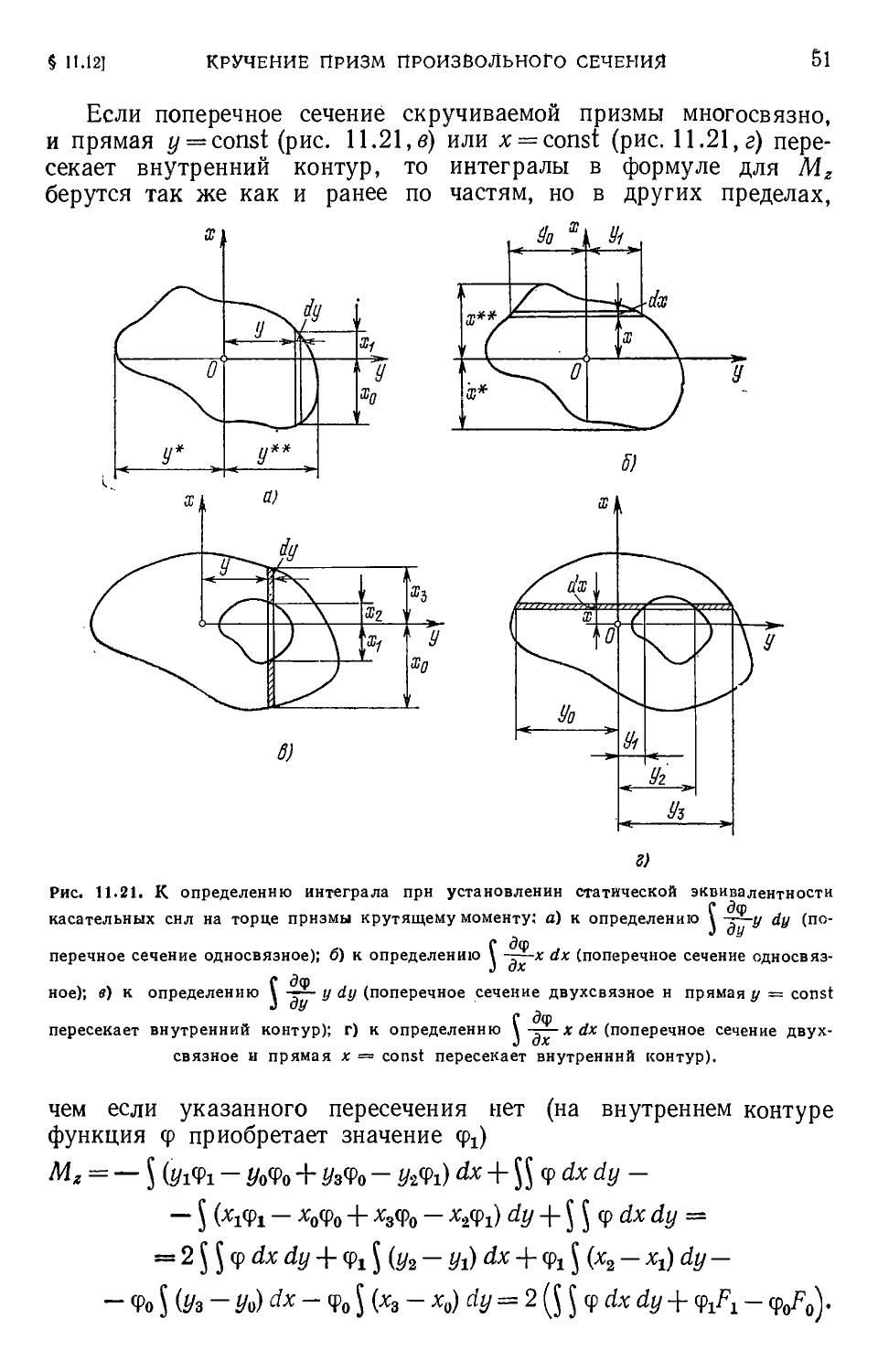
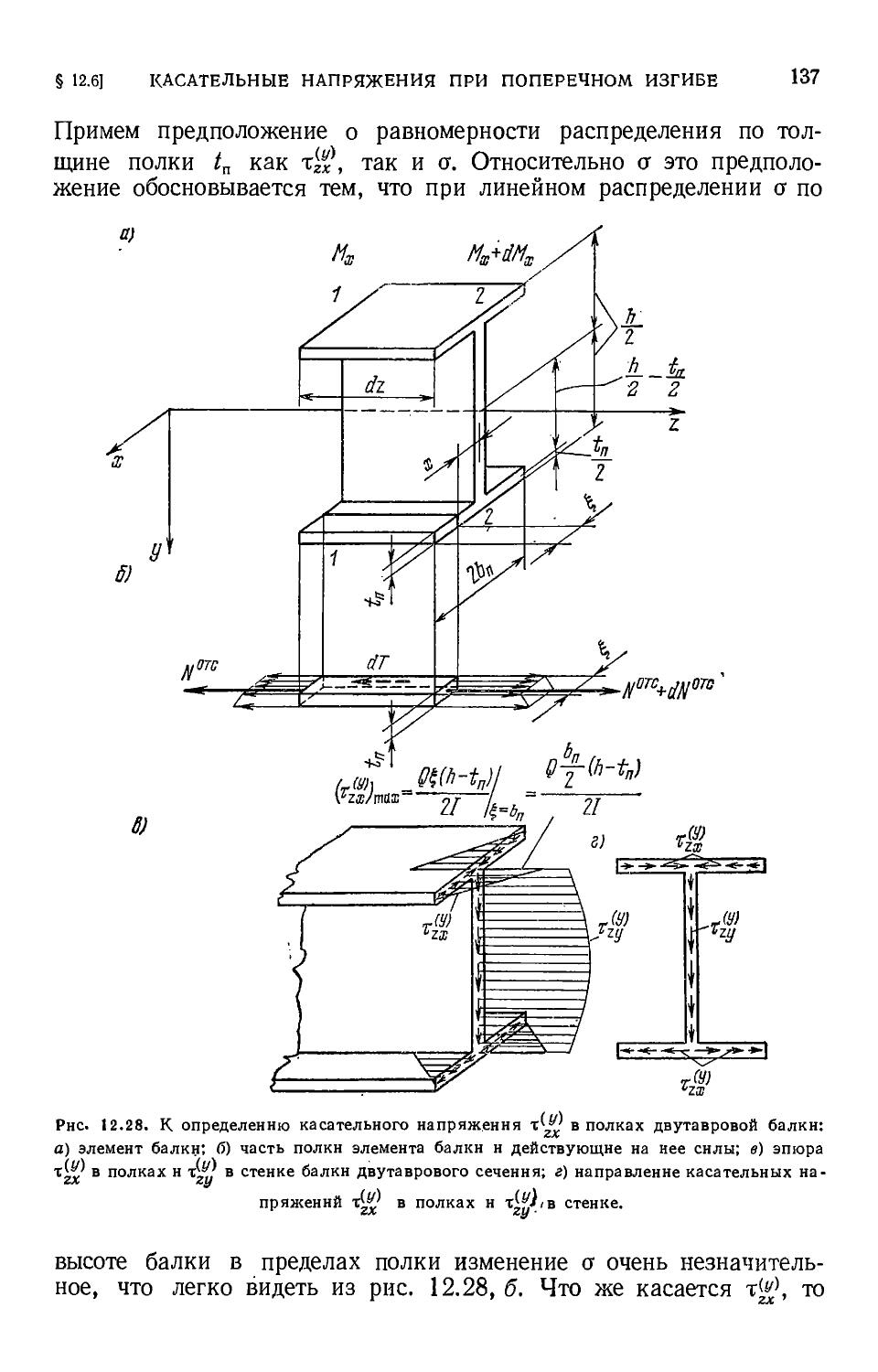
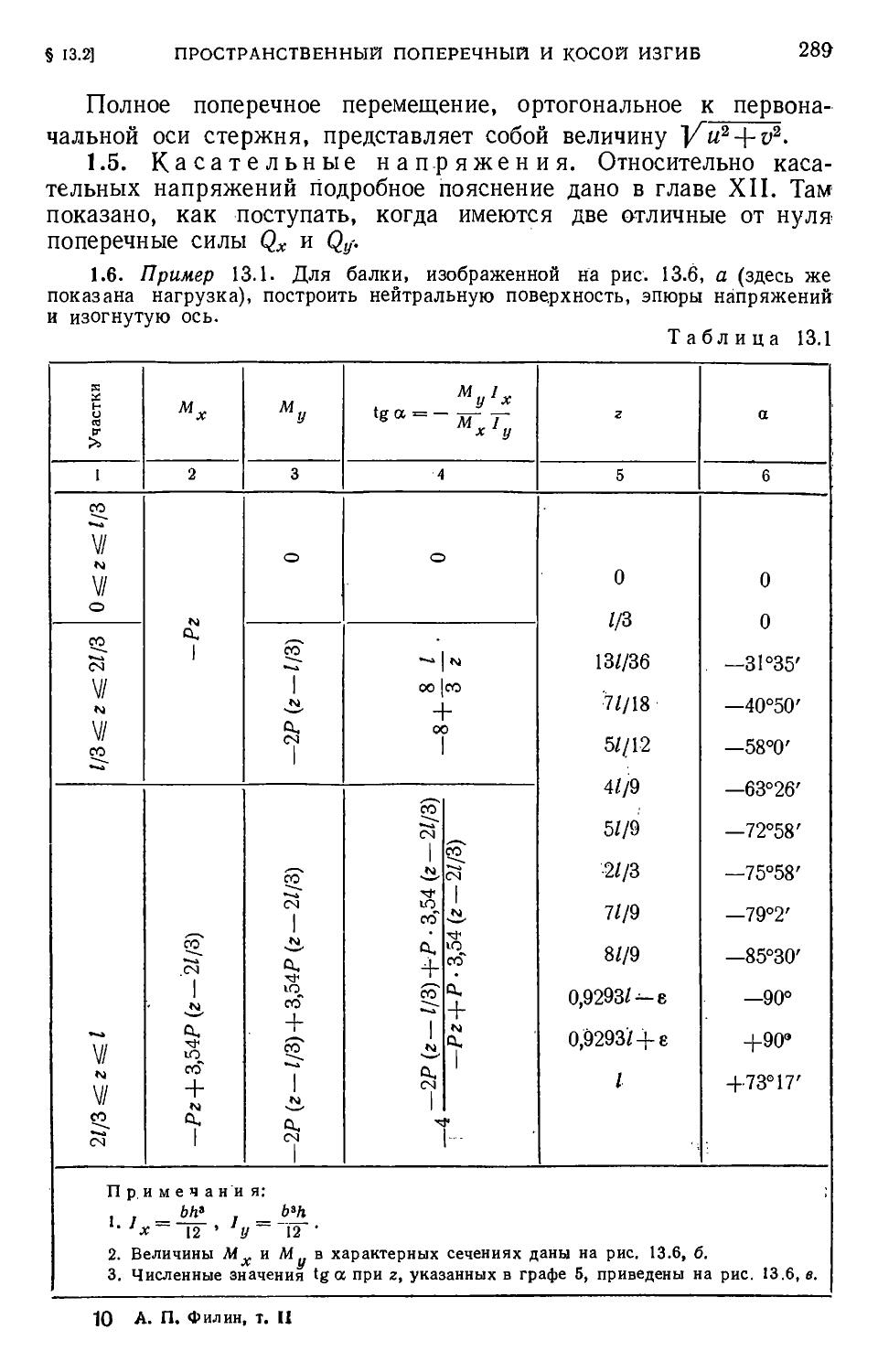
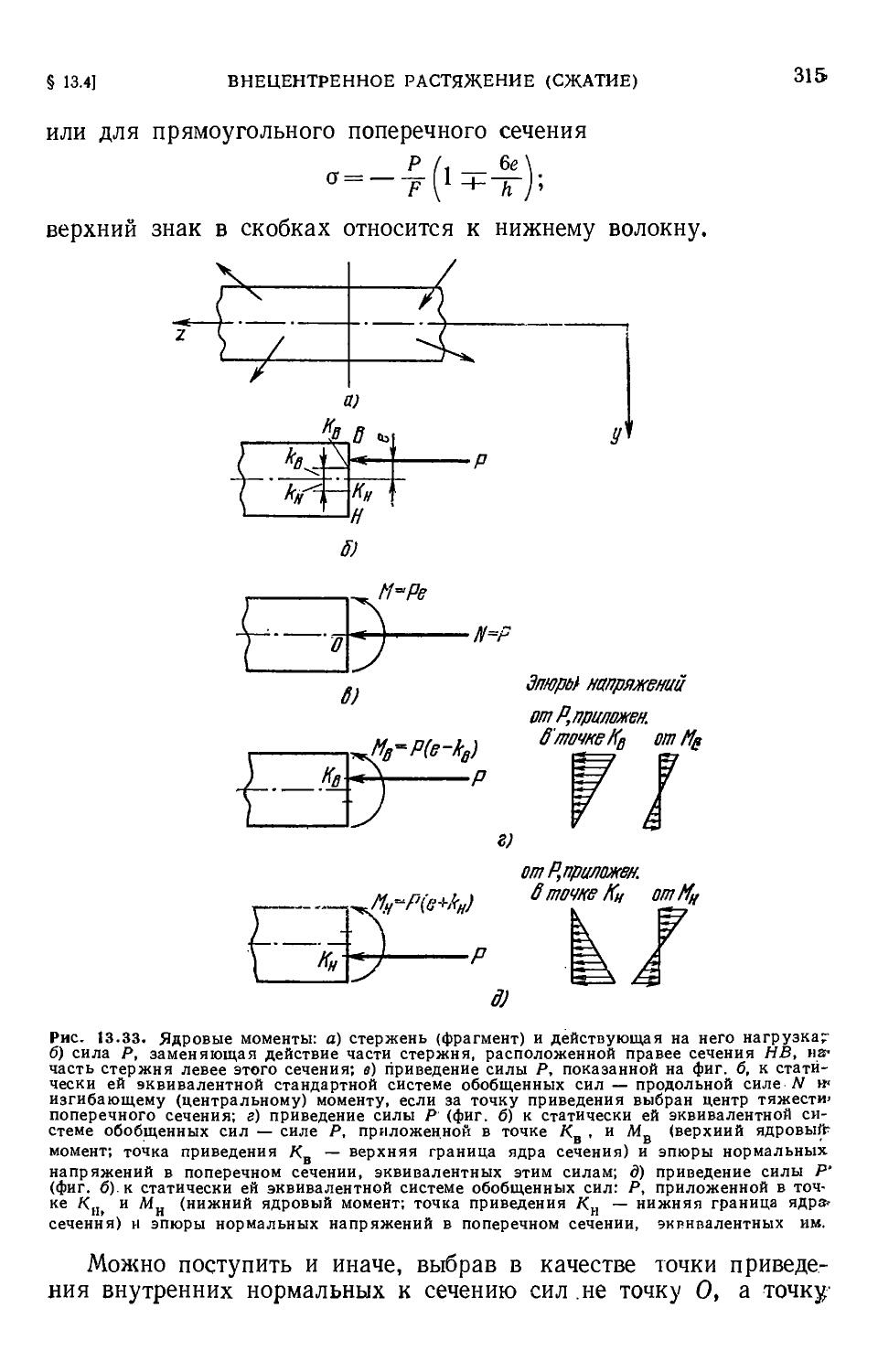
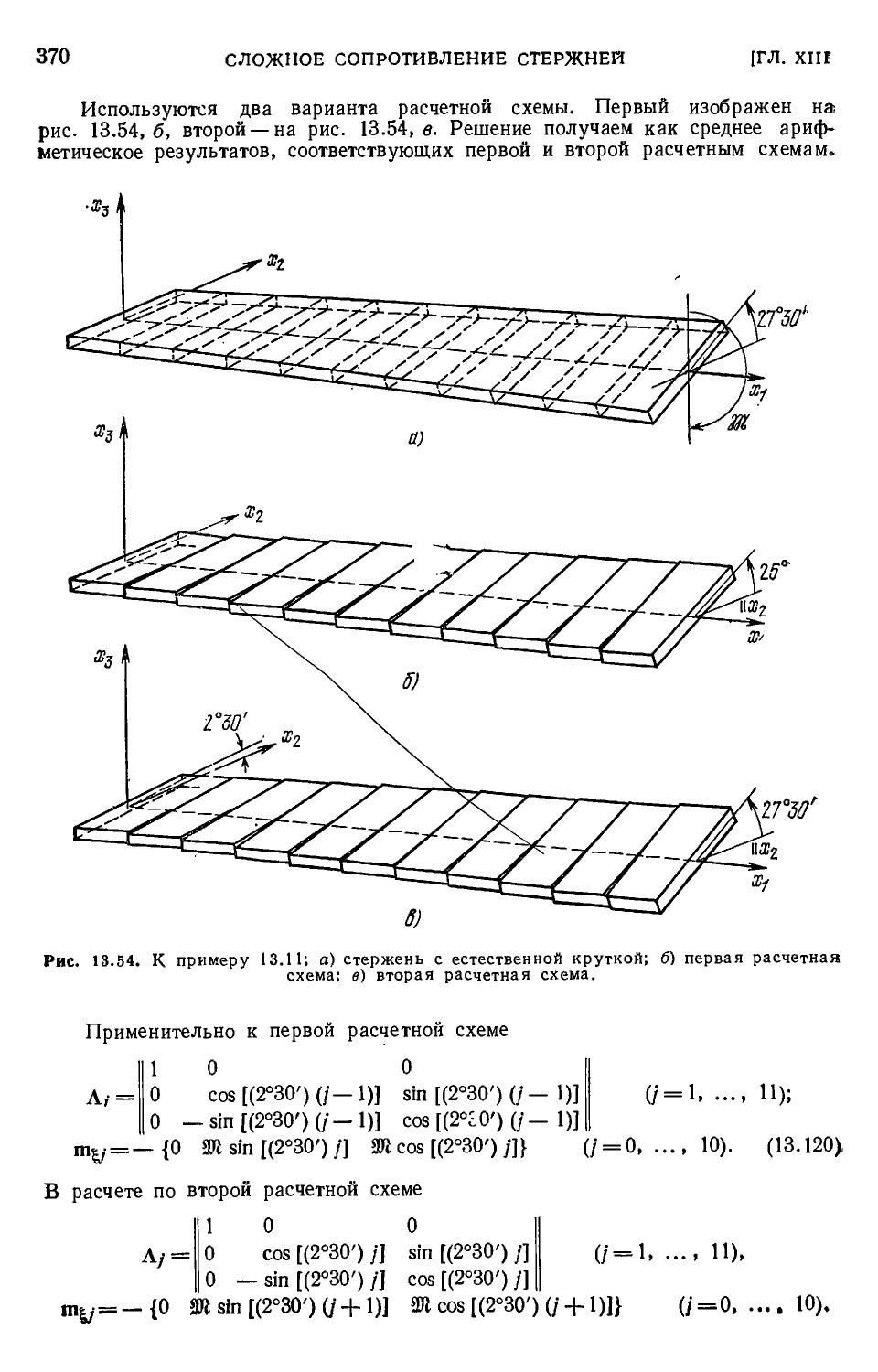
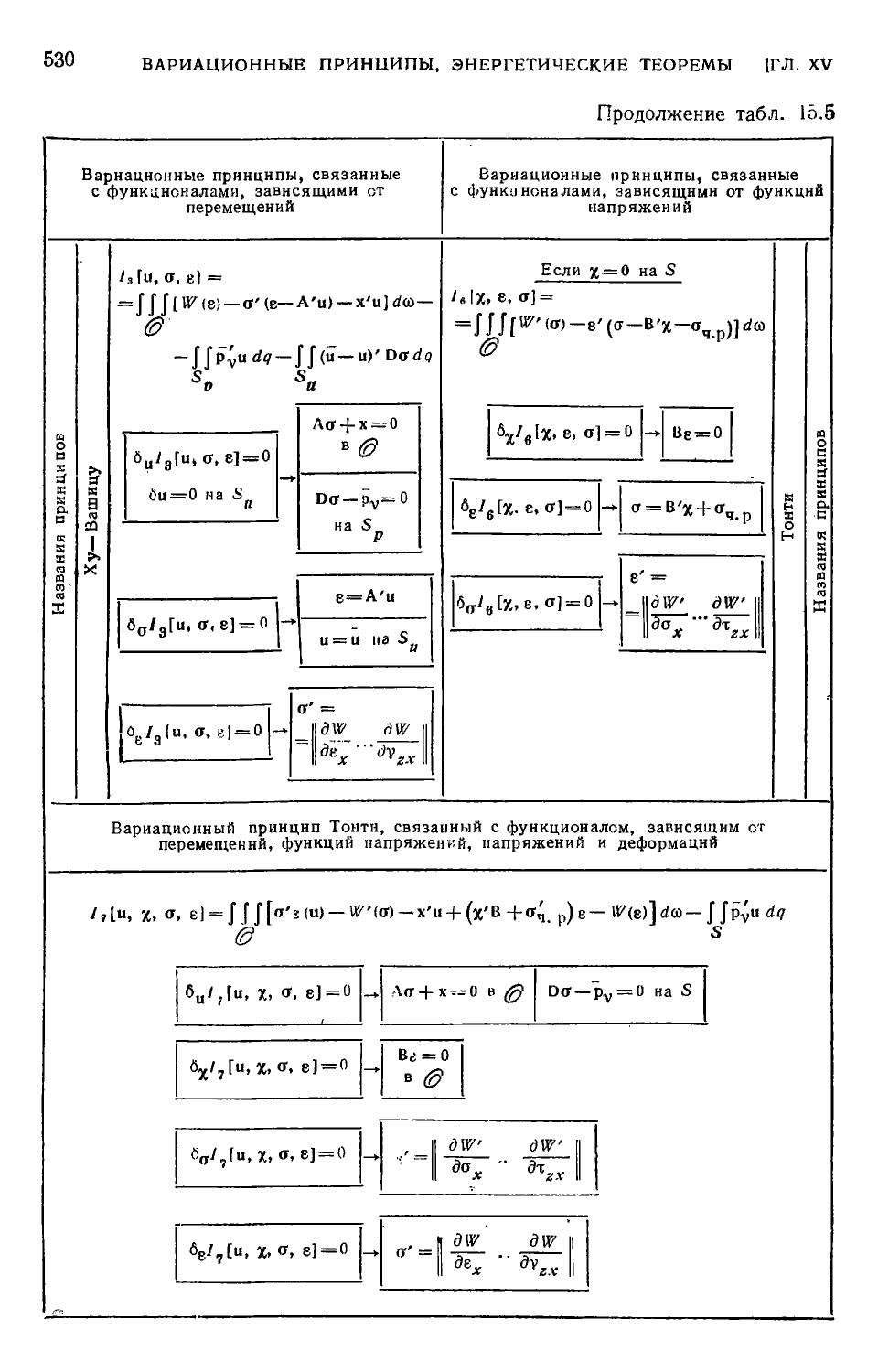
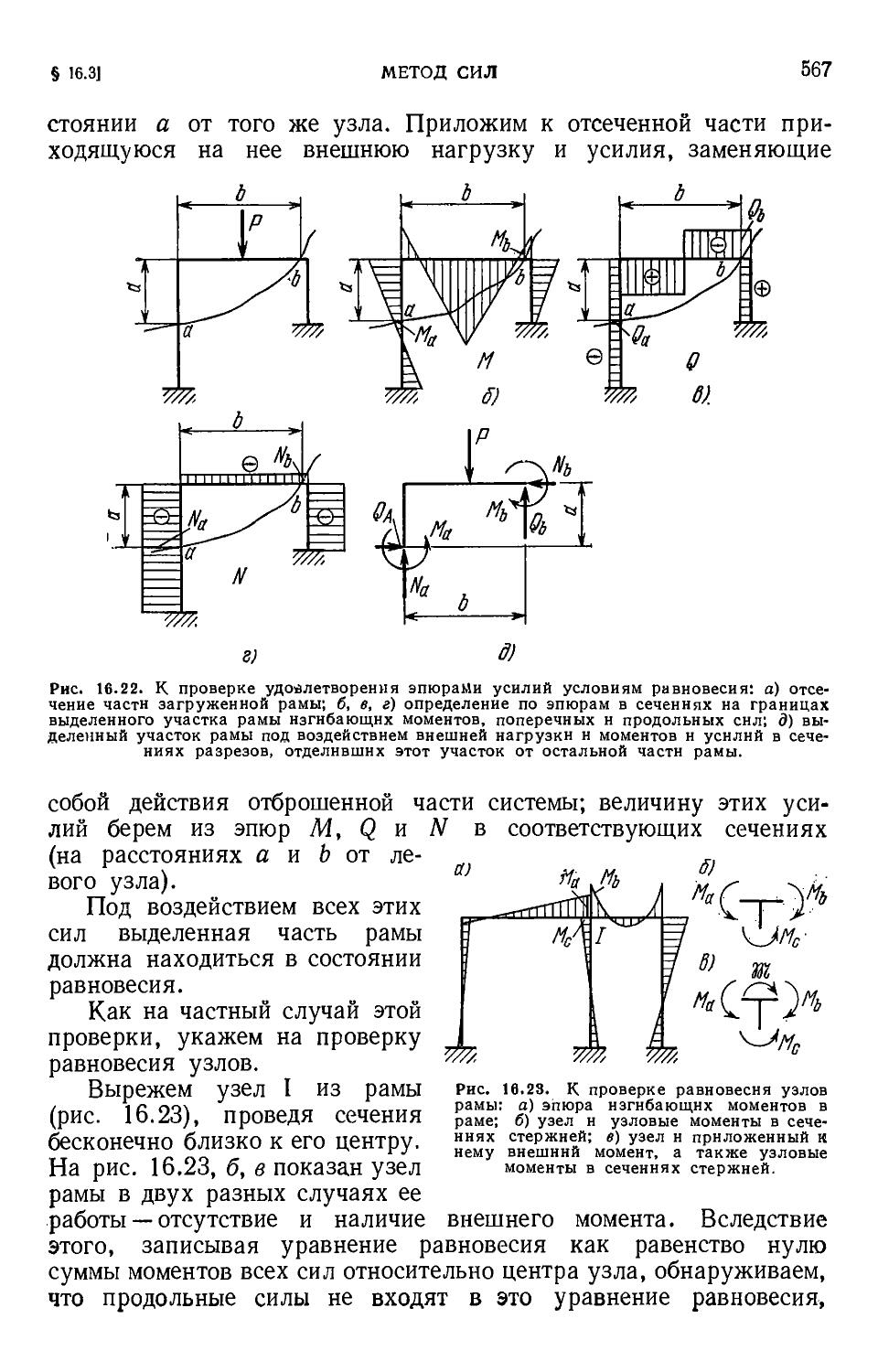
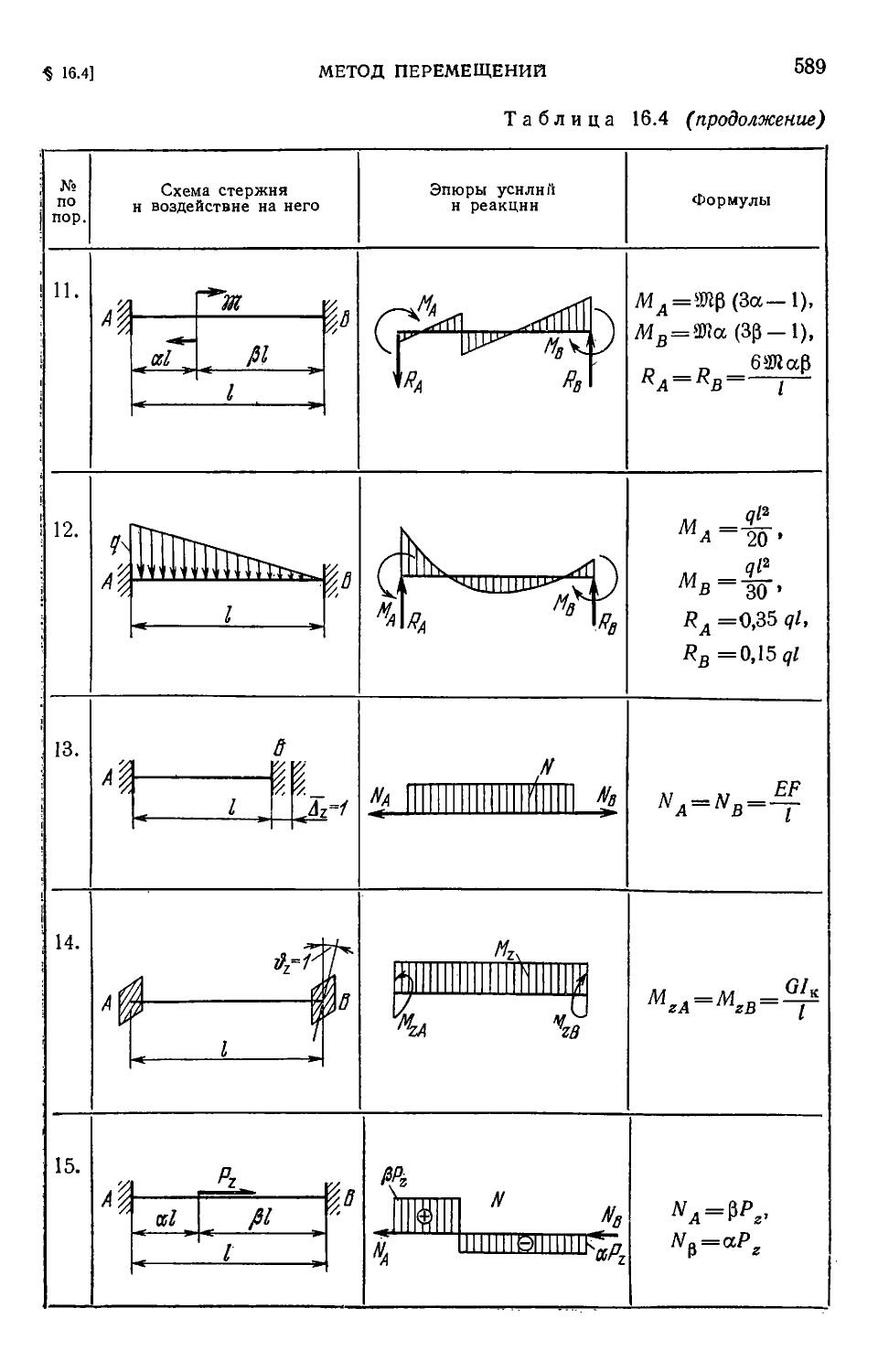
Author: Филин А.П.
Tags: испытания материалов товароведение силовые станции общая энергетика физика строительство механика
Year: 1978
Text
А. П. Филин
ПРИКЛАДНАЯ МЕХАНИКА
ТВЕРДОГО
ДЕФОРМИРУЕМОГО ТЕЛА
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
С ЭЛЕМЕНТАМИ ТЕОРИИ СПЛОШНЫХ СРЕД
И СТРОИТЕЛЬНОЙ МЕХАНИКИ
Τ о м II
^
й
ш
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1978
30.121
Φ 53
УДК 620.10
Филин А. П. Прикладная механика твердого
деформируемого тела: Сопротивление материалов с элементами теории
сплошных сред и строительной механики. Т. II. — М.: Наука.
Главная редакция физико-математической литературы, 1978,
616 с.
В томе II излагается теория деформации стержней,
энергетические основы механики твердого деформируемого тела и
элементы строительной механики (статика стержневых систем). При
обсуждении ряда вопросов используется и аппарат теорий упругости,
пластичности и ползучести, с одной стороны, для оценки
элементарной теории, составляющей основное содержание курса, а с
другой стороны, для решения задач, не разрешаемых при помощи
элементарной теории.
Книга предназначена для студентов втузов, изучающих
сопротивление материалов, теории упругости, пластичности и
ползучести и строительную механику, а также для аспирантов,
научных работников и инженеров, занимающихся проблемой
прочности в различных областях техники (строительство,
машиностроение, судостроение, самолетостроение и др.).
Табл. 41, илл. 422.
Анатолий Петрович Филин
ПРИКЛАДНАЯ МЕХАНИКА
ТВЕРДОГО ДЕФОРМИРУЕМОГО ТЕЛА
Том II
М., 1978 г. 616 стр. с илл.
Редакторы В. С. Калинин, А Г. Мордвинцев
Техн. редактор С. Я. Шкляр
Корректор А. Л. Ипатова
ИБ № 11355
Сдано в набор 14.06.78. Подписано к печати 27.11.78. Т-22035. Бумага 60Χ90'/ιβ. тип. № 1.
Литературная гарнитура. Высокая печать. Условн. печ. л. 38,5. Уч.-изд. л. 38,86. Тираж
12 000 экз. Заказ № 1390. Цена книги 1 р. 70 к.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Отпечатано в ордена Трудового Красного Знамени Ленинградской типографии '№ 2
имени Евгении Соколовой «Союзполнграфпрома» при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли, 198052, Ленинград, Л-52,
Измайловский проспект, 29 с матриц ордена Октябрьской Революции, ордена Трудового
Красного Знамени Ленинградского производственно-технического объединения «Печатный
Двор» имени А. М. Горького Союзполнграфпрома при Государственном комитете Совета
Министров СССР по делам издательств, полиграфии н книжной торговли. 197136,
Ленинград, П-136, Гатчинская ул.. 26
. 30106 — 186 tna _й © Главная редакция
Φ /\eoft\n\ то 138-78 физико-математической литературы
053(02)-7о издательства «Наука», 1978
ОГЛАВЛЕНИЕ
Предисловие 7
Отдел четвертый
ДЕФОРМАЦИЯ СТЕРЖНЕЙ
Глава XI. Сдвиг. Кручение стержней 11
§ 11.1.. Предварительные замечания 11
§ 11.2. Однородный чистый сдвиг прямоугольного параллелепипеда . . 12
§ 11.3. Понятие о свободном (нестесненном) и стесненном кручении.
Чистое кручение 14
§ 11.4. Характер деформации круглого цилиндра при чистом кручении 15
§ 11.5. Гипотезы, используемые при построении теории чистого
кручения круглых цилиндрических стержней 16
§ 11.6. Формула для касательного напряжения в поперечном сечении
круглого цилиндрического бруса при чистом кручении 16
§ 11.7. Условие прочности при чистом кручении круглого
цилиндрического бруса 20
§ 11.8. Деформация при чистом кручении круглого цилиндрического
бруса . 24
§ 11.9. Оценка результатов элементарной теории посредством аппарата
теории упругости 28
§ 11.10. Потенциальная энергия деформации при чистом кручении вала
круглого поперечного сечения 35
§ 11.11. Чистое кручение круглого цилиндрического вала при работе
материала в упруго-пластической стадии 36
§ 11.12. Кручение призматических стержней произвольного поперечного
сечения 42
§ 11.13. Понятие о кручении призматических стержней произвольного
поперечного сечения при упруго-пластической стадии работы
идеально-пластического материала 82
<j 11.14. Кручение круглых валов переменного диаметра . . ; 88
§ 11.15. Свободное кручение призматического стержня из наследственно-
упругого материала (пример применения принципа Вольтерра) 95
\
ОГЛАВЛЕНИЕ
Глава XII. Плоский изгиб стержней 97
§ 12.1. Предварительные замечания 97
§ 12.2. Характер деформации призматического бруса при чистом изгибе 99
§ 12.3. Гипотезы, используемые при построении технической теории
чистого изгиба призматического стержня 102
§ 12.4. Нормальные напряжения в поперечном сечении стержня при
чистом изгибе 104
§ 12.5. Исследование чистого изгиба призматического бруса методом
теории упругости 115
§ 12.6. Касательные напряжения при поперечном изгибе балки .... 124
§ 12.7. Анализ частных случаев поперечного изгиба балки
прямоугольного сечения методом теории упругости. Обоснование
предположений, принятых при построении технической теории 148
§ 12.8. Центр изгиба 166
§ 12.9. Траектории напряжений и деформаций при поперечном изгибе.
Эпюры напряжений, действующих в точках поперечного сечения
на площадках, не лежащих в нем. Линии равных деформаций 180
§ 12.10. Условия невозникновения предельного состояния материала
в локальной области в балках при поперечном изгибе 185
§ 12.11. Потенциальная энергия деформации при изгибе балки 193
§ 12.12. Дифференциальное уравнение изгиба балки 197
§ 12.13. Интегрирование дифференциального уравнения изгиба балки . . 207
§ 12.14. Интегрирование уравнения изгиба в случае балки переменной
вдоль длины жесткости 226
§ 12.15. Изгиб балок, лежащих на сплошном упругом основании .... 231
§ 12.16. Дифференциальное уравнение изгиба стержня в плоскости оси,
имеющей очертание окружности 255
§ 12.17. Изгиб балки при не чисто упругой работе материала 257
§ 12.18. Изгиб призматического стержня из наследственно-упругого
материала (пример применения принципа Вольтерра) 273
§ 12.19. Метод прогонки 273
Глава XIII. Сложное сопротивление стержней 285
§ 13.1. Предварительные соображения 285
§ 13.2. Пространственный поперечный изгиб. Косой изгиб 287
§ 13.3. Совместно происходящие пространственный изгиб и осевая
деформация жесткого стержня 298
§ 13.4. Внецентренное растяжение (сжатие) 302
§ 13.5. Совместно происходящие изгиб и осевая деформация
(растяжение) гибкого стержня 316
§ 13.6. Совместно происходящие пространственный изгиб и кручение
круглого цилиндрического стержня 328
§ 13.7. Общий случай деформации стержня с прямолинейной осью . . 334
ОГЛАВЛЕНИЕ 5
§ 13.8. Изгиб консольной призматической балки силой, действующей
в плоскости торца (результаты решения задачи) 337
§ 13.9. Дискретная матричная форма метода начальных параметров . . 354
Глава XIV. Стесненная деформация тонкостенных стержней 380
§ 14.1. Тонкостенный стержень. Определение 380
§ 14.2. Описание картины стесненной деформации тонкостенных
стержней открытого профиля 382
§ 14.3. Теория тонкостенных стержней открытого профиля 385
§ 14.4. Влияние деформируемости поперечного сечения на напряженно-
деформированное состояние криволинейной тонкостенной трубы 418
§ 14.5. Неравномерность деформации по ширине пояса в тонкостенном
стержне при изгибе/ Понятие о редукционном коэффициенте . . 425
§ 14.6. Примеры расчета стержней открытого тонкостенного профиля 430
Отдел пятый
ОБЩИЕ ПРИНЦИПЫ, ЗАКОНЫ, ТЕОРЕМЫ, МЕТОДЫ СТАТИКИ
ДЕФОРМИРУЕМЫХ СИСТЕМ
Глава XV. Вариационные принципы и энергетические теоремы
статической проблемы упругости 438
§ 15.1. Вводные замечания 438
§ 15.2. Вариационное исчисление и связь его с проблемами механики 439
§ 15.3. О возможности формулирования вариационных принципов
теории упругости 450
§ 15.4. Закон сохранения энергии 457
§ 15.5. Работа внешних сил, совершаемая за отрезок времени 6t, при
загружении сплошной среды 458
§ 15.6. Потенциалы напряжений и деформаций 460
§ 15.7, О связях между механическими, тепловыми и электрическими
величинами 467
§ 15.8. Потенциальная энергия деформации 473
§ 15.9. О двух вспомогательных понятиях 481
§ 15.10. Теорема Клапейрона 483
§ 15.11. Принцип возможных перемещений 484
^ 15.12. Принцип возможных изменений напряжений 488
15.13. Аналогия Еариационных принципов ... 494
§ 15.14. Замечание о двух разновидностях постановки экстремальной
задачи 495
§ 15.15. Теорема о взаимности работ и следствия из нее 490
§ 15.16. Определение перемещений по теореме Кастильяно 501
§ 15.17. Универсальная формула Мора для определения перемещений
в стержневых системах. Прием Верещагина 504
§ 15,18, Перемещения в стержневых системах от изменения температуры 509
6
ОГЛАВЛЕНИЕ
§ 15.19. Отыскание перемещений в статически неопределимых стержне-
ных системах 512
§ 15.20. Формула Папковича и вытекающие из нее следствия 514
§ 15.21. Вариационные принципы, соответствующие функционалам,
зависящим от двух, трех и четырех вектор-функций 522
Глава XVI. Некоторые элементы статики стержневых систем 532
§ 16.1. Вводные замечания 532
§ 16.2. Расчетная схема и кинематический анализ системы.
Статическая и кинематическая неопределимость. Неизвестные методов
сил и перемещений 534
§ 16.3. Метод сил 555
§ 16.4. Метод перемещений 583
Дополнение I. Геометрические характеристики поперечных сечений
стержней 598
Дополнение II. Краткие сведения о симметрии кристаллов 604
Именной указатель 611
Предметный указатель 613
ПРЕДИСЛОВИЕ
Второй том курса, предлагаемый вниманию читателя, содержит
два отдела. Первый из них (отдел четвертый) посвящен деформации
стержней, второй (отдел пятый)— энергетическим основам статики
систем — общим энергетическим законам и теоремам, вариац'ион-'
пым принципам и методам расчета систем при статическом на них
воздействии.
Особенностью изложения материала первого из упомянутых
отделов, как уже об этом предупреждался читатель в предисловии
к первому тому курса, является использование наряду с
элементарной теорией аппарата теории упругости, основы которой были
даны ранее —в девятой главе (первый том).
Органическое сочетание элементарной теории и теории
упругости позволило, с одной стороны, дать оценку результатов
элементарной теории, а с другой — решить не решаемые средствами
последней важные для практики задачи.
Так, в главе XI, посвященной кручению стержней, дана оценка
гипотез сопротивления материалов, используемых при построении
теории чистого свободного кручения круглого цилиндрического
бруса, и наряду с этим рассмотрена теория кручения
призматических (цилиндрических) стержней произвольного поперечного
сечения и теория кручения тел вращения. Изложение материала
главы XI принято таким, чтобы сделать наиболее естественным
и простым переход к главе XIV, посвященной теории
тонкостенных стержней.
В главе XII, кроме оценки результатов теории чистого изгиба
призм, получеь ных средствами элементарной теории, рассматри-
паются такие задачи (изгиб консоли сосредоточенной силой,
приложенной к торцу, изгиб балки на двух опорах равномерно
распределенной нагрузкой —обе на уровне плоской задачи теории
упругости), которые позволили подтвердить правомочность
применения формулы для-нормального напряжения в поперечном сечении
бплки, выведенной для чистого ее изгиба, при построении теории
поперечного изгиба.
8
ПРЕДИСЛОВИЕ
В главе XIII решение задачи об изгибе консоли позволило
дать оценку гипотезы о равномерном распределении по ширине
балки составляющей касательного напряжения, параллельной
плоскости действия сил, и определить другую составляющую
касательного напряжения. Решение этой же задачи позволило
определить положение центра изгиба и установить удельный вес
эффекта крутящего момента, возникающего вследствие приложения
внешней поперечной силы не в центре изгиба, а в центре тяжести,
как в случае тонкостенного, так и массивного стержня.
Важной является и демонстрация на указанных выше примерах
некоторых особенностей примененного в них полуобратного метода
Сен-Венана, имеющего общее самостоятельное значение.
Как задача о кручении стержня, так и задача об изгибе
(чистом и поперечном) решается не только для условий чисто
упругой работы материала, но и применительно к
упруго-пластической стадии его работы, а также применительно к работе стержня
при указанных на него воздействиях, если материал обладает
свойством вязкоупругости.
Из задач элементарной теории, кроме традиционных, обращено
внимание на обоснование метода начальных параметров и
подробное его рассмотрение, в частности — на получение системы частных
решений, удовлетворяющих требованиям метода. Обсуждена задача
о так называемом сложном (продольно-поперечном) изгибе гибкого
стержня, в которой не применим принцип независимости
действия сил.
Масштаб изложения материала пятого отдела принят иной чем
четвертого, поскольку имеется в виду, что этому материалу
посвящается особый самостоятельный курс. Относительно глав этих
отделов уместно сказать следующее.
В главах XV и XVI обращено внимание на формулирование
основных фундаментальных вариационных принципов механики
деформируемого тела, на их дуальность и вытекающую из нее
дуальность методов сил и перемещений. Примеры, приведенные
в главе XVI, призваны помочь читателю уяснить механический
смысл вопросов. Алгоритмический же и вычислительный аспекты
вопроса, в том числе в связи с использованием ЭВМ при расчете
сложных конструкций, обсуждается, из-за ограниченности объема
книги, лишь в общих чертах и даются указания на литературные
источники, где этот аспект освещен подробно. Думается, что даже
такое знакомство с новыми вопросами расширит кругозор
читателю, а указания на основные литературные источники будут
способствовать этому.
Тем не менее проблема использования ЭВМ имелась в виду
и при изложении материала глав XII и XIII. Так, в этих
главах использован в ряде случаев матричный формализм, хорошо
приспособленный к программированию для ЭВМ. Кроме того,
ПРЕДИСЛОВИЕ
9
обсуждены методы (метод прогонки в главе XII и матричный
дискретный метод начальных параметров в главе XIII),
использование которых непосредственно связано с необходимостью
применения ЭВМ. Вместе с тем эти методы позволили решить ряд
примеров повышенной сложности (примеры 12.28, 13.10, 13.11 и
13.12), что было бы невозможно при изложении лишь
традиционных методов. Так удалось рассмотреть решения геометрически и
(или) физически нелинейных задач, решение задачи о
произвольном пространственном стержне, подвергнутом произвольному
силовому воздействию.
В некоторых, редких случаях для иллюстрации обсуждаемых
вопросов приводится краткая информация— уравнения и
комментарии к ним —без подробного вывода и обсуждения метода их
решения (теория тонких стержней Кирхгоффа — Клебша, теория
связанной термоупругости, пиро- и пьезоэлектрического эффектов).
Ссылки на литературные источники, некоторые математические
комментарии и предлагаемый иллюстративный материал (примеры
и рисунки) по замыслу автора призваны помочь читателю в
ознакомлении с основами курса. Отдел шестой—динамика и
устойчивость, включая главу об усталости,—составит содержание
III тома.
В заключение, как и в томе I, приводим таблицу параграфов
и разделов, соответствующих курсу сопротивления материалов,
на изложение которого по учебному плану отводится 70 часов
лекций.
Если в учебном плане имеется курс теории упругости объемом
50 часов, то, как уже указывалось в предисловии к тому I,
целесообразно этот курс читать совместно с курсом сопротивления
материалов и в таком случае, кроме главы IX, рекомендуются
в качестве обязательных следующие параграфы и разделы из глав
настоящего тома: 11.9, 11.11—11.15, 12.5, 12.7, 12.17, 12.18,
13.8, 15.3, 15.5, 15.6, 15.20, 15.21.
При изучении небольшого курса статики сооружений (иногда
включаемого учебным планом в курс сопротивления материалов)
рекомендуем использовать следующие параграфы и разделы глав XV
н XVI: 15.18, 15.19, 16.1, 16.2 и 16.4.
Автор неизменно встречал внимательное отношение к своему
курсу со стороны В. В. Новожилова, чьи рекомендации и
поддержка в процессе работы над книгой были весьма ценными.
-Л. И. Балабух и В. С. Калинин существенно помогли автору
полезными советами и замечаниями, учет которых способствовал
улучшению книги. На всех этапах работы над книгой большую
помощь автору оказывала А. И. Филина. Всем этим лицам автор
очень благодарен.
Автор
10
ПРЕДИСЛОВИЕ
Материал II тома, рекомендуемый в качестве обязательного
при 70 часах лекций, отводимых на весь курс
Главы
XI
XII
XIII
XV
XVI
Параграфы
11.1-5-11.8, 11.40
12.1ч- 12.4, 12.6, 12.8-ί-12.11
12.12
12.13
13.1 Ч- 13.3
13.4
13.5
13.6, 13.7
15.4
15.8
15.9, 15.10
15.11
15.12
15.134-15.17
16.3
Разделы (указаны лишь для тех
параграфов, в которых
используются не все разделы)
1-Г-З
1, 2, 3.1Ч- 3.4
1 -5-6
1-5-6
1
1, 2, -4-5-6
1, 2, 44-6
1-5-3
Отдел четвертый
ДЕФОРМАЦИЯ СТЕРЖНЕЙ
Глава XI
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
§ 11.1. Предварительные замечания
В настоящей Главе рассматриваются такие виды деформации
брусьев, при которых материал работает в условиях чистого сдвига.
К числу их относятся: однородный чистый сдвиг тела (например
прямоугольного параллелепипеда конечных размеров) и чистое
кручение круглых цилиндрических стержней.
Результаты технической теории оцениваются аппаратом
теории упругости.
Кроме упругой, рассматривается и упруго-пластическая
стадия работы материала, а также кручение стержня в случае
ползучести материала.
В этой же главе обсуждаются и более сложные случаи —
свободное кручение призматических стержней произвольного
поперечного сечения в упругой и упруго-пластической
стадиях работы материала, а также кручение круглых
цилиндрических стержней в случае переменного вдоль оси крутящего момента
и кручение тел вращения.
Кручение элементов конструкции и деталей машин встречается
и очень большом числе случаев. Одним из наиболее характерных
п.ч них является кручение вала машины (рис. 11.1, а). На
кручение работает стержень винтовой цилиндрической и конической
пружин. Кручение, наряду с другими видами деформации,
испытывают: в целом корпус корабля при расположении на косой
иолне1) (рис. 11.1, б); крыло самолета в случае, если равнодей-
1) Кручение возникает вследствие того, что по разные стороны от
диаметральной плоскости значения интенсивности сил поддержания, как функции
кпординаты г, различны. Например, в двух точках А и Аг кормы уровень
иоиерхности воды различен —в точке А он выше. Аналогично в точке В уро-
|нчп> выше, чем в точке Вг; вследствие этого силы поддержания в заштрихо-
шшиых частях оконечностей (носа и кормы) больше, чем в симметричных им,
опюсительно диаметральной плоскости, частях; отсюда и возникают внешние
12
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ XI
ствующая сил, приложенных к нему, не проходит через точку,
называемую центром изгиба (см. гл. XIII) (рис. ИЛ, б); балка
Рис. 11.1. Примеры элементов конструкций и машин, работающих на кручение: а) вал
машинь; б) когпус корабля на косой волне; в) крыло самолета; г) балочное перекрытие
(продольная балка изгибается, поперечные изгибаются и скручиваются).
перекрытия при изгибе (например, балки перекрестного
направления, изображенные на рис. 11.1, г). Можно привести и ряд
других примеров.
§ 11.2. Однородный чистый сдвиг прямоугольного
параллелепи педа
Рассмотрим прямоугольный параллелепипед конечных
размеров. Пусть на четыре его грани действует касательная
равномерно распределенная нагрузка с интенсивностью τ (рис. 11.2, а).
Напряженно-деформированное состояние параллелепипеда
однородное.
Если вырезать из него бесконечно малый элемент с гранями,
параллельными граням рассматриваемого параллелепипеда
конечных размеров (рис. 11.2, б), то на гранях элемента будут
действовать напряжения τ, вызывающие его сдвиг в той же плоско-
моменты, вызывающие кручение; они распределены по координате г по
сложному закону, зависящему от формы смоченной водой части поверхности
корабля и от формы поверхности волны.
«ί И.21
ОДНОРОДНЫЙ ЧИСТЫЙ СДВИГ
13
гги, в которой испытывает сдвиг параллелепипед с ребрами alt Ъ
и аг (рис. 11.2, а). Элементарный параллелепипед (а следовательно,
Ч
1'ис. 11.2. Чистый сдвиг параллелепипеда конечных размеров (однородное
напряженное состояние): а) поверхностные силы, действующие на параллелепипед конечных раз-
моров н вызывающие его чистый сдвиг; 6) чистый сдвиг бесконечно малого элемента.
и параллелепипед конечных размеров) находится в равновесии.
Одно из уравнений равновесия всего параллелепипеда (^момг/ = 0)
имеет вид
Ьаххаг — Ъа<{шх = 0.
Для исключения перемещения
параллелепипеда как
жесткого целого мысленно закрепим
точку О
uQ = vQ=wo = 0. (11.1)
11редотвратим в точке О и ^
повороты: элемента dx
относительно осей у и ζ и
элемента dy относительно оси χ
dw
дх
= 0,
dw
дх Jo '
ду
= 0.
(11.2)
Рис. 11.3. Деформация параллелепипеда
конечных размеров при чистом сдвиге.
Деформированный
параллелепипед при соблюдении
(11.1) и (11.2) показан на рис. 11.3. Здесь же изображены силы Qx
и Q,, являющиеся статическим эквивалентом распределенных на
14
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
гранях касательных сил
Qx = J τζχ dFx = τ \ dF1 = xFx = ταφ (χζ) (12). (11.3)
F, F,
Из (11.3) имеем
τ = ~ или τ = ~.
Согласно закону Гука
v — Σ — ®х — J°k-
Ύ~ G GFt GF2'
Величину s{ называют абсолютным сдвигом. Согласно рис. 11.3
■%=αιΥ = %ρ δ2 = α2γ = ^-. (11.4)
Величина GFi (ί = 1, 2) в знаменателе (11.4) называется
жесткостью при сдвиге; она имеет физико-геометрическую природу. G —
модуль упругости при сдвиге, /^ — площадь грани прямоугольного
параллелепипеда, параллельно которой измеряется величина
абсолютного сдвига.
§ 11.3. Понятие о свободном (нестесненном)
и стесненном кручении. Чистое кручение
Свободным, или, иначе, нестесненным кручением
призматического стержня называют деформацию, возникающую в случае,
если к каждому из его торцов приложены поверхностные
тангенциальные силы, статическим эквивалентом которых является лишь
момент, действующий, разумеется, в плоскости торца. Моменты
на противоположных торцах равны по величине и противоположны
по направлению. Никакие связи на скручиваемый брус не
накладываются (деформация его ничем не стеснена). В случае круглого
или кругового кольцевого поперечного сечения скручиваемого
бруса при определенном законе распределения тангенциальных
поверхностных сил на торцах торцы и все поперечные сечения
остаются плоскими. Такой частный случай свободного кручения
называется чистым кручением. В случае любого другого
поперечного сечения, кроме указанных выше, плоскость поперечного
сечения под влиянием кручения искривляется —депланирует
(перестает быть плоской); при одном определенном для каждого вида
поперечного сечения законе распределения касательных сил на
торцах и таком же законе во всех поперечных сечениях депла-
нация всех поперечных сечений оказывается одинаковой. Из
сказанного ясно, что при свободном кручении призматического бруса
нормальные напряжения в поперечных сечениях отсутствуют.
<i 11.4] ДЕФОРМАЦИЯ КРУГЛОГО ЦИЛИНДРА ПРИ КРУЧЕНИИ 15
Если имеются какие-либо связи, препятствующие торцам или
отдельным поперечным сечениям депланировать так, как они депла-
пировали бы при отсутствии этих связей, то кручение называется
стесненным. Стеснение кручения влечет за собой возникновение
и поперечных сечениях стержня нормальных самоуравновешенных
напряжений, которые в случае массивных стержней быстро убы-
нают (затухают) при удалении от тех сечений, где создано
стеснение. В случае же стержней тонкостенного, в особенности
открытого, сечения, затухание эффекта стеснения происходит значительно
медленнее, поэтому стесненное кручение таких стержней на уровне
технической теории рассматривается самостоятельно (см. главу XIV).
§ 11.4. Характер деформации круглого цилиндра
при чистом кручении
Проследим за картиной деформации круглого цилиндра при
чистом кручении, наблюдаемой в эксперименте.
На рис. 11.4 β, показан брус до деформации, изображена
поверхностная нагрузка на торцах (линейный закон распределения
α) δ) δ)
I'm, 11.4. Деформация круглого цилиндра при кручеинн: а) система линий на поверх-
■ ···>'ιII круглого цилиндра и поверхностная нагрузка (на чертеже показан закон распре-
ш'.'ичши на одном из диаметров; такое же распределение имеет место на любом диаметре),
iiiii и.нающая его чистое кручение; б) картина деформации круглого цилиндра при чн-
имм кручеинн;. в) картина деформации вблизи торца при нелинейном распределении
касательных напряжений.
но радиусу) вдоль одного из диаметров на каждом торце.
Ιιικ.ΊΜ же нагрузка имеется на любом из диаметров. На каждом
и ι торцов она складывается в момент дЯ.
I la боковую поверхность цилиндрического бруса и на торцы нане-
"Ίι,ί сетка ортогональных линий, равноотстоящих в каждой системе.
16
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
После деформации брус приобретает вид, показанный на
рис. 11.4, б. Продольные прямые линии на боковой поверхности
искривляются и превращаются в винтовые. Боковая поверхность
сохраняет форму круглой цилиндрической поверхности, высота
цилиндра не изменяется, поперечные линии и торцы остаются
плоскими и поворачиваются относительно оси цилиндра.
Относительный поворот поперечных линий пропорционален расстоянию
между ними. Радиальные линии на торцах поворачиваются и
остаются прямыми. Описанная картина деформации сохраняется
при любом отношении высоты и диаметра цилиндра. При другом
законе распределения внешних поверхностных сил, приложенных
к торцам и создающих такой же по величине, как и в первом
случае, внешний момент ЭУ1, получается несколько иным и
характер деформации бруса (рис. 11.4, в). Однако это отличие
ощутимо лишь в окрестности торцов, что полностью согласуется
с принципом Сен-Венана.
§ 11.5. Гипотезы, используемые при построении теории чистого
кручения круглых цилиндрических стержней
Наблюдаемая в опыте картина, описанная выше, позволяет
сформулировать следующие гипотезы х):
1. Поперечные сечения бруса, плоские до деформации, остаются
плоскими и в результате деформации, и расстояния между ними
не изменяются. Поперечное сечение круглого цилиндрического
бруса ведет себя при чистом кручении, как жесткий диск. При
этом радиальные отрезки в поперечных сечениях, прямолинейные
до деформации, остаются прямолинейными и после деформации и
в пределах поперечного сечения все поворачиваются на один и
тот же угол.
2. Поворот поперечных сечений относительно друг друга вокруг
оси круглого цилиндрического бруса пропорционален расстоянию
между сечениями.
§ 11.6. Формула для касательного напряжения
в поперечном сечении круглого цилиндрического бруса
при чистом кручении
1. Статическое обследование скручиваемого вала. Пусть имеем
круглый цилиндрический брус, подвергнутый чистому кручению.
Рассечем стержень на две части поперечным сечением с
координатой г. Коль скоро брус в целом находится в состоянии равно-
*) Термин гипотеза в рассматриваемом и в аналогичных ему случаях в
прикладной механике твердого деформируемого тела широко используется, хотя,
пожалуй, правильнее было бы применять термин допущение,
§ 11.6] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ЧИСТОГО КРУЧЕНИЯ ВАЛА 17
весия, в равновесии должна находиться и любая из двух
образовавшихся при рассечении частей. На торец рассматриваемой части
бруса действует внешний момент ЭУ1г, а к другому торцу,
образовавшемуся вследствие рассечения бруса на две части,
приложены распределенные внутренние силы, которые по отношению
к рассматриваемой части бруса являются внешними.
Интенсивности трех составляющих (по осям хуг) этих сил в произвольной
точке поперечного сечения суть: xzx, xzy, σζ.
Стандартная система внутренних сил и моментов, являющихся
статическим эквивалентом этих распределенных по поперечному
сечению' сил, определяется из условий эквивалентности
Qx = J τζχ dF, Qy = J xzy dF, N = <\ σζ dF;
F F F
Mx = J azydF, My = \ σζχ dF, Mz = J (xzxy - xzyx) dF.
F F r"
Итак, на рассматриваемую часть стержня действуют дУ1г, Qx, ...
..., Mz, под влиянием которых она находится в равновесии.
Уравнения равновесия имеют вид
£прл; = 0, Q* = 0; £момл; = 0, МХ = 0 (ху)\
£прг = 0, Λ/ = 0; £момг = 0, Мг-Жг = Ъ\ Мг = Жг.
Если в (11.6) подставить (11.5), то получим
\xzxdF = 0, \xzydF = 0, \ozdF = 0,
F F F
J ozy dF = 0, J σζχ dF = 0, $ (xzxy - xzyx) dF = Шг. \
F F F )
Уравнения (11.7)3i4i5 показывают, что, во-первых, нормальные
напряжения либо тождественно равны нулю, либо во всей
площади поперечного сечения являются самоуравновешенными в его
пределах. Поэтому эти уравнения рассматривать не будем.
Остальные уравнения, в которые входят касательные компоненты
напряжений, могут быть удовлетворены при бесчисленном количестве
париантов распределений напряжений по поперечному сечению
стержня. Как уже указывалось в § 2.3, задача сопротивления
материалов является статически неопределимой относительно закона
распределения напряжений по поперечному сечению бруса.
2. Исследование деформации стержня. Для раскрытия
статической неопределимости представим в аналитической форме
функцию, характеризующую распределение деформаций. Вырежем из
стержня элемент двумя поперечными сечениями, расположенными
бесконечно близко одно от другого. Вид этого элемента до и после
(11.5)
(11.6)
18
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
деформации с учетом принятых гипотез, показан на рис. 11.5, а.
Из этого элемента вырежем сектор- (рис. 11.5, б).
Рассмотрим поворот одного из торцов этого сектора по
отношению к другому. Очевидно, что все концентрические слои
цилиндра испытывают сдвиги, тем большие, чем дальше концентрический
Рис. 11.5. Деформация элемента круглого цилиндра при чистом кручении: а) элемент
вала: б) сектор, вырезанный из элемента вала.
слой отстоит от оси. Наружный слой испытывает сдвиг уг, а слой
радиуса ρ — сдвиг γρ. Отрезок ЛВ может быть представлен двояко
ΑΒ=ράϋ·ζ, AB = dz-yp; ρ άϋ·ζ = dz-yp,
отсюда
Vp = P^t· (И.8)
Уравнение (11.8) является тем дополнительным, которое, будучи
присоединенным к уравнениям равновесия, позволяет раскрыть
статическую неопределимость проблемы. Однако в уравнения
равновесия (11.7) входят компоненты напряжения, а в уравнение
(11.8)—деформации. Для совместного использования этих
уравнений необходимо связать напряжения с деформациями
аналитической зависимостью; такой является уравнение закона Гука.
3. Использование физической зависимости. Сдвиг и
касательное напряжение связаны уравнением закона Гука (рис. 11.6) τρ =
= Gyp, или, если учесть (11.8),
TP = Gp-^. (11.9)
Согласно (11.9) касательные напряжения распределяются в
зависимости от ρ по линейному закону. Однако формула (11.9) не
является расчетной, так как в нее входит величина d$z/dz,
которую мы не знаем. Желательно иметь формулу, в которой
касательное напряжение связано с крутящим моментом. С этой целью
Ί ll.dl КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ЧИСТОГО КРУЧЕНИЯ ВАЛА 19
подставим (11.9) в уравнение равновесия (11.7)6, которое для
удобства представим так, чтобы момент касательных сил в поперечном
ссчспии выражался не через компоненты касательного
напряжения, а через полное касательное напряжение (рис. 11.7),
направленное перпендикулярно радиусу. Если бы имелась отличная от
пуля составляющая касательного напряжения, направленная вдоль
радиуса (попутно заметим* что в точке поперечного сечения,
расположённой у контура, такая составляющая должна быть равна
нулю и в силу закона парности касательных напряжений, так как
боковая поверхность бруса свободна от всяких напряжений), то
Рис. 1Ь6. К зависимости между
напряжениями и деформациями
при чистом кручении круглого
цилиндра.
Рис. 11.7. Ортогональность
направлений полного касательного
напряжения и радиуса-вектора
точки его действия.
следствием этого было бы искривление поперечного сечения,
которое не обнаруживается в опыте и которое не согласуется с
принятой гипотезой о сохранении плоской формы поперечного сечения.
Итак, наши рассуждения утверждают нас в том представлении
о направлении полного касательного напряжения, которое было
шлсказано выше. В соответствии с этим представлением
уравнение (П'.7)6 заменим эквивалентным ему уравнением
\TppdF = $)1z. (11.10)
F
Подставим (11.9) в (11.10), в результате получим
dz
(11.11)
Учитывая, что интеграл в этом уравнении представляет собой
полярный момент инерции площади поперечного сечения
/Р = IP2 dF,
F
получим (11.11) в следующей форме:
0^ =
dz
Μ,
(11.12)
20
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
Подставив (11.12) в (11.9), получим окончательную расчетную
формулу
τΡ = -Τ£·. (11ЛЗ)
1р
На рис. 11.8 изображена эпюра распределения касательных
напряжений в зависимости от р; такая эпюра имеет место на
любом из радиусов поперечного сечения.
Индекс ρ в формуле (11.13) в
дальнейшем будем опускать. Очевидно, что
при законе распределения
касательных напряжений (11.13) уравнения
(11.7)lf2 удовлетворяется, и их не
рассматриваем.
§ 11.7. Условие прочности
при чистом кручении круглого
цилиндрического бруса
Рис. 11.8. Эпюра полных
касательных напряжений по
радиусу поперечного
сечения круглого цилиндра при
чистом кручении.
1. Сплошное круглое поперечное
сечение. Максимальное касательное
напряжение имеет место в наиболее удаленной от
центра точке поперечного сечения при р = ртах = ^>
^тах = ^р |р—г == ·< "г/*/Ур.
Введем величину
называемую полярным моментом сопротивления поперечного
сечения скручиваемого круглого цилиндрического бруса. Тогда
формула для максимального напряжения приобретает вид
Ттах=^. (11.14)
w ρ
Материал рассматриваемого бруса испытывает чистый сдвиг,
поэтому условие прочности приобретает вид
Тгпах = ψ- < [τ], (11.15)
где [τ] —допускаемое касательное напряжение, определяемое по
той или иной теории прочности. 3
Учитывая, что для круглого поперечного сечения
г4 тг.гЗ
h =
пг*
w P 2
получим условие прочности в следующем виде:
2УИ,
π/-3
[τ].
(11.16)
(11.17)
§ 11.7] УСЛОВИЕ ПРОЧНОСТИ ПРИ ЧИСТОМ КРУЧЕНИИ ВАЛА 21
Пользуясь этим условием, можно решить как задачу проверки
прочности, так и задачу подбора поперечного сечения. В первом
случае задаются Мг и г и требуется сопоставить величину
т£ (И.18)
с [τ]. Для подбора сечения, который заключается в отыскании
величины г по заданным Мг и [τ], решим
(11.17) относительно г, г^У2Мг/п[т].
2. Рациональная форма центрально-
симметричного поперечного сечения
скручиваемого бруса. Рис. 11.8
свидетельствует о том, что материал внутренней зоны
поперечного сечения участвует в работе
в меньшей мере, чем периферийной. В связи
с этим применяют полые валы. Форма
поперечного сечения такого вала и
распределение касательных напряжений в нем
показаны на рис. 11.9. Из
нижеприведенных примеров станет ясно, что сплошной
вал способен воспринять меньший по
величине крутящий момент, чем полый вал
такой же площади поперечного сечения при одинаковых
максимальных напряжениях.
Для круглого кольцевого поперечного сечения вала полярный
момент инерции и полярный момент сопротивления выражаются
следующими формулами:
Рис. 11.9. Эпюра полных
касательных напряжений по
радиусу поперечного
сечения пустотелого круглого
вала при чистом кручении
1Р— 2
яг*
π
= ϊ(Κ*-ή,
\γ/ — Ip —lL·— ^ Γ ι
= ^0-«4),
(11.19)
где a = r/R.
Условие
полого вала.
прочности (11.15) сохраняет свой вид и в случае
Подставив (11.19) в (11.15), получим
ш- -ы
Тщах —'
(11.20)
π#3(1— α4)
Подбор сечения состоит в отыскании R из (11.20)
*-~~у π(ΐ_α4)[τ] '
3. Главные напряжения. Главные напряжения при кручении
осесимметричного вала постоянного сечения легко находятся в
соответствии с формулами (7.15) для чистого сдвига, ο1 = τ> σ2 = 0,
<r3 = — τ· Нормали к главным площадкам с ненулевыми главными
22
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
напряжениями составляют угол 45° с поперечным сечением
(рис. 11.10, а). В зависимости от того, в хрупком или пластичном
состоянии находится материал, разрушение при чистом кручении
происходит по одной из двух схем: при хрупком состоянии
материала—от отрыва (рис. 11.10, б, б) и при пластичном — от среза
(рис. 11.10, г, д). Разрушение и от отрыва и от среза вследствие
г) д)
Рис. 11.10. Характер разрушения круглого цилиндрического вала при чистом
кручении: а) направления главных напряжений в круглом цилиндре при чистом кручении;
б), в) части разрушенного вала в случае хрупкого состояния материала; г) след плоскости
среза на боковой поверхности при пластичном разрушении вала; д) части разрушенного
вала в случае пластичного состояния материала.
одинаковости условий работы материала по длине вала
теоретически должно было бы произойти сразу во всех сечениях, однако
этого никогда не происходит из-за того, что материал на самом
деле не однороден, а квазиоднороден и разрушение происходит
в наиболее ослабленном месте.
4. Примеры.
Пример 11.1. Имеются два вала с одинаковыми площадями
поперечных сечений — один из них сплошной радиуса г0, а другой — пустотелый
с наружным и внутренним радиусами R и г (а=г//?= 1/2;/? = 2 )/"3r0/3).
Определить на сколько процентов крутящий момент в поперечном сечении
полого вала превышает крутящий момент в поперечном сечении сплошного
§ 11.7] УСЛОВИЕ ПРОЧНОСТИ ПРИ ЧИСТОМ КРУЧЕНИИ ВАЛА 23
вала при условии, что максимальные касательные напряжения в обоих
случаях одинаковы и равны [τ].
Решение. Определяем крутящий момент в поперечном сечении полого вала
M^) = Wfon) [τ] = η& (1_α4) [τ]=5/3 π/.3 [τ].
Определяем крутящий момент в поперечном сечении сплошного вала
М^спл) = ^(спл) [τ] = JW£ [Х].
находим отношение крутящих моментов ■
ЛКСПЛ> (nrl \ /5/3 \ 2/3
-I— = _ [τ] : тег» [τ] = = 0,692.
^пол) \ 2 ι 7 \ 12 / 5
Определяем процент превышения значения Μψ01^ над величиной М(гспл)
(1— Mfnn)lMf03l))- 100=30,8%.
Пример 11.2. Имеются два вала: сплошной (радиус поперечного
сечения—г0) и полый (с радиусами поперечного сечения наружным и
внутренним—/? и г, a = r/R = 2/3). Определить долю, составляемую площадью
поперечного сечения полого вала от площади поперечного сечения сплошного
■вала, при условии, что в сравниваемых случаях равны максимальные
напряжения (равные [τ]) и величины крутящих моментов Мг, возникающих в
поперечных сечениях.
Решение. Определяем радиус поперечного сечения сплошного вала из
условия
Мм _м. 2М£_М. ,-ί/Ж
^(спл)-М' ягз-[т]' '<>-У π [τ]'
Определяем площадь поперечного сечения сплошного вала
"---«-«уШ
Определяем наружный радиус поперечного сечения полого вала из условия
ф> = М *.:(^<1-"Ч)-М; Д-/»(1^)М·
Определяем площадь поперечного сечения полого вала
I /7 Щ \2
^П0Л> = Я^2 _ π/-2 = nR2 (l _ α2) = π ( ! _ α2) Τ/ [—^
α*) [τ]
Определяем отношение площадей поперечных сечений полого и сплошного
пила
3 // 2М~ \2 4
/•'<»<^ = "^-^К (я(1-о?)[т]) = 1-«* _ *"¥
-/(да ' *—* У(>-щ
= 0,643.
24 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ [ГЛ. XI
§ 11.8. Деформация при чистом кручении круглого
цилиндрического бруса
1. Угол крутильного поворота поперечного сечения вала. Из
(11.12) имеем
d$ =Mzdz
аХТг GIP
— угол, на который повернется один торец относительно другого
торца в элементе с размером dz (рис. 11.5).
Величину
*' = -5Г = -077 (11Л2)
естественно назвать интенсивностью угла закручивания стержня,
величину же $г —углом крутильного поворота сечения.
2. Дифференциальное уравнение относительно угла
закручивания. Выведем дифференциальное уравнение, связывающее $г с
интенсивностью распределенной моментной крутильной нагрузки тг.
Для этого воспользуемся уравнениями (11.12) и (1.9)6, которые
запишем так:
<».%->*.. *& — *.. (П.21)
Продифференцируем уравнение (11.21)! по ζ, учтя, что GIP =
= const,
сопоставив (11.22) с (11.21)2, получим
. d2flg _ dM
ρ dz2 ~ mz' dz* GI
GlP-^ = -mz, -f-JL=-7Tf-. (Ц.23)
3. Интеграл дифференциального уравнения в случае одного
участка. Рассмотрим сначала случай, в котором на всей длине
вала функции Мг и тг, а следовательно, и ■6г сохраняют свой
вид, т. е. вал содержит один участок.
Проинтегрируем (11.23)2 дважды. В результате первого
интегрирования найдем
О
и в результате второго
Ъг =- -^- ^ mzdzdz + ClZ + C2. (11.25)
GIP
0 0
§ 11.8]
ДЕФОРМАЦИЯ ПРИ ЧИСТОМ КРУЧЕНИИ ВАЛА
25
Постоянным интегрирования С± и С2 можно дать механическую
трактовку. С этой целью положим в (11.24) и (11.25) ζ = О, тогда
Μι
GI,
Μ
г. о
GIr
— ^1» vzlz-o — ^г,о — ^2·
(11.26)
z-o v'p ' ■ - .- - \
Здесь Ог>0 и ΜΖι0 — крутильный поворот поперечного сечения и
крутящий момент в поперечном сечении, проходящем через начало
координат. Величины ϋ·Ζι0 и Мг<0 —начальные параметры.
Учитывая (11.26), получим выражения для Мг и $г
Mg = Mg,0-[mgdz, 0г = Фг>о +
м
ζ ζ
ζ, ο
GI,
Ζ —
GI,
\\mzdz dz.
Ь о
4. Интеграл дифференциального уравнения в случае двух и
нескольких участков. Рассмотрим теперь случай, в котором в
пределах длины стержня имеются два участка и на каждом из них
функция интенсивности распределенной моментной крутильной
нагрузки своя собственная: тгл, mZi2. Пусть координата границы
между участками z = zv (Поскольку структура уравнения (11.23)2
совершенно аналогична структуре уравнения (2.27), дальнейшие
выкладки выполняем без комментариев, отсылая читателя к
разделу 3 § 2.21, где содержится аналогичный материал, подробно
поясненный.)
d2®z,i тг,г d2ftZt2 тй
dz2 GIP '
&®ζ,2 &ϋζΛ _
dz2 dz2
d4®z.2-$z,i)
dz2
__ '■Z, 2
dz2 ~ GIp '
тг,2 (_ mgj.
GIP [ GIp
_ тг,г—тг,г
GI„
При z\
Vz, 2 — ^ ι + ®z, доп, 2» тг, 2 _ mz, 1 4" mz, доп, 2»
θ
ζ, доп. 2
= ь
Μ
Ζ. ДОП. 2
dz2
г, zx, доп, 2
т
Ζ, ДОП. 2
GIn '
z,zlt доп, 2 '
{ζ-ζχ)
"ί-ν,,ο-t GI г QI
ζ ζ
Щ \\
г ζ
ffm^dzdz + 1 ft,, гь доп, г +
*J г.) \\г1
О О
г, доп, 2
\
dzdz.
+
Μ
ζ ζ
ζ, zt, доп, 2
GIn
(z-zJ-'qj- j j m2, Д0Пр 2 с?г с?г,
2l Ζ,
Λ1,-:- Λίζ. 0 _ J m, dz + |2i Aiz,z„flon.2- ί^ζ,Λοπ.2^.
(11.27)
26
сдвиг, кручение стержней
[гл. χι
Величины ^г, гь доп, 2 и Мг< Zli доп_ 2 — скачки соответственно в
функциях $г и Мг на границе участков. Если не иметь в виду
специального приспособления на границе
участков, то ΰΖιΖΐι доп,2 = 0.
шг>1
δ
h,3
Пример 11.3. Найти функции Мг и 0г
для вала, изображенного вместе с
приложенной к нему нагрузкой на рис. 11.11.
Решение. Поскольку нас интересуют
относительные повороты сечений ог,
связанные лишь с деформацией, закрепим вал
против поворота как жесткого целого
относительно оси г. Пусть при z = 0$z = bz 0 = 0.
Функции Мг и фг находим по формулам типа (11.27), но с учетом того факта,
что в рассматриваемом случае не два, а три участка, при этом
fl*,o = 0, Мг,0 = -Шгш1,
Рис. II.II, Вал и действующая на
него моментиая нагрузка.
**. *ь доп. 2 = °.
*2, г^доп.З^0'
М2,г1,доп,2 = 0'
м2,21, Д0П( з-а»г.2.
тг, доп. 2 = ~ тг>
т2,доп.З = 0·
Кроме того, из условия равновесия вала в целом.имеем:
вследствие чего
аК*,х-9К*,8 + 9Я*,8-/я*у = 0,
^.1 = ^.2-^,3 + ^^ = 0.
А,
GI.
-2»*.2+аи*,8·
тг — )г-
GI
г г
j- \ \ mzdzdz +
о о
г ζ
+
}'р 3 i
тг dz dz-\-\
Ш
•г, 2
//з GIp J .1 ""г ' Ц2//з GID
μ цъ ΐβ p
4<
Μ
г г
t= — №,!-^,3 + m2yj— \ тгсгг+ \ m2d2 +
o //3
2i/3
VZ, 2
5. Условие жесткости. Величина
b b
$г — \ Кг dz = \
Mz
GIn
dz
(11.28)
представляет собой поворот сечения с координатой г = 6 по
отношению к сечению с координатой z = a.
Легко понять, что отношение интеграла (11.28) к отрезку
интегрирования Ь — а представляет собой среднюю интенсивность
угла закручивания
κ*· ср — Ь—а \ κ*
(11.29)
*, 11.«I ДЕФОРМАЦИЯ ПРИ ЧИСТОМ КРУЧЕНИИ ВАЛА 27
Ноли на участке вала a^z^b интенсивность угла
закручивания постоянна, что эквивалентно постоянству Мг, то, как это
следует из (11.29),
Kz,4> = Kz = -Qf-· (11.30)
При хг = const, β = 0, b = l, угол $г получается по (11.28)
следующим:
^z = K(b — a)=^f-,
Величину кг ограничивают, так как при большом ее значении
может возникнуть расстройство нормальной работы машины,
а если внешние воздействия, прикладываемые к брусу, переменны
по величине во времени, то могут возникнуть и колебания со
значительными амплитудами.
Условие, ограничивающее величину хг>ср, называется условием
жесткости, которое имеет вид
»Чср<Ы, (п.31)
где [xj—допускаемое значение интенсивности угла закручивания.
Величина [хг] применительно к различным классам машин или
конструкций нормируется. Для того, чтобы составить
представление о порядке величины [хг], укажем, что для валов [хг]
долгое время принималось равным от 0,15° до 0,3° на 1 м длины
вала в зависимости от режима работы — чем динамичнее внешнее
воздействие, тем меньше [хг]. Последнее время некоторые
специалисты х) считают такую рекомендацию устаревшей, особенно
для тонких валов. В последнее время имеется тенденция к
увеличению [хг]. Так например, имеется рекомендация2) принимать
для длинных трансмиссионных валов [хг].= 0,01 рад/м (0,57° на
1 м), а иногда и еще большую величину (до 2° на 1 м).
В ряде случаев условие жесткости дает более сильное
ограничение, нежели условие прочности. В связи с этим покажем
использование условия жесткости с целью подбора сечения в случае
чистого кручения осесимметричного вала постоянного сечения.
Для вала сплошного круглого (кольцевого круглого) сечения,
подставив (11.30) в (11.31) и имея в виду, что
Лспл) _ ПП (П0Л) _ JlR* п 4.
ip — 2 ' 1р — 2 ^ ''
*) См., например, Решето в Д. Н., Детали машин, «Машиностроение».
1!)74, стр. 435.
а) Справочник по кранам. Под ред. А. И. Дукельского, т. 2, «Машино-
ι троение», Л., 1973, стр. 425.
28
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
получим
откуда
Олг*
кь
2Шг
0π#4(1 — α4)
ы,
V Gn [кг] » п ^ V Gji (1 -а4) [кг] '
§ 11.9. Оценка результатов элементарной теории
посредством аппарата теории упругости
1. Вводные замечания. Пусть имеем брус в виде круглого
цилиндра, загруженный на торцах распределенной тангенциальной
нагрузкой, складывающейся в моменты, вызывающие кручение бруса.
Свяжем с брусом систему
прямолинейных прямоугольных координатных осей.
Начало координат поместим в центре
одного из торцов, ось г направим вдоль
оси бруса, а оси χ и у в плоскости
торца. Необходимо исследовать
напряженно-деформированное состояние
бруса, для чего применим полуобратный
метод Сен-Вен а на.
2. Первый этап решения задачи. На
первом этапе в качестве «угадываемых»
функций примем компоненты
напряжений, соответствующие напряжению τ,
полученному в элементарной теории.
Для этого перейдем от τ к
компонентам согласно рис. 11.12, %гх = — τ sin α, тгу = τ cos α. Учитывая,
что %ζ = τ = Μζρ/Ιρ = 9Ягр/1р, sina = #/p, cos a = x/p, получим
2«*Ρ у , _ы,р_х. (lb32)1>s
Рис. 11,12. Разложение полного
касательного напряжения на
компоненты.
^zx —
У_
Ρ
^гу —'
/,
X
~Р
все остальные компоненты напряжении равны нулю
Οχ = оу = σζ = хху = 0.
(И.32)з_б
3. Второй этап решения задачи. Проверяем, удовлетворяют ли
функции (11.32) уравнениям теории упругости, т. е. уравнениям
равновесия (9.1) и совместности деформаций.
Уравнения равновесия приобретают вид
Х = 0, 7 = 0,
ж, , т
+ ■
/
/,
+ ζ=ο,
(11.33)
т. е. функциями (11.32) удовлетворяются при условии, что
объемные силы (Χ, Υ, Ζ) равны нулю или при неучете этих сил.
Ч 11.0] ТЕОРИЯ УПРУГОСТИ И ОЦЕНКА ЭЛЕМЕНТАРНОЙ ТЕОРИИ ^
Такое ограничение является вполне приемлемым, так как эти
силы и не предполагалось учитывать в рассматриваемой задаче.
Уравнения совместности деформаций (9.27), записанные в
напряжениях, при условии (11.33) содержат в левых частях
однородные дифференциальные операторы второго порядка, функции
же (11.32) имеют либо нулевую, либо первую степень1) и, таким
образом, вторые производные от них равны нулю. Вследствие
сказанного уравнения совместности деформаций функциями (11.32)
удов летвор яются.
Таким образом функции (11.32) не противоречат уравнениям
теории упругости и им соответствует некоторое напряженное
состояние тела.
4. Третий этап решения задачи. Выясним, каким нагрузкам
на поверхности рассматриваемого бруса отвечают функции (11.32)
и сопоставим их с интересующими нас, для того чтобы
установить, является ли система функций (11.32) решением именно
нашей задачи. Уравнения равновесия элементарного тетраэдра
(9.2) позволяют найти составляющие поверхностной нагрузки на
торцах и боковой поверхности бруса, для чего, кроме
компонентов напряжений (11.32), необходимо знать I, m и п —
направляющие косинусы нормалей к площадкам, лежащим на торцах и
боковой поверхности.
Начнем с рассмотрения торцов бруса, для которых
1 = т = 0, п = ±\ (11.34)
(плюс относится к торцу, удаленному от начала координат, а
минус—к торцу, проходящему через начало координат).
Используя (9.2) при учете (11.34) и (11.32), получим
Ρνχ — -+-—7—» Pvy — — —7—» Pvz — и (И.оо;
' Ρ 'ρ
(нижние знаки—для торца, проходящего через начало
координат).
Проверим, что является статическим эквивалентом
распределенных по торцам поверхностных сил (11.35). С этой целью
определим следующие интегралы:
Qx = \pvxdF, Qy = \pvydF, Mz = \(pvyx-pvxy)dF. (11.36)
F F F
l) Такие задачи, в которых компоненты напряжений или компоненты
деформаций являются функциями степени не выше первой относительно
координат точек тела, называются простейшими — уравнения совместности
деформаций при этом выполняются тождественно.
30
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ, XI
Подставим (11.35) в (11.36), тогда получим
Р F P F
± aw,.
(11.37)
Равенство нулю величин Qx и Qy вытекает из того факта, что
интегралы, входящие в первые два уравнения (11.37),
представляют собой статические моменты
площади поперечного сечения бруса
относительно центральной оси, которые, как
известно, равны нулю. Итак,
статическим эквивалентом распределенных по
:} Ъ каждому из торцов касательных
поверхностных сил является момент,
действующий в плоскости торца и
равный Шг. Таким образом, граничные
условия на торцах совпадают с услог
виями решаемой нами задачи.
Ограничением является лишь тот факт, что
внешний крутящий момент,
приложенный к торцу бруса, создается
касательными поверхностными силами,
приложенными к торцу и распределенными не как угодно, а по строго
определенному закону, представленному формулами (11.35).
Рассмотрим боковую поверхность бруса; нормали к
площадкам, лежащим в этой поверхности, имеют следующие
направляющие косинусы (рис. 11.13):
/ = cosa, m = cos (π/2 — α) = sina, n = 0. (11.38)
Обозначим символами χ* и у* координаты точки, являющейся
центром рассматриваемой площадки на боковой поверхности, х* =
= г cos α, у* = г sin а. Учитывая (11.32) и (11.38), из (9.2)
получаем
Pvx = Pvy =-v,
Рис 11.13. Элемент на боковой
поверхности круглого цилиндра.
Pvz =
2Яг«
Zif
I,
cosa-
Ш,х*
I,
sina =
гШ, sin a cos a , гШ, sin a cos a
Λ
+
I,
= 0.
Итак, и на боковой поверхности граничные условия,
соответствующие функциям (11.32), принятым на первом этапе в качестве
§ 11.9]
ТЕОРИЯ УПРУГОСТИ Й ОЦЕНКА ЭЛЕМЕНТАРНОЙ ТЕОРИИ
31
решения, совпадают с граничными условиями .решаемой задачи —
боковая поверхность свободна от нагрузки.
Окончательно приходим к выводу: функции (11.32) являются
решением задачи теории упругости о чистом кручении круглого
цилиндра только при условии, что поверхностные нагрузки,
действующие на торцы и образующие моменты дЯг, распределены
согласно (11.35).
5. Четвертый этап решения задачи. На этом этапе найдем все
остальные функции, описывающие состояние бруса. К ним
относятся компоненты деформации εχ, ъу, ъг, уху, ууг и угх и
составляющие перемещения и, ν и т.
Компоненты деформации найдем из уравнений закона Гука
(9.5):
ε* = 0, 8^ = 0, εζ = 0, у^ = 0,
_ 2(1 + μ) Шгх _ 2(1 + μ) Шгу
™*~~ Ε Ι ρ ' *гх~ Ε Ι ρ '
Система уравнений Коши, используемая для определения и,
ν и w, приобретает вид:
ди _ p. dv p. dw p. dv . ди _ ~
~дх~ ' ~ду~ ' "дГ ' 1х~т"ду~ '
dw dv __ 2(1 + μ) Шгх ди dw _ 2(1+μ) ЗЯгу' '
dy ^"dz Ε Ιρ · dz + дх ~ Ε Ιρ '
Проинтегрируем эту систему уравнений. Предварительно
исключим из и, υ и w перемещения бруса как жесткого целого. С этой
целью закрепим точку О
*ο = ί/ο = ζο = 0, (11.39)
«следствие чего
u0 = v0 = wQ = О,
и не разрешим в той же точке (11.39) поворачиваться элементу dz
относительно осей χ и у и элементу dy — относительно оси ζ;
и связи с чем
£И£).-0· (-1).=°·
11(скольку подробно интегрирование уравнений Коши было
прокомментировано в § 9.6, здесь покажем лишь результаты
интегрирования и, чтобы читатель, выполняя это интегрирование
самостоятельно, имел возможность контролировать правильность
32
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
преобразований, приведем и некоторые другие данные (выражения
для производных).
I.
2.
в)
3.
в)
II.
3.
III
1. £ =
дх
О;
■>£($И «>£(£)
а / ди\
дг\ду)
= 0;
ΛΓ=ΛΓθ
_ 2(1+μ) Жг ди _ 2(1+μ) Жг
х = хо Ε Ι ρ ' ду ~~ Έ ' Ιρ
«>£(£)-<>: «>£(£)
а /ди\
dz\dz J
_ 2(1 + μ) Эй,.
λ: = ΛΓ0 ^ Ы '
= 0,
χ = Χα
ди 2(1 +μ) Шг 2(1 +μ) 2Яг
аг — £ 1р У' и'~ Ε fp yz'
1 δυ 2(1 + μ) Ш1г2_ 0 δυ Λ.
Ь ~а* Ε [ρ > Ζ· ду _U'
а /а»\ 2(ΐ+μ) mg. б) а /d*\_0. . а /а»
ао 2(1+μ) Ж, 2(1+μ) 2Иг
az £ /р х' ν ε ι ρ xz-
. dw
= 0; 2. |ϋ—0; 3.
ay
az υ'
г;
= 0.
до = 0.
Итак, получили функции ы, и, до:
2(1+μ)2Κ2
и = ν ,ί,Λ—*- г/z,
2(1+μ)33ί2
и = ν ι„γ'—ζ-χζ,
EID *"' Είρ
до = 0. (11.40)
6. Анализ картины деформации бруса.
6.1. Координаты любой точки. Любая точка бруса
(х, у, ζ) в результате деформации занимает новое положение,
определяемое координатами х1 = х-\-и\ y1=yJt-v, z1 = z-\-w.
6.2. Ось бруса. Точки оси бруса (х = 0, у = 0) в
результате деформации имеют координаты
х1 = и\х-у-о = 0, yi=v\x-y-o = 0, z1 = z + w\x-y-0 = z. (11.41)
Из (11.41) ясно, что точки оси бруса не перемещаются, ось бруса
остается прямолинейной.
6.3. Поперечное сечение. Проследим за произвольным
плоским поперечным сечением z = г; точки этого сечения в
результате деформации представляют собой поверхность с уравнением
г1 = г+до1 2 = г. (11.42)
§ 11.9]
ТЕОРИЯ УПРУГОСТИ И ОЦЕНКА ЭЛЕМЕНТАРНОЙ ТЕОРИИ
33
Равенство (11.42) показывает, что поперечное сечение, плоское
до деформации, остается плоским и после деформации. Точки
поперечного сечения не выходят из плоскости этого сечения.
Проекция перемещения точки с координатами х, у, ζ на
направление радиуса-вектора, соединяющего точку (θ, 0, г) с точкой
(х, у, г), равна
(11.43)
и I ~ cos α-\-υ I ~ sin а,
2=2 ' 2=2 '
где
cos а =
V&+
У2
= —, sina =
Vx2+y2
= ^. (11.44)
Подставляя (11.40) и (11.44) в (11.43), получим
~ X , 2(\+\1)Ж, ..-. у
2(1 +μ) 8», ~ х_ , 2(1 + μ) SW
Е!п У г "f Е/в
г ΧΖ^-=0.
г
(11.45)
i-^rfz
Проекция перемещения точки с координатами х, у, ζ на
направление, перпендикулярное к отмеченному выше радиусу-вектору,
равна
t = — и |2=~sina -\-ν\ζ=~ cosa· (П-46)
Подставляя (11.40) и (11.44) в (11.46),
получим
2(1+μ)3», ; у , 2(1 + μ)3^ ~ χ _
1 ~ ΈΤΡ Уг г л Wp хг г -
2(\ + μ)Sΰlг~(x*+yz) Шг ~ /11/17ч
_ \ г_ г \ Т!>;= _г χτ (J J .47)
El,
GL
Рис. 11.14. К установле-
Равенства (11.45) и (11.47) показывают,
что поперечное сечение круглого бруса,
подвергнутого КРУЧенИЮ, ОСТаеТСЯ ПЛОСКИМ И нию зависимости между
г J r ·> ' „ углом зкручивання и пе-
ПОВОраЧИВаеТСЯ Как ЖеСТКИИ ДИСК ВОКруГ ремещеннем.
оси ζ на угол $г (рис. 11.14) относительно
торца ζ = 0. Относительный же погонный поворот сечений равен
_ъг _ тг _ 2(ΐ+μ) тг
G/,
/,
Поэтому формулы (11.40) можно представить так:
и = — кгуг, ν = κζχζ, w = 0.
(11.48)
Произведенный анализ. показал, что гипотезы о характере
деформации круглого цилиндра при чистом его кручении,
принятые при выводе формулы для касательного напряжения в
34
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
\ТЛ. XI
поперечном сечении, оказались законом, правда, лишь при
одном строго определенном способе приложения к торцам внешних
крутящих моментов и малости угла закручивания.
При использовании аппарата геометрически нелинейной теории
упругости обнаруживается более точная картина деформации
круглого цилиндра при чистом его кручении. Если торцы не
закреплены против сближения, то первоначально прямолинейные
продольные волокна в процессе кручения не испытывают
растяжения. Но поскольку прямолинейная ось каждого из таких волокон
превращается при кручении в равновеликую по длине винтовую
кривую, концы последней должны располагаться в плоскостях,
перпендикулярных оси цилиндра, расстояние между которыми
меньше расстояния между плоскостями торцов до деформации.
При сопоставлении деформации двух первоначально
прямолинейных продольных волокон, находящихся на разных расстояниях
от оси цилиндра, обнаруживается, что винтовые кривые, в
которые превращаются оси этих волокон, имеют различные кривизны —
большую у более удаленного от оси цилиндра волокна.
Вследствие этого перемещения в направлении параллельном оси
цилиндра точек торцов, находящихся на разных расстояниях от оси
цилиндра, различны и торцы, строго говоря, перестают быть
плоскими. Если же сближению торцов воспрепятствовать, то при
кручении цилиндра первоначально прямолинейные продольные
волокна испытывают растяжение. Однако при малых углах
закручивания перемещения точек торцов в направлении, параллельном
оси цилиндра, оказываются величиной более высокого порядка
малости, чем перемещения этих же точек в плоскостях торцов,
и описанный эффект почти не проявляется, вследствие чего им
пренебрегают. При больших углах закручивания этим эффектом
пренебрегать нельзя и задача в таком случае становится
геометрически нелинейной.
Заметим, однако, что, как показал А. Ю. Ишлинский в статье
«О напряженном состоянии цилиндра при больших углах крутки»
(Прикладная математика и механика, том VII, 1943, вып. 3) эту
задачу можно решить и на основе классической линейной теории
упругости. Он изучил напряженно-деформированное состояние
упругого круглого цилиндра при больших углах крутки в
условиях, когда точки торцов в процессе деформации не перемещаются
в направлении, параллельном оси цилиндра. Кроме отмеченного
уже возникновения в поперечных сечениях вала нормальных
напряжений, складывающихся в продольную силу, обнаружено,
что, вследствие поперечной деформации продольных растягиваемых
волокон, происходит уменьшение радиуса цилиндра. Наряду с этим
возникают радиальные напряжения, равные нулю на боковой
поверхности цилиндра и достигающие максимального значения
в точках на оси цилиндра.
ч II 1и| ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ЧИСТОМ КРУЧЕНИИ ВАЛА 35
§ 11.10. Потенциальная энергия деформации при чистом
кручении вала круглого поперечного сечения
Рассмотрим вал круглого сечения в общем случае переменного
Ι ι,ι in уса 1), подвергнутый воздействию внешних крутящих моментов,
ны и,тающих внутренний крутящий момент, переменный вдоль оси
Ι Ι:ι такого вала вырежем элемент двумя поперечными сечениями,
находящимися одно от другого на расстоянии dz. Действие
отброшенных частей, примыкающих к этому элементу, заменим
внутренними силами, которые по отношению к элементу являются
шн'ишими. Такими внутренними силами оказываются лишь кру-
ηιιιι,ικ- моменты. В указанном элементе при деформации вала
накапливается потенциальная энергия деформации dU, численно
Iщипая работе dA внешних по отношению к элементу сил
dU = dA. (11.49)
ι', другой стороны,
NIC
dA=^Mgdbgt (11.50)
d*.-^i (И.51)
подставив (11.51) в (11.50) и после этой подстановки использовав
ипПленный результат в (11.49), получим
,,, 1 Mldz
Потенциальная энергия, накопленная во всем валу, найдется по
формуле
/
U
-ί
2GIp
о
I с./in поперечное сечение вала и крутящий момент не зависят от
.-, М, = Шг = const, то
м% с ми а»у
Г» MIL
2GI0 J 2Gf0 2Gf0
μ о
') \\ настоящем параграфе предполагается, что зависимости, полученные
ι ш круглого вала постоянного вдоль его оси радиуса, могут быть использо-
MMIH.I и и случае валов переменного радиуса. Такая концепция связана с допу-
iin iiiu'm некоторой погрешности. Более строгое рассмотрение на.пряженно-дефор-
Hii|mii;iиного состояния валов переменного радиуса производится в § 11,14·
36
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
§ 11.11. Чистое кручение круглого цилиндрического вала
при работе материала в упруго-пластической стадии
1. Гипотезы. Рассмотрим постепенное возрастание внешних
моментов, приложенных к торцам круглого цилиндрического вала
и скручивающих его. Будем считать, что в какой бы стадии ни
работал материал— упругой, упруго-пластической или
пластической—сохраняются две гипотезы — гипотеза плоских сечений и
гипотеза о прямолинейности деформированных радиусов.
2. Диаграмма τ = τ(γ). Для расчета круглого скручиваемого
цилиндра на чистое кручение в любой стадии работы материала
необходимо иметь для материала вала диаграмму τ = τ(γ). Эту
диаграмму можно построить, либо используя непосредственно
опыт с тонкостенной осесимметричной цилиндрической трубкой,
изготовленной из исследуемого материала и подвергаемой чистому
кручению, либо путем пересчета результатов опыта с осевым
растяжениям образца. В первом случае в опыте замеряются Мг —
крутящий момент и $г — угол закручивания. Учитывая при этом
практическую однородность напряженного состояния во всем объеме
трубки, вследствие ее малой толщины и, следовательно,
вследствие практически равномерного распределения напряжений по
толщине трубки, определим τ и γ из уравнений одинаково
справедливых в рассматриваемом случае (однородность поля напряжений)
и в упругой и в пластической стадиях работы материала
Мг = 2nR - б ■ τ · R, ftzR = yl.
Здесь 2nR ■ δ — площадь поперечного сечения кольца.
Из этих уравнений
* = ЪЩЧ- 7-*Γ· С1·52»
Имея экспериментальную зависимость Μζ = Μζ(ϋ·ζ) и используя
(11.52), получаем зависимость τ = τ(γ). В случае, если для
построения τ=τ(γ) применяется диаграмма σ = σ(ε), то соответствие
между этими двумя диаграммами можно устанавливать так.
Предположим, что возникновение пластичности в материале
растягиваемого образца подчиняется условию пластичности в форме
энергетической теории (удельной потенциальной энергии формоизменения).
Интенсивность напряжений (см. гл. V, § 5.16, раздел 8) ^
выражается следующими формулами при двух частных видах
напряженного состояния: осевая деформация (οχφ0, σ2 = 0, σ3 = 0)
(растяжение)
σί = σ1 = σ, (11.53)
чистый сдвиг (σχ = τ, σ2 = 0, σ3 = —τ)
о( = УЗх, (11.54)
§ 11.117 УПРУГО-ПЛАСТИЧЕСКОЕ КРУЧЕНИЕ ВАЛА 37
Сопоставляя (11.53) и (11.54), находим
σ = /3τ. (11.55)
Интенсивность деформаций (см, гл. VI, § 6.5, раздел 6) при
осевой деформации (растяжении) найдем, исходя из того, что % = е
и 83 = 83. Для отыскания е2 и е3, обусловленных эффектом
поперечной деформации, вспомним, что
ео= о ' Зб0 = 8+^бз» £2 = 83= 2—· (11.5b)
Учитывая (11.56), получим ег для осевого растяжения
&i = е — ε0.
При этом
._σο_ _σ0(1-2μ) _σ(1-2μ)
Ь° [К Ε 3£ *
Здесь учтено, что σ0 = (1/3) (σ1-\-σί-\-σ3) =σ/3, тогда
ef = е - σ ~Ε μ . (11.57)
Для чистого же сдвига в плоскости Оху (εχ = гу = гг — ууг — угх = 0;
Ы = Уу= (П.58)
или, сопоставляя (11.58) и (11.57), получаем
ε_(1-2μ)σ=-^, y = V2(e-l-=&u). (11.59)
ЪЕ V 2 х \ ЪЕ J v '
Если из (11.55) определить τ
τ-^. (11.60)
то, используя зависимость σ = σ(ε), найденную в опыте с
растягиваемым образцом, и учитывая (11.59) и (11.60), зависимость
τ = τ(γ) легко получить без выполнения опыта с образцом,
испытывающим чистый сдвиг.
3. Диаграмма касательных напряжений вдоль радиуса круглого
поперечного сечения цилиндрического скручиваемого стержня.
Указанная в заголовке диаграмма строится по диаграмме τ = τ(γ)
для материала и известной величине сдвига vmax, возникающего
к наиболее удаленных от центра точках поперечного сечения вала,
11апомним, что распределение γ по радиусу, вследствие
сохранения прямолинейной его формы при деформации, происходит по
ткону прямой линии Ύ ■ = —-—, у — μ Ymax. Совмещаем
Vmax "max Рщад
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
Λ
•а-
в
α
>£
л
•э·
в
«>Е
Λ
л
Η
и
Л
с-4
Л
ы
,в
а
¥
•s
я
я
X
0)
в·
4)
υ
2
О
a
в·
ω
о.
0)
С
О
с
Я
X
0)
№
со
S
X
S
л
ч
О)
ь
Я
CJ
Я
«
о
о.
2
с
Я)
t-»
О
г
s
со
О.
и
са
К
t=c
>>
s
а.
И
§ fl.il} УПРУГО-ПЛАСТИЧЕСКОЕ КРУЧЕНИЕ ВАЛА 39
начало координат диаграммы τ = τ (у) с центром круглого
поперечного сечения и равномерно сжимаем всю диаграмму в
направлении, параллельном оси γ, до достижения отрезком 7тах величины,
равной радиусу вала г. Получающаяся при этом кривая и есть
эпюра τ вдоль радиуса в поперечном сечении вала. По мере роста
интенсивности угла закручивания dftg/dz величина 7тах
располагается последовательно на разных
участках диаграммы τ = τ(γ) (рис. 11.15).
4. Нагружение вала. Пусть свойства
материала характеризуются диаграммой
Прандтля (рис. 11.16, а). Найдем
крутящий момент, соответствующий
возникновению в точках, наиболее
удаленных от центра, касательных
напряжений, равных пределу текучести при
сдвиге τΤ; для. этого воспользуемся
формулой (11.14)
Τ/max —
Μ
гт
W,
= ττ
Μη = %τΨρ = τ,
nrd
Сели Мг > Мгх и область пластической
работы материала еще не захватила
всего поперечного сечения вала (рис.
11.16,6), то
Рт г
Мг = 5 τ - 2πρ3 dp2 ■ р2 + $ ττ2πρχ dpx · ρν
ο ρτ
Рис. 11.16. Эпюра касательных
напряжений в поперечном
сечении вала при работе материала
в упруго-пластической стадии.
а) график зависимости τ = τ (ν);
б) эпюра касательных
напряжений.
Здесь рт—радиус границы между областями упругой и
пластической работы материала, τ —текущее значение касательного
напряжения в упругой области в зависимости от р2. Значение τ находим
из подобия треугольников на рис. 11.16
τ _ Ра _ _ Ра _
ТТ Рт' Рт
1:сли рт = г, то все поперечное сечение работает в упругой стадии и
ιζτ'
ρ "τ·
Сели рт = 0, то все поперечное сечение работает в пластической
стадии и
лл лл 2пттг3 4 jtr3 4 TV7 4 ΛΛ
Ms = Μζο = —J- = -3 -γ ττ = у WpxT = -3- Мгт.
Таким образом, Mg0 превышает Мп на 33%.
40
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
5. Разгрузка. При малых деформациях разгрузку можно
рассматривать как нагружение силами (моментами), равными по
величине и противоположно направленными тем, какие были
в конце нагружения. При разгрузке зависимость между
напряжениями и деформациями становится линейной, с тем же модулем
упругости, который был на начальном участке нагружения. Таким
образом, эпюра напряжений при разгрузке, рассматриваемой как
нагружение противоположного знака, линейна. Максимальное
напряжение в этой эпюре должно быть таким, чтобы момент,
эквивалентный эпюре напряжений, линейно распределенных по
радиусу поперечного сечения вала, был равен окончательному
значению момента при нагружении. Если при нагружении имеет
место диаграмма Прандтля, то
/3 з\
"*г, разгр = W рТтах = 23ХТ.Г I-g -^ J ·
Отсюда
Ттах = ψ- 2πττ (у - Щ. (11.61)
На границе упругой и пластической областей
t = W^ = ^ ' & . (11.62)
г рт
"3 ~Ϊ2
Поскольку эпюра касательных напряжений в конце нагружения
не линейна, а эпюра напряжений при разгрузке линейна, после
снятия нагрузки в валу будут иметь место остаточные
напряжения (эпюра которых представляет собой разность эпюр нагружения
и разгрузки) и остаточные деформации.
Пример 11.4. Построить эпюру остаточных напряжений,- получающихся
после разгрузки вала, работающего в упруго-пластической стадии при
условии, что в процессе нагружения диаграммой напряжений в материале является
диаграмма Прандтля и упругая область соответствует значению рт=г/3.
Решение. Для построения эпюры остаточных напряжений достаточно
определить две ординаты: при р=рт = г/3 и при р=г. При р = г/3 величина тост
найдется как разность величины тт, взятой из диаграммы нагружения, и
напряжения τ (11.62)
тост ~ττ rWp \3 12/_TtL г.лгз\г 12 /J
Г 4w /r» ή \1 _ 136
~TtL &υ*\3 27-12JJ-243Tt'
При p = r τ^τ найдется как разность величины τ , взятой из диаграммы
нагружения, и напряжения (11.61) —из диаграммы разгрузки
1 //-з рз\ Г 2.2Я/Г» ρ»\Ί 26
^1, = ^-Щ 2πΤτ [Υ ~ 12 ) =Тт L1 "IP- [Τ ~ 12JJ = ~ 81 Τ-
Диаграмма остаточных напряжений, а также диаграммы нагружения и
разгрузки, разностью которых она является, показаны на рис. 11.17,
§ 11.111
УПРУГО-ПЛАСТИЧЕСКОЕ КРУЧЕНИЕ ВАЛА
41
Выполним проверку, которая состоит в том, что система остаточных
напряжений, являясь самоуравновешенной, должна сводиться к нулевому
крутящему моменту. В упругой области формула для
касательного напряжения имеет вид
τ=£ρ;
/α 136
при р = г/3 τ = 243ττ.
ь JL - 136
3 ~243Тт'
Таким образом
τΙρ«ξ/73
отсюда
136 тт
81 /■'·
136 р_
"8Г г Χτ·
В области пластических деформаций
формула для касательного напряжения имеет вид
136
26
при р= у τ=^-τΤ; при р = г х = — -^ τΤ;
или
Цт^а+fc-g-, -|γττ = β + ν. (И-63)
Отсюда, вычитая из второго уравнения первое,
получим
f 26 136\ _ 2
ι~8Ϊ~243 Гт ХТГ;
решая это уравнение относительно kv найдем
107 тт
Подставляя найденное kx в любое из уравнений
системы (11.63), получим возможность
определить а
136
107 г тт
243ττ-α 81- 3 г ,
/136 107\ _
а==\243 + 243Гт-1Гт·
Итак, в области пластических деформаций
107 ρ
=г—8Т7-Тт-
а)
τ = χ·
δ)
Рис. 11.17. Построение эпюры
остаточных напряжений,
возникающих в поперечном сечении
вала после разгрузки,
последовавшей за работой материала в
упруго-пластической стадии:
а) эпюра касательных напряже-
нийв конце нагруження;б)эпюра
касательных напряжений при
разгрузке, рассматриваемой как
нагружение моментом
противоположного знака; в)
эпюра остаточных касательных
напряжений.
Теперь определим момент, статически эквивалентный касательным силам,
распределенным по поперечному сечению вала в соответствии с эпюрой.
42
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
изображенной на рис. 11.17
г/г
М,
О л/3
. 136 1 р< к/з Рз
81 г 4 о 3
:=ττ\ 2πρ —--B.pdp + TT \ 2npil—щ- -Μ pdp=
о 107 ! Ρ4
л/3 81 г 4
л/3
68 \ ή . 2я / . /-3\ 107 π / . г*\
= 8ТПТ8ТТТ+ТГ-27)ТТ-ТЙТГ-8Т)ТТ=0-
Равенство нулю поперечных сил Qv и Q^ очевидно.
Проверка подтвердила правильность полученного решения.
§ 11.12. Кручение призматических стержней произвольного
поперечного сечения
1. Вводные замечания. Рассмотрим призматический стержень
произвольного поперечного сечения. Свяжем с ним правую систему
осей xyz; расположим начало координат в центре тяжести одного
из торцов и направим ось ζ вдоль оси стержня, а оси χ и у
совместим с главными осями инерции торца. Объемные силы
учитывать не будем, т. е. положим X = Υ = Ζ = 0.
Пусть на боковой поверхности призмы поверхностные силы
отсутствуют, а на каждом из торцов — распределены по некоторому
заранее ничем не ограниченному закону, при котором статическим
их эквивалентом является лишь момент, действующий в плоскости
торца. Наличие такого момента в каждом из торцов, при условии
их равенства и противоположности направления, вызывает
кручение стержня. Будем считать, что никаких связей, стесняющих
деформацию, на стержень не наложено —он находится в условиях
нестесненного, или, иначе, свободного, кручения, называемого сен-
венановым по имени французского ученого Сен-Венана,
поставившего и впервые решившего эту задачу.
Сначала рассмотрим кручение призм с односвязным
поперечным сечением, а затем обсудим случай неодносвязных поперечных
сечений.
Решение поставленной задачи выполним полуобратным методом
Сен-Венана.
2. Первый этап решения задачи. В качестве «угадываемой»
части решения примем две функции — и и ν, полагая их такими
же, как и в случае чистого кручения круглого цилиндра (11.48)
и = — кгуг, ν = %ζχζ. (11.64)
Кроме того, наложим ограничение на функцию w, считая, что
все поперечные сечения депланируют (искривляются) одинаково,
т. е. полагая функцию w, не зависящей от ζ
w = xzO(x, y)t (11.65)
Φ — называют функцией кручения.
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 43
3. Второй этап решения задачи. Произведем проверку
удовлетворения функциями (11.64) и (11.65) условиям равновесия —
уравнениям Ламе (9.30). Условия совместности деформаций Сен-Венана
при решении задачи в перемещениях удовлетворяются
тождественно.
Используя (11.64), составим следующие дифференциальные
выражения:
. д2ы , r)2u , агы Λ . d*v . №v d*v Λ
. /агф , дчь\
(11.66)
Подставив (11.66) и (11.67) в (9.30) и учтя, что Χ = 7 = Ζ = 0,
получаем тождественное удовлетворение уравнений (9.30)1)2. Что
касается уравнения (9.30)3, то оно, после подстановки в него
(11.66) и (11.67) и сокращения на кг, приобретает вид
i^ + W~0· (11,68)
Таким образом, функции (11.64) и (11.65), принятые на первом
этапе решения задачи, .допустимы — им соответствует некоторое
напряженно-деформированное состояние тела при условии, что
функция кручения Φ является гармонической, т. е. удовлетворяет
гармоническому уравнению (11.68). Приняв решение в форме
(11.64) и (11.65), мы упростили задачу, сведя систему уравнений
(9.30) к одному уравнению (11.68).
4. Третий этап решения задачи. Установим каким граничным
условиям удовлетворяют (11.64) и (11.65) и сопоставим их с
граничными условиями решаемой задачи, сформулированными в
разделе 1.
Поскольку в поставленной задаче сформулированы статические
граничные условия (на торцах —в интегральной форме),
необходимо получить и граничные условия, соответствующие функциям
(11.64) и (11.65) в статической же форме (9.2). С этой целью
выразим компоненты напряжений через составляющие
перемещения (точнее через функцию Ф), воспользовавшись для этого
уравнениями закона Гука (9.6) и уравнениями Коши (9.3).
Из уравнений (9.3), учитывая (11.64) и (11.65), имеем:
е* = 0, 8^ = 0, ег=0, уху = %ζζ - κζζ = 0,
(дФ . \ (дФ \ (11.69)
44
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ Х\
Уравнения закона Гука (9.6) при учете (11.69) записываются так:
tf* = 0, σί/ = 0, σζ = 0, τΧΰ = ϋ,
Теперь все подготовлено для выражения граничных условий (9.2)
через функцию Ф.
Рис. 11.18. Элемент на боковой поверхности призмы
Рассмотрим боковую поверхность призмы. Направляющие
косинусы нормали к элементу боковой поверхности суть (рис. 11.18)
/ = cos(v, л;) = cos α, m = cos(v, у) — cos [γ — ос) = sin α, /г = 0.
Подставляя (11.70) и выражения для I, т и η в (9.2), получим
Pv* = 0, pvy = 0, pvz = τχζ cos (v, *)+t^cos(v, у).
Поскольку по условию поставленной задачи боковая поверхность
призмы должна быть свободна от поверхностной нагрузки, требуем,
чтобы
Pvz = txz COS (V, Χ) + Туг COS (ν, у) = 0, (11.71)
а для этого, учитывая закон парности касательных напряжений,
в поперечном сечении бруса в точках, расположенных у контура Г,
должно выполняться условие
x^cos(v, χ) -f тгу cos (v, #) = 0 на Г, (11.72)
которое (см. рис. 11.19, а) можно трактовать как равенство нулю
составляющей полного касательного напряжения, направленной
по нормали к контуру, во всех точках поперечного сечения,
расположенных у контура.
Иными словами (11.72) — это условие, согласно которому
полное касательное напряжение в точках поперечного сечения,
находящихся у контура, направлено вдоль касательной к последнему.
Рассмотрим торцы призмы. Направляющие косинусы нормали
к элементу торца суть:
/=0, т = 0, л=;±1 (11.73)
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 45
(плюс относится к торцу, удаленному от начала координат, а
минус—к торцу, содержащему начало координат). Подставляя (11.70)
и (11.73) в (9.2), получим
pvx = =b 1 · τ„ = ± Gkz \j£ — y)>
ρν, = ±1·τ,„ = ±:<3κ, (?£■ + *), pv, = 0. (11.74)
Итак, функциям (11.64) и (11.65) соответствует распределение
поверхностной нагрузки по торцам согласно (11.74).
а) $) 6)
Рис. 11.19. К установлен и ю граничного условия для функции Φ в задаче о свободном
кручении призмы произвольного поперечного сечения: а) поперечное сечение призмы и
точка на контуре; б) к зависимости между dv, dx и dy; в) к зависимости между ds, dx и dy.
Остается определить на торцах интегральные факторы
Qx = \ Pvx dF, Qy = \ pvy dF, Мг = J (pvxy - pvyx) dF,
F F F
чтобы удостовериться выполняются ли условия
Qx = 0, Qy = 0 и МгфО.
Анализ условий на торцах выполним позже.
5. Четвертый этап решения задачи. В этом этапе должны быть
определены все интересующие нас оставшиеся еще не найденными
функции.
Функция w по формуле (11.65) выражается через Ф.
Выше были получены формулы и для компонентов
напряжений (11.70), ненулевые из которых (%гх и хгу) также выражаются
через функцию Ф. Наконец, компоненты деформации легко могут
быть найдены по компонентам напряжений из закона Гука.
Таким образом, решение всей проблемы сводится к отысканию
функции Ф. Для ее отыскания получено уравнение (11.68);
граничные же условия для Φ пока сформулированы не были.
Выполним эту операцию, для чего поступим следующим образом.
Воспользуемся (11.72), подставив в него (11.70) и сократив
46 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ [Г.Л XI
получившееся после этого равенство на Gx2; в результате получим
[l& ~ у) cos <v' *) + {% + х)cos (v> ^ = ° на Г'
или
-^cos(v, χ)-f ^-cos (v, у) = у cos (ν, χ)-χ cos (ν, ί/) на Г. (11.75)
Левая часть равенства (11.75) представляет собой производную
функции Φ по координате, совпадающей по направлению с ν, —
нормалью к контуру. Действительно (рис. 11.19,6):
дФ _ дФ dx . дФ dy
dv ~ дх dv ' ду dv '
при этом dx/dv = cos (χ, ν), dy/dv — cos (v, у), откуда
дФ дФ , , , дФ , ч η /п 7С,
17 = Ж cos <*' V)+Wc (ί/' ν) на (11,76)
Теперь преобразуем правую часть (11.75), учтя следующие
соотношения (рис. 11.19)
x = rcos(r, x), y = rcos(r, у) на Г (11.77)
на Г. (11.78)
-^ = cos(/, х) = — cos(v, y) = — jfct
^- = cos(/, i/) = cos(v, *) = -^
Здесь г —радиус-вектор точки контура поперечного сечения (начало
вектора расположено в начале координат). Подставляя (11.77)
в правую часть (11.75), получим
г/cos (ν, χ) —л; cos (v, г/) =
= г [cos (г, у) cos (ν, χ)— cos (r, x) cos (ν, у)] на Г.
Теперь учтем (11.78), тогда
у cos (ν, χ) —χ cos (ν, #) =
= r [cos (r, у) cos (/, #) + cos (r, λ;) cos (ί, χ)] на Г,
или
у cos (ν, χ)— λ; cos (ν, г/) = r cos (r, ί) на Г. (11.79)
Подставляя в (11.75) вместо левой части равенства выражение
(11.76) и вместо правой части равенства —выражение (11.79), будем
иметь:
~ = г cos (г, 0 на Г. (11.80)
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 47
Правая часть (11.80) представляет собой проекцию г на
направление t (см. рис. 11.19, а). Условие (11.80) и является граничным
для функции х) Ф.
/»cos(«#~/7
0)
5)
в)
Рис. 11.20. График функции л cos (г, (), равной производной дФ/dv, на контуре
поперечного сечения в случае, если последнее имеет вид: а) круга; б) прямоугольника; в) эллипса.
На рис. 11.20 показаны поперечные сечения скручиваемых
призм и изображены функции г cos (г, ή на их контурах.
6. Решение задачи о кручении призмы при помощи функции
Ψ, сопряженной с функцией Ф. Путем перехода от функции Φ
к гармонической функции Ψ, сопряженной с нею, задача о
кручении призмы может быть сформулирована как некоторая другая
краевая задача (задача Дирихле2)) для этой вновь введенной
функции. С этой целью в условии (11.72) направляющие косинусы
нормали ν выразим через соответствующие направляющие
косинусы касательной /, согласно (11.78), в результате получим
Tzxcos(t, y) — Tzycos(t, х) = 0 на Г. (11.81)
Подставив (11.70) в (11.81) и сократив после этого все члены на
Gkz, получим
("Ж" ~"у)cos V> ^_("^"+x)cos^' *)==0 на Г;
учтя формулы (11.78) для cos (t, у), cos (t, x), будем иметь
дФ . \ dx
у ds
ох
ду
+ х)
ds
= 0 на Г,
или, сократив на l/ds и произведя некоторые элементарные
преобразования, получим
дФ
дх
dy
дФ
ду
dx = xdx-\-ydy на Г.
(11.82)
*) Краевая задача для гармонической функции, в которой на контуре
в качестве граничного условия задана производная искомой функции по
координате, измеряемой по направлению нормали к контуру, называется
задачей Неймана.
2) Задачей Дирихле называется краевая задача для гармонической
функции в случае, если на контуре задано значение самой искомой функции.
48 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ [ГЛ. XI
Для того чтобы получить в левой части полный дифференциал,
введем новую функцию Ψ, удовлетворяющую следующим
условиям:
дФ _ 0Ψ дФ _ 0Ψ /η βο4
носящим в теории аналитических функций название условий Коши —
Римана. При этом функция Ψ также является гармонической,
т. е. удовлетворяет уравнению Лапласа
S+S"»- (11.84,
Имея в виду (11.83), придадим условию (11.82) следующий вид:
—^—dx-\--^—dy = xdx-\-ydy на Г, (11.85)
или, учитывая, что выражение в левой части представляет собой
полный дифференциал, получаем
άΨ = χ dx + у dy на Г.
Проинтегрировав (11.85), получим
Ψ(χ, у) = ^ + ^- + С на Г. (11.86)
Очевидно, что (11.86) регламентирует значения Ψ (я, у) на контуре.
Таким образом, введя вместо Φ функцию Ψ, получили задачу
Дирихле для Ψ; эта функция должна удовлетворять
гармоническому уравнению (11.84) и приобретать на контуре значения (11.86).
Формулы (11.70) для хгх и тгу, выраженные через*- функцию Ψ,
имеют вид
*«=<Ц4£-- у), тг,= (Ц-^- + х). (11.87)
7. Решение задачи о кручении призмы при помощи функции
Прандтля. Задача о кручении призмы становится особен чо
изящной, если для описания ее используется функция φ,
предложенная Прандтлем. Эта функция задается во всей области D, т, е.
во всем поперечном сечении призмы, и имеет вид
φ(χ, y) = Gxe(V-£±£} в D. (11.88)
При этом
£-<*.(£--*). £-<4f·-»)· (11-89>
Сопоставляя (11.89) с (11.87), легко обнаруживаем, что
Ъ-%, τ„ = -£. (11.90,
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 49
Функцию Прандтля ср по аналогии с функцией Эри называют
функцией напряжений: остается установить, какому уравнению и
какому граничному условию она должна удовлетворять.
Для этого продифференцируем (11.88) дважды по л: и отдельно
дважды по у
£-(»«.£-<*.. £=<*.£-<*. в D. (П.9.)
Сложим теперь уравнения (11.91)1>2, при этом получим
Учтя (11.84), получим
~Φ + 45- = - 20и« в D. (11.92)
дх2 ' ду2
Уравнение (11.92) называют уравнением Пуассона.
Сопоставляя (11.88) с (11.86), обнаруживаем, что
φ(χ, y)-=GxzC ha Г, (11.93)
т. е. функция Прандтля на контуре поперечного сечения
приобретает произвольное, но постоянное во всех точках значение.
Таким образом, решение проблемы о кручении призмы сводится
к отысканию функции Прандтля, которая находится из уравнения
(11.92) при граничном условии (11.93). После отыскания функции
Прандтля, ненулевые компоненты напряжений находятся по
формулам (11.90), ненулевые компоненты деформаций — из уравнений
закона Гука по формулам
__L __L
Угх q τζχ, Угу q ^гу
Наконец, для того чтобы найти w по (11.65), нужно выразить Φ
через функцию Ψ.
Предварительно найдем Ψ из (11.88)
ψ=0£φ(*. У) + Ц^ в D. (11.94)
После отыскания Ψ, функция Φ находится из (11.83) путем
интегрирования, выполняемого элементарно.
8. Определение интегральных силовых факторов на торцах
призмы. Вернемся к определению статического эквивалента
поверхностных сил Ρν_κ η pvy, действующих на торцы призмы, выразив
их через функцию Прандтля. Согласно (11.74) и (11.90) имеем
50 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ [ГЛ. XI
Определим поперечную силу
F F х0 у0
Χι ί/ι Χι
Xo Уя х»
Равенство нулю интеграла вызвано равенством нулю
подынтегрального выражения, так как функция φ приобретает в точках
контура одинаковые значения и, таким образом, согласно (11.93)
ф(*. &) = Ф(*. y0) = GKzC.
Аналогично получаем Qy = 0.
Наконец, определим Мг (формула составлена для торца,
проходящего через начало координат)
Μ
F F
~ \ dy\^xdx==~~ J dx\^y~\ Фф)~ \ dy(y>x-^ ydxj =
= - j [φ (*. yi) ui - φ (*. ί/ο) y0—$4>dy
dx —
- J [ф(*ь #)*ι-φ(*ο. #)*o- J Φ^ di/.
Для внутренних интегралов было применено интегрирование по
частям. Учитывая, что во всех точках контура значение функции
φ одинаково
φ (χ, yi) = φ (χ, у о) = φ fa. у) = φ fa» г/) = Gx*c = %.
заключаем, что
ж**
ί/**
Первый и третий интегралы, входящие в формулы для Мг,
представляют собой площадь, ограниченную внешним контуром
поперечного сечения скручиваемого бруса (рис. 11.21, а, б)
у**
S (yi-yo)dx= $ (xl-x0)dF = F.
χ* у*
Следовательно,
Mz = 2(^<pdxdy-F%y (11.95)
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 51
Если поперечное сечение скручиваемой призмы многосвязно,
и прямая у = const (рис. 11.21, в) или χ = const (рис. 11.21, г)
пересекает внутренний контур, то интегралы в формуле для Мг
берутся так же как и ранее по частям, но в других пределах,
За х
я,
^\ °
У*
■< >-
.
'/^w!
щ
у**
-*
# J
1
) ,
'
Xi
'"У
Хд
^
6)
а
γ
ч
fy
\
Ν \
) )
^f
1
XZ '
\х1
\
,
ч
' ,
' У
Хд
6)
δ)
Рис. 11.21. К определению интеграла прн установлении статической эквивалентности
касательных сил иа торце призмы крутящему моменту: а) к определению \ ητ-y dy
(поперечное сечение односвязное); б) к определению \ ——χ dx (поперечное сечение односвяз-
ное); в) к определению \ -~- у dy (поперечное сечение двухсвязное и прямая у = const
J dy
Saw
-τ—χ dx (поперечное сечение
двухсвязное н прямая χ = const пересекает внутренний контур).
чем если указанного пересечения нет (на внутреннем контуре
функция φ приобретает значение φχ)
м* = — S &ιΦι ~ УоУо + #зФо - £fe<Pi) ^ + SS Φ dx dy -
— J (*ιΦι - *οΦο + *зФо - *«Φι) dy + \\ydxdy =
= 2\\(pdxdy-\-(p1\(y2- yx) dx + ц>г \ (x2 - xx) dy -
- Фо\ (Уз -Уо) dx-ψο] (хз ~ Xq) аУ = 2 (S J Ψ <**Φ + ΨΛ-Ф<Д)·
52 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ [ГЛ. X!
Здесь интегралы от φ берутся лишь в пределах материальной
части области. Ft и /^ — площади, ограниченные соответственно
внутренним и наружным контурами.
ι ι ι
Рис. 11.22. К определению крутящего момента: а) по формуле (11.95) (поперечное
сечение односвяэное); б) по формуле (11.96) (поперечное сеченне неодносвязное).
Если в поперечном сечении скручиваемого вала имеется
несколько внутренних полостей (сечение /г-связное), то формула для
Мг приобретает вид
MB-2\\\ydxdy + 2 Φ^-φοΛ,ν (Η·99)
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 53
Рассматривая (11.95) или (11.96), обнаруживаем, что Мг не
зависит от значения функции φ0 на контуре. Крутящий момент равен
удвоенному объему, ограниченному, с одной стороны, поверхностью
φ (χ, у) и плоскостями, параллельными плоскости ху в пределах
внутренних полостей и, с другой стороны, плоскостью,
проходящей параллельно координатной плоскости Оху на расстоянии φ0 =
= GkzC от нее (рис. 11.22, а, б).
Итак, мы удостоверились, что поверхностные силы (11.76),
действующие на торцы призмы, имеют своим статическим
эквивалентом только внешний крутящий момент.
9. Окончательная математическая формулировка задачи. Таким
образом, проблема кручения призмы сведена к отысканию
функции Прандтля φ (χ, у) из дифференциального уравнения
Δφ = -2£κζ в D, (11.97)
при граничном условии на контуре
Ф = СхгС на Г. (11.98)
Вследствие независимости Мг от значения С это значение может
быть принято равным нулю, тогда на контуре
φ = φο = 0. (11.99)
10. Определение интенсивности угла закручивания. Выразим
крутящий момент через функцию Φ
Мг = J (pvxy - pvyx) dF =
-μ-<^-,)ί+<*.(»+,),]<ΐΡ_
отсюда
*,-sb (п.юо)
где GIK — жесткость призмы при кручении, а так называемая
постоянная кручения /к отражает в выражении жесткости геометрию
ИИ
x* + y2 + {-^-x--^-y)]dxdy
Если поперечное сечение скручиваемого бруса круглое, то
поперечные сечения его остаются плоскими и, следовательно, Φ (χ, j) ==
==0, вследствие чего
54
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. Χί
т. е. постоянная кручения в этом случае равна полярному моменту
инерции. Постоянную кручения можно выразить, разумеется, и
через функцию Ψ. Для этого подставим в (11.95), вместо φ,
выражение через Ψ, согласно (11.88), и положим φ0 = 0, в результате
получим
Mz = 2Gkz ^(ψ-^^jdxdy. (11.101)
Hi Условие однозначности перемещения w в случае неодно-
связного поперечного сечения призмы. Если поперечное сечение
скручиваемой призмы неодносвязно, то проблема по-прежнему
сводится к краевой задаче
Δφ = —2Схг в D,
9 = Q на Tt (i = 0, 1, 2, ..., η — 1).
На каждом из контуров Г,- постоянная Ct своя собственная. При
этом необходимо соблюдать еще и условие однозначности
перемещения, которое при «-связности поперечного сечения, согласно
главе IX, имеет вид
Kt = §^ds = 0 (i = l, .... я-1). (11.102)
При этом интегралы берутся вдоль произвольной замкнутой линии,
лежащей в пределах поперечного сечения и проходящей через
мысленный разрез, проведение которого уменьшает связность
поперечного сечения на единицу. Имеется в виду, что каждая
следующая г-я замкнутая линия (ί = 1, ..., η— 1) проходит хотя
бы через один новый разрез по сравнению с ранее
рассматривавшимися.
Расшифруем условие (11.102)
*<-$(£!+£D*-° с-'. ·■·.»->)■ (".юз)
Здесь, если учесть (11.65) и (11.83),
dw_ дФ_ &Ψ dw_ дФ ΘΨ
д^ — *г 'Ш~У'г~ду' Ъу~У'гду~ Kz дх'
Наконец, принимая во внимание (11.94) и (11.90), получим
— -κ f-L^4-^---^4-wx -^4-ϋκ
дх -Хг \(3нг ду^У}- G ду^уУ1г~ G ^У*г'
dw / ^ ^Ψ_l \ _L?5 Zf£
~dy y'z\GKz~dx~T'X)- ~'Gd~x~Xy'z~ G -χ*ζ>
тогда (11.103) запишется в следующем виде:
Ы4-4-)^ + Ш*4;+^а-?)л=° <!1Л04>
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 55
или, учитывая, что для любой кривой линии внутри поперечного
сечения так же как и для контура Г справедливы формулы (11.78)
£=cos(t, χ), & = cos(t, у),
получаем
(I)t2cos(t2, t) ds = Gkz φ (χ j- — у -£\ ds. (11.105)
Итак, в левой части равенства имеем интеграл по замкнутой
линии от проекции полного касательного напряжения на
направление касательной к этой линии.
В правой части равенства (11.105) каждый из интегралов
&x-^ds = &xdy и ~foy-^ds = — (bydx (11.106)
выражает собой площадь фигуры (рис. 11.23), ограниченной
замкнутой линией, по которой происходит интегрирование. При этом
учтено, что перед вторым интегралом стоит знак минус и,
следовательно, у площадей, изображенных на рис. 11.23, б, знаки
должны быть изменены на обратные. Отметим, что за
положительное направление обхода замкнутой линии принято такое, при
котором ось χ совмещается с у кратчайшим путем.
Итак, равенство (11.104) приобретает вид
φ τ* cos (τ*, t)ds = 2Gxg%· (11.107)
Интеграл, стоящий в левой части называют циркуляцией
касательного напряжения по замкнутой линии; обозначим его
символом J
У = φ τ* cos (τ„. () ds, (11.108)
тогда формула (11.107) приобретает следующий вид:
J = 2(mz% (11.109)
Для любой замкнутой линии, полностью расположенной в
поперечном сечении призмы, циркуляция касательного напряжения
равна умноженной на 2Gkz площади %, заключенной внутри этой
замкнутой линии. Приведенное утверждение составляет
содержание так называемой теоремы Бредта, по имени английского
ученого, сформулировавшего ее.
Если замкнутые линии выбраны так, как это необходимо для
условия однозначности перемещения w (11.102), то последние
условия записываются в следующей форме:
/, = 2Gx.& (i=\, 2, ..... η-\). (11.110)
Возвращаясь к тому, что на каждом из контуров,
ограничивающих область D, функция φ должна приобретать свое постоянное
56
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
Af5f:
dy>U,x>0;
xdy>0
а2в2:
y<0,dx>0
ydx<0
fffcf:
dy<0, x>0;
xdy<0
щ:
dy<0,w<0;
xdy>0
SfAf:
dy<0,x>0;
xdy<0
вгс2:
y>0, dx>Q\
ydx>0
игАг;
y<o;dx<o;
ydx>0
dy
Рис. 11.23. К определению (υ ί χ -jf- — у -r— J ds: а) к определению ш j-ds, б) к опре·
делен
ию (ν) у
ds.
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 57
значение, подчеркнем, что на каждом из граничных контуров
величины этих постоянных оставались пока неизвестными. Как бы
их не изменять, равновесие и совместность деформаций будут
обеспечены. Условиями же для установления величин этих
постоянных являются условия однозначности перемещений w (11.110)
на каждой из замкнутых линий, совпадающих с внутренними
граничными контурами.
12. Определение напряжения и погонного угла закручивания при чистом
кручении цилиндрического стержня эллиптического поперечного сечения.
12.1. Функция Прандтля. В рассматриваемом случае функцию
Прандтля φ легко подобрать, т. е. легко подобрать функцию, которая
удовлетворяла бы и уравнению (11.97) в любой точке эллипса и граничному
условию (11.98) в любой точке контура. Действительно, если принять ее в виде
(р==л(^ + ^-1)' (11Л11)
понимая под А постоянную величину, то на контуре, уравнение которого
х2 и2
-£--}-^-=1, она обращается в нуль, что соответствует граничному условию
(11.99). Для того, чтобы функция (11.111) удовлетворяла и уравнению (11.97),
подставим в него φ и определим из полученного уравнения постоянную А.
Найдем производные от φ
д\ = 2А &φ_2Α
дх2 а2 ' ду2 6й * { }
Теперь, подставив (11.112) в (11.97), получим
1 . 1 \ ™ - / 1 . 1 \ GkmW
Функция Прандтля приобретает вид
_ Gxza2b2 Ix2 у2
φ— a2-\-b2\^ +62 —
12.2. Определение компонентов напряжения. Компоненты
напряжения выражаются следующими формулами:
_3ср_ 2Gx£a2y _ δφ _20кгЬ2х
гх~ду~ а2+Ь2 ' Х*У~~ дх~ а2 + Ь2 " (И Ό)
12.3. Полное касательное напряжение. Эпюры
напряжений по диаметрам сечения. Полное касательное напряжение в
произвольной точке поперечного сечения с координатами χ и у находим так:
T*-V4*+^=^s Κ^ί/2+^ . (п.цз)
Если точка (х, у) лежит на контуре, то χ и у связаны между собой
уравнением . эллипса, используя которое можно одну из координат из формулы для
хг исключить; например, найдя у2
уъ = Ь2-^х2, (11.114)
прийти к формуле
:дд^*8 \fa*b2-а2Ь2х2 + №х2.
58
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
ГГЛ Xt
Теперь легко найти точку с максимальным полным касательным напряжением,
для чего исследуем хг на экстремум,
можем искать экстремум τ|
Так как хг^0, вместо экстремума хг
402χ2
Т2 (fl2_J_62)2
(П)
d*
= 0,
402κ·2
(α2 + 62)2
(aW — aWx* + №x'2),
{—2а?ЬЧ-\-2№х) = Ъ,
4G2x2
или, учитывая, что
^ φ 0, 262* (б2 — а2) = 0. Пусть а Ф b, тогда je= 0
(α2 + 62)2
и, следовательно, если учесть (11.114), у=Ь.
Для того, чтобы судить о характере экстремума, рассмотрим знак второй
производной
d2(τ|) 402κ|
dx2 = (α2 + 62)2
(—2α262 + 26*).
Если α < 6, то d2 (x^/dx2 > 0, если же а > 6, то d2 (τ%)/άχ2 < 0 и тогда в точке
(0, Ь) х\, а следовательно, и хг, в первом случае принимает минимальное,
а во втором — максимальное значения. Из множества значений, принимаемых
полным касательным напряжением в точках, лежащих на контуре
эллиптического поперечного сечения скручиваемой призмы, максимальным является
значение хг в точке А, ближайшей к центру сечения, и минимальным в точке В,
наиболее удаленной от центра.
Итак, если а > Ь, то
тгтах — Ι τζχ
2Gxza2b
α2 + 62 :
Tzmin xzy
= a
0
2Gxzb*a
a2 + 62 '
Из формул (11.90') видно, что в точках каждого из главных диаметров эллипса
полное касательное напряжение совпадает с одним из компонентов и,
следовательно, направлено перпендикулярно диаметру
20щЬЧ
у = 0-Х*У- fl2 + 62 ' Т«
х = о {Хгх] α2 + 62 ' %г
У-
У
= 0;
х = 0
= 0.
(11.115)
(11.116)
Закон изменения полного касательного напряжения хг вдоль главных
диаметров эллипса [см. (11.115) и (11.116)] линейный. Можно показать, что в любой
точке любого не главного диаметра эллипса направление полного касательного
напряжения параллельно касательной к контуру в точке пресечения с ним
рассматриваемого диаметра и, что закон изменения величины полного
касательного напряжения, в зависимости от расстояния точки от центра сечения,
линейный.
У всех точек на некотором произвольном диаметре отношение χ и у
постоянно
— = tga=const.
У
Тогда из (11,113), вынося у из-под радикала, получаем
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 59
Так как %г зависит линейно от у, то τζ линейно зависит и от
пропорциональных величине у расстояний точек диаметра от центра эллипса
\Гх*~+у* = у\/\+\Ф<х.
Параллельность же расположения хг касательной к контуру в точке
пересечения с ним диаметра легко обнаружить, если учесть, что в точках диаметра
отношение компонентов сохраняется постоянным
Ι τ,χ | Фу а2 ,
Распределение касательных напряжений в эллиптическом поперечном сечении
показано на рис. 11.24, а.
w=m
<Ш^
а)
6)
8)
Рис. 11.24. К кручению эллиптического цилиндра: а) распределение касательных
напряжений; б) Депланацня поперечного сечения эллиптического цилиндра при свободном
кручении (аксонометрия); в) ортогональная проекция горизонталей.
12.4. Интенсивность угла закручивания. Перейдем к
определению погонного угла закручивания хг; предварительно найдем функцию Ψ
Ч-=д^Ф(*,«+^
1
0хга262
Gxz α2 + 62
α2 "^б2
+
Хг + Ф
(11.117)
Подставив (11.117) в (11.101) и учтя (11.100), получим
Λ
-*Ш=
+ 62
α2 b2 ^^
-и=
A-2 + t/2 Χ2+ί/;
2 _ 2
Ω262
dx dy=
+ 62
Φ 62 ^
dxdy.
(11.118)
Отдельно найдем интеграл /
Так как интегрирование необходимо выполнить на всей площади эллипса
(поперечное сечение призмы), имеющего уравнение
И*-i=Q,
(11,119)
60 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ [ГЛ. X)
предел при интегрировании по χ определим, решив (11.119) относительно χ
Х2 = а*-^у*, χ=±αγ' \-У~ =±±У»-*.
Таким образом, необходимо найти следующий интеграл1):
+ь т ъ у
+br , „я , .., ^ ,+ £Vb
2_/y2
V
-Ь J-jYbt-yt
dy=
JL\+b
ь\-ь
- - mr [yvw^w^ K^+f arcsin £];
- [-2 £I ^T^¥+f? | (* K^=^+ b* arcsin l.)]+J +
+2{{(i/VW=y~*+b* arcsin |-)+* =
= — 7ΓΓΤ -?г- 2 arcsin 1 — 2 — — 62 arcsin 1 + 2 -;- 62 arcsin 1 =
bo3 2 о3 о о
ab n η ab π , . . π πα6 „, ,_Λ.
= -т2у-12+2й*гт· (lL120)
Подставив (11.120) в (11.118), получим окончательное выражение для Ik
. 0 а262 лоб а363 ,,, 10П
1к = 2а^¥-Т=ЛЖ^' (11Л21)
Теперь по формуле (11.100) после подстановки в нее (11.121) находим
интенсивность угла закручивания
**= oU · (11Л22)
12.5. Момент сопротивления при кручении. Напишем
формулу для максимального касательного напряжения (при а>Ь)
2в-лгаЧ
хг max — I хгх
,-о WW' <11Л23>
у=ь
г) Здесь использованы следующие табличные интегралы:
• У
arcsin ~
b
С fW=TyH dy=^ L yw^-\ь*
f i/*VW=!J*dy -|- ^(62_у2)з+^ L YW=y*+b* arcsin -|-\,
( K(62-i/2)3 di/=1 [ί/ Κ(62-ί/2)3+^. К^^Ч-^ arcsin i-1.
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 61
Шдставим в (11.123) выражение для хг согласно (11.122), в результате получим
'«max πα62 ψ . w 2 ' l '
Величину W называют моментом сопротивления профиля при кручении.
12.6. Депланация поперечного сечения. Составляющая
перемещения w выражается следующей формулой (см. (11.65)):
т=кгФ(х, у).
Найдем функцию Φ (χ, у) по полному ее дифференциалу
ά®=ψχάχ + ^άϋ, (11.125)
дФ с№ ЧФ , дФ 6Ψ 262
■У + У' -лТГ = 5Г= „а , ш х~х-
дх ду а2 + 62 * ' Ό ду дх а?-\-1
Функцию Φ из (11.125) получим путем интегрирования, аналогичного
интегрированию уравнений Коши
^ l· дФ . , V- дФ
2α2
., 2α2 \ α2 —б2
При интегрировании (11.125) учтено, что в центре сечения w, а следовательно,
и Φ равны нулю из-за косой их симметрии относительно центра. Имея
формулу для Ф, находим и
а2 —б2
Функции w соответствует седлообразная поверхность — гиперболический
параболоид, изображенная на рис. 11.24, б в аксонометрии и на рис. 11.24, в при
помощи горизонталей на ортогональной проекции. Каждая из горизонталей
представляет собой гиперболу, отнесенную к осям χ и у как к асимптотам и
имеющую уравнение
хУ = к> k = ^-б2 ' (1U26)
Н* α2 + 62
w* — отметка на поверхности w, соответствующая обсуждаемой горизонтали.
Искривление первоначально плоского поперечного сечения, т. е.
депланация, наблюдается при свободном кручении призм любого поперечного сечения,
кроме круглого или круглого кольцевого, которые остаются плоскими и после
деформации.
12.7. Частный случай —круглое поперечное сечение.
Пусть a = b = r, тогда формулы (11.126), (11.90'). (11.121) и (11.124)
приобретают соответственно следующий вид:
а* —а?
а?-\-а?
2Gxza*y 2G%za*x
α2 + α2 - ΟΧ*ί/> %Ζΰ- α2 + α2
w \=Κζ -ο ■ _.. k = 0;
Ггх=~ „а ,*„я =-Gxgt/, χζΰ = —ς±-Γ = 0^ζ^
а3а*- лг4 , паа* иг* ._
(11.127)
62
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
ГГЛ. XI
13. Результаты решения задачи о кручении призматического
бруса прямоугольного поперечного сечения. Решение задачи о
свободном кручении призмы прямоугольного поперечного сечения
(рис. 11.25) в принципе выполняется по той же схеме, которая
показана в предыдущем разделе в примере о свободном
кручении эллиптического цилиндра. Однако в случае прямоугольного
поперечного сечения практическая реализация этой схемы намного
сложнее. Основная сложность состоит в решении краевой задачи
(11.97), (11.98).
,
1
/
►c>|cvi
к
'
ι
ι
а
1
Г
а
1
'
я
а)
Рис. 11.25. К свободному кручению призмы прямоугольного поперечного сечения:-
а) поперечное сеченне призмы; б) эпюры касательных напряжений в поперечном сечении.
Здесь не приводится весь ход решения и даются лишь
окончательные результаты, представленные в виде формул, таблиц и
рисунков.
Решение для φ ищется в виде ординарного
тригонометрического ряда, в котором вследствие очевидной симметрии задачи
сохранены лишь нечетные члены
Ф= 2 M#)cos-^-. (11Л28)
Граничное условие (11.98) на сторонах контура х = ±а/2
функцией (11.128) удовлетворяется. Правую часть уравнения (11.97)
представляем в виде ряда Фурье
1.3,5,...
~-2Gx,= 2 Akcos-^-. (11.129)
§ 11.12]
кручение Призм произвольного сечения
63
Теперь, подставляя (11.128) вместо φ и (11.129) вместо — 2Guz,
получаем дифференциальное уравнение для отыскания функций
/* (У)
tt(y)-(^)2h(y) = Ak. (11.130)
Две постоянные интегрирования в общем интеграле уравнения
(11.130) находятся из граничного условия на сторонах контура
y = ±b/2 fk (— 6/2) = fk (4- b/2) = 0. В результате отыскания
постоянных интегрирования и подстановки интеграла fk (у) в (11.128)
получаем функцию Прандтля в следующем виде:
<P = Gkz
т) -х-
80хгаа
π3
1, з. 5,
k— 1
(-1) 2
ks
, kny
ch —- ,
a knx
г—τ-COS
ch-^—
2a
Далее находятся компоненты напряжений по формулам (11.90).
Максимальное напряжение, постоянная кручения и момент
сопротивления профиля при кручении выражаются формулами
(если Ь>а)
<-z max
= τ
гу
у = о =ΰκζαΚ, Ik = a3bK1, W = a2bK2,
χ=αβ
в которых К, K-l и К2 — некоторые функции отношения Ь/а, для
которых составлены таблицы
1, 3, 5, ...
А * π2 L· k*
ch
knb
2a
*1=Т И
1, 3, 5, ...
192 a X\ 1
π5, b
1 τέ-th
knb
~2a~
K,=
JSi.
к
Из таблиц значений коэффициентов /С, Κι и К2 (табл. 11.1)
видно, что если поперечное сечение очень вытянуто, т. е.
Таблица 11.1
К
Ki
Кг
Ь/а
1
0,675
0,1406
0,208
1,2
0,759
0,166
0,219
1,5
0,848
0,196
0,231
2,0
0,930
0,229
0,246
2.5
0,968
0,249
0,258
3
0,985
0,263
0,267
4
0,997
0,281
0,282
5
0,999
0,291
0,291
10
1,000
0,312
0,312
00
1,000
0,333
0,333
64
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
отношение Ь/а-*-оо, то
= вкга, /А = 4- a3b = О,3333α36, W = \a2b = 0,3333a2b.
ьгтах
Близкими к этим формулам оказываются и формулы и при
достаточно большом Ь/а, например, при Ь/а = \0 тгтах = бх.а,
Ik = 0,3\28a3b, W = 0,3\28a*b. Ha рис. 11.25, б изображены эпюры
касательных напряжений в прямоугольном поперечном сечении
призмы, испытывающей свободное кручение. тгтах возникает
в точке посредине длинной стороны поперечного сечения.
14. Аналогия Прандтля.
14.1. Аналогия и ее значение. Выведем уравнение
равновесия мембраны большого натяжения, растянутой равномерно
во всех направлениях силами интенсивности ρ и находящейся
под воздействием поперечной равномерно распределенной нагрузки
интенсивности q. Вырежем из мембраны элемент со сторонами dx
и dy, параллельными осям х и у соответственно (рис. 11.26, а).
Действие соседних отброшенных частей заменяем
соответствующими силами (рис. 11.26,6,6: по условию натяжение мембраны
одинаково во всей области по любому из направлений) и запишем
уравнение равновесия (Σπρζ = 0)
О,
pdy dx pdy(dx + дх2 dx)-\-pdx ду
или
ρ 9χ2 dxdy + p ду2 dxdy= qdxdy,
Δη>=—5-.
Ρ
·<"*(£+£*)-
— qdxdy
d2№ a2to _ q
dx2 "■"' at/2 — ρ
(11.
Здесь ft — смещение точек мембраны в направлении,
перпендикулярном той плоскости, в которой она располагалась до
приложения поперечной нагрузки1).
Сопоставление уравнений (11.131) и (11.97) показывает, что
при условии соблюдения равенства
^- = 2Q%Z (11.132)
оба уравнения становятся идентичными. Такая идентичность
свидетельствует о математической аналогии задачи о свободном
кручении и о деформации мембраны большого (одинакового во всех
направлениях) натяжения при воздействии на нее поперечной
*) Использована буква ш, поскольку буква w занята — ею обозначены
перемещения, параллельные оси г в скручиваемом брусе.
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ &>
равномерно распределенной нагрузкиг). Эта аналогия была
отмечена Л. Прандтлем и носит его имя. Аналогия Прандтля имеет
большое практическое значение, так как, во-первых, она
позволяет найти решение задачи о нестесненном кручении призмы
любого поперечного сечения путем проведения эксперимента
с мембраной; натянутой на плоский контур, имеющей такие же
'^тттттттТтттттТТ А А А
й)
дх'
ψ4ί-:
57
--f-
w*
Λ
ду ду\ду
ю
дх дх
Рис. 11.26. К выводу уравнения равновесия мембраны большого и равномерного по
области и направлениям натяжения: а) план; б) проекция элемента мембраны и
действующих на него сил на плоскость Окг; в) аксонометрическое изображение элемента мембраны
и действующих на него сил.
форму и размеры (в каком-либо масштабе), как и контур
поперечного сечения скручиваемой призмы. Во-вторых, отмеченная
аналогия позволяет, исходя из умозрительных соображений,
представить основной характер функций φ, а следовательно, и
распределение касательных напряжений по поперечному сечению
произвольной формы, так как характер провисания мембраны
под поперечной нагрузкой, т. е. вид функции ΐύ достаточно
очевиден, чего нельзя сказать о функции φ. Наконец, умозрительно
представляя вид функции то, в соответствии с ожидаемым
характером провисания мембраны можно придать этой функции упро-
*) Разумеется, для аналогии задач необходима и идентичность граничных
условий. Таковая имеет место, Функции φ и in на внешнем контуре равны О,
66
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
(ГЛ. XI
щенный аналитический вид в случае некоторых видов поперечного
сечения призмы, и найти таким образом приближенное решение.
Аналогия Прандтля позволяет по известной форме провисания
мембраны, определяемой функцией ft, заданной в аналитическом
виде или отыскиваемой экспериментально, установить следующее:
1. Направление полного касательного напряжения в точке
поперечного сечения призмы.
2. Величину полного касательного напряжения в точке
поперечного сечения призмы.
3. Величину крутящего момента.
Остановимся на каждом из этих пунктов.
14.2. Определение направления и величины
касательного напряжения в точке поперечного
сечения призмы. Формулы (11.90)
показывают, что, беря производную от
функции φ по координате х(у),
получаем значение компонента касательного
напряжения, направленного
параллельно у (х). Представим теперь, что
поверхность φ = φ (χ, у) рассечена
плоскостями, параллельными плоскости ху.
Эти плоскости оставляют на поверхности
следы в виде замкнутых линий
—горизонталей. На рис. 11.27 изображены
проекции горизонталей на плоскость
поперечного сечения. Рассмотрим
произвольную точку поперечного сечения
и проходящую через нее проекцию
горизонтали φ = φ* = const. Проведем в
точке А касательную t и нормаль ν к
этой проекции горизонтали, которые
можно рассматривать как оси,
параллельные некоторым центральным осям хг и yv Если считать, что
вся обсужденная выше теория была построена при использовании
не осей х, у, а осей xlt ylt то вследствие произвольности выбора
осей все сохранилось бы и вместо зависимостей (11.90) имели бы
место
_ дц> ___ δφ
φ-ψ
oonst
Рис. 11.27. К обоснованию фор
д(р
~~ для точек
ov
лежащих на проекции горнэон
тали φ = φ* = const поверх
ностн φ = φ (χ, у).
мулы τ =х ,
(11.133)
Здесь сохранено обозначение функций Прандтля, хотя функция,
изображающая соответствующую поверхность, изменит
аналитический вид при переходе от одной системы осей к другой.
Поскольку t\\y1 и ν\\Χι, для точки А формулы (11.133) можно
записать и так
δφ
дф
τ*ν — dt ' %zt ~~
dv '
(11.134)
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 67
С другой стороны, коль скоро кривая, по отношению к которой
в точке А оси ί и ν являются касательной и нормалью,
представляет собой проекцию горизонтали, где φ = φ* = const, имеет
место равенство dcp/dt = 0, или, если учесть (11.134), τζν = 0, и,
следовательно, полное напряжение совпадает с другой
составляющей
T.-Trf = -|f· (11.135)
и, таким образом, направлено по касательной к проекции
горизонтали поверхности φ.
Так как согласно аналогии Прандтля функция ft идентична
функции ср, приходим к выводу, что:
1. Полное касательное напряжение направлено вдоль
касательной к проекции горизонтали поверхности ft = ft (х, у) на
плоскость контура.
2. Величина полного касательного напряжения в точке- А
поперечного сечения равна тангенсу угла наклона касательной
к поверхности ft = ft (χ, у) в точке, проектирующейся в А, при
условии, что эта касательная проведена в плоскости наибольшего
ската поверхности; след этой плоскости на плоскости поперечного
сечения и представляет собой нормаль ν к проекции горизонтали.
14.3. Определение крутящего момента. Рассмотрим
сначала призму, поперечное сечение которой односвязно.
Поскольку имеется зависимость (11.95) и, кроме того,
вследствие аналогии Прандтля имеется равенство
η> = φ, (11.136)
справедлива и такая зависимость:
Мг = 2 J J ft dx dy.
Здесь учтено, что cpo = fto = 0.
Таким образом, удвоенный объем, ограниченный поверхностью
провисания мембраны, натянутой на плоский односвязный
контур (совпадающий с очертанием поперечного сечения
скручиваемой призмы), и плоскостью контура, равен крутящему моменту.
Если поперечное сечение скручиваемой призмы многосвязно,
то аналогия Прандтля приобретает следующий вид. Для
отождествления функций φ и ft, отыскиваемых из уравнений
Δφ = — 2ΰκ^ и Aw = q-,
необходимо натянуть мембрану на все контуры, соответствующие
границам поперечного сечения призмы, и, кроме соблюдения
условия (11.132) и постоянства на каждом из.контуров величины ft,
необходимо еще, чтобы на каждом из внутренних контуров
68
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
функция ft удовлетворяла условию
7| = -§Ιτώ = 7&. (Π.137)
полностью аналогичному условию, определяемому формулами
(11.108) и (11.109). у т р у
Несколько преобразуем это последнее условие
φ τζ cos (Tj, t) ds = 2Схг$г.
Но в нашем случае, поскольку в качестве замкнутой линии
принят t-й внутренний контур поперечного сечения, хг cos (τ Л =
= %zt и, согласно (11.135), " '
T,COS(T„ t)=Tzt = -^-
в результате этой подстановки получим
- § Q ds = 2G*3i- (11.138)
Сопоставляя (11.138) с (11.137), убеждаемся в полной их
идентичности.
Соблюдение условий (11.137) позволяет добиться
однозначности функции ft и определить все постоянные, которым
равняется ft на каждом из контуров. Условие (11.137) по существу
является уравновешиванием нагрузки интенсивностью а
приходящейся на площадь внутри контура, силами натяжения мембраны
натянутой на этот контур. Действительно, если представить себе'
что внутрь каждого внутреннего контура строго по его
очертанию вставлен абсолютно жесткий невесомый диск, которому
разрешено перемещаться только в направлении, перпендикулярном
плоскости контура, то уравнение равновесия - равенство нулю
суммы проекций всех сил на вертикальную ось — приобретает вид
$psinads-<7ft = 0, (11.139)
где
Sina~tga = -^ = _A = Ti. (ПЛ40)
Подставляя (11.140) в (11.139), получим
~§-Wds = j% или §xgds=£$i.
Таким образом, окончательно аналогия Прандтля, в случае
многосвязных поперечных сечений призм, выглядит так: натягивается
мембрана на все контуры-внешние и внутренние в предположе-
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ 69
Рис. 11.28. К обоснованию формулы
с <?ш q
— Ф-т—rfs = — F.
dv
нии, что внутрь внутренних контуров вставлены абсолютно жесткие
невесомые диски, которым разрешено перемещаться лишь в
направлении, нормальном к
плоскости контура (рис. 11.28).
Погонное натяжение мембраны во
всех направлениях одинаково и
равно р. Поверхность
провисания такой мембраны при
загружен ии всей области, лежащей
внутри внешнего контура
равномерно распределенной нагрузкой
интенсивностью q, тождественно
совпадает с поверхностью
функции Прандтля φ, при условии,
(11.132). Отсюда вытекает
следствие. Величина и направление
полного касательного
напряжения находится так же, как и
в случае односвязного
поперечного сечения призмы; что касается
величины крутящего момента, то он находится по формуле,
аналогичной (11.96)
Мг = 2{]]vodxdy + J wfii-»<&}.
Здесь интеграл берется по всей площади поперечного сечения
(т. е. по площади, занятой материалом), w>0 можно принять
равным нулю, а величины \ι\ находятся из условий (11.137).
15. Свободное кручение тонкостенного призматического стержня
открытого профиля.
15.1. Свободное кручение призмы с
прямоугольным поперечным сечением, имеющим большое
отношение сторон. Пусть в прямоугольном поперечном
сечении b/c^l (рис. 11.29, а). Используем аналогию Прандтля.
Приближенно форму провисания мембраны, закрепленной на всем
контуре (рис. 11.29, б), представляем как форму, получающуюся
в случае закрепления лишь на двух противоположных длинных
сторонах (рис. 11.29, в). При этом поверхность провисания
цилиндрическая с поперечным сечением, имеющим такую же форму
как и форма провисания нити при воздействии на нее равномерно
распределенной нагрузки, т. е. эта форма — квадратная парабола
(см. 1 том, стр. 159) (рис. 11.29, г). Распор единицы ширины
мембраны определяется по той же формуле, как и распор нити
(формула (2.46))
_ φ*
8/
(11.141)
70
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
1
>
\
1
у
'
С
X
|\
Очертание нити, как уже было сказано, представляет собой
квадратную параболу \г> = ах2 + d\ при х = с/2 tt> = 0, при л: = 0 \v—f,
или 0 = а·^- rd, f = d,
отсюда d — f, a= j-, и
уравнение параболы
приобретает вид
j^
*а
δ)
У^ дпюра tZy
\
У
ух
А
к
' t
,
X
V
д)
Рис. 11.29. К построению приближенного
решения (с использованием аналогии Прандтля)
задачи о свободном кручений призмы прямоугольного
поперечного сечения с большим отношением
сторон: а) поперечное сечение призмы; б)
горизонтали мембраны, натянутой на контур,
совпадающей с контуром поперечного сечения призмы
(точная картина); в) то же (приближенная картина);
г) поперечное сечение мембраны; д) эпюра
касательного напряжения на линии, параллельной
короткой стороне поперечного сечення; е)
эпюра касательных напряжений по линиям,
параллельным короткой и длинной сторонам
прямоугольного поперечного сечення скручиваемой
призмы.
П> =
4/
*2 + /·
Согласно аналогии
Прандтля касательное
напряжение выражается формулой
*гу
d\x>
dx
8[_
с2
(11.142)
Величину f, найденную из
(11.141),
/=|4 (1М43)
подставим в (11.142), при
этом получим
— A SL fi — <L
%гУ~ С2 ρ 8 х~~р х>
^гтах
— Тг(/тах — ~~ ~
Ρ 2
(11.144)
Теперь остается учесть в
(11.144) условие (11.132),
при котором выполняется
(11.136). Итак,
%гу = 2Gkzx,
Т^гтах — Δ\ΔΆ,Ζ _ — иУСгС.
(11.145)
Найдем крутящий момент как удвоенный объем, ограниченный
поверхностью провисания мембраны, учтя пос ледова! ельно
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ ■?!
формулы (11.143) и (11.132)
Мг = 2'^сЬ = ±сЬ±^ = ±ЬсЮкг. (11.146)
Отсюда' интенсивность угла закручивания
и, = У' ■ (11.147)
G — без
О
Для получения окончательной формулы для т2тах остается
подставить (11.147) в (11.145)2. В результате такой подстановки будем
иметь
T,m.x = Gc—γ5—= -ρ*-. (11.148)
G j be* -5- 6с2
Согласно (11.142) хгу распределено по ширине поперечного
сечения по линейному закону (рис. 11.29, д).
Определим-, какой момент является статическим эквивалентом
касательных поверхностных сил, эпюра которых изображена на
рис. 11.29, д,
Ш* 3 2 1..2 2 '
Таким образом, статическим эквивалентом касательных сил с
интенсивностью хгу является половина крутящего момента. Вторая
половина создается силами с интенсивностью %гх, неучитываемыми
нами, так как действительная поверхность провисания мембраны
заменена цилиндрической поверхностью. Из рис. 11.29, е, видно,
что %гх достигает максимума в серединах коротких сторон и что
в большей части области тгх<^тгу, но вследствие больших плеч
у сил %гх dF ими создается момент, равный Мг/2, т. е. такой же
момент, как и создаваемый силами %zydF.
Величины Ik и W, что видно соответственно из сопоставления
(11.100) с (11.147) и (11.124)х с (11.148), выражаются
следующими формулами:
Ik = ~bc\ Wk = \bc\
15.2. Применение результата предыдущего
раздела к кручению тонкостенного стержня
открытого профиля. Теперь перейдем к рассмотрению свободного
кручения тонкостенных призматических стержней открытого, т. е.
односвязного профиля (рис. 11.30). Все эти поперечные сечения
72
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. Xt
состоят из прямоугольников, и, исходя из аналогии Прандтля,
представляется возможным записать следующую приближенную
зависимость х):
М,
21 Ц Gkz = GIk*,; /* —g- 2 biCh *г = Щ;' {ПЛ49)
Максимальное касательное напряжение в пределах г-го
прямоугольника, входящего в состав
поперечного сечения стержня,
Мгс{
'2 max
ι = GkzCi = ■
(11.150)
15.3. Пример 11.5. Определить
максимальное касательное напряжение в
швеллере, составленном из полос
прямоугольного поперечного сечения (размеры
указаны на рис. 11.31), и интенсивность
угла закручивания, если крутящий
момент равен 0,1 Тм и модуль упругости
материала при сдвиге G= 8· ΙΟ5 к.Г/см2.
ί
Рис. 11.30. Поперечные
сечения тонкостенных
стержней открытого профиля.
I
Ьп=50мм
^=ъ
а"ст=8мм
Рис. 11.31. Поперечное
сечение тонкостенного
стержня открытого
профиля.
Решение. Максимальное касательное напряжение в полке и в стенке
определим соответственно по формулам
Тгтах, π'
гтах, ст
Мгсп
10 000-1,2
1 6псп-2 + |6стсст) у-5. 1.2·.2+ 1.20.О,*
= 1308,6 кГ/слР
3
Мгсст
10 000 · 0,8
|6псп'2+46стсст) 1.5. 1,2».2 + 1.20.0,*
= 872,4 кГ/см\
J) Для учета повышения жесткости за счет сопряжения прямоугольных
участков поперечного сечения иногда вводят коэффициент k в выражение Ik,
Ik = —\ bff (для двутаврового профиля k «s 1,20, для швеллерного—k^a 1,12).
§ 11.12]
КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ
73
Интенсивность угла закручивания найдем по формуле
Мг
я
С'|«-2 + -3-6с^т
10 000
800 000
(j.5.1,2».2+j.20-0,88)
. = 0,001363 рад/см.
16. Свободное кручение тонкостенного стержня закрытого
профиля.
16.1. Общие положения. Как и в случае кручения
тонкостенного стержня открытого профиля воспользуемся аналогией
Прандтля, но с учетом многосвязности поперечного сечения.
Пусть имеем двухсвязное поперечное сечение скручиваемого
стержня (рис. 11.32, а). Проведем прямолинейный отрезок аЪ
ЩшРо~0
Ξ=ΞΞ25^
»т
^ζ
а)
)
\ \
б)
Рис. 11.32. К использованию аналогии Прандтля прн решении задачи о свободном
кручении призмы двухсвязного тонкостенного сечения (трубы): а) поперечное сечение трубы
и вид сбоку на мембрану, натянутую на внешний и внутренний контуры поперечного
сечения трубы; б) к обоснованию ортогональности полных напряжений отрезку а—Ь,
нормальному к контуру, делящему толщину трубы пополам; в) к обоснованию
равномерности распределения касательных напряжений по толщине трубы.
через точку А нормально к контуру, делящему толщину трубы
в поперечном ее сечении пополам. Будем считать, что отрезок аЬ
нормален не только к контуру, но и ко всем пересекающим его
проекциям горизонталей поверхности провисания мембраны
(рис. 11.32, б). В таком случае во всех точках отрезка аЬ полные
касательные напряжения, согласно аналогии Прандтля,
направлены перпендикулярно к этому отрезку.
Учитывая малую толщину стенки по сравнению с габаритными
размерами поперечного сечения стержня, заключаем, что уклон
поверхности провисания мембраны в направлении, нормальном
к оси контура в разных точках по толщине (рис, 11.32, в), изме-
74 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ [ГЛ. 5CI
няется мало и приближенно может быть принят постояннымх).
При таком предположении касательное напряжение распределяется
по толщине стенки равномерно. Эпюра полных касательных
напряжений %г на отрезке ab изображена на рис. 11.32, б.
Величина %г определяется по формуле
T, = tga = ^ = -^, (11.151)
вытекающей из аналогии Прандтля (здесь учтено, что WQ принято
равным нулю).
Крутящий момент приближенно определяется по формуле
Мг = 2&И)! = 2£cPl = 2$τζδ, (11.152)
где % — площадь, ограниченная контуром, всюду делящим толщину
трубы в поперечном сечении пополам.
Μ
Из (11.152) найдем φ1 — -~ и подставим его в (11.151), тогда
_ мг
Величина τζ достигает максимума там, где толщина стенки
двухсвязного тонкостенного поперечного сечения минимальна
Μζ
Tzmax— off A . '
zoumin
Наконец, в связи с двухсвязностью поперечного сечения
необходимо обеспечить следующее равенство:
§
д\ъ
ds = ±%,
dv p
которое в силу аналогии Прандтля представим так:
_ £ J*t ds = 2Gn$; (11.153)
учитывая (11.135) и (11.151), уравнение (11.153) представим так:
&Tgds = 2Gkz%, φχ <т> —- = 2Gk$,
откуда находим пока оставшееся неизвестным значение φχ и
окончательную формулу для %г
Ψι= с ds κ" Хг= С ^ %г' (И-154)
ds
Τ
г) Имея в виду тождественность функций поверхности провисания
мембраны to и Прандтля φ в дальнейшем вместо буквы № будем использовать
букву φ.
§ 11.12] КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ
75
Подставляя (11.154) в (11.152), получим
г (β)2 .. Мг М,
М,
§
ds_
δ
'^ζ>
у,г — ■
(2ΐ?)2
ds_
δ
Git
h =
§
(23)»
(11.155)
16.2. Пример 11.6. Определить максимальные касательные напряжения
в элементах трехсвязного
поперечного сечения тонкостенного стержня
(размеры даны на рис. 11.33, здесь
же указаны номера контуров) и
интенсивность угла закручивания, если
крутящий момент равен 100 Тм и
модуль упругости материала при
сдвиге G = 800 000 кГ/см*.
Решение. Постоянные значения
функции Прандтля φ на контурах φι
и φ2 нам не известны.
Крутящий момент найдем по
формуле (11.96), которая в
рассматриваемом случае приобретает вид
Мг = 2$!\\\ + 2Ъ2Щ = 2#ιφι + 2#2φ2.
(11.156)
Условия однозначности перемещений w
записываются так:
ρ
h= — $2 = 2СхДг = /2.
(11.157)
В
I
II
*3
1
N
с=1000 мм
Л.
О
7Г
= -=4
df=2L·?мм\,£t=2C}мм
■* »
У
С "
ΊΓ
л,=гомм
л -
//м
:-#гЧОмм
Из этих условий определим φχ и ш2,
входящие в выражения J1 · и У2,
Рис. 11.33. Трехсвязное поперечное
сечение тонкостенного стержня: а) размеры
сечения; б) площади ^ и ^f,.
2, предварительно составив последние:
АВ ВС CD DA
AD
DM
а с а
"φι"δΓ+φι^+φιδΤ +
MN NA
_ φ2-φι φ2 φ2
φι
г-
-Φ2
δ2 С'
Lilft
(11.158)
δ2 ' δι " ' δι u_r δι
Подставляя (11.158) в (11.157), учитывая, что %i = ac и Ъ% = Ьс и
группируя члены, содержащие одинаковые φ/, получим
/2а+с с \ с 0„ Φι , /с , 264-с\ ._ ,
φι (-^- + ^]-q» б-а =2G^c, - ^-с + ф2 ^ + _^j = 2Gk,fc.
76 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ [ГЛ. XI
Отсюда находим φί и φ2
φι = 2Gv.!fi1ai, φ2 = 2Gxg82a2,
αι = -
2b + c с \ be
θι TW αδ2 13
2а + с с \(2Ь + с , с \ с2 1940 '
а2 =
δι ^ bj\ δι ^δ2/ δ!
а -|- с с \ , ас
"ζ h V + Ma 21
(11.159)
/2а + с _с_\ (2b + c ,_с_\_^_ 970
\ δι +δ2;\ δχ + 6j δΐ
Подставляя (11.159) в (11.156), найдем
Мг = 2с2 · 2Gxz (α2α! + £>2α2) =
= 4 · 1002 · 800 000 (βΟ2 · -^-+202 -^W = 1647 · Ю»хг.
Отсюда найдем погонный угол закручивания
Μг 107 рад 1 рад __ град
AG (Sjai + ffiaj,) 1647-10» еж 1647 ж ж '
Наконец, находим максимальные полные касательные напряжения по формулам:
на участках АВ и ВС
_ Ц>1 _ 2GjyV'1a1 _ Aig^1a1 _
Tz max —£~ ~ β] ~ 2δ(*?αι + ί^α2) ~~
1 4U 260
2-2(802-1002-w+202-1002w)
на участке Л£>
φι —Фг _ 2Gxz$1<x1 — ff2a2) _ Мг (#ι«ι — ^а«г) _
^max- 02 - δ2 -2δ2(^(Χι + ^α2) ~
ΙΟ7 (β0- ΙΟΟ-ττ^Γ — 20· 100- 2
2 '
"Μ это/ =9EUr/aft
2· 1 ■ί802·1002·-π^ + 202· 1002 2l
1940 ' 970
на участках ΝΑ и ЛШ
_ φ2 _ 2G%J8tfX2 _ Μβ2&2 _
τζ max - "β— - ζ ~ 2δχ (fffa +8$ая) ~~
ΙΟ7· 20 -100- 21
970
13 2Μ = 210 кГ/см*,
2.2^802.1002-Tg4ir+202.1002-970
16.3. Пример 11.7. Сопоставить крутильные жесткости и максимальные
напряжения стержней открытого и закрытого профилей (рис. 11.34, а, б).
Решение. Величины I/it входящие в формулы для крутильных жесткостей
стержней открытого и закрытого профилей, определяются соответственно по
§ 11.12]
КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ
77
формулам (11.149)2 и (11.155)3, а касательные напряжения—по формулам
(11.150) и (11.154)2, которые применительно к обозначениям рис. 11.34, а
приобретают вид
/откР = ^2.|.бз + 2&б9 + а^=^(а + &))
/закр.
АаЧг
26 +г δ + δ
2аЧ*Ь
а-\-Ь
_откр _ МгО
max ι-οτκρ
к
гэакр
Мг
2вт1а*
Μζδ·3
2№(a + b)
_ Мг
2bab '
Рассмотрим отношение жесткостей и
максимальных напряжений при Ь=а и δ = 0,1α
2aWd · 3
/закр
к
готкр
-.закр
max
тоткр
max
(a + b)263(a + b)
3aW
300α*
Μ,
&{a + by 4α4
2&{a + b) δ(α + &)
= 75,
2bab
3Μζδ
ЪаЬ
α2α 1
=—=0,0(6).
30α2 15
Ш
w-l/l
'
Ι '
δ-
If
#2
r~ с
\
ι
-<
ν
a
•ο
V
Рис. 11.34. Поперечные сечения
тонкостенных стержней: а)
открытого профиля; б) закрытого
профиля.
Производя продольный разрез одной из пластин, образующих стержень
замкнутого профиля, тем самым весьма существенно снижаем крутильную
жесткость (в нашем примере в 75 раз) и повышаем касательные напряжения
(в нашем примере в 15 раз).
16.4. Формула для перемещения ш в
тонкостенном стержне замкнутого профиля при чистом
кручении. Рассмотрим тонкостенный стержень замкнутого
поперечного сечения, фрагмент последнего показан на рис. 11.35, а.
На этом рисунке изображены и две системы осей Μξη —
подвижная и Оху — неподвижная. В подвижной системе ось ξ направлена
по касательной к контуру в текущей его точке М, а η —по
нормали к контуру. Обе системы левые. Исходя из аналогии Прандтля
и допуская некоторую весьма несущественную погрешность, будем
считать, что полные касательные напряжения %г по толщине δ
распределены равномерно и параллельны ξ — касательной к
контуру, т. е. тг| = тг, тгп = 0. Аналогично по толщине δ будем
считать распределенными равномерно и перемещения w.
В неподвижной системе начало координат расположено в точке,
относительно которой момент всех касательных сил (интенсивность
их есть τ?) равен нулю. Такая точка называется центром изкиба,
78
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
о ней подробно говорится в главе XII. Оси хну располагаем
произвольно.
Составим выражение %г ds, учитывая, что напряжение %г
направлено вдоль касательной к контурной линии в сторону
возрастания координаты s (против часовой
стрелки при обходе по контуру)
(рис. 11.35, а)
%г ds = (t^cos a-\-Tzys\n a) ds.
(11.160)
Согласно рис. 11.35, б
cos a =
dx
sina =
dy_
ds
(11.161)
Имея в виду (11.70) и (11.161),
формулу (11.160) представим так х):
τ, ds = Gk,
дФ
дх
dx . дФ dy
"57 + "
dy dx
' ds У ds
dy ds
ds. (11.162)
Учитывая обозначения,
изображенные на рис. 11.35, б, имеем
h = ycosa·
dx dy
■χ sin a = y -j χ -~;
тогда формула (11.162) приобретает
вид
τ, ds = Gn,
дФ , ■ . дФ ,
dx + -gy-dy
— G%zh ds,
dx
Рис. 11.36. К установлению связи
между функцией Φ и секторной
площадью; фрагмент поперечного
сечения тонкостенного стержня;
а) полное касательное напряжение
и его составляющие; б) к
установлению геометрических соотношений;
в) пояснение понятия rfco.
Введем обозначение
d(u=h ds.
(11.163)
(11.164)
•Согласно рис. 11.35, в du>
представляет собой удвоенную
площадь заштрихованного треугольника
(сектора). Величину ω называют секторной площадью. Поскольку
выражение в скобках в формуле (11.163) представляет собой
полный дифференциал функции Ф, представим (11.163), учтя при
этом (11.164), следующим образом:
τ, ds = Gy.z (άΦ - dco). (11.165)
г) Здесь учтено, что компоненты ггх и тгу, изображенные на рис, 11,35, а,
положительны (система осей хуг левая),
§ 11.12]
КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ
79
Если контур поперечного сечения представляет собой
замкнутую линию, то, производя по нему интегрирование выражения
(11.165), получаем
§xgds = Gxg§(dO-du>) = — GnzQ, (11.166)
поскольку
§άω = Ω, $dO = 0. (11.167)
В (11.166) величина ι) Ω —удвоенная площадь, ограниченная
замкнутой контурной линией. Равенство (11.167)2 имеет место
вследствие постоянства значения функции Φ вдоль s.
Нетрудно понять, что интеграл (11.166) является циркуляцией
касательного напряжения (см. формулу (11.108), учитывая при
этом расположение %г вдоль касательной к контурной линии),
вследствие чего (11.166) совпадает с (11.109), но на сей раз
в (11.109) под 5 понимается Ω/2 —площадь, ограниченная
контурной линией замкнутого поперечного сечения тонкостенного
профиля. Различие знаков в (11.109) и в (11.166) вызвано
неодинаковым направлением обхода контура в сопоставляемых случаях.
Найдем из (11.165) функцию Φ путем интегрирования по s
обеих частей этого равенства
S
Ф= [-^-ds-ω + Α. (11.168)
ί 0κ*
Поскольку отсчет ω начинается от точки s = 0 постоянная
интегрирования А представляет собой значение функции Φ при
s = 0
Л=Фи = Ф0. (11.169)
Подставим теперь (11.168) в формулу (11.65), с учетом (11.169)
получаем
S
w = хгФ = — κζω + f -^ ds + хгФ0.
о
Последний член представляет собой перемещение w в точке s = 0:
w\s-q=wq = kzOq.
Таким образом,
s
а> = ю0-хго>+ С if-ds, (11.170)
о
х) При обходе контура против часовой стрелки (рис. 11.35, β) 4ω > 0.
80
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
или, подставляя в (11.170) вместо τζ выражение согласно (11.152),
т. е.
_ мг _ мг
ι, — ·
"* ~~ 2?δ ~~ Ωδ '
получим
S
w=wo(z)Jr-^t\[^-^. (11.171)
о
Для исключения wQ (ζ) воспользуемся свойством периодичности
функции w(z) — при полном обходе контура поперечного сечения
стержня вновь получаем то же значение w(z), которое имеется
в точке начала обхода, т. е. w0 (ζ) = w0 (г) -f -qft Φ -£-— κ*Ω,
отсюда
x -J^H^-JL· Γ Ω2 ΠΙ 172}
Подставим в (11.171) выражение для М
GQ%
найденное из (11.172), в результате получим
S
J
ds_
δ
ш (г) = w0 (z) + Ω ° . пг - ηζω,
или
1
α» (г) = йУ0 (г) + Ω -^- κ* — хгсо, (11.173)
Здесь величины 5= \ -^, s° = (T)-r представляют собой приве-
о
денные 'длины соответственно на участке контура длиной s и на
всем замкнутом контуре. Величину Ω/s0 можно назвать средним-
радиусом замкнутого контура и обозначить символом р, тогда
формула (11.173) приобретает вид w (ζ) = w0 (ζ)-{-р5кг — κζω;
w (ζ) = wQ (ζ) — кг (ω — ps), или, например, w (ζ) = w0 (z) — хгб5, где
65 = ω — ρ§ принято называть обобщенной секторной площадью.
Если интересоваться относительным смещением одной точки
относительно другой, то можно положить w0(z) равным нулю и тогда
w(z) = — κζ®, т. е. депланация тонкостенного стержня замкнутого
профиля происходит по закону обобщенной секторной площади.
§ 11.12]
КРУЧЕНИЕ ПРИЗМ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ
81
При свободном кручении Мг сохраняет свою величину по длине
стержня, вследствие чего x£ = Mi/(G/K) =0, поэтому
ю'(2)=_%'г® = 0 (11.174)
и, таким образом, ay (z) = const, т. е. депланация всех
поперечных сечений оказывается одинаковой.
Таблица 11,2
Форма
сечеиня
/к, см*
WK, см»
Точки с
наибольшими
касательными
напряжениями
Примечание
d
* ■■ ■ 5»
J,
4,74d*
2Λ
d
3.35
d? /2Λ\2·82
22,9 I d
и точке А
0,125<-^<0,5
α
D*_
16
D3
в точке А
d/D
0
0,05
0,10
0,20
0,40
0,60
0,80
1,00
α
1,57
0,80
0,82
0,81
0,76
0,66
0,52
0,38
β
1,57
1,56
1,56
1,46
1,22
0,92
0,63
0,38
WAx
χ(Λδ2+6δι-
-δϊ-δ1)-ι,
Λ0 = Λ-2δ2,
ί>0 = ί>-2δ,
№Ki=2A<AA
№κ2=2/ιυί>0δ2
в точке At
в точке И2
Во внутренних
углах имеет место
высокая
концентрация
напряжений; для ее
уменьшения
необходимо делать
закругления
Из формулы (11.174) как частный случай получается формула
и для стержней открытого профиля, для которых Ω=0, а
следовательно, и р = 0, вследствие чего ω = ω, и таким образом
w' (ζ) = — κ'ζω = 0, w (ζ) = w0 (ζ) — кг(й = const.
17. Таблица для расчета призматических стержней
некруглого поперечного сечения на свободное кручение. В табл. 11.2
приведены данные, позволяющие определять максимальные
касательные напряжения, возникающие в поперечных сечениях
некруглых призматических стержней при их свободном кручении.
82
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
§ 11.13. Понятие о кручении призматических стержней
произвольного поперечного сечения
при упруго-пластической стадии работы
идеально-пластичного материала
1. Вводные замечания. Пусть имеем призматический стержень
произвольного поперечного сечения, свяжем с ним систему осей
xyz, поместив начало координат в центре тяжести одного из
торцов, направив ось ζ вдоль оси призмы, а оси χ и у расположив
в плоскости торца. Будем считать, что стержень подвергнут
воздействию внешних крутящих моментов Шг, приложенных к
торцам и вызывающих свободное кручение. В поперечных сечениях
возникают одинаковые по величине крутящие моменты Мг = дЛг.
Будем считать, что диаграмма напряжений τ = τ(γ) имеет вид
диаграммы Прандтля. Отметим два характерных значения Мг: Μζτ —
крутящий момент, при котором в наиболее напряженных точках
поперечного сечения возникают касательные напряжения, равные
пределу текучести τΤ, и Мг0 — крутящий момент, при котором
во всем поперечном сечении касательные напряжения оказываются
равными тт.
Рассмотрим работу стержня при Мгт^Мг^Мг0. Иными
словами, будем считать, что материал в части объема призмы
работает в упругой стадии, а в остальной —в пластической.
Необходимо, во-первых, установить те положения теории, которые верны
для обеих указанных областей, во-вторых, отдельно для каждой
из областей установить положения, верные только именно для
нее, и, наконец, сформулировать условия, позволяющие
установить границу между областями.
2. Положения, справедливые как для области, в которой
материал работает в упругой стадии, так и для области, где
материал работает в пластической стадии.
а) Объемные силы не учитываем, полагая
X = y = Z = 0. (11.175)
б) Считаем, что боковая поверхность призмы свободна от
поверхностной нагрузки. По торцам действуют только касательные
поверхностные силы, статическим эквивалентом которых являются
внешние крутящие моменты дЯг. Именно эта поверхностная нагрузка
должна быть отражена в граничных условиях.
в) Предполагаем, что напряженное состояние характеризуется
функциями, не зависящими от г. При этом из шести компонентов
напряжений отличными от нуля являются только два:
^гу = тгу(х, у)фО\ (11.176)
<7* = σ# = σ, = τ^=0. )
I 11.13] УПРУГО-ПЛАСТИЧЕСКОЕ КРУЧЕНИБ ЛЮБЫХ ПРИЗМ 83
г) Должны быть удовлетворены уравнения равновесия (5.59).
Если учесть (11.175) и (11.176), то два первых из этих
уравнений удовлетворяются тождественно в форме 0ξ=0, а третье
приобретает вид
дхгх дт?..
+ -^Г = 0. (1Ы77)
дх п ду
Это уравнение может быть удовлетворено, если %гх и %гу выразить
через некоторую функцию ψ в следующей форме:
(11.178)
τζχ ду ,
_ д\р
%гу~ ~дТ
действительно, при этом получаем (11.177) в таком виде:
32ψ £2ψ
дх ду дх ду
= 0, 0 = 0.
д) На боковой поверхности призмы, где нормаль к элементу
этой поверхности имеет следующие направляющие косинусы
(см. рис. 11.18):
/ = cos (ν, χ) = cos α,]
tn = cos {ν, у) =ύηα,\ (11.179)
η = cos (ν, ζ) = 0, J
должны выполняться условия
Первые два из них, учитывая (11.176) и (11.179), выполняются
в форме 0==0, третье — приобретает вид
||-cos(v, χ) - -Ц- cos (v, y)=Q на Г. (11.180)
Поскольку, согласно (11.78),
cos(v, x) = dl,
αχ
cos (v, y) = —Is на Г,
(11.180) получаем в следующем виде:
&ύ> dy . 5ψ dx ,, /11 ιοί\
f i + Wd7=0 на *· (11Л81)
84 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ [ГЛ. XI
Применяя правило дифференцирования сложных функций,
условие (11.181) представим так:
~- = 0, ψ = const на Г.
Для односвязных поперечных сечений можно положить
ψ = 0 на Г. (11.182)
3. Условия, которые должны выполняться в области упругой
работы материала. Помимо условий равновесия в упругой
области должны выполняться и условия совместности деформаций.
Из шести условий Бельтрами, если учесть (11.175) и (11.176),
первые четыре выполняются тождественно в форме 0 == 0, а пятое и
шестое приобретают вид
Δτ^ = 0, Лтгл = 0. (11.183)
Если подставить (11.178) в (11.183), то получим1)
Α Δψ(νπΡ> = 0, ~ Δψ(νπρ> = 0.
Следовательно,
A^(ynp) = C = const. (11.184)
Введем обозначение для константы в правой части (11.184) С =
= — 20кг. В результате получим уравнение
Δψ(Υπρ)==_2(}κ2,
в предыдущем параграфе выведенное иным образом
относительно функции Прандтля. Граничным условием для ψ(νπΡ>
является (11.182).
4. Условие, которое должно выполняться в области
пластической работы материала. В области пластической работы
материала должно выполняться условие пластичности. Примем это
условие в форме Мизеса (см. гл. VIII, § 3, формула (8.21))
-—■ V{gx - σ2)2 + (σ2 - σ3)2 + (σ3 - σχ)2 = σ?
или
Κ - σ2)2 + (σ2 - σ3)2 + (σ3 - σχ)2 = 2σ*. (11.185)
Сопоставление интенсивности напряжений при осевой деформации
и при чистом сдвиге приводит, как это, в частности, было
показано в (11.60), к зависимости σ=]/3τ, откуда имеем и
σΤ. = /3τΤ. (11.186)
1) Индекс (упр) указывает на то, что рассматривается тот частный случай
функции ψ, который относится к области упругой работы материала,
§ 11.131 УПРУГО-ПЛАСТИЧЕСКОЕ КРУЧЕНИЕ ЛЮБЫХ ПРИЗМ #5
Таким образом, подставляя (11.186) в (11.185), получим условие
текучести Мизеса в следующем виде:
т [(σχ - σ2)2 + (σ2 - σ3)2 + (σ8 - σ^2] = τ?,
или, вспоминая выражение второго инварианта девиатора
напряжений, получим
j [(σ, - σу)2 + (σ„ - σ,)2 + (σ, - σ*)2] + τϊ„ + τ£2 + τί* = τ?.
В нашем случае, если учесть (11.176), будем иметь
т!, + т!х = < (11.187)
или, подставляя в (11.187) их выражения, согласно1) (11.178),
Левая часть полученного уравнения представляет собой квадрат
градиента 4>(пл), который, как известно, является наибольшим
уклоном поверхности 4>(пл). Итак, поверхность яр<пл> = ψί1™) (χ, #)
в области пластических деформаций представляет собой,
поверхность с постоянным углом ската.
Если бы все поперечное сечение было охвачено пластической
деформацией, то над всем ним следовало бы построить поверхность
с постоянным углом ската. Для наглядного изображения этой
поверхности можно было бы поступить следующим образом:
изготовить из картона пластину (по форме и размерам повторяющую
поперечное сечение скручиваемой призмы) и, расположив ее
горизонтально, насыпать на нее сухой песок в количестве,
превышающем то, которое может удержаться на ней. Образовавшаяся насыпь
будет ограничена поверхностями естественного откоса —это и будет
поверхность постоянного ската яр(пл) (рис. 11.36). Функция ψ*"·"),
что видно из (11.188), не зависит от интенсивности угла
закручивания.
5. Установление границы между областями упругой и
пластической работы материала в поперечном сечении. Отмеченная
в заголовке граница характеризуется тем, что в точках,
расположенных на ней, полные касательные напряжения
Τ-ζ = V Τ>ζχ ~τ~ Т'гу
достигают величины τ.Γ; по одну сторону от этой границы лежит
область в точках которой тг<тт, а по другую τζ = ττ. На
х) Индекс (пл) подчеркивает, что рассматривается тот частный случай
функции ф, который относится к области пластической работы материала.
86
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
Рис. 11.36. К кручению призмы в упруго-пластической области работы материала!
а) поверхности равного ската, построенные при помощи сухого песка, насыпанного.на
плоскую горизонтальную платформу, повторяющую размеры и форму поперечного
сечения скручиваемой призмы; б) экспериментальное установление границы областей
упругой и пластической работы материала — разрез экспериментальной установки; в) план;
г) аксонометрия; / — контур — рамка (из жесткой проволоки), по очертанию повторйю-
щая контур поперечного сечения скручиваемой призмы; 2 — поверхность равного ската,
изготовленная из твердого прозрачного материала и опирающаяся на контурную рамку;
3 — мембрана, натянутая на контурную рамку до приложения к ней поперечной нагрузки;
4 — равномерное давление интенсивности q, передаваемое на мембрану! 3' — положение
мембраны при q = qt\ 3" — положение мембраны при q = qz (q2 > q{); 3'" —
положение мембраны при q =■ q» (q* > q^Y, 5 — область (заштрихована) контакта мембраны
и поверхности равного ската при q = qt; 6 — проекция области контакта мембраны и
поверхности равного ската на поперечное сечение призмы; 7' — проекция гра:!.чцы
области контакта мембраны и поверхности рапного ската при q = qL; 7" — то же πρι η == 172;
7"' — то же при q — 17,.
§ 11.13] УПРУГО-ПЛАСТИЧЕСКОЕ КРУЧЕНИЕ ЛЮБЫХ ПРИЗМ
87
границе областей т<упр} ==т£л,| т^пр) =т<пл\ или
""1у ~~ду~' дх ~ ~ΈΓ' (11.189)
Имея в виду (11.189), заключаем, что
ψ(γπρ) = ^(пл) Ц_ С,
Если в какой-либо из точек границы между областями упругой
и пластической работы материала
ψ<νπΡ)=ψ(™), (11.190)
то С = 0, и равенство (11.190) справедливо на всей границе
областей.
Опытным путем обсуждаемую границу между областями можно
построить так. Изготовить из прозрачного листового материала
(стекло или подобный ему материал) поверхность равного ската
на плоском контуре, совпадающем с контуром поперечного
сечения скручиваемой призмы. Далее на этот плоский контур
натянуть мембрану и снизу действовать на нее равномерно
распределенной нагрузкой. При некоторой нагрузке на мембрану
последняя в некоторой области достигнет поверхности равного ската и
совпадет с нею. Этот момент опыта соответствует такой работе
призмы, при которой под свободной частью мембраны
располагается область упругой работы материала, а под касающейся
поверхности равного ската — область пластической работы
материала. По мере увеличения нагрузки область соприкасания
мембраны и поверхности равного ската (т. е. область пластической
работы) увеличивается (рис. 11.36). Крутящий момент при упруго-
пластической работе поперечного сечения скручиваемой призмы
определяется по формуле (использованы формулы (11.178))
Мг = J \ (%гхУ~Хг^ dxdy=\) (-Jjj-У + 1ьГ х)dx аУ-
В § 11.12 было показано, что в случае односвязного поперечного
сечения призмы и при условии (11.182)
Мг = 2 J J ψ dx dy.
Иными словами, удвоенный объем, ограниченный мембраной (на
части поверхности, упершейся в поверхность равного ската и на
другой части, не касающейся этой поверхности) и плоскостью
контура, на который она натянута, равняется крутящему моменту.
88 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ [ГЛ. XI
§ 11.14. Кручение круглых валов переменного диаметра
1. Вводные замечания. В настоящем параграфе описывается
общая картина напряженно-деформированного состояния круглого
вала переменного диаметра без подробного решения какого-либо
конкретного примера.
Рассматривается тело вращения, к торцам которого приложены
внешние крутящие моменты, при этом распределение касательных
сил на торцах, создающих эти моменты, выполняется по некото-,
рому закону, заранее не задаваемому.
Основной математический аппарат для решения такой задачи
был дан в § 9.12.
Было отмечено, что часть составляющих перемещений,
компонентов деформации и напряжений обращается в нуль
u = w = Q; εΓ = ε^ = ег = γ^ = 0; σΓ = σ# = σζ = τΓΖ = 0.
Остающиеся ненулевыми функции и, уг#, уг$, тнь τζ$ связаны
между собой следующими зависимостями: уравнениями (Коши)
совместности деформаций и перемещений
ди υ dv /ι ι im\
Yr* = ^:-y, Y**=a£. (11.191)
уравнениями совместности деформаций, выраженными через
напряжения,
ΔτΓβ.-;ττ^ = 0, Δτ^-^τ^=0; (11.192)
уравнением равновесия
дг "*" dz "+" г _υ
и уравнениями закона Гука
trb = GyH>, τ^ = Gvrt·. (11 · 193)
Если представить напряжения через функцию φ, называемую
функцией напряжений
τ*>=-"^"Ιτ' τ** = ^' (11.194)
то уравнение равновесия удовлетворяется.
Для отыскания самой функции φ служат условия
совместности деформаций (11.192), которые после подстановки в них (11.194)
оба приобретают вид:
Ш~Тд£ + Ш = °- ("-«95)
Граничным для функции φ является условие отсутствия
касательной нагрузки на боковой поверхности вала, согласно кото-
§ 11.14] КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ ПЕРЕМЕННОГО ДИАМЕТРА 89
рому полное касательное напряжение τ^ в осевом
у контура располагается по касательной к контуру
т. е. проекция этого напряжения на ν —нормаль
равна нулю
T^sina = 0. (11.196)
сечении вала
(рис. 11.37),
к контуру —
V
Tfly cos a ■
Здесь
dz
C0Sa = Ts>
dr
sin a = -j-.
ds
(11.197)
Подставляя (11.194)
(11.196), получаем
и (11.197) в
dcp dz . дц> dr_ ^
dz ds dr ds
(11.198)
Имея в виду формулу
дифференцирования сложных функций, представляем
(11.198) в следующем виде:
д^ = 0
ds υ·
(11.199)
Рис. 11.37. Осевое сечение
круглого вала переменного вдоль его
оси радиуса; касательное
напряжение вблизи контура, осевого
сечения вала.
Зависимость (11.199) и является граничным условием для φ,
используемым при интегрировании уравнения (11.195). Таким
образом, последовательность решения задачи следующая.
1. Находится функция φ путем интегрирования уравнения
(11.195) при выполнении граничного условия (11.199). Этим
обеспечивается выполнение условий совместности деформаций.
2. Находятся компоненты напряжений т®г и τ#ζ по формулам
(11.194). Этим самым обеспечивается соблюдение равновесия тела.
3. Путем использования уравнений закона Гука (11.193)
определяются компоненты деформации у$г и у$г.
4. Определяется перемещение ν путем интегрирования
уравнений (11.191).
2. Понятие о поверхности равных углов поворота. При
кручении круглых валов переменного диаметра в отличие от круглых
цилиндрических валов совокупность точек, располагающихся до
деформации на радиусе поперечного сечения, оказывается в
результате деформации на некоторой кривой линии. По-другому
картину деформации можно пояснить так. Если мысленно
представить вал, состоящим из концентрически расположенных тонких
элементарных трубок, то в процессе кручения вала поперечные
сечения этих трубок, лежащие в одном и том же поперечном
сечении вала, поворачиваются на разные углы.
В утрированном виде это показано на рис. 11.38, где
изображены поперечные сечения трубчатых слоев вала до и после
деформации, на которых, для того чтобы следить за поворотами
сделаны отметки. Из рисунка очевидно, что ψ — угол крутильного
90
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
поворота кольца радиуса г находится по формуле
t = -f. (11.200)
Теперь представим себе, что аналогичные отметки сделаны
в нескольких соседних поперечных сечениях и при этом так, что
Рис. 11.38. Перемещения точек,
лежащих на радиусе
поперечного сечения круглого вала
переменного вдоль его оси радиуса:
а) отметки на концентрических
слоях вала, сделанные на
радиусе поперечного сечения (до
деформации) вала; б)
расположение отметок в результате
деформации.
Рис 11.39. К построению линии равных поворотов
в круглом валу переменного вдоль его осн радиуса;
а) проекции следов фронтальной осевой плоскости
(А — проекция следа на поверхности равных
поворотов; I, II, III и IV — проекции следов на
плоскостях, перпендикулярных оси вала; кривая,
ортогональная А — проекция следа на боковой
поверхности); б) проекция на плоскость, перпендикулярную
оси вала; О — проекция следа осевой плоскости,
составляющей с фронтальной угол ψ; В — проекция
следа фронтальной плоскости; 1, 2, 3, 4 — проекции
концов радиусов, лежащих в плоскостях I, II, III,
IV; Г, 2', 3', 4' — проекции концов упомянутых
выше искривившихся первоначально направленных
вдоль радиусов отрезков (пересечения этих проекций
искривившихся отрезков с линией О^В — суть
проекции точек линии равных поворотов).
радиусы, на которых располагаются отметки до деформации лежат
в одном и том же осевом сечении вала (по одному радиусу в
каждом поперечном сечении вала (рис. 11.39, а)).
§ 11.14] КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ ПЕРЕМЕННОГО ДИАМЕТРА 91
Картина, получающаяся после деформации, изображена на
рис. 11.39,6, где цифрами 1, 2, 3, ... обозначены концы
радиусов, лежащие до деформации вала в одном и том же осевом
его сечении, но в разных поперечных сечениях; теми же
цифрами со штрихами отмечены концы этих же искривленных
радиусов после деформации (под термином искривленный радиус
здесь понимается совокупность материальных точек). Если теперь
провести осевое сечение В, составляющее с сечением 0, где
первоначально располагались радиусы, угол ψ, то точки пересечения
искривленных радиусов (т. е. испытавших деформацию) с
плоскостью отметят те поперечные сечения колец (они лежат в
плоскостях разных поперечных сечений), которые при деформации
повернулись на один и тот же угол.
Увеличивая число поперечных сечений на рассматриваемом
участке по длине вала, за счет их сгущения, получим на
плоскости В плавную кривую, образованную точками пересечения с этой
плоскостью искривленных радиусов или, иначе, образованную
точками вала, совершившими в составе поперечных сечений колец
одинаковый крутильный поворот. Таким образом, в плоскости
осевого сечения вала можно отметить точки, располагающиеся до
деформации вала на кривой, которая в результате деформации
вала, оставаясь плоской, повернется на угол ψ вокруг оси вала.
Эта кривая ортогональна контурной кривой в осевом сечении
вала. Вследствие осевой симметрии крутильной деформации точно
такая же кривая может быть отмечена в любом из осевых
сечений. Эти кривые образуют поверхность вращения, ортогональную
боковой поверхности вала. Совокупность точек, лежащих на этой
поверхности при кручении круглого вала переменного диаметра,
поворачивается как жесткий диск. Эта поверхность, в случае если
вал становится круглым цилиндром, превращается в плоскость
поперечного сечения, а ее меридиан превращается в радиус
круглого поперечного сечения цилиндра. Если вал имеет коническую
форму, эти поверхности становятся сферическими с центром в
вершине конуса.
Уравнение обсуждавшейся выше поверхности вращения, все
точки которой поворачиваются как жесткий диск, может быть
легко получено. Воспользуемся уравнениями закона Гука (11.193),
подставив в них вместо сдвигов у^ и уг$ их выражения, согласно
(11.191), а вместо тг$ и тг# — их выражения через функцию φ;
в результате получим
~~ 7^lh ~ \дг ~ Т)' n"dr~U~dz'
или
Ι δφ _ „ д I и \ 1 δφ _ „ д_ Ι υ\
~~ή~Έ~ог д~г [Τ)· ^ а?-ог aTv~/'
92 СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ"
или, наконец, учитывая (11.200)
[ГЛ. XI
dz дг '
(11.201)
Продифференцируем первое из равенств (11.201) по г, а второе
^Р = Qr3d_f
дг dz
по ζ
^φ _ п д (,дМр
dzdr
дг
дг
д\ _
дг dz
= о£(г>%). (11.202)
Ввиду одинаковости левых частей в обоих равенствах (11.202)
имеем равенство и правых частей, которое после сокращения на G
прибретает вид:
дг
0ψ
дг
+
dz
0ψ
dz
а но,
или
d*ty 3 d-ψ дЦ> _ п
а7* ~*~ Τ дг 'Т' ~dz* ~~
Решением этого уравнения является функция ty = \|)(r, г),
показывающая крутильный угол поворота плоского кольцевого эле·?
мента с координатами г и г (рис. 11.40, а). Если положить
величину ψ постоянной, ψ (г, r) = C = const, то каждому значению С
<Сяя? тбершсти
<p~const
δ]
\
В)
Рис. 11.40. Пояснение к понятию поверхности равных углов ι/оворота: а) бесконечно
узкий кольцевой элемент поперечного сечения с координатой г, поворачивающийся как
жесткое целое относительно оси г при кручении вала; б) поверхность равных поворотов,
образованная линиями, расположенными в разных поперечных сечениях, но имеющими
одинаковый поворот относительно оси г; в) след поверхности равных поворотов на осевой
плоскости,
будет соответствовать поверхность (рис. 11.40, б, в), которая как
жесткое целое поворачивается на угол ·ψ. Вал в целом
представляет собой совокупность таких поверхностей, плотно заполняющих
его объем,
§ 11.14] КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ ПЕРЕМЕННОГО ДИАМЕТРА »о
3. Картина деформации в локальной области. Весь материал
скручиваемого тела вращения испытывает чистый сдвиг. Все тело
вала можно представить состоящим из элементарных пластинок,
подвергнутых чистому сдвигу. Каждая из них располагается
нормально к одному из меридианов поверхности равных углов
закручивания. Эти пластины испытывают тем больший сдвиг, чем дальше
от оси вала они располагаются (рис. 11.41). Весь объем вала
Рис. 11.41. Чистый сдвиг элементов, нормальных линий равных поворотов.
можно представить состоящим из элементарных трубок
(переменного вдоль оси ζ радиуса), срединная поверхность каждой из
которых является поверхностью равных сдвигов, ортогональной
поверхностям равных углов закручивания. Отмеченные выше
элементарные пластинки, испытывающие чистый сдвиг, входят в
состав этих трубок. Рассмотрим две соседние поверхности равных
углов закручивания, находящиеся друг от друга на расстоянии ds,
измеренном вдоль меридиана вала (рис. 11.42, а), такие, что
крутильный поворот всей первой поверхности с координатой s
представляет собой ψ, а второй поверхности — с координатой s-\-ds —
равен ψ + ίίψ. Вырежем сектор из слоя между этими
поверхностями (рис. 11.42, а, б). Поскольку одна поверхность по
отношению к другой повернулась на dty вокруг оси г, перемещение
точки с на меридиане второй поверхности, совершаемое при этом,
равно cc'=rdty. Здесь г —радиус дуги ее'. В частности, если
точка располагается на поверхности вала (рис. 11.42, в),
то
аа' = R dty.
С другой стороны (рис. 11.42,6)
ее' = уг dst аа' = yR ds.
94
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
Отсюда
dty
ds
и
^-Ο,,-flrf, τβ-Οτβ = 0*2.
Напряжение т(г) действует на площадке, нормальной оси ft
Рис. 11 42 Картина деформации круглого вала переменного вдоль его оси радиусаг
а) вал и элементарный сектор вала, заключенный между двумя поверхностями равных
поворотов расположенными бесконечно близко одна от другой; б) изображение
указанного выше сектора — до и после деформации; в) след на осевой плоскости поверхностей
одинакового поворота, ограничивающих выделенный сектор; г) пластинчатые элементы
сектора н напряжения, вызывающие их чистый сдвиг; д) полное касательное
напряжение в осевом сечении вала у его контура н составляющие этого напряжения;
треугольный элемент осевого сечения с ребрами ds, dr, аг.
(рис. 11.42,г), поэтому его можно обозначить: т(г) =τ#.
Напряжение τ# раскладывается на две составляющие в осях гиг: %$г и
τ$ζ (рис. 11.42, д)\ при этом
τ(/) = τ<> = т$г cos a -f 'tflr sin ά.
§ 11.15] КРУЧЕНИЕ НАСЛЕДСТВЕННО-УПРУГОГО ВАЛА 95
§ 11.15. Свободное кручение призматического стержня
из наследственно-упругого материала (пример применения
принципа Вольтерра)1)
Пусть задача решается в функции напряжения Прандтля2):
Для φ имеем
Δφ = —2 внутри D,
φ = const на Г;
D и Г —область, занятая сечением стержня, и ее граница (для
простоты взято односвязное сечение). Ясно, что φ от упругих
постоянных не зависит и полностью определяется геометрией
сечения.
Для интенсивности угла закручивания хг имеем
_ мг
Кг~ GIK '
где GIK — жесткость при кручении, GIK = 2G J jj φ (χ, y)dx dy.
Πόλο
ставляя выражение для %г в формулы для тгх, тгу, находим
%гх~ /к ду ' %гу~ U дх'
Так как φ и /к не зависят от упругих постоянных, то и
напряжения от них не зависят. Значит, согласно принципу Вольтерра3),
в наследственно-упругом теле напряжения будут такими же, как
в упругом. В частности, если крутящий момент меняется во
времени по закону M = M(t), то
т„(0=м(в^|. т.,(о=-м<о£г!.
т. е. изменение напряжений мгновенно следует за изменением
момента.
*) § 11.15 написан Ю. Б. Шулькиным.
2) Имеется в виду, что φ = φ/(κ20) (φ—функция Прандтля в той ее форме,
которая использована в предыдущих параграфах).
3) Вито Вольтерра (1860—1940) итальянский математик и механик.
Описание его жизни и деятельности с анализом полученных им научных
результатов дано в книге: Полищук Ε. Μ. Вито Вольтерра.—Л.: Наука, 1977.
96
СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ
[ГЛ. XI
Перейдем к определению погонного угла закручивания хг для
стержня из наследственно-упругого материала. Снова применяя
принцип Вольтерра, получаем вместо вышеприведенной формулы
для хг следующую формулу:
М*) = 7£^гМ*(9.
или в подробной записи
Mg(t)
G
Μ.
ι
Здесь g(t — τ) — ядро ползучести для чистого сдвига. В чадтном
случае Мг = const имеем
<^Мг
м,
+ §g(t-T)
άτ
^-[1+Λ(/)],
где Λ (ή— функция ползучести при чистом сдвиге, определяемая
экспериментально. Таким образом, при Мг = const в стержне из
наследственно-упругого материала напряжения не меняются, а угол
закручивания нарастает по такому же закону, по какому растут
деформации сдвига в этом материале при постоянных касательных
напряжениях.
Глава XII
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
§ 12.1, Предварительные замечания
Рассмотрим один из элементарных видов деформации стержня —
изгиб, характеризующийся тем, что при нем происходит изменение
кривизны оси; в частности, если первоначально ось стержня
прямолинейна, то при изгибе она становится криволинейной.
Изгибаемый стержень называется балкой г).
Изучение начнем с простейшего случая — чистого изгиба
призматического стержня, т. е. такого изгиба, при котором
изгибающий момент по всей длине балки отличен от нуля и одинаков
во всех сечениях, все же остальные моменты и усилия равны
нулю
Λί* = const; N = Qx = Qy = My = Mz==0 (xy). (12.1)
После этого будут рассмотрены и более сложные случаи изгиба—.
в частности, поперечный изгиб, при котором отличны от нуля и
изгибающий момент и поперечная сила, остальные же усилия и
моменты по всей длине балки равны нулю.
В теории упругости термин чистый изгиб призматического
бруса подразумевает такую деформацию, при которой, кроме
условий (12.1), имеет место строго определенное распределение
на торцах поверхностной нагрузки, статическим эквивалентом
которой являются моменты Ш, а именно распределение этой
нагрузки по линейному —в зависимости от у (или л;) —закону, если
чистый изгиб происходит в плоскости Oyz(Oxz). При этом во всем
брусе отсутствуют не только поперечные и продольные силы и
крутящий момент, но и самоуравновешенные в пределах
поперечного сечения напряжения, в том числе касательные
напряжения, а следовательно, если учесть закон Гука, то отсутствуют
и сдвиги.
*) Балкой принято называть и стержень, преимущественно
испытывающий изгиб, т. е. стержень, испытывающий, возможно, и другие вида
деформаций. Если изгиб возникает лишь при потере устойчивости
первоначальной формы равновесия (сжатый стержень), то стержень балкой не
называется.
98
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
На рис. 12.1, а, б показаны такие случаи нагружения
призматического бруса, которые вызывают в нем чистый изгиб
в понимании сопротивления материалов. При этом случай,
изображенный на рис. 12.1, а, является чистым изгибом и
в смысле теории упругости, а случай 12.1, б с позиций теории
упругости не является чистым изгибом, так как существует
самоуравновешенная доля у нормальной поверхностной нагрузки,
приложенной к торцу. Исследования этого случая
средствами теории упругости намного сложнее исследования
(^
γ
к
■Ж
т
Ψ\
Ы
— ·****»->
ч.
■J
δ)
Рис. 12.1. Чистый изгиб балки: а) чистый изгиб и в смысле сопротивления материалов,
м в смысле теории упругости; 6) чистый изгиб лишь в смысле технической теории (сопро«
тнвлепня материалов).
чистого изгиба. Штриховой дуговой стрелкой на обоих рисунках
12.1 показаны моменты Ш, являющиеся статическим
эквивалентом распределенных по торцу поверхностных сил. Имея в виду
принцип Сен-Венана, можно утверждать, что напряженные
состояния в случаях, изображенных на рис. 12.1, существенно отличаются
одно от другого лишь вблизи торцов.
На рис. 12.2 изображена балка на двух опорах с консолями;
нагрузка, действующая на нее, такова, что в средней (между
опорами) части
М*== Ρα = const, Qje = Qy = N = My = MltssQ.
В смысле сопротивления материалов эта средняя часть балки
подвергается чистому изгибу. В смысле же теории упругости
средняя часть балки не находится в состоянии чистого изгиба —
здесь при строгом решении проблемы обнаруживаются
самоуравновешенные в пределах поперечного сечения, в том числе
касательные, напряжения.
В этой главе предполагается, что материал балки линейно
упруг. Исключением являются последние два параграфа.
Рассматривается геометрически линейная постановка задачи, т. е.
§ 12.2] ДЕФОРМАЦИЯ ПРИЗМЫ ПРИ ЧИСТОМ ИЗГИБЕ 99
те случаи, в которых перемещения, связанные с деформацией,
малы по сравнению с габаритными размерами поперечного
сечения (точнее, в рассматриваемом случае мал по сравнению с
единицей квадрат угла поворота поперечных сечений).
Рис. 12.2. Балка, средний участок которой (между опорами) подвергнут чистому изгибу
в смысле технической теории (сопротивления материалов).
Начало исследования изгиба, как и других видов деформации,
состоит в построении эпюр усилий и моментов в рассматриваемых
балках, подвергнутых тем или иным внешним воздействиям. Эта
часть исследования для самого общего случая деформации и для
частных случаев, включая сюда и изгиб в различных его
разновидностях, была выполнена в §§ 1.13 и 1.15.
§ 12.2. Характер деформации призматического бруса
при чистом изгибе
Проследим за картиной деформации призматического бруса
прямоугольного поперечного сечения при чистом изгибе,
наблюдаемой в эксперименте. С целью получения заметных деформаций
для наглядности в эксперименте используем брус из такого
упругого низкомодульного материала, как резина.
На рис. 12.3, а показан брус до деформации; изображена
эпюра поверхностной нагрузки на торцах (линейный закон
распределения по высоте), создающей моменты Ш, которые изгибают
брус (балку). На боковую поверхность призматического бруса
нанесена сетка, образуемая системой равноотстоящих линий,
параллельных оси призмы, и системой равноотстоящих замкнутых линий,
лежащих в плоскостях поперечных сечений. Нанесена сетка
ортогональных линий и на торцы; линии этой сетки параллельны
сторонам прямоугольного торца.
После деформации брус приобретает вид, показанный на
рис. 12.3, б, продольные линии на боковой поверхности
искривляются; волокна, лежащие.;в.некотором слое, называемом
нейтральным, первоначальной длины своей не изменяют; в
призматическом брусе прямоугольного поперечного сечения нейтральный
слой расположен по середине высоты. Волокна, лежащие по одну
сторону от нейтрального слоя, удлиняются, а по другую —
100
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Рис. 12.3. Характер деформации балки прямоугольного поперечного сечения при чистом
изгибе: а) балка до деформации с сеткой линий, нанесенных на ее поверхности, и нагрузка,
вызывающая чистый изгиб; б) балка, испытавшая чистый изгиб; е) поперечное сечение
балки прямоугольного сечения, испытавшей изгиб; е) балка, загруженная моментами на
торцах, создаваемыми нагрузкой, распределенной не по линейному закону; д) характер
деформации балки, изображенной на фиг. г; е) поперечное сечение около торца (после
деформации) в балке, изображенной на фиг. г.
§ 12.2] ДЕФОРМАЦИЯ ПРИЗМЫ ПРИ ЧИСТОМ ИЗГИБЕ Щ
укорачиваются; удлинение или укорочение волокон получается
тем большим, чем дальше от нейтрального слоя расположено
волокно. Поперечные замкнутые линии, плоские до деформации,
остаются плоскими и после деформации; при этом, если до
деформации они лежали в параллельных плоскостях, то после
деформации — в плоскостях, образующих некоторые углы, отличные
от нуля, тем большие, чем дальше друг от друга расположены
линии. Стороны этих замкнутых линий, лежащие до деформации
в боковых плоскостях, остаются прямолинейными и
ортогональными к искривленным продольным линиям.
На рис. 12.3, в показано поперечное сечение бруса до и после
деформации. Верхняя и нижняя линии контура сечения в
результате деформации получаются криволинейными. В сжатой зоне
бруса, в силу эффекта поперечной деформации, происходит
расширение, а в растянутой —сужение поперечного сечения по
сравнению с первоначальной его шириной. Отмеченное
расширение и сужение тем больше, чем дальше слой расположен
от нейтрального. Угол а, изображенный на рис. 12.3, в, во всех
поперечных сечениях получается одинаковым.
Торцы бруса, плоские до деформации, остаются плоскими и
после деформации. Сетка линий, нанесенная на торцы, оставаясь
ортогональной, испытывает деформацию. Прямые линии,
первоначально параллельные двум боковым граням бруса, остаются
прямолинейными и поворачиваются друг относительно друга
на тем больший угол, чем было больше расстояние между ними
до деформации. Линии сетки на торце, параллельные верхней и
нижней граням, искривляются.
При этом линия, расположенная по середине высоты торца
бруса, длины своей не изменяет, а линии, расположенные выше
(ниже) нее, удлиняются (укорачиваются) и в тем большей мере,
чем больше расстояние линии от середины высоты торца (от
нейтрального слоя). Верхняя и нижняя грани бруса, плоские
до деформации, приобретают форму криволинейных поверхностей
отрицательной гауссовой кривизныг). Боковые грани становятся
линейчатыми поверхностями. Описанная картина деформации
сохранится при любых соотношениях размеров прямоугольного
параллелепипеда, которым является брус.
х) Гауссовой кривизной поверхности в точке А называется величина
/С = 1/(^?1^?г)» гДе #ι и #2 — радиусы главных кривизн в точке А, т. е.
максимальный и минимальный радиусы из числа радиусов кривизн всех кривых
(нормальных сечений), образуемых на поверхности, как следы пересечения
плоскостей, проходящих через нормаль к поверхности в точке А. Если центры
главных кривизн расположены на нормали к поверхности по разные от нее
стороны, то гауссова кривизна отрицательна. При расположении обоих
центров по одну сторону от поверхности гауссова кривизна положительна,
102
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
При другом законе распределения внешних поверхностных
сил, приложенных к торцам и создающих такой же по величине,
как и в первом случае, внешний момент, который вызывает чистый
изгиб бруса (см., например, рис. 12.3, г), получается несколько
иным и характер деформации бруса (см. рис. 12.3, д, е). Однако
это различие ощутимо лишь в небольших областях, примыкающих
к торцам. Здесь, как и в других аналогичных случаях,
разобранных в главе II (осевая деформация) и в главе XI (кручение),
справедлив принцип Сен-Венана.
В случае иной формы поперечного сечения призматического
бруса картина деформации в целом остается аналогичной
описанной выше, а именно: замкнутые поперечные линии, плоские
до деформации, остаются плоскими и после деформации, и
плоскости их поворачиваются друг относительно друга.
Продольные линии искривляются и при этом две из них, лежащие
в некоторой плоскости (нейтральная плоскость),
перпендикулярной плоскости действия приложенных к торцам моментов, длины
своей не изменяют. Все другие продольные линии, искривляясь
в процессе деформации, изменяют свою длину и тем в большей
мере, чем дальше эта линия расположена от нейтрального слоя.
Торцы при чистом изгибе и в стержнях непрямоугольного профиля
остаются плоскими. Как и в описанном выше случае, строго такая
картина наблюдается всюду лишь при линейном распределении
на торцах нормальных поверхностных сил, создающих внешние
моменты, под действием которых происходит изгиб стержня. При
другом законе распределения на торцах поверхностных
нормальных сил описанная картина деформации нарушается, при этом
вблизи торцов в большей мере, чем в остальной области, где
это нарушение практически очень невелико.
§ 12.3. Гипотезы, используемые при построении
технической теории чистого изгиба призматического стержня
Пока нет подтверждения описанной выше картины деформации
теоретическим путем, естественно полагать ее не абсолютно
строгой, так как всякий опыт сопряжен с погрешностями. Поэтому
на основе экспериментальной картины формулируются гипотезы,
отражающие ее характер, и при помощи их строится техническая
теория чистого изгиба призматического стержня. Сформулируем
две гипотезы.
При чистом изгибе Призматического бруса
поперечные сечения плоские до деформации,
остаются плоскими и после деформации.
Продольные волокна в брусе при чистом его
изгибе не взаимодействуют в нормальном по
отношению к ним направлении, т. е. на площадках,
§ 12.3) ГИПОТЕЗЫ ТЕОРИИ ЧИСТОГО ИЗГИБА ПРИЗМЫ
103
6ΞΞ3»
параллельных оси бруса, нормальные
напряжения равны нулю.
Первая гипотеза чисто геометрическая (кинематическая).
Вторая — имеет статическую природу х).
Первая гипотеза формулируется как логическое следствие
наблюдаемого в опыте факта сохранения при чистом изгибе бруса
плоской формы поперечных замкнутых линий и сохранения
плоской формы торцов.
Для суждения о сохранении плоской формы поперечных
сечений при чистом изгибе достаточно исходить из того, что плоскими
остаются торцы. Действительно, пусть имеем призматический
брус, подвергнутый чистому
изгибу, и будем считать, что
торцы его остаются плоскими.
Вследствие симметрии
картины деформации плоским
остается и среднее поперечное ^^-j I
сечение. Теперь мысленно »/т-тя«-
рассечем брус на две части „ .
г l J Рис. 12.4. К обоснованию гипотезы об от?УТ·
Сечением ПОСреДИНе еГО ДЛИ- СТВИи взаимодействия между продольными
НЫ; у КаЖДОЙ ИЗ ЭТИХ Частей волокнами балки при чистом изгибе.
торцы плоские, поэтому
благодаря симметрии деформации плоскими останутся средние
сечения каждой из этих половинок бруса. Продолжая деление бруса
пополам и удостоверяясь, что среднее сечение каждой из Них
остается плоским, в пределе убеждаемся в сохранении плоской
формы у всех сечений.
Предположение об отсутствии взаимодействия между волокнами
при чистом изгибе может быть подтверждено следующим
рассуждением. Предположим, что мы вырезали из бруса продольный
элемент в виде прямоугольного параллелепипеда (рис. 12.4), одна
из граней которого выходит на поверхность. На этой грани нет
никакой, в том числе нормальной, поверхностной нагрузки.
Следовательно, не действует нормальное напряжение и на нижнюю
грань элемента, обращенную внутрь бруса, так как такое
напряжение нечем было бы уравновесить, если предполагать, что на
торцах и боковых гранях элемента не действуют вертикальные
касательные напряжения, поскольку в деформированном брусе
сохраняется ортогональность линий сетки и, следовательно, нет
сдвигов. Выделяя аналогичный элемент под ранее рассмотренным
и применяя к нему такие же рассуждения, придем и по
отношению к нему к аналогичному выводу. Продолжая этот процесс,
обследуем элементы по всей толщине бруса, Так как первый эле-
!) К обсуждению гипотез мы еще вернемся в § 12,7 (раздел 5), в котором
рассматривается Поперечный изгиб,
io4
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. ХН
мент выделен вблизи верхней грани произвольно, проведенные
рассуждения справедливы для всех элементов, из которых можно
представить состоящим брус. Аналогично можно было бы выделять
элементы, начиная от боковой грани бруса и двигаясь к
противоположной грани. Этим было бы доказано отсутствие нормальных
напряжений на боковых гранях всех элементов. Разумеется,
приведенное здесь обоснование является умозрительным и не
претендует на строгость, однако может служить основанием для
принятия соответствующей гипотезы.
Из второй гипотезы вытекает, что одно из уравнений закона
Гука
е* = £-[<**-μ (<** + <**)].
вследствие отсутствия взаимодействия волокон между собой, т. е.
вследствие равенства нулю напряжений σχ и оуу приобретает
следующий вид:
г* — Ε '
Таким образом, вторая гипотеза предписывает каждому волокну
находиться в линейном (одноосном) напряженном состоянии.
§ 12.4. Нормальные напряжения в поперечном сечении
стержня при чистом изгибе
1. Оси координат. Пусть имеем призматический стержень,
испытывающий чистый изгиб (рис. 12.5). Исследуем
распределение нормальных напряжений в поперечном сечении. Свяжем
со стержнем систему ортогональных осей xyz. Расположим оси χ
и ζ в нейтральной плоскости так, чтобы ось ζ являлась проекцией
оси стержня на эту плоскость.
2. Статическое исследование балки. Рассечем стержень на две
части поперечным сечением с координатой г. Поскольку стержень
в целом находится в состоянии равновесия, в равновесии должна
быть и любая из этих двух частей. На торец рассматриваемой
части бруса действует внешний момент Шх, а в поперечном
сечении имеются распределенные внутренние силы, которые по
отношению к рассматриваемой части стержня являются внешними.
Интенсивность трех составляющих (по осям х, у, ζ) этих сил
в произвольной точке поперечного сечения суть хгх, тгу, σζ,
а их статический эквивалент Qx, Qy, Ν, Мх, Му и Мг
выражается формулами (1.4). Уравнения равновесия рассматриваемой
части бруса имеют вид:
Qx = 0; 9)lx-Mx + Qy2=0, Af, = 3W,;
Q„ = 0; My-Qxz = 0, M,, = 0; (12.2)
iV = 0; M,-0.
§ 12.4] НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ЧИСТОГО ИЗГИБА СТЕРЖНЯ
105
Если в (12.2) вместо Qxt ... , Мг подставить их выражения
согласно (1.4), то получим уравнения равновесия в следующем
виде:
\%zxdF = 0, \TzydF = 0, ]azdF = 0,
F F F
\uzydF = mx = Mx, \<szxdF = 0, l(Texy-xzyx)dF = 0. (12.3)
F F F
Эти уравнения могут быть удовлетворены при бесчисленном
множестве вариантов распределения напряжений по поперечному
δ)
Рис. 12.5. Чистый изгиб балки: а) балка и действующие на нее внешние моменты; б) часть
балки, отделенная разрезом, проведенным в плоскости поперечного сечения.
сечению стержня (в § 2.3 и в § 11.6 уже отмечалось, что закон
распределения напряжений по поперечному сечению бруса
статически неопределим).
Из первого, второго и шестого уравнений (12.3) видно, что
касательные компоненты напряжения в поперечном сечении стержня
либо тождественно равны нулю, либо составляют
самоуравновешенную систему сил. Вследствие этого отмеченные уравнения
рассматривать не будем.
3. Исследование деформации балки. Для раскрытия
статической неопределимости закона распределения напряжений произведем
кинематическое (геометрическое) исследование проблемы —найдем
функцию, характеризующую распределение деформаций. Изогнутая
ось расположена в плоскости Оуг. Вырежем из стержня элемент,
эид которого до и после деформации, с учетом гипотезы плоских
106
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[гл. m
сечений, показан на рис. 12.6. Рассмотрим волокно АгА2,
параллельное нейтральному слою и расположенное от него на
расстоянии у, при этом
А[А'% = dz + Δ (dz) = dz -f гг dz = (1 + вг) dz.
Из подобия треугольников А\ОА'^ и СгОСг имеем
А[А'г pjc+y
JifljC
Ρ/
u'i
*ϊ
0
/\
Λ/ ^2
<?
#? ι
u s
\
QCa
P*
(12.4)
Рис. 12.6. Картина
деформации элемента
(юлки, подвергнутой
чистому изгибу, при
использовании
гипотезы плоских
сечений.
где рх— радиус кривизны нейтрального слоя
изогнутого стержня при изгибе в плоскости,
перпендикулярной оси х.
Учитывая, что CxC2 = dz, получаем (12.4) в
следующем виде:
*· ~~Р7~' 1+8г_1+Р^
dz
или
Рх'
(12.6)
Уравнение деформацииг) (12.5), присоединяемое к (12.3),
позволяет раскрыть статическую неопределимость закона
распределения напряжений по поперечному сечению.
4. Использование физической зависимости. Чтобы
использовать уравнения (12.3) и (12.5) совместно, их нужно выразить
через одно и то же неизвестное; с этой целью воспользуемся
связью между ог и гг, даваемую уравнением закона Гука, которое
с учетом второй гипотезы, как уже указывалось выше,
приобретает вид
в,.= £.
о* = Ее,
Учитывая (12.5), получаем
Рх
σζ = £
Ρ*
(12.6)
Формула в скобках в (12.6) относится к чистому изгибу,
происходящему в плоскости Οχζ.
*) Формула (12.6) является хорошей иллюстрацией общей особенности
технической теории стержней, состоящей в том, что путем использования
гипотез, характеризующих деформацию стержня, оказывается возможным
деформацию в любой точке поперечного сечения связать с деформацией оси.
Последняя описывается некоторыми параметрами, являющимися функцией
одной лишь координаты г. В формуле (12.5) таким параметром является
кривизна оси балки 1/ρ* = κ*, возникающая вследствие ее изгиба,
I 12.4] НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ЧИСТОГО ИЗГИБА СТЕРЖНЯ ^7
5. Условия существования чистого изгиба. Раскрытие
статической неопределимости закона распределения σζ по
поперечному сечению. Подставим (12.6) в уравнения1) (12.3)3<4) б, в
результате этого получим:
H-\ydF = Ot ?-\y*dF=Mxt l\xydF = 0. (12.7)
Ух t) ух *) ух J
F F F
Уравнения (12.7)li3 свидетельствуют о том, что соответственно
обращаются в нуль интегралы
lydF = Q, *\xydF = 0. (12.8)
F F
Поскольку интеграл в (12.8)! — статический момент площади
поперечного сечения относительно оси х, совпадающей со следом
нейтрального слоя на плоскости поперечного сечения стержня,
равенство (12.8)! возможно лишь в случае, если ось χ проходит
через центр тяжести поперечного сечения. Выше было принято,
что ось ζ есть проекция оси стержня на нейтральный слой. Сейчас
получили уточнение — ось стержня лежит в нейтральном слое и,
следовательно, совпадает со своей проекцией — осью ζ. Поскольку
интеграл в (12.8)2 —центробежный момент инерции площади
поперечного сечения, выполнение (12.8)2 возможно, если оси χ и у
являются главными осями инерции площади поперечного сечения.
Выше было сделано предположение о совпадении плоскости
действия внешних моментов, вызывающих чистый изгиб бруса,
с плоскостью изгиба, в которой лежит изогнутая ось стержня,
а следовательно, и центр и радиус кривизны оси. Теперь получено
условие (12.8)2, при котором такое совпадение возможно. Только
в том случае, если плоскость действия внешних моментов,
вызывающих чистый изгиб, содержит в себе одну из главных осей
инерции площади всех поперечных сечений стержня, эта плоскость
совпадает с плоскостью изгиба; другая главная ось инерции
площади поперечного сечения сливается с нейтральной линией.
В отличие от обсужденного выше существует и так называемый
косой чистый изгиб, при Котором плоскость действия внешних
моментов и плоскость изгиба не совпадают (имеется в виду, что
обе плоскости содержат ось стержня). Косой изгиб рассмотрен
в главе XIII как частный случай более сложной деформации
стержня — пространственного поперечного изгиба.
Наконец, уравнение (12.7)2 можно записать так:
х) Уравнения (12.3)lf 2.6 не рассматриваем, поскольку они не связаны
с нормальными напряжениями.
108
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ (ГЛ. XII
Подставляя (12.9) в (12.6) получим искомую формулу
Мху
σ =
Λ
σ =
Мух
(12.10)
Индекс ζ у σ опущен. На рис. 12.7 показана эпюра распределения
нормальных напряжений в поперечном сечении при прямом
а)
δ)
Рис. 12.7. Распределение нормальных напряжений по поперечному сеченню балки,
испытывающей чистый изгиб: о) фасад балки; б) аксонометрия.
чистом изгибе. В скобках в (12.10) показана формула в случае,
если плоскость действия внешних моментов, вызывающих чистый
прямой изгиб, совпадает с плоскостью Οχζ.
6. Условия прочности. Пусть изгиб балки происходит в
плоскости Oyz, а ось χ не является осью симметрии поперечного
сечения; тогда в одном из двух крайних волокон, расположенном
ближе к нейтральному слою, чем другое, напряжение по
абсолютному значению меньше, чем во втором. При условии
неодинаковости сопротивления материала растяжению и сжатию возникает
необходимость в определении напряжений в обоих крайних
волокнах и проверки прочности в каждом из них.
Два условия прочности при М*;>0 имеют следующий вид:
О^тах — '
Мху
max
Λί,
w
jemax
ы.
Μ,
O'min —
w
лгтт
Ml; (i2.li)
здесь величины
W xmax — '
w χ min —
'max
^min
(12.12)
называются моментами сопротивления поперечного сечения при
ИЗГИбе (i/max>0, i/min < 0).
§ 12.4] ^нормальные напряжения чистого изгиба стержня Ю9
Если Мх<0, то формулы для атах и amin находятся аналогично
|σ„,„| = ^<|[σβ]|, ашах=^-<[ар]. (12.13)
w jcmax w *min
Если ось χ является осью симметрии, то \Wxmin\ = WXmax=!-Wx.
Если материал одинаково сопротивляется растяжению и сжатию,
то из двух формул (12.11) при Мх>0, или из двух формул
(12.13) при Мх<сО, пользуются той, в которую входит
наибольшая по абсолютному значению величина из двух величин атах и
C^min·
Пользуясь (12.11), можно решить три следующие задачи.
а) Проверка прочности. Даны Мх, Wx, [σ], требуется проверить,
обеспечивается ли прочность. Для этого достаточно удостовериться,
выполняются ли условия (12.11) или (12.13) в зависимости от
знака Мх.
б) Подбор сечения. Даны: Мх, [σρ], [ас], требуется подобрать
поперечное сечение балки.
В зависимости от знака Мх из (12.11) или (12.13) находим
два значения Wxmax, \Wxm\n\, имея которые можно
сконструировать поперечное сечение необходимых размеров. Задача упрощается,
если в (12.12) ут№ = \ уты |, при этом | Wxmin | = Wx max и если,
кроме того, [σρ] = | [σε] |. *
в) Определение коэффициента запаса. Даны Мх, Wxmax,
\Wxmm\, σ0ΠιΡ, σ0Πι(., [σρ], [σ0]. Ищутся kp и kz. При этом
используются (12.11) или (12.13) и в них полагается [σρ] =
= σοπ, ρ/V К] = σοΙ1( JK-
7. Деформация балки. Уравнение (12.9) является весьма
важным — оно связывает изгибающий момент Мх с кх, кривизной
изогнутой оси первоначально прямолинейного стержня (усх=\/рх),
и может быть представлено так:
Μχ = ΕΙχκχ (Му = Е1уХу). (12.14)
Параметру кх можно дать и геометрическую трактовку.
Действительно, кх dz представляет собой относительный угол поворота
сечений, расположенных на расстоянии dz одно от другого.
Согласно рис. 12.6 имеем
dz = Kxpxdz, κ* = — !ку = —). (12.15)
В (12.14) и в (12.15) в скобки помещены уравнения, относящиеся
к изгибу в плоскости Oxz. Уравнения (12.14) —физические
уравнения (уравнения закона Гука), но не для материала,
а для всего стержня, подвергнутого чистому изгибу.
Уравнение (12.9) свидетельствует о следующих фактах. Во-первых, во
всех точках изогнутой оси балки величина 1/р* имеет одинаковое
значение, так как одинаковые значения во всех сечениях имеют
по
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. ХП
Мх (в силу того, что изгиб чистый) и Е1Х (в силу того, что
рассматривается призматический брус). Постоянство вдоль оси
балки величины κ*= 1/р* (кривизны) означает, что изогнутой осью
призматической балки при чистом изгибе является дуга окружности.
Во-вторых, чем больше величина Е1Х, тем меньше 1/р*. Вследствие
этого Е1Х естественно назвать жесткостью стержня при изгибе.
Этот фактор имеет физик о-геометрическую природу.
Множитель Ε характеризует жесткость материала, а множитель 1Х—
жесткость балки, обусловленную геометрическими свойствами
сечения (чем больше 1Х, тем жестче балка). Линейку значительно
труднее согнуть в ее плоскости, нежели расположив плашмя
(рис. 12.8).
►t:|<Nj
*:|c4j
Ζ
Рис. 12.8. Сопоставление нзгнбного
воздействия на одну н ту же балку в разных
плоскостях — большой н малой нзгнбной
жесткости.
ί
Рнс. 12.9. Идеальное
поперечное сечение балки
при чистом изгибе.
8. Идеальный профиль балки. Для создания большого 1Х при
заданном значении F необходимо материал в поперечном сечении
балки относить как можно дальше от нейтрального слоя. Идеальным
при чистом изгибе является профиль, у которого весь материал
расположен в одинаковом удалении от нейтральной оси (рис. 12.9).
Выбор высоты h диктуется условиями эксплуатации балки и
другими обстоятельствами, о которых говорится ниже.
Разумеется, расстояние между двумя частями поперечного
сечения— поясами—должно сохраниться в процессе изгиба
неизменным, т. е. должна быть обеспечена совместность работы двух
поясов балки—верхнего и нижнего. Для этого некоторая часть
материала балки расходуется на создание связей между поясами;
такой связью в балках сплошного сечения является стенка.
Становится ясным, почему нельзя увеличивать h беспредельно для
повышения 1Х и Wx, если этому даже и не мешали бы условия
эксплуатации. Увеличению h от некоторого его значения
препятствует превалирование увеличения расхода материала на стенку
(толщину ее нельзя делать сколь угодно малой, вследствие
опасности выпучивания из плоскости) над уменьшением расхода
материала на пояса. При увеличении высоты балки приходится
§ 12.4] НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ЧИСТОГО ИЗГИБА СТЕРЖНЯ 41
для обеспечения устойчивости стенки увеличить ее толщину и
создавать специальные конструктивные элементы —так называемые
ребра жесткости.
9. Примеры.
Пример 12.1. Подобрать размеры таврового поперечного сечения,
заданного с точностью до параметра а—рис. 12.10, а, призматической балки,
подвергнутой чистому изгибу в плоскости Oyz. Заданными являются МХ=>ЯИ,
[ос], [σρ] ([ [ас] | = 8 [σρ]). Решение требуется найти в двух предположениях:
Мх>0, Мх<.0 (рис. 12.10,б, в) и результаты сравнить.
Рис. 12.10. К примеру 12.1: а) поперечное сеченне балкн — геометрические размеры;
б) изгиб, при котором ребро сжато; в) изгиб, при котором ребро растянуто; г) к
вычислению статического момента площади поперечного сечення относительно оси хл\ д) к вычн»
сленню /„ — момента инерции площади поперечного сечення балкн; е) к определению
моментов сопротивления.
Решение, а) Определяем положение центра тяжести площади поперечного
сечения и, таким образом, — положение нейтрального слоя. С этой целью
найдем площадь поперечного сечения и ее статический момент относительно
некоторой произвольно выбранной оси х0 (рис. 12.10, о)
F = 3a-a + 5a-a = 8a2, S^—— За-α- 2,5α—α ·5α· 0,5а=—«10а«
(размеры см. на рис 12.Ю, г),
*с—£ϊ = -
-10α»
8α2
.— —1,25α.
б) Находим момент инерции .площади поперечного сечения относительно
оси χ (рис. 12.10,5)
. α (За)3 . „ .. ._ .„ . 5а· а3 . _ /л7г w 61 .
1Х = —^ + а. За (1,25а)2+ —— + 5а · а · (0,75а/ = -ψ о*.
112
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XI!
в) Определяем моменты сопротивления поперечного сечения балки
w =J* (461/48) α4 461
Wxmax Утгх (5/4) α 60 '
Ιχ _ (461/48) α* 461 3
Wxmin'mymla ~ (-11/4) α 132 α'
г) Рассматриваем изгиб балки, изображенной на рис. 12.10,6. Условия
прочности имеют вид
Мх Ш _ 60 Ж . .
°m**~Wxmax =(461/60)аз — 461 а? ^ 1<ТР]* (иЛЬ)
мх ш 132 Ш1 ^ . г Έ. /10 ,_.
ι °«°1Я ι=]-^д " ι <-461/132>а* ι° ш"^ ' '' (
Из условий (12.16) и (12,17) соответственно
β /"WW~ (2J ^ /"132 а» " = τ/ϊ32~"вд~ ^/ϊ6,5 ад
α ~Κ 461 [σρ] » α β Κ 461 I [ac] | К 461 8 [σ0] _ Κ 461 [σρ];
так как α(*> >αί2>, определяющим размеры сечения является α=α(1>.
д) Рассматриваем изгиб балки, изображенной на рис. 12.10, е. Условия
прочности имеют вид
ισ |-|Μ«Ι- 1-^1 -60 * <.rgi| (1218)
I min l~^max ~ (461/60)аз ~ 461 аз ^ ' l<?cJ '· (12'Щ
_ мх _ —m _ 132 ж
Оты-ψ^ - (_ 461/132) аз ~ 461 Φ ^ 1<7PJ* (12ЛУ>
Из условий (12.18) и (12.19) соответственно
(Г).,?/"60 ЗЯ -Ί,/60 ^ -\/"7'Ъ Ш (2')-ί/?ϊ
а К 461 | [<тс11 К 461 8 [σρ] У 461 [σρ]' а — У 461 [σρ]'
Так как α(2,)>α(1/), определяющим размеры сечения является а = сР'\
е) Сопоставляем два случая расположения балки при работе на одну и
ту же внешнюю моментную нагрузку и обнаруживаем, что более экономным
оказался случай расположения балки, при котором ребро сжато. Выигрыш
в размере а, а следовательно, площади поперечного сечения определяется
отношением
-72T = l/ —=0'77 или Γ72μΈ = °'772 = 0'593·
α(2 > V 132 [α(2 ]f
Итак, площадь поперечного сечения балки при расположении ребра в сжатой
зоне составляет 59,3% от площади поперечного сечения балки при
расположении ребра в растянутой зоне. Экономия получается равной 40,7%. При
других соотношениях размеров тавра и других соотношениях допускаемых
напряжений при растяжении и сжатии экономия будет иной.
Пример показывает как простой поворот балки на 180*
относительно продольной оси позволяет использовать
ее значительно эффективнее, чем в первоначальном
положен и и.
§ 12.4] НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ЧИСТОГО ИЗГИБА СТЕРЖНЯ ИЗ
Пример 12.2. Сопоставить изгибающие моменты, вызывающие одинаковые
фибровые напряжения, равные допускаемому, в случае чистого изгиба
призматических балок разных поперечных сечении, площадь которых одинакова и
равна 45а2 (рис, 12.11).
χ
У
На
< »►
1М
9а
Ю
«3
1
За
За
1
1 >«
1
За
9а
·* »■
Ϊ3
/
'
1
11а
\
I
'
ι
δ)
Рис. 12.11. Два варианта поперечного сечения, имеющие одинаковую площадь; а)
первый вариант; б) второй вариант.
Решение, а) Найдем моменты инерции площадей поперечных сечений.
Первый вариант:
η 9α (13α)3 8а(9а)з 4627
/'" —
IX =
12
12
= —а
Второй вариант —
2, 9α (11α)» 6а(9а)з 2535
,(2)
IX =
12
12
= — й
б) Определим моменты сопротивления.
В первом и втором вариантах соответственно,
,11)
wr=
13α/2
2_
13
4627α4 4627
4α
= Ί26-α3'
г'21
x lla/2
2_ 2535a*
11 ' 4a
2535 ,
в) Определим изгибающие моменты, вызывающие фибровые напряжения,
равные допускаемым; для этого воспользуемся формулой Mx/Wх^[о], отсюда
соответственно в первом и втором вариантах
Mm iir/d) г ι 4627 „ г .
х =WX [σ]=-^-αΛ[σ],
f'21
2535
^=ΐη'·[σ]=^α3[σ]
г) Отношение изгибающих моментов в двух вариантах Мх1)/Мх ' = 1,28.
Таким образом, за счет перераспределения материала в пределах поперечного
сечения балки удалось увеличить изгибающий момент, могущий возникнуть
в поперечном сечении балки, иа 28% при условии, что фибровые напряжения
в сопоставляемых случаях одинаковы и равны допускаемому.
Пример 12.3. Определить, какой должна быть высота hj у пустотелой
балки, изображенной на рис. 12.12, а, чтобы в условиях чистого изгиба она
воспринимала такой же момент 2)1, как балка, изображенная на рис. 12.12,6.
Установить, какой процент материала экономится при переходе от сплошного
с£чения к пустотелому; при этом учесть, что h/b=a=2; 6 = 50 см.
114
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Решение, а) Определим момент Ш, который может воспринять балка при
чистом изгибе, если поперечное сечение ее имеет вид, показанный на
рис. 12.12,6, Воспользуемся условием прочности —^ ^ [σ], или—πϊΓ^Ισ]ϊ
Wx Wx
отсюда
Wl = Wxv [σ]=^[σ]=^[ο]. (12.20)
б) Установим, каким должен быть момент сопротивления, чтобы во втором
варианте балки изгибающий момент, такой же как и в первом варианте,
вызывал такие же напряжения в крайних
<s|Lrs
I
-Г
Π
rfb|iri
^3
1.
2SS^
i
волокнах, т, е. имея
[о],
или
\П2'
bh\
[σ]. Найдем
ш
а)
δ)
Рис. 12.12. Два варианта поперечного
сечения, в которых одинаков момент
сопротивления: а) первый вариант;
б) второй вариант.
12 12 //1!/2. [σ] * (12.21)
Совершая преобразования, получим
bhl . 3 иы.* ( 6 м ι т\ и , 4 ,а
Ж + 25^~(т25&3 + м)^ + 62564=
= 0,
или, подставляя сюда вместо Ш соответствующее выражение согласно (12.20)
и умножая все члены на 15/6, будем иметь
Учитывая, что а=2, 6=50 см, придем к следующему кубическому уравнению
/if + Ш\ — 26 800/ii + 12 000 = 0,
единственным вещественным корнем которого является hi = 124,5 см. Итак,
момент сопротивления поперечного сечения пустотелой балки получим,
подставив Ь и h-i в левую часть формулы (12.21)2,
„с4>^-4(,2«--Н3]т2Ь=,г,0000·6 «*
Проверкой правильности полученного решения может служить сопоставление
Ψ? с ΨΤ
6 6
в) Определим, чему равна площадь поперечного сечения пустотелой балки
F^^bhy—bthi— -уft] = 50. 124,5— |-.5θίΐ24,5—-|·ΰθ)=3090 см*,-
для сопоставления приведем /?Φ=50· 100=5000 см2.
г) Найдем экономию, полученную за счет перехода к пустотелому сечению4
/ГЦ) /7(2)
tL_£ 100=38,2о/о.
§ 12.5] ТЕОРИЯ УПРУГОСТИ В ЗАДАЧЕ ЧИСТОГО ИЗГИБА 115
§ 12.5, Исследование чистого изгиба призматического бруса
методом теории упругости
1. Вводные замечания. Пусть имеем призматический брус,
загруженный на торцах нормальной распределенной нагрузкой,
складывающейся в моменты, вызывающие изгиб( бруса. Свяжем
с брусом систему декартовых координат, расположив начало ее
в центре тяжести одного из торцов, оси χ и у по направлению
главных осей инерции площади торца, а ось ζ — вдоль оси бруса
в сторону противоположного торца.
Для исследования напряженно-деформированного состояния
бруса применим полуобратный метод Сен-Венана.
2. Первый этап решения задачи. В первом этапе в качестве
«угадываемых» функций примем компоненты напряжений,
полученные в элементарной теории, изложенной в § 12.4,
β
ох = оу = τχυ = туг = χΖχ = О, аг=— у. (12.22)
3. Второй этап решения задачи. Проверим, удовлетворяют ли
функции (12.22) уравнениям теории упругости, т. е. уравнениям
равновесия и совместности деформаций.
Уравнения равновесия (9.1) функциями (12.22) удовлетворяются
при условии
χ = γ = Ζ = 0, (12.23)
т. е., если объемные силы равны нулю или не учитываются.
Такое ограничение является вполне приемлемым, так как эти
силы и не предполагалось учитывать в рассматриваемой задаче.
Уравнения совместности деформаций (9.22) и (9.26),
выраженные в напряжениях, при условии (12.23) также удовлетворяются,
так как они в левых частях содержат однородные
дифференциальные операторы второго порядка, функции же (12.22) либо
нулевой, либо первой степени и, таким образом, вторые производные
от них равны нулю.
Таким образом, функции (12.22) не противоречат уравнениям
теории упругости и им соответствует некоторое напряженное
состояние тела. „
4. Третий этап решения задачи. Выясним, каким нагрузкам
на поверхности рассматриваемого бруса отвечают функции (12.22),
и сопоставим эти нагрузки с интересующими нас для того, чтобы
установить, является ли (12.22) решением именно нашей задачи.
Уравнения равновесия элементарного тетраэдра (9.2) позволяют
найти составляющие поверхностной нагрузки на всех гранях бруса,
для чего, кроме компонентов напряжений (12.22), необходимо
знать /, т и η — направляющие косинусы нормалей к площадкам,
лежащим в этих гранях.
116
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. Χΐί
Начнем с рассмотрения торцов бруса, для которых
1 = т = 0, п=±\ (12.24)
(плюс, относится к торцу, удаленному от начала координат, а
минус—к торцу, проходящему через начало координат).
Используя (9.2) при учете (12.22) и (12.24), получим
β
Ρν* = 0, ρνί/ = 0, ρνζ = ± — у (12.25)
г
(минус —для торца, проходящего через начало координат). Таким
образом, (12.22) является решением задачи теории упругости при
условии, что моменты, действующие на торцы, образуются из
поверхностных сил, распределенных на торцах именно так, как
это предписано функциям (12.25).
Рис. 12.13. К определению направляющих косинусов нормалей к площадкам
поверхности призматического бруса.
Рассмотрим боковую поверхность бруса; нормали к площадкам,
лежащим в этой поверхности, имеют следующие направляющие
косинусы (рис. 12.13):
/ = cosa, m = cos (γ — α] = sin a, n = 0. (12.26)
Учитывая (12.22) и (12.26), из (9.2) получаем на боковой
поверхности pvx = 0, pvy = 0, pVz = 0 и убеждаемся, что функциям (12.22)
как на торцах, так и на боковой поверхности соответствует
интересующая нас поверхностная нагрузка.
Следовательно, функции (12.22) могут рассматриваться не
только как решение какой-то задачи теории упругости, но и
именно интересующей нас.
5. Четвертый этап решения задачи. В этом этапе найдем все
остальные функции, описывающие состояние бруса. К ним
относятся: компоненты деформации &х, гу, гг, уху, ууг и угх и
составляющие перемещения и, ν и w. Предварительно найдем
составляющие внутреннего момента и внутренней силы в поперечном
§ 12.5] Теорий упругости в задаче чистого изгиба 117
сечении, пользуясь условиями эквивалентности
Mx = $azydF=^y*dF=^,
F F
Мя = \ ozxdF=E-^ yxdF=^L = 0,
F F
N=[azdF=^ydF = ^Sx = 0.
F F
Так как за оси χ и у нами приняты главные центральные оси
инерции площади поперечного сечения бруса, центробежный момент
инерции 1ху равен нулю, вследствие чего нулю равен и
изгибающий момент My. Поскольку ось х — центральная, статический
момент Sx относительно этой оси равен нулю; отсюда нулю равна
и продольная сила N.
Компоненты деформации найдем из уравнений закона Гука
ε* = w [σχ - μ (oy + οζ) ] = — -^ у = — μ ^f- у,
EL
Μχ
1 г / ι \ι У Μ χ
#.
Ρ £'*
2(1 + μ) _0 =2(1 + μ) _0 _2(Ι + μ) _0
Система уравнений Коши, используемая для определения и, ν и w,
приобретает вид
ди_ Мх ду _ Мх dw _ Мх
dv \ди _(\ dw . dv _ ^ du , dw _ ~
аё + ^ —υ· ay+аг-υ» dz^~dx~υ·
Проинтегрируем эту систему уравнений. Предварительно исключим
из и, ν и а» перемещения бруса как жесткого целого. С этой
целью закрепим точку O(xo = yo = zQ = 0), вследствие чего и0 = v0 —
= w0 = 0, и не разрешим в той же точке поворачиваться элементу
dz относительно осей χ и у и элементу <&/ —относительно оси г,
в связи с чем
!).=Ш.=0· (1).=°·
Поскольку подробно интегрирование уравнений Коши было
прокомментировано в § 9.6, здесь никаких пояснений не даем и при-
118
Плоский изгиб стержней
[ΓΛ. XII
водим лишь некоторые промежуточные выкладки и окончательные
результаты.
τ ι ди Мх
I. 1. ^- = е* = — μ
дх
Е1>
У\
*·■>£(!)—* φ !(£)-°.
ч д /ди \ Λ ди Мх
χ;
3··)δ(κ) = 0. 6)|(i) = 0· »)|(1)-0.
Ε/,
au
a7
= 0; и = — μ
EL
xy.
ay — 8ί/ μ
з ^ i. ^ =
£Λ
#
ν a /dv\ Λ лча /ао\ Λ ч а /а»\
дг EIX> V 2EIX L z ^ μ ^ ί/ ;j-
ш. ι. |=о;
2 cb = М*г_
' ду Е1Х
г. dw Мху
dz ~~ I7J:
w
Мхуг
EL
Итак, получили функции и, ν и w
Μ
* xy = —?-xy,
χ Ρ
ϋ =
Μ,
2£/,
Γ_ г2 + μ (jf. _ y2}] = Γ_ 22 + μ (χ2 _ ^2)]>
2ρ
αί=
Μ,
1
•г/г = -- z/г.
£/* "' Ρ
(12.27)
6. Анализ картины деформации бруса.
6.1. Координаты любой точки. Точки бруса (я, г/, г)
в результате деформации занимают новое положение,
определяемое координатами х1 = х-\-и, y\--y-\-v, z1 = z-{-w.
6.2. Ось бруса. Точки оси бруса {х = 0, г/ = 0) в результате
деформации занимают новое положение (рис. 12.14)
Хл — U L_
г*М
х-у-0
= 0, ί/ι = » U-ί,-ο = — 2Ж77 ="~ 2^» г1 = г + ®\х-У-о = г>
(12.28)
т. е. располагаются на параболе (рис. 12.14), мало уклоняющейся
от дуги окружности при малых прогибах; действительно, кривизна
этой параболы, если подсчитать ее по приближенной формуле
κκ = ν
\х-У-0>
§ 12.5]
ТЕОРИЯ УПРУГОСТИ В ЗАДАЧЕ ЧИСТОГО ИЗГИБА
119
оказывается постоянной величиной
v \x-v-o ~~
х'■ = — = const,
ΕΙ
что характерно для окружности. При больших прогибах
приходится пользоваться точной формулой для кривизны изогнутой оси,
имеющей следующий вид:
«л "—
К[1+ИаР
Х-У-0
или, учитывая выражение для ν \x-y-Q, получаем функцию
ЛЛ
κ,
ЕЛ
/M-rni
зависящую от г, что свидетельствует о том, что изогнутая ось не
есть окружность. Однако при больших прогибах нельзя
пользоваться линейными уравнениями Коши и необходимо прибегать
Рис. 12.14. Изогнутая ось призматического бруса при чистом изгибе.
к нелинейным зависимостям между параметрами деформации и
составляющими перемещения. Интегрирование этих точных
(нелинейных) уравнений привело бы нас к уравнению окружности для
деформированной оси бруса. Приближенность линейных уравнений
Коши усматривается хотя бы и в том, что точка оси бруса после
деформации имеет координату z1 = z, такую же как и до
деформации (формула (12.28) и рис. 12.14). Тогда, как ясно, что гх
должно быть меньше ζ вследствие того, что осевое волокно длины
своей не меняет.
6.3. Поперечное сечение. Проследим за произвольным
плоским поперечным сечением ζ=*ζ*, точки которого в результате
деформации располагаются на поверхности с уравнением
Мх .._* * Л , Λί,
z1 = z*4-w|2=2. = z*+|^02* = z*(l -lYffy)
= z*
1+-*-
(12.29)
120
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Это — уравнение плоскости, параллельной оси χ (рис. 12.15). При
У>0 ζ1>ζ*, при ί/<0 г1<г*.
6.4. Ортогона л ь ность поперечного сечения оси
бруса после деформации. Покажем, что поперечное
сечение остается в результате деформации нормальным к изогнутой
оси. Для этого (12.29) запишем так
ъ - ι а- у и— р у π
Это есть уравнение прямой, представляющей собой след плоскости
поперечного сечения на плоскости Oyz. Угловой коэффициент этой
прямой равен ρ/ζ* или (см. рис. 12.15)
ctgp=^.
(12.30)
Уравнение касательной прямой к оси бруса в точке z = z* имеет
вид
zl
ρ
tib-f
2 = 2*
(12.31)
Предположим, что след плоскости поперечного сечения на
плоскости Oyz и касательная прямая к изогнутой оси бруса являются
%-f+p
z=z
f*Mrf)
Рис. 12.15. Ортогональность поперечного сечения деформированного бруса к изогнутой
его оси при чистом изгибе.
Я
перпендикулярными прямыми, тогда βχ = γ + β· Если это так, то,
согласно формулам приведения, должно выполняться равенство
π
tgPi = tg(^-+p = —ctgp.
(13.32)
Сопоставляя (12.30) и (12.31), убеждаемся в том, что равенство
(12.32) выполняется, следовательно, сделанное предположение
о перпендикулярности указанных выше прямых справедливо.
Таким образом гипотеза плоских сечений, принятая при
построении технической теории чистого изгиба бруса, является на
самом деле законом, т. е., формулируя гипотезу, мы «угадали»
действительную картину деформации.
§ 12.5]
ТЕОРИЯ УПРУГОСТИ Й ЗАДАЧЕ ЧИСТОГО ИЗГИБА
121
6.5. Деформация боковых г ρ а ней в с л учае, если
брус представляет собой прямоугольный
параллелепипед. Боковые линии в некотором прямоугольном
поперечном сечении до изгиба бруса (рис. 12.16) представляются
уравнениями
z = z*t
х = ±
2 »
после Деформаций они превращаются в линий, имеющие следую*
щие уравнения:
хг = х-\- и
21=Z+ W
. Ь μ Ь
г==г* =zt-2-_,_-Ti/:
~4-*·+£-*·(ι+-*).
2 = 2*
1
ρ
(12.33)
Так как и хг и Ζχ зависят от у линейно, линии боковых сторон
ab и cd поперечного сечения после деформации представляют
Я
S>i/:
О
У
Рис. 12.16. Прямоугольный параллелепипед.
собой прямые агЬг и οχάχ\ как и до деформации их положение
в пространстве можно охарактеризовать положением проекций
на плоскости Оху и Oyz. Проекция на плоскость Oyz лежит в
прямой линии, представляющей собой проекцию на эту же плоскость
всего поперечного сечения бруса, испытавшего деформацию
(см. рис. 12.17, а). Рассмотрим проекцию этой линии на плоскость
Оху (см. рис. 12.17,6). Обозначения проекций точек аъ Ьъ сг и
с?! на плоскость Oyz снабжены верхним штрихом, а на плоскость
Оху — двумя штрихами.
Составляющие перемещений точек а, Ь, с и d при переходе
в новое положение аъ Ьъ сг и аъ произошедшем в процессе
деформации бруса, показанные на рис. 12.17, получены по
формулам (12.27).
Составляющие перемещений точек a (x=b/2, y = — h/2, z = z*)
и с (х^ — Ь/2, ί/ = —/г/2, г = г*), согласно (12.27), выражаются
l" ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
следующими формулами:
[ГЛ. XII
μ Ъ
Ua-~~p~2\~^)-JT= — U"
μ bh
V* = k
Wa=-\ —
&2 _Д2
4 4
__ hz*
2p:
] = t»c,
Wr
-Ζ*2 + μ
P \ 2Γ
Составляющие перемещений точек
* = — у, У = ~2, z = z*j, согласно (12.27), суть:
Ь(х=±, *-*
= z*\
μ b h
μ bh
"i = -7TT=-iT
• — ud,
υ* = Τ9
wb
ι
P 2
[_Ι..+μ^_*)]_ΡΛ
wd.
Угловой коэффициент в уравнении прямой а\Ь\ на рис. 12.17, б
равен ^ζμ6/(2ρ). Иными словами (см. рис. 12.17), tgy=»
~° + %> с ДРУГ0Й стороны, tgv = tg[rt—у). tgy. Отсюда
α
~Щ = + %> Щ = щ; = Г·*-' (12.34)
Формула (12.34) показывает наклон боковой стороны первоначально
прямоугольного поперечного сечения, получающийся в результате
гиа-щ
Рис. 12.17. Картина перемещений точек боковых сторон первоначально прямоуголь·
ного поперечного сечения при чистом изгибе бруса, имеющего форму прямоугольного
параллелепипеда: а) проекция на плоскость Оуг; б) проекция на плоскость Оку.
деформации, по отношению к оси у. Вся боковая поверхность
оказывается линейчатой,
§ 12.5]
ТЕОРИЯ УПРУГОСТИ В ЗАДАЧЕ ЧИСТОГО ИЗГИБА
123
6.6. Деформация верхней и нижней сторон в
прямоугольном поперечном сечении. Верхняя и нижняя
линии ас и bd в некотором прямоугольном поперечном сечений
до изгиба бруса (рис. 12.16) представляются уравнениями
z = z*.
У=±±
2*
После деформации ас и bd превращаются в линии ахехсх и Ь^гаъ
имеющие следующие уравнения:
У1=У + у
Z-l—Z+W
»=±
Α ι J.
2 "τ" 2р |_
.· =ζ*-+~ — — ζ*=ζ*(\-+~—)
*\ ζ - ρ 2Ζ ζ 11-2Ρ;·
# —"+" гс
у — 2
Эти линии представим проекциями на плоскости Oyz и Оху
(рис. 12.18).
W
δ)
Рис. 12.18. Картина перемещений точек верхней, нижней н средней линий
первоначально прямоугольного сечейня при чистом изгибе призматического бруса: а) проекция
на плоскость Oyz; б) проекция на плоскость Оху.
Уравнения проекций линий ахехсх в b-J^ на плоскость Оху
имеют вид
# = ;
2
г*2
+
μχ1
μ/ι2
2р ' 2р 8р
(плюс в формулах используется для линии Ь^гаг и минус для а^с^Ц-
»*2
а линии г^! на ту же плоскость у = — "^~ + _γ-· Все три кри-;
вые представляют собой квадратные параболы, которые при более
строгом решении, основанном на использовании не уравнений
124
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Коши (линейных), а нелинейных уравнений, связывающих
параметры деформации с перемещениями, оказываются дугами
окружностей, при этом дуга r-^tx имеет радиус ρ/μ. Чем меньше μ, тем
больше радиус и в пределе при μ = 0 этот радиус устремляется
к бесконечности, а угол а (см. формулу
(12.34)) устремляется к нулю, вследствие
чего прямоугольное поперечное сечение
остается прямоугольным. В связи со
сказанным интересно вернуться к формуле
(12.34), связывающей радиус кривизны
изогнутой оси бруса, радиус кривизны
срединного слоя в плоскости
поперечного сечения и коэффициент Пуассона.
Соответствующая геометрическая картина
показана на рис. 12.19, из которого
очевидна отрицательность гауссовой кривизны
деформированного нейтрального слоя и,
аналогично, отрицательность гауссовой
кривизны деформированных верхней и нижней
поверхностей бруса. Приведенный здесь
анализ полностью подтверждает картину
деформации, описанную качественно в
§ 12.2.
§ 12.6, Касательные напряжения
при поперечном изгибе балки
1. Вводные замечания. Ограничимся
пока рассмотрением балки, которая имеет
продольную плоскость симметрии,
являющуюся и плоскостью действия всех
внешних сил и моментов, в том числе
реактивных. В § 12.8 это ограничение будет снято.
Будем рассматривать нагрузку, не
вызывающую продольной силы. Иными словами,
рассмотрим балку, в поперечных сечениях которой возникают лишь
изгибающий момент и поперечная сила, действующие также в
плоскости симметрии балки. Возникающая при таких условиях
деформация называется прямым (плоским) поперечным изгибом балки.
Будем считать, что и к поперечному изгибу можно
применять формулу (12.10) для нормального
напряжения, выведенную применительно к чистому
изгибу, т. е., что можно применить гипотезы, введенные в теории
чистого изгиба, и к поперечному изгибу в части касающейся
нормального напряжения. Позднее правомочность такого
допущения будет обсуждена.
Рис. 12.19. Взаимное
расположение и кривизны
изогнутой оси бруса и
нейтральной линии в поперечном
сечении: / — поперечное
сечение бруса; 2 — изогнутая
ось бруса; 3 — нейтральная
линия в поперечном сечении.
§ 12.6] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 125
2. Наличие касательных напряжений в балке при поперечном
изгибе. Возникновение в поперечном сечении балки поперечной
силы свидетельствует о наличии в нем и касательных напряжений,
являющихся интенсивностью распределенных касательных сил,
статическим эквивалентом которых и
является поперечная сила.
Однако к этому вопросу можно подойти
и не столь формально, а воспользоваться
опытом, в процессе которого
обнаруживаются касательные напряжения в
нейтральной плоскости и в плоскостях,
параллельных ей. Используя при этом закон
парности касательных напряжений,
приходим к заключению о наличии касательных
напряжений и в поперечных сечениях.
Представим себе балку на двух
опорах, составленную из двух брусков,
свободно лежащих один на другом (рис.
12.20, а). Если такую систему нагрузить
вертикальной силой Р, то возникнет
изгиб, в процессе которого, учитывая, что
бруски никак друг с другом не соединены,
произойдет проскальзывание одного бруска
по другому так, как это показано на
рис. 12.20, а; имеется в виду, что силы
трения между брусками невелики и ими
можно пренебречь. Если же при
составлении балки склеить бруски друг с другом,
то картина изгиба получится иной, она
изображена на рис. 12.20, б. Различие в
двух картинах деформации определяется
ролью, которую играет клей. Она состоит
в том, что клей, обеспечивая совместную
деформацию брусков, препятствует
удлинению нижних волокон верхнего бруска и
укорочению верхних волокон нижнего.
Постольку поскольку непосредственное
действие клея на бруски локализуется
лишь гранями, которыми они соприкасаются
друг с другом, это действие можно представить при помощи сил,
приложенных к нижней грани верхнего бруска и верхней грани
нижнего. Для достижения отмеченного выше эффекта, являющегося
результатом действия клея, направление сил должно быть таким,
каким оно показано на рис. 12.20, в. Очевидно, что если вместо
склеенной из двух брусков балки изгибать монолитную, имеющую
такую же высоту, как и высота балки, составленной из двух
φ
5)
Ж
τ
Клей
Рис. 12.20. Эксперимент,
выявляющий наличие
касательных напряжений в балке при
поперечном изгибе: а)
поперечный изгиб балки,
составленной из двух несвязанных
между собой этажно
расположенных брусков; б)
поперечный изгиб балки,
составленной из двух склеенных
между собой этажно
расположенных брусков; в)
картина усилий, создающих
эффект, эквивалентный роли
клея, соединяющего бруски
в балку.
126
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
брусков, то тенденция к проскальзыванию двух частей балки —
расположенных выше и ниже нейтрального слоя будет устранена
касательными силами взаимодействия верхней и нижней частей. Если
интенсивность этих сил достигнет определенного для материала
балки значения, то произойдет скалывание — т. е. разрушение —
разделение балки на две части, верхнюю и нижнюю. Разумеется,
что такой характер разрушения мыслим лишь при тех
соотношениях геометрических размеров и сопротивлений материала
различным видам разрушения, при которых раньше указанного
скалывания не наступит разрушение от других причин. Описанная
картина скалывания может иметь место в балках с малым
отношением l/h и выполненных из материала с малым отношением
тск/аР(С). Здесь тск — предел прочности при скалывании, σρ(ε)
—предел прочности при растяжении (сжатии). Примером такого
материала может служить древесина, при совмещении годичного слоя
с нейтральным. Аналогично можно было бы показать наличие
касательных напряжений не только в нейтральном слое балки, но
и в любой из плоскостей, лежащих в теле балки и параллельных
нейтральному. Итак, опыт доказывает наличие касательных
напряжений в нейтральной плоскости и в параллельных ей плоскостях.
В силу закона парности, касательные напряжения возникают и
в поперечных сечениях балки.
3. Формула для составляющей касательного напряжения,
параллельной поперечной силе, в точке поперечного сечения балки.
Установим зависимость величины касательного напряжения от
координат точки в поперечном сечении. Отнесем балку к той же
системе координатных осей, которая была рассмотрена в двух
предыдущих параграфах. Напомним, что рассматривается балка
симметричного поперечного сечения при условии, что ось
симметрии лежит в плоскости действия внешних сил. Будем, следуя
Д. И. Журавскому х), считать, что определению подлежит не полная
величина касательного напряжения, а лишь составляющая его,
параллельная соответствующей поперечной силе Qy. Иными
словами, будем изучать ту составляющую касательного напряжения,
статическим эквивалентом которой является поперечная сила Qy.
Другая составляющая в пределах сечения, если она имеется при
изгибе в плоскости Oyz, образует систему самоуравновешенных,
распределенных в поперечном сечении касательных сил.
Примем гипотезу статического характера о распределении
касательных напряжений в поперечном сечении балки, которую сфор^
мулировал Д. И. Журавский, впервые получивший формулу для
х) Журавский Дмитрий Иванович (1821 —1871) — русский инженер и
ученый в области строительства, в частности мостостроения и строительной
механики, автор проектов и строитель мостов (деревянных) на железнодорожной
линии Петербург — Москва.
§ 12.6] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЙ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 12?
касательного напряжения при поперечном изгибе балки. Эта
гипотеза состоит в следующем.
Во всех точках поперечного сечения, лежащих
на линии, параллельной нейтральной оси, значение
составляющей полного касательного напряжения,
параллельной плоскости действия сил, одинаково.
Из балки1, подвергнутой поперечному изгибу, вырежем элемент
двумя бесконечно близко друг к другу расположенными
поперечными сечениями, одно из которых, обозначенное индексом /, имеет
координату г, а другое, обозначенное индексом 2, — координату
z-\-dz. Пусть изгибающий момент в сечении / равен М, а в
сечении 2 равен M-\-dM. На рис. 12.21, а изображен этот элемент
балки и в сечениях / и 2 показаны эпюры нормальных
напряжений. В сечении 2 величина нормальных напряжений больше, чем
в соответствующих точках (с теми же координатами χ и у)
сечения /, именно поэтому в сечении 2 изгибающий момент больше,
чем в сечении /, на величину dM.
Найдем величину касательного напряжения в точке
поперечного сечения стержня с координатой у. Отсечем от
рассматриваемого элемента некоторую его часть плоскостью, параллельной Охг
и находящейся от нее на этом расстоянии у, и рассмотрим
равновесие сил, действующих на эту часть элемента (рис. 12.21, б).
Такими силами, действующими параллельно оси ζ, являются W0TC,
№TC + dN0TC и άΤ.
Сила Af°TC = W0TC является равнодействующей нормальных сил,
распределенных по линейному относительно у закону, приложенных
к грани A±B-J)X. N™ = N0TC + ά№™ — аналогичная сила,
возникающая на грани A2BJ)2 рассматриваемой части элемента. Сила
dT — равнодействующая касательных распределенных сил,
возникающих на грани A1B1BiA2. Наличие силы dT обусловлено
неодинаковостью сил W?TC и Л^тс; без силы dT элемент под влиянием
сил NiTC и Л^2ТС не находился бы в равновесии.
Уравнение равновесия имеет вид
(№TC + d№lc)-NOTC-dT = Of dT = dN™. (12.35)
Силу dT находим по следующей формуле, происхождение которой
очевидног)
dT = b(y)dz.r$. (12.36)
На основании закона парности касательных напряжений
заключаем, что %*уг> действующее на площадке АхВгА2Вг, равно искомому
1) Здесь и дальше верхний индекс (у) или (х) при символе компонента
касательного напряжения подчеркивает тот факт, что данный компонент
соответствует изгибу в плоскости Оуг и Охг.
128
Плоский изгиб стержней
[Гл. хп
касательному напряжению τ%] в любой точке линии А2В2 в
плоскости поперечного сечения стержня; Ь (у) — размер
поперечного сечения балки вдоль линии, параллельной оси х, проведенной
/ι
H+dfi
Рис. 12.21. К выводу формулы для касательных напряжений при поперечном изгибе:
а) элемент балки в двух ортогональных проекциях; б) аксонометрическое изображение
части элемента балки, отделенной от последнего сечением, параллельным нейтральной
плоскости на уробйе точки в поперечном сечении, в которой определяется касательное
напряжение.
на расстоянии у от плоскости Oxz. Сила d№TC выражается
формулой
dN^=\dadF1=\^dF1=^ Г уdFx = Ш*'S* . (12.37)
S: ^ Χ X 4J Χ
Fi Ft Fi
Здесь Fx площадь грани A2B2D2, т. е. часть площади поперечного
сечения стержня, расположенная по одну сторону от прямой,
проходящей через точку поперечного сечения, в которой опреде-
§ 12.6] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 129
напряжение, и параллельной нейтральной
lydF^S* (12.38)
ляется касательно
линии. Интеграл
представляет собой статический момент указанной выше части
площади поперечного сечения стержня относительно нейтральной
оси.
Подставляя (12.36) и (12.37) в (12.35), получим
.(«/) _ dMx
Ь (у) dz ■ xfj =
(у) _ άΜχ_
st
st
или
QyS\
ъуг
τ(χ)-
dz b (y), Ix
QXS*
(12.39)
(12.40)
3! 5sj
h(X)Iy
При переходе от (12.39) к (12.40), во-первых, учтена
дифференциальная зависимость между Qy и Мх, а, во-вторых, учтен закон
парности касательных
напряжений. В скобки в I \ Нейтральная ось
(12.40) помещена формула
для составляющей
касательного напряжения при
изгибе в плоскости Oxz.
Здесь h (χ) — размер
поперечного сечения балки
вдоль линии, параллельной
оси у, проведенной на
расстоянии χ от нее (рис.
12.22).
Абсолютная величина
интеграла (12.38) не
зависит от того,
рассматривается ли статический момент
площади A2BJD2 или площади A2L2B2 относительно нейтральной
оси, так как эта ось проходит через центр тяжести площади
A2D2B2L2, являющейся суммой площадей A2B2D2 и A2L2B2
^х, пл, АгОгВгЬг
Ю
■δ)
Рис. 12.22, Пояснение к формулам (12.40): а)
изгиб в плоскости Oyz. б) изгиб в плоскости Oxz.
— ^>х, пл АгОгВг~Т~ "Ьд:. пл АгЬгВгу
ИЛИ
>->дс, пл АгОгВ.г~Г £>х, пл A2L2B2—0, Ox> Пл. АгЬгВ.,— — <Ъ'Г, пл АфгВг>
Если в формулу (12.40) ввести символ абсолютного значения
статического момента S*, то можно иметь в виду статический
момент любой из двух частей площади поперечного сечения
(расположенной выше или ниже линии А2В2) относительно
нейтральной линии.
130
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
(ГЛ. ΧΪ1
Полученное распределение касательных напряжений (формула
(12.40)) относится к поперечным сечениям, не проходящим через
точки 1, 2 приложения сосредоточенных сил. Вблизи сечений
приложения сосредоточенных сил имеют место особые области, не
поддающиеся анализу средствами технической теории. Для
исследования этих областей, если материал упруг, необходимо
использовать аппарат теории упругости.
4. Эпюры касательных напряжений в поперечном сечении балки.
4.1. Вводное замечание. Имея формулу (12.40), можно
построить эпюру касательных напряжений по высоте поперечного
сечения балки.
Рассмотрим три характерных формы поперечного сечения
балки; прямоугольник, круг и двутавр. На этих сечениях могут
быть выявлены основные особенности в распределении
касательных напряжений по поперечному сечению любого вида.
4.2. Пр я мо у г о л ьное поперечное сечение.
= Y{Y-y){j + y) = j{~r-y'
b(y) =b = const, Ιχ = -τψ-
h 2\ 4
Qy 2" Π-- У 3 Qy I 4y<
^ = ΊΓ Ш ' =ТЖ ^-ίΗ· <12·41)
12
Функция (12.41) —квадратная парабола (рис. 12.23, а). Согласно
(12.41) наибольшее касательное напряжение, из числа
возникающих на площадках, лежащих в плоскости поперечного сечения,
имеет место в точках поперечного сечения балки, находящихся
на нейтральном слое, а у верхнего и нижнего краев поперечного
сечения касательное напряжение равно нулю.
3 Qy
^zy !ί/-ο — 2 ~bh ' %гу
= 0.
В случае прямоугольного сечения формула (12.40), а следовательно,
и полученная из нее формула (12.41), позволяет найти
составляющую касательного напряжения, совпадающую с полным
касательным напряжением хг (вторая составляющая τζχ равна нулю).
4.3. Круглое поперечное сечение.
/* = -χ-, &(y) = 2rslnaf
2 2 2 (12·42)
S% =-n- r3 sin α — -ή- r3 sin α cos2 a = —rz sin3 α.
§ 12.6]
КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ
131
Первое слагаемое в формуле для 5* представляет собой
статический момент площади сектора круга (с центральным углом 2а)
относительно нейтральной оси, а второе — равнобедренного
треугольника с углом при вершине 2а
Х(У) =
Qy-^r* sins а 4 Q
2r sin а
яг4
3 ηή
у sin2a =
4 QV /I 2 ч
= -5-—г (1 —cos2 a)
3 тег2 v '
4 Q
У
3 я/8
1 -
Г2
(12.42')
График функции (12.42') изображен на рис. 12.24, б сплошной
линией.
О
У
а)
шип
ШИН
ниш
ttmu
ь
■* *■
δ)
Рис. 12.23. Распределение касательных напряжений в прямоугольном поперечном
сечении балки, испытывающей поперечный изгиб: а) эпюра напряжений хгу\ б)
иллюстрация к распределению xSy в поперечных и продольных площадках с учетом закона
парности касательных напряжений.
У контура поперечного сечения полное касательное
напряжение располагается вдоль касательной к контуру (рис. 12.24, в).
При этом условии составляющая полного касательного
напряжения, нормальная к контуру, равна нулю, что и должно быть
(имея в виду закон парности касательных напряжений), так как
боковая поверхность изгибаемого бруса свободна от поверхностной
нагрузки и, следовательно, на ней нет и касательной
составляющей, параллельной оси бруса.
Полное касательное напряжение в точках круглого
поперечного сечения, расположенных у контура, равно
%г~ sina ~~ Ъпг* V i
ML
132
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Рис. 12.24. К распределению касательных напряжений в круглом поперечном сечении
балки, испытывающей поперечный изгиб: а) поперечное сечение балки, заштрихована часть
площади поперечного сечения, статический момент которой относительно нейтральной
оси необходимо найти для определения касательного напряжения х™> в любой точке на
)ямой АВ; б) эпюра распределения τ^=τ^ (у) (линия /) и τ^3χ = ^mayiy)
4 Qu
отрезке npj
У
Уг
О,
(линия 2). Ординаты линии 1 равны кх -^ —j-, коэффициент ki= 1— — при у/г
1/4, 1/2, 3/4 и 1 соответственно приобретает следующие значения: 1; 0,9375; 0 7500;
0,4375; 0; ординаты линии 2 равны кг ^ —~, коэффициент kt=Vl—(t//r)* при у/г = О,
1/4, 1/2, 3/4 и 1 соответственно приобретает следующие значения: 1; 0,96825; 0,86600;
0,66150; 0; в) направление полного касательного напряжения в точке поперечного
сечения, расположенной у его контура; 3 — боковая поверхность; 4 — поперечное сечение;
Μ
ли) „ лу)
г) эпюры полных касательных напряжений χν|' и их компонентов V"' и τν^ в точках
отрезка линии АВ поперечного сечения.
§ 12.6] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ ι*>
Соответствующий график показан на рис. 12.24, б штриховой
линией. Распределение полных касательных напряжений на линии
круглого поперечного сечения, параллельной нейтральной линии,
показано на рис. 12.24, г.
Рассматривая балку такого массивного поперечного сечения
как круглое и исследуя поперечный изгиб ее в плоскости Oyz,
мы, пользуясь формулой (12.40)!, находили т(гиу\ а %ZUJ,
соответствующее этому изгибу, оставалось неопределенным, а при изгибе
в плоскости Οχζ, аналогично мы находим по формуле (12.40)2
τΜ, а тгМ остается неопределенным. При одновременном изгибе
в обеих плоскостях полные касательные компоненты напряжений
выражаются следующими формулами:
+ тё, (12.43)
а полное касательное напряжение хг находится как
геометрическая сумма полных компонентов хг = У~х\у -\-ι\χ. Учитывая, что
доли компонентов, символы которых в формулах (12.43) обведены
рамками, средствами сопротивления материалов найти не удается,
становится очевидной невозможность полного определения
касательных напряжений при поперечном изгибе балки произвольного
профиля. В некоторых случаях, например в случае
прямоугольной балки, когда τ^ и %№ равны нулю, или в тонкостенных
балках открытого профиля, о которых говорится ниже, найти
полное хг представляется возможным. Можно найти полное
значение хг и в массивных профилях общего вида, но не во всех
точках, а лишь вблизи контура, где известно направление
полного напряжения %г.
4.4. Двутавровое поперечное сечение. Двутавр
обладает специфической особенностью — тонкостенностью,
характерной для большого класса балок. В связи с этим приведем
некоторые краткие сведения об этих стержнях.
Тонкостенным называется такой стержень (рис. 12.25), у
которого / ^> s ^> δ, / — длина стержня, s — характерный габаритный
размер поперечного сечения (например, длина контура), δ
—толщина стержня. Контур поперечного сечения в одних случаях
может представлять собой замкнутую, а в других не замкнутую
линию. В соответствии с этим тонкостенный стержень в первом
случае называется стержнем закрытого, а во втором — открытого
профиля1) (см. рис. 12.26).
Распределение касательных напряжений в поперечном сечении
балки тонкостенного открытого профиля обладает некоторой
(у)
tzy — tzy "Τ
^zy
^ζχ —
*ζχ
ι) К определению понятия тонкостенный стержень вернемся в главе XIV.
134
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
спецификой, на которой остановимся сначала на примере
двутавровой балки, а затем рассмотрим вопрос в общем виде.
Рассмотрим распределение касательных напряжений по
двутавровому поперечному сечению балки при поперечном ее изгибе
в плоскости Oyz (в плоскости стенки). Если иметь в виду
упрощенную форму двутавра, изображенную на рис. 12.27, а, и
находить распределение касательных
напряжений τ^ путем
формального применения формулы (12.40),
то эпюра этих напряжений имеет
вид, показанный на рис. 12.27, б.
В эпюре τΜ получился разрыв на
уровне перехода от стенки к полке
вследствие того, что на этом уровне
претерпевает разрыв ширина
сечения Ь — в точке, лежащей
бесконечно близко к уровню перехода от
полки к стенке выше этого
перехода, ширина Ь, используемая в
формуле (12.40), представляет
собой ширину полки двутавра,
а в точке, лежащей бесконечно
близко к тому же уровню, но
расположенной ниже него,
ширина сечения представляет собой
толщину стенки. Разумеется,
такая картина является
упрощенной и при более строгом
решении задачи указанного разрыва
в τ№ не обнаруживается.
Эпюра на рис. 12.27, б относится
к любой линии, лежащей в пределах стенки и параллельной
оси у. В силу сделанного предположения о равномерности
распределения касательного напряжения на любой прямой,
параллельной нейтральной линии, эпюра x^J в пределах полки должна
была бы иметь вид, показанный на рис. 12.27, в. Однако такая
эпюра противоречит закону парности касательных напряжений,
так как касательных напряжений, параллельных оси г, на нижней
грани полки не имеется.
В связи с отмеченными двумя несоответствиями эпюр,
получаемых при использовании формул (12.40), реальному
распределению напряжений представляет интерес рассмотреть, каким
получается это распределение при решении проблемы более
совершенными средствами, например, методом теории упругости. На
рис. 12.27, г показаны эпюры напряжений, соответствующие решению
Рис. 12.25. Соотношение размеров в
тонкостенном стержне; I > s > б.
§ 12.6] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 135
гл
а)
б)
Рис. 12.26. Примеры поперечных сечений тонкостенных стержней: а) открытого профиля;
б) закрытого профиля.
Рис. 12.27. Распределение касательных напряжений в поперечном сечении двутавровой
балки при поперечном ее изгибе: а) поперечное двутавровое сечение; б) эпюра напряже-
ннй τζυ п0 лнинн 1 — 1 поперечного сечеыня, определенных по формуле (12.40); в) то же
по лнинн 4—4', г) эпюры напряжения ν··/., определенного методом теории упругости;
д) поперечное сечение прокатного двутавра и эпюры напряжений t№J в этом сечении.
136
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
методом теории упругости. При этом, поскольку при точном
решении обнаруживается неравномерность распределения
напряжений по ширине сечения, дано несколько эпюр х^\
соответствующих различным линиям, параллельным оси г/, в том числе и
проходящей в пределах полки. В этих эпюрах нет разрыва на
уровне перехода от стенки к полке, нет противоречия закону
парности касательных напряжений в эпюре в пределах полки.
Вблизи входящего угла в том месте, где стенка соединяется с
полкой," имеется особая точка —в ней напряжение стремится к
бесконечности. Разумеется, что и такого положения вещей не может
быть в натуре. Аппарат теории упругости справедлив лишь в
пределах упругости, и как только напряжения превышают этот
предел результаты теории упругости перестают быть верными.
Следовательно, правильнее было бы либо исключить из рассмотрения
указанную выше точку, либо применить теорию у пру
го-пластических деформаций.
В силу наличия отмеченной концентрации напряжений в
прокатных профилях вблизи перехода от стенки к полке делают
закругления и тем самым существенно уменьшают концентрацию
напряжений. На рис. 12.26, д показаны эпюры τ^> в реальном
профиле с закруглениями, построенные на основании решения
теории упругости. Заметим, что в этом случае результат мало
отличается от полученного и по элементарной теории (формула
(12.40)) и от наблюдаемого при экспериментальном анализе
напряженного состояния. Напряжение т№ в пределах полки намного
меньше, чем в пределах стенки.
Особенностью двутавра, как тонкостенного открытого профиля,
является то, что при изгибе в плоскости Oyz компонент τ^
в стенке почти точно совпадает с полным напряжением χ (у)
в полках же компонентом х\у) можно пренебречь вообще; в них
наиболее существенным компонентом, также почти точно
совпадающим с полным напряжением χψ, является χ(£. Иными
словами, в тонкостенном открытом профиле, в частности таком как
двутавр, с большой степенью точности можно считать, что
полное касательное напряжение направлено параллельно оси
контура. В стенке это х{Л), а в полках x[v). Для отыскания х{у) в пол-
ках двутавра выполняется операция, аналогичная той, которая
была использована при выводе формулы (12.40). С этой целью
от элемента балки, заключенного между сечениями /—1 и 2—2
с координатами ζ и z-\-dz (рис. 12.28, а) отрежем часть полки и
рассмотрим равновесие ее, имея в виду, что в сечении /—/ балки
действует изгибающий момент Мх, а в сечении 2—2 — Мх -\- dMx.
Уравнение равновесия отсеченной части полки имеет вид
{№™ + ά№™)-Ν°™-άΤ = 0, dT^dN™, (12.44)
§ 12.6] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 137
Примем предположение о равномерности распределения по
толщине полки tn как х[Ух, так и σ. Относительно σ это
предположение обосновывается тем, что при линейном распределении σ по
*\ s\ .N™+dNm'
β)
γ гл/таж Тут / ^7 "
21
S)
г (У)
Г
ΐΙ
ЛУ)
■у
~(У)
ЛУ)
Рис. 12.28. К определению касательного напряжения v^y в полках двутавровой балки:
а) элемент балки; б) часть полки элемента балки н действующие на нее силы; в) эпюра
в стенке балки двутаврового сечения; г) направление касательных на-
τ^' в полках н rfj
пряжений ν*&> в полках и т^//в стенке.
высоте балки в пределах полки изменение σ очень
незначительное, что легко видеть из рис. 12.28, б. Что же касается τ^, то
138
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
сделанное предположение находится на уровне гипотезы Журав-
ского, достаточно хорошо подтверждающейся для тонкостенных
балок экспериментом.
В формуле (12.44)
άΤ = dz · tn ■ х{£\ dN0TC = ltn άσπ. (12.45)
Здесь άση — приращение нормального напряжения в поперечном
сечении балки в пределах полки при переходе от сечения /—/
к сечению 2—2, обусловленное приращением момента dMx
dM |Ά_Μ
, am*\2 2 dMx ,u , . /ю.сч
dan = '-j- L = —JJ!L(h-tn). (12.46)
Подставляя (12.46) в (12.45) и после этой подстановки (12.45)
в (12.44), получим
d2.tn%H = ltn^-(h-ta),
2/,
откуда
{у) dM l{h-tn) {y)_QyUh-t.)
%хг — dz 2/x ' %гх ~ 2l\. * V*·*')
На рис. 12.28, в показаны эпюры напряжений τ&> в пределах
полок и x[yj в стенке, возникающие при изгибе в плоскости Oyz.
На рис. 12.28, г изображены сами напряжения в поперечном
сечении. Наряду с этим в полках имеются напряжения τψ>t
представленные эпюрами на рис. 12.27.
В пределах всего сечения двутавра, в силу его симметрии
напряжения χ№ в полках само уравновешиваются, т. е. не
складываются ни в какую силу. Однако учитывать эти напряжения
при оценке прочности необходимо.
5. Касательные напряжения в поперечном сечении балки
тонкостенного открытого профиля. Рассмотрим теперь тонкостенный
профиль произвольного вида, сохранив пока лишь условие
наличия оси симметрии у поперечного сечения, лежащей в плоскости
действия внешних сил.
Прежде всего, как и при рассмотрении двутавра, условимся
считать, что по толщине тонкостенного профиля нормальные
напряжения при изгибе балки распределены равномерно; допускаемая
при этом погрешность невелика. На рис. 12.29 показана балка
тонкостенного профиля и эпюра нормальных напряжений,
возникающих в поперечном ее сечении; вследствие малости отношения
-r-jx разница в величинах нормальных напряжений в верхней и
нижней точках сечения 1 — 1 невелика, аналогичная разность
§ I2.<fl КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 1-эУ
в сечении 2 —2, а тем более 3 — 3, еще меньше. В дальнейшем
будем считать, что по толщине тонкостенного профиля
напряжения распределены равномерно и при этом равны величине,
соответствующей точке, лежащей посредине толщины профиля, т. е.
на контуре.
При выводе формулы для касательного напряжения в
поперечном сочении балки тонкостенного открытого профиля при
поперечном изгибе поступим аналогично тому, как это делалось выше,
применительно к балкам массивным или двутаврового сечения.
Рис. 12.29. К обоснованию допущения о равномерности распределения нормальных
напряжений при изгибе балки открытого тонкостенного Профиля: /в> 2В, Зв, —'
Нормальные напряжения в верхних волокнах сечений / — /, 2—2, 3—3; /н, 2Н, Зи — то же в
нижних волокнах.
Пусть требуется найти касательное напряжение в точке А,
находящейся внутри балки. Проводим через эту точку поперечное
сечение и на расстоянии dz от него еще одно поперечное сечение.
Таким образом, из балки выделяется бесконечно малый элемент
(рис. 12.30, а). Пусть в сечении, проходящем через точку Л, дей-.
ствует изгибающий момент Mx-\-dMx, а в другом сечении — Мх.
Теперь через точку А проведем продольное сечение aAdcb
(рис. 12.30, б). Очевидно, что чем меньше площадь aAdcb, тем
больше по величине касательные напряжения, возникающие на
ней. Наименьшей площадь aAdcb становится, если эта площадка
проведена нормально к контуру (рис. 12.30, б). Вследствие закона
парности касательных напряжений, напряжение τ в поперечном
сечении направлено перпендикулярно отрезку ad, т. е. вдоль
касательной к контуру. Вместе с тем, учитывая тонкостенность
стержня можно говорить о равномерности распределения не только
нормальных, но и касательных напряжений по толщине профиля
(рис. 12.30, г). Расположение же касательных напряжений по
направлению касательной к контуру свидетельствует о том, что
это есть полное напряжение. При выводе формулы для касатель-
140
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
ного напряжения %<&} (τ^) в массивных балках сечение,
содержащее dT, располагалось параллельно нейтральному слою Oxz (Oyz).
Итак, отличие рассматриваемого здесь вывода от ранее
выполненного состоит в том, что в формуле (12.40) вместо b (у) надо
иметь в виду δ (s) — толщину профиля в рассматриваемой точке
Рис. 12.30. К выводу формулы для касательного напряжения прн поперечном нзгнбе
тонкостенной балкн открытого профиля: а) элемент балки; б) часть элемента балки и
действующие на нее силы; в) к обоснованию выбора нормального сечения — отделение
части элемента сечением с максимальными касательными напряжениями; г) направление
полного касательного напряжения, определяемого формулой (12.48), и распределение
его по толщине профиля.
контура (рис. 12.30, а). Во всем остальном имеется полное
совпадение. Поэтому
%(*) =
_QySl
δ/>
%(У) =
QxS]
(12.48)
При изгибе как в плоскости Oyz, так и в плоскости Oxz
напряжение τ располагается вдоль касательной к контуру. Поэтому
при изгибе одновременно в обеих плоскостях касательные
напряжения в тонкостенных открытых профилях, определенные по
формулам (12.48), складываются алгебраически (см.
рис. 12,31)
{у)
τ, = τΥι + τ.
.(χ) _ QySx
QxSy
Ыл
δ/,
(12.49)
6. Оценка порядка величины отношения ттах/сГтах. Произведем
сопоставительную оценку порядка величин нормальных и каса-
§ 12.6] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 141
тельных напряжений, возникающих при поперечном изгибе балок
нетонкостенного профиля. С этой целью рассмотрим поперечный
изгиб однопролетной балки прямоугольного поперечного сечения,
шарнирно опертой по концам и загруженной равномерно
распределенной нагрузкой. В такой балке максимальное нормальное
Рис. 12.31. Распределение полного касательного напряжения по толщине профиля;
а) при изгибе в плоскости Oyz; б) при изгибе в плоскости Oxz, β) при одновременном из;
гнбе в плоскостях Oyz и Oxz.
напряжение возникает в сечении посредине пролета (где
максимален изгибающий момент) в волокнах, наиболее удаленных от
нейтрального слоя. Эти напряжения равны
Μ
OYnflY '
л: max
ql*
W
8
bh*
3 qfi
Максимальные касательные напряжения в поперечном сечении
возникают в опорном сечении (где максимальна поперечная сила)
на уровне волокон нейтрального слоя; эти напряжения равны
τ "i/max
3 2
~2~bh
3 ql
II'
Отношение xmax и amax выражается формулой
max
max
3 ql
3 ql*
TW
h
T"
Если не ограничиваться площадками поперечных сечений, то ясно,
что наибольшего значения τ достигает в крайних точках среднего
поперечного сечения на площадках, составляющих с ним 45°.
Здесь τ max — CFmax/2. ОрИ ИНЫХ балке И НЭГруЗКб у Ощах И Тщах
адреса другие.
142
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
7. Искривление плоскости поперечного сечения балки
вследствие неодинаковости в различных точках поперечного сечения
сдвига при изгибе. Представим себе элемент балки между сече-*
ниями с координатами ζ и z-\-dz. Распределение касательных
напряжений, возникающих при поперечном изгибе балки по высоте
поперечного сечения ее, неравномерное. Если элемент балки
(рис. 12.32) мысленно разбить на бесконечно тонкие пластины,
параллельные срединному слою, то каждая из них под влиянием
касательных напряжений подвергается сдвигу. Наибольшему сдвигу
подвергается пластина, расположенная на уровне нейтрального
касательные напряжения в попе-
Наиболее же удаленные от нейт-
не подвергаются сдвигу, так как
в этих местах касательные
напряжения в поперечных сечениях
равны нулю. Совместность
деформации всех испытавших
деформацию пластин, на которые разбит
элемент балки, мыслима лишь при
искривлении поперечных сечений.
На рис. 12.32 показан элемент
после деформации. При этом видно,
что различные пластины испытали
различный сдвиг — наибольший у
нейтрального слоя; не испытали
сдвига вовсе пластины, наиболее
удаленные от нейтрального слоя.
На этом же рисунке штрихами
показан вид деформированного элемента с учетом деформаций,
возникающих и от нормальных напряжений. Итак, вследствие
сдвига при изгибе поперечные сечения в балке искривляются.
8. К вопросу об использовании формулы для нормальных
напряжений, выведенной применительно к чистому изгибу, и
в случае поперечного изгиба. При выводе формулы для
касательного напряжения при поперечном изгибе, на первый взгляд,
обнаружилась некоторая несогласованность с первой гипотезой,
которая нуждается в разъяснении.
Формула (12.10) для абыла выведена применительно к чистому
изгибу, при этом использовалась гипотеза плоских сечений.
При рассмотрении поперечного изгиба в процессе вывода
формулы (12.40) для τ без специального обоснования была применена
формула (12.10) для σ. Вместе с тем был обнаружен факт
искривления поперечных сечений вследствие неравномерности сдвига при
изгибе. Возникает вопрос, можно ли использовать формулу (12.10)
для σ при поперечном изгибе и, как следствие, — является ли
достоверной формула (12.40). Ответ на эти вопросы можно дать
слоя, так как именно здесь
речном сечении максимальны,
рального слоя пластины вовсе
Рис. 12.32. Искривление поперечных
сечений балки при поперечном изгибе
вследствие неравномерности сдвига.
§ 12.6] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 143
положительный и объясняется это
следующим. При выводе формулы (12.10)
для σ на основе гипотезы плоских
сечений существенным был не сам факт
сохранения плоской формы поперечного
сечения, а вытекающая из него
линейность зависимости (12.6) гг от у. При
сохранении плоской формы сечения
эта линейность выполняется с
очевидностью, однако линейность
зависимости ez от у может соблюдаться и при
одинаковом искривлении (депланации)
всех поперечных сечений. Легко
представить себе, что если испытавшие
деформацию волокна, из которых состоит
элемент балки после деформации (торцы
пластинок располагаются на
криволинейных линиях, изображенных на
рис. 12.32 штрихами), расположить
так, чтобы левые торцы их, лежали на
прямой (рис. 12.33), то и правые торцы
могут расположиться либо на прямой,
либо на кривой, мало отличающейся
от нее. К вопросу о гипотезах мы
вернемся еще раз в разделе 5 § 12.7.
^§w
о
k
\
Рис. 12.33. К обоснованию
допустимости использования
формулы для нормального
напряжения в поперечном сечении
балки, находящейся в условиях
чистого изгиба, при выводе
формулы для касательного
напряжения при
поперечном изгибе: несмотря на
искривление поперечных сечений
при поперечном изгибе балки,
относительные удлинения
волокон подчиняются линейному или
близкому к нему закону,
вследствие чего формула (12.5) для ε
остается такою же как н при
чистом изгибе, где сечения
сохраняются плоскими. В этой
иллюстрации для простоты
пояснения сдвиг полосок не показан.
9. Примеры.
Пример 12.4. В круглом поперечном
сечении балки, испытывающей поперечный изгиб в двух ортогональных
плоскостях Οχζ и Oyz, определить полное касательное напряжение в точке А,
расположенной у контура (рис. 12.34, а). Радиус круга г, поперечные
^илы Qx и Qy (их отношение Qx/Qi/=2) заданы. Применить принцип
независимости действия сил.
Решение. Определяем x^J по формуле (12.42)
4 Qy /ι , * 4 Q" Γι 1П\2Л Qy
Ли) — .
w 3 itr2
x<zy) 2
Определяем x^ по формуле x^) = zy — —
Qy
формуле, аналогичной (12.42),
sin α 3 iu2
Определяем
rg> no
lzx
4 Q*
3 jtr2
Определяем χΜ по формуле
['--(T-K&Ntfl-k
Μ) —
Λχ)
ιζχ
2 <2д
2/3 Qx 4J/3 Qy
sin
π
— a
Ϋ2> sir*
nr*
ПГ*
144
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Определяем хг по формуле
v-^-*.
<*>—.
Щ
Злг2
(2/3-1) 1,64
иг2
Условно принятое положительное направление хг показано на рис. 12.34, б.
Пример 12.5. В прямоугольном поперечном сечении балки, испытывающей
поперечный изгиб в двух ортогональных плоскостях Охг и Oyz, определить
й)
δ)
Рис. 12.34. К примеру 12.4: а) поперечное сечение балки, в точке А которого требуется
найти касательное напряжение; б) к определению компонентов касательного напряже-
„ня if н τ£>.
полные касательные напряжения в точках А, В и С (рис. 12.35, а). Стороны
прямоугольника Ь и h, поперечные силы Qx и QH заданы (Qx/Qy=l).
is
b
4
a
A
С
».b
b
V
·/
/'
/
•*=:|·*
да
В
ж
■*r-* к _ _r(X> _
Ус
~z(»-~z
ferW
8)
Рис. 12.35. К примеру 12.5: α) поперечное сечение балки и точки А, В, С, в которых
требуется найти касательные напряжения; б) изгиб в плоскости Oyz; в) изгиб в плоскости
Охг: г) совместное действие изгиба в плоскостях Оуг и Охг.
Решение. Определяем xfj по формуле (12.41) (рис. 12.35, б)
Т*У~2 bh\ №}~ 2 bh 4 8 № τ* ' τ^ _υ·
Такие напряжения имеют место и в точке Л и d точке В.
Определяем x^J по формуле, аналогичной (12.41) (рис. 12.35, в)
гх
3_Q
2
Aft
4х2
ί>2
2 hb A
9 Q,
8 Μ
rM
2#
§ 12.6] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ Н5
Такие напряжения имеют место и в точке Лив точке С."
В точке С х%/=0, г<*>=0.
В точке В т<*)=0. х[х,}=0.
В точке А полное напряжение %г определяется по формуле (рис. 14.35, г)
lz(A)
-Vwr+Wr-Tc&vs (β-β,-ω
8. bh
Полные напряжения в точках В и С находим соответственно по формулам
τ — rUO.
τζ(Β)~ιζ ■
lzy ' «(С)-%ζ ~ιζχ-
Пример 12.6. В равнобедренном треугольном поперечном сечении балки,
испытывающей поперечный изгиб в плоскости Oyz (у—ось симметрии
треугольника, рис. 12,36, а), найти максимальное касательное напряжение. Размеры
треугольника: с (основание), h (высота) и поперечная сила Qy заданы.
^
if г
*zmtti
Рис. 12.36. К примеру 12.6: а) поперечное сеченне балкн; б) к определению статического
момента части площади поперечного сечения, расположенной по одну сторону от точки
с искомым касательным напряжением; в) месторасположение точки с максимальным
■ЛМ(-Ли)
zy
(ti„m>o») н с максимальным полным касательным напряжением х™' 1x^2. )
\ 2i/max/ r г \ ггпах/·
Решение. Для отыскания касательного напряжения воспользуемся
формулой (12.40)ϊ· Момент инерции площади треугольника относительно
центральной оси, параллельной основанию, выражается формулой 1х=с№/36. Ширина
текущего сечения (рис. 12.36, б), параллельного оси х, как функция у
выражается следующей формулой:
^4-<+τΗτ+ί-)·>ь
= с, Ь
УГТ
=0.
у=-тн
Абсолютное значение статического момента площади части треугольника,
расположенной по одну сторону от отмеченного выше текущего сечения, найдем
по формуле
3+Т)ЫН+У)Т[Т-У)
si
1 /2 \ 2 (h \ 1 /2 h Л
Максимума по высоте сечения величина хгу достигает при таком у, при
котором достигает максимума отношение Sx/b (у).
146
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Исследуем отношение St/b (у) на экстремум
'dy
Ь(У)
Ь(У)
-Α-2ί/) = 0; _Α_2ί/=0;
У=*~тг
dy*
S*
St
Ь(У)
max
>-i(-4)-(-
Mrt/
= -|<o,
2f/ max
= t
«i/
# = —
Qj/ St
I u b(y)
Qu
y= —
h —
c/l8/36
h2
·*■■— ч
12 c/i
Однако максимальным касательным напряжением является напряжение
не в точке С поперечного сечения при у — — Λ/6,' а полное напряжение в точке
поперечного сечения D на том же уровне, направленное по касательной к
контуру. В рассмотренном случае этот уровень не совпадает с нейтральным слоем
"гтах
_ T2i/max _^ Qy
cos α "~ *" ch
V-
/i2 +
r2
h
Пример 12.7. Построить эпюру распределения касательных напряжений
по поперечному сечению балки тонкостенного открытого профиля,
изображенного на рис. 12.37, а, при поперечном изгибе в плоскости Oyz. Размеры
сечения г, δ и поперечная сила Qy заданы.
Рис. 12.37. К примеру 12.7: а) поперечное сеченне балки; б) эпюра τ (она же, с точностью
до множителя oV8jx/Q , эпюра распределения по контуру абсолютного значения
статического момента части площади поперечного сечения, лежащей по одну сторону от
текущей точки контура, относительно оси х); в) распределение касательных напряжений
по толщине профиля.
Решение. Для построения эпюры %г найдем функцию хг=т:г(ц))· С этой
целью воспользуемся формулой (12.48)^,
St = \ губ ац> = V г2б cos φ ίίφ = ήδ sin φ,
2л 2π
/Λ-= \ rf/26d(p = r36 I cos29 άφ = ήδ(-~- φ + -κ- sin2(p]
2π
= ήδπ,
T(i/) = Qi/2Ssin<P Qy
δήδϊΐ
=ш5т(*·
12.6]
КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ
147
На рис. 12.37, б, в показана эпюра распределения касательных
напряжений хг по периметру контура.
Пример 12.8. Построить эпюры распределения касательных напряжений
хг^ (х^) по поперечному сечению балки тонкостенного открытого профиля,
изображенного на рис. 12.38, а, при поперечном изгибе в плоскости Oyz(Oxz).
Размеры сечения, указанные на рис. 12.38, а, и поперечная сила Qt/[QX) заданы.
d *
Ч>
$ #Ы+ЬНаг+аг+к
£(а±Ь)4^7гЛ
fy/a^+B
2Va^d^
8)
Рис. 12.38. К примеру 12,8: а) поперечное сеченне балкн; б) эпюра статического момента
S* (у) (л = 26 (а+-т>-) с)'· ") эпюра статического момента S* (я) (в = с& ί-|· +<ί))·
Решение. Касательные напряжения находим по формулам (12.48). Построим
эпюры St и Sy~.
Участок 1—2
-β» + -ί« S*L=o=0;
s$\Si=c=cb(c+d-^) = ^- + cdb.
Участок 2—3
S* = 6 (a-\ )r-4~s«{) a~\ a 2 ■)■
S$=cd (- + dW s26 /rf - d ,- S* .. ) ·
2
Участок 3-
2
На участке 3—4 S# = 0 поскольку центр тяжести отсеченной части
находится на оси у, относительно которой определяется статический момент. Эпюры
Sx и Sy показаны, соответственно па рис. 12.38, б и е. В силу того, что все
остальные члены, входящие в формулы для τ^ и τ^\ являются постоянными,
не зависящими от χ или у, эпюры τ^ и х[х) оказываются аффинно-эквивалент-
ными соответственно эпюрам S* и S*. Определение же 1Х и 1у не вызывает
затруднений и его здесь не приводим.
§ 12.7. Анализ частных случаев поперечного изгиба балки
прямоугольного сечения методом теории упругости.
Обоснование предположений, принятых при построении
технической теории
1. Вводные замечания. В настоящем параграфе обосновываются
некоторые положения, о которых говорилось в предыдущем
параграфе без доказательств. Имеются в виду такие вопросы как:
малость оу по сравнению с ог, линейность функции &г — &г (у) или
малость отклонения этой функции от линейной. Обоснование
указанных положений производится средствами теории упругости,
но не в общем виде, а на примерах, которые позволяют
экстраполировать результаты на другие частные случаи. Сначала
рассматривается плоская задача для балки, в которой поперечная
сила постоянна вдоль ее оси (консоль, загруженная на конце
сосредоточенной силой), затем в условиях опять-таки плоской
задачи исследуется изгиб балки на двух опорах, загруженной
равномерно распределенной нагрузкой. Разумеется, что в обоих
примерах сечение балки прямоугольное. Граничные условия на
торцах балки удовлетворяются в духе Сен-Венана.
На этих примерах удается проследить и за некоторыми
особенностями самого полуобратного метода Сен-Венана, оставшимися
невыясненными в силу большой простоты тех задач, которые выше
были решены этим методом.
2. Изгиб консоли.
2.1. Исходные данные. Имеем консольную балку в форме
прямоугольной пластины со сторонами / и h. В срединной
плоскости этой пластины расположим координатные оси ζ и у, подобно
тому, как это делалось в предыдущих параграфах для балок.
Пусть левый конец балки заделан, а правый свободен и загружен
сосредоточенной силой Ρ (рис. 12.39). Подробно о том, что
понимать под заделкой и под сосредоточенной силой будет сказано
§ 12.7] ПОПЕРЕЧНЫЙ ИЗГИБ. ОЦЕНКА ТЕХНИЧЕСКОЙ ТЕОРИИ Н9
ниже в порядке уточнения этих понятий. Рассматриваемая задача
однородна, так как объемные силы не учитываются (полагаются
равными нулю). Выполним анализ напряженно-деформированного
состояния балки полуобратным методом Сен-Венана.
!
I
-*=Сч!
ί—ί
IP
44
Η
WjS
т
ί(Η
■§
'■Л
νζ
У
■У
δ)
Рис. 12.39. Консольная балка: а) фасад и поперечное сечение балки; б) к определению
знака опорного момента.
2.2. Первый этап решения задачи. Воспользуемся
технической теорией для установления вида компонентов
напряжений
Л2
σζ = -
мл
Л,
у=-
P(l-z)
У, о у = О,
Мх = -Р(1-г), Qy = P\ St = (~-y)b^[T + y =Y[j-y
r _.T _ Qy&
1 fh
— «2
!fi
2/,
(12.50)
b th*
2 \4
2.3. Второй этап решения задачи. Проверяем,
удовлетворяют ли функции (12.50) уравнениям однородной плоской
задачи теории упругости: уравнениям равновесия (9.87) и
уравнению совместности деформаций (9.94).
При подстановке (12.50) в (9.87), получаем
0 + 0 = 0,
Ρ Ρ
ТХУ+ТУ=0'
При подстановке (12.50) в (9.94), имеем 0 = 0.
Иными словами, компоненты напряжений (12.50) удовлетворяют
и условиям равновесия и условиям совместности деформации.
2.4. Третий этап решения задачи. Выясним, каким
поверхностным нагрузкам соответствует система функций (12.50)
150 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. ХН
и сопоставим их с заданными на поверхности силами для того,
чтобы удостовериться, является ли система (12.50) решением именно
той задачи, которая нас интересует. Условия на поверхности
имеют вид (9.88).
Рассмотрим нижнюю и верхнюю кромки y = ±h/2, где
т = ±1, п = 0. (12.51)
Учитывая (12.50) и (12.51), получим (9.88) в следующем виде:
Pvy = 0, pvz = 0.
Перейдем к торцам. Рассмотрим правый торец z = l, где
т = 0, п=\. (12.52)
Учитывая (12.50) и (12.52), получим (9.88) в таком виде
Ρν, = -Ητ '-, Ρν* = 0. (12.53)
2/,
Проинтегрируем pvy в пределах площади всего торца
+ А/2
п.. η пи ~π ι i l_ tt An — ,„, , _^_
8/, 2/.v 3 \ 8 T 8
— /i/2 —ft/2
+ Λ/2 +Ί/2
J pvzbdy = 0, ] pvzybdy = Q.
— ft/2 —ft/2
Итак, на правом торце действительно действует сила, равная Р,
как это и было задано в условии примера. Однако напряжения
(12.50) соответствуют не любому распределению этой силы на
торце, а лишь такому, какое предписано зависимостью (12.50).
При любом другом распределении силы Ρ на торце напряжения
будут другими, чем (12.50). Однако на основании принципа Сен-
Венана на небольшом удалении от торца на величину порядка h
практически закон распределения Ρ по торцу не существенно
влияет на напряжения.
Остается обследовать левый торец балки г = 0, где
т = 0, л = —1. (12.54)
Учитывая (12.50) и (12.54), получим (9.88) в следующем виде:
Pvy — 27 » Pvz — [У'
§ 12.7] ПОПЕРЕЧНЫЙ ИЗГИБ. ОЦЕНКА ТЕХНИЧЕСКОЙ ТЕОРИИ 151
Производя интегрирование в пределах всей площади левого
торцевого сечения, получим
+ /1/2 + ft/2 + ft/2
С С С PI Pi
J pvybdy = — P, j pvzbdy = j Txbydy = -r
Plb i/2 +ft/2
= 0.
—/i/2
"ft/2 -"ft/2 —"ft/2
По смыслу задачи в левом торцевом сечении (сечение заделки)
должен возникнуть опорный момент, равный — PL Проверим,
приводится ли распределенная по этому торцу поверхностная
нагрузка pvz к указанному моменту. Для этого раскроем интеграл
+ /ι/2 + /ι/2
М= — j Pvzybdy = — -~ j у2dy = — 4S^- = - PI
— Л/2 ' —ft/2
12/,
Знак минус перед интегралом принят в связи с тем, что при
положительных у и руг изгибающий момент отрицателен (рис. 12.39, б).
Итак, получили подтверждение, что функции (12.50) представляют
собой компоненты напряжений именно в интересующей нас задаче.
2.5. Четвертый этап решения задачи. Из уравнений
закона Гука
1 г„ λΊ μ Ρ{1 — ζ)
гУ = ~Ё К _ №] = Ε Ιχ У'
1 г ι P(t — z)
«* = -Ε- [Ъ - μσΡ] = щ^- у,
_ 2(1+μ) _ l+μ ^JT^
Угу— Е τ-zy — - Е jj-
получаем компоненты деформации, имея которые, путем
интегрирования уравнений Коши
— J?? — _£ ^ (l — г) _ _аш_ _ _ Ρχΐ — ζ)
гУ~ ду ~ ~Ё" [х У> &г~ дг ~ Е1Х #'
ди . dw 1 + μ
Ч*У ~ ~дг + ~~ду~ ΊΓ~
/, εζ =
'(£-
dw
дг
~Уг)
(12.55)
найдем составляющие перемещения υ и саг.
Для исключения из ϋ и да перемещений как жесткого целого
закрепим балку, предотвратив перемещение центра левого торца
при у = ζ = 0, υ = υ0 = 0, w = wo = 0 и поворот одного из
элементов. Определение ν и w выполним в двух вариантах
закрепления против поворота (рис. 12.40). В первом варианте
закрепления (рис. 12.40, а) воспрепятствуем повороту элемента dz
152
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ -
Выполним интегрирование уравнений Коши
τ ι ЁИ — ±_ ρ(ι~ζ) ,,.
ι· ' ди ~ Ε ' h у'
[ГЛ. XII
0 ч д I ди\ _ г * л>
μ ρ
ди
Ρ (1-2)
ΕΙΧ
ди
"dz
μΡ y*_. Plz
> ~Γ
ΕΙ
Eh
Ρζ*
2ΕΙΧ '
Ρ Γ π \ У2 . Ιζ* ζ8 1
(12.56)
II. 1.
dw
ι+μ
^(-τ-^2
9 dw —
Δ' dz ~
Ε Ιχ
Ρ(1-ζ)
+
μΡ У2
ΕΙΧ 2
Plz Ρζ*
ΕΙ
2ΕΙΛ
Eh
У\
W
= -к[-{1-^У-^ + ^^у\ 02-57)
Во втором варианте закрепления (рис. 12.40, б) воспрепятствуем
повороту элемента dy
dw
ί/=2=ο \ ду /о
Информация, аналогичная приведенной выше (результат
интегрирования), дается и в этом случае, но здесь сначала определена
функция w, а затем v.
Eh
I 1 а) д ldw\ 1+μ 2Р и Ι μ Ρ и Ρ(2+μ) и
L ' а) ду \ду) ~ Ε Ixy^ Ε 1ХУ~ Р' У'
л\ д (dw\_ P(l — z)
dz \ ду
Eh
dw _ _ Ρ(2 + μ) У*_
ду ~ Eh "2
9 dw__ _ Р(1-г)
Δ' dz ~ Elx y'
w =
Eh
(2 +μ) У3
ΕΙ
+ ι
PI . Ρζ*
2Eh
Ψ
(12.58)
ΤΤ 1 J*L — Α Ρ(/-ζ) „.
η* ι' ду ~ Ε Ιχ У'
ρ (--у*)
д^= 1 + μ V 4 У ) Ρ(2 + μ) y» Plz
L' dz Ε Ιχ "τ" E/r 2 "^ EIX
v =
Eh
μ (/ — ζ) «ι te2
— 2— У2 + -2~
EI,
z*
6
f
(l+μ) ft2
Pz2
2EIX '
(12.59)
§ 12.7] ПОПЕРЕЧНЫЙ ИЗГИБ. ОЦЕНКА ТЕХНИЧЕСКОЙ ТЕОРИИ 153
Сопоставляя (12.56), (12.57) с одной стороны и (12.58), (12.59)
с другой, обнаруживаем отличие в соответствующих формулах —
подчеркнутые члены отсутствуют в аналогичной функции из
другой группы формул.
Рис. 12.40. Закрепление балки против перемещения как жесткого целого:, а) первый
вариант закрепления; б) второй вариант закрепления; в) переход от картины
перемещений при одном варианте закрепления к картине перемещений при другом — путем
поворота деформированной балки как жесткого целого.
Наконец, рассмотрим еще три варианта закрепления, в каждом
ί ди\
из которых vQ, wQ и Nj— ι определяются из интегральных условии.
Во всех трех вариантах равны нулю два интеграла
+ ft/2 +ft/2
J v\z.0dy = 0, J w\z-ody = 0,
— ft/2 — /ι/2
а отличается один вариант от других видом третьего интеграла,
также обращенного в нуль. В третьем, четвертом и пятом
вариантах этот интеграл соответственно имеет вид;
+ ft/2
+ ft/2
+ Н/2
■ft/2 —ft/2 —ft/2
Функции ν и w находятся так, как показано выше, но
параметры ν0, ιινύ и (dv/dz)0 оставлены неизвестными
υ = υη
-№)*l+(£l·-
2£Л
Ρ/ζ2
du
дг)оУ +
2EIX
Ρμί/3
Рг?
6£/, '
6£Λ
Plzy , Pz*y
EIX "·" 2EIX
154 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. XII
Производные -~— и -=- и ω* находятся по следующим
формулам:
dw__ (1 + μ)ΡΛ? _ (1-}-μ)Ρί/2 ^ ^\ Ρμί/2 _ Ρ/ζ . Ρζ2
Я, . Τ OP/ PI ~Γ
5ί/ "~ 4£/* Elx \dz Jo ' 2£/* £/* ' 2EIX >
dv _ μΡί/2 , / dv \ Plz Pz*
~dz~ ~ - 2EIX + { dz /0 + E/, 2£/* '
aiw dv _ (1+μ)Ρ / Λ2 _ -\ _9(dv\ Ρμί/2 2P/z Рг^
ω*-^7 a*' £77~l4 #/ ^β*λ>+*/* eix+ Ё77-
Первые два интегральных условия в каждом из
рассматриваемых вариантов одинаковы и в раскрытом виде представляются так:
Отсюда
Ρμ/Λ2 г,
Третье условие, из которого находится (dv/dz)0 в каждом из
трех обсуждаемых вариантов закрепления имеет соответственно
следующий вид:
(1+μ)ΡΚ» (1 + μ)№ (dv\ . Pyh^ _ β _ Ρμ^_ / до\ ,_η
4£/* 12Ε/, \az;0/l'r24£/x ' 24£/ν "τ" \3ζ )0η~υ>
ΕΙΧ \ 4 12/ Vaz /о ^ 12£/л
Отсюда величина (dv/dz)Q в третьем, четвертом и пятом
вариантах соответственно выражается формулами:
/ dv\ ptv л , 5 \ /ао\ _ _μΡΛ2_ /а_и_\ ρ/ι2 /. . з \
\dz jo ~ 6Е1Х \ 1 + 4 μ/' V3z /о ~~ 2AEIX ' V ^ /о ~ 12E/, \ + 2 ^ '
2.6. Анализ картины деформации балки.
2.6.1. Координаты точки балки. Любая точка балки {у, ζ)
в результате деформации занимает новое положение, определяемое
координатами y1 = yJrv, z1 = z-\-w.
2.6.2. Ось балки. Рассмотрим ось балки, точки которой (ί/ = 0)
в результате деформации занимают новое положение уг = ν |,,_0,
z1 = z-\-w\y-0. Первый вариант закрепления
&=-шг[-т--тг]· Zl==z' (12,60)
1 X
Второй вариант закрепления
Ух
Чх-т + -^*]. ζ^ζ' (12·61)
ΕΙ
Позднее, находя перемещения при изгибе балки в § 12.15, мы
вернемся к формулам (12.60), (12.61). Последний член в формуле
(12.61) отражает влияние сдвигов на прогибы (см, рис. 12.41).
§ 12.7] ПОПЕРЕЧНЫЙ ИЗГИБ. ОЦЕНКА ТЕХНИЧЕСКОЙ ТЕОРИИ 155
В третьем, четвертом и пятом вариантах закрепления
уравнение изогнутой оси балки соответственно имеет вид
У ι
Ул.
Ρμ/Λ2
24£/
Ρμ/fr
24EL
+
Ркч
χ GEIX
1+|μ) +
, Ρμ№ζ Р№
Ρ/ζ2
2Ε/Χ
Ρζ*
24ΕΙΧ
Ph4
2EL
_ Ρμ№ ■
^1— 24£/κ "+" \2ΕΙ
ι+4 μ +
Ρ/ζ2
2Ε/,
Ρζ3
"6£77
Ρζ*
6ΕΙ*
2.6.3. Поперечное сечение. Проследим за произвольным
первоначально плоским поперечным сечением ζ = ζ* = const; точки этого
сечения в результате деформации оказываются на поверхности
с уравнением
г1 = г* + ау|2=2*. (12.62)
а) Первый вариант закрепления.
В формулу (12.62) подставляем w
согласно (12.57), тогда уравнение
деформированного поперечного
сечения приобретает вид
Ρ Г (, ζ* \ *
ίγ)ζ у-
1 Е1Х
(2 + μ)ί/3
6
[-(
/
+
(1 + μ)Α*0
]. (12.63)
Рис. 12.41. Прогиб вследствие
сдвигов в балке.
Поперечное сечение перестало быть плоским и искривилось по
кубической параболе. Форма искривленного левого торца
описывается уравнением, получаемым из (12.63) при ζ* =0
-£ф£. + 2±Р»-у]. (12.64)
Е1Л
Напомним, что в первом варианте закрепления в точке у ~
= г = 0 элемент dz не поворачивается. Определим угол,
составляемый элементом dy, лежащим в поперечном сечении, с осью у
в результате деформации. Для этого найдем производную от zlt
согласно (12.64), по у
dzi
dy
Ρ(1+μ)/ι2 2(1+μ)ΡΛ212 3Ρ
ί/=0
ΑΕΙ,
~№ 2bhG
Ъ_Р_
2 FG'
Здесь Ζ7—площадь поперечного сечения балки, a G — модуль
упругости при сдвиге. Результат получен ожидаемый (рис. 12.40, а).
Действительно, в балке прямоугольного сечения на уровне
нейтрального слоя касательное напряжение и сдвиг выражаются
формулами
. — А^__ЗР _ τ 3 Ρ
*~ 2T~2F> У~ ~G~ 2 FG'
156
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
б) Второй вариант закрепления. Используем в (12.62) w из
(12.58), тогда уравнение деформированного поперечного сечения
при z = z* имеет вид
При г* = 0, т. е. на левом торце, имеем
Ρ (2 + μ)0»
Zl
ΕΙΛ
Во втором варианте закрепления в точке у = ζ = Ο не
поворачивается элемент dy, элемент же оси dz поворачивается. Определим
указанный поворот. Для этого из (12.61) найдем производную
dz
_ (ΐ+μ)^2 ρ з р
2 = 0 _ 4 ΕΙΧ~ 2 FG'
Картина описанной здесь деформации показана на рис. 12.40, б.
При различных способах закрепления функции ν и w получаются
различными (например (12.56), (12.57), с одной стороны и (12.58),
(12.59) — с другой), форма же тела, испытывающего деформацию,
остается во всех случаях неизменной. Последнее иллюстрируется
на рис. 12.40, в. Переход от картины, соответствующей первому
варианту закрепления, к картине, отвечающей второму варианту,
осуществляется за счет поворота деформированной балки как
з ρ
жесткого целого на угол ττψβ вокруг точки О.
2.6.4. Еще об оси балки. До сих пор отмечалась схематизация
представления нагрузки и внутренних усилий, используемая
в сопротивлении материалов. Здесь обсуждена ситуация, которая
позднее позволит уяснить еще один тип схематизации,
используемый в сопротивлении материалов —схематизацию характера
закрепления тела на опорах. Из бесчисленного количества способов
закрепления балки в левом торцевом сечении рассмотрено два
и каждому из них соответствует своя кривая изогнутой оси
(рис. 12.40, в). Закрепление балки, для исключения ее
перемещения как жесткого целого, было выполнено при минимально
необходимом количестве связей. Этим случаям закрепления
соответствуют определенные трактовки на уровне сопротивления
материалов. На самом же деле может возникнуть потребность решения
более сложной задачи, например, задачи об изгибе консоли,
которая во всех точках торца припаяна к абсолютно жесткой стене.
Такая задача не может быть решена средствами технической
теории сопротивления материалов и является типичной для теории
сред, в частности теории упругости.
Прогиб конца консоли в двух сопоставляемых вариантах
закрепления балки, соответственно первом и втором, выражается
§ 12.7] ПОПЕРЕЧНЫЙ ИЗГИБ. ОЦЕНКА ТЕХНИЧЕСКОЙ ТЕОРИИ 157
формулами
V
V г =
Ιί/=
ΕΙ,
Ρ
ΕΙ>
Р/з
3ΕΙ'
Β
/3 (1+μ)Λ» ,
3£/* + 2 GF'
Во втором варианте закрепления второй член в выражении для
прогиба на конце консоли учитывает влияние сдвигов. В первом
варианте закрепления сдвиги на перемещения оси влияния не
оказывают, но зато влияют на поворот элемента, лежащего в
поперечном сечении заделки.
В последних трех вариантах закрепления балки прогиб конца
консоли выражается соответственно формулами
ν
р/з , Ρ/ΑΜί + μ) _
Ιί/=ο
Р/з
3£V
+
6£Λ
Р/з Pl_
Pi:
Р/з , Ρ//ι2(1+μ)
'ЗБ/,
+
12ΕΛ
3£/
Ρ/» , Ρ/
3£/
2GF'
3. Изгиб балки на двух опорах.
3.1. Исходные данные. Имеем балку в форме
прямоугольной пластины со сторонами / и h (рис. 12.42). Балка по концам
свободно опирается на опоры и загружена равномерно
распределенной нагрузкой интенсивностью q. Более подробно о характере
- о
A
ντϊ It 11 Ιττ ttϊττίι'
I
c 2 τ
A
ζ
■*—>■
■
IHIUI
ν
'4fr
/Ζ
Рис. 12.42. Балка на двух опорах.
распределения реакций по торцам балки и о характере
закрепления балки на опорах будет сказано ниже (их примем такими,
какими они получаются, если исходить из решения аналогичной
задачи в технической теории). Рассматриваемая задача является
плоской однородной (объемные силы полагаются равными нулю).
Используем для анализа напряженно-деформированного
состояния полуобратный метод Сен-Венана.
158
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
3.2, Первый этап решения задачи. Воспользуемся
технической теорией для установления вида компонентов
напряжений
σ.
Мху
*(£--)»
*гу ■
Qys*x
ых
а„
qz
' χ
2 V 4
Ла
-У
Λ
О,
Яг { 4 у2
2 /.*
(12.65)
Здесь имеется в виду (рис. 12.42), что
3.3. Второй этап решения задачи. Проверяем,
удовлетворяют ли функции (12.65) уравнениям однородной плоской
задачи теории упругости: уравнениям равновесия (9.87) и
уравнению совместности деформаций (9.94). При подстановке (12.65)
в (9.87), получаем
(τ-ή_
о,
fr + lr^0· <12·66>
Второе уравнение равновесия удовлетворено, а первое —нет,
выражение, стоящее в левой части (12.66)!, не нуль.
Неудовлетворения первому уравнению равновесия следовало ожидать, так как
принимаемое в технической теории равенство оу = 0 противоречит
хотя бы тому условию, что на верхней грани балки аи = — q\
разумеется, σ^ΦΟ и на площадках, параллельных верхней грани.
Для обращения в нуль выражения, стоящего в левой части
уравнения (12.66)!, производная да^/ду должна иметь следующую
структуру:
д-^ = А1У* + А» (12.67)
а это означает, что само напряжение σ,, должно быть выражено
следующей функцией:
ty =
А&
\-Α& + Α9.
При таком условии, подставляя (12.67) наряду с хгу согласно
(12.65) в (9.87), получим
^+A-l£+2-fi/3
0; Аг — — 27^,
А -^
§ 12.7]
ПОПЕРЕЧНЫЙ ИЗГИБ. ОЦЕНКА ТЕХНИЧЕСКОЙ ТЕОРИИ
159
Итак, после внесения коррективы, получили систему функций,
которые удовлетворяют условиям равновесия
qz /A»
Я (Р
Ыхи "т"8/,» ' '*3' °г~21х\А Z ly>
^гу
2Л
(τ-ή-
(12.68)
Теперь для проверки удовлетворения условию совместности
деформаций подставим (12.68) в (9.94)
2?
— j-y-j-y = 0 или fy = 0.
(12.69)
Выражение, стоящее в левой части (12.69), при у φ О, не
нуль. Следовательно, уравнение совместности деформаций не
удовлетворяется. Для удовлетворения этому условию требуется в (12.68)
внести коррективу, но так, чтобы при этом не нарушалось
равновесие тела. Не будем изменять σ,, и хгу и тем самым сохраним
удовлетворение первому уравнению равновесия. Изменим лишь аг,
однако, чтобы при этом не нарушалось удовлетворение второму
уравнению равновесия. С этой целью в выражение для σζ введем
слагаемые, производная от которых по ζ равна нулю, а вторая
производная по у имеет вид Ллу. Тогда сами эти слагаемые ока-
А и3
зываются такими —Ψ--{■ Аьу-{■ Ав. Итак, полагаем:
°»-Ы^+й;*+л.. «.-&(£-*■)*+¥+*·*+*.
τ*ί/
21 χ
qz /h2
■У
Условие совместности деформаций (9.94), после подстановки в него
последнего варианта формул для σ^, аг и %гуу оказывается таким:
'χ 'χ 'χ
Откорректированные компоненты напряжений
°у = — (П-У3 + $гУ+А3,
8/Л·'
°*=щ[т ~2")У +щУ3+а*у+А«
^zy —
—Ш-*
(12.70)
удовлетворяют условиям и равновесия, и совместности деформаций.
160 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. XII
3.4. Третий этап решения задачи. Выясним, каким
поверхностным нагрузкам соответствуют компоненты напряжений,
полученные в конце второго этапа, и сопоставим их с заданными
на поверхности для того, чтобы удостовериться, являются ли
указанные компоненты решением именно той задачи, которая нас
интересует.
Условия на поверхности имеют вид (9.88). Рассмотрим нижнюю
кромку y = h/2, где
m=lf Λ = 0. (12.71)
Учитывая (12.70) и (12.71), получим (9.88) в следующем виде:
q h? ,qh2 h , * π
ρ™—~ ш~х "β" + βτ; "5"+Лз' Ρνζ ~ υ*
Из условия обращения в нуль pvy, имея в виду, что на нижней
кромке нет никакой нагрузки, найдем
д _ £_№_ _ q№ _ qh3 q_
3~"6IX 8 16/* ~ 24/х ~ 2 *
После удовлетворения граничным условиям на нижней кромке
получаем
ау=-£;У3+1гхУ-т>
а*=£х{т-г2)у+£хУ3+А*У+л*> \ <12·72)
τ*υ 2/χ \ 4 У
Рассмотрим верхнюю кромку у — — h/2, где
т = —1, л = 0. (12.73)
Учитывая (12.72) и (12.73), получим (9.88) в следующем виде:
q 12/i3 , qh42 h , q _ „ _π
Pvy~ "6"/ι3 8 + 8/гз 2 "+" 2 — *' Pvz ~υ*
Перейдем к торцам ζ = ± 1/2, на которых
т = 0, п=±1. (12.74)
Учитывая (12.72) и (12.74), получим (9.88) в следующем виде:
Pv. = 4=^r(f-#2). Р^«±(з7^8 + 40 + Л.). (12.75)
§ 12.7]
ПОПЕРЕЧНЫЙ ИЗГИБ. ОЦЕНКА ТЕХНИЧЕСКОЙ ТЕОРИИ
161
Проинтегрируем pvy и ρνζ в пределах всей площади торца (тол
щину пластины полагаем равной единице)
+ А/2 +Л/2
J Pvy
— ft/2
+ Л/2 _ ql
ί///ι2ί/ qly*
•ft/2
Ι6Λ
12/,
•ft/2
+ Α72
+ ft/2
S PwL=±//2^=± S (щУ3 + Аьу + ЛвУу = ±А6Н.
-ft/2 -ft/2
(12.76)
(12.77)
Интеграл (12.76) определяет собой поперечную силу, а (12.77) —
продольную силу на торцах. Найдем величину моментов, которые
может создать на торцах поверхностная нагрузка pvz (12.75)
+ А/2 +ft/2
J Pvz
-ftZ2
-J/2
ydy = ±: J (^tf + A^ + Aoyjdy-
— h/2
— 3/* 5 16— Пъ 3 4 '
(12.78)
В решаемом примере ни продольной силы, ни изгибающего момента
на торцах нет. Распоряжаясь постоянными Аь и Лв, обеспечим
равенство нулю этих величин. Для равенства нулю продольной,
силы на торцах, согласно (12.77), необходимо, чтобы Ав = 0. Для
равенства нулю изгибающего момента на торцах, согласно (12.78),
ffi
qh?
требуется, чтобы ±gi-^-±: Л6-^ = 0, Аъ= — щ-. Окончательно
формулы для компонентов напряжений приобретают вид
а - q ,J3-Uqh2 11-3-
я /ι*
^у+±у3- —
20/ХУ* Т*У— 2/,\4 У
(12.72')
Таким образом, откорректированное решение технической теории
соответствует поставленной задаче, если распределение реактивных
сил на торцах подчинено закону (12.75), который с учетом
полученных значений для Аь и А6 приобретает вид
ql /h* ,
р-у=+Ш1-у
Pv,=±u-y>-m.
·χ\ι ι \"χ- so/,;·
При других законах и сохранении величины интеграла (12.76),
а также равенстве нулю продольной силы и изгибающего момента
на торцах компоненты напряжений будут иными, чем даваемые
формулами (12.72), однако, согласно принципу Сен-Венана, уже
в небольшом удалении от торцов численно напряжения будут
мало от них отличаться.
162
ПЛОСКИЙ ИЗГЙб СТЕРЖНЕЙ
[ГЛ. Xlt
3.5.· Четвертый этап решения задачи. Найдем все
остальные функции.
Из уравнений закона Гука
' = ^Κ-μσ*] = 2ΐ77{-(1+2μ)ΊΓ +
2Е1Х
р2
+
[4
О + т^-Кт-^-й}-
■ -j[oe - μσ^ - 2Ш7 \ 3 +
Угу'-
2(1+μ)
"tzy
+[(ί-*Κ(ί+")]'+>4}·
(τ-ή
ΕΙ χ
(12.79)
получаем компоненты деформаций, имея которые путем
интегрирования уравнений Коши (9.89) найдем составляющие
перемещения и и υ. Приведем результаты интегрирования этих уравнений,
выполняемого совершенно аналогично тому, как это было
показано в § 9.6. Для исключения из υ и w перемещений как
жесткого целого закрепим балку, предотвратив перемещение центра
среднего сечения и поворот элемента dz при у = г — 0
'dv\
У-г-0
U)o
о,
υ
£_/-
ΕΙ A
W
(l + M)/t»zy , 1 + μ ο
4 ]г~Т~гУ "
цгуа
+
1+μ
Wzy + Щ.
3.6. Анализ картины деформации балки.
3.6.1. Координаты произвольной точки балки. Любая точка
балки (у, ζ) в результате деформации занимает новое положение,
определяемое координатами уг = у-\-и, zx = z-\-w.
3.6.2. Ось балки. Рассмотрим ось балки, точки которой (г/ = 0)
в результате деформации занимают новое положение
*-<)~--ώ:{-[(τ-*)-τ{τ-ήν-Ψ»ή'
■ £ ~j— о г? ^*
4Е1Х
Последний член в формуле для гг очень мал, так как мал
порядок отношения q/E, и им можно пренебречь. Происхождение
этого члена таково, что вследствие наличия ау и поперечного
сжатия балки под влиянием этого напряжения происходит удлинение
осевого волокна балки. Аналогично происхождение последнего
члена в формуле для ε, (12.79).
§ 12.7] ПОПЕРЕЧНЫЙ ИЗГИБ. ОЦЕНКА ТЕХНИЧЕСКОЙ ТЕОРИИ "^ 163
3.6.3. Поперечное сечение. Рассмотрим произвольное
первоначально плоское поперечное сечение балки г = г* = const;
множество точек этого сечения в результате деформации представляет
собой поверхность с уравнением
Ζχ = Ζ* + W \z-z* =
B^+A{-(1+1Wy+24b'W^^+iia4(12'80)
В формуле (12.80) подчеркнут член, связанный с искривлением
поперечного сечения.
4. Анализ допущений, принятых в технической теории изгиба
балки.
4.1. О зависимости 8г = ег(г/). Как уже указывалось, при
выводе формулы (12.10) существенным было не сохранение
плоской формы сечений, а линейность зависимости ег = ег(г/).
Примеры, приведенные в настоящем параграфе, показывают, что и
в случае искривления сечений, но сохранения неизменной
величины поперечной силы (изгиб консоли силой), гг остается
линейной функцией как и при чистом изгибе (см. (12.55)).
При искривлении сечений в условиях переменной вдоль оси ζ
поперечной силы (изгиб балки на двух опорах равномерно
распределенной нагрузкой) гг оказывается нелинейной функцией
(формула (12.79)), однако отклонение ее от линейной
незначительно. Чтобы доказать это утверждение, оценим удельный вес
подчеркнутого нелинейного относительно у члена в общей
величине выражения в фигурных скобках в формуле для гг (12.79).
В табл. 12.1 приведен процент, составляемый нелинейным членом,
а также последним членом от всего значения выражения,
стоящего в фигурных скобках в формуле для гг (12.79). С целью
перехода к безразмерным величинам все члены в скобках
разделены на /3. Из таблицы становится очевидной возможность
использования формулы (12.10) для σ и при искривлении поперечных
сечений вследствие неравномерности сдвига по высоте балки.
Только вблизи торцов влияние нелинейного члена становится
большим. Сказанным подтверждается утверждение, сделанное в
разделе 8 § 12.6 о целесообразности отказа от гипотезы плоских сечений
в пользу гипотезы о постоянстве вдоль оси балки депланации
сечений.
4.2. Сопоставление величин аутах и σζ max. Имея
функцию a,j, легко построить эпюру (рис. 12.43) распределения этого
компонента напряжения по высоте балки. Из этой эпюры видно,
что максимальное значение ау равно интенсивности внешней
нагрузки q
_ q 12 № qh* 12 q
Gv „= * - 6" h* ' Τ ~~ 16 ' λ*' 2 ~ q'
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
см
W
Я
К
Ч
\о
се
Η
Ϊ?
S
**"
SIS
^
о
о
л)л
ТЕ, S2·
w w
+ β
^•■s
е +
+ S
£ +
II *|3
blss «Я
!·> ""1·^
""|к· II
χ Χ |
- Ι* (Ν к Г*
1 V 1
а>
S* Ч.
N
1
uh
-^J_l_^
-la
" -
а, £
ΙΑ
+
<Ν
О
ι
со — 5,
1
II
-I*
a>
N
-Й
о
<л
CO
г^
(О
m
■*
СО
<м
-
Tf СО 00 О СЛ 00
со со ·"* Is- ι~- оо
·. л -. ·* ·. »·
— о «—· О —< О
(О t~ О (О -ι чС
t> О) 00^ ^ О О)
©" <n" о" со" -J оо"
CN Is- Is- Is- CN Is-
Tt· со —■ —■ ■* со
iO <D ^ ■* О (О
со со ю о — —
rj< CN СО Is- СО О
N Ю « И С» О!
— CN — СМ О —
о, о„ о_ о^ о_ о^
о" о* о" о" сГ о"
t^- г^— г^— г^— г^— г^—
со со со со со со
со со со со со со
со со со со со со
1—1 ι—Ι 1—1 1—1 ι 1 1—1
о о о о о о
о о о о о о
о о о о о о
о о о о о о
Ю О IQ О iO О
N Ю N Ю N Ю
оо со оо со оо со
о о о о о о
о о о о о о
о, о^ о_ о_ о_ ол
о" ρ о* о" о" о"
ι Τ ι ι ι ι
О О iO О О О
О О Is- ιΟ О О
О О 00 Is- ιΟ О
О О — 00 Is- ιΟ
iO Q Is- ■* 00 Is-
СМ Ю —' 00 OS 00
-Ν -UN О -
о о о о о о
о о о о о о
ιΟ Ο Ό Ο Ό О
Is- О Is- О Is- О
оо о оо о оо о
σι ю oj ю οι ю
О Is- О Is- О Is-
о о о о о о
о о о о о о
о о о о о о
о о о о о о
о о о о о о
СМ — СМ —ι СМ —ι
— |оо — Is*
о '
+1 +1
со σι со о
О ■* О ιΟ
оо" ~ ее см"
ιΟ СО
СЧ
1
00 OS Is- Ю
г-^ со^ —^ см
•—Г СО" ιθ" —Г
■* оо
— см
|
Is- Is- 00 Is-
— — Ю СО
Tf Tf Tf CO
о о со со
■* Ν Ο Ν
ю — о о
о — о о
о_ о, о„ о„
о о о о
1
Is- Is- Is- Is-
СО СО СО СО
со со со со
со со со со
ι—· 1—1 ι—· г—4
о о о о
о о о о
О, О^ 0„ О^
со" со" о со"
Ю OIQ О
см ю см ю
оо со оо со
о о о о
о о о о
о о о о
о о о о
I I I 1
ю о
Is- Ю
00 Is-
со оо
■* σ>
ю о
о —
°- °„
со" о" о о
ю о ю о
Is- О Is- О
оо о оо о
со ю σι ю
О Is- О Is-
о о о о
о о о о
о о о о
о о о о
о о о о
см — см —
*■»*
со loo ~ |см
1 1
+1 +1
— |ιΟ
COt^COOOiOCMCOOOCMO
00^ —^ 00^ —_ Tf CM t-^ 00^ — ιΟ
d d о" о о" о о* о" со м"
ю со
ч
1
СО
союооюоиомм
— h-CNOOCMCfiTft^cMCN
■» _ ^ лл»ч»ч»ч_»ч_
ООООООО —ι Ю -1
Tf 00
— см
1
oooooooooooooot'-oo
osoooooTfoooooooo
— со — смслоососмоосо
TfCOiOiOt'-OCMQOCO
МШМГ«(0*Г>1000
(ΟΝιΟ-^ΟΙΝιηΟΟ
о — о — о о о о о о
оооооооооо
^^«ч^^*1«ч«ч«ч*ч
оооооооооо
1
оооооооооооо'оооооооо
00000000000000000000
оооооооооо
CN(N(N(N(NCNfNCN(N(N
оооооооооо
оооооооооо
оооооооооо
о о о„ о о. ооооо
«к «Ч ·. «ч ·. «t ~фь «Ч «Ч ^
оооооооооо
CMlOCMiOCMlOCMIOCMlO
СОСМСОСМСОСМСОСМСОСМ
о — о— о — о — о —
TfCO'ifOOTfCO'iCO'tCO
оооооооооо
оооооооооо
оооооооооо
оооооооооо
ОООООООООО
I I I I I I I I I 1
ООГ~-ЮООГ~-10
ΟΟΟΟΓ~-ιΟΟΟΟΓ~-
оосйсо^ю^со
ю о ю — оо Is- со со
CMLOoots-cocots--'*
со см ю — ■* ел см ю
о — о — оооо
оооооооо
оооооооооо
СМЮСМЮСМЮСМЮСМЮ
Г"-Г"-Г"-Г"-Г"-Г"-Г"-Г"-Г"-Г"-
— 00 — 00 — 00 — 00 — 00
— OJ—ι СЯ « G >-1 О) -4 Си
оооооооооо
оооооооооо
оооооооооо
оооооооооо
оооооооооо
оооооооооо
^CN'*(N'*CN'*fS'*CN
>*ч!
"- |оо —* |-ч*< со loo >-·» |см
о ' ι" ι ι
+1 +1 +1 +1
~^ IO
^1—
§ 12.7] ПОПЕРЕЧНЫЙ ИЗГИБ. ОЦЕНКА ТЕХНИЧЕСКОЙ ТЕОРИИ 165
Оценим порядок величины отношения агтах/\ау\тах = о2тах/д,
'г max
'г |z = 0, y=h/2
1 /qPhl2
q\2h* qh42h\ 3 /2 1
"г ам« ocihso I = Τ Τλ'ΤΎ'·
Рис. 12.43. Эпюра
распределения σ по
высоте балкн.
q q q \ lbft» ' ШЩ 20h^2 J 4 /ι2 ' 5
Учитывая, что ЦК >· 5, легко понять пренебрежимую малость
I ву |тах по сравнению с σζ max. Этим оправдывается пренебрежение
напряжением ау по сравнению с σζ в технической теории балок.
5. Еще о гипотезах элементарной теории балок. Анализ чистого
изгиба балки, выполненный в § 12.5 при помощи аппарата теории
упругости, полностью подтвердил правомочность гипотез,
принятых в § 12.3, на основе которых была построена элементарная
теория чистого изгиба балки. На самом деле
то, что постулировались этими гипотезами в
случае чистого изгиба представляет собой
закон.
При рассмотрении же поперечного изгиба
было обнаружено, что, во-первых, поперечные
сечения вследствие неравномерности сдвигов по
высоте балки искривляются, а на площадках,
параллельных оси г, вообще говоря, возникают
нормальные напряжения. Эти факторы при
формальном подходе к вопросу противоречат
содержанию гипотез, принятых в § 12.3 для чистого
изгиба и далее распространенных на случай поперечного изгиба.
Однако на самом деле результаты, полученные в § 12.4 и § 12.6,
вполне приемлемы применительно к поперечному изгибу. В
сказанном утверждают и оба примера, рассмотренных в настоящем
параграфе.
Коснемся первой гипотезы. В разделе 8 § 12.6 уже
говорилось, что существенным является не сам факт сохранения плоской
формы сечения, а вытекающая из него линейность относительно у
функции ег, и что эта линейность может иметь место и при
искривлении сечений.
Решение задачи об изгибе консоли (раздел 2 настоящего
параграфа) показало, что, если поперечная сила во всех
поперечных сечениях одинакова (Qy = const), то одинаковыми оказываются
и возникающие в результате деформации искривления (деплана-
цпи) всех поперечных сечений. При этом функция гг оказывается
линейной и точно такою же как и в условиях применения
гипотезы плоских сечений. Если же Qy φ const, то, как показало
решение задачи об изгибе балки на двух опорах равномерно
распределенной нагрузкой (раздел 3 настоящего параграфа),
искривления (депланация) поперечных сечений не одинакова по длине
f>;uiiui, но мало изменяется при переходе от одного сечения к
другому и функция ег вследствие этого отличается от линейной
несущественно.
166
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Решение последней из двух упомянутых задач настоящего
параграфа показало и малость отношения нормальных
напряжений ау/аг.
Вследствие сказанного выше для того, чтобы гипотезы были
одинаково приемлемы не только по существу, но и формально и
для чистого и для поперечного изгиба их следует, оставляя
сущность вопроса неизменной, сформулировать несколько иначе,
а именно:
а) депланация одинакова во всех поперечных
сечен и я х;
б) нормальные напряжения на площадках,
параллельных оси балки, пренебрежимо малы по
сравнению с нормальными напряжениями в
поперечных сечениях.
Заметим, что кроме двух упомянутых гипотез в элементарной
теории изгиба стержня, излагаемой в § 12.4 и § 12.6, фактически
используется еще одна гипотеза, которую сформулируем так:
в) поперечные сечения не испытывают
деформации в своей плоскости.
В такой формулировке гипотезы а), б) и в), а следовательно,
и все результаты настоящей главы справедливы не только для
массивных, но и для тонкостенных стержней; однако
применительно к одной из ситуаций работы последних (стеснение депла-
нации) требуется введение и других гипотез 1).
В случае чистого изгиба гипотеза а) переходит в гипотезу
плоских сечений — все сечения имеют одинаковую нулевую депла-
нацию (отсутствие депланации), гипотеза же б) заменяется более
сильной —отношение ау/аг не мало, а просто равно нулю.
Фактически в совокупности все три гипотезы предусматривают
обращение в нуль деформаций е*, гу и уху.
§ 12.8. Центр изгиба
1. Определение. Пусть имеется поле касательных напряжений
в поперечном сечении балки, вызванных поперечным изгибом.
Приняв в качестве точки приведения касательных сил,
распределенных в поперечном сечении, произвольную точку, лежащую
в нем, мы можем ввести статический эквивалент указанных
распределенных сил в виде равнодействующих силы и момента.
Существует одна такая точка*в поперечном сечении, которая
обладает тем свойством, что момент касательных сил, действующих
в поперечном сечении, относительно этой точки равен нулю. Такая
точка называется центром изгиба. Очевидно, что если в качестве
11 Рассмотрению этой особой ситуации в работе тонкостенного стержня
посвящена глава XIV.
§ 12.81
tlEHTP ИЗГИБА
№
точки приведения внутренних касательных сил, действующих
в поперечном сечении, принять центр изгиба, то статическим
эквивалентом этих сил будет только равнодействующая сила, а
равнодействующий момент окажется равным нулю.
Практический интерес центр изгиба представляет лишь для
тонкостенных открытых профилей, по причине, которая будет
пояснена ниже.
2. Отыскание положения центра изгиба в простейших случаях.
В общем случае для отыскания координат центра изгиба
необходим специальный расчет. Однако для некоторых тонкостенных
открытых профилей положение центра изгиба является очевидным
(рис. 12.44), поскольку очевидно положение точки, относительно
которой момент всех касательных сил, распределенных по
поперечному сечению, равен нулю.
ШЩЩШ ШШ
И
Η
и
w
It
н
Η
■С
[Ц
w
*♦
Η
It
w
mi
δ)
6)
Рис. 12.44. Примеры очевидного расположения центра изгиба в поперечных сечениях:
а) двутавровом; б) зетовом; в) уголковом и тавровом.
В случае поперечного сечения балки в виде швеллера
(рис. 12.45, а) положение центра изгиба находится путем
несложного расчета. Равнодействующая касательных сил в каждой из
полок равна 7\, а в стенке — Т2 (рис. 12.45,6). Точка С должна
быть расположена так, чтобы момент, создаваемый силами Tlt
имел знак, противоположный моменту, создаваемому силой Т2, и
уравновешивал его. Ясно, что точка С должна лежать не внутри
порыта, а вне него. Вместе с тем при наличии оси симметрии
у сечения центр изгиба располагается на ней. Таким образом,
точка С лежит на горизонтальной оси симметрии, где-то левее
стенки — на расстоянии е от ее оси. Для определения величины е
достаточно учесть, что относительно точки С момент обеих сил 7\
и Т2 должен быть равен нулю,
Опла Т2 равна поперечной силе Qy, так как она создается именно
ι пи [ряжениями в стенке (доля, создаваемая вертикальными
166
Плоский изгйв Стержней
[ГЛ. XI}
касательными напряжениями в полке ничтожна и ею
пренебрегаем). Силу 7\ находим, исходя из формулы (12.47), выведенной
для касательных напряжений в половине полки двутавра, ничем
. и
' II
N
i
«si
.
,
яр=е-с|
it
1
ι
- С
ι
'
а- '
« Ι
:-5
•^ ■
. *4
>— -
δ1
■«-3 >
f '
Ι
α)
ΰ)
6)
8)
Рис 12.45. К определению координаты центра изгиба в швеллерном профиле балки:
а) распределение касательных напряжений по поперечному сечению; б)
равнодействующие касательные силы в отдельных элементах профиля; в) эпюра касательных
напряжений в полке; г) статический эквивалент распределенных по поперечному сечению
касательных сил в случае совмещения точки приведения сил с центром изгиба.
не отличающийся от формулы для такого напряжения в полке
швеллера1) (рис. 12.45, в)
Т-гх — '
21* '
Таким образом,
*zx max
е =
Qybh
"277
1 Qyb*ht
Τ 2ΙΧ
7Ί =-5-τ
ζχ max
Ы = -г
1 QybVit
4 2/Λ
Q
у
1 №КЧ
8 /*
Итак, статический эквивалент двух сил Тх и силы Т2
представляется в виде силы, равной T2 = Qy и приложенной в точке С
(рис. 12.45,г).
3. Практическое значение понятия центра изгиба. В балках
открытого тонкостенного профиля наблюдается некоторое
явление, сущность которого объясняется ниже. Как будет показано,
с этим явлением связано понятие центра изгиба.
Представим себе консольную балку швеллерного сечения,
нагруженную на свободном конце силой Р, приложенной в центре
тяжести сечения, и расположенную параллельно стенке, т. е. линия
действия силы Ρ совпадает с одной из главных осей инерции
(рис. 12.46, а). Отсечем от консоли некоторую часть произвольным
!) В обсуждаемом здесь случае символом h обозначена не полная высота
профиля, а расстояние между серединами толщин его полок,
§ 12.8]
ЦЕНТР ИЗГИБА
169
поперечным сечением (рис. 12.46, б). Статическим эквивалентом
внутренних касательных сил, распределенных по сечению, если
за точку приведения принять центр изгиба, явится одна сила
Qy = P (рис. 12.46,6). Внешняя сила Ρ и внутренняя Qy не
находятся в равновесии — не выполняется равенство нулю момента
этих сил относительно любой оси, параллельной оси стержня.
Вследствие этого, кроме изгиба, неизбежно возникает кручение,
создающее в поперечном сечении балки дополнительное поле
касательных напряжений, которое совместно с полем изгибных
касательных напряжений уравновешивает силу Р. Явление
закручивания стержня при тех условиях, которые описаны выше,
Рис. 12.46. К пояснению причины возникновения кручення при поперечном изгибе,
вызванном силами, приложенными не в центре изгиба: а) консольная балка, изгибаемая
силой Р, приложенной в центре тяжести торца; б) часть упомянутой выше консоли
(внутренние касательные силы в поперечном сечении приведены к центру изгиба); в) кручение,
сопутствующее поперечному изгибу и возникающее вследствие неуравновешенности
внешней силы полем касательных напряжений, соответствующих лишь поперечному изгибу;
г) способ приложения внешней силы, при котором поперечный изгиб не сопровождается
кручением.
обнаруживается и в опыте, и балка испытывает деформацию,
изображенную на рис. 12.46, в. Для предотвращения этого кручения
внешнюю силу Ρ надо приложить так, чтобы статический
эквивалент внутренних сил, распределенных по поперечному сечению,
мог уравновесить ее без возникновения поля касательных
напряжений, связанных с кручением. С этой целью внешнюю силу Ρ
необходимо прикладывать в центре изгиба (рис. 12.46, г). При
этом будет происходить только изгиб, не сопровождаемый
кручением. В принципе подобное явление имеет шесто и в случае
массивного сечения, однако в этих сечениях, даже если они
произвольного вида и не имеют осей симметрии, центр изгиба и центр
тяжести отстоят один от другого на величину малую по
сравнению с габаритными размерами сечения, вследствие чего крутящий
момент, возникающий от силы Ρ и найденный относительно центра
тяжести поперечного сечения, мало отличается от момента той же
силы относительно центра изгиба поперечного сечения. Вместе
г тем крутильная жесткость стержней массивного сечения или
тонкостенного замкнутого профиля велика, тогда как у тонко-
170
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
стенных открытого профиля —мала (см. пример 11.10). Этим и
объясняется тот факт, что возникновения кручения при изгибе
массйвно"гб_'стержня" сйламйГ¥ё" проходящими
практически"почти не' обнаруживается'; В тонкостенных жёстерж-"
нях открытого профиля "вся картина явления гораздо более
выпукла. Задача определения координат центра изгиба в случае
массивных поперечных сечений не является элементарной и здесь
не рассматривается. Этому вопросу посвящен § 13.8.
Теперь становится понятно, почему, говоря о поперечном изгибе,
мы ограничивали форму поперечного сечения, считая ее
симметричной, и при этом имели в виду, что плоскость действия
внешних сил проходит через оси симметрии поперечных сечений. Это
ограничение делалось с целью еще до введения понятия центра
изгиба исключить случаи возникновения кручения при изгибе,
так как центр изгиба лежит на оси симметрии поперечного
сечения и, требуя расположения внешней силы в оси симметрии
поперечного сечения, мы тем самым гарантировали прохождение
линии действия силы через центр изгиба.
Сейчас стало ясно, что нужно делать для создания лишь
поперечного изгиба без возникновения кручения. Однако вследствие
отмеченной выше незначительности удельного веса этого явления
в случае стержня массивного поперечного сечения мы не будем
его учитывать, т. е. мы будем использовать_построенную_выше
теорию поперечного тшба'бёзП^Ш^либо поправок на
возникающее кручение' й в" том случае, когда при наличии массивного
сечения, внешняя сила не проходит" через центр изгиба.
"Применительно же "к стержням открытого тонкостенного
профиля обсужденное выше явление необходимо учитывать — либо
располагать внешние силы так, чтобы не возникало кручения,
либо, если это невозможно по конструктивным и
эксплуатационным соображениям, и кручение возникает, то отражать его в
расчете.
4. Определение координат центра изгиба в случае
тонкостенного открытого профиля произвольного вида.
4.1. Секторная площадь. Для дальнейшего изложения
вопроса об определении координат центра изгиба поперечного
сечения тонкостенного стержня нам понадобится ввести в
рассмотрение новые понятия — геометрические характеристики поперечных
сечений тонкостенных стержней, называемые секторными,
аналогичные уже использовавшимся характеристикам.
Пусть имеем некоторый открытый профиль тонкостенного
стержня; изобразим контур —среднюю линию его поперечного
сечения (рис. 12.47, а), на котором отметим некоторую
произвольную точку Ov—начало отсчета дуги s контура, определяющей
на нем положение точки К. Из некоторой произвольной точки Р,
называемой полюсом, проведем -радиусы к концам элементарной
§ 12.8] ЦЕНТР ИЗГИБА 171
дуги ds, заключенной между точками К и К'. Удвоенную
площадь треугольника К.РК' будем рассматривать как
дифференциал секторной площади ω.
d(u = h ds,
где h — высота треугольника КРК', a ds —его основание.
Величину h можно рассматривать как расстояние от Ρ до прямой,
содержащей в себе ds. Имея выражение для da>, найдем ω
S
ω = ^ h ds.
о
Интегрирование ведется от точки Ог — начала отсчета дуги s до
текущего значения s. Величина со представляет собой функцию
о) . 5) б)
Рис. 12.47. К определению момента касательных сил в поперечном сеченнн тонкостенной
балкн открытого профиля относительно полюса Р: а) произвольный открытый профиль
тонкостенного стержня; б) варианты эпюры ω, соответствующие различным комбинациям
выбора положения точек Ρ и Οΰ в) к обоснованию формулы (12.81).
от s, зависящую от положения полюса Ρ и начала отсчета Ог
как от параметров. При перемещении текущей точки К по контуру
радиус РК поворачивается вокруг точки Р. Если этот поворот
происходит против часовой стрелки, то с?со;>0, если по часовой
стрелке, то с?со<;0.
Из рис. 12.47,6 вытекает формула для элементарного момента,
создаваемого касательными напряжениями относительно точки D
dM=hxbds. (12.81)
На рис. 12.47, б показан пример построения эпюры ω для
одного контура, но при разных положениях точек Ρ и Ог.
Нам понадобится связь между секторными площадями ω и ω'
относительно двух полюсов А и В (рис. 12.48). С этой целью
покажем сначала чему равняется дифференциал секторной
№ ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. Xlt
площади, если полюс располагается в начале координат некоторой
системы осей ху (рис. 12.48, а).
Плечо h выражается через координаты точки К на контуре
следующей формулой: h = χ sin α -~y cos α. Тогда
d(u = hds — χ sin ads — у cos <xds = — χ dy -\- у dx\
здесь учтено, что sinac?s = — dy, cos a ds = —dx.
Если полюс секторной площади находится не в начале
координат, а в точке Л или в точке В (рис. 12.48, б), то
άωΑ = — (χ — ах) dy-\-(y — ay) dx, άωβ = — (χ — bx) dy-\-(y — by) dx.
Вычитая άωΒ из άωΑ, получим
d (ωΑ — ωв) = — (ау — by) dx -\- (ах — bx) dy = ах dy — ау dx,
τββ ax — bx = ax, ay — by — ay. После интегрирования сол — ωβ =
= ах (у - у0) -ау(х- л:0) + β. Отсюда
о)д = ωβ + ах (у - у0) - ау (х - х0) + β.
Здесь β — постоянная интегрирования, х0 и у0 — координаты начала
в эпюре секторных площадей (рис. 12.48, в).
ю б) 5)
Рис. 12.48. К определению центра нзгнба произвольного тонкостенного открытого
профиля: а) полюс совмещен с началом координат; б) дифференциалы секторных площадей,
соответствующие полюсам А и В; в) секторные площади, соответствующие полюсам А и В,
4.2. Механическое условие, определяющее
положение центра изгиба. Рассмотрим произвольный
тонкостенный открытый профиль (рис. 12.48). Условием для отыскания
координат центра изгиба С является равенство нулю относительно
этого центра момента (формула (12.81)), создаваемого
касательными силами в поперечном сечении,
\bxhds = Q. (12.82)
F
Имеется в виду, что центр изгиба С, относительно которого
выполняется условие (12.82), нам пока не известен. Подставим
в (12.82) вместо τ его выражение согласно формуле (12.49); кроме
§ 12.81 ЦЕНТР ИЗГИБА 173
того, учтем, что hds представляет собой дифференциал секторной
площади (άω), если точку С считать в качестве полюса. Наконец
умножим и числитель и знаменатель на dF — дифференциал
площади поперечного сечения, в пределах которого производится
интегрирование- Итак, после выполнения отмеченного и
сокращения подынтегрального выражения на δ (12.82) приобретает вид:
Qu с Л day Qx с d(u
F F
Возьмем каждый из интегралов по частям
Qu
Ιχ s, Ιχ J dF ' [y у Sl /J df '
(12.83)
si и s2 — координаты точек 1 и 2 контура, являющихся
граничными для него. Статические моменты 5* и SJ, соответствующие
этим точкам, равны нулю, так как отсеченная от поперечного
сечения площадь для одной из этих точек равна нулю, а для
другой равна всей площади поперечного сечения.
Итак, (12.83) приобретает вид
Qu с dS* Qx с dS*
-77Ьж^+Т7Ь^=0· <12·84>
F F
Учтем, что
г· г* dS* dS*
St=\ydF, SU=\xdF,4± = y, -^- = x. (12.85)
Ft F1
Учитывая (12.85)3(4, представим (12.84) в следующем виде:
^- f ya>dF + ^ f x(udF = 0. (12.86)
F У F
Равенство (12.86) при произвольных Qx и Qy мыслимо лишь
в случае, если
ly(odF = 0, lx(udF = Q. (12.87)
F F
Итак, получили условия (12.87), которым должен удовлетворять
центр изгиба.
Практически отыскание центра изгиба путем использования
условий (12.87) осуществляется следующим образом:
а) находим центр тяжести площади поперечного сечения балки;
б) находим главные оси инерции площади поперечного
сечения балки;
174 плоский изгиб стержней [гл. хи
в) при произвольно выбранном полюсе Р' (рис. 12.48)
вычисляем интегралы
Sxa/dF, \yu>'dF; (12.88)
F F
г) имея в виду, что относительно центра изгиба как полюса Ρ
секторная площадь есть ω, и учитывая связь между секторными
площадями для двух полюсов Ρ и Р'
ω = 0)4-0* (у-у0) -ау (х-х0) + β
(хо> Уо"~ координаты начала в эпюре секторных площадей),
составляем условия (12.87)
J уса dF — \ ί/ω' dF + о* \ уг dF — аху0 $ у dF —
F F F F
-ay[xydF-\-ayx0\ydF + ^ydF = Ot (12.89)
F F F
J χω dF — 5 χω' dF-\-ax^xy dF — axyQ J χ dF —
F F F F
— <xy ^x2 dF -f- aux0 J χ dF + β J л; c?F = 0.
Если оси х и у являются центральными, имеем
\xdF = 0, \ydF = Q\ (12.90)
F F
если, кроме того, эти оси являются главными осями инерции,
получаем еще одно равенство
\xydF = 0. (12.91)
F
Имея в гвиду (12.90) и (12.91), уравнения (12.89) записываем
в виде
\уы' dF + ax\y*dF = Q>, \x<u'dF-ay$*2dF = 0,
F F F
откуда
ϊ ί/ω' dF [X(u'dP
CCX = — j , <Xy = j .
'x ' у
Получены окончательно формулы для координат центра изгиба,
отсчитываемых от того произвольного полюса, относительно
которого построена первоначальная эпюра секторных площадей ω' и
вычислены интегралы (12.88).
§ 12.8]
ЦЕНТР ИЗГИБА
175
5. Примеры.
Пример 12.9. Найти координаты центра изгиба для профиля,
изображенного на рис. 12.49.
Решение. Центр тяжести площади поперечного сечения совпадает с О —
геометрическим центром кольца. Одна из
главных центральных осей инерции—ось
χ—совпадает с осью симметрии профиля, т. е.
проходит через линию разреза кольца;
вторая главная ось инерции—ось у
—перпендикулярна оси х.
Совместим полюс Р' с центром тяжести
(или иначе с О), тогда секторная площадь ω,
соответствующая точке В контура, если
начало отсчета ее расположить в точке А,
изобразится формулой
? 1
ω'(φ) = 2 Ι -^rd(fr=r2(f.
о
Координаты точки В суть: *(<p) = rcos<p,
у (φ) = — г sin φ. Тогда интегралы f χω' dF,
Рис. 12.49. К примеру 12.9.
1
yus'dF находим по следующим формулам (учитывая при этом, что dF ■■
·■ г c/φδ):
2π
2π=0.
ϊ χω' dF= \ r cos срг2фгб ίίφ = г*б (cos φ-f·φ sin φ) 1^
2π
у ω' dF =— ϊ r sin <рг2(ргб с?ф=»— г*д (sin φ — φ cos φ) Цп— 2пг*6.
ι
Моменты инерции площади поперечного сечения находятся по формулам
2π
1Х}= \ y*dF = f ή sin2 φδ/- dq> = r4 I — -^ sin 2<p -f -i-cpj |2π=π/-»δ,
С „ 2"
/ = \ x2dF= С /1
y J V ή cos2 φδΓ d® = r36 (-^ sin 2φ
= /*δ (-J- sin 2φ -f i- φ\ f" = π^δ,
Находим координаты центра изгиба
^ у<а' dF
ах=-
— 2πΓ*δ
/.,
ηήδ
= —2r, ay--
[т' dF
Jp
T7~
= 0.
Пример 12.10. Найти координаты центра изгиба для профиля,
изображенного на рис. 12.50, а.
Решение. 1. Координаты центра тяжести площади
поперечного сечения. Ох0у0^произвольная система осей (рис. 12.50*6).
Находим статические моменты площади поперечного сечения относительно'
Рис. 12.50. К примеру 12,10: а) поперечное сеченне тонкостенного стержня; б) оси х0,
Уа'.ь) координаты центра тяжести (в см); г) главные оси инерции; д) эпюра <а'(полюс в центре
тяжести) (линейные размеры в см, ординаты эпюры ω' в смг); е) к определению длины
отрезка /; ок) эпюра уг (ординаты в см); з) эпюра дс, (ординаты в ли); и) длины отрезков;
к) координаты центра изгиба (в еж).
§ I2.S]
ЦЕНТР ИЗГИБА
177
этих осей
S = 2 ft-;t0/ = 10- 1.45+15.· 1-37,5 + 50. Ь 15 + 20· 1-0 +
ί=ι
5
+ 35-2- 17,5 = 2987,5 слА,
8χ0=Σ ^«= 1°· 1-5+15- 1-0 + 50- 1 -20 + 20- 1-50 +
i = \
+ 35-2· 60 = 6250сл».
Площадь поперечного сечения стержня Ρ = Σ ^i=10· 1 + 15- 1 + 50- 1+20 χ
i
Χ 1+35 · 2= 165 см2. Координаты центра тяжести площади поперечного сечения
находим по формулам (см. рис. 12.50, в)
V — _Ji° —
2987,5
Хо
165
-= 18,106 еж, Уо = —к— =
6250
- = 37,879 ли.
2. Главные оси инерции площади поперечного сечения.
Прежде всего найдем осевые и центробежный моменты инерции площади
поперечного сечения стержня относительно центральных осей xv yv параллельных
Таблица 12.2
Участки
профиля (t)
1
2
3
4
5
F. смг
10
15
50
20
70
*1с. см
26,9
19,4
-3,1
-18,1
—0,6
и\с[см
-32,9
—37,9
— 17,9
12,1
22,1
,собств
1х см*
i
83,33
1,25
6666,7
666.7
23,33
,собств
'у. см*
0,833
281,2
3750,0
1,67
7145,8
соответственно осям х0, у0. Поместим в табл. 12.2 площади элементов
поперечного сечения, координаты центров тяжести (в системе осей xv уг)
5 5
lUy=HFix\c +Σ /^бств= Ю-26,92+15-19,42 + 50-(—3,1)2 + 20 (—18,1)2 +
i=l t=l l
+ 70 (—0,6)2 + 0,833 + 281,2 + 3750,0+1,67+7145,8 = 31118,97 сж*.
5 5
!χ=Σ Fiyl + Σ /$обств= Ю (- 32,9)2+ 15 (- 37,9)2 + 50 (- 17,9)2 +
+20· 12,12 + 70-22,12 + 83,33+1,25 + 6666,7 + 666,7 + 23,33 = 92948,80 еж4,
'**.= Σ Fixic{yxc,+ Σ Сбств=ίο(-32>9)·26·9+15(-37>9) ι9·4+
ί=1
1 = 1
+ 60(-17,9)(-3,l) + y
1/1-503 50-13
12
12
2-0,6-0,8 + 20- 12,1 (—18,1) +
+ 70-22,1 (— 0,6) = — 27410,9 см\
178
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[гл. хи
Определим угол, составляемый главной осью инерции xt с осью х±,
tg2a0
—2/
Х1У1
2 (—27410,9)
- = — 0,8867,
" 31118,97 — 92948,8
2a0 = — 41°34\ a0 = —20°47',
sin 2a0 = — 0,6635, cos 2cto = 0,7482, sin cto = — 0,3549, cos a0 = 0,9349.
Находим главные моменты инерции
Ικ =/„ cos2an+/„ sin2otn-f/, .. sin 2a =
χ2 Χι 0 ' U\ 0 ' *i U\ 0
= 92948,8 · 0,93492 + 31119 · (— 0,3549)2+ (— 27410,9) (—0,6635)= 103347,5 см*,
Ι^ = ΙΧι sin2a0+/tfi cos2a0—IXiyi sin 2aQ=
'= 92948,8 (— 0,3549)2 + 31119 · 0,93492 —(— 27410,9) (— 0,6635) = 20709,49 см*.
Для проверки найдем
/ =— sin 2an (I,. —fx) + IXIJ C092a =
х*Уш 2 0 \ Hi xi/ ' xiUt 0
= + i- (_ 0,6635) (—61829,8)-b(—27410,9)(0,9349) = 20510 — 20510 = 0.
3. Вычислим интегралы ] χ2ω' dF, ]у2(й' dF.
F F
Таблица 12.3
«
о
%
2
6
5
4
3
2
1
?!
£
—27,879
—37,879
—37,879
2,121
22,121
22,121
at
Η
26,894
26,894
11,894
—18,106
—18,106
16,894
ιι н
81
°>S2
82
ч U 3
25,143
25,143
11,120
—16,927
—16,927
15,794
II £
во
Те ι
%||0
9,8943
13,443
13,443
—0,753
—7,851
—7,851
at
•α
Η
15,249
11,700
- 2,323
—16,174
— 9,076
23,645
lis
ΰ<4
al
>пЗ
—9,545
—9,545
-4,221
6,426
6,426
—5,996
11 «
*1
UO
51155
—26,064
—35,413
—35,413
1,983
20,681
20,681
at
•0
—35,609
—44,958
—39,634
8,409
27,107
14,685
С этой целью построим эпюры ω', х2 и у2- Выберем полюс в произвольной
точке, например в центре тяжести площади поперечного сечения. Тогда эпюра ω'
приобретает вид (начало отсчета ω' помещено в точку 1), показанный на
рис. 12.50, 5. При этом учтем рисунок 12.50, е, согласно которому из подобия
треугольников находим отрезок f через с, d, e
ТШ4=1' ^ П.894 А» 15,828 с,
е = 37,879 —с=37,879— 15,828 = 22,051 см,
11,894
Ь0_
30 '
d= 11,894. у= 19,824 см,
22
/ 11,894 , ΟΟΛΚι 11,894 ,. _,_
ЖГ = -Т9Ж' /-22,051^324-= 13,212^.
§ 12.8]
ЦЕНТР ИЗГИБА
179
На рис. 12.50, ж и 12.50, а изображены эпюры *а и у2. При построении этих
эпюр учтено, что координаты концов отрезков, образующих контур в системе
осей хг и у1з имеют значения, показанн .ie на рис. 12.50, и, координаты же
этих точек в системе осей х2 и у2 находятся по формулам
*2=*ι сое щ—у\ sin α„, у2=*Χι sin α0+ι/ι cosa0.
Вычисления сведены в табл. 12.3.
Вычисляем1) интегралы
f χ2ω' dF= — {^p- 774,24 (— 2 ■ 9,076 + 23,645) +
F
ι or»
+ l^L [774,24 (— 2 · 9,076-16,174) +1136,36 (— 2. 16,174-9,076)] +
1 . 5Ω
+ _L^i [1136,36 (— 2-16,174-2,323)+ 1796,96 (—2-2,323—16,174)] +
+ -1^Д [1796,96 (— 2 · 2,323+ 11,70)+ 2365,14 (2. 11,70-2,323)] +
+ -Цр- [2365,Щ2 ■ 11,70 +15,249) + 2634,08 (2 · 15,249 + 11,70)]1 «
= — (49617,2 — 245497,1— 640095,3+ 156314,5 + 337605,3) =342055,4 см\
С yja' dF = - {-^l^ 774,24 (2 · 27,107+ 14,685) +
F
ί 9Ω
+ JLlfu [774,24 (2 · 27,107 + 8,409)+ 1136,36 (2 · 8,409+27,107)] +
1 5Ω
+ 11ΣΪ. [1136,36 (2 · 8,409 — 39,634)+ 1796,96 (— 2 · 39,634 + 8,409)] +
+ -Ц^- [1796,96 (— 2 . 39,634— 44,958) +2365,14 (— 2 .44,958 — 39,634)] +
+ -Цг^- [2365,14 (— 2 · 44,958 —35,609) + 2634,09 (— 2 · 35,609—44,958)]! =
= — (622346,8 — 327998,4— 1277120,0 — 324044 —1004806) = 2655625 еж5.
Находим координаты центра изгиба
\ £/2ω' dF
_ _F 2655625 0_7
a* Г = 103347,5 ""~2&,/ СЛ'
\ χ2ω' dF
i 342055,4 1Й_
au 20709,5 =lb'5 ™'
i) Здесь использован пример интегрирования, предложенный А,
Верещагиным и поясняемый в главе XV·
180
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[гл. χι ί
§ 12.9. Траектории напряжений и деформаций при поперечном
изгибе. Эпюры напряжений, действующих в точках поперечного
сечения на площадках, не лежащих в нем.
Линии равных деформаций
1. Траектории главных напряжений. Пусть имеем балку,
испытывающую поперечный изгиб. Рассмотрим в ней напряженное
состояние в ряде точек, расположенных в одном и том же
поперечном сечении на разных расстояниях от нейтрального слоя
(рис. 12.51) и, пользуясь кругами Мора, определим для каждой
7
Напрадл. б $
Напрадл. ss ^^-К \ Напрадл. бг
Напрадл. аъ
Напрабл. б'$
/г
Напрадл. ef=0
б
Направл.б-f
Напрабл. &δ=ϋ
= /71
б
Напрабл.вΊ
б Напрабл. бу
Рис. 12.51- Направление главных напряжений в точках поперечного сечения балки,
подвергнутой поперечному изгибу.
из них направления главных напряжений. В каждой из точек
нижнего волокна направление σχ совпадает с этим (растянутым)
волокном, а направление σ3 перпендикулярно последнему и
располагается в плоскости параллельной плоскости действия сил. Если
двигаться от крайнего растянутого волокна к крайнему сжатому,
то направления σχ и σ3 постепенно поворачиваются; на уровне
нейтрального слоя они составляют с ним углы, равные 45°; в
каждой точке верхнего волокна направление σχ лежит в поперечном
сечении, а направление σ3 совпадает с этим (сжатым) волокном.
Аналогичная картина наблюдается во всех остальных поперечных
сечениях балки. Представим себе два семейства кривых. Кривые
одного из них в каждой точке балки касаются направления σ1(
а кривые другого —направления σ3. Такие кривые, как об этом
уже говорилось в главе V, называются изостатами или
траекториями главных напряжений. Картина траекторий главных
напряжений в балке при поперечном ее изгибе, соответствующая
элементарной теории изгиба, показана на рис. 12.52, а.
§ 12.9] СИСТЕМЫ ОСОБЫХ ЛИНИЙ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 161
Поскольку в изотропном теле имеет место коаксиальность
тензоров напряжения и деформации, т. е. в каждой точке
напряженно-деформированного тела направления главных напряжений
и главных деформаций совпадают, траектории главных
напряжений одновременно являются и траекториями главных деформаций.
Известно, что армирование бетона стальными стержнями
применяется в связи с тем, что бетон хорошо работающий на
сжатие, плохо сопротивляется растяжению. Стержни арматуры
располагают по возможности по направлению траекторий главных
растягивающих напряжений. Другим примером практического
б)
Рис. 12.52. Траектории главных напряжений в балке при поперечном изгибе: а)
картина траекторий (элементарное решение); б) расположение арматуры в железобетонной
балке.
использования траекторий главных напряжений является
подкрепление тонкой стенки стальной балки с целью предотвращения ее
выпучивания, вследствие наличия сжатия в стенке. Ребра
жесткости наиболее эффективны при расположении их по
направлению траекторий главных сжимающих напряжений. По
конструктивным соображениям в практике конструирования от такого
расположения в той или иной мере отклоняются.
Разумеется, для того, чтобы судить о том, как располагать
стержни арматуры или ребра жесткости, необходимо иметь поле
направлений главных напряжений; его и дает система траекторий
главных напряжений. На рис. 12.52, б изображены стержни
арматуры в балке, траектории главных напряжений в которой
показаны на рис. 12.52, а.
2. Эпюры главных напряжений в точках поперечного сечения.
Определив главные напряжения σχ и σ3 в точках поперечного
сечения балки по формуле (12.94), можно построить соответствующие
182
Плоский изгиб стержней
[Гл. хи
Ά
ΪΜ
тШ^
7f'50
Г
.
•ё
■
ι
У
7а
V
X
о
0,000b
0,020b
0,0558
0,0677
0,1521
Ο,δδΟΟ
0,550δ
0,8072
0,7871
1,0W
δ)
1,0U89
0,7871
0,8072
0,5603
Ο,δδΟΟ
0,1521
0,0677
0,0 δ58
0,020b
' 6,000b
-iff
Рис. 12.53. Эпюры главных напряжений прн поперечном изгибе балки: а)
прямоугольного поперечного сечения; б) двутаврового поперечного сечения.
Рис. 12.64. Траектории максимальных касательных напряжений.
§ 12.9] СИСТЕМЫ ОСОБЫХ ЛИНИЙ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 183
Ттх
эпюры. На рис. 12.53 показаны такие эпюры для двух видов
поперечного сечения балки — прямоугольного и двутавровогох).
3. Траектории максимальных касательных напряжений. Имея
поле касательных напряжений и площадок, на которых они
действуют, можно построить два семейства кривых —так называемых
траекторий максимальных касательных напряжений. Каждая из
таких кривых в любой своей точке имеет касательную,
совпадающую с направлением максимального касательного напряжения
в соответствующей точке
напряженного тела. Кривые одного се- t й!
мейства ортогональны кривым дру- mz P
гого. На рис. 12.54 изображены 0,5859
траектории максимальных каса- о,кЪ99
тельных напряжений2).
4. Эпюра максимальных
касательных напряжений в точках
поперечного речения. Наряду с
представленной на рис. 12.23, а
эпюрой касательных напряжений
можно рассмотреть и эпюру
максимальных касательных
напряжений в точках поперечного сечения
(рис. 12.55); разумеется, при этом
площадки, на которых действуют
такие напряжения, не лежат в
поперечном сечении (за исключением
точек нейтрального слоя) и ориентированы так, что делят
двугранные прямые углы между главными площадками пополам.
Ниже в § 12.10 дается формула (12.94) для главных
напряжений при поперечном изгибе. Согласно этой формуле
0,1951
0,1529
0,0 h68
0,1529
0,2951
0,Ш9
0,5859
01
Ρ
0,52М
0,3938-
0,Ш38
0,1930
0,1988
0,1521
0,1988
0,2930
'0,W8
0,3938
0,5Z№
Ю
δ)
Рис. 12.55. Эпюра максимальных
касательных напряжений в точках
поперечного сечения: а) прямоугольное
сечение; б) двутавровое сечение.
Ттах = -^Ц— = Vol + 4τ
2
5. Линии равных деформаций. Имея поле значений и поле
направлений главных деформаций для каждого уровня
деформаций (в пределах от уровня нулевых деформаций и кончая
уровнем максимальной во всем поле главной деформации) можно
построить два семейства кривых — линий равных деформаций.
В каждой точке линии равных деформаций данного уровня
касательная к ней совпадает с тем направлением, вдоль которого
х) Подробного выполнения выкладок ввиду их элементарности и
очевидности не приводим. Эпюры на рис. 12.53 относятся к сечению заделки
консольной балки длиною /, загруженной силой Ρ на конце, при условии //а = 50.
8) Кривые, обсуждаемые в разделах 3 и 5 настоящего параграфа,
предложены В. М. Никитиным,
184
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Μ
δ)
Ί J I j | if u w к у if
Tttttttt ту
6)
Phc. 12.56. Лнннн равных деформаций (построены В. Μ. Никитиным): а) в балке,
подверженной чистому изгибу (уровень деформации соответствует деформации волокна
с у = di); б) то же при уровне деформации, соответствующем деформации волокна с у = а2;
в) линии нулевых деформаций в балке на Двух опорах, загруженной равномерно
распределенной нагрузкой. '
§ 12.Ю] Предельное состояние материала ё точке балки I85
удлинение в соответствующей точке балки равно принятому уровню
деформации.
Кривые одного семейства не являются ортогональными
кривым другого. На рис. 12.56 показаны примеры линий равных
деформаций.
0
§ 12.10. Условия невозникновения предельного состояния
материала в локальной области в балках
при поперечном изгибе
1. Вводные замечания. Обсуждение проверки условия,
отмеченного в названии параграфа, разобьем на две части. Во-первых,
покажем, как проверить невозникновение предельного состояния
материала в любой точке балки, а во-вторых, обсудим вопрос
о выборе наиболее опасной или
наиболее опасных точек
в балке.
2. Проверка невозникновения
предельного состояния в
материале в произвольном элементе
балки. Пусть имеем балку,
испытывающую изгиб. Рассмотрим
произвольное состояние этой
балки, в котором отличны от
нуля и изгибающий момент и
поперечная сила (рис. 12.57).
Элементы, расположенные в
крайних волокнах, испытывают
осевую деформацию (растяжение
или сжатие); элементы,
находящиеся на уровне нейтрального
слоя, подвергнуты чистому
сдвигу. Все остальные элементы, находящиеся в промежутке между
нейтральным слоем и наиболее от него удаленными волокнами,
испытывают плоское напряженное состояние, в котором
σζφ0, σ„ = 0, тгу = тугф0. (12.92)
Для проверки невозникновения предельного состояния в материале
балки в соответствующей точке необходимо применить теории
прочности или условия пластичности, в зависимости от того
ожидается ли хрупкое или пластичное состояние материала.
Напомним формулы для главных напряжений в общем случае плоского
напряженного состояния, используя индексы, соответствующие
плоскости Оуг
σι, и = -V1 ± у V(oy ~ Ozf + Ή
У*
Рис. 12.57. Напряженное состояние
элементов балки при поперечном изгибе.
Г*
(12.93)
№
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
В случае поперечного изгиба, учитывая (12.92), главные
напряжения получаются как частный случай из (12.93), при этом
становится очевидным и то, какое из них является наибольшим и
какое наименьшим в алгебраическом смысле
σι^ + ΙΤ^ί+Щ,, σ2 = 0, σ3 = -^--ΙγΌΐ + ^τΙν;
(12.94)
в дальнейшем в формулах для главных напряжений индексы г и
гг/при компонентах напряжений будем опускать. Входящие в (12.94)
нормальные и касательные напряжения определяются по
формулам (индексы у σ и τ опущены)
Мху
σ =
(12.95)
в случае массивного поперечного сечения
τ =
QySt
Ых » <12·96)
в случае тонкостенного поперечного сечения открытого профиля
QyS%
χ —
6Λ
(12.97)
Условия невозникновения предельного состояния в материале по
четырем классическим теориям в случае поперечного изгиба,
с учетом равенства нулю σ2, имеют вид
σ,
экв!
= σ.
G:
экв!
μσ3 < [σ];
Μ;
= σο
Κ] Ι;)
σ3ΚΒ2 =* σ1 —
σ9ΚΒ3 = σ1 σ3
σ9ΚΒ4 = Υ<Α + σ| — σχσ9 < [σ].
(12.98)
Окончательные расчетные формулы получаются из (12.98)
подстановкой в них вместо σχ и σ3 соответствующих выражений согласно
(12.94). В результате такой подстановки получаем:
I теория:
<W -у + тVσ2 + 4τ2^[σ0]
или
σ,
экв!
= 4-|у^Т4*«£|К]|;
(12.99)
II теория:
σ9ΚΒ2 = | + -jV^T^-μγ + j μΥ^Τ^
отсюда
l
К
οναΛ = ί(1-μ)+Τ(1+μ)ν^ + ^*^Μ\ (12.100)
§ 12.10] ПРЕДЕЛЬНОЕ СОСТОЯНИЕ МАТЕРИАЛА В ТОЧКЕ БАЛКИ 187
III теория:
отсюда
σ3ΚΒ3 = 1/σ3+4τ2^[σ];
IV теория:
найдем предварительно выражение
тогда
σ9ΚΒ4 = Κσ2 + 3τ2 < [σ]. (12.102)
Используя одно из условий (12.99) —(12.102), производим
проверку невозникновения предельного состояния материала в
обследуемой точке балки.
3. Установление наиболее опасных точек в балке. Теперь, когда
уже показано, как произвести проверку невозникновения
предельного состояния материала в любой точке балки, остановимся на
вопросе, какие же точки балки подвергать такому обследованию.
Условия (12.99) — (12.102) показывают, что наиболее опасными
являются те точки балки, в которых одновременно и σ и τ
достигают больших значений. Формулы (12.95) и (12.96) или (12.97)
позволяют установить, что опасную точку следует искать в
сечении, в котором и М, и Q либо оба достигают максимальных по
абсолютной величине значений, либо одновременно имеют большие
значения, мало отличающиеся от наибольших. Для установления
же положения опасной точки в пределах найденного таким
образом сечения балки необходимо иметь в виду, что σ достигает
наибольшего значения там, где τ равно нулю и наоборот. Поэтому
в поперечном сечении следует искать точку, в которой
одновременно достигают большого значения те величины у и St/b,
которым соответственно пропорциональны значения σ и τ. Под
большими понимаются значения у и 5*/&, мало отличающиеся от
наибольших. Если, например, поперечное сечение балки двутавровое,
то в месте соединения стенки с полкой и σ, и τ имеют большие
значения; именно в этом месте и могут располагаться наиболее
опасные точки. Если нет сечения, в котором и М, и Q достигают
одновременно больших значений, мало отличающихся от
наибольших, и в поперечном сечении нет точек с одновременно большими,
т. е. мало отличающимися от наибольших значениями как у, так
и S%/b, то следует проверить точки, в которых достигают своего
максимума только а—-это наиболее удаленное от нейтрального
(12.101)
= σ2 + 3τ2,
188
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
i
ffi
5,2м
Р=10т
слоя волокон в сечении с максимальным изгибающим моментом.
Проверять точку с максимальным касательным напряжением
(в сечении с максимальным Q) нужно только в случае
тонкостенных балок, так как в балках массивного сечения, как это
указывалось ВЫШе, Tmax/ffmax ^ h/L НаГЛЯД-
ное представление об относительной
степени напряженности точек поперечного
сечения дают эпюры предыдущего
параграфа.
4. Подбор сечения балки. Как
правило, подбор сечения балки при
поперечном изгибе производят так же, как
и при чистом изгибе, т. е. из условия
Р1
Р-
1?ПТт>^
Зп. Mm
ΐ
Эп. Qu
Ю
Рис. 12.58. К примеру 12.11:
а) схема балки и эпюры усилий;
б) поперечное сечеине балки.
атах = Mmax/U?i^[a]. После того как
сечение балки таким образом
подобрано, производят поясненную выше
проверку невозникновения предельного
состояния в локальной области и, в
случае необходимости, соответственно
несколько изменяют сечение балки.
5. Примеры.
Пример 12.11. Подбор сечения и
проверка прочности балки.
Подобрать сечение и произвести проверку
невозникновения предельного состояния в
локальной области в консольной балке, изображенной
вместе с нагрузкой и эпюрами усилий на рис.
12.58, а, где указаны и все размеры. Материал
балки —сталь (Ст. 3) с допускаемым
напряжением [σ]=1600 кГ/см2.
Решение. Проверку невозникновения
предельного состояния материала производим в
точке соединения стенки с полкой в сечении
заделки, используя четвертую теорию.
а) Подбор сечения произведем из условия
Μ /W =ζ[σ1, имея в виду, что Мт
•тах/^^М· ИМеЯ В ВИДУ> — »-тах-
= Р1 = 10 000 · 320 = 3 200 000 кГ см, это
условие представим в виде 3 200 000/1*7^1600, Ψ ==г 3 200 000/1600 = 2000 см3.
Сечение балки примем двутавровым по сортаменту. Двутавр с моментом
сопротивления, ближайшим к 2000 см3, является /V50c, у которого Wx =
= 2030 см3 и !х = 50 640 см*, Sx= 1210 слр.
б) Проверим невозникновение предельного состояния в локальной области.
Согласно (12.102) [Ασ2 + 3τ2^ [°V>
Мху
»(т-')
10 000-320.(25 — 2)
I*
QyS*
10 000
50 640
16,2 ·2·24
1450 кГ/см*,
τ=-ττ- = —1,6-50 640 =102 кГ/см2;
У1Щ*^Ъ · 1<§» = 1460 HflCM* < 1600 Щсм\
§ 12.101 ПРЕДЕЛЬНОЕ СОСТОЯНИЕ МАТЕРИАЛА В ТОЧКЕ БАЛКИ 189
yh=Gonst
Проверка показала, что материал в точке перехода от полки к стенке
находится в безопасном состоянии. Ближе к границе допускаемых состояний
находится материал в крайнем волокне в том же сечении заделки. Действительно,
напряжение в этом волокне
σ = M/W = 3 200 000/2030 =
= 1575 кГ/см* < 1600 кГ/см*.
Пример 12.12.
Проектирование балок
равного сопротивления.
Запроектировать консольную
балку (рис. 12.59, а) равного
сопротивления, понимая под
таковой балку, в каждом из
поперечных сечений которой
максимальные напряжения
одинаковы, в частности могут быть
равны допускаемым. Поперечное
сечение балки принять
прямоугольным. Пример решить в трех
вариантах предположения о
поперечных сечениях: а) высота
поперечного сечения постоянна
по длине балки; б) ширина
поперечного сечения постоянна по
длине балки; в) отношение
высоты к ширине поперечного
сечения постоянно по длине балки.
Решение. Условие равно-
прочности во всех вариантах
имеет вида = M/W = const = [σ];
в каждом из вариантов это
условие конкретизируется.
Первый вариант (h=const)
σ =
b(z) =
Μ (ζ)
b (ζ) /ι2
6
6Μ (ζ)
[ο];
6Ρζ
-τ-=α= const
ο
[σ] /ι2 [σ] Α2
Рис. 12.59. К примеру
противления: α) схема
сопротивления при h -
сопротивления при Ъ =
сопротивления
12.12. Балки равного со-
балкн; б) балка равного
= const; в) балка равного
const; г) балка равного
при h/b = const.
Функция Ь (ζ) — линейная (рис. 12.59,6). Найдем два характерных размера
6Р1
max-^ U-ί — [σ]/ι2 ' ^пнп— Ь ^^ — 0,
Второй вариант ф = const)
a=W^[<j]; HZ)
max
ftmin^0·
190 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. XII
Третий вариант Qi/b=a=const)
Pi
- Μ;
6 (г) aW (г)
6
.,. ; /"opt ... i /"брт ξ /6^ργ
&тах=У αϋ[σ] » "max [/ [σ] '*
*mln"-°» Лт1п = 0·
Сравним объемы полученных вариантов равнопрочных балок.
Первый вариант
К =-р;-/ . . ,„ П= . т ,· ИЛИ О = ——-.· -г-=>4 .
2 [σ]Λ2 [σ]/ι [σ]/2 ft α
Здесь введены безразмерные величины v = V/l3 и α=Α//, Λ=3Ρ/([σ]/2).
Второй вариант
о о
Третий вариант
з /г 6Р Ί2 j,—0 J Ι/Ί Γ6ΡΡ z5/3· 3 I'
Пусть Ρ = 10 Г =10 000 κΓ; /=»1 ж =100 еж; [σ] = 30 /сГ/сл2; тогда
3 · 1000 _1_
30- 100а== 100
и формулы для ν во всех трех сопоставляемых вариантах приобретают вид
Проследим внутри каждого варианта за изменением и в зависимости от
безразмерных параметров — соответственно от α, β и а. Этим зависимостям
отвечают графики, представленные на рис. 12.60 и позволяющие произвести
сопоставление вариантов, носящее, разумеется, лишь иллюстративный
характер, так как параметры α, β и α различны. При другом численном значении А
кривые безразмерных объемов материала оказались бы другими, Настоящий
§ 12.10) предельное состояние материала в точке балки Ш
пример показывает, что равнопрочных балок существует бесчисленное
множество, и каждая из них имеет свой собственный объем1)»
>=0,01 i (1)
1/k 1/1
Рис. 12.60. Кривые безразмерных объемов балок равного сопротивления как функции
безразмерных параметров сечений.
Сопоставление объема балки равного сопротивления с объемом
соответствующей балки постоянного сечения, в которой полнонапряженным
является одно сечение (сечение заделки) показывает следующий процент пере-
расхода материала в балках постоянного сечения.
Первый вариант.
Учитывая, что объем балки постоянного сечения выражается формулой
V —им— 6Pl ь/_6Р/а
const - °maxrti - [σ] h2 ni ~ j^,
!) Для получения балки наименьшего объема должна быть сформулирована
задача оптимизации, что не является целью настоящего примера. Заметим
лишь^ что сама постановка задачи оптимизации балки является вариантной и
в этой постановке требование равнопрочности не является обязательным.
Сочетание требований равнопрочности и минимальности площади
поперечного сечения балки (последнее эквивалентно минимальности объема статически
определимой балки) рассмотрено в статье А. Ю. Ишлинского «О равнопрочном
сечении балки» (Ученые записки Московского государственного университета,
вып. 39, Механика, М., 1940). Здесь автор показал, что не существует балки,
в сечениях которой возникают Μ и Q, такой, чтобы в каждой точке
поперечного сечения выполнялось условие
<W#eM (t = l 4).
Поперечное сечение балки, обладающее минимумом площади при
выполнении отмеченного условия и ограничении невыхода контура поперечного
сечения за заданный заблаговременно габаритный контур, не может быть
равнопрочным во всех точках,
192
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
найдем коэффициент перерасхода материала в %
(6РР ЗР/2\ /ЗР/2
^con.t-^lftrtn/_r/W
ЮОо/о
]h [o]hJ'\[o]h
)]
100о/0 = 100о^.
Второй вариант
" const V max
^Ym-'· ν=ν^-τ^·
V t — V
const '
ν
const
100%=LlV iot-tV жглтУ iariJI00%=
50o/0.
Третий вариант
ν -h h i-\f 6Pl Ί,/"6αΡ//-τι./'
•const-°тахПтах'— |/ a2 [σι |/ [σ] ^
6P
2 /5
[σ] J a >
Г6Я1
2ii A
a ' Б '
'-4
ЮОо/о =—3-^ ЮОо/о = 66,7 o^.
V ,—V
v const "
Остановимся на одной детали. В настоящем примере исследовался
поперечный изгиб, однако мы не рассматривали касательных напряжений. Вместе
с тем, поскольку поперечная сила во
всех сечениях в рассматриваемом
случае одинакова, а изгибающие моменты
изменяются от нуля до конечного
значения, имеется область с малыми
значениями изгибающих моментов, где
размеры поперечного сечения балки
определяют не нормальные
напряжения, а касательные. Определим те
минимальные размеры сечений, которые
необходимы по условию прочности,
связанному с касательными
напряжениями. Где эти размеры окажутся
больше принятых по условию
нормальных напряжений, там их
установим по условию касательных
напряжений. Для того, чтобы решить
поставленную задачу, необходимо знать
допускаемое напряжение при чистом
сдвиге. Воспользуемся четвертой
теорией, согласно которой
[τ]=0,577[σ] = 17 кГ/см*.
Рис. 12.61. Увеличение размеров оало,>
равного сопротивления у конца консоли
с целью обеспечения выполнения условия
прочности элементов балки,
расположенных в нейтральном слое и испытывающих
чистый сдвиг: а) балка с h =■ const; б)
балка с Ь = const; в) балка с h/b = const.
Первый вариант
ЗР . .
^°min"
Второй вариант
ЗР . .
= [τ],
τ =
2bh
*mln =
^min —
mm
§ 12.11] ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ БАЛКИ 193
Третий вариант
τ =
ЗР
2ftmiiAiIn
= [τ],
fQy\ %
Ь
■dz
со
У
=ПГ
На рис. 12.16 изображен свободный конец консольной балки в каждом из
трех вариантов с учетом создания условий для воспринятая касательных
напряжений.
§ 12.11. Потенциальная энергия деформации при изгибе балки
Представим себе некоторую балку, которая под воздействием
нагрузки испытала поперечный изгиб. Внешние силы,
деформирующие балку, совершают работу, в балке же накапливается
потенциальная энергия дефор-
мации, численно равная этой "#-
работе..
Определим энергию,
накопленную в балке. Вырежем
из балки двумя поперечными
сечениями элемент, имеющий
идоль оси ζ размер dz (рис.
12.62). Влияние отброшенных
частей, примыкающих к
элементу, заменим внутренними
силами, действующими в
сечениях стержня, статическим эквивалентом которых при
поперечном изгибе являются Qy и Мх. По отношению к элементу эти
силы являются внешними. Работа dA, совершаемая ими на
соответствующих им и вызванных ими перемещениях, равна
потенциальной энергии деформации dU, накапливаемой в элементег)
dA = dU. (12.103)
Рассмотрим два загружения выделенного элемента. В первом —
элемент загрузим моментами Мх, а во втором силами Qy. На
рис. 12.63 показана картина деформации в каждом из этих
случаев загружения элемента. Легко видеть, что при одновременном
действии Мх и Qy на элемент, каждая из сил способна произвести
работу лишь на перемещениях, ею же вызванных; на
перемещениях же, вызванных другой силой, ни Мх, ни Qy работы не
производят. Действительно, моменты Мх могут произвести
работу лишь в случае взаимного поворота сечений, к которым они
Рис. 12.62.
Элемент балки
изгибе.
при поперечном
*) Работа внутренних сил. возникающих в элементе при деформации, т. е.
работа приращений сил взаимодействия между астицами тела при росте
деформации всегда отрицательна, так как действие внутренних сил,
препятствующее деформации, всегда направлено противоположно соответствующим
перемещениям. Работа внутренних сил численно равна и противоположна по
знаку потенциальной энергии деформации.
7 А. П. Филин, т. II
194
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
приложены; такого поворота не происходит под влиянием сил Qy.
Аналогично силы Qy производят работу при взаимном перемещении
по направлению, нормальному к оси балки центров поперечных
сечений; такого перемещения под воздействием Мх не происходит.
Таким образом, энергия dU, накапливаемая в элементе, может
быть найдена как сумма двух
слагаемых — dU м и dU0ii
dU = dUMx + dUQy.
Каждое из этих слагаемых
представляет собой энергию,
накопленную в элементе вследствие
того, что одна из сил Мх или Qy
производит работу на
перемещениях, соответствующих этой силе
и вызванных ею же.
Коль скоро внешняя нагрузка,
действующая на балку, приложена
к ней статически, статическим
оказывается и характер приложения
сил Мх и Qy к рассматриваемому
элементу, так как силы Мх и Qy
в любой момент времени
пропорциональны внешней нагрузке. Таким образом, каждая из
величин άϋΜχ и dUQ может быть найдена как действительная работа
соответственно сил Мх и Qy, статически приложенных к элементу.
Выведем формулу для dUMx. Имея в виду формулу (12.103),
получим
dUMx = dAMx = YMxd$x == 2χΕΙχ .
Ю
δ)
Рис. 12.63. Деформация элемента
балки: а) деформация вследствие поворота
сечений; б) деформация балки
вследствие относительного сдвига сечений.
Здесь ά$χ — угол относительного поворота торцов элемента
(рис. 12.63)
d$ r= M*dz
αχΤχ ΕΙх '
Для того, чтобы найти dUQy поступим следующим образом.
Выделим из рассмотренного элемента пластинку толщиной dy на
расстоянии у от нейтрального слоя (рис. 12.64) и найдем
потенциальную энергию деформации, накопленную в этой пластинке.
На гранях выделенной пластинки (рис. 12.64), лежащих в
поперечных сечениях балки, действуют силы хгуЪ (у) dy = xb (у) dy, а на
гранях, параллельных срединной плоскости,— силы xyzb (y)dz =i
;= xb (у) dz (хгу — хуг = τ — вследствие закона парности касательных
напряжений).
§ 12.11]
ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ БАЛКИ
195
Потенциальная энергия деформации, накопленная в пластинке,
численно равная работе внешних по отношению к пластинке
сил %Ь (у) dz и xb (у) dy на соответствующих им перемещениях
yxdy и y2dz, определяется выражением (рис. 12.64):
2- (тЬ (у) dz) (7x dy) + у (τ& (у) dy) (γ2 dz) = у %b (у) dy dz (уг + γ2) =
= ±Tb(y)dydz-y = ±(TdF)^dz). (12.104)
Формула (12.104) получена с учетом закона Гука τ = γ(?, где
γ =^γ1 + γ2 — относительный сдвиг элемента. Для того, чтобы
получить потенциальную энергию деформации, накопленную во всем
+
·§>
Λ
г χ
Е2 2Ζ3
О
Ь(у)
/г \ tktfidg
Λ>ζ_
p-=i
rb(y)dz
- Λ.
■§»
Ε
rWz
Λ>
Й/.
5;
г;
Рис. 12.64. К определению dUn : а) элемент балки; 6) поперечное сечение; в) пластинка,
вырезанная из элемента балки; г) деформация пластинки, вырезанной из элемента балки.
элементе, изображенном на рис. 12.64, необходимо
просуммировать потенциальную энергию деформации всех пластинок, на
которые мысленно можно разбить элемент, или, иначе,
dUQy = dAQy _ I J (τ dF) (S. dz) _ -g J τ* rff.
учитывая (12.40), будем иметь
dUn.. =
Qydz
I
од:
2G/J J &2(ί/)
dF =
2G/7
/i J
«* ^ 6»(y)
s* dF = -Qy
2GF
у
где
* jK &2 (У)
dF.
(12.105)
Величину /^ называют приведенной по сдвигу в плоскости Oyz
площадью поперечного сечения. Необходимость введения Fy связана
с неодинаковостью сдвига пластинок по высоте поперечного
7*
196
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
сечения, вызванной неравномерным распределением по высоте
сечения касательных напряжений. С этим же фактом (см. § 12.6)
связано искривление поперечных сечений.
Коэффициент Vy является отвлеченным числом, зависящим лишь
от формы поперечного сечения стержня. Например, для
прямоугольного поперечного сечения высотой h и шириной Ь
Vv~ (Ш_Х> \ б2 аг~Ъ'
^ ' — ft/2
Для двутаврового поперечного сечения можно приближенно
полагать vy = F: FCT, где F — полная площадь поперечного сечения,
/^ — площадь поперечного сечения стенки.
Выражение GFy называется жесткостью балки по сдвигу при
изгибе в плоскости Qyz. Эта величина имеет, как и жесткости
стержня при других видах деформации, физико-геометрическую
природу. Первый множитель содержит физическую информацию —
меру сопротивляемости материала сдвигу, т. е. жесткость
материала, второй геометрическую — жесткость, обусловленную формой
и размерами сечения.
Итак,
dU=M*te + Qldz
2Е1Х ' 2GFy '
Потенциальная энергия деформации, накопленная во всей балке,
находится так: "
/ ι а
Qydz
M^r + f
2GFy
о о *
Пример 12.13. Определить коэффициент vy для круглого поперечного
сечения радиуса г.
Решение. Воспользуемся формулой (12.105) при этом F = nr2, 1% = (яг4/4)2 =
jtV8 * 2
= ■, b — 2r sin a, dy = r sin a da, dF = b dy — 2r2 sin2 a da, Sx = —- r3 sin3 α
i О О
(b и S* были найдены в § 12.6 —формулы (12.42)2,3),
π
η /2 \2
γ r3 sin3 α] ηη %
Γ 7 32 Γ
——: —!— 2r2 sin2 ada — -r-- \ sin0 a da —
(2r sin α)2 9π J
sin5, a cos a , 5 / 3 1 . _ , 1
6
+ τ [τ α~τs,n 2α+τ2-Sln 4a)J о= τ·
'§ 12.12] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗГИБА БАЛКИ 197
§ 12.12. Дифференциальное уравнение изгиба балки
1. Точное и приближенное уравнения. При выводе формулы
для нормального напряжения в случае чистого изгиба балки была
получена зависимость, связывающая кривизну у,х = \/рх с
изгибающим моментом и изгибной жесткостью балки
1 Мх (Ai, = 3W). (12.106)
Ρ*
EL
С другой стороны, кривизна кривой, которой является изогнутая
ось балки, может быть выражена через производные функции
Z) = v(z), изображающей эту ось
.(рис. 12.65)
— = ±-f= υ" (12.107)
Рнс. 12.65. Балка, испытывающая
чистый изгиб.
Прежде чем приравнять правые
части равенств (12.106) и (12.107),
имея в виду равенство их левых
частей, установим необходимый
знак в (12.107). Рис 12.65
показывает, что при положительном
изгибающем моменте изогнутая ось
принимает очертание кривой с отрицательной кривизной.
Следовательно, в (12.107) для выполнения соответствия знаков изгибаю-
.щего момента и кривизны необходимо принять знак минус
υ" = _ Jb. (12.108)
VV + (v'n* EIX-
Это дифференциальное уравнение изогнутой оси балки обыкновенно
называют точным, в отличие от приближенного, получаемого из
(12.108) в тех случаях, когда можно пренебречь величиной (ν')2
по сравнению с единицей, и имеющего следующий вид:
мх
V = —
EL
EIxv"
Μ,
(12.109)
Продифференцируем (12.109)2 дважды по г, исходя из того, что
жесткость Е1Х является переменной по длине балки, т. е.
представляет собой функцию от ζ
(FIxu")" = qy. (12.110)
Здесь учтена зависимость Ml——qu, имеющая место при тх = 0
(см. (1.9)2(4). В случае постоянной по длине жесткости балки, это
уравнение приобретает вид
Elxviv=qy. (12.111)
Вспоминая происхождение уравнения (12.106) (оно получено из
198
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ..Х1Г
четвертого уравнения равновесия системы (12.3)) заключаем, что·
дифференциальное уравнение изогнутой оси (точное или
приближенное) является уравнением равновесия балки при изгибе. В
дальнейшем для балок постоянной по длине жесткости в большинстве
случаев мы будем использовать приближенное дифференциальное
уравнение изогнутой оси в виде (12.111).
2. Обзор правил знаков, принятых в теории изгиба стержня^
Уместно дать обзор принятых правил знаков для всех величин,
участвующих в теории изгиба: qyt тх, Qu, Мх, ΰχ, ν (см. табл. 12.4)
и дать обзор всех основных формул, соответствующих принятым
правилам (существенными являются получающиеся в этих формулах
знаки (табл. 12.5)).
Таблица 12.4
О
&
О
0^2
»|74
У\
мх мх
9в
Р^^?
Щ Ц
'У
Ψ *' «* ΰ Ζ
у)
0
т.
6
У\
В таблицах 12.4 и 12.5 приведены два столбца, в первом из
них дается информация применительно к принятому в настоящей
книге сочетанию правил знаков, а во втором приводятся
аналогичные данные применительно к другому варианту комбинации
таких правил, принятому, в частности, в литературе по строительной,
механике корабля. Преимущество первой системы над второй — в
отсутствии знака минус в формулах для напряжений σ и τ, а также
в формулах условий эквивалентности; проигрыш этой системы по·
гравнению со второй — наличие знака минус в ряде
дифференциальных зависимостей.
3, Граница применимости приближенного дифференциального
уравнения изгиба балки. Как каждое приближенное уравнение,,
уравнение (12.111), или эквивалентное ему (12.109)2 имеет
некоторую границу применимости; установим ее.
§ 12.12]
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗГИБА БАЛКИ
199
Таблица 12.5
Условия эквивалентности
Формулы для напряжений
I
Mx=\oydF
Qy = \%dF
F
Mx = ~\aydF
F
Qy-=~SxdF
τ = ·
Mxy
QSy*x
Ы,
о —
τ = —
Mxy
Ιχ
Q S*
^y χ
Ых
Дифференциальные зависимости
А =
V
V'
υ"
ν"'
νιν
0
*
*'
Φ'
<Γ
О
о
Μ
Μ'
Μ"
А = ВС
О О
о
о
о
я
о
о
Q
Q'
в=
υ О
О $
О О
О О
О О
О О
О О
Μ О
О Q
О О
с=
о
1
1
Е1Х
1
Е1Х
1
Е1Х
1
Е1Х
1
ΕΙχ Е1Х
О
О
1
1
-1
0 0
0 0
0 0
1 0
—1 1
с=
о
1
1
Е1Х
1
Е1Х
1
Е1Х
1
£/*
1
ΕΙχ Е1Х
0 0 0
0 0 0
1 О О
1 1 О
1 1 1
Замена точного дифференциального уравнения приближенным
допустима во всех тех случаях, когда максимальное значение (ν')2
является величиной пренебрежимо малой по сравнению с единицей.
Очертание изогнутой оси балки при постоянной вдоль ее оси
жесткости зависит от вида нагрузки и от характера закрепления
балки. Всегда можно изогнутую ось разбить на участки,
границами которых являются точки перегиба или центры концевых
сечений балки (рис. 12.66). Каждый из этих участков может
трактоваться как половина волны или доля от нее. Наибольшие значения
величины ν'\ а следовательно и (ν')2, соответствуют точкам
перегиба или крайним границам отмеченных половин волн. Можно
установить какими должны быть параметры половины волны,
чтобы на ее границах величина достигала предельного значения,
т. е. такого, при превышении которого уже нельзя пренебрегать
пеличиной (ν')2 по сравнению с единицей и, следовательно, нельзя
заменять точное дифференциальное уравнение (12.108)
приближенным (12.109). Для выполнения оценки будем предполагать,
200
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XIГ
что половина волны представляет собой кривую, симметричную»
относительно середины ее длины. Тогда в качестве параметра,,
характеризующего половину волны, можно принять отношение а/Ь
(рис. 12.66). Если, например, полагать, что допустима
погрешность в 5%, то границей применения приближенного
дифференциального уравнения будет являться;
величина (у)2 = 0,05, или v' = tg'&f^^
^0,2236, или ft^l2°36'.
Оценим, каким должно быть
отношение а/Ь, чтобы на границе
половины волны выполнялось равенство.
$ = #* = 12°36'. С этой целью
рассмотрим три различных очертания:
кривой: синусоиду, квадратную
параболу и окружность. Вся информация
сведена в табл. 12.6.
χ—p^v-_L__>iJf·-^ ч Из табл. 12.6 очевидно, что пре-
^ t Г ГТ I 7777, дельному параметру а/Ь соответствуют
довольно крутые половины волн по·
сравнению с теми, которые допустимы,
в конструкциях. В балочных
разрезных пролетных строениях мостов
допустимая величина a/b = l/f не меньше
800—1000. Отсюда становится ясно,
что практически во всех случаях,,
встречающихся в строительных
конструкциях, в машиностроении,
самолето- и кораблестроении с большим:
запасом достаточна точность, даваемая приближенным
дифференциальным уравнением, и лишь в очень гибких элементах (в
которых только и могут иметь место а/Ь, указанные в таблице),,
встречающихся в приборостроении, может возникнуть
необходимость прибегать к точному дифференциальному уравнению.
Установим, каким должно быть отношение а/К, где К — высота:
балки, чтобы в этой балке при а/6 =18,00 (см. табл. 12.6),
материал оставался в пределах упругой работы, точнее — в пределах,
допускаемых напряжений. Из очевидного соотношения (см. рис
в последнем столбце табл. 12.6) р2 = -j- -f (ρ — Ь)2, отсюда
« а
г
^*й-_
7^
с ζ ,
_^^-^
а
г 2 ,
\
<ъ
11
Рис. 12.66. Характерные варианты
очертания изогнутой оси балки.
2рь=т + *г· т-
2Ь
а?
+ f>2
Ρ
2_
b
а?
4ί>2
+ 1
Подставляя сюда α/6 = 18,00 и 6 = α/18,00, получим
j__ 0,439
ρ α '
(12.112),
-^ 12.12] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗГИБА БАЛКИ 201
Таблица 12.6
■<
j£V^
*у .
·*=»,
1
1
Синусоида
Квадратная
парабола
Окружность
max
Ό =
max
= υ'
пред
а
Ύ
b sin —
α
46
α*
(α—ζ) г
6π nz
cos —
a a
£<«-*>
6π
a
4b_
a
bn
a
■■ 0,2236
π
0,2236
= 14,05
46
— = 0,2236
α
0,2236
= 17,89
tg**=-
a
"2"
p—6 »
p2 = -^- + (p-6)2,
Д2 α2 A
2p6=4 + 6*. р = -^г + 4,
86
tgi}* =
α
"2
α
26
аи
α2 1
86 2 862 "2
α2 1 α
862 ιδυ 2 g 26 '
62 tgfl* 6 υ'
α
Τ
α
Τ
α
Τ
α
Τ
2 ·./" 4
tgO* ±(/ tg2f>* + »
2 + 2/1 + 0,05
0,2236 »
2 + 2.1,0247
0,2236 »
4,0494
0,2236
= 18.11
202
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. Х1Г
С другой стороны, если в (12.5) положить ymax=h/2, то
h 1 2егтах 2[σ]
8гтах=^-, — =? I =-Щ-· (12.113)
Приравнивая правые части (12.112) и (12.113), получим
0,439 _ 2[σ] α 0,439£
а ~ НЕ * h ~~ 2 [а] '
Если балка выполнена из стали Ст. 3 (£" = 2,1 -106 кГ/см2, [а] —
= 1,6-103 кГ/см2), то
а _ 0,439-2,1-Ю6 _ 9оо 9qn
τ - 2-1,6-юз- -28b^290·
Отсюда видно, что балка очень гибка. При отношении a/h = 290
балка может быть лишь гибким упругим элементом прибора,
наподобие пружины. Обычные же балки в строительных и
машиностроительных конструкциях имеют это отношение в несколько
десятков раз меньше, чем 290. Если α//ι=10, то а/Ь = 525.
4. О перемещениях вследствие сдвига при изгибе.
Рассматривавшиеся выше перемещения связаны с поворотами поперечных
сечений. Наряду с ними имеется еще одно слагаемое
—перемещения вследствие сдвига при изгибе (сдвиг при изгибе не
сопровождается поворотом поперечных сечений).
Эти перемещения, как будет позднее показано, значительно меньше
перемещений от изгиба и ими по сравнению с последними в
подавляющем большинстве случаев можно пренебречь, за
исключением балок с малым отношением l/h (порядка 5), выполненных
из материала с очень малым отношением G/E (порядка 1/10-f-1/20,
например, в деревянных балках). Поэтому ниже — всюду, где не
сделано специальной оговорки, — имеется в виду перемещение
лишь от поворота сечений при изгибе, определяемые из точного
(12.108) или приближенного (12.110) дифференциального
уравнения изгиба. В настоящем же разделе остановимся на том, как
учесть и влияние сдвигов на перемещения при изгибе, если в этом
возникает необходимость.
Итак, внешняя нагрузка, действующая на стержень и
вызывающая его поперечный изгиб в плоскости Oyz складывается из
распределенных силовой и моментной нагрузок qy и тх и
сосредоточенных сил и моментов Ру, Шх. При этом указываются
участки, на которых имеет место та или иная распределенная
силовая или моментная нагрузка и координата сечения приложения
сосредоточенной силы или сосредоточенного момента.
Внутренние момент и сила имеют отличные от нуля
составляющие: Мх Qy. В процессе деформации балки точки оси испыты-
■§ 12.12] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗГИБА БАЛКИ 203
вают перемещения, а поперечные сечения поворачиваются.
Составляющие указанных перемещения и угла поворота в системе Oxyz,
соответствующие поперечному изгибу в плоскости Oyz,
обозначаются символами ν, $х. Деформация стержня в этом же случае
может быть задана и при помощи параметров деформации кх, уу.
Напряженно-деформированное состояние стержня определяется
условиями равновесия (статика проблемы), условиями совместности
деформаций (кинематика проблемы) и зависимостями между
усилиями и параметрами деформации (физика проблемы).
Из шести уравнений равновесия элемента стержня с
прямолинейной осью запишем два (1.9)2>4, относящихся к поперечному
изгибу в плоскости Oyz и сопровождающему его сдвигу. Эти
уравнения выражают равенство нулю суммы проекций всех сил
на ось у и равенство нулю суммы моментов всех сил относительно
оси χ
dQu dMx
-ЗГ + Яу = 0> -4r-Q, + mx = 0> (12.114)
или, подставляя выражение для Qy, найденное из уравнения
(12.114)2, в уравнение (12.114)!, получим
τ£- + ^4ί,-0. (12.115)
Уравнения, связывающие деформации (κ* и уу) и перемещения
(ν, ϋ·χ) на уровне геометрически линейной постановки проблемы,
имеют вид
κ* = _"2^' θ* + ν^ = -5ί· (12.116)
Природа второго уравнения пояснена на рис. 12.67, из
которого ясно, что часть прогибов обусловлена сдвигом уу. Этот
рисунок перекликается с рис. 12.40, б. Подстановка (12.116)2 в
(12.116)! дает
*—Т^-2Г- (12-47)
Сдвиг, вызываемый поперечной силой, не зависящей от ζ, также
остается неизменным по длине балки, при этом второй член
и (12.117) обращается в нуль, т. е. в этом случае сдвиг не вызы-
оает изменения кривизны оси стержня. Изменение кх — кривизны
оси стержня — вызывается переменным по ζ сдвигом; такой сдвиг
ио.шикает, если и Qy также зависит от ζ.
Физические уравнения (закон Гука для всего изгибаемого
стержня), связывающие усилия (Мх, Qy) и деформации (κ*, yy)t
204
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
имеют вид1)
_ Мх
t^L ν -Ям.
dzGF' yv~~GF
у
(12.118)
Первое из этих уравнений является обобщением уравнения (12.109)
на случай учета влияния сдвига на изменение кривизны оси балки.
Выведем уравнение равновесия, выраженное через функцию υ
и справедливое в случае, если материал подчиняется закону Гука.
fx<0, dvT<0
dvr
dz fy
δ)
Рис. 12.67. Элемент балки при поперечном изгибе с учетом сдвигов: а) прогиб, связанный'
с поворотом сечення; б) прогиб, связанный со сдвигом.
Подставим в уравнение равновесия (12.115) вместо Мх еп>
выражение через параметры деформации, получаемое из (12.118),.
Мх = кхЕ1х--^-ду.
Такая подстановка дает
EI d2y,x 4- dm
dz2
dz
_ΕΙχΟ%
^ Чу пр. и-,2 υ·
GFfJ dz2
(12.119)
(12.120)·
Если (12.115) представляло собой уравнение равновесия для
стержня, испытывающего деформацию (геометрически линейный
*) Приведем сводку всех шести уравнений закона Гука для стержня
в целом, но без учета влияния неравномерности сдвига по длине балки на
кривизну ее оси
М,
*Х~'Е1К '
Уу
_ Qy
GFy>
κ,
_МУ
'-Ely*
Ч* GFX>
Ν
Μ,
Ъ- Ер, **- Qfk
Первые два уравнения относятся к изгибу к плоскости Oyz, вторые два —
к изгибу в плоскости Охг, пятое — к осевой деформации и шестое—к
свободному кручению.
§ 12.12] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗГИБА БАЛКИ 205
случай), но выполненного из материала с любой зависимостью
между напряжением и деформациями, то (12.120) является
аналогичным уравнением равновесия, но уже лишь для стержня,
изготовленного из материала, следующего закону Гука.
Подставляя в уравнение (12.120) вместо параметра деформации
пх его выражение через перемещение согласно (12.116), получим
искомое уравнение
*1χάζ* dz q^GFy dz* Ό· (12.121)
Уравнение (12.121) по природе своей аналогично уравнениям Ламе
в теории упругости и является уточненным (учтен сдвиг)
приближенным дифференциальным уравнением изгиба стержня.
Если не учитывается влияние сдвигов на перемещения при
изгибе, что равносильно предположению о бесконечной жесткости
стержня по условию сдвига, то последний член в уравнении
(12.121) обращается в нуль; при отсутствии моментной
распределенной нагрузки, или ее независимости от ζ, в нуль обращается
и второй член в (12.121), при этом получается приближенное
дифференциальное уравнение изгиба балки, рассмотренное в начале
параграфа.
Последовательность отыскания шести неизвестных функций:
Мх, Qy, ν, $χ, кх, уу, полностью описывающих
напряженно-деформированное состояние прямолинейной балки при поперечном
изгибе в рамках технической теории, при условии задания
функций q и тх и численных значений и координат приложения
сосредоточенных сил Ру и моментов Шх, следующая. Интегрируя
(12.121), находим ν, далее из (12.116)! находим κχ. После этого
из (12.119) определяем Мх, из (12.114)2. находим Qy, из (12.118)2
находим уу, после чего из (12.116)2 определяем ϋ·χ.
5. Граничные условия. Для того, чтобы задача была решена,
т. е. найден интеграл дифференциального уравнения (12.121),.
имеющего четвертый порядок, необходимо иметь по два граничных
условия на каждом из концов стержня. Так, например, при г — гА
чти два граничных условия могут быть выбраны из числа
нижеприводимых четырех, за исключением расположенных в одной и
той же строке *)
ΜΙ (πΐ d3V . ΕΙχ аС1У\
ilv EIxd'v I EIxdqu mx
+
K<l? ' GFydz3 ' GFy GFy dz GFy
Elx
-GF-y«y
г=гл=Ь(А> ■ I - EI
d^v
= — 0{A)
-ZA ЧУ »
A vx , ^ "* dzZ
г=гА = м<хЛ) . (12.122)
') В формулах (12.122)2, з. 4 в левых частях внутри круглых скобок поме-
ιΐιΐ'ΐΐι,ι развернутые выражения соответственно поперечной силы, угла поворота
иппорсчпого сечения и ■ изгибающего момента. Формулы для изгибающего мо-
206
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Таким образом, если известны либо усилия и моменты в двух
сечениях стержня, либо перемещения и повороты, то можно найти
по указанной выше схеме все функции, описывающие напряженно-
деформированное состояние стержня.
Вернемся опять к упрощенному варианту постановки задачи
поперечного изгиба балки, в которой не учитывается влияние
сдвигов на прогибы. Одновременно будем считать равной нулю
распределенную моментную нагрузку. При этом граничные
условия (12.122) приобретают вид
.И>
2 = 2,
&ХЛ\ EIxv"
ΕΙχν'"
ϊ(Λ)
— <2Γ,
-м[А\
В частности, отсюда получаются такие характерные граничные
условия: жесткое защемление конца балки, шарнирное опирание
конца балки, свободный конец балки, для которых имеют место
соответственно следующие граничные условия при г = гд:
(и = 0, и' = 0), (и=*0, \Г = % (ζ/"=0, ι/' = 0).
Упруго-податливому защемлению (податливость 51) и упруго-
податливому опиранию (податливость А) конца балки при ζ~ζα
отвечают граничные условия г)
V-
-ΑΕΙχν'\
—%EL
■ν
мента получаются из (12.119) после подстановки в нее (12.116)];. Формула
для поперечной силы получается после решения (12.114) относительно Qy и
подстановки вместо Мх, отмеченного в настоящем примечании выражения.
Формула для угла поворота поперечного сечения получается из (12.116)2
путем решения относительно ϋχ и подстановки вместо γ^ выражения согласно
(12.118)2, в котором под Qy подразумевается выражение, полученное согласно
приведенному выше указанию настоящего примечания,
*) Податливости А и 51 пояснены на рис. 12.68, а, б.
δ)
Рис. 12.68. Пояснение природы податливосте.й! а) природа податливости ЭД (Щ — угол
поворота упругой заделки при действии на нее момента, равного единице); б) природа
податливости А (Л — просадка упругого проседающей опоры при действии на нее силы,
равной единице).
§ 12.13] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИБА БАЛКИ 207
§ 12.13. Интегрирование дифференциального
уравнения изгиба балки
1. Вводные замечания. Особенностью определения перемещений
при изгибе посредством интегрирования дифференциального
уравнения изгиба является то, что в пределах рассматриваемой балки
может иметься несколько участков с различным видом функции v.
Деление оси балки на участки связано с рядом причин. Для того,
чтобы уяснить их, рассмотрим следующую форму записи
дифференциального уравнения изгиба:
ΕΙχυ" = — Μχ
Очевидно, что если при переходе через какое-то сечение балки
изменяется вид функции в правой части, то при этом изменяется
и вид функции v. Вместе с тем известны все причины, могущие
изменить вид функции Мх при переходе через некоторое сечение
ζ = Ζι', к числу их относится наличие в сечении ζ = ζι
сосредоточенной силы Ρ и (или) сосредоточенного момента Ш, изменение
в сечении г = г,· вида функции qy и (или) тх. На этом перечень
причин, влияющих на изменение вида функции ν можно было бы
закончить, но мы для некоторой общности, целесообразность
которой станет ясной несколько позже, отметим еще два фактора,
которые могли бы явиться причиной изменения вида функции
при переходе через сечение z = zt. Один из этих факторов
представляет собой ступеньку в очертании оси балки на некоторую
величину, а другой — излом в этом очертании на некоторый угол.
Происхождение ступеньки и излома будет обсуждено ниже.
В настоящем параграфе сначала обсуждается интегрирование
дифференциального уравнения изгиба при наличии в пределах
балки лишь одного участка, далее исследуется вопрос
интегрирования указанного уравнения в случае нескольких участков в
пределах длины балки. Все отмеченные выше разделы настоящего
параграфа посвящены определению перемещений в балках
постоянного вдоль оси ζ поперечного сечения. Случай балки, жесткость
которой зависит от г, рассматривается в §§ 12.14 и 12.19.
2. Интегрирование дифференциального уравнения изгиба балки
в случае одного участка. Пусть имеем дифференциальное
уравнение изгиба призматической балки
EIxv™ = qy. (12.123)
Пудем считать, что в пределах всей длины балки имеется один
участок.
Расположим начало координат (z = 0) в центре одного из
концевых сечений балки. Тогда, последовательно интегрируя
208
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
уравнение (12.123) четырежды, получим
EIxvm = - Qy = - Qy0 + \ qy dz,
(12.124)
EIxv" = — Mx = — Mx0-Qyoz + J J qy dz dz,
о о
υ' = ϋχ== ϋχο — -ft- ζ
Mxo Qy0
ζ ζ ζ
-ΉΤχζ2+-Ε77$№^άζάζάζάζ>
*ο ΕΙΧ
0 0 0
ζ ζ ζ ζ
u^Uo + u^-g^T^-g^^ + lTj J ,) J J Qydzdzdzdz·
ο ό о о
В формуле для у первые четыре члена можно рассматривать как
общий интеграл однородного уравнения, соответствующего (12.123),
Ζ Ζ2 Ζ3
имея в виду, что 1, ц-, ^, зу — СУТЬ частные его решения, а
коэффициенты при них — постоянные интегрирования1). Последний
член в этой формуле можно рассматривать как частное решение
неоднородного уравнения (12.123). Другая форма частного
решения дается ниже формулой (12.136).
Решение (12.124) является общим для всех балок, содержащих
один участок. Специфика каждой из исследуемых балок
учитывается в величинах Qyo, Мхо, ϋ·χ(> и vQ, которым легко дать
механическую трактовку — это соответственно: поперечная сила,
изгибающий момент, угол поворота и прогиб в сечении, совпадающем
своим центром с началом интегрирования. Для того, чтобы
удостовериться в сказанном, положим г = 0, тогда все члены в
правых частях (12.124) обращаются в нуль за исключением одного
(Qy0— в первом, Мх0 — во втором, $хо — в третьем и v0 — в
четвертом уравнениях). Вместе с тем смысл левых частей уравнений
(12.124) соответственно таков: минус поперечная сила, минус
изгибающий момент, поворот и прогиб. Отсюда и делается
заключение о природе Qm Мхо, ftXQ и v0. Величины Qm, Мх0, ftXQ и v0t
называются начальными параметрами.
2) Заметим, что при последовательном интегрировании уравнения (12.123)
перед третьим интегрированием обе части уравнения (12.124)2 были разделены
на Е1Х для того, чтобы в результате третьего интегрирования получить угол
поворота поперечного сечения балки θ=υ', а в результате четвертого —
прогиб v. Без такого деления в результате третьего и четвертого интегрирования
имели бы не ν' и v, a EIxv' и ΕΙχν соответственно. Вследствие отмеченного
деления на Е1Х получилось то, что в (12.124)j постоянной интегрирования
является —■ Qy0 и в (12.124)2—величины—Qy<> и — Мх0, а в (12.124)3 таковыми
Qi/o ΜΛθ α /1о 1олч Qyo Mx0
являются —-ρ-ΐ—, ~ έτ~ и Ф*оИ в (12.124)4 — величины—-—_>—--_ νχ0 и ν0.
civ hi x hi v hi x
$ 12.13]
ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИБА БАЛКИ
209
До сих пор мы находили поперечную силу и изгибающий
момент, пользуясь правилами: поперечная сила Qy равна сумме
проекций всех сил, расположенных по одну сторону от
рассматриваемого сечения на ось г/, а изгибающий момент Мх равен сумме
моментов всех сил, расположенных по одну сторону от
рассматриваемого сечения относительно его центра. В соответствии с этими
правилами
г г
Qy = Qr/o - S Чи dz> M* = М*о + Qyo* - S Чу* dz. (12.125)
о о
Формула (12.125)χ для Qy совпадает с (12.124), a (12.125)2 —для
Mx представляет собой другую форму, во многих случаях более
удобную, чем (12.124), дающую тот же самый результат.
Формулы (12.124) представим в матричной форме
w(z) = Kw(0) + I; (12.126)
w(z)HQ*(*) МЛг) *,(*) υ (г)}; w(0)HQw М,0 Ъхо υ0};
1 0 0 0
ζ 10 0
ζ2 ζ
К
2ΕΙΧ
ΕΙΛ
2ΕΙ
1 0
г 1
л:
ζ г г
(12.127)
ίζ ζ ζ ζ ζ ζ
— \ qu dz — I V qy dz dz -щ- \\\qydzdz dz
г г г г \
ёЛ $ ί j j Яу dz dz dz dz\= V11*1*1*}'
0 0 0 0
Примеры 12.14 (рис. 12.69), 12.15 (рис. 12.70), 12.16 (рис. 12.71), 12.17
(рис. 12.72) решить самостоятельно. Во всех примерах для балок,
изображенных на рисунках, найти вектор w (г).
§
У1
τι?
ζ
Ι ι ' ,г
|JfJ V'l'V "n|f 4f
Τ
2
0
Л
1
1
Йтту
Я
Рис. 12.69. К примеру 12.14.
Рис. 12.70. К примеру 12.15.
Указания. Во всех четырех примерах матрица-столбец 1 имеет вид !
f
qz
qz2 qz*
qz*
6EIX 24EL
f
210
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Вследствие симметрии в примерах 12.15 и 12.17 начало координат удобно-
располагать посредине пролета.
1
о
JMjMJjj Jn Jnjf]'''
тттттττ
и
1
.1
ИIV
ί
О
У\
V | ' ' 1'injf и
Hi
Ч
ι
г
ъ
V,
Рис 12.71. К примеру 12.16.
Рис. 12.72. К примеру 12.17.
Векторы w (0) при записи их непосредственно из условий примеров
соответственно имеют вид
1) w(0) = {9/ -f 0 0J
(первые, два элемента находятся как реакции в заделке);
2) w(0)={0 Мх0 0 о0},
ΛίΛ-ο и и0 находятся из условий на любом конце балки, например, на правом::
1 0
I2 .
// \
аЦт)
ίι \
и -
Ы
8£А
Μχ0\\+
ql2
8
?/*
384£/*
=
0
0
Квадратная матрица второго порядка получена из матрицы К — сохранены,
элементы, находящиеся на пересечении строк, соответствующих Мх Ш2) и
ν (1/2) (вторая и четвертая строки), и столбцов, соответствующих Λί^ и %
(второй и четвертый столбцы), при этом ζ = 1/2,
Мх0
1 0
Ι2 ,
8ΕΙ,
ql2
8
384£/,
3) w(0) = {QJ/o Мх0 0 0}, Qyo и ΛίΛθ находятся из условия на правом-
конце балки:
МА1)
v(l)
ι
1
/з
I2
6ΕΙ« 2ΕΙ,
1 ®y° II4-
\мх0\Г
. ql2
2
24E1X
110
11 о
4) w(0) —{0 Mx0 0 v0}, Mx0 и v0 находятся из условий на любом,
конце балки, например, правом
О
ί1 \
νι-ζ-ι
\2/
2Е1Х
I2
8Е1Х
0
1
мх0
+
ql3
48EIX
ql*
Ъ84Е1Х
=
0
0
§ 12.13] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИБА БАЛКИ 211
Ответы в примерах соответственно нижеследующие:
q(t-z)
qlz
1) w (ζ) =
ql* qz*
qlz2
2) w (z) =
2Elx
qlz3
GEIX
— qz
qP_
8
+
+
2 2
ql4
+
qz3
2EIX
qPz*
4EK r 24£/
6EIX
qz*
qz*
2
ql2z qz
8EI
6EL
ql4"- _5_ ψ_
"Γ ogj с; ι
qz9
16£/
384 EL
24EL
3) w (z) =
-g-ql — qz
ql2 5 , 0-22
4) w(z) =
<y/2
8£/*г
g/2
16£/* 2
— i?2
№_q£
24 2
<7/2
5 *' z2 + *
\6EIX
5 ^
6E/,
48 EI,
23 +
24£/j
24£/*
9*4
384E/,
z +
?/2
48£/
-z2 +
24£/j
Пример 12.18. Найти вектор w (г) для балки, изображенной на рис. 12.73
вместе с приложенной к ней нагрузкой.
Рис. 12.73. К примеру 12.18.
Решение. Располагаем начало координат в центре левого концевого
сечения балки, при этом
w(0) = {Qi/0 MM 0 0}, | = {-
0ι&
21
qiz3 ЯР*
4izb
6/ 24EIJ \20EI
>}·
212
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Qyo и Мх0 находим их условия
υ (I)
/2
/
Отсюда
Qyo
Μχϋ
/2
2Е1Х
/»
6ΕΙΧ
ί
ΕΙΧ
/2
2Eh
Qyo Ι! ,
Μλ-οΙΓ
Qp
24ΕΙΧ
ЯР
\20ΕΙΧ
=
0
0
2ΕΙΧ
/3
6ΕΙΧ
/2
2£/*
/3
/2
2Ε/,
-1
<7^3
24ΕΙΧ
111*
\20ΕΙΧ
ι
ΕΙΧ
/2
6£/,
2£/,
1
/*
/*
24ΕΙΧ
Qil1
120ΕΙΧ
=
3 ,
20^
30
,4{ΕΙχγ 6 (Ε/,)»;
Подставляя Q^q и Λί*0 в w (0) и используя после этого (12.126), получим
3^_г^
10 /
w(z) = y
-- + ^/z-
/2 _3_
Ϊ5 + Τθ
/2Ζ
15Е/,
/2ζ2
30£/*
3/
3/
20£/*
/ζ»
20£/*
z2 +
+
12EIJ
ζ*
60EIJ
w(/) =
~20^
20
0
0
Найдем максимальный изгибающий момент в пролете. Условие экстремума
функции Мх имеет вид
dM3
dz
= °* T0qil-2[Z* = 0' zi = |/"ffi/a = 0·546'· ζ2 = -0,546/.
Корень со знаком минус не удовлетворяет условию задачи — сечение
оказывается вне балки.
Определим знак второй производной, -т-у = — ~- <0. Следовательно, при
г = 0,546/ функция Мх достигает максимума.
Мхты = Мх\г-.
= 0,546/'
qi12 + ~ щ1 · 0,54б/-|[ (0,54603 = 0,0214^2.
30
Найдем максимальный прогиб. Условие экстремума функции ν имеет вид
dz
= 0,
30£/j
3. qil
40 Eh
z2-f
qtz*
q&
24EIJ
20EI
jEf'-l^+H-·.
21 = 0, 5z3 — 9/22 +4/3 = 0.
(12.128)
По смыслу задачи одним из корней должен быть z2 = /, так как при
г = / функция ν должна приобретать минимальное значение. Действительно,
подстановкой в (12.128) убеждаемся, что г = / является корнем этого
уравнения: 5/з — 9/з + 4/з = 0, 0===0.
Деля левую часть уравнения (12.128) на ζ—/, получим
(5гз—9/22 + 4/2); (/—г) = 5г2+5г/ — 4/2, (/—г) (5г2 + 5г/ — 4/2) = 0.
§ 12.13] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИБА БАЛКИ 213'
4
Отсюда получаем квадратное уравнение z2-\-lz—=-/2=0, из которого
находим последние два корня z3 = 0,525/, г4=—1,525/. Последний корень
условиям задачи не удовлетворяет, так как точка г = г4 = —1,525/ выходит за<
пределы балки. Для того, чтобы установить вид экстремума рассмотрим знак.
ВТОРОЙ ПРОИЗВОДНОЙ При Ζ = Ζχ, Z2, 23
ν·= 1<
?[l'3-№+TzS]. °"1~.-=Ш77Т,3>0·
20£/..
ϋ" 1«^-2оЙ7/3>0' ϋΊ^2-ο,525,=6δΙ77/Μ-ι.2 8)<о.
Итак, при z = 2i = 0 и z = z2 = l функция ν приобретает минимальные,,
а при ζ = ζ3 = 0,525/ максимальное значения "*
ν |г_г1=о=0, ν |г_г2_/ = 0, ν |г=гз_о.525Г =0,00131 j^j-.
3. Интегрирование дифференциального уравнения изгиба балки
в случае наличия нескольких участков (метод начальных
параметров).
3.1. Вводные замечания. В тех случаях, когда в
пределах длины балки имеется два или большее число (т) участков,
вид функции ν (а следовательно, и $х, Мх и Qy) на каждом из
участков оказывается своим собственным.
Для каждого из т участков имеем свое дифференциальное
уравнение ΕΙχυ[ν = ς,Λ, ΕΙχν\ν = ςυ2, .... EIxv™ = qym.
Если не принимать никаких специальных мер, то, так как
в решении каждого из этих уравнений содержится четыре посто-
яннных интегрирования, пришлось бы составлять Am условий,
для их определения и решать систему Am уравнений с Am
неизвестными. Условиями для отыскания постоянных интегрирования
являлись бы: по два граничных условия на концах балки и по
четыре условия сопряжения функций vt и vi+1 и их первых трех
производных на каждой из границ, участков (t и t + l): vt
с Vi+1, $xi = v'i с v'i+1 = = ϋ·χ<ι+1 (согласование углов поворота),
— Mxi/(EIX) = υ'ι с ό"+1 = — ΜΧι ι+ι/(ΕΙχ) (согласование изгибающих
моментов), —Qyi/(EIx) = Vi" c ν'{'+{ = — Qy,i+i/(Eix) (согласование
поперечных сил). Согласование состоит в том, что функции и
(или) их производные на двух соседних участках должны либо
плавно переходить одна в другую, либо должен иметь место·
скачок.
В табл. 12.7 изображены причины возникновения участков и
отмечено, какие из функций ν, $х, Мх и Qy при этом
претерпевают скачок, а какие плавно (по ординатам) сопрягаются при
переходе через границу участков. Необходимость решения всякий
раз системы линейных алгебраических уравнений порядка Am
представляет значительное осложнение. С целью его преодоления
можно построить решение всей проблемы так, чтобы в нем все
'214
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Таблица 12.7
Фактор сечения
шг,
■ж
Цу· доп. k
-Ρ,
о
о
Μ
X, ДОП. k
—Py(z—zk-i)
т>
*
χ, доп. k
2ET(z-Zk-i)
-E77{z-Zk-l}
a
^доп. k
6EI,
(z — Zk-i)3
2E7Z{z-Zk-l)2
a(z—zk-i)
-P,
Q.y. Zk-χ, доп, k—Чу, доп. k \z — Zk-i
0 0
Μχ, ζ/ι-Ι· ДОП, k *"Xl дОП, k U-2^-l
m,
о
о
0 α
0
0
v"k-l· Д°п· * — ^доп. k \z-Zk-i
о о
Примечание. Силы в пружинах, в шарнире и ползуне обеспечивают
соответственно поворот н смещение до упора.
§ 12.13] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИБА БАЛКИ 215
сопряжения на границах участков происходили автоматически х>
и всего содержалось бы четыре начальных параметра.
Ниже примем следующий способ изложения. Сначала сущность
метода будет показана путем использования механических
понятий, а после этого приведено·
математическое обоснование.
3.2. Зависимости
метода начальных
параметров. Рассмотрим такое
загружение балки, которому
Рнс. 12.74. Представление распределенной Рис. 12.75. Представление
нагрузки при наличии двух участков на прогибов при наличии Двух
балке: а) нагрузка на первом участке; участков,
б) представление нагрузки на втором
участке как суммы нагрузки, продолженной по
закону первого участка и дополнительной
нагрузки.
соответствует два участка (рис. 12.74, а), вследствие чего имеются
два уравнения
.IV
ΕΙχΌι = qyl, EIX = v2 = q,J2
(12.129)
Представим прогиб и интенсивность нагрузки на втором участке
следующим образом (рис. 12.75):
»2 = t;l + tW2. Яи2=Яи1 + Яу.Лоп,2· (12.130).
*) В теории линейных обыкновенных дифференциальных уравнений с
постоянными коэффициентами такое построение решения известно под названием.
метода Коши. Исторически, однако, получилось так, что в сопротивлении
материалов тот Hie по существу метод был разработан на основе механических
идей. В создании метода в такой трактовке принял участие ряд ученых, соеди
них были А- Клебш, И. Г. Бубнов, Н. П. Пузыревский, А. Н. Крылов,
Н. К· Снитко. Этот метод получил название метода начальных параметров.
Он используется в механике твердых деформируемых тел не только при
интегрировании уравнения изгиба балки, но и в других случаях (см. гл. II, XI),
где ситуация аналогична (наличие участков) —при интегрировании
дифференциальных уравнений изгиба балки на упругом основании, сложного
(продольно-поперечного) изгиба балки и других аналогичных.
В учебной литературе использование метода начальных параметров для
определения перемещения w при осевой деформации и φ при кручении
применил впервые, по-видимому, П. М. Варвак в своем учебном пособии
«Методические разработки по сопротивлению материалов» (Киев. Киевский
автодорожный институт. Кафедра сопротивления материалов, 1974).
Метод Коши подробно обсужден и проиллюстрирован примером в книге
А. П. Филина «Приближенные методы математического анализа, используемые-.
ίι механике твердых деформируемых тел» (Л., Стройиздат, 1971),
'216
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Например, для случая, изображенйого на рис. 12.74, а,
Яу1 = Яо ( 1— — J, <7t/2 = 0; qy, Ron, ъ = Яуг—Яу\ = — <7о (1 — —
На втором участке показаны: нагрузка qyi, определенная той же функцией,
которая задает нагрузку на первом участке, и нагрузка qy, доп, 2. прибавление
которой к qyi на втором участке создает qyi.
Подстановка (12.130)1р2 в (12.129)2 дает
ΕΙχ^ι + νΆ0Π,2Υν = qyl + qy,Ron,2\ (12.131)
вычитая (12.129)! из (12.131) получаем уравнение EIv^n> 2 = Яу,лоп,2>
аналогичное уравнению (12.123), вследствие чего и его интеграл
можно представить в форме, аналогичной интегралу (12.124)
уравнения (12.123). Выражению для и, согласно (12.124),
соответствует начало интегрирования в сечении балки с г = 0; поэтому
в рассматриваемом здесь случае (определение г>Д0Пр2) начало
интегрирования нужно расположить на границе первого и второго
участков, а в качестве начальных параметров принять конечные
приращения (скачки) функций v, $х, MXi Qy на границе
участков, т. е.
^доп, 2 \Z) = »\доп, 2W2l ,доп, 2 ~Г 'доп, 2» (1 2.1 32)
"Wflon. 2 \Z) ~ l^t/, доп, 2 MXt Д0Пр 2 ^х, доп, 2 ^доп, 2J»
^ζι, доп, 2 = Щу, ги доп, 2 '"■*. «ι, Доп, 2 ^*, гх, доп, 2 ^«l, доп, 21» ... . „,
(2 2 2 (12.133,1
J Я У, ДОП, 2 "2 J J ?</, ДОП, 2 "2 "2
2, 2, 2j
2 2 Ζ Ζ Ζ Ζ Ζ
Ж" ί ί ί ^доп·2 йг ^г rf2: "^7 ί ί J J ^доп·2 d2: d2 rf2 dz
Z\ 2j 2i
1
(z-zi)
(z-2l)8
2EIX
(2-2i)>
fiP/
2i 2j 2i 2i
0 0 0
1 0 0
(z-zi) j 0
£/,
(2-Zi)2 - , .
op/ (г zi) l
*^доп, 2
Аналогично (12.129)1>2 можно представить функции на третьем и
на любом ί-м участке
Щ = Щ+ ^доп, 3 = »1 + Идоп. 2 + »Д0П, 3*.
ί'ί/, доп, 3 Яу1 ~Г" *?(/, доп, 2 ~Г" *7t/, доп, 3»
ί i
Vi = v1Jt Σ идоп,А» <7ί/ί = <7ί/ι+ Σ Яу,Лоп,к (t = 2, 3, ..., m).
ft=2 ft=2
§ I2.I3J
ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИБА БАЛКИ
217
При этом получается формула для wRonj(z), аналогичная (12.132),.
с заменой в ней индекса 2 на t; аналогично заменяются индексы.
2 на ί и в выражениях матрицы КДОп.2 и векторов w2l)florip2,
I,
■доп, 2·
В последнем из указанных векторов и в матрицах КДОп,2 и
\ν*,,Λοπ,2 вместо гх должна быть координата 2/_χ сечения на
границе участков (t номерами i — 1 и ί.
В таблице 12.7 приведена информация, показывающая чему
равны дополнительные члены в функциях Qy, Мх, &х и ν на
участке z^zk-lt т. е. чему равны Qy,aolilit> MXiRon,k, $х1Л01и k>
νд0П>А, если в сечении z = zk-.x имеет место один из факторов Ру,
wlx't α, а. В частности показано, в каких функциях (из числа Qy,.
Mxt ΰχ, ν) возникают скачки при z = zk^lr вследствие наличия
отмеченных факторов, а также показано чему равны эти скачки
Qy-Zk-V доп' *' X,zk-V Д°п· *' *· "k-V догь *' V*k-V ДО11'*'
Разумеется, возможны случаи, при которых на границе
участков имеются все указанные причины, или любые комбинации
из этих причин, создающих деление балки на участки.
Окончательно для участка i вектор у/(г) выражается
формулой
с
W (2) = KW (0) + I + Σ (Кдоп. /,W*A_1( доп. ft + 1доп. *)· О 2> l 34>
/г =2
Матрица К в (12.134) имеет такой же вид, как и в (12.127),
а матрица Кдоп, к выражается следующей формулой:
*^доп, к
1
Z — Zk-l
2EIX
(z — Zk-ύ3
6£/,
0
1
EIX
(z-Zfe-i)2
2E1X
0
0
1 0
ζ — ζΛ_ι 1
(12.135)
Ρ
3.3. Примеры. Пример 12.19. Найти вектор ν/(ζ) для балки,
изображенной вместе с нагрузкой на рис. 12.76.
Решение. Матрицы К и Кдоп, k имеют
стандартный вид (см. (12.127)3 и (12.135)).
Остальные матрицы, входящие в
формулу для w(z) (формула (12.134)), имеют
следующий вид:
УА
О
'/'/.
y(0) = {Qyo 0 Ъх0 0},
™г1.яоп,2 = {-Р 0 0 0};
1 = {0 0 0 0},
1доп,2={0 0 0 0}, zx = l[2.
У1
{
I
1
я&
Рис. 12.76. К. примеру 12.19.
'218
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Начальные параметры QyQ и ϋ·χ0 найдем и# условия1) на правом конце
«балки
υ(1)
Отсюда
Qyo
ζ 0
г3
6ΕΛ
6EL
\Qyo
|θ*ο
+
2 О
Ζ3
-Χ
г —
/
кг
6£/
г —
X
— Р
О
121·
1_
2
/ \*
2 ;
2~т; _^
6EIX Z 2
— Р|
о
Р_
2
Р1*
Ш1Х
Наконец, используя (12.134), получаем искомый вектор w (z)
w(z) =
т+
2
Ρ/2
2 +
//2
//2
(-^)
<->К)
16£/^ 4Б/*
Ρ/2 ρ
■ζ2 +
16£Λ
12£/,
?8_
1/2 2ΕΙΧ
(-Ρ)
1/2 6£/д
/ \2
Пример 12.20. Найти вектор w(z) для балки, изображенной вместе с на;
грузкой на рис. 12.77.
W-
Mi
У
XT
ч
лгШ<№
а
< =н
Ч.
Рис. 12.77. К примеру 12.20.
х) Квадратные матрицы (2χ2) в этом условии образованы из элементов
соответственно матриц К и КДоп, л> лежащих на пересечении строк, соответч
сгзующих Мх{1) и υ (/), и столбцов, соответствующих Qy0 (Qy2i, лОП, 2) и
«лсо (yxzt, доп. г)*.
§ 12.13]
ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИБА БАЛКИ
219'
Решение. Вектор w (ζ) находим по формуле (12.1 4). Кроме стандартных:,
матриц К и Кдоп,k> B ЭТУ формулу входят векторы, имеющие следующий вид:.
w(0) = {Qil0
w,z доп, з={— Pi
(2-23)а
ι q ί
ι ?* /Г (г-г,)' (г4-г3)2
•доп, δ— Zi-zs \1 2 -г 2
(2-Zs)4 (Z4-Z3)41
М*0
0
2 0
з)2
0 0},
0 0},
о}; 1 =
(г-г,)»
wv
WV
ДОП, 2 {"
ДОП, 4= {"
= 'ДОП. 2 = 'ДОП, 3
1
{г-г-бУ·
Щ
0 0
= {0
1
0 0},
0},
0 0
(г-
0},
-2з)5
][-
EL
24
(г-г3)3 | "(г4-
120
2з)3
)>
— ί-
г/* L
£/« I 24
Здесь учтено, что
24
<7доп, 5 = — Я* И
Я/
Ζ — Ζ4
'/* L
б ■ б
(г — г3)6. (г4—г3)5
120
120
]}·
= -</'
ζ—ζ3
ζ4 — ζ3 / ' ζ4 — ^3
Начальные параметры {Qyo Mx0} определяем из условия
Qy(t)
Mx(l)
01
1
Qyo
мх0
+
Zi — Zs
+
2»! +
1
I — z2
-(1/2) -il-zzf
— (1/6).(Z —2fs)»
+
(-*Ί) +
1 С
/—Z4 ]
—3>l2
q* II [- (1/2) (/-z3)2 + (l/2) (z4-z3)2I
Z4-Z3 I [- (1/6) (/-z8)3+(l/6) (Z4-Z3)3]
После отыскания из этого условия столбца {Qy0 Λί.*ο} имеем все данные
для определения w (ζ) из (12.134). В приведенных выше граничных условиях
в матрицах КДОп,й использованы лишь те блоки, построенные из элементов
первых двух строк (соответствующих Qy (ζ) и Мх (ζ)), которые дают
ненулевые результаты.
3.4. Общая формула для частного-решения.
Найдем выражение для vROnik, вызванного qy,Ron,k' Для этого
воспользуемся решением для vRon> k от сосредоточенной силы,
рассматривая распределенную нагрузку как множество элементарных
Рис. 12.78. Представление частного решения в форме, в которой эффект элементарной
силы от распределенной нагрузки трактуется как эффект сосредоточенной силы.
сосредоточенных сил и пользуясь сложением эффектов действия
каждой из них на основании принципа независимости действия сил.
Пусть на некотором участке действует произвольная
добавочная нагрузка ду, лоа (рис. 12.78), выделим элементарную нагрузку
'220
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Яу, доп άζ и определим добавочный прогиб от этой силы в сечении z
, Я у, коп «ζ , „о
^доп= 6£77"(2~ζ)·
Полный добавочный прогиб, т. е. добавочный прогиб от всей
нагрузки, приложенный на участке от гг до ζ определится по
формуле (общая формула для определения частного решения ичр)
2 2
ν4.Ρ = νΆΟΠ=^άνΆοη = -^^^(ζ-ζ)4ζ. (12.136)
2, 2,
3.5. Математическое обоснованиеметода
начальных параметров. Существенными в построении решения
методом начальных параметров являются два обстоятельства:
а) условия, которым должна удовлетворять система частных
решений, из коих конструируется общее решение однородного
уравнения, соответствующего рассматриваемому, и б) вид
используемого частного решения неоднородного- уравнения. Остановимся
на обоих этих вопросах на примере решенного выше уравнения
(12.123).
Выше говорилось о том, что в формуле для ν (12.124) первые
четыре члена могут рассматриваться как общее решение
однородного уравнения, соответствующего уравнению (12.123),
сконструированное из четырех линейно независимых частных решений
. z гг г3
' 1!"' ~W' "ЗГ*
Эта система частных решений является системой с единичной
матрицей. Так называется система частных решений, которая
удовлетворяет условиям, показанным в табл. 12.8.
Таблица 12.8
f(0) = 1
ua,=z
f(2,=z2/2
V-3,=Z3/6
ο(0)
1
0
0
0
ν' (0)
0
1
0
0
Ό" (0)
0
0
1
0
υ'" (0)
0
0
0
1
Если решается любое другое обыкновенное неоднородное п-го
порядка дифференциальное уравнение с постоянными
коэффициентами, то все остается совершенно аналогичным, только другой
становится система линейно независимых частных решений с
единичной матрицей.
3 12.13] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИБА БАЛКИ 221
Отметим, что систему линейно независимых частных решений
с единичной матрицей всегда можно построить, исходя из любой
произвольной системы линейно независимых частных решенийг).
Второй существенный факт состоит в том, что можно построить
такое частное решение неоднородного дифференциального
уравнения
t(v) = ^r + a1^[ + ... + anv = f(z), (12.137)
которое обладает тем свойством, что сам этот интеграл и первые
л — 1 его производные обращаются в нуль при г = 0.
Такой частный интеграл имеет вид
ν4^ = \ν(η^{ζ-ζ)ί(ζ)άζ. (12.138)
о
В случае уравнения (12.123) интеграл (12.138) записывается
так: »ч. ρ = J щ-: , поскольку »(я_1} = υ8 = -ψ и / (ζ) =
о
Я у {ζ)
- Е1Х *
Имея в виду свойство общего решения v = C0V(Q)-\-C1vil)-{-
+ С2и(2) -f C3u(3) однородного дифференциального уравнения,
соответствующего уравнению (12.123), отмеченное в табл. 12.8, а также
свойство частного решения (12.138) обращаться вместе со своими
л—1 производными (п — 4) в нуль при 2 = 0, получаем
механическую трактовку каждой из постоянных интегрирования.
Действительно, имея функцию υ и первые ее три производные
» = Ww + Ci»u) + c2v(2) + ед3) + »ч. р,
ν' = cov[0) + wId + c2v{2) +c3v{3) + V4. p,
V" = C0V№(o) + Ciufi) + C2U("2) + CSV'(Z) + f5. p.
»'" = <V<6> + Ci»(i) + C2V{2) + <V<8> + iCp,
заключаем, что co = t;(0), с1 = и'(0), са = »"(0), c8 = t;"'(0).
» = »(0)0(о) + »'(0)0(1) + ^(0)0(2, + »'"'(0)о(8, + оч.р. (12.139)
Из четырех начальных параметров два в большинстве случаев
известны2). Если же имеется несколько участков, то, вводя
понятия νΛ0Π и <7у,доп и повторяя все отмеченное выше для каждого
L) См., например, В. В. Степанов. Курс дифференциальных
уравнение!, изд. 3-е, М. — Л.: ОНТИ, 1939, гл. V, § 2 (примечание к теореме 5,
стр. 180); изд. 8-е, М.: Физматгиз, 1959.
2) Неизвестными оказываются все четыре начальных параметра, если
в сечении балки с z = 0 имеют место упруго-податливое защемление и упруго-
податливое опирание,
222
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
из участков, а также имея в виду, что в большинстве случаев
все параметры в начале &-го участка
v*k-i· доп' * ' 2=2ft-i'
vz , доп, k ! 2-z. » ···' Uz , доп, fe'z-г. ,
известны1), понимаем, что сопряжение функции и всех ее
производных до (/г—1)-го порядка на границе участков выполняется
автоматически и что число участков не влияет на общее число
параметров, подлежащих определению.
3.6. Случаи, в которых игк_11ЛОП,кфО и (или)
®х, zk_v доп, кФ 0.
Пример 12.21. Для балки, изображенной на рис. 12.79, находящейся под
воздействием равномерно распределенной нагрузки, найти вектор w (ζ).
1
01
ΤΗΐίΐΜΠΠΠΠΜΠ
ч
%
</1
Рис. 12.79. К примеру 12.21. Балка с ползунком (величина скачка в υ заранее не«из«
вестиа).
Решение. Для отыскания w (ζ) используем формулу (12.134). Матрицы К
и Кдоп,2 имеют стандартный вид (12.127)3 и (12.135), остальные матрицы (вект
торы) представляются так:
w(0) = {QJ/0 ММ 0 0}.
w
«и ДОП
qz2 qz3 qz*
qZ ~~ΊΓ 6EIX 24£/,
,2 = {0 0 0 ^,доп,2},
j, 1доп,2={0 0 0 0},
zx = //4.
Параметры Qy0, Мх0 и vZu A0U< 2 найдем из условий
|*(0
\υ(1)
Ρ
I
2ΕΙΧ
I3
6ΕΙΧ
ΕΙΧ
Ι Qyo Ι
Μχθ\
+
ql3
6ΕΙΧ
24ΕΙΧ
ί
+ |
1 "ίι, доп, 2-
011
ο!»
2£/Λ
В результате решения этих уравнении получаем
q±
I Qyo II 4
\\МХ0\\ д?
24
_ ql*
Jzlt доп, 2 48£/JC »
*) Величина o«fe_,, ДОп, fe неизвестна в том случае, когда в сечении z=Zfc_j
расположен ползунок. Величина υ'ζ k неизвестна в случае, если в сече*
нии z=Zk-\ расположен шарнир,
-§ 12.13]
ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИБА БАЛКИ
223
я, наконец,
w(z) =
Qy(*)
Мх(г)
Ρ (2)
1
ζ
О
1
О
о
ζ2
2£/*
"6£/-
ζ2
'2£/,
+
-9Z
_£Ζ«
2
tfZ3
6£/*
^2*
24£/,
+μ
ι
г~т
!Z±L
2£/*
2~т
6£/.
2~Т
£/*
/ \2
ζ~τ
2EL
О
О
2~Т
1
О
о
о
qt*
48£/J
Пример 12.22. Для балки, изображенной на рис. 12.80, находящейся под
воздействием равномерно распределенной нагрузки, найти вектор w(z).
^u
W^
Рис. 12.80. К примеру 12.22. Балка с шарниром (величина скачка в Ъχ заранее ие
известна).
Решение. Решение представляем согласно формуле (12.124). Матрицы К
и К on а стандартны. Матрицы-столбцы w(0), I и 1доп,2 такие же, как в
предыдущем примере, матрица-столбец w 2 имеет следующий вид;
w.
Параметры Qy0, Мх0 и Ъх ги Д0П) 2 найдем из условий
ν (I) I
I*
2£/*
6£/*
/
£/*
/2
\\Qyo Ι 1
II
I qi*
\бЕ1х
ql*
|24£/л:
+
ι ι
1
ζ'τ
д —
wx, zl( доп, 2
2£/.v
Отсюда
IQi/o
29 ,
11 /2
•ft
» ^|2кДОП,2
ql*
~' №EIX »
224
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
и, наконец,
w(z)
Qy(z)
Мх(г)
Qx (ζ)
ν (ζ)
"4
Ζ2
2ΕΙΧ
Ζ=»
6ΕΙΧ
ζ —
0
1
ζ
ΕΙΧ
ζ2
2ΕΙΧ
0
0
1
ζ
0
0
0
1
29
56*
И
112
0
0
ζ —
/ \2
2ΕΙΧ
Ζ"Τ
6£/*
0
1
Ζ~Τ
£/*
-ΤΤο?'2
/_\2
"4
2£/*
+
— ?ζ
qz*
2
tfZ3
6£/*
ί?Ζ4
24£/χ
0
ο
+
Ζ"Τ
ο
ο
168£/*
0
Припер 12.23. Найти вектор {ν Ο Λί Q} для неразрезной двухпролет-
ной (пролеты /t и /2) балки постоянного поперечного сечения с изгибной
жесткостью EI, опирающейся на шарнирные опоры, из которых одна
неподвижна. Балка загружена в левом пролете равномерно распределенной
нагрузкой интенсивности q на участке, левый и правый концы которого находятся
па расстояниях соответственно а и Ь от крайней левой опоры (а^О, b sc /х);
в правом пролете к балке приложены две сосредоточенные силы Р1 и Р2
(точки приложения их находятся от крайней левой опоры балки соответственно
на расстояниях end).
Решение. Свяжем с балкой систему координатных осей с началом,
совпадающим с центром шарнира крайней левой опоры, ось ζ направим вдоль оси
балки слева направо и ось у вниз. Для решения применим метод начальных
параметров. Поскольку начало координат совмещено с центром крайней левой
шарнирной опоры ν0=0, М0=0; тогда формула для искомого вектора
приобретает вид
ν
Μ
Q
ζ3
6£/
1 —
0
ο
2ΕΙ
ζ
1
\Щ
+ ΙΙα<7
(ζ-α)*
24£/
(ζ —α)3
6£/
(ζ —α)*
+IL R
2
-(ζ-α)
(z-k)3
6£/
(ζ-Ι ι)2
2ΕΙ
(ζ-ω
1
-hi
{ζ-by
24£/
(ζ-6)3
6£/
(ζ —6)2
llc^i
2
-(ζ -b)
{z — cf
+
6£/
{z — cf
2ΕΙ
(ζ-с)
1
-llrf^
(z — d)*
ЬЕ1
{z — dy
2EI
(z-d)
1
§ 12.14] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ИЗГИБА БАЛКИ -25
Неизвестные начальные параметры ϋ0 и Q0, а также неизвестную
реакцию R промежуточной опоры найдем из условий
v\z = ll = 0, v\z = li + h = 0, Μ\ζ = 1ι + Ιΐ = 0.
В развернутом виде эти условия получаются из приведенной выше
формулы; для этого используем дважды первую строку (при z=k и z = li-\-l2),
и третью строку (при ζ~=/ι + /2). В результате получим
к ~
к + к -
О
'1
6EI
(/ι+ω3
/l+/2
0
'2
6EI
к
%
Qo
R
"M[(ll"fl)4"(/l_i)41
_24l7[(/l+/2_a) -(/i+/2-6)J 617 6£7
-S-[(/l + /2-fl)2-(/l+/2-6)2] + Pl(/l+/2-C) + /52(/l + /2-d)
Решение этого матричного уравнения имеет вид
θ0
Qo
R
=
α11 α12 ^13
α21 α22 α23
fl31 α32 α33
9
Ρχ
ρ*
где
au=» —
1
48/i(/i + /a)£/
[_2/}(6>_β2)(3/1 + 4/ί) +
<2l2 = —
%з = —
M/l + '2-C)
+ 8/χ (6з_аз) (/1 + /2)_(64_а4) (3/, + 2/г)],
12/2
^4y^[/i-(/1 + /2-c)2]>
^±Vz|7[ZI_ft+/i_d)4:
^"δ/ϊ^+ω[8/? {b~a) (/ί+/2)_2/ι (62_α2) (^ι+^ί+ί*4-«4)ь
Αη^ο/^/'ΓΛ [(*i + f»-c)a-/il·
fl23;
2/1/2 (/1+/2)
k + h — d
2/1/2 (/1 +/2)
1
[(/i + /2_d)2-/l];
Сз1 = 8Ж [2/? (&2 ~ Q2) + Ulh (62 ~ α2) ~(Μ ~ α4)]'
^2 = Нг7?±[2с (/i + /2)-/?-C2],
Q33:
/1+/2 — d
2/,/*
& А. П. Филин, т. II
\2d{h + h)-l\-d*\.
226 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. XII
Подставляя найденный вектор {00 Qol и выражение для R в формулу для
искомого вектора, получим окончательные формулы для ν, ϋ, Μ и Q.
В качестве иллюстрации укажем, что в случае, если /ι=4 м, 12 = 6 м,
а=1 м, 6 = 3 м, с=6 м, d = 8 м, <7 = 2 Т/м, Ρι = 4 Τ, Ρ2=6 Τ, использова-
44 1 31
ние приведенных выше формул позволяет найти Ф0 = — т? ъ~, Ρα&·, Qo = tkx Τ,
45 Ы 120
fifiQ
#=-— Т. (При отыскании численного значения ϋ0 величина Ε должна
выражаться в Т/м2, а / — в ж4, поскольку при отыскании численного
коэффициента также использовались единицы измерения м и Т.)
В ранее приведенных примерах расчета однопролетных балок было
показано, что, используя метод начальных параметров, можно находить вектор
{v ft M Q} с одинаковой степенью сложности как для статически
определимых, так и для статически неопределимых балок. Рассмотренный пример
проиллюстрировал возможность отыскания методом начальных параметров
указанного выше вектора и для неоднопролетных статически неопределимых
балок. Однако при этом решение оказывается более трудоемким, чем при
комбинированном использовании метода сил для раскрытия статической
неопределимости (применительно к условиям нашего примера величина R
определилась бы из одного самостоятельного уравнения) и метода начальных
параметров для отыскания вектора {ν ■& Μ Q}, когда статическая неопределимость
уже раскрыта (начальные параметры при этом находятся из системы двух
уравнений с двумя неизвестными).
Наконец, заметим, что независимо от того, использован ли метод начальных
параметров в чистом виде или в комбинации с методом сил, в случае
неоднопролетных балок при вычислениях возникают малые разности близких по
значению величин, что связано либо с потерей точности, либо с необходимостью
сохранения при вычислениях большего, чем при использовании других
методов, числа значащих цифр.
§ 12.14. Интегрирование уравнения изгиба
в случае балки переменной вдоль длины жесткости
Дифференциальное уравнение изгиба балки в случае
жесткости, изменяющейся по ее длине, имеет вид
[EIxv"]' = qir
Это уравнение после двукратного интегрирования, выполненного
последовательно, дает
{EIxvn)' = -Qy = -QyQ + \qydzt (12.140)
о
г г
EIxv" = — Mx = — Mxo-Qy0z + ^qydzdz. (12.141)
о о
Дальнейшее же интегрирование выполним уже после деления
обеих частей равенства (12.141) на Е1Х
?,"__^L ν>-ϋ =$ _{M±dz
υ-—ΕΙχ, ν -vx-vXQ j ΕΙχαζ,
о
г г
v^v0 + $XQz- J §jfxdzdz-
(12.142)
§ 12.14] ИЗГИБ БАЛОК ПЕРЕМЕННОЙ ВДОЛЬ ОСИ ЖЕСТКОСТИ 227
Отыскание интегралов в формулах (12.142)2;3 в зависимости от
вида подынтегральной функции может быть выполнено либо
в замкнутой форме, либо по одной из приближенных формул
квадратур.
Пример 12.24. Определить перемещения в балке равного сопротивления,,
рассмотренной в примере 12.12 (первый вариант балки).
Решение. В рассматриваемом случае
£/x = £*sfjnpij_f Мх = -Рг, Qyo^-P, Мх0 = 0, qy = 0.
Таким образом, в соответствии с (12.140), (12.141), (12.142)2>3 Qi/= —Рк
Mx = —Pz,
г
o*=ox0-J
12(-Pz)/dz = A ,_12_«*
Eh3zh "" ~r£/i36 '
па zomax L.n υmax
г ζ
12P/
ο=ο0 + *χοζ— 1 \ -jjj-dzdz=v0-\-$x(iz
***m.x 2 «
о о
Вид функций Мх и ΕΙ χ оказался таким, что их отношение представляет собой
постоянную величину, вследствие чего интегрирование получается предельно
простым. Начальные параметры $х0 и ν0 найдем из условий
0*1.-1=0, Ъх0+-££—=0, *Λ 12Ρ/2 -
Eh*bmax M Eh*bmax
I П ι^/ι 6Р/3 П 12Р/3 6Р/3 6Р/3
max " "max "max " "max
Таким образом,
Ρ/2 . Plz
ъх=-
EI 'ΕΙ *
'*max *max
'jcmax
ι Pl* Pl* ■ - ι - _
'«max **max "*max "jcmax
В балке равного сопротивления прогиб в 1,5 раза больше, чем в
консольной балке постоянного сечения, такого же как и максимальное по размерам
сечение в балке равного сопротивления
_ Р/з _ Р/з
umax op i op/
ι.πιχ ocixmax
Таким образом, при той же прочности, как и балка
постоянного сечения, балка равного сопротивления значительно более
гибка. Это ее свойство используется в специальных элементах,
носящих название рессор. Такие элементы призваны, сохраняя
прочность, за счет большой деформируемости уменьшать эффект
ударных и иных динамических воздействий.
8*
228
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Конструктивно балку равного сопротивления с небольшой
постоянной высотой сечения, используемую в качестве рессоры,
оформляют так, чтобы габаритные размеры в плане (ширина) не
были бы очень большими. В связи с этим балку разрезают на по-
δ) г)
Рис. 12.81. Балка равного сопротивления при малой постоянной высоте (рессора):
а) план с указанием границ полосок, на которые разрезается балка; б) план и фасад при
этажном расположении полосок, составляющих балку; в) фасад рессоры; г) рессора
(аксонометрическое изображение).
лосы одинаковой ширины и располагают их этажно, не соединяя
один ярус с другим. Схематически это выглядит так, как показано
на рис. 12.81, б, в. На рис. 12.81, г представлена аксонометрия
конструкции рессоры.
Пример 12.25г). Определить прогибы судна относительно прямой,
соединяющей концы его оси, при следующих данных. Длина судна L = 80 м.
Значения изгибающего момента и момента инерции площадей поперечных сечений
эквивалентного бруса2) приведены в табл. 12.9.
Таблица 12.9
z/L
Мх {Тм)
1х(м*)
0
0
0,45
0,1
—500
0,50
0.2
—1700
0,67
0.3
-2600
0,82
0.4
—3100
0,85
0,5
—3200
0,85
0.6
—3100
0,85
0.7
—2500
0,79
0,8
-1400
0,70
0,9
—400
0,59
1.0
0
0,50
Решение. Определим постоянные г>0 и $хо, входящие в интеграл (12.142)3,
пользуясь граничными условиями задачи. Так как прогиб отсчитывается от
J) Взят из книги: Филин А- П., Соколова А. С, Строительная
механика корабля, ч. 1, «Речной транспорт», 1957.
2) Так называется некоторая условная балка, являющаяся расчетной
схемой корпуса корабля в расчетах на прочность при рассмотрении общего его
изгиба.
§ 12.14] ИЗГИБ БАЛОК ПЕРЕМЕННОЙ ВДОЛЬ ОСИ ЖЕСТКОСТИ 229
-прямой, соединяющей концы искривленной оси судна, то на обоих концах
прогиб отсутствует. Следовательно,
L z L г
0 0 U О
0 О 0 0
Применим для численного интегрирования правило трапеций, используя прием
определения интегралов с переменным верхним пределом, принятый в
судостроении. Расчет сводим в табл. 12.10, где
п Мхь' п 1ХЪ' 10 й М' L Z Ш сф-1 Ш ж2*
Поясним упомянутый выше прием интегрирования. Напишем формулу трапе-
L
ции для ингеграла 1 -~-йг, она применительно к нашему случаю имеет сле-
о
дующий вид:
СМ*. ΔΙ 1 /Мх0 , η Мх, , „ Мх* . , пМх„ . Мл
о
1* л, ~ AL ! fM*<> 4-2 M*i д.9 М*2 л. -L9 М*» _l м*"\
Ιχ Δ С \ Ιχο Ιχΐ 1χ·2 1χ9 1ХЩ /
Выполним некоторые преобразования. Во-первых, вынесем за скобки
отношение Мхъ11хъ и учтем обозначения для тп = Μхп: Μхь и in = IXn:/xn,
во-вторых, разобьем на слагаемые члены, содержащие коэффициенты 2, тогда
получим
-+("+")+0^)]·
Если теперь представить, что требуется вычислить интеграл
)ΕΓχάζ>
о
то все получится аналогично. Однако, так как верхний предел теперь не L,
a z, внутри квадратных скобок сохраняются лишь те выражения в круглых
скобках, которые соответствуют отрезку [0, ζ). Таким образом, при
увеличении ζ постепенно число учитываемых выражений в круглых скобках
увеличивается; при z = L учитываются все выражения, содержащиеся в интеграле
с верхним пределом L. Выражение в круглых скобках представляет собой
сумму ординат трапеции, номер которой такой же, как и индекс у второго
слагаемого в этом выражении.
Таким образом, каждое число в столбце (4) в /-й строке равно числу
в (/ — 1)-й строке того же столбца (это сумма выражений во всех предыдущих
круглых скобках) плюс сумма чисел в строках / — 1 и / столбца (3)—это
230
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. ХГГ
№
сечення
2
Τ
Интегральная
сумма
(3)
Интегральная
сумма
(4)
(2). 128,548
Таблица 12.10
1
(6) - (5)
X
= (7)Х
Мхъ (ΔΖ.)*
7д-54£
1
о
1
2
3
4
5
б
7
8
9
10
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
0
0,265
0,676
0,840
0,970
1,000
0,970
0,840
0,532
0,180
0
О
0,265
1,206
2,722
4,532
6,502
8,472
10,282
11,654
12,366
12,546
О
0,265
1,736
5,664
12,918
23,952
38,926
57,680
79,616
103,636
128,548
0
12,855
25,710
38,565
51,420
64,274
77,129
89,984
102,839
115,694
128,548
0
12,590
23,974
32,901
38,502
40,322
38,203
32,304
23,223
12,058
0
0
—0,04
—0,07
—0,10
—0,12
—0,12
—0,11
—0,10
—0,07
—0,04
0
выражение в круглых скобках, соответствующее /'-му участку. Так^как
интегрировать приходится два раза, операция повторяется, но на сей раз роль
столбца (3), которая имелась при первом интегрировании, играет столбец (4),
а роль столбца (4) играет столбец (5). Кроме того, при втором
интегрировании перед выражением в квадратных скобках появляется еще раз множитель
AL/2. В столбце (6) помещены приближенные значения выражения
1
ΔΖΛ»
2)
а в столбце (5) —выражения
1 Μ
хъ
L г
г ССМх_
ΐ J J EIX
dz dz,
Ε Ι
ХЬ
I
о о
г г
И&
dz dz.
/ΔΖλ* 1 Мхь
Вычитая из столбца (6) столбец (5) находим в столбце (7) выражение
L г
Мх
1
ΔΙΝ» 1 Mxb [L
2J Ε 1ХЬ
oo oo /
тогда, умножая столбец (7) на (-»-) -w-j—-, находим в столбце (8) прибли-
\ ζ / с ] хъ
женные выражения для ν, точные значения которого определяются по
формуле (12.143).
К вопросу интегрирования линейных дифференциальных уравнений с пере>>
менными коэффициентами мы вернемся в § 12.19,
§ 12.15]
ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ
231
§ 12.15. Изгиб балок, лежащих на сплошном
упругом основании х)
1. Вводные замечания. Балкой, лежащей на сплошном
упругом основании,, называется такая балка, которая опирается по
всей своей длине на упругую среду, сопротивляющуюся
перемещениям, вызванным изгибом балки.
Балки на упругом основании встречаются в технике очень
часто. К числу примеров таких конструкций относятся: элементы
верхнего строения железнодорожного пути (рельсы и шпалы),
ленточные фундаменты зданий, корпуса кораблей. Расчетная схема
в виде балки на упругом основании ис-
пользуется в расчетах многих важных ΰ)
конструкций; например, осесимметрично
деформированных оболочек вращения, /ν-
балочных перекрытий. ^
На рисунках будем изображать бал- ζ
ку на упругом основании сплошной ά -
линией, а сплошное упругое основание л
под ней штрихами (рис. 12.82, α). δ>
Балки на сплошном упругом осно- Рис 12-82ι Балка на сплошном
ВаНИИ. КРОМе ЭТОГО ОСНОВаНИЯ, МОГУТ упругом основании: а) балка на
» г J сплошном упругом основании
ОПИраТЬСЯ еще И На ДИСКреТНЫе ОПОрЫ — без опор; б) балки на сплошном
жесткие и (или) упругоподатливые упругом °™ованнн н °поРа*.
{рис. 12.82, б). Нагрузка, действующая
на балку, уравновешивается и реакциями опор и реактивным
сопротивлением сплошного упругого основания.
2. Свойства упругого основания. Интенсивность реакций
упругого основания τ зависит от механических свойств основания, от
прогиба балки и от ширины опорной площадки балки.
Существует большое число различных схем сплошного упругого
основания; в соответствии с каждой из них создана теория балок на
упругом основании. Обзор этих схем и соответствующих им
теорий выходит за пределы предмета настоящей книги. Многие из
схем и теорий, построенные применительно к грунтам,
рассматриваются в механике грунтов и в курсе оснований и
фундаментов.
Наиболее простой и вместе с тем в ряде случаев достаточно
точной является гипотеза, выдвинутая Э. Винклером. Для
грунтов эта гипотеза не является идеальной, ко тем не менее общий
характер распределения усилий в балке на упругом основании
она позволяет уловить. Сущность этой гипотезы состоит в том,
1) При изложении материала настоящего параграфа использована книга:
Филин А. П., Соколова С. А, Строительная механика корабля, ч. 1,=»
Речной транспорт, 1957»
232
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
что реакция упругого основания считается пропорциональной
просадке в рассматриваемой точке1) (рис. 12.83)
г (г) = kv (г).
Коэффициент пропорциональности k в этой зависимости называется
коэффициентом погонной жесткости упругого основания и имеет
Рнс. 12.83. Реактивное давление на балку со стороны сплошного упругого основания,
согласно гипотезе Винклера: а) балка на сплошном упругом основании; б) балка на
сплошном упругом основании и опорах.
размерность F/L2. Винклерово упругое основание можно
представить как бесконечное множество независимых упруго
проседающих опор (пружин с одинаковыми жесткостными характеристи-
Рнс. 12.84. Механическая модель Винклерова упругого основания: а) самостоятельно
деформирующиеся пружинки с одинаковыми линейными характеристиками; б)
распределение усилий в пружинах, пропорциональное просадкам.
ками), расположенных по всей опорной поверхности балки (рис.
12.84). Если ширина балки равна Ь, то k можно представить так:
k = bkQ.
!) Гипотеза Винклера предусматривает наличие двухсторонних связей
между, балкой и основанием. Для случая односторонних связей аналогичная
гипотеза была предложена задолго до Винклера академиком Российской
академии наук Н. И. Фуссом.
Заметим, что гипотеза Фусса является идеальной для плавающем призма·
тической балки.
Жизни и деятельности Н. И. Фусса (1755—1826) посвящена книга:
Лысенко В. И- Николай Иванович Фусс—Наука. 1975,
§ 12.15] ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ 233
Здесь kQ —коэффициент жесткости упругого основания
(коэффициент жесткости постели), имеющий размерность F/L3. Если b —
функция от г, то функцией от г становится и k. Такое упругое
основание называется основанием переменной жесткости. Мы будем
рассматривать/случай постоянного по длине балки значения /г1)
(основание постоянной жесткости).
Конструкцией, родственной балке на упругом основании,
является балка на упруго проседающих опорах, расстояние между
которыми намного меньше
общей длины балки.
Примерами могут служить: рельс,
опирающийся на шпалы (рис.
12.85), балка, работающая
в составе перекрытия, где
количество пересекаемых ею
балок велико, и другие. Для
упрощения расчета упругие
опоры таких балок в
расчетной схеме заменяют
сплошным упругим основанием с
коэффициентом погонной
жесткости k — c/a, где с —
коэффициент жесткости опоры
(сила, необходимая для
просадки опоры на линейную единицу), а— расстояние между опорами.
Оценка погрешности, возникающей от такой схематизации,
выполненная И. Г. Бубновым, показала, что абсолютная ошибка
при определении изгибающих моментов имеет величину порядка
га2, а сам изгибающий момент — величину порядка ή2.
Следовательно, относительная погрешность оказывается величиной порядка
а2/12 — 1/п2, где п — число участков балки. Даже при трех
промежуточных опорах, т. е. при η = 4, погрешность получается порядка
всего 6%.
3. Дифференциальное уравнение изгиба балки на сплошном
упругом винклеровом основании. Будем исходить из
дифференциального уравнения изгиба балки постоянного сечения
EIxu™ = qy, (12.144)
!) Классической иллюстрацией балки на фуссовом основании переменной
жесткости является плавающее судно. Интенсивность реакции в этом случае
г = уи>. Здесь у— удельный вес жидкости, ω — площадь погруженной части
шпангаута, являющаяся функцией осадки Т.
Случай прямостеыного судна с ватерлинией в форме прямоугольника,
когда г—yBT=kT, соответствует случаю балки на фуссовом упругом
основании постоянной жесткости; в общем случае при наличии развала бортов и
заострений оконечностей В становится функцией координаты по длине судна и
меняется с изменением осадки, поэтому зависимость между г и Τ оказывается
более сложной, хотя основание остается фуссовым.
Рнс. 12.85. Примеры балок с дискретно
расположенными упруго проседающими опорами,
которые приближенно можно рассматривать
как балку на сплошном упругом основании:
а) железнодорожный рельс на шпалах; б) балка
перекрытия, опирающаяся на ряд балок
перпендикулярного направления.
234
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
однако, имея в виду использовать это уравнение для расчета
балки на упругом основании и учитывая, что на балку действует
не только распределенная внешняя нагрузка, но и
распределенные силы реакции сплошного упругого основания, необходимо
вместо qy подставить разность qy — r — qy — kv. При этом
предполагается, что положительное направление реактивных сил
противоположно положительному направлению нагрузки. Тогда вместо
уравнения (12.144) получаем
EIxvlv = qy-kv, или EIxvlv + kv = qy. (12.145)
Если связи между балкой и сплошным упругим основанием
односторонние, то задача становится нелинейно й. Расчет при этом
приходится вести методом последовательных
приближений. В нулевом приближении задаемся длиной и
расположением участков, на протяжении которых балка перестает иметь
контакт с основанием, далее решается задача и выявляются
области, в пределах которых балка имеет перемещения не в сторону
основания. Полученная картина принимается в качестве исходной
в расчете в первом приближении. Далее процесс продолжается
до тех пор, пока области отсутствия контакта балки с основанием
в двух соседних приближениях не окажутся практически
совпадающими.
4. Четыре формы интеграла дифференциального уравнения
изгиба балки на сплошном винклеровом упругом основании в
случае одного участка в пределах балки. Пусть вся длина балки
составляет один участок.
Уравнение (12.145)^ является линейным обыкновенным
неоднородным дифференциальным уравнением с постоянными
коэффициентами четвертого порядка. Общий интеграл такого уравнения
в силу его линейности складывается из общего интеграла
соответствующего однородного уравнения
EIxO™ + kv = Q (12.146)
и какого-либо частного решения Неоднородного уравнения (12.145)2.
Общее решение однородного уравнения (12.146) вследствие
того, что порядок его четвертый, состоит из суммы четырех линейно
независимых частных решений этого уравнения, которые примем
в виде
Ό = Αέν. (12.147)
Подставив (12.147) в (12.146), получим после деления на Ае^фО
следующее характеристическое уравнение:
Е1хц* + к = 0;
$ 12.15] ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ 235
разделив оба члена этого уравнения на Е1Х и введя обозначение
α = γ^ίι/(4ΕΙχ), получим характеристическое уравнение в
следующей форме:
η4 + 4α4 = 0, η4 = —4α4.
Применив тригонометрическую форму изображения минус единицы
как частного случая комплексного числа, получим
η4 = 4α4 [cos (1 + 2λ) π + i sin (1 + 2λ) π]. (12.148)
Извлечем корень четвертой степени из обеих частей равенства
(12.148) по формуле Муавра
η _ Υ2 a [cos -ί!±£ϋ + i sin Л±*ЙД.].
Придавая п четыре значения: 0, 1» 2, 3, получим следующие четыре
значения η и соответствующие им частные решения уравнения
<12.146):
% = α (1 + 0, Щ = Л ^ Vх*,
η2 = α (—1 + 0, vx = Л 2<raVa*,
η3 = α (—1 - i), »a = A3e-aze~iazt
η4 = α (1 — i), ν3 == Л4еаге_
•,α,ζο-ιαζ
Общий интеграл уравнения (12.145) приобретает вид (решение
в показательной форме)
0 = ич. ρ + е~аг (Л 2е1'аг + Л3<г'"аг) + еаг (Л^1'"* + Л 4<riaz).
Здесь ичр —любое частное решение уравнения (12.145). Имея
в виду соотношение Эйлера, связывающее показательные
функции с тригонометрическими
e±iaz — cos a2 + I sin a2>
переходим к показательно-тригонометрической форме интеграла
ν = ич.ρ + е~аг (^i cos аг + ^2 sin az) + еаг (^з cos аг + £4 sin а·?)·
(12.149)
Здесь Я^Лз + Лз, В2 = (Л2-Л3)*\ 5. = ^ + ^, В^{АХ-А,)и
Используя соотношение, связывающее показательную функцию
с гиперболическими e±az = chazdz$hazt перейдем от (12.149)
к гиперболо-тригонометрической форме интеграла уравнения (12.145)
v — ич. ρ + Cicn az cos аг + C2 ch az sin аг + C3 sh аг cos аг +
+ C4sha2sina2. (12.150)
Здесь C^B^B» C2 = B2-\-Bt, C3 = -Bx-\-Bs, С4 = _В2 + Я4.
Постоянные интегрирования в каждой из трех приведенных выше
форм решения находятся из граничных условий.
236
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Наконец, построим решение методом начальных параметров.
Будем исходить из семейства линейно независимых частных
решений, входящих в (12.150)
v0 = ch аг cos аг, ϋχ — ch аг sin аг,
щ = sh аг cos аг, v3 = sh аг sin аг.
(12.151)
Перейдем от этого семейства к другому, в котором частные
решения представлены как линейные комбинации (12.151):
з
I
Vft=2c«*i (k==0> 1> 2>3)'
(12.152)
удовлетворяющие условию единичной матрицы.
Нам понадобится матрица
V0 Vi V2 V3
ν,
0
β
rtr
П
ϋΐ
~*ψψψ
v's
ц
~*trt
η
vl
—rrr
v,
ν,
νΆ
= V.
Выражения производных от функций vit входящих в ν, легко
получить, имея сами функции (12.151). Этих производных для
сокращения объема книги не показываем и предлагаем читателю
найти их самостоятельно.
Матрица ν при г = 0 имеет вид
vU-o =
1
0
0
0
0
α
0
2аз
0
α
0
—2аз
0
0
2α2
0
(12.153)
Такую матрицу имеет система уравнений относительно
коэффициентов в линейных комбинациях (12.152). Искомые коэффициенты
в (12.152) находим из уравнения
1 0
0 α
0 0
0 2аЗ
0
а
0
-2а3
0
0
2а2
0
II
II
С<)0 с10 с20 с30
Coi cii c2i c3i
с02 с12 с22 С32
СОЗ С13 С2з Сзз
1
0
0
0
0
1
0
0
0 Of
0 0
1 0
0 1
решая которое имеем
с00 с10 с20 с30
Coi cii c2i csi
c02 C12 c22 c32
^03 ^18 ^23 c33
1 0
0 α
0 0
0 2α3
0
α
0
2α3
0
0
2α2
0
V1
/
10 0 0
0 10 0
0 0 10
0 0 0 1
(12.154)
§ 12.15] ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ 237
Матрицу, обратную матрице (12.153), легко найти,
выразив через союзную. Приведем готовый результат
1
0
0"
0
0'
α
0
2α3
0
α
0
—2α3
0
0
2α2
0
-1
0 0
0
1
2α
1
2α
0
ο
ο
0
1
4α3
1
4α3
1
2α2
Подставляя (12.155) в (12.154), получаем
соо сю с2о Сзо
с01 с11 с21 с31
с02 с12 с22 с32
СОЗ с13 с23 с33
0 0 г—
0
1
2а
1
2а
0
0
0
0 —
1
2а2
0
1
4а3
1
4а3
0
1
о
о о
о о
0 0 0
1 0 О
1
о
Придадим (12.152) матричную форму
или
Vo
Vx
v2
v3
1
0
0
0
0
1
2α"
0
1
4α3
Vo
Vi
v2
v3
0 0
1
2c
0
1
4α
- (
г
1
2
,3 (
)
[
X2
)
c00 c01 ^02
C03
c10 cll C]2 Cj3
c20 c21 c22 c23
СЗО с31 С32 С 33
chazcosaz
ch az sin az
sh az cos az
shaz sinaz
=
0
1
1
0
ch az cos az
„— (ch az sin az+ sh az cos az)
1
2a2
1
sh az sin az
j-- (ch az sin az — sh az cos az)
например,
(12.155)
0
1
2a
1
2a
(J
0
0
0 -
1
0
1
4a3
1
4a3
0
(12.156)
238
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Если составить матрицу (эту простую операцию здесь не
показываем)
V0 Vi V2 V3
v'o vi v; v3-
v0ff vr vsff v3"
Vi" У/' V;" V3"
то обнаруживаются дифференциальные зависимости между
функциями V0, Vlf V2 и V3, представленные в нижеприводимой матрице
V =
(12.157)
V =
V0
VJ =- 4α* V3
V^' =_4a4V2
V0'* = —4a*Vi
Vi V2 Vg
vi =v0 v; =Vi vj
v; =-4a*v3 v; =v0 v;
V;" = _4a4V2 v;*' = —4a*V8 Vi"
=v2
■Vo
(12.158)
Легко обнаружить и то, что матрица (12.158) действительно
приобретает вид единичной при г —О
10 0 0
0 10 0
0 0 10
0 0 0 1
VI =
* \г-о —
(12.159)
Полностью аналогично выводу формулы (12.136) построим
отыскание частного решения
°ч.р— $
Е/л
V3 [α (ζ - ζ)] d£.
(12.160)
Это частное решение обладает свойством
^ч. ρ U—о ~ ^ч. ρ \г-о ~ ^ч. ρ \ζ~ο — Уч. ρ \ζ-ο ~ ^· (1 ■£· 1 61)
Теперь построим выражение общего интеграла через функции
V0, Vj, V2, V3, носящие название функций Η. П. Пузыревского1) —
А. Н. Крылова2) по именам ученых впервые и независимо один
от другого предложивших их3),
ν = v4m ρ + D0V0 (ок) + 0iVx (ok) + D2V2 (ok) + АЛ'з (az). (12.162)
Ύ) Пузыревский Нестор Платонович (1861 — 1937) — советский гидротехник,
строитель и ученый.
2) Крылов Алексей Николаевич (1863—1945) —советский ученый,
механик, математик, кораблестроитель.
3) Выше представлены функции А. Н. Крылова (12.156). Функции
Н. П. Пузыревского отличаются от функций А. Н. Крылова лишь
коэффициентами и имеют следующий вид:
V0 = ch az cos az, Vi = —т=- (ch az sin az+sh az cosaz),
Va=shaz sinaz, Va
V'2
1
(ch az sin az — sh az cos аг).
§ 12.15]
ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ
239
Легко обнаружить, что при использовании системы частных
решений с единичной матрицей и частного интеграла в форме (12.160),
удовлетворяющей условиям (12.161), постоянные интегрирования
Ь0, Dlt D2 и D9 имеют смысл начальных параметров. С этой целью
найдем ν', ν" и гГ, учтя дифференциальные зависимости (12.158)
между функциями V0, V\, V2, V3,
υ
О, = v'4.p+ D0 (- 4α4) V3 + ОгV0 + ДМ + ^3V2,
ν — — ■
ν'"' = ■
_Μχ
ΕΙ,
Qu
ΕΙΛ
= ^.P+^o(-4a4)V2 +
+ Dx (- 4α4) V3 + D2V0 + D8Vlf
+ Ц)(-4а*)У1 +
υ,
ч. ρ
(12.163)
+ Dx (- 4α*) V2 + D.2 (- 4a4) V3 + D3V0.
Зависимости (12.162) и (12.163) при z — 0, если учесть (12.159)
и (12.161), принимают вид
ν ._
г-0
г=0
Щ = А>,
<M«-o = <U = A.
AJ
Λ0
£Λ
= £>2,
Q,
£/,
Q
ί/Ο
г-0
ΕΙ,
= Ζλ
(12.164)
Таким образом, окончательно имеем
w(2) = Kw0+I0,
или
w(z) =
Qi/
Μ*
θ,
V0
Vi
v2
Уз
4a4V3
V0
Vi
£/*
V2
4a4£/*V2
4α4£/*ν3
Vi
4a4£/jeV1
4a4£/*V2
—4a4V3
V0
0
4yo
Μ
О
■«о
■«о
00
+
— Ε/ о"'
jc ч.
— ΕΙ ν"
X Ч.
ч. ρ
Уч. ρ
(12.165)
Дифференциальные зависимости между функциями Пузыревского представлены
следующей матрицей, аналогичной матрице (12.158):
V0 Vi V2
V0' =-/2aV3 Vi =/2aV0 V2' =Ϋ2 αΫχ
V-=_2a2V2 V? =— 2a2 V3 V,' = 2a2V0
V;" = —2К2азУ! УГ = -2К2азу2 Vi" = —2l/2a»V8
Этой матрице отвечает не единичная матрица (12.159),
гональная матрица [~1 Ϋ2α 2a2 2|A2a3J. Функции Η. П. Пузыревского
безразмерны, а размерность функции А. Н. Крылова определяется
размерностью входящих в них коэффициентов, содержащих а. Функция
V0—безразмерна, функции Vj, V2, V3 имеют размерность соответственно; длины, длины
в квадрате и длины в кубе,
V3
v; =K2av8
Vi =2a2Vi
V;' = 2Y2a*Vo
а некоторая дна-
240
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Здесь Qy, Мх, ϋ·χ и и, а также иЧшР и его производные являются
функциями от 2 (от α зависят как от параметра), a V0, Vlf V2
и V3 —функциями от az.
Структура формулы (12.165) аналогична структуре формулы
(12.126), только вид матриц К и I здесь получился иной вслед-
ствие того, что вместо частных решений 1, -^, -„-, -^·,
образующих общий интеграл однородного дифференциального уравнения
изгиба обыкновенной балки (не на упругом основании), имеют
место частные решения VQ(az), Υ1(αζ), \ί2(αζ), \ί3(αζ), линейная
комбинация которых является решением однородного
дифференциального уравнения изгиба балки на упругом основании.
Начальные параметры находим из граничных условий. Обычно
из четырех начальных параметров значения двух оказываются
очевидными. Функции V0, Vlt V2 и V3 табулированы. Однако, при
использовании ЭВМ удобнее в общую программу включать
подпрограммы вычисления функций V0, .... V3.
5. Интеграл в форме, характерной для метода начальных
параметров в случае нескольких участков. При наличии нескольких
участков, как и в случае изгиба балок
,«.. не на упругом основании, используем
1доп,№' представление (12.134), но при иных
— выражениях для матриц К и Кдоп,й,
I и 1доп, к· При этом формулы для
К и I уже показаны в (12.165).
Матрица Кдоп, к аналогична матрице К
с той лишь разницей, что V0, Vlf
V2 и V3 являются функциями не
аргумента аг, а а (г — г^). Наконец, матрица 1Д0П> k имеет
следующий вид:
1доп,А —{ £>ч.р,доп,6 &'х £>ч.р,доп,/г & ' χ ^ч.р.доп.й ^ч. р. доп. ftj·
(12.166)
Zh-1
Рис. 12.86. К отысканию частного
решения.
Рассмотрим два частных случая нагрузки и соответствующие
частные решения:
1· ?«,, доп, « = 4 = const,
V
ч. р. доп, η '
ζ
η^ \ ν3[α(ζ-ζ)Μ =
---Йг(-т5г)у.[«(*-МСм-
1Е^Г {1 - V, [α (ζ - гм)]| = I {1 - V, [а (г - г»-,)]}.
§ 12.15] ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ
2. ^,доп.я = <7о(£-2я-1) (РИС· 12·86)'
ζ
—^- $ (ζ-ζη^)Υ3[α(ζ-ζ)]άζ.
ΖΠ-1
241
ϋ
ч. р. доп, я
Интегрируя по частям, получаем
<7о ( 1
ν,
ч. р, доп> я'
£/,
4а4
(C-2«-i)V0[a(2-0]|« +
Я-1
+
go
1
<7о
= ^ (г - гм) -Ь
4а4
<7о
ζ
$ V0[a(2-C)]dC =
'я-1
Я/*
1
νχ[α(2-ζ)]
= %u*
4а4/ -- · ---„_ι
^-iJ-VJa^-e,^)]}.
(12.167)
6. Использование функций V/ при любом выборе частного
решения v4.p. Заметим, что функциями V/ (аг) (i = 0, 1, 2, 3) можно
пользоваться как линейно независимыми частными решениями
однородного уравнения (12.146) для построения его общего
интеграла при любом виде ич>р —частного решения неоднородного
уравнения (12.145). Однако если ич-р не обращается в нуль при 2 = 0
вместе со своими первыми тремя производными, постоянные
интегрирования в общем интеграле однородного уравнения (12.146)
не представляют собой начальных параметров с точностью до
некоторых постоянных множителей как это было в том случае (см.
формулы (12.164)), когда ичр было принято таким, что при 2 = 0
обращалось в нуль вместе со своими первыми тремя
производными.
Иными словами, общий интеграл уравнения (12.145) можно
представить и так:
ν = »,.ρ + /C0V0 (аг) + /С^ (аг) + /C2V2 (аг) + tf.V. (аг), (12.168)
где v4.9 — может быть любым частным решением уравнения
(12.145).Вместо функций У$ можно применять и W
гп р г^ш
/7Й1Н jr ] |
Л
ZZf
Zz
Рис. 12.87. К примеру 12.26.
Пример 12.26. Найти вектор w (z) для балки на сплошном упругом
основании, изображенной вместе с действующей на нее нагрузкой на рис. 12.87,
*** ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. XII
Решение. Для получения w (г) воспользуемся формулой (12.134).
Матрицы К и Кдоп, k имеют стандартный вид. Остальные векторы выражаются:
следующими формулами:
1 = j {—4α4£/*λ'ί (αζ) — 4α4£/ *V2 (αζ) 4а4V3 (αζ) [ 1 — V0 (αζ)]},
1доП, s==—f- {-4a4£/^V! [a (z-2l)] -4α4£/*Υ2 [а (ζ-Ζχ)]
4o*V8 [а (г-zrf] [1- V0 (a (z-Zl))]}>
1доП;з = 1доп,4={0 0 0 0}, WjJ0n,3={-P 0 0 Of,
wflOn,4 = {0 й»г 0 0}.
7. Расчет бесконечных и полубесконечных балок на сплошном
упругом основании.
7.1. Общие замечания. В теории бесконечных балок
различают две их разновидности — бесконечные балки,
простирающиеся до бесконечности в обе стороны, и полубесконечные, —
имеющие один конец и простирающиеся бесконечно лишь в одну
противоположную этому концу сторону.
В ряде случаев балки, лежащие на упругом основании,
обладают большой длиной. Примером может служить рельс
железнодорожного пути. Для таких, да и для менее длинных балок
анализ напряженно-деформированного состояния можно выполнить
как для балок бесконечно длинных. Такой подход выгоден, так
как расчет бесконечных балок проще, чем балок конечной длины.
7.2. Полубесконечная балка. Рассмотрим
полубесконечную балку на сплошном упругом основании, загруженную на
конце силой Ρ и моментом дЯ (рис. 12.88). Воспользуемся пока-
Ш Р
Q: ,
if"
Рис. 12.88. Полубесконечная балка на сплошном упругом основании, загруженная
сосредоточенными силой и моментом на конце.
зательно-тригонометрической формой интеграла, при этом, так как
распределенной нагрузки нет, ϋ4ρ = 0,
v=.e-az ф^ cos az_|_B2s'maz) + еаг (В3 cos аг-\-В^'таг).
При беспредельном удалении от загруженного конца балки
прогибы, уменьшаясь, должны устремляться к нулю. В связи с этим
в выражении для ν нужно сохранить лишь затухающие члены,
а возрастающие положить равными нулю. Таким образом, из
условий на бесконечности В3 = В4 = 0, и решение приобретает вид
v = e-az(B1cosaz + B2smaz). (12.169)
§ 12.15]
ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ
243
Для определения Вх и Bz воспользуемся граничными условиями
на конце балки —при г = 0
ΈΙχν" = — 3W, ΕΙχυ"' = Ρ. (12.170)
Для раскрытия этих условий найдем ν" и ν'"
ν' = — ае-аг (Вх cos аг + В2sinaz) + ае~аг (— Вхsinaz + В2 cos аг) --■=
= ае-аг[(В2 — В1) cosaz —(fii + fijjxinaz],
и" = 2а2<гаг [— fi2cosaz + fiiSinc6z], (12.171)
ε»'" = 2а3<гаг [(fix + В2) cos аг + (£2 - Вх) sinaz].
Подставляя (12.171) в (12.170), получим
т
2Е1ха*[-В2] = -ЭЯ,
В*~ 2Е1м*'
2Е1ха3(В1 + В2) = Р, Вх + В2 =
2ЕКа?'
В,--
т
2Е1ха? 2Е1^'
Подставляя Вг и В2 в (12.169) и в (12.171), найдем
0 = 2^ Ъ(«)-5?|п %(«*)·
<К =
ЭД
^Εττ^Μ+^τ-ηοΜ
' }
М* = — — η2 («г) + 2Κη8 (аг),
а
Qy = — ΡΆι (аг) - 2аЭИт]8 (аг),
(12.172)
где
г)0 (аг) = е~аг cos аг, ηχ (аг) = е~аг (cos аг — sin аг),
η2(αζ)=£_α* sinaz, η3 (аг) = е~аг (cos аг +sinaz).
С увеличением аргумента происходит быстрое уменьшение
значений («затухание») функций т)0(аг), .... η2(αζ). Графики их
представляют собой
волнообразные линии с расстояниями *S\
между нулевыми точками,
равными π. Функции r\Q(az),
..., η2 (аг) табулированы. Вид
функций графиков v, Mx, Qv в
двух случаях (Ш = 0, Ρ Φ 0 и
3)] φ 0, Ρ = 0) показан на
рис. 12.89, а, б.
Из графиков в 12.89, а, б,
легко заключить, что при
аг^уЯ Мх и Qi/
пренебрежимо малы по сравнению
с максимальными их значе-
16*
Рис. 12.89. Эпюры υ, Μχ и Q в
полубесконечной балке на сплошном упругом основании;
а) случай «ДО = 0, Ρ = I; б) случай SJJt = 1,
Ρ ~ 0. .
244 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. XII
ниями и, следовательно, Мх и Qy в полубесконечной балке
пренебрежимо мало отличаются от таковых в балке, имеющей
3 я
длину />γ —. Этот факт определяет большое практическое
значение информации, относящейся к полубесконечной балке.
Рис. 12.90. Бесконечная балка на сплошном упругом основании: а) балка, загруженная
сосредоточенной силой; б) основная система в виде двух полубесконечных балок; в)
использование результата, относящегося к бесконечной балке, загруженной сосредоточенной
силой для отыскания эффекта действия произвольной нагрузки; г) эпюра ν в роли линий
влияния прогиба в сечении под сосредоточенной силой: / — линия прогиба бесконечной
балки на упругом основании при действии силы, равной единице, в точке А; 2 — то же
при действии силы, равной единице, в точке В; кривая / полностью совмещается с кри^
вой 2 при смещении вправо на расстояние а. Поскольку νΑφ^ = υβ(Α) (первый индекс —
адрес перемещения, второй — адрес силы, вызвавшей перемещение), кривая / — линия
влияния прогиба в точке А, а кривая 2 — линия влияния прогиба в точке В.
7.3. Бесконечная балка. Пусть имеем бесконечную
балку на сплошном упругом основании, загруженную
сосредоточенной силой Ρ (рис. 12.90, а). Воспользуемся результатом
(12.172), полученным для полубесконечной балки для того, чтобы
проанализировать напряженно-деформированное состояние
бесконечной балки. С этой целью мысленно разрежем бесконечную
§ 12.15] ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ 245»
балку в сечении приложения силы и эту силу поровну (по Р/2)·
приложим к краям проведенного разреза. Вследствие симметрии"
бесконечной балки и нагрузки относительно точки О (см.
рис. 12.90, б) кососимметричные факторы (Ό·* и Qy) в сечении■
г = 0 равны нулю, поэтому, проведя разрез в сечении г = 0,
действие одной части балки на другую заменяем лишь внутренним:
моментом (изгибающим моментом Мх). Получили так называемую-
основную систему1) (рис. 12.90, б) для бесконечной балки.
Величина МХ0 = Х нам не известна, ее найдем из условия равенства*
нулю относительного угла поворота сечений, совпадающих с краями;
разреза; вследствие симметрии каждое из краевых сечений у
разреза поворачивается на одинаковые по величине углы, равные нулю.
Воспользуемся функцией $х при г = 0 для полубесконечной,
балки, учтя, что вместо Р, надо иметь в виду Р/2, а вместо Ш
неизвестную величину X, при этом 1&д:|г_0 = 0.
Итак, имеем (здесь учтено, что η3(0) = 1, η0(0) = 1:
Р +7^ = 0, Х=Р
4сс2£/* ' аЕ1х ' 4а'
Теперь найдем все функции: и, $х, Мх и Qy, для чего в
формулы (12.172) вместо Ρ подставим Р/2, а вместо Ш величину
Р/(4а). В результате такой подстановки найдем для правой части:
балки с г^О
ϋ = 4^ ^(az)-g^ %(«*)==
^ = (-4^С05аг-4^81Паг+4^С05аг)е"аг =
= ~4^ЁГх^^аг^ (12.173).
/ Ρ Ρ Ρ \ Ρ
Μχ = [— 2^sina2 + ^cosa2 + 4^sina2je-a2=^%(a0),
rs ( Р ι Ρ ■ 2<XP ■ \ a- Pis
Qy = [— γ cosаг-Ь-уsinew — -^sinazje-"* = —— г]0(аг),
Ρ Ρ Ρ
V \ζ-ο = ^max = gas£/ » *™χ \ζ-ο = Μ. κ max = ^ > Qt/ |ζ = ο + ε = Qmax =— "у *■·
I — — b — Pk — Pa
r U-o — rmax — K^max — ga3£/ ~ ~2~'
*) Основной системой в строительной механике называют систему! в'
каком-то смысле более простую, чем заданная, и полученную из последней"
при помощи той или иной ее модификации, вследствие которой основная.,
система отличается от рассчитываемой заданной. Далее, вместо
непосредственного расчета заданной системы рассчитывают основную, но в алгоритме этого-
расчета имеется аппарат, ликвидирующий отличие основной системы от
заданной, вследствие чего результат, полученный для основной системы, спра—
подлив и для заданной,
'246
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Имея формулы (12.173), можно найти υ, $х, Мх и Qy от любой
распределенной нагрузки, а также от любой системы
сосредоточенных сил. Покажем как это делается. Пусть имеем
бесконечную балку, загруженную на участке длиной d нагрузкой,
распределенной по любому закону (рис. 12.90, в) и сосредоточенными
силами Pi (i = l, ..., η). Принимаем некоторую точку оси балки
в качестве начала координат; координаты начала и конца участка,
загруженного распределенной нагрузкой, и координата точек
приложения ί-й сосредоточенной силы, суть: a, b и z{ соответственно.
Рассмотрим некоторое текущее сечение балки с координатой ζ и
. для него найдем интересующие нас функции υ, ϋ·χ, Мх и Qy,
пользуясь формулами (12.173). Нагрузку qydt, собранную с участка
длиной άζ, будем рассматривать как сосредоточенную силу, тогда
-от распределенной нагрузки
dt Ь
-Если же учесть еще и воздействие сосредоточенных сил, то
η Ь
VI Pi С Яу
υ= Σ^έτχ^α^-Ζ^+)8^ΕΓχ^α^-ζ^άζ·
t = I a
Аналогично находим и остальные функции
η Ь
®* = ~2ιΤ^Μα(ζ-Ζι)]-Ιϊ^χΆΛν{ζ-ς)}άζ,
i= I a
η Ь
i=I a
η Ь
Qy = — 2 τ ^ο[«(ζ - χι)]- §Ц- η0[« (* - Q]αζ.
i~\
Если qy = const = q и EIX = const и если учесть следующие
дифференциальные зависимости между затухающими функциями:
r\'0(az) = — оиг)з(аг), ηί (аг) = — 2αη0 (аг), η^ (ocz) = αηχ (ocz),
% (аг) = —2αη2 (аг),
§ 12.15] ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ 247"
то формулы для ν, ϋ·χ, Мх и Qy приобретают вид
η
υ=Σ №ΕΓχ^α(ζ~ ζΜ~8^ΕΓχ^οta (г~6)]_т1о[«(ζ-α)]},
η
®χ=— 245^η2[α(2-2/)] + Β^7^{η3[α(2-6)]-η3[α(2-Ω)]},..
ί=1
η
ί=1
η
^ = - Σ T1h["b-2i)] + ±{41[a(2-b)]--ih[a{2--a)]}.
ί=1
Заметим, что функция ν (αζ) = ν (αζ)/Ρ является так называемой
функцией влияния, график ее (линия влияния) обладает тем
свойством, что каждая его ордината представляет собой ν в сечении
г = 0,_когда над этой ординатой располагается единичная сила
(Р = Р= 1). Приведенное утверждение легко уяснить рассматривая
рис. 12.90, г.
8. Расчет однопролетной балки на сплошном упругом
основании.
Пример 12.27. Найти функцию ν, $χ, Мх и Qy для балки,
изображенной на рис. 12.91, а.
Решение. Вследствие симметрии балки и действующей на нее нагрузки·
относительно середины пролета расположим начало координат в этой точке—
Воспользуемся решением в форме (12.168). При этом сохраним в нем лишь-
четные функции и учтем, что частное решение имеет вид1) v4,v = qjk, таким-
образом
ν = у + KoVo (az) + /C22a2V2 (as).
Значения постоянных интегрирования найдем из граничных условий
= 0.
f|,=+//9 = 0, v"=- Μχ
12 =
:*/2-υ· " —~EL
;l/2
'χ
В развернутом виде эти условия, если ввести обозначение u — αΐβ,
запишутся так:
■j + K0Vo («) + K£v?V2 (и) = 0, - /Co4a*V2 (и) + K22a*V0 (и) .-= 0.
Отсюда
„ _ Я Уо(Ц) „ Я 2a2V2 (и)
* Vg(")+4a4Vl(u) ' ^ k VJ(«) + 4a*Vi(u) *
г) Если нагрузка <7 (ζ) в (12.145) выражается алгебраическим полиномом.·.
степени не выше третьей, то ι>4.ρ можно принять в форме
»ч. ρ = ?/*·. (12.174)
В справедливости этого уравнения легко убедиться, подставив (12.174)"·
и (12.145). Использованы табл. V/ с учетом связи V,- с V; (Vj = 2a2Vt·).
,:248 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
■Подставляя полученные выражения для Ко и К-2 в ν, $χ>... найдем
,. _ Я Г, Уо («) У» (αζ) + 4а*У2 (и) У2 (аг) 1 )
*L VJ(«) + 4a*V|(u) J'
- _ <7 4α*ν0 (и) У3 (аг) -4а«У2 (и) Vf (аг)
Х Ь Vg(u) + 4a4Vl(u)
Μχ—ΕΙυ —ς _____ , ^
η _ £,,.» _ 0 Уо («) Vi («Ю + 4a'V, (и) V3 (аг)
Vi/ v 4 V2(u) + 4a4V|(u)
[ГЛ. XII
(12.175)
(12.176)
Найдем величину и место расположения максимального прогиба; с этой
кнелью приравняем нулю υ' или» что то же самое, ву, равенство же нулю $х
γγγττνΐΗΐΙΙτττττττττ'Ι'Πτττττ
''ШУИ
300см
О
300см
„пилот* V» 0,0001865(1см
ОЩтвдсн Μ у Д00019Щ
см
ΟΜΟγ-
0,00173
■£' 0,020 f
qll
?Рис. 12.91. К примеру 12.24. Балка с шарннрно опертыми концами на сплошном
упругом основании: а) вид балки и связанной с нею системы осей; б) эпюры прогибов при двух
значениях коэффициента погонной жесткости упругого основания \q в кГ/см); в) эпюры
изгибающих моментов при двух значениях коэффициента погонной жесткости упругого
ι основания: I — первый вариант (А = 108,6 кГ/см*, 2 — второй вариант (А = 5500 кГ1смг)\
при k = 0 (балка без упругого основания) w — --—■ 2,, ■ .
max 384 с/„
§ 12.15] ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ 243'
мыслимо при условии равенства нулю числителя в выражении $х, т. е.
V0 (и) V3 (αζ) - V2 (u) Vx (αζ) = 0. (12.177)-
Найдем численное решение для двух вариантов значений исходных данных:.
/ = 600 см, Ε =2- 106 Kf/CM2t /x = 21 720 см* (двутавр № 40а). Величина k-
взята в двух вариантах /г = 108,6 кГ/см2 и /г = 5500 кГ/см2. Двум вариантам &_-
соответствует и два значения α
,6 _ 1 1
a —I/ ir?, —I/ , „ 1rt. 21720 ~" 200 см '
-■i/JL_ei/ »
|/ 4£/* |/ 4-2- 10·-
5500 2_ J_
а — !/ 4 · 2 · 106 · 21 720 ~" 150 см '
тогда и в обоих вариантах определится величинами
а/ 1 600 ^ а/ 2 600
"-Т-мо'-Г-1·5^· "==Т==150'-У=4(раа)·
Уравнение (12.177) с учетом вида функции V/ становится таким:
(ch и cos и) j~ (ch αζ sin αζ —sh αζ cos αζ) —
— fj-g (sh " sin ") "о- (ch αζ sin αζ+sh αζ cos αζ) = 0-
После сокращения на γ-^ в первом варианте \& — ппп —)
жесткости
получаем трансцендентное уравнение
2,34675 (ch αζ sinaz—shazcosaz) — 0,14884 (ch αζ sinaz + sh αζ cosaz) = 0,
корнем которого является аг=0. Следовательно, согласно (12.175)!, учитывая,
что V2(az) |a*-o = °> V0 (аг) |аг_0 = 0,
W - V [„о —Я1 ~ у» («) + 4aWf («)] ' итах = ^|2-о = Т[1-(«,о(")]·
V0 (и) Vq(1,5)
Фо(")
Vg (и) + 4a*Vl (u) Va2 (1,5) + 4a*Vl (1.5)
0,1664
■ = 0,0367, vmaY = 4- 0,9633.-
(0,1664)2 + (2,1239)2 * * max k
Во втором варианте уравнение (12.177) имеет вид
(ch 4 cos 4) j-g (ch αζ sin αζ—sh аг cos αζ)—
— ψ-g (sh 4 sin 4) ^— (ch αζ sin αζ + sh az cosaz) = 0,.
после сокращения на l/(4a3) получаем
17,8158 (chaz sinaz—sh az cosaz) —20,6802 (ch az sinaz + shazcosaz) = 0.
Это уравнение, кроме корня (αζ)χ = 0, имеет еще два корня: (αζ)2= 1,65 w
ι аг f Ь65 1,65-150 ... . _ .
(az)3= —1.65 lz = ± = ± η = ±124 ел). Действительно, при>
аг = 1,65
ch az sin az — sh аг cos az = 4a3V3 (az) = 2,8895,
ch az sin az + sh az cos az = 2a Vi (az) = 2,4927;
'250 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. XII
17,8158-2,8895 —20,6802-2,4927 = 51,5 —51,5 = 0. Найдем функцию ν при при-
>веденных выше значениях αζ
„| Ч\\ V"(4) Ί 9 Γι ~17'850 Ί ? ίο»!
v,*-° k [_ Vg(4) + 4a*Vl(4)J *[_ (—17,850)2 +(20,653)2j_ /fe 1,υ^'
,, . Hi Vo(4)Vo(1-65) + 4aW2(4)V2(l,65)l-| 9
"Ία*-ι,65 = Τ[_1 Vg(4) + 4a*Vl(4) J = Τ [1 ~F° (u) 1»-*' =
_£_ Γ. (— 17,850) (— 0,2136)+ (— 20,653) - 2,4996 1 _ q_
k L (—17,850)2 + (—20,653)2 J fc 1,Ub4·
Вследствие четности функций V0 и Vj такой же результат получается и
при *) az =— 1,65.
Таким образом, существует не один, а три экстремума у функции υ. На
рис. 12.91, б изображена изогнутая ось балки в двух вариантах величины
жесткости сплошного упругого основания.
Границей между областью значений и, в которой кривая изогнутой оси
имеет один экстремум и областью и, где кривая изогнутой оси имеет три
■экстремума, является и = 3,1. При и<3,1 кривая ν имеет один экстремум,
при u$s 3,1— три экстремума.
Найдем величину и место расположения максимального изгибающего
.момента; с этой целью приравняем нулю dMx/dz = Q{/; равенство же нулю Qy
мыслимо при условии равенства нулю числителя в выражении (12.176)", т. е.
V0 (и) Vi (аг) + 4a*V2 (u)V8 (az) = 0. (12.179)
Уравнение (12.179) в первом варианте (а = -^т ) приобретает вид
:0,1664 тг— (chaz sinaz+sh azcosaz) +
+ 2a2· 2,1239 -j—- (ch azsinaz—shazcosae) = 0.
-Сокращая на l/(2a), получаем
0,1664 (chazsinaz+shazcosaz) + 2,1239 (ch azsinaz—shazcosaz)=0.
Это уравнение имеет единственный корень αζ = 0. Вследствие этого, согласно
*(12.175)з, учитывая, что V2 (az) |аг_0=0, получаем
Μ У2 (и)
Ч Vg(") + 4a4Vl(") *
Придадим формуле вид, удобный для сопоставления с изгибающим моментом
* балке не на упругом основании
ql* 8 1 2a2V2(u)
Мх = -
'X
8 β 2α2 [Vj»(u) + 4a«V5(u)l
qP_ ^_ 2a«Va(l,5) _ qP_ J 2,1239 = ^ш qP_
8 Z2«2 Vg(l,5) + 4a«VS(l,5) 8 1,5» 0,1664»+ 2.12392 ' " 8
*) Функция F0 (и) выражается следующей формулой:
ρ ,,Λ Ур (и) V0 (az2,3) + 4a4V2 (и) У2 (αζ2ι3) Μ9 ,_я
FM = Vg(") + 4a*V|(u) · <12Л78>
'Здесь (az2pS) — ненулевые корни (аг2=—аг3) уравнения (Г2.177). Величина
этих корней, что видно из уравнения (12.177), зависит от и, вследствие чего
все выражение в правой части формулы (12.178) является функцией лишь й.
Аналогично функцией лишь и является и нижеприводимая Х0» но только
(аг2,з) являются ненулевыми корнями уравнения (12,179).
§ 12.15] ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ 25Г
Таким образом, в рассмотренном случае в балке на сплошном упругом
основании максимальный изгибающий момент составляет 20,8% от максимального-
изгибающего момента в балке не на упругом основании.
Во втором варианте уравнение (12.179) приобретает вид
— 17,850 · -fr— (ch αζ sin az-\- sh <xz cos az) +
+ 2a2 (— 20,653) -j-j (ch az sinaz — shazcosaz)=(X.
Сокращая на l/(2a), получаем
— 17,850 (chaz sin az-fsh az cos az) — 20,653 (ch az sinaz — shaz cos az) = 0.
Это уравнение имеет следующие корни: (az),=0, (az)2 = 3,21 и (az)3=—3,21'.
/ " 3,21 3.2Ы50 ...
[z=h ■— = ± ^ = 241 см
\ a 2
Действительно, при az = 3,21 имеем
chaz sinaz+shazcosaz = 2aVi (az) = — 13,193,
chaz sinaz — shaz cos az = 4a3V3 (az) = 11,487,
— 17,850 (— 13,193) —20,653· 11,487=241,5—237,2=4,3. Погрешность
составляет (4,3/241,5) 100=1,78%.
Найдем функцию Мх при приведенных выше значениях az
м ι ql2 4 2k2V2 (4)
тх\(аг)1=0— 8 /2с£2 Vg(4) + 4a4VH4)
qP 1 (-20,653) qP
~ 8 16 (-17.850)2+ (—20,653)2 8 '
Нижеприводимая функция χ0 табулирована
1 2g2V2 (и)
Хо(Щ- ц2 у2(ц) + 4а4У|(ц) '
qP 4 2a2[V0(4)V2(3,21)-V2(4)V0(3,21)] _
Μ
*|(az),,«=±3,2i — — 8 Ρα2 Vg(4) + 4a*VJ(4) —
__ qP ч__^ 1 (—17,850) (—0,8508) - (—20,653) (—12,381)
— 8 л0(и)- 8 16 (—17,850)^ + (-20.653)2
= -^- 0,02Ог
Хо(«) = ·
1 2д2 [У0 (и) У2 (аг2,3) - У2 (и) V0 (az2,3)]
"2 Vg(") + 4a4Vl(u)
Границей между областью значений и, которой соответствует функция Мх-
с одним экстремумом и областью значений и, коим отвечает функция Мх
о тремя экстремумами, является ΐί=π/2. Если и^л/2, то у Мх — три
экстремума, если «<π/2, — то один. Эпюры Мх изображены на рис. 12.91, е.
Угол поворота опорного сечения балки найдем по нижеприведенной
формуле, получающейся из (12.175) путем подстановки az\z==[,2 = u,
« , _ № ( п 24 1 4дЗ[У0(ц)У3(ц)-У2(«)Уг(Ы)]
v*k=±//2-+ 24Е1Х { >~Р 4a3 V2(u) + 4a4Vl(U) =
qP
'-252 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. XII
Нижеприведенная функция ψ2 (и) табулирована
*и«л—* 1 4аЗ[У0(ц)У3(ц)-У2(ц)У1(ц)]
%l >- 4~"u3 V2(u) + 4a4Vl(u)
В нашем случае при и = 1,5
„ __ <7/3 , п3 1 0,1664.2,1959 — 2,1239-2,4971
^|z = ±Z/2--*- 24£/^ ( >Т 1,53 (0,1664)2 +(2,1239)2 "~
При и=4
- _ _Ф_, nJ_ 1 (—17,850) (—2,829)-(—20,653) (—38,505) _
'х|г=±//2~ 24Я/^ v ; 4 4з (-17.850)2+ (—20,653)2
__ ^*
24ΕΛ
0,012
Наконец, поперечную силу на опоре, т. е. при z = ±l/2, найдем по
формуле (12.176) после умножения и числителя, и знаменателя правой части на
л ι _-Я1 2 1 2°с [Уо (и) Vi (и) + 4а*У2 (и) Уэ(и)] __ ql
чу\г^±Ц2-+ 2 / 2а V2(«) + 4a*V|(w) __н 2 μ°ΐ;'
„л_1 1 2а [У0 (и) Уг (и) + 4а* У2 (и) У3 (и)]
μ°ι > ~ 2 ' и VI (и) + 4a*V| (и)
■Функция μ0 (и) табулирована.
В нашем случае при и = 1,5 и « = 4 соответственно имеем следующие
^значения μ„ и Qy:
, ,. _ 1_ 1 0,1664-2,4971+2,1239.2,1959 _
μβί")|«=ι,5--2 1,5 (0,1664)2+ (2,1239)2 - υ'όΙό>
Qy |2;=±//2==+ -тр 0,373,
... _ 1 J_ (-17,850) (-"8,505) + (-20,653) (-2,829)
М")|«-4—2 4 ' (—17,850)2 +(-20.653)2 "~ ,1Ь'
^ι2=±//2=+4·0·125·
Балка, рассмотренная в примере 12.26, впервые была исследована И. Г.
Бубновым наряду с балкой, защемленной по концам и также загруженной равно*
>мерно распределенной нагрузкой. Позднее П. Ф. Папкович обобщил эти
решения, распространив их на случай упругой податливости опор *).
1) Эти решения приводятся в курсе П. Ф. Папковича «Строительная
.механика корабля», ч. I, том II, «Морской транспорт», 1947, повторяются и
в других книгах по строительной механике корабля: Я- И. Короткий,
Л, 3. Л о к ш и н, Н, Л. Сивере, Изгиб и устойчивость стержней и стерж-
·§ 22.15] ИЗГИБ БАЛОК НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ 253
9. Затруднения, возникающие при расчете балок на сплошном
упругом основании, в случае большого значения аргумента az.
При бесконечно больших значениях аргумента аг функции
Крылова А. Н. (12.174), которые можно представить1) так:
V0 (аг) = ^ cos аг,
1 / еаг 4- е~аг еаг — е~аг \
Vi (аг) = 2^- ί ^ s in аг Η §—- cos azj,
1 еаг е~аг
V2 (аг) = -^5"' 2 Si° аг'
1 / gazj_g-az еаг е~аг \
v3 (аг) = -£-£ f 2 sin аг 2 cos azj '
вырождаются в следующей функции:
V0 (аг) = -s- cos аг, Vx (аг) = ^— eaz (sin аг + cos аг),
\ \ (12.180)
V2 (аг) =-д-теаг sin аг, V3 (аг) — g-g eaz (sin аг — cos аг).
Это вырождение происходит вследствие того, что при аг->-оо
устремляется к нулю величина е~аг. Функции (12.180)
представляют собой «синусоиды» с периодически возрастающими по
показательному закону ординатами. При аг-^оо функции Vi
становятся линейно зависимыми (например.V1 = 2— V0 + aV2, V3 = 2~ V2:—
—4-3-V0), вследствие чего посредством их вообще нельзя
выразить общий интеграл уравнения (12.146). Если аг не бесконечно
велико, но все же имеет достаточно большое значение, то функции
Крылова Н. А. становятся близкими к функциям (12.180).
Использовать функции Крылова для построения интеграла уравнения
(12.146) можно, но при этом происходит падение точности расчета,
в котором используются эти функции, вследствие того, что при
удалении от точки приложения силы влияние ее на υ, $х, Мх и
Qy уменьшается, вместе с тем аг, а следовательно, и максимальные
ординаты функций У0(аг), ..., У3(аг) увеличиваются. Таким обра-
невых систем, «Судостроение», 1958; А. П. Филин, А. С. Соколова,
Строительная механика корабля, ч. 1, Л. Речиздат, 1957.
В этих же книгах имеются таблицы тех функций, которые использованы
при определении в балке примера 12.26 экстремальных прогибов (функции <р0
и F0), изгибающих моментов (функции χ0 и Х0), наибольших значений углов
поворота сечений (функция ψ2) и поперечной силы (функция μ0), а также
таблицы аналогичных функций для балки на сплошном упругом основании
жестко защемленной по концам.
I) Если учесть, что
chaz— -£ . shaz=-^ = .
254
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
4
У
(
I
W*
Ю
\ \\\\\ \\\\м\{\
Ri
5)
зом, получается, что все уменьшающийся с увеличением аг
результат становится разностью все увеличивающихся чисел; вместе
с тем хорошо известно, что наличие малых разностей больших
величин связано с большой потерей точности х). Из-за такой
опасности приходится принимать специальные меры для уменьшения
погрешности. Поступим так. Сначала
при отыскании влияния каждой
сосредоточенной силы балку рассматривают
как бы находящейся в составе
бесконечной и находят все функции в этом
предположении, не принимая во
внимание закрепления балки, т. е.
бесконечная балка служит для балки конечной
длины как бы основной системой. После
отыскания решения такой задачи к балке
прикладываются неизвестные реакции
опор (силы и моменты), и величина их
находится из условия, чтобы при
наложении их влияния в основной системе
на влияние внешних сил в основной же
системе были удовлетворены граничные
условия по концам балки. Этим
обеспечивается идентичность работы балки
конечной длины и соответствующего
участка в бесконечно длинной балке.
Идеи соответствующей методики были
предложены в 1882 г. Г. Циммерманом
и позднее развиты и детально разработаны Г. В. Клишевичем2).
Если удовлетворены следующие три условия: I) в пролете нет
ни сосредоточенных сил, ни сосредоточенных моментов и имеется
лишь распределенная нагрузка; 2) α/^3π/2; 3) функция q
выражается полиномом степени не выше третьей, то можно поступить
следующим образом (для конкретности рассмотрим балку,
изображенную на рис. 12.92, а). Примем основную систему в виде балки,
*) В качестве иллюстрации этого положения приведем пример. Пусть
в процессе расчета мы сталкиваемся с необходимостью такого вычисления:
100—99=1. Представим себе, что и в уменьшаемом и в вычитаемом
вследствие той или иной причины допущена ошибка в 1%, вследствие чего имеем:
101—98 = 3. В результате ошибка достигла 300%. Если бы тот же результат
получался иначе, например, как 3—2=1, то ошибка в одном проценте
и в вычитаемом и в уменьшаемом сказалась бы на результате не так сильно,
действительно, 3,03—1,98=1,05, погрешность в результате достигла 5%.
2) С расчетом балок на сплошном упругом основании по Г. Циммерману —
Г. Клишевичу можно познакомиться в капитальных трудах по строительной
механике (см., например, П. Φ. Π а п к о в и ч, Строительная механика корабля,
ч. I, т. II, «Морской транспорт», 1947, стр. 403). Г. Циммерман (Н. Zirnmer-
mann) — немецкий инженер. Г. В. Клишевич —профессор Ленинградского
политехнического института,
Рис. 12.92. К расчету балок на
упругом основании при большом
значении аргумента аг: а) балка
на сплошном упругом
основании; б) основная система — балка
без опор на сплошном упругом
основании, рассматриваемая как
полубесконечная балка,
простирающаяся бесконечно вправо
при учете влияния Mt и Rt и
бесконечно влево при учете
влияния Мг и R2.
§ 12.16] УРАВНЕНИЕ ПЛОСКОГО ИЗГИБА КРУГОВОГО СТЕРЖНЯ 255
свободно лежащей на сплошном упругом основании и никак не
закрепленной на опорах. Перемещения от нагрузки, возникающие
в такой основной системе, определяются так: v — q/k. Неизвестные
реакции R1 и R2 и реактивные моменты Μλ и М2 найдем из
условий на концах балки, которые записываем следующим образом:
и|г_0 = 0, •&х\г-0 = 0, ϋ !*_/ = (), 0ж|г_, = О,
или в развёрнутом виде:
(12.181)
k
Здесь не учтено влияние силы R2 и момента М2 на прогиб и
угол поворота левого концевого сечения балки в силу того, что
это влияние пренебрежимо мало, так как α/^=3π/2. Аналогично
не учитываем по той же причине и влияние Rx и Мг на ν и $х
на правом конце балки. Влияние же R2 и М2 на υ и $х на левом
конце балки и влияние R2 и М2 на г; и Ό·* на правом конце балки
приближенно (с пренебрежимой погрешностью) находим как для
тюлубесконечной балки. Например, условия (12.181 )х при' этом
представляются следующим образом (см. формулы (12.172)):
± _ Ri , Mi 0 4_ _Ri Mj__п 9 1R
Α 2α3£/* "^ 2cc2£/* ' k Ч" 2α2£/* α£/* " Ι1-*·10*/
При этом имеется в виду, что η0_(0) = % (0) = η8 (0) = 1. Из (12.182)
находим Rx и Afj. Аналогично Находятся и R2 и М2.
§ 12.16. Дифференциальное уравнение изгиба стержня
в плоскости оси, имеющей очертание окружности
При рассмотрении изгиба стержня с прямолинейной осью была
использована зависимость между изгибающим моментом и
изменением кривизны оси κ = \/ρ = Μ/(ΕΙ). Поскольку первоначально
ось стержня прямолинейна, изменение кривизны оси (κ) совпадает
с самой кривизной изогнутой оси. В случае же, если ось стержня
еще до деформации криволинейна, то изменение кривизны
представляет собой разность кривизн оси после и до деформации, и
зависимость между изгибающим моментом в поперечном сечении
стержня и изменением кривизны оси стержня приобретает вид
1 1 Μ
= рт, здесь ρ и рх — радиусы кривизны оси стержня до
и после деформации.
В случае, если ось стержня до деформации представляет собой
окружность радиуса г, формула для 1/р имеет вид
_L — _L — *$.
ρ ~~ r ~ ds *
256
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XIF
Пусть стержень с осью в виде окружности подвергается изгибу
в плоскости оси, вследствие которого точки оси получают
перемещения. Радиальное
(рис. 12.93). На рис.
перемещение обозначим символом «:
12.93 изображен элемент оси стержня до·
деформации (ab) и после
деформации (аф-^).
Очевидно, что кривизна
элемента оси после
деформации определяется по
формуле
1 ίίφ + Δ ίίφ
рх ds-{-Ads'
ds dsidsJ
Вследствие того, что и
представляет собой
функцию положения точки на
кривой, т. е. является
функцией s, касательная
к кривой агЬг в точке аг
составляет с нормалью к
отрезку прямой Оа угол
du/ds, а в точке Ьг
касательная к агЬг составляет с нормалью к отрезку Ob угол
dJ + ds (s") ds = Έ + S ds- Из рис· 12·93 видно' что Угол d(p +
-\-Ad(p, образуемый радиусами кривизны кривой ахЬг в точках
аг и b-i определяется следующей формулой:
du , du , d?u
Рис. 12.93. К выводу дифференционного
уравнения изгиба стержня с осью в виде окружности.
ίίφ + Δ άψ = d(p —
ds
+ Ж +
ds*
ds,
откуда
bdy = ~ds.
Если приближенно считать, что длина дуги ахЬг равна (р — и) dq>, т. е.
пренебрегать разностью длин дуг афх и агЬ\ то Δ ds = —-ud(p =
=—uds/p. Тогда, имея в виду формулу для l/plf получим
d*u
άφ . ds2
1
1
άφ + -г^г ds
Pi
ИЛИ *)
рГ
ds —
Ρ ~~
ds*
и ds
Ρ
1
*,!-£)
d(f
Is
i + f) + *"
ds2
i + -
Π Ρ
Ρ
Ρ
1j Здесь имеется в виду, что 1
пренебрежено всеми членами, начиная, от 2
91 Ρ Ρ2
u2
рЗ
+
§ 12.17]
УПРУГО-ПЛАСТИЧЕСКИЙ ИЗГИБ БАЛКИ
257
Учитывая, что dq>/ds=\/p, получим
или, пренебрегая величиной и/р по сравнению с единицей и
подставляя полученное выражение для изменения кривизны оси
стержня в формулу, связывающую это изменение с отношением
М/(Е1), окончательно получаем
Μ _ и d*u
ΕΙ ~ ρ2 "τ ds2 '
§ 12.17. Изгиб балки при не чисто упругой работе материала
1. Предварительные замечания. Рассмотрим изгиб балки (чистый
и отдельно поперечный), при котором в части ее объема материал
испытывает чисто упругую деформацию, а в остальной— упруго-
пластическую, в частности, чисто пластическую. Как и в случае
упругой работы балки при изгибе, будем считать, что зависимость
продольных деформаций волокон от их расстояния до
нейтрального слоя линейна гг = у/р. В частности, такая зависимость
получается при использовании гипотезы плоских сечений.
Второе предположение состоит в том, что нормальные
напряжения, действующие на площадках, параллельных оси балки,
считаются равными нулю. Если отсутствие этих напряжений в чисто
упругой балке при чистом изгибе подтверждается строгой теорией,
то в случае работы материала балки в упруго-пластической
области обнаруживается, что, вследствие неодинаковости
коэффициента Пуассона в пластической и упругой областях (в первой
μ = 0,5, а во второй μ<0,5), возникают самоуравновешенные
нормальные напряжения на плоскостях, параллельных
нейтральному слою, а также касательные напряжения. Как показывает
эксперимент, неучет этого взаимодействия волокон, параллельных
оси, не влечет за собой заметной погрешности и является
приемлемым.
С целью упрощения выкладок, но без ущерба для выявления
принципиальных особенностей изучаемого вида деформации,
предполагается, что поперечное сечение балки имеет две оси
симметрии и что одна из них лежит в плоскости действия моментов и
'или) сил; при этом вторая ось лежит в нейтральном слое.
Кривая зависимости σ = σ(ε) за пределом пропорциональности
может иметь произвольный вид (рис. 12.94, а), в частности,
представлять собой отрезок прямой линии, продолжение которой
не проходит через начало координат (линейное упрочнение)
(рис. 12.94,6) (если угол наклона прямой равен нулю, то кривая
σ = σ(ε) имеет вид диаграммы Прандтля — рис. 12.94, в; если при
этом угол наклона прямолинейного участка диаграммы, располо-
9 А. П. Филин, т. II
258
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
женного ниже предела пропорциональности, равен 90°, то
получаем диаграмму жестко-пластического тела — рис, 12.94, г). В
основном коснемся работы стержней, изготовленных из материала
упруго-пластического (диаграмма рис. 12.94, б).
ел
0 Л
О
<Si\
f
ε J
а)
δ)
6j
8}
Рис. 12.94. Диаграммы напряжений: α) произвольного вида без площадки текучести;
б) с линейным упрочнением и без площадки текучести; в) диаграмма Праидтля (упруго-
пластнческое тело); г) диаграмма напряжений жестко пластического тела.
Рассмотрим два режима работы стержня — нагружение и
разгрузку.
2. Чистый изгиб.
2.1. Нагружение. Первым долгом проследим за характером
распределения нормальных напряжений в поперечном сечении
в процессе постепенного роста моментов, изгибающих стержень,
от нулевого их значения.
Вследствие того, что сечения остаются плоскими,
относительные деформации продольных волокон балки изменяются по
линейному закону; в наиболее удаленных от нейтрального слоя, т. е.
При t/ = t/max, ОНИ рЭВНЫ 82,maX. ТаКИМ обраЗОМ, Существует ЗЭВИ-
симость
&г - у . (12.183)
2, max
Уп
Разумеется, что каждому текущему значению моментов,
изгибающих брус, а следовательно, и текущему значению Мх
соответствует свое собственное текущее ε2> max. Перестроим диаграмму
напряжения так, чтобы по оси абсцисс откладывалась величина εζ/εΖιΠΙΆΚ.
Итак,
σ* = /(ε,/ε2)Π13χ). (12.184)
Подставляя в (12.184) выражение гг/гг<тах согласно (12.183),
получаем зависимость
<*z=f (У/У max).
Точке на оси ег/ег>тах в диаграмме напряжений и точке на оси
у/Утах в поперечном сечении с одинаковыми (безразмерными)
координатами соответствует одинаковое напряжение (рис. 12.95). В
качестве иллюстрации, на рис. 12.96 показано четыре уровня
§ 12.171
УПРУГО-ПЛАСТИЧЕСКИЙ ИЗГИБ БАЛКИ
25»
βζ~σζ(εζ)
Рис. 12.95. Совпадение диаграммы напряжения на участке О
-тпах
(ε
max
деформация в крайнем волокне поперечного сечения балки) и эпюры нормальных напряжений
в поперечном сечении в безразмерных осях (е/бтах и у/утах).
Рис. 12.96. Совпадение диаграммы напряжения на участке 0 — emaxi (8max^ _ дефор-
мация в крайнем волокне поперечного сечения балки) и эпюры нормальных напряжений
в поперечном сечении в безразмерных осях (8/етах£ и У/Утах) при разных уровнях
нагружения.
9*
260
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
значений изгибающего момента и соответствующие им ε2( max, ι (i =
= 1, 2, 3, 4). В каждом случае точке с 82>тах отвечает
безразмерная координата 1. Иными словами, эпюра нормальных
напряжений в поперечном сечении представляет собой кривую
нормальных напряжений на отрезке 0 —8г,тах, при этом ег,тах,
соответствует текущему значению Мх.
σ<βτ
1
ю
а=бт
LJ
Ж.
δ)
6)
3)
Рис. 12.97. Распределение нормальных напряжений по высоте поперечного сечения
Салки: а) Мх < Мхт; б) Мх
М,
в) Мхт < Мх < Мх$, г) Мх = M^Q.
Таким образом, если зависимость между σζ и гг выражается
диаграммой Прандтля, то отдельные стадии нагружения
характеризуются эпюрами распределения ог по поперечному сечению,
изображенными на рис. 12.97.
Теперь остановимся на определении двух характерных
значений изгибающего момента. Первый из них (ΜΧί) соответствует
возникновению
напряжения, равного пределу
текучести, в наиболее
удаленных от нейтрального слоя
волокнах, а второй
—любому текущему моменту
Мх > ΜΧΎ, в частности
моменту, при котором в
случае диаграммы Прандтля
пластические деформации
охватывают все поперечное
сечение стержня.
Итак, исходя из
формулы для нормального
напряжения в поперечном
сечении балки в случае
упругой ее работы аг = Мху/1Х, находим изгибающий момент,
соответствующий возникновению в крайних волокнах (т. е. при
y = h/2) напряжения σζ, равного пределу текучести στ
Μχ = Μ„ = Ψστ. (12.185)
Изгибающий момент в стадии работы балки после
возникновения в крайних волокнах напряжения, равного σ.,., в случае
Рис. 12.98. Распределение напряжений по
поперечному сечению балки при линейном
упрочнении. К. определению момента, статически
эквивалентного силам, распределенным по поперечному
сечению.
§ 12.17]
УПРУГО-ПЛАСТИЧЕСКИЙ ИЗГИБ БАЛКИ
261
линейного упрочнения (рис. 12.98), если высота той части
поперечного сечения, которая работает в чисто упругой стадии, равна
2η, а фибровое напряжение σ, выражается формулой
Мх = £ (στ ^) Ьух dyx + 2 j (στ + щ^ (уг - η)) г/2& <*&.
В частности, если зависимость между напряжениями и
деформациями характеризуется диаграммой Прандтля, то σ — στ = 0 и
Μ.
η Α/2
= ^ j г/16 di/x + 2στ J ί/2& d#2,
или
Μ
x = ^$yldF1 + 2oT$y2dF2 = ^ I{rp) + oTSr\ (12.186)
F, F2
где
Ft Fz
jtynw _ момент инерции площади той части поперечного сечения,
примыкающей к нейтральной оси, в которой напряжения не
превышают величины στ и материал работает упруго, относительно
нейтральной оси; 5(пл) — статический момент площади той части
- -Y/Z/7/Z/7/Z/7/7/7/7/7/7/7/7/7/-/7/7777Z/7,
Рис. 12.99. Упругая и пластическая области в балке при чистом изгибе,
соответствующие некоторому уровню нагрузки, при котором ΜΧτ < Μ χ< Mxq.
поперечного сечения (две зоны по разные стороны от упруго
работающей части сечения), материал которой работает в пластической
области, относительно нейтральной оси.
Поскольку при чистом изгибе во всех сечениях эпюры
напряжений одинаковы, границы областей упругой и пластической
работы материала представляют собой плоскости, параллельные
оси стержня (рис. 12.99).
262
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Если пластическая деформация охватывает материал во всем
поперечном сечении, то изгибающий момент становится
предельным Мх = Мхо; ему соответствует превращение балки в изменяемую
систему, этот изгибающий момент выражается формулой
(пл)
Мхо — СГтОдгтах·
В случае прямоугольного поперечного сечения (рис. 12.100)
Ь№
с(пл) _ 9 JA A _
Охтах — ^ * 2*4 4
Μ
ХО
(12.187)
При расчете же по допускаемым напряжениям предельным
считается изгибающий момент, соответствующий возникновению
напряжений, равных пределу текучести, в наиболее удаленных от
нейтрального слоя волокнах; этот момент
находится по формуле (12.185). В случае
прямоугольного поперечного сечения
W
ft'
т
ь
ft'
Ж
>
•*5|<*-(
' 1
1
V
Мх, = -ρ- στ.
(12.188)
Рис. 12.100. Прямоугольное
поперечное сечение балки.
К определению статического
момента s^ax при разви-
тии пластических
деформаций во всем поперечном
сечении.
Сопоставляя (12.188) с (12.187),
находим МХ0 = ШХТ = \,5МХТ, ft = 1,5. Учет
пластической деформации позволяет в
полтора раза экономнее использовать балку
прямоугольного поперечного сечения, чем
при расчете с учетом лишь упругой стадии
работы материала.
Теперь выясним, какую экономию
можно получить в случае прокатного профиля
(двутавр I № 50) 5<.пл> = 2 ■ 899 = 1798 см\
Мхо = S<™4 = 1798στ, Μχτ = Ψστ = 1560στ,
ί^1 = k = τέ^κ = 1,15. Учет пластических
Мхт 1560
деформаций в случае тонкостенного прокатного профиля приводит
к меньшему выигрышу, чем в случае массивных поперечных
сечений. К тому же, допуская развитие значительных
напряжений в стенке, а на половине высоты сечения эти напряжения
сжимающие, мы создаем условия, в которых возможна потеря
устойчивости плоской формы изгиба, т. е. выпучивание стенки.
Поэтому часто опасаются допускать возникновение во всей стенке
тонкостенного профиля больших напряжений, и в качестве
опасного состояния балки считают то, при котором напряжения,
равные пределу текучести, возникают лишь в крайних волокнах.
Иными словами, пластических свойств материала не принимают
во внимание.
$ 12.17]
УПРУГО-ПЛАСТИЧЕСКИЙ ИЗГИБ БАЛКИ
263
Интересно отметить, что при изменении η в довольно широких пределах
величина изгибающего момента мало отличается от Мх0- Ниже приводим для
прямоугольного сечения значения Мх соответственно при η=Α/4 и η=/ι/3
J Μ3
ал στ \ 2 ^ 0 1 .. (h 1 1 ,\ 11 ...
м'~т
12
48
12
f στ
*Х1Ч4*Ы^·
Найдем отношение Мх/Мх0 при двух указанных выше значениях η
Мх _ 11/48 = 11 М^ _ 23/108 23
Мл.0 ~ 1/4 ~ 12 · Μχο ~ 1/4 ~ 27 *
Отличие Λί* от Мх0 при η = Λ/4 и η = /ι/3 составляет соответственно г—-—χ
1 23/27
χ.100 = 8,(3)% и j-ί 100=14,8%. Для двутаврового сечения (например,
1
I № 50) это отличие Мх от
(рис. 12.101)
Мх
Мх
στ
0,93 · 25з
Мх0 при тех же значениях η еще меньше
12,5
h— ι
50
'' 3
50
12
0,93 · 33,(3)2
12
fστ·2 899 — 0,93· 12,5
|-στ2 899 —0,93· 16,7
16,7
= 1749,6στ.
= 17ΐ0,8στ.
Здесь учтено, что толщина стенки равна 0,93 см; статический момент площади,
расположенной по одну сторону от оси χ относительно этой оси, равен 899 см3;
для получения статического момента
части площади поперечного сечения,
за исключением той зоны, в которой
деформации упруги, из 899 см3
вычтена соответствующая величина.
Отличие Мх от Мх0 при η = /ι/4
и η = /ι/3 составляет соответственно:
100 (1798 — 1749,6) : 1798 = 2,7% и
100(1798—1710,8): 1798 = 4,8%.
Пусть пластическая область
распространяется на всю
площадь поперечного сечения.
Условие равенства нулю
продольной силы в поперечном сечении
имеет вид N = — Fcxgt-\-Fpgt =
= 0. Отсюда
0,9Ъсм
0,95см
Fynp*
Fn
9
ι*??.'??*·*.
пл
Рис. 12.101. Поперечные сечения двутавра
при различном развитии пластической
области. К определению влияния η на
еж
т. е. нейтральная ось делит площадь поперечного сечения пополам.
Если поперечное сечение балки имеет лишь одну ось
симметрии, лежащую в плоскости действия внешних моментов, то
нейтральная ось не проходит через центр тяжести сечения.
264 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Кривизна оси балки в случае наличия упруго работающей
части поперечного сечения может быть найдена так. Напряжение
упруго работающего волокна равно
σ =
дем
-Ег =
1
~р~
[ ИЗ
Ρ у 1 d2v о
"ρ ' "ρ" ~~ ώ? ~~ ~Еу '
d2v στ
ί/_η ~~ d& ~ £η *
а /(упр)
(12.186) η- τχ ,п.
V ' ' Л/f С(ПЛ)
(12.189)
. Подставляя η;
в (12.189), получаем
d% 1 ΛΓ,—σ Sl.njI)
vi-hsti— (12·190>
2.2. Разгрузка. Если деформации малы, то разгрузку
можно представить как нагружение силами (моментами), равными
и противоположными тем, какие были в конце нагружения. При
разгрузке зависимость между напряжениями и деформациями
становится линейной с тем же модулем упругости, который был
на начальном участке нагружения.
Максимальное напряжение в эпюре напряжений при разгрузке
должно быть таким, чтобы момент, эквивалентный эпюре линейно
распределенных по высоте сечения напряжений, был равен
окончательному значению момента при нагружении. Пусть при нагру-
жении имеет место диаграмма Прандтля, тогда
М — W/n — °т /(УПР) ι п с(пл)
lvlx, разгр— № "max, разгр — ~ 'х ~Г <->т°* »
С^тах, разгр ==ZW ( ~ΖΓ ' х ~\~&τ&χ )· (12.191)
На уровне границы упругой и пластической зон при разгрузке
возникает напряжение
η — rr η _ ^Π_/στ /(УПР) ι „ с(пл)\ /19 109*
аразгр —°max, разгр ^β — ψ^ \ ΊΓ" ιχ Τυτ°* )· Uz-lyz/
Поскольку эпюра нормальных напряжений в конце нагружения
была нелинейной, а при разгрузке — линейной, после снятия
нагрузки в балке имеют место остаточные деформации и
напряжения, эпюра которых равна разности эпюр нагружения и
разгрузки.
Пример 12.28. Построить эпюру остаточных напряжений, получающихся
после разгрузки балки, работающей в упруго-пластической стадии при
следующих условиях: поперечное сечение прямоугольное, в процессе нагружения
материал характеризуется диаграммой Прандтля, упругая зона составляет·
одну треть от высоты балки (2η = Λ/3).
$ 12.17] УПРУГО-ПЛАСТИЧЕСКИЙ ИЗГИБ БАЛКИ 265
Решение. Для построения эпюры остаточных напряжений оост достаточно
определить две ординаты при y=r\ = h/6 и при y = h/2. При y=h/6 oOCT
*:!*>*
•**1^
^1^
°тах,разгр π ит
Рис. 12.102. Эпюры нормальных напряжений по высоте прямоугольного поперечного
сечення: а) при нагружении; б) при разгрузке (Сразгр ). трактуемой как нагружение
моментом, равным по величине моменту в конце нагруження, но противоположным ему по
знаку; в) эпюра остаточных напряжений (оост).
/ 13
найдется как разность величины στ и напряжения (12.192) [о \n=h/6 =o7 στ
{рис. 12.102)
«ост —σ-r ψ^η'χ -Гитс>х J
= στ
η = /ι/6
2/ι·6 /6 b (/ι/3)3
6Μ3 -h\h
12
f2
hb h
r;J=27 στ·
При y = h/2 величина оост найдется как разность величины στ, взятой из
диаграммы нагружения, и напряжения (12.191) (amaxpa3rp = -q-crT j из
диаграммы разгрузки
„ —п L 111. /(Упр) ι σ с(пл)\ _
«ост —στ— ψ I 1Х ^итс>х I —
Γ, 6/6 b (/ι/3)3 26/ι2\Ί 4
= (T41_^U~l2—+ -9-]] = --9-στ·
Выполним проверки, которые состоят в том, что система остаточных
напряжений, являясь самоуравновешенной, должна сводиться к нулевой
продольной силе и нулевому изгибающему моменту
JV=T'-9-aTr3/l-T'27(TTU + 39/lj +
+
14
27'
_7_
39'
отМ-гг+одА) —-o-'-g-oTjg Ί=0.
Λί*= -гг
4 2 . /. . 1 2 Λ 1 14 7 (h . .
-9-στΊ3Λ А-2.у. йЛ)-Т' 27 σ' 39Λ(τ + 2"
+ Г-1^т(т-24-4)- 117-^27.6 ^680-15582-7098)^0.
266
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Коснемся теперь остаточных деформаций. После полного
снятия внешних моментов брус остается криволинейным. Если в конце
нагружения, когда изгибающий момент достиг величины Мх, кри-
1 Mx-oxSxnll)
визна оси бруса согласно (12.190) равна — = — (упр)—, а умень-
1 Мк
шение кривизны оси в процессе разгрузки равно = ~-,
Рразгр Е'х
остаточная кривизна оси выражается формулой
1 _!__!__ Mx-aTS^ _JK_== Mx\lx-ITP)]-0TSK^/X
ΕΙχ £/ /(упр)
το
ост
разгр
£/(упр>
Если упругая область захватывает все поперечное сечение, то
(пл)
irp, = ix, sr=o, ι/ρ
ост
0.
3. Поперечный изгиб. Пусть для материала балки справедлива
диаграмма Прандтля. При поперечном изгибе степень развития
пластических деформации в различных сечениях различна х), так
как изгибающий момент не постоянен по длине балки, как это
<*r. <*г,
Δ 5-5№Ъ-Ъ1-11-1
Рис. 12.103. Упругая н пластическая области в балке при поперечном изгибе, соответ^
ствующне некоторому уровню нагрузки.
имеет место при чистом изгибе. В связи с этим граница между
областями упругой и пластической работы материала представляет
собой некоторую криволинейную поверхность. На простом
примере покажем, как она находится (рис. 12.103).
Изгибающий момент балки в сечении с координатой г=^//2
выражается формулой
Ρζ
Мх=^, Мх\г^т = М
х, max
EL
4 '
*) Напоминаем, что, как это было отмечено выше, влияние касательных
напряжений на условие возникновения пластических деформаций в
рассматриваемом случае невелико и им пренебрегаем,
§ 12.17]
УПРУГО-ПЛАСТИЧЕСКИЙ ИЗГИБ БАЛКИ
267
Именно в крайних волокнах сечения z = l/2 в процессе роста
силы Ρ в первую очередь возникают напряжения, равные пределу
текучести στ. Снабдим обозначение соответствующих изгибающего
момента, внешней силы и радиуса кривизны индексом τ: Мхт,
Ρτ и рт. При этом МХт = Рт1/4. Теперь найдем координату ζτ
поперечного сечения, лежащего на границе областей балки, одна
из которых работает полностью упруго, а в другой напряжения,
равные пределу текучести, захватывают некоторую часть
поперечного сечения, начиная от одного крайнего волокна в сечении
с ζ = ζτ и кончая сечением под силой, где часть его, работающая
при σ=στ, максимальна. С этой целью приравняем изгибающий
момент Мх значению момента МХт
"гт "т* л л ~ fjt_ '
χ — 9 — 4 —/К1*т» ^т— ρ * о "
Установим связь между Мх/МХт и р/рт. Текущее значение
изгибающего момента Мх (Мх > Мхт) выражается формулой Мх =
ft/2
= 2 $ oby dy. Заменим переменную интегрирования,-имея в виду
6
зависимость ί//ρ = ε, # = ερ, dy = pde, e \y=h/2 = emax =/г/(2р), ρ =
= /i/(2emax), тогда получим
emax emax
M* = 2p2 С аЬгаг = щ^ С оЬгаг. (12.193)
о δ
Если ширина поперечного сечения балки постоянна, то Ь в (12.193)
можно вынести за знак интеграла. Разобьем интеграл на два —
первый возьмем в пределах от 0 до ет, а второй от ет до 8тах,
тогда
м, ш
^-тах
ετ етах
(12.194)
\ σε аг + Ι* σε
0 ε„
τ
В первом и во втором интегралах соответственно имеем
а = Ее, σ = στ. (12.195)
Учитывая (12.195)1>2, представим (12.194) в виде
Ь№ г b't /в» 82
Μ
X Ор2
Учтем, что
&Τ~ τ> Жд;~2в2тах[-3+ 2 2j- 12 6ΐ^+4σΧ·
Μ2σ re* ε2 ε2, η 6Λ2 σ ε? Μ2
268
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
Имея в виду, что ΜΧΎ = -^-σΛ, ετ = g- , 8тах=2Б,
[гл. χιϊ
_ Ρ
получим
м,=-%ё+|м,Т=
2р/ ~тах-2р
max
2 Рт
2 (d P?
Ρ
(12.196)
Из (12.196) находим ρ
Исходя из ранее приведенной зависимости у = гр, найдем ρ
при у=у\ и соответственно е = ет:
У
η
Ец
Eh
P=t = g- = -', Р1„-*2=Рт=й;. (12Л98)
Подставим (12.198)1ι2 в (12.197)2 и сократим полученное после
этого уравнение на Ε/στ, в результате находим
■η (ζ).
1-4/
3-2
Λ4*
Λί,-τ
Υ
Здесь учтено, что
Μ,
2 » ίΥ1τ 4 '
(12.199)
Функции η = η(ζ) соответствует граница между упругой и
пластической областями. Эта граница имеет вид квадратной параболы.
<?г
Элюраб
Рис. 12.104. Поперечный нзгнб балкн в упруго пластической области работы материала?
а) границы пластической и упругой областей при разных уровнях нагрузки; б)
образование пластического шарнира при Ρ = Р„.
По мере роста силы Ρ происходит расширение области
пластических деформаций (рис.12.104, а). При некотором значении силы:
Р=Р0 все поперечное сечение под силой работает в пластической
области — образуется так называемый пластический шарнир и;
балка теряет свою геометрическую неизменяемость (рис. 12.104, б)*
§ 12.17]
УПРУГО-ПЛАСТИЧЕСКИЙ ИЗГИБ БАЛКИ
269
Изгибающий момент в сечении под силой должен при этом стать
таким же как и предельный момент при чистом изгибе, а именно
Μχο = ^στ. (12.200)
Формулу (12.200) можно получить и из (12.199), если положить
в ней η = 0, ζ = у, Ρ = Р0\ 0 = -^ 1/ 3 — 4 ~- ^. Решаем
полученное уравнение относительно Р0 и далее находим *МХ0
ro— 2 τ— 2 / — [ ^ϋτ— / υτ» mxo— 4 — 4 τ'
Координата ζΊ при Р = Р0 приобретает значение
— Oil — 11 — 1
Ζ"[~¥ύ2~Ζ2~Ζ'
Иными словами, в момент образования пластического шарнира
в рассматриваемой балке напряжения в крайних волокнах равны
στ на протяжении средней трети длины балки. Разумеется, что
при другой нагрузке и (или) иной форме поперечного сечения
величины Р0, Мх0, гт окажутся иными. Принцип же их отыскания
остается неизменным. Нагрузка Р0 является .опасной "для всей
балки в целом, поскольку последняя при ее воздействии теряет
свою геометрическую неизменность. При расчете балки по
допускаемым нагрузкам условие прочности приобретает вид1)
Ρ < [Я] = Polk.
4. Изгиб статически неопределимых балок.
4.1. Идея расчета. Статически неопределимая балка при
образовании в ней одного пластического шарнира в сечении с
максимальным изгибающим моментом не теряет своей геометрической
неизменяемости, меняется лишь расчетная схема балки, т. е.
изменяется характер ее работы, но балка способна выдерживать
дальнейшее увеличение нагрузки. В сечении, где расположен
пластический шарнир, при дальнейшем увеличении нагрузки изгибающий
момент не возрастает. Будем предполагать, что все силы
монотонно возрастают пропорционально одному общему для них
параметру. При некотором значении параметра нагрузки, превышающем
то, при котором образовался первый пластический шарнир, в
балке образуется второй пластический шарнир и, если при этом не
теряется геометрическая неизменность системы, то балка
способна выдержать дальнейшее увеличение нагрузки, но расчет
ведется по новой расчетной схеме на этот раз в виде балки с двумя
пластическими шарнирами.
*) Идея расчета систем по методу допускаемых нагрузок изложена в § 3.10.
Па
ЖЕ
ПО k
μ° ι щ иг τ 2 ~ί/ι
е)
§ 12.17]
УПРУГО-ПЛАСТИЧЕСКИЙ ИЗГИБ БАЛКИ
271
li+lz=2,5l
Рис. 12.105. К примеру 12.29: а) иераэрезная балка и действующая на нее нагрузка
(такая балка рассматривалась в примере 12.23 прн Ρ — 4 Г н I = 4 м); б) эпюра
изгибающего момента (значения, помещенные в скобки относятся к примеру 12.23, вне
скобок — к общему случаю значений Ρ и /); в) расчетная схема балки после возникновения
первого пластического шара; г) эпюра изгибающих моментов прн образовании второго
пластического шарнира и соответствующая схема балкн (масштаб ординат принят таким,
какой получается прн условии, что на фнг. б Ρ = Рт); д) к построению балочной эпюры
для правого пролета; е) к проверке правильности эпюры, изображенной на фнг. г; ж)
закономерность изменения ординат эпюры Μ как функции параметра Ρ (между значениями
Ρ — Ρ и Ρ = А. не показана; построение эпюры в открытом промежутке LPTf P01 не
является элементарной задачей).
272
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Количество пластических шарниров, при котором балка
перестает быть неизменяемой, зависит от степени ее статической
неопределимости и от вида нагрузки. Если степень статической
неопределимости системы равна п, то максимальное количество связей,
выключение которых превращает ее в геометрически изменяемую,
равно я-Н 1. Однако может быть и такая ситуация (в случае
неразрезных балок она возникает часто), при которой
образование даже меньшего количества, чем п-\-\ пластических шарниров,
приводит к геометрической изменяемости части конструкции, в то
время как другая часть остается статически неопределимой.
4.2. Пример 12.29. Определить опасное значение параметра нагрузки для
балки, рассмотренной в примере 12.23 и изображенной на рис. 12.105, а. По
сравнению с этим примером внесено обобщение. Если в примере 12.23 Р = 4
и /ι = 4 м, то в рассматриваемом здесь случае величины Ρ и ^ = 1 сохранены
в общем виде.
Решение. На рис. 12.105, б представлена эпюра изгибающих моментов,
возникающих в балке. Даны значения ординат как при Р=4Г и /1==/ = 4 м
(помещены в скобки), так и в общем виде. Последние получены из первых
путем деления на 4-4=16 и умножения на Р1. Определение реакций RA и
RB, а также само построение эпюры не показываем, поскольку после
определения R, выполненного в примере 12.23, такие операции элементарны.
Максимальный изгибающий момент имеет место в сечении г — 8м
Μ |2 = 8ж = 0,52152 (7) PL
Обозначим величину силы, при которой в крайних волокнах этого сечения
(предполагаем сечения симметричными относительно оси х) возникает
напряжение равное στ, символом Рт, а соответствующий этой силе изгибающий
момент в сечении ζ = 8 м — символом Μτ. Λίτ=0,52152 (7) PTL
Поскольку при этом материал во всем сечений работает в упругой стадии
Μτ_ 0,52152 (7) /у _ 1 Ψστ_Λ n„WaT
ψ -στ, ψ _στ, ^τ-0522 / -1.У1/ / .
Величину изгибающего момента, соответствующего возникновению в
сечении г = 8 м пластического шарнира обозначим символом М0. При этом М0=
= ηΜτ. η зависит от формы и размеров поперечного· сечения. Напоминаем,
что, например, для прямоугольного сечения я=1,5.
С момента возникновения в сечении г = 8 м пластического шарнира
расчетная схема балки приобретает вид, показанный на рис. 12.105, е.
Дальнейшее увеличение параметра Ρ приводит к возрастанию опорного
изгибающего момента, в сечении же г = 8 м изгибающий момент возрастать не может.
При том значении параметра нагрузки (обозначим его символом Р0), при
котором и в опорном сечении изгибающий момент достигает величины М0, в
опорном сечении также возникает пластический шарнир, и балка теряет
геометрическую неизменяемость. Эпюра изгибающих моментов приобретает вид,
показанный на рис. 12.23, г. Вместе с тем, при действии на однопролетную балку
пролетом 1,5/ сил Ρ и 1,5Р, как это показано на рис. 12.105, д, в сечении
2 2 Μ
под силой 1,5Р изгибающий момент равен -ттР1, поэтому — Р01 = М0-{-—- =
-4«.. Отсюда p.-l.^-^-Mil-MpjL. Тогда pjPt_
= (2ηΨστ/1): (1,9\7Ψστ/1) = \,043η.
§ 12.19]
МЕТОД ПРОГОНКИ
273
Коэффициент 1,043 показывает долю увеличения Р0 по сравнению с Рт,
обусловленную статической неопределимостью системы, т. е. тем, что
геометрическая неизменяемость наступает после образования не первого, а второго
пластического шарнира. После возникновения первого пластического шарнира
увеличение нагрузки лишь на 4,3% влечет за собой возникновение второго
пластического шарнира, сопровождающееся потерей геометрической
неизменяемости.
Условие прочности, пользуясь которым подбираем сечение, имеет вид
„ Р0 2nWoT 2nW. . ,
Ρ = -ς- = —-~- = —ζ—[σ], отсюда находим необходимый момент
сопротивления балки W —Ρ1/2η[σ].
§ 12.18. Изгиб призматического стержня из наследственно-упругого
материала (пример применения принципа Вольтерра)г)
По технической теории балки напряжения не зависят от
упругих постоянных
"г.
/* ' гу ~ Μ (у)'
Значит по принципу Вольтерра напряжения в упругой и
наследственно-упругой балках с одинаковой геометрией и внешней
статикой будут одинаковыми.
Поскольку кривизна в упругой балке выражается следующей
формулой:— = -р/-,для наследственно-упругой балки имеем
О»- tLI v
1 1
Px(t) 1ХЕ*"'Х^> 1ХЕ
Mx(t)
Μ
ι
χ(ί)+^(ρ(ί-τ)Μχ(τ)άτ
где φ(ί —τ) —ядро ползучести при растяжении — сжатии
(предполагается, что смена знака у напряжения не меняет характера
ползучести). В частности, когда Мх = const
J- = ^L-[l + 0(i)]f
WX Е-'Χ
где Φ (/) — функция ползучести при растяжении —сжатии.
§ 12.19. Метод прогонки
1. Предварительные замечания. Для избежания отмеченного в
разделе 9 параграфа 12.15 недостатка метода начальных
параметров—потери точности, а также для эффективного выполнения
х) § 12.18 написан Ю. Б. Шулькиным.
274
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XIГ
расчетов в тех случаях, когда коэффициенты в подлежащих:
интегрированию дифференциальных уравнениях переменны —
представляют собой функции того же аргумента, что и искомая
функция—может быть использован так называемый метод прогонки,-
Ниже, в разделе 2, излагается его сущность.
Пусть имеем краевую задачу для дифференциального
уравнения порядка 2п относительно функции s (ζ) с двухточечными
граничными условиями:
s(2'l) (2) + а2п (z) s^-D (?) + ... + й, (г) s" (г) + а, (г) s' (ζ) +
+ аг (ζ) s (ζ) + α0 (ζ) = 0 в промежутке [0, /],
s(2* -1) (0) + bin_h aS(2,-2) (0) + . . . + b3> ,/ (0) + b% kS' (0) +
+ bhks(0) + b0,k = 0t
s(2'- x> (/) + c2n_lt ks^~v (1) +... + c3i ks" (I) + cit ks' (I) +
+ c1,ks(l) + co,k = 0 .
(й=1, 2, .... /г).
Эту краевую задачу можно сформулировать в других
терминах, перейдя от одного дифференциального уравнения порядка Ire
к системе порядка 2/г, состоящей из 2п дифференциальных
уравнений, каждое из которых, будучи первого порядка, разрешено
относительно производной от одной из искомых функций. Такая
форма системы называется нормальной формой Коши. Разумеется,,
что при указанном переходе подвергаются соответствующей
модификации и граничные условия (12.202). Выполняется это
следующим образом.
Введем обозначение s (ζ) — sx (z).
Далее, применяя новые обозначения для последовательности
производных от s (ζ)
s'(z)=s'l(z)=s2(z); s"(z)=s3(z); ...; s^-1) (z) = s2n (z) (12.203)
и используя совместно (12.201) и (12.203), получим
s,(z)=sr1(z)=s2(z),
S"(z)=s;(2)=Sa(z),
S*(2)=SH?)=M*).
s^^-1) (г) = s^ _ ι (г) = s2rt (г),
s(2«) (г) _ s'2n {ζ) = — (цп (г) s2„ (г) —
— flfe*~i(z)s2«-i(z) —··· —
- Ог (г) s2 (г) - ах (г) s± (г) - а0 (г). :
(12.201)
(12.202>
-§ 12.19]
МЕТОД ПРОГОНКИ
275
Граничные условия (12.202) с учетом (12.203) и (12.204)2Л
приобретают вид
s2n (0) + 62я-1, ks2n-i (0) +... + 62, ks2 (0) + bh ASi (0) + bQt k = 0, "1
s2n (!■) + с2я_ь fcSa^i (/) + ... + c2i fts2 (/) + clt ftSi (0 + c0> ft = 0 J
(12.205)
(6 = 1, ..., η).
В матричной форме (12.204) и (12.205) представляются
соответственно так:
s[ (ζ)
s'Az)
S2n - 1(2)
>2л
(^
0
0
0
at(z)
1
0
0
— a2
(г)
0
1
0
— a3
(ζ)
0
0
0
— «2Я-
-i(z)
0
0
1
— a.
X
а2я (г)
Χ
«ι (ζ)
Si (г)
S2/l-l'(z)
s-in (г)
+
1
I
1
0
0
0
— <% (z)
(12.206)
в промежутке [0, 1],
*1.1
&1,2
*>ί. Я-1
&1.Я
сы
с1.2
ci, я-ι
с1. Я
ί>2. 1 ···
&2, 2 · · ·
^2. Я-1 · · ■
Ьг. η '··
С%, ι
^2. 2 · ·
С2. Я—1 * ·
са. я · ?
&2я-1. 1 ^
^ая-'.а *
&2Я-1, Я-1 *
&2Я-1. Я 1
• с2л-1.1 1
Сая-i, 2 1
• С2я-1. Л-1 '
С2я-1. Я 1
5,(0)
s2(0)
San-i (0)
52я (0)
МО)
s, (0)
«ая-ι (0)
s2* (0)
— &o.j
0. Я-1
-fc,
— b0, η
— Co. ι
— C0. 2
— co. я-1
C0. Я
(12.207)
или
ds
—- = As + g в промежутке [0,1],
dz
Bs(0)=b, Cs(/)=c.
(12.208)
(12.209)
Сопоставляя (12.208) с (12.206) и (12.209) с (12.207), легко
понять, что понимается под символами s, A, g, В, Ь, С, с.
2. Алгоритм1). Разобьем совокупность неизвестных функций
Si {г), ..., s,2n(z) на две группы по η функций. Не поступаясь
х) Излагается вариант алгоритма метода прогонки, обсужденный в статье
В. Л. Бидермана «Применение метода прогонки для численного решения
задач строительной механики», Инженерный журнал «Механика твердого тела»,
1967, № 5, стр, 62 — 66.
276
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. ΧΙΓ
общностью, учитывая возможность произвольной нумерации
функций, будем считать, что эти группы составляются следующими
функциями: Si (г), ..., sn(z) и sn+1 (г),
52я
(г).
Тогда (12.208) и (12.209) можно представить соответственно"
так:
dsj
dz
dsa
dz
41
*21
A1S
A-22
+
gl
в промежутке [0, /], (12.210)=
Bl B2
I MO)
I MO)
=b, 1^ c2
MO
MO
= c.
(12.211)
Переведем граничное условие (12.211) на конце 0 промежутка-
[0, /] в условие на другом его конце /. С этой целью поступим,
так. Прежде всего решим (12.211)х относительное! (0):
или
si(0)=,—8^-8,8* +Bf1 b,
s1(0) = Los2(0) + ro.
(12.212).
(12.213)-
сопоставляя (12.213) и
Вид матриц L0 и г0 легко уяснить
(12.212).
Далее представим решение уравнения (12.210) в следующей,
форме:
s (г) = s<°> (г) + ClSu> (г) + .. . + C„s*n> (г), (12.214)
s(0) (г) — частное решение уравнения (12.208) (или, что то же самое,,
уравнения (12.210)), удовлетворяющее условию (12.213), a s(/) (г)·
(/ = 1, ..., п) — линейно независимые решения однородного
уравнения, соответствующего (12.208) (т. е. уравнения (12.208) при
g===0), удовлетворяющие однородному граничному условию,
соответствующему (12.213) (т. е. условию (12.213) при г(0)=0).
Поскольку рассматриваемая система дифференциальных
уравнений имеет порядок 2п, вектор функций (12.214), содержащий η
постоянных интегрирования, можно рассматривать в качестве ее
интеграла лишь в том случае, если подчинить (12.214) в каждой
точке оси ζ еще η условиям. Последние представим в следующем,
виде:
Si (г) = L (г) s2 (ζ) + г (г). (12.215).
При г = 0 условие (12.215) должно совпадать с (12.213), откуда;
следует, что L (0) = L0 и г (0) = г0.
Матрицы L (г) и г (г) подлежат отысканию. Их найдем из
условия, что s(0) (г) удовлетворяет (12.215), a su) (г) удовлетворяют
однородному условию, соответствующему (12.215) (т. е. условию
(12.215) при г(г)==0).
§ 12.19] МЕТОД ПРОГОНКИ 27 Ί.
Сначала выведем уравнение относительно L (г). Рассмотрим
однородное условие, соответствующее (12.215), полагая, что этому
условию удовлетворяет s(i) (z)
S(0 (г) = L (г) s<<> (г). (12.216)
Продифференцируем (12.216)
Л(0(г) dL(z) ds(0(2)
T = ^rsi"W + L«^. 02.217).
ds(0 (г) ds(0 (г)
Определим —^— и —^-— из (12.210) при условии, что gx (г)—·
= g2(2)=0, и подставим соответствующие выражения в (12.217)-.
ds(0 (г)
-^= AusW(2) + AusiO(2),
ds(0 (г)
-^== А218(/)(г) + А228(0(г);
AllSf> (г) + A12s(0 (г) = ^- sp (г) + L (г) Ая8<<> (г) + Цг) A22s<<> (г).
В полученное равенство вместо s\C) (г) подставим его
выражение, определяемое формулой (12.216); в результате подстановки;
получим
AnL (г) ^» + A12sf = ££L s(/) + L (г) A21L (г) sp + L (г) Arf,
или
[тГ" + L & A*L ^ + L W A*» - A"L & - AiJ s(2° = °· 02·218>'
Поскольку (12.218) выполняется для п линейно независимых,
векторов, матрица, представленная множителем при sp, является:
нулевой; отсюда
^М = - L (г) A21L (г) - L (г) А22 + AUL (г) + А12. (12.219f-
Так.как матрица L (г) гс-го порядка, уравнение (12.219)
эквивалентно системе п2 дифференциальных нелинейных уравнений,,,
каждое из которых первого порядка и разрешено относительно
производной от искомой функции, Эта система уравнений может
быть решена при помощи того или иного численного метода.
В приведенном ниже примере использован предложенный нами-:
метод итераций.
Перейдем к выводу уравнения относительно г (г), во всем-
аналогичному выводу уравнения (12.219) относительно L (г).
Рассмотрим условие (12.215), считая, что ему удовлетворяет s(0) (г),.,
т. е. рассмотрим
s'j0 (г) = L (г) sa0' (г) + г (г). (12.220>
;278 ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ [ГЛ. XII
Продифференцируем (12.220)
&·/>' _ dL(z) ,0I , ds<°' dr(2) Л9 99П
"di HT~S2 +Ъ^-1Г + ~аГ' (12.221)
Определим ds^/dz и ds^'/dz из (12.210) и подставим в
соответствующие выражения в (12.221)
ds'r =A11sT + A12s^ + g1, ^ = A21sr + A22s:T + g.2;
dz "11U1 ' ' 12^ ' S1' d2
A11si0l+Ausiel + gl =
= ^- s'201 + L (г) A21si°'+ L (г) A22s2- + L (г) g2 + £$-.
В полученное равенство вместо s'/" поставим выражение,
определяемое равенством (12.220), а вместо dL (z)/dz — выражение
согласно (12.219); в результате подстановки получим
.AnL (г) s:201 + Aur (г) + A12s20) + gl =
= - L (г) A21L (г) sT - L (г) A22s201 + AnL (г) s201 + A12s201 +
+ L (г) A21L (г) s2<" + L (г) A21r (z) + L (г) A22s20) + L (г) g2 + ^L.
После взаимного уничтожения ряда членов придем к
дифференциальному уравнению относительно г (г)
£$■ = (Аи - L (г) А21) г (г) + gl - L (г) g2, (12.222)
эквивалентному системе η дифференциальных уравнений, которая
может быть решена одним из численных методов. В приведенном
ниже примере для решения этой системы применен метод итерации.
В результате интегрирования уравнений (12.219) и (12.222)
от г = 0 до z = l находим L (/) и г (/); подставляя их в (12.215),
получаем
s1(/) = L(/)s2(/) + r(/). (12.223)
Таким образом, выполнено выдвинутое выше требование
переведения («прогонки») граничного условия (12.211)! с конца г = 0
промежутка [0, /] к концу /, Отсюда и название метода (метод
прогонки).
Описанная выше операция составляет так называемую
«прямую» прогонку. Теперь необходимые для определения искомых 2п
функций, образующих столбец s(z), 2n условий все отнесены
к концу промежутка [0, /] и, таким образом, двухточечная
краевая задача сведена к задаче Коши. Однако для получения
вектора s(z) мы не будем решать задачу Коши, поскольку и при
этом решении происходит потеря точности, имеющая ту же
природу, что и потеря точности при использовании метода
начальных параметров.
§ 12.19]
МЕТОД ПРОГОНКИ
279'-
Поэтому, с целью избежания этого недостатка, для
определения вектора s (г) прибегнем к «.обратной» прогонке, для чего
поступим так. Интегрируя от z = l до г = 0, определим из (12.210)
вектор s2(z), подчиняя его и зависимости (12.215), которая
обеспечит выполнение условий при г = 0. Выглядит это так.
Определим ds2/dz из (12.210) и из полученного при этом уравнения;
исключим sx (г) при помощи (12.215). Итак,
ds2
dz
— ^21Sl "Τ* A22S2 ^2'
и уравнение относительно s2, с учетом (12.215), приобретает вид
ds2
dz
= A21L (г) s2 + А21г (г) + A22s2 + g2;
(12.224)
интегрируя его, находим s2. После этого из (12.215)
получаем sx (г). На этом завершается процесс обратной прогонки;,
таким образом задача
полностью решена.
ЧГЧо
3. Пример 12.30. Определить
вектор s(z) = {vftMQ} для балки
переменного сечения, опирающейся
по всей своей длине на винкле-
рово упругое основание
переменной жесткости, а по концам
упруго опертой и упруго
заделанной. Нагрузка, действующая на
балку, и информация о законах
изменения вдоль пролета Ink
(момент инерции площади
поперечного сечения балки и коэффициент
постели упругого основания)
показаны на рис. 12.106. Поперечное
сечение прямоугольное (ширина
90 см, высота 100 см), Е =
= 360000 кГ/см*, /0= (96 · 1003)/12=
= 8- 10е см1, £0 = 20 кГ/см2, q0 =
=ШкГ/см, 910 = 0,5· \0-Щ/кГсм,
А0 = 0,5 · 10'6 см/кГ, Щ =0,3-
■ \0-10\/кГсм, Лг = 0,3 · Ю-6 см/кГ.
Решение. Имея в виду
дифференциальные зависимости
Эпюра Ι=Ι(ζ}-
длюра к-кау
Рис. 12.106. К примеру 12.30: а) балка и
действующая на нее нагрузка; б) эпюра / = / (г);.-
в) эпюра k = k (г); Ε = 360000 кГ/смг, /0 =':
" " см*, ka = 20 кГ/см2, q% = 300 кГ/см,.
1 Ао = 0,5-10-в см/кГ,
8 · 10е см*, k0
Sl0 = 0,5-Ю-»0
SI; = 0,3· 10-"
кГ/см '
' А
кГ/см ' I
U =
M' = Q,
ΕΙ '
Q' = —q = —(q-ku), (12.225)
ΕΙ,
- = 0,00347 (2). 10-"
0,3· 10-· см/кГ,.
1
κΓόμ '
введя обозначения
υ (г) = si (г), Φ (г) = s2 (г), Μ (г) = ss (г), Q (г) = s4 (ζ) (12.226).
и учитывая тот факт, что от (12.204)3 зависимость между s2 и s3 отличается w
имеет вид
si (г) = —«я («)/(£/),
280
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
ятредставим уравнение (12.206) в виде
о'(г)
О'(г)
М' (г)
Q'{z)
1 !
0J —
_0
ΕΙ (г)
0 0\
k (г) 0 I
0
0
ν (г)
О (г)
Μ (г)
<?(г)
+
О
О
О
•9 (г)
(12.227)
Разумеется, к (12.227) пришли бы и исходя из дифференциального
уравнения изгиба балки на упругом основании
(ΕΙ (г) ν" (г))'=ф (z) = -q (г)+* (г) и (ζ),
«ли
(£/(г)о'(г)Г+*(г)1>(г) = <7(г)
л выполняя процедуру, описанную в разделе 1 -настоящего параграфа.
Граничные условия имеют вид
1 0
0 1
■*о
ν(0)
*(0)
М(0)
Q(0)
0
0
9
1 0; 0 At
о ι ι si, о
ν (Ι)
*(/)
Λί(0
Q(0
0
0
Из (12.228)i
si (0) =
υ(0)
Ο(0)
О — Д,
-«о О
Μ (0)
Q(0)
+
(12.228)
= LoS2 (0) + r0. (12.229)
Переходим к отысканию матрицы L (г). Уравнение (12.219) относительно
1, (г) в нашем случае, если учесть (12.227), имеет вид
dLn(z)
dz
dL21 (z)
dz
dL12 (г)
dz
dL22 (г)
dz
Ui (г) L12 (г)
ί<2ΐ (г) L22 (г)
О О
Λ (г) О
Ln (г) L12 (г)
L2i (г) L22 (г)
ί-ιι (г) L12 (г)
L2i (г) L22 (г)
О 1
О О
+
О II
о о
Ln (г) L12 (г)
^2i (г) L22 (г)
+
1
Е1(г)
(12.230)
Производя в (12.230) простейшие матричные операции, получаем систему
дифференциальных уравнений относительно элементов матрицы L (г)
din (г)
dz
= L21 (z) — L12(z)k(z)Ln(z),
dLd\iZ) = L22 (ζ)-La (z)-Li2 (г) k (г) Li2 (г),
dL2l (г)
dz
dL22 (г)
dz
1
— L22(z)k(z)L11(z),
EI(z)
= — Ln (z) — L22 (г) k (г) Li2 (г).
(12.231)
Систему (12.231) интегрируем методом итераций с учетом начальных
условий (матрица L0 дана в формуле (12.229))
L(2)U-o = L(0) =
Ιιι(0) Lu(0)
^2i(0) Laa(0)
0 -Л0
— Slo 0
= L0. (12.232)
§ 12.19] МЕТОД ПРОГОНКИ
Итерации выполняем по следующим формулам1):
2
47> (г) = - [[ёЩ +L&~ Х) (г)* (г) МГ ° (г)] ώ + ««.
о
4? (г) = - J U^ (г) + ^"~ υ (г)* (г) Ltf" '> (г)] аг,
"о
4? (*> = J Ш? (г)-МГ '> (г)* (г) МГ !) (г)] <*г,
о
4? (г) = \[Ц? (г)-Li? (г)—Z-<g- '> (г) Л (г) Lft" ° (г)] d2 + A0,
о
(л=1, 2, ...).
281:
} (12.233).
В нулевом приближении принимаем L[\] (г) = 0, Ζ/β (г) = А0, Щ1 (г)=0.
Результаты вычислений2) приведены в табл. 12.11. Итерация прекращена
при получении в соседних приближениях Ly шести одинаковых значащих,
цифр в десятичной системе. Такой результат достигнут после двадцати
итераций при разбиении промежутка интегрирования на тридцать равных частей-
В табл. 12.11 приведены значения Li;- (ζ) через 1/10 промежутка
интегрирования.
Таблица 12.1?
2
0
0,1/
0,2/
0,3/
0,4/
0,5/
0,6/
0,7/
0,8/
0,9/
/
-L„ ■ 10'
(1/кГ)
0
0,0867112
0,2322393
0,4373973
0,6817992
0,9203529
1,107362
1,228536
1,302697
1,361435
1,437525
Llz ■ 10*
(см/кГ)
0,05000
0,14406
0,51183
1,27160
2,44966
3,89083
5,31293
6,51429
7,49662
8,41459
9,50758
-ί-,ι ■ Ю1»
(ХКкГсм))
0,50000
0,96050
1,51048
2,12839
2,74494
3,25603
3,58193
3,71589
3,70910
3,62855
3,53607
L„ ■ W
О/кГ)
0
0,0867112
0,2322393
0,4373973
0,6817992
0,9203529
1,107362
1,228536
1,302697
1,361435
1,437525
J) Верхний индекс у Ly (z) обозначает номер итерации.
2) Вычисления выполнены на ЭВМ ЕС-ЮЮ по программе, составленной.:
В. И. Париковым в ВЦ Ленпромстройпроекта в группе, руководимой В. И. Слив--
кером. Обоим этим лицам автор приносит глубокую благодарность^
.282
ПЛОСКИЙ ИЗГИБ СТЕРЖНЕЙ
[ГЛ. XII
Аналогично методом итерации находим и г (г). Согласно (12.222)
dRi (ζ)
dz
dR2 (ζ)
dz
0 1
0 0
tfl(2)
Rii?)
Lu (г) L12 (z)
i<2i (z) L22 (z)
1
0 0
IIЬ (ζ) 0
Ri(z)
R2(z)
Ln (г) L12 (ζ) ||
L2i (ζ)
/•22(2)1
0
— я
(12.234)
После выполнения матричных операций в (12.234) получаем систему
дифференциальных уравнений относительно #ι (ζ) и R2 (ζ)
dRx (z)
dz
dR2 (г)
dz
= R2 (z)-L12 (z) (/?! (z)k(z)-q (г)),
= L22{z){q{z)-R1(z)k{z)).
(12.235)
„При интегрировании учитываем начальное условие
#ι(0)
Яа(0)
= Гл
«■(z)U-o = r(0) =
'Итерации выполняем по следующим формулам:
#<«> (z) = J [L22 (z) (q (ζ)-/?{"- ') (z)k(z))]dz,
(12.236)
о
г
R[n) (*) = $ [#(2я) (z)-L12 (г) (R[n~ ') (г)* (ζ)-? (ζ))] dz.
6
(12.237)
"В нулевом приближении принимаем #iol(z)=0. Результаты вычислений
приведены в табл. 12.12. Итерация прекращена при получении в соседних
приближениях Ri шести одинаковых значащих цифр в десятичной системе. Такой
результат достигнут после тринадцати итераций при разбиении промежутка
интегрирования на тридцать равных частей. В табл. 12.12 значения Rt
шриведены через 1/10 промежутка интегрирования.
* 2
' 0
• ο,ι/
0,2/
) 0,3/
,; о,4/
: о,5/
Ri (см)
0
0,0372156
0,213243
0,756959
1,93668
3,87984
Rz ■ Ю'
0
0,151416
0,790724
2,21861
4,59396
7,67936
ζ
0,6/
0,7/
0,8/
0,9/
/
Таб
Rt (см)
6,43201
9,29586
12,3224
15,6622
19,8161
лица 12.12
Rz · Ю2
10,8642
13,6195
15,8876
18,0712
20,9167
После отыскания L (ζ) и R (ζ) из (12.228) и (12.223) находим столбец
{υ(1) *(/) M(l)Q(l)h
§ 12.19]
МЕТОД ПРОГОНКИ
285-
Итак имеем:
ι о; о Аг
о 11 «ι о
ν (0 II
*(о!"
£ц(0 Ц*(1)
L2i(l) L22il)
viD
O(0
Mil)
Q(i)
0
0
ι
Mil)
Qil)
+
Ri(t)
«2(0
\
(12,238);,
В развернутом виде эти уравнения имеют вид
о(0+ i4|Q(/) = 0, 1
Ф(0 + »|Л4(0 =0,
ν (Ι) - ί-u (/) Μ (/) - L„ (/) Q (/) = /?! (/),
О (0 - *4i (0 Af (0 - L22 (/) Q (/) = R2 (/). ,
Решая систему (12.238), получаем
υ (/) = Л, [R2 (/) Lu (0-/?i (0 Lai (/)-/?i (0 91Л : D,
* (0 = »i [«i (0 *.m (0- «2 (0 i-12 (0 - A[R2 (/)]: D,
Λί (/) = [—/?! (0 Iaa (0 + Яа(0^12 (0 + Л/Яа (01: £>.
Q (0 = [~ *.ii (0 «2 (0 + La (/) I?! (0 +Я1Я1 (01 : D,
Ο = '-ιι (0 ί-22 (0-^-12 (0 ί-21 (0-Я/ Lia (O + HfLa (0-Mi·
Численные значения приведенных выше величин суть:
ν (/) = 8,657381 · ΙΟ"2 см, φ (/) = — 1,608469 ■ 10"» рад.,
М(1) = — 5,361563 · 10' кГсм, Q (/) = — 2,885794 · Ю5 кГ.
Переходим к обратной прогонке, для чего интегрируем уравнение (12.224)»
в промежутке [0, /] от z = l к ζ = 0.
Это уравнение в рассматриваемом случае имеет следующий вид:
112 (ζ) Μ (ζ)
^22 (Z) Q {Ζ)
(12.239)-
dM
dz
dQ
dz
0
k(z)
0
0
I Ln (z)
+
+
Μ (ζ)
Q(z)
+
0
kiz)
Rx(z)
Я2(г)
+
0
-?(z)
Выполняя матричные операции, получим систему дифференциальных
уравнений относительно Μ (ζ) и Q (ζ)
dM^=Q(z),
dz
dQjz)
dz
= k (z) Ln (ζ) Μ (ζ) + £ (ζ) Lia (2) Q (ζ) + * (ζ) #г (ζ) - 9 (ζ).
(12.240),
Систему (12.240) интегрируем методом итерации в промежутке [0, /]„..
начиная от z=l и кончая z = 0,c учетом начальных условий (12.239)34—
Итерации выполняем по следующим формулам:
Μ'»1 iz) = M (/) + $ Q"*-1' (z) dz,
Q<«' (ζ) —
= Q (0 + $ [* (2) Lu (ζ) Λί<«> (2) +Λ (2) L12 (z) Q'«-*' (z) + , (z) /?! (z)-q (z)j dz.
:284 плоский изгиб стержней [гл. хн
Результаты вычислений помещены в табл. 12.13.
Таблица 12.13
г
0
0,1/
0,2/
0,3/
0,4/
0,5/
Λ1 · Ю-7
(кГсм)
—4,04180
—1,78572
0,013309
1,33578
2,16584
2,48219
Q · 10-*
(кГ)
2,06346
1,69309
1,30297
0,899324
0,481600
0,041386
ζ
0,6/
0,7/
0,8/
0,9/
/
м · ю-'
(кГсм)
2,24986
1,41681
—0,082778
—2,32000
-5,36156
Q · Ю-5
(кГ)
—0,435072
-0,961600
— 1,54663
—2,19039
—2,88579
В нулевом приближении принимаем Q (z) = Q (/). Итерация прекращена
*при получении в соседних приближениях Q и Μ семи одинаковых значащих
цифр в десятичной системе. Число итераций в программе было принято априорно
равным 41, что в четыре раза превысило количество необходимых итераций
для получения указанной выше точности.
Завершается расчет отысканием функций ν (ζ) и ϋ (ζ). Это выполняется
путем использования формулы (12.215), которая в рассматриваемом случае
приобретает следующий вид:
о (*) II
После выполнения указанных в (12.241) операций получаем значения ν (ζ)
и Φ (ζ), приведенные в табл. 12.14.
Таблица 12.14;
г
0
0,1/
0,2/
0,3/
0,4/
0,5/
V (СМ)
0,103173
0,435974
0,877053
1,31628
1,63977
1,75638
0-103 (рад)
2,02090
3,33469
3,79663
3,30917
1,93240
—0,021817
ζ
0,6/
0,7/
0,8/
0,9/
/
V (СМ)
1,62909
1,29114
0,835743
0,389435
0,865738
■&· 10» (рад)
—2,01244
—3,45875
—3,95333
—3,33139
— 1,60847
Приведенная выше информация для функций Q и Μ о точности, дости-
> гаемой в итерационном процессе, и о числе итераций относится и к функциям ν
,и ·θ. Как и при вычислении L^ и Ri при отыскании значений функций Q, М,
■ ν и ■& промежуток интегрирования разбивался на тридцать равных частей.
В табл. 12.13 и 12.14 даны результаты для аргументов, взятых через 1/10
; промежутка интегрирования.
Машинное время, затраченное на решение всего примера, составило 1 минуту
51 секунду. Цифровая информация, приведенная в таблицах 12.13 и .12.14 дана
-со значительно большей точностью, чем требуется в инженерных расчетах.
Lu (г)
Ln (z)
La (z)
L22 (ζ) Ι
\M(z)
Q(z)
+
Riiz)
Яа(2)
(12.241)
Глава XIII
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
§ 13.1. Предварительные соображения
В главах II, XI и XII рассмотрены так называемые
элементарные деформации стержня: осевая деформация, свободное
кручение и плоский поперечный изгиб. В первом! случае в
поперечных сечениях стержня возникает продольная сила N, во втором —
только крутящий момент Mz, в третьем — только изгибающий
Рис. 13.1. Примеры конструкций, в которых стержневые элементы испытывают сложное
напряженное состояние: а) водонапорная башня (колонна сжата весом бака с водой и
собственным весом и изогнута давлением ветра); б) рама (элементы аб н вг изгибаются
и скручиваются): в) пролетное строение моста (балки изгибаются в вертикальной плоскости
постоянной и временной нагрузками, сжимаются тормозной силой, изгибаются в
горизонтальной плоскости и скручиваются боковыми горизонтальными (удары подвижного
состава) воздействиями).
момент Мх и поперечная сила Qy (или Му и Qx). В ряде случаев
стержень работает в условиях, когда в его сечениях возникают
иные комбинации усилий, нежели отмеченные выше, а в самом
общем случае могут возникнуть все шесть составляющих
внутренних силы и момента г) - Qx, Qy, Ν, Мх, Му и Мг. Такую работу
*) Соответствующие примеры на построение эпюр последних рассмотрены
в главе I,
286 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ХПГ
Pi
1\
—--*»т'
О
'/,
ж
ШЯ,
δ)
■ Pi
Pi \\
стержней в отличие от элементарных, упомянутых выше видов-
деформаций, называют сложным сопротивлением стержней. На
рис. 13.1 изображены стержневые конструкции, в которых стержни
испытывают сложное сопротивление.
Настоящая глава посвящена определению напряжений и
перемещений в случае сложного сопротивления стержней.
Если в стержне перемещения точек оси малы по сравнению·
с поперечными размерами, а повороты малы по сравнению с
единицей, то применим принцип
независимости действия сил, и, таким
образом, непосредственно могут быть,
использованы результаты теории
элементарных видов деформации стержня
с прямолинейной осью. Теория
сложного сопротивления стержня в этом
случае, при условии соблюдения и
закона Гука, оказывается линейной.
Именно так и строится теория в
§§ 13.2-13.4, 13.8 и 13.9.
В случае, если не выполняются
указанные выше условия, и,
следовательно, принцип независимости
действия сил не применим, приходится
строить специальную теорию, в
которой учитывается взаимное влияние
отдельных факторов.
Представим себе стержень,
загруженный силами Рг и Р2 (рис. 13.2).
Очевидно, что деформация,
вызванная каждой из сил Рг (сжатие, рис.
13.2, а) и Р2 (изгиб, рис. 13.2, б) при
одновременном их действии, влияет
на усилия, возникающие в
поперечных сечениях от другой силы. Действительно, под влиянием
силы Рг стержень укорачивается и, следовательно, плечо силы Р2
относительно центра любого сечения, например, с координатой
2 = 0 уменьшается, вследствие чего изгибающий момент, вызван-
wrn
В)
ю
Рис. 13.2. К установлению границы
использования принципа
независимости действия сил: в) сжатие
стержня силой Рх; б) изгиб стержня
силой Рг; в) совместное действие
сил Pi и Р2 на стержень. Если
Рг da — *ι) < Рг'о н Pte «S Рг/о, то
можно пользоваться принципом
независимости действия сил (обратите
внимание на то, что /0 — h зависит
от Pi н е зависит от Ра).
ный силой Р9 в сечении
г = 0,
Р,
также уменьшается. С другой
стороны, в отсутствие силы f2 сила Рг только сжимает стержень,
при наличии же силы Р2 сила Рх, кроме того, и изгибает
стержень, поскольку линия действия силы Рг не совпадает с его осью
из-за наличия прогиба, вызванного силой Р2. Такое взаимное
влияние имеет место всегда. Однако это влияние составляет
заметный процент от эффекта самостоятельного действия каждой из
сил лишь при условии, что стержень достаточно гибок (велико
отношение l/h, где / — длина, a h — поперечный размер) и что на
<§ 13.2] ПРОСТРАНСТВЕННЫЙ ПОПЕРЕЧНЫЙ И КОСОЙ ИЗГИБ 287
него действует большая по величине нагрузка. При ощутимом
взаимном влиянии эффектов сил пользоваться принципом
независимости действия сил, в котором предполагается полное отсутствие
этого взаимного влияния, нельзя.
Вопрос о границе правомочности (с наперед заданной
точностью) принципа независимости действия сил при одновременном
приложении к стержню продольной и поперечной нагрузки
рассмотрен в § 13.5.
§ 13.2. Пространственный поперечный изгиб. Косой изгиб
1. Пространственный поперечный изгиб.
1.1. Внешние силы и внутренние усилия. Пусть
имеем призматическую балку; неподвижное закрепление ее как
жесткого тела в пространстве осуществим при помощи опорных
стержней. Свяжем с балкой систему координатных осей Охуг,
начало которой расположим в центре тяжести одного из торцов;
направим ось ζ вдоль оси балки, а оси χ и у совместим с
главными осями инерции торца. Будем считать, что вся нагрузка
гх
Рис. 13.3. Стандартная система внешних сил, вызывающих пространственный нзгнб
■(количество сосредоточенных воздействий может быть различным, сосредоточенные силы
и моменты могут быть прнложенылнбо к одному н тому же, либо к различным сечениям;
распределенные силовые и моментные нагрузки могут занимать различные участки на
балке, начиная от полной ее длины, и иметь различные пересечения областей действия).
(внешние силы и реакции опорных стержней, которые полагаем
известными), действующая на стержень, приведена к стандартной
системе.
Точки приложения сосредоточенных (Рг) и распределенных
(q = q(z)) сил лежат на прямой линии, на которой располагаются
центры изгиба поперечных сечений (такое приложение сил
исключает возникновение кручения), а точки приложения
сосредоточенных и распределенных векторов — моментов лежат на оси стержня.
Разложим Ри 9Rh q, m на составляющие в системе осей Охуг
(рис. 13.3): Plx, Piy, Piz, Ш1х, Ш1]}, ЪЖ1г, qx, qy, qz, тх, my, mz.
В настоящем параграфе будем считать, что
Ρ и
О, Ш1г = 0, ?is0, тг~ 0.
288 сложное сопротивление стержней [гл. хш
м,
:0.
При таких условиях в поперечных сечениях
ЛГ^О, Мг^0, <&ξ£0, Qtf=£0, Μ*ξ£0, ,„„.
Деформация балки при описанных выше условиях называется
пространственным поперечным изгибом, поскольку силы и
изогнутая ось балки располагаются не в плоскости, а в пространстве.
Пусть функции Qx, Qy, Мх, Му известны, например для них
построены эпюры.
1.2. Формула для нормального напряжения
в поперечном сечении. Применяя принцип независимости
действия сил, представим рассматриваемую деформацию балки
как сумму двух изгибов —в плоскостях Oyz и Охг. Вследствие
этого, учитывая (12.10), получаем
σ =
Мху
Мух
Ιχ Π 1у
1.3. Нейтральная линия, нейтральная
поверхность. Точки (х0, уа) в поперечном сечении, в которых σ=0τ
образуют прямую (нейтральную ось), уравнение которой имеет вид
Мху0 , Л^х0_
— — Ж,
+
о, * =
Рассмотрим
му1х
1х 'у
(13.1)
tga
Xq
My IX
tga = — W-T.
iY1x ' у
(13.2)
Угол α (рис. 13.4) является функцией г, поскольку от ζ
зависит отношение Му/Мх. Множество нейтральных осей всех попереч-
а?
х0
Jo^
I
Рис. 13.4. Положение
нейтральной оси при
пространственном изгибе стержня.
Рис. 13.5. Нейтральная поверхность при
простраиствениом изгибе стержня.
ных сечений образует нейтральную поверхность, которая, что ясно
из ее определения, является линейчатой (рис. 13.5).
1.4. Перемещения. Изогнутая ось определяется двумя
функциями υ = υ(ζ) и u = u(z), отыскиваемыми из
дифференциальных уравнений EIxv{V = qy, EIyulv = qx.
§ 13.2] ПРОСТРАНСТВЕННЫЙ ПОПЕРЕЧНЫЙ И КОСОЙ ИЗГИБ 289
Полное поперечное перемещение, ортогональное к
первоначальной оси стержня, представляет собой величину ]/Лы2 + и2.
1.5. Касательные напряжения. Относительно
касательных напряжений подробное пояснение дано в главе XII. Там
показано, как поступать, когда имеются две отличные от нуля
поперечные силы Qx и Q,j.
1.6. Пример 13.1. Для балки, изображенной на рис. 13.6, а (здесь же
показана нагрузка), построить нейтральную поверхность, эпюры напряжений
и изогнутую ось.
Таблица 13.1
и
я
в·
>>
М,
М.
Му<Х
со
V/
V/
о
со
см
V/
V/
со
V/
V/
со
см
а.
го_
см
I
а.
ю
со"
+
а.
со
а.
см
го
см
I
а.
ю
со"
+
со
а.
см
оо [со
+
00
со
см
ю
со"
а.
+
со
а.
см
со_
см
ю
со"
а,
+
а.
■«#
0
Ιβ
13//36
7//18
51/12
41/9
51/9
-2//3
71/9
81/9
0,9293/ ^- ε
0,9293/ +ε
ι
0
0
. —31°35'
—40°50'
—58°0'
—63°2б'
—72°58'
—75°58'
—79°2'
—85°30'
—90°
+90·
+73° 17'
Пр. имечани я:
х~ 12 ' У~ 12 *
2. Величины Λί^. и Μ в характерных сечениях даны на рис. 13.6, б.
3. Численные значения tg α при г, указанных в графе 5, приведены на рис. 13.6, в.
10 А. П. Филин, т. II
290 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ХШ
>\
ζΊιΗιΜι
z-gl z-jl z-^l щ1 ~L
0.3Wtl
Рис. IS.β. К примеру 1J.1: а) балка и действующие на нее силы; б) эпюры изгибающих
моментов Мг и М„; в) график функции tg α.
§ 13.2] ПРОСТРАНСТВЕННЫЙ ПОПЕРЕЧНЫЙ И КОСОЙ ИЗГИБ 29t
Решение. Раскладываем силы на составляющие, параллельные осям χ и у.
Нейтральная поверхность определяется уравнением (13.1).
Вся информация по определению Мх, Му, tga и α сведена в табл. 13.1.
График tga = /(z) показан на рис 13.6, в. Вид нейтральной поверхности
показан на. рис. 13.7. Определение напряжений сведено в табл. 13.2.
Рис. 13.7. К примеру 13.1. Нейтральная поверхность (продольный и поперечный
масштабы изображения балки различны здесь и на рис. 13.8 и 13.9).
На рис. 13.8 показаны эпюры напряжений в сечениях балки. На рис. 13.9
дана более исчерпывающая характеристика распределения напряжений в балке,
при этом использован принцип изображения, проиллюстрированный на рис. 13.10;
эпюры напряжений, лежащие в плоскостях боковой поверхности призмы
повернуты на 90° до совмещения с плоскостью поперечного сечения.
Рис. 13.8. К примеру 13Д. Эпюры нормальных напряжений в характерных
поперечных сечениях балки (сечения, в которых изменяется вид функции Μ и (или) Μ ).
У
Так как закон изменения изгибающих моментов вдоль оси балки по
участкам линейный, .достаточно было показать на рис 13.8 эпюры нормальных
напряжений лишь в тех поперечных сечениях, в которых происходит
изменение, вида функций Мх и (или) Му. Ввиду линейности закона изменения по
10*
.292
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
участкам вдоль балки и Мх и Му, линейным по участкам оказывается и закон
изменения напряжений вдоль продольных ребер. Это и изображено на рис 13.9.
Имея эпюры изменения вдоль длины балки нормальных напряжений в углах
Off -^=7 . Lrb
мг ьь1
Рис. 13.9. К примеру 13.1. Эпюры нормальных напряжений в поперечных сечениях балки.
поперечных сечений, легко построить эпюру этих напряжений в любом поне-.
•речном сечении.
Ю 5)
Рис. 13.10. К построению повернутой эпюры нормальных напряжений в поперечном
сечении балки: а) эпюра нормальи'йх напряжений, в которой ординаты направлены вдоль
действительного направления σ; б) эпюра нормальных напряжений в точках поперечного
сечения, расположенных у его контура, в которой ординаты повернуты на 90° и
совмещены с плоскостью поперечного сечения; I — нейтральная ось.
Найдем функций υ и и, решая краевые задачи
Efxvlv=qy\ ο|,_/ = 0, у' U_/ = ^-U-/ = 0;
Elyuxv = qx\ и:|,_, = 0, и'\ζ^ = Оу |*_, = 0.
Не приводя промежуточных выкладок, подробно поясненных в главе XII
в ряде примеров, покажем окончательные выражения функций ρ и и,
§ 13.2] ПРОСТРАНСТВЕННЫЙ ПОПЕРЕЧНЫЙ И КОСОЙ ИЗГИБ 293
со
то
Я
К
ч
ю
то
О
oq
о
«J
to
to
=»
5
«о
j;
,
«ο
!
Λ)
5
Η
5
Ν
С?
1
5"
Τ
(4) - (5
+
ю
+
2
1
ю
+
+
ю
■*
СО
CN
О
О
о
о
о
о
о
о
о
а.
см
•о
•^1
а.
см
Si
•о
1
•^1
см
<Я
-О
•^1
а.
см
<я
•О
1
о
*-л
а.
см
<Я
•О
1
о
а, μ
1
ео_
»--»
*■**
а,
см
<я
st
•о
•^1
а,
<Я
•о
II
-с |-о
^*
1
^
•^1
а,
<я
St
•о
II
·« |·ο
■*
Г
^J_^
•^1
а,
<Я
•О
а.
-*
•е
(Я
Ό
1
•^1
а.
(Я
•о
1
*-чк
а.
см
•^1
а.
см
го
1
со
1
со
см
·—*
а.
^*
(Я
-о
I
1
II
s: |S
см
Ί
II
•^1
Л
Si
СМ
о"
a, ла
00
00
см"
jL^
-с |-о
О)
о"
1
00
1
1
а.|3£
II
•е |·ο
σι
сГ
1
00
о_
·-* |ет
•^1
а.
σ>
о"
•si
<Я
-О
1
at
00
1 '
(Я
St
•О
•^*
а.
ю
о"
1
,ΙΒΡΙ
о
■^*»
•^1
а.
(Я
-Si
•o
00
00
см"
1
1
II
CL Ηί
CM
o"
1
II
294
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. ХШ
(Промежуточные выкладки предлагаем выполнить читателю.)
Ρ/3 Р/2 РгЗ
о = О,1586-^ 0,3035 4гт- ζ '
Е1Х
II 5^2 Ρ/ _2_ \з
ΕΙ χ" ι'βΈΓχ~\ι \2ΕΙΧ \Ζ 3
3
Ρ/3 Ρ/2
κ = 0,171 ^τ °'2481ΓΓ 2 +
3E(y\Z з)
'у
ι 3£7,
з"
Определим функции и и ν в трех характерных сечениях г=0, 1/3, 2//3-
5J/J2P/ __2_ \8
2_ 12£/„ Г 3 '
3
Р/з р/з р/з
«1,-0 = 0,171^ = 0,684^-, 0 1,^ = 0,1586^-,
P/S Р/З
: 0,0636
РР
Е1Х'
Р/з р/з р/з
«|г=2;/3 =0,0183 ^-=0,0730^-, ν |г = 2г/3 =0,0057 ^-.
Здесь учтено, что /г/6 = 2, вследствие чего т^ = -т" : ~W == 1л ~ ' 'χ — ^y
На рис. 13.11 схематично изображена изогнутая ось балки. Очевидно, что
это пространственная кривая.
Рис. 13.11. К. примеру 13.1. Изогнутая ось балки (пространственная кривая); 1 —.
отклонения, характеризующие выход изогнутой оси из плоскости.
2. Косой изгиб
2.1. Условия возникновения. Рассмотрим частный
случай пространственного поперечного изгиба —так называемый
косой изгиб, возникающий при выполнении двух условий:
1) все силы (Ph q), включая реакции в опорных связях и
моменты (Ю1{, т), действуют в одной плоскости, называемой
плоскостью действия сил, которая в рассматриваемом случае: не
совпадает с главной плоскостью инерции;
2) моменты инерции площади поперечного сечения балки
относительно главных осей не равны один другому (1хф1у).
При таком расположении нагрузки отношение изгибающих
моментов Μχ/My имеет одинаковое значение во всех сечениях,
§ 13.2] ПРОСТРАНСТВЕННЫЙ ПОПЕРЕЧНЫЙ И КОСОЙ ИЗГИБ 295
вследствие этого угол α сохраняет свою величину и нейтральной
поверхностью оказывается плоскость. Некоторые другие
особенности косого изгиба проследим на приводимом ниже примере.
2.2. Пример 13.2. Пусть имеется призматическая консольная балка,
загруженная одной силой Р, приложенной к центру тяжести торца
перпендикулярно оси балки и под углом φ к оси у (рис. 13.12) (начало координат
помещено в центре тяжести торца, ось ζ
направлена вдоль оси балки, оси χ и
у — главные оси инерции поперечного
сечения). Найти положение
нейтральной плоскости в этой балке и
распределение в ней нормальных
напряжений.
Решение. Разложим силу Ρ на
составляющие по осям χ и у: Рх и Ру
Рх — Р sin φ, Ρ у — Ρ cos φ.
При этом
Мх — — PyZ —— Ρ cos φ · ζ =— Μ coscp,
My = — Pxz — — Ρ sin φ · ζ — — Μ sin φ.
Здесь Μ = Ρζ.
Нормальные напряжения в
поперечных сечениях находим по формуле
Мху Мих
σ—^4-А. (13-3)
1 χ 'и
Рис. 13.12. Косой изгиб балки (существует
плоскость действия сил, составляющая
угол φ с у — главной осью инерции
поперечного сечения; Ιχ φ 1 ); t — плоскость
действия сил.
Уравнение нейтральной линии получим из условия σ = 0, так как в точках
Рис. 13.13. Расположение нейтральной линии в поперечном сеченнн балки,
испытывающей косой нзгнб: а) к зависимости между х», у» и a (tga =· ytlxt)\ б) вваимное
расположение следа плоскости действия сил и след* нейтральной плоскости
ί — нейтральная линия; t — след плоскости действия сил
(*«_·-££*,);
(*о· Уо) поперечного сечения на этой линии нормальные напряжения равны
нулю; Поскольку Μ φ О, получаем
л Уо Ιχ irt m
:0, -, = __ tg<p,
Χα ι и
у о соз φ . Хр sin φ
Ι χ +
■ у x0 ' у
ло, с другой стороны, отношение уа/ха (см, рис. 13.13, а), представляет собой
296 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XIII
тангенс угла наклона нейтральной линии по отношению к оси х,
обозначавшегося в предыдущем разделе символом ос. Таким образом,
Ιχ
χο 'и
(13.4)
Если угол (π/2) —φ в первой четверти, то ее —в четвертой (рис. 13.13, б).
При 1х — 1у α = — φ и нейтральная плоскость перпендикулярна плоскости
действия сил (плоский изгиб). Во всех остальных случаях | ot | =^ ш и
нейтральная плоскость не перпендикулярна плоскости действия сил. Такой именно
изгиб и называется косым.
Отличие |сс| от φ увеличивается с увеличением отношения 1х/1у- В
качестве иллюстрации рассмотрим случай прямоугольного поперечного сечения со
сторонами /гиб при различных отношениях сторон (табл. 13.3). В
зависимости между | α | и φ существенной является не форма поперечного сечения,
а величина отношения главных моментов инерции площади поперечного
сечения. Поэтому результаты таблицы при рассмотренных отношениях 1х/1у
относятся к любым по форме поперечным сечениям.
Таблица 13.3
h
b
1
2
5
10
Lx ' у'
bb? ψ b3h
~ 12 : "12 ~~
ft*
1
4
25
100
tga
φ= 1°
= 0,0175
—0,0175
—0,0700
—0,4375
—1,7500
φ = 5°
tg<p=-
= 0.0875
—0,0875
-0,3500
—2,1875
—8,7500
φ= 10°
tg<p =
= 0,1763
—0,1763
—0,7052
—4,4075
— 17,6300
α
φ= 1°
— 1°
—4°
—23°36'
—60° 15'
φ = 5°
—5°
—19°17'
—65°26'
—83°30'
φ= 10°
—10°
—35°11'
—77°20'
—86°45'
Рассмотрим форму и положение в пространстве изогнутой оси балки.
Найдем функции и и ν, решая следующие краевые задачи:
•IV--<7* = 0; ц|г_г = 0, и'
■qy = 0; у|г=г = 0, ν'
EIuul
EIxv
IV
\z-l = Qy \z-l = 0,
\ζ-ι = ®χ |г-г = °;
PI3 sin φ PI2 sin φ Ρ sin φ
ЪЕ1у
Ρ Is cos φ
ЪЕ1Х
2EIy
PI2 cos φ
2EIX
6EI
z3,
у
Ρ cos φ я
' 6EIX '
При любом 'значении ζ — ζΐ (0
величину, Действительно,
Ρ Ρ sin φ
и
υ
ΕΙ,
1
ζ^Ι) отношение u/υ сохраняет-свою-
Ρ/3 cos φ
Elx
Ι £8\
τ+τ)
3 2^6
* 11
Введем обозначение (см. рис. 13.14) u/v-
i о U ι Ιχ
*g β = ^- = *δΨ7^ =
υ ι У
= tg β, получим
— tga.
§ [3.2] ПРОСТРАНСТВЕННЫЙ ПОПЕРЕЧНЫЙ И КОСОЙ ИЗГИБ 297
Изогнутая ось представляет собой плоскую кривую, лежащую в плоскости,
проходящей через ось ζ и составляющую, с осью у угол, равный β.
Поскольку β=|α| плоскость, в которой располагается изогнутая ось
балки (плоскость изгиба), перпендикулярна нейтральной плоскости.
\
а
1
'
71%)
г а
Jph
\
7^
•ψ
^а
\у
β=ΰϋ
—Η
f*
)
1
<t
V
Рис. 13.14. Взаимное
расположение следа плоскости изгиба
(плоскости, в которой
располагается изогнутая ось) и следа
нейтральной плоскости: / — след
нейтральной плоскости; 2 — след
плоскости действия сил; 3 —
след плоскости изгиба.
Рис. 13.15. К
количественной оценке
отклонения плоскости изгиба от
плоскости действия сил:
/ — след плоскости
действия сил; 2 — след
плоскости изгиба.
Балки с большим отношением главных моментов инерции особенно
чувствительны к выходу силы из плоскости главных осей инерции.
Действительно, отклонение силы от главной оси инерции всего на 1°, при отношении
Ю
Рис. 13.16. Эпюра нормальных напряжений в поперечном сечении при косом изгибе;
а) аксонометрическое изображение; б) повернутая эпюра.
/_„.: /^=100, влечет за собой отклонение плоскости изгиба (см. табл. 13.3,
учитывая, что β = —α), т. е. плоскости, в которой располагается изогнутая
ось балки, на 60° 15' (рис, 13.15),
298 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XIII
Вернемся к распределению нормальных напряжений на плоскости
поперечного сечения балки. На рис. 13.16 изображена эпюра распределения
напряжений согласно формуле (13.3). Эта эпюра имеет закон плоскости,
пересекающей поперечное сечение балки по нейтральной линии. Проверку прочности
следует производить в точках, наиболее удаленных от нейтральной линии.
§ 13.3. Совместно происходящие пространственный изгиб
и осевая деформация жесткого стержня
1. Предварительные замечания. Рассматривается случай, когда
можно использовать принцип независимости действия сил.
Условно1) в этом случае стержень будем называть жестким..
При комбинации деформаций, указанной в заголовке параграфа,,
в поперечных сечениях стержня, вообще говоря, возникают
отличные от нуля следующие усилия и моменты: Qx, Qu, Ν, Мх и Му.
Отличие от случая, обсужденного в предыдущем параграфе, состоит
в наличии продольной силы Ν, возникшей вследствие того, что
у внешних сосредоточенных сил (включая реактивные) и
интенсивности распределенной нагрузки q, кроме составляющих по
осям хну, имеется и составляющая по оси ζ. От общего случая
деформации стержня рассматриваемый отличается лишь
отсутствием кручения (Мг = 0). Обсудим два вопроса — вид нейтральной
поверхности в брусе и распределение нормальных напряжений
в поперечном сечении бруса. Распределение касательных
напряжений в поперечных сечениях получается таким же, как и в
случае пространственного изгиба.
2. Формула для нормального напряжения в поперечном
сечении бруса. Используем принцип независимости действия сил- и
просуммируем нормальные напряжения при осевом действии сил
и при двух плоских изгибах (в плоскостях Οχζ и Oyz). Получим
распределение нормального напряжения по поперечному сечению
по закону плоскости
N Мху Мух _Ν Λ MXF My F \ -
a-T + "77" + 1J - Ύ \l + -ТТ:У + ~¥ Tyx)■ <13·5)
3. Нейтральная поверхность. Кроме общей для всего стержня
системы координатных осей Oxyz, в каждом поперечном сечении
проведем оси Xj_\\x и уг\у с началом координат в точке Ог
(рис. 13.17), являющейся центром тяжести поперечного сечения.
Уравнение нейтральной линии в поперечном сечении имеет вид
1 + ^£ #о + ^*о = 0 (13.6)
!) Условность состоит в том, что, как уже указывалось, граница области,
в которой допустимо пользоваться принципом независимости действия сил,
совершая при этом ошибку не более установленной заранее, зависит не только
от относительных размеров стержня, но и от уровня нагрузки. Подробно об
этом говорится в § 13.5,
§ 13.3]
ПРОСТРАНСТВЕННЫЙ ИЗГИБ И РАСТЯЖЕНИЕ БРУСА
299
Это уравнение соответствует прямой в плоскости поперечного
сечения, балки, не проходящей через точку Ov Прямую (13.6)
строим по отрезкам, отсекаемым на осях хх и уг (рис. 13.17),
, ΝΙΧ ι NIU .-to j\
MXF '
Myf
В каждом из сечений отрезки, отсекаемые нейтральной линией
та осях хх и ylt свои собственные, поскольку N, Мх и Ми
гу 1$
и;
."
г
К ι
•Рис. 13.17. Призматический стержень: а) системы осей Охуг и OtXiy,; б) нейтральная
линия в поперечном сечении.
(в 13.7) зависят от ζ. Нейтральная поверхность (13.6) является
линейчатой, но в отличие от рассмотренной в § 13.2, она не
содержит в себе ось г.
4. Пример 13.3. Даны брус и действующие на него силы (рис. 13.18),
отношение ///ι=5. Построить нейтральную поверхность и эпюру напряжений.
'Отличие условий настоящего
примера от условий примера 13.2
состоит лишь в наличии сил Pi —Ρ
и Рь — Р. Поскольку эти силы не
влияют на изгибающие моменты,
последние останутся такими же,
как и в примере 13.2. Вместе с тем
появятся вызываемые силами Р4 и
Р5 продольные силы, которых не
■было в брусе примера 13.2.
Решение. Строим эпюру
продольной силы (см. рис. 13.18).
Далее находим положение
нейтральных линий в характерных
сечениях (сечения приложения сил
и заделки).
В торцевом сечении Мх =
= Му = 0 и напряжения ог
возникают только от Ν, при этом
они распределены равномерно, а
нейтральная линия удалена в
бесконечность
ΝΙΚ
Уо==— -ττ-V ->■ СО,
ЗпюрвМ
Хо =
MXF
MyF
-*-OD.
Рис. 13.18. К примеру 13.3: а) балка н
действующие на нее силы; б) эпюра продольной
силы.
Определение отрезков, отсекаемых нейтральной линией на осях хх, у$
в поперечных сечениях через каждые Лг = //36 сведено в табл. 13,4, (При
этом учтено, что //А = 5, hjb — 2.)
300
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ΧΪΙΓ
Таблица 13.4
ζβ
0
1/36
1/18
1/12
1/9
5/36
1/6
7/36
2/9
1/4
5/18
11/36
1/3-ε
1/3 + ε
13/36
7/18
5/12
4/9
17/36
1/2
19/36
5/9
7/12
11/18
23/36
2/3
25/36
13/18
3/4
Τβ
29/36
5/6
31/36
8/9
11/12
17/18
35/36
1
Ν
Ρ
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
ΡΙ
0
—1/36
—1/18
— 1/12
-1/9
—5/36
-1/6
—7/36
—2/9
-1/4
-5/18
—11/36
-1/3
-1/3
— 13/36
—7/18
—5/12
—4/9
—17/36
-1/2
— 19/36
—5/9
—7/12
—11/18
—23/36
—2/3
—0,5992
—0,5284
—0,4576
—0,3868
—0,3160
—0,2452
—0,1744
—0,1036
—0,0328
0,0380
0,1088
0,18
му
PI
0
0
0
0
0
0
0
0
0
0
0
0
0
0
—1/18
-1/9
-1/6
—2/D
—5/18
-1/3
—7/18
—4/9
-1/2
—5/9
— 11/18
—2/3
—0,6263
—0,5830
—0,5397
—0,4964
—0,4531
—0,4098
—0,3665
—0,3232
—0,2799
—0,2366
—0,1933
—0,15
Ό / ΝΙχ\ >
Τ \ mxf) h
со
0,6
0,3
0,2
0,15
0,12
0,10
0,0857
0,075
0,0667
0,06
0,0545
0,05
0,01
0,0923
0,0856
0,0800
0,0750
0,0706
0,0667
0,0632
0,0600
0,0571
0,0546
0,0521
0,0500
0,0556
0,0630
0,0737
0,0860
0,1053
0,136
0,191
0,3216
1,106
—0,880
—0,300
—0,185
χ0 j Nly\ ι
h \ MyFj h
CO
CO
CO
CO
CO
CO
CO
CO
CO
CO
CO
CO
CO
CO
0,15
0,075
0,050
0,0375
0,0300
0,0250
0,0214
0,0187
0,0166
0,0150
0,0136
0,0125
0,0133
0,0143
0,0154
0,0168
0,0184
0,0203
0,0227
0,0258
0,0298
0,0352
0,0430
0,055
§ 13.31 ПРОСТРАНСТВЕННЫЙ ИЗГИБ И РАСТЯЖЕНИЕ БРУСА 301
Рис. 13.19. К примеру 13.3. Нейтральная поверхность (продольный и. поперечный
масштабы изображения балки здесь и на рисунках 13.20 и 13.21 различны).
Рис. 13.20. К примеру 13.3. Эпюры нормальных напряжений в характерных
поперечных сечениях балки (сечения, в которых изменяется вид функции_Μχ и (или) Μ ).
Рис. 13.21. К примеру 13.3. Эпюра нормальных напряжений в поперечных сечениях
балки-.
302
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XII!
Таблица 13.5
г
1
0
1
ί-+·
21
3
ι
г
I
0
ι
21
3
/
Ν
2
Ρ
Ρ
2Ρ
2Ρ
2Ρ
Μχ
3
0
Ρ/
3
PI
3
2ΡΙ
3
0,18Ρί
<Μ
(5) + (6) + (7)
Ρ
bh
9Ρ
~~bh
8Ρ
bh
58Ρ
bh.
1,6Ρ
bh
%
4
0
0
0
ЧР1
3
-0,15 Ρ/
6/1
5
Ρ
Ρ
2Ρ
Wi"
2Ρ
2Ρ
Ж
σ£
(5) - (6) + (7)
Ρ
"Μ
IIP
bh
12Ρ
18Ρ
6/г
12.4Ρ
6Λί.ν
6fta
6
0
2Ρ/
b№
ЧР1
bh*
API
bW
1.08Ρ/
<*θ
(5) + (6) - (7)
Ρ
Ж
9Ρ
Tti
8Ρ
bh
22Ρ
bh
16,4Ρ
Wi
Шу
b*h
7
0
0
0
API
b*h
o,m
Wft
σΓ
(5) - (6) - (7)
Ρ
Ж
HP
fc/l
12P
bh
62P
Μ
5,6P
Wi
Нейтральная поверхность показана на рис. 13.19. Определение
нормальных напряжений в поперечных сечениях бруса выполнено в табл. 13.5. Эпюры
напряжений изображены на рис. 13.20 и 13.21.
§ 13.4. Внецентренное растяжение (сжатие)
1. Вводное замечание. Внецентренным растяжением {сжатием)
называется деформация стержня, вызываемая двумя равными и
противоположно направленными силами, приложенными к торцам
бруса в точках пересечения с торцами линии действия этих сил,
параллельной оси бруса, но не совпадающей с нею (рис. 13.22).
Если эта линия совпадает с осью, то растяжение (сжатие)
оказывается центральным или осевым. Стержень предполагается
произвольным призматическим. Очевидно, что при внецентренном
§ 13.41
ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ (СЖАТИЕ)
303
растяжении (сжатии) в поперечных сечениях бруса возникают
следующие усилия: Мх^Сг = const, My^C2 = const, N^C3 =
= const. Иными словами, внецентренное растяжение (сжатие) есть
комбинация двух чистых изгибов, происходящих в главных
плоскостях инерции бруса и центрального (осевого)
растяжения (сжатия).
2. Формула для нормального напряжения в
поперечном сечении. Внецентренное растяжение
(сжатие) можно рассматривать как частный случай
совместно, происходящих пространственного изгиба
и осевой деформации.
В рассматриваемом случае1) (рис. 13.22)
N = ±P, Мх = ±РуР,
Му = ±РхР. (13.8)
Здесь Хр и уР — координаты точки приложения
силы Р.
Подставляя (13.8) в (13.5), получим
« +ίΡ ^РуРул Рхрк
/,
ι,
P I F F
= ± γ- [Ι + /- УрУ + j- XpX
Напомним, что величины
λί~1- = ί л[1-и- = [
(13.9)
(13.10)
Иис. 13.22.
Внецентренное
растяжение стержня.
называются радиусами инерции площади поперечного сечения
призмы. Учитывая (13.10), формулу (13.9), описывающую
распределение напряжений по закону плоскости, представим в виде
σ=±-£ (l + ^ + ^x). (13.11).
3. Нейтральная линия. Учитывая, что P/F Φ 0 уравнение
нейтральной линии (линии, на которой σ = 0) записываем в
следующем виде:
Ур
1 +7? ^ο + #χο = α
Это прямая, не проходящая через начало координат системы
О1Х1У1 (рис. 13.22), отсекает на осях хг и уг отрезки (рис. 13.23)
Уо |*о-о — ,, — aui
Ур
Ч> |£/о—О
= — -*- = аЛ
(13.12)
1) Здесь и ниже знак плюс относится к случаю внецентренного растяже·»
ния, а минус—к случаю внецентренного сжатия.
20.4 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ХШ
Поскольку брус призматический и, следовательно, каждая из
величин i\ и i'yt а также хР и уР во всех сечениях сохраняет
свое значение, заключаем, что нейтральная поверхность
представляет собой плоскость, параллельную оси бруса и что во
всех поперечных
сечениях распределение
напряжений одинаковое
(рис. 13.24).
4. Проверка
прочности. Наибольшие
нормальные напряжения
возникают в точках,
наиболее удаленных от
нейтральной оси.
Именно в них и надо произво-
дитьпроверку прочности,
Рис. 13.23. Отрезки αχ
и а , отсекаемые на осях
xt н U\ нейтральной
линии в поперечном сечении
внецентренно
растянутого (сжатого) стержня.
Рис. 13.24. Эпюры нормальных напряжений в
поперечных сечениях стержня при внецентренном
сжатии: а) общий вид стержня; б) эпюра
нормальных напряжений в поперечном сечении
(аксонометрическое изображение); в) повернутая эпюра
нормальных напряжений.
сопоставляя напряжения с допускаемыми; если в
поперечном сечении возникают напряжения двух знаков, и материал
сопротивляется по-разному растяжению и сжатию (см. например,
рис. 13.24), условия прочности имеют вид
tfmin | — | &А I =
-т(1 + 1гУл + '$-ХА
ч
Кж]!,
σ
max
р /Ί г ур
I2
У
L^pacTj·
(13.13)
Если напряжения в пределах всего поперечного сечения одного
знака, то используется одно из приведенных выше условий в
зависимости от знака напряжения.
§ 13.4] В НЕЦЕНТРЕ ИНОЕ РАСТЯЖЕНИЕ (СЖАТИЕ) 305
5. Ядро сечения. Пусть при некотором положении точки
приложения силы Ρ нейтральная линия касается контура и нигде
■его не пересекает. Очевидно, что при таком положении
нейтральной линии нормальное напряжение во всех точках поперечного
сечения имеет один знак (при внецентренном растяжении — плюс,
так как все сечение растянуто, а при внецентренном сжатии —
минус —все сечение сжато). Исключение составляет точка
касания (или точки касания) нейтральной линии к контуру, в
которой нормальное напряжение равно нулю.
Если рассмотреть все множество касательных к контуру,
«катая» касательную по нему (рис. 13.25) так, чтобы она нигде его
не пересекала г), то множество точек приложения силы Р,
соответствующих этим касающимся контура нейтральным линиям·,
at δ) δ}
Рис. 13.25. К построению ядра сечення: а) расположение нейтральных осей (каждая
■ось относится к своей собственной точке приложения силы в поперечном сечении)
касательно к контуру поперечного сечеиня при условии непересечения контура в любой
другой точке; б) пример.расположения касательной к контуру в точке С, пересекающей
этот контур в двух других точках Di и D2 (такое расположение нейтральной линии при
построении границы ядра сечения не используется); в) ядро сечення.
представит собой некоторую замкнутую линию (рис 13.25, в).
Часть поперечного сечения, заключенная внутри и на самой линий
называется ядром сечения. Если к любой его внутренней точке
приложить силу, пер пендикулярную плоскости сечения, то она
вызовет во всем поперечном сечении напряжение одного знака.
Если сила прикладывается к границе ядра сечения, то
нейтральная ось касается контура в некоторой точке, и, следовательно,
в этой точке нормальное напряжение равно нулю. Наконец, если
точка приложения силы Р, внецентренно растягивающей
(сжимающей) призму, находится вне ядра сечения, то нейтральная
линия пересекает контур поперечного сечения и, следовательно,
по одну сторону от нее в сечении имеются сжимающие, а по
другую сторону — растягивающие напряжения.
В тех случаях, когда материал хорошо сопротивляется
сжатию и плохо растяжению (например, бетон, камень, кирпич
х) Например, катание касательной по контуру в точках между Л и β не
производится, так как .касательные к контуру между точками А и В
пересекают контур (см. рис. 13.25, б).
306
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. ХПГ
и т. п:),: то-при работе этого материала в составе внецентренно»
сжатого элемента иногда добиваются расположения точки
пересечения линии действия сил, с поперечным сечением внутри ядра·,
сечения.
. 6. Примеры. Пример 13.4., Построить ядро сечения для круглого
поперечного сечения радиуса г (рис. 13.26, а).
Решение. Пусть нейтральная линия касается контура в точке а с
координатами %=— '-г,- уо = 0» тогда формулы (13.12) получат следующий вид:
со— —
уР:
Ур — О,
i* Iy/F (nr*/4): ш*
т. е. выбранное расположение нейтральной линии соответствует приложению·
сты.Р .в точке А (г/4, 0). При этом точки Л и а лежат по 'разные стороны^
а)
δ)
Рис. 13.26. К построению ядра сечения в круглом поперечном сеченин стержня: а)
круглое поперечное сеченне; б) взаимное расположение точек А н а. (точка А. — точка
приложения силы; α — точка касания нейтральной линии к контуру); в) ядро сечения.
от центра О (рис. 13.26, б). Очевидно, что аналогичная картина имеет место·
при любом другом расположении точки касания. Следовательно, ядро сечения
представляет собой круг радиуса г/4, концентричный круглому поперечному
хёчению !(рис 13.26, в).
Пример. 13.5. Построить ядро сечения для прямоугольного поперечного-
сечения (рис. 13.27, а).
Решение. Расположим, нейтральную линию, так, чтобы она касалась одной-
из сторон контура (рис. 13.28,6), и учтем (13.12), тогда
b b il
Х°~ 2 ' 2 ~ хр'
Аналогично (см. рис: 13.27, в) при
b b
Х°~ 2' 2 ~
h h il
ifo---2~, - 2 --^.
2il
xp~'T =
2i%
b
Xp=-
h
*»Λ/12
. bh
b ~
b
6--·
„ 6/13/12
bh
h
b
6 *
h
6 '
§ 13.4]
ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ (СЖАТИЕ)
307
Четырем положениям нейтральной линии
соответствуют четыре точки на границе ядра
сечения—Л, В, С и D. Для того, чтобы, получить
все остальные^точки этой границы, необходимо
проследить за" всем процессом катания
нейтральной линии по контуру при условии отсутствия
пересечений с контуром. Для этого достаточно
проследить за переходом касательной к контуру
на одной его стороне к касательной на смежной
■стороне контура. При этом переходе происходит
поворот касательной вокруг вершины
прямоугольника. (Например, при переходе от 1—1 к 2—
J? —вращение относительно точки К (рис 13.27, г).)
В процессе такого вращения точка, лежащая на
границе ядра сечения,:совершает путь от А до D.
Установим, какова форма этого пути, т. е. как
перемещается точка {хр, ур) положения силы Ρ
при условии, что координата точки, лежащей на
нейтральной линии, не изменяется, поскольку
точка К принадлежит всем этим линиям (xQ = xK,
Уо = Ук)·
Иными словами, в уравнении нейтральной
линии
хр Ур
1+-Тхк + ^тУк = °-
ly ΐχ
х и ук — фиксированные параметры, а хр и
у — переменные. Очевидно, что в такой
трактовке—это уравнение прямой и, следовательно,
повороту нейтральной линии вокруг точки /<"
соответствует перемещение точки приложения силы Ρ
по прямолинейному отрезку, соединяющему А н
D. Аналогично обстоит дело и при повороте
нейтральной линии вокруг Других вершин
прямоугольника. Итак, ядро сечения в прямоугольном
поперечном сечении имеет форму ромба с
диагоналями, равными одной трети длины
параллельных им сторон прямоугольника.
На рис. 13.28 изображен случай воздействия
на стержень прямоугольного поперечного сечения
силы Р, нормальной к сечению при нескольких
таких позициях этой силы, при которых точки
ее приложения располагаются на одной из
главных осей инерции поперечного сечения.
Вследствие этого изгиб происходит лишь в одной
плоскости Οχζ и формула для нормального
напряжения приобретает вид
Р ■ - ' (13.14)
^
X
0
Ώ\
Я
t
' а
ι В
8) f
US
В.
Μ
-^
о
г
К1
6
*4
^
-*т[1+%'У
На рис 13.28 показаны эпюры нормальных
напряжений при нескольких положениях силы.
Обращаем внимание на тот. факт, что среднее
напряжение во всех случаях остается одним и тем
же, равным P/F,
У
Рис. 13.27. К построению
ядра сечения в
прямоугольном поперечном сеченин
стержня: а) прямоугольное
поперечное сечеине; б)
взаимное расположение точки А
(точка приложения силы) и
нейтральной линии
(касается правой стороны
прямоугольника); в) взаимное
расположение точек С, D и В
(точки приложения силы) и
соответствующих
нейтральных линий, касающихся
сторон прямоугольника;
г) поворот нейтральной
лишний вокруг вершины К
поперечного сечения и
соответствующее ему перемещение
точки приложения силы.
308 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XIII
Итак, если поперечное сечение имеет такую форму, что полное
обкатывание его нейтральной линией можно представить как
конечное число положений касательной, в каждом из которых
она имеет не менее двух общих точек с контуром и равное ему
число вращений относительно точек пересечения *
соответствующих соседних по ходу Обкатки касательных, тО ядро сечения
строится так< Находятся точки границы ядра, соответствующие
Л
Ρ
\Р
tlttimttfi
тот
F
т
ίφ^
ч
У'
'
X
jffft^
ч
У]
'
χ
■ уфг^.
Ч
У
ί
X
Sf!fib.~·
%
у
'
Рис. 13.28. Зависимость вида эпюры нормальных напряжений при виецеитреииом
сжатии бруса в случае различного расположения точки приложения силы в поперечно!*
! ι ' сечении. ' '
каждому,'из конечного числа положений, касательных к контуру.
Эти точки являются вершинами многоугольника. Остается лишь
соединить указанные вершины прямолинейными отрезками (рис. 13.29).
7. Цонятие О предварительном напряжении железобетонных
балок, известно, что бетон хороню сопротивляется сжатию и
плохо растяжению. Разрушающие напряжения при растяжении
составляют ^ 1/10 —1/15 долю разрушающих напряжений при
сжатии. Для оказания помощи бетону в той области
конструкции, где ему приходится, работать на растяжение, укладывают
стальную арматуру, воспринимающую на себя значительную часть,
растягивающих усилий. В ряде случаев бетон вовсе выключается,
из работы на растяжение вследствие возникновения в нём трещин,
и растягивающие усилия полностью воспринимаются
арматурой. Однако простое .использование стальной арматуры без·
дополнительных мер все же не позволяет решить всей проблемы.
Во-первых, несмотря на сцепление бетона с арматурой в нем,
как уже отмечено, могут возникнуть трещины. Это объясняется
тем, что предельная растяжимость бетона очень мала. Во-вторых,,
при тех относительных деформациях, при которых в бетоне воз*-
§ 13.4]
ВНЁЦЕНТРЕННОЕ РАСТЯЖЕНИЕ (СЖАТИЕ)
309
никают трещины, в арматуре напряжения значительно ниже
допускаемых. Так как допустимы лишь микротрещины в бетоне„
да и то не во всех конструкциях (например, в резервуарах или
корпусах судов, где требуется водонепроницаемость, трещины
вообще недопустимы), доводить
напряжения в арматуре до допускаемых даже
при использовании обычной стали
нельзя, так как поперечные размеры
трещин становятся уже опасными, (при
них возникнут коррозия арматуры
вследствие попадания к ней по
трещинам влаги и агрессивных газов и
эрозия бетона вследствие замерзания воды
в трещинах). Высокопрочную же сталь
применять в обычных железобетонных
конструкциях вовсе нецелесообразно.
С целью предотвращения
возникновения трещин используют
предварительное напряжение балки для
компенсации растягивающих напряжений в
бетоне в рабочем состоянии.
Пусть имеем бетонную балку прямо-'
угольного поперечного сечения на двух
опорах, нагруженную равномерно
распределенной нагрузкой (рис. 13.30, а).
Под влиянием этой нагрузки в
поперечных сечениях балки возникнут
изгибающие моменты, эпюра которых
представляет собой квадратную
параболу (рис. 13.30, б). Если балка чисто
бетонная, то в ней, как в балке из
однородного (квазиоднородного) материала, в области ниже
срединного по высоте слоя возникнут растягивающие напряжения;
наибольшее из них —в сечении посредине пролета.
Пусть теперь мы пожелали за счет предварительного
напряжения бетона улучшить работу балки. С этой целью домкратами,
упираясь в жесткие опоры (например, стены), разовьем давление
на торцы балки, вызывающее в общем случае такое внецентрен-
ное сжатие балки, напряжения от которого, складываясь с
напряжениями изгиба, вызванными поперечной нагрузкой,, полностью
компенсируют растяжение в нижних волокнах среднего сечения.
Пусть эксцентриситет силы Ρ равен е, рис. 13.30». в.
Напряжения, вызванные нагрузкой q, равны
8 __,_ 3ql2
Рис. 13.29. Ядро сечення: α) в
зетовом поперечном сеченнн;
б) в восьмиугольном
поперечном сеченнн.
OWb —
310 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ХШ
Напряжения, вызванные внецентренным сжатием, определим
Ρ I e \
но формуле, аналогичной (13.14) σρ = 1 +-.т#). или
F \ ϊχ
σ
ρ __
II, В
-У1
eh
2bS-fbh
12
Ρ
bh
-& 1±
бе
Из условия σΗ =
3 ql*
мое Р\ P?=-j-
рис
ί?/2
4 ьт
= -°р„ =
Р_
bh
1 -f-τ-) найдем
необходима
£ = 0,
h/6
4 А(1Ч-6в/А)'
13.31, а, б, 5 показаны эпюры Мр и Np при разных
всем этим случаям эпюры
О)
< '"* г
и /ι/2, а также отвечающие
jLLjL3J''''ί "'χ'' jnjn jr jm" 1Щ
нормальных напряжении σ'
и σ"-|-σρ в сечениях ζ = 0,
//4 и //2. Такого же
эффекта можно добиться,
развивая силы, передаваемые на
торцы бетонной балки при
помощи натяжения
арматуры, помещенной в канал,
созданный в балке при ее
изготовлении. Достигнуть
этого можно так. Перед
бетонированием балки
поместить в опалубку (в
форму) трубки из жести
и в них с некоторым
зазором расположить
арматуру, например,
высокопрочные тросы. Затем
забетонировать балку и дать
бетону отвердеть и
приобрести необходимую
прочность. В теле бетонной
балки при этом образуются
каналы, внутренняя
поверхность которых
представляет собой внутреннюю поверхность уложенных жестяных
трубок. Арматура, находящаяся в этих каналах, не имеет
сцепления с бетоном. Если один конец каждого арматурного
стержня снабдить упорным устройством, а другой— домкратом,
упирающимся в торец бетонной балки (рис. 13.32), то при
-помощи домкрата будет создано напряжение в конструкции —
растяжение в арматуре и сжатие в бетоне.
Эпюра /У'
Эпюра Нр
Рис. 13.30". Нагружение балкн виецентренно
сжимающими ее силами Р: а) балка и действующая
:на нее нагрузка; б) эпюра изгибающих моментов
от нагрузки; в) внецентренное сжатие балкн
силами Ρ и эпюры изгибающего момента и
продольной силы, вызываемые этой силой.
§ 13.4]
ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ (СЖАТИЕ)
311
*·!:§
\^l^rftf$
ъ.
^
с».
II
ЗЕ
^1
^ II
ΗΣ,
cvl
^>-,
■5*
^ I
K)|oq
^ И
V
ю
•с;
йш
■1за\
«D
^ττΤΤΤΐΤίϊϊΤ§Ι
,^ττίΤΤίΜΙ
~ϊϋ οι/
ч
о
с».
5:
t
I
ν*
I
\
Ш
CM
CM
I
I «a
Θ
III Ι Ι Ι Ι 111 ΙΙΤΠ
\:
φ
^^ШШтвп»
О.
IS
to
«IS
^тгШШПк.
^ЙГПТгтггг^
СЧ1
•«а
«у tw
^3
о-
II £
N «>
X *>
к ..
αϊ ·*£
Ζ II
X
3 «г
χ да
о. Ч
<и о
D
И <=
«>
в
я го
к в·
о. £-
га «>
я _
о
■3 «>
в
к га-
s S
5 ^ '
й- s
о о
в я
(X
е- «у
а. »;
■§ к.
~ Ч'
К со
г» W
* о,-
О. *"
^ +-
CS О-
«о ^
!
312 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XIII
Положение того конца стержня, за который его вытягивал
домкрат, фиксируется после достижения проектного значения
усилия (например, постановкой шайб под колодку, которой
заканчивается арматурный стержень), и домкрат снимается.
Промежуток между стержнем арматуры и внутренней
поверхностью канала в бетонной балке инъектируется цементным
раствором, после твердения которого возникает сцепление между
арматурой и окружающим
ее телом балки.
Путем сопоставления
рис. 13.31,6, в можно
заключить, что при
расположении напрягающей силы
в пределах ядра сечения
суммарные эпюры σ?-}-σρ
во всех сечениях балки
оказываются однозначными
(напряжения
сжимающими). При выходе точки
приложения силы из ядра
сечения напряжения на
некоторой части длины в
верхней зоне балки
оказываются растягивающими,
т. е., улучшая работу
материала в одной части
балки, ухудшаем, правда, в
меньшей мере, —в другой.
Можно принять такие
меры, при которых будут
полностью компенсированы
изгибающие моменты во всех поперечных сечениях и, следовательно,
полностью устранены растяжение и неравномерность
распределения напряжений по высоте сечения балки. Отмеченный выигрыш
в работе конструкции достигается ценой усугубления работы
бетона на сжатие. Делается это так. Половину из числа трубок с
арматурой уложим горизонтально на некотором небольшом
расстоянии (обеспечивающем необходимую толщину так называемого
защитного слоя бетона) от нижней грани балки. Другую
половину расположим по квадратной параболе так, чтобы пересечение
последней с торцами балки находилось от оси балки на таком же
расстоянии как и арматуры, уложенной горизонтально
(рис. 13.32, б). Поскольку число стержней арматуры,
расположенных горизонтально, и число отогнутых стержней принято
одинаковым, и во всех стержнях усилия развивались домкратами
одинаковые, равнодействующая всех этих усилий в каждом
^iiilff^^
: ЗпюраМ1'
6)
Тис. 13.32. Предварительное напряжение балки
при помощи натяжения арматуры: а) случай,
когда арматура расположена параллельно оси
балки; домкрат, натягивающий арматуру силой Р,
упирается в торец балки (иа рисунке изображены
две силы по Р/2); б) случай, когда половина
арматурных стержней расположена параллельно
оси балки на расстоянии а от нее, а другая
половина стержней отогнута по квадратной
параболе, пересекающей торец тоже на расстоянии а
от оси балки (пунктиром показана линия
действия равнодействующей усилий во всех
арматурных стержнях, эта линия аффиино-эквивалеитна
эпюре изгибающих моментов от нагрузки); в)
эпюра изгибающих моментов от предварительного
напряжения в случае б.
§13.4] ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ (СЖАТИЕ) 3!3
йз сечении будет иметь точку приложения посредине расстояния
между центрами тяжести горизонтальных и отогнутых стержней
в этом сечении. Множество точек приложения этих
равнодействующих представляет собой квадратную параболу (пунктир нз
рис. 13.32, б), аффинно-эквивалентную (сжатую по вертикали
в два раза) той, по которой расположены отогнутые стержни.
В каждом поперечном сечении действует сила (равнодействующая
усилий во всех стержнях арматуры), имеющая эксцентриситет,
равный расстоянию от точки пересечения параболы,
изображенной пунктиром, с поперечным сечением балки, до оси. Вследствие
наличия эксцентриситета указанная сила в каждом из сечений'
создает изгибающий момент, противоположный по направлению
тому, который вызывается внешней нагрузкой. Эпюра этих
изгибающих моментов, созданных предварительным напряжением
балки, как и от нагрузки, также представляет собой квадратную
параболу, но имеет противоположный знак. Чем больше величина,
суммарной силы натяжения стержней арматуры, тем
пропорционально больше все ординаты эпюры изгибающих моментов,
вызванных предварительным напряжением балки. Можно подобрать,
величину суммарной силы такой, чтобы эпюры Μι и Мр
с точностью до знака оказались тождественными j Μ?|ξ= | Λίρ j„
Так полностью компенсируется изгиб, однако в балке
возникает сжатие с продольной силой Ν = Ρ во всех сечениях,
В приведенном выше рассуждении в связи с большой пологостью
отогнутых стержней пренебрежено разницей между усилием
в отогнутом стержне и его проекцией на горизонтальное
направление.
Работа предварительно напряженных балок в натурных
условиях значительно сложнее описанной здесь.
Во-первых, под влиянием усадки и ползучести бетона и:
релаксации напряжений в арматуре со временем происходит
снижение силы натяжения в арматурных стержнях, а
следовательно и силы, сжимающей бетон. При назначении величины
силы натяжения арматуры это обстоятельство необходимо
учитывать.
Во-вторых, как правило, балка служит не для работы только
лишь на собственный вес интенсивностью qlt а для восприятия,
кроме того, той или иной так называемой полезной нагрузки
интенсивностью д2. Поэтому в расчете приходится различать три
стадии работы конструкции: работа только на нагрузку qlt работа
на нагрузку qx и предварительное напряжение и, наконец,
работа на qv предварительное напряжение и q2. На нагрузку qz
расчет балки ведется как обычной железобетонной балки, в
которой арматура имеет сцепление с бетоном. Разумеется, .что при
назначении величины силы натяжения нужно рассчитывать
на компенсацию и тех растягивающих напряжений, которые
314 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ХШ
вызываются нагрузкой q2. Но при таком условии изгибающие
моменты, создаваемые предварительным напряжением балки,
должны не только компенсировать изгибающие моменты от
нагрузки qit но и создавать необходимый запас сжатия для
будущей работы на нагрузку q2, а это связано с возникновением
изгибающих моментов при совместном действии нагрузки q1 и
предварительного напряжения балки, противоположного знака
по сравнению со знаком изгибающих моментов от qv Вследствие
отмеченного, во второй стадии работы балки некоторые области
ее могут находиться в худших· условиях, нежели в третьей
стадии работы.
В-третьих, натяжение всех стержней арматуры не может быть
выполнено одновременно, при последовательном же натяжении
возбуждение усилия в каждом следующем стержне ослабляет
нат яжение ранее напряженных стержней. Этот эффект также
приходится учитывать в расчете. Имеется и ряд других причин,
усложняющих работу конструкции (наличие касательных
напряжений, технологическая сложность расположения стержней по
параболе и т. п.).
Все изложенное свидетельствует о значительной сложности
вопроса.
Предварительное напряжение применяется с целью улучшения
напряженного состояния не только железобетонных балок, но и
балок из однородного материала, например стали.
Регулированию напряжений в конструкциях при помощи
предварительного напряжения посвящена большая литература г).
8. Понятие о ядровых моментах. В ряде случаев при
рассмотрении внецентренного сжатия (имеется в виду плоская работа
стержня) удобно пользоваться не двухчленной формулой (13.14),
а некоторой одночленной. Для того чтобы достигнуть этого, введем
новое понятие — ядровые моменты. Пусть нормальные
составляющие внутренних сил, действующих в поперечном сечении стержня
(рис. 13.33, а), имеют равнодействующую Р, приложенную в точке
с эксцентриситетом, равным е (рис. 13.33, б). До сих пор эту
систему внутренних сил мы приводили к стандартной системе —
изгибающему моменту Μ.= Ре и продольной силе Ν =— Ρ,
выбирая в ■ качестве точки приведения сил центр тяжести площади
поперечного сечения (рис. 13.33, в). В результате этого формула
для нормальных напряжений в крайних волокнах приобретает вид
N . Μ Ρ Λ , eF\ /ίο 1сч
!) Bauingenieur — Praxis Heft 38. Die Vorspannung im Stahlbau. Theorie
und Konstruktionspraxis von Doz. Dipl. — Ing. Pavel Ferjencik, CSc., Dipl.—Irig.
Miloslav Tochacek, CSc. 1975. Verlag von Wilhelm Ernst und Sohn. Berlin,
Miinchen, Dtisseldorf (библ. 573 лит. источн.).
§ 13.4]
ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ (СЖАТИЕ)
315
или для прямоугольного поперечного сечения
Ρ Λ бе
верхний знак в скобках относится к нижнему волокну.
^г
7^
{ bJ
( kf\
а)
f\
.
Км \
и
У
δ)
М-Рв
N=F
6)
Мв'Р(е-кв)
Зпюры напряжений
от Р,приложен.
в'точнеКв от Mg
от Р,приложен.
^МГР(ЫН) в ™чке КИ отИн
Рис. 13.33. Ядровые моменты: а) стержень (фрагмент) и действующая на него нагрузка;·
б) сила Р, заменяющая действие части стержня, расположенной правее сечения ИВ, на·
часть стержня левее этого сечения; в) приведение силы Р, показанной на фиг. б, к
статически ей эквивалентной стандартной системе обобщенных сил — продольной силе N и<
изгибающему (центральному) моменту, если за точку приведения выбран центр тяжести·
поперечного сечения; г) приведение силы Ρ (фиг. б) к статически ей эквивалентной
системе обобщенных сил — силе Р, приложенной в точке Кв , и Μβ (верхний ядровыГр
момент; точка приведения К — верхняя граница ядра сечения) и эпюры нормальных
напряжений в поперечном сечении, эквивалентных этим силам; д) приведение силы Р'
(фиг. б), к статически ей эквивалентной системе обобщенных сил: Р, приложенной в
точке К., и Μ (нижний ядровый момент; точка приведения Кн — нижняя граница ядра*
сечения) и эпюры нормальных напряжений в поперечном сечении, экрнвалентных им.
Можно поступить и иначе, выбрав в качестве точки
приведения внутренних нормальных к сечению сил не точку О, а точку
316 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ.. XIII
Къ — верхнюю границу ядра сечения или точку /Сн — нижнюю
границу ядра сечения. В первом случае (рис. 13.33, г)
статическим эквивалентом силы Ρ с эксцентриситетом е является сила Ρ
с эксцентриситетом kB (верхний радиус ядра сечения) и момент
ΛίΒ = Ρ (е — kB) —.верхний ядровый момент, т. е. момент внутренних
сил относительно верхней границы ядра сечения. Нормальное
напряжение в нижнем волокне от силы Р, приложенной в Кв,
равно нулю, а от Мв
σ„ = -^-· (13.16)
Аналогично, во втором случае (13.33, д) статическим
эквивалентом силы Ρ с эксцентриситетом е является сила Ρ с
эксцентриситетом kn (нижний радиус ядра сечения) и момент ΜΆ = Ρ (е +
+ kH) — нижний ядровый момент, т. е. момент внутренних сил
относительно нижней границы ядра сечения. Нормальное
напряжение в верхнем волокне от силы Р, приложенной в К», равно
нулю, а от Мн
*- = —ίς-: <13·17)
Формулы (13.16) и (13.17) удобнее формулы (13.15) в случае,
если расчет ведется на подвижную нагрузку, вызывающую при
разном положении на конструкции усилия различных знаков,
так как приходится находить наиневыгоднейшее положение
нагрузки для.одного фактора (Мн или Мв), а не двух факторов (Ν
и М), имеющих, как правило, различные на.иневыгоднейшие
участки загружения конструкции, что осложняет отыскание
экстремальных напряжений по формуле (13.15).
§ 13.5. Совместно происходящие изгиб и осевая
деформация (растяжение) гибкого стержня
I. Предварительные замечания. В начале настоящей главы
было отмечено, что если стержень обладает значительной
жесткостью, то в некоторых пределах можно не считаться с взаимным
влиянием отдельных видов деформации. Например, можно не
считаться с возникновением дополнительных изгибающих моментов
от продольной внешней силы вследствие искривления оси стержня
под влиянием поперечной нагрузки, вызывающей изгиб. Граница
допустимости использования принципа независимости действия
сил оставалась неопределенной. В настоящем параграфе
показывается, как может быть учтено взаимное влияние осевой
деформации и изгиба и поясняется принцип установления границы
.допустимости пренебрежения этим влиянием, если величина
разрешаемой погрешности в процентах к решению, учитывающему
указанное влияние, установлена,
§ !3.5]
ИЗГИБ И ОСЕВАЯ ДЕФОРМАЦИЯ ГИБКОГО СТЕРЖНЯ
317
2. Дифференциальное уравнение изгиба балки и его общий
интеграл: Рассмотрим закрепленный в пространстве
прямолинейный стержень, подвергнутый воздействию произвольной
распределенной поперечной нагрузки q{z), действующей в плоскости Oyz,
и, кроме того, воздействию продольных растягивающих1)· сил,
центрально приложенных к концам стержня (рис. 13.34).
Дифференциальное уравнение
изгиба балки имеет вид
EIxv" = — Mx. (13.18)
Изгибающий момент Мх и
поперечная сила Qy создаются
поперечной внешней нагрузкой
и внешними продольными
силами Р, т; е.
ΜΧ = ΜΧ + ΜΪ, Qy = Ql + QPy
(13.19)
•rm^JSrrrrmTTrn
У1
Рис. 13.34. Совместное действие на гибкий
стержень поперечной н продольной
растягивающей нагрузок.
dMxldz.
Из рис. 13.34 видно, что Мх =— Pv, Qy — — Ри'
Таким образом,
Mx = Mqx-Pv, Qy = Q«-pv'. (13.20)
Формулы (13.20) показывают, что при одновременном изгибе и
осевой деформации гибкого стержня усилия зависят от прогибов.
Подставляя (13.20) в (13.18), получаем дифференциальное
уравнение сложного изгиба балки
EIxu" = — Mx + Pv. (13.21)
Дифференцируя (13.21) последовательно два раза, получаем
(EIxv")' = -Ql + Pv\ (EIxv")" = qy + Pv".
Если функция ν известна, то углы поворота и усилия в
сечениях балки находятся обычным порядком
θ, = ο', Mx--= — EIxv\ Qy = — EIxv\ (13.22)
Ограничимся рассмотрением частного случая призматической
балки {EIX — const), тогда дифференциальное уравнение сложного
изгиба приобретает вид
EIxvW-Pv" = qm »iv_ftv = _^. k = ]i~. (13.23)
EIX> '" Ψ ΕΙΧ·
Общий интеграл неоднородного уравнения (13.23) равен сумме
общего интеграла однородного уравнения
uiv-W = 0 (13.24)
Ц Случай сжимающих сил ниже будет обсужден особо,
318
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
и какого-либо частного интеграла неоднородного уравнения (13.23)..
Характеристическое уравнение и его корни имеют вида4 — k2a2 =
= 0; α1 = α2==0» Яз = ^» fl.4 = — &· Следовательно, общий интеграл:
уравнения (13.24) может быть представлен так: и(0) = Л1 + Azkz +■
+ Афкг + A4e-k*; и<°> = Вг + B2kz + Б3 ch fez + B4 sh /гг.
Ιζ=0 1г-0
W*
Α=Λ-<
'+Λ#/ ~(-£/um+Po'J/ ; Rz~RB~{-Q+Pv')\ -(ElOm+Rv'Jl
k»t Ιζ-σ lz-i /z
ггу δ)
zH
Рис' 13.35. К установлению связи между поперечной силой на опоре, опорной реакцией;
и силой, растягивающей стержень: а) левая опора; б) правая опора.
Частное решение уравнения (13.23) может быть найдено одним;
из известных способов, в частности, способом неопределенных
коэффициентов. Например, пусть q = const, ищем ич-р в следующей
форме:
»4.p = D1zs, + DiZe + DJ^.
Подставляя (13.25) в (13.23), получим
(— <№ΌΧ + 24D3) - 6#ϋ2ζ - 12k2D9z*
Яу
El,
(13.25)
(13.26>
Чтобы равенство (13.26) оказалось тождеством, необходимо-
обратить в нуль коэффициенты при ζ и г2, что эквивалентно
равенствам
D2 = D3 = 0. (13.27).
Учитывая (13.27) из (13.26), находим Dlt а затем и частное
решение
qy qy . _ qy ,2
£>ι =
1) ■= 7
2р' ич. ρ 2Ρ
Ч&Е1Х
Граничные условия для самого общего случая закрепления
конца балки (упругое защемление на упруго податливой опоре)
имеют вид:
для. левого конца (рис. 13.35)
v = ARX = А (— ΕΙ ν'" + Ρν'), ν' = Ш = —ϊ\ΕΙυ"; (13.28)
для правого конца
v = ARt = AiEIxxr + Pv'Y, V -- %Μ^%ΕΙχυ". (13.29)
'§13-5]
ИЗГИБ И: ОСЕВАЯ ДЕФОРМАЦИЯ : ГИБКОГО СТЕРЖНЯ
319:
Μ,ι ■ nil ■■ ■ И ■ '' ■■!' I
1
г
V
У}
SffiL
I яр?
г
Здесь Л — податливость упруго проседающей опоры, т. е. осадка
этой опоры при силе, действующей на нее, равной единице; VI—^
податливость упругого защемления конца балки, т. е. угол
поворота опорного сечения при
моменте, возникающем е. опорном
сечении, равном единице.
4 Из (13.28), (13.29). можно
получить граничные условия при
всех частных случаях закрепления
концов балки:
при неподатливой опоре А = О,
υ = 0;
при абсолютном защемлении
1Й = 0, 1>'=0;
на свободном левом (правом)
конце
Л = Я-^оо, ϋ"ί=0,
=ρ£/χ-Γ-/ν=0. (13.30)
P.
а)
immw^ г
1
I
■г
I
2 Г/
δ)
0..
^35
3. Примеры. Пример 13.6. Опреде-·
.лить перемещения и усилия в Однопро-
летной призматической балке, Шарнирно
опертой по концам, при воздействии на
нее равномерно'распределенной
поперечной нагрузки и продольных растягивают
щих сил, центрально' приложенных, по
концам (рис. 13.36, а).
Решение. Расположим начало
координат в центре среднего сечения балки
и вследствие симметрии, относительно
оси у и конструкции, и нагрузки
сохраним в общем интеграле . однородного
уравнения лишь четные функции > ■
v = B1 + Bschkz, (13.31)·
У)
I:
tfc—
m?
Μ>Μ
Ρ
Р.г.
δ)
Рис.· 13.36. Балки, испытывающие
сложный; изгиб: а) κ примеру 13.6;
б) κ примеру 13.7; в), κ примеру 13.8:
г) κ использованию' результата
примера 13.8.
а частное решение примем в форме ич.р = —^ г2. Тогда, общий интеграл
неоднородного уравнения примет вид
•ν =Вг + Вя ch kz-gp г*
Граничные условия »[2==;/2=0, ν"
(13.32)
= г/2=0 в развернутой форме
записываются тек:
Bi + 5,ch.»^?
ql*
8Р
■0,
ft*B8ch»^=0,
(13.33)
где »=/г//2, или 2»=fc/.
Из (13.33) находим'^ =|^-,^2.
ί»' Вз = Ш сК"»» И окончательно
320 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XIIГ
* = «, Р = Е1Х(^У. (13.35)
ql*
v=-
k.7 1 1
^_1+T(»8_ftiz«)j, (13.36)
В функцию и внешняя растягивающая продольная сила Ρ входит в
знаменатель коэффициента перед скобкой и неявно в k и »-. Выразим Ρ и к
через »
После подстановки (13.35) в (13.34) и учета (13.22) получим
~ch kz
'Е1Х(Щ* ~ch~
0,— ВЦГ—£%£. (13.38)
В характерных сечениях функции (13.36) —(13.38) приобретают следующие
частные значения:
**!«-££ (l-^). (13.41)
Формулы (13.39) — (13.41) можно представить в следующем виде:
5 о/4 й/3
ϋ \*-«=-mETxh (ϋ)' °* k=±//2=- гщ;* <»)·
Μ*|*_β = ^<ρο(»). (13.42)
При этом имеются в виду следующие обозначения *):
24/1 1 \ ч
Λ<e>=65S(ηϊΓΪ-f+-2 β")· *■<»>=£<*-*»>.
«^ЧК1"^)' <13·43>
Пример 13.7. Условия отличаются от предыдущего примера только тем,
что концы балки жестко защемлены (рис. 13.36, б).
Решение. Вид общего интеграла неоднородного уравнения сохраняется
неизменным (формула 13.32), граничные же условия имеют вид
и1г=;/2 = 0' и'1г=//2 = 0>
или в развернутой форме
Bi + Ba ch»-g = 0, B3k sh»- |^ = 0,
откуда
3 2Р/г sh ϋ' βι 8P 2Р/г sh ϋ *
i) Заметим, что ψ0 (»)=/ι (2»)> ГДе функция /х (о) приведена ниже
(формула (13.46)!).
§ 13.5] ИЗГИБ И ОСЕВАЯ ДЕФОРМАЦИЯ ГИБКОГО СТЕРЖНЯ 321
Подставляя в (13.32) найденные выражения для Βχ и В3 и имея в виду
равенства (13.35), получим
ql*
v = —^
eia^Y
/ch kz _ . \ J>_ Ό2 — fe2z2]
\ch» /th» + 2 J»
Mx = — EIxv"= — 7H-T5 —u !
* (2υ)2 \ sh d
(13.44)
В характерных сечениях имеем
, ί/» 24/ϊ » \ ql*
ν |г-о_з84£7;^ [γ -т~2) - mm-J1 {*}>
u=0 24 »а Г sh
h» ) = 24 φι <*>'
Μ\ζ=±1/2
?Ρ3 /,-th»\ ^
~~ 12 »2 \ th» / 12 χ^'
(13.45)
где использованы обозначения
w-£(i-*i). *«-*('-£)-*«-£(тг1*)· "3'46)
Пример 13.8. Определить перемещения и усилия в однопролетной
призматической шарнирно опертой по концам балке, при воздействии на нее
опорного момента и растягивающих осевых сил, приложенных по концам
(рис. 13.36, в).
Решение. Ввиду отсутствия распределенной пролетной нагрузки ич-р = 0 и
общий интеграл уравнений (13.23) имеет вид
v=Bi-\-B2kz-\-Bzohkz-\-Bishkz. (13.47)
Учитывая граничные условия на левом конце балки (z=0)
f|*-o = 0, f"U~o = 0,
которые в развернутой форме приобретают вид Вг-{-В$ = 0, k2B3 = 0, находим
Βί = Βζ = 0. (13.48)
Граничные условия на правом конце балки (2 = /)
* |*-*=о, Eixu"\z.t—an
в развернутом виде с учетом (13.35) записываются так:
522u+54sh2u = 0, E/xBifi*sb2v = — 331, (13.49)
Из (13.49) находим
дуг 1 $щ
β4=~£7^8Έ2ί' Βζ = Έ7χΜ^· (13*50)
Таким образом, с учетом (13.48) и (13.50) функция (13.47) имеет вид
Ш [kz shkz'
υ =
EIxk2 2»
[kz sh/гг]
L2^ shT2»J*
Зная функцию ν, находим
η , 33ί / 1 chkz\ „ „„ sh/гг
Е1М\Ъ sh2»7' * * sh2u'
322
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
(ГЛ. XIII
В характерных сечениях функция Ό* приобретает следующие частные
значения:
„ , _ Ш 6/1 1 \ ЧШ . . , ι
. . к/ з / ι ι\_ т . ,. [ (ШИ)
где!) VtW-K^-^), <i(»)-|(thW-^)·
При загружении моментами каждого из двух концов однопролетной
призматической балки с шарнирными опорами (рис. 13.36, г) углы поворота
находятся по следующим формулам, являющимся следствием формул (13.51):
°* ^зЖ^+бЖ^' **|г-<—бЖ^(")_з£7;% (ϋ)·
4. Влияние продольных внешних сил на перемещения и
усилия в растянуто-изогнутой балке. Все формулы (13.42), (13.45),
(13.51) имеют одинаковую в принципе структуру.
Выражение прогиба, угла поворота, изгибающего момента
в сечении paci я нуто-изогнутой балки содержат в качестве
множителя функции /, φ, χ, ψ, учитывающие влияние продольных
внешних сил. Выражения, на которые умножаются функции,
представляют собой соответственно прогиб, угол поворота, изгибающий
момент в том же сечении, но при условии равенства нулю
продольной внешней силы. Функции /, φ, χ, ψ убывают (затухают)
L -.AT
с увеличением аргумента »= -~- I/ -ετ- .
Графики функций f0, flt φ0, φΧ и χ показаны на рис. 13.37, а.
Чем больше величина растягивающей силы, тем при прочих
равных условиях в большей мере уменьшаются этой силой
прогибы, углы поворота и усилия, вызванные поперечной нагрузкой.
Если считать, что при расчете допустим какой-то процент
погрешности, например 5%, то по графикам или табличным значениям
функций /, φ, χ, ψ можно установить, какие значения аргумента2)
?и = х>Т соответствуют значениям функций, равным 0,95. Тогда при
x>i ^ t>* величина соответствующей функции больше 0,95,
следовательно, влияние продольных сил меньше 5% и этим влиянием
можно пренебречь, т. е. полагать, что изгиб и осевая
деформация происходят независимо друг от друга. Если же fy > *>*, то
неучет влияния продольной силы повлечет за собой погрешность
больше 5%.
Аргумент t>, от величины которого зависит степень влияния
внешней продольной силы на параметры изгиба, имеет сложную
!) Заметим, что ψι(») = χ(2»), ψ2 (») = ψι (2»)·
а) Заметим, что функции φ0, /0, φ,, fv χ принимают значение 0,9500
соответственно при » = 0,3550; 0,3598; 0,6698; 0,7260; 0,8985, а φ*, ff, φ*. /*,
χ* —значение 1,0500 при ν = 0,3384; 0,3422; 0,6404; 0,6900; 0,8365.
§ 13.5] ИЗГИБ И ОСЕВАЯ ДЕФОРМАЦИЯ ГИБКОГО СТЕРЖНЯ -23
1-f0(W
Ζ- ffW)
1-φ0№
5-XW)
са νί- <>-Г ю" ·<*■" ^ ^ ^" °сГ ^ ξί ^" ^
50,0 -
Щ0
Щ0
ΖΟβ
10,0
5,0
1,0
1-f0*№
Z-ff*№
5-p*(W
5-X*№)
j ι ι 1 i__i ι ι L
0 0,50 1,0 1,5 > 2,0 2,50 2,75 3,0 Я W
2.
5)
Рис. 13.37. Графики функции: α) графики функций fQ (у)) ΐχ (V), Φ (»), Φχ (»)( χ (£);
б) графики функций /*, (0)) /* (1,)> φ* (^ φ* (^ χ* (у).
η*
324 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XIII
природу — он представляет собой статико-геометрический фактор.
Относить стержень к той или иной категории (требующей или не·
требующей учета влияния продольной силы на параметры изгиба
при принятой величине допускаемой погрешности) можно лишь
на основе учета не только жесткости и длины стержня, но и
внешних осевых сил, растягивающих стержень. Один и тот же
стержень при одной продольной внешней силе может быть сильно
чувствителен к влиянию этой силы на параметры изгиба, а при
другом значении указанной силы —мало чувствителен. Сказанное
проливает свет на условность деления стержней на гибкие и
жесткие в зависимости лишь от отношения длины и поперечных
размеров. Дело не только в геометрии самого стержня, но и
в модуле упругости материала и величине продольных сил.
5. Случай совместного сжатия и поперечного изгиба. Если
сила Ρ является сжимающей, то в уравнении (13.23)! изменяется
знак перед Ρ и уравнение приобретает вид
EIxv™ + Pv" = qu. (13.23)?
Если под k понимать выражение, определяемое следующей
формулой: k~Y\P\l(EIx), то однородное уравнение,
соответствующее (13.23)*, запишется так:
ulv + fcV = 0. (13.24)*
Характеристическое уравнение и его корни приобретают вид
а4 + /г2а2 —0, аг = а2~0, a3 = ik, ai = — ik.
Общий интеграл уравнений (13.24)* становится таким:
и<о>* = А! + A2kz + Abeikz + A^~ihz
или
ϋ(0) * = Вг + B2kz + В3 cos kz + Bi s in kz.
Параметр ν» заменяется параметром Ό* = ikl/2 = it>. Вместо
функций φ0(ν), f0(v), 4>ι(ο), χ (ρ), Μ»), введенных в случае, если
силы Ρ растягивают стержень, в случае сжимающих сил имеют
место функции, получающиеся из них путем замены k на ik, и
Ό на i». Эти новые функции обозначим теми же символами, что
и исходные, но введем для отличия верхний индекс *.
В результате получим г)
φ° Μ = Щ* [{ ~~ chT») = ^(соГ» — 1
АЧ*) = 5$И^-1 + 4и2
м/ »! . J ι
5»*\ 2 ~ cos v
ϊ) Имеются в виду следующие формулы Эйлера:
еах ι ρ-αχ »
ейх ι g-ax gax e~ax eax e~ax
chax= -ζ ; sha^=· r- ; thcoi:
$ 13.5] ИЗГИБ И ОСЕВАЯ ДЕФОРМАЦИЯ ГИБКОГО СТЕРЖНЯ 325
φ* Μ ~~ (ϋί)2 V sh t» J »» (sin »
л w (t»)a \ thf» J »2
* -1
tgto '
fW = (5i)i-("2-"th-2-j = ir(tgT-"TJ'
Функции /о, Фо с возрастанием аргумента » от 0 до зх/2
возрастают от 1 до бесконечности, а функции /*, φ* и χ* возрастают
ют 1 до бесконечности с возрастанием аргумента Ό от 0 до π
(рис. 13.37,6).
Такое устремление значений функций к бесконечности
происходит при значениях силы Р, равных соответственно зт2£7//2 и
4эх2£7//а. Эти значения сил играют фундаментальную роль в
теории устойчивости первоначальной формы равновесия сжатых
упругих стержней. Здесь же заметим, что бесконечного роста ни
перемещений, ни углов поворота, ни усилий в действительности быть
не может и сам факт такого возрастания указанных величин,
•обнаруживаемый расчетным способом, свидетельствует о
неправомочности расчетного аппарата при условии значительного роста
перемещений, поскольку в этом случае нельзя использовать
лриближенное дифференциальное уравнение изгиба стержня.
Использование же точного дифференциального уравнения позволило
бы получить достоверную картину роста перемещений в области
•больших их значений.
6. Влияние продольной силы на суммарные напряжения в сече-
яиях балки. Внешняя продольная растягивающая сила уменьшает
изгибающий момент от поперечной нагрузки. Однако это не
обязательно означает, что уменьшаются нормальные напряжения
в поперечных сечениях.
Наибольшее и наименьшее напряжения в поперечных сечениях
(в крайних волокнах) растянуто-изогнутой балки определяются
по следующей формуле:
σ—£. + -£. (13.52)
Выразим как Ν, так и Μ через аргумент ъ. Пусть
рассматривается балка, изображенная на рис. 13.38. В нашем случае Ν = Ρ.
Пользуясь формулой (13.35), находим
Ы = Р = Щ^&. (13.53)
giax_L. e~i(tx giax g-tax giax g-tax
COSOa= X ; sinax= g ; tga*= . (eiax+e-iax)
и вытекающие из них
ch iax=cos ax, sh iax=ί sin ax, th iax=i tg ax.
326
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. ХПГ
Изгибающий момент в среднем поперечном сечении балки
выражается формулой
(13.54)·
м,=4-<м»)·
Учитывая (13.52), (13.53) и (13.54), представим растягивающие-
напряжения в крайнем волокне среднего поперечного сечения
следующим образом1):
qt* h
4ΕΙχ л
16 Ιχ
<Ро (*1)·
(13.55).
■ II ИР' ■■ ι I flip· Mf
Шт
,',,,,,Π
Ρ
ш
На рис. 13.39 при помощи графиков показаны слагаемые,
входящие в правую часть формулы (13.55). Для удобства их
суммирования графики отложены по
разные стороны от оси абсцисс. Суммьг-
ординат заштрихованы. Из графиков,
видно, что увеличение силы Ρ сначала
снижает суммарные нормальные
напряжения, а затем приводит к их.
увеличению.
7. Раскрытие статической
неопределимости продольных усилий. Во*
всех вышеприведенных разделах данного параграфа
предполагалось, что сила Ρ задана. В ряде случаев она не известна и
ее требуется найти. Пусть однопролетная балка, шарнирно оперта!
Рис. 13.38. Балка, испытывающая
сложный изгиб.
\"ММ1"ЧЧ1 ι"'
'liUr1"1"1
Sf S
ΑΙ
IIU'I'I
Ж
Рис. 13.39. Зависимость напря-
жения о = -=- + -==г от ν .
г W
Рис. 13.40. К раскрытию
статической неопределимости продольной
силы.
по концам, но обе опоры неподвижны. Под воздействием
поперечной нагрузки противоположные концы стремятся сблизиться^
но вследствие неподвижности опор такого сближения не
происходит, из-за чего в балке возникает наряду с изгибом
растяжение (рис. 13.40). Система статически неопределима относительно
*) Имеется в виду, что балка имеет плоскость симметрии,
перпендикулярную плоскости изгиба.
^ 13.5]
ИЗГИБ И ОСЕВАЯ ДЕФОРМАЦИЯ ГИБКОГО СТЕРЖНЯ
327
растягивающей балку силы и для определения ее необходимо
-составить уравнение совместности деформаций.
Если бы одна из опор была подвижной, то в изгибаемой
балке концы ее сблизились 6li на величину бив ней не
возникло бы продольной силы. Однако так как на самом деле концы
сблизиться не могут, к ним как бы прикладывается неизвестная
растягивающая сила X, возвращающая конец балки,
переместившийся навстречу противоположному концу, в исходное положение.
Сближение концов выражается следующей формулой *):
11 (υ')2 dz.
о
Уравнение совместности деформации и его решение
записываются в следующем виде:
о о
Функция и', входящая под знак интеграла, в свою очередь
•зависит от X (см. формулу (13.37))
ν =·
ql*
<1Уж
sh
Уж
ch
l-V—
2 У Е/х
-Уж
*) δ —сближение концов балки при изгибе можно найти как разность
длин оси изогнутого стержня и длины его проекции на первоначальное
da
ds
—»-
..
§
Μ
'
ι
ι
Рис. 13.41. К определению сближения концов балки1 при отсутствии стеснения; элемент
балки до и после поворота, связанного с изгибом.
■направление оси (рис. 13.41)
db = ds—dz=Y(dz)* + {du)* —dz = ΫΊ + {ό')* dz — dz,
ι ι ι ι
,δ= f Y\ + (v'fdz- f dz«» C l+y(u')2~Uz- f dz =
0 0 0 0
ι ι
= l + ^(v'fdz-l = ^(v'fdz.
328
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. ХШ
Таким образом, окончательно уравнение совместности
деформации приобретает вид
X
_ EF С
~ 2/ ]
qP
EI Al
Υ
χ
ΕΙΧ
sh
Уж
ch
w-
χ
EIX
-у
χ
EIV
άζ.
Получили сложное трансцендентное уравнение относительно'
неизвестной продольной силы X. Решить это уравнение можно·
методом итерации.
Могут встретиться и более сложные случаи, в которых
сближение опор воспрепятствовано не полностью, а в соответствии
с жесткостью некоторых элементов,,
называемых в судостроении
распорами. Соответствующую систему
иллюстрирует рис. 13.42.
§ 13.6. Совместно происходящие
пространственный изгиб и кручение
круглого цилиндрического стержня
Гибкая δαηκα
Ραοπορ
Рис. 13.42. Распор —жесткая связь,
препятствующая сближению концов
гибкой балки при ее изгибе под
воздействием поперечной нагрузки.
1. Усилия. Напряженное
состояние элемента. Деформацию стержня,,
отмеченную в названии параграфа*
рассмотрим на частном примере,
не теряя, тем не менее, общности.
Пусть имеем вал (рис. 13.43, а),
опирающийся на два подшипника и несущий два зубчатых колеса,
одно из которых А расположено на консоли, а другое Б между
подшипниками. Колесо А (радиуса #х) является ведомым; на него
со стороны ведущего колеса В действует сила Рг. Колесо Б
(радиуса R*,) — ведущее, на него со стороны ведомого колеса Г
действует сила Р2. Силы Рг и Р2 имеют горизонтальное
направление. Веса колес А и Б равны соответственно Gx и G2. Требуется
подобрать поперечное сечение вала. Свяжем с валом систему
осей Oxyz (рис. 13.43, а).
Строим эпюры крутящего и изгибающих моментов,
возникающих в валу (см. рис. 13.43, в, г, д). Найдем геометрическую
сумму эпюр Мх и Му, обозначив ее символом МИЗГ (рис. 13.43, е).
Поскольку поперечное сечение круглое и момент сопротивления
его при изгибе в любой плоскости одинаков, можно ординаты,
пространственной эпюры Мизг расположить и в одной плоскости.
Итак, расчетными являются эпюры крутящих моментов Мг = Мкр.
и эпюра полных изгибающих моментов Мтг.
Обращаем внимание на то, что в эпюре Мизг на рис. 13.43, е
нЬт нулевых ординат, кроме концевых сечений. В точке а нену-
·§ 13.6]
ПРОСТРАНСТВЕННЫЙ ИЗГИБ И КРУЧЕНИЕ СТЕРЖНЯ
329
левая ордината в аксонометрическом изображении слилась с
нулевой линией.
Теперь рассмотрим напряженное состояние элемента вала,
находящегося вблизи боковой его поверхности (рис. 13.43, ж).
Мхи My
и)
43h
1Рис. 13.43. Совместное действие изгиба и кручения на стержень (вал): а) вал и зубчатые
«олеса — А (ведомое) и Б (ведущее); колесо В (ведущее) передает силу Pt на колесо А,
•колесо Г (ведомое) оказывает сопротивление Рп колесу Б; б) эпюра Μ , = Μ ·, в) эпюра Μ ·.
г) эпюра Μ \ δ) аксонометрическое изображение эпюр Μχ и Μ · е) эпюра л! —
геометрическая сумма эпюр Мк и Μ ; ж) сечение Ъ изогнуто-скрученного вала, эпюры
нормальных и касательных напряжений по диаметру, представляющему собой след пересечения
с поперечным сечением плоскости действия Л1 _ — изгибающего момента в
рассматриваемом сечении; з) наиболее напряженные элементы в рассматриваемом поперечном
сечении (сечение согласно фиг. д); и) тип напряженного состояния элемента при
совместном действии изгиба и кручения.
Элемент вырезан в поперечном сечении вала у конца диаметра,
являющегося следом плоскости, в которой действует момент Мизг
в данном сечении. На рис. 13.43, ж изображено напряженное
состояние этого элемента. Индексы «изг» и «кр» у σ и τ
подчеркивают, что эти напряжения вызваны соответственно изгибом и
кручением. Это напряженное состояние аналогично тому, которое
330 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ΧΙΙΓ
испытывает при плоском изгибе балки любой элемент,
находящийся между нейтральным слоем и крайними волокнами.
2. Условия невозникновения предельного состояния. Для
проверки невозникновения предельного состояния в материале этого:
элемента (разрушения или пластической деформации течения)
можно воспользоваться соответствующими формулами (12.99) —
(12.102), выведенными при аналогичном анализе в случае
плоского поперечного изгиба. Только вместо σ надо иметь в виду
оизг, а вместо τ — напряжение τ1φ. Тогда эти формулы
приобретут следующий вид:
σ3ΚΒ> ι = т 1аизг + V tfvW + 4τ,^ρ] ^ [σ], (13.56)
σ31{13>2 !μ-ο.3 = 0,35σ„ΒΓ + 0,65 ]/σ*3Γ + 4τ2κρ < [σ], (13.57)
σβΙΜ.8 = ν/"σϊ.Γ + 4^κρ^[σ], (13.58)-
σβΜ, 4 = ^зг + Зт^р^ [σ]. (13.59)
Поскольку входящие в (13.56) —(13.59) напряжения σΗ3Γ и τκρ>
находим по формулам
Мтг Мтг 7Икр Мкр Мкр
σΗ3Γ— ψ — пгщ ι τκρ ·ψρ ягз/2 2W
условия (13.56) — (13.59) получаются в такой форме:
г~2 м^
_}_\Мш.+ 1/ i!k. . 4
иэкв, ι — 2 [ f г Г ψ2 ~ Ί
4Wa
2Ϊ^ — w ^m» μ ο. ου/
г, ft Q5 ^изг ι a gr Ι/ ^нзг ■ л Мкр _
_ 0,35Λ4Η3Γ + 0,65]/Λί2Η3Γ+Λ4κρ _ Мэкъ,2 ^ Γ^Ί ,„ш
— - ^ — ij» ;== L°J» U0-D1r
w w
1/ Λί ИЗГ ι ,7Ийр _ НЗГ ЭКВ. 3 —- Г_1 /1 О СО\
<W3=|/ -ψ—l"4l"WS" = № = —W~^LaJ' (10.04.
-д/"^нзг , Q Мкр Ум1зг + 0,75Мкр МЭкв.4 ^-r^l /1QAQ\
<W4=p -^—Ι"31¥Γ== № =—ψ-^ίσ\· (13.63)
Таким образом, расчетные формулы по всем теориям приобретают
единый вид
**«.* = J%si^M. (13.64)
где под M9KBii (t = l, 2, 3, 4) понимаются эквивалентные моменты,
определяемые выражениями, показанными в формулах (13.60) —
<§ 13.6] ПРОСТРАНСТВЕННЫЙ ИЗГИБ И КРУЧЕНИЕ СТЕРЖНЯ 331
(13.63). Формула (13.64) во всем "аналогична формуле проверки
прочности крайнего волокна изогнутой балки
σ = 4^[σ], (13.65)
где, как известно, Μ — изгибающий момент, a W — момент
сопротивления поперечного сечения при изгибе. Этой аналогией и
объясняется то, что выражения, определяемые формулами (13.60),
(13.61), (13.62), (13.63), названы эквивалентными моментами.
3. Подбор сечения вала. Имея формулу (13.64), которую
представим так:
^■«М. (13-66)
можно подобрать сечение вала. Для этого достаточно решить
неравенство (13.66) относительно г
r*V^ffi- (13·67>
Подбирая г по формуле (13.67) по разным теориям (£ = 1, 2,
3, 4), получаем различный результат. В машиностроении долгое
время широкое распространение имела вторая теория,
справедливая, как известно, в случае хрупкого поведения материала.
Вместе с тем материал в валах в большинстве случаев ведет себя
Бе как хрупкий, вследствие чего правильнее расчет вести по
условиям пластичности (третья или червертая теория). Однако
переход к третьей или четвертой теории показал, что диаметр
вала, найденный по этим теориям, оказывается большим по
величине, чем при использовании второй теории, тогда как сечения
валов, подбиравшиеся по второй теории, удовлетворяли условиям
надежности, что подтверждалось многолетней практикой их
эксплуатации. Такое на первый взгляд парадоксальное положение вещей
легко объясняется тем, что при переходе от одной теории к
другой, более совершенной, уменьшается, естественно, фактор
незнания, т. е. должен быть уменьшен коэффициент запаса и, таким
образом, переходя от одной теории к другой, более совершенной,
изменять нужно не только аЭ1СВ(Ь т. е. левую часть неравенства,
но и правую, т. е. допускаемое напряжение, повышая его.
4. Случай, когда на вал действует продольная сила. Если бы
на вал, кроме сил, лежащих в плоскостях, перпендикулярных
к оси и вызывающих пространственный изгиб и кручение, были
■бы приложены и осевые силы, то в состав нормального
напряжения входила еще доля, равная N/F.
Эпюра нормальных напряжений при этом изменилась бы по
сравнению с показанной на рис. 13.43, ж (нейтральная ось не
проходила бы через центр тяжести поперечного сечения). От этого
-изменения тип напряженного состояния элемента, выделенного
332 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ХПГ
в точке с максимальными нормальным и касательными
напряжениями, не изменится, однако "вид формул получается несколько
иным, поскольку вместо csmr = Mmr/W следует иметь в виду
N
Μ
N W
σ — F ^ W W F ^
Μ
нзг
W
Ν^ ягЗ/4 Мтт
N
W лг*
W
4- + Μ.-Ι3Γ
~1?
Условия невозникновения предельного состояния по всем
теориям приобретут следующий вид:
<Wi=[_W-4- + M„3r +
Λ-γ [Ν ■£)* + 2Ν ^ ΜΗ3Γ + Μ£3Γ + Μ,2Φ]: 2W ==
^·». > = [0,35"(iV -J- + МИ8Р) +
+ 0,65]/Г(л^)Ч2ЛГ ^MH3r + MLr + M'p]:U7:
σ9ΚΒ( з = [У [Ν ^)2 + W L. Мтг + AfSar + M,2{p]: W *
°экв, 4
(13.68)
- []/"(лГ ~J + 2N^ МИЗГ + М*ЗГ + 0,75М£Р] : V < [σ].
Подбор сечения вала при наличии N несколько усложняется..
В качестве примера рассмотрим подбор сечений вала по третьей
теории, исходя из условия (13.68)3. Возведем в квадрат обе части
(13.68)3 получим при этом
W*16 +
N
ηζ
2 Мизгг + М^г + М^р-[а]2-^-г6 = 0,
или
[а]^г6-~г*-^Мттг-№эг + М*кр)=0. (13.69)
Для отыскания г необходимо решить уравнение (13.69),
являющееся уравнением шестой степени. Решить это уравнение можно·
одним из приближенных tметодов, например, методом Ньютона.
3. Пример 13.9. Построить эпюру полных касательных напряжений
в контурных точках круглого поперечного сечения стержня, в котором имеют
место усилия Qx, Qy = 1Qx и момент Mz = Qxr. Здесь г — радиус поперечного
сечения стержня.
Решение. Поскольку в точках поперечного сечения, расположенных у era
контура, полное касательное напряжение как при поперечном изгибе в
плоскости yOz (τ!^), так и при поперечном изгибе в плоскости xOz (^zx))y
а также при кручении (т^кр^) направлено по касательной к контуру, полное
§ 13.6] ПРОСТРАНСТВЕННЫЙ ИЗГИБ И КРУЧЕНИЕ СТЕРЖНЯ 333
а)
A w щ, е.
f Щ з °°
д)
д)
Рис. 13.44. К примеру 13,9: а) поперечное сечение стержня и действующие в нем усилия,
соответствующие касательным напряжениям; б) эпюры напряжений τ J5 B точках
поперечного сечения, расположенных у контура; в) эпюра напряжения тув тех же точках;.
г) эпюра напряжений ν ' в тех же точках; д) эпюра суммы напряжений %*■■*' + τ'*' в тех
же точках; е) эпюра τ
ЛУ)
г С)
с(кр).
τν|' + τκ > -\- τν μ' в тех же точках (на всех эпюрах у ординат
показаны лишь числовые коэффициенты при Q /лл2).
334 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XIII
касательное напряжение при одновременном действии всех трех видов
деформации находятся как алгебраическая сумма τ2=τ£ί')-1-τ£,:)+τ*κρ^.
В разделе 4.3 § 12.6 была получена формула для χ№
xf e J$L = ~ \ sin α =^% sin a.
since 3 jtr2 3π/·2
Аналогичная формула получается и для х^\ однако если сохранить
измерение угла α от вертикального диаметра, то в формуле для τ*** вместо a
нужно иметь (π/2 — α), тогда
(χ) 4 Qx . / π \ 4 О,.
2 3 яг2 \ 2 / 3 яг2
Формула для τ^κρ) имеет вид
τ(κρ) = Мг _^ Qxr 2QX
2 Wp π/*/2 nr» *
На рис. 13.44 показаны эпюры τψ>, τ[χΚ τ<κρ), τ^+τ^ и τ
Ордината эпюры, соответствующая касательному напряжению,
направленному против часовой стрелки (при взгляде на стрелку оси ζ), отложена
снаружи окружности.
§ 13.7. Общий случай деформации стержня
с прямолинейной осью
1. Последовательность расчета и основные формулы. В самом
общем случае воздействия внешних сил на стержень с
прямолинейной осью в его поперечных сечениях возникают все шесть
составляющих внутренних силы и момента: Qx, Qyt Ν, Мх, My,
Мг. Пользуясь принципом независимости действия сил, если
взаимным влиянием эффектов действия этих сил можно
пренебречь, легко получаются формулы для напряжений и
перемещений. Последовательность расчета стержня в этом случае, если
все усилия в опорных стержнях статически определимы,
оказывается такой.
а) Строятся эпюры Qx, Qy, Ν, Мх, Му и Мг (этот вопрос
подробно освещен и в общем виде и на примерах в главе I).
б) Находятся нормальные напряжения
N Мху Мух
σ=-ΊΓ + -τ~ + —Γ~·
Г ' χ 'у
в) Находится положение· нейтральной линии
N Мху Мих
т + ^- + -т-=°·
г ' χ 'у
г) Находятся точки /г1>2 с наибольшим и наименьшим в
алгебраическом смысле нормальными напряжениями — это точки,
наиболее удаленные от нейтральной оси; в них нормальное
§ 13.71 ОБЩИЙ СЛУЧАЙ ДЕФОРМАЦИИ ПРИЗМАТИЧЕСКОГО БРУСА 335
напряжение находится по формуле
0Г<1. 2) = _ + ХУ*1-Ъ + У *М ,
г Ι χ ι у
Здесь xky yk — координаты точки, в которой производится
проверка.
д) Определяются касательные напряжения. Вопрос о них
обсудим подробнее. В главе, посвященной кручению, отмечалось,
что только в случае круглого поперечного сечения решение может
быть получено элементарными средствами, во всех остальных
случаях приходится прибегать к использованию теории
упругости. В главе, посвященной изгибу, уже говорилось, что по
формуле элементарной теории удается найти с некоторой
погрешностью касательное напряжение %гх при поперечном изгибе в
плоскости Oxz (его мы обозначим символом τ^) или напряжение τζ
при поперечном изгибе в плоскости Oyz (его мы обозначим
символом τ^). Остаются неизвестными: напряжения τζχ при изгибе
в плоскости Oyz (символичное его обозначение τ^) и
напряжение %гу при изгибе в плоскости Oxz (обозначим символом %(*у).
Величины τ^? и τ[κ) могут быть найдены лишь средствами теории
упругости. Если считать, что отмеченные выше слагаемые
компонентов касательных напряжений известны, то полное касательное
напряжение находится как геометрическая сумма полных
компонентов напряжений
τ = Vb + ϊΰ - V (τ£> + τ£> + τ£«)· + (τ« + τ<£ +τ< ?>)·.
Разумеется, можно воспользоваться известными результатами
решения задач по кручению и изгибу стержней некоторых видов
поперечных сечений, полученными методами теории упругости.
Имея поле нормальных и касательных напряжений, по
известным формулам определяем главные напряжения, а далее
производим проверку невозникновения предельного состояния в
окрестности точки тела по одной из известных теорий.
е) Перемещения в общем случае деформации стержня
находятся как геометрическая сумма перемещений, определенных при
элементарных деформациях.
2. Потенциальная энергия деформации. Потенциальная энергия
деформации прямолинейного стержня в случае, если в
поперечных сечениях стержня отличны от нуля все три составляющие
внутренней силы: Qx, Qy и N и все три составляющие
внутреннего момента: Мх, Му, Мг, определяется по формуле:
) \2ΕΡ + ~2ЁТХ~ + "2G77 + ~2ЁП + ~2GfJ + "ЩГ/ '
о
336
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
dz dw
Рис. 13.45. К определению шести слагаемых потенциальной энергии деформации,
накапливаемой в элементе стержня с прямолинейной осью, испытывающего общий случай
пространственной деформации.
0
1
1
.
SKSS
iz
Ν=Ρι
Φ
Τζ
lf-P7
δ)
щ
Pi
ζ
Λ
ρ?
ι
ϊ
β)
Рис. 13.46. К обоснованию недопустимости применения принципа независимости
действия сил к определению потенциальной энергии деформации при воздействии на
стержень нагрузок, вызывающих в нем один и тот же вид элементарной деформации:
а) стержень под воздействием силы Pi', б) стержень под воздействием силы Р2; в) стержень
под воздействием сил Pi и Р2.
§ 13.8] ИЗГИБ КОНСОЛИ СИЛОЙ. РЕШЕНИЕ ТЕОРИИ УПРУГОСТИ 337
т. е. равняется сумме потенциальных энергий при отдельных
элементарных видах деформации. Возможность такого
суммирования объясняется тем, что элементарные деформации элемента
прямолинейного стержня ортогональны, т. е. каждая из
величин Qx, Qyt Ν, Мх, Му, Мг, действующих на этот элемент,
выполняет работу лишь на перемещениях ею же самой
вызванных. На перемещениях же, вызванных другими величинами, ни
одна из них работы не выполняет. В этом легко убедиться,
рассматривая рис. 13.45.
Вместе с тем обращаем внимание на то, что, поскольку
потенциальная энергия деформации содержит величины Qx, Qy, Λ/\
Мг, Му и Мг не в первой степени, применить принцип
независимости действия сил к ней нельзя. Так, например, если на брус
действуют две силы Рг и Р2, вызывающие его растяжение
(рис. 13.46), то при самостоятельном действии каждой из этих
сил потенциальная энергия, накапливаемая в стержне,
определится соответственно по формулам (см. рис. 13.46, а, б)
II - С p*dz - JUL и - f p*dz - J!i£L
1 — J 2EF ~ 2EF' 2— J 2EF ~ 2EF'
о о
При совместном же действии сил потенциальная энергия,
накапливаемая в стержне, если учесть вид эпюры N (рис. 13.46, в),
выразится формулой
α /
Р\{1-а)
г, _ С (Рг + Ptfdz С P\dz _ (Рг+Ptfa
1+2 J 2EF "+" J 2EF 2EF ~^
2EF
Р\а . РгР2а , Ρ la ■ P\{l — a)
"τ" ρπ ~Γ ορρ "τ*
Итак,
2EF ' EF ' 2EF ^ 2EF ~
_ Ρ»[α + (1-α)] Ρ\α РгР^а _
2EF """ 2EF """ EF ~
_ Ρ*1 Ρ\α РхРга _ ,, .. , РхРга
~ 2EF ~r 2EF "■" EF ~ ui~T~uz~r EF '
§ 13.8. Изгиб консольной призматической балки
силой, действующей в плоскости торца
(результаты решения задачи)
1. Предварительные замечания. В предыдущей главе осталось
три вопроса, не получивших полного обсуждения. Первый из них
касается главной трудности задачи о поперечном изгибе балки —
определения второго компонента касательного напряжения хгх
при изгибе в плоскости zy или хгу при изгибе в плоскости zx.
Второй вопрос относится к оценке точности формулы для опре-
338
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
деляемого в сопротивлении материалов компонента касательного
напряжения хгх при изгибе в плоскости zx или хгу при изгибе
в плоскости zy. Наконец, третий вопрос, не получивший
исчерпывающего пояснения, касается центра изгиба. В § 12.8 было
введено понятие о центре изгиба и показано, как находить
координаты этой точки в случае, если стержень имеет открытое
тонкостенное сечение. В общем случае определение координат центра
изгиба рассмотрено не было. На все три отмеченных вопроса
можно дать ответ, рассматривая при помощи аппарата теории
упругости изгиб консольной балки силой Р, лежащей^в_гмос^ости
ее торца и~"'име~ю£цёТГ'произвольную точку" приложения и
произвольное" направление. Поскольку деформация, вызываемая такой
силой, не является элементарной,. эт6т~в^прос"'ра^матрй^аётся"
в настоящей~"гла'ве в данном параграфе. Строго говоря, и
материал § 12.8 не относится к плоскому изгибу, о чем там
говорилось, однако его мы поместили в главу XII с целью показа
границы области, в которой возникает плоский изгиб.
Упомянутая выше задача об изгибе консольной балки была
поставлена и решена Сен-Венаном. Позднее она подвергалась
дополнительному рассмотрению рядом авторов, в частности,
С. П. Тимошенко. Имеется ряд вариантов решения и изложения
решения этой задачи. Здесь будут показаны лишь план решения
задачи и основные результаты без промежуточных выкладок.
2, Постановка задачи. Имеется призматический стержень,
закрепленный на одном торце и загруженный силой Р, лежащей
в плоскости свободного торца при условии, что и точка
приложения силы, и ее направление произвольны. Объемные силы
считаем равными нулю: X = V = Z = 0. Требуется найти
напряжения и перемещения, возникающие в балке, и координаты
центра изгиба.
Свяжем с рассматриваемым стержнем систему осей Oxyz.
Начало координат расположим в сечении закрепления балки
в точке, представляющей собой проекцию на это сечение точки
приложения силы Р. Ось χ совмещаем с проекцией линии
действия силы Ρ на сечение закрепления, ось г проводим
параллельно оси стержня, а ось у направляем так, чтобы система Oxyz
была правой (рис. 13.47).
3. Решение задачи. Решение задачи выполняется
полуобратным методом Сен-Венана.
На первом этапе в качестве угадываемой части решения
принимаем
σχ = σ, = τχΰ = 0, ог = Р (α* + βί/ + γ) (L-z). (13.70)
Напряжение σζ в (13.70) пропорционально изгибающему моменту
P(L — z) и распределено в поперечном сечении по закону
плоскости, определяемому функцией ах + $у + γ.
-§ 13.8] ИЗГИБ КОНСОЛИ СИЛОЙ, РЕШЕНИЕ ТЕОРИИ УПРУГОСТИ
339
На втором этапе решения из первых двух уравнений
равновесия устанавливаем, что
τ« = τ„(*. у), xgy = xgy(xt у), (13.71)
т. е. распределение касательных напряжений во всех сечениях
оказывается одинаковым.
а
сс^
V
С
\"
Λ
ί*
в)
Рис. 13.47. Изгиб призматической консольной балки произвольного поперечного
сечения силой Р, лежащей в плоскости торца и имеющей произвольные точку приложения
и направление линии действия: а) балка, сила и система координат; б) часть балки между
спободным концом консоли и сечением с координатой, равной г (в последнем сеченин
показаны составляющие внутренних силы и момента); в) к определению направляющих
косинусов нормали ν и касательной t к контуру поперечного сечения в системе осей ху.
Третье уравнение равновесия удовлетворяется тождественно,
если функции (13.71) принимаются такими:
-^■ + ах2 + ух
Р_
2
*гу
[-# + β^+Ητϊ <13·72)
:1десь % — %(х, #) —неизвестная пока функция.
Первые четыре уравнения совместности деформаций
(уравнения Бельтрами) удовлетворяются функциями (13.70) и (13.71)
тождественно, а два последних уравнения сводятся к уравнению
2μ
Ь%=Т^фх-Щ)+С,
(13.73)
где С — неизвестная постоянная, определяемая из граничных
условий на боковой поверхности. Граничные условия для
функции χ находятся из граничных условий для компонентов
напряжении.
11остоянные α, β и γ находятся из трех уравнений
равновесия (из общего их числа шесть) части балки, расположенной
между торцом и произвольным поперечным сечением
^прг = 0, 2МОМА; = 0' 2μομ# — 0·
(13,74)
340
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. ХИТ
В развернутой форме система уравнений (13.74) имеет вид
S(/a + Sx$ + Fy = 0,
Ix& + IxV + Sxy = 0, (13.75)
I^ + Ix^ + Syy=—\. .
Здесь F, Sx, Sy, Ix, Iy, /^ — площадь поперечного сечения балки,
статические моменты этой площади относительно осей χ и у,
осевые моменты инерции указанной площади относительно осей χ
и у и центробежный момент инерции площади в системе осей ху.
На третьем этапе решения из условия обращения в нуль
напряжений на боковой поверхности устанавливаем граничное
условие на контуре поперечного сечения для χ
ds
(^ + yy)~-(ax2 + yx)dy
ds
ds
на Г.
(13.76)
Сила Ρ вызывает и изгиб и кручение стержня.
Задачу можно разбить на две —на задачу о сен-венановом
кручении и задачу об изгибе. С этой целью функцию χ
представляем в виде линейной комбинации двух функций χ^ψ + βφ,
тогда краевая задача (13.73), (13.76) распадается на две краевые
задачи
^ = -^гфх-ау) в D,
3φ.
~ds~'
С_
В
в D,
0 на Г;
3ψ_
ds
1+μ
-(ax2 + yx)^
на Г.
(13.77):
Полагая С/В = — 2Gnz, удостоверяемся, что φ —это функция
Прандтля. Тогда функция ψ описывает только изгиб.
Ограничиваясь односвязными поперечными сечениями балки и
симметричными относительно нейтральной линии, можно
показать, что φ = 0 и ψ = 0 на Г, а следовательно и χ = 0 на Г.
Из условия равенства нулю момента относительно оси ζ на
торце (условие эквивалентности) находим постоянную С
Шг = ξ ξ {хгуХ - ХгхУ) dF = 0;
} } 20кг
dF
§ ω [W + γί/) ~ -(αχ» + γ*) -§-] ds +
J J φ dF + ± J J фу-ax) xy dF\
F F )'
(13.78)
+
Здесь ω —секторная площадь.
§13.8] ИЗГИБ КОНСОЛИ СИЛОЙ. РЕШЕНИЕ ТЕОРИИ УПРУГОСТИ 34Г
Остальные пять условий эквивалентности на торце \ ^ хгх dF =■■
F
= Р, ]\TzydF = 0, \\azdF = 0, \\a£xdF = 0, \ $ агу dF = 0 удов-
> F F F
летворяются функциями (13.70) и (13.71) тождественно.
На четвертом этапе отыскиваются все остальные функции
(компоненты деформации — из закона Гука (9.5) и составляющие
перемещения путем интегрирования уравнений Коши (9.3)).
Функции и, ν и w имеют вид
ρ [ Lz* zZ \
, Р0+Ц)С ™ { 2 6 )
Τ 2Ε у Ε '
-^-(L-z)(f- + W) + ^, (13.79),
Ε \ 6 ^ 2 ' 2 У 2£
Pa[Z,z —2-jx Ρ(1+μ) f 5χ Ι , , , Ρ(1+μ) / βί/3 . γ^
+ Ε Ε )-di\x-ody + Ε Гз" +
2
б
/ ζ2
μΡ ( βί/з yy2\ _ pyyz Py[Lz 2
го/ ρ ~Γ ρ
Погонный угол закручивания стержня находится по формуле как
среднее в пределах площади поперечного сечения значение вели-
1 (* (* fit л
чины д(аг/дг кг = у ι ι —^-dF. Здесь дыг/дг — скорость измене-
F
ния по координате ζ поворота (£>г = 1/2(ди/дх — ди/ду), т. е.
погонный угол закручивания волокна, параллельного оси стержня и:
пересекающего поперечное его сечение в рассматриваемой точке..
Величина хг выражается следующей формулой:
ъ=-Ц$*-[&?№*--«у1+с]·
4. Схема решения задачи. Мыслимы две несущественные
разновидности последовательности решения задачи. Первая — в
которой хг задано, вторая —при неизвестном κζ.
342 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XIII
Если хг задано, то схема решения задачи следующая.
1. Находим геометрические характеристики поперечного
сечения стержня: F, Sx, Sy, IXt Iy, Ixy.
2. Определяем α, β и γ из уравнений (13.75) через F, SXi
•^ί/г 'χι '\ji I xy
3. Находим функцию φ, решая краевую задачу (13.77)!.
4. Находим функцию ψ, решая краевую задачу (13.77)2.
5. Находим С по формуле (13.78).
6. Находим В по формуле
В---иЬ (13.80)
7. Находим функцию χ по формуле χ = ψ + βφ.
8. Определяем компоненты напряжений по формулам (13.70)
я (13.72).
9. Определяем составляющие перемещения по формулам (13.79).
Если пг неизвестно, то пункты 1 и 2 остаются неизменными.
В пункте 3 решается краевая задача для функции φ
Δφ = — 2 в D,
§- = Q на Г.
ds
Пункт 4 остается неизменным.
В пункте 5 находим С по формуле (13.78), в которой вместо
■4>/(Gkz) имеет место φ.
В пункте 6 находим В по формуле В = —С/2.
В пункте 7 находим χ по формуле χ = ψ + βφ.
Пункты 8 и 9 остаются неизменными.
В заключение (в пункте 10) определяется хг по формуле κζ =
F
Вследствие линейности задачи можно использовать принцип
независимости действия сил применительно к двум изгибам в
произвольных плоскостях xOz и yOz и кручению относительно линии,
проходящей через центры изгиба поперечных сечений.
5. Центр изгиба.
5.1. Условие для отыскания центра изгиба. Как
уже говорилось в § 12.8, центром изгиба называется такая точка
в поперечном сечении стержня, которая обладает тем свойством,
что если линия действия поперечной силы в сечении, проходит
через нее, то имеет место только изгиб, кручения стержня не
происходит.
Выше в настоящем параграфе была решена задача об изгибе
консоли силой, приложенной к торцу и лежащей в его плоскости.
Точка приложения силы и ее направление были произвольны;
ось χ была выбрана в сечении заделки так. что именно на нее
§ 13.8] ИЗГИБ КОНСОЛИ СИЛОЙ. РЕШЕНИЕ ТЕОРИИ УПРУГОСТИ 343
проектировалась линия действия силы. При этом было поставлена
условие, согласно которому никакие другие силы или моменты,
в том числе $Лг, на торец не действовали. Из условия 9Лг = 0 и
была найдена величина произвольной постоянной С. В условиях
такой постановки погонный угол закручивания кгфО.
Можно поставить задачу иначе. Найти такое С, которому
соответствует хг = 0, а затем определить, каким должен быть
внешний момент 5Шг, чтобы поставленное условие имело место.
Коль скоро кручения нет, погонный угол закручивания должен
быть равен нулю хг = off u ' $х— аУ) + Μ = ^· Отсюда,
учитывая, что Ρ (1 +μ)/(2£/Γ) Φ Ο,
1^-фх-ау) + С = 0. (13.81)
Из (13.81) найдем такое значение С, которому соответствует
отсутствие закручивания
С = --^(Рх-ау). (13.82>
По найденному значению С определим момент ЬЛг, приводящий
совместно с силой Ρ к отсутствию кручения стержня. Будем
исходить из общего выражения для Шг как статического эквивалента
распределенных касательных сил в поперечном сечении
ЗИ« = Ц (τ,„χ - хвху) dF = 0. (13.83).
F
Подставим в (13.83) хгх и хгу согласно (13.72) и учтем, что χ
выражается через С, а последнее находим в результате указанных
выкладок; получим момент Шг, к которому наряду с силой Ρ
приводятся касательные поверхностные силы с интенсивностями хгх-
и хгу при условии, что κ2 = 0
ЗЯ, = Ρ§ω [фу' + уу) ~ - (о*« + ух) -§-] ds +
+ РШ^+ТТ^-^7 (fkc" аУс)]dF+ τ Π №- αχϊ ХУ dF-
F F
5.2. Определение координат центра изгиба.
Силу Рх, действующую в плоскости Oxz, и момент 5Шг можно *
заменить статически эквивалентной им силой Р = РХ,
недействующей в плоскости, параллельной плоскости Oxz на расстоянии у^
Если 5Шг> 0, то для того, чтобы и момент, создаваемый силой Рх>.
был положительным, необходимо, чтобы линия действия силы Рх.
была смещена в область отрицательных значений у.
:344
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
Итак,
"■ = — ρ
У1 = -Цг- (13-84)
X
Если бы решалась задача, в которой консоль загружена силой Ру,
то все было бы аналогично показанному при изгибе силой Рх
:и координата х{ плоскости, параллельной Oyz, при расположении
в которой сила Ру вызывает только изгиб, определится по формуле
Xl = —^.. (13.85)
у
5.3. Упрощение формул для координат центра
изгиба. Формулы для координат центра изгиба, как это показал
В. В. Новожилов в своем курсе теории упругости х), могут быть
упрощены. Это упрощение состоит в том, что интегралы,
содержащие функции изгиба гр* и %, можно выразить через интегралы,
содержащие функцию кручения, и, таким образом, для
определения координат центра изгиба достаточно решить более простую
задачу о кручении стержня, нежели задача об изгибе стержня.
Формулы для щ и х{ в этом случае имеют вид
(1 + μ)0κ,
F
-$£(α* + β£ + γ)φ<ί/\ (13.86)
F
*'= <1 + μ)0». ^№(y-yc) + a(x-xc))dF-
F
- JJ(osy+p* + v)q>dF. (13.87)
F
Формулы (13.86) и (13.87) намного проще формул (13.84) и
(13.85). Самое главное их достоинство состоит в том, что при
их использовании для определения координат центра изгиба не
приходится решать задачу об изгибе.
5.4. Сравнительная оценка влияния отклонения
линии действия силы от центра изгиба на погонный
угол закручивания массивного и тонкостенного
стержня открытого профиля. Сопоставим влияние эффекта
кручения, возникающего вследствие приложения силы Ρ не в центре
изгиба, а в центре тяжести, для двух поперечных сечений —
массивного—в виде половины круга и открытого тонкостенного — в виде
лоловины кольца. Не приводя решения, отметим, что ценр изгиба
-.(см. В. В. Новожилов, Теория упругости, гл. VI, § 21, стр. 288)
ί) Новожилов В, В., Теория упругости, Судпромгиз, 1958,
§ 13.8] ИЗГИБ КОНСОЛИ СИЛОЙ. РЕШЕНИЕ ТЕОРИИ УПРУГОСТИ 345'
в случае балки с поперечным сечением в виде половины круга
(рис. 13.48) располагается в точке с координатами
Χι = О, у{
8R
5π
[' +
μ
-0,147
μ
20
3 1 + μ ' 1 + μ 3π.|·
Для уяснения взаимного расположения центра изгиба и центра
тяжести приведем их координаты
;0, ус
F
3 к
±R_
3 π
Найдем численные значения yt (при μ = 0,25) и ус в долях
от R
У'=Ш[ +ТТ§ - °·147 Ш §] - °·5117β· fc-0.4245R.
Таким образом, если вести расчет консольного стержня,
принимая в качестве точки приложения внешней силы Ρ центр тяжести
поперечного сечения, то возникнет
крутящий момент, равный Мг = Ρ (0,5117 —
— 0,4245) R = 0,0872PR. Неучет этого
момента или, иными словами,
пренебрежение кручением вносит, разумеется,
искажение в поле действительных
касательных напряжений в поперечном сечении.
Кроме того, не учитывая кручение, мы
тем самым не учитываем вызываемую им
депланацию, а при наличии стеснения
последней не учитываем возникающие
вследствие этого нормальные напряжения.
Жесткость на кручение стержня с
поперечным сечением в виде половины круга
равняется (см. В. В. Новожилов, Теория
упругости, гл. VI, § 15, стр. 268) G/K =
=2G 55 φ (χ, #)dF = 0,294Gtf4. Таким об-
F
разом,
0,№5Р
Рис. 13.48. Поперечное
сечение призмы в виде
полукруга и расположение в нем
центра тяжести площади и
центра изгиба.
погонный угол закручивания
/С»
М,
_ 0,0№PR
G/K ~ 0,294G#4
0,2966
найдем по формуле
Ρ
GR3 '
Для сопоставления эффекта неучета кручения, возникающего
вследствие того, что плоскость действия силы Ρ проходит не
через центр изгиба, а через центр тяжести, рассмотрим балку,
поперечное сечение которой имеет вид очень узкого полукольца
(k = Rx/R = 0,95) рис. 13.49. Координаты центра изгиба для такого
профиля (см. В. В. Новожилов, Теория упругости, гл. VI, § 21,
346
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
•стр. 288) суть:
*ί = 0,
У ι
где
8 R
5π 1-fc4
{l + 5&2-5&3-А;5+у-^ [1 -5&2 + 5&3-&5]
1+μ 3π 1—/г2 Д4/ \l
1, 2405Я при μ = 0,
при μ = 0,25,
00
к я * Ζύ (2л —
1
я = 0
(2я—1)2(2я+1)2(2гс + 3)2
X
[ (2к — 1)2 (14-fe*"+<) — (2я + 3)3 /г4 (1 + /г/1и~2) + 16 (2я+ 1) fe2"+3 \ _
= 0,000059859Я4
Координаты центра тяжести площади этого же сечения (точнее
центра тяжести дуги однородной плоской
кривой в виде половины окружности) определяется
по формулам
(/
%1№R ,
>А
uf
%х
ЦИ
Ϊ ' 'У
0M08R
#с = 0,
Ус
sx
2 2
пД2/2 —π#|/2
2^(1— fe8)/3
4Д (1— *s)
(1— k2)nR2/2 3π (1— /г2)
0,6208tf.
Рис. 13.49.
Поперечное сечение призмы
в виде тонкого
кругового полукольца и
расположение центра
тяжести площади и
центра изгиба в
плоскости поперечного
сечения.
Крутящий момент, возникающий вследствие
того, что плоскость действия силы Ρ проходит
через центр тяжести поперечного сечения, а не
через его центр изгиба, равен следующей
величине:
Мг = (yi-yc) Ρ = (1,2406- 0,6208) PR =
= 0fi\98PR.
Жесткость при кручении стержня с поперечным
сечением в виде половины кольца GIK
находится с учетом приведенной выше формулы для /к: GIK =
= 0,000059859СЯ4. Таким образом, погонный угол закручивания,
возникающего вследствие того, что сила Ρ приложена не в центре
изгиба, а в центре тяжести, равен
Мг
*у- GIK
0.6198ЯР
0,000059859G#4
10 354Р
GR*
Отношение хг у сопоставляемых стержней массивного и тонко-
§ 13.8] ИЗГИБ КОНСОЛИ СИЛОЙ. РЕШЕНИЕ ТЕОРИИ УПРУГОСТИ 347
стенного получается: хгтонк/хгмасс= 10 354/0,2966 = 34 909. Зта
величина обусловлена, с одной стороны, различием в возникающих,
крутящих моментах, определяемым отношением Мг Ί0ΚΚ/ΜΖ масс ---
= 0,6198/0,0872 = 7,1078; и, с другой стороны, различием
"крутильных жесткостей, оцениваемым отношением GI^^JGI^^,^ —
= 0,294/0,000059859 = 4911,5. Произведение двух последних
отношений и дает приведенное выше отношение интенсивностей
углов закручивания: 7,1078-4911,5 = 34 909. Эффект в основном!
проявляется через жесткость.
6. Изгиб консольной балки эллиптического поперечного сечения.
Пример 13.10. Исследовать изгиб консольной балки эллиптического поперечного-
сечения, при условии, что сила Р, изгибающая стержень, приложена в центре-
тяжести торцевого сечения и действует вдоль главной оси инерции х.
Решение. 6.1. В рассматриваемом случае кручения не возникает.
Уравнение эллипса имеет вид
х? и2
^ + -р = 1· (13.88>.
Воспользуемся первым вариантом схемы, учтя, что хг = 0. Объединяем первые-
два пункта схемы.
6.2. Так как оси χ и у в рассматриваемом случае центральные главные,
Sx = Sy = Ixy = 0 и система (13.75) приводит к следующему решению: а = — \/1у,
β = 0, γ = 0. Следовательно, из всех геометрических характеристик
поперечного сечения нам понадобится лишь
+ а + ЬУ1 — (*2/α2> +α
1у= J x*dx 5 dy= 5 х*у
~а —ЬУ\ — (хг1а*) ~а
dx=
— bVl — (x2/az)
+ а t +а
— а —а
= ?!L Г_ JL y^-}fif+~[x j^2=^ + fl2 arcsin £Υ| |+α =
2b Γ α2
= — -^-α2 (arcsin 1 — arcsin (—1))
nazb
Итак, α =
πα36
6.3. Пункт 3 схемы решения в связи с отсутствием кручения выпадает.
6.4. В пункте 4 решается краевая задача для функции ψ. В нашем случае
она формулируется так:
*♦--& тэг» ■« тКэт"-£ «г- <'389>
С. П. Тимошенко предложил для придания наиболее простого вида
граничному условию для ψ представить эту функцию в виде суммы двух функций
ψ=θ(*. у) + 1(У)· (13.90)
348 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XIII
Подставляя (13.90) в (13.89), получим
д® _L df = 4 & dy 6® = 4 х* dy df dy
ds ' ds ztcfib ds ' ds na3b ds dy ds '
или
"-' 4 *-&ϊ£. (18.81)
(13.92)
ds \ na3b dy J ds '
Если положить
_df__ 4g2 y*_ _ 4a2
dy ~ na3b b2 na3b '
то условие (13.91) приобретает вид
ae г 4 / уад» \i dy ae =r^ /*2 y» γι dy
ds ~ [ na3b { "^ f>2 ^J ds ' 5s L πα^ί, ^ α2 "^ £>2 у J ^ *
Учитывая (13.88), получим
аэ
= 0 на Г. (13.93)
ds
Так как поперечное сечение односвязно, это граничное условие может быть
записано еще проще (подобная ситуация уже встречалась в задаче о кручении)
θ = 0 на Г.
Функция / (у) должна удовлетворять уравнению (13.92), которое можно
представить так:
Подставим (13.94)2 в (13.90)
ψ = θ(*. у)-^^2-уу (13.95)
Теперь, подставив (13.95) в (13.89), получим уравнение, которому должна
удовлетворять функция θ
._ 2α2 2μ 1 ._ 2 ία2 . μ \ ,10 ne.
Ае-т^у = -фт/> ^=ф + тт^)у' <13·96>
Итак, сформулирована краевая задача для функции Θ: (13.96)2 и (13.93).
Представим функцию Θ в виде
в=А{£*+*-1)у- (13·97)
Она удовлетворяет граничному условию (13.93). Постоянную А найдем из
условия удовлетворения дифференциальному уравнению (13.96), для' чего
подставим (13.97) в (13.96). В результате этой подстановки получим
2А , 6Л 2 /α2 , μ \
1*У + 1*у==Гу{ь* + ТТ^)У'
Приравняв коэффициенты при у в левой и правой часгях равенства, будем
иметь
2Α(? + ρ) = ζ;(ρ+ϊ+μ)·
§ 13.8] ИЗГИБ КОНСОЛИ СИЛОЙ. РЕШЕНИЕ ТЕОРИИ УПРУГОСТИ 349
Отсюда
а2 . μ
1 fr2 "*" 1 + μ _ 1 a2b* /μ α2
iy _i , 3 "—/ί/ί>2+3α2νι + μ ^"2
а2 "Г" р
Итак,
1 a2fr2 / μ α2\/χ2 t/2 \
/y ί>2 + 3α2 U +μ Ή W + Ρ l) У>
_ 1 a2fr2 / μ a3\/*2 t/2 \ _<^( У*_ _
ψ /^йя+за'и + μ + P/U2 + ί>2 Vy /.Л 3ft» y
6.5. Находим постоянную интегрирования С (по формуле (13.78)), которая
б нашем случае равна нулю С = 0 вследствие равенства нулю кг.
6.6. Находим В из (13.80) 5 = 0.
6.7. Находим функцию χ = ψ-|-βφ; учитывая, что вследствие отсутствия
кручения φ=0, χ приобретает вид:
1 a2fr2 / μ a2\/s2 t/2 \ _a2_(y^_ \
1 ~ Iy fc2 + 3a2 [l + μ + 'by U2 & Г "^ U'fc2 *7 '
6.8. Определяем компоненты напряжений по формулам (13.70) и (13.72)
ρ
ох = оу = хху=0, oz = P(ax+$y+y)(L — z)=—-I-x(L—z),
xzx-[dy + ax +УХ)2 ~2 /„^ + 3αΛΐ+μ + ί>»Λα»+ ft2 V
Pa2 /г/2 \ x*P _P j /x* 3y* A a* (x* y* \\
-ΤΓνφ-η-τντ-Ά\Α\*+ΊΓ-ιΓΤι\3 + »-η)'
Г ду , Ω , , IP 1 α2£>2 /μ , a*\2xy Ρ пя ху
6.9. Находим перемещения по формулам (13.79)
Тгг/
_ μΡ(Ι-ζ) х* _ μΡ(1 —ζ) у2 _Ρ_ /L22 _ ζ»\ μΡ (L —г)
ί_ £/,, 2 2Е1у ^ EIy\2 > б)' v~ Ely
PQ+μ) Γ/■* , 3^£_ \ . _ tf (уЧ _ Υ] Plfl μΡ&
Ε L\3a2 & j Iy\№ )\ ЪЕ1у ЬЕ1«
-±г Ш-£)х.
На этом решение задачи заканчивается. Ниже приведем анализ полученного
решения.
7. Частный случай — круглое поперечное сечение.
7.1. Формулы для хгх и хгу и для и, v, w. В случае круглого
поперечного сечения a = b = r и формулы для компонентов напряжений
приобретают следующий вид:
ρ
ох = оу=хху = 0, az = —1-x(L — z),
'у
Ρ (я/х* Зу* А г2 Ι& . i/2 A)
т _ рлхУ л- 1 Г%{ μ 4-Λ
Хгу — НА^, A-j- 4 ^j-p^ + 1 j .
350
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. ХШ
alb
Рисунок
а (С — 1)
а/4
[а/2
За/4
0,34616
-3,7
0,32450
-3,7
0,25963
-3,7
0,15144
-3,7
а/4
а/2
За/4
0,37500
-11,1
0,35156
-11,1
0,28125
-11,1
0,16406
-11,1
1/2
а/4
а/2
За/4
0,42856
-22,2
0,40178
-22,2
0,32144
-22,2
0,18750
-22,2
« 13.8]
ИЗГИБ КОНСОЛИ СИЛОЙ. РЕШЕНИЕ ТЕОРИИ УПРУГОСТИ 351
Таблица 13.6
У
μ. = 0 | и = и,5
4
0,34375
—3,03
0,32225
—3,02
0,25781
—3,03
0,15038
—3,02
0,36719
-9,2
0,34422
—9,2
0,27538
-9,2
0,16063
-9,2
0,41072
—18,8
0,38503
-18,8
0,30803
— 18,8
0,17969
— 18,8
4*ύ
2
0,33653
—0,97
0,31550
—0,95
0,25241
—0,95
0,14725
—0,96
0,34375
—3,03
0,32225
—3,03
0,25781
—3,03
0,15038
—3,03
0,35716
-6,67
0,33481
—6,67
0,26784
—6,67
0,15625
—6,67
36 (*ί)
4
0,32453
+2,71
0,30422
+2,7
0,24341
+2,7
0,14197
+ 2,7
0,30468
+9,4
0,28563
+9,4
0,22853
+9,4
0,13328
+9,4
0,26786
+24,5
0,25110
+24,5
0,20091
+25,5
0,11719
+24,5
°{χύ
0,30770
+8,32
0,28847
+8,3
0,23078
+ 8,3
0,13463
8,32
0,24999
+33,4
0,23438
+33,4
0,18749
+33,4
0,10938
+33,4
0,14286
+133,8
0,13393
+ 133
0,10714
+ 133
0,06250
+ 133
Значение у
произвольно
0,33333
0
0,31250
0
0,25000
0
0,14584
0
оззззз
0
0,31250
0
0,25000
0
0,14584
0
0,33333
0
0,31250
0
0,25000
0
0,14584
0
По формуле
сопротивления
материалов
χ
ΖΧ
РаЧ1у
0,33333
0,31250
0,25000
0,14584
0,33333
0,31250
0,25000
0,14584
0,33333
0,31250
0,25000- 1
I
0.14584 1
352
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
Несколько преобразуем формулы для хгх и xzy
21, [\4
+ (--х7^-^+1Ч-£Г-йт*+Й^»- +
\ Ί Ρ Г
Γ"4(1 + μ)_4 ^Τ2]=:27;|._4(1 + μ)Λ' ' 4(1 + μ)
2μ + 3 Л Ρ(3 + 2μ)Γ ^^Ί
^--^^Τ^ + 1^--№ί#^. 03.98)
"*- ννΐ + μ^/^" 4/,(1 + μ)
Формулы для перемещений приобрегают вид
μΡ(ί,-ζ)*» μΡ(ί,-ζ)^ Ρ /Lz* z»\ .
"-—шту шгу— + ΕΓν{Ύ-τ)* (13·99)
μΡ {Ι —ζ)
Ρχ
^-4Ε7[/(1 + μ)["(1+μ);'2 + 3ί/2(1+3μ + 2μ2)~,'2(1 + 3μ + 2μ2)]
lz -~)χ = ^ί1±3μ±2μ2)
EIy\ 2) 4ΕΙ„(1 + μ)
1 + μ
1+3μ + 2μ2
Λ:2 + 3ί/2
-]-
7.2. Оценка гипотезы о постоянстве τ2Д. по ширине балки.
Из формулы (13.98) следует, что τζχ не остается постоянным по ширине балки,
поскольку в эту формулу входит у. Произведем оценку отклонения τζχ от
средней его величины по ширине сечения и от величины, полученной по
формуле элементарной теории.
В табл. 13.6 помещены безразмерные величины τζχ: (Ра2/1у) при двух
значениях μ = 0 и 0,5, трех значениях alb — 2; 1; 1/2, четырех значениях
Xi~-a(i— l)/4 (t = l, 2, 3, 4) и при пяти значениях у на каждом из уровней:
0, b(Xi)/±, b (X{)/2, 3b (Xi)/4, bi(Xi), где b{ (χι) — половина ширины сечения на
уровне, определяемом координатой х{. Здесь же под значением xzx: (Pa2/Iv)
в процентах указано отклонение от среднего значения
6|Λ-(*?/α2)
τζχ, ср = ч /·— 2 . \ tzxdy,
bVl-xVa* j|
совпадающего со значением, определяемым по формуле сопротивления
материалов.
Данные табл. 13.6 позволяют сделать следующие выводы.
1. Погрешности, даваемые формулой элементарного решения (сопротивления
материалов), тем выше, чем больше вытянуто поперечное сечение в направлении,
перпендикулярном плоскости действия сил.
2. В плоскости действия сил и в области, примыкающей к ней,
элементарное решение дает заниженные значения для компонента касательного
напряжения (т. е. не в запас прочности); в областях, примыкающих к контуру,
элементарное решение дает завышенное значение компонента касательного
напряжения. Наибольшие по абсолютному значению погрешности имеют мест-
в точках вблизи контура,
§ 13.8] - ИЗГИБ КОНСОЛИ СИЛОЙ. РЕШЕНИЕ ТЕОРИИ УПРУГОСТИ 353
Таблица 13.7
а/Ь
2
1
1
2"
alb
2
1
1
2
i
1
2
3
4
1
2
3
4
1
2
3
4
i
1
2
3
4
1
2
3
4
1
2
3
4
*;
0
α/4
a/2
3a/4
0
a/4
a/2
3a/4
0
a/4
a/2
3a/4
h
0
a/4
a/2
Зя/4
0
a/4
a/2
3a/4
0
a/4
a/2
3a/4
y.
μ = 0
0
0
0
0
0
0
0
0
0
0
0
0
0
~b{X.)
0
0,09310
0,16654
0,19080
0
0,15129
0,27063
0,31005
0
0,17290
0,30929
0,35434
4-б^>
0
0,18620
0,33309
0,38160
0
0,30258
0,54127
0,62010
0
0,34580
0,61859
0,70868
3 t ,
4 b(X.)
0
0,27930
0,49963
0,57240
0
0,45386
0,81190
0,93015
0
0,51870
0,92788
1,06300
b (*,·)
0
0,37240
0,66617
0,76320
0
0,60515
1,08250
1,24020
0
0,60160
1,23720
1,41730
У
μ = 1/2
0
0
0
0
0
0
0
0
0
0
0
0
0
-Γ"<*ί>
0
0,10086
0,18042
0,20670
0
0,20172
0,36084
0,41340
0
0,40344
0,72169
0,82680
~-b(Xi)
0
0,20172
0,36084
0,41340
0
0,40344
0,72169
0,82680
0
0,80687
1,44340
1,65360
4 b(xt)
0
0,30258
0,54127
0,62010
0
0,60515
1,08253
1,24020
0
1,2103
2,1651
2,4804
b(x.)
0
0,40344
0,72169
0,82680
0
0,80687
1,44340
1,65360
0
1,1614
• 2,8868
3,3072
12 А. П. Филин, т. II
354
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
Наибольшая погрешность, даваемая формулой элементарного решения,
относится к случаю μ=0; при коэффициенте Пуассона, равном 0,5, формула
элементарного решения дает точные значения компонента касательного
напряжения.
4. Если в пределах поперечного сечения (при фиксированном значении а/Ь)
провести линию через точки, координата у у которых составляет одинаковую
долю от ширины & = ί?(χ), то во всех точках этой линии (такие линии на
рисунках в табл. 13.6 показаны штрихами) погрешность, даваемая формулой
Элементарного решения, оказывается одинаковой. Это свидетельствует об
аффинной эквивалентности эпюр компонента касательного напряжения на всех
линиях, параллельных нейтральной. В табл. 13.7 помещены значения!)—10τ(ί*:
(Ра?/1у) для точек первого квадранта. Разумеется, приведенные выводы
относятся именно к эллиптическому поперечному сечению. Однако некоторые
обнаруженные закономерности проявляются и в других поперечных сечениях,
7.3. Приближенное определение t[xJ. В качестве грубого
приближения для оценки величины т**\ не поддающегося определению в
элементарной теории, приведем нижеследующую формулу, полученную как
аппроксимация:
х(х) =TWtea
lzymax lzx ι&α'
α —угол, составляемый касательной к контуру с осью χ в точке, для
которой определяется х^утах\ tzxJ—находится для этой же точки по формуле
сопротивления материалов (12.40).
Поперечные сечения балки искривляются; это вытекает из наличия
в функции w членов, содержащих χ в степени выше первой; тем не менее
точная формула для аг, полученная при решении настоящего примера,
совпадает с формулой элементарной теории. Последний факт еще раз подтверждает,
что при выводе элементарной формулы для ог при изгибе, существенным
является не сохранение плоской формы поперечного сечения, а линейность
в зависимости от χ функции гг, имеющая место при Qx = const.
Наконец, установим вид уравнения изогнутой оси балки, исходя из (13.99)
_ _Р_ 110_ _ z»\
x=o~ElA 2 6"j·
if-0
Наибольший прогиб получаем на конце консоли, т. е. при z = L
_ PL?
х=у=о~ ЗЕГу>
что совпадает с результатом, получаемым на основе элементарной теории.
§ 13.9. Дискретная матричная форма метода начальных
параметров
1. Постановка задачи. Ставится цель создать такой
расчетный аппарат, который позволил бы находить усилия и
перемещения в стержне с произвольными очертанием оси, видом
поперечного сечения и законом изменения сечений вдоль оси при
воздействии на стержень произвольной нагрузки. При этом ста-
и0=и
О max О
I) В табл. 13.6 и 13.7 Ь(х·) /Ь = 1; /15/4; >^3/2; >^7/4 (ί => 1, 2, 3,4).
Значения в табл, 13.6 вычислил А. Г. Яшкин.
§ 13.9] ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ 355
вится дополнительное условие — алгоритм должен быть
приспособлен к эффективному использованию ЭВМ.
2. Расчетная схема объекта. Обозначения. Для эффективного
использования ЭВМ применим дискретную расчетную схему;
с этой целью прибегнем к следующей аппроксимации формы
стержня. На оси стержня отмечаем точки — узлы —на некотором
расстоянии один от другого. В пределах между соседними узлами
стержень представляем призматическим. Число узлов и их
расположение на оси принимаем такими, чтобы расчетная схема не
была слишком грубой, так как это влечет за собой
недозволенную потерю точности, и не была бы излишне детализированной,
если это связано с неоправданным усложнением расчета, не
сопровождающимся ощутимым повышением точности.
Разумеется, что точки, в которых у рассчитываемого стержня
имеется излом оси и (или) ступенька в поперечных сечениях
(в форме и (или) размерах), принимаются в качестве узлов
обязательно. Если на рассчитываемый объект действуют внешние
сосредоточенные силы и моменты, то и точки их приложения
также принимаются в качестве узлов. Распределенные же
силовая и моментная нагрузки приводятся к узлам, принятым на
основе вышеизложенных соображений, или, если они оказываются
слишком редкими, то —и к специально для этой цели введенным
узлам. Таким образом, распределенные нагрузки сводятся также
к сосредоточенным силам и моментам.
Пронумеруем узлы^- от 0 до п, начиная от одного из концов
стержня. Если стержень имеет замкнутую ось, то нумерацию
начинаем от любого из узлов, и тогда этот узел имеет два номера О
и п. Участку, ограниченному узлами /—1 и у, присваиваем
номер у; длину его оси обозначим s,. При рассмотрении участка
с номером у в качестве поперечного сечения призмы принимаем
сечение с центром в узле у --1; можно было бы воспользоваться
и другим условием назначения поперечного сечения на участке
с номером у.
Стержень связываем с некоторой системой декартовых
координатных осей хг, х2, х3. Кроме того, каждый из участков с
номером у" связываем с его собственной системой декартовых
координатных осей ξ1;·, bi/, bij с началом в узле у — 1, считая при этом,
что ось ξ1;· совпадает с направлением оси элемента (у —1, /),
а оси |2у и \zj — с главными центральными осями инерции
поперечного сечения. Направления осей выбираем так, чтобы обе
системы были правыми. Направляющие косинусы осей ξ1;·, |2у, %г}
в системе осей х1, х2, х3 образуют матрицу
'V
hj
hj
mlf
Щ
/n3/
п1}
«2/
«8/
12*
356 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ΧΙΠ
Введем обозначения: Fj — площадь поперечного сечения
расчетной схемы стержня1) на участке /; Ι2}· и /з/ —моменты
инерции указанной выше площади соответственно относительно осей \2}
и Ъ]\ ly — постоянная кручения для поперечного сечения на
участке /; F2j и F3J — площади поперечного сечения стержня на
участке у, приведенные по сдвигу соответственно в плоскостях ξχξ2
и lih{F2] = Fj'.y2]\ F3j = Ff:v3f) 2); MxlJ, MX2j, Mx3/t Pxlj, PX2f, Px~s/
{M%lj, Mw, MUJ, Pw, Pi2/, Pt3j) — составляющие внутренних
момента и силы в сечении, расположенном бесконечно близко
к узлу у со стороны узла у — 1 в системе осей хъ х2, х3 (ξ1;·, ξ^, ξ3/);
иХ], u2J; uzj, a^f, a2y, a3j- — составляющие перемещения узла у и
угла поворота сечения3) с центром в узле у в осях хъ х2, х3.
Правила знаков для перемещений, поворотов, внешних сил и
моментов и внутренних сил и моментов приняты следующие.
Внешние силы и моменты, перемещения и повороты сечений
положительны, если векторы, их изображающие, направлены в
сторону положительных значений на параллельных им осях хъ х2, х3.
Внутренние силы и моменты Ρ'лу, РХ2], Ρ х3],
Mxlf, Mx2j, Мхз/
(Рц/, Р\2]-, Рщ, Щг], Щг]> Щз]) положительны, если векторы,
их изображающие, действуя в сечении у на участок стержня
(у, / +1), направлены в сторону положительных значений на
параллельных им осях х1, х2, х3 (ξι,/+ι, ξ2, /+ι» hj+i)· Имеется в виду,
что если смотреть на конец вектора, изображающего момент или
угол поворота, то сам момент или угол поворота направлен
против часовой стрелки.
Введем в рассмотрение матрицы-столбцы
wxj = {u^-m^p^·}, W|, = {uyttymypy}, \vu = {OOm^fy*};
Uj = {uvu2]u3j\, af = {α^-ο^ο^-};
mx/ = {MxlfMx2/Mx3f}, pxj = {Pxl/PX2jPx3J\;
m&/ = {MwMwMl9/}, ρυ = {P^jPl2jPl3}}\
0 = {000}, ην* = {ЭЯ^Щ^Ц*}, ρ = {%,*%*% *h
*) Ниже слова «расчетная схема» будем опускать, всегда подразумевая их,
поскольку рассмотрению подвергается не сам стержень, а его расчетная схема,
2) Коэффициенты приведения площади находятся по формулам
v^=7r \ Is dF' Va/=7T \ "J dF'
Щ j> b2j /3/ J Ьы
b2] (by) — размер поперечного сечения на участке /, параллельный оси |2у (£з/)·
как функция координат £3у (ξ2/); Sfy(Sfy) —статический момент части площади
поперечного сечения отсеченной линией, которая параллельна оси ξ3; (bs/)
относительно оси ξ3/ (£г/); величина S%j (Sifi — функция расстояния |2у (1з/)
от указанной линии, отсекающей часть площади, до оси £3у (|2/·).
3) Имеется в виду малый поворот сечений,
§ 13.9] ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ 357
3^1/*, ...» фз/* ~~ составляющие в осях xlt хг, х3 внешних момента
.и силы, приложенных в узле /*.
Очевидно, что my = Afmx/, ру^Л/р^,
Ε О О О
О Ε О О
О О А/ О
О О О А/
wy =
wx/-=AfwxJ.
(13.100)
Здесь 0 и Ε — нулевая и единичная матрицы третьего порядка.
Элементы матрицы v/xj вызываются величинами, образующими
матрицу начальных параметров w*0, и все матрицы внешних
нагрузок ivjx (/* = 1, 2, ..., / —1), приложенных между узлами О
и у; поэтому матрицу wxj можно представить так:
/-ι
W
х)
Σ*.
xj{i)
(/ = 1, ..., η),
(13.101)
i = 0
где wXj(i) O' = 0, 1, ..., /—1)—слагаемые матрицы wxft
вызванные соответственно следующими причинами: w^0, щ, Ιυ2, ..., tt>/-i·
3. Матрица преобразования столбца W|0 в столбец W|i.
Отмеченное в заголовке раздела преобразование имеет вид
wu = N1w6o =
Ε
0
0
0
ΟιΜ-
Ε
0
0
Сг, ϊ
Q.i
Ε
0
Сз, ι
C5,i
Сб,1
Ε
Що-
(13.102)
Второй индекс в обозначениях элементов матрицы в
формуле (13.102) и индекс у N является номером участка.
Ниже удостоверимся в справедливости общей структуры
матрицы преобразования Nlt показанной в (13.102) (имеется в виду
наличие и расположение в ней блоков Ε и 0), и, кроме того,
найдем развернутые выражения остальных блоков. Разобьем
обсуждение на четыре этапа. На первом из них покажем (рис. 13.50)
влияние блока и0 на матрицу w^; этим влиянием управляет
первый квазистолбец матрицы Nx в (13.102). Из рис. 13.50 очевидно,
что если конец 0 участка (01) смещается без поворота так, что
составляющие перемещения по осям хъ х2, х3 суть и1з0, u2i0, u3i0,
то и все точки участка (01) и, в частности, узел /, имеют такие же
по величине составляющие перемещения, т. е. ultl = ultQ, u%1 = u2tQ,
*h, ι — ^3,ο·
Именно поэтому блок матрицы Nlt лежащий на пересечении
первых квазистолбца и квазистроки, представляет собой
единичную матрицу. При этом не возникает никаких поворотов и
внутренних усилий и моментов в узле /, поскольку элемент (01) стержня
не: деформируется. Вследствие этого все остальные блоки первого
киазистолбца матрицы Мх —нулевые матрицы третьего порядка.
358
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
На втором этапе рассмотрим влияние блока а0 на матрицу w^,
т. е. обсудим второй квазистолбец матрицы Να. На рис. 13.51, а, в, д
показано, что происходит с участком (01), если в узле 0 этот
участок имеет поворот, составляющие которого соответственно
равны а1>0, а^о, а3>0. Очевидно, что при этом величины а1>0, а.2>0,
а3>0 характеризуют поворот всего участка (01) и, в частности,
в узле /, т. е.
αι. ι— αι,ο»
α2,1 — α2. 0'
аз, ι — аз.
οι 13.103)
Поэтому блок матрицы Nlt расположенный на пересечении
вторых квазистроки и квазистолбца, представляет собой единичную
матрицу. Поскольку при повороте не
происходит деформации участка (01),
внутренние усилия и моменты в пределах
■ц ■ etf этого участка и, в частности, в сечении /,
-^ ' равны нулю. Вследствие этого блоки
второго квазистолбца матрицы Nlt лежащие
в третьей и четвертой квазистроках, яв-
х1 ляются нулевыми матрицами третьего
порядка. Остается определить блок С1Л,
х uzj-i/hg преобразующий повороты в узле 0 в пе-
' .'-я ремещения узла /.
На рис. 13.51, б, г, е изображены
проекции участка (01) до и после
поворота на плоскости, перпендикулярные той
оси, относительно которой произошел
поворот. Поскольку ось участка (01)
совпадает с направлением |ltl, проекции
участка (01) на оси хъ х2, х3
оказываются соответственно равными
выражениям Si/lllf Sim^i, s1n1>1, a проекции
этого же' участка стержня на
координатные плоскости х?х3, х3хг и хгх2 суть:
rlt r2 и г3, представляющие собой радиусы
окружностей, описываемых узлом / при
повороте элемента (01) относительно
соответственно осей xlt x2, х3. Так как эти
повороты равны (13.103), дуги,
описываемые узлом /, соответственно равны
fiOi.o» r2a?.,o» Ά о» а составляющие перемещения узла / в осях
Λά, хг, х3 находятся следующим образом. При повороте
относительно осей хг (рис. 13.51, б), хг (рис. 13.51, г) и х3 (рис. 13.51, е)
составляющие перемещений имеют выражения, помещенные
соответственно в три нижеследующие строки (первый элемент в каждой
строке — перемещение параллельное оси xlt второй — параллельное
Рис. 13.50. Влияние
блока uQ на матрицу w^ (на
первый квазнстолбец
матрицы Νχ); а), б), в) влияние
отдельных элементов
столбца Uo·
S 13.91 ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ
в)
δ)
«δ л
a3,/=»3Lff ^2 а11~а3,0
В)
В)
Рис. 13.51. Влияние блока aQ на матрицу Wy (на второй квазнстолбец матрицы Nj)J
α) влияние поворота конца 0 элемента (01) относительно от х\, аксонометрия; б) то же,
ортогональная проекция на плоскость хгхп; в) влияние поворота конца 0 элемента (01)
относительно оси хг, аксонометрия; г) тоже, ортогональная проекция на плоскость χ%Χιϊ
ϋ) влияние поворота конца 0 элемента (01) относительно оси xs, аксонометрия; е) то же.
ортогональная проекция аа плоскость ΧιΧι.
360 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
оси х2 и третий — параллельное оси х3):
'' Slttl, 1а1, 0>
[ГЛ.:-XIIГ
0; — гга1г! sin βϊ = — /у^о Sl"1'i
ri
rxalt! cos βχ = r^i, 0
fr^l, ί
/"ι
simi, ιαι. οί
r2a2)1 sinp2 = r2a2)0
Sl"l, ί
/■г
■ Sxtilt 1α2) 0;
Vi. ι
0; — r2a2>! cos β2 = — r2a2, 0 -^i- = — Vi, xa% 0;
/"a
— Γ,^β,^ΐηββ
^з^з, о
simi, ia3, o'>
^^θ,Ι^Οδ Рз —^зЩ,0 —— — Sj'l, ι^,Ο» 0*
'3
Таким образом, матрица С1Л преобразования поворотов в узле О
м в перемещении узла / имеет
Щ1,1*1__ПШ*1 вид
~G/dfMWmff
WSf/fef Sf/%2,0 °°1 Gitf^Wlf
ZEh,i ~mz,i
Ci.i =
0 »ι"ί,ϊ — %%,!
-Si"i,i 0 s^bi
^/ηι,ι — Sj/i, i 0
(13.104)
На третьем этапе
рассмотрим влияние блока т&0
на матрицу w&1, т. е.
обсудим третий квазистолбец
матрицы Nv
На рис. 13.52, а, б, в
показано воздействие на
элемент (01) в узле 0
моментов MiltQ, Μ&2)0 и Μΐ3ι0„
а также
уравновешивающие их моменты в узле
/ (М1Ь1, М12Л, Ми>1)..
Здесь же представлены и
вызываемые такими
воздействиями на элемент (01)
перемещения и повороты в.
Рис. 13.52. Влияние блока т,0 на матрицу wtl УЗЛе L Обращаем ВНИМЭ-
(на третий квазнстолбец матрицы Νχ): а), б), 1) НИе НЭ ТО, ЧТО МОМеНТЫ В.
влияние отдельных элементов столбца пи0. ОбОИХ уЗЛЭХ, ОГраНИЧИВЭЮ-
щих элемент, отнесены
все к местной системе координат, соответствующей участку,
соединяющему эти узлы. Легко видеть, что для уравновешивания
Eh
Ъ,1
Eh
Ъ,1
4 13.9] ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ 361
внутренних моментов, действующих в узле 0, достаточно в узле 1
приложить только внутренние моменты, внутренние же силы
в узле
/
равны
Р&. ι =
нулю М61>1 = М61,0, М|2Л = М&2(0, Mi3tl = Mi3i0;
О, Рм.,=0.
Ιβ,ι
Таким образом, в матрице Νχ блок, лежащий на пересечении
четвертой квазистроки с третьим квазистолбцом, является
нулевым, а в пересечении третьих квазистроки и квазистолбца —
единичной матрицей. Поскольку влияние перемещения и поворота
элемента (01) в узле 0 уже учтено, при рассмотрении элемента (01)
на третьем этапе, он представляется как консоль, жестко
защемленная в узле 0.
На рис. 13.52 показаны составляющие перемещений и
поворотов узла / от действия каждого из моментов. Эти величины
определяют собой вид матриц С1(2 и С1>4. Заметим, что прогибы
и углы поворота на рис. 13.52 представлены в системе осей |1Л,
ξ2> χ, ξ3, ι, для перехода к составляющим по осям xlf х2, х3
приходится величины умножать на направляющие косинусы в системе
осей xlt х2, х3 тех направлении,
перемещении и поворотов,
в элементах матриц С2>1 и
Эти
С4,
которым параллельны векторы
множители (косинусы) указаны
J2, 1
о
s\l,
3,1
s\l
2, 1
2£/2,ι
s\mb, i
s?«3, i
2EI
2,1
2£/3,i
2£7Ti
άΊη2. 1
2EI
3.1
кл
ЩЛ
"ΐ,ϊ
'2,1
m2,i
"2,1
^3,1
«'3,1
"3,1
■4,1
Sil
1,1
Syl
2,1
0
0
0
0
0
0
2EI.
2EI
0
3,1
2,1
AiD2(1, (13.105)
3,1
GId.i
slmi,i
EI2,i
δχ/722. χ
01 ал
GId,i
Eh,i
Sl»2, ί
Eh.i
Eh, г
Sitrh, 1
£/3.1
sln3, 1
£/3,1
кл
mi.i
«1,1
*2, 1
т2л
"2,1
'8.1
Щ,г
«3,1
GId,x
0
0
^ι-
Ο
ΕΙ μ
0
Si
EI
3, i
a;d
4,
ία 3.1 об)
Наконец, на четвертом этапе рассмотрим влияние блока р&0 на
матрицу W|i, т. е. обсудим четвертый квазистолбец матрицы. Nv,
362
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. ХПГ
На рис. 13.53, а, б, в показано воздействие на элемент (01)
в узле 0 сил Ρ|ι,ο> Р|2,о» ^|з,о> а также уравновешивающих их
сил и моментов в узле 1.
^6i.i = ^U,o и ΛΪ6ΐ.ι = 0; Ръ2Л=Ръ2,о и MUl = — Pl2toSl;
Pis, 1 = ^,оИ Λί u,! - Р&,о8г. (13.107>
Здесь же показаны и вызываемые такими воздействиями на
элемент (01) перемещения и повороты в узле 1. Поскольку
внутренние силы в узле / равны внутренним силам в узле 0, блок,,
лежащий на пересечении четвертых столбца и строки,
представляет собой единичную матрицу. Что касается матриц СдЛ, С5>1 и
C6il, то они, если учесть формулы (13.107) и рис. 13.53, имеют
следующий вид:
о о
См= о о
0 —St
^3,ι —
hk. i
EFi
hmi. i
EF1
Sl"l,i
EFi V6£73>]
Si
6EI
s\
3,1
6EI.
3,1
(.
GF2ll
_SL_
GFm
&2.1
m2,i
GF
2,1
n,
2.1
0
si
0
>
( si Si
^ 6£/a>1 GFSli
sf si \
6£/2,i GFS,J
s? Si \
6£/
2,1
GF
3,1
3,i
™3,i
"3,1
кл
ЩЛ
«i.i
*2.1
m2,i
"2,i
ki
™3.i
"3.1
si
£Fi
0
Sl
\6£/
3,1
GF.
2,1
0
si
\6£/2,i
= AiD8,i»
ч
GFm
(13.108)
C6,i =
sf/;
3,1
sU
1*2,1
2£/3,i
s?m3,i
2£/3,i
s!"3.i
2£/2,i
sfm2,j
2,1
2EI
s\n2, i
2EI
3,1
2EI
2,1
ii.i
ЩЛ
ЧЛ
k.i
m2,i
"2,i
'3.1
"*3,1
"3.1
0
0
0
2EI
2EI2ll
0
3,1
= AiD6>1. (13.109>
Обращаем внимание на то, что на рис. 13.53, б, в показаны
прогибы и повороты в узле / отдельно от внутренних силы и
момента (13.107), приложенных к узлу /, в матрицах же в (13.108)
и (13.109) написаны суммарные эффекты сил и моментов.
$ 13.9] ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ 363
хз,
ι
4%τ
ι /?χι
/Jj^
pw~Pv;o^
\sfPtV SfPW
EFi EFf
».
Jw
*i
a)
ΊΜ
S1Pkl,0
Eh
3,f
Р$2,гР§гл
«/%:
lEh
3,1
ΖΕΑ
Ы
2Είν -2ΕΙν
Μ δ)
Είι,ι E/2tf ΙΕΙυ lEiUi
SfP§3,f tSfPi3,f_SfP$3,t? SfP~i3tff
X/
ipW siPW $р№
в)
!Рис. 13.53. Влияние блока р* на матрицу Ww (на четвертый квазистолбец матрицы 4^)1
а) влияние силы Ρ&ιρ0; б) влияние силы Pi9a; в) влияние силы Pft
ξ8,ο·
ξ3,ο·
364 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ХПГ
4. Матрица преобразования столбца νν*0 в столбец w^.
Подставим в (13.102) вместо W|X и W|0 их выражения, согласно формуле:
(13.100), и вместо С2 lt C3 lt С4 х иС61 соответственно их
выражения, согласно формулам' (13.105), '(13.108), (13.106), (13.109),,
тогда получим
Ε Cifi Λίϋ2>ί Λίϋ3ιί
0 Ε AiD4>i Λίϋ5ιί
0 0 Ε Q.i
0 0 0 Ε
AiW^! ±=
Axw.
χθ'
(13.110)
Выше уже отмечалось, что когда мы рассматриваем участок (/ — 1, /),.
в частности (01), то усилия как в узле / —1, так и в узле /
относим к системе осей ξν, |2у, |3у, поэтому W|j0=A1wJfi0.
Решая (13.100) относительно w^fl и переходя к развернутой.
форме матрицы Alf получим
w^1 = Ar1N1A
ч«^0 =
Ε 0 0
0 Ε 0
0 0 Λ
0 0 С
0
0
ί о
» a;
Ε Ci,i AiD2li AiD3>1
0 Ё AID4>1 AiD6i
0 0 Ε C6ll
0 0 0 Ε
Ε
0
0
0
или, после умножения матриц,
W*i =
Ε С]
0
0
0
l.i AiD2,iAi A'D3,iAi
Ε AiD4ilAi AiD5ilAi ^
0 Ε ( А^С6, j Ai
0 0 AjEAi
Νχθ·
0 0
Ε 0
0 Αι
ο Ύ
ο
ο
Αχ
W
XQf
(13.111)
Здесь учтено, что матрица Ах ортогональная вследствие чего
АГ=Аь (13.112)·
Учитывая (13.112), получим ΑίΕΑ1 = Αϊ'ΕΑ1 = Ε. Легко доказать,,
что AiCe.jAi = €!,!, действительно,
а;с6ла1 =
h,i
m2,i
"2,i
k,i
mb,i
«3,1
0 0
0 0
0—Sf
0
h
0
(k,ih,i — h.ih,ι) Ч (h,1ГП3,i — /3,1m2,1) Si
(tn2, ils, i — m3, χ12, χ) Si (m2, χ/Пз, i-^ms, i^Vi) si
("2. ih. ί — "з, ih. 1) Si (n2, xmz, i — n3, xm2, x) sx
0
k,i mx,i nltl
h,i ^2,1 "2,1
hd ms,i пзл
(^2.in3, i — h,in2,\) si
(^2,i"3.i —^3.i"2.i)si
("2. in3. i — пз, гпг, 1) si
Si"i,i —htni,i
0 sik.i ==^ι,ι-.
— sJi.i 0
Здесь учтены зависимости /2i 1m3t г — 13ι !/η2ι г — nlt ь m2i!% г —
— m3jl%i = i1,i» th,ih,i~nb.ih,i — mi,iy вытекающие из свойств,
компонентов векторного произведения двух векторов.
§ 13.9]
ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ
365
Наконец, вводя обозначения Сг г = Аг ъ Α[Ό2 гАг — А2 lt
AiDiJilA1 = A3,1, Α[Ό4ι1Α1 = Α4Λ, AiD^A^Αβι1, из (13.111)
получим
Ε Ali A2li A3,i
w
xl
0
0
0
Ε
0
0
A4, i
Ε
0
Α5,ί
Ai(1
Ε
™χθ = ΚχΛν^0.
(13.113)
Учитывая обозначения в формуле (13.105), получим
w*l = W*1(0)·
(13.114)
5. Отыскание матриц столбцов νν*/^). Найдем теперь
последовательно матрицы w^o) для всех узлов j — 2, ..., п. Матрица
^ν^2(0) находится аналогично матрице wxl — wxl^0), только при этом
вместо матрицы wx0 следует иметь в виду матрицу w^^—w^,
а все величины, относящиеся к участку 1, заменить
соответствующими величинами для участка 2, т. е. заменить Ах на А2, Alfl
на А1)2, ..., Аб,1 на А5>2·
Тогда
Аналогично
W*2(0) — K2W.n(0) = Κ2Κι\ν^0.
W*3 (0) — K3K2KiW^0,
(13.115)
(13.116)
Здесь
К,=
Ε Ailf A2l/ Α3,;·
0 Ε А4>/ A5l/
0 0 Ε Αι./
0 0 0 Ει
Αι, / = Clt /, Α2, / = A/DajA/, ASf / = A/D3, /A/, A4iΊ — A/D4i/A/f
A5j1=A/D5p/A/.
Формулы для СЪу, D2>;, D3iy, D4, ,·, D5jy соответственно
аналогичны формулам для С^, D2)1) D3fl, D4il, D6il (13.104), (13.105),
(13.108), (13.106), (13.109) с той лишь разницей, что вместо sx
используется' s; и все вторые индексы вме'сто 1 становятся /.
Введем обозначение
^/. ι = K/K/-i .... Κ2Κι·
(13.117)
Поскольку произведение верхних квазитреугольных матриц такж0
представляет собой верхнюю квазитреугольную матрицу, именно
такой и оказывается &itV Учитывая (13.117), формульг (13.113)—·
366
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
(13.116) представим в следующем виде:
w*i(o)=w*i = £i,iw*o.
W*2(0) = ^2,lW*0»
W*S (0) = ^3,1W*0»
W*re(0) = ftre,lW.*0·
(13.118)
bi Учет влияния на матрицу w^ нагрузки, приложенной к
узлам, находящимся между узлами 0 и J. Рассмотрим теперь
влияние нагрузки, приложенной к узлу /„., на составляющие
перемещения, поворота и внутренних момента и силы в сечении,
совпадающем с узлом j (/> /*). Иными словами, найдем
матрицу-столбец WxfOt). Очевидно, что
w,/(/.>-Λ/,/. + ι»/,. (13.119)
Окончательно формула (13.101) с учетом (13.118) и (13.119)
приобретает вид
/-1
w*/ = ft/, iw^0 + 2 ft/, </+ι)»ί·
ι=1
При образовании матриц fty, r имеет место легко
обнаруживаемая нижеприводимая закономерность, позволяющая существенно
уменьшить при вычислениях на ЭВМ объем требуемой памяти
по сравнению с непосредственным использованием формулы (13.117)
Ε Bft B£>, Bft
о ε eft b<;J
0 0 Ε B[rt)
0 0 0 Ε
^/,r =
k=r k=r k=r
Bi?/-2 a4,„ eft-'2 аб,лн-2а4,,+1вЦ,
fe=r k=r k=r
Ββ-2 A3fft + '2 A2fftBftH-S A1>ft+1B^.
fe=r
fe=r
ft = r
Матрица wxj содержит составляющие перемещения, поворота
и внутренних момента и силы в сечении, расположенном
бесконечно близко к узлу } (где приложены внешние сила и момент)
со стороны начального сечения 0. Если необходимо найти
матрицу wxj,+ для сечения, расположенного бесконечно близко
к узлу /, но по другую от него сторону, то это легко выпол-
§ 13.9] ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ Зб7
няется по формуле w*, у, + = w*( у + voj. Переход от матрицы w*,}) +
к матрице Щ,/,+ совершается так:
wi./. + = ^/+iw*./.+·
7. Область применения матричной формы метода начальных
параметров (МНП). МНП может быть непосредственно применен
для расчета стержня любого очертания, закона изменения
сечений и при любом силовом воздействии, даже в случае, если ось
задана не уравнением, а графически или в табличной форме
(координаты точек оси). В принципе степень сложности во всех
случаях остается одной и той же.
Комбинируя МНП со ступенчатым приложением нагрузки
(шаговая процедура), можно решать существенно геометрически
нелинейные задачи, в том числе при непростом нагружении
(внешние силы изменяются не пропорционально одному и тому же
параметру) и при следящих нагрузках. Алгоритм МНП хорошо
приспособлен к программированию для ЭВМ.
Эталоном для оценки точности МНП может служить решение,
получаемое на основе теории малых деформаций тонких
стержней (теории Кирхгоффа— Клебша).
8. Теория тонких стержней Кирхгоффа — Клебша.
Изложенная в предыдущих резделах настоящего параграфа теория МНП х)
позволяет решить линейную задачу деформации произвольного
пространственного стержня и является дискретным механическим
эквивалентом теории малых деформаций тонких стержней
Кирхгоффа — Клебша 2).
Без вывода приведем уравнения этой теории в векторной
форме.
1) Эта теория была предложена в работе А. П. Филина «Некоторые
элементарные сведения из линейной алгебры» (§ 8), помещенной в сборнике
«Современные методы расчета сложных статически неопределимых систем»
(пер. с англ. Л. И. Филиной; составление и общая редакция А. П. Филина.
Л.: Судпромгиз, 1961). См. также: Филин А. П. Матрицы в статике
стержневых систем и некоторые элементы использования ЭЦВМ (глава вторая,
раздел 13).—Стр.ойиздат, 1966.
2) Кирхгоффом была получена система дифференциальных уравнений
равновесия: Kirchhoff G. irJournal fur Mathematik (Crelle), Т.40, 1850,
T.56, 1859; Kirchhoff G. Geselschaft Abhandlungen, Leipzig, 1882, S. 285;
Kirchhoff G. Vorlesungen uber Mathematische Physik, Band 1: Vorlesungen
uber Mechanik, Vorlesung 28 (S.406), Vorlesung 29 (S.428/1897). Клебшем
получена система уравнений совместности перемещений и параметров деформации:
Clebsch A. Theorie der Elasticitat fester Korper. 1862. Теория Кирхгоффа —
Клебша была изложена Лявом (Love A.E.H. Treatise on the mathematical
theory of elasticity, tt. 1,2, 1892—1893). Имеется перевод на русский язык
(Б. В. Булгакова и В. Я· Натанзона) с 4-го английск. изд., вышедшего
в 1926: Ляв А. Математическая теория упругости: М. Л.: ОНТИ, 1935
(гл. XVIII и XIX). Уравнения теории Кирхгоффа — Клебша в векторной форме
были представлены А. И. Лурье в его работе: О малых деформациях
криволинейных стержней. Труды ЛПИ, 1941, № 3, 148—157,
368 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ \ТЛ. XIII
1. Уравнения равновесия (шесть уравнений в проекциях на оси)
d^ + P = 0' d^ + ei.oXV + m = 0.
2. Уравнения совместности перемещений точек оси стержня,
углов поворота триедра осей и параметров деформации (шесть
уравнений в проекциях на оси)
3. Уравнения закона Гука (шесть уравнений в проекциях
на оси)
S = 1\()Е0.
Эта полная система восемнадцати уравнений двенадцатого
порядка позволяет определить восемнадцать следующих функций:
внутренние усилия в системе осей ξχ (касательная к оси стержня),
Ег» £з (главные оси инерции поперечного сечения): N (продольная
сила), Q2, Q3 (поперечные силы), М1 (крутящий момент), М2, М3
(изгибающие моменты), образующие вектор s или два вектора
V = {NQ2Q3] и М = {М1М2М3}; параметры деформации в той же
системе осей ξχ, ξ2, ξ3: ε (относительное удлинение осевого
волокна), γ2 и γ3 (сдвиги в плоскостях ξ1ξ2 иЩ, κ1)0 (изменение
кручения) и κ2>0, κ3ι0 (изменение кривизн оси стержня в
плоскостях ξχξ2 и ξιξ3). образующие вектор ε0; составляющие перемещения
точек оси стержня: uhQ, ы2>0, u3t0 в системе осей ξχ, |2, ξ3,
образующие вектор и0 и составляющие а1)0, а2)0, схд)0 вектора а0
малого поворота триедра ортов е1)0, е3)0, ед)0 направлений |х, ξ2 и ξ3·
Кроме уже отмеченных, другие величины, входящие в
уравнения, имеют следующий смысл: s0 — координата точки на оси
стержня, отсчитываемая вдоль оси; р = {р!Р2Рз} и m = {m1mim3}—
векторы, интенсивности составляющих силовой и моментной
распределенных нагрузок; вектор Ω={Ω1Ω2Ω3}, составляющие
которого в системе осей ξχ, ξ2, l·^ характеризуют кручение (Ω1 = /ί1) и
кривизны (Ω2 = k2 в плоскости ξχξ2, Ω3 = k3 — в плоскости ξχξ3)
оси стержня; δΩ — приращение вектора Ω, возникающее в
результате деформации стержня. Вектор Ω связан с так называемым
вектором Дарбу Q° = xt-f kb зависимостью Ω = Ω°+ -Σ* (κ и k —
кручение и кривизна кривой оси, отнесенной к натуральному
триэдру ортов — tnb (касательная, нормаль и бинормаль кривой),
φ —угол, составляемый ортами η и е2(0); вектор Дарбу— это
угловая скорость вращения натурального триедра ортов (tnb) при
движении его по кривой с линейной скоростью υ=\\ γ0 — вектор
сдвигов (в системе осей ^, ξ2, ξ3)» определяемых осредненно для
всех волокон пересекающих нормально и (или) лежащих ε по-
§ 13.9] ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ 369·
перечном сечении (последний сдвиг равен нулю); К0 — матрица
жесткости, имеющая вид:
Ко =
Ε
Jf ° ° ° Ε\^Ψ~ Ah^L
F F F
0 GF9, 0 0 0 0
0 0 GF3 0 0 0
С r2 dF
0 0 0 G \ —j- 0 0
F
E Γ ξ2.ο dF 00o Ε f S'10 dF Ε f ^2 °^3 ° dF
F F F
llodF
:^„ о о в$ЩРв$ А
F F F
Ε и G — модули упругости продольный и сдвига, ξ2)0 и ^ —
координаты точек поперечного сечения. Интегрирование ведется
по площади поперечного сечения, г — радиус-вектор точки
поперечного сечения с началом в центре его тяжести; А = klt0r —
— ^3,0^2,0 + ^2,о^з,о — дискриминант метрического тензора, k3>0 и &2>0
(в плоскостях ξ3£ι и Ык) — кривизны волокна с координатами |2)0
и £з,о его следа в поперечном сечении; г = ]/"ξ|,0 + Ы>0·
Приведенные здесь уравнения даны в форме, предложенной А. И. Лурье,
в упомянутой в сноске его работе; в эти уравнения внесена
модификация — учет γ, выполненная И. М. Черневой и О. Д. Та-
нанайко.
Уравнение Кирхгоффа—Клебша в тех случаях, когда
интегрирование их может быть выполнено в замкнутой форме,
позволяют получить решения, являющиеся эталонными для
результатов, отыскиваемых при помощи дискретной матричной формы
метода начальных параметров. Именно поэтому указанные
уравнения и приведены в настоящем параграфе.
9. Примеры. Пример 13.11. В консольном стержне с прямолинейной осью
и равномерной вдоль оси естественной круткой найти составляющие
перемещения центра торца в осях х2, Хз- Свободный торец повернут по отношению
к сечению заделки иа 27,5°. На рис. 13.54, а изображен стержень и
приложенная к нему нагрузка. Любоз нормальное к оси стержня сечение
представляет собой прямоугольник с отношением сторон 6/Л=10.
Решение. Аппроксимируем форму стержня. Представляем стержень
расчетной схемой в виде одиннадцати одинаковых призм, повернутых одна по
отношению к другой на 2°30'. Оси всех повернутых призм располагаются на
одной прямой. Длина оси каждой призмы равна а/11, где а—длина
рассчитываемой консоли. Поперечное сечение каждой призмы такое же как у задана
ιιοιό стержня. При такой аппроксимации s, = yr, /2)i = /2i2,=;... = /2ill = /a,
Λι. ι = /з,2 = ...·= 1я.ц = /з-
370 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. ХПГ
Используются два варианта расчетной схемы. Первый изображен на
рис. 13.54,6, второй —на рис. 13.54, в. Решение получаем как среднее
арифметическое результатов, соответствующих первой и второй расчетным схемам.
Щ0"
27°30г
Рис. 13.54. К примеру 13.11; а) стержень с естественной круткой; 6) первая расчетная
схема; в) вторая расчетная схема.
Применительно к первой расчетной схеме
1 0 0
Λ,· = 0 cos [(2°30') (/- 1)] sin [(2°30') (у - 1)]
0 — sin [(2°30') (/ — 1)] cos [(2°:0') (у — 1)]
ту = — {0 Ш sin [(2°30') у] 2)ϊ cos [(2°30')/]}
В расчете по второй расчетной схеме
1 0 0
0 cos [(2°30') у] sin [(2°30') у]
0 — sin [(2°30')/I cos [(2°30') у]
ту « - {0 Ш sin [(2°30') (/ +1)] Ш cos [(2°30') (/ +1)]}
(/ = 1, ...
(/ = 0, ..., 10).
И);
(13.120>
Λ7· =
(/=1, .... 11),
0=о. .... Ю),
§ 13.9] ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ 371
Все операции в приведенном здесь решении выполнены в матричной
•форме согласно алгоритму, показанному в предыдущих разделах параграфа;
-однако для большей компактности представления информации в книге принят
-следующий способ изложения. Показываются матрицы и операции с ними
в общем виде, а элементы этих матриц при разных значениях индекса участка
или узла приведены в таблицах. Так в табл. 13.8 представлены синусы и
косинусы углов, кратных 2°30\
Таблица 13.8
/
0
1
2
3
4
5
sin (2е30') /
0
0,0436
0,0872
0,1305
0,1736
0,2164
cos (2° 30') /
1
0,9990
0,9962
0,9914
0,9848
0,9763
/
6
7
8
9
10
11
sin (2°30') /
0,2588
0,3007
0,3420
0,3827
0,4226
0,4617
cos (2° 30') i
0,9659
0,9537
0,9397
0,9239
0,9063
0,8870
Поскольку нас интересуют лишь перемещения и при этом поперечные
силы в рассматриваемом случае отсутствуют, формула (13.102), которая в
развернутой форме с учетом (13.105), (13.106), (13.108) и (13.109) при замене
!-*■}, 0-»-/—1 представляется так:
Ε
0
0
0
Pw
Ε
0
0
A/D2,y
A/D4i/
Ε
0
A/D3, /
A/De>;
C6>/
Ε
«/
Ρξ/
упрощается и приобретает вид
U/1_1E Ci>f A/D2./|
u/-f
«/-i
mbf-i
Km
(/ = i ii).
a,
0 Ε
A/D4>/|
u/-i
«/-£
(/=1 11). (13.121)
Рекуррентное использование формулы позволяет найти искомые
перемещения Ιΐχι·
Для первой расчетной схемы
и<у = {о(з,7б53
та?
■f 117,23
Stta2
или
U
т.
11
242£/2 ' ' 242£/3
117,23 , 3,7653 62
'2Е13
Н!
121
121 Ь?
)(-16.,
та?
16,1024
242£/2
1024 16,1024 Ь*
21 121 Λ2
та?
242£/3
)}·
)}·
или, наконец,
та2
"ίν==2ΈΓ{0 4,°808 -13·174}·
Для второй расчетной схемы и^' = {0 5,3881 —17,9876}. Среднее арифме-
fflla2
тичсское из двух полученных результатов un-
'2EL
{0 4,7345 —15,5808}.
Настоящий пример является эталонным, он решается и точно путем
использования системы дифференциальных уравнений Кнрхгоффа—Клебша»
372 СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ [ГЛ. XU1
при этом перемещения и2 и и3 находятся по следующим формуламJ):
ЯЯ*| 2-ψ — sin2 -ψ
Жх% 1 — cos 2г{7 , Шх$
(2ψ)2
L =
При /3//2 = 62//г2 = (Ю)2=100
2Κ
2ΕΙ
з
'-'f'
'2
Κ =
u3 =
2EL
(Щг
■1+-
'2
«2 =
mxt
L = — 0,0101- 2EI3; К = 0,0099 · 2£/3;
1 — cos I
11 xs\
36 a J
+ ·
а»лг?
0,0101 ·2£/3 121 β*| ' 2 · 0,0099.· 2£/ '
1296
π;
αΛ
u3 =
2Κ*§
11 λγ3
ο? π -- — sin
об α
11 χ3
ос π —
do a
—0,0101 ·2£/3
1296 α
2
и, наконец,
"ίΙ*,-α—2£/8
9>ϊα2 / 0,463
"з U,-a —
—0,0101
0,153
+
1
2-0,0099
= 4,69^-,
2£/я
зяа2
2£/3 —0,0101
= -15,15
2£/я
В величинах «г и и3 по сравнению с точным решением допущены ошибка
соответственно Щ^™-. 100 = 0,85%, 15,5^~^5,15 · 100 = 2,84%.
Советуем читателю самостоятельно определить щ, выполнив необходимые
вычисления.. Для того, чтобы при этом имелась возможность промежуточного
контроля, приведем численную информацию, характеризующую конкретный
вид матриц Ci,/, D2>/, D4i/, и/ и α/ при всех / (/=1, ..... , 11). Заметим, что
поскольку узел 0 совпадает с сечением заделки столбцы и<> и сс0 — нулевые.
Матрицы Ci,/, D2,/ и D4>/ имеют следующий вид:
Г —а
0
0
0
0 0
0 1
— 1 0
Щ·'- 242£
D4, / =
11£
2(1+μ)
Id
0
0
0
0
0
0
0
1
h
о
_1_
h
U/ =
α/
Λ
+
1
'2
0 -
Жа*
0
1
Чз
/^ = _ bh*
(/ = 1.
И).
242£
ο/ =
/2
*/
'й
0
+
+
ϊΐ
hi
h
Ша_
11£
*) Пономарев С. Д., Бидерман В. Л., Макушин В. М., Ма<
линии Н. Н., Лихарев К- К-, Феодосьев В, И, Расчеты на проч^
ность в машиностроении т, II, Машгиз, 1959,
§:·Ι3.9]· ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ'ПАРАМЕТРОВ 373
Для обоих вариантов величины aj, cj, dj, ej, fj и gj представлены
в табл. 13.9, а величины bj и hj— в табл. 13.10.
Пример1) 1-3.12. Определить составляющие перемещения центра и угол
поворота концевого сечения консольной призматической балки .пролетом 4 м,
загруженной на свободном конце моментом 3)1 = 24 Тм. Момент инерции
площади поперечного сечения / = 712.еж4 (рис. 13.55, а).
Решение. Использование известной формулы элементарной теории для опре-
Ша? 2 400 000-160 000
деления прогиба показывает, что эта величина ц2 = 9£7= 2 9ПППППП =
= 134,8 см настолько велика (~ а/3), что использование приближенного
(линейного) дифференциального уравнения изгиба балки недопустимо.
1
ю
иг,см
О
а,рай
яьсм
η . 80
и
ио
80
по
160
1W
320
к
5)
160 1U0
fy,CM
320 U00
в)
Рис. 13.55. К примеру 13.12: а) рассчитываемая система и внешнее воздействие; б)
очертание изогнутой оси на разных этапах нагруження; в) графики углов поворота на разных:
этапах нагруження.
Применим 'матричную форму МНП в комбинации с шаговой процедурой.
Поскольку, как и в предыдущем примере, нас интересуют только перемещения,..
а поперечные -силы во всех сечениях равны нулю, можем воспользоваться
формулой (13.121). Так 'как задача плоская, матрицы в этой формуле
упрощаются. Ниже покажем формулу (13.121) применительно к рассматриваемому
примеру. В матрицах Ci,y, D2|/ оставляются первые две строки, отвечающие
ubj и и2,/ и в них — лишь третий столбец, соответствующий α3)/· и Л4з|,/>
а в матрице D4>/- — лишь элемент в третьей строке, отвечающий а3,/ и
соответствующий воздействию M3^,j, т. ё. лежащий в третьем столбце. Матрица Ар
1) Настоящий пример решен А. М. Чинарян,
-374
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
Таблица 13.9
k= 1
1
2
3
4
5
6
7
8
9
10
11
—
k — ϊ
i
fe = 2
1
2
3
4
5
6
7
8
9
10
11
Ak)
а\
0
0,0019
0,0133
0,0493
0,1324
0,2924
0,5662
0,9974
1,636
2,538
3,765
5,363
Μ
Cj .
df
0
0,0436
0,2177
0,6081
1,299
2,372
3,906
5,978
8.657
12,01
16,10
21,36
Sk)
ei '
f(k)
4
0
0,0436
0,1305
0,2599
0,4309
0,6422
0,8922
1,179
1,500
1,854
2.237
—
J.k)
gi
0
0,0019
0,0095
0,0265
0,0566
0,1034
0,1704
0,2608
0,3778
0,5243
0,6929
—
юмер варианта расчетной схемы
приобретает вид
/
1
2
3
4
5
6
7
8
9
10
11
1
1
3,998
8,986
15,95
24,87
35,71
48,43
63.00
79,36
97,46
117,23
Та
»'"
1
1,998
2.990
3,973
4,943
5,896
6,829
7,739
8,622
9,475
—
блица 13.10
ζ
2
bf
0,998
3,986
8,950
15,87
24,71
35,43
48,00
62.36
78,46
96,23
115,58
hf
0,998
1,990
2,973
3,943
4,896
5.829
6,739
7,622
8,475
9,297
—
"2,/
1
0
0
A/
0 -
1
0
Η
- s?mij
«Α./
1
"4,f
>
si/../
2EI9
s\m2,j
2EI3
s
1
I*
"i,/-i
α3,/-ί
Μ.
»Ι·Μ
(13.122)
Внешний момент (нагрузку) будем прикладывать долями. Попытаемся
сначала разбить ее на восемь равных ступеней по 3 Тм. При этом на i-й ступени
4)
1 0
0 1
о о
Vя!. /
s/(i_1)
Τ». /
1
У 2, /
2EI9
<Ί1)
2EI3
EIa
u\,j-
,ίΟ.
% h
(0
3,/-
α
(13.123)
Здесь учтено, что направляющие косинусы оси %χ на каждом участке / берутся
в соответствии с геометрией, полученной в результате учета деформации на
(I—1)-й ступени нагружения.
В нашем случае Sf = ajklt М$ /_ι=—Sfy/^a· *i и ^2 — число участков
в балке а число ступеней нагрузки. Направляющие косинусы находятся по
§ 13.9] ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ 375ч
следующим формулам, происхождение которых очевидно*):
*+Σ «ί/'-Σ <>,-, 'ς O-'ς «iV
Μ. / — ο. » "4. ι —
Ί./ - Τ, » '">./
Sy ·» / S/
2,/ —Μ,/ ι *2. / — ml(/ ·
Щ
Результаты вычислений по формуле (13.123) при ^=10 и k2 = S помещены:
в табл. 13.11.
Рассматриваемый пример тоже является эталонным. Его легко решить
точно в замкнутом виде, используя элементарные функции. Это решение имеет-
следующий вид:
El EI
"ι (*ι) = — -эд [аз (*ι) — sin а3 (*i)], u, (хг) = — ^- [cos а3 (хг) — 1],
Вычисления показали, что повышения точности можно добиться главным-
образом за счет измельчения ступеней нагрузки, т. е. за счет увеличения &2;
увеличение kx при неизменном k2 сказывается на точности несущественно.
В табл. 13.12 представлена информация о погрешностях решения при
разных ki и &2· На рис. 13.55, б, в представлены изогнутые оси балки и графики
функции α3 = α3(·Χι) после каждой из ступеней нагружения. Все вычисления
выполнялись на ЭВМ.
Пример2) 13.13. Определить функции их (z), u2(z), as(z) для консольной
жестко защемленной балки длиной 400 см, прямоугольного поперечного сече-·
ния (/г = 4 см, 6 = 30 см), загруженной на свободном конце моментом 5Ш = 2,4 Тм,
изгибающим балку в плоскости ее наименьшей жесткости.
Решение. Легко убедиться, как и в предыдущем примере, в том, что про-,
гиб конца консоли настолько велик, что пользоваться приближенным
дифференциальным уравнением изогнутой оси не представляется возможным. С другой
стороны, отношение /ι//= 1/100 настолько велико, что при достижении внешним
моментом значения меньшего, чем максимальное, материал в наиболее
напряженной области начинает работать в пластической стадии (см. § 12.12,
раздел 3). Учтем обе нелинейности (геометрическую и физическую). Первую—·
при помощи шаговой процедуры, вторую —путем введения понятия
«эквивалентного» момента инерции в условиях использования шаговой процедуры.
Эквивалентным называем момент инерции, удовлетворяющий условию
daa = Ма
ds EI' '
*) В тексте (пример 13.11) приведена плоская задача. В случае
пространственной задачи матрица Ац направляющих косинусов локальных осей участка
с номером / в глобальной системе осей χ^, χ2, χ3 после загружения ί-й
ступенью нагрузки выражается следующей формулой: Ау; = Лу,;_1 (E + Ay/). Здесь
Ay, t-i — матрица, имеющая такую же природу, как и Ау;, но соответствующая
моменту после загружения (ι — 1)-й ступенью нагрузки; Е—единичная матрица
третьего порядка, А^ — матрица поворота участка / под воздействием i-й
ступени нагружения
0 аз/7 — «2/7
— а3/7 0 а1;7
а2,г — а1;/ 0
2) Пример решен А. М. Чинарян.
А/,-
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ· [ГЛ. XIII
ί~\
С;
се
ч
со
>.
*С1
£;
о
<JJ
оо
ίο
ИЗ
■Φ
СО
<Ν
Я S gee
X χ·— tta
С а -о
и
2
Η „
SB 3
S1^
о
S
О
О
о
о
о
о
о
о
о
о
а
,
ю
о
со
см
о
о
со"
со
г-
см
о"
ю
со
00
г-~
00
г-
г-
ю
со
1—1
о
rF
00
со
ю
см"
ю
■*
"^1
см
3
о
1
со
о
^-•CN
3
^■t.
1 1
со ||
о
00
о
о"
см
г-
о
о"
·■#
со
о
о"
со
ю
о
о"
00
<*
о
о"
о
-*
о
о"
см
со
о
о"
-*
см
о
о"
со
о
сГ
00
о
о
о"
·*—ι
-—·.
-—СО
β
Γ-
ιΟ
00
о
I
Tf
CM
со
cT
00
CO
-*
o"
CO
a>
CM
1
Tf
00
f—1
cT
|
'
со
о
•—'
о"
^r
Ю
о
о
I
CM
CM
о
о"
со
о
о
сГ
1
|
о
о
о"
'—*
см -
"=Г
со
о
Ύ—«
см
со
со
о
о
со'
см
со
-*
ю
сГ
см
о
со
ΓΙΟ
γιο
ю
,_^
■—'
со
см
о
осГ
со
со
ю
СП
00
00
см"
00
см
τ—Ι
f-H
,
см
со
о"
'*—1
оГ "
w(M
й
-—^
см
со ||
,_,
со
Ύ—Ι
о
**
Tf
сГ
00
см
f—Ι
о"
см
f-H
f-H
о"
со
ст>
о
о"
о
00
о
о"
-*
со
о
о
00
-*
о
сГ
см
со
о
о
со
τ—Ι
О
о*
·*—ι
°*«^
wCO
8
о
ΓΙΟ
см"
1
см
γόο
f-H
I
Tf
f—Ι
со
τ
CT)
γ-
οο
сГ
со
ю
ю
о"
1
1
СП
τ—Ι
со
о"
см
со
1—1
о
00
со
о
сГ
ст>
f-H
о
сГ
см
о
о
о
'——
со -
"ίΓ
СО
о
1—^
оо
, ,
г-
СТ>
оо"
со
00
ст>
г-
еГ
со
со
00
ю
со"
см
ст>
см
со
г-^
■—■
ю
со
о
см"
со
о
г-
г-^
со
со
со
^~
со
см
°1
f-H
см
00
-*
о
■"*—ι
^лГ'
—OJ
а
^—ъ.
со
о ||
•w*
t
-*
см
о
г-
см
о"
fO
ст>
т-н
о"
00
со
f-H
о"
-*
-*
т-н
о"
о
см
'—'
о"
со
СТ>
о
о
см
г-
о
о"
00
-*
о
сГ
-*
см
о
о
'*—1
СО "
-—.'СО
8
ΓΟΟ
1—^
ю
1
со
-*
γ-
οο"
1
г-
см
со
см"
00
ю
г-
Ϊ"
ю
о
ί—1
ι-Η
1
1
00
со
со
сГ
1
; Ю
'' СМ
со
о
1
ю
со
о"
1
ст>
со
о
сГ
1
-#
о
о
о"
1
·—-ч
^ -
3
о
о
о
со
см
ΓΟΟ
f-H
ю
г-
о
о^
5^
см
f-H
^г
со
00
00
о
со"
см
ст>
со
о
со"
00
со
см
о
г-
г-
г-
ю"
00
со
ю
см"
см
-*
со
о
·*—ι
"* лГ
^-■см
а
/^*^
-*
2 II
:_
οι
со
о"
СТ)
00
см
о"
ΓΙΟ
см
о"
ю
см
см
о"
со
ст>
f-H
о"
1 1
со
'—'
о"
00
см
f-H
о
со
ст>
о
сГ
-*
со
о
сГ
см
со
о
о
·*—ι
"^^-Г
ч_^ГО
8
.9] . ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ 377
_
·■»»
ч
_,
ϊζ
о
<JJ
оо
ίο
■я
■*
СО
(Ν
4> г- - S
*а к s Ег л
«Я От
Пере
щен]
(см)
повор
(рш
i
χ Ч
OIL
о
S
О
ю
ю
00
1
см
ео
см
со'
1
ю
г~-
ео
■*"
1
00
см
ел
1
i-H
^
00
i-H
1
см
со
о
г-н
1
t
Tf
ю
о"
1
ю
см
см
о
■чг
со
о
о"
1
со
о
О'
о"
1
^р^*»-ч
LO -
"з"
ео
■чр
г-
СЛ
ι—
, ,
г^
со
.■<*"
со
-*
ю
ю
ео
о
см
а>
ео
со
см
00
оо"
см
ео
ео
о
о"
см
00
см
00
СМ
ел
1—1
см
Г-Г'
о
см
ео
ео
о
00
о'
*»-*
ίο -
—CN
3
Ю
2 II
д
О
■ч*
О
д
со
ео
о"
,
см
ео
о"
д
00
см
о"
, ,
-*
см
о"
, ,
о
см
о"
, ,
СО
τ—Ι
сГ
о
см
г—i
о
о
00
о
сГ
о
^г
о
о"
"5~."
ч^СО
е
д
О
00
см
Ί
ео
ео
ео
1
Tf
ю
ю
со"
1
00
00
ео
"чН"
1
ел
ю
г~-
см"
1
ео
ел
ю
τ
, ,
ι—Ι
00
сГ
1
00
ео
ео
о
1
г~-
сл
о
о
о
о
о"
1
^^'—Ί
(О -
' 3
, ,
00
οι
ю
ел
со
ео
ео
|>-
f—1
СМ
-f-H
со
ю
-*
ел
со"
о
ео
ю
"ч|"
ео
-*
,—1
О
"ч|"
см
Tf
00
ео
ю"
о
со
со
00
, ,
ю
00
ео
ео
со
со
о
_
«о -
wCNJ
3
<S
22.1
см
00
Tf
о
ео
ео
-*
о"
ю
00
ео
о"
г~-
ео
ео
о"
с»
00
см
о"
, ,
-*
см
о"
ео
ел
f-H
о"
-*
^ι
о
со
ел
о
о
00
-*
о
о
^^'*—1
<£> —
ν—-СО
β
ю
г^
00
r-i"
Ί
ел
ео
о
ео"
Ί
о
СО
f-H
СП
1
ю
ео
f-H
со"
1
о
со
00
ео"
1
00
см
см
см"
1
ю
ео
τ—Ι
f-H
ео
г~-
-*
о
1
ю
ео
т-н
о
1
Tf
Т-Н
о
о
1
Tf
со
ю
о
~
■*
ео
00
00
со
ι—
f-H
1>-
1>-
см
со
"чН"
ю.
00
•—ι
οι
о"
-*
ел
г^
ел
Г*-"
см
ео
ео
ел
Г-"
ел
ел
о
о
см
ел
^
"чН"
Tf
см
Т-Н
,—.·^· .—.—'
f- .
"з"
f-^r
—Сч>
3
|р
"I
см
со
ю
о
со
о
ю
о"
ел
-*
-*
о"
ео
ел
ео
о"
1^-
ео
ео
о"
, ,
00
см
о"
ю
см
см
о"
ел
со
Ύ—1
о
см
т-н
ι 1
о
со
ю
о
о
'*—1
^-/νΓ
>—-СО
β
г~-
ю
г-
ео
см
,
■*
ео
с»
00
* 1
см
Ί
00
со
Т-Н
оо"
1
о
-*
ю"
1
ел
со
ел
см"
1
ео
ю_
Τ
о
ео
о"
1
о
00
т-н
о
1
00
т-н
о
о
'»-*
όδ -
3
ео
^
Ю
ю"
см
см
ео
о
о
о
со
ю
ео
см
см"
со
ел
ю
00
ю"
-*
со
см
сл_
ео
-*
t^-
Tf
о"
см
ю
ео
ιο_
f-H
СМ
ео
f-H
ю
-*
00
см
ι 1
00 -
—^CN
3
II
«'
СМ
Tf
со
о
00
ΓΙΟ
о"
Tf
ю
о"
ел
■*
Tf
о"
иО
00
ео
о*
, ,
см
ео
о"
г^
ю
см
о"
ео
ел
f-H
о
00
см
f-H
о
Tf
со
о
о
**—ι
^ίΥϊ"
■—-CQ
8
^ ·ί« 00
"1"
^"^
ooo
ео о ^
со ео со
со ео" о
см см
о о со
со о
γιο оо ю
со о" о"
-н О
ι -
о о см
Г- О -н
г> о ю
ео" о" о"
—ι 00
о о оо
СМ Ю Tl·1
СМ Ю Tl·1
со" —" о"
1 <°
о о -*
ел ю оо
см^ -*_ ео^
1Г$ IT) <S
1 ^
-η О О
со оо см
ео со ео
ео" -н" о"
ι ео
ео о со
-* см ю
г- ео^ см
г-" О* о"
1 N
Ю О ΟΙ
оо оо ел
(О *н
О -н" О
ι -
ел ю оо
■чГ — СМ
СМ — ^н
о ю о
1
СМ 00 xf<
<о ·* со
о см о
о" -н^ о"
1
••^ ·>^. ·*-.
ιΗ И СО
3 3 8
Точное
ешение
сх
378
СЛОЖНОЕ СОПРОТИВЛЕНИЕ СТЕРЖНЕЙ
[ГЛ. XIII
Таблица 13.12
Число
участков
10
20
10
5
Число
ступеней
нагрузки
8
8
16
8
Значения перемещений и поворота
конца стержня, найденные
матричной формой метода начальных
параметров
см
-23,759
-23,801
—25,374
-23,582
"г
СМ
125,543
125,532
124,827
125,586
а,
рад
0,642
0,642
0,642
0,642
Точные значения
перемещений и
поворота конца
стержня
«1
см
о
со
со
со"
см
1
см
о
о
00
со"
см
а,
рад
о
■чр
со
о
Расхождение, %
"1
10,8
10,6
4,7
11,5
"г
1,8
1,8
1,2
1,9
а,
0,3
0,3
0,3
0,3
Для поперечного сечения, работающего в упругой стадии, эквивалентный
момент инерции 1'г совпадает с обычным моментом инерции /3. Если же
материал в части поперечного сечения работает в пластической стадии, то при
•*i|csil
•^!<NJ
Рис. 13.56. Эпюра нормальных
напряжений в поперечном сечении балки,
работающей в упру го-пластической области.
Поперечное
сечение
Рис. 13.57. К примеру 13.13.
условии, что для него справедлива диаграмма Прандтля, относительное
удлинение волокна, лежащего на границе упругой и пластической области работы
материала, обозначенное символом ε0. выразится следующими формулами
(рис. 13.56):
εο=-ΕΓ — тг
ν 1 ааъ Мг
Учитывая, кроме того, зависимость — = —г2 = -ψ^ττ
ρ ds ΕΓΆ
, получаем формулу для l'z
П =
M3r\
Величина η находится из условия равенства внешнего момента моменту
внутренних сил. Для рассматриваемого в настоящем примере прямоугольного
поперечного сечения
m=2Ojbhh_
2 4
Отсюда
п 1 2
·2στ6η-^ + 2.-£-ηστί>-£-η.
§ 13.9] ДИСКРЕТНАЯ ФОРМА МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ 379'
и, окончательно,
*-%ν
3ft^
4
Ж
Ν*
160
80
Критерием для установления того значения внешней нагрузки (момента),.
при котором материал в поперечном сечении начинает работать в упруго-
пластической стадии, является сопоставление величин η и Λ/2. Если η^Λ/°
то сечение работает в упругой стадии.
Как только η становится меньше, чем
ft/2, сечение начинает работать в
упруго-пластической стадии и при
уменьшении η до нуля в сечении (в
рассматриваемом случае одновременно во
всех сечениях) образуется
пластический шарнир. При дальнейшем
увеличении нагрузки величина Г3 становится
мнимой и принятая расчетная схема
перестает быть правомочной.
Для расчета разобьем стержень
на Ю одинаковых участков, а
нагрузку— на 24 равных доли, которые
прикладываем поэтапно. На каждом
этапе подсчитываем их и и2
(горизонтальная и вертикальная составляющие
перемещения точки оси, рис. 13.57),
а также углы поворота узловых
поперечных сечений а3 по формулам
предыдущего примера. По перемещениям
определялись направляющие косинусы
локальных осей участков
деформированной схемы. На каждом же этапе нагружения определялась величина η;
и сопоставлялась с Λ/2. С этапа, при котором впервые удовлетворялось
условие η < ft/2, производилось определение эффективного момента инерции
площади поперечного сечения балки. Результаты расчета представлены в табл,
13.13 (иъ и2 и ос3 определены для конца консоли) и на рис. 13.58- Чисто
упругая стадия работы материала прекращается, начиная от значения внешнего
момента, равного 1,6 Тм.
Таблица 13.13
ЯъРаВ ι/ζ
h I
-и
-3
-г
-1
50
-0,3
UO
-0,2 30
10
-0,1
' 10
иьсм
ι
-10
8
-^^
-£
'"^S
^—ι*»^
f>\
ι ι
Ul)/
ι
ν
0,8
1,6 Ι,ϊ
Ш(Гм)
Рис. 13.58.
= П (931).
= "1 (Ш),
Графики кривых:
2 — и2 = u2 (5Ш),
4 — а3 = α, (>Щ,
1 - η =
3 — Ui =
<№,
Тм
ο,ι
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
ι,ι
1,2
— "ι,
CM
0,00
0,05
0,10
0,19
0,31
0,47
0,65
0,86
1,10
1,36
1,66
1,99
«2,
CM
2,38
4,28
6,19
8,09
10,00
11,90
13,80
15,70
1<60
19,49
21,39
23,28
аз,
рад
0,012
0,024
0,036
0,048
0,059
0,071
0,083
0,095
0,107
0,119
0,131
0,143
1], CM
3,39
3,32
3,24
3,16
3,08
3,00
2,91
2,83
2,74
2,65
2,55
2,45
'*'
8
СМ*
160,0
160,0
160,0
160,0
160,0
160,0
160,0
160,0
160,0
160,0
160,0
160,0
Эй,
Тм
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
—"ι,
см
2,34
2,73
3,14
3,58
4,06
4,56
5,10
5,70,
6,36
7,14
8,09
9,46
«2.
СМ
25,17
27,05
28,94
30,82
32,96
34,58
36,50
, 38,48
40,58
42,89
45,58
49,20
«2,
рад
0,155
0,167
0,179
0,190
0,202
0,214
0,227
0,239
0,253
0,267
0,285
0,308
η, см
2,34
2,24
2,12
2,00
1,87
0,73
1,58
1,41
1,22
1,00
0,71
0
7ί·
3
см*
160,0
160,0
160,0
160,0
159,0
155,9
150,2
141,4
128,6
110,0
81,3
0
Глава XIV
СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
линейной осью, в том
ff
,
•*з
1
\
1
h
"*з
У
J
&
I]
■г d .
< ' >
1
«ъ
,
1
ι
§ 14.1. Тонкостенный стержень. Определение
В § 1.4 дано определение понятия стержень и приведена
классификация стержней (призматические, непризматические с прямо-
числе с естественной закрученностью,
криволинейные с осью в виде плоской
или пространственной кривой). Общим
для всех них является условие dmax <^ /,
здесь с?так — максимальный габаритный
размер поперечного сечения, / — размер
стержня вдоль его беи.
Стержни по признаку типа
поперечного сечения подразделяются на две
группы — массивные и тонкостенные.
В массивных стержнях 6min —
'наименьший размер поперечного сечения — имеет
одинаковый с dmax порядок величины
(рис. 14.1,a): 6min ~ dmax. В
тонкостенных же стержнях 6min^c?max и,
разумеется, 6min<^L, где L — длина
контурной линии поперечного сечения
тонкостенного стержня (рис. 14.1,6).
Сопоставляя все три характерных размера,
получаем условие, присущее
тонкостенным стержням δ <; d <; / (δ <; L <^/).
В. 3. Власовг) предложил
следующие оценки, при удовлетворении
которым "стержень относится к
тонкостенным: δ/ά< 0,1,. d/T< 0,1.
d
ί
"*
в)
δ)
Рнс. 14.1. К классификации
стержней: а) массивные
стержни (δ ~ d); б) тонкостенные
стержни (δ ·< d).
*) В. 3. Власов (1902—1958)—советский ученый, механик. Автор теории
тонкостенных стержней открытого профиля и исследований в области теории
оболочек. Первые его публикации, посвященные теории тонкостенных стержней,
-относятся к 1936 г,
Li] ТОНКОСТЕННЫЙ СТЕРЖЕНЬ. ОПРЕДЕЛЕНИЕ 381
Ла рис. 14.2 изображены тонкостенные стержни. Все они пред-
вляют собой оболочки, в которых / превалирует над остальны-
размерами. В тонкостенных стержнях рассматривают так на-
раемую срединную поверхность, делящую во всех своих точках
гщину элементов, образующих стержень, пополам. След этой
:Рнс. 14.2. Тонкостенные стержни: а) открытого профиля; б) замкнутого профиля; в) с
прямолинейной осью н естественной круткой; г) с плоской криволинейной осью замкнутого
постоянного вдоль оси сечения; д) с плоской криволинейной осью замкнутого переменного
вдоль оси сечения; е) стержни с пространственной криволинейной осью открытого и
замкнутого поперечного сечения.
поверхности на плоскости, нормальной к оси стержня,
представляет собой некоторую линию, называемую профильной линией или
контуром поперечного сечения. Тонкостенные стержни
подразделяются на стержни открытого и замкнутого профиля в
зависимости от того, является ли профильная линия незамкнутой или
замкнутой кривой. Характер напряженно-деформированного
состояния тонкостенных стержней открытого профиля при
воздействии на него нагрузки существенно отличается от такового в
тонкостенных стержнях замкнутого профиля. В соответствии с этим
382 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
для каждого из двух типов тонкостенных стержней построена
своя теория.
В настоящей'главе рассматриваются призматические
тонкостенные стержни *), толщина которых в плоскости поперечного сечения*
вдоль контурной линии может быть переменной.
В главах XI и XII деформация тонкостенных стержней уже
обсуждалась. В главе XI рассматривалось свободное кручение
тонкостенных стержней открытого и замкнутого профиля и в
главе XII— определение касательных напряжений в тонкостенных
стержнях при поперечном изгибе и определение координат центра
изгиба в поперечном сечении тонкостенного стержня открытого·
профиля. Ниже излагается теория стесненной деформации
тонкостенных стержней открытого профиля.
§ 14.2. Описание картины стесненной деформации тонкостенных:
стержней открытого профиля
Для того, чтобы деформация тонкостенного стержня
открытого профиля, являющегося оболочкой, могла быть описана
математическим аппаратом, характерным для технической теории
стержней, более простым, чем аппарат теории оболочек, требуется
ограничить класс рассматриваемых объектов. Рассматриваются
тонкостенные стержни, жесткие в поперечной плоскости. Эта
жесткость достигается при помощи конструктивных мер
(постановка достаточно часто расположенных поперечных диафрагм
(рис. 14.3,а) или ребер (рис. 14.3,6), обеспечивающих
недеформируемость, точнее малую деформируемость поперечных сечений в
их плоскости.
На рис. 14.4, а, б, в показаны примеры ничем не стесненной
деформации тонкостенных стержней, происходящей под воздейст-
х) Теории тонкостенных стержней посвящена богатая литература. Отметим1
основные источники, содержащие большую библиографию.
Власов В. 3. Тонкостенные упругие стержни. Изд. второе,
переработанное и дополненное. М.: Физматгиз, 1959 (первое издание с подзаголовком
(прочность, устойчивость, колебания) вышло в 1940 г. в Стройиздате. В этой
книге рассматриваются и непризматические тонкостенные стержни).
Уманский А. А. Кручение и изгиб тонкостенных авиаконструкций.—
М.: Оборонгиз, 1939.
Джанелидзе Г. Ю., Пановко Я. Г. Статика упругих тонкостенных
стержней. — М. Л.: Гостехиздат, 1948.
Урбан И. В. Теория расчета стержневых тонкостенных конструкций.—
М.: Трансжелдориздат, 1955.
Пановко Я- Г. Тонкостенные стержни и системы, составленные из
тонкостенных стержней. — В кн.: Строительная механика в СССР, 1917—1957/Под
ред. И. М. Рабиновича. М.: Гос. изд. лит. по строит, и архитектуре, 1957.
Пановко Я. Г. и Бейлин Е. А. Тонкостенные стержни и системы,
составленные из тонкостенных стержней. — В кн. Строительная механика в
СССР, 1917— 1967/Под ред. И. М. Рабиновича. М.: Стройиздат, 1969,
§ 14.21 КАРТИНА СТЕСНЕННОЙ ДЕФОРМАЦИИ СТЕРЖНЕЙ 383
Рис. 14.4. Примеры нестесненной деформации тонкостенных стержней: а) свободное
кручение тонкостенного стержня открытого профиля (труба с продольным разрезом);
б) Деформация двутавра бнмоментамн, действующими на торцы; в) тонкостенный Двутавр,
вагруженный сосредоточенными внецентренно приложенными растягивающими силами,
и четыре Доли, на которые разбиваются эта нагрузка (первая Доля вызывает растяжение,
вторая — нзгнбное кручение; третья и четвертая — изгибы в главных плоскостях
инерции); г) воздействие бимоментов, приложенных к торцам на двутавровый стержень
с массивной стенкой.
384 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
вием внешней нагрузки. Из этих примеров видно, что в условиях
свободного кручения происходит депланация торцов, а
следовательно, й поперечных сечений. Депланация поперечных сечений
возникает И в случае воздействия самоуравновешенной в пределах
поперечного сечения системы сил, параллельных оси стержня,
напр имер,.в сдучае двутавра, вследствие закручивания стенки, имеющей
малую крутильную жесткость. Для сравнения на рис. 14,4, г
приведен массивный двутавровый стержень, подвергнутый
аналогичному воздействию. Вследствие большой крутильной жесткости
толстой стенки двутавра влияние самоуравновешенной системы сил
Рис. 14.5. Стесненное кручение тонкостенного стержня открытого профиля;· а) стержень
до Деформации; б) стержень после деформации; в) картина взаимодействия стержня с
плитой заделки.
локализуется вблизи торцов стержня (справедлив принцип Сен-
Венана), в то время как в тонкостенном стержне затухание
эффекта самоуравновешенной системы сил происходит медленно. Об
этом говорится и в § 9.9,
Если деформация стержня "стеснена, например, один из торцов
жестко прикреплен (приварен, приклеен) к массивной плите
(рис. 14.5, а), то депланация поперечного сечения при
продвижении от свободного торца к противоположному заделанному торцу
уменьшается и в заделанном торце вовсе равна нулю —сечение
остается плоским (рис. 14.5, б). Уменьшение депланации — это
увеличение степени стеснения деформации, состоящей в
уменьшении перемещений точек стержня в направлении, параллельном
его оси. Вследствие такого стеснения деформации в поперечных
сечениях стержня возникают нормальные напряжения (рис. 14.5, в).
Стеснение деформации возникает и в случае, когда крутящий
момент по длине стержня имеет переменную величину. Поскольку
§ I4.3J ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 385
кручение тонкостенного стержня открытого профиля
сопровождается изгибом некоторых элементов, например, полок двутавра,
такую деформацию называют изгибным кручением1).
§ 14.3. Теория тонкостенных стержней открытого профиля
1. Предварительные замечания. В настоящем параграфе
обсуждается теория тонкостенных стержней открытого профиля, в
которой одновременно рассматриваются осевая деформация,
поперечные изгибы в двух ортогональных плоскостях и кручение.
Качественно новым по сравнению с ранее (в предыдущих главах)
рассмотренными результатами является учет стеснения деплана-
ции. Последний можно было бы выполнить независимо от осевой
деформации и изгиба. Однако представляет интерес сам факт
одновременного построения теории всех видов деформации, в связи с
чем именно такое изложение и принято в настоящем параграфе. К
тому же становится ясным, что излагаемая теория тонкостенных
стержней является обобщением ранее изложенной теории стержней в
случае их тонкостенное™ (имеются в виду стержни открытого профиля).
2. Гипотезы. В основу обсуждаемой в настоящем параграфе
теории положены следующие гипотезы2).
1. Контур поперечного сечения не испытывает деформации в
своей плоскости.
2. Сдвиги в срединной поверхности тонкостенного стержня
отсутствуют.
3. Распределение нормального компонента напряжения в
поперечном сечении тонкостенного стержня по толщине
образующих его пластин равномерное.
4. Продольные волокна в нормальном к ним направлении не
вза имодействуют.
5. Распределение касательной составляющей напряжения πα
толщине пластин, образующих тонкостенный стержень,
подчиняется линейному закону.
1) Впервые экспериментально возникновение кручения тонкостенной балки
открытого профиля и депланацию поперечного сечения в случае, если
внешняя поперечная нагрузка лежит в плоскости, не проходящей через линшо
центров изгиба, обнаружил Бах (С. Bach, VDI, 1909. Bd. 53, №41, S. 1710;
VDI, 1910, Bd. 54, № 10, S. 385; см. также Bach, Baumann. Elasticitat
und Festigkeit, S. 268—271, 369—381. Berlin. 1924).
Теоретическое исследование изгиба и кручения тонкостенных стержней
открытого профиля впервые выполнил С. П. Тимошенко (Об устойчивости
плоской формы изгиба двутавровой балки. Известия СПб Политехнического
института, т. IV—V, 1905—1906), при этом крутильную жесткость стержня
он определил экспериментально. С. П. Тимошенко обнаружил возникновение
нормальных напряжений при стесненном кручении тонкостенного стержня
открытого профиля.
2) Ниже указывается и другой вариант формулирования гипотез.
386 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
Первую из этих гипотез нужно понимать следующим образом.
Контур поперечного сечения стержня не является вообще неде-
формируемым, однако деформация его такова, что проекция
контура, испытавшего деформацию, на плоскость, нормальную к оси
стержня, конгруентна контуру поперечного сечения до
деформации, т. е. сохраняет форму и размеры последнего, но как жесткое
целое в плоскости поперечного сечения может иметь смещение и
поворот.
Таким образом, деформация контура поперечного сечения
стержня происходит лишь в связи с составляющей перемещения,
параллельной оси стержня, и представляет собой депланацию этого
контура.
Вторая гипотеза используется лишь при определении
перемещений и связанной с ними осевой деформации волокон стержня,
параллельных его оси. Эта гипотеза, таким образом,
используется при определении лишь нормальных напряжений в плоскости
поперечного сечения стержня на основании уравнений закона
Гука. Касательные же напряжения в рамках второй гипотезы,
разумеется, не могут быть определены при помощи закона Гука,
поскольку согласно этой гипотезе сдвиги равны нулю. Для
определения касательных напряжений используется уравнение
равновесия. Картина здесь совершенно аналогична наблюдаемой в
теории поперечного изгиба стержней: гипотеза плоских сечений
применяется лишь для определения гг и аг (путем использования
закона Гука), для отыскания же хгх и (или) %гу
рассматривается равновесие элемента балки, так как закон Гука применен быть
не может, поскольку в рамках гипотезы плоских сечений
сдвигов нет.
Ниже обсуждается другой вариант гипотез, который можно
принять для построения теории тонкостенных стержней. В этом
другом варианте нет отмеченной особенности, состоящей в том,
что гипотеза (вторая) в одной части теории используется, а в
другой — нет.
3. Внешние силы. Отнесем стержень к левой системе
прямолинейных ортогональных координатных осей Oxyz. При этом
ось ζ направим параллельно оси стержня, никаких других
ограничений на систему Oxyz не накладываем. Положение точки Μ
срединной поверхности тонкостенного стержня можно определить
координатами г и s. Координата s изменяется вдоль контура
поперечного сечения от некоторой точки Miy являющейся точкой
начала отсчета (рис. 14.6, а).
Будем считать, что к срединной поверхности стержня
приложена распределенная нагрузка, составляющие интенсивности
которой по осям х, у и ζ суть
Ρχ=Ρχ{ζ, s), py==Py{z, s), рг = рг{г, s). (14.1)
§ 14.31
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ
387
В каждом поперечном сечении эту нагрузку приведем к точке,
расположенной на оси г. Таким образом, статическим эквивалентом
Рис. 14.6. Тонкостенный стержень открытого профиля; а) координаты точек на
срединной поверхности н составляющие нагрузки, распределенной по этой поверхности; б)
составляющие Перемещения точки срединной поверхности; а) составляющие распределенных
силовой и момеитиой нагрузок, приведенных к точкам оси стержня.
нагрузки (Н.1) оказываются нижеследующие силовые и мо-
ментные распределенные нагрузки:
4χ(ζ) = ]Ρχ(ζ> s)ds, qy{z)=\py{z, s) ds, qz{z) = \ pz(z, s) ds;
L L L
mx{z) = \pz(z, s) y(s)ds, my{z) = \pz(zy s) x{s)dst
L L
™* (z) = S [Px (*, s) у (s) - py (z, s) χ (s)] ds.
L
Нам понадобятся производные по ζ от тх и ту, покажем их
выражения
dmx
dz
С dp* (2, *) . . . dmy С dpz (ζ, s)
) d2 у(s>ds> -3r=j—-*—*<*>*· (14·2)
S88 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
Согласно правилу, принятому в т. I § 1.12, положительные qx(z),
qy (ζ) и qz (г) направлены в сторону положительных значений на
параллельных им осях. Положительные векторы1) mx(z), my(z)
и тг (г) представлены на рис. 14.6, в.
Кроме распределенных нагрузок, поясненных выше, к
стержню могут быть приложены сосредоточенные силы Pi (i=\, 2, ... , η)
в точках i (г/, S;) срединной поверхности стержня, при этом сила Pt
может быть разложена на составляющие по осям х, г/, г: Pix, Piy,
Piz. Эти составляющие положительны, если они направлены в
сторону положительных значений на параллельных им осях.
4. Перемещения.
4.1. Центр кручения. Рассмотрим точку Μ срединной
поверхности тонкостенного стержня (рис. 14,6, б) и составляющие
перемещения этой точки им, ъм,
wM, возникающие при деформации
стержня.
Поскольку в поперечном сечении
контурная линия стержня не
испытывает деформации, перемещения ее
точек определяются перемещением
контура как жесткого целого в
плоскости поперечного сечения. Такое
перемещение можно описать, задавая
перемещение точки Л,
принадлежащей контуру, или жестко связанной
с ним, и поворот относительно этой
точки.
На рис. 14.7 показано сечение,
содержащее точку М. Проекции осей
χ и у, а также начала координат О
на эту плоскость обозначены теми же
символами, которыми обозначены оси
и начало координат. Для координат точки Л, составляющих
перемещения этой точки, и угла поворота контура поперечного
сечения как жесткого тела относительно этой точки введем
соответственно символы ax, ay\ uA, vA, $г, при этом
uA = uA(z), vA = vA(z), ϋζ = ϋζ(ζ). (14.3)
На рис. 14.7 uA, vA и $г изображены положительными. Зная
04.3), определим перемещение некоторой точки В с координатами
Ьх и by, связанной жестко с контуром поперечного сечения, но
не обязательно расположенной на нем. Из кинематических
соображений находим
"в=-"а + (&# —%)G*. νΒ = νΑ—ψχ — αχ)ΰ;. (14.4)
Рис. 14.7. К установлению связи
между перемещениями точек,
жестко связанных с контуром
поперечного сечения, поворачивающимся
как жесткое целое в своей плос-
• кости.
х) Правила знаков см. т. I, стр: 51.
§ Н.З]
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ
389
При малых иА, vA и 'ftz перемещение контурной линии в
плоскости поперечного сечения и вообще плоского жесткого
диска, можно представить как поворот относительно так
называемого мгновенного центра
вращения. Эту точку
применительно к рассматриваемому
случаю, когда жестким
диском является проекция
поперечного сечения
скручиваемого тонкостенного стержня
на плоскость, нормальную
к его оси, естественно назвать
центром кручения. К
вопросу об определении его
координат мы еще вернемся
ниже.
4.2. Перемещения и
и Ό. Если точку В
совместить с точкой Μ (χ, у), т. е.
считать расположенной на
самом контуре поперечного сечения,
тают вид
Рис. 14.8. К установлению связи между
составляющими перемещения точки срединной
поверхности стержня в двух системах осей —
общей для сечения (неподвижной) и
подвижной (локальной для точек контура).
им (г, s) = иА (ζ) + [у (s) - ау] Ъг (г),
vM (г, s) = vA (г) - [х (s) - ах] ϋζ (г).
то формулы (14.4) приобре-
(14.5)
Здесь x(s) и у (s) — координаты точки Μ контурной линии,
являющиеся функцией координаты s, которая определяет положение
этой точки на контуре при заданном начале отсчета Мг.
На рис. 14.8 показана картина перемещения контурной линии
в плоскости поперечного сечения; имея ее в виду, представим
составляющие перемещения и и \> в системе осей ξη (рис. 14.8)
следующими формулами:
им = —«жcos a — u^sina, \>м = им^а — fjucos a. (14.6)
Подставляя (14.5) в (14.6), получаем
им = — и a cos a — υ a sin a + {[χ (s) — a*] sin a — [y (s) — ay] cos α} ϋ·ζ,
ϊ>Μ = и a sin a — vA cos a-\-{[x(s) — ax] cos a + [y (s) — ay] sin a} $z.
Из рис. 14.8 видно, что выражения, заключенные в
фигурные скобки, соответственно равны h(s) и t (s), т. е.
uM(z, s) =— иА (ζ) cos a- (s) — vA (z) sin a (s) -\-h (s) $z (ζ),
Ъм (ζ, s) = и a (z) sin a (s) — vA (ή cos a(s) + t (s) \% (z).
(14.7)
В приведенной записи показано функциями каких переменных
являются, величины, входящие в формулы (14.7). Последние члены
390 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
выражают известный факт — при малом повороте перемещение равно
произведению угла поворота на длину перпендикуляра,
опущенного из центра вращения на направление искомого перемещения
течки (Л4).
Очевидно, что если точка Д_совпадает с центром кручения, то
иА —0, vA = Q, и формулы (1477)^становя1Гсл одночленными
ил (г, s) = h (s) Аг (г), »Λ (г, s) = * (s) θ, (ζ). (14.8)
4.3. Перемещение wM. Для определения wM воспользуемся
второй из сформулированных выше гипотез.
Сдвиг yzi в срединной поверхности тонкостенного стержня,
согласно уравнению Коши (6.11) и принятым обозначениям для
перемещений, выражается формулой
dwM дим
**—5Г + ТГ- <14·9)
Применение второй гипотезы, согласно которой γ2| = 0, приводит
к уравнению
dwM дим
Т + 1Г=0· <14·10)
Интегрируя (14.10) по s, получим
М ди
wM(z, s) = —l -^-ds+hiz). (14.11)
ΛΓ,
Поскольку функция wM зависит от двух переменных ζ и s,
а интегрирование при отыскании wM выполнялось лишь по s,
в выражение wM> согласно (14.11), входит произвольная
функция /х (ζ), которой можно дать механическую трактовку,
предположив, что точка Μ совпадает с Mlt тогда интеграл в (14.11)
обращается в нуль и
о»л(г. 0) = Мг) = о»А1,(г). (14.12)
т. е. функция/х (г) представляет собой Wm1 — перемещение точки Мх
контурной линии в-направлении, параллельном оси г, являющееся
функцией г.
Подставляя (14.7)а в (14.11) и выполняя дифференцирование
по г и интегрирование по s, получим г)
Щи (г, s) = wMl (ζ) - и'А {ζ) χ is) - υ α (ζ) у (s) - Ъ'г (г) ω (s). (14.13)
х) Обсудим вариант другого подхода к формулированию гипотез,
используемых при построении теории, при котором приходим к тому же результату,
что и в последнем члене формулы (14.13). Гипотезы 1, 3 и 4 из числа
сформулированных в § 14.3 используются, а вместо гипотез 2 и 5 принимаются
соответственно нижеприводимые гипотезы.
2а. Перемещение депланации поперечного сечения (в случае стесненной
деформации стержня) с точностью до постоянного множителя остаются такими
§ 14.3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 391
При этом учтено (см. рис. 14.9, а), что
cos a (s)ds = — dx(s), sin α (s)ds = — dy(s), h(s)ds = da>(s).
(14.14)
Под ω (s) понимается удвоенная площадь сектора,
ограниченного кривой МгМ и радиусами-векторами точек Мг и М,
проведенными из точки1) Л, а под x(s) и у (s) — координаты точки Μ
(рис. 14.9, б).
W(S)
Рис. 14.9. К построению эпюр секторных площадей: а) дифференциал секторной площади;
б) секторная площадь; / — неподвижный радиус; 2 — подвижный радиус. .
5. Деформация гг. Компонент деформации εζ найдем,
используя уравнение Коши (6.11)3
dw,
гг =
'ж
dz
которое, если учесть (14.13), приобретет следующий вид:
ег = wm, (г) - и"А (г) * (s) - v"A (г) у (s) - V (ζ) ω (s). (14.15)
же, что и при нестесненном кручении. Указанный множитель представляется
неизвестной функцией от г. (Эта функция может быть найдена, например,
путем использования вариационного принципа Кастильяно (см. главу XV).
Выше она была получена иным путем и представляет собой Ог (г)=хг (ζ)).
5а. Распределение касательных напряжений в поперечном сечении стержня,
вызванных стеснением депланации, равномерно по толщине пластин,
составляющих стержень.
В случае стержней замкнутого профиля существенным оказывается
фактор искажения формы поперечного сечения стержня в своей плоскости.
Вследствие этого теория становится сложнее, чем теория тонкостенных стержней
открытого профиля.
Попытки построения теории тонкостенных стержней с использованием
гипотезы о недеформируемости профиля в плоскости поперечного сечения
оказались неудачными — результаты, получаемые на основе таких теорий, не
подтверждаются опытом.
х) Для ω принято правило знаков: ω > 0, если при переходе от Μχ κ Μ
радиус-вектор вращается против часовой стрелки,
392
СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
6. Напряжение аг. Для определения напряжения ог
воспользуемся уравнением закона Гука (7.12")3
ε* = -^[σ*-μ(σξ + ση)].
(14.16)
выразив величины w'm. (ζ),
На основании четвертой гипотезы σ^ = σΆ — 0 вследствие чего (14.16)
приобретает вид εζ = σζ/Ε, σζ = Εεζ, или, если учесть (14.15),
σζ = E[w'Mt(z) ~u'A(z) x(s) -v"a{z) у (s) -Ы(г) <o(s)]. (14.17)
Это еще не окончательная рабочая формула для σζ. Ее получим,
и а (г), ν'ζ (ζ) и #г (г) через
соответствующие обобщенные усилия. К
этому вопросу вернемся после
рассмотрения уравнений равновесия
элемента тонкостенного стержня.
7. Напряжение τ^. В
соответствии с пятой гипотезой
распределение τΖξ по толщине пластин,
образующих тонкостенный стержень,
подчиняется линейному закону (рис.
14.10, а). Заметим, что τζ^ = τζ, т. е.
представляет собой полное
касательное напряжение. Трапецеидальную
эпюру тг| разобьем на две части
согласно рис. 14.10, б, в. Слагаемое,
изображенное на рис. 14.10, в,
соответствует свободному кручению,
статическим эквивалентом этого
слагаемого является крутящий момент
свободного кручения, который
согласно (11.100)
Mz = yizGIk = VzGIk, (14.18)
JO
Рис. 14.10. Распределение
касательных напряжений по толщине
тонкостенного стержня открытого
профиля: а) касательные
напряжения, статическим эквивалентом
которых является лишь крутящий
момент", б) доля касательных
напряжений, создающая изгибно-крутиль-
ный момент; в) Доля касательных
напряжений, создающая момент
свободного кручения.
согласно разделу 15.2
определяется по формуле
где Ik,
§ П.12,
Ik = У -„г b{c'j. Символ «тильда» в
обозначении крутящего момента
свободного кручения применен с целью
подчеркнуть, что Mz не есть полный,
крутящий момент, а лишь часть его.
В главе XI, где рассматривалось свободное кручение, Mz
совпадал с полным крутящим моментом (поэтому там символ «тильда»
не использовался).
Как уже указывалось при обсуждении второй гипотезы,
касательное напряжение τ*| найдем не из уравнения закона Гука*
·§ 14.3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 393
а используя уравнение равновесия элемента тонкостенного стержня
с размерами dz, ds, δ (s) (рис. 14.11).
Равенство нулю суммы проекций всех сил, приложенных
к этому элементу, на ось г представляет собой одно из
уравнений равновесия элемента
д(огб) \ ι сд(ъг6) \.
σ*δ Η лт- dzjds — σζδ ds + (τ^δ -\ ^— ds)dz
dz
ds
— τ&δ dz + pz dz ds = 0,
или после взаимного уничтожения некоторых членов и
сокращения на dzds оставшихся после этого,
д{огЬ) д(т|гб)
+ —яг- +Рг=0.
dz
ds
(14.19)
Интегрируя уравнение (14.19) по s и деля все члены на δ,
получаем
1
τ& ~ δ (s)
_ £ iML ώ _ J pj (г§ S)dS+f2(2)
(14.20)
Поскольку τ^δ является функцией ζ и s, а интегрирование
выполнено по s, в состав интеграла (14.20) входит произвольная
функция от ζ (f2 (г)), которой можно
дать механическую трактовку, для
чего достаточно положить s = 0.
В этом случае оба интеграла в
квадратных скобках в (14.19)
обращаются в нуль и
/2 (г) = δ (0) х1г (г, 0) = 50. (14.21)
<5zfr-±-dz
Здесь 50 —погонная
сдвигающая сила 5| в продольном
(параллельном ОСИ Ζ) СеЧенИИ СТерЖНЯ Рис. н.п. К равновесию элемента
ПрИ S = 0. ПоДСТаВЛЯЯ В (14.20) тонкостенного стержня.
выражения согласно (14.17) и
(14.21), учитывая закон парности касательных напряжений и
интегрируя по F (δ (s) ds = dF), получаем
τ*1 (г, s) = ~ lsQ - J pz (ζ, s) ds -E w'Ml (ζ) \dF~
[ 0 L F
s s s
- u'a (z) \ x (s) dF - όα (ή \ydF- ftz" (г) \ ω (s) dF
(14.22)
(14.23)
394 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
Учитывая, что
\dF = F(s), lx(s)dF = Sy(s)t
о о
S 5
ly(s)dF = Sx(s), \co(s)dF = S(i>(s),
о о
придадим формуле (14.22) следующий вид:
τ*ξ (ζ, s) = -щ lsQ -}Pz (ζ, s)ds-E [w'Ml (ζ) F (s) -
- и a (z) Sy (s) - v'a (z) Sx (s) - Ьтя (г) 5ω (s)]j. (14.24)
Формулу для тг| (г, s) можно вывести и иначе, не пользуясь
дифференциальным уравнением равновесия бесконечно малого
элемента стержня с размером δ, ds и dz (14.18) с последующим его
интегрированием, а рассматривая непосредственно равновесие
элемента, заключенного между точками Мг и М, имеющего один
бесконечно малый размер вдоль оси ζ (см. рис. 14.12). Заметим,
что если рассмотреть равновесие отсеченной части элемента между
точками Μ и Μk, то получим формулу для тг| (г, s),
эквивалентную формуле (14.24),
+ Ε К/отс - u'aST - VAST - С'5Г]}· (Н.25)
Формула (14.24) не является рабочей формулой. Для
получения последней нужно производные w"Ml(z), и α (ζ), υ α (ζ) и "&'г(г)
выразить через обобщенные усилия.
8. Дифференциальные уравнения равновесия элемента
тонкостенного стержня в произвольной системе декартовых координат-
На рис. 14.13 представлен элемент стержня, заключенный между
сечениями ζ и z-\-dz. В сечении с координатой ζ в пределах
участка контурной линии, длина которого равна единице,
статическим _эквивалентом, соответствующим аг, является погонное
усилие Νζ, а каждой из долей касательного напряжения,
изображенного на рис. 14.10, б, в, — соответственно погонные усилия Sz и Нг
__ + 6/2 +6/2 +6/2
Nz= \ σζάη, Sz= $ τ^άη = $ τ^Λη,
-6/2 —6/2 —6/2
+ 6/2 +6/2
— 6/2 —6/2
§ 14.3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 395
Рис. 14.12. К определению касательного напряжения в тонкостенном стержне
открытого профиля.
Рис. 14.13. К составлению уравнения равновесия элемента тонкостенного стержня,
выделенного Двумя поперечными сечениями, расположенными бесконечно близко одно
к другому.
396
СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
Образование Нг пояснено рис. 14.14. При этом, беря интеграл от Нг
по всей контурной линии, получаем момент свободного
кручения
\Hz(z, s)ds = Mz(z).
(14.26)
Уравнения равновесия элемента имеют вид
д(тг1Ь)
У прл; = О
2ПР# = 0
^прг = 0
дмом А = 0
L
dz
cos adzds -\-qxdz = 0,
д (тг|б)
—^— sin adz ds-\- qy dz = 0,
*δ)
^1!Р£ч.ага& + дяаг = Ь
i
' (14.27)
д (τζ%δ) dMz
—-^—dzh ds + —τ— dz -\-mAdz = 0;
mA = \[px{zy s)(y-ay)-py{z, s)(x-ax)]ds.
Уравнение (14.27)4 представляет собой равенство нулю суммы
моментов относительно оси, параллельной оси ζ и проходящей
через точку А в плоскости
поперечного сечения, при этом
второй член в левой части получен
т \ с учетом (14.26) следующим об-
Ϊ7(
разом:
J
dz
dz) ds =
dz J
Ηг ds dz = , z dz.
dz
Рис. 14.14. К образованию крутящего
момента свободного кручення.
Сокращая все члены в
уравнениях (14.27) на dz, учитывая
(14.14), а также независимость δ от г, позволяющую вынести δ из-
под оператора дифференцирования по г, и учитывая, наконец,
равенство bds = dF, получаем уравнения равновесия элемента
§ 14.3]
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ
397
тонкостенного стержня в следующем виде:
J
д (τζ1δ)
dz
dx
д (τηδ)
+ ?, = 0, J-^d// + ?9 = 0,
L
J
—^—d(n-\-—-r
OZ ' d2
■f-m^ = 0.
(14..28)
Выполним интегрирование по частям в (14.28)1>2>,
д (τ^δ)
dz
к (» 5 Г δ (тге6) Π
5 (τηδ) К С д Гд (τζ1δ) Ί
—Η—ω
„К-Ь^[
дг
д(τ^δ)
dz
■\ds + M'z + mA=0.
(14.29)
Учтем, что поскольку на продольных кромках касательные
напряжения Т|г равны нулю, напряжения тг| как при s = sK, так и
при s = sH вследствие закона парности касательных напряжений
также равны нулю, поэтому первые члены в каждом из
уравнений обращаются в нуль.
Под интегралами в (14.29) переменим местами
последовательность дифференцирования по ζ и s; к полученным при этом
уравнениям присоединим (14.28)3, поставив его на первое место
F
С д Г β (тпб) 1
С д Γ3(τΛδ) 1
l°iil-s-F+M'+'n*~0·
(14.30)
398
СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
Теперь подставим в уравнения равновесия (14.30) аг, тг| и Мг
согласно формулам (14.17), (14.24) и (14.18) соответственно1)
WMtE J dF - u'aE \xdF- ό'αΕ\ у dF- tt;"£$ G>dF + qg = Qt
F F F F
w"MiE\x dF - u\v E\x* dF -v™ E\xy dF -
F F F
_<>;ν£ ^x«>dF + qx+[x^ds = 0,
F L
w'M,E\y dF -u^E \xydF -v™ E\y* dF -
F F F
-^E^dF + qy+^y^-ds^O,
L
w'm,E\ (udF — u™E^χω dF — vAvE ^(aydF —
F F F
-^vE^2dF-\-^GIk-\-mA+^^-ds = 0.
F L
В матричной форме эта система уравнений (если в последних
трех переменить знаки на противоположные) имеет следующий
вид:
■ (14.31)
FD*
-SyD*
— SXD*
- SuP*
-SUD» -SxDs -5ω03
fyD*
IxP*
ω1
V>4-
Glt
D2
w
Mt
U,
Ъ,
Ε
Ях
Яу + тх
Ях + ту
dpi
тА+^-дг
ds
Здесь символ D обозначает оператор дифференцирования
U— dz\ dz*f U — dz*' U — dz*)'
δ Γδ(τζ1δ)Ί
A) Покажем отдельно выражение для. -^— —■? ds, учитывая формулы
(14.24) и (14.23)
д Γδ(τ,ίδ)1 дрг . ... "I
'dz L"lT-J-1Ss-"& dS~E Wm^-JaiM-VaV Μ-φωάΡ [.
§ 14.3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 399
Кроме того, имеются в виду формулы (14.2) и нижеприводимые
обозначения интегралов:
F = \dF, Sy=\xdF, Sx = ]ydF, Sffl=$a>dF,
Iy = \x* dF,
hy = \xy dF, Ιχω = J χω dF,
F
= J t/ω dF,
Ix = \y*dF,
уш
/ω=$ω2^.
(14.32)
9. Дифференциальные" уравнения равновесия элемента
тонкостенного стержня в главных координатах. Если функция 1, χ (s),
y(s), co(s), входящие в состав подынтегральных выражений
в (14.32), принять не произвольными, как это было сделано
выше1), а за счет выбора системы координатных осей х, у и
положения точек А и Мг добиться того, чтобы эти функции являлись
ортогональными (такие функции будем называть главными
координатами), то система уравнений (14.31) существенно упрощается.
Действительно, из самого определения понятия ортогональности
системы функций вытекает обращение в нуль интегралов,
входящих в (14.31) и расположенных в (14.32) выше ступенчатой линии.
Вследствие этого система (14.31) распадается на четыре
самостоятельных уравнения
И»мг — Яя* Е1уиу=дх + т>у, EIxv^=qy^m'x,
ElXv-GIkK = mA+§
ω-p-ds.
dz
(14.33)
Уравнение (14.33)! описывает осевую деформацию стержня,
уравнения (14.33)2>3 — изгиб стержня соответственно в плоскостях
Oxz и Oyz и, наконец, уравнение (14.33)4 —кручение стержня.
Если ρ ζ (z, s)s=0, то m'x = 0, m^ = 0, qz = 0 и (14.33)
приобретает вид
EFw"Mi = 0, EIyUy = qx, EIv^=qy,
£/ω#ιν - GIk$" = mA. (14.34)
Получение главных координат обеспечивается надлежащим
выбором следующих шести параметров, разбивающихся на три
группы, каждая из которых инвариантна по отношению к дру-
х) Эта произвольность состоит в произвольности выбора системы осей ху,
положения секторного полюса—точки А и положения точки Λίχ — начала
отсчета координаты s на контурной линии,
400 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
гим. Первая группа из трех параметров связана с выбором системы
координатных осей Оху, два параметра это координаты точки О —
начала координат системы осей χ и у и третий — определяющий
ориентацию (имеется в виду угол) системы осей Оху относительно
контура поперечного сечения. Вторая группа параметров состоит
из координат секторного полюса. Наконец, один самостоятельный
параметр— координата, определяющая положение на контурной
линии точки Mi —начала отсчета секторной площади.
Первая группа параметров определяет собой главные
координаты x(s) и y(s). Вторая и третья группы параметров совместно
определяют собой главную координату ω (s). Четвертая же
главная координата — 1, разумеется, не подлежит определению.
С выбором главных координат χ (s) и у (s) связано обращение
в нуль интегралов Sy, Sx и 1хи. С выбором же главной
координаты ω (s) — обращение в нуль
интегралов 5ω, Ιχ(ύ и Iy(0.
10. Отыскание главных
координат. Выше говорилось, что
функции 1, х, у и ω называют
главными координатами, если
они ортогональны.
Ортогональность функций 1, х, у
достигается, если в качестве системы
координатных осей Оху
принимается система главных
центральных осей инерции (см.
Дополнение). Остается найти
такую функцию ω, которая
ортогональна каждой из функций 1,
х, у, т. е. удовлетворяет
условиям равенства нулю
интегралов (14.32)4)7>9. С этой целью отнесем поперечное сечение
тонкостенного стержня к системе главных центральных осей
инерции х, у и установим зависимость между секторными площадями,
соответствующими двум полюсам А и В при одной и той же
произвольной точке Мг начала отсчета секторной площади.
Напомним (см. рис. 14.9), что дифференциал секторной площади
выражается формулой d(u=hds. Если полюс располагается
в точке Л (рис. 14.15), имеем
άωΑ = h,Ads = [(χ — ах) sin а —(у — ау) cos a] ds. (14.35)
Если полюс принят в точке В, то
άωΒ = hBds = [(χ — bx) sin а —(у — by) cos a] ds. (14.36)
Вычитая (14.36) из (14.35), получим:
άωΑ — άωΒ = [(bx — αχ) sin a — (by — ay) cos a] ds,
^
'
\ &
-§:'\ 1
45S
JL
\ °
\-dy-.
**
У
βχ
■*—ν
At
άωΑ
"\ г..
!\~^х
""Ч^й^
b
ι
ν
τ~^
Χ
I
-ds
.
' W
\ 2
Рис. 14.15. К установлению зависимости
между секторными площадями,
построенными при двух .разных полюсах, но одной
и той же точке начала отсчета на контуре.
§ 14.3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 401
или, учитывая (14.14),
d (ωΛ — ωβ) = <Xxdy — <xydx.
Здесь
ax = bx — ax, ay = by — au.
Интегрируя (14.37), находим соотношение
ωΑ = ωΒ + ОД — а.уХ -f β.
(14.37)
(14.38)
(14.39)
Это есть формула преобразования секторной площади при
изменении секторного полюса. Можно поставить задачу, зная ь>в—
секторную площадь, соответствующую произвольному полюсу В
и произвольной точке М1 начала отсчета секторных площадей, —
найти такое положение полюса А и такое положение М* — точки
начала отсчета секторных площадей, при которых секторная
площадь ωΑ представляет собой функцию аргумента (s) —-co(s),
ортогональную функциям 1, χ (s) и у(х), т. е. удовлетворяющую
условиям равенства нулю интегралов в (14.32)4ι7ι9. С этой целью
подставим (14.39) в (14.32)4i7f9 вместо ω и приравняем результат
подстановки нулю, в итоге чего получим
\u>BdF + a,x\y dF -ay\x dF + §\dF = 0,
F F F F
\xu>BdF-\-ax\xydF-ay\x2dF-\-§\xdF = Q>t
F F F F
\y(uBdF + ax \y2dF-ay\xydF + §\ydF = 0.
(14.40)
Поскольку в качестве осей х-и у приняты главные оси инерции
площади поперечного сечения, имеют место равенства нулю
интегралов (14.32)2ι3,6 и, таким образом, система (14.40) с учетом
принятых обозначений (14.32) приобретает вид
5ωβ+β^ = 0, 1Х(,в-ссу1у = 0, 1у(Лв+ах1х = 0, (14.41)
откуда β = — Svb/F, ay = 1х&в/1у, ах = — 1уав/1х· Поскольку
полюс В был выбран произвольно и, таким образом, координаты
Ьх и by известны, определив <хх и ау, можно найти из (14.38) и
координаты точки Л, называемой главным секторным полюсом,
ах = Ьх — <хх, ay = by — <ху. Обращаем внимание на то, что
положение точки Л не зависит от выбора начальной точки отсчета
секторной площади, принятой при определении ωΒ. В этом легко
убедиться, если учесть, что (рис. 14.16) ωβ (sx) = (ub(s2) -f ωβ (s12).
402
СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ, χιν
Действительно, подставляя ω5 (sx) в интегралы ΙΧ(ύΒ и 1у(йв,
получаем
ΙχωΒ = 5 х<*>в (h) dF = S χωΒ (s2) dF + ω5 (sl2) \ χ dF (xy).
Но учитывая равенство нулю интегралов (14.30)2(3, окончательно
имеем равенства
5 χω в (h) dF = J χω в (s2) dF (xy),
F F
справедливость которых и требовалось доказать.
В § 12.8 было введено понятие центра изгиба и даны условия
(12.161) для отыскания его. Нетрудно видеть, что эти условия
совпадают с условиями отыскания
главного секторного полюса. Таким образом,
эти обе точки совпадают. Что касается
М* — главной точки начала отсчета
секторной площади, то она определяется как
такая точка на контуре, в которой
величина ωΑ обращается в нуль. Можно
подойти к определению положения точки М*
и иначе. Напишем формулу для ωΑ (sx)
применительно к точке Л (главному
секторному ПОЛЮСу) (ύА (Sj) = (йА (S2) + ®А (S12)·
Секторная площадь ωΑ является функцией
дуги s12. Если точка М2 является нулевой
точкой начала отсчета секторных площадей,
то ^ ωΑ (s2) dF = 0 и, следовательно,
F
J ωА (sx) dF - ωА (s12) J dF = 0;
F F
5 ωΛ (Si) dF - ω a (s12) F = 0.
QB(Si)
Qg(S12)
Отсюда
Рис 14.16. К установлению
зависимости между
секторными площадями,
соответствующими одному полюоу,
но двум разным точкам
начала отсчета на контуре.
5 ωΛ (5l) dF
ω α (S12)
(14.42)
Точка М2 называется секторной нулевой
точкой. Таких точек на контуре может
быть больше, чем одна. Та из этих точек, которая ближе
остальных к главному секторному полюсу, называется главной
секторной нулевой точкой.
11. О совпадении центра кручения с центром изгиба. Коснемся
теперь отыскания координат центра кручения. Если считать, что
§ 14.3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 403
на стержень действуют лишь внешние скручивающие моменты, то
в поперечных сечениях не возникает ни продольной силы, ни
изгибающих моментов
Ne = 0t lagdF = 0;
F
Мх = 0, \czydF = 0\
F
My = 0, \ <згх dF = 0.
F
Если, кроме того, полагать, что точка А является центром
кручения и, следовательно, иА = 0 и иЛ = 0, то как уже
указывалось, им и \>м определяются по формулам (14.8) и вместо
формул (14.13), (14.15) и (14.17) соответственно имеем
wM = WMt (z)-f>'z(z)<x>(s),
Sz = wm1(z) — W (ζ)ω(ί),
Тогда условия равенства нулю усилий Ν, Мх и Му
представляются так:
w'Ml(z)F-V(z)\«>(s)dF = 0,
F
w'Mt (ζ) 5 χ (s) dF - G£ (ζ) J ω (s) χ (s) dF = 0,
F F
а>'мг (г) J у (s) dF - θ; (г) $ ω (s) у (s) dF = 0.
F F
Если положение точки Мг подобрать так, чтобы интеграл
в первом из этих уравнений обратился в нуль, то тогда и
w'Mi(z) = § и два остальных приведенных условия приобретут вид
J ω (s) x (s) dF = 0, J ω (s) у (s) dF = 0.
F F
Таким образом, при условии, что точка Л является центром
кручения, мы пришли к необходимости удовлетворения тем же
требованиям, что и при отыскании центра изгиба и
совпадающего с ним главного секторного полюса. Иными словами, центр
кручения и центр изгиба в поперечном сечении тонкостенного
стержня открытого профиля совпадают.
12s Отыскание секторного момента инерции в главных
координатах. Подставим в общую формулу для /ω выражение ωΑ
согласно (14.39) и выполним элементарные алгебраические
404 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
преобразования, в результате чего получим
1&А = \ ω2Α dF = \ (ωв + аху - аух + β)2 dF =
F F
= ax {IxUx — IxyUy + $SX -f Iy0)Bj — CCy (—IyCly + IxyO-x + $Sy + /X(UB) -f.
+β(^β + 5ω5+αΛ-α,5,)+α,/ωβί/-α«//ωΰ,+ β5ω5+/ωΒ. (14.43)
Сопоставляя выражения внутри скобок в (14.43) с левыми частями
равенств (14.40)3i2fl, равными нулю, убеждаемся в их
соответственной идентичности, вследствие чего получаем окончательную
формулу для UA
' ω^ = ' «>в "τ" ал7шву <XylфВх -р Ρ^ω^·
13. Обобщенные усилия и бимомент. Формулы для
напряжений. Рассмотрим четыре интеграла по всей площади поперечного
сечения стержня, подынтегральными выражениями которых
являются произведения напряжения σζ соответственно на одну из
функций 1, x(s), у (s) и ω (s). При этом первые три интеграла
представляют собой обобщенные усилия N, Му и Мх а
четвертый — так называемый бимомент
N = \oZ'\-dF, My = \(5zxdF, Mx = \azydFy
F F F
B = \Gz®dF. (14.44)
F
Из четырех понятий, представляемых каждой из формул (14.44),
три первых известны читателю с самого начала изучения курса
(см. § 1.11)—это так называемые обобщенные внутренние
усилия — продольная сила и изгибающие моменты (последние два
действуют соответственно в плоскостях Охг и Oyz). Продольной
силе N соответствует доля напряжений, распределенная по за=
кону 1 (т. е. равномерно распределенные напряжения);
изгибающим моментам Му и Мх отвечают доли напряжений,
распределенные соответственно по закону координатных функций χ и у.
Последняя формула (14.44) выражает новое понятие — бимомент,
являющееся одним из основных в теории тонкостенных стержней.
Бимоменту соответствуют самоуравновешенные
напряжения (§1.16) в поперечном сечении, распределенные
по этому сечению по закону секторной площади ω. Заметим, что
если решать задачу о деформации тонкостенного стержня
открытого профиля на основе строгого использования аппарата теории
упругости, то самоуравновешенные напряжения, распределенные
по закону ω, представят собой лишь часть полной системы само-
уравнопешенных напряжений. Остальная их часть технической
теорией тонкостенных стержней, изложенной здесь, не может быть
§ 14,3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 405·
уловлена. Однако эта часть самоуравновешенных напряжений,
неулавливаемая указанной теорией, оказывается несущественной —
максимальные значения σζ в этой части малы по сравнению
с максимальными значениями тех долей напряжений, которые
создают Ν, Мх, Му и которым отвечает распределение по закону ω.
Подставим в (14.44) выражение для агу согласно (14.17), и
учтем ортогональность главных координат 1, х, у и ω. В
результате подстановки получим
N = EFw'Ml, Mu = — EIyU'At Μχ = -ΕΙχνΆ, В = -Е1„Ъ'Я. (14.45)
Решая полученные уравнения относительно w'mx, u"a, ν'Ά и b"z>.
получаем
N Ми мх в
W> Ua~~ei> Va~~ei> ΎΤζ~~εΤ<[
w'm^-ww WA=—Wf-, v'a = -eTx> ®*=-ΈΤω· (14·46>
Продифференцируем (14.46) по ζ, в результате найдем
W*i-Wr ' Ua~~ Щ- ~Ё7/ Va еТх--еТх>
К = —Ю-=-ТГ· О4·47)
Равенство нулю т"м1 вытекает из (14.34)!. В (14.47) введено
обозначение dB/dz = Μω. Величина Μω называется *) изгибно-крутиль-
ным моментом. Он образуется теми касательными напряжениями,,
которые вызваны стеснением депланации. Подставляя (14.46)·
в (14.17) и (14.47) в (14.25), получаем расчетную формулу для
аг и первый, второй и четвертый члены в нижеприводимой
расчетной формуле ДЛЯ Т|г=Тг|
N МуХ Мху Βω
T^ - "л/ Η -Τ7 l· -Γ- +
Ыи π Ых ^ lk π δ/,
ω
(14.49)
Здесь η —расстояние от контурной линии по нормали к ней до
точки, в которой определяется напряжение. 3°^с=5* (ху).·
Формулу для σζ можно рассматривать и как первые четыре члена
разложения σζ в обобщенный ряд Фурье по ортогональной системе функций, четыре-
из которых суть 1, χ (s), y(s), <b(s), -
σζ = αι1+α2*+α3ί/ + α4ω. (14.48).
Для определения коэффициентов используем обычную процедуру Фурье.
Поочередно умножим обе части равенства (14.48) на каждую из функций 1, x(s),.
у (s), ω (s) и берем интегралы от обеих частей равенства в пределах всей'
') Бимомент имеет размерность сила χ (длина)2, изгибно-крутильный моменг
имеет размерность силаХдлина,
406 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
области представления функций, учтя их ортогональность. Из полученных
таким образом уравнений находим коэффициенты ау, а2, а3, а4. Итак имеем
ladF
[oz.l.dF=ai[\*.dF, α^^—-^;
^ozxdF=a2 jj^dF,
α2 =
ρ ρ \x*ar 'у
F
\ σ,χ dF
*_!_ ^щ_
\ x* dF Λ.
^GeydF = as^y*dF,
ι GgfudF — ai 1 (u2dF, α4
F
Μχ.
B_
Специфика обсуждаемой ситуации состоит в том, что раскладываемая в ряд
функция нам неизвестна, вследствие чего интегралы, находящиеся в
числителях коэффициентов αν α2, as, ai не могут быть вычислены, и для их
определения, т. е. для определения N, Му, Мх, В приходится прибегать к иному
аппарату — N, Му, Мх находятся из условий равновесия (если система
статически неопределима, то после раскрытия этой неопределимости) или все они,
а также В определяются по формулам (14.46). Можно было бы расширить
систему ортогональных функций, но для практического ее использования
потребовался бы способ отыскания соответствующих им числителей в
формулах для коэффициентов аг.
Полный крутящий момент Мг складывается из двух долей
Μ^Μ, + Μα. (14.50)
В формуле (14.49)2 четвертым членом учтена доля
касательного напряжения, соответствующая моменту стесненного кручения
{изгибно-крутильному моменту Μω). Итак, в формуле (14.49)
последние члены учитывают эффект стеснения деформации
тонкостенного стержня открытого профиля — стеснения его депланации.
Теория тонкостенных стержней открытого профиля В. 3.
Власова, и, в частности, формулы (14.49), являются обобщением
теории стержня, изложенной в главах II, XI —XIII.
14. Дифференциальное уравнение углов закручивания.
Граничные условия. Интеграл.
14.1. Уравнение. Выше было показано, что для
отыскания как бимомента, так, следовательно, и связанного с ним
дифференциальной зависимостью изгибно-крутильного момента, нужно
знать функцию углов закручивания. Ее находим из дифферен-
§ 14.3]
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ
407
циального уравнения, получающегося из формулы для Мг, путем
дифференцирования
GIKW -ЕЦ>7 =Мг, EI&&™ -GIK$l = — M'z = тг. (14.51)
14.2. Общий интеграл. Интеграл уравнения (14.51)
вследствие его линейности складывается из общего интеграла
соответствующего однородного уравнения
JV о/Ж
Е/Л
К"2
о
и какого-либо частного решения уравнения (14.51).
Представим уравнение (14.52) в следующем виде:
ftIV _ *1 а"
0, k = l
(14.52)
(14.53)
Уравнение такого типа было рассмотрено в гл. XIII (см. (13.24))
и был найден общий его интеграл. Воспользуемся этим
результатом. Итак, имеем
А* = С, + С2г + С3 sh ■£- + С4 ch */-+ К Р (г)·
Нам понадобятся выражения А', В
+ G/KA2, покажем их:
(14.54)
£/ωΑ", Λίж = — £/*Г +
в = — ε ι ωθ; =
G/.
c2+^i4.p(z)-^-*i:vp(2)].
(14.55)
14.3. Граничные условия. Укажем характерные
граничные условия для функции лг.
1) Жесткое защемление торца (отсутствует и крутильный
поворот торца и его депланация)
лг = 0, Ъ'г = 0. (14.56)
2) Шарнирное закрепление торца (торец не может испытывать
крутильного поворота, но свободно депланирует, вследствие чего-
нормальных напряжений, распределенных по закону секторных
площадей, нет)
Аг = о, Я = 0. (14.57)
3) Свободный конец стержня (не воспрепятствованы ни
крутильный поворот, ни депланация торцов, вследствие чего на
408
СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ .СТЕРЖНЕЙ [ГЛ. XIV
торце нет ни касательных, ни нормальных напряжений,
распределенных по закону секторных площадей)
Мг = 0, В = 0. (14.58)
14.4. Метод начальных параметров. Частные
интегралы, образующие общий интеграл однородного уравнения (14.52),
kz й _,_ kz
суть: Ф*о = 1, Фя
что матрица
sh —, Ov3 = ch
/
Нетрудно видеть,
1
'*1
при г = 0
'г \г-о
sh —
k , kz
TchT
k* . kz
72- <* —
A3 . /fez
73-ch —
1 0 0
k
0 1 f
0 0 0
ife3
0 о -F-
β*»
, fcz
ch— ■
k , kz
Tsh'T
/fe2 . kz
i*-ch-r
13-sh
τι
0
/fe2
/2
0
3,,
<&
Αζί
a'-'
Vzi
не является единичной. Для построения решения в форме метода
начальных параметров нужно перестроить решение однородного
уравнения (14.52) так, чтобы частным интегралам, его
образующим, соответствовал определитель Вронского с единичной
матрицей, а частное решение неоднородного уравнения (14.51) вместе
со своими первыми тремя производными при ζ = 0 обращались
в нуль. С этой целью построим новую систему частных
интегралов ϋ·ζ{, представив их как линейную комбинацию ϋ·ζ1 Фгй =
з
— ^j ckftzl>
Для отыскания коэффициентов см имеем матричное уравнение
1 0
0 1
0 0
0 0
0
k
ι
0
&з
IT
1
0
£2
/2
0
I Coo
Cot
C02
1 c03
ClO C2o C30
Cll C2l C31
c12 C22 C32
c13 C23 C33
=
10 0 0
0 10 0
0 0 10
0 0 0 1
§ 14.3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 40£
решая его относительно матрицы {сг/-}, получаем
С00 ClO С20 Сзо
с01 СП С21 Сз1
С02 с12 С22 С32
СОЗ с13 с23 Сзз
=
1 0 0
0 1 А
0 0 0
ks
о о ir
ая матрица имеет вид
/2
1 ° "Ж
0 1 0 -
0 0 0
0 0
/2
£2~
1
0
/fe2
/2
0
-α
10 0 0
0 10 0
0 0 10
0 0 0 1
0
/2
* k*
/з
£3
0
•
Находим^ новую систему частных интегралов, образующих
общий интеграл однородного уравнения (14.52) и
удовлетворяющих при этом поставленным выше условиям
Ог2
Ог3
1
0
/2
W
0
0
1
0
/2
>
0
0
0
/з
Й»
0
0
/2
0
1 1
?
• kz
sh —
|ch —
=
1
ζ
/2
£2
/2
£2
K-0
f I . kz
TshT—z
(14.59)
Матрица, соответствующая определителю Вронского, который
отвечает системе функций $го, ϋ·ζ1, Фг2, ϋ·ζ3, имеет вид
Ф,
2
1
0
0
ΪΚ-·)
TshTz
. fcz
ch —
Λ . kz
Tsh —
/2 / / , kZ
-Τ7Γ Τ SI -; Ζ
/г2 \k I
ΐΚ-0
¥shT-
ch —
Удостоверяемся в том, что матрица Ог при г = 0 является еди-.
ничной
10 0 0
0 10 0
'*1*-о— 0 0 10
0 0 0 1
410 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
Частное решение уравнения ϋ·[ν w А" = -^- примем таким,
чюоы
ft
г, ч. ρ U-0
ttz, ч.
Ρ \г-о
^г, Ч,р U-0 ^2, Ч.р U-0 U.
Функция лг и первые три ее производные выражаются
следующими формулами:
^ = ^.4.P + ^o+^ + ^2[^-(ch-^-l)] +
+ D414TshTL-2
ΕΙ
JV"' _ ^ ι _^_ д/ _ __ Μω _ л,'" ι
■ω
■ω
(14.60)
+ D2|sh-^. + A)ch-^
Постоянным интегрирования может быть дана механическая
■трактовка, для этого рассмотрим Аг, а2, Аг и Аг" при г = 0
■Α" ι
Αι _ а Г) А' I — κ I — А'
"г 1г-о — "го — Ly0* "г |г-о — Λζ |г-о — иг
А:(
20
ω
ΕΙ
ω
= D2, tt2"|*-o
20 — κζθ
Μ,
оъ
ω
ΕΙ*
Μω0 .
ΕΙ,
Οίό'=Α..
ω
Очевидно, что DQ, Dlt D2 и D3 представляют собой величины,
называемые начальными параметрами.
Вводя в рассмотрение векторы
В (ζ) Μω (ζ)
Ъг (г) = |Аг (г) ^ (г) О,' (г) ОГ (г)} = {Аг (г) κ, (г) -
А =Ла κ __^__ii«0_l
£/,
ω
£/,
ω
-}·
Α*. ,. ρ (г) = {θ*. ,.ρ (г) Λ*,. .ρ (г) С *·ρ (г) <Сч.Р (г)},
получим формулу для вектора Аг (г)
#, (г) = L (г) #,+ #,,,. ρ (г).
Поскольку граничные условия выражаются не через Аг и Λ4ω,
я через β и Мг, можно соответствующим образом перестроить
§ 14.3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ
функции (14.60)з,4, при этом вместе с (14.60)1>2 получим
411
+ D3[
+
F(lshT-
·)]·
в = — £/ωο: =—ε ι ж.,. η - /Ш« сН ^
ω"ζ, ч. ρ
-De^ysh
мг
EU%" + G/K0; = - EIJi'z't\. ρ -
(14.61)
- Ο,ΕΙ» \ sh ^ - Ζ)3£/ω ch -^ + б/**;, Ч. ρ + G/A +
+ G/KD21 sh ^-z- + GIKD3 [A (ch f— 1)] ·
Сохраняя для постоянных интегрирования прежние обозначения,
теперь получим для них иные выражения из условий
^г U-o == "«о == ^о»
^2 U-0 == κ« U-0 == ^zo == κ«0 == ^Л»
Б
2-0
β0 = — 02ΕΙω,
Μ
г 12-о
Μ
20
(14.62)
Отсюда
20 κ20»
So
2 — FI
-D.EI
"Τ /2 κ«0»
ω '
^2o-G/KX20.
'з-^^ω —^"го—*-"κΛ2ο· (14.63)
Подставляя (14.63) в (14.61) после взаимного уничтожения
некоторых членов и введения векторов
*; (ζ) = {Ож (ζ) кг (ζ) Β (ζ) Мг (г)}, Ко = {К Ъо ^ Мг0},
ft* h) =
=Я*,Р (г) Οί. ,.ρ (г) - £/ωΟβ', ,. ρ (г) (- Е1ай'я'/Ч. ρ (г) + G/,Οί, ,. ρ (г))},
получим
*i(z) = L*«*0 + *;i4.p(z)f
где
L* =
1
0
и
0
TshT
fr
£/ω γ sh
0
Az
~T
X ( ukz
G/кГ /"
1 k и kz
GIK I I
, kz
ch-
0
\
l 11 .кг \
-^**-0
Ζ . &z
xsh-r
1
412 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
14.5. Частное решение. Частное решение представим
в виде
ζ
^*·ч ρ= оЬ J ®г·3 (z ~~ ^ Шг ^=
о
ζ
= ^ £ [L sh } (г - ζ) - (г - ζ)] /η, 4ζ. (14,64)
Если, например, тг = const, to
α т, Г /2 , * , „. . (z — ζ)2"]|2
-3.L1 ii! chhl _ Ζ2Ί
~~ G/K I. £2 "*" Λ»~ Ζ " 2 J'
«-»-&(τΛΤ-*)· *-.p=a(chX-')>
a"' _ mz k , kz Λιν _ mz k2 . kz
Z'4-P~ "G77Tbn~T' г7г'ч-Р~"ё77 /2 / :
ф*.ч.р1*-о=о, Аг',ч.р|г_0 = о, А2>ч.рu = о = о, А;';чр|г_о=0;
тгроизведем проверку удовлетворения уравнения (14.51) решением
<14.6б)
(14.65)
т
G/K /2 cn / μ
m.
tn,
m,
z_ ry. kz ι " f"g
G/K Ы1 / "*" /2 G/K £/
G/K тл
tn,
ω
£/ω G/K £/
ω
14.6. Случай нескольких участков. Если в пределах
•стержня имеется не один участок, то, как это делается обычно
в методе начальных параметров, начиная с границы участков
(в сторону возрастания ζ) в интеграл включаются дополнительные
члены. Причинами разделения стержня на участки могут явиться
-следующие факторы.
1. Изменение вида функции, описывающей распределенную
моментную нагрузку.
2. Наличие в промежуточном сечении стержня внешнего
сосредоточенного крутящего момента.
3. Наличие в промежуточном сечении стержня
сосредоточенного бимомента.
Наряду с указанными могут быть и особенности конструкции
•стержня в сечении, вследствие которых в этом сечении имеют
место разрывы функций Аг или ϋ·'ζ. Такие факторы встречаются
в исключительных случаях и их касаться не будем.
Остановимся подробно на отмеченных выше факторах.
На рис. 14.17, α показана ситуация, при которой возникает
распределенная моментная нагрузка —юна вызывается распределенной
лоперечной силовой нагрузкой, лежащей в плоскости, не проходящей
$ 14.3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 413
через линию центров изгиба. Разумеется, что нагрузка q в этом
случае, кроме указанного воздействия, вызывает еще и изгиб. Если
сечение, в котором изменяется вид функции тг(г), имеет
координату гъ то общий интеграл уравнения (14.51) имеет вид
•.-*- + *>£-&(<*£-ΐ)--&(>£-*) +
г
+ -оНК-5Ьт(г-Э-(г-9К^ +
О
г
+ |2ι о77 J \j sh j- (г - ζ) - (г - ζ)] тг, доп>2 άζ,
где тг>поп>2 = тг2 — тг1.
Напомним, что в методе начальных параметров влияние
дополнительных членов, записываемых после символа Бубнова (в нашем
α δ)
Рис. 14.17. К определению внешней крутящей моментной нагрузки: а) случай
воздействия распределенной внешней крутящей момеитной нагрузки; б) случай воздействия
сосредоточенного крутящего момента.
случае это член, содержащий тг,ДОП12), на $г на первом участке
сказывается через те начальные параметры, которые определяются
из граничных условий на конце стержня с г = гтах.
На рис. 14.17, б показана нагрузка, создающая
сосредоточенный внешний крутящий момент в промежуточном сечении стержня
с координатой г = гг ШКп = Ре.
Обозначая функцию О- на первом участке символом дг1,
представим интеграл уравнения (14.51) в этом случае так:
ЗДкоП * / .1
414
СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
Разумеется, что сила Р, кроме указанного воздействия, вызывает
еще и изгиб.
Наряду с внешними силами, перпендикулярными образующим
срединной поверхности тонкостенного стержня, на последний могут
действовать и силы, направленные
вдоль образующих или
параллельные им (рис. 14.18). Такие силы
могут быть приложены как к
торцам стержня, так и в любом из
промежуточных сечений (одном
ШШ Нескольких). Эти силы могут
создать бимомент, действующий
соответственно в том сечении, к
точкам которого приложены силы.
Сначала рассмотрим случай, в
котором точки приложения сил
лежат на контуре поперечного
сечения (рис. 14.18). Вызываемый
этими силами бимомент
выражается формулой х)
k
8«$рж(гь s)<udF+ Σ pi<»i>
F ('= I
(14.66)
здесь Ζχ — координата
рассматриваемого сечения, <ог — значение
ординаты функции ω в точке
приложения -силы Р{.
Если сила приложена в точке,
находящейся вне контура
поперечного сечения стержня, и
передается на него через некоторую
жесткую консоль (см. рис. 14.19),
то эта сила создает бимомент
Рис. 14.18. Тонкостенный стержень
открытого профиля под воздействием
внешних сил, направленных вдоль
образующих срединной поверхности:
а) сосредоточенные силы на торцах;
б) сосредоточенная сила в
промежуточном сечении; в) распределенная и
сосредоточенная нагрузки на торце;
г) распределенная и сосредоточенная
нагрузки в промежуточном сечении.
тура стержня и консоли CD
в сечении г — гг имеет место
S = PcoD,
(14.67)
где сод — секторная площадь в
точке D (конец консоли, к
которому приложена сила Р),
построенная вдоль дуги МХС кон-
(Мг — точка начала отсчета ω). Если
внешний сосредоточенный бимомент,
*) Для того чтобы внешний бимомент отличить от внутреннего, первый
из них обозначим готической буквой 33,
§ 14.3] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 415
то функция $ζ приобретает вид
0, = 0Д +
2(
33
GIK
ch-j-(z— гх).
(14.68)
момен-
возникает
стержень
Рис. 14.16. К определению
внешнего бимомента, вызываемого
сосредоточенной силой, параллельной
оси стержня и приложенной в
точке, не лежащей на контуре.
14.7. Влияние на кручение изгибающих
тов. В тонкостенных стержнях открытого профиля
эффект стеснения депланации и при воздействии на
внешнего изгибающего момента. Следует строго разграничивать
случаи образования внешнего изгибающего момента поперечными
силами (как это было показано выше) и продольными силами.
На рис. 14.20 показан стержень
швеллерного сечения. На рис. 14.20, а
изображена эпюра секторных
площадей этого сечения. На рис. 14.20, б, в
показаны два варианта создания
изгибающего момента поперечными
силами и продольными силами,
действующими в одной и той же
плоскости. При этом изгибающий момент,
созданный поперечными силами,
кручения стержня не вызывает,
поскольку плоскость его действия проходит
через центр изгиба. Продольные же
силы, образующие изгибающий
момент, вызывают кручение, поскольку сила Р, приложенная в точке В,
где ордината эпюры ω не равна нулю, создает бимомент Б = Ρ(οβ.
На рис. 14.20, г, д изображен другой случай расположения линий
действия поперечных и продольных сил, создающих изгибающий
момент. В этом случае момент, создаваемый поперечными силами,
вызывает кручение, поскольку плоскость его действия не проходит
через центр изгиба сечения, а изгибающий момент, создаваемый
продольными силами, кручения не вызывает, так как в точках
приложения обеих сил (точки sx и s2) ординаты эпюры ω равны
нулю, и следовательно, бимомент, соответствующий этим силам,
равен нулю. Пусть момент ШИЗГ представляется как результат
действия пары сил, перпендикулярных образующей, с плечом Лг,
так, что (рис. 14.21) Ρ = 9ЛИЗГ/Лгх. Любая функция (из числа $ζ (г),
$'z(z), B(z)/(GIK), Mz(z)/(GIJ, отвечающая воздействию момента Шнзг
может быть обозначена символом Φ (г, ζΊ) и представлена как
разность соответствующих функций Ф, отражающих воздействие
двух параллельных сил Р, находящихся на расстоянии Azlt одна
от другой
Φ
Фа» = [ФР(*. «1 + 4)'
Р(г,г1)]Ре =
[Φρ(ζ, z^bzJ-Orf, гх)рнзгв
Δζχ
416 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
Рис. 14.20. Отлнчне эффекта, вызываемого парами внешних сил, лежащих в одной
плоскости, но образованных либо поперечными, либо продольными внешними силами,
приложенными к тонкостенному стержню: а) эпюра секторной площади; б) пара
поперечных внешних сил, не создающих крутящего момента поскольку плоскость их действия
проходит через центр изгиба (точка А); в) пара продольных внешних сил, вызывающих
внешний бнмомент и следовательно изгнбное кручение, поскольку сила Ρ приложена
в точке В, где ордината эпюры ω^Ο (другая сила Ρ не вызывает бнмомента, так как
приложена в точке s1( где ордината эпюры ω = 0); г) пара поперечных внешних сил,
вызывающих крутящий момент, поскольку плоскость действия сил не проходит через
центр изгиба; о) пара продольных внешних сил, не вызывающих никакого крутильного
эффекта, поскольку в точках Si и s» приложения сил ординаты эпюры ω равны нулю.
§ 14.3]
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ
417
переходя к пределу при Δζ1-+0, получаем
дФ<
*^Η3Γ^·
(14.69)
фа»= dZl
Если изгибающий момент действует в плоскости, касательной
к срединной поверхности тонкостенного стержня, и образован
двумя силами Ρ 3DtH3r = PAs, расположенными бесконечно близко
Рис. 14.21. К вопросу об определении крутильного эффекта момента, плоскость
действия которого не проходит через центр изгиба: а) сосредоточенный момент; б)
представление сосредоточенного момента парой сил.
к линии касания (рис. 14.22) (т. е. обе силы Ρ лежат в
срединной поверхности тонкостенного стержня), то любая функция (из
числа ΰζ(ζ), $г(г), В (z)/(GIK), Mz(z)/(GIK)), отвечающая
воздействию момента 9ЛНЗГ> может быть представлена как разность
соответствующих функций Фх, отражающих влияние двух
параллельных сил Р, находящихся на
расстоянии \s одна от другой
Фт (г) =
= Φ1(ζ)[-Ρω,Η-Ρ(ωΑ + Δωέ)] =
Ф1(г)РАщ=:Ф1(г)
2Я
НЗГ
Δδ
Δωκ.
О,
Рис. 14.22. Пара внешних
продольных сил, лежащих в срединной
поверхности тонкостенного стержня.
Переходя к пределу при As
получим
ΛκΜ-Φ,ΟΟίΚ.,φ)^. (14.70)
В случаях, изображенных на рис. 14.19, на рис. 14.20, в и 14.22,
в сечении ζ = ζ1 имеется сосредоточенный бимомент 33, а в случаях,
изображенных на рис. 14.20, г, 14.21 — сосредоточенный момент Wlz.
14.8. Примечания. Завершим параграф следующими
существенными примечаниями.
1. Обсужденная выше теория тонкостенных стержней позволяет
учесть влияние стеснения не всякой депланации, а лишь той,
которая соответствует закону секторных площадей.
2. В пределах поперечного сечения заменять одну систему
поперечных сил другой, статически ей эквивалентной, можно.
418 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
поскольку проекция контура поперечного сечения на плоскость,
нормальную к оси стержня, в теории тонкостенных стержней
принято считать неизменной.
3. В пределах поперечного сечения заменять одну систему
продольных сил другой, статически ей эквивалентной, можно
лишь при условии, что при этом не изменяется и бимомент.
В частности, в пределах пластин, пересекающихся в одном ребре,
заменять продольную нагрузку любой статически ей эквивалентной
можно, поскольку при этом бимомент сохраняет свою величину.
§ 14.4. Влияние деформируемости поперечного сечения
на напряженно-деформированное состояние криволинейной
тонкостенной трубы
1. Вводные замечания. Постановка задачи. Говоря о
деформации тонкостенных стержней, в предыдущих параграфах мы
использовали гипотезу о неизменяемости формы проекции поперечного
сечения на плоскость, перпендикулярную оси стержня. Однако
в некоторых случаях такая гипотеза вступает в противоречие
с характером деформации тонкостенного стержня в
действительности. Особенно ярко это обнаруживается в случае, если ось
стержня не прямолинейна, а замкнутое сечение очень тонкостенно.
Приведем результаты исследования Т. Кармана *).
Рассмотрим трубу с осью в виде окружности радиуса R и
кругового поперечного сечения радиуса г при толщине стенки 6.
Труба подвергнута изгибу моментами М, создаваемыми нагрузкой
на торцах, распределенной по закону плоскости. Труба
представляет собой оболочку, однако достаточно надежно можно
рассчитать ее и средствами намного более простыми, чем теория оболочек.
Это и выполнил Т. Карман. При указанном на рис. 14.23
направлении моментов происходит сплющивание трубы — уменьшение
диаметра поперечного сечения трубы в плоскости ее оси и
увеличение в перпендикулярном этой плоскости направлении.
Постановка задачи сводится к следующему. Для указанных
выше трубы и воздействия на нее, при условии, что угол,
составляемый торцами трубы, равный α до ее деформации, в результате
деформации увеличивается до значения α+Δα, нужно установить,
как изменится при этом поперечное сечение и какова величина М,
соответствующая изменению угла на Δα.
*) Впервые на этот факт обратили внимание в начале XX века при
исследовании работы криволинейных труб и сопоставлении наблюдаемой в натуре
картины с результатами расчета по обычной теории изгиба стержней.
Первой, ставшей классической, работой, в которой была вскрыта причина
отмеченного значительного отличия результатов элементарной теории от
результатов эксперимента, была статья Т. Кармана: К arm an Т. Uber die
Formanderung durmwandiger Rohre, insbesondere federnder Ausgleichrohre. —
Zeitschrift fur Vereines deutscher Ingenieure, Band 55, № 45, November, 1911,
§ 14.4] ДЕФОРМИРУЕМОСТЬ СЕЧЕНИЯ КРИВОЛИНЕЙНОЙ ТРУБЫ 419
Решение осуществляется, методом Ритца, сущность которого
пояснена в главе XV. Вследствие однородности полей напряжений,
деформаций, перемещений по координате, измеряемой в плоскости
оси трубы, достаточно рассмотреть задачу о.минимуме
потенциальной энергии деформации, накапливаемой в трубчатом секторе,
Рис. 14.23. К воаннкновению эффекта сплющнвання поперечного сечення тонкостенной
трубы с криволинейной осью; а) фасад; \б) поперечное сеченне.
образованном двумя поперечными сечениями трубы, расстояние
между которыми по оси трубы равно единице. Обозначим эту
величину символом U. Последняя представлена в виде суммы двух*
слагаемых (/х и (/2. Первое из них — потенциальная энергия осевой
деформации волокон, расположенных концентрично оси трубы,
а второе — потенциальная энергия изгибной деформации кольцевых
волокон (длину контура поперечного сечения трубы при дефору
мации его в своей плоскости считаем неизменной).
Удельная потенциальная энергия ult соответствующая Uu
выражается формулой их = σ^/2 — Е&\/2, вследствие чего1)
о о
х) Формула для ί/2 аналогична формуле для потенциальной энергии
деформации прямолинейного стержня
u^lllpLto. (14.72>
О
В формуле (14.71), для того чтобы охватить интегрированием всю длину оси-
кольцевого элемента, интегрирование ведется от 0 до 2π (ds = r dtp).
Выражение (1//Ί— 1 /г) — изменение кривизны оси стержня — играет роль ν"- в (14.72).
420
СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
здесь е1 — относительная линейная деформация волокна,
нормального к поперечному сечению трубы;
".-j£(i-4-)''*=^'j(-W)V ™
здесь гг — радиус кривизны контура поперечного сечения трубы
после деформации. Найдем ех и (1 /гх — 1 /г), входящие в формулы
(14.71) и (14.73). Величину ех пред-
as ставим в виде суммы двух слагаемых
гг = г{ -Hi2'· (14.74)
Первое из них такое же как и в
теории, не учитывающей сплющивания
поперечного сечения. Вторым
слагаемым учтем влияние на 8Х
сплющивания поперечного сечения.
Первое слагаемое (см. рис. 14.24)
выражается формулой
^—, (14.75)
е',11 =
Рис.
14.24. К установлению связи
между As, Δα, у и R.
где s — длина текущего волокна,
расположенного на расстоянии у от
цилиндрической поверхности,
содержащей ось трубы и нормальной к плоскости, в которой эта ось
располагается, As —удлинение указанного волокна в соответствии
с гипотезой плоских сечений.
Величину (14.75) найдем учтя, что
As'1»
Δα 2
2 у
Деля (14.76)! на (14.76)2, получаем
Δα Δβ(1,/2
R + У
(14.76)
α s/(R+y)
Отсюда
Лс(И
\-{R+y)
ys
Δα
— 2α '
сш. . АД'1'
1 s
У
R+y
Δα
' α
^ У Δα
~ R α
(14.77)
Второе слагаемое в (14.74) найдем по формуле ef' = ks{2]/s (см.
рис. 14.25), As(2) — удлинение волокна, до деформации
расположенного на расстоянии у от цилиндрической поверхности,
содержащей ось трубы и нормальной к плоскости, в которой эта ось
располагается. Удлинение происходит за счет того, что след волокна.
§ 14.4]
ДЕФОРМИРУЕМОСТЬ СЕЧЕНИЯ КРИВОЛИНЕЙНОЙ ТРУБЫ
421
в плоскости поперечного сечения трубы при сплющивании
последнего перемещается из точки Ρ в точку Рг. Составляющая этого
Д5(21/2 d
перемещения, параллельная оси у, обозначена ν : —~ = р ,
e'j2; = ρ ^-ρ, Выразим ν через нормальную и касательную
к контуру составляющие перемещения РРХ ν = ΔΓ sin φ + Δ, cos φ,
угол φ пояснен на рис. 14.26.
Итак,
У Δα
*>=R
α
, ν у Δα , ΔΓ sin φ + Δ^ cos φ
(14.78)
Относительная линейная деформация е2 контура поперечного
сечения находится по формуле (9.120)2 для ε^ е2 = —£--\ j-Ц
роль и в формуле (9.120)2 здесь играет.Δ0 а роль ν — величина А(.
Обыкновенная производная
применена здесь вместо частной в формуле
(9.120)2 по той причине, что в "этой
5— —■-. 7// формуле г —переменная величина
Рис. 14.25. К определению As( )
и Δ5(2).
Рис. 14.26. К установлению связи между
Ό, ΔΓ, Δ. и φ; 1 — до деформации, 2 —
после деформации.
(область имеет конечный размер в направлении г), а в
обсуждаемом случае г — постоянная величина — радиус контура, поэтому
величина Δ* является функцией лишь аргумента φ. Условие
нерастяжимости контура имеет вид
_ _ dAt
dtp ~' "r dq>
Подставляя (14.79) в (14.78) и учитывая, что y = rsincp (см.
рис^ Г4.26), получаем
ε2=^ + ^ = 0, ΔΓ =
1 г ' г dq> г
(14.79)
8χ= -
^{^-r sin φ -- -A sin φ + Δ, cos φ]. (14,80)
422 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
Формула для изменения кривизны оси стержня, очерченного по
окружности, была выведена в § 12.19. В обозначениях, принятых
в настоящем параграфе, она приобретает вид
_!__ J - *£._!_£*£.- 1 (dAt I d3A'\ П4 8П
П r~ r2 "ϊ" ds* ~ ή \ άφ "ϊ" ώρ3 )' ν**-°4
Учитывая формулы (14.80), (14.81), а также (14.71) и (14.73),
получаем
2π
,, Ебг С /Δα . dAt · .л Vs л .
^="2ЖЗ ("a~rSin(p~" "^SUKp + A^coscpj ίίφ +
о
2π
+ 24>5 JUf+"d#J Λρ· (14.82)
о .
Вариационная задача отыскания функции Л* = Д* (φ), при которой
достигается минимум функционала U в прямом приближенном
методе Ритца, сводится к задаче отыскания коэффициентов ct
в приближенном решении, представленном в фо же конечной суммы
М<Р) = £ <*М<р) (14.83)
»= ι
из условия обращения в минимум функции U = U (clt ..., cn)t
в которую превращается функционал (14.82)
2π
ί/[Λ((Φ)]=]>(Δ«(φ),^·, ^)*Р
'при подстановке в него вместо Δ, (φ) выражения (14.83). Т.
Карман в качестве функций /г(ф) принял /^sii^cp, /2 = sin4(p, ...
·.·. ,, /„ = sin 2/ζφ. Решение, соответствующее первому приближению,
при котором х)
Δ/(φ) = ^ι,8ίη2φ (14.84)
х) Верхний индекс у с± указывает количество сохраненных членов в том
приближении, к которому относится этот коэффициент. Это необходимо,
поскольку Ci во втором приближении отличается от ci в первом приближении
Д, (φ) = cf sin 2φ -f- c<?' sin 4φ; cf φ с[и.
§14.4] ДЕФОРМИРУЕМОСТЬ СЕЧЕНИЯ КРИВОЛИНЕЙНОЙ ТРУБЫ 423
и c(i[ находится из условия1) dU/dc^' = 0, приобретающего вид
— Зг
Δα , ,с , л-лоч _;,, л .,ιι 3 ._ Δα
+ (5 + 6λ»Κ"=0, ^=5Т6Р-Г
α ' х ' ' * ' 5+ЬЛа α
дает уже достаточно хороший результат. При этом
,, _£π/·3(Δα/α)2 6 Λ 9 \
Если не учитывать деформируемости поперечного сечения трубы
в своей плоскости, то изгибающий момент выражается формулой
Ma=Ell-L-~) = EI^- = EIAa
Ri R J s ^' Ra>
а отнесенная к единице длины оси трубы работа внешних
моментов, совершенная при деформации трубы и численно равная ей
потенциальная энергия деформации,—формулой
Λ—TJ№-7L-T£/T^-№· <14·86)
Верхний индекс н указывает на неучет деформируемости
поперечного сечения в своей плоскости.
Сопоставляя формулы (14.85) и (14.86), убеждаемся в том, что
в случае учета сплющивания поперечного сечения трубы роль
момента инерции площади поперечного сечения играет выражение
яг3б[1 — 10 ι ΐ2λ2)' ^СЛИ ввести Для этого выражения символ /спл,
индекс в котором подчеркивает учет эффекта сплющивания
поперечного сечения и, кроме того, учесть, что момент инерции
площади поперечного сечения трубы при недеформируемости его в своей
плоскости, выражается формулой / = зтг3б, по получим /спл = /. Ь
9
k= 1 — ю-!-ΐ2λ2' К0ЭФФИ1*иент А учитывает эффект сплющивания2).
u 2R*
х) Выражение для U, после подстановки (14.84) в (14.82), приобретает вид
2π
\ (г sinqt + cl11 sin 2φ cos φ — 2c/» cos2q> sin<p] £ίφ +
2π \
+ ^.36cr'f сой»2ф*р1
ο )
или после раскрытия интегралов и введения обозначения для параметра 6Rfr% =λ
2) Если при решении задачи использовать второе приближение, при кото,
ром At=c(?] sin 2a+4si sin 4φ, то формула для коэффициента k приобретает
3+536λ24-4800λ4:
следующий вид; k= i06 + 413w + 480W ·
424 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
Коэффициент k вносит существенное изменение в величину
жесткости трубы. Так, например, если R= 100 еж, г = 10см и 6 = 0,3 см,
то λ = δ^/r2 = 0,3-100/102 = 0,3 и к=1--щ^7^¥=\— 0,812=
= 0,188, т. е. вследствие сплющивания поперечного сечения
жесткость трубы уменьшается более чем
в пять раз.
На рис. 14.27 показан график
зависимости коэффициента k от
параметра λ при первых трех
приближениях. Существенное влияние
сплющивание поперечного сечения
оказывает и на распределение напряжений
в его плоскости. Выше была полу-
ϊβ^!Щ чена формула для elt используя ко-
р торую получаем формулу для напря-
Рис. 14.27. График функции ЖеНИЙ
k=kf™-
Если, используя первое приближение, согласно которому Δ/
выражается формулой (14.84), где с[1] находится по приведенной
выше формуле, написать формулу для σ, то получим
ρ г Δα / . 6
sin3 φ
г-Δα у
σ = Ε —^
α R
1-
5 + 6λ2
т
здесь учтено, что у = гътц>.
сжатие в
б растяжение
5)
Рис. .14.28. Эпюры нормальных напряжений в круговом поперечном сечении
тонкостенной трубы с осью, очерченной по окружности; а) контур поперечного сечения трубы н
ортогональные проекции эпюр напряжений а; 1 — при λ = 1,0; 2 — при λ = 0,5; 3 —
при λ = 0,1; б) аксонометрия; / — при λ = оо, 2 — при λ = 0,5.
При неучете сплющивания формула для σ имеет вид
,Δα у
σ = Ε
a R '
таким образом, функциональный коэффициент 1 — 5 , 6λ2 (γ)
вносит корректив в распределение напряжений по поперечному
§ 14.5] ПОНЯТИЕ О РЕДУКЦИОННОМ КОЭФФИЦИЕНТЕ 425
сечению трубы. На рис. 14.28 показаны эпюры распределения σ
по поперечному сечению трубы при различных λ.
Обсужденное в настоящем параграфе явление сплющивания
трубы с криволинейной осью получило название эффекта
Кармана х).
В заключение параграфа заметим, что вопрос об учете депла-
нации и искажения формы поперечных сечений тонкостенных
балок замкнутого поперечного (в частности, многосвязного)
сечения в своей плоскости при анализе напряженного
деформированного состояния рассматривал и В. 3. Власов, предложивший
дискретно-континуальную полубезмоментную расчетную схему
призматической оболочки2).
§ 14.5. Неравномерность деформации по ширине пояса
в тонкостенном стержне при изгибе. Понятие
о редукционном коэффициенте
При изгибе балок с поперечным сечением типа двутавра
с широкими поясами (рис. 14.29, а), коробчатого сечения (14.29, б, в)
с большими расстояниями между стенками и т. п., если внешние
воздействия, вызывающие чистый изгиб балки, непосредственно
приложены к стенке (стенкам), наблюдается следующая картина
деформации. В сжатом поясе лишь то волокно, которое
непосредственно связано со стенкой, испытывает деформацию, такую же
как и примыкающее к нему волокно стенки. Остальные же волокна
в сжатой полке укорачиваются в меньшей мере. Наибольшее
«отставание» укорочения происходит в крайних волокнах полки.
Наоборот, в растянутой полке —во всех волокнах, не
соединяющихся непосредственно со стенкой, происходит «отставание»
удлинений по сравнению с удлинением волокна полки, соединенного
со стенкой. Вследствие этого торцевые сечения перестают быть
плоскими — происходит их депланация — напряжения в
поперечных сечениях полок распределяются неравномерно. С увеличением
г) После Кармана исследованию подвергались трубы и иных поперечных
сечений. Прямоугольное — исследовано С. П. Тимошенко (см. статью в
юбилейном сборнике трудов, посвященном семидесятилетию А. Феппля — Festschrift
zum siebzigsten Geburstage A. Fopple, 1923, S. 74), эллиптическое и
плоскоовальной формы—В. И- Феодосьевым (Расчет тонкостенной трубки Бурдона
эллиптического сечения энергетическим методом, Оборонгиз 1940), Р. Кларком,
Т. Гилроем и Э. Рейсснером (Clark R., Gilroy Т., Reissner E. Stress and
deformations of toroidal shells of elliptical cross sections, — J. Appl. Mech.
1952, 19), Д. Л. Костовецким (Костовецкий Д. Л., Прочность трубопроводных
систем энергетических установок. — Л·: Энергия, 1973), линзообразного
сечения—Олесяком (Olesiak EIZ.; The bending of thin-walled pipes with lenticular
cross sections. — Bull, de l'Acad. Polon.).
2) В л а с о в В. 3. Строительная механика тонкостенных пространственных
систем.—Стройиздат, 1949, гл. Ill,
426 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ (ГЛ. XIV
ширины полок и уменьшением их толщины эта неравномерность
возрастает —стенка, деформируясь, все менее эффективно увлекает
за собой (вовлекает в работу) полки. Поскольку внутренний
изгибающий момент должен уравновешивать внешний, и величина
Рис. 14.29. Характер деформации и распределения напряжений в тонкостенной балке
при изгибе моментами, приложенными к стенкам: а) изгиб двутавровой балки; б) изгиб
коробчатой балки; в) распределение напряжений в поясах многоконтурной балки; г)
распределение напряжений в поперечном сечении балки, изображенной на фиг. а.
его тем самым фиксирована, уменьшение абсолютных значений
фактических напряжений в какой-то части сечения связано
с неизбежным увеличением их в другой части, примыкающей
к стенке (рис. 14.29, г), по сравнению с величинами напряжений,
которые получаются в элементарном расчете, основанном на
предположении равномерного распределения напряжений по ширине
полки. Сечения торцов остаются плоскими лишь, если моменты
§ 14.5] ПОНЯТИЕ О РЕДУКЦИОННОМ КОЭФФИЦИЕНТЕ 427
фактически приложены так, как это предписывается элементарной
теорией балок.
На рис. 14.30 показаны различные случаи нагружения
тонкостенных стержней силами, приложенными к торцам, и
соответствующие им картины деформации стержней. Как уже
указывалось (§§ 2.7, 9.9), принцип Сен-Венана применим к тонкостенным
г) £) е)
Рис. 14.30. Депланацня тонкостенного двутаврового поперечного сечения при
различных воздействиях на торец с учетом детального характера приложения нагрузки:
а) равномерно распределенная нагрузка, приложенная к стенке; б) равномерно распре»
деленные нагрузки одного знака, приложенные к полкам; в) сосредоточенные силы,
приложенные в местах присоединения полок к стенке; г) сосредоточенные силы одного знака,
приложенные к центру сечения н к краям полок; д) распределенная нагрузка нзгнбногэ
характера, приложенная к стенке; е) равномерно распределенные нагрузки разного знака,
приложенные к полкам.
стержням лишь в случае замены одной системы сил другой ей
статически эквивалентной в пределах площадки торца
(поперечного сечения), характерный размер которой имеет порядок
минимального характерного размера материальной части поперечного,
сечения (имеется в виду толщина пластин, образующих стержень).
Для того, чтобы, заменяя одну нагрузку другой, если обе они
428 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ, XIV
действуют в пределах всего поперечного сечения тонкостенного
стержня, получать при этом выполнение принципа Сен-Венана,
необходима эквивалентность нагрузок и в сверхстатическом смысле
(например, равенство бимоментов в двух сопоставляемых случаях,
кроме равенства усилий Д4, N, ...)· В противном случае
затухание эффекта самоуравновешенной нагрузки или приближение
картины распределения напряжений к номинальной,
соответствующей формулам сопротивления материалов, происходит намного
медленнее по длине балки, чем в массивных стержнях.
В связи с обсуждаемым находится и вопрос о правомочности
перенесения момента в пределах поперечного сечения.
а
) f
< >
6
=ч
^
1
J
1
\
_—ή^
1
==/Г Ι ν
*А
У
е d
а)
6)
Рис. 14.31. К установлению понятия редукционного коэффициента: а) распределение
напряжений в поперечном сечении полки балки двутаврового сечения (abode — действи»
тельная эпюра напряжений; fgchi — условная эпюра равномерно распределенных
напряжений по площади, равновеликая действительной эпюре напряжений): б)
поперечное сечение двутавровой балки.
Расчет конструкций должен выполняться с учетом отмеченной
выше неравномерности работы полок тонкостенных балок. При
этом доводить до допускаемой величины можно лишь
максимальные напряжения. Вследствие этого в остальной части полки имеет
место недонапряжение, возможности материала используются не
полностью. Важно знать меру этого недоиспользования, чтобы
не перегрузить материал в местах возникновения максимальных
напряжений.
В расчетной практике широко распространен прием
проектирования, в котором используются так называемые редукционные
коэффициенты. Если бы действительная эпюра напряжений,
неравномерно распределенных в полке балки, была известна (рис. 14.31),
то можно было бы вместо фактической ширины В в расчет
вводить некоторую ее часть— так называемую приведенную ширину*
определяемую из условия
£ΠρσΙΙί8χ = \ σ dx = ac?B. (14.87)
§ 14.5] ПОНЯТИЕ О РЕДУКЦИОННОМ КОЭФФИЦИЕНТЕ 429
Интегрирование в (14.87) ведется по всей ширине полки.
Иными словами, приведенной называется такая ширина, через
которую может быть пропущен тот же поток напряжений, какой
пропускается через всю полку, однако при условии равномерного
распределения напряжений, равных максимальному напряжению
в действительной эпюре.
Отношение
^ = Ф = ^ (14.88)
" "max
называют редукционным коэффициентом; он показывает, какую
долю действительной ширины полки следует вводить в расчет
балки, в котором предполагается равномерное распределение
напряжений по приведенной ширине и величина напряжения
принимается равной максимальному напряжению в действительной
эпюре с неравномерным распределением. Редукционный
коэффициент является и мерой отклонения среднего напряжения от
максимального.
Может возникнуть вопрос — зачем же вводить в расчет
приведенную ширину полки и редукционный коэффициент, если известна
действительная эпюра. Разумеется, будь на самом деле
действительная эпюра напряжений известна ни приведенной ширины
полки, ни редукционного коэффициента вводить не следовало бы.
Использование этих понятий оказывается целесообразным,
если действительная эпюра напряжений не известна, а величина
редукционного коэффициента каким-то образом приближенно
может быть установлена. Приближенное установление величин
редукционных коэффициентов может быть выполнено различными
методами, например, экспериментальным путем в опытах раз
навсегда проведенных с конструкциями или их моделями.
Разумеется, такие опыты следует производить для каждого типа
конструкции и характерного воздействия на нее.
Другой подход к отысканию редукционных коэффициентов
теоретический — путем выполнения раз навсегда расчета методом
теории упругости некоторого множества типичных конструкций
при характерных воздействиях.
Редукционный коэффициент широко используется в практике
проектирования корпусов судов и самолетов. При этом такое
использование не ограничивается широкополыми тонкостенными
балками. Весь корпус судна представляется в виде балочной
расчетной схемы, называемой эквивалентной балкой или брусом. При
этом продольные связи корпуса и обшивка вводятся в
эквивалентный брус с различными редукционными коэффициентами
в зависимости от протяженности, конструктивных особенностей,
режимов работы. Мировой опыт кораблестроения позволил
накопить информацию для такого подхода к оценке так называемой
430 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
обицей продольной прочности. Казалось бы целесообразно
ограничивать ширину полок в балках, коль скоро при больших
ширинах материал в них используется недостаточно эффективно.
Однако делать пояса балок широкими приходится в ряде случаев
из эксплуатационных, технологических, конструктивных и других
условий.
Из формулы (14.88) очевидно, что в разных поперечных
сечениях балки величина редукционного коэффициента, вообще говоря,
различна, поскольку могут меняться и аср и атах. Редукционный
коэффициент зависит от типа поперечного сечения, соотношения
размеров, характера закрепления балки, и от приложенной к ней
нагрузки.
Исследование величин редукционных коэффициентов для
трубчатых балок выполнил П. Ф. Папкович *).
Рассматривал вопрос о неравномерном распределении
напряжений по ширине пояса тонкостенной балки при ее изгибе и
В. 3. Власов2).
§ 14.6s Примеры расчета стержней открытого тонкостенного
профиля
Пример 14.1. Проанализировать характер деформации тонкостенного
стержня открытого профиля при условии, что, кроме ограничений,
накладываемых на деформацию гипотезами о неизменности проекции контурной линии
на плоскость поперечного сечения, и отсутствии сдвигов в срединной
поверхности, имеет место ограничение εζ = 0 (отсутствие продольных удлинений во
всей срединной поверхности стержня).
Решение. Используя формулы (14.15) и (14.12) и имея в виду условие,
накладываемое на εζ, получаем
w'Mt (z)-uA(z)x*(s)-vA (г) у* (s)-^(z)co(s)=0. (14.89)
Учитывая линейную независимость функций 1, х* (s), у* (s) и ω (s), заключаем,
что условие (14.89) выполняется лишь при равенстве нулю коэффициентов
при этих функциях, т. е.
^Λί, (z) = 0' u"a(z) = °> v"a(z)=0> *£(ζ) = °· (14.90)
Условия (14.90) возможны, если сами функции wM (ζ), иА(г), νΑ{ζ) и ω (s)
имеют следующий вид:
™мЛг)=сЬ uA{z)=C2+CiZ, ua(z) = C3+C5z, Ъг (г) = Сй + С7г. (14.91)
Функции (14.91) получены путем интегрирования уравнений (14.90).
Постоянным интегрирования Ci, ..., С7 можно дать механический смысл. Для этого
достаточно наряду с (14.91) рассмотреть и результат первого интегрирования
уравнений (14.90)2l3,4
и'А{г)=Сь и'А(г) = Съ, %{г)=С„ (14.92)
х) Π а п к о в и ч П. Ф., Теория упругости, Оборонгиз, Л.-М., 1939, глава X,
§ 9, § 12.
2) Власов В. 3., Строительная механика тонкостенных пространствен*
ных систем,. Стройиздат, 1949, гл. VI.
§ 14.6] ПРИМЕРЫ РАСЧЕТА ТОНКОСТЕННОГО СТЕРЖНЯ 431
и положить как в (14.91), так и в (14.92) ζ = 0· Тогда, согласно (14.92),
С4=и'А(0), Cb = v'A(0),. С7 = Ъ'г(0), (14.93)
т. е. С4 и С6 представляют собой углы наклона в сечении 2 = 0 проекций
соответственно на плоскости Oxz и Оуг, касательной к пространственной
кривой, в которую превращается волокно, параллельное оси стержня и
проходящее через точку А; С7 — погонный угол закручивания стержня в сечении z=0.
Согласно (14.91)
т. е. Ci^— перемещение, параллельное оси ζ, точки Μι в сечении ζ = 0; С. и
С3—перемещения точки А в сечении ζ = 0, параллельные осям χ и у
соответственно, и ϋζ — угол поворота контурной линии в сечении ζ = 0. Учитывая
(14.93) и (14.94), напишем (14.91) в следующем виде:
w
м
i(z) = wMi(0), uA(z) = uA(0) + u'A(0)z, vA{z) = vA(0) + u'A(Q)z,
<Uz) = O2(0) + ^(0)z.
Поскольку проекция контурной линии на плоскость z = 0 представляет
собой неизменяемую фигуру, которая может лишь перемещаться в этой
плоскости, величины иА (0), υΑ (0) и wM (0) определяют собой поступательное
перемещение этого начального сечения вдоль осей х, у и ζ. Величины иА (0),
νΑ (0) и 02 (ζ) — определяют собой повороты сечения относительно осей х, у
и ζ соответственно, ϋ1^ (0) — обобщенное перемещение в сечении ζ = 0,
определяющее собой меру депланации сечения, а сама депланация первоначально
плоского поперечного сечения, согласно (14.13), происходит по закону
секторной площади ω = ω(δ).
Величины
"л(0), vA(0), wMi(0), uA(0), ϋ'Α(0), ϋζ(0) (14.95)
определяют собой перемещение сечения ζ = 0 как жесткого целого и,
следовательно, в составе функции (14.91) имеется лишь один параметр C1=b'0(z),
с которым связана деформация стержня.
Для того чтобы исключить из перемещений, определяемых по формулам
(14.91), доли, представляющие собой перемещение как жесткого целого, все
величины (14.95) следует положить равными
нулю
w
м
t(0) = uA (0) = vA(0) = u^ (0) = υ'Α(0) =
^500кГ/м
= Аг(0)=0; (14.96)
тогда из (14.91) с учетом (14.93) остается
O2(2) = ft.£(0) ζ, τ· е· стержень испытывает
лишь кручение с постоянной
интенсивностью угла закручивания $^(ζ) = κζ(ζ) = ϋ'ζ (0).
При этом, согласно (14.13), с учетом (14.91),
(14.92), (14.93) и (14.96) w (z, s) = hz (ζ)ω (s),
т. е. выяснилось, ч.то тонкостенный
стержень открытого профиля в предположениях,
сделанных в условиях примера, испытывает
свободное кручение.
Пример *) 14.2. Определить напряжения от стеснения депланации в
стержне, изображенном вместе с нагрузкой, действующей на него, на рис. 14.32.
Положение центра изгиба, с которым, как было отмечено, совпадает главный
секторный полюс для рассматриваемого в настоящем примере попереч-
Рис. 14.32. К примеру 14.2.
*) Вычисления в примере 14.2 выполнены.И, Ц, Рыбиной,
432
СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
ного сечения, было определено в примере 12.10· Там же были найдены и
главные оси инерции.
-ЗЩ*
■551$
ЦИ 6,9
а) 298.8
γτβ5Ζ,δ
255,9
д)
-19,78
112,55
Рис. 14.33. К примеру 14.3: а) координаты центра тяжести и центра изгиба; б) эпюра
ω; β) эпюра ω«. г) эпюра S °ТС; д) составляющие распределеннной нагрузки и их плечи
относительно центра изгиба; е) эпюры а^'при 2=0 и г = /.
Решение. Нормальные и касательные напряжения, соответствующие
стеснению деформации, находим по формулам σ = βω//ω, τ2|=Λίω5°τν(δ7ω).
Используя центр изгиба в качестве полюса, строим эпюру секторных
площадей ω (s^ при произвольном выборе точки начала отсчета (за таковую
принимаем точку / (см, рис. 14.33, а),
§ 14.61 ПРИМЕРЫ РАСЧЕТА ТОНКОСТЕННОГО СТЕРЖНЯ 433
1. На рис. 14.33, а показаны плечи hi, необходимые для построения этой
эпюры ω (на контуре). На рис. 14.33, б представлена эпюра ω^).
2. Находим интеграл 5ω = ^ω^(δ])ίί^
F
Sb=_2.^-335-552-3+316-720-3I6'7-28'38.50-
-28,38 +634,9, ί5_ 634,9 +.203 ,„__„„ ^
2
3. Находим (йА (s12) no формуле (14.42)
ωΑ («ft) = β = ^ - - ^ = -296,8 «A
4. Определяем положение точки с ординатой ωΑ (s^ на эпюре ω (δχ),
принимаемой за новую точку начала отсчета ω, которой соответствует эпюра
главных секторных площадей. На рис. 14.33, в показана эта операция. После
этого строим эпюру главных секторных площадей (см. рис. 14.33, в).
5. Произведем проверку ортогональности функций ω и χ, ω и у, для чего,
пользуясь правилом Верещагина, вычисляем интегралы V χω dF и \ yω dF.
F F
Эпюры х и у представлены на рис. 12.50, з и ж соответственно.
ί
WdF=~? [296,8 (2 -23,64-9,076) —255,6 (—2 · 9,076 + 23,64)] +
1 -20
+ -Lpi [—255,6 (—2 · 9,06- 16,17)- 19,94 (—2 · 16,17-9,06)] +
1 . 50
+ -Lpi [—19,94 (—2 · 16,17-2,323) +325,2 (-2 · 2,323- 16,17)] +
+ ^r^ [325,2 (—2-2,323+11,70) — 338,1 (2-11,70 — 2,323)] +
+ ^r^ [—338,1 (2 -11,70+ 15,25)-905,9 (2 · 15,25+11,70)] =
= 148000—148000 = 0,
yω dF=^-^- [296,8 (2 · 14,68 + 27,11)-255,6 (2-27,11 + 14,68)] +
1 -20
+ !-~ [—255,6 (2 · 27,11 +8,409) —19,94 (2 - 8,41+27,11)] +
Η—g-^ [—19,94 (2 · 8,409 — 39,63) +325,2 (—2 · 39,63+8,409)] +
.+ 111*? [325,2 (—2 · 39,63- 44,96) - 338,1 (—2 · 44,96 - 39,63)] +
+ Ijp [—338,1 (—2 · 44,96-35,61) -905,9 (2 · 35,61 - 44,96)] =
= 254000 — 254000 = 0.
Равенство нулю интегралов свидетельствует об ортогональности функций ω
и χ, ω и у.
434
СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
6. Строим эпюру S°TC. На рис. 14.33, г показана разбивка контура попе?
речного сечения стержня на участки пятисантиметровой длины. Вычисления
S°TC сведены в табл. 14.1 (столбцы I-j-IV).
7. Находим главный секторный момент инерции, используя прием
Верещагина
С 35
/ω= \ a*dF = 2 · -g-[296,8 (2 · 296,8 — 255,6) — 255,6 (—2 -255,6 + 296,8)] +
20
+ 1 ■ -g- [—255,6 (—2 ■ 255,6- 19,9)- 19,9 (—2 . 19,944 — 255,6)] +
50
+ 1 · -ξ [—19,9 (—2 · 19,9 + 325,2) + 325,2 (+2 · 325,2- 19,9)] +
+ 1 ~ Γ325;2 (+2 · 325,2-338,1)-338,1 (—2 . 338,1+325,2)] +
ο
+ 1 -^[—338,1 (—2-338,1—905,9) —905,9 (—2-905,9 —338,1)] = 8 630 000 еж*.
8. Определяем интенсивность внешней распределенной моментной,
крутящей нагрузки tnz. Раскладываем интенсивность распределенной нагрузки q на
составляющие qx и q и определяем плечи этих составляющих относительно
центра изгиба. Соответствующая информация помещена на рис. 14.33, д
qXi = q cosα0 = 500 ·0,9349 = 467,4 /сГ/ж = 4,674 кГ/см,
qyi = q sin α0 = 500· 0,3549= 177,4 /сГ/ж= 1,774 кГ/см,
/i1 = 5,781 -cosa0—11,78-sin «0 = 5,781 .0,9349—11,78.0,3549=1,225 см,
/ι2 = 5,781 · sin α0+11,78-cos «0 = 5,781-0,3549+11,78-0,9349= 13,06 см,
tnz = qXzhi + qy2fh= 4,674- 1,225+1,774- 13,06 = 28,91 ^^.
9. Находим функцию ϋζ путем интегрирования дифференциального
уравнения
*ίν-£**'=/<*>. 7^-lfe-» Пг)=-Щ' (14·97)
Итак, общий интеграл этого уравнения (14.54) имеет вид1) (здесь мы не
пользуемся формулой метода начальных параметров)
O^Ci + CeZ + Csch-^-z+CASh-y-z-^^-z». (14.98)
!) Последний член в (14-98) представляет собой частное решение
уравнения (14.97), которое, учитывая, что тг = const, получаем следующим образом.
Представляем его в следующей форме:
Α2,4.ρ=Λ4Ζ4 + Αίζ3+Λ2ζ2+Λ1ζ. (14.99)
Найдем первые четыре производные функции (14.99)
Ъг, ч.р = 4Л4гз+ЗЛ3г2 + 2Л2г+Л1, < ч.р= 12Л4г2 + 6Л3г+2Л2,
Сч.р=24Л42 + бЛ3, ^учр = 24Л4. (14Л00)
Подставляя (14.100)2г4 в (14.97)]; получим
24Л4-^- (12Л422+6Лзг + 2Л2) = / (ζ),
k2 mzl2 f (z)/a
отсюда Л4=0, Л3=0, — -^2Аг = тг, Аг=— -^-; ϋ2, ч.р = 2£2~ζ2·
§14.6? ПРИМЕРЫ РАСЧЕТА ТОНКОСТЕННОГО СТЕРЖНЯ 43с>
Таблица 14.1
№ точек
1
I
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
ωό, см*
II ■
—905,9
—622,0
—338,1
— 117,0
104,1
325,2
290,6
256,1
221,6
187,1
152,6
118,1
89,6
49,1
14,6
-19,9
—78,8
— 137,7
—196,7
—255,6
-176,7
—97,8
-18,8
60,1
139,0
217,9
296,8
AS°TC, «.«
ω
III
2 "5
0
—3819
—2400
— 1138
-32
1073
1540
1367
1194
1022
849
677
504
331
159
-13
—247
—541
—836
— 1131
—2161
— 1372
—583
206
995
1784
2572
S°TC. см*
ω
IV
iv._1 + Mb
0
—3819
—6219
—7357
—7389
—6316
—4776
—3409
—2215
— 1193
—344
333
837
1168
1327
1314
1067
526
—310
^1441
—3602
—4974
—5557
—5351
—4356
—2572
0
x*t· кГ/см1
ν
iv.f ^ )
0
3,839
6,250
7,394
7,427
6,349
4,801
3,428
2,222
1,201
0,348
—0,333
—0,839
—1,173
—1,332
-1,319
-1,071
-0,527
0,3114
1,449/0,725
1,810
2,520
2,793
2,689
2,189
1,293
0
Если начало координат принять посредине длины стержня, то вследствие
симметричности задачи в выражении (14.98) для функции θ2 сохраняем лишь
члены, представляющие собой четные функции, т. е.
^z = Ci-{-C3ch—z
т212
2kaEl,
■ζ*.
ω
(14.101)
Граничные условия при заданном характере закрепления концов стержня
имеют вид
ζ \z-iiz
= 0,
^/2 = °·
436 СТЕСНЕННАЯ ДЕФОРМАЦИЯ ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XIV
. В разверну-
Возьмем производную от (14.101) по z, ^ = C3-r-sh-: .
I I R £11 (^
той форме граничные условия выражаются так:
k , kz mzl2z
„ — sh *
2 ~<> /
с1+с>Н-Мга=°- c»rsh4
= 0,
ω
Отсюда
Ся =
m,/4
2£3£/(ushy '
Сг =
mzll
mzl* Ch 2
8№ΕΙω 2№ΕΙω shk_
и функция (14.63) приобретает вид
#, = mz'4
8ftȣ/,
ω
2W7^cthT +
m,/4
2Λ»£/ω8Η-|-
, £ζ m2/2
— СП Ζ2.
k C I 2№Ιω '
или
ф*=
m2/2
i2.
4
xcihT+-——
* sh —
z2
или
m,
2G/K
h —
T_TcthT + T—Γ-Ζ2
Нам понадобятся вторая и третья производные по ζ от θ2
га2
2G/K
sh — ζ
/ Ц- 2ζ
shi
m,
2G/K
£ch
kz
sh
m, £2
sh
kz
10. Определяем бимомент
Β = -£/ωθ2 = -£/
'ω
"г
мент
mz
2G/K
2G/K /
ch -j- ζ
*—ίγ
1 k
sh-g
— 2
•
= -
m2/2
2*2
ch -3-z
sh -τ-
Η, Определяем изгибно-крутильный момент
'ω-
2£2 /
v. *
shT
, kz
mzl I
ΊΓ~~Τ'
shT
§ 14.6]
ПРИМЕРЫ РАСЧЕТА ТОНКОСТЕННОГО СТЕРЖНЯ
437
12. Строим эпюры нормальных напряжений, вызванных стеснением депла-
нации в двух характерных поперечных сечениях 2 = 0 и ζ = 1/2
σ(ω) = β(ΰ =
I
ω
m2/2co
-2Ί*ΰ
ch
kz
I
и k
— 2
,<ω) Ι =,
mzl2(u
ω
_ft
2
i, k
— 1
(ω), =_^oricthl_1].
» °* \z-l/2 ^2/ω [2 2 J*
/K = i- У &£6ί = Jr[10· 13+15.13 + 50· 13 + 20-13 + 35. 23] = 125 см*;
= 1,416;
*='/1£=600/
2,1· 106· 125
2 (1+0,3)· 2,1 .ΙΟβ-8 630 000
sh-|- = 0,7687, cth ^- = 0,6095;
Ki =
mJ2
Mo
k_
2
v, k
— ι
28,91 · 6002
1,4162·8 630 000 10,7687
[»-']-«и«.
*· — %£[т Cth Τ"1]— Mw'VSToOO 10.708-0.6095-4 = 0.3436,
ИЛИ
< U-*i»·
и σ<ω) '
На рис. 14.33, е показаны эпюры σ2ω) )2_0 ,. ~г \г-цъг
13. Определяем касательные напряжения, вызванные стеснением депла-*
нации
kz
(ω) <ύ a> 2 ω
T,t —'
/
lzl
δ/
ω
2fi /ω ft ·
П 2
Определение ординат эпюры τ2|' в сечении заделки (ζ = 1/2) сведена
в табл. 14.1 (столбец V). При этом учтено, что
28,91 · 600
mzi
2677
'ω
2 · 1 · 8 630 000
28,91-600
= —0,001005, 6=1,
2 ■ 2 · 8 630 000
=—0,000502, δ = 2,
Отдел пятый
ОБЩИЕ ПРИНЦИПЫ, ЗАКОНЫ, ТЕОРЕМЫ, МЕТОДЫ
СТАТИКИ ДЕФОРМИРУЕМЫХ СИСТЕМ
Глава XV
ВАРИАЦИОННЫЕ ПРИНЦИПЫ И ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ
СТАТИЧЕСКОЙ ПРОБЛЕМЫ УПРУГОСТИ
§ 15.1. Вводные замечания
Поведение механических систем может быть описано двумя
эквивалентными способами: локальным — при помощи
дифференциальных уравнений и вариационным — при помощи экстремальных
принципов. Первый из них рассматривался в предыдущих главах,
второму посвящена настоящая глава. Между этими способами
имеется глубокая как физическая, так и математическая связь.
Физическая связь может быть проиллюстрирована таким
примером: положение устойчивого равновесия механической системы
есть положение, отвечающее минимуму ее потенциальной энергии
(шарик на дне чаши).
Математическая связь состоит в том, что решение краевой
задачи или задачи Коши для дифференциального уравнения,
описывающего поведение данной механической системы,
оказывается эквивалентным проблеме отыскания функции,
минимизирующей определенный интеграл, которым выражается
потенциальная энергия системы. Если иметь в виду, что минимизация
определенного интеграла (функционала) является предметом
вариационного исчисления, можно сказать, что решение краевой
задачи или задачи Коши для дифференциального уравнения
эквивалентно решению соответствующей вариационной проблемы.
В настоящей главе читатель знакомится с теми вариационными
(экстремальными) принципами, которым подчиняется поведение
механических систем1). Предварительно в § 15.2 читателю напо-
1) Вариационным проблемам механики посвящена большая литература;
в частности вариационные проблемы теории упругости обсуждаются в следующих
использованных нами книгах и статьях:
Курант Р. и Гильберт Д. Методы математической физики, том
первый, перевод со второго немецкого издания 1930 г. (первое немецкое издание
в 1924 г.) Либина 3., Лившица Б. и Рабиновича Ю. Издание третье
исправленное. — М.: Гостехиздат, 1951; Папкович П. Ф. Теория упругости.—
Оборонгиз, 1939; Лейбензон Л, С Вариационные методы решения задач
§ 15.2] ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ПРОБЛЕМЫ МЕХАНИКИ 43£
минается минимум необходимых сведений о вариационном
исчислении. Далее обсуждаются принципы и теоремы, лежащие в
основе статической проблемы механики деформируемого тела,,
для которой фундаментальными являются понятия равновесия,,
совместимости деформаций и физического аспекта напряженно-
деформированного состояния. При этом речь идет как об упругой
системе, состояние которой характеризуется конечным числом
параметров, так и о сплошной упругой среде, описываемой
функциями. Определение перемещений в упругой системе,
вызванных ее деформацией, вытекает из основного содержания главы,.
в связи с чем и этот вопрос рассмотрен именно в настоящей главе.
§ 15.2. Вариационное исчисление и связь его
с проблемами механики
1. Основные понятия. Предметом вариационного исчисления *)
является исследование функционалов на максимум и минимум.
теории упругости.—М.: Гостехиздат, 1943. Пратусевич Я- А.
Вариационные методы в строительной механике.—М.: Гостехиздат, 1948. Мих-
л и н С. Г. Проблема минимума квадратичного функционала.—М.: Гостехиздат,
1952. Гольденблатт И. И. Экстремальные и вариационные принципы.
в теории сооружений. — В кн.: Строительная механика в СССР 1917—1957/
Под ред. Рабиновича И. М. — М.: Гостехиздат, 1957. Ми χ ли н С. Г.
Вариационные методы в математической физике.—М.: Гостехиздат, 1957. Рейс-
снер Э. О некоторых вариационных теоремах теории упругости.—В кн.:
Проблемы механики сплошной среды (к 70-летию акад. Н. И. Мусхелишвили). —
М.: Изд-во АН СССР, 1961. Ланцош К· Вариационные принципы механики,
перевод с англ. Гантмахера В. Ф. Под ред. Полака Л. С—М.: «Мир», 1965.
Gunard Oravas, Leslie McLean. Historical development of
energetical principles in Elastomechanics. — Applied Mechanics Reviews, 1966,
№ 8, 11. Михлин С. Г. Численная реализация вариационных методов. —
М.: Наука, 1966.
Washizu К. Variational methods in elasticity and plasticity.—Oxford,
Peragmon Press, 1968; Second ed., Pergamon Press, 1975.
Tonti E. Variational principles in elastostatics.—Meccanica, 1967, 2r
№ 4, 201—208 (Имеется перевод на русский язык: Вариационные принципы
в теории упругости (перевод В. А. Пальмова).—Механика (периодический
сборник переводных статей), 1969, № 5(117), с. 124 —138, «Мир»).
В некоторых из этих источников имеется большая библиография.
Вариационные принципы, относящиеся к упругим и упруго-пластическим
системам, рассматривались в работах Гвоздева А. А. (1934, 1938), в книге
Новожилова В. В. (Теория упругости. Судпромгиз, 1958). Вариационные
принципы в теории оболочек обсуждены в статьях Алумяэ Η. Α., А й-
нолы Л. Я-, Галимова К. 3., Абовского Н. П.
Вариационные принципы в механике (в широком смысле) рассматриваются
в курсах аналитической механики и в книгах:
Вариационные принципы механики/Под ред. Полака Л. С—М.: Физ-
матгиз, 1959.
По лак Л. С. Вариационные принципы механики, их развитие и
применение к физике.—М.: Физматгиз, I960.
х) Укажем некоторые руководства по вариационному исчислению:
Лаврентьев М., Люстерник Л. Основы вариационного исчисления
т, I, П.—М.: Гостехиздат, 1935; Лаврентьев Μ. Α., Люстерник Л. А.
ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Функционалом называется переменная величина (число), значение
которой зависит от выбора функции, принадлежащей некоторому
классу. Функционал может зависеть и от нескольких функций,
каждая из которых принадлежит своему классу. В качестве
примера функционала можно привести время, требующееся для
•скатывания в вертикальной плоскости шарика по желобу из
точки А в точку В (рис. 15.1),
t-
J V2gy
(15.1)
Функция у = у(х) характеризует форму желоба в плоскости л#.
При разных у время t различно. Функция у(х) в функционале
играет роль, аналогичную роли
аргумента в функции. Вариационная
проблема для функционала (15.1)
формулируется так: найти функцию
У = У(Х)> при которой t оказывается
минимальным. Функция у ищется
на множестве функций,
обеспечивающих условие прохождения
кривых, соответствующих им, через
точки А и В и обладающих
непрерывностью и гладкостью. Отмеченные
условия определяют класс функций,
от которых зависит функционал.
Функция у, которой соответствует
экстремальное значение функционала,
называется экстремалью1).
Экстремаль в вариационном исчислении играет роль, аналогичную
выполняемой в обычном анализе значением аргумента функции, при
котором последняя имеет стационарное, в частности
экстремальное, значение.
В качестве еще одного примера функционала рассмотрим
потенциальную энергию деформации изгибаемого стержня (влия-
Рис. 15.1. К постановке
вариационной задачи о шарике,
скатывающемся по желобу из точки А в
точку В.
Курс вариационного исчисления, изд. второе переработанное.—М.: Гостехиздат,
1950; Б лисе Г. А. Лекции по вариационному исчислению. Пер. с англ.
■Солнцевой Ю. К. под ред. Эльсгольца Л. Э. —М.: ИЛ, 1950; ЭльсгольцЛ. Э.
Вариационное исчисление. —М.: Гостехиздат, L952. Ахиезер Н. И. Лекции
по вариационному исчислению. —М.: Гостехиздат, 1955; Гельфанд И. М.,
Фомин С. В. Вариационное исчисление. —М.: Физматгиз, 1961.
!) Экстремалью в вариационной задаче для функционала (15.1) является
■циклоида, такая экстремаль названа брахистохроной; задача о ней была
предложена Иоганном Бернулли (1696) и решена, кроме него, еще И.
Ньютоном, Яковом Бернулли старшим и Г. Лопиталем. Эта задача явилась истоком
вариационного исчисления.
§ 15.2] ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ПРОБЛЕМЫ МЕХАНИКИ 441
ние сдвигов при поперечном изгибе для упрощения примера
учитывать не будем)
ι ι
17 = J-set· или1> u=) 2 ·
о о
Здесь U представляет собой число — некоторую размерную
величину. Это число зависит от υ" (ζ), а следовательно, от υ (ζ) —
функции, описывающей кривую, являющуюся осью изогнутой балки
(υ" (ζ) = 1 /ρ (ζ) — функция, характеризующая изменение кривизны2)
оси по длине балки). Если задаваться очертанием оси изогнутой
балки, т. е. задаваться видом функции ν (ζ) (а следовательно, иг
функции υ" (ζ)), то каждой такой функции υ(1) (ζ) будет
соответствовать значение (число) потенциальной энергии деформации U{iK
Можно поставить задачу найти функцию3) υ (ζ), при которой
функционал U принимает минимальное значение. В таком случае
задача становится вариационной 4).
Как будет пояснено в последующих параграфах, в механике
сформулированы так называемые вариационные принципы, в
которых экстремальность некоторых функционалов, имеющих
энергетическую природу, выражает определенные свойства механической
системы. Вследствие этого проблемы механики могут
формулироваться как вариационные.
Если^функционал Г [у (х)] достиг экстремума на экстремали у (х),.
то приращение функционала Δ/ = / [у (х)] — I [у(х)]> вызванное,
переходом от кривой у = у(х) к другой кривой у(х), называемой
кривой сравнения, должно сохранять свой знак, какая бы кривая
сравнения ни была взята. Если функционал / достиг на у(х)
минимума, то Δ/>0, а если —максимума, то Δ/<0. Разность
у(х) — у (х) называется вариацией функции и обозначается δ#
(рис. 15.2): Ьу = у{х)-у{х).
1) Здесь учтена зависимость М = —ΕΙν".
2) Имеются'в виду малые прогибы балки, при которых (у')2<^1.
3) Разумеется, сравниваемые функции ν (г) должны удовлетворять
кинематическим условиям, накладываемым на ось балки (условия закрепления в
пространстве; непрерывность (если нагрузка не сосредоточенная) самой функции
и трех ее производных.
*) Указание на экстремальность энергии деформации мы находим у Л. Эйлера
и Д. Бернулли, с именами которых связано возникновение вариационного
исчисления. Д. Бернулли в 1738 г. в письме к Эйлеру предложил ему вывести
уравнение изгиба балки Якова Бернулли путем решения вариационной
проблемы для функционала 1 ——. Эта величина с точностью до постоянного-
множителя £7/2 представляет потенциальную энергию деформации балки.
Доказательство этого положения Л. Эйлер опубликовал в 1744 г. В
рассуждениях Д. Бернулли и Л. Эйлера не имелся в виду функционал U', хотя,
строго говоря, рассматривать нужно .именно его (см. ниж姧 15.6 и 15.12)»
442 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Роль вариации Ьу в вариационном исчислении аналогична
роли приращения независимого аргумента при изучении функции.
Вариация функции Ьу — сама является функцией х.
Если функционал 7 достигает экстремума лишь по отношению
к близким кривым сравнения у = у-\-Ьу, то экстремум называется
относительным (сравните с относительным экстремумом функции).
О
/&*
/
Τΰχ>β
-»-
Χ
Рис. 15.2. Вариация функции, при
которой малы by и Ьу'.
У*
о
УтУ<Ы
А
В
у-у(®
а;
Рис. 15.3. Вариация функции, при
которой Ьу малая величина, а
Ьу' — большая.
Если при этом Ьу — малая величина, а Ьу' — может быть и
большой величиной (рис. 15.3), то экстремум функционала называется
сильным; при условии малости как Ьу, так и Ьу' — слабым (рис. 15.2).
Χι
Приращение функционала1) / = $ F (х, у, у') ах, обусловленное
Хо
варьированием у и у , имеет вид
Xt
ы = $[т£&у+§]<ь+*=ы+*.
Хо
•Ы — называется вариацией функционала и является главной
линейной частью приращения функционала. Величина Ы играет роль,
аналогичную дифференциалу функции —дифференциал функции
тоже представляет собой главную линейную часть приращения
■функции, R — остаточный член. Интегрируя второе слагаемое
подынтегрального выражения в Ы по частями и учитывая
граничные условия для Ьу, Ьу\х==Хо = 0, by\XssXl = 0t получаем
Χι
•ΜΕ-έ®]**
(15.2)
Хо
Необходимым условием экстремума функционала является
обращение в нуль его вариации, т. е. 67 = 0. Так как интеграл
в (15.2) при таком условии должен быть равен нулю при любых
^Имеется в виду, что F(x, у, у') дифференцируема по х, у и у'.
§ 15.2] ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ПРОБЛЕМЫ МЕХАНИКИ 443
Ьу, нулю должно равняться выражение в скобках *)
Уравнение (15.4), называемое уравнением Эйлера, и является
необходимым условием экстремальности функционала. Будем
считать, что граничные условия для экстремали заданы
у\х=Хл=Уо, У\х=Х1=У1- (15.4)
Случай, когда граничные условия для экстремали не заданы,
гГояснен ниже.
Экстремали рассматриваемой вариационной задачи находятся
как интегральные кривые уравнения Эйлера. Если уравнение
Эйлера второго порядка, то семейство экстремалей зависит от
двух параметров, которые находятся из граничных условий (15.4).
Для того чтобы установить действительно ли реализуется на
кривой у = у(х) экстремум функционала и при этом выяснить,
что имеет место — максимум или минимум — необходимо
рассмотреть достаточные условия.
С этой целью изобразим приращение функционала (пользуясь
формулой Тейлора), представив в явной форме как линейный
член, так и член второй степени относительно by и by'.
AI=\F(x, y + by, y'+by')dx-lF(x, у, y')dx =
Хц Xq
Χθ
Здесь R имеет порядок выше второго относительно by и Ьу'.
Интеграл, в подынтегральном выражении которого имеется одно-
*) В развернутом виде (15.3) выражается так:
dF &F d*F , δΨ „ .
У „У =0.
ду дхду' дуду' ду'
В других, более сложных случаях (а) —функционал от я. функций
одной переменной и от их первых производных; б) — функционал от одной
функции одной переменной и от η последовательных производных этой
функции; в) — функционал от функций нескольких переменных и от их производных)
дифференциальные уравнения, выражающие необходимые условия экстремума
функционала, получаются более сложными. Иногда в названии этих
уравнений, кроме имени Эйлера, упоминаются имена и других ученых (С. Д.
Пуассона, М. В. Остроградского), но часто и в этих, более сложных случаях,
упоминают только имя Эйлера.
444
ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
родный многочлен второй степени относительно бг/ и бг/', по
аналогии со вторым дифференциалом называют второй вариацией
функционала и обозначают символом б2/. Если б/ = 0, а б2/ Φ О,
то при достаточно малых бу и $у' знак Δ/ совпадает со знаком
б2/. Для слабого экстремума функционала (для того, чтобы на
экстремали достигался минимум (максимум)) достаточно
выполнения на указанной экстремали условия б2/ > 0 (условие
минимума) и б2/<0 (условие максимума).
Как видно из приведенной ниже схемы, отыскание экстремума
функционала аналогично отысканию экстремума функции.
Отыскание экстремума функции
у = у(х). (15.5)
1. Составляется условие
экстремума:
ах
(15.6)
2. Решается уравнение (15.6) для
отыскания численного значения
аргумента х, при котором функция имеет
экстремум.
3. Определяется знак второй
производной; если
функция имеет минимум, если
dx
— максимум.
4. Определяется экстремальное
•значение функции
У(х)
•в результате подстановки числа х,
найденного в п. 2, в (15.5).
нала
Отыскание экстремума функцио-
Х\
/[</(*)] = $ F(x, у, y')dx. (15.5')
1. Составляется условие
экстремума: δ/= 0 или, вытекающее отсюда,
ι-да- <->
2. Решается уравнение (15.6') для
отыскания функции у (х), на которой
функционал имеет экстремум.
3. Определяется знак второй
вариации функционала; если
62/ > О,
функционал имеет минимум, если
δ2/<0
— максимум.
4. Определяется экстремальное
значение функционала
/ Ы (*)]
в результате подстановки функции
у(х), найденной в п. 2, в "(15.5').
2. Пример использования вариационного пути получения
дифференциальных уравнений и естественных граничных условий в механике твердого
деформируемого тела. Пример 15.1. Получить уравнение равновесия изогнутого
•стержня как уравнение Эйлера вариационной проблемы о минимуме
функционала потенциальной энергии системы1).
Решение. Составим функционал П — потенциальную энергию изогнутой
■балки, состоящую из двух слагаемых — U — потенциальной энергии деформации
балки и V — потенциальной энергии сил собственного веса (распределенная
х) Обсуждение соответствующего вариационного принципа дается ниже
в § 15.11.
§ 15.2] ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ПРОБЛЕМЫ МЕХАНИКИ 445
нагрузка), действующих на балку,
ι ι ι
n = U + V = ^ ^ (v'f dz- ^ g»ife=J|^ (xn2-qo]dz.
0 0 0
Введем обозначение
ι
F(v, v") = ^-{v"f-qv\ Π = f F(v, v") dz. (15.7)
о
Отметим, что вариационный метод позволяет получать не только
дифференциальные уравнения проблемы, но одновременно и недостающиег) граничные
условия. Эти граничние условия, называемые естественными, не
обуславливаются внешними обстоятельствами и вытекают из сути самой вариационной
задачи. Удовлетворение естественным граничным условиям необходимо для
соблюдения экстремума функционала в той же мере, что и удовлетворение
дифференциальному уравнению Эйлера. Совокупность наложенных извне и
естественных граничных условий обеспечивает единственность решения
вариационной проблемы — из поля экстремалей выделяется одна.
Составим выражение первой вариации функционала (15.7)а
ι ι
δΠ = δ J F (ν, xf) dz=\bF (ν, ν") dz;
о о
найдем вариацию подынтегрального выражения
bF(o, ϋ") = ^ + εφ, V' + zy'')-F{u, if) = ε (~ φ +.^φ") .
Здесь вариация функции ν представлена в виде δυ = εφ, где φ —функция
от ζ, а ε —бесконечно малый параметр.
Таким образом, вариация функционала имеет вид
о о
Условием экстремума функционала является обращение в нуль
вышеприведенного интеграла. В развернутой форме при двухкратном применении
интегрирования по частям ;это условие выглядит так:
/ ι ι
δΠ С fdF , dF \ , С dF , t [dF /V f ,d(dF\.
о о о
= |^^ζ+[^^ο-[έ(^-)(ί)]ο+ί(ί,έ(Ι^)ώ=0'
или
δΠ f [dF d* (dFY\ , , [dF , d (dF\ V .
x) Если граничные условия не заданы вовсе или заданы не все,
вариационный путь решения проблемы позволяет всегда автоматически получить
граничные условия в нужном количестве.
446 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
1
2
3
4
5
6
Внд балкн
Наложенные извне
(кинематические) граничные
условия
Требования,
предъявляемые к δν и δν', в
соответствии с условиями строки 2
таблицы
Естественные
(статические) граничные условия,
вытекающие из требования
равенства нулю граничного
члена (15.13)
Нетривиальные решения
однородного
дифференциального уравнения,
соответствующего уравнению
(15.12), при граничных
условиях, наложенных извне и
естественных
Условия, накладываемые
на нагрузку (функция в
правой части
дифференциального уравнения (15.12))
для того, чтобы уравнение
имело решение
"■
0(0) = 0 v(l) = 0
t>'(0) = 0 v'(l) = 0
&(0) = 0 δν(1) = 0
δϋ'(0) = 0 δϋ'(/) = 0
— —
—
—
%~ &
ο(0) = 0 ν([) = 0
ϋ'(0) = 0 -
δϋ(0) = 0 δν(1) = 0
δϋ'(0) = 0 —.
— v"(t) = 0
—
*
Если однородное, дифференциальное уравнение при учете всей
совокупности граничных условий (наложенных извне и естественных) имеет
решения, кроме тривиального (см. строку 5 таблицы), то неоднородное
уравнение имеет решение лишь в случае, если функция в правой части-
этого уравнения ортогональна отмеченным выше нетривиальным решением
однородного уравнения (см, строку 6 таблицы).
§15.2] ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ: И ПРОБЛЕМЫ МЕХАНИКИ 447
Таблица 15.1
| , .
о(0) = 0 —
о'(0) = 0 -
бо(0) = 0 -
δϋ'(0; = 0 -
_ о" (0 = 0
— о'(0 = 0
—
—
4fe *
ϋ(0) = 0 о (0 = 0
бо (0) —Обо (0=0
0"(О) = О ν" (0 = 0
*
—
'/ΆΊΜϊ\ лтттЯТг
'* \
τ/
о(0) = 0 —
би(0) = 0 —
_ ow(0=0
off(0) = 0 о* (0 = 0.
ζ
ι
[ q (ζ) · г ■ dz = 0
Яу^чцу^
— —
uw(0)=0u'"(0=o
о'(0) = 0 ϋ"(0 = 0
1 г
ι
jq(z)-l -dz=Q,
ι
\q (ζ) · ζ· dz = 0
б
В предпоследнем столбце — одно условие ортогональности, его
механический смысл — равенство нулю момента от нагрузки относительно точки О
(т. е. балка находится в равновесии, несмотря на недостаточность
количества связей для обеспечения неподвижности). В последнем столбце—два
условия ортогональности, их механический смысл — самоуравиовешенность
нагрузки.
448 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Если значения ν и ν' фиксированы на концах интервала, то в этих точках
δο и δν', а следовательно, и φ, и φ' равны нулю. Таким образом, в указанном
случае выражение
[dF , d (dF\ у
[wbv'-Tz{w)bvX>
носящее название граничного члена, обращается в нуль. Для равенства нулю
первого члена в (15.8), учитывая произвольность φ, необходимо обращение
в нуль выражения внутри квадратных скобок под интегралом, т. е.
dF d* (dF\
или
до ' агг \dV
Уравнение (15.9) и есть уравнение Эйлера [рассматриваемой вариационной
задачи, а равенство нулю граничного члена
[£"-Ι(£Κ-β
позволяет установить естественные граничные условия.
Воспользуемся (15.9) для получения развернутого дифференциального
уравнения Эйлера.
Учитывая вид функции F (15.7)ί, имеем
dF dF pi j, d* dF ci IV /1K 114
d4=~q; w=EIx/> wW=EIV ' (15Л1)
Таким образом, дифференциальное уравнение Эйлера рассматриваемой
вариационной проблемы приобретает вид уравнения равновесия изогнутой балки
EIvw=q. (15.12)!
Граничный член (15.10) в рассматриваемой задаче, если учесть выражение1
(15.11) для dF/dv", приобретает вид
ΕΙ [ν" δν'-ν'" δν]ι0. r (15.13):
В табл. 15.1 приведена информация, относящаяся к различным случаям'
закрепления концов балок.
Аналогично показанному в настоящем разделе выводу может
быть сделан вывод дифференциальных уравнений равновесия и
совместности деформаций в теории упругости, в теории пластин
и оболочек и т. д. Одновременно с уравнениями могутЧзыть
получены все естественные граничные условия г). Можно показать, что
уравнения Эйлера инвариантны при преобразовании
подынтегральной функции в функцию от новых независимых переменных.
Методы вариационного исчисления удовлетворяют тому
требованию, что минимум скалярной величины (функционала) не зависит
от выбора координат. Это наиболее естественным образом соот-
г) Ниже в § 15.21 показано, что вариационным путем получаются и
физические уравнения, связывающие напряжения с деформациями,
§ 15.2] ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ПРОБЛЕМЫ МЕХАНИКИ 449
ветствует законам природы, инвариантным по отношению к системе
координат.
3. Об учете дополнительных условий при решении
вариационной проблемы. Если решается вариационная проблема для
функционала
Х\
I = \Fdxt р = Р{уъ yit ..., уп; χ)
Χο
и при этом на функции уъ ..., уп наложены дополнительные
условия
/;(#1> Уъ ..., уп;х) = 0 (/=1,-..., /7ϊ),
то проблема называется вариационной на условный экстремум.
Ее можно свести к «свободной» (без дополнительных условий)
вариационной задаче, но для функционала
χ9
Экстремали, на которых достигается экстремум функционала
/, являются решением и исходной вариационной проблемы.
Величины λι называются неопределенными (функциональными)
множителями Лагранжа. Уравнения Эйлера вариационной проблемы
для функционала / и условия для /г позволяют найти yt и λ/
(ί = 1, 2, ..., η; у' = 1, ..., т). Аналогичная ситуация имеет место
и при отыскании экстремума функции, но множители Лагранжа
при этом не являются функциональными.
4. Понятие о прямых методах решения вариационной задачи.
Решение вариационной задачи о минимуме функционала может
быть выполнено не только классическим путем, описанным выше,
согласно которому она сводится к краевой задаче для некоторого
дифференциального уравнения или системы дифференциальных
уравнений, но и так называемым прямым методом. Последний
состоит в представлении искомой функции (экстремали),
минимизирующей функционал, в виде ряда
со
y(x)=ΣaM(χ)> (15.14)
i = \
здесь ί/ί —априорно принятые функции, удовлетворяющие тем или
иным требованиям, например граничным условиям, и образующие
полную систему, а% — неизвестные коэффициенты. После
подстановки (15.14) в функционал / [у (х)] последний превращается
в функцию неизвестных коэффициентов аг. Отыскание этих
коэффициентов производится из условий минимизации функции
450 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
2 a{yt (χ) . Отмеченные условия имеют вид
Щ = ° (/-1.2,...)
и представляют собой бесконечную систему алгебраических
уравнений (линейных, если функционал / — квадратичный).
Практически ряд заменяют суммой конечного числа членов, тогда система
алгебраических уравнений имеет конечный порядок и решение
оказывается приближенным1).
§ 15.3. О возможности формулирования вариационных
принципов теории упругости
Из изложенного в § 15.2 очевидно, что некоторое множество
проблем может быть описано при помощи требования
стационарности некоторых функционалов, т. е. в вариационной форме.
В каждом из таких случаев эта же проблема представима и
в локальной форме — при помощи дифференциальных уравнений,
являющихся уравнениями Эйлера в вариационной задаче для
соответствующего функционала.
Обратное утверждение справедливо не всегда, а именно, не
всякое дифференциальное уравнение или систему
дифференциальных уравнений можно рассматривать как уравнения Эйлера
в вариационной задаче для некоторого функционала. Для того,
чтобы имелась такая возможность, дифференциальные операторы,
входящие в дифференциальные уравнения, должны удовлетворять
определенным требованиям. Эти требования сводятся к
следующему. Дифференциальные операторы А и А*, входящие в
различные группы уравнений (каждая из которых составлена
относительно своих тензоров и функций), должны быть формально
сопряженными, т. е. такими, что
555 ιιΑυ dco = 5 5 5 ν А* и άω
Θ Θ
*) Изложенный подход составляет сущность так называемогометода Ритца
(Вальтер Ритц —немецкий ученый-физик 1878—1909) Ri'tz W. Uber eine neue
Methode zur Losung gewisser Variationsproblerae der mathematischen Physik, —
Journ. f. d. reine und angewangte Mathematik, 1908, Bd. 135, H.l.
Отметим некоторые книги, в которых обсуждаются прямые методы
математического анализа.
Канторович Л. В., Крылов В. И. Приближенные методы высшего
анализа.—М.: Гостехиздат, 1949.
Μ и χ л и н С. Г., Смолицкий X. М. Приближенные методы решения
дифференциальных и интегральных уравнений (серия «Справочная
математическая библиотека»). — М.: Наука, 1965.
Μ и χ л и π С. Г. Численная реализация вариационных методов. —М.: Наука,
1966.
Филин А. П. Приближенные методы математического анализа,
используемые в механике твердых деформируемых тел, —Л.: Стройиздат, 1971.
§ 15.3] О ФОРМУЛИРУЕМОСТИ ВАРИАЦИОННЫХ ПРИНЦИПОВ 451
(при А = А* операторы самосопряженные), и и. υ — функции.
Если и и ν — векторы, то условие представляется так:
5$$u'Avda> = $$$v'A*uii<B.
© 0
Формальность сопряжения заключается в рассмотрении лишь
символа дифференцирования без задания области его определения,
включающей в себя область изменения независимых переменных,
класс функций и граничные условия для функций, на которые
действует оператор.
Указанным условиям удовлетворяют линейные уравнения теории
упругости, а именно, общее решение уравнений равновесия
(совместности деформаций) выражаются при помощи оператора,
являющегося формально сопряженным оператору, входящему в
уравнения совместности деформаций (равновесия).
Для того, чтобы подтвердить сказанное, во-первых, покажем,
что в пространственной задаче теории упругости компоненты
напряжений могут быть выражены через шесть некоторых
функций напряжений (наподобие функции Эри в плоской задаче
теории упругости), образующих так называемый тензор функций
напряжений, а во-вторых, представим все основные уравнения и
зависимости пространственной задачи теории упругости в
матричной форме.
Итальянский ученый Б. Финци показал х), что если компоненты
напряжений представить в нижеприводимой форме, выразив их
через шесть функций хш χ22, χ33, χ23, χ3ι, Ъл* то однородные
дифференциальные уравнения равновесия удовлетворяются.
η —а —д*Ъ& Ι ^χ33 Ι 9 д2*23
°n-Vx- QZ2 "Г ду2 -r^-Qffr'
а -а -а2Хзз , д^ц 0 d\zi
о22-оу- 9χ2 -t- dz2 -t*dzdx,
η — гт — д**п I d2*22 I 9 ^Χι2
Ою-υ*— ду2 -f δχ2 -Г*дхду>
а =т - а2Хп . ^м &Ы &т
«аз Чг— дудг'Г дх* дхду дхдг'
а -т _ д*Хм дяЫ ■ d2bi Ухи
°31 ~~ izx ~ dz дх дудх^ ■ ду* ду дг '
а -т _ ^/зз д2*23 Фъг - d2Xi2
«и—lJ4/— дхду dzdx dzdy^~ dz* '
г) F i n ζ ϊ В., Integrazione della equazioni indefinite delta Meccanica dei
sistemi continue. Rend. Lincei, 1934 ser. 4, 19.
По-видимому, независимо от Б. Финци и примерно б то же время
отмеченный результат получил и Ю. А. Крутков, книга которого («Тензор
функций напряжений и общие решения в статике теории упругости». Изд-во
АН СССР, 1949) появилась в связи с объективными причинами много лет
спустя после ее написания,
452 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Функции Xij являются компонентами некоторого симметричного
тензора второго ранга, который можно представить при помощи
следующей матрицы:
Х =
Χιί Xi2 Xis
Xai X22 Хгз
χ3ι Хз2 Хзз
lij = Χμ-
При этом существенными являются лишь три компонента, а три
других могут быть приняты произвольно. Компоненты тензора X
можно представить и при ■ помощи вектора г)
5C={Xll Х22 ХЗЗ Х23 Хз1 Xl'2/r
Выражения σ через χ можно рассматривать как решение
однородных дифференциальных уравнений равновесия, поскольку при
подстановке этих выражений в однородные дифференциальные
уравнения равновесия последние обращаются в тождества.
Аналогично и формулы (уравнения) Коши, в которых компоненты
деформаций выражаются через составляющие перемещения, могут
рассматриваться как решение дифференциальных уравнений
совместности деформаций Сен-Венана (поскольку подстановка
выражений для компонентов деформаций согласно формулам Коши
в последние уравнения обращает их в тождества).
Теперь представим в матричной форме основные уравнения и
зависимости теории упругости2), предварительно введя в рассмотрение
*) Заметим, что еще до Б. Финци учеными Г. Морера (Мог era G., Rendi-
conti d. Lincei, Ser. 5, 1, 137—141, 1892) и Д. К· Максвеллом (Maxwell J. С,
Scientific Papers, 2, 1870) компоненты напряжений выражались через три
функции напряжений так, чтобы при этом удовлетворялись уравнения
равновесия. Так как распоряжаться тремя из шести компонентов тензора X можно
произвольно, решения Морера и Максвелла могут быть представлены как
частные случаи, соответствующие нижеприводимым частным видам вектора χ
{Xu Χ22 Хзз Х23 X3i Xn} = Wi <Р2 <Рз 0 0 0},
{Хп Х22 Хзз Х23 Хз1 Χ12}={θ 0 0^^-^}.
На возможность соединения решений Морера и Максвелла для получения
тензора функций напряжений указал Э. Бельтрами (Beltrami E. Rendi-
conti d. Lincei, ser. 5, 1, 141 — 145, 1892). Этот вопрос обсуждается в книге:
Лурье А. И-, Теория упругости. «Наука», 1970.
2) В рассматриваемом здесь представлении компоненты тензоров
напряжения и деформации составляют векторы соответственно σ и ε. Аналогично
построен и вектор σ4. ρ.
§ 15.31 О ФОРМУЛИРУЕМОСТИ ВАРИАЦИОННЫХ ПРИНЦИПОВ 453
следующие матрицы (операторы) и векторы·:
А =
д
дх
0
0
υ
д
ду
0
υ
о
д
dz
0
д
dz
д
ду
д
Иг
0
д
дх
д
~ду~
д
дх
0
D =
1
0
0
0
т
0
0
0
η
0
η
т
η
0
/
m
/
0
в=
о
dz*
ду*
, &
дгду
О
_аг_
dz*
О
дх2
д*
ду*
д2
дх*
О
а2
дхдг
О
О
дудх
аа
а# az
0
о
д2
а*2
а2
дудх
а2
dzdx
0
02
dzdx
0
а2
dxdy
а2
а#2
аг
dzdu
0
0
а2
dxdy
&■
dxdz
д*
dydz
аа
дг2
с =
2G
1—2μ
(1-μ)
μ
μ
μ
(ΐ-μ)
μ
μ
μ (ΐ-μ) Ι
ο
ο
ο
ο
ο
ο
ο
ο
ο
ο
ο
ο
ο
ο
ο
ο
ο
ο
1—2μ
2
Ο
1—2μ
2
Ο
1—2μ
(Перегородки в матрицах использованы с целью подчеркнуть
закономерности их структуры.)
Χ = {ΧΥΖ}, Ρν={Ρνχ Ρνμ Ρνζ}»
ε = {ε.
χ &у &ζ Ууг Угх
Уху}* G—\®x ®y ®z tyz "^zx ^xyft
U — [U V W), Оч ρ—\GXi 4>p ^ι4>ρ GZi 4#p Τι/*, 4#p TZXt 4> ρ TXyt4wp\,
Здесь σ4>ρ —вектор, представляющий собой частное решение
неоднородных дифференциальных уравнений равновесия. Учитывая
приведенные выше обозначения, получим следующую запись
уравнений и зависимостей теории упругости.
Ι. Αα = — χ в 0. (15.15)
454 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ 1ГЛ. XV
(дифференциальные уравнения равновесия);
Da = pv на1) Sp (15.16)
(граничные условия);
σ = Β'χ + σ,ρ (15.17)
(решение дифференциальных уравнений равновесия, выраженное
через функции напряжений).
II. Ве = 0 (15.18)
(уравнения совместности деформаций Сен-Венана);
8 = А'и (15.19)
(решение уравнений совместности деформаций Сен-Венана,
выраженное через перемещения);
u = u на Sa
(граничные условия).
III. σ = Οε, Ϊ
е = С1а )
(две взаимнообратные формы записи закона Гука для
изотропного тела).
Наконец, разрешающие, уравнения:
АСА'и = —х (15.22)
(уравнения Ламе2) — уравнения равновесия, выраженные через
перемещения и справедливые при соблюдении ; закона Гука для
изотропного тела);
ВС-1(В'х + ач.р) = 0 (15.23)
(уравнения Бельтрами — Мичелла 3) — уравнения совместности
деформаций, выраженные через функции напряжений и справедливые
при соблюдении закона Гука для изотропного тела).
Используя приведенные выше уравнения, покажем, что
условие формальной сопряженности операторов применительно к проб-
г) 5 —поверхность тела, S=Sp-\-Sn; 5p —часть поверхности тела, на
которой заданы поверхностные силы, Su — остальная часть поверхности тела,
на которой заданы перемещения. Если Sp = S — граничные условия статические,
если Sp = О — кинематические, если 0<5р<5 —граничные условия смешанные.
2) Уравнение получено из Аог = — х подстановкой в него (Г = Се и
подстановкой в последние ε = Α'ιι.
3) Уравнение получено подстановкой в уравнение Ве = 0 выражения для
8 = С~1о' и подстановкой в последнее <τ = Β'χ + σ,4.ρ. Строго говоря, название
«уравнения Бельтрами —Мичелла» применено условно, поскольку Бельтрями
и Мичелл выражали условия совместности деформаций не через функции
напряжений, а через сами напряжения и использовали, таким образом, не
решение уравнений равновесия, а сами уравнения равновесия.
(15.20)
(15.21)
§ 15.3] О ФОРМУЛИРУЕМОСТИ ВАРИАЦИОННЫХ ПРИНЦИПОВ 455
леме теории упругости выполняется. Для этого будем исходить
из очевидного равенства
$$$ε'σίίω = $$$σ'είίω, (Ιδ.24)
© 0
и в левой, и в правой частях которого под интегралами с
точностью до постоянного множителя 1/2 имеется величина удельной
потенциальной энергии деформации. Теперь, воспользовавшись
равенством (15.19), представим (15.24) в следующем виде:
\ \ \ ιι'Ασ άω = \ J $ σ'Α'ιι άω.
Θ ©
Отсюда ясно, что операторы А и А' являются формально
сопряженными, т. е. А' = А*; вместе с тем А —это оператор в
уравнениях равновесия, а А' — оператор в решении уравнений
совместности деформаций.
Теперь, воспользовавшись равенством (15.23), представим
(15.24) в следующем виде:
55$8'(B'x + a4.p)^ = 5^[x'B + (a,p)']8dW,
Θ 0
или
\\ \ ε'Β'χ άω + $ \ $ ε'σ4. Ρ άω = $ $$ χ'Βε άω + $ $ $ (σ4. ρ)' ε άω.
Θ Θ Θ Θ
Но вторые члены в левой и правой частях равны друг другу,
вследствие чего
S$$e'B'Xda> = SS$X'Beda>.
Θ Θ
Отсюда ясно, что операторы В и В' являются формально
сопряженными, т. е. В' = В*, вместе с тем В —это оператор, входящий
в дифференциальное уравнение совместности деформаций, а В' —
оператор, входящий в решение уравнений равновесия. Таким
образом, полученные равенства свидетельствуют о том, что
условия, поставленные в начале параграфа, выполнены и
дифференциальные уравнения теории упругости являются уравнениями
Эйлера, соответствующими вариационным проблемам для
некоторых функционалов.
Обсуждаемый в настоящем параграфе вопрос связан с
симметрией всего аппарата теории упругости, характеризуемой схемой,
показанной в табл. 15.2. В этой схеме σ занимает симметричное
положение по отношению к ε, а и по отношению к χ. Как будет
показано ниже, симметрией обладает и система функционалов и
соответствующих им вариационных принципов.
456 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Таблица 15.2
Закон Гука (обратная
форма зависимости)
Закон Гука,
выраженный через перемещения н
напряжения
Решение уравнений
совместности деформаций
Сен-Венана, выраженное
через перемещения
Уравнения
совместности деформаций
Сен-Венана
Уравнения
совместности деформаций,
выраженные через функцию
напряжений и справедливые
для тел, подчиняющихся
закону Гука
Выше говорилось, что вариационные проблемы подразделяются
на свободные (без дополнительных условий) и на вариационные
проблемы условного экстремума при наложении на функции, от
которых зависит функционал, дополнительных условий.
Функционалы, соответствующие свободным вариационным проблемам, будем
называть полными, а вариационным проблемам на условный
экстремум — частными.
Вариационный принцип, в котором утверждается, что
истинные поля х) и, σ, ε, χ таковы, что полный функционал, завися-
х) Здесь имеются в виду математические поля (векторное и тензорные).
Такие поля представляют собой область пространства (в частности плоскости),
каждой точке Μ которой поставлен в соответствие вектор (в нашем случае —
перемещение и) и (М) или тензор (в нашем случае — тензор второго ранга —
напряжение в точке, деформация в точке, функции напряжений) α (Μ), ε(Μ),
%(М). Математическое поле может быть и скалярным (например, поле
температур в некоторой области). Существует математическая теория—теория поля,
изучающая свойства скалярных, векторных и тензорных полей.
Закон Гука (прямая
форма зависимости)
Закон Гука,
выраженный через функцию
напряжений и Деформации
Решение уравнений
равновесия, выраженное в
функциях напряжений
Уравнения равновесия,
выраженные в
напряжениях
Уравнения равновесия,
выраженные через
перемещения н справедливые
для тел, подчиняющихся
закону Гука
е?=Се
<з-Ъ'Х+ 1
г
АбГ=-ас *^
ЛСА'и=-х *W
! Б=С^(5
> A'it-Г'ег
II
"
^•-V ε=Α"
"
-* Βε=0
[з вс_/[в'х+
+<?ц.р]=0
§ 15.4]
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
457
щий от них, имеет стационарное значение, позволяет получить
все уравнения теории упругости как уравнения Эйлера и
одновременно естественные граничные условия. Такой вариационный
принцип обсуждается в § 15.21.
Вариационные принципы, в которых истинность указанных
полей гарантирует стационарность частных функционалов,
постулируют выполнение и тех или иных дополнительных условий.
В §§ 15.11 и 15.12 подробно рассматриваются два из них
—вариационный принцип Лагранжа (потенциальной энергии системы) и
вариационный принцип Менабреа — Кастильяно (дополнительной
работы) применительно к стержневым системам и
пространственной задаче классической (линейной) теории упругости. В § 15.20
мы возвратимся к этим принципам еще раз. В § 15.21
обсуждаются вариационные принципы, соответствующие другим частным
функционалам.
Вариационные принципы механики, с одной стороны, имеют
большое теоретическое значение, поскольку они выявляют
энергетическую основу теории и устанавливают связь между
различными подходами в описании проблемы теории. С другой стороны,
важным является практическое значение принципов, поскольку
они позволяют, во-первых, имея общие выражения для
функционалов, находить дифференциальные уравнения и естественные
граничные условия в любых конкретных случаях, что
непосредственно в ряде случаев сделать затруднительно, а во-вторых,
находить решения, минуя составление дифференциальных уравнений,
при помощи так называемых прямых методов.
§ 15.4. Закон сохранения энергии
Основным энергетическим законом физики и, в частности,
механики твердого деформируемого тела является закон
сохранения и преобразования энергии, который формулируется
следующим образом,
Энергия любой замкнутой *) материальной системы при всех
происходящих в ней процессах сохраняется, превращаясь лишь
из одной формы в другую. Если жг материальная система
подвергается внешним воздействиям вследствие чего переходит из одного
состояния в другое, то количество поступившей (в алгебраическом
смысле) в эту систему энергии равно количеству энергии,
отданной (опять в алгебраическом смысле) взаимодействующими с этой
системой телами и полями 2).
*) Материальная система может рассматриваться как замкнутая, если
взаимодействием ее с окружающим миром можно пренебречь.
2) Здесь имеются в виду физические поля, которые, как известно,
понимаются как одна из форм существования материи, осуществляющая
взаимодействие частиц вещества и связывающая их в системы,
458 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV·
Энергия является однозначной функцией состояния системы,
и изменения энергии, связанные с переходом системы из одного
(начального) состояния в другое (конечное), не зависят от пути
(способа) перехода.
Воздействие на деформируемое тело окружающей среды состоит
Э том, что к нему подводится некоторая энергия (механическая
и (или) немеханическая, например, тепловая); последняя
затрачивается на увеличение энергии тела, складывающейся из
кинетической и внутренней энергий.
Уравнение закона сохранения энергии в общем случае
представим в следующей форме:
δΑ + δ9 = δΤ + δΰ. (15.25)
Здесь δΑ —механическая энергия, затраченная на деформацию
тела за отрезок времени δ/, численно равная работе внешних сил,
приложенных к телу; δ9 — механический эквивалент
немеханической энергии, подведенной к телу за тот же отрезок времени; δΤ —
изменение кинетической энергии тела, произошедшее в указанный
промежуток времени; δΟ — изменение внутренней энергии тела,
произошедшее за δ/.
В левой части равенства (15.25) имеем энергию, подведенную
(в алгебраическом смысле) к телу за некоторый отрезок времени
Ы, а в правой части — изменение энергии тела за тот же отрезок
времени.
Для механики твердого деформируемого тела большой
интерес представляет термодинамический аспект закона сохранения и
преобразования энергии. Все воздействия на тело в термодинамике
подразделются на два рода — воздействия первого рода связаны
прямо или косвенно с макроскопическими перемещениями точек
тела и характеризуются работой, совершаемой этими
воздействиями; воздействия второго рода связаны только с теплообменом
между системой и окружающей ередой.
§ 15.5. Работа внешних сил, совершаемая за отрезок времени btr
при загружении сплошной среды
Работа внешних сил, совершаемая за отрезок времени δ/,
складывается из двух слагаемых — работы объемныхх) и работы
поверхностных сил
δΑ = δΑ1 + δΑ2, (15.26)
δΑχ = J J J χ~'ρδιι άω, δΑ2 = J $ ρ^διι dq. (15.27)
0 s
*) Составляющие объемной силы могут быть выражены через составляющие
массовых сил (т. е. приходящихся на единицу массы) следующим образом: X =
= Хр, Y = Yp, Z*=Zp, где ρ —плотность материала,
§ 15.5] РАБОТА ВНЕШНИХ СИЛ, ЗАГРУЖАЮЩИХ СПЛОШНУЮ СРЕДУ 459
Здесь χ = {'Χ'ΫΖ} — вектор массовых сил, δη=={δαδνδυυ} — вектор
приращений составляющих перемещения за отрезок времени δί.
Если вместо Ρν подставить выражение, соответствующее
уравнениям равновесия элементарного тетраэдра (15.16) pv = D<y, то
получим
6Л2 = J J ou'Dff dq, δΛ2 = J J J (Ασ)' 6u <4ω + J J ξ σ' (А'би) cto.
s 0 0
(15.28)
При переходе от (15.28)х к (15.28)2 использована формула
Гаусса — Остроградского преобразования поверхностного интеграла
в объемный. Воспользуемся матричной формой уравнений
равновесия1) элементарного параллелепипеда и уравнений Коши (15.15)
и (15.19)
Ασ = — Ы - -dirj ρ, ε = A'u,
тогда, изменив последовательность операций варьирования и
дифференцирования во втором интеграле в (15.28)2, получим его
в следующем виде:
6Л2 = — ^ j (х--^-)'διιρ^ω + J ^ σ'δεάω. (15.29)
0 0
Подставив (15.29) и (15.27)х в (15.26) и произведя взаимное
уничтожение членов, получим
6Л = J ££ {^j διιρ άω + ^ ^ σ'δε dco. (15.30)
0 0
Первый интеграл представляет собой δΤ — вариацию
кинетической энергии тела2). Учитывая это, представим (15.30) в
следующем виде:
δΑ = δΤ-\-\\\α'δΕά(ύ. (15.31)
0
1) Уравнения равновесия написаны с учетом сил инерции, т. е. с
использованием принципа Даламбера.
2) 7,=у ^ J [ p[-|-fe'u)]2^,e= {Hi}.выражение [А (е'и^-квад-
0
рат полной скорости. Варьирование проиллюстрируем на одном из элементов
строки подынтегрального выражения
Λ Г 1 (ди \2-| 1 ди . / ди \ ., d2u du .. ^u Λ
460 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Подставим выражение (15.31) для бЛ в уравнение (15.25);
после взаимного уничтожения членов получим
$$$σδε<ίω + δ.9 = δ£/. (15.32)
0
Если от уравнения (15.32), относящегося ко всему рбъему
тела, перейти к записи аналогичной по природе зависимости, но
представленной для единицы объема, и при этом в Э учесть лишь
тепловую энергию, а в U лишь потенциальную энергию
деформации, то получим1)
σ'δε + δζ) = δ№\ (15.33)
Здесь Q и W — соответственно механический эквивалент
удельной тепловой энергии, подведенной к телу, и удельная
потенциальная энергия деформации.
§ 15.6. Потенциалы, напряжений и деформаций
1. Вводные замечания. Будем считать, что процесс
деформирования тела термодинамически обратим и однозначно выражается
уравнением состояния в терминах своих переменных. Иными
словами, предполагаем идеальную упругость материала в
энергетическом смысле (см. § 2.22). Из термодинамики известно 2), что
6Q = T6S, (15.35)
тогда (15.33) приобретает вид
σ'δε + Τδ8 = δ№. (15.36)
*) В такой форме закон сохранения энергии может трактоваться как
первый закон термодинамики. Впервые применять законы термодинамики (первый
и второй) к изучению процесса деформирования тела предложил английский
(шотландец по происхождению) физик В. Томсон (Kelvin, lord, William
Thomson, 1824 — 1907). Эти идеи были изложены в его статьях в 9-м издании
Британской энциклопедии, позднее изданных отдельной книгой (Elasticity and
heat, 1880).
2) Равенство (15.35) связано со вторым законом термодинамики, сущность
которого состоит в двух утверждениях. Первое называется теоремой Карно-
(у каждой термодинамической системы существуют два свойства—ее
абсолютная температура Τ и ее энтропия S, такие, что в любом бесконечно малом
обратимом процессе изменение количества тепла выражается формулой dQ=TdS).
Второе утверждение носит название принципа возрастания энтропии, который
формируется так: в изолированной системе энтропия всех тел, входящих в нее,
остается постоянной в течение обратимого процесса, увеличивается при
необратимом (реальном) процессе и никогда не может уменьшиться: AS^O.
Отсюда ясно, что приращение энтропии в связи с переходом системы из
одного состояния равновесия (1) в другое состояние равновесия (2) равно
интегралу (Клаузиуса) по любому пути между состояниями 1 и 2.
2
S2-S^[^-. (15.34)
§ 15.6] ПОТЕНЦИАЛЫ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ 461
2. Упругий потенциал.
2.1. Исходная зависимость. Представим формулу (15.33)
для всего объема тела
J J J σ'δε άω + 6Q = δΙΛ (15.37)
©
Здесь (7 — потенциальная энергия деформации всего тела,
a 6Q —механический эквивалент тепловой энергии, подведенной
ко всему телу. Как это станет ясно из нижеизложенного,
существует при определенных условиях так называемый упругий
потенциал, характеризующий деформированное состояние тела, численно
равный работе напряжений, приходящейся на единицу объема
(удельная потенциальная энергия упругих деформаций).
Потенциалом в физике, в частности в механике, называют некоторую
вспомогательную скалярную или векторную величину (потенциальную
функцию), характеризующую физическое силовое поле и облегчающую отыскание
других величин, описывающих .физическое поле. Использование потенциалов
целесообразно, поскольку потенциальная функция связана с источниками,
образующими поля, проще чем с этими же источниками связаны искомые
величины, и вместе с тем искомые величины связаны с потенциальной функцией
проще чем с источниками поля.
Примером может служить φ (χ, у, ζ, t) потенциал скорости в гидро- и
аэромеханике. Скорость ν в этом случае выражается формулой
v^gradcp (grad9=i-^. + j^. + k-§.).
Проекция скорости на направление s равна ν cos (v, s)=dcp/ds; vx=dq>/dx,
Vy—dy/dy, vz = dy/dz.
Потенциалы существуют не всегда. Так, например, потенциал скоростей
существует лишь в случае, когда угловые скорости вращения частиц равны
нулю. Поэтому течение без вращения частиц называется потенциальным.
Для отыскания потенциала составляется специальное уравнение.
Например, для отыскания потенциала скоростей используется условие неразрывности
движения. В случае несжимаемой жидкости уравнение неразрывности имеет
dvx day dvz
ВИА:-Ж + ^- + "аГ==0'О1СЮАа
дх* "1" ду* "f" dz* ~
Если течение происходит в объеме жидкости, имеющем твердые или свободные
границы, то на них функция φ должна удовлетворять не только приведенному
выше уравнению Лапласа Δφ=0, но и граничным условиям.
Существует специальный раздел математической физики, изучающий
потенциалы силовых полей, образованных притягивающими массами, зарядами (поле
тяготения, поле Кулона) и т. п. Если силовое поле потенциально, то
существует такая функция (потенциал поля), что напряженность поля является ее
градиентом, т. е. компоненты напряженности в каждой точке равны значениям
частных производных функции в этой точке. При наличии двух или
нескольких полей их потенциалы складываются.
Изменение потенциала при бесконечно малом изменении дефор·-
мированного состояния имеет вид δΨ = α'δ&.
462 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Таким образом, подынтегральное выражение в (15.37) и есть
вариация упругого потенциала. Функция W является потенциалом
в том случае, если 6W представляет собой полный дифференциал.
Ниже рассматриваются два термодинамических процесса, в
условиях которых bW удовлетворяет этому требованию.
2.2. Адиабатический процесс. В случае
адиабатического процесса отсутствует обмен тепловой энергией, т. е. 6Q — 0,
6S —0. Примером такого процесса могут служить упругие
колебания. В этом случае (15.37) приобретает вид
©
G'£.2—6Wa3 есть ни что иное как удельная внутренняя энергия
упругой деформации.
Из полученного равенства заключаем, что 6WaA представляет
собой полный дифференциал и №ад является потенциалом,
называемым упругим потенциалом.
2.-3. Изотермический процесс. В случае
изотермического процесса деформации, т. е. процесса, происходящего при
неизменной температуре (δΤ = 0), также существует упругий
потенциал, но отличный от того, который имеет место при
адиабатическом процессе деформирования.
Для доказательства существования изотермического упругого
потенциала рассмотрим цикл обратимого изотермического процесса,
при котором уравнение (15.37) приобретает следующий вид:
φ$$$σ'δβίίω-{-φδ<? = φδΙΛ (15.38)
©
Воспользуемся вторым законом термодинамики (см. 15.34),
согласно которому 6Q не нуль, но в пределах цикла обратимого
изотермического процесса, имеющего место лишь в рамках
упругости
§4p- = ^r§6Q = 0. (15.39)
Но так как обратимый процесс происходит в пределах
упругости, то
§δ£/ = 0, (15.40)
и уравнение (15.38) переходит (если учесть (15.39) и (15.40))
в условие §\\\ σ'^ε ^ω ~ 0» которое выполнимо лишь в случае,
©
если σ'δ& = δΨΗ3 является полным дифференциалом от шести
переменных ε*, Byt ег, ууг, угх> уху. Если процесс не является ни
изотермическим, ни адиабатическим, упругого потенциала не
существует.
§ 15.6] ПОТЕНЦИАЛЫ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ 463
3. Термодинамические потенциалы. Наряду с функцией W
рассмотрим еще три функции
F = U7-TS, (15.41)
-W' = W-a's, (15.42)
G = F-a'e = r-TS-a'8 или G = (— W) -TS = W-a'e-TS.
(15.43)
Покажем, что при адиабатическом и изотермическом процессах
6F, δ (— W) и 6G также являются полными дифференциалами.
Прежде всего рассмотрим функцию W. Придадим формуле
δΨ — σ'δΒ следующий вид:
δ№ = 6(σ'β)-β'δσ,
(15.44)
δ(№-σ'β) = — ε'δσ. ν
Но поскольку δ IF и при адиабатическом и при изотермическом
процессах есть полный дифференциал, то и
δ(^«(Η.)-β'β)-δ.(-^Α(«)) = -β'βσ, β^(Η8,=β'βσ
также является при этих процессах полным дифференциалом.
Теперь перейдем к функции F; рассмотрим ее вариацию
5F = 6U7-6T-S-T6S. (15.45)
При адиабатическом процессе 6S---0 и, следовательно, 6FM = 6U?—
— δΤ-S. Из термодинамики известно, что δΤ—полный
дифференциал, но полным дифференциалом является и W. Отсюда следует,
что бРад при адиабатическом процессе — полный дифференциал.
При изотермическом процессе Τ = const и δΤ = 0, поэтому
бРиз = б№ — T-6S. Из термодинамики известно также, что 6S —
полный дифференциал; поскольку δΨ также полный дифференциал,
заключаем, что 6FH3 при изотермическом процессе — полный
дифференциал.
Наконец, рассмотрим функцию G. Запишем ее вариацию
6G = (— 6№')-6TS-T6S. (15.46)
Учитывая, что при адиабатическом процессе 6S = 0, а при
изотермическом 6Т = 0, получаем
6Gafl = (-6U7^-6T-S,
(15.47)
6Gh3=(-6^3)-T6S.
Имея в виду, что 6Т и 6S, входящие в (15.47), суть полные
дифференциалы, а также то, что б№'ад и δΨ'Η3, как было
показано выше, представляют собой тоже полные дифференциалы,
заключаем, что таковыми являются и 6G^ и 6GH3. Как будет
показано ниже, функции F, — W, G являются потенциалами
464 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Таблица 15.3
Термодинамические переменные
со
о
о.
о
н
*
со
<υ
Ч
s
сз
со
3
S
<υ
ч
со
«
Е-
<υ
о.
с
«
3
О-,
о
к
X
ω
я
о
с
2
о
Μ
S
о
X
с
*
о
со
о
о
О-,
о
со
S
<υ
Η
F = F(e, J)
ψ=ψ(ε, S)
6F =
aF
dF
dy
zx
dF
6W =
dW dW
δεχ "' dy
zx\
dW
а) 6F = SW — T6S-
— 6T-S,
б) 6F = T.6S+ff'6e—
— T-6S —6T-S =
= ff'6s-S6T
CO
II
σ' =
aF
aF
de.
<?v
г*
s=—^
a_F
ат
G = F—σ'ε
G = G(ff, T)
6G =
ad
aG
aa,
ат
zx
ьо+рт
а) 6G = OF-(6ff)'e-
— σ' δε,
б) δσ = σ'δε — S6T —
-ε'δσ-σ'δε =
=.—S-δΤ-ε'δσ,
а) 6G = 6(— W')-
-δΤ-S —T-6S,
б) 6G = T-6S-8'6ff-
_6T-S-T-6S =
= _ε'δσ —S-δΤ
6U7 = T6S + ff'6e
σ' =
aw7 a^
3e, '" дуг
dW
"~dS
_| (_ W') = W-a'e
(-W') = (-W')(a, S)
δ(— Ц7') =
d(—W)
d(—W)
do.
d^zx
a (— w)
as
δσ +
6S
CO
^
σ
а) 6(-W') = 6W-
— (δσ)'ε — σ' δε,
б) δ(— \^') = T6S +
+ σ'δε-(δσ)'ε-
— σ'δε = Τδ5-ε'δσ
ε' = —
aG
aG
ao»;'" дх
zx
s=—^
dG
ат
ε' = —
a(-uz') a(—\p")
aa.
т=
дхгх
а (— ии
as
§ 15.6J ПОТЕНЦИАЛЫ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ 465
напряжений и деформаций при определенном сочетании
выбранных для описания состояния тела параметров и при условии,
что термодинамический процесс является либо адиабатическим,
либо изотермическим.
Упругое тело можно представлять как такое тело, для
которого задания одной из двух термодинамических переменных Τ и
S и одного из двух тензоров —напряжений и деформаций, или,
что то же самое, одного из двух векторов — σ и ε, достаточно
для полного определения состояния тела.
Ниже рассмотрим все четыре комбинации:
ε и Τ, ε и S, σ и Τ, σ и S. (15.48)
Характеристические функции могут быть представлены как
функции принятых независимых переменных.
В табл. 15.3 показаны потенциалы напряжений и деформаций.
Дадим пояснения к таблице. С этой целью воспользуемся помощью
рис. 15.4, на котором изображена
структура таблицы с
обозначением отдельных структурных ее
частей.
В ячейках /, //, //' и ///
рис. 15.4, а рассматриваются
потенциалы, зависящие от
параметров, приведенных соответственно
в (15.48). В ячейках / и II —
потенциалы напряжений и в
ячейках //' и ///—деформаций.
В блоках /, //, //' И /// Рис. 15.4. К таблице 15.3.
(рис. 15.4, а) табл. 15.3 потенциа^
лами соответственно являются: U (удельная внутренняя
энергия, которая в рассматриваемом случае идеально-упругою
материала совпадает с удельной потенциальной энергией деформаций
U = W.
Для всего .объема тела, или для всей системы потенциальная
энергия обозначается символом (/); F (свободная энергия);
W' (потенциал, с точностью до знака совпадающий с так
называемой удельной дополнительной энергией — W' = W')\ для всего
объема тела или для всей системы дополнительная энергия
обозначается символом V; G (потенциал, в некотором смысле
аналогичный функции Гиббса в термодинамике. Известно, что
функция Гиббса выражается формулой G = F + pV, где ρ и V —
давление и объем).
В ячейках α, β, α', β' (рис. 15.4, а) помещены формулы,
связывающие потенциалы, обсуждаемые в соседних с этими ячейками
блоках (/, ..., ///). Эти формулы показывают, что с точностью
до знака они совпадают с формулами, характерными для преоб-
У
Ζ
ί
4
1
1
δ
if
i
z
ъ
4
1
Ζ
δ
4
466 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
разования Лежандра г) координатной системы (формулы в ячейках
α и β' по переменным Τ и S, а в ячейках а' и β — по ε и σ).
Из формул в ячейках α, β, α', β' ясно, что F и W'= —W'
получаются из W, a G может быть получен по любой из двух
следующих схем: W ->■ F -> G; W ->■#' = — W -+■ G.
Доказательство того факта, что функции W, F, — W и G
действительно являются потенциалами либо напряжений (W, F),
либо деформаций (— W и G), строится по единообразной схеме
и приводится в блоках /, ..., ///. Упомянутая схема состоит
в следующем: в разделе / каждого блока (см. рис. 15.4, б)
указывается от каких параметров-функций зависит функционал;
в разделе 2 приводится выражение полной вариации
функционала; в разделе 3 — полная вариация функционала дается на
основании формул, помещенных в ячейках α, β, α', β'; наконец,
в разделе 4 из сопоставления формул для вариаций
функционалов, приведенных в разделах 2 и 5, получаются формулы,
свидетельствующие о том, что функционал, рассматриваемый в данном
блоке, действительно является потенциалом деформаций или
напряжений, а также одной из термодинамических переменных Τ или S.
Формулы для компонентов напряжений, помещенные в
разделе 4 блока /, называются формулами Грина (по имени
английского ученого, впервые их получившего), а формулы в разделе 4
блока //' — формулами Кастильяно. Имеются аналоги для
формул Грина и Кастильяно, справедливые Для дискретных, в
частности стержневых, систем (см. §§ 15.11 и 15.12 —формулы (15.66)2
и (15.73)2).
Интересно заметить, что в правых частях формул в разделе 4
блоков /, //, //' и /// имеют место знаки соответственно:
~~Г" » ~~Г" » ~~Г" » » » "~Г" » » "
Поскольку нам неоднократно придется использовать формулы
Грина и Кастильяно, напишем их отдельно, хотя они
представлены в табл. 15.3
_ dW _ Ш_ _ dW_ _ dW _ dW _ dW
a*~ дгх ' °у- dey > σ*~ двг ' х*у- духу ' τν~ дууг ' Тг*-~ду-^>
(15.49)
_ dW _ dW _ dW dW _ dW _ dW
ε*--^7' &У~ day ' &* ~ даг ' V*y~ dxxy ' Vv ~ дхуг ' ^Х~Ж^·
(15.50)
г) Преобразование было открыто и использовано Л. Эйлером в 1770 г.;
однако широко известным оно стало после того, как Лежандр использовал
его в 1787 г., именно в связи с этим это преобразование получило имя
Лежандра; справедливее было бы называть его преобразованием Эйлера, либо,
в крайнем случае, преобразованием Эйлера —Лежандра. Первый примитивный
пример этого преобразования найден в исследованиях Лейбница. О
преобразовании Лежандра см. например, Р. Курант и Д. Гильберт. Методы
математической физики, т, II, изд. 2-е, Гостехиздат, 1951, М, — Л-, гл, I, § 6,
§ 15.7] ОСНОВНЫЕ И ПОБОЧНЫЕ ФИЗИЧЕСКИЕ ПРОЦЕССЫ В ТЕЛЕ 467
4. Различие упругих постоянных при адиабатическом и
изотермическом процессах. Вследствие отмечавшегося выше различия
упругих потенциалов при адиабатическом и изотермическом
процессах упругие постоянные в уравнениях закона Гука при этих
двух процессах в незначительной, правда, мере, но все же
отличаются друг от друга.
Впервые на это обратил внимание У. Томсон. Им
выполнялись опыты с растягиваемыми при разных скоростях нагружения
образцами. При очень большой скорости
нагружения (диаграмма О А рис. 15.5) теплообмен
между образцом и окружающей средой
произойти не успевает и поэтому процесс
получается адиабатический. При очень медленном
нагружении (кривая ОВ) происходит полный
теплообмен, вследствие чего температура образца
все время остается неизменной и процесс таким
образом оказывается изотермическим. При
быстром нагружении температура образца
получается ниже окружающей среды и позднее после
выравнивания температуры образца и
окружающей среды происходит удлинение образца,
соответствующее приращению ε на величину АВ
(упругое последействие при нагружении). При
очень быстрой разгрузке (кривая ВС) к концу
разгрузки температура образца оказывается выше окружающей
среды и лишь после выравнивания температур образца и
окружающей среды длина образца уменьшается на величину,
соответствующую изменению ε, измеренному отрезком СО (упругое
последействие при разгрузке). Адиабатический модуль упругости
равен Eajl = tgaaa, а изотермический £„3 = tgaH3, £ад>£из.
Отличие модулей £ад и £из для такого материала, как сталь, очень
небольшое — порядка г19—\% х).
Рис. 15.5. К
установлению величины
модуля продольной
упругости при
адиабатическом и
изотермическом процессах.
§ 15.7. О связях между механическими, тепловыми
и электрическими величинами
1. Общие положения. Можно, рассматривая термодинамику
равновесных свойств кристаллов и имея в виду тепловые, элект-
; ические и механические их свойства и соотношения между ними,
построить диаграмму2), а также весьма общую, но вместе с тем
^Подробнее об этом см., например, в книге Тимошенко С. П.,
История науки о сопротивлении материалов, Физматгиз, 1957.
2) Диаграмма .была предложена Хекманом (Нес k man n G., Erg. exakt
Naturwiss., 4, 140 (1925)) и развита Дж. Наем (Н а й Дж., Физические
свойства кристаллов и их описание при помощи тензоров и матриц, изд. 2-е,
«Мир- 1967).
468
ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
компактную, систему уравнений. На рис. 15.6 показана эта
диаграмма.
На диаграмме цифра в круглых скобках показывает ранг
тензора, коим является соответствующая величина, цифра в квад-
Электрические
величины
1П
гИапря-
' женность
поля
Ε J диэлектрическая
Л) ^с/-проницаемость Ш
(Напряжение
ё
(2)
Щ^^'
-f
термическое напряжение
Механические
величины
(2)
Термодпруаие
эффекты
т
емпера-
тдра
AT
(0)
Тепловые
величины
(О) .
Рис.
15.6. Диаграмма зависимостей между механическими, тепловыми и электрическими
величинами.
ратных скобках показывает ранг тензора системы коэффициентов
в соответствующих зависимостях. Отмеченная же выше система
уравнении, связывающая все величины, упомянутые на. диаграмме
§ 15.7] ОСНОВНЫЕ И ПОБОЧНЫЕ ФИЗИЧ2СКИЕ ПРОЦЕССЫ В ТЕЛЕ 469·
рис. 15.6, изображается так:
8
Ρ
AS
=
SET
DT
α'Ε
D'T
κσΤ
P'°
αΕ
Ρσ
coE
Τ
or
Ε
ΔΤ
(15.51)
1
1
Здесь цифры, показанные справа и снизу от матриц, обозначают
размеры блоков матриц. В соответствии с рис. 15.6 коэффициенты
упругости—тензор четвертого ранга. Ранг тензора, компонентами
которого являются элементы в блоках квадратной матрицы
в (15.51), равняется сумме рангов тензоров, входящих в
соответствующие зависимости, где эти элементы суть коэффициенты.
Вследствие симметрии тензоров напряжений и деформаций,
порядок матрицы СЕТ коэффициентов упругости (см. (7.3)) получается
не девятый, а шестой.
Верхние индексы в (15.51) указывают на факторы,
остающиеся неизменными при определении индексируемой величины;
так, например SET означает, что упругие податливости
определены при1) Ε = const и Τ = const (вследствие отмеченных равенств
SET—изотермические податливости при постоянном электрическом
поле). Адиабатические податливости при постоянном
электрическом поле обозначаются так: SES (верхний индекс S
соответствует энтропии; при адиабатическом процессе S = const). Рядом
с линиями на рис. 15.6, соединяющими окружности, показаны
символы матриц коэффициентов в зависимости между величинами,
соответствующими окружностям. Так, например, на линии,
соединяющей σ и ε, показаны S и С. Для получения ε,
обусловленного σ, имеем уравнение e = Sa, а для получения σ,
обусловленного ε, — уравнение а = Сг; аналогично для получения ε,
обусловленного Е, имеем уравнение ε = ΏΈ.
Диаграмма (рис. 15.6) и уравнение (15.51) подчеркивают
взаимную зависимость и энергетическую связь большого числа
разнообразных явлений, каждое из которых может изучаться
самостоятельно лишь с определенной погрешностью.
В формуле (15.51) в диагональных блоках расположены
матрицы коэффициентов зависимостей, отражающих основные
эффекты: упругость, диэлектрическую проницаемость и тепло-
!) Обращаем внимание на то, что здесь и в формуле (15.51), Е
—напряженность электрического поля. Условие Ε = const имеется в четырех угловых
блоках матрицы коэффициентов в (15.51), условие T = const—в четырех
верхних левых блоках этой матрицы и, наконец, условие ff = const —в четырех
нижних правых блоках, т. е. при определении элементов блоков матрицы
в (15.51) постоянными остаются одна или две из величин, находящихся
в столбце правой части (15.51),.
470 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
емкость; в остальных недиагональных блохах — побочные
(вторичные) эффекты.
2. Понятие о термоупругости. Связь механических процессов
с тепловыми проявляется в термоупругих эффектах — вследствие
деформаций происходит изменение теплопроводности, а
следовательно, и изменение температурного поля. К тому же при
деформировании тела выделяется теплота. Из-за изменения
температурного поля происходит температурная деформация, а при ее
стеснении возникают температурные напряжения. Возникновение
тепла вследствие наличия поля механических напряжений
называется пьезокалористическим эффектом.
Термоупругие эффекты в самом общем случае заключаются
в указанном выше взаимном влиянии полей деформаций и
температур. Эффект связанности проявляется в образовании движения
тепловых потоков в теле, в возникновении связанных тепловых
и упругих волн, в температурном рассеянии энергии. Кроме того,
вследствие изменения температуры могут изменяться модули
упругости.
Существует ветвь механики — термоупругость, в которой
изучается отмеченное взаимное влияние полей деформаций и
температур, а также в условиях стеснения деформаций возникновение
поля температурных напряжений.
Полная система уравнений термоупругости содержит
следующие системы уравнений или уравнения.
1. Уравнения движения (в частности, равновесия)
Ασ = — χ —pu.
Для общности приведены уравнения движения.
2. Уравнение теплопроводности, в котором учтена связь
температуры с деформацией
ΔΤ--Τ-ηύ=0.
Здесь Φ — первый инвариант тензора деформации, а — коэффициент
температуропроводности (a = k/(cp), k и с — коэффициенты
теплопроводности и теплоемкости) η = γΤ0/&, Τ0 — температура тела
в естественном (ненапряженном) состоянии, γ = (3λ — 2ν)α; λ, ν —
постоянные Ламе, α — коэффициент линейного теплового
расширения, Δ —оператор Лапласа.
3. Уравнения Коши
8 = A'U.
4. Уравнения закона Гука —Дюамеля — Неймана
а = С (е — E/i) = С (А' и — ε(1), или ε = С"% -\- г(1.
§ 15.7] ОСНОВНЫЕ И ПОБОЧНЫЕ ФИЗИЧЕСКИЕ ПРОЦЕССЫ В ТЕЛЕ 471
Покажем вывод уравнений закона Гука —Дюамеля — Неймана.
Рассмотрим сначала частный случай, когда имеет место чисто тепловое воздействие
/=Т—Т0 (при отсутствии механического). Расчленим мысленно тело на
элементы. Чисто тепловые деформации, возникающие в несоединенных между
собой элементах тела, например в элементарных прямоугольных
параллелепипедах, выражаются следующим вектором:
е/1={е*/1в^/1вг,/1, Ууг,пУгх,пУху,п} = № αί α/ 0 0 0}.
Если поставить цель из таких элементов, испытавших деформацию, составить-
сплошное тело, то в процессе объединения обязательно возникнут
дополнительные упругие деформации. Указанные дополнительные упругие деформации
вызывают дополнительные напряжения, с которыми они связаны законом
Гука ff/2 = Cs/2· Условию совместности деформаций в этом случае должны
удовлетворять суммарные деформации ε^=ε/ι-(-ε/2. связанные с
перемещениями уравнениями Коши 8^=А'и^, тогда ε/2=ε^—е(1=\'и(—ε/i и закон
Гука— Дюамеля — Неймана приобретает следующий вид:
о(2=С(А'щ— ε(1).
Присоединение сюда напряжений, вызванных механическим внешним
воздействием и выраженных при помощи закона Гука через соответствующие им
деформации ffM=CeM или ffM=CA'nM, приводит к вышеуказанной записи
закона Гука —Дюамеля —Неймана. При этом учтено, что
ff=ffM + ff/=C8M + C(A'u/—εη), Α'ιι,+εΜ=ε,+εΜ=ε=Α'ιι.
Для решения проблемы к приведенной выше полной системе
уравнений присоединяются соответствующие начальные и
граничные условия.
Во всех четырех группах уравнений, приведенных выше,
величины σ, ε, d, u являются суммарными, вызванными как
механическим, так и тепловым воздействием σ = <*„ + σΛ ε = εΜ4-8/,
Получим уравнения, являющиеся аналогом уравнений Ламе
в условиях постановки проблемы термоупругости. Для этого·
подставим σ, согласно уравнению Гука — Дюамеля — Неймана,
в уравнение движения; в результате будем иметь
AC (A'u — е1() = — χ — ри.
В таком виде уравнения называются уравнениями
Дюамеля—Неймана по фамилиям получивших их ученых1).
Связанность полей деформаций и температур в приведенной
выше полной системе уравнений термоупругости описывается
х) Дюамель—(J. M. С. Duhamel, 1797—1872)—французский ученый,
механик. Опубликовал полученное им уравнение, приведенное в тексте,,
в работе «Memoire sur le calcul des actions moleculaires developpees par les
changements de la temperature dans les corps solids». Mem. acad. sci. savants-
etrangers, t. 5, p. 440 — 498, 1838.
Франц Нейман (Franz Neumann, 1798 — 1895) опубликовал это уравнение
на пять лет позже в Abhandlungen preuss. Akad. Wissenschaften, Math.-Natu-
rer Klasse, B, 2, S. 1—254, 1843. В этом мемуаре основным предметом
обсуждения являлся предложенный Ф, Нейманом оптический метод исследования
напряжений,
472 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
посредством того члена в приведенном уравнении
теплопроводности, в котором имеется коэффициент η. Можно ввести
безразмерный коэффициент β, зависящий от коэффициента η
(μ —коэффициент Пуассона). При этом если β<^1, то
связанность полей деформаций и температур невелика и ею можно
пренебречь. Некоторые полимерные материалы, например, поливинил-
бутираль, обладают большим значением параметра г) β.
Иногда даже при сравнительно небольшой связанности полей
деформаций и температур эту связанность уместно учитывать,
поскольку при этом выявляются новые качественные особенности
явления.
При пренебрежимо малых β задача теплопроводности
оказывается самостоятельной, независимой от задачи упругих
деформаций, а последняя решается в условиях априорно заданного
температурного поля. Такая задача намного проще связанной.
Термоупругости посвящена большая литература 2).
3. О проблемах пьезоэлектрического и пироэлектрического
эффектов. Пьезоэлектрический и пироэлектрический эффекты
связаны с понятием диэлектрической проницаемости. Известно, что
на поверхности диэлектрика, помещенного в электрическое поле
напряженностью Е, индуцируются заряды *(на одной части
поверхности положительный, а на другой— отрицательный),
удельный дипольный момент которых Ρ (вектор поляризации)
пропорционален напряженности Е.
Некоторые твердые диэлектрики характеризуются тем, что
у них имеет место постоянная поляризация даже в отсутствии
внешнего электрического поля. Такими, например, являются
кристаллы кварца. Каждая элементарная ячейка решетки такого
кристалла обладает постоянным дипольным моментом (дипольный
момент равен произведению величины заряда и расстояния δ
между положительным и отрицательным зарядами) и все диполи
одинаково ориентированы. Однако внешнее поле, создаваемое этой
поляризацией, не обнаруживается, -поскольку происходит раз-
}) См., например: Dillon О. W., Thermoelasticity when the material
coupling parameter equals unity. Trans. ASME, ser. E, vol. 32, 1965, pp.
378—382;
Коваленко А. Д., Основы термоупругости, «Наукова думка», 1970,
стр. 277.
2) Укажем лишь некоторые литературные источники: Коваленко А. Д.,
Термоупругость. «Вища школа», Киев, 1975; Новацкий В., Вопросы
термоупругости, изд-во АН СССР, 1962; Новацкий В., Динамические задачи
те ρ мо упругости, «Мир», 1970. В этой книге имеется обзор В. А. Шачнева
«О новых результатах в теории сопряженной термоупругости».
Новацкий В., Теория упругости. «Мир», 1975.
§ 15.8] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ 473
рядка, вследствие того что собираются блуждающие заряды и
нейтрализуют поляризационные заряды. Если же из-за какой-то
причины внутренние дипольные моменты кристалла изменяются,
то внешнее поле легко обнаруживается, поскольку действие
блуждающих зарядов не успевает проявиться. Если при этом
диэлектрик находится в конденсаторе, то свободные заряды
индуцируются на электродах.
Если дипольные моменты изменяются вследствие теплового
расширения при нагревании диэлектрика, то возникновение при этом
внешнего электрического поля называется пироэлектрическим
эффектом. Возникновение же внешнего электрического поля из-за
изменения дипольных моментов кристалла за счет механической"
деформации (изменение расстояния между положительными и
отрицательными зарядами за счет деформации) называется
пьезоэлектрическим эффектом (существуют прямой и обратный
эффекты). Наряду с этим имеют место и такие явления, как
выделение тепла при воздействии электрического поля
{электрокалорический эффект)у выделение тепла при индуцировании дипольных
моментов {теплота поляризации).
Если Gij и е/;· — соответственно компоненты (ί, у = 1, 2, 3)
напряжения и деформации, а Еа и Ра {а= 1, 2, 3) — составляющие
напряженности электрического поля и вектора поляризации, то
пьезоэлектрические постоянные eaij и пьезоэлектрические модули
daiJ· находятся по следующим формулам:
Если Cijkl и Sijkl — модули упругих жесткостей и податливостей
при Е = 0, то
3 3 3 3
i= 1 / = 1 i = l /=1
В этой записи не учтена симметрия тензоров S, С, ε, σ.
Отмеченные выше побочные эффекты приобретают в
современной технике существенное значение.
§ 15.8. Потенциальная энергия деформации
1. Потенциальная энергия деформации линейно-упругой
пространственной стержневой системы. Из результатов гл. II, XI,
XII и XIII известно, что в самом общем случае работы линейно-
упругой стержневой пространственной системы, состоящей иа
стержней с прямолинейными осями, полная потенциальная
энергия деформации выражается формулой
А=1 О
474 ВАРИАЦИОННЫЕ ПРИНЦИПЫ. ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Эта же энергия через параметры деформации стержня
выражается так:
г h
fc= Го
2. Удельная потенциальная энергия деформации
анизотропного тела.
2.1. Вывод формулы. В самом общем случае упругого
-анизотропного тела закон Гука выражается уравнениями (7.2).
Выше было показано, что как при адиабатическом, так и при
изотермическом процессах деформирования 8W представляет собой
полный дифференциал δ№ = σ'δε, при этом упругий потенциал г),
■или иначе удельная потенциальная энергия упругой деформации,
■с точностью до произвольной постоянной выражается так:
W = J [σ* άεχ + σΰ dey + σζ dez + тху dyxu+xuz dyyz+Tzx dyzx]. (15.52)
"Условия интегрируемости (15.52), если учесть формулы (15.49),
имеют вид
дах доу дох дхху дох дхуг
~d&y'~Wx' ду7у~ "dij* дуу~г~ ~д*х'
&-tf· &=%" <**>■ <1553>
Если в (15.53) подставить (7.2), то получим Су = С^. Всего
имеется пятнадцать условий (15.53), следовательно, в самом общем
случае анизотропии тела число различных упругих постоянных
равно2) 36 — 15 = 21. Здесь 36 — число упругих постоянных в (7.2),
15 —число условий (15.53).
*) Здесь и ниже упругие потенциалы при адиабатическом и
изотермическом процессах не различаются.
2) Заметим, что у крупнейших ученых начала XIX века было
неправильное представление о числе независимых упругих постоянных тела,
обладающего свойством общей анизотропии, и изотропного тела. Навье, Коши,
Пуассон, Ламе и Клапейрон считали, что указанные числа равны соответственно 15
и 1 (при этом Пуассон полагал коэффициент поперечной деформации, носящий
•его имя, всегда равным 0,25). Английскому ученому Дж. Грину (1793—1841)
принадлежит строгий результат (в работе, представленной и опубликованной
в 1839 «On the lows of the reflection and reflection of light at the common
surface of two поп-crystallized media; см. и более позднюю посмертную
публикацию «Mathematical papers of the late George Greens», edited by
N. M. Fercers, London, 1871), согласно которому эти числа равны 21 и 2. Эта
работа положила начало длителкцой дискуссии, в результате которой
восторжествовала точка зрения Грина,
§ 15.8]
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
475
Представим закон Гука (7.2) в несколько измененной форме
а, = Си8, + ... + С1ву4
(15.54>
Св1ех + ...-\-С6<}у,
ZX1
сохранив обозначение упругих постоянных таким же как в (7.2),
но понимая под Си, С1Ъ и CiQ (/ = 1, ..., 6) величины в два раза
меньшие, чем в (7.2). Подставляя (15.54) в (15.52) и выполняя
интегрирование, получим
W=~2 СП8' + СПехЕУ + С138Л + СиВхУху + С1ЬйхЧуг + Cie8*V« +
+ У С^У + С^уег + С2^уУху + С2ЪеуУУЛС2бЁуУгх +
+ У С3& + СМ&гУхи + СзЬ&гУиг + С^гУгх +
+ У СА + CuVxyVyz + С*УхуУгх +
+ уС55^г + СббТ^Т^ +
+уС6вт^. (15.55)
Согласно (15.55) W представляет собой однородную функцию
второй степени относительно е*, гу, ..., угх. Аналогично, подставляя
в (15.52) выражения для ε*, ..., угх, согласно закону Гука,
через σ*, ..., τζχ, после интегрирования получили бы W в виде
однородной функции второй степени относительно компонентов-
напряжения.
2.2. Удельная потенциальная энергия в
различных частных случаях анизотропии тела.
2.2.1. Одна плоскость упругой симметрии. Совместим
плоскость хОу с плоскостью симметрии упругих свойств. Тогда
замена г на — г не должна изменять W. Вместе с тем, если учесть
формулу (15.55), очевидно, что при такой замене изменяется знак
У Ууг и yzx, поэтому все члены, содержащие ууг и угх, за
исключением тех, в которых содержится произведение их, и квадраты
каждого из них, должны обратиться в нуль. Иными словами,
должны быть выполнены восемь следующих условий:
С15 = С16 = С 26 = С2в = С35 — С36 — С45 = С46 = 0. (15.56)
Число упругих постоянных уменьшается до тринадцати (21 — 8—
= 13).
2.2.2. Три взаимно ортогональные плоскости симметрии. При
наличии в каждой точке тела трех взаимно перпендикулярных
плоскостей упругой симметрии не должно изменяться выражение
476 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
для W при изменении поочередно каждого из аргументов χ на
— х, у на —у, г на —г. Вместе с тем, как это видно из (15.55),
при таких заменах меняется знак у уху, ууг, угх. Вследствие
этого, кроме уже отмеченных выше, должны обратиться в нуль
члены, содержащие уху и произведение уугугх- Иными словами,
должны выполняться, кроме (15.54), еще и четыре следующих
условия:
С14 = С24 = Сз4 = С56 = U. (15.57)
Число упругих постоянных уменьшается при этом до девяти
(13 — 4 = 9). Такой вид анизотропии называется ортотропией.
2.2.3. Простейшая ортотропия. При одинаковости свойств во
всех трех направлениях, перпендикулярных плоскостям упругой
симметрии в ортотропном теле, величина W не должна
изменяться при круговой перестановке (xyz).
Вследствие этого, кроме (15.56) и (15.57), должны соблюдаться
еще и следующие шесть условий:
^11 ■ = ^22 = ^33» ^12 = ^13 ==^2з! ^44=^5β = ^60·
Число упругих постоянных при этом уменьшается до трех
(9-6 = 3).
2.2.4. Другие частные случаи. Существуют и другие различные
частные случаи анизотропии, характеризуемые семью, шестью,
пятью постоянными.
Известные в природе кристаллы анизотропны. Каждая синго-
ния кристаллов (триклиническая, моноклиническая, орторомбиче-
ская, кубическая, тетрагональная, тригональная и
гексагональная) обладает определенным типом анизотропии.
В табл. 15.4 (заимствована из упомянутой выше книги
Дж. Ная) показана структура матриц упругих постоянных
(упругих жесткостей и упругих податливостей), соответствующих всем
тридцати двум видам симметрии кристалловг). В этой таблице
черным кружком показаны отличные от нуля элементы матрицы,
точкой — равные нулю элементы. Одинаковые по величине и знаку
х) Л. И. Седовым и его сотрудниками показана возможность
представления конечных точечных кристаллических групп и текстур посредством
тензоров, компоненты которых инвариантны относительно этих групп.
Систематическое изложение этого вопроса дано, в частности, в статье В. В. Лох и на
и Л. И. Седова «Нелинейные тензорные функции от нескольких тензорных
аргументов» (Прикладная математика и механика, 1963, т. 27, вып. 3. См.
также Л. И. Седов. Механика сплошной среды. Том. I. Издание третье,
■«Наука», 1976. Добавление I).
В этой статье приведен и список литературы, относящейся к обсуждаемой
проблеме. В статье показано, что свойства текстур и кристаллов можно
задавать при помощи тензоров. Эта задача связана с теорией групп — с
рассмотрением группы сим_метрии, образованной системами преобразований координат.
Элементарные сведения о симметрии в аспекте, используемом в кристалло-
трафии, даны нами ниже в Дополнении II.
§15.81
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ 477
Таблица 15.4
Сингрния
Классы
Структура матриц
С и S
Число
разных
упругих
постоянных
Триклинная
Моноклинная
Орторомбиче-
ская
Кубическая
Тетрагональная
оба
все
все
все
1)4,4
4\т
2) 4 mm
42 т*
422
4\ттт
• · ·
• · · ·
• · · · ·
• · · · · ·
• · · · · ·
• · · · ·
• · · ·
21
13
1) 7
2) б
478 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Таблица 15.4 (продолжение)
Сингоння
Классы
Структура матриц
С и S
Число
разных
упругих
постоянных
Тригональная
1) 3,3
2) 32
3 т
3 т
1)7
2) б
Гексагон'альн; я
все
Изот»"' ..ι^ я
с,.;ода
ненулевые элементы представлены черными кружками,
соединенными линией; если два элемента равны по величине, но
противоположны по знаку, то один из них изображен черным, а
другой — незачерненным кружком и последние соединены один с
другим линией. Большой кружочек с зачерненной серединой,
соединенный линией с черным кружком, означает в случае матрицы S —
элемент, удвоенный по величине гю сравнению с элементом,
изображенным простым черным кружочком (в случае матрицы С —
элемент, равный по величине элементу, изображенному простым
черным кружочком); крестик означает элемент, равный 2 (Sn—512)
в случае матрицы S и тНСц —С12) в случае матрицы С.
2.2.5. Изотропное тело. Исходя из энергетических
соображений, можно удостовериться в наличии двух констант упругости
в случае изотропного тела. Величину W (15.54) можно
представить, если за х, у и ζ принять главные оси, как однородную
функцию второй степени от εχ, е2 и ε3. Если тело изотропно, то
§ 15.8] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ 479
эта функция не должна изменяться при перестановке местами е^
е2 и е3, т. е. должна быть симметрична относительно главных
деформаций. В самом общем виде симметричная однородная
функция второй степени относительно аргументов е^ е2 и е3 может
быть представлена так:
W = А (б! + е2 + е3)2 + В (егг2 + е2е3 + ед).
Приходим к выводу, что упругие свойства изотропного
материала характеризуются двумя упругими постоянными А и В.
Установим связь полученной записи закона Гука для изотропного
тела с рассматривавшимися в гл. VII.
Учитывая, что в скобках (соответственно первых и вторых)
находятся величины первого и второго инвариантов
деформированного состояния в точке, и имея ввиду выражения для этих
инвариантов
8* + 8|/ + 8* = 8ι + 88 + 88 = /1(Τβ),
гхеу + еуег + гггх - т {у%у + fyz + γ») = е^ + е2е3 + г3гг = /2 (Те),
приходим к следующей записи W для изотропного тела в
произвольных осях:
W = А {гх + &у.+ гг)2 + В [ехеу + гугг + гггх - ~ (у% + ylz + ?«)] ·
Если теперь воспользоваться формулами Грина (15.49), то
получим обобщенный закон Гука для изотропного тела в
следующей форме:
σ* = 2А {гх + гу + гг) + В (гу + ег), %ху = — - Вуху.
Отсюда ясно, что постоянные А и В связаны с μ, G или с λ и ν
следующими зависимостями:
B = -2G = -2v, ,4 = G-£=|r = v+-|.
В гл. VII I тома при выводе уравнений закона Гука для
изотропного материала было принято предположение коаксиальности
тензоров напряжений и деформаций, вследствие чего, выделив из
тела элементарный прямоугольный параллелепипед, грани
которого совпадают с главными площадками, мы считали, что в
процессе его деформации не происходит сдвигов, поскольку
вследствие коаксиальности Т0 и Τε ребра пересечения главных площадок
должны совпадать с направлениями главных деформаций. Здесь
из энергетических соображений получены уравнения закона Гука
для изотропного тела, совпадающие с выведенными в I томе, но
без использования предположения о коаксиальности тензоров Τσ
и Τε. Напротив теперь логика рассуждений иная — подобие картин
480 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
кругов напряжений и деформаций является не следствием, а
доказательством указанной коаксиальности. Выше говорилось о
локальных симметриях в точке.. Поэтому всегда можно использовать
декартову систему координат. Подчеркнем, что оси координат мы
располагали в соответствии с локальной симметрией. Если же
записывать закон Гука в произвольной системе ортогональных
координат, никак не согласованной с локальной симметрией, то
матрица упругих констант шестого порядка для всех различных
случаев анизотропности, вообще говоря, получается полной, но
число независимых констант сохраняется таким же, какое
было отмечено выше при рассмотрении отдельных случаев
анизотропности.
2.3. Заключительные замечания. Анизотропные
свойства тела в целом ряде случаев естественно описывать не в
прямоугольной прямолинейной системе координат, а в той или иной
системе криволинейных координат. Например, если не учитывать
конусности ствола дерева, то анизотропность его описывается
в цилиндрических координатах.
В любой точке естественной древесины можно отметить три
характерных ортогональных направления: 1—вдоль волокон, 2 —
вдоль радиуса и 3 —вдоль касательной к годичному слою в
поперечном сечении. Вдоль каждого из этих направлений упругие
свойства свои собственные (различны продольные модули
упругости), точно также как различны модули при сдвиге между
любыми парами из трех этих направлений. Однако во всех точках
упругие свойства, отнесенные к этим характерным направлениям,
одинаковы. Такая анизотропность называется цилиндрической
ортотропностью.
В других материалах ортотропность может быть отнесена
к иной системе криволинейных координат. С другой стороны,
в одной и той же системе криволинейных координат, как и в
декартовой системе координат, у разных материалов анизотропность
может быть различной. Очевидно, что выбор криволинейных
координат для описания анизотропности не является произвольным*
а обусловлен природой самого материала.
Различными типами анизотропии обладают и многие
искусственные, в частности, некоторые композитные материалы.
Напряженно-деформированное состояние в них определяется на основе
теории упругости анизотропного тела, в которой физические
уравнения (уравнения закона Гука) содержат матрицу жесткости или
податливости, соответствующую типу анизотропности тела. К числу
анизотропных материалов относятся фанера, древеснослоистые
пластики, стекловолокнистые материалы и др.
В последние два десятилетия нашли широкое применение так
называемые пространственные регулярные структуры
—пространственные конструкции, состоящие из стержней и объединяющих
§ 15.9] О ДВУХ ВСПОМОГАТЕЛЬНЫХ ПОНЯТИЯХ 481
их узлов. Структуры содержат многократно повторяющиеся
стержневые пространственные ячейки, матрицы жесткостей и податли-
востей которых в зависимости от конфигурации повторяют по
своему строению матрицы жесткостей и податливостей кристаллов
тех или иных сингоний и классов, т. е. обладающих
соответствующей им анизотропией. Вследствие этого при расчете таких
конструкций, учитывая малость размеров ячейки по сравнению
с габаритными размерами, иногда в качестве расчетной схемы
принимают сплошную анизотропную среду, в которой как бы
«размазаны» дискретные свойства
стержневой системы.
Теория упругости анизотропного
тела представляет собой большую
ветвь теории упругости х).
§ 15.9. О двух вспомогательных
понятиях
1. Возможные перемещения.
Ниже будет подвергнуто варьированию
деформированное состояние системы,
описываемое перемещениями.
Представляет особый интерес один класс
этих вариаций, в котором они
удовлетворяют всем условиям
совместности деформаций. Такие вариации
называют возможными
перемещениями.
На рис. 15.7 показаны примеры.
Если речь идет о задаче теории
упругости, то вариации перемещений
и деформаций должны
удовлетворять во всем объеме тела
уравнениям Коши, а на той части
поверхности тела, где заданы перемещения — вариации перемещении
должны равняться нулю.
2. Возможное изменение напряжений. Ниже подвергается
варьированию напряженное состояние, описываемое
напряжениями (или внутренними усилиями). Представляет особый интерес
один класс этих вариаций, в котором они удовлетворяют всем
г) Отметим две книги, посвященные теории упругости анизотропного
тела, во второй из которых имеется большая библиография.
Л е χ н и цк и й С. Г., Теория упругости анизотропного тела, Гостехиздат,.
1950.
Саркисян В. С, Некоторые задачи математической теории упругости
анизотропного тела. Изд-во Ереванского университета, Ереван, 1976 (Список
литературных источников насчитывает' 285 наименований).
συ
ю
Чъ*Щ^
6)
з)
Рис. 15.7. Изменения (вариации)
перемещений: а), б) возможные
изменения перемещений — не
нарушаются ни внешние, ни внутренние
связи; в) нарушена внешняя связь—
на правой опоре перемещение
должно быть равно нулю, а в
вариации перемещений оно не равно
нулю. Такое изменение (такая
вариация) перемещений не является
возможной; г) нарушена
внутренняя связь — нзлом в осн. Такое
изменение (такая вариация)
перемещений не является возможной.
482 ВАРИАЦИОННЫЕ ПРИНЦИПЫ. ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
*A=-pW
ΕΞ
τττττ
a jHt nit itHiti
*+*1чЧ
a)
'ЛГгтъ. V.
Mum
^ дпюры
Μ и М
ffl Эпюрьг
γ QutU
Рис. 15.8. Изменения (вариации) сил (внешних и внутренних): а) возможное изменение
(вариация) сил — не нарушаются условия равновесия; б) совокупность изменений
(вариаций) внешних н внутренних снл, не являющаяся возможной — нарушено равновесие
балкн (вариации реакций ие соответствуют вариациям внешних активных снл); е)
совокупность изменений (вариаций) внешних н внутренних снл, не являющаяся возможной —
нарушено равновесие балки (вариация изгибающих моментов не соответствует вариации
внешних сил).
§ 15.10]
ТЕОРЕМА КЛАПЕЙРОНА
483
условиям равновесия. Такую совокупность вариаций указанных
функций называют возможным изменением напряжений (усилий).
На рис. 15.8 показаны примеры.
Если речь идет о задаче теории упругости, то возможные
вариации напряжений и объемных сил удовлетворяют во всем
объеме тела дифференциальным уравнениям равновесия элемента тела
и закону парности касательных напряжений (который также
представляет собой три условия равновесия), а на той части
поверхности тела, где заданы поверхностные силы, — вариации
напряжений и поверхностных сил удовлетворяют уравнениям равновесия
элементарного тетраэдра.
В частности вариации внешних сил могут быть равны нулю,
тогда вариации напряжений самоуравновешены.
§ 15.10. Теорема Клапейрона
Рассмотрим статическое приложение к линейно-упругому телу
внешних сил и установим зависимость между работой внешних
сил и накопленной в теле энергией деформации.
1. Случай дискретной системы. Пусть процесс таков, что
в (15.25) 65 = 0, δΤ = 0 и δ(7 = δ(/, τ. е. к телу подводится только
механическая энергия, кинетическая энергия тела не возникает
и внутренняя энергия равна потенциальной энергии деформации.
Тогда (15.24) приобретает вид 6Л=6(/. Закон сохранения
энергии (15.25) соблюдается в процессе всего нагружения. Поэтому
работа внешних сил, которая в случае линейно упругой системы
η
(см. § 2.22) выражается формулой Л =*-*-У Q^, численно равна
1 = 1
накопленной в теле потенциальной энергии деформации (/, т. е.
A =U, или
y2Qtf|=l/· Σ<^ = 21Λ (15·58>
Это и есть теорема Клапейрона. Для выражения, стоящего
в левой части (15.58)2, можно ввести специальный символ А>
имея в виду, что А=2А.
2. Случай сплошной среды1). Теорема Клапейрона для
рассматриваемого случая выражается полученной выше формулой
*) Значительно позже Клапейрона немецкий ученый Г. Π ρ а н г е
(1885—1941) указал на то, что теорема Клапейрона представляет собой в общем
случае распространение теоремы Эйлера об однородных скалярных функциях
На сложные однородные функционалы (Prange G., Die Variations- und Mini-
mal-prfnzipe der Statik der Baukonstruktionen. Technische Universitat in
Hannover, 1916),
484 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
(15.55), которую представим здесь в следующем виде:
2W. (15.59)
Можно придать аналитической записи теоремы Клапейрона вид,
полностью аналогичный формуле (15.58), с этой целью получим
формулу для работы, производимой внешними силами (объемными
и поверхностными) при статическом их приложении на упругих
перемещениях. Такая формула может быть выведена аналогично
тому, как это было сделано в § 15.5 (вывод формулы (15.30)),
но с учетом того, что в рассматриваемом здесь случае, во-первых,
отсутствуют силы инерции (первый интеграл в формуле (15.30)
равен нулю) и, во-вторых, вместо вариаций перемещений и
отвечающих им вариаций деформаций должны иметь место
соответственно перемещения и деформации. Тогда искомая формула,
получаемая из формулы (15.30), приобретает вид
Л=$55*'вйш.
Θ
В развернутом виде эта формула записывается так:
JJ \ (Хи + Υ ν + Zw) άω + \ J (ΡνχΗ + pvyv + pvgw) dq =
0 s
= J И (σ*ε* + °УгУ + G*E* + Х*уУ*У + Wif* + tzxYzx) <*<*>,
Θ
или, учитывая (15.59), окончательно получим формулу,
аналогичную формуле (15.58)
\\UXu + Yv-\-Zw)diu-\-\\ (ΡνχΗ + PvyV + PvzW) dq = 2 J \ \ W άω.
0 s ©
(15.60)
§ 15.11. Принцип возможных перемещений1)
1. Общая формулировка. Принцип возможных перемещений
формулируется так. Если система находится в состоянии
равновесия, то сумма работ всех внешних (действующих на нее) и внутренних
сил на всяком бесконечно малом возможном перемещении равна
нулю.
х) Впервые принцип возможных перемещений для твердых тел был четко
сформулирован Ж· Л. Лагранжем в его «Аналитической механике» (Mecanique
analitique, 1788), почему и носит его имя, хотя основные идеи этого принципа
можно обнаружить в значительно более ранних работах (см., например, V а г i-
gnon, Nouvelle mecanique —письмо Иоганна Бернулли к Вариньону, t 2.
Paris, 1725, стр. 174). ^"деформируемым телам этот принцип впервые был
применен С, П, Пуассоном в 1833 г? (Traite de mecanique),
§ 15.11]
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
485
Принцип возможных перемещений можно сформулировать и
иначе, поменяв местами исходное условие и следствие: если сумма
работ всех внешних и всех внутренних сил системы на всяком
бесконечно малом возможном перемещении равна нулю, то система
находится в состоянии равновесия. При этом, разумеется, в
равновесии находится как вся система в целом, так и любая ее часть.
2. Применение принципа к стержневым системам. Пусть имеем
некоторую систему, например балку (рис. 15.9), загруженную
какой-то нагрузкой и находящуюся в равновесии. Внешние силы,
Рис. 15.9. К принципу возможных перемещений: / — ось балки до деформации; // —
ось балки, испытавшей деформацию в соответствии с внешней нагрузкой; /// — кривая
(ось) сравнения; / — элемент балки до деформации; /' — элемент балки, испытавшей
деформацию; /" — элемент балки после возможного изменения перемещений.
понимая их как обобщенные, обозначим символом Qi = Pi(i = \, ...
...,/), а соответствующие им перемещения — символом д> = Л/
(ί = 1, ..., 0· Под влиянием нагрузки система деформировалась
и в ней возникли усилия Мх, Му, Мг, Qx, Qy и Ν; параметры же,
характеризующие деформацию, суть: кх, ку, кг, yXt yyt гг. Эти
параметры деформации можно рассматривать как обобщенные
перемещения, соответствующие указанным выше внутренним усилиям
как обобщенным силам.
На рис. 15.9 линия / и элемент / — это ось балки и элемент
ее до деформации; линия // и элемент /' — ось балки и элемент
ее в равновесном, деформированном под влиянием нагрузки
состоянии.
На рис. 15.9 изображена балка, испытывающая плоский изгиб,
вследствие чего из шести усилий и шести параметров деформаций
отличны от нуля МХ1 Qy и Ν, κ*, уу и гг.
Рассмотрим теперь бесконечно малую возможную вариацию
перемещений (возможные перемещения), отсчитываемую от дефор-
486 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
мированного состояния. На рис. 15.9 линия /// и элемент /"
представляют собой ось балки и элемент ее после указанной
возможной (кинематически допустимой) вариации перемещений.
Возможную вариацию перемещений, соответствующую внешним силам,
обозначаем символом δ^^δΔ/. В случае пространственной
стержневой системы в результате вариации перемещений имеет место
вариация всех шести параметров деформации δκ*, δκ^, δκ2, δγ*,
δγ^ и бег. Так же как и сами параметры кх, ..., ег, вариации
этих параметров являются обобщенными перемещениями,
соответствующими внутренним обобщенным силам Mxt ..., N. При
кинематически возможном варьировании перемещений около
равновесного состояния не принимаем во внимание изменение ни внешних
сил, ни внутренних усилий, поскольку работа, производимая
ими на возможных перемещениях, оказывается малой более
высокого порядка, чем работа самих внешних сил или внутренних
усилий.
Математически принцип возможных перемещений
формулируется в следующем виде г):
t
Σ Q^ + (-δί/) = 0, (15.61)
ι = 1
здесь δ(/ —вариация потенциальной энергии деформации системы
(вызванная возможной вариацией перемещений); взятая со
знаком минус2) она равна вариации работы внутренних сил.
В развернутом виде δ(/ представляется так:
л
+ Q*ev* + Q/Yy + Ar6ee] dz. (15.62)
3. Применение принципа к сплошной среде. Применительно
к сплошной среде уравнение вариационного принципа возможных
перемещений имеет вид
555 (ХЬи + Υδν + Z6w) da> +
©
+ 55 (ρν*δ« + ΡνΑ + Pvzbw) dq-bV = 0, (15.63)
s
x) Если у системы имеются внешние упруго податливые связи, то реакции
в них производят работу на вариациях перемещений по направлению этих
связей. Будем относить эти реакции к числу внешних сил и работу,
производимую ими, включать в первый член формулы (15.61).
2) Работа, производимая внутренними силами, отрицательна, поскольку
внутренние силы стремятся воспрепятствовать перемещениям, происходящим
под воздействием внешних сил, так как внутренние силы направлены в сторону,
противоположную перемещениям точен их приложения.
§ 15.11J
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
487
здесь
Θ
ЛП7 dW Χ* I dW Λο _L dW Ло . dW Лм I dW Я . 9W *
4. Полная потенциальная энергия системы. Можно ввести
обозначение для функционала, вариация которого рассматривалась
в (15.62) в случае дискретной системы и в (15.63) в случае
сплошной среды. Такой функционал — функционал Лагранжа —
обозначим символом П. Функционал Π представляет собой полную
потенциальную энергию упругой системы
π=ι/+ν,
где (/ — потенциальная энергия деформации, a V = —Л
—потенциал внешних сил, действующих на систему.
Принцип возможных перемещений, если иметь в виду
функционал П, может быть записан и в такой форме:
бП = б(1/-Л)=0. (15.64)
Отсюда следует, что из всех возможных состояний равновесию
системы, подверженной воздействию внешних сил (имеющих
потенциал), соответствует то, при котором полная энергия системы
принимает стационарное значение. Это так называемый
вариационный принцип Лагранжа. Уравнение (15.64) полностью
повторяет (15.61) в случае дискретной системы и (15.63) в случае
сплошной среды. Функционал Π для случая сплошной среды
обсуждается в § 15.13 и 15.20.
Из условия стационарности функционала Π получаются
дифференциальные уравнения равновесия как уравнения Эйлера —
Лагранжа вариационной проблемы, из этого же условия
вытекают условия равновесия на границе (см. § 15.20). Уравнения
равновесия для дискретных статически неопределимых систем
выводятся из (15.64) в нашей книге (см. сноску1) на стр. 563).
5. Теорема Лагранжа—Дирихле. Условие 6П=0 свидетельствует
о стационарности П. В частности, Π может иметь экстремум.
Знак второй вариации позволяет судить о характере экстремума
(максимум или минимум). В случае консервативной системы
(на основании закона сохранения энергии) устойчивое
равновесие, неустойчивое равновесие и безразличное равновесие имеют
место соответственно при
Π = min, 6П = 0, δ2Π > 0,
П = тах, δΠ = 0, δ2Π<0,
Π = const, δΠ = 0, δ2Π = 0.
488 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Приведенные условия составляют сущность теоремы Лаг-
ранжа — Дирихле, представляющей собой достаточный признак
(или критерий) устойчивости для консервативной системы. В
качестве иллюстрации к этой теореме может служить пример с
шариком, расположенным на дне чаши, на вершине выпуклой
поверхности и на плоскости.
6. Теорема и формула Лагранжа для дискретных систем (первая
формула Коттерилла — Кастильяно). Выразим U через
обобщенные перемещения и подставим это выражение в (15.61)
/=■1 / = 1 / = 1 / = 1
(15.65)
Из (15.65)3 вследствие произвольности (в рамках кинематической
допустимости) величин б<7/ будем иметь
<Ъ-щ-°- <Ь-щ- <15·66)
Частная производная от потенциальной энергии деформации
по обобщенному перемещению равна соответствующей ему
обобщенной силе1).
Сформулированное положение представляет собой теорему
Лагранжа, а (15.66)2 — формулу Лагранжа (первую формулу
Коттерилла — Кастильяно), которая, как и сам принцип возможных
перемещений, справедлива для любой (линейной и нелинейной)
деформируемой системы.
Природа формулы Лагранжа (первой формулы Коттерилла —
Кастильяно) аналогична природе формул Грина (15.49).
§ 15.12. Принцип возможных изменений напряжений
1. Общая формулировка. Принцип возможных изменений
напряжений формулируется так: если деформация системы согласована
со всеми имеющимися внутренними и внешними связями, т. е.
если соблюдена совместность деформаций системы, то сумма работ,
производимых бесконечно малыми возможными изменениями всех
внешних и внутренних сил на действительных перемещениях
системы (вызванных самими статически действующими силами),
равна нулю.
Принцип возможных изменений напряжений, если поменять
местами исходные условия и следствия, можно сформулировать
1) С формулой (15.66) мы связали имя Лагранжа в том смысле, что она
вытекает из вариационного принципа Лагранжа. Однако непосредственно же
получил ее Кастильяно и, поскольку ниже получена и другая
симметричная (15,66) формула, формулу (15,66) называют первой формулой Кастильяно»
§ 15.12] ПРИНЦИП ВОЗМОЖНЫХ ИЗМЕНЕНИЙ НАПРЯЖЕНИЙ 489
и иначе: если сумма работ, производимых бесконечно малыми
возможными изменениями всех внешних и внутренних сил на
действительных перемещениях системы, равна нулю, то
деформация системы согласована со всеми имеющимися внутренними и
внешними связями, т. е. соблюдается совместность деформаций
системы.
2. Применение принципа к стержневым системам. Пусть имеем
некоторую систему, например, балку (рис. 15.10), загруженную
(до вариации сил) (после бариации сил)
1 Ϊ 1"
Рис. 15.10. К принципу возможного изменения напряжений: / — ось балки до
Деформации; // — ось балки, испытавшей деформацию в соответствии с внешней нагрузкой;
/ — элемент балки до Деформации; /' — элемент балки, испытавшей деформацию под
воздействием внешних сил; /" — то же после возможного изменения (вариации) сил
(внешних н внутренних).
какой-то нагрузкой и испытавшую деформацию,
удовлетворяющую всем условиям совместности. В системе, испытавшей
деформацию (параметры последней кх гг и перемещения и Ф;),
под влиянием обобщенных внешних сил Qi = Pt (/== 1 ή
возникают усилия Мх N. Соответствующие обобщенным
силам перемещения обозначим символом ^ = Δί (г = 1, ..., t).
На рис. 15.10 линия / и элемент / — это ось балки и элемент
ее до деформации; линия // и элемент У —ось балки и элемент
ее в деформированном с сохранением совместности деформаций
состоянии, возникшем под влиянием нагрузки.
Рассмотрим теперь бесконечно малую возможную вариацию
внешних сил (6Q1 = 6P1 8Qt = bPt) и внутренних усилий
(δΜχ δΝ). Будем считать, что при статически возможном
варьировании внешних сил и внутренних усилий в окрестности
490 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
той их комбинации, которая соответствует соблюдению
совместности деформаций, изменение параметров деформации и
перемещений не принимаются во внимание, поскольку работа,
производимая на них вариациями внутренних и внешних сил,
оказывается малой более высокого порядка, чем работа вариаций
внешних сил на самих кх,
JZ1
и,
о..
Математически принцип возможных изменений напряжений
формулируется так г):
^ Я,Щ - W = 0;
/ = 1
h
Σ
s = 1
61/'- 2 $[κ,βΛί, + κνβΛίι, + κ,βΛ1ι +
(15.67)
Q(P)V
Первое слагаемое в формуле (15.67)х представляет собой
вариацию так называемой дополнительной работы деформации (δ А'),
а второе слагаемое —вариацию дополнительной
энергии. Для того что5ы пояснить
функционал (/', рассмотрим нелинейно деформируемую
систему. Легко проверить, что функционал U',
называемый дополнительной энергией, может
быть представлен так 2):
Рис. 15.11. К
происхождению термина
дополнительная
работа.
Происхождение этого названия становится
ясным из рассмотрения рис. 15.11, где показан
график зависимости между обобщенной силой
и обобщенным перемещением в случае, если
эта зависимость нелинейна. Действительно,
I/ —потенциальная энергия деформации — изображается площадью,
заштрихованной вертикально, поскольку δϋ = 6A=Q$q, а
площадь, заштрихованная горизонтально, дополняет первую до
прямоугольника, представляющего работу постоянной по величине
еилы Q, которая совершается на перемещении q. Эта горизон-
*) Если у системы имеются внешние упруго податливые связи, то
варьируем и реакции в этих связях, а работу, производимую ими на
соответствующих им перемещениях, включаем в первый член формулы (15.67).
2) На то, что U' получается из U преобразованием Лежандра впервые
указал итальянский ученый Кротти (1839—1896) (Crotti F., Conversazioni
$aggi di critica scientifico pratica; Regio stabilimento tipolitographico cav. Mi-
Helli Rovogo p. 1—19; Crotti F., Esposizione de teorema Castigliano e suo
raccordo colla teoria dell'elasticita; Atti del collegio degli ingegneri et architetto
in Milano. Tomo 11., fasc. 4, 20 parte, pag. 225).
§ 15.12] ПРИНЦИП ВОЗМОЖНЫХ ИЗМЕНЕНИЙ НАПРЯЖЕНИИ 491
тально заштрихованная площадь и изображает1) (/', поскольку
&Af = SQ-q. Вариация функционала V может быть записана так;
t i t
61/' = 2 Qjbqj + 2 ЩЯ) - 2 Ж ЬЪ- О 5·68)
/ = 1 /=1 / = 1
Подставляя в (15.68) вместо dU/dqj величину Qf на
основании (15.66)2 и производя приведение подобных членов, получим
t
δΐ/'= 2 Щя/> О5·69)
1 = 1
т. е. пришли к формуле (15.67)!·
Значительный вклад в науку в области энергетических теорем и
вариационных принципов во второй половине XIX века принадлежит итальянским
ученым. Одним из первых ученых, пытавшихся сформулировать принцип,
носящий в настоящее время название принципа возможного изменения
напряжений, был итальянский инженер Л. Ф. Менабреа (1809—1896). Первая его
работа, посвященная этому вопросу, была опубликована в 1857 г.
(Menabrea L. F., Principio generale per determinare le tensioni e le pres-
sioni in un sistema elastico. Reale Academia delle Scienze di Torino).
Однако в работе содержались неточности. Во-первых, Менабреа не
осознавал того, что в формулировке этого принципа фигурирует не потенциальная
энергия деформации, а некоторая абстрактная математическая величина,
позднее названная дополнительной энергией; во-вторых, у Менабреа в
формулировке принципа фигурировали не действительные перемещения, как это должно
быть, а их вариации, и, наконец, не была подчеркнута необходимость
удовлетворения вариациями напряжений условиям равновесия, т. е. не отмечалась
статическая возможность вариаций напряжений. В связи с работами Менабреа
и содержащимися в них неточностями возникла большая и длительная
дискуссия, в которой приняли участие многие ученые. Один из участников этой
дискуссии Ж- Л. Ф. Бертран (1822—1900) в письме к Менабреа в 1869 г.
сообщил последнему о необходимости внесения в принцип исправлений в связи
с тремя отмеченными выше фактами (U' вместо U, qi вместо bqi и статическая
возможность bQi). В 1870 г. Менабреа опубликовал статью, в которой учел
все замечания Бертрана (Menabrea L. F. eBertrandJ. L. F. (Выдержка
из письма Бертрана к Менабреа), Atti della Reale Accademia delle Scienze
di Torino, Tomo V, Pag. 702). По сути дела современная формулировка
принципа возможного изменения напряжений принадлежит Бертрану". Однако
в связи с тем, что, насмотря на наличие ошибок в первоначальной
формулировке принципа, Менабреа применял его при решении многих задач и не
допуская ошибок (поскольку рассматривались линейные системы, в которых
£/' = £/, вариации сил принимались статически возможными без указания на
это, а под bqi фактически понимались сами qi), иногда сохраняют в названии
принципа и имя Менабреа.
Незгвисимо от Бертрана в 1882 г. принцип дополнительного упругого
потенциала (дополнительной упругой энергии) был предложен немецким
ученым Вильгельмом Френкелем (1841—1895) применительно к пространственной
задаче теории упругости (Frank el W., Der Princip der kleinsten Arbeit der
inneren Krafte elastischer Systeme und sein Anwendung auf die Losung bausta-
l) В случае линейной зависимости между обобщенной силой и обобщен*
ным перемещением имеем U' = t/.
492 ВАРИАЦИОННЫЕ ПРИНЦИПЫ. ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
tischer Aufgaben. Zeitschrift den Architekten und Ingenieur-Verein zu
Hannover. Neue Serie 28, S. 64, 1882).
В 1921 г. немецкий ученый Оскар Домке (1874—1945) (Die Erganzungs-
energie elastischer Systeme (Miiller-Breslau zum 70 Geburstag). «Eisenbau», vol.
12, S. 100) исследовал принцип возможного изменения сил с термодинамической
точки зрения и установил экстремальный принцип для адиабатических упругих
систем: все внешние силы и температура делают величину W — У)С}д — У] TS
минимальной т. е.
6(Q.T)[f/'-Hi?i?-STSl = 0;
здесь Τ — абсолютная температура, S —энтропия.
Если система нелинейна, например в физическом смысле, то,
раскрывая выражение для 6U' по формуле (15.67), необходимо
пользоваться нелинейными зависимостями между параметрами
деформации стержня (κ*, ку, κζ, ух, уу, гг) и внутренними
усилиями (Мх, Му, Мг, Qx, Qy, N).
3. Применение принципа к сплэшной среде. В случае
сплошной среды принцип возможных изменений напряжений выражается
следующей зависимостью, со всей очевидностью вытекающей из
формулы (15.69):
J J J (ыбХ + νδΥ + wbZ) άω + $ $ (u6pvx + vbpvy + wbpvz) dq - W = 0,
0 s
δι/' = \ \ \ [ε*δσ* + ε^δσ^ + εζδσζ + ухубххи + уигЬхиг + угхЬхгх] άω.
Θ
4. Вариационный принцип Кастильяно. Если положить, что
вариации внешних сил равны нулю, то принцип возможных
изменений напряжений принимает вид б(/'=0. Отсюда следует, что
из всех возможных изменений напряжений (усилий) совместности
деформаций соответствуют те, при которых дополнительная работа
принимает стационарное значение. Сформулированный принцип
называется вариационным принципом Кастильяно г).
5. Применение вариационного принципа Кастильяно к
сплошной среде. Вариационный принцип Кастильяно в случае
сплошной среды напишем в форме
Ш' = \ \ \ [ε*δσ* -f ЕуЪау + εζδσζ + γ^δτ^ +
0
+ Υί,*δτ^ + γ**δτ^]<2ω = 0. (15.70)
Функционал для случая сплошной среды обсуждается в § 15.13
и § 15.20.
х) Наряду с вариационным принципом Кастильяно можно было бы
сформулировать и вариационный принцип, полностью симметричный вариационному
принципу Лагранжа, если ввести в рассмотрение функционал П', и условию
стационарности которого придать вид 6Я'=0, 8U'— 6Л'=0. Варьирование
ведется по внешним силам и внутренним усилиям (случай дискретной системы)
или внешним силам и напряжениям (случай сплошной среды).
§ 15.12] ПРИНЦИП ВОЗМОЖНЫХ ИЗМЕНЕНИЙ НАПРЯЖЕНИЙ 493
6. Теорема и формула Кастильяно (вторая формула Котте-
рилла—Кастильяно) для дискретной (в частности, стержневой)
системы. Если выразить V через обобщенные внешние силы, то
вариацию можно представить так:
/=1
Подставляя (15.71) в (15.67), получим
t t t
ZiAb-Ha^-0·· 2(щ.-<7/)««/=°· 05.72)
/=1 /=1 ,· = 1
Так как величины 6Q/ произвольны, равенство (15.72)2 имеет
место лишь при
dU' Λ dU' .. с ,,оч
щ-ч> = °> ч/=щ- (15-/3)
Частная производная от дополнительной работы по
обобщенной силе равна соответствующему этой силе обобщенному
перемещению. Сформулированное положение представляет собой
теорему Кастильяно, а (15.73)2 — формулу Кастильяно (вторую
формулу Коттерилла — Кастильяно), она аналогична формулам
Кастильяно (15.50).
Английский ученый Д. Г. Коттерилл (1836—1922) в четырех статьях (On
an extension of dinamical principle least action, vol. 29, p. 299; On the
equilibrium of arched ribs of uniform section, vol. 29, p. 380; Further application
of the principl of least action, vol. 29, p. 430; On elliptic ribs, vol. 30)
опубликовал в 1865 и 1866 гг. в журнале Philosophical magazin, ser. 4, полученные
им результаты, которые остались незамеченными, вследствие чего позднее они
независимо повторились другими авторами и им присваивались имена
последних. К числу этих результатов относятся следующие.
1. Установление, что раскрытие статической неопределимости
осуществляется минимизацией U (здесь он допускал ошибку, ибо на самом деле
минимизировать надо U', однако, поскольку рассматривались линейные системы,
для которых U'=U, ошибка в расчете не возникала).
2. Доказательство того, что множители Эйлера — Лагранж·' используемые
при отыскании условного экстремума дополнительной работы, ямеют природу
перемещений.
3. Получение формулы для потенциальной энергии деформации стержневой
системы (учет изгиба (без сдвига) и осевой деформации).
4. Получение (до Кастильяно) формулы dU/dQi = qi (опять допуская
ошибку — вместо U надо иметь U').
5. Получение (до Кастильяно) формулы dU/dgi = Qi.
6. Получение вариационного принципа Менаореа, позднее названного
именем Кастильяно, из условия dU/dX = q=0 (здесь опять ошибочно
использована U вместо U').
Позднее результаты 4—6 были независимо получены Кастильяно также
без уяснения отличия U' от U. Однако, по-видимому, присвоение указанным
результатам имени Кастильяно вполне заслуженно, поскольку он решил
посредством полученного им аппарата огромное количество примеров и. по
существу, создал рабочий расчетный аппарат.
494 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
§ 15.18 Аналогия1) вариационных принципов
Для краткости принцип возможных изменений перемещений
(сил) будем называть первым (вторым) принципом. Аналогию
принципов легко проследить на параллельном приведении их
формулировок2).
В первом (втором) принципе утверждается, что если система
находится в состоянии, удовлетворяющем условиям равновесия
(совместности деформаций), то сумма возможных работ всех
внешних и внутренних сил (статически возможных бесконечно малых
вариаций внешних и внутренних сил) на всяких кинематически
возможных бесконечно малых вариациях перемещений
(перемещениях, вызванных самими силами) равна нулю.
В первом (втором) принципе предполагается, что, варьируя
перемещения (внешние и внутренние силы), считаем неизменными
внешние и внутренние силы (перемещения).
При сопоставлении принципа возможных изменений
перемещений (15.61) и (15.62) и принципа возможных изменений сил
(15.67) применительно к стержневым системам или при
сопоставлении метода перемещений и метода сил, о которых речь идет
в главе XVI, обнаруживается симметрия следующих понятий:
внешняя сила —перемещение
внутреннее усилие —параметр деформации (деформация)
совместность деформаций — равновесие
статическая возможность — кинематическая возможность
бесконечная малость —бесконечная малость
вариация внешних сил и вариация перемещений и парамет-
внутренних усилий ров деформаций.
Эту симметрию следует понимать в том смысле, что если
в формулировке одного из принципов встречается понятие,
помещенное в один из двух вышеприведенных столбцов, то в
формулировке другого принципа или метода имеет место понятие,
помещенное в той же строке другого столбца.
Сопоставление функционалов в вариационных принципах Лаг-
ранжа и Менабреа — Кастильяно при решении пространственной
задачи теории упругости выполнено в §§ 15.20 и 15.21.
ι) В настоящем параграфе для того, чтобы выпуклее подчеркнуть аналогию
вариационных принципов (симметрию формулировок), мы внесли некоторые
изменения в традиционную терминологию. Принцип возможных перемещений
назван принципом возможных изменений перемещений, а принцип возможных
изменений напряжений —принципом возможных изменений сил. Кроме того
вместо слова работа, традиционно используемого в формулировке принципа
использован термин возможная работа. Примечание об этом термине
дано в § 15.15.
2) Часть формулировки, относящаяся только ко второму принципу, дана
в скобках, а к первому — курсивом вне скобок,
§ 15.14] ДВЕ РАЗНОВИДНОСТИ ЭКСТРЕМАЛЬНОЙ ЗАДАЧИ
495
§ 15.14. Замечание о двух разновидностях постановки
экстремальной задачи
1
ι ''V VH
Iм
ψ
о
В теории дискретных, в частности стержневых, систем,
рассматривая один и тот же объект, задачу можно поставить двояко,
либо как вариационную, либо как
задачу об экстремуме функции.
В качестве примера приведем
исследование напряженного
деформированного состояния балки,
изображенной на рис. 15.12.
Задачу можно решить, исходя
из минимизации функционала
Ш
I
й)
U
I
i'li'lii' LiijlljM ίι ί |ii
δ)
аГр«0)
V
π С [ΕΙ (ν")2 \ ,
П=П—γ1—ηυ\αζ, т.е. сред-
ο
ствами вариационного исчисления
путем использования
вариационного принципа Лагранжа, согласно
которому 6П= 0.
Уравнением Эйлера в
поставленной вариационной проблеме
(здесь интеграл зависит от
неизвестной функции υ = ν (ζ) и
представляет собой функционал), как
было показано в разделе 2 § 15.2,
является EIvw = q, после решения
которого, получив υ, можно найти
ф = о' Μ = — ΕΙυ" и Q= — EIv'",
т. е. ось изогнутой балки
представляет собой такую кривую,
которой соответствует
экстремум (минимум) функционала потенциальной энергии системы.
Эту же задачу можно решить, исходя из экстремизации функциих)
Рис. 15.12. К раскрытию статической
неопределимости системы: а)
статически неопределимая система; б)
статически определима (основная) система,
полученная из статически
неопределимой отбрасыванием связи и заменой ее
неизвестной реакцией связи; в)
основная система под воздействием внешней
нагрузки; г) основная система под
воздействием единичной силы,
приложенной по адресу отброшенной связи.
и
-Ч
Xlz-^Jdz
2£7 '
(15.74)
г) Первым обратил внимание на то, что U и V в формулах Лагранжа и
Кастильяно в определенных постановках представляют собой функционалы,
был Луиджи Донати. Он в своих работах 1888, 1889 и 1894 гг. разъяснил
четко связь между этими функционалами и понятиями упругого потенциала
в терминах теории упругости и вариационного исчисления (D о π a t i L., Sur
lavoro di deformazione dei sistemi elastici; Memorie dell'accademia di scienze
di Bologna, Tomo IX, ser. IV, p. 345; 1888. D ο π a t i L., Illustrazione al teorema
del Menabrea; в том же журнале, Tomo X, ser. IV, p. 267, 1889. Donati L.,
Ulteriore osservazioni intorno al teorema del Menabrea, Tomo XV, ser IV, p. 449,
1894).
496 ВАРИАЦИОННЫЕ ПРИНЦИПЫ. ЭНЕРГЕТИЧЕСКИ!: ТЕОРЕМЫ [ГЛ. XV
зависящей от дискретной неизвестной Хх (реакция опоры), решая
уравнение
д\]'
щ = 0· (15.75)
(В (15.74) интеграл не является функционалом, а
представляет собой функцию одной переменной Хх.) В данном случае
использовано не вариационное исчисление, а аппарат отыскания
экстремума функции.
Уравнение (15.75) можно было бы представить и так:
^-Δ -0
где на основании теоремы Кастильяно частная производная от
дополнительной энергии по обобщенной силе представляет собой
обобщенное перемещение, соответствующее этой силе. Однако это
перемещение в данном случае по условию закрепления балки
должно равняться нулю. Покажем, что экстремум, определяемый
условием (15.75), или, что то же самое, условием dU'/dX1 =
= Δ1 = 0, есть минимум. Для этого достаточно убедиться в том,
что d2U'/dXl > 0.
Будем иметь в виду, что Δ1 = δηΧί-\-ΔιΡ. Здесь ΔιΡ
—перемещение, соответствующее силе Χλ и вызванное всей внешней
нагрузкой, би —перемещение, соответствующее Хг и вызванное
силой Χλ = 1. Тогда
dW д fdU'\ д /А ч s
= λϋ7 (Δι) = δι
дХ\ ~ ОХ1 \дХг) дХг у ν ~ υΐ1'
би>0 (рис. 15.12), так как в противном случае воздействие
силы, равной единице, на конце консоли должно вызвать
перемещение конца консоли в сторону, противоположную
направлению действия силы, чего быть не может.
Итак, d2U'/dXl>>0 и, следовательно, величина ХХ имеет
значение, обращающее значение функции дополнительной работы
в минимум.
§ 15.15. Теорема о взаимности работ1) и следствия из нее
1. Область применения. Рассматриваемая в настоящем
параграфе теорема справедлива для линейных систем, определение
которых дано в разделе 2 § 16.2.
х) Теорема была доказана итальянским ученым Бетти в 1872 г. В 1882 г.
более просто эту же теорему и следствия из нее доказал Кастильяно,
используя коммутативность произведения скалярной функции (В е 11 i E. Teoria della
Elasticita. II Nuovo Cimento, Ser. (2), Ν Ν 7, 8, 9, 10; 1872/73; Castig-
] i a π о А. С, Intorno ad una proprieta dei sistemi elastci, «Atti della Reale
Accademia delle Scienze di Torino», Tomo XVII, June, pag. 705, 1882).
§ 15.15] ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ И СЛЕДСТВИЯ ИЗ НЕЕ 497
2. Теорема. Прежде чем сформулировать теорему, рассмотрим
некоторую систему, находящуюся в двух различных состояниях.
В первом состоянии система загружена обобщенной силой Qlt
а во втором — обобщенной силой Q2 (изображать каждую из этих
сил на рис. 15.13 будем в виде одной сосредоточенной силы).
Теперь представим себе, что к системе приложены обе
обобщенные силы. При этом процесс загружения осуществим в двух
вариантах.
Будем считать, что в первом
варианте (рис. 15.13, в) к системе сначала
статически приложена обобщенная сила
Q1 = Plt при этом сила Рх на
перемещениях ею же вызванных совершает
работу Ап\ после того как закончен
рост силы Ри к системе статически
прикладывается обобщенная cnnaQ2 = Р2.
При этом на перемещениях, вызванных
последней, совершает работу и сила Рх
(эту работу обозначим символом А12),
и сила Р2 (работу силы Р2 на
перемещениях ею же вызванных
обозначим А22).
Во втором варианте процесса
загружения (рис. 15.13, г) к системе
сначала статически приложена
обобщенная сила Р2, совершающая при
этом работу А22. После того как
закончен рост силы Р2, к системе статически
прикладывается обобщенная сила Рг.
На перемещениях, вызванных силой Plt
работу производит и сила Рг (эта работа равна Лх1), и сила Р2\
работу силы Р2 обозначим А21.
Работа, совершенная внешними силами в первом варианте
процесса нагружения системы, равна Лг = Ли + Л12 + A2i.
Аналогично работа, совершенная внешними силами во втором
варианте процесса нагружения системы, равна А2 = Аг2-\-А^-\-Ап.
При этом
Α\\=-η-Ρ\Δ\\> А22 = -к- °2^22» ^12=°ιΔ12, Л21 = Ρ2Δη. (15.76)
г)
Рис. 15.13. К теореме о
взаимности работ: а) первое состояние
системы; б) второе состояние
системы; в) первый способ
приложения к системе нагрузок двух
ее состояний; г) второй способ
приложения к системе
нагрузок двух ее состояний.
В линейной системе потенциальная энергия деформации не
зависит от последовательности приложения отдельных частей
нагрузки, а зависит лишь от окончательного значения всех
приложенных к системе сил. Поэтому потенциальная энергия
деформации Ult накопленная в системе при первом варианте
процесса загружения, равна потенциальной энергии деформации U2,
498 ВАРИАЦИОННЫЕ ПРИНЦИПЫ. ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
накопленной в системе при втором варианте процесса загружения
иг = и2. (15.77)
С другой стороны, на основании закона сохранения энергии
в каждом из вариантов процесса загружения действительная
работа внешних сил равна потенциальной энергии деформации
системы
Аг = ии A2 = U2. (15.78)
Учитывая (15.77) и (15.78), имеем
Лг = Л2, ИЛИ Ац 4"·^12"4"·^22= -^22 ~Ь -^21 ~Ь Ац.
Отсюда
А12 = А21. (15.79)
Полученная зависимость аналитически выражает собой
теорему о взаимности работ, которая может быть сформулирована
следующим образом» Работа внешних (внутренних) сил первого
состояния на соответствующих им перемещениях второго
состояния равна работе внешних (внутренних) сил второго состояния
на соответствующих им перемещениях первого состояния.г)
!) В некоторых литературных источниках в формулировке теоремы вместо
слова работа используется термин возможная работа (см., например,
И. М. Рабинович. Курс строительной механики. Часть II. Гос. изд-во
литер, по строительству и архитектуре. М. 1954). При этом по смыслу
изложения под указанным термином имеется в виду абстракция, отличающаяся от
действительной работы тем, что силы, производящие работу, могут относиться
к одному состоянию системы, а перемещения им соответствующие—к другому.
Вместе с тем дается определение этого понятия в параграфе, посвященном
принципу возможных перемещений, как работы сил на возможном
перемещении, хотя в самой формулировке указанного здесь принципа термин возможная
работа не используется и вместо него применено просто слово работа.
Аналогичное последнему дается определение возможной работы и в классическом
курсе П. Α π π е л я (П. Α π π е л ь. Теоретическая механика. Том первый. Пер. с
пятого французского издания И. Г. Μ а л к и н а. Физматгиз. 1960). Как правило,
в формулировке принципа возможных перемещений не используется термин
возможная работа и в других литературных источниках (см., например: К. Л а н-
цош. Вариационные принципы механики. Пер. с англ. В. Ф. Гантмахера.
Под ред. Л. С По лак а. «Мир». 1965; А. И· Лурье. Теория упругости.
«Наука» 1970; В. В.. Новожилов. Теория упругости. Оборонгиз. 1958 и др.)
Для обеспечения симметрии понятий, рассматриваемых в принципах
возможных перемещений и возможных изменений напряжений, можно было бы
склониться в пользу первой, приведенной выше (в начале настоящей сноски),
трактовки понятия возможная работа. Тогда этот термин можно было бы
применить и к работе, совершаемой возможными вариациями сил на
соответствующих им перемещениях, вызванных самими силами. При таком условии
термин возможная работа мог бы быть включен симметрично в формулировки
обоих принципов — и возможных перемещений и возможных изменений
напряжений, что и было сделано в § 15.13. Вопрос этот, разумеется, чисто
терминологический, не влияющий на существо дела,
§ 15.15] ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ И СЛЕДСТВИЯ ИЗ НЕЕ 499
Формулировка содержит в скобках указание на справедливость
теоремы применительно и к работе внутренних сил. Это вытекает
из того, что работа внутренних сил равна работе внешних сил,
взятой со знаком минус.
Теорему о взаимности работ можно сформулировать и так:
работа внешних сил первого состояния на соответствующих им
перемещениях второго состояния равна взятой с обратным
знаком работе внутренних сил второго состояния на
соответствующих им перемещениях первого состояния.
3. Следствия. Из теоремы о взаимности работ вытекают
важные следствия.
3.1. Взаимность перемещений1). Перемещение,
соответствующее первой силе и вызванное второй силой, равной
единице, равно перемещению, соответствующему второй силе и
вызванному первой силой, равной единице.
Здесь силы и перемещения понимаются в обобщенном смысле.
Действительно, учитывая формулы (15.76) и (15.79), будем иметь
PA2 = ^Aa· (15.80)
Так как силы Рх и Р2 приняты равными единице, получаем2)
о12 = о21.
Если размерность у Рг и Р2 различна, то у величин Δ12 и Δ21
размерность тоже различная, но такая, что в обеих частях
равенства (15.80) размерность, как всегда, должна быть одинакова.
Что же касается величин δ12 и δ21, то, учитывая равенства δ12 =
= Δ12/Ρ2 и δ21 = Δ21/Ρχ, вытекающие из определения величин δ12
и δ21, и равенство, вытекающее из правила пропорции и
получаемое из (15.80) Δ12/Ρ2 = Δ21/Ρχ, убеждаемся в одинаковости их
размерности.
3.2. Взаимность реакций. Пусть имеем некоторую
деформированную систему. Рассмотрим ее в двух
напряженно-деформированных состояниях (рис. 15.14). В первом —по направлению
связи / произошло перемещение, равное единице, при этом в связи
/ реакция равна гп, а в связи 2 — г21. Во втором состоянии
перемещение, равное единице, произошло по направлению 2, при этом
в этой связи имеет место реакция г22, а в связи / — реакция г12.
Если в каждом из состояний отбросить связи и заменить их
х) Теорема Максвелла. Теорема была доказана в 1864 г. Д. К· Максвеллом
до доказательства более общей теоремы Бетти. Однако работа Максвелла
осталась незамеченной инженерами и учеными. В 1874 г. независимо от Д. К·
Максвелла и Э. Бетти взаимность перемещений была доказана О. Мором.
(Maxwell J., On the calculation of the equilibrium and stiffness of frames,
Philosophical Magazine, series (4), April, vo . 27, p. 294, 1864. MohrO. C, Beitrag
zur Theorie der Bogenfachwerkstrager, Band 20, S. 223; Beitrag zur Theorie des
Bogenfachwerks, Band 20, S. 243; Beitrag zur Theorie des Fachwerks, Band 20,
S. 509; Zutschrift des Architekten und Ingeniuer Verein zu Hannover, 1874).
2) Перемещение, вызванное единичной силой, обозначаем символом б
с соответствующими индексами.
500
ВАРИАЦИОННЫЕ ПРИНЦИПЫ. ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
т Щ ¥' vk
действие на систему соответствующими реакциями, то, согласно
принципу взаимности работ, можно утверждать, что работа
внешних сил первого состояния на перемещениях им соответствующих
во втором состоянии равна работе
внешних сил второго состояния на
перемещениях им соответствующих
в первом ги ■ 0 + г21 · 1 = г121 + г22 · 0,
r12=r2l и, в общем случае, гц=гц.
Итак, получили: реакция в
связи /, возникающая при единичном
перемещении по направлению
связи /', равна реакции в связи / при
единичном перемещении по
направлению в связи i.
3.3. Взаимность реакций
и перемещений1). Пусть имеем
некоторую линейно деформируемую
систему. Рассмотрим ее в двух
напр яженно-деформированных
состояниях (рис. 15.15). В первом —на
систему действуют нагрузка (силы
Рх, Р2, ..., Р{,..., Рп), под
влиянием которой в связи i возникает
реакция RiP\ во втором —по
направлению связи i произошло
перемещение, равное единице и в этой связи
возникла реакция Гц. Если в
каждом из состояний отбросить связь i
и заменить ее действие
соответствующей реакцией, то, согласно
принципу взаимности работ, можно
утверждать, что работа внешних сил
первого состояния на перемещениях им
соответствующих во втором равна
работе внешних сил второго
сойм соответствующих в первом
Рис. 15.14. К установлению
взаимности реакций: а) система и
наложенные на нее связи; б) состояние
системы, при котором по
направлению связи / произошло
перемещение, равное единице', в) состояние
системы, при котором по
направлению связи 2 произошло
перемещение, равное единице.
Рис. 15.15. К установлению
взаимности реакций и перемещений:
а) действительное состояние;
б) вспомогательное состояние.
стояния на перемещениях
Rip-1+Σ p^Pki = ru-0, RiP = - Σ р£'рк1·
Если в первом состоянии имеется всего одна внешняя сила
Pj = \, то2) rip= — S'-p.h или, упрощая символику,
П/= — δ/t. (15.81)
*) Сформулирована и доказана А. А. Гвоздевым (Общий метод расчета
сложных статически неопределимых систем, МИИТ, М., 1927).
2) Реакция в связи, вызванная единичной силой, обозначается символом г
с соответствующими индексами,
§ 15.16] ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПО ТЕОРЕМЕ КАСТИЛЬЯНО 501
Формула (15.81) выражает взаимность ri} и—Ь1Ь Реакция
в связи ί, вызванная внешней единичной силой Р/ = 1, равна
взятому с обратным знаком перемещению по направлению этой
силы, вызванному перемещением, равным единице, происходящим
по направлению связи i. Для того чтобы подчеркнуть, что
перемещение вызвано перемещением (а не силой), в обозначение введен
верхний штрих.
Пример 15.2. В однопролетной призматической балке пролета / и
жесткости £7, защемленной на обоих концах, определить перемещение, нормальное
оси балки в точке i последней, отстоящей на //4 от левого конца, если правый
(центр его обозначаем символом /) переместился в направлении,
перпендикулярном оси на величину, равную единице.
Решение. Искомое перемещение обозначается символом 6t'-. Согласно
теореме о взаимности перемещений и реакций 6f. = —■ гуг, где /у,·
—вертикальная реакция в правой опоре (в точке /), возникающая от единичной силы
перпендикулярной оси балки и приложенной в точке i. Эта реакция
определяется по формуле Γμ=— 1 · α2 (Ι + 2β), α/ —расстояние точки приложения
внешней силы от левой опоры (Osgasg 1), β/ —расстояние точки приложения
внешней силы от правой опоры (β = 1— α). В нашем случае а = 1/4, β =3/4. Знак
минус в формуле для r}i принят из следующих соображений. Если
перемещение точки / (на величину, равную единице) произошло в положительном
направлении оси у, то и в точке i направление такое же. Поэтому во
вспомогательном состоянии единичную силу, приложенную в точке i, также
направляем в положительном направлении оси у, но в этом случае реакция гп имеет
противоположное направление, следовательно и противоположное направлению
перемещения точки /. Поскольку г μ энергетически соответствует этому
перемещению, г μ < 0. Окончательно имеем
§ 15.16. Определение перемещений по теореме Кастильяно
Формула Кастильяно (15.73) ^ = Л| =^- = ~позволяет
непосредственно находить интересующие
нас перемещения, если известно
выражение для V в функции от Р{.
Для линейных систем численно ^ 'ά.
w = v.
Покажем методику определения
перемещений в линейно упругих
системах на примерах. Уу
г, ico /-ч * Рис· 15.16. К примеру 15.3.
Пример 15,3. Определить прогиб конца
консольной призматической балки,
загруженной силой Ρ (рис. 15.16), имея в виду, что сечение балки прямоугольное.
Решение, Формула для V имеет вид
1 Μ ■ dz ρ Q» dz
^
/
1-Z-*
С μ* αζ с Q,,dz
502 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Поскольку искомое перемещение —прогиб конца консоли—представляет собой
перемещение, соответствующее силе Р, получаем
дМх , dQu
I м Ζ Ι η
dv du cm* dp . с чу дР
V^=-dP==dp-\-ETrdZ+\~GF^-dZ· (15·82)
В формуле (15.82) выполнена операция дифференцирования по параметру под
интегралом, в нашем случае
Мх = — Pz; Qy = —P (15.83)
и
дМх dQu
-gp—.. -з^—1. (15.84)
Подставляя (15.83) и (15.84) в (15,82), получим
Р(-Рг)(-г)аг C(-P)(-\)dz Р/з Р1
v{*-°-)—ёгх—+i —щ mz+щ- (15·85)
о о
Первый член в (15,85)—это прогиб, вызванный изгибом консоли, а второй —
•сдвигом, сопровождающим изгиб. Оценим удельный вес второго члена в
выражении υ |г_0. для этого представим формулу (15.85) в следующем виде:
Р/з Λ . ЗЕ1Х
°U-o = oc7- Μ
ЪЕ1Х \ ^ PGFy
Учитывая тот факт, что поперечное сечение балки прямоугольное, имеем Ix ■.
/ ь!*_ \
, Р13 / , , 0Έ "12 \ Р/з (χ t 3 Ε h*
Поскольку второй член в формуле, отражающий влияние сдвига на прогиб,
■содержит множитель /ι2//2, наибольшее относительное влияние этого члена на
величину прогиба получается при наибольшем допустимом значении h/l. Таким
является h/l =1/5. При h/l > 1/5 элементарная теория изгиба, обсуждаемая
здесь, не дает необходимой точности. При /ι// = 1/5 формула приобретает вид
ι __™!_Λ-ΐ_Α 1 Е\_ Р1Ь Λ ι 3 Е
v\*-»-3EIx \1_1"10'25'G/ 3£/Д +250G
Если для балки использованы такие материалы, как сталь или древесина,
то величина E/G соответственно равна 2,5 и 20 и
ι _ Р13 /,, 3 \ , Р1Ь ί^ , 24
ν1*-ο-3ΕΓχ{ι + ϊοδ)> и1г-°-ШГх[1+Ш
т. е. в этом случае прогиб от сдвига при изгибе составляет соответственно
3% и 19% от полного значения прогиба*).
х) Вопрос о влиянии деформации сдвига при изгибе на величину прогибов
ή тесно с этим связанные вопросы о влиянии сдвигов на кривизну оси балки
и об учете потенциальной энергии стеснения депланации поперечного сечения
■стержня, вызванной сдвигом, обсуждался в рамках элементарной теории в ряде
работ; в некоторых из них предприняты попытки оценки результатов при
помощи аппарата теории упругости,
Отметим некоторые из этих работ,
§ 15.16] ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПО ТЕОРЕМЕ КАСТИЛЬЯНО 503
Пример 15.4. Определить угол поворота торцевого сечения призматической
консольной балки, загруженной силой Ρ на конце консоли (рис. 15.16).
Решение. Углу поворота торцевого сечения как обобщенному
перемещению соответствует обобщенная сила в виде момента, приложенного
к этому же сечению. Вместе с тем такого
момента среди действующих на систему сил нет.
Применительно к такому случаю Кастильяно
предложил остроумный прием, состоящий в присоединении
к числу действующих сил обобщенной силы,
соответствующей искомому обобщенному перемещению. При
этом возникает возможность взятия производной
от V по этой силе, после этого введенную
обобщенную силу полагаем равной нулю. Взятие
производной от функции по аргументу в той точке, где
он равен нулю, проиллюстрировано на рис. 15.17.
Итак, используя приведенную выше' формулу для
U' = U, представим Ьх в следующем виде:
дмх dQu
1 Мх -π£ dz J Q„ ~^r dz
x~ Ж ~ дШ ~ J
ЗШ
EI,
f
ж
GF,
Рис. 15.17. Пояснение К.
введению нулевой силы
при определении
перемещения по Кастильяно а
случае, если отсутствует
соответствующая ему
обобщенная сила.
После введения обобщенной силы т, соответствующей искомому обобщенному
перемещению (рис. 15.18), Мх — —Pz—m, Qy — —Р. Следовательно,
ι
дМх
dm
ι,
9Qy
зт
= o,
♦-$
(— Pz){— \)dz Pz*
Ell ==~2ЁК
PI2
~2ЁТ
Ritter W.,
bearbeitet von
und Festigkeit, Berlin,
Math., vol. 24, 1889;
1895;
'elasticity an calcul des
1475—1478; F
G rash of F., Teorie der Elasticity und Festigkeit 1878;
Anwendungen der graphischen Statik (Nach Prof. Dr. С Culman
W. Ritter), Bd. 1, Zurich, 1888; Bach C, Elasticity
1889; (2-ое изд. 1894); Pearson K. Quart. Journ.
Rankine W. J., Macquorn, Applied mechanics 14-ed,
Mesnager Α., Sur I'application de la theorie d'<
pieces rectangulaires flechies, Compt. rend, 1.132, 1901, p. 1475—1478; hi-
Ion L. N. G. Phil. Trans. Roy. Soc, (A), vol. 201; Karman Th. v., Scripta
Universitatis atque Bibliothecae Hierosolmitanarum, 1923; Timoshenko S.,
The approximate solution of two-dimensional problems in elasticity. Phil. Mag,
vol. 47, № 282. June 1924, p. 1095, К arm an Τ h. v., Uber die Grundlagen
dar Balkentheorie. Abhandl. aerodynam. Inst. tech. Hochschule, Aachen, T.7,1927.
Тимошенко С. П., Сопротивление материалов, часть первая, пер. с англ»
Н. А. Шошина, 3-е русское издание, Гостехиздат, 1934 (пер. с первого изд.
на англ. яз. 1930 г. —Strength of materials, New York), стр. 171 —175;
Тимошенко С. П. Теория упругости, пер. с англ. Н. А. Шошина, Гостехиздат,.
1934 (Theory of elasticity. London, New-York, 1934) стр. 52—53 и 118; Пап·
ко вич П. Ф-, Строительная механика корабля, ч. I, т. 1, Изд-во «Морской
транспорт», 1945; Η е i 1 i g R. Schubverformungseinflup auf die Wolbkrafttorsion
von Staben mit offenem Profil. Der Stahlbau April 1961; Гаврилив Ю. М-,
Энергетическая и графо-аналитическая трактовка основных составляющих
перемещений чистого и стесненного сдвига коротких балок. Прикладная механика,,
том 6, вып. 5, Киев, 1970. Гаврилив Ю- Μ., Τ е ρ л е ц к и й Л. В.,
Определение перемещений чистого сдвига двутавровой балки полуобратным методом
плоской задачи теории упругости. «Известия вузов», серия «Строительство и
архитектура», 1972, № 5. Reissner E. Upper and lower bounds for
deflections of lamination cantilever beam with accounting of deformations of transver-
bal shear. Applied Mechanics. Trans, of. ASME., 1.973, N. 4,
504 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Рассмотренный пример показывает, что от сдвига,
сопровождающего изгиб, повороты поперечных сечений равны нулю. Схе-
Рис. 15.19. К оценке влияния сдвигов иа
перемещения в балке при поперечном
изгибе: а) балка, подвергнутая поперечному
изгибу; б) прогибы, соответствующие
взаимным поворотам поперечных сечений в балке;
в) прогибы, соответствующие сдвигам.
матически наличие двух составляющих (от Мх и от Qy) у
прогибов и одной составляющей у поворотов (только от Мх) легко
уяснить из рис. 15.19.
§ 15.17. Универсальная формула Мора для определения
перемещений в стержневых системах. Прием Верещагина
Пусть имеется некоторая система, несущая определенную
нагрузку (рис. 15.20). Требуется определить проекцию на
направление i — i перемещения некоторой точки г этой системы, вызванного
приложенной к ней нагрузкой. Состояние системы, в котором к
ней приложена действительная внешняя нагрузка, будем
называть грузовым (действительным). Искомое перемещение, согласно
принятому правилу, обозначим символом \iP.
Рассмотрим систему в двух состояниях—действительном
{рис. 15.20, а), когда к системе приложена заданная нагрузка,
и вспомогательном (рис. 15.20, б), когда к системе в той точке,
перемещение которой мы определяем, приложена сила, равная
единице и направленная вдоль i — ί.
В действительном состоянии в системе возникают усилия
Мхр, Qyp, Myp,_Qxp,_ МгР_ и JVp, _a во_вспомогательном
состоянии — усилия Mxi, Qyi, MyU Qxi, Mzi и N{. На основании теоремы
о взаимности работ работа внешних сил вспомогательного
состояния на соответствующих им перемещениях действительного равна
т%
Рис. 15.18. К примеру 15.4.
§ 15.17]
УНИВЕРСАЛЬНАЯ ФОРМУЛА МОРА. ПРИЕМ ВЕРЕЩАГИНА
505
взятой с обратным знаком работе внутренних сил
действительного состояния на соответствующих им перемещениях
вспомогательного
1 · Δ,Ρ =
хР QyiQyp MyiMyp QxiQxp MziMzp NjNp]
+ ~GFy~~ + Е1Ц + GFX + G/„ + ~ЁГ JUZ'
-ΣίΚ
я=1 О
Отсюда получаем универсальную формулу для определения
перемещений в стержневых системах, предложенную О. Мором,
в 1874 г.
ЧР
* 1п
-ш
п=\ 0
MxiM
χρ
Eh
, QyiQyp , MuiMup ■
+
я/„
χρ
GF>
+
MgiMzp N{N
GL
+
EF
\dz.
(15.86)
- Формула для перемещений в фермах была дана Максвеллом в 1864 г.
Однако его работа осталась незамеченной и практически формула получила
применение после работы Мора, относящейся к
самому общему случаю стержневой системы.
Формулу Мора можно получить и иначе,
—используя формулу Кастильяно (15.73)2 и учитывая, что для
линейных систем U' = U. (Формула для U для
стержневой системы дана в § 15.8.) Поскольку система
линейна, представим все усилия как линейные функции
внешних сил
М*Р = а1Р1+ - +aiPi+ - +апРп,
Np-kPl
Полагая Рг =
= 0, Р, = Р,= 1,
Мхр = аг
MyP = ci-
MzP = ei·
Здесь символами
лия от силы Ρι-
+ ...+/Λ+
- Рч== ··· =
получаем
1=^г,
l=Myi,
\=МгЬ
М-хЬ Qyb
= 1.
Таким образом
-Pi-i
%р-
QxP =
Np =
• ■ · J
МхР = Ях1Р1+-+Ях,
·· +lnpn.
= р{+1=-~ =p«=
= *ι'ΐ-Όφ
= *fl = Oxh
=/г1=^.
N{ обозначены уси
Pl+-MxnPnA
Ν,
Рис. 15.20. К выводу
универсальной формулы
для перемещений в
стержневой системе: а)
грузовое состояние системы;
б) вспомогател ьное
(единичное) состояние
системы.
xir
Тогда, дифференцируя подынтегральное выражение в U по параметру Рг,_как
это сделано в примерах 15.3 и 15.4, и учитывая, что дМ pjdPi = M
dQypftPi — Qyh ··· dNp/dPi = Nu приходим к формуле Мора.
Аналогично для перемещения точки i по направлению i — i,
вызванному единичной силой Pj = 1, которое обозначается символом
506 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
%/, имеем формулу
п= I 0
+ -qfT" + —δξ— + ~eF-J dz· <15·87>
В таких системах как балки и рамы при отношении высоты
поперечных сечений стержней к их длине, не превосходящем 1/10,
влияние сдвигов в формулах (15.71), (15.72) по сравнению с
членами, выражающими влияние изгиба, оказывается малым и им
можно пренебречь.
В стержнях ферм возникают только продольные силы; поэтому
все члены формулы перемещений, кроме содержащего Ν,
обращаются в нуль.
В действительных конструкциях ферм шарниров в узлах нет,
поэтому некоторые небольшие изгибающие моменты и поперечные
силы в стержнях появляются, но величина этих усилий невелика,
и влияние их нэ перемещения по сравнению с влиянием про^
дольных сил пренебрежимо мало, поэтому
Δ = У f ^fjL = у ^η)ΝΡ С dz=y Щп)^Рп)1п
п.—10 η— Ι 0 п—\
EFn
Здесь учтено, что в фермах вдоль каждого из стержней не меняются
ни величина усилия, ни площадь поперечного сечения, поэтому
из-под интеграла можно вынести все члены, кроме dz. Интеграл же
от dz равен 1п.
С целью облегчения вычисления интегралов, входящих в
формулу перемещений (называемых интегралами Мора), можно
воспользоваться излагаемым ниже простым правилом, предложенным
в 1925 г. А. К. Верещагиным1) в бытность его студентом
Московского института инженеров транспорта.
Если считать, что сечение каждого из стержней вдоль его оси
не меняется, то под интегралами, входящими в формулы (15.86),
(15.87), имеем произведения двух функций^ например, первый
интеграл берется от произведения функций Mxi и МхР
г
ι
я
El
к
MxiMxP dz.
о
!) Биография Верещагина А. К· помещена в журнале «Строительная
механика и расчет сооружений» 1977, № 2: Калмыков П. В. и Носов А. Н.,
К 80-летию со дня рождения А. К· Верещагина,
§ 15.17] УНИВЕРСАЛЬНАЯ ФОРМУЛА МОРА. ПРИЕМ ВЕРЕЩАГИНА 507
Мл
мя
'XI
&
. . ζ
| αω-\
! ^р
7
t^xAi
с&Т-
л
Функция Μχΐ, изображенная графически эпюрой изгибающих
моментов от единичной силы, в системах, составленных из
прямолинейных стержней, линейна вдоль каждого стержня. Что касается
функции МхР, изображаемой графически эпюрой изгибающих
моментов от внешней нагрузки, то
она, вообще говоря, нелинейна.
Представим себе один из
стержней конструкции и покажем
эпюры изгибающих моментов Мхр и
Mxi в этом стержне. Эпюру МхР
будем считать функцией^
произвольного вида, а эпюру Mxi одной
линейной функцией в пределах
всего стержня (рис. 15.21).
Выделим элементарную
площадку άω в эпюре МхР (рис. 15.21)
άω = МхР dz. _
Ординату в эпюре Mxi, лежащую под выделенной площадкой,
можно представить в виде Mxi = ζtg<x.
Теперь интеграл Мора можно записать следующим образом:
1 С .-> „ ., tea С , ... (15 88)
η
Рис. 15.21. К отысканию интеграла·
Мора по Верещагину.
-щ-)М*МхР<1г = ^^<Ь.
ω
Интеграл берется по всей площади ω эпюры МхР.
Интеграл в (15.88) представляет собой статический момент
площади ω эпюры МхР относительно оси п — п. Известно, что
статический момент площади относительно некоторой оси равен
произведению значения площади на расстояние от ее центра тяжести
до этой оси.
Итак, имеем
ω
Подставляя (15.89) в (15.88), получим
(15.89)
я
MxiMxP dz =
ωζΰ tg a
Ε/χ
но £ctga = T), где η —ордината эпюры Μχι, имеющая такую же
координату по оси z как и центр тяжести площади эпюры МхР.
Окончательно интеграл Мора можно представить в следующем
виде:
l-^MxiMxPdz = -ff-,
ΕΙ
508
ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Обращаем внимание на то, что здесь со —площадь
произвольной по виду эпюры, а η —ордината в линейной вдоль
всего стержня эпюре. Аналогично находятся и все остальные
интегралы в формуле Мора.
Приведем в качестве иллюстрации пример.
Пример 15.5. Определить вертикальную проекцию полного перемещения
■сечения i рамы, находящейся под нагрузкой, указанной на рис._15.22.
Решение. На рис. 15.23, а и 15.23, б показаны эпюры Мр и Mv Определим
перемещение по формуле Верещагина.
Нумерация стержней показана на рис. 15.22, соответствующие ей индексы
приняты в обозначении ординат, площадей эпюр и моментов инерции сечений
л — itt j_ ωζΤΐ2
JD_ Е1г "+" Е1г
HP'
~ 2EI0{2 2 2J\6 Ί
+
1
EIa
Pl и
~2-h
(/).
Следует обратить внимание на то, что при определении интеграла,
соответствующего стержню 1, эпюра Мр должна рассматриваться как эпюра
произвольного вида, так как закон
изменения ее ординат не остается
одинаковым и при том линейным вдоль всей
длины стержня. При определении же
интеграла, соответствующего
стержню 2, в связи с тем, что обе эпюры
(Мр и МЛ характеризуются каждая
линейным законом вдоль всего
стержня, можно брать любую из площадей
я умножать на ординату «под центром
Ь11Л
U 2 В
Мр
"Ж
в)
^МшптЛ1
I
Рис. 15.22. К примеру 15.5.
Система и приложенная к
ней нагрузка.
Mi
-m δ)
Рис 15.23. К примеру 15.5;
а) грузовое состояние системы;
б) вспомогательное (единичное)
состояние системы.
А (/) Щ
тяжести» этой эпюры, взятую в другой эпюре. Результат получается одина-
ковый. Действительно -i—Έ-τ^ = φ-—'—.
Ы% Ει2
Если приходится «перемножать» эпюры более сложного вида, чем
приведенные в примере, можно воспользоваться свойством интеграла: интеграл суммы
JOO/I 1 у
§ 15.181
ПЕРЕМЕЩЕНИЯ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
509
равен сумме интегралов. На рис. 15.24 показаны три случая «перемножения»
эпюр; ниже приводятся формулы, соответствующие этим случаям.
5
α) δ) в)
Рис. 15.24. К использованию приема Верещагина.
К рис. 15.24, а
ι
MpMi dz
£7
ι·Ί , <Yk. + V»
_1_!±_l
ΕΙ ^ ΕΙ
ΕΙ
αϊ
ΊΓ'
ωι = —» ω2 = ο »
К рис. 15.24, б
I
α>! = -
dl
ω2 = -
2 '
К рис. 15.24, β
ι
ί
ΜρΜι dz _ ωχηχ ω2η2
αϊ
ΕΙ
ΕΙ
ΕΙ '
ω1 =
Ы
Ύ
! MpMjdz ^ <yi,_m(3-fr+-3fl) 4
ΕΙ ΕΙ + ΕΙ ΕΙ +
ω8=-
ω2;
2d
ΕΙ
— Ы
§ 15.18. Перемещения в стержневых системах
от изменения температуры
Определение перемещений, происходящих вследствие изменения
температурного поля, выполняется аналогично отысканию
перемещений от нагрузки по формуле Мора. Отличие состоит в том,
что вместо грузового состояния рассматривается температурное1);
покажем как это делается.
') Температурным состоянием системы называется такое ее состояние,
когда внешним является температурное воздействие,
510 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Пусть имеется система, температурное поле которой с течением
времени изменяется. Требуется определить перемещение некоторой
точки ί системы (точка лежит на оси одного из стержней) в
направлении ί — ί, происходящее вследствие изменения
температурного поля.
Рассмотрим систему в двух состояниях: действительном —
температурном и вспомогательном — единичном. Вспомогательное
единичное состояние ничем не отличается от такового при определении
перемещений от нагрузки — к системе прикладываем единичную
силу, имеющую адрес искомого перемещения в действительном
состоянии, т. е. точка приложения единичной силы —точка,
перемещение которой нас интересует, а направление этой силы —
направление искомого перемещения. Такую силу можно назвать
энергетически соответствующей искомому перемещению, поскольку
именно на нем эта сила производит работу.
Рис. 15.25. Схема распределения температурных градиентов в призматическом стержне
произвольного поперечного сечеиня.
»
Что касается действительного температурного состояния, то
в нем нас будут интересовать такие параметры деформации,
которые являются обобщенными перемещениями, соответствующими
внутренним усилиям как обобщенным силам. Будем считать, что
стержневая система состоит из призматических стержней,
приращения температуры в каждом стержне свои собственные, и при
этом приращение температуры в поперечном сечении подчиняется
закону плоскости (рис. 15.25). При таком условии поперечные
сечения остаются плоскими и после температурной деформации.
Вырежем мысленно из стержня системы элемент двумя
поперечными сечениями, находящимися на расстоянии dz одно от
другого (рис. 15.26). Для большей наглядности картины температурной
деформации опишем около нашего элемента прямоугольный
параллелепипед, две грани которого лежат в плоскостях поперечных
сечений элемента, а остальные четыре параллельны попарно
главным осям инерции поперечного сечения. Мысленно закрепим концы
всех продольных волокон элемента, ближние к началу координат,
а далее проследим за той температурной деформацией, которой
подвергается элемент при условии распределения приращений
§ 15.18] ПЕРЕМЕЩЕНИЯ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ 511
температуры по поперечному сечению по закону плоскости.
Очевидно, что вследствие принятого закона распределения по
поперечному сечению приращений температуры концы всех продольных
волокон элемента, удаленные от начала координат, после изменения
температурного поля расположатся в плоскости abed. Таким
Ш 6)
Рис. 15.26. К определении, параметров деформации элемента призматического стержня
под воздействием изменения температурного поля: а) «температурное» состояние
элемента — элемент и картина температурных удлинений его продольных волокон; 6)
вспомогательные (единичные) состояния элемента.
образом, обобщенные перемещения, вызванные изменением
температурного поля и соответствующие продольной силе 7Уг и
изгибающим моментам Μχι и Mui в этом же элементе, но во
вспомогательном состоянии системы, равны соответственно
здесь tlt /2, t3 и ^ — приращения температуры по линиям,
представляющим собой следы на гранях боковой поверхности
прямоугольного параллелепипеда, описывающего брус, оставляемые
плоскостями главных осей инерции поперечных сечений; а
—коэффициент линейного расширения. При принятом законе распределения
температурных приращений обобщенные перемещения,
соответствующие поперечным силам и крутящим моментам, равны нулю.
512
ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Теперь применим теорему о взаимности работ в следующей
формулировке: работа внешних сил вспомогательного состояния
на перемещениях, им соответствующих в действительном
(температурном) состоянии, равна взятой с обратным знаком работе
внутренних сил вспомогательного состояния на перемещениях, им
соответствующих в действительном
ЬЛ"=2 Η Λ α + ь α + ^^ι + —ΊΓ-)α\άζ·
/=10
Если вдоль волокна бруса температурные перемещения не
изменяются, то выражения в скобках под интегралом, содержащие
приращения температур, от
переменной интегрирования не зависят
и могут быть вынесены за знак
интеграла, в связи с чем формула
для Δ^ приобретает вид
k I
Δ„ =
Ht
h-к
α
/=io
k
ίΜ
Mxldz +
+
U-h
a
21*1*02+
/=1 0
N,dz.
«V>
§ 15.19. Отыскание перемещений
в статически неопределимых
стержневых системах
Определение перемещений от
нагрузки в стержневой
статически неопределимой системе в
принципе остается таким же, как и в
случае стержневых статически
определимых систем.
Если подходить к вопросу
формально, то статически неопре^
делимую систему следует
рассчитывать дважды —один раз на
воздействие внешней нагрузки, а второй — на воздействие
единичной силы, приложенной по адресу искомого перемещения.
Рис. 15.27. К определению
перемещений в статически неопределимой
системе: а) статически неопределимая
система, подвергнутая воздействию
внешней нагрузки; б) эпюры усилий в
статически неопределимой системе от
внешней нагрузки; в) варианты статически
определимых систем и внешних
нагрузок, от действия которых возникают
усилия с соответствующими им
эпюрами такими же как и на фиг. б.
§ 15.19] ПЕРЕМЕЩЕНИЯ В СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМАХ 513
Однако мыслимо упрощение, заключающееся в том, что при
определении перемещений от нагрузки во вспомогательном
состоянии можно рассматривать не статически неопределимую, а
статически определимую, получаемую из заданной статически
неопределимой. Такая возможность объясняется следующим образом.
Ю
1
V/,
I
д^чщ^^
б)
'/у
V
1_
k
щ*щщж^
8)
1-\\L
i
4
I'llTiw _,*γττϊ11Ι'
I I I I I I I I ^VJH/^1 Ι Ι 1 Ι Ι Ι II
18
Рис. 16.28. Варианты вспомогательных оостояннй в соответствующие им эпюры
изгибающих моментов: а) вариант единичного состояния в статически неопределимой системе;
б, в, г, д) 1-й, 2-й, 3-й и 4-й варианты статически определимых систем во вспомогательном
состоянии.
После того как в статически неопределимой системе в
действительном состоянии построены эпюры усилий от нагрузки, их
можно истолковывать как эпюры усилий в любой статически
определимой системе, полученной из заданной, путем
отбрасывания связей и замены их соответствующими усилиями. В качестве
иллюстрации на рис. 15.27, а показана статически неопределимая
балка, загруженная силой Р\ на рис. 15.27, б изображены эпюры
Мх и Qy в этой балке, а далее на рис. 15.27, в представлено из
бесчисленного множества четыре варианта статически
определимой системы, полученной из заданной статически неопределимой
путем отбрасывания связей. Нагрузка в каждом варианте состоит
из внешних сил, действующих на заданную статически
неопределимую систему —рис. 15.27, α и из усилий в отброшенных
связях. Каждому из вариантов отвечают точно такие же эпюры
Мх и Qy как и изображенные на рис. 15.27,6.
614 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Коль скоро эпюры усилий в статически Беопределимой системе
могут быть отнесены и к любой статически определимой системе,
получаемой из заданной путем отбрасывания некоторых связей,
отпадает необходимость во вспомогательном состоянии
рассматривать статически неопределимую систему и достаточно ограничиться
полученной из нее статически определимой.
Пример 15.6. В балке, изображенной на рис. 15.27, а, определить прогиб
посредине пролета.
Решение. Построим вспомогательное единичное состояние. При этом
рассмотрим один вариант, в котором это состояние отнесено к статически
неопределимой системе, а далее поочередно используем каждый из четырех
вариантов статически определимой системы, показанных на рис. 15.27, в. На
рис. 15.28 изображены все варианты вспомогательного единичного состояния
и соответствующие им эпюры Мх.
Теперь определим искомое перемещение в каждом из пяти вариантов
единичного состояния, пользуясь формулой Верещагина (рис. 15.28, а):
— 9 9 l Pl L JL l X — PlS
ь v\z = l/2-2'2 ·~2 8 ' 4 * 3 "8""£77~ 192£/* '
о , 0 / 1 / 1 Р/ 1 Pl3
2. ν ,_,,ο = 2·-Γ·-ς-·-?Γ·-7Γ·
2 =
'/2 4 2 2 3 8 Е1Х №Е1Х '
-о l l L λ Pl 1 .._ РР
6' ν\ζ = Ιβ-2'-2' 4 * 2 ' 3 '~5" Е1х ~ 192ΕΙ, '
4. ν
1 X
1 / / 1 Pl 1 Pl3
г = //2 2 2*238 Е1Х №Е1Х >
_ 1 I I Ъ_ Pl 1 , 1 _3_ 3
5· ν\ζ = ι/2-2'-2Ύ' 1б * β '-g-· ει + 2 16 ' ' 8 Х
1 Pl 1 РР
2 8 El \92EIX°
Ответ при всех вариантах единичного состояния получается одинаковым.
§ 15.20. Формула Папковича и вытекающие из нее следствия
1. Предварительное замечание. П. Ф. Папкович г) вывел2)
формулу, при помощи которой представляется возможным получить
формулировку рассмотренных выше вариационных принципов,
избежав при этом простого их постулирования, которое было
использовано в §§ 15.11 и 15.12. Наряду с этим указанное
равенство имеет своим следствием и приведенные выше энергетические
теоремы.
*) Папкович Петр Федорович (1887—1946) — советский
инженер-кораблестроитель и ученый-механик, чл.-корр. АН СССР, автор фундаментального
курса строительной механики корабля (ч. 1, т. 1, 1945; ч. 1, т, 2, 1946,
Морской транспорт; ч. II, 1941, Судпромгиз).
2) Папкович П. Ф., Теория упругости. Оборонгиз, 1939.
§ 15.20] ФОРМУЛА ПАПКОВИЧА И СЛЕДСТВИЯ ИЗ НЕЕ Б1&
2. Формула Папковича. Свою формулу П. Ф. Папкович
получил, исходя из выражения для работы внешних сил
Л = $$$ u'xda>+$$u'pvd<7. (15.90)
© s
К правой части (15.90) добавляются нулевые члены {Зх — 3^
и (J2 — Λ)> οτ чего, разумеется, равенство не нарушается.
При этом Jx представляется в двух тождественно эквивалентных:
формах
J1=\\u'ndq% Jx = \\WOadqt (15.91),
s s
a J2 принято таким:
У2=555<7'8сгсо. (15.92>
0
В (15.91) Σ и 1 выражаются следующими формулами:
Σ =
Οχ
%ху
ххг
хух
°У
хуг
хгх
хгу
Ог
= \\σ(ΐ) σ(2) <*<s)|. \ = {lmn},
где σ(1), σ(2), с(3) — столбцы в квадратной матрице Σ, /, т, η —
направляющие косинусы нормали к площадке поверхности,
ограничивающей тело.
Тождественное равенство двух форм представления Jlt согласно»
(15.91)! и (15.91)2, легко доказать, сопоставляя развернутые
выражения Σ1 и Do.
Преобразуем выражение Jx согласно (15.91)!
Jx = J 5 u'21 dQ = S S u'lσ(ΐ) σ(2) <*(з) II{l dq mdq ηdq) =
s s
= 5 51 u'tf(i) u'a{2) и'а(з) II {dy dz dz dx dx dy} =
s
= 55 "'<*u) dy dz + 5 5 ϋ'σ(2) dz dx + J \ u'a(3) dx dy =
Θ
Переход от интеграла по поверхности к интегралу по
ограниченному ею объему выполнен по формуле Гаусса —
Остроградского.
Продолжим преобразование Jlt
4-Ш№+тг+^)+
Θ
ι ди' , За' .flu' 1 ,
+ ~W σω + If *(2) + ~дГ (3) J "
516 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Учитывая вид матриц σ(1), σ(2), σ(3), и, σ и А, получаем
/х = J J J (ϋ'Ασ + σ'ΑΊι) άω. (15.93)
Θ
Добавляя к правой части (15.90) нулевые члены в
развернутом их выражении —(15.93), (15.91)2 и (15.92), получим
А =5 \ \ и'х άω + 5 J u'pv dq + \ \ \ (и'Ао + а'А'и) άω-
Θ s Θ
— \ \ u'Da dq + \ \ \ σ'ε άω - J $ $ σ'ε άω,
s Θ ©
мли окончательно
Α =$$$[ϋ'(Ασ + χ) + «*'(Α'ιι-ε) + σ'ε]ίίω +
©
+ $$u'(pv- Όσ)άς. (15.94)
s
Это и есть равенство П. Ф. Папковича.
В (15.94) в общем случае фигурируют элементы четырех
произвольных состояний тела. Для первого из них известны
внешние силы χ и pv, для второго — перемещения и, для третьего —
напряжения σ и, наконец, для четвертого — деформации ε. В
частности, все эти векторы или некоторые из них могут относиться
к одному и тому же напряженно-деформированному состоянию тела.
Если χ, ρν и а относятся к одному состоянию тела, то
выполняются условия равновесия внутри (во всем объеме) тела и на
■его поверхности; если к одному состоянию тела относятся и и ε,
то удовлетворяются уравнения Коши, а следовательно, и условия
совместности деформаций.
3. Теорема Клапейрона. Пусть все векторы х, pv, и, σ и ε
относятся к одному состоянию тела, тогда в А выражения в
круглых скобках равны нулю вследствие того, что соблюдается
соответственно — равновесие в объеме, совместность деформации во
-всем теле и равновесие на поверхности. В результате остается
равенство
А = J J J σ'ε άω = 2 $ $ $ W άω = 21/,
© ©
•выражающее собой теорему Клапейрона (см. (15.60)).
4. Теорема о взаимности работ. Пользуясь равенством,
вытекающим из сопоставления (15.90) и (15.94), получаем
\ \ \ и'х άω + \ \ u'pv aq = $ \ \[W (Ασ + χ) + σ' (A'u - ε) + σ'ε] άω +
' © s 0
+ $$u'(pv-Da)d<7· (15.95)
§ 15.20] ФОРМУЛА ПАПКОВИЧА И СЛЕДСТВИЯ ИЗ НЕЕ 517
Пусть имеем два состояния тела. Векторы, относящиеся к
первому из них, снабдим индексом 1, а ко второму — индексом 2.
Воспользуемся равенством (15.95) дважды. Первый раз
положим и = и2, ε = ε2, χ = χχ, Ρν = Ρνι> ο = α1 и равенство (15.95)
приобретет вид
J J J xiu2 άω + J J р;хи2 dq = $ $ $ σίε2 doa, (15.96)
а во второй раз будем исходить из того, что ti = u1( ε = εχ; χ =
— х2, pv = Pv2» 0 = 0% и тогда (15.95) представится так:
J J J X2U! dco + 5 5 p;2ux d<7 = J J J σ^ dco. (15.97)
Θ s Θ '
Если иметь в виду зависимости закона Гука для каждого из
двух состояний
а1 = Свг, σ2 = 0ε2 (15.98)
и далее обе части равенства (15.98)! умножить на ε2, а обе части
равенства (15.98)2 —на ε1( то обнаружим, что интегралы в
правых частях равенств (15.96) и (15.97) равны между собой
\ \ \ σ[ε2 άω = $ $ $ σ^ άω, (15.99)
Θ Θ
следствием чего является одинаковое ;ь и левых частей в этих
равенствах
\ \ \ χίικ άω + \ \ p;tu2 aq = \ \ \ хгЧ άω + $ $ p;2ux dq. (15.100)
e s 0 s
Равенства (15.99) и (15.100) выражают собой теорему о
взаимности работ для сплошной линейной среды в двух различных
редакциях. Выше в § 15.14 теорема о взаимности работ была
сформулирована в общем виде, но аналитически представлена
применительно лишь к стержневым системам.
5. Вариационный принцип возможных перемещений
(вариационный принцип Лагранжа). Пусть χ, ρν и σ относятся к одному
состоянию тела х), т. е. соблюдены условия равновесия в области
и на ее границе, — удовлетворены уравнения (15.15) и (15.16)t
а вместо и и ε рассматриваются их вариации 6и и δε (и),
которые считаем кинематически возможными, т. е. удовлетворяющими
условиям совместности деформаций
Α'διι-δε(ϋ)=0. (15.101)
х) Черта над символами χ и ρν указывает на то, что соответствующие
величины известны (заданы).
518 ВАРИАЦИОННЫЕ ПРИНЦИПЫ. ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Варьируя обе части равенства (15.95) по и и учитывая (15.16),
(15.15) и (15.101), получим1)
J J J х'би άω + ] J p;6u dq = \ $ $ σ'υε (и) αω, (15.102)
ИЛИ2)
- $ $ f&u d? = 0. (15.103)
s
Это есть условие стационарности функционала
/ Ju] = $$${№ [ε (u)]-x'u}dW-$$p;ud<7, (.15.104)
носящего название функционала Лагранжа. При переходе от
(15.103) к (15.104) учтено, что
dW dW
дЕх '" дуг
δε (u) = Wa (ε) δε (и) = № [ε (и)].
Перепишем (15.104) при условии, что ρν задано лишь на 5Р,
т. е. на части поверхности 5, а на остальной части поверхности
Su — S — Sp заданы перемещения и = и
/х [и] = J J J {W[e (и)]-х'и} da>-$ $ р> dq - Ц р& dq. (15.105)
0 'Sp Su
Коль скоро на Sa перемещения заданы, вариация би на этой
части поверхности равна нулю 6ujsf/=6u=0.
Поскольку в условии стационарности функционала (15.105)
последний член не участвует, его можно опустить и полагать
1г (и) в таком виде:
/х [Uj = \ J \ [W [ε (и)] - х'и] άω - $ $ p> dq. (15.106)
Вариационный принцип Лагранжа формулируется так. Если
тело находится в равновесии (равновесие в объеме и на
поверхности), то истинному состоянию тела соответствует стационар-
1) В левой части (15.95) перед варьированием подынтегральные
выражения транспонированы, что не изменяет их вида в развернутой после
выполнения матричных операций форме.
2) Нижний индекс при δ указывает на то, что варьирование произведено
по и, При переходе от (15.102) к (15.103) учтены формулы Грина.
§ 15.20] ФОРМУЛА ПАПКОВИЧА И СЛЕДСТВИЯ ИЗ НЕЕ 519
ность функционала 1г [и] на множестве кинематически возможных
вектор-функций сравнения и, т. е. при кинематически возможных
вариациях би.
Справедливо и обратное утверждение: если функционал
приобретает стационарное значение на множестве кинематически
возможных кривых сравнения и, т." е. при кинематически
возможных вариациях би, то тело находится в равновесии (равновесие
в объеме и на поверхности). Это вытекает из того, что
функционал It [и] соответствует тождественному равенству П. Ф. Пап-
ковича (15.94) в предположении равновесия тела.
Можно доказать справедливость приведенного выше обратного
утверждения, не апеллируя к равенству (15.94). Покажем как
это делается.
Рассмотрим вариацию функционала (15.106) по и и по
условию стационарности приравняем ее нулю
διΛ [и] = $ J J 6U7 [ε (и)] άω - \ \ $ х'би άω - $ $ р^би dq = 0.
© © SP
Здесь
dW dW & . .
δε (и)
bW [ε (и)J
двх '" дугх
= Ι σ*... τζχ || δε (и) = σ'А'би. (15.107)
При получении (15.107) учтено соотношение (15.101),
описывающее кинематическую возможность вариаций δε (и) и би.
Итак,
διΛ (и) = 555 а'А'би άω - $$$ х'би άω - $$ р^ би dq = 0. (15.108)
© © *р
Поскольку выражение а'А'и входит в формулу (15.93) для Jlt
для того, чтобы получить первый интеграл в (15.108), проварьи-
руем (15.93) по и и решим результат относительно интеграла
от σ'Α'δϋ
J55a'A'6udo = 6uy1-J5J(6u)'Aado. (15.109)
© ©
Отсюда, подставляя (15.109) в (15.108) и применяя в этой
подстановке вместо 6u^i выражение согласно (15.91)2, получим
bull (u) = 55 (би)' Da dq - $$$ (би)' Ασ άω -
Sp ©
-$$$x'6udco- 55 р^би ύί^ = 0. (15.110)
© Sp
Здесь первый интеграл берется по 5Р, поскольку на остальной
части поверхности тела S„ = S — Sp вариации перемещений равны
нулю (перемещения здесь являются заданными).
520 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Объединяя в (15.110) интегралы, окончательно имеем1)
6u/1(u) = — Щ(6и)'[Аа + х]йа> + ЭД (6u)' [Da-pJ dq = 0. (15.111)
© Sp
Отсюда следует, что нулю должны равняться выражения в
квадратных . скобках. Получаемые при этом равенства суть
соответственно уравнения равновесия в области и на границе. Таким
образом, доказано сделанное выше утверждение —следствиями
стационарности функционала 1г (и) являются дифференциальное
уравнение равновесия во всем объеме тела (которые представляют
собой уравнения Эйлера в вариационной проблеме для
функционала 1г (и)) и уравнения равновесия на той части поверхности тела,
где заданы поверхностные силы, вытекающие из равенства нулю
граничного члена (последний интеграл в (15.111)).
Если предположить, что материал подчиняется закону' Гука и
удовлетворены уравнения Коши, т. е. соответственно соблюдены
зависимости (15.21) и (15.19), то дифференциальные уравнения
равновесия приобретают вид уравнений Ламе.
Разумеется, поскольку у вектора и, от которого зависит
функционал 1Х (и) и по которому производится варьирование
последнего, три составляющих, то и уравнений Эйлера в вариационной
задаче для 1г (и) тоже три (дифференциальные уравнения
равновесия или три уравнения Ламе, если представлять их не в
векторной форме, а в составляющих).
6. Вариационный принцип Кастильяно. Пусть и и ε относятся
к одному состоянию тела, т. е. известно решение (15.19)
уравнений совместности деформаций Сен-Венана или, иначе,
удовлетворены уравнения Коши, а вместо χ, σ и ρν рассматриваются их
вариации δχ, δσ и δρν, которые считаем возможными, т. е.
удовлетворяющими дифференциальными уравнениями равновесия в
области и уравнениям равновесия элементарного тетраэдра на
границе тела
Αδσ = — бх, D6a = 6pv. (15.112)
Тогда, варьируя равенство (15.95) по σ и учитывая (15.19) и
(15.112), получим зависимость
555 ϋ'δχ άω + JJ u'6pv dq = $$$ (δσ)' ε άω, '(15.113)
© s ©
выражающую собой вариационный принцип возможного изменения
напряжений.
]) При переходе от (15.110) к (15.111) подынтегральное выражение в
последнем интеграле подвергнуто транспонированию, что не отражается на
результате,
§ 15.20] ФОРМУЛА ПАПКОВИЧА И СЛЕДСТВИЯ ИЗ НЕЕ 521
Если положить вариации внешних сил равными нулю, то
(15.113) приобретет следующий вид:
V4(*) = ffi6a(X)'8[<r(x)]dcD = 0.
Θ
Это иная запись (15.70).
При этом
ΙΛ%) = \\\№'[σ(χ))άω, (15.114)
Θ
где W — удельная дополнительная энергия.
Стационарность этого функционала рассматривается в
вариационном принципе Кастильяно., который формулируется так. Если
деформированное состояние тела подчинено условиям совместности
деформаций, то истинному состоянию тела соответствует
стационарность функционала /4(χ), которая имеет место на множестве
вектор-функций сравнения χ, порождающих статически возможные
напряжения σ, τ. е. при вариациях δχ, соответствующих
статически возможным вариациям δσ. Последние к тому же обладают
самоуравновешенностью вследствие равенства нулю вариаций
внешних, сил.
Справедливо и обратное утверждение: если-функционал /4(χ)
приобретает стационарное значение на множестве вектор-функций
сравнения %, порождающих статически возможные напряжения σ,
которым соответствуют самоуравновешенные вариации δσ, то
деформации подчиняются условию их совместности. Это вытекает из
того, что функционал /4[χ] соответствует тождественному
равенству П. Ф. Папковича (15.94) в предположении совместности
деформаций в теле.
Однако справедливость этого обратного утверждения
обнаруживается и без апелляции к равенству (15.94), для этого
представим функционал (15.114) в следующей форме:
V* (X) =- J J J bW> [а Ш Λ» = J H I fl ... fl) δσ (χ) Λ»,
0 0
или
V4(x) = ffiB'B'6^^ = 555(6X)'[B8]dM = 0. (15.115)
0 0
Здесь учтена зависимость (15.17), из которой δσ (χ) = Β' δχ, а также
формулы Кастильяно
dW' dW π „
дах '" дх
ΖΧ
Отсюда нулю должно равняться выражение в квадратных
скобках под интегралом в (15.115), а это равенство и есть у рае-
522 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
нение совместности деформаций (15.18). Таким образом,
действительно следствием стационарности функционала /4 (χ) являются
уравнения совместности деформаций Сен-Венана х), которые
представляют собой уравнения Эйлера в вариационной проблеме для
функционала /4(х)·
Если предположить, что материал подчиняется закону Гука
(15.21)2, то, имея в виду использованное уже представление σ
(15.17)! из (1:5.18), получим уравнения Бельтрами — Мичелла. На
той части поверхности, где заданы поверхностные силы, вариация
их равна нулю, а следовательно,
6pv|sp-D6o = DB'6x^0, или δχ^^Ο.
Разумеется, поскольку у вектора χ, от которого зависит
функционал Ιχ (χ) и по которому производится варьирование
последнего, шесть составляющих, то и уравнений Эйлера в вариационной
задаче для Ι4 (χ) тоже шесть (уравнения совместности диформаций
Сеи-Венана или уравнения Бельтрами—Мичелла, если
представлять их не в векторной форме, а в составляющих).
7. Заключительные замечания. Оба вариационных принципа —
Лагранжа и Кастильяно — являются вариационными принципами,
в которых формулируются условия и следствия стационарности
частных функционалов (1г (и) и /4 (χ)), и, таким образом, в этих
принципах имеет место условная вариационная проблема.
В каждом из принципов условием стационарности функционалу
является одно (векторное) уравнение Эйлера (по числу функций,
от которых зависит каждый из функционалов 1г и /4). Если
в качестве уравнений Эйлера получены "соответственно уравнения
Ламе и уравнения Бельтрами— Мичелла, то в каждом из
указанных вариационных принципов на функционал наложено два условия.
В следующем параграфе рассматриваются другие вариационные
принципы механики деформируемого твердого тела для частных
функционалов и вариационный принцип для полного функционала.
§ 15.21. Вариационные принципы, соответствующие функционалам,
зависящим от двух, трех и четырех вектор-функций
1. Вариационный принцип Рейсснера2). Вариационный принцип
Рейсснера устанавливает условия и следствия стационарности так
*) Такой способ получения уравнений совместности деформаций наиболее
естественно поясняет почему число этих уравнений равно шести, хотя на
первый взгляд могло показаться, что для раскрытия статической неопределимости
напряжений к трем дифференциальным уравнениям равновесия элемента тела,
содержащим вследствие закона парности касательных напряжений шесть
неизвестных функций, достаточно присоединить три уравнения совместности
деформаций.
2) Reissner Ε., On a variational theorem . in elasticity. J, Math, and
Phys., 1950, 29, № 2, 90—95.
«§ 15.21] ФУНКЦИОНАЛЫ ОТ НЕСКОЛЬКИХ ВЕКТОР-ФУНКЦИЙ 523
называемого функционала Рейсснера
/2 (и, σ) = 5JS [σ'ε (и) - W (or) - х'и] άω - JJ &и dq, (15.116)
0 SP
получающегося из функционала Лагранжа путем преобразования
Л ежа и др а
W(e) = a'B-W'(a). (15.117)
Подставляя (15.117) в (15.106), получаем для /2 (и, а)
выражение (15.116).
Условия стационарности этого функционала выглядят так:
6u/a(u, σ)=0, δσ/8(ϋ, <т)=0 (15.118)
а) В развернутом виде (15.118)!, если учесть, что е = А'и,
имеет вид
6J2 (", о) = 555 [σ'Α'διι - х'би] da» - \\ р'би dq = 0.
0 SP
Вариация δ„/8(и, с) совпадает с вариацией би/а(и), взятой
согласно (15.108), вследствие чего би/2(и, о) в результате тех же
преобразований, которые были выполнены с бц^ (и), приводится
к виду
6„/2(uf a)=-SJS(eu)'[Aa + x]dQ + H(6u)'(Dff-Pv)dflf = 0.
0 Sp
и отсюда вытекают те же следствия, а именно —дифференциальные
уравнения равновесия в области и уравнения равновесия на
границе тела, где заданы поверхностные силы.
б) Условие (15.118)2 в развернутом виде выглядит так:
δσ/2 (и, а) = 555 [(δσ)'ε - SW (σ)] άω =0.
0
Здесь*)
вследствие чего
δσ/2 («, σ) = 55S (бег)' (е - W$) άω = 0,
Θ
Reissner Ε., On variational principles in elasticity. Proc. Sympos.
Appl. Math., 1958, 8, 1—6.
Рейсснер Э., О некоторых вариационных теоремах теории упругости,
Сб. «Проблемы механики сплошной среды» (к 70-летию акад. Н. И. Мусхелиш-
вили). Изд-во АН СССР, 1961.
*) Обращаем внимание на то, что штрих у вектора удельной
дополнительной энергии W* не есть символ транспонирования.
524 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
откуда ε — W£ = 0, или, при подчинении материала закону Гука,
Таким образом, вариационный принцип Рейсснера
формулируется так. Если известен общий интеграл уравнений совместности
деформаций, то истинному состоянию тела соответствует
стационарность функционала /2 (и» σ)> следствием которой являются
уравнения равновесия во всем объеме тела, условия равновесия
на той части поверхности тела, где заданы поверхностные силы,
и физические уравнения, связывающие деформации с
напряжениями.
Функционал Рейсснера (15.116) получен из функционала Ла-
гранжа, в котором отсутствует член, содержащий интеграл по Sa,
поскольку функционал Лагранжа варьируется лишь по
перемещениям, а вариация перемещений на 5Ц, где они заданы, равна
нулю, вследствие чего указанный член в 1Х (и) не был
существенным и был опущен. В принципе же Рейсснера варьирование
выполняется и по напряжениям, поэтому на Su варьирование
по σ может быть выполнено. В приведенном выше функционале
Рейсснера на Su варьирование по о не производилось, поскольку
член с интегралом по Su не был использован. Если бы этот член
был включен в функционал, то по σ следовало бы варьировать
и его.
Существует второй вариант функционала Рейсснера Гг [и, σ]^
отличающийся от первого лишь включением члена, содержащего
интегрирование по Su
/£(u, σ) = /2(ϋ, a)-l\(u-u)'Dadq. (15.119)
Sn
Его можно трактовать как член, учитывающий дополнительное
требование — равенство на Su перемещений заданным значениям и,
и=--=и, и —и = 0. Поэтому вместо /2.(и, а) исследуется стационар·
ность функционала
/Пи, а) = /2(и, a) + §{u-u)b*dqt (15.120)
где λ^ — функциональный вектор-множитель Лагранжа, λ* =
Природа λ* очевидна — это неизвестные поверхностные силы
на Sa, выражающиеся через напряжения по формуле
λ„ί=ρν = 0σ. (15.121)
Подставляя (15.121) в (15.120), получаем (15.119). Разумеется,
что из условия ба1ъ(и, <*)=0, кроме зависимостей между
напряжениями и деформациями, получаются и граничные условия на 5„.
§ 15.21]
ФУНКЦИОНАЛЫ ОТ НЕСКОЛЬКИХ ВЕКТОР-ФУНКЦИЙ
625
2. Вариационный принцип Ху—Вашицу1). Функционал Ху —
Вашицу получается из второго функционала Рейсснера, если
потребовать выполнения дополнительного условия (15.19). Тогда
вариационная проблема для функционала /g (u> σ) заменяется
вариационной проблемой для функционала
/а(и, σ)+555λ'(ε-Α'ϋ)ίίω, λ = {λ1λ2 ... λ6'}. (15.122)
0
В развернутом виде (15.122) выглядит так:
555 [σ'ε (и) - W (а) - х'и] άω - \\ р> dq-§ (й -и)' Dadq +
0 Sp Su
+ 555λ'(ε-Α'ϋ)ίίω,
0
или, используя (15.117) и объединяя первый и последний
интегралы, получим
Ш iw (ε)+λ' (ε - A'u) - x'uJάω - SS pvu d4 -
0 Sp
-\\(\i-\\)'Oodq. (15.123)
Su
Вектор λ найдем из условия равенства нулю вариации этого
функционала по ε:
$$$[δ№(ε) + λ'δε]£ίω = 0. (15.124)
Θ
Учитывая, что выражение в квадратных скобках под
интегралом в (15.124) должно равняться нулю, получаем
SW
dW
λ' = — Wa, где W5 =
+ |λ1...λ6[|)δε = 0,
dW
dW
дех '" дуг
С другой стороны, Wd=a'. Следовательно, λ'= — σ' и
функционал (15.123) приобретает вид
/3(и, σ, ε) = 5$$[№(ε)-σ'(ε-Α'ϋ)-χ'ϋ]^ω-
0
— 55 pv u dq — 55 (u — u)' Dor dq.
i) См. список на стр. 439,
526 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Это и есть функционал Ху —Вашицу.
а) Варьируя 13(и, σ, ε) поочередно по и, σ, ε и приравнивая
вариации функционала к нулю, получаем условия стационарности
iV3 (и, <*, ε) = 555 [σ'Α' - χ'] διι dco - JJ pv Sudq = 0. (15.125)
0 Sp
Здесь учтено, что би s = διι==0. Преобразование первого
интеграла в (15.125) ранее было выполнено (см. (15.109) и (15.110)).
В' результате получим
δ„/,(ιι, σ, B)=—\§(buy(Aa + x)d(u + ll(6uy(Da-~pv)dq = 0.
0 Sp
Отсюда следуют условия равновесия в объеме и на части
поверхности тела Sp
Ασ + χ = 0 в 0 и Όα — ρν = 0 на SP.
б) δσ/9(ιι, σ, ε) = — Щ (δσ)' (ε - \'и) άω -]1 {й -ιι)'Όδσάη = 0.
0 su
Отсюда следует общее решение (15.19) уравнений совместности
(15.18) и граничное условие на 5„ (15.20).
в) Наконец, δε/3 (", β, ε) = $$$[δ№ (ε) — σ'δε] άω =0. Отсюда '
0
W (ε) - σ'δε = 0, Wafie - σ'δε = 0, (Wa - σ') δε = 0,
или
, „, „ ,, II dW dW
II иьх υΎ.
гх
т. е. получили соотношения между напряжениями и деформациями.
3. Вариационный принцип1), симметричный2) принципу Рейс-
снера. Функционал 1Ь (ε, χ) в обсуждаемом принципе получается
из функционала Кастильяно путем преобразования Лежандра,
т. е. путем использования (15.117)
0
ИЛИ
Me. X) = SSS [(Х'В + ^.р.) ε - U7 (ε)] ίίω.
0
г) Этот принцип, так же как и принципы, рассматриваемые в разделах 4
и Б, предложены Э. Тонти в упоминавшейся выше его статье.
2) Симметрия понимается в смысле, представленном в § 15,13,
§ 15.21] ФУНКЦИОНАЛЫ ОТ НЕСКОЛЬКИХ ВЕКТОР-ФУНКЦИЙ 527
Условия стационарности /5 (ε, χ) выражаются так:
а) δε/5 (ε, χ) = 0, б) δχ/5 (β, χ) = 0. (15.126)
В развернутом виде (15.126)! выглядит так:
а) бе/а (в, X) = SSS (<* (Χ))' δε da> - $$$ δ№ (ε) άω = 0, или, если
© 0
учесть (15.107),
δβ/β (ε, χ) = ЭД {[σ (χ)]' - W,} δε dco = 0.
©
Условиями стационарности функционала 1Ъ (ε, χ) являются
уравнения, связывающие напряжения и деформации (в частности,
в линейной системе — уравнение закона Гука), a'=Wd, или
a = (Wa)', или, наконец, учитывая (15.17) и (15.21)ь получаем
б) Β'χ + σ4.ρ = Οε. (15.127)
Условие (15.126)2 в подробной форме имеет следующий вид:
δ-Λ(ε, χ) = 5$5(δχ)'Βε^ω = 0.
Θ
Условиями стационарности функционала /5 (ε, χ) являются
уравнения совместности деформаций (15.18).
4. Вариационный принцип, симметричный принципу Ху—Вашицу.
Напомним, что при выводе функционала Ху —Вашицу, был
принят за основу функционал Рейсснера Г% (и, с) и использовалась
зависимость (15.117). В данном разделе применим симметричную
зависимость, и подобно тому как при выводе функционала
Ху—Вашицу поставили дополнительное условие (15.19), в рассматриваемом
случае потребуем выполнения симметричного (см. табл. 15.2)
условия (15.17), используя так же как и при построении
функционала Ху —Вашицу множители Латранжа для сведения
условной вариационной проблемы к свободной.
В результате отмеченного выше получим
§l{W'(a)+V[a-B'x-a4tPm]}da>. (15.128)
0
Вектор λ найдем из условия равенства нулю вариации этого
функционала по а
555 [δΙΓ (σ) + λ'δσ] άω = 0. (15.129)
0
Учитывая, что выражение в квадратных скобках под
интегралом в (15.129) должно равняться нулю, получаем
ί 357"· ai^T Ή1λι·.·λβ1ΐ)δσ = 0.
528 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ [ГЛ. XV
Отсюда
П Π- idW' dW'\ - Jo 1
ΐΛ1 · · · Λβί \-fo^ · · · -Щ^1 - - \&х · · · Угх],
т. е.
λ = —ε, λ' = — ε'
и функционал (15.128) приобретает следующий вид (в таком виде
функционал симметричен функционалу Ху — Вашицу):
/β(χ, σ, ε) = $$${№»-ε'[σ-Β'χ-σ4.ρ]}<ίω.
Ниже приводим условия стационарности этого функционала
а) δχ/β(χ, σ, β) = $$$β'Β'δχΑο = 0.
Отсюда получаем (15.18), т. е. в вариационной задаче для
функционала /„ (χ, σ, ε) уравне иями Эйлера являются условия
совместности деформации.
б) δσ/6(χ, σ, в) = $$$в1Г(а)Л»-$$$в'6аЛо=0,
© ©
или, если учесть, что
г*
δσ,
получаем
W.(X.a..)-J^(ea)'f{^...^-}-e]d»-0.
Отсюда в качестве второго условия стационарности функционала
h (χ» <*» ε) получаем физическое матричное уравнение,
связывающее деформации с напряжениями
idW dW'\ _ _fdW dW'\
\дах ··· дхгх) ε_υ' г-\дох "· дхгх)'
В частности, в случае линейной зависимости е = С~1в.
в) ββ/β(χ, σ, β)«—JJJ (δε)'[σ-Β'χ-σ4<ρ]^ω = 0.
Θ
Отсюда в качестве третьего условия стационарности
функционала h(%, су, ε) получаем общее решение (15.17) уравнения
равновесия.
5. Вариационный принцип Тонти, Функционал /7j(u, χ,,σ, ε),
для которого в обсуждаемом принципе рассматривается
вариационная задача, получается как сумма двух функционалов /2(и, о)
и h(Xt ε) при условии, что SP = S.
§ 15.21] ФУНКЦИОНАЛЫ ОТ НЕСКОЛЬКИХ ВЕКТОР-ФУНКЦИЙ 529
Таблица 15.5
Вариационные принципы, связанные
с функционалами, зависящими от
перемещений
Вариационные принципы, связанные
с функционалами, зависящими от функций
напряжений
и
о
е
&
X
s
о.
е
«
S
■X
я
И
ω
я
hM-
Еслн 6u = 0 на Sn
JJJ{^[E(u)]-x'u}i(ro-
©
Если χ=0 на S
Θ
V4&] = 0
Βε = 0
Если
σ = Β'χ + σ
ч.р
BC-i(B'X+
4-σ )==0
^ ч.р'
Если 6u=0 на S
/г1и, σ] =
=JJJ[a'e(u) — W'(a) — x'u]da —
0
flu/2[u, σ] = 0
Ασ + χ = 0
*0
Da—pv==0
HaSp
Если χ=0 на S
Λ [χ, ε]
= Ш[(*'в+*ч.р)е-^Ы]^
0
6χ/Β[χ, ε] = 0
Βε=
= 0 Β0
6ε/5[χ,ε]=0
Если
σ = Β'χ+σ4ρ
σ' =
d№ dur
•V" **«
.
Β'χ+σ4ρ=Οε
530 ВАРИАЦИОННЫЕ ПРИНЦИПЫ, ЭНЕРГЕТИЧЕСКИЕ ТЕОРЕМЫ 1ГЛ. XV
Продолжение табл. 15.5
Вариационные принципы, связанные
с функционалами, зависящими от
перемещений
Вариационные принципы, связанные
с функиноналами, зависящими от функций
напряжений
за
Ы", σ, ε| =
= JJJ[l^(e) — σ' (ε— A'u) —x'u]da>—
0
-JJp^urf? —JJ(ii—u)' Dadq
6цУ3[и»а, ε] = 0
Cu=0 на £
δσ/3Γιι,σ(ε] = 0
e=A'u
u = u иа S,
Va|u' σ, e| = 0
Если χ-=0 на S
1*\X, ε, σ] =
=Ш["7' № -ε' (σ-Β'χ-σ4 p)]dco
V«'x- ε> σΐ=°
ϋε = 0
1Α%. ε, σ] —0
"ε'β
σ = Β'χ + σ,
ч.р
V,[X,e,ol-0
ε' =
||<Э И?" tW
Ρσ*'"Λ«
Вариационный принцип Тоити, связанный с функционалом, зависящим от
перемещений, функций напряженки, напряжений и деформаций
Ыи, %, σ. e] = J f J[«t's<u) —1»"<σ) —x'u + (x'B+< ρ)ε— ИГ(е)]а(со — J JpyU d?
0 S
V
[u,
χ.
σ,
ε] =
= 0
ty
,Ги,
χ.
σ.
β] =
= 0
v
,f»
A»
σ,
ε] =
= 0
V-
[u,
χ.
σ,
ε] =
= 0
Λσ+χ = 0 в 0
Da —ρν = ϋ на S
Вг = 0
в 0
а' =
dW dW
дгх " ^z.v-
§ 15.21] ФУНКЦИОНАЛЫ ОТ НЕСКОЛЬКИХ ВЕКТОР-ФУНКЦИЙ 531
Итак,
Ми, Ъ о, ε) = $$$ [σ'β (и) - W (а) - х'и] άω -
0
-55Ρν"^ + Κ[(χ'Β + <ρ)ε-^(ε)]^ω.
s 0
Условиями стационарности этого функционала являются
а) б„Ми, Ъ σ· ε) = 0. б) δχ/7 (и, χ, σ, β)=0,
β) 5J7(u, χ, σ, ε)=0, г) 6J7 (u, χ, σ, e) = 0.
Эти условия в развернутом виде и следствия из них повторяют
информацию, полученную при обсуждении стационарности
функционалов /2(и, σ) и /5(χ, ε).
В табл. 15.5 приведена сводка полученных результатов.
Глава XVI
НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ
§ 16.1. Вводные замечания
Настоящая глава посвящена той ветви прикладной механики
твердого деформируемого тела, в которой рассматриваются
стержневые системы, подвергнутые статическому воздействию; при
этом предметом изучения являются усилия и перемещения в этих
системах. Из самого термина ясно, что стержневыми называются
системы, составленные из стержней, соединенных между собой
тем или иным способом. Учебная дисциплина, соответствующая
содержанию этой главы, иногда называется статикой
сооружений (статикой стержневых систем).
Как правило, соединение стержней в узлах является упруго-
податливым, т. е. таким, при котором для изменения угла,
составляемого касательными к осям стержней в узле, требуется
приложение некоторого момента, по устранении которого изменение
первоначального угла исчезает. Однако в расчетной схеме
конструкции в одних случаях соединение стержней может быть
принято шарнирным (рис. 16.1, а), т. е. таким, при котором
в узле конструкция не сопротивляется повороту касательной
к оси одного стержня относительно касательной к оси другого,
а в других — жестким (конечной или бесконечной жесткости)
(рис. 16.1, б). При бесконечной жесткости углы, составляемые
касательными к осям стержней в узле, не изменяются, каким бы
ни был момент, стремящийся изменить этот угол.
Шарнирным соединение стержней в расчетной схеме может
быть принято тогда, когда, полагая наличие в каждом из узлов
(рис. 16.1, а) шарнира, получаем тем не менее такую систему
(рис. 16.1, б), в которой изменение расстояний между узлами
мыслимо лишь за счет деформации стержней. Если же, полагая
в узлах системы (рис. 16.1, б) для получения ее расчетной схемы
наличие шарниров (рис. 16.1, г), обнаруживаем возможность
изменения расстояний между узлами без деформации стержней, т. е.
§ 16.1]
ВВОДНЫЕ ЗАМЕЧАНИЯ
533
убеждаемся, что имеет место механизм, то для обеспечения
сопротивляемости расчетной схемы системы нагрузке следует положить
777/ 777>. д.,
ю δ)
w7/
I
Ш ЯГл
> -ϊ
г)
77Я.
В)
Ш,
Рис. 16.1. К вопросу о выборе расчетной схемы системы: а, б) стержневые системы;
в, г) схемы, полученные из изображенных соответственно на фиг. а, б систем путем
включения в узлы шарниров. (В случае в расстояния между узлами могут изменяться лишь
за счет деформации стержней; поэтому схема, изображенная на фиг. в (ферма), может
являться расчетной схемой системы, показанной на фиг. а; В случае, представленном на
фиг. г, расстояния между узлами могут изменяться и без деформации стержней (см.
пунктир); поэтому схема, изображенная на фиг. г, не мож^т являться расчетной схемой
системы, показанной на фиг. б); d) схема (рама), которая может] быть расчетной для
системы, изображенной на фиг. б.
соединение стержней в узлах обладающим бесконечной или
конечной жесткостью. Разумеется, этого нельзя делать в тех случаях,
777/, tffa Я77, 7Я/, 7777, 7777,
Ю δ) δ)
777/, W,
Рис. 16.2. К выбору расчетной схемы системы: а, б, в) стержневые системы; г, д, е)
расчетные схемы систем, изображенных соответственно на фиг. а, б и в; 1 — трос; 2 —
конструктивный шарнир; 3 — стержень, способный работать лишь на растяжение (расчетная
схема (система) с односторонней связью); 4 — стержень, способный работать и на
растяжение и на сжатие.
когда сама конструкция соединения стержней в узле исключает
такую возможность. Так, например, на рис. 16.2, а, б, в
изображены три системы, а на рис. 16.2, г, д, е их расчетные схемы.
534 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
Поскольку трос гибок и не способен передавать на стойки моменты,
присоединение его к стойкам в расчетной схеме должно быть
принято шарнирным. Аналогично при наличии конструктивного
шарнира и в расчетной схеме конструкции должен быть шарнир.
Если все стержни соединяются между собой лишь в концевых
сечениях и при этом в расчетной схеме в соединениях могут
быть приняты шарниры, а нагрузка представлена в виде
сосредоточенных сил, прикладываемых лишь к узлам, то система
называется фермой. В расчетной схеме плоской фермы в узлах
предполагаются цилиндрические шарниры (ось шарнира
перпендикулярна плоскости фермы), а в пространственной — шаровые.
Как правило, в расчетной схеме стержни в фермах принимаются
призматическими х).
Если в расчетной схеме системы соединение стержней
приходится считать обладающим той или иной жесткостью (конечной
или бесконечной), то система называется рамой. В расчетной
схеме рамной системы часть соединений стержней между собой
в узлах может быть принята и шарнирными (рис. 16.2, г).
Основное содержание главы относится к статически
неопределимым системам.
§ 16.2. Расчетная схема и кинематический анализ системы.
Статическая и кинематическая неопределимость.
Неизвестные методов сил и перемещений
1. Выбор расчетной схемы. Использсвание кинематического
анализа шарнирно-стержневых систем.
1.1. Вводные замечания., Для того, чтобы судить к какой
из категорий относится стержневая система — к фермам или
рамам — необходимо выполнить так называемый кинематический
анализ шарнирной схемы системы.
Шарнирно-стержневые (и шарнирно-дисковые) системы,
используемые при кинематическом анализе расчетных схем конструкций,
можно подразделить на три класса: неизменяемые, изменяемые и
особые: Характерные примеры каждого из этих классов
изображены на рис. 16.3.
В неизменяемой системе изменение ее конфигурации мыслимо
лишь за счет деформации элементов (растяжения или сжатия
стержней) и при этом удлинения (укорочения) стержней имеют
тот же порядок, что и линейные перемещения. На рис. 16.3, а
величины Δ' и ΔΓ или Δ" и ΔΓ одного порядка.
1) На самом деле в конструкции стержней ферм имеются всевозможные
диафрагмы, соединительные решетки и тому подобные детали, не учитываемые
в расчетной схеме,
§ 16.2] КИНЕМАТИЧЕСКИЙ АНАЛИЗ. НЕИЗВЕСТНЫЕ МЕТОДОВ 535
В изменяемой системе изменение ее конфигурации мыслимо
без деформации стержней (рис. 16.3, б). В особых системах
перемещение узла вызывает деформацию стержней, но эти удлинения
оказываются малыми более высокого порядка, чем перемещения
узлов (рис. 16.3, в, г)х).
1.2. Кинематический
анализ шарнирно-стерж-
невых систем.
1.2.1. Необходимое условие
неизменяемости. Пусть имеется
шарнирно-стержневая система,
состоящая из стержней,
соединенных между собой в узлах
шарнирами, расположенными по концам
стержней. Прежде всего
удостоверяемся, не является ли система
(ферма) простой. Если ферма
простая, то она статически
определима и неизменяема. Простая
ферма может быть получена из
исходного шарнирно-стержневого
треугольника (в пространственном
случае тетраэдра) путем
присоединения к нему узла, а далее
последовательного присоединения к
образующимся системам узлов, при
помощи двух (трех) стержней2).
Лишь если ферма не является
простой, возникает необходимость
в кинематическом ее анализе.
Покажем как он выполняется. Пусть
общее количество узлов равно Y,
число стержней, соединяющих эти
узлы между собой или присоединяющих их к опорам; равно С.
Число степеней свободы всех Υ узлов, рассматриваемых
самостоятельно, равно Ν— 2Υ или Ν — 3Υ в зависимости от того,
является ли система плоской или пространственной.
Каждый стержень, соединяющий два узла между собой или
присоединяющий узел к опоре, можно трактовать как одну связь.
1) Приведенные выше идеи, положенное в основу классификации —
сопоставление порядков величин перемещений узлов и деформаций (удлинений)
стержней для установления типа системы при кинематическом ее анализе —
предложены Ю. Б. Шулькиным. Им же разработан математический аппарат
для выполнения этого анализа (см. его статью „Кинематический анализ
стержневых конструкций". .Сб. «Расчет пространственных конструкций». Вып. XVII,
под ред. С А. Алексеева, В. В. Новожилова, Стройиздат, Μ., Ι977),
2) См. 1 том (глава III, § 3.2; стр. 170, рис. 3,3).
Рис. 16.3. К кинематическому анализу
систем: а) неизменяемая шарннрно-
стержневая система; б) изменяемая
система (пунктирными линиями показаны
конфигурации, которые может
приобрести система без деформации
стержней); в, г) особые системы (в —
мгновенно изменяемая н г — мгновенно
жесткая систему).
536 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
От соотношения величин С и N зависит является ли число
связей (стержней) в системе достаточным, недостаточным или
избыточным:
C = N, C<Nt C>N. (16.1)
Условия (16.1)L з являются необходимыми, но не
достаточными для неизменяемости системы (см. рис. 16.4).
Ю в)
Рис. 16.4. К вопросу о неподвижности и неизменяемости системы: а) система, изменяемая
вследствие недостаточности числа связей (У = 6; N — 2У = 12; CQn = 3; С = 8;
С = CQn + Ост =11; С = 11 < 12 = N); б) неизменяемая система при достаточном
числе связей (У = 6; N = 2У = 12; CQn = 3; Сст = 9; С = CQn + Сст = 12; С = 12'=
= 12 = N); в) изменяемая система при достаточном числе связей (У = 6; N = 2У =12;
Соп = 3; Сст ~ 9; С = Соп + Сст = 12; С = 12 = 12 = JV; расположение связей
неправильное — в левой панели одна из диагоналей для неизменяемости является
лишней, в правой же панели не хватает диагонального элемента); г) изменяемая система при
числе связей, превышающем достаточное (У = 10; N = 2У = 20; С = 3; С = 19;
С = Соп + Сст =22; С = 22 > 20 = N); при наличии по одной лишней диагонали
в каждой из трех левых панелей, не хватает диагонали в правой панели; д) неизменяемая
система при числе связей, превышающем достаточное (У = 6; N = 2У = 12; С = 3;
С — 10; С = CQn + Сст= 13; С = 13 > 12 = N); одна из диагоналей в левой панели
является лишней. Система статически неопределима.
1.2.2. Достаточное условие неизменяемости. Достаточное
условие неизменяемости системы вытекает из анализа системы
уравнений равновесия, т. е. матрицы ее коэффициентов и
расширенной матрицы. Соответствующая информация приведена в табл. 16.1.
Учитывая, что размеры матриц А и А0, ранги каторых
подлежат вычислению, как правило, высоки, использование условия,
поясненного в табл. 16.1, практически затрудняется. На помощь
приходит так называемый метод замены стержней. Сущность его
состоит в том, что посредством некоторого преобразования
сложной фермы (отбрасывания некоторых η стержней и введения
такого же количества стержней, но соединяющих другие узлы,
чем отброшенные стержни) удается свести ее к простой форме,
которую называют основной системой. Условия, ликвидирующие
отличие основной системы от заданной, представляются в виде
§ 16.2] КИНЕМАТИЧЕСКИЙ АНАЛИЗ. НЕИЗВЕСТНЫЕ МЕТОДОВ 537
BS Ш
SS 4>
а*
О.
(-· ω
У S
О Η
*
Ρ.0)
α) Ч
s й
ав о
о.»
информация
онструкции
5 а
о
<3
SS
X
9В
урав
системе
решении
о <и
ω
sf
я
S
о.
о
•F·
SB
S
• · ι.
Соот
ноше
ние
/"! И
gs ssc
О Я < v.
■ „\ ■ н
н Щ ω
S Э as as
On S
Us S
z. is
S*2£
"go*
^*5
. —
1
у
/
/
/
/
7
КЧ
IS>
l·^
νθΛ
<D Η
Β" <υ
S Ξ
£ ° Я
w <υ S
е- и. s
О <L)
X
κ π) <υ
■2 S Ξ
Й S «
* 5 5
О. <и
has
ж с «
я о о
X К В·
a s
О О,
Н со
<-> >>
X сх,
Ε (_,
cl се
<d я
та
X
ш 2j
^1
га <d
Ξ Ο.
<υ
(-ι <υ
Η ο
S DC
U DC
<υ <υ
pa «
ε
II
v.
I
4 " &
/*
ГО*
JSS
Ήκ
S <D CTJ
O. !><
s-. . <υ
J)H2
о „та
"Η
gS8.
3 <υ <υ
к s δ
£83g
υ as
В" С К
Ι
<
^Ч
\
X
\
\
\
)
/
/
/
/
HI
^
&
JKS
ο
χ
!S
<u
ра
о
χ
Lh
s
t-f
>> π)
Ρ/Ξ
κ χ
ο S
(Π
S
1
О
<υ
Ξ
ра
о
о
О)
и
се К
°«—
=-§
X
га 2ч
О) 4)
(-; О,
Η ι
S
CCJ
Χ
ν.
ε
V
ν.
e
II
ε
—
(Μ CO
538 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVf
К φ
s Ь
=iSB
конст
ствие
&°5
s «
г π
Cs
к я
5 =*
орма
стру
Х°
X*
о
уравнений
информация о системе
и ее решени)
ι > W.
(- 2J ω
о 3 Ss
,9 о χ „
О SB v.
SB Я *- Я
■ „', н
(- ϊ 0)
ο a s s
О О SB „
Us δ
воз-
эж-
ОГО
учая
-°' ч ЭБ С
"*1
-*-
-^
о
X
X
<υ
РЭ
о
X
t,
Ξ
S
>>
V ' β
\
\
)
/
/
/
/ J^
J *л
О ω tf w
q«s а и w s
χ
ο
«
S
Χ
<υ
χ
pa
Π)
η,
>>
Π)
Ξ
<υ
ίο
s
υ
ν»
II
ы
W
ε
V
1^
e
II
ε
■*
X jS b. S CL,
ω о _ со с
Ξ α« κ о
со о о <υ <υ
К f-, О. X X
+
X X
~ 1
ι ε
« ' en·—'
х Τ
^ А
тг ><
<Х<
ι 1
Μ
<υ
3
X
о,
О)
2
W
1
14
я
X
о о
in cq
+
• ι <D <D '
UJ W S « К
2 4w m a
динствень
системы
ожно при
. Послед
подстано
удовлетво
»я ^ч2 к s
XU Я * " S η w
«-g^s* I x«
g >>< 1 <D £ g В
η ϊ ι л , а —
9, II ° Λ ж к
sS «го m-Sm S
о
III
+
(Ν
<
+
ιΗ
χι
+
«а
Χ
<я
<
"fa
<
CI
<
I
§ 16.2]
КИНЕМАТИЧЕСКИЙ АНАЛИЗ. НЕИЗВЕСТНЫЕ МЕТОДОВ
539
К 01
§£
о.
н ω
<-> as
SB ш
О Η
а о
р. ш
IS
Es
« аз
si*
§ о·
О. Η
о о
&Х
SB °
BS
SB
О)
SB
В)
я
α
£я
BS Ш
о о.
О Hi
О)
as я
=ί
я
г
α
о
•е
χ
н 2J ω
о gas я
,R о * -
они е
SSS5S
ogk5k
и а
Г Д W
о 3 as as
<-> sb E
I »
κ w
& к
К К
° Μ
о
<υ
в*
П)
?
Μ
о,
с
о
<υ
X
а:
<υ
00
и
икс
ч
к
гя
m
« о
X
и о
w
X
s
к "
Si*
3 Ξ
<υ χ
χ
pa
Π)
>>ο
Ρ> с
ю —■
ο
<D Ξ
DC Q,
pa О
сз Ό1, ч
>>ч к
^ к <υ
•й Н tJ
«jog
н о ^
О DC Ξ
к £- <υ
о о о.
+
X
ε
χ
ε
s
χ
pa
Π)
о,
>>
5 ε
и
χ
S
ч
О)
<υ
χ
<υ
<υ
<υ
s
X
3
О)
о,
о
X
ч
S
о,
с
о
X
+
χ <υ
н о
о к
^ X
Ю Ю
О f-
X -
« к
< χ«
—' * X
- - ω
I- S sr
<С w "J
7 χ χ
Ι «ι·
II §2
Χ И £
Λ
4 π)
CO pa
g w к
3 <" 2
*«&
<υ
Ξ
со
S
pa
s
s
Ξ
s
« 5
>> 4
а· «
p. s о <υ
о ^ (2 s
№ О m О
Ξ
О
Я
pa
к
s
ts
>.o
о. аз
f- Χ
о <d
х pa
О О
П)
?
(1)
X
<υ
Ξ
со
S
а
н
П)
н
о
s
s
а
V
Ξ
S
Μ §
>. ч
о, <υ
f- о,
X о
о <υ
« X
►J >r
&
<υ
Ξ
pa
о
о
<υ
χ
'S
s
χ
<υ
χ
pa
Π)
η,
s
χ
Ξ
s
3
<υ
ο,
Ι
π)
ε
V
V
Ю
со
540
НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
α*
° Й
« υ
Ο. φ
ω ее
г μ.
я ο
Q.CQ
Cs
Sf Μ
8-е
о
s
sb
φ
SB
CO
я
α
>>
а 5
S *
Ι3
Я φ
υ ο.
Ο φ
S S
sf
я
г
α
о
■θ
sb
Κ
о Э я я
<-> SB g
°3o£
s
о.
δ
s
о
φ
ч СО
к й
В к
о s
в*
δ
S
со
8
s
и
α>
И
pa
со
о.
>■«
s
CO <D
Ξ
s
S
4)
δ
S
Ο
a
ο.
со
t
00
"»·?
к
<υ <υ oj
Μ tf к
* Εν Й
S CO *» к
* * О J-
>> α. α.
&C 2 *
У 9 δ S
Χ Χ *£ *
0&S
»s
s
X
<υ
χ
pa
со
о.
о о
л л
+
РЭ
СО
о.
!><
3
РЭ
о,
О)
с
со
СЯ·"^
е I
СО
Ξ
<υ
ίο
s
U
<υ
S
Χ
<υ
a
ο,
F-ι »Κ
<υ κ
ω χ
Ξ <υ
s χ
ία)
κ
и Q,
Ο
pa
'S
pa
ο
4
ι ^
' <υ
s
χ
<υ
3
<υ
ο,
Ι
«.ο
κ _ι_
X ~
3 Ι
χ
4
<υ
4
ο
ο
с
II
ν»
Λ
δ
σι
Ι
я
SB
φ
я
α
я
о.
>>
о
ч
и
I
t
я 3
ч ж
ω*
* «
SB ts
ж я
«ч
о я
с£
я -
я я
Ч
и а
SS
s«
аз *·
Is
со *™
о-в:
~ я
о sf
ω 5
б*
2 §
ч *
φ ►
= и о
xnwS
„•s я ω
I |S χ
, ь. О S3
+ я Я «
<=§*&
5*ав*
- Я я <u
К*
Я Я
у *
О) О)
О SB
О pQ
SB га
CQ Q.
а*
5s
Я φ
SB Я
и ο
га ·
00·=·
&5
5 о
υ υ
яш
ой
s a
я 2
α я*
о S
ф Я
«е
га г-*
S С
со ш
s*
ϊχ
s SB
18
я о
=f
ω я о.*
S я «>
я о._ Й
Я °
* t. s *
5Sls
О я
к!?
яЯ
φ
s ϊ
м а:
я η
о
£8
D.O
Η SB
У ЕС
ЭВ о
SS
>>п
г я
φ
S ω
"** я
ϊϊ
СО Ι-Γ
sI
§в
SBW
(U
ω я
2 я
33 Я 2 Я ■ « s
φ о.С °-S s 5
* ι я ΐ 8
ж , я
φ 5 Ε Q
s.."_ с я ε g
11 О. ж» t?
Ξ К я η. ρ?
"SXs(i
со ЕГ и
к Ез ft г о"и
г sb о s и с
С 5 ■ Я φ .ο
Λ см SB cjco £
φ Φ С Ο
Ο. Ο Μ
Λ Ο
Η SB
Яад
Β) φ
Ο SB
Эх
и я
φ «
К У
В ω
Ч а»
о Ε
й 8"
с S
а> о
SB Φ
I-,
Vs.
л?
Φ ^Я
8яй
s,« °
CO rt>
O—SB
.>- к
Hji Я
X О)
я"- о
4 -о
.-ν в
s »- ^
1) —.
м ·· О
§§«§
See
ом ч
33 sC:i
;« ·
ш «
око
5 S *>
S 9· К
«&·*
« ч а)
« и я
?·« «
о. w о
н a sb
о S а;
•и то !ίΐ
SB щ φ
о я и
ы, о
о"5Е
-ss
я ?°
m О Я
Sos
я о.=г
SC «
о.. ϊ^
ш
Φ :
S .
я :
δ
SB
о
§ 16.2] КИНЕМАТИЧЕСКИЙ АНАЛИЗ. НЕИЗВЕСТНЫЕ МЕТОДОВ 541
системы k линейных алгебраических уравнений. При этом анализ
матрицы А исходной системы уравнений п-то порядка (см. табл. 16.1)
заменяется аналогичным анализом упомянутой системы k-το
порядка. Поскольку k<^n, получается огромный выигрыш в
количестве вычислений х).
2. Линейность системы. Будем исходить из того, что в
рассматриваемых системах перемещения настолько малы по
сравнению с габаритными размерами, что ими можно пренебречь и
уравнения равновесия составлять для недеформированной схемы. Если,
кроме того, иметь в виду и соблюдение закона Гука для
материала, придем к выводу, что рассматриваемые здесь системы линейны,
и к ним применим принцип независимости действия сил, согласно
которому любая функция, характеризующая
напряженно-деформированное состояние при нескольких воздействиях на систему,
равна сумме таких функций, соответствующих каждому
воздействию, рассматриваемому самостоятельно, а при увеличении какого-то
воздействия в k раз соответственно в k раз возрастает и
соответствующая воздействию функция, т. е. Ф = Ф14-Фг» Φ = &Φι.
3. Статическая неопределимость. Стержневая система
называется статически неопределимой, если внутренние усилия и
моменты в поперечных сечениях, пусть даже некоторых стержней,
входящих в ее состав, не могут быть найдены из одних уравнений
равновесия, хотя бы при каком-то одном воздействии на систему2).
Для того, чтобы установить какой является система —
статически определимой или неопределимой, введем понятие лишняя
связь. Под лишними подразумеваются такие связи, удаление кото*
рых не превращает систему в механизм. Лишь с этой точки
зрения указанные связи можно назвать лишними, так как и
без них система сохраняет свою геометрическую неизменяемость.
С точки же зрения работы конструкции, обеспечения ее
прочности и жесткости, эти связи не являются, вообще говоря, лишними.
Геометрически неизменяемую систему без лишних связей можно
получить из системы статически неопределимой не единственным
способом.
г) Упомянутая выше система /г-го порядка имеет вид уравнений,
отрицающих наличие усилия во введенной связи:
NixXx + NtiXt + ... + NlkXk + Nip = Q (ί = 1, .... k).
Здесь Х]> ..., Хь — силы, действующие по направлению замененных стержней
и равные усилиям в них, Nip — усилие в ι'-ом заменяющем стержне от
внешней нагрузки. Nij — усилие в t'-ом заменяющем стержне от силы Х,= 1.
2) Здесь и ниже для простоты вместо термина расчетная схема системы
используется термин система. Заметим, что если бы система не была
геометрически линейной, то уравнения равновесия пришлось бы составлять для
деформированной системы и, таким образом, находить усилия из одних уравнений
статики не представилось бы возможным,
542
НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
У/77/
а)
~1Ь.
Щ
■УЛ
ткя
7L·
На рис. 16.5, б показаны различные варианты удаления
лишних связей в одной статической неопределенной системе. Следует
обратить внимание на то, что не
каждую связь можно рассматривать как
лишнюю; так, например, в балке,
приведенной на рис. 16.5, а, нельзя
отбросить горизонтальный опорный
стержень, так как система при этом стано-
~" вится изменяемой, превращается в
механизм, даже если других связей и не
_ удалять (рис. 16.5, в). Такие связи,
которые нельзя отбрасывать, не
превращая систему в механизм, называются
^. безусловно необходимыми *).
Для того чтобы систему с лиш-
_ ними связями превратить в
геометрически неизменяемую без лишних связей,
можно удалять и внутренние связи.
— Если рассечь стержень в
пространственной системе, то тем самым
исключаем шесть связей, так как в
результате рассечения края разреза получают
возможность иметь три относительных
линейных смещения вдоль
направлений, не лежащих в одной плоскости,
и три относительных угловых
перемещения (три относительных поворота
вокруг трех направлений, также не
лежащих в одной плоскости). Аналогично
рассечение стержня в плоской системе
означает исключение трех связей, из
коих две препятствуют относительным
линейным смещениям краев разреза в
плоскости системы и одна препятствует
относительному повороту этих краев
вокруг оси, перпендикулярной
плоскости системы.
Введение шарового шарнира в тело
стержня, входящего в состав
пространственной системы, создает возможность
трех относительных поворотов сечений,
лежащих по разные стороны от шарнира, и, таким образом,
представляет собой исключение трех связей.
К-
IH
и-
1Ь-
$*-
%-
dfe 7%Z
δ)
Р==Ъ>—~Чг--
1L· ife
ν?· 7%7/
Рис. 16.5. Статически
неопределимая система и варианты
основной системы, получаемые
путем исключения внешних
лишних связей; а) статически
неопределимая система (неразрезная
■балка); б) варианты основной
системы; в) геометрически
изменяемая система (механизм),
возникшая вследствие исключения
безусловно необходимой связи.
·) Этот термин предложен И, М. Рабиновичем,
§ 16.2] КИНЕМАТИЧЕСКИЙ АНАЛИЗ. НЕИЗВЕСТНЫЕ МЕТОДОВ 54U
! ί
И !
Ι ιΛ* \ ι
Аналогично включение цилиндрического шарнира в тело
стержня означает исключение одной связи, препятствующей
относительному повороту сечений, лежащих по разные стороны от
шарнира, в плоскости, перпендикулярной оси шарнира.
Включение ползунка (рис. 16.6) в тело стержня означает
исключение одной связи, препятствующей относительному
линейному смещению частей стержня,
расположенных по разные стороны от ползунка,
вдоль направляющей ползунка;
Геометрически
неизменяемая система, не содержащая
лишних связей, является
статически определимой.
Чем больше в статически
неопределимой системе лишних связей, тем больше
необходимо иметь дополнительных условий
сверх условий статики, чтобы получить
возможность отыскания внутренних усилий. Поэтому число
лишних связей показывает степень статической неопределимости:
степень статической неопределимости системы равна числу ее
лишних связей.
Существует общая методика определения числа лишних
связей, а следовательно, и степени статической неопределимости
в любой статически неопределимой стержневой системе.
ίά
Рис. 16.6. Ползунок,
включенный в тело стержня.
11
|умм||и
ч
ю
t
(7//л
— — —··*'■
δ)
Рис. 16.7. Замкнутый контур: а) замкнутый плоский стержневой контур»; б, в)
замкнутые контуры (плоский и пространственный), одним из элементов Которых является «земля».
Для описания этой методики необходимо коснуться понятий
о жестком замкнутом контуре, полной системе независимых
замкнутых контуров и о числе простых цилиндрических
(шаровых) шарниров.
Замкнутым жестким контуром называют систему жестко
соединенных между собой стержней, оси которых образуют замкнутую,
нигде не самопересекающуюся линию (рис. 16.7, а). Замкнутый
жесткий контур, что видно из его определения, не содержит
ни шарниров, ни ползунков. Системы, показанные на рис. 16.7, б, в
(Г-образная рама с защемленными концами и пространственная
;544 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
*--,-
рама), могут рассматриваться как жесткие замкнутые контуры,
так как конструкция, к которой прикреплены рамы, в силу ее
жесткости играет роль замыкающей стороны контура.
В общем случае 'в пространственной или плоской стержневой
системе можно отметить подсистемы двух типов — консоли и замк-
__ .^ нутые контуры. На рис. 16.8 приведен
соответствующий пример. Консоль всегда
статически определимах), в ней усилия могут
быть найдены из одних уравнений
равновесия независимо от рассмотрения остальной
части конструкции. Поэтому, желая
установить степень статической неопределимости
стержневой системы, можно мысленно
отбросить все консоли и рассматривать лишь
оставшуюся после этого часть.
Введем понятие системы независимых
замкнутых контуров. Система замкнутых
контуров стержневой конструкции
независима, если в каждом из них имеется хотя бы
один стержень, не входящий ни в один из
остальных контуров (рис. 16.9). Заметим, что
если опорная часть контура (земля) учтена при рассмотрении
одного контура, то в остальных контурах она уже не считается
в качестве нового «стержня».
W7/, 777/,
Рис. 16.8. Расчетная
схема стержневой системы
с двумя характерными
типами областей
(пунктиром обведены
консольные области, остальная
часть системы —
замкнутые контуры).
/ ~,
1 3 ι
ι "ч
ι Ζ ι
ι ι
1 1
' -4 '
! 1 !
ι. >
У/////
1
4 !
ι
5 !
6 \
9 !
1
8 1
1
7 !
1
·, /
ν////////////////////, ν//////////////;
%
■
\1
I
5
Ь1
а)
ш)ш////)//////% У777///7/777/777/777//.
В)
6)
Рис. 16.9. Установление значения К — числа замкнутых контуров, образующих
полную систему: а) случай, в котором «земля» является замыкающим стержнем лишь одного
контура; б) случай, в котором «земля» входит в качестве замыкающего «стержня» не только
в один контур (при выбранной последовательности нумерации контур в верхнем правой
углу не входит в К, поскольку в нем нет ни одного «нового» стержни, т. е. стержни дан*
ного контура, не входящего в контуры с меньшими номерами; стержень «земля» учиты*
вается как новый лишь в каком-то одном контуре); в) расчетная схема, эквивалентна^
схеме, изображенной на рис. б; (в обозначении контуров штриховым пунктиром отмй*
чены «новые» стержни); г) определение К для пространственной рамы.
Независимую систему замкнутых контуров стержневой
конструкции условимся называть полной, если в конструкции нет
ни одного стержня, не входящего хотя бы в один контур этой
системы (рис. 16.9).
) Утверждение справедливо в случае линейности системы,
§ 16.2] КИНЕМАТИЧЕСКИЙ АНАЛИЗ. НЕИЗВЕСТНЫЕ МЕТОДОВ
545
Если в полной независимой системе контуров стержневой
конструкции содержится К замкнутых контуров и все они жесткие,
то, произведя К разрезов надлежащим образом (каждый новый
разрез обязательно рассекает стержень нового контура), получим
совокупность консолей, т. е. статически определимую систему
(рис. 16.10). Поскольку каждый разрез стержня в
пространственной (плоской) стержневой системе исключает 6 связей (3 связи),
число лишних связей соответственно равно £/7 = 6/С, Л = ЗК.
У///////////////////////, У///////////////////////,
1
5
5.
д
δ
7
6 8\ 7
<7//////>/;/;///////////,
|
}
0)
V777777777777777777777/,
Рис. 16.10. «Надлежащее» проведение разрезов стержней в жестких контурах для
установления степени статической неопределимости системы: а) нумерация контуров,
учитываемых при определении числа К и «надлежащее» расположение сечений (в каждом
контуре рассечен лишь один «новый» стержень; номер сечения совпадает с номером контура);
б) система «консолей», образующаяся при «надлежащем» проведении разрезов (вся
система распадается на самостоятельные консоли).
При наличии в стержневой конструкции шарниров и (или)
ползунков, число Л для пространственной конструкции
определяется по следующей формуле:
Л=6К-Ш]Х-ЗШШ-П + С. (16.2)
Здесь Д/ц — приведенное число простых цилиндрических шарниров,
Шш — приведенное число шаровых шарниров, Я —число ползунков,
включенных в стержни конструкции, С —число стержней,
включая опорные, оба конца которых прикреплены при помощи
шаровых шарниров и которые не имеют точек приложения сил,
за исключением концевых точек (центров шаровых шарниров).
Цилиндрический шаровой шарнир называют простым, если он
соединяет лишь два стержня или две части стержня. Шарнир,
соединяющий более чем два стержня, называют сложным. Если
шарнир соединяет /г + 1 стержень, его называют «-кратным
(эквивалентным η простым шарнирам).-
Приведенное число цилиндрических (шаровых) шарниров равно
суммарному количеству простых цилиндрических (шаровых)
шарниров, которому эквивалентны все имеющиеся в системе
цилиндрические (шаровые) шарниры.
546 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
Поясним происхождение члена С в формуле (16.2). Если
стержень прикрепить к опорам на, каждом из концов при помощи
шарового шарнира, то получается система с одной степенью
свободы, поскольку при таком закреплении ничто не мешает стержню
вращаться относительно оси, проходящей через центры шаровых
шарниров. Такая ситуация встречается в опорных стержнях в
пространственной конструкции и в расчетной схеме пространственной
фермы. Однако поскольку нагрузка прикладывается только к
узлам фермы и представляет собой сосредоточенные силы, эта
степень свободы стержня фермы не является существенной и не влияет
Рис. 16.11. Закрепление стержня, обеспечивающее его неподвижность (геометрическую
неизменяемость) н статическую определимость (К = 5, Шш = 12, С = 6; Л = 6/< —
— ЗШШ + С = 6 ·5 — 3 -12 + 6 = 0); цифрами около шаровых шарниров указана их
кратность; С — общее количество стержней, не несущих внешней нагрузки н имеющих
по концам лишь шаровые шарниры.
на неизменяемость общей конфигурации системы. Поэтому член С
компенсирует такие формально учтенные предыдущими членами
формулы степени свободы.
На рис. 16.11 показано закрепление балки в пространстве,
обеспечивающее ее неподвижность, неизменяемость и статическую
определимость.
Пример 16.1. Установить степень статической неопределимости
стержневого перекрытия1), показанного на рис. 16.12, а.
Решение. Представим себе перекрытие как конструкцию,
содержащую полную систему (К = 23) независимых жестких
*) Перекрытием (стержневым) называется конструкция, состоящая из двух
систем стержней, пересекающихся друг с другом под некоторым (чаще всего
прямым) углом. Если оси всех стержней лежат в одной плоскости, то
перекрытие называется плоским. Конструкция перекрытий обычно такова, что
в каждом из пересечений балок двух направлений имеются все шесть связей.
С этой точки зрения перекрытие представляет собой плоскую, пространственно
работающую раму. Однако при частных видах загружения перекрытий
существенными оказываются не все связи в пересечении стержней. Так, например,
если имеется лишь нагрузка, перпендикулярная плоскости перекрытия, то
наиболее существенной в каждом пересечении стержней оказывается связь,
перпендикулярная плоскости перекрытия. В этом случае расчетная схема
-перекрытия представляет собой две системы балок, из которых балки одной
системы опираются на балки другой,
§ 16.2] КИНЕМАТИЧЕСКИЙ АНАЛИЗ. НЕИЗВЕСТНЫЕ МЕТОДОВ 547
контуров (рис. 16.12, б). Приведенное число шаровых шарниров
(рядом с каждым шаровым шарниром цифрой указана его
кратность) #/ = 54. Число лишних стержней и равная ему степень
статической неопределимости Л = п = 6/С — 3///Ш + С = 6-23 — Зх
Х54 +27 = 3.
Обсужденный выше подход применен для решения данного
примера лишь с целью показа
Однако в рассматриваемом
примере можно поступить и
гораздо проще — отбросить
три связи, соединяющие
балки пересекающихся
направлений, и поскольку в
результате такой операции
получаются самостоятельные
балки, каждая из которых
неподвижна (неизменяема) и
статически определяема, в
рассматриваемой системе
лишних связей всего три, а
поэтому трем равна и степень
статической неопределимости
системы.
Таким образом, другой
подход к установлению
степени статической
неопределимости состоит в том, что
система мысленно
представляется в виде соединенных
между собой при помощи
связей частей, каждая из
которых обладает
геометрической неизменяемостью и
статической определимостью. Степень статической неопределимости
равна числу таких связей.
Можно, наконец, любую систему представить состоящей из
отдельных стержней (рис. 16.13, в) и сопоставить число
неизвестных усилий во всех сечениях, проведенных для разбивки
конструкций на отдельные стержни, с числом уравнений
равновесия для всех стержней.
При таком подходе можно дать следующее определение.
Стержневая система статически неопределима, если число неизвестных
усилий и моментов в сечениях, разбивающих систему на
отдельные стержни, превышает число уравнений статики. Степень
статической неопределимости равна разности между отмеченными
выше числами.
универсальности формулы (16.2).
Рис. 16.12. К установлению степени
статической неопределимости балочного перекрытия:
а) заданная система; б) вид, приобретаемый
системой, если бы в ней все контуры были
жесткими.
548 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
В раме, изображенной на. рис. 16.13, в, проведено 12 разрезов, каждый
из которых рассек 6 связей. Всего неизвестных усилий в этих связях 12-6 =
= 72. Вместе с тем число уравнений равновесия, учитывая, что рассечение
образовало восемь стержней и для каждого из них можно составить 6
уравнений равновесия, равно 8-6 = 48. Таким образом степень статической
неопределимости равна 72 — 48 = 24.
Рис. 16.13. К установлению степени статической неопределимости пространственной
рамы: а) заданная система; б) система в виде четырех консольных элементов; в) система
в виде отдельных стержней.
4. Кинематическая неопределимость. По аналогии с последним
приведенным выше определением понятия статической
неопределимости и ее степени можно дать и определение понятия
кинематической неопределимости.
Систему назовем кинематически неопределимой, если по
концам стержней, ее составляющих, имеются неизвестные линейные
и (или) угловые перемещения. Число независимых таких
неизвестных будем называть степенью кинематической
неопределимости системы *).
Именно поворотом концевых сечений стержня системы и
относительным смещением концевых его сечений и определяется его
напряженно-деформированное состояние. Подробно об этом
говорится в § 16.4. Рассмотрим пока рамы с жестким закреплением
стержней как в узлах, так и на опорах. Пусть число узлов равно У.
*) Термины кинематическая неопределимость и степень кинематической
неопределимости ниже обсуждаются более подробно,
§ 16.2] КИНЕМАТИЧЕСКИЙ АНАЛИЗ. НЕИЗВЕСТНЫЕ МЕТОДОВ 549
Степень кинематической неопределимости рамы складывается из
двух слагаемых
т = тугл + /псмещ. (16.3)
Достаточно знать все составляющие угла поворота У узлов
рамы, чтобы тем самым знать углы поворота обоих торцевых
сечений каждого из стержней. При этом
= ЗУ и тугл = У (16.4)
т
'УГЛ
соответственно для пространственных и плоских рам.
Второе слагаемое в правой части равенства (16.3) —тсмещ
равно числу таких независимых линейных смещений узлов,
которые позволяют найти относительные смещения концевых
сечений во всех стержнях. При учете влияния осевой
деформации стержней на перемещения узлов тшеш = ЗУ и тсмеш = 2У
соответственно для пространственных и
плоских рам.
Итак, а
т = ЗУ + ЗУ = 6У, m = Y + 2Y = 3Y (16.5) Щ
zk
17
т
VP,
т
X
Рис. 16.14. Кинематнче
ски неопределимая
пространственная рама.
соответственно для пространственных и
плоских рам. Если опорные сечения стержней
закреплены упруго-податливо, то и их надо
причислять к узлам.
В ряде случаев в расчетную схему вносят
упрощение —пренебрегают осевой
деформацией стержней. При этом степень
кинематической неопределимости системы становится
иной — отпадают перемещения, обусловленные осевой деформацией
стержней, и остаются лишь перемещения, вызванные изгибом.
С целью отыскания тсмеш в этом случае поступают так. Мысленно
вводят во все узы шарниры (цилиндрические в плоской раме и
шаровые— в пространственной). В результате такой операции
получается механизм, имеющий число степеней свободы, равное тсмеш.
Это число равно минимальному количеству стержней, которые
нужно ввести в упомянутую шарнирно-стержневую схему для
ликвидации ее изменяемости —для превращения ее из механизма
в ферму. Так, степень кинематической неопределимости системы,
изображенной на рис. 16.14, при учете осевой деформации равна
шести (неизвестными являются три составляющих перемещения
узла и три составляющих его поворота), а при неучете осевой
деформации оказывается равной трем — неизвестными остаются
лишь углы поворота узла относительно осей х, у и ζ.
В табл. 16.2 изображены различные стержневые системы и
показана степень их статической и кинематической
неопределимости.
550 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
Таблица 16.2
5. Стержень как элемент конструкции. В общем случае
стержневая система в одно и то же время может быть и статически и
кинематически неопределимой. Для того, чтобы полностью
охарактеризовать напряженно-деформированное состояние системы, т. е.
найти 18 функций х)
Qx, Qy, Ν; Мх, My, Мг; ух, уу, ег; κχ, ку, кг;
и, v, w; ΰχ, Ъу, Ъг (16.6)
*) Qx> Qy N — составляющие равнодействующей внутренней силы в
текущем поперечном сечении; Мх, Му, Мг — составляющие момента внутренних
сил в текущем поперечном сечении; γ*, уу, ег—соответственно сдвиги при
изгибе в. плоскостях Οχζ и Oyz и относительная линейная деформация осевого
волокна в текущем поперечном сечении стержня; %х, ху и яг — изменения
§ 16.2] КИНЕМАТИЧЕСКИЙ АНАЛИЗ. НЕИЗВЕСТНЫЕ МЕТОДОВ 551
в любом сечении каждого из стержней, ее составляющих,
достаточно найти для каждого из концевых сечений стержней либо
перемещения и повороты, либо составляющие внутренних силы и
момента. Допустим и смешанный подход. Поясним сделанное
утверждение, показав схему решения
задачи анализа
напряженно-деформированного состояния призматического стержня.
Имеем три системы уравнений:
статические уравнения
(дифференциальные уравнения равновесия элемента
стержня; см. уравнения (1.9) в I томе)
^-4-а =0
dQy
dz
dN
dz
■<7ι/ = 0,
■<7* = 0,
dz
— Qy + mx = Q,
Qx+my = Q,
dM
-Zf- + mz=0,
(16.7)
Phc. 16.15. Деформация
элемента балки от сдвига при
поперечном изгибе.
приобретающие после исключения из них Qx и Qy следующий вид:
dm
у
dz*
dM,
+
dm.
dz
dz
-f тг = 0,
<7* = 0,
ά*ΜΛ
dz*
dN
dz
drrii
+ ^Γ + ^ = °·
+ q, = 0;
(16.8)
кинематические уравнения (уравнения совместности
деформаций и перемещений; см. уравнение (12.116) и пояснение о знаке,
формулу (11.12') и формулу (2.22))
κ^
®у + Ух =
d2u
dz* '
du
d2u
— Ky— dz* '
α ι dv
dftz
dw
(16.9)
(природа пятого уравнения пояснена рис. 16.15, природа
четвертого уравнения аналогична), которые после исключения из них и
и ν преобретают следующий вид:
dz
d$x
^У^ЧГ'Г dz *
аУу
κζ =
d$,
dz '
8г =
dw
~dz
(16.10)
кривизн оси в плоскостях Oxz и Oyz и погонный угол закручивания оси
стержня в текущей ее точке; и, v, w — составляющие перемещения текущей
точки оси стержня; $х, $у, ·θζ—составляющие угла поворота текущего
поперечного сечения стержня относительно осей х, у, г.
552
НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVf
физические уравнения (закон Гука)
мх
1
м
dQv 1
κ</— ΕΙ~~ ί* r*p * У*
Q>
dz GFy>
Λ V j-i j ~^
dQx 1
GFX>
Qy
κ* =
Ely dz GFX> 4y~GFy>
Mz __N_
GIk ' Ъг~ EF' )
(16.11)
Имея уравнения (16.7) — (16.11), для отыскания всех
восемнадцати функций Qx, ..., Mz; ух, ..., хг; и, ..., $г поступим
так. Первым долгом выведем разрешающую систему уравнений
относительно и, v, w, ϋ·ζ. Для этого в уравнения (16.8)
подставим выражения для усилий, найденные из (16.11)
Мх = куЕ1х-
Мг = KzGIk;
EIX Ely
Qy\ Му = 'ХхЫу Tjp-qx',
GF
(16.12)
N=bzEF.
В результате такой подстановки получим уравнения равновесия
элемента стержня, выполненного из материала, подчиняющегося
закону Гука
EI
£4*
dm ц
EI
d*x
у
GI
х dz*
+
dz
dm.
■\-9y-
Elyd*qx
GFX dz*
EIX d*qy
dz ' чу GFy dz*
ds*
= 0,
= 0,
+ m, = 0, EF^ + qz = 0
(
(16.13)
k'dz -г'"* —"» ~* dz
Теперь воспользуемся (16.9)1)2)3)6 для исключения κ*, ку, κζ,
гг из (16.13). После этого исключения получаем
d*u__dmy_ , Ely d*qx _ а |
d4v dmx
ΕΙχ dz* dz~ ~ qy'
GFX dz*
EIX d*qy
GFy dz*
= 0,
гч d*ftz . Λ CT?d*w . Λ
(16.14)
Уравнения (16.14) по своей природе аналогичны уравнениям
Ламе в теории упругости.
Функции
Яху Я у, Яг, тх, ту и тг (16.15)
предполагаются заданными.
Поскольку система уравнений (16.14) имеет двенадцатый
порядок, необходимо иметь по шесть граничных условий на каж-
§ 16.2] КИНЕМАТИЧЕСКИЙ АНАЛИЗ. НЕИЗВЕСТНЫЕ МЕТОДОВ 553
дом из концов стержня. Так, например, в простейшем случае при
ζ = ζΑ {ζА — координата одной из границ отрезка интегрирования)
эти шесть граничных условий могут быть выбраны из числа
нижеприводимых двенадцати, за исключением расположенных
в одной и той же строке
и
= гА
= и(А\
d*u
Е1У№~тУ
υ\ζ = ΖΑ=υ(Α\ [Е1х~^-тх +
dsu
d&
Ely dqx
Wx~dz
EIX dqy
Wy~~dz
:ZA
= ZA
= -QW;
■<#*>;
w
dw
-zA
= W{A) EF^f-\ =NW;
UZ \г=гд
dv EIx d3v
1
ΕΙ χ dQy
1
dz
GFy d?3
GFy GFy dz
GF
m.
:ZA
= &М
El ^L^iha
-L,y χ aj>. ^r πκ Чу
I du Ely d*u
dz
+
1
dz*
Ely dQ,
GF
\z=zA
\
= — MxV;
(16.16)
GFX dz* ^ GFX GFX dz
GFr тУ
= №),
z = zA У
d*u Ely
y d& ~^~ 7^~ a,x
GFX
z = zA У '
ΟΙ ^
ulk~dT
= MtAK
:ZA
Последовательность отыскания функций следующая. Интегрируя
(16.14) находим и, v, w, ftz. Все уравнения в (16.14) и
соответствующие граничные условия являются самостоятельными — изгибы
в двух главных плоскостях, кручение и осевая деформация в
рассматриваемой (линейной) постановке задачи происходят независимо
друг от друга. В случае нелинейной в геометрическом смысле
постановки задачи этой самостоятельности не было бы. Далее, из
(16.9), дифференцируя уже найденные функции, получаем кх, ку,.
хг и ег. После этого из (16.12) определяем Мх, Му, Мг и N; из
(16.7)4)5 находим Qx и Qy; из (16.11)d(5 получаем ух и уу и,
наконец, из (16.9)4)5 находим ΰχ и $у.
Таким образом, если известны либо усилия и моменты в
концевых сечениях стержня, либо перемещения и повороты, то можно
найти по указанной выше схеме все функции, описывающие
напряженно-деформированное состояние стержня.
Если функции (16.15), все или некоторые из них,
претерпевают в каком-то из сечений балки изменение своего
аналитического вида, то в соответствующем сечении имеет место граница
между участками балки, и интегрирование ведется по участкам,
при этом на каждой границе участков должно быть двенадцать
условий сопряжения. Аналогично обстоит дело и в тех случаях»
554 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
когда имеются сосредоточенные силы и моменты Рх, Ру, Рг, Шх,
Шу, 30ΐζ; в сечениях их приложения имеются границы участков
интегрирования. Для избежания необходимости использовать
условия сопряжения при наличии двух или нескольких участков
можно применить метод начальных параметров.
Если бы стержень имел ось не прямолинейную и (или) имел
бы переменное по форме и размерам вдоль оси поперечное
сечение, то и в этом случае можно было бы составить
дифференциальные уравнения, наподобие приведенных выше для стержня
призматического. Основной же вывод о возможности по известным
усилиям и моментам в концевых сечениях стержня либо по
перемещениям и поворотам тех же сечений найти (точно или
приближенно) все функции, описывающие напряженно-деформированное
состояние стержня, остается в силе.
Переход от самостоятельно работающего стержня к
стержневой конструкции связан с необходимостью согласования
граничных условий, отдельных стержней.
Наиболее просто это сргласование осуществляется, если
известны перемещение и угол поворота каждого из узлов
соединения стержней. В этом случае три перемещения и три поворота
концевого сечения каждого из стержней находятся как
составляющие перемещения и поворота примыкающего к этому сечению
узла, взятые в системе осей соответствующего стержня. В связи
с этим для каждого из стержней задача отыскания функций и,
v, w и Φζ оказывается самостоятельной. Если же заданы сила и
момент, приложенные к узлу, то для последнего можно составить
шесть уравнений равновесия, в которые войдут усилия и моменты
во всех концевых сечениях стержней, сходящихся в узле, и таким
образом определение функций и, v, w и ϋ·ζ не может быть
выполнено для каждого стержня отдельно.
Существует два общих метода строительной механики
стержневых деформируемых систем: метод сил и метод перемещений.
Первый применяется для расчета статически неопределимых
систем, а второй — для кинематически неопределимых систем *).
В первом в качестве неизвестных принимаются Х{ (ΐ = 1, ..., η) —
внутренние усилия и (или) моменты в лишних связях, после
определения которых система становится статически определимой,
а во втором — Z{ (i = l, ..., т) — перемещения и повороты узлов,
г) Как правило статически неопределимые системы одновременно являются
и кинематически неопределимыми. Аналогично кинематически неопределимые
системы во многих случаях статически неопределимы. Поэтому, не принимая
во внимание исключительные случаи, можно говорить о множестве статически
и одновременно кинематически неопределимых систем. Для определения
усилий в таких системах необходимо раскрыть либо их статическую, либо
кинематическую неопределимость. Вопрос о том, что является более
целесообразным, решается индивидуально. Об этом будет сказано ниже.
§ 16.3]
МЕТОД СИЛ
555
после отыскания коих система оказывается кинематически
определимой. Таким образом, число неизвестных в методе сил равно η —
степени статической неопределимости системы, а в методе
перемещений т — степени кинематической неопределимости.
Упомянутые выше методы позволяют находить усилия не
только в концевых, но и в любых других сечениях без
самостоятельного рассмотрения отдельных стержней после отыскания
концевых усилий или перемещений. Перемещения в неконцевых
сечениях стержней могут быть найдены как в методе сил, так и
в методе перемещений непосредственно по специальному алгоритму
и без интегрирования уравнений (16.16), хотя при анализе этого
алгоритма обнаруживается его эквивалентность указанному
интегрированию.
Итак, при расчете стержневой системы сначала находится
конечное множество величин (концевые усилия и(или)
перемещения), зная которые без затруднений можно найти континуальную
информацию о напряженно-деформированном состоянии всех
стержней системы. В силу конечности множества неизвестных,
определяемых в первую очередь, и дискретности расположения сечений,
к которым они относятся, стержневые системы могут быть
названы дискретными. Хотя, строго говоря, при полном объеме
решения проблемы после отыскания дискретной информации
ищутся функции, описывающие напряженно-деформированное
состояние континуально.
Если при рассмотрении двумерных (пластины и оболочки) или
трехмерных (массивы) объектов континуальная информация о
напряжениях и перемещениях на контуре (поверхности) элемента
конечных размеров такой системы за счет упрощающих
предположений сводится к дискретной, то в принципе подход к анализу
системы ничем не отличается от анализа стержневой системы.
В таком случае континуальный объект представляется дискретной
расчетной схемой и алгоритм анализа
напряженно-деформированного состояния ее полностью остается идентичным алгоритму для
стержневой системы. На таком подходе основан так называемый
метод конечных элементов.
§ 16.3. Метод сил
1. Основная система. Лишние неизвестные. Как уже
указывалось, в строительной механике в ряде случаев приходится
вместо непосредственного изучения заданной системы
рассматривать другую, в каком-то смысле более простую систему,
получаемую из заданной путем тех или иных преобразований.. Такую
систему называют основной. Используя в расчете основную
систему, необходимо обеспечить то, чтобы она находилась в
совершенно таком же напряженно-деформированном состоянии, что
556
НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
и заданная система, несмотря на отличие от последней. Тогда
результаты расчета, полученные для основной системы, могут
быть отнесены к заданной.
При расчете статически неопределимых систем методом сил
в качестве основной принимается система, получаемая из
заданной путем отбрасывания лишних связей. Если отброшены все
?h?. ?fo. rh?. jfe -fa
•л
'//
\Xf \XZ IXs \Xi, \XS
г
V,
W7/.
m.
* * U U U U U
Xf Xz Xs Xfy X5\P
w, w, π?. 7Я, π?, w, ш
a)
Jxz
\P x3xf \P
777/.
Χι
\xz
Xz Ρ
V77,
"Ш
777/
δ)
δ)
Рис. 16.16. Варианты основной системы для двух статически неопределимых систем!
а) первая система (неразреэная балка); б) деталь конструкции наразрезной балки в
последнем варианте основной системы (включение шарнира в тело балки над
промежуточной опорой); в) вторая система (плоская рама).
лишние связи, то основная система оказывается статически
определимой и геометрически неизменяемой (последнее следует из
самого определения понятия лишняя связь). Только такие
основные системы мы и будем рассматривать, хотя мыслимы и
статически неопределимые основные системы. Исключение лишних
связей для получения основной системы из заданной может быть
выполнено не единственным образом. Мыслимо множество
основных систем, соответствующих заданной.
На рис. 16.16 показаны две заданные системы и ряд
вариантов основной системы, соответствующих каждой из них, Оче-
§ 16.3]
МЕТОД СИЛ
557
видно, что приведенными вариантами не исчерпываются все
мыслимые основные системы.
Ниже будет показано, что разным основным системам
соответствует различная потеря точности при вычислениях.
Следовательно, выбор рациональной основной системы является важной
задачей. Основная система отличается от заданной тем, что в ней
отсутствует ряд связей (лишние связи). Следовательно, она,
деформируясь, может приобретать и такую форму, которая
невозможна для заданной системы. С целью обеспечения
эквивалентности основной и заданной систем к основной системе, кроме
внешней нагрузки, должны быть приложены вместо отброшенных
связей соответствующие им усилия. Однако величины этих
усилий неизвестны. Указанные неизвестные усилия и являются
основными в методе сил. Отсюда
и его название.
После определения
основных, так называемых лишних
неизвестных задача
оказывается статически
определимой.
2. Система канонических
уравнений метода сил.
2.1. Механический
смысл системы
уравнений. Условием для
отыскания значений лишних
неизвестных и является
обеспечение эквивалентности
основной и заданной систем —
значения лишних неизвестных
должны быть такими, чтобы
при совместном их действии с нагрузкой перемещения,
соответствующие отброшенным связям *), обращались в нуль.
На рис. 16.17, а, б показан характер деформации рамы и со<
ответствующей основной системы в том случае, когда усилия,
приложенные взамен отброшенных связей, имеют истинные
значения.
В системе, изображенной на рис. 16.17,6, связи не
препятствуют возникновению относительного поворота сечений по краям
разреза, не препятствуют относительному перемещению центров
сечений по краям разреза, как в вертикальном, так и в
горизонтальном направлениях, т. е. не препятствуют возникновению
перемещений, соответствующих усилиям Х1( Х2 и X,. Несмотря на
х) Лишние неизвестные и соответствующие им перемещения понимают как
обобщенные силы и энергетически отвечающие им обобщенные перемещения.
Ρ
ι
\
±
WZ
W7~A
Ю
Рис. 16.17. Пояснение смысла канонических
уравнений метода сил: а) деформация
статически неопределимой рамы под воздействием
нагрузки; б) деформация основной системы
под воздействием внешней нагрузки и
действительных значений лишних неизвестных
(усилий в отброшенных связях); обе картины
деформации (фиг, α и б) идентичны.
558 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
отмеченную возможность (с точки зрения закрепления)
возникновения указанных перемещений, их нет вследствие того, что
значения усилий в удаленных связях установлены правильно. Иначе
говоря, деформации отдельных частей системы при
действительных значениях лишних неизвестных оказываются
согласованными между собой или, иначе, совместными.
Итак, определению лишних неизвестных служат условия
совместности деформаций
Δ, = 0 (ί = 1, ..., η). (16.17)
Здесь Δ,-— обобщенное перемещение в основной системе,
соответствующее ί'-й лишней неизвестной и вызванное внешней нагрузкой
и всеми лишними неизвестными, п — число отброшенных связей
(степень статической неопределимости).
Уравнения (16.17) могут быть представлены следующим
образом:
Аа + Лй + ... + Л,я + Л„, = 0 (£ = 1, ..., η), (16.18)
поскольку Лг является результатом совместного действия каждой
из лишних неизвестных и внешней нагрузки. Здесь Δν —
перемещение в основной системе, соответствующее ί-й лишней
неизвестной, вызванное /-й лишней неизвестной, Δ;Ρ — перемещение
в основной системе, соответствующее ί-й лишней неизвестной и
вызванное внешней нагрузкой.
Перемещение Δ;; можно представить так: Δ^ = bi}X}% где bi} —
перемещение, вызванное силой Х; = 1. Таким образом, уравнения
(16.17) могут быть представлены в окончательной форме
δίΐΧι + « + .·. + δΛ + ΔίΡ = 0 (» = 1, 2, .... п). (16.19)
Уравнения (16.19) называются каноническими уравнениями
метода сил потому, что они составляются по единому для любой
системы закону (канону).
Итак, для раскрытия статической неопределимости задачи
привлекаются уравнения (16.19), представляющие собой условия
совместности деформаций.
На рис. 16.18 и 16.19 показан смысл коэффициентов и
свободных членов в канонических уравнениях, соответствующих
стержневым конструкциям, изображенным на рис. 16.16, а, в, при
двух вариантах основной системы.
Матрица системы канонических уравнений
δη δ12 ... δ1η
8и δ22 ... б2я (16.20)
£Л1 ^Л2 ··· Олл
·§ 16.3]
МЕТОД СИЛ
559
w Я « <u я
и и α) хл,
Η * ω с *
»*я
<» 5 к 5 ч
^ СС Ч J3
м *, та ч
а. о.ь as χ
5 «О
s - о. я
я а Ρ га
ж <-* Я
О "О·
о ш « Я
ω и I- Ц·
я О·^ и
560 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
JCf-t
«£j
V:
т^
7W,
$ъг<0
^$г<0Ш
Ш?,
гут-
$г<0
$11
№
<"
Хъ-1
71Ъ.
\
&1Р I А
■* *4 "
ff
4?Д<0
^.
£г;
δ)
"^щищй^
/Ъ
V2=/
т^
^
л:,
яя:
t-Лг?
г
acflfll
1 ?^г
Ζ .1
0
Рис. 16.19. Два варианта основной системы для одноконтурной плоской рамы н
пояснение смысла коэффициентов и свободных членов канонических уравнений: а, б) первый
и второй варианты; θ) эпюры изгибающих моментов в единичных (вспомогательных)
состояниях в первой основной системе.
§ 16.3]
МЕТОД СИЛ
561
обладает рядом свойств; отметим два из них: ее симметричность
δι, = δμ (16.21)
и положительность определителей всех главных ее миноров
δϋ δ12 ... δ,
δ21 δ22
Ь1{ > О,
δ//
>0,
βί£
β/<
δ*ί
δ*/
δ//
δ*/
δ* a
δ/Α
δ*Α
>ο,
■Ία
δ2/ι
J/ll
Jai
>0.
(16.22)
2.2. Определение коэффициентов и свободных
членов уравнений. Коэффициенты и свободные члены в
системе канонических уравнений представляют собой перемещения,
которые могут быть определены по формуле Мора (формулы
(15.87) и (15.86) с использованием приема Верещагина.
Таблица 16.3
Типы систем
Фермы плоские и пространственные
Балки однопролетные, неразрезные;
плоские балочные перекрытия,
работающие на нагрузку, нормальную к плоскости
перекрытия; плоские рамы при не очень
больших продольных силах
Плоские рамы при больших
продольных силах (например, стойки в
многоэтажных рамах); арки
Пространственные рамы при не очень
больших продольных силах
Пространственные рамы при наличии
больших продольных сил (например,
рамные купола, стойки в многоэтажных
рамных каркасах)
Учитываемые виды деформации
при определении перемещений
Осевая деформация
Изгиб (если Ijh > 5) или
изгиб и сдвиг (если Ijh < 5)
Изгиб и осевая деформация
(если Ijh > 5) или изгиб, сдвиг
и осевая деформация (если
Ijh < 5)
Изгиб в двух главных
плоскостях и кручение; сдвиг (если
Ijh < 5)
Изгиб в двух плоскостях,
кручение и осевая деформация;
сдвиг (если Ijh < 5)
Примечание.
/ — длина участка оси стержня между точками перегиба, h — высота поперечного
сечения.
В табл. 16.3 указано, в каких случаях учитывается влияние
отдельных видов деформации на величину перемещений (бгу и Δ/Ρ).
Для определения коэффициентов и свободных членов в
канонических уравнениях необходимо построить эпюры тех усилий
562 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. ΧΥΓ
в основной системе от внешней нагрузки и отдельно от каждой
из единичных сил Χι (ί = 1, ..., η), которые соответствуют
учитываемым видам деформации согласно табл. 16.3.
Состояние основной системы, загруженной заданной внешней
нагрузкой^ называют грузовым, а загруженной одной из
единичных сил ^г=1, ί-м единичным (или i-м вспомогательным).
Пример 16.2. Определить коэффициенты и свободные члены канонических
уравнений метода сил применительно к раме, изображенной на рис. 16.19.
Решение. Учтем при определении δ1( и А.р лишь изгиб. Принимая в
качестве основной системы систему, представленную на рис. 16.19, а, будем иметь
эпюры Mi (ί=1, 2, 3) изгибающего момента, показанные на рис. 16.19, в.
Интегралы, входящие в бг- и А.р, найдем по правилу Верещагина. В
соответствии с рис. 16.19, в, получим (читателю предлагаем выполнить все
операции, необходимые для получения бг/ и Διρ (t=l, 2, 3), которые здесь не
приведены)
. 243 . 135 . 99 1 . 144 „ 27 _ 12
011_£77' 12 W 13==ТТ7Г' ύ22-£77' 023_~£7Γ· 033==Ш7>
99 1
,13~ 2 Е1г
Λ —
' А2Р
, δ22 =
261
ΕΙ, '
216 . 261 . 45
Δ. η = -^-r- . Δ_ г, = ^-r-. Δ„
IP ΕΙχ ' 2P EIX > зр ΕΙΧ *
Таким образом, канонические уравнения после сокращения всех членов
на 1/(Е1х) приобретают вид
99
243Xi —135Х2 + -2-Х3 + 216 = 0,
— 135Х1 + 144Х2 — 27Х3-261=0,
QQ
yXi —27Х2+12Х3 + 45 = 0.
Пример 16.3. Вывести общие формулы для коэффициентов и свободных
членов канонических уравнений метода сил применительно к неразрезной
балке при использовании основной системы, изображенной на рис. 16.18, а.
Решение. Определение коэффициентов в i-м уравнении дает
би = 0, .... 6ifj_2=0, 8Μ-ί = -6^77, 6»=W\Ti+i^]>
б*.М = ёЩ? b,l+2 = 0, .... 6,я = 0. (16.23)
Свободный член в i-м уравнении найдем следующим образом:
4«-ea+tt- (,β·24>
Здесь (ύι — площадь эпюры изгибающего момента в грузовом состоянии
основной системы в i-м пролете, а/ и 6г — расстояния по горизонтали от центра
тяжести эпюры а^ соответственно до левого и правого конца i-ro пролета.
Таким образом, i-e каноническое уравнение (уравнение трех моментов)
имеет вид
§ 16.3]
МЕТОД СИЛ
563
Если все пролеты между собой равны и момент инерции поперечных
сечений во всех пролетах балки одинаков, т. е. /1 = /2 = ... = /т=/, ^ = 1^ = ...
,.. = /т = /, то уравнение приобретает вид
Xi-i + 4Xi+X/+i = ---£- (<Oiai + <oi+1&i+i). (16.26)
Из трех вариантов основной системы для неразрезной балки (рис. 16.18)
лучшей является основная система, изображенная на рис. 16.18, а, поскольку
ей соответствует обращение в нуль ряда коэффициентов в системе
канонических уравнений и, следовательно, уменьшение трудоемкости по составлению
этой системы. Система канонических уравнений приобретает частный вид,
называемый системой трехчленных уравнений—в каждое из уравнений входит
не более трех неизвестных. Такую систему не только легче составить, чем
систему с полной матрицей, но и легче решить. Система обеспечивает и
меньшую потерю точности при решении, нежели в случае иных рассмотренных на
рис. 16.18 основных систем.
При большом числе неизвестных систему канонических
уравнений удобно получать, используя матричную формуг).
Система канонических уравнений после ее составления решается.
Если порядок ее невелик, для этого могут быть использованы
настольные вычислительные машины. Начиная примерно с η = 6,
целесообразнее вычисления производить на ЭЦВМ, пользуясь
специальными программами для решения систем линейных
алгебраических уравнений. В основу этих программ, как и в основу
ручного счета, целесообразно класть алгоритм Гаусса.
3. Отыскание усилий.
3.1. Построение эпюр усилий. Задача отыскания
усилий в сечениях стержней системы, после того как найдены
лишние неизвестные, становится статически определимой.
Используя принцип независимости действия сил, находим усилия по
нижеприводимым формулам
Ф = ФР + Ф1Х1 + Ф2Х2 + ... + ФяХя,
(Ф = МХ, Qy, My, Qx, Мг, Ν). (16.27)
Для применения этого алгоритма в каждом из единичных и
грузовом состоянии строятся эпюры всех шести внутренних
усилий и моментов. В раскрытии же статической неопределимости,
т. е. при вычислении δν и ΔίΡ, необходимых для отыскания Xt
(i = \ η), как уже указывалось (см. табл. 16.3),
использованы могут быть не все усилия (так, например, при неучете
влияния осевой деформации и сдвигов при изгибе на
перемещения бгу и ΔίΡ не используются усилия Qx, Qy, N).
!) См., например: Филин А. П., Матрицы в статике стержневых систем
и некоторые элементы использования ЭЦВМ, Стройиздат, 1966,
564 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
Можно, однако, использовать формулы (16.27) лишь для тех
усилий, которые участвовали в раскрытии статической
неопределимости (т. е. при вычислении значений величин δν и ΔίΡ),
остальные же усилия, коль скоро для них не построены эпюры
в единичных состояниях, находить из условий равновесия так,
как это показано на примере расчета рамы (пример 16.4).
Пример 16.4. Определить усилия в сечении k рамы, изображенной на
рис. 16.20. Основная система рамы показана на рис. 16.20, а. Лишние неиз-
λ λ *XR 1
вестные получены из системы уравнений примера 16.5: Х1=-^Т, Х2=-г^Т,
93
88
Решение.
88 ' л 176
Х3==_^ Тм.
М,
Г 93 41 361 . IID I I V
!"L" 88 + 88 ^*""Т76 Х*+Г Г*™/.
Тм,
О - 361 4-
343г и -41г
Члены в первых двух формулах, стоящие после символа ||, учитываются,
если сечение k находится правее точки приложения силы Р.
Пример 16.5. Построить эпюры усилий в раме, изображенной на рис. 16.20,
Решение. Подсчеты, связанные с определением величины ординат в отме*
ченных сечениях (рис. 16.20, а), приобретают следующий вид:
в сечении/: «-ο^+Ο-^+Ι .(-|)+0— %Тм;
в сечениях 2 и 3: M = 6.|+0.fM+l.(_ g) + 0=f Тм;
в сечениях 4 и 5: ^ = 6.-^-6.^+1^-^+12 = ^ Тм;
о 41 361 / 93\ 3
:3-00 —6-Т7Д+Ь -QO+12 = QQ
в сечении 6: ^ = 3.^-6.^+1^-^+12 = ^.
На рис. 16.20, б показана рама и эпюра изгибающих моментов от узловых
моментов. В пределах незагруженных стержней эта эпюра представляет собой
полную эпюру изгибающ χ моментов. Загруженным является стержень 3—4.
Для получения эпюры изгибающих моментов в пределах загруженного стержня
строим балочную эпюру изгибающих моментов, как это показано на рис. 16.20, в
и складываем ее с ранее построенной эпюрой. Ордината эпюры Μ под силой Ρ
777
получилась равной у=^ Тм.
Эту же величину нашли бы, пользуясь формулой (16.27),
«-•й-"*· ·(-£)+·-!£ г*
Для построения эпюры поперечных сил можно использовать зависимость
Q=dMjdz.
§ 16.3]
МЕТОД СИЛ
565
88'
9Ъ^
Т8Тм
1
, 2
\kT
| /
1
\ 1
176'
' хк
'
г «
l·
Я
270
да.
Тм
Тм
Ϊ2Μ™ 1
88'м п
16 г'м
\p-vr
РХ
Np -f-ZT
в)
—Р=—Т
L ж)
Ш,
Рис. 16.20. К построению эпюр Μ и Q в раме после раскрытия статической
неопределимости и к выбору хорошей основной системы в грузовом состоянии: а) основная система
под воздействием внешней нагрузки и найденных лишних неизвестных; б) эпюры
концевых изгибающих моментов; в) эпюра изгибающего момента от нагрузки в статически
определимой балке (балочная эпюра); г) эпюры Μ и Q; д) хорошая основная система в
грузовом состоянии — удалены слабо работающие связи; е) эпюры усилий в основной системе
(д) в грузовом состоянии; як) основная система в грузовом состоянии, в которой эпюры
Усилий такие же, как и в основной системе (д), за счет переведения некоторой Доли усилий
в отброшенных связях в категорию внешних сил.
566 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
Учтем, что производная функции представляет собой тангенс угла наклона
касательной к кривой, изображающей функцию. Подсчеты, связанные с
определением поперечной силы на различных участках рамы, имеют вид:
153 93
. . _ 88 + 88 41
на участке 1 — 2 Q= g— = 88
на участке 3 — 7Q
306 777
176 + 176 _ 361
3 "~ 176 ;
777 63
_ . п 176 + 44 343 _
на участке 7 — 4 Q = » = Т76
63__3
- ,п 44 88 41
на участке 5 — о Q — 5— = — — / .
Имея эпюру
вия равновесия
JVo
4Λ
щ
Шт
176 '
88 '/
ЗЦЗ
176
Τ
88
Q, можно построить эпюру N. Для этого используются усло-
узлов. Применительно к приведенному выше примеру будем
иметь: из равновесия узла I (рис.
4fil 41
\6.2l, α) Ν2=-^Τ; Ν3=-^Τ;
из равновесия узла II (рис. 16.21, б)
41 „ ., 343
шт
ш<^<
•88 '
Νχ^
ΙΙΙΙ1ΙΙΙΙΙΙΙ
ю
δ)
~ш
Μ
6)
ЗкЗ
175
г
шг
^4 = -^ Τ; Ν5 = --
Т.
Рис· 1Θ.21. К построению эпюры N в раме:
а) к равновесию левого узла; б) к равновесию
правого узла; в) эпюра N.
88 * 5 176
В рассматриваемом примере
вдоль каждого из стержней
нормальная сила не меняется,
вследствие чего для построения всей
эпюры достаточно определить
значение продольной силы в каком-
либо из сечений каждого стержня.
На рис. 16.21, в показана эпюра
продольных сил.
При расчете сложных систем с применением ЭВМ используется
матричная форма расчета (см., например, книгу, указанную на
стр. 363 в подстрочном примечании), позволяющая найти матрицу
всех усилий во всех расчетных сечениях от всех нагружений.
3.2. Проверка правильности построения эпюр
усилий. Расчет любой системы завершается проверкой
правильности прстроения эпюр усилий.
Если усилия в системе определены правильно, то они должны
удовлетворять двум условиям: условию равновесия всей
системы в целом или любой ее части и условию
совместности (согласованности) деформации любых смежных частей
системы.
Остановимся на первой, так называемой статической проверке.
Мысленно отсечем от рамы (рис. 16.22) какую-то часть. Пусть,
например, проведенное сечение пересекает горизонтальный
стержень на расстоянии Ь от левого узла и левую стойку на рас-
§ 16.3J
МЕТОД СИЛ
567
стоянии а от того же узла. Приложим к отсеченной части
приходящуюся на нее внешнюю нагрузку и усилия, заменяющие
-Шл
г)
д)
Рис. 16.22. К проверке удовлетворения эпюрами усилий условиям равновесия: а)
отсечение части загруженной рамы; б, в, г) определение по эпюрам в сечениях на границах
выделенного участка рамы изгибающих моментов, поперечных н продольных снл; д)
выделенный участок рамы под воздействием внешней нагрузки и моментов н усилий в
сечениях разрезов, отделивших этот участок от остальной части рамы.
собой действия отброшенной части системы; величину этих
усилий берем из эпюр М, Q и N в соответствующих сечениях
(на расстояниях а и Ь от
левого узла).
Под воздействием всех этих
сил выделенная часть рамы
должна находиться в состоянии
равновесия.
Как на частный случай этой
проверки, укажем на проверку
равновесия узлов.
Вырежем узел I из рамы
(рис. 16.23), проведя сечения
бесконечно близко к его центру.
На рис. 16.23, б, в показан узел
рамы в двух разных случаях ее
работы — отсутствие и наличие
этого, записывая уравнение
а)
^rrrrmlJK^^
Mr.
г
Ο/ν
Рис. 1Θ.23. К проверке равновесия узлов
рамы: а) эпюра изгибающих моментов в
раме; б) узел н узловые моменты в
сечениях стержней; в) узел н приложенный к
нему внешний момент, а также узловые
моменты в сечениях стержней.
внешнего момента. Вследствие
равновесия как равенство нулю
суммы моментов всех сил относительно центра узла, обнаруживаем,
что продольные силы не входят в это уравнение равновесия,
568 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
а)
У/
V,
М-4
*к-
Α'
2
-/V
0
I
1 -J»'
/«'
^
^
.0
I
так как их направление проходит через точку, относительно
которой берется момент, а поперечные силы не входят в
указанное уравнение, так как соответствующие им плечи
бесконечно малы.
Уравнение равновесия принимает вид —Ма — Мс-\-Мь — 0.
Если к узлу приложен внешний сосредоточенный момент 30?,
то его необходимо учесть при составлении уравнения. Например
(рис. 16.23, в) уравнение равновесия
запишется в форме — Ма — Мс-\-Мь-\-
+ал=о.
Аналогично для узла могут быть
составлены и два других уравнения
равновесия (равенство нулю суммы
проекций всех сил, действующих на узел,
на какие-либо две пересекающиеся оси),
в которые войдут лишь поперечные и
продольные силы, а также внешние
сосредоточенные силы, действующие на
узел.
Если усилия, взятые из эпюр l) M,
Q и N, удовлетворяют условиям
равновесия, то это еще не свидетельствует о
правильности эпюр. Соблюдение
равновесия является необходимым, но
не достаточным условием того,
что построенные эпюры правильны.
Можно привести наглядный пример
удовлетворения условиям равновесия
при неправильных результатах расчета.
На рис. 16.24, а показана неразрезная
балка и неправильно построенные
эпюры Μ и Q, при которых, тем не менее,
условия равновесия удовлетворены.
Действительно, заменяя действие опоры на
балку соответствующими реакциями согласно эпюрам, показанным
на рис. 16.24, а, имеем картину, представленную на рис. 16.24, б.
На этом же рисунке показан характер деформации балки. Вместе
с тем очевидно, * что такая деформация невозможна, ибо центры
сечений а, б и в должны находиться на одной прямой, вследствие
расположения на одной прямой центров опор. Таким образом,
деформация балки несовместима с характером ее закрепления, иными
словами, не соблюдено условие совместности деформаций. Из
бесчисленного множества комбинаций величин реакций в средней и
IP
в
Рис. 16.ii4. К вопросу об
условиях совместности деформаций:
а) неразрезная балка и
неправильно построенные эпюры Μ
и Q (удовлетворяют условиям
равновесия, но не
удовлетворяют условиям совместности
деформаций); б) картина
деформации балки, соответствующая
эпюрам Μ и Q, изображенным
на фиг. а.
х) В общем случае пространственной рамы усилия берутся из всех шести
проверяемых эпюр: Мх, Qy, My, Qx, M2, N,
§ 16.31
МЕТОД СИЛ
569
крайних опорах, возможных с точки зрения равновесия,
действительной является та комбинация, которой соответствует и
соблюдение условий совместности деформаций.
Остановимся на второй, так называемой деформационной
(кинематической) проверке правильности построения эпюр или, иначе,
«^|
W/,
■т ι
ю
θ
^
111 1111 И 11 ГТТТП
Νη
^
777Ζ-
N
У///,
8}
'/,
I
5)
Νη
Т2Ы% 1
ь<Р*
к
д)
δ)
Ш^Ч-с
В)
ш
ж)
Ж?,
3}
Рис. 16.25. К проверке удовлетворения эпюрами М, Q и N условиям совместности
деформаций: а) рама, загруженная внешней нагрузкой (с — сечение проверки совместности
деформаций частей рамы, расположенных по разные от него стороны); б, в, г) определение
изгибающего момента, поперечной и продольной силы в сечении с по эпюрам Λί, Q и Ν:
д) рама с выключенными связями в сечении с, находящаяся под воздействием внешней
нагрузки и момента и усилий, заменяющих выключенные связи; е, ж. э) эпюры усилий
во вспомогательных состояниях системы с выключенными связями, соответствующие
единичным силам, действующим по «адресу» выключенных связей.
на проверке соблюдения условий совместности деформаций.
Мысленно превратим рассматриваемую статически неопределимую
систему в статически определимую геометрически неизменяемую
путем исключения лишних связей. Вместо отброшенных связей
приложим те усилия, которые им соответствуют; величины этих
усилий берутся из всех проверяемых эпюр (в частном случае —
в плоской раме М, Q и Ν).
Проверка эпюр и состоит в том, что выясняется, равны ли
нулю перемещения, соответствующие силам, заменившим связи.
570 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
Проверяя правильность построения эпюр в рассматривавшемся выше
примере, можем превратить раму в статически определимую систему путем
проведения одного разреза (исключения трех связей), например, в правой стойке
на расстоянии с от центра узла II (рис. 16.25). Тогда вместо отброшенных
связей придется приложить к полученной статически определимой системе
усилия Мс, Qc и Nc (рис. 16.25).
Если эпюры построены правильно и, следовательно, правильными являются
их ординаты в месте мысленно проведенного сечения, относительные
перемещения краев проведенного разреза, происходящие под воздействием внешней
нагрузки и сил Мс, Qc и Nc, должны быть равны нулю (отсутствуют
относительные горизонтальные и вертикальные перемещения центров сечений по
краям проведенного разреза, а также относительный поворот этих сечений).
Иными словами, должны быть равны нулю обобщенные перемещения,
соответствующие каждой из обобщенных сил Мс, Qc
действием внешних сил и усилий Мс, Qc и Nc.
и Nc и происходящие под воз-
Известно, что для отыскания перемещений, если пользоваться приемом
Верещагина, необходимо «умножить» эпюру Μ от единичной силы,
соответствующей искомому перемещению, на эпюру Μ от нагрузки, действие которой
вызывает искомое перемещение. Эпюра от той нагрузки, от которой ищем
перемещения, т. е. эпюра, соответствующая загружению системы, показанному
на рис. 16.25, д, и представляет собой проверяемую эпюру Μ (рис. 16.25, б).
Эпюры же Μ от единичных сил необходимо построить- Эти эпюры показаны
на рис. 16-25, е, ж, з- Если «произведения» (по Верещагину) каждой из эпюр
М, изображенных на рис. 16.25, е, ж, з, и проверяемой эпюры Μ окажутся
равными нулю, проверяемые эпюры М, Q и N построены правильно.
При наличии в системе жесткого контура особенно простым оказывается
получение «произведения» эпюры от единичного момента, приложенного к краям
разреза (эпюра М3 рис. 16.25, з), на эпюру М, так как в эпюре Λί3 все
ординаты равны единице *). Отсюда одним из требований правильности построения
эпюр с точки зрения соблюдений условий совместности деформаций является
равенство нулю алгебраической суммы площадей эпюры М, разделенных на
VI Μ Λ
жесткость соответствующего стержня, У -^- = 0.
При постоянной жесткости стержней и наличии жесткого
контура сумма площадей участков эпюры М, расположенных
по одну сторону от оси стержней контура, должна быть равна
х) Контуры при этом можно брать по одному из вариантов, показанных
на рис. 16.26 штриховой линией. В пределах каждого варианта проверка пс
К.
Λ..
"гП
77"!
Г-fV
гу/н
Ж Ж Ж Ш>, Ж. Ш. W/. Ш, Ш
Ю δ) δ)
Рис. 16.26. К проверке удовлетворения эпюрой нагибающих моментов условиям
совместности деформаций по «жестким контурам»; а) первый вариант; б) второй вариант;
в) третий вариант. / — первый контур; 2 — второй контур.
контуру, не отмеченному штриховой линией, сделанная сверх проверки пс
контурам, отмеченным штриховой линией, представляет собой следствие дву>
других проверок по контуру и ничего нового не дает.
§ 16.3]
МЕТОД СИЛ
571
сумме площадей участков эпюры М, расположенных по другую
сторону от этой оси.
Если в раме, изображенной на рис. 16.27.Ω, жесткость всех
стержней одинакова, сумма площадей на рис. 15.27,6,
заштрихованных сплошными линиями, должна быть равна сумме
площадей, заштрихованных штрихами.
Установление равенства нулю «произведения» одной из
единичных эпюр на окончательную эпюру Μ не исключает
необходимости проверки равенства нулю
«произведений» всех остальных единичных эпюр на ^НШШПТГ
эпюру М.
Итак, деформационных проверок
необходимо сделать столько, какова степень стати- ^ а)
ческой неопределимости. /
Удовлетворение как всем условиям рав- i\. Л
новесия, так и всем условиям совместности ч^
деформаций свидетельствует о правильности > .
построения эпюр усилий. _Еь _. А —
4. Вопросы точности и трудоемкости.
Выбор ОСНОВНОЙ СИСТеМЫ И ЛИШНИХ НеИЗВеСТНЫХ. Рис. ι6,27. К проверке
4.1. Групповые неизвестные. f,nl°PbI "згиб„а,?,щи^ мо'
г j ментов в жестком замкну-
Разделение неизвестных. Сохране- том контуре: а) однокон-
ние необходимой точности и уменьшение тру- турная рама; б) эпюра м-
доемкости расчета являются центральными
проблемами алгоритмического и вычислительного аспекта
строительной механики. При расчете стержневых систем методом сил
удовлетворение обоим требованиям достигается, если в матрице системы
канонических уравнений имеется много нулевых элементов, а
ненулевые расположены компактно в области, близкой к главной
диагонали матрицы, и при этом численные значения элементов,
расположенных на главной диагонали, существенно превышают
значения остальных элементов. Идеальным является случай, при
котором ненулевыми являются лишь элементы, расположенные на
главной диагонали. В таком случае происходит полное разделение
неизвестных в системе канонических уравнений, и для отыскания
неизвестных вовсе не приходится решать систему — каждое из
неизвестных определяется самостоятельно. Вместе с тем выше уже
было обнаружено, что вид матрицы коэффициентов системы
канонических уравнений зависит от выбора основной системы и
лишних неизвестных.
До сих пор в настоящем параграфе в качестве лишних
неизвестных принимались полные значения усилий, заменяющие собой
отброшенные связи. Такие лишние неизвестные Хг, ..., Хп
назовем элементарными. Подобный выбор неизвестных вовсе не
является единственно возможным. В качестве неизвестных можно
принимать и так называемые групповые неизвестные Xt, ..., X*,
572
НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
представляющие собой линейные комбинации из элементарных
неизвестных
X1 = Ω11^1 + #12^2 + · · · 4" а1пХпу
Л9 = ^21-^-1 4" ^22-^-2 "Т" · · · 4" ^гя^я»
Хп = β/ιΐ^ΐ 4" ^Я2^2 + · · · 4" йппХ-П'
(16.28)
При этом число таких линейных комбинаций должно равняться η
(степени статической неопределимости) и они должны быть
линейно независимыми, т. е. равенство α1Χ* + α2Χ* + .. .-\-αηΧ% = 0
с постоянными коэффициентами щ (i = I,'..., п) должно иметь
место лишь при одновременном равенстве нулю всех щ (i = 1, ...
..., η).
Формулы (16.28) свидетельствуют о том, что каждое из
неизвестных усилий в отброшенной связи отдельными своими частями
входит в групповые неизвестные. Система канонических
уравнений, соответствующих групповым неизвестным, может быть
представлена так:
6ЙХТ 4- ЫХ 4- · · · + ЫпХп 4- АГр = 0 (ί = 1 л). (16.29)
К групповым неизвестным можно предъявить требование, чтобы
они были^ртонормированными, т. е. чтобы усилия Ж*, Q*, М*у
Q*, Μ*, Ν*, соответствующие единичным значениям групповых
неизвестных, удовлетворяли условию ортонормированности с
некоторыми весами
т I,,
**.
Ч
X
4=1 О
И¥ + ^ + - + ^Ы?£/ (16-30)
При этом произойдет полное разделение неизвестных в (16.29).
Для того, чтобы найти групповые неизвестные, удовлетворяющие
условию (16.30), матрица коэффициентов в (16.28)
аи
dni
аи
а,
должна быть нижней треугольной
α21 α22
anl ап2
ак
■пп
СИ
Съ\ С22
cni ся2
и элементы Сц (i, j = 1, ..., η; j ^ /) должны находиться по
специальному алгоритму (алгоритм Грама — Шмидта).
Переход от элементарных неизвестных к групповым должен
производиться с целью упрощения расчета. Однако при исполь-
§ 16.3]
МЕТОД СИЛ
573
зовании упомянутого выше алгоритма трудоемкость процесса
построения матрицы С оказывается не меньшей, чем при решении
системы уравнений относительно неизвестных Х{ (i = 1, ..., η)
с полной матрицей коэффициентов. В таком случае использование
групповых неизвестных далеко не всегда целесообразно.
Групповые неизвестные могут быть использованы и с целью
неполного разделения системы уравнений, а упрощения,
состоящего в разбиении системы на самостоятельные подсистемы, что
существенно уменьшает трудоемкость при составлении и решении
системы. В ряде случаев такого упрощения удается достичь,
определяя состав группы не посредством какого-либо
вычислительного процесса, а из простых умозрительных соображений.
Именно в таких случаях использование групповых неизвестных
оказывается наиболее эффективным.
4.2. Использование свойств упругой
симметрии. Примером умозрительных соображений, позволяющих
принять групповые неизвестные такого состава, при котором
происходит упрощение системы канонических уравнений — разделение
ее на самостоятельные системы, может служить использование
свойства упругой симметрии системы.
Пусть имеется простая система, обладающая упругой
симметрией г) относительно некоторой оси. В таком случае целесообразно
и лишние неизвестные принимать либо симметричными, либо
кососимметричными относительно этой оси. При таком выборе
происходит разделение системы уравнений на две подсистемы
с симметричными и кососимметричными неизвестными.
Соответствующий пример показан на рис. 16.28. Заметим, что в общем
случае пространственной рамы симметричному (кососимметрич-
ному) лишнему неизвестному соответствуют симметричные (косо-
симметричные) эпюры Мх, My и N и кососимметричные
(симметричные) эпюры Qx, Qy и Мг. Кососимметричная эпюра
характерна тем, что в симметрично расположенных сечениях
абсолютная величина ординат эпюры одинаковая, а знаки
противоположные. Разделение системы уравнений на подсистемы происходит
потому, что функции — усилия, соответствующие симметричной
неизвестной, ортогональны одноименным функциям, отвечающим
кососимметричной неизвестной (соответствующие им интегралы
в формуле (15.86) равны нулю).
При разделении системы уравнений на подсистемы существенно
уменьшается количество необходимых арифметических операций
для отыскания неизвестных. (Например, при разделении системы
на две подсистемы одинакового порядка, —в 4 раза.)
х) Упругая симметрия состоит в следующем. Во-первых, симметричен
рисунок, образуемый осями, стержней, и, во-вторых, у симметрично расположенных
сечений жесткости одинаковы,
574
НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
в
ш
дг » Ш
1 1
\Μιί
шш
X?
1 1
11
X*
_Ш[Ш.
Ξ /% \
ПИ:!!
Хч
1 1
-
-ШЛШ
\ ъ 1
Nihil
β)
Xs Xff
гОтВ
г)
1 1 1
\
ж\\
мА
inii
Ъ
_]Д]Щ]11Ш
zXy
llllllll
NUN
v_
^TQ—^_
Ю
Yj Уг УзУ^^У^
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
В)
Рис. 16.28. К понятию групповых неизвестных: а) упруго-симметричная рама; 6)
симметричная основная система и элементарные неизвестные; в) единичные состояния
основной системы, соответствующие элементарным неизвестным (не обладают ни прямой, ни
косой симметрией относительно оси симметрии рамы); г) групповые лишние неизвестные;
д) единичные состояния, соответствующие групповым неизвестным (обладают прямой
или косой симметрией относительно оси симметрии рамы); е) матрица коэффициентов
канонических уравнений, соответствующая групповым неизвестным, изображенным
на фиг. г.
§ 16.3]
МЕТОД СИЛ
575
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
W7^- ^Щь jP^ ^ яР^ ш:гь ь™ ь77
ПН1Ш7
IIIII ШП IIIII
IIIII lllllllllll
i J
/ /
MB Ξ
=
Ξ
11
I Bill
К. J
11
=
Ξ
Ύ77/, W77 V77/. τΤΤ/ w7> 777/ 7777,
3
ffa
10
11
11
Ma
7777, W7/.
777?, 777/.
7777,
6)
Рис. 16.29, а, б, в. Локализация эпюр усилий за счет использования групповых
неизвестных: а) плоская рама; б. в) единичные состояния с симметричными и кососнмметрнч-
нымн эпюрами изгибающих моментов (без локализации) и структура соответствующей
им матрицы коэффициентов канонических уравнений.
576 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
^
fUf
ййп
7777/. W/
2 h fi
wm
£
Μ,
VT?/ W7/.
aW
tfa
Ma
777/, 777/.
&
кй-ик
a
fl fl
M3
777/. 7777,
fi fi
mm
1^J1
1
1
777/ 7777.
10
7^
м10
7777. 777?.
Φ
Ms
1^1
fiis
fl fl
7777, 7777. μ
Ms
fi h
m
τι
1 ;
11
Μ,
n
^
777/.
a
777/
δ)
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
7777, Z77, 7777,
_MS_
ЛШШН
iVi -
7777 WT/.
d)
Рис. 16.29, г, д. Локализация эпюр усилий за счет использования групповых нензвест»
ных: г, д) единичные состояния с симметричными и кососнмметрнчнымн эпюрами
изгибающих моментов (с использованием локализации) и структура соответствующей им
матрицы коэффициентов канонических уравнений.
§ 16.3]
МЕТОД СИЛ
577
Если расчетная схема конструкции обладает двумя осями
упругой симметрии, то система уравнений разбивается на четыре
подсистемы, а в случае системы с циклической симметрией
порядка k — nak подсистем. В последнем случае для такого
разбиения используются дискретные ряды Фурье г).
4.3. Локализация ненулевых подобластей эпюр.
Другим примером умозрительных соображений, позволяющих
осуществить такой выбор групповых неизвестных, который
приводит к упрощению системы канонических уравнений даже в
случае, если у расчетной схемы нет никакой симметрии, является
iii
4А ЗЛ Sfi
i
h
ψ iju'jj ψ
щ
ti h -
а,)
ΰ)
в)
Л
ί
»?
1,^1
m^jjm
h h
W/, WZ
W/
8)
d)
Рис. 16.30. Пояснение к построению группового неизвестного: а) эпюра изгибающих
моментов от продольных единичных сил в верхнем ригеле; б) эпюра изгибающих
моментов от продольных единичных сил в ригеле на этаж ниже верхнего; в) сумма эпюр,
изображенных на фиг. а к б; г) эпюра от момента, равного h, в разрезе верхнего ригеля; д) сумма
эпюр, изображенных на фиг. виг.
локализация участков эпюр усилий, соответствующих лишнему
неизвестному с ненулевыми ординатами, в пределах жесткого
контура расчетной схемы или другой локальной области. На рис.
16.29 и 16.30 приведен пример такой локализации областей эпюр
с ненулевыми ординатами, при которой упрощается каждая из
подсистем с симметричными и кососимметричными неизвестными.
Этот пример интересен и в том отношении, что в нем обе идеи
(использование упругой симметрии и локализация эпюр) использованы
совместно. Известен алгоритм локализации эпюр в случае
произвольной формы жестких контуров в пространственных рамах2) и
алгоритм автоматического построения эпюр всех усилий от каждого
из локализованных лишних неизвестных во всех контурах3).
*) Филин А. П., Матрицы в статике стержневых систем и некоторые
элементы использования ЭЦВМ. Стройиздат, 1966.
2) Филин А. П., Статика сооружений на основе элементарных
положений функционального анализа. Изв. АН СССР, Механика и машиностроение,
№1, 1964.
3) Филин А. П., Алгоритм построения матрицы при расчете произвольных
пространственных рамных (с жесткими контурами) систем методом сил.
Строительная механика. Сборник статей, посвященных 80-летию И. М, Рабиновича.
Стройиздат. 1966.
578 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
Силы, приложенные
гательных (единичных)
■<*|<N
уРТ/,
ю
/■>
J
h
VZ7,
^TiTTm^
W
ш.
I
Заканчивая пояснения, относящиеся к групповым неизвестным,
отметим, что всю совокупность сил, входящих в состав
группового неизвестного, следует рассматривать как обобщенную
силу.
к основной системе в каждом из вспомо-
состояний, следует рассматривать как
орт обобщенной силы, значения же
обобщенных сил ищем из канонических
уравнений, каждое из которых
выражает собой равенство нулю в основной
системе величины обобщенного
перемещения, соответствующего той или иной
обобщенной силе, принятой в качестве
неизвестной, и вызванного внешней на-
грузкой и всеми лишними неизвестными.
~^ЦЩЁ = 4.4. Переменная основная
Щ^ = __ система. Полная система
координатных функций. Уже с
первых шагов использования основной
системы обнаружилось, что, с одной
стороны, одной и той же основной
системе могут соответствовать различные
неизвестные (различные в разных
вариантах группы усилий, заменяющие
отброшенные связи), вызывающие,
естественно, различные распределения
усилий в единичных состояниях основной
системы (например, рис. 16.31), а с
другой стороны, некоторое распределение
усилий можно отнести к различным
основным системам и, естественно, к
разным лишним неизвестным. Так,
например, усилия, изображенные на рис.
16.32, а, могут быть отнесены к
различным основным системам и лишним
неизвестным (рис. 16.32, б, б) неразрезной
балки (рис. 16.32, г).
Таким образом, существенным в
расчете является не вид основной системы,
не вид групп сил из числа,
действующих по направлению отброшенных связей и принимаемых в
качестве неизвестных, а вид эпюр усилий, им соответствующих.
Фактически эти эпюры отвечают той системе функций, по
которой раскладывается в конечный ряд разность между искомой
функцией и функцией в грузовом состоянии, роль же неизвестных
в расчете играют коэффициенты при указанных функциях.
Рис. 16.31. Различные варианты
лишних неизвестных,
относящиеся к одной и той же
основной системе: а) заданная
система; 6) первый вариант лишних
неизвестных; в) второй вариант
лишних неизвестных.
16.3J
МЕТОД СИЛ
Б79
I
777/
X-,
1
Ю
1_
Or
777/, 7777,Xi
"777/.
-a—a-
7777, 777/
7777/ 7777,
hi
le
777,
-a—a—a л
7777, ^777, 7777, 777/
777/
7777,
777/
jo
v77,
-a—ar
7777. 7777,
%1
~a-
7777,
6)
W
777/ 777,
Xs
V '' Ь\ Хгг
lj \1г l3 t/j
h
0)
1 12
A A
777/, 777/.
h
Ъ
7Г
777/.
8)
k
h
5
75 ZT
777, 777/
777/
777/.
"Δ
777,
Iff
1
777.
Рис. 1Θ.82. Различные варианты трактовки эпюр усилий: а) эпюры усилий; б) первый
вариант основной системы, к которой могут быть отнесены эпюры, представленные на
фиг. α; β) второй вариант основной системы, к которой могут быть отнесены 3Πΐορυ4
изображенные на фиг. а; г) заданная система.
580 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ.,XV!
Существенной является система функций (их графики— эпюры
усилий в единичных состояниях), по которой производится
разложение указанной выше разности функции и которую следует
рассматривать как конечную систему координатных функций
(базис). Совершенно понятно, что функцию можно разложить в
бесконечном числе базисов. Картина здесь совершенно аналогичная
разложению вектора по ортам. Такое разложение может быть
произведено в бесконечном количестве вариантов, в каждом из
которых принята своя система ортов.
Поскольку в случае пространственной стержневой системы
в самом общем случае в каждом i-м единичном состоянии
основной системы рассматриваются шесть эпюр усилий (Qxi, Qyi, ...
..., Mgi), каждый орт, входящий в базис^ представляет собой
шестимерную вектор-функцию \QXi Qyt Ni Mxi My{ Mgi).
К базису предъявляются следующие требования:
1) в методе сил каждая из координатных вектор-функций
должна быть статически возможной, т. е. удовлетворяющей
условиям равновесия;
2) число вектор-функций в базисе при использовании метода
сил должно быть равно степени статической неопределимости;
3) вектор-функции должны быть линейно независимыми.
Выбор базиса — исключительно ответственная операция: удачно
выбранный базис обеспечивает малую трудоемкость и малую
потерю точности при вычислениях.
Если ортогонализация достигается простыми средствами
(умозрительными — из соображений механики), то она весьма
целесообразна и ею необходимо пользоваться. Если же
ортогонализация достигается специальным преобразованием (перестройкой)
некоторого предварительно принятого неортогонального базиса,
то такой путь далеко не всегда следует использовать, во-первых,
потому, что трудоемкость этого процесса часто не ниже, чем
решение системы с матрицей (или обращение этой матрицы),
соответствующей исходному базису, а, во-вторых, в процессе этой
ортогонализации встречаются все те же особенности, которые
приводят к потере точности и при решении системы уравнений
или обращения матрицы.
Следует иметь в виду и еще одно обстоятельство. Если
ортогональный базис получают из некоторого предварительно
принятого произвольного неорто^онального, то вектор-функции
ортогонального базиса чаще всего имеют ненулевые значения во всей
области. Это затрудняет отыскание усилий по формулам (16.27),
так как требует большого числа операций для получения каждой
из ординат, и, что самое главное, является причиной потери
точности и в последней ступени расчета.
Практически наилучшим является базис, в котором функции
предельно локализованы, т. е. часть области, где функция отлична
§ 16.3]
МЕТОД СИЛ
581
от тождественного нуля, является малой по сравнению со всей
областью ее задания. При этом перекрытие подобластей
ненулевых значений функций оказывается небольшим и большая часть
побочных коэффициентов в системе канонических уравнений
обращается в нуль. Как правило, матрица в таком случае остается
хорошо обусловленной. Для обеспечения наилучшей
обусловленности в рамках, принятых с точностью до постоянных
множителей вектор-функций базиса, необходимо выбирать такое
соотношение масштабов этих функций, при котором матрица системы
канонических уравнений по возможности приближалась бы к орто-
нормированной. В таком случае информация, содержащаяся в
каждой из вектор-функций и в каждом из уравнений, используется
оптимально.
4.5. Выбор грузового состояния. Грузовое
состояние можно относить к любой основной системе. Однако хорошей
основной системой в грузовом состоянии является та, которая
по упругим свойствам незначительно отличается от рассчитываемой,
т. е. та, которая получена из последней путем удаления
наименее работающих (наименее существенных при данной нагрузке)
связей. В таком случае членом ФР- улавливается главная часть
искомой функции Φ и остается небольшая доля, подлежащая
разложению по выбранному базису (подлежит разложению Ф — ФР).
Это приводит к снижению потери точности. На рис. 16.20,(9
показан один из вариантов такой системы. Шарниры помещены
в местах предполагаемого расположения нулевых ординат
эпюры М.
Если эпюры усилий от нагрузки (рис. 16.20, е), построенные
для такой основной системы, отнести к основной системе,
использованной в единичных состояниях (рис. 16.20, ж), то по
направлению отброшенных связей в грузовом состоянии будут
действовать некоторые силы (моменты), которые можно рассматривать
в этой основной системе как внешние силы. Вместе с тем, коль
скоро первым (грузовым) слагаемым в формулах (16.27) для
усилий уже учтена в некотором приближении вертикальная сила
в левом опорном сечении, в качестве неизвестной величины
принята не полная величина усилия в отброшенной связи Х2, а лишь
какая-то доля его,У2, равная разности между действительным
значением и имеющим место на рис. 16.20, ж.
До сих пор, рассматривая системы, обладающие упругой
симметрией, говорили о тех упрощениях, которые получаются
в матрице коэффициентов канонических уравнений метода сил
в том случае, если и основная система принята симметричной,
а лишние неизвестные либо симметричны, либо кососимметричны.
Известно, что при этом система канонических уравнений
распадается на две системы, из коих одна содержит только
симметричные, а другая только кососиметричные неизвестные. О
582
НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
свободных членах в системе канонических уравнений пока не
говорилось ничего.
В том случае, когда и нагрузка обладает либо прямой, либо
косой симметрией, получается упрощение и в свободных членах.
Именно в случае симметричной (кососимметричной) нагрузки
в нули обращаются все свободные члены в системе уравнений
t
\ 1"1 X
5 1 1
1 1
f
шин
: /
ΙΙΙΙΙΙΙΙ
Hlllll_,
it Ξ
ΙΙΙΙΙΙΙΙ
1-4
Ξ 1
-пиши
tfIH н
ш#
hL%
w/л
Pk гР Ρ,.
Ы Ι
мг
Δ
Рис. 16.33. Наличие прямой и (или) косой симметрии у внешней нагрузки.
Симметричные и кососимметрнчные единичные и грузовые состояния основной системы; 1, 2, 3 —
эпюры Μ в симметричных единичных состояниях основной системы; 4, 5, 6 — то же в
несимметричных состояниях; Ρ — грузовая эпюра изгибающих моментов в основной
системе при симметричной нагрузке; Ρ — грузовая эпюра изгибающих моментов в
основной системе при кососимметричной нагрузке.
Матрица канонических уравнений
в случае симметричной нагрузки
Матрица канонических уравнений
в случае кососимметричной нагрузки
№
ур-ния
1
2
3
Г 4
5
6
Λΐί Χζ\ Λ3
+ + +
+ + +
+ + +
Λ 4» ■" 5' Λ|
+ + +
+ + +
+ + +
Свободные
члены
+
№
ур-ния
1
2
3
4
5
6
Χΰ Λ
+ -
+ -
+ -
h +
ft
+ + +
+ + +
+ + +
Свободные
члены
+
+
+
с кососимметричными (симметричными) неизвестными. Равенство
нулю указанных свободных членов объясняется ортогональностью
эпюр, т. е. тем, что они представляют собой в этом случае
«произведения» (по Верещагину) симметричной и кососимметричной
эпюр (рис. 16. 33).
Равенство нулю всех свободных членов в системе линейных
алгебраических уравнений указывает на то, что она имеет нулевое
(тривиальное) решение, т. е. все неизвестные равны нулю,
поскольку определитель системы не равен нулю, о чем говорилось
§ 16.4]
МЕТОД ПЕРЕМЕЩЕНИЙ
583
выше, когда отмечались некоторые свойства матрицы
коэффициентов системы канонических уравнений метода сил г)
В конструкции, обладающей упругой симметрией при
симметричной (кососимметричной) нагрузке, все кососимметричные
(симметричные) неизвестные равны нулю.
Отметим, что любую нагрузку в случае наличия оси симметрии
у конструкции можно разложить на симметричную и кососиммет-
ричную доли (рис. 16.34).
'"Г '" f I
Φ Я/2
Ж
к
2
ШШ?А
V,
/λ
Рис. 16.34. Разложение произвольной нагрузки на симметричную и кососимметричную
доли.
В более сложных случаях симметрии, например, в случае
циклической симметрии, нагрузку можно разложить по тем же
тригонометрическим функциям дискретного аргумента, при помощи
которых были представлены единичные вспомогательные состояния.
Тогда от каждой из полученных таким образом долей нагрузки
возникают отличные от нуля усилия, соответствующие той же
функции, которой отвечает и нагрузка; все усилия, отвечающие
остальным функциям, обращаются в нуль.
§ 16.4. Метод перемещений
1. Неизвестные метода. Покажем еще раз, что, зная линейные
смещения и повороты концевых сечений стержня, можно полностью
описать деформацию стержня, а следовательно, и распределение
в нем усилий. На этот раз не будем ссылаться на систему
уравнений (16.14) и граничные условия (16.16), и проанализируем
непосредственно картину деформации. Для простоты остановимся
на плоской рамной системе. Обобщение на произвольную
пространственную систему почти очевидно.
Установим, какие перемещения в плоской стержневой системе
достаточно знать, чтобы определить деформацию всей системы.
*) Если бы определитель был равен нулю, а ранг матрицы коэффициентов
■системы канонических уравнений равнялся бы рангу расширенной матрицы,
то, кроме тривиального решения, имелось бы и бесчисленное множество
ненулевых решений.
584
НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
Пусть имеется нагруженная рама (рис. 16.35). Проследим за
деформацией одного стержня АВ (рис. 16.36), входящего в состав
рамы.
Вследствие действия на раму всей нагрузки центры ее узлов
перемещаются, и узлы поворачиваются на некоторые углы, в том
числе перемещаются и поворачиваются узлы, к которым подходят
концы стержня АВ.
Полную картину перемещения оси стержня АВ, если
рассматриваемая система подчиняется закону Гука, можно представить
как результат сложения нескольких перемещений, каждое из
которых вызвано одной из перечисленных выше причин.
Первое слагаемое полного перемещения изобразим в виде
поступательного перемещения стержня АВ, при котором центр
Рис. 16.35. Кинематически Рис. 16.36. Деформация стерж-
неопределимые рамы. ня рамы.
концевого сечения А занял свое окончательное положение
(рис. 16.37, а). При этом стержень не испытывает никакой
деформации и, следовательно, в нем не возникает никаких усилий. На
рис. 16.36 тонкой штриховой линией показана ось стержня АВ до
перемещения на первом этапе. На рис. 16.37 аналогичное
обозначение принято на каждом из этапов полного перемещения, т. е.
окончательный вид оси стержня на одном этапе принимается в
качестве первоначального вида на следующем этапе.
Второе слагаемое полного перемещения (рис. 16.37, б)
представим как перемещение точек оси стержня, которое получится,
если центр правого концевого сечения стержня из положения В'
переместится в окончательное свое положение Blt но оба концевых
сечения не испытывают поворота. При этом ось стержня изогнется
и изменит свою длину, вследствие чего в сечениях стержня
возникнут усилия (изгибающий момент, поперечная и продольная силы).
Перемещение центра правого концевого сечения из точки В' в Вг
может быть представлено как геометрическая сумма перемещения
В'В", произошедшего вдоль оси стержня (под влиянием которого при
неподвижном левом конце стержня стержень изменил свою длину,
вследствие чего в нем возникла только продольная сила), и
перемещения В"ВЪ произошедшего в направлении, перпендикулярном
оси стержня, под влиянием которого произошел изгиб стержня.
§ 16.4]
МЕТОД ПЕРЕМЕЩЕНИЙ
585-
Ю
$ "Л
δ'
Таким образом, чтобы охарактеризовать изгиб стержня,
произошедший вследствие поступательного смещения концевых сечений'
стержня на величины ΔΑ и Δβ, достаточно знать не полные
величины указанных смещений, а лишь смещение центра одного*
концевого сечения стержня
относительно центра другого в
направлении, перпендикулярном недеформи-
рованной оси стержня.
Итак, при условии, что левое
концевое сечение сместилось
поступательно на ΔΑ, поступательное
смещение Δβ правого концевого сечения
можно разложить на три слагаемых
(рис. 16.37, в)
~Ав = Ш -{-WW" + В~%,
причем первое слагаемое (ВВ' = Δα)
не вызывает никакой деформации
стержня, второе слагаемое В'В"
вызывает осевую (продольную)
деформацию, третье слагаемое В"В1
вызывает изгиб. В дальнейшем в ряде
случаев изменением длин стержней
будем пренебрегать. Кроме того,
всегда будем пренебрегать разницей
длин оси изогнутого стержня и
хорды, стягивающей его концы.
Третье и четвертое слагаемые
(рис. 16.37, г и д) полного
перемещения стержня представляют собой
перемещения точек оси,
происходящие соответственно от поворота
левого концевого сечения на угол
ц>А при неподвижном правом
концевом сечении и от поворота правого
концевого сечения на угол ц>в при
неподвижном левом концевом сечении.
В обоих этих случаях в стержне
возникает изгиб. Определение пятого,
последнего, слагаемого полного
перемещения состоит в учете влияния
нагрузки, непосредственно приложенной
к стержню АВ. Та доля влияния этой нагрузки на деформацию
стержня, которая состоит в участии (совместно с остальной
нагрузкой, действующей на раму) в образовании линейных
перемещений и поворотов концов стержня АВ, нами уже учтена, так
Ψ -U
Б)
Ά0
Рис. 16.87. Анализ деформации
стержня рамы.
586 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
как рассматривались перемещения Ад, Ад, φΑ, φβ, представлающие
собой результат действия всей нагрузки, приложенной к раме,
в том числе и нагрузки, непосредственно приложенной к
стержню АВ. Остальную долю влияния нагрузки, приложенной
непосредственно к стержню АВ, на перемещение точек его оси, а
следовательно, и на соответствующие им усилия, найдем,
рассматривая стержень АВ как стержень с несмещающимися и непово-
рачивающимися концевыми сечениями, так как указанные
перемещения уже учтены, т. е. рассматривая стержень АВ как балку
с защемленными концами, загруженную нагрузкой, приложенной
к стержню. Сложив все слагаемые перемещения, получим
окончательный вид изогнутой оси стержня (рис. 16.37, е).
На рис. 16.37, ж картина деформации, вызванной внешней
нагрузкой, приложенной непосредственно к рассматриваемому
стержню при условии, что концевые сечения не перемещаются и
не поворачиваются, отнесена к первоначально недеформированному
состоянию.
Усилие в любом сечении стержня АВ может быть найдено
как сумма усилий, возникающих в этом сечении от каждой из
следующих причин: от относительного смещения концов стержня
на величину В'В" в направлении его оси и на величину B"Blt
в напряжении, перпендикулярном его оси, в предположении
отсутствия поворота концевых сечений, от поворота левого
концевого сечения на угол ψΑ при защемленном противоположном конце,
от поворота правого концевого сечения на угол φβ при
защемленном противоположном конце и, наконец, от внешней нагрузки,
приложенной к стержню АВ в предположении жесткого
защемления его концов. Можно заранее построить эпюры изгибающих
моментов от разных воздействий на балку с защемленными
концами и пользоваться полученными результатами как известными
данными. Такие данные приведены в табл. 16.4. В этой же таблице
для балок, один конец которых жестко защемлен, а другой
шарнирно оперт, приведены эпюры усилий, вызванных
аналогичными причинами. С такими балками приходится встречаться,
если в состав рамы входят стержни, один конец которого
подходит к жесткому узлу или заделан, а на другом имеется
шарнир.
Подведя итог сказанному выше, подтверждаем ранее сделанный
вывод о том, что если известны углы поворота всех жестких узлов
рамы (что равносильно заданию углов поворота концевых сечений
всех стержней рамы) и известны, кроме того, такие независимые
линейные смещения узлов, зная которые можно найти для всех
стержней относительные смещения концевых сечений как вдоль
оси, так и в направлении, перпендикулярном оси стержня, то,
пользуясь готовыми решениями табл. 16.4, можно построить эпюры
усилий.
Таблица 16.4
№
по
пор.
Схема стержня
и воздействие на него
Эпюры усилий
и реакции
Формулы
Q
Ма
Λί .=3ί,
Ra
Дя
3(
ΕΙ
ι'
2.
( ΙΐΐίΐΙΙΐίΐΤΤΤίΤιΤΓτ^
Ra
Rru
., 3i
MA=— .
RA=RB = ~^
3.
aJ
δ
τ.
PI
ΛίΑ=-2-β(1-β2)>
Ρ/
Мс=^ЩЪ—а),
RA=^V-V2)>
Pa2
шш
iitiiiim^
Ζ
м„=Д^
#.
8
5
Rh
ra=t41,
rb =4-«/
At
al
Ik
δ
m
MA=-2^-[)'
RA=RBZ
ж
2/
(1-β2)
19*
588 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
Таблица 16.4 (продолжение)
№
по
пор.
Схема стержня
н воздействие на него
Эпюры усилий
и реакции
Формулы
6.
"I
IMTOtttttt^ j
I
RA Q
Μ =^-
A ~ is .
Яд = 0,4 ql,
RB = 0,l ql
7.
A
I
в
ш
%
Q
МЛ
W^
Μ,
RB
MA=4i,
MB = 2i,
Ri = #n =
6i
в- ι
cll*^»
Ri
R -R -12/
Щ
al
«* >■
ь
MA = a$2Pl,
MB=a*$Pt,
Μα = 2αψΡΙ,
ί?Α = β2(1+2α)Ρ,
/?β==α»(1 + 2β)Ρ
10.
4
Jjj jiVv V
У Уу
¥
(k^ll^A
RA=RB = ~2-
S 16.4]
МЕТОД ПЕРЕМЕЩЕНИЙ 589
Таблица 16.4 (продолжение)
по
пор.
Схема стержня
н воздействие на него
Эпюры уснлнГ!
н реакции
Формулы
11.
4
αϊ
Ь
cpv-
Rn
MA=m$(Za— 1),
Μ5 = 3«α(3β-1),
63Καβ
12.
9s
4
ή
ШШшТтггг·^
V/
Ρ
^
Ri
ο/2
#д =0,35 ?/,
#5 =0,15^
13.
4
«
Jz-/
/У
■φ—
na~nb- ι
14.
/У:
δ
&
^
^
^=^5 = -^
'ZB
15.
,Я
%
Of/
Ρ
б
βΡζ
W
h
N
N*
lllllll^lllNll^
590. НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI"
Таблица 16.4 (продолжение)
по
пор.
Схема стержня
и. воздействие на него
Эпюры усилий
- и реакции
Формулы
16.
У
ч
ш
чшы
У/,
У,
Ν*
*А
ζ
я 2
17.
ΊζοΑ
*l
ΜΤΤΠΤΤΤΙΤΠΤΓ^
Чго1
ЧгО1
1
Ыь*л,
ΝΑ
^ШЩ
/ν,
'β
Ν , =
ЯгО1
Α 3 »
Β 6
αϊ
/
\Β
βΐ
Μ2Α"
V
«,Μτ
Μ,
'Ζβ
Мг
1.9.
m-,1
M,
2.
%
'zA
W,
zB
MzA f-,
тгВ~ 2
20.
mzol
mz0l
jf^^4
%
'zff
§16.4]
МЕТОД ПЕРЕМЕЩЕНИЙ
591
Таким образом, в качестве неизвестных в методе перемещений
принимаем углы поворота всех жестких узлов системы и
независимые линейные смещения узлов, при помощи которых можно
•определить относительные смещения концов всех стержней системы
как вдоль оси, так и в направлении, перпендикулярном оси
соответствующего стержня.
Неизвестными в методе перемещений являются именно те
параметры, которые определяют собой факт и степень кинематической
неопределимости. Последняя же подробно обсуждена в начале
главы.
Метод перемещений применяют к кинематически неопределимым
-системам. Как правило, они одновременно являются и статически
неопределимыми. Статически определимые системы могут быть
легко рассчитаны (имеется в виду определение усилий) на основе
уравнений статики, т. е. без введения в рассмотрение
предварительно определяемых перемещений. Это особенно очевидно, если
в расчете перемещения не интересуют вовсе или требуется менее
подробная картина перемещений, нежели та, которую дает метод
перемещений.
Само понятие степени кинематической неопределимости в
традиционно установившемся смысле этого термина, в отличие от
понятия степени статической неопределимости, является условным
и зависит от ряда обстоятельств.
Во-первых, на степень кинематической неопределимости влияет
вид принятой расчетной схемы. Если в конструкции имеется
стержень с криволинейной осью, которая в расчетной схеме
заменена ломаной, то степень кинематической неопределимости зависит
от числа узлов или участков этой ломаной.
Во-вторых, на степень кинематической неопределимости влияет
степень точности определения перемещений. Если при расчете
рамы с несмещающимися узлами не учитывать влияния осевых
деформаций и сдвигов, то степень кинематической неопределимости
зависит лишь от числа углов поворота жестких узлов; если же
учитываются и продольные деформации, то степень кинематической
неопределимости увеличивается на число линейно независимых
линейных смещений узлов, происходящих в результате осевой
деформации.
В-третьих, степень кинематической неопределимости зависит
от уровня обеспеченности расчетчика вспомогательными
материалами. Если расчетчик располагает только данными о
распределении усилий в однопролетных балках с прямолинейной осью и
различными условиями закрепления концов при воздействии на них
нагрузки, а также при относительных поворотах концевых сечений
и относительных перемещениях их центров, то степень
кинематической неопределимости оказывается выше, нежели в том случае,
когда имеются данные подобного характера относительно более
592 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
сложных систем. Например, можно иметь необходимые данные и
об элементах с криволийной осью или даже о некоторых
стандартных стержневых системах.
В настоящей книге при установлении степени кинематической
неопределимости используются данные об однопролетных балках
с прямолинейной осью при различных условиях закрепления
на концах х).
2. Идея метода перемещений. Основная система и
канонические уравнения. При расчете системы методом перемещения, как
и в методе сил, вместо непосредственного расчета заданной системы
рассматривается некоторая иная, упрощенная, называемая
основной системой. Основная система метода перемещений получается
из заданной путем введения дополнительных связей,
препятствующих повороту жестких узлов и смещениям узлов, для чего
вводятся жесткие заделки, делающие невозможными повороты узлов,
но не исключающие их линейных смещений, и добавляются
стержни, препятствующие смещению узлов.
Таким образом, в общем случае вся система оказывается
состоящей из изолированных балок двух типов: жестко
защемленных по обоим концам или жестко защемленных на одном и шар-
нирно опертых на другом конце2).
Если учесть, что балки обоих указанных выше типов могут
быть рассчитаны заранее на всевозможные воздействия, то в
основной системе метода перемещений любое перемещение от нагрузки
(прогиб точки оси, угол поворота сечения) можно считать
известным. С этой точки зрения такую основную систему метода
перемещений уместно назвать кинематически определимой.
В методе перемещений могут применяться и основные системы,
кинематически неопределимые (со степенью неопределимости
меньшей, чем заданной системы), подобно тому как при расчете
конструкций методом сил можно использовать и статически неоп-
!) По-видимому, если ставить целью соблюдение симметрии (дуальности)
понятий, то кинематической неопределимостью следует называть отсутствие
в системе некоторых связей, вследствие чего она не является конструкцией,
могущей сопротивляться нагрузке, а представляет собой механизм. Степень же
кинематической неопределимости — это минимальное число связей, недостающих
для того, чтобы механизм был превращен в статически определимую,
геометрически неизменяемую систему. В дальнейшем такая трактовка практически
не применяется и в термины кинематической неопределимости и ее степени
вкладывается общепринятый смысл, несмотря на отмеченные его дефекты и
отсутствие возможности проследить дуальность понятий. Изложенные в данном
примечании соображения были впервые высказаны Ю. Б. Гольдштейном и
Ю. Б. Шулькиным.
2) Могущие встретиться в конструкции балки третьего типа, шарнирно-
опертые по обоим концам, при неучете осевой деформации являются статически
определимыми фрагментами конструкции, распределение усилий в которых
может быть выполнено вне остального ее расчета. Однако, выполняя
последний, необходимо сохранить эти фрагменты в составе всей конструкции.
§ I6.4J
МЕТОД ПЕРЕМЕЩЕНИЙ
im
ределимую основную систему. На таких системах мы в настоящем
курсе не останавливаемся.
Для отыскания неизвестных перемещений Zlt Z2, ... составим
такие условия, которые ликвидируют разницу между основной
и заданной системами. Отличие основной системы от заданной
состоит в том, что она содержит введенные связи, которых нет
в заданной системе.
Если в основной системе все узлы (вместе с заделками)
повернуть на те углы, которые имеют место в заданной системе, и,
кроме того, осуществить линейные смещения по направлению
добавленных опорных стерженьков (вместе с этими стерженьками),
с тем, чтобы эти смещения были бы такими, как и в заданной
системе, то никакой разницы в деформации основной и заданной
систем не будет.
С другой стороны, если нет различия в основной и заданной
системах в отношении деформации, не должно быть разницы и
в распределении усилий, а это означает, что реактивные усилия
в добавленных связях (заделках, стерженьках) должны равняться
нулю, что эквивалентно отсутствию этих связей.
Итак, физический смысл тех условий (тех уравнений), из
которых находятся неизвестные перемещения Zlt Z2 ..., состоит
в отрицании реактивных усилий в связях основной системы,
введенных дополнительно по сравнению с заданной системой.
Уравнения эти записываются в виде
R{ = 0 (t = l, 2, ..., т).
Каждое из реактивных усилий Rl (R{ — усилие в 1-й
добавленной связи), вызванное всеми перемещениями, соответствующими
введенным связям, и внешней нагрузкой, равно нулю. В
развернутом виде это можно изобразить следующим образом:
/?£i + /?f. + ... + /?f» + /?fP = 0. (1 = 1, ..., m), (16.31)
где /fy — реактивное усилие в i-й добавленной связи, вызванное
перемещением Ζ;·, произошедшим по направлению /-й добавленной
связи (вместе с этой связью); Rtp — реактивное усилие в i-й
добавленной связи, вызванное внешней нагрузкой.
Используя принцип независимости действия сил, реактивное
усилие Rif можно выразить формулой
/?v = rvZf. (16.32)
Здесь Гц — реактивное усилие в t'-й добавленной связи, вызванное
перемещением Zj = 1, произошедшим по направлению /-й
добавленной связи (вместе с этой связью).
Учитывая (16.32), уравнения (16.31) представим в виде
riiZi + ri2Zt + ... + rlmZm + Rtp = 0 (t = l, ..., rn). (16.33)
594 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVF
Г~\
Уравнения (16.33) строятся по одному закону (канону) для
любой системы, рассчитываемой методом перемещений, и поэтому
называются каноническими уравнениями метода перемещений.
Пусть t-e каноническое уравнение метода перемещений
изображает равенство нулю реактивного момента в мысленно введенной
заделке, закрепившей некоторый узел. Коль
скоро реактивный момент, являющийся по
отношению к узлу внешним (рис. 16.38), равен
нулю, узел находится в равновесии при
условии, что к нему приложены лишь моменты,
рис. 16.38. к пояс- заменяющие собой действие стержней, подхо-
иенню физического дЯЩИХ К ЭТОМу узлу. ИНЫМИ СЛОВЭМИ, КЭНОНИ-
смысла канонических " "^"" J J J » о
уравнений ческие уравнения метода перемещении
представляют собой уравнения равновесия.
3. Определение коэффициентов и свободных членов в
канонических уравнениях метода перемещений. Коэффициенты и
свободные члены в уравнениях (16.33) определим, выведя специальные
формулы для г;/ и Rip, используя теорему о взаимности работ.
ш?.
δ)
Рис. 16.39. Единичные и грузовые состояния основной системы: а) эпюра Afi; б) эпюра М&
в) эцюра Мй; г) эпюра Мр.
Если рассмотреть основную систему метода перемещений в двух
состояниях, например рассмотреть основную систему на рис. 16.39
в состояниях / и 5, тр, применяя теорему о взаимности работ
-§ 16.4]
МЕТОД ПЕРЕМЕЩЕНИЙ
595
в форме: работа внешних сил состояния 3 на перемещениях
состояния / равна взятой с обратным знаком работе внутренних
сил состояния / на перемещениях состояния 3, будем иметь
* ls
*··-Σ$
MXMZ dz
ΕΙ
1 О
Отсюда, заменяя / на i и 3 на / и распространяя полученную
формулу на самый общий случай, будем иметь
k h
г у ξ(ΜχίΜχ} QyiQyj Л,ЛМ
s= I О У
Интегралы, входящие в выражение r{j, легко определяют по
правилу Верещагина путем «перемножения» эпюр.
Для определения свободного члена RiP рассмотрим основную
систему в грузовом и первом вспомогательном (единичном)
состояниях (рис. 16.39, а и 16.39, г).
На основании теоремы о взаимности работ, используемой в форме:
работа внешних сил грузового состояния на перемещениях
единичного состояния равна работе внешних сил первого единичного
состояния на перемещениях грузового состояния, имеем РдР1 +
+ #1Р-1=0.
Отсюда RlP = — PbPv или, в общем случае
Rip = — Ρδρι*
Таким образом, для определения реакций RiP необходимо найти
перемещение 6ph т. е. перемещение, соответствующее орту
внешней нагрузки и вызванное перемещением, эпюра от которого
представляет собой эпюру М{. Для получения необходимого результата
следует построить эпюру Мр в любой статически определимой
системе, которая может быть получена из данной путем удаления
тех или иных связей. При этом в такой статически определимой
системе обязательно должна быть удалена ί-я связь.
Итак, для определения RiP имеем формулу
* ls . _,
Rip= — P У [ MiMp dz
s=l 0
или, внося Ρ под знак интеграла и заменяя МрР на Мр, получим
k h _ ,
d __ V f ΜιΜρ dz
EI
s=l 0
596 НЕКОТОРЫЕ ЭЛЕМЕНТЫ СТАТИКИ СТЕРЖНЕВЫХ СИСТЕМ [ГЛ. XVI
Применительно к самому общему случаю
s = l О
Для рамы, изображенной на рис. 16.39, система канонических
уравнений (16.33) приобретает вид
^ι "г ~з~ ^2 ё~ 3 £7 = '
у Zx + у Z2 - -ξ Ζ3 + gj = О,
~g~ ^1 ~g~ ^2 "Γ "β" ^3 = U.
Предлагаем читателю самостоятельно, пользуясь данными рис. 16.39
и формулами для ri} и RiP, вывести эти уравнения.
4, Упрощение системы канонических уравнений метода
перемещений. Подобно тому как можно упростить систему
канонических уравнений метода сил упрощению подвергается и система
канонических уравнений метода перемещений.
Если в методе сил i-и элементарной лишней неизвестной
называется полная величина усилия в ι-й отброшенной связи, то
в методе перемещений под t-й элементарной неизвестной
подразумевается полная величина перемещения, устраненного ί-й
добавленной связью. В приведенных выше примерах все неизвестные
метода перемещений являются элементарными.
Будем обозначать элементарные неизвестные метода
перемещений, как это уже сделано выше Zlt Z2, При расчете системы
в качестве неизвестных можно применять не только элементарные,
но и так называемые групповые неизвестные. В частности,
групповые неизвестные можно выбрать такими, чтобы система
канонических уравнений полностью разделилась. Однако, как и в
методе сил, это, вообще говоря, достигается ценой не менее
трудоемких работ, чем непосредственное решение системы канонических
уравнен ш с неразделенными неизвестными. Вследствие сказанного
применять групповые неизвестные целесообразно лишь тогда, когда
они, будучи выбранными из умозрительных соображений,
позволяют в некоторой мере упростить систему канонических
уравнений, например, разбить ее на две или несколько подсистем.
В частности, упрощение легко достигается, если у системы
имеется упругая симметрия. Б таком случае целесообразно все
неизвестные принимать либо симметричными, либо кососимметричными
относительно упругой оси симметрии.
Заметим, что если в методе сил существует проблема
локализации эпюр, то этой проблемы в методе перемещений нет,
§ 16.4]
МЕТОД ПЕРЕМЕЩЕНИЙ
Г>!)7
поскольку структура основной системы этого метода такова, что
локализация выполняется автоматически.
При этом, если предельная локализация эпюр в методе сил
в случае рам с жесткими соединениями стержней происходит
в пределах одного замкнутого контура, то в методе перемещений—
в пределах примыкающих к узлу стержней (рис. 16.40).
Все сказанное об использовании упругой симметрии и, в
частности, циклической упругой симметрии при рассмотрении метода
сил справедливо и для метода перемещений. Каждая
вектор-функция в методе перемещений является кинематически возможной, т. е.
удовлетворяющей условиям равновесия.
'
i
1
ниши
Рис. 16.40. Локализация эпюр: а) локализация в методе сил; б) локализация в методе-
перемещении.
5* Выбор грузового состояния. Некоторое упрощение в системе
канонических уравнений метода перемещений в случае
конструкции, обладающей упругой симметрией, может быть получено путем
разбиения внешней нагрузки на доли, соответствующие симметрии
системы, в том числе циклической, как это было сделано и в
методе сил.
6. Завершение расчета системы. После составления
канонических уравнений и их решения, которое в силу симметрии матрицы
коэффициентов относительно главной диагонали (как и в методе
сил) может быть осуществлено при помощи сокращенной схемы
Гаусса, находятся усилия по формулам
Φ = Φ1Ζ1 + ΦίΖ2 + ... + Φ„Λ1+Φρ (Φ = Λί„ Qy, ..., Ν).
Дополнение I
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПОПЕРЕЧНЫХ СЕЧЕНИЙ СТЕРЖНЕЙ
В теории стержней приходится иметь дело с рядом геометрических
характеристик их поперечных сечений. В настоящем дополнении приводятся
необходимые сведения для определения этих характеристик.
ϋ
Ук
О
Ζ
О
X
1\ И
Ук&'
Of
θα
««—
ι
-С
dF
^J
**',
χ
»■
Ъ
(В
Рис. Д.1.
Рис. Д.2.
Рис. Д.З.
1. Статические моменты площади плоской фигуры.
1.1. Пусть имеется плоская фигура (рис. Д.1). Статическим моментом
площади этой фигуры относительно оси χ (у) называется интеграл, имеющий
следующий вид:
Sx = \ydF /Sy=\xdF\ ( Л)
1.2. Если область разбита на подобласти (рис. Д.2), то
Sx = iydP=lydF+\ydF+...+ lydP = sM+sp + ...+ S<p; (Д.2)
F A F. Fn
аналогичную запись можно сделать и для Sy.
1.3. Если известны статические моменты относительно осей *, у, то
статические моменты относительно осей хх, yt (рис. Д.З), при условии, что
xt = x—а, У1=У — Ь> (Д·3)
находятся так:
SXi =\ yx dF = \ (у - Ь) dF = J у dF - Ь \ dF = Sx - bF,
Syi = \xx dF= J (x-a) dF=\x dF-a \ dF = Sy- aF.
(Д-4)
F F F F
Зависимости (Д.4) справедливы при любых значениях величин а и Ь;
последние, в частности, могут быть такими, что статические моменты SXt и S^
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ 01-Ч 1С 111III
Г)')!)
обратятся в нуль
\ydF — b^dF=0, lxdF-a\dF = 0.
(Д-5)
При этом точка Ох с координатами а и b в системе осей х, у оказывается
центром тяжести площади фигуры. Координаты центра тяжести площади
фигуры находим из условий (Д-5)
\ydF „ \xdF _
)dF r )dF г
F F
Статический момент относительно центральной оси,
т; е. оси, проходящей через центр тяжести площади u
фигуры, называемся центральным статическим момен- О χ
том площади фигуры и равен нулю.
1.4. Если плоская фигура разбита на части PllCi д>4>
(рис. Д.4), для каждой из которых известны площадь
и положение центра тяжести, то статический момент
площади всей фигуры относительно некоторой оси равен сумме произведений
площадей отдельных ее частей на расстояния от центров их тяжести до этой оси
1 л
/
1
•ίο
ι
" 1 '
t
Υ
V \
ι
,
'-*■
β χ = F&X + ^2 +.— + Р'пУп·
(Д-7)
1.5. Пример Д. 1. Определить статический момент площади треугольника
относительно оси, проходящей через его основание (рис. Д.5).
Рис. Д.5.
Рис. Д.6.
Решение.
Л h
Sx= I ybdy= \ yfc—y-jAdy = c \ ydy-^ \ y*dy =
о
ch* с № ,„ / 1 1 \ м/й
=τ-ιι=* τ-τГсН/6'
Этот же статический момент может быть найден по формуле
h 1
ch?
S-=/rT=2-c/l-y = -6-·
Пример Д.2, Определить статический момент Sx площади фигуры,
изображенной на рис, Д.6, -
'600
ДОПОЛНЕНИЕ I
Решение.
о 1 с , . с „ , с2 / а , , \
2. Моменты инерции площади плоской фигуры
2.1. Осевым моментам инерции площади плоской фигуры (рис. Д.1)
относительно оси χ (у) называется интеграл следующего вида:
Ix = \y*dF (ly = ]x?dF\.
(Д.8)
Центробежным моментом инерции площади плоской фигуры относительно
•осей х, у называется интеграл
Ixu = \xydF.
(Д-9)
2.2. Если область разбита на подобласти (рис. Д.2), то
/^ = 5 y*dF = ] y*dF + \ y*dF + ] y*dF+\ y*dF =
F Ft F2 Ft F4
/Ml . ,<8> . /(31 , ,fl>
= lx -\-1k +lx -\-tx '
Аналогичную запись можно сделать и для 1у, а также для 1Х1/.
2.3. Если известны осевые и центробежные моменты инерции площади
плоской фигуры относительно осей х, у, то аналогичные величины относительно
осей хъ ух (рис. Д.З) при условии, что хх = х—а, у1 = у — Ь находятся так:
Ιχ =\y\dF=]{y-bfdF=WdF — 2b\ydF-\-m\dF = Ix—2bSx-\-b^F,
*' F F F F F
/ =\ (x—a) (y — b) dF=^xydF — a $ ydF — b J χ dF-\- ab^dF =
Xl 1 F F F F F
= Ixu — aSx — bSy + abF.
(Д.Ш)
Если оси х и у центральные, то, так как относительно этих осей статические
моменты обращаются в нуль, формулы (Д.10) приобретают вид lx =Ix-\-№F,
Λ,-/„+βν, iXtU =ixu+abF-
Vi
2.4. Если известны осевые и центробежные моменты инерции площади
плоской фигуры относительно осей х, у, то аналогичные величины относительно
осей xlt ί/ι, при условии, что ось Xi(yi) составляет с осью χ (у) угол α (рис.
Д.7), могут быть найдены следующим образом. Между хг и у^ с одной сто-
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СК'ИИШП
(\<Ц
роны, и χ и у — с другой, существуют очевидные зависимости х^-^хсоят. |-
4- у sin α, У\ — у cos α— jc sin α, вследствие чего имеем
/ = \y\ dF=\ (У cosa~x sin с)2 cfF^
F F
= cos2 α ί у8 dF — 2 sin α cos α Ϊ до/ d/7-}- sin2 α ί χ2 dF =
F F F
= /* cos2 OL-\-Iy sin2α — Ixy sin 2a,
/ = J x| dF= J (x cos a-fy sin a)2 dF=
F F
= cos2a $x2dF-f2sinacosa Jxt/dF-f sin2 a J t/2GfF = (Д.11)
F F F
= lx sin2 OL-\-Iy cos2 a -f /^ sin 2a,
/ = J j^dF^ (xcosa-f i/ sin a) (i/ cos a— x sin a) dF =
= cos2 α Ϊ jo/ dF-f sin a cos a f i/2 dF —sin a cos a \ x2 e?F —
F F F
— sin2 a^xy dF=Ix sin a cos a — /^ sin a cos a -f Ixy (cos2 a — sin2 a).
F
2.5. Если иметь в виду, что направляющие косинусы осей xt и у^ в
системе осей х, у выражаются следующими формулами:
/i = cos(jc1, jc)=cosa, wz1 = cos(x1, t/)=cosi-~—a) = sin a,
/2 = cos(i/i, x)=cos (-^~f aj = — sin a, m.,}=cos (t/i, t/) = cosa,
то формулам (Д. 11) можно придать вид
/χ1=^ϊ+//»ϊ+2(-/*»)Ί'ηι.
V = Vi +V*i+2 (-'*„)'Λ, ' (Д-12)
Структура формул (Д. 12) свидетельствует о том, что момент инерции площади
плоской фигуры представляет собой симметричный тензор второго ранга
/* -Л
Т1-\
<ху
'ху
Следствием сделанного утверждения является наличие у моментов инерции
ряда свойств, характерных вообще для тензоров второго ранга. Перечислим
эти свойства.
2.6. Существуют такие оси л:0 и у0, относительно которых центробежный
момент инерции Ιχ равен нулю. Такие оси называются главными, а осевые
моменты инерции относительно этих осей главными моментами инерции IK ■==■
~ 7ι* ^уо~^2' ^ такому выводу можно было бы легко прийти и не пользуясь
тем фактом, что момент инерции площади плоской фигуры представляет собой
симметричный тензор второго ранга. Действительно, если, пользуясь формулой
(Д.11)3, положить, что оси хг и ух совпадают соответственно с некоторым»
такими осями л:0, у0, что
602
ДОПОЛНЕНИЕ 1
то из условия (Д. 13). может быть найден угол а, составляемый х0 с χ и у0 с
■ · ιχ~ιν
у, определяющий положение таких осей 0 = -—sin2ай-\-1хуcos2α0, отсюда*
2/ 2/
tg2a0 = 7-^f-, 2a0=arctg *y . (Д. 14)
7i/ '* 7# 'х
2.7. Главные осевые моменты инерции Ιχ и /2 обладают свойством
экстремальности—один из них максимален, а другой — минимален из всего
множества осевых моментов инерции относительно осей·, проходящих через
рассматриваемую точку —начало координат системы' ху.
К такому выводу можно было бы легко прийти и, не пользуясь тем
фактом, что момент инерции площади плоской фигуры представляет собой
симметричный тензор второго ранга.
Действительно, условия экстремальности Ιχ и / как функций аргумента
а имеют вид
dlx
'' =0; — 2/х cos α sin α + 2/y sin α cos α —
dl
ΰι
da
— 21 xy cos2 α + 21 xy sin2 α = 0, (Д.15>
0; 21 x sin α cos α — 2/y cos α sin α + 21 xy cos2 α —
— 2/^sin2a==0, (Д.16)
Учитывая возможность изменения.знаков у всех членов каждого из равенств
(Д. 15) и (Д.16), убеждаемся в их полной идентичности. Вместе с тем этя
равенства позволяют найти угол а*, определяющий собой положение таких
осей χ =я* и у ==у*., относительно которых Ίχ —Ιχ* и /„ —К* обладают
свойством экстремальности. Этот угол определяется из (Д. 15) (или, что то же
самое, из (Д.16)) (Iy — Ix) sin 2a* —2Ixy cos2a* = 0, или
tg2a* = -7—5iU. (Д.17)
lu~'x
Сопоставляя (Д.17) и (Д-14) убеждаемся в одинаковости углов а* и а0, а
следовательно, и в совпадении осей х* с х0 и у* с у0. Вследствие сказанного
приходим к выводу, что оси х0 и у0, относительно которых центробежный
момент инерции равен: нулю,, одновременно, являются и осями, относительно
которых осевые моменты инер-ции обладают свойством экстремальности.
2.8. Определение главных моментов· инерции выполняется по общей схеме
отыскания главных значений симметричного тензора второго ранга, т. е. из
квадратного уравнения
-С1 ~/wl=0' /2-^+д+('Л-^)=0·
ху у ι
Отсюда /χ, 2 = —~2—± 1/ I ^—.) —1х1у + 1ху, или
/ι.2 =-^^- ±yK('W/+4/V (Д. 18)
Этот же результат можно получить и без использования понятия
симметричного тензора второго ранга, если в выражения для Ιχ и / вместо α подста-
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ С1-ЧШ1ИЙ
cm
вить угол,, полученный, из формулы (Д. 17). Дли этого, достаточно выразить
sin2 a*, cos2 а* и sin 2а* через tg2a*
. „ ш 1-cos2а* -.17. · 1
sm2 а* = —; = —. 1 ,,
2 2 V Kl-ftg22a* /
„ * 1 +cos 2а* 1 ,, ,
cos2 a* = — = — 1 -f
sin 2a*■■
2
tg2a*
1
/l+tg22a* /*
/l-ftg22a* '
(ДЛ9)
или, подставляя (Д. 17) в (Д. 19), получим
1
sin2 a* =■— I 1
1 /
cos2 а* =— 1
1
V
\ = 1п
h~i*
1 +
4/
ху
Vy-Ιχ)2
2\ V(iy-ixr+uly)'
W*
\
Л K(/„-02 + 47lJ'
■ (Д.20)
2/
ху
sin 2a*
ϊν-1-х
2/
ху
V
1
4/iy VVy-Ixf+U
ху
Vy-lx)
Подставляя (Д.20) в (Д.11), приходим к формулам (Д.18)
1 / Л,-/* \ 1 / Λ,-Λν \
Χι
У ι
-**-"
+'Μι-
2\ V(Iy-Ixf+Ulyj У2\ Wy-Ij + U.
ху ,
-I
2/
ху
Л,-И* (/,-/*) (/v-7*)
ху
V(iy-ixf+uly . -r vy
2/L '* + '« 1
21/(/у-/,)а + 4/^
'ху
У(/„-/,)» +4/.
1 —
■*#
> -У(/^-/,)2 + 4/^ = /2,
2
/ν"7*
+Л,- М-
',-'*
2 \ 1/7^7^+4717/ * 2 \ V(I,-!,)* +Ally
+
+ /.
2/
ху
Ιχ+Ι
ху
V{iv-ixf+uly
^+-V(Iv-Ixf + Uxy = h.
2.9. Угол, составляемый главной осью х0 с χ выше уже был найден.
Можно, разумеется, следовать и формальной схеме, поясненной в гл. V в том
месте, в котором определяются.направляющие косинусы главных осей в системе
осей х, у. Этих выкладок здесь не повторяем вследствие их полной
идентичности.
604
ДОПОЛНЕНИЕ II
2.10. Пример Д.З. Определить момент инерции площади треугольника
относительно центральной оси х, параллельной основанию (рис. Д8).
Решение. Ширина фигуры, измеряемая параллельно основанию как
функция у, определяется формулой Ь (у) = Ь (-=- -f -τ-). Искомый момент инерции
определяется по формуле
/t/3 /t/3
/t/3
/*= j y*dF= \ y*b(y)dy = b ^ у'
b y*
-2/t/3
-2/1/3
3 3 -2h/3^ h 4
■ 2/t/3
Λ
di/
^4A
h/3
— 2/i/3
3
2 /, 1
; з" b 3"
2 ,\«
W-(-M>
= 2 , ,я 1 W 15 _ №
— "9 3 Ah 81 — 36 *
Дополнение II
КРАТКИЕ СВЕДЕНИЯ О СИММЕТРИИ КРИСТАЛЛОВ
Симметрией кристаллов, как и других симметричных объектов называется
свойство совмещаться с собой путем поворотов, отражений, инверсий, включая
и комбинацию этих операций.
Симметрия огранки кристалла, т. е. его внешней формы, является
следствием симметрии атомного его строения, последняя определяет собой и
симметрию физических, в частности, упругих свойств кристалла.
Если через углы пространственной кристаллической решетки провести
плоскости, то объем кристалла можно разбить на равные параллелепипеды —
ячейки, длины ребер и углы, в которых обозначаются соответственно а, Ь, с и
α, β, у.
По признаку симметрии кристаллы подразделяются на семь сингоний
(см. табл. Д.1), являющихся наиболее крупными классификационными
подразделениями. Сингония кристалла характеризуется соотношениями между
длинами ребер и отдельно — между углами ячейки. Однако одними и теми же
соотношениями а, Ь, си α, β, у могут обладать не один, а несколько типов
решетки. В таблице Д.2 показаны все 14 видов так называемых решеток
Броне1), принадлежащих одной из семи сингоний кристалла и одному и£
х) А. Б раве—французский ученый (см. работу Bravais A. Etudes cristallo-
graphiques. Paris. 1866.
ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ КРИСТАЛЛОГРАФИИ 605
Таблица Д.1
Сингония
Триклин-
ная
Моноклинная
Ромбическая
Тетрагональная
Тригональ-
ная
боэдрическая)
Гексагональная
Кубическая
Класс симметрии кристалла
(конечные точечные
кристаллографические
группы)
Моноэдрическая
Пинакоидальная
Диэдрическая осевая
Диэдрическая безосная
Призматическая
Ромбо-тетрагональная
Ромбо-пирамидальная
Ромбо-дипирамидальная
Тетрагонально-пирамидальная
Тетрагонально-трапецоэдриче-
ская
Тетрагонально -дипирамидаль-
ная
Дитетрагонально-пирамидаль-
ная
Дитетрагонально-дипирамидаль-
ная
Тетрагонально-тетраэдрическая
Тетрагонально-скаленоэдриче-
ская
Тригонально-пирамидальная
Тригонально-трапецоэдрическая
Дитригонально-пирамидальная
Ромбоэдрическая
Дитригонально-скаленоэдриче-
ская
Тригонально-дипирамидальная
Дитригонально-дипирамидаль-
ная
Гексагонально-пирамидальная
Гексагонально-трапецоэдриче-
ская
Гексагонально -дипирамидаль-
ная
Дигексагонально-п::рамидаль-
ная
Дигексагонально-дипирамидаль-
ная
Тритетраэдрическая
Дидодекаэдрическая
Гек сатетраэдр ич еская
Триоктаэдрическая
Гексаоктаэдрическая
Международные
обозначения
1
Ϊ
2
т
2/да
222 ..
тт'2
ттт
4
422
4/т
4тт
Ajmmm
4
42m
3
32
3m
3
3m
6
6m2
6
622
6/m
Qtmn
6jmmtn
23
m3
43m
432
m3m
Разновидности точечных
групп симметрии
вращения
•
•
•
•
•
•
•
•
•
•
•
инверсионные
•
•
•
•
•
•
•
•
•
•
•
зеркальные
•
•
•
•
•
•
•
•
•
•
Примечание. Среди зеркальных отмечены группы, не сводимые к
инверсионным и не имеющие центра симметрии.
'*'06 ДОПОЛНЕНИЕ II
Типы решеток
Син
Гриклинная
Моноклиииая
Ромбическая
Примитивная
(узлы только
в вершинах
параллелепипеда)
Базоцентриро-
ванная (имеется
еще по одному
узлу в центрах
двух
противоположных
граней)
г*Л
Объем ноцент-
рированная
/ 1\ к/
/А
/' i
ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ КРИСТАЛЛОГРАФИИ 607
Таблица Д.2
гони и
Тетрагональная
Тригональная
(ромбоэдрическая)
Гексагональная
Кубическая
«*м°
/ °с
а<
/
/а=
а
и
90"
γ-mr
608
ДОПОЛНЕНИЕ II
Типы решеток
Снн
Трнклннная
Моноклинная
Ромбическая
Гранецентри-
рованная
афЪфс,
афЬфс,
α=γ = 90ο, β^90°
афЬфс,
α = β=γ = 90°
Признаки
сингонии
Общий случай
косоугольного
параллелепипеда
Призма с основанием
в виде
параллелограмма
Призма с
прямоугольным основанием
четырех типов решетки. В этой таблице в предпоследней строке приведены
признаки, определяющие каждую из сингонии.
В рамках одной сингонии имеется несколько классов симметрии
кристаллов. Всего во всех семи сингониях 32 класса, все они показаны в
таблице Д.1. Вид симметрии характеризуется символами (международные
обозначения).
Факт существования той или иной симметрии определяется наличием тех
«ли иных элементов, порождающих симметрию. В кристаллах к числу их
относятся: ось симметрии, плоскость симметрии, зеркально поворотная ось
симметрии, инверсионная ось симметрии.
Символ η обозначает наличие оси симметрии порядка п, т. е. такой оси,
■при повороте вокруг которой на угол 360°/л тело совмещается само с собой.
В кристаллах встречаются формы, соответствующие одному из следующих
значений л: 1, 2, 3, 4, 6.
Символ т обозначает наличие плоскости симметрии.
Символ η свидетельствует о наличии симметрии, определяемой поворотом
•вокруг оси на угол 360°/« и зеркальным отображением относительно
вспомогательной зеркальной плоскости. На рис. Д.9 а, б показаны тела, обладающие
зеркально поворотной симметрией (оси 4 и 2). В случае 2 симметрию можно
трактовать.как инверсию относительно центра симметрии. Символом последней
■симметрии является I.
Инверсионная ось симметрии обозначается символом η и порождаемая ею
симметрия состоит в повороте на угол 360°/л и инверсии относительно
щентра, т. е.
п-
■ п.. 1 = 1..· л..
ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ 113 КРИСТАЛЛОГРАФИИ <»<>!>
Таблица Д.2 (продолжение)
го ннн
Тетрагональная
Трнгональная
(ромбоэдрн ческая)
Гексагональная
Кубическая
α = β = γ = 90°
a — b — c,
a-—b^c,
α = β=90°, y=120c
a = b = c,
α==β=γ = 90ϋ
Призма с
квадратным основанием
Тело, получаемое
из куба
вытягиванием вдоль
пространственной
диагонали
Тело, состоящее
из трех призм
с основаниями
в виде ромбов
Куб
Наличие и оси симметрии я-го порядка, и плоскости симметрии,
перпендикулярной ей, обозначается символом η : т, пересечение оси и плоскости
симметрии не под прямым углом обозначается символом п/т-
6)
Рнс. Д.9.
Наличие оси симметрии порядка η и плоскости симметрии, проходящей
через нее, обозначается символом пт.
Напомним, что в главе XV отмечается работа В. В. Лохина
и Л. И. Седова, в которой авторы указали совокупности простых
тензоров, характеризующих и задающих каждую точечную группу
симметрии кристаллов.
€10
ДОПОЛНЕНИЕ II
Точечные группы симметрии кристаллов являются одним из частных
•объектов, рассматриваемых в разделе математики, носящем название теории
групп.
Группой называется класс G объектов (элементов) φ, χ, ψ,... тогда и
только тогда, когда представляется возможным сформулировать действие (»)
с любыми двумя элементами' из G, такое, что результат этого действия φ°χ
также является элементом G и при этом для любых φ, χ, ψ,... выполняются
условия
1. (9°x)°^ = 9°(x°^),
2. ε° φ = φ° ε = φ,
3. φ ο φ-1 = φ-1 ο φ = ε.
Здесь ε—так называемый элемент идентичности, принадлежащий G,
φ-1 —элемент, принадлежащий G и обратный элементу φ. Теория групп
изучает свойства действий (например, сложение векторов, последовательное
выполнение преобразований) безотносительно к природе как действия, так и
объекта, с которым выполняется последнее. В теории групп изучаются
действия, обладающие тем свойством, что объекты действий и результаты их
принадлежат группе.
Совокупность всех операций симметрии [gly ... , g^] данного кристалла
образует группу симметрии G в смысле математической теории групп.
Величину k называют порядком группы.
Пусть F (х\, х2> хз)—функция, описывающая форму кристалла, и
операция g [xv х2> x3] осуществляет преобразование всех точек кристалла, тогда g
является действием, a F — симметричным объектом, если
g [Χι, Χ2ι ^3J =r= ·*■!' X2> %Λ> ' (Xl> %> •'"β)= *■ \%l > X4i Хз)·
Из числа различных групп симметрии, используемых для описания
кристаллов, важнейшие C?g (пространственные группы, описывающие атомную
структуру кристалла) и Gjj (точечные группы, описывающие внешнюю форму
кристаллов, их всего 32 группы (см. табл. Д.1), которые иначе называют
кристаллографическими классами).
Подробное обсуждение вопросов, затронутых в настоящем дополнении,
можно найти в книге А.„ В. Шубников, В. А, Копцик, Симметрия
в науке и искусстве. «Наука». 1972.
ИМЕННОЙ УКАЗАТЕЛЬ
Абовскнй Н. П. 439
Айнола Л. Я. 439
Алексеев С. А. 535
Алумяэ Н. А. 439
Аппель П. (Appell P.). 499
Ахнеэер Н. И. 440
Балабух Л. И. 9
Бауман P. (Baumann R.) 385
Бах К. (Bach С.) 385. 503
Бейлнн Е. А. 382
Бельтрамн Е. (Beltrami E.) 84, 339, 452,
454, 522
Бернуллн Д. (Bernoulli D.) 441
Бернуллн И. (Bernoulli Joh.) 440, 484
Бернуллн Я. (Bernoulli Jacov) 440, 441
Бертран Ж. (Bertrand J. L. F.) 491
Бетти Э. (Betti E.) 496, 498
Бидерман В. Л. 275, 372
Блнсс Г. A. (Bliss G. А.) 440
Браве A. (Bravais А.) 604
Бредт P. (Bredt R.) 55
Бубнов И. Г. 215, 233, 252, 413
Булгаков Б. В. 367
Бурдон Е. (Bourdon E.) 425
Варвак П. М. 215
Варнньон П. (Varignon P.) 484
Вашнцу К. (Washizu К.) 439. 525—527,
530
Верещагин А. К. 5, 179, 433, 434, 504,
506. 508, 514, 561. 562, 570. 582, 595
Винклер Э. (Winkler Ε.) 231. 232
Власов В. 3. 380, 382, 405, 406, 425, 430
Вольтерра В. (Volterra V.) 3, 4, 94, 95.
273
Вронский Ю. (Wronski J.) 408
Гаврнлнв Ю. М. 503
Галнмов К. 3. 439
Гантмахер В. Ф. 439, 499
Гаусс К. Ф. (Gauss К. F.) 101, 450, 459.
515, 563. 597
Гвоздев А. А. 439, 500
Гельфанд И. М. 440
Гнббс Дж. В. (Gibbs J. W.) 465
Гилрой Т. (Gilroy Т.) 425
Гильберт Д. (Hubert D.) 438, 466
Гольдепблатт И. И. 439
Гольдштейн Ю. Б. 592
Грам И. (Gram 1.) 572
Грасхоф Ф. (Grashof) 503
Грнн A. (Green A. E.) 466, 474, 479, 488,
518
Гук P. (Hooke R.) 14, 18, 31, 43—45, 49,.
88, 89, 91, 97, 104, 106, 109, 117, 151,..
162, 195, 203, 205, 286, 341, 368, 392,.
454, 467, 456, 470, 471, 474, 475, 479,.
480. 520, 522, 537, 584
Даламбер Ж. Л. (D'Alembert J..L.) 459
Дарбу Ж. Г. (Darboux J. G.) 368
Джанелидзе Г. Ю. 382
Днллон О. (Dillon О. W.) 472
Дирихле П. Г. Л. (Dirichlet P. G. L.) 47,
48, 487
Домке О. (Domke О.) 492
Донатн Л. (Donati L.) 495
Дукельскнй А. И. 27
Дюамель Ж- (Duhamel J. Μ. С.) 4.70—472-,
Журапскнй Д. И. 126, 138
Ишлн некий А. Ю. 34, 19.1
Калинин В. С. 9
Калмыков П. В. 506
Канторович Л. В. 450
Карман Т. (Karman Th. v.) 418, 425, 503-
Карно С. (Carnot S. N. L.) 460
Кастнльяно A. (Castigliano А. С.) 5, 391,.
457, 466. 488. 492 — 494, 496', 501, 505,-
521 522 529 '
Кнрхгофф Г. P. (Kirch-hoff G. R.) 9, 367,
369, 371
Клапейрон Б. П. (Clapeyron В. Р. Е.)
5. 474. 483, 484, 515
Кларк P. (Clark R. А.) 425
Клаузнус Р. Ю. Э. (Clausius R. Ju. E.) 460
Клебш A. (Clebsch A.) 9, 215. 367, 369, 371.
Клишевнч Г. В. 254
Коваленко А. Д. 472
Копцнк В. А. 610
Короткий Я- И. 252
Костовецкнй Д. Л.. 425 . ,
Коттернлл Дж. Г. (Cotterill J. H.) 4,88, 493
Кошн О. Л. (Cauchy A. L.) 31.. 43, 48. 61,
88. 117. П9, 124. 151, 16.2. 215. 274,
278, 341, 390. 391, 452, 459. А7.0, 471,
474, 480. 515, 520
Кроттн Ф. (Crotti F.) 490
Крутков Ю. А. 451
Крылов А. Н. 215. 238, 239. 253
Крылов В. И. 450
Кулон Ш. О. (Coulomb Ch. A.) 461 ■ '
Кульман К. (Culmann К.) 503
Курант P. (Couraht R.)'438. :466'
612
ИМЕННОЙ УКАЗАТЕЛЬ
Лаврентьев М. А. 439
Лагранж Ж. Л. (Lagrange J. L.) 449, 457,
484, 487, 488, 492, 493, 495. 517, 518,
522—524, 527, 529
Ламе Г. (Lam6 Q.) 43, 205, 454, 470, 471,
474, 520, 522
Ланцош К. (Lanczos С.) 439, 499
Лаплас П. С. (Laplace P. S.) 48, 461. 470,
474
Лежандр А. М, (Legendre Α.Μ) 465,
466. 523, 526
-Лейбниц Г, В. (Leibniz G. W). 466
.Лехннцкнй С. Г, 481
Лнбнн 3. Г. 438
Лифшнц Б. 438
.Лихарев К. К. 372
.Локшнн А. 3. 252
Лопнталь Г. Ф. (De l'Hopital) 440
Лохнн В. В. 476, 609
Лурье А. И. 367, 369. 452, 499
Лысенко В. И. 232
Лгостерник Л. А. 439
Ляв A. (Love Α. Ε. Η.) 367
Маклен Л. (Мс Lean L.) 439
Максвелл Дж. (Maxwell J. С.) 452, 498, 505
Макушнн В. М. 372
Малнннн Η. Η. 372, 499
Меиабреа Л. Ф. (Menabrea L. F.) 457,
491, 494 .
Меиаже A. (Mesnager А.) 503
Мизес P. (Mlses R.) 84. 85
Михлин С. Г. 439. 450
.Мичелл Дж. (Mlchell J. H.) 454, 522
Мор О. (Mohr О.) 5, 180. 498, 504—509, 561
Морера Г. (Morera G.) 452
Муавр A. (Moivre A.) 235
-Мусхелншвнлн Н. И. 439, 523
Навье Л, М. (Navier L. Μ. Η.) 474
Най Дж. Φ. (Nye J. F.) 467, 476
Латанзон В. Я- 367
Нейман Φ. (Neumann F.) 47, 470—472
Никитин В. М. 183, 184
Новацкнй В. (Nowacki W.) 472 (
■Новожилов В. В. 9. 344. 345, 439/499. 535
Носов А. Н. 506
'Ньютон И. (Newton I.) 440
Олесяк 3. (Oleslak Ζ.) 425
•Оравас Г. (Oravas G.) 439
'Остроградскнй М. В. 443, 459, 515
Пальмов В. А. 439
Лановко Я. Г. 382
Лапковнч П. Ф. 6. 252, 254, 430, 438, 503,
514—516, 519. 521
Ларнков В. И. 281
Пирсон К- (Pearson К.) 503
Лолак Л. С. 439, 499
Лолнщук Ε. Μ. 95
Лоиомарев С, Д. 372
Пранге Г. (Prange G.) 483
Лрандтль Л. (Prandtl L.) 40, 48, 49, 53.
57, 63—67, 69. 70, 72—75, 77, 82, 84.
94, 257, 258. 260, 261, 264, 265, 378
Лратусевич Я. А. 439
Луассон С. Д. (Poisson S, D.) 49, 124, 257,
354, 443, 471, 474, 484
Луэыревский Н. П. 215, 238, 239
Рабинович И. М. 382, 439, 498, 542, 577
Рабинович Ю. Л. 438
Рейссиер Э. (Relssner Ε.) 425, 439, 503,
522—627, 529
Ренкнн В. (Ranklne W. J,) 503
Решетов Д. Н. 27
Рнман Г. Ф. Б. (Riemann G. F. В.) 48
Рнттер В. (Ritter W.) 503
Рнтц В. (Ritz W.) 419, 422
Рыбина И. И. 431
Саркисян В. С. 481
Седов Л. И. 476, 609
Сен-Венан Б. (Saint-Venant В.) 8, 16. 28.
42. 43, 98. 102, 115. 148—150, 157, 161.
338, 384, 427, 452, 454, 456, 522
Снверс Н. Л. 252
Слнвкер В. И. 281
Смолнцкий X. М. 450
Сннтко Н. К. 215
Соколова А. С. 228. 231, 253
Солнцева Ю. К. 440
Степанов В. В. 221
Тананайко О. Д. 369
Тейлор Дж. И. (Taylor J.) 443
Терлецкий Л. В. 503
Тимошенко С. П. 338, 347, 385, 425, 467
Томсон В. (Thomson W., Kelvin, lord)
460, 467
Тонтн Ε. (Tonti E.) 439, 526, 528—530
Тохачек М. (TochaXek M.) 314
Уманскнй Α. Α. 382
Урбан И. В. 382
Файлон Л. (Filon L. N. G.) 503
Феодосьев В. И. 372, 425
Феппль A. (Foppl А.) 425
Феркер Н. (Fercers Ν. Μ.) 474
Ферьенчнк П. (Ferjenfik P.) 314
Фнлнн А. П. 215, 228, 231, 253, 367, 450.
563. 577
Фнлнна Л. И. 9, 367
Фннцн Б. (Finzi В.) 451, 452
Фомни С. В. 440
Френкель В. (Frankel W.) 491
Фурье Ж· Б. Ж. (Fourier J. В. J.) 62,
405, 577
Фусс Η. И. 232
Хайлнг P. (Heilig R.) 503
Хекман Г. (Heckman G) 467
Ху Хей-Чанг (Hay-Chang Ни) 525—527,
530
Цнммерманн Г. (Zlmmermann Η.) 254
Чернева И. М. 369
Чинарян А. М. 373. 375
Шачнев В. А. 472
Шмндт Е. '(Schmidt E.) 572
Шошнн Η. Α. 503
Шубников А. В. 610
Шулькнн ΙΟ. Б. 94, 273, 535, 592
Эйлер Л. (Euler L.) 235. 324, 441, 443—
445. 448—450. 455. 457. 465. 466. 483,
487, 493. 495, 520, 522, 528
Эльсгольц Л. 3. 440
Эйрн Дж. Б. (Airy G. В.) 49, 451
Яшкнн А. Г. 354
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аналогия вариационных принципов 494,
529, 530
— Прандтля 64—67, 69, 70, 72—74, 77
Жесткость материала ПО
— прямоугольного параллелепипеда при
сдвиге 14
— сплошного упругого осцоишши 232
233, 248, 249, 279
стержня при кручении 53, 76 77 95
169. 345—347, 384, 385
Балка 97
— на упругом основании 231—255, 279 —
284
— неразрезиая 224—226, 269—273, 562
— переменного сечения 189 — 193, 197, 3аДача геометрически нелинейная 373 —
226 230 279 284 '■'''
— равного 'сопротивления 189—193, 227 — — н физически нелинейная 375, 378,
— растянуто (сжато)-нзогнутая 316—324, ^79
325-328 - Днрнхле 47
— статически неопределимая 210—213, — Кошн 278, 4.38
224—226. 269—273, 562. 563 — Шев** Двухточечная 24, 207. 234,
Бнмомент 383. 404—408, 410, 411, 413, 276· ■324· 407
416—418, 436, 437 Для Функции кручения 43. 4G
— внешний 414 _ _ _ _ напряжений при кручений
Брус эквивалентный 228, 429 вала переменного сечення 88. 89
— — — — — — — консоли, сопронож-
дающем нзгнб 340
Вал 11 — 12, 14—27, 35 — 42. 88—96 поперечном изгибе коп-
Варнацнн возможные кинематически пе- соли без кручения о40
ремещеннй и деформаций 481, 517—520 — ~7~.~ ~ — — — — — с кручением
— — статически напряжений (усилий) ai0
481 — 483, 520—522 _ _ _ _ упруго-пластическом
функций напряжений 521 кручении призмы 83 84
Взаимность перемещений (реакций) 498 — Прандтля 49
(499) — _ _ _, сопряженной с функцией
и реакций 500 кручения 48
— — теории упругости плоская 149—
157, 157—163
Гипотеза Вннклера 231 - ~ простейшая 28-34. 115-124
Гипотезы теории тонкостенных стержней Неймана 47
открытого профиля 385. 386, 3.90 ~ термоупругости (теплопроводности)
— технической теории массивного стерж- „ 470 (472)
ня 16, 33, 36, 102—104, 124, 126, 142, Закон Гука обобщенный для анизотропного
163, 165, 166 тела 475· 48°
— — — — изотропного тела 31, 43—45
91, 117, 341, 479, 517, 522
Депланацня поперечного сечення при кру- ~ опаПРопи °о1^;ОЙ деФ°Рмацнн 97· 106,
ченнн свободном призмы некруглого 204· 205> 2°" ,. ,„
сечення 14, 42, 61, 81 сДвнге 14· 18·'95; 386
поперечном изгибе балки ~ сохранения энергии 457, 460. 483
141 — 143, 155, 163, 165, 354 £?« ^Р"°Дннамнкн первый (второй)
— — — тонкостенного стержня откры- 4°"· (4°2)
того профиля 384, 390
Деформации остаточные 40, 264, 266
— тепловые (температурные) 470, 471
Диаграмма Прандтля 39, 42, 257, 260,
261, 264, 266, 378
— Хекмана—Ная 467, 468
Жесткости упругие 475
Жесткость балки по сдвигу при изгибе 196
— — при изгибе ПО, 197, 198
Изменение кривизны оси стержня 203
255, 257. 264, 423
— напряжений (усилий) возможное 481
483
Изменяемость геометрическая 272 534
536, 537, 539, 540, 592
Изостаты 180
Интеграл Клаузнуса 460
Интенсивность угла закручивания 24 26
27. 39, 53, 59, 71, 72, 75. 85. 95. 407-412
614
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Контур в стержневой системе замкнутый
544
Концентрация напряжений 135, 136
Коэффициент линейного теплового
расширения 470, 511, 512
— редукционный 429, 430
Коэффициенты температуропроводности,
теплоемкости, теплопроводности 470
Кривизна оси балки изогнутой 97, 106,
109. ПО, 119, 197, 255, 264, 266, 273
— — — остаточная 266
Кручение при поперечном изгибе балки
169, 170
— свободное призмы (сенвенаново)
прямоугольного сечения 62, 63
— — — ( ) — — с большим
отношением сторон 69 — 71
— — — ( ) тонкостенной закрытого
профиля 73—81
— — — (—) — открытого профиля 71 —
73, 77
— — — (—) эллиптического сечения
57—61
_ — тонкостенного стержня открытого
профиля 382 — 4Ь8
Линия влияния прогиба балки на упругом
основании 244
— нейтральная 107, 127, 129. 133, 134,
261, 263. 288, 295, 298. 299, 303, 305—
308, 331. 334, 340
— равных деформаций 180, 183—185
— — поворотов 90
—. центров изгиба 287, 385, 413
Метод замены стержней 536, 541
— Кошн интегрирования
дифференциальных уравнений 215, 220
— начальных параметров 24, 25, 213, 215,
220, 225, 226. 236, 240. 273, 278, 408
— полуобратный Сен-Венана 28, 42, 105,
148, 149, 157. 338
— прогонки 273. 274, 278
— Рнтца 419, 422, 450
Методы прямые- решения вариационной
задачи 449
Модули упругих жесткостей (податлнвос-
тей) 473, 481
Момент изгибающий предельный 261
— инерции секторный 403
— кручения нзгнбного 405
— — свободного 396
— сопротивления полярный 20, 21
при изгибе балки 112—114, 273,
331
— — — кручении призмы 60, 61
Моменты ядровые 314—316
Нагрузка опасная 39, 262, 2-69
Напряжение остаточное 40, 41, 264, 265
— предварительное 308—310, 312, 314
— температурное 470
— фибровое 113
Напряжения самоуравновешенные 15, 17,
138, 157, 265
Начало отсчета дуг в эпюре секторных
площадей 170, 400, 402
Неизвестные лишние метода сил 555, 556,
571. 572, 574. 577
— — — групповые 571, 572
— ортонормнрованные 572
— — — —, построенные по принципу
локализации эпюр 575—577
Неизвестные лишние метода сил
групповые, лостроениые по принципу упругой
симметрии системы 574
— — — — элементарные 571
Неизменяемость геометрическая 268, 269,
271, 532. 534. 541
Неопределимость статическая
(кинематическая) 17, 18, 271, 272, 541, 554
(548, 554)
Операторы формально сопряженные 450,
451
Ось стержня (балки) изогнутого 105, 107,
118, 120. 154—156, 162, 197. 199. 250,
288, 290, 294, 297
Параметр нагрузки, опасное значение 272
Параметры деформации балин при изгибе
203
— — стержня, вызванной изменением
температуры 511
— — — при общем случае воздействий
550—552
— начальные в теории изгиба балки 25,
208. 215, 218. 221, 410
— — — — тонкостенного стержня
открытого профиля 410, 411
Переменные термодинамические 465, 466
Перемещения возможные 481, 482
— вследствие сдвига при изгибе балки 202
— температурные 509, 510
Площадь секторная 78, 81, 170—174, 340,
391, 399 — 401, 404
Поверхность нейтральная 288, 294, 298,
299, 301, 302, 304
— равных сдвигов 94
— — углов поворота 89. 90, 92—94
Поворот поперечных сечений балки изгнб-
ный 202, 203, 205. 206, 208, 551
Поле деформаций 470, 472
— механических напряжений 470
— направлений главных напряжений 123
— силовое 461
— температурное 470, 472, 510
— тяготения 461
Ползучесть 11, 94—96, 273, 313
Полюс секторных площадей 170, 172, 175,
400, 401
Последействие упругое 467
Постоянная кручения 53, 54
Потенциал даформацнй 460, 464, 465
— напряжений 460, 464, 465
— упругий 461, 462, 474
Потенциалы енловых полей 461
— термодинамические 463
Потеря точности 227, 253, 254, 273
Преобразование секторных площадей 401
Принцип вариационный возможных
изменений напряжений 488—492
— — — перемещений 484—486, 517
— — Лагранжа 457, 487, 495, 522, 529
— — Менабреа—Кастильяно 391, 457, 492, ■
495, 496, 520—522, 529
— — Рейсснера 522, 524, 529
— — —, второй вариант 524
— — Тонтн для полного функционала
528, 529
— — —, симметричный принципу
Рейсснера 526, 529
— — —,— — Ху—Вашюцу 525, 530
— возрастания энтропии 460
— Вольтерра 94, 95, 273
— Даламбера 459
— независимости действия сил 143, 219,
286, 287, 298, 316, 336, 337, 342, 541
— Сен-Венана 16, 98 102. 150, 161, 384i
427
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
•615
Профиль балкн идеальный ПО
Процесс термодинамический необратимый,
обратимый 460
Процессы адиабатический, изотермический
462, 463, 467, 469, 474
Работа внешних сил 193, 195, 262, 458, 515
— внутренних сил 193
— возможная 494, 499
— дополнительная 457, 490, 496
Радиус кривизны нейтрального слоя 106
— — оси изогнутой балкн 124, 255, 267
— ядра сечения 316
Разгрузка 40, 258, 264, 2С5
Расчет по допускаемым нагрузкам 269
Решение дифференциальных уравнений
совместности деформаций Сен-Венана
452, 454—456
— — — равновесия однородных теории
упругости в функциях напряжений 452,
454—456, 529, 530
Ряд Фурье 62, 405
Связь двухсторонняя, односторонняя 232,
234
Сдвиг абсолютный 14
— прн изгибе балкн 155, 195, 203, 551,
552
— чистый 11—13, 20, 21, 36, 37, 84, 92—94,
96. 185, Ϊ92
— — однородный 11, 12
Связь безусловно необходимая 542
— лишняя 541
Силы массовые 458
— самоуравновешенные 98, 105, 447
Симметрия упругая системы (циклическая)
573 (574)
Система геометрически изменяемая 534,
535, 537, 540
неизменяемая и статически
определимая 537, 539, 543
канонических уравнений метода сил
(перемещений) 556, 558 (593, 594)
ымкериатнвная 487
шип у ров жестких независимых 543,
Μ I
— полная 543, 544
мщернмльиая замкнутая 457
μι шин-НПО жесткая 537
изменяемая 537
■ Ί'ΐκιιιιιιΐϊΐ 245, 254. 536, 555 — 557, 578,
1,и"
( in ιΐ'Μΐ,ι особые 534, 535
( in шипи,' мптернала пластичное 22, 185
крупное. 22, 185
и .'hi iM'iTHMicHiioe 470
('.(Инин, кинематическом (статическое)
пещи шдел п мости стерж немом системы
ΙϊΊΗ hlil), Γι Π Б. GO I (271, ГНИ, 540. Г>П0.
И П Γι)
Стержеш, luiiiuK'Teiiiii.iil закрытого
(открытою) профили 711, 7Γι- 77. 79, 81. 133,
ПН), ,'IHI ИНН (li!>, 71. 73. 76, 82, 138,
НО. НУ. Id». 170-172, 176, 344,
381—ана, :i8G)
Стеснение температурных деформаций 470
Схема расчетная стержневой системы 532,
534
Тело анизотропное 474
Температура абсолютная 460, 463—466,
468. 469
Тензор деформаций 464, 465, 469, 479
Тензор моментов ннерцнн площади
плоской фигуры 601
— напряжений 464, 465, 469, 479
— функций напряжений 451, 452, 454
Тензоры упругости 475
Теорема Бредта 55
— и формула Каст'нльяно 493
— — — 'Лагранжа 488
— Карно 460
— Клапейрона 483, 484, 516
— Лагранжа—Дирихле 487
— о взаимности работ 496, 497, 516, 595
Теплоемкость (теплопроводность) 468, 469
(470)
Термодинамика (термоупругость) 458 (470)
Траектории главных деформаций
(напряжений) 180. 181
— максимальных касательных
напряжений 182. 183
Угол закручивания вала 33, 34
— поворота сечения вала крутильный 26
— — — прн изгибе балкн 99, 208, 252,
253, 322
Удовлетворение граничным условиям по
Сен-Венану 148
Уравнение гармоническое (Лапласа) 48
— дифференциальное изгиба (равновесия)
балкн 197, 199, 205. 206, 213
— — — (—) — на упругом основании
215. 233, 234
— — — (.—) — переменного сечення на
сплошном упругом основании
переменной жёсткости 280 — 284
— — — (—) — приближенное 197 — 200,
202, 206, 213, 215. 288, 317, 325
— — — ( —) — продольно-поперечного
(сложного) 317. 324
— — — (—) — точное 197—200. 202. 325
— — — стержня, очерченного по дуге
окружности 255, 256
— — с переменными коэффициентами 230
— — угла закручивания 24
— — — — в теории тонкостенных
стержней открытого профиля 406, 407
— нейтральной линии 298
— Пуассона 49
— теплопроводности 470
— трех моментов 562
Уравнения дифференциальные равновесия
теории упругости 28, 83, 88, 158, 159,
339, 453 — 456, 487. 523
— — — элемента призматического
стержня 551
— — — — тонкостенного стержня
открытого профиля в главных координатах
39!)
— — — — — — — —— произвольных
координатах 394—398
— — совместности деформации Бельтра-
ми—Мнчелла 454,-456, 522
— — — — и перемещений для
призматического стержня 203, 551
_ _ _ _ Сен-Венана 454—456, 520. 522
— — — — — как уравнения Эйлера 529,
530
— Дюамеля —Неймана 471
— закона Гука (см. закон Гука)
— — — в произвольной системе
координатных осей, не согласованной с
локальной упругой симметрией тела 480
— — — — форме Грина (Кастильяно)
как уравнения Эйлера 529, 530
— — — для элемента конструкции 109.
204, 552
— — — Дюамеля —Неймана 470, 471
616
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Уравнения Кастнльяно 528
— Коши 31, 43, 61, 88. 117, 119, 124, 162,
34 1, 391, 452, 459, 470, 471, 481, 516.
520
— — как уравнения Эйлера 529, 530
— Ламе 43, 205. 454. 456, 520, 522, 552
— равновесия элементарного .тетраэдра
29. 105, 160, 459, 515, 520. 524
Условие жесткости 26, 27
— закрепления тела интегральное 154
— неизменяемости стержневой системы
достаточное 535 — 537, 539, 540
— — — — необходимое 535, 536
— равнопрочностн 189, 191
Условия граничные для угла закручивания
и его производных в теории
тонкостенного стержня отирытого профиля 407
— — естестиенные 444, 445, 448, 451,
529, 530
— — на контуре поперечного сечения 46 —
49, 53, 54. 340. 347, 348
— — при упругом опнраннн и упругом
защемлении концевых сечений балкн
280
— на бесконечности 242
— начальные 280
— однозначности перемещений 54, 55, 57,
75
— сопряжения решений на границах
отрезков интегрирования 213
Формула Папковнча энергетическая в
теории упругости 514 — 516, 521
Формулы Грина 464, 466, 479. 488, 526.
529. 530
— Кастнльяно 464, 466, 521, 629, 530
— ЭПлера 324
Функции затухающие 243, 246
— Крылова 238
— Лузыревскопх 238
Функционал Кастнльяно 521, 526, 529
— Лаграпжа 487, 518, 523, 524, 529
— потенциальной энергии деформации 495
— Рейсснера 523—525. 527, 529
— Тонтн, второй 528, 530
— —, первый 526, 529
— —, третий 530, 531
- Ху—Вашицу 525—527, 530
<Гуикцня нлняння 247
— гармоническая 43, 47
Функция Гельмгольца (F), свободная
энергия 463—466
— Гнббса (G) 463—466
— кручения 42, 43, 344
— напряжений 49, 88
— ползучести при осевой деформации 273*
— — — чистом сдвиге 96
— потенциальная 461
— Прандтля 48, 49, 57, 63, 66. 69, 75, 84,
94, 340
—, сопряженная с функцией кручения 47
— Эйрн 49
Центр кручення тонкостенного стержня
отирытого профиля 387, 388, 403
— нзгнба 12, 166—170, 172—176, 179, 287,
338, 343 — 345, 382, 403, 415
Циркуляция касательного напряжения 55
Шарнир пластический 268, 269, 271—273·
Энергия внутренняя (удельная) 458 (465>
— дополнительная (удельная) 490 (464 —
466, 521)
— кинетическая 458, 459
— механическая 458
— потенциальная деформации 35, 193—
196, 335—337, 441, 444, 461
— — — удельная 460, 461, 464—466,
474, 518
— — — — анизотропного тела 474
— — — в общем случае деформации
стержня 335
— — сил собственного веса 444
— — системы полная 444, 457, 487
— тепловая удельная 460
Энтропия 460, 463—466, 468, 469
Эпюра секторных площадей 171, 172,
174—176, 178
Эпюры усилий кососнмметрнчные
(симметричные) 573
Эффект Кармана 423
Ядро сечения 305—308, 312
— ползучести для осевой деформации 273
— — — чистого сдвига 97
А. П. Филин
ПРИКЛАДНАЯ
МЕХАНИКА
ТВЕРДОГО
ДЕФОРМИРУЕМОГО
ТЕЛА
том