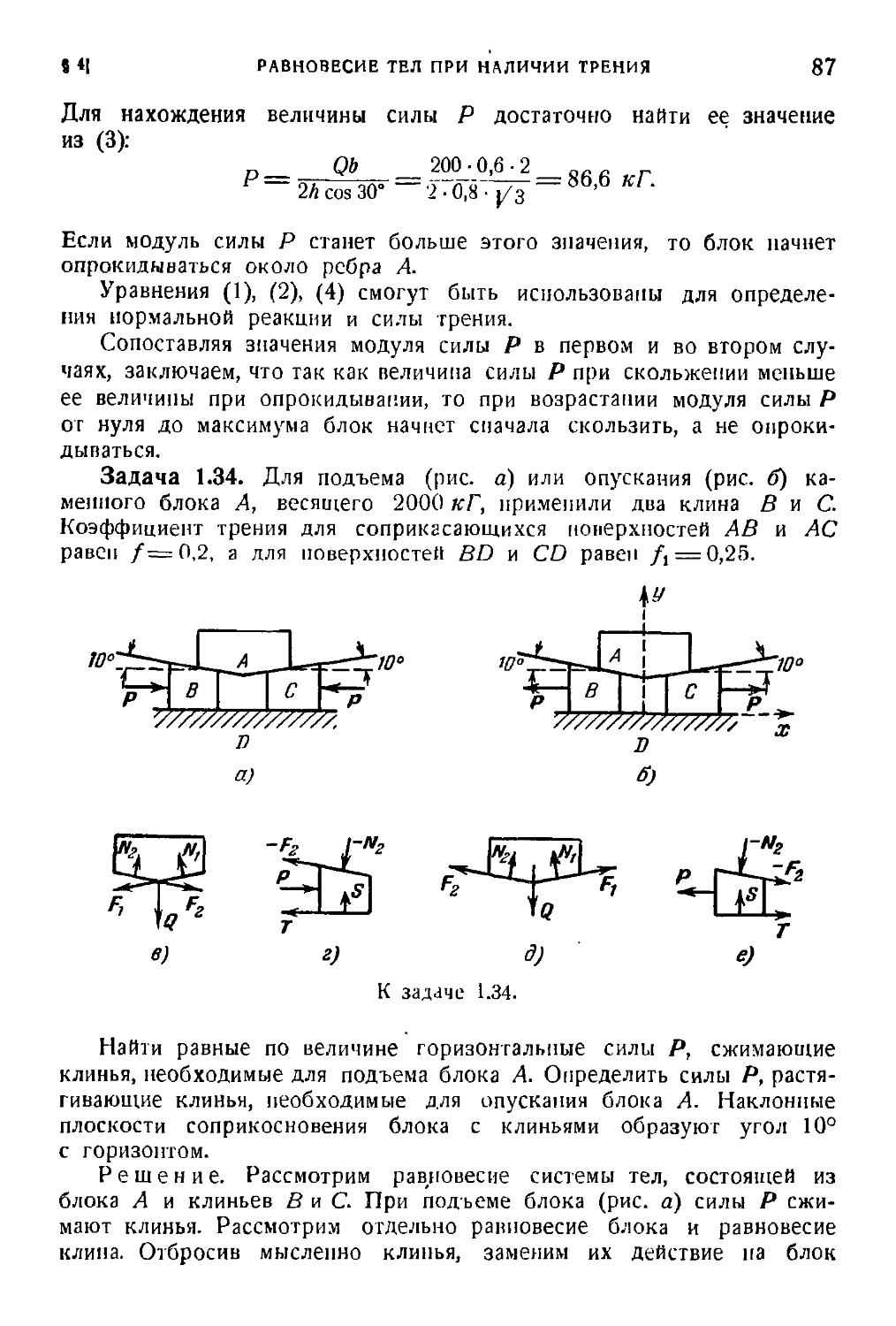
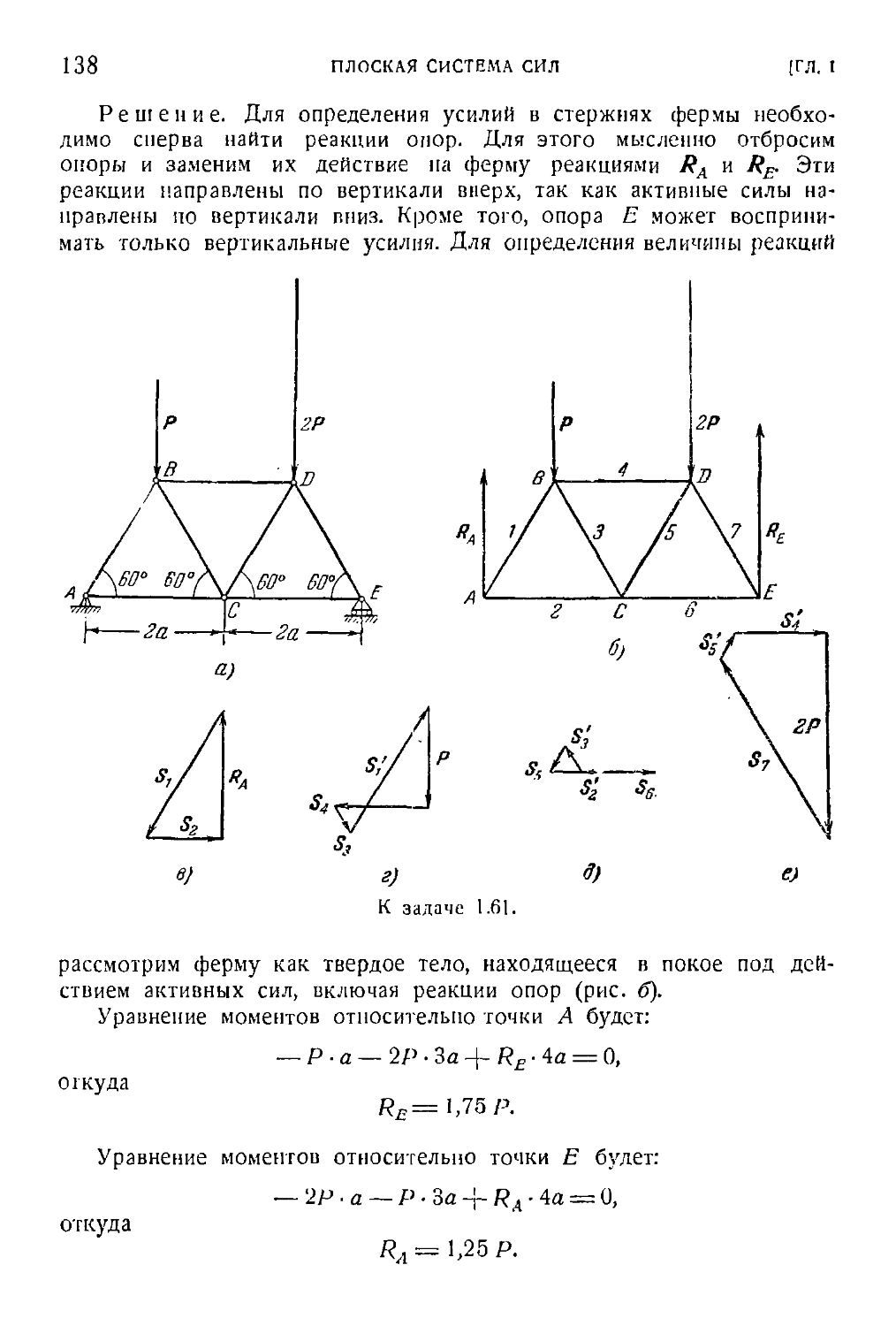
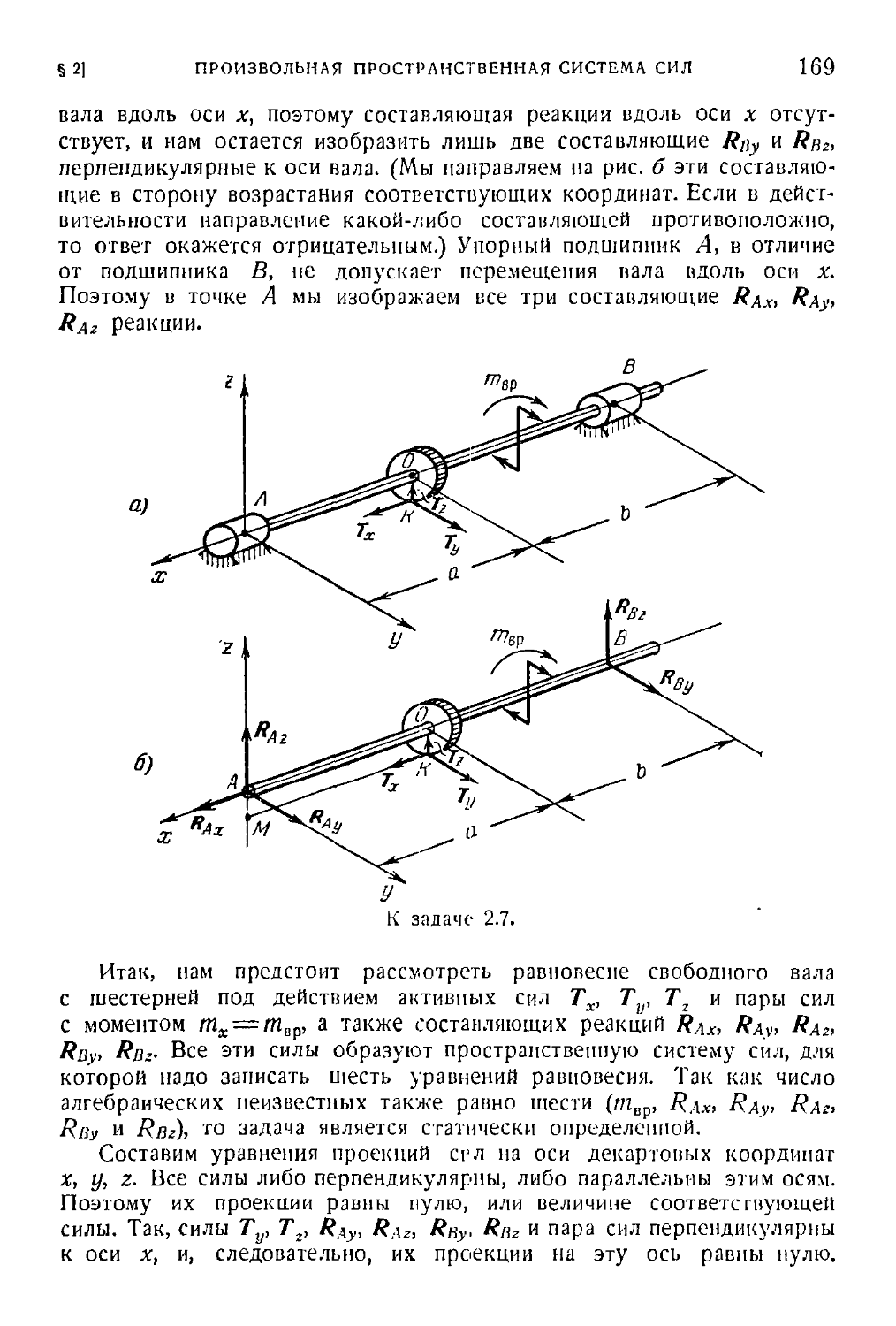
Author: Бать М.И. Джанелидзе Г.Ю. Кельзон А.С.
Tags: кинематика математическо-механическая геометрия движения биологические науки механика
Year: 1967
Text
М. И. БАТЬ, Г. Ю. ДЖАНЕЛИДЗЕ, А. С. КЕЛЬЗОН
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
В ПРИМЕРАХ И ЗАДАЧАХ
Под редакцией
Г. Ю. ДЖАНЕЛИДЗЕ и Д. Р. МЕРКИНА
ТОМ ПЕРВЫЙ
СТАТИКА И КИНЕМАТИКА
ИЗДАНИЕ ПЯТОЕ,
ПЕРЕРАБОТАННОЕ
Допущено Министерством
высшего и среднего спещального образования СССР
в качестве учебного пособия
дл'1 втузов
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
М О С К В А 19 6 7
531
Б 28
УДК 531. 1/2@76.2)
Теоретическая механика в примерах и задачах, т. I
(статика и кинематика), Бать М. И., Д ж а н е л и д-
з е Г. Ю., К е л ь з о н А. С.
Книга представляет собой пособие по решению задач тео-
теоретической механики. Краткие сведения из теории даны в кон-
конспективной форме. Цель книги —научить читателя самостоятеты.о
решать основные типы задач. Всего в книге 234 решенные
задачи.
Книга может быть нотезпа не только студентам и препо-
преподавателям, но и инженерам, ведущим технические расчеты, так
как решения многих задач являются одновременно примерами
инженерных расчетов.
В первом томе рассматриваются следующие разделы статики
и кинематики: система сходящихся сил, произвольная плоская
система сил, равновесие тел ирк наличии трения скольжения и
трения качения, графическая статика, пространственная система
сил, центр тяжести; движение точки, поступательное движение
и вращение твердого гсла вокруг неподвижной оси, сложное
движение точки, плоское движение твердого тела, вращение твер-
твердого тела вокруг неподвижной точки, общий случай движения
твердого тела, сложение вращений твердого тела вокруг парал-
параллельных и пересекающихся осей, 'сложение поступательного и
вращательного движений твердого тела.
Рисунков 312.
Моисей Иосифович Бать,
Георгий Юстинович Джанелидзе,
Анатолий Саулович Нельэон
Теоретическ.т механика в примерах и задача*
Гом 1
М.. 1%7 г., 512 стр. с н.1.1.
Редакюры А. Г. Мордвинцев, Н. И. Ротальская
Техн. редактор И. Ш. Акселърод Корректоры С. Н. Емельянова, И. Я. Крпщтснь
Сдано в набор 19/V 1967 г. Поаписано к печати 26/1Х 1967 г. Бумага 60X«0l/ie. Фнз. печ. .1.
32. Условн. печ. л. А1. Уч.-нзд. л. 29 79. Тираж 200 000 экз. Т-13613. Цена книги 93 коп.
Заказ J* 980.
Издательство сНаука>
Главная редакция физико-математической литературы.
Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типография № 1 «Печатный Двор>
имени А. М. Горького Главполнгра |Шрома Комитета по печати прн Совете Министров СССР,
г. Ленинград, Гатчинская ул., 26.
2И-2
33-87
ОГЛАВЛЕНИЕ
Из предисловия редактора ко второму изданию 6
Предисловие к пятому изданию 8
Введение 9
РАЗДЕЛ ПЕРВЫЙ
СТАТИКА ТВЕРДОГО ТЕЛА
Основные законы статики . . . -. 10
Глава 1. Плоская система сил Ifi
§ 1. Система сходящихся сил 16
Г. Равновесие твердого тела, к которому приложена система
сходящихся сил 16
2°. Теорема о трех непараллельных силах 24
о°. Метод проекций : 28
4°. Момент силы относительно точки. Равновесие твердого тела
с одной неподвижной точкой Зй
§ 2. Произвольная плоская система сил. Случай параллельных
сил 39
Г. Равновесие твердого тем при наличии плоской системы
сил 3!)
2°. Опрокидывание твердых тел 55
3°. Приведение произвольной плоской системы сил к простей-
простейшему виду -г'7
§ 3. Равновесие системы твердых тел 03
§ 4. Равновесие тел при наличии трения 82
1°. Равновесие твердого тела при наличии трения скольжения. . 82
2°. Равновесие твердого тела при наличии трепня качения. . . 108
3°. Равновесие твердых тел при наличии трения гибких тел ... 11Г>
§ 5. Графическая статика и методы расчета ферм 123
Г. Равновесие произвольной плоской системы сил. /Метод
последовательного сложения 123
2°. Применение метода веревочного многоугольника к плоской
системе сил 123
3°. Расчет усилий в стержнях фермы. Способ вырезания
узлов 131
4°. Определение усилий е: стержнях фермы построением
диаграммы Максвелла — Кремоны 110
5°. Определение усилий в стержнях фермы методом сечений . . . 144
1*
4 ОГЛАВЛЕНИЕ
Глава II. Пространственная система сил 147
§ 1. Система сходящихся сил 147
§ 2. Произвольная пространственная система сил . 155
1°. Момент силы относительно точки. Момент силы относительно
оси. Теория пар в пространстве 155
2°. Приведение к одному центру сил, произвольно расположе-
ных в пространстве 163
,3°. Приведение произвольной пространственной системы сил
к простейшему виду , 187
§ 3. Центр тяжести 199
РАЗДЕЛ В Т О Р О ("I
КИНЕМАТИКА
Глава III. Движение точки 216
§ 1. ": )аектория и уравнения движения точки 216
1°. Основные определения 216
2°. Переход от уравнений движения в декартовых координатах
к естественному уравнению движении 229
§ 2. Скорость и ускорение точки 232
Глава IV. Простейшие движения твердого тела 271
§ 1. Вращение твердого тела вокруг неподвижной оси 271
§ 2. Преобразование upociefiiimx движений 285
Глава V. Сложное движение точки ЗОЭ
§ 1. Абсолютное, переносное и относительное движения точки . . . 300
§ 2. Сложение движений. Определение траекторий и уравнений
движения в относительном и абсолютном движениях точки , . 301
§ 3. Сложение скоростей. Определение скорости точки в относи-
относительном, переносном и абсолютном движениях- 311
§ 4. Сложение ускорений 321
Г. Определение ускорений точки при переносном поступатель-
поступательном и произвольном переносном движенимх 324
2°. Скорость н ускорение точки в полярных, сферических и
цилиндрических координатах 341
§ 5. Кинематика колебаний 331
1°. Гармонические колебания 351
2°. Негармонические колебания 361
Глава VI. Плоское движение твердого тела 366
§ 1. Уравнения плоского дпижения твердого тела. Уравнения
движения точки плоском фигуры 366
Г. Определение уравнений плоского движения твердого тела
и уравнений движения точки плоской фигуры 366
2°. Определение положения центра конечного вращения плоской
фигуры 369
§ 2. Скорости точек плоской фигуры 372
§ 3. Подвижная и неподвижная центроиды 392
§ 4. Ускорения точек плоской фигуры 404
§ 5. План скоростей и план ускорений 434
§6. Сложение вращений твердого тела вокр\г ппраллельньх
осей 455
ОГЛАВЛЕНИЕ б
Глава VII. Вращение твердого тела вокруг неподвижной точки
и сложение вращений вокруг пересекающихся осей. Общий
случай движения твёрдого тела 467
§ 1. Определение скоростей и ускорений точек твердого тела,
вращающегося вокруг неподвижной точки 467
§ 2. Сложение вращений вокруг пересекающихся осей 480
§ 3. Общий случай движения твердого тела. Сложение поступатель-
поступательных и вращательных движений 501
Г. Скорости и ускорения точек твердого тела в общем случае
движения 501
2°. Сложение поступательных и вращательных движений
твердого тела , 504
Приложение. Международная система единиц (СИ) 511
ИЗ ПРЕДИСЛОВИЯ РЕДАКТОРА КО ВТОРОМУ ИЗДАНИЮ
Немногочисленные законы и теоремы, лежащие в основе теоре-
теоретической механики, находят весьма разнообразные и обширные при-
применения. Поэтому у лкц, изучающих или использующих п своей
деятельности теоретическую механику, наибольшие затруднения вызы-
вызывает приложение общих положении теории к решению конкретных
задач.
В обширной литературе, посвященной теоретической механике,
имеется мало книг, ставящих своей целью научить читателя методам
решения задач. Между тем потребность в таких руководствах ощу-
ощущается как студентами в процессе обучения (в особенности студен-
студентами заочных и вечерних факультетов), так и инженерами и техниками
в их практической деятельности.
Авторы настоящей книги, опираясь на многолетний опыт препо-
преподавания теоретической механики в Ленинградском политехническом
институте им. М. И. Калинина, поставили своей целью создание ру-
руководства по решению задач.
В соответствии с этим замыслом в книге даны в конспективной
форме лишь краткие сведения из теории — предполагается, что для
ее изучения читатель пользуется одним из курсов теоретической
механики. Из большого числа учебников по этому предмету, опубли-
опубликованных в СССР, следует, прежде всего, рекомендовать курс
Л. Г. Лойцянского и А. И. Лурье «Теоретическая механика», т. I,
изд. 5, Гостехиздат, 1954 г.; т. II, изд. 5, Госгехиздат, 1955 г. (книга,
определившая современные традиции преподавания механики во вту-
втузах и предназначенная для лиц, изучающих теоретическую механику
по полной программе) и книгу С. М. Тарга «Краткий курс теорети-
теоретической механики», изд. 3, Физматгиз, 1963 г. (учебник, предназначен-
предназначенный для .'И'ц, изучающих теоретическую механику по сокращенной
программе).
Наиболее эффективным путем обучения искусству приложения
методов теоретической механики является не сблегчение формально-
формального заучивания правил и приемов (чему часто способствуют обшир-
обширные методические указания), а показ их в действии. Ввиду этого
в руководстве основное внимание уделено решению конкретных за-
ПРЕДИСЛОВИЕ РЕДАКТОРА КО ВТОРОМУ ИЗДАНИЮ 7
дач, специально составленных для того, чтобы, с одной стороны,
избежать разбора задач, входящих в сборник И. В. Мещерского и
иные распространенные в СССР задачники, а с другой—дать воз-
возможность после изучения книги (или ее разделов) самостоятельно
решать главные типы задач.
Для облегчения активного изучения материала (а только такое
изучение и имеет смысл) в каждом разделе книги даны краткие
рекомендации о последовательности решения тех или иных типов
задач и лишь после этого приведено подробное рассмотрение подоб-
подобных задач, причем зачастую сравнены и оценены различные методы
решения.
Предполагается, что параллельно с разбором материала по руко-
руководству читатель па основе изученного самостоятельно решает соот-
соответствующие задачи из сборника задач по теоретической механике
И. В. Мещерского и тем самым научается применять полученные
знания.
Сравнительно большой объем руководства объясняется тем, что
оно составлено в расчете как на последовательное изучение, так и
из выборочное использование. Последний способ и является главной
формой применения ввиду различия объема материала и порядка его
прохождения в различных высших учебных заведениях.
В этом томе основные законы статики, §§ 1, 2 главы I и глава П
написаны М. И. Бать; §§ 3, 4, 5 главы I, главы III, IV, V, VI, VII
написаны А. С. Кельзоном. Введение написано Г. Ю. Джанелидзе.
Он же принял участие к составлении многих других параграфов,
в частности, §§ 1, 2 главы I, §§ 1, 2 главы III и §§ 1 — 4 главы V,
а также осуществил общее редактирование.
Авторы считают приятным долгом принести глубокую благодар-
благодарность Г. М. Валовой, О. Е. Короли, И. Е. Лившицу, Л. И. Мачабели,
Д. Р. Меркину, Т. В. Путята, Г. Н. Савину, Р. С. Шафаревичу и
и В. Н. Щелкачеву за ценные указания и критические замечания.
Хочется надеяться, что и впредь читатели будут помогать совер-
совершенствованию книги своими критическими замечаниями, которые бу-
бут с благодарностью рассмотрены.
Ленинград,
март 1963 г.
Г. Ю. Джанелидзе
ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
Первое издание учебного пособия «Теоретическая механика в
примерах и задачах» вышло в свет в 1961 г. Все последующие
издания печатались без существенных изменений.
За прошедшие годы выявилась необходимость внести в книгу
ряд изменений и дополнений. Поэтому настоящее, пятое, издание
подверглось переработке. Прежде всего, был пересмотрен весь текст
и внесены необходимые исправления. Некоторые, менее удачные за-
задачи заменены новыми. Во многих случаях даны более подробные
решения.
Идя навстречу многочисленным пожеланиям, авторы внесли новые
главы, освещающие дополнительные разделы курса теоретической
механики. Это потребовало увеличения объема книги, в связи с чем
настоящее издание выходит в трех томах. Первые два тома охваты-
охватывают материал, отвечающий основному курсу теоретической механики,
а третий содержит дополнительные главы. Это вызвало необходимость
перенести из первого тома в третий том раздел, в котором рассмат-
рассматривалась кинематика точки в относительных координатах (задачи
преследования). Одновременно в первый том включены новые разделы:
кинематика колебательных движений и общий случай движения твер-
твердого тела.
В первом томе основные законы статики, §§ 1 и 2 главы I и
глава II написаны М. И. Бать, введение написано Г. Ю. Джанелидзе,
остальные разделы написаны Л. С. Кельзоном. Авторский коллектив
понес невосполнимую утрату в лице безвременно скончавшегося про-
профессора Г. Ю. Джанелидзе, соавтора и первого редактора книги.
В новом издании изменена нумерация задач и рисунков — первое
число означает номер главы, второе — номер задачи (рисунка) в
этой главе.
Авторы считают своим приятным долгом принести глубокую
благодарность Н. И. Алексеевой, Е. Г. Бергер и О. В. Григорьевой
за ценные указания.
М. И. Бать, А. С. Кельзон, Д. Р. Меркин
ВВЕДЕНИЕ
Теоретическая механика является наукой, в которой изучаются
перемещения тел с течением времени (механические движения). Она
служит базой других разделов механики (теория упругости, сопротив-
сопротивление материалов, теория пласт лчпости, теория механизмов и машин,
гидроаэродинамика) и многих технических дисциплин.
В основе теоретической механики, как и всякой пауки, лежат
представления и абстракции, отражающие главные черты изучаемых
явлений. Рассмотрим некоторые из них.
Количественная мера механического взаимодействия между фи-
физическими объектами — сила — характеризуется модулем, направлением
и точкой приложения, т. е. является вектором.
Во многих случаях форма и размеры движущегося тела не играют
существенной роли. Поэтому вводится понятие о материальной
точке, не имеющей протяженности, по обладающей массой (мерой
инертности материальной точки).
Все физические тела в той или иной степени деформируемы.
В тех случаях, когда этими деформациями можно пренебречь, мате-
материальное тело рассматривается как абсолютно твердое (или, короче,
твердое), т. е. предполагается, что расстояния между любыми его
точками остаются неизменными.
Курс механики состоит из трех разделов — статики, кинема-
кинематики и динамики.
Возникшая в результате практической деятельности теоретическая
механика развивается в неразрывной связи с техникой. За несколько
столетий до нашей эры возникновение статики было вызвано расцве-
расцветом строительства. Затем новый толчок дало развитие мореплавания,
промышленности, военного дела и астрономии — в результате в XV —
XVII веках возникли кинематика и динамика.
Великие достижения последних лет — внедрение автоматизации
п различные области техники, создание искусственных спутников
Земли, запуск космических ракет и межпланетных лабораторий — обу-
обуславливают дальнейшее разиитие теоретической механики, пауки,
созданной в результате усилий большого числа гениальных ученых
и выдающихся инженеров.
РАЗДЕЛ ПЕРВЫЙ
СТАТИКА ТВЕРДОГО ТЕЛА
Основные законы статики
Статикой называется раздел теоретической механики, в кото-
котором рассматриваются задачи на равновесие тнердых тел и преобра-
преобразования одной системы сил в другую, ей эквивалентную. В оснопе
теоретической механики лежат экспериментально установленные зако-
законы, справедливость которых проверена многовековой практической
деятельностью человека. Основные определения и законы даны ниже.
Изолированной называется материальная точка, действием на кото-
которую других материальных тел можно пренебречь.
Закон 1 (закон инерции). Изолированная материальная
точка находится в покое либо движется равномерно и прямолинейно.
Равномерное и прямолинейное движение материальной точки яп-
ляется движением по инерции. Под состоянием равновесия мате-
материальной точки и твердого тела понимают не только состояние по-
покоя, но и движение по инерции. Для твердого тела существуют раз-
различные виды движения по
инерции, например равномер-
пое вращение твердого тела
вокруг неподвижной оси.
Закон 2. Твердое тело
Рис. 1.1. находится в равновесии под
действием двух сил только
в том случае, если эти силы равны по модулю и направлены в про-
противоположные стороны по общей линии действия (рис. I.I).
Эти две силы называются уравновешивающимися. Вообще силы
называются уравновешивающимися, если твердое тело, к которому
приложены эти силы, находится в покое.
3 а к о п 3. Не нарушая состояния *) твердого тела, можно до-
добавлять и отбрасывать уравновешивающиеся силы.
Следствие. Не нарушая состояния твердого тела, силу можно
переносить по ее линии действия в любую точку тела.
Две системы сил называются эквивалентными, если одну из них
можно заменить другой, не нарушая состояния тнердого тела.
Слово «состояние» здесь означает состояние движения или покоя.
СТАТИКА ТВЕРДОГО ТЕЛА
И
Равнодействующей называется сила, которая эквивалентна дан-
данной системе сил.
Закон 4. Равнодействующая двух сил, приложенных в одной точ-
точке, приложена в той же точке, равна по модулю диагонали парал-
параллелограмма, построенного на этих силах, и направлена вдоль этой
диагонали (рис. 1.2).
По модулю равнодействующая равна
cos
Закон 5 (закон равенства действия и противодей-
противодейтела действуют друг на друга,
Рис. 1.2.
Равновесие нетвердого
с т в и я ). Силы, с которыми два
равны по модулю и направ-
направлены в противоположные сто-
стороны по одной прямой, т. е.
FB=~FA*) (рис. 1.3).
Следует иметь в виду, что
действие — сила, приложенная
к телу Б, и противодейст-
противодействие— сила, приложенная к те-
телу А, не уравновешиваются,
так как они приложены к раз-
разным телам.
Закон 6 (закон отвердевания),
тела не нарушается при его затвердевании.
Не следует при этом забывать, что условия равновесия, явля-
являющиеся необходимыми и достаточными для твердого тела, являются
необходимыми, но недоста-
недостаточными для соотыетствую-
щего нетвердого тела. Так,
абсолютно жесткий стер-
стержень может находиться в
равновесии под действием
Двух сил, равных по мо-
модулю и направленных вдоль Рис- 1-3.
стержня либо друг к другу,
либо друг от друга (т. е. под действием как сжимающих, так и рас-
растягивающих сил), а нить, соответствующая этому стержню, может
находиться в равновесии только под действием двух сил, направлен-
направленных друг от друга. Под действием сил, направленных друг к другу,
нить сомнется.
Твердое тело называется свободным, если его движение ничем не
ограничено. В большей части технических задач встречаются лишь
несвободные твердые тела.
Буквы, обозначающие векторы, набраны в книге полужирным шрифтом.
12 СТАТИКА ТВЕРДОГО ТЕЛА
Несвободным называется такое твердое тело, на которое нало-
наложены связи, ограничивающие его движение в некоторых направле-
направлениях. Так, для лампы, подвешенной на шнуре, связью является шпур;
для книги, лежащей па с голе, связью является стол; для лестницы,
приставленной к стене, связями являются пол и стена. Для шара, ка-
катящегося по бильярдному столу, связью является поверхиосаь стола и
его борта.
Сила, характеризующая действие связи па твердое тело, называ-
называется реакцией связи. Если считать силу, с которой твердое тело
действует на спязь, действием, то реакция связи является противо-
противодействием. При этом сила — действие при-
приложена к связи, а реакция связи прило-
приложена к твердому 1елу.
Все силы, действующие на твердое
тело, можно разделить па две группы:
силы активные и реакции связей *).
При этом активными следует считать все
силы, не являющиеся реакциями связей.
Таким образом, какая-либо неизвестная
сила, не являющаяся реакцией связи, также
ЯНЛяеЮ! ЭК1ИВПОЙ СИЛОЙ.
')ис- 1-4- Закон 7 (закон освобождае-
освобождаемо с i и 0 1 связей). 11есвободпое твер-
твердое "тело можно рассматривать как сиободпое, если его мысленно
освободи 1ь 01 связей, заменив действие связей соответствующими
реакциями связей.
Этт закон дает возможнос1ь, в частности, применить к несво-
несвободному твердому телу условия равновесия, справедливые для сво-
свободного твердого тела. При этом следует, отбросив связи, наложен-
наложенные па твердое тело, заменить их соответствующими реакциями
связей. Затем надлежит рассмотреть равновесие этого несвободного
твердого ге.та, как тела свободного, под действием активных сил
и реакций связей.
В большинстве задач па равновесие твердого тела следует, если
это возможно, сразу указать направление реакций связей, а затем оп-
определи ib их модули в ходе решения задач. Для облегчения опреде-
определения направления реакций связей рекомендуется внимательно озиа-
комшься l приведенными ниже примерами.
1. Если твердое тело опирается па идеально гладкую (без тре-
трения) поиерхпость, то реакция поверхности направлена по нормали к,
пей и ючке соприкосновение т. е. перпендикулярно к, касательной
плоскости в данной точке поверхности (рис. 1.4). Такая реакция на-
называется нормальной реакцией.
*) Ино1да активные силы называют задаваемыми.
СТАТИКА ТВЕРДОГО ТЕЛА
13
/7777777777777/s
с
Рис. 1.5.
2. Если твердое тело в точках А и В (рис. 1.5) опирается на
ребра двугранных углов, а в точке С—на гладкую плоскость, то
для направления реакций связи в точках А и В следует применить
метод обращения, т. е. представить, что дву-
двугранный угол опирается на твердое тело
(рис. 1.6), являющееся для него связью. Эта
обращенная задача сводится к рассмотренному
выше случаю 1, т. е. опорная реакция R' на-
направляется по соответствующей нормали. Снова
обратив задачу, определяют искомое папрапле-
иие реакций в точках А и В, причем на осно-
основании закона равенства действия и противодей-
противодействия: RA= —R'a, Rn= —Re- Реакция Ro
в соответствии со случаем 1, направляется пер-
перпендикулярно к горизонтальной плоскости (см.
рис. 1.5).
3. Если твердое тело упирается острием в угол (например, лест-
лестница в выступ пола), то подобную связь следует рассматривать как
двойную: угол А (рис. 1.7) препятствует перемещению твердого тела
по горизонтали палено и по вертикали вниз.
Поэтому две составляющие опорной реакции
/?1Д и /?.2Д следует направить противоположно
этим перемещениям: первую — направо, вто-
вторую — вверх. (В подобных случаях реакцию RA
зачастую ошибочно направляют вдоль АВ.)
4. Цилиндрическим шарниром называется
совокупность неподвижного валика А и наде-
надетой на него втулки В, соединенной с твердым телом D (рис. 1.8).
При этом твердое тело может поворачиваться вокруг оси валика.
В точке соприкосновения С ьтулки с валиком возникает опорная
¦л
f
a'
Рис. 1.6.
Рис. 1.8.
реакция, направленная по нормали к идеально гладким поверхностям
соприкасающихся тел в точке касания. Так как положение точки С
соприкосновения валика А с втулкой В заранее неизвестно, то
14
СТАТИКА ТВЕРДОГО ТЕЛА
невозможно сразу указать направление реакции R. При решении задач
реакция R заменяется двумя взаимно перпендикулярными составляю-
составляющими Rt и R*. Определив п ходе решения задачи Rt и R%, находят
модуль и направление реакции R. Нетрудно видечь, что реакцию
можно разложить на составляющие по любым двум направлениям,
например на R, и #> или на R3 и /?4 (рис. 1.9) и т. д.
Рис. 1.10.
Обычно, пренебрегая диаметром валика, по сравнению с другими
размерами, составляющие Rt и R% прилагают в центре О.
5. В случае сферического шарнира (рис. 1.10) также нельзя за-
заранее указать положение точки соприкосновения и, следовательно,
направление реакции R. При решении задач реакция R сферического
шарнира заменяется тремя взаим-
взаимно перпендикулярными состав-
составляющими /?„ /?.г и /?3 (рис. 1.11).
6. Если па твердое тело на-
наложена гибкая связь (нить, канат,
с
Рис. 1.12.
трое, пень и др.), то реакция приложена к твердому телу в точке его
прикрепления к гибким связям. Реакция гибкой связи направлена по
касательной к связи в точке ее наложения (рис. 1.12).
7. Если абсолютно жесткий невесомый прямолинейный стержень,
концы которого соединены шарнирами с другими частями конструк-
конструкции, находится в равновесии иод действием сил, приложенных по его
концам, то следует реакции направить вдоль стержня.
Действительно, если к стержню со стороны других частей кон-
конструкции приложены силы в каждом из его концов, т. е. в шарни-
шарнирах, то после сложения сил оказывается, что и каждом из шарниров
статика твердого тела 15
приложено по одной силе. В результате стержень находится в рав-
равновесии под действием двух сил, приложенных в шарнирах. Соглас-
Согласно второму закону эти силы по модулю равны и направлены в про-
противоположные стороны по сбшеИ линии действия, т. е. вдоль стержня.
При этом стержень подвергается растяжению силами Ft и F\ (рис. 1.13, а)
либо сжатию силами Ft и F't (рис. 1.13, б), причем /^= ¦—Fl и
Fq= —F.v Если стержень подвержен растяжению, то реакции стер-
стержня 7\ и Т[, приложенные к шарнирам, на основании закона равен-
равенства действия и противодействия направлены вдоль стержня друг к
Fi A 8 t}' A F2 ' F2' В
*: о о—•— о а- ¦« о
А Т, Т,' В S2 а В S'2
о—^ -в—о -*——о ¦ о—*-
а) 6)
Рис. 1.13.
другу (рис. 1.13, а). Если стержень подвержен сжатию, то реакции
стержня 5.2 и So, приложенные к шарнирам, направлены вдоль стер-
стержня друг от друга (рпс. 1.13, б). Следовательно,
(рис. 1.13, а), а также
(рис. 1.13, б). Так как F[ = —F{ и F^=: —Fit
то получим:
г; =-7, и 5,==-s,
Решение задач па равновесие твердого тела, не-
независимо от взаимного расположения приложенных
к телу сил, рекомендуется проводить в следующем
порядке:
1) выделить твердое тело, равновесие которого надо рассмотреть
для отыскания неизвестных величин;
2) изобразить активные силы;
3) если твердое тело несвободно, то, примени» закон освобожда-
емости от связей, приложить к нему соответствующие реакции связей;
4) рассмотреть равновесие данного несвободного твердого тела,
как тела свободного, находящегося под действием активных сил и
реакций связей;
5) использовать необходимые и достаточные условия (уравнения)
равновесия в соответствии со взаимным расположением сил, приложен-
приложенных к твердому телу, и определить искомые вел.,чины.
16
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
Обращаем внимание читателя на то, что этот порядок является
общим при решении любых задач на равновесие твердого тела. Ме-
Методы применения пятого пункта и дополнительные рекомендации бу-
будут сделаны в соответствующих параграфах.
Напомним, что в технической системе единиц сила измеряется
в кГ, а в системе единиц СИ — в н (ньютонах), причем
1 «-Г = 9,81 н.
Г Л Л В А I
ПЛОСКАЯ СИСТЕМА СИЛ
§ 1. Система сходящихся сил
1°. Равновесие твердого тела, к которому прило-
приложена система сходящихся сил. Сходящимися называются
силы, линии действия которых
пересекаются в одной точке.
После переноса всех сил по
их линиям действия в эту
точку получается эквивалентная
система сил, приложенных в од-
одной точке.
Равнодействующая R системы
сил, приложенных в одной точ-
точке, приложена в той же точке и
изображается замыкающей сторо-
стороной силового многоугольника,
построенного на слагаемых си-
силах, т. е. равнодействующая R равна векторной сумме слагаемых сил:
= У F* С1*)
Рис. 1.14.
При построении суммы векторов (рис. 1.14) надо к концу первого
слагаемого вектора F1 приложить вектор F'b равный второму сла-
слагаемому вектору Fb к концу второго слагаемого вектора F'% присое-
присоединить вектор F'3, равный третьему слагаемому вектору F3, и т. д.
Суммой векторов R является замыкающий вектор, начало которого
совмещено с началом первого слагаемого вектора, а конец — с кон-
концом последнего слагаемого вектора. Если векторы изображают силы,
то многоугольник OABCD, построенный на рисунке для четырех сла-
слагаемых сил, называется силовым, а его замыкающая сторона OD
является равнодействующей R.
и
СИСТЕМА СХОДЯЩИХСЯ СИЛ
17
Если все слагаемые силы лежат на одной прямой, то вершины
силокого многоугольника оказынаются лежащими из одной прямой.
Равнодействующая R этой системы сил лежит на той же прямой.
На рис. 1.15 изображена равнодействующая четырех сил Fb Fit F3
и Fit лежащих на одной прямой. (Для ясности изображения линии
действия сил несколько сме-
смещены друг относительно друга.)
Для равновесия твердого
тела, к которому приложена
система сходящихся сил, не-
необходимо и достаточно, чтобы Рис. 1.13.
векторная сумма этих сил рав-
равнялась нулю: У?=0, т.е. чтобы силовой многоугольник был замкнут.
Это значит, что конец вектора последней слагаемой силы должен
совместиться с началом вектора первой слагаемой силы. На рис. 1.16
изображен замкнутый силовой многоугольник, построенный на пяти
слагаемых силах.
В случае равновесия твердого тела, к которому приложены силы,
лежащие" на одной прямой, вершины замкнутого силового много-
многоугольника оказываются лежащими на прямой, вдоль которой в обоих
направлениях отложены слагаемые силы, векторная сумма которых
равна нулю (рис. 1.17).
Рис. 1.17.
При решении задач на равновесие твердого тела,
ic которому приложена плоская система сходящихся
сил, надо выполнить четыре первых пункта, указан-
ных к начале книги, на стр. 15. Затем:
5) построить замкнутый силовой многоугольник (построение надо
начинать с силы, известной как по модулю, так и но направлению);
6) решив силоной многоугольник, определить искомые величины.
Если число активных сил и реакций связей, приложенных к твер-
твердому телу, находящемуся в равновесии, равно трем, то задача сво-
сводится к построению и решению силового треугольника.
Задача 1.1. Однородный цилиндр М, вес которого Р = 20 кГ,
лежит па гладкой горизонтальной плоскости. Сверху на цилиндр
давит вертикальная сила F=50 кГ, линия действия которой прохо-
проходит через центр тяжести цилиндра.
18
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
6)
м
IP
м
IP
kR
0
Г
р
А"
Fu
.\\\\\\\\\\\\\\\\\\v
Определить давление цилиндра на горизонтальную плоскость.
Решение. Рассмотрим равновесие несвободного цилиндра М
(рис. а). К цилиндру приложены дне активные силы: Р — вес,/7—вер-
вес,/7—вертикальная сила давления. Вес цилиндра приложен в его центре тя-
тяжести С и направлен по вертикали вниз. Сила давления совпадает
по направлению с весом цилиндра.
На цилиндр наложена одна связь — гладкая горизонтальная пло-
плоскость, препятствующая перемещению цилиндра по вертикали вниз.
Применив закон освобождаемое™ от связей, заменим действие гори-
горизонтальной плоскости на цилиндр соответствующей реакцией R (рис. б).
Направим реакцию R в стс-
а) б) рону, противоположную тому
перемещению, которое- огра-
ограничено горизонтальной плоско-
плоскостью, т. е. но вертикали вверх.
Теперь данное несвободное
твердое тело можно рассмат-
R ривать как тело свободное,
к которому приложены актив-
активные силы Р и F и реакция
горизонтальной плоскости R.
К задаче 1.1. Эти три силы лежат на од-
одной прямой.
Если нее слагаемые силы лежат на одной прямой, то вершины си-
силового многоугольника оказываются расположенными на той же прямой.
Изобразим вектор, равный силе Р, поместив его начало в произ-
произвольной точке. Из конца его, т. е. из точки А, проведем вектор,
равный силе F. В конце его, т. е. в точке В, находится начало век-
вектора R (рис. в).
Так как при равновесии твердого тела сумма сил Р, F и R
должна быть равна нулю, то конец вектора R должен совпасть
в точке О с началом первой слагаемой силы Р (на рис. в для яс-
ясности изображения линии действия сил Р и F и силы R несколько
смещены друг относительно друга). Как следует из рис. в, R = P -\-F.
Подставив численные значения, получим R=70 кГ.
Давление твердого тела на горизонтальную плоскость равно
но модулю реакции R этой плоскости и направлено ей противопо-
противоположно, т. е. по вертикали вниз.
Задача 1.2. Однородный шар весом Р — 20 кГ опирается в точке А
иа гладкую наклонную плоскость, образующую угол а = 60° с гори-
горизонтом, а в точке В на выступ, находящийся на одной горизонтали
с точкой А.
Определить опорные реакции наклонной плоскости и выступа.
Решение. Рассмотрим равнокесие шара. К шару приложена одна
активная сила — его вес Р, направленный по вертикали вниз. Шар
»ч
СИСТЕМА СХОДЯЩИХСЯ СИЛ
19
находится в равновесии при наличии двух связей: наклонной пло-
плоскости и выступа. Применив закон освобождаемости, заменим действие
на шар мысленно отброшенных связей соответствующими реакциями.
Реакция RA гладкой наклонной плоскости направлена к ней перпен-
перпендикулярно. В точке В проведем касательную (рис. б) и направим
опорную реакцию перпендикулярно к касательной. Следовательно,
линия действия RB проходит через центр тяжести шара С.
Теперь можно рассмотреть шар как свободное твердое тело, на-
находящееся в равновесии под действием плоской системы трех сил:
Р, RA и RB, линии действия которых пересекаются в точке С. Для
К задаче 1.2.
равновесия шара необходимо и достаточно, чтобы сумма этих трех
сил равнялась нулю. Поэтому силы образуют замкнутый силовой
треугольник.
Построение силового треугольника начнем с силы Р, пзвеаной
как по величине, так и но направлению. Из произнольной точки О
(рис. в) проведем вектор, который равен силе Р. К ксниу силы Р
надо приложить начало силы RA или JRB. Выбираем в качестве сле-
следующей стороны силового треугольника реакцию выступа /?д. Так как
направление силы RD известно, то проведем через точку А прямую
АК, параллельную линии действия реакции RB. Для последующего
построения силового треугольника надо к концу Rn приложить на-
начало силы RA. Сделать это невозможно, так как модуль силы Rn
неизвестен. Несмотря на козникшее затруднение, построение силового
треугольника можно успению завершить. Следует учесть, что при
рапновесии шара силовой треугольник должен быть замкнут. При
20
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
этом конец вектора реакции RA должен совместиться с началом век-
вектора силы Р, т. е. попасть в точку О. Поэтому проведем через
точку О прямую OL, параллельную линии действия силы RA. Точка В
пересечения прямых АК и OL определяет положение третьей вер-
вершины В силового треугольника ОАВ. В построенном силовом треу-
треугольнике должно иметь место единое направление стрелок, т. е.
в каждой из вершин треугольника должен быть расположен конец
только одной из трех сил.
Для определения модулей опорных реакций RA и RD остается
решить силовой треугольник ОАВ. Нетрудно видеть из рис. в, что
углы, образованные линией действия силы Р с линиями действия
реакций RA и RB, равны 60е; таким образом, силовой треугольник
оказывается равносторонним и, следовательно, Ra = Rb = P= 20 кГ.
Если бы при построении силового треугольника мы к концу
силы Р приложили начало силы RA (а не RB, как это было сделано
выше), то получили бы силовой треугольник ОАО (рис. г), равный
силовому треугольнику ОАВ. Решение этого силового треугольника,
естественно, привело бы к тем же результатам.
Задача 1.3. Через гвоздь, вбитый в стену, переброшен трос
(рис. а). Один конец троса прикреплен к полу иод углом 30° к гори-
горизонту. К другому концу троса поднешен груз, вес которого Р= 100 кГ.
Определить величину реакции стены, в которую вбит гвоздь.
Весом гвоздя пренебречь. Трос расположен в вертикал! ной плоскости.
Решение. Предварительно рассмотрим равновесие груза (рис. б).
К грузу приложены: вес Р, направленный по вертикали вниз, и реак-
реакция троса Т, направленная
по вертикали вверх. Вос-
Воспользовавшись вторым за-
законом о равновесии твер-
твердого тела под действием
двух сил, получим:
Т=Р =\00 к Г.
Переходим к рассмотре-
рассмотрению равновесия гвоздя. Мыс-
Мысленно рассекая левую и пра-
правую ветви троса вблизи
гвоздя, заменим действие
отброшенных частей троса
его реакциями 7^ и Т±
(рис. в). Силы 7\ и Т.1 равны
по модулю силе Т, но различны по направлению: |7^|= |7\j| = |7"|.
Связью, наложенной на гвоздь, является стена.
Гвоздь находится в равновесии под действием активных сил Г, и
Т-1 и реакции R стены, направление которой неизвестно. Так как
К задаче
§ 11 СИСТЕМА СХОДЯЩИХСЯ СИЛ 21
линии действия этих трех сил пересекаются в одной точке, то можно
построить силовой треугольник на силах Ть Г3 и R. В данном сило-
силовом треугольнике две силы G\ и Го) известны как по величине, так
и но направлению. Проведя из произвольной точки О силу, векторно
равную силе Ть приложим к ее концу силу, векторно равную силе
Га (рис. г).
Так как при равнонесии гвоздя силовой треугольник должен бы 1ь
замкнут, то, соединив начало О силы TL с концом В силы 7\>, опре-
определим реакцию стены Л. Конец силы должен находиться в исходной
точке О. При этом силовой треугольник ОАВ оказывается замкнутым.
Для решения силового треугольника ОАВ воспользуемся вспомо-
вспомогательными построениями. Проведем из точки В направо горизонталь
и продолжим ОА по вертикали вниз до пересечения с горизонталью
в точке D. В треугольнике ABD угол ABD равен углу наклона ле-
левой нетви троса к горизонту, т. е. 30°. Следовательно, угол BAD
равен 60°. Угол BAD является внешним по отношению к силовому
треугольнику ОАВ. Замечая, что силовой треугольник ОАВ является
равнобедренным (силы 7\ и Г.2 по модулю равны), имеем: /_ ОВА —
= Z ВОА = ту L BAD = 30°. Теперь из треугольника ОАВ без труда
находим искомый модуль реакций R стены:
R = BO = BA cos 30°-|- АО cos 30° = 2Тcos 30° ==
= 2- 100 i^?«173 кГ.
Задача 1.4. Два абсолютно жестких стержня АВ и АС соединены
шарниром в точке А и прикреплены ц полу шарнирами В и С, обра-
образуя с полом соответственно углы 45° и 60° (рис. а). К валику шар-
шарнира А подвешен па нерастяжимой нити груз D, вес которого
Р = 100 к Г.
Определить усилия, возникающие в стержнях АВ и АС. Весом
стержней пренебречь.
Решение. Для определения усилий в стержнях АВ и АС сле-
следует рассмотреть равновесие шарнира А. Однако непосредственно
приступить к исследованию равновесия узла А невозможно, так как
он находится в равновесии под действием трех неизвестных сил:
реакций стержней АВ и АС и реакции нити AD. Поэтому для опре-
определения реакции нити предварительно рассмотрим равновесие груза D.
Груз D находится в равновесии под действием двух сил: веса Р и
реакции нити Т. Эти силы направлены в противоположные стороны
(рис. б). Учитывая условие равновесия груза, получим, что Т=Р =
= 100 к Г.
Теперь, когда одна из трех сил, приложенных к шарниру А,
известна, можно изучить равновесие шарнира А. К нему приложена
одна известная сила — реакция нити Т, направленная по вертикали
22
ПЛОСКАЯ СИСТЕМА СИЛ
(ГЛ. Г
вниз (на основании закона равенства действия и противодействия
Г' =—Г). Реакции Тв и Тс стержней АВ и АС направлены вдоль
стержней (см. на стр. 14 и i5 пример 7 направления реакции связей).
На рис. в эти три силы изображены приложенными в шарнире А
(в общем случае трудно заранее указать, направлены ли силы Тв и
Тс вдоль стержней вверх
или вниз; это будет уточ-
уточнено в ходе последующего
решения задачи).
При равновесии шар-
шарнира А равнодействующая
этих сил должна быть равна
нулю, следовательно, силы
Т, Тв и Тс образуют замк-
замкнутый силовой треугольник.
Построение силового тре-
треугольника (рис. г) начнем
с силы Т\ известной по Re-
личипе и по направлению.
Взяв произвольную точку О,
приложим к ней силу 7".
Затем, проведя через начало
и конец силы Т прямые OL и SK, соответственно параллельные
стержням ЛС и АВ, получим в пересечении третью вершину Q сило-
силового треугольника OSQ. Изобразив на сторонах треугольника SQ
и QO стрелки так, чтобы сумма трех сил V, TR и Тс равнялась
нулю (в каждой из вершин силового треугольника OSQ должен быть
расположен конец только одной из трех сил), получим направления
реакций Тв и Тс.
Перейдя к решению силового треугольника, заметим, что /_ SOQ =
O
S
К задаче 1.4.
р
= /_ DAC=30° и Z OSQ== Z.
= 4a°, как углы с соответст-
соответствепно параллельными сторонами. Следовательно, /_ SQO= 105°. При-
Применив теорему синусов, получим:
Т* = Тс = г
sin 30° sin 45° sin 105° '
откуда
T, sin .40°
~~ ' 1Л7Т0У
sin 45°
sin 105°
Подставив численные значения, находим:
7"в = 51,8 к Г, 7"с = 73,2 кГ.
Задача 1.5. На рис. а изображен механизм антипараллелограмма
ABCD, состоящий из абсолютно жестких стержней АВ, ВС и CD,
шарпирно соединенных между собой в точках В и С и прикреплен-
СИСТЕМА СХОДЯЩИХСЯ СИЛ
23
пых шарнирами А и D к неподвижному звену А ГУ, AD = BC,
AB = CD. К валику шарнира С приложена направленная по горизон-
горизонтали налево сила Fc=10 кГ. (Впредь для краткости валик шарнира
мы будем называть шарниром.)
Определить величину силы FR приложенной в шарнире В и направ-
направленной по вертикали вниз, если механизм находится и равновесии
и положении,
L A DC = 90°.
указанном n,i рис. а, т. е.
Весом стержней пренебречь.
при
BAD = 30° и
К задаче 1.Г>.
Решение. Для определения величины силы Fe следует рассмс т-
реть равновесие шарнира В. Однако непосредственно это сделав
невозможно, так как ни одна из трех сил, приложенных к шарниру В
(сила FR и реакции стержней АВ и ВС), неизвестна по неличное.
Поэтому для определения ветичипы реакции стержня ВС предвари-
предварительно рассмотрим равновесие шарнира С. К шарниру С приложена
активная сила Fc и реакции стержней CD и СВ. Так как стержни
соединены шарнирами, то реакции направлены вдоль соотвектную-
uui.x стержней.
На рисе изображен силовой треугольник для узла С Из произ-
произвольной точки О проведена сила Fc. Через начало и конец силы Fc
проведены прямые ОК и HL, соответственно параллельные стержням
СВ и CD. В точке пересечения этих прямых пайдем третью иеп-
шину N силового треугольника OHN. Направим вектсры TD и Тп
так, чтсбы сумма сил Fc, TD и Та оказалась равной пулю.
24 ПЛОСКАЯ СИСТЕМА СИЛ ;ГЛ. I
Для определения углов в треугольнике OEM вернемся к рис. а.
Соединив точки В и D, рассмотрим треугольники ABD и DCB. Эти
треугольники раины по трем сторонам, так как по условию AD = BC,
АИ = CD, а сторона BD у лих обшая. Воспользоиавшись равенством
треугольников, найдем, что /_ DCB= /_ DAB= 30°. Теперь легко
доказать равепстио треугольников AMD и СМВ. Действительно,
AD = BC, ?DAM= АМСВ = Ж, / AMD= L СМВ = 60°. Сле-
Следовательно, ?_ СВМ = L ADM = 90°.
Обратившись теперь к силопому треугольнику OEN, нетрудно
заметить, что ?, EN0= l_ МСВ = 30°. Так как Fc J_ TD, то получим:
Г 2 О
Теперь мы можем определить искомую силу Fa, рассмотрев равпо-
иесие шарнира В (рис. г). К шарниру В приложены активная сила Fn
п реакции стержней АН и ВС, направленные идоль стержней. При
этм реакции Т'в стержня нам извести^. Она равна по модулю силе TR,
определенной из силового треугольника OEM, и противоположно ей
направлена, т. е. Т'п = —Тв (см. на стр. 14 и 15 пример 7 направ-
направления реакций связей).
Начнем построение силоиого треугольника для узла В с реак-
Ш и Т'в, отложив ее от произвольной точки Р (рис. д). Затем, про-
проведя через начало и конец Т'п прямые PU и RV, соответственно
параллельные линиям действия искомой силы FB и стержню АВ,
получим в их точке пересечения третью вершину 5 силового тре-
треугольника PRS. Направим векторы ТА и Fn так, чтобы силовой тре-
треугольник PRS оказался замкнутым. Так как линии действия сил Т'ц
и ТД соответственно параллельны стержням СВ и АВ, то /_ PRS =
= Z. МВС= 90°. Заметив, что ,/ RPS= Л BAD= 30°, как углы
с взаимно перпендикулярными сторонами, найдем из силового треу-
треугольника PRS:
р т'п 2
Подставив значение Тп из формулы A), получим:
FB = * V'S Fc = 23,1 кГ.
Рекомендуем решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Ме-
Мещерского, издания 1950 г. п последующих лет: 20, 24,
28, 31.
2°. Теорема о трех непараллельных силах. Если твер-
твердое тело находится в равновесии под действием трех неиараллель-
§ ч
СИСТЕМА СХОДЯЩИХСЯ СИЛ
25
Рис. 1.18.
пых сил, лежащих в одной плоскости, то линии действия этих сил
пересекаются в одной точке (ркс. 1.18).
Следует иметь в виду, что пересечение линий действия трех непа-
непараллельных сил в одной точке является лишь необходимым условием
для равновесия твердого тела. Пересечение
линий действия трех сил в одной точке не
является достаточным условием, так как
равнодействующая этих сил может оказаться
не равной нулю. Следовательно, достаточ-
достаточным условием является наличие замкнутого
силоиого треугольника при одновременном
пересечении линий действия трех сил в од-
одной точке.
Теорема о трех непараллельных силах
значительно облегчает решение задач па
равновесие твердого тела п тех случаях, когда
направление одной из трех урав-ювешинающихся сил неизвестно. Дей-
Действительно, определив точку пересечения линий действия двух сил,
направления которых известны, мож-
можно указать направление линии дей-
действия третьей силы, так как она
должна пройти через точку приложе-
приложения этой силы и точку пересечения
линий действия первых двух сил.
Задача 1.6. На рис. а изобра-
изображена схема суппорта универсаль-
универсального металлорежущего станка с. за-
закрепленным в нем резцом. К резцу
в точке D со стороны обтачивае-
обтачиваемого изделия (Па рисунке изделие
не показано) приложено давление N,
образующее угол 30° с вертикалью
и равное по модулю 300 кГ. Схе-
Схематизируя опоры суппорта, считаем,
что опорой А является цилиндри-
цилиндрический шарнир, а в точке В суппорт
поддерживается пружиной.
Пренебрегая весом суппорта,
определить реакцию опоры и силу
упругости пружины. Размеры ука-
указаны па рисунке.
Решение. Рассмотрим равно-
весие суппорта, к которому прило-
приложены силы: N—давление обтачиваемого изделия на
упругости пружины, направленная но вертикали
резец, F — сила
вверх. Применив
26 ' ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. Г
закон освобождаемое™ о г спязей, мысленно отбросим цилиндри-
цилиндрический шарнир А и компенсируем его действие на суппорт соот-
соответствующей реакцией RA. Обычно мы не можем заранее указать
направление этой реакции (см. пример 4 направления реакций на
с i р. 1'.\ п 14). Однако в данном случае суппорт находится в равновесии
под действием трех непараллельных сил: N, F и RA. Поэтому можно
воспользоваться теоремой о трех непараллельных силах, согласно
которой линии действия сил N, F и RA должны пересекаться в од-
одной точке. 'Гак как линии действия сил N и F пересекаются в точке Ь\
то линия действия силы RA также должна проходить через эту точку
(см. рис. б).
Построение силового треугольника (см. рис. в) начнем с силы N,
приложив ее в произвольной точке О, взятой вне основного рисунка.
Через начало О и конец Q вектора N проведем прямые, параллель-
параллельные линиям действия сил F u /}А. В точке пересечения этих прямых
найдем третью вершину М силового треугольника 0MQ- Направим
векторы RA и F так, чтобы силовой треугольник оказался замкнутым,
т. е. чтобы в каждой из его вершин был расположен конец только
одной силы.
Для решения силового треугольника выполним на рис. б вспомо-
вспомогательное построение: проведем через точку D вертикаль до пере-
пересечения в точке /. с прямой АЕ. Нетрудно видеть, что треугольники
0MQ (рис. в) и DLE (рис. б) подобны, ибо имеют соответственно
параллельные стороны. Определим длины сторон треугольника DLE.
И:! прямоугольного треугольника DKE, и котором, по условию,
ПК—СП--\Г) см, имеем DC =-^—=20 см, KE — DK ctg 30° =
sin o(J
— \Ь\'':\ см. Поэтому BE = BK+KE = {2Q-\-loVz) см, т.е.
#? = 46 см. A)
Средняя линия CL треугольника ВАЕ равна CL^,jZ?? = 23 см.
Значит, DL = CL — С?> = 3 см. Для определения LE преднарителыю
вычислим АЕ из прямоугольного треугольника ЛЕВ. Имеем Л? =
= У'АВ* -г BE2 = ylO* -f 46* = 55 см. Так как AE=AL-\-LE =
= 2/./:, то /,С = 27,5 см. Итак, стороны треугольника DLE равны
DI1 = 30 см, DL = :\ см, /.? = 27,5 см. B)
Использовав подобие треугольников 0MQ и DLE, запишем:
-Л — F — N-
Lli DL — DE'
откуда
§11
СИСТЕМА СХОДЯЩИХСЯ СИЛ
27
Подставив значения LE, DE и DL из формул B), а также значение
N= 300 кГ, получим:
C)
= 275 к Г, F='iO кГ.
Задача 1.7. Однородная палочка весом Р и длиной 2а опи-
опирается концом А о гладкую внутреннюю поверхность полусфери-
полусферической чаши радиуса г. Промежуточной точкой В палочка опирается
о ребро чаши.
Определить величину угла а, образуемого палочкой с горизонтом
в положении равновесия, и опорные реакции в точках А и В.
С — центр тяжести па-
палочки, М — центр сферы,
половина которой обра-
образует чашу фис. а).
Решение. Если опу-
опустить палочку концом А
в полусферическую чашу,
то она займет и ней по-
положение равновесия при
некотором фиксирован-
фиксированном значении угла я, об-
образуемого палочкой с го-
горизонтом. При этом угол я
зависит от длины палоч-
палочки 2а и радиуса чаши г.
В случае равновесия
угол я должен быть та-
ким, чтобы линии дей-
действия трех сил, приложенных к палочке, — веса Р и реакций йл
и RB — пересекались в одной точке. Реакцию RA направим по нор-
нормали к поверхности и данной точке, т. е. по радиусу AM, а реак-
реакцию Rn — перпендикулярно к палочке (рис. б). Пусть О — точка пе-
пересечения линий действия этих трех сил. Такого построения оказы-
оказывается достаточно для определения значения угла а. Рассматривая
равнобедренный треугольник АМВ, имеем AM — АШ=г, /_ ВАМ =
= L АВМ. Так как /_ МВА== L В AS = а, то /_ ВАМ= L АВМ =
= а. Угол АВО, вписанный в окружность радиуса г, является но по-
построению прямым. Он должен опираться на диаметр окружности;
поэтому АО = 2г. Из треугольника AOS находим AS= АО- cos 2a —
= 2rcos2a. Из треугольника ACS имеем AS=AC- cos a = a cos л.
(Так как центр тяжести однородной палочки расположен в ее сере-
середине, то АС^а.) Следовательно,
К задаче 1.7.
AS = '2r cos 2а = a cos а.
С)
28 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
Заменив cos 2а через 2 cos2 а—1, получим:
2г B cos'2 а — 1) = a cos а,
или
4r cos2 а — а cos а — 2г = 0.
Решив это квадратное уравнение, найдем:
а ± j/o -г 3'2г2
cosa = L^ .
Так как 0<^a<^ir/2, то 0<^cosa<^l. Поэтому, отбросив отрица-
отрицательное значение cos a, окончательно получим:
Для определения опорных реакций RA и RR построим замкнутый
силовой треугольник (рис. в). Из произвольной точки К проводим
вектор, равный силе Р. Проведя через начало вектора Р прямую /</:,
параллельную реакции Rn, а через конец вектора Р — прямую LD,
параллельную реакции RA, получим в точке пересечения этих прямых
третью вершину N силового треугольника KLN. Из сравнения рис. б
и в нетрудно видеть, что ^ NKL= /_ ЯОС = а, /_ NLK= L QAM —
= 90° — Л MAS — 90° — 2a и, следовательно, ?_ KNL = \ 80° —
— (Z LKN-\- L ЯШ) = 90°-[-а.
Применив к силовому треугольнику K.LN теорему синусов, запишем:
Sin @0"--a)" Sin a. sill (90° — 4a) '
откуда
где cos a определяется по формуле B).
Рекомендуем решить следующие задачи из «Сбор-
пика задач но теоретической механике» И. В. Ме-
Мещерского, издания 1950 г. и
последующих лет: 37, 38, 40, 41.
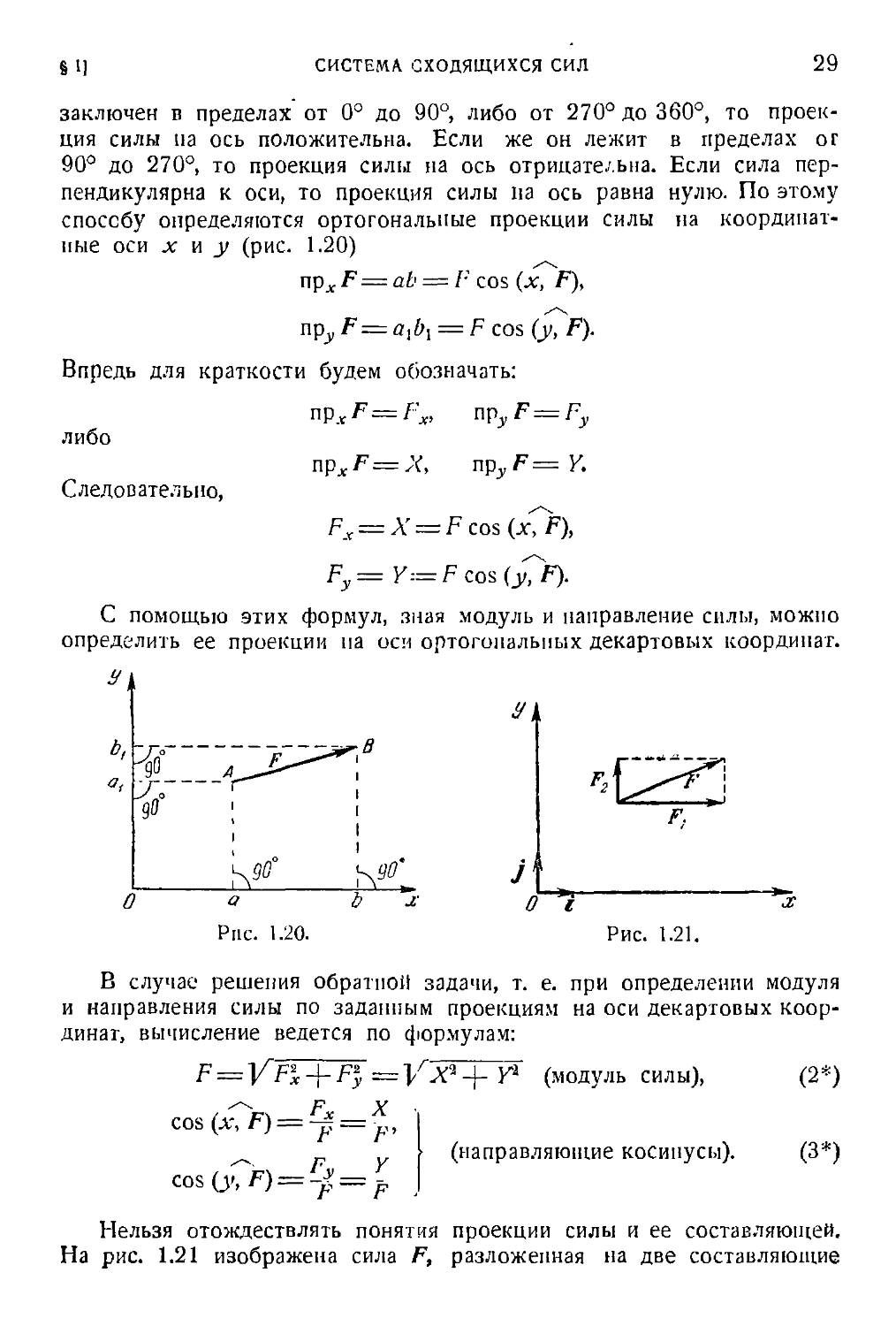
3°. Метод п р о е к ц и й. Ортого-
Ортогональная проекция силы па ось, по-
подобно проекции любого вектора па
ось, раина произведению модуля
силы на косинус угла, образованного
положительным направлением оси про-
проекций и направлением проектируемой силы (рис. 1.19):
иРлг F=^ o-b = F cos (x, F).
Проекция силы па ось является алгебраической величиной. Если
угол между положительным направлением оси проекций и вектором
§ч
СИСТЕМА СХОДЯЩИХСЯ СИЛ
29
заключен в пределах от 0° до 90°, либо от 270° до 360°, то проек-
проекция силы на ось положительна. Если же он лежит в пределах or
90° до 270°, то проекция силы на ось отрицательна. Если сила пер-
перпендикулярна к оси, то проекция силы на ось равна нулю. По этому
способу определяются ортогональные проекции силы на координат-
координатные оси х и у (рис. 1.20)
. F = ab = F cos (x, F),
npy F=aibl = F cos (y, F).
Впредь для краткости будем обозначать:
прх F=FX, пру F=Fy
npxF = X, npy F=Y.
либо
Следовательно,
Fx = A' = F cos (x, F),
Fy= Y-= F cos (y, F).
С помощью этих формул, зная модуль и направление силы, можно
определить ее проекции па оси ортогональных декартовых координат.
У i
а Ъ
Рис. 1.20.
F.
Рис. 1.21.
В случае решения обратной задачи, т. е. при определении модуля
и направления силы по заданным проекциям на оси декартовых коор-
координат, вычисление ведется по формулам:
B*)
C*)
F = VF% -\-Fy= Vx? + У1 (модуль силы),
(направляющие косинусы).
¦/•м
У
Нельзя отождествлять понятия проекции силы и ее составляющей.
На рис. 1.21 изображена сила F, разложенная на две составляющие
30 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
силы F, и F.2, направленные параллельно соответствующим осям ко-
координат, т. е. F=F1-\-Fi. Составляющая силы является вектором,
который можно представить в виде произведения проекции силы на
орт (единичный вектор) соответствующей оси, т. е.
Fl==FJ=Xl, F%=Fyj=Y].
Следовательно, разложение силы на составляющие можно записать
в виде
Орты осей координат всегда направлены в положительных направле-
направлениях соответствующих осей. Знак проекции силы определяет направ-
направление ее составляющей, т. е. если проекция силы положительна, то
направление составляющей силы совпадает с положительным направ-
направлением соответствующей оси, если же проекция силы отрицательна,
то направление составляющей силы противоположно положительному
направлению соответствующей оси.
Переходим к определению равнодействующей плоской системы
сходящихся сил методом проекций. Пусть даны силы F,, F.b ..., Fn.
В плоскости действия сил построена система осей декартовых коор-
координат ху. Разложения данных сил по ортам этих осей координат
имеюг вид
Fi = Fixl-(-Fiyj, Fi = Fixi-j-Fiyj, ..., Fn = Fnxi-f-Fnyj.
Разложение равнодействующей плоской системы сходящихся сил
по ортам этих осей координат дается формулой: R=Rxl-\-Ryj, где
Rx и Ry — проекции равнодействующей на соответствующие оси.
Проекции равнодействующей на оси декартовых координат равны
алгебраическим суммам проекций слагаемых сил на соответствующие
оси
п
О . р I р _|_ _|_ р чд р
Определив по этим формулам проекции равнодействующей, можно
вычислить ее модуль
и направляющие косинусы
cos (х, R) = -* cos (у, R)=~y (fi*)
Уравнения равновесия твердого тела при наличии
плоской системы сходящихся сил. Для равновесия твер-
<S 11 СИСТЕМА СХОДЯЩИХСЯ СИЛ 31
дого тела, к которому приложена система сходящихся сил, необхо-
необходимо и доааючно, чтобы суммы проекций всех сил системы на оси
декартовых координат равнялисо нулю:
или, в более краткой записи,
2Fftje=0, 2^ = 0. G'*)
k = \ к = \
Задача называется статически определенной, если число неизве-
неизвестных равно числу независимых уравнений равновесия. Если же число
неизвестных больше числа независимых уравнений равновесия, то
задача называется статически неопределенной. В последнем случае
одними уравнениями статичи задача не может быть решена. Для ее
решения следует привлечь уравнения, даваемые другими дисципли-
дисциплинами, например сопротивлением материалов.
Задача на равновесие твердого тела под действием плоской си-
системы сходящихся сил является статически определенной, если число
ал1ебраических неизвестных не более двух. Так, если известны на-
направления всех слагаемых сил и модули всех сил, кроме двух, то
можно определить неизвестные модули двух сил. Если одна из сил
не известна пи по величине, ни по направлению, то все остальные
слагаемые силы должны быть заданы.
Преимущества аналитического метода проекций по сравнению
с геометрическим методом силового многоугольника особенно заметны
в задачах на равновесие твердого тела при наличии более трех схо-
сходящихся сил. Действительно, решение силового четырех-, пяти- и
я-угольника представляет известные трудности, в то время как реше-
решение задачи методом проекций лишь незначительно усложняется при
увеличении числа проектируемых сил.
При решении методом проекций задач па равно-
равновесие твердого тела, находящегося под действием
плоской системы сходящихся сил, надо выполнить
четыре первых пункта, указанных в начале книги,
на стр. 15. Затем:
5) убедиться в том, что данная задача является статически опре-
определенной, т. е. что число алгебраических неизвестных не более двух;
6) выбрать в плоскости действия сил систему осей декартовых
координат ху;
7) составить уравнения равновесия твердого тела в проекциях на
оси декартовых координат G*);
8) решить систему составленных уравнений равновесия и опреде-
определить искомые величины; еслм величина какой-либо из неизвестных
32 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
сил окажется отрицательной, то это означает, что направление силы
противоположно тому, которое было указано на рисунке.
Если по условию задачи требуется определить равнодействующую,
то после выполнения первых четырех пунктов решения задачи надо
вычислить проекции равнодействующей Rx и Ry но формулам D*),
затем определить модуль равнодействующей и ее направляющие
косинусы по формулам E*) п F*).
При выборе осей декартовых координат целесообразно их на-
направить так, чтобы они были параллельны либо перпендикулярны
большинству слагаемых сил.
При определении проекции силы иа ось можно пользоваться сле-
следующим приемом: вычислить модуль проекции силы как произведение
модуля силы па косинус острого угла между линией действия силы
Рнс. 1.22.
и прямой, лежащей на оси проекций. Для определения знака проекции
силы надо смотреть па проектируемую силу и ось проекции так,
чтобы плоскость, проходящая через них, была видна в виде прямой.
Если при этом направления силы и осп совпадают, то проекция силы
положительна, если же направления силы и оси противоположны, то
проекция силы отрицательна.
Например, проекции на ось х сил F^ и Fb изображенных па
рнс. 1.22, а, положительны, и можно сразу записать:
Flx = Г, cos alr F,A = F.t cos a.a,
tmecro того чтобы производить вычисления
Fu = Fi cos C60° — aj) = Fi cos a*
Проекции же сил F3 и Ft, показанных на рис. 1.22,6, отрицательны,
так как непосредственно ясно, что
F3x = — F-л cos а3, Flx = — Fl cos а4.
Сложнее было бы вычислить проекции формально:
F3x = F-i cos A80°-|-a3) = — F3 cos a3,
Fix — Fi cos A80° — a4) = — F4 cos a4.
S >]
СИСТЕМА СХОДЯЩИХСЯ СИЛ
33
Задача 1.8. Решить задачу L4 методом проекций.
Решенне. Воспользуемся изображением сил Т, Тс и Тв, дан-
данным па рис. й к задаче 1.4. Направим ось х по горизонтали па-
право и ось у по вертикали вверх. Составим уравнения равно-
равновесия шарнира А в проекциях на оси
х и у:
Л115"
?0
V\
X
К задаче 1.8.
У
l = Тв cos 45° — Тс cos 60° = 0,
+ rccos30°— Г=0.
Решив эту систему уравнений, найдем
7С —73,2 кГ, 7fl = 51,8 кГ.
Решение этой задачи аналитическим
методом проще геометрического ме-
метода (см. решение задачи 1.4).
Задача 1.9. На рисунке изображены четыре силы Fh Fb F3 и Fb
приложенные к твердому телу в точке О и лежащие в одной пло-
плоскости.
Определить модуль и
направление силы F$, кото-
которую следует приложить в
точке О для того, чтобы
твердое тело находилось в
равновесии. Дано: Ft = 2 н,
F3 = F3 = 4 н, Fi = 6 н.
Решение. Для реше-
решения задачи методом проек-
проекций направим оси декарто-
декартовых координат: ось х — по
горизонтали направо, ось
у — по вертикали ьверх.
Уравнения равновесия твердого тела в проекциях на оси х и у
имеют вид
К задаче 1.9.
или
ix
F
lx
F
3y
ix +
= 0,
= 0,
(I)
B)
где Fix и FSy — проекции неизвестной силы Ft на оси х и у.
Так как число неизвестных равно числу уравнений, то задача
является статически определенной.
2 М, И. Бать и др., т. I
34 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
Вычислим проекции четырех заданных сил Flt Fb F3 и Ft па оси
хну:
Flx = 0, F9j(.= F<,cos450=2Vr~2> F3x = F3 cos 60° = Q,
Fix = — Fi cos 30° = — 3
F,, = — Fj cos 30° = — 2 /I, Fijp = — F4 cos 60° = — 3.
Подставляя эти значения в уравнения A) и B), получим:
2 1/" + 2 — 3 ^-1- FBjr = 0, C)
2 + 21Л2-21ЛЗ —
Из уравнений C) и D) найдем F$x=0,37, Fg),= 1,64. Модуль иско-
искомой силы /^ равен
F, = KFL + Fiy = 1,68«.
Вычислим направляющие косинусы:
cos (*Г>В) = >Г = °Щ = 0>22> cos °^в) = 5f = Щ = °'98'
откуда
(хУ,) ^ 77°, (j/Г/7,,) ^ 13°.
Определение искомой силы Ft методом проекций не составило осо-
особого труда. При геометрическом методе решения этой задачи приш-
пришлось бы построить силовой пятиугольник и затем определить модуль
и направление силы Fs. Преимущества метода проекций бесспорны.
Задача 1.10. При монтаже колонны ММ для подъема груза С
весом Р на вершину колонны использованы два крана. Груз подни-
поднимается с помощью троса ВСА, 1фикрепленного концом В к непод-
неподвижному левому крану (кран на рис. а не изображен), а концом А —
к тележке правого крана. При движении тележки по горизонтали
направо груз — полый цилиндр, скользит вдоль колонны MN вверх.
Длина троса равна L. Расстояние от неподвижного левого конца В
троса до колонны MN равно BN=l.
Считая, что груз С находится в покое, определить натяжение
троса и давление груза на колонну. Угол, образованный левой ветвью
троса с колонной равен а. Весом троса и трением груза о колонну
пренебречь.
Решение. Для определения неизвестных рассмотрим равновесие
груза С. К грузу приложена одна активная сила — его вес Р. На груи
наложены связи: трос ВСА и колонна MN. Реакция R гладкой ко-
колонны перпендикулярна к ее оси (см. рис. б). Изобразим ее по гори-
§ И СИСТЕМА СВОДЯЩИХСЯ СИЛ 35
зоптали палено. Мысленно рассечем обе ветви троса вблизи точки С.
Реакции Т и Т направлены вдоль иетвей троса, причем | Т \ = | Т | = Т.
Направим ось х по горизонтали направо, а ось у по вертикали
вперх. Обозначив угол NCA = a, запишем уравнения проекций всех
сил, приложенных к грузу С, нз оси х и у.
ZFkx= Г sin f — Г sin a — R = Q, (I)
V Fftj, == T cos <f -j- T cos а — P = 0. B)
Из уравнения B) найдем:
P
C)
COS <f + cos a
Использовав значение (З) в уравнении A), получим:
о _ Р (sin <р — sin а)
:<is <f \ cos a '
Остается выразить cos ср и sin 9 через /,, /и я. Обозначим: ВС=а,
= Ь. По условию
a — b=-L. E)
Из треугольника SGV имеем:
Sin a '
CN = I ctg а. (б)
Воспользовавшись треугольником ЛСЛ/ и выражениями E) и F), за-
запишем:
Теперь нетрудно вычислить sin o = l^l —cos'2ip. С помощью резуль-
результата G), после несложных преобразований, получим:
Подстапив значения cos у из G) и sin ср из (8) в C) и D), окон-
окончательно получим:
L sin а — /
Т=2Р-
L sin 2а
г, 2„ ]/(/.2 + Р) Sin2 a — 2/./ sin a — (/. sin а — Osin a
Z. sin 2a
По мере подъема груза С угол а увеличивается, стремясь к 90°
(значит, sin 2а ->- 0). При этом модуль реакции троса также растет.
Груз С невозможно поднять на уровень горизонтали АВ, ибо при
этом sin 2a= sin 180° = 0 и величина Г неограниченно возрастает.
2'
36
ПЛОСКАЯ СИСТЕМА СИЛ
(ГЛ. I
Искомые натяжение троса и давление груза С на колонну соот-
ветстпенпо равны по модулям силам Т и R.
Решение этой задачи с помощью силового многоугольника значи-
значительно сложнее, ибо приходится решать замкнутый силовой четырех-
четырехугольник, построенный на си-
силах Р, R, Т и Г.
Рекомендуем решить
следующие задачи из
«Сборника задач по тео-
теоретической механике»
И. В. Мещерского, изда-
издания 1950 г. и последую-
последующих лет: 21, 26.
4°. Момент силы от-
относительно точки. Рав-
Равновесие твердого тела
с одной неподвижной
точкой. Момент силы F
относительно точки О, ко-
который записывается в виде
т0 (F), для плоской системы
сил равен по абсолютной ве-
величине произведению модуля
силы F па расстояние h от
точки О до линии действия
силы F, называемое плечом.
Если сила F стремится по-
повернуть тело вокруг точки О
против часовой стрелки, то
момент силы положителен,
если же в направлении часо-
вой стрелки, то отрицателен.
(В дальнейшем вместо: «сила
стремится повернуть тело во-
воО
1.10.
круг точки О ...», будем го-
говорить: «сила видна направленной вокруг точки О»). Например (рис.
1.23), mo(F1) = Fihb т0(F8) = — F8fts.
Размерность момента силы в технической системе единиц —
— кГм, а в системе СИ — н-м = дж (джоуль), причем
дж.
Следует помнить, что плечо h является отрезком перпендику-
перпендикуляра, опущенного из точки на линию действия силы. Иногда оши-
ошибочно в качестве плеча изображают отрезок, соединяющий точку, отно-
относительно которой вычисляется момент, с точкой приложения силы.
§11
СИСТЕМА СХОДЯЩИХСЯ СИЛ
37
Момент силы относительно точки равен нулю, если линия дей-
действия силы проходит через эту точку, так как при этом плечо
равно нулю. Например:
Теорема Варипьо-
на для системы схо-
сходящихся сил (теорема
о моменте равнодействую-
равнодействующей): момент относительно
точки равнодействующей R
системы сходящихся сил Fu
/\), ..., Fn, расположен-
расположенных в одной плоскости,
равен алгебраической сум-
сумме моментов слагаемых сил
Рис.
относительно той же точки:
т
= т0
Здесь
m
/?=
т0 (Fn) = ? т0 (Fk). (8*)
Удобство применения теоремы Вариньона заключается в том, что,
минуя непосредственное определение равнодействующей, можно иы-
числить ее момент относительно точки,
зная моменты всех слагаемых сил отно-
относительно той же точки.
Выражение момента силы F отно-
относительно точки А через проекции силы
на оси декартовых координат- имеет
вид
тА (F) = (х — a) Fy — (у — Ь) /\, (9*)
где Fx и Fv — проекции силы F на
оси декартовых координат, х и у —
координаты точки В приложения си-
силы F, а и b — координаты точки А Рис. 1.24.
(рис. 1.24).
Этой формулой рекомендуется пользоваться в тех случаях, когда
определение величины плеча h связано с вычислительными трудно-
трудностями.
В частности, если момент силы F определяется относительно
начала координат О, т. с. a = fr = 0, то формула принимает вид
-xFy—yFx, A0*)
38
ПЛОСКАЯ СИСТЕМА СИЛ
|ГЛ. Г
где Fx и Fy — проекции силы F на оси декартовых координат, х и
у — координаты точки приложения силы F.
Перейдем к рассмотрению задач на равновесие твердого тела
с одной неподвижной точкой. Если единственной связью, наложенной
на твердое тело, находящееся в равновесии, является неподвижная
точка (например, шарнир), то ее реакция должна уравновешиваться
с равнодействующей всех активных сил. Следовательно, при равно-
равновесии твердого тела линия действия равнодействующей всех актив-
активных сил должна проходить через неподвижную точку. В противном
случае происходит опрокидывание твердого тела.
Для определения условий, обеспечивающих равновесие твердого
тела с одной неподвижной точкой, к которому приложена плоская
система сходящихся сил, необходимо направить линию действия равно-
дейстпующей активных сил через точку пересечения линий действия
активных сил и неподвижную точку.
Эти же задачи можно решать с номой:ыо теоремы Вариньома,
записанной относительно неподвижной точки. Так как при этом мо-
момент равнодействующей активных сил, проходящих через неподвиж-
неподвижную точку, равен нулю, то сумма моментов всех активных сил отно-
относительно неподвижной точки также равна нулю:
л
V mo(Fk) = 0, A1*1
где О — неподвижная точка.
Задача 1.11. Тонкий однородный стержень АВ весом Р можс:
поворачиваться вокруг шарнира В, прикрепленного к полу.
Определить величину силы F, которую нужно приложить по го-
горизонтали вправо в конце стержня А для того, чтобы стержень
оставался в равновесии, об-
образуя угол а. с вертикалью
(рис. а).
Решение. Рассмотрим
условия равновесия стержня
АВ. К стержню приложены
две активные силы: Р и F,
линии действия которые
пересекаются в точке О.
К задаче 1.11. Единственной связью, налс-
женпой на стержень, яв-
является шарнир В. Линия действия реакции N шарнира согласно тес-
реме о трёх непараллельных силах должна проходить через точку О.
Итак, стержень АВ находится в равновесии под действием трех
сходящихся сил Р, F и N. Для того чтобы не произошло опрокиды-
опрокидывания стержня АВ вокруг шарнира В, линия действия равнодейству-
§ 2| ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ 39
ющеи R активных сил Р и F должна проходить через точки О и В,
т. е. должна составлять с вертикалью угол OBD, который мы обозна-
обозначим через C. Учтя, что вес Р приложен в середине стержня, получим
АС=СВ. При этом АО = OD. Так как tga= ~ = ^ ,
— 99
~Ь'В' то
Построив на рис. б равнодс-йстпующую R активных сил Р и F
под углом C к вертикали, найдем из прямоугольного треуголь-
треугольника KLM:
При выполнении этого условия стержень АВ будет находиться в рав-
р
новесии. Если F^-rptga, то стержень опрокинется вокруг шарнира В
р
в направлении по часовой стрелке, если же F<^-^-tg a, то против
часовой, стрелки.
Данную задачу проще всего решить, применив условие равновесия
рычага (П*), которое здесь имеет вид
mB(P)-\-mB(F) = 0. A)
Так как
тв(Р) = Р-ВЕ=\1Р- АВ sin a, mB (F) = — F. BD = —F• АВ cos a,
то, подставив эти значения в формулу A), получим:
уР-Л5 sin a —F-i4Scosa = 0,
откуда
Рекомендуем решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Мещер-
Мещерского, издания 1950 г. и последующих лет: 62, 63, 64.
§ 2. Произвольная плоская система сил.
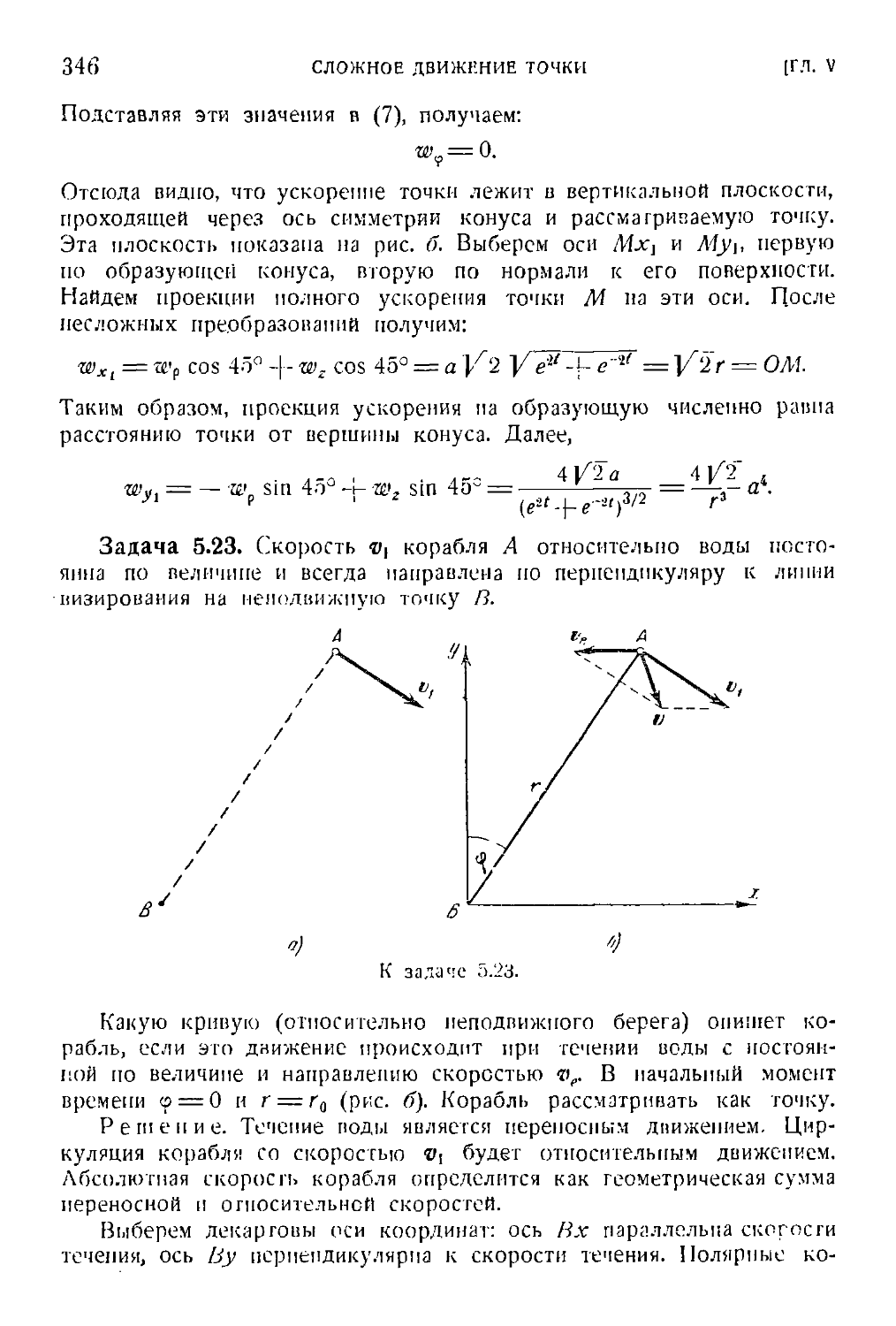
Случай параллельных сил
1°. Равновесие твердого тела при наличии плоской
системы сил. Напомним сначала, что равнодействующая двух па-
параллельных сил, направленных в одну сторону, раина по модулю
сумме модулей данных сил и направлена в ту же сторону. Линия
40
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. Г
действия равнодействующей делит внутренним образом расстояние
между линиями действия данных сил па части, обратно пропорцио-
пропорциональные этим силам. Таким образом (рис. 1.25),
R=Fl+F, *=«;.
Равнодействующая двух параллельных сил, не равных по модулю
(пусть |/^ ?> | Z7! |) и направленных в разные стороны, равна по мо-
модулю разности модулей этих сил и направлена в сторону большей
R
Рис. 1.25.
Рис. 1.26.
силы. Линия действия равнодействующей делит внешним образом
расстояние между линиями действия данных сил на части, обратно
пропорциональные этим силам. Таким об-
образом (рис. 1.26),
Система двух параллельных сил, рав-
равных по модулю и направленных в разные
Рис. 1.27. стороны, называется парой сил (рас. 1.27).
Расстояние между линиями действия этих
сил называется плечом пары. Так как две силы, равные по модулю
и направленные в разные стороны, не лежат на одной линии дей-
действия, то твердое тело, к которому приложена пара сил, не находится
в равновесии. Пара сил стремится повернуть твердое тело, к кото-
которому она приложена.
Мерой действия пары сил является алгебраическая величина, на-
называемая ее моментом. Момент пары сил равен по абсолютной
величине произведению модуля одной из сил пары на плечо. Если
пара сил видна направленной против часовой стрелки, то момент пары
положителен, если по часовой стрелке, то отрицателен. Примеры даны
па рис. 1.28.
Теория пар сил на плоскости сводится к четырем теоремам.
Теорема 1. Алгебраическая сумма моментов сил, составляющих
пару, относительно произвольной точки плоскости не зависит от вы-
выбора этой точки и равна моменту пары.
ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
41
Теорема 2. Не нарушая состояния твердого тела, пару сил
можно переносить в плоскости ее действия.
¦ Теорема 3. Пары сил, моменты которых равны, эквивалентны.
(Пары сил называются эквивалентными, если одну из пар можно за-
заменить другой, не нарушая состояния твердого тела.)
я,=/>/->,
^- f>2 \Fi
Рис. 1.28.
Это значит, что, не нарушая состояния твердого тела, можно из-
изменять величину плеча либо величину силы, сохраняя при этом
неизменным момент пары сил (рис. 1.29).
"'6 h, =6 h2
Рис. 1.29.
Теорема 4 (сложение пар сил на плоскости). При сложении
нескольких пар сил на плоскости получается равнодействующая пара,
момент которой т равен сумме моментов слагаемых нар:
n = ^ mk=
Fkhk.
На рис. 1.30, а показаны три пары сил с моментами m^ = Fxhb
/яа = — Fih-t, m3^Fah3, а на рис. 1.30,6 представлена их равнодей-
равнодействующая пара с моментом т == Рфх — Рф% -j- F3h3 = Fh.
Для равновесия твердого тела под действием пар сил, лежащих
в одной плоскости, необходимо и достаточно, чтобы сумма моментов
данных пар равнялась нулю:
= 0, т. е. 2±% =
42
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. [
Приведение силы к данной точке. При приведении
силы к данной точке добавляется присоединенная пара сил, момент
которой равен моменту данной силы относительно центра приведения.
Рис. 1.30.
Это значит, что, не нарушая состояния твердого тела, можно силу F
приложить в точке В (рис. 1.31), добавив присоединенную пару сил,
момент которой равен моменту заданной силы F относительно центра
приведения В.
Приведением силы к данной точке широко пользуются при пре-
преобразовании произвольной плоской системы сил к простейшему виду.
Главным вектором V называется век-
векторная сумма сил, приложенных к твердому
телу, т. е.
рис [ 3,
Проекции главного вектора Vx и Vv на
оси декартовых координат равны суммам
проекций данных сил на соответствующие оси:
Модуль главного вектора
v=Vvi+ v?.
Направляющие косинусы главного вектора определяются по форму-
формулам:
cos
= •?, cos
Главным моментом т0 относительно центра О называется сумма
моментов сил, приложенных к твердому телу, относительно этого
§ 2] ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ 43
центра, т. е.
В соотиетствии с определением главный вектор V является ста-
статическим инвариантом, т. е. величина и направление главного вектора
не зависят от выбора центра приведения системы. Главный момент
системы при перемене центра, нообще говоря, меняется. Главный мо-
момент тА плоской системы сил относительно нового центра приве-
приведения А равен сумме главного момента этой системы сил относи-
относительно старого центра О и момента относительно нового центра А
главного вектора V, приложенного в старом центре О:
mA = m0-\-mA(VQ).
Приведение к одному центру сил, произвольно
расположенных па плоскости. В результате приведения
сил, произвольно расположенных на плоскости, к одному центру О
система сил преобразуется к приложенной в этом центре силе, рав-
равной главному вектору V, и паре сил, момент которой равен главному
моменту т0.
Не следует отождествлять силу V с равнодействующей R, так
как равнодействующая — это одна сила, которая эквивалентна данной
системе сил, а сила V эквивалентна данной системе сил только в со-
совокупности с парой сил, момент которой равен главному моменту т0.
Частные случаи приведения сил, произвольно рас-
расположенных на плоскости, а) Главный вектор равен нулю,
но гла-вный момент не равен нулю, т. е. V=0, т0 ^ 0. Система сил
приводится к паре сил, момент которой равен главному моменту т0
(в этом случае главный момент системы сил не зависит от выбора
центра приведения).
б) Главный вектор не равен нулю, но главный момент равен нулю,
т. е. V ^ 0, /яо=0. Система сил приводится к равнодействующей
ft= V, приложенной в центре приведения системы.
в) Главный вектор и главный момент системы не равны пулю,
т. е. V -ф 0, т0 jt 0. Система сил приводится к равнодействующей
#= V, линия действия которой отстоит от линии действия силы V
на расстоянии h = mo/V. Положение линии действия равнодействую-
равнодействующей fi должно быть таким, чтобы знак момента равнодействующей fi
относительно центра приведения О совпадал со знаком главного мо-
момента системы сил т0 относительно центра О.
Сила V и равнодействующая R равны по модулю и параллельны
(рис. 1.32).
Теорема Вариньона для произвольной плоской
системы сил. Если система сил приводится к равнодействующей,
44 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
то момент равнодействующей относительно произвольной точки равен
сумме моментов данных сил относительно той же точки (теорема
Вариньона):
л
к = I
г) Главный вектор V и главный момент т0
системы равны нулю V=0, mQ — 0. Твердое тело,
Рис. 1.32. к которому приложена данная система сил, нахо-
находится в равновесии.
¦Уравнения равновесия твердого тела под дейст-
действием произвольной плоской системы сил. Для равно-
равновесия твердого тела под действием произвольной плоской системы
сил необходимо и достаточно, чтобы сумма проекций всех сил на
произвольно выбранные оси декартовых координат х и у и сумма
моментов этих сил относительно произвольно выбранной точки О
равнялись нулю:
2_i * кх — и> 2-i r*y— ' Zj то\гк) — и- U )
к — I к == I к = 1
В случае произвольной плоской системы сил задача является ста-
статически определенной, если число алгебраических неизвестных не бо-
более трех.
Можно ограничиться составлением одного уравнения проекций,
например на ось х, по при этом составить два уравнения моментов
относительно двух произвольных точек:
tl fl fl
?Fkx = 0, % mA(Fk) = O, 2 /яд(/г*) = °- <2*)
При этом следует иметь в ниду, чго ось, относительно которой со-
составляется уравнение проекций, не должна быть расположена перпен-
перпендикулярно к прямой, проходящей через две точки, относительно кото-
которых составляются уравнения моментов. Если это условие не будет
выполнено, то уравнение проекций окажется следствием уравнений
моментов и решение подобной системы уравнений равновесия даст
возможность определить только две неизвестные величины вместо
трех.
Можно, минуя составление уравнений проекций сил, составить
три уравнения моментов относительно трех произвольно выбранных
точек:
2 >nA(Fk) = 0, 2 тв(рь) = 0. 2 '«с(^) = 0- C*)
§ 21 ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ 45
При этом следует иметь d виду, что эти три точки не должны ле-
лежать на одной прямой, так как иначе одно из уравнений равновесия
окажется следствием двух других.
Уравнения равновесия твердого тела под действием плоской си-
системы параллельных сил имеют вид
S Fkx=0, 2 mo(Fk) = 0, D*)
k=l A=l
причем ось х не перпендикулярна данным силам. Задача является
статически определенной, если число алгебраических неизвестных не
более двух.
Можно обойтись без уравнений проекций и составить два урав-
уравнения моментов относительно двух произвольно выбранных точек:
2 тА (Рк) = О, 2 тв {Fk) = 0. E*)
к=\ к=\
Следует иметь в виду, что эти две точки не должны лежать на пря-
прямой, параллельной данным силам, так как в противном случае одно
из уравнений равновесия окажется следствием другого.
При решении задач на равновесие твердого тела,
к которому приложена плоская система параллель-
параллельных сил, надо выполнить четыре первых пункта,
указанных в начале книги на стр. 15. Затем:
5) убедиться в том, что данная задача является статически опре-
определенной, т. е. число алгебраических неизвестных величин не более
двух;
6) выбрать систему осей декартовых координат;
7) составить уравнения равновесия системы параллельных сил;
8) решив уравнения равновесия, определить неизвестные вели-
величины.
Если величина какой-либо неизвестной силы окажется отрицатель-
отрицательной, то это означает, что направление этой силы противоположно
тому, которое было изображено на рисунке.
Оси декартовых координат целесообразно направлять так, чтобы
одна из них оказалась параллельной всем силам, приложенным к твер-
твердому телу. Уравнение моментов рекомендуется составлять относи-
относительно точки, лежащей на линии действия неизвестной силы. Это
дает возможность определить одну из неизвестных величин непосред-
непосредственно из уравнения моментов.
При решении задачи с помощью двух уравнений моментов шестой
пункт решения задачи отпадает. При этом не следует забывать, что
точки, относительно которых составляются уравнения моментов, не
должны лежать па прямой, параллельной силам.
46
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ I
Задача 1.12. В кузове грузовой автомашины весом Р лежит
груз D весом Q = P/2.
Пренебрегая силами трения, определить давления передних и зад-
задних колес автомашины на шоссе. Размеры указаны на рис. а, С —
центр тяжести автомашины.
Решение. Рассмотрим равновесие автомашины. К ней приложены
активные силы: Р — вес автомашины, Q — вес груза. Применив закон
освобождаемости от связей, мысленно отбросим связь — шоссе. Реак-
Реакции шоссе RA и RB, приложенные к колесам, при отсутствии трения
направлены перпендикулярно к шоссе, т. е. вертикально вверх (рис. б).
Конечно, RA и RB являются суммарными реакциями соответственно
двух задних и двух передних колес.
Итак, автомашина находится в равно-
равновесии под действием плоской системы
параллельных сил: Р, Q, RA и RB. За-
Дача является статически определен-
определенной, ибо число алгебраических не-
неизвестных равно двум.
Направим ось х параллельно
силам вертикально вверх, а уравне-
уравнение моментов составим относительно
точки А. Тогда, применив уравне-
уравнения D*), запишем:
=RA-!rRD-P-Q = 0, A)
/?й)=/?в-За —P-2a+Q-o=0.
ставив это значение Rn в
Из уравнения B), приняв во внимание,
что Q = Я/2, найдем RD = Я/2. Под-
уравнение A), получим /?л-= Я. Итак,
у
C)
Искомые давления колес автомашины на шоссе равны по модулю
соответствующим реакциям и направлены противоположно, т. е. вер-
вертикально вниз.
Эту задачу можно было решить с помощью уравнений равнове-
равновесия, в каждое из которых входит лишь одна неизвестная величина.
Для этого вместо уравнения A), содержащего две неизвестные вели-
величины RA и RB, следует составить уравнение моментов относительно
точки В. Это уравнение удобно тем, что в него не входит RD (мо-
(момент силы Rn относительно точки В равен нулю):
i ~\- Q ¦ \а = 0. D)
§ 2] ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ 47
Из уравнения D) при Q = P/2 непосредственно получим /?Д = Я
(ср. формулу C)).
Задача 1.13. Консольная балка AD весом Я=4 Т лежит на
двух опорах В и D, причем опора В расположена на катках. На
конце А к балке приложена вертикальная сосредоточенная сила
F=8 Т. На участке CD на балке находится равномерно распреде-
распределенная нагрузка интенсивности q^Q,o Т/м (интенсивностью назы-
называется величина силы, действующей на единицу длины). На участке АВ
к балке приложена пара сил с моментом m = 6 Тм.
Определить опорные реакции в В и D. Размеры указаны па ри-
рисунке.
Решение. Рассмотрим рашювесие консольной балки AD (уча-
(участок балки АВ, расположенный вне опор, назьшается консолью).
На балку действуют активные
силы: вес балки Р, приложенный '
в ее середине, вертикальная а) | <?" J ?П111 !l 11 П
сила F, равнодействующая Pt А ' \ й i I Ц
распределенной нагрузки (Р\ = ffih. ' i
= q.CD=\ Г), приложенная в се-
середине участка CD и направлен- ¦*«
ная по вертикали вниз, и, нако-
наконец, пара сил с моментом т.
Применив закон освобождае-
мости от связей, направим опор-
опорную реакцию RB по вертикали
иверх. При равновесии балки
главный вектор и главный момент К задаче 1.13.
равны нулю. Главный вектор ра-
равен сумме вертикальных сил F, Р, Рь RB и опорной реакции RD
(главный вектор пары сил равен нулю). Для того чтобы главный
вектор был равен нулю, опорная реакция RD должна быть направ-
направлена вертикально.
Итак, балка находится в равновесии под действием системы па-
параллельных сил (пару сил можно, не нарушая равновесия балки, по-
повернуть так, чтобы силы, входящие в ее состав, были направлены
вертикально), в число которых входят две неизвестные по модулю
силы RB и RD. Следовательно, задача является статически опреде-
определенной.
При решении этой задачи целесообразнее, минуя составление урав-
уравнения проекций на ось, параллельную приложенным силам, составить
два уравнения моментов относительно точек приложения В и D не-
неизвестных сил RB и RD. При этом учитываем, что сумма моментов
сил, входящих в состав пары сил, вычисленная относительно любой
точки, равна моменту этой пары сил. Сумму моментов сил распреде-
распределенной нагрузки CD заменяем на основании теоремы Варииьопа
48
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
моментом равнодействующей силы Ру. Получим:
= F-2 — т — Р-1—Р, -3 +
',-1=0. B)
Удобство составленных уравнений заключается в том, что в каждое
из них входит только одна неизвестная величина.
Из уравнений A) и B) находим:
RD = — 0,75 Т, RB= 13,75 Т.
Отрицательное значение RD указывает, что направление силы RD про-
противоположно тому, которое изображено на рисунке, т. е. опорная
реакция RD направлена по вертикали вниз.
Задача 1.14. Однородная горизонтальная балка АВ весом
Р=800 и в сечении D защемлена в стене (рис. а). К балке прило-
приложены: вертикальная сосредоточен-
сосредоточенная сила F=1200 и и пара сил,
стремящаяся повернуть балку по
часовой стрелке. Момент пары ра-
равен m = 600/ дж, где / — длина
свободного конца балки, рав-
равная 2 м.
Определить реакцию и момент
реактивной пары в защемленном
сечении D. Размеры указаны на
i рисунке. Длиной защемленной
части балки пренебречь.
Решение. Рассмотрим рав-
б) новесие балки. К ней приложены
К задаче 1.14. активные силы: Р, F и пара сил
с моментом т. Глухая заделка
балки в стену препятствует перемещению балки по вертикали вниз,
а также ее повороту в вертикальной плоскости под действием актив-
активных сил по часовой стрелке. Поэтому, применив закон освобождаемое ги
от связей и мысленно отбросив стену, мы должны компенсировать ее
действие на балку реакцией RD и реактивной парой сил, стремящейся
повернуть балку против часовой стрелки (рис. б). Главный вектор
является суммой Р, F и реакции RD (напомним, что главный вектор
каждой из пар равен нулю). Так как при равновесии балки главный
вектор равен нулю, а силы Р и F вертикальны, то реакция RD также
направлена вертикально (рис. б).
Повернув активную и реактивную пары так, чтобы входящие
в них силы были направлены вертикально, мы получим плоскую си-
систему параллельных сил. Данная задача является статически опреде-
определенной, ибо число неизвестных равно двум (RD и т0). Переходим
§ 2] ПРОИЗВОЛЬНАЯ СИСТЕМ* СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ 49
к составлению уравнений равновесия. Составим уравнение проекций
на вертикальную ось у и уравнение моментов относительно точки D:
2 mD(Fk) = тр - т - Р-¦!¦ - F¦ \ 1= 0.
Из первого уравнения находим RD = Р-\- F = 2000 я, а из вто-
второго получим /ир = 3800 дж. Положительные значения RD и тр
указывают, что направления силы Rd и реактивной пары с моментом
/И„ были выбраны правильно.
Рекомендуем решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Ме-
Мещерского, издания 1950 г. и последующих лет: 78, 87,
89, 90.
Переходим к решению задач на равновесие твер-
твердого тела, к которому приложена произвольная
плоская система сил. При решении этих задач надо
выполнить четыре первых пункта, указанных в на-
начале книги на стр. 15. Затем:
5) убедиться в том, что данная задача является статически опре-
определенной, т. е. что число неизвестных величин не более трех;
6) выбрать направления осей декартовых координат и точку
(или точки), относительно которой предполагается составить урав-
уравнение моментов;
7) составить уравнения равновесия твердого тела;
8) решить систему полученных уравнений равновесия и опреде-
определить неизвестные величины.
Уравнения равновесия можно составить в любом возможном виде
(см. выше, стр. 44, формулы A*), B*), C*)).
Следует стремиться к получению таких уравнений равновесия, в
каждое из которых входила бы только одна неизвестная величина.
В этом случае можно каждую из неизвестных величин непосредственно
определить из соответствующего уравнения. Для этого оси координат
целесообразно направить так, чтобы некоторые неизвестные силы ока-
оказались перпендикулярными к этим осям. Тогда величины этих неиз-
неизвестных сил-в соответствующее уравнение проекций не войдут. Центр
моментов, т. е. точку, относительно которой должно быть составлено
уравнение моментов, следует выбрать в точке пересечения линий
действия двух неизвестных сил. Это дает возможность непосредственно
определить из соответствующего уравнения моментов величину третьей
неизвестной силы. Если, однако, этот центр моментов расположен
так, что вычисление плеч при определении моментов сил представ-
представляет значительные трудности, то лучше составить относительно дру-
другого центра такое уравнение моментов, в которое войдут величины
50
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. f
днух неизвестных сил, и затем совместно решить полученную си-
систему уравнений.
Если направление какой-либо реакции связи неизвестно, то следует
заменить ее двумя составляющими, направив их параллельно осям
кг ординат в сторону положительного отсчета. Если в результате ре-
решения знак величины какой-ли.бо силы окажется отрицательным, то
это означает, что направление силы противоположно тому, которое
было предварительно указано на рисунке.
В тех случаях, когда по условию задачи требуется определить
давления твердого тела на опоры, нужно найти равные по модулю
этим давлениям соответствующие реакции связей, а затем направить
искомые давления противоположно этим реакциям.
Задача 1.15, Горизонтальная однородная балка АВ длиной /= 4 м
и весом Р^1 Г, прикрепленная шарниром А к стене, удерживается
у-
//////////¦'////////////////////////////Л
К задаче 1.15.
в ранповесии тросом DE, расположенным под углом 45° к горизонту;
DB=l м. К свободному концу балки В приложена сосредоточенная
сила F = 2T, образующая угол 60° с горизонтом.
Определить давление балки на шарнир А и натяжение троса DE.
Решение. Рассмотрим равновесие балки АВ, на которую дейст-
действуют две активные силы: вес балки Р, приложенный в ее середине
(АС=СВ^ 2 м), и сосредоточенная сила F, приложенная в конце
балки В.
На балку наложены две связи, шарнир А и трос DE. Мысленно
оборвав трос DE, заменяем действие троса на балку реакцией троса
Т, направленной от точки D в сторону обрыва. Направление реакции
шарнира А заранее указать нельзя. Поэтому изобразим две взаимно
перпендикулярные составляющие этой реакции. Направим ось х вдоль
оси балки по горизонтали направо, а ось у по вертикали вверх. Состав-
Составляющие реакции RAx и RAy направим вдоль осей координат в сторону
их возрастания.
§2] ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ 51
Теперь балку можно рассматривать как свободное твердое тело,
находящееся в равновесии под действием пяти сил, причем лишь ве-
величины трех сил Т, RAx и RAy неизвестны. Следовательно, задача
является статически определенной.
Составим уравнения равновесия балки в проекциях на оси х и у
и уравнение моментов относительно точки А. Выбор точки А в ка-
качестве центра моментов удобен, так как моменты двух неизвестных
по величине сил RAx и RAy относительно точки А равны нулю и в
уравнение моментов войдет лишь одна неизвестная Т. Уравнения
равновесия имеют вид
2 Ркх = RAX-{-T cos 45° -j- F cos 60° = 0, (i)
2 Fky =RAy — P-\-T cos 45° — F cos 30° = 0, B)
2mA(Fk)=T-AK — P-AC— F-AM = 0. C)
Из уравнения (З) находим
Так как
Г— рАС +FAM
А С = 2 м, АК = AD sin 45° = ~ У^ м,
[ = 4?sin 60°= 2/3 м,
то
Т = 1 Щ- -\- 21- /б = Д^ A + 2/3) = 4,2 Г.
3
Подставив это значение 7" в уравнения A) и B), получим:
#^ = - 3,96 Т, RAy = - 0,23 Т.
Знак минус, стоящий в выражении RAx, указывает, что нанравле-
1 иг составляющей реакции шарнира RAx противоположно тому, кото-
которое было указано па рис. б, т. е. сила RAx направлена по горизон-
горизонтали налево; аналогично сила RAv направлена по вертикали вниз.
Искомые давления балки на связи направлены противоположно
соотиетствующим реакциям связей и равны им по модулю, т. е. го-
горизонтальная составляющая силы, действующей на шарнир, равна
3,96 Т и направлена по горизонтали направо, вертикальная составля- .
ющая силы, действующей на шарнир, равна 0,23 Т и направлена
вверх, натяжение троса равно по модулю 4,2 Т.
Задача 1.16. На рис. а изображена симметричная стропильная
ферма длиной /=10 м, весом Р=12 7", стоящая на двух опорах,
причем левая опора А расположена на катках, которые могут пере-
перемещаться вдоль горизонтальной плоскости. Перпендикулярно к АЕ
в точке D, на расстоянии AD=2 м, приложена сосредоточенная
сила /7=4 Т,
52
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. Г
Определить опорные реакции в точках А и В.
Решение. Рассмотрим равновесие фермы, к которой приложены
две активные силы: вес фермы Р и сосредоточенная сила F.
Так как катки не препятствуют перемещению фермы в горизон-
горизонтальном направлении, то опорная реакция RA направлена перпендику-
перпендикулярно к горизонтальной плоскости. Указать заранее направления
опорной реакции в точке В невозможно. Поэтому в опоре В следует
изобразить две взаимно
перпендикулярные состав-
составляющие реакции (рис. б).
Направим ось х по
горизонтали направо, ось
у по вертикали вверх,
а составляющие реакции
Rnx и Кцу параллельно
соответствующим коор-
координатным осям.
Итак, к ферме прило-
приложены пять сил, в том
числе три неизвестные по
модулю силы: RA> RBx и
RBV. Следовательно, за-
•"? дача является статически
определенной.
Используем уравне-
уравнения равновесия фермы в
проекциях на оси хну
и уравнение моментов
относительно точки А.
К задаче 1.16. Составление уравнений
проекций на оси л: и у
целесообразно потому, что силы RA и RBy перпендикулярны к оси х,
а сила RBX перпендикулярна к оси у. Следовательно, эти три неиз-
неизвестные по модулю силы в соответствующие уравнения проекций не
войдут. Выбор точки А в качестве центра моментов удобен потому,
что линии действия сил RA и RBX пересекаются в этой точке. Сле-
Следовательно, моменты этих сил относительно точки А равны нулю и
в уравнение моментов войдет лишь неизвестная величина силы RBy.
Уравнения равновесия имеют вид
—Fcos30° —P = 0,
A)
B)
C)
§ 21 ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ 53
Из уравнения C) находим:
Учитывая, что AD — 1 м, АК=5 м, АВ—Юм, F=4 Т, Р=\2 Т,
получаем, что RBy = 6,8 Т. Подставив это значение RBy в уравнение
B), имеем RA=8,66 Т. Из уравнения A) находим, что #вл =
= — F cos 60° = — 2 7.
Знак минус, полученный в выражении для RBx, указывает, что
направление составляющей опорной реакции RBx противоположно
тому, которое было указано на рисунке, т. е. сила REx направлена
по горизонтали налево.
При решении системы уравнений A), B) и C) модули неизвест-
неизвестных сил RBx и РВу были непосредственно определены из уравнений
A) и C). Лишь величину силы RA пришлось вычислить из уравнения
B), подставив в него значение RBy. Однако можно составить такую
систему уравнений равновесия, чтобы из каждого уравнения была,
независимо от других, определена каждая из неизвестных. Действи-
Действительно, сохранив уравнения A) и C), составим вместо уравнения B)
такое уравнение моментов, чтобы в него вошла лишь одна иеизвес!-
ная RA. Для этого необходимо, чтобы моменты двух других неизвест-
неизвестных сил, т. е. RBx и RBV, оказались равными пулю. Этому условию
легко удовлетворить, выбрав за центр моментов точку пересечения
линий действия этих сил, т. е. точку В. Итак, вместо уравнения B)
сосгаиим уравнение моментов сил относительно точки В:
2i 0. D)
Из уравнения D) непосредственно находим:
Учитывая, что KB = 5 м, АВ=Ю м, NB = MB — MN—AB cos 30° —
— AD = 5 Уз — 2 = 6,65 м, P=z12 T, F=4 T, получим RA = 8,66 Т.
Задача 1.17. Ознакомившись с условием и решением задачи 1.6,
определить силы RA и F с учетом веса суппорта, приложенного
в его центре тяжести С и равного Р = 60 кГ.
Решение. В задаче 1.6 мы рассмотрели равновесие суппорта
под действием трех сил: N, F и RA, использовав теорему о трех
непараллельных силах. Теперь к этим силам добавляется вес суппор-
суппорта Р. Это лишает нас возможности применить теорему о трех непа-
непараллельных силах, с помощью которой мы смогли определить поло-
положение линии действия реакции RA цилиндрического шарнира А.
Поэтому заменим силу #д двумя взаимно перпендикулярными состав-
составляющими. Направив ось х по горизонтали направо, а ось у но
вертикали виерх, изобразим на рис. б составляющие RAx и RAy.
54
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
Итак, суппорт находится в равновесии под действием плоской
системы пяти сил: N, Р, F, RAx и RAy. Задача является статически
определенной, ибо число алгебраических неизвестных равно трем: F,
Составим уравнения проекций па оси х и у и уравнение момен-
моментов относительно точки В. Выбор точки В целесообразен, ибо линии
действия двух неизвестных сил RAx
и F пересекаются в точке В. Зна-
Значит, моменты этих сил относительно
точки В равны нулю. В уравнение мо-
моментов войдет лишь одна неизвестная
величина RAy, которую непосредственно
можно будет определить. Уравнения
равновесия имеют вид
^-N cos 60°+1*^=0,
«в
= P-BC—RAy-AB +
+ N-BS=0.
х
Из уравнения C) получим:
_P-BC + N-BS
КАУ — АВ
B)
C)
D)
.17.
По условию: Р=60кГ, N= 300 к Г,
ВС= 15 см, АВ = 30 см. Из треуголь-
треугольника BSE имеем BS = BE ¦ sin Ж =
= 46 '^ =23 см (здесь использована
формула A) задачи 1.6). Подставив эти значения в D), находим:
Яд, = 260кГ. E)
Затем из уравнений A) и B) имеем RAx = N cos 60° = 300- ^= 150 кГ,
/j^p-j-A/cosSO0— RAy = 60+ 150 /3—260 = 60 кГ. Итак,
RAx = 150 кГ, Р = 60 к Г. F)
Использовав результаты E) и F), вычислим модуль реакции Лл
цилиндрического шарнира А по
Получим:
RA = 300 кГ.
G)
§ 21 ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ 55
Как и следовало ожидать, учет силы тяжести Р суппорта сказался
на увеличении реакции RA и силы упругости F. Напомним, что при
решении задачи 1.6 без учета веса суппорта эти силы были по мо-
модулю равны: RA = 275 кГ, F = 3OtcF (см. формулу C) задачи 1.6).
Как и в предыдущей задаче, вместо уравнения B) можно составить
уравнение моментов относительно точки А. Это дало бы нам воз-
возможность сразу определить силу F.
Конечно, задачу 1.6 можно также решить с помощью системы
уравнений A), B), C). Действительно, приняв в этих уравнениях
Р—0, мы получим: RAx=l50 кГ, RAy — 230 kF, F='dO кГ и,
следовательно, RA = у R%x~r К*Ау == '^5 к^-
Рекомендуем решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Ме-
Мещерского, издания 1950 г. и последующих лет: 122,
123, 129, 133, 134, 135, 136, 140.
2°. Опрокидывание твердых тел. При исследовании
покоя твердого тела (конструкций) встречаются задачи, в которых
следует определить предельные значения сил или размеров, обеспечи-
обеспечивающих сохранение этого состояния. В этих задачах обычно при
величине силы, превышающей наибольшее допустимое значение, обе-
обеспечивающее покой твердого тела, происходит опрокидывание тела
вокруг одной из точек опоры.
Такие задачи решаются в предположении, что твердое тело начинает
отрываться от одной из опор. Поэтому реакции этой опоры не сле-
следует учитывать. Тогда при равновесии твердого тела реакция остав-
оставшейся опоры должна уравновешиваться с равнодействующей всех
активных сил. Это значит, что линия действия равнодействующей
всех активных сил проходит через оставшуюся опору и, следовательно,
момент равнодействующей относительно точки опоры равен нулю.
Таким образом, в соответствии с теоремой Варипьоиа сумма моментов
всех активных сил относительно точки опоры О равна нулю:
Из этого уравнения определяются предельные значения сил или
размеров твердого тела, при которых еще не наступает опрокиды-
опрокидывание.
Решение задач на опрокидывание твердых тел
надо проводить в следующем порядке:
1) изобразить активные силы;
2) определить опору, относительно которой может произойти
опрокидывание твердого тела;
3) составить уравнение моментов активных сил относительно этой
точки опоры;
56
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
4) решив уравнение, определить искомую величину (предельную
силу или предельный размер).
Задача 1.18. Горизонтальная консольная балка АС весом Р
лежит на опорах А и В, причем опора А расположена на катках,
не препятствующих перемещению вверх. К консольному концу С
балки приложена сосредоточен-
сосредоточенб
-2м-
К задаче 1.18.
ная вертикальная сила F.
Определить наибольшее зна-
значение силы F, при котором балка
остается в покое. Размеры ука-
указаны на рисунке.
Решение. На балку дейст-
действуют две активные силы: вес
балки Р, приложенный в середине балки, т. е. па расстоянии 1 м от
опоры В, F—сосредоточенная сила, приложенная в конце консоли,
т. е. в точке С.
Нетрудно видеть, что при большом значении силы F произойдет
опрокидывание балки вокруг опоры В в направлении по часовой
стрелке.
Для определения наибольшего значения силы F надо сумму мо-
моментов активных сил относительно точки В приравнять нулю:
Р Р
откуда F = y. Если сила F^>y, то происходит опрокидывание бал-
балки покруг опоры В в направлении по часовой стрелке.
Задача 1.19. Подъемный кран установлен на грузовой автомашине.
Вес противовеса В равен P<j = 2 Т. Вес автомашины с краном без
противовеса, равный /?j = 5 7",
приложен в точке С.
Определить наименьшее рас-
расстояние DE между осями колес
автомашины и наибольший вес Ра
поднимаемого груза А, при нали-
наличии которых автомашина не опро-
опрокинется как с грузом А, так и
без него. Размеры указаны на
I D \ К
1-"—Аи »1- "I I-»-
1,5м 2м
К задаче 1.19.
рисунке.
Решение. К грузовой авто-
автомашине с установленным на ней
подъемным краном приложены активные силы: Рх — вес автомашины
с краном без противовеса В, Р% — пес противовеса В. При наличии
груза А приложен также его вес Р3. ¦
При подвешенном грузе А может произойти опрокидывание авто-
автомашины в направлении против часовой стрелки вокруг точки касания D
8 21 ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ 57
переднего колеса с землей. При отсутствии груза А может совер-
совершиться опрокидывание автомашины под действием противовеса В
и направлении по часовой стрелке вокруг точки касания Е заднего
колеса с землей. Иные варианты опрокидывания не рассматриваем
как практически неинтересные.
Для определения наибольшей величины веса Р3 поднимаемого
груза А и наименьшего расстояния DE между осями колес, обеспе-
обеспечивающего равновесие автомашины, надо составить: 1) уравнение мо-
моментов активных сил относительно точки D с учетом момента неса /*,,,
2) уравнение моментов активных сил относительно точки Е без учета
момента веса Р3. Эти уравнения имеют вид
Р3.4 —/>,.1,5 — P,(D?-L2) = 0,
PX(DE— 1,5) — Pj.2 = 0.
Решив эту систему уравнений равновесия при Р., = о Т, Pq=2 T,
находим: Р3 = 4 Т, DE=%3 м. Таковы предельные значения Ря и DE,
обеспечивающие равновесие автомашины.
В случае Рз^>4 Г произойдет опрокидывание автомашины вокруг
точки D в направлении против часовой стрелки.
В случае DE<^2,3 м при отсутствии груза А произойдет опро-
опрокидывание автомашины вокруг точки Е в направлении но часовой
стрелке.
Рекомендуем решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Мещер-
Мещерского, издания 1950 г. и последующих лет: 94, 95, 96.
3°. Приведение произвольной плоской системы сил
к простейшему виду. Рекомендуется следующий порядок выпол-
выполнения приведения:
1) выбрать оси декартовых координат;
2) выбрать центр приведения системы сил;
3) вычислить проекции главного вектора системы сил по фор-
формулам
k=l ft=I
4) определить модуль главного вектора V=V^Vx-\- V'y и направ-
направляющие косинусы
cos (х, V) = -Л, cos (у, V) = -У;
5) вычислить главный момент системы сил относительно центра
приведения по формуле
я
wo= 2 mo(Fk)>
где О — центр приведения системы сил;
58 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
6) в зпвисимости от значений V и т0 возможны четыре случая:
а) если V ф 0 и т0 ф О, то следует систему принести к равно-
равнодействующей R, равной силе V, отстоящей от нее на расстоянии
h = mo/V и расположенной так, чтобы знак момента равнодействую-
равнодействующей относительно центра О совпадал со знаком главного момента т0;
б) если V^O, то — 0, то система сил приводится к равнодей-
равнодействующей, совпадающей с V;
в) если V = 0, пго^0, то система сил приводится к паре сил
с моментом т0;
г) если V=0 и /яо = 0, то система сил находится в рапновесип.
Уравнение линии действия равнодействующей в случаях а) и 6)
имеет вид
п
xRy — yRx= 2 mo(Fk),
где RX=VX, Rv=Vy, a x и у — текущие координаты точки линии
действия равнодействующей, О — начало координат.
Оси декартовых координат следует папранлять так, чтобы силы
и возможно большем числе оказались параллельными либо перпен-
перпендикулярными к этим осям. Центр приведения системы следует выби-
выбирать гак, чтобы моменты сил относительно этого центра в возможно
большем числе обратились в нуль, т. е. чтобы линии действия этих
сил проходили бы через центр приведения системы.
При переходе от одного центра приведения (О) к другому центру
приведения (А) следует иметь в виду, что главный вектор V от вы-
выбора центра приведения не зависит (главный вектор является стати-
статическим инвариантом), а главный момент системы изменяется и соот-
соответствии с формулой
Задача 1.20- Произвольная плоская система сил была приведена
к центру О. В результате приведения были получены сила V (см. ри-
рисунок) и пара сил, момент которой равен главному моменту mo = 4Va.
Определить главный момент этой системы сил при переходе
к новому центру приведения А, находящемуся на расстоянии ОА = а
от старого центра по оси х.
Решение. Выбираем оси декартовых координат так, как это
изображено на рисунке.
Задачу можно решить двумя способами.
1. Приведем силу V к точке А. Для этого приложим в точке А
две уравновешивающиеся силы V и V так, чтобы одна из них была
векторно равна силе У. Теперь сила V оказалась приведенной
к точке А. При этом добавилась пара сил (присоединенная пара),
в состав которой входят сила V, приложенная в точке О, и сила V,
§2]
ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
59
т.
т.
'А г
приложенная в точке А. Момент присоединенной пары тпр равен
тпр=— Va.
Следовательно, помимо силы V, приложенной в точке А, мы имеем
две пары сил с моментами т0 и тпр. Эти две пары сил экпивалентпы
равнодействующей паре сил с моментом тА,
равным тА=т0-\- отпр = 4 Va— Va^SVa.
Величина тА является искомым главным мо-
моментом системы сил относительно нового
центра приведения А.
Итак, в результате перехода от старого
центра приведения О к новому центру А
главный момент системы изменился.
2. Эту задачу можно решить, восполь-
воспользовавшись тем, что сила V, равная главному
вектору системы сил, является статическим
инвариантом, т. е. не зависит от выбора
центра приведения, а главный момент системы изменяется. Как из-
известно, главный момент произвольной плоской системы сил относи-
относительно нового центра приведения равен алгебраической сумме глав-
главного момента этой системы относительно старого центра и момента
относительно нового центра глав-
главного вектора системы, приложен-
приложенного в старом центре, т.е. тА =
= т0 -\- тА (Vo). Учитывая, что по
условию /rao=4l/a, a tnA (Vo) =
= —Va, находим tnA=3Va.
Задача 1.21. К диску прило-
приложены четыре силы: Fi = Fi = F,
К задаче 1.20.
Привести эту систему сил к
простейшему виду.
Решение. Взяв начало коор-
координат в центре О диска, напра-
направим ось х по горизонтали на- К задаче 1.21.
право, а ось у по вертикали
вверх. За центр приведения системы примем точку О. Определим глав-
главный вектор V и главный момент т0 данной системы сил. Так как
A)
то предварительно вычислим проекции Vx и Vy главного вектора V
п
на декартовые оси координат и сумму моментов V mQ {Fk) всех сил
60
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
относительно точки О:
Vx = 2.Fkx= — Fi cos 30° — Ft cos 30°-f-FL cos 45°, B)
Vy = V Fky = — Ft cos 60° -f- F\ cos 60° — Fz -4- Ft cos 45°, C)
2 m0 (Fh) = Fз • a - F, ¦ a sin 45°, D)
где буквой а обозначен радиус диска. Из B) — D) получим: V* = 0,
Vj, = O, V /ho(F/;) = 0. Теперь формулы A) принимают вид: V=0,
то = 0.
Итак, главный вектор V и главный момент т0 оказались рав-
равными нулю. Как известно, это условие является необходимым и доста-
достаточным для равновесия твердого тела. Значит, диск под действием
данной системы сил находится в покое.
Задача 1.22. Вдоль сторон равностороннего треугольника на-
направлены три равные но модулю силы j ^ | = | /% | = | f1 ^= /"'. Длина
стороны треугольника равна а.
Привес in систему сил к простейше.му виду.
в
Й7"
К задаче 1.22.
Р е in е и и е. Выбрав начало осей декартовых координат в иер-
шине треугольника А, направим ось х по горизонтали направо и
ось у по вертикали вверх. Определим главный вектор и главный
момент данной плоской системы сил. Выберем в качестве центра
приведения точку А.
Модуль глашюго вектора данных сил вычислим по формуле
Vx =
Vy =
-Vj., где
hx = Ft — Fi cos 60° — F3 cos 60° = 0,
ky = Fi cos 30° — F3 cos 30° = 0.
Следовательно, главный вектор равен нулю: V^0.
Вычислим главный момент данной системы сил относительно
центра приведения А. Учитывая, что
= тА (F3) = 0, тА (F.2) = F.VAD = ^- Fa,
§2] ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ 61
получим: г -
тА = тА (FJ + тА (F,) + тА (Fz) = *± Fa.
Итак, выбрав в качестве центра приведения данной системы сил
точку А, мы нашли:
V=0, mA = №-Fa,
т. е. установили, что система сил приводится к паре сил с моментом
т = Ку- Fa. Как известно, в случае приведения системы сил к паре
сил главный момент не зависит от выбора центра приведения.
Эту задачу можно было решить иначе. Так, например, совершив
перенос силы F3 по ее линии действия в точку А, можно сложить
силы FY и F'v приложенные в точке А (рис. б). Суммой этих сил
будет сила Flb, являющаяся диагональю ромба, угол при вершине
которого равен 120°. В этом случае диагональ ромба равна его сто-
стороне, т. е. \Fli3\^F. Итак, данная система сил оказалась приведен-
приведенной к паре сил, в состав которой входят силы /^ и Z7, :„ с плечом
h = AD = aK}-. Момент этой пары сил равен m = Fh — -^-Fa.
Второй вариант решения задачи оказался более коротким. Однако
следует иметь в виду, что в первом варианте использован более
общий прием приведения произвольной плоской системы сил к про-
простейшему виду, которым неизменно следует пользоваться при реше-
решении более сложных задач.
Задача 1.23. Привести к простейшему виду систему сил Ft, F^
и F3, изображенную на рис. а. Силы F\ и /\, направлены по проти-
противоположным сторонам, а сила F3 — по диагонали прямоугольника
ABCD, сторона AD которого равна a. \F1\ = \F%\ — ^-\F3\ = F.
Решение. Выбрав начало осей декартовых координат в вер-
вершине прямоугольника А, направим ось х по горизонтали направо,
а ось у по вертикали вверх. (Выбор таких направлений осей х и у
удобен, так как две силы из трех параллельны оси у \\ не дают
проекций на ось дг.)
Приведем данную систему сил к главному вектору и главному
моменту. Выберем в качестве центра приведения системы сил начало
координат А. Найдем сначала проекции главного вектора на оси
координат:
V, = 2 Fkx = - F, cos 30° = —
Модуль главного вектора V равен
^V$ = 2F, A)
62 ПЛОСКАЯ СИСТЕМА СИЛ
а направляющие косинусы будут:
[ГЛ. I
т. е. (х, V) = 150°, (у, V) = 60°. Сила V изображена на рис. б.
Переходим к определению главного момента системы сил отно-
относительно центра приведения А. Учитывая, что
= тА (F3) = 0,
т
тА (FJ =
находим:
= тА (f,) -f mA
B)
Итак, система сил оказалась приведенной к силе V и паре сил с мо-
моментом тА, направленным против часовой стрелки.
а)
К задаче 1.23.
Известно, что если V^O и тА ^ 0, то'систему сил можно при-
привести к равнодействующей силе R. Для этого изобразим пару сил,
соответствующую главному моменту тА, так, чтобы силы, входящие
в состав пары сил, равнялись по модулю силе V, причем одна из них
(V) лежала бы на одной линии действия с силой V и была направ-
направлена ей противоположно. При этом вторая сила, входящая в состаа
пары сил, приложенная в точке К, окажется векторпо равной силе V.
Плечо пары /2 = ЛК следует подобрать так, чтобы момент этой нары
сил был равен главному моменту тА, т. е. m^= Vh, откуда й =
= АК= пгА/V- Воспользовавшись формулами A) и B), находим
h = aj2. Теперь мы получили систему, состоящую из трех сил. Мо-
Модуль каждой из этих сил равен модулю главного вектора V. Две
силы, приложенные в точке А, равные по модулю и направленные
в противоположные стороны по общей линии действия, уравновеши-
уравновешиваются. Эти силы можно отбросить, не нарушая состояния твердого
тела. Остается одна сила V, приложенная в точке К, эквивалентная
§ 31 РАВНОВЕСИЕ СИСТЕМЫ ТВЕРДЫХ ТЕЛ 63
данной системе сил. Следовательно, эта сила, равная главному век-
вектору V, является равнодействующей Л. Таким образом, нам удалось
привести данную систему сил к равнодействующей R.
Определим уравнение линии действия равнодействующей R, вос-
воспользовавшись уравнением
xRy-yRx=^mA{Fk). C)
Проекции равнодействующей /? на оси декартовых координат равны
проекциям главного вектора V па соответствующие оси, т. е. Rx =
= — Fy 3 , Ry = F. Сумма моментов всех данных сил относительно
начала координат А является главным моментом тА, определяемым
формулой B):
? тА (Fb) = mA = Fa.
Подставив значения Rx> Rv, 2 тА (Fk) в уравнение C), находим
уравнение линии действия равнодействующей /?:
Это — уравнение прямой с угловым коэффициентом, равным —
откуда следует, что угол, образованный этой прямой с осью х, со-
составляет 150°.
Найдем точки пересечения линии действия равнодействующей
с осями координат. Имеем: при х-=0 у=^~а, при у = 0 х = а.
Следовательно, равнодействующая направлена по диагонали DB пря-
прямоугольника ABCD.
§ 3. Равновесие системы твердых тел
В статике твердого тела наряду с равновесием одного тела рас-
рассматриваются сочлененные системы материальных тел, т. е. совокуп-
совокупности твердых тел, касающихся друг друга своими поверхностями
или соединенных друг с другом шарнирами, гибкими нитями или
стержнями.
Важной задачей статики системы твердых тел является определе-
определение реакций связей. Для этого основным является способ расчлене-
расчленения, при котором наряду с равновесием . всей системы тел рассмат-
рассматривается равновесие отдельных тел (или групп тел системы). При
этом все остальные тела системы и соответствующие связи мысленно
отбрасываются, а их действие на тело, равновесие которого рассмат-
рассматривается, заменяется реакциями.
Следует заметить, что при рассмотрении равновесия всей системы
твердых тел реакции связей между телами, входящими в систему, не
64
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
В
Рис. 1.33.
должны учитываться; они не входят в уравнения равновесия, как
внутренние, взаимно уравновешенные силы. А при рассмотрении ран-
иовесия каждого тела в отдельности или какой-либо группы тел,
входящих в систему, соответствующие реакции связей, которые были
мысленно расчленены, становятся внешними силами и входят в ураи-
нения равновесия.
Задачи на равновесие системы твердых тел, находящихся под
действием произвольной плоской системы сил, решаются путем при-
применения уравнений равновесия твер-
твердого тела, разобранных в § 2 (уран-
неиия A*) или B*), или C*)).
Рассмотрим в качестве примера си-
системы твердых тел, изображенные на
рис. 1.33, 1.34.
Шатунно-кривошипный механизм
ОАВ (рис. 1.33) состоит из трех твер-
твердых тел: кривошипа ОА, шатуна АВ и ползуна В. Эти тела соеди-
соединены друг с другом шарнирами А и В. Кроме того, на них на-
наложены еще две связи: шарнирное закрепление в точке О и гори-
горизонтальные направляющие, препятствующие вертикальному переме-
перемещению ползуна В.
Цилиндрический стакан (рис. 1.34) поставлен вверх дном на гори-
горизонтальный пол, внутри стакана покоятся два шара. Эта система со-
состоит из трех твердых тел: шара Ои шара
0.2 и стакана, находящихся друг с другом
в контакте. На эту систему тел наложена
одна внешняя связь: гладкий горизонталь-
горизонтальный пол.
При решении задач на равновесие си-
системы тел недостаточно, как правило, рас-
рассмотреть равновесие этой системы в целом.
Для всей системы условия равновесия сво-
сводятся или к трем уравнениям равновесия для
плоской системы сил, или к двум уравне-
уравнениям для плоской системы параллельных
сил. В этом случае число неизвестных может быть больше числа
перечисленных уравнений.
Однако это обстоятельство еще не делает систему статически не-
неопределимой, так как если разделить систему на отдельные твердые
тела и составить уравнения равновесия для каждого из них, то число
новых неизвестных может быть меньше числа новых уравнений рав-
равновесия. Если число всех составленных таким образом независимых
уравнений равновесия для всей системы и отдельных ее частей будет
равно числу всех неизвестных, то такая задача является статически
определенной.
У/////////////////////////.
Рис. 1.34.
РАВНОВЕСИЕ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
65
Поясним это на примере трехшарнирной арки (рис. 1.35, a). Apica
состоит из двух симметричных молуарок, соединенных в точке С
шарниром. В точках А и В арка шарпирпо прикреплена к фундаменту.
На арку действуют две активные известные силы: горизонтальная
сила Q, приложенная в точке D, и вертикальная сила Р, приложен-
приложенная в гочке Е. Применяя принцип освобождаемоеги от связей, отбро-
отбросим мысленно шарнирные закрепления в точках Л и Б и заменим
их действие силами реакций. Величины и направление Э1их реакций
неизвестны. Следовательно, их можно предиавть двумя составляю-
составляющими каждую: F Ах и FAv, Flix и Fliy. Таким образом, для системы
Рис 1 35.
гьердых чел, сосюящей из дпух полуарок (рис. 1.35, б), можно cocia-
iniib три уравнения рашюиесия, в то иремя как число неизвестных
сил равно четырем. Чем не менее задача является статически оп-
определенной. Рассмотрим равновесие каком-либо одной полуарки
(рис. 1.35, в). На левую ио;;уарку дейстуег одна сила Q. Отбрасывая
мысленно шарниры Л и С пмеае с правей полуаркой, заменяем их
действие реакциями. Реакция в точке А представлена двумя ранее
выбранными составляющими FAx
7Ау, реакция в точке С, также
неизвестная по величине и по направлению, определена составляю-
составляющими FCx и FCy. Для левой полуарки ложно составить три уравне-
уравнения равновесия, между тем как новых неизвестных только два; FCx
и FCy. Таким образом, рассматривая равновесие всей арки и левой
полуарки, имеем шесть уравнений равновесия и шесть неизвестных,
т. е. задача является статически определенной. Эта же задача можег
3 М И Бать и др , т. 1
66 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
быть решена и другим способом, если рассмотреть равновесие левой
полуарки (рис. 1.35, в) и отдельно равновесие правой полуарки
(рис. 1.35, г) И в этом случае число уравнений равновесия равно
числу неизвестных (шести). На основании пятого закона (закон равен-
равенства действия и противодействия) составляющие Fcx, Fiy реакции шар-
шарнира С, приложенные к правой полуарке, равны по модулю и на-
направлены прямо противоположно соответствующим составляющим ре-
реакции того же шарнира С, приложенным к левой полуарке.
При решении задач па равновесие твердых тел
надо выполнить четыре первых пункта указанных
в начале книги, на стр. 15. При этом следует выде-
выделить систему твердых тел и отдельные твердые тела,
входящие в систему, равновесие которых надо рас-
рассмотреть. Затем:
5) сопоставить число неизвестных величин и число независимых
уравнений равнонесия; эти числа должны быть равны, если задача яв-
является статически определенной;
6) выбрать наиболее удобные системы координат; при этом для
каждого тела и для всей системы тел может быть избрана своя си-
система координат;
7) составить уравнения равновесия для каждого твердого тела или
для каждой системы твердых тел, равновесие которых исследуется;
8) решить систему всех уравнений равновесия.
Если система твердых тел разделяется па отдельные тела, то при
замене их взаимодействия реакциями связей следует ввести реакции,
приложенные к одному телу, и на основании закона равенства дей-
действия и противодействия выбрать реакции, действующие па второе
тело, равными по модулю и направленными прямо противоположно
(см., например, рис. 1.35, в и рис. 1.35, г).
В том случае, когда значение неизвестной силы окажется по от-
ответу отрицательным, направление этой силы следует взять противо-
противоположным тому, которое было изображено на рисунке.
При составлении уравнений равновесия целесообразно оси коорди-
координат и точки, относительно которых составляются уравнения моментов
сил, выбирать так, чтебы в каждое уравнение входила только одна не-
неизвестная величина.
Если по условию задачи требуется определить лишь некоторые
неизвестные величины, то надо составить только те из уравнений рав-
равновесия, которые необходимы для получения ответа.
Задача 1.24. Дна гладких цилиндра А и В помещены в ящик
(рис. а). Цилиндр А весит Q = 40 кГ и его радиус R = 80 мм; ци-
цилиндр В весит Р = 30 кГ и его радиус г = 50 мм-
Определить реакции вертикальных стен в точках Си ?, гори-
горизонтального пола в точке D и давление между цилиндрами, если ши-
ширина ящика 250 мм.
РАВНОВЕСИЕ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
67
Решение. Отбросим мысленно стены и пол ящика и рассмотрим
равновесие каждого цилиндра в отдельности. Цилиндр В находится
в равновесии под действием трех сил: веса Р, горизонтальной реак-
реакции стены F и реакции N цилиндра А, направленной по прямой, со-
соединяющей центры О и Oi обоих цилиндров (рис. б).
Чтобы найти угол а, образованный реакцией N с горизонтом, рас-
рассмотрим треугольник ООХН (рис. в). В этом треугольнике сторона
в)
г)
К зацаче 1.24.
OOj = /? -(- г = 130 мм, катет ОН= 120 мм. Пользуясь теоремой
Пифагора, находим длину второго катета О,/У=50 мм. Таким об-
образом,
5 12
sina=T3-,
cosa=T3-
Составим уравнения равновесия для цилиндра В. Так как линии дей-
С1вия сил, приложенных к цилиндру, пересекаются в центре цилин-
цилиндра, то достаточно составить два ураннения, приравняв лулю сумму
проекций всех сил на оси х и у (рис. а):
68 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
Подставляя значение Р=30 кГ, находим:
Л/ = 78 к Г, F = 72 к Г.
Цилиндр А находится в равновесии под действием четырех сил: веса
Q, горизонтальной реакции стены S, вертикальной реакции пола Т
и реакции N' цилиндра В, равной по величине и направленной про-
противоположно силе N. Все четыре силы (рис. г) пересекаются в точке
О, центре цилиндра А. Составим два уравнения равновесия этих сил.
Суммы проекций сил на ось х и ось у равны нулю:
Отсюда находим:
5=72 кГ, 7=70 кГ.
Следует заметить, что эта задача может быть решена и другим,
графическим способом. Действительно, зная величину и направление
силы Р, а также направления сил N и F, строим силовой замкнутый
треугольник. Этот треугольник совпадает с треугольником ОО[Н
(рис. в), если сторону О\Н положить равной силе Р. Тогда сторона
ОН даст в этом же масштабе силу F, а сторона OOt силу N.
Далее строим замкнутый силовой многоугольник для сил, прило-
женных'к цилиндру А. Построение начинаем с известных по величине
и направлению сил N' и Q. Проводя из конца силы Q прямую, парал-
параллельную S, а из начала силы N' прямую, параллельную Т, получаем
замкнутый силовой многоугольник (рис. д), стороны которого в из-
избранном масштабе и определяют неизвестные силы.
Задача 1.25. Блоки А \л В весом соответственно 600 кГ и 300 кГ
удерживаются п равновесии на гладкой плоскости, наклоненной под
углом 30° к горизонту, силой Р, параллельной ООи при помощи ры-
рычага OD, перпендикулярного к наклонной плоскости (рис. а). Тросы,
соединяющие рычаг с блоками, также параллельны плоскости OOt.
Определить, пренебрегая трением, усилия в тросах и величину
силы Р. Расстояния ОЯ=8 см, НС=8 см, CD= 16 см.
Решение. Рассмотрим равновесие каждого блока в отдельности
и равновесие рычага. Блок А (рис. б) находится в равновесии под
действием четырех сил: веса Q.,, натяжения Ть параллельного наклон-
наклонной плоскости, реакции Л/, блока В и реакции наклонной плоскости
N.b перпендикулярных к плоскости OOt.
Выберем оси координат ху (рис. а) и составим уравнения равно-
равновесия:
2/-'**=7"» —QjSin30° = 0, \
v/?ftJ)=A/1 —Qjcos300 —Л/, = 0. J
Из первого уравнения найдем:
7", = Q sin 30°= 300 кГ.
§ 3|
РЛВНОВР.СИЕ СИСТЕМЫ ТВЕРДЫХ ГЕЛ
69
Блок В (рис. в) находится r равновесии мод действием трех сил:
неса Q,, реакции Nb перпендикулярной к плоскости ОО„ и пгпяжепия
jpoca Ть параллельного QOV Составим уравнения равновесия:
%Fkx=T1 — Qi sin30° = 0,
? Pky =Ni—Qi cos 30° = 0.
Отсюда находим:
7"i = Qi sin 30°= 150 кГ, Nt — 150]/3 кГ.
Из второго уравнения системы A) получим:
Мг = Q, cos 30° -f- Nt = 300 • УЪ-\- 150]/з = 450^3 к Г.
Зная натяжение тросов, рассмотрим равновесие рычага (рис. г), на-
находящегося под действием сил: Р, — Ть — Т.ь и реакции шарнира
в)
б)
\30
о.
К задаче 1.25.
О, которую представим и виде ее проекции FOx и FOy. Уравнения
равновесия для рычага будут:
2 Fix = /-'о, + Р— 7, - У, = О,
У] т0 (/=¦„) = 1\ • 8 -f 71! • 16 — Р ¦ 32 = 0.
„ ,. 8-300+16.150 ,-,, ,. ,. tit г.
Отсюда находим: Р = ^ = 1о0 /с/ , 1-Ох— 1 у-\-Т^ — Р =
= 300 /сГ.
70
ПЛОСКАЯ СИСТЕМА СИЛ
|ГЛ. I
Задача 1.26. В приборе (рис. а) тела А и В могут скользить по
сторонам угла К; одна из сторон вертикальна, а другая образует
угол 20° с горизонтом. Наклонная плоскость соприкосновения обоих
тел составляет угол 40° с вертикалью. Сжатая пружина давит вниз
с силой Р = 10 кГ на тело А.
Пренебрегая весом тел и предполагая, что все соприкасающиеся
поверхности гладкие, найти горизонтальную силу Q, удерживающую
систему в равновесии.
Решение. Отбросим мысленно стороны угла К и рассмотрим
отдельно равновесие тела А и тела В. На тело А (рис. б) действуют
а.)
40"
К задаче 1.26.
три силы: давление пружины Р, направленное по вертикали вниз, ре-
реакция вертикальной стены Nt, направленная по горизонтали влево, и
реакция F отброшенного тела В, перпендикулярная к наклонной пло-
плоскости соприкосновения обоих тел. Линии действия этих сил пересе-
пересекаются в одной точке, так как тело А находится в равновесии под
действием трех непараллельных сил, лежащих в одной плоскости.
Следовательно, для них достаточно составить два уравнения равнове-
равновесия, приравняв нулю сумму проекций всех сил на оси хну. Выбе-
Выберем оси так, как это показано на рис. а. Тогда
? Fkx — F cos 40° — Л7, = 0,
^ Fkx = F sin 40° — Р= 0.
Подставляя значение силы Р, находим из уравнений F =15,58 к Г,
Л/, = 12 кГ.
На тело В (рис. в) действуют три силы: реакция F тела А, рав-
равная известной уже силе F, но направленная в .соответствии с зако-
законом равенства действия и протииодейсии.я и противоположную сю-
S 3] РАВНОВЕСИЕ СИСТЕМЫ ТВЕРДЫХ ТЕЛ 71
роиу, неизвестная по величине горизонтальная сила Q и реакция N.h,
перпендикулярная к наклонной стороне угла, составляющая, следова-
следовательно, с вертикалью угол 20°. Запишем для этих трех сил, пересе-
пересекающихся в одной точке, два уравнения равновесия:
?F»x = Q-\-Ni sin 20° — F cos 40° = 0,
? Fky = yv9 cos 20° — F sin 40° = 0.
Подставляя в эти уравнения найденное ранее значение F, опре-
определяем остальные силы Q = 8,3 кГ, ^=10,6 к Г.
Задача 1.27. Двухпролетная Оалка AD (рис. а) с промежуточным
шарниром С закреплена шарнирно в точке А. В точках В и D балка
опирается при помощи катков на горизонтальные направляющие.
J\ \Q ¦*
г- \" \Q Рй'\ ПР \R> t
i ft \ В С \ D | A/1 | I
Tf7fr I С ^C9, ^ ?0, x^J to 6
aj S) g)
К задаче 1.27.
Определить реакции опор А, В, D и усилие в шарнире С, если
на балку действуют: пара сил с моментом УИ = 20 кГм, сила Я = 8 кГ,
сила Q=12 кГ. Даны размеры: Л? = 4 л, ПВ = 2 м, ВС=3 м,
CM=MD=2 м.
Решение. Система твердых тел состоит из двух балок. Рассмот-
Рассмотрим равновесие каждой из балок отдельно. Па балку АС действуют
(рис. б): активная сила Р и активная пара сил с моментом М. Кроме
того, на балку наложены связи — шарниры Л и С, подвижная опора В.
Отбрасывая мысленно связи, заменяем их действие реакциями. Так как
реакция шарнира А неизвестна по направлению и величине, заменяем
ее двумя составляющими RAX и RAv. Аналогично реакция шарнира С
также изобразится двумя составляющими RCx и RCy. Реакцию опо-
опоры В представим вертикальной силой #й. Рассмотрим, далее, равно-
равновесие балки АС как равновесие свободного твердого тела, находяще-
находящегося под действием шести сил и одной пары сил. Выберем оси ко-
координат с началом в точке А, ось абсцисс направим по горизонтали
вправо, ось ординат по вертикали вверх. Составим уравнения равно-
равновесия балки АС:
RCy-P = 0, B)
= RB. AB-\- RCy- АС~ Р¦ АЕ — М = 0. C)
72 ПЛОСКАЯ СИСТЕМА СИЛ |ГЛ. 1
Можно было бы вместо второго уравнения равновесия составить сумму
моментов псех сил относительно точки С В это уравнение вошли бы
только две неизвестные силы RAv и Rn, так как линии действия
остальных неизвестных сил пересекаются в точке С. Однако в обоих
случаях уравнение A) является независимым от остальных уравнений
и содержит два неизвестных; уравнения B) п C) связаны между со-
собой и содержат три неизвестных.
Таким образом, из полученной системы ни одно из неизвестных
не может быть определено. Рассмотрим поэтому равновесие второй
балки CD (рис. в). На балку действует одна активная сила Q. Прм-
меняя закон освобождаемое™ от связей, заменим действие шарнира С
и опоры D реакциями связей. Реакция Rn направлена по вертикали,
перпендикулярно к горизонтальной плоскости, на которую опираются
катки. Реакция шарнира С неизвестна по величине и направлению.
На основании закона равенства действия и противодействия состав-
составляющие этой реакции равны по модулю составляющим реакции шар-
пира, приложенным к балке АС, и направлены в прямо противопо-
противоположные стороны (рис. в). Таким образом, имеем свободное твердое
тело—балку CD, находящуюся в равновесии под действием пяти сил.
('оставим уравнения равновесия, выбрав оси координат с началом
в точке С; ось абсцисс направим по балке вправо, ось ординат —
вертикально вверх. Имеем:
v; mc (Fk) = Rn-CD — Q-CH=0. F)
В этих трех уравнениях равновесия только одна новая неизвестная RD.
А всего в шести уравнениях равновесия шесть неизвестных. Из уран-
нений D) и A) следует:
Из уравнения F) находим:
KD=Q-tz>=12l2/4==6 кГ'
а из E) получаем:
Rcy=RD — Q = Ci—l2 = — 6 к Г.
Знак минус показывает, что в действительности направления состав-
составляющих RCv и R'Cv противоположны принятым па рисунке.
Далее, из C) имеем:
«л = РЁ + ^-*с, 5^ = 8-4/6-1-20/6-L6- 9/6= 17,66 кГ
и, наконец, из B) находим:
RAy =р—Кц — R(.y = 8—17,66 -j- 6 = — 3,66 к Г.
РАВНОВЕСИЕ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
73
Знак минус указывает, что и реакция /fAv направлена не вверх, как
предполагалось, а по вертикали вниз.
Задача 1.28. Через блок с неподвижной осью О и радиуса R
(рис. а) перекинута нить, к копнам которой подвешены два одинако-
одинаковых груза Pi и Pj. Правый конец нити свисает вертикально. ЛевыП
конец нити огибает блок с подвижной осью d и радиуса г. Нес
блока с подвижной осью g. Ось нижнего блока насажена на конец
стержня длиной /, другой конец которого закреплен на оси верхнего
блока.
а)
б)
К злдаче 1.28.
Пренебрегая несом стержня, определить угол я, который образует
стержень с вертикалью в положении равновесия, и усилие в стер-
стержне 00,. Pi =/3,2=10 кГ, я=4 к Г, R = 4 см, г = 3 см, /=10 см.
Решение. Рассмотрим равновесие системы твердых тел, состоя-
состоящей из двух блоков и стержня, соединяющего их центры (рис. б).
Для этого мысленно отбросим ось О, поддерживающую верхний блок,
и заменим ее реакцией N. Кроме того, на систему действуют внеш-
внешние силы Ри Р.ь g. Реакция N вертикальна, так как все остальные
силы заведомо вертикальны. Составим для данной системы параллель-
параллельных сил два уравнения равновесия:
? ,п0 (Ft) = PtR — P,j (/ sin a — r) — gl sin a = 0.
Из первого ураинепия определим реакцию N:
:=24 if Г.
74 ПЛОСКАЯ СИСТЕМА СИЛ 1ГЛ. I
Из второго уравнения находим угол а:
Ю-4 — 10A0 sin а— 3) — 4- 10 sin а = 0,
откуда sin a =1/2, я = 30°.
Для определения усилия в стержне рассмотрим равновесие блока
с подвижной осью. Он находится в равновесии под действием четы-
четырех сил (рис. в): веса g, двух ранных по величине реакций нити Р.г
и Т, а также реакции стержня S, направленной по стержню, но не-
неизвестной по величине. Таким образом, геометрическая сумма этих
четырех сил должна быть равна нулю:
Так как угол я известен и 7"=Р2, то проще всего величину 5 опре-
определить графически, построением силового многоугольника. Отложим
из точки а (рис. г) две вертикальные силы g и Р3 в избранном для
сил масштабе. Далее, из точки с, конца силы Рь как из центра, про-
проведем дугу окружности радиусом, равным по величине Р.г. На этой
дуге должен находиться конец силы Т и начало силы S, составляю-
составляющей угол а =30° с вертикалью. Проведя из точки а под углом 30°
к вертикали прямую до пересечения с дугой окружности в точке d,
соединим прямой точки d и с. Отрезок da и определит величину уси-
усилия в стержне. Измерив его в избранном Для сил масштабе, находим,
что усилие в стержне 5= о кГ.
Задача 1.29. Рама состоит из двух жестких частей АС и ВС
(рис. а), соединенных шарниром С и прикрепленных к фундаменту
шарнирными опорами А и В-
Определить реакции в шарнирах А, В, С, если в точке D прило-
приложена вертикальная сила Р= 1 т. Задачу решить графически.
Решение. Реакции шарниров А и В неизвестны по величине
и направлению. Следовательно, если рассматривать равновесие всей
системы АСВ, отбросив опоры А и В и заменив их действие реакци-
реакциями, то число неизвестных будет равно четырем, а уравнений равно-
равновесия будет три.
Рассмотрим поэтому отдельно равновесие левой части рамы (рис. б).
К этому твердому телу никаких активных сил не приложено. Приме-
Применяя закон освобождаемости от связей, отбросим мысленно шарниры Л и С
и заменим их действие реакциями. Часть рамы АС находится в равно-
равновесии под действием двух сил: RA и Rc. Согласно второму закону
статики эти силы должны быть равны по величине и направлены по
одной прямой в разные стороны. Так как одна сила приложена
в точке А, а другая — в точке С, то общей линией действия этих
сил будет АС.
Рассмотрим, далее, равновесие правой части ВС рамы. К ней при-
приложена одна активная сила Р. Освобождаясь мысленно от двух связей:
шарниров В и С, заменяем их действие реакциями. Реакция R'c "а
I 31
РАВНОВЕСИЕ СИСТЕМЫ ТВЕРДЫХ ГЕЛ
75
основании закона равенства действия и противодействия равна по не-
неличине Rc и направлена в противоположную сторону по АС (рис. в).
в)
-fie
ж)
/
я. ^
Ч\
\
\
\
v
Q
в яя
J»«
К задаче 1.29.
Направление реакции RH может быть определено на основании тео-
теоремы о трех непараллельных силах. Действительно, часть ВС нахо-
находится в равновесии под действием трех непараллельных сил, лежа-
лежащих в одной плоскости. Линии действия двух сил известны- они пе-
пересекаются в точке О. Согласно теореме линия действия третьей силы
76 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
реакции RIS должна также проходить через точку О. Три силы Р, R'c, Rn,
линии действия которых пересекаются в точке О, находятся в равно-
равновесии. Следовательно, они должны образовать замкпутый треугольник.
Откладываем из произвольной точки (рис. г) силу Р, известную по
неличное и направлению. Из конца силы Р проводим линию, парал-
параллельную АС, т. е. линии действия силы R'c. Из начала силы Р про-
нодмм линию, параллельную ОБ, т. е. линии действия силы RB. По-
Получаем замкнутый силовой треугольник, стороны которого и опреде-
определяют п принятом для силы Р масштабе величины искомых реакций:
R'c и Ris- Согласно ранее доказанному реакция шарнира А раина R'c-
Решение задачи об определении реакций шарниров трехшарнир-
иой арки осложняется, если среди активных сил, действующих на
трехшарнирпую арку, имеется одна сила, приложенная к шарниру С.
Рассмотрим в этом случае трехшарнирную арку как соаавленную из
трех тел: диух полуарок и шарнирного болта. Полуарки не соприкаса-
соприкасаются друг с другом. Шарнирный болт соприкасается с каждой из них.
Рассмотрим три возможных варианта задачи.
В первом варианте (рис. д) активная сила Р приложена к шар-
шарнирному болту, а к полуаркам никаких задаваемых сил не приложено.
В эюм случае на левую полуарку, находящуюся в равновесии, дей-
действуют две равные силы RA и Rc (рис. б), направленные по прямой
АС в противоположные стороны. Совершенно аналогично па правую
полуарку действуют две взаимно уравновешивающиеся силы Ro и Rct,
направленные по прямой ВС. Рассмотрим равновесие шарнирного
бол1а С, к которому приложены три силы: сила Р, реакции левой и
правой полуарок — Rc, — RCi (рис. е), причем сила Р извеана по
величине п направлению, а у реакций полуарок известны только ли-
линии действия. Строя замкнутый треугольник (рис. ж), находим вели-
величины реакций Ro RCl и, следовательно, равные им величины RA, Rn.
Во втором вариаше (рис. з) активные силы, кроме шариирною
бол!а С, приложены только к одной правой полуарке (сила Q). Рас-
Рассмотрим равновесие левой полуарки (рис. б). Направление реакцгй
Rc и RA совпадает с прямой АС.
Далее, присоединяем шарнирный болт С вместе с приложенной
к нему активной силой Р к правой полуарке и рассматриваем се
равновесие (рис. и) под действием сил: Р, Q, — Rc и реакции Rn,
которую раскладываем па две составляющие Rlix, Rny.
ь'5ам1_чая, что —Rc образует угол 45° с горизонталью, составляем
три уравнения равновесия:
!>¦** = Rc cos 45° - Q -1- RBX = О,
У] Fky = Rc sin 490 - P + RBy = 0,
откуда и определяются все три неизвестные.
§ 3] РАВНОВЕСИЕ СИСТЕМЫ ТВЕРДЫХ ТЕЛ 77
В третьем варианте (рис. к) активные силы приложены, кроме
шарнирного болта, и к обеим полуаркам.
В этом случае сначала определяем реакции шарниров А и В. Для
этого рассмотрим равновесие всей арки, отбросив мысленно шарниры
А и В и заменив их действие реакциями (рис. л). Три уравнения
равновесия будут:
В этих трех уравнениях четыре неизвестных: RAx, RAy, RBx, RBy.
Чтобы составить четвертое недостающее уравнение равновесия, рас-
рассмотрим равновесие любой полуарки (например, левой), присоединив
к ней шарнирный болт с приложенной к нему силой Р (рис. м). При
этом составляем уравнение равновесия, в которое бы не входила
реакция правой полуарки па болт. Таким уравнением равновесия
будет равенство нулю суммы моментов всех сил относительно шар-
шарнирного болта С
Из этой системы четырех уравнений определяются RAx, RAy, R,u,
RHv. Далее, составляя остальные ураннения раппонесия для левой
полуарки, находим RCx, RCy — составляющие реакции правой полу-
арки на болт.
Для определения реакции левой полуарки па болт (она в этом
случае не равна реакции на болт правой полуарки) необходимо рас-
рассмотреть отдельно равновесие правой полуарки.
Задача 1.30. Цилиндрический стакан радиуса R поставлен откры-
открытой стороной на гладкий горизонтальный пол. Внутри стакана нахо-
находятся два одинаковых шара радиуса г и несом Р каждый.
Определить вес Q цилиндрического стакана, при котором шары
не опрокинут его. Стенки стакана абсолютно гладкие.
Решение. Для определения искомого веса стакана рассмотрим
отдельно равновесие двух шарои (рис. б) и равновесие стакана (рис. в).
На систему двух шаров действуют силы: вес каждого шара Р,
приложенный в центре шара и направленный по вертикали вниз;
реакция гладкого пола Т, направленная по вертикали вверх; реакции
стенок стакана Nj и Nb направленные по горизонтали и приложен-
приложенные в точках D и С-
Проведем оси координат: ось х горизонтально, ось у вертикально.
Уравнения равновесия для системы, состоящей из двух шаров, имеют
78
вгд
ПЛОСКАЯ СИСТЕМА СИЛ
т0 (Fk)= Nt-AB-P-OB = 0.
[ГЛ. I
(I)
B)
C)
Третье уравнение — уравнение моментов — составлено относительно
точки О, где пересекаются линии действия трех сил, в том числе
двух неизвестных. Из первого уравнения следует:
Ni = Ni = N. D)
Из третьего уравнения находим:
Р-ОВ
N=-
АВ
E)
Рассмотрим, далее, равновесие цилиндрического стакана (рис. в).
На стакан действуют силы: вес Q но вертикали вниз, реакции шарон
о
6) о)
К задаче 1.30.
N[ и N'it приложенные в точках D и С, реакции пола в точках И
и К- (Ясно, что N[ = М и Л'2 = М-) В момент опрокидывания ста-
стакана, который мы рассматриваем, давление в точке И на пол и, сле-
следовательно, реакция пола обращаются в нуль и стакан опирается на
горизонтальную плоскость только в точке К-
Составим уравнение моментов относительно точки К
-Q-R = 0. F)
Далее из F), учитывая D), имеем:
N-AB — Q-R — 0.
Подставляя в это равенство значение N, определенное формулой E),
имеем:
, ИВ РОВ- АВ /' ¦ ОН
R ~ RTab ~~ R
131
РАВНОВЕСИЕ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
79
но 05 = 2/? — 1т, и, следовательно, для равновесия необходимо,
чтобы выполнялось Неравенство
(знак неравенства соответствует случаю, когда давление на горизон-
горизонтальную плоскость будет распределяться по всему ободу).
Задача 1.31. Два однородных стержня АВ и CD длиной 2/ и
весом Р каждый опираются в точках D и В на гладкий горизонталь-
горизонтальный пол и соединены посередине шарниром О. Концы стержней А и
С соединены нитью. Между верхними половинами стержней лежит
гладкий диск радиуса г и весом Q. Угол DOB = 2я.
**
"Ox
Определить натяжение нити.
Решение. Для нахождения реакций пола в точках D и В рас-
рассмотрим равновесие системы твердых тел (два стержня, скрепленных
шарниром и нитью, и диск), отбросив мысленно пол и заменив ею
действие вертикальными реакциями Rn и RB (рис. б). Кроме реакций
пола, к системе твердых тел приложены: в центре диска его вес Q,
в шарнире О вес стержней 2Р, оси координат показаны на рисунке.
Составляем дна уравнения:
сумма проекций всех параллельных сил на вертикаль равна пулю
сумма моментов всех сил относительно точки D равна нулю
2>о (^) = «в • ?О - B/> + <2)-? = о.
Решая совместно эти уравнения, находим:
Как и следовало ожидать, реакции пола равны между собой.
80 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
Рассмотрим, далее, равновесие диска, отбросив стержни и заменив
их действие на диск реакциями TV, и /Уа (рис. в). Реакции /V, и /V)
соответственно перпендикулярны к стержням АВ и CD, так как тре-
трение между диском и стержнями по условию отсутствует. Следова-
Следовательно, Af] и Ni образуют с горизонталью равные углы а. Кроме
реакций, на диск действует сила тяжести Q. Линии действия всех
трех сил пересекаются в центре диска. Напишем уравнения равнове-
равновесия диска:
^ Fkx — TV, cos a — jV2 cos а = 0,
2 Fky = TV, sin a -f Nt sin а — Q = 0.
Решая совместно эти два уравнения, имеем:
/V=M = M = 0 ? .
•* 2 sin «
Таким образом, реакции стержней равны между собой, что очевидно
и но соображениям симметрии.
Далее, рассмотрим равновесие одного из стержней, заменив дей-
действие пола известной реакцией RD н давление диска найденной вели-
величиной TV (рис. г). На стержень, кроме того, действуют следующие
силы: неизвестное по величине натяжение нити S, неизвестная по
величине и направлению реакция шарнира О, которую представляем
двумя составляющими RQx и ROy, и вес стержня Р. Благодаря тому,
чго ранее были найдены реакции RD и TV2, число неизвестных сил,
действующих на стержень, равно трем, т. е. задача является статиче-
статически определенной. Так как по условию требуется найти только натя-
натяжение нити, то достаточно составить одно уравнение равновесия,
приравняв нулю сумму моментов всех сил относительно точки 0:
^ т0 (Fk) = SI cos я — RDl sin a — Nu -~- = 0.
fa
Отсюда
Задача 1.32. Нить ЛЕВ прикреплена к потолку в точках Л и В
и пропущена через дна отверстия в балке С!) (рис. а). В середине /:'
нити подвешен груз Р. Вес балки CD равен Q. Расстояние CD между
отверстиями в балке равно АН.
Полагая нить и балку абсолютно гладкими, определить угол о,
образованный в положении равновесия балкой и нижними отрезками
нити, натяжение нити и реакции между балкой и питью в точках
С и D.
Решение. Для определения натяжения нити разрежем мысленно
АС и BD и рассмотрим равновесие нижней части системы (рис. б)
§31
РАВНОВЕСИЕ СИСТЕМЫ ТВЕРДЫХ ГЕЛ
81
под действием песа груза Р, веса балки Q и реакций нитей R, и R.t.
Проведя оси координат (рис. б), составляем два уравнения равно-
равновесия:
^iFby = Ri-rRi-P-Q = 0,
2 /яс {Fk) = R, • CD - (Q + Р) -2- = 0.
Решая совместно эти два уравнения, имеем:
что, впрочем, очевидно вследствие симметрии системы.
Для нахождения уела а рассмотрим равновесие сил, приложенных
к точке Е (рис. в). Следует заметить, что натяжение во всех частях
A
С
L
в
л
т—I
Н
i
i
i—ill , Ji—
К задаче 1.32.
нити по модулю одно и то же, так как в точках С и D, где нить
проходит через отверстия в балке, трение отсутствует. Если бы в
эгих точках между нитью и балкой существовало трение, то натяже-
натяжения нити но разные стороны от отверстия были бы различны.
В точке Е приложены вес Р и натяжения R\ и R!2 нитей, обра-
образующих угол о. с горизонталью. Для определения угла а достаточно
составить одно уравнение равновесия (сумма проекций всех сил на
вертикаль равна нулю):
2R sin а — Р = 0,
82 ПЛОСКАЯ СИСТЕМА СИЛ (ГЛ. I
откуда
Второе уравнение равновесия (сумма проекций всех сил на гори-
горизонталь равна пулю) составлять нет необходимости, так как оно
только вновь подтвердит ранее установленное равенство натяжений
в левой и правой половинах нити R[ = R'i = R. Для определения
реакции между балкой и нитью рассмотрим равновесие нити в точке С,
отбросив балку и заменив ее действие реакцией, составляющие кото-
которой обозначим через Nx н Ny (рис. г). Кроме того, на нить в точке С
действуют натяжения #.2 и —Ri отрезков нитей АС и ЕС. Составляем
уравнения равновесия точки С:
у р = ft cos а дг __ о( A)
2iFky = R-Ny-R sin а = 0. B)
Из уравнения B) находим:
Уравнение A) дзет:
Для приобретения навыков в решении задач на
равновесие системы твердых тел рекомендуется ре-
решить следующие задачи из «Сборника задач по тео-
теоретической механике» И. В. Мещерского, издания
1950 г. и более поздних лет: 108, 109, 112, 143, 144, 145, 147,
150, 164, 166, 167, 169.
§ 4. Равновесие тел при наличии трения
1°. Равновесие твердого тела при наличии трения
скольжения. Силы трения скольжения возникают между шеро-
шероховатым телом и шероховатой поверхностью, если равнодействующая
активных сил R не направлена по нормали к поверхности, на кото-
которой покоится тело (рис. 1.36). При равновесии тела необходимо,
чтобы реакция шероховатой поверхности 5 (рис. 1.37) равнялась по
величине Л и была направлена в прямо противоположную сторону.
Разложим активную силу R на нормальную составляющую N и каса-
касательную составляющую Т, реакцию шероховатой поверхности на нор-
нормальную составляющую Nt и касательную составляющую F, назы-
называемую силой трения скольжения или силой трения первого рода.
При равновесии должны соблюдаться равенства
N—Ni = 0, A*)
T — F = Q. B*)
РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ
83
Из опыта известно, что при изменении величины составляющей Т
в определенных пределах равновесие тела не нарушается. Следова-
Следовательно, и сила трения скольжения согласно уравнению B*) будет
меняться в этих пределах.
Таким образом, сила трения скольжения при покое есть состав-
составляющая реакции связи, возникающая при действии активных сил,
стремящихся сдвинуть тело. Эта составляющая реакции направлена
в сторону, противоположную возможному движению тела. Величина
силы трения может меняться от нуля до некоторого предела, в за-
зависимости от величины и направления активных сил, с тем чтобы
Рис. 1.36.
воспрепятствовать перемещению тела. Огличие силы трения от дру-
других реакций связей заключается и том, что ее модуль не может пре-
превысить определенного предела.
Зависимость между силой трения и нормальным давлением опре-
определяется законом Кулона: наибольшая величина силы трения сколь-
скольжения пропорциональна нормальному давлению тела на поверхность
Fmn=fN. C*)
Сила трения всегда направлена в сторону, противоцоложную возмож-
возможному относительному движению.
17остоянная / называется коэффициентом трения скольжения.
Экспериментально установлено, что этот коэффиииенг зависит от ма-
материала соприкасающихся тел и их шероховатости (чистоты обра-
обработки). Для абсолютно гладких тел коэффициент / ранен пулю. Для
реальных тел
D*)
Коэффициент трения не -зависит от силы нормального давления и пло-
площади соприкосновения *).
*) В последнее время экспериментально установлено, что с нзменепием
нормального давления и площади соприкосновения коэффициент трения не-
незначительно меняется. Этим изменением мы будем пренебрегать.
84 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
Угол ф между нормалью к поверхности и полной ее реакцией
в положении предельного равновесия, когда F — Fma%, называется
углом трения (рис. 1.38). Этот угол определяется равенством
tg'f = /. т. е. cp = arctg/. E*)
Построим в точке соприкосновения нормаль к поверхности и пря-
прямую ОА, составляющую с ней угол <р. Конус, описанный этой пря-
прямой как образующей, называется конусом трения.
Если линия действия равнодействующей активных сил, приложен-
приложенных к твердому телу, лежит внутри конуса трения, то вне, зависи-
зависимости от ее модуля тело останется в покое. Это объясняется тем,
что в этом случае движущая сила будет меньше предельной силы
трения.
©у
1 V
i v
¦///////////////////AW///////.
о
Рис. 1.38. Рис. 1.39. Рис. 1.40.
Действительно, рассмотрим равновесие тела, находящегося на го-
горизонтальной плоскости 5 (рис. 1.39). К телу приложена равнодейст-
равнодействующая активных сил Q под углом а к нормали (нес тела входит
в Q). Коэффициент трения скольжения /=tg'.p иззестен. Полагая
а<^ср, составим уравнение равновесия, приравняв пулю сумму проек-
проекций всех сил на направление нормали (рис. 1 -40):
TV— Qcosa = 0 или 7V=Qcosa. F*)
Проектируя все силы на горизонтальное направление, находим:
Qsina — F = 0 или Qsina — F. G*)
Замечая, что наибольшее зн;1чение силы трения равно
Fma=fQ cos я, (8*)
и учитывая, что tga<^tg», заключаем:
Qsina</Qcosa. (9*1
Следовательно, сила Q, линия действия которой находится внутри
конуса трения, не может сдвинуть тело с места, как бы велика она
ни была. На этом свойстне основаны некоторые самотормозящиеся
устройства.
Нсли из Q выделить вес тела Р, то неравенство (9*) примет вгд
Qi sin a</(P-t-QiCOSa). A0*)
§ 4| PABIIOnF-СИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ 85
Следовательно, сила Q, ме может нарушить равновесие тела при
Сила трения может принимать различные знамения or пуля до
наибольшей величины. Поэтому уравнения равновесия твердого тела,
которые выражались равенствами [§ 2, уравнения A*'), B*), C*)|,
при наличии сил трения превращаются в неравенства. В связи с этим
при решении задач, как правило, рассматривают наибольшее значе-
значение силы трения и находят при этом из уравнений равновесия пре-
предельные (наибольшие и наименьшие) значения искомых величин.
Так, например, рассматривая равновесие лестницы АВ (рис. 1.41),
опирающейся на гладкую стену и шероховатый пол, мы найдем
наименьшее значение угла я, при котором лестница
будет в покое, если нозьмем максимальное значение
силы трения. Положений равновесия лестницы будет
при этом бесчисленное множество, так как при любом
значении угла а, большем найденного, по меньшем 90°,
для равновесия необходима сила трения меньшая, чем
ее максимальная величина.
При решении задач на равновесие т пер-
лого тела при и а л и ч и и сил трения еле- Рис. ].41.
дует выполнить четыре первых пункта,
указанных в начале книг и, па стр. 15. При этом следует
реакцию шероховатой поверхности представить двумя составляю-
составляющими — нормальной реакцией и силой трения, или же, не расклады-
раскладывая эту реакцию па составляющие, направить ее под углом трения <р
к нормали к поверхности (при максимальной силе трепля);
5) сопоставить число неизвестных величии п число независимых
уравнений равновесия, которые должны быть равны для статически опре-
определенных задач; при этом к уравнениям равновесия твердого тела сле-
следует добавить зависимость силы трения от нормального давления C*);
6) выбрать систему координат;
7) составить систему уравнений равновесия для сил, приложенных
к твердому телу или к системе твердых тел;
8) решив систему уравнений равновесия, определить искомые ве-
величины.
Задача 1.33. Определить модуль силы Р, при которой начнется
движение блока (рис. а). Вес блока Q = 200 кГ, нысота h = 0,8 м,
ширина й = 0,6 м. Сила Р, приложенная н точке В, образует угол
30° с горизонтом. Коэффициент трения между блоком и горизон-
горизонтальным полом /=0,2.
Р е ш е и и е. Движение блока может начаться в двух случаях:
а) если начнется скольжение блока по плоскости вправо (рис. о)
и б) если блок начнет опрокидываться вокруг ребра (рпс. в).
86
ПЛОСКАЯ СИСТЕМА СИЛ
1ГЛ. I
Рассмотрим первый случай. В этом случае точка приложения реак-
реакции пола N неизвестна. Составим уравнения равнооесия — прирав-
приравняем суммы проекций всех сил на оси координат (рис. б) нулю
? Fkx = P cos 30° — Fi = 0,
^Fky = N-{-P sin 30° — Q = 0.
Кроме того, учтем зависимость силы трения от нормального давления
Определим из данной системы уравнений силу Р. Исключая силы
и N, находим:
р —
cos 30° + / sin 30° ~ 0,965 '
Если величина силы Р станет больше этого значения, то блок нач-
начнет скользить вправо.
а)
Рассмотрим второй случай. В случае возможного опрокидывания
блока вокруг ребра А нормальная реакция N и сила трения F будут
приложены в точке А (рис. в).
Составим три уравнения равновесия и четвертое уравнение — за-
зависимость силы трения от нормального давления
v Fhx = p cos 30° — F = 0,
V 1-ку = д' — Q -f P sin 30° — 0,
т А (Fk) =: Q ¦ | - Р cos Жк = 0,
A)
B)
C)
D)
РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ
87
Для нахождения величины силы Р достаточно найти ее значение
из C):
Qb 200 -0,6-2
Р=?
2Л cos 30" '2 • 0,8 ¦ j/з
= 86,6 кГ.
Если модуль силы Р станет больше этого значения, то блок начнет
опрокидываться около ребра А.
Уравнения A), B), D) смогут быть использованы для определе-
определения нормальной реакции и силы трения.
Сопоставляя значения модуля силы Р в первом и во втором слу-
случаях, заключаем, что так как величина силы Р при скольжении меньше
ее величины при опрокидывании, то при возрастании модуля силы Р
от нуля до максимума блок начнет сначала скользить, а не опроки-
опрокидываться.
Задача 1.34. Для подъема (рис. а) или опускания (рис. б) ка-
каменного блока А, весящего 2000 кГ, применили два клина В и С.
Коэффициент трения для соприкасающихся монерхностей АВ и АС
равен /=0,2, а для поверхностей BD и CD равен /,==0,25.
Л7°^г
У//УУУУУУУУУУ7УУ.
V
а)
УУУУУУУУУУУУУУУУ/
D
6)
X
в)
К задаче 1.34.
Найти равные по величине горизонтальные силы Р, сжимающие
клинья, необходимые для подъема блока А. Определить силы Р, растя-
растягивающие клинья, необходимые для опускания блока А. Наклонные
плоскости соприкосновения блока с клиньями образуют угол 10°
с горизонтом.
Решение. Рассмотрим равновесие системы тел, состоящей из
блока А и клиньев В \л С. При подъеме блока (рис. а) силы Р сжи-
сжимают клинья. Рассмотрим отдельно равновесие блока и равновесие
клипа. Отбросив мысленно клинья, заменим их действие на блок
88 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. (
нормальными реакциями N и силами трения F (рис. в). Кроме того, на
блок действует известная сила — вес Q. Составим два уравнения
равновесия, приравняв нулю суммы проекций всех сил на оси х и у:
%Fkx = N2s\n 10° — N1 sin Ю0-!-^ cos 10° —F, cos 10° = О,
2Fky = Nt cos I0°-|-Njcos 10° — Q — F{ sin 10° —F2 sin l0° = 0.
Кроме того, запишем зависимость сил трения от нормального дав-
давления
Тогда находим:
Перейдем, далее, к рассмотрению равноиесия клина В (рис. г).
На клин дейстиуют: реакция блока, которая раскладывается на нор-
нормальную составляющую—7V.S и силу трения — /\х, активная сила Р и
реакция пола, разложенная па нормальную силу 5 и силу трения Т.
Напишем уравнения равновесия для клипа В:
Цг\*= —М sin 10° —F.2cos 10°—
HFA;V = 5 + Fjsm 10° — Л/.2 cos 10° = 0.
Кроме того, имеем зависимость силы трения от нормального дав-
давления
' —/|О.
Отсюда, пользуясь найденными ранее значениями реакций, найдем
5=996 кГ, Г=249 л-Г, Р = 641 /сГ.
Таким образом, для равновесия системы при подъеме блока полу-
получено необходимое граничное значение силы /> = 641 кГ. Если же
41 кГ, то начнется подъем блока; система придет в движение.
Перейдем к определению величины силы Р при спуске блока.
Блок А находится в равновесии (рис. д) под действием активной
силы — веса Q, нормальных реакций клиньев N, и Л^ и сил трении
Ft и F4. Силы трения в этом случае направлены вдоль наклонной,
плоскости вверх. Это сразу видно из рассмотрения равновесия кли-
клипа В (рис. <?), так как в связи с изменением направления силы Р на
прямо противоположные силы Г и —F% меняют свое направление
на противоположное по сравнению с предыдущим случаем (рис. г).
Уравнения равновесия для блока А будут:
2lFkx = Fl cos 10° —/\s cos 10° —TV] sin 10°-)-Л/, sin 10° = 0,
vpky = л?, cos 10°-{- Nt cos \0°-\-fl sin 10°-|-/v.2 sin 10° — Q = 0.
Кроме того, зависимость силы трения от нормального давления даечея
равенствами
Fl=fN1, Ft = fN*
§ 41 РАВНОВЕСИЙ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ 69
Отсюда находим:
Л/, = Л'з = 980 к Г, F1 = Ft=l 96 кГ.
Уравнения равновесия для клина В (рис. е) будут:
SFtjr= r-f/-2cos 10° — N.,, sin 10° —P = 0,
SF^ = 5- Mi cos 10° —Г.2 sin 10° = 0.
Сила трения выражается через нормальное давление
T=f,&
Отсюда, пользуясь ранее найденными значениями реакций Л^ и Fs,
найдем:
5=999 кГ, Г=250 кГ, Р = 21Ъ кГ.
Найденное значение Р является граничным при равновесии системы
в случае опускания блока.
Таким образом, на основании проведенного исследования можно
заключить, что система будет находиться в равновесии, если проек-
проекция силы Р лежит в пределах
— 273 кГ ^ Рх й=: 641 кГ.
Если модуль каждой из сил Р будет больше 641 к Г, то при их на-
направлении, указанном на рис. а, начнется подъем блока. Для тою
чтобы блок начал опускаться, нужно приложить силы Р в противо-
противоположном направлении, причем их модуль должен превышать 273 кГ.
Задача 1.35. Полуцилиндр весом Р и радиуса R лежит па не-
негладкой горизонтальной плоскости (рис. а). Однородный стержень ОА
длиной I и весом Q шарпирно закреплен в точке О. Он опирается
па гладкую поверхность полуцилиндра, образуя угол а с вертикалью
OB=h.
Определить наименьшую величину коэффициента трения скольже-
скольжения / между полуцилиндром и горизонтальной плоскостью при рав-
равновесии.
Peuieiine. Полуцилиндр н стержень являются системой твердых
тел, находящихся в равновесии. Под действием веса стержня полу-
полуцилиндр может начать движение вправо (при недостаточной силе
трения между полуцилиндром и полом). Для определения искомой
наименьшей величины коэффициента трения скольжения между полуци-
полуцилиндром и горизонтальной плоскостью рассмотрим отдельно равно-
равновесие стержня и полуцилиндра.
Рассматривая равновесие стержня ОА (рис. б), отбросим мысленно
шарнир О и заменим его действие реакцией. Реакция шарнира при-
приложена в точке О и неизвестна но величине и направлению. Пред-
Представим поэтому реакцию двумя составляющими Fox и FOy. Отбрасывая
90
ПЛОСКАЯ СИСТЕМА СИЛ
1ГЛ. I
мысленно полуцилиндр, заменим е;го действие на стержень реакцией Si,
направленной перпендикулярно к стержню, так как согласно условию
трение между стержнем и полуцилиндром отсутствует. Величина реакции
•S] неизвестна. Кроме указанных реакций, к стержню в его середине
приложен вес Q, направленный по вертикали.
На рис. в представлены силы, действующие на полуцилиндр при
равновесии. Полуцилиндр находится в равновесии под действием трех
сил: веса Р, реакции стержня S.2 и реакции негладкой горизонталь-
горизонтальной плоскости. Вес Р направлен по вертикальной оси симметрии полу-
полуцилиндра и, следовательно, линия действия этой силы проходит через
точку С, лежащую на оси цил^нчра. Реакция стержня St согласно
пятому закону (закон равенства действия и противодействия) равна
по величине Si и направлена противоположно. Следовательно, реакция
У ////////У/У/УУ У У///У///////s
С)
К задача 1.35.
5.j перпендикулярна к стержню, совпадающему по направлению с ка-
касательной к полуцилиндру, и направлена по радиусу DC. Этот радиус
образует с горизонтальным диаметром полуцилиндра угол а, так как
стороны АО и ВО, образующие угол а, соответстгенно перпендику-
перпендикулярны к прямой DC и горизонтальному диаметру. Равнодействующая
реакций негладкой горизонтальной плоскости должна быть приложе-
приложена в точке С. Действительно, полуцилиндр находится в равновесии
под действием трех непараллельных сил, лежащих в одной плоскости.
Следовательно, линии действия всех трех сил пересекаются в одной
точке. Но силы S2 и Р пересекаются в точке С Значит, и линия дей-
действия равнодействующей реакции негладкой плоскости должна про-
проходить через точку С. А это возможно только в том случае, если эта
реакция приложена в точке С. Разложим реакцию горизонтальней
плоскости на две составляющие: нормальную реакцию Nc и силу тре-
трения Fc. Перейдем к составлению уравнений равновесия обоих тел.
Составим для стержня сумму проекций всех сил на оси х и у и
приравняем их нулю:
«41 РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ 91
Уравнение моментов относительно точки О будет:
Q~ slna —5,-00 = 0. C)
Точка О выбрана за центр моментов, так как при этом составляю-
составляющие реакции шарнира О не входят в ураниение моментов. Таким
образом, из последнего уравнения непосредственно находится неиз-
неизвестная сила S|, а только эта сила из входящих в систему уравнения
A) — C) и войдет далее в уравнения равновесия полуцилиндра. Урав-
Уравнения A) — B) могут быть использованы для нахождения неизвестных
составляющих реакций шарнира FOx, FOy
Из уравнения C), пользуясь очевидным равенством
OD cos a. = h — г sin a, D)
найдем:
о ~ АО . ~ /cos a sin а _,
S Q sin a = Q rrjr :—г. E)
2(h — r sin a) v '
1 ^ 1-OD 2(h — r sin a)
Перейдем к составлению уравнений равновесия для полуцилиндра.
Проектируя силы, приложенные к полуцилиндру, на оси координат,
получим два уравнения равновесия:
Si cos a — Fc = 0, F)
JVC — 5а sin a — P = 0. G)
Кроме того, сила трения связана с нормальной реакцией зависимостью
Fc=fNc. (8)
Учитывая равенство 5,=?.2, получим систему четырех уравнений
E)—(8) с четырьмя неизвестными 5, Fc, No/¦ Дли нахождения
наименьшего значения коэффициента трения / исключим из рассмат-
рассматриваемой системы остальные неизвестные. Внося E) и (8) в уравне-
уравнение F), получим:
/sjnWiJL fN Q g)
4 (Л — г sin a) J с v '
Подстаиляя E) в G), найдем:
Исключая из полученных уравнений (9) и A0) реакцию Nc, получим
окончательно:
COS a
f =
SMI a -f- -,-,-
2Р I lh r У
Это и есть наименьшее значение коэффициента треиия, при кото-
котором полуцилиндр и стержень будут находиться в раиновесии.
92
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. Г
Задача 1.36. Крутящий момент мотора электрической лебедки
ранен М=\20кГм. Для остановки мотора служат тормозные колод-
колодки тормоза Л (рис. а), прижимающиеся силами Р к тормозному диску
В, жестко связанному с ротором мотора. Радиус тормозного диска
г = 600 мм.
Определить силу давления Р, необходимую для удержания ротора
в равновесии, если коэффициент трения между деревянными колодка-
колодками и чугунным тормозным диском равен /=0, о.
Решение. Рассмотрим равновесие тормозного диска В (рис. б).
К диску приложена активная пара — крутящий момент М- Отбрасы-
Отбрасывая мысленно тормозные колодки, заменяем их дейстние реакциями.
б)
К задаче 1.36.
Каждая реакция раскладывается на две составляющие: нормальное
давление Р и силу трения F. Зависимость между нормальным давлением и
силой трения выражается при помощи коэффициента трения
F=fP. (О
Для равновесия диска необходимо, чтобы сумма моментов всех
сил, приложенных к диску, равнялась нулю. Силы Р взаимно уравно-
уравновешиваются и в уравнение моментов не входят. Силы трения обра-
образуют пару сил; крутящий момент представляет собой также пару сил.
Сумма моментов сил, составляющих пару относительно любой точки,
равна моменту пары. Таким образом,
F Чг — М = 0. B)
Подставляя значение силы трения A) в уравнение B), имеем:
/P-2r —Af = O,
oiкуда
М
120
Задача. 1.37. Электрическая лебедка (рис. а) весом Q = 2 7* кре-
крепится к фундаменту при помощи шести болтов. Максимальная сила
тяги Т равна 8 Т и направлена под углом 30° к горизонту. Коэф-
Коэффициент трения между основанием лебедки и фундаментом равен
/=0,5.
§4] РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ 93
Определить силу затяжки болтов, при которой срезывающее уси-
усилие в них равно нулю и лебедка удерживается от сдвига одной силой
трения.
Решение. Рассмотрим равновесие лебедки. К ней приложены
две активные силы: вес Q и скла тяги Т. Отбрасывая мысленно
связи — болты и фундамент, заменим их действие реакциями (рис. б).
Полагая затяжку всех шести болтов одинаковой, заменяем их действие дву-
двумя силами ПО ЗР каждая. Реакцию фундамента раскладываем на нормаль-
нормальную составляющую R и силу трения F. Силу трения направляем по
горизонтали влево, в сторону, противоположную возможному сдвигу
^1
^.HJPTi'
»\\ q\ Л\зр
6)
К задаче 1.37.
лебедки. Так как срезывающее усилие в болтах равно нулю, то сле-
следует рассмотреть равновесие лебедки как равновесие свободного твер-
твердого тела, находящегося под действием сил: Q, Т, ЗР, ЗР, R, F.
Выберем оси координат: ось х направим по горизонтали вправо,
ось у вертикально вверх. Составим сумму проекций всех сил па ось
у и приравняем ее нулю:
К — оР — Q — Г sin 30° = 0.
Из этого уравнения определяется нормальная составляющая реакции
фундамента, равная по величине нормальному давлению на фундамент:
-f- Г sin 30° = 6P-|-2 + 8-0,5 = 6P-|-6. A)
Приравнивая нулю сумму проекций всех сил на ось х, имеем:
Из этого уравнения определяется необходимая для равновесия сила
трения
F= T cos 30° = 8 ^<=^6,92 7". B)
Зависимость между силой трения и нормальным давлением дается
формулой
94
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ.
Подставив в это выражение значение силы трения B), нормального
давления A) и коэффициента трения, получим:
6,92 = F Л + б) / = F Л + 6) 0,5,
откуда определим необходимую величину затяжки болтов
«,92 — 6-0,5
Р =
6 • 0,5
1,3 Г.
Таким образом, для того чтобы болты не испытывали срезываю-
срезывающих усилий и лебедка удерживалась от сдвига силой трения, необ-
необходимо и достаточно, чтобы затяжка каждого болта удовлетворяла
условию
1,3 Т.
Задача 1.38. Однородный прямолинейный стержень АВ весом Q
(рис. а) опирается в точке В па шероховатую вертикальную степу.
Коэффициент трения между стержнем и стеной равен /. В точке А
стержень опирается на горизонтальный гладкий пол. Стержень удер-
удерживается в равновесии нитью AD, перекинутой через блок D. К концу
нити подвешен груз Л.
¦Ч
I
I
лг.
б)
К залаче 1.38.
Определить пределы, в которых можно изменять величину груза Л,
чтобы не нарушить равновесия стержня.
Решение. Рассмотрим равновесие стержня АВ. На пего дей-
действует одна активная сила, вес стержня Q, приложенный посредине
стержня в точке С и направленный по вертикали вниз. На стержень
наложены три связи: горизонтальный пол, вертикальная стена и
нить AD. На основании закона освсбождаемости от связей отбросим
мысленно связи и заменим их действие реакциями. Реакция гладкого
иола NA направлена перпендикулярно к полу, натяжение нити Р на-
направлено но горизонтали вправо, реакция шероховатой вертикальной
стены может быть представлена двумя составляющими: нормальной
реакцией Л'д, направленной по горизонтали плево, и силой трения Fn.
Сила трения направлена по вертикали: 1) в случае, когда груз Л
I 41 РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ 95
наименьшей величины и, следовагельно, возможное направление дви-
движения точки — вниз, сила трения FR направлена вверх (рис. б),
в сторону, противоположную возможному движению; 2) в случае,
когда груз Р наибольшей величины, точка В может начать сколь-
скользить но степе вверх и, следовательно, сила трения FB (рис. о) на-
направлена по вертикали вниз, опять-таки в сторону, противоположную
возможному движению.
Рассматривая равновесие стержня АВ как свободного твердого
тела, находящегося под действием пяти сил: Q, NA, N№ Fn, Pm\n
(рис. б), найдем минимальное значение веса груза Рт\п- Выберем оси
координат — ось х направляем по горизонтали вправо, ось у верти-
вертикально вверх. Составим уравнения равновесия (рис. б):
X mR (Fb) = Pmln I sin a -f- Q • 0,5 / cos a — NA / cos a = 0.
Через / в последнем уравнении обозначена длина стержня АВ. Кроме
того, напишем зависимость силы трения от нормального давления
FB=fNB.
Задача является статически определенной, так как система из четырех
уравнений содержит четыре неизвестных: NA, Fn, /V,j, Рт\п- Решая
совместно эту систему уравнений, находим искомое минимальное
значение величины груза Р:
Для определения наибольшей величины груза Р рассмотрим рав-
равновесие стержня АВ (рис. в) как свободного твердого тела, находя-
находящегося под действием пяти сил: NB, Fa, Q, NA, Pmai. Тогда уравне-
уравнения равновесия имеют вид
?/""'** = Ртах— Л'в = 0,
^ тв (Fk) = Рты! sin a -j- Q ¦ 0,5/ cos a — NAl cos a = 0,
кроме того,
f
Решая совместно эту систему уравнений, находим наибольшую вели-
величину груза Р, при которой стержень будет в равновесии:
р — Q m
96 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. (
Из уравнения A) следует, что Ртах неограниченно возрастает,
если tga—*¦/. При tga<[/ для возможности подъема стержня (сколь-
(скольжения точки В ннерх по стене) необходимо, чшбы сила Q была па-
пранлена вверх по пер i икали, чт невозможно. Таким образом, в этом
случае не сущеетует силы [>т1Ш которая могла бы нарушить равно-
равновесие лестницы.
Таким образом, равновесие стержня возможно при изменении веса
груза Р в пределах
Эта задача может быть решена и несколько иным путем. Заме-
Замечаем, что по условию задачи не требуется определения неизвеспюй
реакции гладкого пола NA. Поэтому из возможных уравнений равно-
равновесия стержня (рис. б) выберем такие, которые не содержат NA,
Составим уравнение моментов всех си.ч относшелыю точки Л:
V rnA(Fk) = NHl sin a -|-/-"B/cos а — Q fcosa = 0. C)
Второе уравнение равновесия—равенство нулю суммы проекций
всех сил па горизошальпую ось х. В нею также не пойдет неизве-
неизвестная сила NA:
ZFkx = Pmin-Nn = 0. D)
К этим двум уравнениям добавляется соотношение между нормаль-
нормальной реакцией п силой трения в течке В:
FB=fNB. E)
Подставив значение Fn иэ C) а ('!) и учтивая D), сразу получим.
Аналогично для нахождения наибольшего значения силы Р составим
такие же уравнения равновесия (рис. в):
V т А (F,,) z= NBl sin у — I:Hl cos a — Q ^ cos a = 0,
Is n =
{'сшив совместно aiy систему уравнений, определим максимальное
значение силы /-*:
/п.а>— .2(tge_y> - С)
Таким образом, как и следовало ожидать, мы пришли к результату,
выражаемому формулой B).
Сопоставляя оба решения, мы видим, что в мерном случае мы
применили общий мет.од составления уравнений равновесия для тер-
PABIIOBFXHE ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ
97
дого тела, находящегося под действием произвольной плоской системы
сил, не учитывая особенностей данной задачи. Достоинство общих
методов и заключается в том, что они ведут к цели, несмотря на раз-
различия в условиях задач.
Иногда такой путь не яиляется самым простым и коротким. На
примере второго способа решения мы видим, что при учете особен-
особенности данной задачи (п задаче не требуется определить величину
реакции гладкого пола NA) удалось составить меньшее число урав-
уравнений равновесия, которые проще и скорее привели к пели.
Задача 1.39. Два одинаковых однородных стержня ЛВ и ВС,
весом Р и длиной / каждый, шариирно соединены между собой.
В течке А стержень ЛВ шариирно прикреплен к вертикальной стене.
в)
К задаче 1.39.
Точка А находится на высоте h над горизонтальным полом, па ко-
который концом С свободно опирается стержень ВС.
Зная коэффициент трения / между стержнем ВС и горизонталь-
горизонтальным полом, определить угол $ при равновесии.
Решение. Рассмотрим отдельно равновесие стержня ВС (рис. б)
и стержня АВ (рис. в). Отбросив мысленно связи, заменим их дей-
действие реакциями. К стержню ВС приложены силы: нес Р, нормальная
реакция горизонтального пола N и сила трения F, направленная
в сторону, противоположную возможному движению; реакция шар-
шарнира В не известна ни по величине, ни но направлению (представим
се двумя составляющими SBx и SBy).
К стержню АВ приложены силы: вес Р; составляющие реакции
шарнира В, равные и противоположные силам, приложенным в точке В
к стержню ВС (обозначим эти составляющие через S'bx и S'sy);
составляющие реакции шарнира А, названные RAx и Riy.
Составим уравнения предельного равновесия для стержня ВС:
r-Sllx = 0, A)
N~P — SHy = 0, B)
Fl sin p — N1 cos p + P -^ cos ? = 0, C)
F ==fN. D)
4 M. И. Бать и др., т. I
98 ПЛОСКАЯ СИСТЕМА СИЛ |ГЛ. !
Уравнение моментов C) составлено относительно точки В, уравне-
уравнение D) дает зависимость силы трения от нормального давления.
Уравнения равновесия для стержня АВ будут:
S'Bx—RAx = O, E)
S'By — P + RAy = 0, F)
S'rxI sin а — S'nyl cos а -4- P - - cos а = 0. G)
Здесь сумма моментов сил G) составлена относительно точки А.
Чтобы найти уравнения, определяющие зависимость между углами
аир, решим совместно составленные уравнения, кроме уравнений E)
и (б), так как последние содержат RAx и RAv, которые согласно
условию задами находить не нужно. Из уравнения A), B) и D) най-
лем:
SHyi. (8)
Исключив из уравнения C) неизвестные F, N, получим:
Snxl sin 3 — (Я -u SBy) I cos 3 -\- PJ cos В = 0. (9)
Разделив это равенство на /cos^ и воспользовавшись равенством (8),
найдем:
SBy)tg$-SIly-~ = O. A0)
С другой стороны, разделив уравнение G) на /cos а и воспользовав-
воспользовавшись равенством (8), получим:
SBy-\-^- = 0. (И)
Исключив из уравнении A0) и A1) Snv, паЛдем:
3tg8 — tga = y. A2)
Это — первое уравнение, определяющее углы а, В и положении рав-
равновесия.
Второе уравнение найдем из геометрического равенства
/sin 3-j-/sin a. = h, A3)
откуда получим:
sin В -f- sin о. = -*-. A4)
Исключив из равенств A2) и A4) угол а, найдем:
^-sini=__2
ь >/1 — (Л//— sin fi)a /
РАШЮЯЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ
99
Если j30 — корень этого уравнения, то равновесие системы будет
при любом Р^>Ро-
Задача 1.40. Однородный стержень АВ длиной / опирается кон-
концом А па внутреннюю гладкую понерхность пустотелого полуцилиндра
радиуса г и концом В па шероховатый горизонтальный пол (/<^2г).
В положении равновесия центр тяжести стержня С находится на вер-
вертикальном диаметре полуцилиндра.
Определить угол Э> составляемый стержнем с полом в положении
равновесия, и коэффициент трения скольжения / между стержнем и
полом, полагая, что сила тре-
пия достигает в этом положе-
положении стержня своего предель-
предельного значения.
Решение. Рассмотрим
равновесие стержня АВ. На
стержень действует одна актив-
активная сила, вес стержня Р. Так
как центр тяжести стержня С
лежит на одной вертикали
с центром цилиндра О, то ли-
линия действия силы тяжести
проходит через точку О. На
стержень наложены две связи: гладкая поверхность полуцилиндра и
шероховатый пол. Применим закон освобождаемое™ от связей. Отбро-
Отбросим мысленно связи (рис. б) и заменим их действие реакциями. Реакция
гладкой стенки полуцилиндра направлена нормально к его поверх-
поверхности, т. е. по радиусу АО. Изобразим ее силой Т. Следовательно,
в точке О пересекаются линии действия двух сил: реакции Т и веса Р.
Но стержень находится в равновесии под действием трех сил: Т, Р
и реакции иола в точке В. Согласно теореме о трех непараллель-
непараллельных силах линия действия реакции пола R должна также пересекать
точку О. Направим реакцию R но линии ВО (рис. б). Угол между
нормалью к полу и реакцией R есть угол трения ср, причем /= tg ?¦
Из треугольника 0BD найдем:
_ ВР — §CS°ll —/cos?
'J
К задаче
г . UIJ <
A)
Обозначим угол между силой Т и линией горизонта буквой г.
Тогда, опуская перпендикуляр AN из точки А па вертикальный диа-
диаметр, имеем AN= АО cos a. = AC cos p, или
I
Г COS а = у COS р.
Аналогично ON= r sin i и DN=l sin P; следовательно,
т sin i-\- I sin JJ = r.
4*
B)
C)
100 ПЛОСКАЯ СИСТЕМА СИЛ 1ГЛ. I
Сопоставив A) и B), найдем:
cosa = /. D)
Обозначив для краткости =- == b <Г 1 (так как по условию /<Г 2г),
найдем из B) и C), что
cos a. = b cos p, E)
sin a= 1 — 1b sin p. F)
Возведем равенства E) и F) в квадрат и сложим. После неслож-
несложных преобразований получим:
36 sin р — 4 sin р -(- Ъ = 0,
откуда
. о 2 +- J/ 4 — ЗА1'
sin р = —~ о. .
1 Зо
Следовательно,
cos р = ]/ 3*« - 2 ± V 4 - ЗЛ
Знак минус перед вторым корнем должен быть отброшен, так как
Ж- — 2 — V 4 — 362 < 0
и значение cos 3 будет при этом мнимым. Итак, окончательно
cos 8 = Д 1/ 362 —
f=b cos 3 =-| Y № — 2 Н- К 4 - Зй2 .
Решение этой задачи отличается от большинства задач на равно-
равновесие при наличии трения тем, что мы не разлагаем реакцию шеро-
шероховатой поверхности на нормальную составляющую и силу трении.
Задача 1.41. Дне одинаковые призмы А и В образуют лестницу.
Ступени нагружены силами Р и Q, точки приложения которых за-
заданы (рис. а). Призма А опирается на вертикальную стену и накло-
наклоненную под углом а плоскость второй призмы. Призма В опирается
на горизонтальный пол.
Определить условия равновесия, учитывая трение всех контакти-
контактирующих поверхностей. Коэффициенты трения призм о горизонтальный
пол, вертикальную стену и друг о друга одинаковы и равны /=tg(p.
Собственными весами призм можно пренебречь по сравнению с силами
Р и Q.
§41
РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ
101
Решение. Рассмотрим равновесие каждой из призм, отбросив
мысленно стену, пол и другую призму, заменив их действия нормаль-
нормальными реакциями Nh No, N3 и силами трения Ть Ть Т3. Расчетные
схемы показаны на рис. б для верхней призмы и на рис. в для нижней..
Максимальные значения касательных сил (сил трения) при равно-
равновесии равны
7'1==/М, 7-9=/Afc
В проекциях па коорди-
координатные оси уравнения равно-
равновесия имеют вид:
для призмы А
Л/i — /V2 sin a -j-
M cos a -(- /М — Я +
-\- fN-i sin а= 0;
для призмы ZJ
— //v'2 cos а -}-
-|-Л/2 sin а —/Л/3 = 0,
— /Л4 sin а—A^cosa — Q-(-
Решив эту систему уравне-
уравнений равновесия, найдем:
„ _ 2/ sin а -(- A —Р) cos ot
== A —/2) Sill a — 2/ COS а
или, после подстановки /=
= tg <p и несложных триго-
тригонометрических преобразо-
преобразований,
Р—О —JgJL
~ТгУ
(
в
ГЛ 1
а-2сХ
W
-а-у>
К задаче 1.41.
Отсюда видно, что решение существует, если а^>2ср. Таким обра-
образом, условие равновесия лестницы, образованной двумя призмами,
будет:
Эта задача наряду с приведенным аналитическим решением может
Сыть решена и графически.
102
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
Если заменить касательн>ю и нормальную составляющую реакции
в каждом случае одним вектором (рис. г):
Я, = N, + 7,,
A.
У si.
A
0
^ о
,, ^ »|f
то к каждой из призм будет приложено три силы (см. рис. г) и
можно воспользоваться теоремой о трех силах. Графическое решение --
комбинация двух замкнутых силовых
треугольников — предс7-авлено на рис. д.
Задача имеет решение только при
а^>2ср. Это учтено па рис. г, где
угол а начерчен достаточно большим.
Задача 1.42. Однородный стержень
АС длиной / и весом О опирается кон-
концом А на гладкую горизонтальную
плоскость, а промежуточной точкой В
на прямоугольную призму, стоящую на
той же гладкой плоскости. Угол трения
между стержнем и призмой равен ср.
Определить, какой вес должна иметь
призма, чтобы система была в равно-
равновесии. Стержень составляет с горизон-
горизонтом угол а. Размеры призмы известны
(рис. а).
Решение. Рассмотрим равновесие
стержня и призмы в отдельности. От-
Отбросив мысленно горизонтальную пло-
плоскость и призму, заменим их действие
на стержень реакциями. На стержень
в) действуют (рис. б): нес G, нормальная
реакция гладкой плоскости NА, пор-
К задаче 1.42. мальная реакция призмы Nn, касатель-
касательная реакция призмы Тв (сила трения).
Составим уравнение моментов относительно точки А:
-т»
откуда получим:
NB= .j- cosa- sin a.
Рассмотрим, далее, предельное равновесие призмы, отбросив мыс-
мысленно пол и стержень. На призму действуют (рис. в): нес Q, давление
стержня — NB, сила трения — Тв и нормальная реакция No плоскости.
§ 4| РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРР.НИЯ 103
Где следует приложить равнодействующую нормальной реакции плоскос-
плоскости? Правее силы Q она не может быть приложена, так как относительно
такой точки не будет выполнено равенство нулю суммы моментов
всех сил. Значит, точка приложения реакции лежит на. левой половине
отрезка ОЕ. Крайнее возможное положение ее, соответствующее
критическому равновесию, в точке О, когда призма может начать по-
поворачиваться вокруг ребра О. На рис. в изображены силы в положе-
положении критического равновесия.
Горизонтальная составляющая нормального давления — NH на приз-
призму не должна превышать по модулю горизонтальной составляющей
силы трения — Тв в предельном положении равновесия. Это условие
может быть записано так:
Тв cos a Ss NB sin а.
При этом знак неравенства следует понимать в том смысле, что сила
трения не достигает своего максимального значения и, следовательно,
равновесие системы не будет нарушено.
Подставив в это неравенство максимальное значение Тв, равное
ND ¦ tg cp, получим:
tg 'f - NB cos я 5; NB sin а, или tg
т. e.
Составим уравнение моментов сил, приложенных к призме отно-
относительно точки О:
7д • a- cos a — Л/й ¦ а ¦ sin a — Q ^ = 0.
Подставив предельное значение силы трения
и значение Л/й, найденное ранее, в предыдущее равенство, получим:
a-lgcp- cos a,j- cos a sin a —/- cos a- sin a-a sin а — Q2 =0.
Отсюда найдем:
-
Q = - - (tg cp cos a — sin a) cos a sin a =
2* (s'n ^ cos a — cos ^ s'n
или окончательно
Q =¦ тгт sin (cp — a) sin 2a,. *
^ 2b cos tp VT '
Из этой формулы также следует, что задача имеет решение при
, ибо в противном случае вес призмы получится отрицательным,
104
ПЛОСКАЯ СИСТЕМА СИЛ
II Л. I
что невозможно. Чем ближе угол наклона стержня к углу трения,
тем более легкой может быть призма; в случае когда а = ср, даже
невесомая призма удерживается и равновесии.
Задача 1.43. Квадратный ящик весом Q находится в покое на
горизонтальном негладком полу. Коэффициент трения между полом и
ящиком равен /. Через ящик перекинут трос, закрепленный своими
концами в О и Oj. Ветни троса образуют с полом углы 30° и 60°.
Пренебрегая трением между ящиком и тросом, определить натя-
натяжение троса, при котором ящик будет оставаться в покое (рис. а).
Решение. Рассмотрим равновесие ящика (рис. б). Па ящик дей-
действует одна активная сила — вес Q, приложенная в центре и направ-
направленная но вертикали вниз. Па ящик наложены две связи—трос и
К задаче 1.43.
пол. Отбрасывая мысленно эги связи, заменим их дейстние реакциями.
Так как трение между ящиком и тросом отсутствует, то натяжение
троса Т будет везде одинаковым. Натяжение троса будет действо-
действовать на ящик по направлениям ОА и О,В (рис. а). Разложим реак-
реакцию пола на нормальную реакцию N и касательную реакцию F, яв-
являющуюся силой трения.
Рассмотрим равновесие ящика как свободного тела, находящегося
под действием пяти сил, указанных па рисунке. Составим уравнения
равновесия, приравняв пулю сумму проекций всех сил на оси х и у:
N-
Т cos 60° — Т cos 30° -f- F = 0,
Q—T sin 00° — У sin 30° = 0.
С)
B)
Кроме того, имеем зависимость между силой трения и нормальным
давлением (по модулю равным нормальной реакции), а именно:
C)
D)
Из B) находим:
F = fN.
l\'=Q-\- 7'(sin 60°+ sin 30°).
Подставляя это значение в |3) и затем в A), имеем:
7 (cos 60°— cos30°)-|-/[Q+ 7"(sin 60°+ sin 30°)] = 0. E)
§4]
РАПНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ
105
Решая уравнение (о) относительно неизвестного Т, находим натяже-
натяжение троса в предельном случае
Т=-
/Q
2/Q
"cos30°— cos60°— /(sin 60' — sin 30°) j/з" _ i _ t /j/3 -L. [)'
Ящик будет находиться и покое при
УЗ- 1-/A/3+1)'
Задача 1.44. Дна цилиндра с радиусами г, и г.} и весами Р, и
Р2 опираются на горизонтальный пол и вертикальную стену гак, что
прямая OjO.,, соединяющая центры цилиндров, образует угол у с го-
ризоптом. Коэффициенты трения: между первым цилиндром и гори-
горизонтальным полом /,, между вторым цилиндром и вертикальной сте-
стеной /2 и между цилиндрами /.
Определить минимальные значения этих коэффициентов, при кото-
которых система может находиться в равновесии, а также нормальные
реакции пола, степы и реакции между цилиндрами.
Решение. Рассмотрим равновесие каждого из цилиндров в от-
отдельности (рис. б и в), отбросив мысленно пол, степу и другой
цилиндр, заменив их действие реакциями. Каждую реакцию разложим
на нормальную составляющую и силу трения. Тогда первый цилиндр
можно рассматривать как свободное твердое тело, находящееся
в равновесии иод действием пяти сил: веса, двух нормальных реак-
реакций и двух сил трения (рис. б). Аналогично рассматривается равно-
равновесие второго цилиндра (рис. в). Силы трения направлены по каса-
касательным, проведенным к цилиндрам в точках соприкосновения в сто-
сторону, противоположную возможному движению цилиндра.
106 ПЛОСКАЯ СИСТЕМА СИЛ (ГЛ. I
Составим уравнения равновесия для первого цилиндра:
У, Fky = Ni — Pi — N sin 9 — F cos 9 = 0,
V m (F \ P r f-r A
2d mOl Krk) ^lrl — ' rl u-
Уравнения равновесия для второго цилиндра будут:
2J Ft,x = N cos 9 — N1 — F sin 9 = 0,
? Fky = N sin 9 — Pa + F2 + F cos 9 = 0, B)
К этим уравнениям равновесия следует добавить зависимости пре-
предельных сил трения от нормального давления
C)
Решив совместно систему из девяти уравнений A) — C), найдем:
Ра cos ? . sj П \ П '+sintP
1 1 M
A Ч-sincp)
П \ П
_ P3 cos у
cos<f .
1 -I- sin tp'
s'n <p
l+slncp+cos<f-
Полученные значения коэффициентов трения янляются минимальными;
если они будут превышать эти неличины, то равновесие системы
сохранится, а силы трения при этом не будут достигать своих пре-
предельных значений.
Задача 1.45. Шкив радиуса г насажен на вал радиуса а, который
может вращаться в подшипниках. Коэффициент трения между валом
и подшипниками /.
Определить наибольшую иеличину силы Р, которая удержит шкив
в покое, если к шкиву приложена сила Q, образующая с силой Р
угол а (рис. а). Найти значение силы Р, когда а = т/2 и когда силы Р
и Q параллельны.
Решение. Отбросив мысленно подшипники, рассмотрим равно-
равновесие вала вместе со шкивом, заменив действие подшипников нор-
нормальной реакцией N и моментом сил трения т. Момент сил трения
(относительно точки О) может быть представлен в виде
m=/N a,
(I)
S4|
РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ
107
Момент сил трения будет направлен в сторону, противоположную
возможному движению. Таким образом, этот момент будет совпадать
а)
б)
К задаче 1.45.
по направлению с моментом меньшей силы. Положив Q<^P, соста-
составим уравнение' равновесия вала со шкивом, приравняв нулю сумму
моментов всех сил относительно центра О: '
С другой стороны, нормальная реакция N определится по величине
как равнодействующая двух сил Р и Q
n= Vp* -\- Q3 -г 2/JQ со^* • C)
Подставив это значение в уравнение B) и освободившись от ради-
радикала, получим:
- BQ + 2Q cos a??) P -\- Q* ( 1
- ^"-) = 0.
D)
Величина Р равна большему корню этого квадратного уравнения.
Меньший корень Р будет соответствовать случаю Q^> Р. В слу-
случае, когда Р и Q параллельны, решение упрощается. Действительно,
при этом
Л'—P-fQ • E)
и, следовательно, из B) после несложных преобразований находим:
Р = ЪГТ=Га- ^
R случае a = i:/2 силы Р и Q нзаимпо перпендикулярны, и из D)
получим:
108 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
Знак минус не удовлетворяет условию задачи, так как при эгсм
- 1 < 1 (8)
и, следовательно, P<^Q, что противоречит условию. Неравенство (8)
вытекает из того, что функция
при х=\ принимает значение
убывает. Действительно,
а в рассматриваемом случае
<р(\)=\ и при
при
монотонно
Знак минус в равенстве G) соответствует случаю Q~^>P, когда
момент трения будет совпадать по направлению с моментом силы Р.
Для приобретения навыков в решении задач на
равновесие при наличии трения скольжения реко-
рекомендуется решить следующие за-
задачи из «Сборника задач по тео-
теоретической механике» И. В. Ме-
Мещерского, издания 1950 г-, и боле е
поздних лет: 67, 71, 73, 74, 174, 175,
17G, 177, 178, 180, 181, 186, 187.
2°. Равновесие твердого тела
п р ^ наличии трения качения. Между
кап<ом и плоскостью, на которой он по-
покоится, возникают силы трения, если прило-
приложить к оси катка силу 5 (рис. 1.42), стре-
стремящуюся его двигать по плоскости. Рассмотрим случай, когда сила 5
параллельна горизонтальной плоскости.
Из опыта известно, что при изменении величины силы S от нуля
до некоторого предельного значения S,[p кагок остается в покое,
т. е. силы, действующие на качок, уравновешиваются. Кроме актив-
активных сил: веса Р и силы S, к катку, равновесие которого рассматри-
рассматривается, приложена реакция плоскости. Из условия равновесии трех
непараллельных сил следует, что реакция плоскости R должна про-
проходить через центр катка О, так как две другие силы приложены
к этой точке.
Следовательно, точка приложения реакции С должна быть сме-
смещена па некоторое расстояние /к от вертикали, проходящей череп
центр колеса, иначе реакция If не будег иметь горизонтальной со-
§4] РАВНОВЕСИЕ ТРЛ ПРИ НАЛИЧИИ ТРГ.НИЯ 109
ставляютей, необходимой для удовлетворения условий равновесия.
Разложим реакцию плоскости ¦ R на две составляющие: нормальную
составляющую N и касательную реакцию F, являющуюся силой тре-
трения (рис. 1.43).
Таким образом, в предельном положении равновесия катка к нему
будут приложены две взаимно уравновешивающиеся пары: одна пара
сил Eпр, F) с моментом 6"пр-г (где г — радиус катка) и вторая пара
сил (N, Р), удерживающая каток в равновесии. Момент торой пары,
называемый моментом трения качения, определяется формулой
mmn=fKN, A2*)
где /к — коэффициент трения качения, измеряемый в единицах
длины. Этот коэффициент можно рассматривать как расстояние, на
которое смещается реакция N от вертикали,
проходящей через центр катка.
Для того чтобы имело место чистое ка-
качение (без скольжения), необходимо, чтобы
сила трения F была меньше по величине,
чем максимальная сила трения скольжения
F<fN, A3*)
где /— коэффициент трения скольжения. 'Ш//////////7777гт77т//!у////////:м
Трение качения возникает из-за дефор- ^
мации катка и плоскости, ^следствии чего P|ic- 1.43.
соприкосновение между катком и плоскостью
происходит по некоторой поверхности, смешенной от нижней точки
катка в сторону возможного движения. При решении задач па
равновесие твердого тела при наличии трения каче-
качения надо выполнить четыре первых пункта, указан-
указанны х в начале книги, па стр. 15. При этом следует реакцию
шероховатой поверхности направить из точки, отстоящей на расстоянии
коэффициента трения качения fK от нормалс, проведенной из центра
катка так, чтобы она проходила через гсчку О пересечения двух
других сил, действующих на каток (рис. 1.42), или заменить реак-
реакцию R двумя составляющими — нормальной реакцией N и силой
трения F;
5) сопоставить число неизвестных и число уравнений равновесия,
добавив к ним зависимость момента трения от нормального давления;
число неизвестных должно быть равно числу уравнений, если задача
является статически определенной;
6) составить систему уравнений равновесия для твердого тела;
7) решив полученную систему уравнений, определить искомые
величины;
8) сопоставив величину силы трения с максимальной силой трения
скольжения, убедиться в том, что первая сила меньше второй.
по
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
Задача 1.46. Цилиндрический каток диаметра 60 см и весом
Q= 392 кГ приводится в равномерное движение человеком, который
давит на рукоятку АО = 1,5 м с постоянной силой Р в направлении АО.
Высота точки А над горизонтальной дорогой 1,2 м. Коэффициент
трения качения катка равен /=0,5 см.
Определить величину силы Р, силу трения при качении и нор-
нормальную составляющую реакции горизонтальной плоскости (рис. а).
Коэффициент трения скольжения между катком и дорогой /=0,2.
Решение. При равномерном качении катка все силы, действую-
действующие на каток, уравновешиваются. К катку приложены две активные
силы: нес катка Q и сила давления человека Р. На каток наложена
одна связь — горизонтальная плоскость. Применив закон освобожда-
освобождаемое™ от связей, отбросим мысленно горизонтальную плоскость и
х
а.) б)
К задаче 1.46.
заменим ее действие реакцией R. Эта реакция приложена в точке С,
находящейся на расстоянии /к от вертикали, проведенной через центр
колеса. Реакция R направлена но прямой СО, так как согласно тео-
теореме о трех непараллельных силах в случае равновесия лиши их
действия пересекаются в одной точке О (рис. б). Реакцию плоскости R
раскладываем на две составляющие: нормальную составляющую N,
перпендикулярную к плоскости, и касательную составляющую — силу
трения при качении F, направленную вдоль плоскости.
Рассмотрим равновесие кагка как твердого тела, находящегося
под действием четырех сил: Q, P, N, F.
Выберем систему декартовых координат. Ось х направим по го-
горизонтальной плоскости вправо, ось у — вертикально вверх через
центр катка. Составим уравнения равновесия. Обозначив буквой а угол
между горизонталью (осью х) и рукояткой ОА, получим:
^Fhx=F-Pco^ = 0, A)
2lFky = N—Q — P sin a = 0t B)
][]/ис (/=;) = Р cos a ¦ г — (Q + P sin a)/K = 0. C)
В уравнении C) букпой г обозначен радиус катка.
I 4| РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ 1 I 1
При составлении суммы моментов сил относительно точки С сила Р,
приложенная в центре катка О, разложена на две составляющие —
горизонтальную (Р cos а) и вертикальную (Р sin а), и использована
теорема Вариньона. При этом, как принято всегда делать, при вычис-
вычислении момента горизонтальной составляющей силы Р мы пренебрегли
изменением ее плеча, считая, что оно равно радиусу катка г.
Из уравнения C) "найдем величину искомой силы Р:
р %-_ = —gLW =8,27 кГ.
Г COS а— /к sin а 1,2 0,9
° °5
"° Г, ~ °'5 Г5
Равенство B) даст:
по
N= Q -\- P sin а = 392 -f 8,27 ^ = 396,95 к Г.
1 ,о
Из уравнения A) определяем величину силы трения:
F=Pcosa.--= 8,27 {-'? = 6,63 кГ.
1,0
Проверим, сопоставляя величины силы трения при качении F и
силы трения скольжения, будет ли в данном случае чистое качение
или же будет иметь место скольжение. Сила трения скольжения равна
Fl==fN= 0,2 • 396,95 = 79,4 кГ.
Таким" образом,1 сила трения скольжения больше силы трения при
качении ,
Fi>F
и каток будет катиться без скольжения.
Задача 1.47. Цилиндрический каток радиуса г и весом Q
(рис. а) удерживается в равновесии на наклонной плоскости, состав-
составляющей угол а с горизонтам, нитью, перекинутой через блок А.
К концу нити подвешен груз несом Р. Коэффициент трения качения
катка равен /к.
Определить наименьшую и наибольшую величины веса Р, при
которых каток будет в равновесии. Найти наименьшее значение коэф-
коэффициента трения скольжения /, при котором в случае движения
каток будет катиться без скольжения.
Решение. Рассмотрим равновесие катка в двух случаях.
В первом случае, когда величина Р имеет наименьшее значение,
возможное направление движения катка по наклонной плоскости —
вниз (рис. б). Точка С, где приложена реакция плоскости, в этом
случае смешена на расстояние /к влево от перпендикуляра, опушен-
опушенного из центра катка О на наклонную плоскость. К катку приложены
две активные силы: вес Q и натяжение нити Рт\а-
112
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
Смбрасыпая мысленно связь, наложенную па каток, — наклонную
плоскость, заменяем ее действие реакцией, которую раскладываем
па нормальную состанляютую N и касательную составляющую (силу
трения F). Составляющая N перпендикулярна к наклонной плоскости,
сила трения направлена вдоль наклонной плоскости в сторону, про-
тиноположную возможному движению центра катка.
Рассмотрим равновесие катка как равновесие свободного твердого
тела, находящегося под действием четырех сил: Q, Ртт, N, F. Так
как по условию требуется найги только минимальное и максимальное
значения силу Р при paFii-говесии, то из трех уравнений равновесия
ттжжшшь
К задаче 1.47.
составим одно уравнение, выражающее равенство пулю суммы момен-
icn всех сил относительно точки С:
? тс (Fk) = - /KQ cos a - J- (Q sin а - PmiIIj r = 0. A)
В это уравнение не вошли неизвестные силы N и F, так как они
приложены в точке С.
При составлении уравнения мы разложили силу Q па дне состав-
составляющие: Q cos а, направленную перпендикулярно к наклонной плос-
плоскости (плечо этой составляющей относительно точки С равно коэф-
коэффициенту трения качения /к), и составляющую Q sin а, направленную
параллельно наклонной плоскости и отстоящую па расстоянии г от
нее. Решая уравнение A) относительно Ртп> имеем:
Лпш ='
^
sin а — --^ cos а
¦]•
B)
Рассмотрим теперь второй случай, когда сила Р достигает макси-
максимальной величины, при которой возможно равновесие. В этом случае
возможное направление движения катка — вверх по наклонной плос-
плоскости (рис. в). Силы Q и Ят1Х направлены аналогично первому слу-
случаю и приложены пс-прежнему в центре каша О. Реакция наклонной
§ 4| РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ 113
плоскости на этот раз приложена в точке Сь смещенной на расстоя-
расстояние /к вправо по наклонной плоскости.
Составляем уравнение моментов относительно точки Q:
Л «с, (Fh) =AQ cos a — (Ршах — Q sin а) г = О,
откуда имеем:
Таким образом, каток будет находиться в равновесии на наклонной
плоскости, если величина силы Р лежит в пределах
Q sin а — - cos » UcPs^Q sin а -j- — cos а .
Перейдем к определению наименьшего значения коэффициента
трения скольжения /, при котором в случае движения цилиндр будет
катиться, a i;e скользить. Рассмотрим вначале случай, когда вес
груза Р имеет наименьшую величину.
Приравняем нулю суммы проекций всех сил на ось х, параллель-
параллельную наклонной плоскости, и па ось у, перпендикулярную к ней
(рис. б). Подставляя в первое уравнение
2 Fh* = рш\п Н- F - Q sin а = О
значение Р,,иП, соответствующее B), находим силу трения при каче-
качении
Второе уравнение равновесия
позволяет определить нормальное давление, равное по величине нор-
нормальной реаьции
yV=Q cos a.
Условием, при котором будет чистое скольжение, является:
F<fN, D)
где/—коэффициент трения скольжения. Внося в D) значения F и N,
находим:
? E)
114
ПЛОСКАЯ СИСТЕМА СИЛ
|ГЛ. I
Рассмотрим, далее, случай, ксгда вес груза Р имеет наибольшую
величину (рис. в). В этом случае уравнения проекций будут:
Внося в уравнение F) значение Ртлх C), находим:
^F, = ?q cos а,
Ni = Q cos a.
Подставляя эти значения в D), получаем условие чистого качения
k\\\\\\\\\\\\\\\\\^
которое совпадает с условием E).
Задача 1.48. Стальной цилиндр радиуса г зажат между двумя
параллельными направляющими, из которых нижняя закреплена не-
неподвижно, а верхняя мо-
)р жег перемещаться прямо-
прямолинейно, оставаясь иарал-
? лельной своему перво-
первоначальному положению.
Верхняя направляющая
прижимается вертикаль-
вертикальной силой Р к диску
(рис. а). Коэффициенты
трения качения между па-
палиндром, нижней и верх-
верхнем направляющими соот-
соответственно равны/К1 и/К:!.
Пренебрегая весом ци-
цилиндра и направляющих,
найти максимальную силу Ть приложенную к верхней направляющей,
при которой цилиндр еще будет оставаться в покое.
Решение. Рассмотрим равновесие цилиндра (рис. б), отбросив
мысленно нижнюю и верхнюю направляющие, заменив их действае
реакциями. Тогда на цилиндр будут действовать со стороны нижней
направляющей нормальная реакция А/, и сила трения Ть со стороны
иерхней направляющей нормальная реакция N.2 и сила трения 7V
При этом точка приложения реакции нижней направляющей будет
смещена вправо от вертикального диаметра па расстояние /„,, а теч-
течка приложения реакции иерхней направляющей будет смещена на
расстояние fKi от вертикального диаметра влево, т. е. в сторону воз-
а)
6)
К задаче 1.48.
§ 4| РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ 1 15
можного перемещения цилиндра по отношению к каждой из направ-
направляющих.
С другой стороны, если рассмотреть равновесие цилиндра вместе
с верхней направляющей, то, проектируя силы на вертикаль, получим:
/Vj — Р = 0 или N, = P.
Тогда, возвращаясь к рассмотрению цилиндра (рис. б), имеем, проек-
проектируя силы на вертикаль:
Л/, — Л/2 = 0 или Nl = N.l = P.
Составим, далее, сумму моментов всех сил относительно точки Л:
откуда искомая максимальная сила равна
(МЛ Ч- М/К1) = 2Р~ (Л, -f Л, )•
2
Если коэффициенты трения качения равны
то тогда
Для приобретения навыков в решении задач на
равновесие тел при наличии трения качения реко-
рекомендуется решить следующие за-
задачи из «Сборника задач по теоре-
теоретической механике» И. В. Мещер-
Мещерского, издания 1950 г. и более позд-
поздних лет: 190, 191, 192.
3°. Равновесие твердых тел при
наличии трения гибких тел. Предпо-
Предположим, что па неподвижный цилиндр навита
нить, к одному концу которой подвешен груз Рис. 1.41.
весом Р. Угол охвата цилиндра нитью равен а
(рис. 1.44). Коэффициент трения нити о шероховатую поверхность
цилиндра равен /. Тогда сила Т, необходимая для удержания груза Р
в равновесии, определяется по формуле Эйлера:
Т=Ре~и, A4*)
где е — основание натуральных логарифмов. Таким образом, сила Т,
уравновешивающая груз Р, не зависит от диаметра цилиндра и явля-
является функцией угла охвата и коэффициента трения.
При решении задач на равновесие твердых тел
при наличии трения гибких нитей надо выполнить
116
ПЛОСКАЯ СИСТЕМЛ СИЛ
[ГЛ Г
четыре первых пункта, указанных r начале книги,
на стр. 15. Далее следует:
5) сопоставить число неизвестных величин и число уравнений рап-
иопесия, добавив к уравнениям равновесия зависимость A4*) между
силами натяжения нити с обеих сторон охватываемого тела, и убе-
убедиться в том, что число независимых уравнений рашю
числу неизвестных и, следовательно, задача является
статически определенной;
6) выбрать систему координат;
7) составить уравнения равновесия тпердого тела;
8) решив эту систему уравнении, определить неизве-
неизвестные величины.
Задача 1.49. При швартомке судна матрос наклады-
накладывает канат восьмеркой на чугунные столбы. Натяжение
каната рашю Q, сила, с которой матрос удерживает ка-
канат, равна Р. Угол охпата канатом каждого столба ра-
ранен 210°.
Определить коэффициент трепня каната о столбы, если
известно, что матрос может удержать канат, наложив три
восьмерки. Полагая коэффициент трения каната о чугунный столб
ранным /=0,15, определить величину натяжения, которое матрос
способен удержать, если сила р = 60 кГ.
Р е ш е и и е. Угол oxnava канатом одного столба равен
2Ю° = -1 я.
При наложении трех поплгерок угол охвата канатом столбов будет
в шесть раз больше, т. е. 7л. Тогда зависимость натяжений двух к< п-
цов каната определится формулой
К зада-
задаче 1.49.
Логарифмируя, находим искомый коэффициент трения между канагг<м
и чугунным столбом:
" Q
f= -- - 111
Из A) имеем:
Рш
In wp = lT.f= 3,3 .
Отсюда при заданных значениях / и Р
и О = 27 -60= 1620 к Г.
9-=21
Р
Таким образом, наложив три восьмерки на чугунные столбы, матрос
может удержать в равновесии канат, ко второму концу которого при-
приложена сила, равная 1620 кГ.
§41
РАВНОВЕСИЕ ГЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ
117
Задача 1.50. Через два неподвижных вала с центрами О и О,
(рис. а) перекинут трос, к концам которого подвешены грузы Р и Q,
причем P^>Q.
Определить минимальное значение коэффициента трения между
валами и тросом, при котором грузы будут находиться в равновесии.
Полагая коэффициент трения троса о вал равным /= 0,25, найти
груз Р, который можно удержать в равновесии грузом Q=10 кг.
Решение. Рассмотрим равновесие части троса, охватывающего
левый вал (рис. б). На трос действует активная сила Р. Отбрасывая
мысленно правый вал, разрезаем трос между валами и заменяем дей-
действие правой части силой натяжения троса Т.
К за„аче i 50.
Для равновесия этой части троса должно удовлешорягься равен-
равенство
~-J0L
где угол обхвата а равен 3-/2. Итак,
Рассмотрим, далее, равновесие правого вала (рис. в), отбросив
мысленно левый вал, разрезав трос и заменив его действие силой Т,.
Согласно закону равенства действия и противодействия натяжения Т
и 7"j равны по величине. Для равновесия части троса, охсшынаютсй
правый вал, должно удовлетворяйся равенство
_ _ _ -,, T.S (<)\
Q = Те , * '
так как и у правого вала угол охвата а=3~/2.
Решая совместно уравнения A) и B), исключая натяжение ipoca
между валами Т, находим:
г _ бт.Т
откуда
f=Ar:^Q-
1 18
ПЛОСКАЯ СИСТЕМА СИЛ
|ГЛ.
Эта же задача может быть решена и другим способом. Рассмат-
Рассматривая равионесие всего троса (рис. а) и замечая, что полный угол
охвата тросом двух валов рапеп
3,3 „
находим зависимость между силами Р и Q:
oi куда имеем:
4?
Для определения величины груза Р, который можег быть удержан в
раннопесии грузом Q=lO кГ, из C) находим:
Тогда
In ?- = 3*/= 2,358.
= 10,5 и Р = 10 • I 0,5 = 105 кГ.
Таким образом, грузом Q, равным 10 кГ, можно удержать в равно-
равновесии груз Р, равный 105 к Г.
Задача 1.51. Трос АВ охватывает барабан, вращающийся вокруг
центра О. Коэффициент трения троса о барабан равен /. Концы троса
А и В прикреплены к рычагу BAD, который можег поворачиваться
вокруг точки D. Расстояния AD^a, BD = b.
ВС \А
а)
К задаче 1.Ы.
I с J в
6)
Определить натяжение троса в точках А и В. Пренебрегая весом
рычага BAD, найти расстояние CD = c, на котором надо подвесить
к рычагу груз Q, чтобы давление в точке D равнялось нулю.
Решение. Рассмотрим равновесие троса, охватывающею барабан,
отбросив мысленно рычаг (рис. б) и заменив ею действие реакциями
троса Sj и S2.
§4) РАВНОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ 119
Согласно уравнению A4*) зависимость между этими натяжениями
определится формулой
S4 = V, 0)
так как угол охвата тросом барабана равен тс. Показатель степени в
A) положителен, ибо при заданном направлении вращения барабана
натяжение Si<^Sb
Рассмотрим, далее, равновесие рычага BAD, полагая в согласии
с условием задачи, что давление в точке D, и, следовательно, реакция
шарнира D рапны нулю. На рычаг действует активная сила Q. От-
Отбросим мысленно трос и заменил его действие реакциями S[ и S&
(рис. в). Очевидно, что SJ = S|, Si — S.2.
Выберем оси координат и составим уравнения раьновесия
^Fky = S'l-'rSi~Q = 0, B)
XmD(Fb) = Qc~S[a-S'ib = O. C)
Мы получили систему из трех уравнений A), B), (.4) с тремя неизве-
неизвестными: S[, S'%, с. Из уравнений (I) и B) получим:
'_ Qe
'K
Подставив эти значения натяжений в уравнение C), найдем искомое
расстояние с:
SjQ + S.,b a + bef*
с~ Q ~—ТТ^"
Вместо уравнений равновесия B) и C) можно составить два урав-
уравнения моментов относительно точек А и В. К этим точкам приложе-
приложены неизвестные по величине реакции S[ и S'^. Следовательно, каждсе
уравнение моментов будет содержать только одну неизвестную ве-
величину силы и искомое расстояние с:
2 mB(Fk) = S[ (b-a)-Q(b-c) = 0.
Решая эти уравнения совместно с равенством A), приходим к ра-
ранее полученным ответам.
Задача 1.52. Ремень пропущен через пять неподвижных валиков,
как это показано на рис. а. Коэффициент трения ремня о валик
/ = 0,4. Расстояние между центрами валиков, расположенными на од-
одной прямой, равно /=50 мм. Диаметр валиков rf = 25 мм. Слева
к ремню приложена сила Р== 150 к Г.
Каково минимальное значение силы Q, при котором ремень будет
находиться в поксе.
120
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
Решение. Обозначим угол охвата валика ремнем через а. Тогда
для отрезка ремня, охватывающего каждый валик, можно записать
Q
6)
К задаче 1.52.
соотношение между натяжениями ремня по обе стороны от валика:
Т\ — Тф *,
Tt=T3e*',
Исключая из этой системы уравнений промежуточные усилия
7"i,..., 7 (перемножая все равенства), находим
Q—PebU. A)
Угол а определится из раыных прямоугольных треугольников АО-^В
и AO.fi (рис б):
/sin j-=d,
откуда
sin 2"= у = 0,5,
а = 60° =1,0472 рай.
Тогда из A) находим:
Q= 150. ^5-0,4-1.0472 __ [so . ?.2,0941 _ 150 . $,1207 =1218,11 кГ.
§4]
РЛГШОВЕСИЕ ТЕЛ ПРИ НАЛИЧИИ ТРЕНИЯ
121
Задача 1.53. На неподвижный цилиндр напита веревка, к одному
из концов которой подвешен груз Q.
Сколько раз надо намотать веревку на цилиндр, чтобы груз* Q
можно было удержать вертикальной силой Р, приложенной к дру-
другому концу веревки? Коэффициент трения веревки
о цилиндр равен /.
Решение. Воспользуемся формулой Эйлера,
согласно которой при предельном равновесии ми-
минимальнее значение модуля силы Р равно
где а — угол охвэга веревкой цилиндра. Этот
угол равен
?2
К задаче 1.53.
где п — число полных витков ьеревки, к кото-
которым добавляется но углу тс/2 со стороны действия каждой из сил.
Таким образом,
Логарифмируя, находим:
lnQ — ]nP=fizBn-\-l),
откуда
Задача 1.54. Прямолинейный стержень АВ, длиной / и весом Р,
центр тяжести С которого находится от конца А па расстоянии
а)
Б)
К задаче 1.54.
АС=а, опирается в точке В на шероховатую вертикальную стену,
а в точке А — на гладкий горизонтальный пол. Коэффициент трения
между стержнем и вертикальной стеной /,. В точке А к стержню
прикреплена нить, перекинутая через неподвижный круглый цилиндр
122 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
(рис. а). К концу нити подвешен груз Q. Коэффициент трения между
питью и цилиндром равен /.
Пренебрегая весом нити, определить, в каких границах может
изменяться угол а при равновесии.
Решение. Рассмотрим равновесие стержня АВ, отбросив мы-
мысленно вертикальную стену, горизонтальный пол и горизонтальную
нить и замени» их действие реакциями. Отдельно рассмотрим равно-
равновесие нити, охватывающей цилиндр (рис. г). Решение задачи распа-
распадается на два случая.
Случай минимального угла а. При этом точка А может начать
двигаться влево, точка В— вниз. Следовательно, сила трения F будет
направлена вверх (рис. б), а силы трения, приложенные к ниги на
цкли.щре (рис. г), будут направлены по часовой стрелке. Таким сбра-
зом, стержень АВ (рис. б) будет находиться и равновесии под дей-
действием следующих сил: нормальной реакции N, натяжения нити Т,
веса Р, нормальной реакции Л и силы трения F.
Составим уравнения равновесия для стержня АВ:
^Fkx^=T-R==0, A)
2lFky=N-P + F = 0, B)
J^mB (Fk) = — N1 cos a 4- P (I — a) cos a -f Tl sin * = 0. C)
Кроме того, запишем зависимость силы трения от нормального давле-
давления в точке В:
Z7 = /,/?.
Зависимость натяжения нити 7' от силы Q, учитывая, что силы тре-
трения на цилиндре направлены по часовой стрелке, будет (формула
Эйлера):
Te-f,ft=Qr
Из данной системы уравнений найдем:
N=P—flQef*#.
Подсггв-.ш значения N и 7 в уравнение C), получим окончательно:
Этой формулой определяется минимальное значение угла а при рав-
равновесии стержня.
Случай максимального угла а. При этом точка А может начать
двигаться вправо, точка В — вверх. Следовательно, сила трения F
будет направлена вниз (рис. в), а силы трепня, приложенные к нити
на цилиндре, будут направлены против часовой стрелки.
«5] ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЕРМ 123
Ураппения равновесия стержня АВ будут:
T-R = Q,
N—P-F = Q,
— Л7 cos a -J- Р (/ — a) cos а -j- 77 sin а = 0.
Кроме того, зависимость силы трения от нормального давления
в точке В определяется равенством
F = /,/?.
Натяжение нити будет:
7-= Qe-№.
Из этой системы, исключим R и F, найдем:
yV=P-!-/1Qe-/'c'2.
Далее, подставив в уравнение моментов значения N и Т, получим:
Этой формулой определяется максимальное значение угла а при
равновесии.
§ 5. Графическая статика и методы расчета ферм
1°. Равновесие произвольной плоской системы
сил. Метод последовательного сложения. Если твердое
тело находится в равновесии иод действием произвольной плоской
системы сил, то путем последовательного графического сложения
таких сил можно определить значение неизвестных из условий равно-
равновесия. При эгом число неизвестных не должно превышать трех для
системы сил, приложенных к одному твердому телу, иначе задача
будет статически неопределенной. Этот графический меч од решения
задач целесообразно применять, если общее число сил, действующих
на твердое тело, невелико. По сравнению с аналитическим методом
решения задач на равновесие плоской системы сил указанный графи-
графический способ более нагляден, но его применение при большом числе
сил очень громоздко.
Метод последовательного сложения сил можно
применять в двух вариантах.
Если твердое тело находится в равновесии под действием заданной
плоской системы сил и трех реакций, линии действия которых изве-
известны (/?], 1.ь /3), а величины реакций требуется определить, то реко-
рекомендуется такая последовательность действии (первый вариант):
1) складываем последовательно графически все известные актив-
активные силы и получаем их равнодействующую;
124 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ.1
2) находим точку пересечения линии действия равнодействующей с
линией действия одной из реакций (/]);
3) переносим равнодействующую в эту точку и разлагаем ее на две
силы: одну, направленную вдоль линии /], а другую, направленную в
точку пересечения линии действия двух остальных реакций AЬ /3);
4) составляющая равнодействующей активных сил, направленная по
линии /,, определяет величину первой реакции;
5) вторую составляющую равнодействующей активных сил пере-
переносим в точку пересечения линий действия двух остальных реакций и,
разлагая по направлениям их действия (/.2 и /3)> находим искомые ве-
величины двух последних реакций.
Если твердое тело находится в равновесии под действием заданной
плоской системы сил и двух реакций, причем для одной реакции известна
только точка приложения (Л), а для второй — линия действия D), то ре-
рекомендуется такая последовательность действий (второй вариант):
1) складываем последовательно графически все известные активные
силы и получаем их равнодействующую;
2) переносим равнодействующую в точку пересечения ее линии
действия с линией действия второй реакции (/а);
3) в точке пересечения разлагаем равнодействующую па две состав-
составляющие: одну по линии действия второй реакции, а другую по на-
направлению к точке А. Первая состанляющая определяет вторую реакцию,
а нторая составляющая — величину и направление реакции в точке Л.
Задача 1.55. Вертикал!, ный гладкий стержень CD весом Р опи-
опирается и точках Л и В (рис. а) на цилиндрические шарниры, а коп-
ном D на гладкую плоскость, наклоненную к горизонту под углол а.
Определить графически реакции в точках Л, В, D, если
AB = AD = a.
Р е ш е п и е. Для определения реакций в точках Л, В, D рассмот-
рассмотрим равновесие стержня CD. Ila стержень действует одна активная
сила — сила тяжести Р, направленная по стержню. Стержень находится
в равновесии под действием четырех сил: веса Р, реакций наклонной
плоскости и цилиндрических шарниров Л и В. Применяя закон осво-
бождаемости от связей, отбросим мысленно связи и заменим их дей-
действие на стержень реакциями (рис. б).
Реакция гладкой наклонной плоскости R приложена в точке D и
направлена перпендикулярно к наклонной плоскости. Реакция цилинд-
цилиндрического шарнира направлена перпендикулярно к оси шарнира, так
как перемещению вдоль оси такой шарнир не препятствует. Обозна-
Обозначим эти реакции RA и RB (рис. б). Таким образом, стержень CD на-
находится в равновесии как свободное твердое тело, па которое дейст-
действуют четыре силы: Р, RA, RB, RD.
Продолжаем линии действия реакций RA и RD до их пересечения и
точке К (рис. б). Линия дейстия равнодействующей этих днух сил про-
проходи г через точку К- Линии действия двух других сил Р н R[t пере-
ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЕРМ
125
секаются в В. Следовательно, линия действия их равнодействующей
проходит через точку В.
Итак, все силы, действующие па стержень CD, приведены к двум
силам, одну из которых перенесем по линии действия в К, а дру-
другую — в В. Таким образом, стержень CD находится в равновесии
под действием двух сил, приложенных в В и 1С. Следовательно, эти
силы направлены по одной прямой ВК r противоположные стороны.
Откладываем (рис. в) в избранном масштабе известную по нели-
неличине и направлению силу Р. К ее концу присоединяем силу RB, конец
которой находится в точке пересечения с прямой, параллельной ВК
-*¦-> У
о)
К задаче 1.55.
и проведенной из начала силы Р. При этом условии равнодействую-
равнодействующая сил'Р и RB будет направлена от В к К.
Затем из конца силы RR проводим горизонтальную прямую, соот-
соответствующую линии действия силы RA, до пересечения с линией, па-
параллельной Rn и проведенной из начала силы Р. Равнодействующая
сил RA и RD направлена при этом от К и В. Таким образом, графи-
графически определены реакции RA, /?я, Rn. Замечая, что угол между Rn
и вертикалью равен а, находим:
Задача может быть решена и аналитически. Замечая, что /_ ADK =
= а, составляем три уравнения равновесия (ось х направляем по го-
горизонтали вправо, ось у—вертикально вверх):
2 Fkx = RB - RA -f RD sin a = 0,
= 0-
126
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. Г
щие задачи из «Сборника задач
Решая совместно полученную систему уравнений, находим:
RB = P tga, RA = 2Ptg*, RD = i~'
Для приобретения навыков в решении задач на
равновесие тел методом последовательного сложе-
сложения сил рекомендуется решить графически следу ю-
по теоретической
механике» И. В. М е -
терского, издания
1950 г. и более позд-
поздних лет: 121, 123.
2°. Применение
метода веревочно-
веревочного многоугольника
к плоской системе
сил. Сложение сил, рас-
расположенных в одной пло-
плоскости, при помощи ме-
метода веревочного много-
многоугольника, является столь
же общим методом ре-
решения задач статики на
плоскости, как и анали-
аналитический, рассмотренный
ранее.
Для графического сло-
сложения сил F,, F^ F3 пе-
Рис. 1.45. обходимо изобразить силы
на рисунке (рис. 1.45, а).
Далее, строим силовой многоугольник (рис. 1.45,6), откладывая из
произвольной точки вектор, равный первой силе Ft, из его копна
вектор /\j и из конца вектора Fq вектор F3. Начало первой силы
соединяем вектором R с концом последней силы. Вектор Л опреде-
определяет величину и направление равнодействующей.
Для нахождения линии действия равнодействующей выбираем
произвольную точку О за полюс и соединяем полюс с началом и
концом каждой силы прямыми линиями, называемыми лучами. Первый
луч обозначается через а, луч, идущий в конец первой и начало
второй силы, /—2, и т. д. вплоть до последнего луча, обозначенного
через и>.
Далее (рис. 1.45, а) проводим из произвольной точки d прямую,
параллельную лучу а, до пересечения с линией действия силы Flt из
этой точки проводим прямую, параллельную лучу 1 — 2, до пересе-
пересечения с линией действия силы F^ из этой точки проводим прямую,
а)
«5] ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЕРМ 127
параллельную лучу 2 — 3, до пересечения с линией действия послед-
последней силы f3. Из этой точки проводим прямую, параллельную лучу ш.
Далее, продолжаем полученные лучи а и о до их пересечения в точке В,
которая и является одной из точек, лежащих на линии действия рав-
равнодействующей. Перенеся в точку В найденный из многоугольника
сил вектор R, можем считать задачу о нахождении равнодействующей
системы сил Fb Fb F3 разрешенной. Построенная па рис. 1.45, а
ломаная линия называется веревочным многоугольником. Этот метод
решения применим для любого числа сил, лежащих в одной плоскости.
Если система сил находится в равновесии, то силовой много-
многоугольник и веревочный многоугольник должны быть замкнуты.
Следовательно, на рис. 1.45, вконец последней силы должен совпасть
с началом первой силы; на рис. 1.45, а лучи а и ш должны быть
направлены по одной прямо!!. Система сил приводится к паре сил,
если силовой многоугольник замкнут, а веревочный многоуголь-
многоугольник не замкнут. В этсм случае в силовом многоугольнике лучи а
и ш сольются в одну прямую, а в веревочном многоугольнике лучи а
и «) будут параллельны друг другу.
При решении задач на определение равнодей-
равнодействующей плоской системы сил способом веревоч-
веревочного многоугольника рекомендуется такая последо-
последовательность действий:
1) изображаем в избранном масштабе на рисунке твердое тело
с приложенными к нему силами;
2) строим отдельно силопой многоугольник и находим его замы-
замыкающую R;
3) выбираем произвольную точку за полюс и соединяем ее с вер-
вершинами силового многоугольника прямыми линиями — лучами, обозна-
обозначаемыми а, 1—2, 2—.3, ... , и);
4) строим на первом рисунке, где изображено твердое тело с ирг-
ложенными силами, веревочный многоугольник;
5) продолжая до пересечения лучи а и ю иереночного многоуголь-
многоугольника, находим точку на линии действия равнодействующей;
6) через полученную точку проводим равнодействующую R парал-
параллельно главному вектору силового многоугольника.
При решении задач па определение реакций опор
твердого тела, находящегося в равновесии под дей-
действием "плоской системы сил, следует придержи-
придерживаться такого порядка действий:
1) изображаем в изобранном масштабе твердое тело с активными
силами;
2) отбросив мысленно опоры, заменяем их действие искомыми
реакциями;
3) строим на отдельном рисунке силовой многоугольник, из кото-
которого определяется сумма искомых реакций, но не каждая из них;
128
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
мыкая который, находим
о)
4) выбирая произвольную точку за полюс, соединяем ее лучами
с вершинами силового многоугольника;
5) строим па нервом рисунке веревочный многоугольник, за-
паправление недостающего луча, разде-
разделяющего реакции опор;
6) перенося найденное
направление недостающего
луча на рисунок силового
многоугольника, находим
каждую из искомых реак-
реакций опор.
Задача 1.56. Па балку
АИ дейп вуют силы: /7, = 6 Г,
Ft = 8T, [:3 = 6T, Fi = 5T.
Силы F; и Fi направлены
по вертикали. Силы F-i и Z7-,
действуют соответственно
под углами 60° и 30° к балке
(рис. а).
Определить посароепием
веревочного многоугольника
равнодействующую данной
системы сил.
Решение. Для опре-
определения равнодействующей
данной системы сил строим
Силовой многоугольник
(рис. б). Дли этого в избран-
избранном масштабе для сил из
произвольно выбранной точ-
точки с (рис. б) проводим нек-
тор, по величине и направ-
направлению равный силе F{, из
конца этого вектора прово-
проводим второй вектор, по ве-
величине и направлению рав-
равный силе Fi, из конца этого
вектора откладываем вектор,
равный F3, и из конца по-
К задаче 1...
слелпего откладываем вектор, равный Ft. Построенный силовой много-
многоугольник оказался незамкнутым; следовательно, силы приводятся к
равнодействующей.
Соединив начало вектора F, с концом вектора Fit находим пек-
тор R, замыкающий силовой многоугольник; этот вектор по величине
и направлению равен равнодействующей данной системы сил. При
§5] ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЕРМ 129
обходе силового многоугольника все составляющие силы направлены
в одну сторону, тогда как вектор R направлен в противоположную.
Чтобы найти точку приложения равнодействующей, строим вере-
веревочный многоугольник. Для этого из произвольно выбранной точки О
(рис. 6) проводим луч а в начало вектора Fh луч /—2 в начало
вектора Fb луч 2—3 в начало вектора F3 и луч 3—4 в начало век-
вектора Ft. В конец вектора Ft проводим луч ш. Из произвольной
точки d (рис. в) вблизи силы Fi проводим прямую, параллельную
лучу а, до пересечения ее с линией действия силы Z7,. Из точки их
пересечения проводим прямую, параллельную лучу 1—2, до пересе-
пересечения ее с линией действия силы Ft. Из точки пересечения этих
линий проводим прямую, параллельную лучу 2—3, до пересечения ее
с линией действия силы F3 и из этой точки проводим прямую, парал-
параллельную лучу 3—4, до пересечения с линией действия силы Fim Из
точки пересечения луча 3—4 с линией действия силы Ft проводим
прямую, параллельную лучу о).
Продолжая прямые, параллельные лучам а и «, до их пересечения
в точке е, проводим через точку е прямую, параллельную вектору R.
Точку пересечения этой прямой с балкой обозначим через /. Это
и есть точка приложения равнодействующей заданных сил на
балке АВ.
Измеряя длину вектора R, находим, пользуясь избранным масшта-
масштабом, величину равнодействующей. Она равна 17,4 Т. Принят масштаб
1/3 Т в 1 мм.
Задача 1.57. Балка АВ (рис. а) длиной 12 м закреплена шар-
нирпо концом А и опирается концом В па опору, установленную па
катках. К балке приложены силы: Fi = 2T, F2 = 3 7", F3= 1 Т. Рас-
Расстояния: ЛС=4 м, CD = 2 м, DE=3 м.
Определить построением веревочного многоугольника реакции
опор А и В.
Решение. Рассмотрим равновесие балки АВ. На балку дейст-
действуют активные силы: Fb Fit F3. Применяя закон освобождаемости or
связей, отбросим мысленно опоры А и В и заменим их действие
реакциями. Реакция опоры В, установленной на катках, направлена
перпендикулярно к плоскости, на которую опираются катки, т. е. по
вертикали вверх. Направление реакции шарнира А, вообще говоря,
неизвестно, но так как все силы, действующие па балку, направлены
вертикально, то ясно, что и реакция шарнира А должна быть верти-
вертикальной; если бы эта реакция не была вертикальной, то ее состав-
составляющая по горизонтали ничем не уравновешивалась бы и равновесие
балки было бы невозможно.
Обозначим реакцию опоры А через RA, реакцию опоры В через
RB и построим силовой многоугольник для пяти сил, действующих
на балку. Из произвольно выбранной точки с (рис. 0) проводим
и некотором масштабе вектор, изображающий силу Ft; из конца этого
б М. И. Бать и др., т. I
130
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
вектора проводим второй пектор, изображающий силу F.b и анало-
аналогично изображаем силу F3.
Реакции опор RA и RB известны только по их направлениям.
Ввиду того, что балка находится в равновесии, силовой многоуголь-
многоугольник должен быть замкнут и конец вектора RA должен совпадать
с началом вектора Ft (в точке с), а начало вектора RB — с концом
вектора f3 (и точке d). Таким образом, вектор суммы реакций изве-
известен. Для определения величин каждой из слагаемых этой суммы
проведем из произвольно выбранной точки о луч А — 1 в начало
вектора Fl и конец вектора RA, луч 1—2 в начало вектора F.2,
луч 2 — 3 в начало вектора F3, луч 3 — В к начало вектора RB (сов-
(совпадающее с концом вектора /^ в точке d). Направление луча В — Л
неизвестно, так как неизвестны величины реакций RA и RB.
Далее переходим к построению веревочного многоугольника.
Для этого нз точки е (рис. в) на линии действия реакции RA про-
проводим прямую, параллельную лучу А — 7, до пересечения ее с лг-
нией действия силы Flt из точки их пересечения проводим прямую,
параллельную лучу / — 2, до пересечения с линией действия силы F.,;
таким же образом проводим прямые, параллельные лучам 2 — 3,
3 — В, до пересечения их с линиями действия сил F3 и реакций RB.
Так как система сил находится в равновесии, то веревочный мно-
многоугольник должен быть замкнут, и, следовательно, прямая между
линиями действия реакций RA и /?в должна проходить через точку е.
Теперь мы можем провести из полюса о луч В — А, параллельный
этой прямой; он поделит отрезок dc на отрезки, равные реакциям
RA и RB (для наглядности на рис. б реакции RA и RB сметены не-
несколько влево). Измеряя найденные величины реакций в принятом
масштабе, находим их значения: /?л = 3,17, RB = 2,9T.
ГРАФИЧР.СКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЕРМ
131
Задача 1.58. На балку АК, находящуюся в равновесии, шарннрпо
закрепленную в точке А и свободно опертую при помощи катков
в точке В, действуют силы: Fx = 2 T, /-'.2 = 3 Т, пара сил/ момент
которой равен УИ = 4 Т-м, и распределенная нагрузка интенсив-
интенсивностью Р = 0,5 Т/м.
Определить с помощью построения веревочного многоугольника
реакции опор Ал В (рис. а). Размеры заданы: Л/<Г= 12 м, АС=1 м,
СИ=Ъ м, НЕ=\ м, ЕВ = 4 м.
Решение. Для определения реакций опор, применяя закон осво-
бождаемости от связей, мысленно отбрасываем опоры и заменяем их
М
В-А
Н Е
а)
-к
К задаче 1.58.
действие на балку реакциями опор RA и RB (рис. в). Обе реакции
направлены вертикально вверх, так как все активные силы направ-
направлены вертикально вниз, а сумма проекций сил пары на любую ось
равна нулю. Так как действие пары сил не изменится, если перенести
ее в любое место плоскости, сохранив момент пары неизменным, за-
заменим пару силами Fi и F3, равными по модулю 2 Т кажлая и при-
приложенными соответственно в точках Си Д расположенных на рас-
расстоянии 2 м друг от друга. Сила Fit равная 2 Г и приложенная
в точке С, уравновесится силой Fu равной 2 Т, и о дальнейшем
в расчет приниматься не будет.
Чтобы решить задачу с помощью веревочного многоугольника,
распределенную нагрузку необходимо заменить сосредоточенном си-
силой /v Модуль этой силы равен
Fs = P ¦ ЕВ = 0,5- 4 = 2Т,
и приложена она в точке N в середине отрезка ЕВ.
б*
132 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ.1
Переходим к построению силового многоугольника. Для этого
из произвольной точки 5 (рис. б) откладываем в выбранном масштабе
вектор, но модулю и направлению равный силе F3. Из конца этого
вектора проводим вектор, по модулю и направлению равный силе Ft.
Из конца этого вектора проводим вектор, равный силе Ft. Ввиду
того, что балка находится в равновесии, многоугольник сил должен
быть замкнут, и поэтому начало вектора, соответствующего реак-
реакции Rn, должно совпадать с концом вектора, соответствующего силе Ffl,
а конец вектора, соответствующего реакции RA,— с началом силы F:i
в точке 6". Для наглядности реакции RB и RA (рис. б) проведем не-
несколько левее. Затем из произвольно выбранной точки о проводим
луч А — 3 в начало вектора Fa, луч 3 — 2 в начало вектора Fq, луч
2 — 5 в начало вектора FTl, луч 5 — Б в начало вектора RB, луч
Б— А в начало вектора RA провести пока нельзя, так как неиз-
неизвестны модули сил RB и RA.
Далее переходим к построению веревочного многоугольника. Для
этого из произвольной точки М (рис. б) па линии действия реакции RA
проводим прямую, параллельную лучу А — 3, до пересечения с ли-
линией действия силы F3. Из точки их пересечения проводим прямую,
параллельную лучу 3 — 2, до пересечения ее с линией действия силы F .
Из точки их пересечения проводим прямую, параллельную лучу 2 — .5,
до пересечения ее с линией действия силы Ft. Из точки их пересе-
пересечения проводим прямую, параллельную лучу 5 — В, до пересечения
се с линией действия силы Rn. Так как рассматриваемая система си.т
находится в равновесии, веревочный многоугольник должен быть замк-
замкнут. Поэтому прямая между линиями действия сил RB и RA должка
пройти через точку М, лежащую на направлении силы RA (рис. в).
Теперь можно провести луч В — А параллельно этой прямой из точки о
(рис. б). Этот луч разделит отрезок SL на векторы, равные реак-
реакциям RA и RB. Измерив этя векторы и умножив на выбранный мас-
масштаб, находим, что /^д = 3,9 Т, а /?л = 3,1 Т.
Задача 1.59. На балку AFJ, шарнирно закрепленную в точке А
и опертую при помощи катков в точке В, действуют силы /7, = 6 Т,
F,i = 8 Т, Р3 — 6 Т, F4 = 5 T; силы /=", и /^ направлены по верти-
вертикали. Силы Ft и F3 направлены соответственно под углами 60° и
30е к балке.
Определить построением веревочного многоугольника реакции опор
(рис. а).
Решение. Для определения реакций опор применяем закон
освобождаемости от связей, отбрасываем мысленно опоры и заменяем
их действия реакциями RA и RD. Реакция Rn направлена но верти-
вертикали вверх, так как опора В установлена на катках и, следовательно,
не может препятствовать перемещению вдоль плоскости, на которую
опираются катки. Реакция шарнира RA может быть любого направ-
направления (рис. б).
ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЕРМ
133
а)
Для определения реакций опор способом веревочного млогоугольни-
ка строим сперва с выбранном масштабе силовой многоугольник для ак-
активных сил и реакций опор. Активные силы известны по неличине
и направлению, реакция опоры Rn известна только но напраилению,
реакция опоры RA не известна пи но величине, ни по направлению,
однако можно скапать, что конец
ее в силовом многоугольнике дол-
должен совпасть с началом силы Fb
так как балка находится в равно-
равновесии и силовой многоугольник
должен быть замкнут.
Из произвольной точки с
(рис. б) проводим вектор, по ве-
величине и направлению ранный
силе Fx, из кошт этого вектора
проводим вектор, по величине и
направлению ранный силе Рг. Та-
Таким же образом проводим пек-
торы, по величине и направлению
равные силам F3 и F,k. Из конца
вектора, равного силе Fb прово-
проводим направление реакции Rn, на
котором должен лежать конец
кектора, равного реакции Rn.
Дальше из произвольного полюса
о проводим луч А — / в па-
чало век гора Fu луч / — 2 в
начало вектора F.,, луч 2 — 3
в начало вектора F2, луч 3 — 4
в начало вектора F,t и луч 4— В
в начало пектора Rn. Луч В— Л
в начало вектора RA провести
нельзя, так как величина реак-
реакции Rn неизвестна.
Для определения величины ре- к задаче 1.59.
акции RB переходим к построению
веревочного многоугольника. Для этого проводим через точку А
(рис. в) (так как эго единственная известная точка на линии дейст-
действия реакции RA) прямую, параллельную лучу А — /, до пересечения
te с линией действия силы F{. Через эту точку пересечения прово-
проводим прямую, параллельную лучу 1 — 2, до пересечения ее с линией
действия силы F.v Через эту точку пересечения проводим прямую,
параллельную лучу 2 — 3, до пересечения ее с линией действия
силы Fz. Таким же образом проводим прямые, параллельные лучам
3 — 4 и 4 — В, до пересечения их с линиями действия сил F^ и Ra.
134 ПЛОСКАЯ СИСТЕМА СИЛ (ГЛ. I
Прямая, параллельная лучу 4 — В, пересекает направление реакции Rn
в точке d.
Ввиду того, что при равновесии системы веревочный многоуголь-
многоугольник должен быть замкнут, соединяем точку d с точкой А, где было
начато построение веревочного многоугольника. Теперь можно про-
провести луч В — А через полюс о (рис. б) параллельно прямой dA.
Луч В — А пересекает направление реакции RB в точке е, которая
и определяет конец вектора RB. Величина и направление реакции RA
найдутся, если соединить конец вектора Rti с началом вектора Ft.
Измерив отрезки, изображающие реакции, и учтя принятый масштаб,
найдем RA=\2,8 Т, RB~6 Т.
Для приобретения навыков в решении задач на
равновесие тел и сложение сил способом вере и оч-
очного многоугольника ре-
рекомендуется решить сле-
следующие задачи из «Сборни-
«Сборника задач но теоретической
механике» И. В. Мещерского,
издания 1950 г. и более позд-
поздних лет: 193, 194, 195, 196.
Рис- ]л6- 3°. Расчет усилии и стерж-
стержнях фермы. Способ выреза-
вырезания узлов. Фермой (рис. 1.46) называется геометрически не-
неизменяемая конструкция, образованная прямолинейными стерж-
стержнями, соединенными друг с другом концами при помощи шарниров.
Шарнирные соединения концов стержней называются узлами. Ферма
является статически определимой, если число узлов п и число стерж-
стержней иг удовлетворяют уравнению
/и = 2л — 3.
Если число стержней :ie удовлетворяет этому равепстпу, то воз-
возможны два случая:
/и>2н -3,
ферма является в этом случае статически неопределимой;
/«<2я — 3,
конструкция перестает бить геометрически неизменяемой, получает
подвижность (становится механизмом).
Расчет усилий в стержнях фермы методами статики (н том числе
и графостатики) может быть произведен только для статически оп-
определимых ферм *).
*¦) Расчет статически неопределимых ферм выходит за рамки курса
теоретическом механики, так как требует учета деформаций конструкций
§ 5t ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЕРМ 135
В дальнейшем мы будем полагать, что заданные активные силы
приложены в узлах фермы и лежат в одной плоскости с фермой,
трение в шарнирах отсутствует. При выполнении этих условий стержни
будут пли сжаты, или растянуты, следовательно, реакции стержней
будут совпадав по направлению со стержнями.
Расчет статически определимых ферм проводится одним пз трех
способов:
а) способом вырезания узлов;
б) построением диаграммы Максвелла — Кремоны,
в) методом сечений.
Расчет сводится к определению усилий в стержнях фермы. Актив-
Активные силы и реакции опор являются внешними силами для всей фермы,
рассматриваемой как твердое тело; усилия в стержнях в этом слу-
случае— внутренние силы. Поэтому для определения усилий необходимо,
согласно общему правилу, рассмотреть равновесие части фермы, д.-;я
которой искомые усилия являются внешними силами.
При расчете ферм способом вырезания узлов можно пользоваться
аналитическим и графическим методами.
При аналитическом методе решения задач на расчет
ферм способом вырезания узлов надо выполнить
четыре первых пункта, указанных в начале книги,
на стр. 15. Затем:
5) определить реакции опор, пользуясь уравнениями равновесия
для всей фермы, рассматриваемой как твердое тело, или при помощи
веревочного многоугольника;
6) вырезать узел, в котором сходятся два стержня, и рассмотреть
его равновесие под действием активных сил и реакций разрезанных
стержней; определить эти реакции из двух уравнений проекций сил,
приложенных к узлу, на декартовы оси координат;
7) переходя от узла к узлу, рассматривать аналогично равнове-
равновесие каждого узла; при этом в каждом узле должно быть только два
неизвестных усилия в стержнях; составляя для каждого узла два
уравнения равновесия в проекциях на оси х и у, определить все
искомые усилия в стержнях.
При графическом методе решения задач на расчет
ферм'способом вырезания узлов надо выполнить ч е -
i.i p e первых пункта, указанных в начале книги, на
стр. 15. Затем:
5) определить реакции опор, пользуясь уравнениями равновесия
для всей фермы, рассматриваемой как твердое тело, или при помощи
веревочного многоугольника;
6) вырезать узел, и котором сходятся два стержня, и рассмотреть
его равновесие .под действием заданных активных сил и реакций
разрезанных стержней; определить эти реакции построением замкну-
замкнутого треугольника или многоугольника сил, приложенных к узлу;
13G
ПЛОСКАЯ СИСТЕМА СИЛ
[ГЛ. I
7) переходя от узла к узлу, рассматривать аналогично равновесие
каждого узла; при этом з каждом узле должно быть только дпа
неизвестных усилия в стержнях; строя для каждого узла замкнутый
силовой многоугольник, определить все искомые усилия в стержнях.
Задача 1.60. Определить усилия в стержнях фермы (рис. а) ана-
аналитическим методом вырезания узлов.
2000 иГ
а:,
RA\
б)
У
$5
БС:°
' 1000 к Г
в)
К задаче 1.60.
Решение. Для определения усилий в стержнях сначала надо
найти реакции опор А и И. Для этого мысленно отбрасываем опоры
и заменяем их действие па ферму реакциями RA и R,,. Вниду сим-
симметрии фермы и нагрузки реакции опор равны друг другу и каждая
по величине равна 2000 кГ. Когда реакции опор определены, пере-
переходим к определению усилий в стержнях. Для этого надо рассмат-
рассматривать равновесие каждогс узла, мысленно отбросив сходящиеся и них
стержни и заменяя их действие па узел реакциями. Первым надо
рассмотреть узел, к которому приложены только две неизвестные
силы. Начнем с узла А. Узел А находится и равновесии под дейа-
§ 5] ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЕРМ 137
висм известной реакции RA и неизвестных реакций аержпей / и 2.
Будем обозначать реакции стержней соответственно через 5j и 52
(рис. б) и направлять их от узла, предполагая таким образом, что
стержни растянуты. Затем через точку А проводим сси х и у и со-
составляем систему уравнений равновесия узла Л, приравнивая нулю
сумму проекций всех сил на эти оси.
Уравнение проекций па оси х и у будуг:
5,+ 5, cos 30° = О,
/^-j-S^cos 60° =0.
Отсюда находим:
S, = - 4000 к Г, Si = 3464 кГ.
Отрицательное значение реакции ^ показывает, что в действи-
действительности она направлена в противоположную сторону и стержень 1
не растянут, как мы предполагали, а сжаг.
Теперь переходим к исследованию равновесия узла В. В узле В
сходятся три стержня, из которых стержни / и 3 направлены по
одной прямой, а стержень 4 под углом к ним. Никаких активных
сил к узлу В не приложено. Следовательно, течка В находится в рав-
равновесии под действием трех реакций стержней. Эю возможно только
и случае, если усилие в стержне 4 равно пулю, так как только оно
проектируется на направление, перпендикулярное к стержням / и 3.
Итак, усилия в стержнях 7 и 3 одинаковы, а усилие в стержне 4
равно нулю.
Переходим к узлу С. Узел С находится в равновесии под дейст-
действием двух неизвестных реакций 5В и S6, активной силы 1000 кГ и
известной реакции S'v которая по неличине равна реакции S2, прило-
приложенной к узлу А, но направлена в противоположною сторону (рис. б).
Проводим оси координат через точку С и составляем уравнения рав-
равновесия для узла С.
Уравнения проекций на оси х и у будут:
— S^ -j- 6'B cos 60° -!- SR = 0,
5Bcos 30°— 1000 = 0.
Отсюда находим:
Ss = 1155 кГ, S6 = 2886,5 к Г.
Следовательно, стержни 5 и 6, как мы и предполагали, расшгуты.
Ввиду полной симметрии (|ермы и приложенной в узлах па1р\зки
достаточно определить усилия в стержнях левом половины фермы.
Так, например, усилия в стержнях 1 и 11, 2 и 10 будут ввиду сим-
симметрии равными.
Задача 1.61. Определить графически усилил в аерммнх фермы
(рис. а) способом вырезания узлов.
138
плоская Система сил
[ГЛ. I
Решение. Для определения усилий в стержнях фермы необхо-
необходимо сперва найти реакции опор. Для этого мысленно отбросим
опоры и заменим их действие на ферму реакциями РА и RE. Эти
реакции направлены по вертикали внерх, так как активные силы на-
праплены по вертикали вниз. Кроме того, опора Е может восприни-
воспринимать только вертикальные усилия. Для определения величины реакций
г)
К задаче 1.61.
е>
рассмотрим ферму как твердое тело, находящееся в покое под дей-
действием активных сил, включая реакции опор (рис. б).
Уравнение моментов относительно точки А будет:
откуда
откуда
— Р ¦ а — IP • За -|- RE ¦ 4а = О,
RE=l,75P.
Уравнение моментов относительно точки Е будет:
— '2Р ¦ а — Р ¦ За + RA ¦ 4а = О,
RA = 1,25 Р.
I 51 ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЕРМ 139
Определив реакции опор, переходим к нахождению усилий в стерж-
стержнях. Обозначим стержни цифрами 7, 2, 3, ..., 7.
Первым вырежем тот узел, в котором имеется только две неиз-
кестные силы, например узел А. К узлу А приложены три силы:
реакция опоры RA, реакции S\ и 5.2 перерезанных стержней 1, 2.
Реакция RA известна по величине и направлению, реакции стержней
направлены вдоль стержней, но величина их неизвестна. Напомним, что
совпадение направления реакций со стержнями соблюдается всегда,
если прямолинейные стержни закреплены шарнирпо своими концами
и все силы приложены только в узлах.
Для определения величины реакций стержней строим треугольник
сил, откладывая их в тем порядке, в каком они встречаются при
обходе узла по часовой стрелке. Первой откладываем в масштабе
известную величину RA (рис. в), из ее конца и начала проводим пря-
прямые, параллельные стержням 1 и 2, до их пересечения. Стороны по-
полученного треугольника определяют реакции St и S.2. Чтобы найти
их направление, обходим треугольник сил в направлении, указанном
известной силой RA. При равновесии узла стрелки в замкнутом си-
силовом многоугольнике идут в одном направлении. Перенося реакцию
Si на стержень /, находим, что она направлена к узлу, следовательно,
стержень / сжат. Перенося реакцию S.2 на стержень 2, находим, что
она направлена от узла А, следовательно, стержень 2 растянут.
Следующим вырезаем узел В. К нему приложены четыре силы:
две неизвестные реакции S3 и 54 стержней <? и 4, известная реакция
стержня /, которая равна по величине реакции Su приложенной
к узлу А, по направлена в противоположную сторону (обозначим ее
через S[), активная сила Р. Строим многоугольник этих сил. Первой
откладываем в масштабе силу S\ (рис. г), к концу ее прикладываем
активную силу Р, а затем через конец силы Р проводим прямую,
параллельную стержню 4, а через начало силы SJ — прямую, парал-
параллельную стержню 3, до их пересечения. Стороны полученного четы-
четырехугольника определяют реакции S3 и 54. Чтобы найти их направле-
направление, обходим четырехугольник в направлении, указанном известными
силами. Перенося реакцию S3 на стержень 3, находим, что она на-
направлена от узла В, следова!ельно, стержень ,3 растянут. Перенося
реакцию Si на стержень 4, находим, что она направлена к узлу В,
следовательно, стержень 4 сжат.
Следующим вырезаем узел С. К нему приложены четыре силы:
две неизвестные реакции S^ и 56 стержней 5 и в и две известные
реакции стержней 2 и 3, которые по величине равны реакциям 52
и Sa, приложенным соответственно к узлам А и В, по направлены
п противоположные стороны (обозначим их через 5.2 и S't). Строим
многоугольник этих сил. Первой откладываем известную силу S.j,
к ней прибавляем также известную силу S'it затем через конец силы S;',
и начало силы S'2 проводим прямые, параллельные стержням 5 и в,
140 ПЛОСКАЯ СИСТЕМА СИЛ (ГЛ. Г
до их пересечения. Обходя полученный многоугольник сил в панрав-
лсиии, указанном известными сллгми, находим направление реакций
Ss и 56. Перенося реакцию 53 на стержень 5, находим, что она на-
направлена к узлу С, следоиагелыю, стержень 5 сжат. Перенося реак-
реакцию S6 на стержень в, находим, что она направлена от узла С,
следовательно, стержень 6 растянут.
Следующим вырезаем узел D. К нему приложены четыре силы:
одна пеи:зпеппая реакция стержня 7, активная сила 2Р и известные
реакции St и 53, которые равны по величине реакциям 54 и 53, при-
приложенным соотвстстиеино к узлам В и С, но направлены в противо-
противоположные стороны (обозначим их через SJ и S~). Строим многоуголь-
многоугольник сил. Первой откладываем силу S'$ (рис. е), к пей присоединяем
силу S\ I! активную силу 'IP. Затем соединяем конец силы 2Р с на-
началом силы S3 и получаем искомую реакцию S-. Перенося реакцию 57
на стержень 7, находим, что она направлена к узлу D. Следовательно,
стержень 7 сжат. Построение этого многоугольника одновременно
служит и проверкой правильности построения всех многоугольников,
так как найденная сила 57 должна быть параллельна стержню 7,
если построение сделано верно.
4\ Определение усилий в стержнях фермы по-
построением диаграммы Максвелла — Кремоны. Способ
вырезания узлон, рассмотренный в предыдущем пункте, позволяет
сравнительно просто найти усилия в стержнях фермы. К недостаткам
этого способа следует отнести повторное построение усилий в стерж-
стержнях, которые один раз проводятся в одном направлении, а другой
раз — в противоположном. Кроме того, построение силовых много-
многоугольников для каждого узла в отдельности не создает общей кар-
картины распределения усилий в стержнях фермы. Определение усилий
построением диаграммы Максвелла — Кремоны позволяет устранить
эти гедостагки.
Построение диаграммы Максвелла — Кремоны заключается
в соединении силовых многоугольников, построенных для всех
узлов фермы, в один чертеж так, чтобы ни одно из усилий не
повторялось дважды.
При расчете фермы способом Максвелла — Кре-
Кремоны следует придерживаться следующих правил и
последовательности действий:
1) определяем из условий равновесия всей фермы как твердого
тела, находящегося под действием плоской системы сил, опорные
реакции; это делается графически, построением веревочного много-
многоугольника, причем результат затем проверяется аналитически, при
помощи уравнений равновесия;
2) отбрасываем опоры и изображаем все приложенные к ферме
внешние силы, включая реакции опор, так, чтобы эти векторы рас-
располагались вне контура фермы;
S 5] ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЕРМ 141
3) части плоскости, ограниченные контуром фермы и линиями
действия внешних сил, обозначаем буквами; обозначаем буквами
также части плоскости, ограниченные стержнями фермы; узлы фермы
обозначаем римскими цифрами; стержни нумеруем арабскими циф-
цифрами;
4) строим замкнутый многоугольник внешних сил, откладывая силы
в том порядке, в каком они встречаются при обходе фермы; направ-
направление обхода выбирается произвольно (но часовой или против часо-
часовой стрелки); силы обозначаем двумя малыми буквами того же на-
наименования, что и большие буквы, обозначающие смежные участки
плоскости, между которыми проходит линия действия данной
силы;
5) последовательно строим на этом же рисунке замкнутые сило-
силовые многоугольники для каждого узла; при этом узлы выбираем
в таком порядке, чтобы каждый раз число неизвестных усилий
в стержнях равнялось двум (в последнем узле получится при этом
одно неизвестное усилие); обход каждого узла делаем в том же
направлении, которое было избрано для внешних сил (по часовой или
против часовой стрелки); в этом же порядке откладываем встречаю-
встречающиеся внешние силы и усилия в стержнях;
6) для определения того, сжат или растянут стержень, в каждом
замкнутом силовом многоугольнике мысленно направляем стрелки
в одном направлении, указанном известными силами, и переносим
найденное усилие на стержень; стержень сжат, если усилие направ-
направлено к узлу, и растянут, если усилие идет от узла;
7) измеряем на диаграмме отрезки, изображающие искомые уси-
усилия в стержнях фермы, и находим, учитывая принятый масштаб сил,
величины усилий.
Задача 1.62. Определить усилия в стержнях фермы (рис. а) по-
построением диаграммы Максвелла — Кремоны.
Решение. Для определения усилий в стержнях фермы необхо-
необходимо прежде всего найти реакцию опор. Для этого мысленно отбро-
отбросим опоры и заменим их действие на ферму реакциями. Реакция
опоры В направлена по вертикали вверх, так как опора установлена
на катках, которые не могут препятствовать перемещению вдоль пло-
плоскости, на которую опираются катки. Величина и направление реак-
реакции опоры А неизвестны, поэтому найдем ее составляющие но осям
х и у. Для этого составим уравнения равновесия фермы как свобод-
свободного твердого тела, находящегося в равновесии под действием актив-
активных сил и реакций опор.
Уравнение моментов относительно точки А будет:
— RD ¦ 6а -f Р ¦ а -\- Р ¦ Аа -\- W ¦ 2а = О,
откуда
ЯВ=1,5А
142 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ.1
Уравнения проекций на оси х и у будут:
Rax-p = o,
RB-P-2P + RAy = 0,
откуда
RAx=p. RAy=i.~oP.
Тогда модуль реакции шарнира А равен
Определим направление реакции опоры А Для этого найдем
угол р, образованный реакцией с осью х:
cos P = -^=-j?p =О,бб,
откуда
f> = 5б°20'.
После того как реакции опор найдены, можно перейти непосредст-
непосредственно к. построению диаграммы Максвелла — Кремоны.
Изображаем все приложенные к ферме внешние силы, включая
реакции опор, так, чтобы их векторы расположились вне контура
фермы (рис. б). Части плоскости, ограниченные контуром ^фермы и
линиями действия внешних сил, обозначим буквами С, D, Е, F, Сг,
плоскости, ограниченные стержнями фермы, обозначим буквами Н, I,
/., М; узлы фермы обозначим римскими цифрами /, //, ///, IV, V, VI;
сгержни нумеруем арабскими цифрами /—9.
Строим вначале многоугольник ннешнпх сил (рис. в), который
должен быть замкнут, так как ферма находится в равновесии. Откла-
Откладываем силы в том порядке, в каком они встречаются при обходе
фермы по часовой стрелке, и обозначаем их двумя малыми буквами,
соответствующими тем большим буквам, которыми обозначены две
смежные области, разграниченные линией действия данной силы при
обходе фермы но часовой стрелке. Откладываем в масштабе вектор cd,
соответствующий реакции RA, к нему прибавляем вектор de, соот-
соответствующий силе Р, таким же образом откладываем векторы ef, fg,
gc, соответствующие силам RR, Р и 2Р.
Получив замкнутый многоугольник внешних сил, приступаем
к построению многоугольников сил, приложенных к узлам фермы,
начиная с того узла, в котором есть только две неизвестные силы,
например с узла /. Многоугольники строим, также обходя узлы по
часовой стрелке и обозначая усилия в стержнях двумя малыми бук-
буквами, соответствующими тем большим буквам, которыми обозначены
дне смежные области, разграниченные данным стержнем. Согласно
принятым обозначениям мпоюугольник сил, приложенных к узлу /,
S5|
ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФГ.РМ
143
должен состоять из векторов cd, dh, he, соответствующих по вели-
величине и направлению силе RA и усилиям стержней /, 4.
Поскольку все стержни прямолинейны, соединены между собой
шарнирами и внешние силы приложены только к узлам, то усилия
и каждом стержне напраплены вдоль стержня, так как он находится
У,
б)
1
в)
К задаче 1.62.
п равновесии под действием только двух сил, реакций шарниров.
Стержень при указанных условиях может быть только ежа г или ра-
растянут.
Вектор cd па рисунке уже есть; чтобы найти векторы dh и he,
достаточно через точку с провести прямую, параллельную стержню /,
а через точку d — прямую, параллельную стержню 4, и в точке их
пересечения поставить букву h.
Переходим к узлу ///. Многоугольник сил, приложенных к нему,
должен состоять из векторов gc, ch, hi, ig. Векторы gc, ch на рисунке
уже есть; чтобы найти векторы hi, ig, достаточно провести через
точку /2 прямую, параллельную стержню 7, а через точку g-- пря-
прямую, параллельную стержню 2, и в точке их пересечения поставить
букву /.
144 ПЛОСКАЯ СИСТЕМА СИЛ [ГЛ. I
Переходим к узлу //. Многоугольник сил, приложенных к нему,
должен состоять из векторов lh, hd, de, el, II. Векторы lh, hd, de на
рисунке уже есть; чтобы найти векторы el, li, проводим через точку е
прямую, параллельную стержню 5, а через точку / — прямую, парал-
параллельную стержню 8, и в точке их пересечения ставим точку /.
Переходим к узлу V. Многоугольник сил, приложенных к нему,
должен состоять из векторов fg, gi, il, lm, inf. Векторы fg, gi, il на
рисунке уже есть; чтобы найти векторы lm, mf, проводим через
точку / прямую, параллельную стержню 9, а через точку/—прямую,
параллельную стержню 3, и в точке их пересечения ставим букву т.
Многоугольник сил, приложенных к узлу IV, должен состоять из
векторов ml, le, em. Векторы ml, le па рисунке уже есть; чтобы
найти вектор ет, соединяем прямой точку т с точкой с. Эта пря-
прямая должна быть параллельна стержню 6, так как вектор ет соот-
соответствует усилию в стержне 6". Таким образом, параллельность этого
вектора стержню 6 является проверкой правильности построения
диаграммы.
Переходя к узлу VI, видим, что многоугольник сил, приложенных
к нему, должен состоять из векторов fm, me, ef, которые уже есть
на рисунке. Таким образом, усилия всех девяти стержней найдены и
осталось только определить, какие стержни растянуты и какие сжаты.
Для этого векторы силовых многоугольников каждого узла мысленно
переносим на соответствующие стержни и определяем, куда они на-
ираилены: если к рассматриваемому узлу, значит, стержень сжат, если
от узла — растянут. Силовой многоугольник cdh характеризует равно-
равновесие узла /. Силы в этом треугольнике направлены от с к d, от
d к h и от h к с. Следовательно, вектор dh направлен к узлу /,
значит, стержень 4 сжат; вектор he направлен от узла /, значит,
стержень 1 растянут. Силовой четырехугольник gchi характеризует
равновесие узла ///. Силы в ;>tom четырехугольнике направлены от g
к с, от с к h, от h к I, следонательпо, вектор hi направлен от узла ///,
значит, стержень 7 растянут; вектор lg направлен от узла ///, следо-
следовательно, стержень 2 растянут. Рассуждая таким образом дальше,
находим, что стержни 3, 9 также растянуты, а стержни 5, 6, 8 сжаты.
Чтобы найти величины усилий стержней, измеряем их на диаграмме
и умножаем на масштаб сил.
5°. Определение усилий в стержнях фермы мето-
методом сечений. Рассмотренный способ расчета фермы путем построе-
построения диаграммы Максвелла — Кремоны является графическим приемом.
В отличие от пего метод разрезов фермы позволяет определить
усилия и стержнях аналитически.
При расчете ферм .методом сечений рекомендует-
рекомендуется такая последовательность действий:
1) определяем опорные реакции, рассматривая равновесие фермы
как твердого тела, находящегося под действием плоской системы сил;
ГРАФИЧЕСКАЯ СТАТИКА И МЕТОДЫ РАСЧЕТА ФЁГ-М
145
для этого составляем три уравнения равновесия или применяем спо-
способ веревочного многоугольника;
2) разрезаем мысленно ферму, к которой приложены все внешние
силы, на две части так, чтобы число разрезанных стержней не пре-
превышало трех, и заменяем действие отброшенной части искомыми уси-
усилиями стержней, полагая все стержни растянутыми;
3) составляем уравнения равновесия для части фермы так, чтобы
в каждое уравнение входило одно неизвестное усилие; для этого
составляем уравнения моментов относительно точек, где пересекаются
линии действия двух неизвестных усилий; если дна стержни парал-
параллельны, то составляем уравнение проекции на ось, перпендикулярную
к этим стержням, п которое также войдет одно пеизпестпое усилие;
4) решая каждое из составленных уравнений, находим искомое
усилие в стержнях; если в ответе получается знак минус, то это
означает, что стержень сжат, а не растянут.
Задача 1.63. Определить усилия в стержнях фермы методом се-
чениП (рис. а).
Решение. Для определения усилий в стержнях фермы сначала
надо определить реакции опор. Для этого мысленно отбросим опоры
и заменим их действие па ферму реакциями RA и /?Л. Рассматриваем
г? zp
?Sa L
К задаче 1.63.
ферму как твердое тело, находящееся в равновесии под действием
семи активных сил и двух неизвестных реакций опор. Ввиду сим-
симметрии фермы и нагрузки реакции опор равны друг другу и каждая
по величине равна 6А
После того как реакции опор определены, переходим к опреде-
определению усилий в стержнях фермы. Разрезаем мысленно ферму по
стержням, усилия в которых надо определить (рис. б), например по
стержням 8, 9, 10, и удаляем правую часть фермы, заменив действие
ее реакциями стержней S8, S9, Sln. Направим эти реакции вдоль
перерезанных стержпеп от узлов П и /, предположив таким образом,
что стержни 8, 9, 10 растянуты. Теперь левая часть фермы (рис. б)
146 ПЛОСКАЯ СИСТЕМА СИЛ |ГЛ. I
находится в равновесии под действием реакции опоры RA, трех актип-
ных сил и реакций стержней Ss, S9, Slo. Чтобы найти величины этих
реакций, составим уравнения равновесия- для левой части фермы, при-
приравнивая нулю сумму моментов всех сил относительно точек / и /.,
в которых пересекаются линии действия двух искомых неизвестных
сил. Благодаря этому уравнение моментов будет содержать только
одно неизвестное. Так, уравнение моментов относительно течки /
будет:
RA • 2а — Р ¦ 2а — ЧР ¦ a -j- 58 ¦ а = О,
откуда
Отрицательное значение величины реакции Ss говорит о том, что
в действительности эта реакция направлена в сторону, противопо-
противоположную принятой, т. е. к узлу Е, и, следовательно, стержень 8 сжат.
Уравнение моментов относительно точки L будет:
~2Р-а — 2Р-'2а — Р-За -f RA-3a — Su>-a = О,
откуда
5,о = 9Р.
Стержень 10, как мы и предполагали, растянут.
Так как усилия S8 и Slo параллельны, то не существует течки
их пересечения, поэтому для определения усилия So вместо уравне-
уравнения моментов составляем уравнение проекций всех сил на вертикаль-
вертикальную ось, перпендикулярную к стержням 8 и 10:
RA — P—2P — IP-L-59 cos 45° = 0,
откуда
Отрицательное значение реакции S9 говорит о том, что в дейст-
действительности эта реакция направлена и сторону, противоположную
принятой, т. е. к узлу /, и стержень 9 сжат. Аналогично могут быть
определены методом сечений усилия в любых стержнях этой фермы.
Для приобретения навыков в решении задач на
расчет усилий в стержнях ферм рекомендуется ре-
решить следующие задачи из «Сборника задач по тео-
теоретической механике» И. В. Мещерского, издания
1950 г. и более поздних лет: 199, 202, 204, 205, 206, 207.
ГЛАВА II
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
§ 1. Система сходящихся сил
В § 1 главы I была рассмотрена плоская система сходящихся
сил. Пространственная система сходящихся сил, подобно плоской,
также приводится к равнодействующей R.
Равнодействующая R пространственной системы сходящихся сил
приложена и точке пересечения линий дейстпия слагаемых сил и является
замыкающей стороной силового многоугольника, построенного па
этих силах, т. е.
R=^Fh. A*)
fe —= i
В отличие от соответствующей и.юской задачи силовой многоуголь-
многоугольник не является плоским, т. е. он представляет собой ломаную про-
пространственную линию.
Проекции равнодействующей силы R на оси декартовых коорди-
координат х, у, z равны Суммам проекций слагаемых сил на соответствую-
соответствующие оси, т. е.
я, = i; г*» Ry = ? Fky Rz = i; Fk? B*)
U = 1 * ^ 1 к = [
Модуль равнодействующей У? равен
направляющее косинусы даются формулами:
D*)
Для равновесия твердого тела, к которому приложена простран-
пространственная система сходящихся сил, необходимо и достаточно, чтобы
равнодействующая равнялась пулю: #=0, г. е. чтобы силовой мне-
148
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
гоугольник был замкнут. При этом уравнения равновесия имеют вид
|>*л. = 0, ?/>, = (), 1^~ = 0. E*)
к - I
Л = 1
ft ¦= 1
Задача является статически определенной, если число алгебраи-
алгебраических неизвестных не более трех (предполагается, что все силы не
лежат на одной прямой или в одной плоскости). Так, если известны
направления всех сил, то можно определить модули трех сил.
При решении задач па равновесие твердого тела,
находящегося под действием пространственной
системы сходящихся
сил, надо выполнить
четыре первых пунк-
пункта, указанных в на-
начале к н и г и, и а с т р. 15.
Затем:
о) убедиться в том, что
задача является статически
определенной, т. е. что число
алгебраических неизвестных
величин не более трех;
6) выбрать систему осей
декартовых координат х,
У, г;
7) составить уравнения
равновесия E*) твердого
Р"с- 2.1. тела в проекциях на оси
декартовых координат;
8) решить полученную систему уравнений, т. е. определить неиз-
неизвестные величины.
Если требуется найти равнодействующую пространственной си-
системы сходящихся сил, то после выполнения первых шести пунктов
следует определить проекции Rx, Ry, Rz равнодействующей R по фор-
формулам B*), затем вычислить модуль равнодействующей R и направ-
направляющие косинусы по формулам C*), D*).
Начало осей декартовых координат рекомендуется выбрать в точке
пересечения линий действия слагаемых сил, а координатные оси на-
направить параллельно либо перпендикулярно к большинству этих сил.
Иногда при определении проекции силы на координатную ось,
например силы F на ось х, бывает неизвестен угол между осью х и
линией действия силы, но зато задан угол а, образованный силой F
и координатной плоскостью ху (рис. 2.1), а также угол C между
осью проекций х и проекцией Fxy силы F на координатную пло-
плоскость ху. (Не следует забывать, что, в то время как проекция силы
§ II
система сходящихся сил
149
па ось является алгебраической пеличиной, проекция силы на пло-
плоскость есть вектор.) В этом случае для определения проекции Fx
силы F на ось х надо, во-первых, найти проекцию Fxy силы F на
координатную плоскость ху, а затем вычислить проекцию вектора Fxy
па ось х, 1. е.
Гх —Оа =
"Рл-
Аналогично проекция силы
Далее,
Итак,
Fy = Ob =
х = F cos о. cos
з,
Fxy
F
Fxy
= Fj,y cos
на ось у
= Fxy sin
и меет
Qc=-F sin a.
, = F cos a sin p,
cos
вид
COS
/
a co;
a sin
= /• sin a.
He следует смешивать понятия проекции силы па ось н состав-
составляющей силы (рис. 2.2). Составляющая силы является вектором, рав-
равным произведению соответ-
соответствующей проекции силы на
орт оси проекций, г. е.
р — р : р — р /
' х — ' xl> ' у — * yj>
F — F k
• 2 ' 2К-
Разложение силы F по ортам
осей декартовых координат
имеет вид
Если проекция силы на ось
отрицательна, го соответствую-
соответствующая составляющая силы на-
направлена в сторону, противо- р 22
положпую положительному на-
направлению этой оси.
Задача 2.1. Определить равнодействующую пространственной си-
системы сходящихся сил, изображенной на рисунке.
Силы F% и Fa расположены в плоскости ху, сила Fi лежит б пло-
плоскости yz, а сила /^ — в плоскости xz; Fi = 2 н, F<i = F3 = 4 н,
Р? = 6 И.
Решение. Можно определить равнодействующую R как замы-
замыкающую сторону силового многоугольника, построенного на силах
Fu F.}, Ft и Fb т. е. К= Fl-\- F,-[- Fa-[- F^. Однако этот много-
многоугольник представляет пространственную ломаную и поэтому непо-
непосредственное определение модуля и направления вектора R требует
либо построения модели, либо применения сложных методов начер-
начертательной геометрии.
150
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
|ГЛ. II
Эту задачу можно решить значительно проще, воспользовавшись
методом проекций. Как известно, проекции равнодействующей fl оп-
определяются по формулам B*).
В данном случае эти формулы имеют вид
Ry = Fly -г ^з.у ~
Вычислим проекции сил Fu Fit F3 и Fi па осп х, у, z:
Flx = 0, Fty = F, cos 60°, FXz = F, cos W)
Fajc = F2 cos 30°, F2v = — F2 cos G0°, F.lz = 0;
FiX = ^з cos 45°, F3v = F3 cos 45°, F3z = 0;
F4je = F4 cos45°, r4v = 0, F,LZ = F4 cos 45°.
Подставив эти злачеш.я в формулы A), получим:
Rx = Fa cos 30° -j- F3 cos 45° -j- F4 cos 45°,
Rv = F, cos «0° — Fa cos G(j° -1- F3 cos 45°, B)
R2 = l'\ cos ?i0° -[- Ft cos 4")°,
откуда, использован заданные в условии числовые значения, находим:
Рх = 10,5 н, Ry=\,82 н, Rz = 5,96 п.
Теперь легко найтн модуль равно-
равнодействующей R
и ее направляющие косинусы:
cos (л-Гл) = ^ = 0,86,
cos 0^
cos (/,">)
0,15,
0,57,
откуда
К задаче 2.1.
=56°
Зная модуль и направление равнодействующей ^, можно изобра-
изобразить ее в системе координатных осей х, у, z.
Задача 2.2. Измерительный прибор весом Р установлен па тре-
треножнике— трех стержнях АС, ВС и DC равной длины /, соединен-
соединенных шарниром С (рис. а). Стержни ВС и DC образую! с верти-
вертикалью угол 30°, а стержень АС—угол 45°.
1]
СИСТЕМА СХОДЯЩИХСЯ СИЛ
151
Определить реакции стержней АС, ВС и DC. Размерами прибора
и весом стержней пренебречь. Опорные точки А, В и D располо-
расположены в горизонтальной пло-
плоскости, причем BD = ?^
Р е ш е и н е. Для определе-
определения искомых реакций стерж-
стержней рассмотрим равновесие при-
прибора С. К прибору приложена
одна активная сила — его вес
Р, изображенный на рис. б.
На прибор наложены три
связи — стержни АС, ВС и DC.
Применив закон освобождае-
мости, отбросим мысленно связи
и заменим их действие на при-
прибор реакциями. Направим реак-
реакции Тл, Тв и TD ндоль соот-
соответствующих стержней от кон-
концов ic их серединам, тем самым
предполагая, что стержни рас-
растягиваются (при направлении
сил Тл, Тв и TD мы восполь-
воспользовались седьмым примером
направления реакций связей,
рассмотренным в начале книги,
па стр. 14 и 15).
Теперь мы можем изучить
равновесие прибора как равно-
песие свободного твердого
тела, находящегося под дей-
действием пространственной си-
системы четырех сходящихся сил:
Р, ТА, Тп и TD. При этом сле-
следует составить три уравнения
проекций на оси декартовых
координат. Так как число алге-
алгебраических неизвестных также
равно трем (Тл,
деленной.
Проведем ось х вдоль линии действия силы Р и выберем начало
координат О в точке пересечения оси z с горизонтальной плоскостью,
в которой лежат течки Л, В и D. Направим оси х и у в эгой пло-
плоскости соответственно параллельно и перпендикулярно к веномога-
тьлыюй прямой BD.
Тн и TD), то задача является статически опре-
152 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ [ГЛ. II
Составляя уравнения равновесия, мы встретимся с трудностями
при проектировании сил Тв и Тп на оси х и у, так как неизвестны
углы между линиями действия этих сил и осями х и у. Поэтому
предварительно спроектируем силы Тв и TD на плоскость ху, а затем
эти проекции ТПху и TDxy спроектируем на оси хну. Модули сил
ТВ*У И TDxy РаВ""
Тпху = Тв cos 60°, TDXy = TD cos 60°. A)
Для проектирования векторов Тнху и Тпху на оси х \\ у займемся
определением углов между линиями действия этих сил и осями х и у.
Из прямоугольных треугольников ОБС и ODC следует, что ОБ —
= OD = l- sin 30°^//2, где / — длина каждого из стержней. Так как
но условию Z?D также равно //2, то треугольник OBD является рав-
равносторонним; значит, угол образованный ОБ и осью х, равен С0°.
Переходим к составлению уравнения проекций сил на ось х.
Проекции сил Р и ТА на ось х равны нулю (сила Р перпендику-
перпендикулярна к оси дг, а ТА лежит в плоскости yz, перпендикулярной к этой
оси). Для вычисления проекций сил Тв и TD надо векторы Т!1ху и
Тпху спроектировать на ось х. Эти проекции соответственно раины:
ТВху cos 60° и — iвху cos 60°- Значит, уравнение проекций на ось х
имеет вид
2 Fkx = Твху cos 60= - TDxy cos 60° = 0.
Приняв во внимание равенства A), запишем:
?F^=7-Qcos260°— rDcos*60°=0. B)
При проектировании слл па ось у мы, кроме проекций сил T{i и
TD, соответственно равных: Твху cos 30° и TDxy cos 30°, получим
также проекцию силы ТА, которая раина — Тл cos 45° (сила Р пер-
перпендикулярна к оси у). Значит, уравнение проекций на ось у запи-
запишется в виде
2 Fky = Тпху cos 30° -\- TDxy cos 30° — Тл cos 45° = 0.
Учтя равенства A), получим:
v рку = тв cos 60° cos 30°-|- TD cos 60° cos 30° — TA cos 45° = 0. C)
Легко состапить уравнение проекций на ось z, так как нам из-
известны углы, образованные линиями действия каждой из сил и осью г:
^/>, = — Р — Гл cos 45° — Тв cos 45°— TD cos 30° = 0. D)
Остается решить систему уравнений B) — D). Из уравнения B)
следует Тв^ Тп. Вычтя D) из C) и приняв во внимание, что 7Й= Гп,
2 •—
получим Гй=Гд=— ]/3 Р= — О.38Р. Подставив полученные
I /9"
значения Тв и TD в уравнение C), находим ТА= — -д- Р=—0,47Р,
1]
СИСТЕМА СХОДЯЩИХСЯ СИЛ
153
Знаки минус, стоящие в ответах, показывают, что найденные силы
направлены не так, как мы их предположительно изобразили па рис. б,
а прямо противоположно. Это означает, что стержни АС, ВС и DC
подвержены не растяжению, а сжатию.
Задача 2.3. На гладкой прямоугольной наклонной плоскости ABCD,
расположенной под углом 30° к горизонту, лежит груз Е весом Р.
Груз удерживается в рашю-
песии посредством двух взаимно
перпендикулярных рапных но
длине тросов ЛЕ и BE, лежа-
лежащих на наклонной плоскости
п прикрепленных к пей в точ-
точках А и В.
Определить реакции тросов
и наклонной плоскости. Разме-
Размерами груза пренебречь.
Решение. Для определе-
определения неизвестных рассмотрим
равновесие груза Е. К грузу
приложена одна активная си-
сила — его нес Р (рис. б). На
груз Е наложены три связи:
1лалкая наклонная плоскость и
тросы АЕ и BE. Применив за-
закон освобождаемое™ от связей,
отбросим связи и компенси-
компенсируем их действие па груз соот-
соответствующими реакциями. Так
как наклонная плоскость яв-
является гладкой, то ее реакция JR
направлена перпендикулярно к
плоскости. Реакции гибких спя- К задаче 2.3.
зей направляются по касатель-
касательным к ним в точках обрыва связей. В данном случае реакции тро-
тросов ТА и Тп направлены вдоль АЕ и BE (см. рис. б).
Теперь мы можем рассмотреть равновесие груза Е как равнове-
равновесие свободного твердого тела, находящегося под действием четырех
сил: Р, JR, ТА и Тп, образующих пространственную' систему сходя-
сходящихся сил. Для этой системы мы можем составить три уравнения
равновесия. Так как число алгебраических неизвестных также равно
¦jpeM (RA, Тл и 7";j), то задача является статически определенной.
Учитывая, что тросы АЕ и BE и, следовательно, силы ТА и Тв
взаимно перпендикулярны, направим оси л: и у вдоль линий дейст-
действия этих сил, а ось z—перпендикулярно к этой плоскости, т. е.
вдоль линии действия силы R. При этом выборе направлений осей
154 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ [ГЛ. II
координат проекции сил R, Т^ п Тв будут либо равны пулю, либо
величине соответствующей силы. Некоторые трудности приходится
преодолеть лишь при проектировании силы Р, так как нам неиз-
неизвестны углы, которые образует линия действия силы Р с осями х
и у. Поэтому, предварительно спроектировав силу Р на плоскость ху,
найдем вектор Рху (проекция вектора на плоскость также является
вектором) и затем уже спрсектируем Рху на оси х и у. Модуль век-
вектора Рху равен
Рху = р cos 60°. A)
Переходим к составлению уравнений равновесия пространствен-
пространственной системы сходящихся сил. Для этого суммы проекций всех сил
па оси декартовых координат х, у, z надо приравнять нулю. Эти
уравнения в данной задаче имеют вид
2 Fkx = Рх + Rx + ТАх -[- Твх = 0,
? F\v = Ру - Ry -f TAV -L- Тву = 0,
Е Ркг = я, -;¦- r2 - \- tAz -|- 7 л,=о.
После подстановки значений проекций сил:
Рх=- Рху cos 45°, Rx = 0, Тлх = 0, 7B.V = Тв, Ру = — Рху sin 45°,
Ry = 0. rAv = 7 л- 7"bj. = 0, Pz = - Р cos 30°, R2 = R,
ТАг--=0, ТВг = 0,
эти уравнения примут вид
2 F*, = - .%, cos 45° + 7fl = 0, B)
2 />v = - Р^ sin 453 + Тл = 0, C)
2FAe= —i=>cos30°-|-/? = 0. D)
Для определения неизвестных остается решить систему уравнений
B) — D), приняв при этом во внимание равенство A). Получим
7-л=7д = ^-Р:,>, = ^Р = 0,35Р, R = Xfp = 0,8TP. При состав-
составлении уравнений равновесия нам пришлось столкнуться с труднос-
трудностями при проектировании силы Р на оси х и у, так как предвари-
предварительно пришлось проектировать Р на плоскость ху. Этих труднос-
трудностей можно избежать, направив ось _у, но биссектрисе угла ЛЕВ,
ось z\ — по оси z, а ось ЛГ[ — так, чтобы имеете с осями ух и zy
она образовала правую систему осей координат. Теперь сила Р ока-
оказывается лежащей в плоскости ухг: и, следовательно, ее проекции
па оси хь уъ .с| имеют вид
PXi — 0, РУ1 = — Р cos 60°, P2i = — Р cos 30°.
«21
ПРОИЗВОЛЬНАЯ nPOCTPAHCTBF-ННЛЯ СИСТЕМА СИЛ
155
Уравнения равновесия груза в проекциях на оси хи уь г, запи-
запишутся так:
2 FkXl = - ТА cos 45° -f TB cos 4о° = 0, E)
2 Ръ>1 = — Р cos 60° -|- ТА cos 45° — 7В cos 45е = 0, F)
2/^, = —f> cos 30°4-Я = 0. G)
Сравним системы уравнений B) — D) и E) — G). При тождестве
уравнений D) и G) составление уравнений E) и F) проще и потому
предпочтительнее составлению уравнений B) и C). Объем же вычис-
вычислений при решении систем B) — D) и E) — G) примерно одинаков,
неэтому выбор осей координат Х\, у\, zt является более целесооб-
целесообразным.
Рекомендуем решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Ме-
Мещерского, издания 1950 г. и поел еду кнци х лет: 212, 216,
217, 220.
§ 2. Произвольная пространственная система сил
1°. Момент силы относительно точки. Момент
силы относительно оси. Теория нар в пространстве.
В случае плоской системы сил момент силы относительно точки был
определен как алгебраическая ие-
личина: mo{F) = zhFh.
При пространственном распо-
расположении, сил этого определения
Рис. 2.4.
недостаточно, так как плоскости, проходящие через линии действия
сил п точку, относительно которой вычисляются моменты, различны.
Поэтому момент mo(F) силы F относительно точки О в прост-
пространстве определяют как векторное произведение mo(F) = r \ F,
где г — радиус-вектор, проведенный из точки О в точку приложения
силы. Таким образом, вектор mQ(F) направлен перпендикулярно
к плоскости, содержащей линию действия силы и точку О, так что
сила с конца его видна направленной вокруг точки против часовой
стрелки (рис. 2.3). Модуль вектора mo(F) ранен произведению мо-
156
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
дуля силы на расстояние от ючки до линии действия силы (плечо), т. е.
\mo{F)\ = Fh.
Момент силы относительно осп mz{F) (рис. 2.4) определяется
как алгебраическая величина, абсолютное значение которой равно
произведению модуля проекции силы
кулярную к оси г, на расстояние hp
Fp на плоскость Р, перпенди-
перпендиот точки О пересечения осп
с этой плоскостью до линии действия проекции силы па плоскость Fp,
т. е. | mz (F) | = Fplip.
Если с конца оси z видно, что сила /^стремится поверить тело вокруг
точки О против часовой стрелки, то момент положителен, если но часовой
стрелке, то отрицателен,
т. е.
Момент силы F, изобра-
изображенной на рис. 2.4, отно-
относительно оси г положи-
положителен.
Итак, момент силы от-
относительно точки — век-
вектор, момент силы отно-
относительно оси — алгебраи-
алгебраическая величина. Если
точка лежит на оси, то
момент силы относитель-
относительно оси равен проекции момента силы относительно точки па Э1у ось,
т. е. mz{F) = nvtm0{F) (рис. 2.5).
Зная моменты силы относительно осей декартовых координат
tnx{F), my(F), mz{F\ можно определить величину момента силы mo(F)
относительно начала координат О и его направляющие косинусы но
формулам:
У (П
Рис. 2.5.
I >"о С7)
cos[z,mc(F)} = -
mz(F)
«о (f):
B*)
причем m0 {F) = mx (F) i -j- my (F)j-\- mz {F) ft.
Выражения моментов силы относительно осей декартовых коор-
координат через проекции силы на эги оси даются формулами:
= xFy-yFjr C*)
121
ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
157
Здесь Fx, Fy, F2— проекции силы F на оси декартовых коорди-
координат, х, у, z — координаты точки А приложения силы (рис. 2.6).
Момент силы относительно оси равен нулю, если линия действия
силы и ось лежат в одной плоскости (рис. 2.7), т. е.:
а) если сила параллельна оси (при этом проекция Fp силы F на
перпендикулярную к оси плоскость Р обращается в пуль: Fp=:0);
б) если линия действия силы пересекает ось (при этом /гр^0).
г 1
п
Fzk
А
У'
z
yJ
У
Рис. 2.6.
Рис. 2.7.
В случае пространственной системы сил главным моментом
относительно точки называется векторная сумма моментов всех
сил системы относительно той же точки:
D*)
Главным моментом пространственной системы сил относи-
относительно оси называется сумма моментов всех сил системы относи-
относительно этой оси:
>' *«= 2 «Л/7*)- E*)
*=i
т. е.
нг — zkFky), ту = ^ {zkFkx — xhFk2),
F*)
Зная главные моменты системы сил относительно осей декарто-
декартовых координат, можно определить модуль главного момента относи-
158
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
телыю начала координат О и его направляющие косинусы по фор-
формулам:
K «^ + «j, G*)
cos (x, m0) = -
т.
cos (jm»o) = -?>--, cos (z,mo) = ^f-.. (8*)
mr
Если пространственная система сил приводится к равнодействую-
равнодействующей, то согласно теореме Вариньона момент равнодействующей
силы относительно точки ранен иекторной сумме моментов всех сил
системы относительно той же точки:
Та же теорема относительно осей декартовых координат форму-
формулируется так: момент равнодействующей силы относительно оси ранен
сумме моментов составляющих сил относительно той же оси:
тх (/?) =
х {Fk),
ту
к -« I
Момент пары сил в пространстве определяется как вектор, пер-
перпендикулярный к плоскости пары, причем с конца его пара видна
направленной прочив часовой стрелки (рис. 2.8). Модуль момента
нары сил равен произведе-
произведению модуля одной из сил
пары на расстояние между
линиями действия сил (пле-
(плечо): \т\ = Fh.
Теория пар в гтро-
' I странстве дается
т т2 двумя теоремами.
Рис. 2.8. Теорема 1. Пары, век-
векторные моменты которых
равны, эквивалентны; следовательно, не нарушая состояния твердого
тела, пару сил можно переносить в плоскость, параллельную данной.
Теорема 2. Момент равнодействующей пары равен векторной
сумме моментов составляющих пар.
Для равновесия твердого тела, находящегося под действием пар
сил в пространстве, необходимо и достаточно, чтобы векторная
сумма моментов этих пар была равна нулю
i»fc =
Вычисление моментов сил и главных моментов систем сил отно-
относительно о:ей является важной составной частью решения задач на рав-
равновесие твердых тел под действием произвольных пространсчвенных
§ 2j ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 159
систем сил, а также задач на приведение этих систем сил к про-
простейшему виду.
Вычисление главных моментов систем сил отно-
относительно осей рекомендуется проводить в следую-
следующем порядке:
1) провести плоскость, перпендикулярную к оси, относительно
которой требуется определить главный момент системы сил;
2) найти точку пересечения оси с этой плоскостью;
3) спроектировать силу на плоскость, перпендикулярную к оси;
4) опустить перпендикуляр (плечо) из точки пересечения оси
с плоскостью на линию действия проекции силы на плоское п., опре-
определенную в предыдущем пункте;
5) записать модуль момента силы относительно оси в виде про-
произведения модуля проекции силы на найденное плечо;
6) определить знак момента силы относительно оси;
7) повторить построения и выкладки, сделанные в третьем, чет-
четвертом, пятом и шестом пунктах для каждой из сил системы;
8) вычислить главные моменты системы сил относительно осей
в виде сумм моментов данных сил относительно этих осей.
Если определение проекции силы па плоскость, перпендикулярную
к оси, затруднительно, то следует разложить силу па составляющие.
Затем вместо момента силы относительно оси надо, применив георему
Вариньона, вычислить сумму моментов сил составляющих относительно
этой оси.
Если этот прием также затруднителен, то надо найти проекции
силы Fx, F;y, рг па оси, записать координаты х, у, г точки прило-
приложения силы и вычислить моменты силы относительно осей декар-
декартовых координат по формулам C *).
Если оси декартовых координат в условии задачи не заданы, то
целесообразно выбрать эти оси так, чтобы моменты возможно боль-
большего числа сил обратились в нуль. Значит, надо направить оси па-
параллельно силам либо так, чтобы оси пересекали линии действия сил.
Задача 2.4. Вычислить моменты относительно осей координат .vr,
у и z силы F, направленной по диагонали боковой грани прямоуголь-
прямоугольного параллелепипеда, изображенного на рисунке, если длина ребра,
параллельного оси х, равна а.
Решение. Линия действия силы F пересекает ось х, поэтому
момент силы F относительно оси х равен нулю:
Для определения момента силы F относительно оси у спроекти-
спроектируем эту силу на плоскость xz, перпендикулярную к оси у, т. е.
определим Fxz. Нетрудно видеть, что FX. = F cos 30°. Остается взять
момент силы Fi2 относительно точки пересечения оси у с перпенди-
перпендикулярной плоскостью xz, т. е. точки О. Плечом является ребро
160
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
ОА = а, С конца оси у видно, что сила Fxz стремится повернуть тело
в плоскости хг вокруг точки О по часоной стрелке, следовательно,
момент силы отрицателен. Итак,
ту (F) = — Fxia = — Fa cos 30° = —
Fa
Остается определить момент силы F относительно оси г. Для
этого найдем величину проекции Fxy силы F на плоскость ху, пер-
перпендикулярную к оси z. Легко видеть,
что Fxy = F cos 60°. Теперь вычисляем
момент силы Fxv относительно точки О
пересечения оси z с перпендикулярной
плоскостью ху. Плечом оказывается отре-
отрезок ОА = а. Знак момента положителен,
так как с конца оси г видно, что сила Fxy
стремится повернуть тело в плоскости ху
вокруг точки О против часовой стрелки.
Значит,
, ™ г^ Fa
Задача 2.5. Определить моменты от-
'х 'ху иосителыю осей х, у и z силы F, изо-
К задаче 2.4. браженной на рисунке. Сила F, приложен-
приложенная в точке А, лежащей на оси у, обра-
образует с плоскостью ху угол 30°, причем се проекция на эту пло-
плоскость образует с осью у угол О АС, равный 45°; ОА = а.
Решены е. Как и и предыдущей задаче, находим без труда мо-
моменты силы F относительно осей у и z: mv(F) = 0 (линия действия
силы F пересекает ось у), mz(F) = — Fxy'h, где Fxy = F cos 30°==
„l/з" „
= rbj модуль проекции силы г на плоскость ху, перпендику-
1/2"
лярную к оси z, a h = OA sin 45° = a sin 45° = а -Ц> длина пер-
перпендикуляра, опущенного из точки О пересечения оси z с плоско-
плоскостью ху на линию действия силы Fxv. (Знак момента отрицателен,
так как с конца оси z видно, что сила Fxy стремится повернуть тело
в плоскости ху вокруг точки О по часовой стрелке.) Итак,
/72 y(F)= О,
A)
Труднее найти момент с ялы F относительно оси х, так как неиз-
неизвестен угол между силой F и перпендикулярной к оси х плоско-
плоскостью yz. Здесь целесообразно прибегнуть к приему, упомянутому
в обзоре теории, — разложить силу F на две составляющие. Разло-
§21
ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
161
жим силу на составляющие Fxv л F2 (см. рисунок). Таким образом,
F — Fxv-\-F2, где Fxv = F cos'3Q°, FZ = F соз"бОэ.
Теперь для определения момента силы F относительно оси х
применим теорему Вариньопа, согласно которой момент равнодей-
равнодействующей силы относительно оси равен сумме моментов составляющих
сил относительно той же осп. В данном случае
Так как линия действия силы Fxy пересекает ось х, то mx(Fxy) = i
Момент силы F2 относительно оси х равен тх(Fz) = Fza. Учитывая,
ч го Fz = F cos 60° = j
окончательно получим:
/2,
тАП=т- C)
Для вычисления мо-
момента силы F относи-
относительно оси х можно
было также воспользо-
воспользоваться формулой
где у \\ z — координаты 'х
точки А приложения си-
силы F, a Fy и Fz —
К задаче 2.5.
проекции силы F на оси у и z. В данном случае у = а, 2 = 0,
Fy = — Fxy cos 45° = — F cos 30° cos 45° = -—t
F2 = F cos 60° = ~.
Подставив эти значения в формулу D), получим результат формулы C),
Как показывает решение этой задачи, в случаях, когда вычисле-
вычисление момента силы относительно оси обычным приемом затруднительно,
следует прибегать к разложению силы на составляющие, с после-
последующим применением теоремы Вариньона, либо к выражениям C *)
моментов силы относительно осей через проекции силы на эти оси.
Задача 2.6. Вычислить главные моменты относительно осей х,
у и z и точки О пространственной системы сил, изображенной на ри-
рисунке. Сила Ft лежит на ребре куба, а силы /\, и F3— на диагона-
диагоналях его боковых граней. Ребро куба а равно 2 м, /ч=10 н, F% =
6 М, И, Бать и др., т. I
162
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
Решение. Глашше моменты системы сил относительно осей
равны суммам моментов данных сил относительно этих осей, т. е.
«,= ?>, (Л). «?, = 2 «у с*).
в данной задаче
= У^тг (Fh),
тх = тх
ту = ту
тх
j- my
-f mx
my
/яг = /яг (F,) -)- отг (f-i) -)- тг (F3).
Моменты сил Fj, Ft и F3 относительно осей х, у \\ z имеют
следующий вид: tnx(F,) = 0 (линия действия силы Fx пересекает ось х),
/м (F,) = 0 (сила Z7] параллельна оси у), m2(F,)=r:Fla; долее,
) = Fi sin 45°я = -^]--,
= — FJi = — F,a sin 45° = — —-
ту
т. (F.2) = Ft cos 45°a = F«-a^2 (
= 0
(линия действия силы /^ проходит через точку О, т. е. пересекает
оси х, у и г).
Внеся эти значения моментов сил в формулы A), получим:
т
__ Г.2а 1/2"
¦2
в
К задаче 2.6.
или, подставляя численные зна-
значения:
пгх = 1А дж, п?у = —24 дж,
mz = 44 д.-ж.
Главные моменты системы сил
tnx, my, mz относительно осей де-
декартовых координат х, у, z одно-
одновременно являются проекциями
главного момента т0 относительно начала координат О на соответ-
соответствующие оси, т. е. то = mJ.-\- mvj-\- m^k. Исполыюнэв формулы G*)
и (8 *), найдем теперь модуль главного момента системы сил отно-
«j 2| ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
сителыю точки О и его направляющие косинусы:
т0 = Vm'x -\- т\, -j- tnz = 55,5
cos (*Гш0) = **- = 0,43, cos (>Г«0) = "'¦"¦ = - 0,43,
'"о о
)='"* =0,79,
"о
т. е. (л-, т0) = 05°, (у, то)=П5°, (.г, то) = 38°. И гак, mo = B4i —
_. 24/+44ft).
2°. lip и ведение к одному центру сил, произвольно
расположенных в пространстве. Главным вектором V
п
сгстемы сил называется векторная сумма этих сил, т. е. V= ^ ^*-
* ^--1
Проекции 1'д., V7;, и Vz главного вектора V на оси декартовых
координат равны суммам проекций сил па соответствующие оси:
V, = ? Fkx, Vy=j^ Fkv, 'Vz=% Fbe (9*)
k -- --1 * — I Л- —-1
Модуль главного нектора V и направляющие косинусы опреде-
определяются по формулам:
V=V VI -г V'y + Vj, A0*)
cos(.v7V) = ?, соз(у'>)=^, cos(z?V) = ^. A1*)
Главный момент т0 пространственной системы сил относительно
центра О ранен векторной сумме моментов всех сил относительно
этого центра:
т
о=
Проекции главного момента т0 па (си декартовых координат
называются главными моментами тх, ту, mz относительно соответ-
соответствующих осей, т. е. mo=mxi—rtnvj-\-mzk.
Главные моменты пространственной системы сил тх, ту, mz отно-
относительно осей х, у, 2 определяются по формулам E*), (б*). Зная
тх, ту, mz, можно определить модуль и направляющие косинусы т0
по формулам G *) и (8 *).
В результате приведения сил, произвольно расположенных в про-
пространстве, к одному центру система сил оказывается эквивалентной
силе, равной главному вектору V, и паре сил, момент которой век-
торно равен главному моменту т0.
164 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ ' [ГЛ. II
При перемене центра прннедеиия системы сил главный момент
системы, вообще говоря, меняется, примем зависимость главного мс-
меита пространственной системы сил от выбора центра приведения
выражаемся так: главны!) момент тл пространственной системы сил
относительно поною центра А равен векторной сумме главного мо-
момента та этой системы сил относительно старого центра О и момента
относительно нового центра Л силы V, приложенной в старом цен-
центре О: mA = m0-\-mA(V0).
Статическими инвариантами пространственной системы сил
называются такие характеристики этой системы, которые остаются
неизменными при перемене центра приведения. Статических инвариан-
инвариантов существует два:
первый статический инвариант — главный вектор V системы
сил; в соответствии с определением величина и направление главного
вектора V не зависят,от выбора центра приведения:
V=VJ-\-Vyj-j-V1k,
где Уд-, VY, \'г определяются по формулам (9 *);
второй статический инвариант — скалярное произведение глав-
главного вектора V и главного момента т0—не зависит от выбора
центра приведения:
V то= Vxtnx-\- Vytnv-~ V2m?,
где Vx, Vь, V2 и тх, т , mz определяются соответственно по фор-
формулам (9*) и (о*), F*).
Не следует отождествлять силу V с равнодействующей силой ff,
так как равнодействующая R—это одна сила, которая эквивалентна
данной пространственной системе сил, а сила V эквивалентна данной
системе сил только н совокупности с парой сил, момент которой
равен главному .моменту то-
Различные случаи приведения сил, произвольно расположенных
в пространстве
а) Главный ысктор равен нулю, но главным момент не равен нулю,
т. е. V=0, m0^ 0.
Система сил приводится к паре сил, момент которой равен глав-
главному моменту то- (В этом случае главный .момент системы сил то
не зависит от выбора центра приведения.)
б) Главный вектор не ранен пулю, по главный .момент равен нулю,
т. е. V г? 0, то = 0.
Система сил приводится к равнодействующей /?= V, приложенной
в центре приведения системы.
и) Главный вектор и павпый момент системы не равны нулю
и притом взаимно перпендикулярны, т. е.
V --/- 0, т0 г? 0, (moTv) = 90°.
§2]
ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
165
Система сил приводится к равнодействующей #= V, линия
действия которой параллельна линии действия силы V и отстоит
от нее на расстоянии h = tno/V. Положение линии действия равно-
равнодействующей должно быть таким, чтобы направление момента равно-
равнодействующей /? относительно центра приведения О совпадало с на-
направлением главного момента системы сил то относительно центра О.
Сила V и равнодействующая /? равны по модулю, параллельны
и отличаются, вообще говоря, только линиями действия (рис. 2.9).
Рис. 2.9.
Рис. 2.10.
г) Главный вектор и главный момент системы не равны нулю
и притом не взаимно перпендикулярны, т. е.
V ф 0, т ф 0 и (У\то) ф 90°.
Система сил приводится к дпнаме (силовому винту) — совокуп-
совокупности силы V и пары сил, лежащей в плоскости, перпендикулярной
к этой силе.
Линия действия силы V называется центральной осью. Централь-
Центральная ось является геометрическим местом цепгроп приведения, для
которых главный момент ото имеет наименьшее значение и направлен
вдоль этой оси (рис. 2.10). Уравнения центральной оси имеют вид
—zVx + xVz mz — xVv+yVx
x v V2
где mx, my, mz, Vx, Vy, V2 имеют прежние значения, а х, у, z —
текущие координаты.
д) Главный вектор и главный момент системы равны нулю, т. е.
V=0, mo = 0.
Твердое тело, к которому приложена данная пространственная
система сил, находится в равновесии.
166
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
Уравнения равновесия твердого тела под дейст-
пием произпольной пространственной системы сил.
Для равновесия твердого тела под действием произвольной пространст-
пенной системы сил необходимо и достаточно, чтобы суммы проекций
всех данных сил на произвольно выбранные оси декартовых координат
х, у, z и суммы моментов всех сил относительно этих осей равнялись нулю:
л
A hx
2 «»*(|?*)=(
л
2
m
I/ '
)=o, S
т2
= Q, A2*)
= 0. A3*)
проекций; они
Три последних
Первые три уравнения называются уравнениями
обеспечивают равенство нулю главного вектора V.
уравнения называются уравнениями момен-
моментов; они обеспечивают равенство нулю
главного момента то-
В случае произвольной пространствен-
пространственной системы сил задача является стати-
статически определенной, если число алгебраи-
алгебраических неизвестных не более шести.
В случае равновесия твердого тела
с одной неподвижной точкой, например
со сферическим шарниром (рис. 2.11),
система активных сил приводится к равно-
равнодействующей, линия действия которой
проходит через неподвижную точку. Три
проекции реакции неподвижной точки fiOx,
Roy, Roz на оси декартопых координат
определяются из уравнений A2*).
Из уравнений моментов A3*) могут быть определены неизвестные
величины грех активных сил (напомним, что активными называются
все силы, не являющиеся реакциями связей).
В случае равновесия твердого тела с двумя закрепленными точками,
например с двумя сферическими шарнирами или двумя подпятниками
(рис. 2.12), можно определить величины четырех составляющих опорных
реакций RAx, /?лг Rex, Кву> перпендикулярных к оси, проходящей
через неподвижные точки. Величины составляющих опорных реакций
Raz и Rbz, направленных вдоль этой оси, не могут быть в отдель-
отдельности определены. Можно найти только их сумму Raz-^Rbz- Если
одна из опор выполнена в виде подшипника В (рис. 2.13), допускаю-
допускающего перемещение пдоль оси 2, то отсутствует составляющая реакция
Rbz- В этом случае из уравнений равновесия можно определить вели-
величины пяти составляющих опорных реакций Rax< Ялу, Raz, Rbx> Riiy,
и величину одной активной силы.
ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
167
Различные случаи приведения к одному центру
параллельных сил в пространстве. Эти силы могут быть
приведены:
а) к паре сил, если главный вектор равен нулю, а главный момент
не равен нулю: V = 0, mo^Q;
б) к равнодействующей, если гланный вектор не равен нулю,
а главный момент раиен нулю: V -^ 0, ото = 0;
г
Рис. 2.13.
в) к равнодействующей, если главный вектор п главный момент
не равны нулю: V =j? 0, то^О; в случае системы параллельных сил
вектор V и вектор то всегда взаимно перпендикулярны;
г) твердое тело находится в равновесии, если главный вектор
и главный момент системы раины нулю: V = 0, nio = 0.
Уравнения равновесия системы сил, параллельных оси г, имеют вид
= 0. A4*)
Задача является статически определенной, если число алгебраи-
алгебраических неизвестных не более трех.
При решении задач на равновесие твердого тела,
находящегося под действием произвольной простран-
пространственной системы сил, надо выполнить четыре первых
пункта, указанных в начале книги, па стр. 15.
168 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ [ГЛ. II
Затем:
5) убедиться в том, что данная задача является статически опре-
определенной, т. е. что число алгебраических неизвестных не более шести;
6) выбрать систему осей декартовых координат;
7) составить шесть уравнений равнопесия твердого тела A2*) и A3*).
В случае системы параллельных сил отпадают два уравнения проек-
проекций сил па оси, перпендикулярные к силам, и одно уравнение моментов
сил относительно оси, параллельной силам. Так, если силы параллельны
оси х, то уравнения равновесия имеют вид
2 ^* = °. 2 my(Fk) = 0, 2 »'Л^) = 0;
ft — i ft = i *=i
8) решив систему уравнений, составленных в предыдущем пункте,
найти неизвестные величины.
Оси декартовых координат рекомендуется выбирать так, чтобы
они оказались параллельными либо перпендикулярными к возможно
большему числу неизвестных сил, а также чтобы линии действия не-
пзиестпых сил пересекали эти оси.
Задача 2.7. На рис. а изображена косозубая шестерня радиуса г,
закрепленная на горизонтальном валу. Вал лежит в двух опорах:
упорном подшипнике А и цилиндрическом подшипнике В. В точке К,
расположенной в вертикальной плоскости симметрии шестерни, к ее
зубу приложено давление Т со стороны другой шестерни, находящейся
с ней в зацеплении (на рис. а сила Т и вторая шестерня не изо-
изображены). Давление Т разложено на три составляющие Тх, Ту и Т.,
которые соответственно параллельны осям координат х, у к z (начало
координат взято в точке А, ось х направлена вдоль вала, ось z —
по вертикали вверх, ось у — так, чтобы вместе с осями х \\ z была
образована правая система координат). К валу, вращающемуся равно-
равномерно, приложена пара сил с вращающим моментом твр так, что ее
моменты относительно осей равны: mx = mBp, my = mz = Q.
Определить реакции опор А и В и вращающий момент твр. Даны
модули составляющих Тх, Ту и Тг давления Т на зуб шестерни.
Размеры указаны на рисунке. Весом шестерни и вала пренебречь.
Р е ш е и и е. Для определения неизвестных реакций опор Л и В
и вращающего момента швр рассмотрим равновесие вала с сидящей
па нем шестерней. (Под равновесием вала мы понимаем не только
покой, по и его равномерное вращение, упомянутое в условии задачи.)
К палу и шестерне приложены следующие активные силы, изо-
изображенные на рисунке: три составляющие Тх, Ту, Тг давления Т
и пара сил, момент которой mx = tnBp требуется определить (в данной
задаче момент активной пары сил неизвестен).
Связями, наложенными па вал, являются две опоры: упорный под-
подшипник А и подшипник В. Мысленно отбросим связи и компенсируем
их действия па вал реакциями. Подшипник В допускает перемещение
§2]
ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
169
вала вдоль оси х, поэтому составляющая реакции вдоль оси х отсут-
отсутствует, и нам остается изобразить лишь дне составляющие Rny и Rpz,
перпендикулярные к оси вала. (Мы направляем на рис. б эти составляю-
составляющие в сторону возрастания соответствующих координат. Если в дейст-
действительности направление какой-либо состапляющей противоположно,
то ответ окажется отрицательным.) Упорный подшипник А, в отличие
от подшипника В, не допускает перемещения пала о до ль оси х.
Поэтому в точке А мы изображаем все три состанляющие RAx, Rap
R реакции.
б)
х
К задаче 2.7.
Итак, нам предстоит рассмотреть равновесие свободного вала
с шестерней под действием активных сил Тх, Ту, Тг и пары сил
с моментом mx — mEp, а также состанляющих реакций RAx, RAv, RAz,
Rny, Riiz- Все эти силы образуют пространственную систему сил, для
которой надо записать шесть уравнений равновесия. Так как число
алгебраических неизвестных также равно шести (твр, R,\x, RAy, Raz,
Run и Rbz), to задача является статически определенной.
Составим уравнения проекций с^л на оси декартовых координат
х, у, 2. Все силы либо перпендикулярны, либо параллельны этим осям.
Поэтому их проекции равны нулю, или величине соответствующей
силы. Так, силы Ту, Tz, R,ny, R.\2, Rey Riiz и пара сил перпендикулярны
к оси х, и, следовательно, их проекции на эту ось равны нулю.
170 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ (ГЛ.11
Из проекций на ось х лишь RAx и Тх отличны от нуля, причем обе
проекции положительны. Итак,
2>Fkx = Tx-\-RAx = 0. A)
Аналогично запишем уравнении проекций сил на оси у и z:
? Fky = I, -,- RAy4-RBy = 0, B)
(Напомним, что проекция пары сил на любую ось рампа нулю, ибо
1лавпый вектор пары сил ранен пулю.)
Переходим к составлению уравнений моментов сил относительно
осей х, у, 2. Предварительно заметим, что составление этих уравнений
и данной задаче производится достаточно просто. Действительно, линии
дейгмгля сил параллельны и.-н пересекают оси координат и, значит,
имеют моменты, равные нулю, либо силы лежат в плоскостях, пер-
перпендикулярных к осям п, следовательно, отпадает необходимость
в проектировании этих сил иг. плоскости, перпендикулярные к осям.
При составлении уравнен ля моментов сил относительно оси х
предварительно заметим, что силы Rax и Тх параллельны оси х,
а линии действия сил /tr\v, R^^, Тг, Rny и Rbz пересекают ось х.
Следовательно, их моменты равны нулю. Значит, в уравнение моментов
войдут лишь моменты силы Ту и пары сил.
По условию момент пары относительно оси х равен твр, т. е.
шх = швр. D)
Сила Ту лежит в плоскости, перпендикулярной к оси х. Из точки
О пересечения оси с плоскостью опускаем перпендикуляр ОК=1Г
па линию действия Ту. Момент положителен, так как с конца оси х
видно, что сила Т стремится повернуть тело вокруг точки О против
часовой стрелки. Итак,
тх(Ту)=Ти-г. E)
Использовав формулы D) и (о), запишем уравнение моментов
относительно оси х:
При составлении уравнении моментов относительно оси у заметим,
что силы Ту, Rav, Ray параллельны оси у, а линии действия сил RAx
и /?д_- пересекают ось у. Следовательно, моменты их равны нулю.
Кроме того, по условию момент пары сил гпу равен нулю. Значит,
отличными от нуля являются только моменты сил Тх, Тг и Rnz. Все
эти силы лежат в плоскости xz, перпендикулярной к оси у. Плоскость
xz пересекается с осью у и :.очке А. Поэтому из точки А опускаем
перпендикуляры на линии действия сил Тх, Тг и Rnz. Соответственно
§2) ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 171
получим: AM —г, АО = а и АВ = а~-Ь. Момент силы Тх отрица-
отрицателен, так как с конца оси у видно, что сила Тх стремится повернут»
тело вокруг точки А по часовой стрелке, а моменты сил 7\ и Rnz
положительны, ибо они видны противоположно направленным!!. Птах,
my(Tx) = -Tx-r, my(T2) = Tz-a, my{R,l2) = Rll2(a \-b). G)
Приняв во снимание формулы G), запишем ураниеше моменте»
относительно оси у в виде
^tmy(Fk) = -Tx-r-lrTs-a-\-RBl(a-[-b) = O. (8)
При составлении уравнения моментов относительно оси г пало
учесть, что силы 7\, клг, Rnz параллельны оси г, а линии действия
сил Тх, Rax, RAy пересекают эту ось. Поэтому моменты этих сил
относительно оси z равны нулю. Кроме того, но условию момент пары
сил относительно оси z также равен нулю. Значит, в уравнение пойдут
только моменты сил Ту и Кцу
Сила Т лежит в горизонтальной плоскости, перпендикулярной
к оси z. Из точки М пересечения оси z с этой плоскостью опускаем
перпендикуляр МК=АО = а на линию действия Ту. Момент силы Ту
относительно оси z отрицателен, так как с конца оси z видно, что
сила Ту стремится повернуть тело по часовой стрелке. Значит,
mz(TJ=~Tu-a. (9)
Сила R[iy лежит в плоскости ху, перпендикулярной к оси z. Из
точки А пересечения этой плоскости с осью z опускаем перпендикуляр
АВ^а-\-Ь па линию действия Rny. Момент отрицателен, ибо скопца
оси z видно, что сила Rny стремится повернуть тело вокруг точки А по
часовой стрелке. Итак,
mz {R,iy) = -Rny(a -f- b). A0)
Приняв во внимание формулы (9) и A0), запишем уравнение
моментов сил относительно оси z:
. 2mz(Fh) = -Ttt-a-ROy(a-\-b) = 0. A1)
Итак, уравнения равновесия вала с закрепленной па нем шестерней
имеют вид
24 = ^+^ = 0, (!)
J^Fky = Ty-\-RA}l-j-RBy = O, B)
J^Fkt=T,-\-RAt-\-RBi = 0, C)
ltrnx(Fh) = mBp-i-Tu-r = 0, (б)
l -Tx.r + Tt-a-]-RBt-la-\-b) = O, (8)
-Tu-a-Rlly(a-\-b) = 0. A1)
172 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ [ГЛ. II
Теперь переходим к решению этой системы шести уравнений
с шестью неизвестными (RAx, RAy, Raz> Rey, Rbz и mBp). Из уравне-
уравнения F) имеем твр==—Ту-г. Искомый вращающий момент пары,
как и следовало ож*идать, оказался отрицательным. Действительно,
с конца оси х вращение пары видно в направлении по часовой стрелке.
Из уравнения (8) получим:
Тх-г—Т,-а
Из уравнения A1) находим:
Теперь, подставив значение RBy в уравнение B), a RBz в C), соот-
соответственно имеем:
n _ lii* n _ Тх-г+Тг-Ь
Наконец, из A) следует RAX=— Тх.
Значения RAx, RAy, RAz и RBy оказались отрицательными. Это
означает, что направления сил RAx, RAv, RAZ и /fBy противоположны
тем, которые предположительно были нами указаны на рисунке.
Знак RLiz может быть выяснен только после подстановки численных
значений Тх, Tz, а и г.
Задача 2.8. Багажная полка железнодорожного вагона прикреп-
прикреплена к стене вагона дпумя петлями (цилиндрическими шарнирами)
Л и В и стержнем MS. Стержень, присоединенный шарнирами М и 5
к полке и стене, образует угол 30° с горизонтальной плоскостью
полки.
Определить реакции петель A w В к стержня MS, если вес
полки Р =10 кГ. Размеры указаны па рисунке.
Решение. Для определения искомых реакций петель А и В
и стержня MS рассмотрим равновесие полки KLMN. На полку
действует одна активная сил,! — ее вес Р=10 кГ, приложенный в
центре тяжести С полки (в точке пересечения диагоналей прямоуголь-
прямоугольника KLMN (рис. б)).
Применив закон освобождаемое™, мысленно отбросим связи, т. е.
петли А и В и стержень MS, и компенсируем их действие на полку
соотоетстоующими реакциями соязей. Реакция Т стержня направлена
вдоль стержня от Ж к S. Сразу указать направление реакций
петель А и В мы не можем. Так как, однако, петли — цилиндричес-
цилиндрические шарниры — не препятствуют перемещению полки вдоль оси АВ,
то отсутствуют составляющие реакций вдоль этой оси. Значит, реак-
реакции направлены перпендикулярно к оси АВ и каждая из них может
быть разложена на две взаимно перпендикулярные составляющие.
ПРОИЗВОЛЬНАЯ ПРОСТРЛНСТВЕННАЯ СИСТЕМА СИЛ
173
Выбрав начало декартовых осей координат в петле А, изобразим
ось х вдоль АВ, ось у по горизонтали направо и ось z no вертикали
вверх. В соответствии с выбором осей координат изобразим состав-
составляющие реакций RAv, RAZ в петле А и RBy, RBz в петле В (см. рис. б).
Итак, полка KLMN находится в равновесии под действием актив-
активной силы — веса Р и пяти нечзнесшых сил: RAv, RAZ, Rlly, Rljz и Т.
Так как все эти силы образуют пространственную систему сил, то
число уравнений равновесия равно шести. Значит, задача является
статически определенной, причем одно из уравнений должно быть
зависимым от остальных пяти или тождественно обратиться в нуль.
Займемся составлением уранмений равновесия. Так как все силы
лежат в плоскостях, перпендикулярных оси х, то проекция каждой
силы на эту ось равна нулю, и уравнение проекций на ось х обра-
обращается в тождество
%Ркх=0. A)
Из остальных пяти уравнений равновесия мы сможем определить все
пять неизвестных.
При составлении уравнения проекций на ось у заметим, что силы
Р, RAz и RBZ перпендикулярны к оси. Значит, отличными от нуля
174 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ (ГЛ. (I
являются только проекции сил RAy, RHv и Т. Силы RAy и RBy парал-
параллельны оси^» и их проекции па эту ось равны RAy и RBy, а проек-
проекция силы Т равна —7"cos30c, поэтому уравнение проекций па ось у
имеет вид
Ц F*y = *ау + Kb, ~ T cos Ж = 0. B)
Составляя уравнение проекций на ось z, учтем, что силы
Rny перпендикулярны к оси z и их проекции равны нулю. Силы Д
RBz и Р параллельны оси z и их проекции на эту ось равны RAz,
Rrz и — Р- Наконец, проекция силы Т раина Т sin 60°. Значит, урав-
уравнение проекций на ось z имеет вид
Е Fl" = К А" + RBZ - Р -f 7 Sin 60° = 0. (?,)
Переходим к составлению уравнений моментов относительно осей
х, у и z. Моменты сил RAv, RA2, RBy и RB2 относительно оси л:
равны пулю, так как линии действия этих сил пересекают ось х.
Значит, отличными от нуля являются только моменты относительно
оси .V сил Р и Т.
Сила Р лежит в плоскости, перпендикулярной к оси х. Из точки Е
пересечения этой плоскости с осью х опускаем перпендикуляр ЕС
па линию действия силы Р. Момент силы Р относительно оси х отри-
отрицателен, так как с конца оси х видно, что сила Р стремится повер-
повернуть тело вокруг точки Е по часовой стрелке. И гак,
mxiP)=— P-EC. D)
Сила Т лежит и плоскости, перпендикулярной к оси х. Из точки N
пересечения этой плоскости с осью х опускаем перпендикуляр NQ
на линию действия силы Т. Момент силы Т относительно оси х
положителен, ибо с конца оси х видно, что сила Т стремится повер-
повернуть тело вокруг точки N против часовой стрелки. Значит,
mAT)=T-NQ. E)
Приняв во внимание формулы D) и E), запишем уравнение
моментов относительно оси х:
^mAFk) = -P-EC-\-T-NQ = 0. F)
При составлении уравнения моментов относительно оси у следует
учесть, что моменты сил RAy, RIjy и RA! равны нулю (сила RBy
параллельна оси у, а линии действия сил RAy и RAz пересекают эту
ось). Значит, отличными от нуля являются только моменты относитель-
относительно оси у сил Р, RIiZ и Т.
Сила Р лежит в плоскости, перпендикулярной к оси у. Из точки D
пересечения этой плоскости с осью у опускаем перпендикуляр DC
па линию действия силы Р. Момент силы Р относительно оси у
§21 ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 175
отрицателен, так как с конца сси у видно, что сила Р стремится
повернуть тело вокруг течки D по часовой стрелке. Значит,
ту (Р) = — Р- DC. G)
Столь же просто определяется момент силы RUz относительно
оси у. Действительно, сила RBZ лежит в плоскости xz, перпендику-
перпендикулярной к оси у. Из точки А пересечения этой плоскости с осью у
опускаем перпендикуляр АВ на линию действия силы RBZ. Момент
положителен, ибо с конца оси у видно, что сила RBZ стремится
повернуть тело вокруг течки А против часовой стрелки. Итак,
my(RB,) = RBZ-AB. (8)
Несколько труднее вычислить момент силы Т относительно оси у,
так как сила Т не лежит в плоскости, перпендикулярной к этой оси.
Поэтому предварительно спроектируем силу Т на плоскость, прохо-
проходящую через точку М, перпендикулярно к оси у. Проекцией является
сила 7\ (напомним, что проекция вектора на плоскость — также век-
вектор). Из точки О пересечения этой плоскости с осью у опускаем
перпендикуляр ОМ па линию действия с и л iii 7\. Так как с конца
оси у видно, что сила Ту стремится повернуть тело вокруг точки О
против часовой стрелки, то момент силы Т относительно оси у
положителен, т. е.
my(T)=Tl-OM (9)
Теперь, использопав выражения G), (8) и (9), запишем уравнение
моментов относительно оси у:
^ my (Fk) = — Р ¦ DC -J- RHS ¦ ЛИ -f Tt ¦ ОМ = 0. A0)
Остается составить уравнение моментов относительно оси г. Сразу
отметим, что моменты сил Р, RA!, Rlu и RAy относительно оси z
равны нулю (силы Р, RAz RBZ параллельны оси г, а линия действия
силы RAy пересекает эту ось). Значит, отличными от нуля являются
лишь моменты относительно оси г сил RBy и Т. Сила RBy лежит
в плоскости ху, перпендикулярной к оси г. Из точки А пересечения
этой плоскости с осью z опускаем перпендикуляр АВ на линпо
действия силы RBy. Так как с конца оси z видно, что сила RHy
стремится повернуть тело вокруг точки А по часовой стрелке, го
момент ее отрицателен, т. е.
mz(RBy)=-Rny-AB. A1)
Для вычисления момента силы Т относительно оси z предвари-
предварительно найдем проекцию 7^ силы Т на плоскость ху. Из точки А
пересечения этой плоскости с осью z опустим перпендикуляр AN
на линию действия силы 7~2. Момент силы Т относи )ельно оси z
176 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ [ГЛ. ГГ
положителен, так как с конца оси z видно, чго сила Т.г стремится
повернуть тело вокруг точки А против часовой стрелки. Значит,
щг{Т)=Тя-АМ. A2)
Теперь, приняв во внимание формулы A1) и A2), запишем урав-
уравнение моментов относительно оси z:
2 mz (Fk) = - RLjy . AB -f- T,-AN=0. A3)
Игак, для определения пяти неизвестных RAy, RA2, RBy, RBz и Т
мы составили пять уравнений: B), C), F), A0) и A3). Прежде чем
перейти к решению этой системы, вычислим модули сил Г, и Т.2,
а также длины отрезков (плеч) ЕС, NQ, DC, AB, ОМ, AN, входящих
в уравнения F), A0) и A3). Имеем: Ту== T sin 30°= ^- Г, Т.г =
= Тcos 30°= tJ— 7". Обозначим буквой а ширину полки. Тогда
ЕС — 4- a, NQ = ЛУИ sin 30° = a sin 30° = у а,
пп 80 — 2-10 Qn
DC = л = 30 см,
АВ = 80 — 2-Ю — 60 см, ОМ = 80 — 10=70 см, AN=OM = 70 см.
Кроме того, но условию Р ==¦¦ 10 кГ.
Теперь система уравнений B), C), F), A0) и A3) примет вид
^-'-^-^7 = 0, A4)
Яд*-Яя,-Ю-т--17-=0, A5)
^ = 0, A6)
i-7--70 = 0, A7)
— К,,,.60 + ^-7"-70 = 0. A8)
Остается решить эти уравнения.
Из уравнения AG) имеем Т== 10 кГ. Подставив это значение Т
в уравнения A7) и A8), по/учим: RBZ = — -^ = — 0,83 кГ, RBy =
=г. -уКЗ = 10,09 кГ. Теперь из уравнений A4) и A5), подставив
в них полученные значения RBy и RBz, находим: RAy = — -^-1/3 =
= — 1,44 кГ, RAz = 5 • -g- =.- 5,83 кГ, Знаки минус, полученные в от-
§2] ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 177
вегах для RAy и RBZ, i/оказывают, что направления сил RAy и RBZ
противоположны тем, которые указаны на рис. б.
Составляя уравнения моментов, мы столкнулись с некоторыми
трудностями при вычислении моментов силы Т относительно осей у
.и г, так как пришлось силу Т проектировать па плоскости, перпен-
перпендикулярные к этим осям. Этих трудностей можно избежать, направив
координатные оси yt и z, так, чтобы моменты силы Т относительно
этих осей равнялись нулю. Для этого возьмем начало координат
в точке N, направим ось ху вдоль оси х, а оси у{ и zt — соответст-
соответственно параллельно осям у и z (см. рис. б). Нетрудно видеть, что
моменты силы Т относительно осей у1 и zy обратятся в нуль, так
как линия действия силы Т пересекает эти оси. Составим уравнения
равновесия полки, воспользовавшись осями координат х,, у,, zv При
неизменности уравнений A4), A5) и A6) уравнения A7) и A8) при-
примут вид
2 mn (Fk) = P-CM — RBZ ¦ DN—RAZ ¦ АА'= 0, A9)
2mZl(Fll) = RAyAN-\-RBy'BN=0. B0)
В уравнения A9) и B0) не входит сила Т и поэтому составить
их проще, чем уравнения A7) и A8). Однако решение системы урав-
уравнений A4)—A8) легче, чем решение системы A4), A5), A6), A9) и
B0). Значит, выбрав оси xh yt, ^ вместо осей х, у, z, мы добились
упрощения составления уравнений моментов относительно осей у1 и
zlt но усложнили решение системы уравнений равновесия. Объем вы-
вычислений в обоих случаях примерно одинаков.
Задача 2.9. На рис. а изображена квадратная крышка ABCD
грузового люка. Крышка прикреплена посредством сферического шар-
шарнира А и петли (подшипника) В. Подняв крышку над горизонтом
на угол 30°, ее закрепили с помощью оттяжки DE, образующей
угол 60° с плоскостью крышки.
Определить опорные реакции сферического шарнира А и петли В,'
а также реакцию оттяжки DE. Вес крышки равен Р.
Решение. Для определения неизвестных рассмотрим равновесие
крышки ABCD.
К крышке приложена одна активная сила — ее вес Р. Точка О
приложения силы Р расположена в центре квадратной крышки
(рис. б).
На крышку наложены три связи: сферический шарнир А, петля В
и оттяжка DE. Применив закон освобождаемости, мысленно отбросим
эти связи и заменим их действие на крышку соответствующими реак-
реакциями. Оборвав оттяжку DE в точке D, направим реакцию Т вдоль
нее от D к Е. Сферический шарнир А является неподвижной точкой,
поэтому сразу указать направление реакции невозможно, и ее следует
заменить тремя взаимно перпендикулярными составляющими. Петля В
178
ПРОСТРАНСТВЕННАЯСИСТЕМА СИЛ
(ГЛ. П
допускает перемещение вдоль АВ, значит, в эго.м направлении отсут-
отсутствует составляющая реакции, т. е. в петле В имеются только две
составляющие, перпендикулярные к АВ.
Выберем начало координат в точке В, ось х направим вдоль АВ,
ось у — вдоль ВС, а ось z — перпендикулярно к плоскости крышки,
х
так чтобы она вместе с осями х и у образовала правую систему
осей координат (см. рис. б) В соответствии с этими осями изобразим
три составляющие RAx, RAy, RAz реакции сферического шарнира А и
две составляющие RBy и RBZ реакции петли В.
Теперь мы можем рассмотреть равновесие крышки как равнове-
равновесие свободного твердого тела, находящегося под действием активной
силы Р и реакций Т, RAx, RAy RA2, Rny и RBz. Все эти силы обра-
образуют пространственную систему сил, для которой следует составить
шесть уравнений равновесия. Так как число алгебраических неизве-
S 2] ПРОИЗВОЛ!>Н\Я ПРОСТРЛНСТВЕНП\Я СИСТЕМА СИЛ 179
стиых также ранпо шести (Т, RAx> RAv> RAZ, RBV и RBi), то задача
является статически определенной.
Составляя уравнения равновесия, мы столкнемся с трудностями
при рассмотрении силы Т, так как нам неизвестны углы, которые
образует эта сила с координатными осями х и у. Поэтому разложим
силу Т на две составляющие Txv и Тг так, чтобы сила Txv лежала
в плоскости ху, а сила Тг была к ней перпендикулярна (см! рис. б),
т. е. параллельна оси z. Модули этих сил равны
Тху = Г cos 60°, Тг = Т cos 30°. A)
Аналогично поступим с силой Р, разложив ее на составляющие
силы Pv и Pz (сила Р лежит в плоскости, перпендикулярной к оси х;
поэтому ее проекция па ось х равна нулю). Для модулей Э1их сил
имеем:
Ру = Р sin 30°, Рг = Р cos 30°. B)
Впредь при составлении уравнений равновесия мы вместо проек-
проекции силы Т на ось будем вычислять сумму проекций сил Txv и Тг
на эту ось, а вместо момента силы Т относительно оси будем, на
основании теоремы Вариньоиа, вычислять сумму моментов сил 7\.v и
Тг относительно соответствующей оси.
Займемся составлением уравнений проекций сил на оси декарто-
декартовых координат.
Силы Р, /?д,„ RA!, RBy, RBz и Тг перпендикулярны к оси х и
проекции их па эту ось равны нулю. Значит, отличными от нуля
являются только проекции сил RAX и Тху. Итак,
=/?^—^ cos 45° = 0.
Подставив значение Txv из формулы A), имеем:
? Fkx = RAx — Т cos 60° • cos 45° = 0. C)
Силы Рг, RAX, RAl, RRz и Tz перпендикулярны к оси у и проек-
проекции их на эту ось равны пулю, значит, в уравнение проекций на
ось у войдут только проекции сил RAy, RBv, Py и Txv. Итак,
? рку = RAy _j- RBy — Р sin 30° — Тху sin 45° = 0.
Подставив значение Тху из формулы A), получим:
2Fky = RAy + RIiv— P sin 30°— 7cos60o-sin 45°=0. D)
Силы Pr RAX, RAy, RBv, Txv перпендикулярны к оси z и, следо-
следовательно, их проекции на эту ось равны нулю, поэтому в уравнение
проекций на ось z войдут лишь проекции сил Рг, Тг, RAZ и Rlu.
Итак,
^ Fkt = RAZ -\- RBZ - F cos 30° + T cos 30° = 0. E)
180 ПРОСТРАНСТВЕННАЯ СИСТЕМЛ СИЛ [ГЛ. II
Переходим к составлению уравнений моментов относительно
осей х, у и г.
Линии действия сил RAx, RAy, RAz, Rny, Rnz, Ру и Тху пересекают
ось х, поэтому моменты этих сил относительно оси х равны пулю.
Отличными от пуля являются только моменты сил Рг и Тг.
Сила Рг лежит в плоскости, перпендикулярной к оси х. Эта пло-
плоскость пересекается с осью х в точке М. Опускаем из точки М
перпендикуляр МО на линию действия Pz. Момент силы отрицателен,
так как с конца оси х видно, что сила Рг стремится повернуть
тело вокруг точки М по часовой стрелке. Значит, mx(Pz) =
= — PZ-OM. Если длину стороны квадратной крышки мы обозначим
буквой а, то OM = aJ1. Пряняо во внимание формулу B), запишем:
/ял(Рг)= —Pcos30°-y, F)
Заметим, что для вычисления момента силы Р относительно оси х
не было нужды в разложении силы Р па составляющие Ру и Р~,
первая из которых дает момент, равный пулю. Действительно, сила Р
лежит в плоскости, перпендикулярной к оси х. Из точки М пересе-
пересечения оси х с этой плоскостью опускаем перпендикуляр ML па ли-
линию действия силы Р. Тогда /пх(Р)= — Р • ML. Из треугольни-
треугольника OML имеем ML = ОМ cos 30°= |- cos 30°. Значит, тх(Р) =
= — Р -„- cos 30°, что соответствует формуле F). Разложением силы Р
на ее составляющие Ру и Рг целесообразно будет воспользоваться
при вычислении ее моментов относительно осей у и г, так как сила Р
не лежит в плоскостях, перпендикулярных к этим осям.
Сила Тг лежит в плоскости, перпендикулярной к оси х. Из точ-
точки А пересечения этой плоскости с осью х опускаем перпендикуляр
Л?> = а на линию действия силы 7\. Момент положителен, так как
с конца оси х видно, что сила 7\, стремится понернуть тело вокруг
точки А против часовой стрелки. Значит, mx{Tz)^Tz- а. Приняв
во внимание формулу A), имеем:
mx{Tz)= Г sin 30°-а. G)
Итак, использован формулы F) и G), запишем урапнение момен-
моментов относительно оси х:
^ ,пх (Fk) = — Р cos 30° • -?- + Г cos 30е - а = 0. (8)
При состанлении уравнения моментоц относительно оси у надо
учесть, что линии действия сил RAx, RDv, RBz, Txy пересекают ось у,
а линии действия сил RAy и Ру параллельны оси у. Поэтому моменты
всех этих сил относительно оси у равны нулю. Значит, в ураинение
моментов относительно оси у войдут лишь силы: RAZ, Рг и Тг.
§2] ПРОИЗВОЛЬНАЯ ПРОСТРЛНСТВЕННЛЯ СИСТЕМА СИЛ 181
Сила RAz лежит о плоскости xz, перпендикулярной к оси у. Из
точки В пересечения этой плоскости с осью у опускаем перпенди-
перпендикуляр ВА = а на линию действия RAz. Момент RA, отрицателен, ибо
с конца оси у видно, что сила RAz стремится повернуть тело вокруг
•дочки В но часовой стрелке. Значит,
my(RAi) = -RAi-a. (9)
Сила Рг лежит в плоскости, перпендикулярной к оси у. Из
точки К пересечения этой плоскости с осью у опускаем перпенди-
перпендикуляр K0 = ir на линию действия Рг. Момент положителен, так как
с копна оси у видно, чго сила Р, стремится повернуть тело вокруг
точки К против часовой стрелки. Итак, wy{Pz)=^Pl-^y. Приняв во
внимание формулу A), имеем:
/^ (/>,) = Л cos 30°—. A0)
Сила Тг лежит в плоскости, перпендикулярной к оси у. Из точ-
точки С пересечения этой плоскости с осью у опускаем перпендикуляр
CD —а на линию действия силы Т.. Момент отрицателен, ибо с конца
оси у видно, чго сила Тг стремится повернуть тело вокруг точки С
по часовой стрелке. Значит, гпу(Тг) =— Т2-а. Приняв во внимание
формулу A), запишем:
ту(Тг) = - Г cos 30°-а. A1)
После использования формул (9), A0) и A1) уравнение моментов
относительно оси у примет вид
2lmy(Fk) = — R^-a-j-PcosW0--^ — Гсоэ 30°-а = 0. A2)
Остается составить уравнение моментов относительно оси z. За-
Заметим, что линии действия сил RAx, RBy, RBs и Тху пересекают ось z,
а силы RAz, Pz и Тг параллельны этой оси. Поэтому моменты этих
сил относительно оси z равны пулю. Значит, в уравнение моментов
войдут только моменты диух сил: Ру и RAy.
Силы Ру и RAy лежат в плоскости ху, перпендикулярной к оси z.
Из точки В пересечения плоскости ху с осью z опускаем перпен-
перпендикуляр ВМ = а/2 на линию действия Ру и перпендикуляр ВА = а
на линию действия RAy. Момент силы Ру отрицателен, a RAy поло-
положителен, так как с конца оси z видно, что сила Ру стремится повер-
повернуть тело вокруг точки В по часовой, а сила RAy — против часовой
арелки. Значит,
mz(RAy) = RAy-a, A3)
тг{Ру) = -Ру:} = -Р^Ж^. A4)
(В формуле A4) учтен результат B).)
182 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ [ГЛ. II
Запишем уравнение моментов относительно оси z, использовав
выражения A3) и A4):
/?;(JF.a-Psln30o.-J = 0. A5)
Итак, уравнения равновесия крышки имеют вид
2.Fkx = RAx — 7 cos 60°-cos 45° = 0, C)
? Fky = RAy + RBy — P sin 30° — T cos 60° • sin 45° == 0, D)
X /^г = RAz + /?Вг — P cos 30° + У cos 30° = 0, E)
? mx (Fk) = - P cos 30° • ~ -4- Г cos 30° • a = 0, (8)
Ц/я3,(/7А)=— /?Аг¦ a +/> cos 30° -y— Г cos 3()°-a = 0, A2)
Хтг(Рк)= RAy-a-P sin Ж ¦ % = 0. A5)
Для определения неизвестных остается решить эту систему шести
уравнений с шестью неизвестными.
Из уравнений (8) и A5) непосредственно находим Т и RAy. Сло-
Сложив уравнения (8) и A2), получим RAz. Далее из C) вычислим RAx,
из D) — RBy и из E) — Rli2.
Р Р V 2
Приводим ответы: T= — t RAy = — t RAz = 0, RAx = -^— P =
=0,18 P, Rny= —fP- P --= 0,43 P, RBZ = *~ P = 0,43 P.
Если, решая задачу, мы испытываем затруднения при вычислении
моментов ^относительно осей какой-либо силы, то достаточно выбрать
начало координат на линии действия этой силы для того, чтобы эта
сила в уравнения моментов не вошла. Так, для того чтобы в данной
задаче сила Т не вошла в уравнения моментов, достаточно взять
начало координат в точке D приложения силы Т, а оси xit _Vi и zt
направить соответственно параллельно осям х, у и z. При этом урав-
уравнения проекций на оси хь уь zx будут имечь вид, тождестненный
уравнениям C), D) и E) проекций на оси х, у и z. Так как линия
действия силы Т пересекает оси xit y\ и zb то эта сила не войдет
в соотпетствующие уравнения моментов. Поэтому
2 mXl (Fk)=- RA;- a -RBl.a + P cos 30°. -f =0, A6)
V myi (Fk) = RB2.a-P cos 30° • \= 0, A7)
2 «*, (ft) = P sin 30° • -J +RAx.a- RBy ¦ a = 0. A8)
Теперь для определения неизвестных надо решить систему урав-
нений C), D), E), A6), A7) и A8).
§2] ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 183
Степень трудности составления уравнений моментов (8), A2) и
A5) относительно осей х, у, z и уравнений моментов AG), A7) и A8)
относительно осей xit y\, г{ примерно одинакова. Объем вычислений
при решении системы уравнений C), D), E), (8), A2) и A5) и си-
системы C), D), E), A6), A7) и A8) также примерно одинаков.
Если бы в условии данной задачи петля В была заменена сфери-
сферическим шарниром, то в точке В добавилась бы составляющая реак-
реакции RBX, алгебраических неизвестных стало бы семь (RAX, RAy, RAZ,
Rbxi &ву> Riiz и Т) и задача оказалась бы статически неопределен-
неопределенной. Если бы одновременно с введением сферического шарнира В
оттяжка DE была заменена силой Т, известной по величине и направ-
направлению, то, хотя число неизвестных стало бы равным шести (RAx,
Rat Raz> ^вх> Rrv> ^b*)> задача осталась бы статически неопределен-
неопределенной. Действительно, выбрав прежние направления осей х, у и .г, не-
нетрудно видеть, что RAx и RBx нойдуг только в одно из шести урав-
уравнений равновесия — в уравнение C) проекций на ось х, которое при
этом примет вид
?Fhx = RAx-\-RPjX—Tcos 60°• cos 45° = 0.
Из этого уравнения можно определить только сумму RAX -}- Rnx,
а каждое из этих неизвестных найти невозможно. Тем самым подтвер-
подтверждается указание, сделанное в обзоре теории этого пункта, что задача
на равновесие твердого тела с двумя закрепленными точками (в дан-
данном случае с двумя сферическими шарнирами) является статически
неопределенной.
С учетом того, что в решениях задач 2.7—2.9 дано подробное из-
изложение методики составления уравнений равновесия, в следующих
днух задачах эти уравнения составлены без дополнительных по-
пояснений.
Задача 2.10. На рисунке изображен поворотный крап, ось враще-
вращения которого имеет две опоры: подпятник А и подшипник В. С по-
помощью троса, переброшенного через блок D, при вращении крана
вокруг оси АВ происходит подъем либо опускание груза Е, подве-
подвешенного к концу троса. Вес крана, приложенный в его центре тяже-
тяжести С, равен Pt = 2T. Вес поднимаемого груза Е равен Ла = 4Г.
Конструкция крапа совмещена с плоскостью рисунка, т. е. лежит
в плоскости yz. Ось х направлена на нас. В точке К крепления
троса к крану проведены оси xbybzb соответственно параллельные
осям х, у, z.
Наклонная ветвь троса образует с горизонтальной плоскостью ххух
угол, равный 60°. Проекция этой ветви троса на плоскость х^\\
образует с осями х\ и у\ соответственно углы 120° и 30° (см. ри-
рисунок).
Определить опорные реакции подпятника А и подшипника В,
а также величину вращающего момента mQ, который надо приложить
184
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. П
к крапу вокруг оси вращения z для того, чтобы он находился
в равновесии; а=\ м, Ь=4лг, c? = 3_if, 1г = 4м.
Решение. Рассмотрим равновесие крана, к которому приложена
одна активная сила — его нес Рь приложенный в центре тяжести С
крана, а также искомый вращающий момент т0. На кран наложены
связи: подпятник А, иодш! пник В и трос, прикрепленный к крапу
, в точке К- Так как под-
¦ ' пятник А является не-
неподвижной точкой, то его
реакцию RA представляем
тремя составляющими
Ял* RAy H Raz- Подшип-
Подшипник В допускает переме-
перемещение вдоль оси враще-
вращения z, поэтому здесь от-
отсутствует составляющая
реакции, лежащая па оси,
и следует ввести только
дпе боковые составляю-
составляющие RBx и RBy. Оборвав
трос возле точки креп-
крепления К, направляем его
реакцию Т вдоль троса.
Здесь часто совершают
грубую ошибку, изобра-
изображая вместо силы Т вес
Рг груза Н, приложен-
приложенный в точке Е и направ-
направленный по вертикали
вниз. Надо мысленно рас-
рассечь трос вблизи точки
крепления К и заменить
отброшенный трос реак-
реакцией Т, направленной по
тросу. Из условия равновесия груза Е находим j Т\= \Рг \ = 4 7".
Теперь рассмотрим равновесие крапа под действием вращающего
момента т0 и сил: Рь RAx, RAy, RM, RBx, Rny и Т.
Число неизвестных равно шести (RAx, RAy, RAz, RBx, RBy и mQ),
и задача является статически определенной.
Составление уравнений равновесия затруднено пространственным
положением силы Т, поэтому предварительно разложим силу Т па
три составляющие Тх, Ту, Т:, параллельные осям х, у, z. Модули их
равны
К задаче 2.10.
Тг = Т cos 30°, Тх = Тху cos 60° = Т cos2 60°,
Ту = Тху cos 30°= Т cos 60° cos 30°.
A)
§2] ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 185
Исиользопав A), находим:
7, = 17, 7, = У~3 7, 7, = 2/~3 7. B)
Теперь составим уравнения равновесия крана:
Учитывая при решении системы значения Тх, Ту и 7г из B), а также
численные данные, находим:
m 0 = 4 Т м, RBX = 0,7 5 Г, Я flJ, = —5,31 7,
/?Лл. = 0,25 7, /^==3,58 7, Я,,, = 5,46 7.
Допустим, что условие этой задачи изменено: искомый пратаю-
тий момент т0 задан, а вместо подшипника Б имеется подпятник.
Тогда в точке В добавляется неизвестная составляющая реакции RIU.
Видоизмененная задача оказывается статически неопределенном, хотя
при этом число алгебраических неизвестных остается равным числу
уравнений, т. е. шести (RAx, RAy, RAz, RIix, RHv, RB2). Действительно,
1{Аг и RIU входят только в уравнение проекций па ось z, которое
принимает вид
Z Ъг =" RAz + R,U - Pi— Тг = 0.
Из этого уравнения можно определить только сумму RA, — Rl>2, a
каждое из этих неизвестных найти невозможно.
Полученный результат подтверждает указание, сделанное в обзоре
теории этого пункта, что задача на равновесие твердого тела с двумя
закрепленными точками (в данном случае подпятниками Л и В), не-
несмотря па соответствие числа неизвестных числу уравнений, является
статически неопределенной.
Задача 2.11. Однородный стержень АВ весом Р, образующий
с полом угол 45°, упирается концом А в негладкий плинтус комнаты
(рис. а), а концом В в гладкую вертикальную стену. В точке В
к стержню прикреплен горизонтальный трос BE.
Проверить, может ли стержень оставаться в равновесии, а также
определить реакции плинтуса, стены и троса, если коэффициент тре-
трения скольжения о плинтус /==0,5, а угол OAD равен 30°. Оси
х, у, z изображены на рисунке.
Решение. Стержень не мог бы оставаться в равновесии, если
бы плинтус был гладким. В этом случае конец стержня А начал бы
186
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
скользить вдоль плинтуса. Равновесие возможно лишь при наличии
силы трения /\,p, направленной противоположно возможному движе-
движению, т. е. от Л к О, причем модуль силы трения должен быть
меньше или равен его наибольшей величине:
где/—коэффициент трения скольжения, a RA — модуль нормальной
реакции плинтуса. В случае невыполнения условия A) стержень при-
придет и дпижение.
¦зо°
*Ау
У
а)
х
К задаче 2.11.
К аержпю приложена одна активная сила — его вес Р (рис. б).
Так как по условию стена является гладкой, то ее реакция RB пер-
перпендикулярна к плоскости стены, т. е. параллельна оси х. Реакция Т
троса направлена от В к Е. О направлении силы трения /^р было
указано выше. Нормальная реакция RA плинтуса расположена в пло-
плоскости уг, но направление ее пока неизвестно. Поэтому разложим
силу RA на две взаимно перпендикулярные составляющие RAy и RAz,
Т' ^ *А = *Ау + ПАг- B)
Задача является статически определенной, ибо число неизвестных
равно пяти: RB, T, Frp, RAy и RAZ.
Об через 11, составим пять уравнений
Обозначив
равновесия:
длину стержня
И mx(Fk)=. — P.lcos 45° sin 30°-\-T-2l sin 45° = 0,
21 »iy (Fk)= — P.lcos 45° cos 30° + RD¦ 21 sin 45° = 0.
C)
D)
E)
F)
G)
§ 2j ПРОИЗВОЛЬНАЯ ПРОСТРА11СТНЕННАЧ СИСТЕМА СИЛ 187
Решая систему уравнений C)—G), найдем RAZ из E), Т из F),
RB из G); затем получим FTp из C) и RAy из D). Итак, искомые
силы по модулю равны
RA, = P, RAy=T=0,25P, /?fi = FTp=^p=0,43P. (8)
Остается проверить, может ли стержень оставаться в равновесии.
В соответствии с формулой B) запишем:
RA = VRtAy-f-RtAZ. (9)
Внеся значения RAy и RAZ из (8) в формулу (9), найдем:
/?,, = ¦? 1/77 =1,04 Р. A0)
Подставив в неравенство A) значения FTp и R из (8) и A0), при
/¦=0,5 получим:
0,43 Р < 0,52 Р.
Так как условие A) выполнено, то стержень находится и равно-
равновесии.
В заключение вычислим наименьшее значение коэффициента тре-
трения скольжения /, при котором стержень будет оставаться в равно-
равновесии. Отбросив в формуле A) знак неравенства, найдем:
Если бы по условию коэффициент трения скольжения был меньше
чем 0,41, то стержень не мог бы остаться в равновесии и начал бы
двигаться.
Рекомендуем решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Мещер-
Мещерского, издания 1950 г. и последующих лет: 246, 254, 257,
262, 264, 265, 267, 268, 271, 272, 276, 277, 278.
3°. Приведение произвольной пространственной
системы сил к простейшему виду рекомендуется
выполнять в следующем порядке:
1) выбрать оси декартовых координат;
2) взять центр приведения системы сил в начале координат О;
3) вычислить проекции Vx, Vv, Vz главного вектора V системы
сил по формулам (9*);
4) определить модуль главного вектора V и направляющие коси-
косинусы по формулам A0*) и A1*), причем
5) найти главные моменты tnx, my, тг системы сил относительно
осей х, у, z по формулам E*), F*);
188 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ [ГЛ. И
6) определить модуль главного момента т0 и его направляющие
косинусы по формулам G*) и (8*), причем
7) выяснить, к какому простейшему виду приводится заданная
система сил:
а) если V=0 и то = 0, то твердое тело, к которому приложена
данная система сил, находится в равновесии;
б) если V=0, тоф0, то система сил приводится к паре сил
с моментом т0;
в) если V ф О, /яо=0, то система сил приводится к равнодей-
равнодействующей R= V. Уравнения линии действия равнодействующей в этом
случае будут:
где У„ Vy, Vz — проекции главного вектора V, определенные в третьем
пункте, а х, у, z — текущие координаты линии действия равнодей-
равнодействующей;
г) если V Ф 0, тоф0, то следует выяснить, не являются ли V
и т0 взаимно перпендикулярными.
В случае взаимной перпендикулярности V и т0 их скалярное
произведение Vm0 равно нулю. Поэтому надо проверить, выполняется
ли равенство
Vxmx-\-Vymy-\-V2m2 = 0.
Если равенство имеет место, то система сил приводится к равнодей-
равнодействующей /?. Уравнения линии действия равнодействующей R в этом
случае имеют вид
mx—yVz + zVy my — 2Vx-\-xVz mz — xVy-\-yVx
V~x Vy — Vz • ^10 >
Если равенство Vxmx-\~ Vyttiy-y Vzmz = 0 не имеет места, то
главный вектор V и главный момент т0 не взаимно перпендикулярны
и система сил приводится к динаме. Уравнения центральной оси также
определяются по формулам A6*).
Главный вектор V динамы определен в четвертом пункте. Главный
момент т дипамы для центров приведения, взятых на центральной
оси, лежит на этой оси. Его проекцию на центральную ось (мини-
(минимальный момент) следует определить по формуле
При приведении пространственной системы сил к простейшему виду
оси декартовых координат следует выбрать так, чтобы возможно боль-
большее число сил оказалось параллельно либо перпендикулярно к этим
ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
189
О)
осям, а также чтобы линии действия сил в возможно большем числе
пересекали эти координатные оси.
Задача 2.12. Пространственная система сил была приведена
к центру О, взятому в начале координат системы xyz. В результате
приведения были получены: сила V=\0k и пара сил, момент кото-
которой векторпо равен главному мо-
моменту системы то= 12? —J— 20ft, при-
причем [ V] = н, а \т0] = дж.
Определить силу и пару сил, к
которым приведется данная система
сил, если за центр приведения при-
принять точку А, лежащую на оси у
и отстоящую от начала координат
на расстоянии 0А = 2м (рис. а).
Решение. При приведении
пространственной системы сил к но-
новому центру сила остается равной
главному вектору V, а главный мо-
момент меняется в соответствии с фор-
формулой
К задаче 2.12.
= mo + AOXV0. A)
Поэтому строим в точке А силу V.
Затем переносим т0 в точку А и
изображаем момент относительно
нового центра А силы V, прило-
приложенной в старом центре О, т. е.
mA(V0). Так как mA(V0) надо на-
направить перпендикулярно к плоско-
плоскости, проходящей через Vo и точку А,
т. е. к плоскости уг, и притом так, чтобы с конца его сила Vo была
видна направленной" вокруг центра А против часовой стрелки, то
лектор mA(V0) параллелен оси х, но направлен'в противоположную
сторону (рис. а). При этом \mA(V0)\ = \ V\OA=z 20 дж.
Итак, для определения главного момента тД относительно нового
центра А надо, следуя формуле A), сложить векторы т0 и mA{V0),
приложенные в точке А, т. е.
т.
= то-\- тА (Vo) =V2i-\- 20ft — 20i = — Si -f 20ft.
На рис. а вектор тА получаем как диагональ параллелограмма,
построенного па векторах т0 и mA(V0).
Из найденного результата тА — ~ 81-\-'20k следует, что тАх~
= — 8 дж, тАу = 0, тАг = 20 дж. Таким образом, главный момент тА
190
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
|ГЛ. II
по модулю равен тА = V rri\x -|- т~А -f- ^Az = 4 \ 29 дж. Направляю-
Направляющие косинусы определяем по формулам:
cos (х,
т
л
т, о
cos (у,
cos
откуда
(xTtnA) — Ml °40', (jCmA) = 90°, (С^тА) = 21 °40'.
Эту задачу можно решить, не прибегая к формуле A) — зависи-
зависимости между главными моментами пространственной системы сил,
определенными относительно двух центров.
Можно построить в центре А две уравновешивающиеся
силы V и V (рис. б). Тогда сила V оказывается приведенной
к центру А, но при этом добанляется присоединенная пара в составе
сил: V, приложенной в точке О, и V, приложенной в точке А. Мо-
Момент этой присоединенной пары /»пр перпендикулярен к плоскости
пары, т. е. к плоскости уг, причем с его конца приложенная пара
видна направленной против часовой стрелки, т. е. параллельно оси-*,
но it сторону, противоположную положительному направлению этой
оси. По модулю |тпр| = | V\ ¦ 0А =
= 20 дж. Нетрудно заметить, что
т„р и tnA(V^) (из первого ва-
варианта решения задачи) векторно
равны, т. е. т„9 — тА (Vo). Для
определения главного момента от-
относительно центра А остается
сложить т0 и /ипр, т. е. тА =
= то-\-тЛр = то-\-тА{У\ от-
откуда находим значение т0, полу-
полученное в первом варианте реше-
решения задачи.
Оба метода решения задачи
по объему вычислений примерно
равноценны.
Задача 2.13. На рисунке изо-
К залачс 2.13. бражепа пирамида АОВС, две бо-
боковые грани которой расположены
в координатных плоскостях xz и yz, а основание лежит в плоско-
плоскости ху. Ребра АИ и АС образуют с ребром — высотой АО — углы
30°. К пирамиде приложена система пяти сил. Силы /^ и Ft напрак-
30°-
§21 ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 191
лены по ребрам АВ и АС, силы F3 и Ft — вертикальны, а линия дей-
действия силы Ft совмещена с высотой 0D основания ВОС.
Определить модули сил Fb Fk и Ft, если пирамида находится
в равновесии. Дано: F\ = Fq = F.
Решение. Примем за центр приведения начало координат О.
При равновесии пирамиды главный вектор V и главный момент т0
системы сил, приложенных к пирамиде, равны нулю: V=0, /яо = 0.
Так как по модулю
V= Wi^r Vy-VV% m0 = Vml-\-m*y-{-ml,
то
Vx=Vy=Vz = 0, тх = ту = тг = 0. A)
Вычислим проекции Vx, Vy, V. главного вектора V по формулам:
Vx = X Fkx, Vy = f, Fky, VI=^ Fhz.
A=l fe=l *=1
В данном случае получим:
Vx= — Fi cos 60° + Fv cos 45°, B)
Vy = — /72cos60o-j-Fscos45°, C)
^=гр]С05 300 + ^со5 300 — F3 — F^ D)
Вычислим главные моменты т„ ту, тг относительно осей х, у, z
по формулам:
п п п
* = 1 к = I ft = 1
Введя обозначения: ОВ = ОС=а, для данной системы сил имеем:
.a-^-, E)
my = F,-a-Fi-^Q-, F)
и« = 0. G)
Приняв во внимание условия A), запишем (Q) — F) в виде
— F, cos 60° -f-FB cos 45° — 0, (8)
— Fa cos 60° + /-'„ cos 45° == 0, (9)
Fi cos 30° 4- F\ cos 30° — F3 — F4 = 0, A0)
A2)
192
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
Так как по условию Fl = Fi = F, то из уравнений A1) и A2) нахо-
находим F3 = Fi = F*-?y-, а из уравнения (8) получим /-8 = F-4f-. При
этих значениях F3, P4 и Fs уравнения (9) и A0) тождественно обра-
обращаются в нуль.
Итак, пирамида АОВС находится в равновесии под действием дан-
данной системы пяти сил при условии:
F —F _р V'3 F —p.V'2
1 з — Г4— ~2~> 8— ~2~*
Задача 2.14. Привести к простейшему виду систему сил Fu Fit
F3, Fb Fa и F6, приложенных к вершинам С, В и Е куба, ребро кото-
которого равно a; F, =/^ =/%, = F4 = f;
F]f = F6 = Fy2 , Направления сил
указаны на рис. а.
Решение. Принимаем за центр
приведения точку О. Направляем оси
х, у, z вдоль ребер куба (рис. а).
Определим проекции Vx, Vy, Vz
главного вектора V на оси х, у, z:
'У ^ = 2^ = ^ —Z7. cos 45°,
+ F~o cos 45° -|- F6 cos 45°,
t = H Fu = Fa — F6 cos 45°.
Подставив значения модулей дан-
данных сил, имеем:
Следовательно, глакпыН вектор V
системы сил равен нулю.
Переходим к определению главного момента т0. Находим сначала
главные моменты тх, ту, тг системы сил относительно осей х, у, z:
тх=У1 тх(Fk) = F3a — Faa cos 45° — F6a sin 45°,
mv = 2 my (Fk) = — F3a— Faa cos 45° -\- F6a cos 45°,
t»z = S'«.- (Fk) = — F2a — Fia -|- F6a cos 45° + F8a sin 45°.
Подставив значения модулей данных сил, имеем:
тх= — Fa, ту = — Fa, тг = 0.
Таким образом, главный момент /»0 = — Fai — Faj, а его модуль
т0 =
+ «5 = Fa V~2.
8 2]
ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
193
Итак, данная система сил оказалась приведенной к силе V=0 и
паре сил с моментом т0 = — Fai — Faj, изображенным на рис. б
(пара сил расположена в плоскости, перпендикулярной к /я0, так что
пара с конца т0 видна направленной против часовой стрелки).
Задача 2Л5. Принести к простейшему виду систему сил F,, Fb
Fit Fn и F9, приложенных в вершинах А, К и С прямоугольного
параллелепипеда OABCDEKL;
= 2F, ОС = а,
= а/2.
Решение. Принимаем за центр приведения точку О. Определяем
проекции Vx, Vy, Vz главного вектора V на оси х, у, z:
Подаянии значения модулей сил, получим:
VX = F, Vy = 2F, V2 = F. A)
Таким образом, главный вектор V=Fi-\-2Fj-\-Fk, а его модуль
Найдем теперь главные моменты тх, ту, тг данной системы сил
относительно осей х, у, z:
р ,р f a f a f ? f
- Jj Zt it
или, подставив значения модулей сил, имеем:
тх = О, ту = 0, тг = 0.
Следовательно, главный момент т0 относительно центра О равен нулю.
Так как главный мо-
момент системы оказался рав- г
пым нулю, то сила V яв-
является равнодействующей Л,
т. е. система сил приводится
к равнодействующей, линия
действия которой проходит
через точку О, причем
Теперь найдем уравне-
уравнения линии действия равно- **х
действующей но формуле
A5*). Воспользовавшись
формулами A), получим уравнение линии действия равнодействую-
равнодействующей в виде
X У 2
7 М. И. Бать и др., т. I
194
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
Задача 2.16. Привести к простейшему виду систему сил, изобра-
изображенных на рис. а. Силы приложены к вершинам куба, ребро кото-
которого равно a; Fi = Fi = F3 = F, Fi = Ft = 2F.
с)
?
А
г
V
i
0
^^
¦
1
г*
^^С У
в
м
1
К задаче 2.16.
Решение. Принимаем за центр приведения точку О. Оси декар-
декартовых координат х, у, z изображены на рис. а. Определяем проек-
проекции Vx, Vy, Ve главного вектора V на оси х, у, г:
Подставив значения модулей данных сил, имеем:
откуда главный вектор
а его модуль
V=-Fk,
A)
B)
C)
8 2] ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 195
Определяем главные моменты т„ ту, mz системы сил относи-
относительно осей х, у, z:
mx=z^mx (Fk) = ~
My =
Подставив значения модулей данных сил, получим:
тх = 0, my = Fa, тг = 0. D)
Следовательно, главный момент относительно центра О
mo — Faj, E)
а его модуль
V
т0 = Vm% -\- m\ -\-m\ — Fa. F)
В соответствии с формулами B) и E) на рис. б изображены сила V
и главный момент т0 системы сил.
Так как V и т0 оказались взаимно перпендикулярными, то си-
систему сил можно привести к равнодействующей R, причем R= V.
Найдем уравнения линии действия равнодействующей по форму-
формулам A6*). Воспользовавшись формулами A)*и D), запишем A6*)
в виде
У — а~х ... О т
О — 0 — F' ^ }
откуда х = а, _у = 0, т. е. линия действия равнодействующей Л= — Fk
лежит в плоскости xz, параллельна оси z и отстоит от нее на рас-
расстоянии х = а (рис. б).
Положение линии действия равнодействующей R можно было
определить, не пользуясь уравнением G). На рис. в изображены
сила V и главный момент т0, приложенные в точке О. Так как
главный момент т0 лежит на оси у, то пара сил, соответствующая
главному моменту т0, расположена в плоскости, перпендикулярной
к т0, т. е. в плоскости xz так, что с конца т0 пара видна направ-
направленной против часовой стрелки. Одну из сил V', входящих в состав
пары, изображаем противоположно V, причем V' = —К Тогда линия
действия второй силы V, входящей в состав пары сил, должна от-
отстоять от линии действия первой силы на расстоянии ОМ = ^Л. Так
как mo = Fa, a V=F, то ОМ = а. Итак, система сил оказалась
приведенной к трем силам: силам V и V', приложенным в точке О,
и силе V, приложенной в точке М. Первые две силы уравновеши-
уравновешиваются, и их можно отбросить. Поэтому система сил приводится
к одной силе V, приложенной в точке М, которая, следовательно,
является равнодействующей If. Линия действия равнодействующей /f
параллельна оси z и отстоит от нее на расстоянии ОМ-=а (рис. в).
Т
196
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
Следует иметь в виду, что общим приемом определения уравнений
линии действия равнодействующей R является применение формулы G).
Задача 2.17. Привести к простейшему виду систему, состоя-
состоящую из двух скрещивающихся сил Z7, и Fiy изображенных на рис. а;
Fx=F<i, = F, ОА = а. Сила /^ параллельна оси Ох.
К задаче 2.17.
Решение. Принимаем за центр приведения точку О. Подобно
решению предыдущих задач, определяем проекции Vx, Vy, Vz глав-
главного вектора V на оси х, у, z:
= Fb Vy = ZFky = 0, V2 = ZFkz = -Fx. A)
B)
C)
D)
Учитывая, что \Fl | = |/r21 —:\F\, имеем:
VX = F, Vy = Q,
Таким образом, главный вектор
V=Fi — Fk,
а его модуль
§-2| ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 197
Найдем теперь главные моменты тх, ту, тг системы сил отно-
относительно осей х, у, г.
Так как \Ft \ = F, то
тх = О, ту = 0, тс = — Fa. F)
Таким образом, главный момент
а его модуль
т0 = Vmx + m* -j- ml = Fa. (8)
Итак, система скрещивающихся сил приведена к изображенным
на рис. б силе V = Fi — Fk и паре сил, момент которой равен глав-
главному моменту относительно центра О, т. е. /wo = — Fak.
В данном случае отсутствие перпендикулярности векторов V и т0
очевидно. В более сложных задачах можно воспользоваться скаляр-
скалярным произведением Vm0 = Vxmx -j- Vymy -\- ]/2тг, которое в случае
взаимной перпендикулярности векторов V и т0 должно обратиться
в нуль. В нашей задаче, воспользовавшись формулами B) и F), по-
получим VntQ^Pa. Итак, векторы V и т0 не взаимно перпендику-
перпендикулярны. Это значит, что система сил приводится к динаме.
Найдем уравнения центральной оси по формуле (l(i*). Эти урав-
уравнения в данном случае, если принять во внимание формулы B) и F),
имеют вид
¦=;-= п =—Г-^-, ИЛИ у = — И 2= — X. (9)
Таким образом, центральная ось лежит в плоскости, параллельной
координатной плоскости xz, отстоит от нее па расстоянии а/2 и па-
параллельна биссектрисе MN-
Остается определить главный момент т относительно центров
приведения, лежащих на центральной оси. Как известно, вектор т
лежит на центральной оси. Его проекция на направление главного
вектора определяется по формуле A7*).
Использовав равенства B), D) и F), получим:
Главный момент т изображен на рис. в.
Итак, данная система скрещивающихся сил оказалась приведенной
к динаме, т. е. к силе V = Fi — Fk и паре сил, расположенно!!
в плоскости, перпендикулярной к V. Проекция момента т этой пары
198 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 1ГЛ. II
на направление главного вектора V (минимальный момент) опреде-
определяется формулой A0).
Эту задачу можно было решить с помощью простых построений,
минуя метод проекций. Изобразив на рис. г заданные силы Ft и Fit
приведем их к одному центру. Выбрав за центр приведения точку А
приложения силы Fit построим в точке А две уравновешивающиеся
силы Fj и F[. Находим силу V как сумму сил Ft и Fb приложенных
в точке А. Так как Ft и Ft взаимно перпендикулярны и по модулю
равны, то модуль силы V равен V= V^F\ -\- F\ = FVi (в данном
случае параллелограмм сил превратился в квадрат, параллельный
плоскости xz, а сила V параллельна биссектрисе MN).
При приведении силы Fx к центру А добавилась присоединенная
пара в составе силы Flt приложенной в точке О, и силы F[, при-
приложенной в точке А. Плечо пары ОА равно а (рис. г). Так как
присоединенная пара сил лежит в плоскости yz, то момент этой пары,
являющийся главным моментом тА, направлен перпендикулярно к пло-
плоскости yz, т. е. параллелен оси х. По модулю: mA=Fa.
Разложим главный момент тА на две составляющие: tnA = m-\-mlt
где вектор т совпадает с направлением главного вектора V, a nti
перпендикулярен к главному вектору. Нетрудно видеть, что паралле-
параллелограмм моментов, являющийся в данном случае квадратом, также
лежит в плоскости, параллельной плоскости xz. Находим:
1^2" с 1/2"
mi = m = mAJ~ = Fa-~.
Вектор т от выбора центра приведения не зависит. От вектора т,\,
перпендикулярного к силе V, можно избавиться посредством перехода
к новому центру приведения. Для этого построим пару сил, соответ-
соответствующую моменту Ш\. Одну из сил, входящих в пару, обозначим V
и направим так, чтобы она уравновешивалась с силой V. Тогда плечр АВ
пары расположится по оси у и в точке В окажется приложенной
вторая сила V, входящая в состав пары с моментом т.\ (напоминаем,
что эта пара сил должна лежать в плоскости, перпендикулярной к /м„
и притом ее следует изобразить так, чтобы с конца тх эта пара
была видна направленной против часовой стрелки). Плечо пары АВ
вычисляется без труда: тх= V-AB, откуда АВ = ^. Так как ш1 =
a V=fV5, то АВ = %.
Силы V и V, приложенные в точке А, уравновешиваются, и их
можно отбросить. Теперь система сил оказалась приведенной к силе V,
приложенной в точке В, и паре сил с моментом т, который можно
параллельно перенести и направить вдоль силы V. Линия действия
силы V, приложенной в точке В, является центральной осью, парал-
8 3] ЦЕНТР ТЯЖЕСТИ 199
лельной биссектрисе MN. Так как АВ = ^-, а ОА = а, то OS = 4.
Окончательно V=Fy2, m — Fa ^~-, что совпадает с результатами,
порченными в первом варианте решения задачи.
Следует иметь в виду, что метод непосредственных построений,
примененный во втором варианте решения этой задачи, может быть
успешно использован только в простейших случаях. Так, при равных
по модулю силах Ft и F4 все углы, получившиеся при построениях,
оказались равными 45°. Если бы мы несколько усложнили задачу,
взяв не равные по модулю силы Ft и Fit то определение положения
центральной оси оказалось бы довольно затруднительным.
В этом случае целесообразно пользоваться уравнениями централь-
центральной оси A6*).
Применив формулы A) и F), мы бы получили:
yFj _—2F2 — xFt _ (а —у) F8
F»~ 0 — />, •
откуда z = —р-1 х, у= ,, а (отсюда при условии данной задачи
\Fl\ = \F<k\ = F имеем z = — х, у = ~\, т.е. центральная ось ле-
2.
жит в плоскости, параллельной координатной плоскости хг, и отстоит
aFl
от нее на расстоянии у = . .д.
I "Г" * i
Рекомендуем решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Мещер-
Мещерского, издания 1950 г. и последующих лет: 232, 234,
236, 237, 240, 241.
§ 3. Центр тяжести
Дана система параллельных сил Flt Fit ..., Fn, которые приво-
приводятся к равнодействующей. Будем считать точки приложения сил
фиксированными.
Центром параллельных сил называется точка приложения равно-
равнодействующей силы, обладающая тем свойством, что при повороте
всех параллельных сил на один угол, с сохранением их параллель-
параллельности, равнодействующая поворачивается вокруг центра параллельных
сил С на тот >ье угол.
Координаты центра параллельных сил даются формулами:
2 ( ± Fkxk) 2] (± Г"Ук) I]
С п > УС п • ZC п
*=¦]
200 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ (ГЛ. II
здесь хк, ук, zk — координаты точки приложения силы Fk, где
к= 1, 2, ..., п. В этих формулах Fk — величина силы, г ±Fk —
проекция силы Fk на ось, параллельную силам. При этом проекция
силы считается положительной, если направления силы Fk и парал-
параллельной оси совпадают, и отрицательной, если направления силы Fk
и параллельной оси противоположны.
Если твердое тело находится вблизи поверхности земли, то к каж-
каждой материальной частице этого тела приложена сила тяжести (счи-
(считаем, что материальные частицы распределены в твердом теле непре-
непрерывно). Эти силы тяжести приближенно образуют систему парал-
параллельных сил (линии действия сил тяжести двух материальных частиц,
лежащих на земной поверхности и отстоящих друг от друга на
расстоянии 31м, образуют угол, равный одной секунде).
Центр параллельных сил тяжести Pit Р2, ..., Рп называется
центром тяжести С твердого тела, а сумма сил тяжести всех его
материальных частиц называется весом Р твердого тела:
А1
Координаты хс, ус, zc центра тяжести С твердого тела даются
приближенными формулами:
ft=l k=l ft=l
Эти формулы являются приближенными, так как координаты xk,
yk, zk точки приложения веса Рк А-й материальной частицы опреде-
определяются с точностью до размеров этой частицы.
Положение центра тяжести С твердого тела по отношению к его
материальным частицам не зависит от состояния твердого тела.
Впредь будут рассматриваться однородные твердые тела, для
которых удельный вес всех их материальных частиц постоянен.
Координаты хс, ус, zc центра тяжести С однородного тела при-
приближенно имеют вид
Здесь Az»ft — объем k-i\ материальной частицы, хк, ук, zk — коорди-
координаты точки приложения силы тяжести этой частицы, V—объем
п
твердого тела: l/=^Azift. Для повышения точности результата
подсчета следует разбивать твердое тело на материальные частицы
возможно меньшего объема.
§31
ЦЕНТР ТЯЖЕСТИ
201
Координаты хо уо zc центра тяжести С однородной поверхности
приближенно даются формулами:
k- B*}
Здесь Ask — шютадь поверхности k-й материальной частицы, хк, ук,
zk — координаты точки приложения силы
тяжести этой частицы, 6" — площадь по-
верхности твердого тела:
Рис. 2.14.
В случае однородной пластинки, распо-
расположенной в плоскости ху (рис. 2.14) формулы B*) принимают вид
Здесь суммы ^ хк ksk и ^ yk Asft называются статическими
л
моментами площади: ^ хк &sh = Msv — статический момент пло-
л
щади однородной плоской фигуры относительно оси у, У;Уь ^sk =
= Msx — статический момент площади однородной плоской фигуры
относительно оси х.
Если центр тяжести С однородной плоской фигуры лежит на
некоторой оси, то статический момент площади относительно этой
оси равен нулю. Например, если центр тяжести С лежит на
оси х, то
Координаты хс, уо zc центра тяжести С однородной линии при-
приближенно имеют вид
202 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ [ГЛ. II
Здесь Д/л — длина А-й материальной частицы, xk, yk, zk— коорди-
координаты точки приложения силы тяжести этой частицы, L—длина тела
л
(например, проволоки): L = ^ Д/А. В случае плоской кривой, лежащей
в плоскости ху, координата zc = 0.
В тех случаях, когда объемы, площади или длины каждой частицы,
а также их центры тяжести могут быть определены точно, фор-
формулы A*), B*), C*) дают не приближенные, а точные значения
координат центра тяжести всего тела. Если же упомянутые выше
величины не могут быть определены точно, то читатель, владеющий
методами интегрального исчисления, может вместо приближенных
формул A*), B*), C*) и D*) пользоваться точными формулами:
а) в случае однородного твердого тела
xc~V S xdv' yc = V § Уау' zc = y §**»• E*)
(Ю (V) ifo
где V= ^dv (интегрирование распространено по всему объему твер-
(V)
дого тела);
б) в случае однородной поверхности
\ ^\ F*)
(Si iS)
где 5=Jflfs (интегрирование распространено по всей поверхности
iS)
твердого тела);
в) в случае однородной плоской фигуры, Лежащей в плоско-
плоскости ху:
xc=-g-[xds, yc = -g\yds, zc = 0; G*)
г) в случае однородной линии
±t \\ (8*)
где L= ^/(интегрирование распространено по всей длине тела).
U)
Если линия является плоской и лежит в плоскости ху, то
zc = 0.
Если в однородном твердом теле имеется плоскость симметрии,
то центр тяжести С лежит в этой плоскости. Если же в теле имеется
ось симметрии, то центр тяжести С лежит на этой оси.
Иногда для определения положений центров тяжести линий и
площадей плоских фигур пользуются теоремами Гульдина.
I 81
ЦЕНТР ТЯЖЕСТИ
203
Первая теорема Гульдана. Площадь боковой поверхности тела
вращения (рис. 2.15), описанной плоской кривой (АВ), вращающейся
вокруг оси (у), расположенной в плоскости кривой и ее не пересе-
пересекающей, равна произведению длины дуги L на длину окружности 1ъхс>
описываемой центром тяжести С дуги: S=2kxcL.
У
1
/
/
О
У
с
\
О
Рис. 2Л5.
Рис. 2.16.
Вторая теорема Гульдина. Объем тела вращения (рис. 2.16),
описанного плоской фигурой, вращающейся вокруг оси (у), распо-
расположенной в плоскости этой фигуры и не пересекающей ее контура,
равен произведению площади фигуры 5 на длину окружности 2
описанной ее центром тяжести С, т. е. V=
2irx
c,
Рис. 2.17.
Рис. 2.18.
Положения центров тяжести некоторых твердых
тел простейшей геометрической формы:
а) центр тяжести площади однородного прямоугольника располо-
расположен в точке пересечения его диагоналей;
б) центр тяжести площади однородного треугольника находится
в точке пересечения его медиан;
в) центр тяжести дуги однородной окружности (рис. 2.17) нахо-
находится на оси симметрии, и его положение определяется координатами:
204
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
Sin я.
хс = г , _ус = 0, где г — радиус окружности, а— половина цен-
центрального угла;
г) центр тяжести площади однородного кругового сектора (рис. 2.18)
расположен на оси симметрии и имеет координаты: хс = -^г^^л
ус = 0, где г — радиус окружности, а — половина центрального угла;
д) центр тяжести С однородной призмы находится в середине
отрезка, соединяющего центры тяжести С, н С, верхнего и нижнего
оснований этой призмы (рис. 2.19), т. е. С1С=СС1;,
е) центр тяжести однородной пирамиды лежит на отрезке, сое-
соединяющем вершину О пирамиды с центром тяжести Q ее основания,
О
0
Рис. 2.19.
Рис. 2.20-
Рис. 2.21.
1
на расстоянии -j- этого отрезка ОС\ от центра тяжести С\ основания
пирамиды (рис. 2.20), т. е. CC1 = -jOC1;
ж) центр тяжести однородного кругового конуса лежит на его
высоте и отстоит на расстоянии 1/4 высоты от основания конуса
(рис. 2.21), т. е. АС=~ОА.
При решении задач на определение положения центра тяжести
однородного твердого тела существенную роль играет удачный выбор
осей координат.
Если в твердом теле имеется плоскость симметрии, то одну из
осей координат, например z, следует направить перпендикулярно
к этой плоскости. Так как центр тяжести лежит в плоскости сим-
симметрии, т. е. в плоскости ху, то ^с = 0 и остается определить только
две координаты: хс и ус.
Если и твердом теле имеется ось симметрии, то одну из коор-
координатных осей, например х, следует совместить с осью симметрии.
Так как центр тяжести лежит на оси симметрии, т. е. на оси х, то
Ус = zc = Q и остается определить только одну координату хс.
Наиболее расиространенным приемом использования формул A*),
B*), C*) или D*) является мысленная разбивка однородного
§31
ЦЕНТР ТЯЖЕСТИ
205
твердого тела на такие части, положение центра
тяжести каждой из которых известно, либо легко
может быть определено.
Так, например, при разбивке площади однородной плоской фигуры,
изображенной на рис. 2.22, на три части положение ее центра тяже-
тяжести С (хо ус, zc) определяется по формулам C*):
««j p^ u i^ *^ ilo( ^^ dog ~[ *"^
здесь дг], _y,, Z\ — координаты центра тяжести С] первой части пло-
плоской фигуры; Д$! — площадь первой части и т. д.
о
О
X
Рис. 2.22.
Рис. 2.23.
В некоторых случаях целесообразно заменить твердое тело не
суммой, а разностью отдельных его частей. Так, например, в случае
пластинки с двумя вырезами, изображенной на рис. 2.23, ее площадь
можно записать в виде разности площадей сплошной плоской фи-
фигуры / и двух вырезов 2 и 3, т. е. S=kst — Д<?4 — Д% В этом
случае положение центра тяжести С(хс, ус, гс) однородной плоской
фшуры определяется по формулам
с ASt—As2 — As3 ' с Asi — As2 — Asa ' c '
здесь xt, уi, Z\ — координаты центра тяжести С\ сплошной плоской
фигуры /, площадь которой равна Asjj хь уъ z^ — координаты
центра тяжести С4 выреза 2, площадь которого равна ksb и т. д.
Следует иметь в виду, что прием разбивки однородного твердого
тела на отдельные части приводит при использовании формул A*),
B*), C*) или D*) к точному результату только в том случае, когда
координаты центров тяжести отдельных частей, а также их площади
(либо объемы, либо длины) могут быть точно определены. Поэтому
в случаях твердых фигур с криволинейными контурами или твердых
тел с поверхностями сложной формы точность результатов оказы-
206
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
[ГЛ. II
вается недостаточной (для повышения точности результата приходится
разбивать тело на большее число частей, что усложняет решение
задачи) и рекомендуется применять точные формулы E*), F*), G*)
или (8*).
Теоремами Гульдина удобно пользоваться в тех
случаях, когда в число данных и неизвестных входят:
а) длина вращаемой дуги, расстояние от центра тяжести этой
дуги до оси вращения и площадь поверхности вращения, описанной
дугой (первая теорема Гульдина);
б) площадь вращаемой плоской фигуры, расстояние от центра
тяжести плоской фигуры до оси вращения и объем тела вращения,
описанного этой плоской фигурой (вто-
(вторая теорема Гульдина).
Задача 2.18. Определить положе-
положение центра тяжести С однородного
проволочного контура OABD, состоя-
состоящего из двух прямолинейных отрез-
отрезков OA=-OD = a, расположенных под
углом 60° друг к другу (/_ AOD =
= 60°), и полуокружности ABD диа-
диаметра AD (рис. а).
Решение. Проволочный контур
имеет ось симметрии, вдоль которой
мы проводим ось х. Взяв начало
координат в точке О, направляем
ось у по вертикали вверх.
Так как центр тяжести С контура лежит на оси симметрии х, то
ус = 0. Для определения координаты хс воспользуемся формулой D*):
0)
В данном случае целесообразно разбить весь проволочный контур на
три части: два прямолинейных отрезка ОА и OD длиной а каждый
и полуокружность ABD радиуса а/2. Такая разбивка является удоб-
удобной, так как положения центров тяжести каждой из этих частей
нетрудно определить. Обозначим отрезок ОА номером /, отре-
отрезок OD — номером 2, полуокружность ABD — номером 3. Тогда фор-
формулу A) можно записать в виде
B)
Д/, + Л/, + Л/,
где Xi, х^ — абсциссы центров тяжести Ct и С2 отрезков ОА и OD,
лг3 — абсцисса центра тяжести С3 полуокружности ABD, а А/,, Л/,,
§ 31 ЦЕНТР ТЯЖЕСТИ 207
^4 — длины этих частей проволочного контура. Как видно из ри-
рисунка,
*1=* = ™сов30« = -^. C)
Для определения х3 воспользуемся тем, что расстояние ЕСг от
центра окружности до центра тяжести дуги Са определяется фор-
формулой
Sin a
-
В данном случае ос = л/2 и, следовательно, так как г = а/2, имеем
ЕС3 = й/п. Поэтому
x3=OE-i-ECa—OA cos 30°-j--2-= !±|i^- а. D)
Кроме того, имеем:
Д/1 = Д/3 = а, */3 = f. E)
Подставив C), D) и E) в формулу B), получим:
аУЪ , а УЗ , 2 + д/З па
Итак, центр тяжести проволочного контура OABD находится
в точке С с координатами: хс = 0,76а, ус = 0.
Задача 2.19. Определить положение центра тяжести С площади
поперечного сечения однородного штампа, изображенного на рис. а.
Решение. Заметив, что сечение имеет ось симметрии, проведем
вдоль оси симметрии ось х и перпендикулярно к ней, по вертикали
вверх, ось у. Так как центр тяжести С сечения лежит на оси сим-
симметрии, т. е. на оси х, то необходимо определить лишь коорди-
координату лгс.
"Проведя вспомогательные линии МР и NS, разобьем площадь
сечения на сумму площадей трех прямоугольников. Обозначим пря-
прямоугольник MDBA номером /, прямоугольник ENLK— номером 2 и
прямоугольник NMPS—номером 3. Тогда формулу C*) можно
записать в виде
Так как центры тяжести Q, С4 и Са прямоугольников лежат
в точках пересечения их диагоналей, то имеем:
B)
208 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
Площади прямоугольников равны
Д$! = ^si = 300 см\ As3 = 200 см\
[гл. и
C)
Воспользовавшись B) и C), запишем формулу A) в виде
15 ¦ 300 4- 15 • 300 4- 5 ¦ 200
Хс ~ 300 4- 300 4- 200
¦ см, т. е. хс=\2,5 см.
Итак, центр тяжести площади сечения штампа находится в точке С
с координатами: хс=\2,Ьсм, _ус = 0.
Эту задачу можно решить несколько иначе, проведя вспомога-
вспомогательную прямую AL (рис. б) и представив площадь данного сечения
в виде разности площадей прямо-
прямоугольников EDBK и SPAL. Обо-
Обозначив прямоугольник EDBK но-
номером /, а прямоугольник SPAL
номером 2, запишем формулу
C*) в виде
Хп = -
Ast —x* AS;,
D)
D
Р
С, Сг
S
—^
в
А
*х
L
si—Д«,"
где ЛГ] — абсцисса центра тяже-
тяжести С] прямоугольника EDBK,
х^ — абсцисса центра тяжести
Са прямоугольника SPAL, a Asj
и Д*4 — соответственно площа-
площади этих прямоугольников. Нахо-
Находим:
= \5 cm, xi =
= 400 см\
E)
Подставив E) в формулу D), но-
лучим:
15-1200 — 20-400
ХС — Г200^400 СМ'
откуда хс = 12,5 см.
К задаче 2.19.
Второй прием решения задачи
оказался более коротким. Этот
прием замены площади данной плоской фигуры разностью двух пло-
площадей удобно также применить при решении следующей задачи.
Задача 2.20. Определить положение центра тяжести однородного
кругового сегмента АМВ, если радиус окружности равен г, а цен-
центральный угол равен 2а.
ЦЕНТР ТЯЖЕСТИ
209
Решение. Выберем оси координат: направим ось х вдоль оси
симметрии, начало координат возьмем в центре окружности О, а ось у
направим по вертикали вверх. Так как центр тяжести кругового
сегмента АМВ лежит на его оси сим-
симметрии, т. е. на оси х, то ус = 0.
Остается определить абсциссу хс центра
тяжести С. Для этого представим пло-
площадь 5 сегмента АМВ как разность
двух площадей: площади Д^ кругового
сектора ОАМВ и площади Д^ равно-
равнобедренного треугольника ОАВ, т. е.
5Д A
Теперь формулу C*) можно запи-
записать в виде
Xr —
is, — 4s2
.
К задаче 2.20.
где Xi и х^ — соответственно абсциссы центров тяжести Q и С3
кругового сектора ОАМВ и треугольника ОАВ. Находим:
= г\
о . 2 sin a
i = r-sin а cos а, лг1= — г- ,
о л
j=-j-r cos а B)
(положения центров тяжести треугольника и кругового сектора ука-
указаны выше, в обзоре теории). Подставив B) в формулу A), получим:
2 sini , 2 , .
-тг Г Г*а 5" Г COS a Г2 Sin a COS ot
о a о
Лг-
sin'
вид
с Г* а — Г1 Sin a cos a За — sin a cos а '
Итак, координаты центра тяжести С кругового сегмента имеют
с = 0. C)
с 3 а — sin at cos я'
Задача 2.21. Определить положение центра тяжести однородного
полукольца, если его внешний н внутренний радиусы соответственно
равны П я г.
Решение. Направив ось х вдоль оси симметрии полукольца
(рис. а), имеем ус — 0. Начало координат взято в центре О полу-
полукольца, ось у направлена по вертикали вверх.
Для определения абсциссы хс центра тяжести С представим
площадь полукольца и виде разности двух площадей полукругов
радиусов /? и г, т. е. S = hs1 — Д% где Дх] — площадь полукруга
радиуса R, а Дяа — площадь полукруга радиуса г. Теперь формулу C*)
можно записать в виде
As,—
210
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
(ГЛ. II
и Ci полу-
где xt и Хц — соответственно абсциссы центров тяжести
кругов радиусов R и г.
Можно определить xt как абсциссу центра тяжести кругового
сектора (рис. б) при а = л/2. Так как *с = 4 R^ (см. обзор тео-
теории), то при а = тг имеем ^ = -5-/?. Аналогично х« = -^-г.
z an оя
Итак,
*-, _ D v- г /О\
-Ч "~~ ^п *\, Л2 *~~* ~7Г~ ' * \~)
Значения ху и х2 можно было также получить из формулы C)
предыдущей задачи, считая полукруг круговым сегментом при а = л/2.
Дейс гвительно, хс = ~ R —Ш'
tx = r./2 имеем Xi = -
4
Sin а cos a
При
/?. Аналогично лга =
Записав значения площадей
лукругов радиусов R и г:
по-
подставляем B) и C) в формулу A). Имеем:
Зя
4
Зп
D)
Итак, искомые координаты центра тяже-
тяжести С полукольца имеют вид
К задаче 2.21.
4
хс— з«
__0
Эту задачу можно было решить иначе, применив вторую теорему
Гульдина: V=2ttxcS, где 5 — площадь полукольца, лгс — искомая
абсцисса его центра тяжести С, V—объем тела вращения, описанного
полукольцом вокруг оси у, т. е. объем полого шара, у которого
внешний радиус равен R, а внутренний г. Следовательно,
V .
*с = ^- E)
Учитывая, что 5=-~—~=y(R3—
), a V=-|uR3-
= -тг тс G?3 — г3), подставляем эти значения 5 и V в формулу E)
§31
и получаем:
ЦЕНТР ТЯЖЕСТИ
211
-| к (*¦-/¦¦)
Сопоставляя оба способа решения задачи, следует отдать пред-
предпочтение второму. Решение оказалось короче, кроме того, не было
необходимости пользоваться формулой, определяющей абсциссу хс
центра тяжести С кругового сектора хс = к-/?.
Однако следует заметить, что применение второй теоремы Гуль-
дина оказалось эффективным потому, что вычисление площади пло-
плоской фигуры — полукольца и объема тела вращения — полого шара
не представило затруднений. Если вычисление объема тела вращения
оказывается громоздким, то применение второй теоремы Гульдина
нецелесообразно.
Вместе с тем, если по условию задачи площадь плоской фигуры
и положение ее центра тяжести известны, то применение второй тео-
теоремы Гульдина является
удобным приемом для вы-
вычисления объема тела вра-
вращения (см. задачу 2.24).
Задача 2.22. На рисунке
изображена схема корпуса
баржи. Определить положе-
положение центра тяжести пло-
площади однородной поверх-
поверхности, ограниченной снизу
боковой поверхностью полу-
полуцилиндра, с торцов — пло-
плоскостями ADMSE и BCLTK,
с боков—плоскостями АВКЕ
и DCLM и сверху — плоскостью ABCD. Дано: ADME и BCLK— рав-
равные квадраты со стороной 2а, ABCD — прямоугольник со сторо-
стороной АВ, равной 10а. Оси х, у, z изображены на рис. а.
Решение. Нетрудно видеть, что данная поверхность имеет ось
симметрии, совмещенную с осью г. Значит, центр тяжести С пло-
площади этой поверхности лежит на оси г и две его координаты хс
и ус равны нулю. Таким образом, нам остается определить лишь
координату zc.
Для этого мысленно разобьем данную поверхность на несколько
поверхностей, так чтобы положение центра тяжести площади каждой
из них можно было легко определить: / и 2 — поверхности квадра-
квадратов ADME и BCLK, 3 и 4 — поверхности полукругов EMS и KLT,
К задаче 2.22.
212 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ [ГЛ. II
5 — поверхность прямоугольника ABCD, 6 и 7 — поверхности пря-
прямоугольников АВКЕ и DCLM, 8 — боковая поверхность полуцилин-
полуцилиндра EMSKLT.
Координата центра тяжести zc площади данной поверхности, опре-
делясмая по формуле B*): гс = -^ , в данном случае, при
1
= 8, имеет вид
О)
Вычислим площади поверхностей AsA при k=1, 2, ..., 8. Полу-
Получим: As] = Д«2 = 4аа, Д«3 = Д«4 = -у, Да'в= Д«б^ ^57^20а2, Д«8 =
= 1(W.
Затем определим значения координат zft центров тяжести площа-
площадей поверхностей при ? = /, 2, ..., 8.
Центры тяжести площадей квадратов 1 и 2 расположены в их
центрах, т. е. z^ ="zt = a.
В справочных данных о положении центров тяжести некоторых
однородных тел был рассмотрен случай г): центр тяжести площади
кругового сектора расположен на его оси симметрии и отстоит от центра
2 sin a
окружности на расстоянии, равном -=-г , где г — радиус окруж-
о ос
ности, а а—половина центрального угла. В случае полукруга 3
тс 2 S1" ~2 4
г = а, а^-гг. Значит, О\С^^-^-а = --а, а координата z%
центра тяжести С3 полукруга 3 равна z% = ОС3 = ОО\ -\- OiC3 =
= 2e"bse = 2eA+s)- Итак' -з = ^ = 2
Центры тяжести площадей прямоугольников 5, 6, 7 находятся в
их центрах, т. е. zB = 0, z6--z4 = a.
Для определения координаты zs центра тяжести площади боко-
боковой поверхности полуцилиндра используем случай в), рассмотренный
для дуги однородной окружности. Ее центр тяжести отстоит от цен-
центра окружности на расстоянии хс = г -^-^, где г — радиус окруж-
окружности, а a — половина центрального угла. В данном случае r = a, а
* «I
ЦЕНТР ТЯЖЕСТИ
213
. я
я sm T 2
а = т-. Значит, О]С8 = а = — а, а искомая координата 2S
8=2a + -^-a = 2af 1 4-^-).
равна Zg = OCg = OOi -j-
Итак, подсчеты площадей и координат центров тяжести площа-
площадей отдельных частей данной поверхности дали следующие резуль-
результаты:
на2
Д$1 = Дз» = Аа, Д$ч = Дя< = —
6 1 . 8 ^ -f- „ J.
Подставив эти значения в формулу A), получим 2= 1,35а.
Значит, положение центра тяжести С площади данной однород-
однородной поверхности определяется координатами: хс=ус = 0, zc= 1,35а.
Задача 2.23. Твердое тело состоит из однородного полого ци-
цилиндра 1 высотой Н с внешним и внутренним радиусами оснований,
равными R и г, и однородного сплошного конуса // с основанием
радиуса R и высотой h.
К задаче 2.23.
Определить положение центра тяжести твердого тела, если г =
з 1
= — R и /г = —-//. Система осей xyz изображена па рисунке.
Решение. Так как ось симметрии твердого тела совмещена с
осью у, то хс = zc — 0.
Остается определить ординату ус центра тяжести С. Обозначим
центр тяжести цилиндра через d и через С2 — центр тяжести конуса.
214
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
|ГЛ. II
Для вычисления ус воспользуемся формулой A*), которая в дан-
данном случае имеет вид
л а А лйШ 1 л а Л ^л
L, О)
где у1 и уц — ординаты центров тяжести цилиндра А и конуса В,
а Аг»! и Аг»а — соответственно объемы этих тел. Находим:
Дг,, = 11(^_г2)Я) Дг>2 = -1*/?2/г, у1 = ~, y, = H^-~h B)
(напомним, что центр тяжести С9 конуса отстоит на расстоянии одноп
четверти высоты от основания конуса).
Воспользовавшись соотношениями B), запишем формулу A) в
виде
* — Г») Н + ут:/?2
3 1
Учитывая, что по условию r=-jR и h=-^-H, окончательно имеем:
39 „
Итак, положение центра тяжести С данного твердого тела опре-
определяется координатами:
39
0 Н 0
Задача 2.24. Однородный тор образован вращением круга ради-
радиуса г около оси, лежащей в плоскости этого круга. Расстояние от
центра тяжести круга до оси вращения равно R.
К задаче 2.24.
Определить площадь поверхшсти и объем тора.
Решение. Направим ось z вдоль оси вращения и, следовательно,
оси симметрии тора.
Так как расстояние R от центра тяжести С круга до оси вра-
вращения дано, а также известны длина окружности и площадь круга
«31 ЦЕНТР ТЯЖЕСТИ 215
радиуса г, то, применив обе теоремы Гульдина, можно легко опре-
определить площадь поверхности и объем тора.
Действительно, согласно первой теореме Гульдина S=2icycL,
где ус — расстояние от центра тяжести С линии, описывающей дзн-
иую поверхность, до оси вращения, L — длина этой линии, 5—пло-
5—площадь поверхности тела вращения.
В данном случае ус =/?, L = 2т:г и, следовательно, искомая пло-
площадь 5 поверхности тора равна
Для определения объема тела вращения применим вторую теорему
Гульдина: V=2r.ycS, где ус — расстояние от центра тяжести С пло-
плоской фигуры, описывающей данный объем, до оси вращения, б1 —
площадь этой плоской фигуры, V—объем тела вращения.
В данном случае yc = Fl, lS1=7tr2 и, следовательно, искомый
объем V тора равен
1
Применение обеих теорем Гульдина оказалось весьма эффективным.
Использование других приемов решения этой задачи, например
формул интегрального исчисления, является более громоздким.
Рекомендуем решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Мещер-
Мещерского, издания 1950 г. и последующих лет: 286, 287,289,
292, 293, 295, 296, 300, 302.
РАЗДЕЛ ВТОРОЙ
КИНЕМАТИКА
Кинематика является разделом теоретической механики, в кото-
котором изучаются движения тела безотносительно к причинам, их вызы-
вызывающим.
При движении тел относительно друг друга расстояния между
точками этих тел могут изменяться. Эти изменения обычно опреде-
определяются по отношению к некоторой системе отсчета, системе коорди-
координат, которая и заменяет при изучении движений одно из тел. Если
выбранная система координат условно принята за неподвижную, то
движение других тел по отношению к этой системе отсчета называют
абсолютным движением.
В классической механике время считают одинаковым для любых
систем отсчета, что является приближением к истине, достаточно точ-
точным, если скорости рассматриваемых движений малы по сравнению
со скоростью света.
За единицу времени принята секунда. Начало отсчета времени
выбирается произвольно.
ГЛАВА III
ДВИЖЕНИЕ ТОЧКИ
§ 1. Траектория и уравнения движения точки
1°. Основные определения. Траекторией точки называется
линии, описываемая движущейся точкой в пространстве. Траектория
может быть плоской или пространственной кривой. Движение точки
определяется заданием закона движения. Закон (уравнение) движе-
движения точки устанавливает зависимость положения точки в пространстве
от времени.
Движение точки М в неподвижной системе координат xyz опре-
определяется заданием трех фуннцип (рис. 3.1)
*=МЪ у=МЪ z=M), A*)
которые называются уравнениями движения точки. Подставив в урав-
уравнения A*) значение времени t = tb можно определить координаты
§11
ТРАЕКТОРИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ
217
и, следовательно, положение точки в пространстве в этот момент
времени. Уравнения A*) представляют параметрические уравнения
траектории точки. Для нахождения уравнений траектории точки в
координатной форме необходимо из уравнений A*) исключить время
и получить зависимости вида
<Pi (•*> У) = °> <?« (.У» z) = °-
Совокупность этих двух уравнений определяет кривую, по которой
движется точка.
Существуют и другие способы задания движения точки. При век-
векторном способе задания закона движения радиус-вектор г движу-
движущейся точки М (рис. 3.1)
дается как функция времени
r = r(t). Связь между ра-
радиусом-вектором г и декар-
декартовыми координатами точки
выражается равенством
B*)
Рис. 3.1.
Здесь i, j, k — орты (еди-
(единичные векторы) осей коор-
координат. Если в B*) принять
за х, у, z текущие коорди-
координаты точки М, определяемые
уравнениями A*), то B*)
дает закон движения точки
в векторной форме.
Третий способ задания движения точки называется естествен-
естественным. В этом случае движение точки определяется уравнением
о=/@, C*)
где а — криволинейная координата, отсчитываемая вдоль дуги от не-
некоторой начальной точки О на траектории (рис. 3,2). При этом спо-
способе предполагается, что
траектория движущейся точ-
точки М известна. Ириволиней-
ная координата — это дли-
длина дуги, отсчитываемая в
одну сторону от начальной [)ис. 3.2.
точки положительной, а в
другую — отрицательной (направление положительного отсчета должно
быть задано). Уравнение C*) называется естественным уравнением
движения точки.
При естественном способе задания движения также имеется три
уравнения: первое уравнение — это закон движения точки C*), два
218
ДВИЖЕНИЕ ТОЧКИ
ГГЛ. III
других уравнения определяют траекторию точки, ибо кривая в про-
пространстве выражается уравнениями двух поверхностей, пересечение
которых и является траекторией точки.
Среди других систем координат, при-
применяемых при изучении движений, отме-
отметим полярную систему координат, широко
используемую при описании движений,
происходящих в плоскости. В полярной
системе координат (рис. 3.3) положение
точки в плоскости определяется радиу-
радиусом р—длиной отрезка, соединяющего не-
неподвижный центр О с движущейся точ-
точкой М, и углом ср между неподвижной прямой Ох (полярной осью)
и отрезком ОМ. В этом случае уравнения плоского движения точки М
будут:
D*)
Рис. 3.3.
При исследовании движения точки в пространстве часто пользу-
пользуются сферическими и цилиндрическими координатами.
Сферическими координатами точки М (рис. 3.4) являются: рас-
расстояние г точки М от неподвижного центра О, угол (J> (угол по-
поворота плоскости гОМ по отношению к фиксированной плоско-
плоскости xOz) и угол ср, образованный
прямой ОМ с неподвижной пло-
плоскостью хОу.
Цилиндрическими координа-
координатами точки М называются: поляр-
полярные координаты риф проекции
точки М на неподвижную пло-
плоскость хОу и высота z точки М
над этой плоскостью.
Уравнения движения точки в
сферических координатах:
Рис. 3.4.
ср = ср (i).
Уравнения движения точки в цилиндрических координатах:
E*)
F*)
Для перехода от сферических координат к прямоугольным декар-
декартовым координатам служат формулы: >
х = г cos ср cos
= т cos <p sin
z = r sin <р.
§ II ТРАЕКТОРИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ 219
Формулы перехода от цилиндрических координат к прямоуголь-
прямоугольным декартовым координатам:
X = р COS <|), у = р Sin (|), Z — Z.
Полярные, сферические, цилиндрические системы координат в от-
отличие от декартовых называются криволинейными координатными
Системами.
Уравнения движения точки могут быть представлены графиками.
Если по оси абсцисс откладывать независимую переменную t (время),
а по оси ординат — координату движущейся точки, то на графике
получим кривую зависимости координаты от времени, т. е. уравнение
движения. Такие графики должны быть построены для каждой из
трех координат, определяющих движение точки в пространстве. Гра-
Графики движения могут быть построены и при задании закона движе-
движения в виде C*), D*) или другим способом. Уравнения движения точки
могут быть заданы таблицей, в которой каждому дискретному значе-
значению времени соответствуют определенные значения координат.
Решение задач на определение закона движения
и уравнения траектории производится в такой по-
последовательности:
1) выбирается система неподвижных координат — прямоугольная,
полярная или какая-либо иная; начало координат и та или иная си-
система выбираются, исходя из условий задачи, так, чтобы дальнейшее
решение было возможно более простым;
2) на основании условий задачи для избранной системы коорди-
координат составляются уравнения движения точки, т. е. находится зависи-
зависимость координат точки от времени;
3) имея уравнения движения точки, можно определить ее положе-
положение в любой момент времени, установить направление ее движения,
найти траекторию и ответить на различные вопросы, касающиеся
движения точки.
Задача 3.1. Точка М совершает плоское движение согласно урав-
уравнениям
* = 6 + 3f, (I)
y = 4t. B)
Определить траекторию точки М.
Решение. Уравнение траектории в координатной форме находим,
исключив из обоих уравнений движения время. Из второго уравнения
имеем t=ylA. Подставляя это значение в первое уравнение движе-
движения, получаем уравнение траектории
х = 6--|-0,75>
Это — уравнение прямой линии. Для построения этой прямой заме-
замечаем, что при у = 0 jc = 6 и при х = 0 у= —8.
220
ДВИЖЕНИЕ ТОЧКИ
[ГЛ. Ill
На чертеже находим точку А F,0) и точку В @, — 8), через ко-
которые и проходит указанная прямая. Однако отнюдь не вся эта бес-
бесконечная прямая будет являться траекторией точки М. Определим по-
лэжение точки М в начальный момент времени ^^0. Подставляя эю
значение времени в уравнения движения A) и B), находим начальное
положение точки: хо = 6, уа = 0.
Следовательно, точка М начинает
движение из точки А. Из уравне-
уравнений движения следует, что с уве-
увеличением времени координаты
точки М будут расти, оставаясь
положительными. Так, при ?=1
координаты точки М будут: х = 9,
_у = 4. Находим эту точку на
траектории и обозначаем ее бук-
буквой С. Таким образом, траекто-
траекторией точки М будет полупрямая
ACD. Другая половина прямой
АВ не будет являться траекто-
траекторией точки М.
При прямолинейном движении
точки уравнения движения упро-
упрощаются, если совместить ось координат с траекторией. Найдем уравне-
уравнения движения точки М, если начало координат выбрать в точке А,
начальном положении движущейся точки М, и ось Ху направить по
полупрямой ACD, а ось у^ перпенди-
перпендикулярно к ней. Тогда из треугольника
АСЕ, пользуясь уравнениями движения
A), B), находим:
jrf = (х — 6f 4- va = 9*2 4- 16?2 = 25*J,
а следовательно,
X! It Ot. (Л)
Так как точка М движется в по-
положительном направлении оси хи то
К задачам 3.2, 3.3. знак МИНУС в C) следует отбросить.
Таким образом, уравнения движения
точки М в новой системе координат будут:
Х± ОТ,
У В
К задаче 3.1.
Для прямолинейного движения точки мы, но существу, получили од-
одно уравнение движения.
§ 11 ТРАЕКТОРИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ 221
Задача 3.2. Кривошип ON длиной а вращается вокруг оси, пер-
перпендикулярной к плоскости рисунка и проходящей через точку О.
Угол <р между неподвижной осью Ох и кривошипом изменяется про-
пропорционально времени: <? = kt.
Составить уравнения движения точки N в декартовой системе ко-
координат. Найти уравнение ее траектории. Определить время одного
полного оборота точки N и момент времени, когда обе координаты
точки равны между собой.
Решение. Для составления уравнений движения точки N надо
выразить ее координаты как функции времени. Из рисунка находим
координаты х, у точки N:
х = ON cos <p,
у = ON sin <p,
или
х = а cos kt, A)
у = a sin kt. B)
Это и будут искомые уравнения движения точки N.
Чтобы найти уравнение траектории точки в явной форме, надо
исключить из уравнений движения время. Для этого возведем каждое
уравнение движения в квадрат:
xa = a3cos2K C)
У = a1 sin'At D)
и сложим уравнения C) и D):
Это уравнение траектории точки N определяет окружность радиуса а
с центром в начале координат.
Определим время одного полного оборота точки N. Это время Т,
в течение которого угол у изменится на 2тс радиан:
(f = kT=2r.,
откуда
2я
1 ~Т-
Найдем начальное положение движущейся точки. Для этого надо
в уравнения движения A) и B) подставить значение ? = 0. Тогда
хл = а, ул = 0.
Определим момент времени, когда обе координаты точки N равны
между собой:
х =_у = a cos ktx — а sin ktu
т. е.
222 ДВИЖЕНИЕ ТОЧКИ 1ГЛ. (II
Это равенство возможно при
**,=«! + =¦, E)
где я = 0, 1, 2, 3,...
Из E) определяются моменты времени, когда координаты точки
равны между собой
Задача 3.3. Положив в предыдущей задаче угол <р равным kt-\-§>
где Аир — постоянные величины, определить движение точки М>
являющейся проекцией точки N на ось Ох.
Решение. Точка М движется прямолинейно по оси Ох, следо-
следовательно, ее движение определяется одним уравнением
х= ON cos cp = a cos (kt -\- р).
Это есть уравнение прямолинейного гармонического колебательного
движения. Из него следует, что наибольшее отклонение точки М от
центра колебаний О определяется координатами
Xt = + a, Xi = — а.
Величина а называется амплитудой колебания, kt -\- p называется фа-
фазой колебания, а р — начальной фазой колебания.
Определим период колебаний — промежуток времени, в течение
которого точка совершает одно полное колебание, т. е. возвращается
в исходное положение с той же по величине и направлению скоро-
скоростью. Обозначая период буквой Т, находим его величину из условия
того, что приращение фазы колебаний за это время равно 2те:
т. е.
Задача 3.4. Точка движется согласно уравнениям:
х = a cos (kt — е), A)
у = b cos kt. B)
Определить уравнение траектории точки. Как меняется траектория
точки при увеличении разности фаз е от 0 до 2тс?
Решение. Чтобы найти уравнение траектории точки в явной
форме, надо из уравнений движения исключить время. Для этого пре-
преобразуем первое уравнение движения:
x = aCos(kt — e) = a[cos kt cos s-f- sin W sin sj. C)
* 11 ТРАЕКТОРИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ 223
Решая уравнения B) и C) относительно cos kt и sin kt, находим:
cos kt=^-,
sin kt =
X V
COSe
a b
sin ?
Возведем эти равенства в квадрат и сложим их:
i +
или окончательно:
sin2 е
а • Ь '
Уравнение D) при произвольном значении е есть уравнение эллипса.
Из этого уравнения видно, что наибольшие и наименьшие значения
о)
6)
9)
6)
с) ж]
К задаче 3.4.
Л?
переменных соответственно будут ± а для х и ± Ь для у. Таким
образом, во всех случаях эллипс вписывается в прямоугольник со
сторонами 1а и 1Ь.
Будем теперь менять значения s от 0 до 2ir. При е = 0 уравнение
D) принимает следующий вид:
Следовательно, когда фазы обеих составляющих взаимно перпенди-
перпендикулярных колебаний одинаковы, эллипс вырождается в две совпада-
совпадающие прямые линии, являющиеся диагональю прямоугольника (рис. а).
При увеличении & от 0 до it/2 эллипс, одна из осей которого
совпадает по направлению с диагональю прямоугольника, постепенно
расширяется (рис. б). При е = я/2 уравнение D) примет вид (рис. в)
224
ДВИЖЕНИЕ ТОЧКИ
[ГЛ. III
т. е. уравнение эллипса принимает каноническую форму. При даль-
дальнейшем увеличении е эллипс снова сужается (рис. г) до тех нор, пока
при e==ic не выродится в другую диагональ прямоугольника (рис. д).
При этом уравнение D) принимает вид
= 0.
Далее, с увеличением е от v до 2т: процесс повторяется, являясь зер-
зеркальным отображением первой половины процесса (рис. е, ж, з).
Если, как в разобранном примере, частоты обоих взаимно перпен-
перпендикулярных колебаний равны, то разность фаз е остается постоянной
и эллиптическая траектория точки неизменна. Если же, как это бы-
бывает в большинстве технических приложений, между частотами обоих
колебаний существует малая разница, то траектория колеблющейся
точки может быть представлена с достаточной точностью одним эл-
эллипсом лишь для нескольких периодов. Затем этот эллипс меняется
в соответствии с изменением вели-
величины е со временем, проходя разо-
разобранные выше стадии.
Задача 3.5. Точка М, брошенная
под углом а к горизонту, если пре-
пренебречь сопротивлением воздуха,
движется согласно уравнениям:
x = v0cos%-t, (I)
y = v0sino.-t—^. B)
О
К задаче 3.5.
В этих уравнениях v0, a, g—по-
g—постоянные величины.
Определить уравнение траекто-
траектории точки, наибольшую высоту h
ее подъема над уровнем начального положения, расстояние s по гори-
горизонтали, при котором точка достигнет наивысшего положения, а также
дальность полета точки по горизонтали.
Решение. Для определения уравнения траектории точки в явной
форме надо исключить из уравнений движения время. Получив из
первого уравнения
х
t —
C)
и подставив зто выражение в уравнение B), найдем искомое уравне-
уравнение траекюрии
2uii cos2 а
D)
§ I] ТРАЕКТОРИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ 225
Из аналитической геометрии известно, что это есть уравнение пара-
параболы с осью симметрии, параллельной оси у. Действительно, каждому
значению у соответствуют два значения х. Эта парабола проходит
через начало координат, так как значения координат х = 0, _у = 0
удовлетворяют ее уравнению.
Чтобы определить наибольшую высоту подъема точки h, надо
найти по правилам дифференциального исчисления экстремальные зна-
значения у. Для этого вычислим производную от у по координате х и
приравняем ее нулю; так как -^--jf-^, а лт^0» то мож»о ограни-
ограничиться приравниванием к пулю производной
У = % = ^osina — gti — O. E)
Следовательно, у достигает экстремального значения при
^ ^ (б)
Подставляя это значение времени в уравнение B), находим наиболь-
наибольшую высоту подъема
, »J sin2 а gvr, sin2 a 1 vl sin2 a
Это экстремальное значение у будет, действительно, максимумом, а
не минимумом, так как вторая производная от у при t = t1 отрица-
отрицательна:
?'\t-tt= —8-
Для определения абсциссы s, при которой точка достигает наивыс-
наивысшего положения, надо значение времени, соответствующее этому мо-
моменту F), подставить в уравнение A):
va sin а v\ sin 2i
s = x=vcoso-±-^—= -
Дальность полета но горизонтали / определится из уравнения тра-
траектории D), если положить в нем_у = 0:
tga-x — -2Jc^ai =°-
Отсюда находятся два значения х:
Первое значение соответствует начальному моменту (моменту вылета
точки), второе значение определяет дальность по горизонтали. Сопо-
Сопоставляя значения Ins, заключаем, что /=2s, т. е. наивысшего по-
положения точка достигает на половине горизонтальной дальности.
8 М. И Бать и др., т. I
226
ДВИЖЕНИЕ ТОЧКИ
|ГЛ. Ill
Заметим, что искомые величины дальности и высоты полета мои.-
ио было найти и не прибегая к дифференцированию. Достаточно было
учесть, что траекторией служит парабола, ось которой параллельна
сси ординат, причем парабола проходит через начало координат. Дей-
стпительно, положив в уравнении D) у равным нулю, находим два
значения х, из которых первое равно нулю, а второе определяет
дальность полета по горизонтали. Внеся в уравнение D) Вместо х ве-
величину, ранную половине дальности полета, находим максимальную
высоту подъема h.
Задача 3.6. Снаряд, вылетающий из ствола орудия, стоящего у
подножья возвышенности, поверхность которой наклонена иод носто-
янным углом р к горизонту,
движется согласно уравнениям
(сопротивлением воздуха пре-
пренебрегаем):
х = v0 cos a • t,
A)
-С B)
О
К задаче 3.6.
где а — угол между горизон-
горизонтом и направлением вылета
снаряда.
Определить, под каким углом а следует выстрелить, чтобы полу-
получить наибольшую дальность полета вдоль линии ОА.
Решение. Исключив время t из уравнений A) и B), находим
уравнение траектории в явной форме:
y = tg*-x-TJ??r. C)
Уравнение прямой ОА, являющейся проекцией поверхности воз-
возвышенности па вертикальную плоскость ху, будет:
D)
Снаряд упадет на землю в точке А, при этом ординаты, определя-
определяемые уравнениями C) и D), станут рапными, следовательно,
откуда
о
COS2 a
a = ^(sin 2a—2 cos2a- tg ?).
Для определения наибольшей дальности в зависимости от угла
вылета а вычисляем производную от х по а и приравниваем ее нулю:
— = -i С2 COS
2 sin 2a • tg ft = 0,
§ 1| ТРАЕКТОРИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ 227
откуда
ctg2a=-tgp,
или
2а— — -1-3
Таким образом, наибольшая дальность будет мри угле бросания,
равном половине угла между вертикалью (отрицательной осью у) и
откосом ОА.
Задача 3.7. Точка, брошенная наклонно к горизонту, движется
в воздухе, сопротивление которого пропорционально скорости, со-
согласно уравнениям:
* = ^О-^ (О
-^)-{-. B)
В этих уравнениях va, а, к, g—постоянные положительные величины.
Определить уравнение траектории точки, наибольшую высоту h
над уровнем начального положения, а также абсциссу, при которой
точка достигнет наивысшего положения.
Решение. Для определения уравнения траектории точки п явной
форме надо исключить из уравнений движения время. Из A) находим:
х C)
и, далее, после несложных преобразований
) D)
,= ln(l
kg \ v0cosa
Подставляя C) и D) в уравнение B), получаем уравнение траектории
точки п явной форме
* kv0 cos a ' k2g \ v0 COS a.
Для определения наибольшей высоты h над уровнем начального
положения надо найти максимум величины у, рассматриваемой как
функция координаты х. Для этого, по правилам дифференциального
исчисления, необходимо вычислить первую производную от_у по коор-
координате х и приравнять ее нулю. Так как -]г —-§> zr < * -J/ ~Ф- 0> то
можно ограничиться приравниванием нулю производной от коорди-
координаты у по времени. Найденное из этого уравнения значение незави-
независимой переменной — времени t1 подставляется в уравнение B), и тем
8*
228 ДВИЖЕНИЕ ТОЧКИ [ГЛ. III
самым находится максимальное или минимальное значение у. Если
вторая производная от у по времени в этот момент отрицательна, то
найденное экстремальное значение у является максимумом, в проти-
противоположном случае — минимумом.
Вычисляем, пользуясь уразнением B), производную от у по вре-
времени и приравниваем ее нулю:
j/=(z>osma +-?-
Тогда
е ksft =
kv0 sin a -)- 1 '
или
t\ = г— In (kv0 sin a-f- 1).
Подставляя эти значения в уравнение B), после несложных преобра-
преобразований находим экстремальнее значение
Для того чтобы убедиться в том, что найденное значение, действи-
действительно, является максимальным, вычисляем вторую производную от у
по времени
)
Вторая производная отрицательна, так как k, g, ti0 — положительные
числа, а угол а лежит в первой четверти.
Определим, далее, абсциссу, при которой точка достигнет наивыс-
шего положения. Для этого достаточно в уравнение A) подставить
значение времени tb соответствующее наивысшему положению точки.
Тогда имеем:
v0 COS a 1. 1 \ vl sin 2a
Xl kg \ ~~ Ъо sin a + 1 ) 2g (kv0 sin a + I)'
Пользуясь уравнением траектории точки E), можно получить равен-
стпо, определяюи1ее горизонтальную дальность полета. Если положить
в уравнении E) координату _у = 0, то одно из значений х, удовлет-
удовлетворяющее трансцендентному уравнению
kvsm+l 1 Л kg__x\
kg \ w0 COS a У v '
х
v0 COS a kg \ w0 COS a
будет Xi = 0; это значение соответствует вылету течки из начала
координат в начальный момент времени. Второе значение хг, являю-
являющееся корнем уравнения F), определяет горизонтальную дальность
полета. Это значение может быть, в частности, получено путем гра-
§ II ТРАЕКТОРИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ 229
фического решения уравнения F). Для этого при известных числен-
численных значениях коэффициентов k, g, v0, а следует построить 'функцию
' v ' У,, COS а ' kg% \ Vo COS а /''
откладывая по оси абсцисс значения х, а по оси ординат соответст-
соответствующие им значения f(x). Пересечение этой кривой с осью абсцисс
и дает второй корень уравнения F) — дальность полета по горизонтали.
2°. Переход от уравнений движения в декартовых
координатах к естественному уравнению движения.
Если уравнения движения точки даны в декартовых координатах
*=/i(9. у=Ш z=Mt) О*)
и требуется найти уравнение движения в естественной форме, то необ-
необходимо сначала определить траекторию точки, а затем найти закон
движения этой точки по траектории.
Нахождение уравнений траектории точки производится путем исклю-
исключения времени из уравнений движения A*). Для нахождения закона
движения a=/(Y) необходимо воспользоваться известным выражением
для дифференциала дути
±d3=ds=V(dxY + (dyf +Ш1 = V~A'(t)+fi~(t)+fi\t)dt. B*)
Интегрируя, находим:
о = ± \ Vtf (О -\-П2 @+/за @ dt + с. (з*)
Произвольная постоянная интегрирования С находится из началь-
начальных условий: так, например, если отсчет пути начинается от началь-
начального положения точки, то при ^ = 0 а = 0. Подставив эти начальные
условия п уравнение C*), определяем С.
Задача 3.8. Точка совершает плоское движение согласно урав-
уравнениям:
х = a cos kt, A)
J>=J[A —cos#). B)
Определить уравнение траектории точки и закон ее движеит.я,
отсчитывая расстояние от начального положения.
Решение. Для получения уравнения траектории точки находим
из уравнения A)
costt=? C)
и подставляем C) в уравнение B):
230
ДВИЖЕНИЕ ТОЧКИ
Таким образом, траекторией точки является отрезок прямой
определяемой уравнением D) и дополнительным условием \
вытекающим из A).
а
[ГЛ. HI
линии,
N
к'г
К задаче 3.8.
Для нахождения закона движения точки но траектории имеем:
dx == — ak sin kt ¦ dt,
Тогда
dy = -? k sin kt-dt.
do=V(dxJTWf =
Итерируя это уравнение, получаем:
fj sin kt ¦ dt
Так как координата с отсчитывается, по условию задачи, от началь-
начального положения точки, то up» /=0 <з=0. Подсзавляп эти значения
в E), имеем:
откуда
Внося найденное значение произиольной постоянной С в уравнение E),
находим закон движения точки по траектории
Это — уравнение гармонического колебательною движения точки.
S П
ТРАЕКТОРИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ
231
Точка О, около которой совершаются колебания {центр колеба-
колебаний), находится на расстоянии
от начального положения. Амплитуда колебаний ранка
В момент времени t~0 точка находится в крайнем положении А.
В момент времени t = rJt2k, когда cos kt = O, точка находится в центре
колебаний, в О. В момент времени г = u/А, когда cos/i-f =—1, точка
находится во втором крайнем положении, п точке Б.
Графически движение точки представлено на рисунке. На рис. а
построена траектория ЛОВ. На рис. б представлена зависимость a or
времени.
Задача 3.9. Точка М движется согласно
уравнениям:
х = а cos kt, A)
_у = а sin kt, B)
z = bt, C)
где а, k, b — постоянные.
Определить уравнения траектории точки
и закон движения точки по траектории, от-
отсчитывая расстояние от начального положе-
положения точки.
Решение. Для определения уравнений
траектории точки находим из уравнения C)
время и вносим это значение в A) и B).
Тогда
х = а cos -г z,
-г- К задаче 3.9.
Это — уравнение винтовой линии. Из уравнений A), B) видно, что
проекция точки на плоскость ху описывает окружность за время 2-z/k.
За это время проекция точки на ось z переместится на величину
называемую шагом винтовой линии. Винтовая линия навивается па
поверхность цилиндра радиуса а.
232 ДБИЖЕНИЕ ТОЧКИ [ГЛ. 111
Для нахождения закона движения точки по траектории находим:
dx == — ak sin kt ¦ dt,
dy -- ak cos kt ¦ dt,
dz == bdt.
Тогда дифференциал дуги будет:
da = V(dxf — Jdyf -{- (dzf = VaW — b* dt
Интегрируя это равепстио, пиеем:
o = l/a'2A2-)-^/-)-C. D)
Для определения произвольной постоянной интегрирования восполь-
воспользуемся начальными условиями. При t = 0 о = 0, так как отсчет дуги
начинается одновременно с отсчетом времени. Подставляя эти началь-
начальные условия в уравнение D), находим:
Таким образом, закон движения точки по винтовой линии запишется
в виде
если отсчитывать положительные значения дуги против часовой стрелки.
Движение начинается из точки хл — а, у0 = 0, 20 = 0 и происходит
по винтовой липни против часовой стрелки.
Для приобретения навыков в решении задач на
составление и исследование уравнений движения и
определения траекторий точки рекомендуется ре-
решить следующие задачи из «Сборника задач по теоре-
теоретической механике» И, В. Мещерского, издания 1950 г.
и более поздних лет: 311, 312, 314, 315, 317, 318, 320, 321.
§ 2. Скорость и ускорение точки
Скорость точки есть производная по времени от радиуса-век-
радиуса-вектора г, определяющего ее положение в пространстве. Скорость точки
характеризует изменение ее положения во времени
o = % = vJ-\-Vyj+vtk, A*)
где I, J, ft — орты осей .v, у, z. Проекции скорости на оси непод-
неподвижных декартовых координат равны
dx dy dz . .„.,..
§ 2] СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 233
Модуль скорости дается формулой
ь = У& + Ъ + *1 C*)
Направление скорости определяется направляющими косинусами:
cos (Сх) — ^, cos (v, у) = -*-, cos @Г2) = ^ . D*)
Скорость направлена по касательной к траектории.
Ускорение точки есть производная от скорости но времени или
вторая производная от радиуса-вектора г по времени. Ускорение точки
является мерой, характеризующей быстроту изменения скорости:
w = S = S = e'*l + V-i-«',*- E*)
Проекции ускорения на неподвижные декартовы оси координат раины
wx = vx = x, Wy = vy=y, wz = vz = 2. F*)
Модуль ускорения вычисляется по формуле
w = Yw%-\-w$-1rwl. G *)
Направление ускорения определяется направляющими косинусами:
cos(o», х)=-?, cos(w,y) = ^-, cos(o», z)=~. (8*)
Если уравнение движения задано в естесткенной форме, то ско-
скорость точки равна
v = *atx=v.-T, (9*)
где т — орт касательной, направленный в сторону увеличения a; vz —
проекция скорости на касательную, равная
Если z»T^>0, то точка движется в сторону увеличивающихся значе-
значений с. Если z»T<^0, то точка движется в противоположную сторону,
п направлении уменьшающихся значений а.
Ускорение в этом случае определяется через проекции па естест-
естественные оси координат. Естественными осями координат, или натураль-
натуральным триэдром траектории, называется ортогональная (прямоугольная)
система координат, состоящая из oceil: а) касательно!), направленной
в сторону возрастания дуговой координаты, б) главной нормали, направ-
направленной в сторону погнутости траектории, и в) бинормали, направленной
так, чтобы три оси составляли правую систему координат (рис. 3.5).
234
ДВИЖЕНИЕ ТОЧКИ
|ГЛ. Ш
Плоскость, в которой расположены касательная и главная нормаль,
называется соприкасающейся, или плоскостью крипизны в данной точке
кривой. Плоскость, в которой лежат главная нормаль и бинормаль,
называется нормальной плоскостью. Нормальная плоскость перпенди-
перпендикулярна к соприкасающейся плоскости. Плоскость, перпендикулярная
к главной нормали, называется спрямляющей плоскостью. Если кривая
плоская, то соприкасающаяся плоскость
совпадает с плоскостью кривой.
При переходе от одной точки тра-
траектории к другой естественные оси,
оставаясь между собой ортогональны-
ортогональными, непрерывно поворачиваются, сопро-
сопровождая движущуюся точку.
Ускорение точки лежит в соприка-
соприкасающейся плоскости и определяется
как векторная сумма касательного п
нормального ускорений точки:
щ» = щ» -\-w П 1*1
Проекция ускорения на касательную
дается формулой
dv
Рис. 3.5.
A2*)
Касательное ускорение характеризует изменение скорости по
величине. Оно равно нулю, когда величина скорости остается неиз-
неизменной. Кроме того, оно обращается в нуль в те моменты времени,
когда скорость достигает экстремальных значений.
Величина нормального ускорения определяется формулой
Щ1 =— A3*)
где р—радиус кривизны траектории. Нормальное ускорение харак-
характеризует изменение скорости по направлению. Оно равно пулю при
прямолинейном движении точки, а также в точках перегиба траекто-
траектории, так как в обоих случаях радиус кривизны обращается в беско-
бесконечность. Кроме того, нормальное ускорение обращается в нуль в точ-
точках, где v = 0. Модуль ускорения вычисляется при помощи формулы
w =
A4*)
Направление ускорения определяется направляющими косинусами:
cos
)=: —, COS ("Ш, П)= --.
A5*)
§ 21 СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 235
Важными частными случаями движения являются равномернее
и равнопеременное движения. При равномерном движении величина
скорости постоянна. Уравнение равномерного движения
A6*)
где о — дуговая координата точки, отсчитываемая от начала коор-
координат, а а0 — значение дуговой координаты при 1 = 0. При равно-
равнопеременном движении касательное ускорение точки постоянно по ве-
величине. Уравнение равнопеременного движения будет:
a = ffo + V+^. A7*)
Зависимость скорости от времени в равнопеременном днижении оп-
определяется уравнением
vx = v0-\-wxt. A8*)
Если wx~^>0, то движение, определяемое уравнениями A7*) и A8*),
является равноускоренным, если же а\<^0, то это движение равно-
замедленное (при 1),^>0). Вообще при ускоренном движении каса-
касательное ускорение совпадает по знаку с проекцией скорости на ка-
касательную. При замедленном движении касательное ускорение и
проекция скорости на касательную имеют противоположные знаки.
Зависимость между скоростью и пройденным путем при равно-
равнопеременном движении определяется формулой Галилея
Часто в яадачах требуется найти радиус кривизны траектории.
Радиус кривизны траектории может быть определен из формулы A3*)
р=--. A9*)
Если уравнения движения заданы в декартовых координатах, то при
помощи формул C*) и G*) следует найти величину скорости и уско-
ускорения точки, затем найти значение касательного ускорения по фор-
формуле A2*). Тогда из соотношения A4*) определяются нормальное
ускорение и, далее, при помощи A9*) радиус кривизны траектории.
При движении точки по плоской кривой радиус кривизны траек-
траектории и нормальное ускорение точки могут быть определены другим
способом, нашедшим в последнее время широкое применение в инже-
инженерной практике.
Обозначим угол, составленный касательной к траектории (или,
что то же, скоростью) с некоторым неизменным направлением, бук-
буквой if) (рис. 3.0). Тогда радиус кривизны равен
236 ДВИЖЕНИЕ ТОЧКИ [ГЛ. Ill
I dii dii da
где (Jj = jt- = -j~ -— и, следовательно, величина нормального ускоре-
ускорения равна а
wn = j = v\ty\. B1*)
В этом параграфе решаются задачи на определение скорости,
ускорения точки, нахождение радиуса кривизны траектории по изве-
известным уравнениям движения точки. Определение скорости и ускорения
точки по заданным уравнениям движения сводится к дифференциро-
дифференцированию уравнений движения и может быть всегда выполнено как при
аналитическом, так и при графическом задании Движения точки. Одно-
Одновременно могут быть получены другие данные, характеризующие
движение точки: ее положение в лю-
любой момент времени, наибольшее и
наименьшее значения скорости и уско-
ускорения и т. д.
При решении задач на
определение скоростей и ус-
ускорений полезно придержи-
придерживаться следующего порядка:
1) выбрать систему координат;
р 36 2) составить уравнения движения
точки в избранной системе коорди-
координат;
3) по уравнениям движения точки определить проекции скорости
на оси координат и скорость по величине и направлению;
4) зная проекции скорости, определить проекции ускорения на оси
координат и ускорение по величине и направлению.
Если траектория точки задана по условию задачи, то целесооб-
целесообразно применить естественную форму уравнений движения и искать
ускорение точки через проекции на оси натурального триэдра.
В этом параграфе решаются также задачи на определение урав-
уравнений движения точки и ее траектории, если известно ее ускорение.
При решении задач на определение уравнений
движения точки и ее траектории рекомендуется та-
такая последовательность действий:
1) выбрать систему координат;
2) составить проекции ускорения на эти оси;
3) проинтегрировать полученные зависимости и найти проекции
скорости;
4) в найденных выражениях определить произвольные постоянные
интегрирования, пользуясь известными значениями проекций скорости
в некоторый момент времени;
5) проинтегрировать полученные зависимости для проекций ско-
скорости и получить уравнения движения точки;
§ 21 СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 237
6) определить произвольные постоянные иптегриропания, пользуясь
значениями координат точки r некоторый момент нрсмспи;
7) исключив из уравнении движения время, получить уравнение
траектории в координатной форме.
Задача ЗЛО. Первый искусственный спутник, запушенный 4 ок-
октября 1957 г. в СССР, имел скорость v, равную 8 км/'сек, и период
обращения Т, равный 1 я 36 мин, или 5760 сек.
Определить высоту полета спутника над
поверхностью Земли, полагая его орбиту кру-
круговой, а движения равномерным. Радиус Земли
принять равным /? = 6370 км.
Решение. Обозначим буквой г радиус
орбиты спутника, проведенный из центра Земли,
букпой h — искомую высоту спутника над по-
поверхностью Земли.
Путь s, проходимый спутником за один пе-
период обращения, равен произведению времени Т, К задаче 3.10.
затраченного на один оборот, на скорость дви-
жения спутника v. С другой стороны, этот же путь равен длине
окружности радиуса г. Таким образом,
откуда
г = J^ = 7340 км.
2я
Далее находим искомую высоту полета:
А = /• — /? = 7340 — 6370 = 970 км.
Задача 3.11. Две точки движутся равномерно одна за другой
по одной прямой линии со скоростями ч)} и Ф». причем расстояние
между их начальными положениями
было равно ай. Обе точки начали о и, р, д2
двигаться одновременно. в0 "
Определить время Т, по истече-
истечении которого одна точка догонит к задачам 3.11, 3.12.
другую.
Решение. Пусть прямая Os есть траектория движения. Тогда
уравнение движения первой точки, вышедшей из О, будет:
Уравнение движения второй точки, вышедшей из Ои будет:
о4 = V4 -[- а0,
ибо отсчет координаты следует по-прежнему вести от начальной
точки О. Столкновение произойдет в момент времени Т, когда
238 ДВИЖЕНИЕ ТОЧКИ [ГЛ. 111
в, ==ff.i, ИЛИ
vlT=vqT-\-all,
откуда
Задача 3.12. Решить предыдущую задачу при условии, что пто-
рая точка начинает движение через промежуток премени т после
начала движения первой точки.
Решение. Уравнение движения
первой точки останется не-
изменным:
Уравнение дпижег.ия второй точки изменится, так как время движе-
движения второй точки равно (t — т), и, следовательно,
:= Vt (t — i)-\- <J0.
Приравнивая пути, пройденные обеими точками, находим время,
прошедшее от начала движения первой точки до столкновения:
= v4{T — T)-fa0,
откуда
Задача 3.13. Судно для достройки на плаву спускается на воду
но смазанным полозьям с постоянным ускорением. Первый метр пути
судно прошло за 1 сек.
Сколько времени потребовалось для спуска судна, если длина
полозьев 400 м?
Решение. Уравнение движения судна по полозьям
at*
где 5 — пройденный путь, а — ускорение, t—время.
Применим эту формулу к первому участку пути, когда судно
прошло 1 м за 1 сек
at\
Si = -у',
здесь Si=l м, а ^ = 1 сек. Аналогично для остального пути
по полозьям
an
S
где i'.j = 400 м, U — искомое время.
§ 2] СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 239
Для определения ?4 составим отношение
?s^ \i_
Si t\ '
откуда
Задача 3.14. Подводная лодка, не имевшая хода, погружается
на глубину согласно уравнению
где р, k, s, т — постоянные коэффициенты, s — площадь горизон-
горизонтальной проекции лодки. Ось х направлена по вертикали вниз.
Определить скорость лодки, а также начальное и предельное
значения скорости при неограниченном возрастании времени.
Решение. Для определения модуля скорости вычисляем про-
производную от х по времени:
dx
dt
-±i.
)¦
Начальное значение модуля скорости находим, подставляя в урав-
уравнение A) значение ? = 0. Тогда
Предельное значение модуля скорости лодки при неограниченном
возрастании времени будет:
/-.со кь
Задача 3.15. Корабль движется согласно уравнению
а = М 272,7 \п ]-±^1 , 50t) м. A)
Определить величину начальной скорости судна.
Решение. Для определения модуля скорости вычисляем абсолют-
абсолютное значение производной дуговой координаты по времени:
J 6^
7
420
V —
50
— OU —
1 + 6й"-'
Модуль начальной скорости судна определится из B) при подста-
подстановке ? = 0, откуда
zH = 10 м/сек.
240 ДВИЖЕНИЯ ТОЧКИ 1ГЛ. III
Задача 3.16. Частица, несущая электрический заряд в, движется
п однородном электрическом поле с переменной напряженностью
?=Asin^, где А и k — постоянные коэффициенты. Уравнение
движения частицы имеет вид
еА I, sin kt
где in — постоянная величина.
Определить величину скорости точки, ее начальное значение,
а также наибольшее и наименьшее значения скорости.
Решение. Для нахождения модуля скорости вычисляем произ-
производную от х по времени
ах
Ш
еА
A)
Подставляя в уравнение A) начальное значение времени ? = 0,
получим, что
¦г.0 = 0.
Для определения экстремальных значений модуля скорости на-
находим первую производную от величины скорости по времени и,
приравнивая ее значение нулю, определяем моменты времени, когда
скорость достигает наибольших и наименьших значений:
dv еА . ,, „
Следовательно, ktl = O, г., 2ir, 3ir, 4ir, ..., откуда
, Tin
Tl~T'
где п = 0, 1, 2, 3, ...
Подставляя найденное значение ty в уравнение A), находим:
при л = 0
t>min = ^(l —cosO°) = 0; B)
при л= 1
'"•» = »* A-COSK) = Ж- <3>
При последующих значениях и величины скорости B) и C) будут
периодически повторяться.
Задача 3.17. Точка М движется по окружности радиуса г с ка-
касательным ускорением wz, величина которого неизменна. В началь-
начальный момент точка находилась в Жо и ее скорость равнялась нулю.
Определить, в какой момент времени величина нормального уско-
ускорения станет ранной величине касательного ускорения, и вычислить
длину дуги, пройденную точкой к этому моменту. '
§2) СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 241
Решение. Интегрируя равенство
при w, = const имеем:
vz = w.J-{-C, B)
где С — произвольная постоянная интегрирования, определяемая из на-
чаЛыюго условия: при / = 0 v. — 0. Подставляя эти значения в B),
находим С = 0 и, следовательно,
v, = wj. C)
Нормальнее ускорение точки определяется формулой
v«- w\ta-
ш-=т=—•
Для нахождения момента времени, когда касательное и нормаль-
нормальное ускорения по величине равны, приравниваем их значения
и определяем искомый момент времени
Скорость точки C) можно представить в ниде
Интегрируя, находим:
о = и», Т + С.
Постоянная Ct определяется по начальному условию: при /=0
а = 0.
Тогда
Полагая в этом уравнении /=7i, находим искомую величину дуги:
Задача 3.18. Груз D подвешен па двух тросах ЕАС и НВС,
перекинутых через блоки А и 8. В начальном положении стрела
прогиба ОС = с= 10^3 м и АС = ВС. Расстояние между блоками
242
ДВИЖЕНИЕ ТОЧКИ
[ГЛ. III
А В — 1п = 20 м. Трос НВС наматывается на барабан лебедки с по-
постоянной скоростью v= 1 .ч/сек. Трос ЕАС разматывается с барабана
лебедки с такой же скоростью.
Определить траекторию точки С, к которой подвешен груз, а также
скорость этой точки.
Решение. Выбираем оси координат: начало координат в точке О,
ось х направляем по АВ вправо, ось у перпендикулярно к АВ вверх
У//////////////УУ///////////////////////
а)
К задаче 3.18.
(рис. а). Определяем из треугольника АОС начальную длину тросов:
АС=ВС = Ь,
Ь* = АОг + ОО = а* + са = 102
• 3 = 400,
откуда Ь = 20 м.
Рассмотрим произвольное положение груза (рис. б). Длина троса
\ = b-\-vt, длина троса BCt = b — vt. Обозначив координаты точки
i (х, у), находим зависимость этих координат от времени:
О9. A)
<)\ B)
C)
Вычитая из A) равенство B), имеем:
— — vt = '2t м.
Проекция скорости точки С! на ось х будет:
vx = х — — v = 2 м/сек.
Вноси в уравнение A) найденное значение координаты х, определяем
зависимость координаты у от времени:
у=-
— а1
11 — ~ ] ьЧ1 =•— [ 300 -
D)
§ 1\ СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 243
Проекция скорости на ось у равна производной от координаты у
по времени
3t
V = V =
у
Скорость точки определится формулой
л ' у" ' узоо-
Модуль скорости
1 300— ЗС2 "
Для нахождения уравнения траектории груза следует совместно
решить уравнения A) и C), исключив из них время. После несложных
преобразований находим уравнение траектории
"F+T4""^? = L
Таким образом, груз движется по дуге эллипса.
Решение этой задачи показывает многообразие приемов составле-
составления уравнений движения точки. В данной задаче уравнения A) и B)
являются системой уравнений, определяющей зависимость координат
от времени, разрешая которую относительно каждой из координат,
мы находим уравнения движения груза C) и D).
Задача З.Т9. Точка М совершает колебательное движение согласно
уравнениям:
* = tf cosBA;/ — e), A)
y—bcoskt. B)
Определить траекторию точки М. При каких значениях ? траектория
точки обращается в параболу? Найти скорость точки в начальный
момент времени.
Решение. Для определения траектории точки надо исключить
из уравнений движения время. Для этого преобразуем первое уравне-
уравнение следующим образом:
jc = a[cos Ikt cos e-L- sin 1Ы sin e] =
= a[cos9&/ cos ? — sm^kt cos e -f- 2 sin kt cos kt sin ?J. C)
Из второго уравнения находим:
cos kl=^-, sin kt— l/l — =?- .
Подставляя эти значения в уравнение C), получаем уравнение траекто-
траектории точки М
214 ДВИЖЕНИЕ ТОЧКИ [ГЛ. III
Из уравнений A), B) следует, что при любых значениях е координаты
х и у не превышают соотнетственно значений z\za и ±Ь. Таким
образом, траектории ючки М нписынаются в прямоугольник со сторо-
сторонами '2а и '2Ь. Уравнение D) обращается в уравнение параболы при
е, = 0 и ?} = -:
!(¦
*•==!(¦ ^)
Переходим к определению скорости точки М. Проекции этой
скорости равны первым производным от координат по времени
vx = x= — lak sin (Ikt — е),
vy = p=- — bk sin kt.
Находим значение этих проекций в начальный момент времени,
полагая ? = 0,
vM = — lak sin e, E)
Таким образом, в начальный момент времени скорость точки на-
направлена но оси х, а ее величина определяется по формуле E).
Задача 3.20. Точка движется прямолинейно согласно уравнению
^ = 3sin2^ — 4 cos Ird. A)
Доказать, что движение точки является гармоническим колебатель-
колебательным движением. Определить амплитулу и период колебаний. Найти
скорость и ускорение точки
Р е in e п и е. Гармоническое колебательное движение определяется
уравнением
х = а sin (kt — p), B)
или
х = a sin kt cos p — a cos kt sin p. C)
Сопоставляя уравнения A) и C), замечаем, что они совпадают, если
положить
& = 2я, acosp = 3, asinp = 4. D)
Из уравнений D) находим:
а1 = 25, или а = 5;
tg?=y=l,33, или Р = 0,925.
Подставляя найденные значения а и |3 в уравнение B), имеем:
х = Я sin B:rf —0,925).
2[ СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 245
Период колебаний равен
Находим, далее, проекцию скорости точки на направление движения
vx = х = 1 О* cos (Ir.t — 0,925).
Проекция ускорения точки равна
wx = vx = х = — 20*3 sin Br.t — 0,925) = — 4A.
Задача 3.21. Дано уравнение движения точки
\
Доказать, что точка совершает гармоническое колебательное дви-
движение. Определить амплитуду, период колебаний, а также скорость
и ускорение точки.
Решение. Используя формулу тригонометрии
sin3a = -i-(l —cos 2a),
представим уравнение движения тонки в виде
х=1 — cosF^-f тс) = 1 -{- sin
Из этой формулы видно, что точка совершает гармоническое колеба-
колебательное движение около положения А, определяемого абсциссой
х, = 1.
Если перенести начало координат в точку А, то уравнение движе-
движения точки будет:
(
де х — координата, отсчитываемая от точки А. Амплитуда колебаний
равна единице, период
Проекция скорости точки на направление движения определится
по формуле
Проекция ускорения точки равна
dvx d2x О/, a .
wx =-1*г = —=- 36«» sin
или
wx = Збя3 — 36А:.
246 ДВИЖЕНИЕ ТОЧКИ [ГЛ. III
Задача 3.22. Точка движется согласно уравнению s = 48t — Мл,
где координата s измеряется в метрах, а время — в секундах.
Определить величину скорости точки в моменты времени tv= 1 сек,
tt^2 сек, ^з=3 сек, t^^\ сек. Найти среднюю скорость точки
за первую, вторую, третью и четвертую секунды. Найти среднюю
скорость точки за четыре секунды. Определить момент времени и рас-
расстояние от начала отсчета пути, когда точка остановится.
Pte ш е и и е. Величина скорости определится как производная оТ пути
по времени
«, = -?=48-12ft A)
Внося в это выражение значения моментов времени, находим скорости:
ysl = 48— 12 = 36 м/сек,
. Vsi = 48— 12 - 22 = О,
us;) = 48— 12- 3* = — 60 м/сек,
vsi = 48 — 12 ¦ 4* = — 144 м/сек.
Эти значения определяют величины скорости в заданные моменты
времени. Для определения среднего значения скорости необходимо
разделить пройденный путь на промежуток времени, в течение которого
этот отрезок пути пройден. Таким образом, скорость точки за первую
секунду будет:
VtcP = -r—т-=—j— = 44 м/сек,
где координата точки в момент ?=1 сек, S| = 48- 1 —4 • I3 = 44 м,
начальная координата s0—-0. Аналогично определяются величины
средних скоростей точки за следующие секунды:
So Si 64 44 _„ ,
Vicp — -j-—.— = j = 20 лцсек,
¦^ = Т~Г; = ^Т^ = -™ м/сек,
Vicp = 4—7^ = —f1^ =-100 м/сек.
Знак минус указывает, что скорость направлена в сторону отрица-
отрицательных s.
Находим, далее, момент времени, когда точка остановилась, при-
приравнивая нулю выражение для скорости A)
48— 12^ = 0,
¦откуда
tt = -Ji'2 сек.
§ 21 СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 247
В этот момент скорость точки равна нулю и направление движения
изменяется на противоположное. При значении t^ = 2 сек координата
точки равнялась
s, = 48-2 — 4-23 = 64 м.
Второй отрицательный корень следует отбросить, как лишенный физи-
физического смысла, ибо время растет монотонно.
Переходим к определению средней величины скорости за четыре
секунды. Путь, пройденный точкой за четыре секунды, складывается
из пути s.2 = 64 м, пройденного за первые две секунды, и пути,
пройденного за третью и четвертую секунды, когда точка двигалась
п сторону отрицательных s. Находим этот путь следующим образом.
При ? — 4 сек координата точки была:
s4 = 48-4 —4-43 = —64 м.
Следовательно, за третью и четвертую секунды точка прошла пугь
|Si — s21 = 128 м.
За все четыре секунды точка прошла путь
64+128=192 м.
Величина средней скорости точки равна
192
vcp = —j- =48 м/сек.
Следует заметить, что точка двигалась вначале в сторону положи-
положительной оси s и прошла в этом направлении путь s2 = 64 м. Ее
средняя скорость при этом была положительна. Далее точка двигалась
в противоположном направлении 128 м. Ее средняя скорость, оставаясь
по величине постоянной, была из этом участке пути отрицательной.
Как видно из решения этой задачи, при определении средней скорости
точки следует учитывать тот факт, что при перемене направления
движения точки перемещение складывается из всех пройденных участ-
участков пути и может быть не равно разности координат конечного
и начального положений точки.
Задача 3.23. Точка Мх брошена вертикально вверх. Уравнение
движения точки при отсутствии сопротивления воздуха имеет вид
x = vj-*f, A)
где va и g—постоянные коэффициенты.
Определить скорость и ускорение точки, максимальную высоту
подъема точки и время, когда точка достигнет наивысшего положения.
Решение. Проекция скорости точки находится как производная
от координаты по времени
v* = va-gt B)
248 ДВИЖЕНИЕ ТОЧКИ [ГЛ. III
Проекция ускорения точки при прямолинейном движении равна
производной от проекции скорости по времени или второй производ-
производной от координаты но времени
«'* ==vx = x = — g,
т. с. ускорение точки — постоянная величина. Из уравнения B) видно,
что при t = 0- vx = va. Следовательно, постоянная v0 является зна-
значением проекции скорости точки в начальный момент времени.
Чтобы определить момент времени, когда точка достигнет макси-
максимальной высоты, воспользуемся тем, что скорость точки в этом
положении равна пулю. Обозначая время подъема через Т, из B)
находим:
Таким образом, время, в течение которого точка достигнет наивыс-
наивысшего положения, равно
Г=|. C)
Наибольшую высоту подъема h найдем, подставив значение вре-
времени C) в уравнение движения A):
Задача 3.24. Точка Aft брошена вертикально вверх с начальной
скоростью va.
Через сколько секунд Т надо бросить вертикально вверх из
того же места с начальной скоростью i>i<^o0 вторую точку М^,
чтобы обе точки встретились в наикратчайшее время or начала дви-
движения первой точки?
Уравнение движения теки, брошенной вертикально вверх, при
отсутствии сопротивления воздуха
где v0—начальная скорость точки, g—ускорение свободного па-
падения.
Решение. На первый взгляд может показаться, что вторую
точку следует бросить вверх одновременно с первой. Однако скорость
второй точки может оказаться достаточно малой и она поднимется
па небольшую высоту и упадет па Землю раньше, чем первая точка
успеет ее догнать. Поэтому выбор момента времени бросания второй
точки играет существенную роль.
Так как вторая точка Мг, орошенная вверх через Т секунд после пер-
первой, имеет меньшую начальную скорость, то встреча возможна только
при возвратном движении первой точки вниз. Обозначим буквой tt
§ 2| СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 249
время движения перной точки от ее наивысшего положения до встречи
со второй точкой. Тогда путь, пройденный первой точкой вниз за
время tb будет:
Обозначим буквой т время, отсчитываемое от момента, когда пер-
первая точка находилась в наивысшем положении, до момента начала
движения второй точки. Тогда пугь, пройденный второй точкой до
встречи с первой, равен
Так как в момент времени t\ точки встретились, то, следовательно,
Sl + S2 = /2, A)
где h — наибольшая высота подъема первой точки, равная v-Jig (смотри
предыдущую задачу). Тогда, подставляя в A) значение всех величин,
находим:
Рассматривая это уравнение как неявную зависимость <,=/(t), на-
находим производную от ti по 1 и приравниваем ее нулю:
откуда
z'i.
Но vxjg равно времени подъема второй точки на наибольшую
высоту (см. задачу 3.23). Следовательно, в момент встречи вторая
точка будет находиться в наивысшем положении.
Подставим найденное значение tx — ¦z из C) в уравнение B).
Тогда, после приведения подобных членов, находим:
откуда определяется время
Далее, из уравнения C) находим:
D)
250
ДВИЖЕНИЕ ТОЧКИ
[ГЛ. III
Чтобы найти искомое время Т, но истечении которого с момента
бросания первой течки следует бросить вверх вторую точку, необхо-
необходимо к х прибавить время t0, в течение которого первая точка до-
достигла наивысшего положения:
vi 1 »о
Из формулы D) следует, что
т > 0 при
•z = Q при
при
'2v\,
Таким образом, при т^>0 бросание второй точки происходит после
того, как первая точка достигла наивысшего положения; при т<^0
бросание второй точки происходит до того, как первая точка оказалась
н наивысшем положении; а при т = 0 бросание второй точки происходит
в тот момент, когда первая течка находится в наивысшем положении.
Задача 3.25. Линейка эллипсографа АВ = 1 скользит концом А
по оси абсцисс и концом В по оси ординат. Линейка приводится
к»
К задаче 3.25.
в движение кривошипом ОС = 0,5/, шарнирпо прикрепленным в ее
середине. Расстояния АМ = а, ВМ = Ь известны. Угол 9 между осью
абсцисс и кривошипом изменяется пропорционально времени y = kt.
Найти уравнения движения точки М эллипсографа и уравнение
се траектории. Определить также радиус кривизны траектории точ-
точки М, ее скорость, касательное, нормальнее и полное ускорения при
произвольном положении механизма и, в частности, в моменты вре-
времени tt = 0 и L% = KJ2k.
Решение. Для состаиления уравнений движения точки М рас-
рассмотрим треугольник ОАС. Он равнобедренный: ОС=АС= 0,5/,
следовательно, /, СОА = l_ CAO = y = kt. Тогда координаты точки
М будут:
х = ВМ cos 9 = b cos kt, A)
у = АМ sin 9== a sin kt, B)
§ 2| СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 251
или в векторном виде
r = xi-\-yj=b cos kt-i-\-a sin kt-j,
где i, j—орты осей координат x, у. Этими равенствами определяются
уравнения движения точки М.
Для нахождения траектории точки представим уравнения движения
в виде х
-;- = cos kt, ^-= sin kt,
возведем эти равенства в квадрат и сложим их:
^_ \У 1
Таким образом, траектория точки М — эллипс с полуосями Ь, а.
Для определения скорости точки М вычисляем первые производ-
производные от координат по времени, равные проекциям скорости точки
на соответствующие оси координат:
vx = х = — bk sin kt, vy=p = ak cos .kt
Величина скорости определяется формулой
icos'ikf. C)
Направляющие косинусы вектора скорости будут:
, ^ ч vx — b sin kt
cos (v, x) = -- = ,
v ]/b» sirf'kt + a* cos" kt'
. -^- . vv a cos kt
' У> -^ 1/*2Т1п2 kt + a2 cos2 kt'
В векторном виде скорость может быть представлена так:
<о = vxi -j- ^yj= — bk sin kt ¦ i -(- ak cos kt -j.
Находим проекции ускорения на оси координат, вычисляя первые
производные по времени от проекций скорости или вторые производ-
производные но времени от координат точки:
wx = vx = х = — bk? cos kt, Wy = vy = y = — ak? sin kt. D)
Величина ускорения определится по формуле
w = Vw%-f- wy =
Направление ускорения может быть найдено путем сопоставления
уравнений движения точки A), B) и формул, определяющих проекции
ускорения на оси координат D). Последние могут быть представлены
в виде
wx= — kPx, Wy = — №у;
таким образом,
w = wj -f- wyj= — k- (xi -\-yj) = — A-r.
252
ДВИЖЕНИЕ ТОЧКИ
[ГЛ. III
Следовательно, ускорение точки М направлено по радиусу-нектору,
проведенному из М в О, и по величине прямо пропорционально
расстоянию точки М от начала координат. Проекция ускорения на
касательную определится как производная от проекции скорости на
касательную по времени (и данном случае vz = v)
dv k2 (b2 — a1) sin kt cos kt
w = — = —v ' -—
1 dt Yb- sin2 kt + a2 cos2 kt '
Но величина полного ускорения связана с касательным и нормальным
ускорениями зависимостью
1
Теперь, после несложных преобразований, найдется неличина нормаль-
нормального ускорения точки М:
w. = V w — от; = —==—=— -—. (о)
Уа*саа?Ы-\-Ь*&т3 kt
Зная модуль нормального ускорения точки E) и ее скорость C),
находим радиус кривизны траектории;
в
т?_ (a2 cos2 kt -f- V2 sin2 kt) ~2
" wn ab
Пользуясь полученными формулами, определяющими основные
кинематические величины б любой момент времени, находим их зна-
значения:
X
У
V
И1Т
w
р
Ь
0
akj
0
ksb
— k-Ы
а'2
b
kt — "-
0
а
— bkl
0
ksa
— k2aj
ft»
a
«21
СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ
253
Задача 3.26. Кривошип ОА = г вращается равномерно вокруг
точки О в плоскости чертежа: угол <р = ?^. Шатун АВ шарнирно
соединен с концом кривошипа в точке А и проходит через цилинд-
цилиндрический шарнир, который может поворачиваться вокруг неподвиж-
неподвижного центра Л/. Длина A3—/^>2г.
Определить уравнения движения точки В, проекции ее скорости
и ускорения на оси координат, кacafeльнoe, нормальнее и полнее
ускорения, а также радиус кривизны траектории при произвольном
положении механизма. Определить координаты, скорость, ускорение
точки В и радиус кривизны ее траекто-
траектории при <р = 0 и <р = г..
Решение. Треугольник OAN рав-
равнобедренный, так как ОА— ON=r.
Следовательно, /_ OAN= L ONA =
= 90° — 'f/2. Тогда координаты точки В
ранни ('
х = г cos kt-\-1 sin -у, A) "Г"
kt
y = r sin kt — I cos ^ ¦ B)
Выражения A) и B) являются уравне-
уравнениями движения точки В. Они получены
проектированием ломаной линии ОАВ со-
соответственно на еси абсцисс и ординат.
Проекции скорости на неподвижные декартовы оси координат
находятся как производные от координат по времени:
k kt
vx-=^x = — rk sin kt-\-l-~- cos -„-,
k kt
vv = p = rk cos kt -j- / y sin --.
Величина скорости определится по формуле
К задаче 3.26.
* + -j-rlsin ~.
Проекцию ускорения на касательную найдем как производную
от проекции скорости на касательную по времени (v^:=v):
dv.
.„ , kt
— k-rl cos -у
.,1а , . kt'
rs+T-r/sinT
Если касательное ускорение и\ и проекция скорости на касательную
г>т одного знака, то точка В движется ускоренно. Если же w. и ат
противоположных знаков, то точка В движется замедленно.
254
ДВИЖЕНИЕ ТОЧКИ
[гл т
Проекции ускорения точки на неподвижные декартовы оси коор-
координат равны первым производным по времени от проекций скорости
на соответствующие оси или вторым производным по времени от
соответствующих координат точки:
,. ,, , ft2 . kt
Wx = X == — rkl COS kt — l-r Sin -ту,
kr k?
wy =y=.~ rk* sin kt -f- / -г- cos ~.
C)
Пользуясь уравнениями (З) и D), определяем величину полного
ускорения точки R:
-|- -? - f sin f.
Зная иеличпны полного и касательного
модуль нормального ускорения по фор
wn = Yw'- — w'l
16
ускорений точки, вычисляем
1уле
. kt
SHI 2"--
,.3 ,kt
r-i cos- -
-•¦II* r • 'lt \
> r-+T-r/sin-
C другой стороны, величина нормально "О ускорения равна
"~ Р '
Отсюда можно определить радиус кривизны, так как скорость точки
и нормальное ускорение известны:
" cm
I/ 64r4 -;- \е>гЧ< -|- f1 — 96r3/ sin^- — 12 r/« sin *' + 36r2/2 sin2 *'-
Перейдем к вычислению координат точки В, ее скорости и уско-
ускорения при угле <ро = О- Из уравнений движения A) и B) находим
координаты точки Б при рассматриваемом положении механизма:
¦*о = г, уа = —1.
При этом модуль скороеiи точки
а касательное ускорение точки будет равно
— k*rl
§ 21 СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ
Величина нормального ускорения
255
Величина полного ускорения выразится так:
Радиус кривизны траектории при 'ро = О будет:
з
Соответственно при угле <pi = ?c эти величины равны
хх = — г -f1, ух = О,
«',1 ^ О,
_ Br — IK
Задача 3-27. Точка М, движущаяся с постоянной по величине
скоростью v, описывает цепную линию, уравнение которой имеет вид
X _ X
Определить проекции скорости и ускорения, а также полисе уско-
ускорение точки как функции ее координат. Определить ргдиус кривизны
цепной линии.
Примечание. Использовать выражения
гиперболических функций через показательные:
sh 2
chT-
thz =
Решение. Рассматривая х и у, входя- к залачс 3.27.
щие в уравнение цепной линии, как функ-
функции нремени и дифференцируя ураьпение цепной линии по времени,
имеем:
.. dv d I .
250 ДВИЖЕНИЕ ТОЧКИ [ГЛ. III
Далее, так как сумма квадратов проекций скорости равна квад-
квадрату скорости точки, то
р* = ъ* — х*. C)
Возводя уравнение B) в квадрат и подставляя вместо левой части
ее значение C), находим:
v х х s -- ( )
или
.-,.2 v- va-a°-
-f- sh- — ch2 — ¦"
' а а
Извлекая из обеих частей равенства (о) квадратный корень, легко
находим, что
Это. равенство определяет проекцию скорости на ось абсцисс как
функцию координат точки.
Чтобы определить проекцию скорости на ось у, подставим найден-
найденное значение F) в уравнение B). Тогда
* = 7sh*. G)
или, внося в это равенство значение у из A), находим:
у = г> th—. (8)
Для вычислении проекции ускорения на ось абсцисс продиффе-
продифференцируем но времени соотношение F), помня, что v = const,
va . va va х v-a3 x ,п,
x = ,- у — т • — sh — = i- sh —. (9)
У У У а у3 a v '
Для определения проекции ускорения па ось ординат вычислим,
пользуясь (8), вторую производную от ординаты по времени:
A0)
ch2— "*
а
Учитывая F), находим:
A1)
Для нахождения величины ускорения точки воспользуемся фор-
формулой
» ** + $' A2)
У
V— v
у — „
ch2 —
а
v va
а
X
а
г
f-a*
СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ
257
подставляя в которую (9) и A1), имеем, после несложных преобра-
преобразований:
A3)
= —г 1 4- sir — = —г
х
а
Используя вновь равенство A) и извлекая из A3) киадратный корень,
находим величину ускорения точки
v'-a
w == —
f '
A4)
Так как точка по условию движется с постоянной скоростью, то ее
полное ускорение будет одновременно яиляться и ее нормальным
ускорением:
w = wn = j. A5)
Сопостанляя равенства A4) и A5), определяем радиус кривизны
цепной линии
Задачу можно решить непосредственным дифференцированием
уравнения цепной линии, не переходя к гиперболическим функциям.
Однако такой путь решения является более длинным.
Задача 3.28. Точка Q движется по параболе yl = 2px так, что
положение ее проекции на ось ординат дается формулой y = ct.
К задаче 3.28.
Определить скорость и ускорение точки Q, а также радиус кри-
кривизны параболы.
Решение. Координаты х, у движущейся точки Q, входя-
входящие в уравнение параболы, являются функциями времени. Вычисляя
9 М. И. Бать и др., т. I
258 ДВИЖЕНИЕ ТОЧКИ [ГЛ. Ill
производную по времени от обеих частей уравнения параболы, имеем:
или
pvx. A)
С другой стороны, дифференцируя по времени y = ct, находим:
Тогда из A) имеем:
ус
х~ Р '
и, следовательно, скорость точки определится соотношением
Величина скорости равна
Проекции ускорения на оси координат находим по формулам:
с с2
wx = vx= — >*== — = const,
х х р У р
wy = *> — °-
Таким образом, модуль полного ускорения точки равен
w = \w jc h= —.
I Al p
Обозначая угол между касательной к параболе и осью jc буквой <р,
находим величину нормального ускорения точки Q
wn = w\ cos (90° — ср) ] = w | sin sp j.
С другой стороны,
2
откуда
v-
" wn w\ sin <f | с21 sin <f I '
или, учитывая B), получаем:
Вссстанавлипая в точке В, находящейся па расстоянии ОВ=р/2
от точки О, перпендикуляр к оси абсцисс (директрису параболы),
СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ
259
находим точку А, в которой этот перпендикуляр пересекается с нор-
нормалью к траектории точки. Тогда
1<ЭЛ|=тг
sin <f I
D)
Сопоставляя равенства C) и D), находим:
где точка С—центр кривизны.
Задача 3.29. Точка М движется согласно уравнению а = аеы,
причем утл, образуемый полным ускорением с касательной, остается
неизменным и равным 60°.
Определить скорость, касательное, нормальное и полное ускоре-
ускорения точки, а также радиус кривизны траектории как функции дуги а.
Решение. Проекцию скорости на
касательную находим как производную
от дуги по времени
г1. = з = akek! = ki.
Проекция ускорения точки па ка-
касательную равна
Так как угол между полным уско- к задаче 3.29.
рением и касательной известен по ус-
условию, то модуль полною ускорения определится из равепава
w cos a = wv
откуда
~~ cos 60°
Величина нормального ускорения точки будет:
Wn
Радиус кривизны траектории определяется по формуле
w \/3k! 3
3
Радиус кривизны с течением времени неограниченно возрастает.
Траектория точки — расходящаяся спираль.
9«
260 ДРИЖЕНИЕ ТОЧКИ [ГЛ. III
Задача 3.30. Движение точки задано уравнениями в декартовых
координатах
х = el cos t,
у==с' sin t,
z = el.
Определить радиус кривизны траектории.
Решение. Для нахождения радиуса кривизны траектории вос-
воспользуемся формулой нормального ускорения
Вычислим скорость точки. Проекции скорости на неподвижные
декартовы оси равны
vx = х = е( (cos t — sin t),
vy =y = e' (cos t -J- sin i),
vz = i •= e'.
Тогда
Переходим к определению проекций ускорения точки:
wx=x = — 2е* sin t,
Wy = y = '2ec cos t,
wz= z = e'.
Абсолютная величина ускорения будет
w = 'V w]. -\-w- -r w~z = e' Vn.
Касательное ускорение находим как производную от скорости по
времени:
величины полного и касательного ускорений точки, находим ее
нормальное ускорение
2
откуда
и, следовательно,
be* — Зе" =
B)
СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ
261
Внося значения скорости и нормального ускорения в формулу A),
находим радиус кривизны траектории
Радиус кривизны и нормальное ускорение являются важными
характеристиками движения точки.
В данной задаче из уравнения C) следует, что при неограниченном
возрастании времени радиус кривизны неограниченно возрастает.
Однако нормальное ускорение не стремится к нулю при неограни-
неограниченном возрастании времени, как это видно из B), а, наоборот,
неограниченно возрастает. Траектория точки, заданная параметриче-
параметрическими уравнениями движения, представляет логарифмическую спираль,
радиус кривизны которой неограниченно возрастает с течением вре-
времени.
Задача 3.31. Система состоит из двух блоков (рис. а), один из
которых может вращаться вокруг неподвижной оси О, второй может
В)
К задаче 3.31.
вращаться вокруг подвижной оси Os. Через первый блок перекинут
трос, прикрепленный одним концом к подвижной оси О,. Груз /,
прикрепленный ко второму концу троса, движется в данный момент
вверх со скоростью 6 м/сек и с замедлением 2 м/сек*. Груз 3,
прикрепленный к тросу, перекинутому через подвижный блок, дви-
движется вверх с замедлением 4 м/сек*, имея в данный момент ско-
скорость 3 м/сек.
262 ДВИЖЕНИЕ ТОЧКИ [ГЛ. III
Найти скорость и ускорение центра подвижного блока, точки Oi
и груза 2 в данный момент времени.
Решение. Обозначим ординаты грузов соответственно через у\,
У1> Уз и ординату точки О, буквой у (рис. б). Так как длина троса
между грузом / и центром блока Oj неизменна, то
У\ + У + ~r = const,
где буквой г обозначен радиус блока. Точно так же неизменна и
длина троса, соединяющего грузы 2 и 3. Выражаем длину этого
троса
Уг —У —Уз —У -\-ъг = const.
Дифференцируя оба равенства по времени, находим:
С)
Подставляя заданные значения скоростей pi и у3, имеем:
р = — 6 м/сек,
]/<1 = ^у— у3 — — 15 м/сек.
Дифференцируя уравнения A) по времени, получим:
Внося в эти уравнения известные значения ускорений j/, и ул, находим:
у = 2 м/сек"-,
у~г = 2у—JA) = 8 м/сек'2.
Таким образом, скорость у и ускорение у точки О\ равны ско-
рссти и ускорению груза /, но направлены в прогивоположную
сторону. Скорость J).2 груза 2 направлена вниз и равна 15 м/сек,
ускорение этого груза J/.3 направлено вверх и равно 8 м/сек^.
Задача 3.32. Ускорение точки равно 12 t м/секг и направлено по
оси х в отрицательном направлении. При t = 2 сек скорость точки
равнялась 6 м/сек и была направлена по оси х в положительном
направлении. При t = 'S сек точка находилась на оси х па расстоя-
расстоянии 50 м от своего начального положения.
Определить уравнение движения точки.
Решение. Точка движется прямолинейно по оси х, следова-
следовательно, се ускорение в проекции на ось х равно
¦—— - lit
« 2] СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 2G3
Представим это уравнение в виде
dx = ~\1t-dt, (I)
умножив обе его части па dt и заметив, что
d*x_ d?
~W~Tf
Уравнение A) интегрируем:
» B)
Для определения произвольной постоянной интегрирования Сл
воспользуемся условием, что при t = 2 сек х = 6 м/сек. Внося эти
значения переменных в уравнение B), находим:
G = - 6 • 22 -4- Q
ИЛИ
d = 30.
Тогда уравнение B) примет вид
Умножая обе части этого уравнения на dt, находим:
dx= — 6i2dt-\-30dt.
Интегрируя, получаем:
л- = — 2/' + 30^ -\- С,. C)
Чтобы определить произвольную постоянную интегрирования С,_,
«несем в уравнение C) соотнетствсино условию л- = 50 м при
^ = 3 сек:
50 = — 2 • 27 + 30 • 3 + Сь
отсюда
С,= 14.
Внося это значение в уравнение C), находим уравнение движения
точки
0/-f 14.
Задача 3.33. В течение 20 сек скорость корабля, совершающего
движение (циркуляцию) по дуге окружности радиуса 200 м, падает
с 15 до 12 м/сек.
Предполагая, что величина касательного ускорения пропорцио-
пропорциональна квадрату скорости, определить путь, пройденный за первые
десять секунд, и угол циркуляции.
264 ДВИЖЕНИЕ ТОЧКИ !ГЛ. !Т1
Р е in e и и е. Касательное ускорение корабля пропорционально
квадрату скорости, следовательно,
где к — неизвестный по величине коэффициент ^пропорциональности.
Отделяя переменные, находим:
- - = k at.
v-
Воспользуемся для нахождения коэффициента к условием, что
в течение 20 сек скорость корабля падает с 15 до 12 м/сек. Инте-
Интегрируя в этих пределах уравнение A), имеем:
12 20
15
или
12
1
откуда
= 20/;,
Ii2 is; —2и/г
k = — 1/1200.
Переходим, далее, к определению пути, пройденного кораблем за
первые десять секунд. Для этого вначале находим интегрированием
из (I) скорость как функцию времени. Имеем:
-l--rC = kt. B) ^
Для определения произвольной постоянной интегрирования надо ^
воспользоваться начальными условиями движения: при ? = 0 скорость
v = vn. Внося эти значения переменных в B), находим:
Подставляя это значение в B), определяем величину скорости
1 - - vakt ¦
Для нахождения длины пути, пройденного кораблем за первые
десять секунд, воспользуемся зависимостью
Tt =v "l —v,,kt'
§ 2] СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 265
Отделяя переменные и интегрируя, находим:
I ~v0,
откуда
ю ю
с— С _J^l__ _ 1 (" </(! —togO
J I—«oft«~ A J 1— kvat •
о о
о
Следовательно,
10
s = —-r-ln A — kvut)
Подставляя значения всех величин, получим:
5= 1200 In A + 1/1200 • 15 ¦ 10) = 1200 In 9/8 «а 150 м.
Тогда угол циркуляции в радианах будет равен
о = s/R = 150/200 = 0,75.
Задача 3.34. Точка движется прямолинейно с ускорением
w = 6 угх м/сек*,
где х — координата точки. В момент времени tx = 2 сек координата
точки была .л:! = 27 м, а скорость раннялась т>1 = 27 м/сек.
Определить уравнение движения точки, а также зависимость скс-
рости и ускорения от времени.
Решение. Чтобы найти уравнение движения точки, представим
заданную зависимость ускорения от пути в виде
и умножим обе части уравнения па dx, чтобы отделить переменные
dx ¦ dv я/- - ,
dt =-bfxdx,
откуда
Инте1рируя, находим:
^ = |^/3-{-С,, A)
где Ci — произвольная постоянная интегрирования. Для ее определе-
определения подставим в уравнение A) значения vl = '27 м/сек при xl = '27 м.
Тогда из уравнения A) получаем С, = 0 и, следовательно,
B)
2f»f>
СНИЖЕНИЕ ТОЧКИ
(ГЛ. Ill
Используя зависимость v==dx/dt и умножая урапнепие B) па dt,
отделяем переменные
х
Интегрируя, находим:
3jcI/3 = 3M-C. C)
Произвольную постоянную интегрирования определяем, используя
t 2 = ?1 м. Подстанляя эти значения
в уравнение C), находим С3 = 3.
Уравнение движения точки по-
получим, подставил значение произ-
произвольной постоянной и C):
условие задачи: при tl = :
s
сек
Зависимость скорости от вре-
времени найдем, вычисляя производ-
производную по времени от х:
6)
К задаче 3.35.
Ускорение как функция вре-
времени определится как производ-
ная от скорости по времени:
w = 6 (t + 1).
Задача 3.35. Зависимость
пройденного пути от времени
определяется трапецией, представ-
представленной па графике.
Начертить график, представляющий зависимость величины скоро-
скорости от времени (si = s1).
Решение. В течение г.ремепи от 0 до tl точка движется равно-
равномерно со скоростью, равной по модулю
S!
Начиная с момента tt до t.x точка неподвижна, ее расстояние от
начала отсчета пути остается неизменным. Далее, от момента г2 до
ы< мента г3 точка движется равномерно в обратном направлении со
скоростью, равной по модулю
Искомая зависимость скорости от времени представлена на рис. б.
Задача 3.36. Зависимость величины скорости первой точки от
премепи изображается дугой полуокружности АМВ. Начальное и
2]
СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ
2С>7
конечное значения величины скорости равны v0. Время движе-
движения ty
Определить постоянную скорость с, которую надо сообщить
второй точке, чтобы она прошла тот же путь в то же время.
Решение. Первая точка прошла за время tx путь, равный пло-
площади, заключенной между по-
полуокружностью АМВ и отрез-
отрезком OD, так как
_ds
и, следовательно,
s = ^ vdt,
о
т
1
М t,
К задаче 3.36.
а этот определенный интеграл
и равен указанной площади.
Вычислим искомую площадь как площадь прямоугольника OABD
без площади полукруга:
A)
так как численные значения
С другой стороны, этот
же путь вторая точка должна
пройти за то же время, сле-
следовательно,
s = dv B)
Приравнивая оба значе-
значения пути A) и B), находим:
ТС 11 »
г»0 и
— у i>0
равны радиусу окружности.
откуда величина скорости
второй точки равна
к задаче 3.37.
Задача 3.37. Две точки
движутся по одной прямой
из одного и того же начального положения. Зависимость скорости
каждой точки от времени представлена на графике. Известны мо-
моменты времени tx и t^ (см. рисунок).
Определить время 7" от начала движения первой точки, по иае-
чении которого обе точки встретятся.
268
ДВИЖЕНИЕ ТОЧКИ
[ГЛ. III
Решение. Площадь треугольника ОАВ, численно равная пути,
пройденному первой точкой за время t, дается выражением
1де через а обозначен угол наклона прямой ОА к оси абсцисс. Пло-
Площадь треугольника 0{СВ, численно равная пути, пройденному второй
точкой за это же время t, выражается так:
-2O1B-CB = ~(t-tl){t — tl)tg^,
где через р обозначен угол наклона прямой О\С к оси абсцисс.
Точки встретятся в момент Т, когда их пути будут равны. Сле-
Следовательно, приравнивая площади треугольников, равные численно
пройденным путям, получаем:
С другой стороны, из графика следует равенство
Решаем совместно систему уравнений A) и B). Из уравнения B)
имеем:
_ti — tl
~~~t.r "¦¦
Подаавляя это значение в уравнение A) и сокращая обе части
равенства на tgp, после несложных преобразований находим:
Задача 3.38. На рис. а представлены зависимости величины ско-
pocin or времени для двух прямолинейно движущихся точек, вышед-
вышедших одновременно из одного
и того же места. Зависи-
Зависимость модуля скорости от
времени изображается на
графике для первой точки
прямой, проходящей через
начало координат, для вто-
второй точки — четвертью ск-
О
t,
ружпоаи.
Определить: 1) ускоре-
ускорение второй точки как функ-
функцию времени; 2) ускорение
nepnoil ючки, если известно, что первая точка догоняет вторую точку
и юг момент, когда последняя останавливается; 3) вычислить время ог
К задаче 3.38.
« 21 СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ 269
начала движения до момента, когда величины скоростей обеих точек
равны.
Считать известными v0 и tt.
Решение. Рассмотрим произвольное положение второй точки М,
которое она занимает в некоторый момент времени t (рис. б).
1. Отрезок MN рапеп модулю скорости второй точки уг, отре-
отрезок ON соответствует времени t; радиус ОМ равен, с одной стороны,
величине начальной скорости второй точки v0, а с другой — ире-
мени tlt когда вторая точка оста!!;]вливается. Тогда
v, . t
cosa= —, sina = ~.
Возводя эти дна равенства в квадрат и складывая, находим:
.Wo
"Г
х-1-
откуда модуль скорости второй точки в любой момент времени
равен
Проекция ускорения второй точки, движущейся прямолинейно, на
направление движения будет:
2. Вторая точка останавливается при г'3 = 0, т. е. при l = ti.
Путь, пройденный второй точкой, измеряется площадью четверти
круга
Путь, пройденный за это же время первой точкой, движущейся равно-
равноускоренно, равен
s
где wt — искомая величина ускорения первой точки. По условию,
пути, пройденные обеими точками к этому моменту tb равны, так
как первая точка догоняет в этот момент вторую точку. Следова-
Следовательно, 5! = 52 И
Отсюда определяется модуль ускорения первой точки
270 ДВИЖЕНИЕ ТОЧКИ (ГЛ. III
3. Величина скорости первой точки в любой момент времени t
равна
Величина скорости второй точки была найдена выше:
Приравнивая эти два значения модуля скорости, определяем тот
момент времени Т, когда неличины скоростей обеих точек одина-
одинаковы:
7С T//I -т- Т/Л 1 Г 1 О г-г-Л
После несложных преобразспанпй имеем окончательно:
7-= 2^
I'M-*2
Для приобретения навыков в решении задач на
определение скорости и ускорения точки рекомен-
рекомендуется решить следующие зада.чи из «Сборника задач
по теоретической механике» И. В. Мещерского, изда-
издания 1950 г. и более поздних лет: 322, 323, 325, 330, 341,
346, 352, 353, 363, 367, 370, 371, 372, 373, 374.
ГЛАВА IV
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
§ 1. Вращение твердого тела вокруг неподвижной оси
Простейшими движениями твердого тела являются поступатель-
поступательное движение и вращение твердого тела вокруг неподвижной оси.
Поступательным движением твердого тела называется такое движе-
движение, при котором любая прямая, проведенная в теле, остается во все
время движения параллельной своему первоначальному направлению.
Траектории точек при этом движении представляют собой одинако-
одинаковые кривые, которые могут быть получены одна из другой путем
параллельного смещения. При поступательном движении скорости и
ускорения всех точек твердого тела в данный момент геометрически
равны. Следовательно, при исследовании поступательного движения
твердого тела достаточно определить движение одной какой-либо
точки тела. Таким образом, задача о поступательном дииженип твер-
твердого тела сводится к задаче кинематики точки.
При вращении твердого тела вокруг неподвижной оси точки,
лежащие на оси вращения, неподвижны, остальные точки описывают
окружности с центрами, находящимися на оси вращения и с радиусами,
равными длине перпендикуляра, опущенного из точки на ось враще-
вращения. Эти окружности расположены в плоскостях, перпендикулярных
к оси вращения.
В данной главе мы рассмотрим вращение твердого тела вокруг
неподвижной оси и преобразование простейших диижеиий твердых
тел. При вращении твердого тела вокруг неподвижной оси криволи-
криволинейная координата любой точки, движущейся по окружности, являю-
являющейся ее траекторией, определяется формулой
« = *« + % A*)
где а — дуговая координата движущейся точки, а0 — начальное значе-
значение дуговой координаты, h — кратчайшее расстояние от точки до оси
вращения, <р — угол поворота твердого тела вокруг оси. Угол пово-
поворота связан со временем зависимостью
B*)
272
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
[ГЛ. IV
называемой уравнением вращения твердого тела вокруг неподвиж-
неподвижной оси. Угол ср называется угловым перемещением твердого тела,
вращающегося вокруг неподвижной оси за данный промежуток вре-
времени. Измеряется угол <? следующим образом: проводим неподвижную
плоскость N через ось вращения Oz и неподвижную прямую Ох,
подвижную плоскость М, жестко связанную с вращающимся телом,
проводим через ось вращения Oz и какую-либо точку твердого тела.
Тогда двугранный угол между этими плоскостями определяет пол-
полностью положение твердого тела (рис. 4.1). Линейный угол поворота ?
измеряется в радианах или в оборотах. Один оборот соответствует
1- радианам.
Угловая скорость твердого тела характеризует быстроту изме-
изменения угла поворота твердого тела. Угловая скорость — вектор, на-
направленный по оси вращения в ту сто-
сторону, с которой вращение видно проис-
происходящим против часовой стрелки (для
правой системы осей). Так, на рис. 4.1
вектор угловой скорости должен быть
направлен в положительном направлении
оси z, если угол <р увеличивается, и в от-
отрицательном направлении оси z, если
угол сэ уменьшается. Проекция угловой
скорости на ось вращения z равна произ-
производной от угла поворота по времени
. = - У =
C*)
Рис. 4.1.
При отсчете угла поворота и радианах
и измерении времени в секундах угловая
скорость измеряется в сек~1. В технике
угловую скорость часто определяют чис-
числом оборотов в минуту (п об/мин). Связь между этими единицами
измерения дается формулой
¦2г- -' "" --' D*)
-1
Для характеристики быстроты изменения угловой скорости во
времени служит угловое ускорение. Угловое ускорение — вектор,
совпадающий но направлению с вектором угловой скорости, если
вращение ускоренное, и направленный прямо противоположно угло-
угловой 'скорости, если вращение замедленное. Проекция углового уско-
ускорения па ось вращения рзвпа производной от проекции угловой
скорости по времени или второй производной от угла поворота по
времени;
dn>z dsa s~%\
§ 1| ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ 273
При отсчете угла поворота в радианах и измерении времени в секун-
секундах угловое ускорение измеряется в сек'"-.
Если угловая скорость юг постоянна, то вращение называется
равномерным и происходит по закону
<? = ?о -г 'V- F*)
Если угловое ускорение e.z — величина постоянная, то вращение
называется равнопеременным (равноускоренным или равпозамедленпым)
и происходит согласно уравнениям:
? = ?о + %г' + е-2-. (8*)
Если знаки u>z и в2 совпадают, то вращение равноускоренное, в про-
противном случае — равнозамедлешюе.
Проекция скорости точки твердого тела па касательную к окруж-
окружности, направленную в сторону возрастания дуговой координаты а,
дается пыражепнем
Скорость точки твердого тела определяется векторной формулой
« = ©Хл A0*)
где г — радиус-вектор, проведенный из любой точки, лежащей па оси
вращения, к рассматриваемой точке твердого тела.
Ускорение точки твердого тела складывается пз нормального
ускорения и касательного ускорения. Нормальное ускорение направ-
направлено от точки по перпендикуляру к оси вращения, в сторону этой
оси, а его модуль равен
И)„==-- = ш4Й. A1*)
Касательное ускорение направлено по касательной к траектории, а его
проекция на касательную раина
wx = d^ = ezh. A2*)
Модуль полного ускорения точки
w =]/а'л-|г-а'; = /г]/АиL-|-еч. A3*)
Здесь знак проекции у шг и гг можно опустить, так как шг = ± ">,
e.z = ± в и, следовательно, ш* = ш4, е| = е5.
Полное ускорение составляет угол а с перпендикуляром, опущен-
опущенным из точки на ось вращения, причем угол а отсчитывается от
ускорения точки к перпендикуляру (—90° =sCasg90°). При этом
tga== --=5. (Н*)
274 ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА [ГЛ. IV
Часто показывают направление вращения и направление углового
ускорения дуговыми стрелками w и е (рис. 4.2). Направление дуго-
дуговой стрелки ш показывает направление вращения и определяет направ-
направление скоростей всех точек твердого тела (рис. 4.2).
Если дуговые стрелки ш и е одного направления, то вращение
ускоренное, угловая скорость твердого тела возрастает. Если дуговые
стрелки ш и е противоположно направлены, то вращение замедленное,
угловая скорость твердого тела уменьшается. Направление е опреде-
определяет направление касательного ускорения точек твердого тела (рис. 4.2).
В этом параграфе решаются задачи на определение проекций
угловой скорости и углового ускорения твердого тела на ось враще-
вращения по заданному уравнению движения.
Эта задача сводится к дифференцирова-
дифференцированию угла поворота по времени. Обратная
задача — определение закона вращения
твердого тела вокруг неподвижной оси,
ес:ли известно его угловое ускорение или
угловая скорость. Эта задача решается
интегрированием и последующим опреде-
определением произвольных постоянных инте-
интегрирования но начальным условиям дви-
жения.
рис ^ 2 Зная угловую скорость и угловое ус-
ускорение твердого тела, можно определять
скорости и ускорения отдельных точек твердого тела, вращающе-
вращающегося вокруг неподвижной осн.
При решении задач на вращение- твердого тела
вокруг неподвижной оси рекомендуется придержи-
придерживаться такой последовательности действий.
Первый тип задач—дано уравнение вращения твердого тела,
требуется определить угловую скорость, угловое ускорение, скорость
и ускорение точки твердого тела:
' 1) выбираем систему координат так, чтобы одна из осей (для
определенности ось z) совпадала с осью вращения;
2) составляем уравнение вращения твердого тела (зависимость
угла поворота от времени);
3) дифференцируя по времени угол поворота, определяем проек-
проекцию угловой скорости на ось вращения;
4) вычисляя вторую производную от угла поворота но времени,
находим проекцию углового ускорения на ось вращения;
5) пользуясь выражением проекции угловой скорости на ось
вращения, вычисляем линейную скорость точки и ее нормальное
ускорение;
6) пользуясь выражением проекции углового ускорения на ось
вращения, определяем касательное ускорение точки;
§ 1] СРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НР.ПОДВИЖИОП ОСИ 275
7) по найденным нормальному и касательному ускорениям нахо-
находим полное ускорение точек но величине и направлению.
Второй тип задач — задано угловое ускорение или угловая
скорость твердого тела; требуется найти уравнение вращения, ско-
скорость и ускорение точки твердого тела:
1) интегрируя дифференциальное уравнение, определяющее проек-
проекцию углового ускорения па ось вращения; находим проекцию угловой
скорости; произвольную постоянную интегрирования определяем по
начальным данным;
2) интегрируя дифференциальное уравнение, определяющее проек-
проекцию углоной скорости па ось вращения, находим уравнение вращения
твердого тела; произвольная постоянная интегрирования определяется
по начальным данным;
3) пользуясь выражением проекции угловой скорости на ось
вращения, вычисляем величину скорости и нормального ускорения
точки;
4) определяем величину касательного ускорения точки, зная проек-
проекцию углового ускорения на ось вращения, и далее находим полное
ускорение точки.
Задача 4.1. Искусственный спутник Земли, запущенный в СССР
4 октября 1957 г., имел вначале период обращения 1 ч 36 мин.
Определить его среднюю частоту обращения. Во сколько раз
частота обращения спутника больше величины угловой скорости
Земли (при вращении ее вокруг собственной оси)?
Решение. Период обращения спутника — это время, за которое
он совершает один полный оборот по орбите. Это время равно
1 я 36 мин, или 96 мин.
Следсншелыю, радиус-вектор спутника делает
П = gg О б/MUH.
Выражаем величину этой частоты обращения в сск~х:
ш = ж% сек'х=тосек" = °-00 ] 09
Величина угловой скорости Земли при вращении вокруг собственной
оси соответствует 1 обороту за 24 часа, или
п, = ft об/яас = ^тад об/мин = j^0 об;мин.
Находим, далее, отношение величины частоты обращения сну шика
к угловой скорости Земли
и 24 ¦ 60 , _
276 ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА [ГЛ. IV
Спутник сделает 15 оборотов за сутки, в течение которых Земля
сделает один оборот вокруг своей оси.
Задача 4.2. Сохраняя условия предыдущей задачи, определить
скорость и ускорение искусственного спутника, считая его орбиту
круговой, высоту полета над поверхностью
Земли h = 970 км. Радиус Земли R — 6370 км.
Решение. Величина скорости спутника
определится по формуле
v = (h-\-R)u>,
где h-\-R — радиус описываемой спутником
окружности.
Итак,
К "задаче 4.2. ° = ^97° + 637°) Ш KMI"K = 8 кя1сеК-
Так как касательное ускорение спутника равно нулю (оо^ const),
то величина ускорения
w = wn = (h + R) ^ = (970 -1- 6370) ~ = 0,00874 км/сек* =
= 8,74 м\сек\
Ускорение направлено к центру Земли.
Задача 4.3. При пуске в ход трамвая пожатый выключает посте-
постепенно реостат, вследствие чего угловое ускорение ротора мотора
увеличивается пропорционально времени и его угловая скорость через
6 сек достигает пеличины 36л: сек'1.
Найти число оборотов, которое совершил ротор за это время.
Решение. Модуль углового ускорения е растет пропорционально
времени. Следовательно, обозначая неизвестный коэффициент пропор-
пропорциональности буквой k, имеем:
Умножая обе части равенства па dt и интегрируя, находим проекцию
угловой скорости ротора па ось вращения
В начальный момент при t^=0 шОг = О, так как ротор был непо-
неподвижен. Подставляя эти значения в уравнение A), находим, что С=0
и, следовательно,
С другой стороны, согласно условию при ? = 6 сек угловая скорость
достигла величины и^^Збтс сек'1. Используя это, из уравнения B)
§ 1| ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
определяем коэффициент k:
или
k ¦-= 2т..
Внося это значение в уравнение B), получаем, что
шг = тЛ'\
Учитывая, что шг = -? и интегрируя, находим:
277
C)
Но при ^ = 0 угол поворота неподвижного ротора был равен
нулю (о = 0). Следовательно, С,=0 и окончательно
тЛ* ...
?--=-3". D)
Для определения числа оборотов ротора за 6 сек полагаем в D)
t = 6 сек. Угол поворота в радианах
<Pi= -у-
следовательно, ротор за 6 сек сделал:
Ni = ^ == 36 оборотов.
Задача 4.4. В условиях предыдущей задачи определить скорость
и ускорение точки М обода ротора в момент времени /, = 3 сек.
Диаметр ротора с? = 20 см.
Ре ш спие. Величину угловой скоро-
скорости ротора в момент времени ti = 'i сек
находим, пользуясь формулой C) преды-
предыдущей задачи:
w, = "rf2=m-3- = 9- сек~\
Далее, модуль скорости точки обода бу-
деи
v=\v,_' = \шг\-а2-=9п- 10 = 90* см/сек.
Скорость точки обода направлена перпен-
дикулярпо к радиусу, в сторону вращения.
Величина нормального ускорения точки обода и этот момент
раина
к задаче 4.4.
= 810п- см/сек\
278 ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА [ГЛ. IV
Проекция ускорения этой точки на касательную будет:
wt = е2 ~ — ЧъГ % = 2Cht • 3 = 6'Отг см/сек*.
Величина полного ускорения точки определяется формулой
w = Yw\ -\- w\ — ЗОтс ^729яа -L 4 см/сек1.
Угол, составляемый полным ускорением точки с радиусом, нахо-
находится из уравнения
te а _ Ъ. — U. — 2?L = г- _ _2_ — о 0236
Эта задача может быть решена и другим способом. В предыду-
предыдущей задаче было найдено уравнение вращения ротора D)
Пользуясь формулой (I*) обзора теории, составляем уравнение дви-
движения точки обода ротора в естественной форме:
d Юл ,3
а=1?=т-' см-
Находим, далее, проекцию скорости точки обода на каса!ельную
к траектории, вычисляя производную от а по времени
vz = з = 10-f2 см/сек.
Величина скорости в момент времени tj = 3 сек будет:
т»т — 1 Отс • 9 — 90т: с м/с ек.
Определяем величину нормального ускорения в этот момент времени
у2 90 V „,„, , ,
W" = р" = 1^5rf==81 °Л см1сек'-
Проекция ускорения па касательную равна производной от vz по
времени
Следовательно, в момент времени ^ = 3 сек
w, = 60тс см'.сек*.
Величина полного ускорения определяется формулой
w = V w'ii -I- w\ = 30it ]/ 729za -J~ 4 r.v/c ека.
Угол наклона полного ускорения к радиусу, соединяющему точку
с осью вращения, находится из уравнения
дат 60л 2 _ _,,.,_
*S я = wn == 8Т0л^ = 27л = °'OiЖ
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
279
Первый способ решения является более удобным, так как опре-
определяет скорость и ускорение точки через угловую скорость и угло-
угловое ускорение, общие для исех точек тела.
Задача 4.5. При пуске в ход машины для кручения капроновой
нити шпиндель перетепа приобретает рабочую скорость, соответст-
соответствующую 15 000 o6JMiiH за 30 сек.
Считая угловое ускорение шпинделя во иремя пуска постоянным,
определить число оборотов шпинделя за иремя пуска. Найти ско-
скорость и ускорение точки па поверхности блочка
шпинделя при дальнейшем равномерном пращении,
если его диаметр равен 40 мм.
Решение. Величина угловой скорости шпин-
шпинделя во время пуска расгет пропорционально времени
и достигает значения 15 000 об1мин через 30 сек.
Определяем величину углового ускорения шпинделя
а 15 000.2;: 50 _„ . _,
ег=Т = -боТзо-=У1: = 52'4 сек ¦
Угол попорота шпинделя за время пуска опре-
определится по формуле (8*) при шо = О и <ро = О-'
е<2 50- • SO2
у = -гг =' .' ' — =7500л радиан.
Число оборотов за время пуска будет:
а 7500п г,-гп
^- = ——;=3/50 оборотов.
К задаче 4-5.
Модуль скорости точки на ободе блочка шпинделя (после достиже-
достижения рабочей скорости) равен
v = mr= 15 000|j-20 =10 000- мм/сек=\0х
к = 3\',4 м/сек.
Ускорение этой точки при дальнейшем равномерном вращении будет
состоять только из нормального ускорения, нсличипа которого най-
найдется по формуле
= wH = ^r = (^^f^ м/сек* = 5000,* м/сек*.
Это ускорение направлено но перпендикуляру, опущенному из точки
на ось вращения.
о
71—\Г
Л у
1—I
280 ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛЛ |ГЛ. IV
Задача 4-6- При подъеме лифта угловое ускорение барабана диа-
диаметром d=:0,8 ж, на который наматывается канат, поднимающий
. клеть, изменяется соглас-
сеп' по показанному на ри-
рисунке графику.
#м—i Определить наиболь-
„ . тую скорость подъема
¦iceit лифта, а также высоту
подъема за 20 сек.
Решение. Движе-
Движение лифта распадается па
К задаче 4.6. три этапа. В течение
первых двух секунд ба-
барабан, начиная движение из состояния покоя, вращается с постоян-
постоянным угловым ускорением. Следовательно, величина его угловой ско-
скорости равна
а угол поворота определяется по формуле
О = тг . A)
Полагая t = 1 сек, находим модуль угловой скорости в конце
первого этапа движения
и)[ = 0,4 • 2 = 0,8 сек-1
и величину скорости точки на поверхности барабана, равную модулю
скорости, с которой наматывается канат и поднимается лифт в этот
момент времени,
¦D]=UIr = 0,8-0,4 = 0,32 м/сек. B)
Это и будет наибольшая скорость подъем;), так как на втором, сле-
следующем, этапе угловое ускорение равно пулю, угловая скорость ба-
барабана остается неизменной и, следовательно, скорость подъема лифта
сохраняет свою величину.
Определим путь, пройденный лифтом и течение первых двух се-
секунд. Для этого находим из A) угол поворота барабана за это время
0 4 ¦ 22
и высоту подъема
На втором этапе величина скорости лифта постоянна и опреде-
определяется равенством B). Следовательно, высота подъема за этот этап
будет:
/z.j = ¦&,(?) —*,) = 0,32. 16 = 5,12 м.
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
2Я1
На третьем этапе вращение барабана происходит с постоянным
угловым замедлением. Следовательно, угол поворота будет равен
<р, = со, (t3 - /,) -
? =0,8-2— ^^ = 0,8 рад.
Теперь легко найти высоту подъема лифта на этом этапе:
/ij = ?, у =0,8- 0,4 = 0,32 л.
Таким образом, полная высота подъема лифта
h = /?! 4- /2S -f /г3 == 5,76 м.
Задача 4.7. Вал с присоединенными к нему пластинами вращается
в подшипниках согласно уравнению
где (р — угол поворота вала, а и ш0 — постоянные коэффициенты.
Определить углоиую скорость и угло-
угловое ускорение вала. Найти скорость и
ускорение центра пластины А, отстоящего
на расстоянии R от оси вращения.
Решение. Проекция угловон скоро-
скорости вала на ось вращения равна первой
производной от угла поворота по времени
ш, = —>¦
г (It
A)
Из этого равепстпа иидио, что в началь-
начальный момент при ? = 0 величина угло-
угловой скорости вала равнялась ш(|. Опре-
Определяем проекцию углового ускорения
вала на ось вращения как производную от угловой скорости по
времени
К задаче 4.7.
14-
или, сопоставляя B) и A),
Проекция углового ускорения отрицательна, проекция угловой ско-
скорости вала с течением времени неограниченно уменьшается.
282
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛЛ
1ГЛ. IV
Переходим к определению скорости и ускорения центра А пла-
пластины. Модуль скорости этой точки равен
v -=
Ускорение этой точки складывается из нормального и касательного
ускорений. Величина нормального ускорения
Проекция ускорения на касательную определяется формулой
Модуль полного ускорения
Угол а, составляемый ускорением точки с радиусом, соединяющим ее
с осью вращения, находится из уравнения
Направления скорости и ускорения центра пластины изображены
на рисунке. Отрицательное значение tga указывает па то, что угол a
откладывается а сторону, противополож-
противоположную направлению вращения твердого тела.
Задача 4.8. Ускорение любой точки
нала, вращающегося в подшипниках, со-
составляет постоянный угол 60° с перпен-
перпендикуляром, опущенным из этой точки на
ось вала. Начальное значение проекции
угловой скорости па ось z, направленной
по оси вала, равно — <о„, начальный угол
поворота вала равен нулю.
Определить касательное, нормальное н
полное ускорения точки вала, расстояние
которой от оси вращения г. Найти уран-
пение иращепия пала вокруг пеиодниж-
пой оси, а также зависимость величины
угловой скорости от угла поворота вала.
Решение. Угол а между ускорением точки и перпендикуляром,
опущенным из точки па есь вала, связан с проекцией углового
К задаче 4.8.
§ II ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ 283
ускорения и величиной угловой скорости соотношением
Подставляя значение tga, и учитывая, что tz=-~t имеем:
Переменные отделены. Интегрируя, находим:
V*t=-zr+c, C)
где С—произвольная постоянная интегрирования. Определяем се,
подставляя в равенство C) начальные условия: шг = —ш0 при ^ = 0,
откуда С= и, следовательно,
или
ш, -— ¦
Далее, из A) и D) определяем проекцию углового ускорения вала
па ось вращения
е2 = tg г, ш| = КЗ ^
Проекция ускорения точки, радиус вращения которой г, на на-
направление касательной определяется формулой
w. = тг, =
Модуль нормального ускорения этой точки
Тогда величина полного ускорения точки
w = V w% A- w% — 2ГШ11 = ¦
Для нахождения уравнения движения вала воспользуемся равен-
равенством D), записав его так:
284 ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛЛ [ГЛ. IV
Умножая обе части равенства E) на dt, отделяем переменные:
— ш„ dt
Интегрируя, имеем:
F)
Произвольная постоянная интегрирования С\ определяется путем
подстановки в уравнение F) начальных данных: при ^ = 0 <р = 0.
Эю дает Q=0. Следовательно,
_j/3~ln 1
3 1 i_,
Это и есть уравнение вращения вала.
Переходим к определению зависимости проекции угловой скоро-
скорости на ось вращения от угла поворота. Для этого умножим обе части
равенства B) па rf<p- Находим:
Интегрируя, имеем:
¦/3'<p = lnQu)z>
C,«)z = е^3 v.
или
Произвольную постоянную интегриро-
нания С-1 определяем, подставляя началь-
начальные данные: при ? = 0 ^^=0 и шг= — ш0.
Тогда С.,^ и окончательно находим:
Задача 4-9. Регулятор Уатта вращается
с постоянной угловой скоростью at во-
К задаче 4.9. круг вертикальной оси. Угол АСВ при
этом оказался равен 60°, а ускорение ша-
шаров Л и В равно но величине lOOg, где g = 980 см/сек2. Стержни
АС, ВС, AD и BD одинаковой длины /=10 см.
Сколько оборотов в минуту делает регулятор?
Решение. Для того чтобы найти величину угловой скорости
регулятора, напишем зависимость ускорения шаров от параметров
регулятора. Так как регулиор вращается с постоянной угловой ско-
скоростью, то ускорение шара будет нормальным ускорением, модуль
i 21
ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ
285
которого определяется формулой
wn = лш'2 == / sin 30°ш\
где г — кратчайшее расстояние шара до оси вращения.
С другой стороны, согласно условию
wn=--i00g.
Приравнивая эти два выражения нормального ускорения шара, на-
находим: ,
[ 10 ЮО-980
л[ 100? 1/ ЮО-980 . ,.-. _,
ш= I/ 1—-?.«-= I/ -г» »- •= 140 сек '.
У I sin 30 г 10 - 0,0
В технической системе единиц угловая скорость регулятора будет
равна
п = ш об)мин = —г.-р~ = 1340 об!мин.
Для приобретения навыков в решении задач па
вращение твердого тела вокруг неподвижной оси
рекомендуется решить следующие задачи из «Сбор-
пика задач н о теоретической механике* И. В. Мещер-
Мещерского, издания 1950 г. и более поздних лет: 375, 376, 382,
385, 386, 388, 390, 393.
§ 2. Преобразование простейших движений
Под преобразованием простерших движений следует понимать:
а) преобразование вращательного движения в поступательное (и обрат-
обратное преобразование), б) преобразование вращения вокруг одной не-
неподвижной оси во вра-
вращение вокруг другой не-
неподвижной оси и в) пре-
преобразование одного по-
пупателыюго движения
в другое поступательное
днижение. При решении
задач о движении меха- ^
пизмов, преобразующих Рис. 4.3.
простейшие движения,
следует пользоваться совместно формулами кинематики точки и фор-
формулами кинематики твердого тел;:, вращающегося вокруг неподвиж-
неподвижной оси.
Преобразование вращения одного твердого тела вокруг неподвиж-
неподвижной оси во вращение второго твердого тела вокруг другой неподвижной
оси осуществляется посредством зубчатого или фрикционного зацепле-
зацепления двух колес (рис. 4.3, а, б) или при помощи ременной передачи
(рис. 4.4, 4.5).
286
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
[ГЛ. IV
При внутреннем зацеплении (рис. 4.3, а) и нескрещивающейся
ременной передаче (рис. 4.4) направление вращений обоих колес сов-
совпадает. При внешнем зацеплении (рис. 4.3, б) и скрещивающейся
ременной передаче (рис. 4.5) направление вращения колес противо-
противоположно. Величины скоростей па ободе зубчатых колес, находящихся
в зацеплении, равны. Также равны по модулю скорости на ободе
шкивов ременной передачи,
если нет скольжения ремня по
шкиву. Угловые скорости ко-
колес обратно пропорциональны
числам зубцов или радиусам,
или диаметрам
Рис. 4-4. ша ft 2, rf,
В этой формуле u)j, о)а — мо-
дули- угловых скоростей, г1г
г.г — радиусы начальных окруж-
окружностей, db d,_ — диаметры на-
начальных окружностей, 2j, z.j —
числа зубцов первого и соот-
соответственно второго колеса.
Зубчатые колеса и ремен-
ременные передачи, изображенные на
рис. 4.3 — 4.5, представляют
примеры последовательного соединения колес и шкивов. При после-
последовательном соединении каждое из колес вращается вокруг своей не-
неподвижной оси.
Часто применяется параллельное соединение колес, когда два колеса
вращаются вокруг одной неподвижной оси. Если при эгом они жестко
соединены друг с другом, то их угловые скорости равны.
При решении задач на преобразование простей-
простейших движений рекомендуется такая последователь-
последовательность действий:
1) исходя из условия задачи, выписать уравнение движения или
другие кинематические соотношения для того тпердого тела, движение
которого известно;
2) пользуясь формулами кинематики точки и кинематики вращения
твердого тела вокруг неподвижной оси, паНти уравнение движения
другого твердого тела, которому передается движение, а также найти
скорости и ускорения различных точек этого твердого тела.
Задача 4.10. Зубчатое колесо / находится во внешнем зацеплении
с зубчатым колесом //. Первое колесо имеет диаметр Dj = 400 мм
и вращается с угловой скоростью 0^ = 1: сек'1 вокруг неподвижной
ОСИ Oj.
Рис. 4.5.
21
ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ
287
Определить угловую скорость второго колеса, если его диаметр
равен Dss = 320 мм и оно вращается вокруг неподвижной оси О*
Решение. В месте соприкосновения зубцов обоих колес скорости
точек первого и второго колес одинаковы. Обозначая величину этой
скорости v, имеем:
±
и, следовательно,
А
or
Пользуясь формулой A), находим:
D,
к-400
~320~
- = -г-7с сек
К задачи 4.10.
Так как колеса находятся во внешнем зацеплении, то их угловые
скорости направлены в противоположные стороны. Если колесо /
вращается против часовой стрелки, то ко-
колесо // вращается по часовой стрелке.
Задача 4.11. Зубчатое колесо / на-
находится во внутреннем зацеплении с
зубчатым колесом //. Радиус первого
колеса Г]=150 мм и оно делает п{ =
=-—1500 об/мин, вращаясь вокруг непо-
неподвижной оси О\.
Определить радиус второго колеса,
если оно должно вращаться вокруг не-
неподвижной оси Ог, делая пг = 4500 об/мин.
Решение. В месте соприкосновения
зубчатых колес скорости точек первого
и второго колес должны быть ранпы. Величина скорссти точки обода
колеса / равна
К задаче 4.11.
A)
Модуль скорости точки обода колеса // равен
30 -
Сопоставляя равенства A) и B), находим:
288
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
[ГЛ. IV
Так как величины угловых скоростей пропорциональны числам оборотов
в минуту, имеем:
1500
= 50 мм.
В рассматриваемом случае внутреннего зацепления оба зубчатых
колеса вращаются в одну сторону.
Задача 4.12. Зубчатое колесо /, радиус которого равен гь на-
находится во внешнем зацеплении с зубчатым колесом // радиуса г9.
Первое колесо вращается в дан-
данный момент с угловой скоро-
скоростью oij и угловым ускорением ?,.
Определить угловую скорость
и угловое ускорение второго ко-
колеса, а также нормальное уско-
ускорение находящихся в соприкосно-
соприкосновении точек колес.
Решение. При вращении
зубчатых колес, находящихся в
зацеплении, скорости точек со-
соприкосновения обоих колес долж-
должны быть равны п любой момент
времени. Для этого необходимо, чтобы были равны не только ско-
скорости этих точек, но и их касательные ускорения, ибо если в дан-
данный момент скорости этих точек равны, а касательные ускорения
не равны, то и следующий момент времени нарушится и равенство
скоростей точек соприкосновения. Из равенства модулей скоростей
вытекает соотношение
К задаче 4.12.
откуда
(О., = Ш. —- ,
A)
Угловая скорость второго колеса o.j при внешнем зацеплении
направлена в сторону, противоположную угловой скорости atj первого
колеса. Величины касательных ускорений точек соприкосновения обоих
колес будут:
\
Приравнивая эти значения, получаем:
что легко найти также непосредственно путем дифференцирования
соотношения A).
Угловое ускорение второго колеса е4 направлено в сторону, противо-
противоположную угловому ускорению с, первого колеса.
§21
ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ
289
Модули нормальных ускорений точек соприкосновения обоих
колес определяются формулами:
Нормальные ускорения этих точек не равны друг другу по величине
и направлены по одной прямой н разные стороны.
Задача 4.13. Для спуска груза М, привязанного к копну троса,
намотанного па барабан ///, вытягивают со скоростью л канат А,
намотанный па барабан 1. На одной оси с барабаном 1 радиуса тх
насажено зубчатое колесо / радиуса /?„ жестко скрепленное с ним.
Зубчатое колесо / сцеплено с зубчатым колесом 2 радиуса гъ которое
вращается как одно целое
вместе с зубчатым коле-
колесом // радиуса /?5. Послед-
Последнее сцеплено с зубчатым ко-
колесом 3 радиуса г3, вра-
вращающимся как одно целое
с барабаном /// радиуса Ry
Определить скорость, с
которой спускается груз М,
если оси всех зубчатых ко-
колес неподвижны.
Решени е. Модуль ско-
скорости точки на ободе бара-
барабана 1 радиуса г, равен ве- К задаче 4.13.
личине скорости точек ка-
каната v. Определим скорость точки па ободе зубчатого колеса / ра-
радиуса Rt. Модуль угловой скорости барабана 1 и зубчатого колеса /
равен
v
">¦ = — .
г,
Величина скорости точки па обеде зубчатого колеса /
Зубчатое колесо ,/ находится в сцеплении с зубчатым колесом 2
радиуса гь следовательно, скорости точек па ободе этих колес равны.
Определяем модуль угловой скорости зубчатых колес 2 и //
и, далее, находим величину скорости точки па ободе зубчатого колеса //
радиуса R%
10 М, И. Бать и др., х. I
290
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
[ГЛ. IV
Эт и есть одновременно модуль скорости точки на ободе зубчатого
колеса 3 радиуса г3, сцепленного с зубчатым колесом //.
Следовательно, величина угловой скорости зубчатого колеса 3
и барабана /// равна
щ
3~
Модуль скорости" точки на ободе барабана /// радиуса R3, равный
искомой величине скорости груза М, дается формулой
Задача 4.14. Для преобразования периодического возвратно-по-
сгуиателыюго прямолинейного движения во вращательное движение
в двигателях внутреннего сгора-
сгорания применяют плоский шатупио-
кривошиппый механизм, состоя-
состоящий из кривошипа ОА=г, вра-
вращающегося вокруг неподвижной
7Я77////Я>7Я77У///'//у ™ЧКИ О В ПЛОСКОСТИ рисунка.
К задачам 4.14, 4.15.
шатуна АВ = 1, шарнирно соеди-
соединенною с кривошипом, и порш-
поршня В, двигающегося по горизон-
1альным направляющим цилиндра, совпадающим с прямой ОВ, и шар-
шарнирно соединенного с шатуном АВ.
Полагая угловую скорость кривошипа ОА постоянной и равной оH,
определить уравнение движения и скорость поршня В. Найти скорость
поршня при <р, = 0, <p.2 = r/2, <р3 = тс.
Решение. Угол поворота кривошипа, вращающегося с постоян-
постоянной угловой скоростью %, равен
Опуская перпендикуляр из точки А на линию ОВ, находим уравне-
уравнение движения поршня В
cos
— r'1 sin
* = OD -\-DB = OA cos ? + У/'2 — AD1 = i
Для определения проекции скорости поршня В на ось х необходимо
вычислить производную от координаты поршня х по времени:
dx . , r2<o0 sin ш01 cos <oat
vDx = x = -т- = — гш0 sin ш„г " =
— r2 sirr1
1 -J sin (.)/
~ у p — r* sin* ь>й( J °
A)
Значение проекции скорости поршня при различных значениях
угла поворота кривошипа получаем, подставляя в A) соответствующие
ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ
291
величины:
при cpj = 0 и <р3 = к vD = О,
при <pQ = т/2 х = vBx = —гш0,
т. е. при (р.г = тг/2 скорость точки В равна по величине скорости
точки А; направления скоростей этих точек также совпадают.
Задача 4.15. В условиях предыдущей задачи определить ускоре-
ускорение поршня В как функцию времени, а также величину этого ускорении
в моменты, когда ^, = 0, <ра = ~/2, ср., —тс.
Решение. Поршень В движется прямолинейно, следовательно,
проекция его ускорения равна первой производной от проекция
скорости по времени
d Г . , . г sin 2<йЛ 1
WHr = Х= — Г<")„ -гг Sin (OJ -U —¦—- ° =
иВх-
= — ru)(j cos («„г1
г-<*1 Г 2 cos 2q
2 L]/"/2 —ra~sir
r- sin2
"Т I
2(/2— г2 sin2 VK/1J'
Тогда значения ускорения поршня при различных знамениях угла
поворота кривошипа будут:
при cpj = O wBx= — re
при <?.2 = т./2 ьоВх=--^
При <рз = 1
и>п* = f«l И г .
Задача 4.16. Для подъема груза Р служит электрическая лебедка,
состоящая из ведущего вала с на-
насаженной на нем шестеренкой
с числом зубцов 2]. Груз подни-
поднимается при вращении ведомого
вала с шестеренкой. Число зуб-
зубцов шестеренки г* При этом ка-
канат, на котором подвешен груз Р,
наматывается на барабан радиу-
радиусом R. Уравнение вращения ве-
ведущего вала имеет вид
К задаче 4.16.
Определить уравнение движе-
движения, скорость и ускорение гру-
за Р.
Решение. Пути, проходимые точками, расположенными на ободах
сцепленных зубчатых колес, равны, т. е.
to»
292 ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТГЛА [ГЛ. IV
Здесь через гь га обозначены радиусы I и II зубчатых колес, ?2 —
угол поворота ведомого вала. Из A) находим:
ибо радиусы колес пропорциональны длинам окружностей и, следо-
следовательно, пропорциональны числам зубцов. Далее, находим зависимость
пути, пройденного грузом, от времени (уравнение движения груза)
Проекция скорости груза па вертикаль определится как произ-
ноднан от координаты s2 по времени
Проекция ускорения груза, движущегося прямолинейно, на на-
направление движения равна производной от проекции скорости по
времени
Второй способ решения. Определяем проекцию угловой
скорости ведущего вала па ось вращения как. производную от угла
поворота по времени
Далее, находим величину угловой скорости ведомого вала, исходя из
равенства скоростей точек соприкосновения обоих колес
!?'. _ гл.
<о, г, '
откуда
Скорость груза равна по величине скорости точки на поверхно-
поверхности барабана
ю,= Кша = 4к/#-'-. B)
Ускорение груза, движунегося прямолинейно, равно по величине
касательному ускорению точки па поверхности барабана
г 21
ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ
293
Для определения уравнения днижения груза напишем уравнение B)
в виде
ds.
Умножая обе части равенства па dt, имеем:
ds-i = 4kR -'--1 dt.
Интегрируя в пределах от 0 до s.2 и от 0 до t, находим уравнение
движения груза М
г2
При втором способе решения определяются величина угловой ско-
скорости ведомого вала и значение его углового ускорения. Эти вели-
величины характеризуют движение ведомого вала и, как частный случай,
движение груза Р. Поэтому второй способ решения предпочтителен.
Задача 4.17. Редуктор скорости, предна-
предназначенный для изменения величины угловой ско-
скорости при передаче вращения от нала / к валу //,
состоит из четырех зубчатых колес, вращаю-
вращающихся вокруг неподвижных осей. Зубчатые ко-
колеса имеют следующее число зубцов: 2!= 12,
22 = 72, 23=l0- Вал // делает 100 об/мин,
а вал / должен делать 5400 об/мин.
Найти число зубцов четвертого зубчатого
колеса.
Решение. Величины угловых скоростей
первой пары зубчатых колес, сцепленных друг
с другом, относятся обратно пропорционально
числам зубцов:
— — -. A) К задаче 4.17.
Аналогичное равенство можно написать и для второй пары колес,
находящихся в зацеплении:
_-
B)
Колеса 2 и 3 жестко закреплены на общем валу, следовательно,
их угловые скорости равны ша = @3. Перемножая равенства A) и B),
находим:
«i2a*
294 простейшие движения твердого тела [гл. iv
Отношение модулей угловых скоростей равно отношению чисел обо-
роюв в минуту. Подставляя известные данные в C), получаем:
5400 _ 72 г,
00 ~ 12- 10 '
отсюда следует, что четвертая шестерня имеет 90 зубцов.
Задача 4.18. Ведущий вал фрикционной передачи / вращается с
носюянпсй угловой скоростью, делая 300 об/мин, и одновременно
передвигается в направлении стрелки н
"*р обратно согласно уравнению
ша / <* = D + 3 cos 2*0 ел,
V77?\
где время дано в секундах. Радиусы
колес: г = 5 см, R. = 20 см.
Определить: 1) угловое ускорение
вала // как функцию времени и 2) уско-
ускорение точки на ободе колеса // в мо-
моменты времени г, = 0; ^ = 0,25 сек;
13 = 0,5 сек.
К задаче 4.18. Решение. Скорости точек сопри-
соприкосновения обоих колес равны между
собой, так как колесо / фрикционной передачи катится без сколь-
скольжения по колесу //. Так как величина углоиой скорости ведущего
вала
то модуль скорости точки обода колеса /, соприкасающейся с коле-
колесом //,
v — гш0 == 5 • 1 Огс = 50гс -ем)сек. B)
Величина скорости такой же точки, но принадлежащей колесу //,
равна
v = md, C)
где со — модуль угловой скорости колеса //. Приравнивая значения
B) и C), находим величину угловой скорости колеса II
50л 50л ,
U3 = -T=4 + 3coS2r7tceK~1' D)
Проекция углового ускорения колеса // равна производной от
проекции угловой скорости по времени (считаем, что ось z направ-
направлена в сторону <а)
tf<o 300nJ sin 2nt 300л2 sin 2nt ,
** = -dF = T> = -{4 + зШЩ5-сек ' E)
9 2] ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ 295
Переходим к определению ускорения точки на ободе второго ко-
колеса в различные моменты времени. Сначала находим для каждого
момента времени величины: ш, е. Пользуясь формулами A), D), (о),
имеем:
при ^ = 0 ш, = —-сек1, ?i = 0,
при ^., = 0,2о сек @, = —— сек \ й, = —.-сек \
при ^3 = 0,5 сек со3 = 50т: сек'1, ?3 =0.
Далее, определяем величину ускорения точки на ободе колеса II
по формуле
w=R /e'2-j-со4.
Подставляя значения R, ?, со для каждого момента времени, находим:
при t1 = 0 Wi = ^к— к* «=; 10 000 см/сек* = 100 м/сек1,
при ^ = 0,25 сек wt^= б^^б^ + бгб'2 см/сек'1 = Ш м/сек\
при ^а = 0,5 сек о)я = 50 000л4яа495 000 слД-<?к9 = 4950 л/«
Задача 4.19. При пуске в ход кулачок начинает вращаться из
состояния покоя вокруг неподвижной оси О с постоянным угловым
ускорением ? = 0,1 г сек'"'. Достигнув угловой скорости, соответству-
соответствующей 40 ofiJMiiH, кулачок далее
вращается равномерно. Уравнение
контура кулачка имеет вид
(архимедова спираль). Стержень А
кулачкового механизма движется в К задаче 4 19.
неподвижных направляющих В, как
показано на рисунке, удерживаясь в соприкосновении с контуром
кулачка при помощи пружины.
Определить скорость стержня и время, в течение которого про-
продолжался пуск в ход. Найти ускорение стержня.
Решение. Угол поворота кулачка при пуске равен
B)
Расстояние между центром кулачка и стержнем равно
г = (~ ¦ 0,05rcf2 + 2(А см. C)
296 ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛЛ [ТЛ. IV
Стержень движется прямолинейно, следовательно, проекция его
скорости на ось х равна производной от координаты г по времени
vx = r~2-\,5t = 3t см/сек. D)
Проекция ускорения стержня, движущегося прямолинейно, равна
производной от проекции скорости по времени
wx = vx = 3 см/сек0-. E)
По условию, достигнув угловой скорости, соответствующем 40 об/мин,
кулачок далее вращается ргппомерпо. Модуль угловой скорости по-
последующего равномерного вращения кулачка
(о, = 40 |[ = А* сек\ (б)
Дифференцируя по времени A), находим проекцию скорости движе-
движения стержня па ось х
30 . 30 30 4 ,_ , ._.
vx, = r = -<t= --<!>! = - — ^ = 40 см1 сек. G)
Пуск в ход продолжается до тех пор, пока скорость D) не ста-
станет равной vxl. Приравнивая эти два значения скорости, определяем
время пуска в ход Т
3 7=40 или 7=13,33 сек. (8)
Время пуска в ход можно определить и другим способом. Про-
Проекция угловой скорости кулачка при пуске в ход определяется как
производная от угла поворота B) по времени
со. = 6 = 0,1^. (9)
Для определения времени пуска Т приравняем значение проекции
угловой скорости (9) ее значению (б). Тогда
0,1тг7"=у*: или 7=13,33 сек.
Задача 4.20. Круговой поступательно движущийся кулачок пере-
передвигается согласно уравнению (рис. а)
х = a cos шг,
где координата х отсчитывается по горизонтали от точки Ot (рис. б),
а, <» — постоянные коэффициенты, t — время.
Определить уравнение движения и скорость стержня.
Решение. Вводя угол <?, как указано на рис. б, находим ко-
координату нижней точки стержня (рис. б)
у— г sin ср. A)
«21
ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ
297
С другой стороны, расстояние от центра кулачка до начала коорди-
координат О1 равно
х = г cos <р = a cos utf,
откуда
cos ср = — cos at,
и, следовательно, sin у = У\ — cos'3 ср = l/ I — i -
///////////////У/У/Ш'///////////.
a)
К задаче 4.20.
Л
Подставляя это значение в уравнение A), находим искомое уравнение
движения стержня:
Проекция скорости стержня определится как производная от ко-
координаты у по времени
Задача 4.21. При подъеме груза А лебедкой закон движения
груза определяется формулой
= --(l —cos о),
A)
где h — полная высота подъема, угол ср изменяется пропорционально
времени
При подъеме груза канат наматывается на барабан В, вращающийся
вокруг неподвижной оси О.
Определить скорость и ускорение точки на ободе барабана (ра-
(радиуса R), смысл постоянной а0, полное время подъема груза, а также
298 ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА [ГЛ. IV
моменты времени, когда угловая скорость и угловое ускорение бара-
барабана достигают наибольших и наименьших значений.
Решение. Величина скорости точки на ободе барабана равна
модулю скорости подъема груза. Проекция скорости груза равна про-
производной от координаты у по времени
или, с учетом B),
r vy = y=y -l-suiv.
У Проекция у
r-flV
Проекция угловой скорости барабана равна
К задаче 4.21. Ш* R R \ 2 Sln ^ ^ '
Переходим к. определению углового ускорения барабана. Имеем:
?г := U>z = -j: COS tp.
Модуль угловой скорости, как это следует из формулы D),
достигает наибольшей величины, когда
sin cpi ==t I,
и, следовательно,
?J==-J-{-«'. D)
где п = 0, 1, 2, 3, 4, ... Подставляя в D) значение <р из B), находим
моменты времени, соответствующие наибольшим значениям модуля
угловой скорости,
Эги же моменты времени соответствуют обращению углового уско-
ускорения барабана в нуль, т. е. наименьшим значениям модуля углового
ускорения.
Наименьшее значение модуль угловой скорости получает при
sin срз==О
и, следовательно, при
<?i = пъ, E)
где я = 0, 1, 2, 3, 4, ... Подставляя в E) значение угла B), находим
моменты времени, соответствующие наименьшим значениям модуля
« 21 ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ 299
угловой скорости,
Эти же моменты времени отвечают наибольшим значениям модуля
углового ускорения.
Величина нормального ускорения точки на ободе барабана раина
Л f-ч Цл/2 . Q
wn = m ^ — 7?sm ?•
Проекция ускорения этой точки на касательную равна
п\ = e2R = а0 cos 9.
Эта формула определяет одновременно и проекцию ускорения груза
на ось у. Следовательно, постоянная а0 есть наибольшее значение
ускорения груза. Полное ускорение точки на ободе равно но вели-
величине
W = Vwk + w* = аЧ У 4Л5 Si" * V + C0S" Ч ¦
Направление ускорения составляет с радиусом угол а, определяемый
уравнением
t _Д>т__ Ч_ 2Rcosf
* wn ш2 h sin2 <p '
Полное время подъема 7" определится из равенства A), если
вместо у подставить h, а вместо <р его значение B):
откуда
Для приобретения навыков в решении задач на
преобразование простейших движений рекомен-
рекомендуется решить следующие задачи из «Сборника задач
по теоретической механике» И. В. Мещерского, изда-
издания 1950 г. и более поздних лет: 397, 399, 401, 403, 407,
408, 409, 411, 415.
ГЛАВА V
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 1. Абсолютное, переносное и относительное движения точки
Рассмотрим движение точки но отношению к системе подвижных
осей коордшш хь уь zt (рис. 5.1), которые в свою очередь дви-
движутся относи юлыю осей л-, у, z. Систему осей х, у, г условно
будем считать неподвижной.
Движение точки относительно неподвижных осей координат
называется абсолютным движением. Движение точки но отношению
к подвижным осям координат хи y[s Zi называется относительным
движением. Переносным называется
движение относительно неподвижной
системы осей х, у, z той точки под-
подвижной системы осей хь _у„ гь с ко-
которой в данный момент совпадает
движущаяся точка.
Наблюдатель, связанный с систе-
системой подвижных осей х{, уь zh ви-
видит относительное движение точки.
Наблюдатель, связанный с системой
неподвижных осей х, у, z, видит
абсолютное движение точки.
Величины, относящиеся к абсо-
абсолютному движению точки, будем
снабжать индексом а, к относительному — индексом г, к переносному —
индексом е (например, vr — скорость точки в относительном движении,
we — ускорение и переносном движении и т. д.).
Поясним понятия абсолютист, относительного и переносного дпи-
жеппй па примере. Диск вращается равномерно с угловой скоро-
скоростью о вокруг оси, перпендикулярной к плоскости диска и прохо-
проходящей через его центр О. По диаметру АВ диска с постоянной по
величине скоростью движется точка М (рис. 5.2).
Выберем неподвижную, абсолютную систему координат с центром
в неподвижной точке О п обозначим ее Оху. Подвижную, отпоси-
Рпс. 5.1.
§ 21
СЛОЖЕНИЕ ДВИЖЕНИЙ. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ
301
тельную систему координат выбираем с центром в неподвижной точке
диска О, ось Охх направляем по диаметру АВ, ось Оу\ в плоскости
диска — перпендикулярно к оси Ох,. Система координат Ох,у, жестко
связана с диском и, следовательно, вращается вместе с ним против
часовой стрелки с постоянной угловой скоростью <а.
Относительным движением точки М в данном примере является
прямолинейное и равномерное движение этой точки по диаметру АВ,
т. е. по оси Oxv Переносным движением точки М является вращение
лместе с диском той точки диска, с которой в данный момент совпадает
точка М. Абсолютное движение точки М есть движение по отношению
к неподвижной системе координат
Оху. Оно складывается из относитель-
относительного движения вдоль оси OxY и из
вращения точки М вместе с диском.
В рассматриваемом примере и в
других аналогичных случаях мы,
кроме представления о переносном
движении точки, встречаемся с поня-
понятием переносного движения твер-
твердого тела, в данном случае диска,
по отношению к которому точка М
совершает относительное движение.
Пользуясь определением перенос-
переносного и относительного движений,
а также рассмотренным выше при-
примером, можно указать на следую-
следующий метод изучения этих движений. Желая изучить относительное
движение точки, следует мысленно остановить переносное движение
и изучать движение далее по законам и правилам абсолютного дви-
движения точки. Если необходимо изучить переносное движение точки,
то следует мысленно остановить относительное движение и рассма-
рассматривать далее движение точки но формулам кинематики ючки в абсо-
абсолютном движении. Если точка участвует одновременно в относитель-
относительном и переносном движениях, то ее абсолютное движение называют
сложным движением точки, а ее относительное и переносное движения
называются составляющими движениями.
§ 2. Сложение движений. Определение траекторий и уравнении
движения в относительном и абсолютном движениях точки
Уравнения движения точки М в относительном движении опре-
определяются формулами
*i=/i@, Ух=Ш, *,=/,(*), A*)
где хъ У\, 2, — координаты движущейся точки М в относительной
системе координат O^X\y^zx (рис. 5.1).
Рис. 5.2.
302 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
Зависимость между г — радиусом-вектором точки М (рис. 5.1)
в абсолютной системе координат, г, — радиусом-вектором той же
точки в относительной системе координат и г0 —радиусом-вектором
начала подвижной, относительной системы координат дается фор-
формулами
r = rQi+rv B*)
где
г = xi-\-yj -\-zk, C*)
rol=xoti^yoj+zolk> D*)
r, = xiii -~yji -j- zxkv E*)
х — xQi -f- a,*, -- oyj, -!- а3г„
У =Уо, -lr ?ixi "Г Pitt "Г Рзг-i.
г TiVi -I- Тз-г-i-
В этих формулах х, у, г — абсолютные координаты точки М;
xQ , yQ , zQ — координаты точки О{ начала относительной системы
координат но отношению к системе Оху.
Формулы B*) или C*) определяют уравнения абсолютного дви-
движения точки М в векторном виде.
Формула E*) дает векторное уравнение движения точки в отно-
относительном движении.
Уравнения абсолютного движения точки находятся из B*) с уче-
учетом C*), D*) и E*) проектированием на оси Oxyz или по формулам
аналитической геометрии, связывающим координаты точки М в двух
системах координат — абсолютной и относительной:
(б*)
В этих формулах аг, р,-, т( — соответственно косинусы углов между
осями абсолютной и относительной систем координат; так, например,
a.t = cos (х, _у,), Та = cos (z, zt) и т. д.
В формулах F*) координаты xQ , yQ , zQ , а также углы между
осями абсолютной и относительной систем координат известны как
функции времени, если задано переносное движение; относительные
координаты хь yt, Z\ определяются как функции времени уравне-
уравнениями A*).
Уравнения переносного движения имеют тог же вид, что и равен-
равенства F*), только под xh yu Zi в этом случае следует подразумевать
три числа, определяющих фиксированные координаты точки М в дан-
данный момент времени. В конкретных задачах уравнения абсолютного
и относительного движений точки могут быть получены и из более
простых, геометрических соображений.
Уравнения A*) определяют относительную траекторию точки М
в параметрическом виде. Для определения относительной траектории
§ 2| СЛОЖЕНИЕ ДВИЖЕНИЙ. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ 308
точки М в координатной форме необходимо исключить время из
системы уравнений A*).
Уравнения F*) определяют абсолютную траекторию точки в пара-
параметрическом виде, так как координаты xQ , yQ , zQ и xit уь г,, так
же как и направляющие косинусы а;, р,-, f,-, являются функциями
независимого параметра — времени. Для определения абсолютной
траектории точки М в координатной форме надо исключить из урав-
уравнений F*) время.
Уравнения абсолютного движения точки F*) упрощаются, если
переносное движение является плоским и относительное движение
происходит п той же плоскости. Обозначая через а угол между
положительными направлениями осей х и хь можно записать уран-
нения F*), выражающие зависимость между абсолютными и относи-
относительными координатами точки, и виде
х = хо, + •*• cos а — ->'i sin а>
y=yQi-\-x: sin а-|-_У] COS а.
Если, кроме того, переносное плоское движение является посту-
поступательным, то можно выбрать относительную систему координат так,
чтобы оси х и хь у и _yi были параллельны. Тогда уравнения G*)
принимают вид (
х = хо, + *i. У =У01 +JV (8*)
Если переносное движение является вращением вокруг неподвиж-
неподвижной оси и относительное движение точки происходит в плоскости
перпендикулярной к оси вращения, то, совмещая начало относитель-
относительной системы координат с осью вращения и ось z с осью гъ находим
уравнения абсолютного движения из G*)
jc = jcjcosa—j,', sin a, у = х{ sin a -\-yt cos a. (9*)
В некоторых задачах более простые решения получаются при
пользовании другими системами координат: полярными, сферическими,
цилиндрическими и т. д.
Задачи, относящиеся к данному параграфу, делят-
делятся на два типа.
1. Известны относительное и переносное движения точки. Тре-
Требуется определить уравнения абсолютного движения и абсолютную
траекторию точки.
2. Известны абсолютное и переносное движения точки. Требуется
определить уравнение относительного движения и относительную
траекторию точки.
Первая задача сводится к сложению двух составляющих дви-
движений точки. Вторая задача заключается в разложении известного
804 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
абсолютного движения на заданное переносное движение и неизвестное,
подлежащее определению, относительное движение.
Рекомендуется такая последовательность дей-
действий при решении задач.
А. Заданы относительное и переносное движения;
требуется определить абсолютное движение:
1) раскладываем абсолютное движение точки па два составных
движения, переносное и относительное;
2) выбираем две системы координат, абсолютную, условно при-
принимаемую неподвижной, и относительную;
3) составляем уравнения относительного движения точки;
4) пользуясь одним из видов уравнений F*) — (9*), составляем
уравнения абсолютного движения точки;
5) исключая время из уравнений абсолютного движения точки,
находим уравнения абсолютной траектории точки в явном ииде.
Б. Заданы абсолютное и переносное движения; тре-
требуется определить относительное движение:
1) раскладываем абсолютное движение точки на два движения,
переносное и относительное;
2) выбираем абсолютную, условно неподвижную систему коорди-
наг и относительную систему осей;
3) составляем уравнения абсолютного движения точки;
4) пользуясь одним из видов уравнений F*) — (9*), находим
уравнения относительного движения точки;
5) исключая время из уравнений относительного движения точки,
находим уравнения относительной траектории точки в явном виде.
Задача 6.1. Судно плывет вниз по течению реки. Скорость те-
течения реки 2 м/сек. Скорость судна по отношению к неподвижной
иоде 10 м/сек.
Составить уравнения относительного и абсолюшого движений
судна.
Р е ш е и и е. Выберем начало относительной и абсолютной систем
координат в той точке, где находилось судно в начальный момент
времени. Течение воды примем за переносное движение. Относитель-
Относительная система координат составляет одно целое с движущейся во-
водой, следовательно, она участвует в переносном движении со ско-
скоростью 2 м/сек. Чтобы составить уравнение относительного движе-
движения судна, остановим мысленно течение реки. Тогда легко получить
уравнение относительного днижепия
Абсолютное движение судна — эго движение по отношению
к берегу, к системе координат, жестко связанной с землей. Уравне-
i:.ie абсолютного движения в данном случае будет;
§ 2|
СЛОЖЕНИЕ ДВИЖЕНИЙ. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ
305
где хч— абсцисса начала относительной системы координат по отно-
отношению к неподвижному берегу. Зависимость абсциссы лг.2 от времени
определяется равенством
Х, = 2Г,
следовательно, уравнение абсолютного движения судна имеет вид
х= l0i-\-2t=l2t.
Задача 5.2. Кривошип ОА вращается равномерно н плоскости
рисунка вокруг неподвижной точки О согласно уравнению <p = kt.
Длины крипошипа и шатуна равны: ОА = АВ = г. Ползун В дви-
движется в направляющих вдоль оси Ох.
К ползуну жестко прикреплен паз, дви-
движущийся вместе с ползуном поступа-
поступательно, как одно твердое тело. Внутри
паза движется точка М так, что рас-
расстояние O\M = rsmkt. Расстояние
О,В — а.
Полагая движение точки М по от-
отношению к пазу относительным, опре-
определить уравнения относительного и аб-
абсолютного движений точки М, а также
ее абсолютную траекторию.
Решение. Выбрав относительные
оси координат О^,)/] с центром в
точке О( так, как это показано па рисунке, находим уравнения относи-
юльиого днижения точки М:
xi = 0, у, = г sin kt.
Переносным движением будет являться поступательное перед-
передние точки вместе с пазом. Уравнения абсолютного движения т
можно получить из системы (8*), так как переносное да>'
является плоским, поступательным движением. Следовг
пения абсолютного движения имеют вид
где х0, у0 — текущие координаты -'
системы координат.
Определим координаты
так как ОЛ = АВ.
Xq = О A
К задаче 5.2.
Таким образом,
306
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
|ГЛ. V
Для определения траектории абсолютного движения из этих уран-
нений исключаем время. Имеем:
х — а
2
= г cos kt,
= r sin kt.
Возводим каждое из этих уравнений в квадрат и, складывая, находим
уравнение траектории
' х — <
~2Г
Это — уравнение эллипса, ось симметрии которого параллельна оси Оу
и находится на расстоянии а от начала координат О.
Задача 5.3. Поворотный кран вращается вокруг оси, перпенди-
перпендикулярной к плоскости рисунка и проходящей через точку О
в)
К задаче 5.3.
иной угловой скоростью: <? = kt. По стреле крана, совпа-
осью Охь передвигается тележка М с грузом согласно
-', =а cos kt, yt = 0 (рис. а).
уравнения абсолютного движения тележки М и ее
"округ оси с постоянной угловой
чижение. Прямолинейное дви-
оиваем как относительное
точки М в абсолютной
теме координат Ох^у^
определяется форму-
«21 СЛОЖЕНИЕ ДВИЖЕНИЙ. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИИ
В нашей задаче
xt == a cos kt,
307
Подставляя эти значения в уравнения A), находим уравнения абсо-
абсолютного движения точки М в декартовой системе координат:
х = a cos2 Id,
у =а cos kt sin kt.
Уравнение траектории абсолютного движения точки проще всего
получить в полярной системе координат:
г =
^у1— a cos kt,
откуда
г — a cos ср.
Это —уравнение окружности диаметра а, проходящей через начало
координат О (рис. б).
Время, в течение которого точка М совершает полное колебание
по стреле Охь как видно из условия задачи, равно
~ 2к
= т-
Найдем время Ть в течение которого точка М опишет в абсо-
абсолютном движении окружность диаметра а (рис. в). Так как /,М0,х =
= 2<? = 2kt, как внешний угол треугольника OOtM, равный сумме
двух углов треугольника, не смеж-
смежных с ним, то угол поворота ра-
радиуса OtM равен '2kt и, следова-
следовательно, искомое время
Таким образом, за время одною
полного колебания груза по стреле
он опишет в абсолютном движении
дважды окружность диаметра а.
Задача 5.4. Лента для записи К задаче fvi.
показаний пера самописца М дви-
движется поступательно, параллельно оси х, с постоянной скоростью я,.
Перо самописца М вращается вокруг точки О на расстоянии ОМ = г,
описывая окружность. Скорость пера постоянна по величине и
равна v.
Определить траекторию, вычерчиваемую пером на ленте.
308
СЛОЖНОЕ ДВИЖЕНИИ ТОЧКИ
[ГЛ. V
Решение. Выберем оси координат с началом в центре окруж-
окружности О и направим ось х в сторону движения ленты, ось у пер-
перпендикулярно к ее скорости.
Абсолютное движение пера самописца М является движением но
окружности радиуса г с постоянной по величине скоростью v. Раз-
Разложим это движение на два составных движения: переносное посту-
поступательное прямолинейное движение вместе с лентой и относительное
движение пера по отношению к ленте. Обозначим относительные
координаты пера через хь j»j и абсолютные координаты через х, у.
Координаты начала относительной системы координат точки О, назо-
назовем х0 , у0 . Согласно уравнениям (8*) зависимость между этими
координатами имеет вид
x = xOl-Tx\> У=У01-гУ\- 0)
Обозначая угол, составленный радиусом ОМ с осью .v, буквой у,
находим:
х = г cos 'f> У = r sin <?¦
Так как ду.га AM = r<p=vt, то угол <р определяется по формуле
Далее, находим координаты начала относительной системы координат
xr
У01
= 0.
Подставляя найденные значения координат в уравнения A), имеем:
Г cos a = vt -- <f -;- xlt
г sin to=yi.
Таким образом, параметрическое уравнение относительной траекто-
траектории пера самописца, т. е. уравнение кривой, которая вычерчивается
на ленте, является уравнением цик-
циклоиды:
X, = Г COS <f — Uj — <р,
= r sin ср.
К задаче 5.5.
Задача 5.5. Кривошип ОА ша-
тунпо-кривошипиого механизма вра-
вращается вокруг оси, перпендикуляр-
перпендикулярной к плоскости рисунка и прохо-
проходящей через точку О, с постоянной
угловой скоростью; угол <р^и>0/.
Длина кривошипа г, длина шатуна АВ = 1. Ползун В движется в на-
направляющих по прямой, проходящей через точку О.
Определить уравнение относительного движения ползуна В по
отношению к системе координат х^уь начало которой совпадает
СЛОЖЕНИЕ ДВИЖЕНИЙ- ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ
309
с точкой соединения кривошипа и шатуна и которая перемещается
поступательно.
Решение. Относительное движение шатуна АВ является враще-
вращением вокруг оси, перпендикулярной к плоскости рисунка и проходя-
проходящей через точку А. Положение шатуна в этом движении определяется
углом <•)— /_ xtAB = l_ ABO. По теореме синусов имеем:
откуда
sin у sin if '
= arcsin i— sin
Это — уравнение относительного движения шатуна АВ.
Чтобы получить уравнения относительного движения ползуна В,
достаточно выразить его относительные координаты х1г ух через най-
найденный угол ф:
— I cos <]; = / у 1 — ^-sin\t,
— — I sin <]j = — r sin u)of.
Таким образом, в данной задаче сложное движение шатуна АВ
разложено на два простых врашате.чьных движения: переносное дви-
движение — вращение с постоянной угловой скоростью <«0 вокруг центра О
неподвижных осей Оху и относительное движение — неравномерное
вращение шатуна вокруг центра Л
подвижной системы координат xt \>i-
Задача 5.6. Точка М движется
с постоянной скоростью vr вдоль
диаметра АВ диска, причем в на-
начальный момент точка находилась
в центре диска О. Диск одновре-
одновременно вращается с постоянной угло-
угловой скоростью ш вокруг оси, пер-
перпендикулярной к рисунку и прохо-
проходящей через центр диска. В началь-
начальный момент диаметр АВ совпадал
с осью Ох.
Определить абсолютную траек-
траекторию точки М.
Решение. Вращение диска с постоянной угловой скоростью
принимаем за переносное движение. Движение точки М по диаметру
диска АВ рассматриваем как относительное движение. Эту задачу
проще всего решить, применив полярную систему координат: радиус-
вектор 0М = г, определяющий расстояние точки М от полюса О, и
К задаче 5.6.
310
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
|ГЛ. V
угол y=i_xGxb определяющий угол поворота радиуса-вектора
вокруг точки О. Имеем:
JCl = Г = Vrt, Ф = u>t.
Для нахождения искомой траектории определяем из последнего
уравнения время
У/
и подставляем это значение в первое уравнение
vr
Г = — V.
ш т
Это есть уравнение архимедовой спирали в полярной системе коор-
координат.
Задача 5.7. Точка М совершает гармоническое колебательнсе
движение согласно уравнениям
х = 0, y = acos(kt + $). (I)
Экран осциллографа, на котором записывается движение точки М,
перемещается влево с постоянной
скоростью ve
Определить траекторию, опи-
описываемую точкой М на экране
(рис. а).
Решение. Точка М участ-
участвует в сложном движении. Абсо-
Абсолютным или результирующим дви-
движением будет прямолинейное гар-
гармоническое колебательное дви-
движение точки М по отношению
к неподвижной системе коорди-
координат Оху, определяемое уравне-
уравнениями A). С другой стороны, раз-
разложим мысленно абсолютное дви-
6) жение точки М на относительное
О
У,
\
\
°\
У
м
1
а)
К л i
К задаче 5 7.
движение по отношению к экрану
и переносное движение вместо
с экраном. Зависимость между координатами точки М в абсолютном
и относительном движениях будет:
где х0 , у0 — координаты точки Olt начала относительной системы
координат, xit уу — искомые координаты точки М в относительном
движении. Далее,
§3] СЛОЖЕНИЕ СКОРОСТЕЙ 811
Из A) и B) находим:
0 = —V-r-*,, acos^ + S^O+j/,
и, далее,
л:, = vet, yt = a cos (kt -f- P)-
Исключив из этой системы уравнений время, получим уравнение
относительной траектории точки М
Это уравнение синусоиды. Обозначим длину волны этой синусоиды
(рис. б) через /. Тогда время одного полного колебания (период)
будет:
т — 1—2Л
1 ~ve~ k '
Таким образом, частота колебаний k точки М связана с длиной
волны на экране соотношением
— I •
Для приобретения навыков в решении задач на
определение траекторий и уравнений движения в от-
относительном и абсолютном движениях точки реко-
рекомендуется решить следующие задачи из «Сборника
задач по теоретической механике» И. В. Мещерского,
издания 1950 г. и более поздних лет: 417, 418, 419, 422,
423, 425.
§ 3. Сложение скоростей. Определение скорости точки
в относительном, переносном и абсолютном движениях
Зависимость между абсолютной, относительной и переносной ско-
скоростями точки, совершающей сложное (составное) движение, опреде-
определяется теоремой сложения скоростей, согласно которой абсолютная
скорость равна геометрической суаие переносной и относительной
скоростей
чз =^ ч} —— ч} (\*Л
а е | г \ г
Для определения относительной скорости точки следует мысленно
остановить переносное движение и вычислить относительную скорость
по правилам кинематики точки.
Для определения переносной скорости точки достаточно мысленно
остановить относительное движение и искать переносную скорость по
правилам кинематики точки как скорость той точки перемещающейся
312
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
[ГЛ. V
Рис. 5.3.
системы координат, с которой совпадает в данный момент движу-
движущаяся точка.
Теорема сложения скоростей (рис. 5.3) позволяет решать задачи
такого рода:
1. Известны две стороны треугольника скоростей по величине и
направлению, соответствующие, например, абсолютной и переносной
скоростям точки; требуется определить третью сторону треугольника,
соответствующую относительной ско-
скорости точки.
2. Известна одна сторона тре-
треугольника по величине и направле-
направлению, соответствующая, например,
абсолютной скорости точки, а также
направления двух других сторон.
Определить величины переносной и
относительной скоростей.
Решение этих задач может быть
получено графически, построением
замкнутого треугольника скоростей
(рис. 5.3, а) или параллелограмма
скоростей (рис. 5.3, б). При обходе
треугольника скоростей стрелки, определяющие направление относи-
относительной и переносной скоростей, идут в одном направлении, стрелка,
определяющая направление абсолютной скорости, — в противопо-
противоположном.
Решение задач, таким образом, сводится к построению треуголь-
треугольника или параллелограмма скоростей и определению элементов, сто-
сторон и углов этих геометрических фигур. Это определение может быть
сделано или тригонометрическим путем, или проектированием геоме-
геометрического равенства A*) на декартовы оси координат.
При применении метода проекций надлежит выбрать оси коорди-
координат и спроектировать равенство A*) на эти оси. Тогда зависимости
между проекциями абсолютной, относительной и переносной скоро-
скоростей определяются формулами:
B*)
C*)
Величина абсолютной скорости находится по ее проекциям
Направление абсолютной скорости определяется направляющими
косинусами
cos (va?x) = v™-, cos (* ЛО = Vavy-. D*)
§3] СЛОЖЕНИЕ СКОРОСТЕЙ 3 I 3
При решении задач рекомендуется такая последо-
последовательность действий:
1) разложить движение на составляющие, определив абсолютное,
относительное и переносное движения;
2) выбрать дне системы координат: абсолютную и подвижную;
3) мысленно остановив переносное движение, найти скорость от-
относительного движения точки;
4) мысленно отвлекаясь от относительного движения, найти ско-
скорость переносного движения точки;
5) применим теорему сложения скоростей, определить иском}ю
абсолютную скорость точки.
Если абсолютная скорость известна, то можно, пользуясь теоре-
теоремой сложения скоростей, найти искомую относительную или перенос-
переносную скорость точки.
Задача 5-8. Две подводные лодки нлынут друг за другом in
расстоянии s одна от другой с одинаковой скоростью v. Звук лока-
локатора, установленного на задней лодке А, настигает впереди плыву-
плывущую лодку в точке В\ и, отразившись, возвращается на экран лока-
локатора в точке А\.
а) 6) 6)
К задаче 5.8.
Определить время от выхода звука из А до возвращения его в Аи
если скорость распространения звука в воде с.
Решение. Первый способ. Разложим абсолютное движение
звука со скоростью с па переносное движение вместе с передней
лодкой и на относительное движение по отношению к передней лодке.
Переносная скорость painia скорости первой лодкн v, так как под-
подвижная система координат связана с первой лодкой и движется по-
поступательно.
При распространении звука от задней лодки к передней относи-
относительная скорость звука (рис. а)
С этой относительной скоростью звук проходит относительное
расстояние s, отделяющее лодки, за некоторое время t{. Следова-
Следовательно,
5. A)
31 4 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
В обратном направлении, от передней лодки к задней, звук имеет
относительную скорость (рис. б)
vr, = с -}- v,
так как в этом случае абсолютная скорость звука с направлена
вправо, а переносная скорость задней лодки v — влево. Звук прохо-
проходит относительное расстояние s между лодками зд некоторое время Л>.
Следовательно,
(c-t-v)U = s. B)
Определяя из A) время tt и из B) время tb складываем их н
находим искомое премя от г.ыхода звука до его возвращения
t — t -¦ t — s ' s — 2sc
ч , ч c_v i ?_!_„ сч_v% ¦
Второй способ. Обозначим через tt время, в течение которого
звук проходит расстояние АВ{ (рис. в). Тогда расстояние
AB1 = ctl, C)
так как звук проходит этот путь с постоянной скоростью с. С другой
стороны, это же расстояние равно начальному расстоянию между
лодками АВ плюс расстояние ВВЬ которое прошла передняя лодка
за время ^ со скоростью v, т. е.
ABl = s-\-vtl. D)
Приравиявая C) и D), находим:
и = ^. E)
Обозначим через t.i время, в течение которого звук проходит рас-
расстояние B\Ai, отразившись от передней лодки. Это расстояние
так как звук прошел это расстояние с постоянной скоростью с за
время t3. С другой стороны, это расстояние
51Л1 = АВ{ — AA1 = s-\- vti — v {U -f r2), G)
ибо AA\ — это путь, пройденный задней лодкой с постоянной ско-
скоростью 1) за время (tt -\- ?2). Сопоставляя равенства F) и G), полу-
получаем, что
t,= s + ot'—vVi+t*)
' С
Искомое время от выхода звука из А до возвращения его в At равно
сумме времен tt и U_
t—/i --]-- r.j = -2 —. («)
СЛОЖЕНИЕ СКОРОСТЕЙ
315
Подставляя в это уравнение значение tt, определяемое из E),
t— s
1— c — v '
и решая затем (8) относительно искомой неизвестной t, после неслож-
несложных преобразований находим, что
Как видно, первый способ, основанный па теореме сложения скоро-
скоростей, проще и быстрее ведет к пели.
Задача 6.9. При запуске искусственного спутника Земли ему
необходимо сообщить вблизи поверхности Земли абсолютную гори-
горизонтальную скорость 8 км/сек.
Определить наименьшую и наибольшую относительные горизон-
горизонтальные скорости, которые необходимо сообщить спутнику, если
запуск производится на экваторе; на ши-
широте 60°; на Северном полюсе. Радиус
Земли # = 6400 км.
Решение. Спутник до начала полета
вращается вместе с Землей как одно тело.
Движение спутника вместе с Землей при-
принимаем за переносное движение.
Движение спутника по отношению к
Земле рассматриваем как относительное
движение.
Тогда абсолютная скорость спутника
будет:
"° == 1>е 4~ *>/¦• К задаче 5.9.
Обозначая широту места запуска углом «, получим для определения
наибольшей относительной скорости равенство
= V. —
где
ve = R cos <pше.
0)
Запуск спутника в этом случае производится в направлении с востока
на запад, в сторону, противоположную вращению Земли.
Наименьшая относительная скорость спутника найдется из ра-
равенства
v=vr-\-ve>
где ve также определяется формулой A). В этом случае запуск про-
производится в направлении с запада на восток, в сторону вращения
Земли.
316 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
При запуске спутника у поверхности Земли на экваторе угол
<р = 0 и, следовательно,
vCi == G400 • 3 /24 • 2гс/3600 = 0,405 км/сек.
Наибольшая и наименьшая относительные скорости спутника опре-
определятся из равенства
v = vr±vei
или
8 = vrdz 0,465,-
откуда максимальная относительная скорость
vr = 8,465 км/сек,
а минимальная относительная скорость
ti,. = 7,535 км/сек.
При запуске спутника па широте 60° переносная скорость спут-
спутника, равная скорости точки, находящейся у поверхности Земли,
будет:
vei — R cos 60°ш, = 0,233 км\сек,
и, следовательно, наибольшая и наименьшая относительные скорости
спутника определятся из равенства
8 = г/, ±0,233,
откуда
г>, max = 8,233 км/сек,
ъг min = 7,767 км/сек.
При запуске спутника па Северном или Южном полюсах переносная
скорость равна нулю, так как эти точки земной поверхности распо-
расположены па оси вращения, п, следовательно,
v — Ч!г = 8 км!сек.
Задача 5.10. Кривошип ОА = г вращается в плоскости чертежа
вокруг неподвижной точки О согласно уравнению <? = kt. Ползун А
при этом перемещается в наклонной кулисе В, которая может пере-
передвигаться поступательно вдоль осп Ох. Угол наклона кулисы к оси Ох
равен а.
Составить уравнения абсолютного и относительного движений
точки А, а также найти абсолютную, относительную и переносную
скорости точки.
Решение. Первый способ. Абсолютное движение ползуна
А — вращение вокруг неподвижного центра О. Относительное дви-
движение — прямолинейное движение ползуна вдоль кулисы, определяемое
СЛОЖЕНИЕ СКОРОСТЕЙ
317
переменным расстоянием OiA = -q. Переносное дпижепие — поступа-
поступательное перемещение точки Л вместе с кулисой.
Уравнения абсолютного движения точки А имеют вид
x = rcoskt, y = rsinkt. A)
С другой стороны, обозначая расстояние OOi^xc, имеем:
X = хе -j- "Ц cos а, у = т) sin а. B)
Решая совместно уравнения A) и B), после несложных преобразова-
преобразований находим:
xe = r cos kt — r sin kt ctg a.
C)
D)
Урапнение C) является уравнением относительного движения точки А.
Уравнение D), с точностью до постоянной величины, является уравне-
уравнением переносного движения, ]ак как последнее является поступатель-
поступательным движением.
К задаче 5.10.
Определим, далее, абсолютную скорость точки А. Так как проек-
проекции скорости
vx = \- = —rk sin kt, vy =y = rk cos kt,
то модуль абсолютной скорости
а направляющие косинусы имеют вид
cos (v, x) = — = — sin kt, cos (v, y)="- = cos kt. E)
Из E) видно, что абсолютная скорость точки Л перпендикулярна
к кривошипу ОА.
318 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
Проекция относительной скорости точки А на направление OtA
равна производной от относительной координаты по времени
, cos kt
rri ' Sin»
так как относительное движение является прямолинейным. Проекция
переносной скорости точки А на ось х
vex = i, = — rk sin kt — rk cos kt ctg я,
так как переносное движение является поступательным и, следова-
следовательно, скорости всех точек кулисы одинаковы.
Второй способ. Находим величину угловой скорости криво-
кривошипа ОА
Величина абсолютной скорости точки А как конца кривошипа,
вращающегося вокруг неподвижного центра О,
Направлена эта скорость перпендикулярно к кривошипу. Относитель-
Относительная скорость точки А направлена вдоль прямой ОгА. Переносная ско-
скорость точки А параллельна оси Ох. Строим параллелограмм скоро-
скоростей (рис. б). Откладываем вектор, равный абсолютной скорости
точки А. На этом отрезке, как на диагонали, строим параллелограмм
скоростей, проводя липни, параллельные относительной и переносной
скоростям, величины которых неизвестны. Эти величины определяются
как стороны параллелограмма.
По теореме синусов имеем:
V Vr Ve
sin a cos kt cos (kt — a) '
Отсюда находим модуль относительной скорости
, cos kt
Vr = rk —: .
r sm a
Проекция переносной скорости на ось х будет:
vex — — гк (sin kt-\- cos kt ctg я).
Второй способ решения быстрее и проще ведет к цели, если тре-
требуется определить только скорости в абсолютном, переносном и от-
относительном движениях. Если же необходимо, кроме этих скоростей,
найти и уравнения абсолютного, переносного и относительного дви-
движений, то целесообразно применить первый способ решения.
Задача 5.11. Точка М скользит по наклонной плоскости АВ
призмы с относительной скоростью, модуль которой равен
СЛОЖЕНИЕ СКОРОСТЕЙ
319
где g—постоянный коэффициент,^— ордината точки, отсчитываемая
по вертикали вниз от высшей точки призмы. В начальный момент
точка М находилась в А (рис. а). Призма перемещается но горизон-
горизонтальному полу с постоянной скоростью ve вправо.
Определить абсолютную траекторию точки М, ее абсолютную
скорость в момент касания пола, если AC^h.
Решение. Выбираем абсолютные оси координат с началом в
точке А, ось Ах горизонтальна, ось Ау направим по вертикали вниз.
Движение призмы ABC принимаем за переносное движение. Дви-
Движение точки М по отношению к призме — за относительное движе-
движение. Строим на заданных переносной и относительной скоростях
А х м
о)
К задаче 5.11.
точки М параллелограмм, диагональ которого является абсолютной
скоростью точки М (рис. б). Используя чертеж, найдем проекции
абсолютной скорости на декартовы оси координат:
iix = ve -у- vr cos a, vy = vr sin я.
Подставив в эти уравнения значения vn vx = dx/dt и vy = dyjdt,
перепишем их так:
—г- = "Ve -\- v '^g V cos a, A)
-/. =V 2gy sin a. B)
dt
Разделив A) на B), получим:
dx = ,—e ~ -}- ctg я dy.
l/2g.sm<* Vy
C)
Интегрируя C) в пределах от 0 до х слева и от 0 до у справа
(так как движение начинается из начала координат), будем иметь:
|/2?Sina '
ИЛИ
2о|
(х sin я —у cos о.) = —у.
320 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
Это и есть уравнение траектории. Траектория — парабола с вер-
вертикальной осью симметрии и с вершиной в точке А, так как каса-
касательная к ней в точке А горизонтальна (vy в начале движения рав-
равнялась нулю). Величину абсолютной скорости в момент, когда точка
касается пола, находим из A) и B), учитывая, что в этот момент y = h:
Направление скорости определится в этот момент углом р, кото-
который она составляет с горизонталью
ctg р = ^ = ctg а-|- ^
l/L2gh sin а '
Задача 6.12. Штурман, находящийся на мое гике морского грузо-
грузового транспорта, идущего на северо-восток со скоростью 16 узлов,
определил величину и направление относительной скорости другого
судна. Эта относительная скорость
оказалась равной 16]^ 2 узлам и на-
направлена на запад.
Определить величину и направ-
направление абсолютной скорости второго
судна, т. е. ею скорость относи-
относительно Земли.
Узел — единица скорости, равная
одной морской миле в час, а мор-
К задаче 5.12. екая миля равна 1852 м. Суда рас-
рассматривать как точки.
Р е ш е и и е. Движение второго судна будем рассматривать как
сложное. Примем за абсолютное движение второго судна его движе-
движение по отношению к Земле. Относительным дпижением второго судна
будем считать его движение но отношению к грузовому транспорту.
За переносное движение второго судна примем движение той точки
подвижной среды, жестко связанной с грузовым транспортом, через
которую в данный момент проходит второе судно. Заметим, что пере-
переносное движение является при этом поступательным движением вместе
с грузовым транспортом.
По условию задачи известны: относительная скорость второго
судна, направленная па запад: vr= 16]/ 2 узлов, переносная скорость
при поступательном движении, равная скорости грузового транспорта
г/г=16 узлам, направленная на северо-восток. Согласно теореме
сложения скоростей
Для графического нахождения абсолютной скорости второго судна
построим треугольник скоростей (см. рисунок). Для этого отложим
из произвольной точки А переносную скорость <ое, направленную
§3|
СЛОЖЕНИЕ СКОРОСТЕЙ
321
на северо-восток, а из конца переносной скорости под углом в 45°
на запад откладываем отрезок, равный vr. Замыкающая сторона тре-
треугольника будет абсолютной скоростью.
Модуль абсолютной скорости определится но теореме косинусов
va = V v\ -\- V} — "ivevr cos (ve, vr) = 16 узлов.
Чтобы найти угол а, определяющий направление абсолютной ско-
скорости, замечаем, что va = ve, следовательно, треугольник скоростей
равнобедренный и угол я. = 90°.
Таким образом, абсолютная скорость направлена на северо-запад.
Задача 5.13. При определении скорости судна относительно воды
производят пробег судна вдоль специально оборудованной мерной
К задаче 5.13.
прямой линии в дпух взаимно противоположных направлениях. При
этом время пробега в одном направлении оказалось ранным 9 мин
20 сек, а время пробега п Обратном направлении 11 мин 10 сек.
Длина мерной линии 5=3 морские мили.
Определить величину скорости судна относительно поды vr, по-
полагая, что в районе испытаний имеется неизвестное, по постоянное
по величине и направлению течение.
11 М. И. Вать и др., т. I
322 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
Решение. Будем рассматривать движение судна как сложнее;
За абсолютное движение судна примем его движение по отношению
к Земле. Скорость va этого движения не известна ни по величине,
ни но направлению. За относительное диижение судна примем его
диижение по отношению к г-.оде. Относительная скорость <vr известна
по направлению (она направлена по мерной линии), неизвестна попе-
личине, по при обоих пробегах величина относительной скорости не-
неизменна. За переносное диижение судна примем движение судна по те-
течению имеете с водной массой. Переносная скорость <ое будет равна
скорости течения, величина и направление которого постоянны, г.о
неизвестны.
Запишем теорему сложения скоростей
•Da = ve-\-vr 0)
Умножим это векторное равенство на th время первого npo6eia,
получим
Проектируя последнее равенство на напранлепие мерной линии s,
получим (см. рис.):
S = ?,,/,+ t,?,,f, cos 3, B)
где неизвестный угол между течением и мерной линией обозначен
буквой р.
Применим аналогичный прием ко второму пробегу. Умножая век-
векторное равенство A) на tb время второго пробе! а, получим:
Проектируя это векторное равенство на направление мерной ли-
линии s, найдем:
5 — vr4.2 — veitt cos p. C)
Учитывая, что vri=vri и vei =vei но условию, перепишем уравне-
уравнения B) и C) в виде
S=vrtx-\-veti cos p,
S—Vfti — vJti, cos p.
Решив эту систему уравнений, исключим vc cos J3 и найдем иско-
искомую величину скорости судна по отношению к иоде
Если в этой формуле расстояние ? дано в милях, а иремя t
в секундах, то размерность г\ будет миля/сек. Так как скорость
судна принято измерять в з^злах, г. е. и морских милях с час, то для
СЛОЖЕНИЕ СКОРОСТЕЙ
323
перевода в узлы пало умножить правую часть D) па 3600, т. с. на
количество секунд в часе. Итак,
vr = —Ц~—-- 3600 узлов.
Подставляя числовые данные /j = 9 мин 20
= 11 мин 10 сек = 870 сек, находим:
— о№ сек, tt =
3C60 + 670; „,,„„ ,__
*'= 2.-ЖГ670 3600=17''
Задача 5.14. Судно идет на восток со скоростью 12 узлов, при
этом флюгер па мачте показывает южный ветер. Судно изменило
курс и идет на север с прежней по величине скоростью, флюгер
теперь показывает западный ветер.
/V
W-A-\
о w о
I
5
б)
К задаче 5.14.
Определить величину и направление скорости ветра по отноше-
отношению к Земле, считая скорость L.erpa постоянной.
Примечание. Наименование курса указывает, куда идет судно,
наименование вотра указывает, откуда ветер дуег.
Решение. Рассмотрим движение ветра как сложное движение.
За абсолютное движение ветра примем его движение по отношению
к Земле. Относительным движением ветра будем считать его движе-
движение по отношению к движущемуся судну. За переносное движение
ветра примем его движение вместе с движущимся судном. Абсолют-
Абсолютная скорость ветра не известна ни по величине, ни но направлению.
Относительная скорость vr ветра известна только по направлению
для двух моментов времени. Переносная скорость <ve ветра, ранная
скорости движущегося судна, известна по величине и направлению
для тех же моментов времени.
Согласно теореме сложения скоростей имеем:
11*
324 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
Следовательно, при первом курсе судна теорема сложения скоростей
для ветра запишется так:
•Dal=Vel-{-Vrl. 0)
Выполним построение, соответствующее правой части уравнения A).
Отложим известный вектор vei и из его конца проведем направление
вектора vr\ (рис. а).
Напишем теорему сложения скоростей для петра при втором
курсе судна:
^«¦2 — Vel "Г vri-
Построение правой части этого равенства дано на рис. б. Совместим,
далее, оба рисунка. Другими словами, выполним оба построения сразу
из одной точки Л.
Тогда начало нектора vn совпадает с точкой Л, а пересечемте
направлений vr[ и <vr, определит конец вектора va (рис. в). Согласно
условию абсолютная скорость ветра постоянна, т. е. г>„, = ©а2. Это
учтено при построении рис. в. Из нос [роения находим, что ветер
юго-западный. Его скорость равна
va = 12 У 2 узлов = 12 У'! I— м\сек ^ 8,73 я [сек.
Для приобретения навыков в решении задач па
сложение скоростей рекомендуется реши т ь следу ю-
IH и с задачи из «Сборника задач по теоретической
механике» И. В. Мещерского, издания 1950 г. и более
поздних лет: 427, 428, 429, 431, 435, 43о\ 441.
§ 4. Сложение ускорений
1°. Определение ускорении точки при переносном
поступательном и произвольном переносном движе-
движениях. Зависимость между ускорениями точки в абсолютном, относи-
относительном и переносном движениях определяется теоремой, сложения
ускорений, иначе называемой теоремой Кориолиса,
Wa = VOe-\- Wr -г- Wc. A*)
Согласно этой теореме абсолютное ускорение точки wa равно гео-
геометрической сумме переносного ускорения we, относительного уско-
ускорения wr и кориолисова ускорения wc.
Для определения относительного ускорения точки следует мысленно
отвлечься от переносного движения и вычислить относительное уско-
ускорение по правилам кинематики точки. Для определения переносного
ускорения следует мысленно остановить относительное движение точки
и вычислить переносное ускорение по правилам кинематики точки
§ 4] сложение ускорений 325
как ускорение той точки подвижной системы координат, с которой
совпадает в данным момент движущаяся точка.
Кориолисово (или поворотное) ускорение вычисляется по формуле
wc = 2ые X Vn С2*)
где о)е'—вектор угловой скорости переносного движения, vr — вектор
опюсителыюй скорости точки. Величина кориолисова ускорения равна
0V = 2cvj, sin (<Ae,vr). C*)
Направление кориолисова ускорения определяется по правилу
векторного произиедеипя: кориолисово ускорение wc направлено пер-
перпендикулярно к плоскости, в которой лежат <ае и vr, в ту сторону,
чтобы наблюдатель, стоящий по вектору wc, видел поворот от век-
вектора сое к вектору vr на наименьший угол против часовой стрелки.
Наряду с определением направления ускорения Кориолпса как век-
векторного произведения (ле X ^V существует и применяется для нахож-
нахождения направления этого ускорения правило Н. Е. Жуковского: спроек-
спроектируем относительную скорость vr на плоскость, перпендикулярную
к угловой скорости о),,, и повернем проекцию в этой плоскости
на угол 90° и сторону вращения определяемого ьле — это и будет
направление ускорения Кориолиса.
Если траектории точек подвижной системы координат не прямо-
прямолинейны и относительное движение точки также является криволи-
криволинейным, то целесообразно вычислять переносное ускорение как гео-
геометрическую сумму нормального и касательного переносных ускорений,
относительное ускорение как геометрическую сумму нормального
и касательного относительных ускорений. При этом формула (I*) за-
записывается в следующем виде:
Щ, = Wen -Г We.: -f Wrn -[- Wr,_ -|- Wc, D*)
|де wen, wrn — соответственно нормальные ускорения и переносном
и относительном движениях, atp,, wr, — соответственно касательные
ускорения и переносном и относительном движениях.
При пользовании теоремой сложения ускорений может быть при-
применен метод проекций. Выбирая неподвижную систему координат xyz
и проектируя равенство D*) па каждую из этих осей, находим:
= и\,пх -- we,x -'r wrnx -,- wrzx --wc
t&rnU~\~'®nV ^'CV> IP )
При этом модуль абсолютною ускорения определяется по формуле
326 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
а направляющие косинусы р.шш
cos («С*) = ^, cos цСу) = %?, cos@) = ^. G*)
Необходимо заметить, что в случае переносного поступательного
движения угловая скорость этого движения <ае paisira нулю и согласно
формуле B*) обращается в пуль и кориолисоно ускорение. Теорема
сложения ускорений при переносном поступательном движении упро-
упрощаете:!:
wa = we-\ да,. (8*)
Из формул B*) и C*) следует, чю ускорение Кориолиса обра-
обращается также в пуль, если угловая скорость переносного движения
параллельна относительней скорости.
Кориолисово ускорение обращается в нуль и в те моменты,
когда ые или vr равны нулю.
Пользуясь теоремой сложения ускорений, м о ж и о
решать следую щ и с типы зада ч:
1. Известно относительное ;) переносное движения точки. Необ-
Необходимо определить абсолютное ускорение точки.
2. Известно абсолютное и переносное движения точки. Необхо-
Необходимо определить относительное ускорение точки.
В первом случае, пользуясь уравнениями относительного движении,
следует определить но правилам кинематики точки относительную
скорость и относительное ускорение точки. Независимо от этого,
исходя из уравнений переносного движения, следует найти перенос-
переносную скорость и переносное ускорение точки. Далее, зная угловую
скорость переносного движения и относительную скорость точки,
можно вычислить корнолисово ускорение по величине и направлению.
После этого абсолютное ускорение может быть определено гео-
геометрически, как замыкающая сторона многоугольника, построенного
па векторах переносного, относительного и кориолисова ускорений.
Можно поступить и иначе, используя упомянутый метод проекций.
Для этого достаточно спроектировать геометрическое равенство A*)
па три взаимно перпендикулярные оси координат, найдя тем самым
проекции абсолютного ускорения на эти оси, согласно формулам E*),
п, далее, определить величину и направление абсолютного ускорения
по формулам F*) и G*).
При решении задач рекомендуется такая после-
последовательность действий. Необходимо:
1) разложить движение па составляющие, определив абсолютное,
относительное и переносное движения;
2) выбрать две системы координат: абсолютную и подвижную;
3) мысленно остановив переносное движение, определить скорость
и ускорение точки в относительном движении;
§ 11
СЛОЖЕНИЕ УСКОРР.НИЙ
327
4) мысленно отилекаясь от относительного движения, найти угло-
угловую скорость переносного движения и ускорение точки в переносном
движении;
5) по известным угловой скорости переносного движения и ско-
скорости точки в относительном движении найти кориолисоио ускоре-
ускорение точки;
6) пользуясь методом проекций, определить проекции абсолют-
абсолютного ускорения на осп координат;
7) но найденным проекциям абсолютного ускорения найти иско-
искомое абсолютное ускорение по величине и направлению.
Задача 5.15. Цилиндр вращается с постоянной угловой скоро-
скоростью <а(|. По поверхности цилиндра движется точка М согласно
уравнениям
Xi = 3 cos 2xt, j/[ = 3 sin '2~t,
г, = Ъи A)
Оси координат хь yb zt жестко свя-
связаны с цилиндром и, следовательно,
вращаются вместе с ним с угловой ско-
скоростью (де. Ось 2[ совпадает с осью
симметрии. Проекция переносной угло-
угловой скорости на ось zt равна ")<>2l =
= 2 сек~\
Определить абсолютную скорость и
абсолютное ускорение точки М. Как
изменятся абсолютные скорость и уско-
ускорение точки М, если направление вра-
вращения цилиндра изменить на обратное,
т. е. если ш-г] = —- 2 сек~л?
Решение. Вращение цилиндра
принимаем за переносное движение.
Движение точки Л\ по поверхности ци-
линдра будет относительным движе-
движением. На рисунке показана винтовая линия — относительная траек-
траектория точки М. Она определяется уравнениями A).
Расстояние точки /V/ от оси вращения z^ равно
К задаче 5.15.
м.
Переносная скоростр. точки М есть скорость той точки цилиндра,
с которой совпадает в данный момент точка М. Ее величина равна
ve = гше =3-2 = 6 м/сск.
Эта скорость лежит в плоскости, перпендикулярной к оси вращения zu
и направлена по касательной к поверхности цилиндра. Переносное
328 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ |ГЛ. V
ускорение точки М есть ускорение той точки цилиндра, с которой
совпадает в данный момент точка М. Вращение цилиндра равномерное,
следовательно, переносное ускорение точки будет переносным нор-
нормальным ускорением, равным по величине
Оно направлено по перпендикуляру, восставленному к оси враще-
вращения zt из точки М. Относительная скорость точки М определится,
исходя из системы уравнений относительного движения A). Проекции
относительной скорости на оси хи у\, z{ равны первым производным
относительных координат по времени:
vrx, = ?l = — 6- sin 4-t, B)
vryi =.C'i = 6- cos 2-^, C)
vrZi = h = 3.
Величина относительной скорости
tV=V -^¦i-;-i + ;? = l''3fi--;-9«-l9J mjcck.
Абсолютная скорость точки М является геометрической суммой
переносной и относительной скоростей. Если сложить геометрически
две составляющие относительной скорости vrx и vrY, то из ураппе-
ний B) и C) следует, что результирующая будет paisiia но модулю G-r.
и направлена в плоскости, перпендикулярном к оси вращения, но каса-
касательной к поверхности цилиндра. Следовательно, эта результирую-
результирующая vrxv совпадает по направлению с переносной скоростью ve. Итак,
абсолютная скорость точки ,И равна но неличине
и = | (vrxy \ vef - {- v*rz = У (С- ¦ [- С)'2 -, ¦ З2 «= 25,5 м/сек. D)
Абсолютная скорость лежит в касательной плоскости к цилиндру и
составляет угол ас с образующей цилиндра, причем
tg a = ^ = ^^^2.4,14 = 8,28. E)
Определяем проекции относительного ускорения на оси Охи Oyh
Ozx как производные от относительных координат но времени
wrx = .1'] = — 12л'2 cos 2я/ = — 4-'х,,
wry = v, = — 12г.2 sin 2-1 = -
Величина относительного ускорения равна
wr = VЛ{ -|- Р? -|- % = 12к* м/сек\
S 4] СЛОЖЕНИЕ УСКОРЕНИЙ 329
Направлено это ускорение по перпендикуляру, восставленному из
точки М к оси вращения, и, следовательно, совпадает по направле-
направлению с переносным ускорением (см. рисунок).
Ускорение Кориолиса равно
wc = 2о), X *V
Величина кориолисова ускорения определится по формуле
wc = '2ч>еъг sin (ы^Ф,.) = '2u>evrxy = 2ше • 6 тс = 24л м^сек1.
Направление кориолисова )гскорения находим но правилу векторного
произиедепия или но правилу II. Е. Жукопского. Для злого спроек-
спроектируем вектор относительной скорости на плоскость ху, перпендику-
перпендикулярную к вектору угловой переносной скорости, и повернем эту про-
проекцию [I плоскости ху на 90° в сторону вращения шс. Это и будет
направление ускорения Корполгса. Следовательно, кориолисоио уско-
ускорение направлено по перпендикуляру, восставленному из точки /VI к сен
вращения, и сонплдаег по направлению с переносным и относительным
ускорениями. Итак, абсолют нее ускорение равно но величине арифме-
арифметической сумме переносного относительного и корколпеона ускорении
w = we - ¦- wr - '¦- ъ\: = 11 - \- 12т:'2 -j- 24л д« 206,5 м'.секК @)
Оно направлено по перпендикуляру, восставленному \\л течки М к оси
вращения (см. рисунок).
Рассмотрим теперь случай «>„= — 2 сек. По сравнении с пре-
предыдущим в данном случае произойдут только следующие изменения.
Проекция относительной скорости на горизонтальную плоскость vryy
и переносная скорость будут направлены по одной прямой, но в раз-
разные стороны. Следовательно, формулы D) и E) примут вид
v=V (vrsy - - ve)" - j vU = \ Fit - 6f + З1 ъ 13,2 Ml сек, D')
tg a = -^ = —^=2-2,14 = 4,28. E')
Ускорение Кориолиса, сохраняя свею величину, будет направлено по
тому же перпендикуляру, восставленному из точки М к оси враще-
вращения, но в противоположную сторону, так как d)t, направлено в про-
противоположную сторону. Следовательно, абсолютное ускорение равно
по величине
w = we — ivr — wc=\2-|- 12-- — 24* = 55,5 м'.сек1. F')
В этой задаче переноснее, относительное и кориолисомо ускоре-
ускорения оказались направленными по одной прямо!! и определение абсо-
абсолютною ускорения свелось к алгебраическому сложению этих величин.
Следует помнить, что такое совпадение направлений всех трех состав-
составляющих полного ускорения не является характерным. В подавляющем
330
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
[ГЛ. V
большинстве случаев составляющие абсолютного ускорения направлены
но разным прямым и их сложение производится векторно.
Задача 5.16. Для сообщения поступательного движения и станках
применяют механизм (рис. а), состоящий из прямолинейного стержня,
вращающегося с постоянной угловой скоростью ш вокруг точки О
так, что угол y = u>t. Дойдя до упора, стержень начинает вращаться
с той же угловой скоростью в противоположном направлении. Ползун А
вращается вместе со стержнем и одновременно можег перемещаться
вдоль стержня. Прямая АП, шарпирно соединенная с ползуном, дви-
движется в горизонтальных направляющих, осуществляя возвратно-посту-
возвратно-поступательное движение.
т.
К задаче 5.1G.
Зная расстояние / от шарнира О до прямой ЛВ, определить ее
скорость и ускорение в поступательном движении.
Решение. Первый с п о с о б. 11роведем неподвижные оси коор-
координат с началом в шарнире О. Тогда координаты точки А определяются
уравнениями
Пеличипа скорости точки А тогда будет:
.'7а-
v = -,-- = -
A)
так как точка А движется прямолинейно. Величина ускорения точки А
определится как производная от скорости по времени
dv 2/o)' cos bit
dt sin3 iot
B)
Второй способ. Рассмотрим абсолютное движение точки А
ползуна как составное: переносное — вращение вместе со стержнем ОЛ
§ 4] СЛОЖЕНИЕ УСКОРЕНИЙ 331
и относительное — прямолинейное движение вдоль стержня О A. Toi да
модуль переносной скорости точки А будет:
v, = О А ¦ ш = —'-.
е Sill cf
Направлена переносная скорость перпендикулярно к стержню ОА,
следовательно, она образует со стержнем Л Л угол SO : — <р О i постельная
скорость (в прямолинейном движении но ОА) равна прои.шсдпои oi ОА
по времени и направлена по ОА
d ! 1 \ Ы cos mi
^i -—г\ -—
r dt \sni ut] sin- mi ¦
Проектируя векторное равенсгьо (рис. б)
определяющее абсолютную скорость точки Л, на направление ЛВ,
находим.
v = — v. sin Ы -! - v. cos tof = — /ш. 1 -I—V— ! = °>-™
' \ ' SIlH tat J Si!]"' <«>i '
что совпадает с A).
Переходим к определению г-.бсолюгпого ускорения точки А.
Согласно теореме сложения ускорении
Так как u> = const, то величина переносного ускорения будет:
хс =(СМ)ш-= /")"
е ' S1H mi "
Оно направлено от А к центру О (рис. в). Значение относиюлыюго
ускорения в прямолинейном движении равно
dvr _ _ Ы* A -j- cos" uii)
Wr dt ~ irn^lai *
Оно направлено по прямой ОА. J'cK-орепие Кориолнса равно по величине
„ rno 2<uJ/ cos oi
wr = 2шу. sin 90° = ; .
c r sin- mi
Папр?пление ускорения оп))еделнгся поиороюм вектора оиюси-
тельиой скорости па 90° в сторону переносного вращения, так как
в рассматриваемом случае vr перпендикулярно к т. Проектируя, далее,
векторное равенство C) на направление абсолютного ускорения, совпа-
совпадающего с осью х, находим*
, , . 1?/<о- COS ")t
w¦— (— w,-p w,) cos tat-- wc bin ii)l = -
\ «. i i' i <- sini ы( >
¦по совпадает с ('2).
332
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
[ГЛ. V
Задача 5.17. Самолет описывает па вираже дугу окружности ра-
радиуса /? —800 лг с постоянной по величине скоростью 160 м/сек.
Касательная к траектории самолета при днижении соппадает с про-
продольной осью самолета. Поршень двигателя движется и направлении
продольной оси согласно уравнению
xl=5 cos 2r.t,
причем ось xt направлена к носу самолета.
а)
К задаче 5.17.
Определить относительную, переносную и абсолютную скорости и
ускорение поршня в моменты времени
/„ = 0, fj = 0,25 сек, t., = 0,5 сек.
II р и м е ч а и и с. Расстояние; от поршня до центра окружности считать
ircn.tMeiiin.iM и равным 800 м, пренебрегая малыми изменениями этого рас-
стонпии в связи с ходом поршня.
Решение. Движение самолета принимаем за переносное движе-
движение. Движение поршня но отношению к самолету рассматриваем как
относительное движение. Движение поршня по отношению к Земле,
складывающееся из движений по отношению к самолету и вместе
с самолетом, является абсолютным движением поршня.
Переносная скорость поршня есть скорость той точки самолета,
с которой совпадает и данный момент поршень. Модуль переносней
скорости равен
ve = 160 MJceK.
Величина угловей скорости переносного движении находится по
формуле
V,.
160
V,. 160 ., „
=/<=Ш = 0'2 сек
Переноснее ускорение поршня есть ускорение тей точки самолета,
с которой совпадает в данный момент поршень. Так как в перенос-
СЛОЖЕНИЕ УСКОРЕНИЙ
333
пом движении самолет движется с постоянной по величине скоростью,
то переносное ускорение является нормальным переносным ускорением,
величина которого
Это ускорение направлено к центру окружности, описываемой само-
самолетом.
Определим положение самолета в моменты времени ta, th f.2. Само-
Самолет вращается с постоянной угловой скоростью ые = § вокруг центра О,
следовательно, угол поворота прямой, соединяющей центр О с самс-
летом, ранен
а для соответствующих моментов времени (угол измеряется в радианах)
<•?„ = (), ?, = 0,2-0,25 = 0,05, ?2 = 0,2-0,5 = 0,1.
Откладываем на рис. а, б, в значения этих углов, а также пере-
перекосную скорость и переносное ускорение точки.
Проекция относительной скорости па касательную к траектории
самолета определится как производная от относительной координаты
по времени, так как относительное движение поршня является прямо-
прямолинейным:
¦zv, = -?,=:— Ют. sin 1тЛ.
Проекция относительного ускорения поршня равна второй произ-
производной от относительной координаты по времени
wrz = xi = й„ = — 2 О*2 cos 2rf.
Для заданных моментов времени значения относительной скорости
и относительного ускорения даются таблицей
о
— 20г.3
tl = 0,25
0
^„ = 0,5
Откладываем на рисунках относительную скорость и относитель-
относительнее ускорение. Относительная скорость и относительное ускорение
направлены по касательной к траектории. Их положительные направ-
направления совпадают с переносной скоростью.
Кориолисово ускорение, равное
334 СЛОЖНО!* ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
отлично от нуля в момент времени ?[ = 0,25 п равно пулю при to = O
и ^2 = 0,5 сек (так как относительная скорость п эти моменты вре-
времени обращается в нуль). Величина кориолисова ускорения в момент
f, = 0,25 равна
wc = 2wcvr sin {<йе, 1)г).
Так как вектор угловой скорости (ле направлен перпендикулярно
к плоскости полета (плоскости рисунка) на читателя, а пектор отно-
относительной скорости лежит и этой плоскости, то угол между ними
прямой и синус этого угла ранен единице. Следовательно, модуль
кориолисова ускорения
¦а»с = '2ioevr= 2 • 0,2 • 10-гс = 4т. м/сек*.
Для определения направления кориолисова ускорения пользуемся
правилом Жуковского. Относительная скорость <ог уже лежит в пло-
плоскости, перпендикулярной к сектору угловой переносной скорости.
Поэтому для нахождения направления ускорения Кориолиса достаточно
повернуть vr н плоскости рисунка на 90° в сторону вращения ш0.
Откладываем пектор кориолисова ускорения (па рис. б) но радиусу
от центра. Находим для каждого момента времени абсолютную ско-
скорость и абсолютное ускорение поршня по величине, а также направ-
направлении этих пекторон:
w = V Wi-\-w? == J/324 -j- 400r4 (=& 201 м'сек\
^ = :;=^ = 6,2о;
при г, = 0,25
v = ve — vr =-¦ 1 60 — 1 Or *ы 128,6 м/сек,
¦w = we — we ==32 — 4- «a 19,44 м\сек\
при /» = 0,5
w = У wt -r wy == У 32^ -¦- 400т:4 f^> 201 м'сек1,
, wr 20л- г п-
tS=4 = ^ = T2- = 6'20-
Углы а и a, измеряются между иаиранлепнем абсолютного уско-
ускорения и радиусом, соединяющим центр виража О с самолетом AI.
Задача 5.18. Корабль плывет вдоль меридиана CBN с юга па
север. Его скорость по отношению ко дну раина 36 км]час.
в 41
СЛОЖЕНИЕ УСКОРЕНИЙ
335
Определить составляющие абсолютной скорости и абсолютного
ускорения корабля, учитывая вращение Земли вокруг своей оси.
Широта места <р = 60°. Радиус Земли /? = (й- 10"' м.
Решить эту же задачу, если корабль плывет вдоль параллели 60°
сеперпой широты с запада на восток.
Решение. Корабль, находящийся в точке В, участвует одно-
одновременно в двух движениях. В нервом движении он вращается вместе
с Землей вокруг оси ON, где N—Северный полюс, О — центр Земли;
это вращение, происходящее с запада
па восток, примем за переносное дви-
движение. В переносном днижеиии течка В
земной поверхности описывает окруж-
окружность параллели 60° северной широты
с центром в точке Л п радиусом АВ.
Но ьтороы движении корабль движется
вдоль меридиана CBN. Это движение
примем за относительное движение.
В относительном движении корабль
описывает дугу окружности CBN ра- к задаче 5.18.
диуса R с центром в точке О.
Абсолютная скорость корабля складывается из переносной и
относительной скоростей:
Переносная скорость по неличине ранна произведению радиуса вра-
вращения АВ па угловую скорость Земли, совершающей один оборот
за 24 часа:
ve =AB-^e=R cos 60°ше =
= 64-10"-0,5
24 ¦ 60 ¦ 60
= 1Ъ2 м/сек.
A)
Эта скорость направлена по касательной к параллели 60° северной
широты с запада на восток. Относительная скорость равна но вели-
величине
vr=36 км-час= 10 л/сек B)
и направлена по касательной к меридиану CBN с юга па север.
Переходим к определению составляющих абсолютного ускорения
корабля. Согласно теореме сложения ускорений абсолютное ускоре-
ускорение равно
Переносное движение — равномерное вращение вокруг оси, сле-
следовательно, переносное ускорение является переносным нормальным
336 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [['Л. V
ускорением, величина которого
we = AB-i^=R cos 60° ш| = 64 • 108 • 0,5 [ —^—У = 0,017 м\сск\
Это ускорение направлено о г В к Л.
Относительное днижение происходит с постоянной но величине
скоростью по дуге окружности радиуса R. Следовательно, относи-
относительное ускорение будет нормальным относительным ускорением,
значение которого раипо
Это ускорение направлено от точки В к точке О.
Кориолисово ускорение определяется по формуле
и>, = 2@,, X Юг-
Величина кориолисова ускорения будет:
wc = 2«uevr sin (аСЧ) = 2 .у4~^-^ Ю sin 60°= 1,2E • \0'3 м.'сек*.
При вычислении угла (йе, <ог мы учли, что угловая скорость Земли
направлена по оси крашения к Сеперному полюсу и, следопательно,
состапляет угол в г>(Р с >ог. Кориолисоно ycicopenne направлено но
касательной к параллели 60'' северной широты с востока па запад.
Рассмотрим, далее, случай, когда корабль плывет ндоль парал-
параллели 60° северной широты с запада на восток. Полагая по-прежнему
вращение Земли переносным движением, а перемещение корабля но
отношению к Земле относительным движением, замечаем, чго величины
переносной и относительной скоростей соответствуют ранее вычислен-
вычисленным A) и B). Только и отличие ог предыдущего случая относитель-
относительная скорость па эют pa:t направлена по касательной к параллели
(К)° северной шпроты, т. е. совпадает по направлению с перепоет й
скоростью.
Переносное ускорение по величине и направлению совпадает
с найденным в предыдущем случае.
Относительное движение па этот раз происходит по дуге окруж-
окружное ти радиуса R cos E0° = АИ. Следовательно, относительное уско-
ускорение будет нормальным и равно но величине
V)r = -гг-'у.^- = 3,12• 10"8 м!сек\
г R cos (>0
Оно направлено от В к Л, т. е. совпадает но направлению с пере-
переносным ускорением.
Ускорение Кориолнса равно
™с = '2(аа X * г-
9 41 ¦
Величина его
СЛОЖЕНИЕ УСКОРЕНИЙ
wc = %),,vr sin 90° = 1,46 • 10'3 м]сек*,
337
так как о,, и <Dr взаимно нерпе щикулярмы.* Кориолисоио ускорение
на этот раз направлено ог точки В к А; таким образом, все три
составляющие абсолютного ускорения: we, wr, wc — направлены
в этом случае но одной прямей.
Задача 5.19. В переходном режиме при пуске в ход главного
судового двигателя шары центробежного регулятора Уатта (рис. а)
расходятся так, что угол а изменяется согласно уравнению
A)
где
(-i
Угол поворота регулятора вокруг вертикальной оси является
заданной функцией нремепп:
<?=№, B)
где постоянный коэф(|шциепт k-=0,3 сек~л. Длина стержней ОА =
= ОВ = АС = ВС =: / = 90 см.
Определить в момент ^, = 10 сек абсолютную скорость и абсо-
абсолютное ускорение иырои регулятора, рассматриваемых как точки.
г
К задаче 5.10.
Решение. Абсолютное движение шаров раскладываем па дна
движения: переносное движение-—вращение вокруг вертикальной оси,
происходящее согласно уравнению B), и относительное движение —
вращение вокруг горизонтальной оси, проходящей через точку О и
перпендикулярной к плоскости О ABC, происходящее по закону (I).
Неподвижную систему координат xyz выбираем с началом в
точке О: ось х направляем перпендикулярно к плоскости ОАВС
338 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
(в момент t{ = 10 сек) па читателя, ось у — в плоскости ОАВС по гори-
горизонтали вправо, ось z — по вертикальной оси вращения вверх.
Находим, пользуясь уравнением A), значение угла а в момент
*,= 10 сек
а— «.Ю l * .Щ — JL
90 ' 900 "~ 6 ¦
Далее, определяем проекцию относительной угловой скорости на
ось х, т. е. на ось, вокруг которой происходит относительное вра-
вращение. Эта проекция раина производной от угла а но времени
В момент ^^10 сек проекция относительной угловой скорости
"'* = ?, СеК'У
Проекция относительного углового ускорения на ту же ось х
раина производной от шгх по времени
Для того чтобы найти относительную скорость и относительное
ускорение шаров, остановим мысленно переносное движение. Вели-
Величина относительной скорости шаров
¦в, =/«>„ = 90 ?. = 2тс см\сск = 0,02и л/гек.
Относительная скорость направлена соответственно перпендикулярно
к стержням' ОА и Ofi (рис. б).
Переходим к определению относительного ускорения шаров. Так
как относительное движение есть вращение вокруг оси, то целесо-
целесообразно вычислить отдельно относительнее нормальное и относи-
относительное касательное ускорения. Первое из них ранпо по величине
wra = Н = 90 -^ = ~ см/сек'1 я« 0,0043 м-сек*
и направлено от шара к точке О. Значение относительного каса-
касательного ускорения определится по формуле
wn = k, = 90 tJ?0 == ^ см1се«* = т. ¦ 10 3 м/сек*.
Это ускорение совпадает по направлению с относительной скоростью
каждого шара (рис. б).
Переходим к определению переносной скорости и переносного
ускорения шаров. Переносное движение — вращение регулятора
вокруг вертикальной оси согласно уравнению B). Чтобы вычислить
§ 41 СЛОЖЕНИЕ УСКОРЕНИЙ 339
скорость и ускорение шаров в переносном движении, остановим
мысленно относительное движение. Проекция угловой скорости пере-
переносного движения па ось вращения равна производной от угла <р
по времени
ю„ = $ = ЗАЛ
При ?[=10 сек эта проекция равна
шрг = 3 • 0,3 ¦ 10'! = 90 сек~К
Проекция углового ускорения в переносном движении на ось
вращения определяется как производная от ше2 по времени
?« = «"« = ? = 6kt-
В момент ?,= 10 сек
?„ = 6-0,3- 10=18 сек-\
Переносная скорость есть скорость шара при вращении регуля-
регулятора вокруг вертикальной оси ОС. Она равна по величине произве-
произведению радиуса вращения па переносную угловую скорость. В момент
t1 = 10 сек
ve = ls\n аше = 90 sin 30°-90 = 40,5 м/сск.
Переносная скорость шаров направлена параллельно оси х; для
шара А она совпадает с положительным направлением, для шара В —
с отрицательным направлением оси (при t — tt).
Переносное ускорение складывается из нормального и касательного
ускорений. При ?=10 сек величина нормального переносного уско-
ускорения
wen = I sin аш= = 90 sin 30° ¦ 90* см/сек* яа 3645 м/сек*.
Это ускорение направлено перпендикулярно к оси вращения ОС.
Величина переносного касательного ускорения равна произведению
радиуса вращения на значение углового ускорения
. ww = /sina21. = 90 sin 30°-18 см/сек* = 8,\ м/сск\
Оно направлено параллельно оси х и совпадает с направлением
переносной скорости каждого шара (рис. б).
Переходим к определению кориолисова ускорения
wc = 2(де X ч>г
Величина кориолисова ускорения будет:
wc = 2u>evr sin (юе, vr).
Замечая, что угол между <ае к ч>г равен 60°, находим значение wc
в момент <| = Ю сск\
wc = 2 • 90 • 2тс sin 60° см/сек = 1,8 ]/ Зтс м/сек2.
340 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
Направление кориолисова ускорения определяется по правилу век-
векторного произведения. Кориолисово ускорение иапраплено перпенди-
перпендикулярно к плоскости, определенной векторами ые и t)r, n ту сторону,
с которой поворот от вектора <ав к vr на наименьший угол виден
против часовой стрелки. В нашем случае ускорение Кориолиса
направлено по переносной скорости (рис. б).
Найдем теперь абсолютную скорость и абсолютное ускорение
шара, пользуясь методом проекций. Проекции абсолютной скорости
на оси находим, проектируя на них векторное раиепство
•oa = 4)e-\-vr
Имеем для шара А:
vax = ve = 40,5 MJceK,
vay = — vr cos 30° = — 0,01 Ут м]сек,
vaz = vr cos 60° = 0,01 г. м'^ек.
Неличина абсолютной скорости раина
va = Yv-ax -(- v%y -|^L ^ 40,51 м',сек,
а ее направление определяется значениями напранляющих косинусов:
cos («Cjf)=?™ = 0,999,
cos (чСу) = V"y = - 0,00134,
°а
cos (чС^г) =v- = 0,000775.
va
Согласно теореме сложения ускорений абсолютное ускорение
Проектируя это векторное равенство на оси координат, находим
проекции абсолютного ускорения шара А:
™ах = а',, -|- wc m 17,9
way — wen -L- wrn sin 30° — wr. cos 30° «=* 3645 м/сек*,
waz = wrn cos 30° -}- wn sin 30° я^ 0,0055 м/сек"'.
Величина и направление абсолютного ускорения определяются по
обычным формулам:
cos (wa, x) = —-* «« 0,005,
cos (да^у) = ^у я« 0,999,
cos (а>^2) = — «=i 1,37 • 10 Л
а
8 Я СЛОЖЕНИЕ УСКОРЕНИЙ 841
2°. Скорость и ускорение точки в полярных, сфе-
сферических и цилиндрических координатах. Многие
задачи кинематики сложного движения точки целесообразно решать
в полярных, сферических и цилиндрических координатах. Одним из
способов решения задач н криволинейных координатах является
разложение абсолютного движения точки на переносное и относи-
относительное движения.
При решении задач в этом параграфе рекомен-
рекомендуется такая последовательность действий.
Заданы о г п о с и т е л ь н о с и переносное д в и ж е и и я,
требуется определить абсолютное движение:
1) выбрать подвижную и неподвижную системы координат;
2) составить уравнения относительного движения точки;
3) состашш> уравнения переносного движения;
4) получить уравнения абсолютного движения и найти абсолют-
абсолютную траекторию точки;
5) определить скорость точки в относительном движении и ее
переносную скорость;
6) пользуясь теоремой сложения скоростей и теоремой Кориолпса,
найти абсолютную скорость и абсолютное ускорение точки.
Задача 5.20. Определить проекции скорости точки М на оси
полярной системы координат.
Р е hiеи и е. Рассмотрим движение точки М по плоской траек-
траектории АИ как составное, сложное движение. Относительным движе-
движением назовем прямолинейное движение точки М вдоль радпуса-век-
тсра р. Переносным дкпжеппем тогда
будет движение точки М вместе
с радиусом-векгором вокруг точки О.
Находим проекцию относительней
скорости точки М на направление
радиуса-вектора как произнодмую от
радиуса-вектора по времени. Ее на-
называют радиальной скорое.ью и
обозначают буквой fp:
Переносная скорость — это ско- к задаче 5.20.
рость точки М, жестко связанной
с радиусом-вектором. Эта скорость, перпендикулярная к радиусу-
вектору, называется трапенерсалыюй скоростью и равна но величине
Абсолютная скорость точки М определится как геометрическая
сумма относительной и переносной скоростей. Так как зги скорости
342 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
взаимно перпендикулярны, то величина абсолютной скорости равна
Задача 5.21. Определить проекции ускорения точки М па оси по-
полярной системы координат и оси цилиндрической системы координат.
М
К задаче 5.21.
Решение, а) Полярная система координат. Рассма-
Рассматривая, как и и предыдущем случае, движение точки как составное,
применим для определения ускорения ючкн теорему Кор полиса
= wr ~ we
wc.
Проекция относительного ускорения па мапранлеппе радиуса-век-
радиуса-вектора равна
wr=p,
так как относительное дпижепие прямолинейное. Это ускорение
направлено по радиусу-вектору.
Переноснее ускорение складывается из двух составляющих: пере-
переносного касательного ускорения
wc. = Р?
и переносного нормального ускорения
wc, папраплено перпендикулярно к радиусу-пектору, a wm напраплепо
от точки М к центру вращения О (рис. а). Величина корнолисова
ускорении
§ 4| СЛОЖЕНИЕ УСКОРЕНИЙ 3 13
(так как вектор <it_\_vr), а направление кориолисопа ускорения
<wc = .'о X «V
совпадает с переносным касательным ускорением.
Далее, находим проекции ускорения точки па оси полярных коор-
координат. Проекция ускорения па радиальное направление
wf = w, — zven = р — р?2-
Проекция ускорения на траисвсрсалыюе направление
З -| - 2рсэ = — -jt (P2?)-
Таковы проекции ускорения точки на оси полярных координат.
б) Цилиндрическая система координат. При про-
пространственных диижениях точки иногда удобно использовать цилин-
цилиндрические координаты. В этой системе координат положение точки М
определяется дпумя молярными координатами р и ср и апликатой z
(рис. б). В этом случае проекция скорости точки находится по фор-
формулам:
Т1р = С, V? --- р^, V, = Z.
Величина скорости
v = УЦ + щ + ъ: = V^+pV-I-z4.
а ее направление дается значениями направляющих косинусов
cos (г»Тр) = р-, cos (v,\) = ^ , cos (v, z) = -j.
Проекции ускорения на цилиндрические осп запишутся таю
«'р — р — р?*, ^9 = р? + 2р», w., = г.
Величина ускорения
а папранляю1ние косинусы вычисляются по формулам:
cos(wTp) = -~—-. cos (eC?) = PJL~1, cos (w, г) = ~.
Задача 5.22. Точка движется но поверхности конуса с углом
растнора при вершине 2a = G0D согласно уравнениям:
г" = а9 0?"-|-<?"*), A)
где время измеряется в секундах, а г и а —в метрах.
344
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
|ГЛ. V
Положение точки М определяется координатой z и полярными
координатами г и <р в плоскости, перпендикулярной к оси Oz.
Определить траекторию точки, а также ее скорость и ускорение
в проекциях па цилиндрические оси координат г, <р, z. Найти началь-
начальные координаты и начальную скорость точки, а также проекции
ускорения на образующую и на нормаль к поверхности конуса.
а)
К задаче 5.22.
Решение. Для определения траектории составим уравнение
поверхности конуса
г2 — zq = Q. C)
Исключая из системы уравнений A) и B) время, находим:
Совокупность двух уравнений C) и D) определяет простран-
пространственную траекторию точки Л1. Начальные координаты точки М
находим, подставляя в (I) и B) значение ^ = 0. Тогда го = аУ'2,
Для определения скорости находим проекции ее па оси цилин-
цилиндрических координат:
vf — f, v9= ry, v2 = г.
Кроме тою, из C) следует, что г = г н, следовательно, v =v2.
Далее, получаем из A), дифференцируя по времени, v ¦
vn = r — а'
( ?~
E)
6 Ц СЛОЖЕНИЕ УСКОРЕНИЙ 345
Для определения значения траисверсалыюй составляющей скоро-
скорости находим из B), дифференцируя это уравнение но времени:
откуда
Следовательно, значение траисверсалыюй составляющей скорости
Определяем неличину абсолютной скорости точки
Отсюда начальная скорость точки
7>0 = 1а.
Для определения ускорения находим его проекции на цилиндри-
цилиндрические осп по формулам:
wt = ?-r(?, (б)
а.?=г?-:-2^, G)
даг = z = г. (8)
Далее, дифференцируя E), получим:
Тогда
Подставляя (9) и A0) в F), определяем проекцию ускорения на
радиальную ось
Переходим к определению проекции ускорения па трансверсаль-
ную ось. После несложных преобразований находим, что
a ' I -~e'" ¦ ¦ e" -.-с"-1
346
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
[ГЛ. V
Подставляя эти значения в G), получаем:
z»9=0.
Отсюда видно, что ускорение точки лежит а вертикальной плоскости,
проходящей через ось симметрии конуса и рассматриваемую точку.
Эта плоскость показана на рис. б. Выберем оси Мх, и Му\, первую
но образующей конуса, вторую по нормали к его поверхности.
Найдем проекции полного ускорения точки М на эти оси. После
несложных преобразований получим:
wXt = wf cos 4o° -|- wz cos 45° = a \fi2 V~e*Zr е"г' = V^r = ОМ-
Таким образом, проекция ускорения па образующую численно раина
расстоянию точки от вершины конуса. Далее,
V'Ia 4J/2"
= -j~
= - wf sin
2 sin 4o- =
Задача 5.23. Скорость <0\ корабля А относительно воды посто-
постоянна по величине и всегда направлена но перпендикуляру к липни
низироиания на неподвижную точку В.
К задаче 5.23.
Какую кривую (относительно неподвижного берега) опишет ко-
корабль, если это движение происходит при течении воды с постоян-
постоянной по величине и направлению скоростью vr В начальный момент
времени <р —0 и г = Га (рис. б). Корабль рассматривать как точку.
Решение. Течение поды является переносным движением. Цир-
Циркуляция корабля со скоростью <О\ будет относительным движением.
Абсолютная скорость корабля определится как геометрическая сумма
переносной и относительной скоростей.
Выберем декартовы оси координат: ось Их параллельна скорости
течения, ось By перпендикулярна к скорости течения. Полярные ко-
§ 4] СЛОЖЕНИЕ УСКОРЕНИЙ 347
ординаты корабля будут определяться радиусом-вектором ВА^г и
углом yBA = <f. Проектируя абсолютную скорость точки па направ-
направление радиуса-вектора и на перпендикуляр к нему, имеем:
г = — ve sin <p, A)
r& = vs—ve cos <p. B)
Разделив ураннение A) на урапнение B), получим:
dL — J^Ji'ILI dv
Проинтегрировав это дифференциальное уравнение с разделяющимися
переменными, найдем:
In Cr = — In cos » :
или
Определим из C) произвольную постоянную С, подставив начальные
данные <р = 0, г = г0; в результате имеем:
с== 1 v,,_
Го Ve — Vi #
Внося это значение произвольной постоянной в C), получим уравне-
уравнение абсолютной траектории корабля
V,
I COS о
Это—полярное уравнение кривых второго порядка; эксцентриси-
эксцентриситет кривой е = — равен коэффициенту при cos о.
г/.
Если — <Г1, то найденная траектория — эллипс с фокусом н точ-
vi
ке 5. Параметр эллипса /j = r0 f 1 —-'-:, с другой стороны, параметр
эллипса определяется через эксцентриситет и большую полуось а
формулой р=а{\—с2). Приравнивая эти два значения параметра,
находим длину большой полуоси, перпендикулярной к скорости н'-
чения,
г.
При L'e^> 1 траектория — гипербола.
348
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
[ГЛ. V
В силу принятых к задаче начальных условий (а = 0) случай
ve = Vy приводит к ранепстиу нулю абсолютной скорости корабля в
начальный момент. Следоиагельно, корабль останется в этом случае
неподвижным. Однако можно показать, что при других начальных
данных случай - = 1 соответствует параболической траектории дви-
движения корабля.
Задача 5.24. Прямая d вращается вокруг точки F с постоянней
угловой скоростью ш и движет но эллипсу кольцо М. Полуоси
эллипса а и Ь; фокус эллипса F, рас-
расстояние от центра до фокуса равно с.
Определить модуль скорости точ-
точки М.
Решение. Полярное уравнение
эллипса имеет иид
,- = ... Р
1 — й COS f '
Здесь p = bil'a — параметр эллипса,
е = с/а — эксцентриситет эллипса.
Полярная ось направлена из фо-
фокуса F вдоль большей оси эллипса (на
рисунке вправо). Модуль скорости
К задаче 5.24.
точки в полярных координатах равен
Из уравнения эллипса, дифференцируя, находим:
ыре sin о
dr
dt'
A
A)
B)
С другой стороны, из полярного уравнения эллипса имеем:
Здесь
гс/о w/з
б'? 1 — f cus о
'(If
Подставляя значения B) и C) в формулу A), получаем:
^ 1 — е cos <p)
а V 1 -ге^ — ^е COS ср.
§ 4] СЛОЖЕНИЕ УСКОРЕНИЙ 349
Внося значение параметра р и эксцентриситета е в равенство D),
окончательно получаем:
Скорость направлена по касательной к эллипсу.
Задача 5.25. Точка движется по поиерхности Земли со скоро-
скоростью v. Угол между скоростью и меридианом в каждой точке траек-
траектории постоянен и ранен а.
Определить траекторию точки.
Р е ш е и и е. Декартовы координаты точки, движущейся по сфере
радиуса R, могут быть выражены через сферические координаты по
формулам (рис. а):
х — R cos 0 cos 9, y = R cos б sin 9» z = R sin 0,
где 6 — широта, z> — долгота местоположения точки па сфере. Най-
Найдем выражение скорости при постоянном радиусе R. Производные ог
декартовых координат по времени равны
Отсюда определяется модуль скорости
v = V~?rF5)r+2l = RV^*-U f cos-0.
Скорость v можно разложить на две составляющие:
vi = Я0,
направленную по касательной к меридиану, и
г-.2 = R cos Ц,
лаправленпую по касательной к параллели.
350 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
/
В общем случае движения точки по сфере модуль скорости
будет:
По условию задачи угол а, образованный скоростью с меридианом,
постоянен. Этот угол связан с составляющими скорости точки cooi-
иошением
или, после подстановки значений vy и т>3,
т
R cos 0 ^> °
Отделяя '"переменные, имеем:
jfl
= d<? ctg a.
cos 0
Это—дифференциальное уравнение искомой траектории. Предполо-
Предположив, что точка начала движение из положения <ри = 0, 60 = 0, инте-
интегрируя, находим:
с , и
С м i Г,
\ —г = с'Я а \ d'-o
J COS в ь J '
и и
и
или
1t!|
откуда получаем уравнение траектории
Кривая на поверхности сферы, описываемая этим уравнением, назы-
называется локсодромией. Такова траектория судна, курс которого не
меняется по отношению к меридиану.
Если ctg a ^> 0, то np;i неограниченном возрастании угла у пре-
предельное значение угла Й определится из равенства
, /тс , 0
и, следовательно,
я , 0 тс
" '•! — Т
или
»=¦"-•
-a 11 сложение ускорении 351
Таким образом, в этом случае локсодромия будет сферической спи-
спиралью, закручивающейся вокруг Северного полюса.
Если же ctga<^0, то, рассуждая аналогично предыдущему, най-
найдем, что 6 = — я/2, и траектория будет сферической спиралью, за-
закручивающейся вокруг Юж-
Южного полюса.
На рис. б представлена
локсодромия и проекции' на
плоскость, перпендикулярную
к оси z.
Задача 5.26. Определить К задаче 5.2G.
ускорение точки, движущейся
в плоскости, если ее трапсверсальпое ускорение относительно центра О
ранчо нулю (такое движение точки называется центральным движе-
движением).
Решеми е. Воспользуемся проекциями ускорения на радиальное
и трансверсалыюе направления, полученные в задаче 5.21,
С)
Согласно условию трансверсалыюе ускорение равно нулю
р? -г2 :Л = -J- si
и, следовательно, произведение p*'f остается неизменным
D)
Величина р2ф раппа )'диоеипому значению секториалыюй скорости.
Действительно, приращение площади сектора, онисгииого радиусом-
вектором точки за время Д^ (см. рисунок), с точностью до величин
первого порядка малости равно
Д5 = 1 РДа = -' ¦ РРД? = i р-Д?) E)
где Дз — приращение дуги за промежуток времени Дг.
Предел отношения приращения площади к приращению времени
.. AS dS 1 2 Л? 1 о. ....
и есть секториальпая скорость.
Перейдем, далее, к преобразованию радиального ускорения точки,
которое в случае центрального движения, рассматриваемого в задаче,
352 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
является полным ускорением точки. Уравнение траектории точки н
полярных координатах может быть ирсдстанлспо зависимостью
Р = Р (г)- <7>
и, следовательно, можно считать, что радпус-пектор зависит от ispc-
мепи через промежуточную переменную <р. Тогда
пли, исключив отсюда <f посредством D), найдем:
С da n till
Р = - - - - == С - = С - ¦
н р2 d<j) do do
где введена новая переменная
Дифференцируя (9) еще раз по t и учитывая, что радиус-вектор за-
виент от времени через <?, имеем:
rf2« . с2 d-u ....
р = —¦ с . о <р = — • ?¦ ,-.г. A1)
Здесь производная ф заменена ее значением из D1. Внося это значе-
значение второй производной радиуса-сектора по времени A1) в форму-
формулу A), а также исключая ф согласно D), получим:
(.2)
Это равенство определяет ускорение точки при центральном дш:-
жепии. Оно дает выражение дли ускорения через элементы траекто-
траектории и полярных координатах G) и постоянную секториальную ско-
скорость. Формула A2) носит название формулы Бше, по впервые се
получил И. Ньютон.
Задача 5.27. Определить ускорение планеты, движущейся согласно
трем законам Кеплера.
1. Планеты обращаются вокруг Солнца по эллипсам, в одном из
фокусов которых находится Солнце.
2. Плсшзди, описываемые радиусом-иектором, идущим от Солнца
к планете, пропорциональны временам, в течение которых они были
пройдены.
3. Квадраты периодом обращения планет относятся, как кубы
больших полуосей их орбит.
Планету и Солнце рассматривать как точки.
Р е ш е и и е. Задачу об ускорении небесного тела в кеплеровом
диижении будем решать в полярных координатах. Полярную ось на-
§ Ц СЛОЖЕНИЕ УСКОРЕНИЙ ЗГK
правим из фокуса, где находится Солнце, идоль большой ocii эллипса.
Уравнение эллипса в полярных координатах имеет вид
(де/; = 62/а — параметр эллипса, e = ?1'a— эксцентриситет эллипса,
а и b — большая и малая полуоси эллипса, сх — полонит фокусного
расстояния.
Второй закон Кеплера устанавливает постоянство секюриалыюй
скорости
РУ = с,
где с — постоянная, рапная удвоенной секторналыгоИ скорости.
Переходим пепосредсгвеппо к вычислению ускорения планеты. В
силу шорого закона Кеплера движение любой планеты является цеп-
тральным. Действительно, секториальпая скорость относительно Солнца
постоянна и, следопаюльно, фэпсверсальпая составляющая ускоре-
ускорения планеты равна нулю. Поэтому полное ускорение направлено по
радиусу.
Таким образом, и силу второго закона Кеплера движение планет
является центральным движение:.'. Для нахождении ускорения планеты
применим формулу Бипе (см. предыдущую задачу):
p \ ' df i
Из уравнения эллипса A) находим:
1 1 , е
и = - = — cos э.
р р [ р
Тогда
d'-u e
-,-„ = cos v
df p
и, следовательно,
. d'a 1
и - - - -., = —,
' 'Jr P
Внося эти значения в формулу Вине, получим:
с- ! , d-a с-
w = w„ = —.,- ¦ и -\- , , = „. B)
Р Г \ ' tin РГ к '
Итак, ускорение планеты, движущейся по законам Кеплера, напраплепо
по радиусу-вектору ючки к фокусу, i. e. к Солнцу, и по величине
обратно пропорционально квадрату расстояния до Солпна.
Этот вывод можно было получить из выражения для радиального
ускорения (см. формулу A) предыдущей задачи), не пользуясь формулой
Бине, непосредственным дифференцированием уравнении эллипса A)
по премеии. Однако это! пугь более длинный.
12 М. И Бать и др , т I
354 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ |ГЛ. V
Параметр р = Ь'г/а в формуле B) можно заменить, пользуясь
третьим законом Кеплера, следующим образом. Третий закон Кеплера
может быть записан так:
где а — большая полуось, Т — период обращения планеты. Через k
обозначена постоянная неличина отношения куба большой полуоси
к квадрату периода обращения. Период обращения при постоянной
сектсриалыюй скорости можно вычислить, разделив площадь эллипса
на эту скорость:
rr __ 1-ub
с
Подставляя значение периода в формулу C), имеем:
или
Ь1 _ _Р
а ЛтЛ'
Внося это значение в формулу B), получим:
__ A--k
Р2
Заметим, что в этом выражении постоянная /г одипакопа для всех
плачет солнечной сие гемм.
Для приобретения навыков в решении задач па
сложение ускорений рекомендуется решить следую-
щйс задачи из «Сборника задач но т е о р е г и ч е с к о й м е-
х а 11 и к е» И. В. Мещерского, издания 1950 г. и б о л е е
поздних лет: 447, 450, 455, 458, 461, 462, 467, 473, 479, 481,
483, 488, 490.
§ Б. Кинематика колебаний
1°. Гармонические колебания. Колебаниями, или колеба-
колебательным процессом, называется такое изменение некоторой величины,
при котором она последовательно возрастает и убывает. Простейшим
и в то же время важнейшим типом колебаний является гармоническое
колебательное движение.
Рассмотрим окружность радиуса а (рис. 5.4). Проведем через
центр окружности точки О два взаимно перпендикулярных диаметра.
Направление горизонтального диаметра примем за ось х, а ось у на-
направим по вертикальному диаметру. Пусть радиус ОЛ вращается
равномерно вокруг центра О с уичопой скоростью к. Положение
КИНЕМАТИКА КОЛЕБАНИЙ
355
радиуса UA0 n начальный момент времени t = Q определяется углом 3.
Тогда угол поворота радиуса ОА определяется формулой
tp = ^_)_3. A*)
Опустим из точки Л перпендикуляр па ось х и напишем уравнение
движения точки В
Это — уравнение гармонических колебаний. Здесь а — амплитуда,
наибольшее удаление точки от ее среднего положения. Расстояние
между крайними положениями точки наливается размахом колебаний.
Угол ср. определяемый формулой A*), на-
называется фазой колебания, а угол 3 — на-
начальной фазой. Период колебания — про-
промежуток времени, в течение которого точка
совершает одно полное колебание, ранен
у
Обратная величина
D*)
в
называется частотой колебаний и изме-
измеряется числом колебаний п единицу нре-
мени. Если яа единицу времени примять секунду, то частота колеба-
колебаний измеряется и герцах (в честь Г. Герца, первого исследователя
электрических колебаний). Величина k называется круговой или цик-
циклической частотой. Как видно из D*), величина k раина числу коле-
колебаний п 2г единиц времени (например,
в 2тс секунд).
Если рассматривать ОЛ как вектор,
вращающийся с угловой скоростью к,
то гармоническое колебание изобра-
изображается его горизонтальной проекцией.
Скорость точки при гармоническом ко-
колебании будет:
vx = x — ak cos {kt -j- P) E*)
и ее ускорение
wx = x = — aft9 sin (ftf-}-?)• F*) Рис. 5.5.
Тогда перемещение, скорость и ускорение точки, совершающей гармони-
гармонические колебания, может быть представлена простой векторной диа-
диаграммой (рис. 5.5), 1Де проекция vx скорости движения представляется
12*
356 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
горизонтальной проекцией вектора ОВ длины ак, повернутого на 90°
по отношению к вектору ОА длины а в ту же сторону, что и на-
направление вращения; проекция wx ускорения точки представлена
горизонтальной проекцией вектора ОС длины ok\ повернутого на
180° по отношению к вектору О А. Все эти три вектора вращаются
с угловой скоростью к вокруг центра О. Таким образом, дифференциро-
дифференцирование уравнения движения точки можно трактовать как поворот изо-
изображающего вектора па 90° в сторону вращения с одновременным
его умножением на к.
При решении задач на кинематику гармонического
колебательного движения рекомендуется такая по-
последовательность действий:
1) выбрагь синему координат;
2) составить уравнения гармонического колебательного движения;
3) сложив гармонические колебательные движения, получить уравне-
уравнение результирующего движения;
4) определить скорость и ускорение точки при гармонических
колебаниях;
5) определить траекторию точки при сложении гармонических
колебаний, пе направленных по одной прямой.
Задача 5.28. Точка совершает гармонические колебания вдоль
горизонтальной оси х. Размах колебаний равен 20 см. Продолжи-
Продолжительность десяти размахоп равна 5 сек. Полагая, что точка в началь-
начальный момент ( = 0 находилась в крайнем правом положении, составить
уравнение движения точки.
Определить скороегь и ускорение точки.
Решение. Уравнение гармонических колебаний точки имеет вид
„v = a sin (?/-•-?)• A)
Найдем значения постояппмх а, к, % исходя из условий задачи.
Амплитуда (армопкчеекпх колебаний равна половине размаха колебаний.
Следовательно,
а = 10 см.
Период колебании определится из условия, что продолжительность
десяти размахов, т. е. пяти полных колебаний, равна 5 сек. Следо-
Следовательно, продолжительность одного полного колебания или период
колебаний будет:
Т = 1 сек.
Коэффициент /г определится из формулы (8:р) для периода коле-
колебаний
k=~ = 2- сек '.
К|ШРЧ\ТИКЛ КОЛР.Г.АИИЙ
357
Подставляя найденные значения коэффициентов в A), находим:
х-10 sin Bг<-;-?). B)
Для определения начальной фазы р воспользуемся начальным
условием: при t~0 точка ьахсдилась в крайнем правом положении.
("ледова1елыю, при ^=0 координат х = а=\() см. Нпося эти
значения в B), получим:
10=-= lOsin p,
откуда sinj-i=l и р = -п,2.
Теперь уравнение гармонического колебательного дпижеиия примет
вид
или, окончательно,
При прямолинейном движении проекции скорое in точки па ось
равна первой производной oi коордипаш по времени
vx =i~- 20^ sni ЧтЛ.
Проекция ускорения точки па ось
от коордитиы по времени
х равна строй производной
= X— — 4Ci:! COS 1~t — —
C)
м
Из C) следует, чго ускорение точки при гармонических колебаниях
всегда пропорционально отклонению и направлено к центру колебаний
Задача 5.29. Точка М
движется по окружиосш ра-
радиуса R = 10 см согласно
уравнению s = 51см, i де s —
пуп>, пройденный по дуче.
13 начальный момент iоч-
iочка М находилась в Af0
(рис. а). Описанное равно-
равномерное движение точки М \ / ' л
по окружиосш може1 быть
осуществлено при помощи
механизма, прсдскш.чеппого ^
па рис. б. Механизм соеiонi К задаче 5,'iO.
из ползуна А, коюрый мо-
м.ег неремещап>ся в направляющих по вертикали. В ползуне имеется
юрпзопгалышп паз, в коюром движется точка М, участвующая ирп
одновременном движении ползуна и точки по na.iy в сложном абсо-
абсолютном движении.
6)
358 СЛОЖИЛИ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
Определить уравнения относительного и переносного движении,
которые надо сообщить: первое относительное — точке М вдоль
горизонтального паза, а нторос поступательное — ползуну Л в верти-
вертикальных направляющих, чтобы осуществить заданное абсолютное
дпижепие точки.
Решение. Определяем угол МйОМ = Ъ, который составляет
радиус ОМ с осью Ох:
? — "¦/?" — R— То — °'0^
Зная угол 3, находим уравнения относительного движения точки
х, == R cos 3 = 10 cos 0,5f, ух = 0.
Уранпеиия переносного движения основания механизма будут:
*0 = 0, j-u =/? sin 3=10 sin 0,5>.
Таким образом, равномерное движение точки по окружности
может бьпь разложено па дна взаимно перпендикулярных, прямо-
прямолинейных гармонических колебательных движения.
Задача 5.30. Точка М движется прямолинейно в папраплнюшгх,
прикрепленных 'жестко к доске А, по закону
совершая гармонические колебании около точки Ot (рис. а). Доска
движется в направлении, параллельном ОХХ\, совершая гармонически е
колебания то И же частоты около неподвижной точки 0.
Определить абсолютное движение шчки М, если закон колебании
доски А определяется уравнением
х0 == a., cos (kt -j- 3.,),
i де ,r0 = 00\.
V e in e и и е. Выберем абсолютную систему координат ху с началом
и неподвижной точке О так, чтобы ось х совпала с относительней
осью л: Тогда абсолютное движение точки определится координатой
х = ОМ = х0 -]- хх — ai cos (kt —j— Pi) -*- at cos (kt -|- 3.,). A)
""Таким образом, задача сводится к сложению двух гармонических
колебаний одинаковой частоты н, следовательно, одинакового периода,
отличающихся амплитудами и начальными фазами. Раскрывая в правей
части A) косинусы суммы днух углов, находим:
.v = (a, cos 3, -)- <7.2 cos 3.,) cos kt — (a, sin 9, -|- a9sinB3)sinW. B)
Введем новые постоянные а и J3, связанные с исходными величи-
величинами следующими равенствами:
a cos Й — at cos 3, -f- a^ cos З.г,
a sin й = и, sin 3,-j д., sin В.,
§5] КИНЕМАТИКА КОЛЕЕ М1ИЙ
Тогда уравнение B) примет пил
х = a cos |3 cos kt — a sin |3 sin /гг! = a cos
-•- |3).
359
D)
Таким образом, при сложении двух гармонических колебаний
одинаковой частоты получается гармоническое колебание и.й же
частоты. Амплитуда эюго колебания а и начальная фаза р опреле.1яю1ся
У I
0
0, И
¦ о 1
A
X
К задаче 5.30.
из уравнений C). Возводя эти уравнения п квадрат и складывая, на-
находим амплитуду результирующего колебания
dl^=a]-\~al'\- 2a,a.2(cos 3[ cos j3.3-j- sin 3, sin ,%)^
|-2a,a,cosO, —32). E)
Начальную фазу колебания находим, разделив! второе из ураине-
ний C) па первое:
(.OS (Si
COS
Из формул E) и F) пытекает следующий простой геометрический
способ определения результирующего колебания. Отложим wa начала
координат О (рис. б) под углом [3, к оси х вектор длиной щ и под
углом pj к оси х вектор длиной а.г. Найдем сумму этих днух пекгоров
как диагональ параллелограмма, построенного на этих некторах. Длина
диагонали соответствует амплитуде результирующего колебания, а угол
ее наклона к оси х определяет начальную фазу этого колебания.
Этот прием геометрического сложения диух гармонических коле-
колебаний одинаковой частоты, направленных по одной прямой, может
быть легко распространен на сложение любого числа таких колебаний.
Достаточно из некоторого произвольного полюса отложить пекторы,
пропорциональные азшлитудам составляющих колебаний под углами
наклона, равными их начальным фазам. Сумма этих векторов определит
амплитуду результирующего колебания, а ее угол наклона — начальную
3(iO
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
[ГЛ. V
фазу. Отсюда следует, что точка будет неподвижна, если сумма этих
векторов равна пулю.
Задача 5.31. Точка М совершает прямолинейное гармоническое
колебательное движение около центра О\ согласно уравнению
хх~С1\ cos (mt — ?,).
При этом основание механизма вместе с точкой Ot совершает также
прямолинейное, поступательное гармоническое колебательное движение
около неподвижного центра О со-
согласно уравнению
x(>i=aa cos («/—?„).
Оба колебания совпадают по наирав-
"*"" ; лсшпо, а |)азпосП| частот этих ко-
колебаний т — п весьма мала по срав-
сравнению с самими частотами.
К залаче г>.31. О.федслпь уравнение абсолют-
абсолютного движения точки М.
Решение. Уравнение абсолютного движения точки находится
по формуле
х = х, -'- х0 = ay cos (mt — в,) -; - a., cos (л^ — е0). A)
Пресбразуем этот результат следующим образом. Заменим тождест-
тождественно
cds (nt — ?0) =- cos [mt — (т — n) t — e(l|,
D)
i да
— e0] =
= {a, cos г, -- аи cos \(т — «)/ -:- е„]} cos mt —•
-j- {«! sia z,-~q0 sin [(in — n)t-lE0]} sin int. C)
Нг.сдем новые переменные г п 0, удовлетворяющие равенствам:
г cos 0 = ai cos е, — а0 cos \(т - и) i -'•- е0],
Г sin 0 = а^ sin ?j -J- я0 sin [(ш - п) t -'¦- e0].
Toi.ia уравнение абсолютного движения точки C1 может быть прсд-
стгв.тепо в виде
х -= г cos (mt — 0), (о)
где г и в определяются из D). Возводим сба равенства в квадрат
)i складываем:
г- — a\~al~ 2aifl0 cos [(m — n)i-\-&0 — в{].
(б)
§5) КИНЕМАТИКА КОЛЕБАНИЙ 3G1
Деля равенства D) одно на другое, находим:
. О = ?'_sLn.?' + flnsin[(m — "U + ?ol
ё a, cos e,' -t- fl0 cos [(;« — и)' т Ео1'
Из формулы E) следует, что результирующее колебание можно
приближенно рассматривать как гармоническое, у которого амплитуда
г и начальная фаза 6 япляются не постоянными величинами, а медленно
меняющимися функциями премеии. Частота изменения этих величин
т — п по условию весьма мала по сравнению с частотами составляю-
составляющих колебаний. Из уравнения (б) следует, что амплитуда абсолютных
колебаний изменяется в пределах /¦тах = <21 — -о0, гш\„ = ах— о0.
Этот вид движения, часто встречающегося в различных областях
техники, называется биением. На рисунке буквами 7Ц обозначен пе-
период биения, а буквами 'Гл — период нарастания колебаний.
Для приобретения навыков и решении задач на
гармонические колебания рекомендуется решить сле-
следующие задачи из «Сборника з а д а ч н о тео р ет и ч ес к с> ii
механике» И. В. Мещерского, издания 1950 г. и более
поздних лек 310, 315, 325, 326, 329, 350.
2е. 1 [ е г а р м о и и ч е с к и е к о л е б а и и я. При сложении двух или
нескольких гармонических колебании разной час юты, происходящих
по одной прямей, получается периодическое, по не гармоническое
движение, если частоты слагаемых движений соизмеримы. Наряду
с этим и природе п технике часто встречаются колебания непериоди-
непериодические. Следует напомнить, что периодическим движением называется
тгкос дниженко, кспорсе полностью повторяется чег.ез некоторый
промежуток времени. Кинематика некоторых таких движений рас-
рассматривается в настоящем параграфе.
При решении задач в этом параграфе рекомендуется
такая п о с л е д о в а т е л ь н о с г ь д е й с т в и ii:
1) выбрать оси координат;
2) составить уравнения колебательного движения;
?>) сложив колебательные днпжеиия, получить уравнения резуль-
результирующего движения;
4) определить скорость и ускорение точки.
Задача 5.32. Точка движется согласно уравнению
х = a, sin (ktt -L- 8,) -J- a, sin (k,t -r 3,), A)
причем периоды слагаемых гармонических колебаний соизмеримы,
т. е. их отношение является рациональным числом:
где tii и Ио — целые числа, а дробь B) несократима.
Определить период результирующего колебания.
362 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ [ГЛ. V
Решение. Движение точки складывается согласно A) из днух
гармоник. Из равенства B) следует, что
Обозначая эти равные произведения букной Т, получим период результи-
результирующего колебания, так как за премя Тоба слагаемых в A) вернутся
к. своим первоначальным значениям и за этот промежуток времени
повторится наименьшее целое число периодов обеих гармоник.
Заметим, что если периоды слагаемых колебаний несоизмеримы,
то не существует периода результирующего движения и движение
в этом случае будет непериодическим.
Задача 5.33. Точка движется согласно уравнению.
х = ае nt sin {Vli* — nrt -\- Ъ).
Определить период колебании, закон убывания амплитуды колебаний
с течением времени, скорость и ускорение точки.
Решение. Прежде всего заметим, что это движение является
колебательным, по не периодическим, так как не существует такого
числа Т, при котором будет выполняться равенство
Будем понимать под периодом колебаний промежуток времени, в те-
течение которого происходит полное колебание, г. е. переменная х
изменяется от одного максимума до другого.
Для нахождения периода найдем, прежде всего, моменты времени,
кргда переменная х принимает экстремальные знамения. Для этого
приравняем производную от ,v по времени нулю
jc = ае'п' [— п sin (k\t -J- -i) -f At cos (kvt -f- C)] = 0,
где обозначено для краткости k1=\fk'i — л'2. Отсюда находим:
Обозначая последовательные значения времени, удовлетворяющие
уравнению A), через ti и учитывая, что периодичность тангенса соответ-
соответствует изменению аргумента на величину к, получим:
Так как ti и ?i+, отвечают максимуму и следующему за ним минимуму,
то их разность равна половине периода. Тогда из B) находим:
или
g 51 КИНЕМАТИКА КОЛЕБАНИЙ 3G3
Переходям к определению закона убывания амилигуды колебаний
с течением времени. Находим из A) значение
Тогда соседние экстремальные значения переменной (амилигуды коле-
колебаний) будут:
о, = |j:(g| = *<?-"'.; sin (*,*Н-ЭI = ае-"'.---=|у=-.:
у ki-rn- '
Отношение двух нос.чедопательных амплитуд равно
Логарифм обратной величины пТ;. называется логарифмическим
декрементом, характеризующим быстроту убывания амплитуды.
Найдем скорость точки
vx=x = ас "' [/г, cos (ft,/ -\-?) — n sin (kj --.- р)|.
Ускорение точки определится как вторая производная or коорди-
координаты по времени
wx = х = ае-"' | — 'Jnkj cos (A,< -;- $)-\- (п — к\) sin (/,-,/ - {- р)].
После несложных нрсобраяоиаш.П пахсди.ч:
j;i == ft^JC 2flX
!де обозначено, как и прежде,
ft0 = A-j -_ п\
Таким образом, ускорение течки складывается из диух частей: уско-
ускорения, пропорционального отклонению точки о г центра колебаний,
и ускорения (замедления), пропорционального скорости.
Задача 5.34. Точка движется согласно уравнениям:
х = а sin \'2uy{ —-\t
г — \
у = a sin ( u)r — -л-:.
Определить траекторию, скорость и ускорение точки.
Решение. Запишем уравнении движения точки так:
х = — a cos 2urt, A)
у = — а соь "tf. B)
3G4
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
тл. v
Для исключения времени из этой системы уравнении преобразуем
уравнение A) следующим образом:
х—-а( sin* wt — cos'2 ust) = а A — 2 cos'2 &t).
Подставляя н эю уравнение значение
cos ш(= —у'а,
получим:
или
х--=а 1-
V
2 \
Это уравнение параболы с вершиной в точке (а, 0), у которой
ось х является осью симметрии. Траекторией точки является отрезок
этой параболы, заключенный в квадрате со стороной 1а, как это
следует из уравнений (I) и B).
Проекции скорости точки найдем, дифференцируя уравнения дви-
движения A) и B),
Vy =J? = i
-а
К задаче 5..34.
sin 2wt, D)
Sill Mt. ('))
Отсюда находим скорость точки
•v = au> sin io^D cos «>ti-\-j).
Проекции ускорения точки
будут:
wx = х = 4flu)- cos 2uit = — 4u)'x,
wv =y = аш! cos mf = — u>ly.
Следовательно,
w= — or Dx? ~-yj). F)
Как видно из уравнения C), точка колеблется по дуге параболы ЛСП
(см. рисунок), причем координаты точек равны: Л(—а, а), С(а, 0),
/j(—а, —а). Парабола пересекает ось ординат и точках Ь, В с ко-
ердипатамп: 0, г': о (' 2/2.
Найдем скорость и ускорение точки в те моменты времени, ко1да
она прохгдпт через Л, С, Я.
Подставляя в уравнения (I) и B) координаты этих точек, находим:
для точки .4:
для течки /,':
для точки С:
cos 2o>f -— 1,
cos2io/=l,
cos 2tur = — 1,
cos (¦)?= —
cos «>^ — -I;
cos (o/ = 0.
§5] КИНЕМАТИКА КОЛЕБАНИЙ ЗОЛ
Тогда из уравнений D) и E) имеем: скорости точки в А и В
равны нулю, а в точке С
причем знак зависит от того, в каком направлении движется точка —
от А к В или наоборот.
Ускорения точки is указанных трех положениях находятся подста-
подстановкой координат в (fi):
wc = — 4 m-ai.
Для приобретения навыков в решении задач па
негармонические колебания рекомендуется решить
следующие задачи из «Сборника задач по теорети-
теоретической механике» И. В. Мещерского, издания 1950 г.
и более поздних лет: 314, 328, 357.
ГЛАВА VI
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 1. Уравнения плоского движения твердого тела.
Уравнения движения точки плоской фигуры
1°. Определение уравнений плоского движения
твердого тела и уравнений движения точки плоской
фигур ы. Плоским (плоско-параллельным) называется движение твер-
твердого гола, при котором траектории всех его точек лежат в плоскостях,
параллельных некоторой неподвижной плоскости. При таком движении
псе точки твердого тела, лежащие на
перпендикуляре, восставленном к этсй
плоскости, имеют одинаковые траекто-
траектории, скорости и ускорения. Следона-
тельно, при изучении плоского движе-
движения твердого тела достаточно исследо-
исследовать движение плоской фигуры, являю-
являющейся сечением твердого тела плоско-
плоскостью, параллельной неподвижной.
Всякое перемещение плоской фи-
фигуры можно разложить на поступатель-
поступательное движение вместе с произвольно
выбранной точкой О,, называемой по-
полюсом, и на вращение фигуры вокруг
этой точки (рис. 6.1).
Выбирая исполнившую систему координат ху и систему коорди-
координат х,>'„ жестко связанную с плоской фигурой, имеем уравнения
плоского движения твердого тела:
О*)
-*- л
Рис. 6.1.
?=/>(')•
В этих уравнениях xov yol — координаты полюса — начала подвиж-
подвижной системы осей; угол <р — угол поворота подвижных осей координат
§ Ц УРАВНЕНИЯ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 367
относительно неподвижных. Ползая систему координат правой, т. с.
ось г направленной перпендикулярно к плоскости ху на читателя,
имеем положительное папраиление отсчета угла <р против часовой
стрелки.
Если выбрать за полюс не точку О,, а какую-либо другую точку
плоской фигуры К, то уравнения движения полюса
(
характеризующие поступательное движение фигуры вместе с полюсом,
будут отличаться ог аналогичных первых двух уравнений в (И). Угол
поворота плоской фигуры не зависит от выбора полюса. Поэтому
третье уравнение, определяющее вращение плоской фигуры, может
отличаться для различных полюсов только па постоянное слагаемое.
Если же для всех полюсов начальные значения угла поворота выбрав
одинаковыми, то уравнения ьращенин плоской фигуры бутут тжде-
ствеппы.
Сис1ема уравнении A*) полпоаыо определяе1 положение плоской
фигуры is любой момент времени.
Уравнения движения произвольной /почки Л1 плоской фигуры
имеют вид
x = xOl -\- х, cos <р — у, мп с?, |
У=Уо, -7 *\ мп <р -\-ух cos --p. J
В этих уравнениях: х, у — координаты точки Л1 в пеподнижпой
системе координат; дг01, уо, — координаты полюса Ой хи у{ — коор-
координаты точки М в системе координат x^'i, жестко cH<uaiiiioti с пло-
плоской фигурой; <р — угол поворота подвижной системы коордппаь
Координаты -V,, _>'] — ъ\о дна цосюяппых, неиамеппых ио время дви-
движения числа, определяющих рассмафивасмую точку плоской (|)шуры.
Остальные величины, иходящие в уравнения B*), являются функциями
времени, которые определяются посредспюм уравнении A*). Исключая
из уравнений B*) время, находим фаекгорию точки М.
При решении задач па определение уравнений
плоского движения твердого тела, уравнений движе-
движения и траекторий точек плоской фи!уры рекомен-
рекомендуется такая последовательность действий:
1) выбираем две системы координат, неподвижную и подвижную,
жсс1ко связанную с плоской фигурой;
2) составляем уравнения движения плоской фигуры;
3) нахедим уравнения двнже.ыя точки твердело тела;
4) исключая ш уравнений движения течки время, определяем
уравнение фаекюрии точки.
3E8
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[ГЛ. VI
Задача 6.1. В шатуппо-кривошипиом механизме центр вращения
кривошипа О находится па расстоянии а от горизонтальной траекто-
траектории полпупа В. Угол поворота кривошипа изменяется согласно закону
?i = kt, где k - - постоян-
постоянный коэффициент. Длина
кривошипа ОА = г, ша-
шатуна АВ = 1-
Определить уравнения
плоского движения ша-
шатуна ЛИ.
Ре ш ение. Выбираем
неподвижную систему
координат с началом в
точке О. Ось х направ-
направляем вправо по горизон-
горизонтали, ось у — по верти-
вертикали вверх. Подвижную
систему координат берем
с началом п точке Л, принадлежащей и геривошпну п шатуну. Ось .V)
проводим но шатуну АН, ось _у, — перпендикулярно к нему. Таким
образом, точка А шатуна (начало подвижной системы координат)
является полюсом. Уравнении движения полюса имеют вид
задаче 0.1.
хл = ОЛ cos 'J = г cos ht,
ул = ОЛ sin 0 —г sin ht.
Для нахождения третьего уравнения движения, зависимости угля
поворота шатуна от времени, спроектируем отрезок A Li на ось у.
У Обозначая через 9 угол между ося-
| ми Л", и Л', находим:
АИ sin а = ОА sin 0 - \ - а,
или, так как
имеем:
sm -f = ¦ t sin
= r, t, =
—.
К задаче 6.2.
Отсюда находится угол а ка:с функ-
функция времени.
Задача 6.2. Жесткий прямой
угол АМС движется так, что точка Л
остается нее время па оси у, т01да
как другая сторона угла МС проходит через неподвижную точку В.
Зная, что АМ = ОВ = а, определить траекторию точки М.
Решение. Для определения траектории точки М выберем по-
полярную систему координат с началом в точке В. Обозначая радиус-
§ М УРАВНЕНИЯ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
вектор ВМ через г и угол ОВМ через а, находим:
AM sin a — ЯМ cos а = ОБ,
или
ИЛИ
n-\-r os а •' -1 — sin a
r 1 — sin a
Отсюда после несложных преобразонаннй получим:
а -г , а
tg
3G9
С)
Из
С)
имеем:
п
—
г
г
г
а
1 — sin
cos з
cos a — 1 -
-
| ¦ sin at
1 -- sill a
Это и есть ураипенне траектории точки М—полярное уравнение
строфоиды.
2°. Определен и е положении центра конечного вра-
вращения плоском фигуры. Любое пепооунателыюе перемещение
плоской фигуры может быть осуществлено поноротом нокруг некото-
некоторой точки, называемой центром (конечного иращения.
Для построения положения центра конечного иращения необходимо
ныбрать две произвольные точки плоской фигуры А и В (рис. 6.2, а).
Пусть после перемещения эги точки оказались в А} и Ну Соединяя
точки А и А,, В н В\ прямыми линиями, найдем точки D и П,
делящие отрезки АЛ{ и В['ц пополам. В этих точках восстакляем
перпендикуляры соотнегственно к прямым AAt и ВН\. Точка пересе-
пересечения этих перпендикуляром О и является положением конечного
цешра крашения плоской фшуры.
370 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. 1ГЛ. VI
Эго построение не приводит к цели только в том случае, если
второе положение плоской фигуры является зеркальным отображением
первого (рис. 6.2, б), так как при этом перпендикуляры, носстан-
ленпые в срединах отрезков AAt и ВВЬ сливаются в одну прямую
линию.
В этом случае для нахождения положения центра конечного вра-
вращения плоской фигуры необходимо продолжить прямые АВ и A^BV
Точка их пересечения и будет искомым центром вращения.
Если же (рис. 6.2, в) перпендикуляры, восставленные к прямым,
соединяющим точки А и Аи В и /?,, в их серединах D и /:', парал-
параллельны, то центра конечного вращения нет.
II р и решении задач на определение положен и я
ц о кт р а к о печного вращения рекомендуется т а к а я
и о с л е до и а т е л ьп о с г ь де й с т в и п:
1) выбираем две точки в начальном положении плоской фигуры;
2) находим положение этих же точек после конечного перемеще-
перемещения фигуры;
3) соединяем прямыми линиями начальное и конечное положения
каждой из двух точек фигуры;
4) носставляем в середине этих отрезков перпендикуляры к этим
прямым и в точке пересечения этих перпендикуляров находим искомый
центр конечного вращения плоской фигуры.
Задача 6.3. Колесо кап-пся без скольжения по прямолинейному
рельсу.
Найти положение центра конечного вращения, если колесо совер-
совершило такое перемещение, что ючка соприкосновения колеса с рель-
рельсом стала наиболее удаленной от рельса точкой (рис. а).
О,////////////////////////У////////////////?,
о) б)
К задаче 6.3.
Решение. Соединим начальное и конечное положения цетра
колеса О и О| прямой (рис. б). Проведем прямую между точками
А и Av Эти прямые пересекутся и точке, которую обозначим через С.
Проводя прямые 0.4, ОАг. ОгАь О\А (рис. б), замечаем, что
0.40]/^ — параллело!рзмм. Прямые 001 и АА1 являются диагоналями
этого параллелограмма. Следовательно, точка их пересечения С делит
отрезки 001 и AAi пополам. Если носстапмть в точке С перпендику-
перпендикуляры к OOi и ААЬ то единственной точкой их пересечения и будет С.
УРАВНЕНИЯ ПЛОСКОГО ДВИЖЕНИЯ ТВИ'ДОГО ТР.ЛЛ
371
Значит, С и является центром конечного вращения при перемещении
колеса из первого положения во второе.
Задача 6.4. Движение звеньев кривошипно-шатунного механизма
определяется углом <р, который образует кривошип ОА с траекто-
траекторией ОБ движения ползуна. В начальном положении угол <ро = я/2
(рис. а).
Определить положение центра конечного вращения шатуна АВ
при перемещении кривошипа ОА и:\ начального положения в положе-
положение, когда угол <р, = 0; в положение, когда угол ср.2 = 3^/2.
Решение. Для нахождения положения центра конечного вращения
шатуна АВ при перемещении из положения <po = z/2 в положение
ср, = О изображаем (рис. б) оба положения шатуна. Соединяем началь-
начальное и конечное положения точек А и В, т. е. проводим прямые ААг
К задаче 6.4.
и ВВ\. Далее, находим середины этих отрезков, точки О и ? В этих
точках восставляем перпендикуляры к рассматриваемым отрезкам.
Пересечение перпепдикулярои, точка С, и является центром конечного
вращения шатуна.
Переходим к определению положения центра конечного вращения
при перемещении шатуна из положения <р0 = тс/2 в положение ср.2 = Зт://2
(рис. в). Как видно из построения, точки В и Вг п этом случае совпа-
совпадают. Точка О является серединой отрезка АА\. Если восставить в
точке О перпендикуляр к отрезку ААЪ то па нем должен находиться
центр конечного вращения. Ввиду того, что конечное положение ша-
шатуна является зеркальным отображением его начального положения,
конечным центром вращения является точка В, где пересекаются
прямые АВ и А]/?,.
Для приобретения навыков в решении задач па
составление уравнения движения плоской фигуры
и ее точек рекомендуется решить следующие задачи
из «Сборника задач по теоретической механике»
И. В. Мещерского, издания 1950 г. и более поздних
лет: 492, 493, 495, 498, 500.
372
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТКЛА
[ГЛ. VI
§ 2. Скорости точек плоской фигуры
Скорости точек плоской фигуры могут быть определены апалши-
ческими, графическими или же графоаналитическими методами. В этом
параграфе рассмотрим нахождение скоростей точек плоской фигуры
аналитическим и графоаналитическим способами. Графический метод
определения скоростей точек, заключающийся в построении плана
скоростей, будет рассмотрен отдельно.
Аналитический метод. При аналитическом методе должны
быть заданы уравнения движения плоской фигуры (рис. 6.3)
*о.=/1@. yot=W, » = /э@- О*)
Проекции скорости точки Л? на неподвижные осп координат опре-
определяются равенствами:
vx = vOiX — <о2 (у — j-0(), ' B*)
В этих формулах vx
на неподвижные осп
vy — искомые
координат; v,
Рис. 6.3.
§ 1 этой главы. Проекции
координат находятся по формулам:
проекции скорости точки М
о,* = л'о,' vot v =Уог — проекции
скорости полюса, начала подвиж-
подвижной системы координат х,у, па
неподвижные оси координат;
и). = ф — проекция угловой ско-
скорости на ось z, перпендикуляр-
перпендикулярную к плоскости движения; х,
у — координаты точки М в i;e-
подвижпсй системе координат;
хо > У о — координаты полюса (){
в неподвижной системе осей.
Определение координат х, у льч-
*" ки М по заданным уравнениям
движения плоской фигуры A*)
производится по формулам B*)
скорости точки М па подвижные оси
V C0S ? + VO,y SiF1 '¦? —
v0{X sin cp -f vOiy cos ф
D*)
E*)
В этих формулах x^, w,,, — искомые проекции скорости точки М
па оси хи у\ подвижной системы координат, жестко связанной
с плоской фигурой; д-j, у\ — координаты точки М в подвижкой си-
системе осей; остальные величины имеют то же значение, что и в урав-
уравнениях B*), C*).
СКОРОСТИ ТОЧГ.К ПЛОСКОЙ ФИГУРЫ
373
Величина скорости точки М по известным проекциям определяется
формулой
Направляющие косинусы даются paeeiiciBavii:
cos (v, x)= x\
COS (V, Х])=
cos (v, у) = -У,
СО8(в,^) = -^
(Г)
(8*)
Графоаналитические методы. Первый графоаналитиче-
графоаналитический способ определения скорости точек плоской фигуры основан
на формуле распределения скороаей (рис. 6.4)
В этой формуле v — искомая скорость точки М; v0 —скорость по-
полюса О у, <л — угловая скорость плоской фигуры; Г] — радиус-вектор,
проведенный из полюса Oj в ючку М.
Таким образом, зная скорость какой-либо точки плоской фигуры,
выбираем эту ючку за полюс. Далее, откладываем от точки М,
скорость которой подлежи!
определению, пек юр, равный
скороаи полюса, п вектор
*> X г у, направленный перпен-
перпендикулярно к г, и ранный по
величине ШГ|. Векюрпая сумма
этих сла1аемых и даег иско-
искомую скорость точки М. Если
скороеII. точки М известна но
направлению, то можно не
зна1Ь величины вращательной Рис.6 1,
скорости ы X г\< таК как |! эга
скорость, и искомая скороаь точки М определяются пересечением
прямой, совпадающей с направлением скороеш ючки М, проведенной
из М, и прямой, перпендикулярной к линии ОуМ, проведенной из
копна нектора vQ , сложенного из точки М.
После тою как треуюльпик или параллелограмм скорое 1ей, пы-
ражающий paiieiiciKO (9'), построен, задача можем ciniaibCH решен-
решенной. Величина и направление скорости ючки М MOiyi бьмь найдены
по рисунку (рис. 0.1) или получены из решения ыого треугольника.
Формула распределения скоростей (9-1) запнсываехс» часю ь дру-
другом виде:
374
ПЛОСКОР. ДВИЖРЛШЕ ТВЕРДОГО ТЕЛА
(ГЛ. VI
где vg — искомая скорость точки В\ч)л — известная скорость точки Д
избранной за полюс, а
г'ил =
X
vHA = «1Л.4
¦— вращательная скорость точки /i иокруг точки Л, равная но мо-
модулю произведению мгновенной угловой скорости плоской фигуры
i,a расстояние от точки до полюса и направленная перпендикулярно
к отрезку прямой НА в сторону мгновенного вращения фигуры.
Многие задачи могут быть решены при помощи теоремы о равен-
равенстве проекций скоростей концов отрезка плоской фигуры па направ-
направление отрезка (рис. 6.4).
Второй I рафоаналитпческнй метод определения скоростей точек
плоском фигуры основан на использовании мгновенного центра ско-
скоростей этой фигуры. При непосгупательпем движении плоской фи-
фигуры (ш ZjL 0) и каждый данный момент су-
существует точка тела, скорость которой раина
пулю. Эта точка называется мгновенным
центром скоростей и обычно обозначается
через Р. Единственным исключением является
сл)чай тук называемого мгновенно-поступа-
мгновенно-поступательного движения (и) = 0), который будет
рассмотрен отдельно. Выбирая мгновенный
центр за полюс, имеем закон распределения
скорое гей в плоской фигуре:
Ч = О)<Г], "О-^=<ОШУ, A0*)
где v — искомая скорость произвольней
''ис. 6.5. точки М; to — yi лопая скорость плоской фи-
фигуры; Г] — радиус-пектор, проведенный из
мгновенного центра скоростей в точку АЛ, называемый мгновенным
радиусом. Таким образом, скорости всех точек плоской фигуры яь-
Л1.ЮТСЯ в данный момент вращательными скоростями вокруг мгновен-
мгновенного центра скоростей. Их неличпны равны произведению величины
угловой скорости на модуль мгновенного радиуса, а направлены они
перпендикулярно к мгновенному радиусу- Таким сбразс.м, величины
скоростей точек плоской фигуры пропорциональны величинам мгно-
ix радиусов:
DP ~ ЛР'
-. и).
(И*)
Методы нахождения положения мгновенного цен-
центра скоростей:
а) известны скорость одной точки О и угловая скорость н."сс-
коИ фигуры (рис. 0.5); мгновенный центр скоростей находится па
« 2| СКОРОСТИ TO4F.K ПЛОСКОЙ ФИГУРЫ 375
перпендикуляре, восставленном к скорости точки О, па расстоянии
ОР-.= °°- A2*)
направление перпендикуляра находим, поворачивая vn па угол rJ'l
is сторону «ращения;
б) известны направления скоростей двух точек плоской фугуры А
и В (рис. 6.6); мгновенный центр скоростей находится в точке
Рис.
Рис. 6.7.
пересечения перпендикуляров, косстапленных п точках Л и В к ско-
скоростям этих точек;
I!) скорости двух точек Л и В плоской фигуры параллельны
друг другу, перпендикулярны к отрезку АВ, направлены и одну сто-
сторону и не раины; мгновенный центр нахо-
находится на продолжении АИ со стороны той
точки, чья скорое п. меньше; расстояния от-
отточек до мгновенного центра скоростей про-
пропорциональны скоростям точек; для опреде-
определения мгновенного центра скоростей необ-
необходимо знать не только направления, но и
неличины скоростей точек А к В (рис. 6.7);
г) скорости двух точек А и В плоской
фигуры параллельны друг другу, перпенди-
перпендикулярны к отрезку АВ и направлены в раз-
разные стороны; мгновенный центр скоростей
лежит на отрезке АВ и делит этот отрезок
на части, пропорциональные скоростям; для нахождения мгновенного
центра скоростей необходимо знать и величины и направления ско-
скоростей обеих точек (рпс. 0.8);
Jnc. 6.8.
376
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[ГЛ. VI
д) плоская фигура катится без скольжения по неподвижной кри-
кривой (рис. 6.9); мпюнспный центр скоростей Р находится в точке
соприкосновения фигуры с кривой.
Если скорости днух точек плоской фигуры параллельны друг
другу и не перпендикулярны к отрезку, соединяющему обе точки
(рис. 6.10), или скорости двух точек фигуры параллельны, раним
друг другу и перпендикулярны к отрезку,
соединяющему сбе точки (рис. 6.11), то
мгновенного центра скоростей в данный
момент не существует или можно сказать,
что ои находится в бесконечности. Угло-
Угловая скорость млосксй фигуры в данный
момент равна нулю, движение называется
мгновенно-поступательным, скорости
всех точек плоской фигуры в этот мо-
момент равны.
При мгновенно-поступательном движении ускорения точек плоской
фигуры, вообще говоря, не равны друг другу и траектории точек
плоском фигуры также неодинаковы.
Рис. 6.9.
Рис 6.10.
I'm:. 6.11.
Положение мгновенного центра скоростей может быть также опре-
определено аналитически. В неподвижной системе осей координаты,
мгновенного центра определяются формулами:
X р — X р.
Oi.v
Ур=Уо,
"о,.,
A3*)
В этих формулах хр, уР — координаты мгновенного центра скоростей
в неподвижной системе координат; х0, у0 —координаты полюса,
начала подпижной системы осей; v0 v, v0 ,, — проекции скорости по-
полюса на неподвижные оси координат; ш2 — проекция угловой скоро-
скорости фигуры на ось, перпендикулярную к плоскости, в которой про-
происходит движение. В подвижной системе осей, жестко связанней
§ 2] СКОРОСТИ ТОЧГ.К ПЛОСКОЙ ФИГУРЫ 377
с плоской фигурой, координаты мгновенного центра скоростей
определяются так:
Vn sin <S — Vn ,, COS ')
x>p=Jh±—<^Jhl L, A4*)
_"<),* cos ?+ty,|V sin ?
J'l p — ~ • (' ° )
Здесь л']р, yip — координаты мгновенного центра скоростей в псд-
пижпой системе осей; <р — угол поворота подвижной системы коор-
координат но отношению к неподвижной. Остальные величины те же,
что и в A3*).
Формулами A3*), A4*), A5*) целесообразно пользоваться, ко!Ла
заданы уравнения движения плоской фшуры A*).
Аналитический метод определения скоростей целесообразно при-
применять, если известны но условию или могут быть без особых за-
затруднении составлены уравнения движения плоской фигуры A*). Ана-
Аналитический метод позволяет, вообще говоря, иайш скорость точки
плоской фигуры как функцию времени. Однако получигь такое реше-
решение в обозримом виде не всегда возможно.
П р п а н а л и г и ч е с к о м методе ре ш е п и е задач реко-
рекомендуется вести в следующем порядке:
1) выбрать неподвижную и подвижную системы координат; начало
подвижной системы осей взять в такой точке, уравнения движет»!
которой известны или могу г быть составлены без особых затруд-
затруднении;
2) составить уравнения движения плоской фигуры: два уравнения
движения полюса и уравнение вращения фшуры вокруг полюса;
3) пользуясь уравнениями движения плоской фигуры, получи 1ь
уравнения движения точки, скорость которой требуется найти;
4) определить проекции скорости на неподвижные или подвиж-
подвижные оси координат и иагггп величину и направление искомой скорости.
Графоаналитические способы нахождения скоростей точек плоской
фигуры целесообразно применять в iex случаях, когда требуется
паИти скорости различных точек плоской фшуры в данный момент
времени при определенном положении плоской фшуры.
Решение задач при помощи мгновенного центра скоростей при этом
эффективнее других графоаналитических методов, если требуется опре-
определить скорости нескольких точек, причем вычисление мгновенных
радиусов может быть произведено без сложных выкладок. Если же
согласно условию задачи необходимо найти скорость какой-либо
одной точки плоской фигуры, то обычно быстрее к цели ведет при-
применение теоремы о распределении скоростей (9*) пли теоремы о ра-
равенстве проекций скоростей концов отрезка плоской фигуры на на-
направление самого отрезка.
378 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
При графоаналитических методах решения задач
рекомендуется такая п о с л е д о в а т с л ь п о с т ь действий:
1) выбрать за полюс ту точку плоской фигуры, скорость которой
известна или легко определяется из условия задачи;
2) найти другую точку плоской фигуры, направление скорости
которой известно;
3) пользуясь формулой распределения скоростей, найти скорость
этой точки плоской фигуры;
4) исходя из формулы распределения скоростей, определить
значение угловой скорости плоской фигуры в данный момент времени;
5) зная угловую скорость фигуры и скорость полюса, найти с по-
помощью формулы распределении скоростей искомые скорости других-
точек фигуры.
При графоаналитическом методе решения задач
может быть применен и метод проекций. R этом случае
может быть рекомендован следующий порядок решения задач:
1) выбрать за полюс точку плоской фигуры, скорость которой
известна;
2) пользуясь формулой распределения скоростей, построить ско-
скорость другой точки плоской фигуры, у которой известно направле-
направление ее скорости;
3) спроектировать полученный треугольник скоростей на направ-
направление прямой, соединяющей обе точки, и найти скорость второй точки;
4) спроектировать треугольник скоростей на направление, пер-
перпендикулярное к прямой, соединяющей обе точки, и найти вращатель-
вращательную скорость второй точки но отношению к полюсу;
5) разделив вращательную скорость на расстояние от точки до
полюса, найти мгновенную угловую скорость плоской фигуры;
6) зная мгновенную угловую скорость фигуры, можно найти ско-
скорости любых точек плоской фигуры, пользуясь формулой распреде-
распределения скоростей.
Если же задача решается при помощи м г и о в е н-
пого центра скоростей, то рекомендуется такая по-
последовательность действий:
1) определить положение мгновенного центра плоской фигуры
одним из вышеуказанных способов;
2) найти величину мгновенного радиуса той точки плоской фи-
фигуры, скорость которой известна, и определить угловую скорость
плоской фигуры, разделив величину скорости точки на величину
мгновенного радиуса;
3) найти искомые величины скоростей точек плоской фигуры,
умножая угловую скорость на мгновенный радиус соответствующей
точки или используя формулу (П*).
Задача 6.5. Стержень АВ совершает плоское движение. Скорость
точки А образует угол 30° со стержнем и равна в данный момент
скорости точек птоскои фигуры
379
по величине 5 м'^ек. Скорооь точки В в этот же момент состзи-
лясг угол 00° с продолжением аержпя (рис. а).
Определигь величину скорости точки В, положение мгновенно! о
центра скоростей, а 1зкже угловую скорооь пержпя, если ею
.гимна АВ = '2 м. Найти ыкже скорость точки Д середины сгержпч.
К задаче 6 г).
Решение. Эту задачу следует решать графоаналитически. Се-
т.ысио формуле распределения скоростей
сгропм [реугольпик скоростей, ссошегспуютиП jpauiienrio A). Из
произвольной ючки О1клады1:ге« и избранном масштабе скороаь isv
известную но величине и папрэнлашю Из когца г1, проводим пря-
прямую, парал.'ельную vliA, т. с. перпендикулярную к стержню ЛИ.
Величина пек гора v!iA пеи.чиесша. Воспользуемся тем, чю i знсс i чо
направление скорости vn. Из начала вектора 1>А проводим прямую,
параллельную направлению vn, до пересечения с прямой гзПА. Таким
образом, получен замкнутый ,рсуюлышк скоростей, стороны кок,-
рого в избранном масштабе определяют скоросп. точки В и враща-
вращательную скорость точки В вокруг полюса А В эюм треугольм! ке
извести одна сторона vA и ьсе три учла (рис. б).
Решая ьгот треугольник, находим:
— "л .- — — =10
sm J0" 0,5
Ii ек,
('2)
замечая, что
vD — vA tg G0° = Г) \ГЪ ^ 8,65 м/t ек;
vUA ~ - ч> В А =: ш ¦ 2,
380 ПЛОСКОЕ Д0ИЖЕ11ИЕ ТВЕРДОГО ТЕЛЛ 1ГЛ. VI
из B) и C) определяем неличину угловой скорости:'
Скорость точки D, середины стержня АВ, может быть найдена
при помощи формулы распределения скорое left
Для построения треугольника скоростей (рис. в) из произиолыюй
точки откладываем скорость <оА. Из конца vA откладываем вектор,
рамный -yVIIA. Соединяя начало вектора vA с конном вектора -j vnA,
находим искомую скорость точки D.
Величина скорости точки D легко определяется из треугольника
скоростей. Дне стороны этого треугольника равны но величине vA —
= vliA^o MJсек, а угол между этими сторонами ранен 60Л Сле-
лонателыю, sioi треугольник рашюпороппий. Величина скорости
точки /) равна также 5 м'сск.
г)\у задачу молено решить и при помощи мгновенного центра
скорое ieH. Для нахождения мгновенного центра скоростей стержня АН
iioccuniiivi перпендикуляры к скоростям точек А и В (рис. г). Пере-
Пересечение МПIX прямых определяет положение мгнонсиного центра ско-
скорое reit Р. В прямоугольном треугольнике АВР известны сторона ЛП
и дна прилегающих угла: /тВЛР = 60':>, /_АВР = '№°. Находим
мгновенные радиусы АР и ИР:
АР = Att sin 30° = 2 -0,5 = 1 м,
ВР = АВ cos 30° = 2 *23-^ 1,73 м.
Величина угловой скорости стержня
и, следовательно, величина скорости точки В
vB = in/jp^5' 1,73 = 8,Go м/сск.
Для определения скорости середины стержня, точки D, пропелем
v.i поденный радиус PD. Ил треугольника ЛОР следует, чго АР =
^^Л1)= 1 м. Следопательно, треугольник равпостороиппй и DP= 1 м.
1 огда
vn -- DP ¦ ш = 5 м/сск.
Скорость точки D направлена перпендикулярно к мгновенному ра-
радиусу DP.
§ 2] СКОРОСТИ ТОЧЕК ПЛОСКОЙ ФИГУРЫ 381
В этой задаче оба метода решения равноценны. Они одинаково
быстро позволяют получить ответ на все вопросы, поставленные
в задаче.
Если бы требовалось найти линь величину скорости точки В,
то проще всего было бы применить теорему о равенстве проекций
скоростей двух точек плоской фигуры па направление отрезка, соеди-
соединяющего эти точки:
vA cos 30° = г'в cos 60е,
откуда
v cos 30°
Л
2 • 0o
7
" cos 60 2 • 0,o
Задача 6.6. Кривошиипо-шатунный механизм состоит из криво-
кривошипа ОА и шатуна АВ с одинаковой длиной г. Кривошип (зращае1ся
вокруг неподвижного центра О. Утл 0 (рис. а) изменяется согласно
А
0
ЖГ
?)
¦ К задаче 6.6.
уравнению ф = ?Л Копен шатуна В шарнирно прикреплен к центру
колеса. Колесо радиуса а катится без скольжении но горизонталь-
горизонтальной плоскости, параллельной прямей ОБ и отстоящей от нее на рас-
сюянии а.
Найти уравнения плоского движения колеса, а тскже уравнения
движения той точки сбода М, которая соприкасается с плоскостью,
когда точка В находится в крайнем правом положении. Определи п>
скорость точки М и мгновенную углоную скорость колеса.
Решение. Первый способ. Выберем начало неподвижней
системы координат в крайнем правом положении точки В (рис. б).
Ось х направим по горизонтали влево, ось у — но вертикали вниз.
В качестве полюса выберем точку В. Составим уравнения движения
полюса:
xn = '2r — 2r cos kt — 2r(\ — cos kt), A)
ун = 0. B)
Для получения третьего уравнения движения, зависимости угла
поворота от времени, замечаем, что так как колесо катится без сколь-
скольжения, то перемещение центра колеса точки В может быгь представ-
представлено как произведение угла поворота колеса <р на ргдиус вращения а:
хп = М1М = а-!{. C)
382 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА /ГЛ. VI
Сопоставляя уравнения A) и C), находим третье уравнение движе-
движения колеса
2r (I — cos kt)
а
Переходим к определению уравнений движения точки М. Рассмотрим
произвольное положение точки М, когда радиус ВМ повернулся
па угол о от своего начального положения (рис. а). Тогда коорди-
координаты точки М могут быть определены следующими уравнениями B*;:
хм==хп — а s'n *?•
или, если внести в эти уравнения значения хп и «:
хм= 2г A — cos kt) — a sin — A — cos kt)
A —coskt)
Таковы ураннепия движения точки Л1. Эти уравнения являются пара-
параметрическими уравнениями траектории точки М, дуги циклоиды. Скс-
рость точки М определяется по ее проекциям на неподвижные оси
координат:
vxM = xM = '2rk sin kt — Irk sin kt cos U-(l — cos kt)\
Возводя в квадрат и складывая, получаем:
sin kt sin ~A — cos kt).
Проекция мгновенной угловой скорости колеса на ось z равна
Irk
-
a
Irk . .,
U) =ф = - Sin kt.
z T a
Второй способ. Покажем другой способ решения. Уравнение
движения точки имеет вид
хв = 2гA — cos kt).
Так как точка В движется прямолинейно, то ее скорость равна
vl1 = x[i=2rk sin kt.
Точка /И, — мгновенный центр скоростей колеса, следовательно, мгно-
мгновенная угловая скорость будет:
I = -" = - Sin
a a
§ 2] СКОРОСТИ ТОЧЕК ПЛОСКОЙ ФИГУРЫ 383
Тогда модуль скорости точки М равен
a Irk
vM = MiM- w = 2a sin -,j • r - sin kt. E)
Угол <р находится из D):
cp = \ wdt = — — cos kt - - С. (о)
j a
Полагая ср = О при г! = 0 и подставляя эти значения переменных
в F), находим:
Следопагелыю,
ср=-A — CQSkt).
Внося это значение в E), получим:
vM= irk sin kt sin — A — cos kt).
Задача 6.7. Круглый цилиндр Л обмотан тонкой нитью, конец
которой В закреплен неподвижно. Цилиндр
падает без начальной скорости, разматывая '/////^'///УУ/////'///'
нить. Величина скорости оси цилиндра опре-
определяется формулой
где g—постоянный коэффициент; у—рас-
у—расстояние, пройденное центром цилиндра, отсчи-
отсчитываемое от начального положении. Радиус
цилиндра ранен г.
Определить ураппения плоского движе-
движения цилиндра.
Р с ш с н и е. Выбираем неподпижпую си-
систему координат с началом в точке О, где
центр цилиндра находился в начале движе-
движения. Ось у направляем по вертикали нниз,
ось х — но горизонтали вправо. Тогда проек-
проекция скорости центра цилиндра на вертикаль-
вертикальную ось, равная производной от координаты у по времени, будет равна
Отделяя переменные, имеем:
К задаче 6.7.
384 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
ипте! рируя это диффереициалыюе уравнение, получаем:
В начальный момент, при t = Q, координата у = 0. Используя это,
находим, что произвольная постоянная интегрирования С|=0, сле-
следовательно, уравнение движения центра цилиндра принимает вид
У = {¦**• (О
Для определения второго уравнения движения (зависимости угла
поворота цилиндра от времени) находим угловую скорость цилиндра.
Мгновенный центр скоростей цилиндра находится в точке Д точке,
где пить отходит от цилиндра, следовательно,
Подставляя в уравнение B) значение у из A), имеем:
ш,=~. -g-t.
6 г
Так как ш, — ~2, то
о Г
интегрируя, находим:
Произвольную постоянную C<i определяем, полагая, что в началь-
начальный момент, при t = 0, угол поворота цилиндра был ранен пулю:
ср = 0. Подставляя эти начальные условия в уравнение C), находим,
что С2 = 0. Таким образом, второе уравнение движения цилиндра
имеет вид
Задача 6.8. Круглый цилиндр А обмотан тонкой питью, конец
которой В закреплен неподвижно. Цилиндр надает без начальной
скорости, разматывая ишь (рис. а). Значение скорости оси цилиндра
определяется формулой
v = -^V3gy, 0)
где g—ускорение силы тяжести;у — расстояние, пройденное центром
цилиндра, отсчитываемое or начального положения. Радиус цилиндра
равен г.
§ 21
СКОРОСТИ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
385
Определить скорости четырех точек па ободе цилиндра, располо-
расположенных па концах взаимно перпендикулярных диаметров, изображен-
изображенных па чертеже.
Решение. Мпюиенпый uemp скоростей цилиндра находится
в точке D, где неподвижная часть нити /ID соприкасается с цилинд-
цилиндром. В этом месю скорости точек ш:ш и цилиндра, находящихся
в соприкосновении, равны .между ccooii и, следовательно, равны пулю.
Скорости остальных то-
чек пропорциональны рас- •и^д~
стояииям до мгновенного
центра cKopocic.il и пер-
перпендикулярны к мгновен-
мгновенным радиусам. Величина
скорости точки IS опре-
определится из пропорции
2~г'
откуда, учитывая A), па-
хедим, что
¦°е=-\\'ЧУ- B)
Направление скорости
точки Е перпендикулярно К задаче G.8.
к мгновенному радиусу
DE, т. е. параллельно скорости точки А. Скорости точек С и //
раины по величине, так как они отстоят ог мпювеппого центра
скоростей, точки Г), па одинаковых расстояниях DC=DH= г [ 2.
Величины этих скоростей определяются из пропорции
г\ >
оiкуда
C)
направлены эти скорости перпендикулярно к мгновенным радиусам СП
и HD (рис. о).
Формулы B) и C) определяют величину скоростей точек С, Е, II
как функцию пройденного центром диска расстояния у. Найдем вели-
величину этих скоростей как функцию времени.
В задаче 6'.7, неходя из уравнения A), было выведено уравнение
движения центра диска
13 М. И. Бать и др., т. I
386 ПЛОСКО!- ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. V!
Подставляя это значение расстояния у в формулы B) и C), получаем:
Величину скорости точек С и /-/ можно также найти па осноил-
нии теоремы о равенстве проекции скоростей двух точек плосксй
фигуры на прямую, соединяющую эти точки. Скорости точек С и Н
составляют углы 45° с линией САН, а скорость точки А направлена
по этой прямой. Следовательно,
vc cos
= w// cos 45° =
откуда
v 2|/2/5—- 2 , -r— 2J/2"
Задача 6.9. Стержень АВ скользит точкой А по горизонтальному
полу вдоль оси х и касается
псе время круга радиуса г.
Определить угловую ско-
скорость стержня АВ, если ско-
*\v\ ' \ рость точки А равна vA.
Решение. Обозначив угол
между стержнем АВ и осью л'
буквой «> получим:
К задаче С.9.
— = sin A80° —о>) = sin (р, A)
где х — координата точки А. Продифференцирован A) но времени,
получим:
d<a r dx
C0Si
или, учитывая, что - ¦- —<
dt=v
иаПдем:
.А.
л'-
ол
АК'
rv,
x=cos(\80o--cf) л- АК хУх'2-Г-'
Эту же задачу можно решить другим способом. Скорость точки К
направлена по касательной к окружности, т. е. по стержню АВ. Ско-
Скорость точки А равна сумме скорости полюса, за который примем
точку К, и вращательной скорости вокруг полюса:
где
илк—-
14
СКОРОСТИ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
ЗЯ7
Спроектируем геометрическое равенство B) на перпендикуляр к АВ:
vA sin f = <» • AK,
откуда, учитывая, что угол ? увеличивается,
v sin <р
VAr
Задача 6.10. Шарнирный четырехугольник ABED (рис. а), в кото-
котором АВ = ЕО —¦ а, АО = ВЕ = Ь, имеет неподвижное звено АВ. Ско-
Скорость точки D известна и равна v.
Определить скорость точки /:' и мгновенную угловую скорость
звена ЕО, если в данный момент угол ОАВ = (^0°.
Решение. Мгновенный центр скоростей звена ВО находится
в точке пересечения стержней BE и АО, и точке Р (рис. б), так как
скорость точки О перпен-
перпендикулярна к АО, а скорость
точки Е перпендикулярна
к BE.
Обозначая длину отрез-
отрезка PD через х, можно вы-
выразить величину скорости
точки О как произведение
длины мгновенного радиуса
PD па величину мгновен-
мгновенной угловой скорости сгерж-
мя ВО:
V = X-m. A)
Проведя прямую ВО, за-
заметим, что треугольники
BED и ARD равны (но днум
равным сторонам при третьей общей стороне), и, следовательно,
/, DAB= /_ BED = 60°. Треугольники АРВ и ПРО также равны,
следовательно, ЛР=ПР = Ь — х и величина скорости точки Е можег
быть представлена формулой
vF = (р — л-) ш == Ьч> — хш = Ьш — у. B)
Рассмотрим треугольник ПРО; по теореме косинусов имеем:
х" = ((? — х)- -¦¦- a- — '2a{b — x) cos 00\
Раскрывая скобки и приводя подобные члены, найдем х:
задаче E.10.
и1 -j-b'1 — ab
— 2b~~a '
13'
388
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[ГЛ. VI
Теперь из уравнения A) можно определить значение мгновенной
угловой скорости стержня I'D
21) — а
V
со = -
X
v
= - =г> —-
а" --;- Ь* — аЬ '
Подставляя эю значение в уравнение B), имеем:
/ 'W- — ub . \ V - а-
^'г = :-, -,--¦ •- Г-г1=—-.-г., iv'i
'¦ \а'~ -г и- — at) ; а- -• - у- - - аи
это и есть искомая величина скорости точки /:' при данном положе-
положении механизма.
Задача 6.11. Вершина Л жесткого прямого угла ВЛП (рис. а)
соединена кривошипом ОА~=г с неподвижным цепiром О. Криво-
Кривошип ОЛ вращается равномерно: <$ = kt. Сторона прямого угла АВ
А/
_ J.'i." -С Л' Ьл/
с)
К задаче 0.11.
б)
проходит непрерывно через неподвижную точку М, я стержень АЕ —
через неподвижную точку N. Тогда М и N лежат па окружности,
описываемой вершиной прямого угла А.
Определить угловую скорость жесткого прямого угла ВЛН, а также
скорости тех его точек, которые совпадают в данный момент с шар-
шарнирами М и N.
Решение. Плоское движение стержня АВ можно разложить па
два простых движения: поступательное движение вдоль АВ и враще-
вращение стержня вокруг шарнира М. Соответственно скорость любой точки
стержня складывается из д-iyx составляющих: одной, направлением
вдоль стержня, и втором, вращательной скорости, перпендикулярной
к стержню АВ; величина вращательной скорости пропорциональна рас-
расстоянию от точки до шарнира М. Следовательно, для точки стержня,
которая в данный момент совпадает с шарниром М, вращательная
составляющая скорости раина пулю и ее скорость направлена вдоль
стержня АВ. Аналогично приходим к выводу, что скорость точки
стержня АЕ, совпадающей и данный момент с точкой Л;, направлена
вдоль стержня АЕ.
§ 21 СКОРОСТИ ТОЧГ-.К ПЛОСКОМ ФИГУРЫ 389
Восстаинм перпендикуляры к направлениям скоростей шчек стержня,
соппадающих с М и .V. Точка пересечения этих перпендикуляров Р
лежит на окружности AMN и нгляется мгновенным центром скоро-
cieti прямого угла ПАЕ. Точка Р лежит на окружносш, так как oiu
является першшюп прямого угл i Л/РЛ', опирающегося па диамеф
окружности. Значение модуля скороеin точки А, как принадлежащей
крииошипу ОЛ, pauiio
ьл = OA-\;i\ = г к. A)
Величина скорости этой же точки Л как принадлежащей прямому
углу ВАЕ, равна проп.чнедеишо мгновенной угловой скорости эк»о
угла па мгновенный радиус АР:
г)д = Л/>-шмг = 2гМчг. B)
Из рапепстп A) и B) находится пелпчипа мпювсппоП угловой скоро-
скорости плоской фигуры Л13!:;
u)Mt = A = const.
Скорость точки стержня АН, совпадающий с шарниром М, равна
по величине произведению мгновенной yi.ioiioti скорости на мгновен-
мгновенный радиус МР:
д, = МР ¦ о>мг = 2r sin ^- • -,- = rk sin -?-
(п равпобслреином треугольнике АОМ углы при основании AM равны
с/2, так как их сумма должна быть раина внешнему углу о).
Скорость точки аержпя АН, совпадающей с шарниром N, раина
vt = NP ¦ юм. —--Ir cos -;,- • -.- = г к cos -.-,-.
Направление скороеге!1 точки А п ючек, проходящих в данный мо-
момент мере:) М и Л', показаны на рис. б.
Задача 6.12. Шарнирный четырехзнепшпе (рис. о) coumnr \ул непод-
неподвижного зиепа Af3 = l, крнвошипон AD^o, hli = b и аержпя Dt'^d,
соединенных шарнкрпо. Кривошип BE вращается с постоянной угло-
угловой скоростью и). При этом гочкд D движется по дуге окружности
между дпумя крайними положениями (рис. в и г).
Определить угли ав1, ап>, 9оi¦ '-?.ij> которые образуют крпвопшпы
с прямой ЛВ в крайних положениях. Пай in угловую скорость кри-
кривошипа AD.
Решение. В первом положении углы а,ц и ctol определяются из
уравнении (см. рпс. в):
(d -j- b) cos -f 01 --= — a cos aol -> -1,
id-\-b) sin <foi = a sin y.M,
ПЛОСКОЕ ЛПИЖЕИИР. ТВЕРДОГО ТР.ЛА
VI
которые получаются проектиропапием сторон треугольника ABD на
горизонталь и вертикаль. И:> этих уравнении находим:
cos
ТЧI '
2Ц(Г-\- Ь)
cos а01 =
(rf -(- bf — a2 — !-
'Ла
Ro птором положении углы <ро,2 п ао.> определяются аналогично из
системы уравнений (см. рис. г):
— (d — h) cos art = / — о cos a0.,,
— (d — /;) sin !50.2 = a sin ам,
oi куда получаем:
I2 A-(d — b)" — a2
cos к,,., = —
2/ (d — b)
cos a02 = •
21a
Переходим, далее, к определению угловой скорости крипошипа AU
К задаче 6.12.
(рис. б). Пропедем прямую АН, обозначив ее длину через k. Прямая АЕ
делит угол а на составляющие
a = а, -|- а.2.
Эта же прямая образует утл ^ с криношипом BE и угол E.2 со япе-
пом DE. Обозначим через f угол /IDC и букпой 8 угол между ис-
исправлением скорее™ точки Н и продолжением прямой Z/c.
2] СКОРОСТИ ТОЧЕН ПЛОСКОЙ ФИГУРЫ 391
Тогда скорости точек D и /; буд>г:
где ш,—искомая yi лопая скорость кривошша AD. Спроектируем ско-
скорости гочис D и Е па направление прямой DE и приравниваем эти
проекции
ш,а sin y = шЬ cos о,
откуда искомая у-летая скорость будет:
b cos S .
ш,= ш. A)
Для нахождения углои 8 и f. входящих и ураипение A), иоспользуемся,
прежде всею, георемой косннусои для треугольника ARE:
k = У'Р -f- & — 211? cos ср. B)
Зпгя величину А, находим, пользуясь теоремой косинусов, из треуголь-
треугольника ЛОЕ
lf--\-d- — a- .„.
Далее, по теореме синусов для треуюльиика ABE имеем:
sin 3, sin «[ sin 9
оiкуда
sin °, = -ft- ып ср. D)
Теорема синусов для трсуюль.шка ADII приводит к равепину
sill f _ Sin ?2
откуда
sin f-= е ып J3,. C)
Далее, находим*
g __ q -1. Р, 90°
и, следовате.'ьно,
cos 8= sin C,-f p9). F)
Внося значения F) и (о) в уравнение A), получим:
bk чн
a- sin -,
Зависимость укчо» ^ и pj от угла <? определяется ранее получен-
полученными равенствами B), C) и D).
392 ILTOCKOF. ДВИЖЕНИИ ТВЕРДОГО ТГ.ЛЛ [ГЛ. VI
Л ля п р и о б р е т е и i: я п а и ы коп п р е ш е и и и за д а ч па
о п р с д с л е и и е скорое г е it г о ч е к плоек о И фигуры ре к о -
м е и д у е т с я р е ш и г ь с л е д у ю m и е з а д а ч п и з «С б о р и и к а
задач по г е о р е т и ч с с к о й мехами к е.» И. В. М с щ е р с к о г о,
издания 19ГH г. и более поздних лег: 502, 503, 504, 508,
510, 511, 513, 517, 521, 530, 539.
§ 3. Подвижная и неподвижная центроиды
Геометрическое место ммюпеммых центром скоростей нлоскей
фигуры, отмеченных па мигиммжмей плоское in, пазынается неподвиж-
неподвижной центроидои.
Геомсмрнческое место мгновенных центров скоростей плоской фи-
фигур и, отмеченных па движущемся теле, называется подвижной ценш-
роидой.
При плоском движении твердого тела подвижная центроида ка-
катится без скольжения но неподвижной. Точка соприкосновения под-
подвижной и неподвижной центроид является в данный момент мгновен-
мгновенным центром скоростей. Центроиды можно определить геометрическим
построением пли аналитически.
Геометрический способ нахождения подвижной и неподвижной
центроид заключается и следующем. Для произвольного положения
плоской фигуры или механизма построением находится мгновенный
центр скоростей. Далее, из построения определяется геометрическое
место мгновенных петров при заданном движении плоской фигуры
как но отношению к неноднижчюй системе координат, так и по отноше-
отношению к осям, жестко связанным с движущейся фигурой.
Аналитическое определение подвижной и неподвижной центроид
производится при помощи формул, дающих значение координат мгно-
мгновенного центра скоростей. Координаты мгновенного центра скоростей
и неподвижной системе осей выражаются так:
хп = х0-У±, A*)
Ур=Уо". 77?" B*)
Координаты мгновенного тигра скоростей в системе координат, жестко
снизанных с плоской фгпрей, определяюicm формулами:
J- sin •; v ross
Л IP— - ;- , (J )
хr cos с •!- у. sin ¦?
Уи'=П-~-П --¦ D*)
В этих формулах: х0, у0—координаты полюса, начала подвиж-
подвижной системы координат; х0, уA—проекции скорости полюса па пепод-
§ 3] ПОДВИЖНАЯ И ИППОДВИЖН\Я ЧР.НТРОПДЫ 393
ПИЖШ.ТС оси; <р — угол попорота подшгжной системы координат но
отношению к неподвижной; wz— проекция угловой скорости плоской
фигуры на ось z, перпендикулярную к плоскости, в которой проис-
происходит движение.
Переменные, находящиеся в правой части этих формул, являются
явными функциями времени пли выражаются через параметры, зави-
зависящие от времени. Решая совместно уравнения A*), B*) и исключая
время, находим уранпепие неподвижной центроиды. Решая систему
уравнений C*), D*), исключая время, определяем зависимость между
координатами х[р и ytp, т. е. уравнение подвижной ист pi,иды и явной
форме.
В некоторых задачах дли нахождения уравнений неподвижной и
подшгжной центроид удобнее ноль:к)н;ггься полкрией системен коорднна г.
При решении задач и i определен не подвижной н
н е и о д и и ж н о й ц е и г р о и д рекомендуется г а к а я нос л е-
д о в а т с л ь н о с т ь д е й с т в и й
1) выделить плоскую фигуру, для которой требуется найти под-
подвижную и неподвижную центроиды;
'2) выбрать две системы координат, неподвижную и подвижную,
жестко связанную с движущейся плоской фшурой;
3) найти построением или с помощью формул A*), ('2{:) мгновен-
мгновенный центр скоростей для произвольного положения плоской фигуры;
4) составить зависимость координат мгновенного центра скоростей
п неподвижной системе осей от какого-либо переменною параметра
движения;
5) решив совместно уравнения для координат мгновенного центра,
исключить переменный параметр и пайш уравнение неподвижной цент-
центроиды п явном виде;
6) пользуясь формулами (.4*), D*) или геометрическим ностроеш-км
мгновенного центра скоростей, соаавнть зависимость координат мгно-
мгновенного neinpa скоростей в подвижной системе координат от како-
какого-либо переменного параметра движения;
7) решив совместно эти уравнения и исключив переменный параметр,
определить уранпепие подвижной цеп фонды в янпом виде.
Задача 6.13. Крипошпппо-шатуппый механизм (рис. а) состоит из
кривошипа ОЛ = г, вращающегося вокруг неподвижном точки О,
шатуна ЛВ=1 и ползуна />', перемещающегося по i ор;гюиталык;й
примой Ох. Угол поворота кривошипа b^^kt, где к—постоянный
коэффициент.
Найти уравнение неподвижной и подвижной цен фонд шатуна АП
в параметрическом виде.
Решение. Выбираем неподвижную систему координат ху с на-
началом в точке О п подвижную систему осей хху\ с начале.м и течке Л,
принадлежащей шатуну, причем ось xt направляем вдоль шатуна ЛИ
(рис. б).
394 ПЛОСКОЕ ДВИЖЕНИЕ ТВР.РДОГО ТЕЛА [ГЛ. VI
Находим координаты точки А:
хА — г cos ([> = г cos kt,
у K = r sin (Jj = r sin ??.
Вычисляя производные от координат точки А, определяем проекции
ее скорости на неподвижные оси координат:
хл = — rk sin kt,
уА -= rk cos /г/.
Для нахождения мгновенной углопой скорости шатуна выразим
ординату точки А через угол попорота шатуна ср (угол <р взят со
К залачо 6.1.°».
знаком минус, так как он отсчитьтается от оси х по часовой стрелке):
уА = г sin kt = — / sin о.
Вычисляя от обеих частей этой формулы производные по времени,
получим:
rk cos kt = — / cos -f ¦ ф,
откуда
г cos kt
( )
г , cos kt
/ COS и
Опуская из А перпендикуляр AN на прямую ОВ, находим из тре-
треугольника NAB
NB Vl2 — r'2 sin- kt
С08?
Внося это значение в уравнение (I), получаем:
cos kt
2 = Ч = —г/г -
j//a— r* sin*'lit '
§ Я] ПОДВИЖНАЯ И ПР.ПОДВИ/КМ \Я Ц1ШТРОИДЫ 305
Теперь, пользуясь равенствами A*), B*), находим уравнение меи/д-
иижнон центроиды и параметрической форме:
У л
хр = хА — ш' = г cos kt -f i/ /"' — г2 sin2 kt, B)
ур=ул -'--']:f = r sin kt - tg Id 1 '7-'--Tl~s\nrhT~ C)
Если построить мгновенный центр скоростей Р шагупа АВ (рис. о),
находящийся па пересечении перпендикуляров, восставленных к ско-
скоростям точек А и Д ю уравнения неподвижной центроиды B) и C)
могут быть получены и непосредственно из треугольника ОРВ.
При г = 1 уравнения неподвижной центроидм упрощаются:
Xp = *2r cos kt,
Ур^= 1r sin kt.
Исключая [фемя, найдем:
т. е. неподвижная ценгроида представляет собой окружность с центром
и точке О и радиуса 2г.
Переходим к определению уравнения подвижной центроиды. Из
уравгениИ C*) и D*) для нашей задачи имеем:
— rk sin kt -у sin U -)- rk
- г« sin" W,
, . . . К/- — ra sia2 U , г . . .
rk sin kt : , • rk cos kt • - - sin kt
ytp = —r—= t }/> — r- sin * hi,
y*p rk cos kt r
или, после несложных упрощений,
, г , „ ,, / . v//- — г- sin- kt \
yJp = tg kt (l — ~ sin '2 kt \ -\~ у sin Id yF^r^v^kt.
Эти равенства и являются уравнениями подвижной центроиды
в параметрическом виде.
При г = 1 уравнения подвижной центроиды упрошаю[ся:
x,p=r(l —I sin*«) = '¦ cos 2kt,
y]p=2r sin kt cos kt = r sin 2H
или, исключая время,
„•2 . i ,,-2 ,'2
396
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[ГЛ. VI
Следовательно, подвижная центроида представляет окружность с цен-
центром is тотке Л и радиуса г.
Задача 6.14. Стержень АВ движется н плоскости чертежа так,
что ею конец Л непрерывно скользит по полуокружности HAD, а сам
стержень нее премя проходит через неподвижную точку D диа-
диаметра ED.
Определить неподвижную и подвижную центроиды стержня АВ
(рис. а).
Р с ш е и и е. Скорость точки А, описывающей дугу окружности,
направлена по касательной к данной окружности. Мгновенный центр
скоростей стержня АВ лежит на перпендикуляре, восставленном
а)
К задаче 6.14.
л точке Л к направлению се скорости, i. е. на радиусе ОА или его
продолжении. 'Гак как стержень АВ скользит но yuiy Д не отры-
наясь от пего, то скорость точки стержня, совпадающей в длппый
.момент с точкой Д направлена вдоль стержня. Восставляя перпенди-
перпендикуляр к стержню п точке Д находим мгновенный центр скоростей
стержня АВ в пересечении перпендикуляров к скоростям точек А и
L), т. е. п точке Р. Эта точка лежит па окружности HAD, так как
прямой угол ADP опирается на диаметр окружности АР. Следова-
Следовательно, мгновенный центр скоростей Р при движении стержня АВ
перемещается по окружности PDAH.
Геометрическое место мгновенных центров, отмеченных в непо-
неподвижном пространстве, таким образом, есть окружность с центром О
и радиуса ОА. Это — неподвижная центроида стержня.
Подвижная центроида является геометрическим местом мгновенных
центров, отмеченных па движущейся плоской фигуре. Точка Р нахо-
находится от точки стержня Л на постоянном расстоянии АР — 2 • ОА,
§ 31
ПОДВИЖНАЯ И НЕПОДВИЖНАЯ ЦЕНТРОИДЫ
397
следовательно, точка Р описывает вокруг движущейся точки А окруж-
нссть радиуса вдпое большего, чем радиус полуокружности EAD.
Это — подвижная центроида стержня.
Найдем уравнения центроид. С этой целью выбираем две системы
координат: неподвижные осп с началом в точке О, ось х направляем
илепо по диаметру АВ, ось у — вертикально вверх, и подвижную
систему коордниаг с началом в точке А, ось х{ направляем по стерж-
стержню АВ, ось j>] — перпендикулярно к стержню по прямой АЕ (рис. б).
Тогда уравнение неподвижной центроиды будет:
а уравнение подвижной цепгропды
Задача 6.15. Груз Q подвешен па блоке С с подвижной осью О
(рис. а). Груз поднимается при помощи троса, перекинутого через
два блока, А и В, с неподвижными осями. Радиусы неподвижных
блоков одинаковы и равны г = 20 см. Блок А делает л, = 60 об/мин,
блок В делает и2—15 об)мин. Диаметр блока О равен й? = 75 см.
Определить подвижную и неподвижную центроиды блока С.
6)
К задаче 6.15.
Р е ш е п и е. Найдем скорость ¦»,, с которой движутся точки обода
блока А и точки троса, расположенные на вертикали, являющейся
касательной к блоку А. Величина искомой скорости
vx = ru»! = 20 • 60 ¦ ^ = 40л см1сек.
Величина скорости v.t, с которой движутся точки обода блока В и
точки троса, расположенные на вертикали, касательной к блоку В,
vt = ru).j = 20 • 1 о ¦ ^ = 10я см]сек.
398 ПЛОСКОЕ ДПИЖЕНИЕ ТВЕРДОГО ТТ.ЛЛ [ГЛ. VI
Эти скорости являются скоростями точек П, D блока С, где трос
сходит по касательной с обода (рис. б). Таким образом, известны
скорости двух точек плоской фигуры, В и D. Эти скорости парал-
параллельны- между собой и перпендикулярны к линии F.D, соединяющей
обе точки. Мгновенный центр скоростей блока должен находиться на
пересечении перпендикуляров, восставленных к скоростям Е и D.
В данном случае эти перпендикуляры совпадают. Положение мгно-
мгновенного центра тем не менее может быть определено, так как ско-
скорости точек Е и D известны по величине. Эти скорости пропор-
пропорциональны расстояниям точек Е и D до мгновенного центра скоростей.
Следовательно, обозначив неизвестное расстояние от точки D до
мгновенного центра скоростей Р через / (рис. б), получим:
г/, = (d --)
Решая совместно зги дна уравнения, находим, что
'=^=25 с*. A)
Положение мгновенного центра скоростей Р можно определит!,
и другим способом, путем геометрического построения. Для этого
необходимо, отложив в избранном масштабе скорости В] и vb соеди-
соединить их концы прямыми. Эти прямые пересекаются в точке Р — мгно-
мгновенном центре скоростей. Из подобия треугольников, образованных
скоростями v-i, ©1 и этими прямыми, следует, что
DP vt I v,
или \
что совпадает с A).
После того как определено место мгновенного центра скоростей
для произвольною положения блока, находим неподвижную и под-
подвижную цешроиды. Выбираем неподвижные оси координат: ось х
направим по горизонтали вправо, ось у направим по вертикали вверх,
вдоль прямой, по которой перемещается ось подвижного блока. При
подъеме груза мгновенный центр скоростей Р будет перемещаться
в неподвижном пространстве по прямой, параллельной оси ординат,
отстоящей от последней па расстоянии 1-\--т. Эта прямая и является
неподвижной цент рондой.
Для нахождения подвижной центроиды увеличим мысленно раз-
размеры блока, описан окружность радиуса /-•- -^- с центром О. Все точ-
точки, лежащие на ободе блока радиуса /-1-4-» с течением времени бу-
будут становиться мгновенными центрами скоростей. Следовательно,
окружность радиуса /-J- ¦ с центром О и будет подвижной цент;.о-
§3|
ПОДВИЖНАЯ И НЕПОДВИЖНАЯ ЦЕНТРОИДЫ
39Э
идой — геометрическим местом мгновенных центров, отмеченных на
движущейся плоской фигуре.
Движение блока О можно рассматривать как качение без сколь-
скольжения подвижной центроиды, окружности радиуса 1-\--т, по непод-
неподвижной центроиде, иертнкалн, проходящей через точку Р.
Задача 6.16. Конец стержня BD шарнирно прикреплен к пол-
ползуну В, передвигающемуся по горизонтальным направляющим. Стер-
Стержень проходит непрерывно через цилиндрический шарнир А, который
Р
А
D
а)
К задаче 6.16.
может вращаться вокруг оси, перпендикулярной к плоскости рисунка.
Расстояние О А —а (рис. а).
Найти уравнения неподвижной и подвижной центроид стержня.
Примечание. Механизм, рассмотренный в это;1 задаче, называется
конхоидографом. Он вычерчивает конхоиду прямой линии, т. е. геометриче-
геометрическое место радиусов-векторов прямой линии, увеличенных или уменьшенных
на один и тот же отрезок.
Решение. Выбираем неподвижную систему координат с центром
н точке О. Ось х направляем по горизонтали вправо. Она совпадает
с направлением движения ползуна В. Ось у проводим по вертикали
ьиерх (рис. б).
При произвольном положении стержня BD, определяемом углом ?
(рис. б), находим построением точку Р — мгновенный центр скоро-
скоростей. Для эгого восставим перпендикуляр к направлению скорости
точки Я. Точка В движется прямолинейно по оси х, следовательно,
и ее скорость направлена по этой оси. Перпендикуляр ВР паралле-
параллелей оси у. Вторая точка стержня, направление скорости которой из-
известно,— это та точка, которая п данный момент проходит через
цилиндрический шарнир А Скорость точки стержня, проходящей через
400 плоское дзижешш твердого тпл\ [гл. vi
неподвижную точку А, направлена вдоль стержня (рис. б). Вос-
Восставим к ней перпендикуляр. Точка Р, находящаяся па пересечении
этих перпендикуляров, и является мгпопеппым центром скоростей.
Для определения неподвижной центроиды, 1еометрического места
мгновенных Петром, отмеченных в неподвижной плоскости, найдем
координаты точки Р:
a i\ \
*p=igv A)
ЛИ ЛО а ,,,.
J *' sin о sin- о sirr о '
так как угол АРБ = 'з. Решим совместно эгу спаему, исключив угол о.
Из первого уравнения
о а I ¦ - sirr 9
X м == п' :—-, — ,
» sinJ a '
из второго уравнения
. о а
sin" э = —
и, следовательно,
х], = а (ур — а).
Это и ее п. уравнение неподвижной центроиды. Неподвижная цептро-
лда — парабола с осью, параллельной оси у-
Переходим к определению ураЕ'.пеиия нс-движной центроиды. Пгд-
ннжпую систему координат, жестко связанную со стержнем BD, вы-
выбираем с началом в точке Я. Ось у^ направляем но стержню Ш),
ось х1 — перпендикулярно к стержню (рис. б).
Находим координаты мгновенного центра скоростей в подвижной
системе координат:
Х] = ВР ¦ cos у = -^ cos <a, C)
Из уравнения A) находим sin<p = — и вносим эго значение угля в
равенство C). Получаем:
х, = .,' У 1 — sin - о = -¦ '- I/ 1 ,,
1 а- а У у]'
откуда находим уравнение подвижной центроиды
При решении этой задачи координаты мгновенного центра ско-
скоростей в неподвижной и подвижной системах осей выражались через
параметр <р. Этот угол при движении стержня BD является функцией
§31
ПОДВИЖН\Я И НЕПОДВИЖНАЯ ЦЕНТРОИДЫ
401
времени. Из условий задачи нельзя найти зависимость угла <р от вре-
времени, так как неизвестна величина скорости точки В или какой-лнб.)
другой точки стержня BD. Однако в этом и пет необходимости.
Какова бы ни была зависимость угла о от времени, эго не может
повлиять па вид уравнении недвижной и неподвижной центроид, так
как они находятся путем исключения из системы уравнений игра-
метра <р.
Задача 6.17. В шарнирном четырехугольнике ABCD стороны по-
попарно равны: AB = AD = a, BC = DC = b. Стержень АО закреплен
неподвижно.
Определить уравнение подвижной и неподвижной центроид
стержня ВС, если кривошип АВ вращается вокруг неподвижной
точки А (рис. а).
Решение. Определим положение мгновенного центра скоростей
стержня ВС. Скорость точки В перпендикулярна к АВ. Скорость
точки С перпендикулярна к
DC. Следовательно, мгновен-
мгновенный центр скоростей стерж-
стержня ВС лежит па пересече-
пересечении продолжений сторон АН
и DC в ючке Р (рис. б).
Уравнение неподвижной
и подвижной центроид бу-
будем искать в полярной си-
системе координат. Для опре-
определения неподвижной цен-
центроиды выберем неподвиж-
неподвижную точку А за полюс и
обозначим расстояние АР от
полюса до мгновенного центра скоростей через г, а угол DAP, обра-
образованный радиусом-вектором АР с неподвижной стороной AD, че-
через ср. Обозначим, кроме того, угол BCD через 2а и расстояние DP
через у. Тогда в треугольнике АСР угол АСР равен % а
К задачам 6.17 и 6.18.
L САР =
р = 90° -f|.
По теореме синусов имеем из треугольника АРС
у-\-ь
sin(
COS -,
Sill :
(I)
Из треугольника ABC па основании тей же теоремы следует, что
402 плоског: движении твердого ti:jia 1гл v\
так как усол ВАС ранен углу CAD. Сопоставляя равенства A) и B),
получим:
у_-\-Ь_ *
г а '
или
У=~(г-а)- C)
с другой стороны, из треугольника APD на основании теоремы ко-
косинусов находим, что
/2 = r2-f a1 — lar coscp. D)
Возведем равенство C) is кп.шрат и подставим это значение в урав-
уравнение D); тогда получим:
bl (г — а? = г'2-|- а2 — lar cos и = г2 -|- а1 — ЧаГ (cos2 -?т — sinj-?-) —
= г'3 -f- а2 — 2аг ^ 1 ~2smi^\ = (r — af-\-4ar sin3 -?-.
Собирая члены, содержащие радиус-вектор г, в левую часть, имеем:
l0 4a3 sin2-—
Это и есть уравнение неподвижной центроиды в полярной системе
координат.
Для определения уравнении подвижной центроиды стержня ВС в
полярной системе координат выберем за полюс точку В стержня ВС.
Радиус-вектор мгновенного центра скоростей обозначим через Г[ =
= г-\-а, угол поворота радиуса-вектора (/. CBP = vi) будем отечн-
тынать от прямой ВС.
То1да, прибавляя к обеим частям равенства C) по b и заменяя Г
через Г] — а, получим:
У \-Ь = -а{г-а) \-Ь = --*¦ (г, - 2а) -\-Ь = ~ (г, - а). (Я)
С! другой стороны, из треу! ельника РВС иахс дим:
(у -\ - bf =-- г\ -- Ьг — 2br, cos ь,. (())
Возводим равенство (о) в квадрат п подставляем значение (у-\-Ь)*
в уравнение F). Имеем:
-а, (г, — af == г] -|- Ьг — 2Г[6 cos tp,,
или, после несложных преобразований,
2ай (ft —
г
§ 1| ПОДВИЖНАЯ И НГ.ПОДВИЖНЛЯ ЦР.ПТРОИДЫ 4Q3
Это и есть уравнение подвижной центроиды в полярной системе ко-
координат, центр которой совпадает с движущейся точкой В, а угол
поворота радиуса-вектора отсчитывается от движущейся прямой ВС.
Задача 6.18. В шарнирном четырехугольнике предыдущей задачи,
стороны которого попарно равны, угловая скорость кривошипа ЛВ
равна <й0.
Определить угловую скорость кривошипа DC и скорость точки С
в тот момент, когда все четыре стержня вытянутся в одну прямую.
Решение. В предыдущей задаче было получено уравнение под-
подвижной центроиды стержня ВС
__ 1аЬ
где Г\ — ВО—расстояние or точки В до мгновенного центра ско-
скоростей.
Когда все стержни вытянутся в одну прямую, угол ?i принимает
значение it и расстояние от точки В до мгновенного центра скоро-
скоростей в этот момент станет равным
_ ЧаЬ
Расстояпге от мгновенного центра скоростей до точки С
Величина скорое in точки В, как принадлежащей кривошипу АВ,
раина
Т'„ = ао>0.
Эга же скорость точки В, как принадлежащей стержню ВС, равна
Приравнивая эти значения скорости точки В, находим мгновенную
угловую скорость стержня ВС
мг г, 2Ь
Находим теперь модуль скорости точки С как произведение мгно-
мгновенной угловой скорости стержня ВС па мгновенный радиус
*'с = П ш«г = tj±^ • ;/b (b — a)= -2 (* -| - а).
Величина угловой скорости кривошипа DC раина отношению ско-
скорости точки С к длине кривошипа b
t'c _ ">n (ft + О)
со — CD ~ 2» '
По направлению угловая 1'корость сйсо совпадает с ы0.
404
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
1ГЛ. VI
Для приобретения навыков в решении задач на
определение центроид плоской фигуры рекомепду-
стсяре шить следующие задачи и з «С б о р и и к а з а д а ч по
теоретической механике» И. В. Мещерского, изда-
издания 1950 г. и более поздних лет: 543, 546, 548, 550, 552,553.
§ 4. Ускорения точек плоской фигуры
Ускорения точек плоской фигуры могут быть определены анали-
аналитическими, графоаналитическими и графическими методами. В этом
параграфе рассматриваются аналитические и графоаналитические спо-
способы определения ускорение точек плоской фигуры. Графический
метод нахождения ускорений точек плоской фигуры, заключающийся
в построении плана ускорений, будет рассмотрен отдельно.
Л п а л п т и ч е с к и й м е т о д. Проекции ускорения любой точки пло-
плоской фигуры на неподвижные декартовы оси косфднпа! пыражаются
уравнениями:
wx = wuix — ?, О' — J'oi) — t0° С* — -*"oi)> 0 *)
«¦ = W0,y "I" ^ (X - XOl) — ш= (у -j/Ol). B*)
М
В этих формулах wx, zev — искомые
па неподвижные оси кооодинат х, у; «'Oi.v = -
проекции ускорения
проекции ускорения точки
Г'и с. fi.I1-'.
Проекции ускорения точк
ределяю гея (формулами:
i> woiy ==3'oi —
полюса (начала
подвижной системы координат) на не-
неподвижные оси координат; сог = ф и
е, = 9 — проекции угловой скорости и
углового ускорения па ось z, перпен-
перпендикулярную к плоскости движения; х,
у — координаты точки М; xOl, yQl —
координаты полюса О\ в неподвижной
системе осей (рис. 6.12). Все величины
правой части уравнений A*) и B*)
легко находятся, если заданы уравнения
движения плоской фигуры.
i M па подвижные оси координат оп-
опC*)
D*)
В этих уравнениях xsXl, zvvi — проекции ускорения точки М на
подвижные оси х,, yt; wOlX1, ffi'Oivi — проекции ускорения полюса О1
из подвижные оси хь уй хи ух — координаты точки /И в подвижных
осях; u)z, zz — тс же, что и в уравнениях A*), B*).
УСКОРЕНИЯ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
405
Величина ускорения точки М по известным проекциям определя-
определяется формулой
Направляющие косинусы находятся по равенствам:
cos (а, х) = -- ;v, cos (w, у) = - у-,
да,,
COS (®/, Л,) = --,1 , COS (W, J'j) = -J- ,
(б*)
G*)
Графоаналитические методы. ПорныН графоаналитиче-
naift способ пахождсшди ускоренно точек плоской фигуры основан
па формуле распределения ускорений (рис. 6'.13)
«'.м = «/0-1-«;];?0-;-«»;{,„. (8*)
В этой формуле w%[—полное ускорение произвольной точки Л1 плос-
плоской фигуры; wo — ускорение полюса О; W\V) — цептросгремтельпое
Ри:. 6.13.
ускорение при вращении фигуры покруг полюса, а Ф'§0 — враща-
вращательное ускорение нокруг полюса. При этом
w%0 ~ — o)Vj, w'jm = «>- • ОМ; (9*)
™Ую = е X П, Wfio ='- ¦ ОМ, A0!0
где Г] — радиус-вектор точки М, происдспный пз полюса О.
Относительное ускорение
J МО
A1*)
т. е. равно векторной сумме центростремительного и иращателыюго
ускорений. Цеитросгремиюлыюеускорение wy\l0 направлено от точки М
406 ПЛОСКО!! ДВИЖЕНИИ ТВЕРДОГО ТГ.ЛЛ |ГЛ. VI
к полюсу О. Вращагельчое ускорение Wj^0 направлено перпендику-
перпендикулярно к радиусу-вектору Г\ в сторону вращения плоском фигуры,
если сращение ускоренное, и в обратную сторону, если вращение
замедленное.
Таким образом, для определения ускорения произвольной точки
М необходимо знать ускорение какой-либо точки плоской фигуры,
принимаемой за полюс, мгновенную угловую скорость ы плосксп
фигуры и, наконец, е, — ее мгновенное угловое ускорение. Тогда,
складывая три вектора w0, Wlvm, wjj'/o (P»c 6.13), находим искомое
ускорение точки М как сумму этих векторов.
Такой способ решения может быть применен, если угол попорота
плоской фигуры tp является известном функцией времени, так как
тогда, вычисляя первую и вторую производные от угла попорота по
времени, можно определить <иг и гг.
Во многих задачах зависимость угловой скорости от времени не-
неизвестна. Тогда мгновенная угловая скорость <о может быть найдена
только для данного момента, для данного положения плоской фи-
фигуры. В этом случае е — мгновенное угловое ускорение — не может
быть найдено непосредственно. Задачи на определение ускорений то-
точек плоской фигуры тем не менее могут быть решены, если известно
направление ускорения какой-либо точки плоской фигуры. Проекти-
Проектируя и этом случае равенстг-ю (8*) на направление /*,, получаем урав-
уравнение с одним неизвестным wM, так как W^o перпендикулярно к rt
и его проекция па гг равна пулю. После того как значение wM оп-
определено из уравнения проекций па Г\, составляем второе уравнение
проекций па направление 1H'Bfi0, перпендикулярное к Г\. В этом урав-
уравнении единственным неизвестным будет wB^0, после определения ко-
которого находится угловое ускорение плоской фигуры е в данный
момент. Нахождение ускорений других точек плоской фигуры может
далее производиться по формуле (8*).
Одна из точек плоской фигуры, направление ускорения котором
может быть определено, совпадает с мгновенным центром скоростей.
Ускорение этой точки является касательным ускорением, так как ее
нормальное ускорение да„==— равно пулю, ибо г> = 0. Это ускоре-
ускорение направлено по общей нормали к неподвижной и подвижной цен i ре-
рейдам, так как подвижная центроида катится без скольжения но не-
неподвижной.
Рассмотрим пример. Пусть изображенное па рис. 6.14 колесо ка-
мггея без скольжения по рельсу. В этом случае обод колеса явля-
является подвижной цеитроидой, рельс — неподвижной. Ускорение течки
колеса С направлено по нормали к центроидам, т. е. к центру ко-
колеса О. На рисунке показаны отрезки циклоиды, являющиеся траек-
траекторией точки С. Ускорение wo естественно, направлено по касатчмь-
§ 41 УСКОРЕНИЯ ТОЧЕК ПЛОСКОЙ ФИГУРЫ 407
пой к этим кривым. Пользуясь тем, что направление ускорения точки
тела, совпадающей в данный момент с мгновенным центром скоро-
скоростей, известно, можно решать многие задачи.
Не следует смешивать нормальное ускорение точки с центростре-
центростремительным ускорением вокруг полюса, а касательное ускорение с ира-
шательным ускорением вокруг полюса. Действительно, нормальное
ускорение любой точки плоской фигуры не зависит от ныбора полюса;
оно направлено перпендикулярно к скорости точки, т. е. по мгновен-
мгновенному радиусу к мгновенному центру скоростей. Центростремительное
ускорение при вращении фигуры покруг полюса зависит от выбора
полюса и направлено всегда к полюсу. Касательное ускорение направ-
направлено по скорости точки или прямо противоположно скорости, т. е.
перпендикулярно к мгновенному радиусу, и
не заиисит также от выбора полюса. Вра-
Вращательное ускорение вокруг полюса зависит
от выбора полюса и направлено перпенди-
перпендикулярно к прямой, соединяющей точку с по-
полюсом.
Если ускорение какой-либо точки нахо-
находится по формуле распределения ускорении,
то для определения нормального ускорения
надо спроектировать все составляющие уско-
ускорения па направление мгновенного радиуса и
вычислить их алгебраическую сумму. Для
нахождения касательного ускорения точки следует вычислить алге-
алгебраическую сумму проекций составляющих ускорений на папраиле-
гие, перпендикулярное к мгновенному радиусу.
Решение некоторых задач по определению ускорений точек пло-
плоской фигуры облегчается тем, что иногда известно нормальное
ускорение какой-либо точки плоской фигуры. Тогда задача ставится
в таком виде: даны ускорение одной точки плоской фигуры—по-
фигуры—полюса О, значение мгновенной угловой скорости фигуры ы и, кроме
того, нормальное ускорение какой-либо точки М. Проектируя вектор-
векторное равенство (8*) на направление нормального ускорения точки М,
получаем уравнение с одним неизвестным wB^Q, которое из пего и
определяется. Зная wr^0, вычисляем мгновенное угловое ускорение г
и, далее, пользуясь формулой распределения ускорений (8*), находим
ускорение любой точки плоской фигуры.
Одним из графоаналитических методов, нашедшим широкое
применение при определении ускорений точек плоской фигуры,
является метод, использующий понятие мгновенного центра уско-
ускорений.
Мгновенным центром ускорений называется точка плоской фигу-
фигуры, ускорение которой в данный момент равно нулю. Положение
408 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛ\ [ГЛ. VI
мгновенного центра ускорений Q определяется формулами:
AQ= Л
A3*)
Таким сбразом. откладывая угол а от ускорения (в сторону мгновен-
мгновенного вращения, если оно угкореппое, п в противоположную сторону,
Рис. G.lo.
если оно замедленное), получаем полупрямую, па которой на расстоя-
расстоянии AQ лежит мгновенный центр ускорений Q (рис. С.15). При эк м
если за полюс принять мгновенный
центр ускорении, то ускорение лю-
любой ючкп илосксй фигуры нахо-
находится по формуле
= — '»т,-;-еХг,. (П*)
Ускорение любой точки состав-
составляет с радпусом-всктсром, проведен-
проведенным из мгновенного центра ускоре-
ускорений, един и то! же угол а A2*).
Рис. 6.16. Модули ускорении точек плоской
фигуры пропс рнпональпы расстоя-
расстояниям до мгновенного центр;! ускорений (рис. (>.!(;). Нелпчина ускоре-
ускорения определяется формулой
wA = AQ У'^-УЛм'. A5*)
Положение мгновенного центра ускорений, мгпсвенная угловая ско-
скорость и мгновенное углогюе ускорение woiyr быть найдены, если
УСКОРЕНИЯ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
409
и. пестны ускорения двух течек плоской фигуры (рис. П.17) и рас-
расстояние между aiw.Mii iочками.
Мгновенный центр ускорений находится путем следующего геоме-
трическою поароеппя. Принимая точку Л за полюс, имеем:
пли
W,, — WA - ;- W,,A
~wA.
(Hi*)
Находим (рис. 0.17) сумму wn н ¦- wA, ранную а;/м. Угол между
ti>/j4 и АН ранен 'а = arctg .,-. Откладываем т д углом а к wA u
ш»,) прямые. Точка пересечении inns прямых и «плясгея мгновенным
центром ускорений.
1'и:-. 0.17.
Определение мгновенном углопол скорости и мгновенного угло-
углового ускорения проще неего производится аиалщическн. Для этого
достаточно спроектировать второе из рапепетп (Hj*) па направление
АН и па перпендикулярную к АН ось HI) (рис. 'i.I7):
АИ ¦ и)- — а-«л = прло (wls) — ирдв (
ИЛ • гг .-= а7Д = |<р№ (w;J) — пр/(л
A7*)
При ре ш с п и п задач па о п р е д е л е и и с у с к о р с п и ft
1 о ч е к п л о с к о ii ф и г у р м р е к о м е п. д _\ е i с и т а к а я и о с л е д о-
п а т е л ь п о с т i> д е И с т в и ii.
Л. Заданы скорости и ускорения одно И точки пло-
плоской ф и г у р ы п п а п р а в ле п и е скорости п у с к о р е н и я
410 ПЛОСКОЕ ЛПИЖЕПИК ТПР.РДОГО ТЕЛА [ГЛ. VI
другой точки фигуры. Требуется определить ус к о -
р е и и я т о ч с к и л о с к о A ф и г у р ы.
1) Находим мгновенным центр скоростей, восставляя перпенди-
перпендикуляры к скоростям дпух точек плоской фигуры, и определяем мгно-
мгновенную угловую скорое п> фигуры;
2) определяем центростремительное ускорение шорой точки
покруг первой;
Я) приравнивая нулю сумму проекций всех слагаемых ускорений
на ось, перпендикулярную к известному направлению ускорения,
находим нз этого равенства величину неизвестного вращательного
ускорения;
4) определяем мгновенное угловое ускорение плоской фигуры по
найденному вращательному ускорению;
5) находим ускорение любой точки плоской фигуры при помощи
формулы распределения ускорений.
В. Лада и 1,1 ускорения двух точек плоской фигуры.
Требуется определить п о л о ж с и и е мгновенного
ц с и г р а ускорений и ус к о р е п и е л ю б о И то ч к и п л о с к о й
ф и г у р ы.
I) Рассматривая первую точку как полюс, проектируем па пря-
прямую ЛИ, соединяющую обе точки, равенство
2) находим из полученного равенства величину да'^д и, далее,
величину мгновенной угловой скорости плоской фигуры;
3) проектируя ю же векторное равенство па направление, пер-
перпендикулярное к АН, находим величину вращательного ускорения
течки /1 и, далее, мгновенное угловое ускорение плоской фигуры;
4) находим ускорение любой точки плоской фигуры, пользуясь
формулой распределения ускорений;
5) находим положение мгновенного центра ускорений, используя
формулы A2*) м A3*).
Ирм других нзпесшых данных могут быгь без особых затрудис-
нгй составлены аналогичные последовательности действий для реше-
решения задач.
Задача 6.19. Цилиндр А падает, разматывая пить (рис. а). Вели-
Величина скорости оси цилиндр;) равна
где у—расстояние, пройденное центром цилиндра. Ррдиус цилиндра
равен г.
Определить ускорение точек D, С, П, И цилиндра, а также поло-
положение мгновенно!о центра ускорений цилиндра.
§4]
УСКОРЕНИЯ ГОЧ1?К ПЛОСКОЙ ФИГУРЫ
41
Решение. В задаче 6.7 Сыло получено значение углоиой ско-
скорости цилиндра
v, о а
** = -?=***' О
исходя из того, что мгнопеппый центр скоростей цилиндра находится
и ючкс D. Находим, далее, проекцию углоиого ускорения цилиндра
№
Л
4-^ У
X» I
hr 1
а)
Г
и>>
с)
К задаче 6.19.
как производную от проекции угловой скорости по времени
e*== ~dt = "з" Т'
Переходим к определению ускорения точки А. Из формулы A)
имеем:
Точка А движется прямолинейно по вертикали, следовательно,
или
B)
412 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО TF..1\ [ГЛ. VI
Таким образом, ускорение точки A найдено. Это — единственная
точка цилиндра, ускоренге чотороп нзнсстпо, п, следовательно, се п
надо принять за полюс.
Переходям к определению ускорении мпювеппот центра скоро-
скоростей цилиндра — точки D. Ускорение юткп D складывается геоме-
геометрически из трех ускорении: ускорения полюса, цент рос гремитель-
гою и вращательного ускорении при нрлциг.ш фигуры вокруг
полюса (рис. о):
Ускорение полюса та, нанранлепо по нерп'калп пнпз. Опечаливаем
aim иекгор от ючки D. Находим, дллес, пелпчнпу нрагцателыюго
ускорения точки U вокруг полюса
о
"-D.\ J л' ( '
Луговые стрелки углопо!1 скорости и >тлового ускорения цилиндра
папран.тепы по чгсоноп сделке. Эю следует п.* рассмотрения ско-
скорости точки А как пратателмюй скорости иокруг мгпонепного uenijia
скорое 1 cti D. Следовак'лыю, нращателыюе ускорение направлено or
ючкп D но нерппсалп ьигрх, в сторону, проппюположную w t.
Сопостаиляя ранепстпа C) и B), находим, чю по величине гг;л=:а1^'_1
п, елсдонагслыю, эти две составляющие ускорения точки D взаимно
уппчюжаюген.
Цен 1 рос 1 речптелыюе yci ореипс ючки D вокруг А по иелнчмче
равно
Это ускорение папраплепо о г ючки D к по.госу А. Таким обра.юм,
абсолюшее ускорение ючкп D раппо по .мсду;по цепiросiремп iель-
пому ускорению
Неподипжпой цемпропдоп цилиндра является прямая BD, точки
которой стапоишен с 1ечениом мремспп мгног.ешпимп центрами ско-
poci ей, отмеченными на неподвижной плоскости. Полшгжпая центроид.i
цилиндра — окружность CliliD. Таким образом, ускоренно мгновен-
мгновенного центра скоростей точки D направлено по пормллн к неподвиж-
неподвижной и подвижном центроида .
Переходим к определению ускорения точки Ц.. Приняв ючку Д
кап и ранее, за полюс, имеем (рис. в):
§ 4] УСКОРПНИЯ ТОЧР.К ПЛОСКОЙ ФИГУРЫ
413
Величина ускорения w?A раина величине w'^A D); это ускорение
иаираплеио п этом случае от точки 12 к полюсу Л Величина ^)?л
равна величине х»"]",. Пннраплепо а»™^ так же, к?к и WA, по верш-
кали вниз. Таким образом, иеличппа ускорении точки /:'
Направление о>г определиi ся i.o формулам:
''°Е ч, ! /
^ = .--- = —
Г ' !)/¦-
Перехолим к оиролслепшо ускорении точки /У (рис. г):
Напранления составляющих ускорения точки И прелегаплсиы па рис. г,
величины их известны. Они полечи гыпаются по формулам, аналогич-
аналогичным B), C), D). Величина ускорения точки //
Направление ускорения определи п:я (формулами:
COS (uQx) = -?х- = — ^ = . —!- . „ ,
Аналогично (рис. д)
COS ACV, X) = — = ---—-''
cos (о>г> у) = J = = __г
L с 1/
\ '" 3 г J
44
ПЛОСКОЕ ДВИЖЕНИЕ ТПЕРДОГО ТКЛЛ
[ГЛ. VI
Переходим к определению положения мгпопениого центра уско-
ускорений. Угол, состапляемыН направлением на мгновенный центр уско-
ускорений с ускорением любой точки плоской фигуры, определяется и:>
формулы
— е — ЛИ
Расстояние от точки А до мгновенного центра ускорений Q
l-V-j-ш
У
1 ¦ ±€!'
г 9 г-~
Откладываем угол а от направления ускорения точки А в сто-
сторону дуговой стрелки е, т. е. по часовой стрелке. В этом напраиле-
нии откладываем от точки А отрезок AQ, конец которого и будет
являться мгновенным центром ускорений.
Задача 6.20. Жесткий прямой угол ВАС (рис. а) движется так,
что стержни АВ и АС проходят через неподвижные точки М и N,
лежащие на окружности, по которой с постоянной по величине ско-
скоростью v дппжется вершина, приводимая во вращение кривошипом ОА.
Радиус окружности QA — r.
К задаче 6.20.
Определить ускорения точек стержня АИ и АС, совпадающих
и данный момент с шарнирами М и N. Найти мгновенный центр
ускорений прямого угла ВАС.
Решение. Мгновенный центр скоростей прямого угла лежит па
пересечении перпендикуляров, восставленных к скоростям точки А,
и точек стержней, совпадающих в данный момент с шарнирами М
и jV. Так как скорость течки стержня АВ, совпадающей в данный
момент с шарниром М, напраплепа по АВ, а скорость точки стерж-
стержня АС, совпадающей в данный момент с шарниром Л', направлена по
§ 4] УСКОРЕНИЯ ТОЧЕК ПЛОСКОЙ ФИГУРЫ 4 1 5
АС, то мгновенный центр скоростей находится п точке Р, следсиа-
челыю, величина мпюпеппоИ угловой скорости прямого угла
Отсюда следует, что мгновенное углопое ускорение прямого угла
равно нулю.
Ускорение wM точки стержня, совпадающей и дашшН момент
с шарниром М, складывается из трех ускорения:
где wA — ускорение полюса точки А— единственной точки прямою
угла, ускорение которой известно; wnMA — центростремительное уско-
ускорение; oi^ — вращательное ускорение точки М вокруг полюса.
Находим эти ускорения: величина ускорения полюса
*>л = у\ О
это ускорение направлено от точки А к точке О. Центростремитель-
Центростремительное ускорение по величине равно
w1a = AM ¦ <-«„ = 1r • cos {- ¦ ^ = vl ¦ cos \
w направлено от точки М к полюсу, к точке Л.
Вращательное ускорение
Откладываем эти составляющие ускорения от точки М. Выбираем
оси координат (рис. б) но сторонам прямого угла и находим проек-
проекции ускорения точки М на эти оси:
wMx = WAcos T — Wma = 7 C0S " — 27-C0S "= 2"r COS 2 '
™му=и'л sin-J = T sin -;I.
Отсюда модуль ускорения точки А1 равен
-i- 3 sin*-|-.
416 ПЛОСКО!. ДВИЖЕНИЕ ТЗГ.РДОГО ТГ-.ЛЛ [ГЛ. VI
Направление ycuoficinisi определится по формулам:
cos (о.-.,, л-) = •'- = -
cos (iaM, y) = \'tr--—— --—-•
Ы'"'' 1/ i —;- 3 sin- -[y-
Переходпм к определению ускорения точки стержня, совпадающей
с шарниром А':
Ускорение полюса wл определено формулой A). Откладываем ею
от гочкп Л' (рис. б). Вращагелыгое ускорение рагию нулю, так как
еЧ1Г = 0. Находим пелпчппу центростремительного ускорения, направ-
направленного ог точки Л' к полюсу, к точке Л:
Теперь определяем проекции ускорения wx па осп координат:
Z. У J.
9 r v'2 . о v! . о w2 . о
При помощи эгпх формул определяем .модуль и [ыправлеппе уско-
ускорения wx:
in
^ ю sin o-
cos (wA.,j-) = --i " = - /- :"-
Переходим к нахождению положения мгновенного центра ускере-
iuiit Q. ,\'юл а между ускорением точки .4 п папрамлепнем на мгно-
мгновенный центр ускорений дается формулой
УСКОРЕНИЯ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
417
откуда следует, что мгновенный иеитр ускорений Q лежит на прямой,
проходящей через точки О н А. Расстояние от точки А до мгновен-
мгновенного центра ускорений Q
W W .
AQ = -т=А •- ,- =г f1 = 4г.
KElr-i-"ir ш«
Таким образом, мгновенный центр ускорений находится на рас-
расстоянии дпух диаметров от точки Л, или па расстоянии одного диа-
диаметра от мгновенного центра скоростей Р.
Задача 6.21. Прямоугольник ЛИСП совершас-г плоское движе-
движение. Ускорение точки А в даи:ц.Ш момент равно w.к-='1 см\сек*- и
л
А
D
се
К задаче 6.21.
составляет угол 30° с прямой АВ. Ускорение точки В равно wn =
=--6 см/секг к об[)азуст угол G0D с прямой /?Л. Длины сторон:
Ли =10 см, ВС =5 см.
Определить мгпопеппую углоную скорость и мгновенное уг-локое
ускорение прямоугольника, а также ускорение точки С.
Решение. Выбираем точку А за полюс. Тогда ускорение
течки В
viB = wA — wJIA-~wfA. A)
Проектируем векторное равенство A) па оси х и у (см. чертеж).
В проекции на ось х имеем:
— wu cos 60° — wA cos 30° — и-«д,
откуда
w^A = wA cos 30° -j- wB cos 60° я» 4,73 см/сек*.
Теперь найдем величину мгновенной угловой скорости фигуры
= 1/^
0,69 сек К
14 М. И Бать и др., т. I
418 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
Проектируя векторное равенство A) на ось у, получаем:
— a'Bcos 30° = wA sin 30° — w*fA.
Отсюда определяется вращаюльное ускорение точки В:
wff = wBA cos 30° -4- wA sin 30° «s 6,19 см/сек1.
Далее, находим величину мгновенного углового ускорения фигуры
емг = ^|я«0,б19 сек-\
Угловое ускорение фигуры направлено по оси z u отрицательную
сторону.
Переходим к определению ускорения точки С. Согласно формуле
распределения ускорений, выбирая точку В за полюс, имеем (рис. б);
«'с = в'в + а'яс-Ь«'К:-
Проектируя это равенство на оси х и у, находим:
11>Сж== — wB cos 60° — w^c ^з — 6,095 см/сек11,
wCy = — wDcos 30° -f w*BC ^ — 2,825 см;( ск'1.
Теперь легко найдется величина ускорения точки С:
Паираиление wc определится формулами:
cos (wc, x) = -?- = — 0,900,
cos {W^y) =-^y= — 0,422.
Задача 6.22. Аптипарзллелограмм образован стержнями:
AD = BC=10 см и AB = ED = ~ см,
соединенными шарнирами (рис. а). Звено АВ неподвижно. Угловая
скорость стержня BL посточппа и равна по величине и)л = 2 сек '.
В положении механизма, когда угол ЛВЕ=0,5к, определить углсиг е
ускорение стержня ED, а также угловую скорость и углопое уско-
ускорение стержня AD.
Най1И положение мгновенного центра ускорений стержня ED.
Решение. Ускорение точки И по величине равно
wE = и>1 ¦ BL = 4 • 10 — 40 cMJt ек1 A)
УСКОРЕНИЯ ТОЧР.К ПЛОСКОЙ ФИГУРЫ
419
и направлено от точки /: к точке В. Мгновенный центр скорое гей
сгерж/гя ED находится и точке Р, так как скорость точки D пер-
перпендикулярна к стержню AD, а скорость точки Е перпендикулярна
к стержню BE. Возьмем точку Е, ускорение которой известно по
величине и по направлению, за полюс. Рассмотрим ускорение точки Р,
считая, что она принадлежит плоской фигуре, жестко связанной со
стержнем ED. Направление ускорения точки Р известно, так как оно
всегда направлено по нормали
к центроиде. Е
Если мысленно соединить
течки В и D прямой, то тре-
треугольники ADB и BDE равны по
трем равным сторонам. Вслед-
Вследствие этого, /_ DAB = /_ BED
и /_ ABE— /_ EDA. Тогда
треугольники АРВ и EPD
равны, имея равные стороны
AB = ED и равные углы. От-
Отсюда Следует, чго
PB—PD и АР-\-РВ =
= AD= 10 см;
таким образом, в условиях дан-
данной задачи сумма расстояний
от мгновенного центра скоро-
скоростей стержня ED до двух не-
неподвижных точек А п В ecib
величина постоянная. Следова- К задаче 6.22.
телыю, точка Р описывает на
геподвижпой плоскости эллипс, фокусами которого являются точки А
и В. Этот эллипс является неподвижной центроидой. По свойству
эллипса нормаль к нему в какой-либо точке является биссектрисой
лнутреннего угла между фокальными радиусами, т. е. биссектрисой
угла АРВ. Таким образом, ускорение точки Р направлено по бис-
биссектрисе угла АРВ. Me следует при этом смешивать мгновенный
центр скоростей стержня ED с точкой Р, принадлежащей стерж-
стержню BE.
Ускорение этой точки складывается из трех ускорений: ускорения
полюса, центростремительного и вращательного ускорений вокруг
полюса:
w = w . -|- w*\ . -4- wn?,. B)
Строим (рис. 6) эти ускорения. Ускорение wE, равное 40 см/сек1,
опстадыпаем от точки Я по стержню ЕВ. Для определения w'),L
14*
г)
420 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
найдем вначале мгновенную угловую скорость стержня ED. Рассма-
трипая точку Е как принадлежащую стержню BE и стержню ED,
имеем:
vE=u>n-BE=alir-EP,
откуда
В этой формуле
/и —ct — 2AD — 3 с.и,
что пмтекает из условия
ЕР -|-PD = ЛР-|- РВ = AD = 10 см
и из равенства (треугольник EDP прямоугольный)
Теперь определяем центростремительное ускорение точки Р:
wpE = ЕР ¦ <о?г = 23- • 9 = 60 см/сск*.
Это ускорение направлено от точки Р к полюсу, к точке Е. Враща-
Вращательное ускорение «uJJJ, направлено перпендикулярно к ¦а>}1,/.-; величина
вюго ускорения неизвестна.
Так как угол АРВ, как легко показан, из рассмотрения тре-
треугольника АРВ, равен 60°, то ускорение точки Р составляет угол
Р = 30° с линией РВ. Проектируя векторное равенство B) па напра-
направление, перпендикулярное к wP, находим:
0 = 40 cos 60° — 60 cos 60° -f w% cos 30°,
от куда
20 0,5-2 20 , ,
w^ = —— = —— см/сек .
PE уз уз
Следовательно,
?мг "рЁ — yj ' 20 "
Переходим к определению угловой скорое in и углового ускоре-
ускорения стержня AD. Для этого определим ускорение точки D, принад-
принадлежащей одновременно стержням ED и AD (рис. в). Ускорение
точки D, как принадлежащей стержню ED, выражается так:
w, = W,. -г- чюЧ „ -I- w"p . C)
Ускорение Ф^Е направлено от точки D к точке Е и его модуль
а"/)Е = DE ¦ ш2мг = ~ ¦ 9 = 301/3 см]сек*.
уз
S 4] ус.корг.пня точ?:.к плоском фигуры 421
Ускорение w~fir направлено перпендикулярно к w'l[)r и его модуль
u^. = D?.?vr =-!?--- •V'3 = 1O см.'сек*.
) 3
Ускорение Wp. известно по иелпчппе A) и направлению. Таким
образом, определен!,! псе три составляющие ускорения точки D.
С другой стороны, при вращении стержня вокруг неподвижного
центра Л точка I) описывает окружность. Проектируя C) на нормаль
AD, находим абсолютное нормальное ускорение точки D
w"D = wp cos G0° — w"Pp ==40-0,5 — 10 = 10 см:сек"\
'1'ак как
где ojj — искома» угловая скорость стержня AD, то
!==/?
/?=¦--¦•
Проектируя ранеиство C) на касательную к траектории точки D,
т. е. па линию LD, находим абсолютное касательное ускорение
точки D
wh = wde — wf. cos 30° ^ 30 1/3 ~ —*2*~ = ] ° ^
Так как
й^==г, -AD,
где ?j — искомое угловое ускорение стержня AD, то
. _Ъ_\оУ* _Vi сек>
ч — д0 — — jo— — У* сек ¦
Таким образом, найдены угловая скорость п угломое ускорение всех
гшепьев атипараллело) рамма, зная которые, можно определить скоросчи
и ускорения любой точки механизма.
Переходим к определению положения мгновенного центра ускоре-
ускорений стержня ЕГ). Вычисляем угол между ускорением любой точки
стержня ED и направлением па мгновенный центр ускорений Q:
находим расстояние от точки Е до мгновенного центра ускорений
UQ= -^=== = --==-^ = 4,37 см.
422
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
1ГЛ VI
С троим мгновенный uemp ускорений, откладывая от направления
ED, совпадающего с ускорением точки Е, угол а в сторону вращения
дуговой стрелки гмг (рис. г) и проводи отрезок EQ длиной 4,37 см.
Задача 6.23. Кривошип ОА = г= 10 см вращается вокруг не-
неподвижной точки О согласно уравнению <p = nt. Коней шатуна В
К задаче 6.23.
прикреплен шарнирпо к центру колеса радиуса /?=12 см, которое
катится без скольжения по прямой, параллельной ОВ (рис. а). Длина
шатуна АВ = /=50 см.
Определить при ер, = 0: а) мгновенную угловую скорость и мгновен-
мгновенное угловое ускорение колеса, б) скорость и ускорение точек Е и D,
в) положение мгновенного центра ускоренна колеса.
§ 4| УСКОРЕНИЯ ТОЧ11К ПЛОСКОЙ ФИГУРЫ 423
Решение. Рассмотрим первое положение механизма, когда угол
ср = 0 (рис. б). Выберем неподвижную систему координат с началом
и точке О, ось х направим по ОВ вправо, ось у — перпендикулярно
к х в плоскости движения вверх, ось z — перпендикулярно к плоскости
движения. Проекция углопой скорости кривошипа на ось z
о>2 = ф = 11 сек'К
Величина скорости точки А
vA — ОЛ ¦ \ <ог != 1 Огг см /сек, A)
причел эта скорость направлена перпендикулярно к кривошипу ОА
(рис. б).
Для нахождения мгновенного центра скоростей шатуна необходимо
знагь направление скоростей двух его точек. Первая точка, скорость
которой известна, — это А, принадлежащая кривошипу и шатуну.
Вторая точка шатуна, направление скорости которой известно, — это
точка В- Действительно, точка В движется прямолинейно по оси х
и ее скорость, следовательно, также напраплепа по этой прямой.
Мгновенный центр скоростей шатуна АВ находится па пересечении
перпендикуляров, восставленных к скоростям точек А и В. Перпен-
Перпендикуляр к <vA есть АВ, перпендикуляром к <ов является прямая DP
(рис. б). Эти перпендикуляры пересекаются п точке В. Значит, точка В
в данном положении механизма является мгновенным центром ско-
скоростей шатуна АВ\ скорость в точке В равна нулю.
Переходим к определению мгновенной угловой скорости колеса.
Точка В принадлежит колесу, и ее скорость равна пулю. Точка Р
является мгновенным центром скоростей колеса, катящегося без сколь-
скольжения по горизонтальной прямой. Следовательно, и скорость точки Р
равна нулю. Отсюда заключаем, что н данный момент мгновенная
углопая скорость колеса равна нулю и скорости всех точек колеса
также равны нулю. Действительно,
vH == щ X г„ B)
где щ — искомая мгновенная угловая скорость колеса; гх — радиус-
нектор, проведенный из мгновенного центра скоростей Р в точку В.
Раз г»в равно пулю, то равна нулю и мгновенная угловая скорость щ.
Переходим к определению мгновенного углового ускорения колеса.
Значение скорости точки А, как принадлежащей шатуну, равно произ-
произведению величины мгновенной углоной скорости шатуна <о, на длину
мгновенного радиуса АВ:
Сопоставляя это значение vA с A), определяем величину мгновенной
угловой скорости шатуна
Юл 10- - .
1 АВ 50 о
424 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
Теперь можно пай ги ускорение точки В. Выбираем точку А за полюс,
так как она принадлежит, как п точка В, шатуну и ускорение ее
легко определяется. По величине оно равно
юА = -шпл = ЛО-и\=\ (к* см хек'2.
Направлено wA от точки А к ючке О, так как оно является нормальным
ускорением. Тогда
wH = wA-\-i^BA-\-w^A, ¦ C)
где
гс.н л = в А ¦ mi = 50 • ^- = 2-2 cmU-ck1.
Ускорение w'jjA наиранлспо от точки В к полюсу, к точке Л. От-
Откладываем и избранном маснпабс составляющие w и зд>;1)л ускорения
точки В (рис. я). Третья составляющая и*"]^ направлена перпендикулярно
к W}jA и неизвееша по величине. Сумма трех вектором согласно C)
должна равняться wis. Но точка Я движется прямолинейно по оси х,
следовательно, ее ускорение должно быть направлено но этой оси.
Проектируя равенство (8) па ось у, находим, чго ь^1'Л = 0 и, сле-
следовательно, е, = 0 и ускорение точки В направлено oi В к точке А.
Проектируя равеистпо C) на ось х, имеем:
wjW = — wA - w]jA = — 10-'2 — Ч~г = — 12л2 см:секг.
Точка В принадлежит одновременно колесу и должна быть выбрана
за полюс как единственная течка колеса, ускорение которой известно.
Так как мгновенное угловое ускорение колеса неизвестно, то следует
вначале искать ускорение такой точки, ускорение которой известно
по направлению. Единственной такой точкой является течка Р. Ее
ускорение является касательным ускорением и направлено по нормали
к центроидам, т. е. от точки Р к центру колеса В (рис. г).
Ищем ускорение точки Р по формуле распределения ускорений:
Откладываем от точки Р направления этих трех составляющих
полного ускорения: w и wR^n направлены по касательной к центроидам,
Wf,B — но нормали, полное ускорение wp направлено по РВ. Проектируя
равенство D) на ось х, находим:
0 = wB-w^B. E)
Отсюда следует, что составляющие w и w^ направлены в разные
стороны и равны по величине. Подставляя в E) их значения, имеем:
5 М УСКОРЕНИЯ ТОЧГ.К ПЛОСКОЙ ФИГУРЫ 425
откуда
?-2 = -— = " сек
(г,, как пндпо из направления HJJ,1^, направлено против часовой
стрелки).
С другой стороны, проектируя D) на ось у, находим:
так как мгновенная углоиая скорость колеса (о, и данный момент
равна пулюB). Следоиателыю, мгновенный центр скорое iей и мгновенный
центр ускорений колеса в данном положении механизма совпадают
и находятся в точке Р.
Осталось определить ускорение точек С и D. Они равны
= *i X r
D,
где гР—радпус-кектор течки Е, проведенный из мгновенного центра
ускорений Р; гп — аналогичный радиус-вектор точки D. Модули этих
ускорений будут:
12"г см;<:ек\
WD = ?.2 • 2/а! ^ 24^:- см;сен'\
Направления этих ускорений определяются по правилу векторного
произведения и показаны па рис. г.
Задача 6.24. Решить предыдущую задачу для положения механизма
при угле <ра = ^-.
Решение. Скорость точки Л раина по величине (см. рис. д)
vA = АО ¦ | <и,! = 10;г см; сек
и направлена перпендикулярно к АО. Скорость точки В параллельна
скорости точки А, так как точка В движется по оси л:. Восставляя
перпендикуляры к <оА и <ve, заключаем, что они не пересекаются.
Таким образом, шатун в данный момент совершает мгновенное по-
поступательное движение, скорости всех его точек равны между собой,
в частности
а его мгновенная угловая скорость (Oj равна нулю. С другой стороны,
точка В принадлежит колесу, мгновенный центр скоростей которого
находится в Р. Следовательно,
426 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТР.ЛЛ [ГЛ. VI
гке и).2 — величина мгновенной углоной скорости колеса; отсюда
«* = BP=l2 CeK '
Находим скорости течек /: и D
и, следоиателыю,
T)yj = и).2. R У'2 = 14,1 тс смIсек,
vn = ш.2 • '2/? = 20к смIсек.
Направления этих скоростей определяются по правилу векторного
произведения и показаны на рис. д.
Переходим к определению ускорений. Величина ускорения точки А
определена; папранлепо это ускорение от А к О (рис. ё). Ускорение
точки В находим по формуле распределения ускорений, взяв точку А,
принадлежащую шатуну, за полюс:
Откладываем wA из точки В м проводим прямую но направлению
ti}'}j\ перпендикулярно к шатуну АВ, соединяющему полюс А с точкой /?.
Составляющая wfsA = щ X AR = 0, так как угловая скорость со,
[1 данном положении раина нулю. С другой стороны, wB направлено
но О В. ГТронодя из В прямую по направлению ОБ, находим пере-
пересечение этой линии с направлением wa^A. Таким образом, найдены:
wn и wfA.
Обозначая угол ОБА через "f и замечая, что угол между wa и
w^A ранен этому углу, находим:
^ J1 = 0,204.
Проектируя равенство A) из осп координат, имеем:
¦wn = та>ур, sin f.
0 = W]fA cos y — а'д.
Решая совместно эти уравнения, находим:
wB = wAtg-[=\ Оя2 • 0,204 = 2,04тса см/сек\
-f- 2,043 =
§ 4| УСКОРЕНИЯ TO4FK ПЛОСКОЙ ФИГУРЫ 427
Величина углового ускорения шатуна АВ в данном положении
будет равна
Вращение шатуна ускоренное, так как мгновенная угловая скорой ь
шатуна в данный момент равна нулю.
Переходим к определению ускорений точек колеса. Точка В
должна быть выбрана за полюс, так как это единственная точка
колеса, ускорение которой известно. Далее следует найти ускорение
точки Р, мгновенного центра скоростей, так как это единственная
точка колеса (кроме В, взятой за полюс), направление ускорения ко-
которой известно. Согласно теореме о распределении ускорений
wP = wB-\-wiu-\-vnfB. B)
Ускорение точки Р, совпадающей с мгновенным центром скоростей,
направлено по нормали к центроидам. Неподвижной центропдой в
данном случае является прямая, по которой катится колесо, подвиж-
подвижной цептроидой — обод колеса. Следовательно, wP направлено по РН.
Откладываем WB от точки Р (рис. ж); WjJ^ направлено по тон же
прямой и неизвестно по величине; w^n направлено or Р к В. Проек<
тируя равенство B) на направление ВР, имеем:
Wp = «,«я = R ¦ и» = 12 ¦ 1^~ = 8,33т;2 см\сек\ C}
Проектируя равенство B) на направление, перпендикулярное к ВР,
находим:
wD = и.% = 2,04 к2 см [сек*. D)
Далее находим величину углового ускорения колеса
Дуговую стрелку sQ (рис. ж) следует направить по часовой стрел-
стрелке. Следовательно, вращение колеса замедленное.
Ускорения точек D и? находятся теперь но формулам распреде-
распределения ускорений (рис. з):
Центростремительные ускорения w^a и да«в, как всегда, напран-
лепы к полюсу В, вращательные ускорения "Ш^а и w^a перпендикулярны
428 ПЛОСКОЕ ДВИЖЕНИЕ ¦] ПЕРДОГО ТЕЛЛ [ГЛ \1
к wllnR и w'lr/l соошегсгиешю. Как легко видсчь из формул C) и (-1;,
величины их раины ¦z^'/tJ/! и ¦zc'",p/J-
Пахсдпм знамения ускорении wr) и И)/.-:
= 9,2о~2 см'сск",
= У (8,;«~- — 2,04т:2)" -•- B,04т:3)- = 6,6т:2 смхекК
Определяем угол я, соаанлиеммй ускорением точки с направлением
па полюс В. Для точки I)
Для точки
tg a, = —--— - = j.^% = 0,323.
Таким образом, найдены ускорения точек D и Н по величине и
направлению.
Переходим к определению положения мгновенного центра ускоре-
ускорений колеса. Находим угол а, определяемый ранепстиол.
е., 0,17-~. \2-
откуда
ая« 13--40'.
Откладываем от ускорения точки В (рис. гг) в направлении дугопой
стрелки ej (рис. ж) угол я d под этим углом проводим прямую, на
которой лежит мгновенный центр ускорений. Находим расстояние дз
мгновенного центра ускорений
И)„ 2,01т:-
HQ!L , --:= 2,86 см.
Откладывая это расстояние от точки В под углом я к ускорению oj;i
(рис. и), находим мпювеппыЯ центр ускорений.
Задача 6.25. В кривошипш-шатуппом механизме угол BOA ранен
к данный момент 0,5тс. Угловая скорость и угловое ускорение криво-
кривошипа длиной ОА = г = 20см известны: иH = т: сек'1, ео = О,'2т: сек' \
Ползун В, описывающий дугу окружности радиуса /? = 30 см, в дан-
данном положении находится из горизонтальной примой. Длина шатуна
Л5 = /=40 см.
УСКОРЕНИЯ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
429
Найти ускорение точки В и мгновенное угловое ускорение ша-
шатуна АВ.
Решение. Скорости точек А и В шатуна параллельны друг
другу и не перпендикулярны к отрезку АВ. Следовательно, мгновен-
мгновенный центр скоростей шатуна находится в бесконечности, шатун
сопершает мгповенно-посгупагелыюе движение, скорости всех его
б)
К залаче 6.25.
точек раним (<«мг=0). Величина скорости ючки А и, следовательно,
любой точки iiiaiyna равна
vA = OA- ш„ = 20- см/сек.
Ускорение точки А складывается из нормального и касательного
ускорений, величины которых раины
wnA = А О ¦ («5 = 20z? см/сек\
te^ = ЛО • е0 = 20 • 0,2г. = 4тс см-сек1.
Выбирая точку А за полюс как единственную точку шатуна,
ускорение которой известно, применяем формулу распределения уско-
ускорений для точки В
Л )
В данном случае <ша неизвестно по величине и направлению, wffA не-
неизвестно по величине. Следовательно, непосредственно найти искомые
величины из уравнения A) нельзя. Воспользуемся тем, что можег
быть определено нормальное ускорение точки В
I B0т:J 40
Wb = "я =
¦ = -тг^ см1сек\
Проектируя равенство A) на нормаль к траектории точки В, т. е.
на вертикальную ось, получаем:
wb = wa — и'Чзл sin Т — Кра cos Т. B)
430
ПЛОСКОЕ. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[ГЛ. V[
где sin if = .д = 0,5; т = 30°. Из формулы B) находим величину
пращагелыюго ускорения
о/'оп-г 40 Л
\ 3 / 40 о i о
ИА СМ7 /3" „г„
так как ю^4 = Лв-с)'^г^0 (рис. б). Отсюда найдется значение угло-
углового ускорения
В соответстиии со знаком W}fA, sMr направлено против часовой
стрелки.
Находим касательное ускорение точки Я, проектируя равенство
A) на ОБ:
wTH — w'A — WjfA sin f == 4л — ~г~Г7- ^ ' ®$ = — 25,4 см/сек*.
О О
гГ7-
О у О
Величина ускорения точки В
wп = к (Wl,)'* -\- (w 1,)" =^ 135 CMJceK^.
Угол, составленный этим ускорением с линией О|В, определяется
из уравнения
111 'и 9^ Л
Задача 6.26. Колесо радиуса а катится без скольжения по прямо-
прямолинейному рельсу (рис. а). Скорость центра колеса постоянная и
раина Vql.
У А
У\
х,
р
а-)
К
X
задаче
6.26.
Р
6)
О
Определить уравнения дьи-жения, скорость и ускорение точки М,
жесисо спяланиои с колесом и находящейся па расстоянии О1УИ = /
от цешра колеси.
§4| УСКОРЕНИЯ ТОЧЕК ПЛОСКОЙ ФИГУРЫ 431
Решение. Выбираем неподвижную систему координат ху и по-
подвижную систему координат Х\у\. Подвижная система координат
перемещается поступательно вместе с центром колеса, а ее оси
остаются параллельными осям неподвижной системы. Величина угло-
угловой скорости колеса определится из равенства (рис. б):
так как мгновенный центр скоростей находится в точке Р соприкос-
соприкосновения колеса с неподвижным рельсом. Следовательно,
<в = —-. A)
Умножая A) на dt и учитывая, что <в = -' имеем:
Интегрируя, находим:
<? = — *-t-Cj. B)
1 а ' '
Полагая !? = 0, при г=:0, находим из B), что произвольная постоян-
постоянная интегрирования d — 0 и, окончательно,
а
Координаты точки М и подвижной системе координат:
vJ
h
= l sin о = / sin —-1,
а
у I = / COS cp = / COS -^ t.
C)
Координаты точки М в неподвижной системе координат склады-
складываются из координат точки О], начала подвижной системы, и коорди-
координат C):
х = Xq1-\- X\=volt -\-1 sm —— t,
У =yot -I- Уi = a +l cos -^r *'
тогда радиус-вектор точки М в неподнижной системе координат
будет:
где i, J — орты осей координат.
432 ПЛОСКОЙ ДВ'ЛЖГНИЕ ТВЕРДОГО ТГ.Л\ [ГЛ VI
Скорость точки Л1 определится как произио/иая рздпуса-вектсра
по времени
/ lvn vn \ /vn vn
Скорость точки М направлена перпендикулярно мгноненпому радиу-
радиусу РМ.
Ускорение точки М еегь производная or скорости по времени
w = ?¦'¦ sin -^ ii + cos -^fj). D)
а- \ а а I
Замечая, с учетом (.4), что рщиус-пекгор О,/И ранен
предегаиим ускорение D) в виде
Таким образом, ускорение точки М постоянно по величине и иапраи-
лепию от точки М к центру колеса.
Задача 6.27. Прямолинейный стержень АВ сопершает плоское
диижеиие.
Зная ускорение точек Л а В, определить точку С прямой АВ,
ускорение которой янляется наименьшим, а также величину и nanpiu-
ление ее ускорения.
Решение. Графоаналитический метод. Рассматривая
точку Л как полюс, найдем, пользуясь формулой (8+):
«»А = WA 4- U>BA -!" WHA = WA + Щ)А>
величину и иапраилеиие
Для этого откладынаем из точки В ускорение wB и равную ему
сумму 1а>лл-г-'йУл (P"Ci ^)- Ускорение w0A образует с прямой В А
угол а:
Зная угол а, находим мгновенный центр ускорений стержня. Для
этого откладынаем угол а от ускорений wA и wlt в том же накрап-
лепии, в котором прямая ВА отложена от wBA. Пересечение прямых BQ
a AQ и определяет положение мгновенного центра ускорений Q. Зная
положение мгновенного центра ускорений, можно легко найти точку С
УСКОРЕНИЯ ТОМСК ПЛОСКОЙ ФИГУРЫ
433
стержня, ускорение которой является наименьшим. Действительно,
ускорения точек плоской фигуры пропорциональны их_расстояпиям до
мгновенного центра ускорений. Следовательно, для нахождения точки С
достаточно опустить из мгновенного центра ускорений Q перпенди-
перпендикуляр па стержень АВ. Точка С, находящаяся в пересечении перпен-
перпендикуляра со стержнем, будет иметь наименьшее ускорение.
Для нахождении величины и направления ускорения точки С по-
построим на двух векторах иу4 параллелограмм. Направление ускоре-
ускорения точки С определится углом а, отложенным от примой QC. Нели-
Неличина ускорения точки С равна длине пектора с началом в точке С и
с концом па стороне параллелограмма, соединяющей концы век трои wA
(рис. б). Это следует из того, чт ускорение любой точки сгержпя ИЛ
а)
К задаче 6.27.
складывается из относительного ускорения, параллельного waA и про-
пропорционального расстоянию точки до полюса Л, и ускорения полюса wA.
Конец относительного ускорении любой точки стержни лежи г па пря-
прямой DA. Прибавляя к нему ускорение нолюса wA, находим, что конец
ускорения любой точки стержня АВ лежит на стороне параллело-
параллелограмма, соединяющего концы векторов wA.
Величину ускорения wc мож<ю найти и другим путем. Замечая, что
QC— НА
имеем:
QC
Для приобретения навыков в решении задач па
определение ускорений точек плоской фигуры реко-
рекомендуется решить следующие задачи из «Сборника
задач по теоретической механике» И. П. Мещерского,
издания 1950 г. и более поздних лет: 557, 564, 565, 568,
569, 572, 575, 578.
434 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
§ Б. План скоростей и план ускорений
План скоростей—-это диаграмма, позволяющая графически опре-
определить скорости любой точки рассматриваемой плоской фигуры. План
скоростей может быть построен, если: а) известна скорость точки Л
плоской фигуры и направление скорости другой точки В фигуры или
б) известна скорость точки А плоской фигуры и мгновенная угловая
скорость фигуры. План скоростей может быть построен и для сово-
совокупности плоских фигур, образующих плоский механизм.
о)
б)
Рис. 6.(8.
Для иллюстрации рассмотрим следующий пример.
Пусть фигура ABC (рис. 6.18, а) совершает плоское движение.
В данный момент скорость точки А равна vA, направление скорости
точки В задано пунктирной линией kk. Для построения плана скоро-
скоростей откладываем из произвольного полюса о (рис. 6.18, б) отрезок оа,
равный vA. Из точки о проводим прямую, параллельную направлению
скорости точки В, а из точки а — прямую, перпендикулярную отрез-
отрезку АВ, соединяющему точки А и В. Пересечение этих прямых опре-
определяет точку Ь на плане скоростей. Вектор oh соответствует скоро-
скорости точки В — , 4.
_ ob = vB, (I*)
а некгор ab — вращательной скорости точки В вокруг А, т. е.
ай = вЙЛ = в»Хг1. B*)
8 S| ПЛАН СКОРОСТЕЙ И ПЛ\Н УСКОРЕНИЙ 435
гдеГ| = ЛВ. Полученный на рис. 6.18,6 векторный треугольник
ob = оа -\- ab
соответствует формуле распределения скоростей
Из плана скоростей находится непосредственно величина мгновенной
угловой скорости плоской фигуры
= °ы аЬ
мг АВ АВ' ( >
Для нахождения скорости точки С достаточно провести из точки а
прямую, перпендикулярную к АС, а из точки ft (рис. 6.18, tf) прямую,
перпендикулярную к ВС. Пересечение этих прямых определит точку с
плана скоростей. Отрезок ос будет изображать скорость точки С.
Скорости точек плоской фигуры, обозначенных прописными буквами,
изображаются па плане скоростей иекторами, проведенными из полюса о
н соответствующую точку, обозначенную малой буквой; ob означает
скорость точки В и г. д.
Фигура abc па плане скоростей подобна плоской фигуре ABC
(рис. 6.18, а), так как любая прямая, обозначенная малыми буквами
па плане скоростей (ab, например), перпендикулярна к соответствую-
соответствующей прямой {АВ) па плоской фигуре. Таким образом, фигура abc
подобна ABC и повернута на угол 90° и направлении вращения.
План ускорений — это диаграмма, позволяющая графически опре-
определить ускорение любой точки рассматриваемой плоской фигуры. План
ускорений может быть построен, если имеется план скоростей, известно
ускорение какой-либо точки А плоской фигуры и направление уско-
ускорения другой точки В фигуры. План ускорений может быть также
построен, если, кроме плана скоростей и ускорения точки А плоскей
фигуры, известно положение центра кривизны траектории какой-либо
точки В фигуры. Для построения плана ускорений удобно пользо-
пользоваться формулой распределения ускорений при илоско-параллельнсм
движении:
wB = wA-]-^A~^A. E*)
Построение плана ускорений произведем для той же плоской фи-
фигуры, полагая известными ускорение точки А и направление ускоре-
ускорения точки В (прямая NN). Откладываем из произвольной точки о,
(полюса) ускорение wA=-o\a,\. Далее, определяем величину центро-
центростремительного ускорения точки В при вращении вокруг точки А
436 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА (ГЛ. УГ
где аЪ находится непосредственно из плана скоростей (рис. 6.18, б).
Откладываем найденное по величине центростремительное ускорение W}JA
из точки <2| (рис. 6.18, б) в гаправлении, параллельном НА. Обозначим
этот вектор ajrtj.
Вращательное ускорение 'W"fA направлено перпендикулярно к wlxB.
по неизвестно по величине. Из конца w'jj/[ = ain1 проводим прямую,
перпендикулярную к а^: на пей должен находиться конец вектора <wB,
отложенного из полюса о{. С другой стороны, проводя из ot прямую,
параллельную направлению (NN) ускорения wn, замечаем, что конец
вектора wH должен находиться и на этой прямой. Следовательно, ом
находится и точке Ьь где эти прямые пересекаются.
Далее, находим величину мгновенного углового ускорения плсской
фигуры
мг" АВ АВ "
Направление емг можно изображать при помощи дуговой стрелки емг,
которая в данном примере направлена против часовой стрелки. Зная г„,
можем, пользуясь формулой распределения ускорений E*), найти уско-
ускорение любо!) точки плоской фигуры.
Второй вариант построения плана ускорений получается, если вместо
направления ускорения второй точки (точки 13) известно положение
центра кривизны траектории точки В в данном положении плоской
фигуры — С,. Построение в этом случае отличается от предыдущего
следующим. После того как отложены векторы о,^ и а^ц и прове-
проведено направление 1г»др4 перпендикулярно к aj/2b находим нормальное
ускорение точки В
и откладываем этот вектор от полюса ох в направлении BCV Далее,
из конца wn проводим перпендикулярно к wn прямую w^ (направле-
(направление касательного ускорения). На пересечении этой прямой и ранее
проведенного направления W$A и находится точка Ь,, копен вектора
ускорения wB-
При построении плана скоростей и плана ускоре-
ускорений плоской фигуры рекомендуется такая последова-
последовательность действий:
1) изображаем на чертеже в избранном масштабе плоскую фигуру,
скорость и ускорение одной точки А, выбранной за полюс, направ-
направление скорости и ускорения другой точки В;
2) строим план скоростей, откладывая из произвольной точки о
известную скорость точки А и направление скорости второй точки В,
§s| пдм1 скоростпП и пл\н ускорений 437
затем проводим па конца vA прямую, перпендикулярную к ЛВ, до
пересечения с направлением скорости точки В;
3) находим, далее, мгновенную угловую скорость фигуры, после
чего можем построить скорость любо!! точки фигуры, плн строим
скорости других точек плоской фигуры, откладывая их вращательные
скорости перпендикулярно к прямым, соединяющим точки с полюсом Л;
величины вращательных скоростей берем пропорциональными расстоя-
расстояниям точек до полюса Л;
4) строим план ускорений, откладывая из произвольной точки о,
известное ускорение точки А, из его копна — центростремительное
ускорение w'fM и проводя через копен w'}JA направление вращательного
ускорения; пересечение направления ускорения точки В с направле-
направлением 10^ определяет- искомое ускорении точки В;
5) находим мгновенное угловое ускорение плоской фигуры, после
чего можно построить ускорение любой точки.
Задача 6.28. Кривошип ОИ плеского механизма вращается равно-
равномерно, делая 300 оборотов в минуту.
Для положения .механизма, когда е> = 0, тг/6, ~.'2, определить гра-
графически скорости точек А, В, С, О, построив план скорости. Размеры
звеньев: OtA = 2Q см, ЛЯ =100 см, АО = 50 см, ВС =30 см,
OiC= 50 см. Координаты точки 0.2:60 см и -10 см (рис. а).
Vе шспи с. Для определения скоростей точек плоского механизма
для положения, когда (р — ти/б, вычерчиваем схему механизма и избран-
избранном масштабе в этом положении (рис. а) и строим план скороеiей.
Скорость точки Л кривошипа направлена перпендикулярно к кри-
кривошипу О,А. Ее модуль равен произведению угловой скорости кри-
кривошипа па его длину
vA = u-OiA = я30'-• ОУА --= ^Ц^ • 20 = 200;: см',сек.
M;s произвольной точки О (рис. б) откладываем и масштабе отрезок иа,
изображающий скорость vA.
Скорость точки В направлена вдоль прямой OtB. Она опреде-
определяется формулой
"я = «'л-}-«'/м- С)
Для построения скорости точки В из точки о (рис. б) проводим пря-
прямую, параллельную направлению скорости vB, а из точки а — прямую,
перпендикулярную к ЛВ, до их пересечения в точке Ь. Полученный
таким образом отрезок ob определяет скорость точки В, а отрезок ab
определяет вращательную скорость точки В вокруг точки А, вели-
величина которой равна
438 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
где ш™— мгновенная угловая скорость звена АВ. Измерив длины
отрезкой оа и ab и умножил их на масштаб, имеем:
vn — 115тс см]сек,
vnA = 170тс см]сек.
Скорость точки D определяется формулой
Скорость vA уже имеется на плане скоростей. Чтобы найти вра-
вращательную скорость точки D вокруг А, воспользуемся снойством
плана скоростей, т. е. находим место точки d на прямой ab (рис. б)
из соотношения
АВ _ ab
At) —ad'
так как вращательные скорости точек В и D вокруг точки А про-
пропорциональны их расстояниям до полюса А. Соединив полученную
таким образом точку d с точкой о, получим отрезок od, определяю-
определяющий скорость точки D. Измерив длину отрезка od и умножив ее на
масштаб, имеем:
vD= 135л см/сек.
Скорость точки С, как принадлежащей звену ВС, раина
С другой стороны, скорость точки С, как принадлежащей звену О.,С,
папранлепа перпендикулярно к О.2С. Для построения скорости течки С
из точки о (рис. б) проводим прямую, перпендикулярную звену О^С,
а из точки Ь — прямую, перпендикулярную звену ВС, до их пересе-
пересечения в точке с. Полученный таким образом отрезок ос определяет
скорость точки С, а отрезок he определяет вращательную скорость
точки С вокруг точки В, величина которой равна
где <о?.^ — мгновенная углоная скорость звена СВ. Измерив длины
отрезков ос и be и умножив их на масштаб, имеем:
vc= 13 On см]сек,
i»Cy, = 75ir см]сек.
Переходим к построению плана скоростей механизма для положе-
положения, когда <р = те/2. Вычерчиваем схему механизма в масштабе в этом
положении (рис. а) и строи и план скоростей. Скорость точки А кри-
кривошипа направлена перпендикулярно к кривошипу О\А и ее модуль
ПЛАН СКОРОСТЕЙ И ПЛАН УСКОРКНИЙ
439
равен, как было ранее определено, 200тг см/сек. Из произвольной
точки о (рис. г) откладываем в масштабе отрезок оа, изображающий
скорость vA. Скорость точки В направлена вдоль прямой 0,6. Для
построения скорости точки В из точки о (рис. г) проводим прямую,
а
\< задаче 6.28.
параллельную направлению скорости vD, а из точки а—прямую, пер-
перпендикулярную к АВ, до их пересечения в точке Ь. Сделан это по-
построение, находим, что точка Ь совпала с точкой а. Следовательно,
скорость точки А и скорость точки В равны по величине и направ-
направлению, т. е. шатун АВ в этом положении движется мгновенно посту-
поступательно, откуда следует:
vA — vo = vD = 200~ см/сек.
440 ПЛОСКОЕ Д1ИЖЕНИР. ТВЕРДОГО ТГ.ЛА (ГЛ. VI
Скорость темен С направлена перпендикулярно к звену О.^С. Для
построения скорости точки С из точки о (рис. г) проводим прямую,
перпендикулярную к анену 0>С, а из точки Ь — прямую, перпендику-
перпендикулярную к знему ВС, до их пересечения в точке с. Полученный таким
образом отрезок ос определяет скорость точки С, а отрезок be опре-
определяет вращательную скорость течки С вокруг точки В:
v — СИ ¦ шмг
< си — °" ел1
где <о^ — мгновенная углоиая скорость знепа СВ. Измерив длины
отрезком ос и be и умножен их па масштаб, имеем:
i'c = 190-гс см/сек,
¦ггся = 35— см/сек.
Переходим к построению плана скоростей механизма для поло-
положения, когда ср = О°. Вычсрчипаем механизм и масштабе в этом по-
положении (рис. д) и строим план скоростей. Скорость точки А пер-
перпендикулярна к кримошипу О,Д и равна 200- см/сек. Из произвольно!!
точки о (рис. е) откладымаеи и масштабе отрезок он, изображающий
скорость vA. Скорость точки В направлена вдоль прямой OtB и опре-
определяется формулой A). Для построения скорости точки В из точки о
(рис. е) проводим прямую, параллельную направлению скорости ти,
а из точки а —прямую, перпендикулярную к АВ, до их пересечения
в точке Ь. Сделав это построение, находим, что точка b совпала с точ-
точкой о. Следовательно, скорость точки В раина пулю. Это значит, что
точка В является мпювеппь м центром скоростей точек шатуна АВ.
Ерзщательная скорость то1.км В вокруг точки А равна по модулю
200л см/сек. Скорость точки D в атом случае можно найти, пред-
парительно определим величину мгновенной угловой скорости ша-
шатуна АВ
v . 200*
ли— АВ~ 100 ~1" сеК '
откуда
vD = BD ¦ ш^, = 50 • 2* = 100~ см/сек.
Скорость точки С, как принадлежащей звену ВС, складывается со-
согласно B) из скорости полюса, точки В, и вращательной скорости
вокруг точки В.
С другой стороны, скорость точки С, как принадлежащей звену
ОаС, направлена перпендикулярно к О^С. Для построения скорости
точки С из точки о (рис. е) проводим прямую, перпендикулярную
к звену ОгС, а из точки b—прямую, перпендикулярную звену ВС,
до их пересечения в точке с.
Сделав это построение, находим, что точка с совпала с точкой о,
следовательно, скорость точки С равна пулю.
ПЛЛМ СКОРОСТЕЙ И ПЛАН УСКОРЕНИЙ
441
Задача 6.29. Пользуясь условиями предыдущей задачи, найти для
точек механизма, скорости которых были определены, ускорения тех
же точек, построим план ускорении.
Решение. Строим план ускорений для положения механизма,
когда угол ср = -к '6.
К злдаче 6.29.
Так как кривошип OtA вращается равномерно, то ускорение
точки А будет нормальным и его модуль ранен
w. = w" = О
Л Л 1
= 20 '~ Г = 2000т:5 см/сск
v 30 J I
Ускорение wA направлено от тотки Л к точке О,. Из произвольной
точки О] (рис. б) откладынаем в выбранном масштабе отрезок Ojaj,
равный ускорению wA.
Ускорение точки В направлено вдоль прямой Oj/З, так как точка В
пдшжется прямолинейно, и равно сумме ускорения полюса, лрагца-
телыюго ускорения и центростремительного ускорения при движении
вокруг полюса. Принимая за полюс точку А, имеем:
442 плоское движении твердого телл [гл. vi
Вращательное ускорение чи^А направлено перпендикулярно к звену АН,
а центростремительное ускорение w^iA направлено вдоль звена АН.
Модуль центростремительного ускорения равен
'¦л НА ~ВЛ '
где Ьа снимается прямо с плана скоростей.
Модуль вращательной скорости vllA точки В вокруг точки А,
как определено в предыдущей задаче, для данного положения меха-
механизма равен 170г см/сек; тогда
Для построения ускорения точки В из точки о, (рис. б) прово-
проводим направление ускорения 1ЮИ, а п.ч точки а, откладываем вектор
ускорения o>'/Mi через конец которого, обозначенный буквой п, про-
проводим напраплепие вращательного ускорения w"fA до пересечения его
с направлением ускорения wn н точке Ь\. Полученный таким образом
отрезок О\Ь\ определяет ускорение точки В. Измерив длину этого
отрезка и умножив ее на масштаб, находим:
wR= 1917т:'2 см Ice к1.
Ускорение точки D па(:дем, пользуясь свойством алана ускорения.
Для этого на отрезке аф\ паМдем точку du уловлегворяющую соот-
соотношению
ЛИ а,Ь,
ли /7,777"
На!1деи1н,!й таким образом отрезок a,rf, будет представлять
так как wDA и wliA образуют один и тот же угол с ускорением
полюса WA и пропорциональны расстояниям точек D м-В до по-
полюса А.
Соединив полученную таким образом точку d{ с точкой о\, полу-
получим вектор O|rf|, определяющий ускорение точки D. Измерив длину
отрезка O\dx и умножив iu. масштаб, имеем:
wD = 1900г2 см/сек":
Переходим к определению ускорения точки С, которая одновре-
одновременно принадлежит ;шепу ВС и звену О.гС. Ускорение точки С сперва
найдем как сумму ускорения полюса, вращательного ускорения н
центростремительного ускорения вокруг полюса. Принимая за полюс
§ FSl ПЛАН СКОРОСТЕЙ И ПЛАН УСКОРЕНИЙ 443
точку Я, имеем:
Направление ускорения точки С неизвестно. Вращательное ускоре-
ускорение w^PB направлено перпендикулярно к звену ВС, а центростреми-
центростремительное ускорение и^ направлено вдоль звена ВС. Величина центро-
центростремительного ускорения
св СВ СВ '
где вращательная скорость сЪ берется прямо с плана скоростей.
Модуль вращательной скорости vcb точки С вокруг точки В для
данного положения механизма равен 75т: см/сек. Тогда
«^=^1=187,5^ см/сек*.
Для построения ускорения точки С к вектору wlit который па
рис. 6 уже имеется, нрибапляем известное по величине и направлению
ускорение a>?;j, через конец которого, обозначенный буквой я,, проводим
направление ускорения да^- Где-то па этой линии должен находиться
конец вектора wc, но так как направление ускорения точки С неиз-
неизвестно, то многоугольник замкнуть нельзя.
Рассмотрим теперь точку С как принадлежащую звену СО.,. Уско-
Ускорение точки С найдем, как сумму нормального ускорения, направлен-
направленного к точке Oq п касательного ускорения, перпендикулярного к з«е-
пу СОг:
Нормальное ускорение wnc направлено от точки С к точке О.г и равно
по модулю
w" = ?
Модуль скорости 1)с, как определено в предыдущей задаче, для дан-
данного положения механизма равен 130т: см/сек. Тогда
^« = -^^— == 338~'2 см/сек*.
Касательное ускорение w^. известно только по направлению; оно
перпендикулярно к звену О^С.
Для построения ускорения точки С из точки о, плана ускорений
проводим вектор нормального ускорения wo через конец которого,
обозначенный буксой пг, проводим направление касательного ускоре-
ускорения Wc Где-то на этой прямой должен находиться копен вектора
444 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТР.ЛХ [ГЛ. VI
ускорения wc. Очевидно, это будет в тсч.чС пересечения лекторов
w1Pn и г»^., и точке г,. Соедини» точку fj с точкой оь получим век-
вектор о,!"], определяющий ускорение точки С. Измерим длину отрезка
и умножив ее па масштаб, находим модуль ускорения
wc-= 1830т:- см-сек2.
Переходим к построении плана ускорений механизма для положе-
положения, когда угол а —~'2 (рис. в). Так как кривопл-in ОИ нращаекя
рашюмерпо, ускорение точки А будет, как уже определено в преды-
предыдущей задаче, нормальным и направленным от точки А к точке О,.
Его модуль равен 2000я2 см;сек1. Ия произвольной точки ot (рис. г)
откладываем » масштабе отрезок (^а,, равный ускорению wA. Уско-
Ускорение точки В направлено вдоль прямой OtB, так как точка В дви-
движется прямолинейно, п равго сумме ускорений полюса, вращательного
ускорения и цептрос'|рем1Ш'.1ыюго ускорения вокруг полюса. Прини-
Принимая за полюс lOMicy А, нме:м:
Вращательное ускорение да^Д направлено перпендикулярно к звену
АН, а цепгростремителыюе ускорение w'}jX направлено вдоль звена А В.
Величина центростремительного ускорения
(и f
1 ПА
w'i>A~ в л ал '
где Ьа берется с плана скоростей.
Модуль вращательной скорости iieA точки В вокруг точки А,
как определено п предыдущей задаче, для данного положения меха-
механизма равен пулю, следозательпо, центростремительное ускорение
тоже раипо пулю. Для построения ускорения точки В из конца век-
вектора wA, который уже имеется па рис. г, проводим направление вра-
вращательного ускорения w"l\y а из точки о{ проводим направление
ускорения wK до его пересечения с направлением ускорения w".?.
is точке Ь\. Соединив точку ох с точкой Ь,, получаем вектор o,blt
определяющий ускорение точки В. Измерив его длину и умпожин па
масштаб, находим модуль ускорения
wB = 433 г'2 cmJcck*.
Ускорение точки D найдем, пользуясь свойством плана ускорения.
Для этого на отрезке ulbi найдем точку дц из соотношения
AD aj,
§5] ПЛАН СКОРОСТЕЙ И ПЛАН УСКОРЕНИЙ 445
Тогда отрезок а^^ определит
Соединив полученную таким образом точку d\ с точкой О,, полу-
получим вектор О|</|, определяющий ускорение точки I). Измерив длину
отрезка о,г/] и умножив ее па масштаб, находим модуль ускорения
Переходим к определению ускорения точки С, которая одновре-
одновременно принадлежит зиену ВС и звену 0>_С. Ускорение точки С сперва
найдем как сумму ускорений полюса, вращательного ускорения и
центростремительного ускорения покруг полюса. Принимая за полюс
точку В, имеем:
С В I СИ СВ4
Вращательное ускорение о>?Л/{ направлено перпендикулярно к звену ВС,
а центростремительное ускорение w?B направлено вдоль звена ВС.
Модуль центростремительного ускорения раиеп
с«— ch си •
Модуль пращателыюй скорости vCH точки С покруг точки В, как
определено в предыдущей задаче, для данного положения механизма
равен 35- см/сек. Тогда
да?в= (-^—= 40,8^ см1сек\
Для построения ускорения точки С к вектору wlP который па рис. г
уже имеется, прибавляем вектор известного но величине и направле-
направлению ускорения w?n, через конец которого, обозначенный точкой я„
проводим направление ускорения ^1?в- Где-то па этой линии должен
находиться конец вектора wc, по так как направление ускорения
точки С неизвестно, многоугольник замкнуть нельзя.
Рассмотрим теперь точку С как [принадлежащую звену СО^ и
найдем ускорение точки С как сумму нормального ускорения, напра-
направленного к точке 0-1, и касательного ускорения, перпендикулярного
к О.уС:
Нормальное ускорение направлено от точки С к точке Ог и равно
но модулю
446 плоское, движение твердого тела [гл. vi
Модуль скорости vc, как определено в предыдущей задаче, для дан-
данного положения механизма равен 190тс см/сек. Тогда
?!_ = 722i.« см\сек\
Касательное ускорение известно только по направлению; оно пер-
перпендикулярно к звену ОгС. Для построения ускорения точки С из
точки о, плана ускорений проводим нектор wji, через конец которого,
обозначенный буквой п, проводим направление касательного ускоре-
ускорения w^. Где-то па этой прямой должен находиться конец вектора wc.
Очевидно, это будет в точке пересечения направлений векторов w^
и w^, т. е. в точке cv Соедини» точку ct с точкой ои получим пек-
тор о\С\, определяющий ускорение точки С. Измерив его длину и
умножив на масштаб, находим модуль ускорения
wc = 1 ЗООг* см/сек*.
Переходим к построению плана ускорений механизма для поло-
положения, когда угол <р = 0° (рис. д). Ускорение точки А по-прежнему
равно 2000-гс2 см/сек* и п.эпраплено от точки Л к точке О\. Из про-
произвольной точки о, (рис. о) откладываем отрезок о^аь ранный уско-
ускорению чиА.
Ускорение точки В направлено вдоль прямой О\В, так как точка
движется прямолинейно, и равно сумме ускорений полюса, вращатель-
вращательного ускорения и центростремительного ускорения иокруг полюса.
Принимая за полюс точку А, имеем:
Вращательное ускорение чвп?л направлено перпендикулярно к звену
ЛП, а центростремительное ускорение ччпАП направлено вдоль звена АВ.
Величина центростремительного ускорения
7D)
<чд— В А НА '
где Ьа берется с плана скоростей.
Модуль вращательной скорости <оВА точки В вокруг точки А, как
определено в предыдущей задаче, для данного положения механизма
равен 200т: см/сек.
Отсюда
Для построения ускорения точки В проводим из точки О! (рис. е) направ-
направление ускорения wH, а из точки о, откладываем известное по вели-
величине и направлению ускорение WlliA, через конец которого, обозиа-
§5] ПЛАН СКОРОСТЕЙ И ПЛАН УСКОРЕНИЙ 447
чеиный буквой п, проводим направление ускорения w'jfA до пересечения
его с направлением ускорения wB в точке Ьх.
Как видно из рисунка, точка Ьх совпала с точкой п, следовательно,
вращательное ускорение wBjfA равно нулю. Полученный отрезок офх
определяет ускорение точки В. Измерив длину этого отрезка и умно-
умножив на масштаб, находим модуль ускорения a>B = 2400irQ см/сек'1.
Ускорение точки D найдем, пользуясь свойством плана ускорений.
Для этого на отрезке a^j (рис. е) находим точку dx из соотноше-
соотношения
АВ _a,bl
AD Mi '
Измерив отрезок O|rfj и умножив его длину па масштаб, находим
модуль ускорения
а>д = 2200*4 см/сек'1.
Переходим к определению ускорения точки С, которая принад-
принадлежит одновременно зпепу ВС и звену О.гС. Ускорение точки С сперва
найдем как сумму ускорений полюса, вращательного ускорения и
центростремительного ускорения при движении вокруг полюса. При-
Приняв за полюс точку В, имеем:
Модуль центростремительного ускорения ранен
Си СВ СИ '
где с.Ь берется с плана скоростей.
Модуль вращательной скорости vCB точки С нокруг точки В, как
определено в предыдущей задаче, для данного положения механизма
равен пулю, следовательно, центростремительное ускорение также
равно нулю.
Вращательное ускорение Wffc направлено перпендикулярно к звену
ВС. Для построения ускорения точки С проводим через точку bi
плана ускорений направление ускорения wfy. Где-то па этом направ-
направлении должен находиться конец вектора ускорения wc, по так как
направление вектора wc неизвестно, построение дальше вести нельзя.
Рассмотрим теперь точку С как принадлежащую звену СОг. Уа о-
рение точки С найдем как сумму касательного и нормального уско-
ускорений
Нормальное ускорение гг>? направлено от точки С к точке О4 и равно
448 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
Скорость <ос, как определено в предыдущей задаче, для данною поло-
положения механизма равна нулю, следовательно, ее нормальное ускорение
равно пулю. Kacaie;ibiioc ускорение точки С направлено перпендикулярно
к О.гС. Для построения ускорения точки С ".срез тетку о, гг.!.а ускорений
проводим направление ускорения w'c. Где-то па :лсй прямой должен
находиться конец вектора wc. Очевидно, это будет в точке пересе-
пересечения направлений ускорений w^lt и W"^., т. е. м точке ct. Соединив
точку о, с точкой С], получаем вектор о,с,, определяющий ускорение
точки С. Измерив его длину и умножив на масштаб, находим медуль
ускорения
wc -— ЗООО^'7 см'< ей".
Задача 6.30. Определи!ь скорости и ускорения точек А, П, D
крпвошнппо-шагуппого механизма (рис. а) построением плана скоро-
скоростей и ускорений. Крппопшп 0{Л врагпается с постоянной углом й
скоро., н.ю w — 30 cei:'1. Размеры звеньев О,Л— 40 iм, OiO,~ KiO см,
Л/; =180 см, О:В—7() см, DC =200 см, угол ? = -/(;.'
Решение. Строим план скоростей. Скорость точки Л направ-
направлена перпендикулярно к крипошпну О{Л и раина по модулю
vA = OiA- to = 40-30=1200 см'сек.
Hi произвольной точки о (рис. б) откладываем в маемпабе отрезок оа,
ранный скорости vA. Скорость точки В шатуна равна геометричеекг й
сумме скорости полюса и вращательной скорости вокруг полюса.
Принимая за полюс точку А, имеем:
Скорость <иА па плане скоростей уже есть. Вращательная ско-
скорость vISA направлена перпендикулярно к шатуну АВ. Скорость <оп
направлена перпендикулярно к O:R.
Для построения скорости точки В проводим через точку о (рис. б)
прямую, параллельную скорости vL], а ия точки а прямую, перпенди-
перпендикулярную к АВ, до их пересечения в точке Ъ. Отрезок ob определяет
CKopocib точки В. Измерив длину отрезка oh и умножив на масштаб,
находим:
^, = 460 cMJceK.
Отрезок аЪ определяет вращательную скорость точки А вокруг
точки В. Измерив его длину и умножив па масштаб, находим:
vBA = 760 см/сек.
Скорость ползуна D направлена перпендикулярно к коромыслу CD.
С другой стороны, рассматривая движение ползуна как составное
движение, состоящее из переносною вместе с шатуном АВ и отно-
г 51
ПЛАН СКОРОСТЕЙ И ПЛАН УСКОРЕНИЙ
449
сительного Движения вдоль шатуна, находим, что скорость точки D
равна сумме переносной относительной скоростей
Переносная скорость veD есть скорость точки D' шатуна, сов-
совпадающей в данный момент с ползуном, а относительная скорость vrD
К задаче 6.30.
есть скорость ползуна при его движении вдоль шатуна. Так как пе-
переносная скорость veD есть скорость точки D' шатуна, совпадающей
в данный момент с ползуном, то определяем ее, пользуясь свойством
плана скоростей. Для этого делим отрезок ab на отрезки, пропор-
пропорциональные AD и DB
AD _ad'
DB d'b •
Тогда отрезок od' представляет переносную скорость ползуна D. Че-
Через найденную таким образом точку d' проводим направление отно-
относительной скорости <vrD параллельно шатуну АВ, а из точки о про-
проводим направление абсолютной скорости точки D, перпендикулярно
15 М. И Бать и др [ т. I
450 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VT
к коромыслу CD до пересечения с направлением скорости vrD
в точке d. Полученный отрезок ой определяет скорость точки D.
Измерив длину этого отрезка и умножив на масштаб, находим:
vD = 1780 см/сек.
Переходим к построению плана ускорений. Так как кривошип О\А
вращается равномерно, ускорение точки А будет нормальным. На-
Направлено оно вдоль кривошипа от точки А к точке О\ и равно
по модулю
wA = OiA • ш* = 40 ¦ 30а = 36 000 см/сек*.
Из произвольной точки О] (рис. в) откладываем в масштабе век-
вектор Ojfl], равный ускорению <wA.
Переходим к определению ускорения точки В, которая одновре-
одновременно принадлежит звену АВ и звену O.tB.
Ускорение точки В, как принадлежащей звену АВ, будем искать
как геометрическую сумму ускорения полюса, центростремительного
ускорения, направленного к полюсу, и вращательного ускорения во-
вокруг полюса. Принимая за полюс точку А, имеем:
Ускорение wA на плане ускорений уже есть.
Вращательное ускорение w"^A [оправлено перпендикулярно к зпе-
иу АВ, а центростремительное ускорение «)^л направлено вдоль
зпена АВ и равно по модулю
Модуль вращательной скорости точки В вокруг точки А, как мы
уже определили, равен 760 см/сек. Тогда
Для построения ускорения точки В к вектору wA прибавляем
вектор w^A, через конец которого, обозначенный точкой п, прово-
проводим направление ускорения o»j?v Где-то на этой прямой должен на-
находиться конец вектора wu, но так как величина wB^A и направление
ускорения точки неизвестны, многоугольник замкнуть нельзя.
Рассмотрим теперь точку В как принадлежащую звену ОаЛ
и найдем ускорение точки В, как геометрическую сумму нормаль-
нормального и касательного ускорений
§ 5| ПЛАН СКОРОСТЕЙ И ПЛАН УСКОРЕНИЙ 451
Нормальное ускорение wnB направлено от точки В к точке O.j
и равно но модулю
Ь
Модуль скорости vB, как мы уже определили, равен 460 см/сек.
Тогда
^«=^-=3020 см/сек*.
Касательное ускорение w~B известно но направлению, оно перпенди-
перпендикулярно к 0%В. Для построения ускорения точки В из точки ох
плана ускорений проводим вектор wB, через конец которого, обо-
обозначенный буквой я,, проводим направление ускорения wB. Где-то
на этой прямой должен находиться конец вектора wB. Очевидно,
это будет и точке пересечения направлений векторов wBpA и <wxBt
т. е. в точке Ъ\. Соединив точку о\ с точкой Ьи получаем отре-
отрезок офь определяющий ускорение wB. Измерив его и умножив на
масштаб, находим те'а = 51500 см/сек*.
Переходим к определению ускорения ползуна D. Движение пол-
ползуна рассмотрим вначале как сложное движение, складывающееся из
переносного движения вместе с шатуном АВ и относительного дви-
движения по шатуну. Тогда ускорение ползуна D согласно геореме
Кориолиса равно сумме переносного, относительного ускорений и уско-
ускорения Кориолиса
Переносное ускорение weD — это ускорение точки D' шатуна, сов-
совпадающей в данный момент с ползуном. Определяем его, пользуясь
свойством плана ускорений. Для этого достаточно разделить отре-
отрезок д,&] на плане ускорений на части, пропорциональные AD и DB,
ADа^
DB d\b '
Соединив найденную таким образом точку d[ с точкой оь нахо-
находим ускорение точки П шатуна, г. е. переносное ускорение weD.
Действительно,
по отрезок o(aj соответствует ускорению полюса WA, а отрезок
равен сумме w^A
Таким образом,
15*
452 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
Переходим, далее, к определению ускорения Кориолиса, модуль
которого равен
WD ~ 2 - Ше " Vr Si" ^e ФА
Относительная скорость <ог точки D' определяется из плана ско-
скоростей, ей соответствует отрезок d'd (рис. б). Ее модуль
гг = 1240 см/сек.
Переносная угловая скорость (йг есть мгновенная угловая скорость
шатуна. Ее модуль
VBA 760 , о _.
Следовательно,
0)^=2-4,2.1240= 10 415 см/сек*,
так как
sin (tCvr)= sin 90°= 1.
Находим направление ускорения Кориолиса. Относительная ско-
скорость г», точки D направлена по шатуну от точки D к точке А.
Вектор G)e направлен от нас перпендикулярно к плоскости рисунка.
Следовательно, по правилу Жуковского ускорение Кориолиса точки D
направлено перпендикулярно к АВ вверх. Откладываем его величину
из точки d[ (рис. в).
Третья составляющая ускорения точки D, ее относительное уско-
ускорение wrD, направлена по АВ, но неизвестна по модулю. Поэтому
из конца ускорения Кориолиса, точки k, можно провести только на-
направление wrD. Где-то па этой линии должен находиться конец век-
вектора ускорения wD.
С другой стороны, рассматривая точку D как точку, принадле-
принадлежащую звену CD, найдем ее ускорение как сумму нормального и ка-
касательного ускорений
Модуль нормального ускорения w1^ равен
rain—Р
__Р_1Z_15 840 rulrpiA
d CD — 200 —i^o^u си/сек.
Нормальное ускорение направлено отточки П к точке С. Для построения
ускорения точки D из точки о^ плана ускорений откладываем век-
вектор wnD, через конец которого, обозначенный буквой п.г, проводим
направление ускорения w'D перпендикулярно к звену CD. Где-то
на этой прямой должен находиться конец вектора wD. Очевидно,
это будет в точке пересечения векторов wrn и «>', т. е. в ючке dv
9 5]
ПЛАН СКОРОСТЕЙ И ПЛАН УСКОРЕНИЙ
453
Соединив точку dx с точкой oh получаем отрезок о^, соответ-
соответствующий ускорению wD. Измерив его и умножив на масштаб, на-
находим:
см/сек*.
Задача 6.31. Построить план
линейных и угловых скоростей для
редуктора, изображенного па рис. а.
Редуктор состоит из водила Н, ко-
колеса / радиуса г, = 16 см, закреп-
закрепленного неподвижно, сателлитов //
и /// радиусов гп = 11 см и rm =
= 19 см, жестко скрепленных друг
с другом и свободно насаженных па
колене водила Н, и ведомого ко-
колеса IV радиуса rIV = 8 см, закли-
заклиненного на валу 4. Угловая ско-
скорость водила равна 2 = 40т: сек~\
Решение. Вычерчиваем ше-
шестерни редуктора (рис. б) в опреде-
определенном масштабе: 1 см = тм. Про-
Проведем линию g — g, параллельную
б)
К задаче 6.31.
линии центров ООЬ и спроектируем на нее точки, скорости которых
известны: точкуС^ — центр вращения водила Ни колеса IV, ее скорость
454 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА |ГЛ. VI
?'о = 0, точку Р — мгновенный центр вращения сателлитов // и ///,
ее скорость г>р = 0 и точку О—конец водила И, модуль скорое i и
которой равен
t>0 = 2-00! = 4011@,16-1-0,11) = 33,8 м/сек.
Вектор v0 направлен перпендикулярно к водилу влево. Построим v0
на плане скоростей в выбранном масштабе A cjt = k м/сек). Соеди-
Соединим конец вектора <v0 с центром вращения водила, тогда прямая
линия 8Я даст распределение скоростей на водиле Н. Соединяя ко-
конец вектора v0 с точкой Р прямой линией 9П_]П, получим распреде-
распределение скоростей на сателлитах // и III. Продолжим линию 0(]_т
до пересечения с направлением скорости точки В. Точка их пересе-
пересечения определит скорость vB. Зная скорость точки В и положение
центра вращения колеса IV, проведем прямую 9,v, которая покажет
распределение скоростей на колесе IV.
После построения плана линейных скоростей можно определить
величины угловых скоростей всех элементов редуктора. Для этого
на продолжении линии g — g выберем произвольную точку N и от-
отложим от нее отрезок NM произвольной длины с (в нашем примере
с=\ см). Из точки М проведем линии: MS параллельно 9,|__,ц. ML
параллельно 6|V и КМ параллельно 9/у.
Отрезок Л/5=4,1 в масштабе ¦ даст модуль угловой скоро-
СП1 в об/мин сателлитов 11—111
4,1-30 -k 4,1.30-6,55 nr,an ,,
ин-.и = -1ЛГТГ= «-0,1-1 =2560 об'мин'
/г
или в масштабе — модуль угловой скорости в радианах в секунду
_ 4,1 - ft _ 4,1-6,55 _27Q ,
п-.п— т.с— 0,1-1 —2Ш сеК ш
Отрезок М. = 3,8 см в соответствующем масштабе дает значение
и,v = Ml^i^. = 2380 об/мин,
о.о ¦ D.OO г» 1 о 1
^^-'одтг 8 сек
Отрезок Л7<=1,9 см даст значение угловой скорости водила Н
1,9 30-6,55 __ ,ОЛЛ ,,
пи = '.— ^ 1200 об!мин,
1,9-6,55 1ОЙ _.
^=-\гтг=126 сек ¦
Результаты расчетов зависят от точности построения и измерения
графических величин. Допускаемая ошибка не превышает 2°/о-
§ 6| СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ 455
§ 6. Сложение вращений твердого тела вокруг
параллельных осей
При сложении вращений твердого тела, происходящих вокруг
параллельных осей, могут встретиться три случая.
1. Переносная в)е и относительная о»г угловые скорости одного
направления (рис. 6.19, а); в этом случае величина абсолютной угло-
угловой скорости равна сумме модулей составляющих угловых скоростей
ша = ше-\-шг (I*)
и направлена в ту же сторону, а абсолютный мгновенный центр вра-
вращения Р делит расстояние между переносным мгновенным центром Ре
а) 6) 6}
Рис. 6.19.
и относительным мгновенным центром Рг на части, обратно пропор-
пропорциональные величинам переносной и относительной угловых скоростей:
?4=Т- B*)
2. Переносная и относительная угловые скорости противополож-
противоположных направлений (рис. 6) и не равны друг другу по величине;
и этом случае величина абсолютной угловой скорости равна модулю
разности составляющих угловых скоростей
<оа =: oi, — <йе | C*)
и направлена в сторону большей из составляющих угловых скоростей
(па рис. 6.19, б принято <л,^>">Д а абсолютный мгновенный центр
нращепия Р делит расстояние между переносным мгновенным цен-
центром Ре и относительным мгновенным центром Рг внешним образом
на части, обратно пропорциональные величинам переносной и отно-
относительной угловых скоростей:
РГР
D*)
3. Переносная и относительная угловые скорости противополож-
противоположных направлений (рис. 6.19, в) и равны друг другу по величине;
и этом случае величина абсолютной угловой скорости равна пулю,
твердое тело совершает поступательное движение, скорости всех
456
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[ГЛ. VI
точек рашш, они направлены перпендикулярно к прямой РСРГ и их модуль
v = PePr-<ue = PePr-tar (о*)
При решении задач на определение угловых скоростей планетар-
планетарных и дифференциальных зубчатых передач обычно применяются фор-
формулы Виллиса.
г, г.
г. / \ ,, . г* /
Рис. 6.20.
Планетарной зубчатой передачей называется передача (рис. 6.20, а),
у которой одно колесо неподвижно, а остальные колеса приводятся
в движение кривошипом, ось вращения которого совпадает с осью
неподвижного колеса; оси остальных колес находятся на кривошипе.
Зубчатая передача называется дифференциальной (рис. 6.20, б),
если колесо / вращается вокруг той же оси, что и кривошип.
б)
Рис. 6.21.
Формулы Виллиса определяют зависимость между угловыми ско-
скоростями зубчатых колес дифференциальной и планетарной передач
в случае внешнего и внутреннего зацеплений. В случае внешнего
зацепления двух колес (рис. 6.21, а) зависимость между проекциями
угловых скоростей колес (полагаем ось z направленной на читателя)
определяется формулой
Л Г«
§6] СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ 457
где R, г — радиусы колес, zb гъ — число зубцов. Знак минус взят
потому, что при внешнем зацеплении и неподвижных осях колеса
вращаются в противоположных направлениях.
В случае внутреннего зацепления двух колес (рис. 6.21, б) эта
зависимость имеет вид
м,, — Q, R г.
, — Q, г
G*)
Для получения формул F*) и G*) даем мысленно основанию
механизма вращение с угловой скоростью, равной по величине угло-
угловой скорости кривошипа, но направленной в противоположную сто-
сторону. Тогда кривошип становится неподвижным, а угловые скорости
всех колес уменьшаются на величину Яг. После этого, рассматривая
каждую пару колес, находящихся в зацеплении, можем написать основные
соотношения как для пары зубчатых колес с неподвижными осями.
х Способом Виллиса определяются абсолютные угловые скорости
всех зубчатых колес. Далее, используя формулы и методы определе-
определения скоростей и ускорений точек тела в плоско-параллельном дви-
движении, можно найти скорости и ускорения любой точки звеньев
механизма. Можно поступить иначе. Сначала определить относитель-
относительную и переносную угловые скорости и, далее, пользуясь теоремой
сложения скоростей и теоремой Кориолиса, найти скорости и уско-
ускорения любой точки колеса.
При решении задач на сложение вращений вокруг
параллельных осей рекомендуется такая последо-
последовательность действии.
А) В задачах на определение передаточных чисел,
угловых скоростей, скоростей и ускорений различ-
различных точек планетарных и дифференциальных зубча-
зубчатых передач, решаемых методом плоского движения:
1) даем мысленно основанию механизма вращение с угловой ско-
скоростью, раиной по модулю углоиой скорости кривошипа и напра-
направленной в противоположную сторону;
2) составляем для каждой пары колес, находящихся в зацеплении,
уравнение F*) или G*), выражающее зависимость между угловыми
скоростями зубчатых колес;
3) для определения угловой скорости крайнего зубчатого колеса
перемножаем все уравнения, составленные для каждой пары колес;
значения угловых скоростей промежуточных колес (сателлитов) при
этом сокращаются и находится углоиая скорость крайнею колеса;
4) зная углоцую скорость крайнего колеса и скорость его центра
как точки, принадлежащей одновременно и колесу и кривошипу,
определяем положение мгновенного центра скоростей крайнего колеса;
5) находим, зная мгновенный центр и мгновенную угловую ско-
скорость, скорость любой точки колеса;
458 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
6) определяем ускорение центра крайнего колеса как точки,
принадлежащей кривошипу;
7) принимая центр крайнего колеса за полюс, находим ускорение
точки колеса, которое известно по направлению, и далее угловое ускоре-
ускорение крайнего колеса, после чего находим ускорение любой его точки.
Б) В задачах на определение относительной, пере-
переносной и абсолютной угловых скоростей, скоростей
иускорений точек, решаемых при помощи теоремы
сложения скоростей и теоремы К о р и о л и с а:
1) выбираем одно вращение за относительное и второе вращение
за переносное, результирующее движение за абсолютное;
2) но двум известным угловым скоростям определяем третью
угловую скорость;
3) пользуясь теоремой сложения скоростей, находим или относи-
относительную, или перепосную, или абсолютную скорость любой точки
твердого тела;
4) пользуясь теоремой Кориолиса, определяем или относительное,
или переносное, или абсолютное ускорение любой точки твердого тела.
Задача 6.32. Искусственный спутник Земли, двигаясь по круго-
круговой орбите, имеет период обращения, вычисленный но отношению
к системе координат, движущейся вместе с центром Земли поступа-
поступательно, равный 1,5 часа.
Определить его относительную угловую скорость по отношению
к Земле, вращающейся вокруг своей оси, если орбита спутника сон-
надает с экваториальной плоскостью Земли и спутник летит:
а) с востока па запад, б) с запада на восток.
Решение. Земля вращается с запада на восток, делая 1 оборот
за 24 часа. Принимаем вращение Земли за переносное движение.
Следовательно, значение переносной угловой скорости
ше = <}А об/час.
Абсолютная угловая скорость обращения спутника задана:
<»«=,—, об/час.
Эта угловая скорость совпадает по направлению со, в случае б)
и направлена в противоположную сторону в случае а). Согласно
формулам сложения вращений для случая а) имеем:
ш« = "V — «V
от куда
"V = % + ">,. = уз + 21 = °>708 об!час-
С такой углопой скоростью будет двигаться спутник относительно
Земли. В случае б) переносиэя угловая скорость Земли совпадает по
8 6|
СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
459
направлению с абсолютной угловой скоростью спутника. Следова-
Следовательно,
\
откуда
= <ua — <o, = T-- — ^= 0,624 об/час
Задача 6.33. В планетарной передаче кривошип 0^0^ приводит
во вращение колесо /, вращающееся вокруг неподвижной оси, про-
проходящей через Ot. Колесо / должно
вращаться с угловой скоростью в»1(
соответствующей 10 000 об/мин.
Зная радиусы колес: Г| = 10 см,
г.г = 16 см, г3 = 8 см, г4 = 6 см,
найти угловую скорость Й, которую
надо сообщить кривошипу, чтобы
обеспечить требуемую угловую ско-
скорость первого колеса.
Решение. Обозначим угловые
скорости колес /, //, IV, V через
в»,, Щ, (Од, 0M соответственно. Ко-
леса // и /// составляют одно твер-
твердое тело и имеют общую угловую скорость щ. Выбираем ось z
направленной перпендикулярно к плоскости чертежа, на читателя.
Напишем уравнение Виллиса для первой пары колес:
К задаче 6.33.
Аналогичное уравнение для колес 111 и IV имеет вид
так как угловые скорости колес // и /// одинаковы, а их радиусы
различны. Для колес IV и V, находящихся во внутреннем заиепле-
пии, имеем:
Перемножим равенства A), B), C). Тогда, учитывая, что колесо V
неподвижно и, следовательно, u>b = 0, находим:
в.—
Подставляя в это уравнение значения всех величин, находим:
Знак минус означает, что направление вращения кривошипа и пер-
первою колеса противоположны.
J
460 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
Задача 6.34. Вал газотурбинного дпигателя делает 25 000 o6jmuh.
Зубчатое колесо / с внутренним зацеплением имеет z1=\'20 зубцои
и вращается как одно твердое тело с валом А Спаренные между
собой передаточные шестерни 2 и 3 имеют соответственно z2 = 30
и z3 = 80 зубцов. Они насажены па общую
¦"^ 3 ось и вращаются с одинаковой угловой ско-
т _ I ростью. Зубчатое колесо 3 находится в зацеп-
i " | лепии с колесом 4, соединенным с валом, на
Ij ^котором насажен воздушный винт, делающий
1200 обJмин. Колесо 4 имеет гц = '2О зубцов.
Определить угловую скорость, которую
необходимо при этом сообщить кривошипу,
вращающему ось шестерен 2 и 3.
К задаче 6.М. Решение. Для решения этой задами
применим способ Виллиса. Обозначим через пг
угловую скорость пала / и жестко связанного с ним колеса /, бук-
буквой пг — угловую скорость шестерен 2 и 3, буквой /г4 — угловую
скорость колеса 4 и жестко связанного с ним вала, на котором на-
насажен воздушный винт. Искомую угловую скорость кривошипа, при-
приводящего во вращение ось, на которой укреплены шестерни 2 и 3,
назовем л0. Дадим мысленно основанию механизма вращение с угло-
угловой скоростью — л0, тогда кривошип остановится, а угловые скоро-
скорости колес станут равными:
колеса / «, — п0,
колес 2 и 3 п.г — и0,
колеса 4 п^ — п0.
Для нерпой пары колес, находящихся во внутреннем зацеплении,
имеем:
к,—н0 ?а
A)
Но—По 2,
B)
Для второй пары колес, находящихся во внешнем зацеплении,
находим:
Перемножая равенства B) и C), получаем:
»| — "о _ Zj, _ Z4
п, — н0 z, ' ?j'
Внося в это уравнение значения известных величии, имеем уравнение
с одним неизвестным
25 000 —и „ 30-20
1200—н„ 120-80'
§6]
откуда
СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
об/мин.
461
Задача 6.35. Водило 5 вращается вокруг вертикальной оси GO'
с угловой скоростью Q. Водило песет на себе две вертикальные оси,
на одной из которых свободно насажены _
три шестерни /, 2, 3, а на другой, также о \ ^? 4Г' ?
свободно, насажена шестерня 4. Шестер-
Шестерня 4 находится в зубчатом зацеплении
с шестернями /, 2, 3 и с неподвижной
шестерней 5. Числа зубцов шестерен /,
¦|И
шиш;
i, i . illim
шШ 3
2, 3 и 5 соответственно равны: (z-\- I), z, Vq^^A г
(z ~ 1) и z. я
Определить угловые скорости <о,, а>ь ш3 К задаче 6.35.
шестерен /, 2, 3.
Решение. Запишем для каждой пары шестерен, находящихся
в зацеплении, формулы Виллиса.
Для пары шестерен 5 и 4 имеем:
" ~f. О)
О — Q г4'
где ш4 и г4 обозначают соответственно угловую скорость и число
зубцов шестерни сателлита 4.
Формулы Виллиса для остальных пар шестерен, находящихся
в зацеплении, будут:
для пары /—4
для пары 2—4
для пары 3—4
--J; C)
Умножив равенство A) на каждое из равенств B), C), D), найдем:
о
LZL?._i._l.
г
— Q г+Р —Q z ' —2
Из этих трех формул определяются три искомые угловые скорости:
Ш1=г^*, ш'2 = 0; ша= —
z — 1"
Таким образом, шестерня / вращается в ту же сторону, что и
водило, шестерня 2 перемещается поступательно, а шестерня 3 вра-
вращается в сторону, противоположную вращению водила.
462
¦ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[ГЛ. VI
Задача 6.36. В простой планетарной передаче (рис. а) с тремя
соосными валами ведущий вал / приводит во вращение колесо ра-
радиуса гь находящееся в зацеплении с са-
сателлитом радиуса г3, наглухо закреп-
закрепленным на валу //. Вал // закреплен
в подшипнике водила Н. На общем
валу с сателлитом радиуса г3 закреплен
второй сателлит радиуса г4, входящий
в зацепление с колесом радиуса г8. Опре-
Определить угловую скорость сателлитов
радиусов г3 и г4 и колеса ра-
радиуса г.>
Найти скорости точек L, M, AT (рис. б),
если колесо радиуса гв = 90 см непо-
неподвижно, радиусы колес га = ЗО см,
г3 = 40 см, г4 = 20 см. Угловая ско-
скорость водила й=1200 об/мин =
1
б)
= 40я сек'1.
Решение. Метод плоского дви-
движения. В планетарной передаче, рас-
сматриваемой в нашей задаче (рис. б),
колесо радиуса га и водило Н враща-
вращаются вокруг неподвижной оси О.
К задачам 6.36 и 6.37.
Сателлиты с радиусами г3 и г4 совершают плоское движение. Так
как угловая скорость водила 2 задана, то скорость точки А, при-
принадлежащей водилу, равна
vA = Q-OA = Q (г.3 + г3) = 40я • 70 = 2800* см/сек.
$6] СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ 463
Точка А одновременно является центром сателлитов радиусов г3 и г4,
совершающих плоское движение. Мгновенный центр скоростей этих
сателлитов, образующих одно твердое тело (так как они оба наглухо
закреплены на валу), будет в точке Р касания сателлита радиуса г4
с неподвижным колесом радиуса Гв- Зная величину скорости точки
тела, совершающего плоское движение, и положение мгновенного
центра скоростей этого, тела, можно определить его угловую ско-
скорость
v. v 2800я
где АР — расстояние от точки А до мгновенного центра скоростей.
Угловая скорость шя = (о4, так как оба сателлита движутся как одно
тело. Для определения угловой скорости колеса радиуса гг опреде-
определим скорость точки С. Точка С является общей для сателлита
радиуса г3 и колеса радиуса га. Считая, что точка С лежит на сател-
сателлите, определим ее скорость по формуле:
vc = ш3 • СР = ш3 (га + г4) = 140* • 60 == 8400* см/сек.
Зная скорость точки С и считая ее принадлежащей колесу ра-
радиуса гь определим угловую скорость этого колеса
« «с 8400* л„л _.
Скорость точек L и М, принадлежащих сателлитам, определим по
формулам:
vL = w3' LP = <V41^2 = 140* • 201^2 = 3940тт см/сек,
vM = ш3• МР=ш3Уг\-\-г1= 140п• 44,7 = 6260* см/сек,
где LP и МР — расстояния от соответствующих точек до мгновен-
мгновенного центра скоростей.
Точка К лежит на колесе радиуса г2, вращающемся вокруг непо-
неподвижной оси О с угловой скоростью ш2, следовательно, ее скорость
равна
27030 8100 смjсек.
Как и следовало ожидать, vK = vc.
Метод Виллиса. Даем мысленно основанию механизма вращение
с угловой скоростью
й
— й = — 40гс сек'1,
тогда водило Н становится неподвижным, угловые скорости всех
колес уменьшаются на эту величину, а колеса, находящиеся в зацеп-
зацеплении, можно рассматривать как колеса с неподвижными осями.
464 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. VI
Применяя формулы Виллиса, имеем для первой пары колес
«а — 2 г,
ш3 — Q га'
Знак минус взят потому, что при внешнем зацеплении колеса с непо-
неподвижными осями вращаются в противоположные Стороны. Анало-
Аналогично для второй пары колес находим:
"i — Q_'r5
Здесь взят знак плюс, так как при внутреннем зацеплении оба
колеса с неподвижными осями вращаются в одну сторону. Из послед-
последнего равенства определим <и4:
и, — 1200 90#
— 1200 20'
здесь шв = 0, так как согласно условию колесо радиуса гв непод-
неподвижно.
Отсюда находим:
ш4=—4200 об/мин — —140г сек~\
Такова же и угловая скорость колеса радиуса г3, составляющего
одно тело с колесом г4. Знак минус показывает, что вращение сател-
сателлитов г3 и г4 происходит в сторону, противоположную вращению
водила.
Для определения скоростей точек L и М воспользуемся форму-
формулой распределения скоростей и плоском движении (рис. в). За полюс
примем точку А, так как скорость точки А известна по величине и направ-
направлению. Будем считать, что точки М и L движутся вместе с полюсом
н вращаются относительно полюса, тогда скорости точек L и М
соответственно будут:
<0L = '°A-\-1>LA> *M = '°AJf*MA>
где
vLA = ш3. LА = ш3 • г4 = 140-п: • 20 = 2800тс см/сек,
vMд = ш3 • МА = ш3 • г j — 140тс ¦ 40 = 5600^ см!сек.
Направления скоростей <vA, vLA и vMA указаны на рис. б. Теперь
получим:
vl — ^'д + ^Ь=: 2800~ V^= 394Отс см/сек,
и аналогично
vM=VvA-\-v\fA=r2800-Yt> = 6260к см/сек.
Скорость точки К. равняется скорости точки С, а последняя равна
§6] СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ 466
Находим, далее,
vCA = со3 • С А = ш3 • г3 = 140л • 40 = 5600л см/сек.
Для точки С направления <оА и ягд совпадают, поэтому
vc = vA-\-vCA = 2800т:-[- 5600л = 8400тс см/сек.
Для точки А" найдем vK=zvc = 8400л см/сек.
Задача 6.37. Решить предыдущую задачу, если колесо радиуса г5
соединено с двигателем и имеет угловую скорость сов = 3000 об)мин —
= Ю0к сек~К Такая передача называется планетарной передачей с
двойным приводом или дифференциальной передачей (рис. в).
Решение. Метод плоского движения. В планетарной передаче
с двойным приводом, изображенной на рис. а, колесо радиуса г2,
водило Н и колесо радиуса гв вращаются вокруг неподвижной оси О.
Сателлиты радиусов г3 и г 4 совершают плоское движение. Так как
угловая скорость Q задана, то скорость точки А, принадлежащей
водилу, р ап11a
vA = Q-OA~Q(г.,-]- г3) = 40л• 70 = 2800л см/сек.
Скорость точки В, лежащей па колесе гв, которое вращается
покруг точки О с угловой скоростью ws = i00n сек~\ равна
vB = шв • гв = 1 ООл • 90 = 9000л см)сек.
Но точки Л и 5 одновременно принадлежат и сателлитам г3 и гк,
которые совершают плоское движение как одно твердое тело. Зная
неличину и направление скоростей этих точек, можно определить по-
положение мгновенного центра скоростей.
Определим расстояние АР от точки А до мгновенного центра
скоростей. Величины скоростей точек при плоском движении прямо
пропорциональны их расстояниям до мгновенного центра скоростей.
Тогда
откуда
9000г.
ИЛИ 2800^:
= -~ = 9,05 см.
Определим положение мгновенного центра скоростей и зная вели-
величину скоростей vA и ъв, найдем угловую скорость сателлитов г3 и г4
—&-3Sr =•'<>•» «"•
Для определения угловой скорости со2 найдем скорость точки С,
считая ее принадлежащей сателлиту г3.
466 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА 1ГЛ. VI
Имеем:
г»с = ш3 • СР = <»з (^3 — АР) = 9560п см/сек.
Зная скорость точки С я г2, находим:
»с 9560я
Скорости точек L, М, принадлежащих сателлитам, определяются
но формулам:
vL = ш3 • LP = 31 От. УгГ+АРт= 31 Он ¦ 22 = 6800п см/сек,
vM = ш4 -MP= 31 Он Угз + ЛР'2 = 310н .41 = 12 700н сл/сек,
где LP и УИР—расстояния от соответствующих точек до мгновен-
мгновенного центра скоростей. Скорость vK = vc.
Решение. Метод Виллиса. Применяя формулу Виллиса для
первой пары колес, находящейся во внешнем зацеплении, имеем:
Аналогично для второй пары колес, находящейся во внутреннем
зацеплении, находим:
Из последнего равенства определим <v
¦д4 — 1200 90
3000—1200 20'
или
ш3 = ш4== 9300 об/мин
Знак плюс показывает, что направление вращения сателлитов сов-
совпадает с направлением вращения водила.
Определение скоростей точек L и М можно сделать методом
плоского движения, как показано выше.
Сравнение показывает, что метод Виллиса проще метода плоского
движения.
Для приобретения навыков в решении задач на
сложение вращений вокруг параллельных осей ре-
рекомендуется решить следующие задачи из «Сборника
задач по теоретической механике» И. В. Мещерского,
издания 1950 г. и более поздних лет: 585, 587, 588, 589,
592, 595.
ГЛАВА VII
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
И СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ.
ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
§ 1. Определение скоростей н ускорений точек твердого тела,
вращающегося вокруг неподвижной точки
Выберем неподвижную систему осей xyz с началом в неподвиж-
неподвижной точке О и подвижную систему координат x^Zt с тем же цент-
центром, жестко снязанную с твердым телом. Линия ON, пересечение не-
неподвижной плоскости ху и по-
подвижной плоскости ххуъ назы-
называется линией узлов.
Угол прецессии 6 измеряется
от неподвижной оси х до линии
узлов ON и считается положи-
положительным, если поворот с оси z
оидеп против часовой стрелки
(рис. 7.1). Угол прецессии лежит
в неподвижной плоскости ху.
Угол чистого, или собствен-
собственного, вращения <р расположен в
ПОДВИЖНОЙ ПЛОСКОСТИ XjV! И ОТ-
считывается от линии узлов до
подвижной оси ДГ]. Угол (р поло-
положителен, если он виден направ-
направленным против часовой стрелки рис 7.1.
с конца оси 2, (рис. 7.1).
Угол нутации б отсчитыиается от оси z к оси Zi и считается
положительным, если видеть поворот, смотря с линии узлов ON,
происходящим против часовой стрелки.
Уравнения движения твердого тела при вращении около не-
неподвижного центра определяются заданием углов Эйлера как функ-
функций времени:
ф =Л СО, ?=/«('). е =/,(*). A*)
468
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ (ГЛ. VII
Распределение скоростей и твердом теле, вращающемся около не-
неподвижной точки, определяется формулой
v = <aXr, B*)
где v—скорость точки, г—радиус-вектор течки, проведенный из
неподвижного центра, со — угловая скорость твердого тела (рис. 7.2).
Прямая, но которой напраглена угловая скорость тела, называется
мгновенной осью. Скорости всех точек
твердого тела, лежащих на мгновенной
оси, в данный момент равны пулю.
Из формулы B*) следует, что вели-
величина скорости любой точки тела
г» = ш/г, C*)
где h — расстояние от точки до мгновен-
мгновенной оси. Проекции скорости на непо-
неподвижные оси координат определяются
формулами:
D*)
Рис. 7.2.
где х, у, г — координаты точки; и>х> шу,
иJ — проекции угловой скорости на пе-
подпмжпые оси х, у, z.
Проекции скорости на подвижные оси хь уи zx равны
vxi=^y12i — ^,iyi, Vyi=u>1.lXi — (ojei2l, vil = l»JCiy1 — (oyiXi. E*)
R отличие от формул D*), где координаты х, у, z меняются с тече-
течением времени, в уравнениях (о*) величины хь уь zt — координаты
точки тела в подвижных осях, связанных с твердым телом. Естест-
Естественно, эти координаты остаются неизменными.
Входящие в уравнения D*) и E*) проекции угловой скорости
па неподвижные и подвижные оси координат вычисляются по извест-
известным углам Эйлера с помошью формул:
(б*)
где k, n, ki — орты оси z, линии узлов ON и оси
шх = <р sin (Jj sin в —{— 6 cos (Jj,
u)v= — ? cos (j> sin 0 —[— б sin ф,
(рис. 7.1),
G*)
§ 1] ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ 469
где <ах, шу, шг — проекции угловой скорости на неподвижные оси
координат Далее,
u>
l = (j> sin 6 sin ср -j- 6 cos <p,
iayi = ф sin 6 cos cp — 6 sin 'f,
шг1 = 6 cos 8 -j- <j.
(8*)
Здесь ui^.() ш^, шг,1 — проекции угловой скорости на подвижные оси
координат.
Величина мгновенной угловой скорости
Геометрическое место мгновенных осей, отмеченное в неподвиж-
неподвижном пространстве, называется неподвижным аксоадом. Уравнение
неподвижного аксоида
-- = ¦?- = — . A0*)
Ыд. И,у <йг
Подвижным аксоидом называется геометрическое место мгновенных
осей, отмеченное на движущемся теле. Уравнение подвижного аксоида
Угловое ускорение твердого тела есть производная от вектора
угловой скорости по времени
Рассматривая со как радиус-вектор некоторой точки, можно нахо-
находить е как скорость конца вектора со при движении по его годо-
i рафу.
Если обозначить через со0 орт мгновенной оси, то угловое уско-
ускорение определится формулой
или
где
— первая составляющая углового ускорения, направленная по мгно-
мгновенной оси и характеризующая изменение угловой скорости по
470 ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ 1ГЛ. VII
величине. Вторая составляющая углового ускорения равна
-—$
и характеризует изменение угловой скорости по направлению. Обо-
Обозначая через (Oj угловую скорость вращения вектора о», имеем:
Тогда
Наряду с использованием приведенных формул для нахождения
углового ускорения применяют и другой способ определения е, через
проекции углового ускорения на неподвижные оси координат или
оси, жестко связанные с движущимся твердым телом.
Проекции углового ускорения на неподвижные оси координат
даются выражениями:
вх— dt ' ?У— at'' z~ dt • ( б >
Проекции углового ускорения на подвижные оси, жестко связанные
с телом, равны
dm „ dm , dw ,
***— dt ' еУ>— df г'~ dt • ( >
Ускорение точки твердого тела, вращающегося вокруг неподвиж-
неподвижного центра, равно сумме вращательного и осестремительнс го уско-
ускорений (теорема Ривальса)
«M, = »Si + w5?, A5*)
где
ш% = ыХя = <»Х(«>Хг), A6*)
г»% = гхг- A7*)
Если угловое ускорение задано в виде
в = в1-т-е1,
то вращательное ускорение определяется формулой
«3? = WX + WX = «i X г + е-2 X г.
Величина осестремительного ускорения
w°^ = fm\ A8*)
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ
471
где h — кратчайшее расстояние точки до мгновенной оси. Это уско-
ускорение направлено по перпендикуляру, опущенному ич точки на мгно-
геипую ось (рис. 7.3). Величина вра-
вращательного ускорения
^=V, A9*)
где hi — кратчайшее расстояние точки
до оси вектора углового ускорения
(рис. 7.3). Направление вращательного
ускорения определяется по правилу
векторного произведения. Осестреми-
челыюе и вращательное ускорения,
вообще гоноря, не взаимно перпенди-
перпендикулярны; это следует из формул A6*),
A7*).
Однако существуют такие точки
тиердого тела, для которых эти уско-
ускорения в данный момент взаимно перпен-
перпендикулярны. Геометрическим местом этих точек является плоскость
в твердом теле, проходящая через векторы (о и е.
Зная осестремительное и вращательное ускорения, можно опре-
определить модуль ускорения точки по формуле
Рис. 7.З.
wM =
-f-
cos
Проекции ускорения точки на неподвижные оси равны
«>, = e,,z —s.
= tzx — txz
y-\- uzz) — <
4- шуУ
B0*)
B1*)
Проекции ускорения точки на подвижные оси определяются форму-
формулами:
W,
B2*)
При решении задач на определение скоростей и
ускорений точек твердого тела, вращающегося во-
вокруг неподвижного центра, рекомендуется такая по-
последовательность действий.
А. Заданы уравнения движения в виде углов Эй-
Эйлера как известных функций времени. Требуется
определить угловую скорость и угловое ускорение
твердого тела, уравнения подвижного и неподвиж-
472 ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
п ого а к с о и д о о, а также скорость и ускорение какой-
либо точки ЛЦху, уи г{):
1) определить производные от углов Эйлера по времени;
2) найти проекции углоиой скорости на оси неподвижной и под-
подвижной систем координат;
3) вычислить величину мгновенной угловой скорости;
4) определить положенно мгновенной оси;
5) составить уравнения неподвижного и подвижного аксоидов;
G) найти мгновенное угловое ускорение как скорость конца
вектора ел или через проекции углового ускорения на подвижные и
неподвижные оси координат;
7) определить скорость точки М по величине и направлению;
8) найти вращательное и осестремительное ускорения точки М
или проекции ускорения точки М на подвижные и неподвижные оси
координат;
9) вычислить ускорение точки М по величине и направлению.
В. 3 а д а н ы скорость точки М и положение мгно-
мгновенной оси вращении. Требуется определить мгно-
мгновенную угловую скорость, м гновенное углопое ус-
ускорение, неподвижный и подвижный а к с о и д ы, ско-
скорости и ускорения любых точек твердого тела:
1) выбрать неподвижную и подвижную системы координат;
2) найти мгновенную угловую скорость твердого тела;
3) определить искомые скорости точек тпердого тела;
4) найти мгновенное углопое ускорение тнердого тела как скорость
конца вектора мгновенной угловой скорости;
5) вычислить вращательное и осестремительное ускорения точек
твердого тела и, далее, их ускорения;
6) определить подвижный и неподвижный аксоиды.
Задача 7.1. Твердое тело вращается вокруг неподвижной точки
согласно уравнениям:
if = 2t, 9 = 30/, 0 = -*-,
где углы (рис. а) измеряются в радианах, а время — в секундах.
Определить мгновенную угловую скорость тела, уравнение мгно-
мгновенной оси, неподвижный к подвижный аксоиды, а также скорость
точки тела M(Xi,ylt 2(), координаты которой в подвижной системе
координат, жестко связанной с телом, равны
xt = 2 см, j>i = 3 см, 2j = 5 см.
Решение. Имеем две системы координат с началом в неподвиж-
неподвижной точке О: подвижную лг,_у, Г[, жестко связанную с твердым телом,
и неподвижную систему хуг.
Находим производные по времени от углов Эйлера:
ф=2, $ = 30, 9 = 0,
§ ч
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ
473
и согласно (б*) определяем мгновенную углопую скорость тела
ю = (jife -f$fei = 2ft -f30fc,. A)
Проекции мгновенной угловой скорости на неподвижные оси ко-
координат согласно G*) будут раины
A)^ = 30 sin 2t sin -7Т-, (Oji=—30 cos 2^ sin-77-, <лг = 30 cos -rr -|- 2.
Проекции мгновенной угловой скорости на подвижные оси
?
г
К задаче 7.1.
координат согласно формулам (8*) запишутся так:
<oXl = 2 sin |- sin 30/, ш,, = 2 sin -* cos .W, «к, = 2 cos |- -f- 30.
Величина мгновенной угловой скорости определится по форму-
формулам (9*):
2фсЬ cos 8 =
-|- 900 + 2 . 30]/3
Проекции скорости течки Ж на подвижные оси координат опре-
определятся по формулам E*):
vXl = <лУ1г1 — ш,1у1 = 5 cos ЗОг1 — (У^З-f 30) 3 = 5 cos ЗОг1 — 95,19,
Vyi = <°ziX\— u)*i'i=(l/-|- 20J — 5 sin 30/= 63,46 —5 sin ЗОг1,
вг1 =шл.1_у1 — u)>tjfi = 3 sin ЗОг1 — 2 cos ЗОг1.
474 ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ (ГЛ. VII
Скорость точки М выражается через ее проекции по формуле
v = vXlii -\-vyj} -\-vZiki =E cos 30* — 95,19)i,4-
+ F3,46 — 5 sin ЗООЛ 4- C sin 30* — 2 cos 30*) ft,.
Уравнение мгновенной оси в неподвижной системе координат
согласно A0*) будет:
- у - - B)
15 sin 2.? — locos 'It Ж
Уравнение мгновенной оси в подвижной системе осей согласно
A1*) имеет вид
х, У, г,
sin 3Ot cosiOt 31,73"
C)
Из этих равенств находим уравнения неподвижного и подвижного
аксоидов, исключая время. Уравнение неподвижного аксоида получаем
из B):
Уравнение подвижного аксоида находим из C):
(* \2
—— I —0
31.73J ~~U-
Определим (рис. б) половины углов раствора конусов, образую-
образующих неподвижный и подвижный аксоиды. Полагая j = 0, находим
значение
ctg ? = -?- = ?! = 1,86.
Аналогично, считая j>j = O, определяем угол раствора для подвиж-
подвижною аксоида
ct?<x = --= 31,73.
Рассмотренное в этой задаче движение твердого тела вокруг не-
неподвижной точки называется регулярной прецессией. При этом дви-
движении угол нутации 9 — постоянная величина, а углы прецессии ф и
чистого вращения ср изменяются пропорционально времени. Прецессия
называется прямой, если векторы (Oj и ю3 (рис. б) образуют острый
угол. Прецессия называется обратной, если этот угол тупой. В слу-
случае прямой прецессии направления собственного вращения твердого
тела и вращения его мгновенной оси совпадают. При обратной пре-
прецессии эти вращения противоположны.
Задача 7.2. В условиях предыдущей задачи определить мгновен-
мгновенное угловое ускорение твердого тела, а также ускорение точки
М(х„ yh zt).
§ I] ОПРЕДР.ЛР.НШ; СКОРОСТЕЙ И УСКОРЕНИЙ 475
Решение. Мгновенное угловое усксрение твердого тела равно
скорости движения конца вектора мгновенной угловой скорости ел.
Из решения предыдущей задачи (рис.5) следует, чго вектор (о описы-
описывает конус вокруг оси z с угловой скоростью <uv Рассматривая со
как радиус-вектор точки твердого тела, вращающегося с угловой ско-
скоростью to, вокруг оси z, находим скорость этой точки е:
е = ©1Х<»- (О
Далее, согласно соотношению A) предыдущей задачи
ел = W[ -j- щ. B)
Внося это значение ю в A), имеем:
в = «I X («1 "Г «э) =И|Х «з- C)
Из этой формулы следует, что вектор мгновенного углового ус-
ускорения направлен перпендикулярно к плоскости zzt (рис. а преды-
предыдущей задачи), т. е. по линии узлов. Угловое ускорение совпадает с
положительным направлением линии узлов, если прецессия пряная.
При обратной прецессии вектор е направлен в отрицательную сто-
сторону оси ON. Величина мгновенного ускорения определяется из C)
е = и), • u>3 sin 6 = 2 • 30 sin -*- = 30 сек'.
Мгновенное угловое ускорение может быть найдено и другим
способом, методом проекций. Согласно формулам A3*) и A4*) про-
проекции углового ускорения соответственно на неподвижные и подвиж-
подвижные оси координат определяются как производные по времени от
соответствующих проекций мгновенной угловой скорости. Таким сб-
разом, находим проекции углового ускорения на неподвижные оси
координат:
ел = ^ = A5 sin 2t)' = 30 cos It,
Ej, = u>j, = ( — 15 cos It)' = 30 sin It,
Проекции углового ускорения на подвижные оси координат будут:
ел.) = loXi=( sin 30^' = 30 cos 30*,
?j,1==iJ,i = (cos 300'= — 30 sin 30*,
Величина углового ускорения равна
в = V*\ + 4-\- *\= У'^ + 4. + 4, = 30
476 ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
Направление углового ускорения определяется косинусами:
cos (е, х) = -- = cos 2*,
cos (е, у) = -у- = sin It,
cos (e, г) = Е~- = О,
COS (e^i) = ~-'- = COS 30*,
cos (e, У\) = г—-= — sin 30*,
откуда следует, что угловое ускорение направлено по линии узлов.
Переходим к определению ускорения точки М. Находим проек-
проекции ускорения течки М на подвижные оси координат, пользуясь
формулами B2*):
wXl= — 30 sin 30*-5-f-
4- sin 30*(sin 30*¦ 2-f cos 30^- 3-1-31,73-5)—1008-2,
D)
wyi= —30 cos 30*-5-j-
-j-cos 30*(sin 30*- 2 -f- cos 30* • 3 + 31,73 • 5)— 1008-3,
w,L — 30 cos 30* -3-1-30 sin 30* • 2 -|-
-j-31,73 (sin 30* • 2 -f cos 30* -3+ 31,73-5)— 1008-5.
Ускорение точки М по найденным проекциям определится формулой
где lb jb fei — орты осей xh yb zv
Задача 7.3. Конус с углом при вершине ВОС= -ъ)- закреплен шар-
пирно в точке О и катится без скольжения по плоскости ху.
Точка А, находящаяся в центре основания конуса, описывает при
этом окружность, центр которой расположен па оси z. Перпендику-
Перпендикуляр, опущенный из А па ось z, вращается вокруг оси z согласно
уравнению
Радиус основания конуса г.
Определить угловую скорость и угловое ускорение конуса, а так-
также скорость и ускорение течек А, В, С.
§ч
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ
477
Решение. Точка А описывает окружность с центром, лежащим
на оси z. Угловая скорость вращения радиуса h этой окружности,
соединяющего точку А с центром, равна
а длина этого радиуса (рис. б)
h=OA- cos 45° = г cos 45°.
Следовательно, модуль скорости точки А
равен
vA = ftu>i = У2 rkt.
С другой стороны, скорость точки А,
как принадлежащей твердому телу, вра-
вращающемуся вокруг неподвижной точки О,
равна по модулю произведению мгновен-
мгновенной угловой скорости на кратчайшее рас-
расстояние от точки А до мгновенной оси.
Мгновенная ось конуса направлена по об-
образующей ОС. Следовательно,
где hl = h = r cos 45°. Приравнивая два
полученных значения для скорости точ-
точки А, находим:
Скорость течки А параллельна оси х.
Пусть для определенности она совпадает
с положительным направлением оси. Тогда
<»[ направлена по оси z в отрицательную
сторону, а вектор ю — по оси у в поло-
положительную сторону (рис. б). Перехо-
Перехог/
К задаче 7.3.
дим к определению углового ускорения. Воспользуемся с[ормулой
где
Тогда в пашей задаче
е, = Ik ¦ й>0,
причем орт мгновенной оси щ указывает па то, что вектор ?j направ-
направлен по оси у в положительном направлении (рис. 6).
478 ВРАЩЕНИЕ ТВЕРДОГО ГЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
Вторая составляющая углового ускорения равна по модулю
и направлена по оси х в положительном направлении (рис. б).
Скорость течки С равна пулю, так как эта точка находится на
мгновенной оси. Скорость точки В равна по модулю
vB = 2vA = 2\<r2 rkt,
так как кратчайшее расстояние точки В до мгновенной оси
ОД = 2Л,.
Вектор vB направлен параллельно оси х в положительную сторону.
Переходим к определению ускорений. Ускорение точки С опре-
определяется по формуле
wc = w'g -j- w^> -j- ai|SP.
Точка С лежит па мгновенной оси. Следовательно,
Точно так же и
w°.c = 0.
(так как е, |] гс). Итак,
wc = w^P = e2 X Гс-
Ускорение точки С равно по модулю
wc = ?2 гс sin 90° = 4 rk4%Vl
и направлено параллельно оси z (рис. в).
Ускорение точки В находится по формуле
Осестремительное ускорение точки В равно по модулю
_ ов . Ш2 =
и направлено от течки В к О (рис. в).
Ускорение щ>„р направлено параллельно оси х (рис. в) и равно
по модулю
•дайр = е, • ОД • sin 90° = 2УТ- rk.
Ускорение wB? направлено параллельно отрицательному направле-
направлению оси у (рис. в) и равно по модулю
w«p = s, • ОП ¦ sin 90° = 4)'Т rk4\
л*
Модуль ускорения точки В равен
wu = Vwff -г ™% + ^2 = 2г* V 16А*Л-|- 2.
в М ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ 479
Ускорение точки А находится по формуле
wA = wAc -\- wBAр + wB?,
где оссстремительное ускорение равно по модулю
и направлено по кратчайшему расстоянию от точки А к мгновенной
оси, т. с. по /г, (рис. б); первая составляющая вращательного ускорения
равна
г
и направлена параллельно оси х (в положительную сторону); вторая
составляющая вращательного ускорения равна по модулю
и направлена от А к В.
Заметим, что ускорение точки, движущейся по окружности ради-
радиуса h (рис. б), может быть найдено по формуле
w'A,
где нормальное ускорение равно
=
и направлено от А по кратчайшему расстоянию к оси z.
Касательное ускорение равно
А dt
и направлено параллельно оси х.
Сопоставляя оба решения, замечаем, что
wb.p = w~. W. = wb.p cos 45°
A\ At A A-2
и проекция ускорения течки А па ось z pauiia пулю:
wz = wB? cos 45° — w°Ac = 0.
Ускорение точки А расположено в плоскости, параллельной ху.
Для приобретения навыков в решении задач па
вращение твердого тела вокруг неподвижной точки
рекомендуется решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Ме-
Мещерского, издания 1950 г. и более поздних лет: 596,
698, 599, 604, 607, 610.
480
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
[ГЛ. VII
Рис. 7.4.
§ 2. Сложение вращений вокруг пересекающихся осей
Если твердое тело одновременно участвует в двух вращениях во-
вокруг пересекающихся осей, то одно из этих движений принимается
за переносное вращение, а второе — за относительное. Обозначая
мгновенные угловые скорости переносного движения через (ае и от-
относительного движения через <аг, можно
найти мгновенную угловую скорость абсо-
абсолютного движения <аа по формуле (рис 7.4)
10в = 10. + 0>г A*)
Таким образом, результирующее диижеиие
также является вращением твердого тела
вокруг неподвижной точки. Поэтому все ска-
сказанное в предыдущем параграфе относительно
определения скоростей и ускорений течек
твердого тела, нахождения уравнений по-
подвижного и неподвижного аксоидов, угло-
углового ускорения может быть применено в
данном случае.
Наряду с этим при решении задач в этом
параграфе может быть использован и дру-
другой способ. Определение скоростей точек твердого тела может быть
произведено на основании теоремы сложения скоростей
va = ve-\-vr, B*)
где v0 — абсолютная скорость точки; ve и vr — соответственно ее пере-
переносная и относительная скорости. Для определения ускорений точек
может бить применена теоргма сложения ускорений (теорема Кори-
олиса)
wa = we-\-Wr-\--wc, C*)
где wa — абсолютное ускорение точки; we, wr, wc — соответственно
переносное, относительное и корнолисово ускорения.
Корнолпсово ускорение определяется формулой
При решении задач на сложение вращений во-
вокруг пересекающихся осей могут быть использованы
два с п о с о б а.
Первый способ. По заданным угловым скоростям перенос-
переносного и относительного вращений определяется абсолютная углоная
скорость и, далее, согласно последовательности действий, установлен-
установленной в § 1 этой главы, находятся все искомые величины.
S 21
СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
481
Второй способ. Рекомендуется такая последовательность дей-
действий:
1) выбираются неподвижная система координат так, чтобы ее ось
z совпала с переносной угловой скоростью <ае, и подвижная система
координат так, чтобы се ось z± совпала с относительной угловой
скоростью (О/,
2) по известным переносной и относительной угловым скоростям
находится абсолютная угловая скорость;
3) определяются искомые скорости точек в относительном и пере-
переносном вращениях и, далее, искомые абсолютные скорости;
4) находятся переносное, относительное и кориолисово ускорения
и, далее, искомое абсолютное ускорение точек твердого тела путем
векторного сложения или сложением при помощи метода проекций.
Задача 7.4. Шарикоподшипник (рис. а) состоит из неподвижной
обоймы N, внутренней обоймы М, вращающейся вокруг вертикальной
оси z с угловой скоростью <ае, и шарика О, зажатого между обой-
обоймами.
Определить положение оси z, при котором шарик будет катиться
по обоймам М и N без скольжения. Пользуясь чертежом к данной
а)
К задаче 7.4.
задаче, найти графически абсолютную угловую скорость шарика и
его относительную угловую скорость по отношению к вращающейся
обойме М, если <ае задана.
Решение. Будем исходить из условия, что шарик О катится по
обоймам М и N без скольжения. Следовательно, точки А, В шарика,
находящиеся в соприкосновении с неподвижной обоймой N, имеют
скорости, равные нулю. Абсолютная мгновенная ось шарика должна
проходить через эти две точки. Проводим (рис. б) прямую ш через эти
две точки. Точки шарика С, D, находящиеся в соприкосновении с
вращающейся обоймой М, должны иметь одинаковые абсолютные
16 М. И. Бать и др., т. I
482
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
180°-6
скорости с точками обоймы М. Значит, относительные скорости те-
течек шарика, соприкасающихся с точками обоймы М, равны нулю.
Следовательно, относительная мгновенная ось шарика проходит через
точки соприкосновения с вращающейся обоймой М. Проводим (рис. б)
эту прямую (о,.
Находим точку пересечения К прямых <о и <о,. Движение шарика
без скольжения будет достигнуто, если вертикальная ось z будет про-
проходить через точку К- Точка К будет оставаться неподвижной во
все время движения.
Задача 7.5. В механизме маятниковой мельницы (рис. а) главный
вал / соединен с ведущим валом // посредством шарнира Гука.
На конце главного вала жестко закреплен бегун ///. При достаточно
большом числе оборотов ведущего вала бегун прижимается изнутри
к стенке цилиндрической чаши так, что сечение бегуна МХМ. катится
по чаше без скольжения.
Радиус этого сечения ви-
виден из центра шарнира
под углом а. Угол между
главным валом и веду-
ведущим валом 3.
Найти угловую ско-
скорость вращения бегуна
вокруг его оси симмет-
рии, если известна угло-
угловая скорость ведущего
вала.
Решение. Движе-
Движение бегуна рассматриваем
как сложное, состоящее
из вращения вокруг вер-
вертикальной оси и враще-
вращения вокруг оси симметрии. Вращение бегуна вокруг вертикальной
оси (вала //) принимаем за переносное, вращение вокруг оси симмет-
симметрии (вала /) назовем относительным.
Мгновенная ось абсолютного вращения — это линия, соединяющая
две неподвижные течки О и М. Вдоль линии ОМ направлен вектор
абсолютной мгновенной угловой скорости ьла. Вектор переносной уг-
угловой скорости (йе направлен по оси ведущего вала. Вектор относи-
относительной угловой скорости ыг (это искомая в задаче скорость враще-
вращения вокруг оси симметрии) направлен по главному валу I. Предполо-
Предположим, что для наблюдателя, смотрящего на мельницу сверху, бегун
движется по часовой стрелке. Тогда вектор переносной угловой
скорости ые направлен вертикально вниз; основное векторное соот-
соотношение
К задаче 7.5.
§21
СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
483
представлено на рис. б. Рассматривая треугольник, образованный век-
векторами <оа, (ае и <ол имеем по теореме синусов
sina sin[!80° — a — A80° — 8)]
или
sin а sirl (8 — а) '
откуда окончательно находим:
sin (8 — a)
e sm i
Задача 7.6. Искусственный спутник Земли, двигаясь по круговой
орбите, имеет период обращения, вычисленный по отношению к системе
к. \
NO
V
4
V
,
4
\
s
*•—
>*>
' s
\
\
К задаче 7.6.
координат, движущейся вместе с центром Земли поступательно, равный
1,5 часа. Определить его относительную угловую скорость по отноше-
отношению к Земле, вращающейся вокруг своей оси, при угле наклона его
орбиты к экватору а! = 60°. Вектор его угловой скорости <о образует
острый угол с осью SN Земли.
Р е ш е и и е. Плоскость орбиты К.К образует с экватором WO
угол 60°. Тогда вектор абсолютной угловой скорости спутника <о
составляет угол 60° с осью SN, по которой направлен вектор ше
угловой скорости Земли. Рассматривая вращепие спутника как движе-
движение, складывающееся из переносного вращения вместе с Землей и
искомого относительного вращения по отношению к Земле, имеем:
16*
484
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛЛ ВОКРУГ НР.ПОЛВИЖНОЙ ТОЧКИ [ГЛ. Vtt
где (о — абсолютная угловая скорость спутника; слг — его относитель-
относительная угловая скорость. Величина абсолютной угловой скорости
2к
Величина переносной угловэй скорости
_.
МПН
.
Таким образом, в треугольнике угловых скоростей известны две
стороны «и и шр и угол между ними. Определяем третью сторону
треугольника:
* — 2u)u), cos G0° = |j
f- J.2- — -I ^ 0,0675 мин'1.
Находим угол, образованный oir с экватором:
cos K>O) = ^i^O = 0,89.
(or — это углоная скорость спутника относительно Земли.
Задача 7.7. Конус А с углом при вершине, равным D0C= 90°,
имеет неподвижную точку 0 и катится без скольжения по неподвиж-
неподвижному конусу В, угол которого при вершине также равен 90°. Диаметр
К задаче 7.7.
основания подвижного конуса DC= 40 см. Скорость точки 0t по вели-
величине постоянна и равна vq1 = 80 см/сек.
Найти (ар — переносную угловую скорость конуса (вокруг оси z),
его относительную угловую скорость <±>г (вокруг оси симметрии OOt)
и абсолютную угловую скорость <оа. Определить скорости точек D,
Е, С конуса (рис. а).
Решение. Точка О[ лежит на относительной мгновенной оси
вращения ОО{ и, следовательно, ее относительная скорость vrQ равна
нулю. Согласно теореме сложения скоростей
§ 21 СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРРХЕКАЮЩИХСЯ ОСЕЙ 485
при учете равенства vr0 =0 имеем:
Величина переносной скорости равна произведению радиуса вращения
вокруг переносной мгновенной оси z на модуль переносной мгновен-
мгновенной угловой скорости:
v° =00 • ш ,
откуда
ОО,~ОО1~ 20
Полагая движение точки О{ происходящим против часовой стрелки,
если смотреть с положительного направления оси г, вектор ше следует
направить по оси г вверх.
Скорости точек подвижного конуса, находящихся в соприкоснове-
соприкосновении с поверхностью неподвижного конуса, равны пулю, так как
конус А катится без скольжения по конусу В. Следовательно, образую-
образующая ОС является мгновенной осью абсолютного движения и величина
абсолютной скорости точки Ot равна
где oju — абсолютная мгновенная углоная скорость; ОгК — перпенди-
перпендикуляр, опущенный из точки О( на мгновенную ось ОС (рис. б).
Тогда
OlK=OOi sin 45° = 20^=14,1 см
и, следовательно,
Учитывая направление скорости точки Оь проводим <ла от С к О
(рис. в). Направление относительной мгновенной угловой скорости
совпадает с прямой 00]. Строим (рис. в) на векторе <оа, как на
диагонали, параллелограмм угловых скоростей
откуда следует, что величина u>r = <Dp = 4 сек'1.
Переходим к определению скоростей точек D, Е, С конуса.
Скорость точки С равна нулю, так как эга точка лежит па мгновенной
оси абсолютного движения и соприкасается с боковой поверхностью
неподвижного конуса В.
Найдем величину скорости точки D. Величина скорости точки D
равна произведению величины абсолютной угловой скорости u>fl на
486 ВРАЩР.НИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
кратчайшее расстояние точки D до мгновенной оси абсолютного
движения ОС
vD = OD- «>Q == 20 /2 • -^L = 160 см/сек;
vD направлена перпендикулярно к плоскости ODC (рис. б) за рисунок.
Скорость точки D можно найти и другим способом. Действительно,
скорость точки D равна сумме переносной и относительной скоростей
переносная скорость по величине равна
¦u«D=OOI-u>(j = 20-4 = 80 см/сек
и направлена перпендикулярно к плоскости ODC за рисунок; модуль
относительной скорости течки D
vrD = Op ¦ шг = 20 • 4 = 80 см/сек.
Так как относительная скорость совпадает но направлению с переносной
скоростью, то
v = v°D -j- VD = 160 см /сек.
Переходим к определению скорости точки Е. На рис. г представ-
представлена плоскость О^ЕК, перпендикулярная к абсолютной мгновенной
оси ОС и проходящая через диаметр основания конуса OYE. Из рис. г
видно, что кратчайшее расстояние от точки Е до прямой ОС равно
ЕК = V(OiKf + (EOif = 1/200 -р 400 = 24,5 см,
следовательно, величина скорости точки Е будет:
vF = EK- <fle = 24,5 • 5,66 = 138,5 см/сек.
Эта скорость (рис. г) лежит в плоскости О^ЕК и направлена пер-
перпендикулярно к прямей ЕК-
Задача 7.8. В условиях предыдущей задачи определить абсолютное
и относительное угловые ускорения конуса Л. Найти ускорения
точек Oi, D, С.
Решение. Угловое ускорение может быть определено как ско-
скорость конца вектора угловой скорости. Угловая скорость переносного
движения а,, сохраняет без изменения свою величину (<о(?:=4 сек)
и свое направление (по оси г). Угловое ускорение в абсолютном
движении равно
§ 2] СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
(так как вектор <оа вращается со скоростью (оД или
4^=16 сект*.
487
" а' 10/2"
Оно направлено по оси х в положительную сторону, перпендикулярно
к плоскости ОО)С
°4—°</vjc o4
с
б)
О, О
6)
К задаче /.8.
В mi ш! D
о,
Для определения углового ускорения еа можно воспользоваться
теоремой сложения угловых скоростей:
«а = *». + «г-
где <оа, «о,,, <ог — соответственно абсолютная, переносная и относи-
относительная угловые скорости тела. Вычисляя от обеих частей этого
равенства производную по времени, находим:
Так как в данной задаче -^ = 0 и -^ = 0, то
Этот же результат получается и из A), если вычислить непосред-
непосредственно выражение
откуда
?а = ае X «а = «>Р X (<УР + «,.) = <Ое X Wr,
ей=16 сект*.
Переходим к определению ускорений точек Olt D, С. Ускорение
точки Оу может б[.1ть определено тремя способами.
Первый способ — точка Ог описывает окружность радиуса ОО4
с постоянной по'величине скоростью vot =80 см/сек; следовательно,
488 ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
ускорение точки О\ будет нормальным ускорением с модулем
оно направлено от О, к точке О.
Второй способ — ускорение течки Oit как принадлежащей
тиердому телу, вращающемуся вокруг неподиижного центра О:
wo, = wo\ -т ™ор, = «а X К X г) + е„ X г,
причем величина осестремителыюго ускорения
w™ = А«J = Oj/f • uJ = у'2 .10-32 = 320 j/'2 см/сек*.
Это ускорение направлено по перпендикуляру к мгновенной оси, т. е.
от О] к К (рис. а); модуль вращательного ускорения
и^р = ?,Д = ?а • 00, = 16 • 20 = 320 см/сек*,
оно направлено перпендикулярно к еа и г—ОО„ т. е. по оси г
вверх; замечая, что угол л:ежду wff и «)^c равен 135°, заключаем,
что
w0 =-- wff = 320 см/сек*
и направлено но ООи что совпадает с результатом, найденным первым
способом.
Третий с и о с о б — ускорение точки О, определяем по теореме
сложения ускорений (теореме Кориолиса), рассматривая ее абсолютное
движение как составное из переносного вращения (вокруг оси z)
и относительного вращения (вокруг оси OOi); тогда
переносное ускорение папранлепо от Oi к О и равно по величине
weOi = OOi ¦ < = 20 • 16 == 320 см/сек"-;
относительное ускорение точки Ot равно нулю, так как ючка Ot
лежит на оси ООЬ вокруг которой происходит относительное движе-
движение конуса; кориолисоио ускорение точки Oj равно
^Ь^^Хо'о,;
оно обращается в нуль, так как нулю равна относительная скорость
vr точки O]j таким образом, как и при ранее использованных спо-
способах, величина ускорения О, будет:
wOi == weOi = 320 см/сек"-;
это ускорение направлено от Oi к О.
§ 2| СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ 489
Найдем теперь ускорение точки С. Это ускорение также можно
определить различными способами.
Первый способ — ускорение точки С складывается из осе-
стремителыюго и вращательного ускорений
Осестремителыюе ускорение точки С обращается в нуль, так как
течка лежит па мгнонеппой оси; следовательно,
Величина ускорения
wc — w^ = га ¦ ОС ¦ sin 90° = 16 • 20 V? = 320 V2 см]сек*.
Это ускорение лежит в плоскости ООХС, перпендикулярной к еа,
и образует прямой угол с ОС (рис. б).
Второй способ определения ускорения точки С основан на
теореме сложения ускорений
чюс = W). -)-- Wc -\- wcc.
Переносное ускорение точкп С есть ускорение при вращении вокруг
оси z с угловой скоростью те. Величина переносного ускорения
равна
wec — ОС ¦ sin 45°. <o'j = 20 • 16 = 320 см/сек*.
Это ускорение направлено от точки С по перпендикуляру к оси z,
т. е. параллельно оси у (рис. в). Относительное ускорение точки С
есть ускорение при вращении вокруг оси у с угловой скоростью <ог.
Его величина
wrc = ОХС • <о2 = 20 • 16 = 320 см/сек*.
Оно направлено от точки С к О, (рис. в). Кориолисово ускорение
равно
Следовательно, его величина (замечаем, что v?.= OlC-шг)
wrc = 2u>v'c sin 90° = 2 • 4 • 4 • 20 — 640 см/секь,
оно направлено согласно правилу векторного произведения параллельно
оси у (рис. в).
Находим теперь сумму ускорений чю'с и wcc, направленных по одной
прямой в разные стороны:
wcQ — Wc = 320 см\сек\
490 ВРАЩЕНИИ ТВЁРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
Тогда величина полного ускорения точки С
wr = V(wrrf 4- (wcr — werf = 320 V2 см/секь,
оно направлено под прямым углом к ОС.
Переходим к определению ускорения точки D.
Первый способ. Применим формулу распределения ускорений
в твердом теле, вращающемся вокруг неподвижной точки:
Осестремительное ускорение по величине равно
w<? = OD ¦ <о* = 20Yif—J = 640 У7 см/секС
Оно направлено от D к О (рис. г). Вращательное ускорение опреде-
определяется формулой
следовательно, модуль вращательного ускорения
wfl = га • OD = 16 • 20 V2 = 320 j^2 см/'сек*-
Это ускорение направлено перпендикулярно к OD (рис. г). Величина
полного ускорения точки D
wD = l/'fa'o)*-}"(иф* = 32°KlO см/сек*.
Второй способ определения ускорения точки D основан па
использовании теоремы Кориолиса:
Переносное ускорение по величине равно
weD=0D- sin 45°• <о« = 20• 16 = 320 см/сек*
и направлено от D к оси z по кратчайшему направлению (рис. д).
Модуль относительного ускорения будет:
wrD=OlD-u>l=20-l6 = i20 см/секК
Это ускорение направлено от D к Ot (рис. д).
Ускорение Кориолиса дается формулой
где D^=O1D-")r = 80 см/сек. Оно направлено перпендикулярно
к плоскости OCD за рисунок. Величина ускорения Кориолиса равна
wcD = 2@^ sin 90° = 2 • 4 • 80 = 640 см/сек*.
Его направление совпадает с wcD (рис. д).
§ 2) СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
Таким образом, величина ускорения точки D
491
wD = V^d? + («>Ь + ШЬ)9 == 320 Vх ° с Ml сек9.
Направляющие косинусы определяются формулами:
Wr
960
4 u> * ™D 320/10
, -^ ч wDz 320
cos (wn, г) = -^ = —
D WD 320/10
/10 '
Задача 7.9. На рис. а схематически изображен мельничный бегун
с неподвижным направляющим диском ///. Ведущий вал / и опорная
К задаче 7.9.
плита // могут вращаться вокруг вертикальной оси независимо друг
от друга. На вал ОО^ бегуна V наглухо насажено коническое кслесо
IV радиуса г, которое катится без скольжения по неподвижнсму
диску Ш радиуса а.
Определить относительную угловую скорость (»г вращения бегуна
вокруг его оси OOt, а также угловую скорость и)И, которую должна
иметь опорная плита. Длина вала ООх равна Ь, радиус бегуна R.
Колесо IV обегает неподвижный диск за 4 сек.
Решение. Движение бегуна сложное, оно состоит из вращения
оси бегуна OOi вокруг вертикальной оси, проходящей через точку О,
и вращения бегуна вокруг его собственной оси OOV Первое из этих
диижений — вращение вокруг вертикали — будем считать переносным
492 ВРАЩЕНИЕ ТВЕРДОГО Ti-ЛЛ ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
движением, а второе — вращение вокруг оси симметрии бегуна — от-
относительным движением. Угловая скорость переносного вращения
бегуна равна
С°е=т=г llceK-
Величина скорости центра А конического колеса IV равна
Мгновенная ось вращения колеса IV проходит через неподвижный
шарнир О и точку касания колеса с неподвижной плитой М. Линия
ОМ составляет с осью ОА угол а. Из треугольника ОАМ находим:
sin з=-—[L=~,
о
cosa= =.
Кратчайшее расстояние от центра колеса А до мгновенной оси вра-
вращения ОМ равно
АР = ОА- sin д = -—-а--
Величииа мгновенной угловой скорости колеса IV равна
Если иредположить, что скорость точки Л в положении, показанном
на рис. а, направлена перпендикулярно к чертежу, на читателя, то
векторное равенство
будет иметь вид, изображенный па рис. б.
Отсюда видно, что
u>r = <u,, ctg а = ша cos а.
Подставляя значения тригонометрических функций из A), получаем
Эту же угловую скорость воьруг осп 00] имеет и бегун V, состав-
составляющий с коническим колесом IV одно твердое тело.
Величина скорости центра Oj бегуна V будет:
Z' = ш ¦ Ь.
Oi с
Скорость нижней точки бегуна Q может быть найдена двумя способами.
§ 21 СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ 493
Первый способ. Рассмотрим бегун в абсолютном вращении
вокруг мгновенной оси ОМ. Продолжим эту ось до пересечения с ра-
радиусом OjQ. Из подобия треугольников ОАМ и OO^Mi имеем:
а I
г CV
откуда
0 rb
1 l a
Тогда находим:
Кратчайшее расстояние точки Q от мгновенной оси вращения будет:
Тогда
Второй способ. Скорость точки бегуна Q складывается из
переносной скорости вращения вокруг вертикальной оси и относи-
относительной скорости вращения вокруг горизонтальной оси бегуна ОО\.
Обе эти скорости в положении, изображенном па рисунке, перпенди-
перпендикулярны плоскости чертежа, но направлены в разные стороны:
переносная скорость ve — к нам, относительная скорость — от нас,
причем vr^>ve. Тогда величина скорости точки Q будет:
Точка касания опорной плиты // с бегуном имеет такую же ско-
скорость: vu = Vq. Отсюда вычисляем величину угловой скорости Бра-
щеиия плиты:
vi\ я (aR
Направление вращения плиты — обратное направлению вращения вала
бегуна.
Задача 7.10. В условиях предыдущей задачи найти ускорении
точек А и М конического колеса и верхней точки С бегуна.
Решение. Предварительно определим абсолютное угловое уско-
ускорение бегуна как производную абсолютной угловой скорости по вре-
времени
494
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. Vlf
По величине
ность радиуса
не меняется, конец ее вектора описывает окруж-
окруж, с угловой скоростью <ае. Угловое ускорение
С
К задаче 7.10.
согласно (I) можно рассматривать как скорость движения копна
вектора ыа. Вектор углового ускорения г направлен перпендикулярно
к чертежу, на читателя, и численно ранен (рис. а)
§ 2| СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ 495
Ускорения точек могут быть найдены двумя способами: применением
теоремы Ривальса или применением георемы Кориолиса.
Первый способ (теорема Ривальса). Воспользуемся для опре-
определения ускорения точек А, М и С формулой
w = wbp -f w°c = 8 X г + 6),, X (<&* X г),
где вместо г будем подставлять последовательно радиусы-векторы
точек А, М и С.
1) Для ускорения течки А имеем:
wA =г )< ОА + юа X (®а X
Вектор г X 0^ направлен вертикально вверх и равен но модулю
wnP = t- О А = -^—.
А г
Вектор юа X ОА направлен параллелы:о оси z к нам и равен по
величине
ша • ОА ¦ sin а = ш "I?— = ш ¦ а.
Va'lr*
Вектор б)д X (йа X 0^) направлен перпендикулярно к й„ и оси г
(по которой расположен второй сомножитель векторного прогшшде-
ния) вниз (рис. б) и равен по величине
>/ = ш -ш -a- sin 90 = -е— V аг-V-
лае f r i
-a- sin
Проекции ускорения точки Л на оси координат будут:
wАх = — я>^ = — и»^ sin а = — ш^а;
и>, = и>вЯ — и>°.с = w°p — и>Яс cos a •= — = 0.
Следовательно, ускорение точки А направлено горизонтально влепо
по оси х и равно по модулю
Примечание. Точка А, как и др\гие точки оси OOlt совершает
вращение вокруг вертикальной оси с постоянной угловой скоростью и>е и
имеет поэтому только нормальное: ускорение, равное w. =<o|-a, направлен-
направленное к оси вращения, т. е. горизонтально влево. Естественно, что применение
теоремы Ривальса привело к тому же результату.
2) Для ускорения точки М имеем:
ша X (юа X ОМ)-
496 ВРАЩЕНИЕ ТВЕРДОГО TIM А ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
Векгор г X ОМ направлен перпендикулярно к линии ОМ вверх и
равен по величине
чзувр __ g. qm = —^—1/ а'2 -4- г'1.
М г '
Вектор <яа X ОМ равен нулю, так как направления сомножителей
совпадают, следовательно,
Итак, полное ускорение точки М состоит из ее вращательного уско-
ускорения и равно по величине
Оно направлено от точки М перпендикулярно к ОМ.
3) Для ускорения точки С имеем:
wc = г X ОС + <йа X («а X OQ-
Вектор е X ОС направлен в плоскости ху перпендикулярно к ОС
вверх и равен по величине
«»»Р = е ¦ ОС — '^f-
Таким образом, этот вектор лежит в плоскости ху и образует угол 3
с осью у.
Величина осестремителыюго ускорения будет:
I «>« X К, X ОС) ! = <¦>#,
где h — длина перпеидикуляр.1, опущенного из точки С на мгновен-
мгновенную ось ОМ, равная
h = ОС¦ sin (я-j- р) = ]/ b'~-\- R}(sin a cos [3 -j- cos a sin ^).
Внося в это равенство значения функций угла а, полученные в пре-
предыдущей задаче, а также
Kin р = —
cos За-
Заполучим величину осестремительного ускорения
ю~ == ^ V^Vb*- {rb + aR).
Осестрсмительное ускорение направлено перпендикулярно к линии ОМ
от точки С к мгновенной оси.
§ 2| СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ 497
Изобразим слагаемые вектора wc па рис. г. Для определения
величины ускорения точки С спроектируем составляющие ускорения
на оси х и у. Получаем:
wCx=—-wl? sin ? — w™ sin oc= -(rb-\-aR) =
wc — w^ cos p — да?с cos a = — а- (r? -}- a/?) = Ц
откуда
wc
= Vwlx -j- wlv = -pi Уг1Ьа--\- 4aRr»b -j- 4aVafi4 -f a4/?'.
Второй с и о с о б. Рассмотрим движение бегуна как сложное и
воспользуемся для нахождения ускорения точки С теоремой Корио-
лмса, согласно которой
За переносное движение примем вращение вокруг вертикальней
оси, а за относительное — вращение вокруг оси OOV Отметим, что
для всех точек wer и wr. равны нулю, так как угловые скорости ше
и шг не изменяются ни по величине, ни по направлению.
1) Для ускорения точки А имеем:
wA = wen^rwrn^rwc.
Нормальное ускорение в переносном движении направлено к оси
вращения, г. е. по горизонтали влево, и равно
wen = ща.
Нормальное ускорение в относительном движении равно нулю, так
как точка А лежит на оси относительного вращения. Ускорение
Кориолиса равно пулю, так как относительная скорость точки А
равна пулю. Итак, абсолютное ускорение точки равно (рис. в)
2) Для ускорения точки М имеем:
WM = Wen-T Wrn + wc-
Нормальное ускорение точки М в переносном вращении равно
Wen = шеа
и направлено к оси переносного вращения (см. рис. д). Нормальное
ускорение в относительном вращении равно
498 ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
и направлено к оси относительного вращения (на рисунке вверх).
Ускорение Кориолиса направлено вправо и равно
wc = 2u)e ¦ vr sin 90° = 2шешг ¦ г = 2u)|. а.
Направив оси х и у, как показано на рисунке, проектируем слагае-
слагаемые ускорения на эти оси:
wMx = — wen -\- wc =•— ш*
Абсолютное ускорение точки М равно
3) Для ускорения точки С имеем:
Нормальное ускорение в переносном вращении равно
и направлено к оси переносного врашения, т. е. влево (рис. ё).
Нормальное ускорение точки М в относительном вращении направлено
от Ж к оси относительного вращения ООЪ т. е. вниз, и равно
Ускорение Кориолиса направлено влево и равно
по °R
с е г е г е г '
Проектируя составляющие абсолютного ускорения точки С на оси
координат, находим:
wcx = — wea — wc = — rfeb — 2ш= -^-.
Величина абсолютного ускорения точки С равна
wc = Vwlx-\-wlv=: ^ ]/>**» + 4abr*R -f 4ar/?*r» + a4/?2 =
c
Задача 7.П. В автомобильном дифференциале (рис. а) вращение
от оси мотора 1 посредством конической передачи 2 и 5 передается
§2]
СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
499
водилу И. Парные сателлиты / и // (рис. б) вращаются вокруг осей,
закрепленных на водиле Н, и находятся в сцеплении с колесами ///
и IV, движение которых через полуоси <3 и 4 передается задним
колесам автомобиля.
Для получения кинематической зависимости в передаче достаточно
одного сателлита (/ и //), помещенного па водиле II. Однако для
разгрузки осей 3 и 4 вводят второй сателлит, располагая его сим-
симметрично на противоположном конце водила Н. Вал / с шестерней 2
делает 600 об/мин, передаточное отношение — = 5.
К задачам 7.11 и 7.12.
Определить абсолютную и относительную угловые скорости сател
литов и угловые скорости шестерен /// и IV: а) при прямолинейном
движении автомобиля, б) в случае, если правое заднее колесо, встре-
встретив препятствие, остановилось. Радиусы сателлитов / и II равны
г, = 15 см, радиусы шестерен /// и IV—г3=15|/^3 см.
Решение. Обозначим угловую скорость колеса 5, равную угло-
угловой скорости водила, через Q. Тогда для конической пары 2 и 5
имеем:
? = ?. 0)
откуда
= Q = 120 об/мин.
Зная угловую скорость водила, применим к расчету угловых ско-
скоростей звеньев автомобильного дифференциала метод Виллиса. Дадим
500 ВРАЩЕНИЕ ТВЕРДОГО ТЕЛЛ ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ.
мысленно основанию механизма (рис. б) вращение, противоположное
вращению водила и равное ему по величине. Тогда водило станет
неподвижным, а угловые скорости шестерен ///и IV будут равны
и>з — Q,
uL —2.
Угловую скорость сателлигг относительно водила обозначим через о>.
Тогда для каждой пары колес с неподвижными осями можно запи-
записать равенства:
4i — Q Г, W1
причем с формуле C) взят знак минус, так как колеса /// и IV
(при остановленном водиле) вращаются в противоположных напра-
направлениях. Решая уравнения B) и C) относительно 2 и о>, находим:
?1 = 1@K + 0),), D)
Пользуясь этими формулами, найдем ответы.
а) При прямолинейном движении угловые скорости колес равны
ш3 = ш4 и, следовательно, и:! D) имеем:
ша = иL = Ц= 120 об/мин;
из E) находим:
ш = 0.
Сателлиты не вращаются относительно водила Я.
б) В случае остановки правого заднего колеса автомобиля шА = 0.
Тогда из D) находим:
оK=:22 = 240 об/мин.
Относительная угловая скорость сателлита из E) равна
о)
= J|Jp.i u>3= 120 ]/3 об/мин.
Абсолютная угловая скорость сателлита определится из рис. в,
где ш, = <й= 120 l/з об/мин, @^ = 2=120 об/мин:
Задача 7.12. Для автомобильного дифференциала, рассмотренного
в предыдущей задаче, определить угловую скорость водила G и
S3] ОБЩИЙ СЛУЧ<\Й ДВИЖЕНИЯ ТВЕРДОГО 'ГЕЛЛ 501
отиосшельную угловую скорость сателлитов ш, если при повороте
задние колеса автомобиля описывают на земле дуги радиусов
р! = 20 м и р.2=18 .«, причем скорость центра тяжести автомобиля
г* = 38 м/сек. Радиус заднего колеса /? = 0,6 м.
Решение. Скорости центров задних колес автомобиля опреде-
определятся по формулам
v-, = ; р. = 40 м/сек, v, = j р, = 36 м/сек.
Угловые скорости шестерен III и IV (рис. б) будут:
Тогда из формулы D) предыдущей задачи находим углопую ско-
скорость водила
о = -'- («,, + со4) = 2_L (с, -J- Щ) =?=® = 63,3 сек-\
а из формулы E) — относительную угловую скорость сателлитов
г, , . \b\'Z(v, — a.) f in i
Ш = 2г\ ((йз ~ Ш^ = 2.\!^~R °'76 С?К К
Для приобретения навыков в решении задач па
сложение вращений вокруг пересекающихся осей
рекомендуется решить следующие задачи из «Сбор-
«Сборника задач по теоретической механике» И. В. Мещер-
Мещерского, издания 1950 г. и более поздних лет: 611, 612,
614, 615, «17, 618, 622, 627, 630, G32.
§ 3. Общий случай движения твердого тела. Сложение
поступательных и вращательных движений
1 °. Скорости и у с к о р г и и я точек твердого тела
в общем случае движения. Уравнения движения твердою
тела в общем случае движения записываются в виде
¦*o=/i@. J»o
Ф=Л(О. ?
Здесь х0, у0, z0 — координаты произвольной точки твердого
тела, выбранной за полюс; 6, <р, 0 — углы Эйлера: угол прецессии,
угол чисто! о, или собственного, вращения и угол нутации, опреде-
определяющие поворот твердого тела вокруг полюса.
Скорость любой точки твердого тела в общем случае движения
определяема формулой
502 ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
где v — скорость любой точки твердого тела; v0 — скорость полюса;
<а—мгновенная угловая скорость твердого тела; Г\ — радиус-вектор,
проведенный из полюса в точку, скорость которой подлежит опре-
дслекию.
Ускорение любой точки твердого тела в общем случае движения
определяется формулой
w = wo + eXr, + <BX'(fi»Xr,). C*)
Здесь w — искомое ускорение точки; w0 — ускорение полюса; ? —
мгновенное угловое ускорение твердого тела.
Задача 7.13. Центр тяжести ракеты движется со скоростью v0 и
ракета одновременно вращается вокруг своей оси с угловой скоро-
скоростью о (рис. а). Две точки А и В расположены на одном диаметре,
перпендикулярном к оси, соответственно на расстояниях /j и /9 от
последней.
Какому условию должны удовлетворять расстояния Д и 1Ъ если
известно, что скорости точек А и В взаимно перпендикулярны?
Решение. Задача может быть решена двумя способами: анали-
аналитически и графически.
Первый способ. Движение ракеты соответствует общему
случаю движения твердого тела, причем винтовая ось совпадает
с осью ракеты. В общем случае движения твердого тела скорость
любой его точки определяется формулой B*):
где v — скорость любой точки твердого тела; v0 — скорость точки
выбранной за полюс; ш — угловая скорость твердого тела; Г\ —
радиус-вектор, проведенный из полюса в точку, скорость которой
определяется.
Принимая произвольную течку О на оси ракеты за полюс, запи-
запишем скорости течек А и В:
где Г\ и гг — радиусы-векторы точек А к В, проведенные из по-
полюса О. Скорости vA и vB по условию взаимно перпендикулярны.
Условие перпендикулярности векторов — равенство нулю их скаляр-
скалярного произведения:
ч>А-ч>в = 0.
Подставляя в это равенство значения скоростей, получим:
Раскрывая скобки, находим:
*3 + (©X»pi)-Vt-V(mXr») + (<»Xri)-(<»>X»4)==o. A)
По
§3]
ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
503
так как первый сомножитель в скобке перпендикулярен к вектору ш,
а второй сомножитель i>0 по условию параллелен ш. Аналогично
устанавливаем, что и третье слагаемое
Рассмотрим последнее слагаемое из (I). Имеем
(со X /"])(<* X П) = (("г, sin a) (o)ra sin p) cos 180° =
так как векторные произведения (иХп) и (ш></*
а)
б>
К задаче 7.13.
— <о9/,/а,
параллельны
и направлены в противоположные стороны. Внося значения слагаемых
в равенство A), находим:
откуда окончательно имеем:
Это и есть условие, которому должны удовлетворять отрезки /, и /3.
Второй способ. Графическое решение этой задачи пред-
представлено на рис. б, где дано сложение скоростей точек А к В па
плоскости, перпендикулярной к АВ.
Скорость <оА складывается из взаимно перпендикулярных соста-
составляющих, равных по модулю va и co/jj скорость vB аналогично полу-
получается из составляющих, модули которых ¦&„ и о>/а, причем <о/, и си/3
направлены в противоположные стороны, а скорости vA и 1)й взаимно
504 ВРЛЩШИЕ ТВЕРДОГО ТГСЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
перпендикулярны. Тогда из прямоугольного треугольника MKL
с высотой KN находим, что
KN* — NM ¦ NL ил и v\ = w/j • о>/2)
откуда
/ / vl
1 ' @-
2°. Сложение поступательных и вращательных
движений твердого тела. Рассмотрим движение твердого
тела, участвующего в нескольких вращательных движениях вокруг
произвольно расположенных мгновенных осей и одновременно в не-
нескольких поступательных движениях.
Вращательное движение твердого тела характеризуется мгновенной
осью и угловой скоростью, направленной по мгновенной оси. Вектор
угловой скорости можно переносить в любую точку вдоль мгновенной
оси, следовательно, углоная скорость есть скользящий вектор.
Поступательное движение твердого тела можно охарактеризовать
скоростью. Скорость поступательного движения тиердого тела можно
рассматривать как результат действия пары вращений. Скорость
поступательного движения твердого тела есть свободный вектор.
При параллельном переносе вектора угловой скорости добавляется
п точке приведения поступательная скорость
1 = гХ«, A*)
где г — радиус-вектор, проведенный из точки приведения в течку
приложения вектора угловой скорости.
Таким образом, выбирая произвольную точку за полюс, можно
привести все угловые скорости к этой точке и, сложив, получить
результирующую угловую скорость
Поступательные скорости, как непосредственно заданные, так и
возникающие при приведении угловых скоростей к центру приве-
приведения, складываются и дают результирующую поступательную ско-
скорость
Таким образом, любая совокупность вращательных и поступа-
поступательных движений твердого тела может быть заменена одним вра-
вращением с угловой скоростью (о вокруг мгновенной оси, проходящей
через центр приведения, и одним поступательным движением со ско-
скоростью i>0.
§ 3] ОВШИЙ СЛУЧАЙ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 505
Частные случаи сложения крашений и поступательных дпижепий
твердого тела:
1. Если « = 0, i>0 = 0, то гело находится в мгновенном покое.
2. Если « ф 0, фо = О, то тело вращается вокруг мгновенной оси.
3. Если @ = 0, v0 ф О, то тело дпижется мгновенно-поступательно.
4. Если @ ^ О, vo:?^ и ®в-!-и> то тело вращается вокруг мгно-
мгновенной оси, параллельной и отстоящей на расстоянии vJm от мгно-
мгновенной оси, проходящей через центр приведения. Эта мгновенная ось
лежит в плоскости, перпендикулярной к скорости ч>й.
5. Если ®фО, vu ф 0 и т0 не перпендикулярна к <о, то тело
совершает мгновенное винтовое движение. В этом случае существует
мгновенная винтовая ось — геометрическое место точек, скорости
которых равны между собой п направлены пдоль мгновенной осн.
Кинематическим винтом называется совокупность угловой скорости и
поступательной скорости, направленных по одной прямой.
Сложение вращений и поступательных движений
твердого тела рекомендуется производить в следую-
щ е м п о р я д к е:
1) выбрать оси декартовых координат;
2) взять в начале координат, точке О, центр приведения;
3) вычислить проекции результирующего вектора угловой ско-
скорости;
4) определить модуль результирующего вектора угловой скорости
и его направляющие косинусы;
5) найш проекции результирующей поступательной скорости;
6) определить модуль результирующей поступательной скорости
и се направляющие косинусы;
7) установить, к какому из пяти частных случае» приводится
результирующее движение;
8) если движение приводится к вращению вокруг мгновенной оси,
то ее уравнение находится по формуле
.
где х, у, z — текущие координаты мгновенной оси; и>х, ыу, и>г и vx,
vy, vz — соответственно проекции результирующих угловой скорости
и поступательной скорости на оси координат;
9) если движение приводится к винтовому движению, то уравне-
уравнение винтовой оси находится по той же формуле D*).
Наименьшее значение результирующей поступательной скорости,
рапное проекции поступательной скорости на мгновенную ось врг-
щения, определяется по формуле
506
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛЛ ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
10) определить параметр кинематического винта, равный отноше-
отношению минимальной поступательной скорости vmm к результирующей
угловой скорости твердого тела, по формуле
p -min ^
F*)
Как следует из вышеизложенного, существует аналогия между
приведением пространственной системы сил к простейшему пиду и
сложением поступательных и вра-
вращательных движений твердого
тела. При этом роль сил играют
угловые скорости, а роль момен-
моментов присоединенных пар — посту-
поступательные скорости твердого тела.
Задача 7.14. Тело, размеры
которого указаны на рисунке,
участвует в нескольких враще-
вращениях С УГЛОВЫМИ СКОРОСТЯМИ @|,
ш.2> Щ и ш4.
Привести движение тела к
простейшему виду, если
X 1СО, Ш, = (D4 г= 2@, <в.2 = <И3 := СО.
К задаче 7.14. Решены е. Координатные оси
изображены на рисунке. Примем
за центр приведения точку О. Совокупность заданных угловых ско-
скоростей прииодится в общем случае к скорости v и угловой ско-
скорости ш0.
Определим проекции результирующей угловой скорости:
% = О,
")г = — со, — со3 -| - со.2 -U со4 = — 2со — о) 4- со -\- 2со = О,
следовательно, вектор шв ранен нулю:
Проекции результирующей скорости на оси координат vx, vy, v2
найдем аналогично проекциям главных моментов сил, рассматривая
о,, (о.г, щ п ш4 как силы:
= — со4 • а
•а = —
§ 3| ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
следовательно,
507
Итак, шо = О и i> = 0, т. е. тело будет находиться в мгновенном покое.
Задача 7.15. Твердое тело в форме
куба ,со стороной а участвует ею вра-
вращений с угловыми скоростями с»! —
:= (U2 = (О3 = (U4 = (D И CU8 = ОN =: (О у 1.
Размеры тела и направление угловых
скоростей указаны на рис. а.
Привести движение тела к простей-
простейшему виду.
Решение. Примем за центр при-
приведения точку О. Направим оси х, у, z
вдоль ребер куба. Определим проек-
проекции результирующей угловой скорости:
(ох = щ — шв cos 45°,
Шу = — о), — о>4 —)— a>ecos45°-[-
-\- оN cos 45°,
(O2 = (D3 — '"б cos 45°.
Подставив величины угловых скоро-
скоростей, будем иметь:
шх = шу = Ш2 — 0.
Л/1
"У
X
Следовательно, в результирующем дви- к задачс 7.15.
жеиии вращения не будет.
Определим проекции результирующей поступательной скорости:
vx= ш3а — cuaa cos 45° — шйа sin 45°,
Vy = — со3а — 1»3Д cos 45° -4- ш6д cos 45°,
vz = — (о.га — си4а -j- ю6а cos 45° -4- соаа sin 45°.
Псдставив известные значения иеличин, получим:
vx= — ч>а, Vy = — ша, ve = 0.
Тогда модуль поступательной скорости равен
v = J/ v'x -\- Vy -~ v% = cua
Таким образом, движение тела будет мгновенно-поступательным со
скоростью v^=u>aУ'2, направленной, как показано на рнс. б.
Полезно 01 метить, что результирующее .мгновенно-поступательное
движение получается из сложения одних вращений.
508
ВРАЩЕНИЕ ТВЕРДОГО ТОЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ [ГЛ. VII
Задача 7.16. Тело А вращается вокруг оси / с угловой ско-
скоростью <а„ тело В независимо от него нращается вокруг оси //
с угловой скоростью «2 = 2@,. Ось I] перпендикулярна к оси / и
находится от нее на расстоянии а. Какое движение совершает тело А
по отношению к телу В?
Решение. Графический метод. Дадим телу В дополнитель-
дополнительное вращение с угловой скоростью — со.,, тогда тело В будет не-
неподвижно. Движение тела А но отношению к В будет складываться
К задаче 7.16.
из вращения вокруг оси 1 с угловой скоростью (о, и из вращения
вокруг оси // с угловой скоростью — шо. Приведем вектор — со.,
к точке А, тогда в этой точке, кроме вектора — со.^, следует прило-
приложить и скорость
где г==ВА. Этот вектор v будет направлен по оси / и равен по
модулю
Складывая иекторпые углопые скорости (оь и -—а.ь приложенные
к точке А, получим суммарный вектор со, направленный под углом а,
к, оси / п иод углом а.2 к оси //, причем
§ 3] ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 509
Теперь можно сказать, что движение тела А по отношению к
телу В состоит из вращения вокруг оси /// с угловой скоростью
<я == о, 4- со*,
численно равной
и поступательного движения со скоростью v. Ось /// составляет угол чл
с направлением поступательной скорости v (рис. <5).
Движение тела А можно представить более наглядно, если при-
привести движение к винтовому. Разложим скорость v па две взаимно
перпендикулярные состаиляющие v cos а, и v sin ai (рис. s). Составляю-
Составляющая v cos 04 будет направлена но вектору о. Составляющую v sin ait
перпендикулярную к (о, можно представить как пару вращения,
момент которой равен произведению угловой скорости па плечо /.
Находим длину / из равенства v sin 7^ = со/.
Подставляя в это равенство найденное значение v и выражение
будем иметь:
2'о. • а -^=
V 5
откуда находим:
Таким образом, относительное движение тела А складывается из
вращательного движения с угловой скоростью ш и поступательного
движения со скоростью v cos a,, направленных по винтовой осп
(рис. в). Тело А совершает винтовое движение по отношению к телу В-
Модуль поступательной скорости равен
1 2
v cos a1 = 2w,a -—- = —;acoj.
|/ |/
Эту задачу можно решить и аналитическим способом, аналогично
способу, который применяют в статике при приведении произвольной
пространственной системы сил к простейшему виду. Угловые скорости
являются скользящими векторами аналогично силам в статике. Посту-
Поступательные скорости являются свободными векторами, аналогично мо-
моментам в статике.
Аналитический метод. Движение тела А относительно те-
тела В складывается из двух вращений: с угловой скоростью (о, вокруг
оси / и с угловой скоростью —@.2, направленной в отрицательную
сторону оси //.
510 вращение твр.рдого тела вокруг нрподвижной точки [гл. vrr
Выберем оси координат с началом в точке А, тогда проекции
результирующей угловой скорости на оси координат будут:
Шх = — Щ = — 2(О1г Шу = 0, @^ = 0)!. A)
Модуль результирующей угловой скорости равен
со = у шх -)- щ2 -|- т\ =ш1у 5.
Найдем проекции поступательной скорости на оси координат:
vx=0, 1^ = 0, vz = 2a<al. B)
Модуль поступательной скорости равен
Проверим, образуют ли со и «г прямой угол:
со • v = oixvx -f <OyVy + ^z^z — 2ао),.
Как видно, скалярное произведение этих векторов не равно пулю,
следовательно, они не перпендикулярны друг другу. Значит, тело со-
совершает по отношению к телу В винтовое движение.
Найдем уравнение мгновенной винтовой оси. Воспользуемся фор-
формулой
vx~y<*2-*rzu>y уу—г<йх-\-ху>г _ v2 — д-цу +jw.<
ых а у ыг • V'
Это уравнение, если принять во внимание формулы A) и B), при-
принимает вид
2 _ гга.+А-Ц) _ 2а —2у
2 0 1 W
или
х 4
z= — -2> y = Sa- E)
Таким образом, ось вращения лежит в плоскости, параллельной
4
координатной плоскости xz, отстоит от нее на расстоянии у = -- а
и образует с осью z угол а,, определяемый из равенства tga1 = 2.
Осталось найти поступательную скорость, с которой будет двигаться
тело вдоль винтовой оси. Она определится по формуле E)
*»* + уу + zz .„.
г'т1п= ~ I (О)
после подстановки всех значений в правую часть F) имеем:
Естественно, результаты в обоих случаях совпадают.
ПРИЛОЖЕНИЕ
МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
В декабре 1960 г. XI Генеральная конференция по мерам и весам при-
приняла единую Международную систему единиц (СИ).
Процесс введения этой системы в практику (и особенно тех ее единиц,
которые еще не получили широкого распространения) будет осуществляться
постепенно в течение ряда лет — в переходной период, конечно, будут со-
сохраняться и традиционные единицы систем СГС и МкГС, использованные
в настоящей книге.
Приведем для справок выписку из таблиц Международной системы еди-
единиц по ГОСТу 9867—61:
Наименование
величины
Ь'дмиица измерения
Основные единицы
Длина
Масса
Время
Сила электрического тока
Метр
Килограмм
Секунда
Ампер
Дополнительные единицы
Плоский угол
Телесный угол
Радиан
Стерадиан
Производные единицы
Площадь
Объем
Частота
Объемная масса (плотность)
Скорость
Угловая скорость
Ускорение
Угловое ускорение
Квадратный метр
Кубический метр
Герц ({{сек)
Килограмм на куб. метр
Метр в секунду
Радиан в секунду
Метр на секунду в квад-
квадрате
Радиан на секунду в квад-
пате
Сокращеиные обозна-
обозначения (
русские
М
кг
сек
а
рад
стер
м-
м3
гц
K2JM3
м\сек
рад\сек
м{сек*
рад/сек2
диниц
латинские
или
греческие
m
kg
s
А
rad
sr
ms
m3
Hz
hg,'m3
m/s
rad/s
m/s2
rad;s2
512
ПРИЛОЖЕНИЕ
Наичемонаипе
пе.шчпны
Сила
Давление (механическое на-
напряжение)
Динамическая вязкость
Кинематическая вязкость
Работа, энергия, количество
теплоты
Мощность
Количество электричества
Электрическое напряжение,
разность потемциалои,
электродвижущая сила
Напряженность электриче-
электрического поля
Электрическое 'сопротивле-
'сопротивление
Электрическая емкость
Поток магнитной индук-
индукции
Индуктивность
.Магнитная индукция
Напряженность магнитного
поля
Единица измерения
Ньютон (кг ¦ м\секг)
Ньютон на кв. метр
Ньютон-секунда на мегр
Кв. метр на секунду
Джоуль (н ¦ м)
Ватт (дж/сек)
Кулон (а ¦ сек)
Вольт (emja)
Вольт на метр
Ом (eja)
Фарада (к'в)
Вебер (к:ом)
Генри {вб\а)
Тесла (вб м-)
Ампер на метр
П р о д о
л ж е н и е
Сокращенные обозначе-
обозначения единиц
русские
Н
HJM2
н сек\м*
м'2!сек
дж
вт
к
в
e/ju
ом
ф
вб
гн
тл
а\.ч
латинские
или
греческие
N
К/т2
Ns/ms
m-'/s
J
W
С
V
V/ra
Q
F
Wb
H
T
A/m
Определения основных единиц
Метр—длина, равная 1650 763,73 длин волн в вакууме излучения,
соответствующего переходу между уровнями 2р1(| и 5d% атома кринтона-86.
Килограмм — единица массы — представлен массой международного
прототипа килограмма.
Секунда — 1/31556925,9747 часть тропического года для 1900 г. января
0 в 12 часов эфсмсридного времени.
Л мн ер--сила неизменяющегося тока, который, проходя по двум па-
параллельным прямолинейным проводникам бесконечно^ длины и ничтожно
малого кругового сечения, расположенным на расстоянии 1 м один or дру-
другого в вакууме, вызывал бы между этими проводниками силу, равную 2 • 10 7
единиц силы Международной системы па каждый метр длины.
I к Г =9,80665 н =
I дина = М~° н
1 кТ;см- =98066,5 hjm-
1 динаром- =0,1 н]м°
Некоторые переводные множители
= 9,81 «
1 кГ.«= 0,80665 дж-.
1 эрг = 10"т дж
1 кал =4,1868 дж
;9,81 дж