и начала математического анализа
□
и начала математического
анализа
и начала математического анализа
класс
УЧЕБНИК
для учащихся общеобразовательных организаций
Углублённый уровень
Рекомендовано
Министерством образования и науки
Российской Федерации
18-с издание, стереотипное
Москва 2014
УДК 373.167.1 :[512+517]
ББК 22.14я721+22.161я721.6
В44
Рецензент кандидат физико-математических наук А. Я. Блох
Виленкин Н. Я.
В44	Математика: алгебра и начала математического анализа, геометрия.
Алгебра и начала математического анализа. 11 класс. Учебник для учащихся общеобразовательных организаций (углублённый уровень) / Н. Я. Виленкин, О. С. Ивашев-Мусатов, С. И. Шварц-бурд. — 18-е изд., стер. — М. : Мнемозина, 2014. — 312 с. : ил.
ISBN 978-5-346-02829-1
Учебник соответствует требованиям ФГОС среднего общего образования. В книге выделены типовые задачи для подготовки учащихся к Единому государственному экзамену, предложены алгоритмы их выполнения и варианты заданий для самоконтроля. В учебнике реализованы современные подходы к формированию проектно-исследовательских умений и ИКТ-компетенций. Темы индивидуальных проектов, предложенные в учебнике, входят в базовое академическое образование по экономике.
УДК 373.167.1:[512+517]
ББК 22.14я721+22.161я721.6
Учебное издание
Виленкин Наум Яковлевич, Ивашев-Мусатов Олег Сергеевич, Шварцбурд Семён Исаакович
МАТЕМАТИКА:
алгебра и начала математического анализа, геометрия
АЛГЕБРА
И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
11 класс
УЧЕБНИК
для учащихся общеобразовательных организаций (углублённый уровень)
Формат 60х9071в. Бумага офсетная № 1. Гарнитура «Школьная».
Печать офсетная. Усл. печ. л. 19,5. Тираж 1000 экз. Заказ №5378
Издательство «Мнемозина».
105043, Москва, ул. 6-я Парковая, 296.
Тел.: 8 (499) 367 5418, 367 6781.
E-mail: ioc@mnemozina.ru
www.mnemozina.ru
ИНТЕРНЕТ-магазин.
Тел.: 8 (495) 783 8284, 783 8286.
www.shop.mnemozina.ru
Отпечатано в ОАО «Первая Образцовая типография», филиал «Ульяновский Дом Печати».
432980, г. Ульяновск, ул. Гончарова, 14.
© «Мнемозина», 2000
© «Мнемозина», 2014
© Оформление. «Мнемозина», 2014
ISBN 978-5-346-02829-1	Все права защищены
Предисловие
Данная книга предназначена для изучения курса алгебры и начал математического анализа в 11-м классе на углублённом уровне. Её можно использовать и для обучения в колледжах, готовящих к работе по профессиям, требующим повышенного знания математики. Наконец, она пригодна и для самостоятельного изучения курса математики. Заметим, что излагаемый в книге материал по объёму несколько больше, чем предусмотрено Фундаментальным ядром содержания общего образования и требованиями ФГОС среднего общего образования. Соответствующие пункты отмечены звёздочкой или набраны петитом. Они могут быть использованы для элективных курсов или курсов по выбору.
Учитывая, что изложение алгебры в 7—9-м классах было по необходимости не вполне строгим, авторы сочли полезным осветить и ряд ранее изучавшихся тем на более высоком теоретическом уровне. В соответствующих пунктах даются полные и строгие доказательства утверждений, принимаемых в курсе алгебры без доказательства или с неполными доказательствами. Изучение этих вопросов позволит как повторить пройденный материал, так и повысить уровень развития логического мышления учащихся.
Большинство задач учебника способствует подготовке учащихся к итоговой аттестации на достаточно высоком уровне. Задания, отмеченные звёздочкой, предназначены для учащихся, желающих достичь высоких личностных результатов в предметной области «Математика».
Книга состоит из шести глав. Каждая глава разбита на параграфы, а параграфы — на пункты. Ссылка на формулы (3) п. 4 означает, что речь идёт о пункте того же параграфа, а ссылка на формулу (3) п. 4 параграфа 2 означает, что речь идёт о материале той же главы.
При изучении уравнений и неравенств основное внимание уделено общим методам решения. Стремление к повышенному уровню строгости сочетается в книге с использованием наглядных иллюстраций рассматриваемых понятий там, где это полезно. Большое внимание уделяется приложениям математики как к вопросам вычислений, так и к задачам физики, экономики, социологии, что способствует достижению метапредметных результатов обучения.
В школах с углублённым изучением математики анализ естественно основывать на понятиях предела и непрерывности. Мы сочли целесообразным начать с понятия предела функции на бес
конечности, а лишь потом рассматривать предел в точке. Предел последовательности рассматривается как частный случай предела на бесконечности. Соответствующий материал может быть использован и при изучении ряда вопросов Примерной программы по математике основного общего образования для 8-го и 9-го классов школ с углублённым изучением математики и её приложений.
Авторы выражают благодарность за сделанные замечания В. Р. Болотину, М. Л. Галицкому, Б. М. Давидовичу, Р. К. Гордину.
С целью организации самоконтроля знаний учащихся в Приложении приведены работы для самопроверки. Также в Приложении даны примерные темы для исследовательской и проектной деятельности.
§ 1. Неопределённый интеграл
1. Введение. С помощью дифференцирования можно, зная закон движения тела, найти его мгновенную скорость в любой момент времени. Часто возникает необходимость в решении обратной задачи: зная скорость прямолинейно движущегося тела в каждый момент времени, найти закон движения тела. Эти и аналогичные им задачи решаются с помощью операции интегрирования функций, которая обратна операции дифференцирования.
Раздел математики, в котором изучаются свойства операции интегрирования и её приложения к решению задач физики и геометрии, называют интегральным исчислением.
Напомним выведенные в главах 5 и 6 формулы для производных и вытекающие из них формулы для дифференциалов:
Функция	Производная	Дифференциал
ха	ax" 1	axa ldx
sin х	COS X	cos x dx
COS X	-sin x	-sin x dx
tgx	1	dx
	COS2X	cos2x
ctg x	1	dx
	sin2x	sin2x
arcsin x	1	dx
	Vl - X2	dl - x2
arctg x	1	dx
	1 + X2	1 + X2
2. Первообразная. Введём следующее определение.
Определение 1. Функцию F, заданную на некотором промежутке X, называют первообразной для функции f, заданной на том же промежутке, если для всех х G X выполняется равенство F'(x) = /(х), или, что то же самое, dF(x) = f(x)dx.
Замечание. В концевых точках промежутка X речь идёт об односторонних производных.
Например, из равенства (х3)' = Зх2 следует, что функция х3 на всей числовой оси является первообразной для функции Зх2. Заметим, что функция х3 + 4 тоже является первообразной для Зх2, так как (х3 + 4)' = Зх2. Вообще любая функция вида х3 + С, где С — некоторое число, является первообразной для Зх2. Таким образом, функция Зх2 имеет бесконечно много первообразных. То, что первообразных иного вида, чем х3 + С, у функции Зх2 нет, вытекает из следующей теоремы.
Теорема. Если функция f имеет на промежутке X первообразную F, то для любого числа С функция F + С также является первообразной для f. Иных первообразных функция f на X не имеет.
Доказательство. Так как F — первообразная для f на промежутке X, то F'(x) = f(x) для всех х е X. Но тогда при х е X для любого числа С имеем (Г(х) + С)' = Дх). Это значит, что F(x) + С — тоже первообразная для f на X.
Покажем, что иных первообразных на X функция f не имеет. Предположим, что Ф — тоже первообразная для f на X. Тогда Ф'(х) = Дх), и потому для всех х С X имеем Ф'(х) — F'(x} = f(x) -- Дх) = 0.
В силу следствия из теоремы 1 п. 3 § 3 главы 5 (10 кл.) отсюда следует, что функция Ф - F постоянна на X. Обозначим её С: Ф(х) - Г(х) = С. Тогда Ф(х) = F(x) + С, а это значит, что любая первообразная функции имеет вид F + С.
Доказанная теорема показывает, что вопрос об отыскании всех первообразных функции f решается отысканием какой-нибудь одной из них: если такая первообразная найдена, то любая первообразная получается из неё прибавлением некоторой постоянной.
Определение 2. Совокупность всех первообразных функций f называют неопределённым интегралом этой функции и обо-
Таким образом, ^Дх)йх - F(x) + С, где
F — одна из первообразных для f, а С пробегает множество дей
значают символом ^f(x)dx.
ствительных чисел.
В этом равенстве f называют подынтегральной функцией, выражение f(x)dx — подынтегральным выражением, переменную х — переменной интегрирования и слагаемое С — постоянной интегрирования.
Пример 1. Так как ха — первообразная для Зх2, то ^3x2dx = х3 + С.
Опираясь на определение первообразной, докажем следующие свойства неопределённого интеграла (в предположении, что рассматриваемые интегралы существуют).
1)	Имеет место равенство
dfy(x)dx) = f(x)dx.	(1)
(Это равенство означает, что формула верна при любом значении произвольной постоянной С.)
В самом деле, по определению имеем ^/(x)dx = F(x) + С, где F'(x) - f(x). Поэтому
d(^ftx)dx) = (F(x) + C)'dx = F'(x)dx = f(x)dx.
2)	Имеет место равенство
^F'^dx = F(x) + C.	(2)
Оно непосредственно вытекает из определения интеграла.
3)	Интеграл от суммы функций равен сумме интегралов слагаемых:
^(<р(х) + y(x))dx - ^<p(x)dx + ^y(x)dx.	(3)
В самом деле, пусть ^<p(x)dx = Ф(х) + С и ^\|/(x)dx - Ч'(х) + С. Тогда Ф'(х) - <р(х), Ч'Чх) = у(х), и потому
5(<р(х) + v(x))dx = §(Ф'(х) + T'(x))dx =
= §(Ф(х) + T(x))'dx = Ф(х) + Т(х) + С =
4)	Постоянный множитель можно вынести за знак интеграла: \Af(x)dx = A^/(x)dx.	(4)
В самом деле, если А — постоянная и F'(x) - f(x), то (AF(x))' -- AF'(x) - Af(x). Значит,
^Af(x)dx - AF(x) + C = A^f(x)dx.
Так как (xa+1)' = (a + l)x“, то из свойств 2 и 4 вытекает, что при а Ф -1
JxMx =	$(a + l)x“dx = ~ + С.	(5)
Пользуясь этой формулой и свойствами 3 и 4, можно проинтегрировать любую сумму степеней х, умноженных на некоторые числа, если только среди показателей степеней нет числа —1 (в частности, можно проинтегрировать любой многочлен от х).
Пример 2. Вычислим интеграл
^(Зх4 - 5х2 + 6х - 7)dx.
Решение. По свойствам 3 и 4 имеем
^(Зх4 - 5х2 + 6х - 7)dx = 3^x4dx - 5^x2dx + 6^xdx - 7^dx.
Но по формуле (5) имеем
^x4dx = у + С, ^x2dx = у + С, ^xdx = у + С, ^dx - х + С.
Значит,
jj(3x4 - 5х2 + 6х - 7)dx =	- | х3 + Зх2 - 7х + С.
(Мы пишем произвольную постоянную лишь один раз, поскольку произведение любого отличного от нуля множителя на произвольную постоянную, так же как и сумму произвольных постоянных, можно заменить одной произвольной постоянной.)
Пример 3. Вычислим интеграл
^(xVx —^-)dx.
X2 /
Решение. Имеем
$(х^ —^-Idx “	“ 6x-2)dx - ^x3dx - 6^x'2dx =
Упражнения
1.	Вычислите интегралы:
,. С , , С „г. С х3 + Зх2 - Vx + 1 ,	.. Г х4 - 16 ,
1)	\x7dx; 2) \x34xdx; 3) \--------==------dx; 4) \—:---— dx.
J	J	J x^x	J x2 + 4
2.	Проверьте, что функция F является первообразной для функции f, если:
1)	F(x) = у + 2cos2x, f(x) = х® - 4sin2x;
п.	. 6arctg3x.
2)	F(x) = arctg23x, f(x) = у+~дх~:
,	6 tg2 2x
3)	F(x) = tg3 2x - cos 5x, f(x) = cog2 + 5 sin 5x;
4)	Fix) = arcsin(x1 2 3), fix) =
2x
Vl - x4
5)	F(x) = cos \[x - sin(x2), f(x) = -8Ш,—X - 2xcos(x2); 2Vx
4	. .	5	.	5 sin x
6)	Fix) = x4sinx 4-----, fix) = 4x’smx + x4cosx H-------—
cos x	cos2 x
3.	Непосредственное интегрирование. Непосредственное интегрирование основано на использовании результатов дифференцирования функций. В силу определения интеграла из всякой формулы F'(x) = Дх) дифференциального исчисления вытекает соответствующая формула ^/(x)dx = Г(х) + С интегрального исчисления.
Пример 1. Так как (sinх)' = cosх, то
cosxdx = sinx + С.
Таким образом, с помощью таблицы дифференциалов простейших функций получаем следующую таблицу основных интегралов:
1) \xadx =	+ С, а * -1;	5)	= -ctgx + С;
J	а + 1	’ J sin2 х 6
2) ijcosxdx = sinx + С;
3) \sinxdx = -cosx + С;
6)	= arcsinx + С;
J V1 - х2
7)	^Г+^х2 = arctgx + С-
4)	- tgx + С;
J cos2 х
Позднее мы добавим к этой таблице ещё несколько формул интегрирования.
Пример 2. Вычислим интегралы:
1)	-----гА—)dx;	2) ^(6cosx - 7sinx)dx.
J I COS X sin2 X	J
Решение. 1) По формулам (4) и (5) примера 1 имеем
G—----------)dx = 3^ ——у— - 4^ dx = 3tgx + 4ctgx + С.
J \cos2 x sin2 х/ J cos2 x J sin2 x	&
2) По формулам (2) и (3) примера 1 имеем ^(6cosx - 7sinx)dx = 6^cosxdx - 7^sinxdx = = 6sinx + 7cosx + C.
С л/1 — X2 + 1 4- X2
Пример 3. Вычислим интеграл \ ---------------— dx.
J (1 + х2)71 - x2
Решение. Так как
71 - х2 + 1 + х2 _	71 - х2	1 + X2	=	1	1
(1 + ха)71 - х2	(1 + хг)71 - х2	(1 + х2)71 - х2 “ 1 + х2	-71 - х2 ’
то
vl - х2 + 1 + х2 т с dx , г dx	.
dx = J1T7 + hi =arctg* + arcsm* + c-
Упражнения
3. Вычислите интегралы:
1) (в sin x------) dx;
J\	COS2 XI

3) Jjscosx - ^-A_)dx;
«5^
C ___dx_ . 6) J sin2 x cos2 x ’
C(x6 + l)dx.
’ J x2 + 1 ’
4. Вычислите интегралы:
- X2 + x - 1
X2 + 1
dx;
2) ^tg2xdx;
_______________sin x dx_________________.
sin4 2x + 2 sin2 2x cos2 2x + cos4 2x ’
x2 - 4xTx + 4x , -----7=----5--dx.
Ш - 2)
4. Замена переменной. При вычислении интегралов, не содержащихся в приведённой выше таблице, оказывается полезным метод замены переменной (или, как его называют иначе, метод подстановки). В основе этого метода лежит формула дифференцирования сложной функции. Мы знаем, что если F'(x) = f(x) и если существует функция F(<p(t)), причём функция <р дифференцируема, то
(Р(Ф(О)Г = Г(х)ф'(О = f(xW(t) = /(ф(О)ф'(О-
10
Отсюда следует, что если
\f(x)dx = F(x) + С,	(1)
ТО
$Г(ф(О)ф'(О<« = F(<p(t)) + с.	(2)
Поскольку (p'(t)dt = <йр(0> то формулу (2) можно записать в следующем виде:
5/=(cp(t))d<P(O = ВДО) + С.	(2')
Равенство (2') получается из (1) заменой х на (р(£)- Мы доказали таким образом следующее утверждение.
Теорема. Пусть функция ф дифференцируема на промежутке X, а функция F является первообразной для f на образе <р(Х) промежутка X. Тогда F о <р является первообразной для функции (/ ° ф)ф'-
Так как при <р(£) = kt + Ь имеем <р'(0 = k, то из равенства (2') вытекает, что
tyffkt + b)dt = F(kt + b) + С.
Поэтому
fy(kt + b)dt = ±F(kt + b) + C.	(3)
Пример 1. Вычислим интегралы:
1) §cos(4x - 5)dx; 2) ^(8x - ll)3dx.
Решение. 1) Так как cosx dx = sin x + С, то по формуле (3)
получаем, что ^cos(4x - 5)dx = sin(4x - 5) + C.
2) Так как ^x3dx = ^- + С, то ^(8x - ll)3dx =	(8x - ll)4 +
+ C= ~(8x - И)4 + C.
Приведём примеры более сложных подстановок.
Пример 2. Вычислим интеграл
^x2sin(x3)dx.
Решение. Замечаем, что (х3)' = Зх2. Поэтому делаем подстановку х3 = t. Имеем
^x2sin(x3)dx = ^sin(x3)(x3)'dx.
11
Так как (x3)'dx = dt, то
x2sin(x3)dx =
| 'isin/c// = “ cos £ + С = cos(x3) + С. о J	о	о
Пример 3. Вычислим интеграл
\ sin2x cos х с/х.
Решение. Так как (sinx)' = cosx, то напрашивается подстановка sinx - t. Имеем dt = (sinx)'dx = cosxdx, и поэтому
С	с t3	1
\sin2x cosxdx = \t2dt = — + С = — sin3x + С.
J	Joo
Пример 4. Вычислим интеграл
л/а2 - х2 dx, а > 0.
Решение. Здесь формула (2') применяется справа налево.
Л л
Именно, положим х = ср(/) = a sin/,	< t < Тогда <р (t) = a cos г,
и потому имеем
^л/а2 - х2 dx = а2^^/1 - sin2t costdt = a2^cos2 tdt.
TT 2,	1 + cos 2t
Ho cos2 / - -g-----, и потому
с !-----—’	а? с	а? с а? с
\ уа2 - х2 dx =	\(1 + cos2/)d/ = \dt +	\ cos2/d/.
Применяя формулу (3), выводим, что ^cos2/d/ = sin 2/ + С, и потому
С П 9 -1 CL2t , а2 sin 2 £ , „ а2 ,, . . .
\\1а2 - х2 dx = — -I-------- + С = — (/ + sin / cos/) + С.
Чтобы завершить интегрирование, нам осталось вернуться от аргумента / к аргументу х, где, напомним, х = a sin/. Имеем
х	I----т---	/ х%	х
sin / = —, cos / = yl - sin21 = , 1-t = arcsin —, и потому
a	V a2	a
\!a2 - x2 dx - arcsin — + Va2 - x2 + C. (4)
J	Zj	d
Упражнения
5. Вычислите интегралы: C __dx__ „г dx
} J V25 - х2;	j3x2+25’
оЛ dx .	м С dx
2)J25 + x2’	4) J Vl - 16x2 ’
5) cos3x dx;
S sin2 (5x - 6) ’
12
6. Вычислите путём разложения в алгебраическую сумму интегралы:
1)	С X7 - 7х2 + X 4	rdx-	5) ^sin2x cos2xdx;
	J	X2		
2)	С х4 + 6х3 + Зх J	х7х	+ 4^/x2	dx;	6) ^cos8x sin6xdx;
3)	sin23xdx;		7) ^sinl2x sin2xdx;
4)	cos24xdx;		8) ^cos6x cos3xdx.
Следующие интегралы вычислите с помощью замены переменной			
(7-	-9).		
7. 1)	§(4х - 7)8dx;		C	dx
		о)	j cos2 (6x - 1)’ f	dx
2)	7бх + 11 dx;	7)	
			J sin2 2x cos2 2x ’
3)	С dx	8)	(sin x + cos x)2dx;
	' %8х - 15’		
	cosoxdx;		C	dx
4)		9)	J V15 - 6x - 9x2
5)	sin (V2x) dx;	10)	c	dx
			Jx2 - 6x + 10'
8. 1)	с х dx	4)	^(2x + l)cos(x2 + x - l)dx;
	J 1 + х4 ’		
2)	г х2 dx	5)	C arcsin3 x dx.
	J >/1 - Xе ’		
			J Vl - x2
3)	^xsin(x2) dx;	6)	c arctg4 2x dx J 1 + 4x2 '
9. 1)	С ctg4 Зх dx. J sin2 Зх	2)	sin2x cos52xdx.
§ 2. дифференциальные уравнения
1. Введение. Многие законы физики связывают значения величин со скоростями и ускорениями их изменения. Пусть, например, материальная точка массы т движется по прямой линии под действием силы F, направленной по той же прямой. По второму закону Ньютона ускорение точки в момент времени t равно отношению величины силы F, действующей в этот момент на точку, F к массе т: а = — т
Так как ускорение равно второй производной координаты x(t) точки по времени, а = х", то это равенство можно записать в виде
тх" = F.	(1)
13
Рассмотрим несколько примеров.
1) Точка движется по инерции в сопротивляющейся среде, причём сопротивление среды пропорционально скорости движения точки и направлено в сторону, противоположную этой скорости. Тогда F = -kv, и потому равенство (1) примет вид
тх" - -kv.
Поскольку v = х', то получаем уравнение тх" = -kx'.	(2)
Это уравнение можно записать иначе, если вспомнить, что х' = v и х" - (х')' - и':
mv' = -kv.	(2')
В уравнениях (2) и (2'), как и в уравнении (1), дифференцирование производится по времени.
2) Точка массой т падает на Землю под действием силы тяготения. По закону всемирного тяготения сила F в этом случае ..	„ Мт
задается формулой F =	у — гравитационная постоян-
ная, М — масса Земли, х — расстояние от точки до центра Земли (знак «минус» поставлен потому, что сила тяготения направлена в сторону, противоположную положительному направлению оси, рис. 1). Поэтому равенство (1) принимает в этом случае вид
Уравнение (3) можно записать в ином виде, если принять во внимание, что при х = R, где R — радиус Земли, сила F равна -mg.
Значит, у = mg и потому уМ = R2g. Следовательно, уравнение
(3) можно записать так:
3) Точка движется под действием силы, пропорциональной отклонению точки от положения равновесия и направленной к этому положению. Если выбрать начало координат в положении равновесия, то имеем F = -kx, и потому равенство (1) принимает вид
тх" = -kx.
Если обозначить ~ через со2, то получим уравнение
х" + (о2х = 0.	(4)
14
Мы получили уравнения (2), (3), (4), которые содержат аргумент (в нашем случае время), функцию этого аргумента (в нашем случае координату точки) и производные этой функции до некоторого порядка включительно (в нашем случае до второго порядка). Такие уравнения называют дифференциальными, а наивысший порядок производной, входящей в такое уравнение, — порядком этого уравнения. Таким образом, уравнения (2), (3), (4) имеют второй порядок, а уравнение (2') — первый порядок.
Дифференциальные уравнения встречаются не только при изучении движения материальных точек, но и в иных областях физики, биологии, химии и т. д. Составим, например, дифференциальное уравнение радиоактивного распада. Установлено, что мгновенная скорость изменения массы радиоактивного вещества пропорциональна этой массе в данный момент времени, т. е. v = -km (знак «минус» поставлен потому, что масса уменьшается). Поскольку мгновенная скорость изменения равна производной массы по времени, то уравнение v = -km можно переписать в виде
т' = -km.
Получили дифференциальное уравнение первого порядка. Заметим, что оно отличается от уравнения (2') лишь обозначением функции. Это говорит о том, что движение материальной точки в сопротивляющейся среде описывается теми же формулами, что и радиоактивный распад.
Функции, описывающие оба эти явления, будут изучены в главе 2.
Упражнения
10.	Среди следующих уравнений укажите дифференциальные и назовите порядок этих уравнений:
1)	{уУ = У2 + х - 1;	3) slny = х3 + 4;
2)	У' = Г2Х^,У	4) у'" - 4у" + 4у' = tgx.
11.	Для некоторых химических реакций мгновенная скорость реакции пропорциональна произведению концентраций двух реагирующих веществ, причём в процессе реакции одна молекула первого вещества реагирует с одной молекулой второго вещества. Напишите дифференциальное уравнение для количества у вещества, возникшего к моменту времени t (в молях), если начальная концентрация первого реагента равнялась а, а второго — b (о = 1 л).
12.	Напишите дифференциальное уравнение для падения тела в сопротивляющейся среде, если сопротивление среды пропорционально квадрату скорости тела.
15
2. Решения дифференциальных уравнений. Введём следующее определение.
Определение 1. Решением дифференциального уравнения называют любую функцию, при подстановке которой в это уравнение получается тождество.
График решения дифференциального уравнения называют интегральной кривой этого уравнения.
Пример 1. Покажем, что функция у - х является решением дифференциального уравнения у =
Решение. Имеем у' - (х)' - 1. Подставляя значения у = х и у' - 1 в данное уравнение, получаем равенство 1 = “» которое выполняется для любого х * 0.
Простейшими являются дифференциальные уравнения вида
У' = f(x).	(1)
Чтобы решить их, надо найти функцию у по её производной f(x):
у = ^f(x)dx.
Если F — одна из первообразных для f, то это равенство записывают так:
у = F(x) + С.
Видим, что уравнение (1) имеет бесконечное множество решений. Их графики (т. е. интегральные кривые уравнения (1)) полу
чаются друг из друга параллельным переносом в направлении оси ординат (рис. 2). При этом через каждую точку М0(х0, у0) такую, что функция f непрерывна при х = ха, проходит одна и только
одна интегральная кривая.
Рис. 2
Аналогичным образом обстоит дело для других дифференциальных уравнений первого порядка.
Например, для уравнения у = ~ решением является не только указанная в примере 1 функция у = х, но и любая функция вида у = Сх, где С — произвольное число, или, как говорят, произвольная постоянная.
Сх
В самом деле, у' = С = — • Иных решений данное уравнение не имеет. Чтобы доказать это, введём вместо у
16
новую искомую функцию v, положив у = их. Так как у' = v'x + v, а = v, то уравнение у' = принимает вид v'x + v = v, т. е. v'x = О, или v' - 0. В силу п. 3 § 3 главы 5 (10 кл.) это означает, что v постоянная, v - С, и потому у - Сх.
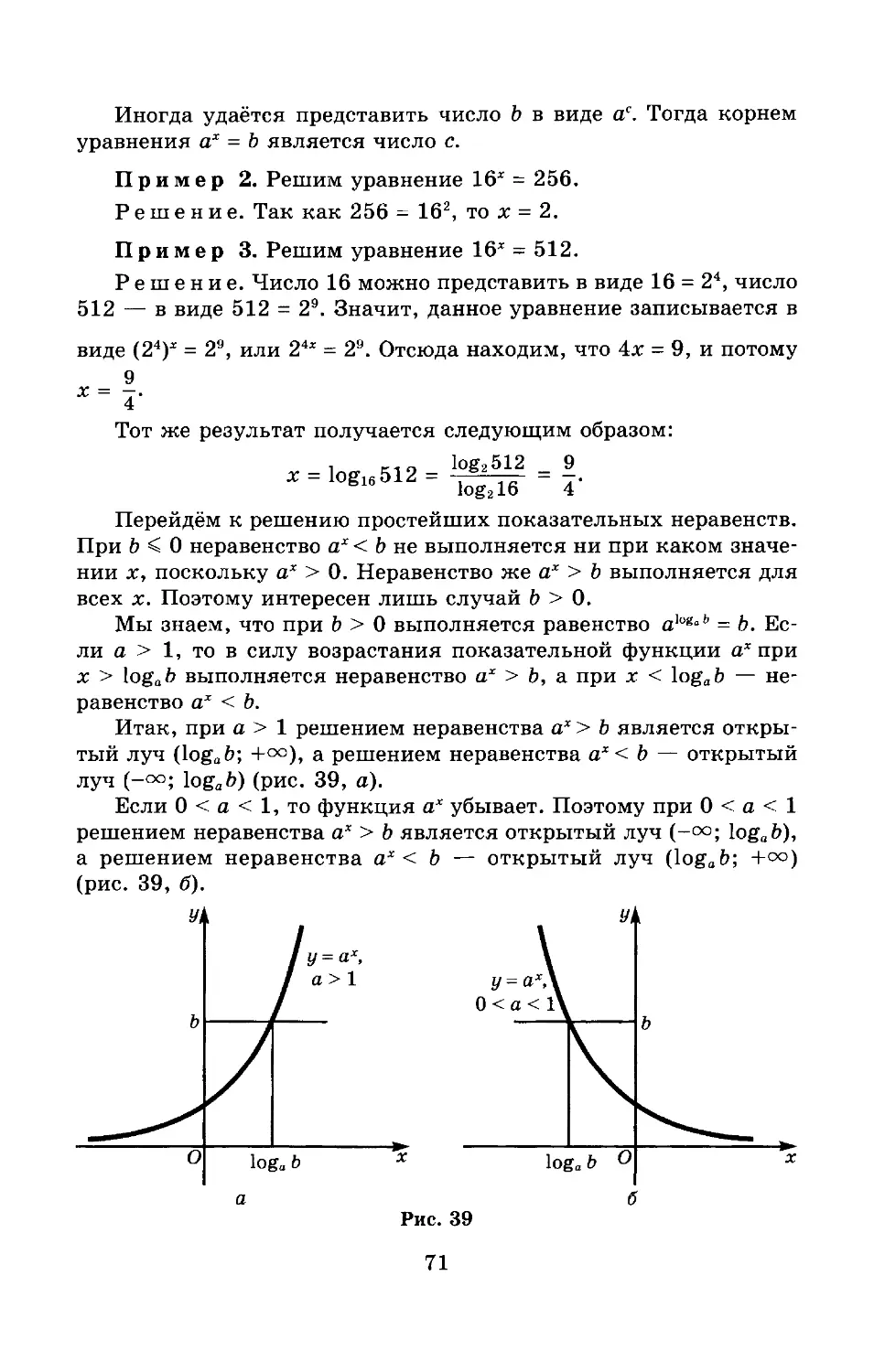
На рисунке 3 изображено семейство интегральных кривых уравнения у’ = Видим, что и в этом случае через любую точку, отличную от начала координат, проходит одна и только одна линия у = Сх. Через начало же координат проходит бесконечное множество линий у = Сх. Поэтому начало координат называют особой точкой для уравнения у' = р В этой точке х = 0, у = 0, и потому выражение не имеет числового значения. Существуют особые точки, через которые не проходит ни одна интегральная линия. Например, интегральными кривыми для дифференциального уравнения у' = являются окружности с центром в начале координат (рис. 4). Ни одна из них через начало координат не проходит.
Введём следующее определение.
Определение 2. Функцию у = <р(х, С), где С — произвольная постоянная, называют общим решением дифференциального уравнения у' = f(x, у) в области Q, если:
а)	для любого С она является решением этого уравнения, т. е. ф'(х, С) = f(x, <р(х, С));
б)	для любой точки М0(х0, у0) из области Q существует единственное значение Со, при котором линия у = <р(х, Со) проходит через точку Мо, т. е. у0 = <р(х0, Со).
17
Таким образом, у = Сх — общее решение уравнения у' = на всей плоскости, проколотой в начале координат.
Определение 3. Решение дифференциального уравнения, получаемое из общего решения путём придания определённого значения произвольной постоянной, называют частным решением этого уравнения.
Пример 2. Найдём частное решение дифференциального уравнения 1/ = у, удовлетворяющее условию у(1) = -2.
Решение. Общим решением этого уравнения является у = ±л/С - х2. Чтобы найти частное решение, положим в этом равенстве х = 1, у = -2. Получаем С = 5. Поскольку значение у = -2 отрицательно, то получаем частное решение у = ->/5 - х2.
Наряду с частными решениями дифференциальное уравнение может иметь решения, не получаемые из общего ни при каком значении произвольной постоянной. Такие решения называют особыми. Например, общее решение дифференциального уравнения (у')2 + у2 = 1 имеет вид у = sin(x + С) (семейство синусоид). Кроме того, это уравнение имеет два особых решения: у = -1 и у = 1, графики которых в каждой точке касаются проходящего через эту точку графика частного решения (рис. 5).
Рассмотрим теперь дифференциальные уравнения второго порядка. Простейшими из них являются уравнения вида
У" = f(x).	(2)
Чтобы решить такое уравнение, введём новую функцию z = у'. Тогда имеем z' = (у')' = у", и уравнение (2) примет вид г' = f(x).
Из него находим
z = fy(x)dx = F(x) + Сн
где F — одна из первообразных функции f, — произвольная
18
Ho z = у', и потому имеем у' = F(x) + Сь Значит, у = §(F(x) + Ci)dx = Ф(х) + CiX + С2, где Ф — одна из первообразных функции F, а С2 — вторая произвольная постоянная.
Пример 3. Решим уравнение
у" = х3.
Решение. Имеем
у' = ty'dx = ^x3dx = y + Clt откуда
J/ =	+ Cjjdx =	+ C2.
Из разобранных примеров видно, что в решение уравнения первого порядка входит одна произвольная постоянная, а в решение уравнения второго порядка — две произвольные постоянные. Это верно и для уравнений более общего вида: общее решение дифференциального уравнения п го порядка зависит от п произвольных постоянных.
Для дифференциальных уравнений второго порядка, описывающих прямолинейное движение материальных точек, существование бесконечного множества решений имеет простой физический смысл. Оно означает, что закон движения точки не определяется однозначно заданием сил, действующих на эту точку, надо ещё знать её начальное положение и скорость. По этим данным можно найти значения обеих произвольных постоянных, входящих в общее решение уравнения, и получить частное решение, описывающее движение точки.
Пример 4. Найдём общее решение уравнения1
х" = -g,	(3)
описывающего свободное падение материальной точки, и частное решение этого уравнения, отвечающее начальным условиям х(0) = 10, о(0) = 5.
Решение. Полагая х' = о, имеем о' = -g. Отсюда
v = ^(-g)dt = -gt + Ci.	(4)
Значит,
х' = v = -gt + Ci, и потому
х =	+ Ci)dt =	+ Cit + С2.	(5)
1 Мы пишем знак «минус», поскольку направление силы противоположно положительному направлению оси координат.
19
Чтобы найти значения постоянных Сг и С2, положим в (4) и (5) t - 0. Получаем равенства Ci - о(0) = 5, С2 = х(0) =10. Значит, частное решение имеет вид
х =	+ 5t + 10.
Пример 5. Покажем, что функция
х = Cjcoscot + C2sincot	(6)
при любых значениях С\ и С2 является решением дифференциального уравнения х" + со2х = 0, и найдём частное решение, соответствующее начальным условиям х(0) = х0, у(0) = v0.
Решение. Имеем
х' = -Cicosincot + C2cocoscot и
х" = -CiC02cos(d£ - C2o)2sincot.
Подставляя в уравнение х" + со2х = 0 выражения для х и х", получаем тождество
-CiO)2coswi - C2co2sin cot + co2(CiCoscot + C2sincot) = 0.
Значит, функция (6) при любых значениях Ci и С2 является решением уравнения х" + со2х = 0. Заметим, что в силу п. 7 § 3 главы 6 (10 кл.) это решение можно представить в виде х = A sin (cot + а). В п. 3 будет доказано, что уравнение х" + со2х = 0 не имеет иных решений.
Теперь найдём частное решение, соответствующее данным начальным условиям. При t = 0 имеем:
х(0) = Ci cos 0 + C2sin0 = С^, х'(0) = -C^cosinO + C2cocos0 = C2co.
Так как по условию х(0) = х0 и х'(0) = и0, то Сг = х0, С2 = а потому искомое частное решение имеет вид
Го .
X = х0 cos cot + — sin cot.
co
Итак, мы доказали, что общее решение уравнения х" + со2х = 0 можно записать в виде х = A sin (cot + а). Из курса физики известно, что колебания, совершаемые по закону х = A sin (cot + а), называют гармоническими. Поэтому дифференциальное уравнение х" + + со2х = 0 называют уравнением гармонических колебаний. В п. 1 было показано, что это уравнение описывает движение точки под действием силы, пропорциональной отклонению от положения равновесия и направленной к этому положению. Мы доказали, таким образом, что движение под действием такой силы является гармоническим колебанием.
20
У пражнения
13.	В следующих примерах проверьте, что функция f является решением указанного дифференциального уравнения:
D/=—’Л*) = Т+ 2^+С;
2)	у у' = х + 1, f(x) = +^хг + 2х + С;
3)	У^У = sinx, Дх) = (|(с “ cosx)j3;
4)	2хуу' = у2 - 1, Дх) = ±^Сх + 1;
5)	у' = У2, f(x) = х ± (у найдите значение С по начальному условию |/(0) = 1.
14.	Докажите, что при любых значениях С1Г Сг, С3 функция f является решением указанного дифференциального уравнения:
1)	У'" = (У"Г, Дх) = |(С, - 2хУ + С2х + С3;
О
2)	у"'(1 + О/')2) = 3/(/')2, Дх) = С, ± VC! - (х - С3)2.
g
15.	Проверьте, что функция х = т(1}^2 - р2) (“sinPf ~ psintoi) удовлет-воряет дифференциальному уравнению х" + со2х = — sin (3/ и начальным условиям х(0) = х'(0) = 0.
16.	Проверьте, что функция х = ~ 2тй? (Ш*СО8Ш{ - sinwf) удовлетворяет дифференциальному уравнению х" + ю2х = В sin of и начальным условиям х(0) = х'(0) = 0.
17.	На материальную точку массой 10 г действует сила, пропорциональная отклонению точки от положения равновесия и направленная к этому положению. При отклонении точки от положения равновесия на 15 см сила равна 2400 Н. Напишите дифференциальное уравнение колебаний и найдите его общее решение. Найдите частные решения при следующих начальных условиях:
а) х0 = 5 см, и0 = 0; б) х0 = 0, и0 = 6 уу-
3. Уравнения с разделяющимися переменными. К операции интегрирования сводится и решение дифференциального уравнения первого порядка вида
/ = <р(х)щ(у)	(1)
(в левой части — производная искомой функции, в правой — произведение двух функций, из которых одна зависит от х, а другая — от у).
21
Если при у = уо функция v обращается в нуль, т. е. щ(г/0) = О, то функция у = у0 является одним из решений уравнения (1). В самом деле, подставляя в это уравнение у0 вместо у, получаем равенство
(УоУ = ф(х)ф(г/0)-
Оно тождественно выполняется при любом значении х, так как (у0У - 0 (производная постоянной равна нулю), а щ(г/о) = 0 по условию.
В области, где ф(г/) * 0, уравнение (1) равносильно уравнению
-7-7 = ф(х). ф(у) т
Умножим обе части этого уравнения на dx и учтём, что y'dx = dy. Получаем уравнение
= ^dx’ ™
в котором переменные х и у разделены — выражение в левой части зависит от у, а в правой — от х. Поэтому уравнение (1) называют уравнением с разделяющимися переменными.
Перейдём к решению уравнения (2). Если Ф — первообразная функции ф, а 'Р — первообразная функции то
<*Ф(х) = Ф(х)с^х = ф(х)<2х, d'Viy) = 'V'tyjdy = dy =
Значит, уравнение (2) можно записать так:
d>¥(y) = d^>(x).
Здесь слева и справа стоят дифференциалы функций, зависящих от х (ведь у является некоторой функцией от х). Эти дифференциалы равны друг другу лишь в случае, когда сами функции отличаются только на постоянное слагаемое, т. е. когда ^Р(у) = Ф(х) + С (см. п. 3 § 3 главы 5, 10 кл.). Но это равенство можно записать так:
S^j=S<p(x)dx-	(3)
Итак, мы доказали, что в области, где ф(у) * 0, любое решение уравнения (1) удовлетворяет соотношению (3). Легко видеть, что и обратно, если функция у удовлетворяет соотношению (3), то она удовлетворяет и дифференциальному уравнению (1). Для доказа
22
тельства достаточно взять дифференциалы от обеих частей равенства (3) и принять во внимание, что
С dy _ dy
Эу(у)
а
d!\fi(x)dx - <p(x)dx.
Итак, мы доказали следующее утверждение.
Теорема. В области, где у 0, дифференциальное уравнение у' = <р(х)у(г/)	(4)
имеет решение, удовлетворяющее соотношению
= S<p(x)£/x-	(5)
Кроме того, его решениями являются все функции вида у = у0, где у0 — число, для которого у(Уо) = 0.
Пример. Решим дифференциальное уравнение
У' = (1 + х2)(1 + г/2)	(6)
и найдём его частное решение, удовлетворяющее начальному условию у(0) = 1.
Решение. Так как функция 1 + у2 не обращается в нуль, то можно обе части уравнения (6) разделить на 1 + у2'.
Теперь умножим обе части этого уравнения на dx и примем во внимание, что y'dx = dy.
= (1 + x2)dx.	(7)
Наконец, возьмём интегралы от обеих частей равенства (7):
= S(1 + x2)dx-
По формулам из п. 3 § 1 имеем	= arctgy + Ci, а
^(1 + x2)dx - ^dx + ^x2dx = x +	+ C2. Значит,
arctgi/ = x +	+ C	(8)
(пишем лишь одну произвольную постоянную, так как разность С2 — Ci можно обозначить одной буквой С).
23
Подставляя начальные значения х = 0, у - 1, получаем, что С = arctgl = Поэтому искомое частное решение имеет вид
arctgy = х + у + р т. е. у = tg (х + у +
Общее решение (8) можно записать в виде
у = tg (х + £ + С),
где произвольная постоянная С выбирается на промежутке ? (прибавление л к аргументу не изменит значения тангенса).
Упражнения
18.	Решите дифференциальные уравнения:
1)	У' = 4 + у2;	3) у' =	5) у' = xeJl- у2-,
2)	у' = ху4;	4) у' =	6) V1 - х2 у' = 2^.
bJ.ll оу
19.	Найдите решение дифференциального уравнения у' = хгу'‘, удовлетворяющее начальному условию у( 1) = 2.
20.	Решите дифференциальные уравнения:
1)	у" + 4у = 0;	2) у" + 36у = 0.
4.	Составление дифференциальных уравнений. В примерах из п. 1 дифференциальные уравнения движения устанавливались с помощью второго закона Ньютона, в формулировку которого входит понятие ускорения, т. е. второй производной координаты по времени. Во многих случаях приходится составлять дифференциальное уравнение, делая «мгновенный снимок» некоторого явления.
Решим следующую задачу.
Задача 1. Резервуар, наполненный водой, имеет форму цилиндра с высотой Н и площадью основания S. В дне резервуара 7 сделано отверстие площадью s, через которое за 1 ч вылилось
всей воды. Через сколько времени вся вода вытечет из резервуара, если скорость течения жидкости через отверстие выражается формулой и = k4h, где h — высота жидкости над отверстием, a k — числовой коэффициент?
Решение. Пусть через t часов после начала истечения уровень оставшейся воды равен Л. За промежуток времени [t; t + Ai]
24
уровень воды изменится на АЛ, где ДЛ < 0. По формуле объёма цилиндра получаем, что объём вылившейся воды выражается равенством Ди = -SAh (рис. 6). Эта вода вылилась в виде цилиндрической струйки, площадь основания которой равна з, а высота I равна пути, пройденному за время струйкой, вытекавшей из отверстия (мы пренебрегаем сопротивлением воздуха). Если промежуток времени [t; t + At] достаточно мал, то можно пренебречь изменением за этот промежуток времени уровня жидкости над отверстием, которое влечёт за собой изменение скорости истечения. Тогда приближённо
получаем, что I ~ v&t - kjhkt. Значит, объём вытекшей за этот промежуток времени жидкости приближённо выражается формулой
ДУ - ky/hsAt.
(*)
Сравнивая получившиеся выражения для ДУ, приходим к следующему приближённому равенству:
-S\h ~ ky/hs&t,
т. е.
S
At
Полученное равенство становится тем более точным, чем меньше величина At промежутка времени. Поэтому точным является
равенство	Ит М = д* -> о	о
(разумеется, в пределах сделанных предположений о ходе процесса).
Так как lim = h', то получаем, что
h' =
о
(1)
Задача свелась к решению дифференциального уравнения (1).
Нам известно, кроме того, что в начале процесса высота воды равнялась Н, а через 1 ч осталось всей воды, и потому
25
о
высота стала jg Н. Таким образом, имеем ещё условия: /г(0) - Н ий(1) = ±Н.
Разделяя переменные в уравнении (1), получаем
dh _ fes j, А " sat-
После интегрирования обеих частей находим
2х/й = -^-t + С.
(2)
Мы получили соотношение между моментом времени t и высотой уровня воды h. В это соотношение входят две неизвестные нам ks
постоянные Си —. Их значения определяются из условий А(0) = Н о
9
и Л(1) = — Н. Подставляя в соотношение (2) значения t = 0, h = Н, получаем
2л/я = С.
г I ks
Значит, \]h = yjH - Подставляя в это равенство значения
t = 1, h = -^Н, находим, что М =
10	ZO 4
Итак, Jh. = у/н - t, и потому
Л = н(14)!-	(3>
Теперь уже легко найти, когда вытечет вся вода из резервуара, т. е. когда будет выполняться равенство h = 0. Полагая h = 0, находим, что t = 4, т. е. вся вода выльется через 4 ч. На рисунке 7 изображён график зависимости h от t.
Замечание. Если бы истечение воды было равномерным (в уравнении (1) не было бы y/h), то вся вода вылилась бы из бассейна 16 за -у часа.
26
Упражнения
21.	Составьте дифференциальное уравнение кривой, для которой отрезок касательной, заключённый между осями координат, делится точкой касания пополам. Каковы начальные условия, если кривая проходит через точку 4(3; 2)?
22.	Составьте дифференциальное уравнение кривой, для которой абсцисса пересечения касательной в произвольной точке кривой с осью абсцисс в k раз больше абсциссы точки касания.
23.	Составьте дифференциальное уравнение кривой, для которой отрезок касательной между точками касания и осью ординат делится пополам в точке пересечения с осью абсцисс. Каковы начальные условия, если кривая проходит через точку 4(1; 3)?
24.	Составьте дифференциальное уравнение кривой, для которой отрезок касательной, заключённый между осями координат, имеет длину а.
25.	Составьте дифференциальное уравнение кривой, для которой отрезок касательной, заключённый между точкой касания и точкой пересечения с осью абсцисс, имеет длину а.
26.	Составьте дифференциальное уравнение кривой, для которой площадь треугольника ОМТ, ограниченного осью абсцисс, касательной и радиусом-вектором точки касания (рис. 8), постоянна.
27.	Составьте дифференциальное уравнение движения пули, считая, что сила сопротивления движению пули пропорциональна квадрату скорости.
28.	Полусферическая чаша диаметром 2 м заполнена водой (рис. 9). За какое время вода вытечет из неё через круглое отверстие радиусом 0,1 м, вырезанное на дне чаши (в формуле (*) принять k = 0,6)?
29.	Вода вытекает из цистерны длиной 8 м и радиусом 1 м, лежащей горизонтально, через отверстие внизу цистерны площадью 0,1 м2. Через сколько времени вся вода вытечет из заполненной цистерны (рис. 10)?
5. Математическое моделирование (беседа). Понятия, созданные современной математикой, зачастую кажутся весьма далёкими от реального мира. Но именно с их помощью людям удалось проникнуть в тайны строения атомного ядра, рассчитать движение космических кораблей, создать весь тот мир техники, на котором основано современное производство. Одним из основных
Рис. 9
Рис. 10
27
методов познания природы является опыт, эксперимент. С помощью экспериментов были установлены многие законы природы (закон сохранения вещества и энергии, Периодическая система элементов Д. И. Менделеева и т. д.). Однако не всегда целесообразно проводить эксперимент. За последнее столетие в самых различных областях науки и техники всё большую роль стал играть метод математического моделирования.
Чтобы изучить какое-нибудь явление природы или работу машины, предварительно изучают всевозможные связи между величинами, их характеризующими. Затем полученные связи выражают математически и приходят к системе уравнений. Решая эти уравнения или системы уравнений, учёные и инженеры делают выводы о том, как в дальнейшем будет развиваться это явление или как будет работать машина, что надо сделать, чтобы получить требуемые результаты.
При этом уравнения и системы уравнений бывают алгебраическими и дифференциальными. Чтобы получить уравнения, допускающие решения, приходится упрощать задачу, отбрасывая некоторые величины как несущественные. Но чем точнее нужен результат, тем больше величин приходится учитывать, тем сложнее получается математическая модель.
Математические модели, которые строили в XIX в., были сравнительно простыми. Но возрастающие требования к точности ответа, развитие техники, познание разнообразных явлений привели к построению всё более сложных математических моделей. Большую помощь в их изучении оказывают компьютеры.
Сейчас с помощью математического моделирования решают такие задачи, как описание природы морей и океанов, изучение входа космического корабля в плотные слои атмосферы, ядерные реакции и т. п. Появилась возможность строить математические модели экономики, применять математику в изучении общественных явлений, проблем истории, в изучении языков и т. д. Трудно указать область человеческой деятельности, в которой не применялся бы метод математического моделирования.
§ 3. Определённый интеграл
1. Площади плоских фигур. Как мы увидим ниже, интегральное исчисление позволяет решать многие задачи геометрии и физики. Одной из этих задач является вычисление площадей плоских фигур. В курсе геометрии понятие площади плоской фигуры было определено с помощью следующих четырёх аксиом.
28
1.	Площадь любой фигуры F неотрицательна, т. е. S(F) > О (здесь и ниже через S(F) мы обозначаем площадь фигуры F).
2.	Равные фигуры имеют равные площади: если Fi = F2, то S(Fr) = S(F2).
3.	Площадь фигуры равна сумме площадей её частей: если фигура F разбита на части и F2, то S(F) = S(Fi) + S(F2). (Эти части могут иметь общие граничные точки.)
4.	Площадь квадрата со стороной 1 равна 1.
Однако в курсе геометрии не обсуждался вопрос о том, все ли фигуры имеют площади. А главное, существует ли понятие площади, обладающее указанными выше свойствами (вообще если какое-нибудь математическое понятие определено своими свойствами, то возникает вопрос о существовании понятия с этими свойствами).
Мы будем считать, что для плоских многоугольников площадь с указанными выше свойствами существует (доказательство этого утверждения относится к геометрии, а не к математическому анализу). Тогда каждой ограниченной плоской фигуре F можно поставить в соответствие два числовых множества. Первое из них состоит из площадей многоугольников, целиком лежащих внутри F, а второе — из площадей многоугольников, целиком содержащих фигуру F. Обозначим первое множество через XF, а второе — через YF. Очевидно, что XF лежит слева от YF. В самом деле, пусть х С XF, у 6 Yf. Тогда существуют многоугольники Фи? такие, что Ф лежит внутри F, Т содержит F (рис. 11), причём в(Ф) = х, S(T) = у. Так как Ф содержится в Т, то х С у.
Определение 1. Плоскую фигуру F называют квадрируемой, если множества XF и YF разделяются лишь одним числом. Это число, разделяющее XF и YF, называют площадью фигуры и обозначают S(F).
Таким образом, площадь квадрируемой фигуры является числом, которое не меньше, чем площадь любого многоугольника,
лежащего внутри этой фигуры, и не больше площади любого многоугольника, содержащего эту фигуру. Для неквад-рируемых фигур это определение не годится, так как чисел с указанным свойством может оказаться бесконечно много.
Приведём без подробных доказательств пример фигуры, не имеющей площади. Возьмём квадрат со стороной 1 и удалим из него
29
внутреннюю область квадрата площадью (рис. 12).
Из оставшейся фигуры удалим внутренние облас-
ти восьми квадратов общей площадью
1
х, располо-О
Рис. 13
у. = (|; +°о)
женных, как показано на рисунке 13. Продолжая этот процесс дальше, мы получим после бесконечного множества операций фигуру, не содержащую ни одной внутренней точки (каждая её часть «продырявлена»), и тем самым в ней нет ни одного многоугольника. В то же время общая площадь удалённых квадратов равна
сумме бесконечной геометрической прогрессии -т + т? +
4 о
1^7 + ..., т. е. равна Поэтому площадь любого
многоугольника, содержащего оставшуюся фигуру,
должна быть больше
1 2'
В нашем случае XF = {0},
и потому есть бесконечно много чисел, разделяющих XF
и YF.
Из теоремы 2 п. 4 § 1 главы 1 (10 кл.) следует необходимое и достаточное условие квадрируемости.
Для того чтобы ограниченная плоская фигура F была квадрируемой, необходимо и достаточно, чтобы для любого е > 0 нашлись многоугольники Ф и Т такие, что Ф содержится в F.'V содержит F, причём S('P) - £(Ф) < е.
Замечание. Чтобы избежать ссылки на геометрию при определении площадей многоугольников, можно рассмотреть не все многоугольники, а лишь ступенчатые фигуры, составленные из прямоугольников, стороны которых параллельны осям координат. Площади таких фигур равны сумме площадей составляющих их прямоугольников.
Легко доказать, что для площадей квадрируемых фигур выполняются аксиомы 1, 2 и 4. Доказательство выполнения аксиомы 3 несколько сложнее. Мы проведём его в частном случае, когда линия Г, разбивающая фигуру F на части Д и F2, является ломаной. Итак, докажем следующее утверждение.
Теорема 1. Пусть ломаная Г разбивает фигуру F на части Fx и F2. Если эти части квадрируемы, то квадрируема и фигура F, причём её площадь равна сумме площадей Д и F2.
1 Здесь и далее материал, отмеченный знаком *, является необязательным для изучения учащимися.
30
Доказательство. Зададим е > 0. Найдутся многоугольники Ф1, Ti, Ф2, Ч'г такие, что Ф, содержится в Fh а содержит Flt
причём S(T,) - в(Фг) < где i = 1, 2. Не теряя общности, можем считать, что ломаная Г является частью границы всех этих многоугольников (рис. 14). Составим из Ф! и Ф2 многоугольник Ф, а из и 'Р2 — многоугольник 4х. Тогда Ф содержится в F, 4х содержит F, причём в(Ф) = 8(Фх) + 5(Ф2), S(4x) = «(ЧЛ) + <S('?2) и потому S(V) - в(Ф) = дао + S(T2)) - дао + 5(Ф2)) = дао - в(Ф0) + + (S(4X2) - <3(Ф2)) < к + к = е. Тем самым доказано, что фигура F
квадрируема. Обозначим её площадь через S(F).
Нам осталось доказать, что S(F) = S(F1) + S(F2). Но это следует из того, что числа S(F) и S(F1) + S(F2) разделяют множества вида {8(Ф0 + в(Ф2)} и {S^O + <8(4^)}, где Фь Ф2, 4х!, 4Х2 имеют смысл, аналогичный указанному выше. Поскольку эти множества разделяются лишь одним числом, то S(F) - StFi) + S(F2)*.
У пражнения
30. Докажите, что множество точек М(х; у) таких, что 0<х<1,0<у<1 и х, у рациональны, не является квадрируемым.
31. Докажите, что множество точек М(х; у) таких, что 0 < х < 1 и у = О
1	Р	Р
при иррациональных х, 0 < у , если х = —, где дробь — несо-q	q	q
кратима, имеет площадь, равную нулю.
2. Площадь криволинейной трапеции. Пусть функция f неотрицательна на отрезке [а; Ь]. Фигуру, ограниченную снизу осью абсцисс, сверху графиком функции /, а с боков прямыми х = а и х = b (рис. 15), называют криволинейной трапецией, или, иначе, подграфиком данной функции. Имеет место следующая теорема, дающая достаточное условие квадрируемости криволинейной трапеции.
31
Теорема 1. Если функция / монотонна на отрезке [a; Ь], то соответствующая ей криволинейная трапеция F квадрируема.
Доказательство. Предположим для определённости, что функция возрастает на [а; Ь]. Нам надо доказать, что для любого е > О найдутся два многоугольника Ф1 и Ф2, из которых Ф1 лежит внутри
криволинейной трапеции F, Ф2 содержит F и Я(Ф2) - 5(Ф1) < е. Для построения этих многоугольников разделим отрезок [а; &] на п равных частей точками а - х0 < хг< ... < хп_х < хп = Ь и проведём через эти точки прямые, параллельные оси ординат. Эти прямые разбивают криволинейную трапецию F на части Fo, Flt ..., Fn-r. На каждом отрезке [хЛ; х*+1] построим два прямоугольника: один с высотой /(хА), а другой с высотой f(xk+1). В силу возрастания функции f первый из этих прямоугольников содержится в соответствующей части Fk криволинейной трапеции, а второй содержит эту часть. Поэтому, объединяя первые прямоугольники для всех k, О < k < п - 1, получим ступенчатую фигуру Фь содержащуюся в F. Аналогично, объединяя вторые прямоугольники, получаем
ступенчатую фигуру Ф2, содержащую F.
Покажем, что при достаточно большом п разность площадей построенных ступенчатых фигур станет меньше, чем е. Для этого заметим, что площадь первой ступенчатой фигуры равна
8(Ф0 = ^(/(х0) + ... + Дх,.!)), а площадь второй —
8(Ф2)= ^-“(/(х1) + ... +/(х„)).
Поэтому
8(Ф2) - 8(Ф0 =	(/(х„) - /(Хо)),
или, поскольку /(х0) = f(a), f(xn) = f(b),
8(Ф2) - 8(Ф0 =	(1)
п
Отсюда ясно, что при достаточно большом п указанная разность станет меньше, чем е.
Квадрируемость криволинейной трапеции при указанном в теореме условии на функцию f доказана. Очевидно, что она имеет
32
место и в том случае, когда отрезок [а; Ь] можно разбить на т частей так, чтобы на каждой из них функция f была монотонна (каждую часть мы считаем отрезком, т. е. причисляем к ней её концы). В этом случае функция имеет на отрезке [а; Ь] конечное число экстремумов.
Более сложные рассуждения, которые мы опускаем, показывают, что квадрируемость имеет место и в случае, когда функция f непрерывна на отрезке [а; Ь] и имеет на этом отрезке бесконечно много максимумов и минимумов. Примером такой функции может служить на отрезке [0; 1] функция
Лх) =
х sin — при х Ф 0,
х
0 при х = 0.
(2)
Упражнения
32.	На сколько равных частей нужно разбить отрезок [0; 2], чтобы для криволинейной трапеции, ограниченной линиями х = 0, х = 2, у = 0, у = х2, выполнялось неравенство 5(Ф2) _ <8(Ф1) < 0,001?
33.	Докажите, что круг имеет площадь.
34.	Докажите, что функция (2) имеет бесконечно много экстремумов на отрезке [0; 1].
3. Теорема Ньютона — Лейбница. Одним из основных результатов математического анализа, имеющем важные приложения, является следующая теорема, в геометрической форме сформулированная английским математиком Барроу (1630—1677), а в окончательном виде независимо друг от друга полученная Ньютоном (1643—1727) и Лейбницем (1646—1716).
Теорема 1 (Ньютона — Лейбница). Пусть функция f неотрицательна, непрерывна на отрезке [а; &] и имеет на нём конечное число экстремумов. Обозначим через S(x) площадь криволинейной трапеции, расположенной над отрезком [а; х], где а < х < Ь, и ограниченной сверху графиком функции f. Тогда S(x) является первообразной для f(x), т. е. на отрезке [а; Ь] выполняется равенство S'(x) = Дх).
Замечание. Для существования первообразной у функции f достаточно, чтобы эта функция была непрерывна на отрезке [а; ё]. Однако доказательство этого утверждения несколько сложнее и мы его опускаем.
В дальнейшем мы будем называть S(x) площадью криволиней ной трапеции с переменным верхним пределом (рис. 16).
Доказательство. Нам надо доказать, что для любой точки х из [а; д] (рис. 17) выполняется равенство S'(x) = f(x).
33
Рис. 16
Для определённости
тт	C'z X 1-	s(x + h) - S(x)
Напомним, что S (x) = lim ------г------
v ’ h^o	h
будем считать, что h > 0. В этом случае разность S(x + й) - S(x) равна площади криволинейной трапеции PTQN (рис. 17). Пусть наибольшее значение функции f на отрезке [х; х + й] равно М, а её наименьшее значение на этом отрезке равно т (эти значения существуют в силу предположения о непрерывности функции f на [а; й], см. п. 2 § 3 главы 5, 10 кл.). Тогда площадь фигуры PTQN заключена между площадями прямоугольников с общим основанием [х; х + й] и высотами т и М соответственно. Так как эти площади равны соответственно mh и Mh, то имеем неравенства
mh < S(x + й) S(x) < Mh,	(1)
где т и М зависят от выбора й.
Поскольку й > 0, из этих неравенств следует
S(x + й) - S(x) т < ---------< М.
(2)
При й, стремящемся к нулю, в силу непрерывности функции f в точке х наибольшее значение М этой функции на отрезке [х; х + й] и её наименьшее значение т на том же отрезке стремятся к общему пределу Дх):
lim т = lim М = Дх). h ->0	h->0
S(x + й) - S(x)
Но тогда и заключенное между ними значение -----------------
. .. S(x + й) - S(x) ,, . стремится к Дх), lim -----г------ = Т(х).
h ->0	Й
Случай, когда й < 0, разбирается аналогично. Следовательно, S'(x) = f(x). Теорема доказана.
Из теоремы 1 непосредственно следует важное утверждение.
Теорема 2. Любая функция f, непрерывная на отрезке [а; й] и имеющая на нём конечное число экстремумов, имеет на этом отрезке первообразную.
34
Доказательство. Если функция f положительна на отрезке [а; &], то утверждение теоремы 2 вытекает непосредственно из теоремы 1: одной из искомых первообразных является площадь S(x) криволинейной трапеции для функции f с переменным верхним пределом.
Общий случай легко сводится к разобранному. Так как функция f непрерывна на отрезке [а; б], она ограничена снизу на этом отрезке, и потому существует такое число А, что вспомогательная функция (р, где ф(х) = f(x) + А, положительна на [а; &]. По доказанному выше она имеет первообразную Ф. Но тогда функция F, где F(x) = Ф(х) - Ах, будет первообразной для f. В самом деле, Ф'(х) = ф(х) = Дх) + А, и потому F\x) = (Ф(х) - Ах)' - Ф'(х) - А = = f(x) + А-А = f(x).
Среди всех первообразных для функции f указанная в теореме 1 первообразная (площадь криволинейной трапеции с переменным верхним пределом) выделяется следующим условием: она равна нулю при х - a, S(a) = 0. Отсюда вытекает, что площадь всей криволинейной трапеции ABCD на рисунке 17 равна значению при х = b той первообразной функции f, которая обращается в нуль при х = а.
Пример. Найдём площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми х - 1 и х = 5 и графиком функции х2.
Решение. Первообразными для функции х2 являются функ-ции вида F(x) = -g- + С. Нам надо подобрать постоянную С так,
I3
чтобы выполнялось равенство Е(1) = 0, т. е. -5- + С = 0. Отсюда О
1	X3	1	б3
С = -х, и потому F(x) = — - При х = 5 получаем Е(5) = -5- -О	О	О	о
-	=41^. Значит, искомая площадь равна 414-
О	О	о
Данное выше правило для отыскания площади (найти ту первообразную функции f, которая обращается в нуль при х = а, и взять её значение при х = Ь) несколько громоздко. В следующем пункте мы упростим его, введя понятие определённого интеграла.
Упражнения
35.	Может ли площадь криволинейной трапеции с переменным верхним пределом равняться F(x), если слева она ограничена прямой х = а, сверху — графиком функции f и
1)	а = 2, Дх) = х3, F(x) = х4 - 16;
2)	а = 0, Дх) = cosx, F(x) = sinx + 1;
35
3)	a = 1, f(x) = x3, F(x) = 3x2;
36.	Найдите площадь криволинейной трапеции с переменным верхним пределом, если слева она ограничена прямой х = а и сверху — графиком функции f, где:
1) а = 0, /(х) = х + 4;
2) а = 3, ftx) = х2 + 1;
3) а = -1, f(x) = 9 - х2;
4) а = 0, f(x) = cosx.
37.	Найдите площадь криволинейной трапеции, ограниченной сверху графиком функции f и с боков прямыми х = а и х = Ь, если:
1)	а = 1, b = 4, /(х) = х2 - 1;	3) а = 0, b =	/(х) = sinx;
2)	а = 0, b = 1, f(x) = т-Цт;	4) а = О, b =	/(х) = - -1— 
1 + х	z VI - х2
4. Физические и геометрические задачи, приводящие к понятию определённого интеграла. Мы уже указывали выше, что интегральное исчисление применяется для определения пути, пройденного в течение промежутка времени [а; 6], если известна скорость в каждый момент времени t этого промежутка, v = f(t). Такие и более общие задачи возникают, например, в космической навигации (там приходится определять путь по заданным значениям ускорения). Решим следующую задачу.
П ример 1. Известна скорость прямолинейно движущейся точки в каждый момент времени t промежутка времени [а; Ь], v = f(t). Найдём перемещение точки за этот промежуток времени.
Решение. Выберем на прямой, по которой движется точка, систему координат и обозначим через F(t) координату точки в момент времени t. Тогда перемещение точки за промежуток времени [а; Ь] будет равно разности F(b) - F(a). Но так как скорость есть производная координаты по времени, т. е. /(х) = F'(x), то F — первообразная для функции f. Поэтому перемещение точки равно разности значений первообразной F в точках b и а. Замечателен тот факт, что эта разность F(b) — F(a) не зависит от выбора начала координат на прямой. При другом выборе этого начала ко всем координатам прибавляется одно и то же число С, а разности (F(b) + + С) - (F(a) + С) и F(b) - F(a) равны друг другу.
Пример 2. Найдём площадь криволинейной трапеции, ограниченной осью абсцисс, графиком неотрицательной непрерывной функции f и вертикальными прямыми х - а и х = Ь.
Решение. Выберем на оси абсцисс точку Т(с) и обозначим через F(x) площадь криволинейной трапеции, ограниченной сверху тем же графиком функции /, а с боков прямыми, парал-
36
лельными оси ординат и проходящими через точки Т(с) и Р(х) (рис. 18). Искомая площадь равна разности площадей криволинейных трапеций TQCB и TQSA, т. е. F(b) - F(a). Но мы доказали в п. 1, что F является одной из первообразных для функции f. Значит, площадь криволинейной трапеции ASCB равна разности значений первообразной для функции f в точках b и а. Как и выше, убеждаемся, что эта раз-
ность не зависит от выбора первообразной (т. е. точки Т(с) на оси абсцисс).
Мы разобрали две задачи, в которых ответом оказалась разность значений первообразной F для функции f в точках b и а.
Определение. Разность значений первообразной для функции f в точках b и а называют определённым интегралом этой функции от а до Ъ.
Покажем, что определённый интеграл не зависит от того, какую именно первообразную для функции f мы выбрали. В самом деле, пусть функции F и Ф являются первообразными для функции f. Тогда они могут отличаться друг от друга лишь постоянным слагаемым С, Ф = F + С. Но тогда
Ф(Ь) - Ф(а) = (F(b) + С) - (F(a) + С) = F(b) - F(a), и потому разность не зависит от значения С.
Именно этим свойством объясняется название «определённый интеграл»: в то время как неопределённый интеграл является некоторой совокупностью функций, отличающихся друг от друга постоянным слагаемым, определённый интеграл имеет определённое значение, не зависящее от выбора этого слагаемого.
Определённый интеграл функции f от а до b обозначают так:
С	С6
\ f(x)dx, а иногда так: \ f(x)dx. При этом букву х можно заменить
J	За
а b	b
любой иной, например написать f(t)dt, f(s)ds и т. д. а	а
b
Обозначение f(x)dx читают так: «определённый интеграл от а а
до бэ эф от икс дэ икс». Числа а и b называют пределами интегрирования (а — нижним, b — верхним), знак — знаком интеграла. Если а < Ь, то отрезок [а; Ь] называют отрезком интегрирования
37
и вместо «интеграл от а до 6» говорят «интеграл по отрезку [а; Ь]». Функцию f называют подынтегральной функцией, а выражение f(x)dx — подынтегральным выражением.
Итак, по определению
ъ
5 f(x)dx = F(b) - F(a),	(1)
а
где F — одна из первообразных функции f. Частными случаями этого равенства являются формулы
ь
s = 5 f№	(2)
а
И
ь
S = f(x)dx	(3)
а
для перемещения точки и для площади криволинейной трапеции. В формуле (2) f(t) — мгновенная скорость точки в момент времени t, [а; й] — промежуток времени, а в формуле (3) f(x) — функция, график которой ограничивает сверху криволинейную трапецию, a [a; £>] — отрезок, над которым лежит эта трапеция.
Формулу (1) называют формулой Ньютона — Лейбница.
Из данного выше определения следует, что для вычисления ь
значения определённого интеграла f(x)dx нужно: а
1)	найти какую-нибудь первообразную F для функции f;
2)	вычислить значения F(b) и F(a) этой первообразной в точках b и а;
3)	найти разность F(b) - F(a).
Iь
Разность F(b) - F(a) для краткости обозначают так: F(x)l .
Значит,
С	I»
y(x)dx = F(x)|a. а
л
Пример 3. Вычислим интеграл sinx с/х.
о
Решение. Первообразной для функции sin х является —cosx. Поэтому
Л	I л
^sinxdx = -cosx о - -(cost: - cosO) = -(-1 - 1) = 2.
о
38
2
Пример 4. Вычислим интеграл x3dx.
-2
Решение.
2
-2
2 _ 24	(-2)'
-24	4
Пример 5. Вычислим интеграл
(х3 + 6х2
-2
5)dx.
Решение.
4
(х3 + 6х2 + 5)dx =
-2
5х
4	44
-2 = Т
6 • 43
S-x3- +5-4-
О
16 16 _ „ 4	4 “ и-
4
3
6 • C-2V	\
----+ 5  (-2)1 = 64 + 128 + 20 - 4 + 16 + 10 = 234.
О	/
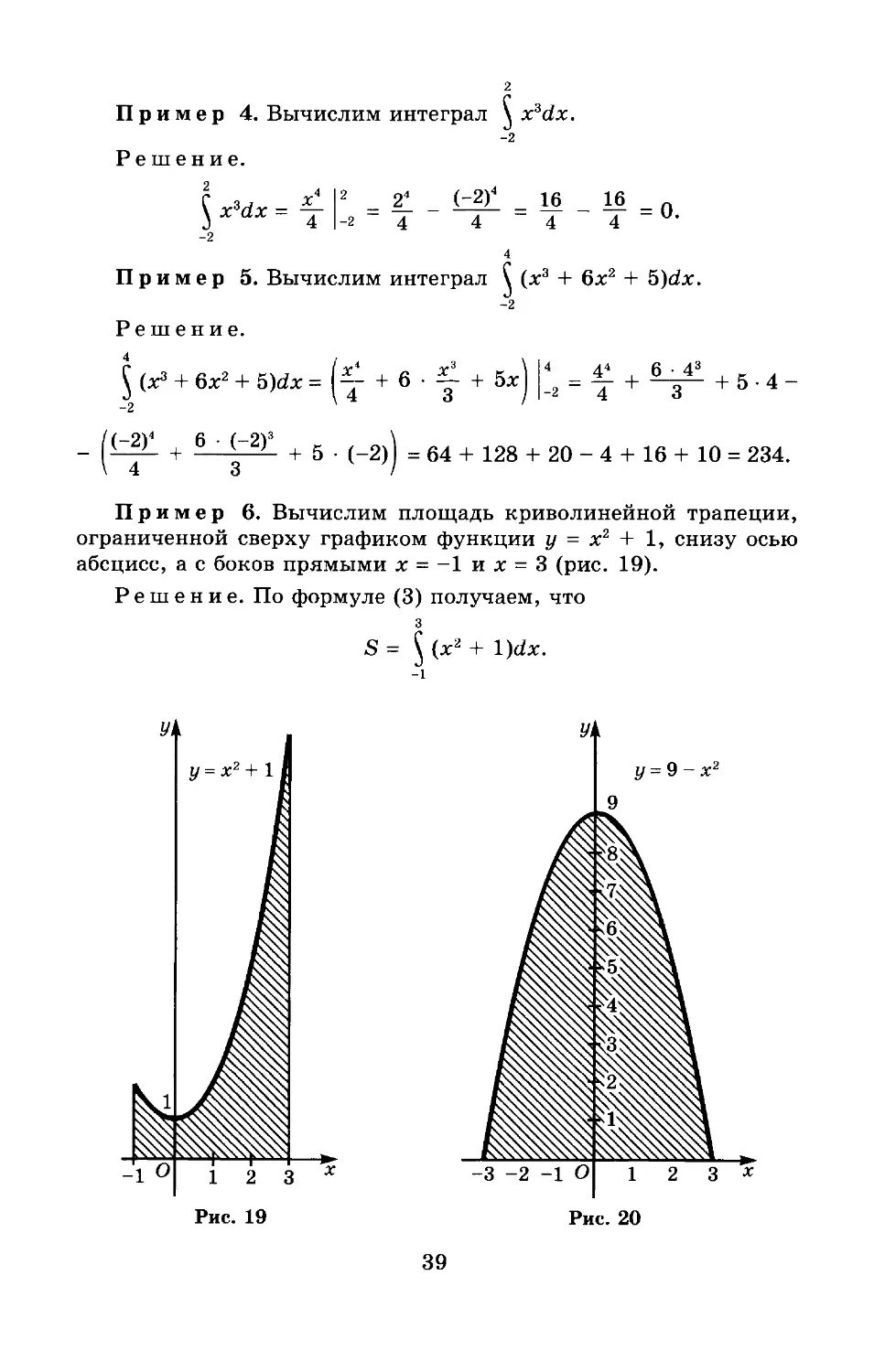
Пример 6. Вычислим площадь криволинейной трапеции, ограниченной сверху графиком функции у = х2 + 1, снизу осью абсцисс, а с боков прямыми х = -1 и х = 3 (рис. 19).
Решение. По формуле (3) получаем, что
з
S = $ (х2 + l)dx.
-1
Рис. 19
39
Первообразная функции х2 + 1 равна -5- + х, и потому О
S =
(-1)) =1з|.
Пример 7. Найдём площадь фигуры, ограниченной сверху параболой у = 9 - х2, а снизу осью абсцисс (рис. 20).
Решение. Сначала найдём точки, в которых парабола пересекается с осью абсцисс. Решая уравнение 9 - х2 = 0, получаем Xi= -3 и х2= 3. Поэтому искомая площадь выражается так:
S = $ (9 - x2)dx = (эх -	|_33 = 27 -	- (-27 -	= Зб.
R
Пр и м е р 8. Найдём значение интеграла § \R2 - х2 dx.
-к
Решение. Уравнение у = -7я2 - х2 можно записать в виде х2 + у2 - R2. Оно означает, что расстояние от точки М(х; у) до начала координат равно R, т. е. что точка М лежит на окружности радиуса R с центром в начале координат. Часть криволинейной трапеции, расположенная над отрезком [-Я; Я], является полу
кругом радиуса R, площадь которого равна 1 л/?2. Значит,
я
$ \iR2 - х2 dx = |лЯ2.
R
Тот же результат получается, если использовать для вычисления формулу (4) п. 4 § 1:
R
5 y/R2 - х2 dx =
-R
(— arcsin — + —л/Я2 - x2 j |Д = \ 2 R 2	/ I
R2 .	. .	. , ... R2 In I лП nR2
= -g-(arcsin 1 - arcsm(-l)) = ~2~ (2 ~ ("2)' = ~2~'
Замечание. Если функция /принимает на отрезке [а; 6] не только ъ
положительные, но и отрицательные значения, то f(x)dx равен разности а
между площадью части криволинейной трапеции, лежащей над осью абсцисс, и площадью её части, лежащей ниже оси абсцисс.
л
Пример 9. Вычислим интеграл sin х dx.
-л
Решение. Так как синусоида симметрична относительно точки 0(0; 0), то часть криволинейной трапеции, расположенная
40
выше оси абсцисс, имеет ту же площадь, что и часть, расположенная ниже этой оси. Разность площадей равна нулю, и потому 71
sinxdx = 0.
— 71
Пример 10. Найдём путь, пройденный при свободном падении телом за первые пять секунд (ускорение равно 9,8 м/с2).
Решение. Так как свободное падение равноускоренно, то скорость в момент времени t равна gt, v = gt = 9,8t. Значит, путь, пройденный за промежуток времени [0; 5], выражается определённым интегралом
а
$9,8fdt = U = 4,9 • 25 = 122,5 м.
Пример 11. Найдём давление, оказываемое водой на плотину, имеющую форму треугольника, обращённого вершиной вниз, если основание треугольника равно I, а его высота равна h.
Решение. Возьмём полоску «бесконечно малой высоты» dx, находящуюся на глубине х (рис. 21). Из подобия треугольников получаем, что длина 1(х) этой полоски удовлетворяет равенству /(х) h - х	,, , (h - x)l	„
——	- —j-—,	откуда t(x)	= —j-—•	Значит,	площадь полоски
(Л - х)1 ,	..	х(Л - х)1 ,
равна dS = —— dx, а давление на нее равно dP = ----------dx.
Чтобы получить давление на всю плотину, надо проинтегрировать dP по х от х = 0 до х = h:
41
Значит, искомое давление равно lh2.
Из формулы ^f(t)dt = F(x) - F(a) и равенства F'(x) = f(x) вы-а
текает, что
= ft*)-
Таким образом, если функция f непрерывна на отрезке [а; Ь] и имеет на нём конечное число максимумов и минимумов, то производная определённого интеграла от этой функции по верхнему пределу равна значению подынтегральной функции в соответствующей точке.
Упражнения
38.	Функция F(x) задаётся формулой F(x) = (arcsin21 + 4t3)dt. Найдите F'(x).
39.	Найдите производные функций:
1)	F(x) = § dt-, 2) F(x) = § dt.
1	VJ
40.	Найдите точки экстремума функции F, где:
о 1 т 1
41.	Вычислите интегралы:
i
1)	(x2 + 4)3dx;
-i
2)	f ____dx____.
> J V16 - x2 ’
-2
5
С t4 - 5t2 + 4
2) F(x) = \ —Л— -/---dt.
’ v ’ J 1 + sin2 t
0
П
2
4) sin2xdx;
о
Л
2
5) \ cos x dx.
42.	Подберите А и В так, чтобы выполнялись равенства:
1	1
(Ах + B)dx = 0 и (Ах + B)xdx = 1.
-1	-1
42
43.	Подберите А, В и С так, чтобы выполнялись равенства:
1	1
(Ах2 + Вх + C)dx - 0, (Ах2 + Вх + C)xdx = 0 и
-1	-1
1
(Ах2 + Вх + C)x2dx = 1.
44.	Найдите площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми х = 0, х = 2 и графиком функции у = х4 + 2х2 + 4.
45.	Найдите площадь криволинейной трапеции, ограниченной осью абс-
цисс, прямыми х = 0, х = 1 и графиком функции у = т——у.
46.	Найдите площадь, ограниченную одной волной синусоиды у = sin х и осью абсцисс.
47.	Найдите площадь, ограниченную параболой у = х2 + 2х - 8 и осью абсцисс.
48.
Найдите площадь, ограниченную кривыми у =
------------- у и у - V2x.
49.	Вычислите площадь фигуры, ограниченной следующими линиями:
1 \	32	о -	о	1	71	71.
1)	У = У = -X3, х = 1;	3) у = 2cosx, у = 1, -у < х < у’
2)	у = у = х - 1, х = 1;	4) у = х4 - 13х2 + 36, у = 0.
50.	С какой силой вода давит на вертикальный прямоугольный шлюз с основанием 18 м и высотой 6 м?
51.	Вычислите, с какой силой вода давит на вертикальную плотину, имеющую форму трапеции, верхнее основание которой равно 70 м, нижнее — 50 м, а высота — 20 м.
52.	Вычислите работу, которую необходимо затратить, чтобы выкачать воду из резервуара, имеющего форму конуса, обращённого вершиной вниз. Высота конуса Л, радиус основания В.
53.	Вычислите работу, которую необходимо затратить, чтобы поднять тело массой т с поверхности Земли на высоту Л (радиус Земли примите равным R = 6400 км). С помощью полученного результата определите вторую космическую скорость (скорость, при которой вертикально поднимающееся тело может подняться на любую высоту).
5. Вычисление геометрических и физических величин с помощью определённого интеграла. Мы видели, что с помощью определённого интеграла можно находить площади криволинейных фигур, путь при неравномерном движении. Чтобы найти некоторую геометрическую или физическую величину с помощью интеграла, поступают следующим образом.
1.	Выражают искомую величину как значение в некоторой точке b функции F.
2.	Находят производную f этой функции.
43
3.	Выражают функцию F в виде определённого интеграла от f и вычисляют его.
4.	Подставляя значение х = Ь, находят искомую величину.
Пример 1. Обозначим через 8(х) площадь сечения некоторого тела V плоскостью, параллельной плоскости уОг (рис. 22) и отстоящей от неё на расстояние х. Найдём объём этого тела при условии, что оно заключено между плоскостями х = а и х - b (О < а < &). (Точное определение понятия объёма и формулировка основных свойств объёмов относится к курсу геометрии, и мы опускаем их обсуждение.)
Решение. Обозначим через Ф(х0) сечение тела V плоскостью х - х0, S(x0) — площадь фигуры Ф(х0). Ради простоты изложения потребуем, чтобы выполнялись следующие условия: функция у = S(x) непрерывна и при хг < х2 проекция сечения Ф(х^ на плоскость уОг содержится в проекции на ту же плоскость сечения Ф(х2) (иными словами, тело расширяется при движении от а к Ь). Обозначим через V(x) объём части тела, соответствующей отрезку [а; х] (рис. 23).
Найдём производную функции У(х). Для этого выберем какое-нибудь значение х0 и дадим ему приращение h > 0. Тогда V(x0 + h) - И(х0) будет объёмом слоя данного тела, заключённого между плоскостями и я2 (рис. 24). Из условий, которым удовлетворяет данное тело, следует выполнение неравенства
S(xQ)h < К(х0 + Л) - Цхо) < S(x0 + h)h.
В самом деле, 5(х0)й — объём цилиндрического тела, целиком лежащего внутри слоя, a S(x0 + й)й — объём цилиндрического тела, содержащего этот слой (рис. 25). Значит,
S(x0)h < -----< S(x0 + й).	(1)
44
Функция у = S(x) непрерывна в точке х0. Поэтому, когда h стремится к нулю, значение S(x0 + h) стремится к S(x0). По утверждению
из п. 3 § 2 главы 4 (10 кл.) ----°--------— стремится к S(x0).
Значит,
,,,, \ г У(х° + h) - 7(х0)
F(x0) = lim -------т-------- = S(x0).	(2)
h ->0
Из равенства (2) следует, что функция у = V(x) является первообразной для функции у = S(x). Отсюда в силу формулы Ньютона — Лейбница
ь
$ S(x)dx - V(b) - V(a). а
Но И(Ь) = V, V(a) = 0, и потому
ь
V = $ S(x)dx.	(3)
Пример 2. Найдём объём конуса, имеющего радиус основания R и высоту Н.
Решение. Поместим вершину конуса в начало координат О (рис. 26). Из геометрии известно, что площади кругов относятся
как квадраты их радиусов. Из рисунка 26 получаем, что =
Г2 X2	с, X ЛД2Х2
- Д2 = Н2 И П0Т0МУ S(x) = н2~'
По формуле (3) имеем
С TtR2x2 , лД2 С , л лД2 х3 Iя j dx - z j x dx - pj2 з I о
о	0
nR2H
3 ’
45
Вообще если функция f непрерывна и неотрицательна на отрезке [a; Ь], то объём V тела, полученного при вращении соответствующей криволинейной трапеции вокруг оси абсцисс (рис. 27), выражается формулой
ь
V = я f2(x)dx.
а
Для доказательства достаточно заметить, что S(x) = пу2 =
Пример 3. Найдём объём шара радиуса R.
Решение. Шар получается при вращении вокруг оси абсцисс полукруга. Уравнение полуокружности имеет вид у = \ЛЙ2 - х2. Поэтому
я
V = л § (7?2 - x2)dx = л
-я

* = |лй3.
-Л О
В физике описанную выше схему применяют обычно в упрощённом виде. Искомые величины рассматривают как «суммы бесконечного числа бесконечно малых величин», а определённый интеграл считают именно такой суммой. Хотя этот подход не имеет точного математического смысла, но весьма нагляден и приводит к верным результатам.
Упражнения
54.	Вычислите работу, которую надо затратить, чтобы растянуть пружину, находящуюся в положении равновесия, на 10 см. Известно, что при растяжении пружины на 1 см сила натяжения равна 5 Н.
55.	Вычислите работу, которую необходимо затратить, чтобы выкачать воду из вертикально стоящей цистерны, радиус основания которой равен R, а высота Н.
46
56.	Вычислите работу, которую надо затра- -------тгг-----------
тить, чтобы выкачать воду из резервуара,	/ 'К
имеющего форму усечённого конуса вы-	/
сотой Н, если радиус нижнего основания /	Ч.
равен г, а верхнего — R, R > г.	/	'ч
57.	Вычислите кинетическую энергию од-нородного диска массой т и радиуса г,	рис> 28
вращающегося с угловой скоростью со вокруг оси, проходящей через его центр перпендикулярно к его плоскости.
58.	Найдите силу давления воды на вертикальную треугольную пластинку с основанием а и высотой h, погружённую в жидкость так, что её вершина лежит на поверхности (рис. 28).
6. Свойства определённого интеграла. Выведем некоторые свойства определённого интеграла, непосредственно вытекающие из его определения. Мы будем, не оговаривая этого особо, считать, что функция f имеет первообразную на отрезках, где она рассматривается.
1.	При перестановке пределов интегрирования определённый интеграл меняет знак:
а	Ь
f(x)dx - - f(x)dx.	(1)
ь	“
В самом деле, ь f(x)dx = F(b) - F(a), а
а
^f(x)dx = F(a) - F(b). ь
Ho F(a) - F(b) = ~(F(b) - F(a)).
2.	Для любого значения а справедливо равенство ^f(x)dx = 0.	(2)
В самом деле,
а
^f(x)dx = F(a) - F(a) = 0. а
Очевиден геометрический смысл равенства (2): при а = b криволинейная трапеция превращается в отрезок и её площадь равна нулю.
3.	Для любых значений а, b и с верно равенство Ь	с	Ь
§ f(x)dx = f(x)dx + f(x)dx.	(3)
а	а	с
47
В самом деле, Ь	с
§ f(x)dx = F(b) - F(a), <\)f(x)dx = F(c) - F(a), a	a
b
5 f(x)dx = F(b) - F(c), c
a
F(b) - F(a) = (F(c) - F(a)) + (F(b) - F(c)). Геометрический смысл равенства (3) при а < с < b показан на рисунке 29.
Следующее свойство определённого интеграла легко следует из свойств первообразной.
4. Справедливы, равенства ь	ь	ь
(ф(х) + ф(х)с/х) dx = (p(x)dx + ф(х)с?х	(4)
а	а	а
U ь	ъ
Аф(х) = А q(x)dx.	(5)
а	а
Докажем сначала равенство (4). Пусть первообразная функции ф равна Ф, а первообразная функции ф равна Т. Так как (Ф + Т)' = = Ф' + Т' = ф + ф, то функция Ф + Т является первообразной для Ф + ф. Следовательно, с	I*
§ (ф(х) + Ф(х))с/х = (Ф(х) + Т(х))|а =
- Ф(Ь) + Т(Ь) - (Ф(а) + Т(а)) -b	ь
= Ф(д) - Ф(а) + 'Р(д) - Т(а) =	y(x)dx.
а	а
Равенство (5) аналогично выводится из того, что (АФ)' = АФ' - Аф. у к	г/п
У = fix) О а	с	Ь *х Рис. 29	Аг V=UX^^^B2 Bi У = Л(х) О а	Ь х Рис. 30
48
Равенство (4) позволяет вывести формулу для вычисления площади таких фигур, как фигура, изображённая на рисунке 30. Эта фигура ограничена сверху графиком функции /2, снизу графиком функции flt а также вертикальными прямыми х - а, х = b (а < Ь); функции Л и /2 непрерывны и неотрицательны на отрезке [а; &].

1
Рис. 31
Площадь S этой фигуры равна разности площадей S2 и где S2 — площадь трапеции аА2В2Ь, a Sj — площадь трапеции аАхВхЪ. Но
si = 5 A(x)dx, ^2=5 f2(x)dx.
Значит,
S = S2 - St= f2(x)dx - fi(x)dx = (f2(x) - fi(x))dx.
Замечание. Формула
S = J (А(х) - A(x))dx
(6)
справедлива не только для случая, когда функции Д и /2 неотрицательны на отрезке [а; Ь].
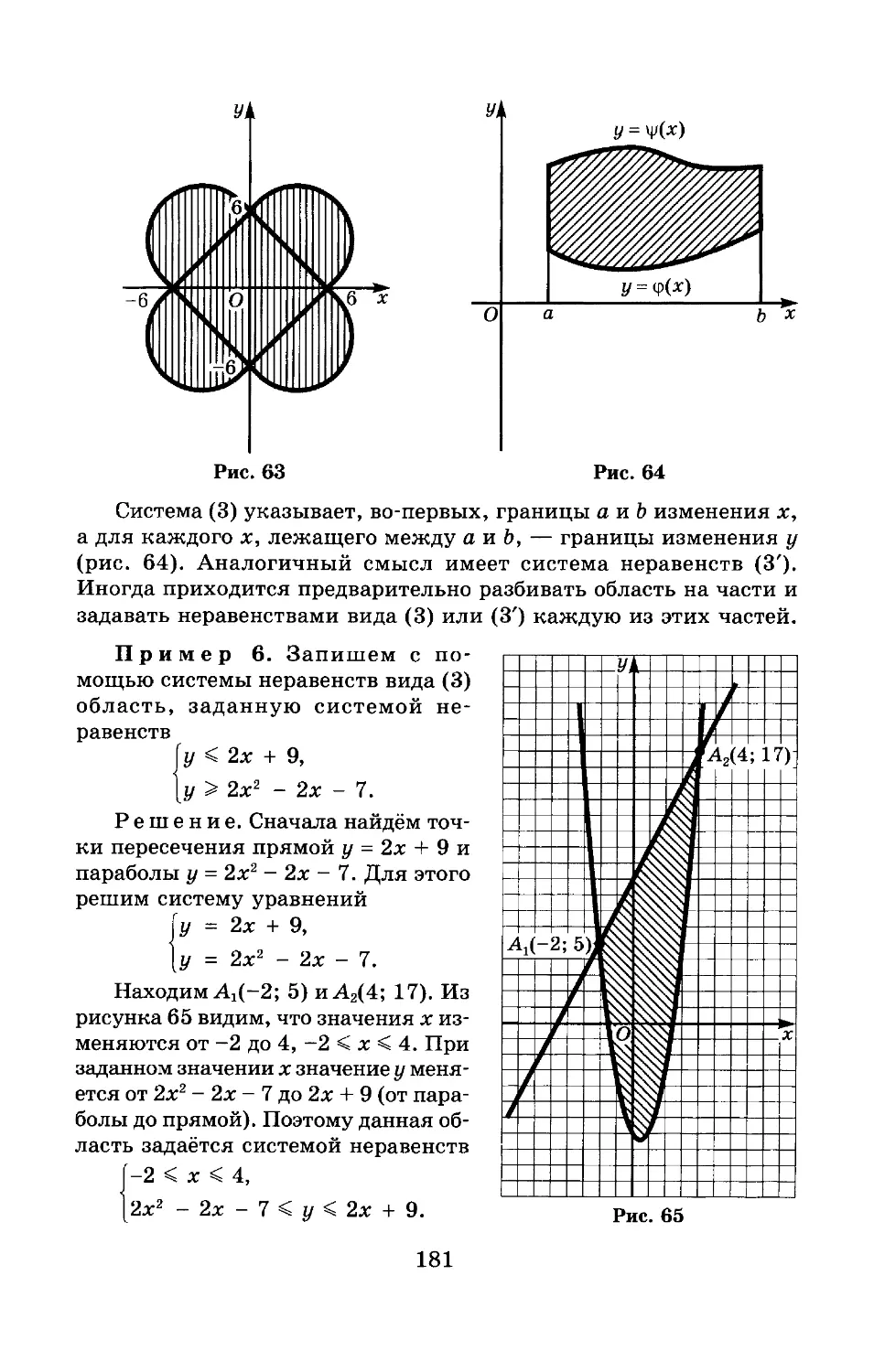
Пример. Найдём площадь фигуры, ограниченной линиями у = х2 и у = 4х (рис. 31).
Решение. В данном случае не указаны пределы интегрирования. Чтобы найти их, надо вычислить абсциссы точек пересечения кривых у = Vx и у = х2.
Так как ординаты обеих кривых в точках пересечения одинаковы, то решение этой задачи сводится к решению уравнения 4х = х2. Оно имеет два корня: Xj = 0 и х2 = 1. Поэтому надо интегрировать от 0 до 1. Применив для отыскания площади формулу (6), получим:
S = §(>/х -x2)dx =
0	3’
Упражнения
59.	Докажите, что если Дх) — чётная функция, определённая для всех значений х, то для любого а
f(x)dx = 2 f(x)dx,
49
а если f(x) — нечётная функция, то а
5 f(x)dx = О
-а
(дайте геометрическое доказательство).
60.	Вычислите интегралы:
Л
6	2
1)$<«- + 3х-в№	2)	+
2
61.	Докажите, что если т — целое число, отличное от 0, то л	я
cosmxdx = sinmxdx = 0.
-л	-л
62.	Докажите, что если т и п — целые числа, причём т * п, то Л	л
sinтхsinпхdx = cosmxdxcosnxdx = 0. -л	-л
63.	Докажите, что при любых целых тип
п
sinmxcosnxdx = 0.
—л
64.	С помощью геометрических рассуждений выведите формулу для
X
- t2 dt. о
7.	Оценка значения определённого интеграла. В случае, когда первообразная функции F для подынтегральной функции не выражается через элементарные функции, для отыскания значе-ь
ния интеграла f(x)dx приходится прибегать к приближённым а
методам. Они основаны на следующих утверждениях, дающих границы, между которыми лежит значение интеграла.
Теорема. Если а < b и на отрезке [а; &] функция f неотрица-ь
телъна, то f(x)dx > 0. а
В самом деле, пусть первообразная для функции f равна F. Тогда по условию на отрезке [a; t>] выполняется неравенство F'(x) = f(x) > 0, и потому функция F не убывает на [а; Ь]. Значит, при а < Ь имеем F(b) > F(a) и, следовательно,
ь
J f(x)dx = F(b) - F(a) > 0. а
50
Из этой теоремы непосредственно получаем следствия.
Следствие 1. Если а < Ъ и на отрезке [a; ft] выполняется неравенство (р(х) < \|/(х), то ь	ь
<p(x)dx < yfxydx. а	а
В самом деле, из условия следует, что на отрезке [a; 6] имеем ф(х) < ф(х), и потому ф(х) - ф(х) > 0. Но тогда по доказанному ь
выше получаем, что (ф(х) - <p(x))dx > 0, и, следовательно, в силу а
b	Ь	Ь	b
свойства 4 п. 6 J y(x)dx - (p(x)dx > 0, т. е. <p(x)dx С y(x)dx. а	а	а	а
Следствие 2. Если а <Ъ и на отрезке [а; Ь] выполняются неравенства т < f(x) < М, то
& m(b - а) < f(x)dx < M(b - а).	(1)
а
В самом деле, из условий вытекает, что ь	ь	ь
mdx < f(x)dx < Mdx. а	а	а
b	Ъ	.	ь
Но mdx = m^dx = тх^ = m(b - а) и Mdx = М(Ъ - а), а	а	а
Следовательно, справедливы неравенства (1).
Геометрический смысл неравенств (1) ясен из рисунка 32 — площадь криволинейной трапеции APQB заключена между площадями прямоугольников ASTB и AZRB.
Пример 1. Докажем, что
2
1 < ^x3dx < 8.
Решение. Функция х3 возрастает на отрезке [1; 2], и потому её наименьшее значение т на этом отрезке равно I3 = 1, а наибольшее значение М равно 23 = 8. По неравенствам (1) получаем
2
1 • (2 - 1) < §x3dx< 8 • (2 - 1),
1
2 т. е. 1 < ^x3dx < 8.
1
51
Рис. 33
Полученная оценка интеграла весьма груба. Чтобы получить более точную оценку, прибегают к предварительному разбиению отрезка [a; fe] на части. Если эти части достаточно малы, а функция f непрерывна на [а; Ь], то на каждой из частей наименьшее и наибольшее значения этой функции мало отличаются друг от друга. Поэтому для каждой из частей получаем
сравнительно точную оценку интеграла по данной части. Суммируя эти оценки и учитывая, что сумма интегралов по всем частям равна интегралу по отрезку [а; 6], получаем границы, в которых лежит значение интеграла.
Такие оценки значения интеграла дают различные приближённые формулы для вычисления этих значений. Предположим, что функция f монотонно возрастает на отрезке [а; &]. Разобьём этот отрезок на п равных частей точками а = х0< хх< ... < хп — Ь. Тогда на отрезке [xk; xk+1] наименьшим значением функции будет f(xk), а наибольшим — f(xk+1). Поскольку при этом длина каждого
отрезка [хк; хЛ+1] равна -—получаем, что при любом k выпол-п
йены неравенства (рис. 33)
f(Xb) 	< ?+\(x)dx < /(х*+1)^.	(2)
xk
Суммируя их, получаем, что
Е Ы < ( f(x)dx <	£ f(xk).	(3)
п л = о	J	п	» = 1
Если функция f убывает, то роли левой и правой частей в неравенствах (3) меняются.
При возрастании п разность оценок сверху и снизу стремится к нулю. В самом деле, суммы слева и справа в неравенствах (3) отличаются лишь тем, что слева есть лишнее слагаемое /(х0), т. е. f(a), а справа — лишнее слагаемое f(xn), т. е. f(b). Поэтому разность оценок сверху и снизу равна а (/(b) -
52
Она стремится к нулю при п —> Это показывает, что, беря достаточно большое значение п, можно получить сколь угодно точные оценки интеграла снизу и сверху.
Пример 2. На сколько частей надо разбить отрезок [1; 2],
2
чтобы по формуле (3) вычислить значение интеграла ^x3dx с точ-1
ностью не менее 0,01?
Решение. В данном случае а = 1, b = 2, f(x) ~ х3, и потому f(a) = 1, f(b) - 8. Нам надо найти такое п, что ~ а (f(b) - f(a)) < 0,01, т. е. —-—(8 - 1) < 0,01. Получаем п > 700. Отрезок достаточно разбить на 700 частей.
Неравенства (3) сводят приближённое вычисление интеграла ъ
f(x)dx к вычислению значений функции f в точках х0 = а, хъ ..., а
хп — b и арифметическим операциям. Разумеется, по мере увеличения числа частей, на которые разбит отрезок [а; Ь], разность оценок сверху и снизу уменьшается и точность вычислений увеличивается.
2
Пример 3. В примере 1 мы получили для интеграла x3dx 1 границы 1 и 8. Разбивая отрезок [1; 2] на 10 равных частей, по неравенствам (3) получаем оценки 2
0,1(13 + 1,13 + 1,23 + ... + 1,93) < ^xsdx <
1
< 0,1(1,Is + 1,2s + 1,3s + ... + 1,93 + 23), которые дают для интеграла более точные границы:
2
3,407 < \x3dx < 4,108.
1
Легко понять, что примерное значение для интеграла даёт среднее арифметическое найденных границ. В нашем случае оно равно i (3,407 + 4,108) - 3,7575. Точное значение интеграла равно Л
%	г4 |2	04 _ 14
$x3dx = |i =	4	= 3,75.
1
Оно отличается от найденного приближённого значения на 0,2 %.
53
В общем виде формула приближённого вычисления интегралов с помощью среднего арифметического нижней и верхней границ в (3) имеет вид
С хЧх = (Ла) + f(b} + f(X1) + ... + /(%„_!)).	(4)
Эту формулу называют формулой трапеций, так как её геометрический смысл состоит в том, что на каждом отрезке [хА; криволинейная трапеция заменяется обычной (рис. 34).
Упражнения
65.	Найдя наибольшее и наименьшее значения функции у =	—
з г dx
на отрезке [-1; 3], докажите, что 0,4 < \	+ хг < 4.
-1
66.	Найдите оценки для интегралов: л 2	4	2
1)	sin4xdx; 2)	^x3sinxdx;	3)	^(х2-4х+	l)2dx.
п	1	0
4 1
67.	С помощью равенства = arctgl = § .	2 докажите, что л < 4.
4	„ 1 + х
68. Вычислите по формуле трапеций при п = 10 интегралы:
3 1) $хМх; 1	л 4	2 3)	,, dx ,,;	5) ^cos3xdx; J (1	+ х)2	J 2 '	0
2 2) ( ЛЛх 2', ’ J 1 + X2 0	х	л 2	4 4) sin3xdx;	6) tgxdx о	о
(значения функций брать с точностью до 0,001). Для интегралов 2) и 4) сравните ответ с точным. Проведите вычисления с помощью микрокалькулятора или компьютера.
Показательная, логарифмическая и степенная функции
§ 1. показательная функция и её свойства
1. Процессы органического роста и убывания. В природе, технике и экономике встречаются многочисленные процессы, в ходе которых некоторые величины изменяются так, что отношение значений величины в моменты времени t и t + Т не зависит от t. Иными словами, для всех Т > 0 в течение любого промежутка времени [£; t + Т] значение величины меняется в одно и то же число раз (не зависящее от t). (Значения t могут быть как положительными, так и отрицательными или равными нулю. Отрицательные значения t соответствуют значениям времени, которые предшествуют моменту начала наблюдения.)
Если величина у = f(t) меняется по такому закону, то выполняется равенство
/(t + Т) _ k(T\ f(t) ( ’
(1)
f(T)
Полагая в равенстве (1) t = 0, получим = k(T).
Поэтому из (1) следует:
f(t + Т) = k(T)f(t) =
(2)
Приведём примеры, в которых величины изменяются по указанному выше закону.
Пример 1. Обозначим через m(t) массу колонии бактерий в момент времени t. Если нет ограничений в количестве питательных веществ и объёме сосуда и притом отсутствуют живые существа, поедающие эти бактерии, то за равные промежутки времени масса колонии будет возрастать в одно и то же число раз. Если за единицу измерения массы принять массу одной бактерии, то m(t) будет равно численности этой колонии.
Аналогично обстоят дела для любой совокупности живых существ при условии, что нет ограничений в пище и пространстве
55
и нет истребляющих их врагов. Поэтому процессы, в которых величина увеличивается за равные промежутки времени в одно и то же число раз, называют процессами органического роста.
Пример 2. В процессе радиоактивного распада вещества его масса m(t) за равные промежутки времени меняется в одно и то же число раз. Поэтому и здесь происходит изменение по закону (2), но при этом масса уменьшается. В таких случаях говорят о процессах органического убывания.
Пример 3. Сумма вклада в банке за данный промежуток времени возрастает в одно и то же число раз (например, за год на 2%, т. е. в 1,02 раза). Эта сумма подчинена закону органического роста.
Следует иметь в виду, что во всех разобранных примерах закон (2) выполняется лишь приближённо — мы пренебрегаем тем, что количество живых существ или атомов вещества выражается натуральным числом, что вклад в банке увеличивается не непрерывно, а лишь ежесуточно и т. д. Однако эти отклонения от закона органического изменения так же не мешают применению этого закона на практике, как отклонение формы Земли от геометрически правильной формы шара не мешает вычислению 4 её объёма по формуле V = лЯ3.
Для описания процесса органического роста и убывания используют функцию, значения которой меняются по закону (2). При этом достаточно знать значения этой функции при добавочном условии, что /(0) = 1. Если это не так, то значения функции получатся из найденных умножением на одно и то же число, равное начальному значению функции (если известна сумма f(t) вклада в момент времени t при начальном значении вклада 1 р., то при начальном вкладе а сумма вклада в момент времени t будет равна aftt)).
При указанном добавочном условии ДО) = 1 закон изменения величины (2) примет более простую форму:
f(t + Т) =	(3)
Отметим некоторые свойства величин, которые были рассмотрены выше. Все значения этих величин (масса колонии бактерий, масса радиоактивного вещества, сумма вклада в сберкассе) — положительные числа. При этом за малый промежуток времени эти величины мало меняются. Наконец, скорость изменения этих величин может быть различной. Если за единицу времени величина меняется в а раз, то её значение в момент времени t = 1 равно а. При а > 1 величина увеличивается, при 0 < а < 1 — уменьшается, если же а = 1, то значения величины не меняются, остаются постоянными.
56
В заключение укажем ещё несколько примеров величин, изменение которых происходит по закону (2).
1)	При прохождении света через мутную среду сила света при прохождении любого участка данной длины I уменьшается в одно и то же число раз.
2)	В ходе цепной реакции количество атомов, распавшихся в течение промежутка времени данной длины, увеличивается в одно и то же число раз.
3)	Если канат прилегает к металлическому барабану на протяжении дуги в ср радиан, то, прилагая к одному его концу силу F, можно удержать в k раз большую силу, приложенную к другому концу, где k зависит лишь от ф, а не от величины приложенной силы.
Разумеется, справедливость закона (2) имеет место лишь в случае, когда выполняются соответствующие условия, например в примере 2, когда не все атомы распались, а в примере 3, когда прилагаемые силы меньше предела прочности каната.
Упражнения
69.	Приведите другие примеры процессов органического роста или органического убывания.
70.	Величина х меняется с течением времени t по закону органического роста. Известно, что при t = 0 её значение равнялось 4, а при t = 3 оно оказалось равным 32. Найдите значение величины при t = 1, -1,
71.	Масса радиоактивного вещества при t = 1 равнялась 54 г, а при t = 4 она равнялась 2 г. Во сколько раз меняется эта масса за единицу времени? Какое значение она имела при t = 0, -4, 3, 7 i?
72.	При прохождении света через мутную среду сила света на участке длиной 10 см уменьшилась в три раза. Во сколько раз уменьшится сила света на участках длиной 5, 20, 25 см?
2. Обобщение понятия степени. Предположим, что некоторая величина характеризует процесс органического изменения и в момент времени t = 0 принимает значение т0, а за единицу времени изменяется в а раз. Тогда при t = 1 она принимает значение тоа, при t = 2 — значение тоа  а, т. е. т0а2, при t = 3 — значение т0а2  а, т. е. т0а3, и т. д. С помощью метода математической индукции убеждаемся, что при t = k эта величина принимает значение тоак, т. е. что
m(k) = mQak.	(1)
Естественно предположить, что значение этой величины в момент времени х выражается равенством т(х) - тоах. Покажем,
57
что это действительно так. Сначала напомним обобщения понятия степени, изученные в 9-м классе.
Пусть а > 0. Обозначим через ап выражение tfa"':
а7 = tfa™.	(2)
Покажем, что для любого натурального числа р справедливо т тР
равенство а" - апр , т. е. что значение аг зависит от значения показателя степени, а не от той или иной формы записи его в виде дроби. Для этого заметим, что
I ЩР\ПР , ----хпр
\апр)	- [пЦатр) - атр
и
(а«) = (л/а^Г = ((\/а")П) = (ат)р = атр.
Из равенства натуральных степеней двух положительных чисел т	тр
вытекает равенство их оснований, а потому а" - апр.
Далее полагаем а~г = и а0 = 1.
Тем самым определены степени с любым положительным основанием и рациональным показателем. Для этих степеней были установлены следующие свойства:
1) аг • as = ar+s; 2)	= ar s; 3) (ar)s = ars;
4) (ab\ = а8  b';	5) (f)' =
Напомним, например, доказательство свойства (1). Представим
показатели г и s в виде дробей с общим знаменателем п: г =
пр	т + р
s = п' Тогда имеем аг • as = а" • ап, ar+s - а п . Но
(<Л  Л = (а?)'  (Л =	. («’ =«- 
(аЛ = (Л—<•)" = «"*’
Отсюда следует равенство аг  as= ar+s. Остальные свойства доказываются аналогично.
--- т
Если а > 1, то и ат > 1 при натуральном т, а тогда Уат - ап > 1.
Значит, если а > 1 и г > 0, то аг > 1. Отсюда следует, что при а > 1, г < s имеем
as = аг  as~r > аг • 1 = аг.
Аналогично доказывается, что если 0 < а < 1, г < s, то ar > as.
58
Нам осталось определить значение ах для случая, когда х — иррациональное число. Это можно сделать следующим образом. Пусть а > 1. Обозначим через X множество чисел вида аг, где г — рациональное число, меньшее, чем х, а через У — множество чисел вида а3, где s — рациональное число, большее, чем х. Если ar 6 X, а3 € У, то г < х < s и потому аг < а3. Это означает, что множество X расположено слева от множества У и потому эти множества разделяются хотя бы одним числом. Можно доказать, что это разделяющее число определено однозначно. Его называют значением ах. При 0 < а < 1 поступают аналогичным образом, только меняют роли X и У.
Итак, мы определили для каждого х значение а*. Этим определяется функция у = ах, заданная на всей числовой оси. Можно доказать, что эта функция непрерывна, принимает по одному разу все положительные значения, возрастает, если а > 1, и убывает, если 0 < а < 1. Она обладает свойствами 1) — 5), ранее доказанными лишь для рациональных значений аргумента. Отсюда следует, что если f(x) - тоах, то для любого Т имеем
f(x + Т) _ тоа”т _ ах  ат _ т _ .. f(x) moa* ах	Д ’’
Это показывает, что функция у = пгоах действительно описывает процессы органического изменения.
Однако детальное доказательство единственности разделяющего числа для множеств X и У, непрерывности функции у = ах и т. д. довольно кропотливая работа. Чтобы избежать её, мы определим показательную функцию иначе и покажем, что так определённая функция обладает всеми нужными свойствами. Сначала придётся определить иную функцию, называемую логарифмической .
Упражнения
73.	Какое из чисел больше:
1)	(3,2)"7 или (3,2) 4;	3) (л/2 + >/з) ’ или (>/2 + >/3 )
2)	2~7,5 или (0,25)3 73;	4) (^2 - л/з) 3 или (^2 - >/з) \
74.	Расположите в порядке возрастания числа: (0,45)"3, (0,4а)1, (0,45)°, (0,45)2.
75.	Какое из чисел больше:
75
1)	2м1 или (0,25)" 2 ;	2) 3й или 3й ?
76.	Положительна или отрицательна разность:
1)	- (л/зГ; 2) (I)275-!?
59
77.	Определите знак:
1)	а, если = 2; 2) а - 1, если а + 40’3^ = 5.
78.	(0,37)“ < (0,37)₽. Что больше: а или р?
79.	Можно ли найти такое х, чтобы выполнялось равенство 2S‘"! х = sin х?
3.	Определение функции In х, её свойства и график. Мы умеем находить первообразные от функций вида у = ха при условии, что а * -1. Среди степенных функций нет такой, что её производная
равна т. е. х1. Введём следующее определение.
Определение 1. Натуральным логарифмом положительного числа х называют значение интеграла у-. Это значение обо-1 значают 1пх: X
lnx=$f-	(!)
Так как функция | непрерывна на луче (0; +°°) и убывает
на нём, то значение 1пх определено для всех х > 0 (см. теорему 1 п. 3 § 3 главы 1). Значит, функция у = 1пх определена на луче 1
(0; +°°). При х = 1 значение этой функции равно —, т. е. равно 1
X
нулю. Значит, 1п1 = 0. Интеграл — является одной из первооб-
1
разных для подынтегральной функции (см. п. 3 § 3 главы 1). Это значит, что при х > 0
(1пх)' =
1
X ’
Значит, функция In х дифференцируема на луче (0; +°о), причём
(1пх)' = i.
(2)
Так как всякая дифференцируемая функция непрерывна, то функция у - 1пх непрерывна на луче (0; +°°).
Поскольку х > 0 на луче (0; +°°), то на этом луче (1пх)' =	> 0.
Значит (см. п. 4 § 3 главы 5, 10 кл.), функция 1пх возрастает на луче (0; +°°). Так как in 1 = 0, то функция In х положительна на луче (1; +оо) и отрицательна на промежутке (0; 1).
60
Докажем теперь, что при любом а > 0 функция In ах тоже является первообразной для функции на луче (0; +°°). В самом деле,
(Inax)' = — (ax)' = — = —. ах	ах х
Так как две первообразные одной и той же функции могут отличаться друг от друга лишь постоянным слагаемым, то на луче (0; +°°) должно иметь место равенство In ах = 1пх + С. Полагая х = 1 и учитывая, что Ini - 0, получаем: С = Ina.
Мы доказали следующее важное свойство функции 1пх.
Если а > 0 и х > 0, то
Inax = Inx + Ina.	(3)
Иными словами, натуральный логарифм произведения равен сумме натуральных логарифмов множителей.
Из равенства (3) вытекает:
если а > 0 и х > 0, то
In — = Ina - Inx;	(4)
х
если х > 0 и п — натуральное число, то
lnx"=nlnx.	(5)
Полагая в равенстве (5) хп = у и учитывая, что х = получаем
In л/х = — Inx, х > 0. п
(6)
Из формул (5) и (6) вытекает, что
In \>'х" = — Inx, х > 0. п
(7)
В самом деле,
In Vx" =
- Inx" = n
m л
— Inx.
n
Докажем, что функция In x принимает сколь угодно большие по модулю как положительные, так и отрицательные значения. В самом деле, так как 2 > 1, то In 2 > 0 и из равенства In 2" = п In 2 получаем, что среди значений функции у = 1пх есть сколь угодно
большие положительные числа. Равенство In — = -a In 2 пока-2
зывает, что среди этих значений есть и сколь угодно большие по
модулю отрицательные числа.
Итак, функция у - Inx непрерывна на луче (0; +°°), возрастает на нём и принимает сколь угодно большие по модулю положительные и отрицательные значения. Отсюда следует, что эта функция по одному разу принимает любое действительное значение.
61
Наконец покажем, что график функции 1пх на луче (0; +°о) обращён выпуклостью вверх. В самом деле,
(1ПХ)" = ((1пх)')' = (У = ~±.
Ясно, что на луче (0; +°°) имеем (1п)" < 0, откуда и следует наше утверждение (см. п. 5 § 3 главы 5, 10 кл.).
Поскольку функция In х принимает по одному разу все действительные значения, то найдётся такое число, что его натуральный логарифм равен 1. Это число было введено в математику действительным членом Петербургской академии наук Леонардом Эйлером (1707—1783) и получило обозначение е.
Итак, через е обозначают число, натуральный логарифм которого равен 1, т. е. для которого выполнено равенство 1пе = е
=	= 1. Очевидно, что е > 1. Так как площадь квадрата ABCD
1
на рисунке 35 равна 1, то видим, что In 2 < 1 и потому 2 < е. С другой стороны, площадь фигуры, заштрихованной на рисунке 35, равна 1, и потому видим, что 1 < 1пЗ, откуда е < 3. Значит, число е заключено между 2 и 3. Более точные методы, которые мы приведём в п. 5 § 3, показывают, что е = 2,7182818284590... Это число иррациональное.
Из равенства (7) следует, что 1п е" = ~ 1пе = Поэтому имеем следующую таблицу значений функции 1пх:
X	1 е3	1 е2	1 е	1	е	е2	е3
In X	-3	-2	-1	0	1	2	3
Используя указанное выше значение е и свойства функции 1пх, строим график этой функции (рис. 36). Из этого графика видно, что по мере увеличения х значения 1пх медленно увеличиваются.
\ У =| 1  - в — с 0	12	3 Рис. 35	Ум у = 1пх __ ° А	*х V	/ Рис. 36
62
А когда x приближается к нулю, оставаясь положительным, значения Inx стремятся к Таким образом,
lim Inx = +°°, lim Inx -X -> too	X —> +0
У пражпения
80.	Найдите производные следующих функций:
1)	ln(4x + 1);	3) In sin х;	5) 1п3х;	7) arctg4 (Inx);
2)	ln(x2 - х + 1);	4) Inarctgх;	6) sin(Inx);	8) arcsin(In5x).
Постройте графики функций (81—85).
81.	у	=	In(16 -	8х	+	х2) - ln(2x - 8).
82.	у	=	In (2 -	+	in (x2 - 12x + 36).
83.	у	=	In (x -	+	In -\/4x2 - 4x + 1.
84.	у	=	In -	xj	+	In >/9x2 - 6x + 1.
85.	1) у = ln(|x - e| + x);	2) у = |ln(x - 2)| + ln(3x - 6).
4.	Логарифмическая функция и степень с любым показателем.
Пусть а > 0 и а Ф 1. Функция принимает значение 1 при х = а. Её называют логарифмической функцией по основанию а и обозначают logax. Таким образом, по определению ,	In х
logox - 5--.
In а
Если а > 1, то Ina > 0. Поэтому ясно, что свойства функции log„x при a > 1 те же, что и у функции 1пх: эта функция непрерывна на луче (0; +°°), возрастает, принимает положительные значения при х > 1 и отрицательные при 0 < х < 1, причём она принимает все действительные значения. При этом lim logax = +°°, X —> +оо
lim logax = -00.
х —> +0
Если же 0 < a < 1, то Ina < 0. Поэтому свойства функции logax при 0 < a < 1 в некотором смысле противоположны свойствам функции Inx. В этом случае функция logflx, оставаясь определённой и непрерывной на луче (0; +°°), убывает на этом луче, причём её значения положительны на промежутке (0; 1) и отрицательны на луче (1; +оо). При этом lim logax = -00, lim logax = +°o.
На рисунке 37 изображены графики функций log2x и log, х.
2
Из равенства (7) п. 3 следует, что = lna| In a
logfl a
— Ina n _ m
In a n
63
Обозначим число ап через b, Ъ = ап. Так как = logob, то Ь = а1ое‘ь. Таким образом, в случае, когда а>0, а*1,Ь>0и логарифм числа Ъ по основанию а — рациональное число, логарифм является показателем степени, в которую надо возвести основание а, чтобы получить число Ъ. Обобщая это утверждение на любые показатели, приходим к сле
дующему определению.
Определение 2. Пусть а > 0, а 1. Через ах обозначают такое число Ь > 0, что logab = х (как мы знаем, такое число всегда существует и однозначно определено). Запись ах читают «а в степени х». При а = 1 полагаем Iх = 1 для всех х.
Итак, имеют место два основных равенства
\ogaax = х,	(1)
a,ogab = b, b > 0.	(2)
В частности, Inx = logex и потому
In ех = х,	(1')
e'nb = b,b>0.	(2')
Отметим, что при любом а > 0, а * 1 выполняются равенства logoXJ/ = logaX + logal/, X > 0, у > 0,	(3)
logo - = logaX - logal/, X > О, у > О, У
т
logax" = logaX, X > 0.
(4)
Для их доказательства достаточно заменить логарифмы с основанием а их выражением через натуральные логарифмы.
Отметим ещё формулу
log b = а > 0, b > 0, с > 0, с * 1, ьа logc а
(5)
позволяющую выразить логарифмы с основанием а, а > 0, а * 1, через логарифмы с основанием с, с > 0,	с *	1.	Для доказательства
1 l	In b	.	In а	1пЬ	п
заметим,	что	logao =	i,	logca	=	:—,	logcb	=	?—.	Подставляя
In a	in c	in c
эти значения в формулу (5), убеждаемся в её справедливости.
64
Отметим некоторые частные случаи формулы (5). Полагая с = Ь, получаем в силу равенства log^d = 1:
log„b =	, а > О, Ь > 0, а * 1, b * 1.	(6)
log.,, а
Далее при а = са имеем в силу равенства logc с“ = а:
log а Ъ =	= - logcfe, Ъ > 0, с > О, с * 1.	(7)
logcc“ а
При Ь = са, с > 0, с * 1, имеем
108-с“=М^ = ьЬ=а10е-е-	<8)
Из(7)и(8) следует, что
log,., ba = logcfc.	(9)
Логарифмы по основанию 10 называются десятичными и обозначаются 1g. Таким образом, lg х = log]0x. Десятичные логарифмы раньше использовались для выполнения громоздких вычислений.
Пример 1. Вычислим значение: a) logioo Ю00; б) log^ V2. Решение, а) Имеем
log1001000 =
logi01000 _ lglO3 _ 31g 10 _ 3
log10100 lglO2 21g 10	2’
б) Имеем
log^V2 =
log2 ^2 log2 </2
I log2 2
I log2 2
1
3’
Пример 2. Выразим логарифм
по основанию а выражения
.	1(х2 + 1)4(г/4 + I)7	2t„4/-
А= --------------—---------— • a2tgIJVa
V (X2 + г/2)6
через логарифмы выражений х2 + 1, у4 + 1, х2 + у2.
Решение. По свойствам логарифма
.	.	.	(х2 + 1)Чг/4 + 1)® 2tgx + l
logaA = loga i----	6 a 4 =
(x2 + у2У
= I loga(x2 + 1) + I log„(y4 + 1) - I logo(x2 + г/2) + 2tgx 4-
Взятие логарифма некоторого выражения с последующим упрощением, как в разобранном примере, называют логарифмированием.
65
Пример 3. Найдём выражение, логарифмом которого по основанию а является
А = у loga(x4 + 2у2 - 1) - | cos5x - | loga(x + 6z/2).
Решение. По свойству логарифмов имеем cos5x = logaacos6x. Поэтому
А - |(61ogo(x4 + 2у2 - 1) - 31ogaacos5x - 21oga(x + 6г/2)) =
= | (logo(x4 + 2у2 - l)e - logaa3cos6x - log„(x + бу2)2) =
1	(х4 + 2у2 - 1)» =	1(х4+2у2-1)°
7 Йа a3ras5x(X + 6j/2)2	^дЗс^бх^ + 6г/2)2
Итак, А = logaB, где
= I (х4 + 2у2 - 1У~ ^a3cos5l(x + бу2)2'
Отыскание выражения по его логарифму называют потенцированием.
Упражнения
86.
Вычислите:
87.
1) logi 64; 2) logs V243; 3) logi00o V10; 4) log7 > 2
При каких значениях х справедливы неравенства:
1)	log7x < log72x;
5)
41og448 glogglS *
88.
89.
90.
91.
92.
2)	logo.sx > logo,5 2;
3)	logx5 < log* 6;
4)	logx V2 <logxl,2;
5)	logxsin < logxsin
6)	logx0,3 > logx3?
Что больше: logaN или log„ —, если:
1) a > 1, 7V>1;	3) a > 1, 0 <2V < 1;
2) 0 < a < 1, ЛГ > 1;	4) 0 < а < 1, 0 <	< 1?
Найдите область определения следующих функций: 1) logi (4х - 8);
2)	logi2(8 - 2х);
3)	log5(-4x - 6);	5) log2(x - 4) +
logi (4 - х).
9
4)	logl (4x + 6); 5
Начертите графики функций из предыдущего упражнения.
Начертите график функции log2(x - 4) + log2(8 - х).
Какая из функций быстрее возрастает, когда х —> +°°: 1) log3x, log2x; 2) logi х, log; x? 3	2
Какая из этих функций больше на промежутке 0
1?
66
93.	Постройте графики функций:
1)	logi|x|; 2) |log3x|; 3) |log3(x - 2)|.
3
94.	Постройте линии, задаваемые равенствами:
1)	Ы = log3(* - 1);	2) |j/| = |log4(2x - 1)|.
95.	Зная, что lg2 ~ 0,3010, lg3 = 0,4771, найдите 1g75.
96.	Является ли равенство
log2(x1 2- 4) = log2(x - 2) + log2(x + 2) тождеством? В какой области оно тождественно выполняется? 97. Прологарифмируйте по основанию а следующие выражения:
п	зМ2^.
f	N Ь2 + с2'
24m2\lb + с, п*Уь - с
2) х = ^b-JbTb;
!а4Ь'3сг\т + п
4)	х = s--------;----
V	d~3y*
98.	Прологарифмируйте выражение х = 27 b5 с2 >/27 + z:
1)	по основанию 3;	2) по основанию т?.
О
99.	Найдите х, если:
1)	logax = |(logab - |logac + logad + 4);
2)	10gaX = |(10gaJ/ + |(10ga Z - 2)jj
3)	logaX = 3[iloga</ + ^(logaz - |(loga t + 2logaU>)) О \	О	/
100.	Докажите, что
101. Что больше:
loga N logo* N
- 1 + lOgafc.
1) logj 2 или log3
3	z
2) log45 или log5 6?
102.	Докажите, что:
loga N + loga! N + loga» N + l°go< N + loga» N ^OgvO.
2)	loga, ...a, X = —--------------7---;
------+ ... + -------- loga, X 10ga, X
3)	logaW log^ + log(^ logcN + logcN loga# = loS° loS» ] lOga*e N
103.	Зная, что logs 2 = a, log6 5 = b, найдите log35.
67
104.	Зная, что log122 = а, найдите log616.
105.	Зная, что logi02 = 0,301, найдите logi0125.
106.	Докажите, что если а и Ь — длины катетов, ас — длина гипотенузы прямоугольного треугольника, то
logt + ca + logc_|,a = 2log* + са logс - ьа.
107.	Упростите выражение:
ill	2	.	3	. п + 1
1)	logoT + 10go- + ... + loga-;
12	п
2)	(logi,a - loga b)2 + (log i a - log„2 b)2 + ... + (log ±a - log„2» b)2; ь!	1,2"
logb log» q
3)	а 1°8ь<’ .
108.	Вычислите пределы:
x->+o 4 + ln2x’	*-»+<> 4 + ln2x’
..	1 + ln2x	.. ..	1 + Inx
2)	lim --------, — ;	4) lim ------------.
3 + 51n2x	n+o 3 + 51nx
5.	Показательная функция, её свойства и график. В п. 4 мы определили значение ах при всех a > 0 и любых х. Если а = 1, то ах= 1 при всех х. При других положительных значениях а получаем функцию ах, отличную от постоянной. Её называют показательной функцией с основанием а. Из доказанных в п. 4 равенств logaax = х,
= ь, ь> о,
вытекает, что показательная функция с основанием а, а> 0, a 1, является обратной к логарифмической функции с тем же основанием. Отсюда следует, что функция ах задана на всей числовой прямой, принимает все положительные значения по одному разу и непрерывна. Она возрастает, если а > 1, и убывает, если 0 < a < 1.
На рисунке 38 изображены графики показательной функции при a = 2 и a =
Отметим, что при a > 1 имеем lim ах =
X —> +оо
= +°о, lim ах = 0. Если же 0 < a < 1, то х -оо
lim ах = 0, lim ах = +°°. х —> +ОО	X -ОО
Каждому свойству логарифмической функции соответствует свойство показательной функции. Докажем сначала, что для всех значений х и t при a > 0 имеем ах  а*= ах+‘.	(1)
68
Если а - 1, то это равенство очевидно, поскольку Iх = 1‘ = 1х+' = 1.
Если же а Ф 1, то по (3) п. 4 имеем
logaax+1 = х + t и loga(ax • а') = logaax + logaa‘ = х + t.
Но два числа, имеющие одинаковые логарифмы по основанию а, где а > 0, а 1, равны. Отсюда получаем (1).
Докажем теперь, что при а > 0 для любых х и t выполняется равенство
(а1)' = ах'.	(2)
В самом деле, при а = 1 обе части равенства равны 1. Если же а > 0, а 1, то по (8) п. 4 имеем
logaax< - xt и loga(ax)' - tlogaax = xt.
Значит, логарифмы по основанию а чисел (ах)' и ах‘ равны, а потому равны и сами эти числа.
Из свойства (2) вытекают равенства
а~Х = (аХ) ' = F	<3>
И
у/а/ = ап	(4)
(достаточно взять соответственно t = — 1 и t =
Теперь докажем, что для любых положительных чисел а и Ь выполняется равенство
(ab)x=axbx.	(5)
Для этого достаточно заметить, что по (3) и (8) п. 4 имеем ln(ab)x = xln(ab) = x(lna + lnb) и
ln(ax • bx) = lnax + lnbx - xlna + x lnb - x(lna + Inb).
Из доказанного утверждения вытекает, что для любых положительных чисел а и b верно равенство
/а\х _ ах
\ь/ - F'	(6)
Упражнения
109.	Докажите равенство (б).
110.	1) Постройте на одном чертеже графики функций у = 2х и у = 3х при -1 < х < 1 в масштабе 1 : 5 см.
2)	Изобразите на одном чертеже графики функций у = 2х, у = 3 • 2х, у = 0,8 • 2х, у = -3 • 2х, у = -0,8 • 2х.
111.	Как по графику функции у = с  а* определить основание а и коэффициент с?
69
112.	Докажите, что для любой показательной функции /(х) = ах и любой геометрической прогрессии blt Ь2, Ь3, ... с положительными членами найдётся такая арифметическая прогрессия хь х2, х3, ..., что для всех п будет f(xn) = bn.
113.	Решите следующие уравнения, пользуясь, где это необходимо, графиками показательных функций:
1)	5х = 25; 2)	З1’1 = 81; 3)	2х = 0,125; 4)	2х = 0,4;	6)	33x l = 1; 7)	4х = 8; 8)	8х = 10; 9)	83~2х = 14;
5) 52х = 5;	10) 0,012 = 70.
114. Упростите выражения:
1) (2х)2 - 3 4х + (ТгГ;	3) 52х - 1 - (5х - 1)(5Х + 1);
2) 22х • 3х + 12х - 2Х+1Х • 6х;	4) а2х + 2ах^ + № - (ах + ^)2.
Вычислите пределы (115—120).
115.	lim	1		116.	lim	2х	+ 1	117.	lim	2х	- 1
	X —> +ОО	X2 +	3х		х -> -ОО	2х •	4- 4		X ->+оо	2х	+ 1
118.	lim	0,3*	+ 2	119.	lim	0,3	* + 2	120.	lim	3х	+ 1
	х —» +ОО	0,3х	+ 5		X -ОО	0,3	" + 5		X -> +ОО	5х	+ 2
§ 2. Показательные а логарифмические уравнения и неравенства
1. Простейшие показательные уравнения и неравенства. Простейшим из показательных уравнений (т. е. уравнений, содержащих неизвестное в показателе) является ах = Ъ, где а > 0, а * 1.
Если b < 0, то это уравнение не имеет решений, поскольку значения а1 положительны. Если же b > 0, то существует един
ственное значение х, удовлетворяющее этому уравнению, а именно х = logab.
1g ъ
Значение loga b равно и потому может быть вычислено с помощью таблиц десятичных логарифмов или микрокалькулятора.
Пример 1. Решим уравнение 5х - 8.
Решение. Единственным корнем данного уравнения явля-
ется число log58, т. е
1g 8
1g 5'
По таблицам десятичных логарифмов
находим
1g 8 = 0,903
1g 5	0,699
= 1,29.
Итак, приближённое значение единственного корня данного уравнения равно 1,29.
70
Иногда удаётся представить число b в виде ас. Тогда корнем уравнения ах = Ь является число с.
Приме Р 2. Решим уравнение 16х - 256.
Решение. Так как 256 = 162, то х = 2.
Пример 3. Решим уравнение 16х = 512.
Решение. Число 16 можно представить в виде 16 = 24, число 512 — в виде 512 = 29. Значит, данное уравнение записывается в
виде (24)х = 2е, или 24х = 29. Отсюда находим, что 4х = 9, и потому
Тот же результат получается следующим образом:
х = logi6512 =
log2512 _ 9
log216 4'
Перейдём к решению простейших показательных неравенств. При Ь < 0 неравенство ах < b не выполняется ни при каком значении х, поскольку ах > 0. Неравенство же ах > Ъ выполняется для всех х. Поэтому интересен лишь случай b > 0.
Мы знаем, что при b > 0 выполняется равенство a}og-b = b. Если а > 1, то в силу возрастания показательной функции ах при х > logo б выполняется неравенство ах > Ъ, а при х < logo Ь — неравенство ах < Ъ.
Итак, при а > 1 решением неравенства ах> b является открытый луч (logo&; +°°), а решением неравенства ах < b — открытый луч (-°°; loga£>) (рис. 39, а).
Если 0 < а < 1, то функция ах убывает. Поэтому при 0 < а < 1 решением неравенства ах > Ъ является открытый луч (-°°; logofe), а решением неравенства ах < b — открытый луч (logo&; +°°) (рис. 39, б).
71
Пример 4. Решим неравенство - < —.
\4 /	16
Решение. Сначала решим уравнение (у) - Так как
=	’ то х = 2. Поскольку в нашем случае а = 1 < 1, то ре-
шением неравенства (1) < является луч (2; 4-о°).
'4 /	10
У пражнения
121.	Решите уравнения:
1)	3* = 729;	2) ± = 8;	3) 9х = 243;	4) (V2 Г = 1.
2	4
122.	Решите неравенства:
1)	2х < |;	2) (М > 1;	3) (|) >	4) 3’ > 92‘.
2.	Решение показательных уравнений и неравенств. В основе решения показательных уравнений лежит следующая теорема.
Теорема. Если а > 0 и а Ф 1, то уравнения
а^=аЛх)	(1)
и Кх) = g(x)	(2)
равносильны. Доказательство. Если а — корень уравнения (2), то имеет место равенство Да) = g(a), а тогда аЯа) = аЛа\ Обратно, если а — корень уравнения (1), то аЛи) - agW, а тогда в силу монотонности функции ах имеем Да) = g(a). Теорема доказана.
Пример 1. Решим уравнение 33^ + 2 =	+	(3)
Решение. Это уравнение равносильно уравнению Зх2 + 2 = = х2 + 5х, корнями которого являются xt - ~, х2 = 2. Эти числа Ct являются и корнями уравнения (3).
К уравнениям вида (1) сводятся уравнения вида аЯ1> =&**>.
Мы знаем, что b = alogab. Поэтому уравнение (4) можно переписать в виде af(x)= ag(x)i°s‘b. А это уравнение при а > 0, а Ф 1 равносильно уравнению
Дх) = я(х) loga&.
72
Пример 2. Решим уравнение
32х’5 = 5х.
Решение. Это уравнение равносильно уравнению g2x-S _ gx!og3S
а потому и уравнению 2х - 5 = xlog35. Корнем этого уравнения 5
является X = ---;
2 - log3 5
Рассмотрим теперь уравнения вида f(ax) = 0. Они решаются с помощью подстановки ах = t, которая сводит их к уравнению f(t) - 0. Пусть Д, tn — корни полученного уравнения. Так как ах принимает лишь положительные значения, то надо отобрать из этих корней положительные, скажем tr, ..., tk, и решить уравнения ах - fi, ..., ах = tk. Отсюда находим хг = logatj, ..., хк = logat*.
Пример 3. Решим уравнение
4х _ 2x+i - 24 = 0.
Решение. Так как 4х = (2х)2, 2х+1 = 2 • 2х, то это уравнение
можно переписать в виде
(2х)2 - 2 • 2х - 24 = 0.
Подстановка 2х = t сводит его к квадратному уравнению t2 - 2t -— 24 = 0, имеющему корни = 6 и t2= —4. Из них положителен лишь корень 6. Поэтому осталось решить уравнение 2х = 6, из
которого находим х = log26 =
1g 6 lg2’
Для решения показательных неравенств используется свойство монотонности показательной функции. Если а > 1, то неравенство aflx} > аЛхУ равносильно неравенству f(x) > g(x), а если 0 < а < 1, то неравенству Дх) < g(x).
Пример 4. Решим неравенство
0,5х2 + 2х + 1 > 0,5х2’3.
Решение. Так как 0 < 0,5 < 1, то это неравенство равносильно неравенству х2 + 2х + 1 < х2 - 3. Решая это алгебраическое неравенство, находим, что х < -2.
Пример 5. Решим неравенство
£2х2 + Зх + 2 > 2х2
Решение. Так как 2 > 1, то это неравенство равносильно неравенству 2х2 + Зх + 2 < х2, т. е. х2 + Зх + 2 < 0. Решая его, получаем, что -2 < х < -1.
Неравенства вида f(ax) < 0, где f — некоторая функция, решаются с помощью подстановки ах = t. Получаем для t неравенство
73
f(t) < 0. Так как а1 > 0, то надо найти пересечение решения этого неравенства с открытым лучом (0; +°°) (т. е. взять часть решения, лежащую на этом луче). Если (<х*; 0Л) — один из промежутков полученной части решения для f(t) < 0, то для отыскания решения исходного неравенства получаем ak < ах < Р*.
При а > 1 отсюда имеем logaa* < х < loga ₽*, а если 0 < а < 1, то logaPb < х < logaak. Далее надо объединить все полученные промежутки.
Пример 6. Решим неравенство
4х - 2Х+1 - 24 < 0.
Решение. Подстановка 2х = t сводит данное неравенство к неравенству t2 - 2t - 24 < 0. Его решением является интервал (-4; 6). Пересечением этого интервала с лучом (0; +оо) является (0; 6). Решая неравенство 0 < 2х < 6, получаем, что -оо < х < log26.
Упражнения
123.	Решите показательные уравнения:
1)	4х-1 + 4» = 320;	6) 23х • 3х - 23х1 • Зх+1 = -282;
2)	5х + 3 • 5х-2 = 140;	7) 0,5х’ 20х~й1'5 = Д;
V2
х-1	хД
3)	5х - 53 х = 20;	8)	4х - 3	2 = 3 2	- 22х’*;
4)	2 • Зх+1 - 5 • 9х2 = 81;	9)	4^ +	16 = 10 •	2/х~2;
5)	52х - 7х - 35 • 52х + 35	• 7х = 0;	10)	52+4+6+	+2х = 0,04	45.
124.	Решите показательные неравенства:
1)	> 2'8х2 + э; 3) 22х+1 - 5 2х + 2 < 0;
2) 4х - 7 • 2х + 12 > 0;
4) |2Х - 2| - |2Х - 1| > |2Х + 1| - 5.
3.	Простейшие логарифмические уравнения и неравенства. Простейшим логарифмическим уравнением (т. е. уравнением, содержащим неизвестное под знаком логарифма) является logax = b, где а > 0, a Ф1. Так как равенство logax = Ъ равносильно равенству х = аь, то получаем следствие:
если а > 0, a 1, то корень уравнения logax = b равен аь.
Пример 1. Решим уравнение log3x = 7.
Решение. Корнем уравнения является число х = З7.
Пример 2. Решим уравнение 1gх - 0,5.
Решение. Корнем уравнения является число х = 100,s = >/10.
В силу монотонности логарифмической функции решение логарифмических неравенств вида logax < Ь (а также вида logax > Ь, logax < b, logax > Ъ) сводится к решению уравнения logax = Ъ.
74
Корнем этого уравнения является число х = аь. Если а > 1, то функция logox возрастает, и потому при х > аь имеем logax > Ъ, а при 0 < х < аь имеем logax < Ъ. Мы доказали следующее утверждение.
Если а > 1, то решением неравенства logax > b является открытый луч (аь; +°°), а неравенства logax < Ь — интервал (0; аь) (рис. 40, а).
При 0 < а < 1 функция logax убывает, и потому верно следующее утверждение.
Если 0 < а < 1, то решением неравенства logox > Ъ является интервал (0; а6), а неравенства logox < Ъ — открытый луч (аь; +°°) (рис. 40, б).
Пример 3. Решим неравенство logj х < 3.
4
Решение. Корнем уравнения logj х = 3 является число 4
= тгт- Так как основание а = -у < 1, то решением неравенства \4/	64	4
/ 1 является открытый луч —; +°о \64
Пример 4. Решим неравенство log4x < 0,5.
Решение. Корнем уравнения log4x = 0,5 является число 40,5 =	=2. Так как в данном случае а - 4 > 1, то решение дан-
ного неравенства имеет вид (0; 2).
Упражнения
125.	Решите уравнения:
1)	logj х = 2>5; 2) log^ х = -6.
2
75
126.	Решите неравенства относительно х:
1)	log3x >	3) log^x > logaVx;
2)	logj х <	4) log5x < logs 10.
3 о
4. Решение логарифмических уравнений и неравенств. В силу монотонности логарифмической функции при любом а > 0, а Ф 1 равенство loga Дх) = logag(x) выполняется лишь при условии Дх) = g(x). Поэтому уравнение logo Дх) = logag(x) в области, где Дх) > 0 и ё(х) > 0» равносильно уравнению Дх) = g(x).
Итак, справедлива следующая теорема.
Теорема 1. Уравнение logaf(x) = logag(x), где а > 0, а * 1, равносильно системе
Дх) = g(x),
Дх) > 0,	(1)
£(х) > 0,
состоящей из уравнения и двух неравенств.
Замечание. В этой системе можно опустить одно из неравенств, так как каждое из них вытекает из уравнения и другого неравенства.
Таким образом, для решения уравнения loga Дх) = logag(x) при а > 0, а * 1 нужно:
1) решить уравнение Дх) - g(x);
2) из найденных корней отобрать те, которые удовлетворяют неравенству Дх) > 0 (или, что то же самое, неравенству g(x) > 0; обычно используют более простое из этих неравенств), а остальные корни отбросить, так как они являются для данного уравнения посторонними.
Пример 1. Решим уравнение
log3(x2 - Зх - 5) = log3(7 - 2х).
Решение. По теореме 1 это уравнение равносильно следующей системе:
!х2 - Зх -5=7- 2х,
|7 - 2х > 0.
Корнями уравнения х2 - Зх - 5 = 7 - 2х являются числа -3 и 4. Осталось отобрать из этих чисел те, которые удовлетворяют неравенству 7 - 2х > 0. Ему удовлетворяет корень -3 и не удовлетворяет корень 4. Значит, 4 — посторонний корень. Итак, х = -3.
Пример 2. Решим уравнение
lg(x + 4) + lg(2x + 3) = lg(l - 2х).	(2)
76
Решение. Логарифмы, входящие в это уравнение, определены для значений х, при которых
х + 4 > 0, 2х + 3 > 0, 1 - 2х > 0.	(3)
При этих значениях х данное уравнение преобразуется к виду lg((x + 4)(2х + 3)) = lg(l - 2х)
и далее к виду
(х + 4)(2х + 3) = 1 - 2х.
Из этого квадратного уравнения находим: Xt = -1, х2= -5,5.
Осталось отобрать из найденных корней те, для которых выполняются неравенства (3). Им удовлетворяет корень хх и не удовлетворяет корень х2. Значит, х = — 1.
Логарифмические уравнения вида f(logax) = 0 решаются с помощью подстановки log„ х = t. Она приводит уравнение к виду f(t) = 0. Если tu ..., tn — корни полученного уравнения, то корнями заданного уравнения являются числа а'1, ..., а1".
Пример 3. Решим уравнение
logi X + log3 X + 1 = ---.
log Л о
Решение. Так как log3 = log3x - log33 = log3x - 1, то данное О
уравнение можно переписать в виде
logfx + log3 X + 1 =  -7-—_-.
iog3 X 1
Положив log3x = f, получаем уравнение
t2 + t + 1 =
т. е. (t - 1)(£2 + t + 1) = 7, или, что то же самое, t3 - 1 = 7. Отсюда находим, что t3 = 8, т. е. t = 2. Из уравнения log3x = 2 получаем х = З2 = 9. Итак, х = 9.
Пример 4. Решим уравнение
log|x - 51og3x + 21 = 0.
Решение. Так как
l0g9X=^ = l£^,
log, 9	2
то это уравнение можно представить в виде
- 51og3x + 21 = 0.
Подстановка log3 х = t приводит к уравнению
t2 - 20t + 84 = 0.
77
Его корнями являются ti = 6, t2 = 14.
Значит, корнями данного уравнения являются Xi = З6 = 729 и х2 = З14.
В силу монотонности логарифмической функции решение неравенства вида
logflf(x) > logag(x)	(4)
сводится к решению соответствующего неравенства, связывающего /(х) и g(x). Если а > 1, то из (4) следует /(х) > g(x), а если О < а < 1, то /(х) < g(x). При этом в обоих случаях надо учесть, что должны выполняться неравенства /(х) > 0 и g(x) > 0.
Таким образом, справедлива следующая теорема.
Теорема 2. Если а > 1, то неравенство loga/(x) > logag(x) равносильно двойному неравенству
/(х) > g(x) > 0.	(5)
Если 0 < a < 1, то неравенство logaf(x) > logog(x) равносильно двойному неравенству
0 < /(х) < g(x).	(6)
Пример 5. Решим неравенство log] (4х - 14) < -1.
Решение. Так как = 2, то -1 = logj 2 и данное неравен-
2
ство можно записать так:
log, (4х - 14) < 10gl 2.	(7)
2	2
Поскольку в данном случае основание логарифмов а = ± меньше
чем 1, неравенство (7) равносильно двойному неравенству
4х - 14 > 2 > 0,
из которого находим, что х > 4.
Итак, решение заданного неравенства имеет вид х > 4, или иначе [4; +<»).
Пример 6. Решим неравенство
1g(х + 27) - lg(16 - 2х) > 1gх.
Решение. Все логарифмы, входящие в это уравнение, определены для значений х, при которых выполняются неравенства х + 27 > 0, 16 - 2х > 0, х > 0. Для этих значений х имеем
lg(x + 27) > Igx + lg(16 — 2х)
и далее
1g (х + 27) > lg(x(16 - 2х)).
78
Поскольку основание 10 десятичного логарифма больше единицы, то данное неравенство эквивалентно следующей системе неравенств:
х + 27 > х(16 - 2х), х > 0,
16 - 2х > 0.
Из неё получаем
|2х2 - 15х + 27 > 0, [О < х < 8
и далее
2(х - 3)(х - 4,5) > 0, О < х < 8.
Отсюда следует, что 0 < х < 3 или 4,5 < х < 8. Это решение можно записать в виде (0; 3) U (4,5; 8).
В заключение рассмотрим неравенства вида f(logax) > 0. Сделаем подстановку logax = t. Тогда неравенство примет вид f(t) > 0. Решая это неравенство, получаем конечное или бесконечное множество интервалов вида (осЛ; Для каждого из них имеем ak < logax < Если a > 1, то отсюда следует, что a“* < х < ар‘, а если 0 < а < 1, то a₽‘ < х < а“*. Решение является объединением найденных интервалов.
Пример 7. Решим неравенство
log, х - 6 log, х - 16 < 0. 3	3
(8)
Решение. Подстановка log, х = t приводит это неравенство 3
к виду t2 - 6t - 16 < 0. Решая его, получаем, что -2 < t < 8. Так
как основание логарифмов а = д меньше единицы, то решением неравенства (8) является < х < (|'| , т. е. < х < 9.
\3/	ООО1
Замечание. Если для t получаем неравенство вида < t < рА, то при a > 1 ему соответствует неравенство 0 < х < ар‘, а при 0 < a < 1 — неравенство < х < +°°. Аналогично для неравенств вида ак <t < +°°.
Пример
8. Решим уравнение
log, х2 - 141og16xxs + 401og4xVx = 0.
2Z
(9)
79
(10)
Решение. Было бы ошибочно, воспользовавшись формулой перехода к новому основанию логарифмов, сразу заменить это уравнение на
Iogx х2 _ 14 logxx3 40 logx Jx _ _ log, — x	log,16x log,4x
2
Дело в том, что указанная формула не может применяться, если основания логарифмов равны 1. Поэтому надо сначала выяснить, не является ли число 1 корнем уравнения (9). Подстановка показывает, что Xi = 1 — корень. Только после этого переходим в области, где х * 1, к уравнению (10), равносильному в этой области уравнению (9). По свойствам логарифмов получаем 2__________________________42	20	_ п
1 - log, 2	1 + 4 log, 2	1 + 2 log, 2
Полагая logx2 = у, имеем 2_________________________42	20 п
1 - У 1 + 4у l + 2i/
Если у *1, у * ~, у то это уравнение равносильно квадрат-
уравнению 2у2 + Зу - 2 = 0. Его корнями являются числа
ному
-2 и
logx2
1	1	~~	1
Если logx2 = -2, то log2x = — и х2 = 2 2 = -/=• Если 2	>/2
= тр то х3 = 22 = 4. Данное уравнение имеет три корня.
Пример 9. Решим уравнение х<х = Vx*".
Решение. В этом уравнении х может принимать только положительные значения. При этих значениях его можно переписать в виде
хЛ = х2.	(11)
Если х Ф 1, то из этого равенства вытекает, что Vx = и пото-му х = 4. Однако равенство (11) справедливо и при х = 1. Итак,
уравнение имеет два корня: х = 4 и х = 1.
Упражнения
127.	Решите логарифмические уравнения:
1)	lg(4,5 - х) = lg4,5 - Igx;
2)	IgVx - 5 + lgV2x - 3 + 1 = lg30;
3)	xlgx = x100;	4) 0,lxlgx“2 = 100;	5) 2log8’ =
80
6)	х1ог“х = агх, а > 0;
8)	log„ (б42^2х!-40х) =0;
10)lgl0 + 11g (271 + 3^) =2; О
12)	^logx V§x log3x = -1;
14)	lgV75 + 5Vx - 1 = 1;
16)	log,a + logo„.s,(x2>/a) = 4;
18)	(1 + logca)logaxlogt,c = logi,x -
19)	2 log,a + 31og2a + ,logxa =
° x log, ax
7) log5(x2 - llx + 43) = 2;
9) 4 - Igx = 3^'lg x;
11) log4(x + 12)log,2 = 1;
13) x^ = 10x‘;
15) log,x2 + log2x = 2,5;
17) log^a + loga, x = 1;
a
;cxlog„e;
128.	Решите логарифмические неравенства:
1)	logi x + log3x > 1;
2)	logox + loga(x + 1) < log„(2x + 6)
(разобрать случаи a > 1 и 0 <
i 6	.	2
3) log* g < log, 3!
5) lg(2x - 3) < 1;
7) 1----------- < ---------;
’	5 - Igx 1 + Igx’
9) log2 log3 < logj logi 7
Л- I J.	2	3 "
10) log^x > log, 3 -
12)	< 1;
14) log^.JSx - 1) < log^-jX2;
a < 1);
4) log,+24 > log,2;
6) 41og2 (x - 1) - logj(x - 1) > 5;
2
8) x10g“I + 1 > a2x;
+ 1.
- Г
11) log,+p2 < log,4, 0 < p <
<0-
15) log^2x2 - x - I) > 1.
§ 3. Дифференцирование и интегрирование показательной и логарифмической функций
1. Логарифмическое дифференцирование. В п. 3 § 1 было показано, что
(1ПХ)' =	(1)
81
Для того чтобы продифференцировать логарифмическую функцию с произвольным основанием, вспомним, что ,	In X
10g‘* =
Поэтому flnxY 1	1 _	1
( ogax)	ina x xlna‘
Итак, (logax) = j •	(2)
Отсюда следует, что d(lnx) =	(3)
d<log^=7&-	<4>
Из равенства (2) получаем, что
(logax)"= (-jM = \xlna/ x2lna
Так как х2 = 0 при любом х, то знак (logax)" противоположен зна-
ку Ina. Иными словами, (logax)" < 0 при a > 1 и (logax)" > 0 при
О < a < 1. Отсюда вытекает следующее утверждение.
График функции logax обращён выпуклостью вверх при а > 1 и выпуклостью вниз при 0 < a < 1.
Пример 1. Найдём производные функций:
1)	1п3х;	2) Insinx; 3)	.
'	' Inx
Решение. Имеем
1)	(1п3х)' = 31п2х(1пх)' =
2)	(Insinx)' = -Д— • (sinx)' = cosx = ctgx; sinx	sinx
3)	(hb) = (ln‘lx)' = -ln-2x(lnx)' =
Пример 2. Найдём производную функции Л где
, Чх - 1(х + З)4 ЛХ) 1П (х2 + 4)5eslnx
82
Решение. В данном случае отыскание производной упростится, если сначала воспользоваться свойствами логарифмической функции:
ftx) = I ln(x - 1) + 41п(х + 3) - 51п(х2 + 4) - sinx,
О
и потому
/'(х) = -А-: 1	+ —------1°*- - COSX.
3(х - 1) х + 3 х2 + 4
Если известна производная функции Inftx), то легко найти и производную функции f. В самом деле, по правилу дифференцирования сложной функции
Значит,
Г(Х) = ftx) • (in ftx))'.	(5)
Эту формулу называют формулой логарифмического дифференцирования.
Пример 3. Найдём производную функции f, где
.. . = Ух - 1(х + З)4 (х2 + 4)5esini '
Решение. Так как
Inftx) = | 1п(х - 1) + 41п(х + 3) - 51п(х2 + 4) - sinx, то
(inftx))' 3(х - 1) + х + 3	х2+Х4 COSX’
и потому
Г(Х) = ftx) • (In ftx))'.
Ух - 1(х + З)4	/	1	4
(х2 + 4)5esinx \3(х - 1) х + 3
210х - cos х). х2 + 4	)
Пример 4. Найдём производную функции /, где ftx) = xtgI. Решение. Так как Inftx) = tgx Inx, то
(Inftx))' - (tgxInx)' =
По формуле логарифмического дифференцирования получаем
(Xtgx)' = Xtgx	+ —)•
\COSJX X I
83
При мер 5. Найдём минимум функции xlnx.
Решение. Производная данной функции равна
(xlnx)' = Inx + х • ± = 1пх + 1.
Приравнивая её нулю, получаем уравнение Inx + 1 - 0, корнем которого является х = е-1. Так как
f"(x) = (xlnx)" = (Inx + 1)' = i
положительно при х = е1, то найденное значение х является точкой минимума. Значение функции в точке минимума равно е Чпе-1, т. е. у„ип = -1.
е
Пример 6. Проведём касательную к графику функции In2 х в точке х0= е.
Решение. Имеем х0 = е, /(х0) = ln2e = 1. Далее, f(x) =
= (ln2x) = ———, и потому f (x0) = —-— = - Уравнение касатель-2	2
ной у - 1 - - (х - е), или у = - х - 1.
Пример 7. Найдём приближённое значение 1п(е + 0,01).
Решение. Нам надо найти /(х0 + Л), где х0 = е, h = 0,01, /(х) = 1пх0. Так как /(х0 + Л) ~ /(х0) + ЛЛ(х0), а (1пх)' = р то получаем
1п(е + 0,01) = 1пе + 0,01 • | = 1 +	= 1,0037.
В заключение запишем формулу интегрирования, соответствующую выведенной ранее формуле дифференцирования:
^=1пх + С.	(6)
Замечание. Так как (1п(-х))' = ~ • (-1) = то при х < 0 имеем С с/х
= 1п(-х) + С. Поэтому в общем виде пишут
= 1п|х| + С.	(7)
Пример 8. Вычислим интеграл
Решение. Так как (х2 + 1)' = 2х, подстановка х2 + 1 = г даёт dz
dz = 2xdx, и потому xdx = Значит,
= 2 St = |in(x2+ D + c.
84
Замечание. Вообще для любой дифференцируемой функции имеет место равенство
=1п|/(х)| + С.	(8)
J / (Л)
Например,
с,	, с sin х dx , I i , z-.
\tgxdx = \--------- = -ln|cosx| + C.
J	J COS X
Пример 9. Найдём площадь, ограниченную прямыми х - О, у = 0, х = 3 и графиком функции у =	* .
Решение. Искомая площадь выражается интегралом
dx х + 4’ о
Подстановка х + 4 = t даёт dx = dt, и потому
= 1пН = lnlx + 41-
J х + 4 J t 11	1	1
Значит, (----- = in х + 4	= In 7 - 1п4 = In-г.
J х + 4	1	1 |о	4
о
Упражнения
129. Найдите производные функций:
1) ln(x3 - 1);	5) Insinx;	9) ln3x + ln(x3);
2) xlnx;	6) Intgx;	10) In ^-=4; ’ x + 1
3) x5Inx;	7) ln7x;	11) In (x + Vx2 + 1);
4) sin3(Inx);	8) ln4x - 41nx;	12) In (x2 + 7x4 + 4)
130.	Найдите производную от у = log,а. (Указание. Воспользуйтесь формулой перехода к новому основанию логарифмов.)
131.	Исследуйте на экстремум функции:
1)	х - 1п(1 + х);	4)
2)	х1п2х;	5) i Inx - arctgx;
3)	In *—	6) Incosx - cosx.
x - 3
132.	Выведите формулу для производных n-го порядка функций:
1)	Inx; 2) 1п(х - 1);	3) In
85
133.	Найдите производные функций:
1Ч] , (х4 + 1)5(х2 + 6х + 14)3.
1)1п\	е«2х(х3 + 5)4
3) (cosx)tgx;
5) Xх’.
2) J(*7 - !)3(х2 + 4х + 5)7.
(х + 3)10eBin5x
4) Xх’;
134.	Вычислите интегралы:
2)	в)
С x3dx .	С--------------dx_
j 1 + х4 ’	' ’ j (1 + х2) arctg х
f xdx .	r	dx
4)	\ 1 + x4 ’	8) \	2
J Л	J yl - x arcsin x
135.	Найдите площадь фигуры, ограниченной гиперболой у =
и прямыми х = 3, х = 8, у = 0.
136.	Найдите площадь фигуры, ограниченной графиком функции х-11пх, осью абсцисс и прямыми х = 1 и х = е.
137.	Найдите производную функции In (х + Vx2 + а). Пользуясь полученным результатом, вычислите следующие интегралы:
.. С , dx .	с	dx
' J Vx2 + 4 ’	' J Vx2 + 6x + 34 ’
24 C , dx .	C	dx
J Vx2 - 9 ’	’ J y/x2 + 6x + 8
138.	Представьте дробь —7 в виде разности дробей со знаменателя-х2 - (Г
ми х - а и х + а. Пользуясь полученным результатом, вычислите интегралы:
8>S«-X+8;
с dx .	с dx
’ J 4х2 - 1’	' J4x2 + 8х + 3
139.	Докажите, что функция /(х) является решением данного дифференциального уравнения:
1)	У"' + (г/")2 = 0, f(x) = (х + G)ln(x + СО + С2х + С3;
2)	у’ = еу, /(х) = In
3)	у'" = S^nfX» /(х) = Insinx + CiX2 + С2х + С3; sin х
4) х3у"' -I- ху' - у = 0, /(х) = x(Ci + С21пх + С31п2х).
86
2. Дифференцирование показательной функции. Так как показательная функция обратна логарифмической, которая дифференцируема, то и показательная функция дифференцируема. Чтобы вычислить её производную, воспользуемся формулой логарифмического дифференцирования. Поскольку Ina* = xlna, то (In a*)' = = (xlna)' = Ina, а потому по формуле (5) п. 1 имеем
(a*)' = a* (In а*)' = ах1па.
Итак,
(а*)' - a* In а.	(1)
Отметим частный случай полученной формулы:
(<?х)' = ех.	(1')
Значит, производная показательной функции с основанием е равна самой этой функции.
Из формулы (1) вытекает, что
(a1)" = (a1 In а)' = a* In2 а.
Но ах > 0 при любом значении х и In2 а > 0 при любом положительном значении а, отличном от 1. Поэтому для всех х и всех а > 0, а Ф 1 выполняется неравенство (а1)" > 0. Следовательно, при любом а > 0, а Ф 1 график функции ах на всей числовой оси обращён выпуклостью вниз.
Пример 1. Найдём производные функций:
1) е*2;	2) cose1; 3)
Решение. Имеем
1)	(е*2)' = ех\х2)' = 2хех2;
2)	(cose*)' - -sine*(e*)' - -e*sinex;
I ex V _ (x2 + 4)(ex)' - ex(x2 + 4)' _ ex(x2 - 2x + 4)
3)	\x2 + 4/	(x2 + 4)2	“	(x2 + 4)2
Пример 2. Найдём приближённое значение для е101.
Решение. Применим приближённое равенство f(x0 + h) ~ = f(x0) + й/'(х0). В нашем случае Дх) - ех, х0 = 1, h = 0,01, и потому /'(х) = ех, f(x0) = е1 = е.
Значит, имеем е1,01 ~ е + е  0,01 = е  1,01.
Поскольку е ~ 2,7182, то искомое приближённое значение равно е1,01 = 2,7454. Точное значение таково: е1,01= 2,7456....
Пример 3. Найдём, под каким углом график функции ех пересекает ось ординат.
Решение. Точкой пересечения графика и оси ординат является точка М(0; 1). Так как в точке х = 0 производная функции
87
принимает значение е° - 1, то касательная к графику в этой точке образует с осью абсцисс угол ср, такой что tgcp = 1, т. е. ф = Но тогда и с осью ординат касательная образует угол
Замечание. Свойство числа е, выясненное в этом примере, можно принять за другое его определение: числом е является основание показательной функции, при котором её график пересекает ось ординат под углом
Упражнения
140.	Найдите производные функций:
1)	ех(х2 + х + 16);	6) 4х(х2 - 1);
2)	exsinx;	7) —2----г;
х2 + 1
4)	esinx;	9) Infe* + 1);
5)	sin(e*);	10) arctg(e*2).
141.	Докажите, что функция у = еах удовлетворяет уравнению у' = ау.
У
142.	Докажите, что функция у = хе31 удовлетворяет уравнению у = —Н у.
143.
144.
Проведите касательную к кривой у = хге х в точке х0 = 1.
Найдите точки экстремума функций:
1)	х2е~
2)	х4е
3)	хе"
Докажите, что функция у = exsin х является одним из решений дифференциального уравнения
4)	х3е"х;
5)	хе х + е 2х;
6)	e"xsinx;
7)	e“sx;
8)	ех 4- е~х - 2 cosx;
9)	1п(1 + ех).
145.
у" - 2у' + 2у = 0.
146.	Докажите, что функция у = exsin х 4- sin 2х является одним из ре шений дифференциального уравнения
у" - 2у' + 2у - -2sin2x - 4cos2x.
147.	Вычислите неопределённые интегралы:
l)^2xdx;	3) ^e"3xdx;	5) ^х4Inxdx;	7) ^Inxdx;
2)^e2xdx;	4) ^exsin(ex)dx;	6) ^xe3xdx;	8) ^xInxdx.
148.	Вычислите определённые интегралы:
2	1	2	7. 3
С	С	с	x'tg^x
1)	y3xdx; 2) j Inxdx; 3)	+ 5x4 dx.
0	4	2
4
149.	Оцените интеграл \ x3e"xdx.
88
150.	Вычислите по формуле трапеций при п = 10:
2	1
1)	Igxdx; 2) § e~*2dx.
i	о
151.	Найдите площадь криволинейной трапеции, ограниченной сверху графиком функции 2х, снизу осью абсцисс, с боков прямыми х = О и х = 1.
3. Дифференциальное уравнение процессов органического изменения. В п. 1 § 1 процессы органического изменения были
охарактеризованы равенством f(t + Т) =
Введём вместо
/(0) •
функции f функцию (р, связанную с f равенством f(t) = f(O)<p(t). Подставляя это выражение вместо f, получаем для <р соотношение <p(t + Т) — <p(^)(p(7*). В п. 2 и 5 § 1 было показано, что этому равенству удовлетворяют лишь функции вида а1, где а > 0. Отсюда
следует, что процессы органического изменения описываются функциями вида /(t) = /(О)а', где а > 1, для процессов органического роста и 0 < а < 1 для процессов органического убывания.
Обозначим f(t) через у, ДО) через уои Ina через k. Тогда а = ек, а' = ем и закон изменения величины у с течением времени при
нимает вид
У = Уоек‘,
(1)
где k > 0, если величина у возрастает, и k < 0, если она убывает.
Функции вида (1) удовлетворяют дифференциальному уравнению у' = ky, причём решений иного вида оно не имеет. В самом деле, разделяя переменные в уравнении у' - ky, получаем — = kdx, У
откуда V— = ^kdt, т. е. 1п|г/| - kt + In С. Но это и означает, что
у = Сек‘.
Поскольку у' является мгновенной скоростью изменения величины у, то мы доказали следующее утверждение.
Мгновенная скорость изменения величины в процессе органического роста или убывания в каждый момент времени пропорциональна значению величины в этот момент времени. При этом коэффициент пропорциональности равен значению k в равенстве (1).
Сформулированное свойство является, как мы видели выше, характеристическим для процессов органического изменения.
К рассмотренному типу процессов близки процессы выравнивания, при которых мгновенная скорость изменения величины у пропорциональна не значению этой величины, а разности между некоторым числом а и этим значением:
= k(a - у), где k > 0.	(2)
89
Поскольку имгн = у', из уравнения (2) получаем дифференциальное уравнение процессов выравнивания:
у' = k(a - у).
Подстановка а - у - г сводит это уравнение к уже изученному случаю. В самом деле, г' = -у’, и потому получаем уравнение г' = -йг. Из него находим z = Се~к‘, откуда
у=а-г=а- Се~к‘.	(3)
Пример. Скорость остывания нагретого тела в каждый момент времени пропорциональна разности между температурой Тг окружающей среды и его температурой Т в этот момент времени. Выведем закон остывания тела с течением времени.
Решение. По условию имеем дифференциальное уравнение Т'= k(T} - Т). Значит, как было показано выше, закон остывания выражается формулой
Т= 7\ - Ce~kt.
Значение С легко найти, если известна первоначальная температура тела То: при t = 0 получаем То = - С, и потому С = Т\- То, т. е.
Т = Т. + (То -	(4)
Чтобы найти значение k, надо ещё задать температуру тела Т2 в некоторый момент времени t2. Из уравнения (4) получаем, что I2 _ I1 = е~к‘г, и потому kt2 = In Значит, У0 71	-*2 “ А
ь = .L }п 2»_2L
t2 1 тг-тс
(5)
К уравнениям разобранного в этом пункте вида сводятся некоторые дифференциальные уравнения второго порядка, в частности, описывающие движение тела в сопротивляющейся среде. Если сопротивление среды пропорционально скорости тела, то имеем уравнение mx" - -kx' (см. уравнение (2) п. 1 § 2 главы 1). Подстановка х’ - v сводит это уравнение к уравнению первого по-
рядка mv = -kv, общее решение которого имеет вид v = Се т . Если
t
начальная скорость движения равна v0, то v = voe т . Поскольку v = х , то х = voe т , и потому
с 1 ,	mv„
х = \1>ое т dt = Ci - —е
(6)
90
Если начальная координата точки равна х0, х(0) = х0, то из (6)
„ тио	г> 1 mvo
вытекает, что х0 = Ci-, и потому Cj = х0 Н—
mv0	~~‘ 1
х = х0 + U - е т ). К
-—t
При t —> +°° слагаемое е т стремится к нулю, и потому движущаяся mv0 тт	mv0
точка стремится к точке с координатой х0 Н—• Число х0 Ч—
тем больше, чем больше начальное количество движения mv0 и чем меньше коэффициент k, характеризующий сопротивление среды.
Упражнения
152.	Решите дифференциальные уравнения:
1)	У' = -9у; 2) у' = 3(у - 4).
153.	Проверьте, что если и г2 — корни квадратного уравнения г2 + рг + + q = 0, то функция у = С1ег'х + С2еГ2Х при любых значениях С\ и С2 является решением дифференциального уравнения у" + ру' + qy = 0.
154.	Пользуясь результатом задачи 153, решите дифференциальные уравнения:
1)	у” - 6/ + 5у = 0;	3) у" - 16у = 0;
2)	у" + 2у' - 15у = 0;	4) у" + 8у' + 15р = 0.
155.	Гибкий шнур длиной I лежит на столе так, что отрезок шнура длиной а свисает вниз. Под действием силы тяжести шнур начинает соскальзывать вниз. За какое время он соскользнёт со стола? (Силой трения пренебречь.)
156.	Количество света, поглощаемое слоем воды, пропорционально количеству падающего на него света. Слой воды толщиной 3 м поглощает половину первоначального количества света. Какая часть первоначального количества света дойдёт до глубины 60 м?
157.	На сколько увеличится длина I эластичного шнура, имеющего массу т, если подвесить шнур за один конец, а затем к нижнему концу подвесить груз массой М? (Использовать закон Гука.)
158.	Сосуд, имеющий форму усечённого конуса с высотой h, радиусом верхнего основания R и радиусом нижнего основания г (R > г), наполнен водой. За какое время вытечет из этого сосуда вода через отверстие площадью S, сделанное в нижнем основании? Решите ту же задачу, если R < г.
159.	В баке находится 60 л раствора, содержащего 5 кг соли. В бак непрерывно подаётся вода со скоростью 3 л/мин, которая мгновенно перемешивается с имеющимся раствором. Смесь вытекает из бака с той же скоростью 3 л/мин. Сколько соли останется в баке через час?
160.	Моторная лодка движется в стоячей воде со скоростью 5 м/с. На полном ходу её мотор был выключен, и через 40 с её скорость стала
91
равной 2 м/с. Считая, что сила сопротивления воды пропорциональна скорости движения лодки, определите скорость лодки через 2 мин после выключения мотора. Решите ту же задачу, считая силу сопротивления воды пропорциональной квадрату скорости лодки.
161.	Материальная точка массой т подброшена вертикально вверх с начальной скоростью и0. Найдите закон изменения скорости, если на точку, кроме силы тяжести, действует тормозящая сила сопротивления воздуха, пропорциональная скорости (коэффициент пропорциональности равен k).
162.	Радиоактивное вещество А имеет в момент времени t = 0 массу т0. Оно распадается, образуя радиоактивное вещество В. Найдите закон изменения массы вещества В при заданных коэффициентах и k2, характеризующих скорости распада веществ Л и В. В какой момент времени количество вещества В будет наибольшим? (Начальная масса вещества В равна нулю.)
163.	За 30 дней распалось 50% первоначального числа атомов радиоактивного вещества. Через сколько дней останется 1 % от первоначального числа атомов, если известно, что число атомов, распадающихся за единицу времени, пропорционально числу атомов этого вещества, имеющихся в данный момент?
164.	Культуре из 100 бактерий предоставлена возможность размножаться при благоприятных условиях. Через 12 ч число бактерий достигло 500. Сколько бактерий будет через 2 суток после начала опыта?
165.	Энергия света, поглощаемая при прохождении через «бесконечно тонкий» слой воды dl, равна lnV2  w  dl, где w — энергия падающего света. Какая часть этой энергии дойдёт до глубины 30 м?
166.	Сосуд вместимостью 40 л содержит 80% азота и 20% кислорода. В сосуд ежесекундно поступает азот объёмом 0,2 л и вытекает столько же смеси. Через сколько времени в сосуде будет 99% азота?
167.	Составьте дифференциальное уравнение движения парашютиста, считая, что сила сопротивления воздуха пропорциональна скорости движения (за искомую функцию примите скорость движения). Найдите предел, к которому стремится скорость падения с течением времени, если начальная скорость падения равнялась нулю. Найдите коэффициент пропорциональности в равенстве F = -kv, если известно, что парашютист массой 80 кг опустился со скоростью 5 м/с. Найдите закон изменения высоты парашютиста над уровнем земной поверхности, если начальная высота была равна h м.
168.	Для некоторых химических реакций скорость реакции пропорциональна произведению концентраций двух реагентов. При этом в процессе реакции одна молекула первого вещества реагирует с одной молекулой второго вещества. Найдите закон изменения массы т первого вещества с течением времени, если начальная концентрация первого реагента равнялась а, а второго — Ь. Разберите также случай, когда а = Ь.
92
4. Некоторые пределы, связанные с числом е. Мы знаем, что (Inx)' = В частности, производная функции у = Inx принимает в точке х = 1 значение 1. Но по определению производной
1	/1	\' т In (1 + й) - Ini ,. In (1 + й)
1 = (lnx)I = 1 = hm —*---------- = hm —~
h -> О	Л	Л —> 0	fl
Значит, имеет место равенство
lim 1П(\+ ° = 1.	(1)
Положим в равенстве (1) ln(l + t) = х. Тогда 1 + t = ех. При этом если i -> 0, то и х ч 0, а если х —> 0, то и t —> 0. Значит, равенство (1) равносильно равенству lim gXx = 1, т. е.
lim = 1.	(2)
х -»О	X
Докажем в заключение, что
1
lim = (1 + ty = е.	(3)
i —> 0
Для этого заметим, что в силу непрерывности логарифмической функции выполняется равенство
In lim (1 + ty = lim ln(l + t)‘ = Jim ln(1*+ f) = 1.
Отсюда и следует равенство (3).
Полагая t = получаем из (3) равенство lim (1 +	= е.	(4)
\ х/
Упражнения
	Вычислите пределы (169—174).							
169.	1)	lim X -» ОО	1 п	1 »2х2	;	2)	lim X • > ОС	2х-1 / х2 + 2х - 1 V+1 в \2х2 - Зх - 21	3) lim -I	(sinx)tgI.
		lim х-»0	1		lim х —			In cos ax
170.	1)		(1 - 2х)х;	2)		х - а 9	3) lim x—>0	In cos bx
171.	1)	lim	(sin x)tg х;	2)	lim (tgx)tg2x. X —> 2 л			
172.		lim X —> оо	1п(х2 - X	+ И.		lim (1 + 3tg2x)ctg!x; х—»0	3)!lni (	1 COS X V2
	1)		1п(х10 + X	+ 1)’	2)			cos 2x)
93
.. ..	eax - ebx	.. In(1 +	sin3x)
z™	sin ex - sindx*	z1™ ln(l +	tg4x)‘
174. 1) lim	+ arcsm5x)	Um Igcosx.
z->o	In (1 - arctg 2x)	z—>o x2
5*. Некоторые неравенства для показательной функции. Так как функция ех возрастает, то при любом х > О выполняется неравенство ех > е° = 1. Кроме того, ясно, что ех < 3х. Эти неравенства являются частными случаями следующего утверждения.
Теорема. Если х > 0, то для любого натурального п выполняются неравенства
ех > 1 + х +	+ ... +	(1)
и
ех < 1 + х + % + ... +	(2)
Доказательство. Неравенство (1) при п = 0 принимает вид ех > 1 и, как отмечалось выше, справедливо в силу монотонности функции ех. Предположим, что неравенство (1) доказано при п = k:
ех > 1 + х + % + ... +	(3)
покажем, что оно справедливо при п = k + 1:
r2	yfe	-у-А +1
г- > 1 + z + ^ + ... + ^ + (JTW-	(4>
Для этого образуем вспомогательную функцию ср — разность левой и правой частей неравенства (4):
у.2	у-А +1
<р(х) = ех - 1 - х - gy - ...	+ !)[•
При х = 0 эта функция обращается в нуль: <р(0) = 0. Её производная имеет вид
Л _ z П 1 2х	Ах*"1 (А + 1)х* _
(р(х)-е	0	1	2!	... А! (А + 1)! “
1х...	(£_!>! ft!-
В силу предположения индукции для всех х > 0 имеем ф'(х) > 0, и потому функция ф не убывает на луче [0; +о°). Поскольку ф(0) = 0, то для всех х > 0 имеем ф(х) > ф(0) = 0, а это и значит, что выполняется неравенство (4).
Итак, неравенство (1) выполняется при п = 0 и из его справедливости при п = k вытекает, что оно верно и при п = k -I- 1.
94
Значит, оно выполняется при всех натуральных п. Неравенство (2) доказывается аналогично, но вспомогательная функция имеет вид yfe	+ 1лХ
<р(х) = ех - 1 - х - ... -	+
Итак, мы доказали, что при х > О выполняются неравенства
•у-П	уП	+ 1
1 + х + ... + ^ <	< 1 + х + ... + ^ +
(5)
С помощью этих неравенств можно найти с любой точностью значение ех при любом х. Это вытекает из следующего утверждения.
Предел при п —> °° равен нулю', lim = 0.
П I	п —> со ПI
К»	JC П
В самом деле, найдём отношение значений —г для соседних п!
значений п + 1 и п:
х"*1 . х" _ х  п! _ хп!	_ х
(п + 1)! а! (п + 1)! п!(п + 1) п + 1'
Если п > 2х, то это отношение меньше чем i, и потому каждый последующий член по крайней мере вдвое меньше предыдущего. Поэтому с возрастанием п эти члены стремятся к нулю, т. е.
lim = 0.
Из доказанного утверждения вытекает, что разность
еххп*1 (п + 1)!
правой и левой частей неравенства (5) стремится к нулю при п —> °°, а это и значит, что они дают при достаточно больших значениях п сколь угодно хорошие приближения к ех.
Замечание. В правой части неравенства (5) имеется слагаемое, которое само содержит е1. Но это слагаемое нужно лишь для оценки погрешности, и потому его можно заменить каким-либо приближённым значением по избытку. Например, если х < т, то вместо ех можно взять 3" (увеличены и основание, и показатель).
Пример 1. Найдём значение е0,6 с точностью до 0,01.
е°'5(0,5)л +1
Решение. Сначала найдём такое п, что +	< 0,01. Так
как е0,5 < е < 3, то для этого достаточно, чтобы выполнялось нера-(°,5Г + 1	1	„	_	1	11
венство	Но при и = 3 имеем = — < —.
Значит, число 1 + 0,5 +	=1,65 является прибли-
жением по недостатку для е0,5 с точностью до 0,01. Более точные подсчёты показывают, что е0,5 = 1,6487.
95
I (-0,5/|	1
I A! I	1000’
Отметим ещё неравенства, выполняющиеся на луче 0):
-у2	у2п -1	^.2
1 + Х + 2? + •" + (2л - 1)! <ех<1+х+2[ +
у2п ~ 1
+ .	+ -------- 4- -.
(2л - 1)!	(2л)!
Мы опускаем доказательство этих неравенств.
Пример 2. Найдём приближённое значение для е“0,5 с точностью до 0,001.
Решение. Сначала найдём такое А, что
Это неравенство выполняется при k = 5. Значит, достаточно взять сумму первых пяти членов:
е °’5 = 1 - 0,5 + ^ -	= 0,607.
3!	4!
Более точные подсчёты показывают, что e~0,s = 0,6065... .
Замечание. Мы установили, что при х > 0 выполняется неравен-Х^1	х^
ство 1 + х + -gj- + ... +	< е“, причём по мере возрастания л значения
суммы в левой части неограниченно приближаются к ех. Приближается эта сумма к е1 и при х < 0. Поэтому говорят, что при любом х функция е1 является суммой бесконечного ряда
е‘= 1 + х +	+ ... +	+ ....	(6)
Упражнения
175.	Докажите, что при х > 0 выполняются неравенства:
1)	е г > 1 - х;	3) е~х < 1 - х +
176.	С помощью доказанных в этом пункте неравенств вычислите с точностью до 0,001:
1)	е° 02;	2) е“0’3.
а 4	ga -j. g®
177.	Докажите неравенство е 2 < —%— (-о° < а < Ъ < °°).
6*. Неравенства для логарифмической функции. Мы уже зна-
1 — Оп 1	(1п
ем, что 1 + q + q2 + ... + gn“l = -=- = --4— (см. п. 2 § 2
*	4	4 1-gl-gl-g'	а
главы 2, 10 кл.). Отсюда следует, что при q = -t имеем
1 - t - ... + (-l)-t- =
96
Если п чётно, п = 2k и t > 0, то
1 - t + t2 - t3 + ... - t2*'1 < j-yp
Если же n нечётно, n = 2k + 1, то при t > 0 имеем
1 - t + t2 - t3 + ... + t2k > 777
Итак, доказано, что при t > 0 выполняются неравенства
1 - t + t2 - t3 + ... - t2^1 C < 1 - t + t2 - t3 + ... + t2k.
(1)
Проинтегрируем эти неравенства от 0 до x. Так как
j +* t = ln(l + £)Г = 1п(1 + х) - 1п1 = 1п(1 + х) о
то при х > 0 имеем
у3	Y2k
+ -р -	< 1п(1 + х) <
Выведенные неравенства позволяют найти приближённые значения 1п(1 + х) при 0 < х < 1 с любой степенью точности.
Пример 1. Найдём значение In 1,2 с точностью до 0,01.
Решение. При х = 0,2 выполняются неравенства 0,2 -	< lnl,2 < 0,2 - ^ +
Поэтому имеем 0,18 < 1п1,2 < 0,183. Значит, 1п1,2 = 0,18. Более точное значение In 1,2 таково: 0,1823....
На интервале (-1; 0) для 1п(1 + х) имеем неравенства
Х 2 + 3	•" +	п(1 + х)	+
< ж . Х1 _	. (-р-х-1
х	23	•• п
(3)
доказательство которых опускаем. Чтобы найти значение 1п(1 + х) .	1 + у тт
при х > 1, делают замену 1 + х = 1 Несложно показать, что
при х > 1 значения у принадлежат промежутку
ЭТОМ
In(1 + х) = In = In(1 + у) - ln(l - у),
а приближённые значения 1п(1 + у) и In (1 - у) находят, как было указано выше.
97
Пример 2. Найдём приближённое значение In 3 с точностью до 0,01.
Решение. В нашем случае 1 + х = 3, и поэтому х - 2. Решим
1 + У
1 - У
уравнение 3 =
Имеем у = Поэтому
1пЗ = In ~	= In (1 + -j - In (1 - 1).
(1_1)	\	2]	\	2]
Но по (3) имеем
! (ИЛ (ИЛ
2	2	3	4	5 ’
откуда находим, что 0,401
0,407. Далее по (3)
имеем
In (1 + -1)
\	2/
Отсюда получаем
-0,695 < In (1 - Д < -0,688. \	2/
Из полученных неравенств вытекает, что 0,401 + 0,688 <
<1п(1 +	- In (1 - Д < 0,407 + 0,695, т. е. 1,089 < 1пЗ < 1,102.
I 2)	\	2/
Значит, 1пЗ ~ 1,10. Более точные подсчёты показывают, что 1пЗ = - 1,098....
Упражнения
178.	Вычислите с точностью до 0,001:
1)	1п1,2;	2) 1п0,85.
179.	Докажите неравенство In а	(0 < а < & < оо).
98
§ 4.	Степенная функция. Иррациональные выражения, уравнения и неравенства
1.	Степенная функция с произвольным показателем. Пусть а — некоторое действительное число. Тогда для любого положительного числа х определено значение х“. Как было показано в п. 4 § 1, это значение равно ealni:
х“ = e“lni, х > 0.	(1)
Тем самым для каждого а существует функция х“, заданная на множестве положительных чисел. Её называют степенной функцией с показателем а.
Замечание. Если а = п — натуральное число, значение х" определено для всех (а не только положительных) значений х. Именно, х" = х • ...  х (п множителей). Если а = ~п — целое отрицательное число, то х " определено для всех отличных от нуля значений х по формуле
х " = Поскольку равенство (-х)“ = (-1)"хл, где п — целое число, сводит изучение степенной функции с целым показателем на луче (-°°; 0) к изучению той же функции на луче (0; +°°), мы ограничимся в дальнейшем рассмотрением положительных значений х.
В этом пункте будут изучены свойства степенной функции с произвольным показателем. Формула (1) показывает, что эта задача сводится к использованию свойств логарифмической и показательной функций.
1)	Степенная функция определена для всех положительных значений х аргумента.
Это свойство следует из определения.
2)	Все значения степенной функции на луче (0; +°°) положительны.
Это следует из положительности значений показательной функции.
3)	Степенная функция непрерывна на луче (0; +°°).
Следует из того, что на этом луче непрерывна логарифмическая функция, а показательная функция непрерывна на всей числовой прямой. Значит, функция х“ непрерывна как композиция непрерывных функций t = 1пх и у = еа‘.
4)	При a > 0 имеют место равенства
lim х“ = 0, lim xa = +оо,	(2)
X —> + 0	х —> + ОО
а при а < О — равенства
lim х“ = +°°, lim xa = 0.	(3)
х —> +0	X —> +оо
99
В самом деле, мы знаем, что lim Inx = -°о и lim Inx = +°°.
X —> +0	х —> +оо
Если а > 0, то отсюда следует, что Ита1пх = -°ои lim cclnx = +°o. х —> +0	х —» +О0
Но х“ = ealnx, lim ех = 0, lim ех = +°о, и потому при а > 0 полу-X -4 -ОО	х —> +ОО
чаем
lim х“ = lim ealnx = lim е' = 0, х —> +0	х —> +0	t —> -со
lim х“ - lim e“lnx = lim е‘ = +°о.
X—>+со	х—>+оо	i —> +оо
Случай а < 0 рассматривается аналогично.
5)	Производная функции xrj- выражается формулой (х“)' = аха-1.
В самом деле, по формулам дифференцирования показательной и степенной функций и по правилу дифференцирования композиции функций имеем
(х“)' = (еа1пх)' = е“1пх(а • Inx)' = еа1пх^ = хи^ = аха1 (4) ха
(мы воспользовались тождеством — - х“ ).
Из формулы (4) следует, что
(ха)" = (аха-1)' = а(а - 1)ха-2.
6)	Если а > 0, то функция х° возрастает на луче (0; +°°), а при а < 0 она убывает на этом луче.
Замечание. Это утверждение можно получить в силу равенства х“ = еа1пх из того, что функции Inx и е' возрастают.
В самом деле, при х > 0 имеем х0"1 > 0. Поэтому если а > 0, то (ха)' = ах“-1 положительно на (0; +°°), и потому функция ха возрастает на этом луче. Если же а < 0, то (х“)' = аха-1 < 0 на (0; +°°), и функция ха убывает на этом луче.
7)	График функции х” обращён выпуклостью вверх при 0 < а < 1 и выпуклостью вниз при а < 0 и при а > 1.
В самом деле, ха“2 > 0 при х> 0. Множитель же а(а - 1) положителен при а < 0 и при а > 1, отрицателен при 0 < а < 1. Значит, (х“)" = а(а - 1)х“~2 < 0 при 0 < а < 1 и (ха)" > 0 при а < 0 и при а > 1. Отсюда вытекает наше утверждение.
8)	Если а = 0, то график степенной функции параллелен оси абсцисс, а при а = 1 он совпадает с биссектрисой первого координатного угла.
Доказанных выше свойств достаточно для того, чтобы построить графики степенных функций при различных значениях а.
з
На рисунке 41 изображён график функции х2. Аналогичный вид имеют графики степенных функций при а > 1. На рисунке 42 1
изображён график функции х2. Аналогичный вид имеют графики
100
степенных функций при 0 < а < 1. Наконец, на рисунке 43 изо-1
бражён график функции х 2. Аналогичный вид имеют графики этой функции при любом а < 0.
Замечание. Если х > 1 и а < р, то ха < х®. Это показывает, что при а < Р график функции х₽ расположен на луче (1; +°°) выше графика функции х“. Аналогично доказывается, что при а < Р на промежутке (0; 1) график функции х[( расположен ниже графика функции х“.
Упражнения
180.	Начертите схематически графики функций:
1)	х’;	2) х4;	3) х3;	4) х10“;	5) х4; 6) х~3;	7) х 4;	8) х 3.
181.	Начертите схематически графики функций:
1)	|х|3;	3) |х - 1|3 + 6;	5) |16х - 32|4;
2)	|х - 1р;	4) |х - 1р + |х + 1|3;	6) (х - I)3 + 6.
101
1
.. х4 + 2 .
3) lim —;---------;
х"+0 4х4 + 1
4) lim х 4 + 2 .
х—>+о	-4
182.	Вычислите пределы:
1)	lim	;
2)	lim 2^Н +	+
х^+оо З3/х + 6Vx + 3
2. Некоторые тождества для степенной функции. Из тождеств для показательной и логарифмической функций вытекают соответствующие тождества для степенной функции.
1) Для любых положительных чисел х и у и для любого а выполняется равенство
(ху)а = хауа	(1)
(следует из равенства (5) п. 5 § 1).
2) Для любого х > 0 и любых а, Р выполняется равенство
(х“)₽ = ха₽	(2)
(следует из равенства (2) п. 5 § 1).
Следствие. Для любых положительных чисел х и у и любого а выполняется равенство
Мы знаем, что при натуральном п имеет место формула бинома Ньютона (см. п. 9 § 3 главы 5, 10 кл.):
(х + у)п = х" + пхп1у +	— хп~2уг + ... +
2	(4)
(n - fe_+ 1) п-у +	+ „
1 • 2 • ... k	у	у
Аналогичная формула имеет место для любого а при х > у > 0:
. .	.	п-1 .	> а(а - 1) •	• (а - /г + 1) „_к к ,
(х + у)а = ха + аха у + ... -I—*-j—-—— -------ха у + .... (5)
Однако в отличие от формулы (4) правая часть формулы (5) является суммой бесконечного множества слагаемых (бесконечным рядом). Эта сумма имеет следующий смысл. Существуют суммы Sk первых k членов; сумму всего ряда полагают равной пределу Sk при k —> оо; § = iim Sk (при х > у > 0 этот предел существует).
k —> ОО
С помощью формулы (5) можно находить приближённые значения (х + у)а, беря достаточно много членов суммы (5) и отбрасывая остальные члены.
102
3
Пр и м е р. Найдём приближённое значение 4,182 с точностью до 0,0001.
Решение. Так как
з	з
4,182 = (4 + 0,18)2,
Q
то положим в формуле (5) х = 4, у = 0,18, а =
3
4,182
з	з,	— • I — — 1 з _ о
42 + -  42	 0,18 + -—-------  42	 0,182 +
2	1-2
0,183 + ... =
*64 + -у/4  2
0,18 +	-	• 0,0324 - —  -Д= • 0,0058 + ...
8 VJ	48
= 8 + 0,54 + 0,00608 - °’.?av- + ... « 8,54603. оо4
Микрокалькулятор даёт ответ: 4,181,5 = 8,5460302.
Формулы (1), (2), (3) верны для любых значений а, в том числе для рациональных. Но хп = >[х. Поэтому из указанных формул выводим следующие свойства корней из положительных чисел.
1)	Если х > 0, у > 0, то tfxy = Vx^.	(6)
В самом деле, по формуле (1)
tfxy = (хуУ = х"у* = y/xtfy.
2)	Если х > 0, то
\ X —	\ X.	(?)
Действительно, по формуле (2)
\^/х = (Х")™ = Х«" = ту[х.
3)	Если х > 0, у > 0, то
УУ п4у	(8)
По формуле (3)
_ X" _ \/х
Уу 'у' tf/'
103
Упражнения
183.	Составьте таблицу значений и начертите графики функций:
1)	|х|3;	3) х4;	5) |х|3;	7) |х - 1|3 + |х + 1|’;
12	3
2)	|х|4;	4) х3;	6) |х|4;	8) Vx4.
184.	Постройте по точкам графики функций:
» ЛГ71;	2) -^—4.	3)	4)
185.	Вычислите пределы:
А	з/~6 ~Т
2)	lim (х + 9)2;	4) lim  +-~.
х —> 3	х —»+ оо	^.2
3. Сравнение роста степенной, показательной и логарифмической функций. При возрастании х на луче [0; +°°) значения функций х10 и 10* неограниченно увеличиваются. При этом сначала быстрее растёт функция х10, что видно из следующей таблицы:
X	1	2	3	4	5
X10	1	1024	50 049	1 048 576	9 765 625
10*	10	100	1000	10 000	100 000
При х - 10 значения этих функций одинаковы (равны 1010), при дальнейшем увеличении 10* растёт быстрее, чем х10. Например, при х = 100 имеем 10* = 10100, а х10 = 1ОО10 = 1020, а при х = 1000 будет 10* = 101000, а х10= Ю0010= 1030.
чем
Определение. Функция f растёт при х —> +°° быстрее, f(x) функция g, если lim = +°°.
Х^+оо g(X)
Из сказанного выше видно, что функция 10* растёт при х —> +°° быстрее, чем х10. Это утверждение является частным случаем следующего общего утверждения.
Теорема. Если а > 1, то при х —> +°° функция а* растёт быстрее любой степенной функции хп, где п — натуральное число.
Иными словами, верно равенство lim = +°°.	(1)
X —> +ОО X
Достаточно доказать равенство (1) при а = е (в силу формулы (2') п. 4 § 1). В этом случае оно вытекает из неравенства
^2	уП	yfl + 1
! + х +	+ ... +	+ _2С_.
104
Графически утверждение этой теоремы означает, что при достаточно больших значениях х график функции ах, где а > 1, расположен выше графика функции хп.
Логарифмическая функция обратна показательной, а функция
X" — функции хп. Но графики взаимно обратных функций симметричны относительно прямой у = х. Отсюда сразу вытекает, что график функции logax, а > 1, при достаточно больших значениях х
1
расположен ниже графика функции хл, т. е. функция logax растёт
1 при х —> +°° медленнее, чем функция хп :
1
1
Например, при х = 10е, п = 3 имеем хп = 100, a log10x = 6.
Замечание. Соотношение (2) сразу вытекает из соотношения (1), если положить в (1) ах = t. Тогда имеем х = logat, причём условия х —> +°о
и t -» +°° равносильны. Поэтому lim = +°°- Но это и значит, что
tn
lim z----- = +°о.
log„ t
Упражнения
186. Вычислите пределы:
1)	lim	2х5 - х2 + 4. 2х	5)	lim X —> оо	21' - х4. 2х2 + х4 ’
2)	lim х -> -оо	2х(х100 + 5);	6)	lim X —> со	In X х/х
3) Jim	(х25 + 2х15 + 6); 4) lim g* 2х - 21 187. Постройте графики функций:			7) 8)	Р	1п3х lim —f=	; + 1 lim xlnx. х->+0	
1) хе~х;	4) хе~х‘;	7) Inx - arctgx;	10) ln(l + e *);
2) х2е~х;	5) xlnx;	8) e‘*sinx;	11) cosx - Incosx,
ех + е“х . 3)	2	’	6) х21пх;	9) ec°sx;	
4. Алгебраические выражения. Введение корней расширяет выразительные средства алгебры, поскольку теперь можно рассматривать выражения с переменными, содержащими знак корня. Назовём получаемые при этом выражения иррациональными.
105
Объединяя рациональные и иррациональные выражения, получаем класс алгебраических выражений. Точнее этот класс определяется следующим образом.
Определение. <Алгебраическое выражение> : : = <число> | <буква> | <алгебраическое выражение> + <алгебраическое выражение> | <алгебраическое выражение> • <алгебраическое выражение> | <алгебраическое выражение> : <алгебраическое выражение> | < ^алгебраическое выражение >.
Вместо знака деления применяется также знак дроби.
Из этого определения вытекает, что все рациональные выражения являются алгебраическими выражениями. Все алгебраические выражения, не являющиеся рациональными (см. п. 1 § 1 главы 2, 10 кл.), называют иррациональными выражениями. Примерами иррациональных выражений могут служить
^/Зх2 + у2, д/х2 + у/~у2 + Vz.
Из определения легко вытекает, что, подставляя в алгебраическое выражение вместо букв алгебраические же выражения, снова получаем алгебраическое выражение.
При отыскании областей существования алгебраических вы-ражении надо учитывать, что выражение <!А имеет числовое значение лишь при тех значениях букв, для которых А имеет неотрицательное числовое значение.
Пример 1. Найдём область существования выражения л/х2 - 6х - 7.
Решение. Это выражение имеет значение лишь для значений х, при которых х2 — 6х - 7 > 0. Решая это неравенство методом промежутков, получаем ответ в виде (-°°; -1] U [7; +°°). Это множество и является областью существования для Vx2 - 6х - 7.
Пример 2. Найдём область существования для выражения
у'х2 - 9 - V16 - х2.	(1)
Решение. Искомая область существования состоит из значений х, для которых х2 - 9 > 0 и 16 - х2 > 0. Решением неравенства 16 - х2 > 0 является отрезок [-4; 4], а решением неравенства х2 — 9 > 0 — множество (—°°; —3] U [3; +°°). Областью существования для (1) является пересечение найденных множеств, т. е. [-4; -3] U [3; 4].
Каждому алгебраическому выражению от х соответствуют функции, заданные этим выражением. Наибольшей возможной
106
областью определения этих функций является область существования этого выражения. Мы будем называть алгебраическими1 функции, заданные алгебраическим выражением в его области
существования.
Одна и та же функция может быть задана различными алгебраическими выражениями. Например, выражения ^/(х + I)3 и х + 1 задают одну и ту же функцию, хотя первое из них иррационально, а второе рационально. Понятие тождественного равенства алгебраических выражений определяется так же, как и для рациональных выражений: должны совпадать области существования этих выражений, а при любом х из этой общей области существования значения выражений должны быть одинаковыми.
Правила тождественных преобразований алгебраических выражений основаны на равенствах 1) — 11) п. 2 § 1 главы 2, 10 кл. (они верны и для иррациональных выражений), а также на нижеследующих равенствах, непосредственно вытекающих из свойств корней (см. п. 3). В этих равенствах буквами А, В обозначены любые алгебраические выражения от х, у, ..., z. Все эти формулы справедливы в случае, когда подкоренные выражения неотрицательны, а также в случае, когда все показатели корней и степеней нечётны.	____
1)	(^/а)" =А;	5) т^А^ = "у/А;
6)
7) 2у[а™ = |А|.
Пример 3. Выясним, при каких значениях х имеет место равенство
7(х - З)2 = х - 3.
Решение. Так как >/(х - З)2 = |х - 3|, то равенство имеет место, если х - 3 > 0, т. е. на луче [3; +°о).
Пример 4. Выясним, при каких значениях х имеет место равенство
л/х - 4 Vx + 4 = yjx2 - 16.	(2)
1 В высшей математике понятию «алгебраическая функция» придают более широкий смысл. Там алгебраической называют любую функцию f такую, что при подстановке этой функции вместо у в некоторое уравнение
вида Р(х, у) = 0, где Р(х, у) — ненулевой многочлен от х и у, получается
тождество.
107
Решение. Равенство (2) имеет место, если х-4>0их + 4>0, т. е. на луче [4; +оо). Заметим, что выражение \/х2 - 16 имеет числовое значение и на луче (-°°; -4].
Упражнения
188.	Найдите /(—1), ДО), /(1), Д-2), Д2), Да + 1), если Дх) = Vx2" - х.
189.	Пусть Дх) = х2 + рх + q. Докажите, что
f(~2+K~q}=°-
190.	Выразите площадь прямоугольника, вписанного в круг радиусом R, как функцию от длины его основания.
Сравните область задания функции с областью существования выражения этой же функции.
191.	Выразите площадь равнобедренного треугольника, имеющего периметр 2р:
1)	как функцию от длины его высоты;
2)	как функцию от длины основания треугольника.
192.	Выразите длину стороны правильного шестиугольника как функцию от длины его апофемы.
193.	Выразите площадь правильного шестиугольника как функцию от длины его стороны.
194.	Выразите произведение корней через один знак корня:
П *13а2ь я12а“Ь3с. J 5а3х 14ау3
’ У с3х ' V х2 ’	’ У 6с5у2 V 2Ь2х2 ‘
195.
Сделайте подстановку и =
в выражения:
1)	2(ui> - \!и2 - 1 \jv2 - 1);	2) (uv + -Ju2 - 1 \lv2 - 1).
196.	Внесите множители под знак корня:
1)	2a3b&;	2)
с2 у а2Ь
197.	Вынесите множители из-под знака корня:
J128g8ft9.	J729a17fr3
V729c5x16’	’ V 64c4x14 ’
198.	Упростите выражения:
л—0 2—Г’где а) < 1( б) ixi > 1;
(1 + х2)У1 - 2х2 + х4
2) у'х2 - 10х + 25 + ^х2 + 6х + 9, где а) х < -3, б) -3 < х < 5, в) х > 5;
'ЗагЬ3 'l	(J2a7c2 .
сх4 )	\У bx5 I ’
/4/2с2х3 \ . (J4x2b3 \ . \\ abs / ’ \У са2 I
5) a/x2V^V^;
6) ух~\'^а^Ь^х.
108
199. Не используя знака модуля, запишите выражения для функций:
1) |(Х - |х|);	4) |х2 - 5х + 6|;
2) ||х - |х||;	5) |хЛг
3) |х + 3 + |х + 2|;
200. Найдите область задания функций:
1) ГТ	: у1\х\ + х 2) Vx2 - х - 12;	3) \/2 - х - х2; 4) >/х2 + 6х + 9 + Vx2 - 2х - 8.
201. При каких значениях х имеет место равенство:
1) у]х(х - 1) = 7х Vx - 1;	2) ^х(х - 1) = V-x V1 - х?
202. Постройте функцию, заданную одним аналитическим выражением, для которой:
1)	D(f) = (-3; 7); 2)	D(f) = [2; 5]; 3)	D(f) = (-00; -3);	4)	D(f) = [3; +00); 5)	D(f) = (-00; -5] U [5; +00); 6)	D(f) = (-00; -4) U [0; 8].
5.	Упрощение иррациональных выражений. При упрощении иррациональных выражений применяются следующие основные приёмы:
1)	приведение корней к одному показателю (по формуле (6) п. 4);
2)	замена произведения или частного корней с одинаковыми показателями корнем из произведения или частного (по формулам (3) и (4) п. 4);
3)	сокращение показателей (по формуле (6) п. 4);
4)	замена корня из корня одним корнем (по формуле (5) п. 4).
Такие преобразования позволяют заменить любое выражение, составленное из чисел и переменной х с помощью операций умножения, деления и извлечения корня, тождественно равным ему
выражением вида \Jaxk или вида
Пример.
^210 • 625 • х35 = ^(22  62 • х7)5 = ^22 •65 • х7.
Полученное выражение можно записать также в виде 12х2 л/18х, поскольку
V22 • б5 • х7 = 6х2л/22  62х = 6х2ч/24 • 32х = 12x2V18x.
Если показатель корня чётен, используется формула (7) п. 4. Например,
= VM- у2- к
109
Упражнения
203.	Упростите выражения:
1)	V64a4b6c24;	2) >/256а864с21.
204.	Приведите к общему показателю корни: yJ2a2b3c и Va&3c2.
205.	Какое из чисел больше:
1)	V2 или >/3;	2) V7 или V5; 3) V11 или V8?
206.	Упростите выражения:
1)	у/а2 + 6а + 9 + у/а2 - 6а + 9, рассмотреть случаи а <-3, -3<а<3, а > 3;
р > 0, q > 0, pq > 1;
3) -;=±= + , 1	: Ц—
' yix - 1 у!х + \ I \ у/х - 1
где х =
а2 + Ь2 2аЪ
а> b > 0;

4)	1 + (а + Уа2 - 1)2(& + y/b2 - 1)' (а + yja2 - 1 )(t> + y/b2 - 1)

10) У19а'Ь + a +
207. Докажите, что:
1>
2) 7^5 - VI = |(V2 + V20 - V25);
О
110
3) 7%/28 - </27 = |(</98 - </28 - 1); О
/3 + 2</5V _ </5+1.
1з - 2</5/	</£ - Г
61 (й + й)! ' (1 + й +
7)	у]ах2 + by2 + cz2 = </а + <//? + </с, если ах3 = by3 = cz3 и ^ + — + ^ = 1: 1 11
8)	(2((а2 + 52)2 - а)((а2 + Ь2)2 - t>))2 = а + Ь - >/а2 + Ь2, а > О, Ь > О;
1 11? 1
9)	(3((а3 + ft3)3 - а)((а3 + b3)3 - b))3 = (а + b)3 - (а2 - ab + 52)3.
208.	Докажите, что
3Li +	+ J-2. _ йГП?
V 2 У 4	27 У 2 У 4	27
является корнем уравнения х3 + рх + q = 0.
209.	Докажите, что при А>0, В>0иА2-В>0 верно равенство
Ja + Jb = JA +	~ в ±	~	~ В.
210.	Упростите выражения:
1)	^2 - >/2; 2) ^2 - 73; 3) Va - Va2 - F; 4) Va + Va2 -
5)	у]a + 5 + c + 2 Jac + be + yja + b + c - 2'1 ac + be, a > 0, b > 0, c > 0.
211.	Докажите, что:
1)		2 + J% +----2- Л  =
Л + \2 + 7з V2-V2-V3
2)	</20 + 14^2 + V20 - 14^2 = 4;
4)	ч|9 - 5^3 = >/3 - 1.
N9 + 5^3	\/з + 1’
I-------1	I-------,	[2 при 1 < х < 2,
5)	\1х + 2>/х - 1 + чх - 2>/х - 1 = / .----
[2>/х - 1 при х > 2.
212.	Найдите значение sin 15°, cos 15°, sin22°30' и преобразуйте получен ные выражения.
111
6. Уничтожение иррациональности в знаменателе или в числителе. Замена дроби, знаменатель которой — иррациональное выражение, тождественно равной ей дробью, знаменатель которой — рациональное выражение, называется уничтожением иррациональности в знаменателе. Аналогично определяется уничтожение иррациональности в числителе. Приведём примеры такого преобразования иррациональных выражений.
Пример 1. Уничтожим иррациональность в знаменателе ,	8
дроби
\1Х
Решение. Умножим числитель и знаменатель дроби на ух1 2 Получим
8 = sVx2 = sVx2 _ 83/х2
Vx ЧхЧх2 Vx3 * X
Пример выражения
2. Уничтожим иррациональность в знаменателе
1
>/х2 + 1 - six2 - 1
Решение. Имеем
1 _ ________________л/х2 + 1 + Ух2 - 1_______
Vx2 + 1 - >/х2 - 1 (Vx2 + 1 - six2 - 1)(n/x2 + 1 + six2 - 1)
Ух2 + 1 + six2 - 1	_ Ух2 + 1 + six2 - 1
(six2 + l)2 - (Vx2 - l)2	2
Уничтожение иррациональности в знаменателе или в числителе дроби применяется при вычислении пределов иррациональных функций.
Пример 3. Вычислим предел
lim (six + 4 - Vx).
X +00
Решение. Так как
л/х + 4 - s/x
(six + 4 - slx)(s/x + 4 + s/x) six + 4 + s/x
4
six + 4 + s/x
и lim (six + 4 + s/x) = +°°, to X +OO
lim (s/x + 4 - s/x) = lim	, -  .........t= = 0.
X-J+oo	X-»+<x>	+ 4 + ylX
112
Упражнения
213. Уничтожьте иррациональность в знаменателе:
2 - ТЗО .	1
Тб - Тб + 77’	о) i/a - 7ь’
2) 	9	. Vio + 715 + 714 + 721’	6) 7^ +	+ 7^’
7аЬсг . ' Тза2Ь7с10’	7) 7^ + 7^’
к + Ljs	8) 7^ + 7& + 7Г
214. Вычислите пределы:
1)	lim X -> ОО	7х3 + X . х + 2	5)	,. 71 + x -71 +..x2	
				x—>0	71 + x - 1
2)	7х2 + 1 + Тх. hm	; Х^+оо	+ Х _ Х		6)	lim X —> OO	(Tx2 + 1 - Tx2 - 1)
3)	lim х - > - 1	+ + Hl Hl	7)	lim x(7x2 + 1 - x); X -» +0O	
4)	lim х-»0	71 + Зх4 - 71 - 2x. X + X2	8)	2	2 lim ((x + l)3 - (x - l)3 X -» +OO	
7. Иррациональные уравнения. Уравнение А(х) = В(х), в котором хотя бы одно из выражений А(х), В(х) иррационально, называется иррациональным. Примерами таких уравнений могут служить
7х - 3 + Тх + 4 = 7, Vx2 - 9 + >/х2 + 9 - 10 = 0.
Уравнение же
V2x4 + 73х2 + -—^1 = 0 уз + V2
рационально, поскольку в нём х не находится под знаком корня. Понятия корня уравнения и его решения для иррациональных уравнений определяют так же, как и для рациональных.
Пример 1. Число 1 является корнем уравнения Тх + 3 = 2, поскольку 71 + 3 = 2. Иных корней это уравнение не имеет, и потому его решением является х = 1.
113
Пример 2. Уравнение л/х + 2 = -3 не имеет корней, так как 4х + 2 принимает лишь неотрицательные значения.
Пример 3. Не имеет корней и уравнение
Vx2 + 4 + л/х2 + 9 = 4,
так как при любых значениях х имеем л/х2 + 4 >2и Vx2 + 9 > 3, а потому >/х2 + 4 + <х2 + 9 > 5.
Решение иррациональных уравнений основано на следующем утверждении.
Теорема. Если п > 0 — нечётное число, п = 2k + 1, то уравнения Ап(х) = Вп(х) и А(х) = В(х) равносильны.
Если же п > 0 — чётное число, п = 2k, то любой корень уравнения Ап(х) = ВЛ(х) удовлетворяет хотя бы одному из уравнений: А(х) = В(х) и А(х) = -В(х).
Доказательство. Пусть а — корень уравнения А(х) = В(х). Тогда .А(а) = -В(а), и потому Ап(а) = В"(а), т. е. а — корень уравнения Ап(х) = В"(х). Таким образом, всякий корень уравнения А(х) - В(х) является корнем уравнения А"(х) = В"(х).
Обратно, пусть а — корень уравнения Ап(х) = Вп(х), т. е. Ап(а) = = В"(а). Если п нечётно, то отсюда вытекает, что А(а) = В(а), и потому а — корень уравнения А(х) = В(х). Значит, при нечётном п уравнения А(х) = В(х) и А"(х) = В"(х) равносильны.
Если же п чётно, то равенство А^а) = В"(а) может иметь место либо при А(а) = В(а), либо при А(а) = -В(а), а потому а является корнем по крайней мере одного из уравнений: А(х) = В(х), А(х) = - -В(х).
Из этой теоремы следует, что если в ходе решения иррационального уравнения А(х) = В(х) приходилось возводить обе его части в степень с чётным показателем, то могут появиться посторонние корни, т. е. корни уравнения А(х) = -В(х). Чтобы отделить их, следует проверить найденные корни, подставив их в исходное уравнение. Появление посторонних корней при возведении обеих частей уравнения в степень с чётным показателем возможно и из-за изменения области существования.
Чтобы отделить посторонние корни, не всегда необходимо подставлять найденные корни в данное уравнение. Разберём два важных вида иррациональных уравнений: уравнение вида 2^А(х) = В(х) и уравнение вида 2f]A(x) = 2^В(х), где А(х) и В(х) — рациональные выражения, a k — натуральное число. Так как значения 2^А(х) всегда неотрицательны, то справедливо следующее утверждение.
114
Уравнение вида 2^А(х) = В(х) равносильно системе, состоящей из уравнения А(х) = В2к(х) и неравенства В(х) > 0:
2^А(х) = В(х) »
А(х) = В2*(х),
В(х) > 0.
В самом деле, по определению корня из числа равенство 2^А(х) = = В(х) означает, что А(х) = В2к(х), причём В(х) > 0.
Аналогично доказывается, что уравнение 2у]А(х) = 2^В(х) равносильно системе, состоящей из уравнения А(х) = В(х) и неравенства В(х) > 0:
А(х) = В(х), В(х) > 0.
Пример 4. Решим уравнение
>/х2 + х + 1 = х - 4.
Решение. Это уравнение равносильно системе х2 + х + 1 = (х - 4)2, х - 4 > 0.
Но уравнение х2 + х + 1 = (х - 4)2 имеет единственный корень
5
х = ^, который не удовлетворяет неравенству х - 4 > 0. Поэтому О
данное уравнение не имеет корней.
Пример 5. Решим уравнение
л/х2 + 2х + 10 = 2х - 1.
Решение. Это уравнение равносильно системе |х2 + 2х + 10 = (2х - I)2, [2х - 1 > 0.
Корнями уравнения х2 + 2х + 10 = (2х - I)2 являются числа 1 и 3, из которых лишь 3 удовлетворяет и неравенству 2х - 1 > 0.
Значит, данное уравнение имеет один корень х = 3.
Пример 6. Решим уравнение
V-9x2 + Зх - 6 = \/-6х - 24.
Решение. Это уравнение равносильно системе
-9х2 + Зх - 6 = -6х - 24, -6х - 24 > 0.
115
Корнями уравнения -9х2 + Зх - 6 = -бх - 24 являются числа -1 и 2. Однако при этих значениях х не выполняется неравенство -бх - 24 > 0, и потому данное уравнение не имеет корней.
При решении иррациональных уравнений полезно перед возведением обеих частей уравнения в некоторую степень «уединить радикал», т. е. представить уравнение в виде С(х) = n]D(x). Тогда после возведения обеих частей уравнения в n-ю степень радикал справа исчезает.
Пример 7. Решим уравнение
х2 + 2х + л/х2 + 2х + 8 - 12 = 0.
Решение. Метод уединения радикала приводит к уравнению четвёртой степени. Поэтому решим уравнение иначе. Положим л/х2 + 2х + 8 = у. Так как у2 - 8 = х2 + 2х, получаем уравнение у2 - 8 + у - 12 = 0, корни которого -5 и 4. Поскольку уравнение >/х2 + 2х + 8 = - 5 не имеет корней, задача свелась к решению уравнения Vx2 + 2х + 8 = 4.
Возведя обе части этого уравнения в квадрат, получим квадратное уравнение х2 + 2х - 8 = 0. Оно имеет корни -4 и 2, причём оба удовлетворяют исходному уравнению.
Проверка корней иррационального уравнения возможна, если множество этих корней конечно. Если же их бесконечно много, то приходится поступать иначе: устанавливать дополнительные условия, налагаемые на корни, и проверять, когда они выполняются.
Пример 8. Решим иррациональное уравнение
>/х2 - бх + 9 + л/25 + 10х + х2 = 8.	(1)
Решение. Если дважды уединить радикал, возведя после этого обе части уравнения в квадрат, то получим равенство
25 + 10х + х2 = х2 + 10х + 25, которое имеет место для всех значений х. Однако, например, число 4 не является корнем исходного уравнения (1), так как
V42 - 6 •4 + 9 + л/25 + 10 • 4 + 42 = 1 + 9*8.
Посторонние корни появились потому, что в данном уравнении оба радикала должны принимать неотрицательные значения, а это условие снимается при возведении в квадрат обеих частей уравнения.
Из условия неотрицательности радикалов получаем, что должны выполняться неравенства 8 - V25 + 10х + х2 > О и 8 -- л/х2 - бх + 9 > 0.
116
Из первого неравенства получаем хг + 10х - 39 < 0. Его решением является отрезок [-13; 3]. Решением второго неравенства является отрезок [-5; 11]. Оба неравенства выполняются на пересечении этих отрезков, т. е. на отрезке [-5; 3]. Поскольку, кроме этих неравенств, никаких ограничений на х не накладывается, а уравнение, получаемое освобождением от иррациональностей, тождественно выполняется на всей числовой прямой, решением уравнения служит найденный отрезок [—5; 3].
Замечание. Уравнение (1) можно решить иначе. Воспользуемся тем, что Vx2 - 6х + 9 = |х - 3| и Ух2 + 10х + 25 - |х + 5|. Данное уравнение принимает вид
|х - 3| + |х + 5| = 8.	(Г)
Разбивая числовую прямую на промежутки (-°°; -5], [-5; 3], [3; +°°), на каждом из которых х-3их + 5не меняют знак, и освобождаясь от знака модуля, убеждаемся, что (1') имеет место лишь на отрезке [-5; 3].
У пражнения
215.	Докажите, что не имеют решений уравнения:
1)	У2х + 3 + Ух — 3 = 0; 4) Ух - 3 - Ух + 9 = Ух - 2;
2)	Ух + 2 + Ух — 1 = -2; 5) Ух + Ух + 9 = 2.
3)	У4 - х - Ух - 6 = 2;
216.	Решите иррациональные уравнения:
1)	У2х - 7х = -52; 2) 2х + У4х - 8 = О
3)	72х + 7 + у/Зх - 18 = у/7х + 1; 4)	+	+ з =	?—.
Vx - 3	Vx - 3
5)	Ух + 9 = 2-Ух - 3;
«Л + 1 +	- 1	+ + 1 - Ух2 - 1	4J	2 _
Vx2 + 1 - Ух2 - 1	Ух2 + 1 + Vx2 - 1
7)	Vx + 7 - Vx + 12	=1; 8) x2 + 3 - V2x2	- 3x	+ 2	= | (x + 1);
9)	x(x + 1) + зУ2х2 + 6x + 5 = 25 - 2x;
10)	Vx + Vx + 7 + 2Vx2 + 7x = 35 - 2x;
11)	x2 - 8(x + l)Vx + 18x + 1 = 0;	12) Vx + 1 + Vx - 1 = 1;
13)	Vl - Vx*-- x2 = x - 1; 14) Vx2 + 4x + 4 - Vx2 - 12x + 36 = 8;
117
15)	\lx2 + 4x + 4 + л/х2 - 12x + 36 =16;
16)	Vx2 + 4x + 4 - Vx2 - 12x + 36 = 6;
17)	Vx + л/бх - 9 + Vx - >/бх - 9 = 'Уб.
8.	Иррациональные неравенства. Решение иррациональных неравенств осложняется тем обстоятельством, что неравенства А(х) < В(х) и А"(х) < В"(х) не являются равносильными: ведь только для неотрицательных чисел а и b из а < Ъ следует а" < Ьп, а из ап < Ьп следует а < Ь. Поэтому при решении иррациональных неравенств надо учитывать знаки правой и левой частей.
Пример 1. Решим неравенство
у/х2 - 55х + 250 < х - 14.	(1)
Решение. Поскольку квадратные корни можно извлекать лишь из неотрицательных чисел, то должно выполняться условие х2 - 55х + 250 > 0. Решением этого неравенства является множество
А = (-оо; 5] и [50; +ОО),
Кроме того, поскольку Vx2 - 55х + 250 > 0, имеем х - 14 > 0. Определяя общую часть множеств А и [14; +°°), получаем луч [50; +°°). Таким образом, решение неравенства (1) должно быть частью луча [50; +°°).
Если х > 50, то обе части неравенства (1) существуют и неотрицательны, а потому оно равносильно неравенству х2 - 55х + 250 < (х - 14)2.
Поэтому осталось решить систему неравенств J50 < х, |х2 - 55х + 250 < х2 - 28х + 196.
Из второго неравенства получаем х > 2. Поскольку (2; +°°) А А [50; +°°) = [50; +°°), то решением неравенства (1) является луч [50; 4-00).
Вообще любое неравенство вида 2^А(х) < В(х) равносильно системе неравенств А(х) > 0, В(х) > 0, А(х) < В2*(х):
2^А(х) < В(х) <=>
А(х) > 0,
В(х) > 0, А(х) < В2*(х).
(2)
Первое из них выражает неотрицательность подкоренного выражения, второе — неотрицательность корня, третье следует из того,
118
что при а > О, b > О неравенства а < Ъ и а2к < Ь2к выполняются одновременно.
Неравенство 2^А(х) > В(х) имеет место либо когда В(х) > О, А(х) > В2к(х), либо когда А(х) > 0 и В(х) < 0. Поэтому надо решить системы неравенств
|В(х) > 0,	ГА(х) > 0,
[А(х) > В2*(х) И |В(х) <0	( }
и объединить их решения.
Пример 2. Решим неравенство
Vx2 + бх 40 > х + 2.	(4)
Решение. Это неравенство сводится к следующим системам неравенств:
(х + 2 > 0,	[х2 + бх - 40 > 0,
}х2 + бх - 40 > х2 + 4х + 4; [х + 2 < 0.
Решением первой системы является открытый луч (22; +°°), второй системы — множество (-°°; -10). Объединяя эти множества, получаем решение данного неравенства: множество (-°°; -10] и U (22; +оо).
Более сложно решение иррациональных неравенств вида
+ л/ад < С(х).	(5)
Поскольку \1-А(х)	0, у/В(х) > 0, то должны выполняться усло-
вия А(х) > 0, В(х) > 0, \Jb(x) < С(х) (соответственно у]А(х) < С(х)). На множестве, где эти условия выполняются, данное неравенство равносильно неравенству
А(х) < (С(х) - Тад)2 (соответственно неравенству В(х) < (С(х) - ^А(х)) ), которое сводится к разобранным выше типам неравенств.
Пример 3. Решим неравенство
Vx + Vx + 7 < 6.	(6)
Решение. Данное неравенство равносильно следующей системе неравенств:
х > О,
х + 7 > О,
^<6,	<7>
х + 7 < (б - >/х) = 36 - 12>/х + х.
119
имеет вид
Последнее неравенство этой системы приводится к виду 12\[х < 29, откуда находим, что 0 < х < yll. Решение неравенства (6) является общей частью решений всех неравенств системы (7), т. е.
Го;
L 144/
У пражнения
217.	Решите иррациональные неравенства:
1)	>/х2 - Зх + 2 > 2 - х; 2) >/25 - х2 + >/х2 + 7х > 3;
3)	>/х2 - Зх - 10 < 8 - 5х; 4) V1 + х + >/1 - х > 1;
5)	>/х + >/х + 7 + 2>/х2 + 7х < 35 - 2х; 6)	----1 > 1;
У 2 - х
7)	у/2х + 1 < 2(х +	8) 7э - Vx2 - 6х + 9 > х - 3;
2-х
9)	711 - Jtx2"- 4х + 1 + X < 5; 10) 712 + 8х + 16 > х - 1.
§	5. Метод последовательных приближений
1.	Приближённое решение уравнений. При изучении курса математики мы встречались с самыми разными видами уравнений: линейными, квадратными, иррациональными, показательными, логарифмическими, тригонометрическими. При этом мы стремились найти общие формулы, позволяющие выразить корни уравнения через входящие в это уравнение числа. Например, для уравнения ах + Ь - 0, а £ 0, формулой решения является х = для уравнения ах2 + Ъх + с - 0, а / 0, — формула Xt 2 -а
_ ^Ь±—b - 4ас, для уравнения а‘=Ь, а> О, а* 1, — формула
x = J^, lg а
а для уравнения cosx = а, |а| < 1, — формулах = iarccosa +
+ 2пп, п 6 Z.
Вычислительная ценность этих формул различна — в одних случаях достаточно выполнения действия деления, в других требуется ещё извлечение корней, а в третьих — отыскание значений логарифма или обратной тригонометрической функции.
120
Результаты всех этих операций лишь приближённо могут быть записаны в виде десятичных дробей. При этом класс уравнений, для которых можно найти формулу решения, весьма узок. Уже для алгебраических уравнений пятой степени нет общей формулы, выражающей корни этого уравнения через его коэффициенты с помощью арифметических действий и операции извлечения корня. Нет формул и для решения таких уравнений, как 2х = х + 3,
. sin Зх	_
х = 1 + —— и т. д., хотя подобные им уравнения часто встре-
чаются при решении практических задач.
Однако для решения практических задач не столь важно обладание формулой решения, сколь умение найти корни уравнения с заранее заданной точностью. Иными словами, надо уметь решать такую задачу.
Дано уравнение f(x) = 0, имеющее корни хн х2, ..., хп, и число е > 0. Найти числа tlt t2, ..., t„, отличающиеся от корней этого уравнения меньше чем на е, т. е. такие, что \tk - xk\ < е, 1 < k < п.
Решение указанной задачи является одним из вопросов вычислительной математики. В этом параграфе мы изложим наиболее важный метод приближённого решения уравнений — метод последовательных приближений.
2.	Метод последовательных приближений. Уравнение /(х) = 0 можно различными способами записать в виде х = ф(х), где (р — некоторая функция. Например, уравнение х2 - 2 = 0 можно записать в следующих видах:
г = х2 + 2 v _ Зх2 + 2 г = 10*(2 - х2) + х2 + 2 2х ’	4х ’	2х
и т. д. Для уравнений, записанных в виде х = <р(х), применяют следующий метод приближённого решения, называемый методом последовательных приближений. Выбирают некоторое начальное приближение х, и подставляют его вместо х в ф(х). Полученное значение х2 = ф(х0 этой функции считают вторым приближением. Далее находят третье приближение по формуле х3 = <р(х2) и т. д. При определённых условиях, которые будут указаны ниже, получающаяся таким образом последовательность чисел х1; х2, ..., х„, ... имеет предел а. Тогда, если функция ф непрерывна, из равенства хл+1 = ф(х„) вытекает, что lim x„ + l - lim ф(хп) - ф( lim х„), т. е.
п —> ОО	Л —> ОО	п —> ОО
а = ф(а). Это означает, что а является решением уравнения х = ф(х). При достаточно больших значениях п разность \х„ - а| становится сколь угодно малой, т. е. хп является достаточно хорошим приближением для искомого корня.
121
Пример 1. Найдём методом последовательных приближений корень уравнения х = 1 + arctgx с точностью до 0,001.
Решение. Положим Xi = 1. Тогда имеем: х2 = 1 + к arctgl = 1 + ? ~ 1,39, Z	о
х3 = 1 + 4 arctg 1,39 ~ 1,474, di
Xi = 1 + 4 arctg 1,474 » 1,487, х5=1+ 4 arctg 1,487 = 1,489, d
х6 = 1 + ij arctg 1,489 = 1,490, di
x7 = 1 + 4 arctg 1,490 ~ 1,490. di
Так как значения x6 и x7 совпадают с точностью до 0,001, то с указанной точностью х = 1,490.
Метод последовательных приближений применяется для извлечения корней. Квадратный корень из положительного числа а является положительным корнем для уравнения х2 = а. Легко х2 + а проверить, что это уравнение равносильно уравнению х = ——•
Поэтому для извлечения квадратных корней применяется следующий метод: берём какое-нибудь положительное приближение Xi для Та и строим последовательность чисел х15 ... , хп, ..., где хп+1 =
+ д
= -----. Процесс ведётся до тех пор, пока модуль разности зна-
2хп
чений хл+1 и х„ не станет меньше заданной точности вычислений.
Пример 2. Найдём значение Тб с точностью до 0,001.
Решение. Положим х3 = 2. Тогда
* = Уг = 2-25-
_ 2,252 + 5 _ 9 236
Хз~ 2-2,25
2,236г + 5
2 • 2,236
« 2,236.
Значит, с точностью до 0,001 получаем <5 = 2,236.
Для вычисления корней k-й степени уравнение х* = а запи
сывают в виде
а + (k - 1)х* Х ~ kxk~l
122
После этого вычисления ведутся по формуле
_ а + (А - 1)*;	m
n+1 kxkn~l ‘
Пример 3. Найдём с точностью до 0,001 значение \/970.
Решение. Положим в формуле (1) k = 3, а = 970 и выберем X! = 10. Тогда
= 970 + 2 • 103 = g.g, х3 = 970 + 2 J»’9* = 9,899.
З Ю2	3  9,9
Значит, с точностью до 0,001 получаем х = 9,899.
Замечание. Формулу х„+1 = —- применяющуюся для извле-^Хп
чения квадратных корней, можно записать в виде x„+i = -^х„ +
Она означает, что следующее за х„ приближение является средним арифметическим чисел х„ и —, для которых средним геометрическим
является х„  —, т. е. 4а. Таким образом, процесс последовательных V хп
приближений заключается в данном случае в том, что на каждом шагу среднее геометрическое заменяется средним арифметическим.
Метод последовательных приближений не всегда приводит к сходящейся последовательности чисел. Исследование даёт следующие достаточные условия сходимости метода последовательных приближений.
Теорема. Пусть на отрезке [а; Ь] функция f монотонна, причём отрезок [Да); f(b)] является частью отрезка [а; Ь], и пусть существует такое число q, что 0 < q < 1 и |/Дх)| < q на отрезке [а; Ь]. Тогда на этом отрезке лежит единственный корень уравнения х - f(x), причём процесс последовательных приближений, начинающийся с любого значения с из [а; Ь], сходится к этому корню.
Упражнения
218.	Решите методом последовательных приближений уравнения, преобразовав уравнение к подходящему виду (оформите вычисления на ПК в виде электронной таблицы):
D х = j -• 2; 2) х = (х + I)3; 3) х - 4 + ter 4) х - 2 +
(X + 1)	IX т 1
5) х =	е-1; 6) 4 - Зх = tgx; 7) х2 - sinx; 8) х3 = sinx;
х "Ь 1	,	, sin х ,,, л _	I,,
9) х = arcsin ——; 10) х = 1 +	; 11) х2 = ln(x + 1);
12) 1пх = 4 - х2; 13) х2 = ех + 2; 14) 2х = 4х.
123
§ 6. Уравнения и неравенства с параметрами
1. Рациональные уравнения и неравенства с параметрами. Обычно в уравнении или неравенстве буквами обозначают неизвестные. Решить уравнение (неравенство) — значит найти множество значений неизвестных, удовлетворяющих этому уравнению (неравенству). Иногда уравнения (неравенства), кроме букв, обозначающих неизвестные, содержат другие буквы, называемые параметрами. Тогда мы имеем дело не с одним, а с бесконечным множеством уравнений (неравенств). При этом бывает, что при одних значениях параметров уравнение не имеет корней, при других — имеет только один корень, при третьих — два или больше корней. При решении таких уравнений (неравенств) надо сначала найти множество всех допустимых значений параметров, а затем разбить это множество на части, в каждой из которых ответ выражается через параметры одной и той же функцией.
Разберём следующий пример.
Пример 1. Решим уравнение ах2 - 4х + 3 = 0.
Решение. В данное уравнение входит лишь один параметр а. Если этот параметр принимает значение 0, получаем линейное з уравнение, имеющее лишь один корень, а именно х - При а Ф 0 уравнение является квадратным и его корни выражаются через параметр а формулами
„ _ 2 + V4 - За „ _ 2 - 5?4 - За X1 —-	, X? —	•
а	а
4	4
Если а < д. то имеем два действительных корня, при а = 3 эти 4
корни совпадают, а при а > 3 подкоренное выражение отрицательно и действительных корней нет.
Ответ записываем так:
если а = 0, то х =
если а < а * 0, то х1>2 = ^-=—-—— 3	’	а
4	3.
если а = —, то х = 3	3
4
при а > действительных корней нет. 3
124
Замечание. Случай а = 0 можно рассматривать как предельный. Именно если а —> 0, то корень	~ За стремится к а корень
а
2 — V4 — За 3	й
---------- — к-т. Мы, однако, не будем этого учитывать и будем а---------4
считать, что при а = 0 имеем единственный корень.
Пример 2. Решим уравнение
Зтх - 5	, Зт - 11 _ 2х + 7
(т - 1)(х + 3) т - 1 х + 3
(здесь и ниже неизвестные обозначены буквами х, у, z, параметры — буквами а, Ь, с, k, т, п и т. д.).
Решение. Выражения в левой и правой частях уравнения имеют значения при т Ф 1 и х -3. При этом условии, умножая обе части уравнения на (т - 1)(х + 3), получаем уравнение, равносильное данному. После упрощения получаем уравнение
(4тп - 9)х = 31 - 2т.
При т Ф | оно имеет корень х - Т<р
Осталось выяснить, при каких значениях т этот корень допустим, т. е. отличен от числа -3. Решая уравнение _2^ = -3, находим, что т = ~.
5	9	2
Итак, если т*1,т* т Ф то уравнение имеет един-
-	31 - 2т тт 1	9	2
ственныи корень х =	_ §• При т = 1, т = р т = - корней нет.
Аналогично решаются линейные неравенства с параметрами.
Пример 3. Решим неравенство 2х - т________________________т <	3
(тп - 2)(х + 3) т - 2 х + 3’
Решение. Допустимыми значениями тих являются такие, что т / 2, х -3. Перенеся все члены в левую часть и приведя дроби к общему знаменателю, получаем неравенство
(т - 2)х - (6 - 7т) (т - 2)(х + 3)	> °’
равносильное в области т/2, х -3 неравенству
(х-^=^)(х + 3)>0.	(1)
125
Решим неравенство (1) методом интервалов. Решая уравнения х+3=0их- -—= 0, получаем х} = -3, х2 = —~ ??*. Воз-тп — z	щ — 1
6 - 7m „ . 6 - 1т „ можны два случая:-3 С _ 2 и-3 > т _ %• Решая неравенство
3 > 6—7m т е ~4?п < о, находим, что т < 0 или т > 2. т &	т ~ сл
Неравенство же -3 <	выполняется на промежутке [0; 2].
Значит, если т < 0 или если т > 2, то неравенство (1) выполняется
на лучах -оо;
6 - 1т\ т - 2 /
и (-3; +°°). При 0 < т < 2 оно выполняется
на лучах -3) и I-—+оо \ т - 2
Если нужно выяснить, нет ли значений параметров, при которых какой-либо корень уравнения имеет «запрещённое» значение, то проще всего подставить это значение корня в преобразованное уравнение — искомые значения параметров сразу определятся.
Пример 4. Решим уравнение
х , 2х _ 3d - 4
b + 1 х - 2 (ft + 1)(х - 2) ‘
Решение. Здесь недопустимы значения b - -1 и х - 2. В области, где Ь * -1, х * 2, данное уравнение равносильно уравнению х2 + 2bx - ЗЬ + 4 = 0,	(2)
корни которого имеют вид
Xi = -ft - y/b2 + 3ft - 4, x2 = —ft + Vft2 + 3ft - 4.	(3)
Чтобы выяснить, при каких значениях ft один из этих корней равен 2, подставим х = 2 в уравнение (2). Получаем 8 + ft = О, откуда ft = -8. При этом значении ft «запретному» числу 2 равен первый корень, а второй принимает значение 14.
Осталось выяснить, при каких значениях ft корни Xj и х2, задаваемые формулой (3), действительны. Это имеет место при ft2 + 3ft - 4 > 0. Так как корнями уравнения ft2 + 3ft - 4 = 0 являются ftj = 1 и ft2= -4, то корни действительны при ft < -4 (причём ft * -8) и при ft > 1.
Итак, заданное уравнение имеет два действительных корня, задаваемые выражениями (3) при ft < -4, ft -8 и при ft > 1. Эти корни совпадают при ft = -4 и при ft = 1. При ft = -8 имеем один корень х = 14. При остальных значениях ft действительных корней нет.
126
Упражнения
219.	а) Найдите все значения а, при которых один из корней уравнения х2 - 2ах + 1=0 больше 1, а второй — меньше 1.
б)	При каких значениях а оба корня уравнения х2 - бах + 2 - 2а + + 9а2 = 0 больше 3?
220.	При каких значениях а корни уравнения (1 + а)х2 - Зах + 4а = 0 существуют и удовлетворяют условию 2 < х < 5?
221.	Найдите все значения а, при которых корни уравнения х2 + х + а = 0 больше а.
222.	При каких значениях а корни уравнения х2 - 2х - а2 + 1 = 0 лежат между корнями уравнения х2 - 2(а + 1)х + а(а - 1) = 0?
223.	Решите неравенства:
1)	х2 + ах + 1 > 0;	2) ах2 + х + 1 > 0.
224.	При каких значениях а выражение х2 - (а + 2)х + а + 3 положительно при всех х > 0?
225.	При каких значениях а выражение ах2 - 2(а - 1)х + За — 1 положительно при всех х > 1?
226.	Для каких значений а неравенство 2х2 — 4а2х - а2 + 1 > 0 справедливо при всех х, |х| < 1?
227.	Найдите все значения а, при каждом из которых любое х, удовлетворяющее неравенству ах2 + (1 - а2)х - а > 0, по модулю не превосходит 2.
228.	При каких значениях а неравенство (а2 - 4)х2 - 4ах + 2 > 0 истинно при всех х > 2?
229.	Найдите все значения а, при которых из неравенства х2 - а(1 + а2)х + + а4 < 0 следует неравенство х2 + 4х + 3 > 0.
230.	Найдите все значения а, при которых неравенство выполняется при любом х > 0:
1)	(а3 + (1 - Т2)а2 - (3 + у[2)а + 3>/2)х2 + 2(а2 - 2)х + а > -^2;
2)	(а3 - (1 + V2)a2 + (V2 - з)а + 3>/2)х2 + 2(а2 - 2)х + а > -^2.
231.	Найдите все значения а, при которых система имеет единственное решение:
fx2 + 2х + а < 0,	|х2 + 4х + 3 < а,
|х2 - 4х - ба < 0;	|х2 - 2х < 3 - 6а.
232.	Найдите все значения а, при которых решения системы образуют на числовой оси отрезок длины 1:
[х2 - 2х < а - 1,	(х2 + 6х + 7 + а < 0,
1)	1	2) i
[х2 - 4х < 1 - 4а;	[х2 + 4х + 7 < 4а.
233.	При каких значениях р уравнение (х - р)2(р(х - р)2 - р - 1) = -1 имеет больше положительных корней, чем отрицательных?
234.	При каких значениях р уравнение ((х - р)2 - 2р 4)(х - р)2 = 2р - 3 имеет больше отрицательных корней, чем положительных?
235.	Найдите все значения р, при которых имеет 4 корня уравнение х(х + 1)(х + р)(х + 1 + р) = р2.
236.	Найдите все значения р, при которых уравнение х4 + (р - 1)х3 + х2 + + (р - 1)х +1 = 0 имеет не менее двух различных отрицательных корней.
127
237.	При каких р уравнение х(х + 1)(х + 2)(х + 3) = р имеет не менее трёх отрицательных корней?
238.	При каких р уравнение xi - рх3 - (2р + 1)х2 + рх + 1 - 0 имеет не менее двух корней, больших 1?
239.	Найдите все значения а и Ь, при которых система уравнений имеет единственное решение:
xyz + z = а, xyz2 + z = Ъ, х2 + у2 + z2 - 4.
240. Найдите все значения а, при решение:
каждом из которых система имеет
1)
х2 + 2ху - 7у2 > ^4 а + 1
Зх2 + Юху - 5у2 < -2;
5х2 - 4ху + 2у2 > 3, 7х2 + 4ху + 2у2 <
2. Иррациональные уравнения и неравенства с параметрами.
Пример 1. Решим уравнение
>/Зх - 2 + Vx + 2 = а.	(1)
Решение. Оба слагаемых являются возрастающими функциями от х. Тем же свойством обладает и их сумма. Поэтому л/Зх - 2 + Vx + 2 может принять каждое значение а не более одного раза. Корни в левой части уравнения определены в области, 2	2
где х > j и х > -2, т. е. при х > д-
Отсюда следует, что наименьшим значением, принимаемым
левой частью уравнения (1), является + 2, т. е. « уб. Это и
V 3	о
есть наименьшее значение а, при котором уравнение разрешимо.
2 г Итак, уравнение (1) имеет единственный корень при а > g <6
и не имеет корней при а < т? V6. о
Чтобы найти выражение для корня через а, уединим радикал и возведём обе части уравнения в квадрат:
Зх - 2 = a2 2aVx + 2 + х + 2, т. е. 2х - 4 - а2 = -2aVx + 2.
Отсюда следует, что должно выполняться неравенство х < 2 + -%. Запишем левую часть получившегося уравнения в виде 2(х + 2) -- (8 + а2) и возведём обе части уравнения в квадрат. Получим после раскрытия скобок и упрощения:
4(х + 2)2 - 8(4 + а2)(х + 2) + (8 + а2)2 = 0.
128
Отсюда
, „	4(4 + а2) ± ^16(4 + а2)2 - 4(8 + а2)2
Xj,2 +	—
2(4 + а2) ± л/За4 + 16а2 2
и потому
Xi = а2 + 2 - 5 а V3a2 + 16, х2 = а2 + 2 + yj3a2 + 16. Cl	Ci
2 г—
Поскольку при а > g л/6 уравнение заведомо имеет один корень,
. о-2
а х2 не удовлетворяет условию х < 2 + то корнем является хх.
2 г
Итак, уравнение (1) имеет при а > 3 уб единственный корень
х = 2 + а2 - к х] За2 + 16,
2 г— а при а < э л/6 корней не имеет.
О
Пример 2. Решим уравнение у] а - у[х + а = х.
Решение. Так как подкоренные выражения должны быть неотрицательны, то должны выполняться неравенства х + а > О, а > 0, а > >/х + а. Кроме того, должно быть их > 0. Значит, наименьшее значение Vx + а равно у[а и необходимо выполнение неравенства а у/a. Значит, а = 0 или а > 1. При а = 0 получаем уравнение yj-yfx = х, имеющее единственный корень х = 0. Пусть теперь а > 1. Возводим обе части уравнения в квадрат и получаем а - у/х + а - х2. Значит, а - х2 = у[х + а, откуда а - х2 > 0. Из уравнения а - х2 = yjx + а следует, что (а - х2 + х)(а - х2 - х) = = (у/х + а + х)(у!х + а - х) = (х + а - х2), откуда
(х + а - х2)(а - х2 - х - 1) - 0.
Значит, либо х + а - х2 = 0, либо а-х2-х-1-0.
Решая первое квадратное уравнение, получаем
Xi =	- + а, х2 = ~ -	+ а.
2	\4	2	\4
Из второго квадратного уравнения имеем
г - -- +	_ 3	_ _1^ _ L. _ 3.
3~ 2 \	4’ 4” 2	\	4’
129
Выясним, какие из корней х1г х2, х3, х4 удовлетворяют условию О < х < 4а. Поскольку Xi > 4а, х2 < О (напомним, что а > 1), то X] и х2 не являются корнями уравнения; х4 также не является корнем данного уравнения, так как х4 < 0. При а > 1 имеем 1	/"3
0 <	+ \1а	4 < а, и потому х3 — корень данного уравнения.
1	I 3
Итак, при а > 1 имеем единственный корень х = — + .а----,
2	v 4
а при а = 0 имеем х = 0. При остальных значениях а корней нет.
Замечание. Единственность корня при а > 1 можно установить так: функция у - х возрастает, а функция у = va - Va + х убывает. Значит, графики этих функций могут пересечься лишь в одной точке.
Теперь решим иррациональное неравенство с параметром.
Пример 3. Решим неравенство
ух - а + V2x + 1 > >/Зх - 4.	(2)
Решение. Чтобы все корни, входящие в неравенство, имели значение, должны выполняться неравенства х > а, х > х >
т. е. х > а и х > Так как при таких значениях х и а все корни О
в (2) неотрицательны, можно возвести обе части неравенства в квадрат. После упрощения получаем систему неравенств
2^/(х - а)(2х + 1) > а - 5, х > а,
(3)
4
что при а < з решением системы (3) является луч
Разберём два случая: а<5иа>5.В первом случае а — 5 < 0 и потому первое неравенство системы справедливо для всех х, удовлетворяющих двум другим неравенствам. Отсюда получаем, 4	\
+оо , а 3	/
4
при з < а < 5 — луч [а; +°°).
Пусть теперь а > 5. В этом случае обе части первого неравенства в системе (3) неотрицательны и можно возвести их в
™	4
квадрат. Так как условие х > 3 заведомо выполнено, то имеем
систему неравенств
|8х2 - 4(2а - 1)х - (а2 - 6а + 25) > 0, х > а.
130
Заметим, что
а2 - 6а + 25 = (а - З)2 + 16 > О при всех а и потому свободный член квадратного трёхчлена отрицателен. Отсюда вытекает, что корни уравнения
8х2 - 4(2а - 1)х - (а2 - 6а + 25) = 0 (4) имеют разные знаки.
Поскольку мы хотим, чтобы один из корней был не меньше чем а, то (рис. 44) в точке а трёхчлен должен
принимать неположительные значения.
Отсюда получаем для а неравенство 8а2 — 4(2а - 1)а - (а2 — 6а + + 25) < 0, т. е. -(а - 5)2 < 0. Оно выполняется для всех а. Значит, один из корней уравнения (4), а именно больший, удовлетворяет условию х > а. Этот корень имеет вид
Х1 = -(2а - 1 + л/ба2 - 16а + 51).
4
^,4	4,.	4
Итак, мы доказали, что если а < д, то < х < +°°; если <
а < 5, то а С х < 4-оо; если а > 5, то х
|(2а -1 + у]ба2 -16а+ 51).
Упражнения
241.	Решите уравнения:
1)	х + у/х - а;
2)	у/а + х _ у/а - х у/а + у/а + х у/а - у/а - х
3)	х + у/х + у/х + 2 + у/х2 + 2х = а;
4)	х2 - 2у/Зх2 - 2ах + 4 + 4 = ^(х + % + 1
5)	(а + х)’ + 4(а - х)3 - 5(а2 - х2)3 = 0;
6)	|х + 3| - а|х - 1| = 4;
7)	|х - 2| + а|х + 3| = 5.
242.	Решите уравнения (при положительных значениях параметров):
1)	(а + Ь)у/а2 + Ь2 + х2 - (а - Ь)у/а2 + Ь2 - х2 = а2 + Ь2;
2)	у/х2 - Зах - а2 + у/х2 - Зах + а2 = у/2(а2 + Ь2);
Р + Я	1	1
3)	2cx2pq = хр + xq;
131
у/a + х - \la - x
243.	Найдите все значения а, при которых уравнение
х|х + 2а| + 1 = а
имеет единственное решение.
244.	Найдите все значения а, при которых уравнение
х2 + 4х - 2 |х - а\ + 2 - а = О имеет ровно два различных решения.
245.	При каких значениях а уравнение х - 0,5а = 4|4|х| - а2| имеет ровно три корня? Найдите эти корни.
246.	При каких значениях а уравнение имеет единственное решение:
1)	|1 - ах\ = 1 + (1 2а)х + ах2;
2)	|(а + 1)х - 2| = (1 + а)х2 - 2ах + 2?
247.	При каких значениях а неравенство имеет хотя бы одно отрицательное решение;
1)	3 - |х - а| > х2;	2) 2 > |х + а| + х2?
248.	Найдите все значения а, при которых система имеет ровно два решения:
Пх2 - 7х + 6| + х2 + 5х + 6 - 12|х| = 0,
[х2 - 2(а - 2)х + а(а - 4) = 0.
249.	Найдите все значения а, при которых система имеет единственное решение:
Пх2 - 5х + 4| - 9х2 - 5х + 4 + 10х|х| = 0,
[х2 - 2(а - 1)х + а(а - 2) = 0.
3. Трансцендентные уравнения и неравенства с параметрами. Функции у - ах, у = logax, у = sinx, у - arcsinх и т. д. называют трансцендентными. Решим некоторые трансцендентные уравнения и неравенства с параметрами.
При решении показательных уравнений и неравенств с параметрами надо проверять случай, когда основание равно 1.
Пример 1. Решим уравнение
а2х~3 - а2х~2 + а2х - b.	(1)
Решение. Запишем уравнение (1) в виде
а2х~3(а3 - а + 1) = Ь.	(2)
Если а = b - 1, то при любом х имеем l2x‘3(i3 - 1 + 1) = 1. Значит, при а = b = 1 корнем уравнения является любое значение х.
132
Пусть теперь а > 0, а Ф 1. Покажем, что при этих значениях а выполняется неравенство а3 - а + 1 > 0. В самом деле, функция >/з у = х3 - х + 1 при х > 0 имеет только минимум в точке х = —,
равный 9 ~	> 0- Поэтому а3 - а + 1 > 0 при а > 0. Отсюда
следует, что если а > 0, а * 1, Ъ > 0, то а2х~3 = а3 + 1 и потому х = |(3 + logafl3 _ba + J.
В случае, когда а = 0, равенство (1) выполняется лишь при b = 0, х >
Наконец, рассмотрим случай, когда а < 0.
В этом случае допустимы лишь целые значения 2х - 3. Иными словами, если a < 0, то х = я * 3, где п — целое число. При этом b = ап(а3 - а + 1).
Итак, если а = b = 1, то х — любое действительное число. Если а > 0, а Ф 1, то х = ^(з + logn 3 ----к Если а - b = 0, то х > х-
\	а а Ч" 1 /
Если a < 0, Ъ = ап(а3 - а + 1), где п — целое число, то х = га
В других случаях уравнение корней не имеет.
Обычно в таких задачах делают оговорку, что a > 0 и случаи a = 0, a < 0 не рассматриваются.
Пример 2. Решим неравенство 2х + 1 4х + 3 a1 + 6 < а1 + 6 .	(3)
Решение. Допустимы значения х такие, что х Ф -6. Если а = 1, то данное неравенство выполняется при всех значениях х таких, что х Ф -6. При а > 1, х Ф -6 оно равносильно неравенству %х + J- > ^х + , которое приводится к виду 2(х + 1)(х + 6) < 0. х + о х + о
Методом интервалов получаем, что х < -6 или х > -1.
Если 0 < a < 1, х * -6, то данное неравенство равносильно неравенству 2х	+ 6 ’ т' е> +	+ 6)	0. Решая его
методом интервалов, получаем -6 < х < -1.
2х + 1
*При а = 0 неравенство (3) справедливо, если +	> 0
и q > 0. Решая эту систему неравенств, получаем, что х < -6
133
з
или х > Если а < 0, то неравенство (3) может иметь место 2х + 1 лишь в случае, когда показатели — целые числа. Если = т и +а = п> то имеем х =	—- = ^.га ~ откуда 24m + п - 4 =
х + 6	2 -т 4 - п
= 3m + 12л 6, т. е. 21m - lln + 2 = 0. Найдём целые значения m и п, при которых выполняется равенство 21m - lln + 2 = 0.
Подбором находим одно решение: т0 = 2, п0 = 4. Остальные решения выражаются формулами
m = 2 + lit, п = 4 + 21t,	(4)
где t — целое число.
Теперь надо выяснить, при каких значениях t выполняется неравенство (3), т. е. при каких тип имеем ап < а".
Если -1 < а < 0, то это неравенство справедливо в следующих случаях:
а)	п чётно, m либо чётно, либо нечётно и m > п;
б)	m и п нечётны, причём m < п.
При а = -1 неравенство имеет место, если п чётно или если т нечётно.
При а < -1 оно справедливо в следующих случаях:
а)	п чётно, m либо чётно, либо нечётно и m < п;
б)	m и п нечётны, причём m > п.
Во всех указанных случаях выполняется неравенство (3). Предоставляем читателю выяснить, при каких значениях t в формулах (4) выполняются указанные выше условия.
Замечание. Методы решения уравнений вида ах + by = с в целых числах изучаются в теории чисел. Они основаны на следующем утверждении: наибольший общий делитель d натуральных чисел а и b можно представить в виде ах + by, где х и у — целые числа.
Пример 3. Решим уравнение
2 loga |х| + 21oga(x + 2) = 1.
Решение. По определению логарифма должны выполняться условия а > 0, а * 1, х * 0, X > -2. При этих условиях заданное уравнение равносильно уравнению
|х| (х + 2) = у/а.
Если -2 < х < 0, то отсюда находим х(х + 2) = у/а. Это уравнение имеет действительные корни лишь при у/а < 1. В этом случае Xi = -1 - л/1 ~ у/а, х2 = -1 + а/1 ~ >/“, причём легко заметить, что при 0 < а < 1 оба корня лежат на промежутке (-2; 0). При а = 1 эти корни совпадают и Xj = -1.
134
При х > 0 получаем уравнение х(х + 2) = 4а, откуда х3 = -1 -- 71 + Va, х4 - -1 + 71 + 4а. Положителен лишь корень х4.
Итак, при 0 < а < 1 уравнение имеет три корня х4, х2, х4. При а > 1 — лишь один корень х4.
Пример 4. Решим неравенство loga2 (х2 + 2х) < 1.
Решение. По определению логарифма должны выполняться неравенства а Ф 0, а Ф 1, а Ф -1 и х2 + 2х > 0. Рассмотрим два случая: |а| > 1 и 0 < |а| < 1.
Если |а| > 1 (т. е. а > 1 или а < -1), то имеем систему неравенств
Гх2 + 2х < а2,
[х2 + 2х > 0.
Первое неравенство выполняется на промежутке (х4; х2), где х4 = -1 - л/1 + а2, х2 = -1 + V1 + а2, а второе — на лучах х < -2 и х > 0. Поэтому система выполняется на пересечении указанного промежутка с объединением этих лучей. Поскольку Х] < -2, х2 > 0, то это имеет место на объединении промежутков (хв -2) и (0; х2).
Пусть теперь 0 < |а| < 1 (т. е. -1 < а < 1, а Ф 0). В этом случае получаем систему неравенств
Jx2 + 2х > а2, (х2 + 2х > 0.
Поскольку а2 > 0, достаточно рассмотреть первое неравенство. Его решением служит объединение лучей (-°°; х4) и (х2; +°°), где х, и х2 те же, что и выше.
Итак, если |а| > 1, то х4< х < -2 или 0 < х < х2; если |а| < 1, а Ф 0, то —< х < х4 или х2 < х < +°о, где х4 = -1 - V1 + а2, х2 = -1 + >/1 + а2.
Пример 5. Решим уравнение
(а - l)cosx + (а + l)sinx = 2а.
Решение. Разделим обе части уравнения на выражение 7(« - I)2 + (а + I)2 = -J2(a2 + 1). Так как
z	1	\2	/	. 1	\2
( а ~	а + 1 |=1
[ л/2(а2 + 1) )	1\/2(а2 + 1))
то найдётся такое а, что sin а = , а 1 =, cos а = , -- + 1 <2(а2 + 1)	х/2(а2 + 1)
135
Именно если а > -1, то а = arcsin , а 1 при а < -1 имеем ч'2(а2 + 1)
а = л - arcsin а ~ 1 =. Поэтому sin а cosx + cos а sinx = , а'^‘ ,
<2(а2 + 1)	Va2 + 1
т. е. sin(x + а) =	. Это уравнение имеет действительные
Уа2 + 1
корни при условии, что
ал/2
Va2 + 1
чае существует такое 0, что sin0 =
< 1, т. е. -1 < а < 1. В этом слу-
ду[2 у/а2 + 1’
Поэтому при -1 < а < 1
данное уравнение принимает вид sin(x + а) = sin0. Отсюда получаем, что х = 2лп + 0 - а или х = 2лп + л - 0 - а, где п — целое число. Эти решения можно представить в виде
х - 2лп + arcsin ,а^	- arcsin 7 а *
у/а2 + 1	у)2(а2 + 1)
или
z о , \	• а — 1
х = (2п + 1)л - arcsin	- arcsin —	 
-J а2 + 1	у/2(а2 + 1)
Пример 6. Решим неравенство
asin2x + 2cosx - а + 1 > 0.
(5)
(6)
Решение. Неравенство легко приводится к виду acos2x - 2cosx - 1 < 0.
Если a = 0, то имеем 2cosx + 1 > 0, откуда получаем + 2лп < х < ^ + 2лп, О	О
где п — целое число.
При а * 0 положим cosx = г. Получаем систему неравенств Гаг2 - 2г - 1 < 0, [-1 < г < 1.
Различные возможные случаи определяются знаками функции Дг) = az2 - 2г - 1 в точках —1 и 1, знаком а и положением и значением экстремума функции у = f(z). Имеем Д-1) = a + 1, Д1) = a - 3. Далее, так как f(z) = 2az — 2, то экстремум находится в точке
г = и является минимумом при а > 0, максимумом при а < 0.
Значение функции в точке экстремума равно -а * Уравнение az2 - 2г - 1 = 0 имеет действительные корни при a > -1, причём эти корни равны _ 1 - 71 + a а
„	1 + 71 - а
Z2 = -----------
а
136
Значения функции f(z) = az2 - 2z - 1 в точках -1, 1 и в точке экстремума меняют знак при следующих значениях а: -1, 0, 1 и 3. Поэтому разобьём числовую прямую на следующие промежутки: (-со; -1), (-1; 0), (0; 3) и (3; +°°). Если а < -1, то f(-l) и /(1) отрицательны, отрицательно и значение экстремума, находящегося в точке промежутка (-1; 1). В этом случае функция у = f(z) отрицательна во всех точках отрезка [-1; 1].
При -1 < а < 0 значение функции положительно при г = -1 и отрицательно при г = 1. Точка экстремума лежит вне отрезка [-1; 1]. Поэтому функция имеет один корень на отрезке [-1; 1], а именно Поэтому функция у - f(z) отрицательна на промежутке (21! 1).
При 0 < а < 3 дело обстоит аналогичным образом. Пусть теперь а > 3. В этом случае функция у = f(z) положительна на концах отрезка [-1; 1], имеет на этом отрезке точку минимума, причём её значение в этой точке отрицательно. Поэтому неравенство f(z) < 0 имеет место на промежутке (zn z2).
Итак, мы выяснили, каково решение системы (6). Возвращаясь к неравенству (5), получаем, что:
при а < -1 неравенство выполняется для всех х;
при -1 < а < 0 и при 0 < а < 3
2лп - arccos 2j < х < 2лп + arccos 21, а при а > 3
2itn - arccos Zj < х < 2лп - arccos22 или
2лп + arccosz2 < х < 2лл + arccos zlt
где Zj = —(1 - л/а + 1), г2 - -(1 + >/а + 1). а	а
Отметим ещё, что:
если а = -1, то х * л(2п + 1);
если а = 0, то 2лп -	< х < 2лп + Др
если а = 3, то
2лп - arccos
х < 2лп или 2лп < х < 2лп + arccos
Упражнения
250.	При каких а уравнение имеет единственное решение:
1)	lg(x2 - 6х + 8)lnl“ = In (ах - 17);
2)	logjax - 7) = 21og16(12x - х2 - 32)?
137
Найдите все значения а, при которых неравенство имеет хотя бы одно решение (251, 252).
251.	4х - а • 2х - а + 3 < 0.
252.	1 + log2(2x2 + 2х + 3,5) > log2(ax2 + а).
Найдите все значения а, для которых неравенство справедливо при всех х (253, 254).
253.	а • 9х + 4(а - 1)3Х + а > 1.
254.	1 + log5(x2 + 1) > log5(ax2 + 4х + а).
Найдите все значения а, для которых оба неравенства выполняются при любых х и у (255, 256).
255.	2a cos 2(х - у) + 8a2 cos (х - у) + 8a2(a + 1) + 5a < 0, х2 + у2 + 1 > 2ax + 2у + а - а2.
256.	2а sin2 (х + у) + а > 4a3sin(x + у) + а3, х2 + (а4 + 1)г/2 + а > 2ху.
257. 1 Р Ь Р 258. 259.	[айдите все значения а и Ъ, при которых система имеет единственное ешение: I Xя + 1 | х2 + у2 = Ь, х > 0. [айдите все значения а, при которых система имеет хотя бы одно ешение для любого Ь (258, 259). (х2 + 1)“ + (Ьг + 1)” = 2, а + Ьху + х2у = 1. r2bx + (а + l)bi/2 = a2, (a - 1)х3 + у3 = 1.

111II1111111111 н+н-н-
Многочлены
от нескольких переменных. Системы уравнений и неравенств
I I I II I I I I I I I I I I I I I I I I I
§ 1. Многочлены от нескольких переменных
1. Стандартный вид многочлена от нескольких переменных.
В п. 1 § 1 главы 2 (10 кл.) было введено понятие целого рационального выражения от переменных х, у, ..., г. Примером такого выражения от х, у, z может служить
(х + у + z)(x2 + у2 + z2 - ху - xz - уг).
Раскрывая скобки и приводя подобные члены, получаем целое рациональное выражение х3 + у2 + z3 - 3xt/z, имеющее вид суммы нескольких одночленов от х, у, z, причём никакие два слагаемых не являются подобными (напомним, что два одночлена от х, у, z называются подобными, если они отличаются друг от друга лишь значением коэффициентов, например 3x4i/z2 и -5x4i/z2). Такую сумму называют многочленом от х, у, г.
Определение 1. Многочленом от переменных хп ..., х„называют сумму выражений вида axj‘...x^, где а — число, kx, ...,kn — неотрицательные целые числа, причём буквенные части любых двух слагаемых различны. В записи обычно опускают множители с нулевыми показателями.
Справедливо следующее утверждение.
Любое целое рациональное выражение от хн ..., х„ тождественно равно многочлену от х1; ..., х„.
Многочлены от одной переменной х записывают так, чтобы степени х убывали слева направо, например пишут — 2х3 + 6х - 4. Такую запись многочлена мы назвали стандартной. Аналогичная запись есть и для многочленов от переменных хь .... х„.
Определение 2. Одночлен ах*' хг2... х% считается старше, чем одночлен bxj"1 х"2... х”» (здесь а и Ь отличны от нуля), если либо ki > т1г либо существует такое s, 1 С s < п - 1, что ki = mi, ..., ks = т» но k,+1 > тп,+1.
139
Пример 1. Одночлен 2х3х|х3 старше, чем одночлен 0,lxfx2x|, так как показатели у х} для них одинаковы, а показатель у х2 в первом одночлене больше, чем во втором.
Если слагаемые многочлена от хн ..., хп расположены так, что любое слагаемое старше, чем все слагаемые, стоящие правее него, то говорят, что слагаемые расположены в словарном (лексикографическом) порядке.
Пример 2. Расположим в словарном порядке слагаемые многочлена
-3xfx3 + 6xfx2x3 - 0,1Х]Х|х3 + 7хfx2Xg.
Решение. Наивысший показатель у хх имеет 6xfx2x3. В слагаемых -0,lxfx2x3 и 7Х]Х2х3 показатели у Xj одинаковы, но первое старше, так как в нём больше показатель у х2, и т. д. Значит, получаем
6xiX2x3 - 0,lxfx^x3 + 7х2х2х| - Зх2х3.
Можно показать, что два целых рациональных выражения тождественно равны в том и только в том случае, когда совпадают их записи в виде многочленов, расположенных в словарном порядке. Таким образом, запись в виде многочлена, расположенного в словарном порядке, является стандартной формой целых рациональных выражений.
Определение 3. Назовём многочлен от переменных х]; ..., х„ однородным степени т, если суммы показателей всех его членов равны т.
Например, Зх + 4г/ - 5г — однородный многочлен первой степени, х2 + у2 + г2 - ху - у г - хг — однородный многочлен второй степени, х3 + у3 + г3 - Зхуг — однородный многочлен третьей степени.
Если ах*' х22... х*" — одночлен степени т, kY + ... + kn- т, то при любом t имеем
a(tx1)*1...(tx„)*" = /*1 + -• + A”aXi1...x*'' = tmaxk' ...х^.
Отсюда можно вывести, что многочлен f(xlt ..., х„) является однородным степени т в том и только в том случае, когда для любого t выполняется равенство
f(txr, ..., txn) = tmf(xlt ..., х„).	(1)
Любой многочлен от Xj.....хп единственным образом записы-
вается в виде суммы однородных слагаемых. Часто вместо словарного порядка применяют следующий: сначала разбивают многочлен на сумму однородных слагаемых и располагают их в порядке убывания степеней, а уж потом члены в каждом слагаемом располагают в словарном порядке.
140
Например, располагая указанным способом многочлен
2х + Зу - х2 + z2 - xz + х3 + Зх2у - 5хуг, получаем
х3 + Зх2у - 5xyz - х2 - xz + г2 + 2х + Зу.
Теорема. Если F(x, у) — однородный многочлен степени т от х и у, то существует многочлен f(t) такой, что F(x, у) = *“/(*)•
Доказательство. Подставим в многочлен tx вместо у. В силу формулы (1) имеем
F(x, у) = F(x, xt) = x”F(l, t), где F(l, t) — многочлен от t. Обозначая его через f(t), получаем требуемое равенство.
Приведение целых рациональных выражений к виду многочлена применяется для доказательства тождеств.
Пример 3. Докажем тождество
(х2 + y2)(z2 + t2) = (xz + yt)2 + (xt - yz)2.	(2)
Решение. Раскрывая скобки, получаем
(х2 + y2)(z2 + t2) = x2z2 + x2t2 + y2z2 + y2t2 и
(xz + yt)2 + (xt - yz)2 = x2z2 + 2xzyt + y2t2 + + x2t2 - 2xtyz + y2z2 - x2z2 + y2t2 + x2t2 + y2z2. Поскольку в обоих равенствах справа стоит один и тот же многочлен, тождество доказано.
Тождество (2) является частным случаем тождества (х2 + ... + х2п)(у2 + ... + у2) =
= (ХгУ! + ... + хпуп)2 + ^(xkyt - X;j/J2, где в правой части суммирование распространено на все пары чисел k и I такие, что 1 < fe, k < I и I п. Тождество (3) также доказывается путём раскрытия скобок, приведения подобных членов и сравнения левой части с правой.
У пражнения
260.	Докажите тождества:
1)	(а2 + Ь2 + с2 + d2)(x2 + у2 + г2 + t2) = (ах - by - сг — dt)2 + + (bx + ay + ct - dz)2 + (ex + dy + az - bt)2 + (dx - cy + bz + at)2;
2)	(x + у + z)3 - x3 - y3 - z3 = 3(x + y)(y + z)(z + x);
3)	(a + b + c + d)2 + (a + b - c - d)2 + (a + c - b - d)2 + (a + d - b - c)2 = = 4(a2 + b2 + c2 + d2);
4)	(a2 - b2 - c2 - d2)2 + 2(ab + de + ad - be)2 = (a2 + b2 + c2 + d2)2 -- 2(ab - ad + be + de)2;
5)	((a2 - b2)cd + (c2- d2) ab)2 + ((a2 - b2Mc2 - d2) - 4abcd)2 = (a2 +	+ d2).
141
261.	Докажите, что при любых значениях р и q х2 + ху + у2 = z3, где х = q3 + 3pq2 - р3, у = -3pq(p + q), г = р2 + pq + q2.
262.	Докажите, что если а + b + с = з, то
s(s - 2b)(s - 2с) + s(s - 2a)(s - 2b) + s(s - 2a)(s - 2c) = = (s - 2a)(s - 2b)(s - 2c) + 8abc.
263.	Докажите тождество
a2t>2	, a2c2 , b2c2	, , , ,
7----VL---\ + 7-----Е77-ГТ + 7T--77--7	— ab + be + ac.
(a - c)(b - c) (a -	b)(c -	b) (b	- a)(c -	a)
2. Симметрические многочлены. Если в многочлене х3у - ху2 букву х заменить буквой у, а букву у — буквой х (или, как говорят короче, поменять буквы х и у местами), то получится многочлен у3х - ух2, который отличен от исходного. Но если сделать то же самое с многочленом х3у + ху3, то получится многочлен у3х + ух3, тождественно равный исходному. Говорят, что многочлен х3у + ху3 не меняется при перестановке букв х и у, что он симметричен относительно этих букв.
Определение. Многочлен F(xi, ..., х„) называют симметрическим, если при любой перестановке входящих в него букв получается тождественно равный ему многочлен.
Так как сумма не изменяется при перестановке слагаемых, а произведение при перестановке множителей, то ясно, что многочлены Xi + х2 + ... + х„ и Xi • х2 • ... • х„ симметричны. Более общий способ получения симметрических многочленов состоит в следующем. Выражение
(t + Xi)(t + х2) • ... • (t + x„)	(1)
при любой перестановке букв хь ..., х„ переходит в тождественно равное ему выражение (отличающееся от исходного лишь порядком множителей). Поэтому если раскрыть скобки, то коэффициенты при степенях t будут симметрическими многочленами от переменных хи ..., х„. Эти многочлены называют основными симметрическими многочленами.
При га = 2 имеем выражение
(t + Xi)(f + Х2) = t2 + (Xj + X2)t + XiX2.
В этом случае основными симметрическими многочленами являются уже известные нам выражения Х] + х2 и Xj  х2. Обозначим их п, и ст2:
Oj — Xi + Х2, СУ2 — Хх • х2.
При га = 3 имеем
(t + Xj)(Z + x2)(t + х3) =
= t3 + (Xi + X2 + X3)t2 + (XiX2 + X1X3 + X2X3)t + XiX2X3.
142
В этом случае получаем уже три основных симметрических многочлена:
О1 = Х1 + Х2 + Х3,
О2 = XiX2 + XjX3 + Х2Х3,	(2)
о3 = Х!Х2Х3.
Наряду с основными симметрическими многочленами рассматривают также степенные суммы, т. е. симметрические многочлены вида
$! = Х1 + х2 + ... + х„,
S2 = X2 + x22 + ... + X2,	(3)
sk = х\ + хк2 + ... + хк.
При п = 2 имеем
Sj = X] + х2, s2 = х2 + х22, 83 = х? + х2 и т. д.
В курсах высшей алгебры доказывают следующую теорему.
Теорема 1. Любой симметрический многочлен от переменных хь ..., хп можно единственным образом выразить как многочлен от основных симметрических многочленов с теми же переменными.
Мы проведём сейчас доказательство этой теоремы для случая двух переменных. Сначала докажем следующее утверждение.
Теорема 2. Любая степенная сумма sk = х" + ук может быть представлена в виде многочлена от су = х + у и а2 = ху.
Доказательство. Применим для доказательства метод математической индукции. При п = 1 наше утверждение справедливо, поскольку Si = х + у = CTj. Справедливо оно и при п = 2:
з2 = х2 + у2 - (х + у)2 - 2ху - ст2 - 2ст2.
Предположим теперь, что утверждение доказано для степенных сумм s*, 1 < k < п, где п > 2, и докажем, что оно справедливо для зп+1. Для этого заметим, что
8п + 1 = xn + 1 + yn + 1 = (х" + у")(х + у) + хпу - хуп = = (х" + г/")(х + у) - хг/(х"-1 + р"-1).
Это равенство можно записать в виде
8л + 1 = S„Oj - S„ 1CF2.	(4)
Так как по предположению s„ и sn-i можно выразить в виде многочленов от Ст1 и ст2, то и sn+i можно выразить в том же виде.
Итак, доказываемое утверждение верно при k = 1, /г = 2 и из справедливости при k - п следует, что оно верно для k = п + 1. Значит, оно верно для всех k.
143
Пример 1. Выразим через ст4 и ст2 степенные суммы 8Ь s2, S3, S4, 85, Sg.
Решение. Мы уже знаем, что St = ст4 и s2 = ст? - 2ст2. По формуле (4) получаем последовательно:
s3 = s2ct4 - 3!ст2 = (ст? - 2ct2)ctj - ст4ст2 = ст? - ЗСТ1СТ2, (5)
s4 = з3ст, - 82ст2 - (ст? - ЗСТ1СТ2)СТ1 - (ст? - 2ст2)ст2 =
= ст? - 4ст?ст2 + 2ст?,
S5 = S4CT1 - з3ст2 = (ст? - 4ст?ст2 + 2ст?)СТх - (ст? - Зст4ст2)ст2 =
= ст? - 5ст?ст2 + бстхст?,
Sg = SsCTt - S4CT2 = (ст? - 5ст?СТ2 + 5СТ1СТ?)СТ1 -
- (ст? - 4ст?ст2 + 2ст?)ст2 = ст? - бст?ст2 + Эст? ст? - 2ст?.
Теорема 1 при п = 2 принимает следующий вид.
Теорема 1'. Для любого симметрического многочлена F(x, у) существует такой (вообще говоря, несимметрический) многочлен Ф(Н1, ст2), что F(x, у) = Ф(х + у, ху).
Доказательство. Пусть симметрический многочлен F(x, у) содержит слагаемое axkyl. Если k = I, то это слагаемое равно а(ху)к и потому равно а ст?.
Если же k ФI, скажем k > I, то наряду со слагаемым ахку‘ в F(x, у) входит и слагаемое аукх1, получаемое из него перестановкой букв х и у. Но ахку1 + аукх‘ = а(ху)‘(хк~1 + ук~‘) = а ст? з^_;. По теореме 2 8*_/ можно выразить через ст, и ст2. Следовательно, и сумма ахку‘ + + аукх1 выражается через ст, и ст2. Так как это рассуждение применимо к любому слагаемому ахку1, то и весь многочлен F(x, у) выражается через Стх и ст2.
Пример 2. Выразим через Стх и ст2 симметрический многочлен F(x, у) = х* + у4 + 2х3у + 2ху3 + х2у2.
Решение. Имеем
F(x, у) = х4 + у4 + 2х3у + 2xz/3 + х2у2 = з4 + 2ст2з2 + ст?. Применяя формулы для з4 и s2, получаем
F(x, у) - ст? - 4ст?ст2 + 2ст? + 2ст2(ст? - 2ст2) + ст? = = ст? - 2ст?ст2 - ст?.
Покажем теперь, как выражаются через основные симметрические многочлены ст4 = х + у + г, а2 = ху + хг + уг, и3 = хуг от трёх переменных степенные суммы s2 = х2 + у2 + г2 и з3 = х3 + у3 + z3. Так как
ст? - (х + у + z)2 = х2 + у2 + z2 + 2ху + 2xz + 2yz = s2 + 2о2,
144
то имеем
s2 = of - 2о2	(9)
(эта же формула верна и для двух переменных). Далее имеем of = (х + у + z)3 = (х + у + г)(х + у + г)2 =
= (х + у + z)(x2 + у2 + г2 + 2ху + 2xz + 2уг) =
= х3 + у3 + г8 + Зх2у + Зху2 + Зх22 + Зхг2 + Зу2г + Зуг2 + бхуг =
= х3 + у3 + г3 + (Зх2у + Зху2 + Зхуг) +
+ (3x2z + Зхг2 + Зхуг) + (Зу2г + Зуг2 + Зхуг) - Зхуг =
= X3 + У3 + 23 + Зху(х + у + 2) + 3xz(x + у + 2) +
+ Зуг(х + у + г) - Зхуг = х3 + у3 + г3 + + 3(х + у + z)(xy + XZ + уг) - Зхуг = s3 + 3OjO2 - Зо3. Поэтому
S3 = of - 3OiO2 + Зо3.	(10)
Из формулы (10) вытекает тождество
х3 + у3 + г3 - Зхуг = (х + у + г)(х2 + у2 + г2 - ху - хг - уг). (11) В самом деле,
х3 + у3 + г3 - Зхуг = s3 - Зо3 = of - 3oiO2 = = ojof - Зо2) = (х + у + 2)((х + у + г)2 - 3(ху + уг + хг)). Раскрывая скобки, получим тождество (11).
Упражнения
264.	Выразите через Ci и ст2 степенные суммы s4, s5, s6, s7, s8 от x, у, г.
265.	He решая квадратного уравнения x2 - 6x + 7 = 0, составьте новое уравнение, корнями которого были бы кубы корней данного уравнения.
266.	Не решая уравнения х2 - Зх + 1 = 0, найдите сумму четвёртых степеней его корней.
267.	Выразите через ог и о2 симметрические многочлены:
1)	х3 + 4х2у + 4ху2 + у3;	2) х6 + 6х4у - 10х3у2 - 10х2у3 + бху4 + у6.
268.	Дано квадратное уравнение 2х2 + Зх - 5 = 0, имеющее корни а и р. Составьте новое квадратное уравнение, корнями которого были бы
СЦ = 2а + | и Pj = 2Р +
269.	Решите предыдущую задачу в случае:
1)	Зх2 + 7х + 4 = 0, а, = и Pj =
2)	2ха - 4» - 3 = 0, а, . и (J, - jjL.
270.	Разложите на множители (выразите через щ и о2):
1)	10х4 - 27х3у - 110х2у2- 27ху3 + 10у4;
2)	2х4 + 7х3у + 9х2у2+ 7ху3 + 2у4.
145
271.	Разложите на множители (представьте в виде произведения многочленов, переходящих друг в друга при замене х *-» у):
1)	2х4 + Зх3у + 6х2у2 + Зху3 + 2г/4;
2)	Зх4 - 8х3у + 14х2у2- 8ху3 + 3/.
272.	Решите уравнения:
1)	10t4 27t3 - 110t2- 27t + 10 = 0;
2)	2t4 + 7t3 + 9t2 + 7t + 2 = 0.
3.	Доказательство неравенств с несколькими переменными. В этом пункте мы докажем некоторые неравенства, выполняющиеся при всех значениях переменных. Как и в случае одного переменного, в основе доказательства этих неравенств лежат
утверждения о положительности суммы и произведения двух положительных чисел, а также то, что квадрат любого числа неотрицателен: а2 > 0 для всех а.
Применим последнее утверждение к а = х - у, где х > 0, у > 0: (х - у)2 > 0, т. е. х2 — 2ху + у2 0, откуда следует, что
X2 + у2 ху < -----2---
(1)
При этом знак равенства может иметь место лишь в случае х - у. Любое неотрицательное число а можно записать в виде а = х2. Тогда х = 4а. Поэтому из неравенства (1) вытекает, что для любых неотрицательных чисел а и b выполняется неравенство т а + ь
Jab ч 2 '	W
Оно означает, что среднее геометрическое двух неотрицательных чисел не больше, чем их среднее арифметическое.
Замечание. Неравенство (2) допускает простое геометрическое доказательство. Отложим отрезки длиной а и b на прямой и примем объединение этих отрезков за диаметр полуокружности (рис. 45). Тогда среднее геометрическое чисел а и b равно длине отрезка СМ, а их среднее арифметическое — радиусу окружности. Ясно, что СМ < R, причём СМ = R тогда и только тогда, когда а = Ь.
На рисунке 46 изображено геометрическое доказательство неравенст-х2 У2 ва (1). Здесь ху — площадь прямоугольника ОАМВ, a -g- + -g- — сумма площадей треугольников OAN и ОВР, и видно, что площадь прямоугольника не превосходит суммы площадей треугольников.
Доказанное выше неравенство (2) является частным случаем следующего неравенства Коши:
„/---------- а, + а2 + ... + а„
 ...  ап < ------,	(3)
имеющего место для любых неотрицательных чисел а2, .... ап (при этом знак равенства имеет место, лишь если а^ = а2~ ... = ап).
146
Оно означает, что среднее геометрическое п неотрицательных чисел не больше, чем их среднее арифметическое.
Докажем неравенство (3). В и. 5 § 3 главы 2 было доказано неравенство ех > 1 + х, имеющее место при всех значениях х.
Обозначим через S среднее арифметическое неотрицательных чисел а1( ап и подставим в неравенство ех > 1 + х вместо х ak числа -х--1,	Получим п неравенств:
О
Л	а* - 1
< es , 1 < k < п.	(4)
О
Левые части этих неравенств по условию неотрицательны, и потому, перемножая п неравенств (4), получаем
at 	• а„ т"Г
S" " * = 1
е s
(5)
Напомним, что п ak означает произведение а^ • ... • ап.
ТТ	di 4" ... 4" Л-
Но —------------- = S, и потому —------------- = п. Значит, из (5)
П	о
следует
а это и означает, что „Г	— < о _ а1 +	+ ап
\ai ’ ••• ’ а„ S - п
Замечание. Поскольку равенство ех = 1 -I- х имеет место лишь при t а.	а.
х = 0, то es = -£ для всех k, 1 < k < п, лишь при условии, что = 1 о	о
для всех k, 1 < k < п, т. е. при условии, что Ui — а% = ... = ап = S.
Это условие необходимо и достаточно для того, чтобы среднее геометрическое п неотрицательных чисел равнялось их среднему арифметическому.
147
Пример. Докажем, что при х > О, у > О, г > О выполняется неравенство
х3 + у3 + г3 - Зхуг > 0.	(6)
Решение. Положим в (3) а = х3, b - у3, с - г3. Имеем
х3 + у3 + г3 г— „ „ ---3------ > ljx3y323 - хуг,
а это и есть неравенство (6).
Упражнения
273.	Докажите, что для любых неотрицательных х, у
2ху s /L7 х + у /х2 + у2 < ^ху < —2- <	•
274.	Пусть х, у — неотрицательные числа и х + у = 1. Докажите, что:
1)	хг + у2 >	2) х4 + у4 >	3) Xs + у8 > y|g-
Докажите неравенства (275—277).
275.	1) —~т н---+ • + А- > и при п > 2;
п + 1 п + 2 2п 2
2)	А" + А" + ••• + А' < —-- для всех п > 2;
22 З2	п2 п
3)	и! > п2;
4)	1 + 4= + А= + ••• + А= > 2Vn + 1 - 2;
V2 л/З лУп
5)	|а| - |Ь| < |а + Ь| < |а| + |Ь|;
6)	д3 о h3- > (а > 0, ь > 0); 2	о
7)	а4 + ft4 >	(а > 0, b	> 0);
8)	3(а2 + Ь2 +	с2)	> (а + b + с)2;
9)	— + ¥ +	—	> а + b + с (а	> 0,	b > 0, с > 0);
’ а о с	v	7
10)	< a±b	(а > b > 0);
11)	-J(a + c)(b + d) > 4ab + 4cd (a > 0, b > 0, c > 0, d > 0);
12)	(a + b)(a + c)(t> + c) > 8abc (a > 0, b > 0, c > 0);
148
14)	\(a + k)(b + l)(c + m) > dabc + ylklm (a > 0, b > 0, c > 0, k > 0, I > 0, m > 0);
15)	- + | + - >-7- (a > 0, b > 0, c > 0);
abca+b+c
16)	Jn < Vn! <
19)	(Xi + x2 + ... + x„)(t- + ••• + -M > n2 (X; > 0, I = 1, 2.n);
\ Л1	лп /
a b c d a + b c + d 1	i
21)	(am + bm)m < (a" + b")" (a > 0, b > 0, m > n > 0);
22)	(ab + be + ac)3 > 27a2b2c2 (a > 0, b > 0, c > 0);
23)	(a + bp < 2',~1(an + bn) (a > 0, b > 0);
24)	-г- + -7= > >Az + Vb (a > 0, b > 0); y/b \la
25)	a4 + b4 > a3b + ab3	(a > 0, b > 0);
26)	x5 + г/5 > x4y + xyi	(x > 0, у > 0);
27)	ab(a + b) + ac(a +	c) + bc(b + c) > 6abc	(a	> 0,	b	> 0, c > 0);
28)	a + b + c > Tab +	Vbc + Vac (a >	0,	b	>	0,	c	>	0).
276.	(xij/i + ... + x„y„)2 <(xf + ... + x2)(y2 + ... + y2n) (неравенство Коши).
277.	(xf + ... + x£)p(*/? + ••• + </’)’ > Xjt/i + ... + xny„, где p > 0, q > 0, — + — = 1, X; > 0, уi 0 (неравенство Гельдера).
§ 2.	Системы уравнений и неравенств
1.	Геометрический смысл одного уравнения с двумя переменными. Мы знаем, что каждой непрерывной функции f соответствует линия Г — график этой функции. Равенство у = f(x), которому удовлетворяют координаты любой точки М(х; у) этого графика и не удовлетворяют координаты иных точек плоскости, называют уравнением линии Г.
Не все кривые на плоскости являются графиками функций. Например, не является графиком функции окружность, поскольку
149
одному значению х могут соответствовать два значения у (рис. 47). Но окружность состоит из двух полуокружностей АВС и ADC, являющихся графиками функций. Можно было бы написать отдельно уравнения этих полуокружностей, но мы вместо этого напишем одно уравнение с переменными х и у, которому удовлетворяют координаты любой точки окружности, но не удовлетворяют координаты ни одной точки, не лежащей на окружности.
Чтобы вывести это уравнение, предположим, что центр окружности находится в точке А(а; Ь), а её радиус равен R (рис. 48). Для любой точки М(х; у) окружности выполнено равенство AM2 = J?2. Но
AM2 = (х — а)2 + (у - Ь)2,
а потому выполняется равенство
(х - а)2 + (у - b)2 - R2.	(1)
Уравнение (1) и является уравнением окружности — ему, как уже говорилось, удовлетворяют координаты любой точки этой окружности, но не удовлетворяют координаты точек, не лежащих на ней.
Пример 1. Напишем уравнение окружности с центром А(-4; 2) и радиусом 6.
Решение. По формуле (1) получаем
(х + 4)2 + (г/ - 2)2 = 36.
Если раскрыть в этом уравнении скобки, получим
х2 + у2 + 8х - 4у = 16.
Вообще уравнение окружности с центром А(а; Ь) и радиусом R после раскрытия скобок принимает вид
х2 + у2 - 2ах - 2Ъу - С,	(2)
150
где С = R2 - а2 - Ъ2. Обратно, выделяя в уравнении вида (2) полные квадраты, приводим его к виду
(х - а)2 + (у - b)2 = D,	(3)
где D = С + а2 + Ъ2. Если С + а2 + Ь2 > 0, то существует такое R, что D = R2. В этом случае уравнение вида (2) является уравнением окружности с центром А(а; Ь) и радиусом R. Если D = 0, то получаем уравнение (х - а)2 + (у - Ь)2 = 0, которому удовлетворяют лишь координаты точки А(а; Ь). В этом случае уравнение задаёт «окружность нулевого радиуса», т. е. точку. Наконец, если D < О, то получаем уравнение, которому не удовлетворяют координаты никакой точки плоскости, т. е. уравнение, задающее пустое множество точек (позднее, когда мы познакомимся с комплексными числами, можно будет сказать, что этому уравнению удовлетворяют точки с комплексными координатами, но мы пока работаем лишь в области действительных чисел).
Уравнение вида F(x, у) Ф(х, у) = 0 задаёт объединение линий F(x, у) = 0 и Ф(х, у) = 0.
Пример 2. Найдём линию, заданную уравнением
(х- 4)(у + 3) = 0.
Решение. Так как произведение обращается в нуль при обращении в нуль хотя бы одного из множителей, то надо решить уравнения х-4 = 0иу + 3 = 0, а потом объединить их решения. Равенству х - 4 = 0 удовлетворяют координаты всех точек прямой, параллельной оси ординат и проходящей через точку А(4; 0) оси абсцисс, а уравнению у + 3 = 0 — все точки прямой, параллельной оси абсцисс и проходящей через точку В(0; —3).
Упражнения
278.	Составьте уравнение, которому удовлетворяют координаты лишь трёх точек: Aj(l; 2), А2(-3; 4), А3(0; 0).
279.	Найдите центр и радиус окружности:
1)	х2 + у2 + 4х - 8у = 5;	3) х2 + у2 - 8х - бу + 25 = 0;
2)	х2 + у2 - 8х - бу + 29 = 0;	4) х2 + у2 - 6х + 8 = 0.
280.	Напишите уравнение окружности с центром А(а; Ь) и радиусом R: 1) а = 1, b = -1, R = 5;	2) а = -4, b = 3, R = 10.
2. Системы и совокупности уравнений. Пусть заданы два уравнения: Fi(x, у) = ФДх, у) и F2(x, у) = Ф2(х, у). Первое из этих уравнений задаёт на плоскости линию Г\, а второе — линию Г2. Чтобы найти точки пересечения этих линий, надо найти все пары чисел (а; Ь) такие, что при замене в данных уравнениях х на а и у на b
151
получаются верные числовые равенства. Если поставлена задача об отыскании всех таких пар чисел, то говорят, что задана система уравнений, и записывают эту систему в виде
[FJx, у) = Ф^х, у), (F2(x, у) = Ф2(х, у).
(1)
Совокупность всех пар чисел (а; Ь) таких, что при подстановке а вместо х и Ъ вместо у получаются верные числовые равенства, образует решение данной системы. Если решение системы состоит из пар чисел (а^ bj, ..., (а„; Ьп), то ответ пишут либо в виде {(ai; bi), ..., (а„; &„)}, либо в виде хх = у{ = Ъ^, ...; х„ = а„, уп = Ъп.
Аналогично определяются системы уравнений с тремя и большим числом переменных. Как правило, число уравнений системы должно равняться числу переменных. Разобранный выше геометрический смысл системы двух уравнений с двумя переменными показывает, что при совпадении числа уравнений с числом переменных мы получаем в общем случае или конечную совокупность решений, или бесконечную совокупность решений, которую можно всё же занумеровать. Последний случай показан на рисунке 49 — гипербола ху = 1 пересекает в бесконечном множестве точек синусоиду у - sinx, и потому система уравнений
ху = 1, у = sinx
(2)
имеет бесконечно много решений. Однако это множество решений не заполняет никакой линии.
Может случиться, однако, что не существует значений переменных, при подстановке
(3)
которых в уравнения данной системы получаются равенства. Например, очевидно, что не имеет решений система уравнений
(х - у = 2,
[2х - 2у = 7.
Системы уравнений, не имеющие решений (или, что то же самое, с пустым множеством решений), называют несовместными.
Как правило, несовместными оказываются системы уравнений, в которых число уравнений больше числа переменных.
152
Пример 1. Докажем, что система уравнений х - у = 2,
 X + у = 6,	(4)
х2 + у2 - 9
несовместна.
Решение. Из первых двух уравнений этой системы находим, что х = 4, у = 2. Но при подстановке найденных значений в третье уравнение получаем неверное равенство
43 + 22 = 9.
Геометрический смысл этого результата состоит в том, что окружность х2 + у2 = 9 не проходит через точку пересечения А(4; 2) прямых х-у = 2их + у = 6. Лишь при значении С = 20 правой части в уравнении х2 + у2 = С окружность прошла бы через эту точку.
Пример системы уравнений (3) показывает, что и в случае, когда число уравнений совпадает с числом переменных, система может оказаться несовместной. В случае двух уравнений с двумя переменными это означает, что соответствующие линии не пересекаются. Несовместной может оказаться и система уравнений, в которой число уравнений меньше числа переменных; например, несовместна система уравнений
(х2 + у2 + 2z = 1,
[Зх2 + Зу2 + 6г = 15.
В некоторых случаях система имеет бесконечно много решений, зависящих от одного или нескольких непрерывно меняющихся переменных. В этом случае её называют недоопределённой. Чаще всего недоопределённой оказывается система уравнений, в которой число уравнений меньше числа переменных.
Пример 2. Покажем, что система уравнений
v +	= 8>	(в)
[х2 + Зу - z = 3 недоопределена.
Решение. Из первого уравнения находим, что х2 = 8 — 2у. Подставляя это значение х2 во второе уравнение, получаем, что у - z = -5. При любом значении у найдётся значение г, удовлетворяющее этому уравнению, а именно z = у + 5. Итак, решение системы уравнений (6) можно записать в виде х2 = 8 — 2у, z - у + 5. Так как 8 - 2у = х2 > 0, то у должно принадлежать лучу (-оо; 4].
153
Пример 3. Система уравнений
Jx2 + у2 + г2 = 169, [х + у + г = 19
недоопределена. Если придать х определённое значение, то получится система двух уравнений с двумя переменными, из которой можно найти значения у и г. Например, при х = 3 получаем систему уравнений
J32 + у2 + z2 = 169, [3 + у + z = 19, из которой находим у^ = 4, гг = 12 или у2 - 12, г2 = 4. При х = 12 получаем систему, имеющую решение yt = 3, z} = 4 или z2 = 3, у2 - 4 и т. д. Таким путём находим бесконечное множество троек чисел, удовлетворяющих данной системе уравнений.
Недоопределённой может оказаться и система уравнений, в которой число уравнений равно числу переменных или даже больше него. Например, недоопределены системы уравнений
Jx2 + у2 =9,
[2х2 + 2у2 = 18	(7)
и
х2 + у2 = 9, 2х2 + 2у2 = 18, Зх2 + Зу2 =27.
(8)
Это объясняется тем, что в (7) второе уравнение системы получается из первого умножением обеих частей на 2, а потому каждое решение первого уравнения является и решением второго. Таким образом, второе уравнение излишне и остаётся недоопределённая система из одного уравнения с двумя переменными. Геометрически в этом случае оба уравнения системы задают одну и ту же линию. Аналогично обстоит дело и в системе (8).
Иногда бывает, что заданная система уравнений обладает некоторой симметрией, например, уравнения системы не меняются при перестановке переменных или при изменении знака у одного или нескольких переменных. Тогда соответствующей симметрией обладает и множество решений этой системы уравнений.
Пример 4. Пара чисел (3; 4) удовлетворяет системе уравнений
jx2 + у2 = 25,
[ху = 12,
154
так как 32+ 42 = 25,3-4 = 12.В силу симметрии уравнений системы ясно, что пара чисел (4; 3) тоже удовлетворяет этой системе. Кроме того, оба уравнения системы не изменяются при одновременной перемене знака у х и у. Отсюда следует, что пары чисел (-3; -4) и (-4; -3) также удовлетворяют нашей системе. Ответ можно записать либо в виде
{(3; 4), (4; 3), (-3; -4), (-4; -3)},
либо в виде
Xt = 3, У1 = 4; х2 = 4, у2 = 3; х3 = -3, у3 - -4; х4 = -4, у4 = -3.
Позднее мы увидим, что эта система не имеет иных решений.
Мы уже неоднократно пользовались тем, что решение уравнения вида
Л(х) ... Д(х) = 0	(9)
сводится к задаче об отыскании значений х, удовлетворяющих хотя бы одному из уравнений Л(х) = 0, ..., fAx) = 0. Если поставлена такая задача, то говорят, что задана совокупность уравнений fAx) = 0, 1 < k < п. Чтобы отличить совокупность уравнений от системы, будем обозначать её с помощью квадратной скобки
’А (х) = о,
........	(10)
fAx) = о
или точек с запятой
Л(х) = 0; ...; Л(х) = 0.	(10')
Аналогичный смысл имеет понятие совокупности уравнений с несколькими переменными и совокупности систем таких уравнений. Запись
означает, что требуется найти все пары чисел (а; Ъ), которые удовлетворяют хотя бы одному из заданных уравнений. Если уравнение Рг(х, у) = 0 задаёт линию Г,, а уравнение F2(x, у) = 0 — линию Г2, то совокупность (11) задаёт объединение этих линий (в то время как система уравнений
FAx, у) = 0,
Е2(х, у) = 0
задаёт пересечение тех же линий).
155
Запись
IX (х> у) = О,
[ФДх, у) = О, ............................. (12)
Х(х, у) = О, _|ф„(х, у) = О
означает, что надо решить каждую систему уравнений IX (х, у) = О, [Ф*(х, у) = О
для 1 < k < п и объединить найденные решения.
Пример 5. Решим совокупность систем уравнений
Гх2 + у2 = 25,
[ху = 12, (х + у = 10, [ху = 16.
Решение. Выше было указано, что решение первой системы уравнений имеет вид {(3; 4), (4; 3), (-3; -4), (-4; -3)}. Решение же второй системы уравнений имеет вид {(2; 8), (8; 2)}. Чтобы получить решение заданной совокупности систем уравнений, надо объединить найденные решения. В результате получаем ответ: {(3; 4), (4; 3), (-3; -4), (-4; -3), (2; 8), (8; 2)}.
Упражнения
281. Решите совокупность систем уравнений:
1)		х + у = 6,	2)		х2 + у2 = 58,
		ху = 8,		х2 - у2 = 40,
		х + Зу = 1,		х3 + у3 = 126
		х ~ 2у = -4;		х3 - у3 = 124
282. Объясните, почему несовместна система уравнений х + Зу = 7, Зх - у = 1, х3 + 2у3 =15.
283. Является ли несовместной система уравнений х + Зу - 7,
- Зх - у = 1, х3 + 2у3 = 17?
156
284.	При каком значении С совместна система уравнений 6х - у = 7,
 х + Зу = 17, х2 - у2 = С?
285.	При каком значении С совместна система уравнений Сх + 2у = 1,
 х + у = 5, х2 + у2 = 17?
286.	Выразите из системы уравнений
X2 + 2у2 + 2 = 6, 2х2 - Зу2 + 5г = 1
х и у через z. Какие значения может принимать z?
287.	Дополните систему уравнений
[х + у = 6,
[2х + у = 1
двумя уравнениями так, чтобы она: 1) стала несовместной; 2) имела конечное множество решений. Ответ поясните графически.
288.	Какой симметрией обладает множество решений системы уравнений:
1)	со +	+ СО н	к	= 97, = 793;	3)	х2 + у2 = 17, х4 + у4 =5;
2)	ху = 8,		4)	х2 + у4 = 20,
	х2 + у2	= 20;		х4 + у2 = 20?
289.	Дополните уравнение х2 + у2 + 2ху = 12 ещё одним уравнением так, чтобы получившаяся система уравнений вместе с решением х = а, у = Ъ имела бы ещё решения х = Ъ, у = а; х = -а, у - -Ъ и х = -Ъ, У = ~а.
290.	При каких значениях С система уравнений
Зх + у = Сх, 6х - 2у = Сх
имеет: 1) единственное решение; 2) бесконечно много решений?
3.	Равносильные системы уравнений. При решении систем уравнений их обычно заменяют равносильными системами урав-(х = а, нений, пока не придут к системе уравнений вида 4	или
[У = b
к совокупности таких систем. При этом понятие равносильности систем уравнений определяется аналогично тому, как это было сделано для уравнений с одной переменной.
157
Определение. Две системы уравнений f^i(x, у) = Ф^х, у), |F2(x, у) = Ф2(х, у)
(1)
и
F3(x, у) = Ф3(х, у),
F^x, у) = Ф4(х, у) называются равносильными, если любая пара чисел (а; Ъ), удовлетворяющая первой системе, удовлетворяет и второй, а любая пара чисел, удовлетворяющая второй системе, удовлетворяет и первой (иными словами, если решения этих систем уравнений одинаковы).
Очевидно, что при замене одного из уравнений системы равносильным ему уравнением (т. е. уравнением, задающим то же самое множество) система переходит в равносильную ей систему уравнений. Поэтому мы можем заменить систему (1) равносильной ей системой
[А(х, у) = О,
U(X, у) = о,
где Л(х, у) = Л(х, у) - ФДх, у), f2(x, у) = Fz(x, у) - Ф2(х, у).
Может случиться, что решения X, и Х2 двух систем уравнений различны, но пересечения этих решений с некоторым множеством Y равны. В этом случае будем говорить, что данные системы равносильны на множестве Y.
Пример 1. Системы уравнений
х + у = 9, у и
ху = 18
х + у = 9, ' _________ху__________
[(х - З)2 + (у - б)2
__________18__________
(х - З)2 + (у - б)2
не являются равносильными, так как пара чисел (3; 6), удовлетворяющая первой из них, не удовлетворяет второй (при х = 3, у = 6 обращается в нуль знаменатель (х - З)2 + (у 6)2). Но на множестве, получаемом из плоскости выбрасыванием точки (3; 6), эти системы уравнений равносильны.
При решении систем уравнений, как и при решении уравнений с одной переменной, применяется метод разложения на множители. Он основан на следующей теореме.
Теорема. Если функции Ft(x, у), ..., F„(x, у) определены на некотором множестве X, то на этом множестве система уравнений
jFJx, у)  ... • Fn(x, у) = О,
[Ф(х, у) = 0	(3)
158
равносильна совокупности систем уравнений 1Х(х, у) = 0,	. fF„(x, у) = О,
[ф(х, у) = 0;	’ [Ф(х, у) - О.
Доказательство. Пусть пара чисел (а; Ь) удовлетворяет системе уравнений (3), т. е. пусть
Fr{a, Ь)  ...  Fn(a, b) - О,
Ф(а, Ь) = О.
Тогда найдётся такое k, 1 < k < п, что Fk(a, b) = 0, и потому та же пара чисел удовлетворяет системе уравнений
Fk(x, У) = О,
Ф(х, у) = О
и тем самым совокупности систем уравнений (4).
Обратно, если пара чисел (а, Ь) удовлетворяет совокупности систем уравнений (4), то найдётся такое k, 1 < k < п, что эта пара чисел удовлетворяет системе уравнений
fFJx, у) = О, ]ф(х, у) = О,
т. е. Fh(a, b) = 0, Ф(а, Ь) = 0.
Поскольку все функции Fk, 1 < k С п, определены на множестве X, то они определены в точке М(а; Ъ), и потому произведение Fx(a, Ь)  ...  Fn(a, b) тоже равно нулю. Это значит, что пара (а; Ь) удовлетворяет системе уравнений (3).
Пример 2. Решим систему уравнений (х2 + у2 - 25)(х + у - 8) = 0, ху = 12.
Решение. Данная система уравнений равносильна совокупности систем уравнений
х2 + у2 - 25 = 0, fx + у - 8 = 0;
ху = 12;	[ху = 12.
Первая система имеет решение {(3; 4), (4; 3), (—3; —4), (—4; — 3)}, а вторая — решение {(2; 6), (6; 2)}.
Значит, данная система имеет решение {(3; 4), (4; 3), (-3; —4), (-4; -3), (2; 6), (6; 2)}, или иначе:
Jxj = 3,	[х2 = 4,	[х3 = -3,	Гх4 = -4,	|х5 = 2,	1х6 = 6,
|_У1 = 4;	[у2 = 3;	[у3 = -4;	[у4 = -3;	[у5 = 6;	[ув = 2.
159
Замечание. Повторно применяя теорему, получаем, что решение системы уравнений
fFi(x, у)  ...  Fn(x, у) = О,
{фДх, у)  ...  Ф„(х, у) = О
сводится к решению совокупности, состоящей из тп систем вида
ГКДх, у) = О,
[Ф,(х, у) = О,
где k пробегает все значения от 1 до п, а I — все значения от 1 до т.
Упражнения
291.	Являются ли равносильными следующие системы уравнений:
(х + Зу = 6,	|(х + Зу)(х2 + у2) = 6(х2 + у2),
[Зх -1 = 1 И [(Зх - 1)(х - у) = х - у?
292.	Какой совокупности систем уравнений равносильна система уравнений
Г(х - у + 1)(х2 + у2 - 25) = О,
[(Зх + у + 5)(ху - 12) = О?
4. Метод исключения. Наиболее мощным методом решения систем уравнений является метод исключения неизвестных, позволяющий последовательно сводить решение данной системы к решению системы (или совокупности систем), содержащей на одну переменную меньше. Этот метод последовательного исключения основан на очевидном утверждении, что система уравнений
[" =,(х)- (1)
|Ф(х, у) = О равносильна системе уравнений
[у = f(x),
Г	(2)
[ф(х, Дх)) = О
и аналогично для большего числа переменных. Но решение системы (2) сводится к тому, что мы решаем уравнение Ф(х, Дх)) = О, содержащее лишь х, после чего подставляем найденные значения х в равенство у = f(x) и ищем соответствующие значения у.
Чтобы свести заданную систему уравнений
jF(x, у) = О, [Ф(х, у) = О
к системе уравнений вида (1) или совокупности таких систем, надо решить какое-либо уравнение системы относительно одного из переменных, т. е. выразить его через другую переменную.
160
Пример. Решим систему уравнений [ху = 12, [х2 + у2 - 25. 12
Решение. Из первого уравнения находим у = — Подстав-144 ляя это значение во второе уравнение, получаем х2 +	= 25,
или после упрощения х* - 25х2 + 144 = 0. Корнями этого биквадратного уравнения являются числа X] = 3, х2 = 4, х3 = -3, 12	12
х4 = -4. Им соответствуют значения У1 = ~д- =4, Уг = -^ - 3, 12	19	«
у3 =	- -4, у4 = -=7 = -3. Значит, решением данной системы
—3	—4
уравнений является множество пар чисел {(3; 4), (4; 3), (-3; —4), (-4; -3)}. Выше мы указывали эти пары чисел, но лишь теперь убедились, что ими исчерпывается решение.
Упражнения
293. Решите системы уравнений:
1)	Г4х2 + 7 у2 = 148,	3)
[Зх2 - у2 = 11;
X + у = X2, Зу - х = у2;
- + Т = 1’ а о “ +	= 4.
х у
5. Метод алгебраического сложения уравнений. Вторым мощным методом решения систем уравнений является метод алгебраического сложения, который основан на следующей теореме.
Теорема. Пусть функция у(х, у) определена для всех пар (а; 5), при которых определены обе функции F и Ф. Тогда система уравнений
(F(x, у) = 0,
[Ф(х, у) = 0 равносильна системе уравнений [F(x, у) = 0, [Ф(х, у) + \|/(х, y)F(x, у) = 0.
Иными словами, при решении систем уравнений можно прибавлять к одному из уравнений системы другое уравнение той же системы, умноженное на некоторый множитель.
161
Доказательство. Пусть пара чисел (а; Ь) удовлетворяет системе уравнений (1), т. е. пусть F(a, b) = 0, Ф(а, Ь) = 0. Тогда верно равенство \у(а, Ь)  F(a, b) = 0 и, следовательно, равенство Ф(а, Ь) + у(а, Ь)  F(a, b) = 0. Это и значит, что пара (а; Ь) удовлетворяет системе уравнений (2).
Обратно, пусть пара чисел (а; Ь) удовлетворяет системе уравнений (2), т. е. пусть F(a, b) = 0, Ф(а, Ь) + у(а, Ь)  F(a, b) = 0. Тогда верно и равенство Ф(а, Ь) - 0, а потому данная пара удовлетворяет и системе (1). Теорема доказана.
Следствие. Если к одному из уравнений системы (1) прибавить другое уравнение той же системы, умноженное на некоторое число Л, а другое уравнение системы оставить без изменения, то получим систему, равносильную данной.
Пример, Решим систему уравнений [х3 + у3 — 28, [х2у + ху2 = 12.
Решение. Метод исключения приводит в данном случае к сложным выкладкам. Поэтому поступим иначе: прибавим к первому уравнению системы второе уравнение, умноженное на 3. В силу формулы для куба суммы получаем систему уравнений |(х + у)3 = 64, [xz/(x + у) = 12,
равносильную заданной. Она равносильна системе уравнений 1х + у = 4, т е (х + у = 4, [ху(х + у) = 12, Т‘ е‘ \ху = 3.
Теперь уже можно исключить переменное. Из первого уравнения находим у - 4 - х. Подставляя это значение во второе уравнение, получаем квадратное уравнение х2 - 4х + 3 - 0, имеющее корни Xj = 1, х2= 3. Соответствующие значения у равны: уА = 3, у2 = 1. Значит, и решение данной системы имеет вид {(1; 3), (3; 1)}, или, что то же самое,
Jxj = 1, Jx2 = 3,
U1 = 3; [j/2 = 1-
Упражнения
294. Решите системы уравнений:
1) Jx2 + ху + 2у2 = 74, 2) |х2 + ху = 15, 3) [2х2 + 2ху + у2 = 73; [ху - х2 = 2;
х + 2у +	= 16,
У
Зх + у + — = 23.
У У
162
6*. Метод замены переменных. Системы симметрических уравнений. Для решения систем уравнений применяется также метод замены переменных — некоторые выражения от исходных переменных принимаются за новые переменные, в результате чего получается более простая система уравнений относительно этих переменных. После того как эта система решена, надо по найденным значениям выбранных нами выражений найти значения исходных переменных.
Пример 1. Решим систему уравнений
(х3у + ху3 = 300,
(1) [ху + х2 + у2 = 37.
Решение. Если вынести в первом уравнении за скобки ху, получим уравнение ху(х2 + у2) = 300. Теперь видно, что левые части обоих уравнений выражаются через ху и х2 + у2. Поэтому положим ху = t, х2 + у2 = s и получим для отыскания t и s более простую систему уравнений
[is = 300,
[t + s = 37.	<2)
Решая эту систему методом исключения, находим, что it = 12, sx - 25, t2 - 25, s2 = 12.
Так как t - ху, s = х2 + у2, то для отыскания х и у надо решить совокупность двух систем уравнений:
[ху = 12, [ху = 25,
[х2 + у2 = 25;	|х2 + у2 = 12.	(3)
Решим первую из этих систем методом алгебраического сложения. Получаем, что она эквивалентна системе уравнений
(х2 + 2ху + у2 = 49,	[(х + у)2 = 49,
<	т. е.	(4)
[х2 - 2ху + у2 - 1,	'	[(х - у)2 =1.
Но из (х + у)2 = 49 следует, что х + у = 7 или х + у = -7, а из (х - у)2 = 1 следует, что х - у = 1 или х - у = -1. Поэтому полученная система уравнений равносильна совокупности четырёх систем уравнений первой степени:
1х + у = 7,	(х + у = -7,	[х + у - 7,	(х + у = -7,
[х - у = 1;	[х - у = 1;	|х - у = -1;	[х - у = -1.
Решая её, получаем ответ:
{(4; 3), (-3; -4), (3; 4), (-4; -3)},	(5)
или, иначе,
*i = 4, ух = 3; х2 = -3, у2 - -4; х3 - 3, у3 = 4; х4 = -4, у4 = -3.
163
[ху = 25, Легко проверить, что вторая система, т. е.
[г2 + у2 = 12,
не имеет решений. Поэтому (5) является и решением заданной системы уравнений.
Общего правила выбора новых переменных не существует. Существуют два вида систем, когда есть разумный выбор переменных: 1) система симметрических уравнений и 2) система уравнений, одно из которых однородно.
Если оба уравнения системы
Jf(x, у) = О,
1	(б)
[Ф(х, у) = О являются симметрическими многочленами от х и у, полезно принять за новые переменные основные симметрические многочлены Qi = х + у и о2 - ху от х и у. Как было показано в п. 2 § 1, оба многочлена F(x, у) и Ф(х, у) можно выразить через О! и о2, в результате чего получается система уравнений от о2, которая обычно более проста, чем исходная. Решив её, находим х и у из соотношений х + у = Oj, ху - а2.
Пример 2. Решим систему уравнений
[х2 + ху + у2 = 21,
J »	»	’	(7)
|х + ху + у = 9.
Решение. Так как левые части обоих уравнений симметричны относительно х и у, введём новые переменные = х + у, о2 = ху и выразим через них левые части уравнений:
х2 + ху + у2 = (х + у)2 - ху = of - о2 и
X + ху + у = О] + о2.
Таким образом, заданная система свелась к следующей:
Гст? - о2 = 21,
(8)
[о] + о2 = 9.
Сложив эти уравнения, получаем квадратное уравнение of + Ci - 30 - 0.
Из него следует, что О] = 5 или - —6. Так как щ + а2 = 9, то о2 = 4 или о2 = 15. Итак, получены две пары: (5; 4) и (-6; 15), удовлетворяющие системе уравнений (8).
Поскольку х + у = щ и ху = а2, то заданная система уравнений свелась к совокупности двух систем:
[х + у = 5, (х + у = -6,
[ху - 4; [ху = 15.
164
Для первой системы находим решение: Xt = 1, х2 = 4, У1 = 4; у2 = 1.
Вторая система решений не имеет.
Пример 3. Решим иррациональное уравнение
$//с + V97 - х = 5.
(9)
Решение. Обозначим у/х через и, а л/97 - х через V. Тогда заданное уравнение примет вид и + v = 5. Кроме того,
и4 + и4 = (л/xf + (V97 - х)4 = х + 97 - х = 97,
поэтому решение заданного уравнения сводится к решению системы уравнений
и + v = 5,
и4 + и4 = 97.
Так как левые части этих уравнений симметричны относительно и и v, введём новые переменные сь = и + v, cs2 = uv. Используя формулу (6) п. 2 § 1, приходим к системе уравнений
Joi = 5,
- 4ofo2 + 2ст2 = 97.
Подставим значение ах = 5 во второе уравнение и получим для отыскания о2 квадратное уравнение - 50о2 + 264 - 0. Решая его, получаем о2 = 6 или о2 = 44. Таким образом, для отыскания и и v надо решить совокупность из двух систем уравнений:
и + v = 5, fu + и = 5, uv = 6; [uv - 44.
Первая из них имеет два решения: пх = 2, v} = 3; и2 = 3, v2 = 2, а вторая не имеет решения. Так как у/х, то получаем два значения для х, удовлетворяющие уравнению (9):
хх — 24 = 16, х2= З4 = 81.
Рассмотрим, как решаются системы уравнений, одно из которых однородно относительно х и у, т. е. системы уравнений вида
Р(х, у) = О,
Ф(х, у) = 0,
(Ю)
где, например, F(x, у) — однородный многочлен от х и у степени п.
Разберём два случая.
а)	В многочлене F(x, у) есть член вида ауп. Тогда F(0, у) = ауп обращается в нуль лишь при у = 0 и либо пара чисел (0; 0)
165
удовлетворяет системе уравнений (это будет, в частности, если и уравнение Ф(х, у) = 0 однородно), либо в решении данной системы вообще нет таких пар, что х - 0. В этом случае введём новую переменную t, положив у = tx. Получаем систему уравнений
[Г(х, tx) = 0,
[Ф(х, tx) = О,
или в силу однородности многочлена F систему
|xnF(l, t) = О, |ф(х, tx) = 0.
Поскольку х Ф 0, получаем систему уравнений
[F(l, t) = О,
}ф(х, «) = 0.	(11)
Из первого уравнения системы находим значения t, подставляем их во второе уравнение и находим соответствующие значения х. По формуле у = tx находим значения у.
б)	Если в F(x, у) члена ауп нет, то все члены многочлена F(x, у) делятся на некоторую степень х, скажем на хк; надо вынести хк за скобки: Е(х, у) = xkF1(x, у) — и свести решение системы (10) к решению совокупности двух систем вида
(хк = О, |^(х, у) = о,
[ф(х, у) = 0; |ф(х, у) = 0.	(12)
Первая из них решается очевидным образом, а вторая — способом, указанным в а).
Пример 4. Решим систему уравнений
[Зх2 - 4ху + у2 =0, |х2 + 2у2 = 19.
Решение. Так как слагаемое у2 в первом уравнении не делится на х, то применяем подстановку у = tx. Получаем систему уравнений
[Зх2 - 4tx2 + t2y2 =0,	(t2 - 4t + 3 = 0,
[x2 + 2t2y2 = 19,	T’ e’ [x2(l + 2t2) = 19.
Корнями первого уравнения являются tr = 3, t2= 1. Подставляя во второе уравнение t - 3, получаем х2 = 1, и потому х = 1 или
166
х - -1. Подставляя же t = 1, получаем х = Так как у = tx, имеем следующее решение системы:
			/19		/19
		*3 =	,—>	Хо 		
*1 = 1,	[*2 = "I,		V з		<1 з
У1 = 3;	[</2 = _3;	Уз =	№	Уз = -у	
Пример 5. Решим систему уравнений Зх3 - 4х2</ + ху2 = О, х2 + у2 - 2.
Решение. Первое уравнение системы однородно, но все члены его левой части делятся на х. Поэтому выносим х за скобки и сводим задачу к решению совокупности двух систем уравнений: х = 0,	|3х2 - 4хг/ + у2 =0,
х2 + у2 = 2;	|х2 + у2 = 2.
Первая система равносильна системе х = 0, у2 = 2, откуда находим: *1=0, уг = \[2 или х2 = 0,г/2= —*/2. Вторая система уравнений решается так же, как в примере 4, и ей удовлетворяют четыре пары чисел:	__ _______________
|х3 = 1,	Jx4 = -1,	1*5 = >/0^2.	1*8 = -л/б/2,
|г/3 = 1;	\yi = —1;	у5 = 3>/0,2;	ув = — 3>/0,2.
Объединяя полученные ответы, находим решение заданной системы в виде {(О; V2), (О; -V2), (1; 1), (-1; -1), (^2; З^/оГг), (-Т0?2; -З^О^)}.
Задача. От пристани А одновременно отправились вниз по течению реки катер и плот. Катер спустился вниз по течению на 96 км, затем повернул обратно и вернулся в А через 14 ч. Найти скорость катера в стоячей воде, если известно, что он встретил плот на обратном пути на расстоянии 24 км от А.
Решение. Сначала составим систему уравнений. В качестве искомых выберем скорость и катера в стоячей воде и скорость течения V. Тогда скорость катера при движении по течению равна и + v, а при движении против течения и ~ v. Значит, чтобы пройти вниз по течению 96 км, ему надо - часов, а вверх по течению 96	т,	96	,	96	„
	 часов. Всего он затратит 	 + —-— часов. 1ак как и - v---------------------------и л- v и — v
167
по условию задачи он вернулся назад через 14 ч, то имеем первое уравнение:
96	96 _
и + V U~ V
Чтобы получить второе уравнение, найдём, какое время затратил катер до встречи с плотом. Он прошёл 96 км вниз по течению 96	72
и 72 км против течения. На это он затратил --- +------часов.
и + v и - v
Плот же проплыл 24 км со скоростью v, на что затратил часов. Так как плот и катер одновременно отправились из А, то затраченное ими до встречи время одинаково, и мы имеем второе уравнение:
96 + 72 = 24 и + V U V V ' Итак, для решения задачи получим систему уравнений f 96 + 96 _
I и + v и - v ’ I 96 + 72	= 24
[и + V и - V V
При замене и на tu и v на tv обе части второго уравнения умножаются на |. Поэтому оно является однородным уравнением. Так как и v = 0 не удовлетворяет этому уравнению, делаем подстановку и = vz. Тогда второе уравнение примет вид
А +	= 24.
z + 1 z - 1 Освобождаясь от знаменателей, получаем 24г2 - 168г = 0.
Это уравнение имеет корни 0 и 7. При г = 0 получаем и = 0, а это значение и ни при каком значении и не удовлетворяет первому уравнению. Поэтому г = 7, т. е. и = lv. Подставляя это значение и
96 . 96	1 л
в первое уравнение системы, получаем	- 14, откуда
v = 2 (км/ч). Но тогда и = 7  2 = 14 (км/ч). Итак, скорость катера в стоячей воде равна 14 км/ч.
У пражнения
295. Решите системы уравнений:
1) tx2 - ху + у2 = 21,	2) ( 2 + у2 = 25XJ/j
V - 2ху + 15 = 0;	2	*2
х2 -у2 =7;
168
а,
X + у + х - у X - у X + у х2 + у2 = 45;
10
3 ’
5)	(X + у)2 + (х - у)2 = |(х2 - у2), 6)	х4 + у4 = ^х2у2
	х2 + у2 = 20;	х3 + у3 = 9;
х4 + у4 + х3у + ху3 = ±j^x2y2,
8) |х3 + х2у + ху2 + у3 = 0, (х2 + 4i/2 = 5.
X + у = 4;
7. Графическое решение системы уравнений. Мы уже знаем, что решение системы уравнений с двумя неизвестными
1>(х, у) = 0,
[Ф(х, у) = 0	(1)
геометрически истолковывается как отыскивание координат точек пересечения линий Гх и Г2, заданных уравнениями F(x, у) = 0 и Ф(х, у) = 0 соответственно. Этим можно воспользоваться для приближённого решения системы уравнений (1). Для этого надо начертить линии Гх и Г2 на клетчатой (а ещё лучше на миллиметровой) бумаге и по чертежу определить координаты точек пересечения этих линий. Разумеется, при этом получатся лишь приближённые значения х и у.
Пример 1. Решим графически систему уравнений у = хг + 4х + 4, 2х + у + 4 = 0.
Решение. Линия у = х2 + 4х + 4, т. е. у = (х + 2)2, является параболой, получаемой из параболы у = х2 сдвигом на 2 единицы влево, а уравнение 2х + у + 4 - 0 задаёт прямую линию у = -2х — 4. На рисунке 50 показаны эти линии. По нему устанавливаем, что линии пересекаются в точках А(-4; 4) и В(-2; 0). Значит, имеем решение системы: хх - -4,	Гх2 = -2,
У1 = 4;	|у2 = о.
Проверка показывает правильность найденного решения. Предоставляем читателю решить ту же систему уравнений аналитически.
169
Пример 2. Решим графически систему уравнений у = х2 - 2х + 4, У = 2х.
Решение. Прямая у - 2х и парабола у - х2 - 2х + 4 = = (х - I)2 + 3 изображены на рисунке 51. Видим, что прямая касается параболы в единственной точке А(2; 4). Отсюда находим решение системы: х = 2, у - 4.
Пример 3. Решим систему уравнений
у = х2 - 2х + 4, У = 2х - 1.
Решение. Из рисунка 52 видим, что прямая у = 2х - 1 и парабола у = х2 - 2х + 4 не имеют общих точек. Система несовместна.
Пример 4. Решим графически систему уравнений (ху = 12, |х - 2у - 2 = 0.
12
Решение. Уравнение ху - 12, т. е. у - задаёт гиперболу.
Из рисунка 53 видим, что точками пересечения этой гиперболы с прямой х - 2у - 2 = 0 являются А(-4; -3) и В(6; 2). Значит, fxt = -4,	(х2 = 6,
|У1 = -3;	[уг = 2.
Пример 5. Решим систему уравнений у = х2 + 5х, х = у2 + 5г/.
170
Решение. Уравнение у = х2 + 5х задаёт параболу с осью, параллельной оси ординат, а уравнение х = у2 + 5у — параболу с осью, параллельной оси абсцисс. Эти параболы изображены на рисунке 54. Имеем четыре точки пересечения О, А, В, С, а потому решение имеет вид:
Рис. 54
Xj = 0,	1	|х2 = -4,
У1 = °;	1	1уз = -4;
х3 » -4,7,	i	[х4 = -1,3,
Уз ~ _1>3;	1	1у< = -4,7.
В этом примере значения координат точек В и С найдены приближённо. Аналитическое решение показывает, что
х3 = —3 — >/з,
Уз = —3 + л/З;
х4 = -3 + >/з, J/4 = -з - >/з
(чтобы прийти к ответу, надо вычесть почленно второе уравнение из первого).
Пример 6. Решим систему уравнений
х2 + у2 + 4х - бу = 13, ху - Зх + 2у - 11.
Решение. Первое уравнение системы можно записать в виде (х+ 2)2 + (у - 3)2 = 26.
Оно задаёт окружность радиусом >/26 = 5,1 с центром в точке
К(-2; 3). Второе уравнение перепишем в виде у =	+ i,1, т. е.
X “Ь Ct
5
у = 3 + х 2' '^то УРавнение гиперболы, полученной из гиперболы
у = — путём растяжения вдоль оси ординат с коэффициентом 5 и последующего параллельного переноса, при котором начало координат переходит в точку К(-2; 3). Обе линии изображены
171
на рисунке 55. По нему находим координаты точек пересечения: А(-7; 2), В(-3; -2), С(-1; 8), В(3; 4).
Итак,
Jxx =	-7,	[х2	=	-3,
[У1 =	2;	[z/2	=	-2;
1х3 -	-1,	|х4	=3,
[Уз =	8;	[z/4	=	4.
Для аналитического решения системы надо почленно прибавить к первому уравнению удвоенное
второе уравнение.
На рисунках 56 и 57 показано графическое решение систем уравнений
\у - х2 - 2х = 1,	[х2 + у2 + 2х - бу - 6 = О,
[х2 + у2 - 2х - бу + 5 = О И |х2 + у2 + 8х + 2у - 32 = 0.
Замечание. При решении уравнений графическим методом следует иметь в виду, что решения, получаемые этим методом, являются лишь приближёнными. Более того, иногда графики могут ввести нас в заблуждение. Например, при графическом решении уравнения (= log^ х
надо найти точку пересечения кривых у - и у = logj х. Если сде-
172
лать эскиз, то покажется, что эти кривые имеют лишь одну общую точку, лежащую на биссектрисе первого координатного угла. Однако на самом
1 1
деле это уравнение имеет еще два корня: х2 = % и х3 =
Упражнения
296. Решите графически следующие системы уравнений и проверьте полученные ответы путём аналитического решения:
1) 1	\х = у2 + 5 г/,		5)	|х2 + у2 [х2 + (у	= 25, - 9)2 = 36;
	[у =	х2 + 5х;			
2) 1	х2 -	8х - 4у = 6,	6)	\х2 - у2	= 25,
	У2 +	5у - 5х = 0;		[х2 + у2	= 47;
3) 1	'х2 +	У2 = 36,	7) J	[х2 - у2	= 25,
	X2 +	бу = 36;		[х2 + у2	= 25;
4) J	'х2 -	4х - бу = 20,	8) 1	|х2 + у2	+ 4х - бу = 13,
	ху =	: -8;		[ху - Зх	+ 2у = 11.
297. Найдите условие, при котором прямая у = kx + т касается: х2 у2	х2 у2
1) эллипса	= 1; 2) гиперболы - рг = 1; 3) параболы
у2 = 2рх; 4) окружности (х - а)2 + (у - b)2 = R2.
8. Системы иррациональных, тригонометрических, показательных и логарифмических уравнений. Методы решения систем уравнений, описанные в предыдущих пунктах, годятся для уравнений более общего вида. Разберём несколько примеров.
Пример 1. Решим систему уравнений
sin х + sin у = а,
х + у = Ъ, Ъ * О.
Решение. По формуле суммы синусов первое уравнение данной системы можно записать в виде 2 sin х cos ж = а. Заменим х + у его значением из второго уравнения, получим х — у	х — у а
sin - cos —5-^ = а. Отсюда следует, что cos ——- - --------г,
2	2	2	2 sin I
и поэтому х - у = ±2 arccos ——г + 4пл, п € Z. Отсюда видно, 2sin|
173
что система (1) имеет решение при условии, что |а| < 2 sin - О.
2
Данная система свелась к совокупности систем уравнений
х - у = ±2 arccos —-— + 4пл, п е Z, 2 sin—
2
х + у - Ь,
из которой для каждого значения п € Z получаем два решения исходной системы:
х =	± arccos ——г + 2тш, г/ = л + arccos ——г- - 2пл.
г	2 sin |	2	2 sin |
Пример 2. Решим систему уравнений
lg х + 1g у - а, Ю'2*»2 = Ъ.
(2)
Решение. Так как логарифмическая функция определена лишь при положительных значениях аргумента, то должны выполняться неравенства х > 0, у > 0. При таких значениях х и у первое уравнение системы (2) можно переписать в виде 1g ху = а, откуда находим ху = 10°. Кроме того, из второго уравнения системы следует, что х2 + у2 = lg Ъ, b > 0. Таким образом, заданная система равносильна следующей системе уравнений и неравенств:
ху = 10°, х2 + у2 = lg Ъ, х > 0, у > 0.
Из уравнений вытекает, что (х2 ± 2ху + у2) = lg b ± 2 • 10“, т. е. что (х + у)2 = lg b + 2  10“, (х - у)2= lg b - 2  10°. Отсюда получаем, что х + у = ±^lg b + 2  10“, х - у = ±^lg b - 2  10“. Но по условию имеем х > 0, у > 0, и потому х + у > 0. Значит, нужно выбрать положительное значение первого радикала. Решая две системы уравнений
х + у = ^/ig Ь + 2 • 10“, х - у = 71g Ь - 2 • 10“,
х + у =	+ 2  10“,
х - у = - 71g b - 2 • 10“
174
находим, что
Xi = |(71g Ъ	+ 2 • 10“	+ 71gb - 2 • 10“),
Ух =	+ 2 • 10“	- 71g Ь - 2 • 10“);
Х2 = |(7!g Ъ	+ 2 • 10“	- Jlgb - 2  10“),
Уг =	Ь &	+ 2 10“	+ Jlgb - 2 • 10“).
Данная система имеет решения при условии, что lg ft > 2 • 10“, т. е. ft > 102 10“.
Пример 3. Решим систему уравнений 71 - 16у2 - 71 - 16х2 = 2(х + у), х2 + у2 + 4х = -.
5
Решение. Из первого уравнения следует, что должны выполняться неравенства |х| < р |у| < р причём знак разности 71 - 16у2 ~ -71 - 16х2 должен совпадать со знаком суммы х + у, а потому |х| > |у|, если х + у > 0, и |х| < |у|, если х + у < 0.
Возведя обе части первого уравнения в квадрат, получим уравнение
1 - 8(х2 + у2) - 71 - 16(х2 + у2) + 256х2у2 = 2(х2 + у2) + 4ху.
Заменим в нём х2 + у2 его значением 4 - 4ху из второго уравнения. После упрощений получаем
-1 + Збху =	+ 64ху + 256х2у2.
v 5
Возведя ещё раз в квадрат обе части уравнения, получаем уравнение 650х2у2 - 85ху + 2-0.
При этом должно выполняться условие Збху - 1 > 0.
После подстановки ху = t получаем квадратное уравнение относительно t: 650t2 - 85t + 2 = 0, причём должно выполняться 1	12
условие t > -XX- Оба корня t, = —, t2 = квадратного уравне-оО	1U	оэ
ния удовлетворяют этому условию. Но из |х| < р |у| < имеем
175
|i| = |хг/| < а этому неравенству удовлетворяет лишь корень
2
t = gg. Поэтому надо решить систему уравнений
х2 + у2 + 4ху = -, 5
ху = Д оо
Первое уравнение этой системы перепишем в виде (х + у)2 + 2ху =
1	2	т-г
- Ё и подставим в него значение для ху. Получаем уравнение
О	ОО
(х + у)2 = откуда х + у = ±-Д=.
°5	<65
Итак, осталось решить две системы уравнений:
X + у = ~Y=, <65
ху = —
65
Решая их, находим четыре решения:
Х1 = <65	х2 = -4=, <65	Х3 =	 <65	х4 = — <65
z/i = -4=; <65	У2 = <65	у3 = <65	1/4 = —4= <65
Дополнительному условию, что |х| > |у| при х + г/ > 0 и |х| < |г/| при х + у < 0 удовлетворяют лишь решения (х4; j/J и (х4; г/4). Значит, имеем решения
Г 2 ;	—М
(<65 <65 J <65	<65 J
Замечание. Можно было бы не следить за условиями, возникающими из данных уравнений, а получить все решения и проверить их подстановкой в данную систему уравнений. Но иногда такая подстановка затруднительна.
Упражнения
298. Решите системы уравнений:
1) (ху = 243,
2)
хя + Л = Д
+ Л = х’;
(1024)’ = (|х)\
176
3) flog2(i/ - x) - log8(3i/ - 5x) = 0, |x2 + y2 = 5;
4)
iw.252#2-1 - 2-Cl
log8 x • log2 (У + l)2 = |;
5) floga x + logo, у = 1, [59 1о^л + x2 = 2a;
6)
cos (x - y) = 2 cos (x + y), cos x cos у =
7)
8)
9)
a2 - x2 \y2 ~b2 xy = ab;
У2
a;
2y)x2 + y2 + xy = 1,
- +	= a;
У x
У2 ~ b2 a2 - x2
a2 + x2
У2 + b2
y2 + b2
--------- = 4,
a2
.2
10)
a,
x + у + Зу/bxy = b;
И)
cos2 у + 3 sin x sin у = 0, 21cos2x - cos 21/ = 10;
12)
tg x + ctg у = a. ctg x + tg у = 2;
13)
a,
14)
arcsin x arcsin у =
о	(1
x + у = 2 arcsin »	2
arcsin x + arccos у
it2
12’
= 0;
151 |Va - x - -Jy - x = y[y, (Jb - x + -Jy - x = Jy;
16)
yjx + 4y - -jx - Jy = 1, Jx2 - у + л/х2 + у = 1.
9. Решение неравенств с двумя переменными. Линия Г: F(x, у) = 0 делит плоскость на несколько областей, внутри каждой
из которых F(x, у) сохраняет знак — в некоторых из этих областей выполняется неравенство F(x, у) > 0, а в остальных неравенство F(x, у) < 0. Поэтому, чтобы решить неравенство F(x, у) > 0, можно сначала изобразить линию Г: F(x, у) = 0 и в каждой из областей, на которые она делит плоскость, выбрать пробную точку. Знак, который принимает F в этой точке, она принимает и во всей области. После этого остаётся отобрать области, в которых F положительно. Присоединяя к полученному решению саму линию Г, получаем решение неравенства F(x, у) > 0.
177
|  11
A(2; -3)1 ^ZZZZZZZJ
H<g<gig<g Kigigigig
00Z0gg ЯЯЯЯЯЯЯЯЯЯЯ
hgjgsgifl


<gig<g<g<g^4PVK^%!%%%%% %%%%%% %%%%%%%%%%% %%%%%% %%%%%%%%%%% ЙЙЙЙЙЙ 'ЖвЮЗШШЯМа
Рис. 59
Рис. 58
Пример 1. Решим неравенство х2 - 4х + у2 + бу - 12 > 0.	(1)
Решение. Выделяя полный квадрат, получаем
(х - 2)2 + (у + З)2 > 25.
Уравнение (х - 2)2 + (у + З)2 = 25 задаёт окружность с центром А(2; -3) и радиусом 5. В качестве пробной точки для внутренней области выбираем центр А (2; -3). Так как (2 - 2)г + (-3 + З)2 = 0 < 25, то во внутренней области данное неравенство не выполняется. Во внешней области выбираем пробную точку В(8; -3). Для неё имеем (8 - 2)2 + (-3 + З)2 = 36 > 25. Отсюда следует, что во внешней области выполняется неравенство (1). Решение изображено на рисунке 58. На рисунке 59 изображено решение неравенства х2 - 4х + у2 + бу - 12 > 0
(обычно чертят сплошную линию, если граница принадлежит рассматриваемому множеству, и штриховую линию в противном случае).
Пример 2. Решим неравенство
(х2 + у2 - 4)(х2 + у2 - 16) < 0.	(2)
Решение. Поскольку произведение равно нулю лишь в случае, когда хотя бы один из множителей равен нулю, уравнение (х2 + у2 - 4)(х2 + у2 - 16) = 0
задаёт линию, распадающуюся на две окружности х2 + у2 = 4 и х2 + у2 = 16 (рис. 60). Они делят плоскость на три части. С помощью метода пробных точек устанавливаем, что неравенство (2) выполняется в кольце, ограниченном этими окружностями (эта область заштрихована).
178
Для графического изображения решения системы неравенств
F(x, у) > О, Ф(х, у) > О
находят сначала множество Xi точек плоскости, на котором выполняется первое неравенство, потом множество Х2 точек плоскости, где выполняется второе неравенство, и, наконец, берут пересечение этих множеств (т. е. их общую часть).
Пример 3. Изобразим графически решение системы неравенств
х + у + 1 > О, х2 + у2 < 25.
Решение. Неравенство х + у + 1 > 0 перепишем в виде у > -х - 1. Ясно, что оно выполняется на прямой у = -х - 1 и в точках, лежащих выше этой прямой. Неравенство же х2 + у2 С 25 выполняется на окружности радиусом 5 с центром в начале координат и внутри неё. Общая часть этих множеств заштрихована на рисунке 61.
Пример 4. Изобразим графически решение системы неравенств
Зх + 2у > О,
Зх + 2у С 12,
х + 4у > -2,
х + 4у < 24.
179
Решение. Каждое из заданных неравенств изображается полуплоскостью, причём граничные прямые первой и второй полуплоскостей параллельны, равно как и граничные прямые третьей и четвёртой полуплоскостей. В данном случае общей частью всех четырёх полуплоскостей является параллелограмм (рис. 62). Рекомендуем читателю разобрать, какие области задают системы, получаемые из заданной всевозможными изменениями
знаков неравенств на противоположные (всего получится 9 различных областей).
Иногда бывает удобно разбить область на части, задать каждую из них неравенством или системой неравенств, а потом объединить эти части.
Пример 5. Зададим с помощью неравенств область, изображённую на рисунке 63.
Решение. Эта область состоит из квадрата и четырёх полукругов. Легко проверить, что квадрат задаётся системой неравенств х + у - 6 < О, х + у + 6 > О, х - у - 6 < О, х - у + 6 > О,
а полукруги — соответственно неравенствами
f(x - З)2 +	(у -	З)2	< 9,	Г(х + З)2	+ (у +	З)2	<	9,
[х + у - 6	> О;	|х + у +	6 < 0;
|(х - З)2 +	(у +	З)2	С 9,	|(х + З)2	+ (у -	З)2	<	9,
|х - у - 6	> 0;	[х - у +	6 < 0.
Во многих случаях бывает удобно задавать области системой
неравенств вида	[а < х < Ъ, [<р(х) < у <	у(х)	(3)
или вида	С < у < d, ф(!/) < х <		(3')
180
Рис. 63
Рис. 64
Система (3) указывает, во-первых, границы а и b изменения х, а для каждого х, лежащего между а и Ъ, — границы изменения у (рис. 64). Аналогичный смысл имеет система неравенств (3'). Иногда приходится предварительно разбивать область на части и задавать неравенствами вида (3) или (3') каждую из этих частей.
Пример 6. Запишем с помощью системы неравенств вида (3) область, заданную системой неравенств
(у < 2х + 9,
[у > 2х2 - 2х - 7.
Решение. Сначала найдём точки пересечения прямой у = 2х + 9 и параболы у = 2х2 - 2х - 7. Для этого решим систему уравнений
(у = 2х + 9,
\у = 2х2 - 2х - 7.
Находим Aj(-2; 5) иА2(4; 17). Из рисунка 65 видим, что значения х изменяются от -2 до 4, -2 < х < 4. При заданном значении х значение у меняется от 2х2 - 2х - 7 до 2х + 9 (от параболы до прямой). Поэтому данная область задаётся системой неравенств
|-2 < х < 4,
[2х2 - 2х - 7 < у < 2х + 9.
181
Пример 7. Зададим системой неравенств вида (3) круг радиусом 6 с центром в точке А(-4; 3).
Решение. Уравнение границы этого круга имеет вид
(х + 4)2 + (у - З)2 = 36.
Отсюда находим
У - 3 = ±736 - (х + 4)2, и потому
У = з ± 736 - (х + 4)2.
Уравнение
У = 3 - ^36 - (х + 4)2 задаёт нижнюю полуокружность, а уравнение
У = 3 + 736 - (х + 4)2 —
верхнюю полуокружность. Так как, кроме того, ясно, что х изменяется от -10 до 2, получаем систему неравенств
-10 < х < 2,
3 - 736 - (х + 4)2 < у < 3 + V36 - (х + 4)2.
Упражнения
299.	Вычертите области, заданные системами неравенств: 1) Г-6 < х < 2,	3) fl < х С 3,
' xi _ 1 < „ < о _ г. [х2 < у < х + 9;
4	1 у <4 х,
2)	ГО < у < 4,	4) ГО < х < 3,
[у < X < 10 - у;	[о С у < V25 - х2.
300.	Задайте неравенствами:
1)	треугольник с вершинами 0(0; 0), А(1; 0), В(1; 1);
2)	трапецию с вершинами 0(0; 0), А(2; 0), В(1; 1), С(0; 1);
3)	параллелограмм с вершинами А(1; 2), В(2; 4), С(2; 7), 0(1; 5);
4)	круговой сектор АОВ с центром 0(0; 0) и концами дуги Л(1; 1) и В(-1; 1);
5)	параболический сегмент АОВ, 0(0; 0), ограниченный дугой параболы АОВ и хордой, соединяющей точки А(-1; 2) и В(1; 2).
301.	Область D задана неравенством или системой неравенств. Задайте её системой неравенств вида (3):
1)	х > 0, у > 0, х + 9 > у1;	2) х2 + у2 < а2;	3) х2 + у2 < х;
4) у > х, х > 1, у -1;	5) [у < х С у + 4,
О < у < 2.
1 То есть
х > О,
У > О, х + 9 > у.
182
302. Область D задана системой неравенств вида (3). Задайте её систет неравенств вида (3'):
1) ГО < х < 4,	3) ГО < х < 1,
[Зх2 < у < 12х;	[—71 - х2 < у < 1 - х;
2) ГО < х < 1,	4) ГО < х < 1,
Ьх < у < Зх;	< < у < ТзТ^.
2 у
Упражнения к §2
	Решите системы уравнений (303—321).			
303.	1)	Зх - 4у + 5г = 18,	3)	х + 2у + г + 7 = 0,
		2х + 4у - Зг = 26,		2х + у - г - 1 = 0,
		х - бу + 8г = 0;		Зх - у + 2г - 2 - 0;
	2)	2г + 5 = Зх,	4)	х + у + г =6,
		х + бу + 4г = 10,		2х + у - г = 1,
		8у - 5х + 2 = 0;		Зх - у + г = 4.
304.	1)	х + у + г = 14,	3)	х, + х2 + х3 + х4 - 36,
		х + у + t - 10,		х, + х2 - х3 - х4 = 24,
		у + г + t -15,		х, - х2 + х3 - х4 = 12,
		х + г + t = 12;		х4 - х2 - х3 + х4 =0.
	2)	х + 2у - z + 2t = 10,		
		Зх - у + 2г + 6t = 19,		
		2х + 8у - Зг + 5t = 31,		
		4х + у + 12г - 3t = 40;		
305.	1)	(х - у)(х2 - у2) = 16,	3)	х3 + у3 + ху(х + у) = 13,
		(х + у)(х2 + у2) = 40;		х2у2(х2 + у2) = 468;
	2)	(х2 + 1)(у2 + 1) = 10,	4)	lOi 1 + н
		(х + у)(ху - 1) = 3;		ху	2’
				х2 - у2 = 3.
306. 1)
3) (ху + х + у = 11, [х2у + ху2 = 30.
-^ + -6_
X - у X + у
4 9
х - у х + у
= 1Д,
= 0,1;
2) Гх2 + 4у2 - Зх - 2 = 0,
[2х + Зу = 5;
183
307. 1) fa	- У = 8a2, /x + \[y = 4a;		
2)	/х + у - yjx - У = a,		
	Jx2 + y2 + ylx2 - y2 = “2;		
3) (	X = a-Jx + У + z,		
	у = bjx + у + z,	> 0,	c > 0.
	2 = Cyjx + у + z, a 0, b		
			3) fx>/x + yjy - 341, [xTy + У'Гх = 330.
308. 1)	+ + h"1 i	+ '«"1	H 1	1 ii	и Н/ bo		
2)	^x + 4у ~ yx ~ Jy ~ i’		
309. 1)	Jx2 - у + Vx2 + у = 1; X" = 243, 1024* = (jx)2;	2) ।	у1>-Гх + 12 = i, x + у = 6.
310. 1)	f82'^ = 32 • 24*-1, [5 • 5”* = s/252* + 1;	2)	xy = 40, x'8s - 4.
311. 1)	log#x + log, у = 5-,	2)	log VxV7 = mn + 1, lg(xle>) _ fm?
	xy = 64;		,1g (y'e#) ^nl
312. 1) [(у + IF = 10 000,	2)	= 58,
(у - I)21	Lqqqq*!'1)’^6’1-6(! = 1-
|(!/2 -	= (y^W' l(
313. 1) yx^ = x2Jx, 2) (^1оё2У10^2 = ^(1 " 10g’2)’ log4 у log/у - Зх) = 1; log^s 2 logjg x = 1.
314. 1)	2) 10g„x log. (xyz) = 48,	,	_ 5 log9x + log, у - 2’
	log, У log, (xyz) = 12,	x + у = a2 + a.
	log, z log, (xyz) = 84, a > o, a * 1;	
315. 1)	(log, x + log, у - 2) log18a = 1,	2) j	lg2x + lg2y = 2,51g2 a2
	x + у = 20a, a > 0, a 1;	xy = a, a > U.
	1 2)	tg x - tg 2y = 1,
316. 1)	sinx sin у = —j, g	4 tg(x - 2y) = 3.
	cosx cosy =	
184
317. 1)	и /А ЬЭ	2)	|х + 2у| < 2,
318. 1)	4х + Зу > 1, |х| < 3; •	л/З	2)	;	| /Л / W О
319. 1)	sin X > —, > л/з cos х > — sin х cos у = d,	2)	sinx 2> COS X > 1. sin х cos у - а,
320. 1)	X - у = Р; х + ay + a2z - а3,	2)	cos х sin у - а. х + ay + a2z + a3t = a4,
321. 1)	х + by + b2z - b3, x + су + c2z = c3; (y + z)2 - x2 = a,	2)	x + by + b2z + b3t = b4, X + cy + C2Z + c3t = c4, x + dy + d2z + d3t = d4. x + у + —-— - a + 1, x - у	b x - у + —-— = b + —. x + у	a оскости множество решений системы
322. Изо	(z + x)2 - y2 = b, (x + y)2 - z2 = c; бразите на координатной пл		
неравенств и найдите площадь 1) Гх2 + у2 < 4,	3) [у > 2|х - 1; 2) (х2 + у2 < 4х,	4) \ху > 4;			полученной фигуры: х2 + у2 < 16, ху < 1; х2 + у2 < -4х, |х| + |у| < 2.
323, Два товарища, имея один велосипед, одновременно отправились из пункта А в пункт В; первый из них поехал на велосипеде, а второй пошёл пешком. На некотором расстоянии от А первый оставил велосипед и пошёл до В пешком. Второй, дойдя до велосипеда, поехал дальше на нём. Оба товарища прибыли в В одновременно. На обратном пути из В в А они поступили точно так же, только первый товарищ проехал на велосипеде на 1 км больше, чем в первый раз, из-за этого второй товарищ приехал в А на 21 мин позже, чем туда пришёл первый. Определить скорость ходьбы каждого из товарищей, если на велосипеде они ехали с одной и той же скоростью, равной 20 км/ч, а при ходьбе первый затрачивал на каждый километр на 3 мин меньше, чем второй.
324. Школьник затратил некоторую сумму денег на покупку портфеля, авторучки и книги. Если бы портфель стоил в 5 раз дешевле, авторучка — в 2 раза дороже, а книга — в 2,5 раза дешевле, то та же покупка стоила бы 8 р. Если бы по сравнению с первоначальной стоимостью портфель стоил в 2 раза дешевле, книга — в 3 раза дешевле, авторучка — в 4 раза дешевле, то за ту же покупку школьник уплатил бы 12 р. Сколько стоит покупка и за что было уплачено больше: за портфель или за авторучку?
185
1. Введение. До сих пор мы рассматривали лишь действительные числа. С помощью положительных действительных чисел можно выразить результат любого измерения, а с помощью произвольных действительных чисел — изменение любой величины. Арифметические операции (сложение, вычитание, умножение и деление на число, отличное от нуля) над действительными числами снова дают действительные числа. Отсюда следует, в частности, что рациональная функция с действительными коэффициентами принимает действительные значения при всех действительных значениях аргумента, для которых она определена.
Операция же извлечения квадратного корня определена не для всех действительных чисел, а лишь для неотрицательных — из отрицательного числа квадратный корень извлечь нельзя. Поэтому в теории квадратных уравнений приходится рассматривать три случая: если D = Ь2 - 4ас > 0, то уравнение ах2 + Ьх + с = 0 имеет два различных действительных корня, при D = 0 оно имеет лишь один действительный корень (второй кратности), а при D < О это уравнение действительных корней не имеет.
Ряд вопросов, возникших при решении уравнений третьей и четвёртой степени, привёл математиков к необходимости расширить множество действительных чисел, присоединив к нему новое число i такое, что i2 = -1. Поскольку действительных чисел с таким свойством не существует, новое число назвали «мнимой единицей» — оно не выражало ни результатов измерения величин, ни изменений этих величин. Но включение числа i потребовало дальнейшего расширения множества чисел — пришлось ввести произведения этого числа на все действительные числа, т. е. числа вида Ы, где b € R, а также суммы действительных чисел и таких произведений, т. е. числа вида а + Ы, где а, b & R. Получившиеся при этом числа были названы комплексными, так как они содержали как действительную часть а, так и чисто мнимую часть Ы.
186
Поскольку выражение а + Ы напоминает многочлен первой степени от i (с той существенной разницей, что i не является переменной), математики XVI века производили операции над такими выражениями по тем же правилам, что и над многочленами, причём когда у них появлялось выражение I2, его заменяли на -1. Например, сумму и произведение комплексных чисел определяли следующим образом:
(а + Ы) + (с + di) = (а + с) + (b + d)i,	(1)
(а + Ы) (с + di) ~ ас 4- adi 4- bci 4- bdi2 —
= (ас - bd) 4- (ad 4- bc)i.
Частное двух многочленов первой степени не выражается, вообще говоря, в виде многочлена. Но для комплексных чисел частное снова выражается в виде комплексного же числа. Именно,
а + Ы	_	(а	4- Ы)(с -	di)	_	(ас + bd) + (be -	ad)i _
с + di	(с	+ di)(c -	di)	с2 - d2i2
_ (ас + bd) + (be -	ad)i	_	ac + bd , be -	adj	т
c2 + d2	c2d2 c2 +	d2 ’	1	’
Из формулы (2) вытекает, что
i3 = i2  г = (-l)i = ~i,
i4 = j3  i = (~i)i = -i2 = -(-1) = 1,
i5 = i4 • i = 1 • i = i.
Вообще
j4n + k= (jiyi . jk _ p . jk = jk.
Например,
j67 _ £64 + 3 _ £4  16 + 3 _ £3 _
Равенства (1), (2), (3) имеют пока что лишь формальный характер. При дальнейшем анализе понятия комплексного числа возникли следующие вопросы.
а)	Можно ли употреблять в записи комплексных чисел операции сложения и умножения до того, как они получают определения?
б)	Является ли i единственным комплексным числом, квадрат которого равен -1?
в)	Достаточно ли комплексных чисел для записи корней любых уравнений с комплексными коэффициентами? (При отрицательном ответе на этот вопрос пришлось бы далее расширять полученное числовое множество.)
И наконец, последний, но первый по важности вопрос.
г)	Какие практические приложения может иметь теория комплексных чисел?
В этой главе мы разберём указанные вопросы.
187
У пражнения
325. Выполните действия над комплексными числами:
2)	(1,(3) + 0,2(6)i) - (-2,1(3) + 0,6(2)г);
3)	(2^3 - 4iV2) - (V27 - iV32) + (-7= + -7М;
^V3	V3/
4)	(Щ. _	+ (A _ А A _ //1 _ ± А _ M _ 1 A\
\n m I \m n I \\n ml \m n II
5)	(4 + 3i) • 0,(2); 6) (-2 - 3i)(-l,(4));	7) (-3,5i)(-4,5);
8)	(1 + i)(l - i); 9) (>/3 - i)(V3 + i);	10)(1 - >/3i)(V3 + >/6i);
n> (1/1 - #)(1 +
12) i^2 + 7зf4- -
{42 42
13)	(2 + 5i)2(3 - i);	14) (3 + i)3;	15) (1 + 2i)2(l - 2i)2;
16)	(2 + i)4 + (2 - 1У;	17) i127, i218, i736.
2. Определение комплексных чисел и операций над ними. Неясности, связанные с преждевременным употреблением знаков сложения и умножения, устраняются весьма просто. Ведь в записи а + Ы нас интересуют лишь действительные числа а и Ъ, идущие в определённом порядке. Поэтому введём следующее определение.
Определение. Комплексным числом z называют пару (а; Ь) действительных чисел а и Ь, взятых в определённом порядке. Две пары (а; Ь) и (с; d) задают одно и то же комплексное число в том и только в том случае, когда они совпадают, т. е. когда а = с и b = d.
Из этого определения следует, что одно равенство (a; b) = (с; d) для комплексных чисел равносильно двум равенствам а = с и b = d для действительных чисел. Если z - (а; Ь) — комплексное число, то а называют его действительной частью, а b — мнимой частью. Приняты обозначения а = Rez, Ъ = Im z (от французских слов reel — действительный и imaginaire — мнимый). Числа (а; Ъ), для которых 6*0, называют мнимыми числами, а числа вида (0; Ь), b * 0, — чисто мнимыми числами.
Определим теперь операции сложения и умножения комплексных чисел (т. е. пар (а; Ь)) в соответствии с «наивными» формулами (1) и (2) п. 1: если г = (а; Ь) и w = (с; d), то
z + w = (а; Ь) + (с; d) = (а + с; b + d)	(1)
и
zw = (а; b)(c; d) = (ас - bd; ad + be).	(2)
188
Итак, мы ввели понятие комплексного числа и определили для этих чисел операции сложения и умножения. Теперь можно перейти к записи комплексных чисел в виде z - а + Ы, о которой говорилось выше. Для этого заметим следующее:
а) для пар вида (а; 0) определённые выше операции сложения и умножения сводятся к соответствующим операциям над дейст-
вительными частями, т. е. имеют место равенства
(а; 0) + (с; 0) = (а + с; 0),	(3)
(а; 0)(с; 0) = (ас; 0);	(4)
б) имеют место равенства
(b; 0)(0; 1) = (0; Ь),	(5)
(0; 1)(0; 1) = (-1; 0).	(6)
Эти утверждения непосредственно вытекают из формул (1) и (2). Из утверждения а) следует, что пару (а; 0) можно кратко обозначить через а. Тогда равенство (6) примет вид (0; 1)  (0; 1) = -1.
Наконец, обозначим пару (0; 1) через i. В этих обозначениях равенство (5) принимает вид Ы = (0; Ь). Поскольку (а; Ь) = (а; 0) + + (0; Ь), то получаем, что пару (а; Ь) можно обозначить а + Ы: (а; Ь) = а + Ы.
Теперь уже операции сложения и умножения в правой части равенства имеют смысл.
В дальнейшем мы будем записывать комплексные числа в виде а + Ы. Формулы (1) и (2) принимают в этих обозначениях вид, указанный уже в п. 1:
(а + Ы) + (с + di) = (а + с) + (b + d)l	(Г)
и
(а + Ы) (с + di) = (ас - bd) + (ad + bc)i	(2')
(это неудивительно, поскольку сами формулы (1) и (2) были введены на основе «наивного» определения операций сложения и умножения).
Свойства операций сложения и умножения для комплексных чисел такие же, как и для действительных: имеют место тождественные равенства:
1)	z + w = w + г,	1')	zw = wz,
2)	(z + w) + t = z	+ (w + t),	2')	(zw)t - z(wt),
3)	z + 0 = z,	3')	z • 1 = z,
а также равенство
4)	z(w + t) = zw + zt.
Кроме того, каждое комплексное число z = а + bi имеет противоположное ему число -г, а именно -г - -а - Ы. В самом деле, (а + bi) + (-а - bi) = (а - а) + (b - b)i = 0.
189
Наконец, каждое отличное от нуля комплексное число z имеет обратное ему число, т. е. такое число w, что zw = 1. Действительно, будем искать число w в виде w = х + yi. Равенство zw = 1 принимает при этом вид (а + Ы)(х + yi) = 1, т. е.
(ах - by) + (bx + ay)i = 1.	(7)
Но комплексные числа равны в том и только в том случае, когда у них одинаковы как их действительные части, так и мнимые части. Поэтому из равенства (7) получаем два уравнения для отыскания х и у:
ах - by - 1, bx + ay = 0.
Решая эту систему уравнений, получаем, что х = д2 ^2. у = аг'^г (при этом а2 + Ь2 Ф 0, так как число z предполагается отличным от нуля, а следовательно, хотя бы одно из чисел а, b отлично от нуля).
Мы доказали, что если г = а + Ы, то
_ X _ а___________b .
w ~ г ~ а2 + Ь2 а2 + Ь2 1‘
Итак, все 9 основных свойств операций сложения и умножения действительных чисел, на которых основана алгебра, верны и для комплексных чисел. Отсюда следует, что любое алгебраическое тождество остаётся справедливым и в комплексной области. Например, для комплексных чисел z и w верны тождества
(z ± w)2 = z2 ± 2zw + w2,
(z + w)(z - w) = z2- w2
И T. Д.
Операции вычитания и деления комплексных чисел определяются равенствами
z — W = Z + (—w) и
Из этих равенств вытекает, что
(а + Ы) - (с + di) = (а - с) + (b - d)i и
= (а +	Ы) • -~т = (а	+ Ы)( 2 с ,2	- 2 d i\	=
с + di '	' с + di '	'\с2 + d2 с2 +	d2 I
_ ас + bd , be - ad:
~ с2 + d2 с2 + d2 ’
190
что совпадает с формулой (3) п. 1. На практике вместо полученной формулы используют указанный в п. 1 приём: умножают числи
тель и знаменатель дроби °- * на с - di.
Упражнения
326.	Найдите действительные числа х и у такие, чтобы выполнялись равенства:
1)	— - 4г + 4 = Зг - - + 2у;
X	Xя
2)	(1 + i)x + (1 - i)y = 3 - г;
3)	(2 + Зг)х + (2 - Зг)(х + у) = 7 - 8i.
327.	Найдите действительные числа х и у такие, что
(2х - Зг/г)(2х + Зуг) + xi = 97 + 2г.
328.	Найдите значения выражений:
3 + 2г,	3 + г , 3 — г.
7 - 2г’	3 - г 3 + г’
3)
1 - 2г
1 + 2г
з
16) (б - 0,2л/б0г) х
х ((V8i - V18i + 4)^г +	+ 5(V^6i - ТМг + 2));
17) 2(Тбг + УЗгЛЛб - 4)(л/3г + г)(1 - Уз)
(7 + 5>/2)(72г - г/
329. Покажите, что если 1 + е + е2 = 0, то
(а + b -I- с)(а + be + се2)(а + be2 + се) = а3 + Ь3 + с3 - ЗаЪс. 330. Решите систему линейных уравнений
х + у + z = А, • х + г/е + ze2 = В, х + уе2 + ге = С, где 1 + е + е2 = 0.
191
3. Сопряжённые комплексные числа. Введём следующее определение.
Определение. Два комплексных числа называются сопряжёнными, если они отличаются лишь знаком мнимой части.
Число, сопряжённое комплексному числу 2, обозначают z. Таким образом, если z - а + Ы, то z = а - Ы. Например 3 + 4i = = 3 - 4i. Ясно, что число, сопряжённое числу z, равно z:
2 = Z.
Число, сопряжённое действительному числу а, совпадает с а, а число, сопряжённое чисто мнимому числу Ы, противоположно ему:
а = а, а 6 R, Ы = -Ы, Ъ 6 R. Докажем следующие утверждения о сопряжённых комплексных числах.
Теорема 1. Число, сопряжённое с суммой комплексных чисел, равно сумме чисел, сопряжённых со слагаемыми: z + w = z + w.
Доказательство. Пусть г - а + Ы, и> = с + di. Тогда z = = а - bi, й> = с - di, и потому
z + w - (а + Ы) + (с + di) - (а + с) + (b + d)i = = а + с - (b + d)i = (а - Ы) + (с - di) = z + й>.
Теорема 2. Число, сопряжённое с произведением комплексных чисел, равно произведению чисел, сопряжённых с множителями: zw - г • w.
Доказательство. Если z = а + bi, w = с + di, то zw = = (а + bi)(c + di) = (ас - bd) + (ad + bc)i - ас - bd - (ad + bc)i. С другой стороны,
z • w = (a - bi)(c - di) = ac - bd - (ad + bc)i.
Получили одинаковые результаты, что и доказывает наше утверждение.
Теорема 3. Если г * 0, то число, сопряжённое с числом, обратным г, обратно числу, сопряжённому с з:
i 1 (т. е. 1 : z = 1 : z ).
г г
Доказательство. Из равенства г • - = 1 по теореме 2 еле дует, что 2	1 = 1=1. Но тогда j = =•
192
Из доказанных утверждений вытекают такие следствия.
Следствие 1. Число, сопряжённое натуральной степени комплексного числа, равно степени с тем же показателем числа, сопряжённого данному:
2п = 2п.
Это утверждение вытекает из теоремы 2 и того, что степень — произведение равных множителей.
Следствие 2. Если заменить в многочлене Р(г) с комплексными коэффициентами значение z - г0 на сопряжённое значение га, а все коэффициенты — сопряжёнными им числами, то значение многочлена заменится на сопряжённое.
Если положить P(z) = anzn + an-xzn~l + ... + а0 и P(z) = anzn + + ап.12п'1 + ... + а0, то утверждение записывается следующим образом: P(z0) = P(z0).
Для его доказательства достаточно заметить, что в силу теорем 1 и 2 и следствия 1 имеем
Р(20) = anzs + an_lZg~1 + ... + а0 = anzs +	+
+ ... + а0 = anz% + a^iz"^1 + ... + а0 = P(z0).
Поскольку действительные числа сами себе сопряжены, то из следствия 2 получаем ещё одно.
Следствие 3. При замене в многочлене с действительными коэффициентами значения z = z0 на сопряжённое число г0 значение многочлена заменяется на сопряжённое.
Утверждения, аналогичные следствиям 1, 2, 3, верны для любых рациональных функций от г.
Теорема 4. Сумма и произведение двух сопряжённых комплексных чисел являются действительными числами.
Доказательство. Имеем
z + z = (а + Ы) + (а - Ы) - 2а, 22 = (а + Ы)(а - bi) = а2 - b2i2 = а2 + Ь2.
Упражнения
331.	Докажите, что если сумма и произведение двух комплексных чисел являются действительными числами, то эти комплексные числа — взаимно сопряжённые.
332.	1) При каких действительных значениях х и у комплексные числа 5 + ixy, х + у + 41 будут сопряжёнными?
2)	Сколько решений будет иметь п. 1), если не требовать, чтобы х и у были действительными? Приведите несколько примеров.
193
333.	Разложите на множители выражения:
1)	т2 + п2;	2) 4а2 + 9Ь2;	3) х2 + 4х + 13; 4) х2 - бх + 25.
334.	Упростите выражения:
1)	(а + 1 + г)(а - 1 + г)(а - 1 - i)(a + 1—1);
2)	(х + 2 - 3i)(x - 2 + 3i)(x + г) (х - i);
3)	(35 + 4 + 5г)(3д + 4 - 5i).
335.	Составьте квадратное уравнение с действительными коэффициентами, одним из корней которого является число:
1)	i; 2)1 + 1;	3) 2 - Z; 4) 1 + 2iV3.
336.	Найдите комплексное число, равное квадрату сопряжённого с ним числа.
4. Извлечение квадратных корней из комплексных чисел и решение квадратных уравнений с комплексными коэффициентами. Введём следующее определение.
Определение. Число w называется квадратным корнем из комплексного числа г, если его квадрат равен г:
W2 = Z.
Квадратный корень из z обозначают >/z. Так как равенство w2 = 0 выполняется лишь при w - 0, то д/о = 0. Таким образом, из числа 0 можно извлечь лишь один квадратный корень. Если w — квадратный корень из числа г, то и -w является квадратным корнем из г: из w2 = z следует (-и»)2 = 2- Мы покажем сейчас, что квадратных корней из z иного вида не существует.
Теорема. Пусть z = а + Ы — отличное от нуля комплексное число. Тогда существуют два взаимно противоположных комп лексных числа, квадраты которых равны г, а иных квадратных корней из z не существует. Если Ь*0, то эти числа выражаются формулой
W = ±^п2 + Ь2 + а + . sign b^a2 + b2 - aj (1)
где
signb =
1, если b > 0,  -1, если b < 0, 0, если b = 0.
При b = 0, a > 0 имеем w = ±>/a, а при b = 0, a < 0 имеем
Доказательство. Пусть w = и + vi и w2 ~ z. Тогда выполняется равенство (u + vi)2 - a + bi, t. e. u2 - v2 + 2uvi - a + bi. Но два комплексных числа равны в том и только в том случае,
194
когда соответственно равны их действительные и мнимые части. Поэтому для отыскания и и о получаем систему уравнений второй степени
(и2 - v2 = а,
[2iw = b.
Если b = 0, то либо и - 0, либо v = 0. При и = 0 имеем и2 - а, и потому а > 0, и = ±4а. Если же и = 0, то -V2 - а, и потому а < 0, v = Разберём теперь случай, когда Ъ Ф 0. В этом случае и * 0,
Ь ТТ
и из второго уравнения находим, что v = Подставляя это выражение в первое уравнение, получаем уравнение 4и4 - 4аи2 -- Ь2 = 0. Оно имеет лишь два действительных корня:
_ 1 Уд2 + ft2 + а _ Мд2 + b2 + а
U1~ \	2	и и2 —	----g-----•
Первому значению для и соответствует значение
___b _ ________Ъ______ _ frVVa2 +~b2 - а
1	2U1	9 /7д2 + b2 +а
2
Но ~^= = ттт = sign ft, значит,
Vft2 1Ы
.	, IVa2 + b2 - а
L>! = Sign ft ---2-------’
и потому
l^a2 + b2 + а	Мд2 + ft2^ - д
и?! = ---2----- + I sign ft \	2
Второму значению и соответствует противоположное значение ДЛЯ IV.
Теорема доказана.
Пример 1. Вычислим >/3 - 4i.
Решение. В формуле (1) положим a = 3, ft = -4. Так как число -4 отрицательно, по формуле (1) получаем
4^. ±f жзи _ js. i s - 4 ±(2 _ ().
I’ 2	’	2	7
Замечание. В отличие от случая корней из действительных чисел под корнем из комплексного числа понимаются оба значения, отличающиеся знаками. Таким образом, в данном случае запись определяет не одно, а два числа.
195
Квадратные уравнения az2 + bz + с = 0, а Ф О, с комплексными коэффициентами решаются по той же формуле
_ -Ь + у/b2 - 4ас
2а
что и уравнения с действительными коэффициентами. (Перед корнем можно было бы оставить лишь знак «плюс», но мы пишем оба знака, чтобы сохранить вид ранее известной формулы.) В частности, теперь можем решать и уравнения с действительными коэффициентами, имеющие отрицательный дискриминант.
Приме Р 2. Решим уравнения:
1) х2 + 4х + 29 = 0;
2) z2 - (3 + 2г)г + 6i = 0.
Решение. Для первого уравнения имеем
х = -2 ± V22 - 29 = -2 ± 7^25 = -2 ± 5г.
Для второго уравнения
3 + 21 + 7(3 + 2г)2 - 24г	3 + 21 ± >/9 - 4 - 121
2= ----------------------- = --------------- =
= 3 + 2г ± Уб - 12г
2
По формуле (1) получаем, что
К---—	(д/52 + (-12)2 Гб . ly/52 + (-12)2 ^5 о о.
У 2	У 2
(берем лишь одно значение корня), и потому
3 + 2г + (3 - 2г)
2 ~	2
Значит, 21 = 3, z2 - 21.
Формулы Виета
21 + г2 =
21 ' 22 = а
сохраняют силу и для уравнений с комплексными коэффициентами.
Легко проверить, что в случае, когда коэффициенты квадратного уравнения являются действительными числами, а корни — комплексными, эти корни сопряжены друг другу.
Упражнения
337.	Решите квадратные уравнения:
1)	х2 - 2х + 2 = 0;	3) 9х2 - 12х + 7 = 0;
2)	х2 + 10х + 50 = 0;	4) х2 + 3 = 0.
196
338.	Вычислите квадратные корни:
1)	V-7 - 24г;	3) 71 + i73;
2)	V24 + 70г;	4) 7г + гТ2;
339.	Решите квадратные уравнения:
1) z2 - (2 + i)2 + 2i =0;	2) z2
6) 7^7.
- (5 + 2г)г + 5 + 5i = 0.
§ 2. тригонометрическая форма комплексных чисел
1.	Геометрическое изображение комплексных чисел. Мы дали
определение понятию комплексного числа и научились выполнять над комплексными числами арифметические действия, а также извлекать из них квадратные корни. Тем самым даны ответы на вопросы а) и б) из п. 1 § 1. Как там отмечалось, одним из важней
ших является вопрос о практическом значении комплексных чисел. Чтобы ответить на него, нужно сначала научиться изображать эти числа геометрически подобно тому, как изображаются действительные числа точками на координатной прямой.
Комплексное число z = х + yi задаётся парой (х; у) действительных чисел. Та же пара чисел может рассматриваться в качестве координат точки М(х; у) на координатной плоскости. Поэтому поставим в соответствие каждому числу z = х + yi точку М и обозначим её M{z) (рис. 66). Ясно, что при этом каждая точка координатной плоскости изображает одно и только одно число, а каждое число изображается одной и только одной точкой. Действительным числам соответствуют точки оси абсцисс, а чисто мнимым — точки оси ординат. Сопряжённые числа изображаются точками координатной плоскости, симметричными относительно оси абсцисс.
Часто вместо точек на плоскости берут их радиус-векторы, т. е. векторы ОМ, идущие из начала координат 0(0; 0) в точку М(х; у). Разумеется, вместо радиус-векторов можно брать любые векторы,
имеющие то же направление и ту же длину.
Изображение комплексных чисел с помощью векторов удобно
тем, что при этом получают простое геометрическое истолкование
операции над ними. Мы знаем, что при сложении комплексных чисел отдельно складываются их действительные и мнимые части:
(а + bi) + (с + di) = (а + с) + (b + d)i.
Точно так же при сложении векторов отдельно складываются их координаты: если ОМ = ai + bj и ON = ci + dj, то
197
ОМ + ON = (а + c)i + (b + d)j. Это означает, что при указанном соответствии операциям сложения и вычитания комплексных чисел соответствуют те же операции над векторами. Иными словами, если числу г соответствует вектор ОМ, а числу w — вектор ON, то числу г + и> соответствует вектор ОМ + ON, а числу z - w — вектор ОМ - ON.
Аналогично при умножении комплексного числа г на действительное число а соответствующий ему вектор ОМ умножается на это же число. Иными словами, числу аг соответствует вектор а  ОМ. В самом деле, на а умножаются как обе координаты вектора ОМ, так и действительная и мнимая части числа г.
Вопрос о геометрическом смысле операции умножения на комплексное число будет рассмотрен ниже.
Упражнения
340.	Как расположены точки комплексной плоскости, соответствующие числам г - а + Ы п г = а - bit
341.	Как расположены на комплексной плоскости точки, соответствующие противоположным числам z и -z?
342.	Во что переходит круг единичного радиуса с центром в начале координат при преобразовании z —> г - 2 + 3i?
2. Полярная система координат и тригонометрическая форма комплексных чисел. Положение точки на координатной плоскости можно задавать не только её декартовыми координатами. Можно задать это положение, указав расстояние г этой точки М до фиксированной точки О (полюса) и направление луча ОМ. Последнее задаётся величиной угла ср, образованного лучом ОМ с фиксированным лучом I, выходящим из точки О. При этом угол отсчитывают против хода часовой стрелки (рис. 67).
Пару чисел (г; ф) называют полярными координатами точки М. Мы видим, что для задания полярной системы координат на плоскости надо задать полюс О, полярный луч I и выбрать единицу измерения длин и углов. Углы обычно измеряются в радианах. В дальнейшем мы будем называть число г длиной радиус-вектора ОМ, а (р — величиной полярного угла (или полярным углом, если это не вызывает недоразумений). Значение неотрицательного числа г однозначно определено для всех точек плоскости, а значение ф определяется с точностью до слагаемого, кратного 2л, для всех точек, отличных от полюса, и не определено для точки О.
В случае когда на плоскости задана декартова система координат, в качестве полюса обычно выбирают начало этой системы координат, а в качестве полярного луча — положительное
198
направление оси абсцисс. При таком взаимном расположении декартовой и полярной систем координат выполняются равенства
X = ГСОЗф,	(1)
у = rsincp.	(2)
В самом деле, луч ОМ пересекает координатную окружность в точке Р(ф), декартовы координаты которой равны costp и sincp (рис. 68). Координаты же точки М, лежащей на луче ОР и находящейся от точки О на расстоянии г, в г раз больше. Из равенств (1) и (2) вытекают соотношения
coscp = р	(3)
8Шф = р	(4)
Кроме того, из треугольника OMN видим, что
х2 + у2 = г2.	(5)
Полученные соотношения позволяют находить декартовы координаты точки по её полярным координатам и обратно. Из формул (3) и (4) вытекает, что
4еФ =	(6)
У
По этому равенству можно найти значение ф с точностью до слагаемого, кратного л. Знаки х и у позволяют установить четверть, где расположена точка, и тем самым значение ф с точностью до слагаемого, кратного 2л.
Пример 1. Найдём полярные координаты точки м(л/3; -1).
Решение. По формулам (3), (4), (5) имеем:
г = 7(V3)2 + (-1)2 = 2,
л/3	1
coscp - —, sincp = л	£
По заданным значениям соэф и эшф находим, что ф = ~. Значит,
полярные координаты точки М равны
199
Пример 2. Найдём декартовы координаты точки М, если её полярные координаты равны 4 и .
4
Решение. По формулам (1), (2)
х = 4 cos (-j) - 4 •	= 2л/2,
у = 4 sin
Иногда отыскание полярных координат точки легче делать по чертежу, чем по формулам.
Пример 3. Найдём полярные координаты точки М(-1; 1).
Решение. Из рисунка 69 сразу видим, что
г = 7(-1)2 + I2 = х/2, ф =
Так как комплексные числа изображаются точками координатной плоскости, их можно задавать не только с помощью декартовых координат этой точки, но и с помощью её полярных координат. Из формул (1), (2) следует, что если z - х + yi, то
2 = ГСО8ф + 4ГЗШф = г(С08ф + 131пф).
Определение. Длина радйус-вектора точки М, изображающей число 2, называется модулем этого числа, а полярный угол точки М — аргументом или фазой числа 2^0. Модуль числа 2 обозначают |г|, аргумент числа z обозначают Arg г; ArgO произволен.
Таким образом, в записи
г - г (совф + 181пф)	(7)
число г является модулем г, а число ф — аргументом этого числа. Запись (7) называют тригонометрической формой числа г.
Модуль любого комплексного числа есть неотрицательное действительное число, равное нулю лишь при 2 = 0. Аргумент числа z имеет бесконечное множество значений, отличающихся друг от друга на слагаемые, кратные 2л.
В случае если хотят получить однозначно определённое значение аргумента, выбирают значение, лежащее между числами -л и л, и обозначают его arg 2, -л < arg2 < л. При переходе через отрицательную полуось значение arg меняется скачком — выше этой полуоси оно близко к л, а ниже неё — к —л.
Пример 4. Найдём тригонометрическую запись чисел:
1) х/з - г; 2) -6;	3) -2(cos^ - zsin^
\	5	5
200
Решение. 1) Имеем г = 2,
ср = ~. Значит,
+ i sin
2) Имеем г = 6, ф = л. Значит,
-6 = 6(cosit + isinn).
3) Запись г = -2
cos - - i sin 5
не является тригонометрической формой записи комплексного числа г, поскольку здесь множитель -2 отрицателен, равно как и знак перед I. Перепишем г в виде
2 = 2
-cos — + I sin — 5	5
Теперь осталось найти такой угол ф, что совф = -cos зтф = м
= sin Ясно, что ф = 4 л. Значит,
5	5
z = 2 cos -л + i sin -л
\	5	5 ,
Замечание 1. Так как при z = х + yi, z = х - yi и zz = х2 + у2 = |z|2, то справедливо равенство
|z|2 = zz.	(8)
Замечание 2. Для действительных чисел понятие модуля совпадает с введённым в 6-м классе. Аргумент действительного числа х равен 0, если х > 0, и равен л, если х < 0.
В заключение выясним геометрический смысл выражения |z - w|. Мы знаем, что число г - w изображается разностью векторов ОМ и ON, изображающих числа z и w соответственно, т. е. вектором NM (рис. 70). Число же \z - равно длине этого вектора, т. е. расстоянию между точками М и N. Итак, число \z - и>| равно расстоянию между точками M(z) и N(w).
Пример 5. Найдём множество точек г, для которых:
1)	|г - 2 4- 5i| = 6;	2) \z - 2 + 5i| < 6.
Решение. 1) Данное множество является окружностью радиуса 6 с центром в точке А(2; -5).
2)	Это множество является кругом радиуса 6 с центром в точке А(2; -5).
201
Упражнения
343.	Представьте в тригонометрической форме комплексные числа:
1)	>/3 + i; 2) 2 - 2г; 3) 6 + 6г; 4) 1 - г>/3;	5) 3 + 4г;
6) -3(cos I + г sin 5);	7) 3cos |
О- • я. 3isin —;
о
8) sin | - г cos
344.	Представьте в алгебраической форме числа:
1)	з(соз^ + isin^); 2) efcos^ + г sin ^1. \ о	о/	\	3	3 /
345.	Докажите, что для любых комплексных чисел
IzJ - |г2| < |zt + z2| < IzJ + |z2|.
346.	Докажите, что если |z| = 1, то z = j.
347.	Докажите, что если |z| = 1, z 1, то г можно
представить в виде
а + г z = ----г, где а — действительное число.
а - г
348.	Докажите, что если |z| = 1, то для любого действительного числа <р имеем
I z cos ср + sin ср I _ | z sin ср + cos ср |
349.	Вычислите модули комплексных чисел:
1)	z = (1 + г)4 + Зг; 2) z =	+	+
(а - b) + 2i^Jab
350.	Докажите, что для любых комплексных чисел Z\ и z2 выполняется равенство
|z! + z2|2 + |zj - z2|2 - 2(\zv\2 + |z2|2).
351.	Из всех комплексных чисел, удовлетворяющих условию |z - 25г| < 15, найдите число, имеющее наименьшее значение аргумента (если значения аргумента брать заключёнными между -л и л).
352.	Изобразите на чертеже множество точек комплексной области, удовлетворяющих условию:
1)	Re z > 1;	2) Im z < -2; 3) |z - 4г = 7; 4) \z - 4 + i\ < 5;
5)	zz + 3z + 3z = 0; 6) |	| = 3.
353.	Найдите условия, задающие области на рисунке 71.
202
3.	Умножение, возведение в степень и деление комплексных чисел в тригонометрической форме. В то время как сложение и вычитание комплексных чисел удобнее выполнять в алгебраической форме, умножать и делить эти числа удобнее, используя тригонометрическую форму записи.
Возьмём числа z и w, заданные в тригонометрической форме:
2 = r(cosy + i sin у), w = B(cosy + г sin у). Перемножая эти числа, получим
zw = r(cosy + isincp)  R(cosy + isin\p) =
= rR(cosy cosy - siny sin у + i(siny cosy + sin у cos y)).
Но по формулам n. 1 § 3 главы 6 (10 кл.)
cosy cosy - siny siny = cos (y + y), siny cosy + siny cosy = sin (y + y) и поэтому
zw = rR(cos (y + y) + isin(y + y)).
Таким образом, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Так как при этом модули и аргументы преобразуются отдельно друг от друга, выполнение умножения в тригонометрической форме проще, чем в алгебраической.
Поскольку г = |z|, R - |u>|, у - Argz, у = Argw, то полученный результат можно записать следующим образом:
\zw\ = \z\  |u>|,	(1)
Arg (zw) = Argz + Argw.	(2)
Смысл равенства (2) состоит в том, что аргумент числа zw отличается от суммы аргументов чисел г и w лишь на кратное 2л. Поскольку деление — действие, обратное умножению, то при w Ф 0 имеем
= 4 (cos(у - у) + i sin(у - у)), W tx
и потому
1-1 = —, I W I |u) |’
Arg I — \ = Argz - Argw.
(3)
(4)
Иными словами, модуль частного равен отношению модулей делимого и делителя, а аргумент частного — разности аргументов делимого и делителя.
203
Наконец, поскольку возведение в степень с натуральным показателем сводится к умножению равных множителей, имеет место формула
zn - Л1 (cosntp + i sin nep).	(5)
Таким образом,
|zn| = |z|n,	(6)
Arg(zn) = nArgz.	(7)
Иными словами, модуль степени с натуральным показателем п равен степени с тем же показателем модуля основания, аргумент этой же степени — аргументу основания, умноженному на п.
Пример. Вычислим значение выражения
_	(1 + f)15 (Уз - z)°
,	^.10
(-1 + iV3) (-2 - 2i)2
Решение. Раскрывая скобки, мы получили бы очень громоздкое выражение, вычисление которого было бы затруднительно. Поэтому поступим иначе — преобразуем все числа к тригонометрической форме:
1 + i = V2(cosJ + zsin^J; у/з - i = 2(cos(-^j + zsin(-^jj,
cos — + i sin — j;
3	3 )
Данное выражение можно записать в виде
(cos + z sin g)j (2(cos (-g) + i Sin (-g)j) (2(cos + I sin (2^/2(003 (~^) + £ sin (~^f)))
Отсюда получаем, что
A = 2^+ S-10’3(cos(^ _	_ 20л + 3л\ +
\	\ 4	6	3	2 /
+ zsin(l^ _	= 2 2 (cos (--л) + z sin (——njj =
\ 4	6	3	2 II \	\ 4 I \ 4 II
= = 1-1;
72^ 2	2 J 2 2 ‘
204
Упражнения
354, Вычислите следующие выражения, представив их в тригонометрической форме:
Уз + i. Уз + Уз/. 1 + cos а + i sin ос
1 - i ’	’ i - у/з ’	1 + cos а - isincc'
355.	Вычислите	где г = coscp + i sin ср.
356.	Вычислите следующие выражения:
(1 + г)5 (УЗ + г)10 .	(1 ~ г)7 (~УЗ - if. (1 + г)124
’ (1-гГ(1-;Уз)	+	' (1 - О98 - id -ь 0е8'
357.	Найдите (1 + sincp + i cos ср)8.
358.	Докажите, что если z + - = 2 cos а (где z — комплексное число), г
то z7! + —— — 2 cos па.
г"
4. Формула Муавра. Применения комплексных чисел к доказательству тригонометрических тождеств. Если положить в формуле (5) п. 3 г = 1, то получим частный случай этой формулы, называемый формулой Муавра’
(coscp + isincp)" = cosncp + isinncp.	(1)
Этой формулой можно воспользоваться для выражения синусов и косинусов аргумента пер через синусы и косинусы аргумента ср. Для этого применим к левой части формулу бинома Ньютона и учтём формулы для степеней числа i. Получаем, что
cosncp + i sin nep = cos" ср + Cocos'1'1 ср sincp —
- C3cos'*“2cp sin2cp - C3icos'I-3cp sin3cp +
+ C4cos"“4cp sin4cp + ....
Отсюда следуют равенства:
cosncp = cosncp - C3cos"“2cp sin2cp + C4cosn'4cp sin4cp - ..., sinnep = C’cos"-1cp sincp - C3cos'*'3cp sin3cp + ....
Суммирование ведётся до тех пор, пока показатель при coscp не обратится в 0 или в 1 (в зависимости от чётности п). Поскольку в выражение для cosncp входят лишь чётные степени sincp, то их можно выразить через coscp и получить выражение для cosncp через coscp. Для sinnep при нечётном п можно получить выражение через sincp, а при чётном п — в виде произведения coscp на выражение от sincp.
205
Найдём такие выражения для некоторых значений п.
При п = 3 получаем:
cos3<p = cos3(p - 3 cos ср sin2 ср =
= cosa(p - 3coscp(l - cos2cp) = 4cos3cp - 3coscp, sin3(p = 3cos2(p sincp - sin3cp - 3(1 - sin2cp)sincp - sin3cp = = 3sincp - 4sin3cp.
При n = 4 получаем:
cos4cp = cos4cp - 6cos2cp sin2cp + sin4cp =
- cos4cp - 6cos2tp(l - cos2cp) + (1 - cos2cp)2 =
= 8cos4(p - 8cos2(p + 1, sin4cp = 4cos3cp sincp - 4coscp sin3(p =
= 4cos<p ((1 - sin2cp)sincp - sin3cp) = 4coscp (sincp - 2sin3cp).
Упражнения
359.	Пользуясь формулой Муавра, выразите через cos<p и sin ср:
1)	cos5cp; 2) sin5<p; 3) cos6cp; 4) sin6cp.
360.	Найдите сумму:
1)	sincp + sin2<p + ... + sinncp; 2) coscp + cos2cp + ... + cosncp.
361.	Докажите тождество
tg«20° - 33tg420° + 27tg220° = 3.
5.	Извлечение корня из комплексного числа. Как и для действительных чисел, корнем п-й степени из комплексного числа z, где п — натуральное число, называют такое комплексное число w, что w" = z. Корень n-й степени из z обозначают Vz. Таким образом, если w = Vz, то 2 = wn. Покажем, что из любого комплексного числа z можно извлечь корень n-й степени, причём если z Ф 0, то Vz принимает п различных значений.
Будем записывать числа в тригонометрической форме. Пусть z = r(cosa + isina). Число и> будем искать в виде w = -R(cos<p + + sincp). В силу формулы (5) п. 3 равенство wn = z принимает вид
Kn(cosncp + i sin nep) = r(cosa + isina).
Но два комплексных числа равны в том и только в том случае, когда их модули равны, а аргументы отличаются лишь слагаемым, кратным 2л. Значит,
Rn = г,
п(р - а + 2fen, k 6 Z.
Поскольку число R должно быть неотрицательным, получаем, что
R =	(1)
ср = о+. gfeg, k е z.	(2)
206
Итак, для модуля R искомого числа мы получили определённое значение. Что же касается аргумента (р этого числа, он может принимать различные значения в зависимости от значения целого числа k. Выясним, при каких значениях kx и k2 получаются значения ф, отличающиеся друг от друга на кратное 2л (т. е. одинаковые значения w). Для этого разность
а + 2л^ _ а + 2nfe, _ 2л(/г1 - fe,) п	п	п
должна быть кратна 2л. Это имеет место в том и только в том случае, когда kr - k2 делится на п. Отсюда следует, что при г Ф О значениям k = 0, 1, ... п - 1 соответствуют различные значения корня, a k - п даёт то же значение корня, что k = 0, при k = п + 1 получаем то же значение корня, что и при k = 1 и т. д. Число различных значений корня равно п.
Мы доказали, таким образом, следующее утверждение.
Теорема. Для любого натурального числа п и любого отличного от нуля комплексного числа г существуют п различных значений корня п-й степени.
Если z - r(cosa + isina), то эти значения выражаются формулой
cos a + 2nk + isina + 2nfe п	п
(3)
где k = 0, 1, ..., п - 1.
Все точки u>k лежат на окружности радиусом yfr с центром в начале координат. Аргументы соседних точек отличаются друг от друга на а потому указанные точки делят окружность на п равных частей. Иными словами, они являются вершинами правильного n-угольника, вписанного в эту окружность (рис. 72).
Пример 1. Найдём все значения для V-l + I-
Решение. Находим для -1 + i, что г = V2, ф = Значит,
=
+ 2nk — + 2лй
Д-------- + t sin А--------
3	3
207
Отсюда получаем, что
Wo = ^(cosj + г sin j = ^-(1 + 0.
= V^cos^ + isin^j = ^(->/6 - 7Й + i(V6 - ч/Й)), w2 = ч/й(сов + i sin = ^(-sin —— i cos —1 = \	12	12 )	\	12	12/
= &(y/6 - ч/Й - i(y/& + ч/Й)).
4
Рассмотрим некоторые частные случаи.
1) Квадратный корень из комплексного числа. При п-2 формула (3) определяет два значения для -Jr (cos а + i sin а):
w0 = ч/r ^cos + i sin
а + 2л wt - ч/rlcos—-—
. ; а + 2л\	а , ; а\
+ I sin------- = —yjr cos — + i sin — .
2 I \	2	2)
Эти значения оказываются (как и следовало ожидать) взаимно противоположными. Применяя формулы, выражающие cos и sin через cos а, легко преобразовать эти формулы к виду, указанному в п. 4 § 1.
2) Корень п-й степени из положительного действительного числа. Если х — положительное действительное число, то |х| = х, ср = 0. Формула (3) принимает в этом случае вид
w* = Vx (cos — + isin— ], k = 0, 1, ..., п - 1. \ п	п )
При k = 0 получаем положительное действительное значение w0 - у[х, т. е. арифметическое значение корня. Если п — чётное число, п - 2т, то при k - т получаем ещё одно действительное (отрицательное) значение корня:
wm = Mos^ + isin^j = -^с. \ 2т	2т /
Если же п — нечётное число, то найденное выше значение корня при k = 0 является единственным действительным значением для корня п-й степени.
К извлечению корней сводится решение так называемых двучленных уравнений, т. е. уравнений вида azn + Ъ = 0.
208
В самом деле, такое уравнение равносильно уравнению гп = и потому для его решения надо лишь найти все значения для
Пример 2. Решим двучленные уравнения:
1) z2 + 1 = 0;	3) z3 — 1 = 0;	5) z6 - 1 = 0;	7) z6 + 1 = 0;
2) z4 - 1 = 0;	4) z3 + 1 = 0;	6) г4 + 1 = 0;	8) г5 - 1 = 0.
Решение. Каждое из этих уравнений решается путём разложения соответствующего многочлена на множители первой и второй степени.
1)	Разложение многочлена z2 + 1 на множители имеет вид z2 + 1 = (z - i)(z + i). Отсюда находим два корня уравнения:
2)	Так как
z4 - 1 = (z2 - l)(z2 + 1) = (z - l)(z + 1 )(z2 + 1),
то в силу 1) имеем четыре корня уравнения: zt - 1, z2 - -1, z3,4 - ±г.
3)	Разложим z3 - 1 на множители: z3 - 1 = (z - l)(z2 + z + 1). Решая уравнения z1-l=0nz2 + z + l=0, получаем три корня:
1 ,	-1 + ь/з
2i — 1, 22,з —	2
4)	Решается аналогично 3). Корнями являются числа _ 1	_ 1 ± i>/3
2i — 1» £2,з —	2
5)	Так как z6 - 1 = (z3 — l)(z3 + 1), это уравнение сводится к двум предыдущим. Корнями являются
+1 ± iyfa Zl,2 — ±1,	23,4,5,6 —	2
(берутся все четыре сочетания знаков).
6)	Для разложения многочлена z4 + 1 на множители прибавим и вычтем 2z2, т. е. (2V2) :
z4 + 1 = z4 + 2z2 + 1 - (zV2)2 = (z2 + l)2 - (zV2)2 =
= (z2 - zV2 + l)(z2 + zV2 + 1).
Теперь надо решить два квадратных уравнения: z2 - ^2z +1 = 0 И z2 - V2z + 1 = 0. Решая их, получаем четыре корня:
Zl.2,3,4 = ^(±1 ± i).
209
7)	Многочлен ze + 1 раскладывается на множители следующим образом:
г6 + 1 = (z2 + l)(z4 - z2 + 1) =
= (z - i)(z + i)((z4 + 2z2 + 1) - 3z2) =
- (z - l)(z + i)(z2 - л/Зг + l)(z2 + V3z + 1).
Решая квадратные уравнения, получаем шесть корней уравнения:
z - +i z -	± Z
*1,2 -	*3,4,5,6 “	2
8)	Разложим многочлен z5 - 1 на множители:
z5 - 1 - (г - l)(z4 + z3 + z2 + z + 1).
Отсюда следует, что zt = 1. Чтобы найти остальные четыре корня, надо решить уравнение
z4 + z3 + z2 + z + 1 = 0.
Разделим обе части этого уравнения на z2 и положим z + | = w. Так как и>2 = г2 + 2 + р-, то получаем уравнение
и>2 - 2 + w + 1 = 0, т. е. w2 + w - 1 = 0.
Оно имеет два корня: мь.г = 1 7,	 Теперь осталось решить два
,1	-1	+ Тб	,1	-1 -	Тб
уравнения: z + -	= -5-- и	г + -	=	 5-----, т.	е.
2	£	2	21
z2 + 1 z + 1 = О, Z2 + 1 +2 — z + 1 = 0.
Решая их, получаем
1 + Тб ± iT10 + 2Т5
Z2,3 -	4
-1 - Тб ± iV10 - 2V5
Z<5 -	4
К извлечению корней сводится и решение так называемых трёхчленных уравнений, т. е. уравнений вида az2n + bzn + с = 0. Здесь надо сначала сделать подстановку z" = w, решить квадратное уравнение aw2 + bu> + с = О, а потом решить уравнения z" = u>i и z" = w2, где Wr и w2 — корни квадратного уравнения.
Пример 3. Решим уравнение
z6 - 9z3 + 8 = 0.
210
Решение. Подстановка z3 = w приводит к квадратному уравнению и>2 - 9iv + 8 = 0, имеющему корни 1 и 8. Решая уравнения z3 = 1 и z3 = 8, получаем корни данного уравнения:
21 = 1> 22,з = 1	2“ = 2’ Zs’e = -1 ±
Упражнения
362.	Сколько и какие значения имеет произведение >/-16  V-9?
363.	Можно ли утверждать, что для комплексных чисел справедливы равенства:
1)	7(а + bi)(c + di) = у/а + Ы  -!с + di; 2) >/(а + bi)2 = (Va + bi) ?
364.	Вычислите значения: >/i, >/i, V-2 + 2i, V-l.
365.	Решите квадратные уравнения:
1)	х2 + 4ix + 12 = 0; 2) х2 + 7ix - 12 = 0; 3) х2 - 8гх -15 = 0. 366. Решите двучленные уравнения:
1)	8z3 - 27 = 0; 2) z12 - 1 = 0; 3) z5 + 32 = 0; 4) г10 - 1024 = 0. 367. Решите трёхчленные уравнения:
1)	г8 - 17z4 +16 = 0; 2) z12 - 65ze + 64 = 0.
6. Основная теорема алгебры многочленов. Во всех примерах, разобранных в предыдущем пункте, уравнение n-й степени имело п корней (действительных или мнимых). Аналогично обстоит дело для уравнения (х - 3)2(х + 4)3 = 0, если считать каждый корень столько раз, какова его кратность,— оно имеет пять корней: корень -4 третьей кратности и корень 3 второй кратности. И здесь число корней совпадает со степенью уравнения. Подмеченная закономерность не случайна, она имеет место для всех алгебраических уравнений, причём не только для уравнений с действительными коэффициентами, но и для уравнений с комплексными коэффициентами. Доказательство этого утверждения основано на следующей теореме, которую называют основной теоремой алгебры многочленов.
Теорема 1. Любое уравнение с комплексными коэффициентами, степень которого больше нуля, имеет хотя бы один комплексный корень.
Отметим, что в формулировке этой теоремы действительные числа рассматриваются как частный случай комплексных, и потому из неё следует, что любое уравнение с действительными коэффициентами имеет хотя бы один (быть может, комплексный) корень.
Доказательство основной теоремы алгебры многочленов довольно сложно, и мы его не приводим.
Отметим некоторые следствия из теоремы 1.
211
Следствие 1. Любой многочлен п-й степени с комплексными коэффициентами раскладывается в произведение п линейных множителей:
ап2п + dn-jz""1 + ... + а0 = a„(z - zj • ... • (z - z„),	(1)
где a0, ..., an, Zi ..., z„ — комплексные числа.
Доказательство. Проведём доказательство по индукции.
При п - 1 утверждение истинно, так как а^г + а0 = ai z + — |.
k ai)
Предположим, что утверждение верно при п = k. Докажем истинность этого утверждения при п = k -I- 1. По теореме 1 многочлен
P(z) = ak+1 zk+1 + akzk + ... + a0
имеет хотя бы один комплексный корень zk+1. Но тогда по теореме Безу (см. п. 3 § 3 главы 2, 10 кл.), доказательство которой дословно переносится на случай комплексных z, этот многочлен делится на z - z*+1, и потому P(z) = (z - za+i)Q(z), где Q(z) — многочлен степени п. По предположению индукции имеем
Q(z) = b(z - Zj) • ... • (z - zk).
Значит,
P(z) = b(z - z^ • ...  (z - zk)(z - zk+1).
To, что b = ak+1, получаем путём раскрытия скобок и сравнения коэффициентов при z*+1.
Итак, в силу принципа математической индукции утверждение истинно для всех п.
Следствие 2. Любое уравнение п-й степени (где п > 1) с комплексными коэффициентами имеет п комплексных корней (при этом каждый корень считают столько раз, какова его кратность).
Доказательство. По следствию 1 уравнение
anzn + ... + а0 - 0
можно записать в виде
а „(г - Zi)  ... • (г - zn) = 0.
Видим, что корнями этого уравнения являются числа z1; ..., z„ и что иных корней оно не имеет.
Пример 1. Составим уравнение наименьшей степени, корнями которого являются числа 3, 2 + i, 2 - i, а старший коэффициент равен 4.
Решение. Искомое уравнение имеет вид
4(2 - 3)(z - 2 - i)(z - 2 + i) = 0.
Раскрывая скобки, получаем уравнение
4z3 - 28z2 + 68z - 60 = 0.
212
Пример 2. Составим уравнение наименьшей степени, для которого число i является корнем второй кратности, а число 1 — корнем третьей кратности, коэффициент же при старшем члене равен 3.
Решение. Искомое уравнение имеет вид
3(z - i)2(z - I)3 = 0.
Раскрывая скобки, получаем уравнение
3z5 - (9 + 60г4 + (6 + 180z3 + (6 - 18i)z2 - (9 - 6i)z +3=0.
Замечание. Поскольку любой многочлен допускает разложение на линейные множители (1), между его корнями и коэффициентами имеют место соотношения Виета (см. п. 3 § 3 главы 2, 10 кл.).
В заключение рассмотрим вопрос о разложении на множители многочленов с действительными коэффициентами. Сначала докажем следующее утверждение.
Теорема 2. Если комплексное число а является корнем многочлена P(z), имеющего действительные коэффициенты, то и сопряжённое с а число а является корнем того же многочлена.
Доказательство. Вп. 3 § 1 было показано, что для многочленов с действительными коэффициентами верно равенство
Р(а) = Р(а).
Так как по условию а является корнем многочлена Р, то Р(а) - 0, а тогда Р(а) = Р(а) = 0 = 0, и потому а — корень многочлена Р.
Данную теорему можно уточнить: а не только является корнем многочлена P(z), но имеет при этом ту же кратность, что и а. Отсюда вытекает, что корни многочлена P(z) можно разбить на действительные корни и на пары взаимно сопряжённых комплексных корней. Действительному корню а соответствует в разложении многочлена Р(г) множитель (z - а), а паре а и а сопряжённых комплексных корней — два множителя (z - a)(z - а). Если а = р + yi, то
(z - а)(г - а) = (z - Р - yi)(z - Р + yi) =
= (z - р)2 - y2i2 = (z - Р)2 + у2 = z2 - 2Pz + Р2 + у2.
При этом очевидно, что квадратичный трёхчлен z2 - 2Pz + Р2 + у2 не имеет действительных корней. Тем самым доказана следующая теорема.
Теорема 3. Любой многочлен с действительными коэффициентами может быть представлен в виде
Р(х) = ап(х - х0 • ...  (х - х*)(х2 + 61Х + с0 • ... • (х2 + Ьтх + ст), где х15 ..., хк и Ьг, Ьг, ..., Ът, си с2, ..., ст — действительные числа, причём множители второй степени не имеют действительных корней.
213
(Мы пишем х вместо г, поскольку теорема касается многочленов с действительными коэффициентами и можно считать значения х действительными числами.)
У пражнения
368.	Составьте уравнение пятой степени, имеющее корни х4 = i, х2 = 2i, Х3 = Х4= 1, Х5 = -I.
369.	Составьте уравнение четвёртой степени, имеющее корни Xi = х2 = = х3 = 1 + I, х4 = 2.
370.	Составьте уравнение наименьшей степени с действительными коэффициентами, имеющее корни х4 = х2 ~ 2 - i, х3 = i.
371.	Разложите на линейные множители многочлены:
1)	х4 + 4х2 + 5; 2) х4 + бх2 + 25.
372.	Докажите, что:
1)	многочлен (coscp + х sin ср)" - cos nep - х sin пер делится на x2 + 1;
2)	многочлен х"sincp - pn lxsinncp + p"sin(n - 1)<р делится на х2 - 2рх coscp + р2.
373.	Найдите сумму р-х степеней корней уравнения хп = 1, где р — натуральное число.
7. Комплексные числа и геометрические преобразования. Функции комплексного переменного. Мы видели выше (см. п. 1 § 2), что сложению комплексных чисел отвечает сложение векторов точек, изображающих эти числа на комплексной плоскости. Отсюда следует, что отображение г —> г + а, сопоставляющее каждой точке z точку г + а, имеет простой геометрический смысл — оно является параллельным переносом на вектор, равный радиус-вектору точки А(а).
Выясним теперь геометрический смысл умножения на комплексное число. При этом для простоты речи не будем различать само число г и изображающую его точку М(г). Пусть R — положительное число. Мы знаем, что если г = r(coscp + i sin ср), то Яг = J?r(cos<p + i sin ср). Таким образом, модуль числа г умножается на R, а аргумент остаётся неизменным. Учитывая геометрический смысл модуля и аргумента комплексного числа, видим, что отображение г Rz, где R > 0, является гомотетией с центром в начале координат и коэффициентом R.
Далее, пусть а - cos а + г sin а, г = r(coscp + isintp). Тогда аг = r(cos(<p + а) + z sin (ср + а)). Это показывает, что умножению на число с единичным модулем и аргументом а соответствует поворот вокруг начала координат на угол а. Ясно, что умножению чисел г на числа вида B(cosa + isina) соответствует композиция указанных выше преобразований, т. е. последовательное выполнение гомотетии с коэффициентом R относительно начала координат О и поворота на угол а вокруг точки О.
214
Более сложное преобразование получается, если поставить каждому числу г * 0 в соответствие число j. Так как
—-----L__—- = 1 (cos (-ср) + isin(-<р)),
r(cos ф + I Sin ф) г
то при этом преобразовании точка с полярными координатами (г; ф) переходит в точку с полярными координатами (р -ф^. На рисунке 73 изображено, в какую фигуру переходит при этом преобразовании квадрат ОАВС. Видим, что форма фигуры изменилась, но углы между линиями остались неизменными.
Преобразования плоскости, при которых сохраняются углы между линиями, называют конформными преобразованиями. Они играют важную роль в картографии, так как позволяют получать карты земной поверхности, на которых углы между линиями такие же, как на этой поверхности. Теория конформных преобразований плоскости тесным образом связана с дифференцируемыми функциями, аргумент которых и значения являются комплексными числами. Понятие дифференцируемости определяется так же, как для функций действительного аргумента.
Конформные отображения используются при решении многих задач теории упругости, аэро- и гидродинамики, электростатики и иных областей физики и техники. Для этого сложные области конформно преобразуют в более простые (например, в круг), после чего решают задачу для этой простой области и обратным конформным преобразованием получают решение для исходной области. Комплексные числа находят применение и в квантовой механике.
Упражнения
374.	Какое геометрическое преобразование определяет формула: 1) и = oiz: 2) w = -3iz + 2 - 4i?
215
375.	Выразите в виде и - f(z) геометрическое преобразование комплексной плоскости, состоящее в последовательном применении:
1)	гомотетии относительно точки О с коэффициентом 2 и переноса на вектор 3 + 4i;
2)	тех же преобразований, но выполненных в обратном порядке.
376.	Выразите в виде и = f(z) гомотетию комплексной плоскости относительно точки 1 - i с коэффициентом 5 и представьте её в виде последовательного выполнения гомотетии относительно точки О и параллельного переноса.
377.	Докажите, что последовательное выполнение двух преобразований, каждое из которых получается последовательным выполнением гомотетии, поворота вокруг того же центра и параллельного переноса, можно заменить одним преобразованием того же типа.
378.	Постройте образ квадрата с вершинами А(0; 0), В(0; 2), С(2; 2) и Z>(2; 0) при следующем преобразовании:
1)	w - iz; 2) w = 2iz — 1 — 3i; 3) w = z2; 4) w = i.
z
1.	Множества и операции над ними. В § 1 главы 1 (10 кл.) было введено понятие числового множества и определены операции над такими множествами. Введём теперь понятие множества с элементами любой природы. Это понятие не определяется, а лишь иллюстрируется примерами. Например, можно говорить о множестве яблок в мешке, множестве натуральных чисел, множестве квадратов на плоскости и т. д. Множество считается заданным, если о каждом элементе можно однозначно сказать, принадлежит он этому множеству или нет. Обычно множества обозначают прописными латинскими буквами, а их элементы — строчными буквами. Если элемент х принадлежит множеству X, то пишут х € X, в противном случае пишут х t X.
Пример 1. Если X — множество русских слов из словаря В. И. Даля, то «семья» е X, a «sieben» < X, 8 f X.
Пример 2. Если N — множество натуральных чисел, то 4 G N, а -0,3 $ N, Сириус $ N.
Два множества называются равными, если они состоят из одних и тех же элементов. Например, множество равносторонних треугольников равно множеству равноугольных треугольников, а множество параллелограммов — множеству четырёхугольников, имеющих центр симметрии. Если множества X и У равны, то пишут X = У.
Множество, не содержащее ни одного элемента (например, множество пятилетних гроссмейстеров по шахматам или множество натуральных корней уравнения 4х2 -1=0), называют пустым множеством. Его обозначают 0.
Множество яблок в мешке, рыб в океане, видов живых существ конечны — количество их элементов можно выразить натуральным числом (хотя мы не всегда знаем значение этого числа). Множества натуральных чисел, ромбов на плоскости, шаров
217
в пространстве бесконечны. Конечное множество можно задать списком его элементов (например, множество учеников в классе задаётся их списком в классном журнале). Два списка элементов одного и того же множества X могут отличаться друг от друга лишь порядком элементов. Например, {1, 2, 3} и {3, 1, 2} — списки одного и того же множества {1, 2, 3} - {3, 1, 2}.
В дальнейшем мы будем обозначать число элементов конечного множества X через п(Х), а множество X, содержащее п элементов, будем называть п-элементным множеством.
Пример 3. Пусть X — множество простых чисел, меньших, чем 20. Оно состоит из восьми чисел: 2, 3, 5, 7, 11, 13, 17 и 19. Поэтому п(Х) = 8, а X является восьмиэлементным множеством.
Если элементы конечного множества как-либо перенумерованы, мы будем говорить, что это множество упорядочено. Одно и то же множество можно упорядочивать различными способами. Например, множество учащихся в классе можно упорядочить по росту (как по возрастанию, так и по убыванию), по весу, в алфавитном порядке фамилий и т. д.
Бесконечное множество нельзя задать списком. Его задают обычно характеристическим свойством, т. е. свойством, которым обладают все элементы множества и не обладают элементы, не принадлежащие этому множеству. Множество, заданное характеристическим свойством Р(х), обозначают {х|Р(х)}. Например, запись {х|х2 - 7х + 12 = 0} обозначает множество корней уравнения х2 - 7х + 12 = 0 (т. е. множество {3, 4}), а запись {ААВС|АВ = = АС = ВС} — множество равносторонних треугольников.
Если каждый элемент множества X является в то же время элементом множества У, то говорят, что X — часть, или, иначе, подмножество множества У. В этом случае пишут X с У. Например, множество квадратов является подмножеством множества ромбов, а множество ромбов — подмножеством множества параллелограммов. Множество натуральных чисел, делящихся на 10, является подмножеством множества чётных натуральных чисел.
Очевидно, что если X с У и У с Z, то X с Z. Если X с Y и У с X, то X = У. Далее, для любого множества X верны включения 0 с X и X с X.
Обобщим на любые множества операции пересечения, объединения и вычитания числовых множеств.
Определение 1. Пересечением множеств X и У называется множество X А У, состоящее из элементов, которые принадлежат как X, так и У.
Например, множество квадратов является пересечением множества прямоугольников с множеством ромбов, а множество
218
a) XU Y	б) X П У	e) X \ У
Рис. 74
правильных шестиугольников — пересечением множества шестиугольников с множеством правильных многоугольников.
Определение 2. Объединением множеств X и У называют множество X U У, состоящее из элементов, которые принадлежат хотя бы одному из множеств X, У.
Например, множество треугольников является объединением множеств косоугольных и прямоугольных треугольников.
Аналогично определяются операции пересечения и объединения над любыми совокупностями множеств.
Определение 3. Разностью множеств X и У называется множество Х\У, состоящее из всех элементов множества X, не принадлежащих множеству У. Если У с X, то разность Х\У называют дополнением множества У в множестве X и обозначают У£.
Например, разностью множества чётных чисел и множества чисел, кратных 3, является множество чётных чисел, не делящихся на 6. Оно является объединением множества чётных чисел, дающих при делении на 6 остаток 2, и множества чётных чисел, дающих при делении на 6 остаток 4. Дополнением к множеству квадратов в множестве ромбов является множество ромбов с хотя бы одним острым углом. А дополнением того же множества квадратов в множестве прямоугольников является множество прямоугольников с неравными соседними сторонами.
На рисунке 74, а, б, в изображены схематически операции над множествами X и У. Такие изображения множеств и операций над ними называют диаграммами Эйлера — Венна.
Упражнения
379.	Для каких из следующих пар множеств имеет место одно из соотношений А с В, В с А, А = В, А е В, В G А:
1)	А =	{а,	Ь, с, </}, В	= {а, с, d}; 2) А =	0,	В =	0;
3) А =	0,	В =	{а, Ь, с};	4) А = {а, Ь, с},	В	= {Ь,	с, а};
5) А =	0,	В =	{0};	6) А = {{а}, а, 0}, В	=	{а};
7)	А =	{{а, Ъ],	{с, d},	с, d}, В = {{а, 6}, с};	8) А	= {{а}, а, 0}, В = 0?
380.	Верно ли, что:
1)	{1, 2} с {{1, 2, 3}, {1, 3}, 1, 2};	3) {1, 3} е {{1, 2, 3}, {1, 3), 1, 2};
2)	{1, 2} 6 {{1, 2, 3}, {1, 3}, 1, 2);	4) {1, 3} с {{1, 2, 3}, {1, 3}, 1, 2}?
219
381.	Даны множества А = {0, 1, 2, 3, 4, 5, 6, 7}, В = {3, 4, 5, 6, 7, 8, 9}, С = {-3, -2, -1, 0, 1, 2, 3, 4}, D = {2, 3, 4, 5, 6}. Задайте списками множества:
1)	A U В U С U D; 2) А П В П С П D-,	3) (А П В) U (С П D);
4)	(A U В) П (С U D); 5) (А\В) и (В\А); 6) D'A U (С\В).
382.	Изобразите с помощью диаграмм Эйлера — Венна множества А, В, С, если:
1)	А с В и В с С; 2) А с С, В с С и А\В = 0; 3) А с С, В с С hC=AUB; 4)АсС,ВсСиАПВ*0; 5) А П В * 0, А П С * 0, В п С *0, А п В п С # 0; 6) А п В = 0, А п с = 0, В n С * 0.
2. Алгебра множеств. Операции над множествами обладают свойствами, которые отчасти напоминают свойства действий над числами, а отчасти отличны от этих свойств.
I. Для любых множеств X и Y выполняются равенства 1)Хиу = УиХи1')ХПУ=УПХ
(аналог тождеств x + z/ = z/ + xhxz/ = ух).
II. Для любых трёх множеств X, У, Z выполняются равенства
2)	(X U У) U Z = X U (У U Z) и 2') (X П У) П Z = X П (У Г) Z) (аналог тождеств (х + у) + г = х + (у + г) и (xy)z = x(yz)), а также равенства
3)	(X U У) П Z = (X П Z) U (У П Z) и
3') (X П У) и Z = (X U Z) П (У U Z)
(из этих равенств одно можно считать аналогом тождества (х + y)z -- xz + yz, но тогда второе не имеет аналога в обычной алгебре).
В случае когда все рассматриваемые множества являются частями одного и того же универсального множества U, результаты выполнения операций пересечения и объединения снова дают подмножество из того же множества. Дополнение к любой части множества 17 снова является частью того же множества. При фиксированном универсальном множестве дополнение к X обозначают X', опуская индекс 17. Отметим следующие свойства операции дополнения.
III.	Для любого множества XcU имеет место равенство
4)	(Х')' = Х.
IV. Выполняются равенства
5)	0' = U и 5') U' = 0.
V. Для любых двух множеств X и У из U имеем
6)	(X П У)' = Х' U У' и 6') (X U У)' = X' П У'.
Мы не будем доказывать все перечисленные свойства, а докажем лишь равенство из пункта 6):
a f (X П V)' " И X Л У о а ? X или НУ»
<=> а € X' или а £ У' « а е X' U У'
220
(знак <=> читается: «тогда и только тогда, когда»). Значит, (X А У)' = X' U Г.
Отметим, что если X с У, то X Q Y = X, X U У = У. В частности, поскольку для любого множества X справедливо 0 с X и X с X, то всегда верны равенства
0 А X = 0, 0 и х = х, хпх = х, х и х = х.
Так же как с помощью правил обычной алгебры, преобразуют алгебраические выражения, в которых буквы принимают числовые значения, с помощью алгебры множеств преобразуют выражения, в которых буквы обозначают множества, причём буквы соединены друг с другом знаками А, и, \, а к некоторым буквам применена операция дополнения (в универсальном множестве U). При этом стремятся привести такое выражение к нормальному виду, а именно к виду объединения пересечений некоторых из данных множеств и дополнений к другим данным множествам. Если два выражения имеют одинаковую нормальную форму (с точностью до перестановки), то они тождественно равны — при подстановке вместо букв любых множеств из них получается одно и то же множество.
Упражнения
383. Пусть А и. В — подмножества универсального множества U, имеющие непустое пересечение. Изобразите с помощью диаграмм Эйлера — Венна следующие множества и укажите среди них равные:
1) (А А В)'; 2)ААВ'; 3)А'ПВ'; 4) (A U В)'; 5) A U В'; 6) A' U В'. 384. Докажите, что для любых множеств верны следующие соотношения:
1) А = (А\В) U (А А В); 2) (А\В) А (А А В) = 0; 3) (А\В) А В = 0;
4) А\В = А\(А А В); 5) А А (В U С) = (А А В) U (А А С);
6)	A U (В А С) = (A U В) A (A U С);
7)	(А\В)\С = А\(В U С) = (А\С)\В = (А\В) А (А\С);
8)	A U (В\С) э (A U В)\С; 9) (А\В) U С z> (A U С)\В.
385.	Пусть А, В и С — подмножества универсального множества U. Докажите, что:
1)	А\В = А А В';	2) (А\В)' = A' U (А А В);
3)	A' U (В U С)' = (А А В)’ А (А А СУ.
386.	Обозначим множество (А\В) U (В\А) через А Д В (симметрическая разность множеств А и В). Докажите, что:
1)АДВ = ВДА; 2)(АДВ)ДВ=А; 3)АД0=А; 4)АДА = 0;
5)	(А Д В) ДС = А Д (В Д С); 6) А Д В = (A U В)\(А А В);
7) A U В = (А Д В) Д (А А В); 8) (В\А) Д (С\А) = (A U В) Д (A U С). 387. Упростите следующие выражения:
1) A A (A U В);	2) (Р A Q) A (Q' А В);	3) (А А В') U (А' А В);
4) (A' U В') A (A U В).
388. Пусть А с В, С с В. Докажите, что (А А В) U (С А В)\(А А С) = А Д С.
221
3. Разбиение множества на подмножества. В основе всевозможных классификаций, применяемых в биологии, лингвистике и других науках, лежит операция разбиения множества на попарно непересекающиеся части.
Определение. Пусть U — некоторое множество и Ха, а е А — система подмножеств из U, обладающая следующими свойствами:
а)	объединение всех множеств Ха совпадает с U, U - U Ха;
б)	если а Ф Р, то пересечение множеств Ха и Хр пусто:
ха П Хр = 0.
Тогда говорят, что множество U разбито на части Х„, а € А.
Пример 1. Множество учеников разбивается на части по первым буквам их фамилий (Алексеев и Антонюк принадлежат одной части, Белов, Боженко и Бакрадзе — другой и т. д.). При этом некоторые части пусты, например часть, состоящая из учеников с фамилиями, начинающимися на ъ, ъ или на ы.
Пример 2. Если X — подмножество в U, то U разбивается на множества X и X' (дополнение к X).
Пример 3. Множество всех многоугольников разбивается на множества треугольников, четырёхугольников, пятиугольников и т. д.
Пример 4. Пусть в множестве U заданы любые подмножества Хп ..., Х„. Каждый элемент множества U принадлежит одним из этих множеств и не принадлежит другим. Этим определяется разбиение множества U на части, имеющие вид
7\ П Т2 П ... П Т„, где для любого k множество Тк совпадает либо с X*, либо с Х'к.
Разбиения на непересекающиеся подмножества встречаются при решении производственных задач: детали разбиваются на классы по материалу, из которого они изготовлены, форме и размерам, технологии обработки и т. д.
Упражнения
389.	Разбейте множество заглавных букв русского алфавита на следующие классы: 1) имеющие только вертикальную ось симметрии;
2)	имеющие только горизонтальную ось симметрии; 3) имеющие как вертикальную, так и горизонтальную оси симметрии; 4) не имеющие осей симметрии.
390.	Сделайте классификацию, как в упражнении 389, для цифр и для букв латинского алфавита.
391.	На рисунке 75 изображены 8 фигур. Придумайте 3 вопроса (ответ: да — нет), позволяющие однозначно определить заданную фигуру.
222
4. Кортежи и декартово произведение множеств. К понятию упорядоченного множества близко, хотя и отличается от него, понятие кортежа.
Определение 1. Пусть даны множества Xit ..., Хп.
Кортежем длины п, составленным из элементов этих множеств, называется конечная последовательность а = (хь ..., хл), где для всех k, 1 < k < п, имеем хк € Хк. Элемент хк называется k-тл. координатой (или А-й компонентой) кортежа а.
Пример 1. Из множеств {а, Ь, с} и {1, 2} можно составить 6 кортежей длины 2:
(а, 1), (а, 2), (b, 1), (Ь, 2), (с, 1), (с, 2).
Пример 2. Любое слово является кортежем, составленным из букв; десятичная запись любого натурального числа — кортежем, составленным из цифр, и т. д.
Пример 3. Любое упорядоченное конечное множество является кортежем, все координаты которого различны.
Кортежи длины 2 называют упорядоченными парами, длины 3 — упорядоченными тройками,..., длины п — упорядоченными n-ками. Для краткости речи слово «упорядоченные» часто опускают.
Определение 2. Два кортежа равны в том и только в том случае, когда они имеют одинаковую длину, причём их координаты, стоящие на местах с одинаковыми номерами, равны.
Таким образом, кортежи а = (х,, ..., хт) и Р = (с/1; ..., уп) равны в том и только в том случае, когда т = п, причём хк - yk для всех k, 1 < k < п.
Пример 4. Кортежи (I2, 22, З2) и (>/1, >/16, >/81) равны, поскольку I2 = V1, 22 = >/16, З2 = >/81.
223
Пример 5. Кортежи (1, 2, 3) и (3, 1, 2) различны, хотя имеют одинаковую длину и одно и то же множество координат — эти координаты стоят в разном порядке. Различны и кортежи (1, 2, 3) и (1, 2, 3, 4) — они имеют разную длину.
Координатами кортежа могут быть множества, кортежи и т. д. При этом, например, кортежи ({а, Ь}, с) и ({&, а}, с) равны, так как {а, Ь} = {Ь, а}, а кортежи ((а, Ь), с) и ((Ь, а), с) различны, так как (а, Ь) * (Ь, а).
Кортеж, не содержащий ни одной координаты (т. е. кортеж длины 0), называется пустым.
Подчеркнём ещё раз отличия понятий кортежа и множества: а) в множестве порядок элементов не играет роли, а кортежи, отличающиеся порядком элементов, различны даже в случае, когда они имеют одинаковый состав;
б)	в множестве все элементы различны, а в кортеже координаты могут повторяться.
Чтобы различать множества и кортежи, мы будем в дальнейшем элементы множеств заключать в фигурные скобки, а элементы кортежей — в круглые (в частности, в круглые скобки заключают элементы упорядоченных множеств).
Введём теперь понятие декартова произведения множеств.
Определение 3. Пусть Аг ..., Ап — некоторые множества. Их декартовым произведением называют множество, состоящее из всех кортежей вида (щ, ..., а„), где а* € Ah, 1 < k < п. Декартово произведение множеств А1} ..., Ап обозначают А] х ... х А„.
Пример 6. Если А = {1, 2, 3}, В = {х, у}, то
А х В = {(1, х)(1, у), (2, х), (2, у), (3, х), (3, у)} и
В х А = {(х, 1), (х, 2), (х, 3), (г/, 1), (у, 2), (у, 3)}.
Этот пример показывает, что, вообще говоря, декартовы произведения А х В п В х А различны, хотя они содержат поровну элементов.
Различны и множества А х В х С, (А х В) х С и А х (В х С) — первое состоит из троек (а, Ь, с), второе — из пар вида ((а, Ь), с), а третье — из пар вида (а, (Ъ, с)), где во всех трёх случаях а € А, Ь е В, с € С.
Если хотя бы одно из множеств А, В пусто, то считают, что и их декартово произведение пусто:
Ах0 = 0хА = 0х0 = 0.
Пример 7. Декартово произведение R х R состоит из пар (х, у) действительных чисел, причём (х,, yt) - (х2, j/2) в том и только в том случае, когда xt = х2, у-> = Уг- Каждой такой паре
224
соответствует точка М(х; у) на плоскости, для которой числа х и у являются декартовыми координатами (отсюда название «декартово произведение»). Декартово произведение R х R х R состоит из троек чисел (х, у, г), которые можно рассматривать как координаты точки М(х; у; г) в трёхмерном пространстве. Декартово произведение R х R х ... х R (п множителей) называют п-мерным арифметическим пространством. Его обозначают Rn.
Упражнения
392.	Из цифр 1, 2, 3, 4, 5 составьте все двузначные числа. Как связано получившееся множество с декартовым произведением А х А, где А = {1, 2, 3, 4, 5}?
393.	Равны ли следующие кортежи:
1)	(а,	{а, Ь,	с},	Ь,	с)	и	(а,	{а, Ь,	с},	{й, с});
2)	(а,	{а, Ь,	с},	Ь,	с)	и	(а,	{6, а,	с},	Ь,	с);
3)	(а,	{а, Ъ,	с},	Ъ,	с)	и	(а,	{а, Ь,	с},	с,	Ь);
4)	(а,	{а, Ь,	с},	Ь,	с)	и	(а,	{а, Ь,	с},	а,	Ь, с)?
5.	Отображение множеств. Числовая функция f ставит в соответствие каждому числу из её области определения однозначно определённое число f(x). При геометрическом преобразовании плоскости (например, параллельном переносе) каждой точке М этой плоскости соответствует однозначно определённая точка той же плоскости (образ точки М). Оба эти понятия (числовая функция и геометрическое отображение) являются частными случаями общего понятия отображения множества в множество.
Определение 1. Соответствие, сопоставляющее каждому элементу х множества X один и только один элемент множества Y, называется отображением множества X в множество У.
Пример 1. Если каждое пальто в гардеробе висит на одном крючке, то, ставя в соответствие каждому пальто крючок, на котором оно висит, получаем отображение множества пальто X в множество крючков У.
Пример 2. Ставя в соответствие каждому треугольнику вписанную в него окружность, получаем отображение множества треугольников X в множество окружностей У.
Пример 3. Ставя в соответствие каждому треугольнику его площадь, получаем отображение множества треугольников X в множество R.
Пример 4. Соответствие, сопоставляющее четырёхугольнику вписанную окружность, не является отображением множества четырёхугольников в множество окружностей, поскольку не в каждый четырёхугольник можно вписать окружность. Это
225
соответствие является отображением множества У четырёхугольников, у которых суммы длин противоположных сторон одинаковы, в множество окружностей.
Пример 5. Соответствие, сопоставляющее треугольнику длину его высоты, не является отображением множества треугольников в множество чисел, так как у треугольника три высоты, и потому ему соответствуют три числа, а не одно.
Пример 6. Соответствие, сопоставляющее окружности описанный треугольник, не является отображением множества окружностей в множество треугольников, так как около данной окружности можно описать бесконечное множество треугольников.
Элемент множества У, соответствующий при отображении f элементу х из X, обозначают f(x) и называют образом элемента х при этом отображении. Если f(x) = у, то элемент х называют про образом элемента у при отображении f. Совокупность всех прообразов элемента у при отображении f называют полным прообразом этого элемента и обозначают
= {x\f(x) = у}.
Правая часть читается: совокупность таких х, что f(x) = у.
Каждому подмножеству А множества X соответствует его образ f(A) при отображении f. Этот образ состоит из всех элементов множества У, которые являются образами элементов из А:
f(A) = {у| у = Да), а € А}.
Каждому подмножеству В из У соответствует его полный прообраз f ’(В) при отображении f. Он состоит из всех элементов, образы которых принадлежат В:
f \B) = {x\f(x) е в}.
Рис. 76
Множество А называют областью определения отображения f, а множество f(A) — множеством значений этого отображения.
Пример 7. Пусть f — ортогональная проекция плоскости на прямую I (рис. 76). Образом четырёхугольника ABCD является отрезок EF. Полным прообразом отрезка EF является полоса, ограниченная прямыми EL и FM.
Отметим некоторые виды отображений.
226
Определение 2. Если при отображении f различные элементы множества X переходят в различные элементы множества У, то отображение f называют обратимым.
Определение 3. Если при отображении f каждый элемент множества У является образом хотя бы одного элемента из X (т. е. если все полные прообразы f~1(y), у € У, непусты), то f называют отображением X на У.
Определение 4. Обратимое отображение множества X на множество У называют взаимно однозначным отображением X на У.
Замечание. В математической литературе встречаются и иные названия указанных выше типов отображений: обратимые отображения называют инъективными (от слова injectio — вложение), отображения на — сюръективными (от французского предлога sur — на), а взаимно однозначные — биективными.
Пример 8. Отображение, при котором каждому пальто сопоставляется крючок, на котором оно висит, является обратимым, если на каждом крючке висит не более одного пальто (некоторые крючки могут быть пустыми). Оно является отображением множества пальто X на множество крючков У, если на каждом крючке висит хоть одно пальто (на некоторых крючках может быть несколько пальто). Наконец, оно является взаимно однозначным отображением X на У, если на каждом крючке висит ровно одно пальто.
Если отображение f множества А в множество В обратимо, то каждому элементу Ъ из ДА) соответствует один и только один элемент а из А такой, что f(a) = Ъ. Полагая f ;(&) = а, получаем отображение Л1 множества /(В) на А. Его называют обратным отображению f. Если отображение f взаимно однозначно, то тем же свойством обладает и обратное ему отображение Л1-
Отметим, что если существует взаимно однозначное отображение конечного множества А на конечное множество В, то в А и в В поровну элементов. Если же существует обратимое отображение конечного множества А в конечное множество В, то можно лишь сказать, что в В не меньше элементов, чем в А. Это утверждение формулируют часто следующим образом.
Если предметов больше, чем ящиков, то при любом распределении элементов по ящикам хоть в одном из них окажется более одного предмета (принцип Дирихле).
На языке отображений эта формулировка означает, что если в А (множестве предметов) больше элементов, чем в В (множестве ящиков), то не существует обратимого отображения А в В.
В случае когда существует отображение f конечного множества А на конечное множество В, то в А не меньше элементов, чем
227
в В. Чтобы убедиться в этом, достаточно выбрать в каждом из полных прообразов элементов множества А по одному элементу. Выбранные элементы образуют часть множества А, содержащую столько же элементов, что и множество В. Это и значит, что в А не меньше элементов, чем в В.
Упражнения
394.	Каждому треугольнику ставится в соответствие его площадь. Укажите область определения и множество значений этого отображения. Как называются треугольники, образы которых при этом отображении совпадают?
395.	Каждому алгебраическому уравнению ставится в соответствие его степень. Укажите множество значений для этого отображения.
396.	Среди следующих отображений укажите отображения на:
1)	X — множество кругов, У — множество действительных чисел, каждому кругу сопоставляется его площадь;
2)	X — множество кругов, У — множество положительных действительных чисел, каждому кругу сопоставляется его площадь;
3)	X = {х| - 3 < х < 5}, У = R, f: х -> х2;
4)	X = {х| - 3 < х < 5}, У = {х| 0 < х < 25}, f: х -> х2.
397.	Найдите образ X для отображения /: х —> х2 - 4х + 5, где X = У = R.
398.	Является ли соответствие «Человек у — сын человека х» отображением /: х —> у множества всех людей в себя? Является ли таким отображением соответствие «Человек у — старший сын человека х»? Является ли отображением f:x—$y соответствие «Человек у — отец человека х»?
399.	Является ли отображением соответствие «Столицей государства х является город у»?
400.	Приведите известные вам примеры отображений из геометрии. Для отображения f: х —> х2 - 5х + 4 множества R в R найдите: 1) образы чисел 3 и 7;
2)	образ отрезка [3; 7];
3)	полные прообразы чисел -2 и 4;
4)	полный прообраз отрезка [-2; 4].
401.	Каждой букве алфавита, кроме буквы «я», ставится в соответствие следующая за ней буква, а букве «я» — буква «а». Найдите образ множества гласных букв и пересечение этого образа с множеством гласных букв.
402.	Докажите, что объединение некоторой фигуры и её образа при симметрии относительно прямой I симметрично относительно этой прямой.
403.	Докажите, что пересечение некоторой фигуры и её образа при симметрии относительно точки А симметрично относительно этой точки.
404.	Среди следующих отображений укажите обратимые и взаимно однозначные:
1)	каждой окружности ставится в соответствие её центр;
2)	каждой окружности радиуса 1 ставится в соответствие её центр;
228
3)	каждому квадрату ставится в соответствие его периметр (здесь X — множество квадратов, У = Я). Все фигуры рассматриваются на плоскости.
405.	Постройте обратные отображения для следующих отображений:
1)	х -> хг - 4х + 3, X = [2; +°°), У = R;
2)	х х4 - 4х2 + 3, X = [>/3; +оо), у = R.
406.	Существует ли отображение, обратное отображению:
1)	х -> х4 - 4х2 + 3, X = [>/2; +оо), Y - R;
2)	х -> х4 - 4х2 + 3, X = (-оо; -7з], У = Я?
§ 2.	Основные законы комбинаторики
1.	Введение. При решении многих практических задач приходится выбирать из некоторой совокупности объектов элементы, обладающие тем или иным свойством, располагать эти элементы в определённом порядке и т. д. Поскольку в таких задачах речь идёт о тех или иных комбинациях объектов, их называют комбинаторными задачами. Область математики, в которой изучаются комбинаторные задачи, называют комбинаторикой.
Приведём несколько примеров комбинаторных задач.
1.	Расположить 10 точек и 5 отрезков так, чтобы на каждом отрезке было по 4 точки.
2.	Расположить числа 1, 2, 3, 4, 5, 6, 7, 8, 9 так, чтобы они образовали «магический квадрат», т. е. квадрат, в котором суммы по всем строкам, всем столбцам и обеим диагоналям одинаковы.
3.	Найти все расположения восьми ферзей на шахматной доске, при которых ни один из них не может взять другого (т. е. не стоит с ним на одной горизонтали, либо одной вертикали, либо одной диагонали).
4.	Найти число расположений восьми ладей на шахматной доске, при которых ни одна из них не может взять другую.
5.	Узнать, сколькими способами можно из 7 мальчиков и 9 девочек выбрать команду для эстафетного бега, если в команду должны войти 4 мальчика и 4 девочки.
6.	Путешественник должен объехать несколько городов, побывав в каждом из них по одному разу, и вернуться назад. Найти кратчайший вариант путешествия, если известны расстояния между городами, причём из каждого города можно попасть в любой другой, минуя остальные города.
Эти примеры показывают, что комбинаторные задачи можно решать на разных уровнях: искать хотя бы одно решение поставленной задачи (примеры 1 и 2), искать все её решения (пример 3), отыскивать число решений данной задачи (примеры 4 и 5), среди
229
Аа	Bb	Cc	Dd	различных способов решения искать оптимальный (пример 6). Ино-гда приходится доказывать, что данная комбинаторная задача не имеет решения. Например, ещё Л. Эйлер доказал, что нельзя расположить 36 офицеров, имеющих 6 различных воинских званий и принадлежащих 6 различным
Bd	Ac	Db	Ca	
Cd	Da	Ad	Be	
De	Cd	Ba	Ab	
Рис. 77				
родам войск (по одному офицеру данного звания в данном роде войск), в 36 клетках квадрата так, чтобы в каждой вертикали и каждой горизонтали были представлены все звания и все рода войск. На рисунке 77 показано решение этой задачи для четырёх воинских званий (А, В, С, D) и четырёх родов войск (a, b, с, d).
Мы будем заниматься в этой главе лишь задачами, в которых надо найти число способов решения той или иной комбинаторной проблемы. Эти задачи образуют часть комбинаторики, называемую перечислительной комбинаторикой или теорией перечислений.
Характерной чертой математического подхода к решению практических задач является абстрагирование, т. е. отвлечение от конкретных черт, выявление глубинного содержания, общего для задач, внешне отличающихся друг от друга. Это приводит к построению математической модели задачи, к введению общих понятий, охватывающих частные случаи. В комбинаторике такие модели обычно строят с привлечением разобранных в § 1 понятий
множества, подмножества, упорядоченного множества, кортежа, отображения и т. д. В следующих пунктах мы разберём, опираясь на эти понятия, два основных закона комбинаторики — правило суммы и правило произведения.
У пражнения
407.	Из шахматной доски вырезаны две угловые клетки, расположенные на одной диагонали. Можно ли замостить эту доску прямоугольниками, состоящими из двух клеток?
408.	Шахматную доску с 3 горизонталями и 3 вертикалями обходят ладьёй и на пути её следования пишут одно за другим числа 1, 2, 3, 4, 5, 6, 7, 8, 9. Найдите путь ладьи, при котором трёхзначное число, получившееся в третьей горизонтали, равно сумме трёхзначных чисел, получившихся в первых двух горизонталях.
409.	Поставьте на шахматную доску 5 ферзей так, чтобы они держали под ударом все её поля.
410.	Докажите, что максимальное число слонов, которых можно поставить на шахматную доску так, чтобы они не били друг друга,
230
равно 14. Обобщите результат на случай доски с п горизонталями и вертикалями.
411.	Докажите, что среди 9 человек есть либо 3 попарно знакомых, либо 4 попарно незнакомых.
2.	Правило суммы. Если на блюде лежат 7 яблок и 4 груши, то выбрать один плод можно 7 + 4 = 11 способами. Вообще справедливо следующее утверждение, называемое в комбинаторике правилом суммы.
Если элемент а можно выбрать т способами, а элемент Ъ — п способами, причём любой выбор элемента а отличен от любого выбора элемента Ь, то выбор «а или Ъ» можно сделать т + п способами.
На языке теории множеств это правило формулируется следующим образом.
Теорема 1. Если пересечение конечных множеств А и В пусто, А А В = 0, то число элементов в их объединении равно сумме чисел элементов множеств А и В:
А А В = 0 п(А U В) = n(A) + п(В).	(1)
Запись X => У читается: «Если X, то У».
Применяя метод математической индукции, выводим из этой теоремы следствие.
Следствие 1. Если конечные множества Alf ..., А„ попарно не пересекаются, т. е. если А, А Ak = 0 при j * k, то имеет место равенство
niAx U ... U Afc) = n(Aj) + ... + n(Ah).	(2)
Правило суммы и его следствие применяются для решения комбинаторных задач — часто приходится разбивать всё множество перечисляемых комбинаций на попарно непересекающиеся группы комбинаций, подсчитывать число элементов в каждой группе и потом складывать получившиеся ответы. Правило суммы можно сформулировать и на языке отображений.
Следствие 2. Если задано отображение f конечного множества X на множество У, то число элементов в X равно сумме чисел элементов в полных прообразах элементов множества У.
В самом деле, всё множество X распадается на попарно непересекающиеся части — полные прообразы элементов множества У.
Разберём теперь случай, когда множества могут иметь непустые пересечения. Начнём со случая двух множеств (рис. 78).
231
Теорема 2. Для любых конечных множеств А и В верно равенство
п(А U В) = п(А) + п(В) - п(А А В).	(3)
Доказательство. Множество A U В является объединением трёх попарно непересекающихся множеств: А\(А А В) (элементы, принадлежащие только А), В\(А А В) (элементы, принадлежащие только В) и А А В (элементы, принадлежащие обоим множествам). Первое из этих множеств содержит тг(А) - п(А А В) элементов, второе содержит п(В) - п(А А В) элементов, а третье — п(А А В) элементов. Значит, число элементов в множестве A U В равно п(А) — п(А А В) + п(В) - п(А А В) + п(А А В), т. е.
п(А U В) = п(А) + тг(В) - п(А А В).
Например, если множество А состоит из букв {а, б, в, г, д, е}, а множество В из букв {г, д, е, ж, з}, то их объединением является множество {а, б, в, г, д, е, ж, з}, а пересечением — множество {г, д, е}. При этом тг(А) = 6, 7i(B) = 5, п(А А В) - 3, п(А и В) = 8, что согласуется с формулой (3).
Формула (3) является частным случаем более общей формулы 7i(Aj U ... U Am) = 71(Aj) + ... + тг(Аи) - п(А1 А А2) - п(А{ А А3) - ...
... - 7i(Ai А А„) - тг(А2 А А3) - ... - тг(А2 А AJ - ...
(4)
... - 7i(Am-! A Am) + n(Aj А А2 А Аз) + ...
... + (-1)*+1ti(Ai А ... А А*) + ... + (-1Г + 1п(А1 А ... A AJ, которую называют формулой перекрытий или, иначе, формулой включений и исключений. В эту формулу, кроме самих множеств Ai,..., Ат, входят их всевозможные пересечения по 2, по 3, ..., по т. При этом, если число пересекаемых множеств нечётно, соответствующее слагаемое входит в формулу (4) со знаком «плюс», а если оно чётно, то со знаком «минус».
Например, при п = 3 имеем
п(А U В U С) = тг(А) + 7i(B) + тг(С) - п(А А В) -- п(А А С) - п(В А С) + п(А А В А С).
Чтобы доказать равенство (5), заметим, что AUBUC = (AUB)U U С, и потому по формуле (3) имеем п(А U В U С) = тг(А U В) + + п(С) - п((А U В) А С). Но по свойствам операций над множествами
(A U В) А С = (А А С) U (В А С),
и потому
тг((А U В) А С) = п(А А С) + п(В А С) - Ti((A А С) А (В А С)) = = тг(А А С) + тг(В А С) - п(А А В А С).
232
Значит,
п(А U В U С) = п(А U В) + п(С) - п(А П С) -- п(В П С) + П(А п В Г) С).
Заменяя п(А U В) по формуле (3), получаем (5).
В общем случае формула (4) доказывается аналогично методом математической индукции.
С помощью формулы (4) легко найти и число элементов некоторого множества U, не принадлежащих ни одному из подмножеств А1г ...,Ап этого множества, — сначала надо найти число элементов в Аг U ... U Ат, а потом вычесть найденное число из числа элементов в U.
Пример 1. В классе обучаются 42 ученика. Из них 16 участвуют в секции по лёгкой атлетике, 24 — в футбольной секции, 15 — в шахматной секции, 11 — ив секции по лёгкой атлетике, и в футбольной, 8 — ив легкоатлетической, и в шахматной, 12 — ив футбольной, и в шахматной, а 6 — во всех трёх секциях. Остальные школьники увлекаются только туризмом. Сколько школьников являются туристами?
Решение. Обозначим через U множество всех учащихся, через А — членов легкоатлетической секции, через В — футбольной, через С — шахматной и через D — туристической. По условию задачи
IZ=AUBUCUD, причём
D П (A U В U С) = 0
и п((7) = 42, га(А) = 16, п(В) = 24, п(С) = 15, п(А П В) = И, п(А П С) = 8, п(В П С) = 12, п(А П В П С) = 6.
По формуле (5) получаем, что
п(А U В U С) = 16 + 24 + 15 - 11 - 8 - 12 + 6 = 30, и потому
n(Z>) = n(Z7) - п(А U В U С) = 42 - 30 = 12.
Значит, туризмом занимаются 12 школьников.
Упражнения
412.	В отделе научно-исследовательского института работают несколько человек, причём каждый из них знает хотя бы один иностранный язык: 6 человек знают английский язык, 6 — немецкий, 7 — французский, 4 знают английский и немецкий, 3 — немецкий и французский, 2 — французский и английский, 1 человек знает все три языка. Сколько человек работают в отделе? Сколько из них знают только английский язык? Сколько человек знают только один язык?
233
413.	Староста одного класса дал следующие сведения об учениках: «В классе учатся 45 школьников, в том числе 25 мальчиков. 30 школьников учатся на хорошо и отлично, в том числе 16 мальчиков. Спортом занимаются 28 учеников, в том числе 18 мальчиков и 17 школьников, учащихся на хорошо и отлично. 15 мальчиков учатся на хорошо и отлично и занимаются спортом».
Докажите, что в этих сведениях есть ошибка.
414.	Сколько чисел среди первых 100 натуральных чисел не делятся ни на 2, ни на 3, ни на 5?
415.	Сколько чисел среди первой тысячи натуральных чисел не делятся ни на 2, ни на 3, ни на 5, ни на 7?
3.	Правило произведения. Вторым основным правилом комбинаторики является правило произведения. Оно выражается следующей теоремой.
Теорема 1. Если множества А и В конечны, то число пар в их декартовом произведении Ах В равно произведению чисел элементов этих множеств:
п(А х В) - п(А)  п(В).	(1)
Доказательство. Множество А х В состоит из пар вида (а, Ь), где а € А, b € В.
Если А = {аи ..., ат} и В = {t>i, ..., bk}, то эти пары можно записать в виде следующей таблицы:
(щ, bj, ..., (а1; bk),
(ат, bj, ..., (ат, ЬА-
Видим, что число этих пар равно mk, т. е. п(А)  п(В).
С помощью метода математической индукции формула обобщается на любое число множеств.
Теорема 2. Если множества Аг, ..., Ат конечны, то имеет место равенство
п(А1 х ... х Ага) = n(Aj) • ... • п(Ат).	(2)
Пример 1. Сколько номеров, состоящих из двух букв, за которыми идут пять цифр, можно составить, использовав 32 буквы и 10 цифр?
Решение. Обозначим множество из 32 букв через А, а множество из 10 цифр через В. Каждый номер требуемого вида является кортежем из декартова произведения Ах Ах В х В х В. Так как п(А) = 32, п(В) = 10, то по формуле (2)
п(А х А х В х В х В) = 32 • 32 • 10 • 10 10 = 1 024 000.
При решении некоторых комбинаторных задач приходится иметь дело с более общей ситуацией, чем рассмотренная выше. Она описывается следующей теоремой.
234
Теорема 3. Пусть задано отображение конечного множества X на множество У, причём в каждый элемент множества Y отображается одно и то же число элементов множества X. Тогда число элементов в X равно произведению числа элементов в У на число элементов, отображающихся в каждый элемент множества У.
Доказательство. Множество X распадается на попарно непересекающиеся подмножества — полные прообразы элементов множества У при отображении f. Поэтому число элементов в X равно сумме чисел элементов в этих прообразах, а число прообразов равно числу элементов в У. По условию все прообразы имеют поровну элементов. Поэтому п(Х) равно сумме п(У) равных слагаемых, т. е. произведению п(У) и числа элементов в каждом прообразе.
Отметим, что теорема 1 является частным случаем теоремы 3: достаточно рассмотреть отображение (a, b) —> Ь множества А х В на В. Видим, что прообраз каждого Ъ е В содержит п(А) элементов, а в В содержится п(В) элементов. Поэтому п(А х В) = п(А)  п(В).
Приме р 2. Сколько упорядоченных пар можно составить из 32 букв, если в каждой паре буквы различны?
Решение. Поставим в соответствие каждой паре букв первую букву этой пары. Получим отображение множества У пар требуемого вида на множество X букв. Полный прообраз каждой буквы содержит 31 букву (все буквы, кроме данной). Поэтому число пар требуемого вида равно 32 • 31 = 992.
Заметим, что множество пар в этом примере не было декартовым произведением двух множеств. Аналогично можно найти число троек, в которых никакие две одинаковые буквы не идут подряд. Такие тройки записываются в виде (а, Ь, с), где а Ф b и b Ф с. При отображении (а, Ь, с) (а, Ь) каждая пара (а, Ь) имеет полный прообраз из 31 тройки. Так как число пар равно 32  31, то число троек равно 32 • 312 = 30752.
Решение задач такого типа можно проводить также на основе следующего утверждения, обобщающего теорему 2.
Если первую координату кортежа длины k можно выбрать П1 способами, при любом выборе первой координаты вторая выбирается п2 способами, при любом выборе первых двух координат третья выбирается п3 способами и т. д. до k-й координаты включительно, то общее число получаемых таким образом кортежей равно ПЩ2 ••• пк.
При построении троек, не содержащих рядом стоящих одинаковых букв, первую координату можно выбрать 32 способами, при
235
каждом таком выборе вторая координата выбирается 31 способом, а при каждом выборе первых двух букв третья выбирается тоже 31 способом. Вновь получаем ответ 32 • 31 • 31 = 30 752.
Упражнения
416.	Имеется 5 видов конвертов без марок и 4 вида марок. Сколькими способами можно выбрать конверт и марку для посылки письма?
417.	Сколькими способами можно выбрать согласную и гласную из слова «здание»? из слова «паркет»?
418.	Сколькими способами можно указать на шахматной доске два квадрата — белый и чёрный? Решите ту же задачу, если нет ограничений на цвет квадратов. Решите её, если надо выбрать два белых квадрата.
419.	Сколькими способами можно выбрать на шахматной доске белый и чёрный квадраты, не лежащие на одной горизонтали или одной вертикали?
420.	Из 3 учебников алгебры, 7 учебников геометрии и 6 учебников физики надо выбрать комплект, содержащий по одному учебнику по каждому предмету. Сколькими способами это можно сделать?
421.	В корзине лежат 12 яблок и 10 апельсинов. Ваня выбирает либо яблоко, либо апельсин, после чего Надя выбирает из оставшихся фруктов и яблоко, и апельсин. Сколько возможно таких выборов? При каком выборе Вани у Нади больше возможностей выбора?
§ 3.	Основные формулы комбинаторики
1.	Размещения с повторениями. В этом параграфе мы рассмотрим некоторые типовые комбинаторные задачи.
Задача 1. Найти число всех кортежей длины k, которые можно составить из элементов множества X, если число этих элементов равно т, п(Х) = т.
Решение. Нам надо найти число элементов декартова произведения X х ... х X, состоящего из k одинаковых множителей. По формуле (2) п. 3 § 2 это число равно п(Х) х ... х п{Х) (k множителей), т. е. равно n(X)k = mk.
Определение. Кортежи длины /г, составленные из элементов тп-элементного множества X, называют размещениями с повторениями из т элементов по k. Число этих кортежей обозначают А* . (Буква А от французского слова arrangement — размещение. Черта указывает на возможность повторения элементов.)
Мы доказали формулу
А‘ = тк.	(1)
236
Пример 1. Сколько пятизначных номеров можно составить из девяти цифр 1, 2, 3, 4, 5, 6, 7, 8, 9?
Решение. Такие номера являются кортежами длины 5, составленными из элементов множества X = {1, 2, 3, 4, 5, 6, 7, 8, 9}. По формуле (1) их число равно Ад = 95 = 6561.
К подсчёту числа кортежей данной длины сводятся многие другие комбинаторные задачи.
Задача 2. Найдём число отображений множества X в множество Y, если п(Х) = k и n(Y) = т.
Решение. Перенумеруем элементы множества X: X = = {хь ..., хк}. Каждому отображению f множества X в Y соответствует кортеж длины k, составленный из образов этих элементов (взятых в том же порядке), т. е. кортеж (ДхО, ...» f(xk)). Обратно, задание кортежа (i/ц ..., yk), составленного из элементов множества Y, однозначно определяет отображение f: элемент х, переходит в элемент у,.
Значит, число отображений множества X в множество Y равно числу кортежей длины k, составленных из элементов множества Y. Так как п(У) = т, то по формуле (1) это число равно тк.
Пример 2. Сколькими способами можно разделить 6 различных конфет между тремя детьми?
Решение. Каждый способ раздела является отображением множества конфет в множество детей. Число таких отображений равно З6, т. е. 729.
Вообще любое отображение fe-элементного множества X в тп-элементное множество Y можно истолковать как раскладку k элементов по т ящикам. Мы видим, что число таких раскладок равно тк.
Задача 3. Найдём число всех подмножеств множества X, если X содержит k элементов.
Решение. Будем раскладывать элементы множества X в два ящика. Каждому подмножеству А множества X соответствует способ раскладки, при котором элементы подмножества попадают в первый ящик, а остальные элементы — во второй. Обратно, каждая такая раскладка однозначно определяет подмножество элементов, попавших в первый ящик. Поэтому общее число подмножеств в X равно числу способов раскладки элементов множества по двум ящикам, т. е. равно 2П,Х) = 2к.
Это утверждение легко доказать и с помощью математической индукции по k.
237
Пример 3. Выпишем все подмножества множества {а, Ь, с}. Решение. Данное множество имеет восемь подмножеств:
0, {а}, {Ь}, {с}, {а, &}, {а, с}, {Ь, с}, {а, Ъ, с}.
Так как 8 = 23, это соответствует доказанному выше утверждению.
У пражнения
422.	Сколько существует пятизначных номеров, не содержащих цифру 8? не содержащих цифр 0 и 8? составленных из цифр 2, 3, 5, 7?
423.	Сколькими способами можно разложить 12 различных деталей по 3 ящикам?
424.	Имеется набор из 16 карточек: четыре с буквой «А», четыре с буквой «Б», четыре с буквой «В» и четыре — с буквой «Г». Сколько различных комбинаций букв можно получить, выбирая из набора 4 карточки и располагая их в некотором порядке?
425.	В некотором сказочном королевстве не было двух человек с одинаковым набором зубов. Каково могло быть наибольшее число жителей этого королевства, если у человека с детства 32 зуба?
2.	Размещения без повторений. Будем теперь составлять из элементов m-элементного множества X не кортежи длины k, а упорядоченные подмножества той же длины. Иными словами, в отличие от п. 1 будем брать лишь кортежи длины k без повторяющихся элементов.
Определение. Упорядоченное множество длины k, составленное из элементов m-элементного множества X, называют размещением без повторений из т элементов множества X по k. Число таких размещений обозначают А^.
Задача 1. Найдём число размещений без повторений из т элементов по k.
Решение. Первой компонентой кортежа может стать любой из элементов множества X. Так как их число равно т, то получаем т возможностей выбора. Если первый элемент X] уже выбран, второй элемент можно выбрать лишь т — 1 способами (повторение элемента X; не допускается). Аналогично устанавливаем, что при выбранных элементах Xj и х2 элемент х3 можно выбрать т - 2 способами и т. д. вплоть до элемента хк, который можно выбрать т - (k - 1), т. е. т - k + 1 способами (до него выбран k - 1 элемент: Xi, ..., xk-i, ни один из которых не должен повториться).
По правилу произведения получаем, что число размещений без повторений из т элементов по k выражается формулой
= т(т - 1) ... (т - k + 1).	(1)
238
Эту формулу можно записать иначе, если воспользоваться обозначением п! (эн факториал) для произведения натуральных чисел от 1 до п, n! = 1 • 2 • ... • п. Если умножить обе части равенства (1) на (т - А)! - (т - k)  ...  1, то получим, что
(т - k)\  А^ = т  (т - 1)  ... • (т - k + 1)(т - k) • ... • 1 = ml.
Отсюда вытекает, что
Пример 1. Найдём, сколькими способами можно выбрать из 40 учеников класса старосту, его заместителя и физорга.
Решение. Любой такой выбор является размещением без повторений из 40 элементов по 3 (он задаётся кортежем длины 3 без повторений, составленным из элементов множества учеников). Значит, число способов выбора равно
А30 = 40 • 39 • 38 = 59 280.
В п. 1 была установлена связь между кортежами длины k, составленными из элементов множества Y, и отображениями в У A-элементного множества X. Размещениям без повторений соответствуют такие отображения, при которых разные элементы множества X отображаются в разные элементы множества У, т. е. обратимые отображения множества X в У. Тем самым доказано следующее утверждение.
Пусть множество X содержит k элементов, а множество У — т элементов. Тогда число обратимых отображений множества X в множество У равно А^.
Наглядное истолкование обратимых отображений X в У состоит в том, что элементы множества X раскладываются по т ящикам, причём ни в один ящик нельзя положить более одного элемента.
У пражнения
426.	Сколькими способами можно составить трёхцветный полосатый флаг, если имеются ткани пяти различных цветов? Решите ту же задачу при условии, что одна полоса должна быть красной.
427.	В цехе работают 8 токарей. Сколькими способами можно поручить трём из них изготовление трёх различных видов деталей (по одному виду на каждого)?
428.	Из 10 различных книг выбирают 4 для посылки. Сколькими способами это можно сделать?
429.	В профком избрано 9 человек. Из них надо выбрать председателя, его заместителя, секретаря и культорга. Сколькими способами это можно сделать?
430.	Сколькими способами можно отправить 5 писем 11 адресатам, если каждому отправляют не более одного письма?
239
3.	Перестановки без повторений. Если длина размещения без повторений равна числу т элементов множества X, то в этом размещении встречаются по одному разу все элементы из X. Два таких размещения отличаются друг от друга лишь порядком этих элементов. Дадим таким размещениям особое название.
Определение. Перестановкой без повторений из т элементов называют размещение без повторений из этих элементов по т.
Число перестановок из т элементов обозначают Рт (от французского слова permutation — перестановка). Так как Рт = А”, то по формуле (1) п. 2 получаем, что
Рт = т • (т - 1) • ... • (т - т + 1) = т • (т - 1) • ...  1 = ml. Итак,
Рт = ml.
Пр им ер 1. Сколькими способами 6 человек могут сесть на 6 стульев?
Решение. Занумеруем стулья числами 1, 2, 3, 4, 5, 6 и обозначим человека, севшего на fe-й стул, через xk. Тогда (х1; ..., х6) — перестановка из имён этих шести людей, причём каждой такой перестановке соответствует один и только один способ размещения на стульях. Значит, число способов равно Р6 = 6! = 720.
Каждая перестановка элементов множества X задаёт взаимно однозначное отображение этого множества на себя. Именно, занумеруем элементы множества X числами 1, 2, ..., т: X = (хь ..., хт) и возьмём какую-нибудь перестановку этих элементов. После этого элементу х, поставим в соответствие первую координату этой перестановки, элементу х2 — вторую, ..., элементу хт — т-ю координату. Этим задаётся взаимно однозначное отображение X на себя.
Например, если X - (1, 2, 3, 4), то перестановке (4, 3, 2, 1) соответствует взаимно однозначное отображение множества X на себя, при котором 1 переходит в 4, 2 — в 3, 3 — в 2, 4 — в 1.
Упражнения
431.	Сколькими способами можно обить 6 стульев тканью, если имеются ткани шести различных цветов и все должны быть использованы?
432.	Сколькими способами могут расположиться в турнирной таблице 10 футбольных команд, если известно, что никакие две команды не набрали поровну очков?
433.	На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите ту же задачу, если Б должен выступить сразу после А.
240
4.	Сочетания без повторений. Будем теперь строить из элементов множества X не кортежи, а подмножества. Получим так называемые сочетания без повторений.
Определение, й-элементные подмножества от-элементного множества X называют сочетаниями без повторений из элементов этого множества по k. Их число обозначают С* (от французского слова combinaison — комбинация; применяется также обозначение (")).
Пример 1. Из множества {a, b, с, d, е} можно составить 10 сочетаний по 3 элемента в каждом:
{а, Ь, с}, {а, b, d}, {a, b, е}, {а, с, d}, {а, с, е}, {а, d, е}, {Ь, с, d}, {b, с, е}, {b, d, е}, {с, d, е}.
Из каждого такого сочетания путём различных упорядочиваний элементов получается 6 размещений из 5 элементов по 3. Например, из сочетания {а, Ь, с} получаем следующие размещения: (а, Ь, с), (а, с, Ь), (Ь, а, с), (Ь, с, а), (с, а, Ь), (с, Ъ, а). Отсюда видно, что число размещений без повторений из 5 элементов по 3 равно 6 • 10 = 60, что согласуется с формулой (1) п. 2: А* = 5 • 4  3 = 60.
Задача 1. Найдём число сочетаний без повторений из т элементов по k.
Решение. Из каждого сочетания без повторений из т по k путём упорядочиваний получаются k\ различных размещений без повторений из т элементов по k. При этом различные сочетания порождают различные размещения и каждое размещение может быть получено указанным образом. Отсюда следует, что число размещений без повторений из т элементов по k в k\ раз больше, чем число сочетаний без повторений из т элементов по k. Иными
A.k
словами, мы доказали, что Akm - k\ • С*. Но тогда СД = -угр Под
ставляя для выведенное в п. 2 значение
'т k\(m - k)\'
т\
получаем
(1)
Формулу (1) можно записать также следующим образом:
гк _ т(т - 1) • ...  (от - fe + 1)
1 • 2  3  ...  k ‘	1 ’
Пример 2. Сколькими способами можно составить команду из 4 человек для соревнования по бегу, если имеются 7 бегунов?
Решение. Число выборов равно:
С!
7-654 =
12 3 4
241
Замечание. Если бы команда выбиралась для эстафетного бега на 100 + 200 + 400 + 800 м, то число способов выбора было бы в 4! = 24 раза больше, поскольку играл бы роль порядок спортсменов, — кто какую дистанцию будет бежать.
Понятие сочетания без повторений тоже можно истолковать на языке отображений, только теперь придётся отображать упорядоченные множества. Именно, пусть даны два упорядоченных множества X и У, причём п(Х) - k, n(Y) = т. Тогда число отображений X в У, сохраняющих порядок элементов, равно С*. В самом деле, каждое такое отображение однозначно определяется выбором k элементов из множества У. После этого первый элемент множества X отображается в наименьший из выбранных элементов, второй — в следующий из выбранных элементов и т. д. вплоть до А-го, который отображается в последний из выбранных элементов.
Например, подмножеству А = {2, 3, 6} упорядоченного множества У = (1, 2, 3, 4, 5, 6) соответствует следующее отображение упорядоченного множества X = (10, 11, 12) в У: 10 переходит в 2, 11 — в 3 и 12 — в 6.
Многие комбинаторные задачи сводятся к подсчёту числа сочетаний без повторений из т элементов по k.
Задача 2. Найдём число кортежей длины k + п, содержащих k раз букву а и п раз букву х.
Решение. Так как состав кортежей известен, они могут отличаться друг от друга лишь порядком букв. Но этот порядок однозначно определяется заданием мест, на которых стоят буквы а (остальные места занимаются буквами х). Иными словами, надо выбрать A-элементное подмножество в (А + поэлементном множестве мест. А это можно сделать С£+п способами.
Пример 3. Сколькими способами можно попасть из точки А в точку С (рис. 79), если можно двигаться лишь вправо и вверх по отрезкам сети?
Решение. Каждый путь состоит из 8 горизонтальных и 4 вертикальных единичных отрезков. Если обозначить горизонтальный д	q отрезок буквой а, а вертикальный —
буквой х, то получим кортеж из 8 букв а и 4 букв х. Согласно приме-ру 2 число таких кортежей, а тем --------------------- самым искомое число путей, равно
А	В с* - 12 • 11 ' 10'9 = 495
Рис. 79	12 3 4
242
У пражнения
434.	Сколькими способами можно выбрать 5 делегатов из состава конференции, на которой присутствуют 15 человек?
435.	Сколькими способами можно поставить 8 шашек на чёрные поля доски?
436.	Сколькими способами можно поставить на чёрные поля доски 12 белых и 12 чёрных шашек?
437.	У одного человека есть 11 книг по математике, а у другого — 15 книг. Сколькими способами они могут выбрать по 3 книги каждый для обмена?
438.	Сколькими способами можно заполнить карточки «Спортлото» (зачеркнуть 6 номеров из 49)? Во скольких случаях из выбранных шести номеров после тиража три окажутся угаданными правильно? Во скольких случаях правильно будут угаданы 4 номера? 5 номеров? 6 номеров?
5. Сочетания и биномиальные коэффициенты. Обозначение С* встречалось нам при изучении бинома Ньютона. Совпадение обозначений не является случайным: в п. 9 § 3 главы 5 (10 кл.) было доказано, что
_ __ml
kl(m - й)!’
а сейчас мы получили ту же формулу для числа сочетаний без повторений из т элементов по k. Таким образом, коэффициент при хт~к  ак в разложении бинома (х + а)т равен числу сочетаний из т элементов по Л. В этом можно убедиться, не используя формул для биномиальных коэффициентов и для числа сочетаний.
В самом деле, запишем (х + а)т в виде произведения множителей (х + а):
(х + а)т = (х + а) • ... • (х + а) (т множителей).
Если раскрывать скобки в этом произведении, не используя обозначения степени и не переставляя множителей, то получим всевозможные кортежи длины т, составленные из букв х и а. Например,
(х + а)3 = (х + а)(х + а)(х + а) =
= ххх + хха + хах + хаа + ахх + аха + аах + ааа.
Чтобы выяснить, какие из этих слагаемых войдут в член разложения бинома, содержащий xm~kak, надо узнать, сколько из таких кортежей содержат т - k букв х и k букв а. В п. 4 было показано, что число таких кортежей равно Ckm_k) + k, т. е. С*. Это и показывает, что коэффициент при хт~к  ак в разложении бинома (х + а)т равен числу сочетаний из т элементов по k.
В п. 10 § 3 главы 5 (10 кл.) были доказаны на основе формулы бинома Ньютона и явного выражения для С* различные свойства
243
чисел. Мы покажем сейчас, что эти свойства можно доказать на основе комбинаторных рассуждений.
1)	Чтобы доказать равенство
с° + С> + ... + Скт + ... + С" = 2",	(1)
заметим, что множество из т элементов содержит 2т подмножеств (см. п. 1). Разобьём совокупность всех подмножеств на классы, отнеся к Л-му классу подмножества, содержащие k элементов. Тогда в 0-м классе будет С® подмножеств, в 1-м классе — подмножеств, ..., в т-м — С™ подмножеств. Поскольку каждое подмножество попадает в один и только один класс, по правилу суммы получаем равенство (1).
2)	Чтобы доказать равенство
= С£~к,	(2)
поставим в соответствие каждому /г-элементному подмножеству А тп-элементного множества X его дополнение в X. Это дополнение содержит т - k элементов, причём отображение, ставящее в соответствие подмножеству его дополнение, взаимно однозначно (если А * В, то и А' Ф В'). Значит, число тп-элементных подмножеств в X равно числу (иг - Л)-элементных подмножеств. А это и значит, что
Ск = c™~k.
3)	Несколько сложнее доказывается равенство
скт = скт-_\ + С*.,.	(3)
Выберем в тп-элементном множестве X какой-нибудь элемент а и разобьём все й-элементные подмножества множества X на два класса. К первому отнесём те подмножества, которые содержат элемент а, а ко второму — все остальные. Если из каждого подмножества 1-го класса удалить элемент а, останется (k — 1)-элементное подмножество (т - 1)-элементного множества X, получаемого удалением из X элемента а. Поэтому 1-й класс содержит С*~_\ множеств. Множества же 2-го класса являются fe-элементными подмножествами (т - 1)-элементного множества X (ведь они не содержат а). Поэтому их число равно С* Так как каждое k-эле-ментное подмножество из X попало в один и только один класс, а их число равно С*, то по правилу суммы имеем равенство
С А — Г1*-1 _1_ С* т ~	- 1	'	-1 •
Аналогичным образом можно с помощью комбинаторных рас-суждений вывести дальнейшие свойства чисел С*.
244
Упражнения
439.	Докажите следующие тождества для чисел С*:
1)	с? + с”+1 + с;,2 + ... + с;+т_, = с:^;
2)	С°РС?_Р + с'сг; + ... + С‘СГ-7 + ... + С?с°п~р = С";
Q\ рРрп~р,рр рп-р .	^р лп-р , л. ПР р^~Р—рп + \.
°/ '~'р'~'т ~ р ~ р + I'-'m. - р - 1 ’ ♦ • ’ ' '-'р + к^т - р - к ' • • • ' ^р + т -п'-'п - р	+ 1 >
4)С„°С" - С’с”? + - + (-1)‘с„‘сг; + ... + (-1)"‘љѰ_т = 0.
440.	Докажите, что
(С“)2 + (С*)2 + ... + (СП2 = с2"„.
6.	Перестановки с повторениями. При перестановке букв в слове «толпа» получается _Р5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов» потому, что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова». Мы имеем здесь дело с перестановками с повторениями.
Определение. Перестановкой с повторениями состава (Aj, ..., V) из букв (ан ..., ат) называют любой кортеж длины k = kr + k2 + ... + + km, в который буква at входит к, раз, ..., буква ат - km раз. Число таких перестановок обозначают P(ki, ..., km).
Пример 1. Кортеж (а, Ь, а, а, с, Ь, Ь, Ь, с) является перестановкой с повторениями из трёх букв а, четырёх букв b и двух букв с. Его состав выражается кортежем (3, 4, 2) (мы считаем, что буква а — первая, Ь — вторая и с — третья).
Задача. Найдём число P(kit ..., km) перестановок с повторениями, имеющих состав (Ан ..., km).
Решение. Перестановку состава (ki, ..., km) можно получить следующим образом: сначала выбираем kv место из общего числа мест k =	+ k2 + ... + km и пишем на них букву а, — этот выбор
может быть сделан Ск1 способами. Затем из оставшихся к - kt мест выбираем k2 места и пишем на них букву а2 — этот выбор может быть сделан С^_ способами. Выбор мест для буквы аг может быть сделан	способами и т. д.
По правилу произведения получаем, что выбор перестановки состава (V k2, ..., km) может быть сделан

. Г'*’"
способами. В силу формулы CJk = jy получаем
P(klt k2........km) =
fe!	(fe - fe,)!	(fe - fe, - ... -
M* - M! ’	- *2)! ’	’ VO!
245
После сокращения получаем формулу
Р(Ъ. k \ ~ _______—_____ — (^1 + ^2 + •" + ^тУ	/1 \
W  ... • kJ ~	W.-...-kJ •	(1)
Пример 2. Сколько слов можно получить, переставляя буквы в слове «математика»?
Решение. Слово «математика» является кортежем длины 10, имеющим состав (2, 3, 2, 1, 1, 1) (буква «м» входит два раза, буква «а» — 3 раза, буква «т» — два раза, буквы «е», «и», «к» — по одному разу). Значит, при перестановках букв получится
Р(2, 3, 2, 1, 1, 1) = х-.-ъ!~о11 1 г - 151200 «слов».
Как и другие понятия комбинаторики, перестановки с повторениями могут быть истолкованы на языке отображений множеств.
Пусть даны упорядоченные множества X и У, причём п(Х) = k -= ky + ... + km, n(Y) = m,Y = {y1; ..., ym}. Тогда P(k1.kJ равно
числу отображений X в У таких, что полный прообраз элемента У/ содержит k, элементов. Именно каждому такому отображению f сопоставляется перестановка с повторениями длины k, состоящая из букв z/1; ..., ут, причём буква у, стоит на месте тех х,, для которых ДхЭ = у).
Пример 3. Сколькими способами можно разложить 28 различных предметов по четырём различным ящикам так, чтобы в каждом ящике оказалось по 7 предметов?
Решение. В силу сказанного выше число способов равно
Р(7 7 7 7)- -----—---- = 28~.
)	7! 7! 7! 7!	(7!)4
В примере 3 было существенно, что ящики можно отличить друг от друга (например, они покрашены в разные цвета).
Пример 4. Сколькими способами можно положить 28 различных открыток в 4 одинаковых конверта так, чтобы в каждом конверте лежало по 7 открыток?
Решение. Сначала пометим конверты цифрами 1, 2, 3, 4. Тогда согласно примеру 3 число различных раскладок равно Р(7, 7, 7, 7). После этого сотрём пометки. Теперь конверты можно произвольно переставлять друг с другом, не меняя результата раскладки (ведь они теперь неотличимы друг от друга). Так как число различных перестановок четырёх конвертов равно Р4 = 4!, то число различных раскладок уменьшается в 4! раз, и потому оно равно
Tl^7’ 7’ 7’ 7>= nW’
246
Замечание. Ясно, что число различных раскладок является целым.
Поэтому 4!(7',)т
— целое число. Таким же образом доказывается, что при
(тп)!
любых натуральных т и п число	челое-
Заметим теперь, что так как с*= = Р(т ’ k’ k}' то формулу бинома Ньютона можно записать следующим образом:
(х + а)т = ^Р(т - k, k)xm как.	(2)
* = о
Такая запись обобщается на случай большего числа слагаемых в скобке. Именно для любых k и t верна формула
(xi + х2 + ••• + х,)* =	kt)xi' ... х^,	(3)
где сумма распространяется на все числовые кортежи (&1; ... kt) из неотрицательных целых чисел такие, что ki + ... + kt = k.
Формула (3) доказывается так же, как формула бинома Ньютона: записывают выражение (xj + ... + xt)k в виде произведения k множителей, раскрывают скобки без обозначения степени и изменения порядка множителей, доказывают, что при этом получились все кортежи длиной k из букв хи ..., х(, и выводят отсюда, что коэффициент при х*' ... хк‘ равен P(klt ..., kt). Мы опускаем детали этого рассуждения.
Пример 5. Раскроем скобки в выражении (а + b + с)3.
Решение. Ответ имеет вид
(а + Ь + с)3 = ZP(fei, k2,	,
где сумма распространена на все кортежи (klt k2, k3) такие, что (fei + k2 + k3) = 3. Ими являются кортежи (3, 0, 0), (0, 3, 0), (0, 0, 3), (2, 1, 0), (2, О, 1), (1, 2, 0), (1, 0, 2), (0, 1, 2), (0, 2, 1), (1, 1, 1).
Так как
Qf
Р(0, 0, 3) = Р(0, 3, 0) = Р(3, 0, 0) = 0,^3! = 1,
Р(2, 1, 0) = Р(2, 0, 1) = Р(1, 2, 0) = Р(1, 0, 2) = Р(0, 1, 2) =
= Р(0, 2, 1) =	= 3,
P(i, 1, D= nflii -6, то
(а + b + с)3 = а3 + Ь3 + с3 + За2Ь + ЗаЬ2 + За2с 4- Зас2 + + ЗЬ2с + ЗЬс2 + баЬс.
247
Пример 6. Докажем, что сумма всех чисел Р(А1( kt), для которых + ... + kt = k, равна £*.
Решение. Положим в формуле (3) хг = х2 = ... = xt = 1. Получаем
t* = SP(fe1; ..., kt),	(4)
где k1 + ... + kt = k.
Упражнения
441.	Сколько слов можно получить, переставляя буквы слова «парабола»? слова «математика»? слова «метаморфоза»?
442.	Сколькими способами можно расставить шахматные фигуры (короля, ферзя, две ладьи, двух слонов и двух коней) на первой горизонтали шахматной доски?
443.	У мамы было 2 яблока, 3 груши и 4 апельсина. Каждый день она давала ребёнку по одному фрукту. Сколькими способами она могла это сделать?
444.	Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?
445.	Сколькими способами можно переставить буквы слова «огород», чтобы три буквы «о» не шли подряд?
446.	Сколькими способами можно переставить буквы слова «обороноспособность», чтобы две буквы «о» не шли подряд?
447.	Найдите число членов разложения:
1)	(а + Ъ + с)3;	2) (а + b + с + d)4.
448.	Найдите наибольший коэффициент в разложении:
1)	(а + Ъ + с)10;	2) (а + b + с + d)n.
449.	Найдите коэффициент при х4 в разложении (1 + 2х + Зх2)10.
450.	Найдите коэффициент при хк в разложении
(1 + х + ... + х"1)2.
451.	Найдите сумму различных четырёхзначных чисел, получаемых при всевозможных перестановках цифр 1, 1, 4, 4. То же самое для цифр 0, 0, 4, 4.
7.	Сочетания с повторениями. В заключение рассмотрим так называемые сочетания с повторениями. Пусть имеются предметы т видов и из них составляется набор, содержащий k элементов. Два таких набора считаются одинаковыми в том и только в том случае, когда они имеют одинаковый состав. Такие наборы назовём сочетаниями с повторениями из т элементов по k. Число сочетаний с повторениями из т элементов по k обозначим С„.
Задача 1. Найдём число сочетаний с повторениями из т элементов по k.
Решение. Каждый состав сочетания задаётся кортежем (kit k2, ..., kn), состоящим из неотрицательных целых чисел, где
248
т. е.
k} показывает количество элементов первого вида, k2 — второго, ...., km — т-го. Таким образом, С‘ равно количеству числовых кортежей (Аь ..., km) длины т, для которых + k2 + ... + km - k (как указывалось, здесь все k. — неотрицательные целые числа).
Итак, надо решить следующую задачу.
Задача 1'. Найдём количество тех числовых кортежей (fei, ..., km) длины т, для которых ky + k2 + ... + km = k.
Решение. Будем кодировать каждый кортеж (klt ..., km) кортежем, составленным из единиц и нулей. С этой целью заменим в кортеже каждое число kt последовательностью из kj единиц (если k, = 0, то единицы не пишутся), а каждую запятую нулём. Получится кортеж из ki + ... + km = k единиц и т - 1 нуля (запятых в кортеже (klt ..., km) на 1 меньше, чем чисел). Например, кортеж (4, 1, О, 2) кодируется так: (1, 1, 1, 1, 0, 1, 0, 0, 1, 1). Обратно, каждому кортежу, составленному из k единиц и т — 1 нуля, соответствует числовой кортеж (kit ..., km) такой, что kr + ... + + kn - k. Поэтому искомое число кортежей вида (klt ..., km) равно числу кортежей из k единиц и т - 1 нуля. По формуле перестановок с повторениями число таких кортежей равно P(fe, т - 1), ";<?-• Но это число равно С*+т_4. k\(m - 1)!
Итак, мы доказали равенство
С— k _ flk т —	+ т - 1 •
Пример 1. Сколько наборов из 7 пирожных можно составить, если в продаже имеются 4 сорта пирожных?
Решение. Искомое число равно С74, т. е. С’ + 41. Но
Р? — рз _ 10-9-8 _ 120 Сю _ С10 - 1.2-3
Итак, можно составить 120 наборов.
Пример 2. Сколькими способами можно разложить k одинаковых шаров по т различным ящикам?
Решение. Различные способы раскладки различаются лишь числом шаров, попавших в каждый ящик. Значит, число таких способов равно С£, т. е. С* + т_1.
У пражнения
452.	В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нём 12 открыток? 8 открыток? Сколькими способами можно купить 8 различных открыток?
453.	Сколько существует треугольников, длины сторон которых независимо выбираются из следующих значений: 4, 5, 6, 7 см?
249
454.	Сколько можно построить различных прямоугольных параллелепипедов, длины рёбер которых выражаются натуральными числами от 1 до 10?
Задачи к главе 5
(Некоторые задачи имеют повышенную трудность)
455.	Сколькими способами можно отобрать несколько фруктов из семи яблок, четырёх лимонов и девяти апельсинов (мы считаем, что фрукты одного вида неразличимы)?
456.	Сколько слов, содержащих не менее чем одну букву, можно составить из двух букв «А», пяти букв «Б» и девяти букв «В»?
457.	20 различных деталей раскладывают в три ящика, причём в первый ящик кладут 3 детали, во второй — 5 деталей, а в третий — все остальные детали. Сколькими способами это можно сделать?
458.	Сколько пятибуквенных слов, каждое из которых состоит из трёх согласных и двух гласных, можно составить из букв слова «уравнение»?
459.	20 пассажиров собираются совершить поездку в поезде. В кассе есть 12 билетов на нижние полки и 8 — на верхние. При этом 4 пассажира не желают ехать внизу, а 5 пассажиров — наверху. Сколькими способами их можно разместить в поезде, если: 1) порядок размещения пассажиров по местам как внизу, так и наверху не учитывается; 2) порядок размещения учитывается и внизу, и наверху; 3) учитывается только порядок размещения пассажиров внизу?
460.	Сколько шестизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9, если каждое число должно состоять из трёх чётных и трёх нечётных цифр, причём никакие две цифры в нём не повторяются?
461.	В лаборатории работают 8 физиков и 10 химиков. Надо создать рабочие группы по трём темам. В первую группу должны войти 4 физика, во вторую — 5 химиков, а третья должна состоять из трёх человек, которые могут быть как физиками, так и химиками. Сколькими способами можно создать такие группы?
462.	В течение десяти недель школьники должны написать 10 контрольных работ по 9 предметам, в том числе 2 по математике. Сколькими способами можно составить расписание этих работ так, чтобы контрольные работы по математике не шли друг за другом?
463.	У филателиста есть 8 разных марок на космическую тему и 10 разных марок на спортивную тему. Сколькими способами он может наклеить 3 марки первого вида и 3 марки второго вида в альбом на 6 пронумерованных мест?
464.	Сейф открывается при помощи цифрового кода, циферблат которого состоит из 100 клавиш с числами, расположенными по окружности. Для того чтобы открыть сейф, необходимо нажать какие-то 3 клавиши, причём известно, что между любыми двумя искомыми клавишами располагаются не менее 10 клавиш. Сколько комбинаций из трёх клавиш необходимо перепробовать, чтобы заведомо открыть сейф, если: 1) порядок нажатия клавиш несуществен; 2) этот порядок существен?
250
465.	В мастерской по изготовлению ключей есть 12 типов заготовок для ключей. Из каждой заготовки можно сделать ключ, вырезав выступы в пяти определённых местах, причём на первом месте величина выступа может принимать 2 значения, а на остальных — 3 значения. Сколько различных ключей может изготовить мастерская?
466.	Две команды А и Б играют серию матчей по волейболу до четырёх побед одной из них (ничьих в волейболе нет). Сколько различных серий таких матчей может быть?
467.	Сколько среди километровых столбов 0|999, 11998, 2|997, ..., 999|0 таких, что на них лишь две различные цифры?
468.	Найдите максимальное число шахматных королей, которое можно поставить на обычную доску так, чтобы они не били друг друга. Решите такую же задачу для доски с т вертикалями и п горизонталями.
469.	Какое наименьшее число шахматных слонов надо поставить на обычную доску так, чтобы они держали под боем каждое поле доски и каждый слон был защищён другими?
470.	Расставьте на шахматной доске наименьшее число ладей так, чтобы каждое поле доски было бито по крайней мере два раза. Решите задачу в двух вариантах: считая, что ладья не бьёт полей, заслонённых от неё другими ладьями, и считая, что она бьёт такие поля.
471.	Какое наибольшее количество дамок можно поставить на чёрные поля шахматной доски так, чтобы каждую дамку могла побить хотя бы одна из остальных дамок?
472.	Из числа 1234567891011...9899100 вычеркните 100 цифр так, чтобы оставшееся число было наибольшим.
473.	В шести секторах круга расставлено 6 шашек, по одной в каждом секторе. Одним ходом разрешается любые две шашки передвинуть в соседние секторы так, что одна движется по часовой стрелке, а другая — против часовой стрелки. Можно ли собрать такими ходами все шашки в одном секторе?
474.	Даны 20 различных натуральных чисел, меньших 70. Докажите, что среди попарных разностей этих чисел есть 4 одинаковые.
475.	Из двухсот чисел 1, 2, 3, ..., 200 выбрали одно число, меньшее 16, и ещё 99 других чисел. Докажите, что среди выбранных 100 чисел есть два, из которых одно делится на другое.
476.	Докажите, что из 981 числа, каждое из которых не превосходит 1958, можно выбрать три числа такие, что сумма двух из них равна третьему.
477.	Докажите, что 77 телефонов нельзя соединить друг с другом так, чтобы каждый был соединён ровно с 15 другими.
478.	Докажите, что 20 взвешиваниями без гирь нельзя упорядочить по массе 10 предметов.
479.	Сколькими способами можно представить число 1000000 в виде произведения трёх множителей, если разложения, отличающиеся порядком множителей, считаются различными?
480.	Сколькими способами можно разложить 19 различных предметов по 5 ящикам так, чтобы в 4 ящика легли по 4 предмета, а в оставшийся — 3 предмета?
251
481.	Сколькими способами можно разложить 3 марки по 20 копеек и 10 марок по 10 копеек в 4 пакета разных цветов? Решите эту же задачу, если пакеты неразличимы.
482.	Сколькими способами можно выбрать из п различных предметов нечётное число предметов?
483.	Сколькими способами можно переставить буквы слова «Юпитер», чтобы гласные шли в алфавитном порядке?
484.	Сколькими способами можно переставить буквы слова «перешеек», чтобы 4 буквы «е» не шли подряд?
485.	Сколькими способами можно переставить буквы слова «параллелизм», чтобы не менялся порядок гласных букв?
486.	Сколькими способами можно переставить буквы слова «пастух», чтобы между двумя гласными буквами были две согласные?
487.	Сколькими способами можно переставить буквы слова «огород», чтобы никакие две буквы «о» не стояли рядом?
488.	Сколькими способами можно переставить буквы слова «космос», чтобы две одинаковые буквы не стояли рядом?
489.	Сколькими способами можно расставить 10 букв «р» и 10 букв «п», чтобы для любого k < 20 среди первых k букв было не меньше букв «п», чем «р»?
490.	Сколькими способами можно расставить 20 белых шашек на шахматной доске так, чтобы расположение было симметрично относительно центра доски? Решите ту же задачу при условии, что шашки ставятся лишь на чёрные поля.
1.	Введение. События в материальном мире можно разбить на три категории — достоверные, невозможные и случайные. Например, если подбросить игральную кость, то достоверно, что число выпавших очков будет натуральным числом, невозможно чтобы это число равнялось 7, и возможно, что оно будет равно 5. Однако при одних бросках это число будет равно 5, а при других будут выпадать другие значения очков: 1, 2, 3, 4 или 6.
Потребности практики привели математиков к изучению случайных событий. Например, при организации телефонной связи в некотором районе нужно знать число вызовов в каждый момент времени, а оно случайным образом изменяется с течением времени. При стрельбе из артиллерийского орудия надо знать число снарядов, попавших в цель, а попадание в цель является случайным событием.
На первый взгляд может показаться, что в задачах о случайных событиях ничего нельзя сказать об их исходе. И действительно, если бросить кость лишь один раз, то с одинаковой вероятностью можно ожидать выпадения 1, 2, 3, 4, 5 или 6 очков. Но при многократном повторении этого опыта оказывается, что одни исходы будут появляться чаще, а другие — реже. Например, если бросить игральную кость 1200 раз, то очень маловероятно, что всё время будет выпадать одно очко. Гораздо вероятнее, что значения 1, 2, 3, 4, 5 и 6 будут появляться примерно с одной и той же частотой.
Раздел математики, изучающий закономерности случайных событий, называют теорией вероятностей. Эта теория имеет дело не с отдельными событиями, а с результатом проведения достаточно большого числа испытаний, т. е. с закономерностями массовых случайных явлений. По определению, приведённому в БСЭ, теория вероятностей есть математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким-либо образом с первыми.
253
В повседневной жизни мы часто пользуемся словами «вероятность», «шанс» и т. д. «К вечеру, вероятно, пойдёт дождь», «Вероятнее всего, мы поедем в воскресенье за город», «Это совершенно невероятно», «Много шансов, что я успешно напишу контрольную работу» и т. д. — все эти выражения как-то оценивают вероятность того, что произойдёт некоторое случайное событие. Однако, чтобы можно было применять к оценке вероятностей математические методы, надо дать этому понятию строгое определение. Мы сделаем это позднее, а сейчас приведём цитату из энциклопедии, дающую представление о том, что такое вероятность.
«Вероятность математическая — числовая характеристика степени возможности появления какого-либо определённого события в тех или иных определённых, могущих повторяться неограниченное число раз условиях».
Нашей задачей является превратить это описание понятия вероятности в точное математическое определение и выяснить, как связана вероятность с частотой появления данного события в длинной серии испытаний.
Упражнения
491.	Приведите примеры: 1) достоверных событий; 2) невозможных событий; 3) случайных событий.
492.	Что вероятнее — появление герба при бросании монеты или появление нечётного числа очков при бросании игральной кости?
493.	Что вероятнее при бросании двух монет — выпадение обеих цифр или цифры и герба?
494.	Что вероятнее получить при делении домино между 4 игроками — все «дубли» или же все кости с «шестёрками»?
495.	Проведите следующий эксперимент: бросьте 50 раз две игральные кости и запишите сумму для каждого броска. Какая сумма появилась чаще всего? Какая — реже всего? Какое число очков появилось чаще: 3 или 12?
496.	Из мешка с 33 жетонами, на которых написаны русские буквы, вытаскивают один за другим 4 жетона. Сколько раз, по вашему мнению, нужно повторить этот эксперимент, чтобы из этих букв получилось слово «барс»? Во сколько раз будет меньше число необходимых экспериментов, если 4 жетона вытаскивают сразу (т. е. порядок их появления несуществен)?
497.	Что вероятнее — угадать 6 номеров из 49 или 5 номеров из 36?
498.	При 10 бросаниях правильной монеты выпадал герб. Что вероятнее при следующем броске — выпадение цифры или герба?
2. Вероятностное пространство. Основным понятием, с которым мы будем иметь дело в дальнейшем, является понятие опыта, или испытания. Этому понятию нельзя дать математическое определение, однако ясно, что значат слова «подбросим
254
монету и посмотрим, упала она вверх гербом или цифрой» или «включить электрическую лампочку и поглядеть, через какое время она перегорит». Для нас будет существенно лишь то, что данное испытание может иметь различные исходы. При этом для простоты будем рассматривать лишь случаи, когда множество U этих исходов конечно: U = {Х1( ..., Хп}. С каждым опытом можно связать различные множества исходов. Важно лишь то, что при каждом испытании происходит один и только один исход.
Пример 1. При бросании игральной кости возможны следующие множества исходов:
1)	{Ai, А2, А3, А4, А5, А6}, где Ай означает выпадение k очков;
2)	{Во, BJ, где Во — выпадение чётного числа очков, а Вх — выпадение нечётного числа очков;
3)	{С15 С2}, где Cj состоит в том, что число выпавших очков меньше или равно 4, а С2 — что это число больше или равно 5.
В то же время в этом опыте не являются множествами исходов:
4)	множество {А1; А2}, так как А] и А2 не исчерпывают всех возможных исходов;
5)	множество {Во, С\}, так как при выпадении, например, двух очков одновременно происходят Во и Си а мы условились, что может произойти лишь один исход.
При многократном повторении опыта одни его исходы могут происходить чаще, а другие — реже. Например, если монета изогнута, то может случиться, что герб выпадает вдвое чаще, чем цифра. Мы будем говорить в этом случае, что вероятность выпадения герба вдвое больше, чем вероятность выпадения цифры. Чтобы выразить вероятность каждого исхода числом, надо выбрать «единицу измерения». Для этого условимся считать, что сумма вероятностей всех исходов равна 1. Тогда каждому исходу Xk будет соответствовать неотрицательное число pk — вероятность этого исхода, причём выполняется равенство рг + ... + рп = 1.
Одним из важных вопросов теории вероятностей является то, откуда берутся значения вероятностей исходов испытаний, ведь вероятности всех остальных событий мы будем получать, опираясь именно на эти вероятности. Здесь возможны два случая:
а)	по каким-либо соображениям симметрии мы считаем все элементарные исходы равновозможными, в этом случае имеем Pi = Р2 - ••• = рп, а так как pi + р2 + ... + рп - 1, то все равны р„ - —, 1 < k < п; г п
255
б)	вероятности р15 .р„ исходов Хь Хп определены предварительным проведением серии опытов, в этом случае за рк принимают относительную частоту случаев, в которых произошло элементарное событие Хк (т. е. отношение числа mk таких случаев к общему числу М проведённых испытаний).
Подход а) называется классической, схемой теории вероятностей, а подход б) — статистическим подходом. Например, если после проверки 1000 деталей оказалось, что среди них 3 бракованные, то принимают, что вероятность брака равна 0,003, или же 0,3%. В статистике изучается вопрос: какое число испытаний нужно произвести, чтобы полученные статистическим путём вероятности были достаточно надёжными?
Введём следующее определение.
Определение. Вероятностным пространством называют конечное множество U = {Хи ..., Х„}, каждому элементу Хк которого поставлено в соответствие неотрицательное число рк, причём сумма этих чисел равна 1.
Вероятностное пространство можно обозначить так: (Хь ... ..., ХП; р^ ..., р„). Но в дальнейшем для краткости вместо этого будем писать (U, Р), где U = {Хп ..., Х„}> Р = \р4, ..., рп}.
Приме Р 2. Если монета симметрична, то выпадение герба или цифры равновероятно. В этом случае вероятностное пространство состоит из двух исходов Г и Ц, каждому из которых сопоставлена вероятность, равная
Пример 3. Если кость симметрична, то вероятностное пространство можно выбрать так: {А, А2, А3, А4, Аь, Ае} (см. пример 1), где каждый исход Ah имеет вероятность g.
Сложнее вопрос о построении вероятностного пространства при бросании двух монет. Здесь можно выбрать пространство событий А2.0, -Au, А0.2, где А2,о означает двукратное выпадение герба, А0.2 — двукратное выпадение цифры, аАц — то, что один раз выпал герб и один раз цифра. Однако эти события не являются равновероятными. Чтобы обнаружить это, возьмём две монеты: 5-рублёвую и 2-рублёвую. Ясно, что выпадение цифры или герба на каждой из этих монет никак не зависит от того, какой исход имело бросание другой монеты. А это значит, что равновероятными являются не исходы А2.о, А1Д, Ао.2, а исходы ГГ, ГЦ, ЦГ, ЦЦ, каждый из которых имеет вероятность -j. Вероятности же событий А2,о> -Au, Ао,2 неодинаковы. Так как Л20 совпадает с ГГ, А0,2 — с ЦЦ,
256
причём вероятности этих событий равны —, то на долю события
остаётся вероятность 1 -	Значит, в этом случае
вероятностное пространство состоит из исходов А2,о, А1Д, Ао,2 с 111
вероятностями —,	и — соответственно.
Упражнения
499.	Укажите некоторые множества исходов для следующих испытаний: 1) производится выстрел по мишени, представляющей собой круг, разделённый на 10 концентрических частей, которые занумерованы числами 1, 2, 3, ..., 10;
2)	проводится турнирный футбольный матч между двумя командами;
3)	наудачу извлекается одна кость из полного комплекта костей домино;
4)	пять раз подбрасывается монета.
500.	На десяти жетонах выбиты числа 1, 2, 3, ..., 10. Наудачу извлекается один жетон. В каких случаях указаны все возможные исходы испытания:
1)	чётное, нечётное;
2)	чётное, не делится на 3;
3)	простое, составное;
4)	не более трёх, не менее четырёх?
501.	Для испытания, состоящего в пятикратном бросании монеты, запишите все возможные исходы, если учитываются: 1) результат каждого броска;
2)	число выпадений герба;
3)	какой стороной вверх монета большее число раз падала.
502.	В каких из следующих примеров указаны все возможные исходы испытания:
1)	выигрыш, проигрыш в шахматной партии;
2)	выигрыш, проигрыш встречи по волейболу;
3)	выпадение (в указанном порядке) герба — герба, герба — цифры, цифры — цифры при двукратном подбрасывании монеты?
503.	Образуют ли события «на обеих монетах выпала цифра», «на обеих монетах выпал герб» множество исходов при бросании двух монет? Какое событие надо добавить к этим двум, чтобы получилось полное множество исходов?
504.	Образуют ли следующие события множество исходов при двух выстрелах по мишени: «ни одного попадания», «одно попадание», «нет промаха», «есть хоть одно попадание»?
505.	Образуют ли множество исходов следующие события при вынимании одной косточки домино: «вынута кость 0:0», «вынута кость 6:6», «сумма очков на вынутой кости — натуральное число, которое не больше чем 11»?
506.	Приведите пример опыта с тремя исходами.
507.	Приведите пример опыта с тремя попарно несовместными событиями, которые не образуют множества исходов опыта.
257
508.	Приведите пример опыта, в котором есть такие четыре события, что в результате опыта одно из них обязательно происходит, но они не образуют множества исходов этого опыта.
509.	Монета искривлена, и потому вероятность выпадения цифры втрое больше вероятности выпадения герба. Чему равны эти вероятности?
510.	Игральная кость налита свинцом, в результате чего вероятность выпадения каждого числа очков пропорциональна этому числу. Найдите указанные вероятности и вероятностное пространство. Решите задачу, если вероятность выпадения любого числа очков обратно пропорциональна этому числу.
511.	Вероятность выигрыша партии в шахматы мастером А у перворазрядника В втрое больше вероятности того, что партия кончится вничью, а вероятность ничейного исхода вдвое больше, чем проигрыша мастера. Найдите вероятностное пространство для этого испытания.
512.	Задаёт ли следующая таблица вероятностное пространство?
Исход	Х1	х2	х3	х4
Вероятность	0,2	0,42	0,28	0,3
513. Вероятностное пространство задано следующей таблицей:
Исход	Х1	Х2	х3	х4
Вероятность	0,2	0,1	0,5	0,2
Во сколько раз исход х3 вероятнее исхода х2? Какие исходы равновероятны?
514.	Для следующих испытаний укажите множества равновероятных исходов:
1)	бросаются (правильные) монета и игральная кость;
2)	пять раз бросается монета;
3)	из мешка с 33 жетонами, на которых написаны буквы русского алфавита, один за другим извлекаются пять жетонов;
4)	то же испытание, но жетон после извлечения и записи возвращается в мешок;
5)	то же испытание, что в случае 3, но жетоны после извлечения расставляются в алфавитном порядке;
6)	правильный тетраэдр, куб и правильный октаэдр, грани которых помечены цифрами, бросают на плоскость;
7)	в розыгрыше первенства участвуют 18 команд, которые случайным образом разбиваются на две группы по 9 команд в каждой.
3. Вероятность событий. С бросанием игральной кости связаны не только исходы А1; А2, А3, А4, А&, As из примера 1 п. 2, но и иные события, например событие X — «число выпавших очков является простым числом» или событие Y — «число выпавших очков больше чем 3, но меньше чем 6» и т. д. Каждое из этих событий выполняется при тех или иных исходах испытания и не выполняется при других. Тем самым каждому такому событию соответствует некоторое подмножество множества U исходов.
258
Например, для события X это множество состоит из исходов А2, А3 и А5, а для события У оно состоит из исходов А4, А;>.
Введём следующее определение.
Определение 1. Событием при данном испытании называется любое подмножество X множества U исходов.
В дальнейшем, говоря об исходах, из которых состоит событие X, мы будем говорить, что они благоприятствуют этому событию. Про остальные же исходы будем говорить, что они не благоприятствуют событию X.
Определение 2. Вероятностью события X называют сумму вероятностей исходов, благоприятствующих этому событию.
Пример 1. Найдём вероятности событий X и У, указанных выше.
Решение. Событие X состоит из трёх элементарных исходов
А2, А3, А5. Вероятность каждого из них равна поэтому вероят-
13	1
ность события X равна 3 • g = g = Событие У состоит из двух исходов А| и А5, и его вероятность равна 2-^ = 4.
О о
Событие, состоящее в том, что выпало простое число очков и это число больше чем 2, но меньше чем 5, происходит лишь при исходе А3, и его вероятность равна
Пример 2. Выясним, что вероятнее выбросить при метании двух костей — 7 очков или 8 очков.
Решение. Трудность этой задачи состоит в правильном выборе множества исходов. Чтобы сделать правильный выбор, будем бросать кости по очереди и записывать получившиеся исходы. При бросании первой кости возможны 6 исходов, которые мы обозначим Аь А2, А3, А4, А5, Ав. Все эти исходы равновероятны. Равновероятны и исходы Вь В2, В3, В4, В5, В6 при бросании второй кости. Так как кости не скреплены друг с другом, то каждая пара исходов (А,, Вк), где 1 < у < 6, 1 < & < 6, имеет одну и ту же вероятность. А так как число таких пар по правилу произведения равно 36, то вероятность каждого исхода (А;, В*) равна
о О
Теперь осталось подсчитать число исходов, благоприятных выпадению 7 очков и 8 очков. 7 очков выпадают при шести исходах: (Ai, В6), (А2, В5), (А3, В4), (А4, В3), (А5, В2), (А6, BJ, а 8 очков — при пяти исходах: (А2, В6), (А3, В5), (А4, В4), (А5, В3), (Ав, В2). В первом случае имеем вероятность 6 •	а во втором —
259
1	5
36 = 36’ Значит, вероятность выбросить 7 очков больше, чем вероятность выбросить 8 очков.
При решении этой задачи мы использовали интуитивное понятие независимости двух испытаний. Позднее мы уточним это понятие, а пока что отметим лишь, что если одно испытание имеет равновероятные исходы Аг, ..., Ат, а второе — равновероятные исходы В1( В2, ..., Вп, то независимость этих испытаний означает, что все пары исходов (Ау, Bk) равновероятны, а потому вероятность появления каждой пары (Ау, Bk) равна
Примером независимых испытаний является извлечение из мешка помеченных жетонов при условии, что вынутый жетон после записи его пометки возвращается обратно. Иначе обстоит дело, если вынутый жетон обратно не возвращается.
Пример 3. В мешке лежат 33 жетона, помеченные буквами русского алфавита. Из него извлекают жетоны и записывают соответствующие буквы, причём вынутые жетоны обратно не возвращают. Какова вероятность того, что при этом получится слово «око»? Слово «ар»?
Решение. Ошибочно было бы решать задачу так: вероятность извлечения любой буквы равна поэтому вероятность сложить оо
слово «око» равна вероятность сложить слово «ар» равна оо	оо
Это было бы верно, если бы последовательные извлечения жетонов из мешка были независимы друг от друга. Но так как жетоны обратно в мешок не возвращаются, то, вынув в первый раз букву «о», мы уже не получим её при третьем извлечении. Поэтому вероятность получить слово «око» равна нулю. Чтобы найти вероят
ность получения слова «ар», заметим, что при двух извлечениях букв получаются всевозможные размещения без повторений из 33 букв по две, причём очевидно, что любые два таких размещения равновероятны. Так как общее число этих размещений равно А|3 = 33 • 32 = 1056, то вероятность сложить слово «ар» равна 1^6’
Этот пример показывает, что при решении многих задач теории вероятностей оказываются полезными формулы комбинаторики — при определённых условиях у нас с равной вероятностью получаются размещения с повторениями (если, например, жетоны извлекаются и потом возвращаются обратно), размещения без повторений (если жетоны не возвращаются обратно), перестановки
260
с повторениями или без повторений, сочетания и т. д. Долгое время комбинаторику вообще рассматривали как вспомогательную дисциплину для теории вероятностей, лишь теперь она приобрела самостоятельное значение.
Пример 4. Из мешка с 33 жетонами, помеченными буквами русского алфавита, вынимают 6 жетонов и располагают их в порядке извлечения. Какова вероятность получить слово «Москва», если: 1) жетоны после извлечения возвращаются обратно; 2) жетоны после извлечения обратно не возвращаются?
Решение. В случае 1 множество равновероятных исходов испытания состоит из всех размещений с повторениями из 33 элементов по 6. Их число равно А33 = 33е. Поэтому искомая вероятность равна ЗЗ-6. В случае 2 множество равновероятных исходов состоит из всех размещений без повторений из 33 элементов по 6. Их число равно А33 = 33 • 32  31  30 • 29 • 28, и потому искомая вероятность равна 33 . 32 . 31 130.29 . 28~
Пример 5. Из квадратиков с буквами сложили слово «Миссисипи», после чего эти квадратики положили в мешок и перемешали. Какова вероятность, что после поочерёдного извлечения квадратиков из мешка получится то же самое слово?
Решение. В данном случае равновероятными исходами являются появления любых перестановок с повторениями из одной буквы «м», 4 букв «и», 3 букв «с» и одной буквы «п». Число та-9!
ких перестановок равно Р(1, 4, 3, 1) =	4,	= 2520. Поэтому
вероятность получения слова «Миссисипи» равна
Пример 6. В мешке лежат 5 жетонов, помеченных буквами «а», «б», «в», «г» и «д». Из него 4 раза извлекают жетон, который после записи его буквы возвращается обратно. Какова вероятность, что при этом ни одна буква не повторится дважды?
Решение. В этом случае множество равновероятных исходов состоит из всех размещений с повторениями из 5 элементов по 4. Оно содержит = 54 = 625 размещений. Благоприятными являются при этом размещения без повторений, число которых равно
А| - 5 - 4 • 3 • 2 - 120. Значит, вероятность равна = 0,192. ozo
Пример 7. При тех же условиях найдём вероятность того, что в полученной записи никакие две соседние буквы не будут одинаковыми.
261
Решение. Здесь надо сначала найти число размещений с повторениями из 5 букв по 4, в которых нет одинаковых соседних букв. В каждом таком размещении первую букву можно выбрать 5 способами, а каждую следующую букву — 4 способами (не повторяя предыдущую). Значит, по правилу произведения число благоприятных комбинаций равно 5 • 4 • 4 • 4 - 320, а искомая
320 вероятность равна = 0,512. oZ t>
Пример 8. Из мешка с 33 жетонами, на которых написаны буквы русского алфавита, извлекаются 4 жетона, которые располагаются в алфавитном порядке. Какова вероятность того, что при этом получится слово «винт»?
Решение. Так как жетоны располагаются в алфавитном порядке, то существенны лишь извлечённые буквы, а не порядок, в котором их извлекали. Поэтому общее число равновероятных исходов равно числу сочетаний без повторений из 33 букв по 4, „ „4	33 32 31 30 4ААОА о
т. е. Сзз = —1.2-3—4— = 40920. Значит, искомая вероятность
раВНа 40920'
П р и м е р 9. Карточки, на которых написаны буквы слова «обороноспособность», располагаются произвольным образом. Какова вероятность того, что при этом все 7 букв «о» идут подряд?
Решение. Очевидно, что существенно лишь расположение семи букв «о». Так как общее число карточек равно 18, то выбор ,	й	га 18!
семи мест для буквы «о» может быть сделан С[8 = ц, способами. Благоприятны выборы, при которых все выбранные места идут подряд. Но группа из 7 букв «о» может занимать лишь 12 различных положений среди остальных 11 букв (в самом начале, между первой и второй, ..., в самом конце). Отсюда следует, что искомая вероятность равна
12 _ 7! • 11! 12	1
CJ8 18!	2652'
Пример 10. Из мешка с 33 жетонами, на которых написаны буквы русского алфавита, извлекают 4 раза жетоны, причём каждый жетон после извлечения и записи изображённой на нём буквы возвращается в мешок. Какова вероятность, что из полученных таким путём букв можно будет сложить слово «март»? Слово «мама»?
Решение. Множество всех равновозможных исходов состоит из размещений с повторениями из 33 букв по 4, и число этих
262
исходов равно ЗЗ4. Благоприятны исходы, при которых получаются в любом порядке буквы «м», «а», «р», «т». Так как из этих 4 букв можно составить 4! = 24 перестановки, то искомая вероят-
ность равна -^Ц-. А для того чтобы можно было составить слово 33
«мама», надо дважды вынуть букву «м» и дважды — букву «а». 4!
Так как из этих букв можно составить лишь Р(2, 2) = 2! 2! ~ ® пеРе"
л	6
становок, то вероятность получается в 4 раза меньше: ^7.
Упражнения
515.	Будут ли события равновероятными:
1)	«выпал герб» и «выпала цифра» при броске монеты;
2)	«выпал герб» и «выпала цифра» при броске неправильной (например, вогнутой) монеты;
3)	«промах» и «попадание» при выстреле отличного стрелка;
4)	«выпало два герба» и «выпало две цифры» при броске двух монет;
5)	«выпало не менее трёх очков» и «выпало не более четырёх очков» при броске игральной кости;
6)	опыт: вынимается косточка домино из полного набора в 28 косточек; событие А — «вынута кость, на которой есть 6», событие В — «вынута кость, на которой есть пусто»?
516.	Для броска игральной кости вычислите вероятности следующих событий:
1)	«выпало два очка»;
2)	«выпало пять очков»;
3)	«выпало чётное число очков»;
4)	«выпало простое число очков»;
5)	«число выпавших очков кратно трём».
517.	Бросили две монеты. Какова вероятность того, что на одной монете выпал герб, а на другой — цифра?
518.	Бросаются две игральные кости. Найдите вероятности событий:
1)	сумма выпавших очков равна 2, 3, ..., 12. Полученные результаты изобразите на координатной плоскости точками, у которых абсцисса равна сумме очков, а ордината — вероятности этой суммы;
2)	разность выпавших очков равна 0, 1, ..., 5;
3)	сумма выпавших очков больше их произведения.
519.	Из пяти отрезков длиной 1, 3, 5, 7 и 9 наудачу выбирают три. Какова вероятность того, что из них можно построить треугольник?
520.	Куб, все грани которого окрашены, распилен на 1000 равных кубиков. Найдите вероятность того, что наудачу взятый кубик имеет две окрашенные грани.
521.	Какова вероятность того, что в январе наудачу выбранного года окажется пять воскресений?
522.	На шести одинаковых карточках написаны буквы «А», «В», «К», «М», «О», «С». Карточки раскладываются наугад в ряд. Какова вероятность того, что получится слово «Москва»?
263
523.	Слово «агава» разрезали на буквы и их выложили наудачу в ряд. Какова вероятность опять получить это же слово?
524.	Слово «лилии» разрезали на буквы и их выложили наудачу в ряд. Какова вероятность опять получить это же слово?
525.	Слово «молния» разрезали на буквы и выложили наудачу четыре из них в ряд. Какова вероятность получить слово «миля»?
526.	В ящике лежат 20 одинаковых на ощупь шаров: 12 белых и 8 чёрных. Какова вероятность вынуть наудачу: 1) белый шар; 2) чёрный шар; 3) два разноцветных шара?
527.	В ящике лежат 20 одинаковых на ощупь шаров: 12 белых и 8 чёрных. Из ящика вынули наудачу восемь шаров. Чему равна вероятность того, что: 1) ровно три из них чёрных; 2) чёрных шаров вынули не более трёх?
528.	В ящике лежат 13 зелёных, 10 красных и 7 синих одинаковых на ощупь шаров. Наудачу вынимают 8 шаров. Чему равна вероятность того, что вынули: 1) 3 зелёных, 2 красных и 3 синих шара; 2) 1 зелёный, 5 красных и 2 синих шара?
529.	На карточках выписаны цифры 1, 2, 3, 4, 5, 6, 7, 8 и 9. Наугад берут четыре карточки и выкладывают их в ряд. Какова вероятность того, что: 1) получится чётное число; 2) получится число 1234?
530.	Из семи лотерейных билетов два выигрышных. Семь человек по очереди берут по билету (не возвращая его обратно). Чему равна вероятность выигрыша и зависит ли она от места в очереди?
531.	В периодически разыгрываемой лотерее из п билетов один выигрышный. Человек покупает по одному билету каждого выпуска. Какова вероятность того, что за т розыгрышей он хоть один раз выиграет?
532.	В ящике лежит 31 деталь первого типа и 6 деталей второго типа. Наудачу вынимают три детали. Чему равна вероятность того, что: 1) все три детали первого типа; 2) хотя бы одна из трёх вынутых деталей первого типа; 3) хоть одна из трёх вынутых деталей второго типа?
4. Алгебра событий. Вычислять вероятность события, строя каждый раз множество равновероятных исходов и подсчитывая число благоприятных исходов, довольно затруднительно. Поэтому для вычисления вероятностей пользуются правилами, позволяющими по известным вероятностям одних событий вычислять вероятности других событий, получаемых из них с помощью некоторых операций. Поскольку событиями мы назвали подмножества в множестве элементарных исходов испытания, а над множествами мы уже умеем выполнять операции объединения, пересечения, нахождения дополнения, то такие же операции будем выполнять над событиями.
Сейчас мы дадим определения указанным выше операциям над событиями. Поскольку теория вероятностей была создана задолго до теории множеств, в ней сложилась своя терминология и свои обозначения, которые нам придётся учитывать.
264
Определение 1. Событие, которому не благоприятен ни один из возможных исходов, называется невозможным. Событие же, которому благоприятен любой исход испытания, называется достоверным.
На языке теории множеств это означает, что невозможному событию отвечает пустое множество исходов, а достоверному — всё множество возможных исходов. Поэтому будем обозначать невозможное событие через 0, а достоверное через U.
Определение 2. Объединением событий X и Y называется событие, которому благоприятны все исходы, благоприятные хотя бы одному из событий X и У.
Например, при бросании двух костей объединением событий «выпало чётное число очков» и «выпало простое число очков» будет событие «число выпавших очков отлично от 9». В самом деле, среди натуральных чисел от 2 до 12 только число 9 не является ни чётным, ни простым. Если два зенитных орудия стреляют по одному и тому же самолёту, то объединением событий «первое орудие поразило самолёт» и «второе орудие поразило самолёт» будет «самолёт поражён».
Множество исходов испытания, благоприятных объединению событий X и У, является объединением множества исходов, благоприятных X, с множеством исходов, благоприятных У. Поэтому, как и в случае множеств, объединение событий X и У обозначают X U У. Применяют также название «сумма событий» и соответствующее обозначение X + У.
Определение 3. Пересечением событий X и У называют событие, которому благоприятны лишь исходы, одновременно благоприятные и для X, и для У. Его обозначают X П У или XY.
В разобранных выше примерах пересечениями будут события «при бросании двух костей выпало два очка» (единственным чётным простым числом является 2) и «самолёт поражён обоими зенитными орудиями».
Определение 4. Два события X и У называют несовместными, если их пересечением является невозможное событие (т. е. если никакой исход не может быть благоприятен обоим событиям одновременно).
Например, несовместны события «число выброшенных очков делится на 3» и «число выброшенных очков даёт при делении на 3 остаток 1».
Множества исходов, соответствующие двум несовместным событиям, имеют пустое пересечение: X П У = 0.
Если любые два события из множества {Xlt ..., Хл] несовместны, то эти события называют попарно несовместными. Например, попарно несовместны события «число очков делится на 3», «число
265
очков при делении на 3 даёт остаток 1» и Г\	«число очков даёт при делении на 3 оста-
f X \/ ¥	\ ток 2». А события X — «число очков —
I	J простое число», Y — «число очков —
чётное число» и Z — «выброшено более k	J 3 очков» несовместны в совокупности (их
пересечение пусто), но не являются по-
Рис. 80	парно несовместными, так как, например,
2 является и простым, и чётным числом, а 5 — простым числом, которое больше чем 3. Диаграмма Венна для множеств исходов этих событий имеет вид, изображённый на рисунке 80.
Если события Х1У ..., Хп попарно несовместны, причём их объединение совпадает с полным множеством исходов U, то любой исход благоприятен одному и только одному из этих событий. В этом случае множество всех элементарных исходов разбивается на попарно непересекающиеся подмножества исходов, благоприятных этим событиям. Поэтому можно выбрать другое множество элементарных исходов, а именно исходы Х1У ..., Хп. Если все элементарные исходы были равновероятны, а всем событиям Х1;..., Хп соответствует одно и то же число благоприятных элементарных исходов, то все элементарные исходы Хх, ..., Хп тоже равновероятны. Например, при бросании одной кости события «выпало чётное число очков» и «выпало нечётное число очков» образуют полную систему исходов, причём они равновероятны, поскольку первому из них соответствуют три случая выпадения очков (2, 4 и 6) и второму тоже три (1, 3 и 5).
Определение 5. События X и У называются противо наложными друг другу, если любой исход благоприятен одному и только одному из них.
Например, противоположны события «выпало чётное число очков» и «выпало нечётное число очков». События «число выпавших очков меньше чем 3» и «число выпавших очков больше чем 3» не являются противоположными, поскольку выпадение 3 очков не является благоприятным ни для одного из них. Не являются противоположными и события «сбитый самолёт поражён первым орудием» и «сбитый самолёт поражён вторым орудием», поскольку может случиться, что в самолёт попали оба выстрела.
В теории вероятностей принято обозначать событие, противоположное событию X, через X.
Определение 6. Событие У называется следствием события X, если любой исход, благоприятный событию X, благоприятен и событию У.
266
Например, выпадение при бросании трёх костей нечётного числа очков является следствием того, что число очков простое (любое простое число, которое не меньше чем 3, является нечётным). Событие «футбольная команда осталась в высшей лиге» является следствием события «футбольная команда выиграла чемпионат страны».
Если событие У является следствием события X, то множество исходов, благоприятных событию X, является подмножеством в множестве исходов, благоприятных У. Поэтому в таком случае пишут X с У.
Мы ввели основные операции над событиями. С их помощью можно определить другие операции. Например, событие X П У можно назвать разностью событий X и У (оно имеет место, если событие X произошло, а событие У нет).
Но в дальнейшем мы будем пользоваться лишь определёнными выше операциями. Поскольку операции над событиями сводятся к соответствующим операциям над множествами благоприятных им исходов, то все утверждения алгебры множеств, отмеченные в п. 2 § 1 главы 5, остаются справедливыми и для операций над событиями. Например, для событий верны равенства
ХПУ = X U У, X U У = X П У;
операции объединения и пересечения обладают свойствами коммутативности и ассоциативности, причём каждая из них дистрибутивна относительно второй операции. Для любого события X выполняются равенства
X = X, X П X = 0, X 0 0 = 0, X П У = Х;
XU 0 = X, хи и = и.
Кроме того, если У с X, то X П У = У, X и У = X, а потому X 0 X = = X и X = X.
Упражнения
533.	При каких условиях для событий А и В верны равенства:
1)	А = (Л и В)\В;	2) А и (В\С) = (A U В)\С;	3) А\В = А;
4)	А\В = 0;	5) А\В = В? Ответы поясните диаграммами Венна.
534.	Верно ли утверждение: если A U В = С, то А = С\В?
535.	Докажите утверждение: если В с А, то А = В U (А\В).
536.	Расшифруйте краткие записи:
1)	иД; 2) .П Д:	3) U А*.,; 4) П A2s + 1.
i=5	j = 2	k=1	s-o
537.	Запишите короче (как в № 536) события:
1)	A, U А2 U ... U А57;	3) As U A, U ... U А55;
2)	А, П А2 Я ... Я А47;	4) Ад Я Ад О ... Я Аю7.
267
538.	Бросили медную и серебряную монеты и рассмотрели события: А — «герб выпал на медной монете»;
В — «цифра выпала на медной монете»;
С — «герб выпал на серебряной монете»;
D — «цифра выпала на серебряной монете»;
М — «выпал хотя бы один герб»;
F — «выпала хотя бы одна цифра»;
G — «выпал один герб и одна цифра»;
Н — «невыпадение ни одного герба»;
К — «выпало два герба».
Каким событиям из этого списка равны события:
1)AUC; 2) А ПС; 3) М П В; 4) G и М; 5) G П М;
6)	В Л D; 7) М U К?
539.	По мишени производятся три выстрела. Рассматриваются события Ak — «попадание при k-тл выстреле», k = 1, 2, 3.
Пользуясь действиями и и Л над событиями А* и Ah, запишите события:
А — «все три попадания»;
В — «все три промаха»;
С — «хотя бы одно попадание»;
D — «хотя бы один промах»;
М — «не менее двух попаданий»;
F — «не более одного попадания»;
G — «попадание в мишень не раньше третьего выстрела»;
Н — «ровно одно попадание»;
К — «ровно два попадания».
540.	В поле наблюдения микроскопа находятся четыре клетки. За время наблюдения каждая из них может как разделиться, так и не разделиться. Рассматриваются события:
А — «разделилась ровно одна клетка»;
В — «разделилась хотя бы одна клетка»;
С — «разделились не менее двух клеток»;
D — «разделились ровно две клетки»;
М — «разделились ровно три клетки»;
F — «разделились все четыре клетки».
Запишите словами, в чём состоят события в 1—7 и верны ли равенства в 8, 9:
1)	F; 2) А и В; 3)АПВ; 4) В и С; 5) В О С;
6)	(D U М) U В; 7) В П F-, 8) В П F = С П F; 9) В П С = D.
541.	Назовите для указанных событий противоположные:
А — «выпало два герба», опыт: бросок двух монет;
В — «вынули белый шар», опыт: вынимают один шар из ящика, в котором лежат белые, красные и синие шары;
С — «три попадания», опыт: сделали три выстрела по мишени;
М — «не более двух попаданий», опыт: пять выстрелов по мишени;
D — «хотя бы одно попадание», опыт: пять выстрелов по мишени; F — «выигрыш Петрова», опыт: партия в шахматы Петров — Васин.
268
Рис. 81	Рис. 82
542.	На рисунках 81—84 изображены электрические схемы. Выключатели изображены кружками, в которых указан номер выключателя. Запишите через события А* — «выключатель с номером k включён» для каждой схемы события: 1) А — «ток идёт»; 2) А — «ток не идёт».
543.	Прибор состоит из двух блоков. Первый блок состоит из двух однотипных деталей и работает при исправности хотя бы одной из них. Второй блок состоит из трёх однотипных деталей и работает при исправности хотя бы двух из них. Весь прибор работает, если работают оба блока. Выразите через события Ак — «исправна k-я деталь первого блока», k = 1, 2, В„ — «исправна п-я деталь второго блока», п = 1, 2, 3 и АЛ, Вп события: А — «первый блок работает»;
В — «второй блок работает»;
С — «первый блок не работает»;
D — «второй блок не работает»;
Н — «прибор работает»;
К — «прибор не работает»;
М — «прибор не работает, но для того чтобы его исправить, до-
статочно заменить одну деталь».
544.	Прибор состоит из двух блоков. Первый блок состоит из четырёх одинаковых деталей и работает при исправности хотя бы двух из них. Второй блок состоит из пяти одинаковых деталей и работает при исправности хотя бы трёх из них. Весь прибор работает, если работают оба блока. Выразите через события Ак — «исправна k-я р&талъ первого блока» (k = 1, 2, 3, 4), Вп —_«исправна п-я деталь второго блока» (п = 1, 2, 3, 4, 5) и события Аг и Вп события А, В, С, D, указанные в № 543.
545.	Рассмотрим события А — «взятая наудачу деталь оказалась первого типа», В — «взятая наудачу деталь оказалась второго типа» и С — «взятая наудачу деталь оказалась третьего типа». Запишите словами, что представляют собой события:
1)	A U В; 2) A U В;
546. Докажите равенства:
1)	A U В = А П В;
2)	A U (А А В) = А;
3)	(A U В)\В = А\В;
3)	A U С; 4)AUBUC.
4)	A U В = (А\В) U (В\А) U (А А В);
5)	(А\В) U В = A U В;
6)	(A U В) А (С U В) = (А А С) U В.
269
547. При каких условиях справедливы равенства:
1)АиВ=АПВ;	3)AUA=A;
2) (A U В)\В = А;	4) А П А = А?
548. Упростите выражения:
1) (A U В) П (A U В);	3) A U (В\(А Л В)) U (С\(А Л С));
2) (A U В) П (В U С) П (С U А);	4) ((A U В) Л В) U (А Л (А Л В)).
5. Теоремы сложения. Приведём теперь теоремы, с помощью которых можно по вероятностям одних случайных событий вычислять вероятности других случайных событий, каким-либо образом связанных с первыми. Начнём с теорем, которые образуют группу с общим названием «теоремы сложения».
Теорема 1. Если события А и В несовместны, то
Р(А U В) = Р(А) + Р(В).	(1)
Доказательство. Обозначим исходы, благоприятные для события А, через аь ..., ат, а для события В — через ..., Ь„. Вероятности этих исходов обозначим соответственно через plt ... ..., рт и Qi, ..., qn. Тогда событию А и В благоприятны все исходы alt ..., ат, ..., bn. В силу того что события А и В несовместны, среди этих исходов нет повторяющихся. Поэтому вероятность события A U В равна сумме вероятностей этих исходов, т. е.
Р(А U В) = pi + ... + рт + qi + ... + q„.
Но Pi + ... + рт = Р(А), qi + ... + qn = Р(В), а потому
Р(А U В) = Р(А) + Р(В).
Теорема доказана.
Пример 1. Стрелок стреляет в мишень. Вероятность выбить 10 очков равна 0,3, а вероятность выбить 9 очков равна 0,6. Чему равна вероятность выбить не менее 9 очков?
Решение. Событие А «выбить не менее 9 очков» является объединением событий В — «выбить 10 очков» и С — «выбить 9 очков». При этом события В и С несовместны, так как нельзя одним выстрелом выбить сразу и 9, и 10 очков. Поэтому по теореме 1 имеем
Р(А) = Р(В) + Р(С) = 0,3 + 0,6 = 0,9.
Если события Аь ..., А„ попарно несовместны, то событие A] U ... U A„-i несовместно с событием А„. В самом деле,
(Ai U ... U А,.!) Л А„ = (А Л А„) U ... U (А„-! Л А„).
Но при s < п имеем А„ П А„ = 0, и потому (Ai U ... U An-j) Л А„ = 0. Пользуясь этим замечанием, получаем из теоремы 1 следствие.
270
Следствие. Если события Ai, А„ попарно несовместны, то вероятность объединения этих событий равна сумме их вероятностей:
Р(Аг U ... U А„) = Р(АД + ... + Р(АЯ).	(2)
Доказательство. Как было отмечено выше, события Aj U U ... U А„ ! и А„ несовместны, а потому по теореме 1 имеем
Р(АГ U ... U А„_! U А„) = Р(АХ U ... U А„^) + Р(А„).
Применяя это же рассуждение к первому слагаемому и продолжая далее, получаем после п - 1 шага, что
Р(АХ U ... U А„) = P(At) + ... + Р(А„).
Пример 2. В цехе работает несколько станков. Вероятность того, что за смену потребует наладки ровно один станок, равна 0,2. Вероятность того, что за смену потребуют наладки ровно два станка, равна 0,13. Вероятность того, что за смену потребуют наладки больше двух станков, равна 0,07. Какова вероятность того, что за смену придётся проводить наладку станков?
Решение. В этом примере опыт состоит в том, что прошла смена и отмечено, сколько станков за эту смену потребовало наладки. В этом опыте события: А — «за смену потребовал наладки ровно один станок», В — «за смену потребовали наладки ровно два станка» и С — «за смену потребовали наладки более двух станков» — несовместны. Нас же интересует вероятность события А и В и С. По теореме 1
Р(А U В U С) = Р(А) + Р(В) + Р(С) = 0,2 + 0,13 + 0,07 = 0,4.
Выведем теперь связь между вероятностями противоположных событий.
Теорема 2. Для любого события А имеем
Р(А) = 1 - Р(А).	_	(3)
Для доказательства вспомним, что A U А - U, P(U) - 1 и А А А = 0. Тогда по теореме 1 получаем
1 = P(U) = Р(А U А) = Р(А) + Р(А), откуда следует требуемая формула.
Пример 3. Берётся наудачу трёхзначное натуральное число от 100 до 999. Какова вероятность того, что хотя бы две его цифры совпадают?
Решение. Опыт здесь состоит в том, что наудачу выбирают натуральное число от 100 до 999 и смотрят, есть ли у него совпадающие цифры. События «взяли наудачу число N» (N = 100, 101, ..., 999) равновероятны (в этом смысл слова «наудачу»)
271
и образуют множество исходов этого опыта. Число исходов п = 900. Нас интересует событие А — «у выбранного числа совпадают хотя бы две цифры». Проще, однако, подсчитать вероятность противоположного события А — «у выбранного числа все цифры различны». Каждое такое число есть размещение без повторений из 10 цифр по 3, не имеющее первым элементом нуль. Следовательно, т = A3W -А* = 10 • 9 • 8 - 9 • 8 = 92 • 8
(из числа всех трёхэлементных размещений без повторений надо вычесть число тех, у которых на первом месте стоит нуль) и
™ - W - °-72-
Тогда по теореме 2 получаем Р(А) = 1 - Р(А) - 0,28.
В ряде случаев приходится вычислять вероятность объединения событий, которые могут быть совместными.
Теорема 3. Для любых двух событий справедливо равенство
Р(А U В) = Р(А) + Р(В) - Р(А А В).	(4)
Доказательство. Событие А состоит из компонент А А В и А Л В, а событие В — из компонент А И В и А Л В. Поэтому
A U В = (А А В) U (А А В) U (А А В) U (А А В) =
= (А А В) U (А А В) U (А А В),
и поскольку входящие в это разложение компоненты попарно не пересекаются, то
Р(А U В) = Р(А Л В) + Р(А А В) U Р(А А В).	(5)
С другой стороны, имеем Р(А) = Р(А Л В) + Р(А А В) и Р(В) -- Р(А А В) + Р(А А В), а потому Р(А) + Р(В) = 2Р(А А В) + + Р(А А В) + Р(А А В). Сравнивая эти равенства с (5), получаем доказываемую формулу (4).
Равенство (4) напоминает формулу (3) п. 2 § 2 главы 5 (оно может быть получено из той формулы в случае, когда вероятности элементарных исходов одинаковы). Аналогом отмеченной там же формулы перекрытий является равенство
Р(А, U ... U А„) = S(-l)*+1P(Aii А ... A AJ.	(6)
Здесь суммирование распространено на все комбинации событий Ац ..., Ап по одному, по два, по три и т. д., по п. В частности, при п = 3 имеем
Р(А U В U С) = Р(А) + Р(В) + Р(С) - Р(А А В) -
- Р(А А С) - Р(В А С) + Р(А А В А С).
272
Упражнения
549.	Стрелок попадает в десятку с вероятностью 0,05, в девятку с вероятностью 0,2, а в восьмёрку с вероятностью 0,6. Сделан один выстрел. Какова вероятность следующих событий: А — «выбито не менее восьми очков», В — «выбито более восьми очков»?
550.	Выведите формулу для Р(А U В U С) в общем случае.
551.	В день физкультурника Сизов пошёл на стадион. Можно было купить билет на футбол с вероятностью 0,3, или купить билет на баскетбол с вероятностью 0,4, или купить билет на волейбол с вероятностью 0,2. Какова вероятность того, что: 1) Сизов попал на соревнование; 2) Сизов попал на соревнование, в котором запрещена игра ногой?
552.	В мастерской работают три станка. За смену первый станок может потребовать наладки с вероятностью 0,15. Для второго станка эта вероятность равна 0,1, а для третьего станка — 0,12. Найдите вероятность того, что за смену хоть один станок потребует наладки, считая, что одновременно станки наладки потребовать не могут.
553.	Известны вероятности Р(А) и Р(А А В). Найдите Р(А А В).
§ 2. Независимые испытания
1. Независимые случайные события. Формула (4) п. 5 § 1 сводит отыскание вероятности объединения нескольких событий к отысканию вероятности пересечений различных событий. Последняя задача не имеет определённого решения: если А с: В, то А А В = А, и потому Р(А А В) = /’(А), а если А А В = 0, то Р(А А В) = 0. Возможны и различные промежуточные случаи. Однако есть случай, когда по заданным вероятностям событий А и В можно вычислить вероятность их пересечения, — это случай, когда данные два события независимы.
В п. 3 § 1 мы говорили о независимых испытаниях и отметили, что если первое испытание имеет т равновероятных исходов, а второе п равновероятных исходов, то любая пара исходов этих ис-
1	т->
пытании имеет одну и ту же вероятность Рассмотрим теперь два события А и В такие, что первому из них благоприятствуют k исходов первого испытания, а второму — I исходов второго испытания. Пусть для определённости это будут исходы аг, ..., ak и Ьг, Ь2, ..., bh Тогда событию А А В благоприятствуют все исходы (aj; bj) такие, что 1 < i < k, 1 < j < I. Их число по правилу произведения в комбинаторике равно kl. Поскольку каждый из этих исходов имеет вероятность то вероятность события kl
А А В равна Заметим теперь, что вероятность события А
273
равна —, вероятность события В равна -, а — - —  Прите	п тп тп
ходим к следующему выводу: в рассматриваемом примере независимость испытаний проявилась в том, что вероятность события А А В оказалась равной произведению вероятностей событий А и В:
Р(А А В) = Р(А)Р(В).
Обобщим теперь понятие независимости на более широкий класс событий.
Определение 1. События А и В из одного и того же вероятностного пространства называются независимыми, если выполняется равенство
Р(А А В) = Р(А)  Р(В).	(1)
Это равенство наверняка выполняется, если одно из событий А или В невозможно (обе части равенства (1) обращаются в нуль) или достоверно (если достоверно А, то обе части равенства (1) равны Р(В), поскольку в этом случае А А В = В и Р(А) - 1).
Пример 1. Докажем, что при бросании кости события А — «выпало чётное число очков» и В — «число выпавших очков делится на 3» являются независимыми.
Решение. Очевидно, что Р(А) = i, Р(В) = 4- Событие А Л В состоит в том, что число очков чётно и делится на 3, а потому оно равно 6. Его вероятность равна Так как	 i, события
А и В независимы.
Покажем, что если события А и В независимы, то независимы события А и В, а также события А и В, равно как и А и В.
В самом деле, по правилам алгебры множеств имеем (А Л В) U U (А А В) = А, причём А А В и А А В несовместны. Поэтому Р(А) = Р(А А В) -I- Р(А А В). Но в силу независимости событий А и В выполняется равенство Р(А А В) - Р(А)  Р(В), и потому
Р(А А В) = Р(А) - Р(А А В) = Р(А) - Р(А) • Р(В) = = Р(А)(1 - Р(В)).
Поскольку Р(В) = 1 - Р(В), то равенство (2) можно записать в виде
Р(А А В) = Р(А) • Р(В).
Значит, А и В независимы.
274
Аналогично доказывается независимость А и В. Повторно применяя проведённое выше рассуждение, получаем, что Р(А И В) = = Р(А) • Р(В), т. е. что и события А и В независимы.
Пусть события А и В независимы. Из формулы Р(А U В) = = Р(А) + Р(В) - Р(А А В) вытекает, что
Р(А U В) = Р(А) + Р(В) - Р(А) • Р(В).	(3)
Итак, при независимости событий А и В верно равенство (3).
Пример 2. Два зенитных орудия стреляют одновременно и независимо друг от друга по самолёту. Самолёт сбит, если в него попал хоть один снаряд. Какова вероятность сбить самолёт, если вероятность попадания первого орудия равна 0,8, а второго 0,75?
Решение. Обозначим через А событие «в самолёт попал снаряд первого орудия» и через В — «в самолёт попал снаряд второго орудия». Нам надо найти вероятность события A U В. В силу независимости этих двух событий можно воспользоваться формулой (3). Но Р(А) - 0,8, Р(В) = 0,75, и потому
Р(А U В) = 0,8 + 0,75 - 0,8 • 0,75 = 0,95.
Определим теперь понятие независимости для нескольких событий.
Определение 2. События А, В, ... называются независимыми в совокупности, если для любого подмножества этих событий вероятность их пересечения равна произведению их вероятностей.
Пример 3. Четыре охотника стреляют одновременно и независимо друг от друга по зайцу. Заяц подстрелен, если попал хотя бы один охотник. Какова вероятность подстрелить зайца, 29 если вероятность попадания для каждого охотника равна •'
Перенумеруем охотников и рассмотрим события Ak — «попадание k-ro охотника», k = 1, 2, 3, 4. Эти события по условию задачи 2
независимы и P(Ak) = ~ при любом k. Нас интересует вероятность О
события «заяц подстрелен», т. е. А} U А2 U А3 U А4:
Р(А, U А2 U Аа U А4) = 1 - Р(Д U А2 U А3 U А4) =
= 1 - Р(А, А А2 А А3 А А4) =
= 1 - Р(Л)  Р(А2)  Р(А3) • Р(А4) = 1 - (|)4= 1 -	= 0,988.
Здесь, как и раньше, мы воспользовались тем, что при замене независимых событий противоположными независимость событий не нарушается (докажите это самостоятельно).
275
Применённый при решении примера 3 приём перехода к противоположному событию очень полезен при вычислении вероятностей объединения независимых событий.
Пример 4. Событие А может произойти в опыте с вероятностью р. Опыт повторили независимым образом п раз. Какова вероятность того, что при этом событие А произойдёт хоть один раз?
Рассмотрим события Ак — «событие А произошло при й-м повторении опыта», k = 1, 2, ..., п. События А* независимы, так как опыты повторяются независимым образом. Р(Ак) = р для всех k. Нас интересует событие «опыт повторили независимым образом п
раз, и при этом событие А произошло хотя бы один раз» — U Ак.
k - 1
Заметив, что Ак независимы и что P(Ak) = 1 - р = q, получаем
Р( и А) = 1 - Р( и Ак) = 1 - Р( П А) = k = 1	k-1	k -1
= 1 - Р(А) • Р(А) • ...  Р(А) = 1-9".
Интересно отметить, что lim Р( U Ап) = lim (1 - qn) = 1 (посколь-п —> оо k — 1	п —> °о
ку 0 < q < 1), т. е. при достаточно большом числе повторений опыта событие А произойдёт почти наверняка (с вероятностью, как угодно близкой к 1) хоть один раз. Про события, которые происходят почти наверняка, принято говорить, что они практически достоверны.
Замечание. Из попарной независимости событий не следует их независимость в совокупности.
У пражнения
554.	Бросили монету и игральную кость. Покажите, что события «выпал герб» и «выпало чётное число очков» независимы.
555.	Из полного набора костей домино вынимается наудачу косточка и одновременно бросается игральная кость. Докажите независимость событий «число очков на косточке домино кратно трём (хоть одно)» и «на игральной кости выпало простое число очков».
556.	Два станка работают независимо друг от друга. Вероятность того, что первый станок проработает смену без наладки, равна 0,9, а второй — 0,8. Какова вероятность того, что: а) оба станка проработают смену без наладки; б) оба станка за смену потребуют наладки?
557.	События А и В независимы. Докажите, что независимы А и В.
558.	События А, В, С независимы. Докажите, что независимы тройки событий: а) А, В, С; б) А, В, С; в) А, В, С и т. п.
559.	Три стрелка независимо друг от друга стреляют по цели, каждый сделал по одному выстрелу. Вероятность попадания для первого
276
стрелка равна 0,8, для второго — 0,75, для третьего — 0,7. Какова вероятность: 1) хотя бы одного попадания; 2) ровно одного попадания; 3) ровно двух попаданий; 4) трёх попаданий? Какова вероятность, что все промахнулись?
560.	Могут ли быть два несовместных события независимыми?
561.	В мастерской работают три станка. За смену первый станок может потребовать наладки с вероятностью 0,15 (и после этого до конца смены наладки не потребуется). Для второго станка эта вероятность равна 0,1, а для третьего — 0,12. Какова вероятность, что хоть один станок за смену потребует наладки, если станки требуют наладки независимо друг от друга?
562.	Прибор, работающий в течение суток, состоит из трёх узлов, каждый из которых независимо друг от друга может за это время выйти из строя. Неисправность хотя бы одного узла приводит к отказу прибора. Вероятность безотказной работы в течение суток первого узла равна 0,9, второго — 0,95, третьего — 0,85. Найдите вероятность того, что в течение суток прибор будет работать безотказно.
563.	Завод изготавливает изделия, каждое из которых с вероятностью р имеет дефект. В цехе три контролёра. Попадание изделия на контроль к первому, второму или третьему контролёру равновероятно. Вероятность обнаружения дефекта (если он имеется) для fe-ro контролёра равна рк (k = 1, 2, 3). Если изделие не было забраковано в цехе, то оно попадает в ОТК завода, где дефект (если он имеется) обнаруживается с вероятностью р0. Найдите вероятности следующих событий:
А — «изделие будет забраковано»;
В — «изделие будет забраковано в цехе»;
С — «изделие будет забраковано в ОТК завода».
564.	Вычислительная машина состоит из п блоков. Надёжность (вероятность безотказной работы в течение времени Т) k-ro блока равна рк (k = 1, 2, ... п). Блоки выходят из строя независимо друг от друга. Какова надёжность машины?
2. Условная вероятность. Формула умножения. Получение добавочной информации может изменить значение вероятностей тех или иных исходов испытания. Например, если известно, что выпало нечётное число очков, то вероятность выпадения 5 очков,
, 1
которая до получения этой информации равнялась становится
- 1	с
равной -т, поскольку общее число возможных исходов уменьши-О
лось с шести (1, 2, 3, 4, 5, 6) до трёх (1, 3 и 5). Вероятность же выпадения 2 очков при получении этой информации становится равной нулю.
Получение некоторой информации о результате испытания означает, что вместо всего множества исходов U надо брать его часть,
277
которую мы обозначим через X. Если исход х не принадлежит X, то его вероятность обращается в нуль. Если же он принадлежит X, то его вероятность увеличивается. При этом ясно, что все вероятности таких исходов увеличиваются в одно и то же число раз, поскольку отношения их вероятностей не меняются при получении новой информации. Обозначим исходы, благоприятствующие событию X, через Х1; ..., Хк, а их вероятности — через р1; ..., рк, После получения новой информации эти вероятности станут равными числам Лр1; ..., '/.рк. Значение X легко определить из того, что сумма новых вероятностей должна равняться 1. Поэтому Xpi + ... + Хрк - 1, т. е. Л(/?! + ... + рк) = 1. Но pi + ... + рк = Р(Х), и потому X =
Мы доказали следующее утверждение.
Если известно, что произошло событие X, то вероятность любого исхода, не благоприятствующего этому событию, обращается в нуль, а исхода, благоприятствующего ему, умножается на
Р(Х)"
Рк Р(Х)'
Найдём теперь новую вероятность некоторого события А. Ему благоприятствуют исходы двух видов — благоприятствующие X и не благоприятствующие X. Как мы видели выше, если произошло событие X, то вероятности исходов первого вида умножаются 1
на D , а исходы второго типа получают нулевую вероятность. "(Л )
Но исходы первого вида составляют события А П X. Таким образом, мы доказали следующее утверждение.
Если известно, что произошло событие X, то вероятность
,	,	.	Р(А П X)
любого события А принимает новое значение: ——•
Определение. Число, выражающее вероятность события А при условии, что произошло событие X, называется условной вероятностью события А относительно события X и обозначается Р(А|Х).
Проведённые выше рассуждения показывают, что
Р(А\Х) = Р(р(х}Х)-	(!)
Из формулы (1) вытекает равенство
Р(А П X) = Р(Х)Р(А\Х),	(2)
называемое формулой умножения.
278
Меняя ролями А и X, получаем, что верно и равенство Р(А ПХ) = Р(А)Р(Х|А).
Сравним формулу (2) с формулой Р(А П X) = Р(Х)Р(А), верной для независимых событий. Видим, что для таких событий верно равенство Р(А|Х) = Р(А). Оно означает, что для независимых событий наступление одного из них не влияет на вероятность другого.
Пример 1. Пусть имеется а белых и b чёрных мешков, причём в каждом белом мешке лежит х красных и у синих шаров, а в каждом чёрном мешке — и красных и и синих шаров. Сначала случайным образом выбирают один мешок, а потом из него вынимают шар. Найдём вероятности Р(Б П К), Р(Ч А К), Р(Б А С) и Р(Ч А С).
Решение. Очевидно, что Р(Б) = д Р(Ч) = -и Р(К|Б) = хх+ у и Р(К|Ч) = ц~~. Далее, событие БАК состоит в том, что выбран белый мешок, а из него извлечён красный шар. По формуле умножения вероятность этого события равна
Р(Б А К) = Р(Б)Р(К|Б) =
Аналогично находим, что
PfTJ п тга	ь	и
а	+ ь	и + V
РШ п гч	а	У
ЛЬ А С) - а	+ ь	X + у
PfTT п	ъ	V
а	+ ь	и + V
Пример 2. Найдём в примере 1 вероятность вытащить в результате испытания красный шар.
Решение. Событие К — «вытащен красный шар» является объединением попарно непересекающихся событий Б А К и Ч А К. Поэтому по теореме сложения вероятностей имеем
Р(К) = Р(Б А К) + Р(Ч А К).
Но значения Р(Б А К) и Р(Ч А К) найдены выше. Отсюда получаем
а	х		+	ь	V
х	“ а + b х +	У		а + Ъ	и + и
Аналогично доказывается, что				
а	У		+	b	V
1	а + Ъ х +	У		а + Ь	и + V
279
Иными словами,
Р(К) = Р(Б)Р(К|Б) + Р(Ч)Р(К|Ч) и
Р(С) = Р(Б)Р(С|Б) + Р(Ч)Р(С|Ч).
Разобранный пример является частным случаем следующей общей теоремы, называемой теоремой о полной вероятности.
Теорема 1. Пусть вероятностное пространство U представлено в виде объединения попарно несовместных событий Х1; ..., Хп:
и = хг и ... и х„,	(3)
где Xt Г) X, = 0 при i / j. Тогда для любого события А верно равенство
Р(А) = Р(Хг)Р(А\Хг) + ... + Р(Х„)Р(А|Х„).	(4)
Доказательство. В силу дистрибутивности операции пересечения событий относительно объединения из (3) имеем
А = А Л U = А А (X! U ... U Х„) = (А Л XJ U ... U (А Л Х„).
При этом из X, Л Xj = 0 следует, что
(А Л X,) Л (А Л Xj) = А Л Xj Л Xj = 0.
Значит, событие А является объединением попарно несовместных событий А Л Хь ..., А Л Х„, и потому его вероятность по теореме сложения равна
Р(А) = Р(А Л XJ + ... + Р(А Л Х„).
Осталось заменить в этом равенстве по формуле (2) Р(А Л Хк) на Р(Х*)Р(А|ХЛ), чтобы получить (4).
Одной из форм формулы полной вероятности является равенство
р(х |да = _________Р(ХДР(А|ХД__________
(	р(Х1)р(А|Х1) + ... + р(Хл)Р(А|Хл)‘	W
Чтобы доказать его, достаточно заметить, что
Р(А Л ХД - P(Xk)P(A\Xk) - Р(А)Р(Х*|А), поэтому
,	_ Р(ХДР(А|ХД
Р(Хк\Л) - Р(А)
Если Хи ..., Х„ — попарно несовместные события, объединение которых совпадает со всем вероятностным пространством U, то
280
в этом равенстве можно заменить Р(А) по формуле полной вероятности и получить равенство (5).
Равенство (5) называют формулой Байеса. Она истолковывается следующим образом: если существуют попарно исключающие друг друга гипотезы Х1г Х„, охватывающие всевозможные случаи, и если известны вероятности события А при каждой из этих гипотез, то по формуле (5) можно найти вероятность справедливости гипотезы Хк при условии, что произошло событие А.
Пример 3. В магазин поступила партия электрических лампочек: 20% изготовлено заводом I, 30% — заводом II и 50% — заводом III. Для завода I вероятность выпуска бракованной лампочки равна 0,01, для завода II — 0,005 и для завода III — 0,006. Какова вероятность того, что взятая наудачу из партии лампочка окажется бракованной?
Нас интересует событие А — «взятая из партии лампочка бракованная». Рассмотрим три события: Xj — «взятая лампочка изготовлена заводом I», Х2 — «взятая лампочка изготовлена заводом II» и Х3 — «взятая лампочка изготовлена заводом III». Эти события попарно несовместны и Xj U Х2 U Х3 = U. Кроме того, в условии примера сказано, что Р(Х0 = 0,2, Р(Х2) = 0,3, Р(Х3) = 0,5, P(A|Xj) = 0,01, Р(А|Х2) = 0,005 и Р(А|Х3) = 0,006. Подставляя эти значения в формулу полной вероятности, получаем
Р(А) = 0,01 • 0,2 + 0,005 0,3 + 0,006  0,5 = 0,0065.
Замечание. Формула полной вероятности сохраняется, если вместо л	п
условия j^Xj = и выполнено условие А с U Xk.
Пример 4. В цеху стоят а ящиков с исправными деталями и Ъ ящиков с бракованными деталями. Среди исправных деталей р % отникелированы, а из числа бракованных никелированы лишь д% деталей (в каждом ящике). Вынутая наугад деталь оказалась никелированной. Какова вероятность, что она исправна?
Решение. Имеем события Xj — «деталь исправна» и Х2 — «деталь бракованная», а также событие А — «деталь отникелирована». Нам надо найти значение PIXjA). По условию имеем
™ = Ль- - Ль- Р,А'ХЛ  ife- ИА1 = W0-
Подставляя эти данные в формулу (5), получаем
а . _Р_
P(Xj |А) = -----a+±J£0--------.
а Р + b д
а + Ь 100 а + b 100
281
Значит, искомая вероятность равна	Например, если
а = 50, b = 3, р = 90, q = 5, то
Р(Х,|Л)= м ” ;'° 5
Если же а - Ь - 50, р - 75, q - 15, то
= 50.75 + 50 15 -°'833-
Упражнения
565.	Бросили игральную кость. Найдите условную вероятность того, что выпало простое число очков, при условии, что число выпавших очков нечётно.
566.	В ящике лежат 12 красных, 8 зелёных и 10 синих шаров, одинаковых на ощупь. Наудачу вынимается один шар. Какова вероятность того, что он красный, если известно, что он не синий?
567.	В ящике лежат 12 красных, 8 зелёных и 10 синих шаров, одинаковых на ощупь. Наудачу вынимаются два шара. Какова вероятность того, что: 1) они зелёные, если известно, что при этом не вынут синий шар; 2) вынутые шары разноцветные, если известно, что не вынут синий шар?
568.	В магазин поступили батарейки от трёх поставщиков: 40 % — от первого, 45% — от второго и 15% — от третьего. Известно, что у первого поставщика 80% батареек повышенной ёмкости, у второго — 70%, у третьего — 90%. Какова вероятность того, что наудачу вытащенная батарейка повышенной ёмкости?
569.	Детали на сборку попадают из трёх автоматов. Известно, что первый автомат даёт 0,3% брака, второй — 0,2%, третий — 0,4%. Найдите вероятность попадания на сборку бракованной детали, если из первого автомата поступило 1000 деталей, из второго — 2000 и из третьего — 2500.
570.	По самолёту производятся три выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором — 0,6, при третьем — 0,8. При одном попадании самолёт сбивается с вероятностью 0,3, при двух — с вероятностью 0,6 и при трёх сбивается наверняка. Какова вероятность сбить самолёт?
571.	При включении двигатель начинает работать с вероятностью р. Какова вероятность того, что: 1) двигатель начнёт работать со второго включения; 2) для запуска двигателя потребуется не более двух включений?
572.	Докажите, что условные вероятности события обладают основными свойствами вероятности события:
а)	0 < Р(А\В) < 1 при любых событиях А и В;
б)	если А П В = 0, то Р(А U В|С) + Р(А|С) + Р(В|С).
573.	Обобщите теорему умножения (теорема 1) на случай трёх, четырёх, .... k событий.
574.	Докажите, что если Р(А\В) > Р(А), то Р(В|А) > Р(В).
282
575.	В белом ящике лежат 12 красных и 6 синих одинаковых на ощупь шаров. В жёлтом ящике лежат 15 красных и 10 синих одинаковых на ощупь шаров. Бросается игральная кость. Если число выпавших очков кратно трём, то наудачу вынимают шар из белого ящика. Если число выпавших очков не кратно трём, то наудачу вынимают шар из жёлтого ящика. Какова вероятность вынуть красный шар?
576.	Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго — 0,03, для третьего — 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего в два раза меньше, чем второго. Определите вероятность того, что взятая наудачу деталь будет бракованной.
3. Формула Бернулли. Закон больших чисел. При введении понятия вероятности отмечалось, что если вероятность некоторого события А равна р, то вероятнее всего, что при повторении испытания много раз относительная частота благоприятных этому событию исходов будет мало отличаться от значения р. Это утверждение, называемое в теории вероятностей законом боль ших чисел, лежит в основе всех практических приложений этой теории — оно позволяет с помощью вычисленных вероятностей предсказывать частоту наступления данного события в длинной серии независимых испытаний.
Выведем формулу Бернулли, позволяющую вычислить вероятность того, что в серии из п независимых испытаний событие А, имеющее вероятность р, встретится т раз. Результат серии из п испытаний можно записать в виде кортежа из букв Аи А, имеющего длину п. Например, если проведено семь испытаний, причём событие А произошло во втором, третьем и пятом испытаниях, то запишем результат данной серии в виде ААААААА. Условие, что испытания данной серии независимы друг от друга, означает, что для вычисления вероятности данного исхода испытаний надо заменить в записи этой серии каждую букву А её вероятностью р, а каждую букву А — её вероятностью 1 - р и перемножить эти числа.
Пример 1. Проводится серия из 8 независимых испытаний. Событие А имеет вероятность р = 0,7. Чему равна вероятность того, что получится исход серии вида АААААААА?
Решение. Заменяем каждую букву А на 0,7, а каждую букву А на 1 - 0,7 = 0,3. Получаем произведение 0,7 • 0,7 • 0,3 • 0,7 х х 0,7  0,3 • 0,7 • 0,3, которое можно записать короче в виде 0,75 х х 0,33. Вычисляя, находим, что искомая вероятность равна 0,00453789 = 0,005.
283
Вообще если событие А имеет вероятность р, то вероятность появления конкретной серии из п испытаний, в которой это событие произошло т раз, равна pmqn~m, где q = 1 - р.
Докажем теперь следующую теорему.
Теорема 1. Пусть вероятность события А равна р, и пусть Ртп — вероятность того, что в серии из п независимых испытаний это событие произойдёт т раз. Тогда справедлива формула Бернулли
Ртп = C”pmq"-m.	(1)
Доказательство. Благоприятными сериями испытаний являются в данном случае те серии из п испытаний, в которых событие А произошло т раз. Каждая такая серия задаётся кортежем из т букв А и п - т букв А. Поэтому общее число таких серий равно Р(т, п - т), т. е. С™ (п. 6 § 3 главы 5). Поскольку, как было показано выше, вероятность каждой такой серии равна pmqn~m, а любые две различные серии несовместны, то равенство (1) доказано.
Приме Р 2. Какова вероятность того, что при десяти бросаниях игральной кости 3 очка выпадут ровно 2 раза?
Решение. Вероятность выпадения 3 очков при одном броске 1	15
равна -. Поэтому р =	? = с- Так как, кроме того, га = 10 и
о	о о
т = 2, то по формуле (1) имеем
р =Г2 (1У(5\8 _ 10 • 9 • 58
^2,10 Clo	1 • 2  610 ‘
Вычисления по формуле (1) при больших т и га затруднительны. В математике установлены приближённые формулы, позволяющие находить приближённые значения для Ртп и, что ещё важнее для
практики, суммы значений Ртп таких, что дробь (относительная
частота появления события А) лежит в данных границах.
По формуле Бернулли вероятность того, что в серии из 100 под-
/1 \100
брасываний монеты все 100 раз выпадет герб, равна 1-1 , т. е.
примерно 10~30. Не столь мала, но всё же ничтожна вероятность того, что цифра выпадет не более 10 раз. Наиболее вероятно, что число выпадений герба будет мало отличаться от 50.
Вообще при большом числе испытаний относительная частота появления события, как правило, мало отличается от вероятности этого события. Математическую формулировку этого качественного утверждения даёт принадлежащий Я. Бернулли закон больших чисел. Приведём его в уточнённой П. Л. Чебышевым форме.
284
Теорема 2. Пусть вероятность события А в испытании s равна р, и пусть проводятся серии, состоящие из п независимых повторений этого испытания. Через т обозначим число испытаний, в которых происходило событие А. Тогда для любого положительного числа а выполняется неравенство
р( И - р > а
I п
pg
а2п
Поясним смысл этого неравенства. Выражение
(2)
т
— равно отно-
сительной частоте события А в серии опытов, а — п
- р — откло-
нению этой относительной частоты от теоретического значения р.
Неравенство
> а означает, что отклонение оказалось
больше, чем а. Но при постоянном значении а с ростом п правая часть неравенства (2) стремится к нулю. Иными словами, серии, в которых отклонение экспериментальной частоты от теоретической велико, составляют малую долю всех возможных серий испытаний. Из доказанной теоремы вытекает утверждение, полученное Бернулли: в условиях теоремы при любом значении а > О имеем
lim Р\
П -А » I
> а = 0.
- - Р
п
— р
п
Для доказательства достаточно заметить, что lim = 0. л —»оо а п
Пример 3. Сколько достаточно провести опытов, чтобы из них получить вероятность события р ~ с точностью до 0,1 с вероятностью 0,9?
Для решения достаточно найти такое п, чтобы (см. нера-
pq
венство (2)) было выполнено неравенство q ^2fl < 0,1. А так как
q = 1 - р, то pq = р(1 - р) < и потому достаточно указать п, удо-
влетворяющее неравенству 4 q <0,1; отсюда п > 250.
Как видим, получение вероятности события из опыта даже с такой незначительной точностью требует большого числа экспериментов. Правда, более глубокие теоремы показывают, что можно ограничиться меньшим числом опытов.
285
Упражнения
577.	Разберите доказательство формулы Бернулли для частного случая п = 4, т = 1, выписывая полностью формулу (1).
578.	Какова вероятность того, что при 10 бросках игральной кости пять очков выпадут ровно: 1) три раза; 2) один раз?
579.	Какова вероятность того, что при 10 бросках игральной кости одно очко выпадет не более трёх раз?
580.	Какова вероятность того, что при 10 бросках игральной кости число очков, кратное трём, выпадет больше 2 раз, но меньше 5 раз?
581.	Что вероятнее — выиграть у равносильного противника (ничейный результат исключается): 1) три партии из четырёх или пять из восьми; 2) не менее трёх партий из четырёх или не менее пяти партий из восьми?
582.	В мастерской работают 6 моторов. Для каждого мотора вероятность перегрева к обеденному перерыву равна 0,8. Найдите вероятность того, что к обеденному перерыву: 1) перегреются ровно 4 мотора; 2) перегреются все моторы; 3) ни один мотор не перегреется.
583.	Вероятность появления события А в опыте равна 0,3. Опыт повторили независимым образом 5 раз. Какова вероятность того, что событие А появится не менее двух раз?
584,	В приборе стоят 6 одинаковых предохранителей. Для каждого из них вероятность испортиться после 1000 часов работы равна 0,4. Если испортилось не менее двух предохранителей, то прибор требует ремонта. Найдите вероятность того, что прибор потребует ремонта после 1000 часов работы, если предохранители портятся независимо друг от друга.
585.	Событие А происходит с вероятностью 1/4. Опыт повторили независимым образом 8 раз. Найдите вероятность того, что событие А при этом произойдёт: 1) не более двух раз; 2) хотя бы два раза; 3) более четырёх раз; 4) хоть один раз, но не более трёх раз.
586.	Сколько надо сделать опытов, чтобы оценку р - ~ с точностью до 0,01 получить с вероятностью 0,95?
587.	Какова вероятность равенства р ~ ~ с точностью до 0,1 при 100 опытах?
588.	Равенство Р ~ получено при 40 опытах. Оцените приблизительно его точность с вероятностью 0,9.
4. Геометрические вероятности. Многие практические задачи приводят к вопросам теории вероятностей, которые не укладываются в разобранную выше схему конечного числа попарно несовместных исходов испытаний. Пусть, например, стержень наудачу разламывается на три части. Какова вероятность того, что из получившихся отрезков можно будет построить треугольник?
286
В этой задаче мы имеем бесконечное А	В
множество исходов, так как разлом может	„
,	тт	Рис. 85
попасть на любую точку стержня. Поэтому
данное выше определение вероятности события как суммы вероятностей исходов не годится. Мы будем пользоваться иным определением вероятности, которое назовём геометрическим. Разберём следующую модель. Пусть на отрезок АВ бросают наудачу точку. Назовём вероятностью попадания этой точки на часть этого отрезка (рис. 85) отношение длины этой части к длине всего отрезка (если часть состоит из нескольких кусков, надо сложить длины этих кусков). Это естественно, так как чем больше цель, тем вероятнее её поразить. Оказывается, что свойства введённого таким образом понятия вероятности очень похожи на рассмотренные в предыдущих пунктах. Именно справедливы следующие утверждения.
1. Для любой части отрезка значение вероятности является неотрицательным числом, не превосходящим 1. Для самого отрезка значение вероятности равно 1.
2. Если части X и Y не имеют общих точек (несовместны), то Р(Х U У) = Р(Х) + Р(У).
На основе этих двух утверждений для геометрических вероятностей можно определить те же понятия, что и в случае конечного вероятностного пространства, доказать аналоги формул сложения и умножения вероятностей, формулу Байеса и т. д.
Вместо отрезка АВ можно взять некоторую геометрическую фигуру, имеющую конечную площадь, и считать вероятностью попасть в часть X этой фигуры отношение площадей указанной части и всей фигуры. Можно брать и объёмы тел в трёхмерном пространстве. Все эти случаи, как и многие другие, охватываются аксиоматическим определением понятия вероятности, на котором мы не будем останавливаться.
Поясним сказанное на решении задачи о разламывании наудачу отрезка, о которой говорилось в начале пункта.
Пример 1. На отрезок длины 1 бросают наудачу две точки. Они разбивают отрезок на три отрезка. Какова вероятность, что из полученных трёх отрезков можно сложить треугольник?
Решение. Заданный отрезок рассматриваем как отрезок [О; 1] числовой прямой. Тогда наудачу брошенные точки имеют координаты — числа х и у, принадлежащие отрезку [О; 1]. Но любую пару чисел можно рассматривать как координаты точки на плоскости. Поскольку 0<х<1и0<у<1, то эти точки (х; у) наудачу брошены в квадрат со стороной 1. Посмотрим теперь, какую фигуру образуют точки, координаты которых удовлетворяют условию примера.
287
Для того чтобы из трёх отрезков можно было построить треугольник, необходимо и достаточно, чтобы длины этих отрезков удовлетворяли неравенству треугольника. При х < у получаем
х < (у - х) + (1 - у), у - х < х + (1 - у), 1 - у < х + (у - х), что после преобразований даёт систему неравенств
х < 0,5, у < х + 0,5, 0,5 < у,
X < у, которая на плоскости определяет треугольник (рис. 86, а). При х > у аналогично получается система неравенств х > 0,5,
У < 0,5, у > х - 0,5, х > у, которая на плоскости определяет ещё один треугольник (рис. 86, б). Общая площадь фигур, заштрихованных на рисунке 86, а, б, равна 0,25. Следовательно, вероятность построить треугольник равна 0,25.
Пример 2 (игла Бюффона). На плоскости (бесконечной) проведено семейство параллельных прямых (тоже бесконечное). Расстояние между соседними прямыми равно I. На эту плоскость бросается наудачу отрезок длины I. Какова вероятность, что отрезок пересекается хоть с одной из прямых семейства?
Решение. Обозначим через у расстояние от верхнего конца отрезка до ближайшей снизу прямой (рис. 87). Проведём луч с началом в верхней (левой) точке отрезка, параллельный прямым семейства и идущий направо. Обозначим через х угол между этим
288
лучом и отрезком. Мы получили пару чисел, удовлетворяющих неравенствам ОСх<л, 0<yCZ. Точка (х; у) с такими координатами наудачу брошена в прямоугольник (рис. 88). Для того чтобы отрезок пересекался хотя бы с одной из прямых семейства, необходимо и достаточно выполнение неравенства у < Zsinx, которым на рисунке 88 определена заштрихованная фигура. Подсчитаем её площадь:
Так как площадь прямоугольника (в который наудачу брошена точка) S = nZ, то искомая в примере вероятность ^=^=^=2= 0,6366.
О nl п
Упражнения
589.	Докажите, что геометрические вероятности обладают основными свойствами вероятности события:
I.	0 < Р(А) < 1 для любого события А;
II.	P(U) = 1, Р(0) = 0;
III.	Р(А U В) = Р(А) + Р(В), если А П В = 0.
590.	Двое договорились о встрече на следующих условиях: каждый приходит в указанное место независимо друг от друга и наудачу в любой момент времени от 13 :00 до 14:00. Придя, ожидает не более получаса, а уходит не позднее 14:00. 1) Какова вероятность того, что они встретятся? 2) Время ожидания сокращено до 20 мин. Какова вероятность встречи?
591.	Решите задачу об игле Бюффона, если на плоскости проведено второе семейство прямых, перпендикулярных первым.
592.	Противотанковые мины поставлены на прямой через 15 м. Танк шириной 3 м идёт перпендикулярно этой прямой. Какова вероятность, что он подорвётся?
593.	На окружности радиусом R зафиксирована точка А. Какова вероятность того, что случайно брошенная на окружность точка В такова, что АВ = Р?
594.	В окружность наудачу вписан треугольник. Какова вероятность, что он остроугольный?
289
595.	В окружность вписан квадрат. В круг, ограниченный этой окружностью, наудачу бросается точка. Какова вероятность, что она попадёт в квадрат?
596.	В окружность вписан правильный треугольник. В круг, ограниченный этой окружностью, наудачу бросается точка. Какова вероятность, что точка попадёт в треугольник?
597.	В окружность наудачу вписывается треугольник. Какова вероятность, что он: 1) прямоугольный; 2) равнобедренный; 3) тупоугольный?
598.	У квадратного трёхчлена х2 4- рх + q коэффициенты р и q выбраны наудачу из отрезка [-1; 1]. Какова вероятность, что получившийся квадратный трёхчлен имеет действительные корни?
599.	В шар вписан куб. Точка наудачу бросается в шар. Какова вероятность, что она попадёт в куб?
600.	В шар вписана правильная треугольная пирамида. Точка наудачу бросается в шар. Какова вероятность, что она попадёт в пирамиду?
Задачи к главе 6
601.	В последовательности чисел 1, 2, ..., п отмечено число k. Найти вероятность того, что из двух наудачу выбранных чисел этой последовательности одно меньше k, а другое больше.
602.	Бросается п игральных костей. Найти вероятность того, что выпадет n-t единиц, п2 двоек, ..., п6 шестёрок.
603.	Последовательность чисел 1, 2, ..., 4Л’ разбивается наудачу на две равные группы. Найти вероятность того, что: 1) в каждой группе будет поровну чётных и нечётных чисел; 2) все числа, кратные N, окажутся в первой группе; 3) числа, кратные N, поделятся поровну между группами.
604.	Сколько раз нужно бросить игральную кость, чтобы появление шести очков имело вероятность: 1) большую 0,5; 2) большую 0,8; 3) большую 0,9?
605.	Сколько раз нужно повторить испытание, чтобы с вероятностью, не меньшей г, утверждать, что хотя бы один раз произойдёт событие А, вероятность которого в каждом испытании равна р?
606.	Лаборант многократно измеряет длину образца. Вероятность ошибки при считывании показаний равна р. Какое наименьшее число измерений надо сделать, чтобы с вероятностью, большей а, можно было утверждать, что хотя бы одно из измерений неверно?
607.	Детали упакованы в ящики, по 100 штук в каждый. В каждом ящике лежит по одной бракованной детали. Контролёр проверяет детали, выбирая наудачу по одной в каждом из 100 ящиков. Какова вероятность того, что хотя бы одна из извлечённых деталей бракованная?
608.	При каком минимальном числе людей в группе вероятность того, что хотя бы два из них родились в один и тот же день, не меньше 0,5 (годы рождения могут не совпадать)?
609.	Вам захотелось найти человека, день рождения которого совпадает с вашим. Сколько незнакомцев вам придётся опросить, чтобы вероятность встречи такого человека была бы не меньше 0,5?
290
610.	Двое вслепую поочерёдно вынимают (без возвращения) шары из ящика, содержащего М белых и N - М чёрных шаров (отличающихся только цветом). Какова вероятность того, что первым белый шар вытащит начинающий? Рассмотреть случаи: a) N = 3, М = 1; б) N = 4, М = 1; в) = 6, М = 2.
611.	Докажите, что если А П В Л С с D, то Р(А) + Р(В) + Р(С) < 2 + P(D).
612.	Каждую секунду с вероятностью р независимо от других моментов времени по дороге проезжает автомашина. Для перехода дороги пешеходу необходимо 3 с. Какова вероятность того, что подошедший к дороге пешеход будет ожидать возможности перехода: а) 3 с; б) 4 с; в) 5 с?
613.	Производится стрельба по некоторой цели, вероятность попадания в которую при одном выстреле равна 0,2. Стрельба прекращается при первом попадании. Найти вероятность того, что будет произведено ровно 6 выстрелов.
614.	В приборе 14 узлов двух типов: 6 — первого и 8 — второго. Вероятность выхода из строя в течение времени Т для каждого узла первого типа равна 0,002, для второго — 0,004. Найти вероятность выхода из строя прибора в результате выхода из строя хотя бы одного узла.
615*. Найти вероятность того, что наудачу взятое целое число окажется простым, предполагая, что вероятность того, что оно кратно п, 1 равна —.
616.	В условиях предыдущей задачи найти вероятность того, что два наугад взятых натуральных числа окажутся взаимно просты.
617.	На 10 карточках написаны числа: 3, 3, 3, 4, 4, 5, 5, 6, 6, 6. Вынимаются наугад одна за другой две карточки. Число, написанное на первой карточке, берётся за числитель, на второй — за знаменатель дроби. Какова вероятность того, что полученная дробь правильная?
618.	Два шахматиста А и В играют матч на следующих условиях: А должен набрать для победы 12 очков (выигрыш — одно очко), В — 6 очков, ничьи не считаются. Обычно А вдвое чаще выигрывает у В, если считать только результативные партии (так что вероятность выигрыша А у В в одной партии можно считать равной 2/3). Игру прекратили после того, как А набрал 8 очков, а В — 4 очка, и победу решили присудить тому, у кого вероятность на окончательный выигрыш больше. Кто победитель?
619.	А и В играют ряд партий на следующих условиях: за выигрыш засчитывается 1 очко; победителем считается тот, кто первым обгонит противника на 2 очка. Найти вероятность победы для А и для В, если А выигрывает отдельную партию с вероятностью а, В — с вероятностью р < а, а + Р = 1.
620.	Решить задачу 619, если победителем считается тот, кто первым выиграет две партии подряд.
621.	Технический контроль проверяет взятые наугад детали из партии, содержащей, как указано отправителем, а деталей первого типа и b деталей второго типа. Предполагается, что от указанного состава есть отклонения: количество деталей первого типа, возможно, равно
291
a - 2, или a - 1, или а, или a + 1 с вероятностями, соответственно равными pi, р2, Рз, Pi- Проверка первых т деталей, т < Ь, обнаружила, что все они второго типа. С какой вероятностью технический контроль может утверждать, что деталей второго типа больше Ъ? Рассмотреть случай: а = 5, Ь = 25, рг = 0,1, р2 = 0,2, р3 = 0,6, р4 = 0,1; 1) проверено 40% всех деталей; 2) проверено 50% всех деталей.
622.	Кусок проволоки длиной 20 см согнули под углом 90° в наудачу выбранном месте. После этого, перегнув проволоку ещё в двух местах (не ломая её), сделали прямоугольную рамку. Какова вероятность того, что площадь полученного прямоугольника не превосходит 21 см2?
623.	Найти вероятность того, что из трёх наудачу взятых отрезков, длина каждого из которых не превосходит а, можно составить треугольник.
624.	Круглая монета диаметром 25 мм наудачу бросается на стол, который расчерчен на квадратные клетки со стороной 50 мм, толщина разбивающих линий 5 мм. Какова вероятность того, что монета не пересечётся с разбивающими линиями?
625.	В круге наудачу проводится хорда. Какова вероятность того, что её длина больше радиуса?
626.	Какой толщины должна быть монета (правильная), чтобы вероятность падения на ребро равнялась 1/3?
627.	Неоднородный прямой круговой цилиндр случайно бросается на горизонтальную плоскость. Радиус его основания равен г, его центр тяжести расположен на оси симметрии на расстояниях а и b, b > а, от его оснований. Найти вероятность падения цилиндра на одно и на второе основание.
628.	Вдоль канала шириной L идёт судно с постоянной скоростью щ. Паром курсирует без остановок поперёк канала с постоянной скоростью v2 и гудит. Этот гудок слышен на расстоянии d < L. Найти вероятность того, что судно услышит этот гудок, если пересечение курсов возможно в любой точке канала.
629.	Некоторое событие может произойти в любой из дней недели с одинаковыми вероятностями. Найти вероятность того, что это событие произойдёт 12 раз подряд только по вторникам и четвергам. Согласуется ли это с предположением о равновероятности осуществления события в любой день недели?
630.	В условиях задачи 629 событие произошло 12 раз и ни разу не произошло в воскресенье. Согласуется ли это с предположением о равновероятности осуществления события в любой день недели?
631.	На справочную телефонную станцию в течение определённого часа дня поступает в среднем п вызовов. Найти вероятность того, что: 1) в течение промежутка времени t (некоторая доля часа) поступит ровно т вызовов; 2) в течение этого промежутка t поступит хотя бы один вызов; 3) две телефонистки с одинаковой нагрузкой (у каждой в среднем п вызовов в час) окажутся перегруженными вызовами в течение небольшого промежутка времени t, если каждая из них может в этот промежуток обслужить не более k вызовов.
ПРИЛОЖЕНИЕ
РАБОТЫ ДЛЯ САМОПРОВЕРКИ
Контрольная работа № 1
1.	Найдите решение дифференциального уравнения у' = ху2, удовлетворяющее начальному условию у(1) = -2.
2.	Материальная точка массы иг = 1 движется по прямой под действием силы, которая меняется по закону F(t) = 8 - 12t. Найдите закон движения точки х = x(t), если в момент времени t = 0 её координата равна 0 и скорость равна 1. В какой момент времени скорость точки будет максимальной?
3.	Функция у - f(x) удовлетворяет дифференциальному уравнению у" + 9у - 0 и начальным условиям /(0) = 3, /'(0) - 9.
Найдите её наименьшее значение на отрезке —; — .
ла гт	г	(%Х ПРИ Х <
4	.Для функции /(х) = <	найдите первообраз-
Isinx при х > 0
ную F, график которой проходит через точку М\ —; 1
Постройте график первообразной.
Контрольная работа № 2
2
1.	Вычислите интеграл ^х2л/1 + x3dx.
о
1
2.	Решите неравенство fytz3 + z2)dt > 0.
о
3.	Вычислите площадь фигуры, ограниченной графиками функций у = х2 - 6х + 4 и у = 4 - х2.
4°. Напишите уравнение касательной, параллельной оси абсцисс,
X
к графику функции /(х) = ^(sin * - s^n х е
о
Зл. 7л 2 ’ 4
Контрольная работа № 3
1.	Решите уравнение (х2 - 4) log3(l - х2 - Зх) = 0.
2.	Решите неравенство 63х~2 < 22i35i“8.
3.	Решите уравнение log2(2* + 1) + log^3 = 31og23 - х.
Т
293
4.	Решите неравенство log2sinx - 31ogsinx 2 > 2.
5.	Решите уравнение log2cosx = 31og4sin2x.
6°. Сравните числа log7 8 и log6 7.
Контрольная работа № 4
4 тт ~	In (1 + tg 2х)
1.	Найдите предел пт————-------
х —> о In (1 + sin Зх)
2.	Найдите наибольшее и наименьшее значения функции
.	25х - 2 • 5X + 1	гп
f(x) =---------- на отрезке [0; 2].
In 5
3.	Скорость охлаждения тела по закону Ньютона пропорциональна разности температур тела и среды. В резервуаре с температурой 10° тело остыло от 100° до 70° за 30 мин. Через сколько минут оно остынет до 50°?
4.	Найдите площадь фигуры, ограниченной линиями ху = 2, у = 4, х = 1.
5.	Найдите все корни уравнения 2|sinx| cos х - sin2x, принадлежащие отрезку [0; 2л].
6°. При каких значениях а уравнение
25х - (а - 4)5* - 2а2 + 10а - 12 = 0
не имеет действительных корней?
Контрольная работа № 5
Решите уравнения:
1.	х + 7з + Vx2 - 2х + 1 - 4.
2.	 '/з sin х = V2 cos х.
3.	л/2х2 - 5х + 12 + 2х2 = 5х.
Решите неравенства:
4.	>/5 - х2 > х + 1.
5.	2х + л/х + 4х < 6 • 4Л.
6°. V3 - х + у/х-1 > 32-х + 3х-2.
Контрольная работа № 6
Вариант 1
1.	Постройте график уравнения х2 + у2 - 2у - 8 = 0.
2.	При каких значениях а система уравнений
J (а + 1)х + у = 3, [2х - (а - 2)у = 6
294
не имеет решений?
3.	Решите систему уравнений х + у - 2ху = -1, х2 + у2 + Зху = 11.
4.	На нефтепромысле сначала работали две буровые установки, а через некоторое время вступила в строй третья установка, в результате чего производительность нефтепромысла увеличилась в 2 раза. Сколько процентов производительность второй установки составляет от производительности первой, если известно, что за три месяца первая и третья установки выдают нефти столько же, сколько вторая за полтора года?
5.	Решите уравнение tgx = tg3x.
6°. Решите систему уравнений
[х + у = 10, |хг/ - z2 - 25.
Контрольная работа № 7
Вариант 1
1.	Решите систему уравнений х + у _ 1 хуг 2
У + z _ 5 хуг 6 х + г _ 2 хуг 3
2.	Решите систему уравнений
|log3(l + yjx + у) = 1 - logg X, [х3 + х2у = 4.
3.	Решите систему уравнений [	л
х - у = -, *	6
,	9 V3
cos х + sin 2у = —.
4.	Изобразите на координатной плоскости множество решений системы неравенств и найдите площадь полученной фигуры:
Jx2 + у2 < 1, [у > |х| -1.
295
5°. При каких значениях а система уравнений
у - 4х = а,
У - х = 1
имеет единственное решение?
Контрольная работа № 8
1.	Представьте в тригонометрической форме:
2.	Пусть z, = >/3 + i, z2 = -sin — + i cos —.
24	24
Вычислите (z1z2)8.
3.	Изобразите на рисунке множество точек z комплексной плоскости, удовлетворяющих условию
[2<|z-i| <4, [О < Re z < 2.
4°. Найдите наименьшее и наибольшее значения |г|, если z - sin 2а + i(sina + cos а).
Контрольная работа № 9
1.	Решите уравнение на множестве комплексных чисел 10х4 + 39х3 + 49х2 + 39х + 10 = 0.
2.	Решите в комплексных числах уравнение |г| - 2z = 2i - 1.
3.	При каком значении b 6 R число
является корнем уравнения х3 - (Ь + 6)х2 + 8Ь2х - 7 + + Ь2 - 0? Найдите остальные корни уравнения при найденном значении Ь.
4.	Решите уравнение 5sinx - 12 cosx = 13sin5x.
Решите неравенство ------------> О.
2х2 - 5х + 3
6°. Решите в целых числах уравнение 2ху - Зу2 - 4у + 2х - 2.
296
Контрольная работа №10
Вариант 1
1.	Сколько чисел, меньших 105, можно записать из цифр 7, 6, 4? Сколько среди них нечётных?
2.	Найдите сумму четырёхзначных чисел, полученных при всевозможных перестановках цифр 3, 7, 7, 5.
3.	Найдите все корни уравнения
л/З sin 2х + 2 cos2x = 2-J2 sin х,
принадлежащие
л. Зтг!
2’ "2J
4°. Докажите, что 5" + 12п + 15 при любом натуральном п кратно 16.
Контрольная работа №11
1.	На карточке спортлото написаны числа от 1 до 49. Какова вероятность того, что наугад зачёркнутое число на этой карточке кратно 6?
2.	В магазин вошли 11 покупателей. Вероятность совершить покупку каждым из них равна 0,1. Какова вероятность того, что 7 из них совершат покупку?
3.	Решите неравенство 3х < 62х-1.
4.	Решите уравнение
* л	л I	71 I л ль.	3т1
sin4х + cos4 х + - = 0,25, если хе л: — .
I 4J	L 2 J
5°. При каких значениях а неравенство log3 _ а | х2 + — ] < 2 вы-з 4' полняется при любом действительном значении х?
Контрольная работа № 12
1 тт J.	\ х2 tg X  -Уз - X2
1.	Дана функция /(х) = .	+ -2—------.
sin Зх 1-х4
а)	Найдите область определения функции f.
б)	Назовите хотя бы одно рациональное и одно иррациональное число из области определения f.
в)	Выясните, является ли функция f чётной или нечётной.
г)	Найдите lim Дх).
х->0
297
2.	Сумма членов бесконечно убывающей геометрической про-
3	.. ..	1 „ „
грессии равна второй ее член равен —. Найдите сумму 4	3
квадратов всех членов этой прогрессии.
3.	Каждая из боковых сторон и меньшее основание трапеции равны а. Найдите большее основание трапеции так, чтобы её площадь была наибольшей.
4.	Найдите площадь фигуры, ограниченной кривой у = х1 2 + 1, касательной к ней в точке с абсциссой х0= 1, и прямой х = 0.
5°. Решите уравнение 3sinx = 4 - cos2 —.
Контрольная работа № 13
1.	Найдите все действительные значения а, при которых равны комплексные числа
2! = 3 + 2а + г(а4 5 + 2) и z2 = 6 - а2 + i(4 - а).
2.	Решите неравенство logz(5 - х2) > log2 (| х | - 1).
3.	Найдите все значения а, при которых уравнение
х2 - xcosa - 0,5 cos 4a = О
имеет два действительных различных корня, сумма квадратов которых равна 0,25.
4.	Найдите объём фигуры, полученной при вращении вокруг оси абсцисс криволинейной трапеции, граница которой задана уравнениями у = х3 + 1, х = 2, у = 0.
5.	ABCA^BiCi — правильная треугольная призма. Через ребро основания АВ и точку М, взятую на ребре Ву(\, проведено сечение. Найдите наибольшую и наименьшую площади сечения, если высота призмы равна 2 см, а высота основания 3 см.
ПРИМЕРНЫЕ ТЕМЫ ДЛЯ ИССЛЕДОВАТЕЛЬСКОЙ И ПРОЕКТНОЙ ДЕЯТЕЛЬНОСТИ
1. Число е.
2. Циклоида.
3. Теория групп.
4. Нестандартные уравнения, нестандартные методы решения уравнений и неравенств.
5. Криптография.
ОТВЕТЫ
1.4)	-g- - 4х + С. 2. Указание. Найти производную функции F по правилу дифференцирования сложной функции. 3. 1) -8cosx - 9tgx + С; 2) 6arcsinх + 3arctgх + С; 3) 6sinx - 4arctgх + С; 4) -5ctgx
- 3arcsinx + С; 5) 75- - х + arctgx + С; 6) -2ctg2x + С; 7)	+
О	О о
+ х + С; 8) arcsinx + С. 4. 1) у- - х + С; 2) tgx - х + С; 3) -cosx + С;
4)	+ С. 5. 1) arcsin £ + С; 2) j arctg £ + С; 3) -4= arctg + С;
z	о	5 о	5V3	5
4) у arcsin4х + С; 5) sin3x + С; 6) ctg(5x - 6) + С. 6. 2) x3Vx + 4	о	о	।
+ х2 'fx + бТх + 24 Vx + С; 3) 77 -	+ С; 5) -4 cos4x + С;
О	Z	о
6) I (cos 2х - | cos 14х) + С. 7. 1) ^(4х - 7)9 + С; 2) | (6х +
+ 11) >/бх + 11 + С; 3) А л/(8х - 15)2 + С; 4) I sin5x + С; 6) | tg(6x -АО	О	О
- 1) + С; 7) -ctg4x + С; 8) Указание. Возвести выражение в скобках в квадрат и воспользоваться основным тригонометрическим тожде-
ством; 9) т: arcsin * +.&х + С; 10) arctg(x - 3) + С. 8. 1) A arctg(x2) + С; о	4	&
2) A arcsin(x3) + С; 3) —1 cos(x2) + С; 4) sin(x2 -I- х - 1) + С; 5) A arcsin4x + о	z	4
+ С; 6) arctg5(2x) + С. 9. 1)	+ С; 2) cos6(2x) + С.
И. у' = Л (а - |)(b -
\	xu ' '	Ct >
12. тх" - -mg + Л(х')2. 14. Указание. Вы
числить вторую и третью производные функции /(х). 18. 1) у = 2tg(2x +
+ С); 2) у =	3) у =	4) у = | arccos (-|х4 + с);
5) у - sin (у- + с); 6) у = (arcsinx + С)2. 35. Указание. Сравнить первообразную функции /(х), обращающуюся при х = а в нуль, с В(0).
х3	тт л sin-Ух 2 cos х - cos Vx
36.2)	+х-12;4)sinx.37.2)	4)	39.1) —х----; 2)-------л---— 
о	4	0	ZX	ZX
40. 2) х = 2, х = -2, х = 1, х = -1. 41. 2)	3)	5) 1. 42. А = В = 0.
О	ZU	Ct
43. А =	“Д, В = 0, С =	44.	19 Ц.	46.	2. 48.	1|.	60. 1)	334^-.
4	4	15	3	4
299
64. Указание. Точки (у; t), удовлетворяющие уравнению у = va2 - t2, лежат на полуокружности радиусом а с центром в начале координат.
I	2
66. 1)	sin4xdx <	3) 0 < §(х2 - 4х + l)2dx< 18. 73. 2) Равны;
л	О
4
4) G/2 - >/з) > (V2 - >/з) . 75. З73 > 3й. 77. 1) a < 0; 2) a - 1 > 0.
79. Указание. Воспользоваться тем, что sinx < 1, а sin2x > 0.
80. 2)	—Ц-; 4)	; 6)
х2 - х + 1	(1 + х2) arctg х
cos (In х).	4 arctg3 (In x).
x ’	) x(l + ln2x)
8) —n,%A • 86. 4)	5) 3. 87. 1) x > 0; 3) при x > 1; 5) при x > 1.
X-s/1 - ln10x	°
88. 2) log„tf < logo 4) logaAr > log„ 89. 1) x > 2; 5) 0. 96. Является
2	1	1	1
тождеством при x > 2. 97. 1)	-	+	-	loga& +	±	log„m -	x	loga(&2 + c2);
о	о	О	о
4) |(4 - 31og„& + 21ogoc + j log, On + n) + 31og„d + |logai/
99. 3) x =
t5u>5
102. 1) Указание. Воспользоваться формулой
1 log*
= Alog/<a. 3) Указание. Перейти к основанию АГ. 103. 2) Указание.
Перейти к основанию 2. 107. 1) log<,(n + 1); 3) logda. 108. 2) i; 4) 77. О	о
111. Указание. При х = 0 у = с; при х = 1 у = са. 113. 5) х -Л
114.1) -22х; 3) 0. 115. 0. 116.	117.1. 118. -. 119.1. 120. 0. 121.1) х = 6;
4	5
2) х = -3; 3) х = |; 4) х = -4. 122. 1) х < -2; 2) х > -2; 3) х <	4) х < 0.
123. 2) х = 3; 4) xj = 4, х2 = 4 - log35; 5) х = 0; 6) х = log24564; 8) х = |; 9) х = 3, х = 11; 10) х = 9. 124. 1) 1 < |х| < 3; 2) х < log23, х > 2; 4) х < log23. 126. 2) х > i; 4) 0 < х < 10. 127. 1) х = 1,5, х = 3; 2) х = 6; 4) х = 1000, у о
х = 0,1; 5) х = J=; 6) х = а2, х = 1; 8) х = 4, х = 36; 9) х = 10; 10) х = 18; V3	а
1	-1± Л?
11) х = 4; 12) х = gj 13) нет решений; 14) х = 26; 15) х = V2; 16)х=а 8 ;
300
17) х = a, x = ax/a; 18) x = 1 (при be / 1), тождество при be = 1;
1	1	°гг3
19) x = -7=, x= -±=. 128. 1)0 <x< 21108’3; 2) x > 3 при a > 1, 0 < x < 3 Va	ava
при 0 < a < 1; 3) 0 < x < 1; 4) 0 < x < 1, x > 2; 5) | < x < |; 6) 1 < x < 1 + Cl
2V2’
X > 3; 7) 0,1 < x < 100; 103 < x < 105; 8)	< x < a'^2 при 0 < a < 1;
0 < x < сГ12 и x > er'2 при a > 1; 9) x < -2; 10) 0 < x < 1, V3 < x < 9;
12) x > 2; 13) x < -2, 0 < x < 1, x > 1; 14) 1 < x < -Л, x > 3--„-- ; Cl
15)	< x < I < x < 1. 129. 1) Jx_2 ; 3) x4(51nx + 1);
3 sin2 (In x) cos (In x) _2^.	2	2x_ 131 t _
’	x	’ sin 2x ’ X2 - 1	’	+ 4	’
точка минимума; 3) нет экстремума; 4) х = е2 — точка минимума;
5)	нет экстремума; 6) х = 2nk (k — целое) — точка экстремума.
132. 1) (г/)" = (-1)"	- 1)! х~п. 133. 3)
In COS X COS2X
tg2 x (cos x)tgx;
5)(| + (1 + In x) In xj xx + x’. 134. 2) |ln|4x- 5| + C; 3) |ln(x4 + 1) + C;
5)	ln|cos7x| + C; 7)ln|arctgx| + C. 136.	137. 1) ln|x + -7x2 + 4 | + C.
138.	1) 71п|^-=-|| + C; 4) ^-ln|9* Щ + C. 139. Указание. Вычис-лить вторую и третью производные функции /(х) и подставить в данное
уравнение. 140. 1) ех(х2 + Зх + 17); 3) Зх2ех’; 4) e“nxcosx; 5) excosex;
ех(х — I)2	рх
7)	-----z—; 9) — -. 142. Указание. Вычислить производную
-у* 2 t _	(?	4~ X
2	X
функции и подставить в уравнение. 143. у = —. 144. 1) х = 0 — точка
минимума, х = 2 — точка максимума; 3) х =	— точка максимума,
Ct
V2
х = —g- — точка минимума; 7) х = 2nk (k — целое) — точки максимума,
2х
х = п(2к + 1) — точки минимума; 9) нет экстремума. 147. 1) —- + С;
In Zj
301
3) е3х + С; 6) I е3х(3х - 1) + С; 7) xlnx - х + С. 149. Зе1 < x3e~xdx < о	У	J
1
< 81е"3. 150. 1) =0,17. 151.	• 154. 1) у =	+ С2ех; 4) у =	+ С2е'3х.
156.	159. =2,738 кг. 160. 0,32 м/с. 161. i> = №-g + ide’"' " пг-
1U24	\к '	к
169.1)е«;2)|; 3)1.170.1)е 2;2)	3)^-. 171.1) е^; З)^1.172.1)	2)<?-,3) е*.
д.2	х2п ~
175. Следует из неравенства 1 + х +	+ ... +	_ д^, < ех, спра-
ведливого для х < 0. 177. Указание. Воспользуйтесь неравенством, связывающим среднее арифметическое и среднее геометрическое двух положи-
тельных чисел. 182. 2)	4) 1 185. 3) 1; 4) 1. 186. 1) 0; 3) 0; 5) 1; 7) 0.
о 4
190. 8(х) = х Ля2 - х2
191. S(h) = %h- ±h3, S(y) = 0,5г/Vp2 - py.
195. 2 fa + при x > 1, у > 1 и t. д. 198. 1) a)	6)
4)	• 2^C2>i^3	5) xVx; 6)	199. 1) 0, если x > 0, и x, если
x < 0; 3) -2x - 5, если x < -3; 1, если -3 < x < -2; 2x + 5, если x > -2.
200. 4) x < -2, x > 4. 201. 2) При x < 0. 202. 3) Например, у = , —   v-x - 3
203. 4a2|b|c5 \lc. 206. 1) -2a, если a < -3; 6, если -3 < a < 3; 2a, если a > 3;
3) j; 4) 2ab + 2^a2 - l)(b2 - 1); 5) a + 5; 6)	8) (ч£ -
9) x^’^a; 10) |9x°’5 + 25a°-25|:|9a°’25 • x°’25|. 207. 1) Указание. До-множьте обе части равенства на ч/2 + 1. 210. 3) Ца + |Ь| - Ja - |Ь|): ч/2;
5) 2%/a + b при а + b > с; 2ч/с при а + Ь < с. 212. sin 15° = ^(ч/з - 1), cos 15° = ^-(ч/з + 1), sin22°30' = 0,5^2 - ч/2. 213. 2) 9  (>/7 - ч/б) х х(>/3 - ч/2) :2; 5)	+	+	. 214. 2)-1; 3) |; 7)0,5.216. 4) х = 5;
а - о	о
5) х = 16; 6) х = +ч/2; 9) 2 и -5; 11) х = 7 + 4ч/3; 15) 10 и -6; 17) |^|; з].
302
217. 1) х > 2; 3) х < -2; 4) -1 < х < 1; 5) 0 < х < 5^; 6) 0,75 < х < 2; 7) -0,5 < х < 0,25(11 - V153), 0 < х < 2. 218. 1) х = 0,4655...; 2) х = -2,32... (х = Vx - 1); 3) х = 4,87...; 4) х = 3,35...; 5) х = 0,091...; 6) х = 0,907... (х = (4 - tgx) : 3); 7) х - 0,876... (х = Vsinx); 9) х = 0,342...; 11) х = 0,746...; 13) х = 1,49....
В задачах 219—240 полезно учесть, что если Xi и х2 — корни квадратного уравнения /(х) = 0, D — его дискриминант и график Дх) — парабола с ветвями, направленными вверх, то f(x) < 0 между корнями, причём хср = (Х[ + х2) : 2 — середина отрезка XjX2 на оси Ох, которая легко находится по теореме Виета. Эти обозначения применяются далее в ответах.
219. а) а > 1; должно быть /(1) < 0, при этом и корни существуют; 2) а > 1; должно быть /(3) > 0, хср > 3 и D > 0 (или вместо этого Дхср) < 3). 220. Необходимо D > 0, 2 < хср < 5, знак а + 1 определяет знаки /(2) и /(5) (2 случая). 222. Корни первого уравнения легко находятся, в этих точках второй трёхчлен должен быть отрицателен. 224. Либо D < 0, либо Л > 0 и произведение корней положительно, а их сумма отрицательна. 229. Переформулируем: все решения первого неравенства должны лежать вне [-3; -1]; или если f2(x) < 0, то /,(х) > 0. 230. Коэффициент при х2 (он должен быть положителен) раскладывается на множители; корни уравнения f(x) = 0 (если они есть) оба должны быть отрицательны. 233, 234. Положить у = (х - р)2. 235. Сгруппировать крайние и средние скобки, у = х2 + хр + х. 239. В урав
нения х и у входят симметрично, единственное решение должно иметь вид (0, 0, г). 240. Сделать замену х = ky, привести систему к виду /\(fe) <
<	< fAk). 241. 2) х = ал/з : 2;
а3 + 2а2 + 2а + 2 - а((а + 2)V2a + з)	/-	63
3)х=---------------------------------, гдеа>72; 5)x = 0,x=|fa.
242. 1) х = ±^- b2)f-2ab. 2) х =	± ^13а< .13а2Ь^+ 2^.
3) х = (с ± д/с2 - 1)	; 5) х = а + Ь. 263. Указание. Умножьте
обе части равенства на (a - b)(b - с)(а - с). 264. S, = ст? - 4ст?ст2 + 2ст|, S5= ст? - 5ст?ст2 + бст^, Se= ст? - 6ст?ст2 + Эс^ст? - 2ст|, S7 = ст? - 7ст?ст2 +
+ 14ст?ст| - 7ст!ст|, S8= ст? - 8ст?ст2 + 20ст?ст| - 16ст?ст| + 2ст|. 265. х2-90х +
+ 343 = 0. 267. 1) ст?
+ 2у2)(2х2 + ху + у2).
1.01
с 2^; 2) используйте
+ CTjCT2. 268. 5х2 + 6х - 8 = 0. 271. 1) (х2 + ху +
275. 1) Указание. Сравните каждое слагаемое
1 „ соотношения:	<
1 = 1___________1. а.
k(k - 1) k - 1 fe’ 8) рас'
кройте скобки, выделите квадраты; 10) рассмотрите а - Ь как разность квадратов; 12) раскройте скобки и выделите квадраты; 14) возведите обе части неравенства в куб; 17) можно использовать ме-2 тод математической индукции; 21) исследуйте функцию (1 + с )х,
303
[20 - 132 7
+ 1)<р: sin 0,5<р. 366. 3)z = 2 cos (25 + l)f + i sin (25 + 1)£ \	5	5
где с =	25) домножьте на 2 и выделите квадраты; 28) вос-
пользуйтесь неравенством, связывающим среднее арифметическое и среднее геометрическое двух чисел. 280. 2) (х + 4)2 + (у - З)2 = 100. 281. 1) {(4; 2), (2; 4), (-2; 1)}; 2) {(7; 3), (7; -3), (-7; 3), (-7; -3), (5; 1)}. 282. Указание. Найти решение системы первых двух уравнений и
подставить в третье уравнение. 284. При С = -21. 286. х =
у = ±J11' | 3^’ “^3	13- 290-1)С *4; 2) С = 4. 291. Нет. 293.1){(3; 4),
(3; -4), (-3; 4), (-3; -4)}; 2) {(5; 3), (2; 6)}; 4) х = 0,5а, у = 0,55. 294.1) {(3; 5), (-3; -5), (-8; 5), (8; -5)}. 295.3) {(6; 3), (6; -3), (-6; 3), (-6; -3)}. 325. 12) 7з + 1,5л/3 + iyjl + 0,5>/3; 14) 18 + 26i; 16) -14. 326. 2) При х = 1, у = 2. 327. Пользуясь условием равенства двух комплексных чисел, составьте систему. 328. 7) i; 13) -	15) 1; 17) 8. 332. 1) {(1; 4); (4; 1)}.
333. 2) (2а - 3yfo)(2a + 3Vdi); 4) (х - 3 - 4i)(x - 3 + 4i). 334. 2) (х2 + 5 + + 12i)(x2 + 1). 335. 3) Например, х2 - 4х + 5 = 0. 339. 1) z = 2, г = i. 343. 4) z = cos (-60°) + i sin (-60°); 7) 2 = з(соз(-^) + i sin
345. У Казани e. Используйте геометрический смысл модуля комплексного числа. 351. Указание. Используйте геометрическую интерпретацию комплексного числа. 356. 1) -Ulcos + i sin ||л). 359. 4) sin6<p = - 6cos5(p sincp - 20cos3<p sin3 cp + 6cos<p sin5cp. 360. 2) sin0,5n<pcos0,5(n + j, где 5 = 0, 1, 2,
3, 4. 367. 2) (Oo.i = ±1, «2,3 = ±0,5(1 + i>/3),	5 = ±0,5(1 - ic/з), co6,7 = ±2,
ш8,9 = ±(1 + iVs), ш10,и = ±(1 - h/з). 370. (x2 - 4x + 5)2 • (x2 + 1) = 0. 372. 1) Указание. Покажите, что корни двучлена х2 + 1 являются корнями данного многочлена. 373. Сумма равна 0, если р не делится на п, и равна п, если р делится на п. 379. 1) В с А; 2) А = В; 3) А с В; 4) А = В; 5) А € В; 6) В ё А, В с А; 7) В с А; 8) В с А, В £ А. 380. 1) Да; 3) да. 381. 3) {2, 3, 4, 5, 6, 7}. 384. 3) Указание. Воспользуйтесь диаграммами Эйлера — Венна. 385. Указание. Покажите, что если некоторый элемент принадлежит левой (правой) части, то он принадлежит и правой (левой) части. 386. Указание. Воспользуйтесь определением симметрической разности и указанием к задаче 385. 387. 3), 4) А Д В. 393. 1) Нет; 2) да. 395. Множество N. 396. 2) и 4). 399. Да. 401. {а, б, ё, ж, й, п, ф, ь, ю, я}; {а, ё, ю, я}. 405. 2) х —> ^2 + VT~+ х. 406. Да. 407. Указание. Прямоугольник закрывает одну белую клетку и одну чёрную. Угловые же клетки одного цвета. 412. 11; 1; 4. 414. 26. 416. 20.
304
417. 9; 8. 418. 1024; 2016; 496. 419. 768. 420. 126. 422. 52488; 32 768; 1024. 423. З12. 425. 232 = 4 млрд. 427. 336. 429. 3024. 431. 6! 433. 60; 24. 434. 3003. 436. - 3-[ . 437. 75075. 438. С°9. 442. Указание. Вос-(12!) 8!
пользуйтесь формулой перестановок с повторениями. 444. С3„ 	.
3’4 ’о ’
447. Указание. Посчитайте число кортежей (kt, k2, k3, k4) таких, что ki + k2 + k3 + k4 = 4, kj = 0, 1, 2, 3, 4. 448. Указание. Коэффициенты разложения — числа Р (fei, k2, k3, k4), где kt + k2 + k3 + k4 = 11. Найдите наименьшее значение fej kj k3l k41. 451. 16665; 12444. 452. 293930; 24310; 45. 453. 20. 457. 7054 320. 458. 1560. 459. a) C4n; 6) C4t 8!  12!; в) C4t  12!. 460. C4  C3 • 6! = 28800. 461. C4  Cj0 C3. 462. 9 9! 463. C| • C?o • 6! = = 4 838 400. 464. 2) 469 200. 465. 1944. 466. 70. 468. Указание. В одном ряду можно поставить не более j королей. Можно занять рядов не более	(для доски т х п). 469. Указание. Покажите,
что 8 слонов могут держать под боем каждое поле доски. Для их защиты достаточно ещё 4 слона. 470. Одна ладья держит под боем одну вертикаль и одну горизонталь. 471. Дамки не могут стоять на крайних горизонталях и вертикалях. 472. Указание. Наибольшее число должно начинаться с наибольшей цифры. 473. Указание. Занумеруйте секторы: 1, 2, 3, 4, 5, 6. Проследите изменение чётности суммы мест при движении и в итоге. 479. 784. 480. Cj9  Cf5  С4,  С4. 482. 2n l. 484. 1560. 486. 144. 487. 60. 488. 84. 490. С3°; C}g. 499. 2) Ничья, результативный матч. 500. 1), 4). 501. 2) {Aq, Alt Аг, А3, А4, А5}, где А, — герб выпал i раз.
505. Образуют. 510. рп = ± п; рп =	• |. 511. (в„, Н, П„; |, |,
-1	-L^x I lb	\	О У У/
Вм, Н, Пм — выигрыш, ничья, поражение (мастера). 512. Указание. Найдите сумму вероятностей исходов. 514. 1) {Г1, Г2, ..., Гб, Ц1, Ц2, ..., Ц6}; 2) ГГГГГ, ЦГГГГ, ГЦГГГ.ЦЦЦЦЦ. 515. 1) Да;
2) нет; 4) да. 516. 2)	4) |. 518. 2) |,	1’ I- Л- 519. 0,3.
U	О 16 У О У 1о
520. 0,104. 521.	522.	523. 0,05. 524. 0,1. 525.	526. 3) тк-
{	(оои
528. 1) С33 • С20  С2: Cf„; 2) С*, • С}3  С2 : С|о. 529. 1) |. 530. р = от места в очереди не зависит. 531. 1 - (1 -	. 532. 1) С|х: С^7; 2) (С31 • С% +
+ С231  С'в + С331): C|j. 538. 2) А П С = К-, 7) М U К = М. 549. Р(А) = 0,85, Р(В) = 0,25. 551. 1) Р = 0,9; 2) Р = 0,6. 552. Р = 0,37. 554. Указание.
305
Проверьте, что вероятность события «выпал герб и выпало чётное число очков» равна произведению вероятностей этих событий. 555. См. указание к задаче 554. 559. 1) 0,985; 2) 0,14; 3) 0,425; 4) 0,42. Вероятность
всех промахов равна 0,015. 562. 1) Р ~ 0,7. 565.	566. 0,6. 568. 0,77.
О
569.	=0,003. 570. 0,594. 575. ||. 576. =0,024. 579. Р = £ С*, • (|) (|)	•
581.	1) Три партии из четырёх; 2) не менее пяти партий из восьми.
582.	1) =0,25; 2) =0,26; 3) =0,000064. 583. =0,472. 584. =0,77. 585. 4) =0,8.
587. = |. 592. 0,2. 595.	598.	600. Р =	601. 2 - —
4	л 24	9л	п(п - 1)
g02 -------—_______
... п6!6"
(CN V
603.1)
((W .	.	с42 
(W(4N)!’ ' С2" ’ С™	‘
004. 1) 1 - (I)"
> 0,5 =» п > 4; 2) п > 9; 3) п > 13. 605. п >
In (1 - г) In (1 - р)'
606.	+ 1. 607. 1 - (О,99)100 = 0,634. 608. 23. 609. 253.
610. а) |; б) 1; в) 612. а) р<?3; б) (1 - g3)pg3; в) (1 - q3 - pq3)pq3-, о Z О
q = 1 ~р. 613. 0,85 0,2 = 0,066. 614. =0,044. 615. 0. 616. Л- 617. =0,411.
л2
618. В, вероятность его выигрыша
1^1 619 243’
а2 Р2
а2 + Р2 ’ а2 + р2’
620.	д,	И) а  621.1) =0,52; 2) =0,61. 622. 0,6. 623. 0,5.
or + Р2 + аР а2 + Р2 + «Р	’
2
624. 0,16. 625. =. 626. Толщина монеты =35 % от её диаметра, о
627. |
а
2-Ja2 + г2
, /
-	628. 1 при L < d, UM + 1
2р2 + г2	’I’P
и 1 - jl -	при L >	+ 1- 629. (|)1Z = 3 • 10 7,
не согласуется. 630.	= g’ согласуется. 631. 1) С" tm • (1 -
(	*	V
2) 1 - (1 - 0"; 3) 1 - £ С"Г(1 - t)"-m
I т = 0	/
306
ОТВЕТЫ К КОНТРОЛЬНЫМ РАБОТАМ
К-1.
1-«- -4-
2
2. х = 4t2 - 2t3 + t, t = — (с).
3
3. 3.
К-2.
2.	z g (-2; 0) и (0; +оо).
3.	9.
4.	у = -0,25.
К-3.
1. -3; -2; 0.
2. х > 2.
3. log23.
4. х е — + 2лл; — + 2лл и — + 2лл; — + 2лл , п е Z.
6	2	2	6
5. arctg 0,5 + 2лл, п. е Z.
К-4.	К-5.
, 2	1. 2.
1. -.	
3	л 2. 2лл, — + 2лл, n g Z.
2 375 -25	3
1п5’ 1п5	3. 1; 1,5.
3. 60.	4. х е [-Тб; 1J.
4. 2 - In 4.	
5. 0, л, 2л, arctg 2, 2л - arctg 2.	5. х G [о; 0,б(3 + Тб)].
6. а е [2; 3].	6. х = 2.
К-6.
2.	а = 1.
3.	(2; 1), (1; 2), (о,2б(-7 ± Тб9);0,25(-7 + Тб9)).
4.	40.
5.	nk, k g Z.
6.	(5; 5; 0).
К-7.
1. (1; 2; 3), (-1; -2; -3).
2. (1; 3), (4; -3,75).
3.
л	л
—I- лл; —и лл 2	3
л
— + 2лл; 2лл
6
л е Z.
5. а = 0,75, а > 1.
307
К-8.
1. а) 2 cos — + i sin — ;
2	2
б) -2 cos a (cos (л + а) + /з1п(л + а)).
2. 128(1 - м/з).
4	j-
4. --, <3.
2
К-9.
1. -0,4; -2,5; -0,5(1 ± ;7з).
3.	Ь = -1; Xi = 3, х2,3 = 1 ± г.
.	1	5	лл	1	5	л._	„
4.	— arccos	—	+ —,	— arccos —	+ —(2л	+ 1), п е	Z.
4	13	2	6	13	6
5.	х е (1; log35) и (1,5; +°°).
6.	(1; 0), (-3; -2).
К-10.	К-11.
1.	363, 121.	8
2.	73 326.	1. — = 0,163.
3.	х = л - arctg0,25.	2. « 22 • 10 *.
3.	х > log126.
4.	л; 1,25л.
5.	а е (1,5; 3).
К-12.
1.	а) [-73; 7з] кроме точек 0; ±1; +^; ±^; в) нечётная; г) 0.
2.	1,125.
3.	2а.
5. 4,5л + блл, п е Z.
К-13.
1.	а = 1.
2.	х е (-2; -1)	(1; 2).
3.	а = ±0,5 arccos (-0,75) + лл, п e Z.
, 405л
4.	----.
14
5.	4^3, >/39.
308
Предметный
Алгебра событий 262
алгебраическое выражение 104
Биномиальные коэффициенты
241
Вероятностное пространство 254
вероятность события 257
— теоремы сложения 268
Гармонические колебания 18
геометрическая вероятность 284
Дифференциальное уравнение 13
----общее решение 15
----решение 14
----с разделяющимися пере-
менными 20
----частное решение 16
дополнение множества 217
достоверное событие 263
Закон больших чисел 282
Интеграл 4, 35
интегральная кривая 14
интегрирование 3
—	метод подстановки 8
—	непосредственное 7
иррациональное выражение 104
— неравенство 116
Квадрируемая фигура 27
комбинаторные задачи 227
комплексное число 186
----аргумент 198
— — геометрическое изобра-
жение 195
----модуль 198
----сопряжённое 190
----тригонометрическая фор-
ма 198
----фаза 198
корень из комплексного числа
192,205
кортеж 221
криволинейная трапеция 29
Лексикографический порядок
138
логарифм числа 58, 61
логарифмирование 63
указатель
логарифмическая функция 58, 61
•	— выпуклость 60
—	производная 58, 80
логарифмическое дифференцирование 81
логарифмическое неравенство 73
—	уравнение 72
Математическая вероятность 252
метод замены переменных 161
—	последовательных приближений 119
мнимое число 186
многочлен 137
множество 215
—	п-элементное 216
—	значений 224
—	характеристическое свойство 216
Невозможное событие 263
недоопределённая система 151
независимые события 272
неопределённый интеграл 4
неравенство Гельдера 147
— для логарифмической
функции 94
— для показательной функции 92
— Коши 144, 147
несовместная система 150
несовместные события 263
Ньютона — Лейбница теорема 31
—	формула 36
Область определения 224
образ, прообраз элемента 224
обратимое отображение 225
объединение множеств 217
—	событий 263
однородный многочлен 138, 163
определённый интеграл 35
—	свойства 45
основная теорема алгебры 209
отображение множеств 223
-	Хна У 225
— взаимно однозначное 225
отрезок интегрирования 35
309
Первообразная 3
переменная интегрирования 4 пересечение множеств 216
— событий 263
перестановки без повторений 238
— с повторениями 243
площадь фигуры 27 подмножество 216 подынтегральная функция 4, 36 подынтегральное выражение 4, 36 показательная функция 66
—	выпуклость 85
—	производная 85
показательное неравенство 71
—	уравнение 68
полная вероятность 278
полярные координаты 196
постоянная интегрирования 4
потенцирование 64
правило произведения 232
—	суммы 229
пределы интегрирования 35 произведение множеств 222 противоположные события 264
процесс органического роста 54, 87
пустое множество 215
Равносильность систем уравнений 156
— на множестве 156
радиус-вектор 195
размещения без повторений 236
— с повторениями 234
разность множеств 217
— событий 265
решение системы 150
Симметрический многочлен 140, 162
система уравнений 150
--графическое решение 167 --методы решения 158—161
следствие события 264
словарный порядок 138
случайное событие 251
событие 257
совокупность уравнений 153
сочетания без повторений 239
— с повторениями 246
стандартный вид многочлена 138
степенная функция 97
----выпуклость 98
----производная 98
степенные суммы 141
Теория вероятностей 251
----классическая схема 254
— — статистический подход 254
Уничтожение иррациональности в знаменателе 110
упорядоченное множество 216
уравнение иррациональное 111
— линии 147
— окружности 148
— с параметром 122
условная вероятность 276
Формула Байеса 279
— Бернулли 281
— Виета 194
— включений и исключений
230
— Муавра 203
— перекрытий 230
— трапеций 52
— умножения 276
функция алгебраическая 105
— комплексного переменного 213
Число е 60
— комплексное 186
— чисто мнимое 186
ОГЛАВЛЕНИЕ
Предисловие ...................................................3
Глава 1. Интеграл и дифференциальные уравнения
§ 1.	Неопределённый интеграл ..................................5
1.	Введение (5). 2. Первообразная (5). 3. Непосредственное интегрирование (9). 4. Замена переменной (10).
§ 2.	Дифференциальные уравнения ..............................13
1.	Введение (13) 2. Решения дифференциальных уравнений (16). 3. Уравнения с разделяющимися переменными (21). 4. Составление дифференциальных уравнений (24). 5. Математическое моделирование (беседа) (27).
§ 3.	Определённый интеграл....................................28
1.	Площади плоских фигур (28). 2. Площадь криволинейной трапеции (31). 3. Теорема Ньютона — Лейбница (33). 4. Физические и геометрические задачи, приводящие к понятию определённого интеграла (36). 5. Вычисление геометрических и физических величин с помощью определённого интеграла (43). 6. Свойства определённого интеграла (47). 7. Оценка значения определённого интеграла (50).
Глава 2. Показательная, логарифмическая и степенная функции
§ 1.	Показательная функция и её свойства......................55
1.	Процессы органического роста и убывания (55). 2. Обобщение понятия степени (57). 3. Определение функции 1пх, её свойства и график (60). 4. Логарифмическая функция и степень с любым показателем (63). 5. Показательная функция, её свойства и график (68).
§ 2.	Показательные и логарифмические уравнения и неравенства...70
1.	Простейшие показательные уравнения и неравенства (70). 2. Решение показательных уравнений и неравенств (72). 3. Простейшие логарифмические уравнения и неравенства (74). 4. Решение логарифмических уравнений и неравенств (76).
§ 3.	Дифференцирование и интегрирование показательной и логарифмической функций ...............................................81
1.	Логарифмическое дифференцирование (81). 2. Дифференцирование показательной функции (87). 3. Дифференциальное уравнение процессов органического изменения (89). 4. Некоторые пределы, связанные с числом е (93). 5*. Некоторые неравенства для показательной функции (94). 6*. Неравенства для логарифмической функции (96).
§ 4.	Степенная функция. Иррациональные выражения, уравнения и неравенства .........................................................99
1.	Степенная функция с произвольным показателем (99). 2. Некоторые тождества для степенной функции (102). 3. Сравнение роста степенной, показательной и логарифмической функций (104). 4. Алгебраические выражения (105). 5. Упрощение иррациональных выражений (109). 6. Уничтожение иррациональности в знаменателе или в числителе (112). 7. Иррациональные уравнения (113). 8. Иррациональные неравенства (118).
§ 5.	Метод последовательных приближений .....................120
1.	Приближённое решение уравнений (120). 2. Метод последовательных приближений (121).
§ 6.	Уравнения и неравенства с параметрами...................124
1.	Рациональные уравнения и неравенства с параметрами (124).
2.	Иррациональные уравнения и неравенства с параметрами (128).
3.	Трансцендентные уравнения и неравенства с параметрами (132).
311
Глава 3. Многочлены от нескольких переменных. Системы уравнений и неравенств
§ 1. Многочлены от нескольких переменных .....................139
1. Стандартный вид многочлена от нескольких переменных (139).
2. Симметрические многочлены (142). 3. Доказательство неравенств с несколькими переменными (146).
§ 2. Системы уравнений и неравенств ..........................149
1. Геометрический смысл одного уравнения с двумя переменными (149). 2. Системы и совокупности уравнений (151). 3. Равносильные системы уравнений (157). 4. Метод исключения (160). 5. Метод алгебраического сложения уравнений (161). 6*. Метод замены переменных. Системы симметрических уравнений (163). 7. Графическое решение системы уравнений (169). 8. Системы иррациональных, тригонометрических, показательных и логарифмических уравнений (173). 9. Решение неравенств с двумя переменными (177).
Глава 4. Комплексные числа и операции над ними
§ 1. Комплексные числа в алгебраической форме ................186
1. Введение (186). 2. Определение комплексных чисел и операций над ними (188). 3. Сопряжённые комплексные числа (192). 4. Извлечение квадратных корней из комплексных чисел и решение квадратных уравнений с комплексными коэффициентами (194).
§ 2. Тригонометрическая форма комплексных чисел...............197
1. Геометрическое изображение комплексных чисел (197). 2. Полярная система координат и тригонометрическая форма комплексных чисел (198). 3. Умножение, возведение в степень и деление комплексных чисел в тригонометрической форме (203). 4. Формула Муавра. Применения комплексных чисел к доказательству тригонометрических тождеств (205). 5. Извлечение корня из комплексного числа (206). 6. Основная теорема алгебры многочленов (211). 7. Комплексные числа и геометрические преобразования. Функции комплексного переменного (214).
Глава 5. Элементы комбинаторики
§ 1.	Множества, кортежи, отображения .........................217
1.	Множества и операции над ними (217). 2. Алгебра множеств (220). 3. Разбиение множества на подмножества (222). 4. Кортежи и декартово произведение множеств (223). 5. Отображение множеств (225).
§ 2.	Основные законы комбинаторики............................229
1.	Введение (229). 2. Правило суммы (231). 3. Правило произведения (234).
§ 3.	Основные формулы комбинаторики ..........................236
1.	Размещения с повторениями (236). 2. Размещения без повторений (238). 3. Перестановки без повторений (240). 4. Сочетания без повторений (241). 5. Сочетания и биномиальные коэффициенты (243). 6. Перестановки с повторениями (245). 7. Сочетания с повторениями (248).
Глава 6. Элементы теории вероятностей
§ 1. Вычисление вероятностей .................................253
1. Введение (253). 2. Вероятностное пространство (254). 3. Вероятность событий (258). 4. Алгебра событий (264). 5. Теоремы сложения (270).
§ 2. Независимые испытания ...................................273
1. Независимые случайные события (273). 2. Условная вероятность. Формула умножения (277). 3. Формула Бернулли. Закон больших чисел (283). 4. Геометрические вероятности (286).
Приложение ...............................................293
Ответы....................................................299
Предметный указатель .....................................309