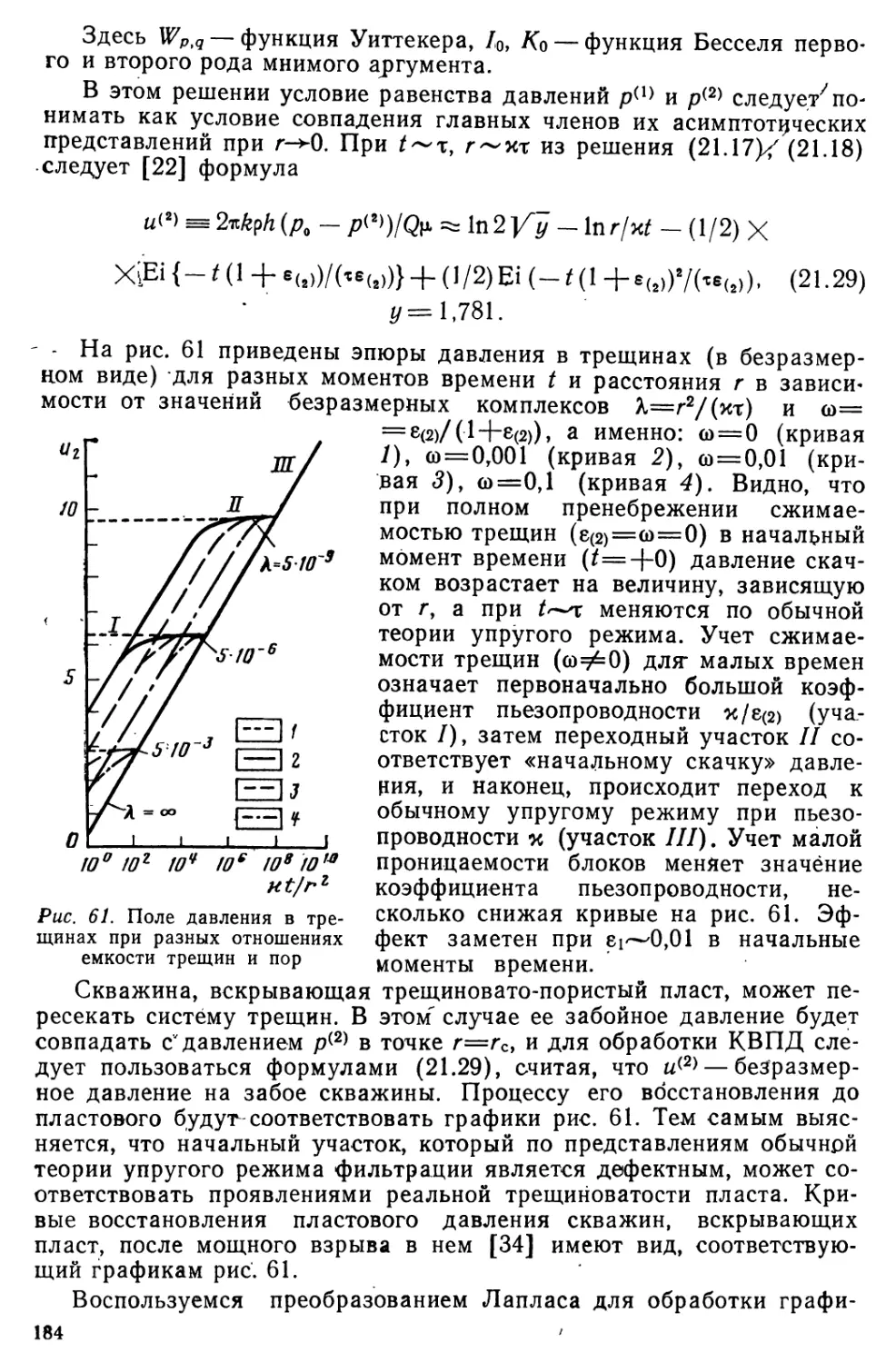
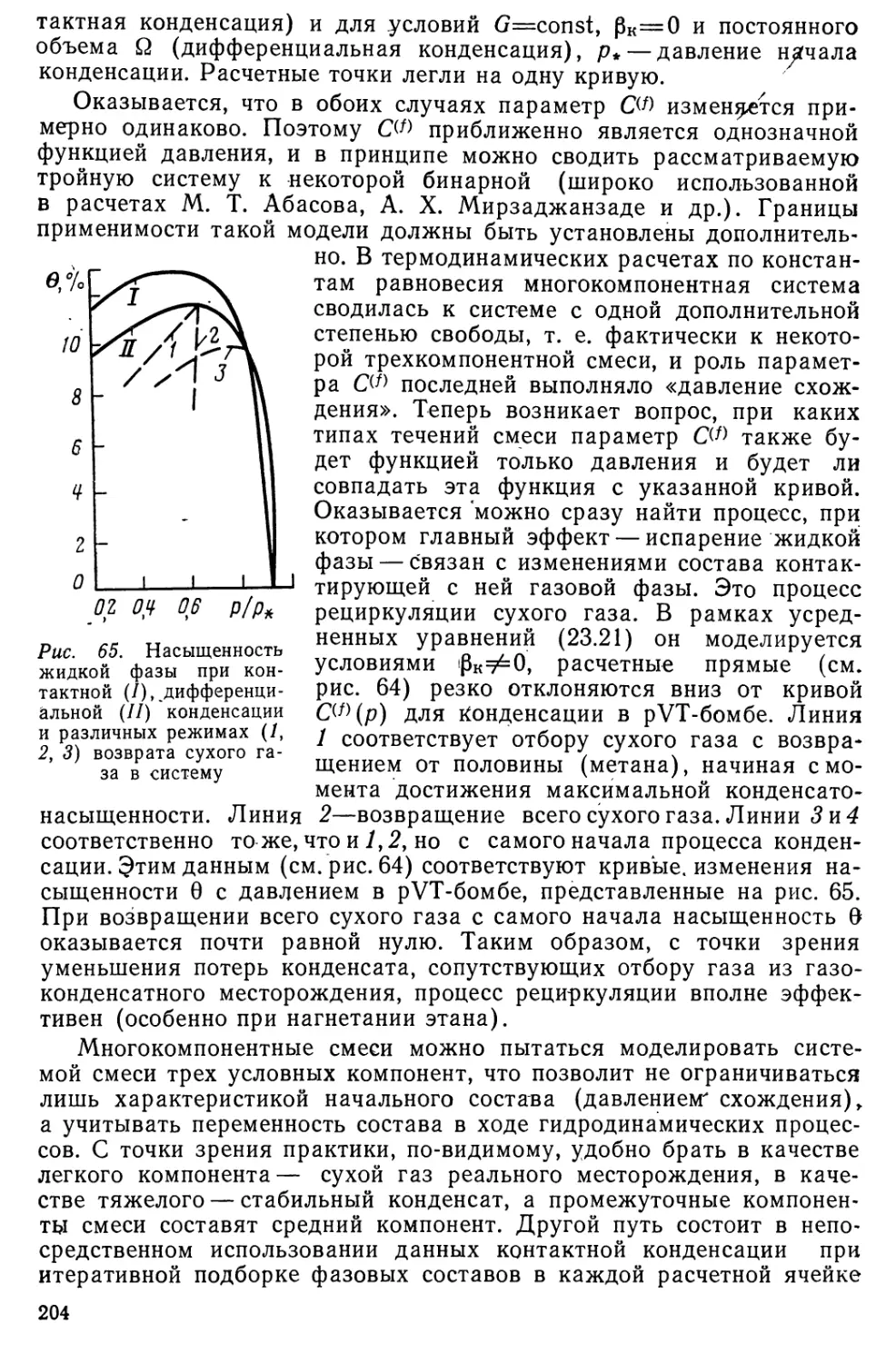
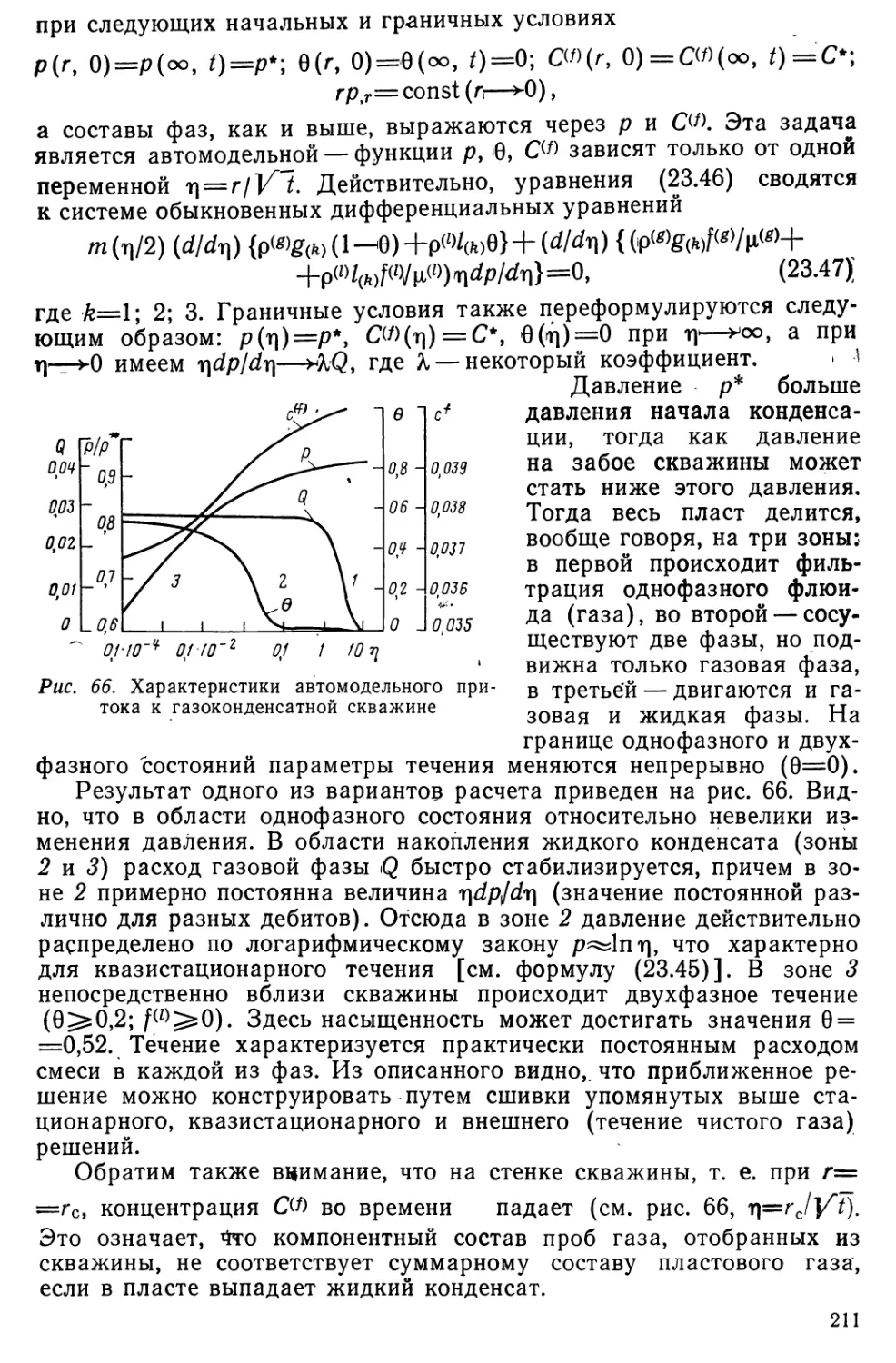
Author: Николаевский В.Н.
Tags: общая механика механика твердых и жидких тел физика механика
Year: 1984
Text
В... Н* Николаевский
МЕХАНИКА
ПОРИСТЫХ
И ТРЕЩИНОВАТЫХ
СРЕД
МОСКВА «НЕДРА» 1984
УДК 531.01
Николаевский В. Н. Механика пористых и
трещиноватых сред.—М.: Недра, 1984. 232 с.
Изложены основы деформации и разрушения
трещиноватых горных пород под воздействием статических и
динамических нагрузок. Особо рассмотрены эффекты
изменения пустотности при сдвиге и насыщении пор и трещин
жидкостью. Приведена теория фильтрации в
деформируемом коллекторе, рассмотрены процессы диффузии и
переноса. Сформулированы определяющие законы
деформирования и критерии разрушения горных пород.
Для специалистов в области геофизики,
нефтепромысловой механики и механики сплошных сред, горного и
взрывного дела; будет полезна студентам старших курсов
нефтяных вузов, обучающихся по специальности
«технология и техника добычи нефти».
Табл. 12, ил. 71, список лит.— 50 назв.
Р е ц е н з е н т — д-р техн. наук В. М. Ентов (ИПМ АН СССР)
ВИКТОР НИКОЛАЕВИЧ НИКОЛАЕВСКИЙ
МЕХАНИКА ПОРИСТЫХ И ТРЕЩИНОВАТЫХ СРЕД
Редактор издательства Н. Е. Игнатьева Переплет художника О. М. Соркиной
Художественный редактор В. В. Шутько Технический редактор А. В. Трофимов
Корректор К. С. Торопцева
И Б № 4844
Сдано в набор 21.10.83. Подписано в печать 20.01.84. T-0194I
Формат 60 X 90Vie * Бумага типографская № 3 Гарнитура «Литературная» Печать высокая
Усл. п. л. 14,5 Усл. кр-отт. 14,5 Уч.-изд. л. 16,0 Тигаж 2300 экз. Заказ 3311/8856—6 Цена 2р.80 коп»
Ордена «Знак Почета» издательство «Недра»-, 103633, К-12, Третьяковский проезд, 1/19
Ордена Октябрьской Революции и ордена Трудового _ Красного Знамени Первая Образцовая
типография имени А. А. Жданова Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли. Москва, М-54, Валовая, 28
2504030300-087 тт inoj
Н043(0П-84 178-84 © Издательство «Недра», 1984
ПРЕДИСЛОВИЕ
Предлагаемая вниманию читателей книга посвящена теории
процессов деформирования, разрушения и течения пористых и
трещиноватых сред, которая в последние годы приобрела особый интерес для
прикладной науки, прежде всего в связи с увеличением технических
возможностей воздействия человека на окружающую среду. В самом
деле, строительство грандиозных сооружений, интенсификация
отборов нефти за счет увеличения фильтрационной проводимости пластов
. и изменения составов жидкости, проходка глубоких шахт, борьба с
горными ударами, проблемы прогноза землетрясений и многие
аспекты динамики земной коры, сейсмобезопасность, сейсморазведка,
взрывные подземные работы, проблемы создания подземных хранилищ и
охраны окружающей среды от загрязнения — для решения всех этих
вопросов народнохозяйственной деятельности необходимы
представления о разрушении горных массивов и подземной гидромеханики.
Весьма близки к этой тематике многие проблемы химической
технологии, порошковой металлургии и т. д.
В течение многих лет работы в АН СССР автору приходилось
преимущественно заниматься разработкой новых разделов механики
сплошных сред, которые были непосредственно связаны с
требованиями прикладной геомеханики. Результаты этих исследований собраны
в данной книге. Основное внимание в ней уделяется формулировке
исходных физических представлений процессов деформации и
течений и их записи в форме уравнений континуальной механики.
Результирующие теоретические построения дополняются решением
примерных задач, цель которых состоит прежде всего в выявлении
коренных особенностей теории, доступных прямой экспериментальной
проверке. Хотя выбор задач проводился также с учетом их
непосредственного прикладного смысла, всегда имелась в виду необходимость
продолжения начатых работ исследователями, непосредственно
участвующими в разработке конкретных промышленных проектов. Во
многих случаях работы автора были действительно существенно
продолжены и внедрены в прикладную науку, что принесло ему
глубокое моральное удовлетворение. В книге упомянуты имена
специалистов, принявших участие в разных этапах этих работ. Ряд их
результатов, но не все и не в должной мере включены в текст книги, что
связано прежде всего с ограниченным объемом. Поэтому далеко не
полон также и список упоминаемых в книге ученых, внесших
значительный вклад в развитие науки о пористых средах и подземной
гидродинамики. Их имена можно найти в обзоре, составленном Г.
К.Михайловым и авторов для сборника «Механика в СССР за 50 лет»,
а также в реферативном журнале «Механика» ВИНИТИ, в
редактировании которого автор принимает участие.
Для выбора ряда тем исследований, равно как и подходов к ним,
3
большое значение сыграла стажировка автора и чтение лекций в
Университете Джонса Гопкинса и Брауновском Университете (США)*
Именно поэтому читатель найдет в данной книге изложение ряда
достижений американских -ученых и отметит довольно широкое
использование их экспериментальных результатов, прежде врёго
данных дорогостоящих испытаний геоматериалов в условиях высоких
давлений и температур. *
В предлагаемой книге читатель найдет ряд разделов и
результатов, по праву уже принадлежащих классической теории фильтрации,
однако книга написана так, чтобы не повторять заслуживших
известность монографий и руководств (А. П. Крылова, П. Я. Полуба-
риновой-Кочиной, Ю. П. Борисова, В. М. Добрынина, Ю. П.Желтова,
Ю. П. Коротаева, Б. Б. Лапука, А. X. Мирзаджанзаде, М. Д. Розен-
берга, Ф. А. Требина, М. И. Швидлера, В. Н. Щелкачеваидр.),
многие из которых были опубликованы издательством «Недра».
Избежать повторов удалось во многом за счет общего подхода,
позволяющего дать единое изложение разделов, традиционно относившихся
к различным ветвям науки — геофизике, нефтепромысловому делу,
механике грунтов или горных пород, взрывному делу и т. д. Может
быть это нарушит информационные барьеры между указанными
областями знаний и приведет к их взаимному обогащению.
Приложенный в конце книги список литературы не претендует на
полноту и содержит преимущественно обзорную литературу, где
можно найти подробную библиографию, а также работы отдельных
ученых, непосредственно связанные с излагаемым материалом.
*
Обращаем внимание читателя на частое использование
следующих форм сокращенной записи операций дифференцирования:
d<pfdt=<f),t\ <3ф/д#г = ф,,-; d\/dxidxj=<pfij.
,Г Л АВ А 1
ОСНОВНЫЕ ПОЛОЖЕНИЯ МЕХАНИКИ
СПЛОШНЫХ СРЕД
1. УРАВНЕНИЯ КОНТИНУАЛЬНОЙ МЕХАНИКИ
Уравнения" баланса массы, импульса. Закон
парности касательных напряжений. Определения
деформации по полю смещений. Термодинамический
анализ. Вязкоупругие и пластические тела.
Соотношения на сильных разрывах. Ударные адиабаты в
гидродинамическом приближении.
Уравнения механики сплошных сред являются балансовыми
соотношениями массы, импульса и количества движения для
элементарных объемов AV, линейный масштаб которых / должен быть
много меньше внешнего масштаба L задачи, но много больше
характерного масштаба X микродвижения частиц, слагающих
изучаемую сплошную среду: L>/>i. Балансовые уравнения для объема
AV можно'упрощать за счет предельного перехода 1/L—ИЭ (или
иначе //L<cl), который осуществляется выбором достаточно большого
внешнего масштаба L. Условие lfL<^l есть условие
дифференциальное™ элементарного объема: AV=dV. Второе ограничение 1^>Х есть
условие представительности фактических интервалов усреднения
(самого объема AV или же его сечений). Если не выполняется
условие L>/, балансовые уравнения для AV не могут быть
интерпретированы как точные континуальные макроуравнения. Если же не
выполнено условие /^>Я, то усреднение по пространственным
интервалам не может приводить к регулярным средним значениям.
Итак, при условии L>/>^, l3^>AV уравнения баланса для AV
могут считаться дифференциальными с внутренним масштабом X
(размер кристаллита зерна, поры).
При нестационарных микродвижениях также допустимо
усреднение по достаточно представительному интервалу времени. При этом
получаются уравнения корреляционных связей в элементе
пространства масштаба X для усредненной микроструктуры, отличающиеся от
континуальных макроуравнений.
Микроструктура пористых и трещиноватых сред представлена как
порами и трещинами, так и частицами (блоками). При составлении
для них континуальных уравнений обычно либо составляют
уравнения для феноменологически средних параметров объема АУ, либо
формулируют эти уравнения сначала в масштабе /<СЯ, а затем
усредняют их по объему AV. В первом случае усреднение проводится
в неявном видеш возможные неточности устраняются специально
поставленными реологическими опытами для замыкания системы
уравнений, так называемыми определяющими законами среды в целом.
5
Во втором случае вид замыкающих связей, а иногда и конкретные
значения реологических параметров определяют теоретически.
В обоих случаях исходными уравнениями являются
дифференциальные уравнения
баланса масс
P,rHpaj),j=/, (1.1)
баланса импульсов
(f>i>i) .*+ (Pvivj) ,i= Ы ,1+fi (1.2)
н баланса моментов количества движения. Последнее в простейшем
случае сводится к закону парности касательных напряжений, или
мначе — к симметрии тензора напряжений оц:
Здесь р — плотность среды, vi — скорости смещения частицы.
Уравнения (1.1) — (1.2) ^-истинные балансовые соотношения для объема
dV=dxirix2dxz с центром масс в точке хи х2, *з, в которой указанные
функции р, Vi, ... непрерывны. Индексы i, / принимают значения 1,
2, 3, символ (...),* означает частное дифференцирование по времени
'» (•••)»*— частное дифференцирование по координате Xj. В
уравнения входят потоки массы pvi и импульса pv&j, источники (стоки)
массы / и массовая сила //. Компонента напряжения сг^ есть
проекция на ось г вектора силы, действующей на единичной площадке,
нормалью к которой служит ось /.
Деформация ец элемента среды, находящегося в момент времени
# в объеме dV> вообще говоря, не мала и выражается через
смещения согласно соотношению Аль^анси
еи= (1/2) (uitj+tiiti—Uh,iUk,j). (1.4)
С другой стороны, можно ввести скорость деформации eij по
правилу
ёц= (1/2) (Vij+vjj), Deij = eijdt, (1.5).
причем приращение Ввц определяется следующим образом
Е*е% j= (ei-itf\-Vbfiijth—eiuQkj—е^ы+ешём+е^ёы) dt. (1.6)
Как известно, определения (1.4) и (1.6) не противоречат одно
другому, так как тензоры ец и ёц связаны между собой формулой
eij==£eij/dt=dileijJdt-\-eikeij-{-ejheku (1.7)
где djdt — производная Яуманна, a Qkj— скорость вращения,
d^eij/dt—eij^Vkeij^—eikQkj—ejhQhh (1.8)
Qhj=(l/2) {vklj—vjik).
Сложность этих соотношений связана с тем, что реологические
связи устанавливаются для фиксированной частицы среды (т. е.
ь лагранжевой системе координат), а в используемой здесь эйлеровой
еистеме им соответствуют приращения Бец. Например,- простейший
закон упругости имеет вид
Deti = Emdohh Eijhl=[(l+v)dik8ji—v8ij8ki]E-i (1.9)
(Е — модуль Юнга, v—коэффициент Пуассона) и соответствует
модели линейного гипоупругого материала (по К. Трусделлу).
Интегрирование связей (1.9) в интервале, где Я, \i — постоянны,
приводит к обычной форме закона Гука, связывающего напряжения и
деформации. Во многих практических случаях можно ограничиться
субстанциональными производными
eij=deijfdt=eij,t-\-v%eij9h; (1.10)
т. е. сохранять лишь перенос со скоростью центра масс частицы в dV+
но пренебречь ее формоизменениями и поворотами.
Перейдем теперь к термодинамическому- анализу элемента среды
в объеме dV. Баланс полной энергии имеет вид
{pe-\-pViVi/2) >rf (pev-j+pViViVj/2) ,;•= (oijVi) ,j+FiVi+qiti,
(Ы1)\
где е — удельная внутренняя энергия, q% — потоки теплоты.
Если умножить уравнение (1.2) на скорость и*, получим
уравнение баланса кинетической энергии, или иначе —уравнение живых
сил:
(pvtViJ2) tt+(pViViVj/2) fj= (aijVi) ^—OijVi^+FiVi. (1.12$
Разница уравнений (1.12) и (1.11) есть уравнение внутренней
энергии, или иначе — уравнение притока тепла:
(ре) ,*+ (peflj) ,j=ory0i,i—?/,«- (1.13 J
Если воспользоваться теперь уравнением баланса масс (1.1) при
/=0 и определением (1.5) скорости деформации, то в силу
симметрии тензора oij уравнение притока тепла будет иметь вид
Р« = °//*ц-<7/.*-- О-14)
Полная деформация среды etj = e^} + ^состоит из двух составляю^
щих —обратимой (упругой) g(e) и необратимой е{р). Работа
напряжений на приращениях de{?} переходит в упругую энергию, тогда как
'/
работа на приращениях необратимых деформаций o^de./ диссипи-
руется.
Соотношение (1.14) выражает первый закон термодинамики.
Второй закон термодинамики может быть записан в виде
—qi[idt = pTds—dW^pTds, (1.15)
где Т — абсолютная температура, 5 — удельная энтропия, dW —
необратимо затраченная работа! в среде. В частном случае dW^o^de^,
а в более общем случае dW должна включать работу p\iijd%ij,
производимую при изменениях дополнительного внутреннего параметра
Xij [41]. Конкретизация выражения dW преобразует (1.15) к
уравнению баланса ^нтропии
■p71s=o^y+FLl/3e//-^/il. (1.16)
7
Если исключить потоки теплоты из уравнений (1.14) и (1.16),
получим соотношение Гиббса
r*=£f«-(ol//P)rf^)+Fily£a/yt / 1i.i7)
определяющее энергию е как функцию параметров состояния е^
s и %ij. Поэтому
°" = 9 (~Ш) т = (~^~) с) ^ = ~ (И?) «у {1Л 8)
Часто в качестве параметра состояния используют температуру Г,
т/е. * = е (*<<>, JC,/f Г).
Если представить изменение компонент тензора x*j уравнением
где г,-,-,*, af-jfc,fe — скалярные и векторные интенсивности, порождающие
изменение параметра %0'> то уравнение (1.18) примет вид
Р5+ ЫТ) |Л+ (linOifk/T) tk = П.
Здесь П=2Х/ — интенсивность роста удельной энтропии,
определяемая диссипацией энергии в рассматриваемой точке; X —
термодинамические силы, / — потоки,
ГП=а47еу + Pl,rll + atlhT(rlJIT\ k - qk{T, кЩ (1.19)
Термодинамические силы могут быть связаны с
термодинамическими потоками кинетическими дифференциальными уравнениями,
учитывающими инерционные эффекты, что означает нарушение
принципа квазистационарности микромасштабных процессов. Самым
простым является случай интегрируемости кинетических уравнений.
Тогда термодинамические силы являются нелинейными функциями
потоков. Если разлагать эти функции в ряд, то в первом приближении
потоки Ik будут пропорциональны силам Л&, причем коэффициенты
пропорциональности — кинетические коэффициенты — могут быть
функциями параметров состояния Tte^tri} частицы (например,
вязкость жидкости зависит от температуры).
Гц = mfiki + 2К8,Л8У/) *кг + (PbtlbM + 2МЬ1кЬп) 4l,
qk=A (TjJT)+BT(w/T)jAiit (1.20)
ацк = —ВЬц(Т9к1Т)+СТ(\1ц1Т),к,
где Л, В, С, £, g — кинетические коэффициенты, 8ц — единичный
тензор. Соотношения (1.20) составлены с учетом принципа Онзагера
о симметрии кинетических коэффициентов и принципа Кюри,
согласно которому сила не может вызывать поток другой тензорной
размерности. На кинетические коэффициенты накладывается дополни-
8
тельное условие, согласно которому правая часть уравнения (1.19)
должна быть положительно определенной.
Если кинетические коэффициенты являются константами
материала и, кроме того, qi=rij = ciijk = 0, то соотношения (1.20) описывают
некоторые вязкоупругие тела. Введение структурного параметра %ц
позволяет феноменологически учесть релаксационные свойства
сплошной среды. Соотношения (1.20) сводятся к обобщенной
релаксационной связи
/?а—вст,*= (ER+Q2)e—EQetU (1.21)
т. е. из (1.21) при в = 0, QAR = 0i=7^O следует уравнение состояния
среды Кельвина — Фойгта, а при £7?+Q2=0 — среды Максвелла. Среда
Максвелла описывает релаксацию напряжений, обусловленных
необратимыми деформациями, а среда Кельвина — Фойгта —
запаздывающую упругость.
Если внутренняя энергия ре = (1/2) Ете(ре{£-\-!(s) квадратичная
функция упругих деформаций, то при Xrj=const; Т=const выражения
(1.18), (1.20) означают
ои = Ете%\ е^=^{е!;;)ЬиЬк1+2х(е^)Ь1кЬ}1}о1Г (1.22)
(е)
Скаляры :|, X могут зависеть только от инвариантов тензора £.
или — в силу первого из соотношений (1.22)—от напряжений oijt
в частности от давления и сдвигового напряжения.
Введем диссипативную функцию'
D(^») = (l/2)a,,iy. (1.23)
Если диссипативная функция D — однородная функция первого
порядка по скорости деформации, т. е. при изменении масштаба
времени в t~l раз диссипативная функция меняется также в t раз
D(te{p)) = tD, (1.24)
то D должна быть пропорциональна самой е[р). Сопоставление (1.22)
и (1.23) приводит к выводу, что напряжения а^ не меняются при
изменении всех скоростей необратимых деформаций в одном и том
же отношении, а кинетические коэффициенты g, X также являются
однородными функциями первого порядка от скаляров —от скорости
объемной необратимой деформации е(р) и от интенсивности сдвиговой
необратимой деформации ^р)=-2\/ \е\р) - -^-е^ъЛ (е[р) — 2-^вД
Возможность выражения зависимостей £, А, от вц [см. (1.2)] и
от е\р) означает, что коэффициенты £, % не функции параметров
состояния, а функционалы, т. е. они являются дополнительными
искомыми величинами, определяемыми при решении краевых
задач. Для щ. нахождения нужно ввести два дополнительных
уравнения. Если последние формулируются как алгебраические
предельные условия, связывающие между собой компоненты тензора напря-
9
женйй ац и~ необратимых деформаций e{f), то соответствующие
необратимые деформации e!f) именуются пластическими. /
Простейшие условия (соответствующие пластичности сплошных
металлов) имеют вид условия Треска и условия отсутствия^бъемной
деформации
т = хУ, <fe jj% = 0, и = sgn х, (1.25)
где х =(2|/2")-1{(аи —cy22)2 + ...+6°2i2 + ...}I/2 -интенсивность
напряжений сдвига.
Если диссипативная функция D — однородная функция второго
порядка по скорости деформации, т. е.
D(te[p)) = t2D, (1.26)
то D должна быть пропорциональна квадрату скорости необратимой
деформации е[р)е[р). Тогда кинетические коэффициенты, как следует
из сопоставления (1.22) и (1.23), оказываются независимыми от eif\
т. е. могут быть константами материала или же функциями от оц и
температуры Г, измеряемыми в ходе специальных реологических
опытов. Такие необратимые деформации называются вязкими, а
величины, обратные кинетическим коэффициентам, — коэффициентами
вязкости — объемной £ и сдвиговой т|:
в/=#%+ч(«У "т '*%)• <L27>
Коэффициенты вязкости включают характерное время изменения
внутренней структуры и соответствуют явлениям ползучести
геоматериалов.
Традиционная вязкость горных пород и минералов, обусловленная движением
дислокаций и других дефектов кристаллической решетки, имеет порядок
IG14—1018 Па-с, весьма чувствительна к температуре и, вообще говоря, меняется
ври изменениях скоростей деформации на порядки. При ползучести гранита
108—109 Па-с для каменной соли характерна вязкость т)=1012 Па-с (при
комнатной температуре). Значение сдвиговой вязкости известняка составляет
(1,3—2,1) 107 Па-с.
Пористые геоматериалы обладают обьемной вязкостью. По М. Рейнеру для
асфальта (при расширении) £=2,9-107 Па-с, для бетона (при объемной усадке)
- £=9,4- Ю2 Па-с. Поры меняют также и величину сдвиговой вязкости.
Вязкость глинистых грунтов обусловлена относительным
движением частиц по пленкам влаги в местах контактов. Наиболее
интригующей является коррозионно-хрупкая ползучесть (пластичность)
юрных пород, обусловленная переносом влаги в системе внутренних
трещин. Влажность снижает трещиностоикость породы и приводит
ж дальнейшему росту трещин, что означает рост неупругих
деформаций.
Если в точке х\, *2, *з функции изменяются скачкообразно, то че-
pes эту точку проходит поверхность разрыва 2. Для потоков через 2
составляются балансовые соотношения, или иначе — соотношения на
разрывах. Разрывы появляются там, где для описания движения.
ю
среды как непрерывного используемая система уравнений
оказывается неадекватной.
Решения вне разрыва непрерывны и удовлетворяют соотношениям
на разрыве как граничным условиям с соответствующей стороны от
поверхности разрыва, которая двигается в пространстве со своей
собственной скоростью Ui. Обозначим область, на которую набегает
разрыв, символом «—», а область за разрывом — символом «+». v
В число соотношений на разрывах входят балансы массы, импульса
и энергии. Если разрыв имеет реальную толщину 2А, то для
подсчета потоков через разрыв удобно ввести две контрольные поверхности
h+ и /i~, включающие весь разрывный переход. Локальные потоки
массы, импульса и энергии через элементарную неподвижную
площадку с нормалью tij имеют вид
pvjtij, {pviVj—Oij)njy p(e+lI2v2i)Vjnj—OijVinjy
а для контрольных поверхностей, двигающихся со скоростью Ujy они
включают уже относительную скорость Vj—Uj.
р(Vj—Ui)njy {9Vi(v—Uj) —Gij}njy p(£+ (1/2)vb) (vj—UjYnj—OijVinj
В предположении, что внутри разрыва нет источников массы,
импульса и энергии, можно приравнять потоки через поверхности й+
и h-.
Поскольку скорость Uj коллинеарна вектору /ij, эти соотношения
распадаются на соотношения для касательных и нормальных
потоков. Первая группа дает
(УЩ
рч+ (e++-f vw)-p>:=?-v7 (в-+-^-о7)-о-0,
где индекс т означает компоненту вектора vt, касательную к
плоскости разрыва. Вторая группа приводит к соотношениям
p+(v+-U)=p-(v-n-U), U=Ujni,
p+v+i (v+n— U) —a+,„=p-u-i (Vn—U) — <Г7„, (1.29)
P+(vf -U)(s+ + ±v+v^-*y = ^(v; -U)(s- + ±v-v-yo-v7.
обычным для теории ударных волн. При заданных значениях пара-
метров, например в области перед разрывом, и при известной
реологии среды (функции р(р, 7), е(р, Т) заданы), система трех
уравнений (1.29) содержит четыре искомых величины р+, Г+, v+n и U.
Иначе говоря, система (1.29) может быть разрешена в форме ударной
адиабаты — зависимости трех переменных от четвертой.
Экспериментальные измерения ударных адиабат весьма часто
дают линейную связь между v+n и U:
\ U=a+bv, u=y+n, (L30)
справедливую для весьма сильных ударных волн. Здесь а, Ь —
числовые параметры (табл. 1). Зависимость (1.30) или же иные формн
И
записи измерений ударных адиабат позволяют решать обратную
задачу— находить уравнения состояния веществ для высоких давлений
ш, температур, часто недостижимых в статических условиях. /
Таблица 1
Вещество
Кварц
Вода
Стишовит
Вольфрам
Нефть
Гранит
Каменная соль
Доломит
Ро» кг/м»
2600
1000
4290
19 350
850
2610
2240
2593
Г0
0,653
1,00
1,18
1,54
5,44
1,4
5,5
а, км/ с
1.21
1,50
9,00
4,00
2,19
4,93
3,49
5,97
Ь
2,02
2,0
1,14
1,285
1,52
0,372
1,264
0,876
Внутренняя энергия е материалов при давлениях, намного
превосходящих их прочность, представляется [10] в виде суммы «холодной»
8(ЭС)(У), V = 1/р энергии (удельной энергии на изотерме абсолютного
нуля) и «тепловой» энергии
e=eW (V) + V (p—pW) ITJV). (1.31)
Это уравнение состояния в форме Ми — Грюнайзена. Здесь р<х>=
=T-de№fdV — «холодное» давление, Г (У)—коэффициент
Грюнайзена, причем во многих случаях допустимо задавать Г (V) в простом
виде
Г/Го=17У<ь Го=Г(Уо). "~ (1.32)
«Холодное» давление р(*> для конкретных материалов можно
подбирать по данным об ударной адиабате, или иначе — об адиабате
Гюгонио:
Рн=Рн(Ун)',-ен(Ун)=(1/2)Рн(Уо-У);. (1.33)
Поскольку связи вдоль ударной адиабаты также должны
удовлетворять уравнению Ми — Грюнайзена, из (1.31) и (1.33) находим
соотношение .
р(*)=—<Эе(*>/<ЭУ=рн—Г (ен—е«) V-\ (1.34);
тогда как из представления ударной адиабаты (1.30) для рн следует
такое выражение:
Pn=a*(VQ-V){Vo-(Vo-V)b}-\ (1.35);
Чтобы определить е<х> из дифференциального уравнения (1.34);,
а затем и р<х>, можно прибегнуть к разложению в ряды по
относительному сжатию.
12
2. ОБЪЕМНОЕ УСРЕДНЕНИЕ И МАСШТАБ ОПИСАНИЯ
Баланс массы, импульса и энергии в интегральной
форме. Среднеповерхностные и среднеобъемные
величины. Усреднение по ансамблю. Пористость и про-
светность. Различие макроскопических и среднеобъ-
емных напряжений. Цепочка макроуравнении
равновесия. Некоммутативность усреднения и
дифференцирования. Смена масштабов описания.
Пористые и трещиноватые среды представляют собой конгломерат
сплошного твердого материала и пустот, заполненных при их
насыщении жидкостью или газом. Поэтому уравнения континуальной
механики для всей среды в целом должны отличаться от уравнений для
сплошного твердого материала или для заполняющего пустоты
флюида.
Проинтегрируем уравнения движения и энергии для каждой из
фаз по объему У=УУЦ-У<2) [22], где объемы Va разделены
поверхностью Sm(t)y а внешняя поверхность объема V сложена
поверхностями фаз S<a). При этом можно использовать тождество,
справедливое для произвольной функции t|) в объеме V, ограниченном
поверхностью Sj, перемещающейся со скоростью Wj по нормали /:
V(t) V(0 5
Если поверхности Sa фиксированы в пространстве, получим
следующие с балансовые соотношения
v(a) s<a)
jf j ?v'dV+ j" W№ + WM= J pF.dV+ j 0.jdSjt (2.2)
y(«) 5(a) V(a) S(a)
4f J" ?{*+-!r°iV.i)dV+ J p(. + 4-0i0/)a,dSy+Ew = .
y(a) s(a)
= j -pF^dVH- J «i/f/rfSy + J. PQ^- j" qjdSj,
v(«) s(a) v(a) s(°0
4 j P^v + j WS/+^>= J ^;;>f-+ j q^-
s(«) v(a) v(«)
Здесь Q — объемные источники энергии, возникающие, например,
из-за внешних воздействий, h — мощность необратимой работы на до-
13
полнительных степенях свободы, а АИа\ W£a\ е<а) и Э<а>— стоки
массы, импульса, энергии и энтропии на поверхности S<w> пор (трещин):
М(*)= J tty-wjdS,, W™ = $. {fodvi-w^-o^ds/
E<"> = J {p(• + 4"v'v' ) <°/ - «*/) ~°'/°< + ?/ }dS/-
(2.3)
s(m)
где *9<m) — некоторый дополнительный источник энтропии на
поверхности (например, из-за сухого трения), М1=М =—М2, Е1 = Е = —Е2.
Конвективный расход массы, импульса, энергии и энтропии через
S<m) определяется, как обычно, относительной скоростью Vj—Wj
движения частицы материала Vj и движения границы, т. е. поверхности
поры Wj. Эта разница отлична от нуля, если, например, происходит
потеря массы на поверхности пор (растворение или испарение
твердого материала). Если деформирование пор таково, что на их
поверхности S<m> остаются одни и те же частицы материала, то для этих
частиц будет выполнено условие Vj=w-j. Подобное деформирование
(в том числе необратимое) происходит без внутреннего разрушения
пористой среды. Если же Vj—т^фО в какой-либо изолированной
точке а поверхности S(w> пор, то это есть точка разрушения. Здесь от
поверхности поры в глубь объема будет отходить трещина, а разница
ij=Wj—Vj есть компонента скорости роста трещины (движения ее
вершины) относительно материала среды.
Возьмем в качестве объема V элементарный макрообъем AV=
= AXiAX2AA'3, соответствующий макроскопическим координатам Х{ и
такой, что AXi^X^dxu где X — характерный масштаб поры или
трещины. Тогда балансовые интегральные соотношения (2.1)
приобретают смысл конечно-разностных балансовых соотношений для
объема AV. Введем объемную концентрацию mW=AV(a)fAV фазы а и
среднюю по объему плотность
pWe<p>«=5^. j PdV. (2.4)
ду(а)
Тогда первое слагаемое баланса масс из (2.2) принимает вид
AV(«),
Внешняя поверхность ASj = 2(а)5(а) объема AV в декартовой
системе координат представляет собой поверхность куба с гранями
ASl(Xl—(\J2)AXl)=AX2AXZl ASl(Xl+(l/2)AXl)=AX2AXz и
соответственно для пар граней A52=A^iA^3 и AS$==tAXiAX2.
14
Введем поверхностные концентрации т[а) == AS{cl)[ASj фазы а и
средние по поверхностям потоки массы.
р(^;а)=(р^);а)=^г j ?vinidSt (2.5)
где по / суммирование не проводится. Тогда второй интеграл
баланса масс из (2.2) может быть представлен в виде трех разностей
Д (р{а,)и{а)т(л)) потоков на парных гранях AS/, отстоящих друг от
друга на расстоянии AXj
Что касается стока АКа) в балансе (2.2), то он обратится в нуль,
если скорость Vj движения частицы, находящейся на поверхности
S(w>(£) раздела фаз внутри объема AV\ совпадает со скоростью
перемещения самой поверхности S^m)(t) в этой же точке. Если же Vj-ф
Фхи$, то существует поток массы через поверхность раздела, т. е.
фазовый переход интенсивности
1 = Ж \ ?(pj-wj)nidS.
Если AV<^L37 где L — внешний масштаб движения, то допустимо
положить, что AV=dVy т. е. и первое уравнение (2.2) принимает вид
дифференциального макробаланса массы фазы
(я»("У")).<+(<(р<х)>-/=°- (2-6)
Если ДК>А,3, то средние по объему величины, например (2.4), и
средние по поверхности, например (2.5), являются" регулярными
функциями макрокоординат — соответственно координат центра масс
объема AV или же центра масс площади поперечного сечения
Sj(объема AV, смещенного, на интервал ±AXj/2).
При построении математических моделей многофазной механики
следует в явном виде сохранять пористость т, т. е. относительный
объем пор в единице объема всей среды. Тогда т=\—mi = m2. Для
сред с хаотической внутренней структурой можно утверждать, что
m=(G)=^r^G(xit t; <*>)dVt щ = (0>у='-щ j G{xi% t; .)dS
LV AS.
где G(xu t\ o))=l, если микроточка Xi, t принадлежит паровому
пространству, и G(Xi, t\ co)=0, если точка xu t принадлежит матрице.
Параметр <о Отражает случайный характер принадлежности точки
Xu t той или иной фазе среды. Усреднение G по ансамблю реализаций
среды с параметром © (статистическое среднее) определяется как
, . 8(*„ *)= J G(jtlf <; •)</«. Jd<o=l. /
ш «о
Будем предполагать, что объем AV настолько велик, что^величины
т и in уже не зависят от параметра случайности со. Нетрудно видеть
|22], что средняя по всем параллельным сечениям ASj объема А К
просветность равна пористости:
т = Щ$'*1Л1- (-^Xll2)<J:i^xl-Xj<(AXil2). (2.7)
' AXi
Если просветность fhj одинакова на всех сечениях ортогональных
оси Xjy то m=mj. Если просветность меняется непрерывно
^ (л:А) = ту1(^л)Ч-(^^/^^^) Сл Ч- (1/2) (^Я/^^%) ^ И" -•-
то из интегрального соотношения (2.7) следует, что
т№)=^№)+0{(ЛХ,)2/^}, /=1, 2, 3. + (2.8)
Внутреннее строение пористой среды может быть анизотропно, и
при этом просветность fuj может, вообще говоря, зависеть от
ориентации площадки ее определения. Условие (2.7) тогда означает, что
средняя просветность инвариантна к выбору оси Xj, а согласно
равенству (2.8) просветность ffij с точностью до величин второго
порядка малости является скаляром.
Поскольку величинами^ второго порядка малости в континуальных
уравнениях можно принебрегать, то будем полагать т=т.
Другая ситуация возникает при усреднении уравнений
движения. Рассмотрим частный случай уравнений равновесия упругого
микронеоднородного материала, в котором отсутствуют поры.
Допустим, что в микромасштабе (т. е. для дифференциального элемента
dv=dxidx2dxz) выполняются уравнения равновесия
Oij,j+\Fi=0, ои=ац. (2.9)
Если умножить уравнение (2.9) на координату хк, то получим
oih=(atjXk) ,j-\-iFiXk. (2.10)
Домножение этого уравнения на альтернирующий тензор ен*
приводит к уравнению баланса момента количества движения
\^lhiGijXh) ,j-f-^lkiJFiXk=0, ^lkiOik=0. (2.11)
В силу предполагаемой непрерывности поля а^-, пренебрежения
инерционными силами и отсутствия потоков через поверхность S<w) пор
второе из уравнений (2.1) упрощается
{o.^. + Jf^V^O, (2.12)
5 V
где dV=dxidx2dxs, dSj = ndSj. Разделив (2.11) на AV и определив
среднее по объему и по площадке ASj=AXkAXm следующим образом:
AV AS.
16
получим результирующее макроуравнение в виде
(d/dXj) <aij>j+<Fi> = 0. (2.1-3)
Здесь макродивергенция —сумма следующих выражений:
•£и$*<м=к{м>1 **.-<•">• L 4 (214>
при переходе к дифференциальной записи, справедливой в
асимптотическом смысле (при AXi/L—Я), где L — внешний масштаб задачи).
Средняя объемная сила <Fi> есть регулярная функция
макрокоординаты Xi=Xi—li центра масс объема 1ДУ. Здесь £*• —вектор,
соединяющий центр масс с произвольной точкой внутри ДК. Из
конечно-разностного представления (2.14) видно, что средние усилия
<Ojj>j'на ориентированных площадках (гранях объема AV) можно
считать регулярными функциями координат центра масс объема,
смещенного на расстояние ±(lJ2)&Xk.
Усреднение уравнения (2.10) по объему приводит к следующему
результату:
<aih> = <aik>k+(d/dXj) <а^к>~'<F£k>\ (2.15)
где <Oih>—тензор напряжений, усредненный по объему. Согласна
(2.15) макронапряжение <Gih>k выражается [21] через среднее
объемное напряжение и тензор более высокого ранга. Величины
\iijk=<Oik£>h>j — двойные напряжения, <Р&к>—двойная массовая:
сила. Из дифференциального уравнения (2.14) видно, что
напряжения считаются функциями центра масс, т. е. вычисляются как
средние по ориентированной площадке, проведенной через центр
масс AV.
Двойные напряжения являются моментом распределения усилий
на ориентированной площадке AS/ более высокого порядка, чем
макротензор <(Jij>/; они в свою очередь могут быть выражены через:
свое среднее объемное значение <-а*/£ь>- и моменты еще более
высокого ранга — тройные напряжения. Для получения нужного
соотношения следует домножить уравнение (2.9) на диаду хъ.хт и
усреднить. Если продолжить эту процедуру, то в результате получится
цепочка макроуравнений, включающих в себя макротензоры /г-п>
ранга, вообще говоря, несимметричные из-за условия введения их
как средних по ориентированным площадкам. Домножение
уравнения (2.15) на альтернирующей тензор е«й приводит к уравнению
момента количества движения
^iik<<Jik>h+(d№3fdXi)-№=Q. (2.16).
Отсюда [41] антисимметричная часть макронапряжения отлична от
нуля, если существуют моментные напряжения ^/ = <^шст,/^>/ т
распределение по объему моментов сил ЗИг=<еш^7<?л>.
Если в макрообъеме AV • рассматриваемый материал однороден,,
jo элементарный объем можно свести к точке (I?—>0, \лц—ь0,.
<o/b>j-—K7ij=<o'tj>) и достаточно только обычного уравнения
равновесия (2.13), совпадающего с исходным (2.9). Вектор
макросмещения Vi вводится как среднее по объему смещение
С/4=<рЦг>/<р> = <^>, p=const. (2.17)
2—3311 17>
Поле микросмещений Ui(x) определится как сумма регулярной и
нерегулярной u*i составляющих
MSi)==£M-№№)ij+u*i, <«*i>=0, /(2.18)
деформация е.ц — следующим образом /'
е«=(1/2) {dUildXj+dUjIdXi) +(1/2) (ди\/дх^ди^/дхг).
(2.19)
Усреднение по объему дает
<eti>= (1/2) {дЩдХз+ди,/дХ{) + (1/2) {д<ии>*[дХ,+
+d<u*i>4dXi). (2.20)
Определение средней по объему деформации. (2.20) упрощается, если
<u*i>j=<ti*i>==0. (2.21)
В этом случае второе слагаемое из (2.20) выпадает, т. е. средняя
по объему деформация есть симметричная часть градиента поля
«средних смещений.
Условие (2.21) можно заменить на менее ограничительное
!<M*<>j=<a*/>, i=j\ <и\>эФ<ии>, 1Ф1 (2.22)
Второе слагаемое (2.20) тогда отлично от нуля (например,
циркуляция от тангенциальных компонент смещения по замкнутому
контуру отлична от нуля, если внутри имеется дислокационное
несогласие).
Число сохраняемых дополнительных кинематических средних
параметров должно соответствовать числу уравнений равновесия/Если^
число степеней свободы меньше числа уравнений из цепочки, то в
результате получаются градиентальные. модели среды [21].
Если же дополнительной кинематической переменной будет
поворот фь; микрочастицы, отличный в общем случае от среднего
поворота Qkj, то помимо уравнения количества движения (2.13) нужно
вводить в анализ баланс момента количества движения (2.16).
Подобного типа континуальные модели известны как среды Кос-
сера или иначе" модели 'асимметричной (микрополярной) механики.
Предполагают, что такие усложненные модели позволят учесть
повороты зерен материалов, а также учесть подробнее граничные
эффекты (например, шероховатость штампа, передающего нагрузку).
Сопоставим теперь средние по объему и по плоским сечениям. Из
равенства
Ы = ж$ °udV= 5*7 J Ы'Ж/ (2-23)
следует, что
:<<y/i>=<<r/i>J (2.24)
при <aij>j=const. Если же <(r/j> ,-==/(&), то условие (2.24)
справедливо лишь приближенно. В самом деле, подставим разложение
- [<х!ц>} (**+£*) =<ou>i (Xh) + (d<Oij>jJdXh)b+
+ (1/2) (d^«ui>ildXh)^h+ .v.-
18
в интеграл (2.23). Тогда получим оценку нарушения равенства (2.24)
!<<т«>—<0/i>j=(l/2) (д*<оц>з/дХ*к) (Ах2/12). (2.25)
Если бы можно было устремить AXk—нО, получился бы результат
(2.24), однако правая часть (2.24) оказалась бы тождественно сов-
падающей с локальным значением Oij, поскольку при АХд—*0
стремится к нулю и площадь усреднения Д5,-.
Итак, по оценке (2.25) возможное нарушение равенства (2.24)
имеет порядок АХ2, т. е. по крайней мере порядок квадрата
масштаба микроструктуры К2. Если же учесть, что среднеобъемный тензор
напряжения <оц> симметричен, так как симметричен локальный
тензор Gij напряжений, то именно правая часть оценки (2.25) будет
главным членом антисимметричной компоненты тензора
макронапряжений, которая и входит в уравнение моментов количества движения
(2.16).
Условия перестановочности операций усреднения и
дифференцирования следуют из процедуры интегрирования
/df\ 1 *УТ//2)^ WiiXi + bXj/V-ifjyXt—bXjM
W/=aF, J !Zf i= лх>' =
Х.-(ЬХ./2)
=^L( (2.26)
где <f>j—<f>j(Xk). При усреднении происходит изменение
масштаба описания, а потому
A<f>jfAXj^d<f>j/dXj—дифференциальная операция в новом масштабе и, кроме того, вне зависимости от
параметра ансамбля <о
. . K/>j№±A*;/2; ©)=/№±ДВД
Последнее выполняется для представительной площадки ASjy
включающей в себя весь ансамбль реализаций. Кроме того, произошел
естественный переход от усреднения по объему ДV к усреднению па
ориентированной площадке. Полная аналогия с правилом
перестановочности dfldx=(d/dX)<f> достигается, если принять гипотезу
Усреднение по объему фактически проводится при разработке
алгоритмов численного счета уравнений математической физики, когда
по дифференциальным уравнениям строятся их конечно-разностные
аналоги. Вполне допустимо понимать эти уравнения как новые
континуальные уравнения в йовом (большом-)г масштабе. Но и при
совпадении типов уравнений баланса импульса в микро- и
макромасштабе средние деформации <ец> могут быть связаны с
макронапряжениями <Oij>j совсем иными реологическими законами, чем их
локальные значения. Так, элементы матрицы геоматериала могут
обладать чисто упругими свойствами, а объем AV масштаба I —
включать в себя трещины, т. е. он будет проявлять и неупругие свойства.
Его прочностные параметры, вообще говоря; зависят от /, поскольку
с ростом AV в него могут попадать трещины возрастающего размера.
Если же материал в достаточной степени однороден (трещины или
поры вообще отсутствуют или же намного меньше масштаба /), то
свойства среды будут инварианты к выбору объема AV.
19>
3. РАЗРУШЕНИЕ СПЛОШНОГО МАТЕРИАЛА
Термодинамика вязкоупругого тела с трещиной.
Поверхностные энергия и диссипация. Критерий
роста трещины, выраженный в скоростях^Разрушение
упругих и вязких сред. Трещина в'вязкоупругой
плоскости. Контурный интеграл для энергии. Поток
энтропии. Локализованная диссипация и /-интегралы.
Контурный интеграл для вязкоупругих сред.
Критические коэффициенты интенсивности.
Разрушение сводится к потере целостности элемента или образца
и реализуется путем возникновения и роста трещины в первоначаль?
но сплошном материале. Вершина (точка роста) трещины есть
особая точка и через нее из среды может происходить уход энергии, и
вообще говоря—массы, импульса и энтропии. Классический критерий
Гриффитса для хрупкого разрушения упругого тела использует
только условие расхода энергии в точке разрушения. Условия для
расхода (или поступления) массы вещества могут потребоваться, если
разрушению сопутствует, например, химическая реакция, а
независимый баланс импульса — при некоторых видах динамического разру- "
шения.
В простом случае квазистатического разрушения для системы
«тело-|-трещина+воздей(Ствие» можно составить баланс энергий
PA+Q=E,
где Р — внешнее воздействие, А — соответствующее перемещение.
Уравнение роста энтропии S системы имеет вид
TS=TIl+Q.
Исключение притока тепла Q позволяет выразить производство
энтропии П через мощность и скорость изменения свободной энергии
тела Ф=Е—75. В изотермических условиях (T=Tq) результат особо
прост
TJ1 = Рк~ (Ё - TQS) = РА - Ф. (3.1)
Другое определение П связано с рассеянием Ч? механической
энергии в теле. Согласно вариационному принципу наименьшего
рассеяния [15] энергии (Онзагера)
^ б(П—40=0, (3.2)
причем варьирование проводится по силе Р и длине трещины /.
Свободная энергия Ф состоит из W — упругой энергии тела с разрезом
длины / и поверхностной гриффитсовской энергии 2у^1
ф=ф(/, P)=W(l, Р)+2у01, (3.3):
где yo=Yo(7o> #)> а — линейный масштаб (толщина) поверхностной
зоны материала. Причем
aO/dP=dW/dP=A&, dW/dl=—Gt
где G — сила Ирвина. Здесь Д<е> упругая часть полного смещения Д=
=эД<е)-ЬД(Р>, a W — функция силы Я
20
Рассеяние W будем задавать следующим образом
Т.ЧГ = Л (Р, I) + 2чJ + 2 J Ш, (3.4)
О
где Л —диссипация в теле с разрезом^ 2yJ — скорость диссипации
механической энергии, обусловленная скоростью роста трещины /,
но не зависящая от ее длины; £ — специфическая диссипация энергии
в единице длины поверхностного слоя. Будем считать, что
выполнено условие автономности роста трещины, т. е. величины уо» у*, £
не зависят от Р,
Подстановка выражений (3.1)., (3.3) и (3.4) в уравнение (3.2)
приводит к такому результату
8(Л + ^-)—Д8^ = -28 fw/-28(Y/). (3.5)
о
Далее учтем, что 8(у1)=0у т. е. 7=70+7* не зависит от длины I.
Вариационное уравнение (3.5) распадается на два независимых
соотношения. Первое из них определяет неупругую составляющую
скорости смещения
дА/дР = А - dW/dP = А — А<•> = АО,
а второе дает [30] критерий роста трещины в неупругом теле
ь- (d/di) (Л+dwjdt) = гф = -^ J ш). (3.6)
Трещина растет, если сумма изменений диссипации и скорости
убывания потенциальной энергии тела достигает критического уровня,
обусловливаемого правой частью равенства (3.6). Величина *2£ есть
сосредоточенная диссипация механической энергии, приходящаяся
на единицу приращения длины поверхности слоя. Она должна быть
независима от длины трещины /, но может быть функцией скорости
роста трещины /. Для вязкой диссипации g оценивается так
Здесь в — время релаксации.
Рост трещины в материале сопровождается перестройкой
внутренней структуры вблизи поверхности разрушения. На эту
перестройку затрачивается энергия у, причем у* есть удельная вязкая
диссипация при этой перестройке. В дальнейшем полоска материала с
перестроенной структурой будет диссипировать механическую энергию
иначе, чем до перестройки. Этим объясняется различие
поверхностной вязкости т]в и объемной.-T]V=T); причем [ц] =r\s—r\v.
Начальное условие (/=/0 при /=0) для дифференциального
уравнения (3.6) — относительно длины трещины — определится из
решения задачи об упругом теле с разрезом.
21
Укажем простые частные случаи. Если Х=£,=0, то критерий
(3,6) сводится к критерию разрушения упругого тела ;
G = —dW/dl=2y, (3.8)
где гриффитсовская энергия 2у появляется как константа
интегрирования. Если, наоборот, №=0, то получаем критерий разрушения
вязкого тела
—дА/д1=2\. (3.9)
Если £=0, но Л=т^0, ю трещина растет при условии
dA/dl=G. (3.10)
Рассмотрим рост трещины в зязкоупругой максвелловой
плоскости, растягиваемой усилиями Р. Удельная диссипация и упругая
энергия оцениваются так
D=P*/(2r\), U=P2/2E.
Поскольку избыточные значения упругой энергии и скорости
диссипации тела пропорциональны площади концентрации напряжений
(т. е. /2), то
Л = В^2Р2/(2г1)+Сь W==—B2l2P2/(2E)+C2, (3.11)
где 5,1, В2 — числовые коэффициенты, а С\г С2 — постоянные, не
зависящие от длины трещин.
Подстановка величин (3.11) в условие роста трещины (3.6) при
Y = const приводит к такому дифференциальному уравнению
21-В11(Р2/ц)+В21(Р2/Е) =0. (3.12)
Если скорость роста трещин / не влияет на поверхностную диссипацию (%= '
= %о=const), то | = const и решение уравнения (3.12) имеет экспоненциальный
вид
■U= (U — К) ехР у вй 7j *)> 1*= вхРг в вх Р2
(3.13)
Трещина в вязкоупругом теле растет^ если ее начальная длина /0 больше
порогового значения /*, при котором изменение диссипации в теле на единицу длины
трещины достигает уровня поверхностной диссипации. Если /о</*, то длина
трещины убывает. При /0>/*, /g оказывается возможным рост трещины за
счет-высвобождения упругой энергии.
С другой стороны, если длина /0 больше /*, но меньше критического граффитсов-
ского значения длины /g, определяемого1 из уравнения
G(la)^B2(P4a/E)=2b (3.14)
то решение (3.13) описывает подрастание трещины до значения /g. Если же /o=/g,
то из уравнения (3.12) можно определить конечную стартовую скорость роста
трещины
7,™ JE- (Ы в* \ Y JEW'М Вх \ а .
Второй .частный случай £=£/2, £= [rj]/a = const. Наконец, при l = r[J из (3.12)
следует решение
/ В. Р* Е \
1=****(■£ р* -ъвТЧ- - (ЗЛ6)
22
При постоянстве поверхностной дис-1
сипации трещина равновесно растет
только при спаде растягивающего
усилия согласно (3.15). При
зависимости поверхностной диссипации от
скорости / трещина в вязкой
плоскости равновесно растет и при
фиксированном разрывающем усилии, Р.
Уравнение (3.12) дает условие
применимости- расчета разрыва по
-вязкости модели: трещина должна быть
намного длиннее своего поиращения
за время релаксации />/0.
Рассмотрим теперь
условия разрушения для
движущейся трещины. Для контура
Г=Г0+Г0<+Гг+1\о,
охватывающего (рис. 1) область Л_о,
можно составить баланс
полной энергии
Рис. 1. Пути интегрирования в
стационарной области вблизи вершины трещины
(точка 0)
4 j (в+ер^л = |{(в+^)К-,/)+
А1-. Г
+ okjvk-qj}njdT + j QdA, (3.17)
Al-o
где rijdr — ориентированный по внешней нормали щ элемент длины
контура. Произведение оь,}П$Г означает удельное усилие на
элементе ЛТ.
Если на края трещины Го* и 1\0 не оказывается силового,
массового и/теплового воздействий (okjnjdr = Oy (Wj—Vj)fijdr=0, qjiijdY=
=0), то баланс сводится к разнице Г/-о контурных интегралов Г*
и Г0:
=1Г J {*+?^ул- J W.
L.-l
ni-o
стацио-
Для движущейся области Л,_0, в которой поля е, v,
нарны, а источники Q отсутствуют, контурный интеграл
J{(e + Pi^)(a;/~y/) + %^--9/ }^Г = |{...}^Г = const (3.18)
оказывается инвариантом.
С другой стороны, контур Го является уже односвязным, если
считать, что точка разрушения 0. принадлежит телу. Если в области
Ао указанные поля стационарны, a Q=0 (т. е. в граничной точке 0
тела нет ухода энергии), то контурный интеграл (3.18) по Го будет
равен нулю, а потому и для любого контура Г*, ограничивающего
область стационарности, будем иметь
вне зависимости от выбора реологической, модели тела и от связан*
ного с этим выбором появления сингулярностей.
В теории разрушения удельную внутреннюю энергию произвола
ной частицы е, как правило, отождествляют с объемной внутренней
энергией zv. Если же учесть различие между ними, то балансовое
равенство (3.19) представляется в виде
=J (•*-•) И-^Г- (3.20)
Отсюда, при использовании функции ev баланс притока полной
энергии к вершине стационарно растущей трещины оказывается
отличным от нуля за счет ненулевой разницы в правой части (3.20) на
тех участках контуров 1\, где выходят частицы, претерпевшие
переход «объем-кюверхность». Рассмотрим контур Го, взяв в качестве
последнего □ ABCD (см. рис. 1). В пренебрежении потоками через
границы ВС и AD имеем следующее равенство:
Ё. = $ К - е) К - vj) nidV = J (ss - *v) (wi - »i) d*2>
AB
поскольку через границу CD поступают частицы с внутренней
энергией е = ег, а выходят —с измененной е=е5 через границу АВ (где
П\ = — 1). Введем скорость l = wx—v\ роста трещины относительно
материала тела. Если j существует конечный предел
lim f(ee-e0)(a;1-o1)rf^1 = lim2[t]a/ = 2T0/ = Eei (3'21>
—a
то он соответствует скорости работы на образование новой
поверхности. Предположение, что Ё0 = Ё;- сводит (3.20) к окончательному
инвариантному виду (более тонкий анализ при Е0т^Е; позволит
учесть эффекты разгрузки поверхностных слоев).
Поверхностная энергия уо является функцией параметров состоя*
ния поверхностной фазы (Гиббса), что приводит, например, к
эффекту охрупчивания пород из-за добавок влаги. Для учета этого
следует вводить в рассмотрение химические потенциалы компонент
слагающих материал у бортов трещины.
Составим баланс притока теплоты с использованием энтропии
j [s[wJ-oi)-^}nldr = ^. j" sdA- J j-dA -/?,_„ (3.22)
24
где Ri-o — расстояние в области Л/_о,
А1-.
Отсюда, даже в условиях стационарности полей в Л/_0 и при
отсутствии объемных тепловых воздействий Q = 0, контурные
интегралы, по Ti для потоков энтропии не являются инвариантами —
рассеяние Ri-o зависит от области Л;-о.
Частный случай Ri-0 = 0 соответствует адиабатическому или
изотермическому состоянию (qa~Tj = 0) в области Л*_о упругого
(е{р s= 0) или почти упругого (eff =0 вне Го) тела. При этом
[ [s (Wj. - v,) - Щ rijdT = J [s (wj - v}) - Щ tijdT = const. (3.24)
r, r0
Постоянное значение интеграла определяется условием для Го,
охватывающим стационарное поле в Ло,
J {s (Wj - о,). - Ц-} rtjdT = -Я, (3.25)
Введем теперь удельную энтропию s^ частицы в объеме тела
d.,=dUv + Tds0, dU0 = 4jde%,
(3.26)
Tdsv = -qhfit-\.okfie^.
Тогда интегралы (3.24) — (3.25) можно представить в виде
J \sv К - о/) ~Щ njdT = - Я, + J (sv - s) (wj - v^dT, (3.27)
Го
а оценка для □ ABCD даёт
J (sv — s) {wj — Vj) tijdT = 2 lim [s] al\ [s] = ss -- sv.
r0
Для изотермических условий (Т==Т0).'имеем
Т0 J {S„ (а,, - 0/) - ?,} rt/dT= J (.„ -У) (и,, - 0/) я^Г =
Г0 Г»
= -ГЛ + 2(Т.-Тг)'. To-Yr = limNar.) (3.28)
а->0
причем удобно исцрльзовать понятие диссипации D0 в точке
разрушения
TJt.= \ok)i™dA=D,. (3.29)
kj
A9 J
25
Из соотношений (3.28), (3.29) окончательно получаем
§{(Uv + ^)(wi-Vi) + <>k,Vk}n,dr=Dt + 2-tTi, T = Tt. (3.30)
/
Обратимся теперь к адиабатическим условиям, когда qj = 0. При
этом дифференциальные соотношения (3.28) дают
dev-dUv = okjde{Mft (3.31)
т. е. разница приращений внутренней энергии и упругого потенциала
равно диссипации механической энергии в частице. Интегральный
аналог для контура Го должен еще учитывать количество теплоты,
выделяемой при гриффитсовском разрушении,
[ (•* ~ Uv) К - Vj) njdT = - D0 + 2 (То - у7) /; 4j = 0. (3.32)
Г0
Из интегральных соотношений (3.20) — (3.21) и (3.32) получаем
j { (U0 + Effe-j (w. - Vj) + 0kjVk} n.dT = D, + 2T,/, q, = 0. (3.33)
Г0
Условие адиабатичности выполняется в тех случаях, когда el^>]
^g^KTj, где Л,— коэффициент теплопроводности материала, т. е.
для быстрого роста (в тепловом отношении) трещин. , ..
Таким образом, при использовании упругого потенциала баланс
полцой энергии (3.20) принимает для изотермических и
адиабатических случаев следующий вид
J \ (^ + PJF) (wj-vj) + okjvkyjdT = D0 + 21l T = Tr> V(3.34)
Правая часть (3.34) равна постоянной, если диссипация в
.вершине не меняется в процессе роста трещин. Это означает условие
автономности области Л о.
Использованное для вывода (3.34) условие /?г_о = 0, i?o#0
соответствует почти упругим, телам, или иначе — локализации
диссипации в вершине трещины.
Первое слагаемое правой части (3.34) допускает простую оценку
D. = 2lDdA = 2(D).A.. (3-35)
Ао
где <D>o — среднее'значение удельной диссипации D в А0.
Определяющими параметрами для Do могут служить скорость роста
трещины /, линейный масштаб области ]/Лв, а также реологические
коэффициенты. Если считать, что гриффитсовский процесс хрупкого
разрушения, имеющий характерный линейный масштаб уЕ <С ]/ А0У
полностью подавляется процессом диссипации (здесь Е — модуль
Юнга), то справедлива оценка
e(kf^ilVA0, VA.^a.
26
Если в вершине трещины локализовано пластическое течение [41]
(частиц Ирвина — Орована), то D — однородная функция первого
порядка по скорости деформирования, т. е.
а потому интеграл (3.35) сводится к следующему выражению:
$ ckie{kfdA^2В3VAj = 2fl, (3.37)
причем размерности у и у* совпадают. Коэффициент y* обычно
считается пропорциональным пределу текучести Y материала.
Если в вершине трещины локализовано вязкое течение, то D —
однородная функция второго порядка по скорости деформации,
ФЪ^ёМе^ъГ/УХ., (3.38)
а потому диссипативный интеграл (3.35) сводится к следующему:,
£o=<D>oAo = ri*/2, (3.39) .
где коэффициент сопротивляемости rj* пропорционален
динамической вязкости течения. В рассматриваемом случае Л0 не меняется с
ростом трещины /, но масштаб У.Ао прямо пропорционален скорости
роста трещины
VA0^k!E.
Однако общее выражение для коэффициента сопротивляемости
,,=„(^ ^ iH(M) <3-40>
означает, что т]* будет являться функцией скорости / только в
условиях корреляции хрупкого разрушения и сопутствующей вязкости
диссипации. Если же такой корреляции нет (УА0^>уЕ), то у не
является определяющим параметром и динамическая
сопротивляемость г]* в условиях локальной стационарности и автономности
разрушения выполняет роль материальной константы.
В подвижной системе координат х\, х2 в силу стационарности
и условия Ш1>^1, аУ1 = /, w2=0 имеем
d/dt = —l(d/dxi), Vi=l(dUi/dxi),
где щ— смещение. Тогда контурный интеграл (3.36) принимает
форму
1=1 (([/"+££fi) **. —*/«*. .*i*r }=т+2т (3-41)
Го
для изотермического и адиабатического случаев.
Рассмотрим прбдифференцированное по времени уравнение
локального притока теплоты
^Г dt \ dt —°Ы-дГ+Щ(-и> L — °- (3-42)
27
Перейдем в подвижную систему координат V и х'\ по правилу
t=t\ xk=x'k+lkt',
dldt'=d/dt+U {д/dxj), d/dx'k=d(dxh. /
В предположении о стационарности в подвижной систре коор-»
динат
д /ii_\ / * JL (1 дг \
dt1 [ di' )—lnnidx'j yk dx'k J'"*
уравнение (3.42) принимает вид (штрихи опущены)
/Я дЧ ) д* ( dUl ]— d*qj
-l"°"i dxjdxi l» dxjdxt \0'/ dxn ) dxjdxt #
E^o интегрирование по области Л/_0 приводит к контурному интегра-»
лу второго рода
J ik ('л'6 " °'/ tr'»~ q>) n>4T = J-fcu)*'dr=const* (3'43)
Поскольку в области Л0 (внутри контура Го, непосредственно
охватывающего вершину трещины) также справедливо уравнение L=0,
то при обычных ограничениях на бортах разреза (отсутствие
потоков) постоянная в правой части интеграла равна нулю.
Если ввести удельную внутреннюю энергию sv, то интеграл (3.43)
принимает следующий вид:
h=j -£ (*А/« - '11%; i - я,) уг = J 1аьп1 -^ к -.) Щйт. (з.44>
Г, Г0
Рассмотрим далее продифференцированное по времени уравнение
производства энтропии
В подвижной системе координат в зоне Л,_о стационарного и
изотермического (Т=Т0) состояния имеем
-^ (Tjnbnls - 4i) гЧйТ + Шк,п<Я = 2 &l, (3.46)
I
причем в дравой части стоит производная от сингулярной
диссипации (внутри Го), включаемая в интегральный аналог
дифференциального соотношения (3.45). Введение объемных удельных функций
sv и Dv сводит контурный интеграл (3.46) к следующему
=J T,/„ -|^ (s0 - s) M/dr + 2 j* (Ц, - Z>) b^dT + 2 g* /*• (3.47)
re r0
28
Наконец, разность интегралов (3.46) и (3.47) приводит к
результирующему контурному интегралу вокруг вершины трещины в вяз^
коупругом теле
Nk = Fk - Ik = j (2D5ki - *L bjkr oml ^) njdT = F*k -1\ = N%
(3.48)
или иначе
Nk = J (2D + §) МГ - оя/ *g- /yff = JV%, (3.49)
где £ — индекс оси, вдоль которой растет трещина, а нижний индекс
v объемной фазы опущен. Константа N*k оценивается путем
рассмотрения потоков через контур Го
N*k
= lira j {2 [D\ + ± [/.]) dxu + 2-$*-=!* +2-g-, (3.50)
где [D]=DS—DV — скачок диссипации, £/=g—r0s=/o, [/o]—/so—
—/vo — скачок изотермического свободного потенциала (упругой
энергии U) из поверхности разрушения, lim[/0]^=To.
Если принять далее, что поле скоростей смещений разложимо на
х (е) | (р)
упругую и вязкую составляющие vm=vx ' -\-v£'t то контурный
интеграл (3.49) представляется в виде двух слагаемых
Nk=_(dAldlk)+lk(dGldlk)=N*h9 (3.51)
вычисляемых отдельно,
Для прямолинейно распространяющейся трещины можно
опустить индекс k. Тогда контурный интеграл (3.48) приводит к
следующему критерию разрушения:
N=—(dAldl)—i(dGldl)=2l+2(dy/da)a, (3.52)
что совпадает с результатом (3.6) при неизменном линейном
масштабе a=const.
Возвращаясь теперь к примеру о растяжении вязкоупругой плоскости (3.11),
заметим, что величины Л, G могут быть определены из решения задачи в
напряжениях
дА К* dW К2
_=_(x+l)-i_, G=_--r_(x+1).i1[r(1 + v)f (з.53>
где E/(2+2v)—модуль сдвига, К — коэффициент интенсивности напряжений х=
=3—4v —для плоской деформации, х=(3—v)l(l-\-v) — для плоского напряженно*
го состояния, v — коэффициент Пуассона. Использование выражений (3.53)
превращает условие (3.52) в дифференциальное уравнение
К2 . 2 (1 +v) дК* / ■ , dv Л
— -1 Ed/ °^0+«)(^-^д). (3-54)
Корни этого уравнения определяют критические (разрушающие) значения К=
=/Сс. При Y=const и вязком подрастании трещины /CC^£V2, т. е. Кс постоянно при
£=const, пропорционально скорости / при £^/2 и пропорционально Z1/2 при £^/.
При растяжении линейной вязкоупругой полости с трещиной К= ^ W(//2)>
и уравнение (3.12) при Y=const принимает вид
п* Р* п (1+v) Р2 ♦ /
2£— 16 (1+х)т) /+"8" (1+х) Е / = 0- <3-55)
Сравнение (3.11) и (3.55) показывает, что Вх= (я/16) (14-х)-1, В2= (я/8) (1 +
+x)-i(l+v).
Обычно трещиностойкость конкретных материалов характеризуется
данными для критического коэффициента интенсивности
напряжений Кс- Эти величины либо оказываются константами материала,
что соответствует истинно-хрупкому разрушению по Гриффитсу или
пластической диссипации в вершине трещины, либо они оказываются
•функциями скорости. Последнее говорит о вязком характере
разрушения. Данные для Kc=const при разрушении на отрыв, т. е. для
Кгсг таковы МПа-м1/2: для песчаников 0,4—1,5; для известняков
0,36—1,24; для доломита 0,71. Понятно, что резкое различие в их
прочности определяется главным образом количеством и размерами
трещин.
Критические коэффициенты интенсивности при разрушении на
плоский сдвиг К^ и на разрыв К^.1 (антиплоское разрушение)
являются иными, независимыми характеристиками материалов. Так,
для мелкозернистого песчаника ^=1,47 МПа-м1/2, тогда как
Кпс=4,75 МПа»м1/2, т. е. в три раза больше.
Динамические значения этих параметров несколько отличаются
от квазистатических. Для песчаника 1^=4,8—9,15 значительно
выше статических. Широкий диапазон динамических значений связан
с зависимостью Кс от скорости роста трещин.
ГЛАВА 2
ДИЛАТАНСИЯ ГЕОМАТЕРИАЛОВ
4. МЕХАНИЗМЫ НЕУПРУГОСТИ И МОДЕЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
Способы описания постепенного разрушения
среды. Механизм пластического затекания пор.
Необратимая переупаковка жестких частиц. Предельное
условие Кулона. Площадки предельного равновесия.
Относительное скольжение частиц. Углы трения и
дилатансии. Модель плоского предельного
деформирования.
Для описания процесса неупругого деформирования
пористо-трещиноватой среды можно воспользоваться двумя способами.
Во-первых, можно изучать акты возникновения и роста отдельных
поверхностей скольжения пор, трещин в обычной упругопластическрй или
вязкоупругой среде. Это позволяет, например, найти критериальное
условие появления индивидуального дефекта, рассчитать его рост,
а при правильной постановке даже учесть неравновесность
соответствующего элементарного механизма неупругости. Следующий шаг при
30
таком подходе состоит в решении проблемы коллективного
взаимодействия дефектов (пор, трещин), определяющего изменения всей
системы в целом. Если размер дефектов сравним с масштабами
тела, то тем самым будет решена конкретная задача разрушения/
Если же масштабы тела намного превосходят размеры дефектов,.
то тело можно разделить условно на элементарные макрообъемы
AV, включающие в себя представительный ансамбль дефектов. При
этом объем AV среды, содержащий внутри себя поры, трещины или
поверхности скольжения, считается сплошным, а для нахождения
адекватного реологического закона необходимо уметь вычислять
средние параметры, для ансамбля взаимодействующих дефектов.
Второй путь изучения неупругости состоит в использовании с
самого начала феноменологических представлений, например,
соответствующих теории пластичности, но при этом вносятся поправки,
диктуемые представлениями об элементарных механизмах и
соответствующие реологическим экспериментам с разрушаемыми образцами.
,В трещиновато-пористых телах существует несколько
механизмов, обусловливающих их неупругое деформирование, включая
внутреннее разрушение. Это образование и рост трещин, необратимое
затекание пор, переупаковка зерен среды в условиях действия сил
сухого трения и, наконец, скольжение части массива (блока) с
образованием поверхности обрушения.
Представим пористую среду в виде множества кубов упруго-
пластической твердой фазы (матрицы) с расположенными в центрах
шаровыми полостями радиуса а. Приближенно куб можно заменить
на сферическую ячейку радиуса Ь. Пусть давление в поре р, а извне
к ячейке приложено давление о.
Вокруг поры возникает зона радиуса ар; где выполнено условие
пластичности \аг—ае|=Уо, что соответствует следующему полю
радиального напряжения:
Ог=— р+2У0 sgn (or—(Те) In (г/ар). (4.1)
В упругой зоне ap^.r^b радиальное напряжение имеет вид
Ог=-о+ (4/3) G {a\—a*)/r\ ap^r^b. (4.2)
Здесь G — упругий модуль сдвига, a Y0 — предел текучести
материала матрицы в.сплошном состоянии sgn(ar—(Те) = sgn(er—ее) =6.
Положение упруго-пластической границы определяется условием
ap = 2(G/y0) (a»—a»0)/sgn(ar-ae). (4.3)
Если в ячейке нет пластических деформаций, т. е. ар^ау-то эти
формулы дают искомую связь внутреннего и внешнего давлений в
ячейке
' a_p=(4/3)G(a3o-a3)/a3, a3<a3*=2Ga30/(2G—QY0). (4.4)
Если же происходят пластические деформации, то суммирование
соотношений (4.1) rf (4.2) при г=ар приводит к искомой формуле
a—р = — (2/3)y0e{l+ln[2G(a3-Ta3o)/(yoea3)], а?^а\. (4.5)
Поскольку можно также представить знак в в виде e = sgn(a30—
—a3) =sgn(a—р), условие а^р соответствует уменьшению диаметра
31
tiopbi (0=1), при a<Cp происходит ее расширение (6=— 1).
Пористость т выражается через радиусы ячейки
,т = а3/63. / (4.6)
Определение (4.6) соответствует числу п= (3/4) {nbz)f~l пор на
«единицу объема среды. Если радиус Ь велик, то число пор мало.
Если и радиус а велик, то пор относительно мало, но они крупные.
Из условия неразрывности Ьг—Ь3о = а3—а\ имеем
а*/аз0=Кт/К°т, Km=ml(l-m)t (4.7)
где Km — так называемый коэффициент пористости.
Отождествим величину а со средним давлением в твердой фазе,
т. e.o=—Oif6ijf ар — с поровым давлением жидкости и введем
эффективные давления atf)=(l—т)(о—р). Тогда соотношения (4.4) —
(4.5) дают закон необратимого объемного сжатия среды за счет
затекания пор
(К{°}1Кт) - 1 =(3/4) (o("/G) (1 - т)-\ o(f> <оУ> = - (2/3) 6У. (1 - да),
(4.8)
(К^-К*т)/(К^ -Кт) = ехр{(о<» -о<°)/о?>}).
о(/) ^of, К*т.= 2GK'ml(2G - 6У).
Ограничиваясь малыми изменениями пористости Дт=т—то^С
•Сио, Д*т = т—т*<то, т*—т0<С'п0, получим
о <'> = - (4/3) G, Дда/да,, о(f> < o|f> = - (2/3) У6 (1 - да,),
exp {(o(f) - оУ>)/о|/)} = - (Дда)/(да0 - да.), o(f) ^o<f)
(4.9)
да* = 2mfil(2G - 6У0 + 6У0да).
Можно оценить остаточную пористость тр (после упругой разгрузки
от значения т), если учесть нужным образом изменения в.
Подстановка первого из соотношений (4.9) в уравнение неразрывности (2.6)
позволяет оценить эффективный упругий объемный модуль К
пористой среды, матрица которого представлена несжимаемым (pi =
=const) материалом,
ецЬи=т1{\ -т) ^ ~*{f)/Kt K = (3/4)G"V(1 -m.)-1. (4.10)
Одновременное приложение сдвиговых напряжений приводит к
изменению формы пор и интенсифицирует уплотнение пористой
среды.
32
Рис.- 2. Схема переупаковки
контактирующих частиц
Для исследования эффекта
переупаковки зерен предположим, что
микроструктура среды представлена
конгломератом жестких частиц, на контактах
между которыми при их относительном
скольжении действуют силы сухого
трения. Регулярную упаковку одинаковых;
шарообразных частиц (рис. 2) можно
математически моделировать сплошной
средой, каждая макроточка которой
будет характеризоваться
векторами-ориентирами £,-а)> Cf\ коллинеарными прямым,
соединяющим центры контактирующих
шаров [32].
Выберем оси координат /, 2 так, чтобы равнонаклонная линия
(рис. 2) служила биссектрисой угла if. Тогда для проекций имеем
^ = cos («/4 - ф/2), Cf = sin «4 - ф/2),
(4.11)
С/^ = cos (*/4 + ф/2), Cf =sin(ic/4 + <|>/2).
Кинематическое ограничение для деформаций связано с
жесткостью шаров и состоит в том, что относительные мгновенные
смещения центров шаров ортогональны прямым., соединяющим эти центры
(сохранение расстояния между центрами соприкасающихся шаров).
Скорость относительного смещения двух точек сплошной среды,
расположенных на единичном расстоянии на векторах-ориентирах, суть
bv{a)=Zpl Х(а), Ai>!*l=-£,0* £{Ь) , (4.12)
а условия ортогональности, векторов ки{а) и С: , а также Аи:
Ф)
принимают вид
Ф) г(Ь)
Ч j i Ч Ч j i
0.
(4.13)
Разделяя тензор градиента скорости смещений на антисимметричный
тензор вращения Q/j и тензор скорости деформаций ёц9 преобразуем
условия к виду
V ^ ' Y (°) Г (а)
1ГЧ^1 / - ' Utri-ri Цу —U*
(4,14)
Подставляя в (4.14) значения (4.11), получим кинематическое
условие
ёп cos2 (я/4) — -ф/2) -Js-2ei2 sin (яу 4—-ф/ 2) cos (я/4—
-*/2)+e22:sin2'(ny4—^/2)? = 0,
которое в силу симметрии <?ц = е22 = е/2 преобразуется в дилатан-
сионное ограничение для тензора скоростей деформации
<?=Ay, Л=—2 cos if, 7 = ^12, * (4.15)
где Л — скорость дилатансии.
3—3311 33
Изменения угла if могут быть также учтены
Да!0) = dC^/dt = (1/2)£/ф/Л = 2у sincpr (4.16)
Для рассматриваемой микроструктуры существенно наличие
предельного угла if 0=60°, при котором дальнейшие деформации того же
знака оказываются запрещенными, среда становится жесткой.
Только изменение знака сдвига может привести к разрыхлению среды.
При максимальном разуплотнении if = я/2 скорость объемной
пластической деформации равна нулю — материал пластически
несжимаем, дилатансии нет. Изменение знака -у ведет к изменению зна^
ка ё.
Условие для напряженного состояния (предельного равновесия)
формулируется так: на площадках, нормалью к которым служат
векторы — ориентиры, компоненты тензора напряжений оц должны
быть связаны законом сухого трения. Например, дляС!а) имеем
[т<°)]==£0о<а>, х<в)=о/ус]а)с;в),
(4.17)
0<fl):=O..C(a) С(а\ -С(а)С(а)=0, О<а)>0
где k0 — истинное значение коэффициента сухого трения. В силу
симметрии 0ii = a22 = су, o^ = o+Oi2 cos if, %(а)=.—aissinif, условие
предельного равновесия принимает вид
T=£a, £ = e£0(tgif—0)-1 (cosif)"1, T=ai2. (4.18)
Таким образом, эффективный коэффициент сухого трения должен
зависеть от параметра if микроструктуры среды так же, как и
скорость дилатансии Л. Иначе ^говоря, #=А(Л).
Обратимся теперь к условиям относительных подвижек среды
вдоль поверхности скольжения [28]. Согласно первоначальным
представлениям Кулона, эта поверхность является граничной для
массива и на ней выполнены условия скачка тангенциальных компонент
скорости смещения, а также силовое предельное условие
|Tn|+antgq>o = c0, (4.19)
где Tn, оп—: касательная и нормальная компоненты напряжений,
Фо — угол трения, с0 — сцепление на поверхности скольжения.
При формулировке условий пластического деформирования
сплошной среды с внутренним сухим трением естественно заменить
условие Треска (1.26) на условие Кулона (4.19), а условие
пластической несжимаемости на дилатансионную связь типа (4.15). Тогда
кулонов угол трения приобретает новую интерпретацию — из угла
трения на граничной поверхности, разделяющей две скользящих друг
относительно друга части массива, он превращается в угол
внутреннего трения на площадке предельного равновесия в каждой точке
(элементе) сплошной среды.
Рассмотрим плоскую задачу. Будем считать, что сила сухого
трения /?, действующая на площадке предельного равновесия, на-
34
клонена к ней под углом р и пропорциональна ортогональной к ней
силе N согласно условию Кулона, т. е.
R = NQtg^o+c0ei 6=sgn/?, N>0y (4.20)
причем силы/? и TV могут быть выражены через компоненты тп, оп
тензора напряжений
/?=Tncos p+dnsinp, N=xn sin p—on cos p. (4.21)
Если площадка предельного равновесия составляет с осью х2
максимального сжимающего напряжения о2 угол ф, то
г|5={(я/4)-(1/2)(р+еФо}8епг|). (4.22)
Примем условие коаксиальности тензора напряжений и
скоростей деформаций. Тогда дилатансионное условие (4.15) и условие,
что хи *2 — главная система координат, записываются в виде
^и +^22 = sinv(^xl — е22)Ъ,. 6 = sgn(^n — е22),
(4.23)
*.. = 0. ^ii—»i.i. eM = i>Sit, el2 = (l/2){vlt2+v2tl),.
где, однако, учтена пропорциональность скорости объемной
деформации модулю скорости пластического сдвига (введение знака
соответствует опытам с обычным состоянием песка), v — угол дилатансии.
Уравнения (4.23) определяют две характеристики поля скоростей
dxjdx, = ±l/"(l+8sinv)/(l -6'sinv), (4.24)
наклоненных к оси х2 под углом
8 = arctgy^l - sin v)/( 1+sin v) = (те/4) - (v/2). (4.25)
Скорость относительного движения двух частиц сплошной среды,
лежащих на единичном отрезке г/, определяется по правилу
Avi = eijrjy /-i = sinу, r2 = —cosy,
<•
где у — угол между ir,- и осью х2. Рассмотрим проекции вектора Avi
на характеристику (4.24) и на ортогональное к ней. направление.
Имеем
riAvi = viti sin2 y+v2}2 cos2 у=0, у = ±Л,
rtAVi= (1/2) {vul—u2,2)sm26, r<r,= 0. (4.26)
Отсюда относительная скорость частиц, находящихся на
характеристике поля скоростей, ортогональна к рассматриваемой
характеристике. Будем считать, что относительная скорость Д£>< коллинеарна
силе сухого трения R
sga/?=sgnAy(7=fl)=sgn(t;i,i—v2,2). (4.27)
Тогда 6—(я/2)+р+^ = 0, и в силу уравнения (4.22) имеем
р=(я/4)+Фо+г. (4.28)
Из условий Кулона (4.20), выражений для тп, оп (4.21) и для
угла р (4.28), получаем условие предельного равновесия в форме
|Tn|+ffntg<p = c, (p = 2(p0+v, / * -
ccoscp=Co cos фр=У, (4.29)
что эквивалентно такому предельному условию в инвариантной
форме
T=psin<p+co:costp; р = — (ои +022)/%,
х = (1/2)1/(ап-о12Г + 4о212, (4.30)
а дилатансионное! условие, аналог (4.15)—может быть записано в
виде
*'=-|T|smv, f=(eil-e22y + 4e\2. (4,31)
5, ДИЛАТАНСИОННАЯ УПРУГОПЛАСТИЧЕСКАЯ МОДЕЛЬ
Закон пластического течения при двух
независимых предельных условиях. Правила активного и
нейтрального нагружений и разгрузки. Разрыхление,
уплотнение и критическое состояние. Определение
замыкающих связей (внутреннего трения, и скорости
дилатансии от параметра упрочнения). Учет
допредельной пластичности (сжатия пор гидростатическим
давлением). Классификация разрушения
геоматериалов в зависимости от уровня давления и
температуры. Конкуренция прочности монолита и сухого
трения в разломе. Сверхпластичность.
Приращения полных деформаций йец среды аддитивно
складываются из приращений упругих de{el и пластических de[p} деформаций:
deij = de^-{'deip). Приращения упругих деформаций будем определять
через приращения напряжений doij согласно линейному закону Гу-
ка (1.9).
Приращения пластических деформаций будем связывать с
напряжениями otj тензорно-линейными соотношениями, которые в
изотропном. [30]. случае' имеют вид
■de™ = -(Н + р) 8/yrf6 + (ои + /Аи) d%. (5.1)
Здесь p=—(oij8ij)/3 — давление, а кинетические функции Я, £
являются дополнительными искомыми переменными. Два дополни-
нительных уравнения формулируются для инвариантов тензора
напряжений и для инвариантов приращений пластической деформации.
Фа = вхТ—/а (Р, а', У) , <De=#P)-fe№), Л) .
Среда находится в кулоновом предельном состоянии, если fa
пропорционально давлению, а напряжение соответствует точке
Фа - (2/V3) е^х - ар - Y = 0, et = sgti х,
(5.2)
36
х = (2/К2)"1 {(on - о„У + К - оза)г +(о„ - о22)2 + 6 (ог12 +
+ 6%з + °21,)}1/2-
Форма (5.2) называется конусом Мизеса — Губера — Шлейхера и
интерпретируется как обобщение для пространственного случая
закона сухого трения Кулона, где а — коэффициент внутреннего
трения, У =а# — сцепление.
Второе условие зададим в виде дилатансионного соотношения
(Л — скорость дилатансии)
<b9 = deW - (2/1/3) A^dfpK eT--=sgnrfY(P).
dV»=(llV2){(de.™ -degy+ide'l? ~de^f +
+ Ve$ -degy + b{de$ 2+de\» 2 + deg 2)}1/2. (5.3)
Условия (5.2) и (5.3) при наличии связей (5.3) совпадают, если
dl = — (2l3)Aadh, aI1=Y.
Определяющие уравнения для пластических деформаций
принимают вид
delf = {ои + (2/3) АаНЬи (1 + (2/3) Аа) РЬЦ) dX, dX > 0. (5.4)
Функции упрочнения (ослабления) а=а(х)> Л=Л(х) зависят от
X — параметра упрочнения (ослабления). Если считать, что
упрочнение (ослабление) изотропно и определяется объемной пластической
деформацией, то % = eip)/eiF) , причем за состояние отсчета е[р) мож^
но брать критическое, когда Л=0. Пластическое течение происхо-
дит, если выполнено условие (5.2) и идет процесс активного нагру-
жения, т. е.
фа=0, d'<t>o=-(dq>oldp)dp+(d<bo/d%)di;>0 (5.5)
для деформационно упрочняющейся среды (dajde^X)) или
Фа=0, d'<ba=.{d<bold.p)dp+(d<bo/d%)d%<0 (5.6)
для среды с уменьшающей прочностью (da/d^<0). Впрочем, в
последнем случае процесс непрерывного деформирования может быть
неустойчивым. Нейтральное нагружение характеризуется условиями
Фа=0, d'Oo=0, d%=0 (5.7)
и соответственно при разгрузке
Фа<0, dX=0. (5.8)
Связи (5.4) могут быть представлены в виде
de™ = (дЧ1дои) dX, ЧГ = У, _ 2аЛ (р + Я )2 = \(р + Н) (а - Л), (5.9)
где Ч? — пластический потенциал. Следует подчеркнуть, что функция
пластического потенциала определена только в точке то, ро,
находящейся на соответствующей поверхности текучести (5.2).
Пластическая эквипотенциаль является фиктивной — она не. совпадает с
какой-либо поверхностью текучести, а потому не соответствует фикси-
37
рованному значению параметра упрочнения хо вдоль всей своей
длины. Значения а, Л, Н в формуле (5.9) соответствуют %0 только в
точке to, /?о. Линия, касательная к эквипотенциалям в точке то, ро,
ортогональна вектору приращений деформаций, на плоскости е^р)у/^(р) —
вектору с компонентами d&v\ dy{p). При А<0 пластические
эквипотенциали имеют вид эллипсов; пластический сдвиг dyW ^элементе
среды сопровождается уменьшением объема de^<.0. При Л>.0
пластические эквипотенциали имеют форму гипербол; пластический
сдвиг dyW вызывает увеличение объема de^p)>0 элемента, среды.
Частный случай а=Л>0 соответствует вырождению гипербол в
прямые линии. Только в этом случае пластическая эквипотенциаль
сливается с поверхностью текучести (с прямой Мора — Кулона) и
имеет место так называемый ассоциированный закон течения. Наконец,
случай А=0 соответствует критическому состоянию среды —
эквипотенциальна является прямая линия, параллельная оси давлений.
Выразим модель упругопластического дилатансионного тела
через пластическцй модуль А. Условие (5.5) активного нагружения
имеет вид ,
d'Q>o= (yV~3)Qdx—a:dp= (pda/dx+dY/dx)d%. (5.10)
Из определяющих связей (5.4) имеем
dX = {- (2/^3) Gdx - adp} {2ah (p + H)}-1,
A = (pda/dx + dY/dx) A, (5 л ^
deW = (Л/А) {(2//3) 6dx - adp)},
d^p) = (1 /A) {(2/1/3) bdz - adp}.
Для определения функций a(%), A(x) рассмотрим напряженно-
деформационные состояния, реализуемые при реологических
испытаниях сред,
(Tii = (Ti, а22=азз=сгз,
ai2 = ai3 = a23=0, (5.12)
de\\ = dei, de22=de33=de3, dei2=di3=de23=0.
Упругие приращения деформаций определяются формулами
de[e) = (doJE) - (2v/£)do2, def = (1 - v) (doJE) -(v/E) do,,
£ = 2(l+v)G,
Условия пластичности (5.2) и дилатансии (5.3) принимают вид
(5.13)
def + Uef = (2А/3) 6Т (de\p\ - def),
т.е. по измерениям ol% °2> de\p\ def можно непосредственно
находить значения а и А. Так, по данным Бишопа связь а (А) для
разных речных песков дана на рис. 3. Она удовлетворительно аппрок-
38
симируется зависимостью ф=2фо+^ (см. формулу (4.29), которая.
в данном;'случае представляется в виде
Л = 0,69-'^2-2)11а. (5.14)
Здесь в, = sgn(о, - о,) = вт = sgn {de™ - def) = в.
Из определяющих связей (5.4) следует
ЙЯ = de <") у"3 (26Л)"' (о,
■О-1..
б,-бг ЛШ
04
еЪ^о os
-075 -0У5 -015
Рис. 3. Соответствие коэффициента вну- Рис. 4. Данные стандартных трехосных
Треннего трения а и скорости дилатан- испытаний рыхлых и плотных (штрих)
сии Л для речных песков песков по А. Вешику и Дж. Клафу
Если продифференцировать условие пластичности, то в
предположении, что 7=const, а=а(^}), получим
deWjdOi —(ЪУ3-2*) [61/3 + а- (бУЗ-2а)К/]/[3 ^36(^/^^)0,],
(5.15)
где Ki=do2/doi — инкрементальный коэффициент бокового давления.
Пренебрегая далее сцеплением (У=0), находим компоненты полных
деформаций
deJdo1 = (l-2vKl)E-1 + (Y3 + bA){deW/dG1)(3bA)-1,
(5.16)
de2/do2 = [v - (1 - v)КЦ Е-l - (УЗ - 26Л) {de^jdo,) (6вЛ)"\
При стандартных трехосных испытаниях ai убывает (осевая
сжимающая нагрузка возрастает), тогда как о2 = о3= const, т. е. /0=0.
В опытах на октаэдрический сдвиг реализуется условие p=c0nst,T. е.
На рис. 4 и е? табл. 2 приведены экспериментальные данные
А. Вешика и Дж. Клафа [28] для стандартных испытаний рыхлых,
уплотняющихся при сдвиге песков (кривые 1—4) и результаты
опытов на октаэдрический сдвиг тех же песков (кривые 5, 6).
39
Таблица 2
Опыт
Начальный
коэффициент
пористости
Боковое
напряжение
а2, МПа
0,10
0,10
0,10*
Объемная
деформация при
разрушении
е. %
4,0
3,3
2,4
Осевое
напряжение при
разрушении
ох, МПа
0,316
0,332
0,186
Осевая
деформация при
разрушении
el. %
у
22,6
21,0
14,3
Стандартные
трехосные испытания
Октаэдрическии
сдвиг
1,05
1,02
1,03
* Среднее давление.
По стандартным трехосных испытаниям значения a=j/~3|ai—
—021 /(ai+2a2) есть функция отношения e^/eip), где
^—критическое значение объемной деформации, определяемой здесь как
предельная деформация в процессе уплотнения перед разрушением.
Экспериментальные точки на значительном интервале значений
хорошо аппроксимируются (см. рис. 3) зависимостью
a = 0,27 + 0,47 (eW/elp)). (5.17)
Н. М. Сырников провел расчеты однородных состояний образцов
для стандартных испытаний и для опытов.на октаэдрическии сдвиг.
Результаты (рис. 4, кривые 1—6, сплошные линии)
удовлетворительно согласуются с опытами при Е = 300 МПа, v=0,25.
При одномерном уплотнении (сжатие в жестком цилиндре)
полная боковая деформация отсутствует de2=0. Тогда инкрементальный
коэффициент бокового давления имеет вид
_ (Кз"—29Л) (У* — 28а)-(Уз + 9а) — \%Уъ\ (da/deW) о, (v/E)
■Ki =
(Уз
/О aZtMf](L
ЛГ- =7= ' ' (5Л8)
28Л)(Кз —26а)2 —18.КЗЛ (da/de(P)) а, (1—v)/E
Результаты численных расчетов
для случая (5.18) представлены на
рис. 5 в виде зависимости о\ от
полной осевой (объемной)
деформации е\ при значениях £<р>* = 0,30;
1,00, 3,3% (кривые 1, 2, 3.
соответственно) .
Следует отметить, что
экспериментальные данные 4 (Р. Столла и
И. Эбейдо), приведенные на рис, 5,
были получены для песка с
начальным коэффициентом пористости
гтго=0,495 и согласуются с
расчетом. На рис. 5 приведены также
результаты расчетов разгрузки.
Согласно рассматриваемой модели,
вначале разгрузка происходит по
упругому закону, но при
дальнейшем уменьшении о\ возникает
обратное пластическое течение,
которое наблюдается и эксперимен-
/о eh%
Рис. 5. Расчет одноосного уплотнения
грунта (сплошные линии) и
эксперимент
40
тально. Однако здесь расчет возвратного пластического течения не
проводился (возможный ход кривых 5 намечен штриховыми
линиями). Для выявления роли модуля Юнга был выполнен расчет и при
Е = 200 МПа~ его результаты представлены на рис. 5 штрихпункти-
ром 6 (е[р) = 1°/0).
- Зависимость бакового напряжения (Т2 от величины о\ при
одноосной деформации сжатия и последующей разгрузкой по упругому
закону дана кривой 7 на рис. 5 (расчет для Е^=300 МПа, е[р) = 1°/о)*
В некоторых работах (см., например, [4], в качестве параметра
упрочнения х рекомендуется использовать величину пластического
сдвига у<р). Нетрудно видеть, что в указанных случаях использование
параметров &р) и y(p) математически эквивалентно, но остаточные
изменения объема (фактически пористости) экспериментально
фиксировать более просто.
Поведение песков в первоначально плотном состоянии
оказывается более сложным (кривые 7 для сп—<Тг и 8 см. рис. 4), поскольку
для них характерно наличие участков для еу возрастания и убывания
внутреннего трения, которые разделяются пиком прочности, а'также
сменой первоначального уплотнения на последующее разуплотнение.
Соответствующее изменение знака Л (и пластических приращений
объема) происходит при некотором значении е{р) — ер) (/?), которое
зависит от давления. Так, при весьма высоких давлениях добиться
разрыхления песков вообще не удается: при сдвиге плотные пески
деформируются так же, как и. рыхлые, с дилатансионным
уплотнением. В общем случае %(е(р), ?(р))> но простейшая дилатансионная
упругопластическая модель для плотного песка определяется
следующими связями:
а =^= а, (*<">), Л = Л, (*<">)<0, eW<e{f(p)
(5.19)
а = а2 (£(*)), Л = Л2 (eW) > 0, eW > ef (/?).
Следующая характерная точка реакции плотных песков на
нагрузку соответствует пику их прочности, т. е. максимальному
значению a=Ow и смене знака производной dajde^ (или da/dyW).
Модель наиболее проста, если принять, что точка ат как раз
соответствует значению е[р) .
Иное (и, может быть, более правильное) описание следует
из-представления, что в песке происходят два конкурирующих
микропроцесса. Один из них обусловлен пластическим скольжением
контактирующих зерен или блоков (и описывается дилатансионнои
предельной моделью), а второй — пластическим затеканием пор под
действием всестороннего^давления, причем добавление касательных
усилий интенсифицирует этот процесс. Дилатансионное затекание пор
происходит, когда фигуративная точка достигает поверхности
Текучести, представленной в виде замкнутых линий (кривая 3, ристб^.
Аналитически соответствующие поверхности текучести рекомендую*
задавать в виде эллипсов
<Мт, р, т) = (р//7о)2+(т/то)2-1=0, ' (5^20)
41
Рис. 6. Общий вид поверхностей
разрушения (пика прочности) — У, предела
упругости (начала дилатансии) — 2, затекания
пор — 3 и путей нагружения
где ,ро, то — экспериментально
подбираемые функции/m, а
иногда применяют для них
ассоциированный закрй' течения
йе^ = фФ91доц)йХ. (5.21)
Если рассмотреть общую
картину поверхностей
текучести (см. рис. 6), то становится
понятным смысл моделей
кгравий Гранта» и «глины
Кэм» по А. Скофилду и ГГ.
Роту [28], различающихся
между собой учетом упругих
деформаций. В этих моделях
участки плоских поверхностей
предельной текучести,
соответствующие разуплотнению
плотного песка, и эллипсоидальные
поверхности, соответствующие
затеканию пор,
объединяются в единое семейство
поверхностей текучести Мора — Кулона с замыкающим выпуклым
«дном». Линия критических состояний |т|=а*(р+#) служит
границей между областями разуплотнения и квазигидростатичеекого
затекания пор.
Будем, однако, интерпретировать пластические изменения объема
вследствие затекания пор, равно как вследствие микропроскальзыва-
ния зерен, как явления допредельной пластичности. В
экспериментах с песком непосредственно показано, что допредельные
поверхности текучести (пунктирные линии) соответствуют пластическим из-
. менениям объема в 0,4%, а сдвига — всего в 0,03%. При предельной
пластичности характерная величина необратимого сдвига составляет
.0,8%, что на порядок выше. Участки, представленные на плоскости
%р (см. рис. 6) сплошными линиями, соответствуют скольжению
согласно неассоциированному закону (5.4), а пунктиром—согласно
ассоциированному закону. Если последнее верно, то пунктирные линии
достаточно круто пересекают оси всестороннего сжатия р.
Допредельные' приращения деформаций объема и сдвига могут
быть выражены через приращения напряжений
den =*U,flp+fl4l*, rfyW =tJP+№-
(5.22)
В зоне стыковки областей предельной и допредельной
пластичности, можно просуммировать допредельные приращения деформаций
с предельными
de& =hPdp-\-fud^ + A\dt(")\, rfY<*> = ^ + ^т + «Й.
(5.23)
42
Поскольку сдвиговые эффекты, сопутствующие затеканию пор,
пренебрежимо малы по сравнению с соответствующими эффектами
при предельной пластичности, то эффективная модель необратимых
деформаций пористых сред в условиях выполнения предельного
условия (5.2) имеет вид [27]
de(P) = — (dFldp)dp+A\dyi*>\, dy(P)=xdK Fp=fip, (5.24)
причем dX=0, если предел пластичности не достигнут. В связях
(5.24) практически используется F{p) — крицая ОП (или ОГ),
получаемая при испытаниях на всестороннее сжатие (см. рис. 6). Эта
кривая имеет различные ветви нагружения ОС и разгрузки СР.
Начальные участки ветвей разгрузки соответствуют упругим модулям.
В общем случае соотношения (5.22) или (5.23) неголономны, ш>
скольку функции fiP, fiX включают в себя как производные
пластического потенциала [см. (5.9)], так и значения d\ согласно (5.10)
В экспериментах, когда путь нагружения задан, измеряются
функции
еЮ = е\р) (р, х), т<"> = у<р) (р, х), (5:25)
непосредственное использование которых как замыкающих связей
оправдано в частных случаях простых путей нагружения, когда все
действующие силы меняются пропорционально одному параметру
(так называемые деформационные теории).
Скальные породы под нагрузкой деформируются подобно
плотным грунтам, хотя интенсивность напряжений, вызывающих
необратимые деформации, должна быть намного выше. Необратимые
деформации дилатансионного разуплотнения объясняются развитием
системы внутренних трещин под действием сдвигающих напряжений. Для
этого напряжение сдвига т должно достигнуть предела упругости —
поверхности начала дилата'нси-и (кривая 2). На рис. 6 приведена
характерная кривая всестороннего сжатия ОТ монолитной горной
породы (гранита), которая в отсутствие начальных пор и трещин
является нелинейно-упругой (обратимой). Если сжать образец^ гранита
вдоль ОА, а затем приложить сдвиговое усилие вдоль АВ, то внача:
ле сжатие будет происходить (до В') вдоль гидростатической
кривой ОГу а затем, после пересечения поверхности начала дилатансии,
произойдет переход к состоянию В разуплотнения, несмотря на
весьма высокое среднее давление. Нагружение пористой горной породы
(например, песчаника) характеризуется кривой ОП. Перемещение
точки вдоль пути нагружения соответствует возрастанию давления.
Приложение сдвиговых усилий вдоль линии СЕ вначале
интенсифицирует (от С до точки пересечения D с поверхностью начала
предельной дилатансии) ее уплотнение, а уже затем (от точки N к Е)
происходит дилатансионное разуплотнение. При очень высоких
давлениях наблюдается «только сдвиговая интенсификация уплотнения
(кривая FG). Процесс разгрузки соответствует ветви СРУ резко
уходящей от ОП вследствие закрытия пор. Наоборот, при очень малых
гидростатических давлениях песчаник упруг, затекания пор не
происходит, и под сдвиговой нагрузкой песчаник будет вести себя как
хрупкий гранит.
43
Детальное описание допредельной пластичности, по-видимому,
связано с введением математических моделей, использующих
поверхности текучести с угловыми точками, что означает также
пропорциональность приращений пластических деформаций прирап^ейиям
напряжений [31]. Вопрос о том, какого типа поверхности текучести
следует применять, определяется задаваемой степенью точности.
Достижению пика прочности в образцах песков или же в горных
породах соответствуют точки поверхности разрушения (кривая U
рис. 6). При напряженных состояниях, близких к поверхности
разрушения, происходит перестройка внутренней структуры среды. Нв
горных породах отмечается или ориентация микротрещин и пор в неко-
^Т
Сулое трение
Предел упругости-
Для гронито8\01гпа
200° с
05ГПа\ 01ГПЩ 1йГПа\15ГПа
400° С
о
800° С
600° С
500 °С
Вертикальные
разломы
Циклонные
трещины
Механизм ы разрушения
Локализация
детормпциа
Псевдо-
пластииность
(катаклаз)
±
Пластичность
CSpoc на оря,
кении
П.
4-
I е,
Ш
Хрупкое
разрушение
\ (плавноо скольжение)
\Прометуточ-\
нос разруше\
ние(преры- \
Вист ое сколу
/кение)
Пластическое разрушение
(плавное течение)
Рис. 7. Зависимость реологии геоматериалов от уровня давления, и температуры
44
торых избранных направлениях, или их равномерное распределение
по объему. В грунтах в одних случаях возникает система полос
скольжения; в других — пластическое неограниченное течение захватывает
объемные области. Так, образцы рыхлых песков при малом боковом
сжатии разрушаются объемно, принимая бочкообразную форму,
а при высоком боковом обжатии разрушаются, как и плотные,—
с образованием плоскости скольжения.' > ,
Реологические исследования позволяют провести схематическую
классификацию., неупругости и разрушения теоматериалов (рис. 7)«
Тип дилатансионных трещин, возникающих в интервале между
пределом упругости и пределом прочности, зависит от давления и
температуры. При весьма малых боковых давлениях-
возникают.микротрещины, параллельные сжимающей нагрузке или иначе — ортогональные
направлению растяжения. Борты этих трещин отходят, друг от друга,
между ними не действуют силы сухого трения, а потому даже слабые
сдвиговые усилия приводят к их развитию в-макротрещину, также
параллельную главной сжимающей
нагрузке (эффект раскалывания).
При большем обжатии борта
трещин смыкаются, и сдвиговая
макротрещина будет возникать там,
где касательные усилия достигают
впервые предела прочности
материала. Поэтому макротрещина
наклонна,, а ее ориентация зависит от
соотношения главных напряжений и
углов внутреннего трения и дила-
тансии.
При возникновении
макротрещины происходит хрупкое
разрушение. Машина нагружения в момент
разрушения испытывает, удар —
происходит резкий х:брос
напряжения d. Если же в образце создать
предварительный разрез, то под
нагрузкой произойдет скольжение
по закону сухого трения. В этом
диапазоне давлений сухое трение
между бортами разреза намного
меньше прочности сплошного
материала породы. Однако при больших давлениях р и температурах Г,
когда силы сопротивления сухого трения между бортами возникшей
трещины уже сравнимы с прочностью монолитной среды, система
"мелких трещин постепенно концентрируется в полосы (локализации
деформаций), развитие которых завершается созданием в их
плоскости магистральной трещины. О том, что сухое трение между
бортами имеет порядок прочности материала, говорит прерывистое
скольжение вдоль предварительного разреза: оно сопровождается
разрз'шением материала бортов разреза. Характерный интервал р, Т
Для прерывистого скольжения по В. Брейсу представлен на рис. 8 для
45
Р,
МП а
чоо
200
zoo wo т°с
Ги"о1/ DD 2 ГаУ
Рис. 8, Граница перехода в гранитах
(/, 2) и габбро (3) от плавного
разрушения (/) к прерывистому
скольжению (//) и стандартная
континентальная геотерма (///)
/ — скольжение по магистральной
трещине, 2 — скольжение по подготовленному
распилу, 3 — прерывистое скольжение
L А на
ю д л о а о л
О А. Ж /Ы Ш
д/ •
V. i -I i
■г
■
▲ ■
■
/
-1— .1 , 1
гранитов и габбро. Зачерненные точки соответствуют плавному
разрушению, незачерненные —прерывистому. Указаны также
промежуточные экспериментальные результаты. На рис. 8 показано пересечение
геотермы стандартной континентальной коры и границы /области
прерывистого скольжения (пунктир). /
При разрушении в этом интервале значений рТ машина фиксирует
сброс напряжений (удар) не до нуля, а до значения,
соответствующего остаточной прочности (растресканного материала). При более
высоких значениях р, Т создание магистральных трещин разрушения
оказывается вообщее невозможным — сухое трение на порядок
превосходит прочность сплошного материала (граница Орована — Байер-
ли — Моги). При разрушении не отмечается сброса напряжений —
разрушение псевдопластическое, однако деформирование —
суперпластическое, определяемое скольжением вдоль границ гранул, на
которые разбивает геоматериал сеть мелких трещин. Согласно данным
[43] пористый материал утрачивает ярко выраженные дилатансион-
ные свойства. Для „суперпластичности характерно снижение
сопротивления сдвигу, зависящее от характерного размера «гранул».
Наконец, эксперименты [31] с гранитом показали, что переход от
микротрещиноватости внутри зерен к неупругости, обусловленной
дислокационным механизмом, происходит при температурах 600 °С и
слабо чувствителен к изменениям давления. Что касается межзерен-
ных трещин, то на них влияют и давление и температура. При р и Т
порядка 1 ГПА и 600°С, 1,5 ГПа и 500°С или 700 МПа и 800°С эти
трещины не возникают — неупругие деформации образца в целом
идут за счет дислокаций (и изолированных микротрещин внутри
отдельных зерен минералов). Сама смена элементарных механизмов
деформирования говорит о переходе приказанных давлениях и
температурах от хрупко-дилатансионного состояния (конкретно от
псевдопластического) к истинно-пластическому.
Данные, приведенные на рис. 7, соответствуют обычным
лабораторным скоростям деформирования (е« Ю-4с-1). При более
медленных нагружениях при низких температурах проявляется ползучесть,
обусловленная переносом влаги в системе трещин в образце.
Влажность заметно снижает величину поверхностной энергии образца,
а потому рост трещин облегчается, и, соответственно, дилатансия
начинается при меньшем касательном напряжении. Вместе с тем
замедление скорости деформирования до 10~8 с"1 незначительно
сказывается на пределе прочности геоматериала и переходе к
локализации. Высокотемпературная внутрикристаллическая ползучесть также
оказывает умеренное влияние на необратимое деформирование гранив
тов в диапазоне температур от 200 до 600 °С. В условиях высоких
температур мгновенные пределы упругости горных пород на нагру-
жение существенно снижаются и дилатансионное деформирование
облегчается.
В пористых горных породах смена режимов деформаций и
разрушения в зависимости от уровней давления и температуры должны
I быть еще больше, поскольку в этих породах помимо трещинообразо-
\ вания происходят неупругие процессы вокруг пор. Иногда (например,
I в туфе) под влиянием высокого давления происходит фактический
( 46
04
08 012 0J6
(переход среды в новое состояние
(спрессованный порошок), что
приводит к увеличению внутреннего
трения [31]). Прессование высоким
давлением разрушенного материала
выявляется и на кривых нагру-
жение— разгрузка.
На рис. 9 представлены пределы
прочности (кривая 1) и пределы
упругости (кривая 2) песчаников
различных типов при комнатной
температуре. Кривая 3
соответствует остаточной прочности
песчаника. Дилатансионные эффекты
проявляются между пределами
прочности и упругости при упрочнении и
разупрочнении материала вплоть
до достижения уровня остаточной
прочности. Скорости дилатансии
Л/ на пределе прочности песчаников
различных типов (рис. .10) оказались немного выше значений Л для
речных песков. Наблюдается характерный спад дилатансионных
эффектов с ростом давления, причем их исчезновение примерно соот>
ветствует выполаживанию предельных поверхностей (см. рис. 6)
—переходу к условию Треска: т = const.
Рис. 10. Спад скорости дилатансии
с давлением на пределе прочности
песчаников (р*=Зр/т/о, где т/о —
разрушающее касательное усилие
при 0*3=0)
Рис. 11. Уменьшение сдвиговой
прочности песчаника при росте пористости
Рис. 9. Пределы упругости (начала
дилатансии), прочности и остаточной
разрушающее касательное усилие при
аз=0)
Ma
?00
150
W0
50
• /И
П-0 П-01
-
„Вэгон Уил"
^RBE-ol
^ч. л-оч
ыРулисон" \s.
„СульФУР Крин'*
I I . 1 1
10 12 /V Рщ.
10
tS m0.°U
На рис. 11 показано уменьшение прочности на сдвиг с ростом
начальной пористости песчаника при давлении р=150 МПа. Индексами
"-О, ..., /)-8юбозначены номера образцов по испытаниям А. Н. Став-
рогина. Другие точки соответствуют породам, в которых были
произведены американские ядерные взрывы. Полная количественная
47
упругопластическая модель по данным опытов [43] построена
G. М. Капустянским и автором.
Должны быть очень интересны эффекты объемных
фазовых/переходов в дилатирующих геоматериалах, подвергаемых сдвиговой
нагрузке. Практически важный пример — дилатансионная ^блзучесть
мерзлого грунта [17]. Из опытов В. П. Епифанова следует, что
разрушаемый поликристаллический лед также хорошо удовлетворяет
дилатансионной связи (5.3).
6. ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ И ТЕЧЕНИЕ
ДИЛАТИРУЮЩИХ МАССИВОВ
Дилатансионная модель, в плоской задаче.
Характеристики поля скоростей и напряжений. Пучок
характеристик (центрированное течение). Истечение из
бункера. Полоса скольжения. Ориентация ее в
пространстве.
В плоском случае уравнения равновесия включают три
неизвестных компоненты напряжения
<^ll,l + °r12,2=fl, <Т12,1 + а22,2=/2 _ (6.1)
при заданных массовых силах Д-. Условия пластичности (5.2) и ди-
латансии (5.3) принимают такой вид:
КаМНо^-о,^ (6.2;
deff +de£ = sin v У(defl -degf +4de,(f 2, (6.3)
где ф — угол внутреннего трения, v — угол дилатансии, причем
sinср = а/3(3-Л2)/(3 -аЛ), sinv = Л ]/3/|/"З^Л\ (6.4)
Инкрементальный закон пластического деформирования имеет
теперь вид
йец = Ь + НЬн sin"* sin v - О/2) *иьч (! + sin? sin v)}'di' (a'5>ч
где dX определяется условием (6.2).
Если пренебречь теперь упругими составляющими деформаций,
т. е. принятьde{e} =0, то справедливо такое упрощение:
dexl — de\f = vx, xdt, de22-=de(2f = vit 2dt,
- ' del2=del?=(l/2)(vlt2+v2tl)dt
и, кроме того, любая функция у¥=у¥(%), %=е(Р) может быть
выражена как Ч^р), где р — плотность среды. '
Известная подстановка
(тп=—Р+ (р+Н) sin Ф cos 29, о22=—р—(р+Н) sin ф cos 20,
cr12= — (p+#)sincpsin2e, р = —(l/2)a,/fif/ (6.6)
48
позволяет тождественно удовлетворить условию пластичности
(6.2) и приводит уравнение равновесия (6.1') к такому виду:
(1 - Wf р cos 26) p9l + VtP sin 26/7,2 - W р cos 26р,, +
+ W р sin 26Р> 2 - 2W sin 266,, - 24 cos 266,2 = - f,
(6.7>
W p sin 26/?,, + (1 + W, p cos 26) /7,2 - Wt p sin 26P, , +
+ ^pcos26P,2 + 21Fcos26,1-.2«,sin266,2=-/2.
Здесь Чг=(р+Я) sincp, 9 — угол наклона направления действия
максимального напряжения агг к оси х2 (или, что то же самое,
напряжения аи к оси х\). Функция 4я зависит от давления и плотности.
Изменения плотности определяются полем скоростей согласно уравнению-
неразрывности
Р,/ + У1РЛ + ^2р,2 + Р^1,1 + рУ1,2 = 0. (6.8)
Для выражения компонент скоростей' через углы 9 и v подставим
уравнения (6:6) в закон течения (6.5). После очевидных
преобразований получим
sin 29ui,i+cos 29t;i,2+cos 29y2,i—sjn 29t>i,2=0,
sin 29ui,i+sin vui,2+sin v^ij+sin 29u2,2=0. (6.9)
Обратим внимание, что исключение величины ^1,2+^2,1 из системы
(6.9) приводит последнюю к дилатансионному соотношению (6.3) „
выраженному через максимальную скорость сдвига для произвольной
системы координат
cos 29(^1,1+^2,2) =sm'v(ui, 1+^2,2). (6.19)
Перейдем к представлению системы уравнений предельного
равновесия (стационарного течения) в характеристической форме. Можна
показать, что уравнения характеристик поля напряжений имеют вид
где cos 2г=дЧг/дру \ дЧ/др | ^ 1.
Уравнение характеристик поля скоростей имеют вид
(dx2\ ___ — sin29 + Kl — cos2 25 , /й , *ч /сюч
Ы)гл cos^-cos28 =Ctg(e±a), (6.12)
где cos2S=sinv, т. е. 6= (я/4) — (v/2). Наконец, пятая
характеристика (плотности при др/д<=0) совпадает с траекторией частицы
{dx2ldxi)b=v2/vi. * (6.13)
Условия на характеристиках в отсутствие сил тяжести могут быть
представлены в следующем общем виде:
{(cos 26 - cos 28) dx\ - (cos 26 + cos 28) dx\ -f- 2 sin 2Uxxdx2) X
X {dp (v2dx, -v.dx,) [(—cos 26 — cos 2s) dxx + sin Шх2} +
+ W 9{vldxl-\-v2dx2)d9dx2 — W(v2dx, — vxdx2)dbdx2) —
- 2p (dv.dx, -\-dv2dx2) (dx\ + dx\) + W p cos 2bdx2 = 0. (6.14)
Для получения из формулы (6.14) конкретного
характеристического условия необходимо подставить в нее значение dx2/dx\,
соответствующее рассматриваемой характеристике. При учетУ эффекта
упрочнения (Чг=Чг(р)) соотношения вдоль характеристик
оказываются в общем случае дифференциальными и для реш^йия краевых
задач следует применять численные методы.
Подстановка уравнений характеристик поля скоростей в общие
•соотношения (6.14), за счет обращения в нуль первой фигурной
скобки, приводится к таким условиям
dv\dx\-\-dv2dx2=0, (6.15)
где dx2/dx\ определяются уравнениями (6.12), т. е.
dvi/dss+ctg (9+6) dv2/dss=0ydvi/dsA+ctg{Q—6)dv2/dsA=0. (6.16)
Здесь sa — длина дуги вдоль соответствующей характеристики.
Вместо vu v2 в условия на характеристиках (6.16) можно ввести
компоненты скоростей Us и На на направления характеристик
Uz=vi sin (б—0)— у2соэ (б—О), uA=—v\ sin (б+Э) +
+v2cos (6+6)} (6.17)
Тогда условия на характеристиках (6.16) примут такой вид
dU3/ds3—(UA cosec 26—U3 ctg 26) д (9—6) /ds3 = О,
dUA/dsA+iUs cosec 26-~f/4 tg 26)d(9+6)/ds4=0. (6.18)
Если угол дилатансии v=const, то соотношения (6.18) упрощаются
dUs+(U3 tg v— Ua sec v) d9=0,
dUA+(Uzsecv— U4tgv)dQ=0. (6.19)
Рассмотрим в качестве примера плоское течение, когда движение происходит
-лишь вдоль первого семейства характеристик поля скоростей: Uf£0, £/4=0. При
этом второе семейство характеристик является пучком прямых линий
£/4=0, du=Q, 0=jt/2-f6+const, (6.20)
-выходящих из центра 0 (рис. 12). Из первого уравнения (6.19) следует такое
распределение проекции скорости на характеристику первого семейства:
[/з=Лехр (—Btgv), (6.21)
где А -^ константа вдоль характеристики первого семейства. Замена декартовых
координат хи х2 на полярные x{=rcosdt x2=r sin 9 с полюсом в точке 0
преобразует уравнение (6.12) характеристик первого семейства к дифференциальному
уравнению, интеграл которго имеет вид
логарифмических спиралей
г ехр (—9 tg у) = const. (6.22)
При рассматриваемом течении вектор
скорости Ui должен быть в каждой точке
ортогонален характеристике второго
семейства (его проекция UA=0). Поскольку
указанные характеристики — пучок прямых
линий, то вектор скорости должен касаться
окружностей (пунктир на рис. 12), у=
= я/2—2Д.
Условия, выполняющиеся вдоль
Рис. 12. Поле скорости пластичееко- характеристик ПЛОТНОСТИ (траекто-
го течения при центрированном се- Ad^dMcpn^" млтл#п тат;гтт v v
мействе характеристик ОА, ОВ л рии частиц), имеют ВИД
50
(cos 29+cos 26) [ (v2/v{) +tg(0+6) ] [(v2/v{ +
+tg(6—6)dp—p cos 2M{v\+v22)=Q. (6.23)
Рассмотрим характеристики поля напряжений при дЧ?/др=Ог
когда соотношения (6.14) распадаются на три отдельных, первое из
которых
dp [— (cos 26+sin ф)dxi-\-sm2Qdx2] — (р+Н) sin ydQdx2—0
(6.24)
определяет условия вдоль характеристик поля напряжений (6.11),.
второе v2dx\—v\dx2=0 определяет траектории частиц, а третье
(cos 20—sin v) dx2\— (cos 26+sin v) dx\-\-2 sin 2Qdx\dx2=0, как можно
показать, совпадает с уравнениями (6.12) характеристик поля
скоростей. При дф/др=0 угол 6=(ф/2)+я/4, уравнения (6.11)^ могут
быть также представлены в виде
dx2=dxi tg (Э=1^р=Ря/4). (6.25)
Подстановка (6.17) в соотношения (6.15) преобразует последние
d{p+H)4^2(p+H) tg(pd0=O, (6.26)
соотношение вдоль характеристики (6.11), а интегрирование
уравнения (6.26) дает
р+Н=С exp (=F0 tg ф). (6.27)
При учете силы тяжести соотношения (6.18) имеют более общий
вид
d(p+H)+2(p+H) tgфde1=(Y/cosф){sin(el=Fф)^l+ *
+cos (е1=Рф)Лк2}, (6.28)
где /1=Y^in9i, f2=y cos 8i, 8i — угол наклона оси х\ к горизонту.
Система характеристических уравнений (6.25) — (6.28) является
основой расчетов плоских, статически определимых задач [42].
В осесимметричном случае уравнения равновесия включают в
себя четыре независимых компоненты напряжения, а потому,статически
определимые решения получаются лишь при реализации полного
пластического равновесия (гипотеза Кармана—Хаара [28]), соответет-.
вующего точкам пересечения двух кусков поверхности текучести
Фа=0 в пространстве напряжений. Это возможно при использовании
в качестве Фа=0 пирамиды Кулона — Треска [28]. При
использовании конуса Мизеса — Боткина — Шлейхера (5.2) как предельной
пластической поверхности правильным является только замыкание
задач кинематическими связями, т. е. введение закона течения.
Приведем в качестве примера решение (А. С. Кузнецова) о радиальном
истечении сыпучего материала из плоского бункера, когда линии тока совпадают
с поверхностями if> = const в полярной системе координат, г, -ф. Уравнения статики
(6.7), которые принимают в данном случае вид
{/?(1 +sln<pcos29)},r+ (1/r) (/?sin(psin28), ф+ (2p/r) sin<pcos29 +
+ y cos ф= О,
(6.29)
(psin<psin29),r + (1/r) {/>(Г — 81п<рсо8 29)}ф+ (2p/r) sin<j? sin29 — y sinф = О,
.должны быть дополнены уравнениями течения (6.9), т. е,
vr,r+(vr/r) = (l/2)sinvK{tV,r-(tv/0}2+ О/')1 (*лф)2,
(6.30)
(tg28) Vf,r- (I/O ог, ф = tg29 (iv/r),
У
где © — угол наклона максимального главного нормального напряжения (и
скорости деформации) к радиусу. Система четырех уравнений (6.29), (6.30) содержит
три искомые функции р, 0, vr, что возможно, если-,9=6 (ф), sinv = —sin vo cos 26.
VS cp°=ZcpQ+i0
Рис. 13. Характеристика застойной зоны в зависимости от
внутреннего трения и дилатансии
1 — песок; 2 — стеклянные, шарики
Если далее искать решение в виде
■ Sin vo
^=ТгХ(ф), t;r = f (Ф) г 2+sinv°
(6.31)
то уравнения (6.29), (6.30) сводится к трем обыкновенным нелинейным
дифференциальным уравнениям относительно функций 6(ф), хСФ) и /СФ)« При этом
считается, что cp=2(po-r-v, гДе <Ро— постоянная сыпучей среды согласно (4.29).
Численное интегрирование последних проводится при следующих граничных
условиях: 6(0)=я/2 (равенство нулю касательных напряжений на оси симметрии),
Д0)=1 (условие нормировки). Третьим граничным условием было условие
совпадения внешней границы бункера (линии тока) ф=ф* с характеристикой уравнений
(6.29). Если же при интегрировании выявляется область, где поле скоростей
приводит к отрицательной диссипации энергии, то она считается застойной, а
положение ее внешней границы фиксированной: t|)=i|?**. На рис. 13 приведены
расчетные зависимости ф**(*р°). для бункера с горизонтальным дном: ф*=90°, а также
измерения ф** для сыпучих материалов с различными значениями эффективного
угла трения <p°=2<p0-Hvo. Видно, что разброс экспериментальных точек
относительно расчетной зависимости в отсутствие дилатансии (при v^=0) является
кажущимся, и данные измерений хорошо соответствуют дилатансионной теории. Заметим,
что предположение о радиальности линий тока, по-видимому, оправдано в нешэ-
средственной окрестности как бы точечного стока из бункера. Граница застойной
зоны оказывается линией слабого разрыва радиальной скорости, причем на ней
v=0.
52
Традиционно считалось, что характеристики поля напряжений
(6.11) являются линиями скольжения (Кулона), а это возможно
только если характеристика напряжений одновременно является линией
сильного разрыва поля скоростей. Для этого необходимо, чтобы
характеристики напряжений и скоростей совпадали. Условие
совпадения выражений (6.11) и (6.12) означает
sin ф+ (р+#) (ф,р) cos qp=sin v. (6.32)
Если угол внутреннего трения ф не зависит от давления
(поверхности текучести на плоскости Мора —прямые линии), условие (6.32)
является условием выполнения ассоциированного закона течения:
sir^=sinv( или иначе <х=Л — коэффициенты внутреннего трения и
скорость дилатансии совпадают). Совпадающие характеристики
оказываются Линиями скольжения — на них, как на характеристиках
поля напряжений, выполняется закон сухого трения Кулона (4.19),
а поскольку они же являются характеристиками поля скоростей, то
вдоль них может реализоваться сильный разрыв последнего.
Ассоциированный закон течения не соответствует экспериментальным
данным, полученным при неупругом деформировании геоматериалрв и
пористых сред (афк)у и характеристики полей скоростей и
напряжений не совпадают. Следовательно, на сильном касательном разрыве
скоростей (линии скольжения), отделяющем, например, движущуюся
массу грунта от покоящегося массива, должно выполняться условие
Кулона (6-.30), но с эффективным коэффициентом трения ф*,
отличным, от коэффициента внутреннего трения ф. Указанные линии
сильного разрыва могут либо совпадать с характеристиками поля
скоростей, либо быть геометрическим местом точек их пересечения [32].
Если считать, что сильный разрыв касательных скоростей
эквивалентен узкому слою, в котором скорости претерпевают резкие, но
непрерывные изменения, описываемые теми же уравнениями (6.1) —
(6.5), то такой слой в дилатирующей среде будет расширяться. Пусть
ось х2 направлена по нормали к этому слою, а ось х\ вдоль него.
Тогда внутри этого слоя и2)2, *>i,2>t>2,i, flu» т. е. после скоростей будет
функцией только поперечной координаты, а условие дилатансии (6.3)
приводит к уравнению
vjdx2 = sin v У (dvjdx2f + '(dvjdx^1,
или иначе
dv2/dv{ = tgv. , (6.33)
Интегрирование последнего поперек слоя —А^х2^+Л приводит
к такой связи:
Ы = Ы tgv, Ы=^(+1/г)-^(-/1). (6.34)
Иными словами, скачок касательной компоненты [v\] на линии
сильного разрыва в дилатирующей среде приводит к необходимости
стачка нормальной компоненты скорости [а2]. Тем самым
переходный хлой будет либо расширяться, либо сужаться — в зависимости
от знака скорости (угла) дилатансии. Только при v=0 толщина слоя
сохраняется неизменной, а сам слой допустимо моделировать
бесконечно тонкой линией. В общем случае скачок сильного разрыва ско-
53
ростей следует задавать в виде полосы скольжения конечной
толщины. т /
Нахождение переходного слоя может быть связано с
исследованием возможности ^неоднозначности (бифуркации) решеКий в узкой
полосе при сохранении неизменных однородных полейво внешних
примыкающих областях [37].
Пусть деформации внутри полосы ограничены условием
Mvu)=gi(x2)&i2, i, /=1, 2, 3, (6.35)
где А — разница между полем в полосе и вне ее, a gi(x2) —функция,
не равная нулю только внутри полосы. Условие непрерывности
напряжений означает, что скорость изменения напряжения аг/
считается одинаковой вне и внутри полосы
А°2/ = L2jki^ki = L2jk2gk = 0, (6.36)
где использована зависимость а'// от скорости упругопластических
деформаций ёц
через тензор упругопластических модулей Ьцы. Уравнение (6.36)
имеет неоднозначное решение /*, если
|L2/m|=0. . (6.37)
Здесь
£.//. = О (8/282/ + 8,,) + (К - (2/3) G) ttfiIt - (1 //',) (Go2i +
+ AKVJ%i)(Goji + aKV7r2bj2)(h + G + aAK),
причем h — пластический модуль [см. (5.11)], согласно [37] он
считается независимо определяемым в эксперименте.
Уравнение (6.37) дает такой результат:
l+A/(G + aKA) = {(Gait4-^
+ /C](G + a/CA)}{;ft[(4/3)G + /C)(G + aAK)}"1. (6.38
Анализ [32, 37] условия (6.38) для различных случаев ориентации
полосы относительно главной системы координат приводит к такому
результату для максимального пластического модуля, при котором
возможно неоднозначное решение
ftm/G=("l+v) (A-a)»(l/9) (1—v)-1—(1/2) (1+v) {N+(1/3) (Л + a)}2,
(6.39)
где v — коэффициент Пуассона. Угол наклона 0О полосы бифуркации
определяется следующим образом:
tgK = V(t-NmJI(Nmax _*),), Nmax = ot(VK
(6.40)
N = °jVK'Nmla = °,lVr:, 6 = (l/3)(l+v)(a + A)-tf(l-v).
Параметр N определяет характер деформирования: при чистом
сдвиге N=0, при трехосновном сжатии или растяжении N=±1/3, соот-
54
ветственно. При N=0 в случае а=0, Л=0 бифуркация возможна
только при Л=0 (нет упрочнения), причем 0о=я/4. При
ассоциированном законе течения а=Л и hm<0 — бифуркации в слое возможны
лишь на ниспадающей ветви связи г(у). При неассоциированном
законе течения hm может быть положительно, т. е. при а=й=Л
бифуркации возможны ив условиях упрочнения среды. Несколько иной
подход был развит в работе [25].
Неоднозначность решений в полосе при неизменности состояний
вне ее интепретируется как тенденция к локализации деформаций
в полосы сдвига, приводящая в тому, что вместо непрерывного
деформирования массива происходит смещение одной части массива
относительно другой вдоль полосы (или семейства полос). Известны
эксперименты по сдвиговому деформированию сыпучей среды, когда
вместо непрерывного поля скоростей появлялась одна или целая си-
стема линий скольжения (А. С. Ревуженко, С. Б. Стажевский,
Е. И. Шемякин, [45]). Внутри сдвиговой полосы деформирование
должно развиваться с перестройкой внутренней структуры при
стремлении эффективной скорости дилатансии Л к нулю.
Если же пластически деформировать дилатирующий слой, то
в нем могут расти периодические возмущения, что приводит к
созданию ячеек ускоренного и замедленного деформирования [11]. В
природе этому соответствуют явления будинажа слоев, гексагональные
системы трещин и правильные блоковые структуры.
7. ТРЕЩИНЫ, СТРОЕНИЕ ЗЕМНОЙ КОРЫ И ЗЕМЛЕТРЯСЕНИЯ
Трещиноватость земной коры. Сейсмические
границы как смена реологических состояний
геоматериалов. Природа волноводов и границы
Мохоровичича. Земная кора разных регионов. Типы очагов
землетрясений. Дилатансионные сейсмоаномалии.
Энергетика землетрясений. Блоки земной коры и
разломы.
Сопоставим данные рис. 7 с сейсмоскоростным разрезом
нормальной континентальной коры на рис. 14. Давлению 1 ГПа и
температуре 600 °С, при которых происходят подавление хрупко-дилатансион-
ных трещин в гранитах и переход к истинно-пластическому
состоянию, соответствуют глубины в 35 км [29]. Эта глубина и есть нижняя
граница земной коры, открытая А. Мохоровичичем (1911 г.) по
отражениям сейсмических волн во время землетрясений в Скопле. Таким
образом, выше границы Мохоровичича породы находятся в хрупком
трещиноватом состоянии. На этой гранцце (символ М) породы
земной коры пластически деформируются (состояние 7), а потому
становятся водонепроницаемыми.
Границы внутри земной коры, также фиксируемые по отражениям
сейсмических воли, соответствуют последовательным уровням трещи-
новатости. Так, граница Конрада (символ С или К), иногда
интерпретируема^ как переход от вышележащей гранитной толщи к
расположенной ниже габбро-базальтовой, а иногда вообще отрицаемая
[5], соответствует давлению в 0,5—0,6 ГПа и температуре в 400 °С.
А это как раз граница перехода (см. рис. 7) от псевдопластического
55
состояния 6 к состоянию 5 яркой дилатансии, характеризуемой
прерывистым скольжением, локализацией дилатансионных деформаций
(мелкой трещиноватости) в полосы разрушения, развитие/которых
завершается возникновением наклонных (к главной действующей
нагрузке) трещин. /
Скорость продольны* Волн, к м/с к
40 60 8,0
Z00 ,
со
о
чао %
600
zoo wo
Сдвиговое усилие, МПа
Рис. 14. Сейсморазрез стандартной континентальной коры по Ботту [5] и смена
реологии разрушения гранитов
Граница Форша (символ F) соответствует давлению в 0,2 ГПа,
температуре в 200 °С и переходу к режиму сколового
макроразрушения. Тем самым волноводу, выделяемому на рис. 14, по данным [5],
соответствуют возникновение наклонных трещин (4) и превышение
прочности над силами сухого трения. По другим данным [46]
волноводу соответствует толща между F и С, т. е. толща ярко дилатан-
сионного состояния. Выше F трещины вертикальны (3), т. е.
параллельны направлению вертикального литостатического давления, что
соответствует наблюдаемым выходам разломов коры на свободную
поверхность.
Указанное расположение границ получается при относительно
«грубой» классической интерпретации сейсморазреза. Также «грубой»
и усредненной является классификация механических состояний (см.
рис. 7). Казалось бы, для более точной интерпретации,сейсморазре-
зов земной коры следует учитывать вариации составов пород. Однако
знаменитая Кольская скважина показала, что горизонтальные сей-
смограницы, соответствующие смене трещиноватости, а
следовательно и границы гидротермального метаморфизма, пересекают на одних
уровнях наклонные пласты различных пород кристаллического
фундамента [19].
На рис. 14 дано распределение 8 скоростей продольных волн для
сплошного гранита. Откуда видно, что именно рост трещинной пу-
стотности приводит к спаду скоростей сейсмических волн. Уровень
раскрытия трещин связан с наличием касательных напряжений. На
56
рис. 14 приведена кривая 9 начала дилатансии (предела упругости)
для сплошного образца гранита, без поправок на температуру,
которые снижают необходимое сдвиговое усилие (примерно в 2 раза —
кривая 10). Тем не менее для объяснения резкого скачка скоростей
волн (до 1,5 км/с) на границе Мохоровичича следует учитывать иные
факторы.
Прежде всего вода играет активную роль на тех глубинах, где
могут быть трещины. Даже противоположное утверждение, что
трещины в кристаллическом фундаменте
закрываются из-за переотложения
минерального вещества, неявно
содержит утверждение о наличии
высокопроницаемой системы, по
которой может циркулировать вода или
ее пар. Тогда именно граница
Мохоровичича является предельной
глубиной (линия U рис. 15) действия
водяного пара (как транспортного
агента для физико-химических
превращений), а находящаяся на ней
пластическая порода
водонепроницаема. Обратимся с этих позиций
[29] к гипотезам о природе
границы Мохоровичича.
Гипотеза о фазовом переходе
«базальт, габбро-^эклогит»,
который объясняет нужный скачок
скоростей, отвергалась для
континентальной коры по следующей
основной причине [5]. Согласно фазовой
диаграмме Грина — Рингвуда (граница 2, рис. 15) в отсутствие воды
при температурах и давлениях, характерных для всей коры,
стабильным является эклогит, а не базальт, тогда как в природе кора
представлена гранитами и базальтами [5]. Однако закрытие трещин на
границе Мохоровичича согласно рГ-условиям делает верхнюю мантию
«сухой»; указанный фазовый переход становится возможным,, и если
геотерма имеет вид 3, то он происходит, минуя промежуточную
фазу 4 гранатового гранулита. Нижняя часть коры при заметном
давлении водяного пара будет представлена амфиболитами или гранитами.
Отметим в этой связи, что на некоторых разрезах коры между Мохо
и С вводится еще одна промежуточная граница.
Возможна ли трещиноватость континентальной литосферы ниже
Мохо? Для ответа необходимы Механические испытания эклогитов
при 7^500° и р^0,7 ГПа. Поскольку эклогиты более жесткие
породы, нежели геоматериалы земной коры, они могут хрупко
разрушаться и ниже Мохо. Такую точку зрения подтверждает
сейсмическая анизотропия ^ерха мантии, соответствующая возможно
определенной ориентации сети мелких трещин.
Может ли в коре отсутствовать базальто-габбровый комплекс,
который обычно считается расположенным между Мохо и границей
1100
со
о
£800
!
^5
п \
Г | Солидус
Г1 | * T^V
i§ ^ 1
ъ /
/
^
'А?
/v
•* s
\s Эклогйт
^2
L 1
» 1 г
Давлен'ие,ГПа
0 3S 70
Глубина ,км
Рис. 15. Фазовое равновесие габ-
5роидных пород и эклогита, и со-
:тояние на континентальной
границе Мохоровичича (М) при
учете водного фактора
57
Конрада? Обычно в пользу гипотезы о базальтовом комплексе
приводят данные о радиогенной теплоте, источником которой служат
граниты, и бытует мнение, что заполнение всей коры гранитами
привело бы к «перегреву» коры. Однако, если обратиться к конкретным
данным, то массовая концентрация радиоактивных изотопов урана
в граните 10_6—10-7, а базальте 10~7 и в породах верхней
мантии 10~8. Иначе, говоря, есть" гранцты, которые выделяют теплоту
так же как и базальты.
Геоматериал, подстилающий океаническую кору, представлен
перидотитом (оливином). Происходит [5] химическая реакция Хесса:
«оливин+вода = серпентин»*, которая может идти только там, где
породы проницаемы (т. е. выше Мохо). Почему же океаническая кора
намного тоньше континентальной? Поскольку реакция Хеоса идет при
7^500 °С, граница Мохоровичича могла была бы быть» изотермой
в~500°С. Однако это не так.
Лимитирующим фактором оказывается вновь эффект
закрытия трещин. Дело в том, что
породы с серпентином переходят из хрупко-
дилатансионнрго состояния в
пластическое при значительно меньшем давлении
(при 0,28 ГПа в температурном дипазо-
не от 0 до 500°С [18]). Это как раз
давление на подошве океанической коры.
В областях молодых складчатых гор
сейсмоактивная (трещиноватая) зона
простирается до глубин 1 (рис. 16) в
15—20 км, граница Мохоровичича
отбивается на глубинах в 50—70 км, а
между ними — пластическая зона коры.
Подобная ситуация объясняется
повышенным геотермическим градиентом в
корнях гор. В самом деле, глубинам в 20 км
соответствуют давления в 0,6 ГПа и
температуры порядка 700°С. Этим
значениям р, Т соответствуют устойчивые (и в
то же время пластические состояния 2
базальто-габбровых или гранитных пород. Граница Мохоровичича
будет определяться пересечением кривой геотермического градиента
3 и границей устойчивости эклогита в отсутствие воды. Этой точке
соответствуют глубины 5, 6 в 50—70 км (давление 1,5—2,0 ГЦа и
температуры 800—1000°С). Между базальтом и эклогитом в £том
случае должен быть слой гранатового гранулита 4.
Весьма существенно для тектонической расслоенности земной
коры оказывается наличие между хрупкими породами верха коры и
верха мантии мягких пластических слоев, допускающих большие
горизонтальные подвижки. Дальнейший рост температуры с глубиной
в мантии переводит породы мантии также в пластическое состояние,
а затем и в состояние высокотемпературной ползучести (переход
к астеносфере).
Трещины в земной коре залечиваются благодаря переносу геома-
58 -
Сопидус
п 1 2
Давление, Г па
J I I
20 50 70
Глубина, км
Рис. 16. Фазовое равновесие
габброидных пород и эклогита
и состояние на границе
Мохоровичича (М) при повышенной
геотермальной активности
териалов потоками воды и сопутствующими физико-химическими
процессами, но тектонические силы 1 поддерживают уровень трещи-
новатости. При этом возможен медленный рост трещин,
контролируемый так называемой коррозионной ползучестью, или же быстрый,
неравновесный, приводящий к землетрясениям.
Указанным выше трем зонам дилатансионно-хрупкого состояния
(а также типам разрушения образцов при испытаниях — рис. 7)
можно поставить в соответствие очаги землетрясений трех типов: с
образованием магистрального разрыва без предварительного
возникновения микротрещин в объеме области подготовки (относительно
большие касательные усилия и малые давления); объемное
трещинообразование с выделением магистрального разрыва (промежуточный
случай); трещинообразование вообще без магистрального разрыва — так
называемый рой землетрясений (относительно малые касательные
усилия и большие давления). Промежуточному случаю соответствует
локализация деформаций (и их носителей — малых трещин) в
полосы. В очагах первого типа мелкая трещиноватость может возникать
у вершины магистрального разлома как перед, так и в процессе его
роста. Действительно, сильные землетрясения зарождаются в земной
коре примерно на границе Конрада, тогда как умеренные
концентрируются в зоне волновода и прерывистого скольжения — между
границами Форша и Конрада [50].
Широко известная сейсмоскоростная аномалия — спад
сейсмических скоростей (изменение cPi cs или отношения cv/cs на 10—20%) —
является предвестником землетрясений 1-го и 2-го типа и
сопутствует землетрясениям 3-го типа. С точки зрения дилатансионной упру-
гопластической модели указанная аномалия соответствует
неупругому разрыхлению (раскрытию трещин) из-за концентрации
напряжений, в земной коре в очаге (например, у вершины разлома)- перед
землетрясением. Более того, сейсмическая аномалия может быть
разных знаков, поскольку разрыхление в одной части массива может
переходить в уплотнение в другой. Каждое индивидуальное
зарождение дилатансионной трещины приводит к изучению как упругого
сигнала (форшока), так и электрического сигнала, а возникновения
свежей трещины приводит к выделению радона, гелия и других газов,
растворенных в кристаллической решетке минералов. Попав в
систему циркуляции воды, они становятся одним из признаков
готовящегося землетрясения.
Экспериментально сейсмоскоростная аномалия перед
землетрясением была выявлена в Гарме (СССР). Контрольное подтверждение
было получено в 1971 г. в районе Голубого горного озера (США),
после чего была выдвинута (A. Hyp и др.) гипотеза о связи сейсмо-
скоростной аномалии с дилантансионной природой явлений в
очаге [29].
Возникновение и развитие дилатансионных зон в условиях
действия сухого трения является главным источником диссипации
механической энергии землетрясения.
1 Помимо медленных (геологических) изменений тектонических сил по дияатан-
сионным признакам выделяются их осцилляции (волны)—короткопериодные,
определяемые земными приливами, и долгопериодные [33], коррелируемые с
сейсмической активностью.
59
Исходными значениями для оценки энергии землетрясения и
сброса напряжений в очаге служит энергия ес излучаемых волн,
вычисляемая по формуле Гутенберга — Рихтера
/
aM=lg(Ec/E0), a=.l,5,-Е0 = 25 кДж, * / ' (7.1)
/
где М — магнитуда. Энергия Ес вычисляется как полная энергия волн
вне гипоцентральной области, где потери на диссипацию
незначительны. Ес составляет только часть, и по-видимому, весьма малую от
полной энергии Е, выделяющейся при землетрясении, т. е. Ес = т]Е, где
х\ — коэффициент излучения сейсмических волн, или иначе —
сейсмический к. п. д. Для нахождения величины ц наиболее целесообразно
пользоваться в качестве исходных данными о сейсмическом
моменте, которые приводят к оценке сброса напряжений [о] ~0,1—10 МПа
в очаге, причем порядок 0,1 МПа является наинизшим.
Таблица 3
Параметр
М, магнитуда
Ее. Дж
TriT, Мт
/?с. км
Е, Дж
ТНТ, Мт
R> км
А, км
в, сут
Землетрясение
Умеренно
сильное
5
1012
Ю-3
0,1
1014
0,1
1
10
100
Сильное
7
1015
1
1
1017
100
10
30
1000
Катастрофическое
9
1018
103
10
1020
105
100
100
—
Поскольку сейсмический момент вычисляется по амплитудам
сейсмических волн, сброс напряжений [о] можно рассматривать как
оценку амплитуд этих волн при выходе из зоны диссипации в
упругую зону. С другой стороны, измерения волн разгрузки [29] при
хрупком разрушении твердых тел показывают, что их амплитуды
имеют порядок прочности os разрушаемого тела. С учетом остатбчной
прочности массива aR амплитуда излучаемых волн пропорциональна
разности os—Or. Поскольку энергия упругих волн пропорциональна
квадрату амплитуды, то отсюда получаем оценку коэффициента ц,
П = Ес/Е={[(т]/(а5-ан)}2-10-б-10-2, ^ (7.2)
приняв, что [а] ~0,1—10 МПа и (os—oR) ж (Ю—100) МПа.
Согласно данным о горных ударах, сейсмические к. п. д. имеют еще
меньший порядок: Ti~10-4.
Выберем верхнюю грань оценки (7.2), т. е. примем, что
коэффициент т] при землетрясении имеет тот же порядок, что и при
взрыве, —г) = 0,01. Тогда подстановка Е=100ЕС в формулу [29]
€0
\
R~(eG/o2s)l/3'
(7.3>
позволяет оценить R— истинный масштаб области выделения
упругой энергии.
Сводка характерных значений приведена в табл. 3 для разных
магнитуд и энергий землетрясений. Там же приведены линейные
масштабы А зоны афтершоков и 0 — продолжительности
предвестника землетрясения (времени существования аномалии cp/cs). Из
таблицы видно, что при наибольшей энергии землетрясений масштаб R
области выделения упругой энергии имеет порядок 100 км. Это как
раз средний размер между вертикальными разломами по поверхности
коры для сейсмоактивных областей [29, 37]. Отсюда следует, что
расстояние между этими разломами и максимальная энергия
землетрясений взаимосвязаны. Масштаб в_ 100 км соответствует также
представлениям, что при максимальных энергиях землетрясений
происходит разгрузка целых литосферных блоков.
Итак, верхняя часть литосферы (выше границы Мохоровичича)
состоит из мозаики хрупко-жестких блоков, а ниже — из тех же
горных пород, но в пластическом состоянии. Поэтому -движение
континентальных плит может приводить к кинематическим несогласиям
выше Мохо, которые и разрешаются землетрясениями. Возникающие
при этом концентрации напряжений имеют порядок as [29, 37].
Неустойчивые ситуации на границе Мохоровичича, равно как и
внутри земной коры, возникают при больших и сравнительно
быстрых деформациях. Так, в пластическом материале может произойти
возврат к хрупкому состоянию, связанный с распадом гидратосодер-
жащих минералов, например, серпентина в океанической литосфере,
что приводит к глубинным землетрясениям [18] (под Японией).
Если разломы землетрясения прорывают границу Мохоровичича, та
по ним в мантию может поступить вода, а в кору могут быть
выдавлены ультраосновные породы мантии. Это, вообще говоря, может
привести к фазовым переходам со значительными приращениями
объема и закрытию разлома. Граница Мохоровичича будет иметь при
этом характерные неровности. При достаточной скорости реакции,
которая возможна в условиях высоких температур и давлений и
в присутствии воды, произойдет быстрое расширение вещества вдоль
первоначальной трещины, что превратит ее в очаг землетрясения.
Разломы, ортогонально выходящие на свободную поверхность,
с глубиной становятся наклонными с постоянной ориентацией вплоть
до границы Форша, после чего расширяются в «корневую» систему к
выполаживаются к границам Конрада [46]. Существенно, что очапг
сильных землетрясений также располагаются вдоль выполаживаю-
щихся поверхностей. Это подтверждает общую идею о реологической
расслоенное™ коры и говорит* о преобладании горизонтальных
подвижек в нижней части коры.
ГЛАВА 3
ДИНАМИКА ДИЛАТИРУЮЩИХ И ХРУПКО-РАЗРУШАЕМЫХ
МАТЕРИАЛОВ /
/
8. ОДНОМЕРНЫЕ ВОЛНЫ. ВОЛНЫ В СТЕРЖНЯХ ;
Уравнения одномерного динамического движения.
Их характеристическая форма. Неголономность
уравнения состояния дилатирующих материалов.
Соотношения на сильных разрывах. Ударная
адиабата при неголономности уравнения состояния.
Волны в дилатирующих стержнях.
Рассмотрим одномерные нестационарные движения с плоской и
сферической симметрией. Пусть х— расстояние от плоскости или
центра симметрии, в\=оп — соответствующее главное напряжение,
022=!<Тзз = °:2' а касательные напряжения в плоскостях координат
отсутствуют: (7i2=ff23=ffi3=0. Пусть v — отличная от нуля
компонента скорости движения частиц среды. Для скоростей полной
деформации справедливы представления
ei = v,u e2 = e3=(-k-l)(v/x)/2; <?f/ = 0, i¥=j, (8.1)
где k=\ для плоских и k=3 — для сферических волн.
-Введем вместо главных напряжений <У\, о2 среднее р и
касательное т (действующее под углом в 45° к оси х) напряжения
а1=^р+4т/3, а2=—р—2т/3, x=(oi—а2)/2. (8.2)
Тогда уравнения сохранения массы и импульса в отсутствие
массовых сил принимают вид
P,t+vp,x+pv,x+ (k—l) р {v/x) =0, (8.3)
Р (v,t+wtX) =—р,х+ (4/3)т,*+2 (к— 1) (х/х). (8.4)
Определяющие связи упругопластической модели дилатансии
v,x + (k-l)(vlx) + 3(l-2v)(p/E)=(2Ayy.3{v,x-
- (l/2)(ft - l)(vlx) - 2(1 +v) (x/£)}. (8.5)
Для учета эффектов упрочнения выразим объемно-пластическую
деформацию через переменные
eip)=e—ew=v,x+(k—l) (v/x)+3(l—2v) (р/Е). (8.6)
В силу уравнения (8.3) интегрирование дает связь
e(p>=3(l-2v) (р/Е)+\п(ро/р)+е0^\ (8.7)
выполняющуюся вдоль траектории частицы. Здесь постоянная
е(р) =е(р) при р=0> р=Ро;
Предельное соотношение (5.2) позволяет исключить из уравнений
(8.4), (8.5) переменную т и свести задачу к решению уравнений
^+wix+(l/p){l-(4et/3)/ffip}plx-(4/3)(et/p)X
X/a,pp,x = 2(fe—l)8Tfa/(p^), (8.8)
{3/3(1-2v)/^-f(4/£)6^A(l+v)/a>/7}(p,,+^)jC) +
+ (/3 + 26^A)t;,, + (4/£)e^(l+v)fa(p(p., + t;p,x)-
= -(А-1)(У^т-втА)(^).
62
Уравнения вдоль первой характеристики системы (8.3), (8.6),,
(8.8) имеют вид
Sp-{(K3-2eTA/p-(4/£)e,etJA(l+v)fefP}p =
= -3{k-l)pA(vlx),
(8.9)
5 = 3/3(1 -2v)/£ + (41Е) 6,6, Л (1 + v) fe> р>
а второй и третьей — соответственно
{x)2,z=v±c,
o1dz9cv=(k-l)x-1{±2QJac-9vc>-.%(3-4bJat9)A(vlS)},
(8.10>
где
.fii=f х
(Кз~-28ТЛ) (1-48, (3fg> р)) -* (46tp/£) [Гз(1-2у) + 8тЛ (1 + v)] f„,
• 3K3(l-2v)+48,9TA(l + v)f0(p
X
(8.11>
В плоском случае (k=l) правые части соотношений на
характеристиках обращаются в нуль, и они становятся аналогичными харак*
теристическим уравнениям газовой динамики с заменой давления на
напряжение в\. Знаки 6t и Ьу выбираются из условия диссипацию
механической энергии. Если упрочнение существенно, то вдоль
первой характеристики (8.9) выполняется также соотношение (8.7).
Запишем выражение квадрата скорости распространения малых
возмущений в упругопластической дилатирующей среде,
подчиняющейся условию Мора —Кулона (5.2),
2^ Е (1-29та/КЗ) (1-29тЛ/Кз)+68т9/Л(1-у)а^(/7/£)
С — р 3j(4-2v)+29,eT (l+v)A[a + 3(l-2v) а' (/>/£)]
Здесь штрих означает диффе- с,м/с
ренцирование по е?\ величина У
принята постоянной.
На рис. 17 приведена
построенная согласно (8.11) зависимость
скорости распространения малых
сферических возмущений в
пластической зоне от давления р и
плотности р при значениях £=300 МПа,
v=0,25, р0=1500 Kf/м3, а также
зависимость скорости слабых не-
упругих волн с от давления р
(штриховая линия) для
одномерных плоских волн. Видно, что с
JS0F
300
„ /003
Р\ /оог чроч
J
0.5
to
ft5 /7,МПа
Рис. 17. Зависимость скорости
слабых волн от плотности и давления
при неголономном уравнении
состояния. Штриховая линия — расчет для-
плоских одномерных волн
6$
увеличением давления скорость распространения возмущений
возрастает* Это соответствует, как известно, тенденции к возникновению
ударных волн. ,
В одномерных плоских волнах плотность р при нагру&ении
связана с давлением р однозначной зависимостью [что, например,
следует из условия (8.9) на первой характеристике], т. е: уравнение
состояния интегрируется отдельно от уравнения движения. Указанная
зависимость будет отличаться от зависимости р(р) для движений
других типов.
Так, при сферически-симметричном движении дилатансионное
соотношение (5.3) может быть также представлено в виде
e + 3(l-2v)(/J/£)=(2AeT/K"3)'.{T-2('l+v)W£)}
4 = v.x-(v/x) (8.12)
или с учетом уравнения неразрывности (8.3)
- (1 /Р)"р +.3 (1 - 2v) (pjE) = (2Лвт/]/3) "{T-2(l. + v)(i/£)}.(8.13)
Соотношение (8.ГЗ) включает приращения dp, dx,a также
величину е^\ Проинтегрировать его и найти связь р(р) удается только
при решении дилатансионного соотношения совместно с условием
пластичности и уравнениями движения, т. е. при решении полной
системы уравнений.
Таким образом, уравнение состояния среды (8.13) оказывается
неголономным соотношением [28, 41].
Неголономность уравнения состояния приводит к особой ситуации
на сильных разрывах, при которой ударную адиабату невозможно
построить независимо о*г течения за фронтом волны. Например, при
распространении сферической ударной волны со скоростью v на
разрыве должны выполняться условия баланса массы и импульса (и
энергии — в нёбаротропных средах)
[p(t,_y)]=0, [рУ(с-(/)]=-[р] + (4/3)[т], (8.14)
где квадратные скобки обозначают скачки величины, заключенной
в эти скобки, например, [G]=:G+—G_. Связь (8.13) между р и
напряжениями даже в том случае, если она интегрируется, требует
знания граничного значения (за разрывом) величины сдвига 'у+.
Поэтому соотношения (8.14) должны быть дополнены еще одним условием
на разрыве. Воспользуемся с этой целью физическим условием
непрерывности смещения
[и]=г--и+—и-=0г (8.15)
из которого следует известное кинематическое условие
[у]=-[У*ди/<Э*], V1C = V—v. (8.16)
Поскольку
у=и,х— (k— l)u!(2x), u=uiX+(k—l) (и/х),
то из непрерывности смещения (8.15) следует
[у]=,[ди/дх] = [е], (8.17)
64
т. е. приращения сдвига и объема равны между собой. Если в дила-
тансионное соотношение не вводить величину у в явном виде, то
условие (8.17) становится излишним.
В общем случае, в силу неголономности уравнения состояния,
ударная адиабата зависит от течения за фронтом и ее можно найти
только после решения всей задачи.
В частном (голономном) случае, когда A=const, уравнение ^8.12)
приводит к конечному соотношению вдоль траектории частицы
le-eo)+3(V-2v) (р-Ро)/Е=(2Аву/УЪ){{у-у0)-2(1+1) (т-т0)/£},
(8.18)
где индексом «ноль» отмечено состояние отсчета, или
иначе—начальное состояние [41]. Проходящая ударная волна меняет, вообще
говоря, это начальное состояние. Поэтому с разных сторон от скачка
оно оказывается различным. Скачок начальных состояний
необходимо определять независимо, как функцию интенсивности ударного пе-^
рехода. Физически это означает учет дополнительных эффектов
(физико-химические реакции и т. д.), происходящих в самом фронте
волны.
Условие (8.13) интегрируется вдоль траектории частиц также и
в случае Л=Л(^р>), так как в левой его части стоит как раз величина
deW/dt, но при Л=Л(^), р) условие дилатансии справедливо лишь
в дифференциальном неголономном виде
Если скорость ударной волны меньше скорости продольного звука,
волна принимает двухфронтальную структуру — вперед уходит
упругий предвестник. При этом выделяются два характерных случая.
Если скорость распространения второго фронта — фронта
неупругости (роста трещин, движения дислокаций, проскальзывания зерен)
больше или незначительно отличается от скорости (8.11), то в точке
непосредственно перед разрывом выполняется предельное условие
пластичности.
Тогда значения параметров перед разрывом и~, у_> Р-> т-, так же
как и их значения за разрывом и+, у+, Р-ь ■■*+, связаны условием
(8.18), что с учетом (8.17) приводит к равенству
E<y5-t$[el=--3V5{l-.2v)lp]--4A(l+v)t М, (8.19)
которое вместе с условием пластичности замыкает балансовые
соотношения (8.14). Это позволяет построить ударную адиабату. В не-
дилатирующей среде соотношение (8.19) сводится просто к
следствию из закона Гука
E[e]=-3(l-2v)[p]. (8.20)
Если скорость фронта неупругости меньше скорости (8.11), то
выполнение условия пластичности перед разрывом необходимо, но
не достаточно для начала дилатансионного деформирования.
При изучении законов распространения разрывов в упругопласти-
ческих средах весьма часто фактически принимается предположение
о том, что внутри ударного перехода также происходит упругопласти-
ческое деформирование, иногда с аддитивным введением вязких эф-
5-ЗЗИ 65
фектов 1. Если внутри ударного слоя при этом выполняется неголо-
номное —за счет Л=Л(^Р), р) —условие (8.12), то для этой зоны
нужно сделать предположение о пути деформирования (н^ружение).
Если принять гипотезу, что внутри фронта сферической/ударной
волны происходит одноосная деформация, то ударные адиабаты всегда
(даже при неголономном уравнении состояния) будут независимы от
течения за фронтом, а решение задачи о структуре фронта волны
позволяет получить дополнительные граничные условия.
Для учета необратимого затекания пор следует использовать
модельное представление дилатансионного процесса в виде (5.24), т. е.
вместо упругих деформаций в (8.5) вводить необратимое объемное
уплотнение. Такой модели соответствуют следующие характеристичен
ские уравнения для сферически-симметричной динамики:
{x\ = v, 9FtPpp-(l+A)p = 3pvAlxf
(x)ut = vzhc, ca = -oip-o)P(l+A)/(pF,pp),
(8.21)
a zt 9cv = ± (4c*/x) - {2po( p - o. p (2 - A) F'lpp} (vjx).
В частности, даже при вогнутости кривой гидростатического
уплотнения р=—i/\p(p) к оси давлений (см. рис. 6), соответствующей
возникновению сильного разрыва в плоских одномерных волнах, при
сферически-симметричном движении нагружение может происходить
не скачком, а непрерывно.
Анализ автомодельной задачи о расширении сферического поршня
при гипотезе об одноосной деформации в структуре ударной волны
(В. В. Башуров, Н. А. Скоркин, [4]) позволил фактически выявить
случаи возникновения сильного разрыва или непрерывной ударной
волны нагружения. Автомодельная задача о расширении газовой
(взрывной) полости в рыхлящейся среде при уплотнении на фронте
волны в k раз, т. е^ при постоянной ударной сжимаемости е=(£—1*)/&,
была рассмотрена Ю. С. Вахрамеевым и СВ. Демьяновским [4].
Для изучения волн в стержнях из дилатирующего материала
воспользуемся непосредственно даяными . о стандартных трехосных
испытаниях как для связи «осевое напряжение о — осевая
деформация #1», так и для дилатансионной связи «объемная деформация е —
осевая деформация е\». На рис. 4 приведены такие данные для
песков;^ данные для горных пород и плотных песков качественно
аналогичны. Итак, из опытов связи будем считать известными •
<х=о(е), е=е(г), е=еи (8.22)
Согласно определению осевая деформация е удовлетворяет
уравнению
e,t-\-vetX=v>x, v=vu (8.23)
1 Анализ внутриударных переходов, т. е. структуры ударного фронта, требует
более общей математической модели, нежели используемая вне разрывов. Введение
вязкости является соответствующим простейшим, но не всегда адекватным
обобщением.
66
поскольку в рассматриваемом приближении р=р(л;, t)y v=v(x, t), е=
*=*е(х, t)—функция только осевой координаты и времени.
Динамическое уравнение продольного движения имеет вид
9{v,t+vvtX)=aiX. (8.24)
В силу осевой симметрии составляющие скорости v2 в любом
радиальном направлении jc2 одинаковы. Тогда уравнение
неразрывности может быть представлено в виде
P,*+fp,*+P {v, x+vr,r+ (Vr/r)} = 0, (8.25)
Оно может быть переписано следующим образом:
>/'р=-ё, (8.26)
что после интегрирования приводит к соотношению
ро=рехре, е=е(е), (8.27)
где ро — начальная плотность. Согласно связям (8.22) и (8.27)
динамическое уравнение (8.24) принимает вид
(lJp)(vtt+vvtX)=aieEtX. (8.28)
Система уравнений (8.23), (8.28) относительно двух искомых
функций v и е сводится к двум уравнениям
(1/р) (<*.t+vo.x) =c2v,Xy (l/c) (vlt+vv*) =<W(pc), (8.29)
где введена скорость
c{o) = (l/p)V(hj(h: (8.30)
Если теперь ввести функцию
^(£)=\—т-т—гт- » е — е(о),
то система (8.29) преобразуется к виду
Ftt-\-vFiX=cv,xr v,t+vviX=cFtX..
Отсюда непосредственно следует система
(v±F),t+(v4?c)(v±F)tX = 09
свидетельствующая о сохранении инвариантов Римана
I+=v+Fy I_=v—F
соответственно вдоль характеристик
(x)i=v—c, (x)2=v-\-c. (8.31)
Видно, что с (о)—скорость распространения возмущений
относительно частиц среды. Начальному прямолинейному участку
зависимости а(е) соответствует скорость упругих волн
do[de = E, d*o/de2 = 0, p = pe = cons,
(8.32)
, с0 == V~E/p0 = const.
67
После появления дилатансионных деформаций уплотнения (о$ь
7^<У\) скорость с (о) снижается в силу условий
d<yjde>0, d2o/de2<0, dp/de>0, / У (8.33)
dc/de = (Г/у'рЗо/Л) {(1 /р) d2o/de2 - (1 /р2) (rfp/Л) (do/de)} < 0.
Соответственно нагружение в волне будет начинаться с ударного
фронта, только при сверхзвуковом ударе V^cQy где V — начальная
скорость ударного фронта. При V<Co происходит развал фронта —
вперед уходит начальное возмущение (упругий предвестник) малой
амплитуды (Г^сть а возмущения большей амплитуды (о><У\)
распространяются все с меньшей скоростью, монотонно стремясь к
предельной нагрузке os.
Если же в стержне при а>в\ начинается дилатансионное разупт
лотнение, то dp<tfe<0, р<р0 и величина dc/de может стать
положительной даже при da/de>09 d2<j/rfs2<0, т. е. из непрерывного
профиля может образоваться ударный фронт. В данном случае следует
также учитывать инерцию радиального движения.
9. ЭЛЕМЕНТАРНЫЙ РАСЧЕТ ПОДЗЕМНОГО ВЗРЫВА
Схематизация взрывного движения. Числовой
расчет сферически-симметричного взрыва в монолитных
горных породах. Кинематические интегралы для
массовой скорости и плотности. Камуфлетное урааг
нение взрыва * пористой среде. Экспериментальные
данные.
При взрыве химических взрывчатых веществ (ВВ) широко
принято моделировать источник взрыва в виде расширяющейся полости
радиуса a(t), заполненной взрывными газами "с известными
показателями адиабаты. При ядерном взрыве газы, заполняющие каверну,
образуются при испарении окружающих взрывную камеру горных
пород, что приводит к некоторой (относительно малой) затрате
энергии и к зависимости эффективного значения показателя адиабаты
от окружающей- породы.
Принимаем, во-первых, что энергия и адиабата газов для взрывов
обоих типов априори известны. Во-вторых, ударный фронт
наблюдается в горных породах только в волнах с амплитудой более 10 ГПа|
соответствующая оценка дает весьма малые размеры области
существования ударных волн. С другой стороны, доля энергии, которая
уносится в виде сейсмических волн, есть сотая часть энергии взрыва>
что говорит об интенсивных диссипативных свойствах горных пород.
Отсюда при элементарных расчетах можно пренебречь так
называемой ближней зоной, где из-за чрезвычайно высоких давлений среда
ведет себя подобно жидкости и при использовании уравнений
гидродинамики единственным источником диссипации энергии взрыва
оказывается ударный переход. Будем считать [24], что
гидродинамический (нулевой) этап развития взрыва, имеющий место в «ближней
зоне», завершается, когда давление р на полости будет иметь
порядок от = 0,1рс2, где <тт — максимальное сдвиговое усилие,
выдерживаемое породой (см. рис. 7) и соответствующее ее пластическому тече-
68
нию, обусловливаемому дислокационным механизмом неупругости.
Начиная с этого момента ударная волна в горной породе (или
грунте) будет вызывать разрушения, зависящие от касательных т=
= (or—(Те)/2 и нормальных Ол, ае напряжений. Поскольку начальное
давление газов р0=0,1рс2, а противодавление, моделирующее лито-
' статическое давление, равно pi, то начальная энергия газов в полости
равна
Е= (3/4)naMpo-pi) (y-l)-K
где ао—начальный размер полости, у — показатель адиабаты газов,
р=Ро(а0/а)Ъ=—вг. (9.1);
Для выбора значений Оо, Ро при ядерных взрывах в разных поро-*
дах можно воспользоваться данными [4]. Уравнения движения
имеют вид
(V/V)=vtr+2(v/r), t)=V(ar,r+t/r), (9.2)
где V= р"1 (1 — т)'1 —удельный объем среды.
В упругой зоне будем использовать закон Гука в конвективной
форме
т= G {v>r-v/r), p=-K(vtr+2v/r). (9.3)
В пластической*зоне выполнено предельное условие Мора —
Кулона (5.2), и дилатансионное уравнение (8.5) при & = 3 в
пренебрежении упругим сдвигом будет иметь вид
vtr + 2(v/r) = (llK)(ptt+Vptr) = (2lV^)A\vtr^vlr\. (9.4)
Система уравнений при начальных уравнениях: р=ри v=0, t=0
и граничном условии (9.1) при £5Ю, r=a(t)—допускает простое
решение на ЭВМ. ' •■ - .
На рис. 18, 19 представлены результаты расчетов при следующих
значениях параметров:
#=52,0 ГПа; G = 24,0 ГПа; р0=64,0 ГПа; pt=20 МПа;
Оо=3,2 м; а=0,5; 7=1,4;
(2/1^3) Л = 0,1; Л = 0. (9.5)
На рис. 18 показаны распределения давления в три
последовательных момента времени ^=28/0; t2 = b6t0\ /3 = 84/0, (to = ao/c).
Момент t3 соответствует практической остановке полости. Эпюра
остаточного удельного объема V соответствует моменту tz. Первый
характерный максимум давления, меняющий свое положение во времени,
соответствует движению фронта волны сжатия. Второй, практически
стоящий на месте и уменьшающийся по величине, ведет к
образованию вала остаточных сжимающих напряжений, а следовательно и
плотности вблизи пол©сти. В расчетах принималось A=const, и
график остаточного удельного объема V(r) показывает при Л>0 только
разрыхление (результаты расчетов при Л=0 даны пунктиром). На
самом же деле, резкое повышение давления и изменение плотности
69
приводят к изменению знака скорости дилатансии, т, е. уплотнению
при сдвиге, а поэтому V(r) должно иметь более сложный вид.
Весьма примечательно, то дилатансия приводит к рост/
расчетных амплитуд взрывной волны. Это. подтверждается данными
зависимости максимальной скорости vm (кривая 1), пиковр/о давления
рт (кривая 2) и максимума сдвигового напряжения хт (кривая 3)
от расстояния г (рис. 19). Видно, что относительный эффект
дилатансии возрастает с расстоянием, пройденным волной. Если на ран-
V,!0~JMJ/Kr
040
039
SJ8
037
Рис. 18. Взрывная волна на три
последовательных момента времени.
V — остаточный удельный объем,
pi — литостатическое
противодавление. Штриховые линии — расчет при
Л=0
1,5 г/г'^м/кг'Л
ней стадии дилатансия сказывается в 15%-ном повышении
амплитуд, то к концу взрывного движения составляет 45%. Характерный
излом эпюр зависимостей pm(r)> vm(r) объясняется тем, что на при-
w 3,—
веденных расстояниях г /у Е ^0,4—0,5 годограф фронта волны
сжатия отрывается от годографа пластической зоны (внешний радиус
последней резко замедляет свое распространение) и в дальнейшем идет
как упругая волна. Отметим, что некоторое несоответствие значений
амплитуд давлений на рис. 18, построенном без учета отклонений из-
за пересчета, и на рис. 19 (для момента времени t=28tG) объясняется
возмущением, которое вносит сама принятая процедура перерасчета
[4].
На рис. 20 приведены годографы различных характерных точек:
кривая 1 — радиус пластической зоны rv\ 2 — радиус полости а; 3 —
фронта волны Ькатия (первый максимум); 4 — второго максимума
давления га в зоне повышенного напряжения вблизи полости. Здесь
tQ=aofc, где с — скорость продольных волн. Видно, что дилатансия
приводит к увеличению радиуса пластической зоны, к усилению
максимума зоны пересжатия и уменьшению радиуса полости.
Координаты фронта волны сжатия при расчетах с учетом дилатансии и без
нее совпадают. Увеличение амплитуды взрывной волны, радиуса пла-
70
стической зоны и уменьшение, радиуса полости при расчетах с дила-
хансией связаны с тем, что из зоны дилатансионного разрыхления
материал вытесняется как в упругую внешнюю зону, так и к полости.
Уменьшение радиуса пс^лости вследствие дилатансии,
отмечавшееся при приближенных оценках, возможно сказывается на
относительно слабом (30%) увеличении радиуса rv зоны пластичности,
отождествляемой с эффективным сейсмическим излучателем [24]. Однако
максимальные скорости смещения vm при г=гр возрастают примерно
в 1,5 раза, что существенно увеличивает интенсивность излучаемого
сейсмического сигнала.
PmSm,
МПа
1В00
/00
OL Z
tf-f 2 Ч 6 8 10° ги,/з,м/кг,/з
Рис. 19, Максимальные параметры взрывной волны в функции от приведенного
расстояния
1 — ХфО; II — А = 0
На поздней стадии при обратном движении полости образуется
область, где —аг, —<Гв ниже литостатического давления pi. Вблизи
самой полости эти напряжения вновь оказываются, выше литостати-
еского давления. Наличие характерных указанных областей говорит
о возможности образования трещин и их последующего закрытия при
71
возвратном движении полости. Сопутствующая смена знака т
означает возникновение обратного пластического течения. Поскольку
взрывное движение — расходящееся, ов убывает и может стать
растягивающим. Если достигнут предел прочности на разрыв/то
возникнут радиальные трещины, которые мало меняют такие параметры
взрыва, как размеры полости, зоны дилатансионного разрушения и
параметры эффективного сейсмического излучателя, поскольку
энергия, затрачиваемая на хрупкое разрушение, несравнимо меньше
энергии, диссипируемой из-за сухого трения в зоне дилатансионного
разрушения. Последняя пропорциональна разности а—Л, т. е.
диссипация чувствительна к дилатансии.
Рис. 20. Годографы характерных границ при камуфлетном подземном взрыве
(стрелками обозначены расчетные моменты остановки полости)
Проведенный выше расчет показал соответствие перелома эпюр
максимальных параметров взрывной волны и внешней границы
дилатансионного пластического разрыхления монолитного массива.
Этот факт хорошо подтверждается данными американских
подземных взрывов в граничном массиве, выявивших повышение
проницаемости (за счет появления трещиноватости) вплоть до приведенного
радиуса ?кж1 м/кг1/3 (рис.21) и сведениями [4], что перелом
наблюдаемых эпюр агт{гк) —максимума радиальных напряжений
в гранитных.массивах имеет место примерно на тех же приведенных
расстояниях г^1 м/кг1/3.
72
При A=const дилатансионное уравнение (9.4) сводится к
уравнению с разделяющимися переменными
vmr + 2 (v/r) = (2/1/5) Л (v, г- vjr) 6Г ^ (9.6)
интегрирование которого приводит [27] к первому дилатансионному
интегралу
v = C(t)r-n, /г = (2/1/3 + 2Л6т)/(1/3-2Лет), (9.7)
где C(t)—произвольная функция. В частном случае несжимаемой
среды Л=0 и л=2, т. е. интеграл (9.2) определяет поле скоростей,
/о
-г
10
Ъ 7
^
10~
10
-5
Взрыв Хардхэт
Измерения
Измерения
LjJ
l_.J
I (7) I
1964?
1
2
1965 г.
Ъ
Чг
s
i №
\
*Ш)
1
J
О 30 60 30 /20 150 /60 г/о
Среднее радиальное расстояние от точи и взрыва, м
Рис. 21. Увеличение проницаемости гранитного массива после камуфлетного взрыва
«Хардхэт».
/ — граница полости перед охлопыванием; //— данные по взрыву «Хоггар», /, 3 —измерения
по вертикали; 2, 4 — измерения по горизонтали; /, 2 — измерения 1964 г.;' 3, 4 — измерения
1965 г.: 5 —номер скважины
характерное для взрыва в металле или жидкости. Прямые
эксперименты по камуфлетному взрыву в песке [4, 23, 24] выявили, что за
максимумом во взрывной волне я=1,5—1,8. Объяснение этого
эффекта таково. Взрывная волна уплотняет песок, а дальнейшее его
пластическое течение при v/r>vir вызывает дилатансионное
разрыхление, и поэтому ev=—1, п={2 У"3-2Л)/.(1/3+2Л)<2, Согласно
73.
(9.7), указанному диапазону для п соответствуют Л = 0,18—0,09, что
согласуется с экспериментальными данными для плотных песков и
намного меньше угла внутреннего трения песка (<х^0,5). Дл'я
большей точности следует указать, что при взрыве в песке появляются
кольцевые зоны с разными значениями п из указаннопУдиапазона.
Это говорит об изменениях Л с разрыхлением и о применимости
интеграла (9.2) в каждой из систем кольцевых зон. Для монолитного
материала, согласно А. А. Спиваку и В. М. Цветкову [4], дилатан-
сионное разрыхление еще интенсивнее: л=1,4, т. е. Л=0,21.
В пористых горных породах будет происходить вначале дилатан-
сионное уплотнение, а уже потом разрыхление. В области уплотнения
породы также .можно приближенно пользоваться интегралом (9.7),
задаваясь иным значением Л<0. Граница раздела зоны уплотнения
и разрыхления будет определяться условием е=ед(р), см.* (5.19),
Второй кинематический интеграл, определяющий плотность р
среды в поле скоростей (9.2), можно найти методом, предложенным
Е. А. Самаровым.
Подстановка дилатансионного интеграла (9.7) в уравнение
неразрывности (9.2) приводит к следующему результату:
C(t) dt Р+(Д+1)з^ + (2-Д)-айГй- = 0. (9-8)
Пусть значение произвольной функции времени C(t) интеграла
(9.7) определяется как скорость v(R) на движущейся границе R(t)
и=и(Я)(Щг)п9 dR=№, C(t)=v(;R)R". (9.9)
Тогда вместо времени t в качестве второй координаты можно
ввести радиус R, т. е. свести уравнение (9.8) к следующему:
{/?/Ы#)#"]}(Э(^^
(9.10)
Здесь, кроме того, добавлен член C~{(t)d(Inr2-n)Jdt=0f что
сводит уравнение (9.3) к уравнению относительно новой переменной
функции
Ч^прг"*1. (9.11)
Если R{t)—координата фронта ударной волны, на котором
выполняются соотношения баланса (9.14), то из уравнения баланса
масс следует
v(Ry=^E(R)Ry e(i?) = (p-po)/p (9.12)
при и=0, r>R. Функция e(R) —ударная сжимаемость материала.*
Подстановка условия (9.7) в уравнение (9.5) позволяет прийти
к следующему эффективному уравнению:
ёЧг/дФ+дЧг/дг"+1 = 0, с1Ф=& (R) dRn^ (9.13)
Общее'решение уравнения (9.13) имеет вид
w = w (r"+i _ Г е (#) dR"*1), (9.14)
что дает следующий общий интеграл для плотности:
9 = rn-2f(rn+1-^s(R)dRn+1). (9.15)
Здесь / — произвольная функция интегрирования.
74
Пусть, например, e=const (часто используемое упрощающее
предположение для фронта ударной волны) и R(t=0)=Q. Тогда
р=ро(1—e)-1=i?r,2/(Jf)=const> *=*/?*+V(l— е)
и вид функции / оказывается следующим:
2-п
Пх) = рр-п={хЩ _,)}»tl ро/(1 _,),
или иначе — интеграл для плотности р имеет вид
2—п 2-я
(1-е)р(г,0 = Р.М#/гГ+,-1Г+1 («-1Г'. (9Л6)
Результат (9.16) был получен впервые иным путем, с использова*
нием лагранжевой системы координат [14].
Подстановка интегралов (9.2) и (9.11) в уравнение баланса им*
пульса (9.2) позволяет весьма просто получить так называемое ка-
муфлетное уравнение — относительно радиуса взрывной полости a(t}
[14,24].
Постановка, соответствующая взрыву в пористой горной породе,
требует учета помимо ударного уплотнения на величину е
последующего дилатансионного уплотнения до величины еА (р), после чего
в ходе взрывного движения начинается дилатансионное разрыхление*
Область зафронтального движения разделяется соответственно на
две зоны — уплотнения R^r^R\(t) и разуплотнения R\(t)^r^af где
a(t)—координата стенки полости. В зоне уплотнения выполняются
интегралы (9.2) и (9.11) при n=rii и е=еь В зоне разрыхления
выполняется интеграл (9.2) при /г=/г2, причем произвольная функция
C(t) определяется через закон движения стенки полости, т. е.
v(r) = a(alr),n2 a<r<RA. (9.17)
На границе r=i/?A должны выполняться условия непрерывности
скорости смещения, т. е.
a(a/RAr = eiR(R/RAf\ (9.18)
— условие непрерывности радиальных напряжений; которое будет
использовано ниже, а также условие р=рд, определяющее
собственно закон движения этого фронта
(1 - .) рА = р0 {в, (/?/ЯА)»+* - l}"*'1^., - l)2A'lVJ. (9.19)
Решая это уравнение относительно радиуса /?а, находим простое
соотношение
1 1 __
- [?4l -•,)]/37<Ul) (1 -O^'+V , (9.20)
причем 4*=const при упрощающем предложении, что рд =const. Тем
самым движение полости оказывается также связанным с движением
фронта ударной волны
a**d = BvRr*R, (9.21)
75
_как и в случае только одного значения п для всего зафронтального
. движения. Здесь введено новое значение е=е2, учитывающее
дополнительное изменение плотности в зоне уплотнения
-\к
(9.22)
Интегрирование уравнения (9.17) в предположении, чК) a=R=a0
при *=0, приводит к конечной связи между R и а
7Г+1=й"*+'-|-е-'Л
1 лП\ — rtt
(а
~2 ». v -~0 )• (9.23)
Из условия (9.21) следует также, что в зоне разрыхления
справедливы те. же связи (9.9), (9.12) и (9.16), но с новым значением
п=п2 и е=е2. Поэтому здесь справедливо и распределение плотности
-(9.16) при п=п2, 8='82, тогда как в зоне уплотнения справедливо
условие (9.16) при п=пи e=ei.
- Подстановка интегралов во второе уравнение (9.2) позволяет
получить камуфлетное уравнение
P. /e<(RA)"'+1-iWy3rr
=-7Г^№/) +
«. + 1
(11 + 1) Л
+ •'!
'fflf't-nt)
-1 ~
2Г,
(l+2*t/Vz)rl
r^zRx, i—2 при RA:
^i лГтг
бос.
Уъ + 2*i'
(9.24)
причем 1=1' при #>-гЖа, i—2 при RA^r^a, а-на границе раздела
выполнено условие непрерывности нормальных усилий
С(1)=0<2):
°г(*а).
(9.25)
Рмс. 22. Послевзрывные
параметры пористого камня: плотность р
(а) скорости звука в радиальном
сц (б) и кольцевых направлениях
ci (б), остаточная проницаемость
k (г)
76
Интегрирование уравнения (9.24)
по радиусу позволяет найти поле
напряжения ar{r, t), причем
произвольные функции времени
выражаются через граничные условия на
полости и на фронте ударной
волны. Наличие этих зон уплотнения
и дилатансионного разуплотнения
было подтверждено при
лабораторном камуфлетном взрыве в
пористой среде [4]. В качестве
последней, использовался искусственный
камень (пористость 25%; скорость
звука с=3000 м/с; коэффициент
= Пуассона v = 0,17; плотность р0 =
= 1,850 кг/м3; прочность на
одноосное раздавливание 25,0 МПа).
Измерения гамма-плотномером
выявили (рис. 22) зону остаточного
уплотнения [4],
0,32<г = г/Е1/3^0,47 (м/кг1'3) (9.26)
и разуплотнения
0,12<г=г/Е1/3<0,32 (м/кг1/3), (9.27)
Остаточное разрыхление
тогда как взрывные трещины практически отсутствуют (они
локализованы в зоне г<Зао). Тем самым была зафиксирована кольцевая
сферическая зона уплотнения с характерным максимумом.
Зона разуплотнения совпадает с зоной дробления среды до
порошка, спрессованного высоким давлением. Плотность порошка
меньше начальной плотности среды на 16%, а скорость продольных волн
в нем —на 20%, В зоне уплотнения плотность выше начальной на
5%. Из образца выпиливался диск и измерялась скорость
ультразвуковых волн, распространяющихся в радиальном направлении.
В зоне уплотнения она
оказалась выше начальной до
35%. На эту же зону
приходится максимум
остаточных напряжений. Графики
a, b (см. рис. 22)
согласуются друг с другом, тогда
как график с для скорости
звука в поперечном
(кольцевом) направлении корре-
лируется с данными d по
относительному изменению
проницаемости k.
Взрывная волна внесла
явную скоростную
анизотропию, а измерения
проницаемости, проводимые
продувкой пористого материала
между модельными
скважинами, не уловили этот
эффектно реальном его
существовании говорит
значительный- разброс опытных
точек относительно
усредненной кривой на рис. 22Д
ж 2 м/кг1/3) оказалась ниже
скольку эффект дилатансионного разуплотнения в зоне (9.27)
подавляется дополнительным дроблением зерен среды. Трещинообразова-
ние, создающее высокую полевзрывную проницаемость (см. рис. 21)
в скальных породах, в высокопористом геоматериале оказалось
несущественным. Расчеты (при зависимости скорости дилатансии Л от
плотности и с учетом ударного уплотнения на фронте взрывной
волны), выполненные Е. Е. Ловецким, В. К. Сироткиным и Е. В.
Суминым [4], привели к данным рис. 23. Он показывает остаточное
распределение удельного объема У=1/р для разных начальных пористо-
стей. Видно, что гао=15% играет роль граничного значения, выше
которого среда уплотняется, а ниже — разуплотняется. Впрочем эта
граница чувствительна к литостатическому давлению.
^Интенсивность затухания £ максимальных радиальных
напряжений вблизи заряда для порцетых материалов
* Ч,(М/КГЗ)
Остаточное уплотнение
\
m0=2S%
Рис. 23. Распределение плотности после
подземного взрыва для сред различной начальной
пористости т0
/-5%; 2-15%; 3-25%
Проницаемость всюду (до г ж
начальной k0 = 15 • 10-10 см2, по-
v^^Aoir/EW)^ £=3,5; 0,21<г<0,47
(9.28)
77
значительно выше, чем для скальных горных пород (£^2). Здесь
Ла=6,4, а Огт выражено в МПа. Вне пределов г>0,47 м/кг степень
£=1,96. Интенсивность затухания максимума кольцевых напряжений
ere™ составляет £=0,6 в диапазоне 0,21^г^0,47. Тем сам^м в этом
диапазоне действуют значительные сдвиговые напряжения гт—
=1/2 (огт—овт), вызывающие большие остаточные (дилатансионные)
деформации.
7 аблаца 4
Геоматериал
Песок
Песчаный грунт
Аллювий
Туф
Каменная соль
(пористая)
Каменная соль
(монолит)
Тиосульфат натрия
Граниты
1
р.
кг/мз
1,7
1,5
1,6
1,85
1,72
1,87
2,12
2,14
1,8
2,67
2,7
км/с
0,215
0,08
',2
2,14 |
3,04
3,56
4,42
4,5
4,5
5,4
5,0
Е,МПа
78,6
9,6
2300
8470
15 900
23 700 .
41420
43 300
36 450
77 860
67 500
С
3,4
1,8
3,3
3,035
2,084
2,6 '
2,6
1,25
2,5
1,6
2,16
1,7
1,96
• 2
А*
36,5
9,5
2,8
9,047
140,7
110
140
187
297
122,5
364,5
421,2
617,3
700
Интервал
0,7<7<3
3<г<10
0,5<r<2
r<0,15
г<0,8
1<г<9
1<г<9
1<г<1,5
1,5<г<9
7<1,5
7<0,6
г>0,6
"<1
1<г<20
Опыты
Лабораторные
Натурные
То же
»
Лабораторные
Натурные
Лабораторные
Натурные
Го же
Различие законов затухания максимумов в волне при камуфлет-
ном взрыве в пористых и скальных массивах подтверждается
данными табл. 4 [4], где значения Огт оценены по экспериментальным
измерениям максимумов скорости vm частиц с помощью приближенной
формулы вгт=*рсит. Оказывается, что степень затухания £ для
искусственной пористой среды (9.28) близка к значениям £ для песка и
аллювия.
Внешняя граница (гт=0,47) дилатансионного пластического
течения соответствует перелому эпюры <rrm. В то же время при взрыве
в песке той же пористости (/щ=25%) перелом эпюры вгт(г)
наблюдается при гт=3 (м/кг1/3). Однако эти данные согласуются, если
ввести безразмерный радиус f=r(pc2/E1/3), который учитывает
различия геоматериалов в акустической жесткости (для песка рс2=
=7,86 МПа). Действительно, координата г имеет в обоих случаях
совпадающее значение: гт=12,4 (м-МПа1/3кг-1/3).
Внешняя граница ухудшения проницаемости сцементированного
песка (г=2 или г^50) соответствует внешней границе
допредельных (малых) пластических деформаций при взрыве в сухих
суглинках (по данньш Ю. И. Васильева и др. г = 5—6). Поскольку рс2=
=5,94 МПа для суглинков, указанная граница также соответствует
г=50. Таким образом, изменения проницаемости высокопористой су-
78
хой среды обусловлены малыми остаточными деформациями порового
пространства.
Интенсивная диссипация энергии взрыва в ближней зоне в
пористом геоматериале сказывается на магнитуде сейсмического сигнала.
Характерное его снижение (на порядок) при помещении заряда в
сухой аллювий хорошо известно специалистам [4].
10. ДОПРЕДЕЛЬНОЕ СУХОЕ ТРЕНИЕ И ЗАТУХАНИЕ
СЕЙСМИЧЕСКИХ ВОЛН
Модель обобщенного упругопластического
реологического тела. Возможность взаимогенерации
поперечных и продольных волн. Одномерные слабые
волны. Монохроматический звук и метод гармонической
линеаризации. Затухание монохроматических волн
в геоматериалах. Анализ сигнала общего вида при
локальном сухом трении.
Затухание сейсмических волн в сухих грунтах и горных породах
с пройденным расстоянием х происходит по закону Л=Л0ехр (—Ьх)>
где А — амплитуда волны, а коэффициент затухания Ь прямо
пропорционален частоте колебаний о). Такой результат соответствует
обобщенной упругопластической дилатансионной модели [28], в
которой учитываются две составляющие напряжения Ом — малой
пластической части %ы я большей упругой части dki:
crw=TM-Hw, О0-1)
что соответствует допредельному сухому трению. Напряжения dki
определяют полные деформации ем по упругому закону
d=(l/3)dhl$hi=Key e=en+e22+e3Z> (10.2)
d/hi=2G(ем—(1/3)еЬм), &ы=йы—&Ъы-
Составляющие хы также вызывают упругие деформации е^:
(1/3)А = (1/3)хА = ^(е). (Ю.З)
е{е) =е\? +е% -f <#. ,'W=2G(*J> -(l/3)swaw.
Будем полагать, что
К*=Кги G.=Ge2, е,<1. (10.4)
Разницу между деформациями ekl и е^ будем определять как
пластические деформации eff , связанные с напряжениями хл/
соотношениями
1 р(р) —р(р) h{p)
2i^-b—=e" *22 =...=ilL>0, (10.5)
причем предельное условие для напряжений хм имеет общий вид
1/777= аж | /ж |. sgn^O, VFt=-rat]l9 sgn ;,<(>. (10.6)
79
Относительные смещения площадок АА и AJA' символизируют
девиаторные компоненты полной деформации, а площадок ВВ и
В'В'-г полную объемную деформацию (рис. 24). Буквой К
обозначен элемент сухого трения. Обычно его представляют в виде Поршня,
двигающегося с сухим трением по плоскости скольжения прд
воздействием нормальной силы N и касательной Т (рис. 24,а) .Смещение
поршня символизирует необратимую сдвиговую деформацию. Дила-
тансии соответствует следующий образ: элемент сухого трения
состоит из клиньев (рис. 24,6) и косоугольных вставок, на щеках кото-
Рис. 24. Обобщенное упругопластическое дилатирующее реологическое тело
рых действуют силы сухого трения. При этом относительное горизон-'
тальное смещение вставок символизирует необратимую сдвиговую
деформацию, а связанное с ним смещение самого клина —
происходящую при проскальзывании объемную деформацию, т. е. локальную
дилатансию.
- Рассматриваемая модель определяет некоторую квазиупругую
среду, отдельные частицы элементарного объема которой могут
проскальзывать одна относительно другой. Условия e;<Cl обусловливают
относительную малость эффектов проскальзывания. Нарушение
этого условия приводило бы к возрастанию роли сухого трения и даже
его превалированию над упругими эффектами. Понятию сцепления
У в данной модели соответствует «прочность на сдвиг» упругой
связи, характеризуемой модулем G. * > '
При смене сжатия на растяжение меняются как контактные силы,
так и площадь поверхностей проскальзывания. Это учитывается
сменой абсолютных значений коэффициента внутреннего трения и
сменой знака перед /i в формуле (10.6).
В силу дилатансионного взаимозацепления реологических
элементов сдвига и объема, вообще говоря, продольное движение будет
приводить к поперечным подвижкам, и наоборот —поперечная
волна приводит к малым пульсациям давления, как это будет видно
ниже. Известны эксперименты (Т. 3. Вербицкий, Б. Д. Бойко [29]),
выявляющие взаимогенерацию разных типов волн в реальных
геоматериалах. Приводимый ниже анализ, однако, не учитывает
упомянутые тонкие эффекты.
во
В случае одномерного продольного движения v\ = v(x, t)t v2 =
==Уз=0, а все остальные искомые величины — функции Xi=x и
времени t. Уравнение движения (8.4) при этом имеет вид
?v.t = °. х + (2/3) Ах, о/7 = 0, гф\\ ю
Д=-°11— °22> °»2=°зз' ° = (1/3)(о11+о|1 + в||).
Согласно (10.2) и (10.3) упругие связи приводятся к следующим
dii—d22=2G(eri—e22)=2Ge9 d=Ke,
\f- *« = 2G# (е$ - eg), (1/3) J, = ^w. (10.8)
а соотношения (10.6) переписываются
тп—T22 = af|/i|sgn(ef, — ef2), (10.9)
1^->а1 = У7Л/А- (10-Ю)
Нетрудно видеть, что система (10.7) —(10.8) сводится к
следующему уравнению:
е,и=с2е,хх+(1/Р) {(1/3)/!+(2/3) (тп-тгг)},**,
(10.11)
c2=(/(+4G/3)/p,
дополнительному условиями (10.9) — (10.10), где
/, = е - (1/3) (JJKJ, е\? - eg -= е - &\ - *22)/(2GJ.
Применим метод гармонической линеаризации [20]. Идея этого
метода состоит в следующем. Пусть нелинейная функция имеет вид
2=ф1(й)ф2(м;). Найдем аппроксимацию вида z=CiW-\-C2v. Если
при' линеаризации предположим, что величины v, w меняются по
закону a = ao cos со/, до=ш0 cos со/, т. е. без отставания по фазе, то
20 = CiWq cos со/—(uC2v0 sin (ot=Ciw'o cos | со 11— | со I C2Vo sin | со 11.
С другой стороны, функция z может быть представлена в виде
ряда Фурье, который при сохранении первых членов дает следующее
представление:
z=fo^-fi cos co/-f-/2 sin| со | if,
2ic
/o = ij4i(-hl^sin^)?2Kcos^)^,
0
2ie
/i = V J?* (" Iю Г°« Sin^CP2 К COS ф) COS^cty,
(Г
2* .
f2 = 4" Ui (— h I £>o sin ф) <p2 К cos ф) sin ф/*ф.
Сопоставление первых гармоник для z и линейной функции z0
показывает, что Zo будет аппроксимировать функцию г, если
/0=0, Ci=/,/w0>. С2 = —/2(|со|р0).
6-3311 81
Пользуясь, далее линейностью аппроксимирующей функции z0
(при фиксированной частоте со), можно искать решения типа
линейных комбинаций периодических*функций одинаковой частоты/ со, и
в частности обычного (для бегущих гармонических волн) 'вида v=
= v0 exp i (at—hx). у
Проводя вычисления при
/, = 7{0) cos erf, № - e[f = - © {e[f - e\f) sin *>t,
1 11 4, 22 .\ 11 . 11 / (10.12)
a/ = ai» cosmt^>0; a/r=a2, cosatf<0,
получаем для нелинейного соотношения (10.9) следующую
аппроксимацию
'»-*» = («,+ ^УГ>'(*1»|Г1 («,Т -ё^Г1 (e\?-ej»).t, (10.13)
а для (10.10) при
/, = _«> {е - У,/(3/С*)> sin (о/; . х,, - х22 = (, <J> - т <°>) cos mt
получим
«{f -e(2f = 2 VT|»| («| А | Г1 {e. - /f/WKK, - .J (x<?> - *<°>)"' .
(10.14)
Будем искать допускаемые линейными уравнениями (10.13),
(10.14) решения типа » = aoexpi(e>f—Нх). Тогда уравнения (10.11) —
(10.14) сводятся к следующей системе линейных (относительно
амплитуд колебаний) алгебраических уравнений:
^. = ^. + (l/P^){(l/3)+(2/3)f(a14-aa)1l-1sgn«»}J1'J).
te„ + (l/2G#)(a1+a8)*-1/<0) sgnш-(2^3>|Л|){е. - (10.15)
-(A<0)/3)A}sgn<o,
где г]2 = со2/(Л2с2). Линейность полученных уравнений соответствует
пренебрежимо малой зависимости скоростей и коэффициентов
затухания сейсмических волн от их амплитуд.
При нетривиальном решении системы уравнений выполняется
следующее дисперсионное соотношение:
т]2=1+Р(Л+;В), р<1,Л, 5-1,
1/р = (К + 4G/3) {2/(3tfJ+ IА | (a, + 0^/(2 yTG#)} > 1,
A = (2/3){l+:|A|(a1+a1)/Vr3}Lfl= (10.16)
.= {(4/3) К + a,) irl - | Л | */31/3 } sgn a).
Здесь малость множителя p есть следствие условий (10.4).
Используя его, получим для волны, бегущей в сторону положительного
направления оси х, следующее приближенное значение параметра:
п=х/ (hc)^l±(l/2)^A+i(l/2)^B. (10.17)
82
Отсюда видно, что локальное проскальзывание вносит малую, не
зависящую от частоты поправку к скорости упругой волны, а
коэффициент затухания b оказывается прямо пропорциональным частоте:
С(й=с{гезг1+(1тг1)2Д^г1}^с{1 + (1/2)рЛ}, (10.18)
u=(coImri/c){(res^)2+(ImTi)2}-1^(l/2)pBo|(o|/c,
B = BoSgn(o. (10.19)
При распространении поперечных волн имеем условие ^i = 0, t>2 =
= v2(x, t) и все остальные искомые величины также суть функции
времени t и координаты х=Х\.
Уравнение движения имеет вид
2ре12уи^=(У12,х^ (10.20)
Поскольку oi2=2Gel2y on—dn+xn, уравнение (10.20) преобра-
зуется далее к следующему:
ei2,tt=c2sei2,xx+(l lp)xi2,xX, (10.21)
Так как при подобном движении имеем ец=е22=£зз=0, то du=
=d22 — d33=d=0 и, кроме того, ац = 0. Но сг22 = азз могут быть
произвольными функциями от ху tf как это следует из уравнений
равновесия. Отсюда /1=ra=2(T22, Т22=(Т22. Предельное условие (10.6)
принимает вид
1/"(1/12)Л-)-Л, + «Л=0. , (10.22)
Далее
е = - е'е) = - JJ(3KJ, е% - е{? = /,/(4G*),
а дилатансионная связь, следующая из соотношений (10.7) и пре-
дельного условия, принимает такой вид
А{(1/3) (/i/4G02+M1/2 = A/(3tf«). (10.23)
Очевидно, что при распространении монохроматических волн
изменения локального среднего напряжения h всегда удовлетворяют
условию sgn/i = sgn(—Л). Отсюда гармоническую линеаризацию в
данном случае следует применять не непосредственно к условиям
(10.22), (10.23), а к соотношению
х12 = | Л11/Т2Л.0.1Л2^Л | е™ | sgn^/]/l6G2*-3A2tf*. (10.24)
Подстановка в уравнения (10.20), (10.24) выражений
е12 = efj exp i (vt — hx), т12 = ^ ехР * № — ^гх)
снова приводит к дисперсионному уравнению (10.16) при следую-
щих значениях кс^ффициентов:
p = iG#/G^l, Ф = /С*</*]Л21Л2а2 - 1 sgn<*Y\bG\ -ЗА2К\,
А = 2Л2Ф2/КС2^+ЧЛ2Ф2), (10.25)
В = 2% | Л| <1>GJ(t:2G\ + Л2Ф2), т] =y/(hc\).
6* S3
Отсюда получаем для скорости и коэффициента затухания
поперечных волн выражения, подобные (10.18), (10.19).
<a)*Mi+(7,)H. ^mp^hk;' fl=5.sgn». Ко.2б)
/
Подчеркнем, что неучет эффекта дилатансии (при K=Q) не
приводит к качественному изменению характера продольных волн, но
поперечные волны распространяются как чисто упругие [Л=0, В =
=0 при Л=0, см. (10.25)]. Приведем замеряемые в экспериментах
(со>0) величины декремента затухания: Q = co/(26c) = l/(pS),
обратного коэффициенту В. Для пойеречных колебаний в песке Q=
= 20—50. Для продольных волн в граните, песчанике, известняке
<3=100—200, тогда как для поперечных — величина Q в два раза
больше. Для сравнения укажем, что коэффициент затухания b в
кальците (главном породообразующем минерале известняка) на
порядок меньше, т. е. Q^-2000.
Использованный метод гармонической линеаризации применим
для монохроматических сигналов. Для изучения иных сигналов
следует применять методы нелинейной волновой динамики. Рассмотрим
пример модельного уравнения Кнопова — Макдональда [23]
u,tt—c2uxx=—ec21 ихх\sgn и,и (10.27)
-где и — смещение, е — некоторая малая константа.
Если начальные условия имеют вид
4i(х9 t=0)=y(x), u,t(x, t=0)=— су'(х)у (10.28)
то приближенное решение уравнения (10.27) можно искать в виде
и(х, t)=u(l, т), $=x—ct9 %=ect. (10.29)
Преобразуем уравнение (10.27) к новым координатам <£, т, где
£ — координата относительно фронта волны, т — быстрое время,
M.^"-2s^^ + s^."-^u=-sl"tUlsgnN,,-^^ (Ю.ЗО)
В дальнейшем будем считать, что sgn (еда т—duti)=sgn(—ди%).
Умножив уравнение (10.30) на ди& получим
2U, t.U, *? + I и. Ъи, * I = eU, \и. тх • (10.31)
Обратив внимание, что
ш = (ил)\ ",^f^=.(1/«)«i,. U9bu.t-=(4J*.V
получаем упрощенное уравнение
е,т+( 1/2) 8,^=0 (10.32)
в пренебрежении правой частью (10.31), содержащей малый
параметр е. Начальные условия (10.28) принимают при этом такой вид:
вв,т=0)=[ф'(Б)]2. (10-33)
Воспользуемся теперь методом характеристик [40].
Характеристическая система будет иметь вид
.i£/d/=(l/2)!SgnP, dP/d% = 0, de/dx=0, (10.34)
84
где Р—де,ъ. Отсюда
i = |o+(l/2)TSgnP0, Ро=гл(Ь, т = 0), е0=е(|0, т = 0). (10.35)
Пусть начальное распределение имеет вид параболы
Ф(|, T=0)=l-g2, |i||<l; Ф(|, т=0)=0, |||>1, (10.36)
чему соответствует такое начальное распределение функции:
е(€,-т=0);=4|2, |||.<1; B(iT=0)=0, |||>1. (Ю.37)
A W.V
в 1
г
1"
§
Рис. 25. Правило выбора ветвей решения распространения импульса в среде с сухим
трением
Решение (10.35) принимает вид (рис.25)
E = ?0+(l/2)xsgn^0, Р = 8*.. 9P=4i\t |U<1, (Ю.38)
6 = 6о, Р = 0, 8 = 0, |6о|>1.
Для получения окончательной зависимости e(i£, т) необходимо
решить первые из уравнений (10.38) в виде go—6о(6> 0'- Нетрудно
видеть, что имеется область неоднозначности (отрезки АВ, ВС, CD)
этой "связи (рис. 25,а). Для однозначного выбора ветви решения
воспользуемся способом Рождественского-Яненко [40], а именно
будем брать ту ветвь решения (отрезок CD)y на котором функция е
принимает наименьшее значение (в данном случае е==0).
Результирующее распределение функции е и смещения и даны на рис. 25Д е.
Аналитически оно записывается так:
е(6, т)=0, ы=0г — оо<£< — 1;
8(6, т)=4(6+т/2)2, ц=(т/2-1)2-(6+т/2)2,-1<6<-т/2;-
е(6, т)=0, и=(х/2)—1,-т/2<'£<т/2; (10.39)
8(6,т)=4(6-т/2)2, и=(т/2-1)2-(6--т/2)2, т/2<6<1;
е(6, т)=0, и=0, 1<«£<<х>.
Нетрудно видеть,-что решение (10.39) соответствует
затухающему за конечный промежуток времени (т=2) импульсу, причем
начальная ширина импульса в данном приближении остается
неизменной. Если бы начальное возмущение смещения гладко сопрягалось
с невозмущенной * областью, то имело бы место даже (физически
неоправданное) сужение импульса.
Для оценки степени достоверности указанного приближения рассмотрим,
к чему оно приводит в случае линейного волнового уравнения
и и—c*uiXX=—$c2u,t. (10.40)
85
Тогда начальному распределению (10.28) будет соответствовать решение
и(х, t)=exv(-^$t/2)*p(x—ct)-{-A(x, t)y (ИШ)
где А {х, t) — малые в начальный момент шлейфовые колебания, выражающееся
в виде интегралов от произведений функций Бесселя на функцию *$(х),. Таким
образом, начальный сигнал затухает во времени, а его расширение ^следствие
дисперсии) происходит путем появления шлейфа.
Уравнение (10.40) может быть преобразовано к виду
— 2сри ^ + fat тт =.= jcb р — fu% т> £ = х — cU i=fo (10-42>
и согласно использованному выше приему оно заменяется на следующее:
«.,= -«. е=0/2) {ил)*. (10.43)
Уравнению (10.43) соответствует решение
и(х, 0=Ч>(Е)ехр(—т/2)=<р(л;—с/) exp Н0//2). (10.44)
Сопоставление точного (10.41) и приближенного (10.44) решений показывает,
что использованный приближенный способ действительно приводит к потери
слагаемых А(х, /), определяющих расширение сигнала.
П. СКОРОСТЬ РАЗРУШЕНИЯ И ДИНАМИЧЕСКАЯ ПРОЧНОСТЬ
Двухфронтальные ударные волны. Условия на
фронте разрушения. Статическая прочность как
необходимое условие разрушения. Предельная скорость
роста трещин и замыкание задачи разрушения.
Одномерная плоская волна разрушения. Задача о
горном ударе. Динамическая прочность как
высокоскоростная перегрузка материалов. Опытные данные по
хрупкому ударному разрушению.
Выше принималось, что при взрыве в горной породе разрушение
начинается после достижения напряжений, соответствующих
пределу упругости Ф<т(т, р; а, %)=0, определяемому в опытах на
статическое нагружение. Однако' непосредственные измерения выявляют
особый «динамический предел упругости», значительно
превышающий его статическое значение. В качестве примера приведем
обобщение Д. Грэди [31] для роста прочности при взрывных скоростях
нагружения (рис. 26). Какой смысл следует придавать-динамической
прочности?
Начнем с анализа лабораторных опытов по взрыву сферически-
симметричных зарядов в прозрачных монолитных блоках, в ходе
которых удавалось непрерывно фиксировать (оптическим методом)
движение как фронта ударной волны, так и фронта разрушения
породы радиальными трещинами.
Опыты с плексигласом В. В. Адушкина и А. П. Сухотина [31, 45]
свидетельствуют о том, что фронт образования радиальных трещин
идет со своей собственной скоростью, отличной от скорости ударной
волны. Величина этой скорости вероятно, определяется распростра-*
пением некоторой фазы растягивающих азимутальных напряжений,
а не собственной скоростью развития трещин. Это утверждение
легло в основу расчета взрывного движения [23], согласно которому
перед фронтом разрушения выполняется условие предельного
разрушающего напряженного состояния:
/(<,-) =а.. (11.1)
86
Здесь а* — константа, соответствующая прочности материала
(строго говоря, статической). В частности, при образовании радиальных
трещин а~е=ст*, где а~е — азимутальное предфронтальное
напряжение, о* — прочность на отрыв [23, 45]. Это условие замыкает систему
балансовых соотношений — массы и импульса
p+(t>+—cF) =p-(v-—cF)\
p+v+(v+~cF)—o+n=p-v-(v-—cF)—o-n,
(H.2)
(11.3)
10
1
1
5
I1
/ -L
-o-g
-2"
■ й й
_j
/. [
oTl /
j
■СЁ
w~
w
-2
/0(>
I0l
Wh
IQ1
JO8
Скорость дефарморовония t n~1
Рис. 26. Кажущееся изменение прочности при переходе о/г квазистатических к
взрывным скоростям деформирования
/ — доломит; 2 — известняк; 3 — гранит; 4 — базальт
выполняемых на фронте разрушения как на сильном разрыве [23,
45]. Здесь <Тп — нормальное к фронту усилие, символы «+» и «—»
соответствуют за- и предфронтальным значениям параметров.
При этом реология материала перед скачком и за скачком
считается известной (плотности р+, р~ могут быть выражены через
другие параметры движения). Скорость фронта cF оказывается
непрерывно меняющейся и подбирается из условия сшивки с
непрерывными решениями вЪе скачка. Будем называть подобный режим
движения фронта режимом предельного разрушающего напряжения.
С другой стороны, эксперименты А. П. Сухотина и С. Д.
Викторова [45] со стеклом К-8 показали, что при г>2а0, где До— начальный
радиус взрывной полости, скорость фронта разрушения cF практиче-
87
ски оставалась постоянной: cF=
= 1,6—1,8 км/с (что составляет
примерно половину скорости
поперечной волны). На рис.
27представлен экспериментально полученный1
В. И. Куликовым годограф "фронта
ударной ^ волны (затемненная
прямая полоса) и фронта разрушения
(граница черной области) в
аналогичных экспериментах по взрыву в
стекле ТФ-5, с несколько иными
параметрами. Здесь видно также, что
фронт разрушения периодически
излучает упругие сигналы
(акустической эмиссии). Скорость cF=lJ
км/с измерена при взрыве
стеклянной трубочки и при детонации
заряда у края стеклянной
пластины [45]. Кроме того, в опытах
В. М. Цветкова с канифолью [31,
45] было выявлено, что скорость Cf
фронта радиальных трещин в диа*
пазоне 10ао</*<20а0 составляет
0,4с и «практически совпадает со
скоростью релеевских волн»,
которая была в данном случае cR =
= 0,41 с. Здесь с — скорость
продольных волн (2,37 км/с). В
указанном интервале расстояний
массовая скорость во взрывной волне
имела порядок 10 м/с. Был сделан
[31, 45] вывод о том, что фронт
распространяется с предельной
скоростью распространения трещин
отрыва под действием растягивающих
азимутальных напряжений. Если
принять это утверждение, то
необходимо отказаться от критического
условия а^~ =а* на самом фронте
разрушения. В самом деле, если
скорость фронта разрушения равна [45] предельной скорости роста
трещин N относительно материала, т. е.
cF-v-=N, . (1.1,4)
то условие (11.4) замыкает систему (11.2), (11.3) вместо условия
(11.1). В случае радиальных трещин {N=cRy где cR — скорость волны
Релея.
Меняющимся параметром, подбираемым из условия сшивки
скачка с непрерывными решениями, будет теперь не скорость
распространения фронта трещин, а предфронтальное напряжение. Кри-
! Теневым способом на аппарате Теплера.
88
Рис. 27. Экспериментальный годограф
сферического ударного предвестника
и фронта разрушения (ось времени
вдоль кинопленки, радиальное
расстояние — поперек)
терий разрушения — необходимый, но еще не достаточный —
принимает вид
f(a-7)^a*, (11.5)
Он должен выполняться в зоне перед фронтом разрушения.
Разница в скоростях движения границы зоны (11.5) и фронта
разрушения определяет ненулевое кажущееся «время разрушения» или же
время «запаздывания разрушения».
Переменность скорости фронта радиальных трещин и ее
кажущееся неравенство величине cR объясняются следующим образом.
Если учесть, что. скорость JV надо вычислять относительно
движущегося материала среды (11.4), то оказывается, что, в опытах В, М. Цвет-
кова и др. [31, 45] фронт трещин отрыва двигался с предельной
скоростью N=cR в той части интервала 4a0<r<10a<), гДе cf^
^Л2СЮ м/с. В самом деле, скорость частиц здесь менялась от 30 до
150 м/с, тогда как Сд=1000 м/с. Не исключено также, чтов этом же
интервале произошла смена механизмов разрушения: вначале на
фронте разрушения происходил «скол», которому соответствует своя
предельная скорость. Следует заметить также, что остаточные
размеры зоны сколового разрушения не могут служить основанием для
выбора соответствующего интервала, так как фронт «скола» мог
идти и по материалу, первоначально разбитому радиальными
трещинами.
В опытах с плексигласом отмечалось, что на расстояниях от г=
= 3а0 до г = 5а0 скорость фронта трещин изменялась от 2000 до
500 м/с, а далее сохранялась постоянной: 500 м/с. Зададимся
значением сп=500+и~ — как предельным1. Массовые скорости
составляют и~=100 м/с при г=5а0 и выше — при меньших г. Не исключено
поэтому, что. и в этих опытах реализовался режим предельной
скорости фронта радиальных трещин. Кроме того, в таких относительно
легко сжимаемых средах, как плексиглас, следует учитывать
зависимость <N(oif): трещины распространяются по материалу,
предварительно сжатому упругой ударной волной [45].
До расстояний 4а0 в опытах с канифолью и За0 в опытах с
плексигласом фронт разрушения не отставал от фронта ударной волны.
В этом диапазоне либо имеет место режим принудительно-быстрого
роста радиальных трещин (что требует особой передачи энергии
извне в вершину трещины), либо механизм разрушения носит другой
характер.
В одномерной плоской задаче при скорости ударной волны,
большей, чем скорость звука, структура волны разрушения также одно-
фронтальная. Если же скорость ударной волны меньше, чем
скорость продольных волн, то структура становится двухфронтальной:
вперед уходит упругий предвестник, амплитуда которого
соответствует «гюгониевскому пределу упругости» (HEL), а за
предвестником идет фронт разрушения. Обратимся к рассмотрению именно этой
задачи в приближении линейной теории упругости.
1 X. Шарден указывает на предельную скорость роста трещин в 515 м/с для
плексигласа. По данным Л. Далберга предельная скорость роста трещин отрыва
составляет 600—700 м/с, а при cF=400 м/с начинается ветвление трещин [45].
89
Пусть линия АВ есть годограф упругого предвестника, а линия
АС — фронта хрупкого разрушения (рис. 28).
В зоне О имеем условия покоя /
р = ро, v=0, ап = 022 = Озз=Оо. / (11.6)
На фронте упругого предвестника АВ выполняются следующие
соотношения:
p-(v-—U)=—p0Uy — p-£/ir-v-cr-=— сто, (11.7)
где (Хц = а, U — скорость упругого предвестника. Если принять упро-.
щение: f/^c, то первое из уравнений (11.7) будет удовлетворено при-
в
FT,
б+
Рис. 28. Годограф (а) и схема
двухфронтальной волны
разрушения при ударе (б) и
внезапной разгрузке (в)
ближенно, второе определит величину массовой скорости ir, а плот*
ность р~ определится по закону Гука
v~=— .(or—<то)/(рос), Р~/ро=1 —(<г-—Оо)/{/С+-
+ (4/3)G}, c*={K+(4lS)G}/po, (11.8)
На фронте хрупкого разрушения вновь выполнены условия ба*
ланса массы и импульса (11.2), (11.3), если заменить в последних
аг на а. Из них следует, что в зоне «+» параметры движения будут
определяться так: л
V+=v-—(e+—o-)](pcF), \ои—(722|=2т**,
(11.9)
oll = a+, p+/po=l--p(a+—а0)±(4/3)рт**,
где т** — предельное касательное напряжение, характеризующее
материал в хрупко-разрушенном состоянии, p-1 = /C+2/3G. Здесь
упрощенно принимается, что плотность р+ разрушенного материала
изменяется по тому же закону, что и неразрушенного, а отсчетная
плотность р0 на фронте разрушения не претерпевает скачка.
Скорости cF фронта разрушения определяются по уравнению
(11.2) следующим образом:
(cF-v~) 2= (р+/р-) (0+-0-) I (р--р+).
(11.10)
90
Отсюда для полного решения задачи нужно считать известным
либо а~ (как разрушающее) перед фронтом АС (режим
предельного разрушающего напряжения), либо скорость фронта разрушения
cF, а напряжение сг~ перед фронтом разрушения будет искомым
(режим предельной скорости фронта разрушения).
Согласно теории предельного разрушающего напряжения [23],
перед фронтом разрушения должно быть выполнено условие разру-
- шения сколом
|ац—^а22| =2т* (П.И)
или
cr=ao±{/C+(4/3)G}(T./G). О1-12)
Тогда для массовой скорости в зоне имеем
tr= 4= {i^+(4/3)G}(t./G)/(рос) ==F(t*/G) с, (11.13)
скорость фронта разрушения cF согласно формуле (11.10).
преобразуется следующим образом:
cp-tr = cvV^k0\\Г\ ±(4/3)К - Ч*)К°+ -о') = с„ (11.14)
где cv= 1 /V^PP~ —локальная объемная скорость, сО0= 1/V$P0 — ее
значение в состоянии покоя, c2v0=c2— (4/3)c2s, Cs — скорость
поперечных волн. Отсюда получаем, что только при т*=т** и в
отсутствие скачка плотностей р+^ро фронт разрушения распространяется,
как и фронт пластической волны, со скоростью c*=cv. В общем
случае с* меняется с амплитудой ударной волны за счет всех
сомножителей в формуле (11.13).
Для ударных волн сжатия а-—сг0<0, о+—ао<0, v~>0 и в
условиях (11.12) — (11.14) нужно выбрать нижний знак. Материал за
фронтом упругого предвестника двигается в одном с ним
направлении, а для скорости фронта разрушения имеем
sgn{(cF - v~) - cvV?+l?o} = sgn(v- ***)• (H.15)
Другими словами, скорость фронта разрушения cF—а~=с*
меньше объемной скорости в материале, если т*>т**, что естественно для
хрупко-разрушаемых материалов.
При разрушении в волне разгрузки, если принять, что оно
происходит также разрывным образом на фронте разрушения (по
Л. А. Галину, Г. П. Черепанову [45]), а~—сто>0, tr-<0 — частицы
двигаются к разгруженной плоскости, а+— а~>0у причем в
формулах (11.2) —(11.14) нужно выбирать верхний знак. Такое решение
при о+=0 и р+!=р0 было предложено С. С. Григоряном.
Рассмотрим теперь режим предельной скорости разрушения [45].
При этом решение (11.8) —(11.10) замыкается условием (11.4).
Перед фронтом разрушения, т. е. в зоне упругого состояния «—»,
должно быть выполнено условие
Td= G\o-—oo \!{К+ (4/3) G}S*t*, (11.16)
91
которое является частным случаем необходимого условия
разрушения (11.5). Соотношение (11.10) принимает вид
(iV/^)»=(p+/po){l + (4/3)[G(or^ao)(/C+ . /
+4G/3)-1=Ft**((7+—do)-1}"1, /' (11.17)
причем неравенству (11.11) соответствует неравенство
N<c,<c0V^K. ^ -(11-18)
Величина та есть так называемая «динамическая прочность»
материала* на сколовое разрушение. Покажем, что величина т<г не
есть, однако, параметр материала, а меняется с амплитудой
ударной волны. Выразив в соотношении (11.17) амплитуду ударного
предвестника — согласно левой части (11.16)—через т<*, получим
i?=(c/^)2(p+/po) = l±(4/3)(Td-T*OX
X[a+-ao±(/C+4G/3)Td/G]-1, (11.19)
где 7?, вообще "говоря, также зависит от амплитуды а+—во.
Разрешая (11.19) относительно «динамической прочности», получим*
Td/G=[T**±(3/4) (R-l) (o+-oo)]/[G-
" -(3/4) (iR-l) (K+4G/3)]\ (11.20)
причем, как и выше, верхний знак соотЁетствует волне разгрузки,
а нижний знак —волне нагрузки. Только при R=l выполнено
равенство Td=t**; в общем случае «динамическая прочность» зависит
от финитной амплитуды ударного перехода. Разницу Td—т* следует
понимать как динамическую перегрузку материала [45].
Какую же скорость следует выбирать в качестве предельной
N(o~) для плоских волн? При разрушении «сколом» возникают
трещины поперечного сдвига. Предельной скоростью роста трещин
продольного сдвига является сама скорость cs поперечных волн, а
трещин поперечного сдвига — скорость волны Релея cRy которая весьма
близка к cs (Cfl=0,92cs=0,58c при v=0,25).
В упомянутых выше данных по сферически симметричным
волнам разрушения в стеклах скорость фронта разрушения в стекле
К-8 (А. П. Сухотин и С. Д. Викторов [45]), составляла 1,5—
—1,8 km/c^0,5cs, где cs=3,7 км/с, с=5900 м/с. Опыт А. А. Спи-
вака и В. М. Цветкова [45] по самоподдерживающемуся
разрушению тиосульфата натрия (в цилиндрической симметрии) выявил
двухфронтальную структуру волны, причем данные о движении
фронта разрушения вполне допускают следующую интерпретацию:
скорость фронта практически постоянна ('—'500 м/с) и составляет
примерно 0,5cs= Ю50-4-1150 м/с при с=3200—3450 м/с. Меньшую
долю, чем половина cs> составляет и скорость фронта разрушения в
опытах В. И. Куликова по взрыву в стекле ТФ-5 (cF — от 1,2 до
0,83; с = 3,71; cs=2,22 км/с; р = 4,4-103 кг/м3). Скорость трещин
достигала значения 0,5cs при взрывном разрушении гранита и
мрамора по Н. Даниелу и Р. Роуландсу [45]. Значение предельной ско^
роста. N=0,5cs может объясняться явлением ветвления трещины
[31, 45].
При возникновении пластического состояния за вторым фронтом
зависимость осевого напряжения ап от удельного объема должна
92
переходить в кривую гидростатического сжатия при смещении (па
вертикали вниз) на постоянную величину, равную 4/Зт*, где т*—
предел текучести, оцениваемый по величине HEL.
При хрупком разрушении требуемое смещение равно 4/Зт** и
не коррелирует с амплитудой HEL. Так, при ударном разрушение
кристаллов сапфира (А1203) значения HEL меняются при ударном
сжатии по разным осям анизотропии, но все состояния за вторым
фронтом соответствуют одной кривой при «смещении по вертикали»,,
равном нулю (по Р. Грэхему и В. Бруксу [45]). Последнее иногда,
интерпретируется как «жидкостноподобное» состояние материала за
фронтом второй волны, что на самом деле означает пренебрежимо
малое значение прочности среды в раздробленном состоянии. Этот
же эффект отмечается при ударном разрушении кристаллов MgQ
(по Т. Аренсу [45]) и вольфрама (по Д. Дандекару [45]), причем
в последнем случае было отмечено уменьшение «смещения по верти-
кали» с ростом финитной амплитуды удара. Это следует понимать
как более интенсивное уменьшение остаточной прочности т** или
более мелкое дробление при более сильном ударе. "
Критерием для режима разрушения может служить величина
«динамической прочности» HEL. Так, при ударном сжатии кварца
ХДж. Уокерли [45]) была четко зафиксирована зависимость
амплитуды упругого предвестника от финитной амплитуды ударной волньг
'(-(Г" менялось от 3,5 до 10,0 ГПа) при статической прочности:
~4,0 ГПа. При ударном сжатии сапфира значения HEL зависят не
только от ориентации кристалла, но и от финитной амплитуды.
Опытные точки HEL сапфира заполняют интервал *от 12,0 >до 21,0 ГПа при*
17,5^а+^42,0 ГПа. Можно сделать вывод, что в этих случаях
разрушение происходило по режиму предельной скорости фронта.
В то же время плоские ударные волны в поликристаллическом-
АЬОз (работа Т. Аренса, В. Гаста и Э. Ройса [45]) не выявляют
полной потери прочности за вторым фронтом, причем можно
отметить обратный эффект: некоторое снижение- HEL с ростом
финитной амплитуды удара. Данные о динамической прочности для
кварцевого стекла (плавленного кварца) весьма неопределенны И'
оцениваются в 6,0—8,0 ГПа. Для обычных стекол значения HEL
составляют от 3,6 до 7,5 ГПа или 4,0—0,5 ГПа. Некоторые базальты
и «малопрочные» кристаллы проявляют чрезвычайно низкие
значения HEL (в несколько сот мегапаскалей), так что упругий
предвестник даже не фиксируется (это, конечно, зависит от порога
точности измерений). Чтобы интерпретировать эти результаты,
необходимо использовать нелинейную упругохрупкую модель,
учитывающую переменность скорости* возмущений в неразрушенной области.
Так, плавленный кварц является типичным материалом, ударные-
волны в котором имеют пологий (непрерывный) фронт нагружения,
скорость вступления упругого возмущения уменьшается, а массовая
скорость v растет с -интенсивностью удара. Гораздо чаще в горных
породах скорость упругого предвестника заметно растет с финитным
напряжением о+, тогда как массовая скорость v~ остается
практически постоянной. Из формул (11.7) следует, что этот случай соот-^
ветствует росту амплитуды упругого предвестника HEL, т. е. «дина-
мической прочности» с интенсивностью удара. Наконец, отмечаются
эффекты затухания HEL с пройденным расстоянием (см., например,
данные Т. Аренса и Дж. Дювалла для кварцита [45]). /
Вне рамок лидейно-упругого расчета скорость cF фронта
разрушения растет линейно с массовой скоростью у+, как и скорость
обычных ударных волн. Это имеет место в волнах, например, в
кристаллах кварца (по наблюдениям Дж. Уокерли [45]) и связано с
эффектом большей объемной сжимаемости раздробленного кварца,
чем кристаллического. Возрастание cF с амплитудой а+ отмечается
для многих хрупко-разрушаемых материалов.
Абсолютные значения HEL в хрупко-разрушаемых материалах,
как правило, на порядок превосходят статические значения
прочности, что не может быть объяснено, как в случае металлов, эффектом
скорости нагружения (вязкостью среды). Например, для гранита
(гранодиорита массива заложения ядерного взрыва «Хардхэт»), по
данным К. Петерсена и др., HEL<^4,0—5,0 ГПа, что намного
превосходит любое из статически достижимых напряженных состояний.
Иными славами, между фронтами упругого предвестника и
разрушения материал испытывает кратковременные динамические
перегрузки. Чем выше перегрузка, тем большая достигается фрагментация
материала во фронте разрушения. В самом деле, более высокие
напряжения вызывают рост более мелких трещин, а длина этих
третий тем больше, чем больше продолжительность фазы динамических
перегрузок. О появлении мелких трещин свидетельствуют, например,
зафиксированные при взрывах в стекле ТФ-5 упругие волны
(слабые потемнения на рис. 27) „ излучаемые фронтом разрушения вслед
за упругим предвестником (сильное потемнение на рис. 27). Укажем,
что мелкие трещины возникают перед магистральной в момент
остановки последней, как это установлено наблюдениями за
индивидуальными трещинами. Это означает, что движение фронта
разрушения на самом деле может состоять из остановок и проскоков, а
скорость N является всего лишь средней величиной. Было опубликовано
утверждение об остановках роста радиальных трещин при
взрыве в диске из плексигласа '[45], причем скорость трещин на
интервалах их роста была близка к сп.
Радиальные трещины, возникающие под действием
растягивающих азимутальных напряжений, ортогональны к фронту разрушения
и в силу сферической симметрии случайным -образом повернуты
вокруг нормали к фронту. Это приводит к характерному
игольчатому (пирамидальному) виду осколков. Случайность контролируется
распределением дефектов.
Анализ мелкой трещиноватости по Н, Шорту при ядерном взрыве
«Хардхэт» [23] показал, что трещины в кварцевых зернах
появлялись в тех зонах, где давления достигли 5,0 ГПа. Мы будем
связывать это явление с динамической перегрузкой гранодиорита при
взрыве.
Возникновение трещин, рассеянных по массиву, характерно для
откольного разрушения. В этом отношении замечательны опыты [10]
по отражению плоской взрывной волны от свободной поверхности
металла, при которых испытуемый образец выдерживал растягиваю-
, 94
щие напряжения, в 100 раз превышающие статический предел
прочности. Чтобы понять этот факт, следует обратить внимание на то,
что подобное растяжение в отраженной волне действует в течение
—ДО-6с. За это время трещина, зародившаяся на каком-нибудь
микродефекте, может пройти расстояние порядка 1 мм. Если диаметр
испытуемого образца >> 1 см, то он может остаться неразрушенным.
Иначе говоря, хотя трещина внутри него и возникла,
экспериментатору кажется, что образец был необычайно прочным. Только! в том
случае, если число мест зарождения трещин (микронарушений)
велико, при короткодействующем импульсе растяжения возможно
образование макротрещин, разделяющих образец на части. Верно и
обратное [10]—с уменьшением диаметра образца число дефектов
также падает, а разрывающее удельное усилие растет, причем
асимптотическая экстраполяция дает значения теоретической прочности
£7(2я), что соответствует разрыву вдоль кристаллических плоскостей.
Аналогично чрезвычайно высокая прочность на отрыв была найдена
у плавленного кварца (3,1 ГПа), лишенного микротрещиноватости.
Таким образом, сверхпрочность при кратковременных нагрузках
находится в соответствии с представлением об эффекте конечной
скорости роста трещин.
Обратимся к опытам о арканзасским новакулитом, в ходе
которых фиксировались сбросы напряжений в образце кварцита [45] >
происходящие в момент возникновения откольной локальной
трещины. Оказалось, что амплитуда излучаемых при этом волн
соответствует сбросу на величину статической прочности (на растяжение)
монолитного образца. Поскольку трещина откола ветвилась, скорость
ее роста приближалась к предельной. Продолжительность импульса
растяжения —'Ю-6 с. За это время трещина достигла длины ^-4 мм,,
что при ширине образца в 1—3 см сохраняло его целостность. Прет
амплитуде растяжения, на 50% превосходящей статическую
прочность, возникала сеть трещин, приводящая к фрагментации образца,,
причем большая амплитуда приводила к более мелкому дроблению.
Степень фрагментации больше сказывается на изменении
зависимости р+=р+(р) по сравнению с р~=р~(р). В расчетах,
приведенных выше предполагалось, что эти зависимости одинаковы. Более
строго следовало бы учитывать их различие.
12. ДИНАМИЧЕСКАЯ СЖИМАЕМОСТЬ, СКОРОСТЬ СКОЛЬЖЕНИЯ
И АКУСТИЧЕСКАЯ ЭМИССИЯ
Ударная адиабата при пластическом затекании пор.
Взрыв в вакуумированном и обжатом песке.
Соответствие волны неупругости и скорости волны Релея.
Предельная скорость скольжения. Запаздывание
схлопывания пор. Динамическая сжимаемость
пористых материалов. Псевдовязкость разрушения.
Слабые волны в пластических областях. Акустическая
^ эмиссия как сигнал микроскольжений частиц.
Преобладающие сейсмические частоты геоматериалов.
Для теоретического расчета статической сжимаемости пористой
среды в условиях действия сил сухого трения можно воспользоваться
ячеистой моделью, описывающей ситуацию вокруг индивидуальной
95
поры, вводя (по Дж. Бхатту, М. Кэрроллу и Дж. Шатцу, [45]) для
возникающей пластической зоны предельное условие
Мора—рулона в виде /
(1+р)аг-ав=У. , (12.1)
Если материал матрицы несжимаем, то текущая г и начальная
Го координаты частиц связаны со смещением и условием
Гз = Г3о—£, И=;Г—Гр, (12,2)
где В — постоянная. Внутренний а и внешний Ъ радиусы ячейки с
пористостью т=а3/Ьг тогда определяются так
a3=a3o(m/m0) (1—m0)/(l—m),
fc3= (a3o/m0) (1— m0)/'(l— m). (12.3)
Деформации и уравнение сферически-симметричного упругого
равновесия соответственно имеют вид
err=u>r=(2/3) (S/r3), еее=и/г=-(1/3) (Б/г3); (12.4)
(dorr/dr)+4G{B/rb) =0. (12.5)
Распределение напряжений
ar= (4/3) GB(r-3-a-3), ae=—(2/3) GB(г-з+2а"3), (12.6)
удовлетворяет условию аг(а) =0. Граничное условие аг(Ь)=—р
связывает давление с текущей пористостью
р=(4/3) (G/m) (то—т) (1-т)7 (1-т0), (12.7)
.причем £ = (а3о/т) (т0—т)/(1 — т).
Если пора окружена пластической зоной радиуса ар, то для
внешней упругой области справедливо решение (12.6), а для внутренней
следует искать решение уравнения пластического равновесия
Ог,г+ (2/г) (У-р(Тг) =0, а^г^ар. (12.8)
Интегрирование позволяет найти нормальное напряжение на
упругопластической границе
ar(ap) = (y/'P)[(ap/a)2P-l] (12.9)
при ar(a)=0. Само положение границы ар определяется текущей
пористостью
(ap/a)2№=(2G/Y) (т0—т) (1— т)/(1— т0). (12.10)
Сшивка решений для упругой и • пластической зон проводится с
помощью граничного условия
-^PMap)+2GB/aV=y, г=ар (12.11)
и позволяет связать внешнее давление р с пористостью
р=-(4/3)(0/т)[(то-т)/(1-то)](Ф-т) + (У/р)Х
Х(ф-(2Э/з)_1), 0(2P+3)/3=(y/2G)m(l~m0)/(mo-m). (12.12)
При полностью пластическом состоянии материала ячейки
соотношение (12.12) упрощается
Р=(^/Р){[(1-^)/^]2р/3-1}, m^mvX), (12.13)
где тр — корень уравнения ар=Ь, или иначе:
(m0-mp)(l-mp)/n2p?/3 = y/(2G). (12.14)
36
Разгрузка может быть упругой или упругопластической, причем
предельное условие (12.1) заменяется на следующее:
(1+Р)ав-сгг=У, (12.15)
поскольку ае является теперь максимальным сжимающим
напряжением. Можно показать, что в этом случае
р = (У/р) [(1/т)2р/8_1]_(у/р) (2+р) (ар/а)**+
+ (2/3)G(m-mO(l-m)-1(l-m*)-1[(3+P)(l-m)X
X(fl/flp)8/('P^)+2(l-m)], (12.16)
где m* — значение пористости, с которой начинается разгрузка, а
отношение {а/ар) может быть выражено через величины /пит*
1 _2G{l-m)-i-r, ^ /*p\2p+3 1 ( apy + W+t
Результаты расчетов па формулам (12.12) и (12.16) для
песчаника (т0=18%) приведены на рис. 29 для значений параметров
У=21, 7 МПа, р=3,825, а также G=30,0 ГПа (сплошная линия) и
20,0 ГПа (пунктир). Приведенные экспериментальные данные для
нагрузки (1) и разгрузки (2) являются пересчетом зависимости р =
р(р) для песчаника по правилу
МшРЧ(1-т) = УШ(1
(12.18)
°i/Pi=
[р] =
•m)—diP-(plPo)(l-mo) + 'Pdi
при следующих данных для кварцевого материала матрицы:
= l+d1pm-d2p2m, pm=(l—m)p, rf, = 2,55-10~3, d2 = 10"5,
= 102 МПа.
Рис. 29 показывает вполне удовлетворительное соответствие
объемной статической сжимаемости матрицы реальной пористой среды
с расчетном по ячеистой
упругопластической, модели.
• Данные о зависимости
пористости от давления необходимы для
расчетов, ударных адиабат
пористых материалов по соотношениям
на фронте ударной волны (1.29),
причем параметры материала
матрицы рту 8т, рт связаны с
параметрами среды так: р=(1—т)рШу
е=(1—m)em, р=(1— m)pw, а
уравнение СОСТОЯНИЯ pm = f(pm/Sm)
предполагается таким же, как и для
монолитного состояния.
Для весьма сильных ударных
волн р+>>~, 8+>е~, т+=0
соотношения (1.29) упрощаются и
сводятся к виду, испольаованому при
расчетах ударных переходов столь
большой интенсивности, что.
существен эффект теплового давления
[10]. Он выражается в
расхождении ударных адиабат .пористых
материалов и ударной адиабаты
7—3311
Рис. 29. Расчет
гидростатической
и эксперимент по
сжимаемости
пористого песчаника
97-
для сплошного материала. На рис. 30 приведены данные для
ударной адиабаты песков (1) (по К. Харту и И. Скидмору) и для
сплошного (расплавленного) кварца (2) (по Дж. Уокерли). /
При меньших давлениях, когда эффекты теплового, давления
несущественны, динамическая сжимаемость пористых ^орных пород
оказывается несовпадающей со статической сжимаемостью. На
•рис. 31 проиллюстрированы расхождения динамических (кривая /)
и статических (кривая 2) дилатансионных кривых для песчаника
«Наггет» (по Р. Кристенсу, С. Свансону и В. Брауну [31]).
дмпа
75
ГПп
40 с-
J0
го
w
о '
\
\
\
—
f
\
\
\
Я
\
\
' \ 2
\ °\
\
i i °i i
50
15
0Ц
0.5
06
oj v/v0
Г ойкима
h
/ /
• i ..1 :.. I
00015
0t005 e^ez^e3
Рис. 30. Ударные адиабаты кварцевого
песка (т=40%) и плавленного кварца
в чрезвычайно мощных волнах
Рис. 31. Динамические (1) и статические
(2) кривые дилатансионного
деформирования
Принято объяснять подобные расхождения проявлениями
инерционных мелкомасштабных сил (при сферически-симметричном схло-
пывании пор). Учет динамических сил согласно ячеистой модели,
рассмотренной выше, приводит, однако, к парадоксальному
результату: динамическая сжимаемость оказывается больше статической
даже при введении дополнительных вязкостных сил [45]. Эти
трудности снимаются, если ввести усредненное пульсационное давление
в макроуправление импульса.
Другим объяснением различий сжимаемостей может служить
наличие предельной скорости скольжения, что приводит к
запаздыванию развития неупругих деформаций, охватывающих пору.
Решение К. Броберга [4, 45] показывает, что скорость фронта U
неупругого сдвига (скольжения) не может, по крайней мере,
превышать скорости волны Релея. Реальная предельная скорость, по-
видимому, ниже релеевской скорости. В экспериментах по
динамическому сдвигу вдоль плоского разреза образца гранита (с=5,3 км/с;
Cs=3,l км/с) были выявлены типичные скорости (2—3 км/с) для
фронта прерывистого скольжения. В образцах дунита [4, 45] эта
скорость менялась от 1 км/с до скорости с5=4,6 км/с волны
поперечного сдвига.
Обратимся к опытам по сферически-симметричному взрыву в
обжатом песке — как внешним избыточным давлением, так и путем
создания вакуума в поровом пространстве [4, 45]. Обжатие обеспе-
98
чивает равномерное (по объему) действие сил сухого трения.
Скорость вступления упругого предвестника с = 810 м/с, тогда как
скорость максимума волны сжатия была также практически постоянна
и при давлении обжатия в 2 МПа составляла £/=^451,6 м/с.
Объемный модуль /(=0,51 ГПа соответствует указанному значению с
(измеряемый в статических испытаниях при четвертом цикле нагруже-
ния до 2,0 МПа), поскольку модуль сдвига G = 0,386 ГПа. Отсюда
коэффициент Пуассона v = 0,198, а скорость поперечной волны cs=
= ]/ (1— 2v)/(2—2v) =0,614, с=497 м/с. Скорость волнььРелея при
v=0,-198 имеет значение Ch=0,9105cs, т. е. cR = 452,5 м/с. Отсюда
видно, что U=cR, а потому максимум волны можно отождествить с
фронтом скольжения.
При взрыве в вакуумированном песке также был выявлен
диапазон расстояний постоянства скорости U (200 м) максимума волны
при скорости продольного звука с, в
2 раза большей.
В плоских ударных волнах (по
Р. Столлу и И. Эбейдо [4]) в ваку-
умированных песках (плотность р0=г
= 1800 кг/м3) были зафиксированы
два фронта — вступления и
«стационарного» состояния. Скорость упруго-
то предвестника составляла с = 260;
350 и 400 м/с в зависимости от
степени вакуумирования. Скорость U
второго фронта (неупругих) деформаций
при с=400 м/с и минимальной
амплитуде; в 0,14 МПа составляла
230 м/с=0,575 с, причем скорость U
линейно'растет с амплитудой ах
удара" i/^0,6 с (0,6+0,2850*), где 0,14<
^0x^0,6 [ох]> МПа. С другой
стороны, U как скорость сильного разрыва
определяется условиями баланса
p{v-U)=poU9,px>U=Ox-6°x (12.19)
по зависимости деформации е= (р—р0)/ро от ох, известной из
статических испытаний (рис. 32, пунктир). Можно привести обратный
расчет —по экспериментальным данным для o(U) и формулам
(12.19) найти динамические деформации еа (рис. 32, сплошные
линии). Динамическая сжимаемость песка оказывается заметно
меньше статической. Аналогичный эффект * известен и для насыпного
песка. Экспериментально было также выявлено, что уменьшение
скорости времени нарастания в волне от 1 до 0,1 мкс приводит к
уменьшению сжимаемости песка на порядок.
Представим теперь, что и при схлопывании пор должен
проявляться эффект предельной скорости неупругого деформирования. Из
решений (12.6) следует
е- Ю*
Рас. 32. Динамическая и
статическая сжимаемость песка при двух
уровнях вакуумирования порового
пространства,
/ — с=260 м/с; 2 — с=400 м/с.
р= -or(ap) + (4/3) GB(a
■ьЛ
(12.20)
где ог(ар) —определяется выражением (12.9), ap = af(m).
7*
99
Продифференцируем равенства (12.6) и (12.20) по времени. Тогда
(dp/dt)-2Y(ap/a)2^ (d/dt) (ар/а) = -(4GB/a*p)dap\dt. , (12.21)
Если положить dap/dt=vLi где vL — предельная скорость
скольжения, и учесть d(ap/a)=f (m)dmf то получаем /'
dp/dt = dF/dt + (/С/6), б = ljvL% I = a%[b\
К = (4/3) GB (а[Ь)\ F = 2Y J {/(/ю)}2*"1/' (го)dm. (12.22)
Оценку времени релаксации 9 можно провести так: Vl^W3 м/с,
I—Ю-3 м, 0—10~6 с. Согласно Б. Д. Христофорову разрыв фронта
плоской ударной волны в прессованном порошке соли NaCl (р =
= 1870 кг/м3, с=3,25 км/с) соответствовал вязкости jw=0,10—
1,0 Па-с, причем, действительно, чем давление было выше, тем
меньше была вязкость. Для этого материала р0с2 = 19,75 ГПа и
6 = ц/£=0,5 (10~7—10~6) с. Укажем, что вязкость монолитной
каменной соли* имеет порядок 109—1010 Па-с, что на десять порядков
выше вязкости, наблюдаемой в указанных ударных экспериментах.
Это подтверждает особый механизм вязкого течения (правильнее —
псевдовязкого) при динамическом сжатии пористого вещества. В не-,
которых расчетах множественного хрупкого разрушения скальной
породы также выбиралось значение jut=0,10 Па-с из условия
соответствия экспериментальным данным. Была отмечена псевдовязкость
порядка 0,10 Па-с по измерениям адиабат разгрузки ударно-сжатых
минералов. Ударная псевдовязкость, проявившаяся в плоских волнах
в вакуумированном песке составляет \х=3 Па-с (если задаться
экспериментальным временем релаксации 9=10~4 с).
Для расчетов ударных волн в грунтах иногда рекомендуется
использовать вязкоупругую модель при динамической вязкости \i=
= 1,0—10 Па-с. Изложенное оправдывает подобную рекомендацию.
Укажем, что для глин динамическая вязкость оценивается в 1,3 Па-сг
что намного меньше вязкости, измеряемой при квазистатических
испытаниях (5-Ю8 Па-с).
Имеются, однако, явления, обусловленные предельной скоростью
скольжения и хрупкого разрушения, для описания которых
вязкостное приближение недостаточно. К их числу относятся задачи о
фронтах упругих предвестников, а также о распространении слабых волн
догрузки в областях пластических деформаций. В этих областях
скорость упругих волн соответствует наклону касательной к ветви
разгрузки g=g(£i), но не скорости слабой пластической волны. В этом
смысле сейсмические волны в горном массиве «не чувствуют» его
пластических состояний [45].
Динамическое воздействие на геоматериал приводит к
возникновению волн различных частот, среди которых имеются и частоты,
определяемые внутренней структурой среды. Для выявления этих
собственных сигналов среды важную роль сыграли эксперименты
[8] по пропусканию ультразвукового импульса в морском песке
различной влажности. Ультразвук (20—150 кГц) затухает весьма
быстро: после прохождения 10 см в сухом песке и'порядка 1м —во
влажном. Однако он генерирует цуг "низкочастотных колебаний
100
(рис. 33) с максимумом амплитуды, приходящимся (через 1 м пути)
на 25 Гц. Чему соответствуют эти частоты? Ответ был найден после
сравнения спектров этого цуга и акустической эмиссии (АЭ) при
квазистатическом сжатии того же песка нагрузками, не выводящими
его на режим предельной пластичности. Спектры практически
совпали (рис. 34).
Фронт низкочастотных колебаний распространяется со скоростью
волны переупаковки, которая в сухих песках совпадает с
наблюдаемой скоростью сейсмических волн, а в насыщенных — со скоростью
волн II рода. При полном насыщении были зафиксированы только
ультразвуковые колебания (низкочастотных не было вследствие
аьа
о —
/5:
го-
25-
чо ^
Ип
-too
ZW
20
Tt —-=ге
' '{| »" '" "' '" 1" «" "' "' '" о
20
Z5-
3D'.
ЦОь
Z 6 fZJS 25 50 100 WO WO IB 3/5 6,3 125
Гц ■ м кГц J
• W
■го
"» "ii" "i in u, ,ii . .i ,,. о
Рис. 33. Вступления
ультразвукового /i и низкочастотного
цугов волн в песке влажностью
24 % (а) и влажностью 14 %
(б) по массе
2 В 125 25 50 /00 200 800 !6 3/5 63 125
I Гц '' «Гц 1
Рис.. 34. Спектры низкочастотного цуга волн
(а) и акустической эмиссии (б) песка при
малых необратимых деформациях
исключительно сильного затухания). При неполном вадонасыщении
были видны обе волны (см. рис. 33), а в полностью сухом —
практически только волна АЭ. Частота сигнала АЭ зависит от влажности и
гранулометрического состава песка. Поскольку эффективный угол
трения сыпучей среды cp=2(po+v зависит от истинного угла трения
Фо, который при ультразвуковых колебаниях резко убывает, то
возможное объяснение ультразвуковой генерации необратимых
деформаций, а следовательно, и АЭ состоит в уменьшении ср при
сохранении дилатансионных (чисто кинематических) параметров системы.
Тем самым возникают неустойчивость внутренней структуры
«упаковки) материала, а следовательно, и ее'перестройка.
С другой стороны, известно, что частота 25 Гц является
преобладающей при взрывах в песках. Более того, при взрывах несколько
зарядов с замедлением, равным периоду преобладающей частоты,
происходит резонансное усиление (по В. Н. Заякину) амплитуды,
соответствующей этой частоте, называемой еще собственной
частотой грунта. Другим источником резонансов служит стратификация
среды, которая усиливает сигнал с периодом Т^Л H/cs, где Я —
101
толщина пласта. Таким образом, преобладающая частота грунта,
знание которой необходимо при сейсмобезопасном строительстве,
имеет по крайней мере два физических источника. /
Ярким свидетельством наличия резонансной частоты внутренней
структуры геоматериала служит эксперимент [48] ло ут^йливанию
легкой вибрирующей пластинки в морском песке. Оказывается,
скорость осадки пластинки (без пригрузки)- имеет несколько
максимумов, а абсолютный максимум приходится на 25 Гц. Дополнительно
проведанные опыты показали, что при механическом воздействии
всех-видов на песок излучаемый сигнал в конце концов приобретает
частотный состав, соответствующий резонансным частотам массива.
Для глин подобной частотой оказывается 40 Гц, для гранитов
400 Гц, эродированных гранитов—100 Гц. Если обратиться к
данным по АЭ в ходе дилатансионного квазистатического
деформирования песка, то вслед за АЭ с максимумом амплитуды, приходящимся
на 25 Гц и соответствующей допредельной неупругости, происходит
рост частотного диапазона до 80 Гц. С началом заметных
предельных деформаций в спектре АЭ уже присутствуют частоты от 2 до
20 кГц с двумя максимумами (в пределах 10 Гц и 600 Гц). Картина
слабо меняется вплоть до момента полного разрушения, когда в
спектре остаются частоты 2—50 Гц, а высшие исчезают. Дилатан-
сионное деформирование гранита (по В. П. Епифанову) и бетона
(по Л. Д. Лившицу и др.) характеризуется АЭ с частотами 1 —
12 кГц на стадии, предшествующей разрушению, в момент появления
трещин —в 400 Гц (в бетоне) или от 100 до 800 Гц (в граните). Эти
цифры хорошо коррелируются с указанными значениями
преобладающих частот взрыва. В конце разрушения испытуемых образцов
спектр сигнала АЭ сосредоточен в диапазоне от 2 до 50 Гц, т. е.
соответствует АЭ сыпучего материала.
В природе наиболее сильные эффекты АЭ известны у «поющих "
песков», они связываются Р. Багнольдом [28] с проязлениями дила-
тансии при сдвиге.
Г Л А В А 4
МЕХАНИКА НАСЫЩЕННЫХ УПРУГИХ СРЕД
13. УРАВНЕНИЯ ДВИЖЕНИЯ ДВУХФАЗНЫХ СРЕД
Усреднение уравнений импульса гетерогенной
системы. Межфазовое взаимодействие. Граничные
условия. Уравнения кинетической и полной энергии
фаз. Уравнения баланса энтропии фаз. Рост
энтропии системы. Принцип Онзагера и кинетические
уравнения. Термодинамическое обоснование закона
Дарси. Нелинейные отклонения.
Уравнения баланса масс, усредненные по объему, имеют вид
(т(в)р(в)).*+(^<в)Р(в)^в>)^=-0, 'а=1, 2' ' (13Л)
Усреднение локального уравнения импульса (1.2) по объему ДУ
приводит к следующим двум (а=1,2) балансовым соотношениям
Ю2 .,-,, iTi!л
(13.2)
где символ (...)(<x) означает интеграл по сбъему, занятому фазой а,
{...)(а) —интеграл по площадке, нормалью к которой служит ось Xj
Уравнение (13.2) за счет введения т(а) и т(а) относится к полному
объему А У, а не к его части, занятой фазой а. Будем далее считать
Средняя объемная сила межфазного взаимодействия
F? = W ] Ь -Р(°/ ~ wMnjdS; (13.3)
5(0
/7(D _ _ )7<2) __ /Г
должна быть определена дополнительно. В отсутствие фазовых
переходов Vi = wi. Физически оправдано предположение, что значения
плотности ра и скорости vla\ полученные усреднением по объему и
поверхности, совпадают v\*\
P('4W= <!»,>«•>-«;■>. (13.4)
При использовании средней фазовой скорости ufa) поток
количества движения преобразуется.следующим образом:
<рр1о/>;->= Рл;а)+о{(р - P(a))(of -v,)<*ч; Р« (0/-о;а)) (*,.-<>».
Пульсационными поправками к среднему потоку импульса,
равно как и антисимметричной составляющей динамических
напряжений, будем пренебрегать. Что касается средних фазовых напряжений
.^-ЫГ- . .• (13-5)
то они определяются как средние по площади, занимаемой фазой
на поперечном сечении Sj.
Будем пользоваться балансом мрмента количества движения в
отсутствие объемных моментов и моментных напряжений, т. е.
законом парности касательных напряжений в каждой из фаз
o(a)EEEo(a), a = 1.2. (13.6)
Пусть измеряемое в опытах поровое давление р есть фазовое
напряжение для жидкости
^ = -(1/3) А/- (13.7)
Это означает также пренебрежение касательными напряжениями
в жидкости. Суммарное (полное) напряжение
r/y = Sew(«)oJ> = -трЪи + (1 -т)о;;> (13.8)
103
и давление р определяют эффективные напряжения в пористой мат
рнце у
°ц = Гц+Р*ц = (1 -т)(*™+рЪч). / 413.9)
/■
Средние фазовые массовые силы (fi)(a) = f{a), в частности,
сводятся к силам тяжести (gt — ускорение свободного падения)
m("f,(1) =(1 -m)^gi,m^ff=m^g, (13.10)
Разделим силу межфазового взаимодействия на следующие две
Fi=Ri+pdmldty (13.11)
здесь Ri — объемно-распределенная межфазовая сила, работа
которой приводит к диссипации механической энергии. Тогда уравнения
количества движения переписываются в виде
{(1-»)р(,Ч(,)}.Ж(1-«)р<,Ч(Х)}./=
= о'/Л/-(1-да)р>/ + (1-т)р(»)Л_/г/1 . (13.12)
(VV2)). t + (m9(2)vfvf)_, = - /и/;.,- + mPigi + Rt. (13.13)
Проинтегрируем по объему Д1/ уравнение кинетической энергии,
полученное умножением локального уравнения баланса количества
движения на величину локальной скорости:
(w(a)P(a)^(a)^a)/2)4, +(m(a)P(a)^(a)^a)^V2),/ + ^(a)^a)=
= (m{a)o{a)v{a)) , -т{л)о{л) (v{a)) :-т(а)А{а) + m{a)fla)v[a)+W{al,
v ij i ' • •» ij y i ' * > * ' w i ' ' f f
(13.14)
где Л(а) —скорость изменения пульсационной кинетической энергии
с учетом ее переноса и работы пульсационных инерционных сил на
гранях объема АУ. Работа Л(а) внутренних сил, соответствующая
изменениям средних полей вследствие наличия частиц иной фазы, и
работа W{a) мёжфазовых сил имеют вид
л("=-4г J (o,,.-o<;>M-t>;;;.)dv; (Ш5)
ду(°0
^*
(«)_
=^ J {^,-^<«>,-»/)Ь<«. <:=-^:2!- (13.16)
5(r") (t)
Уравнение для средней кинетической энергии должно совпадать
с уравнением кинетической энергии среднего движения фаз
- /7Z(a)o(aVa)+ //i(a)/(aVa) + F(aVa). (13.17)
ij i, j l ' i i l i i ' v '
104
Это приводит к балансу энергии пульсационного движения в фазе
mta)A(a) = Ww -pv(a)mia) - tf(0Va) -т(а)Л<а),
V , t I . I LI *
m(*)=m=l —my. (13.18)
Слева стоит накопление энергии в объеме AV с учетом работы
пульсационных инерционных сил, справа — источник роста за счет
работы сил межфазового взаимодействия и сток, обусловленный
диссипацией — переходом в теплоту.
Остановимся на возможных вариантах граничных условий:
а) нагрузка Гц прилагается только к матрице среды (условие
типа «высокопроницаемый» поршень). Тогда на границе
оу = Г17 = о*,7) р = 0. (13.19)
Отсюда видна простота измерения эффективного напряжения в
опытах;
б) нагрузка Гц прилагается и к матрице и к жидкости
ey-/*i/=?rt/ = rȣ/. (13.20)
В случае условия типа «сплошной поршень» справедливо
дополнительное условие непроницаемости
v\l)=vf>. ' (13.21)
В случаях «проницаемого поршня» необходимо формулировать
условия непрерывности порового давления, а кинематические
условия выписываются с учетом требований баланса масс;
в) при приложении нагрузок к двухфазной среде со стороны,
жидкости («жидкий поршень») справедливо условие для
нормальных компонент напряжений
Р = Гип, = /Р, °;;Ч = °- (13-22)
Компоненты скоростей, параллельные границе, меняются скачком—от
ут в свободной жидкости до сИ2) в поровой жидкости. Касательное
усилие afr на границе имеет вид
of =pdoJdn, (13.23)
где \i — вязкость жидкости, п — координата, ортогональная границе.
Кроме того, должно задаваться условие прилипания свободной
жидкости к частицам матрицы среды
v=v?\ (13.24)
что, по-видимому, ^оправдано для реальных малопористых сред.
Вообще говоря, граница со свободной жидкостью является для
пористой среды на небольших интервалах практически линией равного
давления и потому в пористой среде вектор скорости движения будет
почти ортогонален границе раздела, а течение в свободной жидкости
105
в пограничном слое будет двумерным. (Отметим полуэмпирическое
предложение Т. Биверса и Д. Джозефа использовать в этом случае
условие смешанного типа у
о<»/и = dvjdti = (Б/Vk) (о- v™ - то?),
где Б — некоторая новая постоянная пористой среды, k — ее
проницаемость) .
Усредним теперь баланс полной энергии в объеме AV
(дас>рС) <. + *Л/2)(">), , + {да(»ув> <(г4-ОЛ/2)0/>]">}1 , =
= {т™ (о^)'«>), ,+от<»> </,,,,.)<"> +,»WqW + Е«- *«. (13.25)
где межфазовый переход полной энергии имеет вид
E[a)t =Ж j {°</*< ~ Р (е + *Л/2) (°/ - «V) + Я}) n,dS,
S(m) (t)
Ey = -E®=Eti. (13.26)
Уравнение баланса (13.25) упрощается, если
т(а) = т^, (а^>;->= of*>tf, </Л)(а) = /<аУа),
=(a(e)+dJe)o;e)/2)o(e), (13.27)
но при этом нужно, вообще говоря, вводить величину Л^а) — скорость
изменения пульсационной полной энергии.
Предположим, что скорости изменения пульсационной полной и
кинетической энергий, равно как и межфазовые работы, и переход
полной энергии отличаются на величину Д^ :
m^A^^E^A^^W^+^K Д(1) = -Д(2) =Д.. (13.28)
Вычитание из уравнения (13.25) уравнения (13.14) приводит к
уравнению притока теплоты -
(//i(a)P(a)8(a)),, + (w(e)p(e).(e)o;e))>, = /n(e)o;/e) i^+m{a)Q{a) +
Перейдем теперь к конкретизации уравнений притока теплоты в
фазы. Воспользуемся условиями (13.7),. (13.8), а также определим
величину Де и работу Л(2) внутренних сил в жидкости, полагая
последнюю равной работе силы Rt межфазовых сил на скорости
относительного движения:
д = pd2m[dt, djdt = д/dt + v^d/dXi,
m{2)A™=Rt{vf -v^). (13.30)
106
Тогда уравнение притока теплоты для жидкой фазы примет вид
Vt=l/P<»>.
а уравнение притока теплоты в матрицу при Л(1)=0 будет
(1 -т)^1) {d^1)jdt + pdy^1)]dt) —
= ^^ + {\-m)Qm. V1=l/P(,). (13.32)
Сформулируем уравнения роста sa — фазовых энтропии так:
(l-«)p<I,7,<4*(,)/* = (l-/»)Q(1) +of(J)«f ;■ (13-33)
mP(2)T{2)diS{2)ldt = mQ(2) - Rt (v™ - if). (13.34)
. Отсюда источниками диссипации служат работа #;(t^(1) —aj2))~ в
жидкой фазе и работа ъ^цёРц в твердой. Работу порового давления
на изменениях объема материала фаз будем считать обратимой.
Тогда соотношения Гиббса для фаз принимают вид
dJl)/dt + pdyl)/ti = (o«]l9)k{;i (1 -тух + T{l)d<sil)fdt; (13.35)
d2e^/dt+pd2 VW/dt = n2)d2sW/dt. (13.36)
Из (13.41) следует, что состояние жидкости в порах определяется
теми же параметрами, что и в свободном объеме, хотя значения е(2),
р(2^, р, Г, s%(2) есть фактически средние для жидкости, заполняющей
множество поровых каналов в объеме AV. Будем предполагать, что
эти усредненные параметры связаны между собой тем же уравнением
состояния, что и в жидкости в свободном СОСТОЯНИИ 8(2) = 6(2) (К(2), s<2))
ИЛИ ё<2> = 8<2>(р<2>, Г<2>).
Для твердой фазы характерна зависимость e(1) = e(1)(V(1), s(1), еец)
или е(1) = е(1)(р(1), Т(1), oUj):, причем зависимости от скалярных
инвариантов тензоров упругих деформаций еец или эффективных
напряжений ofij отражают свойства твердой среды как матрицы.
Усредним уравнение локального баланса энтропии по объему
(m(a)p(a)S(a)), /.+ (w(e)p<e,oJe)s(e))e/ = т\ - (q^lT{a))tIt (13.37)
которое совпадает с постулированными (13.33) и (13.34), если
r(a)2a = D{a) +Q(a) + /(a); Q(a) = - (q{a)/T{a)) T(a) + (ofa,+ .
+ 0i,)i{;/lTiu)i D(l>=d<^;;>;- D^=((oil-o\i;)(dotldxf-
/{а)=1Ж J {~^-рФ/-»/)}*/«.
s(m) (o
107
где /а —приток теплоты в фазу а через поверхность S<m>(/). Сумма
уравнений (13.33) и (13.34) дает уравнение роста энтропии во
всем AV /
{mP<V2) +(1 -ffl)p(V»)b+{fflfV8/w + (l -m)?{l)smvfy,L
= - {(<)/7,(1)) + (-7;2)/7,(2)}./ + S; /(1> = -/<2> = //
s=-(i/r(1)j2<7(,)r0) -(l/T(2))V2)r(2! +
+(/?/r(2))(t)f)-t;;l>)+/(i/r(1) -i/r(2)). (13.38)
Если воспользоваться принципом Онзагера [15] с учетом правил
о тензорных размерностях, то в предположении о том, что градиент
температуры в одной из фаз не может вызывать непосредственно
потока теплоты по другой, получим замыкающие кинетические
соотношения:
/?(.^г(..(:;(1)-г»!2))+1!?)(1/Г(,))Г(,);
J I I Ij ,j
qf ^-Df^-Lf] {v™-vf)IT™-, (13.39)
41 ij ' ,j ' // // IK '*
/ = и(Г<2> -Г*1)), k=LI(T11)TW).
Использование линейных связей (13.39) означает предположение о
микростационарности движения жидкости в поровых каналах.
Термомеханическое взаимодействие физически обусловлено
термодиффузией, а в газонасыщенных средах и тепловым скольжением.
Как правило, эти эффекты малы но сравнению с вязкостным
сопротивлением, а потому будем считать, что Ь^) = 0. Тогда первое
соотношение (13.39) означает пропорциональность силы межфазового
сопротивления относительной скорости движения фаз
*/ = /-//(tf-tf)), ._ - (13.40)
причем зависимость кинетического коэффициента' тц от температуры
жидкой фазы может быть интерпретирована как температурная
зависимость вязкости жидкости. Тензорный характер коэффициента
Гц (будем называть его тензором сопротивления), равно как и
коэффициентов теплопроводности фаз, определяется анизотропией
пористой среды. Принцип Онзагера в приложении к кинетической
связи (13.40) означает, что тензор Гц должен быть симметричен.
В опыте Дарси по измерению силы сопротивления
фильтрационному потоку осуществляют медленную одномерную прокачку
жидкости через горизонтально расположенный образец пористой среды.
Предположим, что образец пористой среды ориентирован вдоль /-й
главной оси анизотропии. Уравнение количества движения (13.13)
108
в этом случае имеет вид
mvf = - (т{2)/ги) pt у = - (кпМ р, ,, (13.41)
где jx-—вязкость прокачиваемой жидкости, kij = \im2/rjj — главное
значение тензора проницаемости кц, поскольку главные оси тензоров
Гц и kij совпадают. Для определения кц как величины, обратной
тензору Гц, существенна невырожденность последнего, т. е. гцфО при
/=1, 2, 3. Если же одно из главных значений, например Гзз
обращается в нуль, то этот случай соответствует условию
неограниченного возрастания значения -проницаемости вдоль той же оси (&зз->
->оо), т. е. давление вдоль этой оси практически постоянно. Если же,
наоборот, проницаемость вдоль одной из главных осей обращается в
нуль (&зз-ИЗ), то это соответствует неограниченному росту
сопротивления (гзз-^оо) вдоль той же оси. Это случай предельной
анизотропии, когда движение происходит лишь в плоскости, ортогональной к
оси вырождения (здесь л:3). В простом, изотропном случае кц=кЬц-
Теперь видно, что закон Дарси (13.41) — следствие уравнения без-
инерционного движения жидкости в порах и определения
межфазовой силы по правилу Онзагера.
Размерность проницаемости [k]=L2, где L — размерность длины.
Проницаемость — геометрическая характеристика порового
пространства. Поскольку при фиксированных перепадах давления и
вязкости отношение k/m определяет среднюю скорость движения
жидкости относительно пористой матрицы, в качестве гидравлического
линейного внутреннего масштаба среды будем брать длину /* =
= yr k/m. В пористом слое, сложенном из сферических частиц одного
диаметра, масштаб /* пропорционален диаметру d [9].
При увеличении скорости движения жидкости закон Дарси
нарушается, что свйзано с инерционными потерями и особенно
существенно для крупнопористых и трещиноватых сред [9]. В этом
микроинерционном, но стационарном режиме следует задавать
соответствующую диссипацию (13.37) в следующем виде:
Ri{<P?-vf) + b (??-v?)\v?-v? I}- (13.42)
и формализм термодинамики необратимых процессов вместо (13.40)
дает
Rt-r^vf-v^ + r^vf-vVWr-v? |. (13.43)
Указанная диссипация — приближенная оценка потерь механической
работы при отклонениях от ламинарного течения жидкости в
каналах, а связь (13.43) соответствует так называемому двучленному
закону фильтрации. Объединение связи (13.43) и уравнения
количества движения (13.13) в пренебрежении макроинерционными силами
и движением самой матрицы действительно дает
vf + Ы>? | vf I = - V.//^)- <13-44)
Асимптотически при весьма больших скоростях закон (13.44)
переходит в закон «турбулентного» режима фильтрации (Краснополь-
109
cp(Re)
8\
1/
Dz ПК
~A~~\3
>
16
-КЗД
д-р+о—;
2 4 6 8 Ю'г Z
S
У £ tf /#_/
Re
J
' z
10°
я
_AJ
>
I 1 7 Г~Д I 1П .
о 1 я 1 + 1 //
^ 1 0 | ~ | //
D | 3
2T~
1 1 1 1 III =]
—^—
SaJ"^+^
1
dzSd
в
Щ
ptt
Ш
ttft°$g
ti
1 1
—и
_ьЬ+<&
г?н
i—
Б 8 w~1 г
Ц 6 8 W°
Ч 6 8 W
Пе
Рис. 35. Отклонения от закона Дарси для песчаников (а) и сыпучих материалов (б)
ского — Шези):
Wi\Wi\=-(mlb) {kitiripj. (13.45)
Области справедливости закона Дарси, двухчленного закона и
«турбулентного» режима определяются внутренним числом Рей-
нольдса
Re = p</^=;(P|^(2) -W)\Jv)Vk(mt . (13.46)
причем кинетическая связь (13.43) может быть представлена в виде
R. = ср (Re) р (/и/А) (v^-v™). (13.47)
Функция cp(Re) для различных пористых сред [9] дана на рис. 35
(номера на рис. 35 соответствуют данным из табл. Ь\.
№
I
2
3
4
5
6
d, см
0,01
0,0065
0,025
0,014
0,017
0,014
т
0,197
0,192
0,119
0,159
0,269
0,136
k, Ю"8 см*
0,182
0,130 •
1,13
0,35
2,5
0,355
.№
7
8
9
ю •
'И
"
d, см
0,016
0,246
0,319
0,246
0,319
-
гп
0,221
* 0,405
0,389
0,394
0,385
Таблица 5
k, Ю-5 СМ»
3,3
2,7
4,1
2,5
3,64
Оценка коэффициента межфазного теплообмена х проводится
£22] на основе задачи о распространении звука в теплопроводном
газе в цилиндрических или плоских щелевидных порах. Имеем
q = - (Д//,) (дТ/дп)3 = х (7\ - Т.),
(13.48)
по
где Т\ — средняя по поровому каналу температура, Г0 — температура
твердой фазы, предполагаемая в данном расчете, неизменной, х —
коэффициент теплообмена — комплексная функция частоты
K = (Dlll2)F(n), п = 1]/Я\101, ' (13.49)
что соответствует запаздыванию по фазе потока q от изменений
поля температур. При этом
для цилиндрических пор
F(n)=2nQ>(n)[l-2Cb(n)/(in)]-\ Ф(п) =
(Ъег'п+ibei'n) / (hern+ihein) у (13.50)
где / — радиус поры [22],
для щелевидных плоских пор
F(n) = in2\h(n ]/7)1[пУТ -&(л]/Т)], (13.51)
где 2/ — ширина щели [22]. При длинах волн, намного больших, чем
характерная длина / (я<с1), в соответствии со свойствами функций
Ьегп, ..., thx имеем
n=F0Dl/l2^k-\ (13.52)
где ^о — числовой коэффициент (F0=3 для щелевидных пор; для
цилиндрических — F0 =8. Поскольку l2^k, то коэффициент
теплообмена х обратно пропорционален проницаемости среды. Были
изучены отклонения от оценки (13.52), связанные с приближением
масштаба возмущений к характерному внутреннему масштабу [22].
Проблемы практического использования [44]
взаимоперекрестных эффектов.; установление границ применимости: квазилинейных
онзагеровских связей (13.39) и их замена, например, в
осциллирующих режимах (сравнить с резонансными явлениями) составляют
тематику нелинейной геофизической акустики.
14. ОБЩИЙ АНАЛИЗ МЕХАНИКИ ПОРОТЕРМОУПРУГИХ СРЕД
Линеаризация уравнений движения. Обобщенные
законы Гука для поротермоупругого тела. Параметр
жесткости матрицы. Эксперименты по сжатию
насыщенного геоматериала. Уравнения динамики волн.
Инерционная релаксация. Равновесные и
замороженные скорости звука. Дисперсионное уравнение для
звуковых волн. Температурная релаксация. Звук в
термоактивной среде. Квазистационарнсге упругое
уплотнение.
Для малых отклонений от стационарных состояний можно
пользоваться макроуравнениями баланса масс, импульса и энергии в их
линейном приближении. При этом
tn = m. + m, v^=v^+v{p , ... (m0^>m, ...)
и полагается, что стационарные значения о|"* так же малы, как и
возмущения, или же еще меньше (что позволяет за стационарное
состояние принимать медленные установившиеся движения). Прене-
111
брегая величинами второго порядка малости и опуская символ
«волны» у возмущений, получим линеаризованную систему уравнений.
Уравнения баланса масс (13.1) принимают вид (mi=l— т/т2 =
= т) * ;
Балансы импульса (13.3), (13.4) с учетом (13.47) упрощаются
(1-й,) ?У<;> == oj . - (1 - т0)р%1+\\-т.) Ро( V- -
Cv?.<= -Р.' + Р>' + W„ (vf> - *»). (14.2)
а фазовые деформации е[а) определяются скоростями v{a,).
Соотношения Гиббса (13.41) при е??=е(?} принимают вид
(1 ^m0)po<,)rfe(i>=T<,) (1 -mJP;w> +0;;w')-
-(1 -m,(pde^-pd(l-m), (14.3)
//^W» =T(2WoPfVS<2) -mj^(2) -/**«,
где de{a) =de[*)&iI — объемная деформация фазы а. Их суммирование
приводит к уравнению Гиббса для всей среды в целом
prfs = (1 _щ0)р^Т* W> + m0p^T^+o\flde^ -
- /7(1 - /ю,)^1) - pm0deW, (14.4)
где р0 = (1 — *я0)р0(1) + /гс0Ро2)» ^е —приращение средней внутренней
энергии: p0cfe = (l — гПд)р{^г{1)-\-т0р{^е{2). Введем свободную
энтальпию
Л = .-(1 -,*,) р^Т(1)^(1) -m^T^ds™ +е^ - . "
— (1 — 1Яв) в*1)/? — mee <■)/?- (14.5)
Свободная энтальпия И(Т(1), Т(2), о^\ /?) также является потен-
циалом, а потому (14.4) преобразуется вновь к полному
дифференциалу
dH=-(\ -w,)P<V,)d7'(1> -тор0(2)АГ(2>- e^dtf -f
+ (1 -m0)e{1)dp + m0e{2)dp; e^ = - dH/dtf;
ё={\-«,) e<*) + от0е<г> = (?Я/(?/7,
112
что в линейном приближении приводит к линейно-упругим связям
e^Atw'S-BwPtkt + m*™^,. (14.6)
ёЬ„ = ВчкР% - Cmpbkl + (1/3)/я0а(2)Г% + ч
+ (1/3)(1-т,)аС)ТС)8//. (14.7)
Из (14.6) видно, что при отсутствии второй фазы (или при
пренебрежимо малом давлении р) среду характеризуют компоненты
тензора Aijki и скаляр си, которые являются константами матрицы —
однофазной среды — с таким же распределением твердого
материала в пространстве, как и в присутствии второй фазы,
Am= (1/2G) (6i,6;7-v(l+v)-16i/6w),
где G — модуль сдвига матрицы (сухой пористой среды), v — ее.
коэффициент Пуассона.
Если эффективное напряжение равно нулю, то
напряженно-температурное состояние в матрице такое же, как и в поровбй
жидкости. В этих условиях каждая из фаз будет расширяться или
сжиматься так, как если бы все пространство было полностью занято ею
одной, связи (14.6) и (14.7) сводятся к скалярным соотношениям
e(i) = _(3B1+2B2)p+a(1)^(1),
moe(2) = -{(3Ci+2C2)-(l-mo)(3Bi+2B2)}p+moa(2)T(2),
а коэффициенты можно будет приравнять к известным из опытов
значениям
(3Bi+2S2)=po), (3C1+2C2)=m0p<2)+(l+m0)p(1) = p,
где р(1), р(2) — сжимаемость, а(1), а(2) — коэффициенты объемного
расширения материалов первой и второй фаз соответственно, р —
средняя сжимаемость. Теперь соотношения (14.6) и (14.7) имеют
вид
*<;> = (l/2G)(oJ - v(l +v)-VJi\lbij) - (l/3)(V/, + (1/ЗУа<1>Г(,),
(1 -m0)e^-\-m0e^ = ^o(f) -p/7 + (l -mJa^Ti1)+m0a(2)TW,
где o(^ = 1/3 (ofP'-h0^ H"0^ )• Разрешая первое из этих
соотношений относительно напряжений и снова вводя во втором скорости
смещений, получим окончательно замыкающие связи в виде
о<;> =(К- 20/3) еЬц + 2Ge4 + .» рЬч - a< "tfT<%, (.» = К${1)), (14.8)
(1 -т.) 00) +яцр»=(1 _ „,,, (в<')Т«) - р< Vd+P'Yi +
+ m,(*mT<*-$"p.t). (14.9)
Уравнение (14.8) — обобщенный закон Гука для насыщенной
пористой среды. Если использовать суммарное напряжение и положить
вц =е\\\ то поровое давление играет ту же роль, что и темпе-
8—3311 113
ратура при учете температурных напряжений.
2Get, = Тч - {vTkkbit + (1 - 2v) (1 - .#) pbl{ - (1 - 2v) (1 - f
-all)K)Tm„}I(l + v). (1*10)
Уравнение (14.9) — не что иное, как результат суммирования
уравнений баланса масс (14.1), поскольку справедливы линейные
соотношения
(l/p<V/=°(1)r(?+P(V<- <iypom)P.?=*WT»-pV*. (14.11)
где а —шаровая часть тензора истинного напряжения в материале
твердой фазы 0^=0^ (1— то)-1— рЬц. В сухой пористой среде (р=0)
эффективные напряжения^* совпадают со средними
макронапряжениями, а потому опыты-по деформированию сухой пористой среды
п изотермических условиях позволяют сразу определять
эффективные параметры КУ G. Введение в расчет цорового давления4^ как
легко измеримой в опытах величины также удобно.
Рассмотрим теперь, как распределяется полная нагрузка. Пусть
цилиндрический образец ограничен сбоку непроницаемыми
жесткими стенками, и сжимается с торцов вдоль оси Х\ непроницаемыми
поршнями. Пр1ьэтом в образце вызвана одноосная деформация
(^22 = ^зз=0, Un — u). При условиях отсутствия дренажа v^) = v(®
из соотношений (14.9) и (14.10) следует
р = пГ, 0<[>=-(1-/г)Г, Г = -Гп> (1412)
где е* —жесткость (сцементированность) матрицы, т. е. отношение
сжимаемостей материала матрицы Pi и всей матрицы в целом 1/К^
~B=(X+2G)-K
Значения коэффициента п при типичных для насыщенных
песчаников параметрах (m0=0,2; v = 0,2; pi = 5-10~5 МПа-1, р2 =
=4,4-10~4 МПа-1) приведены ниже.
•*=рЛ «0,01 0,08 0,16 0,24 ' 0,32 0,4
п 1,00 0,83 0,70 0,60 0,47 0,43
1_еф 1,00 0,92 0,84 0,76 0,68 0,60
Если в ходе опыта жидкость может вытекать из образца в
резервуар, где поддерживается постоянное давление ро, то для
деформации е = еп имеем
* = *»=("{? - .#A)/(K + 4G/3) = -Д/Л (14ЛЗ)
Р{П = - o|f + КР. = Г-(1-ОА.Г=-Гп, Ро = const.
То есть эффективное давление p(f) при общей нагрузке Г и
при.условии дренажа вызывает такую же деформацию образца, как и в
отсутствие жидкости. 'При таком реологическом испытании песчаника
с начальной пористостью т0 = 0,26 и проницаемостью ko=
=0,8-10~8 см2 приращения m одинаковы и при ро =0,1 МПа, и при
р0=\2,0 МПа, если полагать pW = q—0,85 р0, т. е. е* = 0,15.
114
Балансы притоков теплоты в линейном приближении, согласно
уравнениям (13.43), в пренебрежении нелинейными источниками
теплоты имеют вид
(1 -т.)9?Т.*У = (1 -m0)DiV2T(i) -х(Г«> - Г<2>),
Если воспользоваться известным термодинамическим
соотношением
pTds = CdT—aTodp,
где С — теплоемкость при постоянном давлении, а а — коэффициент
объемного расширения, то уравнения (14.14) принимают вид
(-1 tojCjV^il-mJD^W+il -m0)a(1)7>,-
-х(Т(,) -Т(2)), (14-15)
щС^^т^Т™ +"*Л* t+*(Tm - Г(2)).
В случае изотермического движения в изотропной среде и в
'отсутствие массовых сил результирующая система [22] имеет вид
^гН(1Ч(?-Р0) (1 -m9)p9i-(l -me)*;;>=of
Mt+^P.t + "W{* = 0'
(1-^9^=0^. -(1- -mQ) PtU-m\*k-x {v{p-vf\ (14.16)
■ rno9l v?l= - m0p, t + ml »k~l (*<'>- tf),
ojy = (K - 2G/3).rf/yS+ 2Ge „ + .#/Лф (и. 17)
причем деформации ех-;- обычным образом выражаются через
скорости смещений v{P. Эта система уравнений эквивалентна системе
Я. И. Френкеля [22], если в последней выразить лишний пятый
упругий модуль через четыре, фигурирующие в (14.16). Система
уравнений М. Био [22] включает в себя дополнительную инерционную
силу, соответствующую эффекту «присоединенной массы», что
приводит к некоторым неоправданным эффектам.
Уравнения баланса импульса фаз можно представить как
уравнения движения, выраженные относительно смещений &|а)фаз,
(1 - in.) р ?Ч7 „=«,«»,+ {(к- го/3)«;;>„+g (««+ «<;>j)t, +
+e,«;:>I/-«4(«l(,)-«Jmb;
m^u^= о,и» у+ а^]ч+ а,(«<'> - ««).,; (14.18)
а, = - /и, < 1 - /и.) (1 - s.) (р - р\)-', а, = ю2 (р - p^)"1
«8 = — (1 — ^o)s (1 — О* О — pt^O-1; л4 = даУ*-\
8* 115
Одномерные плоские волны описываются (по Гаргу и др.)
уравнением гиперболического типа, которое следует из системы (14.18),
(U,tt-C2oU,xx),t+(l/x)(Ultt-C2+U,xx)(U,tt-C*-UtXX)=0. (1^19)
Здесь x — kp^p^llmA1 —m0)p<0)] — время релаксации, р(0) =(^/—т0)Х.
X Pq1' + /и0Ро2) — равновесная плотность, а волновые скорости
определяются следующим образом:
^^(l/pcoifi-' + r'Cl-^^'/W-'CS/n.-i-e*)8}.
с] = ajim^y, с\ = aj(l - /и.) Р<2),
с?2=а1/(/я,р<1)), 4=а,/(1 -m,)Pow.
Отсюда видно, что очень быстрые возмущения (характерное,
время намного меньше времени релаксации т) распространяются со
скоростью с0. Если характерное время возмущения намного больше
времени релаксации т, возмущение будет переноситься двумя
отдельными волнами со скоростью с+ ис.
Распространение волны поперечного сдвига описывается
характерным релаксационным уравнением
* {К!»- clv2<0. <+ К\- сУ<а)}=°- (14-2°)
«Замороженная» скорость поперечных колебаний c$OQ соответствует
колебаниям самой матрицы при нулевой скорости смещения
жидкости. Это объясняется тем, что касательные усилия воспринимаются
только матрицей. За время, большее, чем время релаксации т,
жидкость будет, полностью вовлечена в движение. Поэтому
«равновесная» скорость поперечных колебаний cso характеризуется тем же
модулем сдвига G матрицы*, но эффективная плотность равна
суммарной массе фаз в единице объема ро. Скорости cs по порядку так
же соотносятся со скоростью с, как и скорости поперечных и
продольных волн в обычном твердом теле.
Введем волновые потенциалы <р(а) и ЧГ^а)
и{а) = (grad<p(a) +rot4^a))t,. (14.21)
Рассмотрим распространение продольных монохроматических
волн, когда потенциалы движения меняются по закону
?<«> = ? W ехр р (^ _ щ _ i {xjc)}%
где с — скорость распространения волны, б — коэффициент
затухания, а <Роа) —постоянная. Тогда система уравнений (14.21) сводится
к системе однородных алгебраических уравнений, которая имеет
отличное от нуля решение, если ее детерминант обращается в нуль,
116
что дает следующее дисперсное уравнение относительно величин
<о и г\:
(V - Va) (? ~ ^Ж'М Mt (? - MJMS) = о,
5 = (*./*)+(«/«К..- c* = MVW*, р* = (1-я?.)рГро2)/Крм)>
6»в + €*б=1 -(Роо/РыЖ^-М!-™,)]-*- (14-22)
^(р_.#рс))Д-'(1_/я,)-'} = _Л[1,
^ = (р>(,х){(1-У2+ф-**Р(,))5-,}1
^з = (Рда/Р*) (Р - ^Р(*>) Я"' = ^ "(Pj = (1 - Ю. W + W.PoW.-
Прежде всего отметим, что в предельном случае т=0
дисперсионное уравнение имеет вид (g—12а) (£—£2&)=0, т. е. g2a, g2^ —пара
корней, соответствующих распространению продольных волн без
затухания. Будем искать корни дисперсионного уравнения (14.22) в виде
ряда
£2 = £2o+'Vr£2i-cD2T2£22+... . (14.23)
относительно сот —малых значений безразмерной частоты [22].
Поскольку время релаксации т обратно пропорционально
фильтрационному сопротивлению г, малые значения сот соответствуют реальному
случаю весьма больших фильтрационных сопротивлений при
конечных частотах со. Приравнивание членов с одинаковыми степенями сот
приводит к цепочке коэффициентов разложения
¥о=М3/М2, £21 = U2o-g2*) {l\-lh)/M2 =
= (Го+М^2о+Мз)/ЛГ2, ...
Ограничимся вторым членом разложения (14.23) и
приравниванием коэффициентов при (сот)-1 и (сот)° = 1. Таким образом находим
0/*) + (»И = *1/^ (14.24)
Для скорости са распространения волны и для коэффициента
затухания 8а соответственно получим следующие выражения
ce = Re{(l/c) + (/8/»)}-,= l^(p-.^(,>)fl-1+(l-.J*/K(p-.^«1))P««).
8а = 1ш{(ш/с) + Й} ^(хшг/2)с;3{^+'«о/(р<1>Р<2)^<)+ (14.25)
+ 0/р(,))(Р —•Р(,,Ж(2 -*.0 -^о)-1 - (Р- •*Р(,,)Я-1] -
-(1/P«,)(P—^(,,)-,>.
Эти результаты соответствуют корню |=£а, относящемуся к
волнам малого затухания, — волнам первого рода. Для получения
характеристик волн второго рода следовало бы пользоваться
разложением по параметру (сот)-1, что соответствует поиску решения с
большим затуханием. Большое различие в коэффициентах затухания
связано с тем, что в волне первого рода смещения твердых и
жидких частиц происходят в одном направлении, а в волне второго
рода—в противоположных.
117
Важным частным случаем, который полностью удается изучить
аналитически, являются мягкие среды.» Малым параметром при этом
служит жесткость среды е<С1. Выделим соответствующие члены в
дисперсионном уравнении " х
14+^{-1+^1е*+Чроо/р(°))(1+Л2бО/(сот)} +
+Л3е*{1-//(ют)}=0,
Ал=(р^^){[2-в^(1-то)]-[(Щ1))-в,У(КВ)}9
А2=е*-2+[т1))-е*У(КВ), Л3=(Роо/:р(0>) [(Р/Р<!>)-в.]/(*В).
Корни дисперсионного уравнения в пренебрежении величинами
порядка е2* имеют вид
(^)a.6 = (l/2)±(l/2)±8№(^2 + 4)/(^+l) + U-l/(2^)±
± 1/(2Q±.»C(A - Л4)/(С* + 1)}. (14-26)
C==(p(*>/pJ^. Л4=(р(«)/Роо-)Л,.
Для волн первого рода, которым соответствуют корень ga и
верхний знак выражения (14.26), результат оказывается совпадающим
с дисперсионной зависимостью, соответствующей релаксационному
уравнению (14.20), но с заменой cS(X> и cSq на сОо=1/т/грр0О, ce= l/l^pp^
и потенциала Ч?2* на ф<2>. Укажем, что для коэффициента затухания
8а волн малых частот справедливо представление
ба=(р(0)_роо)(тсо)/(2р00со), £<1. (14.27)
Термоупругие волны описываются уравнениями неразрывности, .
/я , + (l/3)P(V'! -р0) (1 -«,)/?., +а1""(1 -К)Г(1; -
-(1-4)^ = 0,
т.^ + р^Чл* -imm,T?> + mji>f=0, 1(14.28)
и обобщенным законом Гука в форме (14.8), уравнениями динамики
из (14.16), а уравнения (14.15) притока тепла замыкают систему.
В линейной форме и в пренебрежении теплопроводностью последние
имеют вид
(1-т>)С«>Т" + т£»Т*=аТ.р.,.
(1 -m0)C<"T(i;=(l -m,)*wT0p.t + K(TV _ r<.>)#
В простейших случаях термоупругие волны обладают
релаксационными свойствами, вполне аналогичными ицерционно-вязкостным.
Так, если фазовые скорости равны, но температуры Г<!) и Г<2)
различны, то уравнения неразрывности и динамики упрощаются
РЛ * - (1 - m.)*wT"t -m0a(2)r<2; +ом = 0, {ЫЩ
118
Совместно с уравнением (14.29) они дают релаксационное
уравнение
Tr{p^eooPf»-V2p},<+{p(0)eoP,«-V2p}=0, (14.31)
60=р-Го(а2/С), 0оо=^р— Го [(1—то) (а<1)а(1)/С(1))+т0(а(2>а(2)/С(2))],
C=(l— moJDO+moD2),
Тг=(т0/к) (1—то) (вво/во) (CO>Da>/C).
Согласно уравнению (14.31) скорость зЬука (соответствующая
условию icotr—-*0) получается из двухфазной модели при Т^=Т(2\
г максимальная (сотт—*о°) при равенстве (С<1)/а<1))Г(1)=(С(2)/а(2))Л2).
Введение скалярных ср<а> .и векторных Ч^(а) потенциалов в
уравнения динамики термопороупругои среды, приводит: для поперечных
волн — вновь к уравнению (14.20), поскольку и тепловые эффекты
носят объемный характер, а для продольных волн — к громоздкой
системе пяти уравнений (по П. П. Золотареву [22]). Если
коэффициент объемного расширения материала твердой фазы намного
меньше, чем жидкой а<2)<Са(1), и, ^ кроме того, величина
(а(1>а(1>Г0)/(Р(1)С<1)) = (1—у-1) близка к нулю (эти условия хорошо
выполняются, например, для песчаника), то эта общая система
уравнений для монохроматических колебаний приводит к тому же
дисперсионному уравнению (14.22), но при значениях коэффициентов
Afi=—<1/р.) {p<1)+n2p(2)(l-m0)-im0-i}+(p(2Vp*) WB) (l-M)/m0,
М2=(Роо/р(°)) {(я+лю)2+(1-то) (Р/Я) (1-Af)}, (14.32)
Af8=(ft/B)(l-Ai)(poo/p.)f
Ему соответствуют следующие представления, справедливые для
малых частот (Л<Cl, £<С1) первой продольной волны:
с\ = (я + «.Ш>.0)+(1 -я».)/(р^). 8а = 5ар+8аг,
* —^-£-__^ _J_\
„ - ю« / \—тЛН
^^(^^ItV 04.33)
mp» В ~» we(l- —mejp.
Тем самым коэффициент затухания состоит из двух частей —
инерционно-вязкостной (6ар и ^тепловой баг, причем \6ат—(1—72-1)- Для воды
значение уг" близко к единице, а потому для'водонасыщенной среды
6^6ар и допустимо пренебрежение температурными эффектами.
Последние, однако, существенны для среды, насыщенной нефтью (у2=
= 1,25).
119
Второе предельное значение скорости волны (сот—*оо) можно
найти, воспользовавшись следующим приемом. Представим £2 при
больших частотах в виде /
g2=go+t*gi/(coT).
Тогда дисперсионное уравнение (14.32) в пренебрежение величинами
(сот)-2 дает для членов порядка (сот)°=1 и (сот)-1 соответственно:
£2o+Migo+M3=0, €i=(A*iEo—А*з)/(2&>+Af 1). (14.34}
Так как
Мг(сУ^\+М1(с2/с2л\+1 = 09 (14.35)
то получим
(1 /с) + i («/«) = (lW^ + h,/W » VX/^ + (S,)/(2™'. j/"Q.
При со—ноо скорость о—*~Соо. Конкретно скорость с» в среде
произвольной цементации с учетом термоупругих эффектов имеет вид
ri = ' ' + W+[fr+'..f)-4w(l-M«)p<'>/(;ip«)]1/2
00 ?*-е 2е„[(1-т,)/я] (р(')/р*)
Р* -Р(,) + («/») р2, г = /»..(!-«О р7(лч>(,)). (14.36)
•« = «./A f = i^(l-^«K*),
л 0/, Л»о(1)а(')7'ф а(!)а(2)Г0\
Предельное значение коэффициента затухания таково:
Ь = 8С = 5.Д23.) = {(Afrf. - M,)/(2S0 + ЗД (1/2x6.), е. = (cjcj.
Воспользуемся зависимостями (14.35) и (14.36) для оценки
дисперсии упругих волн в пористых пластах, насыщенных водой и
нефтью. При пористости т=0,2 для скоростей с0 и с«> получаются
значения, приведенные в табл. 6. Из этих данных следует, что наи-,
Таблица 6
Насыщенная
кварцевая
среда
Водой
Нефтью
Скорость
м/с
Со
Со
е*«0,1
2000
2160
1570
1880
е,= 0,1
2200
2340
1830
2Ю0
е#=0,2
2400
2500 |
2050
2300
е#=0,3
2Б00
2660
2350
2520
е*=.0,4
2800
2830
2870
2720
«•=0,5
3000
3000
2800
2920
большую дисперсию следует ожидать при насыщении мягких сред
нефтью. Поэтому удается выделить пласты мягких пород,
насыщенных нефтью, методами сейсморазведки на продольных волнах. Это
положение подтверждается практикой выявления нефтяных залежей
„ с аномально высоким пластовым давлением (АВПД), например,
в баженовской свите Западной Сибири. Такие залежи
характеризуются недоуплотненной матрицей, представленной мягкими глинами.
120
Для мягких термопороупругих сред дисперсионное уравнение
имеет вид
? - (1 + */С) F + (Р/Д) R (С, А) + (//С) /?, (С, А)}= О,
Ъ = АЛк)-ВЛ11)]1. ^ = (Р(0)/Рда)^(Л)+«(Роо/Р(0))^(Л). (14.37)
l()_ Рр* (1+л)2 ' вЛп)-п-^ l+h3—
С=.р(*)вд)/р00. А = /я,(1 -т,)С<,)С(«)о)/(«С) = 'гвв./вов-
Соответственно для скорости распространения сЛ и коэффициента
затухания б0 имеем следующие формулы:
*я=(1/у1р7) Ко +с,)/(/г,с1+/?1). (14.38)
8° = W2)' /(i + P);gP + Jg,){(£ -l)^WC+(l + ^ ?) * (*)}.
При £<Cl, Л<С1 из формулы (14.38) следует такое представление для
коэффициента затухания ба=бар+баг:
бор= (рО—Роо) ТО)2/ (роо2С0) , баТ= (в0—боо) ТтО)2/ (26аоСо) •
Изложенные результаты широко применяются в расчетах
сейсмических параметров осадочных пород, содержащих нефть и газ [1, 44].
При квазистатических приложениях нагрузки допустимо
пренебрегать инерционными силами, при этом уравнение количества
движения жидкой фазы (14.2) упрощается
т^Т-^)=~(тР.1 (14.39)
и уравнение непрерывности (14.17) принимает вид
/и. ф<2) - (3(1)) p. t - (р(,,/3)Гм. t+v^. = (ф) vV- (14-40)
Введение изотермических пороупругих объемных деформаций
Ke,t=(Tkkl3),t+(l-B*)p,t (14.41)
сводит уравнения (14.40) к уравнению
(rhkl3),t+{l+Km0(f>^
(14.42)
из которого видна роль различия фазовых сжимаемостей р(а).
В отсутствие дренажа из (14.39) следует уравнение Лапласа
V2/? = 0, (v{p=v^)t (14.43)
а уравнение (14.42) дает распределение нагрузки между фазами
р-р0 = Я.(Г*л-Г°л)/3, В,= (1_8А){(1^е,)+/(то(р(2)-р(1))}-1.
(14.44)
Коэффициент В* иногда именуют параметром Скэмптона.
Согласно правилу (14.44), можно подобрать такой коэффициент Пуассона
121
vu, при котором закон деформирования {14.16) принимает частный
вид (предложение М. Клири и Дж. Раиса):
2Geii = rii-vu(\+vu)-Tkkbu, (t/'Wf). ^ (14.45)
Коэффициент v4 соответствует условиям, когда жидкость не
может уйти из среды/Сравнение дает
vtt={3v-5.(l-2v) (l-e.)}/{3+B#(l-2v) (1-е.)}, (14.46)
причем при е*—^0, vu~~^0 (несжимаемость) и Б*—>1.
Закон Гука (14.16) в общем случае представим в виде
2 GeiF=rtj-v (l+v) -lTkiA<j+3 (vu-v) В-1 (1 +v) -1 (1 +v„) -■pfcj.
(14.47)
Условия совмесности, формулируемые для компонент тензора
деформаций, сводятся к шести независимым уравнениям
относительно-полных напряжений и порового давления
V1 [(1 + v) Г(7 - уТккЬч\ + Tkk_ it + 3 (vB - v) (1 - yu)-1 B~l [v>(/+
+ /Ы = 0. (14.48)
Уравнения (14.48) дают полезное соотношение
V'[rfeft-f GK-v^'d _ v>-« (i + V„)-V] = 0. (14.49)
Уравнения движения жидкости (14.42) при использовании vu
принимают вид
(*/|i) V2p= {(3/2) (l+v)"1 (l+vu)-1 (vu-v)/GB} (Гнь+ЗМВ.),t.
(14.50)
Комбинирование уравнений (14.49) — (14.50) приводит к
уравнению Фурье
(Ткк+Зр/В*)л = хУЦГкк+Зр/В*),
(14.51)
x=(*/|i) (2G/9) (l-v)S2,(l-Vu)/(vu-v).
15. УПРУГИЕ ДЕФОРМАЦИИ НАСЫЩЕННЫХ ГРУНТОВ
Инспекционный анализ уравнений пороупругости.
Мягкие грунты. Волны давления и переупаковки.
Плоский одномерный удар. Волна уплотнения.
Применимость уравнения пьезопроводности.
Неодномерные задачи. Замедление диссипации порового
давления.
Проведем [22] инспекционный анализ системы уравнений
динамики мягких сред е*<1. Введем безразмерные переменные о!?. ...
следующим образом
где Fij, Р, Tt Lt ... — соответствующие масштабы изменений. Тогда
величины o(J\ ... имеют порядок единицы. Будем также считать, что
характерные масштабы длин и скоростей при движениях разных ти-
122
пов сохраняются: Li—L, f/|a) ^t/. В безразмерных переменных, если
опуетить для простоты символ «черта сверху», уравнения
динамической упругости имеют вид
(1 —m.) р<'w;>, - (Ft,TiD«;;;.+о - «.) (pt/l)/>. , -
-w^(T£//*)(O;,>-of>) = 0,
P<W)<4-(Pr/L)/7.J. + /KoM^/fe)(t;;1)-yf)) = 0/ (15.1)
PP. t + P.^'i + (UT/L) {(1 - т.) с»!;». + m,o« } = 0,
°i! -e*PF7?bu(l -*.)/> = 0 -m<l){(K-2GI3)FYlebij + 2aF-leii}.
Для волн первого рода (масштабов движения \Ua, Та> La) имеем
(i[/(a)L(a)/(^P(a)) > pt/<a>L<a>/(T(a>P<a>) ~ 1
и система (15.1) сводится к уравнениям [39]
рМ^+л * -Ч(1 -лг1 (W*)>f,-»f))
Область, где справедливы уравнения (НхЗ), оценивается из
условий (15.2) следующим образом: La^TalY^9^ т- е- определяется
сжимаемостью материала фаз и их плотностью. Эта оценка дает и поря- •
док скорости са расширения зоны, где изменения истинного напряже-.
ния в твердой фазе практически равны изменениям порового
давления: Заметим, что если в какой-либо зоне пористой среды скорости
движения фаз равны ui(1)=t;i(2) (это есть условие отсутствия
дренажа), тогда* справедлива оценка UaTa/La~$P, т. е. одно из условий
(15.2). Таким образом, перераспределение давления в отсутствие
дренажа регулируется сжимаемостью материала фаз.
Система уравнений (15.4) может быть также преобразована к
волновому уравнению инерционно-вязкой релаксации при равновесном
условии t>(1) = oj2) и «замороженном» Pq1)o^1)= Pq2)^^2)
т (p,tt-c2oo V2p) ,,+ (p,„-c2o V2p) =0, (15.4)
которое соответствует продольной волне первого рода [см. (14.25) ]
для звуковой волны р = р0ехр i{a>t—idx—х/са). Отсюда справедливы
следующие представления
*_ 1 (/ l+^2 \L, i + gy^/c'o
й, _, tt' f / 1 + x2a>2 \ L _ 1 + с^^/с\
a 2c\ \[l+ с^^/с\ J2 1 + c^W/c\
123
(15.2) . '
= 0, (15.3)
( 15.5)
(15.6)
Характерные кривые представлены на рис. 36, 37. Для масштабов
движения W&\ T<b\ L<b> таких, что:
Р(&)~ЯЬ>; Яь)=217г,-г; FW~K, G; /
/■ (15.7)
e~W(bmb)lL(b>~G(byF(b)~l, /
система (15.1) переходит в следующую, более простую
(1 - да.) 0<;> + mpfA = 0, 0<» = (К- 2G/3) еЗ,.у + 2G*,,,
(1 - m0) P<V ]> = «£ . - (1 - m.) р, t - (ml ф) (tf - of),' (15.8)
w»po v?!t= - m*p. i+Kp/*) (у;(1) - °? ')•
Р°°щтэз
001 \
0,005
I
A
£
w/,
£
*£
-—
-yr=08fS97
га
0,85378
0 SO000
0,92593
J L. 1 1
-4 -z о г ч
Pwc. 55. Дисперсия скорости волны
давления в мягком грунте
-2 -/
0 f ,2nnJ V '5 О
Рис. 37. Частотная зависимость
коэффициента затухания волны давления в
мягком грунте
если пренебречь величинами порядка е*. Использование оценок (15.7)
в уравнениях баланса импульса (15.1) - приводит к результату:
рЦ7(Ь)1(Ь)/(ЛЬ)7(Ь))^Ц7(Ь)7(Ь)/1(Ь)_0/Яь), который дает оценку
Ub)T(b) У (К - 2G/3)/p ~ Тф) VW? масштаба области движения.
Таким образом, скорость расширения зоны, где приращения
эффективного напряжения и порового давления имеют один порядок,
определяется деформируемостью собственно матрицы и плотностями фаз.
Система (15.8) сводится к телеграфному уравнению для
объемной деформации
е, и - ^lc\) V2e - ц (1 - m0)l(km0) ел = О,
с.= 1/УЩ. (15.9>
Скорость с распространения малых возмущений рассматриваемого
типа определяется модулем одноосной сжимаемости В пористой ма-
124
трицы и эффективной плотностью
P. = p51)PoW/(Poc^.)=Po1)PoW{(1 -*.)/??+т.1??}(1 -т^т..
Для монохроматических волн уравнение (15.9) дает
соотношение
Ъ*ь=\—ц*ъ |=Т)С/<о, ^=(Ро/Роо)о)т,
из которого следует
1\={\1У2){У\ТЩ+1)-ЩУЪ)(УТ+Т]%-\). (15.10>
Для скорости сь (рис. 38) волн второго рода имеем
сь = с^ V2 (VT+T/СЧ- l)-1'2,
причем cb-+ct= l/VBp* при С— оо и св~*0 при С-*0.
Ь\*г4рЦР\
(15.11)
-2 5 2 У
2Ьл ^Д°
Рис. 55. Дисперсия скорости волны
переупаковки в мягком грунте
-5,(7 -2 J 0„nnZS SJJ
P*
Рис. 39. Частотная зависимость
коэффициента затухания волны переупаковки
в мягком грунте
Коэффициент затухания волн второго рода в мягких средах имеет
вид (рис. 39)
■A = «(Kl+W-- l)1/2(£*K2yV (15.12)
и соответственно Ьъ—*0 при m—>0 и
Укажем, что насыщенному кварцевому песку, характеризуемому
параметрами:
"10=0,3; pi=2,5 г/см3, р2=1 г/см3,
Pi=2,10-5 МПа-1, р2=4 -10-4 МПа-1, 6=0,01 МПа~г,
соответствуют следующие характерные волновые скорости:
Со= lqpO м/с, Соо = 2200 м/с, с*= 140 м/с.
Затухание волн второго рода на порядок больше, чем волн
первого рода [22]. ь
Таким образом, в полностью водонасыщенных грунтах могут
распространяться только волны первого рода. В сухих грунтах волны
125.
первого рода отсутствуют, а волна второго рода переходит в
обычную сейсмическую волну. Действительно, при р2—►£ эффективная
плотность р *(1—т0)рь а скорость с*— скорость с продольных
волн в сухой пористой среде. /
Отсюда скорость распространения наблюдаемых продольных волн
при переходе через зеркало грунтовых вод возрастает в N раз, где
N = calcb = c.lc„ = VBl$V$)li„ (15.13)
т. е. скорость меняется скачком на порядок [22].
Обратим внимание, что скорости поперечных волн в водонасы-
щенном грунте имеют тот же порядок величины, что и в отсутствие
жидкости. Так, «замороженная» скорость c°°s есть скорость
поперечных волн в сухой среде. Поэтому при переходе через зеркало
грунтовых вод скорость поперечной волны испытывает незаметное
изменение в Ns раз
N. = V{(l-mt)tf>+mttf>}{(l-mt)pll)}-1- "' (15.14).
Скачок скоростей продольных волн и отсутствие скачка для
поперечных волн на зеркале грунтовых вод подтверждаются
наблюдениями.
Если на границе пороупругой среды приложены усилия [22]
порядка F*ij—P*fiij, тогда в первой области движения La, Та
характерные изменения давления и эффективного напряжения будут
Ра ~ (- Р*и) 8/, + Р* ~ О К (F*tlbt, - Р*)},
Р?!^ О{U(F*tl-!»*„)}. (15.15)
Во второй области движения L&, Ть, которая расширяется
медленнее, вносятся дополнительно изменения
Р> ^ (_ F"w) 5,,. - О {., (F•„ - Р*)},
согласующиеся с граничными условиями. В частности, при
приложении нагрузки со стороны жидкости (F*ij=0) изменения эффективных
напряжений имеют е* — малый порядок (отсутствие дренажа), тогда
как давление меняется на конечную величину.
Оценка смещений в первой и второй зонах движения дает
и(<о ~ W^TW ~ FHG-1/» ~ pP(a)L,
tt(b)^fl7(b)7(fr)/wf(b)G-iL(b) >ipP(a>L.
Иначе говоря, смещения матрицы в-первой области uW движения
пренебрежимо малы по сравнению со смещениями во второй волне
«W F^l 0{**(F*!j-P'*ii)} n.17,
и(Ь) ~ F<*> ~ F*4 + 0{e, (F*i} - Р*дч)} ' * * >
если только нагрузки не таковы, что Р*ц—e*P*6/j, или если не
выполнены условия отсутствия дрецажа (t>(1)sst;j2)).
126
Для одномерных плоских движений v[l)s==vil) (х, t), v{2)=v(2) {х, t);
^<а)=0, 1ф\, ч(Ц =я(х, t); 0^=0, 1ф\ уравнения пороупругости
сводятся к двум уравнениям для напряжений:
°. и - c\ot хх + sjip, и + (1 /т#) a, t -f (e*q[v*)p, t = О,
в. « + e*fP. и - cVP. хх +. (г/*,) о, V +' («.?/%) Л *= °-
«•.= !№ l/'» = {l»(l -«.)/(«.P»)>{! + «.•./(! -«.)}-
Pa/Poo^-**/(!-"*»). Л/(1-»«.)^(р1/р)0-р|/(/п.Р,). (15.18)
' = (P*/Po2)) m< i1 '- m»)Hl ~т°- 6*)>
q = (1 - «.)• (1 - да.) {1 - (1 - m, - tj (p,/P) tfS},
f(l _«,-i..,) = (l _/i){l -(1 -«.-..Mp./pj/Cfi}.
Начальные условия будем задавать в. виде
р(х, 0)=о{х, 0)=pft=ott=0, 0<*<oo.
Если применить к искомым переменным преобразование Лапласа,,
то граничные условия для ударов «проницаемого», «жидкого» и
«сплошного» поршней (13.23) — (13.26) соответственно примут [22J
вид
ЩО, Ч)=а*(л), Р(0, л)=0; Р=£(Р), П=1(а),
П(0, <п)=Р(0, л)=Г*/л, dn/di\+MdP/dr\=Q, (15.19>
П(0, т|)=0, Р(0, у\)=Р*М,
причем М = (1 — т0)(р{01) — Pq2))/Pq2). Если воспользоваться условием
e*<Cl, характерным для мягких грунтов, т. е,
т*=т, р*=р, ?=(1—т0)2(1—б*В/р*)>
7=1 —(1—т)е.В/р.,
то решения системы уравнений (15.18) [22] будут иметь вид
для удара «проницаемым» поршнем
П(х,^=(а*/7)){1-е*(^^
+ e»(6^)(^ + ^J(^+TitJr-1(l+TixJ-iexp(--Afljc); (15 20>
P(X>7]) = (c^)r-Mr + ^(l + 73xJ-1{l-(eJr)(l + 7]xJ-2^
X hV (h - р<!)/р#) - 1Ч [(Pl/P#) - (г - 1) (h - q) - (hr - q) +
+ qr\ [exp (1 - Xax) — exp (1 - Xbx)\\
для удара «жидким» поршнем
П(х, т,) = - s^*/^{(l - m0)(r - 1)г-Ч1 +ЧТ.)-'-А} [ехр(-Яв*) -
— ехр(— Хьх)\\
/Ч^)-(/ЭД0^
+-(чЛ0 (p*h) (1 + А^*) (' + ^J (1 + tjxJ-2 exp (-Я,*)- (15.21)
127
Для «сплошного» поршня имеем с точностью до членов порядка е3/2
П (х, ij) = Уч (Г*/Ч) /"(Po'Vp.) (Vjr) (1 + V* + 2М-' • Mr (1 ^
+ ^)Kl+1>'.) + Af(r + 11't»)]-,exp(-V«) + «#(r#/i|)(?H-
+ Ачт#) (1 + т)',)"' ехр (- Хах), (15.22)
Я(х, ^^(^Л^КрГ^/р/Х! + ^*+26Л)(1 +^Г2}1/2Х1
ХМг(1+7,х,){(1 + 7)х,)г + М('' + ^)}-1ехр(-Я^) +
+ (8#Г*/7,)((7 + /г(7х#)(1+^*)-1ехр(-Яах).
В этих формулах Ха, Хь— те значения %, действительная часть
которых положительна.
Я2 = С, 2Ьв = (1 -т0)Р*С- 1)/(p0(1VxJ.
± !/"[/- (1 + ЧЧ) + в#(?г + h^)]2- 4чг^ [?У (1 + -ПЧ)1?* - ""
"- (г -О (А -?)]'}•
Определим теперь величины скачков напряжений и давления на
•фронтах волн. Согласно решению (15.20) движение представляется
в виде двух волн
а(х, t)=oa(x, t)+ob(x, t), (15.23)
а в силу теоремы обращения справедливы интегральные формулы
ааУ*'Ч— 2ni J С*Ч(Кь-Ка) е Щ '
«-<«> (15.24)
а—too
Все особенности подинтегральных выражений находится в левой
полуплоскости. Если окажется, что справедливо представление
gf — xkx = y\(t — хс~х) —xZk(Ti), k = a,b, (15.25)
где 1а(ц), 1ь(г\) стремятся к конечному пределу при |ti|—юо, то это
означает, что интеграл оа обращается в нуль при t<x/ca, а интеграл
tfb—при t<x/Cb. Иначе говоря, са, Съ—скорости фронтов волн сга, оь.
Действительно, рассмотрим, например, интеграл оа- Поскольку
в правой полуплоскости rj=Re (r\)-\-ilm (ц) особенностей у подин-
тегрального выражения нет, аа сводится к интегралу по контуру
полуокружности бесконечно большого радиуса, который равен нулю
в силу ограниченности 1а(ц) при \т\\—*оо и условия t<x/ca. В то же
время, если t>x/ca, интеграл аа отличен от нуля. Это означает, что
в точке t=x/Cb величина аа претерпевает скачок. Аналогично
интеграл оь изменяется скачком в точке t=x/cb. Линии t=x/ca,b—
годографы фронтов первой и второй волн.
128
Пусть* на фронте первой волны напряжение меняется скачком о>
значения а~а до значения о+а, т. е. скачок аа имеет величину
[а]а=а+а—а-а. (15.26)
Так как интеграл аа в точке разрыва сходится к полусумме значений
справа и слева, то
Са (x=cat) = (1/2) (а+а—а-а) = (1/2) [<т]«. (15.27)
С другой стороны, величина oa(x=cat) равна интегралу по
полуокружности i\=R ехр кр, —л/2^ф^я/2 при R—и». При вычислениях
будем пренебрегать величинами порядка е2. и выше
-«/2
^ MV + (ч-^)р^ J 2c* ri4
c'=7^=c" ba=CJ* • (15-28)
Отсюда скорость распространения фронта первой волны
совпадает со скоростью Соо монохроматических волн первого рода бесконечно
большой амплитуды. Скачок [а]а затухает во времени
[a]a=e.a*(A/r) (г—1) ехр (—W), (15.29)
а коэффициент затухания Ьа, как и следовало ожидать, получается
умножением коэффициента затухания по длине пути б» на
скорость Соо.
Существенно, что напряжение в первой волне в мягкой среде
возрастает лишь на малую величину (порядка е*). Таким же путем
получаем, что в точке x=cbt второй интеграл сь принимает значение
1 -«/2
=4~°*(1 -8*7")exP(-V*)' ^ = c. (15.30)
Отсюда на фронте второй волны напряжение меняется скачком на
величину
[<т]ь=о*(1—е.Л/г) ехр (—Ььт.), (15.31)
6ь=1/(2т*)=^6ь^.
Значения сь и 6Ь соответствуют скорости и коэффициенту затухания
монохроматических волн второго рода при <о—мх>.
Аналогично получаем для скачков давления поровой жидкости
\р\а = ~ (°*1г) {1 - («./г) (h - р^/Р*)} ехр <- bat), (
[р\ь = К/0 {1 + (••//•) (й - Po'Vp*)} ехр (- bbt).
9—ЗЗП 129
Итак, при приложении нагрузки со стороны «проницаемого»
поршня эффективные напряжения на фронте первой волны меняются
незначительно, тогда как изменения давления в жидкости имеет тюря-
док приложенной нагрузки. Такой же характер носит распределение
усилий между жидкостью и матрицей пористой среды и при других
способах приложения внешних нагрузок, что соответствует общему
правилу.
Действительно, для «жидкого» поршня из (15.21) .следует
[о]а=— е*р*Лехр (—bat); [р]а=р*(1 — е*А/г) exp (—bat),
(15.33)
[а]ь=е.р*Лехр (—М); [р]ь=е*р*(Л/г) exp (—М)
и для «сплошного» поршня:
К = а*Г*/г exp (- bat), [р]а=- Г* {] - .J/(r + Щ exp (- bj),
Н*= 1ЧГ* Кро1)/^2))^(^4/'Г1 exp (-V), (15.34)
Затухание на фронте первой волны обусловлено исключительно
относительными смещениями фаз из-за различия их инерционных
свойств: Ьа=*6а=0 при pi = p2, обе фазы двигаются как единое целое.
На фронте второй волны затухание будет иметь место всегда при
\хФ0, k=£0, так как здесь происходит переупаковка твердых частиц
с отжимом жидкости. Возможность ухода жидкости из среды
(дренажа) обеспечивается граничным условием типа «проницаемый»
поршень; только в этом' случае амплитуда скачков давления и
напряжения на фронте второй волны имеет порядок приложенной нагрузки.
Знак эффективного напряжения между фронтами первой и второй
волн зависит от совпадения со знаком приложенной нагрузки при
/£>0, или иначе — при (Pi/p)/CB>p2/(/n0p), й противоположен при
/г>0. Поскольку для кварцевого водонасыщенного песка всегда
!ft>0, то эффекта динамического разжижения (of<0) в упругой
постановке в задаче о плоском ударе уловить не удается.
Полное решение задачи удается построить для частных случаев
равенства плотностей (pi = p2) фаз [22] или сжатия среды,
составленной из несжимаемых фаз (ip1=p2=0). В последнем случае l^l-1-*
•—*оо, е*—*0, т. е. первая волна уходит на бесконечность,
«мгновенно» изменив начальное состояние покоя. Нетривиальным
оказывается только решение [22] задачи об уплотнении среды при сохранении
возможности дренажа. Оно имеет для эффективного напряжения otf
такой вид:
•* v \ " сь ) г сь .) у г1 — (х!/сЕ)
*1сь
(f>x}c) о' = 0, (t<xfc). (15.35)
130 •
причём жидкость движется (навстречу поршню) со скоростью
(15.36)
для порового давления
* о
+ -^-J Л (*»/<■-(*/*') а2-*У)"2 **. (15.37)
О
Отсюда за самим фронтом второй волны давление в жидкости будет
р = _ 0* {1 _ ехр (_ 2bbt) + (Р< V.P*) [exp (- 2V) - exp (-Mb
jc-c/ = + 0, (15.38)
а перед фронтом
^=-^{l-[(Po1)-Po2))/P*lexP(-2V)}> *-rf=-0, (15.39)
т. е. скачок давления в жидкости совпадает с (15.32) при е*—*0.
При pi#p2, 'Pi¥=0, Рг¥=0 нетрудно построить решение для малых
времен /<Ст, для чего нужно представить [22] решение в виде рядов
по величине 1/ту. В общем случае следует прибегать к численным
приемам. Характерные кривые распределения давления и
эффективного напряжения приведены на рис. 40.
Для анализа распространения практически наблюдаемых волн
в водонасыщенных грунтах можно ограничиться системой (18.3), или
иначе—уравнением для волн давления (18.5). При этом следует
считать, что вся нормальная нагрузка воспринимается жидкостью.
Результаты будут справедливы с точностью до е* — малых величин.
В частности, задача об ударе по полупространству ставится при
следующих граничных условиях:
р(0, t)=p\ р(х, 0) =/?,*=0, р{х—*оо, /)=0. (15.40)
Решение такой задачи можно представить [22] в виде
><*•<>=-£К'*~"£. *«^*§1^ (,s-41>
L
где путь интегрирования L проходит по действительной оси
плоскости со с обходом начала координат по верхней полуплоскости.
Решение сводится к следующему:
р(х, /)=0, t<(x/Coo)y
р(л,0 = ^ехрЬ(1/2)(х/свт)(1-р^рв}/§(-2//Щ
»
A=(l- pJp.)(l/4 + (3/4)pJp.)(*/Ce,,). (15.42)
где /0 (г) —функция Бесселя.
9" 131
При /*=/— Хх/Соо) <т имеем /0 (— 2/]/Vtf*)^I и решение (15.42);
существенно упрощается.
При лг^сУ/ разрыв практически размывается и решение
аппроксимируется следующим:
р(х, t) = (l/2)p*0(z), /
(15.43)
*=(<**—*) {(po/poo-UcoXt}-1/^!,
\\NN\n \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ х /7*. > \ \\\-чл\ \\ \ \ \ \ \\\\\\ \\\\\\\\\\\ Уч\ \\ .\\
ччччч'чч'ччччч'чучччЧч'чччч '■ ЧЧ JT
ЧЧЧ<ЛЧЧЧЧЧ\ЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧЧ
5¥\
{ -
И-
Л =£^ [~
"
х = £•<*,£
X
р/\р\
-I
*/|л1 Ь—р—
х=с£
K^C^t
\\\^\\\\\\\\\\\\\\\\\\\\\\\\\\\
^ччЧ'ч\ччч\ \\ ч чч ч чч'ч ч ч\ чч\ чл
»/|1
■* *Н
x=c<*t
Рис. 40. Эпюры распределения
напряжений в мягком грунте при ударе
высокопроницаемым (а), жидким (б) и
непроницаемым (в) поршнем
где Ф(г) —решение уравнения Фурье (ф|4=ф|И)':
/"— z
Ф (*)■== |/ -|- f ехР ("""4"ч") d^
о
Аппроксимация (15.43) соответствует «вязкостному описанию»
релаксационного процесса. Можно показать [22], что при 7>т (где
Т *—характерное время процесса) уравнение инерционно-вязкостной
релаксации (15.4) переходит в уравнение
P,tt-c2oV2p+(<r\Jp*) (V2p),t=0 (15.44)
распространения волн в жидкости с объемной сжимаемостью р,
плотностью ро и объемной вязкостью tj=pot(c2oo—с2о) = (т/Р) (ро—
роо)/рсх>.
Квазистатические деформации в мягких средах при условии е*<<
:<С1 наиболее просты. Для них справедливы аппроксимации
vu=0,5, B*=l—/Cmo(.p2^Pi)^l, (15.45)
132
а пренебрежение малыми порядка е* в законе Гука сводит последний
к простому виду относительно эффективных напряжений Терцаги
20е„ = *;';- v(l + vr'o^'V ^ (15.46)
Уравнения движения жидкости (14.39) — (14.40) также
упрощаются
(ГА*/3+Р) .*= №v) V2P, (15.47)
Ke,t=(rkkJ3+p)it. (15.48)
Поэтому начальное условие (отсутствие дренажа) для мягких
сред означает
е=0, *=0. (15.49)
Уравнения (15.47), (15.48) сводятся к уравнению относительна
порового давления ' ^ *
(V*p)9t=(Wv>)V4p. (15.50)
Согласно упрощенной схеме Терцаги — Рендулика — Флорина
[22] в любой момент времени /^0 справедливо решение
соответствующей задачи упругого равновесия в напряжениях, причем на места
последних подставляются суммарные напряжения, которые являются
тем самым только функциями координат. Время может входить
параметрически через граничные условия: о^* — рб^=Г^ (хъ.). Поровое
давление по этой схеме описывается не уравнением (15.50), а более
простым
p>t=xV2p, к=(Кк/ц). (15.51)
В начальный момент времени, в соответствии с условием (15.49)
полагают фильтрационное течение мгновенно установившимся [22].
Касательные напряжения возникают мгновенно и во времени уже
не меняются, что на самом деле не так.
Хотя подобные решения часто используются в инженерной
практике, схема является точной только в случае одномерного плоскога
уплотнения. При этом уравнение равновесия дает необходимые [22J
условия
Гп = of? -/> = <,*, (15.52)
поскольку все переменные зависят только от одной координаты х\.
Уравнение (15.50) после двойного интегрирования сводится к
уравнению (15.51), причем V2= (..,),**. Решение (15.37) при медленном
сжатии среды высокопроницаемым поршнем переходит в решение
уравнения (15.51). При этом скачки давления и напряжения можно
считать полностью размывшимися и решение принимает вид
Р^-Ще-^. t = ^=. (15.53)
* о
что соответствует граничным оЦ0, /) =<j* = const. р(0, t)=0, и
начальному р(ху 0)=—о* условиям. Первые обеспечивают
дренирование жидкости, а начальное поровое давление генерируется быстрой
волной давления.
133
Для скорости оседания поверхности v (О, t) под поршнем при
больших t(tbb^l) справедливо асимптотическое выражение
Другими случаями строгой применимости уравнения
диффузионного типа относительно порового давления являются деформации
в отсутствие чистого сдвига, а также осесимметричные процессы
уплотнения в условиях плоской задачи, причем при плоской
деформации
х2={р-е*+(1/3) (1-И) (1—v)~41—е*)2^}-1^/^),
(15.55)
а при плоско-напряженном состоянии
и2={р-е,+ (2/3) (1+v) (1-е.)2*-1} (%). (15.56)
При точном решении плоской неодномерной задачи соотношения
2Ge=(l-2v)(Tkk+2p)f й=1, 2
(Tkk+2p))t=K0V2(Thk+2p)t хо= (*/|i)2G(l-v)/(l+2v)
(15.57)
сводятся к уравнению относительно объемной деформации
ett=xV2e, е(хи 0)=0. (15.58)
Для решения системы (15.57) часто применяют способ Мак
Нами— Гибсона [22]: компоненты смещений выражают
через'функции S, Е так, что
Ши1(1)=-Я ,+at.S^ «2I)=-£'.2+^S,2-5, (15.59)
(V2£),f=K0V4£, e=V2E, V2S=0, (15.60)
^ = 2G|^e + S.2-2G[^v2^+5.2. (15.61)
Отсюда следует интегрировать уравнения (15.60), Так, осадка
поверхности пороупругого полупространства под действием постоянной
нагрузки q на интервале —а<^.х2<л будет
и. (•*.. 0 = W/(«G)} V (хш, t), V (Xt, t) = V, (хг) + Vt (х„ t),
V. (xt) = (1/2) {(xz - a)la} In {.*, - a)/a} - {(xt + a) I a} In {(x2 + a)/a},
y,(*..0-^J^fO/?)c«(iO*
0 (15.62)
?© = em-r^{l-exp(—^-^erfc^.
При aq-+Pj2y a->0, отсюда получается (по В. И. Керчману) решение
об осадке под действием сосредоточенной силы Р постоянной при
Ui(x29 0 = {^/(2nG)}{—ln|jc2| —(l/2)Ei(—*22/4кОЬ v=0. (15.63)
134
Дифференцирование последнего по t приводит к решению об осадке
под действием мгновенной силы оп=—P8(x2)8(t)
щ(х2у t)={P/{2nG)}i-lh\x2\6(t) +
+ (l/20exp(-jc22/4x/)}, v=0. (15.64)
Главным эффектом, который пропускается при расчетах по
теории Терцаги — Рендулика — Флорина, является появление зон
значительного повышения порового давления после приложения
внешней нагрузки (эффект Манделя — Крайера).
16. ПОГЛОЩЕНИЕ И ОТРАЖЕНИЕ ЗВУКОВЫХ ВОЛН
ПОРИСТЫМИ МАТЕРИАЛАМИ
Газонасыщенные пористые среды. Скачки
давления и напряжений. Термоупругие эффекты. Волна
по газу. Отражение волн от пористых слоев.
Для нахождения величин скачков давлекгия и напряжения в
газонасыщенных средах в зависимости от прилагаемых нагрузок
проанализируем задачи о плоском одномерном слабом ударе. Система
уравнений (14.16) относительно трансформенты Лапласа Р, П от pf
а соответственно имеет вид [22]
г)[л+(^+т)(г/т)]П = с2г(^Р/^2)-е,л(/л+^/т)Л
<+r(#Pldxf)— c2r{{r+s*f)y)+[r(n+m) +
+**qr]/x}(d*P/dx*)+B.r\4(f-h)ri+
\ +[Q(>r-l) + (n+m)(f-hr)lT}P=0. (16.1)
Для газонасыщенных сред (pi>p2; P2^'Pi5) коэффициенты
таковы: p^pi, h^(l—m)p2/{mpi), с2=1/(рВ), r=m2(l—m)pi/&&, /=
= (1— m)ln, q=(\— m), r=m(l.—m) pi/(np2).
Поскольку /np2/B»l, (16.1) сводится к уравнению
£ ~ * {&+-& ^o^}^-7^.^ + ^)P = 0( (16.3)
где с* = 11УЩ>, ет = 1 lYfaf, а ^ = 2р<2> Й/ftun) - коэффициент
затухания. Ограниченное на бесконечности решение имеет вид
р(•*. f\)=Ai ехр(—fax) +А2 ехр(—%2х),
(16.4)
%\=л/сК, к22=ц(у]+2Ь00)/с2<х.
Если удар производится «жидким» поршнем, то в силу первого
уравнения (16.1) имеем соотношение
cVYW-t)0) + 2&*)P=0, ;c = 0, (16.5)
т. е. ;4i=0, А2=р* 1т\. Решение (16.4) сводится к следующему:
Р(х. 71) ~ {р*Ы) ехр {- (x/cj у-п (т) + 26J}.
135
Само давление распределяется по закону
р(ху /)=0, t<x/Coo,
p(xjy=p*hxp(J^y^ j exp(-60e)X
/
/
X— >- =g- rfz, +>xc^. (16.6)
При ударе «проницаемым» поршнем из системы (16.1) следует
р(х> r))=Ai{exp(— Х\х)— ехр(—ta*)b
(16.7)
с2со(Я21— Я22)Л1==В(1— т0)-1п(тр2)^п{л+(п+т)(г/т)}(а1/л).
При Ро^^Р^Рг справедливо приближение
Coo(.?i2i— Л22)^—л (Л+2М,
Л1 = -В(1-т0)-1/г(тр2)-1{т1+(Аг+^)(/'/т)}(т1+26оо)-1(аНс/л).
Удару «сплошным» поршнем соответствует решение
Л^О, Р(х, ri)^0, П(*, г\)ъ(о*1ц)екр(-1\х/с)9
(16.8)
р(*, /)^0, а(х, /)^а*, t>x/c*\
в(х, 0^0, t<x/c*.
Таким образом, при падении волны из газа на пористую среду,
насыщенную газом, в ней возникает волна «по газу». Среда ведет
себя подобно акустическому поглотителю с абсолютно жесткой
матрицей: нагрузка на матрицу будет пренебрежимо мала.
Соответственно чрезвычайно слабой, хотя и «не затухающей», будет волна по
матрице (второго рода). Если же удар наносится по матрице ^азо-
насыщенной среды, то, как следует из решения (16.8), давление в
газовой фазе практически не меняется, а приложенная к границе
нагрузка распространяется по матрице в виде незатухающего скачка
(амплитуды удара) со скоростью с#=1/у р^В.
Для оценки истинного затухания звуковых волн в пористой
газонасыщенной среде следует учитывать дополнительно термоупругие
эффекты. Общее дисперсионное уравнение для термопороупругой
среды за счет условий
Ро ^Ро > Р ^Р »Я» ,169)
а(2)»а(1\ С(2)>С(1)
может быть значительно упрощено
I4 + {1 + (Р<,,Р(,,/Р(1,Я) Л* (А) [1 + («7««.)]} $г (P<1>P/P(,)S) 11 +
+ (»/•<,)] М (А) = 0.
M(/0=:(l+AV)(l+/*2r'+<[l -0/Т.)]А/0+#. (16.10);
5 = {-nHlVW^B. *, = *.P0W/(«#).
136
Для первой и второй продольных волн справедливы условия
^ = (Ро2>/Ро1))(Р<2)/^){1 +(«7v)>Af (h), fb= 1. (16.11)
В соответствии с результатом (16.8) в насыщенной газом упру*
гой пористой среде звуковые колебания, соответствующие второй
волне, распространяются без затухания со скоростью, определяемой
только упругими постоянными матрицами и ее плотностью.
Затухание подобных колебаний связано с диссипативными процессами
внутри твердой фазы. Сч ростом жесткости е* пористой среды скорость
второй волны приближается к скорости звука в сплошном материале
матрицы. В то же время скорость первой волны определяется
сжимаемостью газа; при малом давлении в газе эта волна будет мед-*
ленной. Эта волн! иногда именуется волной «по газу» или
«воздушной» волной. Матрица среды при ее распространении практически
неподвижна и является «абсолютно жесткой».
Уравнения движения газа в абсолютно жесткой пористой среде
нужны для анализа эффекта поглощения звука пористыми
материалами. При m=const, а<2)=0, $<& = 0 имеем
р-!+р?Ч?,=°. ро1 Ч(2),=- р., - w*> »*>? .
р(2)/р(2)=р(2)/7_а(2):Г(2)) (16Л2)
mfimT™ =mtDi2)v2Ti2) - и (Г(2> - 7(1>),
(1 -/я,)С(1)Г<» =(1 -m0)D(Vr(,) +н(Т<2> -T(I,)+«.a(,,7>,.
(16.13)
Для анализа звуковых колебаний можно пренебречь
температуропроводностью. Тогда можно рассматривать уравнения баланса
масс и импульса для газа (16.12) совместно с уравнением релакса»
ции его температуры
Г;2| +*r7(2;, = (m^TJC) р,,- (а<2)Г0/С<2>) *тр\ „, (16.14)
где хт=Шй(\—т,) С<'>С(2>/ (кС).
Если теплоемкость матрицы бесконечно велика С«к(1—то)Х
"XCW&ntoCW, то уравнение распространения звука принимает вид
P. u-cWp-{w,lk^)p. ,= (а(2>/р(2))Г.(2г<+(а<2)/Р(2))(^./^,)) Т»
(16.15)
T<2> = (a^T0/C<2>)it,,<-r<2Vxr
где ст — изотермическая скорость звука в свободном газе. Для волн
малых частот имеем»
с —О, 5^(1/сг)|/^7(2^), о)х<1, «*г«1, (16.16)
т. е. пренебрежение температуропроводностью недопустимо. Обра*
щение скорости с в нуль соответствует вязкостному торможению га-»
137
за. Если пренебречь полностью вязкостью газа, то справедлива иная
оценка • /
c~cq = VT2cT; 8~ l/(2^) + (Ti - l)/(2xfy), Х16.17)
сот^>1, С0Тт>1,
т. е. волна распространяется с адиабатической скоростью звука в
свободном /азе cq. При пренебрежении вязкостью газа величина
определяется только вторым слагаемым (т-^оо).
Для нахождения тг нужно знать коэффициент
теплообмена к
TT=m0C(2)/>c=e/2C(2)7D(2), (16.18)
где-для щелевых каналов ширины 2/ имеем 6=1/3, а для круговой
поры радиуса / коэффициент 9=1/8. Поскольку для газов D2lc2^/
^'М'2/р2, т. е. теплопроводность имеет порядок кинематической
вязкости, а I2—й, то %т—т. Отсюда для больших частот
Ь=у2/(2с8%). (16.19)
Оценки по формуле (16.19) показывают,, что газонасыщенные
пористые материалы обладают исключительно высокими
поглощающими свойствами для звуковых колебаний.
При динамическом воздействии на газонасыщенную пористую
среду жесткости е*'—'1 скорость распространения волны давления
будет определяться формулой (16.17), а переносимый ее скачок будет
затухать со следующим коэффициентом затухания:
6=й.+ (72-1)/(2тг), Ь* = /тнг/(2р(2>£). (16.20)
Отражение волн от пористого насыщенного слоя изучается с
помощью уравнений относительно смещений фаз (14.18). Если
смещения tf(e) представить в виде
u[e) — (grad <р(а) + rot г|>(а)) ехр (- Ы), (16.21)
где <р(а\ ЧГ|а) —функции только коордвдат х}, то уравнения (14.18)
сводятся к векторному
Q2 _ рО) (1 — m0) в>*у« + ib(* (1 + v*) y, _ i i frMPo (]f\99\
Я^-- (l-mo)lxv, ■ V.--1 + Р^(1-т0) {lb'ZZ)
и к скалярным уравнениям Гельмгольца
V2xk+(*2X2hxh=0, k=ay b,
(16.23-16.24)
Здесь А,а, kb соответствуют волнам первого и второго рода и
являются корнями следующего биквадратного уравнения:
138
N, - N2X* + NUX4 = 0, Nt = 1 - p<2> К + |ш- X)*1.
^ l^m,. l
2 В (1—т0)р(,) + ш4(о-1"Г
3 Vj> I [(1— тв)р(1) + ^со-1]Вш4(о-1 ""[(I—/и0)р(1)+ш4(о-1] j^co-1'
где dk определено формулами (14.18), а компоненты Ма,ъ связаны
с корнями Ка, ь следующим выражением:
м = 1 - (1 -ж,) В-1 [(1—iwq) р(') + йц»-1]-1*»
iKI* (1-е,) (1 -m.) m,»-» [(1 -m0) p<») + i«->flj«^ + *л4ю-*
Ограничимся [22] плоскими, падающими по нормали к
поверхности раздела волнами
%k=Ak^xp(±UoXhX)9 k = a9 b. (16.26)
Пусть плоскость х=0 разделяет две среды с различными
свойствами. Параметры для полуплоскости л:>0 будем обозначать индек*
.сом «+», в полуплоскости х<.0 — индексом «—», а разницу
значений— индексом [...], например: иг—и+=[м]. Тогда условия
непрерывности смещений частиц твердой фазы, которые должны
выполняться на границе х=0, примут вид
^ [dldx(xa+xb)]=0. (16.27)
Должны также выполняться условия сохранения массы жидкости
[m0(d/dx)(MaXa+Mb%b)]=0, х=0; (16.28)'
непрерывности давления в жидкости, что для смещений дает
[{то (1-«о) (1 -е*) р-1+т2ор-1Ма}Я2оХа+
(16.29)
+ {т0(1-/По) (1-е*)р-,+'п2ор-1Л1ь}Я2ьхь]=0
и, наконец, непрерывности суммарных напряжений
[{(1_те,)Д-' + (1-«.)«.?-*(!-0 + «.p-*(l-«JO-».)^« +
- +w,.p-,Afe}a.,A + {(i_«,)^-+(i-«.)m.p-,(i-0 +
+ /и,(1 -в,)р-'(1 -то)Мь + т\$-*Мь}Х\Хь] = 0. (16.30)
Если из насыщенной среды на границу среды падает волна
первого рода единичной амплитуды, то эти соотношения упрощаются
%~ = ехр (-— ЬХах) + А~ ехр (— wX~x);
» Х+ = Л+ ехр (— тХ+х);
хГ = ЛГехР(-млг*); (16-31)
X+ = A+exp(—i<Afx).
139
Часть энергии падающей волны расходуется на возбуждение бы-
строзатухающей волны второго рода у поверхности раздела. Эта
ситуация существенна при отражении волн от контакта газа с ж#Ьдо-
стью в пористой среде [22].
Прохождение волн низких (сейсмических) частот через/контакт
двух жидкостей в одной и той же пористой среде, а также через
тонкую непроницаемую границу, разделяющую две пористые
насыщенные среды, описываются такой формулой [22];
Л"— (РоО+—(Polg)" Л+_9Са (Росд)"~ Mfi49\
г
. 1"^pis
В' Ш*С1> Ш7
Рш\ 47. Коэффициенты отражения и прохождения сейсмических волн для двухфаз-
ного и «эквивалентного» пластов
а, б ** продольная волна, в, г — поперечная волна
140
которая точно соответствует известным формулам динамической
упругости, но с введением са вместо с.
В. А. Барзам разработал алгоритмы расчета коэффициентов от*
ражения волн, например, продольной волны Pi первого рода — Rp\p\
и прохождения, например, поперечной волны 5 после падения волны
Р\ первого рода — fpis для пластов произвольной толщины h и
пористости т. Характерные результаты для пласта нефтенасыщенного
песчаника, находящегося между газонасыщенным и ' водонасыщен-
ным полупространствами, приведены на рис. 41 и соответственно
обозначены индексами айв. Для сравнения даны результаты
расчета для модели «эквивалентной» однофазной среды (индексы б
и г). Цифрами обозначены значения углов падения волн Рь 1) *ф=
= 0°;о2) -ф=10°; 3) t|)=20o; 4) ^=30°; 5) г|)=40°; 6) г|) = 50°; 7)ф =
= 60°. Величина К — длина волны, параметр сцементированности
е* = 0,17. Видно, что эффект реальной двухфазности среды приводит
к более сильным относительным изменениям |#pipi| и \TP\S\ при
варьировании длины волны. ~
При падении волн на контакт глинистых пород (кровли пласта) и
песчаного коллектора в большом диапазоне углов падения
интенсивность отраженных волн намного меньше при насыщении коллектора
водой, чем при насыщении его нефтью или газом. Для проходящих
продольных (1 рода) волн эти различия менее заметны.
"Поскольку газ и пластовая нефть (из-за растворенного в ней
газа) термически активны, как это отметил Л. А. Сергеев [44], то
расчет по более сложной системе уравнений при Тфconst должен
еще больше усилить эффекты двухфазности для нефтегазовых
коллекторов.
В. А. Барзам рассмотрел также задачу
слоя водонасыщенного песчаника (Л=10 м),
&• 5
о колебании
лежащего на
тонкого
гранит-*
К'Г
ZF \-
Z0
/г
— 1
Ь Ь=\ г
Г 1 H--J-
А
А
Z8
го
IZ
j i
Ji
jk -
W /ZO со, Гц 80 fZO <*>,Гц(
Рис. 42. Неоправданный резонанс колебаний пористого насыщенного пласта на
полупространстве при учете «^присоединенной» массы
/ —Я-1:' Я~Я-2; 3-Я-З
141
ном основании, под действием поперечной S V волны, падающей под
углом -ф = 30°. Для гранита е*=0,7, для песчаника е*=0,21. Цри
этом расчет велся как по системе уравнений (11.26), так и с учетом
присоединенной массы pi2=—т0р(2)о(Е—1) по М. Био [22].
Результаты расчета в виде зависимостей модулей горизонтального и
-вертикального смещений \и°х\ и \u°z\ от частоты —даны на рис.42.
Видно, что при Еф\ (т. е. р12=т^0) графики имеют ярко
выраженные максимумы (при со=133 и 146 Гц). Согласно натурным
наблюдениям, резкого изменения колебаний при наличии хорошо
сцементированного песчаника в указанном диапазоне частот не
наблюдается [резонансная частота слоя сон оценивается как cs/(4#)—36 Гц].
Таким образом, расчеты при pi2 = 0, по крайней мере для
низкочастотного диапазона сейсмических волн, представляются вполне
оправданными.
Г Л А В А 5
НЕУПРУГОСТЬ И НЕОДНОФАЗНОЕ НАСЫЩЕНИЕ
ПОРИСТЫХ СРЕД
17. НЕУПРУГОСТЬ И РАЗРУШЕНИЕ НАСЫЩЕННЫХ СРЕД
Критерий разрушения насыщенных сред. Упруго-
пластическая дилатансионная модель. Нелинейные и
неупругие изменения пористости и проницаемости.
Эффекты влагопереноса в очагах землетрясения.
Изменения проницаемости после взрыва. Разжижение
грунта. ,
Условие возникновения пластических деформаций насыщенной
пористой среды формулируется (согласно принципу Терцаги) путем
простой замены полных сщ на эффективные напряжения о(у в том
предельном условии, которое справедливо для рассматриваемой
среды в отсутствие жидкости, т.-е.
фа=фа(т(/), р</>, у)—о. (17.1)
Здесь р(/)=а+р, т(/)=т — эффективное давление и интенсивность
касательных напряжений в матрице. Было экспериментально показано,
что в качестве Фа можно применять условие Кулона
фа= (2/1/3)еттС>—«р<Я— У=0. (17.2)
В соответствии с критерием (17.2) сдвиговое разрушение
насыщенной среды происходит при напряжениях, меньших на
величину р, чем разрушение той же среды с пустыми порами.
Действительно, в насыщенной пористой среде только -часть р* нормальной
нагрузки приходится на матрицу (скелет) породы, а другая
воспринимается жидкостью, тогда как касательные усилия полностью
воспринимаются матрицей. Что касается развития деформаций в ходе
нагружения при выполнении условий (17.1), то характерная
картина (по Дж. Хандину, [31]) приведена на рис. 43. Видно, что
введение эффективных напряжений действительно позволяет почти пол-
М42
ностью свести деформацию е\(р> оц) к зависимости только от
эффективного напряжения е\ = е\{?^) —такой же, что и для сухой
среды (при р^=0, когда о^ =о/у).Чем ближе поровое давление
(выдерживаемое постоянным в ходе указываемых опытов) к давлению
бокового обжима, тем ближе характер разрушения к хрупкому
(отмечается сброс усилий на, машине нагружения), а чем больше
различаются поровое давление и давление бокового обжима, тем
разрушение ближе к пластическому течению.
тгМПа
дОО
<?/= SOMHa
бj ~ SO: Р-0 (сухая порода)
J I I I I I I
8 to tl № 16 /в 20 П е?°/9
Рис. 43. Описание разрушения насыщенной среды при использовании эффективного
напряжения
Полные деформации матрицы насыщенной среды ец
разделяются на упругие и пластические
detl = de\e}+del>K (17.3)
Закон Гука (14.8) в приращениях имеет вид
Л'„ = Kbtlde{;l + 2G(de(* - <te%/3) + f'Kb^dp, (17.4)
где pi — объемная упругая сжимаемость материала матрицы.
Пластическая деформация определяется условием (17.2) и неас-
социированнымч'законом течения
de\P! = К + (2/3) АаНЬч + (! + 2Ла/3) Pm*i№- (17-5)
143
Соответственная деформационная упругопластическая модель
[34] представляется в виде ,
dy=dy^.+dyiP\ dy^=dx/Gf
/ (17.6)
de =deW+deP\ de&=K+doW+K^dp,
где вводятся коэффициенты /С*, /(** и модуль упрочнения Л,
dyW=(l/h)(di—adoW),
(17.7)
d№=A\dy^\.
При реологических испытаниях образцов в условиях дренажа
поровое давление сохраняется постоянным, что позволяет измерять не-;
посредственно параметры /С, G, а, Л, Н и следить за выполнением
«принципа Терцаги». При опытах без дренажа уход жидкости из
испытуемого образца исключается и это означает
0го«0(,) =е. (17.8)
Уравнения непрерывности (14.1) в линейном приближении
m0f]dp -\-dm-y m0vl4,\ dt = 0;
(17.9)
-.р<аШ>>,+ (1 ~-m№)dp-dM-\-(\ -m,)de = 0
приводят условие (17.8) к ограничению на объемную деформацию
de=deM+deW=!pnjoW-$dp. (17.10)
Поскольку коэффициенты pi, р2 намного меньше, чем 1//С, а тем
более эффективная пластическая сжимаемость Л/Л, в дилатансион-
но-уплотняемых средах при сдвигах должно наблюдаться
чрезвычайно быстрое возрастание порового давлениями зыход
фигуративной точки на предельную пластическую поверхность Фа(т, of)
'происходит при весьма малых эффективных давлениях (хотя полные
давления oiftkj и могут быть весьма высоки). Это эффект дилатанси-
онного ослабления насыщающей среды. Наоборот, сдвиги дилатанси-
онно-разрыхляемых сред относительно безопасны — при них поровое
давление будет падать, а среда дилатансионно упрочняться.
Экспериментальные исследования [4, 31] показывают, что при
сдвиге в условиях малых эффективных напряжений поровое
давление падает (матрица разрыхляется), а при больших — поровое
давление растет, и матрица разрушается при меньшем сдвиговом
усилии. Из (17.10) следует, что в отсутствие дренажа невозможно
пренебрегать малыми допредельными неупругими дилатансионными
деформациями.
Проницаемость в условиях одноосного деформирования с ростом
эффективного осевого давления <з( у меняется [9] примерно по
экспоненциальному закону [9, 22], причем показатель экспоненты аъ
на порядок меньше, чем показатель ат уменьшения пористости т,
k=k0exp(—ak^f)), т = т0ехр(—ата(/)), (17.11)
k/ko=(m/m0)n, n=ak/am^l0, am~10"3 МПа.
144
Если матрица включает в себя сильно сжимаемые составляющие,"
например неподвижные пузырьки газа, проницаемость системы
будет зависеть и от порового давления (за счет большого
коэффициента Pi), и от эффективного давления. Изменения пористости т
при больших сдвиговых деформациях примерно соответствуют
изменениям объемной пластической деформации. По мере
сдвига т вначале убывает, поскольку происходит дилатансионное
уплотнение порового пространства, а затем, после достижения
значения тд, пористость начинает возрастать —происходит дила-
80В
Vzfcf-Gj},
ПЁЗ>
ГТ12
'ЦП*
га*
МП а
■l±2
[jU
m
5'
6
7
/
/
/
/
/■
/
Рис. 44. Спад прочности гранита «Уестерли» под действием влаги
Содержание H2Of %: 7—0; 2 — 0,8; 3—1,0; 4-~ 1,3; 5 — 2,6; tf—залит водой; 7 — валит керо*
chhoiT (по А. Дуба, X Херду, М. Сантору)
тансионное разуплотнение (см. рис. 6, так как dm—de*>). Проницае*
мость, однако, не повторяет этой зависимости.-При дилатансионном
разуплотнении уменьшается лишь темп убывания проницаемости.
Это объясняется дроблением зерен (катакластическим течением),
сопутствующем деформированию, и заполнением поровых каналов бо-
10—3311 ... 145
лее мелкими частицами. Иначе говоря, уменьшение эффективного
диаметра d поровых каналов препятствует возрастанию
проницаемости: k^d2f (m), где /(m) — возрастающая функция, примерно
Соответствующая (17.11) (при фиксированном id). При этом характерно
появление сильной анизотропии среды по проницаемости. /
При разрушении в очаге землетрясения происходит появление
характерных дилатирующих зон. Так, очаг, соответствующий ката-
кластическому разрушению, представлен множеством мелких
трещин, образование каждой из которых дает сейсмический удар, а их
совокупность — рой землетрясений. В этом случае очаг в целом
представляет [29] дилатансионный объем. Возникновение трещинной
пустотное™ на .глубине очага приводит к продвижению воды (при
высоких температурах — водяного пара) в область очага. Вода
снижает трещиностойкость, а следовательно, и прочность (рис. 44)
геоматериала. В результате оказывается, что развитие очага
землетрясения контролируется волной водяного пара [29]. Оценки и
зависимости времени 8 длительности предвестников землетрясения от
линейного масштаба А массива, вовлеченного ъ землетрясение (зоны
афтершоков), — показывают вполне реальную возможность такого
хода событий [29, 37]. Если при землетрясении на фоне
сейсмических толчков выделяется главный удар, то в очаге ему
соответствует появление магистральной трещины. В этом случае дилатансион-
ные мелкие трещины концентрируются в виде облака вблизи
вершины главного разлома. Перенос влаги также контролирует
развитие этой зоны, а следовательно, и наступление момента
неравновесного динамического роста разлома (главного удара).
Сами прогностические признаки предстоящего землетрясения
определяются появлением дилатирующего объема. Это приводит к
подъему свободной поверхности земли или океана, увеличению в
грунтовых водах радона или гелия, выделяющихся при образовании
све^кйх трещин в горной породе. Электромагнитные сигналы связаны
с изменениями электросопротивления дилатирующих горных
массивов, а также с разрядами, обусловленными поверхностными
зарядами в бортах трещины. Миграция ионов во влаге, содержащейся
в системе трещин, усиливает электрические эффекты.
Сейсмоскоростная аномалия — падение скоростей продольных и
поперечных волн в зоне очага перед землетрясением—является
прямым показателем появления самой дилатирующей зоны. Ранее была
предложена теория [29], согласно которой приток воды к дилати-
рующему очагу приводит к восстановлению скорости продольных
волн к самому моменту подземного удара. Позже стало ясно, что
восстановление сейсмоскоростей объясняется локализацией
деформаций в полосы сдвига, но именно движение влаги контролирует
развитие очага землетрясения.
Представления о трещиноватости земной коры (рис. 14) и о
возможности проникания поверхностных вод вплоть до границы Мохо-
ровичича [29] приводят к отождествлению волноводов с областями
повышенной дилатансионной пустотности, причем возможно
насыщенной водой и водяным паром. В этой связи следует вспомнить
объяснение М. Хабберта и В. Руби для наблюдаемых в природе
146
р.кг/см3
ZJ
го
больших надвигов (сорванных покровов) слоев горных пород. Эти
авторы связывали эффект с присутствием воды, которая
воспринимала на себя нормальную нагруаку и, в соответствии с формулой
(17.2), снижала касательное усилие, необходимое для пластического
течения. Альтернативное объяснение, которое можно предложить,
связано с приобретением геоматериалами (в условиях р, Т между
границами Конрада и Мохоровичича) сверхпластических свойств,
т. е. снижения в несколько раз касательных усилий, вызывающих
большие пластические деформации..
Динамическое деформирование
насыщенного массива (при взрыве,
ударе) происходит, по-видимому,
в отсутствие дренажа, хотя
наблюдается относительное инерционное
смещение фаз. Приведем здесь
характерные результаты
лабораторного моделирования [4] камуфлетнога
взрыва в насыщенной (керосином)
искусственной высокопористой
среде (т—25%). Оказалось, что
остаточная взрывная полость близка по
форме к сферической, взрывные
трещины вокруг полости
отсутствуют, причем до радиуса г=г/Е=
=0,8—1,0 м/кг1/3 матрица среды
дробится. Применение
гамма-плотномера к дискообразному срезу
среды после взрыва показало (рис. 45), что вокруг полости
последовательно выделяются зоны разуплотнения и уплотнения. Зона
разуплотнения (до 10% от начального состояния) простирается да
г=0,22 м/кг1/3, зона уплотнения — в интервале (0,22^:^0,8—
—1,0) м/кг1/3. Максимальное уплотнение достигает 5% от
начального состояния. По сравнению с действием взрыва в сухой пористой
среде радиус зоны уплотнения увеличивается в два раза, а само
уплотнение уменьшается в три раза.
Таблица 7
—/
Г =Г°
р*
\^ г -
——=
01 04
ОБ
08
/О
Рис. 45. Остаточные распределения
плотности и проницаемости после
взрыва в насыщенном пористом
камне
Зоны
Полость а
Разуплотнение
Уплотнение
Трещиноватость
Внешний радиус зон г, м/кг1/3
насыщенная среда
0,Ю5
0,21
0,9(+0,1)
Нет
воздушно-сухая среда
0,12
0,32
0,48
Единичные случайные
радиальные трещины
До и после опцта измерялось сопротивление фильтрационному
потоку между последовательно расставленными скважинами.
Оказывается, что сферически-симметричный взрыв приводит к
возникновению трех различных зон (рис. 45). Ближняя к полости зона
(табл. 7) характеризуется существенным улучшением
фильтрационной проводимости (до 10 раз). Внешний радиус этой зоны г=
147
= 0,45 м/кг1/3. Во второй зоне (0,45^/^1,0) м/кг1/3 взрыв ухудшает
фильтрационную проводимость Гф среды по сравнению с
исходным— в среднем на 30—40%, Наконец, внешняя зона /(г^5
^1,0 м/кг1/3) — зона возможного слабого улучшения
фильтрационной проводимости. Ее появление обусловлено слабым, нр/ много-
цикловым воздействием взрывной волны на дальних расстояниях,
которое приводит также к изменениям порового давления.
Укажем теперь и другие следствия динамического повышения
порового давления. Так, при взрыве «Ардварк» (США) был
отмечен крупномасштабный подъем грунтовых вод. На 40-й день
после взрыва на расстоянии в 307 м (по горизонтали) от точки
заложения заряда (35 кг на 71 м выше зеркала грунтовых вод)
уровень воды был на 17 м выше статического. Оценки [4], основанные
на расчетах фильтрационного растекания этого «горба»,
показывают, чтр максимальный подъем уровня вблизи стенок полости, в
зоне ударного уплотнения £г=50—-80 м), достигал сразу после
взрыва 200 м. Таким образом, уплотнение пор мягкого грунта
может приводить к резкому подъему грунтовых вод.
Таблица 8
Песок
Мелкий среднеоКатанный
Мелкий хорошоокатанный
Мелкий плохоокатанный
(подводный намыв)
Среднезернистый .
Пористости т, %
44—45
' 38
46
37—38
Глубина уровня
грунтовых вод,
1 м
0,5
0,2
1,0
0,3
Средняя осадка
на радиусе
5 м, см
22
5
24
7
Средний радиус
осадки, м
22—30
10
20
3—10
При взрыве и землетрясениях возможна также опасность
разжижения грунта. Например, при взрыве заряда мощностью
500 ТНТ, заглубленного на 7 м ниже уровня грунтовых вод [4],
возникла необычно широкая и плоская воронка. Через 20 мин на
расстоянии 80 м ударил гейзер, а повышение порового давления
отмечалось в зоне радиуса в 820 м. При ядерном взрыве КОА
(1300 кт) в насыщенных песках и рифах песок буквально «кипел».
Подробно взрывное разжижение грунтов описано П. Л. Ивановым.
Наиболее опасными с точки зрения разжижения являются рыхлые
грунты (плотность менее 15 г/см3). Взрывная полость .при камуф-
летном взрыве пульсирует как и при взрыве в воде, что говорит
о разжижении грунта в ее окрестности [4].
Если осадка от стандартного взрыва (5 кг заряда на глубине
4,5 м) на расстоянии 5 м в среднем составляет менее 8—10 см, то,
•согласно П. Л. Иванову, опасности разжижения нет (табл. 8). Если
взрыв производится на самом зеркале грунтовых вод, то глубина
возможного разжижения примерно в 1,5 раза больше глубины
заложения заряда [4]. Радиус разжижения Rfe может быть оценен
по формуле
Значения коэффициента |Wi приведены в табл. 9.
148
При групповом взрыве разжижение интенсифицируется, причем
наиболее эффективно расположение зарядов с промежутком 5 по
горизонтали
Таблица 9
Песок
Мелкий
Средний
Относительная
плотность
0—0,2
• 0,3—0,4
0,4
0,3-0,4
0,4
Nx
25—15
9—8
7
8—7
6
АГЯ
5—4
3
2,5
3—2,5
2,5
На дальних расстояниях от взрыва [4], как и при
землетрясениях, опасность разжижения связана с многоцикловым
сейсмическим воздействием.
Согласно классическому объяснению Казагранде, при сдвигах
в рыхлых песках люровое давление повышается,, а если нагружение
кратковременно, то поровое давление не успевает йиссипировать.
Повышенное давление ведет к уменьшению нагрузок оУ\
сжимающих матрицу, т. е. при фиксированных полных напряжениях oij
грунт достигает предела прочности (на сдвиг, на отрыв) и
переходит в жидкое состояние. Отсюда разжижение может происходить
в грунтах, плотность которых ниже критической. Опыты показали,,
что разжижение таких песков происходит на девятом цикле
воздействия. Вместе с тем оказалось, что плотные пески также
разжижаются, но для этого требуется более 800 циклов [4]. Утверждается,
что нагрузка обеспечивает более легкие условия для разжижения.
Это соответствует общему положению о том, что с ростом внешнего
обжатия критическая плотность растет (плотные пески под
обжатием ведут себя подобно рыхлым — могут дополнительно
уплотняться). Вместе с тем значительное предварительное увеличение
внешнего давления в условиях дренажа само по себе приводит к
большей плотности, т. е. к большему числу циклов, нужных для
разжижения. Чем больше амплитуда вибровозмущений, тем
меньше циклов нужно для разжижения.
18. УДАРНОЕ СЖАТИЕ НАСЫЩЕННЫХ СРЕД
Гидродинамическое приближение. Соотношения на
фронте ударных волн. Инерционно-релаксационная
структура волны. Тепловые эффекты при сильном
ударном сжатии. Гипотезы замыкания ударных
соотношений. Учет сопротивления пор схлопыванию.
# Ударное охлаждение одной из фаз. Расчеты для
экстремально неоднородных смесей.
Если давления при ударном сжатии значительно превосходят
прочность материала, то вполне допустимо пользоваться гидроди*
намическим приближением* считая оц=—p6tj, что упрощает систему
149
уравнений балансов массы, импульса и энергии
{(l-«)p«,>}.< + {(l-m)P«,)of,}.»^/{V\/44«PWof,}.i = ^(1M)
(1 -m)9(l)dlv{;)ldt = -p«] - (1 -т)р™. -Rlt/ (18.2)
mp^d^/dt = - да/jj2} +#„ (18.3)
(1 -m)p(l,rf,(«<1> + ^'У1>/2)/'Л + {(1 -mjp0'»)0}. i +
+ /><2) (1 - w),, + (1 _ 9)R,vf> + в^».(,) +/ = 0, (18.4)
«p<4 (e<2) + t,<V2>/2)/<« +<VY>)., + /7<V * -
- (1 - 9)#,t><2) - 9/?1t><1) - / = 0, (18.5)
где p(f>=(\— т) (pi—p2)=p—p2t p==(i_m)p1_|_/np2) разница
между фазовыми давлениями pi и р2 уравновешивается движениями в
приповерхностном слое, а теплопроводностью фаз пренебрегают.
Система дополняется соотношениями
р(а) = р(а)(р(а), е<°>), <Z=1, 2. ,(18.6)
Межфазовое - взаимодействие определяется связями (13.46),
(13.48), 6 — параметр распределения диссипации по фазам.
Замыкает систему (алгебраическая или дифференциальная)
связь между фазовыми давлениями
g(pV>, р<2>, т)=0. ** (18.7)
Будем искать решения системы уравнений (18.1) — (18.7) в виде
одномерной плоской бегущей волны, т. е. зависящие только от
одной переменной: t,=x—Ш. Тогда из этих уравнений следуют
интегралы сохранения массы, каждой из фаз, а также суммарных
импульсов и энергий
p(D(l_m)(y(i)_t/)==M1), p(2>m(a<2>^£/)=.M<2>, (18.8)
р(') (1 -m) (oW—V) 2+p2m (о2—U) 2+
+ (1—m)pW+mpW = Q (18.9)
M<'> («О + аОуО/г) -f M<2> (e(J) 4-a<s)y(2)/2) 4- (1 - m) pWoM +
4-m/7<2>o<J) = r, (18.10)
где D(1)=y(1), i>(2)=w<2\ a Mi, M2, Q, W — постоянные. Уравнения
баланса импульса и полной энергии для второй фазы (жидкости)
при этом сводятся к обыкновенным дифференциальным уравнениям
(dldl) (i><2M2)/2) + (l /р(2>) (dpW/dQ =R, (18.11)
(d/dl) {М2>(е(2>+о<2>и<2>/2) —
—M^vWU—mpW (y(2)_ U)} +
+R{U+(l-&)v<»+evW}+J=0. (18.12)
150
Если решение описывает непрерывную структуру ударной волны,
то интегралы (18.8) —(18.10) и уравнения (18.11) и (18.12)
выполняются всюду в структуре волны. Если же решение содержит
разрыв, соответствующий фронту ударной волны, то указанные
интегралы и уравнения справедливы справа и слева от разрыва,
движущегося со скоростью U.
- Рассмотрим решение, содержащее разрыв. Соотношения на
разрывах, независимые от уравнений движения
[p(«)m(«)(r;(«)—C/)]=[Af(«)]=0> а=1,2,
[р<!> (1—т) {vW—U) 2+ (1 —т)pW—mpW] = [Q] =0,
(18.13)
.[Л|(1)(е(1)+0(1)0(1)/2>+(1—^)Р(1)о(1)+А*(2)Х
X (e(2>+a<2W2>/2) +mp<2W2>] = [W] =0,
означают, что масса фаз, суммарные импульс и полная энергия
среды не возникают на линиях разрыва. Отсюда^ следует, что интегралы
(18.8) — (18.10) справедливы не только вне разрыва, но связывают
также параметры среды перед и за разрывом. Таким образом, на
разрыве могут претерпевать конечное изменение параметры v^a\ р<а>,
Ry ..., входящие в. уравнения *(18.11) — (18.13), а производные по
координате £ обращаются в бесконечность.
Предположим теперь, что дополнительные необходимые
соотношения на разрыве могут быть получены как предел непрерывных
решений, удовлетворяющих уравнениям (18.1) —(18.7) в области—
h^JE^h малой толщины при /i->0. Их интегрирование приводит к
результату
[M2>(e<2>+i>(2>a(2>/2—MWvmU—mp(2)(a<2>—£/)]==0, (18.15)
если i?, v(a\ J в области 2h принимают конечные значения.
В мягкой среде имеется диапазон ударных давлений, при
которых допустимо пользоваться изобарическим приближением ра=
—ра(ра). Возьмем замыкающее условие (18.7) по Г. М. Ляхову
в виде
p(i)=p(2)=Pt (1816)
которое строго справедливо для слабых волн давления в мягких
грунтах.
Если задаться, уравнениями состояния (18.6) в виде [22]
р« =р<-> (1 +р<->Х« (р- Л)}1/Х<а> (18Л7)
и считать х(а) постоянными, то соотношение (18.14) принимает вид
><»>0О/2] = [{pWp*> (Х(2) - 1)}- {1 + р(2)Х<*> (р - р.)}1'111™]. (18 18)
Таким образЬм, можно сформулировать задачу о структуре
ударной волны в мягкой среде, состоящей из ударного перехода — с
алгебраическими условиями на разрыве (18.15) —(18.18) —от начального
151
40
35
JO
25
V 029
i£v №u
Рис. 46. «Замороженная» pA и «равновесная» рв ударные адиабаты насыщенного
грунта и ширина б инерционно-релаксационной структуры фронта в функции от
безразмерной скорости
состояния 0 до «замороженного» А и последующей релаксационной
зоны, от «замороженного» А до «равновесного» В —согласно
интегралам (18.8) — (18.10) и дифференциальным уравнениями (18.11),
д (11 УУЦ
5/0~' 5IO~l S-W3
Р-Ра)(р~р0)
Рис, 47. Значения параметров
насыщенного грунта на «замороженном»
и «равновесном» фронтах волны
в функции от давления
Рис. 48. Распределение параметров по
толщине структуры фронта ударной
волны в насыщенном грунте
152
5I0~Z 5!0'г 5/0~' р
(18.12). Интегрирование дает для структуры ударной волны в водо-
насыщенном песке (при следующих параметрах: т0=0,3; ро ' —
= 2,65 г/см3; Pi = 0,l. 10"4 МПа"1; р2=5-10~4 МПа"1; ^=7,23; х2=
= 7,00; £==i&0(m/m0)n, л=10; \i==l0-7 Па-с) результаты,
представленные на рис. 46—48. Зависимости рл(£/), Pb(U) позволяют
непосредственно иллюстрировать структуру ударной волны ширины б и,
кроме того, показывают, что существует предел U0 скорости £/,
ниже которого структура с начальным ударным фронтом от ро до рл
невозможна.
Нижний предел скорости движения стационарной структуры с
разрывом совпадает- с «замороженной» скоростью звука U0
f/2o=l/ (ЭР-). (18.20)
Можно показать, что при скорости U<.Uq структура ударного
фронта непрерывна и нестационарна.
Скорости движения фаз в равновесном состоянии [22] совпадают
оЦ» *=*«=*,. (18-21)
Сопоставление состояний покоя и равновесия за структурой
разрыва приводит к следующим ударным соотношениям:
U>=V20(Pb-Po)I(Vo-Vb),
[vB-Uy=V*B(pB-po) (Vo-VB). . V*M)
Таким образом, имеются два представления об ударном переходе
в мягких насыщенных средах. Первый — это скачок из состояния О
в состояние А и последующая релаксация к состоянию В. Второй —
это скачок из состояния О сразу в равновесное состояние В. При
этом вся реальная структура, имеющая толщину 2Л-И5, заменяется
одним разрывом толщины 2/^ = 2/1+ 6, причем считается, что
Ai/L<l, где L — внешний масштаб задачи.
При. сильном ударном сжатии необходимо учитывать
температурные эффекты. Уравнения состояния (18.6) берутся в форме Ми—
Грюнайзена (1.32) [10].
Ударную волну будем представлять в виде разрыва, считая, что
фазовые скоррсти выравниваются внутри ударного перехода, а
фазовые температуры не успевают: Г+^Г+г. Тем самым зона
инерционно-вязкостной релаксации включается в сам ударный переход,
а условие (18.21) заменяет собой условие на разрыве (18.14), и
потому справедливы условия на разрывах (18.22). Если ввести
массовую скорость v*=v-\-U, то они принимают вид
6*.= U*(p-p0)/(Vo-V), U*=V*o(p-Po)/{Vo-V), (18.23)
P=(l-m)pW+mp(2\
V-l=(l—m)/VM+m/Vi2\
причем массовое содержание фаз при ударном переходе неизменно
* (i_m)p(i) Л40)
jj( ) = - '-I Const
у (1 — т)^) + т^г)— Mil) + MO сипы'
*' (2\_ Щ(2> Mi*)
У — (1 — m)?(1) + m?(i)— Mil)+M(*)— conSt*-
153
Уравнения для энергии среды в целом (18.13) и второй фазы
(18.15), если.е<а), р(а)»е<а)о, р(а)о, сводятся к уравнениям
,(«) = (рМ/2) (V(a) + V(a)) - p{a)V(a) (a = 1, 2). (1&24)
Замкнем систему (18.23) — (18.24) условием пропорциональности
p(i) = /(p(2). - (18.25)
Тогда уравнения (18.24) ударной адиабаты принимают вид
A=(l-m)jp(,)+m/y(,)= ( * )р(, ^-т-, (18.26)
Л(«)=(2/Г(а)) + 1, l/ZW={l-m)+mK,
1/Z(2)=(1— т)К+т.
Значения параметра К задавались в соответствии со следующими
вариантами. Вариант а соответствовал гипотезе о равенстве
фазовых давлений (18.16), т. е. условию /С=1, принятому выше для рас^
чета волн в мягких средах. Вариант б соответствовал механизму
«микросамосогласования» внутри ударного перехода. А именно: для
ударной волны, идущей по отдельной частице, справедливо соотноше*
ние p<a>^p(a)0a(a)£/(a). Если обеспечено условие (самосогласования)
UW=U,vW = v, то К= V(2)o/V(1)o. Вариант в соответствовал
распределению энергии ударного сжатия по фазам, пропорциональному их
массовому содержанию е(а>= (р(а)/2) (У(а>о+У(а)). Это дает paVa=
=pV или K=V2/Vi.
Для всех вариантов система нелинейных алгебраических уравнен
ний (18.23)'—(18.26) решалась численно. Параметры для водона-
сыщенного песчаника с пористостью т=19% брались из табл. Ь
Результаты расчета приведены в табл. 10. В этой же таблице при-
Таблица 10
Эксперимент
Р*
ГПа
7,6
8,0
20,1
30,0
30,3
33,3
42,9
44,0
48,7
V,
КМ/С
3,77
4,00
6,10
5,63
5,77
5,96
6,74
6,77
7,07
V,
км/с
1,03
1,01
2?01
2,71
2,67
2,85
3,24
3,31
3,52
Приращение энергии
Расчет
*=1
V
3,45
3,51
4,97
5,82
5,84
6,07
6,71
6,78
7,06
V
1,11
1,14
2,03
2,59
2,60
2,75
3,21
3,25
3,46
Для воды
е<"\
<о
K=V(2)IV(\)=26
V
3,44
3,50
4,96.
5,80
5,83
. 6,05
6,70
6,76
7,05
е(«)>0,
V
1,11
1,15
2,03
2,59
2,61
2,76
3,21
3,26
3,47
а=1,2
K=v(2)jV{\)
V
3,44
3,51
4,97
5,82
5,84
6,06
6,71
6,78
7,06
е«">>0;
'*
V
1,11
Д ,14
2,03
2,59
2,60
2,75
3,21
3,26
3,46
1=1,2
Правило аддитивное
V
3,40
3,47
4,92
5,76
5,79
6,01
6,65
6,72
7,00
е<«>>0;
V
1,12
1,16
2,05
2,61
2,63
2,78
3,23
3,28
3,49
а=1,2
ведена экспериментальная- ударная адиабата песчаника. Расчеты
адиабаты по всем вариантам совпадают с экспериментом при
ударных давлениях 20,0 ГПа и выше.
154
В литературе известно также «аддитивное» правило расчета
ударных адиабат смеси, согласно которому ударное сжатие материалов
каждой составляющей происходит так же, как и в ее монолитном
состоянии. Это означает справедливость условий
еы-ев(а) = (1/2)(/7(а)+/7о(а))(У(а)-У(а)), a=l, 2, (18.27)
которые согласуются с балансом суммарной энергии (18.10), если
р(«)=р. Иначе говоря, адиабата Гюгонио смеси задается в виде сум- •
мы ударных адиабат фаз в монолитном состоянии. Результаты
расчетов по «аддитивному» правилу также хорошо соответствуют
опытным данным при р^20,0 ГПа (см. табл. 11).
При давлениях порядка 8,0 ГПа расхождение расчетов и
опытных данных достигает 15%', что значительно превосходит
экспериментальную ошибку (2,5%—4%). Рассмотрим, может ли это
объясняться пренебрежением прочности матрицы песчаника.
В одномерных плоских волнах прочность матрицы в целом
приводит к различию компонент фронтального on (в направлении
удара) и бокового (722=сгзз напряжений. Этим эффектом можно
пренебречь, если ударные давления (порядка 8,0 ГПа) намного
превосходят сцепление песчаника (F^0,02 ГПа).
Проведем оценку поверхностно-прочностного эффекта (прочности
окрестности индивидуальных пор), который может обусловливать
различие фазовых давлений — среднего pi = — l/3(ai 1+2022) в
матрице и р2 — в поровой жидкости. При этом будем считать, что
пористая среда моделируется набором сферических ячеек с внешним
радиусом &, внутри которых находятся сферические поры радиуса а.
Если использовать безразмерную геометрическую характеристику
9 = 63/(Ь3—а3) =1/(1—т), то уравнение состояния насыщенной
пористой матрицы представляется в виде
* ^(•)=^,) + (4/3)0(вв-в)в-'1(в-1)-1, е0<в<6*, (18.28)
У2) = />(1) (apIap + PWiiapl*)*- 1} + (4/3)0(в.-в)в-1(в-Г)-1Х
Х{в(ар/а)-8-(в-1)}, (18.29)
(ар/а)2з+3=2О(е0-е)(е-1)-1(^1) + У)-1,
р(»)={рС1)+(У/-р)}{в/(в-1).}^+Г/р,
(18.30)
Здесь формула (18.29) соответствует упругому деформированию
поры, формулы (18.29)—упругопластическому (причем ар->радиус
упругопластической границы) и наконец, (18.30)—полному
пластическому напряжённому состоянию вокруг поры. Значение 6*
соответствует критерию начала необратимого деформирования поры,
б** —пределу несущей способности ячейки.
e*=(2eG+y+pp^)/(2G+y+PP(1)), (18.31)
{(во-в.О/(в..-1)}{20/(У+рр(«)} = -
= {6**/ (б**-1)}(2Р+3>/3. (18.32)
155
При выводе этих расчетных формул материал матрицы предпо-*
лагается несжимаемым с модулем сдвига G, а давление в твердой
фазе отождествляется с радиальным напряжением аг на внещнем
контуре ячейки. Условие пластичности задается в виде /
(i+p)0;n-o<»=y. у (ш.зз)
При давлениях в 20,0 ГПа и выше эффекты сухого трения в
окрестности поры становятся несущественными и следует брать
значения F* и р*, соответствующие дислокационной текучести
материала, а именно:
У.=.ЗУ/(3+2р) + {Зр/(3+2р).}, р.=0,
при этом формула (18.30) переходит в следующую:
р<2)=рО>+Ппе/-(е-1). (18.34)
Таблица 11
Расчет с
использованием
Формулы (18.30)
Формулы (18.34)
р>
ГПа
7,6
8,0
20,1
30,0
30,3
33,3
42,9
44,0
48,7
V,
км/с
3,85
3,91
4,66
5,45
5,47
5,68
6,32
6,39
6,67
V,
км/с
0,99
1,02
2,16
2,76'
2,78
2,94
3,40
3,45
3,66
Р»
ГПа
6,72
7,08
17,5
26,7
27,0
29,8
38,7
39,7'
44,1
Ри
ГПа
.8,32
8,83
22,5
32,6
33,0
36,1
46,0
47,1
52,0
г/см»
1,08
1,09
1,48
1,73
1,74
1,79
1,95
1,96
2,02
р2>
г/см3
4,12
4,15
5,76
5,89
5,90
5,94'
6,06
6,07
6,13
sgne!
—
Результаты расчета приведены в табл. 11. Видно, что вычислен-
ные значения U, v находятся в лучшем соответствии с
экспериментальными данными при р^8,0 ГПа, нежели расчетные данные
табл. 11. Вместе с тем разница фазовых давлений относительно
небольшая, и результаты оказываются весьма близкими к
гидродинамическому приближению (см. табл. 11 при К=1). >
Для выбора наилучшего варианта замыкания соотношений
необходимо поэтому привлечь дополнительные аргументы.
Прежде всего, пористый материал с пустыми порами также
можно считать смесью, одна из фаз которой не обладает массой:
и следовательно,
y(2)i/(2)=m/(i_m)p(i)> Vr=l/(1—т)р& = №/т.
Кроме того, давление в порах в этом случае должно быть равно
нулю /72=0. Последнему условию не удовлетворяют расчеты при
р{ = р2=р и по аддитивному правилу [4], но соответствуют расчеты
с использованием формул (18.30) или (18.34). Однако расчетное
ударное сжатие водонасыщенного песчаника приводит к
отрицательному приращению энергии в одной из фаз (в воде е2) как при учете
поверхностно-прочностного эффекта, так и при pi = p2=p (см.
табл. 11, 12).
J 56
Рис. 49. Ударные адиабаты вольфрама Рис. 50. Ударные адиабаты парафина
в сплошном состоянии и (расчетные при в сплошном состоянии и (расчетные при*
равных фазовых давлениях) в смеси равных фазовых давлениях) в смеси
Для исследования указанного эффекта была выбрана
экстремальная (по различию свойств веществ) смесь —взвесь вольфрама в
парафине.
На рис. 49 приведены
адиабаты вольфрама в монолитном
состоянии в координатах давлег
ние — удельный объем pw=
=pw(Vw). (сплошная жирная
линия), а. также полученные при
расчете адиабаты вольфрама в
смеси с парафином (пунктир, по
варианту б) для концентраций
вольфрама по массе yw=0,662
(кривые 1) и yw=0,840
(кривые 2). В этих расчетах
использовались данные для уравнения
состояния вольфрама, а также
опубликованные
экспериментальные данные об ударной адиабате
смеси. На шкале справа дано
среднее давление в смеси. Штрих-
пунктирными линиями здесь
изображены адиабаты, рассчитанные
по варианту е.
На рис.50 представлены
соответствующие адиабаты парафина:
Рис. 51. Расчетные ударные адиабаты
вольфрама при неравных фазовых
давлениях в смеси
Of {0 $ VW/VWD
Pn=Pn(Vn). В вариантах расчета б, в приращения внутренней
энергии парафина было положительным (в отличие от варианта при К=
=1). Однако адиабаты вольфрама (рис. 50) отклоняются (во ^fcex
вариантах а, б, в) от его адиабаты в монолитном состоянии при
i/w=0,662 меньше, чем при yw=0,840. На самом деле порядок
отклонений должен быть обратный (такой же, как у парафина).
Рп,ГП°
Рис. 52. Расчетные ударные адиабаты парафина при неравных фазовых
давлениях в смеси
• В связи с этим была проведена серия расчетов для набора
значений К (рис. 51, 52). Здесь адиабата монолита — сплошная жирная
линия, yw=0y662 — сплошные тонкие линии, yw=0,840 —
пунктирные линии. Кривые 1—7 получены соответственно при /С=1; 3; 5; 8;
10; 15; 20. При К^ 3 порядок отклонений ударных адиабат
парафина в смеси от его же адиабаты в монолитном состоянии
соответствует возрастанию содержания вольфрама, В то же время для
вольфрама подобный порядок соблюдается при К ^ 10.
Зависимости расчетного приращения внутренней энергии
парафина от К приведены на рис. 53, для yw=0,662 сплошными линиями,
а для yw=0,840 — пунктиром.
*nfQ"U*/*r Цифрами U 2, 3 обозначены
51 I I -^ОИ кривые, соответствующие
средним давлениям в смеси р=
=23,1; 50, 57,4 ГПа (yw=
= 0,662) и р = 31; 65,6;
81,6 ГПа (yw=—0,84).
Отсюда видно, что положительные
приращения энергии
парафина еп соответствуют К ^ ИХ
Поэтому в окончательном
расчетном варианте было
принято /С= 10, 15.
Соответствующие 53. Приращения внутренней энергии Щие УДарНЫе адиабаты ДЛЯ
парафина в ударной волне вольфрама и парафина при-
158
ведены на рис. 49 и 50 тонкими сплошными линиями.
Различие фазовых давлений в смеси носит неравновесный
характер. Для взвеси вольфрама в парафине фазовые давления
различаются на порядок (сравнить шкалы слева на рис. 49, 50). Для водо-
насыщенного песчаника отношение фазовых давлений должно быть
менее чем 2,6 (см. табл. 11), но заметно превосходить различие,,
обусловливаемое статической прочностью пор. Необходимый учет
неравновесности требует, по-видимому, анализа инерционных эффектов
при схлопывании пор и эффекта предельной скорости разрушения
(относительного скольжения частиц).
Отклонения ударных адиабат фаз смеси от ударной адиабаты
того же материала в монолитном состоянии вполне аналогичны
проявлению аномально высокого теплового давления при ударном сжатии
пористых материалов. Прямым экспериментальным подтверждением
этого также могут служить различия точек фазовых переходов,
чувствительных к температуре (изломов адиабаты смеси на плоскости
pV)t при различных начальных концентрациях.
Известно, что при ударном сжатии графит переходит в алмаз.
При ударном сжатии пористого графита давление перехода
изменяется за счет более высокого нагрева пористого материала и
чувствительности фазового перехода к температуре. Так, если при
начальной эффективной плотности графита (1—то) ро=0,55 г/см3 точка
излома (интерпретируемая как точка фазового перехода) имеет
координату—2,5 ГПа, то при (1—т0) ро=0,680 г/ см3 — координату
—'7,0 ГПа. Выше этой точки адиабата хорошо описывается
уравнением состояния алмаза. Ясно, что ударное сжатие графита, поры
которого заполнены иным материалом, также должно выявлять
снижение точки фазового перехода.
19. МЕХАНИКА СРЕД, НАСЫЩЕННЫХ НЕОДНОФАЗНОЙ
жидкостью
Уравнения динамики при двухфазном заполнении*
пор. Термодинамика движения. Учет капиллярного
давления. Закон деформирования при тепловых и
капиллярных воздействиях. Закон Дарси для
двухфазного потока. Волны в пористой среде, с
защемленными пузырьками газа. Растрескивание грунта
при высыхании.
При насыщении пористой среды многокомпонентной
неоднофазной смесью уравнения баланса масс формулируются для каждой из;
компонент ф) в каждой фазе* (кх) в отдельности
Ow(a)o(a)r(a)i 4-fm(aVa)r(0Vah — Е Г/(ра) — j{aV)-UN{a)
Щ р L{k))tt-+-{m р b{k)v. jtl. —*ри(л) l{k) )-rlv{k)>
Е*С((2 = 1, 1<£<К, (19.1)
где С^ —массовая концентрация А-го компонента в фазе a, у*£ —
интенсивность потока массы &-го компонента из фазы ос в фазу р,
ЛГ(") — порождение или аннигиляция массы &-го компонента из-за
химической реакции.
159
Уравнения баланса импульса составляются в виде "
<p(Vtfx,+<?< V"4(")if>- /=^'Ф- <+VT8)+«(Ув)л.
/ (id.2)
где а{л) — истинные фазовые напряжения, F("s) — сила объемного
взаимодействия между фазами а и р (а=^[3). Так как силы Т7'*9'
являются внутренними, то F{?9) =-- - FJ9a), EajJ f|ap) = 0.
На фазу а со стороны остальных фаз действует сила
F|"> = 2LF!"w = - о<"Wa> + Д {а) + R{a), (19.3)
где /?*a) — силы, определяемые относительными скоростями движения
фаз v(a), а д!а) — догюлнительные силы.
Суммирование уравнений (19.2) должно приводить к балансу
импульса системы
(1.рМя<->0;->)., + (XyWy*)., = Г„., + ЕУУ V (19.4)
где Г(/^ Ea/re<aVa) —полное (суммарное) напряжение. Отсюда
Г,., ,-2от(а)о(а) =So(aWa) = S д!а), (19.5)
причем правая часть (дисбаланс) тождественно обращается в нуль
при условии равенства фазовых напряжений. Нулевому суммарному
дисбалансу (19.5) соответствует присутствие дополнительных
поверхностных (по Гиббсу) фаз [13]. Их движение может быть
ассоциировано с движением одной из рбъемных фаз. Тогда силы A?a) следует '
считать действующими на соответствующую объемную фазу.
Если учитывать разность фазовых давлений р%—Рз=Рс где рс —
капиллярные силы, то дисбаланс будем задавать так:
ЛГ = °,7 0 - «). / - (Р{2) - Л И). * = (°?! + Р*ц) (!-«).,-
-/п(У2)-/7(3,)б,,.; (19.6)
д!2) = д|3) = 0, т, = 1 — т\ тг==тЬ; тг=^т(\—Ь),
где Р=бр<2>+.(1— 0)//3>— полное давление в жидкой фазе, в —
насыщенность.
Тогда
F<I)=P8i/(I -т1,-(рП _^»>Тй1в. ,+/?;•>, (19.7)
Ff=pm(mbll + Rf), (19.8)
if =pw{«(l-e)b + ««
Определение (19.8) соответствует движению поверхностной фазы
совместно с матрицей. Матрица является «несущей» фазой.
160
В случае (19.8) система уравнений движения имеет вид
р<•> (1 -т) {,« + (,;'>>),,>=с/;;. - о - m)/>., - т (Р™ - /Л е. ,+
+«;,)+(i-«)p(V ' (19.9)
P(2)m6 {о» + (*«**).,} = - «•/,« +Я!2) +тЪ^81,
Р™т (1 - в) {**>, + <p?v»\,} = - in (1 - 8) /,» +*f' +
+ да(1-. в) ?<•>*„
где введено полное эффективное напряжение при двухфазном
насыщении пористой среды
??, = Ти+Р*и = С1 - "») (°<7 + ^/)-
Р=3ер(2>+(1— 9)р<3>. (19.10)
Можно ввести фазовые эффективные напряжения в пористой среде
о . (2) относительно второй и а[(} (3) — относительно третьей фаз
о}» (2) = !•„ + /,%. ^>(3) = Г17+У%. (19.11)
Если полное эффективное напряжение о!? вызывает переукладку
зерен матрицы пористой среды, то о!^ (2) — переукладку матрицы сов-
местно с частицами третьей фазы, а о"; (3) — соответственно
матрицы и частиц второй фазы.
При наличии фазовых переходов и химических реакций уравнения
движения должны включать в себя дополнительные потоки
импульса й энергии, пропорциональные интенсивности перехода частиц*
компонент из одной фазы в другую. Соответственно межфазовые силы
в уравнениях (19.2) должны иметь такой вид:
F? = РЬИ (1 - т)., - (р(2) - /3)) пЛ., + ^ <р?1™ -
Ff> = р™ (rub), t +-2Ц (of С; - v? /*>) + 2$* . (19.12)
Ff> = ,» {«(1 -8)}., +V*f Ф^ф + J^f».
причем суммирование для фазы а проводится по всем 0=^а.
Перейдем теперь к анализу уравнений энергии. Умножим
уравнение (19.12) на v*:a) и получим уравнение баланса кинетической
энергии фазы а
#
(Р(в)те(а)Л(а>/2), ,+ fp<»Va)t>;e)0)"Va)/2),, = vla) (m("Va))., +
+s/i-»0;->+i»wpWA0;->. ' (i9.i3)
и-ззп 161
Уравнение полной энергии фазы а записывается в виде
{рС>/и« (.О + Л!"' /2)} t + {fWmw (*(а) + Л(в)/2)yja)}. / +
+{<7><a)>. i={«wo;")°J")>. /+*.(?+<?.+"*(w ^э.н)
где p(aWa) —поток теплоты по фазе a, HP(a) —работа в единицу вре-
мени на межфазовых поверхностях раздела, производимая над фазой
a, Qa — объемный приток теплоты в фазу а из фаз р.
Составляя разность уравнений—(19.14) и (19.13), получим
уравнение баланса внутренней энергии еа фазы a
(/rc(Va)e(a)), t + (/rc%(aVaVa)),, - mMofJv™ =
= - {m^qf\ i + W[a)t+Qa - F^v{;\ (19.15)
Если учитывать различия давлений жидких фаз, то
SaA^a) = - oJ> (I-т)9 Л/ + P (1 - m)., + (pi2) - /?(3)) тЬш, +>c,
(19.16)
где 8c — удельная энергия поверхностной фазы, т. е. энергия,
приходящаяся на единицу порового пространства среды (без учета
фазовых переходов и реакций). При присоединении поверхностной фазы
к матрице среды имеем
ДГ = £аДГ. А«=С=0. (19.17)
Тогда для жидких фаз
W<"> = - /Лу? + 28#(а?,у?> (а = 2> 3)' (19Л8)
что означает
т(а) {<?(л) (daB(a)/dt) + p(a)vf\) + pwdamia)/dt =
= - («(V). f - ¥Г (y!a) - ^') +<2*. (19Л9)
Из уравнений неразрывности (19.1), просуммированных по
компонентам для каждой из фаз в отдельности, следует
djn^ldt = - (/n(a)/P(a)) (djtojdf) - /Л^-
Поэтому уравнение внутренней энергии преобразуется следующим
образом:
т<«> {Р<»> (rf..w-/<*) + /><a) (djtli) (i/p(a))} = - (m(a)<7!a))., + Qa -
- 2$"» (oje) - o®). (19.20)
При введении фазовых энтропии sa и температур Та уравнения
(19.20) принимают вид обычных соотношений Гиббса
Р<а) (</.«<",/Л) + /><в) (dJdt)(ll9{a)) = T(a)9(a) (dasMldt), (19.21)
162
причем уравнения роста энтропии фаз записываются так:
m(«)9(*)T(*) (djMjdt) + (//i(a)<7t(a)),, = Qa - 2<tf(ap) (vla) - vf).
Уравнение энергии матрицы принимает вид
(l-m){p(4«(V'-^
(19.22)
При этом учтено, что для баланса энергии е<с> ассоциированного
поверхностно-капиллярного слоя справедливо соотношение
dlsV/dt=(pM—pW)diQ/dt+QV/my (19.23)
где Q(c) — приток теплоты к поверхностному слою.
Соотношение Гиббса для поверхностного слоя имеет вид
dzW=TmsW+pW (9)d6, (19.24)
что вполне оправдано в рассматриваемом случае. Действительно,
для поверхности раздела фаз справедливо, вообще говоря,
соотношение
de(-c) = T(CWC) +HFdF + Hldr1 +Hidri-\-Xk?%dtifl), (19.25)
где dF—приращение площади поверхности раздела при
деформировании объемов фаз за время dt\ dru dr2 — приращение (за то же
время) приведенных радиусов кривизны менисков, характеризующих
возможные изменения геометрии поверхности раздела. Величины HF,
Ни Н2 — соответствующие термодинамические силы. Кроме того
здесь введены приращения адсорбировавшихся на поверхности
раздела молей к-то компонента dn^} состава жидких фаз, причем <р|^
ее химический потенциал [13].
Если приращения dF, dru dr2 могут быть выражены через
приращения dQ относительного объема жидких фаз в паровом
пространстве, то в отсутствие адсорбции (dn£] =0) соотношения (19.24) и
(19.25) эквивалентны.
Преобразование уравнения (19.22),'введение энтропии Si и
температуры Т\ позволяют, придти к следующим термодинамическим
соотношениям:
(1-т)р(1){<*ЛЛ + т^
+ {l-m)p^mi)(ds^ldt)f (19.26)
(l-m)9^T(1)(d1s^/dt) = -{(l-m)q?)},l+Q1,
совпадающим с соотношениями (13.33), (13.35) для однороднонасы-
щенной пористой среды, но при введении среднего порового давления
А=6р2+(1—0)р3. В <*илу этого можно воспользоваться
определяющими связями для упругих деформаций матрицы при замене
порового давления р на полное двухфазное давление Р. Поскольку,
однако, здесь принята модель движения трех фаз и поверхностный слой
ассоциирован с матрицей среды, то выражение для внутренней энер-
п* 163
гии фазы «матрица+капиллярный слой» есть результат
суммирования соотношений (19.23) и (19.26), т. е.
(i-m) р(,) (dyi)/dt)+т №«(с>/л)=(о® мь?.,+»;;},) -/У
^P(dJdt)(l/?(1)) + p(c)(dlbldt) + {l-m)^lml){d1s(1)/cH)^
+ mT(c)(dlSVldt), (19.27)
где s<c>, 7<с)— энтропия и температура поверхностного слоя. Отсюда
следует, в частности, что упругие деформации матрицы совместно
с капиллярным слоем будут определяться, помимо эффективных
напряжений о.(^ , полного давления Р, температуры 7W=7W=7(2),
ч
также и, насыщенностью 8, которая входит как независимо, так и
в, выражение для Р.
Соответственно будем определять полную деформацию ец
пористой матрицы согласно правилу аддитивности деформаций
> =е\п-\-е)?>+е™
где ер —деформация переупаковки, вызываемая эффективными
напряжениями ар, е{*) —деформация, вызываемая изменением плотности
материала твердых частиц, е{Ь) —деформация, вызываемая
изменением капиллярных сил. Сумма первых двух слагаемых есть
деформация, определяемая связями (14.8) с заменой порового давления р
на среднее поровое давление Р. Деформации е{.) определим
следующим образом:
ер = - (1/3) р(9) {/7(с) (в) - /7(с) (в#)} 8ф (19.28)
где р(9) — коэффициент набухания (;р<е)<0) или усадки (р<е>>0)
матрицы. Суммирование деформаций приводит к следующему
обобщенному закону Гука для упругой пористой среды при ее
двухфазном насыщении:
oj;> = (К- 2G/3) еиЪи + 2ве„ + ,mP*tl + аК (Г(1> - Г.) Ьи + *
+ ГМ/>(с)(в)-/>(с,(№//- (19.29)
Суммируя выражения для энтропии фаз, получим соотношение
Гиббса для всей гетерогенной среды. Уравнение производства
энтропии s=2am<a)p(a)s(a) в единице объема имеет вид
*. t + Sa (pWV),, +2. (т^/Т™). t = (mJT(c)) {p{2) -
- /><3> - p" (6)} dm+s? ^ (Rf'iT (2>) (o« - 0») +
S (#3) '
+ S.(Q<a)/T(e)) + (Q(,c)/r(c)). (19.30)
164
+ Sp (««/T») (of - o») - 2. (fmw/rw) r;-> +
В силу формализма термодинамики необратимых процессов из
уравнения (19.30) следуют замыкающие феноменологические
соотношения:
OT<«>f <•> = - БэЯ<«е> (l/T(e>) Т{*\,
Л!-» = - Sp ^ (a(ap)/Tw) (0<-> - «,«). (19.31)
е={/7(2) -Р(3) -^(С) (в)}/х(с>4-(1/т(в> - i/t*,)/,w,
Qw=«w(1/r(a,-I/7,(P,)+^(2) -р(3) -p(c)(6)}/^w.
Здесь вводятся £)(<*)=Z)(aa) — коэффициент теплопроводности
в фазе а, т<с) — время запаздывания действия капиллярных сил,
х(ар> — коэффициент теплообмена между фазами а и р, a(ap) —
коэффициент сопротивления 'из-за относительного движения фаз а и
р. Коэффициенты перекрестных эффектов будем полагать равными
нулю: Z)<aP>=0, a¥=p, тх=0. Следует, однако, иметь в виду, что
коэффициент Z)(aP), например, учитывает эффект генерации потока
теплоты по фазе а, если задан поток по фазе § (и обратно).
Феноменологические коэффициенты определяются в ходе
специально доставленных опытов. Так, коэффициенты сопротивления
a(cc0) = 0(ap) находятся из опытов по совместному движению несмеши-
вающихся фаз в пористой среде (vjl)=0) в стационарных условиях.
При этом уравнения движения (19.9) без инерционных сил и сил
тяжести сводятся к обобщением записи закона Дарси
^mbpV = atlv?+a(u){vf-vf),
(19.32)
-m{\-b)p^ = a{u)vf+a^(pf-vf).
Разрешив систему уравнений (19.32) относительно скоростей, пои
лучим
vf = (а,п,/Д) {- m (1 - 0) /Z3;.} + (a(tl> + а(м>) (-ив/>^)/.Д.
vf = (а(м)/А) {- mbpf\} + (аы) +a(t,,)(-«(l - 6) ,(»}/Д.
где Д= (a13+ai2) (a23+ai2)—а^а^. При пренебрежимо малом
эффекте увлечения одной жидкости другой (а12=0) выражения (19.33)
переходят в обобщенный закон Дарси для двухфазной жидкости
„(2) __ „*(2) _ _ /w2fi2//7, ч „(2)
^ = mbv^ = -(^r/a{li))p^
ОТ
т*Ъг1ам = £/<2> (6)/ti<2), (19.34)
ш<3> = т"(1 - 6) cf = - {/»■ (1 - Ьу/аы}р«\;
И,(1-«),/в(и) = */(,,(№1
165
Здесь. fa(в), а=2,3 — относительные фазовые проницаемости
(рис. 54). Равновесное капиллярное давление рс(В) можно
представить в виде /
р{с)(Ъ) = чУ^Гк](Ъ, ?), pl = (pJi)Vkfa. / (19.35)
где у — межфазное натяжение, 7(6, <р) —безразмерная функция Ле-
веретта (рис. 55), параметрически зависящая от краевого угла <р
жидких фаз (на плоскости из того же материала, что и матрица
среды).
/0
Р
\\?н h
05
10
Рис. 54. Относительные фазовые
проницаемости для нефти и воды
N
Рис. 55. Капиллярное давление, для
смачивающей 1 и несмачивающей 2У
вытесняемых жидкостей
Учет фазовых переходов и химических реакций требует
обобщения балансов энергий. Для обмена между фазой 1 — матрицы, и
остальными фазами — а=2,3 (при суммировании по а=^р) имеем
W*! =Р(1 - т)л - (/><■> -/><•>)/ив., +е<с> + Zfim -f
+ 2^{(•»> +^»о(Р)/2 + р«)/р(Ю)/э^ ^ (.а) +»|<Юа|»)/2 + /iCO/pCD)/(ip)},
W[V=PWW +^{(«(P,+o/%(W/2 + p<«/pW)/((|") - (19.36)
_ (t(., + tF,<->tFie)/2 + ><•)/?<•))/Йэ)}+ Sp«Je»^> +^QW.
Для фаз, между которыми существует массообмен, должны
выполняться следующие ограничительные условия:
Последнее равенство утверждает, что химические реакции,
приводящие к возникновению массы й-го компонента за счет масс других
166
компонент, и фазовые переходы, меняющие компонентный состав
фазы за счет перетока из существующей фазы, должны в сумме
компенсировать друг друга. Выражения (19.36) составлены так, что
выполнено условие обращения в нуль внутренних сил системы:
20f/p) =0. Требование взаимокомпенсированных внутренних
переходов для баланса энергии означает
2«з{И> +i><«tf >/2+ (р®1рЩ /»"> - [s(a> + t£>0j»>/2 +
+ (/*•>/?<•>) / <■»} + Za&W = 0, 2#.р = Q. (19.37)
Массообмен между матрицей и жидкими фазами соответствует
таким процессам, как плавление матрицы или ее части (например,
таяние мерзлого грунта) или же горение матрицы (например,
горение порохов).
Пример ы. Для анализа слабых волн в насыщенной пористой среде при
наличии пузырьков газа можно использовать линеаризованную систему уравнений.
Уравнения баланса масс (19.1) приобретают вид
«.£> + inje,n<*> + m<e> v\*\ = 0,
(19.38)
п<*> = Р<«>/Р<«>.
Газовая фаза двигается v вместе с матрицей среды, если насыщенность газа
8о^О,1—0,2 (см. рис. 54), а потому достаточно рассматривать уравнения импульса
только для матрицы и жидкости
(1 .-щ) р<" vVt = (1 - щ) hh , + г (vf > - if >),
(19.39)
^2Ч^=-'*.л.--г(»/2)-*Г)).
если пренебрегать капиллярными силами и использовать соотношения
0-«.)>«.е.. р£>. 42)>to<3).
При этом уравнения (19.38) сводятся к одному
П. t + я#> v\]\ + mf vf?t = 0, П = т^П*» + т<2>П<2> + т<3)П<3> , (19.40)
И справедливы линеаризованные уравнения состояния фаз:
П(1)= —р(,)а+а(ЧЛ1), П(** = 0(*)/? — аЛП1),
(19.41)
П(3) = 3<8)/7 —а(8)Л3).
Линеаризованные балансы энергии записываются в виде
m(a)c(«) Г(«) =m(a)z)^v2r(a) _ ^(«) Т(Л) a(«) ff(a) +
+ Sp(9fce)«(ep)(7,(P)-7,(e)). (19.42)
Замыкает систему обобщенный закон Гука (19.29) при рс(9)=0. Рассмотрим
распространение продольных гармонических волн в мягких средах (е»<С1) и
дополнительно будем предполагать
•Stf-jB-^l, 3 = Eam<a) &(a)- . (19.43)
Условие (19.42) выполняется, например, при т3(о) = то0о^1О-2—10~3, если (3^
%5.10-5 МПа-1, ^2^4-Ю-4 МПа-1, 103^8 МПа-1, As—^В-1—1,0—10 МПа.
При таком малом содержании газовых пузырьков в среде будут
распространяться волны двух типов, причем условие (19.43) означает <т=^—р для волны
первого рода. Так как давления в фазах принимаются равными, а термические ха-
167
рактеристики жидкой и твердой фаз близки между собой, то можно полагать, что
Т z&T2. Тогда уравнения энергии (19.42) сводятся к двум следующим:
<mJ'>C<» + 4»> C(2))r<V=K)Z)(1)+m<2>D(2))v'r<"+ ^ 7
+ (^'> «(1) + Ч2> »(2)) ЛЛ * + * (7-(2) " 7-(,)). /
(19.44)
^С(3)Г(3) _ тйд(3) ^(3) + m(3)roa<3V, , - х (Г<2> - Г*1»),
причем x=«i-f-'<2- Если далее пренебречь теплопроводностью, то для периодических
изменений переменных по закону ехр (щх—Ш) получаем такие выражения для
скорости распространения с и коэффициента затухания 5:
с = {\/Vp) V(l + ?»)/(Q,?i + Q1). (19.45)
д _ <о Vfc f(Р<°> ~ Pop) A (h) (б/Роо) (р<«> + PopS8; В. W/P<°> 1
Соответственно
с-»соо=1/Ур^ (»-оо), С^с0=1/Кз"в7 (»->0), (19.47)
причем: для низких сейсмических частот (£<1, ft<Cl) справедливо правило
суммирования вязкоинерционного и теплового затуханий:
* ^ (1/2) (р(') - Роо) VpO + (в, - 'В J хт/в } (»t/Ci).. (19.48)
Здесь Qi, Q2, ^(/i), B*(h)> 60, 6«> определены в [22].
- Приведем численные оценки. Пусть р^!) =2,8, р^2) = 1, р*3) = 1,3 кг/см2, ш^ =
= 0,8, т® = 0,2, т^ =0,02, at = 5-10-6, ae = 2Л0-*, а3=3,7.10-а 1/°С;
С1==0,56, С2=4,2, C3=12,6t02 Дж (см3.°С); ipi=5-10~5, ip2=4*10-4, ^3=8 МПа~».
Если ti^<i2/v, Тт^^2/^з, d — характерный размер поры (пузырек газа занимает
всю пору), то при кинематической вязкости воды v^lQ-2 см2/с получим, что а^
^10-1 см2/с, ф^20%.
Сама величина 6 при фиксированной частоте со с изменением т^ * не остается
постоянной.
Рассмотрим задачу о возникновении трещин под действием капиллярных сил
во влажном полупространстве мягкого грунта. При этом фааа 2 — вода, фаза 3 —*■
воздух. Для мягких грунтов сжимаемостью материала матрицы можно пренебречь.
Тогда обобщенный закон Гука (19.29) принимает вид
о<р = (К-2Э/3) ebij + 2Geij + f)K{p^(b) - /><с) (8,)} «,,. (19.49)
Если задача одномерна, то все величины — функции только х^О, не зависящие
от Х2> — выполняется условие одноосного деформирования: е22=£зз=0. Поэтому из
(19.49) получаем
°22 = 49 = °п (* ~ 20/3)/(/Г + 4G/3) + Щ{В)К {Р{с) (в) -
-/><с> (8.)}/(ff + 4G/3). (19.50)
Пусть на свободной поверхности отсутствуют усилия
Ги==с<[>--е/?(1) = 0, Г12=о#=0 (х, = 0). (19.51)
Здесь учтено, что pW (д:1=0)=0. Тогда при *i=0 имеем
^ = 1^Р{1) (9) (K-2G/3)/(K + 4G/3)] + [2G^K{p{c) (9)-
-/>(с) (8)}/(tf + 4G/3)]. (19.52)
168
f Критерии возникновения вертикальных трещин отрыва в матрице среды
имеет вид
•$>*♦. (19.53)
где а* — прочность на разрыв. Из выражения (19.52) следует, что возрастание
капиллярных сил из-за убывания насыщенности 0 (см. рис. 55) может приводить
к растягивающим усилиям а^ . Если же окажется достигнутым предел прочности
(19.53), то на поверхности грунта возникнут вертикальные -трещины, что типично
для разрушения почвы при засухе. Для нахождения глубины трещин нужно
вычислить боковое напряжение а2ф по заданному распределению насыщенности 0"
с глубиной, воспользовавшись уравнением равновесия
(К + 40/3) .(К - 2G/3) -1 a$t = (1 - т0) {9/><с> (9)}, , + 20р(в) К (К-
-2е/3)-*^с)(в),1 + шр<с)(в)в.1-^1> (l-m.)*i = <>. (19.54)
ГЛАВА 6
ДВИЖЕНИЕ ЖИДКОСТИ И ГАЗА В ДЕФОРМИРУЕМЫХ
ПЛАСТАХ
20. УПРУГИЙ РЕЖИМ ФИЛЬТРАЦИИ ЖИДКОСТИ И ГАЗА
Основной вывод уравнения пьезопроводности*
Гипотезы о напряженном состоянии.
Нелинейно-упругий режим фильтрации. Уравнение Лейбензона и-
его обобщения. Стационарный приток к скважинам.
Искривления индикаторных линий. Изменения про»
ницаемости пласта. Оценка инерционных эффектов.
Течения между рядами скважин. Автомодельный
приток к скважине. Кривые восстановления
давления. Законы газового пласта.
Каждый элемент насыщенного пласта находится под
воздействием вертикального и горизонтального горных давлений,
отождествляемых с суммарными напряжениями Гг> При изменениях порового
давления происходит перераспределение нагрузки между жидкостью и
матрицей пласта, а следовательно, и деформирование последней.
Распространение волны порового давления описывается уравнением
пьезопроводности.
Для вывода уравнения пьезопроводности используются уравнения
балансов импульса и массы для жидкой фазы без учета инерции
(wp<2)), + (mP(2)^2)), = 0,
/ IUM ' пп (20.1)-(20.2)
где Wi = m0v]® — скорость фильтрации.
При наиболее простом варианте (по В. Н. Щелкачеву [22])
скоростью относительного смещения твердой фазы пренебрегают, а
замыкающими являются связи
т = т (р) = т0 {1 + ат (р - /?0)}; ^Q ^
р<*)=р<2){1+^>(/7-/70)},
10
169
что в линейном приближении приводит к уравнению пьезопроводко-
сти ,
p,t=xV2p, x==*o/(|i0/WtfP), P=Om+mop(2). /(20.4)
Во втором варианте (по А. П. Крылову и Г. И. БаренблдФту) [22]
исходят из постоянства главных компонент горного давления
Гц=о*ц—рЬц=const, *=/, (20.5)
что определяет объемную деформацию элемента пласта
е=(1-е,)(р-Ро)//С, (20.6)
а в уравнение пьезопроводности (20.4) входит иной коэффициент
упругой сжимаемости
р= {l-g.+TCmo^2)-^1))} (Кт^-К (20.7)
При этом учитываются смещения матрицы пласта, а пористость
т линейно растет с ростом порового давления
{т-т0)/mQ=-e-i№) (р-р0) = {- (ЦК) + (р^-р^)} (р-ро) , (20.8)
При третьем варианте (по Г. В. Исакову [22]) принимается, что
в своей плоскости пласт деформироваться не может, т. е. e\=e2=Qy
а е3=£з(Р)> гДе Р — давление в жидкости. В этом случае закон Гука
дает
(1-**)/> = (К+ 4G/3), e = 6v
«,{{> = с $ = (K-2G/3)*+«./'. 1 • '
что приводит к такому коэффициенту эффективной сжимаемости
в (20.4) *
р=(р(2)_1р(1)) + (1_е,) (i/m0) (/(4-4G/3)-1. (20.10)
Поскольку коэффициент пьезопроводности на практике находится
при обработке данных изменений порового давления, выбор
конкретной формулы для и имеет значение лишь для предварительных
оценок и зависит от того, какие параметры изменялись в ходе
лабораторных экспериментов.
Реальные перепады давления могут быть столь' значительны, что
необходимо учитывать нелинейные соотношения (17.11). Их
использование при пренебрежении смещением матрицы породы приводит
& нелинейному варианту [22] упругого режима фильтрации
жидкости
<p,t=Kv VV, ф=ехр р (р—ро),
(20.11)
Т=а/р, ip=am+p(2>m0, а=ак-\-ат+а»у
где учитывается экспоненциальное изменение вязкости жидкости
|х=ц,о ехр {ац (р—ро)}. (20.12)
Уравнение нелинейно-упругого режима фильтрации эквивалентно
уравнению Л. С. Лейбензона [16] фильтрации газа. В самом деле,
в последнем случае пренебрегаем деформациями порового
пространства, а для изменений плотности газа имеем
р=р(гЦТ)-*9 (20.13)
170
где z — коэффициент сверхсжимаемости. Если 2=const, то уравнения
(20.1) — (20.2) сводятся к уравнению Лейбензона
pf<=xoV2p2, w=*hl(2n%№). (20.14)
Если же плотность газа меняется по политропическому закону
р=рп. const, /z=const, (20.15)
то уравнение нестационарной фильтрации газа несколько
усложняется
pntt=XlV2p(n+l)M
(20.16)
xi=iM (m0po)-1 (1 -f n) -\
Учет изменений пористости и проницаемости газового пласта
приводит к дальнейшему усложнению уравнения фильтрации
{р exp р(р—p0)}tt=x{p exp [а(р—Ро)]р,гЬ,
(20.17)
P=^m—CLzj a=ct>k—az—dp.
Наиболее общее уравнение фильтрации жидкости и газа имеет
такой вид:
P>t=V{x(P)VP},
Р=СЬЩр1а Х(Р)= Ир) ~ (2018)
где Р — функция Лейбензона, а коэффициент пьезопроводности
также может быть выражен через Р.
Стационарные течения жидкости и газа описываются уравнением
Лапласа
V2P=0, (20.19)
решения которого в плоскорадиальном случае
(11г)(д/дг)(тдР/дг)=0
связывают массовый дебит Q скважины с распределением давления
р=р (Р) в пласте толщиной h
P=pl-Q[x(2nk<>p0h)-1 In (г/гс). (20.20)
Логарифмическая зависимость поля Р от радиуса означает, что
Р—*оо при г—*оо. В связи с этим вводим условную величину
«контура питания» пласта гк такую, что P(rK)=PK=const для разных
значений дебита Q. Хотя ошибка в конкретном выборе значения гк
.слабо влияет на результаты расчетов (так как r^>lrc), его следует
выбирать из анализа соответствующей нестационарной задачи.
Если задаться аналитическим представлением функции
Лейбензона, то удается получить расчетную формулу для дебита скважины.
Обработка с ее помощью данных полевых наблюдений позволяет
определить некоторые параметры пласта. При притоке к скважине
капельной жидкости Р=(1/а)ехр(—аДр) ее дебит определяется
формулой
С=Ч2л$ороЛю) {1—ехр (—аЛр)}/{а1п(гк/гс)},
(20.21)
Др=рк—рс,
171
если пластовое давление рк совпадает с давлением р0 отсчета. При
а—>~0 формула (20.21) переходит в классическую формулу Дюпюй
Q = 2nko9oh lim Г-ехр(-«А/,) = ^ (20 22)
Н«1П(ГК/ГС) а->0 а / ■
где K=2jvk0p0h/ (|х In гк/гс)—коэффициент продуктивности скважины.
Для нахождения К и а по индикаторной линии Q=Q(Ap)
скважины (рис. 56) воспользуемся приемом графического
интегрирования, предложенным А. Т. Горбуновым й автором [22]. Интеграл от
дебита Q по Др (20.21) можно представить в виде
F (Ар) = FJF, =.{Г - ехр (- аДр)}"1 - {аД/>}-\
АР
F1= jQd(Ap). F2 = QAp. (20.23)
о
Функция .F(Ap) представлена на рис. 57, причем рс>Ро
соответствует нагнетанию в пласт жидкости, рс<Ро— отбору. Величина F\
определяется как площадь, ограниченная индикаторной линией и
осыа Др, a F* — площадь соответствующего прямоугольника (см.
Рис. 56. Выпуклая индикаторная
линия стационарного притока к
скважине (I — увеличение отбора, II —
уменьшение отбора, цифры на кри-
Q, mlcym вои — последовательность снятия то-
рис. 56; для этих данных а=0,186 МПа-1). Хотя коэффициент
продуктивности является тангенсом угла наклона касательной и
индикаторной линий в точке pc=p0j из-за трудностей дифференцирования
экспериментальных точек при малых дебитах рйсчет удобнее вести
по формуле
/C=Qcx{l— ехр (—аДр)}"1. (20.24)
В рассматриваемом на рис. 56 случае /(=84,5 т/(сут-МПа).
Иногда изгиб индикаторных линий интерпретируется как
проявление инерционных сопротивлений — закона турбулентной
фильтрации (13.51). Соответствующая формула для притока имеет вид
AP^Q/K+bQ2, (20.25J
172
о—^ о -о»
Lt , 2см
Линия нагнетаний
) о
и она действительно качественно, но не количественно [22],
соответствует выпуклой индикаторной линии (см. рис. 56). Однако формула
(20.25) даже качественно не может объяснить вогнутые
индикаторные линии при нагнетании и отборе. Отрицательные значения а
могут быть объяснены относительно большим увеличением вязкости
с ростом порового давления, чем увеличение проницаемости.
Параметр <х растет, в зонах тектонических несогласий (трещиноватости)
пласта.
Газовые скважины отличаются весьма большими дебитами (и
скоростями фильтрации);, а поэтому расчеты по формуле (20.25)
имеют смысл. Для практических расчетов она представляется в виде
(Р2к—P2c)/(<Q*xcpZcp) =a+(6Q/M, (20.26)
где цср, 2ср — значения (х и г, приведенные к среднему давлению.
Характерные величины коэффициентов: а=60, 6=0,15 при р=5 МПа,
Q — 10 000 тыс. м3/сут.
. Для расчета течений жидкости в пласте, вскрытом системой
скважин, необходимо решать уравнение Лапласа (V2P=0) при задании
адекватной системы источников
или стоков. Чаще всего требуется \ к^~^к п п3/1Яд п
рассматривать двумерные зада- jf .,г% ° °2рдд °~~pJ
чи, причем наиболее важным ока- ' ~г— , zcT,—° °—J^
зываются эффекты интерферен- г ^ ^
ции скважин [35], которые
приводят, вообще говоря, к
снижению дебитов действующих
скважин при вводе в эксплуатацию
каждой НОВОЙ скважины (пере- Рцс. 58, Схема притока жидкости к ря-
хват отборов). Через некоторое дам скважин
время после пуска системы
скважин каждая из них оказывается окруженной своей зоной
дренирования, причем при постоянных дебитах границы дренирования
неподвижны.
Простым и оправдавшим себя способом расчета притока
жидкости от контура питания к цепочке скважин является метод
эквивалентных фильтрационных сопротивлений (Ю. П. Борисова) [35].
Проиллюстрируем метод на типичном примере течения от линейного
контура питания к рядам п скважин с интервалом 2<т (рис. 58). Вся
область фильтрации условно разбивается на прямолинейное течение
от контура питания к условной дренажной галерее и осесимметрич-
ное от галереи, которая играет роль условного контура питания для
индивидуальной скважины. Дебит \Q участка длиной 2оп
определится по формуле для линейного потока
Q= (2ая£оРо/*Ы (P«—P*)fL, (20.27)
где Рк— значение функции Лейбензона на контуре питания, Р*—
на условной дренажной галерее.
Индивидуальная скважина радиуса гс окружена контуром
питания длиной 2а, ца котором поддерживается значение Р=Р* и
который является, одновременно частью условной дренажной галереи.
Поэтому радиус гк условного контура питания индивидуальной сква-
173
жины определяется равенством 2ягк=2ог, т. е. г^=о/п. Согласна
(20.20) тем самым имеем
Q/n=(2rt£0poftM)) (Р.—Рс)/1п c/(nrc\ (2J0C28)
и окончательно * /
Q/n={k^fa)(P^Pc)[(L/2o)^ У (20.29)
Точное решение, определяемое методом отображений стоков,
Q/n=(2nfHfaNv<o) (Рк—Рс) [ln2sh(nL/o)+ln0/(jtrc)]-i (20.30)
при L»a переходит [35] в результат (20.29).
Если роль контура питания играет ряд нагнетательных скважин
(что типично для поддержания пластового давления заводнением
[35]), то метод позволяет аналогично найти дополнительное
фильтрационное сопротивление потоку—от скважин нагнетания до
условной галереи нагнетания.
На газовых месторождениях число работающих скважин
невелико (вследствие их больших дебитов), а вопросы интерференции
скважин из-за локализации депрессии в непосредственной близости
скважин (Р—р2) не столь существенны, как при отборах жидкости.
Поэтому расстановка газовых скважин диктуется иными
технологическими соображениями [16].
. Нестационарные задачи в общем случае упругого режима
фильтрации жидкости приводят к необходимости решения нелинейного
уравнения
иг=т{ч-\)/УЧ2щ w=(pv# (20.31)
При 7 = 1 это уравнение оказывается линейным.
При начальных4и граничных условиях
<pv(jc, 0)=1; <р*(°°, 0=1;
(20.32):
чр7(0, t)=4>vc = const
одномерная линейная задача является автомодельной, т. е. введение'
переменной ^=x/V2Kt сводит уравнение (20.31) к обыкновенному
дифференциальному
TT(0) = cpT, TT(oo)=l. l^-*5)
Числовые расчеты [22] показывают, что при весьма большом
диапазоне значений 7 (1; 2; 4; 10; 100) и реальных перепадов
давлений решения практически близки.
Осесимметричная задача при начальных и граничных условиях
<pv(r, 0)=1, ф*(оо, /)=1,
(20.34)
(гдц)у/дг) r_^0=-^o)Q[io/ (2nk0poh)
также является автомодельной, т. е. уравнение (20.31) "и указанные
условия сводятся к такой системе
cpT-i {d V/*1 + (1 /6) d<p4dl}'-\ - Witt = °>
■?т (00) = 1, W<p4c£ = - aQn0/(2^oPo/i), (20.35)
^ = r/y"2x?-^0,
174
если ввести переменную £ = ]/г/2иГ. Решения вновь [22] оказались
совпадающими при всех значениях, у
В силу отмеченного совпадения решений при всех 7 это линейное
уравнение
uti=KV*u (20.36)
практически оказывается достаточным для задач нестационарной
фильтрации в неограниченном пласте. Замена уравнения (20.31) на
(20.36) называется линеаризацией Лейбензона [24], и ее смысл
состоит в подстановке в эффективный коэффициент пьезопроводности
пластового давления р=ро и в выборе потенциала стационарного'
течения cpv в качестве искомой функции.
Так, распределение давления в полубесконечном пласте после
включения постоянно действующей галереи (20.32) будет
описываться решением уравнения (20.36) вида
[и - и (0)]/[ц (оо) - и(0) = 1 - erf?,
5=jc/(2|/W). '
а поле давления при включении точечной скважины — условия
(20.34) — согласно уравнению (20.36) имеет вид
и-и(оо) = (Qpfhkhp)Ei (- Ц2), 6 = г/(2 Vltf),
Ei (- V) = - [е-г — & In —+ 21n:
J z 4
г ,
У
при достаточно малых значениях £, £/.=0,5772 — постоянная Эйлера.
При обработке кривых восстановления давления в скважине,
расположенных вдали от границ пласта, при всех значениях у также
допустимо пользоваться линейным уравнением (20.36). Задача
формулируется следующим образом.
Действующая скважина с дебитом \Q0 останавливается в момент
£=0, Поле и (г, t) в пласте представляется в виде
u(ry t)=u0(r)^-(QVioJ27ik{)poh)u(rt /), ОЮ, (20.39)
где щ(г) —поле давления при ^=0. Функция и (г, t) также
удовлетворяет уравнению (20.36) при следующих условиях:
и (г, 0) = 0, и (гс, t) = (2*ftePoA/Qne) ис (t); (20.40)
где Uc(t)—измеряемая функция времени (изменения давления на
забое скважины). Граничное условие на стенке скважины для
расхода принимает вид
(rdl!dr)r=rc = ~U (20.41)
что соответствует идеальным условиям закрытия скважины.
Приближенное решение для точечного источника единичной интенсивности
имеет вид ^ -
и (г, t) ъ\п (2,25x^/r2). (20.42)
175
Ди.МПа
30
Отсюда на скважине г=гс закон изменения давления таков:
uc-(t)=A+Blnt,
A=(Q\uJ4nkopoh) In (2,25x/r2c), \20A3)
B=tQno/ (4jt£0poft). /
Поэтому экспериментальные точки uc(t) в полулогарифмической
системе координат должны лечь на прямую линию, что дает простой
способ [6, 22] определения
комплексных параметров
пласта koh\i и х/г2с.
Однако весьма часто
реальные кривые восстановления
пластового давления (КВПД)
имеют начальный нелинейный
участок (рис. 59), который
объясняется либо
^мгновенным закрытием скважины
[Q(t)=0 при *>0], либо
несоответствием в начальный
момент времени
фильтрационного потока жидкости простой
теории упругого режима
фильтрации.
Обратим внимание на то,
что в полулогарифмической
системе координат
«дефектный» начальный участок
слишком растягивается. Поэтому разумно проводить обработку
КВПД, построенных в обычном масштабе времени -(uc-*-t).
Воспользуемся [6, 22] приемом интегрирования, введя безразмерную
функцию
(20.44).
о
где Auc=Uc(t)—Uc(Q) соответствует текущей точке КВПД, для
которой численно подсчитывается интеграл (20.44). Из уравнения
(25.46) следует формула
z(t) = {ln(2,25x^/r2c)— l}/ln(2,25^/r2c), (20.45)
откуда следуют, непосредственно значения комплексов параметров
х/г2с= (1/2,250 ехр 1/(1-2),
Рис. 59. Кривые восстановления пластового
•давления в скважине
««~£-bw*-
{kopch/щ) =Q/ [4я (1 —z) Ли].
(20.46)
Кривым (для двух дебитов на рис. 59) соответствуют значения
а=0,177 МПа-1, Гфр0/щ=4,6-10-* (см4.г)/Па.с.
Для немгновенного закрытия скважины были разработаны
специальные приемы обработки КВПД, требующие замеров спада де-
176
бита Q(t). Среди них укажем способ прямого интегрирования [22] >
подобный (20.44), а также метод, использующий преобразование
Лапласа [6].
Если пласт имеет конечные границы, то линеаризация Лейбензона
недостаточна. В этой связи была численно решена [16, 22], задача
о фильтрации газа к скважине, вскрывающей круговой пласт
единичного радиуса (рис. 60). Видно, что область движения делится на
VW
035
О90
0.85
jf/
/fl
/l1гл
III / Lr/rK=0tZ53Z
Щ Г^ omi
mil \j^^o.m35
ЩугХ^отбз
шлл^0-тп
Dili
\^~ UUID6L
Yj^^-0,005366
1
]^ОШШ
-
^^^7
QjilZJ!Hh/i)=-Ofl5 j
V~Z
0,801
О 025 05 075 £
Рис. 60. Две фазы неустановившегося притока к скважине в конечном пласте
I фазу (автомодельное решение, зависящее только от Ъ) и II фазу
(неавтомодельные решения, где кривые р=уги зависят и от г),
примем на больших радиальных расстояниях от скважины смена
фазы происходит через меньший интервал времени.
Линеаризация, применимая в случае конечного пласта, состоит
(по Л. С. Лейбензону [22]) в замене уравнения (20.31) ца
следующее:
utt=K {и (р)} <v-i)/v V4 (20.47)
где р (t) — среднее по зоне движения давление. Введение нового
масштаба времен^ т сводит (20.47) к обычному линейному уравнению
(по К. С. Басниеву и Г. П. Цыбульскому)
их=кУ2иу dx/dt={u(p)}<y-W. (20.48)
12—3311 ' 177
Для фильтрации идеального газа (y=2,0, Q = const) новое
время т определяется так: ,
T=Pot (1—Qt/2Q0), (20.49)
где йо — начальное содержание (запасы) газа в рассматриваемой
замкнутой залежи. Для малых интервалов времени (<2//Й0<1) тем
самым сохраняется линеаризация (20.36).
Закон падения среднепланового давления используется для
оценки запасов нефти и газа в залежи. А именно, интегрирование
уравнения (20.31) по объему приводит к связи
t
(?>.-<?> = -ИгГ°Ю' aW=fQ(')# (20.'50>
0
между <ф>—средним значением функции ф по пласту, ее
значением в начальный момент /=0 и суммарным отбором Q(t) за
время t эксплуатации залежи. Если при полном отборе жидкости из
пласта <ф>«0, то отсюда следует правило материального
баланса, широко используемое на практике,
Об=Кф>00(0«Ф>о— <Ф>(0)"1-
Материальный баланс используется при построении
приближенных решений методом смены стационарных состояний [16, 22].
21. НЕСТАЦИОНАРНАЯ ФИЛЬТРАЦИЯ С ГИДРАВЛИЧЕСКИМ
ЗАПАЗДЫВАНИЕМ
Напряженное состояние пласта с двойной пори»
стостью. Уравнения фильтрации. Малые параметры»
Упрощенная система уравнений. Изменения
начальных и краевых условий. Приток к дренажной
галерее. Отбор через скважину. Восстановление давле-
_ ния. Фильтрация газа. Учет изменений
проницаемости трещин. Метод линеаризации.
Весьма часто встречаются среды с системами пор разных
масштабов, например, среды с двойной пористостью /п(1) и т(2), обладающие
соответственно двумя проницаемостями &(1) и £(2). Эти системы
гидравлически [2,9] связаны друг с другом, что отражается, во введении
характерного перетока /. Крупные поры, которые чаще всего
представлены трещинами, разделяют среду на блоки; мелкие — на
гранулы.
Суммарные напряжения 1\/, отождествляемые с горным
давлением, в первой матрице (из блоков) уравновешиваются по правилу [9]
Г.. = (1 _ т(»,) П// - тПрЪЪц = ПЯ} - /?(Ч7> (21 Л)
где П/у —истинные, а П-р —эффективные напряжения в блоках, /;(1> —
поровое давление в крупномасштабных порах. Напряжения IItj
играют роль суммарного напряжения во второй матрице
(гранулярной), т. е.
Щ=Ъ$-рЪЪи. (21.2)
178
При неизменном горном давлении параметры первой среды будут
только функциями давления р(1), параметры второй — двух давлений
рО) и р<*>
/яО = mSl) (р<1)), № = £<*) (р<1)), /тг<2) =т^ (/?<'>, /?<2>);
ki*) = kW(pW, /?<2>).
Обмен жидкостью между порами (в блоках) и трещинами будем
описывать распределенными по объему источниками (стоками),
интенсивность которых определяется разностью давлений р(1), р(2>
соответствующих потоков
/=(а*рМ(р(1)-Р(2)), (21.3)
где а* — безразмерный коэффициент, зависящий от проницаемости
блоков k2 и густоты трещин, мерой чему служит удельная (на
единицу объема) поверхность трещин 5. При линейном приближении из
анализа размерностей имеем
a*«#2>S*~fe<*>/I*/ (21.4)
где L — средний размер блоков.
Уравнения баланса масс жидкости-в обеих матрицах
(ртС)),< + (рш<»)_/ + /=0) (рот(г)),, + (Рш(2)),/-У = 0 (21.5)
включают в себя две скорости фильтрации
a>y(a) = - (А(в)М) РУ, a = 1, 2. (21.6)
Система уравнений фильтрации в средах с двойной пористостью
сводится в линейном приближении ik таким двум
(1 + в)/><}>+«<,)/>!?> =x(t(1,vV(l).+ vV(1)). (21.7)
в=(дтМ/дрМ)/(дтЫ/дрЮ); £0)=г(1)£;
№=k\ m<2>p<2>=e(2)mP; т^=т\ $^)=$.
При 8=0 система (21.7) описывает фильтрацию в двух
эквивалентных пористых средах, вложенных друг в друга и представляющих
среду с двойной пористостью, в которой 0<С1. При e(i),6(2)<l
система уравнений (21.27) соответствует фильтрации жидкости в
трещиновато-пористой среде. Действительно, проницаемость трещин (&(2))
намного больше проницаемости пор (&i(1))> тогда как упругоемкость
блоков (т(1)Р(1)) намного больше упругоемкости трещин (т(2)Р(2)).
Упростим систему уравнений для трещиновато-пористых сред,
воспользовавшись наличием малых параметров 8(1), е<2) и
пренебрегая величиной 9 по сравнению р единицей. Введем линейный
масштаб L, масштаб времени Т и масштабы изменений давления рь Рг,
т. е. гР и Р. Тогда в безразмерных переменных
Wit*) (vV(,) + «(,)«vV(,)) = •<,>/>!?> + *рУ ■ . (21 8)
12* 179
Отсюда видно, что в уравнениях (21.7) членами с
коэффициентами e(i), 6(2) можно пренебречь, если ,
e^l; (x77L*)~l; (7/т)<хЛ; Ь^Ум.
Если же e<Cl, то в уравнениях (21.7) можно полагать ео)=0, но
нельзя пренебрегать членом с коэффициентом б(2). Если считать, что
е~е(2), то из уравнений (21.8) следует оценка области L0, Г0, для
которой справедливы изменения давлений такие, что ,р(1)~е'р<2\
Наконец, если e<Cl, то при 8(i)6~l получаем оценку масштабов
L*, Г* области, где р^~гр(1\
(xTJLl)^(l/s{l)); (TJx)^l; L^Vw*- щ -
Таким образом, в весьма малые интервалы времени давление р(2>
в трещинах распределяется согласно уравнению пьезопроводности
•(.)A(?,=»«VV(1) + (^(1)M; Тв = «(1)т<т; L0<^Vm (21.9)
со стоком в блоки, зависящим только от давления в трещинах, и при
эффективном коэффициенте пьезопроводности ио=х/е(2)Э>«.
Дальнейшие (при Т~%) изменения давлений р<!), р<2> в той же
области описываются системой уравнений
xV2/?(2)=/7jJ), хуУ2)+(/?(,) -/?(2>)/т = 0, (21.10)
или же эквивалентным уравнением, одинаковым и для давления
в трещинах, и для давления в блоках [2, 6, 22],
p,t—K%{d/dt)SJ2p—K42py p=pll\ р<2>. (21.11)
Поскольку эти изменения привносятся в область, где давление
р<2> уже возмущено, то начальное условие для уравнения (21.10)
определяется как асимптотическое решение (при t-^oo) уравнения
(21.9). •
В это же характерное время (Г~т) в узкой зоне L*~ V E(dkx<^
«CL около возмущающей границы будут существенны изменения
давления р(1) в блоках, описываемые уравнениями
**(г)УР{1) -(Р{1)М = рУ> Т1*^. L*<^V7^, (21Л2)
тогда как давление р(2) определяется уравнением Пуассона
V2p<2>=—рМ./%.
Для области L, Т этот процесс можно считать одномерным вдоль
нормали к границе среды. Если усреднить уравнение (21.12) по сротг
ветствующей координате (х=х\), получим
('шШр?]% = {р11))$ + {р{1Ч*)+' (21-i3)
где <Ср(1)>+ — среднее по области L* давление в блоках.
Для области L, Г; фильтрация в которой описывается уравнением
(21Л1), проницаемость 6(2)А незначительна, а потому потоками в ле-
180
вой части (21.13) можно пренебречь. Тем самым уравнение (21.13)
принимает упрощенный вид
<Р(1)>+,<+<Р(1)>+Л=0
и его интегрирование по времени дает следующее эффективное
граничное условие для уравнения (21.10) относительно р(1)
Л<»(0, /) = <^')(/)>+ = (/><,)>-+«Р(,)>-- А)ехр(-*/т). (21.14)
Здесь ро — начальное пластовое давление, <р(1)>~=р*— давление
на внешнем контуре пласта. Иначе говоря, скачкообразное изменение
давления в скважине на величину [р]о=р*—Ро приводит к разрыву
давления в системе пор, причем последний не размывается
мгновенно, а релаксирует во времени по закону
[p<i>] =р*-Ро= [р] о exp l-t/%): (21.15)
В то же время разрывные изменения давления в системе трещин
размываются мгновенно
[р(2)]=0, *>0. (21.16)
Чтобы это показать, проинтегрируем первое из уравнений (21.10)
в интервале О^х^к вблизи границы и в интервале времени 0^/^
*Р% \о = I iP{t) (х> '•) - Р{2) <*■ °)> **•
о
Поскольку в области интегрирования функция р(2) ограничена
и. непрерывна во времени, а момент t0=£0 произволен, то
[dpi*)/dn]=09 />0
— скачок нормальной производной р(2) у границы размывается
мгновенно. Поэтому аналогичное интегрирование первого уравнения
(21.10), умноженного предварительно на координату х, приводит
непосредственно к условию (21.16).
Таким образом, решение уравнения (21.11), справедливо в
основной области движения, относительно давления р(1) в блоках требует
изменений граничного условия по правилу (21.14). Если же решать
уравнение (21.11) относительно давления в трещинах р(2), которое
в силу условия (21.16) измеряется в скважинах, то необходимо
заменять обычное начальное условие (например, p(2>(x)=0) на
асимптотическое решение уравнения (21.9).
В связи с этим практически удобно пользоваться [22] несколько
более сложной системой, в которой учтена малая упругоемкость
системы трещин,
Р$ + •<,>/\<?> =*VVS> • Ч*)РУ = *vV> - (/f > - рП)Ы (21 • 17)
Дополним проведенные качественные рассуждения анализом
плоской одномерной задачи:
' р(1)=р(2)=р0) t=09 х>0.
p(i)=p(2)=sLp*f t>0y x=0t i (21.18)
13-3311 181
Решение этой задачи для системы (21.7) при 8=0 было дано
Э. А. Бондаревым и автором [22] и имеет вид
t
Р*
т /
1^ = .uFAx. *) + — ГЛ(л. z)dz + F(x, t),у (21.19)
о
{^=*L = Ft(X9 t)r\-± Г^(Х, z)dz-(«(l)/.)F2(*> ')•
Р*—Р* *в J
о
где использованы следующие обозначения: i ;
F(*f f) = exp (-1[%) erfc (jc/2 j/^x?),
о
_,/ ^Le4>/__£_U.
При малых характерных временах /<Ст решение (21.19) переходит
в решение уравнения (21.9)
Р*
^Л = JL /ехр Л- *Л erfc (ф* - l/-±-) +
**-Р. 2\ FV V*i) \2Vxt V xs(2) / r
+ exp(?^)erte(4f.+ -/^:)}+0(.(„), (21.20,
тогда как (p(1>—po) = (p*—Po)0(e(2)). Асимптотика решения (21.20)
при /->oo имеет вид
Р(2) = А + (Р* - А) ехр (- */}/*).' (21.21)
При характерных временах /~т решение (21.19) переходит в
решение [22] упрощенных уравнений (21.11) для давления р\ в блоках
J^t^=^9{XtZ)d2 + 0{s{l))f х>0
Р — A J
0 (21.22)
о
о _
и для давления р<2> в трещинах
Р
^. = ?1 (х. t) + j Tl (Л, z)£fe. (21.23)
182
Давление в блоках (21.22) удовлетворяет исходному начальному
условию (21.18) и граничному условию (21.14). Давление в трещинах
(21.22) удовлетворяет исходному граничному условию (21.18) и на*
чальному условию (21.21).
Если на границах задается поток жидкости, то это означает зада*
ние суммарной скорости фильтрации
w, = wf) + wf> = - Ш Ыру + р$). (21.24)
При использовании выражений (21.11) или (21.17) оно упроща»
ется и допускает двойное представление
Wj « - Ш p<f = - (kjv) (р<}> + *Р% (21.25)
Осесимметричная задача о пуске (в момент времени /=0)
скважины малого радиуса гс с постоянным дебитом Q в бесконечном
пласте определяется такими условиями:
pn = pi*) = p.{t = 0); /,<«> = />(■> (r=Jrc, f>0). L
*i>)rpy+rpW = -Qp/(2^h) (r==rc,t^0).
Решение системы (21.7) при 6=0 было построено Э. А. Авакян
[22]. Оно включает помимо е<1), е<2) еще один малый параметр Я=*
=r2c/ {nt) <С 1. Наиболее простое решение соответствует включению
точечного стока, т. е. пуску скважины нулевого радиуса (гс-Ю). Вы*
раженное в трансформантах Лапласа р(1), р<2> функций р*1*, р<2) это
решение имеет вид
Ом.
""'; " " ' Г ^_ ' (21.27)
Он Р - s До\ V7 У S.+ 1 У
причем при е(2)=0 решение (21.27) справедливо для моментов
времени t//~st~1. Здесь 5 — параметр преобразования Лапласа.
Трансформантам (21.27) соответствуют такие поля давлений:
t
^{Р.-Р{1)) = *мРЛг, /) + -f ]>д(г. z)dz+ylFt(r, t),
о
2nk?h
'р _7(^то °\Кх V sx+i у
0 (21.28)
4xf z J z *
Ft(r, 0—j(l/2)Vr^exp(-^/x- rV88(l)^)U7_I/?fo(rV4e(l))rf)(
f, (r, 0 = (1 /2) (//*) y^rf exp (- tj* - rV8t(l,irf) ^_3/2.o (r'fbu)*)-
13* 183
Здесь Wp,q — функция Уиттекера, /0, Ко — функция Бесселя
первого и второго рода мнимого аргумента.
В этом решении условие равенства давлений р^> и р<2>
следует7понимать как условие совпадения главных членов их асимптотических
представлений при r-Ч). При /~т, г~хт из решения (21.17у (21.18)
следует [22] формула
и(2) в 2icfepA(A - /?<2>)/Qn ^ In 2 }/£ - In г/к* - (1/2) X
XiEi{—f (1 + «c,))/(«(m))} + (l/2)-Ei (--/(1+«(,))V(~(.)). (21.29)
0=1,781.
- - На рис. 61 приведены эпюры давления в трещинах (в
безразмерном виде) для разных моментов времени t и расстояния г в зависи*
мости от значений безразмерных комплексов К=г2/(кх) и о=
= ^(2)/(1+6(2)), а именно: ш = 0 (кривая
1), ю = 0,001 (кривая 2), © = 0,01
(кривая 3), (о=0,1 (кривая 4). Видно, что
при полном пренебрежении
сжимаемостью трещин (е(2)=(о=0) в начальный
момент времени (*=-f-0) давление
скачком возрастает на величину, зависящую
от г, а при tr^x меняются по обычной
теории упругого режима. Учет
сжимаемости трещин (оэ=й=0) для- малых времен
означает первоначально большой
коэффициент пьезопроводности х/е^)
(участок /), затем переходный участок //
соответствует «начальному скачку»
давления, и наконец, происходит переход к
обычному упругому режиму при
пьезопроводности % (участок III). Учет малой
ю° юг ю* 10е ю* )ow проницаемости блоков меняет значение
Ht/rz коэффициента пьезопроводности, не-
Рис. 61. Поле давления в тре- сколько снижая кривые на рис. 61. Эф-
щинах при разных отношениях фект заметен при ei—0,01 в начальные
емкости трещин и пор моменты времени. '
Скважина, вскрывающая трещиновато-пористый пласт, может
пересекать систему трещин. В этом" случае ее забойное давление будет
совпадать с" давлением р(2) в точке г=гс, и для обработки КВПД
следует пользоваться формулами (21.29), считая, что ^ —
безразмерное давление на забое скважины. Процессу его восстановления до
пластового будут соответствовать графики рис. 61. Тем самым
выясняется, что начальный участок, который по представлениям обычнрй
теории упругого режима фильтрации является дефектным, может
соответствовать проявлениями реальной трещиноватости пласта.
Кривые восстановления пластового давления скважин, вскрывающих
пласт, после мощного взрыва в нем [34] имеют вид,
соответствующий графикам рис. 61.
Воспользуемся преобразованием Лапласа для обработки графи-
184
иг\
10 \
5
0
~--jCt
ж/
л /
/ //
* i
/ А =
Г i
EZU
_J—I , I I
ков КВПД [6, 9]. Тогда можно применять формулу (21.27) или же
при 62=0 ее упрощенный вариант
sp<2)(r, s)=Qix(2nkph)-l{—In (у/2) — (1/2) In (rs/n) +
+ (l/2)ln(l+sx)}, (21.30)
где 5 — параметр преобразования Лапласа.
Поскольку
i=Q\i/ (2nkph) = (рс—ро) /In (гк/гс) (21.31)
можно определить по испытаниям-на стационарный приток, то
обработка КВПД сводится к подбору значения т, которое дает для
графика зависимости р(2) In (5_1+т) уклон i/2s (по А. Бану [9]).
Если скважина не пересекает систему трещин, то измеряемое
в ней давление будет давлением в блоках"р(1), и для обработки
КВПД следует пользоваться формулой, следующей из (21.17) при
82=0, а именно
s(l+sr)pM=Q\i(2nkph)-l{—\n(y/2) —
— 1/2 In (r/x) + (l/2) In (s-'+t)}. (21.32)
И в этом случае удается по кривой КВПД определить величину i,
проведя сопоставление с данными об установившемся притоке.
Сопоставление двух вариантов обработки КВПД при известном радиусе
Гк может в принципе, выявить, контактирует ли скважина с системой
трещин в пласте или же она попала в блок. В первом случае
эффективный радиус скважины может быть на порядок больше значений
гс (~0,1 м), типичных для обычных пористых сред.
Характерные времена запаздывания т по данным А. Бана [9] для
нефтяных месторождений с трещиновато-пористыми коллекторами
меняются от 5 мин (Венгрия) до десятка часов (Иран), а
коэффициента проницаемости — k=(l—5)-10~12 м2. В случае фильтрации
при параметрах пласта, зависящих от давления, интенсивность
перетока / задается пропорциональной разности соответствующих
потенциалов. Так при фильтрации идеального газа эффективная система
уравнений, аналогичная системе (21.11), была предложена П. П. Зо*
лотаревым и Ю. П. Желтовым [22]
(/>(,>)' - (РтУ -•<.)' = д {pmyjdt - xxv1 (/><■>)'.
Исследование индикаторных линий скважин показывает, что
наибольшие значения а соответствуют трещиновато-пористым
коллекторам, т. е. именно в этом случае эффекты нелинейности наиболее
существенны. Система уравнений фильтрации в трещиновато-пористых
средах при нелинейно-упругом режиме фильтрации имеет вид
■ vd(u^Y^4dt—Te1xV2u(1)+w<1>— (и<2>)я=0, . (21.34)
те(2)72д (tf2)) W'/dt—nm М2и&—и^+ (и&) »=0,
где л = а(|)/аО; Tl = <xi'> (а<|> + а9)~*; Г2 = а<2> «> +а9)~1;
"•<■> = (Y./T.)(^ow/^1)); •(,> = ^W;
1/х = *rf (а<!> + а9)/№; * = mi1 V (а&} +а9)/*\
185
Условие er=0 означает пренебрежение проницаемостью блоков,
e2s=0 — упругоемкостью трещин. /
Поскольку в начальный момент времени t=0 давления равны
рО)=р(2)=р0у то для бесконечного пласта вполне допусти^
проводить линеаризацию, заключающуюся в приравнивании давлений,
выраженных в коэффициентах, начальному пластовому давлению ро.
Так, уравнения фильтрации газа (21.33) можно представить в виде
р(П + ,wp<8) = xV« (,<»>)•, (p<M)i. =(,<•>)» + е{г),р(2) _ K,v. {ру
и они хорошо аппроксимируются такими линейными уравнениями:.
(l/2Л)(pW)t/.+ .•(i,(l/2A)(p(•»)«/=xv,(p(,)),.
(/,<»>)» = (/,('>)« + в(2)х (/P))*t - xxV' (/»(•))».. (2L35)
Более сложная система (21.34) линеаризуется следующим образом.
Введем новые переменные, воспользовавшись также приближениями,
соответствующими приему линеаризации Л. С. Лейбензона,
<f(1) = -uW + (iii2))n; <р^ = 1-ы(£>; /г = а<1)/а(г);
Y, (и(М)|/Тх ^ а(П; („(■>)« ^ АШ(2)в (21-36)
Тогда система (21.34), учитывающая экспоненциальные изменения
проницаемости трещин и пористости блоков с давлением, принимает
следующий линейный вид:
<р(1)+^(2)+(9(1)/т)=0, #
•(•)?!?. - "*vV2) - (<р(1)Л)=0- (21
Эта система уравнений несколько неточно описывает скорости
изменения искомых функций во времени, но срхраняет неизменными
выражения для интенсивности перетока J и фильтрационных
сопротивлений в системе трещин. Таким образом, квазинестационарные
решения систем уравнений (21.34) и (21.37) будут практически
одинаковыми.
Перетоки между пластами также приводят к эффектам
гидравлического запаздывания [36], допускающим аналогичное описание.
22. НАПРЯЖЕНИЯ В ПРИЗАБОЙНЫХ ЗОНАХ СКВАЖИН
И НЕЛОКАЛЬНО-УПРУГИЕ ЭФФЕКТЫ
Формулировка задачи теории упругости. Условия
на контактах пласта с массивом и со скважиной.
Преобразование Вебера — Орра. Нагрузки на
колонну при стационарном отборе жидкости. Течение
в тонком пласте в упругом массиве. Нелокально-
упругий режим фильтрации. Ход кривых
восстановления давления. Пластичность вокруг действующих
скважин.
Рассмотрим напряженно-деформированное состояние пороупруго-
го пласта толщиной 2h в окрестности работающей скважины радиуса
г=гс. Выше- и нижележащие горные породы будем считать
упругими и непроницаемыми.
186
(22.4)
Решение этой осесимметричной задачи (согласно В. Н.
Николаевскому и Т. К. Рамазанову) будет удовлетворять линейной системе'
уравнений равновесия (14.16), а именно
V%*-Ke,z/(1— 2v)}+2(l—v)Sp,zl(l—2v)=0 (22.1)
V2«r-(«r/r2) + {e>r/(l-2v)}+2(l-v)5p.r/(l-2v) =0 *
m.t-t o([>-p(,) (l-m,) p„+(l -m,)e,t = 0
(22.2)
m,t + f} m,p;t-\-wr,r-\-(wrfr)-\-w„=0
of = 2G К z + ve/(l-v)}-•*/>.
o<f) = 20 {{urfr) + v (1 - 2v) e) -, шщр, (22.3)
o« = 2G{«f. r +> (1 -» e} - 4p,
°#=G {«,,, +«,,,}•
vr = urJ, V = UzJ,
б = Иг.г+(Иг/0+ ««.«•
о' = (1/3)(о<Л + о(»+о(Л).
v« = d'/<?rl + (1 /r) <?/<?r + ^/dz*.
S = {(l-2v)/(l-v)}{(l-t#)/2G}.
Уравнения (22.1) и (22.3) описывают
напряженно-деформированное состояние упругих массивов выше и ниже пласта при S==e==0,
о^> = ог/,но при иных упругих модулях v и Е. В силу симметрии
относительно плоскости z=0, проходящей через середину пласта,
можно рассматривать лишь верхнее полупространство. Введем верхние
индексы «+> и «—» соответственно для пласта и массива.
На контакте пласта с массивом должны выполняться условия
непрерывности смещений, непроницаемости и равенства усилий
0(f, (+, = 0ш (_,, 0,{+, _ , = „(_) (г = Я). (22'5)
На стенке скважины заданы давление, отсутствие касательных
напряжений и отсутствие радиальных смещений:
р=Рс] а.гг=0, иг=0 (г=гс) ,* (22.6)
а при г-+оо смещение и возмущение давления и напряжений
обращаются в нуль. Для нахождения решения можно применить
интегральное преобразование Вебера —Орра. Тогда уравнения
равновесия (22.1) относительно трансформант
rW,{r\)pdr
)+Y\(irc)'
Wi (fr) 9 У, (С/") У, (?ГС) - Yt (1Г) /, (|Ге)
)+l".(^c)
187
принимают такой вид
dz2 1— 2vч г 1 — 2v dz 1— 2v ^ /
~ (22.7)
\ — 2vdz2 z. 1 — 2v dz ' 1 ~ 2v dz
где Л, У,- — функции Бесселя первого и второго рода от
действительного аргумента.
Если заменить давление р,на среднее по толщине пласта
h
(Р)=-£- ^P(r, z, t)dz,
—л
то с учетом формул обращения решение будет иметь простой вид
ur=[{(A + UB)e*+(C + bDe-*} Wx (rt)dt-S^(p) WJr^dl
о о
оо (22.8)
"*=J {[-A + (3-4v-tz)B]elz +
о
+ [С + (3 - 4v + fe) Я]е-**} W. И dl,
где Л, В, С, D — параметры интегрирования, равно как и <Ср> —
функции |, Л Формулы (22.8) для смещений пласта и массива (с
учетом симметрии) дают выражения
«;+)'= J (А+ chE2 + tefi+ shбг)^ (rE)# - S ^(p) Wx (гЕ)Л.
5 (22.9)
иН-> = f {- Л+ sh&z+ [(3 - 4v+) shfcz -fechfe]#+} AT, (rE) dfc,
о
i/M = J (Л- +ЕгВ-) exp(-te) W\ (гЕ)Л,
1 * (22.10)
«H ==■ J [A- +(3-4v- +fe)B"] exp (- fc) W. (rE)dS,
о
причем условия (22.5) означают следующее:
Л+ = -(Я+/2С+){[4/г(1 _v)+-C+]exp(-2E/i) + C+(2E/i-3 + 4v+)}+
+ 5ехр(-ЕА)(/7); С+ = /г - 1 - 4(1 -v+j; 2(1 - v+)B+ = -С+В~;
р+__ , 2SC+ (я — 1 )<?) sh 6^
_ С+{2(1— /i)5A+[l— лг Н- 4/г(1— v+)] sh2£/z}+C- ехр( —2£Л) '
C-=8/i(l-v+)(l,-v-), /z = (l+v+)(£-/£+)/(14-v-), ^
А' = 1^21 /*и1 (3 - 4v- - 2ЕА) - **Л1 Д+.
Величина я— отношение жесткостей массива и пласта. Условие
п<1 соответствует более жесткому массиву (или более мягкому
пласту) .
188
Построенное решение позволяет найти напряжения на стенке
скважины и в самом пласте, возникающие из-за фильтрационных (Щл при
движении жидкости:
о<+» (гс> г. /) = -i^j<*(*. /O^sh*- (^-^"^ ^
ь
00
+ % — — ^ ch tel <?> rf5+ -^^- Г <?> ^"ЕА chto/5, (22.11)
2 ) ) nrc J
так и в окружающем упругом массиве:
00
o<-)(rc,.z, ^)^-4GS;i-;") \Ф{1 A)/f^l(3-4v-. + 26A)
e-«*_2?gl(te-2v-)} «-*<?>
Л.
(22.12)
Для характерных значений п=0,5—3,5 функцию Ф(|, Л) можно
упростить
Ф(1 Л) =2 (п— 1) [ехр (—|Л) —ехр (—З^Л) ] [1-п+4(1-у+)+Д]-1«
«2(я-1)-[ехр (-^)-ехр(-3|Л)] {l-rt+4(l-v+)], (22.13)
поскольку *
1— n+4(l—v+)>A=4(l^n)£Aexp (—2£А) + (1/С+) {2С~—
—С+[1-я+4(1—v+)]} ехр (—46л),
причем имеет место асимптотическое выражение
Ф(£, «)«2ехр(—£rt)/*(3—4v),rt-*oo. (22.14)
Пусть скважина работает на установившемся режиме, т. е.
распределение давления стационарно,
Р(г) = (рк—Рс) 1П (г/Гк)/1п(Гк/Гс), Гс<Г<Гк
р(г)=0, г>гк. (22.15)
В этом случае
/~р\ = Рк~Рс у»(Ус)Л(6гк) - /,(£ге)У.(6гк) + 2(«6гс) -' (22 jg.
Далее будем учитывать, что (гк/гс) ~102—103. Интегралы (22.11)»
(22.12) могут быть разделены на две части границей £о. Для первой
допустимо асимптотическое представление функций Бесселя
У, (&гс) »-2/(яГс6), /i (<ГсЕ) « (1/2)£гс,
y2i№rc)-r-/2,(erc)«4/(nVcg2), Е<6о, 1&0Гс<1,
а интегралами от £0 до оо можно пренебречь. Если воспользоваться
разложением J^x) в ряд по функциям /гк(*), то, проводя почленное
интегрирование,* получим для напряжения, действующего на колонну
скважины внутри пласта вблизи контакта пласта при (h—г)»<СГс, та-
189
кое выражение -
во /
«^(rctz)ln(rg/rc) _ 4(1 —v)/7 ^п 1 /
2GS(p]
+ h(l-z.)]-»+[Vh\(l+z.) + l+h(l + z,]-»} +
\—П (о о 3 — 2% M*+gt)
1_л + 4(1—v)
fo оЗ-г', ^.П+г») МГ-" z.) j^
/л% (3+ *.)■+• 1 ^K/fc\<3-*.)■+ 1 ^Л/'
•0
3
-}]^[У1г\(г + г.У + 1+к$(3 + г.Г\-гл+
+ 5]-^т,.(3-г.)г+1+МЗ-г.)]-"+0(-^).
где ho=h/rKy Zo—z/h. Напряжение, действующее на колонну сква*
жины внутри массива вблизи контакта с пластом, определяется не*
сколько иным выражением
«<Я(гс. h)\n(rK/rc) „_i f 3 гл 7 /_г^\\1п-гк__
-"»+>--У^МтК'+'С-^))-
оо
~тЕ^(4Л*+^г+^)~'я+М4Л1°+1)_1/2~ (22Л8)
-^2+,- .Ла-7:!) ^ [to +е С1 - t))]K+
' S '"ST(2А* +>ГГР^)-,Я+ о (£).
2
*=1
где у — эйлерова постоянная.
190
На рис. 62 приведены
результаты расчетов для
различных п при гс=0,005А.
Видно, что нагрузка на колонну,
возникающая из-за
фильтрационного потока, максимальна
на контакте пласта с
массивом, и она тем больше, чем
мягче пласт (/г»1) по
сравнению с окружающим массивом.
Можно также показать, что
нагрузка на колонну больше
для большего относительногб
радиуса rK/h контура питания.
Из формул (22.9) следует
такое представление для
объемной деформаций:
-о.г
Ь(МАр)
Рис. 62. Нагрузка на колонну скважины
при разных относительных жесткостях
пласта и массива (п) в функции от перепада
порового давления
в (г, z, 0:=- 5 (р) + 2S (1 - v+) J, W. (Ь)ЩЩ)(р) dl
2С+ (п ■
(22.19)
■l)sh$/tchfrg
= Ф (Ш ch (tz) —
К ' > V ' С+{2(1—я)5Л"+_[1—/i-+4(l—v+)sh2^}+C1exp( —26Л)"
Если объединить уравнения неразрывности и закон Дарси, и
усреднить результат по толщине пласта, то получим такое уравнение
движения жидкости:
<т>,Н-Р<2>т0<р>,*— (k/v) {<Р>,гг+
+ (1/г) <р>,г}-<е>,г=0. (22.20)
Выражение (22.19) приводит уравнение (22.20) к интегродифферен-
циальному уравнению относительно порового давления
00
д(р)
dt
-|^.«г)<*>^Л = 7- rf(r>&.). (22.21)
(«"> = ■
2С+(д — \)sh*th/(bh)
С+{2(1—л)6А+[1 —л + 4(1 —v+)]sh2gA}+C.exp( —26Л)' ^ " '
aa1=2S(l-2v+)(l-eJ, «1 = р - ej(') +(1 - .#).S, %=Щ^).
В том случае, если скважина моделируется точечным линейным
стоком (гсДк->0), указанные выражения упрощаются за счет
приближения Wo(lr) »/о(£г). Это приближение соответствует задаче
о восстановлении давления в скважине, работавшей с постоянным
дебитом Q — условие (20.41) —в пласте бесконечной протяженности.
При п=1 уравнение (22.21) переходит в обычное уравнение пьезо-
проводности. *
Более простым, однако, является случай пласта бесконечно малой
толщины. В этой постановке строятся решения уравнений (22.1),
191
(22.3) при S=p=0 для упругого массива, включающего пласт, а сам
пласт моделируется бесконечно тонким разрезом (на глубине z=?—Н
от свободной поверхности) с условиями (по В. М. Ентову) на бортах
непрерывности нормальных напряжений (суммарных,
отождествляемых с горным давлением)
[агг] = [azy] = [о2Х] =0, п. Ы = [огг-р], (22.23)
где п* — жесткость пласта на поперечное деформирование (вдоль оси
z)> [а] —символ скачка величины а. На свободной поверхности
массива НаПрЯЖеНИЯ ОТСУТСТВУЮТ Ozz=Gzy=Ozx—0, 2=0.
В самом пласте выполняется уравнение (22.20), которое может
быть представлено в виде [24]
(Яр+я)р,*—Ьа, oyh=(kolm0\io)V2P + Q/(m№)> o^ = azz-py (22.24)
где Ь=(дт/до^)Ру Q — распределенные источники (стоки).
Напряжения в упругом массиве, возникающие из-за
возмущающего поля давлений р* в пласте, определяются (по В. М. Ентову и
Т. А. Малаховой) решениями уравнений упругости,
удовлетворяющих условиям (22.23),
°гг = - J ^я (Ш) ? /0 (5r) р (Е,t) dt,
о
w — Я6{1-(Г+27/6+ 2//»6»)ехр(-2^6)}
" т — Н1{1 — (1-2Н1.+ 2Нг¥)ехр( — 2Щ)} '
(22.25)
оо
P = §rpJQ(l,r)dr, d=(nJG)
K + 4G/3
K + G/3'
о
Выражение (22.25) приводит уравнение движения жидкости (22.20)
к виду
М- + ± ГЧГя(^)5/.(8г)1<£>.л = Л -L(rJ£-) + -£- (22.26)
dt J J дг г дг \ дг / р/я0р0
вполне аналогичному уравнению (22.21). Полное совпадение
достигается, если в распределении напряжений (22.25) принять #->-оо, что
справедливо для весьма глубоких (от свободной поверхности) пла-
стов
Ун (Ё) ^-|Я/ (d-lH), (22.27)
а уравнение (22.21) применить к бесконечно тонкому пласту (Л^О)
(Хр /6)\ ^ 2(к-1){/*-1 + 4(1-у-)}^ _
№-l+4(l-v-)} {2(1— п) +4(1 — v + ) +8я(1 —v + )(l—v-)}'
(22.28)
Сопоставление позволяет связать параметры двух постановок
задачи
а(А2 — 1) b_t nji 2/2(1 — v + )
(1 — п) + 2(1— v + ) ~~ р ' G ~~ {п— 1—4П —v-)} {1—^+2(1 — v + )}*
(22.29)
192
Таким образом, уравнение движения жидкости в тонком глубинном
пласте к скважине принимает вид
о о
= * д. /д(р)\, Q rf=s 2л(1-у + )(1-у->
г дг \ drj^mtf,' {1-/2 + 2(1 — v-)> {;i —/г—4(1 — V+»*
(22.30)
который показывает, что полная упругоемкость проявляется только
при нелокальных изменениях порового давления (в некоторой
окрестности элемента пласта). Иначе говоря, изменения порового
давления Ар в малом элементе пласта не будут приводить к равным (или
пропорциональным) приращениям эффективных напряжений Аа(/)
в том же элементе, поскольку толща горных пород не только
генерирует горное давление Г(л:/) на пласт, но и работает по отношению
к пласту как перекрытие (балка).
Поэтому используемое в элементарной теории упругого режима
фильтрации условие уравновешивания/ постоянного горного давления
локальными эффективными напряжениями и поровым давлением
°1? ~ РЬч = Ги (*/) = c°nst (I. / = 1, 2) (22.31)
не отражает того, что окружающая толща функции является не
только нагрузкой, но и работает 'как перекрытие (свод). В -связи с этим
условие (22.31) можно попытаться заменить на нелокальный
эквивалент [22]
°(f)(*.-. 0 +Jf*(fEt:=Ji-)/'№<./)«1^1 = r(Jf/), (22.32)
где Ф — функция влияния, а интегрирование проводится по всей
плоскости пласта.
Чтобы пояснить сказанное, представим упрощенно вышележащую
толщу горных пород по Ф. Энгелунду и Т. Серенсену в виде
бесконечной упругой пластины жесткости £*. В плоском одномерном случае
уравнение изгиба пластины и^еет вид
E*d*u/dx*=Y—o«)—py (22.33)
где и — смещение пластины, роль нагрузки сверху на пластину
играет горное давление Г, а снизу приложено усилие a(f)-f-p,
определяемое напряженным состоянием пласта. Поскольку смещение пластины
равно смещению кровли пласта, то по закону Гука
1 af=Eu/hf (22.34)
где Е — модуль Юнга пласта, h — его толщина.
В силу (22.34) уравнение (22.33) позволяет определить a(f) в
уравнении движения жидкости (22.24). Если продифференцировать урав-
193
нение (22.33) по времени, а затем применить интегральное
преобразование Фурье
/
u{l) = yL Г u{x)exp(itx)dx^ /22.35)
то получим
Й + uEj{hE,) = ->/£». (22.36)
Поскольку
-оо
1 f e-'^tf6 — l/ 2 С_
cos %xd£
+E/(kE0)
О
- у техЧ"тг1/ ^dsln(4wl/ -^г+ т)•
обратное преобразование Фурье с использованием теоремы о свертке
дает
-^-т]-"{-т1к)'"н-т-^г+т}х
—00
х El&udx.' (22.37)
Учитывая (22.34), получим (результат Е. Ф. Афанасьева)
нелокальное условие (27.32) при следующей функции влияния
Ф = Ф(*)/8. 8 = (4A£#/JS)»/4f (2238)
Фо (*) = (1/]/~2)ехр(- \х | )sin( \х | + */4),
причем возможна такая аппроксимация:
Ф(х) « [1/(26)] ехр (—ях2/4). (22.39)
Иначе говоря, приближенно допустимо задавать функцию влияния
в виде функции Гаусса, что значительно упрощает расчеты [22].
В осесимметричном случае уравнение изгиба пластины имеет вид
Е*{1/г)(д/дг) {г(д/дг) [(1/г) (д/дг) (rdu/dr)}=T-af-p. (22.40)
Применение преобразования Ханкеля приводит к результату
О о
который позволяет выразить функцию влияния в виде
W— А*
La <* л\ */,- -ч-оГМ^гцмКгю
194
Ф.(г.р). Ф(г,р) = 2|М11^А£АЖЛ( (22.42)
8 = (4£,#A/Z?)I/4, причем допустима такая аппроксимация
Ф. « (,/2) I. («ГР./28») ехр {- («/«■) (г9 +у)}. (22.43)
где /о — функция Бесселя мнимого аргумента.
Рассмотрим задачу о восстановлении давления в скважине
(дебита Q) после мгновенного ее закрытия (условие 20.41). В этом случае
функция и{г, /), определяемая равенством
! Р=Ро (г) + (Q[i/2nkhp)u (г, t),
будет удовлетворять интегродифференциальному уравнению
(l_a)_-^]/.^jexp(-^-^j-^Pdp = x — у(г^).
о
(22.44)
при следующих граничных условиях:
u(oo, 0)=0, (гди/дг)=—1, r=0, *>0.
Применяя преобразование Ханкеля, получим
й(1, 0=(1Д2){1-ехр.[-<р(|)<]},
<р(£)=х£2{1-а[1—ехр(—62|2/4)}- • (22.45)
Отсюда график КВПД в скважине описывается таким решением:
«(rc.Q = |(l-«-*-w)^4*. ^W = r^W' (22-46>
0
где т=х£/г2с. Величина е=а[1—ехр(—0х2)]<1, так как а<1, 0=
=б2/4г2с>0. Справедливы также разложения
^(x)=xx2f ч*. (22.47)
e-v=e-™%+e-*xt f ч* S(- 1)И(«Т(«Л - И)"1. (22.48)
где суммирование по т распространено на все решения в целых
положительных числах уравнений: Н-2/+ ... +ln=&, *+/+ ... +п=*
=т. Кроме того, имеет место разложение
Ч* = а*2 (-^"«[^(Л-л^-'ехр^Авл?). (22.49)
п=0
Подстановка рядов (22.48), (22.49) в решение (22.46) и
интегрирование приводят к рядам
оо к
fc=l m л=0
Х '(t + ne)—»/» М—>/2 (8(7+7*)] (22-50>
195
с использованием функции Уиттекера
1У1т-\12\Л)— (m__l)| dXm-lX } ,
/
В предельных случаях — при 6 = 0 и при 0 = оо — имеем
соответственно
■«• = Г-5-И(-4.), »„=-^(-Щ. (22.51)
Приведем оценку выхода функции и(х) на указанные
асимптотики при произвольном 6. При достаточно больших т+я9 имеем
М.
1-1/2 (8(т + /гв))- 2К2"(т + лв)1/2 +°((z + nefl2 У
и решение (22.50) принимает вид степенного ряда
Л=1 m л=0
1 У а* \1(—1)^(^ — 1)1 yi (-.l,)*fel /., »^i
2^2" Zj Zj «Л...*! U n\(k-ri)\ \^~ <) ~
0(-L). (22.52)
Если 9<Ст, то 1+v8/t«1 для главных членов разложения (22.52).
Тогда в силу равенства'
k
2 (— 1) /fel [/г! (/г — лг)!]"1 = 0
т=0 /
получим
и=ио+0(1/г), т>9. ~~ (22.53)
В начальные моменты времени 8»*. Тогда в разложении (22.52)
главными будут члены при п=0, а члены пфО будут иметь порядок
0 (т~/9)*и выше. Первый"член разложения дает:
ч*=а*; Y=ta:2/(1—а),
w=Uoo+0(t, 0), т<Св.
т Соответственно, на КВПД можно выделить три характерных
участка (рис. 63). Участок I соответствует интервалу времени О^т^
^0,19 и описывается формулой
Ьр= (Qp/Ankhpo) (In 2,25—ln(l—а«)+1пт). (22.54)
и Участок II соответствует интервалу 0,18^т^10 9. Это переходной
участок, который можно приближенно описать тремя членами ряда
196
(22.52). Участок III— интервалу lOG^t^oo. Здесь
Др= (Q[i/4nkhp0) (In 2,25+ln т).
(22.55)
Асимптота CD соответствует меньшей сжимаемости пласта, т. е.
большей пьезопроводности и/(1—а). Асимптота АВ— максимальной
сжимаемости, т. е. меньшей.пьезопроводности х. Нелокальный эффект
(или иначе — упругость окружающего массива) приводит к
теоретической возможности отклонений реального начального участка EF
вверх от асимптоты Л В, соответствующей элементарной теории
упругого режима фильтрации.
Проведем числовые оценки. Пусть 6=20 м, гс=0,1 м, и=
= 104 см2/с Тогда 9=104 и продолжительность интервала / будет
ti=0,l 6=103, что означает t\=\Q с. Участок /// начнется при %2=
= 10 8=105, т. е. <2=Ю00 с. Таким образом, продолжительность
переходного участка /// будет ~17 мин. Этот характерный пример
показывает, что на практике участок / может отсутствовать. При этом
его первую половину участка //на
рис. 63) можно принять за
дефектную часть кривой (например,
из-за немгновенности закрытия
скважины), а вторую за асимптоту
АВ. Тогда проведение по
экспериментальным точкам ложной
асимптоты EF (пунктир) приведет к
завышению пьезопроводности х и
уменьшению проводимости пласта
kh/\i по сравнению с их
действительными значениями.
Выше были рассмотрены малые,
а потому упругие возмущения в
пластах. Неупругие деформации
порового пространства
(допредельная пластичность) приводят к необратимым изменениям пористости
и проницаемости пласта [2, 12]. Возникновение предельных
пластических состояний в призабойных зонах скважин [38] могут вызывать
течения самого пласта (его матрицы, например, песка) в скважину.
Были найдены напряжения во внешней упругой зоне и во внутреннем
пластическом кольце, а также положение упруго-пластической
границы, отодвигающейся от скважины с ростом ее глубины. Было
оценено также влияние притока жидкости к скважине, причем оказалось
принципиально возможным определять соответствующие изменения
давления на обсадные колонны.
При перетоках жидкости между пластами [36] последние
деформируются, и на их взаимодействии сказываются относительные
жесткости ц вязко-пластические свойства коллекторов и массива.
Рис. 63. Объяснение кривой
восстановления пластового давления
упругой сжимаемостью массива и пласта
197
ГЛАВА 7
ФИЗИКО-ХИМИЧЕСКАЯ ПОДЗЕМНАЯ ГИДРОМЕХАНИКА/
23. ФИЛЬТРАЦИЯ МНОГОКОМПОНЕНТНЫХ НЕОДНОФАЗНЫХ СМЕСЕЙ
Фазовые переходы при медленном
деформировании. Термодинамический анализ. Равновесные и
неравновесные условия. Правило фаз Гиббса в
гидродинамических системах. Бинарные и трехкомпо-
нентные смеси. Моделирование многокомпонентных
смесей. Условия на разрывах. Стационарные и
квазистационарные течения. Автомодельный приток
к скважине. Процесс рециркуляции газа.
В случае недеформируемой и неподвижной матрицы из уравнений
движения жидких фаз можно исключить инерционные силы
т P,i~\Ki \т р Si' (23.1)
т(а)=/тг6(а), т1*=1-т ф = 2,ЗМ=а).
В уравнениях баланса энергии фаз будем учитывать фазовые
переходы (химические реакции не рассматриваются)
(p<"e(,V,))., = -(e(Y))./ + iW -G»<2) -Pm)m».t + Zfiw. (.23.2)
Уравнение баланса энтропии соответственно имеет вид
r(1)(p(,)e(1)s(,)),<+T(w; = -(6(1)^))./+(p(2) -pi3) -
-pie))mb.t + 2fiw. (23.3)
Для фазы а = 2, 3 имеем
(•%<•>.<•»)., + (6(V*V"V->).,+ 6< V'V^ = - (6("><7<в>). , -.(2з
- р*» (d.iw/*)+v(.« +^/р(9))/Г - (е<а> -ь ^<а)/р(а>) СУ+
j_£ffW(£,W_0W)4-£RQ(?e>.
Воспользуемся следующим следствием уравнений баланса масс
(19.1)
(е(а)Р(а>).<+(б(а)р(%;"))./=^ог-/;:Г).
Тогда из соотношений (23.4) получаем
е'Пр'Ч^+лЛ^и/Р^)}--^^
+ (P«)l?{4-l*w+(P*)l?{*)\}j\i;)+zf>m
Соотношения Гиббса для фазы а имеют вид
в<*> {9(л)й/л)1<и+Р(л) (djdt) (17Р(а))} = в("Ув,т.<*> (daS(a) /л) +
+ 9wp(a>Sft?SdaCS/^. (23.6)
198
Поэтому уравнения баланса энтропии фазы. а можно записать
в виде
r<V">e<Xs(">Att = - (е(%(а))..+£p(sft [(.<w +ЛрФ)) - («(в) +
(23.7)
В силу следствий уравнений баланса масс (19.1) и дополнительного,
следствия
можно провести следующие замены1 '
T(a){(6(e)P<a)s(o)). , + (e(e)p(e,s<*,oJ(e)).»} =7'(")*[%(/JJ)- ф +
+ e(a)P(a)T(")(das(o)/dO.
0 P *(*> ЙаС(4) lat — f{k) Т?0(й - /(ft) ) "«'и, ?(ft) V"tt> '(ft) ''*
Если, кроме того, учесть термодинамическое тождество J,
Ts+2kcp(k)C{k)=e+ (р/р),
то уравнение (23.7) можно записать также в виде
Г(.) {(6(«)p<-)s<:))i t± (6<V"V%f >). .} = (A<«>f (•>). . + ^{(8(8) +
+ Лр%Г - (•w+/'w/p("))/ff}+^Q(eW +
+VS С- /Г)+vr>!B-°r>- (23-8)
Уравнение производства энтропии в элементе объема среды может
быть получено путем суммирования уравнений (23.8) для всех фаз и
включая капиллярный слой
(sae(a)P(a)s(a)+m5(c)). ,+(sae(a)p(a)5(a)^;a)+ (с)),, +.sa (в^^/rW)., =
+/,«WX? - (•«+у>/р«) /ff ]+=e^(4pS>/rc->)(/(y - /s») +
+ Sa(l/T(a))S^ (^-o;e))+(l/,(c)) (/>(2).-/>(3) -р®(Ь))пЛш<.
'• (23.9)
Правая часть уравнения (23.9) представляет собой интенсивность
производства энтропии в единичном объеме пористой среды.
Применение формализма [15] термодинамики необратимых процессов
199
(принципы Онзагера и Кюри) приводит к следующим
феноменологическим замыкающим связям:
е(ауа) = -2D(ap) (ijTWfT®
/
/
/
«]4)=a(eW(of,-o;'))I (23.10)
е# , = [/><■>-/><»> -Р(с)(б)]/х(с),
te> + (/?(a)/P(a))+Q(a) =2рт](ар) (1/Г(а)- 1/T(W).
Коэффициенты в выражениях (23.10) вполне аналогичны
коэффициентам в (19.31). Процесс выравнивания химических потенциалов
фаз соответствует частичному (или полному) их взаимному
растворению.
Отметим, что a<aP> выражаются через фазовые проницаемости
/а(8), которые зависят от концентраций компонент при
выравнивании составов фаз р(е)-*е и Р(8)~>(1—9), т. е. /(«>=/<«> (8CW),
Изменение состава фаз будет сказываться на межфазном натяжении,
которое будет меняться от «замороженного» значения у<х> до
равновесного yo, причем рс=Рс(6С<Л).
При совместном движении взаиморастворимых жидкостей,
отличающихся друг от друга по поверхностному натяжению, в течение
интервала времени t^x должны проявляться характерные
капиллярные аффекты. Они действительно наблюдались в опытах по
смешению параллельных струй взаиморастворимых жидкостей в пористой
среде (в виде капиллярной пропитки, интенсифицирующей
перемешивание) [13].
Будем называть локально-равновесным такое движение, когда
скорости фаз в каждой точке отличны друг от друга, но поля
температур и давлений макронеоднородны. Согласно соотношениям (23.10)
в этом случае должны быть выполнены следующие локальные
условия термического, механического и химического равновесий:
r<«> = r<f»=r> jp _^(3)=/?(о(е). ?g=?«;. (23.li)
Общее число равенств химических потенциалов в (23.11) равно
/С(сх—-1). Число независимых концентраций в фазе а равно К—1, а
потому в условиях теплового и механического равновесия химический
потенциал этой фазы будет функцией К—1 концентраций,
температуры и фазового давления. Фазовое давление представляется через
некоторое среднее давление и фазовые насыщенности 6а. Число
последних равно a—1. Следовательно, число переменных во всех
уравнениях равно а(К—1)+2+(а—!)• Отсюда число / независимых
переменных (так называемое число степеней свободы гетерогенной
системы) равно
fic)=K(a—l)—a(K—l)+2+(a—l)=K+l. (23.12)
200
Если же капиллярные силы пренебрежимо малы, то число
степеней свободы будет соответствовать правилу фаз Гиббса
f=K(a— 1)— а(К— 1)+2=К—а+2. (23.13)
Величина/ (или /с)—число переменных, которым можно
придавать произвольные значения, сохраняя существующее число
фаз а,
При фильтрации двухфазной многокомпонентной смеси, удобно
пользоваться следующими обозначениями
. cg'=/(*„ Cg =*(*>; *<*>//<*> = (р(37е№) *<*>(* ТС<п), (23.14)
где фаза 2 — жидкость, фаза 3 — газ, /=1, ..., К— 2. Действительно,
для таких систем условия равенства химических потенциалов (23.11)
разрешаются в виде констант равновесия (коэффициентов
распределения) R^) — измеряемых функций давления, температуры и С<Л—
фазовых концентраций или их комбинаций (согласно правилу фаз
Гиббса их может быть К—2).
В случае бинарной системы эти дополнительные параметры
выпадают— распределение компонентов по фазам зависит только от
давления и температуры. Условие равенства химических потенциалов
сводится к закону растворимости Генри
а=у(Т)р, (23.15)
где а — молярная концентрация растворенного газа.
Учет «реальности» газа и жидкости приводит к введению [13]
функции a=F(p, Т).
Константы равновесия трехкомпонентных систем помимо
давления и температуры могут зависеть от одного параметра, например
С<Я=/2/ (12-\-/г) [13], — отношения промежуточной (по молекулярной
массе) компоненты к сумме концентраций промежуточного и
тяжелого компонент в жидкой фазе.
Как параметр состояния системы, фазовая насыщенность может
играть существенную роль в области, где весьма велики капилярные
силы.
В условиях локального термодинамического равновесия * элемен-'
тарном макрообъеме изменения суммарного содержания компонент,
давления и температур, возникающие из-за обмена веществом и
теплотой с соседними объемами, происходят намного медленнее, чем
процессы установления межфазового равновесия в рассматриваемом
объеме среды. Иначе говоря, межфазовые перетоки вещества
завершаются как бы мгновенно, и уравнения баланса масс компонент
следует формулировать для смеси в целом. Эти уравнения являются
результатом суммирования балансов (23.4) по фазам а=2,3,
ч
т(£юС^р^9^),, + (ЕаС^р(а)<)).^0, (23.16)
14— 3311
201
где скорости фильтрации фазы ww определяются как и выше
w™ = - (Л/(")М'")) grad,- р{л); /(23.17)
Число уравнений (23.16) равно /С, а в число фигурирующих в них
переменных помимо давления и фазовых концентраций а (К—1)
вошли также а—1 фазовых насыщенностей. Общее число переменных
таким образом равно аК. Видно, что переменных больше, чем
уравнений. При учете температуры число переменных будет а/С+1, но
тогда нужно вводить и уравнение притока теплоты, т. е. число
уравнений будет равно /С+1.
Только при равенстве истинных скоростой движения фаз (у(ос) =
ssojW; <х=£р; wl*] =mb(a) v[a) ^т№ vf =wf) и независимости
вязкости и проницаемости от содержания компонент и фаз введение
суммарных концентраций компонент
С*(Л, = (SCg Р(а) 6(«>)/(SaP(a) 6(а)), а=2, 3, (23.18)
число которых равно К—1, оказалось бы достаточным для
замыкания системы уравнений (23.16). Тогда в системе координат,
движущихся со скоростью t>!a)=p!p), каждый малый пространственный
элемент среды представлял бы собой замкнутую термодинамическую
систему, варьирование состояний в которой происходит за счет
изменений давления и температуры.
Фильтрация бинарной, смеси (/(=2), существующей в виде двух
фаз, будет описываться такой системой уравнений:
т{Щ{1) + (1 - 6)£P(fi)}, , +{'P(V" +£P(gVe)}., =0, (23.19)
«{6(1 -/)Р<"+(1 - б)(1 -g)pie)}.t + {(l -t)?il)w<l) +
а концентрации g, I газовой и жидкой фаз определяются
константами равновесия
£//=#(i)(p, Г0), (1-£)/О-0 =#(2)(Р, Г0), р-(С*)<р<р+(С*).
Границы двухфазной области р+, р_ являются функциями
суммарного состава С* смеси.
При ретроградной конденсации, происходящей в смеси
углеводородных газов (и объясняемой взаимодействием между молекулами
различных компонент), жидкая фаза появляется при снижении
давления, а потому р+—давление начала конденсации. Дальнейшее
снижение давления вновь приводит к испарению жидкости: р_—
давление конца испарения.
Вне зоны двухфазного состояния имеем
8=С; 1=0, р<р_(С*), р>р+(С*).
202
При трехкомпонентной двухфазной смеси система уравнений
движения несколько сложнее
(0;
,(0
,<*>,
„(6)1
™{9р(%оЧЧ1-9)Р(^л + ^^^^
(0/
„(0
Je),
.ite)i
т№> /(2) +(1 - 6) pw*(l,b + {P(%> <' +>"'*<.) О. ,— 0,
w{eP^+(l_6)p(g,}w + {p(/)^/) + P(",^(g)}./ = 0) (23.20)
'(к)=Цк)(Р> С(Л, Г0), g(K)=giK)(p, С(/), Го), Р-<Р<Р+,
£(к)=С*к (Р<Р-, Р>Р+).
При контактной конденсации в pVT-бомбе суммарный состав С*к
сохраняется неизменным и давление падает за счет увеличения
объема pVT-бомбы. При дифференциальной конденсации давление
в бомбе изменяется за счет отбора газовой фазы при неизменном
начальном объеме смеси; суммарный состав смеси меняется. Этим
процессам будут соответствовать решения системы уравнений,
получающейся усреднением (23.16) по объему Q,
(d/dt){Q(9(hlik)b + 9iz)g{k)(l — в))}=—er<ik,G(l -Pa,}, (23.21)
где G — суммарный массовый отбор газа, р(К) — коэффициенты,
учитывающие возможное несовпадение составов отбираемого и
содержащегося в объеме Q газа. На рис. 64 представлены расчетные
данные об изменениях параметра CW смеси «метан-н-бутан—декан» при
дифференциальной конденсации (черные кружки) и контактной
конденсации (белые кружки). Расчеты проводились Г. Р. Гуревичем и
автором на основе уравнений (23.21) для объема Q(t), G = 0 (кон-
035
030
UZ5
/ST' \
'/ ■ / У
• / / ,i
^\
*У
1
/j Л
\
1
. 1 .
01
о//
0,5
08
Р/Р*
Рис. 64. Сводный график «свободной» концентрации С</> в различных газоконден
сатных потоках
14*
203
0,%Г
тактная конденсация) и для условий G=const, {Зк=0 и постоянного
объема Q (дифференциальная конденсация), р* — давление начала
конденсации. Расчетные точки легли на одну кривую.
Оказывается, что в обоих случаях параметр С<Л изменится
примерно одинаково. Поэтому Of) приближенно является однозначной
функцией давления, и в принципе можно сводить рассматриваемую
тройную систему к некоторой бинарной (широко использованной
в расчетах М. Т. Абасова, А. X. Мирзаджанзаде и др.). Границы
применимости такой модели должны быть установлены
дополнительно. В термодинамических расчетах по
константам равновесия многокомпонентная система
сводилась к системе с одной дополнительной
степенью свободы, т. е. фактически к
некоторой трехкомпонентной смеси, и роль
параметра Of) последней выполняло «давление
схождения». Теперь возникает вопрос, при каких
типах течений смеси параметр CW также
будет функцией только давления и будет ли
совпадать эта функция с указанной кривой.
Оказывается можно сразу найти процесс, при
котором главный эффект — испарение жидкой
фазы — связан с изменениями состава
контактирующей с ней газовой фазы. Это процесс
рециркуляции сухого газа. В рамках
усредненных уравнений (23.21) он моделируется
условиями |рк=7^0, расчетные прямые (см.
рис. 64) резко отклоняются вниз от кривой
Of)(p) для Конденсации в pVT-бомбе. Линия
1 соответствует отбору сухого газа с
возвращением от половины (метана), начиная с
момента достижения максимальной конденсато-
насыщенности. Линия 2—возвращение всего сухого газа. Линии Зи4
соответственно то же, что и 7,2, но с самого начала процесса
конденсации. Этим данным (см. рис. 64) соответствуют кривые, изменения
насыщенности 0 с давлением в pVT-бомбе, представленные на рис. 65.
При возвращении всего сухого газа с самого начала насыщенность Э
оказывается почти равной нулю. Таким образом, с точки зрения
уменьшения потерь конденсата, сопутствующих отбору газа из газо-
конденсатного месторождения, процесс рециркуляции вполне
эффективен (особенно при нагнетании этана).
Многокомпонентные смеси можно пытаться моделировать
системой смеси трех условных компонент, что позволит не ограничиваться
лишь характеристикой начального состава (давлением" схождения) >
а учитывать переменность состава в ходе гидродинамических
процессов. С точки зрения практики, по-видимому, удобно брать в качестве
легкого компонента— сухой газ реального месторождения, в
качестве тяжелого — стабильный конденсат, а промежуточные
компоненты смеси составят средний компонент. Другой путь состоит в
непосредственном использовании данных контактной конденсации при
итеративной подборке фазовых составов в каждой расчетной ячейке
01 04
Рис. 65. Насыщенность
жидкой фазы при
контактной
(/),,дифференциальной (//) конденсации
и различных режимах (7,
2, 3) возврата сухого
газа в систему
204
на основе данных о контактной конденсации для мгновенного
суммарного состава смеси.
При движении многокомпонентных смесей может возникать
фронт—поверхность разрыва. Разрыв—математическая идеализация
узкой зоны конечных изменений параметров течения. Реальная
ширина этой зоны—структура разрыва—определяется процессами
диффузионного перемешивания или капиллярной пропитки.
Скачкообразные изменения функции на поверхности разрыва должны* быть
равны разности значений этих функций в крайних сечениях структуры
разрыва. Эти изменения должны быть связаны балансовыми
соотношениями, аналогичными соотношениям на фронтах ударных волн. .
Поскольку в узкой структуре разрыва изменения величин
происходят в основном в направлении нормали к разрыву, для вывода
соотношений на разрыве достаточно рассмотреть одномерный поток.
Пусть скорости движения частиц газовой и жидкой фаз через
поверхность разрыва, перемещающейся со скоростью U, равны
соответственно
{ш«>/(т6)}— [/, {(w®lm)/(l—Q))—U.
На поверхностях разрыва должны выполняться балансовые
соотношения для массовых расходов компонент
[l(k)?{l) iP[l) -mVJ)] + [gik)pW{wW -т(\ — 6)f/}] =0, (23.22)
где k=l, ..., 3, а символ [а] означает разность (скачок) величины
а=а- слева и а=а+ справа от поверхности разрыва, считая, что
поверхность разрыва двигается слева направо.
Из обобщенного закона Дарси (19.34) следует, что в подвижной
системе координат £=*—Ut справедливо выражение
- ' др/д% = — (ww + w^ {(f(Wl[№) + (pk/\L^9 (23.23)
правая часть которого ограничена. Именно поэтому переход к
пределу при h—r+O результата интегрирования выражения (23.23) по g
в интервале (—/г, -f-Л) приводит к условию
[р]=р+-р_=0, (23.24)
что означает непрерывность давления при переходе через
поверхность разрыва.
Отсюда при переходе через поверхность разрыва в потоке
бинарной смеси ее плотность, вязкости и фазовые составы остаются
непрерывными и только насыщенность 8 может претерпевать
скачкообразное изменение. При трех и более компонент в потоке
возможны скачки плотности, вязкости и фазового состава, поскольку могут
происходить скачкообразные изменения параметров О.
Если значения С^>_, р_(=р+), 6~, wW- с одной стороны от
поверхности разрыва известны, то соотношения (23.22) содержат К—а
неизвестных С<#+, а* также искомые <г+, ш+ и if/ — всего их число:
К—а+3=/С+1, тогда как число соотношений баланса: К. Отсюда
для однозначного определения всех величин на скачке необходимо
задавать одну из этих неизвестных величин или же определять ее
из условий сшивания непрерывных решений на поверхности
разрыва.
205
Перепишем (23.22) в виде
/
'(ft)1" "к" *"<*> "W
/
(23.25)
и»») =(l — F)w, w^=Fw, a» = a»(')-[-te)(*>,
F = да<г)/(о)(') + a»W) = {1 + (f('> n<«>)/(f<*> (*.<*>)}-".
Л(*) = Р(«(1 -^tfw + P^*). Blk)=m{9w(l -6)^fc) + p<')e/(ft)}.
Функцию T7 принято называть функцией Баклея — Леверетта.
При трехкомпонентной смеси для разрешения (23.25)
относительно указанных неизвестных воспользуемся [13] следующим приемом.
Условием существования ненулевого решения однородной линейной
системы алгебраических уравнений (23.25) относительно величин
w+, w~, U Является равенство нулю определителя системы. Это
приводит к следующему соотношению:
р«ру (F+-e+){P«<i -по(*«; §Ъг 1)+p^n(fi ;
eii U)}+pl5,p^)(f"-e-){p?(i-f+)n(4)^7ft)'/7ft,) +
+р^+П(<й) ; 4>; Т»=0- (23-26)
где □ — определитель третьего порядка, например,
+^72) (4) 'J -st) ^) + ^7з) tej, U -*S> i'i)-
Далее будем считать w~ известным. Тогда система (23.25) уже
линейно зависима и сводится к решению двух неоднородных
линейных уравнений, в качестве которых можно принять
A+)w+-\Bl)-B-))U = A-w-, "
(23.27)
SH(*)^=P««(l-/?) + P</>/?.
ВД*>=т{р<г>(1-е)+р('>б}-.
Решая систему (23.27) относительно w+ и I/, получим
»+ = (Qw/Q)ar, {/== (Q(i)/Q) аг, (23.28)
0-=т.{р?.Р? С7+- 0+) (*J> - '!,) + ?_ (1-П [р? (1 -
-^+) (*J> -^)) + p")f+(/a) -^))1+Р-° Г bf (!.-
-^tob-^ + py^^,-^,)]}.
Q(.) = -w{p<.',p<_') (F~-n (g~} - /-) + ple,(i -6+)(i -
206
-n too) -ri»)+p-) F~«v -4»>+pf6+ fr? о-fl:<ffo, -
-/J))+ P^_('a,-'J,)};
Q. = Pf (1 -Ofr^O -П tej, -^a)) + P-)/7~^a) -
- 'a)) + P+/)f+{Pte>(l ~ПРт -^o») + P-)/?"(/a, -Ф-
Соотношения (23.28) имеют смысл при условии, что £2ф0.
Можно показать, что условие Й=0 соответствует непрерывному течению.
Рассмотрим возможные частные случаи.
1. Смесь одного состава вытесняется смесью другого состава. При этом обе
смеси находятся в однофазном состоянии. Тогда
е-=о, f-=o, е+=о, f+=o
и выполняются условия, характерные для поршневого вытеснения,
w+=w-, U=w-/nL (23.29)
2. За скачком смесь находится в однофазном (газообразном) состоянии, а
перед ним — в двухфазном. Жидкая.фаза неподвижна. Тогда
9-=Р, F-=0, Q+фО, F+ = 0,
p(g) p|g) (i _ 6+) (g+} -g-) + Pff e+ (/+) -g^)
(23.30).
3. Перед скачком происходит двухфазное движение
9-=0, F- =0, 9+^-0, F+фО,
pIg){p|e)(l-8+)(4)-g]I))+
pf {# > (1 -Р+) (gj, -«й,) + Р^+ С(1) -«0))> + "*
+ P^9+(^)-gq))}
+ F(f)p(^)(F+_8+)(g+_/-h))
га- о~Л>+П — F+}
(23.31)
™- Pj'fr^l-^) (g,+ -gf) + Р^+ d+ -ёТ)У
т ?е 0 + F+) (fiff ~*Г> + ?tP+ <<i+ ~ g?) + Р/+ ft <f+- 9+) <8>+ - 'i+)'
Кроме того, при F+=*=»0+ происходит поршневое вытеснение.
4. Перед скачком находится смесь в двухфазном состоянии, а за скачком —
другая смесь в двухфазном состоянии. Жидкая фаза в обоих случаях неподвижна
• v
Q-ф0, F-=0, Q+фО, F+ = 0,
р/+ в D (*Г. в/+. //+) + рП" □ (в?. вГ. ?Г> = °>
207
р7 (рГ9- («Г- Т) - р« С' -e+) (er-ef) - Pi1"в <«г — Т)>
в+-а'~ ft i- Р7в+ tef- Ф + h О -в") (вГ-«П + Pi~e- (gf-'/l} '
' (23.32)
у.= «1 . Р-' (gQ) -gQ))
• и {- Р^8+ Otf> -'£>) + Pig) (1 -8") <4>--в0)> + Р-9" (gO)-'o"))>*
5. За скачком среда находится в двухфазном состояний, но движется лишь
газовая фаза. Перед скачком движутся обе фазы
в-ф, F-=0, е+=£0, F+ФО,
ptf> 9f (F+-e+) п <««>; g%; $>) -'p^»8+ {?(f n-r+)D(ei) •
sTty'Tt)) + ?+F+ □ (l%'> g(i); 'w» = 0; . <23-33>
»+ = чг Pie) {pVe) (J -9+) (*o) - ей)) + p+ 9+ Vf» ~
-giT)) + P-9-(go)-/w)>'
ш- pig>
u = — — {?(?(i-F+)(eti)-gT») +-?fF+ (ifu -4,)}.
Стационарные течения многокомпонентной смеси в условиях
подвижности обеих фаз описываются следующей системой уравнений:
{(*<*> Р(г) *f(*>Mw -М<*> Р('> */<'>М(/)) Р. ,}.» = 0. ' (23.34)
Введем, согласно С. А. Христиановичу, отношение 1\ массового
расхода £-го компонента в потоке к общему массовому расходу
Г(*, = (£<*>РЧ-'<*))/(Р+1).
(23.35)
p^P^'Haf/af). 2*ГЫ = 1..
Отношение ip в силу коллинеарности векторов до^ и Шг(;)
является скаляром. Использование величины 1\ позволяет в силу
уравнения для всей смеси в целом
получить условие
(pW*/WM<«> + P<'>^')/l*<'))r(4).1p., = o. (23.36)
Это означает, что проекция вектора Г^),г на линию тока, вдоль
которой движутся обе фазы, равна нулю, т. е. линии тока
одновременно являются линиями равных значений величин Г(Л>.- Поэтому
в области движения, на границе которой постоянны суммарный
поток и состав смеси, выполняются условия
rK=const, fc=l, 2, 3, (23.37)
из которых два независимых. Если теперь учесть условия равенства
химического потенциала (23.11), которые дают еще К(а—1)
условий, то получается, что в уравнениях (23.36) для всей смеси
независимой является только одна переменная, например давление. По-
208
этому это уравнение сводится к уравнению Лапласа
V2# = 0, H = l(9<*4{g)IP{8)+P{t)f{i)№l))dp + C (23.38)
относительно функции Я. Отсюда можно получить простую формулу
С(Л) = Г(Л)2яЛр(ЛА(Як-Яс)/1п(/гк/гс) (23.39)
для стационарного притока, ife-ro компонента к скважине радиуса
Гс, дренирующей пласт толщиной h с контуром питания RK. Здесь
Як, Яс —соответствующие значения функции Я.
Для практических расчетов необходимо выразить в явном виде
Я как функцию давления. Обратим внимание, что выражение для
суммарной массовой,концентрации (23.18) можно представить в виде
С% = (*(*>? + /(*))/(?•+ 1); Р* = Р(г) (1 - W' в). (23.40)
Сопоставление (23.35) и (23.40) выявляет их аналогию, причем
условие постоянства компонентного состава 1\ в стационарном
потоке соответствует условиям постоянства суммарного состава C*h.
Но последнее реализуется в процессе простого изменения объема
PVT-бомбы (так называемая контактная конденсация). Отсюда
можно использовать данные опытов по контактной конденсации
многокомпонентной смеси для расчетов. ее стационарных течений, если
суммарный состав в опытах выбран равным относительному
компонентному расходу C*h=Tk (по С. Н. Бузинову и др.).
В обоих процессах все параметры являются функциями давлений.
Если фазовые составы gk, h являются в этих процессах только
функциями давления (см. рис. 64), а в опытах по контактной конденсации
удается измерить функцию (3*=я|)(р), то удается найти следующее
соотношение:
.p.=p(*>/<*),i<0/ (9(l)f{l¥8)) =Ф (Р) • (23.41);
Если известны плотности и вязкости фаз при этих же давлениях,
то известны соотношение фазовых проницаемостей /(g)//(0 = cp(p).
С другой стороны, это отношение — функция фазовой насыщенности
в потоке /<^/^)='Ф(|9). Сопоставление функций ф и <ф определяет
искомую связь насыщенности с давлением 0=6 (/?). При известных
зависимостях вязкости и плотности фаз от давления возможно
вычислить функцию Н=Н(р) и рассчитать, например, индикаторную
линию'1- зависимость притока компонент к скважине от давления
при стационарном режиме фильтрации от контура питания, на
котором заданы состав потока и давление. Существенно, что во всей
зоне стационарного движения обе- фазы должны быть подвижны.
Условия (23.35) при неподвижности одной из фаз, например
жидкой, сводятся к следующим
£(*>.<=<>. (23.42)
Согласно условиям локального химического равновесия следует
Поэтому при насыщенности порового пространства жидкой
фазой, меньшей равновесной 8Р (/(6)=0 при 8^0Р), стационарного
209
фильтрационного движения быть не может. Этот факт был отмечен
в примере движения газированной жидкости М. Д. Миллионщиковым
[13]. /
Квазистационарные решения системы уравнений локально'
равновесной фильтрации для области е^6р, где ft(6) =0, fg(Q)^i9
определяются условиями p=p(xi), gh^gkixi), lh=lh(Xi)9 но 6=6 (*г, /).
В этом случае система уравнений в частных производных
разделяется и переходит в систему обыкновенных дифференциальных
уравнений. Например, для осесимметричного потока трехкомпонентной
смеси имеем
w(p(/) /(i) _ рw g{i)^ _ qi {r) = {k/r) {djdr) {g{.) pw/^w) (dp/ft), (23.43)
m(pO /(2) _ pW g{2) et, = A (r) = (k\r) (d/dr) (g{2) pw/^«) {dp/dr),
m(PC> _ pw) 9, = ?(/■) = (*/r) (d/dr) (p<*>/|i<*>) (d/i/dr),
где gA, /a, ц(*>, p<*>, pte)— функции p и <Ж Таким образом, из системы
(23.43) нужно найти функции p(r), CW(r), 0(г, /),
удовлетворяющие граничным условиям. Насыщенность 0 является функцией
времени,
ОС r)=q{r) (tjm) &Чг)-рЩг)}-*+во9 (23.44)
т. е. квазистационарные решения описывают процесс накопления
жидкой фазы (конденсата — в случае ретроградной конденсации)
или ее испарения.
Примерный расчет был выполнен Г. Р. Гуревичем и другими [13]
для фильтрации трехкомпонентной системы: метан — я-бутан —
декан. Характерно, что фильтрационное сопротивление движению в этой
области несколько падает вследствие уменьшения вязкости и
плотности фильтрующегося газа. Были также проведены расчеты отбора
газа через скважину из пласта с начальной равномерно
распределенной жидкой фазой. В этом случае происходит испарение жидкости,
причем возможно увеличение фильтрационного сопротивления за
счет обогащения газовой фазы тяжелыми компонентами.
Анализ результатов расчета показал, что в зоне г0^г*<:г+, где
г+ — радиус начала конденсации, г0 — радиус начала двухфазной
фильтрации, выполнено условие rdp/dr^const. Отсюда следует также
рър++{гдр/дг\4п (г/г+\. (23.451
Если в упомянутых выше расчетах стационарного течения
предполагалась та же зависимость параметров CW(p) от давления, как
и при контактной конденсации, то при расчетах квазистационарного
течения принималось, что ОТ является независимым параметром.
Тем не менее, он оказался функцией давления-, практически
совпадающей (пунктир на рис. 64) с кривыми СМ(р) для контактной и
дифференциальной конденсацией.
Нестационарная задача о пуске скважины с постоянным
массовым дебитом газовой фазы Q соответствует решению (Б. Е. Сомова
[13]) системы уравнений
т{р<« (1 - 6)еш + Р<'> 6/(ft)}., = (IIг) {г (р<« gik) f un/iiO +
+ P('>WW.r}.r = 0 (23.46)
210
Q
004
003
0,02
0,01
о
0,039
06 -{0038
0031
О 03 В
О А 0 035
при следующих начальных и граничных условиях
p(r, 0)=р(оо, t)=p*; В (г, 0)=9(оо, 0=0; О» (г, 0)=С<Л(оо, t)=C*\
rp,r= const (Г\ ^0) ,
а составы фаз, как и выше, выражаются через р и С</>. Эта задача
является автомодельной — функции р, в, С<л зависят только от одной
переменной т] = г/"|/1. Действительно, уравнения (23.46) сводятся
к системе обыкновенных дифференциальных уравнений
т(ф) (сЦсЩ) {pWg{k)(l-4)+p®lik)B}+(d/dr\) {(P{e)g(k)f{6)№g)+
+p®l{h)WiL®)4dpld4}=0, (23.47);
где Л=1; 2; 3. Граничные условия также переформулируются
следующим образом: р(г\)=р*, С(/)(т))=С*, е(*|)=0 при ту—*оо, а при
Ч~т*0 имеем r\dpfdy\—*A/Q, где Я —некоторый коэффициент. .-1
Давление р* больше
давления начала
конденсации, тогда как давление
на забое скважины может
стать ниже этого давления.
Тогда весь пласт делится,
вообще говоря, на три зоны:
в первой происходит
фильтрация однофазного
флюида (газа), во второй —
сосуществуют две фазы, но
подвижна только газовая фаза,
в третьей — двигаются и
газовая и жидкая фазы. На
границе однофазного и
двухфазного состояний параметры течения меняются непрерывно (9=0).
Результат одного из вариантов расчета приведен на рис. 66.
Видно, что в области однофазного состояния относительно невелики
изменения давления. В области накопления жидкого конденсата (зоны
2 и 3) расход газовой фазы Q быстро стабилизируется, причем в
зоне 2 примерно постоянна величина r\dpjdr\ (значение постоянной
различно для разных дебитов). Отсюда в зоне 2 давление действительно
распределено по логарифмическому закону р^Лпт), что характерно
для квазистационарного течения [см. формулу (23.45)]. В зоне 3
непосредственно вблизи скважины происходит двухфазное течение
(0^0,2; р^О). Здесь насыщенность может достигать значения 6 =
=0,52. Течение характеризуется практически постоянным расходом
смеси в каждой из фаз. Из описанного видно,, что приближенное
решение можно конструировать путем сшивки упомянутых выше
стационарного, квазистационарного и внешнего (течение чистого газа)
решений.
Обратим также внимание, что на стенке скважины, т. е. при г=
=гс, концентрация СШ во времени падает (см. рис. 66, T|=rc/]/Y).
Это означает, Фго компонентный состав проб газа, отобранных из
скважины, не соответствует суммарному составу пластового газа,
если в пласте выпадает жидкий конденсат.
Рис. 66. Характеристики автомодельного
притока к газоконденсатной скважине
211
Данные о зависимости СМ(р), полученные в расчете
нестационарного автомодельного притока к скважине, приведены на рис. 64
(треугольники). Видно, что и они весьма близки к кривым СЩр)
при контактной и дифференциальной конденсациях (при одинаковых
исходных составах смеси). у
Рассмотрим [13] плоский одномерный процесс вытеснения трех-
компонентной двухфазной смеси сухим газом. При /=0 через
галерею, расположенную в сечении пласта #=0, нагнетается сухой газ
постоянного состава при постоянном давлении нагнетания, тогда
соответствующая задача оказывается, автомодельной. В самом деле,
начальные и граничные условия
р(х, 6) = р(оо, t) = Poa, Цх; 0) = в(во, t) = b„
Clf){x, 0) = C(f)(oo, t) = C«y, Р(0, t) = p* = const,
(23.48)
g{k)(0, t) = const, /ft(0, 0 = 0
при введении переменной 1\=х/У~ 2t сводятся к следующим:
р(-п)=рл. ст h)=c%. ш^ь* (ч-во),
Р{ъ) = Р* = const, gb) = const, /щэО (i)->0).
В то же время система уравнений движения двухфазной смеси
(23.19) сводится к системе обыкновенных дифференциальных
уравнений
+ «(1/2)(W{p(1(l-j)/i + pi')«,t)} = 0l (23.49)
в которой все коэффициенты зависят от р, 9, С<# и г\.
Однофазное движение газа будет описываться обычным
уравнением фильтрации газа, к которому сводится и система (23.49) при
9=0. В рассматриваемом здесь случае ему будет соответствовать
следующее автомодельное уравнение:
dujdr = - и ({*<«>/р<*>) {и (d/di) (p(«/i»»>) + т (dp<«/di|)}, '
u — dpjdfi.
Подвижная граница раздела областей движения однофазной
фильтрации газа и движения двухфазной смеси является
поверхностью разрыва. Здесь будут выполняться либо условия (23.30), если
жидкая фаза неподвижна, либо (23.33), если обе фазы двигаются.
Скорости фильтрации и поверхности разрыва относительно
переменной выражаются формулами
щЫ = _ (ll^Hdpfdny1 (1/1/3), w? = - и?/р?)(*р№)+(11У%),
(23.51)
ю(/) = _ (f^l^l))(dp/dii)+ (1 //Э), U = dXl (t)/dt = ъ/УШ,
212
где Xi=x{ (t) — закон движения поверхности разрыва. Нетрудно
видеть, что условие на поверхности разрыва оказывается зависящим
только от переменной т].
Для упрощения конкретных расчетов можно решать, однако,
задачу Коши, задаваясь одновременно условиями
dp/dr]=const, p=p*=const, g(/)=const,. (т|'=0), (23.52)
а на скачке, координата которого ir]+, задаваясь еще одним
дополнительным условием
64-=0o(Tl=Tl+). - (23.53)
Это условие определяет полностью все величины слева и справа от
скачка. Характерной особенностью . решения является следующее:
фазовый состав gfi), 1%) перед скачком определяется давлением и
одной независимой концентрацией (Ж Давление на скачке
меняется непрерывно, а условие D(fif^)» gfiy tfi)) =^ определяет
значение С<Я по g—() и давлению р. Таким образом, состав смеси
непосредственно перед поверхностью разрыва зависит не от начального
состава смеси в пласте, а от состава нагнетаемого в пласт газа и его
давления перед скачком.
')
091ЧЧ
0tZ40
0Z36
0,Z3Z
OZZ8
0,ZZ4>
DZZO
'Pip- г
- 0,9Z\
-0.ы\
-ом\
-08б\
- 08V I
-06z\
_ 080\
с
1
T \
l/V
■
1 I
'ft- 2
в
\ ,
O4^ p
N. -dp/d7j
i т—x i
4 6 8
7
в "|
otm -
°,
0,156 -
\0J5Z -
Ww -
wm-
0,140 —
-dp/d?]
0,06
005
0,04
0,0J
ooz
001
1 f'
/7 *
Рис. 67. Расчет процесса одномерной плоской рециркуляции сухого газа в газокон-
денсатном пласте
Примерный расчет был проведен [13] для процесса вытеснения
двухфазной смеси «метан+я-бутан+декан»~ сухим газом'«метан+
+я-бутан». Оказалось, что в области^двухфазной фильтрации после
поступления в нее ^нагнетаемого газа могут происходить как
испарение жидкой фазы (если сухой газ имеет больше тяжелого
компонента или же если начальная насыщенность мала, скажем, 0=0,02),
так и растворение нагнетаемого газа в жидкой фазе (если нагнета-
213
ется более легкий газ или же если начальная насыщенность велика,
8=0,08 и 0,15). При движении обеих фаз (6=0,4) наблюдается
повышенное содержание («вал») промежуточной компоненты. Укажем,
что появление минимума насыщенности 8 перед поверхностью
разрыва (фронтом, сухого газа) соответствует повышенной ко^ентра-
ции легкой компоненты (рис. 67). Известно экспериментальное под-,
тверждение появления вала промежуточных компонент (на
практике— этана).
24. ТЕОРИЯ ФИЛЬТРАЦИОННО-КОНВЕКТИВНОЙ ДИФФУЗИИ
Случайные блуждания частиц в фильтрационном
потоке. Уравнение диффузии. Тензорный вид
коэффициента диффузии. Параметры рассеивания.
Интервалы влияний чисел Рейнольдса и Пекле.
Режимы автомодельности и степенных зависимостей.
Диффузия в газовых потоках. Анизотропия среды.
Учет адсорбции.
Рассмотрим закономерности перемещений жидких частиц в об^
щем потоке однородной жидкости в пористых средах. Представим*
что имеется возможность фиксировать смещения меченых" жидких
частиц. Перемешивание меченых частиц с остальной жидкостью
в масштабе отдельной поры описывается обычным уравнением
диффузии в потоке жидкости
С',,= (Dmbifi\i) ,i—ViC'tif (24.1)
где, как и выше, х%— микрокоординаты, С — локальная
концентрация меченых частиц, Dm — коэффициент молекулярной диффузии,
Vi — локальная скорость жидкости.
Проинтегрируем уравнение( 24.1) по объему \AW\ занятому
жидкостью элементарного макрообъема,
■£ j" C'dV = Dm \d-CLnidS + Dm\dC_nidS-
AV(2) AS<2) Sm
- f Cv^dS - Г Cv.n^S - f С ^*dV, (24.2)
где ASW=mAS — площадь граней объема AV, занятого жидкостью;
Sm — поверхность раздела между фазами, П\ — нормаль. Здесь было
использовано также, что vi=0 в точках Sm, т. е. матрица среды
неподвижна и недеформируема.
Если принять предположение о несжимаемости жидкости
(dvi/dxi=0), то последний интеграл справа тождественно равен
нулю. В пренебрежении адсорбцией меченых частиц на поверхностях
раздела Sm второй интеграл справа также обращается в нуль — нет
стока меченых частиц на Sm:
Можно ввести концентрацию С меченых частиц по всему поро-
вому пространству ДУ<2), занятому жидкостью,
С = ^Г J c'dV- " ' (24-3>
дИ2)
214
Тогда уравнение (24.2) можно понимать как конечно-разностный
баланс меченых частиц в объеме AV. Если разделить его на AV и
рассматривать величины АХ{ как дифференциалы dXt в системе
макрокоординат, это уравнение принимает вид
Ctt={(D%+Dtj) CtJ},i-ViWCti9 (24.4)
причем в (24.4) введены эффективный коэффициент молекулярной
диффузии в пористой среде D°ij и поток перемешивания (DijC,j)y
обусловленный наличием v*i=Vi-~v№ пульсаций — скорости жидких
частиц по сравнению со средней скоростью v№=wif'm [49], а именно
;> д5(2)
Z)'iC./ = W J (C'-C)(vi-vf))nidS = 1±r j C^^dS.
A5(2) A5(2)
(24.6)
Подобный подход позволяет учесть различие между
коэффициентами молекулярной диффузии D°ij в пористой среде и Dm в
свободной жидкости
Doij=:3ijDmf (24.7)
3ij — тензор извилистости пористой среды. Его оценки: з<^0,7— для
рассыпных, сред и з^ОЛ— для горных пород. Реальный тензорный
характер этого параметра проще всего выявить по диффузии в
анизотропных средах.
Для" изучения связи потока DijCyj с параметрами течения vj2), Dm
пористой среды перейдем к анализу перемещения отдельной меченой
частицы в поровом пространстве. Начнем с более простого случая
изотропной пористой среды. Изотропия понимается как
независимость всех параметров случайных полей, характеризующих
микростроение среды, относительно жестких вращений и зеркальных
отображений выбранной системы координат.
В силу хаотичности микростроения можно считать, что
фактические (локальные) скорости жидких частиц vi образуют случайное
векторное поле в трехмерном пространстве. В силу вязкости
жидкости оно непрерывно во всех точках.
Случайное поле локальных скоростей в изотропной среде имеет
ось симметрии —направление средней скорости. В самом деле,
область течения (изотропная пористая среда) неподвижна, и
направление средней скорости, задаваемое ортом woi=i0i/\wi\=v^2) l\v{2) ,
является единственным характерным направлением, неравноправным
с другими направлениями. Анализ макроброуновских блужданий
меченых частиц в таком поле был дан ранее [7, 9, 49]. Здесь
рассмотрим непосредственно скалярную величину Вф\й^
характеризующую диффузию, где bu dj> — компоненты произвольных единичных
215
векторов. Эта скалярная величина в силу инвариантности
относительно жестких вращений и зеркальных отображений конфигурации
векторных аргументов Ьи dj, w°i зависит лишь от углов между ними,
так как модули всех этих векторов равны единице. Поэтому
Dijbid^yibidf, biW°i\ diw\). / (24.8)
Но так как левая часть уравнения (24.8) линейна относительно
произведения bidj, то должно выполняться равенство
Dijbidj=AbiW0idjw0j-i-Bdibi. (24.9).
Отсюда коэффициент диффузии как аксиально-симметричный тензор
имеет вид
Dij=A wOiW^+Bbij, (24.10)
где Л, В —скаляры (возможные функции четных степеней
вектора Wi).
С другой стороны, размерность коэффициента D^ фильтрацион-
но-конвективной диффузии есть Ь2Т~1, а потому коэффициенты Л, В
должны быть пропорциональны скорости Vii2\ а. коэффициенты
пропорциональности Хг им-еть размерность длины. Поэтому равенство
(24.10) может быть представлено [26] в следующем виде:
А-; = (Я, - A,) (tf vf)l\v?\ + X2 |if | Ьи, (24.11)
где Ки Л/2 —соответственно, продольный и поперечный параметры
рассеивания пористой среды.
В общем случае для процесса перемешивания в пористой, среде
справедливо следующее выражение для коэффициента диффузии:
JD;/ = D^.;. + QI,.ft;шVf, , (24.12)
где Qtjki — тензор рассеивания пористой среды, w°k = v^/\v^\. В
изотропном случае он выражается через указанные выше два
скалярных параметра Ль %2-
Существенно, что эти параметры, имеющие размерность длины
и пропорциональные поэтому масштабу микроструктуры d или
~\fkjm, в общем "случае могут зависеть от скорости потока, что
в безразмерном виде означает зависимость от локального числа
Пекле Pe=vWd/Dm или числа Рейнольдса Re=py<2W/|ui=^2>d/v.
В зависимости D = f(v) можно выделить [9] следующие пять
характерных интервалов (см. рис. 68,а).
I. При отсутствии или же при крайне ж медленном движении
Dm^dvW или Pe^Pei перемешивание чисто молекулярное: Pei —
первое критическое число Пекле. Эффект фильтрационно-конвектив-
ной диффузии — второй член в выражении (24.12) — пренебрежимо
мал. Микроблуждания частиц обусловливаются только
молекулярными взаимодействиями.
II. При несколько большей скорости v{2)d—Dm или Pe2»Pe>Pei
молекулярное и механическое перемешивания взаимосвязаны, что
должно отражаться на зависимости коэффициентов от числа. Пекле.
216
В выражении (24.12) сохраняются оба* слагаемых и, кроме тогог
fa = Xi(Pe). Для фильтрашюнно-конвективной диффузии справедлива
следующая оценка
D/v~ Xi(Pe)v^/v = Xi(Pe)Re = h(RePr)Re = X0i(Pr)Ren. (24.13)
Поэтому для режима II справедлива степенная зависимость
коэффициента фильтрационно-конвективной диффузии от скорости и
потока. Броуновские блуждания а
обусловлены молекулярными
силами и перескоками по
системе микротечений.
III. Скорости значительны,
молекулярными эффектами
можно пренебречь, течение
еще локально безинерционно
vWd^Dm или Ре»Ре2, но
Re<Reb где Rei—
первоекритическое число Рейнольдса.
В этом диапазоне: Xf = constH
является линейным масштабом
внутреннего течения.
IV. Скорости еще больше,
Re»Reb инерционные силы
взаимодействуют с
вязкостными, Xi=Xi(Re). Поэтому для
коэффициентов
фильтрационно-конвективной диффузии
имеем степенную зависимость
(24.13) от скорости потока
D/v ~ Xtv'2) /v = Х\ (Re) Re ^ Re".
Ре
I
f К
Е
г
Ш
ш
Y
6 Re, Rez
Ре, Рег
I
Е
ш
¥
в Ret Rez
I
П
ш'
¥
Ре, Рег
I
Е
| ш':
Y
Re, flez
Рис. 68. Режимы конвективно-фильтрацион-:
ной диффузии и переходные числа
Рейнольдса и Пекле
(24.14)
Здесь помимо макроблужданий по поровым каналам частицы
совершают блуждания из-за нестационарных эффектов в масштабе
микротечения.
V. Скорости, весьма значительны, вязкостные силы намного
меньше инерционных, Re»Re2 и вновь ?w = const. Однако значения этих
параметров уже-иные, так как микрокартина течения иная, нежели
при режиме III. Режимы III и V являются предельными по числам
Re и Ре.
Для оценок критических чисел Рейнольдса воспользуемся
данными (см. рис* 35), согласно которым для малопроницаемых сред
(/г = Ю-13 м2) Rei = 10-2, для среднепроницаемых сред (fe=10~12 м2)
Rei = 10~1, а для высокопроницаемых сред (&=10-9 м2) Rei = 0,5 и
Re2=10Rei. Для оценок критических чисел Пекле воспользуемся
условием ki~ 102 Yk, Pei = Xv/Dm^>0,l't Pe2 = Kv/Dm^\0y а потому
будем считать, что Pe = v Vk/m/Dm^l0-3 и Ре2=10"1.
Существенно также, что A,2/A,i-—-Ю-1. Это может приводить^ к
несовпадению указанных режимов для поперечной и продольной
диффузии даже при одинаковых скоростях фильтрации. Укажем, что
15-3311 217
различие значений h2 и Xi обусловлено тем, что поперечная диффузия
контролируется молекулярным переходом частиц с одной линии тока
на другую (Х2=0 при £>т=0). /
Нетрудно видеть, что числа Пекле и Рейнольдса пропорциональны
друг другу /
Pe=PrRe, Pr=v/£>m, (24.15)
где Рг — число Прандтля, которое характеризует физические
свойства собственно флюида. Значения Рг приведены ниже.
Dm* CMVC v» см*/с Pr=v/Dm
Газ • Ю-1 Ю-1 1
Жидкость Ю-4—Ю-8 Ю-2 102—108
Для газов число Рг—'1, а потому можно непосредственно
сравнить числа Rei, ..., Re2. Видно, что для продольной диффузии в
потоке газов в высокопроницаемых средах Rei»Pei, Рег, иначе говоря,
режим I постоянного значения эффективного коэффициента диффу-
/0~v /О'3 tO~2 ЮГ', /0° ad/p0~
Рис. 69. Коэффициент продольной диффузии в фильтрационном потоке газа в
функции от числа Пекле
1 — Л-0,018-10-12 м2; 2 —£«0,128-10-18 м2; 3 —£=0,4-10-™ м2; 4 —А—(12; 23)-10-12 м2; 5 —для
жидкости
зии в этом случае сменяется на режим III согласно варианту а
схемы на рис. 68. Эта ситуация реализовалась для песков при k^
^20 мкм2 в опытах М. А. Пешкина. Продольное перемешивание в
среднепроницаемых материалах характеризуется отсутствием
режима III (автомодельное™), поскольку Ре2—Rei— вариант б рис. 68.
При этом условие постоянства суммарного коэффициента диффузии
сменяется на его пропорциональность величине vn. Подобное явление
наблюдалось в опытах М. А. Пешкина, с проницаемостью от 10 до
0,01 -К)"12 м2, причем из результатов для £=0,018; 0,29-10~12 м2,
можно убедиться в условии пропорциональности: %\^^y~k. Поэтому
для всей области II+IV можно искать единый степенной закон
218
(24.13) — (24.14). Наконец, для продольного перемешивания в
малопроницаемых средах имеем варианты в или г рис. 68. Режимы I
сменяются последовательно на режим II, а затем на IV/ или IV", когда
автомодельность нарушается одновременно за счет зависимостей Кг-
и от Ре, и от Re. Наконец, отметим одну из ситуаций б, в, г для
потока газа в корундовом порошке (проницаемости & = 0,035 и
0,050-10~12 м2), когда выделяется, по-видимому, и режим
автомодельное™ V.
Экспериментальная зависимость по С. Н. Бузинову и М. А. Пеш-
кину для коэффициента продольной диффузии от числа Пекле
приведена на рис. 69 для газа (кривые 1—4) и для жидкостей
(кривая 5). Расхождения кривых 1—4 обусловлены различиями в
проницаемости сред. Несовпадение диапазона 1—4 и диапазона 5
обусловлено различиями в числах Рг. В самом деле, поскольку числа
Прандтля для жидкостей на два-три порядка больше, чем число Рг
для газов, то использование вместо Ре числа Рейнольдса Re
приводит к совпадению диапазонов зависимостей D = f(v) для жидкостей
и газов.
Пересчет (24.15) характерных чисел Pei и Ре2 ставит им в
соответствие такие числа Рейнольдса:
Re0o= Ю-5-10-6, Re0= 10~3—10~4.
Их малость по сравнению со значениями Rei, Re2 сразу приводит
к выводу, что для продольного перемешивания в потоках
жидкости в пористых средах справедлив только вариант а (см. рис. 68).
%Кроме того, если для жидкостей Dm = const, то у газов Dm = Dm(p)»
Действительно, в экспериментах при варьировании давлений
нагнетания эта зависимость была выявлена.
Обратимся теперь к поперечному перемешиванию. В этом случае
критические числа Пекле, вычисленные по коэффициенту
проницаемости, оказываются на порядок больше: Pei—10~2, Ре2^10° (за счет
отношения WXi = 0,l). Это приводит в случае перемешивания в
потоке газа к неосуществимости режима III (автомодельности по Ре и
Re) за исключением высокопроницаемых сред. Для поперечного
перемешивания в потоках жидкости этим критическим числам
Пекле соответствуют такие числа Рейнольдса:
Re00 = 10-4-10-5, Re0=10-2-10-3,
что обеспечивает реализацию режима III в случае средне- и высоко-
проницаемых сред.
Измерения в режиме III одновременно поперечной и продольной
диффузии были выполнены для потока воды в песке [13], причем
оказалось Л,г=0,127 см, Я2 = 0,0089 см, т. е. AiA2 = 14,3 (и<2> = 340—
470 см/с). Для шариков (проницаемости & = 3,43—2,45-10~5 см2) и
песка (&=10-6—Ют5 ем2) были найдены (Д. Харлеманом и Р. Ру-
мером [7, 13] соответственно эмпирические формулы
(DJv) = 54Rel'2, (DJv) = 83Rei'2 ,
Re* = iA2)|/£/v,
15* 219
тогда как для поперечной диффузии в упаковке из шариков
D2/v = 2,95Re2'7,
причем диапазон чисел Рейнольдса 1,6-10~2^Re^l,6-Ю-1, по-^ди-
мому, соответствовал переходу от режима III к режиму ГУ (ва--
риант а, рис. 68). /
Если бы молекулярная диффузия абсолютно отсутствовала, то
яри реализации режима III обращение средней скорости потока
приводило бы к смене знака всего поля локальных скоростей. При этом
теоретически можно добиться обратного, собирания меченых частиц,
распространившихся в фильтрационном потоке, в область начального
лоложения, как это было отмечено Дж. Тейлором. Однако
молекулярная диффузия препятствует подобному явлению — обратить
молекулярные броуновские блуждания невозможно.
В осесимметрично трансверсально изотропной пористой среде
имеется одно характерное направление г/, например, вектор
ортогональный напластованию осадочных горных, пород. Тогда из
рассуждений, подобных проведенным [26], при выводе (24.16) следует
более общая формула
Di5=Aw\w°j+Bbij+CriTi+Ew^ri+Fwfu (24.16)
где Л, В, ... — коэффициенты, которые могут быть функциями
произведете w°kwky win.
В ходе переноса в фильтрационном потоке меченые частицы
могут поглощаться, причем различают три основных механизма
поглощения. Во-первых, это адсорбция частиц на поверхностях твердой
фазы — матрицы среды. Во-вторых, поглотителем могут являться
мелкие поры зерен твердой фазы. Это случай трещиновато-пористых
сред или же специальных упаковок мелкопористых гранул,
используемых в химической технологии. Третьим типом поглотителя могут
•служить зоны так называемой неактивной пористости, скорость
движения жидкости в которых в среднем близка к нулю. Попавшая в
эту зону меченая частица может оставаться в ней достаточно долго,
что приведет к запаздыванию ее возврата в основной поток. Если
второму и третьему случаю соответствует фактически разделение
всего порового пространства на два подпространства, с введением
для каждого из них своей концентрации, а также заданием
интенсивности обмена мечеными частицами, то для учета обычной
адсорбции задать интенсивность поглощения частиц на поверхностях
раздела S* между фазами [см. уравнение (24.2)].
Уравнение макробаланса меченых частиц, транспортируемых в
фильтрационном потоке, имеет соответственно вид
a,t+Ctt= (DiiCti)ti—VjCti9 (24.17)
где а — концентрация сорбируемых частиц на единицу объема
пористой среды. Эта величина связана с концентрацией С этих частиц в
потоке жидкости уравнением кинетики сорбции
a,t = fi(C-y), (24.18)
где (3 — скорость сорбции (функция температуры), а у —
равновесное значение концентрации С, при котором интенсивность перетока
220
вещества обращается в нуль. Функция, связывающая концентрации
а и у, называется изотермой сорбции: a = f(y). Изотерма 'Ленгмюра
a=y/(yo+py), (24.19)
где г/о, р — постоянные, соответствует представлениям о
мономолекулярном слое адсорбированных частиц. Линейный вариант,
аппроксимирующий (24.19) при малых у, носит название изотермы Генри
У=а/у, (24.20)
где y — константа Генри.
Система урайнений (24.17), (24.18) и (24.20) в одномерном
случае сводится к следующему уравнению:
%а{Сл- (DC,xx-vCtX) h+{C,t- (1 + у) -1 (DC>xx-vCiX)}=0, (24.21)
где Ta = YP~1(l+Y)~1 — адсорбционное время релаксации.
Из (24.21) непосредственно видно, что при Г<та, где Г—
характерное время процесса, адсорбция несущественна, тогда как при
весьма медленных Т^>та эффективная емкость пористой среды
возрастает в (1+?) раз. В этом случае эффективной оказывается
система уравнений
C,^=Z)(l+7)-1C,^-t;(l+Y)-10. (24.22)
Нетрудно видеть, что введение нового масштаба времени *
/(v)=//(l+Y) (24.23)
сводит уравнение (24.22) к обычному фильтрационно-конвективному
уравнению переноса. Если в фильтрационный поток мгновенно
запустить смесь веществ с различными константами Генри: уь 42, ..., то
из пористой среды максимумы концентрации этих веществ выйдут в
потоке в различные моменты времени. Если пренебречь
взаимодействием частиц между собой, то распространение каждого пакета
будет описываться решением уравнения (24.22) с подстановкой
соответствующего времени t(yi), t(y*)t ... Это и есть эффект
хроматографии, на основе которого можно разделять' вещества или же
устанавливать присутствие какого-то из них в смеси.
Изложенная теория нашла широкое применение в теории
фильтрации [7, 36] при решении практических задач. Примеры даны ниже.
25. ЗАДАЧИ ФИЛЬТРАЦИОННО-КОНВЕКТИВНОЙ ДИФФУЗИИ
Размыв облака примеси в одномерных плоских
потоках. Использование эквипотенциалей и линий
. тока в неодномерных плоских потоках.
Асимптотические решения. Задачи сорбции. Оценка
радиоактивной опасности. Закритические течения.
В одномерном плоском случае уравнение фильтрационно-конвек-
тивной диффузии имеет вид
mC,t+wC,x={DCrX)tXi D = mD°u+hw (25.1)
и при постоянстве коэффициента D допускает построение простых
решений. Если бы D = 0, то перенос меченых частиц происходил бы
вдоль характеристики
t
хс (t) = J у(2> dt, v& = w[m. (25.2)
о
221
Tax, при задании граничного и начального условий
С(х, * = 0)=0, С(л:=0, 0 = 1, 0<л:<оо (25.3)
меченые частицы распространялись быв виде «ступеньки», со
Скачкообразным фронтом (пунктирные линии, рис. 70). Перемешивание^
однако, приводит к размыву фронта, скачок заменяется на ^переход-
ную зону шириной А. Когда Kiw^D°n, имеем А ^ YDt/m =*
—Y\xv^4 и при К\ = const, у(2) = const зависит только от расстояния,
пройденного фронтом, т. е. средней линией переходной зоны: А ^Ухх-е*
Отметим, что подстановка
• С ,,«С(*.0«р{-(-£—£)} (25.4)
преобразует уравнение (25.1) к обычному
уравнению Фурье
ф, = Дф.
(25.5)
Рис. 70. Схематизация
размыва фронта меченых
частиц в потоке
Задача о размыве в бесконечной среде
прослойки г меченых частиц с начальным
распределением
С(ху 0) =f(x), — oo<x<oo (25.6)
сводится к решению уравнения (25.5) при
следующих граничных условиях:
WX
Ф(х, 0) = f(x)exp(
Соответствующее решение хорошо известно
2mD
■)•
Ф(*, t):
iVnDt
Ж 1ехрГ
(*-6)
2Dm
•)ш
dt
и распределение концентрации имеет вид
00
c^f)=imr jexp(-
х — % — vty
4Dt
)№
dt.
(25.7)
В частности, если прослойка прямоугольная —
f(x) = l; (\x\<a);f(x)=0 (\х\>а),
решение имеет вид
ыо-Ц^Шг^Щг))- '—*• (25'8)
где erf (z) — интеграл вероятности. Известно [9] хорошее
соответствие экспериментальных данных с расчетом, выполненным при D =
= 1,92-Ю-2 см/с (а; = 0,179 см/с).
На границе х=0 или x=L пористой среды условие
формулируется по Г. Бреннеру как балансовое соотношение на разрыве, с'.одной
222
стороны которого — в свободном потоке жидкости — происходит лишь
конвективный перенос со скоростью w, а с другой — в пористой
среде—и перенос, и фильтрационно-конвективное перемешивание,
wC+= wC--D (дС/дх) -. (25.9)
Зто условие справедливо, если диффузионное перемешивание в
свободной жидкости пренебрежимо мало. Практически, однако, на
входе считается заданной концентрация [см., например, (25.3)], т. е.
диффузионным потоком пренебрегают. На выходе условие (25.9)
дополняется (по П. Данкуэртсу) требованием: С+ = С~У т. е.
условие (25.9) заменяется на следующее:
дС/дх=0 (x=L). (25.10)
Последнее может быть сформулировано непосредственно как
условие запрещения диффузионного возврата меченых частиц в по-
• ристую среду.
" Решение задачи (25.3) также хорошо известно и имеет вид
c=i К(-Ш+ехр № eHww-)} <25">
и при D/(wx) <50 упрощается
c^-r&vic{-Ww)' (25Л2)
где -erfс (г) = 1 —erf z.
Использование более точного условия (25.9) на входе приводит
(по В. И. Абрамовой и Г. П. Цыбульскому [13]) к следующему
решению:
cue о=4-{«* [-WW-) -ехр (■£■)('+ :=**)><
Х.*(-ЭД}+1/?«р(-ЭД. (25..3)
Распределение концентрации в пористом слое конечной длины,
при граничных условиях (25.9) на входе —при С+ = 0, #=0 и
(25.10) на выходе (х=Ь), а при начальном—С=Со{х, 0),
построено Г. Бреннером [13] и имеет вид
С0-1 =2ехРРе(27Г ~ 1) 2j (*V+ Ре* + Ре) (Х»л + Ре2) X
k=\
X^cos (2Xk -f) +Ре sin (2l-£)} exp (- -gL) , (25.14)
где Pe=vL/(4D), ft* — положительные корни (k=ly 2, 3, ...)
трансцендентного уравнения
^2я = -гаг. (25л5)
223
за исключением тривиального корня Я = 0. Особый интерес
представляет изменение концентрации С во времени на выходе из пористого
слоя. /
Неодномерная диффузия в плоском потоке от мгновенного
источника важна [36] для нахождения ореала примеси при/ёе
сбросе через скважину в пласт. Решение уравнения фильтрационно-кон-
вективной диффузии при постоянных величинах Ъ\ и D2
Ctt+vCtX = DlC,xx+P2Ctyy (25.16)
имеет вид
где скорость v направлена вдоль оси х, Q — число сброшенных
частиц примеси при / = 0.
Распределение концентрации примеси от постоянно л
действующего источника постоянной интенсивности Q можно найти,
проинтегрировав решение (25.17),
О г
где использовано асимптотическое представление функции Макдо-
нальда.
Если в плоском потоке на линии х=0 задано граничное условие
f(y) = 1, у<0; f(y) = 0, у>09 (25.19)
то стационарное решение [13] имеет вид
с (х, у)=4—зёгехр [ж) 1** (-т \/ ж+ък)х
Х(^+^г)-"2^. -(25.20)
При больших значениях аргумента функции Макдональда /Су(г)я^
*^ 1/гс/2гехр(—г) решение (25.20) упрощается и принимает вид
С(х. у) = ±еПс(фУЩ (25.21)
Решение (25.21) может быть получено непосредственно в
предположении, что С)УУ^>С)Хх.
При произвольном плоском фильтрационном поле v = v(x, у)
следует воспользоваться криволинейной системой координат, выбрав в
качестве независимых переменных ф — потенциал скорости к -ф —
функцию тока. Подобный прием был предложен Ж. Бусинеском для
молекулярной диффузии с конвективным переносом и применен в
задачах фильтрации Н. X. Арутюняном, С. Н. Нумеровым и
224
А. Н. Патрашевым [36]. Изложим этот прием применительно к
фильтрационно-конвективной диффузии с учетом изотропной
молекулярной диффузии [7, 13, 36].
Уравнение (25.1) может быть записано в виде общего уравнения
переноса
С., = (1/Я Яф) {(Яфа*а)> ф + {Н9а%)г ф}, (25.22)
где Яф, Н^ -— коэффициенты Ламэ, аф*, щ* — «физические»
составляющие потока концентрации (в терминологии Н. Е. Кочина). В
рассматриваемом случае имеем
н _и __1_ ( дС \* ' 1 дС f дС у 1 дС
ч> * И ; [ ^ ) — Яф di ; \ д± ) - Яф дф •
^Ф=о, *% = М. (tg*=Q, (n%)*=i.
(*<*rj =<°*)(-зг) +(^Ьг) =^г"зг-
В силу этого
а%= (Av2+D°\v\) {дС/дц) + (Bv2+D°\v\) (дС/дц) —vC,
a%=Av2{dC/dq)
и уравнение (25.22) представляется в виде
С,^ = t;2 {[ (^i I ^ 1;+^°) Аф] ,ф+ [ (^211; | +Z^a) С ф] )Ч1,_С^}. (25.23)
Начальные и граничные условия должны задаваться на
плоскости .ф, а|), причем предварительно надо найти поле а(ср, я|э) из
решения фильтрационной задачи. Приведем один пример.. Согласно
гидравлической теории [36] одномерных установившихся безнапорных
течений
Ф = — kh, /i2 = ca+P> \v\ =ak/(2h),
где^k — коэффициент фильтрации, h — уровень свободной
поверхности, a, р — постоянные. Уравнение (25.23) принимает следующий вид:
C>t— 4h2 у1 2k dh [ h dh J^2 2A- <?ф2 + k HfT.f9
если пренебречь молекулярной диффузией. Стациона-рное
одномерное распределение соли в перемычке длиной L между соленым и
пресным резервуарами будет следующим:
^-Ы-ъУ^-ЪУЫ-Зг)-
-ех"(-^-)Г- (25-24)
Эффективный меюд асимптотических разложений применительно
к уравнению (25.1) был развит Л. Гелхаром и М. Коллинзом [47].
В фильтрационном потоке переменного сечения уравнение (25.1) в
силу несжимаемости потока сводится к следующему:
Cj+vC,x = evC,xx+eD(C,xx—(l/v)v,xC,x), (25.25)
225
где безразмерная координата х направлена вдоль линии тока, Г, и
безразмерные величины, e=A,i/L*0, D=D°T*/ (k\L*)\ Г*, L*—
масштабы времени и длины. Считается, что D^.1, e<Cl. ТакимобразЬм,
левая часть уравнения имеет порядок 1, а правая — е, т. е. нужно
найти асимптотическое решение, соответствующее малому значению е.
Следующий шаг состоит во введении координаты
х
CyT=jf.-.,7 (2526)
— Хо
двигающейся вместе с фронтом вытеснения R(t}, dR/dt=U в
отсутствие диффузии, т. е. с характеристикой уравнения (25.25) при е =
= 0. Уравнение (25.25) принимает при этом вид
С.г = {(1/о) + Ф/о,)}С к-V^IOAO + Wo1)}». «С с. (25.27)
Скорость v является функцией координаты х. При использовании
подвижной координаты (25.26) она становится функцией положения
фронта R (тем самым времени) и расстояния £"j/~e. Введем в
уравнение (25.27) соответствующее разложение
J _1
V ~~ V2
V'K-r-*-)..+""-r--k-iy7K-r-£).+-
Тогда в пренебрежении величинами порядка ]/~е уравнение
(25.27) принимает вид
. C,T={(v(R)+D)/(vHR))}C,K. (25.28)
Введение нового времени
rffl= (v(H) +D)dT(v^(R) = (v(R)+D)dR/v*(R)
позволяет теперь перейти к уравнению Фурье
С,а = С,а. . (25.29)
Последнее в размерном виде выглядит следующим образом:
C.. = *iC>4V -4 = x-i,
(25.30)
Хо Хо
Рассмотрим конкретные течения со следующим распределением
скоростей:
v(x)=Alxh, A, A=const. (25.31)
Если пренебречь молекулярной диффузией, то
~ — *к+1 — Rk+l R2k+1
A(k+l)9 A(k+\)' A2{2k+\)
226
й решение кдля граничных условий (25.3) типа «ступеньки» при
достаточно больших расстояниях, пройденных фронтом [см. (25.13)],
имеет вид
C = -^erfc6,
(25.32)
Таблица 12
Геометрия потока
Одномерный плоский
Осесимметричный
Сферически-симметричный
А
V
v/ (2пт)
Q/ (4ят)
k
о •■
1
2
Положение
фронта R
At
*(2At)]/2
(3At)l/3
Переменная в
(х-Я)/^*)1'2
(x2-R2) (16^73)1/2
(Хз_яз) (36Л^5/5)1/2
где в дана в табл. 12. Расчет показывает, что ширина зоны размыва
наибольшая в плоском потоке, наименьшая — в
сферически-симметричном. Это и понятно — уменьшение скорости вследствие
расхождения потока не только замедляет движение фронта, но и снижает
интенсивность диффузионного перемешивания.
Одномерная задача сорбции в полубесконечном слое, при задании
начальных' и граничных условий типа «ступеньки» относительно
концентрации С в потоке
С(х, 0)=а(х, 0)=0, С(0, *) = 1, С(оо)=0 (25.33)
и описываемая уравнением (24.21), имеет простое решение [13]
С(6, .) = Ир(.)-^|г(2)л}, « = 1£г,
о
Хехр(--|1--т]а^7].
(25.34)
Здесь x=v2t/4D.
При задании условий типа «ступеньки» для концентрации а,
существующий при £ = 0 разрыв, однако, не размывается мгновенно,
как это должно быть по классической теории диффузии, а затухает
по экспоненциальному закону. В самом деле, считая, что всюду в
области фильтрации выполнены уравнения (24.17), (24.18) и (24.20),
условий на разрыве*можно получать [13] интегрированием
уравнений по малой окрестности (—А, +А) поверхности разрыва с
последующим предельным переходом А->0. В этом случае уравнение
(24.17) дает вполне понятное условие непрерывности потока
[D(dC/dx)—vC] = 0, (25.35)
227
а интегрирование уравнения (24.30), умноженного на координату ху
приводит к условию непрерывности концентрации С в потоке /
[С]=0. ,(25.36)
/
Рассматриваемая система уравнений может быть сведена к
уравнению относительно концентрации а адсорбированных частиц
я,"+Р (1+V"1) a,t— {DatXX-vax) yt+ ($/у) (Daxx—vatX) =0. (25.37)
Интегрирование уравнения (25.37) по интервалу (—/i, -\-h) и
предельный переход при /i->0 дают в результате [13] первое условие
для скачков
[Dax-va],t+($/y) [Dax-^va] = 0. (25.38)
Интегрирование уравнения (25.37), умноженного на координату, дает
второе условие
D[at+($/y)a]=0. (25.39)
Интегрируя дифференциальные уравнения (25.38), (25.39)
относительно скачков [а] и [а)Х], получаем окончательно
[а] = [а]0ехр(—$t/y)y [да/дх] = [да/дх]0ехр(—$t/y).
Неодномерная диффузия в плоском фильтрационном потоке при-'
начальных нулевых условиях а=С=0 при ^=0 и задании
граничных условий С(0, y)=f(y), С(х, оо)=0 в предположении, что
^гУУ^ V,XX» Т. е.
a,t+C,t+vC,x=D2C,yy; a,, = p(C-a/Y),
исследована ранее [13]. В частности, при
f(y)=0,y>0;f(y) = l,y<0.
решение имеет вид
С(х. y,t)=-L erfc(-^у^р-) F(х, <). x~vt<0.
(25.40)
С(х, у, 0 = 0, x-vt>0,
где
**. о=Ч- v) h (- т (< - v))/. [> /»Тр!)]+
х/и
Функция F(x, t) —распределение концентрации С в одномерном
фильтрационном потоке в пренебрежении диффузией, но в условиях
адсорбции.
228
с,г/м3
-9
W
W
-Б
W
-8
W
-W\
Ш
о
w
ГМ
Оценка радиоактивной опасности
подземных ядерных взрывов
основывается на расчетах фильтрационно-диф-
фузионного переноса радионуклидов в
потоке газа из взрывной полости с учетом
их возможной сорбции, конденсации и
радиактивного распада. Поскольку
кинетические коэффициенты компонент
различны, трещиновато-пористый массив,
через который идет фильтрация, играет
роль хроматографической колонки.
Исходная смесь распадается на пакеты
разных радионуклидов, которые
выходят на свободную поверхность
неодновременно. Опасность оценивается
ло биологически активным изотопам
(цезЯя 137) с большим периодом
полураспада (30 лет). Результаты расчета
[3] концентрации цезия (кривые 1, 2) и
ксенона 137 (кривые 3, 4) через 25 мин
после взрыва в окрестности
взрывной полости даны на рис. 71. Пренебрежение диффузионным
переносом (кривые 3, 4) приводит к занижению радиоактивной опасности:
(на порядок). Расчеты подобного типа позволяют выбрать
необходимую глубину для проведения промышленных ядерных взрывов.
Наконец, обратим внимание на возможное приложение теории
фильтрационно-конвективной диффузии к расчетам подземных
потоков смесей жидкостей в закритических состояниях, при которых
различия между фазами утрачивается. При этом капиллярные силы
должны исчезнуть [13], фазовые проницаемости (см. рис.
54)—выродиться в прямые линии (/W=£)(fe)), а уравнения неоднофазной
фильтрации перейти в уравнения конвективного переноса (в<*>=С(*>)..
В подобных случаях существенными становятся эффекты диффузии
и сорбции. Подземная гидромеханика жидкостей в закритическом:
состоянии становится актуальной в связи с проблемами разработки,
глубинных месторождений (Прикаспийской впадины, Апшерона
и т. д.).
Рис. 71. Поле концентрации:
цезия (/, 3) и ксенона (2, 4)
с учетом (1у.2) и без учета
(5, 4) диффузии в окрестности:
полости
СПИСОК ЛИТЕРАТУРЫ
1. Авчан Г. М., Матвеенко А. А., Стефанкевич 3. Б. Петрофизика осадочных
пород в глубинных условиях. М, Недра, 1979.
2. Баренблатт Г. И., Ентов В. М., Рыжик В. М. Теория нестационарной
фильтрации жидкости и газа. М., Недра, 1972.
3. Басанский Е. Г., Колобашкин В. М., Кудряшов Н. А. Распространение
радионуклидов через раздробленную породу под действием избыточного давления
продуктов взрыва. — Механика жидкости и газа, 1980, № 2, с. 62—69.
4. Бовт А. Н., Николаевский В. Н. Дилатансия и механика подземного
взрыва.— Итоги науки и техники. Сер. Механика деформируемого твердого тела, т. 14,
1981, с. 129—167.
5. Ботт М. Внутреннее строение земли. Пер. с англ. М., Мир, 1974.
6. Бузинов С. #., Умрихин И. Д. Гидродинамические методы исследования
скважин и пластов. М., Недра, 1973.
7. Бэр Я., Заславский Д., Ирмэй С. Физико-математические основы
фильтрации, воды. М., Мир, 1971.
8. Вйльчинская Н. А. Волна переупаковки песков и акустическая эмиссия. —
ДАН СССР, т. 262, 1982, № 3, с. 568—572.
9. Влияние свойств горных пород на движение в них жидкости/ А. Бан,
А. Ф. Богомолова, В. А. Максимов, и др. М., Гостоптехиздат, 1962.
10. Высокоскоростные ударные явления. Под ред. Р. Кинслоу. Пер. с .англ. М.,
Мир, 1973.
11. Гарагаш И. А. Образование ячеистых структур в упругопластической
среде с внутренним трением и дилатансией. — ДАН СССР, т. 266, 1982, № 1,
с. 59—63.
12. Горбунов А. Т. Разработка аномальных нефтяных месторождений. М.,
Недра, 1981.
13. Движение углеводородных смесей в пористой среде4./ В. Н. Николаевский,
Э. А. Бондарев и др. М., Недра, 1968.
14. Дунин С. 3., Сироткин В. К. Расширение газовой полости в хрупкой
породе с учетом дилатансионных свойств грунта. — Прикладная механика и техническая
физика, 1977, № 4, с. 106—109.
15. Дьярмати И. Неравновесная термодинамика. Теория поля и вариационные
принципы. Пер. с англ. М., Мир, 1974,
16. Закиров С. Н., Лапук Б. Б. Проектирование и разработка газовых
месторождений. М., Недра, 1974.
17. Зарецкий Ю. К., Городецкий С. Э. Дилатансия мерзлого грунта и
построение деформационной теории ползучести. — Гидротехническое строительство, 1975,
№ 2, с. 15—18.
18. Каракин А. В., Лобковский Л. И., Николаевский В. Н. Образование сер-
пентинитового слоя океанской коры и некоторые геолого-геофизические явления. —
ДАН СССР, т. 256, 1982, № 3, с. 572—576.
19. Карус Е. В., Кузнецов О. Л., Кузнецов Ю. И., Нартикоев В. Д. О
возможной природе глубинных сейсмических границ. — ДАН СССР, т. 265, 1982, № 3,
с. 577—579.
20. Коловский М. 3. Нелинейная теория виброзащитных систем. М., Наука,
1966.
21. Левин В. М., Николаевский В. Н, Осреднение по объему и континуальная
теория упругих сред с микроструктурой. — В кн.: Современные проблемы механики
и машиностроения, М., Машиностроение, 1982, с. 182—193.
22. Механика насыщенных пористых сред/ В. Н. Николаевский, К. С. Басниев,
А. Т. Горбунов, и др. М., Недра, 1970.
23. Механика подземного взрыва/ В. В. Адушкин, В. Н. Костюченко, В. Н.
Николаевский и др. — Итоги науки и техники. Сер. Механика деформируемого
твердого тела, 1973, т. 7, с. 87—107.
24. Механический эффект подземного взрыва/ В. Н. Родионов, В. В. Адушкин^
В. Н. Костюченко и др. М., Недра, 1971.
25. Никитин Л. В., Рыжак Е. И. Разрушение горной породы с внутренним
трением и дилатансией. — ДАН СССР, т. 230, 1976, № 5, с. 1203—1206.
26. Николаевский В. Н. Конвективная диффузия в пористых средах. —
Прикладная математика и механика, т. 23, 1959, вып. 6, с. 1042-^1050.
27. Николаевский В. Н. О связи объемных и сдвиговых пластических
деформаций и об ударных волнах в мягких грунтах.— ДАН СССР, т. 177, 1967, № з„
с. 542—545.
28. Николаевский В. Н. Механические свойства грунтов и теория
пластичности. — Итоги науки и техники. Сер. Механика деформируемого твердого тела, 1972,.
т. 6, с. 85.
29. Николаевский В. Я.-Дилатансия и теория очага землетрясений. — Успехи:
механики, 1980, т. 3, вып. 1, с. 71—101.
30. Николаевский В. Н. О разрушении вязкоупругих тел. — Прикладная
математика и механика, т. 45, 1981, вып. 6, с. 1121—1128.
31. Николаевский В. Н., Лившиц Л. Д., Сизов И. А. Механические свойства
горных пород. Деформации и разрушение. — Итоги науки и техники. Сер.
Механика деформируемого твердого тела, 1978, т. 11, с. 123—250. ^
32. Определяющие законы механики грунтов. Пер. с англ. М., Мир, 1975.
33. Периодические вариации цараметров сейсмических волн при просвечивании
литосферы мощными взрывами/ Н. Г. Гамбурцева, Е. И. Люке, В. Н.
Николаевский и др. —ДАН СССР, т. 266, 1982, № 6, с. 1349—1359.
34. Применение подземных ядерных взрывов в нефтедобывающей
промышленности/ А. А. Бакиров, Э. А. Бакиров, В. Н. Виноградов и др. М., Недра, 1981.
35. Проектирование разработки нефтяных месторождений. Под ред. А. П.
Крылова, Ю. П. Борисова, Н. М. Николаевского. М., Гостоптехиздат, 1962.
36. Развитие исследований по теории фильтрации в СССР (1917—1967). Под.
ред. П. Я. Полубариновой-Кочиной. М., Наука, 1969.
37. Райе Дж. Механика очага землетрясений. Пер. с англ. М., Мир, 1982.
38. Рамазанов Т. К. О пластической зоне вокруг скважины в глубинных
пластах. — Известия АН АзССР. Сер. Науки о Земле, 1977, № 1, с. 29—36.
39. Рахматулин X. А. Основы газодинамики взаимопроникающих движений
сжимаемых сред. — Прикладная механика и математика, т. 20, 1956, вып. 2.
40. Рождественский Б. Л., Яненко Н. Н. Системы квазилинейных уравнений и?
их приложения в газовой динамике. М., Наука, 1968.
41. Седов Л. И. Механика сплошных сред. М.,. Наука, 1970.
42. Соколовский В. В. Статика сыпучей среды. М., Физматгиз, 1960.
43. Ставрогин А. Н., Протосеня А. Г. Пластичность горных пород. М., Недра„
1979.
44. Сургучев М. Л., Кузнецов О. Л., Симкин Э. М. Гидродинамическое
акустическое, тепловое циклические воздействия на нефтяные пласты. М., Недра, Л975.
45. Удар, взрыв, разрушение. М., Мир, 1981.
46. Шаров В. И., Гречишников Г. А. О поведении тектонических разрывов на
различных глубинных уровнях земной коры по данным метода отраженных волк
(MOB). —ДАН СССР, т. 263, 1982, № 2, с. 412—416.
47. Gelhar L. W., Collins М. A. General analysis of longitudinal dispersion irt
nonuniform flow. Water Resources Research, 1971, vol. 7, No. 6, 1511—1521.
48. Gomes L., Graves L. Stabilization of beach sand by vibrations. Highway-
Research Board, Bull. No 325, Wash. D. C, 1962, 44—54.
49. Scheidegger A. E. Statistical hydrodynamics in porous media. Advances Hyd-
roscience, vol. 1, New York — London, Academic Press, 1964, 161—181.
50. Sibson R. H. Fault zone models, heat flow and the depth distribution of
earthquakes in the continental crust of the United States. Bull. Seism. Soc. America,.
1982, vol. 72, No 1, 151—164.
f
231
ОГЛАВЛЕНИЕ
Предисловие .... . .... 3
Глава 1. Основные положения механики сплошных сред . 5
1. Уравнения континуальной механики ... 5
2. Объемное усреднение и масштаб описания 13
3. Разрушение сплошного материала .... 20
Глава 2. Дилатансия геоматериалов . . 30
4. Механизмы неупругости и модельные представления ..... 30
5. Дилатансионная упругопластическая модель . 36
" 6.- Предельное равновесие'и течение дилатирующих массивов . Л 48
7. Трещины, строение земной коры и землетрясения ..." .55
Глава 3. Динамика дилатирующих и хрупко-разрушаемых материалов . 62
8. Одномерные волны. Волны в стержнях 62
9. Элементарный расчет подземного взрыва 68
10. Допредельное сухое трение и затухание сейсмических волн . . 79
11. Скорость разрушения и динамическая прочность . . . . . 86
12. Динамическая сжимаемость, скорость скольжения и акустическая
эмиссия . ■ . ■ _ . . 95
Глава 4. Механика насыщенных упругих сред .... .... 102
13. Уравнения движения двухфазных сред 102
14. Общий анализ механики поротермоупругих сред 112
15. Упругие деформации насыщенных грунтов 122
16. Поглощение и отражение звуковых волн пористыми материалами 135
Глава 5. Неупругость и неоднофазное насыщение пористых сред , 142
17. Неупругость и разрушение насыщенных сред . .142
18. Ударное сжатие насыщенных сред .149
19. Механика сред, насыщенных неодн-офазной жидкостью . . . 159
Глава 6. Движение жидкости и газа в деформируемых пластах .... 169
20. Упругий режим- фильтрации жидкости и газа 169
21. Нестационарная фильтрация с гидравлическим запаздыванием . . 178
22. Напряжения в призабойных зонах скважин и нелокально-упругие
эффекты . . 186
Глава 7. Физико-химическая подземная, гидромеханика 198
23. Фильтрация многокомпонентных неоднофазных смесей . .• 1^8
24. Теория фильтрационно-конвективной диффузии ... . 214
25. Задачи фильтрационно-конвективной диффузии ... . 221
Список литературы ... «.»»•*» 230