И. Е. ИРОДОВ
СБОРНИК ЗАДАЧ ПО АТОМНОЙ И ЯДЕРНОЙ ФИЗИКЕ
ИЗДАНИЕ СЕДЬМОЕ ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством высшего и среднего специального образования СССР в качестве учебного пособия для студентов физических специальностей высших учебных заведений
МОСКВА ЭНЕРГОАТОМИЗДАТ 1984
ББК 22.38
И83
УДК 539.1(076.1)
Рецензент: Кафедра общей физики Московского Физико-технического института
Иродов И. Е.
И83 Сборник задач по атомной и ядерной физике: Учеб, пособие для вузов.—7-е изд., перераб. и доп. — М.: Энергоатомиздат, 1984. — 216 с., ил.
В пер. 85 к. 11 000 экз.
Содержит задачи по широкому кругу вопросов атомной и ядерной физики: квантовой природе электромагнитного излучения, волновым свойствам частиц, квантовой механике, атомным спектрам, электронным оболочкам атомов, молекул, кристаллов, физике ядра, нейтронной физике, термоядерным реакциям, элементарным частицам, движению заряженных частиц во внешних полях и др.
В этом издании заменены некоторые задачи и включены новые. Увеличено число ответов в общем виде. Шестое издание вышло в 1976 г.
Для студентов, изучающих курс атомной н ядерной физики.
1704070000-334	ББК 22.38
И 0(51)01-84	53‘84	530.4
© Атомиздат, 1976
© Энергоатомиздат, 1984, с изменеинямн
СОДЕРЖАНИЕ
Предисловие к седьмому изданию....................................
Об обозначениях...................................................
1.	Квантовая природа электромагнитного излучения..................
Тепловое излучение ...........................................
Корпускулярные свойства электромагнитного излучения...........
2.	Модель атома Резерфорда—Бора...................................
Рассеяние частиц. Формула Резерфорда..........................
Водородоподобные системы......................................
3.	Волновые свойства частиц.......................................
Волны де Бройля. Соотношение неопределенностей................
Уравнение Шредингера. Прохождение частицы через барьер . . . .
4.	Основы квантовой механики.....................................
Квантовомеханические операторы................................
Средние значения и вероятности................................
Изменение во времени состояния и механических величин.........
Центрально-симметричное поле. Атом водорода...................
5.	Спектры. Электронная оболочка атомов...........................
Состояние электронов в атоме..................................
Интенсивность н ширина спектральных линий.....................
Характеристические рентгеновские спектры......................
6.	Атом в магнитном поле..........................................
Магнитные свойства атома. Эффект Зеемана......................
Диа- и парамагнетизм..........................................
7.	Двухатомные молекулы...........................................
Вращательные и колебательные состояния........................
Молекулярные спектры'. Комбинационное рассеяние...............
8.	Кристаллы......................................................
Структура кристаллов. Дифракция рентгеновского излучения . . .
Энергия связи и теплоемкость кристаллов ............ .	. . . .
9.	Металлы и полупроводники.......................................
Свободные электроны в металлах и полупроводниках .............
Свойства металлов и полупроводников ..........................
10.	Основные характеристики ядер..................................
Радиус, масса и энергия связи ядер............................
Спин и магнитный момент ядра .................................
11.	Радиоактивность ..............................................
Законы радиоактивного распада ................................
а- и 0-Распады..................................................
у-Излучение: внутренняя конверсия, эффект Мёссбауэра . . . .
Статистика регистрации ядерного излучения. Счетчики ..........
12.	Взаимодействие излучения с веществом..........................
Прохождение заряженных частиц через вещество..................
Прохождение у-излучения через вещество........................
Дозиметрия излучений..........................................
13.	Ядерные реакции...............................................
Законы сохранения в ядерных реакциях...................  .	. .
Уровни ядер. Сечения и выходы ядерных реакций............. . . .
14.	Нейтронная физика.............................................
Нейтронная спектроскопия .....................................
Взаимодействие нейтронов с ядрами.....................
Прохождение нейтронов через вещество..........................101
Замедление и диффузия нейтронов...............................103
15.	Физические основы ядерной энергетики..........................106
Деление ядер. Цепная реакция..................................107
Термоядерные реакции ......................................... ПО
Физика плазмы.................................................112
16.	Элементарные частицы..........................................115
Взаимодействие релятивистских частиц..........................117
Распад частиц.................................................119
Свойства элементарных частиц..................................121
17.	Движение заряженных частиц во внешних полях...................124
Законы движения. Анализаторы..................................124
Ускорители заряженных частиц..................................129
Ответы и решения..................................................133
Приложения........................................................202
1.	Обозначения единиц физических величин......................202
2.	Край К- и £-полос поглощения рентгеновского излучения . . . 202
3.	Некоторые свойства металлов................................203
4.	Плотность некоторых веществ................................203
5.	Константы двухатомных молекул..............................204
6.	Радиоактивное семейство урана..............................204
7.	Таблица свойств нуклидов..................................205
8.	Нейтронные сечения.........................................207
9.	Постоянные делящихся нуклидов.............................207
10.	График пробег — энергия а-частиц в воздухе................208
11.	Коэффициенты ослабления и поглощения для у-излучения . . . 209
12.	Сечения взаимодействия у-квантов в свинце.................209
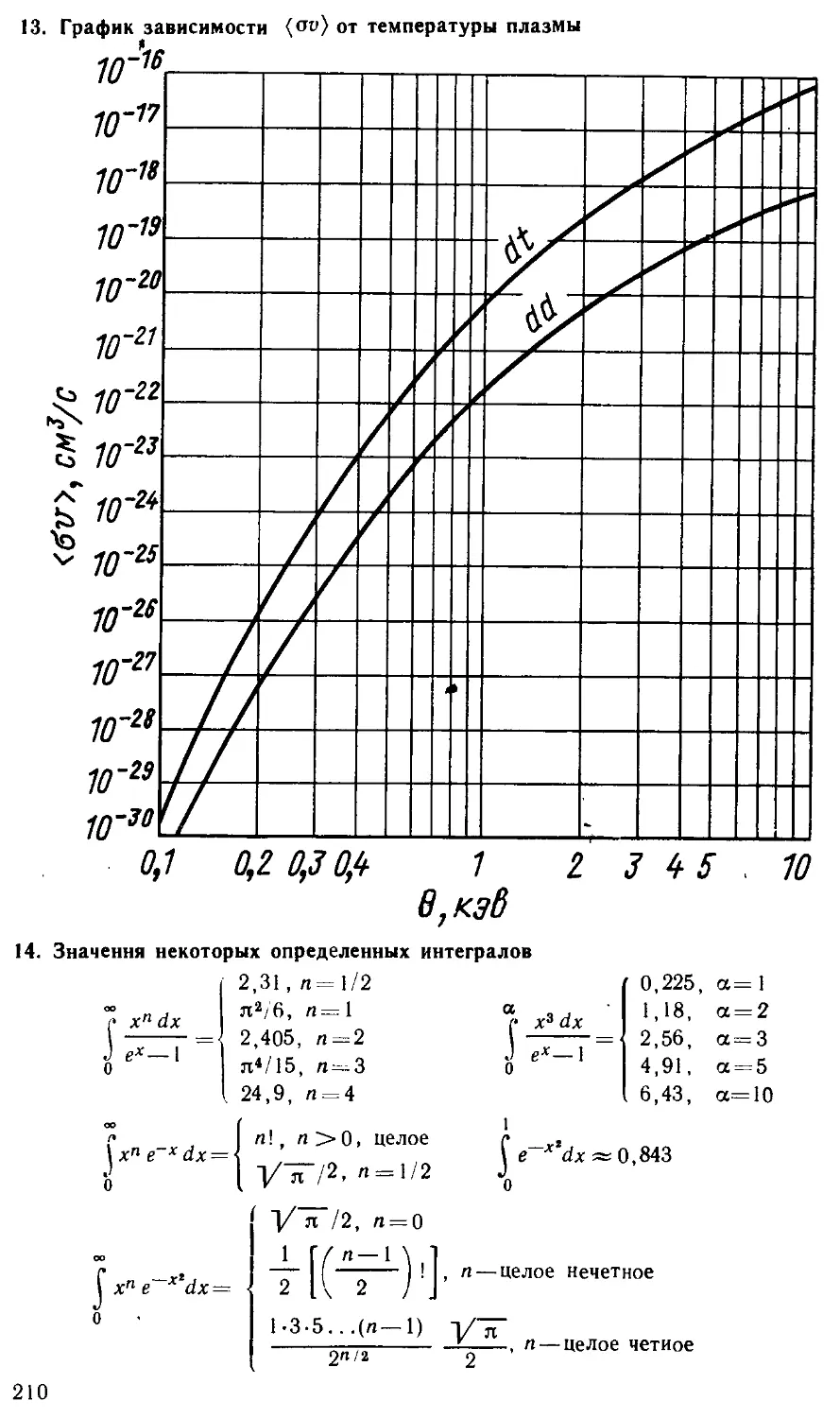
13.	График зависимости (от) от температуры плазмы.............210
14.	Значения некоторых определенных интегралов................210
15.	Единицы радиоактивности и дозы............................211
16.	Соотношения между некоторыми	единицами....................211
17.	Основные физические постоянные............................212
18.	Таблица тригонометрических функций .......................214
19.	Таблица показательных функций............................ 215
ПРЕДИСЛОВИЕ К СЕДЬМОМУ ИЗДАНИЮ
Данный сборник задач предназначен в основном для студентов, изучающих общий курс атомной и ядерной физики. Вместе с тем достаточно большое число задач, выходящих за рамки общего курса, позволяет использовать его и при изучении некоторых спецкурсов.
Сборник содержит свыше 1000 задач с довольно подробными указаниями для решения наиболее трудных из них. Для облегчения работы в начале каждого раздела помещен краткий обзор основных понятий и соотношений, необходимых для решения задач данного раздела. В конце сборника даны сводка основных физических констант, ряд справочных таблиц и графиков.
Все формулы по-прежнему даны в гауссовой системе. Исходные данные и числовые ответы приведены с учетом точности соответствующих величин и правил действий над приближенными числами.
В настоящем издании сборник несколько переработан и дополнен: заменены некоторые задачи на более интересные в физическом и методическом отношении, включен ряд новых задач (в связи с этим изменена нумерация задач в нескольких разделах), увеличено число ответов в буквенном виде, модернизирована таблица элементарных частиц и ДР-
Весьма признателен всем товарищам, которые сообщили свои замечания и тем самым способствовали улучшению сборника.
И. Иродов
ОБ ОБОЗНАЧЕНИЯХ
Векторы обозначены жирным прямым шрифтом (например, v, В); та же буква светлым шрифтом (и, В) означает модуль соответствующего вектора.
Средние значения величин отмечены скобками < >, например <Х>, <х>.
Терминами Л- и Ц-системы обозначены лабораторная система отсчета и система центра инерции соответственно. Все величины в Ц-системе помечены сверху значком ~ (тильда), например р, Е.
Энергия: Т — кинетическая, U — потенциальная, Е — полная. Вр — произведение индукции магнитного поля на радиус кривизны траектории частицы.
Волновые числа: спектроскопическое v = 1/Х, принятое в теории k = — 2л/Х, где к — длина волны.
Все операторы (кроме координат и функций, зависящих только от координат) отмечены сверху значком например А, рх.
1.	КВАНТОВАЯ ПРИРОДА ЭЛЕКТРОМАГНИТНОГО
ИЗЛУЧЕНИЯ
•Энергетическая светимость М теплового излучения:
М = ^си,	(1.1)
где с — скорость света; и — плотность энергии теплового излучения.
•	Формула Вина для спектральной плотности энергии теплового излучения и закон смещения Вина:
и(в = ы3/(ы г); ХтГ = 6,	(1.2)
где ы — частота излучения; Т — абсолютная температура; — наиболее вероятная длина волны в спектре u^; Ь — постоянная.
•	Закон Стефана—Больцмана:
М = а Г4,	(1.3)
где а — постоянная Стефана—Больцмана.
•	Формула Планка для спектральной плотности энергии:
Лш3 1
л2 с3 ^tv>>lkT— j ’	( • )
•	Коротковолновая граница тормозного рентгеновского спектра излучения:
Амин = eV,	(1.5)
или лми„ = 1,239/V, где Лмин — в им; V — в кВ.
•	Формула Эйнштейна для внешнего фотоэффекта:
Л<о = Л —1 2то2акс,	(1-6)
где А — работа выхода.
•	Соотношения между полной энергией Е, кинетической энергией Т и импульсом р релятивистской частицы с массой покоя т:
£2— /гс2 = т2?; рс = Д/г (Т + 2тс*).	(1.7)
•	Комптоновское смещение длины волны рассеянного фотона:
ДА. = кс (1 — cos #),	(1.8)
где Ас =- 2лй'тс — комптоновская длина волны частицы.
Тепловое излучение
1.1.	Воспользовавшись формулой Вина, показать, что:
а)	наиболее вероятная частота теплового излучения ®т схэ Т;
б)	энергетическая светимость М cv Г* (закон Стефана — Больцмана).
1.2.	Показать с помощью формулы Вина, что в спектре распределения теплового излучения по длинам волн:
а)	наиболее вероятная длина волны Zm cv 1/7";
б)	максимальная спектральная плотность энергии их макс сс Тъ.
1.3.	Начальная температура теплового излучения Т = 2000 К. На сколько кельвинов изменилась эта температура, если наиболее вероятная длина волны в его спектре увеличилась на ДА, = 0,25 мкм?
1.4.	Найти наиболее вероятную длину волны в спектре теплового излучения с энергетической светимостью М = 5,7 Вт/см2.
1.5.	Солнечный спектр достаточно близок к спектру абсолютно черного тела с наиболее вероятной длиной волны А,т = 0,48 мкм. Найти мощность теплового излучения Солнца. Оценить время, за которое его масса уменьшится на 1% (за счет теплового излучения). Масса Солнца 2,0-1030 кг, его радиус /? = 7,0-10® м.
1.6.	Имеются две полости 1 и 2 с малыми отверстиями одинакового радиуса г = 5,0 мм и абсолютно отражающими наружными поверхностями. Полости отверстиями обращены друг к другу, причем расстояние между этими отверстиями I = 100 мм. В полости 1 поддерживают температуру 7\ = 1250 К- Найти установившуюся температуру в полости 2. Иметь в виду, что абсолютно черное тело является косинусным излучателем.
1.7.	Зная, что давление теплового излучения р = и/3, где и — плотность энергии излучения, найти:
а)	давление теплового излучения во внутренних областях Солнца, где температура Т х 1,6-107 К;
б)	температуру полностью ионизированной водородной плазмы плотностью р = 0,10 г/см3, при которой давление излучения равно кинетическому давлению частиц плазмы (при высоких температурах вещества подчиняются уравнению состояния для идеальных газов).
1.8.	Медный шарик радиусом г = 10,0 мм с абсолютно черной поверхностью поместили в откачанный сосуд, температура стеиок которого поддерживается близкой к абсолютному нулю. Начальная температура шарика То = 300 К. Через сколько времени его температура уменьшится в п = 1,50 раза? Удельная теплоемкость меди с = 0,38 Дж/(г-К).
1.9.	Вин предложил следующую формулу для распределения энергии в спектре теплового излучения:
иш = Лю3е—а<°/7’, где а — 7,64-10~12 К*с.
Найти с помощью этой формулы при Т = 2000 К:
а)	наиболее вероятную частоту излучения;
б)	среднюю,частоту излучения.
1.10.	Воспользовавшись условием предыдущей задачи, иайти: а) наиболее вероятную длину волны излучения;
б)	среднюю длину волны излучения.
1.11.	Определить число собственных поперечных колебаний струны длиной I в интервале частот (ю, ю + da), если скорость распространения колебаний равна v. Предполагается, что колебания происходят в одной плоскости.
1.12.	Найти число собственных поперечных колебаний прямоугольной мембраны площадью S в интервале частот (<о, <о -f- da), если скорость распространения колебаний равна v.
7
1.13.	Показать, что в полости, имеющей форму прямоугольного параллелепипеда объемом V с абсолютно отражающими стенками, число собственных колебаний электромагнитного поля в интервале частот (<о, со + dco) равно dZw = (V/nV) ordw.
1.14.	Тепловое излучение, заполняющее некоторую полость, можно представить в виде совокупности осцилляторов — собственных колебаний с различными частотами. Найти при температуре Т среднюю энергию осциллятора с частотой ю и плотность энергии в интервале частот (ю, со + d<o), если предположить, что энергия е каждого осциллятора может иметь:
а)	любые значения (непрерывный спектр);
б)	только дискретные значения nha, где п — целое число.
Иметь в виду, что распределение осцилляторов по энергиям подчиняется закону Больцмана N (е) сс е—г/кт, а их распределение по частотам— формуле из предыдущей задачи.
1.15.	Получить приближенные выражения формулы Планка при to « и й(о » kT.
1.16.	Преобразовать формулу Планка к виду, соответствующему распределению:
а)	по линейным частотам;
б)	по длинам волн.
1.17.	Определить с помощью формулы Планка, во сколько раз возрастет спектральная интенсивность излучения с длиной волны X = = 0,60 мкм при увеличении температуры от 7\ = 2000 К до Т2 = = 2300 К.
1.18.	Вычислить с помощью формулы Планка мощность излучения единицы поверхности абсолютно черного тела в интервале длин волн, отличающихся не более чем на т] = 0,50% от наиболее вероятной длины волны при Т = 2000 К-
1.19.	Определить с помощью формулы Планка числовое значение постоянной Стефана — Больцмана.
1.20.	Найти с помощью формулы Планка среднее значение частоты со в спектре теплового изучения при Т = 2000 К.
1.21.	Определить с помощью формулы Планка температуру теплового излучения, средняя длина волны которого (X) = 2,67 мкм.
Корпускулярные свойства электромагнитного излучения
1.22.	Воспользовавшись формулой Планка, найти:
а)	число фотонов в 1 см3 в спектральных интервалах (ю, <о -(- do) и (X, X Ч" dX);
б)	полное число фотонов в 1 см3 при Т = 300 К.
1.23.	Вычислить с помощью формулы Планка при Т = 1000 К: а) наиболее вероятную энергию фотонов;
б)	среднюю энергию фотонов.
1.24.	Показать, что число фотонов теплового излучения, падающих в единицу времени на единичную площадку стенки полости, равно
пс/4, где с — скорость света; п — число фотонов в единице объема. Убедиться, что произведение этой величины на среднюю энергию фотона равно энергетической светимости М.
1.25.	Найти плотность потока фотонов на расстоянии г = = 1,0 м от точечного источника света мощностью Р = 1,0 Вт, если свет:
а)	моноэнергетический с длиной волны X = 0,50 мкм;
б)	содержит две спектральные линии с длинами волн Xj = 0,70 мкм и Х2 = 0,40 мкм, интенсивности которых относятся как 1:2 соответственно.
1.26.	Длины волн фотонов равны 0,50 мкм, 0,25 нм и 2,0 пм. Вычислить их импульсы в эВ/с, где с — скорость света.
1.27.	Найти длину волны фотона, импульс которого равен импульсу электрона с кинетической энергией Т = 0,30 МэВ.
1.28.	Показать с помощью корпускулярных представлений, что импульс, переносимый в единицу времени плоским потоком электромагнитного излучения мощностью Р, не зависит от спектрального состава этого излучения. Чему он равен?
1.29.	Лазер излучает в импульсе длительностью т = 0,13 мс узкий пучок света энергией Е = 10 Дж. Найти среднее за время т давление такого пучка света, если его сфокусировать в пятнышко диаметром d ~ 10 мкм на поверхности, перпендикулярной пучку, с коэффициентом отражения р = 0,50.
1.30.	Короткий импульс света энергией Е = 7,5 Дж падает узким пучком на зеркальную пластинку с коэффициентом отражения р = 0,60. Угол падения ft = 30°. Найти импульс, переданный пластинке.
1.31.	Найти с помощью корпускулярных представлений силу светового давления, которую оказывает плоский световой поток с интенсивностью I — 1,0 Вт/см2 на плоскую зеркальную поверхность, если угол падения ft = 30° и площадь освещаемой поверхности 5=10 см2.
1.32.	Плоский световой поток интенсивностью /, Вт/см2, освещает одну половину шара с зеркальной поверхностью. Радиус шара R. Найти с помощью корпускулярных представлений силу светового давления, испытываемую шаром.
1.33.	Световой поток интенсивностью /, Вт/см2, падает нормально на плоскую абсолютно матовую поверхность. Площадь освещаемой поверхности 5, коэффициент отражения — единица. Найти с помощью корпускулярных представлений силу светового давления.
1.34.	Над центром круглой абсолютно зеркальной пластинки радиусом R находится точечный источник света мощностью Р. Расстояние между источником и пластинкой I. Найти с помощью корпускулярных представлений силу светового давления, которую испытывает пластинка. Рассмотреть также случаи R < Ч и R I.
1.35.	Фотон испущен с поверхности звезды, масса которой М и радиус R, Считая, что фотон обладает массой с присущими ей гравитационными свойствами, найти относительное уменьшение его энергии на большом расстоянии от звезды. Вычислить гравитационное смещение длины волны АХ/Х излучения, испускаемого с поверхности:
а)	Солнца, у которого М = 2,0-1030 кг и R = 7,0-108 м;
9
б)	нейтронной звезды, масса которой равна массе Солнца, а средняя плотность превышает солнечную в 1,0-1014 раз.
1.36.	Найти длину волны коротковолновой границы сплошного рентгеновского спектра, если известно, что после увеличения напряжения на рентгеновской трубке в т) = 2,0 раза эта длина волны изменилась на АХ = 50 пм.
1.37.	Определить напряжение на рентгеновской трубке, если известно, что зеркальное отражение узкого пучка ее излучения от естественной грани монокристалла NaCl наблюдается при уменьшении угла скольжения вплоть до а = 4,1°. Соответствующее межплоскостное расстояние d = 281 пм.
1.38.	Вычислить скорость электронов, подлетающих к антикатоду рентгеновской трубки, если длина волны коротковолновой границы сплошного рентгеновского спектра Хмин = 157 пм.
1.39.	Найти наиболее вероятную длину волны тормозного рентгеновского излучения со спектральным распределением = А (<омакс — —ю), где А — постоянная; <омакс — граничная частота спектра. Напряжение на трубке V = 31 кВ.
1.40.	Вычислить с помощью таблиц приложения:
а)	длины волн красной границы фотоэффекта для Cs и Pt;
б)	максимальные скорости электронов, освобождаемых с поверхности цинка, серебра и никеля светом с длиной волны 0,270 мкм.
1.41.	Найти работу выхода с поверхности некоторого металла, если при поочередном освещении его электромагнитным излучением с длинами волн Aq = 0,35 мкм и Х2 = 0,54 мкм максимальные скорости фотоэлектронов отличаются в т) = 2,0 раза.
1.42.	Медный шарик, отдаленный от других тел, облучают электромагнитным излучением с длиной волны А = 0,200 мкм. До какого максимального потенциала зарядится шарик?
1.43.	При некотором максимальном значении задерживающей разности потенциалов фототок с поверхности лития, освещаемого электромагнитным излучением с длиной волны Ао, прекращается. Изменив длину волны излучения в п = 1,5 раза, установили, что для прекращения фототока необходимо увеличить задерживающую разность потенциалов в т) = 2,0 раза. Вычислить Ао.
1.44.	Найти максимальную кинетическую энергию фотоэлектронов, вырываемых с поверхности лития электромагнитным излучением, напряженность электрической составляющей которого меняется во времени по закону: Е — а (1 + cos «>/) cos ю01, где а — постоянная; ю = = 6,0- 10 14 с-1; ю0 = 3,60-1015 с-1.
1.45.	Электроды вакуумного фотоэлемента (один цезиевый, другой медный) замкнуты снаружи накоротко. Цезиевый электрод освещают моноэнергетическим электромагнитным излучением. Найти:
а)	длину волны излучения, при которой появится фототок;
б)	максимальную скорость фотоэлектронов, подлетающих к медному электроду, если длина волны излучения равна 0,220 мкм.
1.46.	Ток, возникающий в цепи вакуумного фотоэлемента при освещении цинкового электрода электромагнитным излучением с длиной волны 0,262 мкм, прекращается, когда внешняя задерживающая раз-10
ность потенциалов достигает значения Va = 1,5 В. Определить значение и полярность внешней контактной разности потенциалов данного фотоэлемента.
1.47.	Никелевый шарик, играющий роль внутреннего электрода сферического вакуумного фотоэлемента, освещают моноэнергети-ческимэлектромагнитным излучением различных длин волн (/—3). Полученные графики зависимости фототока от подаваемого напряжения V показаны на рис. 1.1. Найти с помощью этих графиков соответствую-
щие длины волн.
1.48. Фотон с длиной волны X = 17,0 пм вырывает из покоящегося атома электрон, энергия связи которого Е 69,3 кэВ. Найти импульс, переданный атому в результате этого
процесса, если электрон вылетел под прямым углом к направлению налетающего фотона.
1.49.	Воспользовавшись законами сохранения, показать, что свободный электрон не может поглотить фотон.
1.50.	Объяснить следующие особенности эффекта Комптона:
а)	необходимость использовать достаточно коротковолновое рентгеновское излучение для проверки формулы
комптоновского смещения;
б)	независимость величины смещения от рода вещества;
в)	наличие несмещенной компоненты в рассеянном излучении;
г)	увеличение интенсивности смещенной компоненты рассеянного излучения с уменьшением атомного номера вещества, а также с ростом угла рассеяния;
д)	уширение обеих компонент рассеянного излучения.
1.51.	Узкий пучок рентгеновского излучения с длиной волны X падает на рассеивающее вещество. Найти X, если длины волн смещенных составляющих излучения, рассеянного под углами = 60° и О2 = 120°, отличаются друг от друга в т] = 2,0 раза.
1.52.	Фотон с длиной волны Л. = 3,64 пм рассеялся на покоящемся свободном электроне так, что кинетическая энергия электрона отдачи составила т] = 25% от энергии налетевшего фотона. Найти:
а)	комптоновское смещение длины волны рассеянного фотона;
б)	угол Ф, под которым рассеялся фотон.
1.53.	Фотон с энергией Йсо рассеялся под углом д на покоящемся свободном электроне. Определить угол ср, под которым вылетел электрон отдачи (по отношению к направлению налетевшего фотона).
1.54.	Фотон с энергией Йсо = 0,46 МэВ рассеялся под углом 0 = = 120° на покоящемся свободном электроне. Найти:
а)	энергию рассеянного фотона;
б)	энергию, переданную электрону.
1.55.	Фотон с импульсом р = 60 кэВ/с (с — скорость света), испытав комптоновское рассеяние под углом ft = 120° на покоящемся свободном электроне, вырвал затем из атома молибдена электрон, энер-
гия связи которого £св = 20,0 кэВ. Найти кинетическую энергию фотоэлектронов.
1.56.	При облучении вещества рентгеновским излучением с длиной волны X обнаружено, что максимальная кинетическая энергия комптоновских электронов Тмакс = 0,44 МэВ. Определить X.
1.57.	Фотон испытал рассеяние на покоящемся свободном электроне. Найти импульс налетающего фотона, если энергия рассеянного фотона равна кинетической энергии электрона отдачи при угле 90° между направлениями их разлета.
1.58.	В результате столкновения фотона с покоящимся свободным электроном углы, под которыми рассеялся фотон и отлетел электрон отдачи, оказались одинаковыми и угол-между направлениями их движения 0 = 100°. Найти длину волны фотона до столкновения.
1.59.	Найти энергию налетающего фотона, если известно, что при рассеянии под углом 6 = 60° на покоящемся свободном электроне последний приобрел кинетическую энергию Т = 0,450 МэВ.
1.60.	Фотон с энергией Нш = 1,00 МэВ рассеялся на покоящемся свободном электроне. Найти кинетическую энергию электрона отдачи, если в результате рассеяния длина волны фотона изменилась на т) = = 25%.
1.61.	Фотон с энергией, превышающей энергию покоя электрона в т| = 1,5 раза, испытал лобовое столкновение с покоящимся свободным электроном, который находится в однородном магнитном поле. В результате электрон отдачи стал двигаться по окружности радиусом R = 2,9 см. Найти индукцию В магнитного поля.
1.62.	Фотон с энергией Нш испытал столкновение с электроном, который двигался ему навстречу. В результате столкновения направление движения фотона изменилось на противоположное, а его энергия осталась прежней. Найти скорость электрона до и после столкновения (v и v').
1.63.	При столкновении с релятивистским электроном фотон рассеялся на угол Ф = 60°, а электрон остановился. Найти:
а)	комптоновское смещение длины волны рассеянного фотона;
б)	кинетическую энергию электрона до столкновения, если энергия налетающего фотона составляет т] = 1,0 энергии покоя электрона.
2.	МОДЕЛЬ АТОМА РЕЗЕРФОРДА — БОРА
• Угол О, на который заряженная частица рассеивается кулоновским полем неподвижного ядра, определяется формулой:
tg (0/2) = q14!S/2bT,	(2.1)
гДе и ?2 — заряды взаимодействующих частиц; Т — кинетическая энергия налетающей частицы; b — прицельный параметр.
в В общем случае формула (2.1) будет справедлива и в Ц- системе, если в ней сделать замену 6 -*-0 и Т -*-Т, где 6 и Т — угол рассеяния и суммарная кинетическая энергия взаимодействующих частиц в Ц-системе,
f=1/2po2TH--=p2/2p, p = m1m2/(m1 + m2)-	(2-2)
12
Здесь р. — приведенная масса; потн — относительная скорость частиц; р — их импульс в Ц-снстеме.
• Векторная диаграмма импульсов для упругого рассеяния нерелятивистской частицы массой т на первоначально покоящейся частице массой М (рис. 2.1). Здесь ртн р'т — импульсы налетающей частицы до и после рассеяния; р’м — импульс частицы отдачи; О — центр окружности с радиусом, равным импульсу р частиц в Ц-системе. Точка О делит отрезок АС на две части в отношении АО : ОС = т : М. Угол О — угол рассеяния налетающей частицы в Ц-системе.
• Формула Резерфорда дл.я относительного числа частиц, рассеянных в.
Рис. 2.1
п
4
J
2
Серия
Паше на
JLU-----
Серия Бальмера
элементарном телесном угле dQ под углом О к первоначальному направлению их движения:
dN! I q} q„ \2 dQ
----=п 142----------------— ,	(2.3) N \ 4Т J sin4 (-0/2)
где п — число ядер фольги на единицу поверхности; Т — кинетическая энергия налетающих частиц;
dQ = sin OdOdcp.
Серия Лаймана
• Схема возникновения основных (рис. 2.2).
• Обобщенная формула Бальмера:
Ряс. 2.2
серий водородоподобных ионов
o) = RZ* — \ «12
1 \ пг J’
ре
2Л3
(2.4)

где <о — круговая частота перехода между состояниями с квантовыми числами «1 и л2; Z — заряд ядра (в единицах е); R — постоянная Ридберга; р — приведенная масса.
• Резонансная линия — линия, обусловленная переходом атомов из первого возбужденного состояния в основное.
Рассеяние частиц. Формула Резерфорда
2.1.	Исходя из томсоновской модели атома, определить;
а)	радиус атома водорода, энергия ионизации которого 13,6 эВ;
б)	частоту колебаний электрона, если радиус атома водорода равен г. При каком значении г длина волны испускаемого света равна 0,6 мкм?
2.2.	На какое минимальное расстояние приблизится а-частица с кинетической энергией Т = 40 кэВ (при лобовом соударении):
а)	к покоящемуся ядру атома свинца;
б)	к первоначально покоящемуся ядру 7Li?
13
2.3.	Вывести с помощью законов сохранения энергии и момента импульса формулу (2.1).
2.4.	а-Частица с импульсом 53 МэВ/c (с — скорость света) рассеялась под углом 60° в кулоновском поле неподвижного ядра атома урана. Найти прицельный параметр.
2.5.	а-Частица с кинетической энергией Т налетает с прицельным параметром 0,90-10-11 см на покоящееся ядро свинца. Найти:
а)	модуль приращения вектора импульса рассеянной а-частицы, если Т = 2,3 МэВ;
б)	при каком значении Т модуль приращения вектора импульса рассеянной а-частицы будет максимальным для данного прицельного параметра. Каков при этом угол рассеяния?
2.6.	Найти минимальное расстояние, на которое протон с кинетической энергией Т — 0,87 МэВ приблизится к покоящемуся ядру Hg при рассеянии на угол Ф = л/2. Сравнить это расстояние с соответствующим значением прицельного параметра.
2.7.	Нерелятивистская частица массой пг и кинетической энергией Т испытала упругое рассеяние на первоначально покоящемся ядре с массой М. Найти в Ц-системе импульс каждой частицы и их суммарную кинетическую энергию.
2.8.	Нерелятивистская частица массой /Hj и кинетической энергией Т испытала упругое лобовое соударение с первоначально покоящейся частицей массой ш2. Найти кинетическую энергию налетающей частицы после соударения.
2.9.	Найти максимальное значение угла рассеяния а-частицы на первоначально покоящемся дейтроне.
2.10.	Нерелятивистский дейтрон упруго рассеялся под углом О' на первоначально покоящемся ядре 4Не. Найти этот угол, если известно, что соответствующий угол в Ц-системе О = 45°.
2.11.	В результате упругого рассеяния протона с кинетической энергией Т = 13,0 кэВ в кулоновском поле покоящегося ядра 4Не последнее испытало отдачу под углом О' = 60° к направлению движения налетающего протона. Вычислить прицельный параметр.
2.12.	а-Частица с кинетической энергией Т = 5,0 кэВ упруго рассеялась в кулоновском поле покоящегося дейтрона. Найти прицельный параметр, соответствующий максимально возможному углу рассеяния а-частнцы в Л-системе.
2.13.	При рассеянии а-частицы с кинетической энергией Т = = 29 кэВ в кулоновском поле покоящегося ядра 6Li последнее испытало отдачу под углом Ф = 45° к направлению движения налетающей частицы. На какое минимальное расстояние сблизились обе частицы в процессе взаимодействия?
2.14.	Неподвижный шар радиусом /? облучают параллельным потоком частиц, радиус которых г. Считая столкновения частиц с шаром абсолютно упругими, найти:
а)	угол О отклонения частицы в зависимости от ее прицельного параметра Ь;
б)	относительную долю рассеянных частиц в интервале углов от
14
ф до Ф + d6, а также вероятность рассеяния частицы в переднюю полусферу (О < л/2).
2.15.	Получить из формулы (2.1) выражения для относительного числа а-частиц, рассеянных в интервале углов (0,0 + dO) и соответствующего сечения ядра.
2.16.	Узкий пучок протонов с кинетической энергией J 00 кэВ падает нормально на золотую фольгу толщиной 1,0 мг/см2. Протоны, рассеянные под углом 60°, регистрирует счетчик, круглое входное отверстие которого имеет площадь 1,0 см2, отстоит от рассеивающего участка фольги на расстоянии 10 см и ориентировано перпендикулярно к падающим на него протонам. Какая доля рассеянных протонов попадает в отверстие счетчика?
2.17.	Вычислить сечение ядра атома золота, отвечающее рассеянию протонов с кинетической энергией Т = 1,20 МэВ в интервале углов от $ = л/3 до л.
2.18.	а-Частицы с кинетической энергией Т = 1,70 МэВ рассеиваются кулоновским полем ядер атомов свинца. Определить дифференциальные сечения этих ядер da/dft и dald£l, отвечающие рассеянию на угол 0 = л/2.
2.19.	Дифференциальное сечение рассеяния а-частиц кулоновским полем неподвижного ядра do/dSl = 7,0- Ю-22 см2/ср для угла Фо =30°. Вычислить сечение рассеяния а-частиц в интервале углов Ф > Фо-
2.20.	Найти вероятность того, что а-частица с энергией Т = 3,0 МэВ при прохождении свинцовой фольги толщиной 1,5 мкм испытывает рассеяние в интервале углов:
а) 59—61°; б) 60—90°.
2.21.	Узкий пучок а-частиц с кинетической энергией Т = 1,00 МэВ падает нормально на золотую фольгу толщиной d — 1,0 мкм. Поток а-частиц / = 3,6-104 с-1. Найти число а-частиц, рассеянных фольгой в течение т = 10 мин под углами:
а)	в интервале 59—61°;
б)	превышающими Фо = 60°;
в)	меньшими Фо = (предполагается, что формула Резерфорда вблизи этого значения угла Фо справедлива).
2.22.	Узкий пучок протонов с кинетической энергией Т = 1,0 МэВ падает нормально на латунную фольгу толщиной pd = 1,5 мг/см2. Найти долю протонов, рассеивающихся на углы свыше Фо = 30°, если массовое отношение меди и цинка в фольге равно соответственно 7:3.
2.23.	Узкий пучок моноэнергетических а-частиц падает нормально на свинцовую фольгу толщиной 2,2 мг/см2. При этом т) = 1,6-10_3 — часть первоначального потока, рассеивающегося под углами Ф > 20°. Найти дифференциальное сечение dold£l ядра свинца, отвечающее углу рассеяния Фо = 60°.
Водородоподобные системы
2.24.	Оценить время, за которое электрон, движущийся вокруг ядра водорода по орбите радиусом 0,5-10-8 см, упал бы на ядро, если бы он терял энергию на излучение в соответствии с классической теорией:
15
dEldt = — (2 е2/ЗсЗ) а2, где a — ускорение электрона. Считать, что вектор а все время направлен к центру атома.
2.25.	Частица массой т движения по круговой орбите в центрально-симметричном потенциальном поле U= иг2/2. Найти с помощью воровского условия квантования разрешенные радиусы орбит и уровни энергии частицы.
2.26.	Считая ядро неподвижным, вычислить для атома водорода и ионов Не+ и Li+ + :
а)	радиусы первых двух боровских орбит и скорости электрона на них;
б)	кинетическую энергию электрона и его энергию связи в основном состоянии;
в)	первый потенциал возбуждения и длину волны резонансной линии.
2.27.	Показать, что частота фотона со, соответствующая переходу электрона между соседними орбитами водородоподобных ионов, удовлетворяет неравенству со,, > со > <о,1+1, где ып и соп+1 — частоты обращения электрона на этих орбитах. Убедиться, что со —> соп при п —> —► оо.
2.28.	В спектре некоторых водородоподобных ионов известны длины волн трех линий, принадлежащих к одной и той же серии: 99,2, 108,5 и 121,5 нм. Какие спектральные линии можно предсказать еще?
2.29.	Вычислить для атомарного водорода:
а)	длины волн первых трех спектральных линий серии Бальмера;
б)	минимальную разрешающую способность Х'бХ спектрального прибора, при которой можно разрешить первые N — 20 линий серии Бальмера.
г 2.30. В спектре испускания атомарного водорода известны длины волн двух линий серии Бальмера: 410,2 и 486,1 нм. К какой серии принадлежит спектральная линия, волновое число которой равно разности волновых чисел этих линий? Какова ее длина волны?
2.31.	Атомарный водород возбуждают на n-й энергетический уровень. Определить:
а)	длины волн испускаемых линий, если п = 4; к каким сериям принадлежат эти линии?
б)	сколько линий испускает водород, если п = 10?
2.32.	Какие линии содержит спектр поглощения атомарного водорода в диапазоне длин волн от 94,5 до 130,0 нм?
2.33.	Определить квантовое число п возбужденного состояния атома водорода, если известно, что при переходе в основное состояние атом излучил:
а)	фотон с длиной волны X = 97,25 нм;
б)	два фотона, с \ = 656,3 нм и Х2 = 121,6 нм.
2.34.	У какого водородоподобного иона разность длин волн головных линий серии Бальмера и Лаймана равна 59,3 нм?
2.35.	В спектре некоторых водородоподобных ионов длина волны третьей линии серии Бальмера равна 108,5 нм. Найти энергию связи электрона в основном состоянии этих ионов.
16
2.36.	Энергия связи электрона в атоме Не равна Ео = 24,6 эВ. Найти энергию, необходимую для удалению обоих электронов из этого атома.
2.37.	Вычислить скорость электронов, вырываемых электромагнитным излучением с длиной волны X = 18,0 нм из ионов Не+, находящихся в основном состоянии.
2.38.	Фотон, испущенный ионом Не+ при переходе из первого возбужденного состояния в основное, ионизирует атом Н, находящийся в основном состоянии. Найти скорость фотоэлектрона.
2.39.	С какой минимальной скоростью должен двигаться атом водорода, чтобы в результате неупругого лобового соударения с другим, покоящимся, атомом водорода один из них испустил фотон? До соударения оба атома находились в основном состоянии.
2.40.	Атом водорода, двигавшийся со скоростью и0 = 3,26 м/с, испустил фотон, соответствующий переходу из первого возбужденного состояния в основное. Найти угол ср между направлением вылета фотона и первоначальным направлением движения атома, если кинетическая энергия атома осталась прежней.
2.41.	Определить скорость, которую приобрел покоящийся атом водорода в результате излучения фотона при переходе из первого возбужденного состояния в основное. На сколько процентов отличается энергия испущенного фотона от энергии данного перехода?
2.42.	При наблюдении излучения пучка возбужденных атомов водорода под углом '0' = 45° к направлению их движения длина волны резонансной линии оказалась смещенной на ДА. = 0,20 нм. Найти ско-рось атомов водорода.
2.43.	С какой минимальной скоростью должны сближаться ион Не+ и атом водорода, чтобы испущенный ионом Не+ фотон, соответствующий головной линии серии Бальмера, смог возбудить атом водорода из основного состояния? Указание: использовать точную формулу доплеровского эффекта.
2.44.	Учитывая движение ядра атома водорода и боровское условие квантования, найти:
а)	возможные расстояния между электроном и ядром;
б)	энергию связи электрона;
в)	на сколько процентов отличаются энергия связи и постоянная Ридберга, полученные без учета движения ядра, от соответствующих уточненных значений этих величин.
2.45.	Вычислить отношение массы протона к массе электрона, если известно, что отношение постоянных Ридберга тяжелого и легкого водорода т] = 1,000272, а отношение масс ядер п = 2,00.
2.46.	Найти для легкого и тяжелого водорода разность:
а)	энергий связи электронов в основных состояниях;
б)	первых потенциалов возбуждения;
в)	длин волн резонансных линий.
2.47.	Вычислить для мезоатома водорода (в котором вместо электрона движется мезон, имеющий тот же заряд, но массу в 207 раз больше);
а)	расстояние между мезоном и ядром в основном состоянии;
б)	длину волны резонансной линии;
в)	энергии связи основных состояний мезоатомов водорода, ядра которых протон и дейтрон.
2.48.	Найти для позитрония (система из электрона и позитрона, вращающаяся вокруг центра инерции):
а)	расстояние между частицами в основном состоянии;
б)	ионизационный потенциал и первый потенциал возбуждения;
в)	постоянную Ридберга и длину волны резонансной линии.
3.	ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ
•	Соотношения де Бройля для энергии и импульса частицы:
Е = ha; р = hk,	(3.1)
где <о — частота дебройлевской волны: k = 2я/Х.
•	Соотношение неопределенностей:
Ах • Ар* > й.	(3.2)
•	Временное я стационарное уравнения Шредингера:
дЧ	h2	2т
ih —	V2’F + t/’F: У2ф +~— (E-U) ф = 0,	(3.3)
at	2m	h2
где Y — полная волновая функция; ф — ее координатная часть; у2 — оператор Лапласа; Е и U — полная и потенциальная энергия.
•	Со'бствеииые значения энергии и собственные функции частицы массой т в одномерном потенциальном поле U (х) = ‘х.з^/2 (гармонический осциллятор с частотой <о = Д/х/т):
(1 \	(]П
« + — ; фп(1)=ап(—1)"еЕ*/2——(е-Н,	(3.4)
где п = 0, 1, 2, ...; £ = ах; а = Д/та/h; ап — нормировочный коэффициент.
•	Коэффициент прозрачности D потенциального барьера U (х):
D ~ ехр
(3.5)
где Xj и х2 — координаты точек, между которыми U > Е.
Волны де Бройля. Соотношение неопределенностей
3.1.	Вычислить дебройлевскую длину волны электрона и протона, движущихся с кинетической энергией 1,00 кэВ. При каких значениях кинетической энергии их длина волны будет равна 100 пм?
3.2.	При увеличении энергии электрона на 200 эВ его дебройлев-ская длина волны изменилась в два раза. Найти первоначальную длину волны электрона.
3.3.	Найти длину волны молекул водорода, движущихся с наиболее вероятной скоростью в газе при температуре 0° С.
3.4.	Определить кинетическую энергию протона, длина волны которого такая же, как у а-частицы с Вр = 25 кГс-см, где В — магнитная индукция; р — радиус кривизны траектории.
18
3.5.	Какую дополнительную энергию необходимо сообщить электрону с импульсом 15,0 кэВ/с (с — скорость света), чтобы его длина волны стала равной 50 пм?
3.6.	Протон с длиной волны 1 = 1,7 пм упруго рассеялся под углом 90° на первоначально покоившейся частице, масса которой в п ~ = 4,0 раза больше массы протона. Определить длину волны рассеянного протона.
3.7.	Нейтрон с кинетической энергией Т = 0,25 эВ испытал упругое соударение с первоначально покоившимся ядром атома 4Не. Найти длины волн обеих частиц в их Ц-системе до и после соударения.
3.8.	Два атома, ХН и 4Не, движутся в одном направлении, причем дебройлевская длина волны каждого атома 1 = 60 пм. Найти длины волн обоих атомов в их Ц-системе.
3.9.	Релятивистская частица с массой покоя m имеет кинетическую энергию Т. Найти:
а)	дебройлевскую длину волны частицы;
б)	значения Т, при которых погрешность в длине волны, определяемой по нерелятивистской формуле, не превышает 1,0% для электрона и протона.
3.10.	Найти кинетическую энергию, при которой дебройлевская длина волны электрона равна его комптоновской длине волны.
3.11.	Вычислить длину волны релятивистских электронов, подлетающих к антикатоду рентгеновской трубки, если длина волны коротковолновой границы сплошного jjeH-тгеновского спектра равна 10,0 пм.
3.12.	Найти с помощью распределения Максвелла функцию распределения молекул газа цо дебройлевским длинам волн, а также наиболее вероятную длину ролны молекул водорода при Т = 300 К-
3.13.	Функция распределения атомоц по скоростям в пучке имеет вид: f (и) zr> и3 ехр (—и2), где и — отношение скорости атома в пучке к наиболее вероятной скорости ^ в источнике (fm=V2AT/m). Найти функцию распределения по дебройлевским длинам волн. Вычислить наиболее вероятную длину волны в пучке атомов гелия при температуре источника 300 К.
3.14.	Поток моноэнергетических электронов падает нормально на диафрагму с узкой щелью шириной b — 2,0 мкм. Найти скорость электронов, если на экране, отстоящем от щели на I = 50 см, ширина центрального дифракционного максимума Ах = 0,36 мм.
3.15.	Найти кинетическую энергию электронов, падающих нормально на диафрагму с двумя узкими щелями, если на экране, отстоящем от диафрагмы на I = 75 см, расстояние между соседними максимумами Ах = 7,5 мкм. Расстояние между щелями d = 25 мкм.
3.16.	Узкий пучок моноэнергетических электронов падает под углом скольжения О' = 30° на естественную грань монокристалла алюминия. Расстояние между соседними кристаллическими плоскостями, параллельными этой грани монокристалла, d = 0,20 нм. При некотором ускоряющем напряжении Vo наблюдали максимум зеркального отражения. Найти Vo, если известно, что следующий максимум зеркального отражения возникал при увеличении ускоряющего напряжения Vo в т] — 2,25 раза.
19
3.17.	Пучок электронов с кинетической энергией Т = 180 эВ падает нормально на поверхность монокристалла никеля. В направлении, составляющем угол а = 55° с нормалью к поверхности, наблюдается максимум отражения четвертого порядка. Найти межплоскостное расстояние, соответствующее этому отражению.
3.18.	Пучок электронов с кинетической энергией Т = 10 кэВ проходит через тонкую поликристаллическую фольгу и образует систему дифракционных колец на экране, отстоящем от фольги на I = 10,0 см. Найти межплоскостное расстояние, для которого максимум отражения третьего порядка соответствует кольцу с радиусом г = 1,6 см.
Рнс. 3.1
3.19.	Пучок электронов, ускоренных разностью потенциалов V, падает на поверхность никеля, внутренний потенциал которого V,= — 14 В. Вычислить:
а)	показатель преломления никеля при V = 150 В;
б)	отношение VIVit при котором показатель преломления отличается от единицы не более чем на 1,0%.
3.20.	Частица массой пг движется в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы I. Найти значения энергии частицы, имея в виду, что возможны лишь такие состояния, для которых в яме укладывается целое число деброй-левских полуволн.
3.21.	Интерпретировать квантовые условия Бора на основе волновых представлений: показать, что стационарным боровским орбитам соответствует целое число дебройлевских волн. Найти длину волны электрона на n-й орбите.
3.22.	Показать, что измерение х-координат частиц с помощью узкой щели шириной b вносит неопределенность в их импульсы Дрх, такую, что &рх> h.
3.23.	Убедиться, что измерение х-координаты частицы с помощью микроскопа (рис. 3.1) вносит неопределенность в ее импульс Дрх, такую, что &х-крх > h. Иметь в виду, что разрешение микроскопа d = X/sin Ф, где X — длина волны используемого света.
3.24.	Плоский поток частиц падает нормально на диафрагму с двумя узкими щелями, образуя на экране дифракционную картину (рис. 3.2). Показать, что попытка определить, через какую щель прошла та или иная частица (например, с помощью введения индикатора И) 20
приводит к разрушению дифракционной картины. Для простоты считать углы дифракции малыми.
3.25.	Оценить наименьшие погрешности, с которыми можно определить скорость электрона, протона и атома урана, локализованных в области размером 1 мкм.
3.26.	Оценить неопределенность скорости электрона в атоме водорода, полагая размер атома порядка 10~8 см. Сравнить полученное значение со скоростью электрона на первой боровской орбите.
3.27.	Оценить минимальную кинетическую энергию электрона, локализованного в области размером I ~= 0,10 нм.
3.28.	Электрон с кинетической энергией Т = 10 эВ локализован в области размером / = 1,0 мкм. Оценить относительную неопределенность скорости электрона.
3.29.	Частица находится в одномерном потенциальном ящике размером / с бесконечно высокими стенками. Оценить силу давления частицы на стенки ящика при минимально возможном значении ее энергий р ь м и н •
3.30.	Частица массой пг движется в одномерном потенциальном поле U (х) = хх2/2 (гармонический осциллятор с частотой <о = Vx/m). Оценить минимально возможную энергию этой частицы.
3.31.	Исходя из соотношения неопределенностей, оценить энергию связи электрона в основном состоянии атома водорода и соответствующее расстояние электрона от ядра.
3.32.	Оценить минимально возможную энергию электронов в атоме Не и соответствующее расстояние электронов от ядра.
3.33.	Свободно движущаяся нерелятивистская частица имеет относительную неопределенность кинетической энергии порядка 1,6* 10-4. Оценить, во сколько раз неопределенность координаты такой частицы больше ее дебройлевской длины волны.
3.34.	Свободный электрон в начальный момент был локализован в области размером I = 10-8 см. Оценить промежуток времени, за который ширина соответствующего волнового пакета увеличится в т] = = 102 раз.
3.35.	Параллельный пучок атомов водорода со скоростью v — — 1,2 км/с падает нормально на диафрагму с узкой щелью, за которой на расстоянии I = 1,0 м расположен экран. Исходя из соотношения неопределенностей, оценить ширину щели, при которой эффективная ширина изображения на экране будет минимальной.
Уравнение Шредингера. Прохождение частицы через барьер
3.36.	Какие решения временного уравнения Шредингера называются стационарными? Показать, что такие решения получаются в том случае, когда U не зависит от времени явно.
3.37.	Как изменится полная волновая функция Y (х, /), описывающая стационарные состояния, если изменить начало отсчета потенциальной энергии на некоторую величину ДО?
21
3.38.	Найти решение временного уравнения Шредингера для свободной частицы, движущейся с импульсом р в положительном направлении оси х.
3.39.	Показать, что энергия свободно движущейся частицы может иметь любые значения.
3.40.	Частица массой т находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Координата х частицы может меняться в пределах от 0 до /, где / — ширина ямы. Показать, что собственные значения энергии частицы и ее нормированные собственные функции имеют вид:
Еп = (я№2тЕ)пг; фп(х) = 1/277 sin (ллх/7), где п = 1,2,...
3.41.	Воспользовавшись условием предыдущей задачи, найти: а) вероятность пребывания частицы с наименьшей энергией в области */3 I < х < 2/ 31;
б)	число энергетических уровней в интервале (Е, Е + dE), если ширина ямы такова, что энергетические уровни расположены весьма густо.
3.42.	Частица массой т находится в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками. Координаты х, у частицы меняются в пределах 0 < х < а, 0 < у < Ь, где а и b — стороны ямы. Определить:
а)	собственные значения энергии и нормированные собственные функции частицы;
б)	вероятность нахождения частицы с наименьшей энергией в области 0 < х < а/3, 0 < у < 6/3;
в)	значения энергии частицы для первых четырех уровней, если яма квадратная со стороной I.
3.43.	Воспользовавшись условием и решением предыдущей задачи, найти число состояний частицы в интервале (£, Е + dE), если размеры ямы а н Ь таковы, что энергетические уровни расположены весьма густо.
3.44.	Частица массой т находится в трехмерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Взяв начало координат в вершине одного из углов ямы, найти:
а)	собственные значения энергии частицы, если стороны ямы равны а, Ь и с;
б)	разность энергий третьего и четвертого уровней;
в)	число состояний, соответствующее шестому уровню, если яма кубическая.
3.45.	Воспользовавшись условием предыдущей задачи и результатом решения пункта а), найти плотность уровней dNIdE, т. е. число уровней на единичный интервал энергии, в зависимости от Е.
3.46.	Показать, что в точке, где потенциальная энергия частицы > U (х) имеет конечный разрыв, волновая функция остается гладкой, т. е. ее первая производная по координате непрерывна.
3.47.	Частица массой т находится в одномерном потенциальном поле U (х), показанном на рис. 3.3, где U (0) = со. Найти:
22
а)	уравнение, определяющеё возможные значения энергии частицы в области Е < Uo; привести его к виду
sin kl = ± kl Vh2/2ml2 Uo , k = У2тЁЩ.
Показать с помощью графического решения этого уравнения, что возможные значения энергии частицы образуют дискретный спектр;
б)	минимальные значения величины PU0, при которых появляются первый и n-й дискретные уровни. Сколько уровней содержит яма, у которой l2U9 = IbtPirn?
3.48.	В предыдущей задаче энергия единственного уровня Е = = Uo!2. Воспользовавшись решением этой задачи, определить:
а)	значение PU0 у такой ямы;
б)	наиболее вероятное значение координаты частицы, изобразить примерный график зависимости ф2 (х);
в)	вероятность нахождения частицы в области х> I.
3.49.	Частица массой т находится в одномерном симметричном потенциальном поле (рис. 3.4). Найти уравнение, определяющее возможные значения энергии частицы в области Е < Uo. Привести его к виду
kl = пл — 2 arcsin (hkll/2mU0), k = ~V'2mE!h, где п — целое число. Показать с помощью графического решения этого уравнения, что возможные значения энергии частицы дискретны.
3.50.	Воспользовавшись решением предыдущей задачи, найти значение l2U0, при котором:
а)	энергия основного состояния частицы Е = UOI2\
б)	появляется второй уровень, n-й уровень. Сколько дискретных уровней содержит данная яма, если PU0 = 75ft2/m?.
3.51.	Частица массой т находится в некотором одномерном потенциальном поле U (х) в стационарном состоянии, для которого волновая функция имеет вид: ф (х) = А ехр (—ах2), где А и а— заданные постоянные. Имея в виду, что U (х) = 0 при х = 0, найти U (х) и энергию Е частицы.
3.52.	То же, что в предыдущей задаче, ноф (х) = 4хе-ах при х > 0, ф = 0 при х < 0 и U (х)	0 при х оо.
3.53.	Найти с помощью уравнения Шредингера энергию гармонического осциллятора с частотой <о в стационарном состоянии:
23
a)	ф (x) = A exp (— a2x2);
6)	ф (x) = Bx exp (—a2x2), где А, В и a — постоянные.
3.54.	Уравнение Шредингера для гармонического осциллятора с частотой <о может быть приведено к виду ф£ + (X — £z) ф = О, где Е = ах; а — постоянная; X — параметр. Имея ввиду, что еобствеввые значения параметра X равны 2n + 1, где п = 0, 1,2, ..., найти собственные значения энергии осциллятора.
3.55.	Воспользовавшись формулой, приведенной во введении к данной главе, найти для первых трех уровней осциллятора с массой т и частотой со:
а)	собственные функции И их нормировочные коэффициенты;
Рис. 3.5
Рис. 3.6
б)	наиболее вероятные значения колебательной координаты х. Изобразить примерные графики распределения плотности вероятности различных значений х в этих состояниях.
3.56.	Частица находится в основном состоянии в одномерном потенциальном поле U (х) со х2. Какова вероятность пребывания ее вне классических границ поля?
3.57.	Зная собственные функции и собственные значения энергии гармонического осциллятора, найти собственные значения энергии частицы с массой т, движущейся в одномерном потенциальном поле U (х) = хх2/2 при х >> 0 и U = оо при х 0.
3.58.	Частица массой т движется в трехмерном потенциальном поле U (х, у, г) = Ч2 х (х2 + у2 + z2), где х — коэффициент квазиупру-гой силы. Определить:
а)	собственные значения энергии частицы;
б)	кратность вырождения n-го энергетического уровня.
Указание: воспользоваться формулами для одномерного осциллятора.
3.59.	Частица массой т и энергией Е падает слева на прямоугольный потенциальный барьер (рис. 3.5). Найти:
а)	коэффициент отражения R и коэффициент прозрачности D этого барьера для случая Е > Uo. Убедиться, что значения этих коэффициентов не зависят от направления падающих частиц;
б)	коэффициент отражения R, если Е < Uo. Определить для этого случая эффективную глубину проникновения частиц под барьер Хдф — расстояние от границы барьера до точки, в которой плотность вероятности нахождения частицы уменьшается в е раз. Вычислить хэф для электрона, если Uo — £ == 1,0 эВ.
24
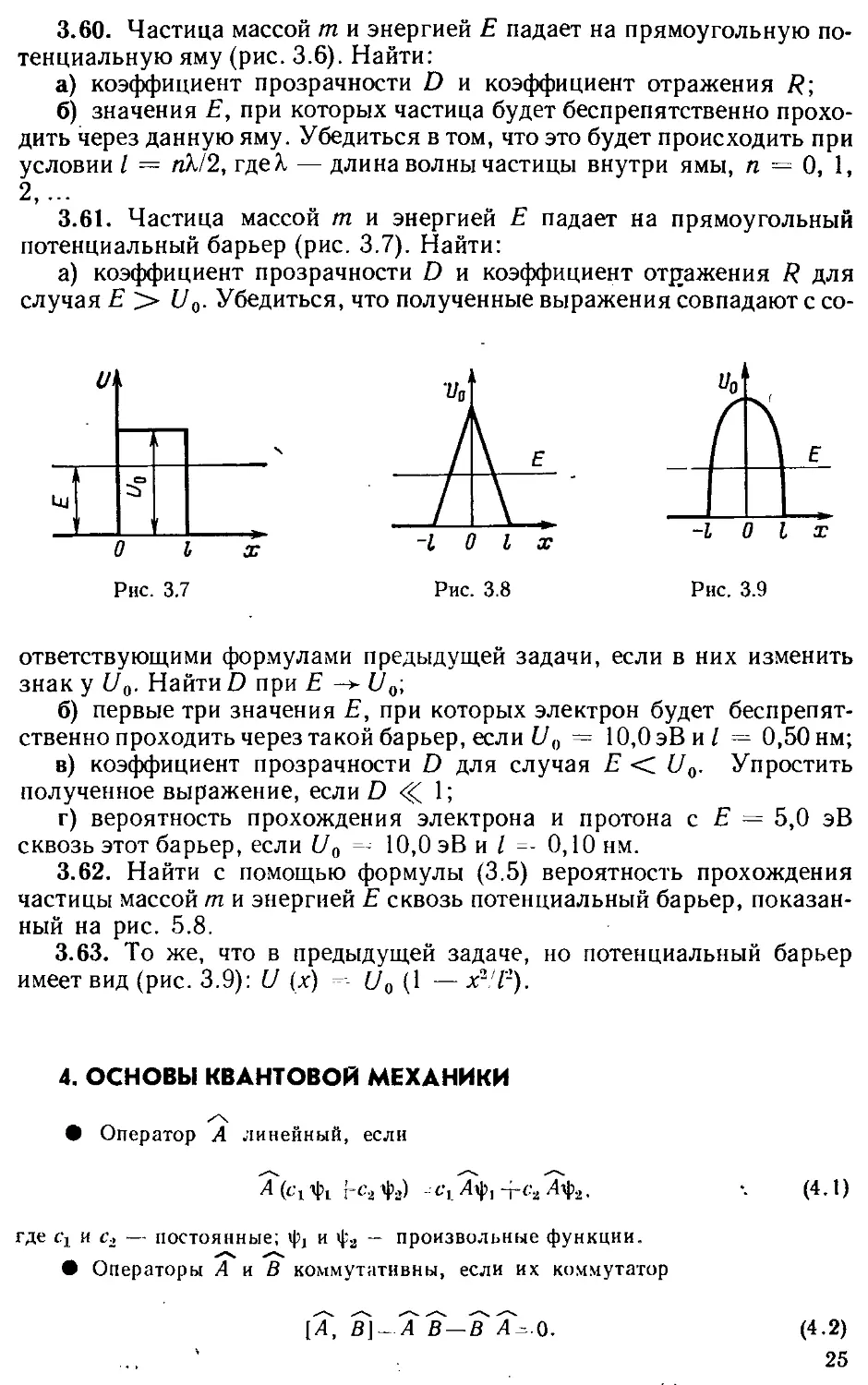
3.60.	Частица массой т. и энергией Е падает на прямоугольную потенциальную яму (рис. 3.6). Найти:
а)	коэффициент прозрачности D и коэффициент отражения
б)	значения Е, при которых частица будет беспрепятственно проходить через данную яму. Убедиться в том, что это будет происходить при условии I = пК/2, где! — длина волны частицы внутри ямы, п = 0, 1, 2, ...
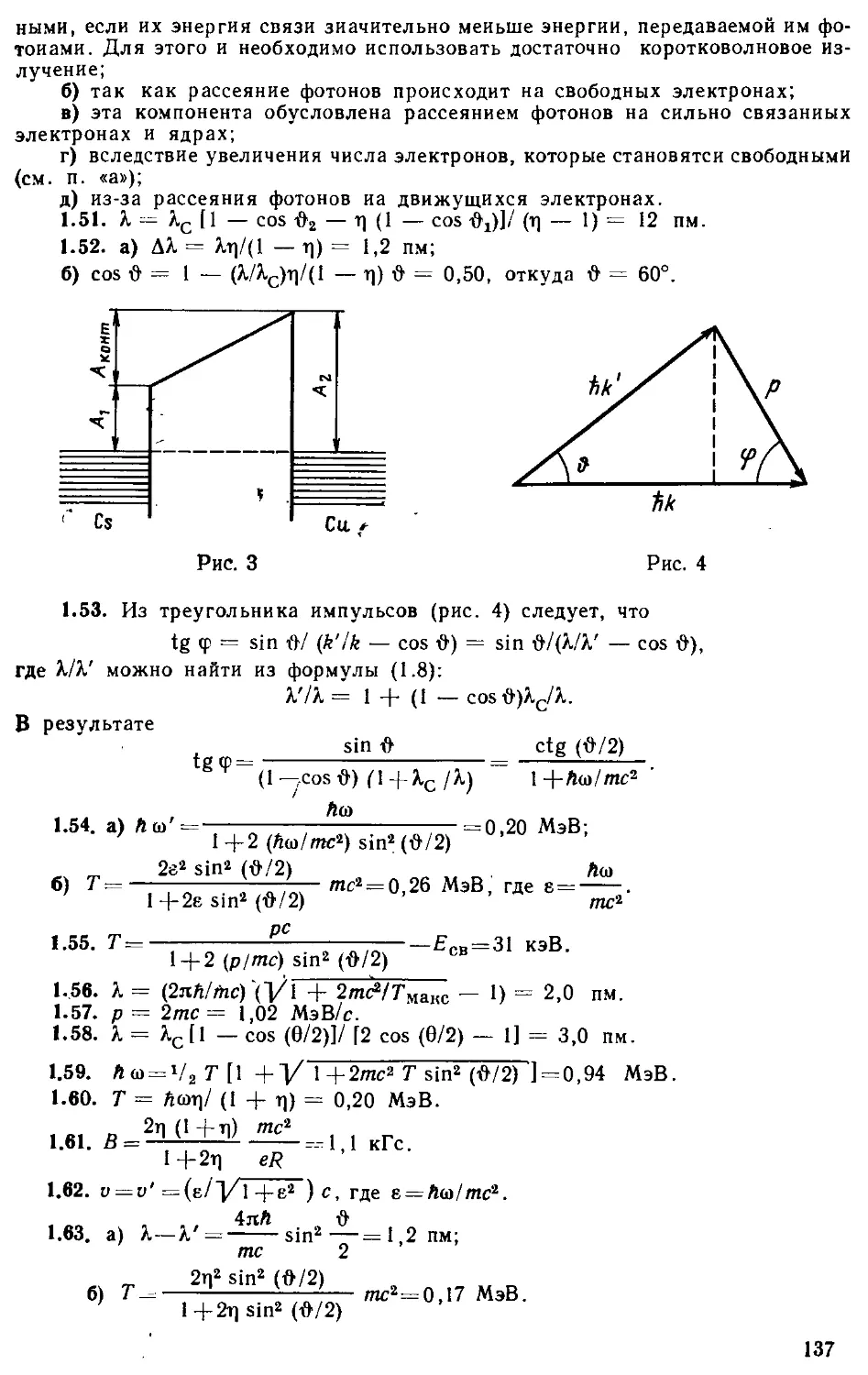
3.61.	Частица массой т и энергией Е падает на прямоугольный потенциальный барьер (рис. 3.7). Найти:
а)	коэффициент прозрачности D и коэффициент отражения R для случая Е > Uo. Убедиться, что полученные выражения совпадают с со-
ответствующими формулами предыдущей задачи, если в них изменить знак у Uo. Найти D при Е -> !/0;
б)	первые три значения Е, при которых электрон будет беспрепятственно проходить через такой барьер, если U() = 10,0эВи/ = 0,50нм;
в)	коэффициент прозрачности D для случая Е < Uo. Упростить полученное выражение, если!) < 1;
г)	вероятность прохождения электрона и протона с Е = 5,0 эВ сквозь этот барьер, если Uo 10,0 эВ и I =- 0,10 нм.
3.62.	Найти с помощью формулы (3.5) вероятность прохождения частицы массой т и энергией Е сквозь потенциальный барьер, показанный на рис. 5.8.
3.63.	То же, что в предыдущей задаче, но потенциальный барьер имеет вид (рис. 3.9): U (х) --- Uo (1 — x2/f).
4. ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
• Оператор А линейный, если
A гс2ф2) с, Лф,4-с2Дф2.
(4.1)
где fj и с., — постоянные; ф, и ф2 — произвольные функции.
• Операторы А и В коммутативны, если их коммутатор
[X S] — А~ 'В— В Д-=0.
(4-2)
25
• Оператор А эрмитов (самосопряженный), если
Уф* A ф1</х = |ф1Л*ф{ dx,	(4.3)
где ih и ф3 — произвольные функции.
•	Разложение фуиуции ф по собственным функциям фп дискретного спектра некоторого оператора:
ф (х) = 2сп фп (х); сп = J фф^ dx.	(4.4)
(4-6)
•	Среднее значение механической величины А в состоянии ф:
(Д) = |ф*Дф5т,	(4.5)
где А — соответствующий оператор; ф — нормированная волновая функция; dx — элемент объема.
•	Уравнение Шредингера в операторной форме:
ift — = НЧ, dt
где Н — оператор полной энергии (гамильтониан).
•	Производная по времени от оператора А:
dA	dA	i —.
+VIя- л1-
dt	dt	ft
(4-7)
где [И, Д] — коммутатор операторов; Н — гамильтониан.
•	Основные квантовомехаинческие операторы:
проекции и квадрат импульса рх = —ift	р = р* + р* +
dx	* я
полная энергия (гамильтониан) И — -£— + U = — V1 +
проекция момента импульса Lx — ypz — zpg, Lg — zpx — xpz; 'Lz xpg —"yPx —iA
квадрат момента импульса L? = L* + L* + L* = — Здесь Vs — оператор Лапласа, его вид в сферических координатах: дг	2	д ।
V» —------4-------к 1 VI '
dr*	г dr	г*
1 й ( . „ 3 \	1	3*
*•* sin О 50 \	50 )‘зт*3 5<р*
где — угловаи часть оператора Лапласа.
• Собственные значения н собственные функции оператора L*: 1(1+ 1)Л’, Г- 0, 1,2, ...;
>rZm(0. ф)===e,|m|Weim’ m=o- ±2.............±Z-
(4.8)
(4.9)
Функции О (О) для S-, р- и //-состояний приведены в табл. 4.1 (с точностью до нормировочного множителя).
• Уравнение Шредингера для радиальной части волновой функции R (г) в центрально-симметричном потенциальном поле U (г):
d*R	2 dR , 2m t	„ L* \
-----+-------------I E—U—--------Iff—0.
dt*	r dr h' \ 2mr* I
(4.Ю)
26
Таблица 4.2
Таблица 4.1
Состояние	1. т	в/(т| <♦»	Состояние	n, I	К (P). P=r/rt
S	0,0	1	Is	1,0	e^p
	1,0	cos 0	2s	2,0	(2—p)e-P/2
р 1	1.1	sin 0	2p	2,1	ре"*/2
	2,0	Зсов10—1	3s	3,0	(21—81р+2р»)е-“/3
d	2,1	sin 0 cos 0	3p	3,1	p (6—p) еГ&3
	2,2	sin10	34	3,2	p»e-0/3
Функции R (г) для водородоподобных атомов приведены в табл. 4.2 (с точностью до нормировочного множителя); здесь i\ — первый боровский радиус.
Квантовомеханмческме операторы
4.1. Проверить следующие операторные равенства: а)77х=1 + х“
е, л
ах
d dx _ч л а 1	d	«
б) х2----X-----— 1;
dx х	dx
)(1 + ^гУ=1+2^+ТГ; \ dx )	dx dx*
г)	(х-ь =Х + ^^2х-Т- + -?Т-\ dx /	dx dx*
. I 1	d	\«	d*	. 2	d
д)	I—т~ x = -7-^-----T“:
\ x	dx	J	dx* x	dx
e)	p.+_2.у__г_+2
\ dx dy J dx* dxdy dy* d* I'd \2
4.2.	Найти результат действия операторов — хг и I х I на функции:
a) cos х и б) е1.
4.3.	Найти собственное значение оператора А, принадлежащее собственной функции фд, если:
d* а) А =;----, фд = sin 2х;
dx*
б)	— -^— + xt, фд = ехр(—х2/2);
dx*
ч V d* . 2 d . sin ах в)Я=——-J-----—, фд~---------.
dx* х dx	х
27
4.4.	Найти собственные функции ф и собственные значения следующих операторов:
а)	— i , если ф (х) = ф (х + а), а — постоянная;
б)	—	, если ф = 0 при х = 0 и /.
4.5.	Показать, что если операторы А и В линейные, то операторы А + В и АВ также линейные.
4.6.	Доказать следующие коммутационные соотношения:
а)	14, £BJ = £[4, Д];^
б)	(aJIC] = [4, В]С + В[А, С].
4.7.	Доказать, что если операторы 4 и В коммутируют, то:
а)	(4 + В)2 = 42 + 24В + В2; (4 + В) (4 — В) = 42 — В2;
б)	1(4 + В), (4^— В)Ь= 0.
4.8.	Оператор 42 = ^Af. Доказать, что если операторы 4; коммутируют с оператором В, то с ним коммутирует и оператор 42.
4.9.	Доказать, что если коммутатор [4, В] = 1, то:
а) [4, В2] = 2В; б) [4, В3] = ЗВ2; в) [42, В2] = 2 (4В + В4).
4.10.	Проверить следующие равенства для коммутаторов:
а)	[х, рж1 = 1Й, [х, ру] = 0, [/?ж, ру] = 0;
б)	]f(x), рх]=--	[/(*)	р.¥ + й2
дх	дх .	дх2
В) [X2, [х, р2]] = — 4й2х.
Здесь / (х) — произвольная функция координаты.
4.11.	Проверить следующие правила коммутации для гамильтониа-
на Н в потенциальном поле U (х):
а)	[Н, х] ---— рх',
т
б)	[И, рх] = 1/1
дх 9
\ г ”**^*21 n't dU . .л д2 U
в)	Я, = 21Й—- Рх+ й -г-;-.
дх	дх2
4.12.	Оператор 4 коммутирует с операторами В и С. Можно ли отсюда заключить, что операторы В и С коммутативны?
4.13.	Доказать следующие теоремы?
а)	если операторы 4 и В имеют собственные функции, то такие операторы коммутируют;
б)	если операторы 4 и В коммутируют, то они имеют общие собственные функции (доказательство провести для случая, когда вырождение отсутствует).
28
4.14.	Найти общую собственную функцию операторов:
а) х и ри; б) рх, ру и /?2; в) рх и р2.
4.15.	В некотором состоянии фд система имеет определенное значение механической величины А. Имеет ли в этом состоянии определенное значение также и величина В, если соответствующие им операторы А и В коммутативны?
4.16.	Доказать, что если оператор А эрмитов, то его собственные значения вещественны.
4.17.	Доказать эрмитовость следующих операторов:
а) /?д.; б) х рх, в) р2х, г) И.
Указание: иметь в виду, что на бесконечности волновые функции и их производные обращаются в нуль.
4.18.	Найти оператор, сопряженный с оператором:
а) хрх; б) ipx.
4.19.	Доказать, чтоесли операторы А и Вэрмитовы и коммутирующие, то оператор АВ — эрмитов.
4.20	Доказать, что если оператор А эрмитов, то и оператор Л" также эрмитов (п — целое, положительное).
4.21.	Доказать, что если операторы А и В эрмитовы, то и операторы А В и АВ -т ВА также эрмитовы.
4.22.	Доказать, что если операторы А и В эрмитовы и некоммутирующие, то оператор:
а) [А, В] не эрмитов; б) i [А, В] — эрмитов.
4.23.	Найти собственные значения и нормированные собственные функции операторов:
а) Д; б) L2.
4.24.	Найти собственное значение оператора L2, соответствующее его собственной функции У (ft, ср) = A (cos ft-i 2 sin ft cos q).
4.25.	Доказать, что оператор Lz эрмитов. Доказательство провести ; а) в полярных и б) в декартовых координатах.
4.26.	Доказать эрмитовость оператора L2, имея в виду, что операторы Lx, Ly и Lz эрмитовы.
4.27.	Проверить следующие правила коммутации:
а) [х, Lx] = 0; б) \у, Вх] = — iftz; в) [z, Lx] = ihy.
4.28.	Доказать следующие правила коммутации:
а) 1Д,	= 0; б) [Ах, Pu] = ift/?.; в) [L.v, pz] = —\hpv.
4.29.	С помощью правил коммутации, приведенных в предыдущей задаче, показать, что:
а) Их, pH = 0; б) [Lx, Pl = 0; в) [L2, ?] = 0.
29
4.30.	Доказать, что оператор U коммутирует с оператором кинетической энергии Т.
4.31.	Проверить следующие правила коммутации:
a) ILX, Ly]= ih Lx; 6) Lx] =ih Lx; в) [L2, Lx] ih Ty.
4.32.	С помощью правил коммутации, приведенных в предыдущей задаче, показать, что:
а)	оператор L2 коммутирует с операторами Lx, Ly и Z2;
б)	|£+, £_] =2ft Lz, где L+ = Lx +i Ly и L_ = Lx —i £„.
4.33.	Модель пространственного ротора — это частица с массой р, движущаяся все время на одном и том же расстоянии г0 от центра. Найти собственные значения энергии такого ротатора, считая известными собственные значения оператора L1.
Средние значения и вероятности
4.34.	Доказать, что если механическая величина А описывается эрмитовым оператором Л, то:
а)	ее среднее значение вещественно;
б)	среднее значение квадрата этой величины <Л2> = j|Aip|2dx.
4.35.	Показать для одномерного случая, что
<р»>=-^-	—Ф*-^-)</х.
2 J \ ах	ах /
4.36.	Доказать, что в стационарном состоянии дискретного спектра среднее значение проекции импульса частицы равно нулю. Указание: воспользоваться выражением оператора рх через коммутатор операторов И и х.
4.37.	Найти среднюю кинетическую энергию частицы в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками (0 < х < [), если частица находится в состоянии:
а) ip (х) Л sin 2 (лх/7); б) ip (х) = Лх (/ — х).
4.38.	Вычислить средние значения кинетической и потенциальной энергий осциллятора е частотой <о в основном состоянии ip (х) — = Л ехр(—а2х2), где а2 -- х/2йю, х — коэффициент квазиупругой силы (I/ = хх2/2).
4.39.	Вычислить средние значения <(Ах)2> и <(Арх)2> и их произведение:
а)	для частицы, находящейся в n-м уровне в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками (О < х < /);
б)	в основном состоянии осциллятора, ip (х) = Л ехр (— а2х2);
в)	для частицы в состоянии ip (х) = Л exp (ikx — а2х2).
4.40.	Определить среднее значение механической величины, описываемой оператором L%, в состоянии ip (<р) = Л sin2<p.
30
4.41.	Вычислить средние значения <(Л<р)3> и <(Л£Х)2> и их произведение для системы, находящейся в состоянии ф (ф) = A sin <р.
4.42.	Показать, что в состоянии ф, где оператор £. имеет определенное собственное значение, средние значения <£ж> и (Lv) равны нулю. Указание: воспользоваться коммутационными соотношениями из задачи 4.31.
4.43.	Вычислить среднее значение квадрата момента импульса в состоянии ф (ft, ср) = A sin ft cos ф.
4.44.	Возможные значения проекции момента импульса на произвольную ось равны nth, где т = 1,1 — 1, ..., — I. Имея в виду, что эти проекции равновероятны и оси равноправны, показать: в состоянии с определенным значением I среднее значение квадрата момента импульса <£2> = h2l (I + 1).
4.55.	Доказать, что собственные функции % и ф2 эрмитова оператора А, принадлежащие различным собственным значениям и А, дискретного спектра, ортогональны.
4.46.	Непосредственным вычислением убедиться в ортогональности собственных функций:
а)	оператора Н для частицы в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками;
б)	оператора Lz.
4А1. Система находится в состоянии, описываемом нормированной волновой функцией ф (х), которую можно разложить по собственным функциям эрмитова оператора Л, т. е.
ф (х) —	(х). Считая функции фл нормированными на единицу:
а)	получить выражение, определяющее коэффициенты
б)	показать, что среднее значение механической величины <Л> = — 2Лл|сл|2, где Ak — собственные значения оператора А. Каков физический смысл |cft|2?
4.48.	В одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками (0 < х < 1) находится частица в состоянии ф (х). Определить вероятность ее пребывания:
а)	в основном состоянии, если ф (х) = A sin2 (лх/1);
б)	на п-м уровне, если ф (х) = Ах (I — х). Вычислить значения вероятности для первых трех уровней.
4.49.	Определить возможные собственные значения оператора Lz и их вероятности для системы, находящейся в состоянии:
а) ф (ф) Л зт2ф; б) ф (ф) = Л (1 + cos ф)2.
4.50.	Имея в виду, что собственные функции оператора волнового числа k (k p/h) есть фл (х) —• (2л)-1/2 eikx, найти распределение вероятностей различных значений волнового числа k:
а)	для частицы на га-м уровне в одномерной прямоугольной потенциальной яме шириной I с абсолютно непроницаемыми стенками;
б)	для осциллятора в состоянии ф (х) — А ехр (— а2х2).
31
Изменение во времени состояния и механических величин
4.51.	Выяснить, является ли волновая функция, представляющая собой суперпозицию стационарных состояний, У (х, t) = 2	(х) e‘“ft/
решением временного и стационарного уравнений Шредингера.
4.52.	Частица находится в одномерной прямоугольной потенциальной яме шириной I с абсолютно непроницаемыми стенками. Найти волновую функцию частицы в момент времени t, если в начальный момент она имела вид: У (х, 0) = Ах (I — х).
4.53.	Плоским ротатором называют систему из двух жестко связанных частиц, вращающуюся в плоскости вокруг своего центра инерции. Оператор энергии такого ротатора имеет вид: Н = (fi2/2/)d2/d(p2, где / — момент инерции системы. Полагая, что в начальный момент волновая функция ротатора имела вид Ф (ср, 0) = A cos2 ср, найти эту функцию в момент времени t.
4.54.	Вычислив с помощью временного уравнения Шредингера производную по времени от среднего значения некоторой механической величины А, изображаемой оператором Л, показать, что
. dA	дА , i	д / ж / dA \
а) Т ~ТГ~^{НА~АИУ' б> ДГ<л> = <	/•
dt	dt h	dt	\ dt /
4.55.	Доказать операторные равенства:
а)	б)-1(ЛВ) = -^-В + Д-^-.
dt	dt dt dt	dt	dt
4.56.	Доказать справедливость следующих уравнений движения в операторной форме:
a) dxdt == рх!т\ 6)dpx!dt = —dUldx.
4.57.	Согласно теореме Эренфеста, средние значения механических величии подчиняются законам классической механики. Доказать, что при движении частицы в потенциальном поле U (х): a) (dx/d.?) = = т\ 6) {dpxidtA> -= — (dUidxy.
4.58.	Доказать, что для частицы, движущейся в потенциальном поле U (х), выполняются операторные равенства:
а) 4" (-V2) — (х рх+ рхх); dt	т
б)	рх)
dt
Рх	ди .
-----х —; т----дх
~ dl' . dU	\
Рх ~Z. I Рх ) •
ОХ ОХ	]
°*
4.59.	Показать, что производная по времени от оператора Lx равна оператору проекции момента внешних сил, т. е.
d -р	[dU	ди \
— Lx - Мх -У--------z — .
dt	\ дг	ду J
32
4.60.	Частица находится в состоянии, описываемом собственной функциейх|? оператора А, который не зависит от времени явно. Показать, что соответствующее собственное значение А этого оператора будет сохраняться во времени, если оператор А коммутирует с гамильтонианом Н.
4.61.	Какие из механических величин (энергия Е, проекции импульса, проекции и квадрат момента импульса) сохраняются при движении частицы:
а)	в отсутствие поля (свободное движение);
б)	в однородном потенциальном поле U (z) az, а — постоянная;
в)	в центрально-симметричном потенциальном поле U (г);
г)	в однородном переменном поле U (z, f) -- a(f) z?
4.62.	Частица находится в некотором состоянии Y (х, t), причем У (х, /) не является собственной функцией оператора А. Зная, что оператор А не зависит от времени явно и коммутируете гамильтонианом Н, показать:
а)	среднее значение механической величины А сохраняется;
б)	вероятности определенных значений механической величины А также не зависят от времени.
Центрально-симметричное поле.
Атом водорода
4.63.	Преобразовать оператор полной энергии для частицы в центрально-симметричном потенциальном поле U (г) к виду
H^Tr+-J—+
2mr2
Какой вид имеет оператор Тг?
4.64.	Частица массой ц движется в центрально-симметричном потенциальном поле U (г). Найти;
а)	уравнения Шредингера для угловой и радиальной частей волновой функции ф (г, ft, <р) = 7? (r)-Y (ft, ф)- Считая собственные значения оператора L2 известными, привести уравнение для функции R (г) к ВИДУ (4.10);
б)	зависимость волновой функции от азимутального угла ср.
4.65.	Частица находится в центрально-симметричном потенциальном поле в состоянии ф (г, ft, <р) = R t(r) Y lm (ft, <р). Каков физический смысл функции |У/т|2? Воспользовавшись табл. 4.1, вычислить нормировочные коэффициенты функций:
а) Y г,®- ®) Y 2д.
4.66.	Частица массой m находится в сферически-симметричной потенциальной яме, где U (г) = 0 при г < го, U - оо при г — го, го — радиус ямы. Найти:
а)	возможные значения энергии и нормированные собственные функции частицы в s-состояниях (/ — 0), гдеф-функция зависит только
2 Зак. 1896	33
от г. При решении уравнения Шредингера воспользоваться подстановкой 4> = %/г;
б)	наиболее вероятное значение гнер и вероятность w нахождения частицы в области г < гвер для основного состояния. Изобразить примерные графики функций яр2 (г) и г2ф2(г) в этом состоянии.
4.67.	Воспользовавшись решением предыдущей задачи, найти средние значения (г), (г2> и среднего квадратического отклонения < (г — (г>)2> для частицы, находящейся на и-м s-уровне (/ = 0).
4.68.	Частица массой т находится в сферически-симметричной потенциальной яме, где U (г) = 0 при г < го, U = оо при г = го, Го — радиус ямы. Воспользовавшись решением задачи 4.66, найти:
а)	радиальную часть ф-функции, RA (г), описывающей р-состояние частицы (/ = 1). Для этого продифференцировать уравнение (4.10), определяющее функции Ro (г) s-состояний, и полученное выражение сравнить с уравнением, определяющим функции R} (г).
б)	энергию первого /?-уровня, сравнить ее с энергией основного состояния.
4.69.	Частица массой т находится в сферически-симметричной потенциальной яме, где U (г) = 0 при г < r0, U (г) = Uo при г го.
а.	Найти с помощью подстановки ф (г) = х (r)ir уравнение, определяющее собственные значения энергии частицы в s-состояниях (/ =0) в области Е < Uо', привести это уравнение к виду
sin kr0 = ± kr0 Yh2/2tnro Uo, k — V 2mE /h.
б.	Убедиться, что данная яма не всегда имеет дискретные уровни (связанные состояния). Определить интервал значений roUo, при которых яма содержит только один s-уровень.
в.	Полагая roUo = 8л2Й2/27т, вычислить наиболее вероятное значение гвер для частицы в s-состоянии, а также вероятность нахождения ее в области г > г о.
4.70.	Привести уравнение, определяющее радиальную часть волновой функции электрона в кулоновском поле ядра Z, к безразмерному виду. В качестве единиц измерения взять атомную единицу длины (первый боровский радиус) и атомную единицу энергии (энергию связи электрона в атоме водорода).
4.71.	Используя подстановку R (г) = х (г)/г, найти асимптотический вид радиальной части волновой функции, R (г), для связанных состояний электрона в кулоновском поле ядра:
а) на больших и б) на малых расстояниях от ядра.
4.72.	Электрон в атоме водорода находится в стационарном состоянии, описываемом сферически-симметричной волновой функцией ф (г) = = А (1 + аг) е™, где А, а и а — постоянные. Найти:
а)	постоянные а, а и энергию электрона (с помощью уравнения Шредингера);
б)	нормировочный коэффициент А.
4.73.	Найти для ls-электрона в атоме водорода:
а)	наиболее вероятное расстояние от ядра гвер и вероятность нахождения электрона в области г < гвер;
б)	вероятность нахождения его вне классических границ поля.
34
4.74.	Определить для ls-электрона в атоме водорода средние значения:
а)	расстояния от ядра <г>, <г2> и <(г — <г»2>;
б)	модуля силы взаимодействия и потенциальной энергии;
в)	кинетической энергии и средней квадратической скорости.
4.75.	Воспользовавшись формулами из табл. 4.2, вычислить для 2р-и Зх-электронов атома водорода:
а)	наиболее вероятное расстояние от ядра;
б)	среднее квадратическое отклонение <(г — <г»2>.
4.76.	Найти средний электростатический потенциал, создаваемый ls-электроном в центре атома водорода.
4.77.	Определить средний электростатический потенциал на расстоянии г от ядра атома водорода, находящегося в основном состоянии. Указание', для нахождения потенциала <ре, создаваемого «электронным облаком», дважды проинтегрировать уравнение Пуассона V2<pe = — 4лр.
5. СПЕКТРЫ. ЭЛЕКТРОННАЯ
ОБОЛОЧКА АТОМОВ
•	Спектральные обозначения термов: х {L}Jt где х — мультиплетность (х — 2S + 1); L, S и J — квантовые числа орбитальное, спиновое и полного момента):
L ---- 0, 1, 2, 3, 4, 5, 6, ...
символ:	S, Р, D, F, G, Н, I, ...
•	Правила отбора квантовых чисел S, L н J:
AS = 0; AL ~ ±1; Д7 = 0, ±1; 7 = 0 + 7 = 0.	(5.1)
•	Термы атома (иона) с одним валентным электроном:
Т = ^ф/(п-А)2,	(5.2)
где R — постоянная Ридберга; Za(j> — эффективный заряд (в единицах е) остова атома (иона), в поле которого движется внешний электрон; п — главное квантовое число валентного электрона; А — квантовый дефект. Схема уровней такого атома (иона) показана на рис. 5.1 (без учета тонкой структуры).
•	Дираковская формула тонкой структуры уровней атома (иона) с одним электроном:
RZ2 rjPRZ4 2	3 \
+ —— --------------- ,	(5.3)
га2 «3	\/4.1/2 4га Г	'
где Z — заряд ядра (в единицах е); а —постоянная тонкой структуры; гаи / — квантовые числа (главное и полного момента).
•	Механические моменты атома (орбитальный, спиновый и полный):
pL=ftl/L(L + 1); Pg—fl 1/S(S4-1); Pj-h^J (7 + 1).	(5.4)
•	В задачах этой главы связь между моментами предполагается нормальной, L — S (спин-орбитальная связь).
•	Правила Хунда:
наименьшей энергией обладает терм с максимальным значением спина S при данной электронной конфигурации и максимально возможным при этом 5макс значением L;
для основного (нормального) терма 7 — |Z. — S|, если подоболочка заполнена менее чем наполовину, и 7 - L + S в остальных случаях.
2*	35
• Эквивалентными называются электроны с одинаковыми квантовыми чис-
лами и п, и I.
• Распределение Больцмана:
(Е,-Ег)/*Г
Мг g2
(5-5)
где gi и g2 — статистический вес (кратность вырождения) уровней с энергиями Et и Е2.
•	Вероятности радиационных переходов между уровнями 1 и 2 (Е2 > £j), т. е. число переходов за I с в расчете на один атом (Z/(V), для спонтанного и индуцированного излучения и поглощения:
Z^l N.^ Л21; 2^д 'Л'2^б21ии; Z™™ IBl2u^	(5,6)
где Л21, В21, В12 — коэффициенты Эйнштейна: и— объемная спектральная плотность излучения, отвечающая частоте со перехода между рассматриваемыми уровнями.
•	Связь между коэффициентами Эйнштейна:
g.	л2 с3
Вц--~	В12-—- — Л21.	(5.7)
g2	Йсо3
•	Соотношение между средним временем жизни т и шириной Г уровня: тГ ~ h.
•	Схема рентгеновских термов показана на рис. 5.2.
•	Закон Мозли для К - линий:
coKa-3/4 7?(Z-o)2,	(5.8)
где /? — постоянная Ридберга; Z — порядковый номер атома; а — поправка (при решении задач считать а - 1).
36
Состояние электронов в атоме
5.1.	Определить потенциал ионизации и первый потенциал возбуждения атома Na, у которого квантовые дефекты основного терма 3S и терма ЗР равны соответственно 1,37 и 0,88.
5.2.	Вычислить квантовые дефекты S-, Р- и D-термов атома Li, если известно, что энергия связи валентного электрона в основном состоянии равна 5,39 эВ, первый потенциал возбуждения 1,85 эВ и длина волны головной линии диффузной серии 0,610 мкм. Какой из перечисленных термов наиболее близок к водородоподобным и чем это обусловлено?
5.3.	Найти энергию связи валентного электрона в основном состоянии атома Li, если известно, что длины волн головной линии резкой серии и ее коротковолновой границы равны соответственно 0,813 и 0,349 мкм.
5.4.	Сколько спектральных линий, разрешенных правилами отбора, возникает при переходе атомов лития в основное состояние из состояния:
a) 4S; а) 4Р?
5.5.	Вычислить для иона Ве+ квантовые дефекты S- и Р-термов, а также длину волны головной линии резкой серии, если известно, что длины волн головной линии главной серии и ее коротковолновой границы равны 321,0 и 68,8 нм.
5.6.	Термы атомов и ионов с одним валентным электроном можно представить в виде Т =- R (Z — a)2/zz2, где Z — заряд ядра (в единицах е); а — поправка экранирования; п — главное квантовое число валентного электрона. Вычислить с помощью этой формулы поправку а и квантовое число п валентного электрона в основном состоянии атома Li, если известно, что ионизационные потенциалы Li и Be4 равны соответственно 5,39 и 17,0 В и поправка а для них одинакова.
5.7.	Найти расщепление, эВ, уровня 4Р атома К, если известно, что длины волн компонент дублета резонансной линии равны 769, 898 и 766, 491 нм. Сравнить полученное значение с энергией резонансного перехода.
5.8.	Головная линия резкой серии атомарного цезия представляет собой дублет с длинами волн 1469,5 и 1358,8нм. Найти интервалы, см-1, между компонентами следующих линий этой серии.
5.9.	Выписать спектральные обозначения термов электрона в этоме водорода для п 3. Сколько компонент тонкой структуры имеет уровень атома водорода с главным квантовым числом «?
5.10.	Вычислить для иона Не4 интервалы, см-1, между:
а)	крайними компонентами тонкой структуры уровней с п 2, 3 и 4;
б)	соседними компонентами тонкой структуры уровня с п 3.
5.11.	Вычислить разность длин волн компонент дублета линии 2Р — 1S атомов водорода и ионов Не+.
5.12.	Какому водородоподобному иону принадлежит дублет головной линии серии Лаймана, разность волновых чисел которого составляет 29,6 см-1?
37
5.13.	Определить для ионов Не+ число компонент тонкой структуры и интервал (в см-1 и длинах волн) между крайними компонентами головной линии серии:
а) Бальмера; б) Пашена.
5.14.	При какой разрешающей способности спектрального прибора можно обнаружить тонкую структуру головной линии серии Бальмера атомарного водорода?
5.15.	Найти возможные значения полных механических моментов электронных оболочек атомов в состояниях iP и 5D.
5.16	Выписать возможные термы атомов, содержащих кроме заполненных оболочек:
а)	два электрона, s и р\
б)	два электрона, р и d;
в)	три электрона, $, р и d.
5.17.	Сколько различных типов термов возможно у двухэлектронной системы, состоящей из d- и /-электронов?
5.18.	Выписать возможные типы термов атома, содержащего кроме заполненных оболочек два /?-электрона с различными главными квантовыми числами.
5.19.	Определить возможную мультиплетность:
а)	терма Оз/2;
б)	термов атомов Li, Be, В и С, если возбуждаются электроны только внешних, незамкнутых, подоболочек.
5.20.	Найти максимально возможный полный механический момент электронной оболочки атома в /^-состоянии, если известно, что этому состоянию соответствуют пять термов одинаковой мультиплетности, но с различными значениями квантового числа J.
5.21.	Известно, что в Р- и D-состояниях двух различных атомов число возможных значений квантового числа J одинаково и равно трем. Определить спиновый механический момент атомов в этих состояниях.
5.22.	Найти угол между спиновым и полным механическими моментами в векторной модели атома:
а)	находящегося в состоянии :iD с максимально возможным значением полного механического момента;
б)	содержащего, кроме заполненных подоболочек, три электрона (р, d и /) и имеющего максимально возможный для этой конфигурации полный механический момент.
5.23.	Атом находится в состоянии V, имея при этом максимально возможный полный механический момент. Определить кратность вы-рождения этого состояния по J. Каков физический смысл полученной величины?
5.24.	Определить максимально возможный орбитальный механический момент атома, находящегося в состоянии, мультиплетность которого пять и кратность вырождения по J равна семи. Указать спектральный символ этого состояния.
5.25.	Найти максимально возможный угол между спиновым и полным механическими моментами в векторной модели атома, находящегося в состоянии, мультиплетность которого три и кратность вырождения ио J равна пяти.
38
5.26.	Определить число возможных состояний:
а)	атома с заданными значениями квантовых чисел L и S;
б)	двухэлектронной системы из р- и d-электронов;
в)	электронной конфигурации nd3.
5.27.	Найти число электронов в атомах, у которых заполнены: а) К- и /.-оболочки, 3s-подоболочка и на 50% 5р-подоболочка;
б)	К-, L-, /И-оболочки, 4s- и 4р-подоболочки. Что это за атомы?
5.28.	Найти максимальное число электронов, имеющих в атоме следующие одинаковые квантовые числа: а) п, I; б) п.
5.29.	Выписать электронные конфигурации и с помощью правила Хунда найти основной терм атомов: а) С и N; б) S и С1. Электронные конфигурации этих атомов соответствуют застройке электронных оболочек в нормальном порядке.
5.30.	Используя правила Хунда, найти основной терм атома, электронная конфигурация незаполненной подоболочки которого:
a) nd2-, б) nd3.
5.31.	Определить основной терм атома, незамкнутая подоболочка которого заполнена ровно наполовину пятью электронами.
5.32.	Найти кратность вырождения основного состояния атома, электронная конфигурация незаполненной подоболочки которого nd6.
575.33.	Найти возможные типы термов атома, электронная конфигурация незаполненной подоболочки которого:
а)	пр2; б) пр3; в) nd2.
5.34.	Убедиться на нижеследующих примерах, что две электронные конфигурации, у одной из которых столько эквивалентных электронов, сколько не хватает другой для заполнения подоболочки, имеют одинаковые наборы возможных типов термов:
а) р1 и р5; б) р2 и р4; в) d1 и d9. Объяснить этот факт.
5.35.	Выписать возможные типы термов для следующих электронных конфигураций:
a) ns1, пр2; б) пр1, пр2. Здесь п =/= п .
Интенсивность и ширина спектральных линий
5.36.	Определить отношение числа атомов газообразного лития в состояний 2Р к числу атомов в основном состоянии при Т =-= 3000 К-Длина волны резонансной линии (2Р — 2S) А = 670,8 нм.
5.37.	Найти долю атомов водорода, находящихся в состоянии с главным квантовым числом п = 2 при Т = 3000 К.
5.38.	Показать, что число атомов, возбужденных на некоторый уровень, убывает со временем по закону N = No e~t/x, где т — среднее время жизни на этом уровне.
5.39.	Интенсивность резонансной линии убывает в р = 65 раз на расстоянии I = 10 мм вдоль пучка атомов, движущихся со скоростью v = 2,0 км/с. Вычислить среднее время жизни атомов в состоянии резонансного возбуждения. Оценить ширину уровня.
5.40.	Разреженные пары ртути, атомы которой находятся в основном состоянии, освещают резонансной линией ртутной лампы (к = = 253,65 нм). При этом обнаружено, что мощность испускания этой
39
линии парами ртути 1 = 35 мВт. Найти число атомов в состоянии резонансного возбуждения, среднее время жизни которого т = -- 0,15 мкс.
5.41.	Газообразный литий, содержащий N = 3,0-1016 атомов, находится при Т = 1500 К- При этом мощность испускания резонансной линии X = 670,8 нм (2Р — 2S) равна / = 0,25 Вт. Найти среднее время жизни атома лития в состоянии резонансного возбуждения.
5.42.	Система атомов со своим излучением находится в термодинамическом равновесии при температуре Т. Пусть переходу между двумя энергетическими уровнями атомов, Ех и Ё2, со статистическими весами gr и g2 соответствуют частота <о и коэффициенты —j—2	Эйнштейна А21, В21 и В12. Имея	в виду, что при рав-
I	новесии системы числа прямых и	обратных переходов
। ______7	(£\ ч=ь Е2) в единицу времени одинаковы, найти вы-
j	ражение для объемной спектральной плотности энер-
I	гии теплового излучения:
j	а) с учетом индуцированного испускания; опреде-
।	_g лить также связь между коэффициентами Эйн-
штейна;
Рис. 5.3	б) пренебрегая индуцированным испусканием (при
каких условиях это можно сделать?).
5.43.	Атомарный водород находится в термодинамическом равновесии со своим излучением. Вычислить:
а)	отношение вероятностей индуцированного и спонтанного излучений атомов с уровня 2Р при температуре Т = 3000 К;
б)	температуру, при которой эти вероятности одинаковы.
5.44.	Через газ, находящийся при температуре Т, проходит пучок света с частотой <о, равной резонансной частоте перехода атомов газа (fiw kT). Показать с учетом индуцированного излучения, что коэффициент поглощения газа
x(T) = x0(l-e^“/w),
где Хо — коэффициент поглощения при Т — 0 К-
5.45.	При каких условиях возможно усиление электромагнитного излучения, проходящего через вещество? Найти отношение заселенности уровней Ч)2 и 1Р1 (Ed > Ер) атомов газа, при котором пучок моно-энергетического излучения с частоте й, равной частоте перехода между этими уровнями, будет проходить через газ, не-ослабляясь.
5.46.	Пусть в квантовой системе (рис. 5.3) производится «накачка» на уровень 2, причем обратный переход возможен только через уровень 1. Показать, что в этом случае усиление света с частотой <о21 возможно при условии ^Лю > g2^2i, где gr и g2 — статистические веса уровней 1 и 2; Ащ и Л21 — коэффициенты Эйнштейна для соответствующих переходов.
5.47.	Пусть q — число атомов, возбуждаемых в единицу времени на уровень 2 (см. рис. 5.3). Найти число атомов на уровне 1 через промежуток времени t после начала возбуждения. Коэффициенты Эйнштейна А2о, А21 и Аю предполагаются известными. Индуцированными переходами пренебречь.
40
5.48.	Спектральная линия X = 532,0 нм возникает в результате перехода между двумя возбужденными состояниями атома, средние времена жизни которых равны 12 и 20 нс. Оценить естественную ширину этой линии АА.
5.49.	Распределение интенсивности излучения в пределах спектральной линии с естественным уширением имеет вид:
т - I О/2)2
V Q) — V П	,
(<о-<о0Р+(у/2р
где Jo — спектральная интенсивность в центре линии (при со а>0); у — постоянная, характерная для каждой линии (для линии, обусловленной переходом из возбужденного состояния непосредственно в основное, у 1/т, т — среднее время жизни возбужденного состояния. Найти с помощью этой формулы:
'а) естественную ширину линии би с известным значением у;
б)	среднее время жизни атомов ртути в состоянии 61/3, если известно, что при переходе в основное состояние испускается линия X = = 185,0 нм с естественной шириной 6А. = 1,5-10~6 нм.
Примечание', шириной линии называют ширину ее контура на половине высоты.
5.50.	Воспользовавшись формулой из предыдущей задачи:
а)	показать, что в пределах ширины линии, т. е. ширины ее контура на половине высоты, заключена половина полной интенсивности линии;
б)	найти полную интенсивность линии, естественная ширина которой бы и спектральная интенсивность в ее центре Jo.
5.51.	Распределение интенсивности излучения в спектральной линии с доплеровским уширением имеет вид:
J<>> = Jq ехР Г—а (ш —,(i)o)2/(i)ol; а = mc42kT,
где Jo — спектральная интенсивность в центре линии (при со — а>о); пг — масса атома; Т — температура газа, К-
а.	Получить эту формулу, используя распределение Максвелла.
б.	Показать, что доплеровская ширина спектральной линии Хо, т. е. ширина контура линии на половине высоты,
6АД0П - 2ZoV(ln 2)/а.
5.52.	Длина волны резонансной линии ртути А, = 253,65 нм. Среднее время жизни резонансного уровня т —- 0,15 мкс. Оценить отношение доплеровского уширения этой линии при Т = 300 К к ее естественной ширине.
5.53.	При какой температуре доплеровское уширение каждой компоненты дублета спектральной линии 22Р — 12S атомарного водорода равно интервалу между этими компонентами?
5.54.	Для получения спектральных линий без доплеровского уширения используют узкий слаборасходящийся пучок возбужденных атомов и наблюдение ведут в направлении, перпендикулярном к
41
пучку. Оценить угол раствора пучка атомов натрия, при котором доплеровское уширение резонансной линии А, = 589,6 нм на порядок меньше ее естественной ширины, если скорость атомов v = 1000 м/с и среднее время жизни в состоянии резонансного возбуждения т — 16 нс.
Характеристические рентгеновские спектры
5.55. Используя закон Мозли, вычислить длины волн и энергии фотонов, соответствующих Да-линиям алюминия и кобальта.
5.56. Определить длину волны Д „-линии элемента периодической системы, начиная с которого следует ожидать появления Л-серии ха-
рактеристического рентгеновского излучения.
5.57.	Считая поправку ст в законе Мозли равной единице, найти:
а)	каким элементам принадлежат Ка-линии с длинами волн 193,5; 178,7; 165,6 и 143,4 пм; какова длина волны Да-линии элемента, пропущенного в этом ряду;
б)	сколько элементов содержится в ря-
ду между элементами, у которых длины волн /<а-линий равны 2,50 и 1,79 пм.
5.58.	Для элементов конца периодической системы поправка в законе Мозли значительно отличается от единицы. Убедиться в этом на примере олова, цезия и вольфрама, длины волн Ка-линий которых равны соответственно 49,2; 40,2; 21,0 пм.
5.59.	Определить напряжение на рентгеновской трубке с никелевым антикатодом, если разность длин волн Да-линий и коротковолновой границы сплошного рентгеновского спектра равна 84 пм.
5.60.	При увеличении напряжения на рентгеновской трубке от 10 до 20 кВ разность длин волн Да-линии и коротковолновой границы сплошного рентгеновского спектра увеличилась в три раза. Какой элемент используется в качестве антикатода?
5.61.	Как будет вести себя спектр рентгеновского излучения при постепенном увеличении напряжения на рентгеновской трубке? Вычислить с помощью таблиц Приложения минимальное напряжение на рентгеновских трубках с антикатодами из ванадия и вольфрама, при которых начинают появляться Да-линии этих элементов.
5.62.	Какие серии характеристического спектра возбуждаются в молибдене и серебре Да-излучением серебра?
5.63.	На рис. 5.4 показаны коротковолновый край К-полосы поглощения рентгеновского излучения и положение Да- и Др- линий испус
кания.
а.	Объяснить природу скачка поглощения.
б.	Рассчитать и построить в масштабе схему Д'-, L- и ЛКуровней атома, для которого ~= 275 пм; = 251 пм и = 249 пм. Что это за атом? Какова длина волны его Ла’линии испускания?
5.64.	Зная длины волн коротковолновых границ поглощения Д- и Л-серий ванадия, вычислить (без учета тонкой структуры):
42
а)	энергию связи К- и L-электронов;
б)	длину волны Ка-линии ванадия.
5.65.	Найти энергию связи Л-электронов титана, если известно, что разность длин волн между головной линией К-серии и ее.коротковолновой границей АХ = 26 пм.
5.66.	Рентгеновские термы в первом приближении можно представить в виде Т = R (Z — а)2/п2, где R — постоянная Ридберга; Z — порядковый номер атома; а — поправка экранирования; п — главное квантовое число удаленного электрона. Вычислить поправку а для К- и L-термов титана, длина волны края К-полосы поглощения которого Хк = 249 пм.
5.67.	Найти кинетическую энергию электронов, вырываемых с К-оболочки атомов молибдена Ка-излучением серебра.
5.68.	При облучении углерода /<а-излучением алюминия возникает спектр фотоэлектронов, содержащий несколько моноэнергетических групп. Найти энергию связи тех электронов углерода, которые вырываются с кинетической энергией 1,21 кэВ.
5.69.	При облучении атомов криптона рентгеновским излучением с длиной волны X обнаружено, что в некоторых случаях из атомов вылетает по два электрона: фотоэлектрон, освобождаемый с К-оболоч-ки, и электрон, освобождаемый в результате эффекта Оже с /.-оболочки. Энергия связи К- и Л-электронов соответственно равна 14,4 и 2,0 кэВ. Вычислить:
а) кинетическую энергию обоих электронов, если Х = 65 пм;
. б) X, при которой энергии обоих электронов одинаковы.
5.70.	а. Показать, что спектры испускания характеристического рентгеновского излучения дублетные.
б.	Почему в спектре поглощения рентгеновского излучения край К-полосы простой, Л-полосы — тройной, М-полосы — пятикратный?
5.71.	а. Указать спектральный символ рентгеновского терма атома, у которого с одной из замкнутых оболочек удален электрон с /= 1 и j = 3/2.
б.	Выписать спектральные обозначения возможных рентгеновских термов атома, у которого удален один электрон из Л-оболочки; из Al-оболочки.
5.72.	Определить число спектральных линий, обусловленных переходами между К- и L-; К- и М-; L- и М-оболочками атома.
5.73.	Вычислить с помощью таблиц Приложения:
а)	длины волн дублета Ка-линии вольфрама;
б)	разность длин волн дублета Ка-линии свинца.
5.74.	Вычислить с помощью таблиц Приложения энергию связи 1s, 2s, 2pi/2 и 2р3/2 электроной атома урана.
6. АТОМ В МАГНИТНОМ ПОЛЕ
• Магнитный момент атома:
ZJ (J -f-1)
W Ив — магнетон Бора; g — множитель (фактор) Ланде.
(6.1)
43
• Формула зеемановского расщепления спектральных линий:
Д<а = («ig-i — m2g-2)jxB5/A,	(6.2)
где mi и gj — магнитные квантовые числа и множители Ланде соответствующих термов.
•	Обозначения зеемановских компонент: л-компонента (Дт 0); сг-ком-понента (Дт = ±1).
•	Правила отбора квантовых чисел (кроме указанных во введении к предыдущей главе):
Дт5 = 0; Дт£ =0, ±1; Дт^ = 0, ± 1;	(6.3)
если Д7 - - 0, то переход trij = 0 ->• nij = 0 не осуществляется.
•	Ларморова частота процессии:
<ол = еЪ/Чтс,	(6.4)
где е — элементарный заряд; т — масса электрона.
• Диамагнитная восприимчивость N изолированных атомов:
Де2
<6-5’
где <г? > — средний квадрат расстояния i-ro электрона от ядра атома.
• Парамагнитная восприимчивость в слабом магнитном поле:
% = ai'T; а = ЛГрА-'ЗА,	(6.6)
где Т — абсолютная температура ; а — постоянная Кюри; W — число молекул; |х — магнитный момент молекулы; k — постоянная Больцмана.
Магнитные свойства атома.
Эффект Зеемана
6.1.	Имея в виду, что отношение магнитного момента к механическому для спинового момента вдвое больше, чем для орбитального, получить с помощью векторной модели формулу (6.1).
6.2.	Вычислить множитель Ланде для атомов:
а)	с одним валентным электроном в состояниях S, Р и D:
б)	в состоянии 3Р;
в)	в S-состояниях;
г)	в синглетных состояниях.
6.3.	Выписать спектральные обозначения терма, у которого:
a) S = 1/2, J = 5/2, £ = 6/7; б) S = 1, L = 2, g = 4/3.
л6.4. Найти магнитный момент р и возможные значения проекции рв атома в состоянии:
а)
6.5.	Максимальное значение проекции магнитного момента атома, находящегося в состоянии D2, равно четырем магнетонам Бора. Определить мультиплетность этого терма.
6.6.	Определить возможные значения магнитного момента атома в состоянии 4Р.
6.7.	Вычислить магнитный момент атома водорода в основном состоянии.
44
6.8.	Убедиться, что магнитные моменты атомов в состояниях 4О1/2 и 6б3/2 равны нулю. Интерпретировать этот факт на основе векторной модели атома.
6.9.	Найти механические моменты атомов в состояниях 5F и 1Н, если известно, что в этих состояниях магнитные моменты равны нулю.
6.10.	Вычислить с помощью правила Хунда магнитный момент основного состояния атома, в котором незаполненная подоболочка имеет электронную конфигурацию: а) пр5; б) nd3.
6.11.	Показать с помощью векторной модели и соотношения diidt = М, где J — момент количества движения атома и М — механический момент внешних сил, что угловая скорость прецессии векто-	
pa J в магнитном поле В равна Y////////A2/A	-----
о» = £ЦвВ'Й, g — множитель Ланде. —*—	~—“_____Р
<6.12. Найти угловые скорости У///////////Л ь Г прецессии механических моментов Н----------------------------
атома в магнитном поле В 1000 Гс, если атом находится:	Рис. 6.1
а) в состоянии 1Р, гР3/2, 5Fp, в основном состоянии, электронная конфигурация незаполненной подоболочки которого npi (использовать правило Хунда).
6.13.	Механический момент атома в состоянии 3F прецессирует в магнитном поле В = 500 Гс с угловой скоростью и = 5,5-109 рад'с. Определить механический и магнитный моменты атома.
6.14.	Объяснить с помощью векторной модели, почему механический момент атома, находящегося в состоянии eFl/2, процессирует в магнитном поле В с угловой скоростью <о, вектор которой направлен противоположно вектору В.
6.15.	Атом в состоянии 2Рц2 находится на оси кругового контура с током I = 10,0 А. Расстояние между атомом и центром контура с током z = 5,0 см, радиус контура R = 5,0 см. Вычислить максимальное значение силы взаимодействия между атомом и этим током.
6.16.	В опыте Штерна и Герлаха узкий пучок атомов серебра (в нормальном состоянии) проходит через поперечное резко неоднородное магнитное поле и попадает на экран Э (рис. 6.1). При каком значении градиента напряженности магнитного поля расщепление пучка на экране 6 = 2,0 мм, если а = 10 см, b = 20 см и скорость атомов v = 300 м/с?
6.17.	Узкий пучок атомов пропускают по методу Штерна и Герлаха через резко неоднородное магнитное поле. Определить:
а)	максимальные значения проекций магнитных моментов атомов в состояниях 4 A, ®S и 5D, если известно, что пучок расщепляется соответственно на 4, 6 и 9 компонент;
б)	на сколько компонент расщепится пучок атомов, находящихся в состояниях 3D2 и 5Fj?
6.18.	В одном из опытов по расщеплению узкого атомарного пучка по методу Штерна и Герлаха использовали атомы ванадия в основном состоянии *Р3/2. Найти расстояние между крайними компонентами пучка на экране (см. рис. 6.1), если а = 10 см, Ь = 20 см, дВ/dz = = 23 кГс/см и кинетическая энергия атомов Т = 0,040 эВ.
45
6.19.	Атом находится в магнитном поле В = 3,00 кГс. Определить: а) полное расщепление, см-1, терма lD;
б)	спектральный символ синглетного терма, полная ширина расщепления которого составляет 0,84 см-1.
6.20.	Построить схему возможных переходов в магнитном поле между следующими состояниями:
а) гР; б)
Сколько компонент содержит спектральная линия, соответствующая каждому из этих переходов?
6.21.	Спектральная линия X = 0,612 мкм обусловлена переходом между двумя синглетными термами атома. Определить интервал АХ между крайними компонентами этой линии в магнитном поле В = = 10,0 кГс.
6.22.	Интервал между крайними компонентами спектральной линии X = 525,0 нм, обнаруживающей простой эффект Зеемана, составляет АХ = 22 пм. Найти интервал, эВ, между соседними подуровнями зеемановского расщепления соответствующих термов.
6.23.	Спектральным прибором с разрешающей способностью Х/6Х = = 1,0-105 необходимо разрешить компоненты спектральной линии X = 536,0 нм, обусловленной переходом между двумя синглетными термами атома. При каком минимальном значении напряженности магнитного поля это возможно, если наблюдение ведется:
а) параллельно и б) перпендикулярно направлению поля?
6.24.	Магнитное поле в случае сложного эффекта Зеемана считается слабым, если магнитное расщепление терма значительно меньше естественного мультиплетного расщепления. Выяснить:
а)	при какой напряженности магнитного поля интервал между соседними компонентами термов 3 2Р1/2 и 3 2Р3/2 атома Na будет составлять 1/10 естественного расщепления 3 2Р-состояния, если длины волн дублета резонансной линии натрия равны 589,593 нм (2Р1/2 —>-2Si/2) и 588,996 нм (2Р3/2->2S1/2);
б)	то же для термов 2Р1/2 и 2Р3/2 22Р-состояния атома водорода, имея в виду, что естественное расщепление определяется дираковской формулой тонкой структуры;
в)	то же для 2Р2/2 и 2Р3/2 22Р-состояния иона Не+. Сравнить с результатом для атома водорода.
6.25.	Воспользовавшись выражением для магнитного момента атома, получить формулу расщепления спектральных линий для сложного эффекта Зеемана в слабом магнитном поле.
6.26.	Какой эффект Зеемана (простой, сложный) обнаруживают в слабом магнитном поле спектральные линии:
а)	'Р 2D5/2 ->2Р3/2; 3Dr ^3Р0, *15
б)	атомов Н, Не, Li, Be, В и С?
(6.27. Построить схему возможных переходов между термами 2Р3/2 и 25j/2 в слабом магнитном поле. Вычислить для соответствующей спектральной линии:
а) смещения зеемановских компонент в единицах реВ/й;
'(^ринтервал, см-1, между крайними компонентами, если В — = 5,00 кГс.
46
6.28.	Найти минимальную разрешающую способность V6A, спектрального прибора, который позволит разрешить зеемановскую структуру спектральной линии .589,0 нм (2Р3/2	натрия в магнит-
ном поле В = 2,0 кГс.
6.29.	Изобразить схему возможных переходов в слабом магнитном поле и вычислить смещения (в единицах рв^/й) зеемановских компонент спектральной линии:
а) 2^з/2 ~^2Р3/2;	2^б/2 “*"2^)з/2-
6.30.	Вычислить смещения (в единицах рБ5/й) в слабом магнитном поле зеемановских л-компонент спектральной линии:
a) 3D3 ->3Р2; б) 3Г>2->3Р2.
6.31.	Показать с помощью векторной модели, что в силовом магнитном поле, когда связь L — S полностью разрывается, энергия магнитного взаимодействия атома = (ть + 2ms) Ив В. Показать, что это приводит к простому эффекту Зеемана.
6.32.	При какой индукции магнитного поля интервал между ст-ком-понентами резонансной линии лития будет в п = 10 раз превосходить естественное расщепление этой линии? Длины волн дублета этой линии равны 670,795 и 670,780 нм.
6.33.	Показать, что частота перехода между соседними подуровнями зеемановского расщепления терма совпадает с частотой прецессии механического момента атома в магнитном поле.
6.34.	Для исследования магнитного резонанса вещество из атомов с собственными магнитными моментами подвергают одновременному воздействию двух магнитных полей: постоянного поля В и перпендикулярного к нему слабого переменного поля Ва. Показать, что наблюдаемые при этом резкие максимумы поглощения энергии возникают при частоте переменного поля а> = g^BIh.
6.35.	Газ из атомов в состоянии 2Г>3/2 подвергли одновременному воздействию постоянного магнитного поля В и перпендикулярного к нему переменного поля Bv с частотой 2,8 ГГц. При каком значении' В возникает резонансное поглощение энергии?
6.36.	Найти магнитный момент атомов Ni (в состоянии 3F), которые обнаруживают резонансное поглощение энергии при одновременном воздействии постоянного магнитного поля В = 2,00 кГс и перпендикулярного к нему переменного поля Bv при частоте последнего v = 3,50 ГГц.
Диа- и парамагнетизм
6.37.	Вычислить магнитные моменты атомов Не и Хе в магнитном поле В •= 10,0 кГс. Их диамагнитные восприимчивости равны соответственно — 1,90 и — 43,0 единиц 10~6 см3/моль.
.6.38. Небольшой шарик из диамагнетика медленно переместили вдоль оси катушки с током из области, где магнитного поля практически нет, в точку с индукцией В. Показать, что совершенная при этом работа А = — %ГВ2/2, где % — магнитная восприимчивость единицы объема диамагнетика; V — объем шарика.
47
6.39.	С какой силой круговой контур с током I = 10 А и радиусом R = 5,0 см действует на атом Ne, находящийся на оси контура на расстоянии z ----- 5,0 см от его центра? Диамагнитная восприимчивость неона х = — 7,2-10~6 см3, моль.
6.40.	Показать с помощью выражения для ларморовой частоты прецессии, что диамагнитная восприимчивость атомарного газа % » « — Ze'-N (j-'y.finic1, где Z — порядковый номер атома; N — число атомов; (г2) — средний квадрат расстояний электронов от ядра.
6.41.	Вычислить молярную диамагнитную восприимчивость атомарного водорода в основном состоянии. Его волновая функция имеет вид: ф (г) =- (лг3)-1/'2 е~ г/г*, где г\ — первый боровский радиус.
6.42.	Имея в виду, что основной вклад в диамагнетизм вносят внешние электроны атома (почему?), оценить радиусы наружных электронных оболочек Не, Na+ и С1_, диамагнитная восприимчивость которых равна соответственно:—1,9; —6,1 и —24,2 единиц 10~6 см3/моль.
6.43.	Атом со сферически-симметричным распределением заряда поместили в магнитное поле В. Выразить напряженность магнитного поля Во в центре атома, обусловленную прецессией электронной оболочки, через электростатический потенциал Ео, создаваемый электронной оболочкой в той же точке.
6.44.	Если парамагнитный газ находится при температуре Т в магнитном поле В, то в отсутствие пространственного квантования среднее значение проекции магнитного момента молекулы
<рв) = рЕ(а) = р (cth а — l/а); а = \tBlkT,
где р — магнитный момент молекулы; L (а) — функция Ланжевена.
а.	Получить это выражение с помощью распределения Больцмана. Изобразить график L (а).
б.	Упростить эту формулу для случаев слабого (а < 1) и сильного (а 1) магнитных полей.
6.45.	Магнитный момент поля некоторого парамагнитного газа при Т — 300 К в слабом магнитном поле В=100 Гс равен 0,150 эрг/(Гс X X моль). Определить постоянную Кюри, отнесенную к молю газа, и магнитный момент каждой молекулы.
6.46.	Определить парамагнитную восприимчивость 1 см3 газа из молекул О, с магнитными моментами 2,8 рв в слабом магнитном поле. Газ находится при нормальных условиях.
6.47.	Парамагнитный газ из атомов в состоянии 2<S i/2 находится при Т = 300 К в магнитном поле В = 25 кГс. Вычислить отношение т] = AjV/jV, где ДУ — разность чисел атомов с положительной и отрицательной проекциями магнитных моментов на направление поля; N — полное число атомов. Вычисление провести:
а)	с учетом пространственного квантования;
б)	классически — без учета пространственного квантования.
6.48.	Найти магнитный момент парамагнитного газа, состоящего из N атомов в состоянии при температуре Т в магнитном поле В. Упростить полученное выражение для случая рВ kT.
6.49.	Парамагнитный газ находится при Т = 300 К в магнитном поле В -- 20,0 кГс. Вычислить с учетом пространственного кванто-48
вания отношение т] = &N/N (см. задачу 6.47). Вычисление провести для случаев, когда атомы находятся в состоянии:
а) 1Р; б) 2Рз/2.
6.50.	Показать, что в слабом магнитном поле средняя проекция магнитного момента атома (с учетом пространственного квантования) <рл> =- p2B/3kT, где ц = gVj (J+ 1) рБ.
6.51.	Парамагнитный газ состоит из атомов лития в основном состоянии. Вычислить:
а)	постоянную Кюри для одного моля данного газа;
б)	магнитный момент 1 г этого газа при температуре 300 К в магнитном поле В = 1,00 кГс.
6.52.	Вычислить парамагнитную восприимчивость 1 г атомарного кислорода в слабом магнитном поле при температуре 1600 К. Атомы находятся в основном состоянии 3Р2-
7. ДВУХАТОМНЫЕ МОЛЕКУЛЫ
• Вращательная энергия двухатомной молекулы:
Ej ~ hBJ (J -I- 1), В - Й/2/,	(7.1)
где В — вращательная постоянная; / — момент инерции молекулы; J — вращательное квантовое число: 7	0, I, 2, ...
•	Правило отбора J:	- ±1.
•	Колебательная энергия двухатомной молекулы:
Ev =- До (v 1- 1/2) [1 — х (v + 1/2)],	(7.2)
где <о — "j/x/p — частота колебаний; х — коэффициент квазиупругой силы; |х — приведенная масса молекулы; v  0, 1,2, ... — колебательное квантовое число; х — коэффициент ангармоничности (для гармонического осциллятора х 0).
•	Правила отбора и:
( ± 1, если х 0, До - <
( ±1, ±2,... в остальных случаях.
•	Зависимость энергии взаимодействия от расстояния между ядрами двухатомной молекулы показана на рнс. 7.1, где D —энергия диссоциации.
49
•	Средняя энергия квантового гармонического осциллятора:
, flat ,	Л<о
£ =—+ h^/kT ~ ‘	(7-3)
z е — 1
• На рис. 7.2 показана схема возникновения красного (а) и фиолетового (б) спутников при комбинационном рассеянии света.
Вращательные и колебательные состояния
7.1.	Найти с помощью таблиц Приложения для молекул Н2 и NO: а) энергию, необходимую для возбуждения их на первый вращательный уровень (J = 1);
б)	угловую скорость вращения в состоянии с J = 1.
7.2.	Найти для молекулы НС1 квантовые числа J двух соседних вращательных уровней, разность энергий которых 7,86 мэВ.
7.3.	Определить момент импульса молекулы кислорода в состоянии с вращательной энергией 2,16 мэВ.
7.4.	Найти значения температуры, при которых средняя кинетическая энергия поступательного движения молекул Н2 и N2 равна их вращательной энергии в состоянии с квантовым числом J = 1.
7.5.	Вычислить с учетом кратности вырождения g вращательных уровней (g = 2J + 1) отношение количеств молекул водорода, находящихся в чисто вращательных состояниях с J = 1 и J = 2 при Т = 300 К.
7.6.	Имея в виду, что кратность вырождения вращательных уровней g = 2J 4 1, найти вращательное квантовое число Jm наиболее заселенного вращательного уровня молекул О2 при Т = 300 К- Изобразить примерный график зависимости заселенности вращательных уровней Nj/N0 от J при этой температуре.
7.7.	Найти коэффициенты квазиупругой силы молекул Н2 и СО.
7.8.	Потенциальная энергия взаимодействия атомов в двухатомной молекуле может быть приближенно представлена формулой:
U (р) = Uo (1 - е-Р)2, р = (г - г0)/г0,
где г0 — равновесное межъядерное расстояние; Uo — глубина потенциальной ямы; а — постоянная, характерная для каждой молекулы. Вычислить значения Uo и а для молекулы водорода.
7.9.	Найти энергию, необходимую для возбуждения молекулы Н2 из основного состояния на первый колебательный уровень (v = 1). Во сколько раз эта энергия больше энергии возбуждения данной молекулы на первый вращательный уровень (J = 1)?
7.10.	Определить температуру, при которой средняя кинетическая энергия поступательного движения молекул равна энергии, необходимой для возбуждения молекул С12 из основного состояния на первый колебательный уровень (V = 1).
7.11.	Найти разность энергий состояний с квантовыми числами и' - 1, J' -=0 и v = 0, J = 5 у молекулы ОН.
7.12.	Вычислить для молекулы HF число вращательных уровней, расположенных между основным и первым возбужденным колебательными уровнями.
50
7.13.	Определить максимально возможное колебательное квантовое число, соответствующую колебательную энергию и энергию диссоциации двухатомной молекулы, собственная частота колебаний которой со и коэффициент ангармоничности х. Вычислить эти величины для молекулы Н2.
7.14.	Вычислить коэффициент ангармоничности молекулы С12, если известны ее частота колебаний и энергия диссоциации.
7.15.	Вычислить разность энергий диссоциации молекул, состоящих из тяжелого и легкого водорода D2 и Н2, если известна частота колебаний молекулы Н2.
7.16.	Найти отношение количества молекул НВг, находящихся в чисто колебательных состояниях (без вращения) с квантовыми числами v = 2 и v = 1 при Т = 910 К. При какой температуре это отношение станет равным 1 : 10?
7.17.	Определить с учетом вырождения вращательных уровней (см. задачу 7.5) отношение количеств молекул водорода в состояниях с квантовыми числами v' — 1, J' = 0 и v = 0, 7 = 5 при Т = 1500 К.
7.18.	Вывести формулу (7.3).
7.19.	Вычислить с помощью формулы (7.3) температуру, при которой:
а)	средняя колебательная энергия молекулы С12 вдвое превышает ее нулевую колебательную энергию;
б)	уровень, соответствующий средней колебательной энергии молекулы О2, совпадает с пятым вращательным уровнем этой молекулы (J = 5, v = 0).
7.20.	Исходя из формулы (7.3), получить выражение для молярной колебательной теплоемкости двухатомного газа при постоянном объеме. Найти приближенный вид этого выражения для низких и высоких температур (kT и kT Й<о).
7.21.	Вычислить с помощью формулы (7.3) молярную колебательную теплоемкость при постоянном объеме газа, состоящего из молекул С12 при температурах 150, 300 и 450 К. Изобразить примерный график Скол (Т).
Молекулярные спектры.
Комбинационное рассеяние
7.22.	Найти момент инерции молекулы СН и расстояние между ее ядрами, если интервалы между соседними линиями чисто вращательного спектра этих молекул Av = 29,0 см-1.
7.23.	Известны длины волн двух соседних линий чисто вращательного спектра молекул НС1: 117 и 156 мкм. Определить:
а)	постоянную вращения В', см-1, и момент инерции этих молекул;
б)	вращательные квантовые числа уровней, между которыми происходят переходы, соответствующие этим линиям.
7.24.	Определить, на сколько изменяется момент импульса молекулы СО при испускании спектральной линии % =1,29 мм, которая принадлежит чисто вращательному спектру.
51
7.25.	Сколько линий содержит чисто вращательный спектр молекул ОН?
7.26.	В колебательно-вращательном спектре поглощения молекул НВг волновые числа нулевых линий, соответствующих запрещенным переходам (ДУ = 0) между основными и ближайшими возбужденными колебательными уровнями (v = 0 и v' ~= 1,2), равны 2559,3 и 5028,2 см-1. Определить частоту колебаний и коэффициент ангармоничности этих молекул.
7.27.	Рассмотрим колебательно-вращательную полосу спектра двухатомной молекулы, для которой справедливо правило отбора ДУ -= +1. Показать, что если вращательная постоянная одинакова для состояний, между которыми происходит переход, то частоты спектральных линий полосы равны
w ± 2Bk\ k — 1, 2, 3, ...,
где <в0 — частота нулевой линии, запрещенной правилом отбора для У; В — вращательная постоянная.
7.28.	Вычислить момент инерции и коэффициент ангармоничности молекулы HF, если волновые числа четырех последовательно расположенных спектральных линий вращательной структуры полосы колебательного спектра равны 3874, 3916, 4000 и 4042 см-1. Известно, что эти линии отвечают переходам ДУ = ±1ио'	1 -+и = 0. Час-
тота колебаний данной молекулы соответствует волновому числу v —
4138,5 см-1. Вращательную постоянную считать одинаковой для всех уровней.
7.29.	Найти относительный изотопический сдвиг ДАА линий чисто вращательного спектра смеси молекул Н35С1 и Н37С1. .
7.30.	Рассмотрим спектральную линию, обусловленную переходом v' = 1, У' -= 0 -+v ~= 0, У = 1 в молекулах СО. Вычислить в волновых числах изотопические сдвиги Дукол и AvBp колебательной и вращательной компонент линий (v = vK0JI — vBp) и их отношение для смеси молекул 12С16О и 12С17О. Ангармоничностью пренебречь.
7.31.	Найти частоту колебаний и коэффициент квазиупругой силы молекулы S2, если известно, что в колебательном спектре комбинационного рассеяния света длины волн красного и фиолетового спутников, ближайщих к несмещенной линии, равны 346,6 и 330,0 нм. Ангармоничностью пренебречь.
7.32.	Определить частоту колебаний молекулы HF, если в колебательном спектре комбинационного рассеяния к несмещенной линии красного и фиолетового спутников Хо — 154,0 нм. Ангармоничность молекулы Дх — 0,0218.
7.33.	Найти отношение интенсивностей фиолетового и красного спутников, ближайших к несмещенной линии, в колебательном спектре комбинационного рассеяния света молекул С12 при Т — 300 К. Во сколько раз изменится это отношение при увеличении температуры вдвое?
7.34.	Показать, что для молекул, у которых правило отбора вращательного квантового числа ДУ = ±1, во вращательном спектре 52
комбинационного рассеяния света действует правило отбора AJ = 0, ±2.
7.35.	Во вращательном спектре комбинационного рассеяния света частоты смещенных компонент (красных и фиолетовых спутников) двухатомных молекул определяются в случае правила отбора AJ •---= 0, +2 формулой:
и =	± 2В (2k 4- 1), k -= 1, 2, 3, ...,
где <в0 — частота несмещенной компоненты; В — вращательная постоянная.
а.	Получить эту формулу.
б.	Определить момент инерции и расстояние между ядрами молекулы О2, если разность волновых чисел двух соседних красных спутников равна 5,8 см-1.
7.36.	Во вращательном спектре комбинационного рассеяния света с длиной волны = 546,1 нм разность длин волн красного и фиолетового спутников, ближайших к несмещенной линии, составляет для молекул N2 АЛ 0,72 нм. Имея в виду правило . ’’бора AJ = 0, ±2, найти вращательную постоянную В', см“’, и момент инерции данных молекул.
8. КРИСТАЛЛЫ
•	Период идентичности — расстояние между соседними одинаковыми атомами вдоль определенного направления в решетке.
•	Межплоскостиое расстояние для простой кубической решетки:
d -ai'Vhi-- k2 ГР,	(8.1)
где а — постоянная решетки; h, k, I — Миллеровские индексы рассматриваемой системы плоскостей.
•	Формула Вульфа— Брэгга:
2d sin f) ----- п).,	(8.2)
Где V)— угол скольжения; п — порядок отражения: X — длина волны.
•	Условия, при которых возможны отражения n-го порядка от системы плоскостей (h*k*l*), где h* = nh, k*  nk, I* nl для объемноцептрирован-ных решеток — если сумма ft*, k*, I* четная; для гранецентрированпых решеток — если Л*, X*. Z* одинаковой четности.
•	Формула Борна и Лайде — энергия связи ионных кристаллов, отнесенная к одной паре разноименных ионов:
,,	<72 В	( 1,748 для решетки типа NaCl:
t/ = —а-----;----, а —{	(8.3)
г /П	I 1,763 для решетки типа CsCI,
Где q — заряд нона; г — ближайшее расстояние между разноименными ионами; а, р, п — постоянные (а — константа Маделунга). Структура кристаллов NaCl и CsCI показана на рис. 8.1.
• Коэффициент сжимаемости при всестороннем сжатии
где V — объем кристалла; р — давление.
53
• Формула Дебая — молярная колебательная энергия кристалла:
£ = 9/?0
х3 dx е*—I
^ммакс k
(8-5)
где Д’ — универсальная газовая постоянная; 0 — характеристическая (дебаевская) температура; юмакс — максимальная частота колебаний, определяемая
Рнс. 8.1
из того условия, что полное число колебаний равно числу колебательных степеней свободы кристалла.
• Молярная колебательная теплоемкость кристалла прн Т < 0:
С = 12/5л*/? (Т/0)3.	(8.6)
Структура кристаллов.
Дифракция рентгеновского излучения
8.1.	Зная плотность и тип решетки, определить постоянные кристаллических решеток натрия и меди.
8.2.	Найти плотность кристаллов NaCl и CsCl (см. рис. 8.1).
8.3.	Получить формулу, приведенную в первом пункте введения к этой главе.
8.3.	Зная постоянную а, вычислить межплоскостные расстояния di00, d110, dul и их отношение для:
а) простой; б) объемноцентрированной и в) гранецентрированной кубических решеток.
8.5.	Вычислить периоды идентичности вдоль прямых [111] и [011] в решетке кристалла AgBr, плотность которого 6,5 г/см3. Решетка кубическая типа NaCl.
8.6.	Определить отношение периодов идентичности вдоль направлений [100], [110] и [111] для простой, объемно- и гранецентрированной кубических решеток.
8.7.	Определить структуру элементарной ячейки кристалла, принадлежащего к кубической системе с осями симметрии 4-го порядка, если известно, что межплоскостное расстояние для системы плоскостей (100)	158 пм, а для плоскостей (ПО) d2 = 223 пм. Плотность
кристалла 19,3 г/см3.
54
п
+2	.....................
+7	.........................
О .............,	е ,...........
-7	........................
-2	....................
Рнс. 8.2
8.8.	Параллельный пучок рентгеновского излучения с длиной волны X падает в произвольном направлении на плоскую прямоугольную решетку с периодами а и ft. Какая картина будет наблюдаться на экране, расположенном параллельно решетке? Найти направления на дифракционные максимумы.
8.9.	Плоский пучок рентгеновского излучения падает на трехмерную прямоугольную простую решетку с периодами a, ft, с. Найти направления на дифракционные максимумы, если направление падающего пучка параллельно ребру а элементарной ячейки. Для каких длин волн будут наблюдаться максимумы?
8.10.	Плоский пучок рентгеновского излучения падает в произвольном- направлении на простую кубическую решетку с постоянной а. Для каких длин волн возможны дифракционные максимумы?
8.11.	Показать на примере простой кубической решетки, что формула Вульфа — Брэгга является следствием условий Лауэ.
8.12.	Найти постоянную решетки AgBr (тип решетки NaCl), если известно, что /Са-линия ванадия отражается в первом порядке от системы плоскостей (100) под углом скольжения О = 25,9°.
8.13.	Вычислить длину волны рентгеновкого излучения, которое отражается во втором порядке от системы плоскостей (100) кристалла NaCl (см. рис. 8.1) под углом скольжения 0 = 25,0°. Найти также угол, под которым это излучение отражается в максимальном порядке от данной системы плоскостей.
8.14.	Монокристалл NaCl (см. рис. 8.1) снимают по методу Лауэ вдоль оси четвертого порядка (ось z) на фотопластинку, отстоящую от кристалла на L = 50 мм. Найти для максимумов, соответствующих отражениям от плоскостей (031) и (221):
а)	их расстояния до центра лауэграммы;
б)	длины волн рентгеновского излучения.
8.15.	Пучок рентгеновского излучения с длиной волны X падает на кристалл NaCl (см. рис. 8.1), поворачивающийся вокруг оси симметрии четвертого порядка, причем направление падающего пучка перпендикулярно к оси вращения. Определить X, если направления на максимумы второго и третьего порядков от системы плоскостей (100) образуют между собой угол а = 60°.
8.16.	Пучок рентгеновского излучения с X = 71 пм падает на вращающийся монокристалл металла с кубической решеткой, который расположен на оси цилиндрической съемочной камеры радиусом 57,3 мм. Направление падающего пучка перпендикулярно к оси вращения (оси камеры). Полученная рентгенограмма состоит из системы максимумов, расположенных по слоевым линиям (рис. 8.2). Установить тип решетки металла (объемно- или гранецентрированная) и ее постоянную а, если расстояние между слоевыми линиями п = 2 и
55
п --- —2 при вращении вокруг направлений [НО] и [111] равно соответственно 65,0 и 23,5 мм.
8.17.	Какие порядки отражения моноэнергетического рентгеновского излучения пропадут при переходе от простой кубической решетки к объемно- и гранецентрированной? Постоянные всех трех решеток предполагаются одинаковыми. Рассмотреть случаи отражения от плоскостей (100), (ПО) и (111).
8.18.	Установить Миллеровские индексы h, k, I плоскостей, отражение от которых дает первые пять линий дебаеграммы для гране- и объемноцентрированной кубических решеток.
8.19.	Вычислить углы дифракции 20 для первых пяти линий дебаеграммы:
а) алюминия и б) ванадия, если X = 154 пм.
8.20.	Определить индексы отражений h*, k*, I* и соответствующие им межплоскостные расстояния для трех линий дебаеграммы алюминия, которым отвечают углы дифракции (20) 17 30', ЗЗс50' и 54с20' при X 71 пм.
8.21.	Узкий пучок электронов с энергией 25 кэВ проходит через тонкую поликристаллическую пленку и образует на плоском экране на расстоянии L --- 20,0 см от пленки систему дифракционных колец. Диаметр первого кольца/? = 13,1 мм. Вычислить постоянную решетки. Известно, что она кубическая объемноцентрированная.
8.22.	В электронограмме дебаевского типа от поликристалличес-кой пленки с кубической решеткой отношение диаметров первых двух дифракционных колец равно 1 : 1,4. Имея в виду, что диаметры этих колец значительно меньше расстояния между пленкой и экраном, определить тип решетки (объемно- или гранецентрированная).
Энергия связи и теплоемкость кристаллов
8.23.	Вычислить константу Маделунга для одномерного кристалла — цепочки ионов, чередующихся по знаку заряда. При расчете иметь в виду разложение In (1 + х) в ряд.
8.24.	Найти с помощью формулы (8.3):
а)	выражение для энергии связи ионного кристалла в равновесном состоянии;
б)	показатель п для кристаллов NaCl и CsCl (см. рис. 8.1), энергия связи которых в равновесном состоянии равна соответственно 765 и 627 кДж/мбль.
8.25.	Кристалл NaCl, коэффициент сжимаемости которого Л = 3,47 • 10~11 Па-1, подвергли всестороннему сжатию, в результате чего его объем уменьшился на 1,0%. Найти:
а)	давление, под которым находится кристалл;
б)	приращение объемной плотности энергии связи кристалла.
8.26.	Коэффициент сжимаемости кристалла NaCl (см. рис. 8.1) в равновесном состоянии К = 3,47 • 10-11 Па-1. Вычислить с помощью формулы (8.3):
а)	показатель п;
б)	энергию связи моля кристалла в равновесном состоянии.
56
8.27.	То же, что в предыдущей задаче, но для кристалла CsCl (см. рис. 8.1), коэффициент сжимаемости которого = 5,02 • 10-11 Па-1.
8.28.	Кристалл NaCl (см. рис. 8.1), коэффициент сжимаемости которого в равновесном состоянии К = 3,47 • 10-11 Па-1, подвергли всестороннему растяжению. Найти с помощью формулы (8.3), насколько увеличится расстояние между ионами, когда кристалл окажется растянутым до теоретического предела прочности (при котором отрицательное давление станет максимальным). Каково значение этого давления?
8.29.	Наряду с формулой (8.3) часто пользуются другим выражением для энергии связи ионных кристаллов:
U = —aq4r + Ле”г/₽,
где а и q имеют прежний смысл; Лир — некоторые новые постоянные. Используя эту формулу, найти:
а)	выражение для энергии связи ионного кристалла в равновесном состоянии; вычислить постоянную р для кристалла NaCl (см. рис. 8.1), энергия связи которого в равновесном состоянии равна 765 кДж/моль;
б)	выражение для коэффициента сжимаемости кристаллов с решетками типа NaCl в равновесном состоянии.
8.30.	Определить колебательную энергию и теплоемкость кристалла при температуре Т, считая каждый атом решетки квантовым гармоническим осциллятором и полагая, что кристалл состоит из N одинаковых атомов, колеблющихся независимо друг от друга с одинаковой частотой и. Упростить полученное выражение для теплоемкости при feT » Йи и feT « Йсо.
8.31.	Рассмотрим одномерную модель кристалла — цепочку из /V одинаковых атомов, у которой крайние атомы неподвижны. Пусть а — период цепочки; пг — масса атома; х — коэффициент квазиупру-гой силы. Учитывая взаимодействие лишь между соседними атомами, найти:
а)	уравнение колебаний данной цепочки и спектр собственных значений волнового числа k;
б)	зависимость частоты колебаний цепочки от волнового числа, а также полное число возможных колебаний; определить максимальную частоту колебаний и соответствующую ей длину волны;
в)	зависимость фазовой скорости от волнового числа и отношение фазовых скоростей, соответствующих самым длинным и самым коротким волнам;
г)	число собственных колебаний цепочки в интервале частот (го, го -г
8.32.	Считая скорость распространения колебаний не зависящей от частоты и равной v, найти для одномерного кристалла — цепочки из N одинаковых атомов длиной L:
а)	число продольных колебаний в интервале частот (<о, <о + dot);
б)	характеристическую температуру 0;
в)	молярную колебательную энергию и молярную теплоемкость при температуре Т; упростить полученное выражение для теплоемкости, если Т 0 и Т 0.
57
8.33.	Для двумерного кристалла число нормальных колебаний одной поляризации в интервале частот (<о, со + dco) определяется формулой:
dZa = (S/2nv2)codco,
где S — площадь кристалла; v — скорость распространения колебаний. Считая v не зависящим от со, найти для плоской квадратной решетки из одинаковыых атомов, содержащей п0 атомов на единицу площади:
а)	характеристическую температуру 0;
б)	молярную колебательную энергию и молярную теплоемкость при температуре Т; упростить полученное выражение для теплоемкости при Т 0 и Т <?’ 0.
8.34.	То же, что в предыдущей задаче, но для трехмерного кристалла — кубической решетки, содержащей пп одинаковых атомов на единицу объема. Известно, что для трехмерного кристалла число нормальных колебаний одной поляризации в интервале частот (со, со + dco) определяется формулой:
dZu, =
где V — объем кристалла.
8.35.	Считая, что скорости распространения продольных и поперечных колебаний не зависят от частоты и равны соответственно v( и vt, найти число колебаний dZ в интервале частот (со, со + dco) и характеристическую температуру 0:
а)	двумерного кристалла — квадратной решетки из N одинаковых атомов, площадь решетки S;
б)	трехмерного кристалла — кубической решетки из N одинаковых атомов, объем решетки V.
8.36.	Вычислить характеристическую температуру железа, в котором скорости распространения продольных и поперечных колебаний равны соответственно 5,85 и 3,23 км/с.
8.37.	Вычислить с помощью формулы Дебая:
а)	отношение &Ei'E0, где ДЕ — энергия, которую необходимо сообщить кристаллу при нагревании от О К до 0; Ео — энергия нулевых колебаний;
б)	энергию, которую необходимо сообщить молю кристалла алюминия, чтобы нагреть его от 0/2 до 0.
8.38.	Используя формулу Дебая, вычислить молярную теплоемкость кристаллической решетки при температурах 0/2 и 0. На сколько процентов отличается теплоемкость при температуре 0 от классического значения?
8.39.	Вычислить характеристическую температуру и энергию, Дж/моль, нулевых колебаний у серебра, если известно, что при температурах 16 и 20 К его теплоемкость равна соответственно 0,87 и 1,70 Дж/ (К-моль).
8.40.	На рис. 8.3 показан график, характеризующий зависимость теплоемкости кристалла от температуры (по Дебаю). Здесь — классическая теплоемкость; 0 — характеристическая температура. С помощью этого графика найти:
58
а)	характеристическую температуру для серебра, если при Т — = 65 К его молярная теплоемкость равна 15 Дж/ (моль • К);
б)	молярную теплоемкость алюминия при Т = 100 К, если при Т = 280 К она равна 22,5 Дж/ (моль • К);
в)	максимальную частоту колебаний <омакс Для меди, у которой при Т = 125 К теплоемкость отличается от классического значения на 25%.
8.41.	Оценить максимальные значения энергии и импульса фонона (звукового кванта) в алюминии.
8.42.	В кристалле из N одинаковых атомов число фононов в интервале частот (<о, и + dco) при температуре Т равно
n(a)da = 9N — --------—-
v	\kQ hu/ki ,
'	' е — I
где 0 — характеристическая температура кристалла.
а.	Получить это выражение с помощью формулы для dZa из задачи 8.34.
б.	Определить наиболее вероятные значения энергии и частоты фононов при температуре 0/2.
в.	Найти темпеоатУоу. начиная с
наиболее вероятная частота фононов равна их максимальной частоте. Температура 0 предполагается известной.
г. Найти характер зависимости полного числа фононов в кристалле от Т при Т « 0 и Г» 0.
8.43.	Рассеяние света прозрачным твердым телом можно рассматривать как результат процесса рассеяния фотонов на фононах, считая при этом, что фотоны в веществе обладают импульсом 1тм с', где с' — скорость света в среде. Используя законы сохранения энергии и импульса, показать, что свет, рассеянный под углом 0, будет содержать кроме несмещенной компоненты две смещенные, относительный сдвиг которых Аи/со = 2 (vic') sin (0/2), где <в — частота падающего света; v — скорость звука в среде.
8.44.	Некоторые вещества (например, парамагнитные соли) при очень низких температурах обнаруживают теплоемкость Сг, во много раз превосходящую решеточную теплоемкость Среш. Установлено, что теплоемкость С; обусловлена внутренними степенями свободы, в частности взаимодействием спинов с внутрикристаллическими полями. Полагая, что каждый атом независимо от других может ориентиро
ваться своим спином параллельно или антипараллельно относительно некоторого направления и что разность энергий атома в этих состояниях равна АЕ, найти:
а)	зависимость С; от температуры Т;
б)	отношение kTI&E, при котором С; имеет максимум;
в)	отношение С;макс/Срсш для случая, когда С;макс отвечает температуре Т = 0/100; 0 — характеристическая температура.
59
9.	МЕТАЛЛЫ И ПОЛУПРОВОДНИКИ
•	Концентрация свободных электронов с энергией в интервале (Е, Е + dE)\
„	„	"|/2т3	"|/Е dE
п (£) dE=f (Е) g (Е) dE =	-----У	,	(9.1)
\+<AE~Ef)‘
где f (Е) = [1 + е >	J-1 — функция Ферми—Дирака; g (Е) — плот-
ность состояний; Ef — уровень Фермн. Для металлов
Г	л2 / kT \2 |	„ Й2	...
£/=-£/« 1— „ I р I ;	£/о— (Зл2л) z ,
|	lz \ £уо / |	2Ш
гдеЕ^ — уровень Ферми при О К; л — концентрация свободных электронов. В этих формулах за начало отсчета Е и Ef принято дно зоны проводимости. • Постоянная Холла для полупроводника:
R	—-----Ь-е Пд Ьд ,	(9.2)
jB ес (пеЬе + пдЬд)г
где е — заряд электрона; пе н пд — концентрация электронов и дырок; Ье и Ьд — ИХ ПОДВИЖНОСТИ.
Свободные электроны в металлах и полупроводниках
9.1.	Найти с помощью соотношения неопределенностей число свободных электронов с кинетической энергией в интервале (Т, Т 4- dT) в металле при О К. Металл взять в форме прямоугольного параллелепипеда объемом V. При определении числа квантовых состояний считать, что физически различны только те состояния, у которых проекции импульса электрона различаются не меньше чем на &рх = 2л/г//х, 1Х — ребро параллелепипеда объема V (аналогично для и Дрг).
9.2.	Получить с помощью формулы (9.1) выражение для максимальной кинетической энергии свободных электронов Тмаас в металле при О К, если их концентрация равна п. Вычислить Тмакс для серебра, полагая, что на каждый атом приходится один свободный электрон.
9.3.	Найти с помощью формулы (9.1) при О К:
а)	среднюю кинетическую энергию свободных электронов в металле, если известна их максимальная кинетическая энергия Тмакс;
б)	суммарную кинетическую энергию свободных электронов в 1 см3 золота, полагая, что на каждый атом приходится один свободный электрон.
9.4.	Найти долю свободных электронов в металле при О К, кинетическая энергия которых больше половины максимальной.
9.5.	Вычислить температуру идеального газа, у которого средняя кинетическая энергия частиц равна средней кинетической энергии свободных электронов в меди при О К. Считать, что на каждый атом приходится один свободный электрон.
9.6.	Найти интервал в электрон-вольтах между соседними уровнями свободных электронов в металле при О К вблизи уровня Ферми, 60
з Г	5л2 / kT V
— £ j о 1 — ---I-----
5 1 I 12 1 Еп /
если объем металла И = 1,00 см3 и концентрация свободных электронов п = 2,0 • 1022 см-3.
9.7.	Часто при расчетах пренебрегают различием значений £у и Е10. Оценить, на сколько процентов отличается Et от £/0 для вольфрама при температуре, близкой к его температуре плавления. Считать, что на каждый атом приходится два свободных электрона.
9.8.	Найти для металла при 0 К, максимальная скорость свободных электронов которого равна vm, средние значения:
а)	скорости свободных электронов;
б)	их обратной скорости 1/п.
9.9.	Вычислить наиболее вероятную и среднюю скорости свободных электронов в меди при 0 К, если известно, что их концентрация 8,5 • 1022 см-3.
9.10.	Показать на примере простой кубической решетки, содержащей по одному свободному электрону на атом, что минимальная дебройлевская длина волны свободных электронов приблизительно равна удвоенному расстоянию между соседними атомами.
9.11.	Получить функцию распределения свободных электронов по дебройлевским длинам волн в металле при 0 К. Изобразить ее график.
9.12.	Средняя энергия свободных электронов в металле при температуре Т равна:
<£> —
Найти с помощью этой формулы для серебра с концентрацией свободных электронов 6,0 • 1022 см-3:
а)	отношение теплоемкостей электронного газа и кристаллической решетки при Т = 300 К;
б)	температуру, при которой теплоемкость электронного газа равна теплоемкости решетки.
9.13.	Концентрация свободных электронов в металлическом натрии п = 2,5 • 1022 см-3. Найти давление электронного газа р; показать, что р = 2/3£, где £—объемная плотность его кинетической энергии.
9.14.	Концентрация свободных электронов в металле со скоростью в интервале (v, v Ч- dv) определяется следующим выражением:
п (v) dv = 2 (——'j --—-------, dv = dvx dv„ dvz.
I 2лЛ / . , (Е-ЕА/ЪТ	x y 2
'	' 1+e j
а.	Получить это выражение исходя из формулы (9.1).
б.	Найти при 0 К концентрацию электронов с проекциями скоростей в интервале (vx, vx + dvx), если максимальная скорость свободных электронов равна vm.
9.15.	Доказать с помощью формулы из предыдущей задачи, что при контакте двух различных металлов их уровни Ферми находятся на одной высоте.
9.16.	Показать с помощью формулы из задачи 9.14, что число термоэлектронов, вылетающих за единицу времени с единицы поверхно
61
сти металла со скоростями в интервале (v, v + dv), равно
v (v) dv ~2л(т/2лЬ)я	v3 dv, ,
где Te — кинетическая энергия термоэлектрона; A — работа выхода. Иметь в виду, что А > kT.
9.17.	Найти с помощью формулы из предыдущей задачи:
а)	среднюю кинетическую энергию термоэлектронов;
б)	плотность тока термоэмиссии с поверхности металла;
в)	работу выхода, если увеличение температуры от 1500 до 2000 К приводит к возрастанию термоэмиссионного тока в 5,0 • 103 раз.
9.18.	Определив концентрации освободных электронов и дырок, показать, что при достаточно низких температурах уровень Ферми в чистом беспримесном полупроводнике находится посредине запрещенной зоны.
9.19.	Концентрация свободных электронов в полупроводнике п-типа при достаточно низких температурах равна
ne = /2^ (mkT! 2лЬ2)3/* е-д^2*г,
где п0 — концентрация донорных атомов; А£ — их энергия активации.
а.	Получить это выражение с помощью распределения Ферми.
б.	Найти положение уровня Ферми.
Свойства металлов и полупроводников
9.20.	Электропроводность металла а = ne2xitn, где п — концентрация свободных электронов; епт — заряд и масса электрона; т — время релаксации, которое связано со средней длиной свободного пробега электрона соотношением <Х> = т (v>; <и> — средняя скорость электронов. Вычислить т, (Х> и подвижность свободных электронов меди, если п = 8,5 • 1022 см-3 и удельное сопротивление Р = 1,60 • 10-в Ом • см. Сравнить полученное значение (X) с расстоянием между атомами меди.
9.21.	Вычислить коэффициент преломления металлического натрия для электронов с кинетической энергией Т = 135 эВ. Считать, что на каждый атом приходится один свободный электрон.
9.22.	Пусть свободные электроны под действием некоторой причины сместились на расстояние х перпендикулярно к поверхности плоского слоя металла. В результате возникнут поверхностный заряд и соответствующая возвращающая сила, что приведет к возбуждению так называемых Плазменных колебаний. Определить частоту этих колебаний в меди, концентрация свободных электронов у которой п = = 8,5 • 1022 см-3. Какова энергия плазменных'волн в меди?
9.23.	Опыт показывает, что щелочные металлы становятся прозрачными в ультрафиолетовой части спектра. Исходя из модели свободных электронов, найти граничную длину волны света, начиная с которой будет наблюдаться это явление у металлического натрия (концентрация свободных электронов п — 2,5 • 1022 см-8).
62
9.24.	Щелочные металлы обнаруживают парамагнетизм, не зави-
сящий от температуры. Он может быть объяснен так. При включении внешнего магнитного поля В свободные электроны с антипараллель-
ными вектору В спинами начнут поворачиваться вдоль В, но при этом в соответствии с принципом Паули они будут переходить на более высокие незанятые уровни. Этот процесс будет происходить до тех пор, пока уменьшение магнитной энергии электронов не сравняется с уве-
личением их кинетической энергии. Найти отсюда парамагнитную вос-
приимчивость металла объемом 1 см3 в слабом магнитном поле, если
концентрация свободных электронов п = = 2,0 • 1022 см-3.
9.25.	Красная граница фотопроводимости чистого беспримесного германия при очень низких температурах соответствует Хо « 1,7 мкм. Вычислить температурный коэффициент сопротивления этого полупроводника при Т = 300 К-
9.26.	Найти минимальную энергию, необходимую для образования пары электрон — дырка в чистом теллуре при 0 К, если известно, что его электропроводность возрастает в г) = 5,2 раза при увеличении температуры от 7\ = 300 К ДО 7\ 400 К-
9.27. На рис. 9.1 показан график зависимости логарифма электро-
проводности от обратной температуры (Т, К) для кремния с примесью бора (полупроводник n-типа). Объяснить характер этого графика. Найти с его помощью ширину запрещенной зоны кремния и энергию
активации атомов бора.
9.28. Образец из чистого беспримесного германия, у которого ширина запрещенной зоны 0,72 эВ, а подвижности электронов и дырок 3600 и 1800 см2/ (В • с), находится при 300 К в поле электромагнитного излучения. При этом его удельное сопротивление 43Ом • см. Определить, какая доля электропроводности образца обусловлена фотопроводимостью. Указание-, использовать решение задачи 9.18.
9.29. Удельное сопротивление чистого беспримесного германия при комнатной температуре р = 50 Ом • см. После включения источника света оно стало pj = 40 Ом • см, а через t = 8 мс, после выключения источника, р2 = 45 Ом • см. Найти среднее время жизни элек-
тронов и дырок.
9.30.	Вычислить с помощью формулы, приведенной в задаче 9.19, энергию активации донорных атомов в полупроводнике л-типа, если известно, что подвижность электронов 500 см2/(В • с), концентрация донорных атомов 5,0 • 1017 см~3 и удельное сопротивление при 50 К равно 1,5 кОм • см.
9.31.	При температуре Т= 300 К некоторый образец германия rt-типа имеет удельное сопротивление р = 1,70 Ом • см и постоянную Холла R = 7,0 • 10-1* СГСЭ. Найти:
а)	концентрацию и подвижность электронов проводимости;
б)	их среднюю длину свободного пробега.
63
9.32.	Пластинку из полупроводника p-типа шириной d = 1,0 см и длиной I — 5,0 см поместили в магнитное поле В = 5,0 кГс. К концам пластинки приложили постоянное напряжение U = 10,0 В. При этом холловская разность потенциала оказалась V 0,050 В и удельное сопротивление р = 2,5 Ом • см. Определить постоянную Холла, концентрацию и подвижность дырок.
9.33.	Рассмотрев характер движения электронов и дырок в полупроводнике с током во внешнем магнитном поле, найти зависимость постоянной Холла от концентрации и подвижности носителей тока.
9.34.	Вычислить разность подвижностей электронов и дырок в чисто беспримесном германии, если известно, что в магнитном поле В 3,0 кГс отношение поперечной напряженности электрического поля EL к продольной Е равно 0,060.
9.35.	В некотором образце германия, у которого подвижность электронов в 2,1 раза больше подвижности дырок, эффект Холла не наблюдается. Найти для этого образца:
а)	отношение концентраций электронов проводимости и дырок;
б)	какая часть электропроводности обусловлена электронами?
10.	ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕР
•	Радиус ядра, фм:
R - 1,4Л1/3,
где А — массовое число ядра.
•	Энергия связи ядра (в единицах массы):
£'св = 2тнч-(Д—Z) тп~Л1,
(Ю.1)
(10.2)
где Z — зарядовый номер ядра; А — массовое число; тн, тп и М — массы атома водорода, нейтрона и соответствующего атома. Для расчетов удобнее пользоваться формулой:
Есв = ZAH - (А - Z)A„ - А,	(10.3)
где Ан, Дл, А — избыток массы М — А атома водорода, нейтрона и нуклида,
соответствующего данному ядру.
•	Полуэмпирическая формула для энергии связи ядра, МэВ:
/а	/д___2Z)2	33 5
Е 14,0Л — 13,042/3—0.584-----— 19,3 —-------- +----— б, (10.4)
Д1/3	А	дЗ/4
+1 при четных А и Z;
0 при нечетном A (Z любое);
— 1 при четном А и нечетном Z.
• Полный механический момент атома:
F = J4- I, F - J г /, J b I — 1 , ..., | J — /|,	(10.5)
где J — механический момент электронной оболочки атома; I — спин ядра. Для разрешенных переходов AF 0, ±1; F — 0 у». Е = 0.
• jVfarHHTHbift момент ядра (точнее, его максимальная проекция):
И glp»,	(Ю.6)
где g — гидромагиитиый множитель; I — спии ядра; ря — ядериый магиетои. 64
•	Модель ядерных оболочек (рис. 10.1). Здесь j — квантовое число полного момента нуклона; цифры в кружках — число нуклонов одного сорта (протонов или нейтронов), которые за-' полияют все уровни, расположенные ниже соответствующей пунктирной линии—границы оболочки. Заполнение уровней протонами и нейтронами происходит независимо и в соответствии с принципом Паули.
•	Четность Р частицы с орбитальным моментом I и внутренней четностью Р, определяет-
•	Четность Р системы из двух частиц (и вообще из двух подсистем) с внутренними четностями Pi и Р2 и с относительным орбитальным моментом I:
P^P^i-l)1.	(Ю.8)
*	Четность системы п нуклонов (или электронов) с орбитальными моментами 12, ..., 1п:
Р =(-l)Z1 + '2 + " + '",	(10.9)
поскольку внутренние четности нуклона (и электрона) равны +1.
Рис. 10.1
Радиус, масса и энергия связи ядер
10.1.	Оценить плотность ядерного вещества, концентрацию нуклонов и объемную плотность электрического заряда в ядре.
10.2.	Рассеяние протонов тонкой свинцовой фольгой отвечает формуле Резерфорда при значениях Вр протонов, не превышающих 450 кГс • см. Оценить отсюда радиус ядер свинца.
10.3.	Результаты опытов по рассеянию быстрых электронов ядрами достаточно хорошо согласуются с распределением объемной плотности электрического заряда ядра р (г) со [1 + е<г~г»>/6|-1, где гп - 1,08Л 1/3 фм; б = 0,545 фм. Найти наиболее вероятный радиус распределения электрического заряда в ядре Ag. Сравнить полученный результат с радиусом этого ядра.
10.4.	В современной системе масс атомов за единицу а. е. м. принята 1/12 массы атома 12С (вместо старой единицы массы ME, равной 1/16 массы атома 16О). Найти связь между единицами а. е. м. и ME. Как изменились численные значения масс атомов при переходе от старой единицы массы к новой?
10.5.	Найти процентное содержание (атомное и массовое) изотопа 13С в природном углероде, который состоит из изотопов 12С и 13С. Атомная масса природного углерода и массы атомов обоих изотопов считать известными.
10.6.	Найти массы нуклонов ‘Н, 2Н и 16О, если известны разности масс, а. е. м. трех фундаментальных дублетов: JH2 — 2Н = 0,001548; 2Н3 — х/2 12С = 0,042306; 12С?Н4 — 16О = 0,036386.
3 Зак. 1896	65
10.7.	Найти с помощью формулы (10.3):
а)	энергию связи ядра, которое имеет одинаковое число протонов и нейтронов, а радиус — в полтора раза меньший радиуса ядра 27А1;
б)	энергию связи на один нуклон в ядрах 6Li, 40Ar, 107Ag и 208РЬ.
10.8.	Определить с помощью табличных значений масс нуклидов: а) энергию связи нейтрона и а-частицы в ядре 21Ne;
б)	энергию, необходимую для разделения ядра 1вО на четыре одинаковые частицы.
10.9.	Найти энергию возбуждения ядра 207РЬ, возникающего при захвате ядром 206РЬ нейтрона с пренебрежимо малой кинетической энергией.
10.10.	Вычислить энергию связи нейтрона в ядре 14N, если известно, что энергия связи ядер 14N и 13N равны 104,66 и 94,10 МэВ.
10.11.	Найти энергию, необходимую для разделения ядра 16О на а-частицу и ядро 12С, если известно, что энергии связи ядер 16О, 12С и 4Не равны 127,62; 92,16 и 28,30 МэВ.
10.12.	Определить энергию, выделяющуюся при образовании двух а-частиц в результате синтеза ядер 2Н и 6Li, если известно, что энергии связи на один нуклон в ядрах 2Н, 4Не и 6Li равны соответственно 1,11; 7,08 и 5,33 МэВ.
10.13.	Показать, что при равномерном распределении заряда по объему ядра энергия кулоновского отталкивания протонов £/кул =-= 0,6/2г2//?, где Z и /? — заряд и радиус ядра.
10.14.	Вычислить разность энергий связи зеркальных ядер 33Sh 33С1, если известно, что масса 33S меньше массы 33С1 на 0,00599 а. е. м. Сравнить полученную величину с разностью энергий кулоновского отталкивания протонов в этих ядрах (см. формулу из предыдущей задачи). Объяснить причину совпадения результатов.
10.15.	Считая, что разность энергий связи зеркальных ядер 23Na и 23Mg определяется различием только энергий кулоновского отталкивания в этих ядрах (см. формулу из задачи 10.13), вычислить их радиусы. Сравнить полученный результат с вычисленным по формуле для радиуса ядра.
10.16.	Вычислить с помощью полуэмпирической формулы:
а)	энергию связи ядер 40Са и 107Ag;
б)	энергию связи на один нуклон в ядрах 50И и 200Hg;
в)	массы атомов 45Sc и 70Zn.
10.17.	Определить с помощью формулы (10.4) заряд ядра, имеющего наименьшую массу среди ядер с одинаковым нечетным значением массового числа А. Предсказать с помощью полученной формулы характер активности (электронная или позитронная) следующих 0-ак-тивных ядер: 103Ag, 127Sn и 141Cs.
Спин и магнитный момент ядра
10.18.	Сколько компонент сверхтонкой структуры имеют основные термы следующих атомов: 3Н (2Si/2); 6Li (2Si/2); 9Ве С50); 15N (45з/2) и 35С1 (2Pi/2)- В скобках указан основной терм электронной оболочки атома.
66
10.19.	Определить спин ядра 59Со, основной терм атома которого 4/7э/2 содержит восемь компонент сверхтонкого расщепления.
10.20.	Найти число компонент сверхтонкого расщепления спектральных линий 2Pi /2 -> 2Si/2 и 2Рз/2 ->2Si/2 Для атомов 39К- Спин ядра предполагается известным.
10.21.	Два герма одного и того же атома имеют различные квантовые числа J (Jj и J2). Какое квантовое число (J или /) можно определить по числу компонент N сверхтонкого расщепления каждого терма в том случае, когда числа компонент для обоих термов:
а) одинаковы = N2)-, б) различны (А\ =/= М2)?
10.22.	Отношение интенсивностей компонент сверхтонкого расщепления спектральной линии ~P\ji -*-2Si/2 натрия равно приблизительно 10 : 6. Имея в виду, что сверхтонкая структура вызвана расщеплением терма 231 /2 (расщеплениетерма 2Р</2 ничтожно мало), найти спин ядра 23Na.
10.23.	Электронная оболочка атома создает в месте расположения ядра магнитное поле Во, направление которого совпадает с направлением механического момента электронной оболочки J. Добавочная энергия взаимодействия магнитного момента ядра с этим полем зависит от ориентации механических моментов J и I, которая определяется правилами пространственного квантования. Исходя из этих соображений, показать, что интервалы между соседними подуровнями, характеризуемыми квантовыми числами F, F — 1, F + 2, .... относятся как (F  1) : (F т 2): ...
10.24.	Терм 2Dz/2 атома 209Bi имеет четыре компоненты сверхтонкого расщепления, причем отношение интервалов между соседними компонентами равно 4:5:6. Найти с помощью правила интервалов (см. предыдущую задачу) спин ядра, а также число компонент сверхтонкого расщепления линии 2Si/2 ->2Оз/2.
10.25.	Найти полное число компонент зеемановского расщепления подуровней сверхтонкой структуры терма 2Р3/2 атома МС1 в слабом магнитном поле.
10.26.	В сильном магнитном поле каждый из подуровней терма 2Si/2 атомов 42К и 85Rb расщепляется соответственно на пять и шесть компонент. Найти спин ядер этих атомов.
10.27.	Вычислить угловые скорости прецессии электрона, протона и нейтрона в магнитном поле В = 1,00 кГс.
10.28.	В опытах по изучению магнитным резонансным методом магнитных свойств атомов 25Mg в основном состоянии 230 обнаружено резонансное поглощение энергии при напряженности постоянного магнитного поля В = 5,4 кГс и частоте переменного магнитного поля v0 = 1,40 МГц. Определить гиромагнитный множитель и, зная спин, магнитный момент ядра.
10.29.	Магнитным резонансным методом исследовали магнитные свойства молекул 7Li19F, у которых момент импульса электронной оболочки равен нулю. При напряженности постоянного магнитного поля В 5,00 кГс были обнаружены два резонансных пика на частотах переменного магнитного поля V] 8,30 МГц и v2 -- 2,00 МГц, которые, как показали контрольные опыты, относятся соответственно з*	67
к ядрам лития и фтора. Найти магнитные моменты этих ядер. Спины считать известными.
10.30.	В газовой модели ядра принимается, что нуклоны образуют газ, заполняющий объем ядра и подчиняющийся распределению Ферми. Оценить из этих соображений максимальную кинетическую энергию нуклонов в ядре, считая такой газ полностью вырожденным. Для оценки принять, что число протонов в ядре равно числу нейтронов.
10.31.	С помощью модели ядерных оболочек написать конфигурации основных состояний ядер 7Li, 13С и 25Mg.
10.32.	Определить с помощью модели ядерных оболочек спин и четность основных состояний ядер 13С и 13N.
10.33.	Найти с помощью модели ядерных оболочек спин и четность основного состояния следующих ядер:
а) 3Н; б) 3Не; в) 15N и 15О.
10.34.	Определить с помощью модели ядерных оболочек спины и четности основных состояний ядер: 17О, 29Si, 39К, 45Sc и 63Си.
10.35.	Используя векторную модель, показать, что гиромагнитный множитель нуклона, находящегося в состоянии /, /,
gj = gi± gs~gl.,
s; si 2Z+1
где знак плюс для j = I + 1/2; знак минус для / = I — 1/2; gs и gt — спиновый и орбитальный гиромагнитные множители.
10.36.	Воспользовавшись формулой из предыдущей задачи, вычислить магнитный момент в состояниях Si/2, Pi/2 и рз/2'-
а) нейтрона (gt = 0); б) протона (gt = 1).
10.37.	Определить с помощью формулы в задаче 10.35 квантовое число I протона в /-состоянии, если известно, что в этом состоянии его магнитный момент р = 5,79ря.
10.38.	Определить с помощью модели ядерных оболочек магнитные моменты ядер: а) 3Н и 3Не; б) 17О и 39К в основном состоянии.
10.39.	Спин ядра 19F вопреки предположению о равномерном заполнении ядерных оболочек равен не 5/2, а 1/2. Считая, что магнитный момент ядра, равный 2,63 ря, определяется непарным протоном, определить уровень, на котором этот протон находится. Гиромагнитные множители протона gs = 5,58 и gt = 1.
11. РАДИОАКТИВНОСТЬ
• Основной закон радиоактивного распада:
e“w; Х=1/т = 1п 2/7,	(И.1)
где X — постоянная распада; т — среднее время жизни радиоактивных ядер; Т — их период полураспада.
•	Удельная активность — активность единицы массы вещества.
•	Распределение Пуассона:
(п\ •
р (п) = (п)п е ' On!,	(11.2)
68
где р (п) — вероятность совершения п случайных событий в течение некоторого промежутка времени, среднее число событий для которого <п>.
•	Гауссово (нормальное) распределение:
р (е) =--т---ехр (—е3/2п2),	(П-3)
о У 2л
где е - \п— (п>| —отклонение от среднего; а — средняя квадратическая (стандартная) погрешность отдельного измерения,
а- ~|/(п) st Д/ п .
•	Средняя квадратическая погрешность суммы или разности независимых измерений:	___________
о =-- Д/of 4-o'J -+...,	(11.4)
где о,- — средние квадратические погрешности независимых измерений.
Законы радиоактивного распада
11.1.	Найти вероятность распада радиоактивного ядра за промежуток времени t, если его постоянная распада равна л.
11.2.	Показать, что среднее время жизни радиоактивных ядер т= 1'А., где X — их постоянная распада.
11.3.	Какая доля первоначального количества ядер 90Sr;
а)	останется через 10 и 100 лет;
б)	распадается за одни сутки; за 15 лет?
11.4.	Имеется пучок нейтронов с кинетической энергией 0,025 эВ. Какая доля нейтронов распадается на длине пучка 2,0 м?
11.5.	Вычислить постоянную распада, среднее время жизни и период полураспада радиоактивного нуклида, активность которого уменьшается в 1,07 раза за 100 сут.
11.6.	Определить возраст древних деревянных предметов, у которых удельная активность 14С составляет 3 5 удельной активности этого же нуклида в только что срубленных деревьях.
11.7.	Свежеприготовленный препарат содержит 1,4 мкг радиоактивного 24Na. Какую активность он будет иметь через сутки?
*	11.8. Определить число радиоактивных ядер в свежеприготовлен-
ном препарате 82Вг, если известно, что через сутки его активность стала равной 7,4 • 109 Бк (0,20 Ки).
11.9.	Вычислить удельную активность чистого 239Ри.
11.10.	Сколько миллиграммов 0-активного 89Sr следует добавить к 1 мг неактивного стронция, чтобы удельная активность препарата стала равной 5,06 • 1013 Бк г (1370 Ки'г)?
'	11.11. В кровь человека ввели небольшое количество раствора,
содержащего 24Na активностью Л = 2,1 • 103 Бк. Активность 1 см3 крови, взятой через t = 5,0 ч после этого, оказалась а — 0,28 Бк см3. Найти объем крови человека.
11.12.	Препарат содержит две 0-активные компоненты с различными периодами полураспада. Измерения дали следующую зависимость скорости счета N от времени t:
t, ч.........	0	1	2	3	5 Ю 20	30
-V, с-1 ... 60,0	34.3	21.1	14.4	8.65	5,00	2.48	1.25
69
Определить периоды полураспада обеих компонент и отношение количеств радиоактивных ядер этих компонент в момент t = 0.
11.13.	При радиоактивном распаде ядер нуклида Xi образуется радионуклид А.2. Их постоянные распада равны и Х2. Полагая, что в начальный момент препарат содержал только ядра нуклида Xj в количестве N10, определить:
а)	количество ядер Л2 через промежуток времени t;
б)	промежуток времени, через который количество ядер Л2 достигнет максимума;
в)	в каком случае может возникнуть состояние переходного равновесия, при котором отношение количества обоих нуклидов будет оставаться постоянным. Чему равно это отношение?
11.14.	226Ra, являясь продуктом распада 238U, содержится в последнем в количестве одного атома на каждые 2,80 • 106 атомов урана. Найти период полураспада 2:i8U, если известно, что он значительно больше периода полураспада 226Ra, который равен 1620 годам.
11.15.	При |3-распаде 112Pd возникает (3-активный нуклид 112Ag. Их периоды полураспада равны соответственно 21 и 3,2 ч. Найти отношение максимальной активности нуклида 112Ag к первоначальной активности препарата, если в начальный момент препарат содержал только нуклид ll2Pd.
'! 11.16. Радионуклид ll8Cd испытывает превращения по цепочке:
118 Cd--->- 118 In --► 118 Sn (стабилен)
30 мин	4,5 мин
(под стрелками указаны соответствующие периоды полураспада). Считая, что в момент t = 0 препарат содержал только Cd, найти:
а)	какая часть ядер превратится в стабильные ядра через 60 мин;
б)	во сколько раз уменьшится активность препарата через 60 мин.
11.17.	Радионуклид испытывает превращения по цепочке: Аг -> А, -> А3 ... (под стрелками указаны соответствующие по-
Xj	Хд
стоянные распада). Полагая, что в начальный момент препарат содержал только ядра нуклида Аг в количестве Л\о, найти выражение, определяющее закон накопления нуклида А 3.
11.18.	Определить массу свинца, который образуется из 1,0 кг 238U за период, равный возрасту Земли (2,5  109 лет).
11.19.	Препарат содержит 226Ra в количестве 10 мкг и продукты его распада, с которыми он находится в состоянии переходного равновесия. Определить с помощью таблиц Приложения:
а)	a-активность 222Rn и p-активность 210РЬ данного препарата;
б)	суммарную a-активность препарата.
11.20.	Радионуклид 27Mg образуется с постоянной скоростью q 5,0 • Ю10 ядро/с. Определить количество ядер 27Mg, которое накопится в препарате через промежуток времени:
а)	значительно превосходящий его период полураспада;
б)	равный периоду полураспада.
11.21.	Радионуклид 124Sb образуется с постоянной скоростью q = = 1,0 • 109 ядро/с. С периодом полураспада Т = 60 сут он превращается в стабильный нуклид 124Те. Найти:
70
а)	через сколько времени после начала образования активность 124Sb станет А = 3,7 • 108 Бк (10 мКи);
б)	какая масса нуклида 124Те накопится в препарате за четыре месяца после начала его образования.
11.22.	Радионуклид Alt образующийся с постоянной скоростью q ядро/с, испытывает цепочку превращений по схеме:
A1-j^-A2-j^- А3 (стабилен)
(под стрелками указаны постоянные распада). Найти закон накопления количества ядер Аг, Л2 и А3 с течением времени, полагая, что в начальный момент препарат их не содержал.
11.23.	Радионуклид 138Хе, образующийся с постоянной скоростью q = 1,0 • 1010 ядро/с, испытывает превращения по схеме:
138 Хе----► 138 Cs--► 138 Ва (стабилен)
1 7 мин	32 мин
(под стрелками указаны периоды полураспада). Вычислить суммарную активность данного препарата через 60 мин после начала накопления.
11.24.	Радионуклид "Мо с периодом полураспада 67 ч в результате Р-распада превращается в стабильный нуклид "Тс. При этом 75% P-превращений идет через изомерное состояние "Тс"1, период полураспада которого 6,04 ч. Определить:
а)	относительное число стабильных ядер в препарате через 5,00 ч, полагая, что в начальный момент препарат содержал только "Мо;
б)	число стабильных ядер "Тс в препарате через 20 ч после начала накопления, считая, что "Мо образуется с постоянной скоростью 1,0 • 1010 ядро/с.
а- и р-Распады
11.25.	Покоящееся ядро 213Ро испустило а-частицу с кинетическое энергией Та = 8,34 МэВ. При этом дочернее ядро оказалось непосредственно в основном состоянии. Найти полную энергию, освобождаемую в этом процессе. Какую долю этой энергии составляет кинетическая энергия дочернего ядра? Какова скорость отдачи дочернего ядра?
11.26.	Ядра 210Ро испускают а-частицы с кинетической энергией Т — 5,30 мэВ, причем практически все дочерние ядра образуются’ непосредственно в основном состоянии. Определить:
а)	количество тепла, которое выделяет 10,0 мг препарата 210Ро за период, равный среднему времени жизни этих ядер;
б)	первоначальную активность препарата 210Ро, если за время, равное его периоду полураспада, препарат выделил 2,2 кДж тепла.
11.27.	Распад ядер 210Ро происходит из основного состояния и сопровождается испусканием двух групп а-частиц: основной с энергией 5,30 МэВ и слабой (по интенсивности) с энергией 4,50 МэВ. Найти энергию а-распада этих ядер и энергию у-квантов, испускаемых дочерними ядрами.
71
11.28.	Распад ядер 226Th происходит из основного состояния и сопровождается испусканием а-частиц с энергией 6,33; 6,23; 6,10 и 6,03 МэВ. Рассчитать и построить схему уровней дочернего ядра.
11.29.	При распаде ядер 212Ро испускаются четыре группы а-частиц: основная с энергией 8,780 МэВ и длиннопробежные с энергиями 9,492; 10,422 и 10,543 МэВ. Рассчитать и построить схему уровней ядра 212Ро, если известно, что дочерние ядра во всех случаях возникают непосредственно в основном состоянии.
11.30.	Оценить высоту кулоновского барьера для а-частиц, испускаемых ядрами 222Rn (закруглением вершины барьера пренебречь). Какова у этих ядер ширина барьера (туннельное расстояние) для а-частиц, вылетающих с кинетической энергией 5,5 МэВ?
11.31.	Определить отношение высоты центробежного барьера к высоте кулоновского барьера для а-частиц, испускаемых ядрами 209Ро, с орбитальным моментом I 2. Закруглением вершины кулоновского барьера пренебречь.
11.32.	Для испущенной ядром а-частицы, кинетическая энергия Т которой значительно меньше высоты кулоновского барьера, коэффициент прозрачности барьера
D = ехр ( —хУТ), х = 2nZe2V2m A,
где Ze — заряд дочернего ядра; m — масса а-частицы.
а.	Получить эту формулу из общего выражения для D (3.5).
б.	Вычислить отношение проницаемостей для а-частиц, испускаемых ядрами 226Th, с энергией 6,33 и 6,22 МэВ.
11.33.	При а-распаде ядер 212Ро с первого возбужденного уровня наблюдается два конкурирующих процесса: непосредственное испускание а-частиц (длиннопробежная группа) или испускание а-частицы после перехода возбужденного ядра в основное состояние (основная группа а-частиц). При этом на каждые 1,0- 10“ а-частиц основной группы испускается 35 длиннопробежных а-частиц указанной груп-ры. Найти постоянную распада данного возбужденного уровня по отношению к испусканию длиннопробежных а-частиц, если среднее вре-ся жизни этого уровня т = 1,8 пс.
11.34.	Найти ширину первого возбужденного уровня ядер 214Ро по отношению к испусканию у-квантов, если известно, что при распаде с этого уровня на каждую а-частицу основной группы испускается 4,3 • 10~7 длиннопробежных а-частиц и 0,286 у-квантов. Постоянная распада по отношению к испусканию длиннопробежных а-частиц равна 2,0  105 с-1.
11.35.	Вычислить суммарную кинетическую энергию частиц, возникающих при p-распаде покоящегося нейтрона.
11.36.	Как определяются энергии, освобождаемые при р~-распаде, Р+-распаде и К-захвате, если известны массы материнского и дочернего атомов и масса электрона?
11.37.	Зная массу дочернего нуклида и энергию Р-распада Q, найти массу нуклида:
а)	“Не, испытывающего р~-распад, Q 3,50 МэВ;
б)	22Na, испытывающего Р"-распад, Q = 1,83 МэВ.
72
11.38.	Установить, возможны ли следующие процессы:
а)	0_-распад ядер 51V (—0,05602k
б)	0+-распад ядер 39Са (—0,02929);
в)	A-захват в нуклиде 63Zn (—0,06679). В скобках указан избыток массы нуклида М — А, а.е.м.
11.39.	Ядро 32Р испытывает p-распад, в результате которого дочернее ядро оказывается непосредственно в основном состоянии. Определить максимальную кинетическую энергию р-частиц и соответствующую кинетическую энергию дочернего ядра.
Рис. 11.2
11.40.	Вычислить максимальное значение импульса электронов, испускаемых ядрами 10Ве, если известно, что дочерние ядра оказываются непосредственно в основном состоянии.
11.41.	Ядро ПС испытывает позитронный распад, в результате которого дочернее ядро оказывается непосредственно в основном состоянии: Вычислить:
а)	максимальную кинетическую энергию позитронов и соответствующую кинетическую энергию дочернего ядра;
б)	значения энергии позитрона и нейтрино в том случае, когда дочернее ядро не испытывает отдачи.
11.42.	Ядро 6Не испытывает 0~-распад, в результате которого дочернее ядро оказалось непосредственно в основном состоянии. Энергия распада Q = 3,50 МэВ. Под каким углом к направлению вылета электрона испущено антинейтрино, если электрон с кинетической энергией Т 0,60 МэВ вылетел под прямым углом к направлению движения ядра отдачи?
11.43.	Вычислить энергию у-квантов, сопровождающих 0-распад ядер 28А1 (рис. 11.1).
11.44.	Определить число у-квантов на один 0-распад ядер 38С1 (рис. 11.2), если относительное число 0-распадов с данным парциальным спектром 0-частиц равно: 31% (0J, 16% (02) и 53% (03).
11.45.	При 0-распаде ядер 56Мп из основного состояния испускаются три парциальных спектра 0-частиц, максимальная кинетическая энергия которых 0,72; 1,05 и 2,86 МэВ. Сопровождающие распад у-кванты имеют энергию 0,84; 0,81; 2,14; 2,65 и 2,98 МэВ. Рассчитать и построить схему уровней дочернего ядра.
11.46.	Ядра 37Аг испытывают /(-захват, в результате которого дочерние ядра оказываются непосредственно в основном состоянии. Пре
73
небрегая энергией связи /(-электрона, определить кинетическую энергию и скорость дочернего атома.
11.47.	Найти энергию нейтрино при /(-захвате в атомах 131Cs, если полная энергия, выделяющаяся в этом процессе, равна 355 кэВ, энергия связи /(-электрона в дочернем атоме 35 кэВ, причем дочернее ядро оказывается непосредственно в основном состоянии.
11.48.	/(-захват в атомах 7Ве частично происходит через возбужденное состояние дочернего ядра, которое испускает при этом у-квант с энергией 479 кэВ. Определить кинетическую энергию дочерного ядра после испускания у-кванта, если угол между направлениями движения нейтрино и ядра отдачи равен 90?. Какова эта энергия в том случае, когда дочернее ядро возникает непосредственно в основном состоянии?
у-Излучение: внутренняя конверсия,
эффект Мёссбауэра
11.49.	Изомерное ядро 81Sem с энергией возбуждения 103 кэВ переходит в основном состояние, испуская или у-квант, или конверсионный электрон с /(-оболочки атома (энергия связи /(-электрона 12,7 кэВ). Найти скорости ядра отдачи в обоих случаях.
11.50.	Изомерное ядро 109Agm, переходя в основное состояние, испускает или у-квант с энергией 87 кэВ, или конверсионный /(-электрон с Вр = 860 Гс  см. Вычислить энергию связи /(-электрона.
11.51.	Атомы 203Т1, возникающие в результате p-распада атомов 203Hg, испускают четыре группы конверсионных электронов с кинетической энергией 266,3; 264,2; 263,6 и 193,3 кэВ. Какой оболочке атома Т1 — К, Llt L2, L3 — соответствует каждая группа? Энергия связи электронов на этих оболочках соответственно равна 87,7; 15,4; 14,8 и 12,7 кэВ. Вычислить также энергию у-квантов, сопровождающих этот распад.
11.52.	Возбужденные ядра 141Рг, возникающие при p-распаде ядер 141Се, переходят в основное состояние, испуская или у-кванты, или конверсионные электроны. Определить энергию возбуждения ядра 141Рг, если конверсионные /(-электроны имеют Вр = 1135 Гс • см, а энергия связи /(-электронов равна 42 кэВ.
11.53.	Возбужденные ядра 117Sn, возникающие при р-распаде 1171п, переходят в основное состояние, испуская последовательно два у-кванта. Этот процесс сопровождается испусканием конверсионных /(-электронов, для которых Вр равно 3050 и 1300 Гс-см. Энергия связи /(-электронов 29 кэВ. Определить энергию у-квантов.
11.54.	Найти число конверсионных электронов, испускаемых в 1 с препаратом 59Fe активностью 3,7 • 107 Бк (1,0 мКи). Схема р-распа-да ядер 59Fe приведена на рис. 11.3. Коэффициенты внутренней конверсии у-квантов равны 1,8 • 10~4 (у,); 1,4 • 10-4 (у2) и 7 • 10~8 (у3/. Вероятности испускания у-квантов у2 и у3 относятся соответственно как 1 : 15.
74
Примечание', коэффициентом внутренней конверсии называют отношение вероятности испускания конверсионного электрона к вероятности испускания у-кванта.
11.55.	Свободное ядро 1911г с энергией возбуждения Е = 129 кэВ перешло в основное состояние, испустив у-квант. Найти относительное изменение энергии данного у-кванта, возникающее вследствие отдачи ядра.
11.56.	Свободное ядро 119Sn с энергией возбуждения Е = 23,8 кэВ переходит в основное состояние, испуская у-квант. Ширина данного
уровня Г = 2,4 • 10-8 эВ. Возможно ли резонансное поглощение такого у-кванта другим свободным ядром 119Sn, находящимся в основном состоянии, если первоначально оба ядра покоились?
11.57.	С какой скоростью должны сближаться источник и поглотитель, состоящие из свободных ядер 1911г, чтобы можно было наблюдать максимальное поглощение у-квантов с энергией 129 кэВ?
11.58.	Как показал Мёссбауэр, в спектре у-квантов, которые испускают возбужденные ядра, входящие в состав твердого тела, каждая у-линия содержит две компоненты; очень узкую с энергией, равной энергии перехода в ядрах, и несравненно более широкую, смещенную относительно первой. Для у-линии 57Fe, соответствующей энергии 14,4 кэВ, относительный сдвиг смещенной компоненты составляет ДХ/Х = 1,35 • 10-7. Убедиться, что эта компонента обусловлена эффектом отдачи ядер при испускании у-квантов.
11.59.	На рис. 11.4 приведена зависимость поглощения у-линии Мёссбауэра с энергией 129 кэВ от относительной скорости источника и поглотителя (1911г). Имея в виду, что испускание данной линии связано с переходом возбужденных ядер непосредственно в основное состояние, найти ширину и время жизни соответствующего возбужденного уровня.
11.60.	Источник у-квантов расположен над поглотителем на расстоянии 20,0 м. С какой скоростью необходимо перемещать вверх источник, чтобы в месте расположения поглотителя полностью скомпенсировать гравитационное изменение энергии у-квантов, обусловленное полем тяжести Земли?
75
11.61.	Относительные значения ширины у-линии Мёссбауэра для 5,Fe и 67Zn равны соответственно 3,0 • 10~13 и 5,0 • 10-16. На какую высоту от поверхности Земли необходимо поднять источник (57Fe и 67Zn), чтобы при регистрации на поверхности Земли гравитационное смещение линии Мёссбауэра превосходило ширину этих линий?
11.62.	При испускании у-квантов, соответствующих мёссбауэровской линии, импульс отдачи сообщается всему кристаллу в целом, поэтому импульс излучающего атома не изменяется. Средняя же кинетическая энергия такого атома возрастает вследствие некоторого уменьшения его массы за счет излучения. Это приводит к тому, что
.____+з/2
1-3/2 /Z^/z ~Г\-----------7/2
'-----3/2
fiat
IYTHT
~5,20 -3,03 -0,87 0 0,87 3,03 5,20мм/с
Рис. 11.5
частота мёссбауэровской линии оказывается меньше частоты перехода <о0, а именно: со = ю0 (1 — (t?2>/2c2), где <и2> — квадрат средней квадратической скорости атома.
а)	Получить это выражение из энергетических соображений.
б)	На сколько градусов температура источника должна быть больше температуры поглотителя, чтобы температурное смещение мёссбауэровской у-линии 57Fe полностью компенсировало гравитационное смещение, если источник находится над поглотителем на расстоянии I = 20 м? Считать, то средняя кинетическая энергия атомов в кристалле равна 3l2kT.
11.63.	На рис. 11.5 показан скоростной спектр поглощения эффекта Мёссбауэра для случая, когда линия испускания у-квантов с энергией Йсо = 14,4 кэВ не расщеплена (источник 57Со введен в немагнитную сталь), а поглотителем является пластинка естественного изотопного состава железа. Положительные значения скорости отвечают движению источника к поглотителю. Используя схему уровней, на которой основана интерпретация данного спектра, найти магнитный момент возбужденного состояния ядра 57Fe и индукцию магнитного поля, действующего на ядро в железе. Магнитный момент основного состояния ядра 57Fe равен р = 0,090ря.
Статистика регистрации ядерного излучения
Счетчики
11.64.	При измерении активности некоторого препарата счетчик дает в среднем 6 имп./мин. Оценить с помощью формулы (11.2) вероятность того, что скорость счета будет иметь значения между 9 и 11 имп. мин.
76
11.65.	Предполагается провести 2000 измерений активности препарата в течение одинаковых промежутков времени. Среднее число импульсов за время каждого измерения равно 10,0. Считая время проведения всех измерений малым по сравнению с периодом полураспада исследуемого радионуклида, определить число измерений, в которых следует ожидать точно 10 и 5 импульсов.
11.66.	Среднее значение скорости счета импульсов от исследуемого радионуклида с большим периодом полураспада составляет 100,0 имп./мин. Определить вероятность получения 105,0 имп./мин и вероятность того, что абсолютное отклонение от среднего числа имеет значение, большее 5,0 имп./мин.
11.67.	Вычислить вероятность получения абсолютной погрешности измерения, превосходящей: а) о и б) 2<т, где о — средняя квадратическая погрешность.
11.68.	Счетчик, находящийся в поле исследуемого излучения, зарегистрировал 3600 импульсов за 10 мин. Найти:
а)	среднюю квадратическую погрешность в скорости счета, имп./мин;
б)	продолжительность измерения, обеспечивающую определение скорости счета с погрешностью 1,00%.
11.69.	При измерении интенсивности исследуемого излучения (вместе с фоном) счетчик зарегистрировал 1700 импульсов за 10,0 мин. Отдельное измерение фона дало 1800 импульсов за 15,0 мин. Найти скорость счета, имп./мин, обусловленную исследуемым излучением, и ее среднюю квадратическую погрешность.
11.70.	Показать, что при наличии фона, интенсивность которого равна интенсивности исследуемого излучения, необходимо зарегистрировать в 6 раз больше импульсов, чтобы обеспечить ту же точность измерения исследуемого излучения, что и без фона.
11.71.	Скорость счета импульсов фона пф = 15 имп./мин, а скорость счета исследуемого препарата при наличии фона пИф = = 60 имп./мин. Пусть /ф и /иф — время измерения фона и исследуемого препарата при наличии фона. Найти оптимальное отношение /ф//Иф, при котором точность определения скорости счета от самого препарата будет максимальной для заданного полного времени измерения /ф + /иф.
11.72.	Используя данные предыдущей задачи, найти минимальные значения и /Иф, при которых относительная погрешность определения скорости счета от самого препарата т] = 0,050.
11.73.	Счетчик Гейгера—Мюллера с разрешающим временем т = 0,20 мс зарегистрировал п = 3,0 • 104 имп./мин. Определить истинное число N частиц, прошедших через счетчик в 1 мин.
11.74.	Какая доля частиц, проходящих через счетчик с разрешающим временем т = 1,0 мкс, не будет зарегистрирована при скорости счета п = 100 и 1,0 • 105 имп./с?
11.75.	При измерении активности некоторого препарата с фоном счетчик Гейгера—Мюллера, разрешающее время которого 0,20 мс, зарегистрировал 1000 имп./с. Отдельное измерение фона этим же счет-
77
чиком дало 600 имп./с. Определить число частиц от исследуемого препарата, которые проходят через счетчик в 1 с.
11.76.	Вблизи счетчика поместили два радиоактивных источника. При попеременном закрывании экраном то одного, то другого источника счетчик дает соответственно п1 и п2 имп./с.При совместном действии обоих источников п12 имп./с. Определить разрешающее время данного счетчика.
11.77.	Число частиц, проходящих в единицу времени через счетчик, равно N. Определить число импульсов в единицу времени на выходе регистрирующего устройства счетчика, если известно разрешающее время счетчика Xi и регистрирующего устройства т2. Рассмотреть случаи: а) Ч > т2; б) Tj < т2.
11.78.	В сцинтилляционном счетчике с фотоумножителем время высвечивания сцинтиллятора Xi = 6 нс, разрешающее время самого фотоумножителя х2=30 нс. Определить число электронов, падающих на сцинтиллятор в 1 с, если число импульсов на выходе фотоумножителя п = 5,0 • 106 имп./с.
счетчик с разрешающим временем т вклю-
A
Рис. 11.6
11.79.	Электромагнитный чен непосредственно на выходе усилителя счетного устройства (без применения пересчетной схемы). Найти в данном случае зависимость числа импульсов п, зарегистрированных в единицу времени, от среднего числа частиц N, проходящих через счетчик Гейгера—Мюллера в единицу времени. Указание: иметь в виду, что если в электромагнитный счетчик, который начал регистрировать импульс, но еще не закончил полный цикл регистрации, поступает следующий импульс, то, хотя последний и не будет сосчитан, он увеличивает мертвое время, вызванное первым импульсом.
11.80.	Импульсы от счетчика Гейгера—Мюллера после усиления подаются непосредственно на электромагнитный счетчик. Определить разрешающее время электромагнитного счетчика, если известно, что при приближении радиоактивного препарата к счетчику Гейгера—Мюллера число регистрируемых импульсов проходит через максимум «макс = 46 ИМИ. С.
11.81.	Два одинаковых счетчика, работающих в схеме совпадений, поместили в поле космического излучения. Определить число случайных совпадений Ап, если число импульсов, поступающих в единицу времени на вход схемы совпадений, от одного счетчика пь от другого п2 и разрешающее время схемы т.
11.82.	Радиоактивный препарат поместили симметрично перед двумя одинаковыми счетчиками, включенными в схему совпадений. Разрешающее время схемы т = 0,10 мкс. Эффективность регистрации каждого счетчика 25%. Определить число частиц, падающих в 1 с, на каждый счетчик, если скорость счета схемы совпадений Ап = = 2,0 • 103 имп./с.
78
11.83.	Радиоактивный препарат А поместили перед двумя одинаковыми счетчиками Sj и S2, как показано на рис. 11.6. Счетчики включены в схему совпадений с разрешающим временем т = 1,0 • 10-8 с. Для определения активности препарата измеряют скорость счета фона А«Ф и скорость счета препарата при наличии фона п „ф. Оба измерения проводят в течение одинаковых промежутков-времени При каком значении t скорость счета от самого препарата будет определена с погрешностью 5,0%, если число импульсов, даваемых каждым счетчиком, равно 1,00 • 105 имп. с от фона и 100 имп. сот самого препарата?
11.84.	Между двумя одинаковыми счетчиками у-квантов, включенными в схему совпадений, помещен радиоактивный препарат, р-рас-пад ядер которого сопровождается испусканием двух квантов и у2. Вероятности регистрации каждым счетчиком данных у-квантов в условиях опыта равны г)! - 5 • 10^4и ц2 = 7 • 10-4. Определить число отсчетов схемы совпадений (в процентах числа импульсов, зарегистрированных за то же время одним из счетчиков), полагая, что корреляцией между направлениями вылета квантов Yi и у2 можно пренебречь.
12. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
• Ионизационные потери энергии тяжелой заряженной частицы в веществе (иерелятивистский случай):
где z — заряд частицы, единицы е; v — ее скорость; п — концентрация электронов в веществе; те — масса электрона; I х 13,5Z, эВ, — средняя энергия ионизации атома вещества с порядковым номером Z.
•	Эмпирические формулы для среднего пробега в воздухе при нормальных условиях а-частицы и протона с кинетической энергией Т, МэВ:
Ra = 0,31Т3/2 см (4 МэВ < Т < 7 МэВ);	(12.2)
/?р (Т) = Ra (4Т) — 0,2 см (Г > 0,5 МэВ),	(12.3)
где Ra (4Т) —средний пробег в воздухе а-частицы с кинетической энергией 4Т.
Средний пробег а-частицы, мг/см2, в веществе с массовым числом А:
/?а==0,56Д1/3 Ra,	(12.4)
где Ra, см, — пробег а-частицы с той же энергией в воздухе (12.2).
•	Радиационные потери энергии электрона (при Т >> тс2), МэВ/см:
/ дЕ \	,7	183
— ----- =2,32-10*27 nTZ In ---------	(12.5)
\ дх /рад	2'/3
где Т, МэВ, — кинетическая энергия электрона; п, см-3, — концентрация электронов в веществе: Z — порядковый номер атомов вещества.
•	Соотношение между радиационными и ионизационными потерями энергии электрона:
(12.6) (дЕ/дх)И0К 800
где Т, МэВ, — кинетическая энергия электрона; Z — порядковый номер атомов вещества.
79
•	Если потери энергии электрона в основном радиационные, то кинетическая энергия электрона в веществе уменьшается по закону:
Т = Тое “х//₽аД,	(12.7)
где /рад — радиационная длина.
•	Средний пробег, г/см2, электрона с кинетической энергией Т, МэВ, в алюминии:
( 0,407 7'1'38 (0,15 МэВ < Т < 0,8 МэВ);
R._{	(12.8)
I 0,542 Т—0,133 (0,8 МэВ < Т < 3 МэВ).
Эти формулы с хорошей точностью описывают пробег и в любых веществах, если потери энергии электрона в основном ионизационные.
•	Закон поглощения 0-частиц:
J-. J„e Vd,	(12.9)
где J — поток 0-частиц; ц — линейный коэффициент поглощения; d — толщи на слоя вещества.
Массовый коэффициент поглощения, см2/г:
И/Р --22Тр-ук3с{0.5 МэВ < 7-рмакс<7 МэВ).	(12. Ю)
где Ермаке МэВ, —граничная энергия спектра 0-частиц.
•	Закон ослабления узкого пучка моноэнергетического у-излучения:
./ 70 е цл’, ц--т + а,	(12.11)
где ц. т. а — линейные коэффициенты ослабления, поглощения и рассеяния.
•	Единицы дозы излучения и предельно допустимые уровни приведены в Приложении 15.
Прохождение заряженных частиц через вещество
12.1.	Найти максимальный угол, на который может отклониться а-частица при соударении с покоящимся свободным электроном.
12.2.	а-Частица с кинетической энергией Та = 25 МэВ пролетела мимо покоящегося свободного электрона, имея прицельный параметр b = 20 пм. Найти кинетическую энергию Те электрона отдачи, считая, что траектория а-частицы прямолинейная и за время пролета электрон остается неподвижным.
12.3.	Быстрая а-частица движется со скоростью и через среду с концентрацией электронов п. Определить энергию, теряемую а-час-тицей на единице пути в результате взаимодействия с электронами, относительно которых ее прицельный параметр заключен в интервале (b, b + db). При расчете воспользоваться результатом решения предыдущей задачи.
12.4.	Вычислить ионизационные потери энергии дейтрона с кинетической энергией 4,0 МэВ на единице пути в азоте при нормальных условиях.
12.5.	Найти отношение ионизационных потерь энергии:
а)	а-частицы и протона с кинетической энергией 5,0 МэВ в неоне;
б)	а-частицы с кинетической энергией 10,0 МэВ в меди и алюминии.
12.6.	В центре сферической ионизационной камеры радиусом 140 мм расположен точечный источник а-частиц с кинетической энергией 80
5,3 МэВ. При каких значениях давления воздуха в камере ток насыщения не будет зависеть от давления?
12.7.	Найти с помощью эмпирических формул:
а) число пар ионов, которые образует а-частица с начальной кинетической энергией 5,5 МэВ на первом сантиметре своего пути в воздухе (энергию образования одной пары ионов считать равной 34 эВ) б) относительное число пар ионов, которое образует протон с начальной кинетической энергией Т 2,5 МэВ на первой половине среднего пробега в воздухе.
12.8.	Радиоактивный препарат 238Ри, испускающий а-частицы с кинетической энергией 5,5 МэВ, электролитически наносят на толстую металлическую подложку. При какой минимальной толщине слоя дальнейшее добавление 238Ри не приведет к увеличению интенсивности потока а-частицы, испускаемых этим препаратом?
12.9.	Найти кинетическую энергию а-частиц, средний пробег которых в железе равен 11,0 мкм.
12.10.	Определить пробег а-частицы в свинце, если ее энергия соответствует пробегу 17 мкм в алюминии.
12.11.	На алюминиевую фольгу падают нормально а-частицы с кинетической энергией 13,7 МэВ. При какой толщине фольги кинетическая энергия прошедших частиц равна 7,0 МэВ?
12.12.	На расстоянии 5,0 см от радиоактивного препарата, испускающего а-частицы с кинетической энергией 9,0 МэВ, помещают алюминиевую фольгу. Какой минимальной толщины должна быть эта фольга, чтобы задерживать все а-частицы? Окружающая среда— воздух.
12.13.	Найти с помощью формулы (12.1) зависимость между пробегами в среде протона и дейтрона, скорости которых одинаковы. Воспользовавшись полученной зависимостью и формулами (12.2) и (12.3), вычислить пробег в воздухе дейтрона с кинетической энергией Т — = 2,0 МэВ.
12.14.	Найти средний пробег протонов с кинетической энергией 3,0 МэВ в свинце.
12.15.	Быстрая тяжелая заряженная частица с зарядом q и скоростью v при движении в среде с концентрацией электронов п образует на своем пути 6-электроны. Считая процесс их образования результатом упругого рассеяния первичной частицы на свободных электронах, определить:
а)	сечение do образования 6-электронов с кинетической энергией в интервале (Т, Т + dT)\
б)	полное число 6-электронов, создаваемых первичной частицей на единице длины ее траектории; предполагается, что известно минимальное значение кинетической энергии Тпор, которой должен обладать электрон для образования видимого следа.
12.16.	При прохождении быстрой тяжелой заряженной частицы через фотоэмульсию на единице длины ее траектории образуется:
N. =: 2пп(1г е* I ________!___
mev2 \ Т’цор 2mev2
81
6-электронов, где п — концентрация электронов; q и v — заряд и скорость первичной частицы; 7п0р — пороговая кинетическая энергия электрона, необходимая для образования видимого следа в эмульсии; те — масса электрона. Определить с помощью этой формулы:
а) минимальную энергию а-частицы для образования 6-электронов в фотоэмульсии, у которой Tnop =11,0 кэВ;
в) энергию а-частицы, при которой на единице длины траектории образуется максимальное число 6-электронов в фотоэмульсии с п = = 6,0 • 1023 см-3 и Тпор = 17,5 кэВ; вычислить максимальное число 6-электронов на 1/10 мм длины траектории а-частицы;
в) заряд первичной частицы,если известно, что максимальная плотность 6-электронов, образуемых ею, в 4 раза меньше максимальной плотности 6-электронов от а-частицы (в той же эмульсии).
12.17.	Вычислить радиационные потери энергии электрона с кинетической энергией 20 МэВ на единицу пути в алюминии. Во сколько раз радиационные потери энергии электрона в свинце больше, чем в алюминии?
12.18.	Оценить кинетическую энергию электронов, при которой радиационные и ионизационные потери энергии одинаковы: в азоте (при нормальных условиях), алюминии и свинце.
12.19.	Оценить кинетическую энергию электронов, при которой радиационные потери энергии в алюминии составляют 1/4 всех потерь.
12.20.	Оценить полную потерю энергии электрона с кинетической энергией 27 МэВ на единицу пути в алюминии.
12.21.	Найти зависимость радиационной длины /рад электрона от порядкового номера вещества Z. Вычислить /рад для электрона в азоте (при нормальных условиях), алюминия в свинце.
12.22.	При прохождении слоя некоторого вещества толщиной 0,40 см энергия быстрых электронов уменьшилась в среднем на 25%. Найти радиационную длину электрона, если известно, что потери энергии электрона в основном радиационные.
12.23.	Оценить первоначальную энергию электронов, если после прохождения свинцовой пластинки толщиной 5,0 мм энергия электронов в среднем составляет 42 МэВ.
12.24.	При торможении электронов достаточно больших энергий в поле ядра сечение испускания у-квантов в интервале частот (со, ® + d&) вблизи максимальной частоты тормозного излучения определяется формулой: do =(Ь7г/рад)с/®/®, где п — число ядер в единице объема. Найти вероятность того; что электрон потеряет свыше 90% своей первоначальной энергии при прохождении через цинковую пластинку толщиной I = 1,0 мм.
12.25.	Вычислить с помощью эмпирических формул кинетическую энергию электронов, средний пробег которых в алюминии равен 100 мг/см2.
12.26.	Найти средний пробег релятивистских электронов с Вр = = 5,0 кГс-см в графите.
12.27.	Пучок электронов с кинетической энергией 0,50 МэВ падает нормально на алюминиевую фольгу толщиной 50 мг/см2. Оценить 82
с помощью эмпирических формул средний пробег электронов, прошедших эту фольгу, в воздухе.
12.28.	Оценить минимальную массовую толщину ^-активного препарата 204Т1, начиная с которой дальнейшее увеличение его толщины не повышает интенсивности потока 0-частиц, испускаемых этим препаратом.
12.29.	Какая доля 0-частиц, испускаемых 32Р, поглощается в алюминиевой фольге толщиной 20 мг/см2?
12.30.	При увеличении толщины окошка счетчика Гейгера—Мюллера на 60 мг/см2 скорость счета 0-частиц уменьшалась в 2 раза. Какова максимальная энергия 0-частиц иссследуемого радиоактивного источника?
12.31.	Найти толщину слоя половинного поглощения 0-частиц, испускаемых радиоактивным препаратом 32Р, для воздуха, алюминия и свинца.
12.32.	Заряженная частица, равномерно движущаяся в среде с показателем преломления п, излучает свет, если ее скорость v превышает фазовую скорость света с' в этой среде (эффект Вавилова—Черенкова). Показать с помощью законов сохранения энергии и импульса, что угол, под которым происходит испускание света, определяется выражением cos & = с'tv. Иметь в виду, что импульс фотона в среде равен Ьли/с’.
12.33.	Вычислить пороговую кинетическую энергию электрона и протона, при которой возникает излучение Вавилова—Черенкова в среде с показателем преломления п = 1,60. Для каких частиц пороговая кинетическая энергия в этой среде равна 29,6 МэВ?
12.34.	Найти кинетическую энергию электронов, которые, проходя среду с показателем преломления п = 1,50, излучают свет под углом О' = 30° к направлению своего движения.
Прохождение у-излучения через вещество
12.35.	При увеличении толщины свинцовой пластинки на 2,0 мм интенсивность проходящего через нее узкого пучка моноэнергетичес-кого рентгеновкого излучения уменьшалась в 8,4 раза. Найти с помощью таблиц Приложения энергию фотонов.
12.36.	Какой толщины следует взять алюминиевую пластинку, чтобы она ослабляла узкий пучок рентгеновского излучения с энергией 200 кэВ в такой же степени, как свинцовая пластинка толщиной 1,0 мм?
12.37.	Степени ослабления узких пучков рентгеновского излучения с энергиями 200 и 400 кэВ при прохождении свинцовой пластинки отличаются друг от друга в четыре раза. Найти толщину пластинки и степень ослабления пучка с энергией 200 кэВ.
12.38.	Вычислить толщину слоя половинного ослабления узкого пучка рентгеновского излучения с длиной волны 6,2 пм для свинца, воды и воздуха.
12.39.	Сколько слоев половинного ослабления в пластинке, ослабляющей узкий пучок моноэнергетического рентгеновского излучения в 1000 раз?
83
12.40.	Построить график зависимости (р/р)1/» от длины волны рентгеновского излучения для меди по следующим данным:
пм ..................... 40	80	120	160	200	240	280
di -j,	мкм................. 78,0	11,0 3,34 12,7	7,21	4,55	3.00
Здесь dt/., — толщина слоя половинного ослабления.
12.41.	Подобрать с помощью таблиц Приложения металлическую фольгу, которая пропускает /Са-линию, значительно ослабляя при этом /(р-линию:
а)	кобальта (кКа = 179 пм, = 162 пм);
б)	никеля (ХКа = 166 пм, -= 150 пм).
12.42.	Рассчитать толщину медной фольги, при которой ослабление Лф-линии цинка = 129 пм) в 10 раз больше ослабления ЛД-линий -- 143 пм). Воспользоваться графиком, приведенным в решении задачи 12.40.
12.43.	Для длинноволнового рентгеновского излучения дифференциальное сечение рассеяния фотона на свободном электроне описывается формулой:
daldQ = 1/2 г* (1 + cos 2,0'),
где ге — классический радиус электрона; О— угол рассеяния фотонов. Найти с помощью этой формулы:
а)	полное сечение рассеяния;
б)	относительное число фотонов, рассеянных под углами 0' < 60°;
в)	относительное число электронов отдачи, вылетающих в интервале углов от 45 до 90°.
12.44.	Вычислить массовый и линейный коэффициенты рассеяния низкоэнергетического рентгеновского излучения для неона и кислорода при нормальных условиях. Иметь в виду, что атомный коэффициент рассеяния определяется формулой Томсона, см2/атом:
оа iliziZeilrn1c'‘.
12.45.	Массовый коэффициент поглощения рентгеновского излучения с X = 20,9 пм для железа равен 1,26 см2/г. Вычислить соответствующий атомный коэффициент поглощения.
12.46.	Имея в виду, что атомный коэффициент поглощения то
CZ4X:* при	где — длина волны края К-полосы погло-
щения; С — постоянная, одинаковая для всех веществ, определить: а) массовый коэффициент поглощения т/р ванадия для рентгеновского излучения с X = 100 пм, если у алюминия т/р = 40 см2/г для X =- 144 пм;
б)	отношение массовых коэффициентов поглощения рентгеновского излучения в костях и тканях человеческого тела; известно, что веществом кости является Са3 (РО4)2, а поглощение тканей обусловлено в основном входящей в ее состав водой.
12.47.	Моноэнергетический пучок у-квантов при прохождении алюминиевой пластины толщиной 2,9 см ослабляется в 2,6 раза. Най-84
ти с помощью таблиц Приложения соответствующий массовый коэффициент рассеяния.
12.48.	Точечный источник у-квантов с энергией 0,80 МэВ помещен в центр сферического слоя свинца, толщина которого Дг = 3,0 см и внешний радиус г = 5,0 см. Найти плотность потока нерассеянных у-квантов на внешней поверхности этого слоя., если активность источника А = 3,70 • 107 Бк (1,00 мКи) , причем на каждый распад испускается один квант.
12.49.	Узкий пучок у-квантов, содержащий в одинаковом количестве кванты с энергиями 0,40 и 0,60 МэВ, падает нормально на свинцовую пластинку толщиной 1,00 см. Найти отношение интенсивностей обеих компонент пучка после прохождения этой пластинки.
12.50.	Узкий пучок у-излучения, содержащий кванты всех энергий в интервале 0,60—0,80 МэВ, падает на алюминиевую пластинку толщиной 2,0 см. Найти степень ослабления интенсивности пучка после прохождения пластинки, если в этом интервале коэффициент ослабления линейно зависит от энергии квантов и спектральная интенсивность падающего излучения не зависит от частоты.
12.51.	Определить с помощью таблиц Приложения сечение взаимодействия, б/атом, у-квантов энергией 1,00 МэВ в алюминии.
12.52.	Узкий пучок у-квантов с энергией 0,15 МэВ при прохождении серебряной пластинки толщиной 2,0 мм ослабляется в 4 раза. Найти сечение взаимодействия, б/атом, этих у-квантов в серебре.
12.53.	Вычислить с помощью таблиц Приложения среднюю длину свободного пробега у-квантов с энергией 1,00 МэВ в воздухе, воде и алюминии.
12.54.	Определить среднюю длину свободного пробега у-квантов в среде, слой половинного ослабления которой равен 4,50 см.
12.55.	Найти с помощью графиков Приложения среднюю длину свободного пробега у-квантов с энергией 2,0 МэВ в свинце, а также средние пробеги этих квантов для комптоновского рассеяния, фотоэффекта и образования электронно-позитронных пар. Каким соотношением связаны эти пробеги?
12.56.	Найти с помощью графиков Приложения вероятность фотопоглощения у-кванта с энергией 2,0 МэВ в свинцовой пластинке толщиной 2,0 мм.
12.57.	Пучок моноэнергетического у-излучения при прохождении свинцовой пластинки толщиной 3,2 см ослабляется в 6 раз. Вычислить с помощью графиков Приложения массовый коэффициент комптоновского рассеяния этого излучения в свинце.
12.58.	Полное сечение комптоновского рассеяния у-кванта на свободном электроне описывается формулой:
е-—2е—2
2е3
In (1 -р 2е) 4
3 ®комп '	,
4
е34 9е2 + 88 + 21
е2(1+2е)2	]’
где е •= htolmc2, — энергия у-кванта в единицах энергии покоя электрона; ат — сечение томсоновского рассеяния.
а.	Упростить эту формулу для случаев е <с 1 и е » 1.
85
б.	Вычислить линейный коэффициент комптоновского рассеяния у-квантов энергией е = 3,0 для бериллия.
в.	Найти массовый коэффициент комптоновского рассеяния у-квантов энергией е = 2,0 для легких веществ.
12.59.	Вычислить с помощью графиков Приложения сечение образования электронно-позитронной пары у-квантом энергией 6,0 МэВ в свинцовой пластинке, толщина которой равна слою половинного ослабления.
12.60.	При какой толщине свинцовой пластинки вероятность образования электронно-позитронной пары у-квантом с энергией 7,0 МэВ равна 0,10?	z
12.61.	Тонкую свинцовую пластинку облучали в камере Вильсона у-квантами энергией 3,0 МэВ. При этом было обнаружено, что электронных треков в г, = 3,7 раза больше, чем позитронных. Найти отношение вероятности образования электронно-позитронной пары к суммарной вероятности других процессов в этом случае.
12.62.	Получить выражение, определяющее пороговую энергию у-кванта для образования пары в поле ядра массой М.
12.63.	Показать, что у-квант не может образовать пару вне поля ядра, даже если такой процесс энергетически возможен.
12.64.	Определить суммарную кинетическую энергию пары электрон—позитрон, которую образует у-квант с пороговым значением энергии в поле покоящегося протона.
12.65.	Вычислить энергию у-кванта, образовавшего в поле покоящегося тяжелого ядра пару электрон—позитрон, если известно, что для каждой частицы пары Вр = 3,0 кГс-см.
Дозиметрия излучений
12.66.	В ионизационной камере, помещенной в однородное поле у-излучения, ток насыщения I = 0,32 мкА. Камера имеет объем V = -- 5,0 л и наполнена воздухом под давлением р = 250 кПа. Температура Т = 300 К. Найти мощность экспозиционной зоны у-излучения.
12.67.	Найти в воздухе и воде в точках, где плотность потока у-фотонов с энергией £ = 2,00 МэВ составляет J = 1,30. • 104см~2  с-1, мощность:
а) поглощенной дозы; б) экспозиционной дозы.
12.68.	На некотором расстоянии от радиоактивного у-источника, период полураспада которого 7 - 26 ч, мощность экспозиционной дозы в начальный момент составляет Ро = 72 нКл (кг • с), или 1,0 Р/с. Найти:
а)	экспозиционную дозу, мкКл кг, за время т = 6,0 ч;
б)	время, за которое поглощенная доза в воздухе D -- 150 мГр (15 рад).
12.69.	Точечный источник активностью А = 3,10 • 109 Бк испускает у-кванты с энергией £=1,00 МэВ. Выход у-квантов на один распад ц = 0,50. Пренебрегая поглощением в воздухе, найти мощность экспозиционной дозы на расстоянии г = 200 см от источника.
86
12.70.	Точечный радиоактивный источник активностью 0,67 X 109 Бк испускает на каждый акт распада два у-кванта энергией 0,80 и 1,00 МэВ. Пренебрегая поглощением в воздухе, найти расстояние от этого источника, на котором мощность экспозиционной дозы равна предельно допустимой для 36-часовой рабочей недели.
12.71.	Найти мощность экспозиционной дозы Рэкс, пКл (кг • с), на расстоянии г = 100 см от точечного у-источника активностью А = = 3,70 • 10' Бк, если источник состоит из радионуклида: a) 24Na, б) 42К, в) 38С1. Схемы распада этих радионуклидов показаны на рис. 12.1.
12.72.	Источник у-квантов энергией Е = 1,00 МэВ равномерно распределен вдоль отрезка прямой длиной I = 100 мм. Число фото-
Рис. 12.1
нов, испускаемых источником в секунду, J = 4,00 • 10е с-1. Найти мощность экспозиционной дозы в точке, которая расположена на перпендикуляре, проходящем через середину источника, на расстоянии R = 50 мм от последнего.
12.73.	Источник у-квантов энергией Е = 2,00 МэВ равномерно распределен по поверхности круглого диска радиусом R = 3,0 см. Активность источника А — 3,70 • 109 Бк/см2, выход у-квантов равен единице. Найти мощность экспозиционной дозы в точке, отстоящей на расстоянии h = 6,0 см от центра источника и расположенной на оси диска.
12.74.	В некоторой точке О, через которую проходит узкий пучок у-квантов энергией 1,00 МэВ, мощность экспозиционной дозы Р = = 0,98 нКл/ (кг • с). Какой толщины свинцовый экран нужно поместить на пути пучка, чтобы мощность экспозиционной дозы в точке О стала равной предельно допустимой Рпр для 36-часовой рабочей недели?
12.75.	Точечный у-источник активностью А = 3,70 • 10е Бк находится в центре сферического свинцового контейнера с наружным радиусом г = 10,0 см. Найти минимальную толщину стенок контейнера, при которой мощность экспозиционной дозы снаружи не будет превышать 0,20 нКл/ (кг • с), или 2,8 мР/ч. Энергия у-квантов Е = = 2,00 МэВ, их выход, т. е. число квантов на один распад, т] = 0,60.
87
12.76.	Узкий пучок у-квантов энергией 2,0 МэВ падает нормально на свинцовый экран толщиной I = 5,0 см. Найти мощность поглощенной дозы в свинце вблизи точки выхода пучка из экрана, если мощность экспозиционной дозы в месте входа пучка в экран PdKC -
0,23 мКл/ (кг • с), или 0,9 Р/с.
12.77.	На каком расстоянии от точечного изотропного источника быстрых нейтронов интенсивностью 4,0 • 107 с-1 уровень нейтронного излучения равен предельно допустимому при 18-часовой рабочей неделе?
12.78.	Поток нейтронов с кинетической энергией Е = 0,33 МэВ и плотностью J -- 1,4 • 105 см~2 • с-1 пронизывает тонкую графитовую пластинку. Найти дозу, поглощенную графитом за время t --= 60 мин,если сечение упругого рассеяния нейтрона на ядре углерода о 4,8 б. Средняя доля энергии, передаваемой нейтроном ядру с массовым числом А при соударении, определяется как / -= 2Л/ (1 + А)2.
12.79.	Сколько а-частиц с кинетической энергией Е 4,0 МэВ, поглощенных в биологической ткани массой т = 1,00 г, соответствует эквивалентной дозе D3KB = 0,50 эВ? Коэффициент качества для данных а-частиц К = 20.
12.80.	На поверхность кожи площадью S = 2,0 см2 падает нормально N - 3,2 • 104 а-частиц с кинетической энергией Е = 5,1 МэВ. Найти средние значения поглощенной и эквивалентной доз, мГр и мЗв, в слое, равном глубине проникновения а-частиц в биологическую ткань. Иметь в виду, что пробег а-частиц в биологической ткани в 815 раз меньше пробега в воздухе; коэффициент качества для данных а-частиц К ; 20.
12.81.	Пучок 0-частиц от радиоактивного источника 90Sr падает нормально на поверхность воды. Плотность потока частиц J =-= 5,0 • 104 см-2 • с-1. Найти поглощенную дозу в воде вблизи ее поверхности за промежуток времени t = 60 мин. Среднюю кинетическую энергию 0-частиц (£> считать равной 4/3 макс.
13. ЯДЕРНЫЕ РЕАКЦИИ
• Энергетическая схема ядерной реакции:
т М -> М* '-* т' + ЛГ + Q,
протекающей через промежуточное ядроМ*, показана на рис. 13.1, где т + М и т' + М' — суммы масс покоя частиц до и после реакции; Т и Т' — суммарные кинетические энергии частиц до и после реакции (в Ц-системе); Е*— энергия возбуждения промежуточного ядра; Q—энергия реакции: Е и Е'— энергии связи частиц m и т' в промежуточном ядре. На рисунке показаны также уровни промежуточного ядра (7, 2, 3).
•	Пороговая кинетическая энергия налетающей частицы (в Л-системе), при которой становится возможной эидоэиергетическая ядерная реакция:
ТПОр-----------IQI,	'	(13.1)
где т и М — массы налетающей частицы и ядра мишени; Q — энергия реакции.
88
•	Векторная диаграмма импульсов* для частиц, участвующих в реакции М (т, т')М', показана на рис. 13.2. Здесь рт, рт, и рм, — импульсы налетающей частицы и частиц, возникающих в результате реакции (в Л-системе); О — центр окружности с радиусом, равным импульсу р возникающих частиц (в Ll-системе):
р = У2р' (T + Q) ,	(13.2)
где р' — приведенная масса возникающих частиц; Q — энергия реакции; Т— суммарная кинетическая энергия частиц до реакции (в Ц-снстеме). Точка О делит отрезок АС на две части, АО : ОС = т' : ЛТ; § — угол вылета частицы т' в Ц-системе; 0 — угол разлета возникающих частиц в Л-системе.
3
•	Принцип детального равновесия: для реакции
mj (sj) 4- ЛЦ (Id т., (s2) + Af2 (/2)
сечения прямого процесса а12 и обратного а21 связаны соотношением:
(25, + 1) (2/х+ 1) о12 Р? - (2s2+ 1) (2Z2+1) а21 pi,	(13.3)
если оба процесса протекают прн одном и том же значении полной энергии взаимодействующих частиц в Ц-системе. Здесь st и — спины частиц; р2 и р2 — импульсы частиц в Ц-системе.
Законы сохранения в ядерных реакциях
13.1.	а-Частица с кинетической энергией То = 1,0 МэВ упруго рассеялась на покоящемся ядре eLi. Определить кинетическую энергию ядра отдачи, отлетевшего под углом & = 30° к первоначальному направлению движения а-частицы.
13.2.	Найти кинетическую энергию налетающей а-частицы, если в результате упругого рассеяния ее на дейтроне:
а)	Вр каждой частицы оказалось равным 60 кГс • см;
б)	угол между направлениями разлета обеих частиц 9 = 120° и энергия, которую приобрел дейтрон, Td = 0,40 МэВ.
13.3.	Нерелятивистский дейтрон упруго рассеялся на покоящемся ядре под углом 30°. Под таким же углом к направлению движения налетающего дейтрона отлетело и ядро отдачи. Какому атому принадлежит это ядро?
13.4.	Построить векторные диаграммы импульсов для упругого рассеяния нерелятивистской а-частицы на покоящемся ядре:
*Аналогичную диаграмму для упругого рассеяния см. с. 116.
89
a) eLi, б) 4He, в) 2H, если угол рассеяния а-частицы в Ц-системе равен 60°. В каком случае связь между энергией рассеянной а-частицы и углом ее рассеяния неоднозначна? Найти для этих трех случаев значения максимально возможного угла рассеяния а-частицы.
13.5.	Какую долю кинетической энергии теряет нерелятивистская а-частица при упругом рассеянии под углом 0' = 60° (в Ц-системе) на покоящемся ядре 12С?
13.6.	Протон с кинетической энергией 0,90 МэВ испытал лобовое упругое соударение с покоящимся дейтроном. Найти кинетическую энергию протона после соударения.
13.7.	Нерелятивистский нейтрон упруго рассеялся под углом на покоившемся ядре 4Не, в результате чего последнее отлетело под углом 60° относительно направления движения налетающего нейтрона. Определить угол 1'1,,.
13.8.	Нерелятивистская а-частица упруго рассеялась на ядре 6Li. Определить угол рассеяния а-частицы:
а)	в Л-системе, если в Ц-системе 1'Ц = 30°;
б)	в Ц-системе, если в Л-системе = 45°.
13.9.	Дейтроны с кинетической энергией 0,30 МэВ упруго рассеиваются на протонах. Найти кинетическую энергию дейтронов, рассеянных на максимально возможный угол в Л-системе. Чему равен этот угол?
13.10.	Найти энергию реакции 7Li (р, а)4Не, если известно, что средняя энергия связи на один нуклон в ядрах 7Li и 4Не равна соответственно 5,60 и 7,06 МэВ.
13.11.	Определить энергии следующих реакций: а) 3Н (р, у) 4Не;
б) 14N (a, d)16O; в) 12С (а, d)14N; г) eLi (d, па)3Не.
в 13.12. Вычислить с помощью таблиц Приложения массу атома 17N, если известно, то энергия реакции 17О (п, p)17N равна Q = —7,89 МэВ.
13.13.	Найти скорости продуктов реакции 20В (п, a)7Li, протекающей в результате взаимодействия нейтронов с покоящимися ядрами бора, если кинетическая энергия нейтронов пренебрежимо мала.
13.14.	Найти энергию нейтронов, возникающих при фоторасщеплении бериллия по реакции 9Ве (у, n)8Be, Q •= —1,65 МэВ, у-кван-тами с энергией Йы = 1,78 МэВ.
13.15.	При облучении дейтериевой мишени у-квантами с энергией Йы — 2,52 МэВ испускаются фотопротоны, у которых Вр =
= 63,7 кГс • см. Пренебрегая различием масс нейтрона и протона, найти энергию связи дейтрона.
13.16.	Вычислить энергию следующих реакций:
а)	2Н (d, р)3Н, если энергия налетающих дейтронов Td == 1,20 МэВ и протон, вылетевший под прямым углом к направлению движения дейтрона, имеет энергию Тр = 3,30 МэВ;
б)	14N (а, р)17О, если энергия налетающих a-частиц Та ~= = 4,00 МэВ и протон, вылетевший под углом О'	60° к направлению
движения a-частиц, имеет энергию Тр = 2,08 МэВ.
13.17.	Определить кинетическую энергию протонов, вызывающих реакцию 9Ве (р, a)eLi + 2,13 МэВ, если пробег a-частиц, которые вы-90
летают под прямым углом к направлению движения протонов, равен 2,5 см в воздухе при нормальных условиях.
13.18.	Дейтроны с кинетической энергией Td= 10,0 МэВ, взаимодействуя с ядрами углерода, возбуждают реакцию 13С (d, а)пВ, Q = +5,16 МэВ. Определить угол между направлениями разлета продуктов реакции, если:
а)	возникающие ядра разлетаются симметрично;
б)	а-частица вылетает под прямым углом к пучку дейтронов.
13.19.	Получить формулу (13.1).
13.20.	Вычислить пороговую энергию а-частиц и нейтронов в следующих реакциях:
V а) а + 7Li	10В + п; б) а + 12С -» 14+ + d;
в) п + 12С	9Ве + а; г) п + 17О -> 14С + а.
• 13.21. Вычислить пороговую кинетическую энергию налетающей частицы в реакции р + 3Н —3Не + п, если налетающей частицей является: а) протон; б) ядро трития.
13.22.	Определить кинетические энергии ядер 7Ве и 15О, возникающих в реакциях:
а)	р + 7Li —7Ве + п, Q = —1,65 МэВ;
б)	п + 19F	15О + р + 4n, Q = - 35,8 МэВ
при пороговом значении энергии протона и нейтрона.
13.23.	Литиевую мишень облучают пучком протонов с кинетической энергией, в 1,50 раза превышающей пороговое значение. Найти энергию нейтронов, вылетающих в результате реакции 7Li (р, п) 7Ве— 1,65 МэВ под углом 90° к пучку протонов.
13.24.	Оценить минимальную кинетическую энергию налетающей а-частицы, необходимую для ее прохождения над кулоновским потенциальным барьером ядра 7Li. Возбудит ли а-частица такой энергии реакцию 7Li (а, п)10В?
13.25.	Нейтроны с кинетической энергией Т = 10,0 МэВ возбуждает реакцию 10В (n, d)9Be, для которой Taav> = 4,8 МэВ. Найти для обратного процесса кинетическую энергию налетающих дейтронов при условии, что полные энергии взаимодействующих частиц в Ll-системе одинаковы для обоих процессов.
13.26.	Получить в Ц-системе выражение для импульса р частиц, возникающих в результате реакции М (пг, т) М' + Q, если кинетическая энергия налетающей частицы Тт (в Л-системе).
13.27.	Определить кинетическую энергию ядер кислорода, вылетающих в результате реакции 14N (р, п) 14О — 5,9 МэВ под углом 30° к направлению бомбардирующих протонов, кинетическая энергия которых 10,0 МэВ. Решение получить с помощью построенной в масштабе векторной диаграммы импульсов.
13.28.	Найти максимальную кинетическую энергию а-частиц, возникающих в результате реакции 16О (d, a) 14N + 3,1 МэВ при энергии бомбардирующих дейтронов 2,0 МэВ.
13.29.	Определить ширину энергетического спектра нейтронов, возникающих в реакции ПВ (а, п) 14N + 0,30 МэВ, если кинетическая энергия бомбардирующих а-частиц равна 5,0 МэВ.
91
13.30.	Литиевую мишень облучают а-частицами с кинетической энергией Та. В результате ядерной реакции 7Li (а, п) 10В, Q = ~ — 2,79 МэВ из мишени вылетают нейтроны. Найти:
а)	кинетическую энергию нейтронов, вылетающих под углом 0, 90 и 180° к направлению движения бомбардирующих а-частиц, если Та =-• 10,0 МэВ.
б)	при каких значениях Та нейтроны будут испускаться только в переднюю полусферу (О'	90°)?
13.31.	Для получения мощных потоков быстрых нейтронов в реактор помещают дейтерид лития LiD, в котором медленные нейтроны реактора возбуждают реакцию 6Li (п, а) 3Н + 4,80 МэВ. Возникающие ядра трития, в свою очередь, возбуждают реакции:
a) D (/, п) 4Не + 17,6 МэВ и б) 7Li (/, п) 9Ве + 10,4 МэВ, которые и являются источниками быстрых нейтронов. Найти максимальную энергию этих нейтронов.
13.32.	Нейтроны кинетической энергией 1,50 МэВ бомбардируют мишень, содержащую нуклиды 6Li и 2Н. Определить с помощью векторной диаграммы импульсов ширину энергетического спектра нейтронов, возникающих в результате следующих последовательных превращений:
п + 6Li 4Не + 3Н; 3Н + 2Н 4Не + п.
13.33.	Найти максимально возможные углы вылета (в Л-системе) продуктов следующих реакций:
а)	9Ве (р, п\ 9В — 1,84 МэВ, если Тр = 4,00 МэВ;
б)	4Не (n, d) 3Н — 17,5 МэВ, если Тп = 24,0 МэВ.
Здесь Т —кинетическая энергия бомбардирующей частицы.
13.34.	Пучок нейтронов кинетической энергией 7,5 МэВ возбуждает в углеродной мишени реакцию 12С (п, а) 9Ве — 5,70 МэВ. Найти: а) относительное число а-частиц, вылетающих в переднюю полусферу (Фа 90°), считая, что в Ц-системе угловое распределение продуктов реакции изотропно;
б)	угол, под которым вылетает а-частица в Ц-системе, если соответствующий угол в Л-системе 30е.
13.35.	Найти пороговую энергию у-кванта, при которой становится возможной эндотермическая реакция фоторасщепления покоящегося ядра массой М, если энергия реакции равна Q.
13.36.	Вычислить кинетическую энергию нейтронов при пороговом значении энергии у-кванта для следующих реакций фоторасщепления:
а) у + d п + р; б) у + 7Li п + 6Li.
13.37.	Показать, что для реакции фоторасщепления ядра у + Л4 — ->• mi -- т2 в случае, когда продукты реакции нерелятивистские, импульсы возникающих частиц в Ц-системе определяются формулой: р «]/’2^“(ё + Й®), где р' — приведенная масса возникающих частиц; Q — энергия реакции; Й® — энергия у-кванта.
13.38.	у-Кванты с энергией 6,40 МэВ, взаимодействуя с ядрами трития, возбуждают реакцию 3Н (у, п) 2Н — 6,26 МэВ. Считая, что в Ц-системе распределение нейтронов по углам изотропно, найти ве-92
роятность вылета дейтрона в переднюю полусферу в Л-системе < 90°).
13.39.	Бериллиевую мишень облучали узким пучком дейтронов с энергией Td = 190 МэВ. В направлении этого пучка за мишенью наблюдали пучок нейтронов с угловой шириной ДО 16°. Найти, используя предположение о механизме реакции срыва, разброс нейтронов по энергии.
. 13.40. Найти возможное значение спина основного состояния ядра 17О, возникающего в реакции срыва при взаимодействии дейтронов с ядрами 16О, если известно, что орбитальный момент захватываемых нейтронов 1п = 2. Сравнить результат со значением спина по оболочечной модели ядра.
• 13.41. Рассмотрим следующие два канала реакции, протекающей через промежуточное ядро 8Ве*:
2 4Не	(1)
p-C7Li-^8Be*Z
48Ве + у	(2)
Спин и четность основных состояний ядер 7Li и 8Ве равны соответственно 3/2- и 0+, спин а-частицы 0; внутреннюю четность протона считать положительной. Установить с помощью законов сохранения момента-импульса и четности для случаев, когда орбитальный момент прогона / равен 0 и 1:
а)	возможные значения спина / и четности Р промежуточного ядра;
б)	состояния (спин и четность) промежуточного ядра, соответствующие обоим каналам реакции.
Уровни ядер. Сечения и выходы ядерных реакций
13.42. Найти энергию возбуждения покоящегося ядра массой М, которую оно получит при захвате у-кванта с энергией Й®.
13.43. Определить энергию возбуждения ядра 4Не, возникшего в результате захвата протона с кинетической энергией 2,0 МэВ покоящимся ядром 3Н.
< 13.44. Какой минимальной кинетической энергией должен обладать нейтрон, чтобы в результате неупругого рассеяния на ядре 9Ве сообщить последнему энергию возбуждения 2,40 МэВ?
13.45.	Мишень 7Li бомбардируют пучком нейтронов кинетической энергией То= 1,00 МэВ. Определить энергию возбуждения ядер, возникающих в результате неупругого рассеяния нейтронов, если энергия нейтронов, неупруго рассеянных под прямым углом к падающему пучку, Т = 0,33 МэВ.
13.46.	Вычислить кинетическую энергию протонов, неупруго рассеянных под прямым углом на покоящихся ядрах 20Ne. Известно, что нижние уровни ядра 20Ne соответствуют энергии возбуждения 1,5;
93
2,2 и 4,2 МэВ. Кинетическая энергия бомбардирующих протонов То = 4,3 МэВ.
13.47.	Найти кинетические энергии нейтронов, при которых сечения взаимодействия с ядрами 16О максимальны, если нижние уровни промежуточного ядра соответствуют энергиям возбуждения 0,87; 3,00; 3,80; 4,54; 5,07 и 5,36 МэВ.
13.48.	При бомбардировке мишени из углерода дейтронами возбуждается ядерная реакция 13С (d, п) 14N, выход которой максимален для следующих значений кинетической энергии дейтронов: 0,60; 0,90; 1,55 и 1,80 МэВ. Найти соответствующие уровни промежуточного ядра, через которые идет данная реакция.
13.49.	Борную мишень облучают пучком дейтронов с кинетической энергией 1,50 МэВ. В результате реакции (d, р) на ядрах 10В установлено, что под прямым углом к пучку дейтронов из мишени испускаются протоны с кинетической энергией 7,64; 5,51 и 4,98 МэВ. Найти уровни возбужденных ядер ПВ, которые отвечают этим значениям энергии.
13.50.	Найти отношение интенсивностей моноэнергетических групп нейтронов, неупруго рассеянных под прямым углом к падающему пучку ядрами 27А1, нижние уровни которых соответствуют энергии возбуждения 0,84; 1,02 и 1,85 МэВ. Кинетическая энергия бомбардирующих нейтронов 1,40 МэВ. Известно, что сечение неупругого рассеяния нейтронов вблизи порога пропорционально скорости неупруго рассеянных нейтронов.
13.51.	Выразить сечение реакции А (а, Ь) В, зная сечение образования промежуточного ядра оа и ширину его уровня, через который она идет, Г и Гь. Здесь Г — полная ширина уровня; Гь — парциальная ширина, отвечающая испусканию частицы Ь.
13.52.	Определить среднее время жизни возбужденных ядер, возникающих при захвате нейтронов с энергией 250 кэВ ядрами 6Li, если известно среднее время жизни данных ядер по отношению к испусканию нейтронов и а-частиц; тп = 1,1-10—20 с; та = 2,2-10-20 с (других процессов нет).
13.53.	Скорость ядерной реакции можно охарактеризовать средней продолжительностью т бомбардировки данного ядра до того момента, когда это ядро вступает в реакцию. Найти т для реакции 60Ni (а, п) “Zn при токе а-частиц J — 16 мкА/см2, если сечение реакции о = 0,5 б.
13.54.	Найти плотность потока нейтронов на расстоянии 10 см от небольшого Ро—Be-источника, содержащего 0,63-1010 Бк (0,17 Ки) 210Ро, если выход реакции 9Ве (а, п) 12С равен 0,8-10-4.
13.55.	При облучении ускоренными до энергии 10 МэВ дейтронами бериллиевой мишени последняя становится интенсивным источником нейтронов. Найти число нейтронов, испускаемых в 1 с на 100 мкА дей-тронного тока, если выход реакции 9Ве (d, п) 10В равен 5-10_3. Сколько радия должен содержать Ra—Be-источник, чтобы он имел ту же активность (выход этого источника считать равным 2,0-107 нейтр./с на 1 г Ra)?
13.56.	Газообразный BF3, находящийся при нормальных условиях в объеме V = 10 см3, облучают тепловыми нейтронами, плотность по-94
тока которых J = 1,0-1010 с_1-см~2. Найти:
а)	число ядерных реакций(п, а) с бором в данном объеме за 1 с;
б)	тепловую мощность, выделяющуюся в этом объеме в результате реакций (и, а) с бором.
13.57.	При облучении дейтронами энергией 1 МэВ тонкой мишени из тяжелого льда выход и сечение реакции 2Н (d, п) 3Не равны соответственно 0,8-10-5 и 0,020 б. Определить сечение данной реакции для кинетической энергии дейтронов 2 МэВ, если выход при этой энергии составляет 4,0-10-5.
13.58.	Выход реакции (у, п) при облучении медной пластинки толщиной d = 1,0 мм у-квантами энергией 17 МэВ w -= 4,2-10 4. Найти сечение данной реакции.
13.59.	Через камеру, в которой находится газообразный азот при нормальных условиях, проходит узкий пучок моноэнергетических нейтронов (0,025 эВ). Поток нейтронов равен 2,0-108 с 4. Найти сечение реакции (п, р), если известно, что за время 5,0 мс на 1,0 см длины пучка возникает 95 протонов.
13.60.	Тонкую пластинку из 113Cd облучают тепловыми нейтронами, плотность потока которых 1,0-1012 с_)-см~2. Найти сечение реакции (и, у), если известно, что через шесть суток облучения содержание ядер изотопа 113Cd уменьшилось на 1,0%.
# 13.61. Тонкую пластинку бора естественного изотопного состава облучают в течение одного года потоком тепловых нейтронов J = = 2,00-1012 с-1. В результате реакции на ядрах 10В содержание последнего к концу облучения стало 16,4%. Определить сечение данной реакции.
13.62.	Определить выход реакции (и, а) при облучении пучком тепловых нейтронов мишени толщиной 0,50 см, состоящей из лития естественного изотопного состава.
13.63.	Железную мишень облучают пучком протонов энергией 22 МэВ. В результате ядерной реакции (р, п), выход которой w = = 1,2-10~3, образуется радионуклид 56Со с периодом полураспада 77,2 сут. Определить активность мишени через т = 2,5 ч после начала облучения при токе протонов J = 21 мкА.
13.64.	Мишень из металлического натрия длительно облучали пучком дейтронов энергией 14 МэВ при токе 10 мкА. Найти выход реакции (d, р), в результате которой образуется радиоактивный нуклид 24Na, если активность мишени через 10 ч после окончания облучения составляет 5,9-1010 Бк (1,6 Ки).
13.65.	Тонкую пластину фосфора толщиной 1,0 г/см3 облучали вте-чение т = 4,0 ч потоком нейтронов 2,0-1О10 с 1 кинетической энергией 2,0 МэВ. Через t = 1,0 ч после окончания облучения активность пластинки оказалась 3,9-10® Бк (105 мкКи). Известно, что активность обусловлена нуклидом 31Si, который возникает в результате реакции (п, р). Определить сечение данной реакции.
13.66.	При облучении толстой* алюминиевой мишени пучком а-
‘Толстой называют мишень, толщина которой больше пробега в ней бом бардирующей частицы.
95
частиц с энергией 7,0 МэВ в результате реакции (а, п) испускается поток нейтронов 1,60-10® с-1. Найти выход и среднее сечение данной реакции, если ток а-частиц равен 50 мкА.
13.67.	Толстую бериллиевую мишень бомбардируют а-частицами кинетической энергией 7,0 МэВ. Определить среднее сечение реакции (а, и), если ее выход составляет 2,50-10~4.
13.68.	Толстую мишень, состоящую из нуклида 7Li, бомбардируют а-частицами кинетической энергией 7,0 МэВ. Найти среднее сечение реакции 7Li (а, п) 10В — 4,4 МэВ, если ее выход w = 2,8-10~5.
13.69.	В камеру, наполненную воздухом при нормальных условиях, впускают пучок а-частиц с кинетической энергией 7,8 МэВ. Длина камеры вдоль пучка больше длины пробега а-частиц данной энергии. Найти среднее сечение реакции 14N (а, р) 17О— 1,20 МэВ, если выход этой реакции 2,0-10_6. Содержание азота в воздухе составляет 78% по объему.
13.70.	Бериллиевую пластинку облучают потоком нейтронов с кинетической энергией 14 МэВ, падающим нормально к ее поверхности. Оценить толщину пластинки, необходимую для 10%-ного воспроизводства нейтронов по реакции (п, 2п), сечение которой при данной энергии нейтронов о = 0,50 б. Считать, что других процессов нет и что вторичные нейтроны в пластинке не поглощаются.
13.71.	Толстую мишень с концентрацией ядер по облучают тяжелыми заряженными частицами. Определить зависимость сечения протекающей ядерной реакции от кинетической энергии Т бомбардирующих частиц, если известны зависимость выхода реакции от энергии частиц w (Т) и выражение для ионизационных потерь энергии этих частиц dT/dx = f(T).
13.72.	При облучении дейтронами дейтериевой мишени протекает реакция d + d-+ 3Не + п, Q = + 3,26 МэВ. Используя принцип детального равновесия, найти спин ядра 3Не, если сечение этого процесса при энергии дейтронов Т = 10,0 МэВ равно оь а сечение обратного процесса при соответствующей энергии бомбардирующих нейтронов равно а2 = 1,8(71. Спины нейтрона и дейтрона считать известными.
13.73.	Найти с помощью принципа детального равновесия сечение Ст! реакции а + 6Li ®Ве + р — 2,13 МэВ при энергии бомбардирующих а-частиц Т = 3,70 МэВ, если сечение обратной реакции при соответствующей энергии протонов о2 = 0,050 мб.
13.74.	Показать с помощью принципа детального равновесия, что сечение эндоэнергетической реакции типа А (р, п) В, возникающей при облучении мишени протонами с энергией Тр, вблизи порога пропорционально V Тр — Тр цор, если для тепловых нейтронов сечение обратной реакции пропорционально l/un, vn—скорость нейтронов.
13.75.	Сечение реакции фоторасщепления дейтрона у + d -+ п + + р, Q — 2,22 МэВ, при энергии у-квантов Й® = 2,70 МэВ равно (Ji = 0,150 мб. Найти с помощью принципа детального равновесия сечение о2 обратного процесса при соответствующей энергии Тп бомбардирующих нейтронов. Вычислить это значение Тп.
96
14. НЕЙТРОННАЯ ФИЗИКА
• Прицельный параметр нейтрона:
Ь = XV/ (/+ 1),
(14.1)
где X - X 2л — его длина волны; / — орбитальное квантовое число.
•	Формула Брейта — Вигнера для изолированного уровня — сечение образования промежуточного ядра на тепловых s-нейтронах (/ = 0):
ГГП	27 +1
ао nX2g __+ (Г/2)2 ’8 2(27 + 1) ’	(’42)
тп+М
где X и 7" — длина волны и кинетическая энергия налетающего нейтрона; То — кинетическая энергия нейтрона, соответствующая рассматриваемому уровню промежуточного ядраЛ1* (рис. 14.1); g — статистический фактор; / — спии ядра-мишени; J — спин рассматриваемого уровня промежуточного ядра; Г и Г„ — полная и нейтронная ширина уровня; Гп зависит от длины волны налетающего нейтрона: ХГП = ХОГП1), Хо и Г„() — длина волны нейтрона и нейтронная ширина уровня при Т = То.
•	Скорость протекания ядерной реакции, т. е. число реакций, протекающих в единице объема за единицу времени, см-3 • с-1:
R = <Е>Ф,	(14.з)
где < S > /V < о > — среднее макроскопическое сечение реакции; N — концентрация ядер; Ф = = п <v> — плотность потока нейтронов; п — концентрация нейтронов; <ц> — их средняя ско-
п
Рис. 14.1
рость.
•	Среднее значение косинуса угла рассеяния нейтронов при упругом соударении с покоящимися ядрами, массовое число которых А:
2
(cos ©)- —•
(14.4)
•	Логарифмической потерей энергии называется In (То/Т), где То и Т — начальная и конечная кинетическая энергии нейтрона.
•	Средняя логарифмическая потеря энергии нейтрона, испытывающего однократное упругое соударение с ядром:
а	/	| \2
g=l + ------In а; а=(—— ,	(14.5)
1—а	\ Д + 1 /
где А — массовое число рассеивающего ядра.
•	Возраст нейтронов, замедленных от энергии до Т\
т„
О 1 dT
------------— см2, Sr( = S5 (1—(cos О)),	(14.6) J 3£2.s 2цг 1
Т
где £ — средняя логарифмическая потеря энергии; Ss и — макроскопическое и транспортное сечения рассеяния.
•	Плотность замедления qE — число нейтронов в 1 см3, пересекающих за 1 с при замедлении заданный уровень энергии Е. Для точечного источника быстрых моноэнергетических нейтронов в бесконечной однородной замедляющей среде
’ <14’7)
4 Зак. 1896
97
где — интенсивность источника, с-1; т — возраст нейтронов, см2; г—расстояние от источника, см.
•	Уравнение диффузии нейтронов для случая неразмножающей среды:
dn!dt=DV2 Ф—2аФ; D = l/3S(r;/.ДИФ = УЩ2;,	(14.8)
где п — концентрация нейтронов; D — коэффициент диффузии; V2 — лапласиан; Ф — плотность потока нейтронов; Sa — макроскопическое сечение поглощения; /.диф — диффузионная длина.
•	Альбедо нейтронов 0 — вероятность их отражения в результате многократного рассеяния в среде.
Нейтронная спектроскопия
14.1.	Одна из первых конструкций механического селектора нейтронов представляет собой два диска, которые укреплены на одной оси и вращаются со скоростью п, об/с. Расстояние между дисками L. На каждом диске имеется по одной радиальной щели, которые смещены относительно друг друга на угол а. Найти энергию нейтронов, пропускаемых таким селектором, если п = 100 об/с, L = 54 см и а = 8°.
14.2.	В механическом селекторе нейтронов, который представляет собой пакет из чередующихся пластинок алюминия толщиной 0,75 мм и тонких слоев кадмия, длина пластин равна 50 мм. Какую скорость вращения необходимо сообщить пакету, чтобы задержать нейтроны с энергией, меньшей 0,015 эВ? Какова при этом длительность нейтронного импульса?
14.3.	Разрешение по пролетному времени механического селектора нейтронов равно Дт/L, мкс/м. Найти зависимость разрешающей способности этого селектора по энергиям (АТ’/Т1) от энергии нейтронов Т, эВ. Полагая \tJL = 1,0 мкс/м, найти \Т/Т для Т = 5,0 эВ, а также максимальное значение Т, при котором А77Т не хуже 10%.
14.4.	Пригоден ли механический селектор нейтронов с разрешением по пролетному времени 0,50 мкс/м для исследования формы резонансной кривой серебра при 5,0 эВ с полушириной 0,20 эВ?
14.5.	Суммарная ширина нейтронного импульса и канала временного анализатора в установке с мигающим циклотроном равна 1,0 мкс. Оценить расстояние от замедлителя до временного анализатора в этой установке, необходимое для разрешения двух резонансов с интервалом 0,50 эВ вблизи энергии 50 эВ.
14.6.	Вычислить энергию нейтронов, испытывающих отражение от системы плоскостей кристалла NaCl cd=325 пм под углом скольжения 4,0°. В падающем пучке содержатся нейтроны с энергиями не более 3,0 эВ.
14.7.	В монохроматоре с кристаллом бериллия используют отражение нейтронов в первом порядке от системы плоскостей с d — 75 пм. Оценить разрешающую способность этого монохроматора по энергиям (ДТ/Т) для нейтронов с энергией вблизи Т = 0,30 эВ, если падающий пучок нейтронов коллимирован до Aft = 0,5°.
14.8.	Монохроматором с кристаллом LiF, в котором используется отражение нейтронов в первом порядке от системы плоскостей с d = 232 пм, необходимо разрешить две группы резонансных нейтро-98
нов с кинетическими энергиями 0,49 и 0,51 эВ. При какой угловой расходимости падающего пучка нейтронов это можно осуществить?
14.9.	При пропускании пучка тепловых нейтронов через толстый слой прессованного кристаллического порошка нейтроны с достаточно большой длиной волны проходят блок, не испытывая отражений от кристаллических плоскостей. Найти кинетическую энергию нейтронов, проходящих через толстый блок графита. Максимальное межплоскостное расстояние графита d = 335 пм.
14.10.	На рис. 14.2 изображена схема сцинтилляционного спектрометра быстрых нейтронов. Исследуемый пучок нейтронов падает на стильбеновый сцинтиллятор фотоумножителя А. В результате упру-
гого соударения с протонами стиль-
бена нейтроны, рассеянные на угол О, регистрируются фотоумножителем В, а протоны отдачи — фотоумножителем А. Импульсы обоих фотоумножителей поступают в схему совпадений (импульсы от фотоумножителя А поступают с задержкой на время пролета рассеянным нейтроном расстояния L). Найти:
а) кинетическую энергию первичных нейтронов, если время задержки, при котором наблюдается максимальное число совпадений импульсов, равно 22,0 нс, L = 50 см и #	45°;
б) относительную погрешность определения энергии нейтронов при диаметре кристалла фотоумножителя В, равном 3,0 см.
Взаимодействие нейтронов с ядрами
14.11.	Получить с помощью квазиклассических рассуждений выражение для прицельного параметра b бомбардирующего нейтрона. Вычислить первые три возможных значения b для нейтронов с кинетической энергией 1,00 МэВ.
14.12.	Найти максимальное значение прицельного параметра при взаимодействии нейтронов с кинетической энергией 5,0 МэВ с ядрами Ag.
14.13.	Показать, что для нейтронов с длиной волны X геометрическое сечение ядра S « л (R + X)2, где R — радиус ядра. Оценить эту величину для нейтрона с кинетической энергией 10 МэВ, налетающего на ядро Au.
14.14.	Оценить максимальную высоту центробежного барьера для нейтронов с кинетической энергией 7,0 МэВ при взаимодействии ядрами Sn.
14.15.	Оценить угол в пределах которого летят нейтроны, испытывающие упругое дифракционное рассеяние на ядрах свинца. Энергия нейтронов 50 МэВ.
14.16.	Найти вероятность того, что в результате взаимодействия медленных нейтронов (/ - 0) с ядрами, спин которых / = 1, проме-4 *	,99
жуточные ядра образуются в состоянии со спином J = 3/2. Считать, что спины нейтронов и ядер имеют всевозможные взаимные ориентации.
14.17.	Исходя из формулы Брейта—Вигнера для сечения образования составного ядра оа, получить выражения для сечений процессов упругого рассеяния и радиационного захвата нейтрона.
14.18.	Выразить с помощью формулы Брейта—Вигнера сечение радиационного захвата нейтрона o,1V от его кинетической энергии Т, если известны сечение со данного процесса при Т = Тй и аначен-й'Я То и Г.
14.19.	Вычислить сечение реакции 1151п (п, у) 1161п для энергии нейтронов 0,50 эВ, если сечение в резонансе оо = 27,6 кб, То — = 1,44 эВ и Г = 0,085 эВ- Известно также, что нейтронная ширина Г„ значительно меньше радиационной Гт.
14.20.	При взаимодействии тепловых нейтронов с энергией 0,025 эВ с ядрами mCd найдено, что сечение рассеяния составляет 0,22% сечения радиационного захвата. Определить отношение вероятности распада составного ядра с испусканием нейтронов к вероятности испускания у-квантов при резонансном значении энергии нейтронов То 0,178 эВ.
о 14.21. Воспользовавшись формулой Брейта—Вигнера, найти:
а)	значения кинетической энергии нейтрона \Тмак(. w	при
которых сечение радиационного захвата имеет максимум и минимум (То и Г предполагаются известными); установить, в каком случае Т маке То',
б)	на сколько процентов сечение о0 процесса (п, у) при Т То отличается от резонансного значения омакс этого процесса, если Г -= То',
в)	значения отношения Г/То, при которых селективность радиационного захвата нейтронов отсутствует.
14.22.	Найти с помощью формулы Брейта—Вигнера для сечения радиационного захвата нейтрона отношение оМ11 н/о0, где аМИц — минимальное сечение процесса (п, у) в области Т < То; а0 — сечение этого процесса при Т =- То, если Г <</ То.
14.23.	Определить с помощью формулы Брейта—Вигнера ширину Г уровня промежуточного ядра, возникающего при захвате нейтрона ядром 113Cd, если сечение радиационного захвата при энергии нейтрона Т 27о в 15 раз меньше сечения этого процесса при Т То, где То - 0,178 эВ. Считать, что Г не зависит от энергии нейтронов.
14.24.	Показать с помощью формулы Брейта—Вигнера, что если ширина АТ резонансного максимума кривой (Т) на иалавлцге. его, высоты мала (АТ 7'0), то АТ ж Г.
14.25.	Резонансная энергия нейтронов, взаимодействующих с ядрами 59Со, То " 132 эВ, соответствующая нейтронной ширине Г„о = -- 0,9Г, причем Г- < То. Найти с помощью формулы Брейта—Вигнера:
а)	резонансное сечение упругого рассеяния нейтронов;
б)	спин состояния промежуточного ядра, через которое идет процесс, если полное резонансное сечение по ~= 10 б.
100
14.26.	Найти отношение резонансного сечения упругого рассеяния нейтронов ядрами 58Мп к геометрическому сечению данных ядер, если То = 337 эВ, Г,10 « Г < То и спин уровня промежуточного ядра, через который идет процесс, 7 = 2.
14.27.	Сечение радиационного захвата нейтронов ядрами 149Sm в резонансе (То = 0,097 эВ) равно оо = 1,2-105 б. Найти нейтронную ширину Гп0 при резонансной энергии нейтронов, если Г„о Г = - = 0,064 эВ и спин ядра 149Sm I = 7/2.
14.28.	Оценить время жизни промежуточного ядра, возникающего при захвате нейтрона ядром 103Rh, если при резонансной энергии нейтронов То = 1,26 эВ сечение процесса (п, у) равно о0 = 2700 б, Г7 » Г„о = 7,8-10-4 эВ и g = 1/4.
14.29.	Найти с помощью формулы Брейта—Вигнера зависимость сечения радиационного захвата медленных нейтронов от их кинетической энергии в том случае, когда промежуточное ядро имеет «отрицательный» уровень энергии, То < 0 (уровень на рис. 14.1). Установить характер зависимости o„v от Т при Т |То| и Т |То|.
14.30.	Выяснить с помощью формулы Брейта—Вигнера условия, при которых сечение радиационного захвата нейтронов подчиняется закону l;v.
14.31.	При облучении нейтронами (2,5 МэВ) магниевой мишени было обнаружено, что кроме упругорассеянных нейтронов имеется группа неупругорассеянных нейтронов, энергия которых соответст-' вует определенному возбужденному уровню промежуточных ядер (1,3 МэВ). Определить относительную ширину данного уровня для неупругого рассеяния, если известно, что полное сечение процесса оПо.1Н ' 2,2 б и сечение упругого рассеяния оу11Р = 1,6 б. 44% которого составляет потенциальное рассеяние.
Прохождение нейтронов через вещество
14.32.	Какова должна быть толщина кадмиевой пластинки, чтобы поток тепловых нейтронов при прохождении через нее уменьшился в 100 раз?
14.33.	Во сколько раз ослабится узкий пучок тепловых нейтронов при прохождении слоя тяжелой воды толщиной 1,0 см?
14.34.	Оценить, во сколько раз ослабится узкий пучок быстрых нейтронов с кинетической энергией 10 МэВ при прохождении свинцовой пластинки толщиной 4,0 см. Считать, что эффективное сечение ядра о -= 2л (/? + X)2; Е — радиус ядра; X — длина волны нейтрона.
14.35.	В центре сферического слоя графита, внутренний и внешний радиусы которого - 1,0 см и г2 = 10,0 см, находится точечный источник нейтронов с кинетической энергией 2,0 МэВ. Интенсивность источника /о = 2,0-104 с-’. Сечение взаимодействия нейтронов данной энергии с ядрами углерода о = 1,6 б. Определить плотность потока нейтронов на внешней поверхности графита, проходящих данный слой без столкновений.
14.36.	Интенсивность узкого пучка медленных моноэнергетических нейтронов уменьшается в 20 раз при прохождении через пластин
101
ку из естественного изотопного состава бора. Массовая толщина пластинки 1,0 г'см2. Определить энергию нейтронов, имея в виду справедливость в данном случае закона l/v.
14.37.	Узкий пучок нейтронов с кинетической энергией 10,0 эВ проходит I = 15,0 см вдоль оси счетчика, наполненного газообразным BF3 при нормальных условиях (бор естественного изотопного состава). Определить эффективность счетчика, если известно, что сечение реакции (п, а) подчиняется закону Ь'р.
14.38.	В счетчике нейтронов, чувствительным элементом которого является кристалл Lil, используется реакция (п, а) на ядрах 6Li. Определить эффективность такого счетчика для пучка тепловых нейтронов, если известно, что толщина кристалла 2,0 см и его плотность 4,0 г'см3 (литий естественного изотопного состава). Рассеянием нейтронов пренебречь.
14.39.	Найти уменьшение эффективности, %, детектора нейтронов — тонкого слоя 10В, который облучали в течение недели плоским потоком тепловых нейтронов с плотностью J = 1,00-1013 см~2-с-1.
14.40.	Немоноэнергетический пучок медленных нейтронов падает на тонкую мишень, возбуждая ядерную реакцию, сечение которой о cv 1 V. Показать, что в этом случае среднее сечение реакции (усредненное по всем скоростям нейтронов) <о (и)> = о «V».
14.41.	Пучок нейтронов с энергиями в диапазоне, для которого сечение реакции (и, а) пропорционально 1.и, проходит через тонкую фольгу из "Li толщиной 10 мг см2. Какова средняя скорость нейтронов, если известно, что выход реакции (п, а) = 0,40?
14.42.	Счетчик нейтронов объемом 100 см3, наполненный газообразным BF.4 при нормальных условиях, помещен в однородное поле тепловых нейтронов (бор естественного изотопного состава). Имея в виду, что сечение реакции о,1а tv 1'«, определить:
а)	объемную плотность нейтронов, если в счетчике протекает 1,0-1012 реакций в 1 с;
б)	число реакций, протекающих в счетчике за 1 с, если Ф = — 1,1  1О‘° см~2-с-1 и температура нейтронов 300 К.
14.43.	Показать, что при облучении тонкой мишени в изотропном поле нейтронов скорость протекания реакции в 2 раза больше, чем при облучении в параллельном потоке нейтронов того же энергетического состава, если в обоих случаях число нейтронов, падающих на мишень в единицу времени, одинаково. Во втором случае имеется в виду поток нейтронов, падающих нормально к поверхности мишени.
14.44.	Сколько времени необходимо облучать тонкий слой нуклида 10В в поле тепловых нейтронов с концентрацией п = 4,0-10я см-3, чтобы количество ядер 10В уменьшилось вдвое? Известно, что сечение реакции ona v 1 v.
14.45.	Тонкий образец металлического натрия, масса которого 0,40 г, поместили в изотропное поле тепловых нейтронов с Ф — 1,0 X > 10’° см_2-с-1. Считать скорость образования радионуклида 24Na постоянной, определить:
а)	активность образца при насыщении и относительную долю накопившихся в этом состоянии ядер 24Na;
102
б)	промежуток времени облучения, через который активность образца будет равна 75% активности при насыщении.
14.46.	Удельная активность золотой фольги, предварительно активированной нейтронами, А = 1,1 -108 Бк/г (3,0 мКи/'г). Сколько времени необходимо дополнительно облучать эту фольгу в поле тепловых нейтронов с Ф = 1,0-1010 см_2-с-1, чтобы увеличить ее активность в г, = 10 раз?
14.47.	Тонкую пластинку меди облучают в изотропном поле тепловых нейтронов с Ф = 0,9-1012 см-2-с-1. Определить удельную активность пластинки через t = 2,0 ч после начала облучения.
14.48.	Тонкую индиевую фольгу 1151п с массой 0,20 г облучали изотропным потоком тепловых нейтронов в течение т = 2,0 ч. Через t — 0,50 ч после окончания облучения активность фольги оказалась А = 2,6-10® Бк (0,07 мКи). Определить плотность потока нейтронов Ф.
14.49.	Небольшой образец ванадия 81V массой 0,50 г активируют до насыщения в поле тепловых нейтронов. Непосредственно после окончания облучения в течение т = 5,0 мин было зарегистрировано N = = 0,8-109 импульсов при эффективности счета Р = 0,010. Определить концентрацию нейтронов, имея в виду, что сечение активации в данном случае подчиняется закону 1/ф.
14.50.	Индиевую фольгу 1151п, покрытую с обеих сторон тонкими слоями кадмия, облучали в изотропном поле нейтронов. Имея в виду, что сечение активации индия в области тепловых нейтронов подчиняется закону 1/и, определить удельную активность фольги при насыщении, если концентрация тепловых нейтронов п = 3,1 -104 см-8 и кадмиевое отношение Red = 20. При расчете полагать, что кадмий поглощает все тепловые нейтроны, а все надтепловые пропускает. Примечание: RCd представляет собой отношение активностей при насыщении для открытой фольги и фольги, покрытой кадмием.
Замедление и диффузия нейтронов
14.51.	Какую долю кинетической энергии теряет нейтрон при: а) упругом лобовом соударении с первоначально покоившимися ядрами 2Н, 12С и aeU;
б)	упругом рассеянии под углом fl на первоначально покоившемся дейтоне, если fl равен 30, 90 и 150°?
14.52.	Нейтроны с кинетической энергией То упруго рассеиваются на ядрах с массовым числом А. Определить:
а)	энергию нейтронов, рассеянных под углом fl в Ц-системе;
б)	относительное число нейтронов, кинетическая энергия которых в результате однократного рассеяния лежит в интервале (7, Т + dT), если рассеяние в Ц-системе изотропно. Построить график функции распределения рассеянных нейтронов по энергиям.
14.53.	Нейтроны с кинетической энергией То = 1,00 МэВ упруго рассеиваются на первоначально покоившихся ядрах 4Не. Определить среднее значение энергии однократно рассеянных нейтронов, считая рассеяние в Ц-системе изотропным.
103
14.54.	Определить вероятность того, что в результате однократного упругого рассеяния нейтрона на дейтроне энергия нейтрона окажется меньше половины первоначальной, если рассеяние в Ц-системе изотропно.
14.55.	Нейтроны испытывают рассеяние на первоначально покоившихся протонах. Считая это рассеяние изотропным в Ц-системе, найти с помощью векторной диаграммы импульсов:
а)	вероятность рассеяния нейтрона в интервале углов (fl, в -г + о!#);
б)	долю нейтронов, рассеиваемых под углами 0 > 60е;
в)	среднее значение угла рассеяния нейтронов в Л-системе.
14.56.	При упругом рассеянии нейтрона на ядре с массовым числом А угол рассеяния нейтрона определяется выражением:
cos # = (1 + Д cos 1Т)/|< 1 АД2 4-2 Л cos#,
где # — соответствующий угол рассеяния в Ц-системе.
а.	Получить это выражение.
б.	Определить долю нейтронов, упругорассеянных в результате однократного соударения на ядрах 9Ве под углами # > #(	90",
если рассеяние в Ц-системе изотропно.
в.	Показать, что при изотропном рассеянии в Ц-системе среднее значение косинуса (cos# > = 2/3 А.
14.57.	Вычислить < cos г'} > для нейтронов, упругорассеиваемых в окиси бериллия ВеО, если рассеяние в Ц-системе изотропно.
14.58.	Полагая упругое рассеяние нейтронов на ядрах изотропным в Ц-системе:
а)	получить формулу (14.5), упростить эту формулу для случая достаточно больших А;
б)	вычислить | для нейтрона в графите и тяжелой воде.
14.59.	Определить среднее число упругих соударений нейтрона при замедлении его от энергии 2,00 МэВ до 0,025 эВ в уране, в графите и тяжелой воде.
14.60.	Найти среднее время замедления нейтрона от энергии То ~ = 2,0 МэВ до 7\ == 0,025 эВ в бериллии, считая средний свободный пробег нейтрона между двумя соударениями не зависящим от энергии и равным 1,15 см.
14.61.	Нейтроны с кинетической энергией 2,0 МэВ замедляются в графите до тепловых энергий 0,025 эВ. Вычислить возраст тепловых нейтронов и длину замедления L.
14.62.	Показать с помощью выражения для плотности замедления qE в случае точечного источника быстрых моноэнергетических нейтронов, что средний квадрат расстояний (по прямой), проходимых нейтроном при замедлении до энергии Е, ( г2 > = 6т, где т — возраст данных нейтронов.
14.63.	Для определения возраста нейтронов точечный источник быстрых нейтронов помещают в большом объеме замедлителя и на различных расстояниях от источника активируют тонкие листки ин-104
дия, покрытые кадмием. При этом степень актйвации индия обусловлена главным образом его резонансным уровнем с энергией около 1,5 эВ. Найти возраст резонансных нейтронов индия в графите, если известно, что на расстоянии г от источника, равных 50, 100 и 150 мм, активность фольг А (в относительных единицах) равна соответственно 100, 94 и 85.
14.64.	Показать, что для ядер, сечение поглощения которых подчиняется закону l/v, резонансный интеграл для надкадмиевых нейтронов (энергия которых больше 0,40 эВ) равен о0/2, где о0 — сечение поглощения при энергии нейтронов 0,025 эВ.
14.65.	Тепловые нейтроны диффундируют в однородной среде, макроскопическое сечение расстояния которой равно Ss, а сечение поглощения пренебрежимо мало. Найти:
а)	вероятность того, что нейтрон в этой среде пройдет без столкновения путь от х до x^dx, а также среднюю длину свободного пробега между двумя последовательными соударениями;
б)	средний квадрат свободного пробега <х2> нейтрона в графите.
14.66.	Тепловой нейтрон с энергией 0,025 эВ диффундирует в графите. Определить среднее время диффузии данного нейтрона (время жизни) и среднее число соударений, которое он претерпевает за это время.
14.68.	Нейтроны диффундируют в среде, сечение поглощения которой пренебрежимо мало. Считая рассеяние нейтронов изотропным в Л-системе, определить:
а)	число нейтронов, пересекающих за 1с с одной стороны площадку 1 см2, если плотность потока нейтронов одинакова во всех точках среды и равна Ф;
б)	результирующую плотность тока нейтронов через площадку, перпендикулярную VO, если Ф -- Фо + (d<D/dn)0 х, где величины с индексом 0 относятся к точкам рассматриваемой площадки (х = 0).
14.69.	Источник тепловых нейтронов находится в безграничной однородной неразмножающейся среде, макроскопическое сечение поглощения которой 2а и коэффициент диффузии D. Считая рассеяние нейтронов изотропным в Л-системе, найти выражение, описывающее стационарное распределение плотности потока Ф нейтронов в среде, если источник нейтронов:
а)	представляет собой бесконечную плоскость, которая испускает за единицу времени с единицы поверхности п нейтронов;
б)	точечный, испускающий за единицу времени п нейтронов;
в)	сфера радиусом /?, которая испускает за единицу времени с единицы поверхности п нейтронов, причем все нейтроны, влетающие внутрь сферы, поглощаются.
14.70.	Точечный источник тепловых нейтронов окружен большим объемом тяжелой воды. Вычислить диффузионную длину нейтрона в этой среде, если отношение плотности потоков нейтронов на расстояниях = 15 см и г2 = 30 см от источника Фх/Ф2 = 2,2.
14.71.	Показать, что средний квадрат смещения теплового нейтрона в среде от точки, где он стал тепловым, до точки поглощения связан с диффузионной длиной соотношением <г2> = бА^ф.
105
14.72.	Нейтрон диффундирует в среде, альбедо которой равно 0. Определить вероятность того, что данный нейтрон пересечет некоторую воображаемую плоскость в среде п раз, а также среднее число пересечений нейтроном этой плоскости.
14.73.	Индиевую фольгу толщиной 0,13 г/см2 активируют до насыщения в баке с водой, в которой имеется поле тепловых нейтронов. При этом оказалось, что активность фольги в 6,9 раза больше активности такой же фольги, но экранированной с одной стороны слоем кадмия. Найти альбедо тепловых нейтронов в воде.
14.74.	Воспользовавшись решением задачи 14.68, найти альбедо отражателя, если среда, генерирующая тепловые нейтроны:
а)	отделена плоской границей от безграничного отражателя — графита, распределение плотности потока нейтронов в котором Ф = — Фое~х''£, где х—расстояние от границы раздела; L—диффузионная длина;
б)	имеет вид шара радиусом R, который окружен безграничным отражателем; известны коэффициент диффузии D, диффузионная длина L и распределение плотности потока нейтронов в отражателе Ф cv (1/г) где г — расстояние до центра шара.
15. ФИЗИЧЕСКИЕ ОСНОВЫ ЯДЕРНОЙ ЭНЕРГЕТИКИ
•	Энергию, освобождающуюся в одном акте деления ядра урана, считать равной 200 МэВ.
•	Коэффициент размножения нейтронов в безграничной среде:
koo = epfi},	(15.1)
где е — коэффициент размножения на быстрых нейтронах; р — вероятность избежания резонансного захвата; f — коэффициент использования тепловых нейтронов (вероятность поглощения теплового нейтрона делящимся веществом); т] — среднее число нейтронов деления на один тепловой нейтрон, поглощенный делящимся веществом.
•	Энергии реакций dd и dt (d — дейтерий, t — тритий);
/p-f 4,0 МэВ,
d-\-d^	d-\-t а -(-« +17,6 МэВ.
3He-f-n + 3,3 МэВ,
Оба канала реакции dd практически равновероятны.
•	Эффективное сечение реакции dd, б:
1	/	31,3 \
add = 1,2-102— exp - —77 ,	(15.2)
Т	\	Г1/2 /
где Т, кэВ, — кинетическая энергия относительного движения дейтронов, т. е. их суммарная кинетическая энергия в Ц-системе.
•	В этом разделе распределение частиц плазмы предполагается максвелловским; температура плазмы дана в энергетических единицах 6 = kT.
106
•	Средние значения величины <то для дейтериевой и дейтериево-тритиевой плазмы, см3/с:
_,4 1	/	19 \
<OT)dd=3’io	—гт ехР I — —:— ;
'	о2/3 I о1/3/
°	°	/	(15.3)
,, 1 I 20 \
<OT)d( = 3.10 |2—-exp	,
02/з	е'/з /
где 0, кэВ, — температура плазмы. Графики этих зависимостей даны вЩрило-жеиии 13.
•	Объемная плотность мощности тормозного излучения водородной плазмы, Вт/см3:	___
а>= 4,8-Ю-31 пе nt "|/ 0е .	(15-4)
где ne<i, см-3, — концентрация электронов и ионов; 0е, кэВ, — электронная температура.
•	Электропроводность полностью ионизованной водородной плазмы, Ом-1 • см-1:
а = 4,0 • 1О503/2,	(15.5)
где 0, кэВ, — температура плазмы.
•	Основное уравнение магнитной гидродинамики для плазмы в квазиста-ционарном состоянии и условие на границе плазмы:
1	В2
v р=—IJBJ; р +т~=c°nst<	(15.6)
с	ол
где р — газокинетическое давление плазмы; j — плотность электрического тока; В — индукция магнитного поля.
• Связь между температурой 6 и продольным током / для равновесного цилиндрического шнура полностью ионизованной водородной плазмы:
0 = /2/4с2У,	(15.7)
где М — число электронов на единицу длины шнура.
Деление ядер. Цепная реакция
15.1.	Определить:
а)	энергию, выделяющуюся при сгорании 1,0 кг 235U; какое количество нефти с теплотворной способностью 42 кДж/г выделяет при сгорании такую энергию?
б)	электрическую мощность атомной электростанции, если расход нуклида 235U составляет 192 кг в год при КПД 30%;
в)	массу нуклида 235U, подвергшуюся делению при взрыве атомной бомбы с тротиловым эквивалентом 30 кт, если тепловой эквивалент тротила равен 4,1 кДж/г.
15.2.	Найти полный поток нейтрино и уносимую им мощность из реактора с тепловой мощностью 20 МВт, считая, что на каждое деление приходится пять Р-распадов осколков, для которых суммарная энергия нейтрино составляет около 11 МэВ.
15.3.	Найти с помощью полуэмпирической формулы для энергии связи (10.3) отношение Z2/A, при котором деление ядра с четными Z и А на два одинаковых осколка становится энергетически возможным.
15.4.	Ядро оказывается совершенно неустойчивым к делению на два одинаковых осколка, если отношение его электростатической энер-
107
гии к поверхностной энергии равно двум. Найти с помощью формулы (10.3) значение Z^/A такого ядра. Сравнить со значением Z2lA ядер, находящихся в конце периодической системы; объяснить причину деления этих ядер.
15.5.	Найти период полураспада 238U относительно спонтанного деления, если известно, что число таких распадов в 1 г чистого 238U равно 25 за 1 ч. Какое число а-распадов за то же время происходит в этом образце?
15.6.	Ядро 235U захватило тепловой нейтрон. В результате деления образовавшегося ядра возникло три нейтрона и два радиоактивных осколка, которые превратились в стабильные ядра 89Y и 144Nd. Найти энергию, освободившуюся в этом процессе, если известны:
а)	избытки масс нейтрона и ядер 235U, 89Y (— 0,09415 а.е.м.) и 144Nd (- 0,09010 а.е.м.);
б)	энергия связи на один нуклон в ядрах 238U (7,59 МэВ), 89Y (8,71 МэВ), 144Nd (8,32 МэВ) и энергия связи нейтрона в ядре 236U (6,40 МэВ).
15.7.	Ядро, возникающее при захвате нейтрона ядром 238U, испытывает деление, если кинетическая энергия нейтрона не меньше 1,4 МэВ. Найти энергию активации делящегося ядра.
15.8.	Определить наиболее вероятную и среднюю кинетическую энергию нейтронов деления 235U, энергетический спектр которых имеет вид: ti(T)^VT ехр (—0,77Г), где Т — кинетическая энергия нейтрона, МэВ.
15.9.	Вычислить сечение деления на ядро урана природного изотопного состава для тепловых нейтронов.
15.10.	Найти средние числа мгновенных нейтронов деления на один поглощенный тепловой нейтрон в 233U, 235U и 239Pu.
15.12.	Сравнить среднее число мгновенных нейтронов деления на один поглощенный тепловой нейтрон в естественном и обогащенном (1,50% 235U) уране.
15.13.	Пластинку из 238U облучают тепловыми нейтронами, падающими по нормали к ее поверхности. При какой толщине пластинки на каждый падающий тепловой нейтрон будет возникать в среднем один быстрый нейтрон деления?
14.14.	Параллельный поток тепловых нейтронов плотностью Jo = 1,2-Ю10 см_2-с-1 падает нормально на пластинку из урана естественного изотопного состава. Толщина пластинки d = 8,0 г/см2. Найти мощность, выделяемую при делении ядер 238U с 1 см2 пластинки.
15.15.	В реактор, работающий на постоянном уровне мощности, ввели тг = 0,90 г 239Рц и, чтобы мощность реактора не изменилась, ввели еще т2 = 0,060 г бора естественного изотопного состава. Считая сечение поглощения плутония и бора известными, найти среднее число нейтронов деления 239Рц на один поглощенный тепловой ней трон.
15.16.	Реактор, в котором делящимся нуклидом является 238U, работает на постоянном уровне мощности. Найти долю нейтронов, 108
покидающих активную зону реактора, если половина нейтронов деления захватывается ядрами урана и примесей без последующего деления.
15.17.	В чем физический смысл коэффициента размножения k? Сколько нейтронов будет в сотом поколении, если процесс деления начинается с 1000 нейтронов и k = 1,05?
15.18.	Оценить промежуток времени, необходимый для деления 1,0 кг вещества в безграничной среде 235U, если средняя энергия нейтронов деления 1,6 МэВ, сечение деления ядра 235U для этой энергии около 2 б и коэффициент размножения k = 1,0010. Считать, что в начальный момент разделилось одно ядро. Как изменится результат, если k — 1,010?
15.19.	На каждый акт деления ядра 238U возникает в среднем около 2,6 нейтрона деления. Сечение деления ядра 238U порядка 0,5 б (для нейтронов спектра деления), сечение неупругого рассеяния составляет несколько барн. Имея в виду, что по крайней мере половина возникающих нейтронов обладает энергией ниже порога деления ядер 238U, показать невозможность самоподдерживающейся цепной реакции деления в среде, состоящей из этих ядер. —
15.20.	Объяснить, почему невозможна самойоддерживающаяся цепная реакция в среде, состоящей из естественного урана.
15.21.	Гомогенная смесь содержит z = 500 молей углерода на каждый моль урана. Вычислить:
а)	коэффициент /, если уран естественного изотопного состава;
б)	степень обогащения урана нуклидом 235U, при котором f = 0,95.
15.22.	Для гомогенной уран-графитовой смеси вероятность избежания резонансного захвата:
р = ехр [— 24,7 (jVo/Ss)0,585],
где Nа — число атомов 238U в 1 см3; Ss — макроскопическое сечение рассеяния среды. Вычислить значение р для смеси, содержащей 400 молей графита на каждый моль урана естественного изотопного состава.
15.23.	Воспользовавшись формулой из предыдущей задачи и полагая коэффициент е = 1, вычислить для гомогенной смеси, содержащей z = 400 молей графита на каждый моль урана, коэффициент размножения kx, если уран естественного изотопного состава.
15.24.	Активная зона гетерогенного реактора на тепловых нейтронах представляет собой бак с замедлителем, в который введено 200 стержней из урана естественного изотопного состава. Длина каждого стержня 1,50 м, диаметр 2,0 см. Пренебрегая самопоглощением нейтронов в уране, оценить среднюю плотность потока Ф и концентрацию тепловых нейтронов, если мощность реактора 0,60 МВт.
15.25.	Тонкую фольгу 233U массой 0,10 г облучали в течение т = 60 с потоком тепловых нейтронов, падающим по нормали к ней. Плотность потока I — 1,1 • 1010 см-2-с-1. Через t = 10 с после окончания облучения активность одной из групп запаздывающих нейтронов с периодом полураспада 55 с оказалась равной А =4,0-105 Бк. Найти выход запаздывающих нейтронов этой группы на одно деление.
109
15.26.	Оценить среднее время жизни одного поколения нейтронов деления в гомогенной среде, содержащей 100 молей графита на каждый моль урана (уран естественного изотопного состава). Иметь в виду, что время замедления нейтронов до тепловых энергий значительно меньше времени диффузии.
15.27.	При делении 235U под действием тепловых нейтронов возникает шесть групп запаздывающих нейтронов:
Т„ с...................... 55,7	22,7	6,20	2,30	0,61	0,23
и>(, 10-3 ................ 0,52	3,46	3,10	6,24	1,82	0,66
Здесь Ti — период полураспада осколков, испускающих t-ю группу запаздывающих нейтронов; wt — выход этих нейтронов на одно деление. Найти, насколько увеличится среднее эффективное время жизни одного поколения нейтронов в среде 235U с замедлителем благодаря запаздывающим нейтронам. Известно, что среднее время жизни одного поколения нейтронов деления т х 1 мс.
15.28.	Найти период реактора Т (время, в течение которого его мощность увеличится в е раз), если коэффициент размножения k = = 1,010 и среднее время жизни одного поколения нейтронов т = 0,10с.
Термоядерные реакции
15.29.	Какая энергия выделяется при сгорании 1 г ядерного горючего в термоядерных реакциях:
a) dt; б) dd; в) 6Li (d, а) 4Не? Сравнить полученные результаты с энергией, выделяющейся при сгорании 1 г урана.
15.30.	На сколько лет хватит запаса термоядерной энергии в отношении реакции dd, если использовать 1% дейтерия, содержащегося в воде океанов, объем которых порядка 1018 м3, при уровне потребления энергии 10Q в год (1Q ~ Ю18 кДж)? Замечание; современный уровень потребления энергии человечеством около 0.1Q в год. Уровень 10Q в год — величина, при которой климат на Земле существенно не изменится: эта величина составляет 1% солнечного излучения, поглощаемого и излучаемого Землей за год.
15.31.	Предложенный Бете углеродный цикл звездных термоядерных реакций состоит из следующих превращений:
р + 12С ->-13N + у, р + 14N ->15О + у,
13N -► 13С + е+ + v, 15О	15N + е+ + v,
р + 13С	14N + у, р + 15N -> 12С + 4Не'.
Вычислить энергию, выделяющуюся в этом цикле при образовании одного моля гелия.
15.32.	Какую долю выделяющейся энергии уносят из зоны термоядерной реакции нейтроны, образующиеся в результате реакции:
a) dt; б) dd?
15.33.	Энергию нейтронов, возникающих в термоядерной реакции dt, можно использовать, если окружить зону реакции оболочкой, которая их поглощает с положительным тепловым эффектом, например оболочкой, содержащей 6Li (л + 6Li ->/4-а). Во сколько раз увеличится используемая энергия при введении такой оболочки?
110
15.34	Оценить минимальную температуру дейтериевой плазмы, при которой дейтроны с наиболее вероятной скоростью относительного движения смогут преодолеть высоту кулоновского барьера. Радиус дейтрона « 2,0 фм.
15.35.	Для заряженных частиц, кинетическая энергия относительного движения которых Т значительно меньше высоты кулоновского барьера, коэффициент прозрачности барьера:
D « ехр (—а/]/”т), а nqt q.2
где <?! и q., — заряды частиц; р — приведенная масса.
а.	Получить эту формулу из общего выражения (3.5).
б.	Вычислить значения D для дейтронов с наиболее вероятной скоростью относительного движения дейтронов плазмы с температурой 1,0 и 10,0 кэВ.
15.37.	В дейтериевой плазме с концентрацией ядер n= 1,0 -1015 см-3 дейтроны реагируют с частотой f = 1,0-10_3 с-1. Найти объемную плотность освобождаемой термоядерной энергии и температуру плазмы 0.
15.38.	Определить кинетическую энергию относительного движения дейтронов, соответствующую максимальной скорости реакции dd в дейтериевой плазме с температурой 0 = 2,0 кэВ.
15.39.	Дейтериевая плазма с концентрацией ядер п = 1,0-1015 см-3 находится при температуре 0. Вычислить для 0 = 1,0 и 10 кэВ:
а)	среднее время жизни дейтрона по отношению к реакции dd\
б)	число реакций dd, происходящих за 1 с в 1 см3, и выделяемую объемную плотность мощности.
15.40.	В дейтерий-тритиевой плазме, имеющей температуру 0 и концентрацию ядер п= 1,00-1015 см-3, концентрация ядер трития составляет п/100. Вычислить для 0 = 1,00 и 10,0 кэВ:
а)	число термоядерных реакций (dd + df) за 1 с в 1 см3;
б)	освобождаемую объемную плотность мощности.
15.41.	Дейтерий-тритиевая плазма с концентрацией ядер п = = 1,00-1015 см-3 имеет температуру 0. Найти для 0 = 1,00 и 10,0 кэВ отношения концентраций ядер трития и дейтерия, при которых мощность освобождаемой термоядерной энергии максимальна, а также значения этой мощности, Вт'см3. Что можно сказать об относительном вкладе реакции dd и dt в освобождаемую мощность при этих условиях?
15.42.	Найти температуру 0 дейтерий-тритиевой плазмы с концентрацией ядер п = 1,0-1015 см-3 (nd = nt), при которой выделяемая объемная плотность мощности w = 1,0 Вт/см3. Считать, что эта мощность выделяется в основном за счет реакции dt.
15.43.	Каким был бы радиус сферического термоядерного реактора, заполненного дейтериевой плазмой с концентрацией дейтронов п при температуре 0, если бы теплоотвод из активной зоны осуществлялся только в виде теплового излучения в соответствии с законом Стефана—Больцмана? Вычислить 0т, при которой радиус реактора минимален. Чему он равен, если п= 1,0-10а° см-3? Обсудить полученный результат.
111
15.44.	Найти температуру 0 дейтериевой плазмы, при которой мощность, выделяемая в термоядерных реакциях, равна мощности тормозного излучения электронов.
15.45.	Имеется дейтерий-тритиевая плазма при температуре 10,0 кэВ, концентрация дейтерия в которой поддерживается на постоянном уровне nd = 1,00-1015 см~3 за счет внешнего источника. Последний обеспечивает скорость поступления ядер дейтерия q, с-1-см-3. Принимая во внимание только реакции dd и dt, найти: а) равновесную (установившуюся) концентрацию ядер трития и значение <?; б) объемную плотность выделяемой мощности ш. При каком значении п величина wd = 100 Вт/см3?
Физика плазмы
15.46.	Пусть плазма имеет вид плоскопараллельного слоя и под действием некоторой причины произошло смещение всех электронов на х относительно ионов в направлении, перпендикулярном к поверхности слоя. Найти с помощью этой модели частоту возникающих электронных колебаний.
15.47.	Диэлектрическая проницаемость плазмы в электрическом поле£ Ео cos w^b условиях, когда можно пренебречь столкновениями частиц и движением ионов, имеет вид: е (w) = 1 — (w0/w)2, где <оо — ленгмюровская частота электронов.
а.	Получить это выражение.
б.	Показать, что электромагнитная волна с частотой со < w0 испытывает в плазме полное внутреннее. отражение.
в.	Вычислить концентрацию электронов в плазме, для которой наблюдается запирание пучков радиоизлучения с длиной волны, большей л0 — 1,7 см.
15.48.	Вычислить поток термоядерных нейтронов из дейтериевой плазмы объемом V = 1,0 л при температуре 9 = 10,0 кэВ, если известно, что запирание зондирующих пучков радиоизлучения наблюдается для длин волн, больших л0 = 5,0 мм.
15.49.	Показать с помощью уравнения Пуассона, что средний потенциал электростатического поля вблизи иона водородной плазмы Ф со (1'г) Q~rld , где г — расстояние до иона; d — дебаевский радиус экранирования. Найти выражение для d, если концентрация электронов (и ионов) равна п и температура плазмы 0 (0е = 0г). Считать, что пространственное распределение частиц подчиняется закону Больцмана, причем |еср | 0-
15.50.	Водородная плазма с концентрацией ядер п = 1,0-1015 см-3 находится при температуре 0 = 10 кэВ. Вычислить дебаевский радиус и число ядер в пределах сферы с этим радиусом.
15.51.	Вычислить сечение, соответствующее рассеянию электронов с кинетической энергией Т = 1,00 кэВ на углы О' > 90° при соударениях с ионами водородной плазмы.
15.52.	Водородная плазма с концентрацией ядер п — 1,0-1015 см-3 находится при температуре 0 = 1,0 кэВ. Оценить минимальный угол ^мин, под которым рассеиваются электроны с наиболее вероятной ско-112
ростью на ядрах, а также значение кулоновского логарифма In (2/0Мин)- Считать, что кулоновское поле ядер простирается до дебаевского радиуса и затем резко обрывается.
15.53.	Эффективное сечение для передачи импульса электрона при рассеянии на ионах плазмы определяется следующим выражением: о = J (1 — cos тТ) а (ft) d$, где а (О) = da/dd) — дифференциальное сечение, определяемое формулой Резерфорда. Вычислить с помощью этой формулы для электронов с наиболее вероятной скоростью в водородной плазме при температуре 0 = 1,0 кэВ и с концентрацией ядер п= 1,0-1015 см-3;
а)	данное эффективное сечение;
б)	среднюю длину «свободного пробега», средний промежуток времени между «столкновениями» и число столкновений в 1 с.
Считать, что рассеяние электронов происходит на кулоновском поле ядер, которое простирается вплоть до дебаевского радиуса и затем резко обрывается.
15.54.	Электрон в водородной плазме излучает мощность = = 4,5-10“31 riiV^T Вт, где nt — концентрация ядер, см-3; Т — кинетическая энергия электрона, кэВ. Найти объемную плотность мощности тормозного излучения электронов водородной плазмы, если температура электронов равна 0, кэВ, и их концентрация пе, см-3.
15.55.	Мощность, передаваемая электронами ионам в единице объема дейтериевой плазмы, Вт/см3:
w = 1,7-10-“ п2 (0е — 0Л 0-3/2,
где п — концентрация электронов (ионов), см-3; 0е и 0; — электронная и ионная температуры, кэВ. Найти с помощью этого выражения для дейтериевой плазмы с п = 1,0-1015 см-3 промежуток времени, за который 0; станет равной 2/-30е, если начальная температура ионов пренебрежимо мала, а электронная температура: а) поддерживается постоянной на уровне 0е = 1,0 кэВ; б) в начальный момент равна 0еО = 1>0 кэВ и теплообмен с окружающей средой отсутствует.
15.56.	Ток /0 протекает вдоль тонкого скин-слоя цилиндрического плазменного шнура радиусом г0. Найти магнитное давление р, т. е. силу Лоренца, действующую на единицу поверхности шнура. Показать, что р = Во/8л, где Во — индукция магнитного поля на поверхности шнура.
15.57.	Пусть газокинетическое давление р дейтериевой плазмы при температуре 0 = 10,0 кэВ уравновешивается магнитным давлением, соответствующим В = 50 кГс. Вычислить концентрацию дейтронов, давление р и объемную плотность мощности, выделяемой в результате протекания термоядерных реакций dd.
15.58.	Ток протекает вдоль тонкого скин-слоя равновесного цилиндрического шнура водородной плазмы радиусом гъ а в обратном направлении — по внешнему коаксиальному цилиндру радиусом га. Найти отношение магнитной энергии к газокинетической энергии плазменного шнура. Плазму считать полностью ионизованной.
15.59.	Плазма имеет вид тонкого цилиндрического слоя, вдоль которого течет ток /х. По оси этого слоя расположен проводник с током
113
12 обратного направления. Пренебрегая магнитным полем внутри плазмы, определить:
а)	отношение токов Iх/12, при котором плазменный слой будет находиться в равновесии;
б)	значение тока /х, при котором температура водородной плазмы в этой системе 0 = 1,00 кэВ, если равновесный радиус плазменного слоя г0 = 6,0 см и концентрация ядер п = 1,00-1015 см-3.
15.60.	Ток 10 протекает вдоль водородного плазменного шнура цилиндрической формы с равновесным радиусом г0. Пренебрегая внешним газокинетическим давлением, определить:
а)	среднее значение газокинетического давления в шнуре;
б)	температуру плазмы, если 10 = 300 кА и число ядер на единицу длины шнура N = 0,7-1017 см-1.
15.61.	Ток I течет вдоль цилиндрического полностью ионизованного водородного плазменного шнура, имеющего N электронов на единицу его длины. Считая температуру плазмы и плотность тока постоянными по сечению:
а)	показать, что распределение концентрации электронов по сечению имеет вид: п (г) = (2Л7лго) (1 — г2/г§), где г0 — равновесный радиус шнура; найти также среднее по сечению значение п2 (г);
б)	найти силу тока, при которой мощность, выделяемая в воде джоулева тепла, равна мощности тормозного излучения плазмы. Какова при этом температура плазмы, если М = 5-Ю1’ см-1?
15.62.	Стеклянная трубка радиусом г0 = 2,5 см заполнена дейтерием с концентрацией молекул п0 = 4,0-1014 см-3 и помещена внутрь одновитковой «катушки» длиной I = 10 см, сделанной из плоской медной шины. После предварительной ионизации дейтерия через виток разряжают батарею конденсаторов. Магнитное поле витка с током сжимает образующийся плазменный шнур до радиуса г = 0,50 см, причем сила тока через виток в этот момент достигает / = 1,0- 10е А. Оценить температуру плазмы, пренебрегая магнитным полем внутри нее. Объяснить механизм сжатия плазмы в этом случае.
15.63.	В результате резкого возрастания тока до значения /0 = = 50 кА цилиндрический шнур полностью ионизованный водородной плазмы сжался до равновесного радиуса г0 = 1,0 см, причем ток в процессе нарастания протекал в тонком скин-слое. Оценить время установления магнитного поля по сечению шнура, число ядер в котором на единицу длины N = 1,00- 101в см-1. Указание: время диффузии магнитного поля на расстояние I порядка PD, где D = с2/4ла - коэффициент диффузии; о — коэффициент электропроводности.
15.64.	Водородная плазма с концентрацией ядер .2,0-1010 см-3, заполняющая стеклянную трубку радиусом 2,5 см, находится во внешнем продольном магнитном поле Bz0 = 4,0 кГс. При пропускании через эту плазму тока /2 = -5,0-108 А, протекающего в тонком скин-слое, плазма сжалась до радиуса 0,50 см,увлекая за собой заключенное в ней магнитное поле Вг. Оценить время «вмораживания» поля в плазме.
15.65.	Показать, что условие устойчивости цилиндрического плазменного шнура с током / в отношении перетяжек при наличии «вмороженного» в плазму продольного магнитного поля Ве имеет сле-114
дующий вид: Bi <; у2 Bz, где Вг — магнитное поле тока I. Считать, что ток I течет в тонком скин-слое. При каком значении Bz не будет перетяжек плазменного шнура с током / = 100 кА и радиусом г = 1,0 см?
15.66.	Убедиться, что тороидальный плазменный виток во внешнем кольцевом магнитном поле Вф, создаваемом тороидальным соленоидом, не может находиться в равновесии независимо от того, имеется в витке ток или нет.
15.67.	Кольцевой плазменный водородный виток с током I. 10 кА и концентрацией ядер п = 1,0-1015 см-3 образован в тороидальной кварцевой камере с радиусом поперечного сечения а = 5,0 см и большим средним радиусом R = 50 см. Пусть в начальный момент средний большой радиус витка также равен А?. Оценить промежуток времени, за который виток будет выброшен на стенку камеры. Считать, что в процессе расширения витка его малый радиус, равный г = 1,0 см, и ток / не меняются, и газокинетическое давление плазменного витка уравновешивается магнитным давлением тока /. Считать также, что ток / течет по поверхности витка — условие, при котором индуктивность витка L = 4 л/? [1п (8/?/г) — 2].
15.68.	Плазменный виток с током / — 10 кА находится во внешнем однородном магнитном поле Bz, перпендикулярном к плоскости витка. Считая, что ток течет по поверхности витка, найти значение В2, при котором виток будет находиться в равновесии, если его большой и малый радиусы равны 7? - 50 см и г = 1,0 см. Формулу для индуктивности витка см. в предыдущей задаче.
15.69.	Кольцевой плазменный шнур образован в тороидальной камере, на которую намотана обмотка, с током, создающим продольное магнитное поле Вф. Если вдоль шнура течет ток I, то магнитные силовые линии в этих условиях имеют вид спиралей, и шнур может испытывать неустойчивость, при которой возмущения плазмы имеют спиралевидную форму. Такая неустойчивость не возникает, если длина шнура меньше шага спирали силовых линий на его поверхности. Найти предельное значение тока /, если Вф = 20 кГс, большой и малый радиусы шнура R = 50 см и г — 1,0 см. 16
16. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
• В этом разделе во всех формулах энергия, импульс и масса выражены в энергетических единицах: р и т — сокращенные записи рс и /пс2, под массой всюду понимается масса покоя.
• Кинетическая энергия относительного движения — это суммарная кинетическая энергия частиц в Ц-системе.
• Лоренц-инвариант:
Е2р2 = inv,	(16.1)
где Е и р — полная энергия и суммарный импульс системы. При переходе из одной инерциальной системы в другую эта величина не меняется.
• Скорость Ц-системы относительно Л-системы:
6 —; vic — р/Е,	(16.2)
где р и Е — суммарный импульс и полная энергия системы частиц.
115
• Лоренцевы преобразования импульса, полной энергии и углов при переходе от Л-системы к Ц-системе (рис. 16.1):
Px—Efi г- E—pxfi L . -к 1/1—₽2 sin fl —	- • L- -- ' ~ ‘ tg V —= ——————— ,
-|/1_02	1/1— p2	cosfl—(£/p)P
(16.3)
где (J — скорость Ц-системы относительно Л-системы.
• Пороговая кинетическая энергия частицы т, налетающей на покоящуюся частицу М, для реакции т -f- М 2т;:
_ (SX)2-(m + M)2 отпор	2М
(16.4)
Рис. 16.1
•	При двухчастичном распаде частицы с массой М импульсы возникающих частиц в Ц-системе:
Р =	1/[Л42-(щ1 + /п2)2][(Л42 -(/^-т,)2],	(16.5)
где mt и т2 — массы возникающих частиц.
•	Векторная диаграмма импульсов для двухчастичного распада релятивистской частицы массой М на частицы с массами т1 н т2 (рис. 16.2). Геометрическое место точек возможных положений конца вектора импульса рг частицы т1 образует эллипс, у которого:
Ь==р-, а-р/1/Г=Р: f=7p/l/n^F,	(16.6)
где b и а — малая и большая полуоси; f — фокусное расстояние; р — импульс возникающих частиц в Ц-системе; р — скорость распадающейся частицы (в единицах с).
Центр эллипса делит отрезок АВ на части в отношении : a2 = Е± : £2, где Ei и Е2 — полные энергии возникающих частиц в Ц-системе.
Максимальный угол вылета частицы mi определяется формулой:
М р
sinfl1MaKC —	,	(16.7)
OTi Рм
где — импульс распадающей частицы.
•	Обозначения квантовых чисел частиц:
Q — электрический заряд, единицы е;
L — лептонный заряд (Le — электронный, £ц — мюонный);
В — барионный заряд;
Т — изотопический спин (изоспин), Тг — его проекция;
S — странность;
С — очарование (шарм).
•	Связь между квантовами числами сильно взаимодействующих частиц и резонансов:
Q Т, ч \'2 (В -+ S 1 С).	(16.8)
116
•	Прн взаимодействии частиц выполняются законы сохранения лептонного и барионного зарядов. В сильных взаимодействиях - также законы сохранения странности S, изоспина Т и его проекции Tz.
*	Согласно обобщенному принципу Паули, для системы из двух изотонически тождественных частиц:
(	—	‘ для частиц с полуцелым спином,
I --1 для частиц с нулевым спином,
где / — орбитальный момент; з — спин системы; Т — ее изоспин.
* Квантовые числа кварков:
Кварк	Q	В	т	Tz		с
и	2/3	1/3	1/2	1/2	0	0
d	-1/3	1/3	1/2	-1/0	0	0
S	-1/3	1/3	0	0	—1	0
с	2/3	1/3	0	0	0	1
Спин каждого кварка равен 1/2. Соответствующие антикварки ц, d, з, с имеют противоположные по знаку значения Q, В, Tz, S и С.
Взаимодействие релятивистских частиц
16.1.	Вычислить импульсы, ГэВ/c, протона, мюона и электрона кинетические энергии которых равны 1,0 ГэВ.
16.2.	Релятивистская частица с массой m и кинетической энергией Т налетает на покоящуюся частицу с той же массой. Найти кинетическую энергию их относительного движения, импульс каждой частицы в Ц-системе и скорость этой системы.
16.3.	Какую кинетическую энергию необходимо сообщить протону, налетающему на неподвижный протон, чтобы кинетическая энергия их относительного движения была такой же, как при столкновении двух протонов, движущихся навстречу друг другу с кинетическими энергиями Т = 30 ГэВ?
16.4.	Релятивистская частица с массой пгг и кинетической энергией Т налетает на покоящуюся частицу с массой т2. Найти:
а)	кинетическую энергию их относительного движения;
б)	импульс и полную энергию каждой частицы в Ц-системе.
16.5.	Определить в Ц-системе кинетические энергии частиц с массами тг и т2, если известно, что кинетическая энергия их относительного движения равна Т.
16.6.	Одна из частиц системы движется с импульсом р и полной энергией Е под углом О' (в Л-системе) к вектору скорости Ц-системы Рс. Найти соответствующий угол О в Ц-системе.
16.7.	Релятивистский протон с кинетической энергией Т рассеялся под углом О1! на покоившемся ядре атома водорода. При этом ядро отлетело под углом 02.
а.	Показать, что ctg г<>1 ctg О2 1 -+- Т12т.
б.	Вычислить минимально возможный угол между направлениями разлета обеих частиц.
в.	Определить Т и кинетические энергии обеих частиц после соударения, если = 30° и 0'2 = 45°.
16.8.	Показать, что при упругом рассеянии релятивистской частицы с массой гпг на покоящейся частице с массой т2 <; пгг максимальный угол рассеяния налетающей частицы определяется выражением sin Фмаке = т^т^.
16.9.	Отрицательный мюон, кинетическая энергия которого Т = = 100 МэВ, испытал упругое лобовое соударение с покоившимся электроном. Найти кинетическую энергию электрона отдачи.
16.10.	Релятивистские протоны с кинетической энергией Т упруго рассеиваются на покоящихся ядрах атомов водорода. Пусть О — угол рассеяния протона в Ц-системе, соответствующий углу О в Л-системе. Показать, что:
a)	tg (0/2) -- )/1 + T2m tg О, т — масса протона;
б)	дифференциальные сечения этого процесса в Ц- и Л-системах связаны соотношением, см2/ср:
~/За	(1 -г«sin2 #)2	„/о
° =	'---«Г- ° W- а = 772т\
4 (1 ;-а) cos v
в)	рассеяние в Ц-системе не изотропно, если дифференциальные сечения ох и о2, отвечающие углам О] = 15° и 02= 30°, равны соответственно 26,8 и 12,5 мб/с при Т 590 МэВ.
16.11.	Релятивистские протоны с кинетической энергией То упруго рассеиваются на ядрах атомов водорода.
а.	Показать, что дифференциальное сечение о (Т), см2/МэВ, соответствующее кинетической энергии Т рассеянного протона в Л-системе, определяется выражением:
а (Т) — а (д) -4л/То,
где о (О’) - дифференциальное сечение в Ц-системе, в которой углу 11 соответствует кинетическая энергия Т.
б.	Найти распределение рассеянных протонов по энергиям в Л-системе, если их угловое распределение в Ц-системе изотропно.
16.12.	Позитрон с кинетической энергией, равной его энергии покоя, аннигилирует на покоящемся свободном электроне. В результате возникают два у-кванта, энергия одного из которых в п = 2 раза больше энергии другого. Вычислить угол между направлениями разлета обоих у-квантов.
16.13.	Показать, что при аннигиляции релятивистских позитронов с импульсом р на свободных электронах дифференциальное сечение рождения у-квантов с энергией Ev обратно пропорционально импульсу позитронов, если угловое распределение у-квантов в Ц-системе изотропно.
16.14.	Вычислить пороговую энергию у-кванта для рождения пары л+я~ в поле покоящегося протона.
16.15.	Получить формулу (16.4).
16.16.	Вычислить пороговую кинетическую энергию бомбардирующих частиц в следующих реакциях (налетающей частицей является первая):
118
1)	р	+	2Н —<-3Не +	л°; 5)	+	р	+	Кп + К°\
2)	р	+	10В -+11 В + л+;	6)	р	+	р ^р	+	2° -4 К+;_
3)	р	+	р -+ Л + Л;	Т)р	+	р^р	+	р + р+-р\~
4)	л~ 4- р —4-	КА\	8)	р	+	р —>•р	4-	р 5 — 4- 5 —.
16.17.	Найти кинетические энергии мезонов, возникающих в водородной мишени при пороговой энергии налетающей частицы:
а) У + Р ~+п + л+; б) р 4- р р 4- 2° + К+.
16.18.	Пусть в прямом процессе релятивистская частица налетает на покоящуюся частицу А, а в обратном — частица b на покоящуюся частицу В (а -+- А В 4- Ь). Считая, что полная энергия взаимодействующих частиц одинакова в Ц-системе для обоих процессов, т. е. Ёа + ЁА = Еь + Ёв, найти:
а)	связь между кинетическими энергиями налетающих частиц Та и Ть в Л-системе в прямом и обратном процессах, если известны массы частиц А и В и пороговая кинетическая энергия частицы а;
б)	для реакции у 4- р п + л+ кинетическую энергию л-мезо-на в обратном процессе, если энергия у-кванта в прямом процессе hw = 200 МэВ; массы протона и нейтрона считать одинаковыми.
16.19.	Протоны с кинетической энергией Т = 500 МэВ бомбардируют водородную мишень, возбуждая реакцию р 4- р ->-d 4- л+-Найти максимально возможный угол вылета дейтронов.
16.20.	Исследование зависимости сечения взаимодействия л+-ме-зонов с протонной мишенью от кинетической энергии л-мезонов позволило обнаружить максимумы сечения при 198, 600 и 900 МэВ. Эти максимумы соответствуют нестабильным частицам — резонансам. Определить их массы покоя.
Распад частиц
16.21.	Остановившаяся 2~-частица распалась на нейтрон и л-мезон. Найти кинетическую энергию и импульс нейтрона.
16.22.	Вычислить максимальные значения кинетической энергии и импульса электрона, возникающего при распаде остановившегося мюона.
16.23.	Гиперядро 5Нел испытывает распад 5Нел->4Не + Р + 4- я~. Вычислить энергию связи Л-гиперона в данном гиперядре, если его энергия распада Q = 34,9 МэВ.
16.24.	л-Мезон с кинетической энергией Тя — 50 МэВ распался на лету на мюон и нейтрино. Под каким углом вылетел мюон, если угол вылета нейтрино равен 90°?
16.25.	л°-Мезон с кинетической энергией, равной его энергии покоя, распадается на лету на два у-кванта. Найти: а) минимально возможный угол между направлениями разлета у-квантов; б) в каких пределах может находиться энергия каждого кванта.
16.26.	Релятивистский №-мезон с кинетической энергией Т распадается на лету на два л°-мезона. Найти:
а)	при каком значении Т один из возникающих л-мезонов может оказаться в состоянии покоя;
119
б)	угол между направлениями симметрично разлетающихся л-ме-зонов, если Т = 100 МэВ.
16.27.	2+-Гиперон с импульсом р% = 900 МэВ/c распадается на лету на положительный л-мезон и нейтральную частицу. Мезон вылетает с импульсом рп = 200 МэВ/c под углом О = 60е к первоначальному направлению движения гиперона. Найти массу нейтральной частицы и энергию данного распада.
16.28.	В результате распада некоторой нейтральной частицы обнаружены протон и л_-мезон, угол между направлениями разлета которых 0 =- 60". Импульсы обнаруженных частиц равны соответственно 450 и 135 МэВ/c. Полагая, что других продуктов распада нет, вычислить массу распавшейся частицы.
16.29.	Получить в Ц-системе выражение (16.5).
16.30.	Обосновать построение векторной диаграммы импульсов для двухчастичного распада релятивистской частицы (см. рис. 42).
16.31.	Рассчитать параметры эллипса импульсов и построить соответствующую векторную диаграмму для следующих случаев:
а)	л°-мезон с Т — тл распадается по схеме л° ->• 2у;
б)	л+-мезон с Т = тя/2 распадается по схеме л ->• р. + v;
в)	протон с Т = тр упруго рассеивается на протоне;
г)	дейтрон с Т = md!2 упруго рассеивается на протоне;
д)	протон с Т =- тр возбуждает реакцию р + р ->л+ + d. Здесь Т — кинетическая энергия.
16.32.	л+-Мезон с кинетической энергией Т распадается на лету на мюон и нейтрино. Найти в Л-системе:
а)	максимально возможный угол вылета мюона, если Т = 50 МэВ;
б)	предельное значение Т, при котором появляется предельный угол испускания мюонов.
16.33.	Релятивистский л-мезон со скоростью 0 = vic распадается на лету на мюон' и нейтрино.
а.	Показать, что для нейтрино углы вылета О и д в Ц- и Л-систе-мах связаны соотношением:
cos & = (cos б — 0)/(1 — 0 cos О).
б.	Считая, что в Ц-системе распределение продуктов распада изотропно по углам, показать, что дифференциальное сечение распада, соответствующее вылету нейтрино под углом О в Л-системе, см2/ср:
о (Ф)	(1 — 02)/(1 — 0 cose)2.
в.	Вычислить вероятность испускания нейтрино в переднюю полусферу в Л-системе (#v	л/2), если кинетическая энергия л-мезона
Т = Шя и распределение нейтрино по углам в Ц-системе изотропно.
16.34.	При взаимодействии медленных л~-мезонов с ядрами водородной мишени наблюдались следующие реакции:
л- + р
п + л0, л°—>-2у.
(1)
(2)
п у
120
Энергетический спектр возникающих у-квантов изображен на рис. 16.3, где Ег = 54 МэВ; Е2 = 84 МэВ и Е3 = 130 МэВ.
а.	Какому каналу реакции принадлежит каждый максимум?
б.	Считая известными массы протона и нейтрона, определить мас-
су л“-мезона.
в. Найти массу л°-мезона.
16.35.	Изучение реакции взаимодействия быстрых л-мезонов с протонами привело к обнаружению нестабильной квазичастицы р, имеющей настолько малое время жизни, что ее образование и распад про-
исходят практически в одной точке. Каким образом, рассмотрев много случаев этой реакции, можно установить, что процесс л- - р —<-л~ — + л+ -п идет частично через связанное состояние (л_л+), т. е. л- 4-+ Р ->-Р + п, р ->л~ + л+? Предполагается, что в каждом случае известны полные энергии и импульсы рi возникающих л-мезонов в Л-системе.
Рис. 16.3
16.36.	При изучении реакции К+ - Р -+ А — л+ -4- л- под действием К-мезонов с кинетической энергией 7\ = 790 МэВ обнаружено, что эта реакция частично идет через связанное состояние (л- А) в две стадии: К~ + р ->(л-А) -г л+, (л~А) ->-л_ + А, причем возникающие л+ -мезоны имеют в Ц-системе кинетическую энергию Тя --= 300 МэВ. Вычислить массу покоя (л- А)-резонанса и его энергию
распада.
Свойства элементарных частиц
16.37.	Определить собственное среднее время жизни:
а)	мюонов, если при кинетической энергии Т --- 7тм их среднее время жизни т -= 17,6 мкс;
б)	л+ -мезонов, если, имея импульс р — 55 МэВ/c, они пролетают в среднем расстояние I — 3,0 м до распада.
16.38.	Найти вероятность распада л+-мезона в полете от места рождения до мишени (расстояние 6,00 м), если кинетическая энергия мезона равна 100 МэВ.
16.39.	Предположим, что протон часть времени пребывает в состоянии «идеальный протон» с магнитным моментом ц)( и остальную часть времени — в состоянии «идеальный нейтрон» (ц = 0) плюс л-мезон (р п 4~ л+). Какую часть времени протон находится в состоянии «идеальный протон»?
16.40.	Определить с помощью принципа детального равновесия (см. введение к гл. 13) спин л+ -мезона, если известно, что в реакции р -4- р —+d -у- л+ полное сечение прямого процесса <тр;, для протонов с кинетической энергией Тр = 500 МэВ (в Л-системе) в 9 раз меньше полного сечения стя<г обратного процесса при соответствующей энергии. Спины протона и дейтрона известны.
121
16.41.	При взаимодействии у-квантов с водородной мишенью протекает реакция у 4 р —>-л° 4 р. Полное сечение этой реакции отр = 0,20 мб при энергии у-квантов Еу = 250 МэВ. Определить с помощью принципа детального равновесия сечение обратного процесса (л°-мезоны бомбардируют водородную мишень) при соответствующей кинетической энергии мезона. Найти эту энергию.
16.42.	Выяснить с помощью законов сохранения лептонного и барионного зарядов, возможны ли следующие процессы:
1)	п -+р 4 е~ 4 ve; 4) К+ Ц+ + vM 4 л°;
2)	-- /)	- р+;	5)	л~ - я -> Д'- 4 Д°;
3)	р+ ->-е+ + ve 4 vM; 6) К~ + р -+S+ + л-.
16.43.	Какие из приведенных ниже реакций запрещены законом сохранения странности:
1)	л- 4 р ->-Л 4 Д'0;	4) ~р 4 п А 4 2+:
2)	я- 4 р 4 2+;	5)	+ р ->-Л + п;
3)	~р 4 р	2° 4 К0 4 п; 6) я- 4 п Н- + К+ 4- Д~?
16.44.	Являются ли реакции распада Д+-мезона на р+ + и л+ 4- л° реакциями слабого взаимодействия?
16.45.	Какие каналы приведенных ниже реакций запрещены и по какой причине:
,п~л~	(1)	р4-2л-	(1)
а)	б) S-
\\4jt	(2)	А->-р4-я~	(2)
16.46.	Найти возможные значения изоспина Т и его проекции Тг для систем: нуклон—нуклон; л-мезон—нуклон.
16.47.	Найти с помощью обобщенного принципа Паули изоспин Т системы:
а)	пр в состояниях 3Р и 3D;
б)	л+л° в состояниях 1Р и lD;
в)	л+л~ в состояниях 'Р и lD.
16.48.	Убедиться с помощью метода Шмушкевича1, что изотопическая инвариантность приводит к следующим соотношениям между полными сечениями о и вероятностями w процессов:
а)	реакции типа N 4- У ->-л + л (N — нуклон):
р 4- р 4 я+ + л- (<тх) р 4 р-+ л° 4- я° (а2) р~п^ л-4 л»(сг3)
2о1 — 4а24а3;
б)	реакции типа л -4 N —А 4 К'.
л+4 пА 4/<+(<Ч) 1
л°4р->- А4Г (cr2) I
Oj = 2<т2;
гВ этом методе мишень и пучок рассматриваются изотопически неполяри-зованными и учитываются все возможные реакции изучаемого процесса; кроме того, возникающие частицы каждого сорта предполагаются также изотонически неполяризованными.
122
в)	реакции типа л + N S + К-
ло + р_^2о + /<+(а2) ло_Цр^2++/(о(а3)
<т3 — <rs, <г1 -+ 04 — 2<т2 “Г <т3;
г) распад т-частиц (т+, т°, т_) на три л-мезона:
т+ -> л+ -j- л° + л° (teij) т~ —л~4 л++л_(ш2) т° —л'; + л° + л° (и>3)
ш2 = w1 + и»3;
д) распад (о°-частицы на три л-мезона; показать, что распад и0 —Зл° невозможен (w° — изотопический синглет).
16.49.	Найти изменение изоспина Т и его проекции Тг в следующих процессах:
а)	л- 4- р -+К+ + 2-; в) /<+ ->л° + л+;
б)	л- 4- р ~-К+ + № + 3-; г) K°s ->2л°.
16.50.	Определить для мезон-нуклонных резонансов значения изоспин Т, странности S, барионного заряда В, а также полного момента 7 и четности Р, если относительный орбитальный момент I = 1.
16.51.	При облучении медленными (/ = 0) л~-мезонами дейтериевой мишени идет реакция л~ + d -+ 2п. Имея в виду, что четность дейтрона положительная, показать с помощью законов сохранения момента импульса и четности, что л~-мезон имеет отрицательную четность.
16.52.	Экспериментально установлено, что изоспин р-частицы, представляющей собой связанное состояние двух л-мезонов, равен 1.
а.	Имея в виду, что распад () ->- 2л относится к сильному взаимодействию, предсказать с помощью закона сохранения момента количества движения спин и четность р-частицы; внутренние четности л-мезонов одинаковые.
б.	Выписать возможные распады р+-, р°- и р--частиц на два пиона.
16.53.	Зная квантовые числа кварков, сконструировать:
а)	из трех кварков следующие барионы: р, п, 2+, S0 и S~;
б)	из кварка и антикварка следующие мезоны: л+, л~, 7<+, /<-и К°.
16.54.	Найти отношение магнитных моментов нейтрона и протона, считая, что магнитный момент кварка пропорционален его электрическому заряду. Иметь в виду, что для частицы, образованной из трех кварков, вероятность состояния, у которого спины двух одинаковых кварков параллельны, в 2 'раза больше, чем вероятность состояния, у которого спины двух одинаковых кварков антипараллельны.
16.55.	Воспользовавшись таблицей кварков, сконструировать:
а)	из кварка и антикварка очарованные мезоны с очарованием С = -j- 1 и — 1;
б)	из трех кварков очарованные барионы с очарованием 1, 2 и 3.
123
17. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ ВО ВНЕШНИХ ПОЛЯХ
• Уравнения движения частицы с зарядом q в аксиально-симметричных электрическом Е и магнитном В полях (в цилиндрических координатах):
•„ Я Iс , Ц<Р „ \
г—пр2 =— £r Н-------Bz ;
т \ с /
—	(г2 ф)=— (oz Br—vr Bz);	(17.1)
г dt	тс
•	Связь между импульсом р заряженной частицы (в том числе и релятивистской), радиусом р кривизны ее траектории и индукцией В магнитного поля: p=-^-qpB.	(17.2)
•	Бетатронное условие. Электрон в процессе ускорения будет двигаться все время по круговой орбите, если магнитная индукция на орбите ВОрб равна половине средней индукции <В> внутри орбиты:
Sop6= g	(17-3)
Предполагается, что в начале ускорения скорость электрона и магнитная индукция равны пулю.
Законы движения. Анализаторы
17.1.	Электрон движется в однородном электрическом поле, напряженность которого возрастает с постоянной скоростью Е = = 20МВ/(см-с). Какую энергию приобретет электрон, когда он пройдет расстояние I = 10,0 см, если в начальный момент его скорость и электрическое поле равна нулю?
17.2.	Электрон начинает двигаться под действием однородного электрического поля Е = 10,0 кВ/см. Определить энергию, которую приобретает электрон, и пройденный им путь за промежуток времени т = 100 нс после начала движения.
17.3.	Протон, вылетающий из точки О (рис. 17.1) с кинетической энергией Т 6,0 кэВ, попадает под действием однородного электрического поля с напряженностью Е в точку А с координатами х = = 10,0 см и у = 7,5 см. Определить:
а)	напряженность £, если угол а0 = 60°;
б)	значения а0 и Е, при которых вектор скорости протона в точке А будет составлять с вектором Е угол а = 30°;
в)	время движения протона до точки А, если Е = 1,00 кВ/см.
17.4.	Электрон с кинетической энергией Т пролетает через однородное поперечное электрическое поле Е и попадает затем на экран Э (рис. 17.2, где а = 10 см, b = 20 см). Определить угол отклонения а электрона и его смещение б на экране, если:
а)	Е = 20 В/см и Т = 1,00 кэВ;
124
б)	£ растет с постоянной скоростью £ = 1,00 МВ/(см-с) и электрон с Т = 40 эВ попадает в это поле в момент, когда £ = 0;
в)	£ меняется со временем по гармоническому закону с частотой v = 10,0 МГц и амплитудой £0 = 5,0 В/см, а электрон с Т = 100 эВ попадает в поле в момент, когда £ = 0.
17.5.	Пучок электронов, ускоренных разностью потенциалов V = = 1,0 кВ, проходит через два небольших конденсатора, отстоящих друг от друга на расстоянии I = 20 см. В обоих конденсаторах синфаз-
Рнс. 17.1
Рис. 17.2
но возбуждается переменное электрическое поле от одного генератора. Изменением частоты генератора добиваются того, чтобы пучок электронов проходил эту систему без отклонения. Определить etn электрона, если два последовательных значения частоты, при которых выполняется это условие, равны 141 и 188 МГц.
17.6.	Определить кинетические энергии протона и релятивистского электрона, у которых Вр = 5,0 кГс^см.
17.7.	Протон с кинетической энергией Т — 50 кэВ пролетает поперечное однородное магнитное поле В = 400 Гс и попадает на экран Э (рис. 17.3, где а = 10 см, b = 20 см). Определить угол отклонения а протона и его смещение 6 на экране.
17.8.	Из точки А, лежащей на оси прямого соленоида, вылетает электрон с кинетической энергией 500 эВ под углом а = 30е к оси. Индукция магнитного поля В = = 50 Гс. Вычислить:
а)	шаг винтовой траектории электрона;
б)	расстояние от оси до точки попадания электрона на экран, расположенный перпендикулярно к оси на I = 20 см от точки А.
17.9.	Слаборасходящийся пучок электронов, ускоренных разностью потенциалов V — 500 В, выходит из некоторой точки на оси прямого соленоида и фокусируется на расстоянии I = 15,0 см при следующих двух последовательных значениях В: 158,0 и 189,6 Гс.
Определить:
а)	удельный заряд электрона;
б)	минимальную индукцию магнитного поля, при которой будет осуществляться фокусировка на этом расстоянии.
125
17.10.	Источник моноэнергетических 0-частиц находится на оси соленоида. Известно, что 0-частицы, испускаемые под углом а = 30° к оси соленоида, фокусируются в точке, находящейся на расстоянии I -- 50 см от источника, при минимальном значении В = 200 Гс. Найти их кинетическую энергию.
17.11.	На оси прямого соленоида в точке О расположен источник 0-частиц и в точке О' — входное отверстие счетчика. Расстояние ОО' I = 50 см. Посредине между О и О' находится диафрагма с узким кольцевым отверстием радиусом R = 7,5 см. Найти:
а)	кинетическую энергию 0-частиц, которые фокусируются в точку О' при минимальном значении магнитной индукции В = 250 Гс;
Рис. 17.4
б)	первые два значения магнитной индукции, при которых 0-частицы с кинетической энергией, равной их энергии покоя, сфокусируются в точку О'. Найти также соответствующие углы вылета а таких 0-частиц из источника.
17.12.	В масс-спектрометре с полукруговой фокусировкой в поперечном однородном магнитном поле расстояние между источниками и местом фокуса х = 40,0 см. Найти дисперсию прибора:
а)	по массам бх/бЛ для моноэнергетических ионов урана;
б)	по энергиям бхбТ для 0-частиц с кинетическими энергиями вблизи Т = 1,0 МэВ.
17.13.	Узкий пучок моноэнергетических ионов проходит секторное поперечное однородное магнитное поле, как показано на рис. 17.4 (вход и выход пучка — по нормали к границе поля). Найти угловую дисперсию прибора по массам ба/бЛ (град/а.е.м) для изотопов Аг, если угол <р = 60°.
17.14.	Слаборасходящийся плоский пучок ионов входит в точке А (рис. 17.5) в электрическое поле цилиндрического конденсатора. Разность потенциалов на пластинах конденсатора подбирается такой, чтобы частицы, вектор скорости которых в точке А перпендикулярен к радиус-вектору в этой точке, двигались далее по круговой траектории радиусом г0. Показать, что:
а)	угол, на котором фокусируется пучок, Y — л/р^;
б)	дисперсия прибора по скоростям в месте фокуса Дг/Ди =2г0/и.
17.15.	В поперечное аксиально-симметричное магнитное поле, спадающее к периферии по закону г~п, входит слаборасходящийся пучок ионов (см. рис. 17.5). Индукция магнитного поля подбирается та-126
кой, чтобы ионы, скорости которых перпендикулярны к радиус-вектору в точке А, двигались далее по круговой траектории радиусом г0. Показать, что:
а)	угол, на котором сфокусируется пучок в горизонтальной плоскости, V = л/|Л1 — п;
б)	при п = 1/2 имеет место двойная фокусировка (как в горизонтальном, так и в вертикальном направлении);
в)	при п = 1/2 дисперсия по скоростям ионов в месте фокуса Дг/До = 4г0/и.
17.16.	Пучок дейтронов проходит поперечные однородные взаимно перпендикулярные электрическое и магнитное поля, созданные
Рис. 17.6
в одной и той же области пространства. Найти кинетическую энергию дейтронов, если при Е = 1,00 кВ см и В--=500 Гс траектория пучка остается прямолинейной.
17.17.	Показать, что с помощью установок, схемы которых изображены на рис. 17.6, можно одновременно определить е т. и скорость заряженных частиц:
а)	в установке I частица проходит последовательно электрическое поле Е цилиндрического конденсатора и однородное магнитное поле В. Известны разность потенциалов V на обкладках конденсатора, радиусы обкладок 7?! и R2, индукция магнитного поля В и радиусы кривизны траектории частицы гх и г2;
б)	в установке II частица проходит электрическое поле плоского конденсатора и попадает на экран Э, причем вся установка (конденсатор и область между ними и экраном) помещена в однородное магнитное поле В (В _L Е).
Известны значения напряженности Е электрического поля и индукции В магнитного поля, при которых траектория частицы в конденсаторе прямолинейна, расстояние / и смещение 6.
17.18.	Радиусы цилиндрических катода и анода магнетрона равны соответственно гх = 1,0 мм и г, -= 20 см. Между ними приложена разность потенциалов V = 200 В. Пренебрегая начальной скоростью термоэлектронов, найти предельное'значение индукции продольного однородного магнитного поля в магнетроне, при котором анодный ток прекращается.
17.19.	Цилиндрический диод состоит из длинной прямой нити накала и коаксиальных катода и анода, радиусы которых равны 0,10 и 1,0 см. Протекающий по нити ток накала 14,5 А создает в окружаю
127
щем пространстве магнитное поле. Пренебрегая начальной скоростью термоэлектронов, найти предельную разность потенциалов между анодом и катодом, при которой анодный ток прекращается.
17.20.	Из точки О пространства, где созданы однородные параллельные электрическое поле с напряженностью Е и магнитное поле с индукцией В (рис. 17.7), вылетает в направлении оси х протон с начальной скоростью V. Найти уравнение его траектории х (/), у (/), z (t). Какой вид она имеет?
17.21.	Узкий пучок одноименных ионов, имеющих различные скорости, входит в точке О в область, где созданы однородные параллельные электрическое поле с напряженностью Е и магнитное поле с индукцией В (см. рис. 17.7). Направление пучка в месте входа совпадает
Рис. 17.7
с осью х. На расстоянии I от точки О находится экран, плоскость которого перпендикулярна оси %. Найти уравнение следа ионов на экране. Показать, что при z I это уравнение имеет вид параболы.
17.22.	Заряженная частица движется в пространстве, где созданы однородные взаимно перпендикулярные электрическое поле напряженностью Е и магнитное поле с индукцией В (рис. 17.8). Считая, что частица покидает току О без начальной скорости, найти:
а)	уравнение траектории частицы х (/), у (();
б)	длину траектории между точками, в которых скорость частицы равна нулю;
в)	среднюю скорость частицы в направлении оси х.
17.23.	В пространстве, где созданы однородные взаимно перпендикулярные электрическое поле напряженностью Е и магнитное поле с индукцией В, движется заряженная частица. Пусть частица покидает точку О (см. рис. 17.8) с начальной скоростью, вектор которой лежит в плоскости %, у и имеет компоненты х0 и у0. Найти уравнение траектории частицы х (/), у (() и изобразить ее вид, если:
а)	х„	и 2, у„ = 0; в) х0 = 0, уи = v;
б)	х0	— v, yQ 0; г) х0 --- у0 = v,
где v =- cElB.
17.24.	Показать, что в условиях предыдущей задачи все частицы с одинаковым значением е!т, независимо от величины и направления начальной скорости, попадут в точку на оси х с координатой xt -
2лпигЕ еВг.
128
17.25.	Протон начинает двигаться в области, где созданы однородные взаимно перпендикулярные электрическое и магнитное поля, причем магнитное поле постоянно и имеет индукцию В, а электрическое поле меняется по закону Е = Ео cos at с частотой а=еВ!тс. Найти уравнение траектории протона х (t), у (/), если в начальный момен времени (/ = 0) он находился в точке О (см. рис. 17.8).
Ускорители заряженных частиц
17.26.	Определить для электрона и протона, движущихся по круговым орбитам в однородном магнитном поле с индукцией В= 10,0 кГс:
а)	периоды обращения и радиусы орбит, если кинетическая энергия частиц Т = 10,0 МэВ;
б)	кинетическую энергию, если радиусы их орбит г = 10,0 см.
17.27.	Пусть в бетатроне магнитный поток внутри равновесной орбиты радиусом г — 25,0 см возрастает от нуля с постоянной скоростью Ф = 5,0-10” Мкс/с. Определить:
а)	напряженность вихревого электрического поля на орбите и энергию, приобретенную электроном за 5,0-105 оборотов;
б)	пройденный электроном путь за т = 3,00 мс и полученную им за это время энергию.
17.28.	Индукция магнитного поля в бетатроне на равновесной орбите радиусом г = 100 см изменяется от нуля до Вт = 5,0 кГс по закону В = Вт sin at с частотой v = 50 Гц. Определить:
а)	кинетическую энергию электронов в конце цикла ускорения;
б)	пройденный электроном путь и число оборотов за полный цикл ускорения, полагая начальную скорость электронов равной нулю.
17.29.	Доказать справедливость бетатронного условия (17.3), воспользовавшись законом электромагнитной индукции и соотношением (17.2).
17.30.	Показать с помощью бетатронного условия (17.3), что напряженность вихревого электрического поля в бетатроне имеет минимум на равновесной орбите. Иметь в виду, что показатель спада магнитного поля вблизи равновесной орбиты п = — (г/В) (дВ/'дг) < 1.
17.31.	Индукция магнитного поля в плоскости симметрии бетатрона вблизи равновесной орбиты изменяется по закону В со 1/г", где п — показатель спада. Доказать, что устойчивость движения электронов обеспечивается:
а)	в радиальном направлении при n < 1;
б)	в вертикальном направлении при п > 0;
17.32.	В плоскости симметрии бетатрона индукция магнитного поля вблизи равновесной орбиты изменяется по закону В со г~п, где п — показатель спада; 0 < п < 1. Пусть угловая скорость движения электрона по равновесной орбите равна w0. Определить для электронов, движущихся вблизи равновесной орбиты, частоты:
а)	радиальных и
б)	аксиальных колебаний.
17.33.	Беспредельному увеличению энергии заряженных частиц в циклических ускорителях препятствует эффект, обусловленный по-5 Зак. 1896	129
терями энергии на излучение. Энергия, теряемая заряженной частицей за один оборот, равна 4/3 л (Е/тс*)* ёЧг, где г — радиус орбиты; Е — полная энергия частицы; т — ее масса покоя. Вычислить энергию Е, до которой можно ускорить электроны в бетатроне, если радиус равновесной орбиты г = 100 см и скорость возрастания магнитной индукции на орбите В = 1000 кГс/с.
17.34.	Определить для протонов, дейтронов и а-части'ц, ускоряемых в циклотроне до максимального радиуса кривизны р = 50 см:
а)	кинетическую энергию в конце ускорения, если магнитная индукция В = 10,0 кГс;
б)	минимальную частоту генератора для достижения в конце ускорения кинетической энергии Т = 20 МэВ.
17.35.	Генератор циклотрона имеет частоту v = 10 МГц. Определить эффективное ускоряющее напряжение на дуантах циклотрона, при котором расстояние между соседними траекториями дейтронов с радиусом кривизны р « 50 см равно Др = 1,0 см.
17.36.	В циклотроне, частота генератора которого v = 10 МГц, ускоряются а-частицы до максимального радиуса кривизны р = 50 см. Эффективное напряжение между дуантами V = 50 кВ. Пренебрегая зазором между дуантами, определить:
а)	полное время ускорения частиц;
б)	полный путь частиц за весь цикл ускорения.
17.37.	При каких значениях кинетической энергии период обращения электронов, протонов и а-частиц в однородном магнитном поле на 1,00% больше периода обращения при нерелятивистских скоростях?
17.38.	Циклотрон, как известно, непригоден для ускорения электронов, так как их период обращения т с ростом энергии быстро увеличивается и резонанс расстраивается. Последнее, однако, можно устранить, если изменение периода обращения электрона Дт сделать кратным периоду ускоряющего поля т0. Ускоритель, работающий по такому принципу, называется микротроном. Сколько раз электрону необходимо пройти через ускоряющий промежуток микротрона, чтобы приобрести энергию Д£ = 4,6 МэВ, если Дт = т0, индукция магнитного поля В = 1,07 кГс и частота ускоряющего поля f = 3,0 X X 103 МГц?
17.39.	Чтобы в циклотроне не возникла расстройка в процессе ускорения частицы, связанная с изменением ее периода обращения при возрастании энергии, медленно изменяют частоту ускоряющего поля. Такой ускоритель называют фазотроном (синхроциклотрон).
а.	На сколько процентов следует изменять частоту ускоряющего поля фазотрона, чтобы ускорить протоны и а-частицы до энергии Т = 500 МэВ?
б.	По какому закону необходимо изменять частоту ускоряющего поля фазотрона, <о (/), если индукция магнитного поля равна В и средняя энергия, приобретаемая частицей за один оборот, е?
17.40.	Чтобы в ускорителе типа циклотрона осуществлялось резонансное ускорение частиц, можно медленно изменять магнитное поле, так чтобы период обращения частицы оставался постоянным и 130
равным периоду ускоряющего поля. Такой ускоритель называют синхротроном. Полагая, что магнитное поле синхротрона однородное и его индукция изменяется по закону В = Вт sin со/, а частота ускоряющего поля равна <а0, найти:
а)	закон изменения радиуса орбиты частицы со временем;
б)	в каких пределах изменяется радиус орбиты электрона, ускоряемого от 2,0 до 100,0 МэВ, если со0 = 7,00-108 с-1 и со = 314 с-1. Какой путь проходит электрон за полный цикл ускорения?
17.41. Синхрофазотрон — это ускоритель, в котором одновремен-
но изменяются : частота ускоряющего электрического поля со (/), и
магнитное поле В (/). При каком соотношении между со (/) и В (/) уско
рение частиц будет происходить по орбите с постоянным радиусом г? Влиянием вихревого электрического поля пренебречь.
17.42. В кольцевом синхро-
А _l!_1_______
Рис. 17.9
фазотроне, ускоряющем прото-
ны от 0,500 до 1000 МэВ, радиус орбиты г — 4,50 м. Считая, что индукция магнитного поля в процессе ускорения растет с постоянной скоростью В = 15,0 кГс/c, определить:
а)	пределы, в которых изменяется частота ускоряющего электри
ческого поля, и полное время ускорения;
б)	энергию, приобретаемую протоном за один оборот;
в)	пройденный путь и число оборотов протона за весь цикл уско
рения.
Влиянием вихревого электрического поля пренебречь.
17.43.	В синхрофазотроне Объединенного института ядерных исследований протоны ускоряются от 9,0 до 10 000 МэВ. Периметр равновесной орбиты с учетом прямолинейных участков П = 208 м. Радиусы орбиты на закругленных участках г = 28,0 м. Индукция магнитного поля на этих участках орбиты растет в процессе ускорения с постоянно!) скоростью В — 4,00 кГс/c. Рассмотреть те же вопросы, что и в предыдущей задаче.
17.44.	В линейном ускорителе заряженные частицы движутся через систему пролетных трубок, присоединенных попеременно к противоположным клеммам высокочастотного генератора Г (рис. 17.9). Ускорение частиц происходит в зазорах между трубками. Пусть протоны впускаются в ускоритель с энергией?^ = 2,0 МэВ и их необходимо ускорить до энергии Т 20 МэВ, причем в каждом зазоре частицы получают энергию А£ 0,50 МэВ, частота генератора f = 100 МГц. Пренебрегая величиной зазоров между трубками, определить длину:
а)	n-й пролетной трубки, в частности первой и последней;
б)	всех пролетных трубок (длину ускорителя).
17.45.	Пусть пролетные трубки в линейном ускорителе имеют одинаковую длину I =- 6,00 см. В каких пределах необходимо изменять частоту генератора такого ускорителя, чтобы ускорить протоны и электроны от 5,00 до 50,0 МэВ?
5*	131
17.46.	Линейный ускоритель с бегущей волной представляет собой цилиндрический диафрагмированный волновод, вдоль которого распространяется электромагнитная волна с осевой составляющей Ех. С помощью кольцевых диафрагм с отверстиями достигается увеличение фазовой скорости волны вдоль волновода, причем ускоряемая частица находится все время приблизительно в одной и той же фазе волны. Найти:
а)	значение Ех, необходимое для ускорения протонов от 4,0 до 1000 МэВ при длине волновода L = 67,0 м;
б)	зависимость фазовой скорости волны от расстояния до входного отверстия в волновод. Во сколько раз должна изменяться фазовая скорость волны для протонов и на сколько процентов для электронов при ускорении их от 4,0 до 1000 МэВ?
17.47.	Одна из возможностей значительного увеличения энергии соударяющихся частиц заключается в использовании встречных пучков этих частиц. Какую кинетическую энергию следовало бы сообщить протону, налетающему на покоящийся протон, чтобы их суммарная кинетическая энергия в системе центра инерции была такой же, как у двух протонов, движущихся навстречу друг другу с кинетическими энергиями 50 ГэВ?
ОТВЕТЫ И РЕШЕНИЯ
1.1. а) Из условия dujda = 0 получим следующее уравнение: 3f (х) + + xf* (х) = 0, х — а>1Т. Корень этого уравнения есть некоторое значение х0, следовательно, шт<ч)Т;
оо	«о
б) согласно (1.1) М оо и, a I ш3/ (wlT)dti> = Т4 { x3f(x)dx, где х = о	о
= а/Т. Отсюда видно, что М со Г*.
1.2. а) Преобразовав формулу Вина от к и^, найдем: -- k~5f (XT). Из условия du}/dK=O получим уравнение 5F (x) + xfm (х) - 0, х КТ. Корень этого уравнения равен некоторому значению х0, значит, Km го 1/Т;
б)	ик = Xm5F (КтТ) со Х~3 оо Р, Где \тТ = const,
1.3.	Уменьшилась на ЛТ — 7*2ЛХ/ (Ь -г ТЛХ)~ 3,0 • 102К-4 ________________
1.4.	Кт~ b Д/а/М — 2,9 мкм.
1.5.	Р -= 4лЯ2о (bfKm)4 =- 4,6 • 1020 МВт (5  109 * * * кг/с); ~)ОП лет.
1.6.	При тепловом равновесии поток энергии излучения, проникающего в Полость 2, равен потоку энергии, выходящей из этой полости: LtAQAS - A42AS, где Ly — яркость отверстия полости 1; М2 — энергетическая светимость отверстия полости 2; AS — площадь каждого отверстия; AQ - &SIP. Для косинусного (ламбертовского) излучателя Lj = Mja. Остается учесть, что 1Л = <тТ , и мы получим Т2 =-- Тх Д/ril = 0,28 кК-
1.7.	а) р - 4о7’4/3с - 1,6 • 104 ГПа (1,6 • 108 атм);
3 ________
б) Т ; ]/Зсрй/2от = 19 • 106 К, m — масса атома водорода.
1.8. срг (п3 — 1)/9оТ’ =-- 1,6 ч, р — плотность меди.
1.9. а) швер = ЗТ.'а - 0,785 • 1013 с-1;
б) = I ши. dw I и da> - 477а — 1,05 • 10)3 с-1.
О w 'о ш
1.10. а) К.п - 2лса 57'	1,44 мкм;
б) </.) 2пса13Т 2,40 мкм. Здесь распределение энергии излучения по длинам волн ил сол~5 е-2ясаА7\
1.11. Ищем решение волнового уравнения sx ~ (1/о2)б в виде £ — = X (х) sin ш/. После подстановки последнего выражения в волновое уравнение получим:
Хх -I IPX - 0, k - ш/v.
Решение этого уравнения с учетом граничного условия X (0) — 0 запишем сразу как X ~ a sin kx. Постоянную k находим из другого граничного условия X (I) — 0. откуда & — пп/1, где п — положительные целые числа (отрицательные числа не приводят к новым линейно-независимым решениям). Видно, что каждому значению п отвечает определенное значение k, а значит, и ш. Поэтому в интервале частот do» число собственных колебаний dZ dn, или dZ — (/1Ло)аш^
1.12. Будем исходить из двумерного волнового уравнения ijx + iy - О )S-Его решение ищем в виде s X (х)У (у) sin ш/. После подстановки его в волно вое уравнение получим:
XxiX у;/у - (Ш/v)2.	U)
Левая часть этого уравнения содержит функции, зависящие ™ль^ °т„* Поскольку эти переменные независимые, каждая из этих функци Д
133
постоянной. Обозначив их соответственно kl и kl, мы можем записать:
Хх + *М = 0; Y'y± k22Y=0,	(2)
причем согласно (1) постоянные k2 и k2 удовлетворяют условию
k\ - kl = И)2.	(3)
Решения уравнений (2) с учетом граничных условий X (0) = 0 и Y (0) = 0 запишем сразу в виде X = sin krx. Y = sin k2y (амплитуды мы опустили, ибо для нашей задачи оии ие существенны). Постоянные kx и k2 находим из граничных условий X (а) ~ 0 и Y (&) = 0, где а и b — длины сторон мембраны. Итак,
| — sin kxx sin k2y sin at,	(4)
где
— лгл a, k2 - n2n.b,	(5)
a и n2 — целые положительные числа (отрицательные числа ие приводят к новым. линейно-независимым решениям).
Выражение (4) — это общий вид стоячей волны на мембране. Каждой паре целых положительных чисел п2 и п2 соответствует одна, стоячая волна (собственное колебание).
Изобразим определенное собственное колебание точкой на плоскости с осями k, и k.>. Тогда (3) есть уравнение окружности с радиусом k ~ ш/v. Число собственных колебаний Zti) с частотой, меньшей <о. равно числу точек внутри круга радиусом k со/у в его первой четверти (так как все П(> 0). Площадь ячейки, содержащей одну точку, есть SkjSkt -= (л2 а&)6л1бп2 = л2'5, ибо 6zij6zi2 = 1.
Поделив площадь четверти круга радиусом k = a/v на площадь одной ячейки, найдем:
лй2'4 S
Z,, =------=--------ы2.
“	л2/5	4лп2
Отсюда d.Za - (S:2nv2)ada.
1.13. Вывод аналогичен решению предыдущей задачи. Но в данном случае вместо 1 4 площади круга следует взять 1 '8 объема шара и, кроме того, полученное выражение надо еще умножить на два; каждой частоте соответствуют две стоячие волны со взаимно перпендикулярными плоскостями поляризации.
1.14. а) (в) kT, da (kT: л2 с3) со2 da — формула Рэлея — Джинса;
у е — nhas/kT	уе—апЛ<о
б) (8)
где а 1 kT. Здесь суммирование проводится по п от 0 до оо. Последнее выражение можно преобразовать к более простому виду следующим образом:
•	апЛол ==-------]п
' да
ha eha/kT
'ы'/гТ
л2 с3
1__е —«Лш
со3 da
-----------— формула Планка. ^a/kT _ [
(Лыз/л2^) е -ha>lkT,
<уЗ
1.15.
1.16.	а)
--- (kT/nV) а2;
16л2 Л
“v ----------
v	С3
'fixhv/kT
е
; иш da =
%
Л
Л. "5
б) Ну —= 16л2сЛ -----------------
е2лЛс/*ГХ _]
134
J.17 /2//1 = (	1)/(е“/7"2— 1) = 4,8, где а = 2лсЛ/ЛЛ.
8л2 с2 КГ* т)
1.18.	ДР =--------------1—= 0,60 Вт/см2.
М(е2ЯСЙ/*6_1)
1.19.	Энергетическая светимость М = i/4 с j u^dco = аТ*. где а-----= (nVeo^'c2^3.
1.20.	< со > = 3,83 kT/ft = 1,00 • 1013
1.21.	7=2,33 ей й< К>=2,00 кК.
п, d к = 8л-------22_
2яйс *77. е	— 1
б) п = 0,243 (kTihc)3 = 5,5 • 10“ см“3
Рис. 2
1.23. а) Из условия dna da = 0 получим: 2 —х — 2е~х, где х = ha/kT. Корень этого уравнения находим подбором или графически: х„ = 1,6. Отсюда
Йсовер = 1,6&7 = 0,14 эВ;
б) <Йы> = 2,7*7 = 0,23 эВ.
1.24.	Из п фотонов, заключенных в единице объема, число фотонов, которые движутся внутри элементарного телесного угла dQ, есть dn = tidQ'An.. Выделим только те фотоны, которые движутся в телесном угле dQ, составляющем угол О с нормалью к площадке AS. Эти фотоны движутся практически параллельно друг к другу, и поэтому за время А/ площадки AS достигнут из иих все те фотоны, которые заключены в косом цилиндре с основанием AS и высотой cSt cos ft <рис. 1):
dK = dn.SS cos ОсДЛ
Проинтегрируем это выражение по ft (от 0 до л/2) и по ср (от 0 до 2л), имея в виду, что dQ = sin ftdftdcp. В результате получим:
АЛ’ 1 4 лс Ar AS.
Отсюда следует, что число фотонов, падающих в единицу времени на единицу яоверхиости, равно пс.
Умножив последнее выражение на среднюю энергию фотонов <Йсо>, найдем !/4л (Йсо)с = >/4 ис = М.
. __ . . Рк „ .____________ о ..1
1.25. а) / =--------= 2-1013 см" - с
8л2 Лег2
Р (Х,-|-2Х»)	.	,
б) /= v 1 ------—=2  Ю13 см - с "
’	24л2 he г-
135
1.26.	2,5 эВ с, 5 кэВ/с и 0,6 МэВ/с.
1.27.	X = 2лсЛ/Д/Т (Т + 2/ПоС2) = 2,0 • Ю-i» см.
1.28.	dp/dt = J (h<i>/c)dNa} = Р/с, где dN а = P^du/hu — поток фотонов с частотами в интервале (<о, <о + d<o).
1.29.	<р> = 4£ (1 + р)/л1рст = 5 МПа (=50 атм).
1.30.	р -- (£/с)"|/1 + р2 + 2р cos 20= 3,5 • 10~3 г • см/с.
1.31.	При зеркальном отражении каждого фотона поверхности передается импульс Др = 2 (Йы/с) cos О. Тогда искомая сила
F = dp/dt J ApdNa = 2 (I/c)S cos2 0=5- 10^3 дин, где dNa — поток падающих фотонов с частотами в интервале (со, <о + da>): dNa = (/ada>/liu>)S cos О.
1.32.	От спектрального состава света переносимый импульс не зависит (см. задачу 1.28), поэтому для простоты будем считать его монохроматическим. Сначала найдем силу dF, действующую на элементарное кольцо dS (рнс. 2) в направлении оси х. При зеркальном отражении каждый фотон передает поверхности dS импульс Др = 2р cos О, х-составляющаи которого Дрх = 2р cos2 0, где р — Й<о/с. Поток фотонов dN, падающих за единицу времени на кольцо dS, равен dN (I/hu>)dS cos О', где dS — 2л/?2 sin ftdft. Тогда
dF = Ap^dN = 4л/?2 (l/c) cos3 0 sin ftdfh
Проинтегрировав это выражение по 0 от 0 до л 2, получим F = tiR-1/с. Интересно, что полученный результат такой же, как и в случае абсолютно поглощающей поверхности.
1.33.	F - 3iiISic.
1.34.	F = Р/ [2с (1 -т /2//?2)].
1.35.	—d (Йоэ) = у (mM/r2)dr; Ды/ы = 1 — е~чМ!Ксг, где — гравитациои-наи постоянная, m = Ьш/с- — масса фотона;
а)	ДА/А = уЛ4//?с2 = 2,1 • 10-в;
б)	ДА/А = 0,10.
1.36.	А = ДАт]/ (т] — 1) •-= 0,10 нм.
1.37.	V = лЛс/ed sin а = 31 кВ.
1.38.	v = с 1/а (а+2)/ (а + 1) = 0,50 с, где а = 2лЙ/тсАмин.
1.39.	/? со (1/АМин — 1/А)/А2. Из условия dix/dA = 0 получим Ат=3/2АМИН= = Злсй/eV = 60 пм.
1.40.	а) 0,66 и 0,235 мкм; б) 5,5 • 10® м/с (Zn), 3,4 • 10® м/с (Ag), HaNi не вылетают.
1.42.	V = (2лЙс-А — А)/е = 1,74 В.
1.43.	Ао = (2лЙс/А) (т] — п)/ (г] — 1) -- 0,26 мкм.
1.44.	7'макс = Й (<о + <оо) — А = 0,38 эВ.
1.45.	Верхние уровни в обоих металлах находятся на одинаковой высоте (рис. 3). Поэтому электроны, вырванные с верхнего уровня цезия, совершают работу Aj т Аконт ~ А%, где Аконт — работа по преодолению внешней контактной разности потенциалов: а) 0,28 мкм; б) 6,4 • 10® м/с.
1.46.	Из условия Й<о = AZn 4- е (VKOHt 4" ^з) находим VK0HT = —0,5 В, т. е. полярность контактной разности потенциалов противоположна внешней разности потенциалов.
1.47.	0,196, 0,213 и 0,224 мкм.
1.48.	р = "|/ (йсо)2 + 2те с2 (Йы—Е) /с~ 96 кэВ/с.
1.49.	Из законов сохранения энергии и импульса
йы+ тс2 = тс2/Д/1—Р2 , Л<о/с = то/Д/1— 02 ,
где Р = v/c, следует, что Р равно 0 или 1. Оба результата физического смысла не имеют.
1.50.	а) Формула комптоновского смещения получена в предположении рассеяния фотонов на свободных электронах. Электроны в веществе будут свобод-136
ними, если их энергия связи значительно меньше энергии, передаваемой им фотонами. Для этого и необходимо использовать достаточно коротковолновое излучение;
б)	так как рассеяние фотонов происходит на свободных электронах;
в)	эта компонента обусловлена рассеянием фотонов на сильно связанных электронах и ядрах;
г)	вследствие увеличения числа электронов, которые становятся свободными (см. п. «а»);
д)	из-за рассеяния фотонов на движущихся электронах.
1.51. А — Ас [ 1 — cos О2 — т] (1 — cos ОД]/ (т] — 1) = 12 пм.
1.52. а) АА = Ат]/(1 —т]) = 1,2 пм;
б) cos <1=1 — (А/Ас)т]/( 1 — т]) ф = 0,50, откуда О = 60°.
Рис. 4
1.53. Из треугольника импульсов (рис. 4) следует, что tg ср = sin О/ (k'Ik — cos О) = sin О/(А/А' — cos О), где А/А' можно найти из формулы (1.8):
А'/А = 1 + (1 — cosO)Ac/A.
В результате
sin &
tg(p=---------—-----------= cfg (»/2)
(1— cos О) (1+Ас/А) 1+Лы/тс2 
Лео
1.54. а) Л со =-------------------—=0,20 МэВ;
1 4-2 (Лсо/лгс2) sin2 (0/2)
2s2 sin» (0/2)	Лео
14-2esin2 (0/2) mc2 = °’26 МЭВ’ W е = ^-
7=------------------------
14-2 (p/mc) sin2 (0/2)
А = (2яй/йс) (1/1 + Зтс^/Тмакс — 0 = 2,0 пм.
р = 2тс = 1,02 МэВ/с.
А = Ас [1 — cos (0/2)1/ Г2 cos (0/2) — 1] = 3,0 пм.
Л со = V2 Т [ 1 4- V 1 4-2/лс2 Т sin2 (О/2) 1 = 0,94 МэВ.
Т = йсот)/ (1 4- г]) = 0,20 МэВ. 2т](1+г)) тсг
В = ———----------= 1,1 кГс.
14-2т] eR
о —о'=(е/1/1 4-е2 )с, где е = Лсо/тс2.
4яЛ	О
а)	А — А =-----sin2—=1,2пм;
тс	2
„	2г]2 sin2 (0/2)
б)	Т —----------------- тс2=0,17 МэВ.
1 4-2т) sin2 (О/2)
б) Т=
1.55.
1.56.
1.57.
1.58.
1.59.
1.60.
1.61.
1.62.
1.63.
£св = 31 кэВ.
137
2.1. а) r=3e2/2£'= 1,6-10~~8 см;
б) ы="|/е2/тг3; 3-10 8 см.
2.2. а) 5,9-Ю-10 см; б) гМИн = (<7i qJT) (1 +	/mL{)=3,4-10-" см.
2.3. Из закона сохранения энергии следует, что модуль импульса рассеянной частицы остается таким же, как и до рассеяния. Отсюда модуль приращения вектора импульса рассеянной частицы
| Лр | = 2р0 sin (0'/2).
С другой стороны, из рис. 5 следует, что
, Л n f г _ Г <71 г cos X	f sin (ф—0/2) dtp
\Sp\ ^Fndt—^	dt-qiq2^
где Fn — проекция вектора силы взаимодействия на направление вектора Лр. Знаменатель подынтегрального
выражения, согласно закону сохранения момента импульса, равен г2ф = —bv0, где о0 — скорость частицы вдали от ядра. Проинтегрировав, получим
I Л р | = (2^/ta0)cos (0/2).
Из сравнения последнего выражения с первым получим искомую формулу.
2.4. b = qiqtm!f? tg (0/2) = 0,6 пм.
2.5. а) | Лр | = V8m77[l—(67VZe2)2] = 1,3-10* МэВ/c;
б) 7== ZeFlb ^- 1,3 МэВ; 90°.
2.6.	Согласно законам сохранения энергии и момента импульса, Т — Т + qTq2/Гмин> t>v = rMHH °'> где штрихованные величины соответствуют гМИн- Из этих '’мин = (ЯМ'2Т) (1 + esc (0/2)) = 0,16 Отношение гмин/Ь = [1 4- sin (0/2)]/ cos’(0/2) = 2,4.
2.7.	р- V2mT МЦт + М)-, T=TMl(m+M).
2.8.	Т' = Т (тг — mFfi (т2 + ffii)2.
2.9.	0Макс = arcsin (mjm^ = 30°.
2.10.	tg О = sinO I ( cos О + О = 36°.
2.11.	b = (^/7) (1 4 Mp/mJ tg О' = 0,24 пм.
2.12.	b = (fF/T) (1 + ma/md) etg (0/2) = 0,5	пм,
+ arcsin (md/ma).
2.13.	Решение аналогично решению задачи 2.6, только производится в Ц-системе с заменой:	Т 7 и О -*• О, где р. — приведен-
ная масса; 7 и О — суммарная кинетическая энергия частиц и угол рассеяния в Ц-системе. В результате получим:
Гм ин = (Зе2,^) (1 -1- 'na/mLi) (1 + esc О') = 0,6 пм.
2.14.	a) cos (0/2) = Ы (R + г);
б)	dw -= 1 sin OdO, w = 1/2.
2
2.15.	dN/N = ndc, где da = (ZeF/2T)2 2л sin OdO/ sin4 (0/2). Л/V pd / Ze2 V S//2
77~= ----- ~FF~ I —:	=4- IO-4, m—масса атома Au.
N m \4T / sm4 (O/2)
Ла - л (Ze2/27)2 etg (O/2) = 2,1 • 10~22 cm2.
уравнений следует: пм.
где О' = л/2 +
в этом случае расчет
2.16.
2.17.
ЦЕ
2.18.	do/d® = (Z<?l‘2T)22n sin 0/ sin4 (0/2) = 3,0 • 10~22 см2/рад; da/dQ = — (da/d^)/2n sin O' = 4,8 • 10~2з см2/ср.
2.19.	Да = (dc/dQ)n sin2 O0 = 5,5 • 10~22 cm2.
2.20.	a) 6  10~5; 6) w = nn (Ze2/7’)2[ esc2 (Oj/2) — esc2 (0-2/2)] =- 5 • 10~4.
2.21.	а) ДА = Ixn. (q1q2/4T)22n sin ОД07 sin4 (&/2) = 1,3 • 104;
б)	ДА = /тля (qtq2/2T)2 etg2 (O0/2) = 1,6 • IO5;
в)	ДА = lx [1 — nn (qxq2l2T)2 etg2 (O0/2) ] = 1,5 • 10’.
2.22.	ЛА/А = л (e4/4T2) (0,7Zf//nj) + 0,3Zi/m2)pd etg2 (O„/2) = 2,7 • 10~3, где Zj и Z2 — порядковые номера меди н цинка; m.\ и т2 — массы их атомов.
do
2.23.----=-
dQ
П 4лп
tg2 (0/2) sin4 (O0/2)
- 1,0-10—23 см2/ср , где n i>dnv, m —
масса атома свинца.
2.24.	Полная энергия электрона в атоме водорода Е = —f?/2r. Убыль энергии за время dt вследствие излучения: —dE --= (2e2/3c3)a2dt. Приняв во внимание, что а = е2/тг2, получим: r2dr = —(4ei/3m2c3)dt. Интегрирование этого уравнения дает т = m2c3rj/4e4 ~ 10~14 с.
2.25. гп ~ У (Л / ты) п, Еп = лй<о,
где п = 1,2,		...; <о = У к/т .	
й2	п2	е2	Z	те4
2.26. гп = 			 •	1 Ь,.а	
те2	Z	h	п	2h2
Z2
п2
Система	Г1 и Г2, 1 О-"8 См		и v2,	1 0е м/с	Т и £СВ( эВ	Vi. в	Х12, им
н	0,529	2,12	2,19	1,09	13,6	10,2	121,5
Не+	0,264	1,06	4,38	2,19	54 4	40,8	30,4
Li++	0,176	0,70	6,57	3,28	122,5	91,5	13,5
2.28.	116, 540 и 1014 им.
2.29.	а) 0,657, 0,487 и 0,434 мкм;
б)	Х/6Х = ы/бы ® (А + 3)3/8 = 1,5 • 103.
2.30.	Серия Брэкета, ^-6_>4 = 2,63 мкм.
2.31.	а) 0,122, 0,103 и 0,097 мкм (серия Лаймана); 0,657 и 0,486 мкм (серия Бальмера); 1,875 мкм (серия Пашена);
б)	п (п — 1)/2 = 45.
2.32.	121,6, 102,6 и 97,3 нм.
2.33.	а) 4; б)_3.________
2.34.	Z = 1/176лс/15АДХ = 3, Li++.
2.35.	Есв = hRZ2 = 54,5 эВ, где Z2 = 8лс (2 + N)2/RkM (А + 4) = = 2 (Не+), А = 3. •
е.36. Е = Ер + 4HR = 79 эВ.
2.37.	v = У (2h/m) (2лс/Х — RZ2) = 2,3 • 106 м/с.
2.38.	v — 2yhR/me = 3,1 • 10е м/с, те — масса электрона.
2.39.	оМин — y3hR/m = 6,25 • 104 м/с, т — масса атома.
2.40.	ср = arccos (3/gftR/mcv0) = 60°.
2.41.	Согласно законам сохранения энергии и импульса,
Е = Лы + mv2/2, Лы/с = mv,
где Е = s/JlR — энергия возбуждения атома; Й<о — энергия фотона; т и v — масса и скорость атома. Из этих уравнений находим:
v = с ("|/1 -\-3hR/2mc2— 1) = 3/4 hR!mc=3,24м/с,
139
где учтено, что 3hR!2tn<?	1;
ЬЕ/Е = mv*/2E = 2/shRlmc2 = 5,5 • 10“7 % .
2.42.	v = з/8/?ДХ/л cos О = 7,0 • 105 м/с
2.43.	Из формулы ы' = ы У(1 + £)/ (1 — 0), где 0 = о/с и (о'/со = 27/20, получим v = 0,29 с.
2.44.	а) Момент импульса системы равен /<о2, где I = р,/2 — момент инерции; р. — приведенная масса; I — расстояние между электроном и ядром. Запишем воровское условие квантования и уравнение движения:
р/2<о = tin-, цы2/ = е2//2.
Из этих двух уравнений находим: I — (h2/fi^)n2, п = 1,2, ...;
б)	кинетическая энергия системы Т =; /<о2/2 = е1/21. Полная энергии системы Е = Т + U — ё*/21 — е2// = —е2/21. Энергия связи Есв = |Е| — hR/n2, где R = це4/2Й3;
в)	без учета движения ядра значения Есв и R больше на m!М = 0,055%, где т и М — массы электрона и ядра.
2.45.	m-plme = (п — г])/п (г) — 1) = 1,84 • 103.
2.46.	a) £d — Ен = 3,7 • 10~3 эВ;
б)	VD — VH = 2,8 мВ;
в)	Х|_| — ^*D	33 ПМ.
2.47.	а) 2,85  1011 см; б) 654 пм; в) 2,53 и 2,67 кэВ.
2.48.	а) 1 ,06 - 10 8 см; б) 6,8 и 5,1 В; в) 1,03 • 1013 с-1, 0,243 мкм.
3.1.	39 пм и 0,91 пм; 0,15 кэВ и 0,082 эВ.
3.2.	X = лйУ2 (т]2 — 1)/тЛЕ = 0,15 нм.
3.3.	Х = 2лПГ\/2ткТ = 132 пм.
3.4.	Т = 2с2 (BpJVmc2 =0,12 МэВ, т — масса протона.
3.5.	ЬЕ = 2л2Й2/тХ2 — р2/2т = 0,38 кэВ.
3.6.	X' = X У(п + 1)/ (п — 1) = 2,2 пм.	_____
3.7.	X = Xn (1 + mn/fftHe) = 0,07 нм, где Xn = 2nhl~\/2mnT.
3.8.	X = X (1 + т])/ (1 — т]) = 0,10 нм, где т] = шн/тНе.
2лЛ____________1_______
3.9.	а) -	1/1 + 7’/2тс2 ’
(10 кэВ (электрон),
б)	Т С мэр (протон).
3.10.	7= (УГ— Qfftc2 = 0,21 МэВ.
3.11.	Х= Хк/У1 + тсХк/лЙ = 3,3 пм.
3.12.	/ (X) со X-4 ехр (—2Хщ/Х2), Хт = лй/у тйТ = 90 пм.
3.13.	/ (X) со Х~5 ехр (—5Хт/2Х2), Хт = 2nh.iy btnkT = 57 пм.
3.14.	о= АлМЬтЛх = 1,0 • 10е м/с.
3.15.	Т = 2 (nhlldkx)2lm =24 эВ.
3.16.	1% = л.2 h2/2 med2 (Уг| — I)2 sin2 О — 0,15 кВ.
3.17.	d = л,Ыг/У2тТ cos (а/2) = 0,21 нм, k = 4.
3.18.	d = лй£/У2тТ sin О = 0,23 им, причем tg 20 = rll.
3.19.	а) л = У1 + Vt/V = 1,05; б) V/Vt > 5.
3.20.	Еп = (n2h2!2mP)n2, где п= 1,2, ...~
3.21.	2лг = лХ, где п = 1,2, ...; X = гл^л, гг — первый боровский радиус.
3.23.	У фотона, рассеянного и прошедшего через объектив, рх < (hale) tg О. Первая часть этого неравенства характеризует одновременно неопределенность Дрх для электрона, Дрх ~ (Й<о/с) tg О ж (2лЙ/Х) sin 4. Неопределенность координаты электрона Дх ~ d = X/ sin ft. Отсюда ДхДрх ~ 2лй.
3.24.	Чтобы установить, через какую щель прошла частица, ее //-координата должна быть определена (индикатором И) с погрешностью Ду < d/2; d — рас-140
стояние между щелями. В соответствии с соотношением неопределенностей это означает, что индикатор должен вносить неопределенность в р-проекцию импульса частицы \pg^2hld.
В то же время условие того, что дифракционная картина не будет нарушена, есть \р'у < где р = 2лй/Х; sss X/d; X — длина волны частицы, т. е. кр’у < 2nh/d.
Таким образом, вносимая индикатором неопределенность импульса Дру оказывается значительно.большей, чем неопределенность ^р’у, при которой дифракционная картина сохранилась бы.
3.25.	Полагая Дх = 0.5 мкм, получим: 2 • 104, 1 • 10 и 5  10-2 см/с.
3.26.	До ~ 10е м/с; Di = 2,2 • 10’ м/с.
3.27.	Тмин ~ 2Й2/т/2 = 15 эВ. Здесь Дх = //2 и р ~ \р.
3.28.	Дц/ц л 2Й//’1/2/п7' = 1,2 • 10~4. Здесь Дх = li2.
3.29.	При сжатии ящика на величину 6/ необходимо совершить работу 6Д = Ffil, которая пойдет на приращение энергии частицы dE. Отсюда F = = dEldl ~ AtFlml3 = 2ЕМИН//. Здесь учтено, что Дх — V2 и р ~ \р.
3.30.	Полагая Дх ~ х и v ~ До, для полной энергии частицы имеем: Е = Т + U й’/2тх2 + хх2/2. Из условия dE/dx = 0 получаем: Емин Л<о. Точный расчет дает Асо/2.
3.31.	Полагая Дг ~ г и v ~ До, получаем:
£св = 11/| — Т » tp/r — tf/imr2.
Из условия dECBldr = 0 находим г ~ Л2/те2 = 0,5 • 10-8 см и Есв sss те4/2Й2 = = 13,6 эВ.
3.32.	Полагая для обоих электронов Дг ~ г и v ~ Ди, запишем выражение для полной энергии:
Е as 2 (p2/2m — г^/г) + е2!2г » tp/mr2 — 1е2/2г,
где член е2!2г характеризует энергию взаимодействия самих электронов. Минимум Е соответствует г sss 4X2/7me2 = 0,3  10~8 см; £мин ~ —49/1вте4/Л2 = = —83 эВ. Эксперимент дает: —79 эВ.
3.33.	Дх/Х as 1/УлДТ/Т = 2 • 103.
3.34.	Д/ as r\mP/h as 10~16 с.
3.35.	Ширина изображения Д=Ь+Д'«Ь4- 2Л//pb, где Д' — дополнительное уширение, связанное с неопределенностью импульса Дру (при прохождении через щель); р — импульс падающих атомов водорода. Здесь положено, что Др = 6/2. Функция Д (&) имеет минимум при b as yF^M/mv = 10-3 см.
3.36.	Если U ие зависит от времени явно, то полное уравнение Шредингера допускает решения в виде У (х, t) = ф (х) f (/). Подставив это выражение в полное уравнение Шредингера, получим два уравнения:
2т	 Е
Ф" (£-m=0; f+i —/=0. л2	п
Решение первого нз них — собственные функции фп (х), соответствующие собственным значениям энергии Еп. Решение второго: f (/) оо е 1Ип , ып — En!h.
В результате:	(х, /) = ф (х)е
3.37.	Изменится лишь временной множитель полной волновой функции. А так как физический смысл имеет лишь квадрат модуля этой функции, то изменение временного миожителя никак не проявляется.
3.38.	Полагая U = 0, ищем решение полного уравнения Шредингера в виде ¥ (х, t) = ф (х)/ (/). В результате
V(x, 0 = Ae-i ((0<-А:х); ш = Е/Л; k=--p!h.
3.39.	Полагая в уравнении Шредингера U = 0, находим решение ф = = Ае±!**; k-  ~\/2mE/h. Видно, что это решение конечно при любых значениях Е > 0.
141
3.40.	Запишем уравнение Шредингера в области 0 < х < I:
ф" = ^ф=0, к=У2тЁ~/И.
Его решение ищем в виде
4' (х) = A sin (kx + а),
где Лиа — произвольные постоянные. Из граничных условий ф (0) == Он ф (/) = 0 находим: а = 0 и sin kl = 0. Отсюда kl = пл, п = 1,2, ... (значение п =- 0 отбрасываем, так как оно соответствует 4 = 0, т. е. отсутствию частицы вообще). Остается учесть связь между k и Е, и мы получим выражение для Еп.
Чтобы определить постоянную А, воспользуемся условием нормировки:
I	__
J Л2 sin2£x<7x - 1 , откуда А -.- Д/2//. 0
,	2 Г лх 1	3
3.41.	a) w= —— I sin2-----dx --- — + ----= 0,61;
I J I 3 2л
Xi
б)	из выражения для энергии Е следует, что dE/E = 2dn'n. Отсюда dN = = dn = (1/лЛ)У т/2Е dE.
3.42.	а) Запишем уравнение Шредингера внутри ямы:
4; + % + ^4=°- k = y2mE!h.
Его решение удобно искать сразу в виде произведения синусов:
4 (х, у) - A sin ktx  sin k2y,
так как при х = 0 и у = 0 волновая функция должна обращаться в нуль. Возможные значения kY и k2 находим из граничных условий:
4 (а, у) =0,	= п±л/а, nY = 1, 2, ...;
4 (х, Ь) =0, k2 = п2л/Ь, п2 = 1, 2, ...
После подстановки 4 (*> У) в уравнение Шредингера получим й2 =	или
Еп, п2 = <я2 Л2/2«) (nl/a2 + п2/Ь2).
Постоянную А находим из условия нормировки. В результате
4Л n„(x> У) = Т/4/а& sin (nx nx/a)-sin (п2 лу!Ь)-,
б)	w =- (1/3 — Д/зМл),2 = 0,038;
в)	Е = 9,9; 24,7; 39,5 и 49,4 единиц №/т1г.
3.43.	Каждому значению двойки чисел nY и п2 соответствует одно состояние (4-функция). Число состояний в интервале (dnt, dn2) равно dN = dn±  dn2. Имея в виду уравнение kf 4- k% = k2, где k± — п^я'а и k2 = п2л/&, отложим на осях координат величины k± и k2. Построим затем в этом «^-пространстве» окружность радиуса k с центром в начале координат. Все точки этой окружности соответствуют одному и тому же значению k, т. е. энергии Е. Нас будет интересовать только 1/4 часть окружности, так как следует рассматривать только положительные значения чисел kt и k2 (отрицательные значения не дают новых состояний, как видно из выражения для ф-фуикции). Число точек (состояний), заключенных между двумя окружностями с радиусами k и k + dk в 1/4 плоскости, есть
dN = f dn±dn2 = j (abl^2)dk1dk2 = i/4 (abi^2)2nkdk.
Имея в виду, что k2 = 2тЕ/Л2, получим:
dN = (abm/2nfl2)dE.
142
3.44.	а) Решение аналогично решению, приведенному в задаче 3.42: Ent пг	'2т) (nf: a^nl/b^+nl!^),
где «j, пг, п3 — целые числа, не равные нулю;
б)	А£ -= л2/г2’т/2;
в)	для шестого уровня л2 4- л| + п3 = 14. Это число, как нетрудно установить подбором, является суммой квадратов единственной тройки чисел: 1,2 и 3. Число различных состояний, отвечающих данному уровню, равно в нашем случае числу перестановок этой тройки, т. е. шести.
3.45.	= (а&ст3/2, _|/2л2й3)1/'ё. Вывод аналогичен приведенному в
задаче 3.43.
3.46.	Проинтегрируем уравнение Шредингера по узкой области, внутри которой имеется скачок потенциальной энергии:
+6
ф'(4-6)—ф'(—в)--— [ (2m/A2)(£— U) tydx.
-6
Ввиду конечности скачка U интеграл при |6| -► 0 тоже стремится к нулю. Отсюда ф' (+0) — ф' (—0).
3.47.	а) Напишем уравнение Шредингера для двух областей:
0	ф" + k2 тр! = 0, k-~\/2mE ih\
х * I, $2 —х24>2 = 0, х ~\/2т (ил—Е) /й.
Их общие решения
ф|(х)- a sin (kx :а), ф3 (х)- Ье~ мх - сехх
должны удовлетворять стандартным условиям. Из условия ф3 (0) -- 0 следует, что а 0. Чтобы волновая функция оставалась всюду конечной, необходимо соблюдение условия с = 0. И наконец, из условия непрерывности волновой функции и ее производно!? по координате в точке х — I получим:
tg&/—— £/х, или sin kl=- ± У h2/2ml2 Uo kl.
Изобразив графически левую и правую части последнего уравнения (рис. 6), найдем координаты точек пересечения прямых с синусоидой. Оии определяют корни уравнения, отвечающие собственным значениям энергии Е. Кории соответствуют тем точкам пересечения, для которых tg kl < 0, т. е. будут находиться в четных четвертях окружности (эти участки оси абсцисс выделены на рисунке жирными отрезками). Как видно, корни уравнения (т. е. связанные состояния) существуют ие всегда; пунктиром показано предельное положение прямой;
б)	л-й уровень появляется при условии kl = (2п — 1)я/2, откуда PU0 = = (2л — 1)2я2Й2/8л1. Четыре уровня.
3.48.	а) Из уравнения, приведенного в условии предыдущей задачи, следует, что sin (ll/mllg/Л) = ~\/'2l2. Отсюда mUg/h 2/^ (другие значения отбрасываем, так как уровень единственный, поэтому аргумент синуса находится во второй четверти) и l2U0 — */lan2tPlm',
143
б)	из условия d^\ldx = 0, где фх со sin kx, находим хвер = л/2й = 2/3Z (рис. 7);
в)	пусть wa. и wt — вероятности нахождения частицы вне и внутри ямы. Тогда
оо	I I
wa!wt=^ b2e~2Hxdx / J a2 sin2 kxdx = 2/ (2-(-Зл), l	I о
где отношение bia определено из условия ф^ (Z) = ф2 (Z), a k = x = 3n/4Z. Остается еще учесть, что wa +	= 1, и мы получим:
wa = 2/(4 + Зя) = 14,9%.
Возможность нахождения частицы в области, где ее энергия Е < U, представляет собой чисто квантовый эффект. Он является следствием волновых свойств частицы, исключающих одновременно точные значения координаты и импульса, а следовательно, и точное разделение полной энергии частицы иа потенциальную и кинетическую. Последнее можно сделать только в пределах точности, даваемой соотношением неопределенностей.
3.49.	Напишем решения уравнения Шредингера для трех областей:
х < 0, ~аекх, х~"|/2л? (U0~E) lh\
О <1 х Z, ф2 = 6 sin (kx^-a), k=~\/2mE /Л;
х > I, ф3 = се — кх.
Из непрерывности ф н ф' в точках х = 0 и х = Z получим: tg а = й/х; tg (kl + а) = —й/х, откуда sin а = hkl~\/2mUa, sin (kl + а) = —Лй/"|/2л?(70. Исключив из последних двух уравнений а, получим
kl = пл — 2 arcsin (AZfe/ 1/2mt70),	( * )
где n — 1, 2, .... n, значения arcsin берутся в первой четверти (от 0 до я/2). Поскольку аргумент у arcsin ие может быть больше единицы, то значения k ие могут превосходить ймакс = ~V2.mU(Jh.
Изобразим левую и правую части последнего уравнения как функцию от k (рис. 8, ylt р2 и Уз — правая часть уравнения при п = 1, 2, 3). Точки пересечений прямой с кривыми уг, у2 и т. д., определяют корни этого уравнения, которые, как видно из рисунка, дают дискретный спектр собственных значений Е.
При уменьшении Uo ймакс перемещается влево — число точек пересечения будет уменьшаться (при заданном Z положение прямой остается неизменным). Когда ймакс становится меньше k' (см. рис. 8), яма будет иметь только один уровень энергии.
Таким образом, данная яма всегда содержит по крайней мере одни уровень энергии.
3.50.	а) Основному состоянию соответствует п = 1 в формуле ( * ) решения предыдущей задачи. При Е = U0/2 величина kl = л/2, откуда l2Un = я2Й2/4т;
б)	из той же формулы (* ) и рис. 8 следует, что при появлении второго, третьего, ..., л-го уровней kl = л, 2л, ..., (п — 1)л, и аргумент у arcsin в этих случаях равен единице, т. е. hk — ~\/2mUa. Отсюда
PU0 = (п— l)2n2Zi2/2m, л = 2, 3, ...
Число уровней определяется из неравенства
л > 1/2т12и0/лЕ > п — 1.
В нашем случае л = 4.
3.51.	U (х) = 2 (а2Е2/т)хР, Е = a.h2/m.
3.52.	U (х) = —ah2/mx, Е = —a?t?l2m.
3.53.	а) Е = Л<о/2; б) Е = 3/2Йо>.
3.54.	Еп = Й<о (л + 1/2).
144
3.55.	a) ф0 -- (a2/n)1/,‘* exp (—g2/2); ф] -- (а2/4л)'^4 2g exp (—g2/2); ф2 = = (а2/64л)*/4 (4g2 — 2) exp (—g2/2);
б)	значения хвер для состояний с n - 0, 1, 2 соответственно равны 0; ±1/а и ±2,5/а. Распределение ф« (х) показано на рис. 9, где х0 — 1/а.
3.56.	0,157.
3.57.	Уравнение Шредингера для этого поля в области х > 0 такое же, как и в случае линейного осциллятора. Поэтому его решения будут теми же, что и для осциллятора при нечетных значениях п, так как ф (0)	0. Это же относит-
ся и к собственным значениям энергии, выражение для которой можно записать в форме Е = h<s> (2п' л- 3. 2), где п’ 0, 1, 2, ... Видно, что при одном и том же значении <о энергия основного состояния (п’	0) втрое превышает энергию ос-
новного состояния осциллятора.
3.58.	а) Решение ищем в виде ф = X (x)Y (y)Z (г). После подстановки в уравнение Шредингера получаем
Х;+2 (m/Л2) (Ex—kx х2/2) Х = 0
и аналогичные уравнения для функций У и Z, причем Ех + Еу + Ег = Е. Эти уравнения совпадают с уравнением для одномерного осциллятора, собственные функции и собственные значения энергии которого известны. Поэтому можно сразу записать:
.	tn, л, л, tn, W tn, (Ю tn, (z) > En = ha (n+3/2), л=л1+л2 + л3;
б)	кратность вырождения уровня с определенным значением п — это по существу число различных комбинаций чисел nlf п2 и л3, сумма которых равна л. Для определения этого числа комбинаций подсчитаем сначала число возможных троек чисел пг, п2, п3 при фиксированном значении пг. Оно равно числу возможных значений п2 (или л3), т. е. равно п — nt + 1, так как п2 может меняться от 0 до л — лх. Тогда полное число комбинаций из Л1, л2, л3 при заданном п есть
у .	,	(п+1) (л+ 2)
W = 2j (п —nj+l) =-----------------.
Л1 — 0
3.59.	а) Запишем решения уравнения Шредингера:
х + 0, фх= й^е1*’ * + &1 е—— ~^2mE/fr,
х > 0, ф2 = a2eifc2X+ &2e — i*2*, k2 -Д/2т (E— UQ) /fl.
Будем считать, что падающая волна характеризуется амплитудой alt причем Вещественной, а отраженная — амплитудой Ь±. Так как в области х > 0 имеется только проходящая волна, то Ь2 = 0. Из условия непрерывности ф и ф' в точ
145
/? =
ке х --- 0 находим fej/aj, а затем R и £>:
fei \2_ / kt—k2 V D= = 4kr k2 ai )	\ ^1 + ^» /	(^1 + ^г)2
в) в данном случае решения уравнения Шредингера имеют вид:
х <: 0, -ф! =at е,кх-4- bj е“ >кх , k = "|/2/п£7й;
х > О, ф2 =а2 eKX-rb2 е“ Кх, х =	2 т (Uo—E) h .
Пусть падающая волна характеризуется вещественной амплитудой а<. Из требования конечности волновой функции следует, что а2 -- 0. Из условия непрерывности ф и ф' в точке х = 0 находим:
7? = | Ьх!аг |2 Д (k— ix) (fe-r-ix) |2 1 .
Плотность вероятности нахождения частицы под барьером w2 (х) 'ч. е- 2ил. Отсюда хиф - 1,'2х. Для электрона х.,ф se 0,1 нм.
3.60.	а) Запишем решения уравнения Шредингера для трех областей:
х д 0, ф! — а} е'кх-г-/?, е~1Ах,	£-•- ~\/2тЕ 'Л;
0<х < I, ф.2 а, е1*" '1' — Ь., е" х , ko	i
x > Z, ф3- - a:i е'кх-
Эти выражения написаны для случая, когда падающая волна характеризуется е,кх, поэтому в волновой функции ф3 оставлен только один член, соответствующий проходящей волне. Из условия непрерывности ф и ф' на границах ямы находим
а3 ________ 4kklte~M_______________
«1	(k±k0)- е~ ik"'~(k—k0)2eik°l
(*§-*2)2 . , .l”1	A , Ul sin2 Z v1
4kl k-	)	\ 4E (E+U„) I
4k2 k2 \- 1	[ 4E (E + Uo) \ -1
(kff — k2)'- sin2 ku I /	\,	‘ sin2 k0 I )
б)	из условия D ~ 1 имеем sin k„l — 0. Отсюда kol = rm, или E =
--- (n-h2l2ml-)n2 — Uo, где n — целые числа, при которых Е > 0.
3.61.	а) Аналогично решению предыдущей задачи (см. п. «а»). В результате получим те же формулы, только в них k0 --= Д/2/n (Е — U0)/fl. При Е —> Uo величина D -э- (1 — т/2(7(/2Л2)-1:
w б) Еп = (л2Й2/2т/2)л2 4- Uu -=^ 11,5; 16,0 и 23,5 эВ. Здесь п = 1,2, 3, ...
(п =# 0, поскольку при п = 0 Е = Uo и D < 1, см. предыдущий пункт);
в)	в этом случае характер решения уравнения Шредингера будет отличаться от случая Е ~> Uo только в области 0 < х < I:
^2= а2 eHX-\-b2 е-**, x = j/2m (Z70—Е) /Л.
а, 2 D — .
«11
Z?=l-D = (l т-
Поэтому коэффициент прозрачности можно найти, заменив в выражении для аз/а} (см. решение задачи 3.60, п. «а») k0 на ix:
ая	4ix k e~ikl
ai	(A4~ix)2exZ—(k—i x)2 e—xi
1 ^gsh2xZ \
+ 4E(Ua-E) }
146
При х/ > 1 величина D <g 1. В этом случае sh х/ = i/^e^ и
D ~ 16fe2X2 е-2хГ [6 _£_/j _2Це- 2lV2m (U,-E)ltl .
(й2н-х2)2	г/(Д uj
г)	для электрона D ж 0,27, для протона D ~ 10~47.
3.62.	D=exp [— 8,'з I "|/2 mlhU^ (Uo—Е)3/.2].
3.63.	D = ехр [— (n//ft)V2m/i/0 (Uo — £)].
4.1.	Указание: учесть, что А2 ф = А (Л Ф)-
4.2.	а) (2 — х2) cos х — 4х sin х; (1 — х2) cos х — Зх sin х;
б)	(2 4- 4х + x2)e-v; (1 + Зх + x2)e-v.
4.3.	а) Д - 4; б) А = 1; в) А = —а2.
4.4.	а) 4 — СеЛх, X = 2лп/а, п	0, ±1, ±2, ...;
б) гр = С sin (Д/Хх), X = (пл//)2, п = ±1, ±2, ...
4.6. а) A (S'Si)-(Z'Si)	=	В/1;
б) А (вс)-(вс) д'=д'в'с'-'в'сд' +ВАС^ВАС=:
['д.'в] сДв'[д'Д].
4.8.	[/Г, Д^21 = 2 1Ж Л2]= 0, ибо
[/Г,д7 J - Пз", £] д'/+д'/ [s', Д/]=о.
4.9.	а) Умножив равенство А В — В А ~ 1 на оператор В сначала слева, затем справа, получим: В А В — В2А - В и АВ2 — В АВ - В. Теперь сложим эти равенства: А В2 — В2А = 2 В.
4.12.	В общем случае нет. Например, оператор ptJ коммутирует с операторами х и рх, которые между собой не коммутируют.
4.13.	а) Если гр — общая собственная функция операторов А и В, то
А Вф = ДВф= ВДф = ВДф; В Дф=ВДф = ДВф = ДВф.
Следовательно, ДВф=ВДфи [Д, В] = 0;
б)	пусть ф — собственная функция оператора Д, принадлежащая собственному значению Д. Из коммутивности операторов Д и В следует, что Д В гр = = В А ф - В А ф = А Вф, т. е. А ф' = Дф', где ф' = В ф. Таким образом, собственное значение А принадлежит и функции ф, и ф', которые, следовательно, описывают одно и то же состояние. Это может быть только в том случае, если эти функции отличаются лишь постоянным множителем, например В: ф' = Вф. Но ф' = Вф, поэтому Вф = Вф, т. е. ф — общая собственная функция операторов Д и В.	___
4.14.	a) f (х, г) ехр (ikyy);
б)	А ехр [i {kyX + kyy + kzz)}\
в)	f (у, z) exp (±ifcxx). Здесь kv - pjtv, v — x, y, z\ f — произвольная функция.
4.15.	Имеет только в том случае, если функция фд одновременно и собственная функция оператора В. В общем случае нет. Например, в случае вырождения (в одномерной прямоугольной потенциальной яме каждому энергетическому уровню соответствуют два значения проекции импульса, ]~рх и —рх, несмотря на то, что операторы Н и рх коммутируют).
147
4.16.	Пусть ф — произвольная собственная функция оператора А, отвечающая его собственному значению А. Тогда вследствие самосопряженности этого оператора
Jф* А фб/х= ( ф А* ф* dx и A Jф* ф dx--- A* J фф* dx, откуда А = А*. Но последнее возможно только при вещественном А.
4.17.	а) 1 ф! рх ф2 dx= — i h I ф* (дф2/дх)</х= — i h I ф‘ ф2 | + “ —
ф* dx= i ф2 p* ф* dx.
4.18.	Оператор A + , сопряженный оператору А, определяется следующим образом:
J Ф1 А ф2 йх = |ф2(л + фх) dx.
а) Рхх б) — i рх.
4.19.	Из условия эрмитовостн операторов А и В следует, что
j" Ф* Л (бфз) J Вф2 (Л* фф) dx =J д* ф|(^|,2)</т =] ф2 В* (л* ф|)</т.
Л и В коммутируют, значит, В* Л* = Л* В* и J ф* Л Вф2 dx = | ф2 Л* В*ф*йт.
4.20.	Каждый оператор коммутирует сам с собой, значит если оператор Л эрмитов, то эрмитовыми будут операторы А '1 = А А и А п.
4.23.	а) Уравнение £2ф -- В2ф имеет решение ф = Л ехр (1В2ф/й). Из требования однозначности, ф (ср) = ф (tp + 2л), следует, что Lz = mh, где т = = 0, ±1, ±2, ... Из условия нормировки Л (2л)-1/2. В результате:
фП|.(2л)-1/2 exp (imtp);
б)	собственные значения Lz = /п2Й2, где т = 0, ±1, ±2, ... Собственные функции имеют тот же вид, что и для оператора В2, т. е. функция фт = = (2л)-1/2 exp (imcp) является общей собственной функцией операторов Lz и Lz. Все состояния с собственными значениями Lz, кроме т 0, двукратно вырождены (по направлению вращательного момента, Lz = ±|/п|Л).
4.24.	2Й2.
4.25.	a) J ф| Lz ф2 d ф= — i h ф* ф2 |o”+Jф2 (^дф^/дф) d<P =
Ф2/-2*Ф1 d<f.
Здесь ф*ф2| оП ~ 0, так как функции и ф2 удовлетворяют требованию однозначности;
б)	f ф;в2 ф2 dr= J (ф| х Ру ф2—ф7у 'р'х Ф2) dx.
В силу эрмитовостн операторов рх и ру подынтегральное выражение можно преобразовать так:
«ta Р'у Ч1!— У^гР*х = Р*у—У р'^ Фг-ф2 ф;.
4.26.	( ф; l 2 ф2 dx^у (ф; l 2 ф2 +ф; l 2 ф2 +ф; l 2 ф2)dx.
148
Так как операторы Lx, Ly, Lz эрмитовы, то эрмитовыми будут и квадраты этих операторов, а следовательно, и оператор L'2.
4.29.	а)[/-х, pi)- ILX, рх] рх-\-рх [£х, рх] 0, ибо [£ж, рх] - 0.
4.30.	Оператор Т можно представить в сферических координатах в виде суммы Т = Tr + Lrllmr2, где Тг — оператор, действующий только на переменную г. Так как оператор L2 ~ —A2V&, ф’действует только на переменные О и <р, то
h2i (/ -г'
4.34 сюда <Д>
4.36.
[ L2, T\-[L\ Tr] + [ L2, £2/2/лг2] = 0.
4.31.	a) [£х, Ly] — Lx Ly—Ly Lx = (ypz — zpy) (zpx — xpz) — (zpx — xpz) X X (ypz — zpy)-^[z, pz] (xpy — ypx)=—ifl (xpv — ypx) = ihLz.
4.32.	a)	[Lyt Lx] + lTz, ?XL где [?x, TX]^Q;
[ Ly , Ax] Ly | Ly, Ax| - j [Ly > Л я] Ly — i h [Ly Lz -f-Lz Ly);
I Az , Ax.] — Az [ Az, Ад.] [Az, Ад.] Az i Л (Az Ly-\-Ly Lz).
Отсюда видно, что [L2, £x] —- 0. Аналогично для Ly и Lz.
4.33.	В случае г ----- r0 const Н - —02/2p.ro)V#,q> --	Поэтому
Яф = (Лрг2)£ф. Так как собственные значения оператора L2 равны ‘I -Г 1), то Е = М (I - 1)/2рг2.
Вследствие эрмитовости оператора A J ф*А ф</т= J фА*ф*</т. От-— <Л‘>, что возможно лишь при вещественном <А>.
Воспользовавшись тем, что Нх— х И-- —(ili/m)px, запишем:
(рх) — J ф* рх фс/х-- (i m h) J (ф*Я хф—ф* х Н ф) dx.
Вследствие эрмитовости гамильтониана подынтегральное выражение можно переписать в виде хфЯф* — хф*Яф -= 0, поскольку Яф*-£ф* и Н ф = £ф. Итак, <рж) 0, что и требовалось доказать.
4.37.	а) Из условия нормировки А2 ~ 8/3/.
(Т) =J фТф dx = —(h2/2m) f фф/ dx — 2/3n2h.2/ml2;
б)А2 -= 30//5; <Т> = 5h2/ml2.
4.38.	Из условия нормировки А2 а^/З/л; <Т> — <//> =
4.39.	а) Здесь фп (х) - (2/Z)1^2 sin (nnx/l)-,
<(Лх)2) = (х2) —(х>2=(1 —6/л2 л2) /2/12;
((Apx)2) = <pJ) = (nA//)2 л2;
б)	из условия нормировки А2 =а j/2/л; ((Ах)2) = 1/4а2; ((Лрх)2)--а2 А2;
в)	А2^а ]/27Т; ((Лх)2) = (х2)- 1/4а2; <(Лрх)2) =(р!> - <Рх)2 --= «3Л2.
Указание: при вычислении среднего значения квадрата импульса целесообразно воспользоваться свойством эрмитовости оператора рх, благодаря чему (р2) ф* Pxtydx -- J | рхф I dx.
4.40.	Из условия нормировки А2 - - 4/3л; <Lz> 4Й2/3.
149
4.41.	Из условия нормировки Д2 — 1/л; <(Atp)2>= < tp2 > — < tp >2 — ----- л2/3 — 1/2;	< (ALZ)2 > = < Lz > = h-.
4.42.	Имея в виду, что ihLx = [Ly, Lz], запишем:
(//*)= — (i/Л) J (гр* Lv Lz гр—гр* Lz Ly ip)dx.
Так как по условию Lzip = Л2гр и оператор Lz эрмитов, то подынтегральное выражение можно преобразовать так:
Ф* Lu Lz гр—гр* Lz Ly гр-L, гр* Ly ty—(Ly ^)~LZ ^* {L4 гр) (Аггр*—Л* гр*)-Но последняя скобка равна нулю вследствие вещественности собственного значения эрмитова оператора (Lz — L*). Аналогично и для оператора Ly.
4.43.	< L2 > — ( грЛ2 грс(П = 2/г2, где — sinO-dO-dtp.
4.44.	Так как х, у, и г равноправны, то < L- > = < Lx > -1- <L^> + — < L2 > -= 3 < L2 >. С учетом равновероятности различных возможных значений Lz имеем:
Й2 Л	2Й2	/ (14-1) (2/4-1)
(Ч? Й (,п2;	2 /п2 -	J-----7—— и (й2)^й2/(/ + 1).
ZI “j- 1	_Z.I -+• 1	о
4.45.	Имеем Д гр( -= Ajtpj и Дгр2 — Д2гр2. В силу эрмитовости оператора А его собственные значения вещественны и
[ гр* Д гр2 dv—j 'Ра Д* Ф* d т, или Д2 J гр, гр2 dx = Дг Jгр2 гр/ dx.
Так как Аг Д2, то последнее равенство возможно лишь при условии | гр^гр2с(т = 0. Значит, функции гр! и гр2 ортогональны.
4.47.	а) Умножим обе части разложения гр (х) =	(х) нагр*(х) и про-
интегрируем затем по х:
| гр/ ф7х - У J Ф* Фь dx-
В силу ортонормированности собственных функций оператора А все интегралы в правой части последнего равенства обращаются в нуль, кроме одного, у которого k - I. Таким образом, сг = | гр*гр7х;
б)	(Д)-=•[ гр* Дгрйх--- f (2 7 Фа) 2 с‘ А‘ Ф') dx=~
2 ck ct Аi J Фа ф/7х-~ 2 I ck I2^a-
a, 1
Причем S |f;, |2 —- 1, что непосредственно вытекает из условия нормировки функции гр (х):
J гр* гр dx = 2 ck с' J Фа Ф1 dx = 1 •
Отсюда следует, что коэффициенты |Cfe|2 — это вероятности обнаружить определенные значения механической величины А^.
4.48.	Прежде всего следует вычислить нормировочный коэффициент Д. Вероятность нахождения частицы на л-м уровне определяется квадратом модуля коэффициента разложения сп функции гр (х) по собственным функциям грп (х) оператора Н: сп j фгрпг/х, где гр„ = (2//)1/2 sin (плх//);
а)	А- - 8/3/. Искомая вероятность wt = cj = 256/27л2 = 0,96;
б)	Д2 - 30 75; wn =- Сп 240 (лп)~6 [1 —(—1)лр, т. е. wn отлично от нуля только для нечетных уровней (п -= 1, 3, 5, ...); дл'я них wn = 960/ (лп)в; uij ~ 5= 0,999, И13 аг 0,001.
150
4.49.	а) Вычислим сначала нормировочный коэффициент А = 2/'р/Зл. Затем разложим функцию ф ((f) по собственным функциям оператора Lz — они имеют вид фт (<р) = (2л)-1/2 е1Ш<р:
ф (ф) -- A sin2 ф-(Зл)-1/2 (1— cos 2(f) - (Зл) —1/2 (1— 1/2 e2i4>—1/2 е-21ф)--= УГзфо — уГб ф^2—уТ7б ф_2.
Отсюда видно, что Lz = 0, ---2й и —2Й. Их вероятности: = 2/3, ш+, =	=
= 1/6;
б)	Lz = О, ±Й, ±2Й и ш0 — 36 70, а»+1 = Ш-j = 16/70, ш+2	ш_2 — - 1/70.
4.50.	а) Найдем коэффициенты разложения волновой функции фп (х) = = (2/Z)1 /2 sin (пях/l) по собственным функциям оператора й:
Г .	п/— 1-(—1)" e~ik! '
фп Ф* dx =п Ул( -------- -----------,
J	Л2Л2—
отсюда
4л/п2	( cos2 (Й//2), если п нечетно,
ttfb —- | СЪ I2 - ~	1
(л2л2—й2/2)2 I sin2 (kl 2), если п четно;
б)	из условия нормировки находим: А'2 = а~[/2/л; Wk -- |с^|2 = = (1/аУ2л)е—*2/2“!.
4.51.	Удовлетворяет только временному уравнению Шредингера.
4.52.	Разложим искомую функцию по собственным функциям стационарных состояний:
¥(х, /) = Фп (х) e-i“n< , фп (х) = (2//)1/2 sin (плх/1).
Коэффициенты сп найдем из начального условия:
р	j3/2 z5/2
сп = I V (х, 0) фп (х) dx — A-——-------[1— ( — 1)"].
J	пл
Отсюда видно, что сп — 0 только при нечетных п. Из условия нормировки функции ¥ (х, 0) находим Л2 = 30//°. В результате
¥(х, 0) = (Я/ л2) (30/ /)1 /2 2 (1 /Л3) sin (плх//) е “,
где а>„ = En/h — (л2й/2т/2)л2, п = 1, 3, 5, ...
4.53.	Сначала, разделяя переменные ф и /, находим стационарные решения уравнения Шредингера:
1Й<?¥/д/ = Я¥, ¥(ф, /) = 2“1/2е’
где а>т — Emth = (й/2/)т2, т = 0, ±1, ±2, ... Затем разложим искомую функцию Y (ф, /) по ф, /): ¥ (ф, /) = ЗУтп’Рт (Ф> 0> гДе коэффициенты ст определим из начального условия ¥ (ф, 0) = 2сте'т<₽ (см- решение задачи 4.49). В результате:
¥(ф, /) = !/2 А (1 4-cos 2ф.е12Л</').
Из этого выражения, в частности, видно, что ротатор возвращается в исходное состояние через промежуток времени А/ = Tilth.
4.54.	а) Имея в виду, что <Л > = ( ¥*Л ¥</т, получим:
J	Г д¥*	— Г	дА	С	~ <?¥
—-(Л)= I -------Л¥</т+|¥*--------¥</т+| ¥* Л -----dr.
di	J dt J	di	J dt
151
А так как d'VIdt^ — (i/й) ЯТ и дЧ*/dt = (iiй) H'V*, то
-Д-(Л) = 4- f (#¥*)%№+f'F*-^-WT-— (*Т*л'яЧ'Л.
Л	ft J	J dt	fl J
Первый интеграл этого выражения вследствие эрмитовостн оператора /7 можно переписать в виде j Чг*//Л'Р^т, тогда
d Г dA i----------
_(л)=|т. _т_(нл_ля)
Wr.
Отсюда видно, что d A/dt -- d A/dt-У (i/й) (НА — АН).
4.56.	Иметь в виду, что операторы х и рх не зависят от времени явно.
4.59.	Оператор Lx не зависит от времени явно, поэтому
dLx!dt —(ilfl) [Н~, C]-(i/»)[p2/2m, L~x\ + (i/й) [£7, fj.
Так как p2 и Lx коммутируют между собой (см. задачу 4.29), то скобка, содержащая их, равна нулю. Остается вычислить последнюю скобку.
4.60.	Дифференцируя по времени уравнение A Y~ Л1? с учетом того, что dAldt = 0, получаем Ad'Vidt = (dAldtyV = Ad'Vldt. Подставим сюда d'Vidt = — —(ithyH'V, тогда (dA/dtyV _ (i/й) (Л Н — Н AyV. Если Л коммутирует с Н, то л'д’Р //ЛТ = ЛЙ и dAldt ~ 0.
4.61.	Решение этого вопроса сводится к проверке, коммутируют ли операторы указанных механических величин с гамильтонианом Н= рУ/2т1- U — - Т + U, где Т —оператор кинетической энергии. Операторы рх, ру, р2, Lx, Ly, Lz и L2 коммутируют с оператором Т (см. задачи 4.29 и 4.30), поэтому остается выяснить, коммутируют ли эти операторы с оператором U.
a)	dH.dt -~= 0 и U -- 0. Все величины сохраняются во времени;
б)	dHldt = 0. Сохраняются во времени Е, рх, ру и Lz;~
в)	dHldt 0. С оператором U (г) коммутируют операторы Lx, Ly, Lz и L2 (это сразу видно, если их записать в сферических координатах: они действуют только на ft н ф). Сохраняются во времени Е. Lx, Ly, Lz, L2.
г)	dH:dt =(= 0. Сохраняются во времени только рх, ру и Lz.
4.62.	a) d< A ydt - (i/й) | Т* (Н, Л]ЧУт = 0, т. е. <Л> = const;
б)	так как операторы А и Н коммутируют, то они имеют общие собственные функции ф„ (х): Лф,( = Лфп и Hifn — Е„фп. Разложим функцию Y (х, t) по собственным функциям фп, которые являются функциями стационарных состояний (Яф’п = й'пФп). поэтому
(х,	фп (х) е 1<1>п* = 2Сп (/)фп (х),
где <оп = En!h, Сп (t) = сп (0)е 1<1>п< . Последняя сумма — это разложение по собственным функциям оператора Л, поэтому квадраты модулей коэффициентов разложения определяют вероятности различных значений механической величины Лп в момент t, т. е. w (Лп, t). Таким образом,
w Ип , 0 = | <=п (0 |2 = | (°) |2=const.
4.63.	Тг = —(h2/2m) [cfHdr2 + (2lr)dldr)\ — это оператор кинетической энергии радиального движения.
152
4.64.	а) Представим гамильтониан в уравнении Шредингера /7ф = Е"ф в форме Н = Tr + L2/2pr2 + U, где Тг — оператор кинетической энергии радиального движения (см. ответ предыдущей задачи). Подстановка функции ф = = RY в уравнение Шредингера приводит к выражению:
YTrR + (R/2iir)2L^Y + YUR = YER.
Имея, в виду, что L2Y = h2l (I + 1)У, получим
[Tr + h2l (/ + 1 )/2рг2 + £/]/? = ER.
Это уравнение определяет собственные значения энергии Е. Его нетрудно при-
вести к искомому виду;
б) подставим в уравнение L2Y — А.У, где L2 = —Й2Уй,<г, функцию У в виде У - 6 (О)Ф (ф) и произведем разделение переменных О н <р. Обозначив постоянную разделения т2, получим уравнение
для функции Ф (ф):
д2Ф /дф2 = —т2Ф, откуда Ф (ф) = Ae>m<f.
Из требования однозначности следует, что m - О, ±1, ±2, ... Таким образом, ф R (г)6 (0)eim<*'.
4.65. Функция |Г4,„Г2 характеризует плотность вероятности нахождения частицы в состоянии с квантовыми числами I и т, рассчитанную на единицу телесного угла, вблизи 0:|К|2 — dw/dQ.
а) "|/з/4л; б) "|/15/8л.
4.66. а) После подстановки в уравнение Шредингера получим: %" -Т £2% —
--- 0, где k -= ~\/2mElh. Решение этого уравнения ищем в виде х A sin (kr 4* а). Из требования конечности функции ф (г) в точке г - 0 следует, что а --= 0. Таким образом, ф (г) - (A/r) sin kr. Из граничного условия ф (ги) - 0 имеем kr0 пл, п 1,2,..., откуда
л2 Л2
е ns	——- п2, ф.ч (г) - (2лг0)
,sin kr г
Коэффициент А найден из условия нормировки J ф24лг‘-’б!г — 1; о
r,J 2
б)	Из условия d (г2ф2)'б!г	0 находим гвер ~ л/2£ rj2, w I ф24лг2б!г —
- 1/2. Графики функций ф2 и г2ф2 показаны на рис. 10.	°
4.67.	(г) J гф2 4лг2 dr г{)'2, о
<г2> 1'з гп (1—3 2л2п2). ((г-(г»2> (г2)-<г)2 (г2 12) (1 — 6 л2 п2).
4.68.	а) Преобразуем уравнение (4.10) для функции А4 (г) к виду
/?['  (2,г)/?( -- (Z4r2 - 2)Ri 0, где k2 2mEiti2. Записав аналогичное уравнение для Ru (г), продифференцируем его по г:
+ (2/г)4 (й2 г2 —2)0.
Из сравнения этих двух уравнений видно, что
Ri (И -	(kr cos kr — sin kr),
где A — нормировочный коэффициент;
153
б)	из граничного условия RT (г0) = 0 получим tg kr0 krg. Корни этого уравнения находим подбором или графически. Наименьшее значение kr0 = 4,5. Отсюда Е1Р « lOt^/mr^ = 2E1S.
4.69.	а. Решения уравнения Шредингера для функции % (г): г<г„, Х1 = Лзш (fer + a),	#-'|/2тЕ/Л,
г>г0, %2 = Вех'' + Се "-xr, х = }/2т ((7—£) /Л.
Из требования ограниченности функции ф (г) во всем пространстве следует, что a = 0 и В — 0. Таким образом;
ф] — (А' г) sin kr, ^2-=(Clr)t
Из условия непрерывности ф и ф' в точке г — г0 получим tg kr„ — —fe/x, или sin kr„ •- £"|/й2 '2тг§(7 krn. Это уравнение, как показано в решении задачи 3.47, определяет дискретный спектр собственных значений энергии.
б.	л2Л2,’8т < r%UH < 9л2й2'8т.
в.	В данном случае имеется единственный уровень: sin kru — (3"1/3/4л)£г0, krg 2 Зл. Е - 2п2й- 9mr2. Из условия д (г2ф2)/дг-0 находим гНер = 3/4Г0; 34%.
4.70.
д1 R др2
2 dR	/ 2Z
4 • I £  •
р др	р
————R" 0, p^r/rx, e-E/Ej.
Р2 1
4.71.	а) Пренебрегая малыми величинами, приведем уравнение Шредингера к виду у.” — х2х -- 0, где х - ~\/2m\E\/h. Его решение есть % — Лех/’ +
Де" хг. Из условия ограниченности R (г) следует, что /	0 и R (г) со
со (1/г)е хг;
б)	преобразуем уравнение Шредингера к виду х* — [/(/+ 1 )/^1х = 0- Ре* шенне его ищем в виде у - Ага. В результате подстановки в уравнение находим два значения а (1 4 / и —/). Функция R (г) будет ограниченной лишь при a = = 1 + /. Отсюда R (г) <х> г1.
4.72.	а) Подставив эту функцию в уравнение Шредингера, получим:
В (а, а, Е) -t- rC (a, a, Е) + г-’ D (а, а) = О, где В, С и D — некоторые полиномы. Это уравнение выполняется при любых значениях г только в том случае, когда В - С - D - 0, откуда а - а = — 1 '2гг -= —rne^h и Е - — те*! St?-,
б)	А - (8nrf)~l/2, где Г] — первый боровский радиус.
4.73.	а) гвер rv — первый боровский радиус; 32,3%;
б)	23,8%.
4.74.	а) <г> -- 3/2гь < г2 > = Зг2, < (Аг)2 >	' ( г>2,, — < г >2 ~ з/4г |,
где Гх — первый боровский радиус;
б)	(E) -2e24f, (U) —е*/гх;
в)	(Г) ~-Jф7фдт = те4/2Л2, икв—е2/А -2,2-106 м/с.
4.75.	а) 4fj и 9Г|; б) 5rJ и 15,75г|. Здесь гг — первый боровский радиус.
4.76.	<р0 I (p/r)4nr2dr - —e!rlt где р-еф2« (г) — объемная плотность
электрического заряда; гг — первый боровский радиус.
4.77.	Напишем уравнение Пуассона в сферических координатах:
1 д2
~	(''Ф₽) 4я(4'|Х (г), е>0.
Проинтегрировав это уравнение дважды, получим:
<ре(г) - .(е/гх-[ е/г)&~ 2г/г‘ A-A-^Bi’r, •	(*)
где Гу — первый боровский радиус; А и В — постоянные интегрирования. Выберем эти постоянные так, чтобы <ре (оо) 0, а <ре (0) было конечным. Отсюда 154
A = О, В = —е. Добавив к полученному выражению ( * ) потенциал, создаваемый ядром, получим:
<р (г) = (е/гг + е/г)е 2г/г‘.
5.1.	5,24 и 2,1 В.
5.2.	0,41, 0,04 и 0,00.
5.3.	Вычислив квантовый деффект S-термов, найдем Есв = 5,4 эВ.
5.4.	а) 6; б) 12.
5.5.	0,27 и 0,05; 0,178 мкм.
5.6.	а = 1,74; м 2.
5.7.	7,2 мэВ; 1,62 эВ.
5.8.	555 см-1.
5.9.	3S|/2, Зр|^2 3/2, 3d3/., 5/2; п компонент.
5.10.	а) АТ -- a2/?'Z4 (п — 1)/п4 = 5,85, 2,31 и
б) 1,73 и 0,58 см-1 (три подуровня).
5.11.	ЛА = а2.97?' = 0,54 пм (одинакова для Н
5.12.	Z = 3, т. е. Li++.
п=3
1 !2 Ч
1—4-
Г3/2
\5
— 3/2
^—1/2
Рнс. 11
1,10 см-1;
и Не+).
5.13.	а) См. рис. 11; v51 = v5 — Vj = 7,58 см-1, ЛА51 = 20,4 пм;
б) Av = 2,46 см-1, ЛА = 54 пм.
5.14.	А/6А > v/ (vз — v2) = 4,2 • 105 (см. рис. 11).
5.15.	В единицах Л: У35/2, ]/15/2 и Уз/2(4Р); 2 Уб, 2 Уз, Уб, У? и 0 (5О).
5.16.	a) и 3P0,i,2;
б)	4О2, 1F3, 3P0,i,2, »D1>2,3, 3F2i3,4;
в)	2pi/2, 3/2 ’ 2°3/2, 5/2’ 2р5/2, 7/2’ *Р 1 / 2, 3/2, 5/2 -	/2, 3/2, 5/2, 7/2 ’
4^3/2, 5/2, 7/2, 9/2.
5.17.	20 (5 синглетных +15 триплетных).
5.18.	'Р1у 4О2, ’S,, 3Р0, j, 2, 3О112,3.
5.19.	а) 2, 4, 6, 8; б) соответственно 2; 1 и 3; 2 н 4; 1,3 и 5.
5.20.	ЛУЗО.
5.21.	Соответственно: ps Й У2 и ps йУ2.
5.22.	а) 35,2е; б) 34,4'.
5.23.	10 (это число состояний с различными значениями гаД.
5.24.	йУ30; :'Н3.
К ОК I оке | к/
5^26. а) V (2J -+- 1) - (2S --- 1) (2L + 1); j
б)	2 (2/, -г 1) • 2 (2/3 - I) 60;
в)	число состояний с одинаковыми квантовыми числами п и I равно = ---= 2 (27 — I). При размещении k электронов по этим состояниям необходимо, учесть принцип Паули. Следовательно, задача сводится к нахождению числа сочетаний из N элементов по k:
CkN - N (N — 1) (N — 2) • ... • (N — k + !)/£! = 120.
5.27.	a) 15; 6) 46.
5.28.	a) 2 (21 + 1); б) 2пг.
5.29.	a) С : Is^s^p2 (3P0); N : X&i&lp* (4S3/2);
6)	S : Is^s^pWSp4 (3P2); C : Is^s^pWSp6 (2P3/2).
5.30.	a) 3F2; 6) 4F3
5.31.	«S5/2.
5.32.	Основной терм 5O4. Кратность вырождения 2J + 1 = 9.
1 55 5
5.33.	Составим таблицу возможных распределений электронов по квантовым состояниям (числам) с учетом принципа Паули (табл. 1 и 2). При этом можно не выписывать тех распределений электронов, которые дают отрицательные значения сумм проекций ML и М$. они не дают ничего нового, в чем можно убедиться непосредственно.
Для наглядности проекцию спина ms каждого электрона обозначим стрелкой, направленной вверх (если ms = +1/2) или вниз (если ms = —1/2).
а)	См. табл. 1. Наличие состояния с ML = 2 и Ms — 0 указывает на то, что имеется терм1/); следовательно, должны быть еще два состояния: ML = 1 и ML = 0 (у обоих Л15 = 0). Из оставшихся расположений состояние с ML = 1 и Ms — 1 указывает на наличие терма 3Р; поэтбму должно быть еще одно состояние с ML =- 0, Ms = 1. Оставшееся состояние с ML = 0и Ms = 0 принадлежит терму 1S. Следовательно, заданной конфигурации соответствуют три типа термов; 1S, +) и 3Р;
tn
Ms м,
Таблица 1
Таблица 2
о
о
i

о
о о
о
2
о о
б)	см. табл. 2. Рассуждая аналогично, получим 2D, 2Р и 4S;
в)	1D, 1G, 3Р и 3F.
5.34.	Обе конфигурации имеют следующие одинаковые типы термов: а) 2Р; б) 1S, ’О и 3Р; в) 2D. Этот факт является результатом того, что отсутствие электрона в подоболочке можно рассматривать как «дырку», состояние которой определяется теми же квантовыми числами, что и состояние отсутствующего электрона.
5.35.	Составим таблицу возможных распределений электронов по квантовым состояниям с учетом того, что принцип Паули налагает ограничения лишь на эквивалентные электроны.
а)	См. табл. 3, где тонкими стрелками показаны проекции спина р-электро-на, жирными — s-электрона .
Таблица 3
т1	ms							
+1 0 .-I	1 f ф	•t	t t 4	•i	4	-t		1 I t
Ms.	3/2 I	1/2 1	3/2 0	1/2 0	1/2 1	1/2 0	1/2 2	1/2 0
156
Возможные типы термов: 2О, 2Р, 23 и *Р.
б)	2S, 2Р (три терма), 2D, 2F, 4S, 4Р и 4О.
5.36.	W2/^=(g2/g1)e-ftft>M7’ = 2,4.10-3, где g1=2, g2 = 4+2.
5.37.	3 • IO-4’.
5.38.	Из условия — dN = ANdt, где A — постоянная, находим Л+~Л’ое—At. С другой стороны, т = ]' tdN = 1/4, где интегрирование проводится по t от 0 до оо. Дальнейшее очевидно.
5.39.	т = l/v In т] = 1,2 мкс; Г яа 5,5 • Ю”10 эВ.
5.40.	N = тМ/2лЙс = 7 • 10е.
5.41.	т = (Nha>/I) (g'/g)e~~^L<‘i’kT = о,07 мкс, где g’ = 4 + 2, g= 2. Здесь учтено, что концентрация атомов на основном уровне практически не отличается от полной концентрации, так как й<о > kT.
5.42.	а) Число прямых и обратных переходов в единицу времени есть Z21 = И21 + B21ua)N2 и Z12 =	Учитывая распределение Больцмана
и то, что Z21 = Z12, получаем
и^21.
(.gil'gz) В12еЛи>/кТ— В21
При Т оо величина иы °°, поэтому gLB12 = g2B21. Кроме того, из сравнения с формулой Планка следует, что В21 = (л2с2/Й<о3)Д21;
б) = (^21/^12) fe/gi) е—Л<й/*Г = (йш3/л2 с3) е—йт/*Г—формула Вина.
5.43.	а) шинд/шсп=1/(еЗЙ/?/4*г-1) ~ 1Q-34;
б)	T=2/t fiR/k In 2= 1,7-105 К.
5.44.	Пусть /о — интенсивность проходящего света. Убыль этой величины при прохождении через слой вещества толщиной dx равна
—JZ® = x<o Ло (Л'1 B12—N2 B21) (Ja/C)ti<i>dx.
где Д') и jV2 — концентрации атомов на нижнем и верхнем уровнях; В12 и В21 — коэффициенты Эйнштейна. Отсюда
х<о = (Й<о/с)^В12 (1 — giNt/g^Ni).
Далее следует учесть распределение Больцмана и тот факт, что й<о 2> kT, при этом ai Af0 (полная концентрация атомов).
5.45.	Из решения предыдущей задачи следует, что для усиления света необходимо, чтобы хо < 0, т. е. gi<V2 > g2^i- Это возможно, если в системе осуществить термодинамически неравновесное состояние. Уо: Np -= gD: gp ~ 5 : 3.
5.46.	В стационарном случае концентрации атомов на верхнем и нижнем уровнях равны соответственно N2 = q/A21 н Л\ = <7/Л10. Для усиления света необходимо, как следует из решения задачи 5.44, чтобы giA^ > g2Ni. Дальнейшее очевидно.
5.47.	Решив систему уравнений N2 = q — A2N2 и N\ = 421/V2 — Д20Л\, где А2 = Д20 + Д21, получим
1' ' д д I	ДА	I
Л1О -^*2 \	Л2 ^*10	/
5.48.	Ал = (Л2/2лс) (1/Tj	1/т2) = 20 фм.
5.49.	а) 6<о = у; б) т = Л2/2лс6Л = 1,2 нс.
5.50.	б) I = 2 f Iadti> = 1/2л6(й/0, где интегрирование проводится от <о0 до оо.
5.51.	а. Пусть vx — проекция вектора скорости излучающего атома на направление линии наблюдения. Число атомов с проекциями скоростей в интервале (vx, vx + dvx):
л (vx) dvx^>exp ( — nw2;2kT)dvx.
157
Частота фотона, испускаемого атомом с vx; есть <о = <о0 (1 + vx/c). С помощью этого выражения найдем распределение излучающих атомов по частотам как — п (vx)dvx. И наконец, остается учесть, что спектральная интенсивность излучения /ш <х> па.
5.52.	6ЛдопЖест~ Ю3.
5.53.	Т » 1,25  10-3а4тс2/А = 39 К, где а — постоянная тонкой структуры: m — масса атома.
5.54.	а - Л/2ЛОТТ] = 2 угл. мин, где т] = 10.
5.55.	845 и 180 пм; 1,47 и 6,9 кэВ.
5.56.	1,22 нм (Na).
5.57.	a) Fe, Со, Ni, Zn; отсутствует Си (154 пм); б) три элемента.
5.58.	0,25. 0,0 и —2,0.
5.59.	15 кВ.
5.60.	Z - 29, т. е. Си.
5.61.	5,5 и 70 кВ.
5.62.	В молибдене — все серии; в серебре — все, кроме 7<-серии.
5.63.	б. Ti; 2,9 нм.
5.64.	а) 5,47 и 0,52 кэВ; б) 0,25 нм.
5.65.	El =- Йог (2лс wAX — 1) ~ 0,5 кэВ, где <о = з/4/? (Z — I)2.
5.66.	ак --- 2,84, aL ~ 10.
5.67.	1,54 кэВ.
5.68.	0,26 кэВ.
5.69.	а) 7ф0Т -= йш - Ек = 4.7 кэВ:	ТОже = (Ек — EL) — EL =
10,4 кэВ, где Ек и EL — энергия связи К- и L-электронов; б) 50 нм.
5.71.	а) -Р3/2: б) -S1/2 и 'Рз/2, 1/2' 2,S1 /2’ 2^3/2, 1/2 И 2°5/2, 3/2’
5.72	К L, М — по две линии; L -* М — семь линий.
5.73.	а) 21,5 пм (Ка1) и 20,9 пм (Ка.у): б) 0,49 пм.
5.74.	115,5, 21,9, 21,0 и 17,2 кэВ.
6.1.	Из векторной модели (рис. 12, где для наглядности ps и р£ изображены совпадающими по направлению с S н L) следует, что
р — pL cos (L, J) — ps cos (S, J),	(1)
где pL •-=- 1/L (L 4- 1) Цб> F.s =_= 2Д/5 (S 4- 1) pg. Введя обозначения L* = - ~\/ L (L • 1). S* -- Д/S (S 4 1) и J* — ~|/y (J — 1), запишем, согласно теореме косинусов:
L*2_ 7*24.5*2—27* 5* cos (SJf; S*2= 7*24-Z*2—27* L* cos (L, J).	(2)
Исключив из (1) и (2) косинусы, получим искомое выражение. - * 158	
6.2.	a) 2 (S), 2/3 и 4/3 (P), 4/5 и 6/5 (D);
6)	0/0 (3P„), 3/2 (3PL и 3P2);
в)	g — 2, за исключением синглетного, где g - 0/0;
г)	g = 1 
6.3.	а) 2Р5/2; б) 3О3.
6.4.	а) 2 У1рб; б) 2 Д/З^Мб-
6.5.	S -- 3; мультиплетность 2S - 1 - 7.
6.6.	4 Д/З, 13’УТ5 и 4УГ5“ магнетонов Бора.
6.7.	УЗрб-
6.8.	Для обоих термов g -- 0; pz | J.
6.9.	йД/2 и йУб”.
6.10.	а) Основное состояние 'Рз/2, S ~ 4'3, р — У34Нб;
б)	основное состояние 4F3/.,, g - 2/5, р У’^Нб-
6.11.	С одной стороны, dJ = [р, В]б!1, где р — магнитный момент атома. С другой стороны (рис. 13), |dj| - J sin fl • a>dt, где J =- йУJ (J -j- 1). Сравнив оба выражения, получим искомую формулу.
6.12.	а) 0,88 • 1010,_1_, 17 • Ю10 и 0 рад'с; б) 1,32 • 1010 рад,с (3Р2).
6.13.	2У5Й и 5У5/4рб- Здесь g 1.25, J - 4.
6.14.	Здесь g ---- —2 '3, поэтому р А j J (не +Д, как обычно).
6.15.	F ----- figdB^dz - 2n/P2zpo/c (R1 ~ z2)5/2 — 4,1 • 10 "22 дин.
6.16.	dBidz = тЛа (а -г 2й)рб 7 кГс/см.
6.17.	а) 0,6, 5 и 6 магнетонов Бора; б) соответственно: на пять компонент; не расщепляется, так как р ~ 0 (g — 0).
6.18.	6 - [а (а — 2й)рб 2Т]дВ/дг ----- 5 мм, рВ = gPpo-
6.19.	a) Av — ДрбВ/лйс - 0,56 см-1; б) lF3.
6.20.	В обоих случаях три компоненты.
6.21.	АЛ №еВ12л.пи? = 35 пм.
6.22.	АЕ = лсйАЛ/Л2 ~ 5  10~5 эВ.
6.23.	а) 2 кГс; б) 4 кГс.
2лйс АЛ (28кГс для терма Рч,,(
6.24.	а) В = 0,1	 12 — 155кГс для теома Р
Л2 ^ooKic для терма г 1!2;
в лЛса2Р24 10,59 кГс для терма Р3/21 £РбП3 |1 ,18 кГс для терма Р1/2.
в)	9,4 кГс (для Р3/2) и 19 кГс (для РХ/^-
6.26. а) Соответственно: простой, сложный, простой, простой (в последнем случае дляобоих термов факторы Ланде одинаковы);
б) атомы с нечетным числом электронов — сложный эффект Зеемана; остальные атомы — и простой (на синглетных линиях), и сложный (на линиях иной мультиплетиости).
6.27. См. рис. 14. а) Для определения возможных смещений, т. е. значений mxgt — m2g2, составим следующую схему:
m = +3/2	+ 1/2	-1/2	-3/2 ,г х
m,gj=+5/5	+2/3	-2/3 -6/3 \Р^г)
\IXIX ^«2=	+?	-1	(’S^)
Смещения: А<о --- --5 3, -г3/3, J-i/3, —1/3, —3/3. —5/3 единиц ц^В/'h^ В приведенной схеме стрелками соединены только те значения mg, разность между которыми (т. е. соответствующий переход) удовлетворяет правилу отбо-
159
pa Am = 0, ±1. Вертикальные стрелки отвечают л-компонентам, косые — с-компоиентам-
б)	0,78 см-’-.
6.28.	= Злсй/ХрбВ = 2,7 • 105.
6.29.	а) А<о = ± (4, 8, 12, 16, 24)/15;
б) А<о = ± (1, 3, 15, 17, 19, 21)/15.
6.30.	а) А<о = ± (0, 1, 2)/6; б) А<о = ± (1, 2)/3, центральная л-компонен-та здесь отсутствует, ибо переход ДУ = 0, Ат = 0 запрещен.
Г» 6.31. В сильном магнитном поле. Оба вектора, L и S, ведут себя в первом приближении независимо друг от друга, н энергия взаимодействия атома с полем
АЕ = —(|xL)B В — (ns)B В = (mL +2ms) рб В .
т +3/2 +1/2 -1/2
~3/2
б Я б
Рис. 14
При переходе .между двумя уровнями смещение зеемановской компоненты А<о — (&mL 2Ams)p.(jB//i. Правила отбора AmL - 0, ±1 и Ams -= 0 приводят к простому эффекту Зеемана-
6.32.	В - (лЛс/рб) (АХ/А3)п ~ 36 кГс.
6.34.	В постоянном поле В магнитные моменты атомов ориентированы вполне определенным образом относительно вектора В (пространственное квантование). Изменение ориентации магнитного момента может произойти только в результате поглощения кванта энергии переменного поля, когда величина его равна разности энергии обоих состояний (ориентаций). Таким образом, й<о = = (|xg — рв)В, где рв = gmy6; т — магнитное квантовое число. Учитывая правило отбора Ат = ±1, получим Йш — gpe8-
6.35.	В 2nhv/gHQ = 2,5 кГс.
6.36.	р 5,6рб (J = 4)7
6.37.	Соответственно 3,4 • 10-“ и 7,7 • Ю-5 Рб-
6.39.
дВ	12л2/«Я4г х	7 ,а_31
F р----------------------п— = 7-10 31 днн .
дг	c2(R2gzi)i Ал
6.40.	Ларморова круговая частота прецессии электронной оболочки атома эквивалентна диагмагнитному току / ~ Zew^ 2л. Магнитный момент кругового тока р = л <р2 > //с, где <р2>	<х2> — <(/2> — средний квадрат рассто-
яний электронов от оси г. взятой в направлении поля В. При сферически-сим-метричном распределении электронов в атоме < х1 > ~ < у~ > — < г2 ) и <г->	<х2> + <(/“><< г2 >	3/2 <Р2>- Отсюда	—
= —(Z<?2.V 6/№) <r2>.
6.41.	< г- > I г2ф24лг2с!г 3r?, %	—2,37 • 10-“ см3;моль.
6.42.	Соответственно 5В. 52 и \04 пм.
6.43.	В„ - —eBVgZmc-, где 4л fp (rVrfr, р (г) — объемная плотность электрического заряда атома на расстоянии г от ядра.
160
6.44.	а) Число молекул, у которых векторы р заключены в элементарном телесном угле dQ = 2л sin ddd, равно dN = Сеа cos e sin ddd, где С — постоянная, а = fiB/kT. Это число тех молекул, проекции магнитных моментов которых рв = р cos д. Отсюда
f рв dN	I	ц
/рв' =-------= р cth а——
' J dN	\	а )
Здесь интегрирование проводится по д от 0 до л;
б) соответственно:	и р.
6.45.	0,45 см3 • К/моль; 1,9 рр.
6.46.	1,6  10-’.
6.47.	а) ц = th а, где а = /п£Рб BikT', т — магнитное квантовое число; g— фактор Ланде. В данном случае т] « а = 0,0056; б) г; - cth Ь — csch Ь, где Ь =- g~\/ J (J -+- 1)рбВ/67'. В этом случае г; « 6/2 = 0,0049.
6.48.	/ = /Vpo tg а, где а -- рдВ/бТ; / = МцвВ'кТ при а < 1.
2 sh а	2
а) . о й—~ —а = 0,0037, где а = 7gp6 В/kT',
1 —j— 2. СП Q.	О
sh b+sh 36
б)	11 ch ch зГ ~	~ 0,0060’ ГДе
gp6^eam
’	2ецВ/АГ 2еат
6.49.
где а = g^BlkT. Здесь суммирование проводится по т (магнитное квантовое число) от —J до -+-7. Для слабого магнитного поля а 1, поэтому еа"‘ = 1 + + ат. Тогда ^пгеат = а~£т2 — aj (J -г 1) (27 + 1)/3 и £еат =27+1.
Дальнейшее очевидно.
6.51.	а) 0,375 см3 • К'моль; б) 0,18 эрг/Гс.
6.52.	6,6 • 10—5 см3/г.
7.1.	а) 15 и 0,42 мэВ; б) 3,3 • 1013 и 6,4 • 1011 рад/с.
7.2.	2 и 3.
7.3.	М = VZEpd2 3,46Й.
7.4.	Т= 2ft2;3pd2b = 117 и 3,8 К.
7.5.	A//A/2 = (g1lg2)^hBlkT = 1,9.
7.6.	Jm d’l/kTu/h — 1/2 = 8. График зависимости Nj/Nn от 7 показан на рис. 15
7.7.	х = р<о2 = 5,7 и 19 Н'см.	_____
7.8.	U„ — D + Й<о.2 = 4,75 эВ; а = <ог0Д/р/2/70 = 1,43.
7.9.	ДЕ = /Ко (1 — 2х) = 0,514 эВ; в 33,7 раза.
7.10.	Т = 2/3Й<о (1 — 2x)/k = 534 К
7.11.	ДЕ = Й<о (1 — 2х) — hBJ (7 + 1) = 0,37 эВ.
7.12.	13 уровней.
7.13.	цмакс ~ 1/2х; Емакс я» Й<о/4х и D = /Ко (1 — 2х)/4х.
Для молекулы водорода цмакс = 17, Емакс = 4,8 эВ, D = 4,5 эВ.
7.14.	х « 0,007.
7.15.	Dd — DH = (Й<он/2) (1 — l/pH/pD) = 0,080 эВ.
7.16.	A^/A/j = exp {— /Ко (1 — 4x)/kT] = 0,02. При 1545 К. N2 1
7.17.	-^-= 2J+1 ехр{ — {Лео (1 — 2х)—ЙВ7 (7+1)]/W}=0,01.
7.18.	Решение аналогично приведенному в задаче 1.14, п. б.
Й<о „	Лео
7.19.	а) Т~—; -=740К;	6) 7’=-------------------- -630К.
k In 3	k In [1 +<o. B7 (7 + 1)]
161
3 Зак. 1896
7.20.	Скол= * (^/kTy^/kT ~ (Я/Ли>/^г р-^/^ К°Л (еЛы/*Т_ ])2	(у?
Здесь /? — универсальная газовая постоянная.
7.21.	0,134, 0,56 и 0,77/?: R — универсальная газовая постоянная.
7.22.	1,93-10-** г-см2; 112 пм.
7.23.	а) В' = (Х2 — k1)/2klki = И см-1; 2,6-10-*® г-см2;
б)	соответственно 4 -* 3 н 3 -* 2.
7.24.	Уменьшается на 1,0Й (J = 2 J = 1).
7.25.	13 линий.
7.26.	(0=-2nc(3voi-vO2) = 5,O-lO14c-1; х =	--УО1~2°2 =0,017,
2 3voi—V02
7.27.	Из условия Л<о = Й<оо + AEj.j получим: со = соо + В [,/' (J1 — 1) — J (J — 1)].
С учетом правила отбора AJ = ± 1 находим:
J' = J + 1, со = со„ -+- 2В (J - 1), J = 0, 1,2, ...
J' = J — 1, со = со0 — 2BJ, J = 1, 2, 3, ...
Обе формулы, как нетрудно заметить, можно объединить в одну, которая приведена в тексте задачи.
7.28.	В' = 21 см-1, / -= h 4зхсВ' — 1,33-10—10 г-см2. Волновое число нулевой линии, отсутствующей в силу запрета AJ + 0, равно v10 = 3958 см-1. Из соотношения v10 = v (1 — 2х) получим х = 0,022.
7.29.	ДА/А = Ар р = 1,5-Ю-з. р — приведенная масса молекулы.
7.30.	| Avkoji | = (Ар/2р)“кол = 28 см-1; |AvBp| = (Др/р) 7вр = 0,10 см-1; АмкоЛ/Лмвр = 280. Здесь р — приведенная масса молекулы.
7.31.	со лс (1/Аф — 1/Ак) = 1,37-Ю14 с-1; 5,0 Н/см.
1/1 + (ДА/А)2 — 1
7.32.	со = 2лс—------1----т------= 7,8-1014с-1.
(1—2х)ЛА
7.33.	/ф//к ~ е	2x)/kT 0 07 Увеличится в 3,8 раза.
7.34.	При переходе Ео Ех (первая стадия процесса) Jx = Jo ± 1. При переходе в конечное состояние Ех Е (вторая стадия) J = /.х±1 = (/о ± 1) ± ± 1, т. е. AJ = 0, ± 2.
7.35.	а) Из условия Лсо = Лсоо — &Ej,j получим:
со = сов — В (J' + 1) — J (J + 1)].
Отсюда с учетом правила отбора А/ = ± 2 (для смещенных компонент) имеем
J' = J + 2, со = сов — 2В (2J + 3), J = 0, 1,2, ...
Г = J — 2, со = сов + 2В (2J — 1), J = 2, 3, 4, ...
Обе формулы, как нетрудно заметить, можно объединить в одну, которая приведена в тексте задачи;
б)	1,9-10-з» г-см2, 0,12 нм.
7.36.	В' = ДА/12 А| = 2,0 см-1; 1,4 • Ю”3» г-см2.
8.1.	429 и 362 пм.
8.2.	2,17 и 1,65 г+м3. If.Qcb
8.3.	Плоскость (Ай/), ближайшая к началу координат, взятому в одном из узлов решетки, отсекает на осях координат отрезки а/Л, alk и all. Расстояние от начала координат до этой плоскости равно межплоскостному расстоянию d. Обозначив углы между нормалью к плоскости и осями координат х, у, г соответственно а, Р, у, получим: cos а = hdla\ cos Р = kda-, cos y = ldia. Остается учесть, что сумма квадратов этих косинусов равна единице.
162
a a a a a a a
8-4-a) a' W W; 6) TT-IW’ B)T’Tyr*
а
Уз~'
8.5. 1,0 и 0,8 им.
8-6. /що ! /цо • Ли =
1 : "|/2 :~]/3 (простая),
1 : "|/2 : З/З /2 (объемноцентрированная), .1 : "|/2”/2 : ~\/3 (гранецентрированная).
8.7.	Предположим, что ребро элементарной ячейки а = ndlt где п — целое число. Нетрудно установить, что при п = 1 на ячейку будет приходиться 1/4 атома, что невозможно; при п = 2 — два атома. Так как кристалл кубический и обладает осями симметрии четвертого порядка, то второй атом может находиться лишь в центре ячейки. Если это так, то d2 должно равняться dx "|/2, что и имеется. Следовательно, решетка кубическая объемноцентрированная.
8-8. Дифракционные максимумы располагаются в точках пересечения двух систем гипербол: a (cos а — cos а0) -- ktk, b (cos 0 — cos 0О) = k2k, где а0, 0О — углы между направлением падающего пучка и направлениями решетки вдоль периодов а и b соответственно; а, 0 — углы между дифрагированным пучком и теми же направлениями решетки.
8.9.	a (cos а — 1) = k3k; b cos 0 - Л2Х; с cos у = k3k. Имея в виду, что cos2 а cos2 0 — cos2 у — 1, получаем:
х ______________2 (ki а}________
(kila)2+ (fe2./ft)24-(fe3/c)2 ’
8.10.	Имея в виду условия Лауэ: a(cos а—cos ky-.\ a (cos 0—cos 0О) = k2k-, a (cos у — cos уд) — k3k и соотношения cos2a -т- cos2 0 4- cos2 у -- 1; cos2a0 + cos2 0O -J- cos2 yn — 1, получаем:
&i cos an — £2 cos 0n - ^Зсо5у0 a — —2a-------------------------— .
k2 + kl^.kl
8.11.	Найдем сумму квадратов отдельно левых и правых частей уравнений Лауэ:
2a2 [ 1 — (cos a0 cos a + cos 0O cos 0 = cos Yi.cosy)] =• (kl — kl 4- k%) X2.
Нетрудно видеть, что сумма произведений косинусов равна non -= cos 20, где п0 и п — единичные векторы, соответствующие направлениям падающего и дифрагированного пучков лучей, угол между которыми равен удвоенному брэгговскому углу 2 О. Тогда первое выражение примет следующий вид:
2a sin ЫЗ/kl + kl + kl к .
Так как al~\/kl kl г k% din, где п — наибольший общий делитель чисел klt k2, k3 (kt — nh, k2 = nk, k3 - nl, n, k, I — миллеровские индексы), то в результате получим 2d sin 0 пк.
8.12.	0,58 нм.
8.13.	119 пм; 58°.
8.14.	а) Соответственно 37 и 40 мм;
a sin О (56,3/лпм для (031)
б)	п 1/Л24- k2 + l2~ (62,6'п м для (221), п = 1, 2, ...
.	asin(a/2)
8.15.	к - —7======= --yk2 k2 — 2kx k2 cos (a/2)
= 0,17 нм, ki и fc2 —порядки отражения.
8.16.	Сначала найдем периоды идентичности / вдоль направлений [110] и [111]. Согласно Лауэ. I cos пк, где - угол между осью вращения и направлением на n-ю слоевую линию; /цо 0,29 нм,/И1	0,71 нм. Их отноше-
6*	163
ние соответствует гранецентрироваииой решетке (см. решение задачи 8.6); а = 1/2/7x10 = 0,41 нм.
8.17. Тип решетки	(ЮО)	(НО)	(Н1)
Объемноцентрированная	Нечетные	—	Нечетные
Гранецентрированная	Нечетные	Нечетные	
8.18.	Гранецентрированная: (111), (100), (110), (311), (111).
Объемноцентрированная: (НО), (100), (211), (НО), (310).
8.19.	а) 38; 45; 63; 78 и 82’; б) 42; 61; 77; 92 и 107э.
8.20.	Из формулы sin 0 - (Л'2а) "j/ft*2 k*2 + I*2 определяем значения суммы квадратов индексов h*, k*. I* и затем подбором находим сами индексы; (111); (311); (511); (333). Соответственно 233; 122; 78 и 233 пм.
8.21.	Первое дифракционное кольцо отвечает отражению от системы плоскостей (111) в первом порядке; а - (2Л7.'D) ~\/h2 ч- k2 +- Р 0,41 нм.
8.22.	Объемноцентрированная.
8.23.	Энергия взаимодействия иона цепочки со всеми остальными ионами;
U 2 (е2 а) (1 - >/, -+- 1/3 - 1/4 + ...) - а^/а, где а 2 In 2	1,385; а — расстояние между соседними ионами.
8.24.	а) |//| Х'а (</- г,,) (1 — 1л), где <V — число пар ионов в кристалле; г„ — равновесное расстояние между соседними разноименными ионами; б) 8,85 и I 1.4.
8.25.	а) р ( \V V) К 0.29 ГПа (3-103 атм); б) разложим функцию U (И) — энергию связи кристалла — в ряд вблизи равновесного значения U»'.
Имея в виду, что в равновесном состоянии (dU dV)„ = 0 и 1/К ~ (d3UidZ-)oV„. получим выражение для приращения энергии U — U„, откуда для объемной плотности
и — u„ (XV V)2,2K	1.4 Дж см3.
8.26.	а) Имея в виду, что р —dU dV. получим:
1	,. d2U	аеЦп—l)	9а4
— -- V------------------, л = 1 +-------— 9,1,
К dV2 18rJ	’	8ае2К
где г0 — равновесное расстояние между соседними ионами, а — постоянная решетки; б) 0,77 МДж моль.
8.27.	п 1 - 27а4/2Уз'ае2К	11,9; U 0,63 МДж/моль.
8.28.	Из условия максимума выражения р — dUidV получим:
(гт 'го)п --(л4-3)/4, п = 1 +9а4/8ае2К =9,1,
где гп — равновесное расстояние между соседними ионами; а — постоянная решетки. В результате найдем: гт!гп --- 1,147. Соответствующее давление
|Рмакс I = (ае^бг4,) [ 1 — (г0/гт)" '1 ] = 4,1 ГПа (4,1 • 104 атм).
8.29.	a) U = N (аеЧг0) (1 — р/г0), Р = 0,112г0 = 31,5 пм;
б)	К — •/4ра4/ае2 (а — 4р). Здесь г0 — равновесное расстояние между
соседними ионами; а — постоянная решетки.
(Лео	/Ко
---+-----------
2	e»<o/A7_ !
С = ЗМ6
/Ко \2
Й7 )
eftb>/kT
(e^/W- l)2 '
При высоких и низких температурах С равно соответственно: 3Nk и 3Nk (hu/kT)2 e~hljylkT-
164
8.31.	а) Напишем уравнение движения л-го атома:
х (£n+i — Нп)-- х (?п-1	^7г) = х (Нп4-i 2gn -j- £n_j).
Решение этого уравнения будем искать в виде стоячей волны ёп — A sin kx X X sin со?, где k — волновое число (2лЛ); х = па — координата л-го атома (л = 0, 1, 2, Л' — 1). В таком виде решение автоматически удовлетворяет граничному условию g0 = 0. Граничное условие для другого конца цепочки = 0 будет удовлетворено, если sin ka (N — 1) = 0. Отсюда получим спектр собственных значений волнового числа:
ki = ш'/а (W — 1), i = 1, 2, .... N — 2
(при i = 0 и N — 1 значение sin kx = 0, т. е. решение вообще не допускает движения). Таким образом, смещение л-го атома можно представить в виде суперпозиции стоячих волн вида
ini = ^i 5>п (ki na)-sin co, t;
б)	подставив выражение g;1; в уравнение движения, найдем:
<о; = 2 (x/m)1/l2 sin (kia 2).
Отсюда видно, что число различных колебаний равно числу возможных значений волнового числа kit т. е. N — 2, или, другими словами, числу колебательных степеней свободы данной цепочки; <оМакс ~ 2 (и/т)1^2, ХМИн = 2а;
со/ I х \i/2 sin а/2)	/ х \1/2 упл л
kt \ т ]	kt	\т ] укор 2
О = (2-V/л	<о2акс —со2) Ао.
8.32.	a) dZa — (Liiw) dot; б) 0 = nhNvIkL', в) имея в виду, что Е = = j < еи > dZ^, где < еи > —средняя энергия квантового гармонического осциллятора с частотой (о, получим
Для определения С = дЕ/дТ надо продифференцировать интеграл по параметру Т (см. Приложение 14). В результате получим:
0/Г	\
Т Г xdx ЫТ \	( R
е J ех-1~ев/г-1	’/.л’/гт/е.
о	'
Значение интеграла при 0/Т -> оо дано в том же Приложении.
8.33.	a) 0=(Л//г) 1/4да»2п0 ;
C=R
(е/г г2 г x*dx е/т 3 _ I —	_
02 J ех—1	ев/г-1
= 1R и 28,9/?Т"2/02. См. решение предыдущей задачи.
8.34.	а) 0 (h:k) Убл2и^п„;
6В Зак. 1896	165
б) £ = 3
х3 dx ех— 1
е/т
Т* 7* х3 dx
04 J е*—1
е/т \ _ j з«, е0/7—1 I (12/5) л2/?7'3/03
См. решение задачи 8.32.
S / 1	1 \	й
8.3S.	+	©=— |/	S(t,T--+vr.}
б)	а _Г (Ц-+-Мл.; е- л-1/ '8"’"	.
“	2л2 у vf vf J	k у V (v~3 +2t<73)
8.36.	470 К (см. формулу для 0 из ответа к предыдущей задаче).
8.37.	а) 1,8; б) 4,23 кДж/моль.
8.38.	20,7 и 23,8 Дж/(моль-К); меньше иа 5%.
8.39.	Легко убедиться, что в этой области температур теплоемкость С о. Т3, поэтому можно воспользоваться формулой для теплоемкости при низких температурах. 0	210 К; £0 = 1.9 кДж/моль.
8.40.	а) 0 = 2,2-102 К; б) С = 13 Дж/(моль-К); в) <оМакс = 4,1-1013 с-1.
8.41.	«(Омаке = 5,2- 10“14 эрг; рмакс = ««макс « л«/г0 я» 10-1» г-см/с.
8.42.	б. Из условия dnlda» = 0 получим уравнение ех (2 — х) = 2, где х= tUn/kT. Его корень находим графически или подбором х0 а; 1,6. Отсюда Й(овер = О,8«0, в. При Т = 0,6250. г. Соответственно п оэ Т3 и пхТ.
8.43.	В результате взаимодействия фотона с фононом энергия фотона изменяется на энергию фонона: Йо/ = Я(о ± Й(озв. В то же время из треугольника импульсов следует, что
(Йсозв/р)2 — («со'/с')2 + («(о/с')2—2 («<о' /с') («<о/с') cos О.
Исключив из этих двух уравнения (o', получим:
(1/и2— 1/с'2) о)2в = 2 (ш/с')2 (1 ±((0зв/(0) (1 —cos О).
Имея в виду, что v с' и (озв <g (о, пренебрежем соответствующими малыми членами в последнем выражении, после чего получим искомую формулу.
8.44.	а) При тепловом равновесии отношение числа атомов /V2 на верхнем уровне к числу атомов Nr на нижнем уровне равно в соответствии с распределением Больцмана:
^/Л'1=е^А£МГ; А'2 = Л'/(1+еД£/*7'),
где N = Л\ + (V2 — полное число атомов. Внутренняя энергия системы £ = = N^E, откуда
дЕ 7 Д£\2 еД£/*г i=dT=Nk\kT) (1+eAJW)2 ;
б)	обозначим kT!&E= х. Из условия dCi!dx= 0 получим уравнение (1 — 2х) е1/* = 1+2х. Его корень находим графически или подбором: х0 яе 0,42;
в)	Сг,макс/Среш = 0,44/2,34.10-4 « 2-103.
9.1.	В интервале импульсов (р, р + dp) число состояний
4лр2 dp V
dZ„ =----—-— =------------р2 dp.
Р крх &Ру &Рг	2л2 Й3
166
Поскольку в каждой фазовой ячейке объемом &pxkpykpz могут находиться два электрона с аитипараллельными спинами, число электронов в этом интервале импульсов п (р) dp=2dZp. Переходя к кинетическим энергиям, получаем: п (Г) dT = (vV2m3i'n2h3) Д/Т dT.
9.2.	Тмакс = (Й2/2т) (Зл2п)2^3 = 5,5 эВ.
9.3.	а) <Т> = з/5Тмакс; б) 31,2 кДж/см3.
9.4.	г] = 1 — 2-3/2 „ о,65.
9.5.	“	-	"
Г as 30 кК.
2л2 Л2
Д£ =------------T7V = 1,8- Ю“22 эВ.
mV (Зл2 п)1/3
На 0,1%.
9.6.
9.7.	.... ___
9-8. п (о) dv = л (zn/лЛ)3 v2dv; а) < v> = 3/4vm; б) < l/v > — 3/2vm.
9.9.	wBep =умакс= 1,6-Ю® м/с; (v)= 1,2- 10е м/с.
9.11.	п (К) d), = 8лХ~Ш.
9.12.	а) Сэл = 1/2л2^Т/£/0; Сэл/Среш = 1/6 л2 kT/Ef0 = 7,6-10-3. Здесь учтено, что данная температура больше дебаевской, поэтому Среш = 3R (закон Дюлонга и Пти);
б)	из характера зависимости теплоемкости решетки от Т следует, что равенство указанных теплоемкостей наступает в области низких температур. Воспользовавшись (8.6), получим Т = (5йв3/24л2£у0)1/2 — 1,7 К.
9.13.	Число падающих в 1 с на 1 см2 поверхности металла свободных электронов со скоростями в интервале (v, v + dv), направления которых составляют углы (6, 6 + dfl) с нормалью к поверхности, равно
2л sin ftdft dv — п (v) dv----------v cos ft.
4л
Умножив это выражение на импульс, передаваемый стенке при отражении каждого электрона (2mv cos ft), и интегрируя, получим:
(*	Л2	-
р= | 2znocosftdv= —---(Зл2 л)°^3	5 ГПа (5-Ю4 атм),
J	15л2 m
где интегрирование проводится по ft от 0 до л/2 и по о от 0 до омакс.
9.14.	а. Рассмотрим пространство скоростей с осями vx, Vy и vz. Тогда приведенное в условии выражение означает, что число свободных электронов, проекции скоростей которых находятся в заданных интервалах, пропорционально объему dvxdvydvz. В то же время, число свободных электронов, модули скорости которых лежат в интервале («, v + dv), пропорционально объему сферического слоя в этом же пространстве, т. е. величине 4nv2do.
Зная распределение электронов по модулям скоростей п (v) dv, запишем:
dvx dvv dv,
n (v) dvx dvy dvz = n (v) dv —-——- •	(•)
”	4nv2 dv
Остается учесть, что n (v) dv = n (£) dE, E = tmfi/2 и dE/dv = ~\/2mE. Подставив эти соотношения и п (£) из формулы (9.1) в правую часть (♦), получим искомое выражение.
б.	п (vx)dvx = 2 (m/2nh)3 dvx J dvy dvz = 2n (m/2nH)3 (v^—v2)dvx.
Здесь интегрирование удобно провести в полярных координатах:
dvvdvz = pdpd<p, где р = ]А'2+^ (р от 0 до рт = ]/
9.15.	Взяв ось х вдоль нормали к поверхности раздела металлов, запишем условия, которым должны удовлетворять электроны, переходящие из одного ме-
6В*	167
талла в другой:
mojj mv32
——+Ф1 = —— Н-ф2; vyi = vy2; vzl=.vz2,	(1)
где (р — потенциальная энергия свободных электронов. Число электронов, падающих в единицу времени иа единицу поверхности раздела, есть
dvi = Vxi п (Vj) dv,, dv2 = vx2 n. (v2) dv2.
При динамическом равновесии dv, — dv2, а так как согласно (1) v tdvt— = vx2 dv2, то и n (Vj) = n (v2). Отсюда следует, что £, — £Z1 =- £2 — E/2. Поскольку £j + <p, = £2 -f- <p2, получим: Ец <p± -= E/2 — <p2.
9.16.	Взяв ось x по нормали к поверхности металла, запишем условия, которым должны удовлетворять электроны, вылетающие из металла:
mvx2/2--mv'^/2 \-U, v'u = vy, v'z^vz,	(1)
где штрихами отмечены компоненты скорости электрона внутри металла; U — потенциальный барьер на границе металла (£у •+• Л). Число электронов, вылетающих в единицу времени с единицы поверхности металла со скоростью в интервале (v, v -р dv), есть
( т \з v'xdv'
dv=v’ п (v') dv' = 2 --- -------------——— =
х	\2«»/ 1+e(£'~£/)/ftr
= 2{m/2nh)3e~{A+E}/kT vxdv.	(2)
Здесь учтено, что согласно (1) vxdv' = vxdv, а также что £' — Ef = Е + А н kT <g Л. Запишем (2) в сферических координатах (vx = v cos S-, dv = v2 X X sin Odd dt»d<pj и проинтегрируем по <p от 0 до 2л и по О от 0 до л/2.
9.17.	a) 2kT-, б) / = (етЛ2/2л2Й3)Т2е~л/*г; в) 4,1 эВ.
9.18.	Примем за начало отсчета энергий потолок валентной зоны. Пренебрегая единицей в знаменателе выражения (9.1), получаем для концентрации свободных электронов:
пе = J л (£) dE — 2 (mkT/2nd2)3/2 exp [(£/—Eg)/kT],
где интегрирование проводится от Eg (уровня, соответствующего дну зоны проводимости) до оо. В то же время, концентрация дырок
nd = J^gdd£ = 2 (mdT/2nd2) 3/2ехр (—EflkT),
где /й^1—fe = exp [(£—£y)/dT] и gd dE = ge dE = C\/2m3/n2 Л3) V—£ dE,
причем интегрирование проводится по £ от — оо до 0. Так как пе — п.д, то Ef — Eg — — Ef и Ef = £g/2, т. e. уровень Ферми находится посредине запрещенной зоны. Следовательно,
ле=пй—2 (/nife772nd2)3/2 ехр (—Д£0/2Л7’),
где Д£о — ширина запрещенной зоны.
9.19.	а. Приняв за начало отсчета энергии уровень донорных атомов, найдем концентрацию электронов проводимости:
пе=Jn (£) dE = 2 (т£Т/2лЛ2)3/2 ехр [(£/— Eg)/kT],	(1)
где интегрирование проводится от Eg (уровня, соответствующего дну зоны проводимости) до оо. В то же время,
ne=-n0[l — f (0)1 — ехр (—Ef/kT).	(2)
168
Перемножив (1) и (2), получим:
п2 2 л „ (mkT/2л/?2) 3,2 ехр (— EgikT), откуда и следует формула, приведенная в задаче.
б.	Из сравнения (1) и (2) получим:
1.2	—1'.2	1п[(2/л0) (mkT 2лЛ2)3/2].
Отсюда видно, что при Т 0 уровень Ферми Ef ~ Eg/2, т. е. находится посредине между дном зоны проводимости и уровнем доноров.
9.20.	2,6 '10-4 с; 3,110~6 см; 46 см2/(В-с).
9.21.	n V1 ~	‘ '>02. где ^макс^ А• А—работа выхода.
9.22.	Так как тх - — еЕ, где Е — — 4лР — 4лпех, то <оо — 1/4лле2/т -- 1,6- 10’“ с-1, е - hox 11 эВ.
9.23.	Так как тх --- еЕ0 cos со/, то х -- — (e£o/zn<o2) cos со?. Имея в виду, что поляризованность Р = пех, получим:
е --- 1 + 4л АЕ — 1 — 4лпе2/щ<о2 = 1 — ((Oo'w)2,
где <о(| — плазменная частота электронов. Металл прозрачен для излучения, если показатель преломления п = "|/е веществен (в противном случае будет наблюдаться отражение излучения). Отсюда л0 2лс'\/т/4ппе2 -= 0,21 мкм.
9.24.	При переходе на свободные уровни v электронов (г значительно меньше полного числа свободных электронов) их кинетическая энергия увеличится на v-AE, где Д£ — интервал между соседними уровнями (см. решение задачи 9.6). При переходе следующего электрона кинетическая энергия увеличивается на 2vA£, а магнитная энергия уменьшится на 2рВ, где р — магнитный момент электрона. Из равенства 2vA£ •= 2рВ находим v, затем суммарный магнитный момент непарных электронов 1 = 2vp н парамагнитную восприимчивость %:
х - I: Н	(щр2:лЧг) (Злгп)1^ = 6-10~7.
9.25.	а (1 р) (dtTdT) - — А£о 2kT- = — л/иг.'^Т2 -= — 0,047 К->, где (> ~< ехр (А£1( 2kT), Д£о — ширина запрещенной зоны.
9.26.	£	|2^7’17’2/(Г2 — Tj)J 1п »] - 0,34 эВ.
9.27.	1,2 и 0.06 эВ соответственно.
9.28.	Да/о — 1 — еп(Ье — Ь^) р = 0,15;
п 2 (тйТ/2лЛ2)3/-’ ехр (— &ElkT).
9.29.	т t In |(р — р2) р2/(р — р2) pj = 10 мс.
9.30.	0,10 эВ.
9.31.	а) 1.0-1018 см-3; 3,7- 103 см2/(В-с); б) из формулы для электропроводности о = пегтХт, где т -	получим:
</.) ~ (cRiep) (ЗтН'П)1^2 = 0,23 мкм.
9.32.	R IpVdBU 1,4-Ю-l’ СГСЭ, 5-Ю1? см-3; 5-102 см2/(В с).
9.33.	Как электроны, так и дырки при наличии тока отклоняются магнитным полем в одну и ту же сторону. При динамическом равновесии из плотности потоков в поперечном направлении будут одинаковы:
пеие^пдид^	(1)
где и — поперечная скорость направленных движений носителей тока. Так как и — ЬЕj_ L b (F — еЕ , ) с (где Ь — подвижность; £ — магнитная часть силы Лоренца; Е— поперечная напряженность электрического поля), то равенство (1) можно переписать так:
nebe(eve В с—еЕ^) - ndbd(ev& В/с-\-еЕ±),
где v - ЬЕ; Е— продольная напряженность электрического поля.
Найдя отсюда отношение Е^/ЕВ, получим:
^ = £1//В=:£1/а£В = (1/ес)(пе 62 — пдЬ%)/(пе Ье ~пд 5д)2.
169
9.34.	be — Ьд = cEjEB = 2,0-103 см2/(В-с).
9.35.	a) I : 4,4; 6) 0,32.
10.1.	Соответственно 1,5- 1014 г/см3; 8,7- 1037 cm~3, 7- 1018 Кл/см3.
10.2.	1,2- 10-12 cm.
10.3.	4,5 фм.
10.4.	1 a. e. m. = 1,00032 ME, уменьшились в 1,00032 раза.
10.5.	Атомное содержание 1,11%, массовое— 1,2%.
10.6.	1.007825, 2,014102 и 15,994915 а.е.м.
10.7.	а) 8Ве, £св = 56,5 МэВ; б) 5,33, 8,60, 8,55 и 7,87 МэВ.
10.8.	а) 6,76 и 7,34 МэВ; б) 14,4 МэВ.
10.9.	6,73 МэВ.
10.10.	10,56 МэВ.
10.11.	7,16 МэВ.
10.12.	22,44 МэВ.
10.14.	А£св = 6,36 МэВ, АС/цул = 6,34 МэВ. Совпадение объясняется приблизительным равенством ядерных сил между нуклонами.
10.15.	4,1 фм (А£св = 4,84 МэВ).
10.16.	а) 341,8 и 904,5 МэВ (табличные значения: 342,05 и 915,36); б) 8,65 и 7,81 МэВ (табличные значения: 8,70 и 7,91); в) 44,955 и 69,932 а. е. м. (табличные значения: 44,956 и 69,925).
10.17.	Из условия dMfidZ = 0 получим:
Zm = А/(1,97 -L- 0,0149А2/3).
Вычислив по этой формуле Zm, получим соответственно 44,9 (47), 54,1 (50) и 59,5 (55), где в скобках указаны Z данных ядер. Отсюда следует, что первое ядро имеет позитронную активность, остальные — электронную.
10.18.	2, 2, 1, 2 и 4.
10.19.	7/2.
10.20.	Четыре.
10.21.	У равно числу различных значений квантового числа £, т. е. 21 -f- 1 или 2J — 1 соответственно при / < J и I > J. Если при разных значениях J обоих термов а) = N2, то N ~ 21 ч- 1; б) Nt 4 У2, то = 27, 4~ 1.
10.22.	Здесь отношение интенсивностей компонент равно отношению статистических весов подуровней расщепленного терма: 10/6 = (2Fr -1- 1)/(2£2 4- 1)= = (/ — 1)/7, отсюда I = 3/2.
10.23.	Энергия магнитного взаимодействия £ = РуВ0 cos (I> J), гДе cos (I, J) = [£ (£ + !) — /(/+ 1) — J (J 4- 1)]/2"|// (7+1) J (J + 1). ‘ Имея в виду, что I и J для всех подуровней одни и те же, получим, что
£ оо [£ (£ 4- 1) — / (7 4- 1) — J (J 4- 1)1-
Отсюда интервал между соседними подуровнями f>Ep pJr^ со F 4~ 1.
10.24.	Число компонент данного терма определяется, как нетрудно заметить, выражением 2J 4 1. Отсюда можно заключить, что 7^3/2. На основании же правила интервалов 4:5:6= (£4- 1) : (£ 4~ 2) : (£ -4 3), где £ = I — J. Отсюда / = 9/2. Указанная линия расщепляется на шесть компонент.
10.25.	1 4 3 + 5 + 7 = 16.
10.26.	2 и 5/2.
10.27.	<о = gseB2mc, где gs — гиромагнитный множитель. Соответственно: 1,76-Ю10; 2,68-10’ и 1,83-10’ рад/с.
10.28.	gs = 2лЙУ0/ряВ = 0,34, р = gs7pH = 0,85ря.
10.29.	р - 2лЙу7/В, отсюда pLi = 3,26ря, pF = 2,62ря.
10.30.	Тмакс = (Л3/2т) (Зл2п)2/3 = 25 МэВ, где т — масса нуклона; п — концентрация протонов (или нейтронов) в ядре.
10.31.	lsf/2 lP3/2>lsl/2 *Рз/2 lP}/2> *S1 /2 *Рз/2 1Р*/2 ^5/2-
10.32.	1Р — 1/2-. Эти величины определяют квантовыми числами нуклона в состоянии lpiy2 (см- Рис- ’0-1).
170
10.33.	a) l/2+; б) l/2+: в) 1/2-. Искомые значения определяются квантовыми числами «дырочного» состояния в замкнутых оболочках и lpj/2—соответственно (см. рис. 10.1).
10.34.	5/2+, 1/2+, 3/24-, 7'2-. 3/2-.
10.35.	Из векторной модели, аналогичной той, которая показана на рис. 12, следует, что ц = ps cos (s, j) 4- Ц; cos (1, j). Подставив сюда выражения
Ps = gs s* Ия- Hi = gi l* Вя, cos (s, j) = (/*2 + /*2—s*2)/2s*/*, cos (1, j) = = (/*2 4-s*2 — /*2)' 21* j*, где s* = Vs (s4-l) ; I* = УI (/+1) ; j* = У j (/+1) , получим n = gj yi(/-^-i) Вя- Здесь
gs-gi gs—gi S (s-j-1)—Z (f-i-1) 8i~	2	2	/(/ + 1)
Теперь остается учесть, что s= 1/2 и j= I ± 1/2.
10.36.	В ядерных магнетонах:
M-	/ = / + '/2		s 1/2	Pl/2	P3/2
Bn	— 1,91	1 ,91 /+1 '	—1,91	0,64	-1,91
Цр	/+2,29	/	2,29 \ (' жР	2,79	-0,26	3,79
10.37.	Для /5^,2 цр = 0,86ця; для f7^2 цр = 5,79 ця; отсюда / = 7'2.
10.38.	а) 2,79 н — 1,91ря; б) — 1,91 и 0,126ця (опытные значения: 2,98, —2,13, —1,89 и 0,39).
10.39.	В соответствии с моделью ядерных оболочек естественно предположить, что непарный протон данного ядра находится на уровне 2sl/2. В этом случае магнитный момент ядра равен 2,79ця (см. решение задачи 10.36). Если же предположить, что этот протон находится на следующем уровне ld3/2, то магнитный момент равен 0,124ря, что сильно отличается от значения, приведенного в тексте задачи.
11.1.	1 — ехр (— X/).
11.3.	а) 0,78 н 0,084; б) 6,8-10-\ 0,31.
11.4.	9-10-‘.
11.5.	0,80-10~8 с-1, 4,0 н 2,8 года.
11.6.	4,1 • 103 лет.
11.7.	1,5-10“ Бк (4 Ки)
11.8.	2-1013 ядер.
11.9.	2.2-109 Бк/г (0,06 Кн/г).
11.10.	0,05 мг.
11.11.	V = (Aia) ехр (— X/) =6 л.
11.12.	Построим график зависимости логарифма скорости счета от времени. Экстраполируя прямолинейный участок, соответствующий более долгоживущей компоненте, к t = 0, найдем разностную кривую (в данном случае это прямая). Последняя соответствует другой компоненте. Из наклонов обеих прямых получим 7"i = 10 ч, Тг = 1,0 ч; Nln : jV20 =2:1.
11.13.	а) Скорость накопления нуклида Л2 определяется уравнением:
У =	— X2jV2, нлн + X2?V2 = ^iN10 exp (—
Его решение с учетом начального условия :V2 (0) = 0 имеет вид:
У = Уо [ехр (— Хг/) — ехр (— Х2/)] Xj/fX-j — М;
б)	tm = [In (Xj/Xjs)]. (Xj — X2);
171
в)	чтобы отношение Л'г'М2 оставалось постоянным. Л\ и ,V2 должны одинаково зависеть от времени. Это возможно лишь в том случае, если ехр ( — Х2/) << ехр (— Х^). Для выполнения последнего неравенства необходимо, чтобы Zj было заметно меньше Z2 и промежуток времени / значительно превосходил среднее время жизни более устойчивого нуклида.
11.14.	4,5-10” лет.
11.15.	^змакс А ю ~ [ехр ( Z । tni) |	ехр ( A2/m)J Z2 (Z2 — Xj)	0,7,
где tnl I In (А, X2)I (X, — Z2).
11.16.	а) Накопление стабильного нуклида описывается уравнением Л'3 --~ Х2Л’2. Подставив сюда выражение Л'2 (/) из решения задачи 11.13 и. проинтегрировав полученное выражение по t, получим:
Л’з Х2 X, Г 1 — ехр (— А) , 1— ехр ( — X., /)
:--------1--------:-------	0,7;
10	А.»	/*1	Ао
б)	А А„ - ехр (— Zj/) - [ехр (— Х^) — ехр (— Х2/)| Х2 (Х2 — Xj) - 0,55, т. е. активность уменьшится в 1,8 раза.
1t1_	,, , , Г ехр ( —Xt/) ехр ( —Х2 t) ,
11.17.	m3==m1()A1x^ (Х1_Хг) (Х1_Хз) + (ь2_М(Хг_ьз) -г
ехр ( —Х3 /)
11.18.	Около 0,3 кг.
11.19.	а) Активность каждого по 3,7-105 Бк (10 мкКи); б) 1,9-10'’ Бк (0,05 мКн).
11.20.	а) 4,1 • 1013; б) 2,0-1013.
11.21.	а) 40 сут.; б) М = Л4Те [ехр (— X/) + kt — 1] q/k = 1,0 мкг.
11.22.	Л\ = (g/ХО [1 — ехр (— XrQj;
M2=(g/X2) 1 4-
, 2 . ехр ( — X! ОД
— Л>2
X!	I
ехр (—Х2 t) ;
Х2 [1—ехр (—Xi Q]
Xi (Х3—Х2)
Xi [1—ехр ( —Х2 /)]
Х2 (Х2— Х3)
11.23. A=q 2
2Х2—X,
—----— ехр (—Xi 0 +
Aj — Ao
X,	1
------;— ехр (—Х2 0	1,4-1010 Бк —(0.4 Ки). Х2 A,	J
11.24.	а) 1,6%; б) 4-1013.
11.25.	Q- Т (1 ma!М) - 8,5 МэВ, где М — масса дочернего ядра; 1,9%; 3.8-103 м с.
11.26.	a) Q = N0T (1 - та1М) [1 — ехр (— X/)] = 16 МДж, где	—
первоначальное число ядер, М — масса дочернего ядра; б) 0,8 мКи.
11.27.	5,40 и 0,82 МэВ.
11.28.	Энергия уровней: 0, 0,11, 0,24 и 0,31 МэВ.
11.29.	Энергия уровней: 0, 0,726, 1,673 и 1,797 МэВ.
11.30.	29 МэВ; 3,6-10~i2 см.
11.31.	— dU^ dr -- F = m^lr -= Mi m^j3, где Mt — орбитальный момент. Интегрируя это выражение н имея в виду, что Л4; = hyl (I А- 1), получаем С/цб —	1) 2таг2. Искомое отношение:
t'Ky.i- Л2 I (/-!) 4 (Z-2) е2 maR= 1,6-10 '2, где R — радиус ядра.
172
11.32.	а) Введя новую переменную по формуле cos2 ([• - T.'U(r). где U (г) — энергия кулоновского взаимодействия, г — расстояние между а-ча-стицей и дочерним ядром, получим после интегрирования:
D = ехр [— (х/лЗ/Т) (2<р0 — sin 2<р0)],
где сро соответствует высоте кулоновского барьера. Дальнейшее очевидно.
б.	Соответственно 3,4 : 1.
11.33.	Хгх = 1/т (1 + Nx/Na) = 2-10’ с-L
11.34.	Г? = hkaNvNa = 0,9-10-« эВ.
11.35.	0,78 МэВ.
„	/ Мм—Мд при ^--распаде и /(-захвате,
11.36.	Q= <
1 Мм—Мд—2те при позитронном распаде.
11.37.	а) 6,0189 а.е.м.; б) 21,994444 а.е.м.
11.38.	а) Нет; б) да; в) да.
11.39.	1,71 МэВ, Тя= Q (Q + 2/ПеС2)/2Мс2 = 78,5 эВ, где Q — энергия распада.
11.40.	р= ~[/Q (Q + 2mecl)lc = 0,84 МэВ/c, Q — энергия распада.
11.41.	а) 0,97 МэВ н 94 эВ; б) 0,32 и 0,65 МэВ. _______________
11.42.	О = л — arccos (pe!pv) = 110°, pelpv = ~\/Т (Т + 2znc2)/(Q — Т).
11.43.	1,78 МэВ.
11.44.	0,78.
11.45.	Энергия уровней: 0, 0,84, 2,65 и 2,98 МэВ.
11.46.	Т а; Q'2’2Mc2 = 9,5 эВ, где Q — энергия, освобождающаяся в этом процессе, М — масса атома; v =• 7,0 км/с.
11.47.	0,32 МэВ.
11.48.	Т = Q (2й<о — Q)/2Mc2 = 6,6 эВ, где Q — энергия, освобождающаяся в данном процессе, М — масса атома; 56 эВ.
11.49.	0,41 н 1,25 км/с.
11.50.	26 кэВ.
11.51.	279 кэВ.
11.52.	145 кэВ.
11.53.	566 и 161 кэВ.
11.54.	1,2-10s с-1.
11.55.	Дй<о/й<о = Е/2МС2 = 3,6-10—7, где М — масса ядра.
11.56.	Вероятность такого процесса будет ничтожно мала, так как уменьшение энергии у-кванта, равное удвоенной энергии отдачи ядра, значительно больше ширины уровня Г.
11.57.	цотн = Й<о/Мс = 0,22 км/с, где М — масса ядра.
11.59.	Г « 2Й<оц/с = 0,01 МэВ, где v — скорость, при которой ордината контура линии равна половине максимальной; т яа 0,06 нс.
11.60.	v =- gllc — 6,5-10-? см/с.
11.61.	Относительное приращение частоты у-кванта, «падающего» с высоты I, есть Д<о/<о — gl/c2 > Г/Е. Отсюда 1Ре >- 2,8 км, ZZn 4,6 м.
11.62.	а. Масса атома при излучении у-кваита уменьшается на 6М — = Й<оо/с2, поэтому его средняя кинетическая энергия (Т = <р2>/2Л4) возрастает на 67’ = <р2> 6М/2М2 — Йй>0 <ц2>/2с2. Следовательно, энергия испущенного у-кванта:
Й<о = Й<оо — бТ = Й<оо (1—(и2)/2с2).
б. Считая, что М <ц2> = ЗйТ, выразим частоту испущенного у-кванта через температуру, <о (Т). После этого найдем относительное приращение частоты у-кванта, обусловленного приращением температуры 6Т:
(б(о/ы0)темп=--(Зй/2Мс2) 6Т.
Гравитационное приращение частоты у-кванта, «падающего» с высоты I, есть (б<о/<оо)Гр — gllc2. Из этих выражений находим: 6Т = 2l3Mgllk —• 0,9 К.
11.63.	и' =— 0,15ця, В = 3,3-105 Гс.
173
11.64.	Др як р (п) \п = 0,08.
11.65.	2,5-10* и 0,8-102.
11.66.	С помощью распределения Гаусса находим, что для е0 =5,0 имп./мии. и о — 1/100 вероятность р (е0) = 0,035;
“	е./о
р(е>е0) = 2 I р (е) de = 1 ——-— | е ~ х'/2 dx = 0,62.
J	1/2л J
е,	0
11.67.	а) 32%; б) 4,6%.
11.68.	а) ± 6 имп./мин; б) 28 мин.
11.69.	50 ± 5 нмп./мин.
11.70.	Пусть без фона зарегистрировано N„ импульсов. Соответствующая относительная средняя квадратическая погрешность т]0 = 1/~[/ N„. С фоном
Т)= У^ф+^фЛ^иф—Л'ф) = У 6/ЛГиф,
так как Л/Иф = 2Мф. Из требования т] =• т]0 получим Уиф = 6УИ.
11.71.	Запишем выражение для квадрата среднего квадратического отклонения скорости счета исследуемого источника и его дифференциал:
ст^ПиФ^иф + пф^ф, 2аи da„=—(пифД2ф) Лиф—(пф//|) d/ф.
Из условия минимума погрешности (dali = 0) и того, что суммарное время за дано, т. е. б//иф + d/ф = 0, получим /ф//иф = VПф/пиф як 1/2.
Пф+УпфЛиФ	Пиф+У"иф"ф
11.72.	1ф =------------= 7 мин; /иф=--------------= 14 мни.
т| («иф—«ф)2	т]2 (яиф—Пф)2
11.73.	В течение каждой секунды счетчик на время хп утрачивает способность к счету. За это время через него пройдет xnN незарегистрированных частиц. Таким образом, N = п + xnN, откуда N = 3,3-104 мни-1.
11.74.	0,010 и 9%.
11.75.	и TLиф/'(1 —тпиф)=Пф/(1 —тпф) = 5,7-102 с-1.
т (1 1/ , _ „ » n12 \ V	П1 n2 ’ 2пгпг
Последнее справедливо прн достаточно малом т, когда ni + пг мало отличается от п12.
11.77.	а) В этом случае регистрирующее устройство зарегистрирует все импульсы счетчика и п = N/(i + xNy,
б)	число импульсов, даваемых счетчиком, пг = ^/(1 + XiN). Из иих регистрирующее устройство зарегистрирует
п2 = nj/(l + Т2П1) = У/[1 + (Т! + т2) У].
11.78.	N = n/[l — Ch + т2) п] = 6-10е с-1.
11.79.	Чтобы электромагнитный счетчик зарегистрировал импульс от счетчика Гейгера—Мюллера в интервале времени (/, t + dl), необходимо, чтобы в предшествующий промежуток времени от t — х до t в него не поступило ни одного импульса. Вероятность последнего р = ехр (— Nx). Отсюда полное число частиц, зарегистрированных в единицу времени электромагнитным счетчиком, п = Np — N ехр (— Nx).
11.80.	Из условия dn/dN — 0, где выражение для п (N) см. в решении предыдущей задачи, находим N = 1/т. Отсюда т 1/епМакс ~ 8 мс.
11.81.	Вероятность, с которой импульс от одного счетчика сопровождается импульсом от другого, отстоящим от импульса первого счетчика на время ±т, равна 2тп2. Отсюда An — 2Tntn2.
11.82.	N = VЬп/Чхх) = 4-10®, где г) — эффективность счетчика.
174
11.83.	Имеем 0,05 = V (пиф + Дпф) tl n-At, где пиф = п„ + Дпф, пф — число совпадений в 1 с от фона (Дпф = 2тп2ф). Отсюда t = (пи + 4тлф)/0,052Пи = = 20 с.
11.84.	v = т]1т]2/(т]1 + т)2) = 0,03%.
12.1.	дмакс = arcsin (те/7Па) = 0,5 угл.мин.
12.2.	Электрон приобретает импульс р в направлении, перпендикулярном к направлению движения а-частицы (рис. 16):
р	р де cos дт>
г2 4
Рис. 16
р=
— “	л/2
Имея в виду закон сохранения момента импульса г2д = const = — vb, где знак минус обусловлен тем, что О < 0, получим после интегрирования: р= 2qelvb и Те = maq2e2lтеЬ-Та = = 6 эВ.
12.3.	Рассмотрим слой толщиной dx, перпендикулярный траектории а-частицы. Число электронов с прицельным параметром в интервале (b, b + db) равно бп = ndx-2nbdb. Энергия, переданная а-частицей этим электронам, б£ = Тебп, где Те — кинетическая энергия, приобретенная каждым электроном. После подстановки выражения для Те из ответа к предыдущей задачи получим:
dE I 4пр2 е2 п db dx | me v2 b
12.4.	(—д£7дх)ион = 0,17 МэВ/см.
12.5.	а) (—dEldx)al(dEldx)p = 11;
б)	(— дЕ1дх)С1л1(— дЕ/дх)м = 2,4.
12.6.	р 5= 27 кПа (0,27 атм).
12.7.	а) 2,8-104; б) т] = 1 — Т'/Т = 0,36, где Т' — кинетическая энергия протона, соответствующая пробегу второй половины пути.
12.8.	14 мг/см2.
12.9.	5,5 МэВ.
12.10.	8 мкм
12.11.	75 мкм.
12.12.	24 мкм.
12.13.	Поскольку —dE/dx = z2f (»), где f (о) — функция скорости частицы, то пробег
о
f dE
,	_ m
R= — |--------------= — E <v),
J z2f(y) z2	v
V
m — масса частицы; F (о) — функция, зависящая только от скорости частицы и свойств среды. Отсюда Rd (о) = 2Rp (v), или Rd (Т) = 2RP (Т/2). Здесь учтено, что m.dlmP = 2.
Пробег дейтона Rd = 4,6 см.
12.14.	42 мкм (см. решение предыдущей задачи).
12.15.	а) В Ц-системе формула Резерфорда имеет вид:
/ qe \2 d Q	[ qe \2 2л sin d ft
ри2 ) 4 sin4 (§/2)	\mev2) 4 sin4 (0/2)
где p — приведенная масса; me — масса электрона. Преобразуем Эту формулу от интервала углов (О, О + dft) к соответствующему интервалу кинетических 175
энергий 6-электронов (Т, Т + dT), имея в виду, что О = л — 2<р и
Т =
4те т
(me + m)2
Т0 cos2 ср,
где <р — угол, под которым отлетает электрон отдачи в Л-снстеме; т и То — масса и кинетическая энергия первичной частицы. Формула для О следует из векторной диаграммы импульсов, а формула для Т — из законов сохранения энергии н импульса. Так как То = mv2/2 н me <С ш, то в результате получим:
da = (2лд2е2//лер2) dT!T\
2лпо2 е2 !	1
(Л =----------------
me v \ ^пор
1___
т 1 макс
где интегрнрованне проводится по Т от Тпор Д° Т'макс = 2mev2. 12.16, а) Тмин = (пга/4пге) Тпор = 20 МэВ; б) из условия dNldv= 0 по-лучим та = (ma/2me) Тпор = 64 МэВ и Умакс = лп?2е2/Т2ор = 5,1; в) q = е.
12.17.	2,0 МэВ/см; в 19 раз.
12.18.	114, 62 н 9,8 МэВ.
12.19.	20 МэВ.
12.20.	10 МэВ/см.
12.21.	Продифференцировав формулу (12.7), получим: — дТ/дх = 77/рад. Сравнив последнее выражение с формулой (12.5), найдем: /рад = 4,31 • 102в/ nl In (183/Z1/3). Соответственно 360 м, 9,8 н 0,52 см.
12.22.	14 мм.
12.23.	Убедившись, что потери энергии электронов в основном радиационные, из формулы (12.7) находим То = 0,11 ГэВ. Здесь /рад определяется с помощью выражения из решения задачи 12.21.
12.24.	Вероятность испускания у-квантов в интервале частот (ш, со + dco) равна dw = nl da. Отсюда
1
I Cd (Лео)	о
w=--------- -3—-=6-10~3.
(рад J Йш 0,9
12.25.	0,36 МэВ.
12.26.	Убедившись, что для этих электронов потерн энергии в основном ионизационные, используем вторую из формул (12.8); 2,8 мм.
12.27.	В воздухе R = 106 мг/см2, или 0,8 м.
12.28.	0,3 г/см2.
12.29.	0,2.
12.30.	1,6 МэВ.
12.31.	50, 2,4-10-2 и 5,7-10-з см.
12.32.	cos О = (с'/р) [1 + Йсо (п2 — 1)/2£] га c'/v, где Е — полная энергия частицы.
12.33.	7'пор =	2 —j- — 'j m<-2- Соответственно 0,14 МэВ и 0,26 ГэВ.
Для мюонов.
12.34.	Т=(------—°S	__ j j тпс2 = 0,23 МэВ.
\ Уп2 cos2 — 1	/
12.35.	0,2 МэВ.
12.36.	3,2 см.
12.37.	1,7 мм; в 6 раз.
12.ЗС.	Соответственно 6,5-10-2, 5,1 и 4,4-103 см.
12.39.	d/dI/2 = (In n)/ln 2 » 10.
12.40.	См. рис. 17, где — край /(-полосы поглощения.
176
12.41.	а) Железо; б) кобальт.
12.42.	Около 10 мкм.
12.43.	а) а =	б) 0,3; в) это число равно числу фотонов, рассеян-
ных в интервале углов, который легко найти с помощью формулы:
etg (072) - (1 + й<оо//лес2) tg ф,
где О — угол рассеяния фотона, а ф — угол, под которым отлетает электрон отдачи. Для низкоэнергетнческого рентгеновского излучения h<o„ <с тес2 и tg тф etg (0'2). Найдя отсюда углы Од н О2> которые соответствуют ф = л/4 н л/2, получим:
т)е = &а!а = (1/а) j da (О) = 1/2.
12.44.	а/р = 0,42/Лсм2 г, для обоих случаев ар яг 0,20 см2/г. Линейные коэффициенты рассеяния равны соответственно 1,8-10—4 и 2,9-10-4 см-1.
12.45.	1,17-10—«а см2/атом.
12.46.	а) 70 см2/г; б) 8,7 : 1.
12.47.	Вычислив массовый коэффициент ослабления, находим по таблицам Приложения соответствующую энергию у-квантов (0,2 МэВ) и по ее значению — массовый коэффициент поглощения. Их разность равна а/p я» 0,095 см2/г.
12.48.	J = (Л/4лг2) ехр (— цДг)= = 6 -103 см-2-с-!.
12.49.	Соответственно 1 : 4,7.
12.50.	J = Jo [ехр (— p2d) — ехр (— щй)]/^ — р2) d = 0,7.
12.51.	2,75 б/атом.
12.52.	1,2.10» б/атом.
12.53.	1= 1/р. Соответственно 1,2-104, 14 и 6 см.
12.54.	/ = d]/2/ln 2 = 6,5 см.
12.55.	I = 1/па, где п — концентрация ядер; /полн = *.9 см; /КОМп=2,5см; /фот = 1.5 см; /пар = 1,8 см. Связь между пробегами:
1 / /поли — 1 / /комп “Ь 1 //фот + 1 / /пар •
12.56.	Юфот = (Офот/^полн) [1 — ехр (— |id)] « 0,013, где р = паполн.
12.57.	Сначала вычислим полное сечение — 17 б/атом. По графику это сечение соответствует двум значениям энергии у-квантов: 1,75 или 10,25 МэВ. Соответственно 0,039 нли 0,012 см2/г.
12.58.	а) Соответственно ar (1 — 2е) и аг (3/8е) (1п 2е+ 1/2); б) 0,084 см-1; в) 0,063 см2/г.
12.59.	и*пар = стпар/2аПОЛ8 = 0,28.
12.60.	3,5 мм.
12.61.	^пар/^фот 4- комп = 1/01	1) ~ 0,37.
12.62.	Воспользуемся инвариантностью величины Е2 — р2с2 и запишем ее в Л- и Ц-системах отсчета при пороговых значениях энергии и импульса у-кванта:
(Лшдор+М <?2)2— (Лц>пор)2 — (М 4- 2 т)2 с4,
откуда Й<оПор = 2/nc2 (1 + т/М). Здесь т — масса каждой частицы пары.
12.63.	Для рождения пары необходимо, чтобы энергия у-кванта была больше 2/пс2, где т — масса каждой частицы. Очевидно, всегда можно перейти в такую систему отсчета, где энергия у-кванта меньше 2тс2 и рождение пары невозможно. Но если этот процесс невозможен в одной системе отсчета, он невозможен и в любой другой.
12.64.	Т = те^а,2/(\ + а) — 0,6 эВ, где а = 2те/тр.
12.65.	Й<в= 2"|/(ер5)2 + (тс2)2 = 2,1 МэВ.
12.66.	Рэкс = IRT/Mp = 22 мкКл/(кГ'С), нли 85 мР/с, где R — универсальная газовая постоянная, М — молярная масса воздуха (29 г/моль).
177
т (98 нГр/с (35,3мрад/ч) в воздухе,
12.67.	а) Р = —EJ — -1	„ ,
р U08 нГр/с (38,9мрад/с) в воде, где т/р — массовый коэффициент поглощения;
б)	Рэкс = 2,9 нКл/(кг-с), или 40 мР/ч.
12.68.	а) £>экс = [1 —ехр (— Хт)| Ро/А = 0,33 мКл/кг (1,28 Р), где Х = (1п/2)/7';
1	/	А) КС '
б) t= In 1 —----------= 2,4ч, где ОЭкс = £’/а, а = 34 Дж/Кл.
А-	\	Р о	/
= 0,40 нКл/(кг-с), или 1,55мкР/с, где а = 34 Дж/Кл.
12.70. 2,5 м.
12.71. Рэкс = 1,38-103 2 (т,/р) Д/Т]; пКл/(кг-с), где т]; — доля у-квантов энергией £(-, МэВ; т,/р — соответствующий массовый коэффициент поглощения, см1 2/г.
а) 131 пКл/(кг-с), или 1,83 мР/ч; б) 9,5 пКл/(кг-с), или 0,13 мР/ч; в) 50 пКл/(кг-с), или 0,69 мР/ч.
1 (т/р) JE , I --------------arctg 	 a 2nlR--------2R
12.72. Рэкс
= 1 ,ЗнКл/(кг-с) или 5,0мкР/с, где а = 34 Дж/Кл.
12.73. РЭкс =-^
— АЕ In Р
= 46мкКл/(кг с) или 0,18,Р/с, где а = 34 Дж/Кл.
12.74.	d = (1/pi) In (Р/Рпр) = 2,0 см, где ц — линейный коэффициент ослабления для свинца.
12.75.	Из-за сферической симметрии число рассеянных фотонов, уходящих из любого элементарного телесного угла, будет компенсироваться фотонами, попадающими в рассматриваемую точку вследствие рассеяния из других телесных углов. Поэтому можно считать, что пучок ослабляется только за счет истинного поглощения, и мы получим:
1
Аг = — In т
(т'/р') Лт|£ 4лг2Ра
= 2,4 см,
где т — линейный коэффициент поглощения в свинце; т'/р' — массовый коэффициент поглощения в воздухе; а = 34 Дж/Кл.
12.76.	Р = аРЭкс е—= 0,6 мГр/с (0,06 рад/с), где а = 34 Дж/Кл; т/р и т'/р' —• массовые коэффициенты поглощения соответственно в свинце в воздухе; р •— линейный коэффициент ослабления в свинце.
12.77.	2,0 м.
12.78.	D — JNAaEft/М = 0,9 мГр (0,09 рад), где NА — число Авогадро; М — масса моля углерода.
12.79.	N = mD3KB/EK = 3,9-10’.
12.80.	D = NE/pSl = 3,0 мГр (0,30 рад), где р — плотность ткани, практически равная плотности воды; I — длина пробега а-частицы в ткани Оэкв = = KD ~ 60 мЗв (0,6 бэр).
12.81.	Учитывая закон (12.9), получим D — (p/p) J < Е > t = 0,26 Гр (26 рад), где р/р = 2,2^-^ м2/кг, если £₽макс, МэВ.
13.1.	Т = [4m1mi/(m1 + /п2)2] То cos2 -0 = 0,7 МэВ.
13.2.	а) Та= (2 + ma/2ma) (epB)2/mac2 = 0,26 МэВ;
б)	Та = Td [1 + (ma — md)2/4mamd cos2 0 ] = 0,6 МэВ.
13.3.	m = md/(4 cos2 0 — 1) = md/2, ядро атома водорода.
178
13.4.	Связь неоднозначна, если масса налетающей частицы больше массы бомбардируемого ядра (случай в). В случаях а и б угол Омане = л, а в случае “ ^макс = arcsin	=30°.
13.5.	ДТ/Т = [4mim2/(mi + т2)2] sin2 (0/2) = 0,19.
13.6.	0,10 МэВ.
13.7.	49°.
13.8.	a) tg О = (sin O)/(zna/znL. + cos О), отсюда О» 18°;
б)	sin О = sin О (я cos О ± Д/1 — т|2 sin2 О), где т| =
Минус перед корнем физического смысла не имеет: здесь sin О не может быть отрицательным. В результате О = 73°.
13.9.	Т' — Т/3 = 0,10 МэВ, Омаке = arcsin (тПр/т^) = 30°.
13.10.	Q = + 17,3 МэВ.
13.11.	а) + 19,8 МэВ; б) —3,1 МэВ; в) — 13,5 МэВ; г) + 1,8 МэВ.
13.12.	17,00845 а.е.м.
13.13.	va = 9,3-10е м/с, oLi = 5,3-10е м/с.
13.14.	Пренебрегая импульсом у-кванта, найдем Т — 8/в (йо> — IQI) = = 115 кэВ.
13.15.	£ = Й<о — (ерВ)2/тс2 = 2,23 МэВ.
13.16.	a) Q = */3 Тр — i/3 Td = 4,0 МэВ;
б)	С=18/17Гр—1з/177'(х—*/i7 /Т^ cos О=-1,2 МэВ.
13.17.	Тр = 2 (Та — 3/5Q) = 5,5 МэВ, где Та — 4,0 МэВ (из графика по пробегу).
13.18.	а) 141°; б) 145°.
13.19.	Ниже приведены два способа решения этой задачи.
1.	Законы сохранения энергии и импульса при пороговом значении кинетической энергии налетающей частицы:
Тпор = |<2|+Тт + Л(, Рт=Рт+м-
Решив эти уравнения, найдем искомое выражение.
2.	В Ц-системе пороговое значение суммарной кинетической энергии взаимодействующих частиц fnop = IQI. Но Тпор = ЦУотн''2 = (р/^) Тпор. Отсюда легко получить выражение для Тпор.
13.20.	а) 4,4 МэВ; б) 18,1 МэВ; в) 6,2 МэВ; г) 0.
13.21.	а) 1.02 МэВ; б) 3,05 МэВ.
13.22.	а) ТВе = i/g|Q| = 0,21 МэВ; б) TQ = 3/7e|Q| =- 1,41 МэВ.
13.23.	0,68 МэВ.
13.24.	ТМин = и/т « 2,8 МэВ, где R — сумма радиусов ядра Li и а-частицы. Эта энергия меньше пороговой (Тпор = 4,4 МэВ), т. е. недостаточна для возбуждения реакции.
13.25.	Запишем условие равенства полных энергий в Ц-системе для прямого и обратного процессов (см. рис. 13.1): Т = Т' + IQI, где Q — энергия реакции (здесь Q < 0). Выразив Г, Т' и |Q| соответственно через Т, Td и ТпоР, получим Td = (т^тЪе) (7 — Тпор) = 5,7 МэВ.
13.26-	р = Д/2р' [(pi//n) Tm + Q], где р н р' — приведенные массы системы до и после реакции.
13.27.	£= 0,566рр; 0,18 или 0,9 МэВ.
13.28.	р = 1,95ра. Из векторной диаграммы импульсов находим: Ра. макс = Р + Pdma/(ma + mN);Ta макс = 4,7 МэВ.
13.29-	р = 0,431ра. Из векторной диаграммы импульсов следует:
Рп = Р ± Ра mn/(mn + mN)t
где знаки плюс и минус относятся соответственно к максимальному и минимальному значениям импульса нейтронов. Отсюда Тп макс — 5,0 МэВ, Тп мин = = 2,7 МэВ.
179
13.30.	a) 5,7, 2,9 и 1,5 МэВ; б) как следует из векторной диаграммы импульсов, это будет при р ратп/(тп + /лв). Отсюда Та 4,65 МэВ.
13.31.	Пренебрегая кинетической энергией медленных нейтронов, найдем прежде всего кинетическую энергию возникающих тритонов:
~ Чта!(та + mt) = 2’75 МэВ<
Затем используем векторную диаграмму импульсов.
а)	р — 1,35р^, рп макс = P~\~Pt mrJ~ 1 »55р/, Тп макс = 19>$ МэВ;
б)	Р = 1 > 1бр;, Рп макс — 1 »26р/, Тп макс = 13,1 МэВ.
13.32.	Из векторной диаграммы импульсов для первой реакции находим максимальное н минимальное значения импульсов ядра трития: 3,07р и 2,21р, где р — импульс налетающего нейтрона.
Затем нз векторных диаграмм импульсов для второй реакции (при максимальном и минимальном значениях импульса тритона) находим максимальное и минимальное значения импульса возникающего нейтрона и соответствующие значения кинетической энергии: 21,8 и 11,0 МэВ.
13.33.	а) Из векторной диаграммы импульсов следует, что
sin Ов макс = wlyPlPp = 0,70, 0g макс = 44 ,5 .
Угол вылета нейтрона может иметь любые значения (от 0 до л);
б)	46,5° (d) и 29° (3Н).
13.34.	а) Сначала найдем угол Оо в Ц-снстеме, соответствующий углу О0 = = л/2 в Л-системе. Из векторной диаграммы импульсов следует, что cos О0 = = 4'1зРп/р = 0>46, где рп — нмпульс нейтрона в Л-снстеме; р — импульс продуктов реакции в Ц-системе. Искомая вероятность:
w = (1 /4л) | 2л sin O/d0 = х/2 (1 —cos Оо) = 0,27;
б)	137°.
13.35.	Из законов сохранения энергии и импульса при пороговом значении энергии у-кванта имеем:
пор + Мс2 = У М'2с4 + (Йй>)2ор, где М' — сумма масс покоя возникающих частиц. Отсюда:
Ло>,101) =(М'2—М2) c2/2M = (l+|Q|/2Mc2) |Q|.
13.36.	Тп « mnQ212M2c2, где шп н М —массы нейтрона и расщепляющегося ядра, Q — энергия реакции; а) 0,68 кэВ; б) 0,58 кэВ.
13.37.	Воспользовавшись инвариантностью величины Е2 — р2с2, запишем:
(Йы + Мс2)2—(Йы)2 = [(/п1+/л2) с2 -f-T'l2,
где Т’ — суммарная кинетическая энергия продуктов реакции в Ц-системе. Отсюда:
Т’ =. —(n^-i-zn.,) с2 ~-"|//И2 с44-2Мс2 Йсо ~ <2 | Йсо.
Имея в виду, что Т' = р2/2р', получаем искомое выражение.
13.38.	Воспользовавшись векторной диаграммой импульсов, найдем угол Од в Ц-системе, соответствующий углу 0^ = л/2 в Л-системе, по формуле cos Oj = (Ру Р) -j- тп), где р = V2р.' (Й<о + Q). Искомая вероятность:
w --(1 /4л) ]*2л sin О dft =i/2 (1 —cos frj ) = 0,34 .
13.39.	Пусть рг' и prl — импульсы нуклона, обусловленные соответственно его внутренним движением в дейтроне и движением нуклона вместе с дейтроном. Тогда максимальное отклонение от направления пучка дейтронов 0 ----- Д0/2 180
нуклон получит при условии, что в момент срыва р/, । р„. Поэтому tg О —P'rJPn V^T’n!Ta. Отсюда найдем Т' — кинетическую энергию внутреннего движения нуклона в дейтроне. Кинетическая же энергия возникающих нейтронов
7'n = (P/1n-Pn)2/2m - 7'ц/2 4 PnPn 'm,
где m — масса нуклона. Отсюда максимальный разброс энергий нейтронов;
А7ц = ± рл р’п tn -- ± |/ 2Т,/ Т'п -- 4 27 МэВ .
13.40.	/ (i-О) I (,ВО) - /„ 1-Л/,	0 - 2 - 1'2 - 5'2 п 3 2. Согласно
оболочечной модели, /	5 2.
13.41.	а) Спин промежуточного ядра 1 sp 4 I ’ lLj, четность Р
- РрР1л (— !)Z- Отсюда
1	/	р	Состояния *Ве*
0	2, 1	-1	2 . 1
1	3. 2, 1, 0	+1	3-. 2’. 1’, 0+
б)	четность системы из двух а-частиц положительна, так как эта система описывается четной волновой функцией. Поэтому Р.)а Р£ (— l)z<>	+ I,
1а 0, 2, 4, ... Из закона сохранения момента импульса I - /, откуда / О и 2. Таким образом, канал (1) возможен через два состояния промежуточного ядра: 2+ и 0+, когда I = 1. Испускание дипольного у-кванта сопровождается изменением четности и спина ядра на единицу. А так как у основного состоянии ядра чВе спин и четность равны ()+, то испускание дипольного у-кванта происходит из состояния промежуточного ядра I -, когда I 0. Испускание квадру-вольного у-кванта не меняет четности, а спин ядра изменяет на 2. Поэтому этот процесс происходит из состояния промежуточного ядра 2+. когда / I.
13.42.	Е - Ггы (I — /гы.2.Мс2).
13.43.	Е £св т 3iр 21,3 МэВ, где £св — энергия связи протона в ядре ‘Не.
13.44.	ТМ11Н = ’»'„£возб -2 ,67 МэВ .
13.45.	ЕВОЗб -	.Т^О,48 МэВ.
13.46.	ТГ	2» ^Ef-2,5 и 1,8 МэВ.
13.47.	Т„ 17 1Ъ (Ево:,б — £<в) 0,42,0.99 и 1,30 МэВ.
Здесь Е,.в - энергия связи нейтрона в ядре 17О.
13.48.	16,67. 16.93. 17,49 и 17,71 МэВ.
13.49.	2,13, 4,45 и 5,03 МэВ.
1о.50.	7ji02	1 : 0,8.
13.51.	ctab - <таГь. Г.
13.52.	т т„то'(тп ь- ха) - 0,7-10-20 с.
13.53.	т 2e,aJ - 4- Ю10 с.
13.54.	4-I02 см-2с-1.
13.55.	ЗЮ12 с-i; 1,5-102 кг.
13.56.	a) R — anuVJ - 2-10® c~i, где а — эффективное сечение реакции, п0 — число Лошмидта; б) 0,9 мВт.
13.57.	о» -=	--- 0,10 б, где w — выход реакции.
13.58.	<т = wln^d = 0,05 б, где п0 — концентрация ядер.
13.59.	1,8 б.
13.60.	20 кб.
13.61.	о = (1/7т) In [(1 — а[)/а2а(1 - 3,9 кб, где т — продолжительность облучения; и а{ — относительное содержание 10В к началу и концу облуче ния; а2 — относительное содержание 1ХВ до облучения.
181
13.62.	w = 1 — exp (— n0od) = 0,8, где n0 — концентрация, ядер в мишени.
13.63.	А = 1.V = (In 2/7') Jwx = 1,5-109 Бк (4 мКи).
13.64.	В результате длительного облучения число образующихся в единицу времени радиоактивных ядер равно числу распадающихся; w=(A 'j) ехр (Хт)= 1,5 10-3.
13.65.	о = А ехр [1 — ехр (— Хт)] = 20 мб, где п — число ядер ие единицу поверхности мишени.
13.66.	w = 1,0- 10-5; (о) = w n0L ~ 46 мб, где п0 — концентрация ядер в мишени; L — пробег а-частнц с данной энергией в алюминии.
' 13.67. 0,54 б.
13.68.	< о> = w п„1 = 0,10 б. где п„ — концентрация ядер в мишени; / — толщина мишени, в пределах которой возможна данная ядерная реакция; / -	— /2; /, и /2 — пробеги а-частиц с энергией соответственно 7 МэВ и
Т’пор = 4,39 МэВ.
13.69.	7,5 мб. См. решение предыдущей задачи.
13.70.	d — (In 0,9)'лсг =- 1.7 см, где п — концентрация ядер Be.
13.71.	Полный выход на одну частицу:
R	Т
f	С	dT
w (Т) --= па а (х) dx -- п0 а (Т)	.
,1	J	dT;dx
о	О
Продифференцировав это выражение по 7', найдем: о (7’) — (1 f (Т) dw/dT.
13.72.	Используем следующие соотношения:
^=2^, pl -2\x.1Ti,T.i = f1ArQ,
где щ и р2 — приведенные массы соответственно d + d и п + 3Не; plt Т\ и р2. Т.г — импульсы и суммарные кинетические энергии взаимодействующих частиц в Ц-системе соответственно в прямом и обратном процессах. С помощью принципа детального равновесия получим:
2/Не | Э 2 (or! сг2) отНе) Tl(T-[-2Q) =2,0, откуда /Не - 12.
12.73.	а, 8 з	J (Т— 7'пор)/7' = 2,0мкб.
13.74.	Согласно принципу детального равновесия:
Oin. nnvPk'P'^v- <	А+р<^'уГТв + п :ТА + р = У'ТА + р- \Ql/TA+p.
Вблизи порога -* |<?1, ибо ТВА.п->- 0, поэтому знаменатель можно считать приблизительно постоянным. Тогда
о jut j/" Т А р | Q | Д/Гр Тр по)).
13.75.	Имея в виду, что ру х hwc и рп - 2р (Ом + Q), получим:
<л2 3 (йсо)2/(йсо4-(?) гпп с2 З.бмкб, Тп -2 (Ом-IQ)--0,96 МэВ.
14.1.	Т 2n2n2L2m!a2 = 0,03 эВ.
14.2.	1.6-102 об е; 0,03 мс.
14.3.	АТ Т 2,77-10~2 ^/Т7 (Дт/7.) -: 6,2• 10-2, где Т1—в эВ; Дт — в мкс; L—в м; 7'мак(. — 13 эВ.
14.4.	Не пригоден.
14.5.	20 м.
14.6.	0,4 и 1,6 эВ.	____
14.7.	\Т'Т 2 ctg ОАО л 5%: здесь sin О - ^h‘d У2тТ.
14.8-	ДО < 0,1.
14.9.	Т < ,Т2/г 2md- - 1,8 МэВ.
182
14.10.	a) 5,4 МэВ: б) 6%.
14.11.	0, 6,4 и 11,2 фм.
14.13.	Рассмотрим нейтроны с орбитальным моментом I и прицельным параметром bi- Геометрическое сечение ядра для них можно представить в виде кольца со средним радиусом bj. Площадь этого кольца:
&Si = l/t л (62_ j — bf_ j)=-(2Z+ 1) лХ2.
Максимально возможное значение I определяется условием &;макс /?. где R — радиус ядра. Отсюда /макс « /?'Х и
R/K
S = у ±S,~ л (Я4-Х)2; /?Ди = 2,9б.
zSb
14.14.	В = K~l (Z -+- 1)/2т/?2 = 5,3 МэВ, где I = 3, т — масса нейтрона, R— радиус ядра. См. решение задачи 11.31.
14.15.	При условии X « R имеем О ~ Х/7?	4,5°, R — радиус ядра.
14.16.	При взаимодействии медленного нейтрона (/==0) и ядра мишени в данном случае возможны (2s — 1) (2/ — 1) различных способов образования промежуточного ядра (s — спин нейтрона). Так как кратность вырождения (статистический вес) состояния с заданным J равна 2 J~ 1, то вероятность образования данного состояния-
2J4-1	2/4-1	2
8 ~(2s4-l) (2/4-1) ~2(2/+1) - 3 '
14.17.	опп = <та Гп, Г; аПу = <уа Г, где оа — сечение образования промежуточного ядра (см. формулу Брейта— Вигнера).
14.18.	а„? = а» (ТУТ)1'2 Г2'[4 (Т - Тиу- 4- Г2].
14.19.	96 б.
14.20.	Гпо/Г? = (^пп/СУду) V'T,T — 0,006.
14.21.	а) Из условия d<Jnv'dT -= 0 получим:
Т““с = То (0,6 ± 1/0,16 - 0,05Г2/П )•
Отсюда видно, что ТмаКс « Ти при Г < То;
б)	Сто < Омаке на 1,8%:
в)	Г/То > 1,8.
14.22.	<тмин/а0 = 0,87 Г2 Т2. здесь <тмин при Тмин = 0,2То-
14.23.	0,12 эВ.
14.25.	а) апп = 4лХ§§Г«о/Г2 = 8-103 (1 ± 1/8) б; в данном случае с ядрами взаимодействуют только s-нейтроны;
б)	из формулы о0 = 4лХ§#Г,|0/Г находим фактор g, откуда J = 4.
14.26.	Опп/<7геом = 4X§g/7?? = 3,5-103, где R — радиус ядра.
14.27.	Гпо « Сто Г;4лХ(2§- « 0.5 МэВ.
14.28.	т яэ о0тТ0'2лЙ§ГЛ0 а 4,4- 10-1® с, где m — масса нейтрона.
14.29.
2лй2§	Гпо Г7
/пУтТтЛ 4(Т + |Т0|)2 + Г2 •
где m — масса нейтрона, Г„о соответствует энергии Т = | То|. В первом случае <r„v со Т—1/2, во втором o„v со Т"-0^.
—1 /2
14.30.	Так как о „ со-----	——, то <7rtV практически пропорцио-
т 4 (Г — То)- 4- Г2 v
иально Т~1 2, если Т мало по сравнению с большей из двух величин, То или
Г, и, кроме того, если Гп <с Г (тогда Г практически не зависит от Т). В слу-
чае То •< 0 значение Т должно быть мало по сравнению с |Т0|.
183
поверхности мишени, имеем:
| <j(v)vn(v)dv	а v
- п W) 
| vn (v) dv	\v)
14.31.	I /Г -- <т /<та (<тполн прМ^нолп 0»44<ТуПр)  0,4, где <т — сечение неупругого рассеяния; оа — сечение образования промежуточного ядра.
14.32.	0,40 мм.
14.33.	Приблизительно в 2 раза.
14.34.	В 2,3 раза.
14.35.	J --- (/0,'4лг|) ехр [— on (г2 — ri)l — 5 см-’-с-1, где п — концентрация ядер углерода.
14.36.	5 эВ.
14.37.	w 1 — ехр (— on/) 1,5%, где и — концентрация ядер, о — сечение для энергии 10 эВ (оно определяется через табличные данные: о -
14.38.	w -= (o,ia oIIO.iH) П — ехр (— ап(,лцп/)] = 86%; где <тполн = опа + -+- апу, п— концентрация молекул Lil.
14.39.	Убыль числа ядер 10В со временем есть — dn - Jnadt. Интегрируя, получаем п =- п0 ехр (— Jot), где п0 — первоначальное число ядер. Относительное уменьшение эффективности счетчика \wiw -- Ап/п — 1 —ехр (— Jot) ат » Jot 2,3%.
14.40.	Из формулы /? JN <о>, где J — плотность тока нейтронов и Л' — число ядер па единицу
, RIN (ц)>---------
Здесь учтено, что ov - <%По-
14.41.	Выход реакции равен отношению скорости протекания реакции к Rn„ ( Л’о (v)vti (v) dv No0v„
плотности тока нейтронов: w ~ ------—	---------------= --------, где Л —
J	п< р >	< v >
число ядер мишени на 1 см2. Отсюда < v ) ~= 5 км/с.
14.42.	Имея в виду, что ov — onv„. получим выражение для числа протекающих в 1 с реакции: R - Л’о01'пл, где Л’ — число ядер в объеме счетчика; п — концентрация нейтронов.
а) 2-10“ см-3: б) R Ло„с„Ф «’>	2- 10’° с-1.
14.43.	Отметим символами * и величины, относящиеся к изотропному и параллельному потокам нейтронов.
Тогда скорость протекания ядерной реакции для нейтронов, падающих на 1 см2 поверхности мишени под углами (й, ft — dft) к ее нормали, dR* — — dJtonl cos ft. где о — сечение реакции; п — концентрация ядер в мише-ии; I — ее толщина: dJ„ — число нейтронов, падающих на I см2 мишени в интервале углов (ft. ft — dft). Так как dJ* =- a cos ft 2л sin ft dft. где a — константа, определяемая из условия задачи (7ц = = 2 f dJt (ft) — 2ла), то /?* — .( dRt (ft) 27|<тп/ -= 2/?(|.
14.44.	т [)п (Л% .V)] o„i'0n = 24 сут,
14.45.	а) Лмакс = ФоЛ’,1 = 5,5-107 Бк (1,5 мКи), Л’макс Фа/Л. = = 4-1010, где No— число атомов в образце;
б)	t----(I X) In (1 — АЛмакс) --= 2Т = 30 ч.
14.46.	М - (1/X) In [(</ — Л), (</ — Т]Л)] = 1,7 сут, где q ~ Фон; и — число атомов па 1 г фольги.
14.47.	А = ФА {0.6901 [I — ехр (— М/)] + 0,31<т2 [1 — ехр (— Х2()]} -= 0,8- Ю10 Бк/г (0,2 Ки г), где Л' — число атомов в 1 г меди; о,, kj и о2, л2 — сечения активации и постоянные распада соответствен ио изотопов 63Си и “®Си.
14.48.	Ф - А ехр (kt),aN0 [1 — ехр (— Хт)] -= 3-107 см-2-с~1, где Ао — число ядер в фольге.
14.49.	п кЛ’/рЛ’о<тоь'о [1 — ехр (— лт)| = 0,7-105 см-з.
14.50.	Активность при насыщении открытой фольги А — Ат + Лнт, где Лт и Лнт — активность при насыщении для тепловых и надтепловых нейтронов. Так как /?cd — Л Лнт, то
Лас -Лнт-Лт (/?cd — 1) - Azo0u0 n, (/?cd— 1) = 8мКи,г,
Где N — число ядер па 1 г фольги.
184
14.51.	а) т) — 4'x/(l + x)2, соответственно 0,89, 0,284 н 0,0167;
б)	Л = 2х (1 + и)-2 [1 + х sin2 О — cos О }/1 — х2 sin2 О] = 0,127, 0,67 и 0,87. Здесь х = 1/Л, А — массовое число рассеивающего ядра.
14.52.	а) Т — То (1 + А2 2А cos 0)/(1 + А)2;
б)	доля ^нейтронов, рассеянных в интервале углов (О, 0 + dO), есть di) = */2 sin О dO. Этим нейтронам соответствует интервал энергий dT, который находим из формулы, приведенной в предыдущем пункте. В результате dr) =- [(1 + Л)2/4Л7’0] dT. См. рис. 18, где а = (А — 1)2/(Л + I)2.
"	_	_	1 + А2
14.53.	< Т > = j Т (О) dr) (О) =	Тв = 0,68 МэВ, где Т (О) и
О	(1 “Г Л)
dr) (О) — выражения, приведенные в решении предыдущей задачи.
14.54.	г) = (64 — А2 — 1 )/8Л = 0,44, где А — массовое число ядра.
14.55.	a) dr] = sin 2OdO; б) Ar) = 0,25; в) < О > = 45°.
14.56.	а. Из векторной диаграммы им-
пульсов (см. рис. 2.1) находим для треуголь-
ника А$0:	ctT -------------------
sin (О — О)___pm 1
sin ф	p Л-}-1
_ ►
ГДе P =	° ,aT0	T0 T
л -f- 1
Рис. 18 Дальнейшее очевидно.
б.	Доля нейтронов, рассеянных в интервале углов (0х, 02) в Ц-системе:
г) х/2 Г sin О d0 = 1/2 (cosOj— cos 02).
В рассматриваемом случае 02 = л, а угол 0х связан с углом 0х соотношением, приведенным в тексте задачи. В результате г) = (А — 1)/2Л яа 0,45.
в.	По определению, <cos О > = */2 J cos О sin О d О. Подставив вместо cos О выражение из условия задачи и сделав замену х = 1 + А2 + 2А cos О, получим после интегрирования искомый результат.
SsВе	SsO
14.57.	<cosOBe0)= —-------<cosdBe) 4- —--------(cosd0) = 0,06.
BeO	BeO
14.58.	а)«По определению, <ln (T0/T)y = f In (To/T) dr) (T), где di] — вероятность того, что энергия нейтрона после однократного рассеяния лежит в интервале (Т, Т 4 dT). Подставив выражение для di) (см. решение задачи 14.52) и проинтегрировав по Т от а.Т0 до То, получим искомую формулу. При А 3> 1 величина £ « 2/4;
б)	в графите | = 0,158, в тяжелой воде
(?D Ssd+ ?o2so)/Ss полн”^'®-
14.59.	z~ In (Тд/Т); соответственно 2,2-10®, 1,2-102 и 31.
14.60.	Нейтрон, замедлившийся до скорости п, за промежуток времени dt испытывает vdi!^ соударений. Если средняя логарифмическая потеря энергии нейтрона за одно соударение равна 5, то — d In Т = 5od//Xs, и после интегрирования получим:
/ = (Xs/g) У“^Г (l/Ут?- 1/ут7)=5-10-5.
14.61.	т=ln (7'0/rT)/[3g Ss (1—(cos О))1-:2,6-1О2 см2, Е=У~ = 16 см.
7 Зак. 1896	>85
14.62.	Выделим вокруг точечного источника нейтронов тонкий сферический слой с радиусами в интервале (г, г + dr). Число нейтронов, пересекающих за 1 с заданный уровень энергии в данном слое, равно 4лг2<Дт/£. Тогда
( г2) = п ~1 J г2 qE4nr2 dr — Sr.
14.63.	Так как активность А пропорциональна плотности замедления q, то зависимость In А от г2 должна быть линейной. Построив график этой зависимости, из наклона прямой (— 1/4т) находим т= 3,1-Ю2 см2.
14.64.	Jpe3 = f <т (Т) dT/T—ft,5o0,
где о (Т) = о0 ~\/Та/Т .
14.65.	a) dw — Ss ехр (— ^isx)dx, Xs = J x dw= 1/ Ss;
6)	(x2) = 2/Ss2 = 13 см2.
14.66.	т = ka/v = 1/oSa = 15 cm, z = <3s!<3a = 1,3-103.
'	(1 — <cos 0 >)] = 2,8 cm; 6) 55 см и 33 м.
14.68.	а) Рассмотрим элементарный кольцевой слой (рис. 19) объемом dV, точки которого расположены на расстоянии г от площадки dS. Число нейтронов, рассеянных в этом слое и достигающих площадки dS, есть
dJ = (Ф ^dV) (dS cos О/4лг2) ехр (— Ssr),
где первая скобка—число рассеивающих столкновений за 1 с в объеме dV, вторая скобка — вероятность того, что нейтрон в результате рассеяния в объеме dV будет в дальнейшем двигаться по направлению к площадке dS, экспонента — вероятность того, что нейтрон пройдет расстояние г без столкновений. Отсюда:
J = !/2 Ф Ss J ехр (— Ss r) s'n cos О d ft dr = <&!$,
б) повторяя рассуждения предыдущего пункта и имея в виду, что теперь Ф = Фо + (дФ/дп)0 г cos О, получаем:
j - Ф° 1	/ дф \	_ Фо ,	1	/ дФ \
+	4 6Ss \ дп /о'	~	4	" 6Ss \ дп )0'
где J+ и J_ — число нейтронов, пересекающих площадку в 1 см2 за 1 с в положительном и отрицательном направлениях оси х. Результирующая плотность тока нейтронов:
/=J + _j_=_(l/3	(дФ/дп)0.
При анизотропном рассеянии в Л-системе вместо Ss будет Str-
14.69.	а) Прн стационарном распределении уравнение диффузии и его решение имеют вид:
ОФ"—2аФ=0, Ф = аех^-|-6е— X^L,
где L = ~^D/2a. Постоянные а и Ь находим из граничных условий: а = 0, так как Ф при х -> оо должно оставаться конечным. Для определения Ь рассмотрим плоскость, параллельную плоскости источника и расположенную на малом расстоянии х от него. Ток нейтронов через эту плоскость (см. решение предыдущей задачи) равен j = — ОдФ!дх = D (ЫL) e~x^L. При х -► 0 ток / -► п. Отсюда b = nUD. В результате Ф = (nUD) e~x/L-, 186
б)	в этом случае Ф" + (2/г) Ф' — (1/L2) Ф — О, где £2 — Dl^a. В результате подстановки х = гФ получим уравнение %" — Е-2Х = 0. Его решение:
X = а ехр (r/L) + b ехр (— r/L), нли Ф = (a/r) ехр (r/L) + (Ыг) ехр (— r/L).
Как и в предыдущем случае, а = 0. Для определения b окружим источник малой сферой радиусом г и найдем ток нейтронов через нее:
j = — ОдФ/дг = D (blг2) (r/L + 1) exp (— r/L).
При r -► 0 полный ток 4л2/ n. Отсюда b = n.AnD и Ф = (п/4лг£>) exp (— r!L) в) Ф (r > /?) == \nR2L/2D (R + £)] exp [— (r — R)/L], где L = VD/SO.
14.70.	Имея в виду, что в этом случае Ф со (1/г) ехр (— r/L) (см. решение предыдущей задачи), получим: L = (г2 — r^/ln Оуг О) = 1,6 м.
14.71.	Рассмотрим точечный источник тепловых нейтронов. Выделим вокруг него тонкий сферический слой с радиусами в интервале (г, г + dr). Число нейтронов, поглощаемых в таком слое за 1 с, есть dn = 4>Sa4nf2dr. Если интенсивность источника М, то < г2 > = f r2dn/n, где dn/n — вероятность того, что испущенный нейтрон, пройдя расстояние г, будет захвачен в слое (г, г + dr). При интегрировании следует использовать выражение для Ф (г), приведенное в решении задачи 14.69, п. б.
14.72.	wn = (1 —Р) рп — 1; (п) =2 пдап/2 да,,.. 2 zip'1-1/2 р" ' 1	1 /(1 — р).
где суммирование проводится по п от 1 до оо. При вычислении суммы в числителе использовано соотношение:
1 +2Р + ЗР2 + .. . =^(₽+0Ч-...)=^[—М-ар	ар \ 1 —р /
14.73.	Если бы ни один из п нейтронов, падающих на фольгу в 1 с с каждой стороны, не проходил сквозь нее, то на фольгу падало бы 2п нейтронов. Однако из-за многократных отражений от ядер воды число нейтронов, пересекающих фольгу за 1 с, должно быть больше, чем 2п. Пусть w — вероятность поглощения нейтрона, пересекающего фольгу. Тогда каждый из 2п нейтронов, падающих на фольгу, с вероятностью 1 — w проходит через нее и с вероятностью Р отражается обратно. Поэтому вероятность вторичного падения данного нейтрона на фольгу равна Р (1 — да), третьего Р2 (1 — да)2 и т. д. Полное число ударов о фольгу с учетом отражений от среды
М = 2п [1 + Р (1 — да) + Р2 (1 — да)2 + ...] = 2п/( 1 — Р (1 — да) ].
Имея в виду, что N/n •— 6,9 и да = pdoaN д/А, получим Р = 0,8.
14.74.	Из решения задачи 14.68 следует, что альбедо
P = J_/J , =fl4 2O -7-In®1) /fl — 2D — 1пф) , \	дп /о / \ дп /0
где D = 1/3Sjr и градиент In Ф соответствует точкам на границе раздела двух сред. С помощью этого выражения получим:
а)	р = (1 — 2D/L)/(\-\-2D/L) =0,935, где D/L- ~l/cra	(1 — (cos tj>);
6)	P=(l — a)/(l +a), где a = 2O (1 /L + 1 /R).
15.1.	а) 0,8-Ю11 кДж, 2106 кг; б) 150 МВт; в) 1,5 кг.
15.2.	З Ю18 с-1; 1,1 МВт.
15.3.	Z4A > 15,7 — 367Л-1>«.
15.4.	45.
15.5.	I-1016 лет; 4,5-107 а-распадов.
15.6.	а) 196 МэВ; б) 195 МэВ.
15.7.	Еакт “ Т 4 £св " 6,2 МэВ, где Т — кинетическая энергия нейтрона; Есв — его энергия связи в ядре 23eU.
15.8.	0,65 и 2,0 МэВ.
15.9.	4,1 б.
15.10.	90, 84 и 72%.
7*
187
15.11.	2,28, 2,07 и 2,09.
15.12.	1,33 и 1,65.
15.13.	Пусть на пластинку падает поток нейтронов, плотность которого Jo. Число нейтронов деления в 1 с в тонком слое dx площадью 1 см2, отстоящем на расстояние х от поверхности, равно vj ехр (— поах) nGfdx, где п — концентрация ядер; <та и <Ту— сечения поглощения и деления. Проинтегрировав это выражение по х от 0 до d (толщина пластинки) и приравняв результат Jn получим: d — — (l/naa) In (1 — <ra/v<ry) - 0,20 мм.
15.14.	W = QJ0 (Sf/Sa) [1—ехр (—Sad)] = 0,03 Вт/см2, где Q~200 МэВ, Sy и Sa — макроскопические сечения деления и поглощения.
15.15.	v = 1 + Мв<тв/^PuCTPu “ 2,1, где N — число ядер; <т — сечение поглощения.
15.16.	9,5%.
15.17.	Отношение числа нейтронов некоторого поколения к числу нейтронов предыдущего поколения. N --= Ю3^'-1 = 1,3- 10s, где i — число поколений.
15.18.	Число ядер, которые испытывают деление к концу «-го звена цепной реакции:
1 + k + k- + ... + kn =- (kn — l)/(& — 1) - Ml tn,
гце M — масса вещества, подвергшегося делению; т — масса ядра. Имея в виду, что п - /'ту, где t — искомый промежуток времени; Ту — длительность пробега нейтрона от момента рождения до акта деления, получим t -- 0,3 мс. При k — 1,01 время t & 0,03 мс.
15.19.	На каждый нейтрон, вызывающий деление, возникает число вторичных нейтронов, равное (2,6/2)-(0,5/М) < 1, т. е. k< 1 (N — порядка нескольких единиц).
по. +(1 — п)<т,
15.21.	а) f -	(1 _л)	+ гСТз = 0,80, где т)-доля ядер 236U в ура-
не, а <Tj, <т2 и стз — сечения поглощения 236U, 238U и углерода; б) 4 8%.
15.22.	0,74.
15.23.	k epft\ = 1 0,744 0,835-1,335 - 0,83.
15.24.	1,0-Ю12 см-з-с-1: 4,6-106 см-з.
15.25.	Скорость накопления «-активных ядер с постоянной «-распада X есть N = qw — KN, где q — число делений в единицу времени, w — выход интересующих нас «-активных ядер на деление (это и есть выход запаздывающих нейтронов иа деление). Интегрируя данное уравнение по времени от 0 до т, получаем число «-активных ядер к концу облучения. Через промежуток времени t после конца облучения число этих ядер
aw i >т\ к	ew	,
А' -^—(1 —е ?'т) е ' , w —------------—=-6 -10 4,
где А -= KN; q = Inctf, п — полное число ядер в фольге.
15.26.	т l/oSa 0,7 мс, где о - 2,2 км/с, Sa -- 6,3-10~3 см-1.
15.27.	Среднее время запаздывания
Ат -_ (S W[ т,)/(2,474 S wi) -83 мс, где т; = 7';/1п 2.
15.28.	Прирост числа нейтронов за время жизни одного поколения равен « (k — 1). Из уравнения dnldt ~ « (k — 1)/т находим л - «ое^”Ч(/т, откуда Т = 10 с.
15.29.	а) 3,4-108 кДж; б) 0,9-10® кДж; в) 2,7-10® кДж. Для урана 0,8 X X 10® кДж.
15.30.	Порядка 10® лет.
15.31.	Сложив отдельно левые и правые части уравнений реакций, получим 4р 4Не i 2е+ + 2ve. Энергетический выход этого превращения Q 4лгн — — тНе — 4лге 0,02650 а. е. и. —- 24,7 МэВ, а в расчете на моль — 2,4-10е кДж/моль.
15.32.	Имея в виду, что Ц-система взаимодействующих ядер в среднем совпадает с Л-системой и кинетическая энергия относительного движения Т Q 188
(при 108 К T ~ 10 кэВ, a Q ~ 10 4- 20 МэВ), получим: a) £n/Q « ma/(ma + + mn) = 0,8; 6) EM -+- Q2) = 0,34.
15.33.	T) - (Qdl J- Qn Li)/0,2Qdt = 6-4.
15.34.	0 '= e2//? = 0,7 МэВ.
15.35.	а. Указание: в исходной формуле для D в общем случае вместо т следует брать приведенную массу р взаимодействующих частиц и вместо Т — кинетическую энергию относительного движения Т. Дальнейшее см. в решении задачи 11.32;
б.	D » ехр (— 31,30“1В/2); соответственно 10—14 и 5-10~5.
15.36.	Соответственно 3- 10—12 и 610~4 б.
15.37.	w " il2nfQdd ~ 0,3 Вт/см3; 0 ~ 10 кэВ.
15.38.	Скорость реакции пропорциональна произведению nva, где v —• относительная скорость взаимодействующих дейтронов. Величина же nva со ехр (— Т/0) ехр (— 31,3т-1/2), где_Т и 0, кэВ (0 — температура плазмы). Это выражение имеет максимум при Тт = 6,2502/3 — 10 кэВ.
15.39.	а) т — l/zi<ow>; соответственно 6106 и 1  103 с; б) R -= 1/2п2 <от>; соответственно 0,8-10® и 5-1011 см~3-с-1; 5- 10—5 и 0,3 Вт/см3.
15.40.	a) R l/2nd <avydd+ndnt <W)dt: соответственно 1,5-10® и 1,1-1012 см-3-с-1; б) 2,2- 10-4 и 2,0 Вт/см3.
15.41.	ntlnd -= 1 — а, где а- (av)ddQdd/(т > dtQdt. При обеих температурах a<gl, поэтому п.( xt nd. Максимальная мощность
п2 (avjdt Qdt 1 , , . _
“’макс— 2 (2—а)	— 4 n~'V^dt^dt'
соответственно 4,5-10~3 и 43 Вт/см3. Вклад реакции dd пренебрежимо мал.
15.42.	Задача сводится к решению уравнения 0 ехр (300' '/3) -- 3,065 < X 109ш—3''2, где 0 выражено в кэВ, w — в Вт/см3. Методом подбора находим 0 » 3 кэВ.
15.43.	г - ЬоТЧпг <av^ddQdd, где о (в числителе) — постоянная Стефана—Больцмана. Из условия dr!dQ =- 0, где 0 = kT, получим 0т - 2,5 кэВ; Гмин-3-106 км (!).’
15.44.
15.45.
0 — 40 > 45 кэВ.
а) В стационарном случае имеем систему из двух уравнений: Wdd + ^d nt (av)dt ,
Ча nd (ov)dd ^d nt (<J»)d/.
Отсюда nt -=4/4 nd {ov)dd \<sv)dt 4-10’2 cm"3, q ---5/4 n-d (OT)dd= 1 ’ Ю12 cm 3-c-1;
6)	wnd ( <» )dd (Qdd-+-1. 2 Qdf) '^24 Вт cm3, —1,0-10l,; cm"j\____________
15.46.	Из уравнения mp x —eE - —4nne2x получим <о0 = ~^^лпег1пге. 15.47. а. См. решение задачи 9.23.
б.	Уравнение волны Е = E:le кх\ где k = 2л/1. При ы < ы0 показатель преломления п = ~\Л- — ix и k (2л/Х0) п ~ 12лх/10, где — длина волны в вакууме. В этом случае Е - £ое"2ЯК/^Х cos ы/, т. е. возникает стоячая волна с экспоненциально убывающей амплитудой.
в.	пе= лс2 те/е2 =5• 1012 см “3.
15.48.	Л'— ’/4 zid (ov)dd 1,=51011 с-1, где nd ^пе. -me c2/e4.%.
15.49.	Уравнение Пуассона в сферических координатах:
(1/г) (гф)/ = —4ле (ni—ne).
Так как пе ;ne+erf>'/0 ж п (1 +еф/0); п4 =
.--л е—e'f>/e ~ п (1—е<р/0),
189
то исходное уравнение принимает вид:
(1/г) (гф)* = а2ф, а2 = влпе2/©.
Введя новую функцию f = rtf, получим уравнение f" = а2/, решение которого /ме-®'. т. е. ф со (1/г) е-аг. Итак, ф ее (1/г) €~r/d, d= 1/а = 1/о/8лпе2.
15.50.	1,7-10-3 см; 2-10’.
15.51.	о = лг4/4Т2 =1,6- 10~2" см2.
15.52.	0мнн = j/enne’O3''2 = 6-10~з угл.с; 15.8
15.53.	а) а=(л eW) In (2/©МИн) = 1 • Ю“18 см2, 0Мин=е3 Д/в^/ 03/2;
б)	lsi= 1,'пг <т — 10 м, те; = /е;/овер = 0,5 мкс, vei= l/tei = 2< 10е с-1.
15.54.	w = 5- 10~31 пгпе "|/9е Вт/см3.
15.55.	а) Интегрируя уравнение d£\ = weidt с учетом того, что £г = = з/2 гцв,, получаем: 0, = 0е [1 — ехр (— ап//03/2)], где а = 7,09-10-13; п — в см-3: / -вс; 0е — в кэВ. Отсюда t х 1,6 мс;
б)	задача сводится к интегрированию уравнения dEe = — weidt с учетом того, что Ее == 3/„ пе0е и dQt = — dQe, так как 0е + 0г = const = 20, где 0 — средняя температура плазмы, равная в нашем случае 0ео/2. Введя переменную у = ~1/0е'0, получим:
у 03/2 f у* dy an J у2—1 Ус
В3/2 ап
2
у 1	у3 г
In---—у——	—0,8 мс,
У~{	3 к
где а = 7,09- Ю-13; 0 — в кэВ; п — в см-з.
15.56.	Сила Лоренца, действующая на 1 см2 цилиндрического слоя (г, г — dr), равна = dF/dS = (1/с) jrB'rdr. Имея в виду, что Br = 21г/сг, где 1Г — сила тока внутри цилиндра радиусом г, и что /г = dIT/2nrdr, получим: = Irdlrlnc?r2. Интегрируя это выражение с учетом того, что переменную г можно заменить на г0, найдем: р — 7£/2лс2г2 = В§/8л.
15.57.	3,1- 1015 см-3; 10 МПа (1,0-102 атм); 2,7 Вт/см3.
15.58.	-"'з In (r^ri).
15.59.	а) Из условия равенства магнитных давлений на внутренней и внешней поверхностях плазменного слоя В2 = Bi — В2 и 11 = 272;
б) Zj = 4сг01/лп0 = 5,4-106 А.
15.60.	а) Исходя из основного уравнения Vp = [jB]/c, имеем: — др/дг = — jB^/c. где В^ = 2/т1сг, 1Г — сила тока внутри цилиндра/ радиусом г. Имея в виду, что / -- dlr 2nrdr, получим: —r2dp = Irdr/rt<P. Интегрируя это уравнение (левую часть—по частям) и учитывая, чтор (г0)== 0, найдем <р>=/§/2лс2г§;
б)	так как р = 2п0, то 0 — I^/At^N = 2 кэВ.
15.61.	а) Задача сводится к интегрированию уравнения — др/дг = jB/c, где р = 2п0, В — 2rtrj/c. При этом необходимо учесть, что 0 = I2/4<?N-, Среднее значение <п2> = 4/3 (А/лг§)2.
б)	искомая сила тока 1~ 1,3-106 А. При расчете использована формула “’рад = 4,8 • 10-31 < п2 > О^эв Вт/см3, где значение < п2 > взято из п. а. Соответствующая температура равна 5 кэВ.
15.62.	Имея в виду, что В = 4nl/cl, п = 2n0 (г0/г)2 — концентрация ядер в момент максимального сжатия и В2/8л = 2п0, получим:
0 as л (rllclro)2l2na ~ 10 кэВ.
15.63.	t ~ г§4ло (O)Zc2 ~ 1 мс, где 0 = I^/t&N = 0,39 кэВ.
15.64.	Около 0,8 мс.
15.65.	В месте перетяжки, где радиус шнура уменьшается иа Аг, магнитное поле возрастает на ABZ 2В2Аг/г, так как вследствие вмороженности поля В2 его магнитный поток не изменится. Собственное магнитное поле В{ тока I также возрастает в этом месте на АВ; —- В, Аг/r. При этом газокииетическое
190
давление не изменяется, так как плазма может свободно вытекать в обе стороны из этой области. Для компенсации неустойчивости необходимо, чтобы Д (В1/8л + р) > ДВ//8л, откуда В, < 1/2*Bz, Bz < “|/2 Чс = 14 кГс.
15.67.	Обозначим буквой f суммарную силу растяжения на единицу длины витка. Тогда 2лЯ/Д7? = Д (L72)/2c2 4- рДУ = 2л2г2ДЯ, р = 12/2лс2г2 (из условия равновесия по малому радиусу г). Отсюда f = [In (87?/r) — i/2] l2!c2R. В рассматриваемом случае можно пренебречь изменением f, так как R меняется мало. Поэтому R At const и t ~ (2a/R)^2 = (2лг2ар//)1/2 = 0,7 мкс, где р — плотность плазмы.
15.68.	В решении предыдущей задачи найдено выражение для растягивающей силы f на единицу длины витка. Эта сила должна уравновешиваться силой Ампера, действующей на ток 1 со стороны поля Bz, на единицу длины витка она равна f = IBzlc. В результате Bz — [In (8/?/г) — 1] 1/cR = 0,11 кГс.
15.69.	Из условия 2л7? 2лгВ(р/В/, где = 21/сг, получим: 7^<т2В /2/?= = 2 кА. ___________________
16.1.	р= ~^Т (Т + 2m). Соответственно 1,7; 1,1 и 1,0 ГэВ/с.
16.2.	Воспользовавшись инвариантностью величины Е2 — р2, запишем: (Т -I- 2m)2 — р2 = [2 (Т 4- т)]2, где левая часть равенства записана в Л-систе-ме, а правая —в Ц-системе. Имея в виду, что р2 = Т (Т + 2m), получим:
T=2m(Vl -т-Т 2m — 1), р = 1/т772, рс= "|/ Т/(Т+2т) .
16.3.	Из выражения Е2 — р2 = inv имеем: (Т' + 2m)2 — р2 = [2 (Т + + т)]2 н Т' = 2Т (Т4- 2m)/m = 2,0-103 ГэВ.
16.4.	a) 7’='|/(m1-!-m2)2+2m2 Т — (т1-)-т2);
~ | m2T(T + 2mi) Г/2 о) р= I--------------
[('П1+т2)2 + 2т2 Т _
£1,2 =1^ Р2 + л1?,2 .
16.5.	— 1/i Г (71 ~Ь2т2	т2-|-Т).
16.6.	Из формулы для рх и равенства ру = ру (см. рис. 16.1) следует формула (16.3) для tg0.	_
16.7.	а. Из выражения для tg О следует:
Л/~ 1 —Р2 sin О	1/ 1 —Р2 sin(n—0)
tg 01 = _1--------------, tg02 = l--------------.
cos'O + Pefj/p	Cos(n — 0) + pc E2/p
Остается учесть, что p/Er = p/E2 = Pi,2 = Pc = V T!(T + 2m).
б.	Из формулы etg 0t etg 02 = а, где a = 1 + Tl2m, получим 0 = = 0i + 02 =	4- arctg (a/ctg 0X). Из условия d0/d0j = 0 находим
etg 0j = ~\/a, следовательно, и etg 02 = ~\/a. Таким образом, угол 0 минимален при симметричном разлете частиц (если массы одинаковы): 0Х = 02 = = бмин/2. Итак, etg (0Мин'2) =1/1-4 т/2т, откуда 0МИн = 53°.
в.	Т= 1,37 ГэВ, 71= 0,87 ГэВ, Т2 = 0,50 ГэВ.
16.8.	Из законов сохранения энергии и импульса имеем:
7’ = 7’1 + 7’2, p2=p2 + p2-2pPl cos 0j
где Тир — кинетическая энергия и импульс налетающей частицы. Имея в виду, что р=1/Т’/(7’ + 2тг), выразим cos 0t через 7\. Из условия d cos 01/d7’i = =0 получим значение Ti, отвечающее максимуму угла 0Х. Подставив это значение в выражение для cos 0Ь найдем искомое соотношение.
16.9.	Те = 2me Т (Т + 2m )/[(тц + те)2 + 2теТ] = 2,8 МэВ.
191
16.10.	а) Из выражения для tg О следует:
tg О =	sin #/(cos"d - 0С Ё!р) =	tg (S/2),
так как ~р!Ё = 0С. Остается учесть, что 0С = Д/ТЦТ + 2m);
----	~ —------- d cos О
б)	так как о (О) sin О da = о (&) sin О da, о (О) = а (О) ---— Bu-
ri cos О
разив с помощью формулы из предыдущего пункта cos О через cos О, найдем производную d cos а/d cos О и подставим в выражение для о (О);
в)	вычислим о (О), соответствующее углам и О2: 5,5 и 3,2 мб/ср. Отсюда видно, что в Ц-снстеме рассеяние не изотропно.
16.11.	а. Из условия о (Г) dT = о (О) riQ, где Т — кинетическая энергия рассеянного протона, dQ — элементарный телесный угол в Ц-системе, следует, что о (Т) = ~о (ft) dQ/dT. Из преобразований (16.3) имеем:
dT = dE = dE	0ср 7;
dQ dQ 2pd cos О 2л “|/ 1 —02 4л
Здесь принято во внимание, что 0С = ~^Т0/(Т0 + 2m) и р = '^/т7’0/2.
б.	dtt'/dT (d(»'dQ)/(dQ/dT)--1Т0 - const. Здесь учтено, что при изотропном рассеянии в Ц-системе относительное число протонов, рассеянных в телесном угле dQ, равно dw -- dQ/4n.
16.12.	cos 0 = (l/2n) [(1	n)2 T/(T + 2me) — 1 — n2], 0 = 120°.
16.13.	o(Ev) = да/дЕу = (до/dQ) (dQ/dEy) = 2ло (0) cos t>|, где dQ — элементарный телесный угол в Ц-системе. Из формулы = (£? + 0ср? cos О)/ |/ 1 — ₽ с получим дЕу/д cos а = $сру1\^ 1—0? = pH. Здесь учтено, что 0С = р/(Ее + те) и ~р = Ёу = Ее = те/]/1 — 0с . В результате о (Еу) = = 4 лег (а)/р.
16.14.	£пОр — 0,32 ГэВ (см. решение задачи 12.62).
16.15.	Воспользовавшись инвариантностью Е2 — р2, запишем это выражение в Л- н Ц-системах при пороговом значении энергии частицы т:
(Ттп пор +т-|-ЛЦ2 Pmnop = (S mi)2,
где pin пор Tm IIOp (Tm пор 4 2т). Отсюда находим искомое выражение.
16.	16. 1) 0,20 ГэВ; 2) 0,14 ГэВ; 3) 0,78 ГэВ; 4) 0,91 ГэВ; 5) 1,38 ГэВ; 6) 1,80 ГэВ; 7) бтр -- 5,63 ГэВ: 8) 7,84 ГэВ.
16.17.	а) 1,36 МэВ; б) 197 МэВ.
16.18.	а) Из условия равенства полных энергий в Ц-системе для обоих процессов запишем, воспользовавшись инвариантностью Е2 — р2'.
(ma-[-mA +-Та)2—Та (Ta-i-2ma) (mb-i~тв-\-Ть)2—Ть (Tb+2mb). Отсюда Ть -- (Та - Тапор)
б) Тп- йю — тя (1 4- тя'2тр) — 50 МэВ.
16.19.	Из выражения для sin 0Макс> гДе М = ~l/2m (Т 4 2т), находим ^макс ~ Ю,5“.
16.20.	Воспользовавшись инвариантностью Е2 — р2, получим: М — — (тр 4 тя)2 4 2трТ. Соответственно 1,24, 1,51 и 1,69 ГэВ.
16.21.	19,5 МэВ, 193 МэВ/с.
16.22.	52,4 МэВ, 53 МэВ/с.
16.23.	Еа - тЛ — (Q 4~ еПр + тп) = 2,8 МэВ.
192
16.24.	tg =£v /)ЛТл (Т„ + 2тя) , где
£v =1/2(^-тц)/(тл + Гл)- Отсюда 10°.
16.25.	а) Из законов сохранения энергии и импульса находим: sin (0/2) = = 1/гшя/1/^1^2. гДе £1 и Е2 — энергии у-квантов. Отсюда видно, что 0МИН будет при Ei = Е2 = (тп + Тя)/2 = тл. Следовательно, 0мин = 60°;
б)	при 0 = л энергия одного кваита будет максимальной, а другого — минимальной. В этом случае sin (зт/2) = 1/2тя/'|/£'1 (Е — £i), где Е — полная энергия л-мезона. Отсюда:
£ = ’/2 ря + Гя± ]Лтя(Гя+2тя)] =252 и 18,1 МэВ.
16.26.	а) Т = (тк — 2тл ) тк /2тл = 0,42 ГэВ.
б)	cos 0 = 2Т (Т + 2wi/s.)/[(7’ + гп^)2 — 4тп1 — 1, откуда 0 = 103°.
16.27.	Из законов сохранения энергии и импульса получим: m2=m2 -j-m2 — 2	+р| ) (m2 + p^)—pz pncos Оj.
Отсюда т = 0,94 ГэВ (нейтрон), Q= 0,11 ГэВ.
16.28.	Так как 0 =/= л, то распад произошел на лету. Из законов сохранения энергии и импульса получим:
т2 = т2 + т2л + 2	(т2 + р2) (т2л+ р2л) -рррясоз0 ].
Отсюда т = 1115 МэВ (Л — гиперон).
16.29.	Указание-, в Ц-системе М = Е =	+ р1 + V mf + р2.
16.30.	Исходим из соотношений:
Pix —(Pix + P^i У1/1 Р2 > Piy—Piy-
Имея в виду, что р\х + р\у = р2, получим уравнение эллипса:
Piy/b2 + (Pix—«i)2/a2=l, где b = py а -p/Vl—Р2 , ai = £i Р/1—Р2 =Ej f/b.
Фокусное расстояние f — ]/а2 — Ь2 = рР/"|/1 — Р2. Отрезок <ха = рм — а.г — = Рм — (М — Ег) fib — EJ/b. Нетрудно убедиться, что > f и <х2 > /, где знак равенства — только для частиц с нулевой массой покоя.
16.31.	а) рл = "^/Зшя, Р = "|/3/2, р = т^/2. Параметры эллипса: а = = 25 = ря/Д/3, «j = <х2 = f = ря/2;
б)	рл = тл 1/5/2, Р = "|/5/3, р — (тп — /Пц)/2тя = 0,19ря. Параметры эллипса: b = 0,19ря, а = 0,29ря, f = 0,21ря, av = f;
в)	этот случай можно рассматривать как распад частицы с массой покоя, равной полной энергии взаимодействующих частиц в Ц-системе: М = Е = = 1/(2 тр)2 + 2m.pT = 1/бтр, рр = l/3mp. Параметры эллипса: Ь = =рр/У&, а = рр/2, f = рр/2"|/з,	= <х2 = а; _	_
г)	аналогично предыдущему случаю имеем: М = Е = 1/11 тр, Pd = 1^5fnp. Параметры эллипса: b = pd/l/lT, а = 4pd/U, f = Pd 1/5/11, ар = а;
Д) b = 0,224рр, а = 0,275рр, f = 0,1589рр, а„ = 0,1685рр.
16.32.	а) Около 20°; б) полагая sin Омакс = •> получаем 7’я	> (тл —
— "гц)2/2т^ — 5,5 МэВ.
193
16.33.	а. Из формул р cos О = (р cos О — $Е)/р sin и р sin ft — = р sin О (см. рнс. 16.1) имеем: tg О = \ 1 — р2 sin ft/(cos О — Р), где учтено, что Е!р = 1, так как у нейтрино масса покоя равна нулю. Дальнейшее очевидно.
---	_ _	— ~ d cos О
б.	Так как о (6) sin О d = о (ft) sin 6 di), то <т (О) = <т (О) —-тг.
'	'	' '	' ' d cos и
Остается найтн производную с помощью формулы, приведенной в п. «а».
в.	w = (1 + Р)/2 = 0,93.
16.34.	а. Узкий максимум — каналу (1) реакции, широкий — каналу (2).
б.	Пренебрегая импульсом п~ -мезона, запишем сохранения полной энергии и импульса для канала (1): тп + тр = Еп + £?, рп = ру. Отсюда тл = =	+ Еу — тр = 0,14 ГэВ.
в.	Из характера спектра у-квантов, возникающих при распаде л°-мезона (широкий максимум), следует, что л°-мезоны распадаются на лету (иначе испускались бы моноэнергетнческне у-кванты). Из законов сохранения энергии и импульса следует, что тл = 2~\/Ei Е2 = 135 МэВ.
16.35.	Если процесс идет через связанное состояние р (в две стадии), то в системе отсчета, связанной с р-частицей, масса покоя р-частицы равна сумме полных энергий частиц, на которые она распадается:
£о = £я+ +Ёя-=Ёгр =Мр , Р = ря+ + ря_=О.
Воспользовавшись инвариантностью величины Е2 — р1 при переходе от Ц- к Л-системе, имеем для л-мезонов: Е2 — р2 = Е2, где Е = Ел+ + Еп_, Р = 1Рл+ + Ря-1-
Если бы реакция шла только через связанное состояние, то, рассматривая много случаев и определяя каждый раз Е2 — р2, мы получили бы одно и то же значение этой величины. Если же реакция идет частично через связанное состояние, то в распределении числа случаев по различным значениям величины Е2 — р2 мы получим максимум, свидетельствующий о наличии резонанса — связанного состояния.
16.36.	Воспользовавшись инвариантиостью Е2—р2, найдем полную энергию взаимодействующих частиц в Ц-системе: Е — 1(тк + тр)2 + 2трТкГ . Полная энергия резонанса (У*-частицы) в Ц-системе равна EY = Е — Еп = = Е - (Тп + шя) н Му = (£2 - р^)'/2 = 1,38 ГэВ, где ~р2 = 72 = 7Я X X (Тп + 2шя). Энергия распада равна 125 МэВ.
16.37.	а) т0 = т Д/1 — Р2 =	+ Т) = 2,2 мкс;
б) т0 = / "|/1—Р2/Рс = 1тл!рс = 25 нс.
16.38.	w = 1 — ехр (— th) = 0,43, где t — время пролета, т — среднее время жизни движущегося мезона.
16.39.	Из условия = <хр.я + (1 — а) }тя, где а — доля времени пребывания протона в состоянии «идеальный протон», находим а » 2/3. Здесь учтено, что Ня/Ня = гпр/тл.
16.40.	2зя + 1 = «/3 (оРР/ом) (рр/р^)2 = 1,05, откуда зя = 0. Здесь рр (импульс протона в Ц-системе) находим с помощью инварианта Е2 — р1 при переходе из Л- в Ц-систему; р2 = трТр!2. Импульс л-мезона в Ц-системе в обратном процессе можно определить из (16.5), рассматривая этот процесс как распад системы с массой покоя М, равной полной энергии End взаимодействующих частиц в Ц-системе. В соответствии с принципом детального равновесия Е^ = ЕРр, поэтому М = Ерр = V Ерр — р2 = V2тр (Тр + 2тр).
194
16.41.	Для у-кванта 2s? + 1 — 2 в соответствии с двумя возможными поляризациями, поэтому <тяр = 2ovp (р?/ря)1 2 = 0,6 мб. Здесь ру находим с помощью инварианта Е2 — р'2, импульс ря в обратном процессе — из условия равенства полных энергий в обоих процессах в Ц-системе (Еур = Елр):
тР	(ЪпрЕу-т*яу-4т*т*я
«2  Г й ПГ “  ' '  ............ 1
тр+ v	4mp (mp + 2£?)
16.42.	Запрещены реакции 1, 3, 5 и 6.
16.43.	Запрещены реакции 2 и 6.
16.44.	Да, поскольку к слабым взаимодействиям относятся все процессы с участием нейтрино, а также процессы, в которых странность S не сохраняется.
16.45.	а) Канал (2) —энергетически; б) канал (1), так как |AS| = 2
т	пп	рр	пр	л+р	Л р	Л°р	л+п	л п	л’п
Tz	—1	+1	0	+3/2	-1/2	+ 1/2	+ 1/2	-3/2	— 1/2
т	1	1	1; 0	3/2	3/2; 1/2	3/2; 1/2	3/2; 1/2	3/2	3/2; 1/2
16.47.	а) Система может иметь Т = 1 или 0. Для 3Р : (— 1)2+*+г = — 1, Т = 1; для 3D : (—1)2+1 + г = —1; Т = 0.
б)	система может иметь Т = 2 или 1 (Т = 0 исключено, так как Tz = -I- 1). Для 2Р : (— 1)‘+°+7’ = + 1, Т = 1. Для Ч) : (— 1)2+°+г = + 1, Т = 2;
б)	здесь Т = 0, 1 и 2. В ^-состояниях Т = 1; в ^-состояниях Т = 2 и 0.
16.48. а) Выпишем все возможные реакции этого типа:
	л+	л	л"
1) рр—>-л+л~,	1') П П—>-Л-Л+ . . Oj	2	2	—
2) рр—>л°л°,	2') пп—>л°л° . . . <т2	—	—	4
3) рр—>л_л0,	3') пр->л+л° . . . о3	1	1	2
Все эти реакции имеют три различных сечения, Oj, о2 и о3. Сечения процессов 1 и Г равны вследствие зарядовой симметрии. Аналогично равны сечения о2 процессов 2 и 2' и сечения о3 процессов 3 н 3'.
Составим таблицу, в которую выпишем числа а, возникающих пионов каждого знака в реакциях с разными сечениями Ст;. Полное число пионов каждого знака равно сумме Из условия неполяризации возникающих частиц числа пионов каждого знака должны быть равны между собой, отсюда
2ot + 1 сг3 = 2<Т1 + 1сг3 = 4о2 + 2о3 или 2ot = 4сг2 + а3;
б)	в данном случае, как нетрудно убедиться, рассмотрение прямых реакций не позволяет получить искомое соотношение. Поэтому, выписав все реакции этого типа, составим таблицу для обратных процессов:
1) л+п->АК+,
2) л» р^АК+,
л p —	. ,о1
л°п —>Л№ . . ,о2
19 5
Из условия отсутствия поляризации для обратных процессов с помощью этой таблицы получим = 2а2;
в) в данном случае, выписав все реакции этого типа, необходимо составить таблицу для прямых и обратных процессов:
				2+	2	2»	л+	л	31°
1) л+	к+,	л“ п -	..		1	1	—	1	1		
2) л» р S» К+ ,	л° п —	2°	•	—	—	2	—	—	2
3) л°р—>S+ К°,	л° п —	► 2~К+ .	 стз	1	1	—	—	—	9
4) л-р->2“К+,	л+ п-	-> 2+ №.	• ®4	1	1	—	1	1	—
5) л” р —>-S° /(о t	л+п -	>S0 к+ .	<7,	—	—	2	1	1	—
Из условия отсутствия поляризации для прямых и обратных процессов получим: <Т1 + <г3 +	= 2 (<г2 + <т5),	-j- <т4 + <т6 = 2 (<т2 + ст3). отсюда
<т3 =~ СТ1 + СТ4 — 2о2 ~ стз>
г)	полагая, что т-частицы изотопическн неполяризованы, выпишем все возможные реакции распада данного типа и составим соответствующую таблицу для этих процессов:
1)	Т+—>-л+Л°Л°, Т“—>Л^Л°Л° . . .W!
2)	т_—>л~л+л_, т+—>л+л"л+ . . .ш2
3)	т° —> л° л° л«.............w3
4)	т° —> л° л“ л+.............wt
л+	Л	л»
1 3 1	1 3 1	4 3 1
Отсюда ffi'j + 3®2 +	= 4ш1-|-Зш3 + t»4, или ш4 + t»3 = w2;
д)	выпишем мыслимые каналы распада ш°-частицы на три пиоиа с указанием вероятности каждого и составим соответствующую таблицу:
л“
^л° л+ л ^Зл°....................
w2
1	1	1
—	—	3
Из условия отсутствия поляризации возникающих пионов получим	+
+ Зш2, отсюда ш2 = 0.
16.49	. а) и б): ДТг = 0 и AS = 0, следовательно, взаимодействие сильное, а для него АТ = 0;
в)	изоспин системы (л°л+) Т равен 2 и 1. Из обобщенного принципа Паули следует, что (— l)z+s+r = (— 1/+г = + 1. Согласно закону сохранения момента импульса, I должно быть равно нулю. Отсюда (— 1)Г = + 1, 7=2. Итак, ДТ = 3/2, ДТг = 1/2;
г)	проекция изоспииа системы 2л° Тг=0. Из возможных значений изоспина (2, 1 и 0) реализуется только 0 и 2, так как согласно обобщенному принципу Паули (— 1)г+°+7’ =4-1. Из закона сохранения момента импульса следует, что I — 0. Отсюда Т должно быть четным, т. е.Оили 2. Итак, ДТ равно 1/2 или 3/2.
196
16.50	. Из условия (Тл — TN| С Т < Тл + TN, где Тл и TN известны, находим Т = 1/2 и 3/2; S = S„ + SN = 0; В = 1; 1 = 1 ± 1/2 = 1/2 и 3/2; Р = PN(~ 1)'= + 1-
16.51	. Из законов сохранения четности Р и момента импульса имеем: pnpd (— 1)1л = Рп(—)1п, отсюда Рл = (—1)/п’, Sn + sd += 2sn +/п, отсюда 1 = sn + sn, -|-/п .
Если бы нейтроны образовались в s-состоянии (/п—0), то в соответствии с принципом Паули они должны иметь противоположные спины, но в этом случае полный момент будет равен 0, что невозможно. Если 1п — 1 (p-состояние), то закон сохранения момента импульса выполняется: 1 = '/а — V2 + 1. Другие значения 1п не годятся. Отсюда Рл = (— 1) п = — 1.
16.52	. а. Из обобщенного принципа Паули следует, что (— i)z+°+7' = = + 1. Имея в виду, кроме того, закон сохранения изоспина в сильных взаимодействиях, находим Т = 1 и /, равное 1, 3, 5, ... Из закона сохранения момента импульса имеем для спина р-частицы Ip = I = 1, 3, 5, ... Эксперимент дает '₽ = L
б.	р+ -> л+ + л°; р° -> л+ + л-; р- -> л-------Н л°. Распад р° -> 2л° за-
прещен, так как для этого / должно быть четным (симметричная волновая функция вследствие неразличимости частиц); но / не может быть четным вследствие закона сохранения момента импульса (для р-частицы спин, как показано в предыдущем пункте, нечетный, точнее, Ip — 1).
16.53	. a) (uud), (add), (uus), (dds), (ass), (dss);
6)	(ud), (ud), (us), (us), (ds).
16.54	. Магнитные моменты кварков и и d, из которых образованы нейтрон п (udd) и протон р (uud), есть Цх = 2/3Ц0 и |12 — — 1/3Цо> где р0 — некоторая постоянная. Учитывая вероятность возможных состояний, находим магнитные моменты нейтрона и протона (в единицах р0):
Рп = 2/з (- У - >/3 - 1/3) + 1/3 (2/3 - >/3 + !/3) = - 2/3;
Рр = 2/з (% + 2/3	V3) ~ V3 (*/s - 2/3 - 1/3) = 1.
Отсюда рп/рр = —2/3 = —0,667 (экспериментальное значение — 0,685).
16.55	. а) Мезоны с С = + 1 : (си)°, (cd)+, (с$)+; мезоны с С = —1: (~си)°, (cd)~, (cs)-;
б)	барионы с С = 1: (csd)°, (csu)+, (cdu)+, (css)0, (cdd)°, (cuu)++; барионы c C= 2: (ccs)+, (ccd)+, (ccu)+ + ; барион с C = 3: (ccc)++.
17.1	. T = i/2m (9el2E/2m)2/3 = 18 эВ.
17.2	. Проинтегрировав релятивистское уравнение динамики, получим: v — ст]/ \ 1 + т]2/2, где т] = eElmc. Искомая энергия Т — тс2 (~\/1 + т]2т2 — 1) = = 2,5 МэВ; 2,5 м.
17.3	. а) Е = 4 (Т/ех) sin2 a0 (ylx — etg <х0) = 0,31 кВ/см;
б)’etg <х0 = 2у!х — etg a, a0 = 103°, Е — 0,22 кВ/см;
в)	t2 = 2 (mr\/E) (1 ± ]/1 — (х2 + у2)/т]2), где т] = у + 2Т/еЕ\ отсюда t = 0,27 или 0,10 мкс.
17.4.	а) tg а = еЕа!2Т, a « 6°, 6 = (a/2 -f- b) tg a — 2,5 cm;
6) tg a = (eEa2/2m) (m/2T)3/2, a « 3°, 6 = (a/3 4- b) tg a = 1,2 cm;
b) tg a = (eE0/mv(i>) [1 — cos <oa/v], a = 7°, 6 = (eE0/ma>2) (сот — sin <or) + + b tg a = 2,8 см, где v — начальная скорость, ш = 2nv, т = a/v.
17.5.	e/m = 2 (v2 — Vj)2 l2/V = 5-1017 СГСЭ/г.
17.6.	Tp = 1,2 МэВ, Te = me2 (У 1 + (epB/mc2)2 — 1) = 1,1 МэВ.
17.7.	sin a = eBa/c~^2mT, a — 7°, 6 = (v/a>) (1 — tj) + a>ab/vr\, где т] — = У1 — (aa>/v)2, <0= eB/mc. В нашем случае (ао/и)2	1, поэтому
197
17.8.	а) Аг = (2ли/ш) cos а = 8 см;
б)	г = 2р |sin (<р/2)| = 1,5 см. Здесь v — скорость; <о = еВ/тс-, р = (vl tn) X X sin а; <р = tol/v cos а.
17.9.	a) elm = 8n2c2V7/2 (Вг — Bj)2 = 5,3 -1017 СГСЭ/г;
б)	Вмин =32 Гс. _________________________
17.10.	Т = тс2 [~[/1 + (еВ1/2п.тс2 cos а)2 — 1] = 0,24 МэВ.
17.11.	a) Т = тс2 [Д/1 4- (Z2 4- л2^2) (еВ/2лтс2)2 — 1] = 0,32 МэВ;
2лп	z Т (Т-)-2тс2)	|335Гс при п—1.
el |/	1-J-(плТ?//)2	\б42 Гс при п = 3;
tg а = nn.R/1, п = 1, 3, 5, ...; 25 н 55°.
17.12.	а) бх/бЛ = х/2Л = 0,85 мм/а. е. м.;
б) 6х/6Т = [(Т + тс2)!Т (Т -4- 2тс2)] х — 0,3 мм/кэВ.
17.13.	ба/бЛ = sin ф/2Л = 0,62 угл. град/а. е. м.
17.14.	а) Для частицы, которая движется по траектории, отличной от круговой, г — rtf2 — — еЕ (r)/m. Имея в виду, что г2ф = const = г2ф0 и <р0 — = v cos а/г0 ж v/rQ = ш0, ибо 1, получим ф = (ra!r)2 <оо. Теперь подставим это выражение в исходное уравнение движения.
Введем параметр 6	1, характеризующий отклонение г от г0, по формуле
г = ra (1 4- 6). После соответствующих преобразований с учетом 6 < 1 получим Е = Еп (1 — 6) и б-:- 2<ojj6 = 0, где Е„ — напряженность поля при г = г0, <оо = v/r0 -- ~VeE№/mr0. Решение этого дифференциального уравнения есть б ---= 6m sin (срД/2), <р = ш0/, где учтено, что б (0) = 0. Из требования б (Т) =0 найдем: V —- л/"|/2;
б)	рассмотрим два иона, вылетающих из точки А (см. рис. 17.5) по нормали к радиус-вектору со скоростями о и v (1 + т]), где т] 1. Если первый ион движется по окружности радиусом г(| и для него r2tf = rov, то для второго иона г2Ф = rov (1 4- т]). Подставив это выражение в исходное уравнение движения и учитывая, что г = r0 (1 4- б), где б <§; 1, получим:
б 4~ 2<о^б = 2со§т), б -= т] (1 — cos ~l^2(f), <р = <оо/.
При ф = л/Д/2 величина б = 2т], или Дг/г0 = 2&v/v.
17.15.	а) Уравнение движения частицы в горизонтальной плоскости:
г — и2/г = — (ev/mc) В (г), е > 0.
Здесь учтено, что Bz = — В (г) и, кроме того, что при движении вблизи равновесной [траектории г v, поэтому rtf v.
Введем параметр б < 1, характеризующий отклонение г от г0, по формуле г -- r0 (1 4 б). Тогда г = гоб и В (г) = Во (1 — пб), где Во — индукция поля при г ~ г„. После подстановки этих выражений в исходное уравнение движения с учетом б <§; 1 получим:
б 4~	(1 — п) б = 0, <оо = v/ra = еВ0/тс.
Решение этого уравнения: б = бт sin (<р Д/1 — п), <р = а>0(, где учтено начальное условие б (0) = 0. Из требования б (Ч7) = 0 найдем, что Т = л/Д/1 — п;
б)	уравнение движения частицы в вертикальном направлении имеет вид: г = — (ev/mc) Вг, где учтено, что rtf At v. При малом отклонении г от плоскости симметрии Br = (dBr/dz)0 г. Так как rot В = 0, то дВг/дг = dBjdr «к гк dB/дг и Вг = п (В0/г0) г.
Поэтому уравнение движения примет вид:
г-|-п<о§ г = 0, a0 = v/r0 = eB0/mc.
Его решение: г = zm sin (ф"|/п), ф = Видно, что при п = 1/2 оба смещения (б и г) обращаются в нуль, когда ф = лД/2;
198
в)	решение аналогично решению, приведенному в п. б предыдущей задачи Полагая Ац/о = т], получим:
6 + (1 — п) <о§6 = cogr), 6 = (1 — cos <р V1 — «) Л/(1 — п), <р = соо/.
При п = 1/2 угол <р = л~|/2 и 6 = 4т], или Аг/г0 = 4Ао/о.
17.16.	Т = i/2 (Е/В)2/тс2 = 42 кэВ.
17.17.	a) v = с (Е/В) (rjr2), elm = (с2 El В2 ) (rjr^, где E = V!t\ In (RjRj,)
6)	v = cEIB, elm = 2 (c2E/B2) 6/(62 + Z2).
17.18.	Bnp = 1/8ЙГЙ7ё cr2/(r22 — r2) = 48 Гс.
17.19.	Vnp = 2 (el2/me2) In2 (r2/ri) = 4 В.
17.20.	Уравнения движения частицы:
х=—mz, у= a; г = мх.
где а = eElm, <о = eBlmc. Их решения:
х — (о/ш) sin со/; у = at2l2;
17.21.	tg l/(e/m) (у/А) = z/l, где А — X (z/Z)2.
17.22.	а) Уравнения движения частицы:
х = ыу, у = а—ых, где <о = еВ/тс, а = еЕ/т. Их решения:
х --- (а/ш2) (со/ — sin Mt), у — (а! со3) (1 — cos со/).
z = (о/ш) (1 — cos со/).
2c2 £7 В2. При z < I у = A (mle) X
Это уравнение циклоиды (рнс. 20). Движения частицы можно представить как движение точки на ободе круга радиусом р = а/<о2, катящегося без скольжения вдоль оси х так, что его центр перемещается со скоростью v = EIB;
б)	I — 8а/<о2; в) (х) = а/м.
17.23.
а Г	/	<ох0 \ . Йо	,.
х -= — Mt — 11 — --------- sin Mt + --------(1 —cos Mt) ;
<o2	\ a J	a
a
COUn	(	<0*0 1
	sin Mt + I 1 —- (1 — cos Mt) a------------------------------\ a /
где a = eElm, м — eBlmc.
a)	x = (а/м2) (Mt — 1/2 sin co/), у — (а/2м2) (1 — cos co/);
6)	x — (а/ш2) (Mt — 2 sin <o/), у = 2 (а/со2) (1 — cos Mt);
в)	x = (а/м2) (1 + Mt — sin Mt — cos Mt), у = (а!м2) (1 -|- sin Mt — cos Mt);
r) x — (а/w2) (1 -j- Mt — cos co/), у = (alto2) sin Mt.
Соответствующие траектории (трохоиды) показаны на рис. 21.
199
17.24.	Из законов движения, полученных в решении предыдущей задачи, следует, что уравнение у (<ot) = 0 имеет два типа корней, один из которых зависит от начальных условий, а другой не зависит. Нас интересует последний, он равен <atn = 2лп, п — целое число. Для п = 1 имеем: Xj = (ala?) a>tr = = 2л (а!со2).
17.25.	х = (а/2а?) (sin ш/ — a>t cos a>t), у= (а/2а?) a>t sin ш/, где а = = еЕ0/т. Траектория имеет вид раскручивающейся спирали.
17.26.	а т = 2л (Т1-)-тс2)/сеВ; 7,3-10~10н 6,6-10-8 с; г= Д/Т (Г + 2тс2)/еВ; 3,5 и 46 см;
б)	Т = тс2 (У] + (егВ/тс2)2 — 1); 2,9 МэВ и 5,9 кэВ.
17.27.	а) |£| = Ф/2пгс = 0,32 В/см, Т = пеФ'/с = 25 МэВ;
б)	I — (У 1 — а2т2 — 1) с/а = 0,9-103 км, где а = еЕ/тс (см. решение задачи 17.2), Т = еЕ1 = 28 МэВ.
17.28.	а) Т - тс2 (У I + (егВт/тс2)2 — 1) = 0,15 ГэВ;
Т/4
1 с 1
б)	L = 1 vdt —— arcsin _ , .... ,
I ш Vl+Л2 о
где А тс2/егВт, a v определяется по формуле р = (е/с) гВ. В нашем случае А 1, поэтому arcsin я; л/2 и L = c/4v = 1,5-103 км; 2,4-105 оборотов.
17.29.	С одной стороны, dpidt = — еЕ, где напряженность Е вихревого электрического поля определяется из закона 2пгЕ = (е/с) Ф, Ф = лг2 <В>. С другой стороны, dp!dt можно найти, продифференцировав по времени соотношение р -- (е/с) гВОрб при г = const. Их сравнения полученных выражений приходим к условию dB0^ldt = 1/2d < В y/dt, откуда следует, что Ворб = 1/2 < В >.
17.30.	Продифференцировав по г выражение Е = Ф/2лсг и учитывая, что дФ/дг — 2ягВ (г), получим дЕ/дг = 0 и д2Е/дг2 > 0, т. е. £ = min.
17.31.	а) В системе координат, вращающейся вокруг осн поля, на электрон действует кроме силы Лоренца центробежная сила инерции. Результирующая сила F (г) — mv2/r — (е/с) vB (г), причем при г = гп сила F (г0) = 0. Для устойчивости движения необходимо, чтобы сила F была возвращающей, т. е. при г > г0 сила F < 0, и наоборот. Это будет так, если В (г) убывает к периферии медленнее, чем 1/г, значит, п <Z 1;
б) вследствие спада поля к периферии оно имеет бочкообразный вид, т. е. вне плоскости симметрии поля существует радиальная компонента ВТ. Последняя создает вертикальную компоненту силы Лоренца Fz = (е/с) vBT. Вблизи плоскости симметрии Br (dBr/dz)0 z. Так как rot В = - 0, то дВг/дг = dBz/dr. Поэтому Fz (е/с) v (дВ/дг) z. При п > 0 производная дВ/дг < 0, и сила Fz всегда направлена к плоскости симметрии.
17.32.	а) <ог = <оо Д/1 — п; б) <oz = <оо Уп, где <оо = еВ/тс (см. решение задачи 17.15).
17.33.	Е = тс2 У 1,5г3 В/се = 0,29 ГэВ.
17.34.	а) Т = (ерВ)2/2 тс2 = 6,12 и 12 МэВ;
б)	v = Ут/2т/яр = 20, 14 и 10 МГц.
17.35.	V = 2n2mv2pAp/e = 0,2 МВ.
17.36.	a) t - n.2mp2v/qV — 10 мкс, где q — заряд частицы; б) L = X
N	j ________ N _
X Ъп = 2^ y2qV/m 2 Уп, где vn — скорость частицы после n-го прохождения ускоряющего промежутка; N — полное число прохождений. В данном случае N велико (N -- T’MaKC/<7V), поэтому Si/" У Упйп. В результате £«* » i/3n3mv2p3/qV — 0,2 км.
17.37.	Т -- m<?txx/xa. Соответственно 5,1 кэВ, 9,4 и 37 МэВ.
17.38.	п 2nfkE/ceB = 9.
17.39.	a. (v0—v)/v0 = Т/(Т + тс2), соответственно на 35 и 12%.
200
б.	Угловая скорость обращения частицы связана с ее полной энергией Е как Е = сеВ ы. Отсюда dE dt = (сеВ/ы2) dw/dt. С другой стороны, dE/dt — — еТ ~ ew'2n. Из этих формул получим: du>ldt = — (е2лсеВ) ш3, и после интегрирования найдем, что ш (/) ----- ш0-У1 —- At, где ш0 = eBlmc, А — = еы^лтс2.
17.40.	а) г - (c/mq) ~\/1 — (тсш0/еВm)3/sin2 wt;
б)	от 42,0 до 42,9 см, L = ш0 <г>/2ш = 1,5-103 км.
17.41.	ш (/) = с/г0 ~\/1 + А2 (/), где А = тсЧегВ (/).
17.42.	а) От 0,35 до 1,89 МГц, 0,82 с;
б)	б£ = 2лег2В,с =- 0,19 кэВ;
б)	1,5- 10s км, 5,2-10® оборотов.
17.43.	a) v — (с П) с 1/1 4- A2 (t), где А - mc2/erB (t) от 0,20 до 1,44 МГц; 3,2 с;
б)	б£ - егПВ с 2,33 кэВ; в) 9• 103 км, 4,3-10® оборотов._______________
17.44.	а) Длина л-й пролетной трубки - (с/2/) Д/1 — (тс2/Еп)2, где £„ — полная энергия протона в л-й трубке (Еп — тс2 — Тп — лД£). В нашем случае Т„ — л&Е < тс2, поэтому 1П 4,9}/4 --- л см. Число трубок Л' 35. /j = 11 см, /35 — 31 см;
б)	L ® 4,9 | У4ТЧ dл 7,5 м, где интегрирование проводится по л от 1 до N.
17.45.	От 258 до 790 МГц. от 2,49 до 2,50 ГГц.
17.46.	а) Ех (Т2 — Ti);eL 0,15 МВ см;
б)	v - с У1 — \тс2!Е (х)]2, где £ (х) - тс2 -	: еЕх х; в 9,5 раза,
на 0,65"<>.
17.47.	5.5- 103 ГэВ (см. решение задачи 16.3).
ПРИЛОЖЕНИЯ
1. Обозначения единиц физических величин
А — ампер А — ангстрем а.е. м,— атомная единица массы атм — атмосфера б — барн Бк — беккерель В — вольт Вт — ватт Гр — грэй
Гс — гаусс Гц — герц Дж — джоуль дин — дина Зв — зиверт К — кельвин Ки —кюри Кл — кулон л — литр м — метр
Десятичные приставки к названиям единиц:
Г — гига, 109
М — мега, 106
к — кило, 103
м — милли, 10~3 мк — микро, 10-6 н — нано, 10-9
мин — минута Мкс— максвелл Па — паскаль Н — Ньютон Р — рентген с — секунда ср — стерадиан Тл — тесла ч — час
эВ — электронвольт
п — пико, 10-’2
ф — фемто, 10“15
а — атто, 10’13
2. Край К- и L-полос поглощения рентгеновского излучения
Z	Элемент	Кран полосы поглощения, пм			
		К	Ч	Lll	Чп
23	Ванадий	226,8			2390	2410
26	Железо	174,1	—	1710	1740
27	Кобальт	160,4	——	1546	1580
28	Никель	148,6	—.	1411	1440
29	Медь	138,0	—	1297	1326
30	Цннк	128,4	—	1185	1210
42	Молибден	61,9	430,5	471,5	491
47	Серебро	48,60	323,6	351,0	3695
50	Олово	42,39	277,3	298,0	3153
74	Вольфрам	17,85	102,22	107,3	1215
78	Платина	15,85	88,8 .	93,2	1072
79	Золото	15,35	86,1	90,5	1038
82	Свинец	14,05	78,1	81,4	950
92	Уран	10,75	56,8	59,1	722
202
3. Некоторые свойства металлов
Металл	А. эВ	Плотность. г/см8	Кристаллическая структура			Температура	
			Т ип	Ячейка, пм		дебаевская в, К	плавления, °C
				а	|			
Алюминий	3,74	2,7	КГЦ	404			374	658,7
Барий	2,29	3,75	КОЦ	502	—	116	704
Бериллий	3,92	1,85	Г пл	228	3,58	1100	1278
Ванадий	3,78	5,87	коц	303	—	413	1715
Висмут	4,62	9,8	гекс	454	11,84	80	271
Вольфрам	4,50	19,1	(Х-КОЦ	316	—	315	3370
Железо	4,36	19,1	(Х-КОЦ	286	—	467	1535
Золото	4,58	19,3	КГЦ	407	—	164	1063
Калий	2,15	0,86	коц	525	—	132	62,3
Кобальт	4,25	8,9	(Х-Г пл	251	4,07	397	1480
Литий	2,39	0,53	коц	350	—	404	186
Магний	3,69	1,74	г пл	320	5,20	350	650
Медь	4,47	8,9	кгц	361	—	329	1083
Молибден	4,27	10,2	коц	314	—	357	2620
Натрий	2,27	0,97	коц	424	—	226	97,5
Никель	4,84	8,9	кгц	352	—	425	1452
Олово	4,51	7,4	тоц	582	3,18	111	231,9
Платина	5.29	21,5	кгц	392	—	212	1775
Свинец	4,15	11,3	кгц	494	—	89	327,5
Серебро	4,28	10,5	кгц	408	—	210	960
Титан	3,92	4,5	г пл	295	4,69	300	1720
Цезий	1,89	1,87	коц	605	—	60	28,5
Цинк	3,74	7,0	г пл	266	4,94	213	419,4
Условные обозначения: Л — работа выхода электрона с поверхности металла; кгц — кубическая гранецентрнрованная решетка; коц — кубическая объемноцентрнрованная; гекс — гексагональная; г пл — гексагональная плотная; тоц — тетрагональная объемноцентрированная.
4. Плотность некоторых веществ
Вещество	Плотность, г/см3	Вещество	Плотность, г/см3
Бор	2,45	Ртуть	13,6
Вода	1,00	Селен	4,5
Воздух (норм, усл.)	1,293:10-’	Сера	2,1
Германий	5,46	Стронций	2,54
Графит	1,60	Теллур	6,02
Индий	7,28	Торий	11,7
Кадмий	8,65	Тяжелая вода D2O	1,10
Кремний	2,35	Уран	19,0
Окись бериллия ВеО	3,03	Фосфор	1,83
Парафин СНг	0,89	NaCl	2,18
Плутоний	19,8	CsCl	4,04
Примечание: плотности других металлов приведены в предыдущей таблице.
203
5. Константы двухатомных молекул
Молекула	Основной терм	Межъялер-ное расстояние d. 10-8 cm	Частота колебаний v. см-’	Ангармоничность х, 10-3	Энергия днссоциаци» D.
н2	•s	0,741	4395,2	28£	4,48
n2	s	1,094	2359,6	6,15	7,37
о2	32	1,207	1580,4	7,65	5,08
f2	'П	1,282	1139,8	8,51	~ 1,6
р2	2	1,894	780,4	3,59	5,03
s2	3V	1,889	725,7	3,93	~4,4
С12	'2	1,988	564,9	7,09	2,48
Вг2	2	2,283	323,2	3,31	1,97
12	'2	2,666	214,6	2,84	1,54
HF	'2	0,917	4138.5	21,8	5,8
НС1	'2	1,275	2989,7	17,4	4,43
HBr	2	1,413	2649,7	17,1	3,75
HJ	'2	1,604	2309,5	17,2	3,06
CO	'2	1,128	2170,2	6,22	~9,7
NO	2n	1,150	1906	7,55	5,29
OH	2n	0,971	3735	22,2	4,35
6. Радиоактивное семейство урана
204
1. Таблица свойств нуклидов
Z	Нуклид	Спнн ядра	Избыток массы нуклида М-А, а.е.м	Массовое содержание в естественной смесн изотопов, и 0	Тип распада	Период полураспада	Энергия а- н 0-частиц 70макс МэВ
	п	1 2	0,008665	—	р-	11,7 мин	0,78
1	н	1 2	0,007825	99,985			
	ж	1	0,014102	0,015			
	зн	1 2	0,0160049	—	р-	12,3 года	0,018
2	3Не	12	0,016030	310-1			
	Же	0	0,002604	~ 100			
3	eLi	1	0,015126	7,52			
	’Ll	3'2	0,016005	92,48			
4	7Li	3 2	0,016931	—	к	53 сут	
	"Be	0	0,005308	—	2 а	10-16 с	0,039
	9Be	3 2	0,012186	100			
	1<>Ве	0	0,013535	—	₽-	2,5- 10б лет	0,555
5	юв	3	0,012939	20			
	i'B	3 2	0,009305	80			
6	nc	3 2	0,011431	—	Р+	20,4 мин	0,97
	12C	0	0	98,89				
	i3c	1,2	0,003354	1.И			
		0	0,003242	—	₽-	5570 лет	0,155
7	13N	—	0,005739	—	Р*	10 мин	1.2
	UN	1	0,003074	99,63			
	is N	1/2	0,000108	0,37			
8	150	—	0,003072	—	Р+	2,1 мин	1,68
	ie0	0	—0,005085	99,76			
	i’O	5/2	—0,000867	0,037			
	18Q	0	—0,000840	0,204			
9	18F	—	0,000950	—	Р+	1,87 ч	0,649
	19F	1/2	—0,001595	100			
	20F	—	—0,000015	—	Р“	12 е	5,42
10	aoNe	0	—0,007560	90,52			
	2iNe			-0,006151	0,26			
	22Ne	0	—0,008616	8,82			
11	22Na	3	—0,005565	—	Р+	2,6 года	0,540
	23Na	3/2	—0,010227	100			
	24Na	4	—0,009033	—	Р~	15 ч	1,39
12	28Mg	—	—0,005865	—	Р+	11 с	2,95
	2<Mg	0	—0,014956	78,60			
	26Mg	5/2	-0,014160	10,11			
	2«Mg	0	—0,0117409	11,29			
	27Mg	Ь'2	—0,015655	—	Р-	8,5 мнн	1,75 и 1 ,59
13	26A1	—	-0,013100	—	Р+	6,7 с	3,20
	27A1	5/2	-0,018465	100			
	28 Al	3	—0,018092	—	Р-	2,3 мни	2,86
14	28Si	0	—0,023073	92,27			
	2»Sj	1/2	—0,023509	4,68			
	30Sj	0	—0,026239	3,05			
	31Si	—	—0,024651	—	Р-	2,65 ч	1,47
15	30p	—	—0,021680	—	Р+	2,5 мин	3,24
	31p	1/2	—0,026237	100			
	32p	—	—0,026092	—	Р-	14,3 сут	1,71
205
Продолжение приложения 7
Z	Нуклнд	Спнн ядра	Избыток массы нуклида М-А, а.е.м	Массовое содержание в естественной смеси изотопов, %	Тнп распада	Период полураспада	Энергия а- н 0-частиц Ермаке МзВ
16	32S	0	—0,027926	95,02			
	33S	3 2	—0,028540	0,75			
	34S	0	0,032136	4,21			
	3SS	3,2	-0,030966	—	р-	87 сут	0,167
17	35С1	3'2	-0,031146	75,4			
	ЗвС1	2	—0,031688	—	р-> к	3,1 • 105 лет	0,714
	37С1	3 2	— 0,034104	24,6			
18	ЗвДг	0	—0,032452	0,34			
	37 Аг	3 2	—0,033228	—	к	32 сут	
	39 А Г	—	—0,035679	—	р-	265 лег	0,565
	40 Аг	0	0,037616	99,60			
19	3«К	3,2	—0,036286	93,08			
	42К	2	- 0,037583	—	р-	1,52 ч	3,55 и 1,99
24	51Сг	7 2	—0,055214	—	к	28 сут	
25	S5Mn	5’2	-0,061946	100			
27	58Со	2	—0,064246	—	К Р+	72 сут	0,47
	59Со	7/2	-0,066811	100			
	6»Со	4	—0,066194	—		5,2 года	0,31
29	63Си	3/2	—0,070406	69,1			
	66Си	3,2	—0,072214	30,9			
30	85Zn	5/2	-0,070766	—	К, р+	245 сут	0,325
35	82Вг	6	—0,083198	—	р-	36 ч	0,456
38	88Sr	0	—0,09436	82,56			
	8»Sr	5/2	-0,09257	—	р-	51 сут	1,46
	8,Sr	0	-0,09223	—	р-	28 лет	0,535
39	90у	2	-0,09282	—	₽-	64 ч	2,24
47	107Ag	1/2	—0,09303	51,35			
53	127 J	5/2	—0,09565	100			
	128]	1	—0,09418	—	Р-. к	25 мии	2,12 и 1,67
79	1,7 Au	3/2	—0,03345	100			
	i»8Au	2	—0,03176	—	р-	2,7 сут	0,96
81	204*£]	—	—0,02611	—	р-	4,1 года	0,77
82	206ph	0	—0,02554	23,6			
	20’pb	1 '2	—0,02410	22,6			
	20spb	0	—0,02336	52,3			
83	20»Bj	9/2	—0,01958	100			
	210Bj	4	—0,01589	—	(X	2,6 • 10е лет	4,97
84	210po	—	—0,01713	—	а	138 сут	5,3
86	222Rn			0,01753	—	а	3,8 сут	5,49
88	22«pa	0	0,02536	—	а	1620 лет	4,/77 и 4,589
90	2S2Th	0	0,03821	100	а	1,4-10’° лет	4,00 и 3,98
	233ТИ			0,04143	—	₽-	22 мин	1,23
92	234(J	0	0,04090	0,006	а	2,5- 10s лет	4,76 и 4,72
	238U	7/2	0,04383	0,71	а	7,1  108 лет	4,20—4,58
	238 (J	0	0,04573	—	а	2,4-107 лет	4,45 и 4,50
	238 (J	0	0,05076	99,28	а	4,5 • 10’ лет	4,13 н 4,18
	239] 1			0,05432	—	р-	23,5 мин	1 >21
94	23spu			0,04952	—	а	89,6 года	5,50 н 5,45
	23»pu	1/2	0,05216	—	а	2,4-10* лет	5,15—5,10
206
8. Нейтронные сечения
Элемент	Изотоп	Массовое содержание в естественной смеси изотопов. %	Период полураспада образующегося изотопа	Сечеине» б		
				поглощения °а	активации °акт	рассеяния «V
н	2H	1	0,015	12,3 года	510-"	5,7-10-“	7
Li	—	—	—	71	—	1,4
	«Li	7,52	—	945 (па)	2,8-10-2	—
	7 Li	92,48	0,85 с	——	3,3-1 о-2	—
Be	’Be	100	2.7 • 106 лет	10~2	9-10-“	7
В	—	——	—	755	—	4
	iob	20	—	—	0,5	—
	>'B	80	0,03 с	3813 (па)	5-Ю-2	—
С	—	—	—.	3,8-10-3	—.	4,8
	12C	98,89	—	—	3,3-1 о-3	—
	13C	1,11	5570 лет	0,5-103	9 10-“	—
О	—	—	—	2-10-«	—	4,2
F	19F	100	И с	<10-2	9-Ю-3	3,9
Na	«Na	100	15 ч	0,53	0,53	4
Al	-7A1	100	2,3 мин	0,23	0,21	1,4
V	—				4,98			5
	50y	0,24	——	250			—
	51 у	99,76	3,76 мни	—.	4,5	—
Си	—	—	—.	3,77	—	7,2
	e3Cu	69,1	12,8 ч	4,5	4,5	—
	65Cu	30,9	5,15 мин	2,2	1,8	—
Ag	—	—	— .	63			6
Cd	—					2540	—.	7
	113Cd	12,26	—	20 000		—
In	—	—		196			2,2
	115In	99,77	54,2 мин			155	—
I	127J	100	25 мин	6,22	5,6-103	3,6
Au	127Au	100	2,7 сут	98,8	96	9,3
U	—	—	—	7,68	—	8,3
	238 (J	99,28	23,5 мин	2,75	2,74	11,2
Здесь: &а н <7акт - сечения сечение для достаточно широкого
для тепловых нейтронов (2200 интервала энергий.
м/с);
«jg> — усредненное
9. Постоянные делящихся нуклидов (на тепловых нейтронах, 2200 м/с)
Нуклид	Массовое содержание в естественной смеси изотопов, %	Сечение, б		Среднее число нейтронов на акт деления	
		поглощения аа	деления	мгновенных V	запаздывающих ц
233JJ			588 ±4	532±4	2,52	0,0066
235U	0,71	694 ±3	582±4	2,47	0,0158
239Pu	——	1025±8	738±4	2,91	0,0061
207
10. График пробег — энергия а-частиц в воздухе
Пробег, см
208
11. Коэффициенты ослабления и поглощения у-нзлученяя
Энергия, МэВ	Алюминий		Свинец		Вода		Воздух	
	М/Р	т/р	М/Р	Т/Р	М/Р	т/р	М/Р	Т/Р
0,1	0,169	0,0371	5,46	2,16	0,171	0,0253	0,155	0,0233
0,2	0,122	0,0275	0,942	0,586	0,137	0,0299	0,123	0,0269
0,4	0,0927	0,0287	0,220	0,136	0,106	0,0328	0,0953	0,0295
0,6	0,0779	0,0286	0,119	0,0684	0,0896	0,0329	0,0804	0,0295
0,8	0,0683	0,0278	0,0866	0,0477	0,0786	0,0321	0,0706	0,0288
1,0	0,0614	0,0269	0,0703	0,038'4	0,0706	0,0310	0,0635	0 ,0276
1,5	0,0500	0,0246	0,0550	0,0280	0 0590	0,0283	0,0515	0,0254
2,0	0,0431	0,0227	0,0463	0,0248	0,0493	0,0260	0,0445	0,0236
3,0	0,0360	0,0201	0,0410	0,0238	0,0390	0,0227	0,0360	0,0211
4,0	0,0310	0,0188	0,0421	0,0253	0,0339	0,0204	0,0307	0,0193
6,0	0,0264	0,0174	0,0436	0,0287	0,0275	0,0178	0,0250	0,0173
8,0	0,0241	0,0169	0,0458	0,0310	0,0240	0,0163	0,0220	0,0163
10,0	0,229	0,0167	0,0489	0,328	0,0219	0,0154	0,0202	0,0156
Здесь: ц/р и т/р — массовые коэффициенты ослабления (для узкого пучка) н поглощения. см2/г.
12. Сечения взаимодействия у-квантов в свинце
209
0,1	0,2 0,3 0/t-	1	2 3 0-5 . 10
в, кэб
14. Значения некоторых определенных интегралов
хп dx
ех— 1
2,31, л=1/2 л2/6, п=1
2,405, п = 2 л4/15, л —3
24,9, п = 4
'е х3 dx
J ех— 1
0,225, а= 1
1,18, а=2
2,56, а = 3
4,91, а = 5
6,43, а=10
j хп е х dx = о
п!, п > 0, целое
У'Г/г, п = 1/2
e~*’dx ж 0,843
хп е
X'dx--
Д/ л /2, л = 0
п—целое нечетное
о
1.3-5...(л-1) у— _________________L___, п — целое четное
2«/2	2
210
Дифференцирование интеграла по параметру:
д	df	д хг	дхх
— f(x,a)dx- —— <Д+/(лг) —----------------—/(Х1)-—
оа ,<	J д а	да	да
х, (а)	х,
___а
Значения интеграла вероятности J (a) ~)/2ii f е~ х'^2 dx о
а	J (а)	1 “	J (а)	а	Э (а)
0,1	0,797	0,9	0,6319	1,7	0,9109
0,2	0,1518	1,0	0,6827	1,8	0,9281
0,3	0,2358	1,1	0,7287	1,9	0,9426
0,4	0,3108	1,2	0,7699	2,0	0,9545
0,5	0,3829	1,3	0,8064	2,25	0,9756
0,6	0,4515	1,4	0,8385	2,50	0,9876
0,7	0,5161	1,5	0,8664	2,75	0,9940
0,8	0,5763	1,6	0,8904	3,00	0,9973
15. Единицы радиоактивности и дозы
Единица активности радионуклида — 1 Бк (беккерель), соответствует одному распаду в секунду, 1 Бк = I расп./с.
Внесистемная единица = 1 Ки (кюри), 1 Ки — 3,700-1010 Бк.
Экспозиционная доза фотонного излучения — 1 Кл/кг (кулон на килограмм), соответствует образованию полного заряда 1 Кл ионов одного знака в 1 кг воздуха, 1 Кл/кг эквивалентен поглощенной энергии 34 Дж иа 1 кг воздуха.
Внесистемная единица — 1Р (рентген), соответствует образованию в 1 см8 воздуха при нормальных условиях 1 СГСЭ заряда каждого знака, т. е. 2,08-10’ пар ионов, 1 Р эквивалентен поглощенной энергии 0,113 эрг в 1 см8 воздуха при нормальных условиях.
Мощность экспозиционной дозы измеряют в Кл/(кг-с) и Р/с.
Поглощенная доза — 1 Гр (грэй), соответствует энергии 1 Дж, переданной излучением 1 кг вещества, 1 Гр = 1 Дж/кг.
Внесистемная единица — 1 рад (рад), соответствует поглощенной энергии 100 эрг на 1 г вещества.
Мощность поглощенной дозы измеряют в Гр/с и рад/с.
Эквивалентная доза — 1 Зв (зиверт), соответствует поглощенной тканью дозе излучения, биологически эквивалентной дозе I Гр фотонного излучения.
Внесистемная единица — 1 бэр (бэр), соответствует поглощенной биологической тканью дозе, биологически эквивалентной дозе 1 рад фотонного излучения.
Мощность эквивалентной дозы измеряют в Зв/с и бэр/с.
Соотношение между эквивалентной и поглощенной дозами:
/->ЭКВ = K’D, где К — коэффициент качества излучения.
16. Соотношение между некоторыми единицами
1 А = 3-10’ СГСЭ	1 Вт=107 эрг/с	1 мм рт. ст. = 133,3 Па
1 А= Ю~8 см	1 Вб=108 Мкс	1 Н=105 дии
(1,660-10-21 г		1
1 a. е.м.=(	1 Гн =10’ см	1 Ом=	см
(931,50 МэВ		9 • 1011
	1 год = 3,11  107 с	1 Тл^Ю4 Гс
1 атм = 101,3 кПа	1 Дж=107 эрг	1 ф = 9.Ю11 см
1 б= 10 24 см2	1 кал = 4,18 Дж	1 фм = 10~13 см
1 бар= 100 кПа	1 Ки = 3,70-1010 Бк	1 Э= 103/4л А/м
1 В= 1/300 СГСЭ	1 Кл=3-10’ СГСЭ	_1^эВ = 1,6-Ю ’12 эрг
		
211
Соотношения между единицами радиоактивности и дозы
Величина	Название и обозначение единицы		Связь между единицами
	Единица СИ	Внесистемная единица	
Активность А	Беккерель (Бк), 1 Бк = 1 расп./с	Кюри (Ки)	1 Ки = 3,7-1010 Бк
Экспозиционная доза Пэке	Кулон на килограмм (Кл/кг)	Рентген (Р)	1 Р = 258 мкКл/кг
Поглощенная доза О •*	Грэй (Гр), 1 Гр = 1 Дж/кг	Рад (рад)	1 пал- /100эРг'/г 1 рад “ 11/100 Гр
Эквивалентная доза ОЯКв	Зиверт (Зв), 1 Зв=1 Гр/К	Бэр (бэр)	1 бэп-Р рад//< 1 ЭР /1/100 Зв
Здесь К — коэффициент качества.
Предельно допустимые уровни излучения, соответствующие дозе I мЗв (100 мбэр) в неделю
Излучение	Энергия излучения	Мощность дозы или плотность потока частиц при 36-часовой рабочей неделе	Коэффициент качества К
Рентгеновское и	<3 МэВ	0,20 нКл/(кг-с)	1
у-излучение		(0,78 мкР/с)	
Р-Частицы и элект-	< 10 МэВ	20 см-2-с-'	1
роны			
(тепловые	0,025 Л	750 см-2-с~‘	3
Нейтроны 1быстрые	1 — 10 МэВ	20 см~2-с-'	10
17. Основные физические постоянные
Скорость света в вакууме
Гравитационная постоянная
Постоянная Авогадро
Число Лошмидта
Универсальная газовая постоянная
Постоянная Больцмана
Элементарный заряд
Масса покоя электрона
Удельный заряд электрона
с = 2,998-101° см/с
(6,67-10 8 см3/(г-с2) У = 16,67-10~11 м3/(кг-с2)
= 6,023-1023 моль-1
л0 = 2,69-101° см-3
о _ (8,314-Ю7 эрг/(К-моль)
/8,314 Дж/(К-моль)
(1,3807-10-1° эрг/К
k = 1,3807-10-23 Дж/К
(0,8617-10-* эВ/К
, _ /4,803-10-1° СГСЭ
“11,602-10-1° Кл
(0,911-Ю-27 г те= (5,486- 1Q-4 а. е. м.
10,511 МэВ
е /5,27-101’ СГСЭ
11,76-104 Кл/кг
212
Продолжение приложения 17
Масса покоя протона
Удельный заряд протона
Разность масс нейтрона и протона
Постоянная Стефана — Больцмана
Постоянная закона смещения Вина
Постоянная Планка
Постоянная Ридберга
Первый боровский радиус
Энергия связи электрона в атоме водорода
Комптоновская длина волны электрона
Классический радиус электрона Сечение томсоновского рассеяния Постоянная тонкой структуры
Магнетон Бора
Ядерный магнетон
Магнитный момент
электрона протона нейтрона дейтрона
Гиромагнитный множитель
электрона
протона
нейтрона
дейтрона
Атомная единица массы
Электрическая постоянная
Магнитная постоянная
11,6726-10—24 г тр- 1.007276 а. е. м.
(938,28 МэВ
е /2,87-1014 СГСЭ тр — 10,959-108 Кл/кг
/п„—/пр= 1,293 МэВ
/5,67- 10~Б эрг/(с-см2-К4)
15,67-Ю-8 Вт/(м2-К4)
6= 0,290 см-К
(1,0546-10~27 эрг-с
h =^1,0546-10—»* Дж-с (0,6582-10-« эВ-с
R тее*/2 Л8 = 2,067- 101в с~» R’ R/2 л с= 1,097-10s см~1
г1 = Л2/тее2 = 0,529-Ю-8 см
Е meel/2 №= 13,56 эВ
Хс=2 ntilme с = 2,426-10-10 см Хс = Лс/2 л —3,862-10-11 см ге = е2/те с2 = 2,82-Ю~*3 см <гт=8/3 л rj =6,65-10—2Ь см2 а = е2/Йс= 1/137,036
„ _ eh /0,9274-Ю-20 эрг/Гс Иб^“2^Г =(0,5788-10-4 эВ/Гс
__ eh _/5,051 • Ю"21 эрг/Гс Ия^2^“|3,152-Ю-8 эВ/Гс
ре= 1,00116 рБ
Рр =2,7928 ря Рп — 1,913 рд
Pd = 0,8574 ря
ge = 2,0022
gp = 5,5855
gn^—3,8263
gd 0,8574
.	_/l,660-10-24 г
i a. e. m.-^931>50 МэВ
e0 =0,885-10-и Ф/м
-7—— = 9-10» м/Ф 4лео
р0 = 1,257• 10-«Гн/м
2s- - Ю-’Гн/м
4л
213
18. Таблица тригонометрических функций
Угол	sin	tg	ctg	COS	
0=	0,0000	0,0000	oo	1,0000	90°
1	0,0175	0,0175	52,29	0,9993	89
2	0,0349	0,0349	28,64	0,9994	88
3	0,0523	0,0524	19,08	0,9986	87
4	0,0698	0,0699	14,30	0,9976	86
5	0,0872	0,0875	11,43	0,9962	85
6	0,1045	0,1051	9,514	0,9945	84
7	0,1219	0,1228	8,144	0,9925	83
8	0,1392	0,1405	7,115	0,0903	82
9	0,1564	0,1584	6,314	0,9877	81
10	0,1736	0,1763	5,671	0,9848	80
11	0,1908	0,1944	5,145	0,9816	79
12	0,2079	0,2126	4,705	0,9781	78
13	0,2250	0,2309	4,331	0,9744	77
14	0,2419	0,2493	4,011	0,9703	76
15	0,2588	0,2679	3,732	0,9659	75
16	0,2756	0,2867	3,487	0,9613	74
17	0,2924	0,3057	3,271	0,9563	73
18	0,3090	0,3249	3,078	0,9511	72
19	0,3256	0,3443	2,904	0,9455	71
20	0,3420	0,3640	2,747	0,9397	70
21	0,3584	0,3839	2,605	0,9336	69
22	0,3746	0,4040	2,475	0,9272	68
23	0,3907	0,4245	2,356	0,9205	67
24	0,4067	0,4452	2,246	0,9135	66
25	0,4226	0,4663	2,145	0,9063	65
26	0,4384	0,4877	2,050	0,8988	64
27	0,4540	0,5095	1,963	0,8910	63
28	0,4695	0,5317	1,881	0,8829	62
29	0,4848	0,5543	1,804	0,8746	61
30	0,5000	0,5774	1,732	0,8660	60
31	0,5150	0,6009	1,664	0,8572	59
32	0,5299	0,6249	1,600	0,8480	58
33	0,5446	0,6494	1,540	0,8387	57
34	0,5592	0,6745	1,483	0,8290	56
35	0,5736	0,7002	1,428	0,8192	55
36	0,5878	0,7265	1,376	0,8090	54
37	0,6018	0,7536	1,327	0,7986	53
38	0,6157	0,?813	1,280	0,7880	52
39	0,6293	0,8098	1,235	0,7771	51
40	0,6428	0,8391	1,192	0,7660	50
41	0,6561	0,8693	1,150	0,7547	49
42	0,6691	0,9004	1,111	0,7431	48
43	0,6820	0,9325	1,072	0,7314	47
44	0,6947	0,9657	1,036	0,7193	46
45	0,7071	1,0000	1,0000	0,7071	45
	COS	ctg	tg	sin	Угол
214
19, Таблица показательных функций
X	ех	е х	X	г	е х
0,00	1,0000	1,0000	4,00	54,598	0,01832
0,10	1,1052	0,9048	4,10	60,340	0,01657
0,20	1,2214	0,8187	4,20	66,686	0,01500
0,30	1,3499	0,7408	4,30	73,700	0,01357
0,40	1,4918	0,6703	4,40	81,451	0,01228
0,50	1,6487	0,6065	4,50	90,017	0,01111
0,60	1,8221	0,5488	4,60	99,484	0,01005
0,70	2,0138	0,4966	4,70	109,95	0,00910
0,80	2,2255	0,4493	4,80	121,51	0,00823
0,90	2,4596	0,4066	4,90	134,29	0,00745
1,00	2,7183	0,3679	5,00	148,41	0,00674
1,10	3,0042	0,3329	5,10	164,02	0,00610
1,20	3,3201	0,3012	5,20	181,27	0,00552
1,30	3,6693	0,2725	5,30	200,34	0,00499
1,40	4,0552	0,2466	5,40	221,41	0,00452
1,50	4,4817	0,2231	5,50	244,69	0,00409
1,60	4,9530	0,2019	5,60	270,43	0,00370
1,70	5,4739	0,1827	5,70	298,87	0,00335
1,80	6,0496	0,1653	5,80	330,30	0,00303
1,90	6,6859	0,1496	5,90	365,04	0,00274
2,00	7,3891	0,1353	6,00	403,43	0,00248
2,10	8,1662	0,1225	6,20	492,75	0,00203
2,20	9,0250	0,1108	6,40	601,85	0,00166
2,30	9,9742	0,1003	6,60	735,10	0,001360
2,40	11,023	0,09072	6,80	897,85	0,001114
2,50	12,182	0,08208	7,00	1096,6	0,000912
2,60	13,464	0,07427	7,20	1339,4	0,000747
2,70	14,880	0,06721	7,40	1636,0	0,000611
2,80	16,445	0,06081	7,60	1998,2	0,000500
2,90	18,174	0,05502	7,80	2440,6	0,000410
3,00	20,086	0,04979	8,00	2981,0	0,000335
3,10	22,198	0,04505	8,20	3641,0	0,000275
3,20	24,533	0,04076	8,40	4447,1	0,000225
3,30	27,113	0,03688	8,60	5431,7	0,000184
3,40	29,964	0,03337	8,80	6634,2	0,000151
3,50	33,115	0,03020	9,00	8103,1	0,000123
3,60	36,598	0,02732	9,20	9897,1	0,000101
3,70	40,447	0,02472	9,40	12088	0,000083
3,80	44,701	0,02237	9,60	14765	0,000068
3,90	49,402	0,02024	9,80	18034	0,000055
			10,00	22026	0,000045
215
Таблица элеме нтарных частиц
Частица		Символ			Масса, МэВ	Заряд				в	Спин, четность I?	Изоспин		Странность s Я	Среднее время жизни т« с	Основная схема распада
		Частица		Античастица		Q						т	Тг			
Фотон		Y			0	0	0			0	1	-		—	оо	
			ve	§	0	0	+1	0	0	0	1/2	—	—	—	ОС	
	Нейтрино		V	V JA	0	0	0	+1	0	0	1'2	—	—	—	ОО	
Леп-			+	VT	0	0	0	0	+1	0	1/2	—	—	—	оо	
ТОНЫ	Электрон	е~		е+	0,511	— 1	+1	0	0	0	1 '2+	—	—	—	оо	
	Мюон	г		Ц+	105,66	— 1	0	+1	0	0	1 '2 +	—	—	—	2,2.10-е	р—>е-	v~
	т-лептон	Т“		т+	1807	0	0	0	-и	0	1.2	—	—	—		T--»,u-vu VT, e~vevx
				л°	135,0	0		0		0	о-	1	0	0	0,8-10~1в	:t,J-.-yy
	Пи-мезоны		. я+	Л“	139,6	— 1		0		0	о-	1	+1	0	2,6- 10~s	л+-ц+
Мезо-			к+	к-	493,8	+ 1		0		0	о-	1/2	4-1/2	+1	1,2 • 10-9	K+-->p+ v^, л+ я®
ны	Ка-мезоны		: №	к°	497,8	0		0		0	о-	1/2	— 1/2	+1	Ks : 0,86-10-1°	Ks—>я+ jt~, n° л°
															Kt : 5,4-10—8	Kl—neve, npvu, 3n
	Эта-мезон			п	549	0		0		0	о-	0	0	0	2,4-Ю-19	t]-*YY- Зп°, п+ я- я®
	Протон	р		р	938,26	+ 1		0		+1	1/2 +	1/2	+ 1/2	0	ОО	—
	Нейтрон	п		п	939,55	0		0		+1	1/2+	1/2	— 1/2	0	0,93-103	n-^pe- ve
	Ламбда-гиперон	л		л	1115,6	0		0		+1	1/2+	0	0	—1	2,5-10-1°	К-^рл-, nn°
			S +	2 +	1189,4	+1		0		+ 1	1/2 +	1	+ 1	—1	0,8-10-1°	2+->pn°, nn+
Барионы	Сигма-гипероны		2»	2°	1192	0		0		+1	1/2+	1	0	— 1	<1 • Ю-14	S°—>Лу
			У-	2-	1197	—1		0		+1	1 /2 +	1	— 1	—1	1 ,5- 10-10	S-—
	Кси-гипероны	, -30		30	1315	0		0		4-1	1/2+	1/2	+ 1/2		9	3- io—10	3°—>Лл0
		J 13-			1321	—1		0		+1	1/2 +	1/2	— 1/2	—2	1,7-10-1°	3~-*Лл~
	Омега-гиперон	Q-		Q-	1672	—1		0		+L	3/2+	0	0	—3	1.3-10-1°	Й-->30л~, 3- я11, \К~
Примечание. Античастицы имеют одинаковые с частицей значения массы, спина, четност, изоспнна, времени жизни и противоположные по знаку значения электрического Q. лептонного Д н барионного В зарядов, проекции изоспина 7+ и странности S.