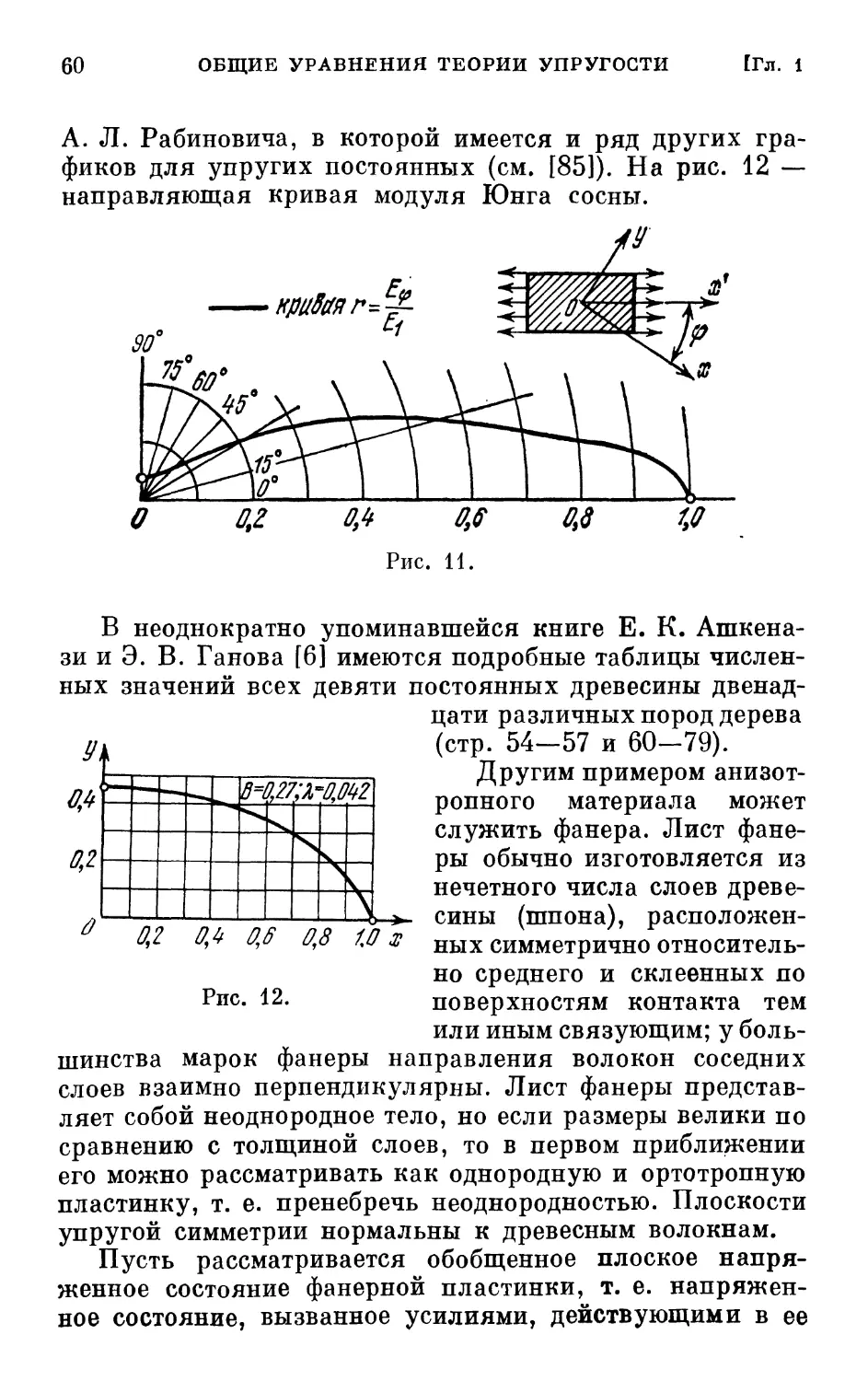
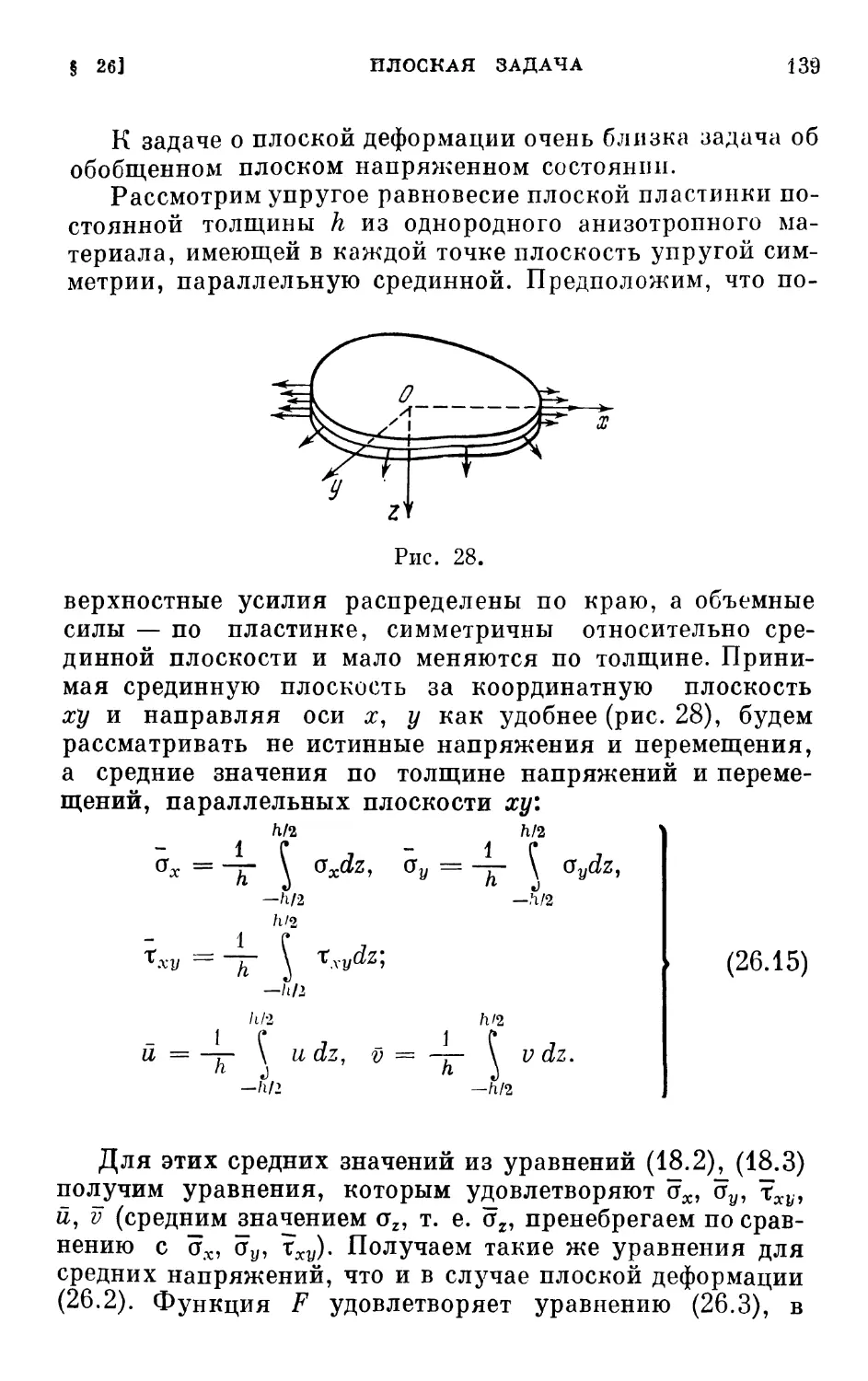
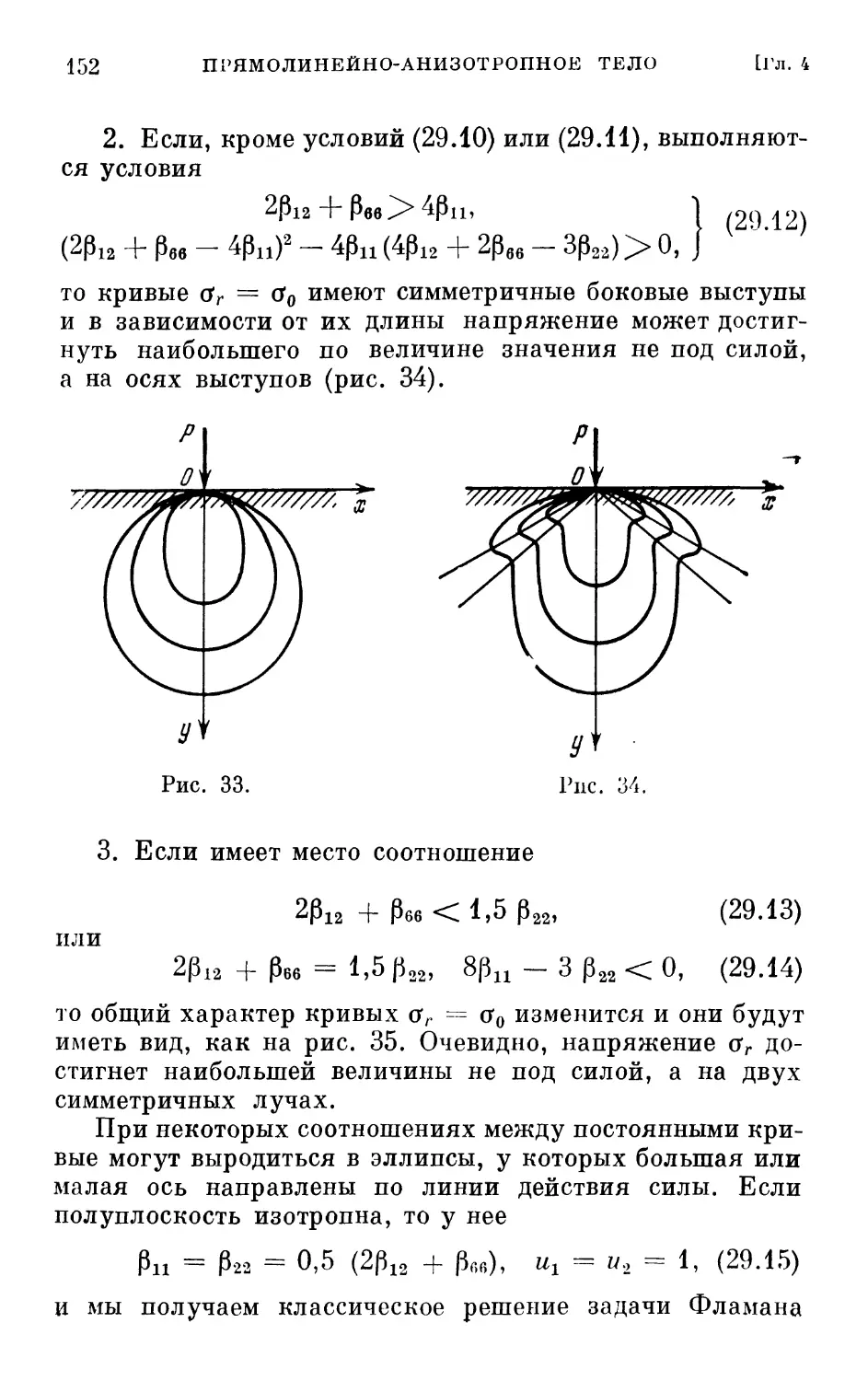
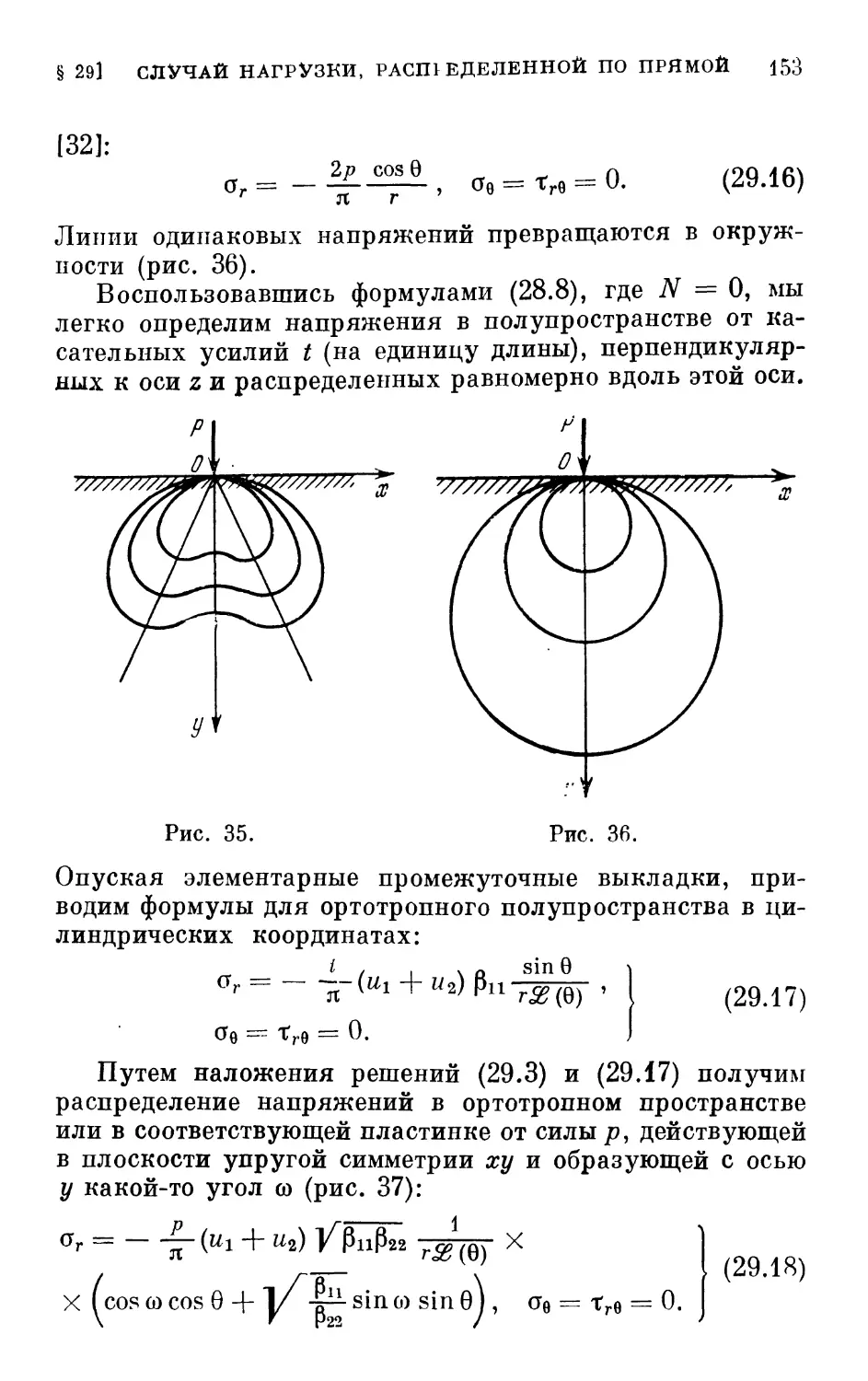
Author: Лехницкий С.Г.
Tags: механика деформируемых тел упругость деформация физика математика механика задачи по физике
Year: 1977
Text
С. Г. ЛЕХНИЦКИЙ
ТЕОРИЯ УПРУГОСТИ
АНИЗОТРОПНОГО
ТЕЛА
Издание второе, переработанное
и дополненное
ИЗДАТЕЛЬСТВО «HAV^A»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1977
5JM"
Л 53
53
УДК 539.3
Теория упругости анизотропного тела. Л е х н и ц-
к и й С. Г. Изд. 2-е, Главная редакция физико-мате-
физико-математической литературы издательства «Наука», М., 1977,
416 стр.
Монография посвящена, систематическому изложе-
изложению механики (статики) твердого упругого тела, обла-
обладающего различными упругими свойствами для разных
направлений, т. е. анизотропного.
В книге приводятся общие уравнения теории уп-
упругого равновесия тел, обладающих упругой анизотро-
анизотропией различных типов, как однородных, так и неод-
неоднородных. Дается математическая формулировка
общих задач равновесия упругого анизотропного те-
тела и наиболее важных проблем — растяжения, круче-
кручения, изгиба, плоской задачи, осесимметричной дефор-
деформации и их обобщений. Даны решения большого числа
частных задач, относящихся ко всем разнообразным
проблемам, полученные как самим автором, так и дру-
другими исследователями. Как правило, все задачи дово-
доводятся до явных формул, а в ряде случаев — до таблиц
и графиков.
Книга рассчитана на научных работников и инже-
инженеров, работающих в области механики, машинострое-
машиностроения, приборостроения, судостроения, самолетострое-
самолетостроения и других областях техники.
Табл. 27, илл. 113, библ. 131.
© Главная редакция физике-
20304 141 математической литературы
п ала 77 издательства «Наука», 1977,
Л 053@2)-77 144~// с изменениями
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию 8
Из предисловия к первому изданию 10
Глава 1. Общие уравнения теории упругости анизотропного
тела 13
§ 1. Напряженное и деформированное состояния спло-
сплошного тела 13
§ 2. Преобразование составляющих напряжений к но-
новым осям 19
§ 3. Обобщенный закон Гука 22
§ 4. Основные случаи упругой симметрии 30
§ 5. Преобразование упругих постоянных при переходе
к новой системе координат 37
§ 6. Преобразование упругих постоянных при поворо-
повороте координатной системы 41
§ 7. Преобразование комплексных параметров при по-
повороте координатной системы 48
§ 8. Поверхности и кривые, изображающие изменение
упругих постоянных с изменением направления . 50
§ 9. Некоторые анизотропные упругие материалы . . 56
§ 10. Криволинейная анизотропия 65
§ 11. Общие уравнения теории упругости и постановка
основных задач. Важнейшие вариационные прин-
принципы 71
Глава 2. Простейшие случаи упругого равновесия 77
§ 12. Растяжение стержня под действием осевой силы и
собственного веса 77
§ 13. Сдвиг 81
§ 14. Всестороннее сжатие 83
i 15. Изгиб стержня моментами, приложенными к кон-
концам 87
§ 16. Изгиб прямоугольной пластинки моментами, рас-
распределенными равномерно по сторонам 91
§ 17. Растяжение и изгиб стержня, обладающего цилин-
цилиндрической анизотропией 93
ОГЛАВЛЕНИЕ
Глава 3. Упругое равновесие тела, ограниченного цилиндри-
цилиндрической поверхностью, в котором напряжения не ме-
меняются вдоль образующей 96
§ 18. Распределение напряжений в однородном теле с
прямолинейной анизотропией, зависящее только
от двух координат 96
§ 19. Функции напряжений 102
§ 20. Общие выражения для функций напряжений в од-
однородном прямолинейно-анизотропном теле ... 108
§ 21. Общие формулы для составляющих напряжений и
проекций перемещения; граничные условия ... 114
§ 22. Распределение напряжений в непрерывно-неодно-
непрерывно-неоднородном прямолинейно-анизотропном теле, завися-
зависящее от двух координат 118
§ 23. Распределение напряжений в однородном теле, об-
обладающем цилиндрической анизотропией, зави-
зависящее от двух координат г, 6 121
§ 24. Распределение напряжений в непрерывно-неодно-
непрерывно-неоднородном теле, обладающем цилиндрической анизо-
анизотропией, зависящее от двух координат 128
Глава 4. Обобщенная плоская деформация и плоская задача
для тела с прямолинейной анизотропией .... 131
§ 25. Обобщенная плоская деформация однородного пря-
прямолинейно-анизотропного тела 131
§ 26. Плоская деформация и обобщенное плоское напря-
напряженное состояние 136
§ 27. Плоская задача для непрерывно-неоднородного пря-
молинейно-ортотропного тела. Растяжение и изгиб
моментами 140
§ 28. Распределение напряжений в упругом однородном
полупространстве под действием усилий, прило-
приложенных к ограничивающей плоскости 143
§ 29. Случай нагрузки, распределенной равномерно по
прямой 147
§ 30. Распределение напряжений в упругом однородном
пространстве с полостью в виде эллиптического ци-
цилиндра 157
§ 31. Растяжение однородной ортотропной пластинки с
эллиптическим отверстием 165
§ 32. Некоторые случаи распределения напряжений в
ортотропной пластинке с круговым отверстием . 175
§ 33. Определение напряжений в однородной пластинке
с эллиптическим и круглым ядром 189
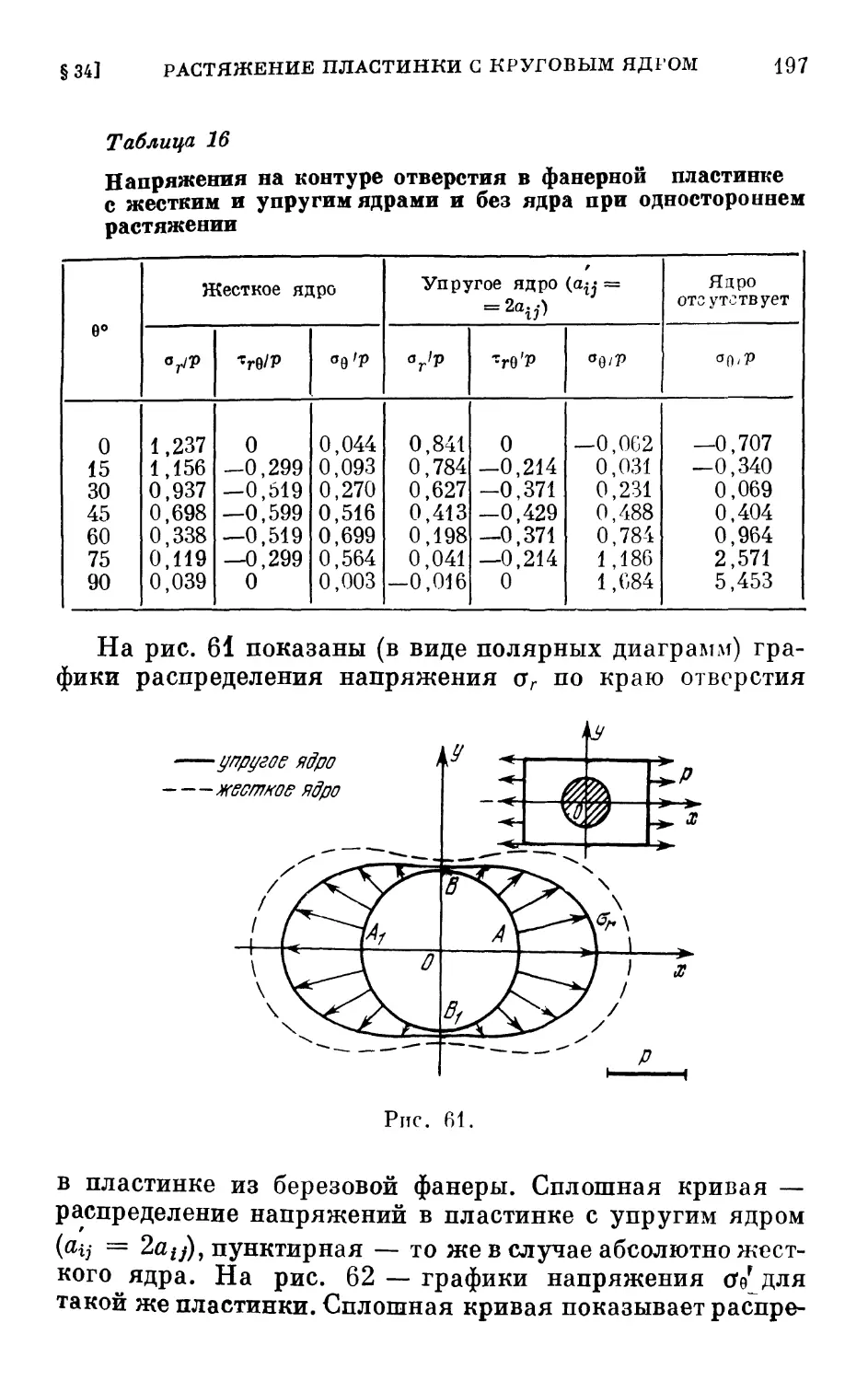
§ 34. Растяжение ортотропной пластинки с круговым яд-
ядром 194
§ 35. Замечания относительно решения плоской задачи
и задачи обобщенной плоской деформации для беско-
бесконечной плоскости с вырезом . . . ^ 200
§ 36. Радиальное распределение напряжений в непрерыв-
непрерывно-неоднородной упругой полуплоскости 202
ОГЛАВЛЕНИЕ
§ 37. Растяжение и изгиб моментами прямоугольной пла-
пластинки 206
Глава 5. Обобщенная плоская деформация, плоская задача
и родственные задачи для однородного и непрерыв-
непрерывно-неоднородного тел, обладающих цилиндричес-
цилиндрической анизотропией 211
§ 38. Обобщенная плоская деформация в однородном
теле, обладающем цилиндрической анизотро-
анизотропией 211
§ 39. Задача о плоской деформации тела с цилиндричес-
цилиндрической анизотропией и родственные задачи 216
§ 40. Плоская задача для непрерывно-неоднородного
тела, обладающего цилиндрической анизотро-
анизотропией 223
§ 41. Осесимметричное распределение напряжений в од-
однородном полом цилиндре, обладающем цилиндри-
цилиндрической анизотропией 226
§ 42. Распределение напряжений в полом однородном ци-
цилиндре под действием внутреннего и наружного
давлений 230
§ 43. Распределение напряжений в полом однородном ци-
цилиндре под действием осевой силы и изгибающего
момента 233
§ 44. Распределение напряжений в непрерывно-неодно-
непрерывно-неоднородном полом цилиндре под действием давления . 238
§ 45. Распределение напряжений в круговом неоднород-
неоднородном цилиндре, обладающем цилиндрической анизо-
анизотропией, под действием осевой силы и изгибающего
момента 241
§ 46. Осесимметричное распределение напряжений в кру-
круговом цилиндр о с упругими характеристиками, ме-
меняющимися вдоль радиуса и по длине 245
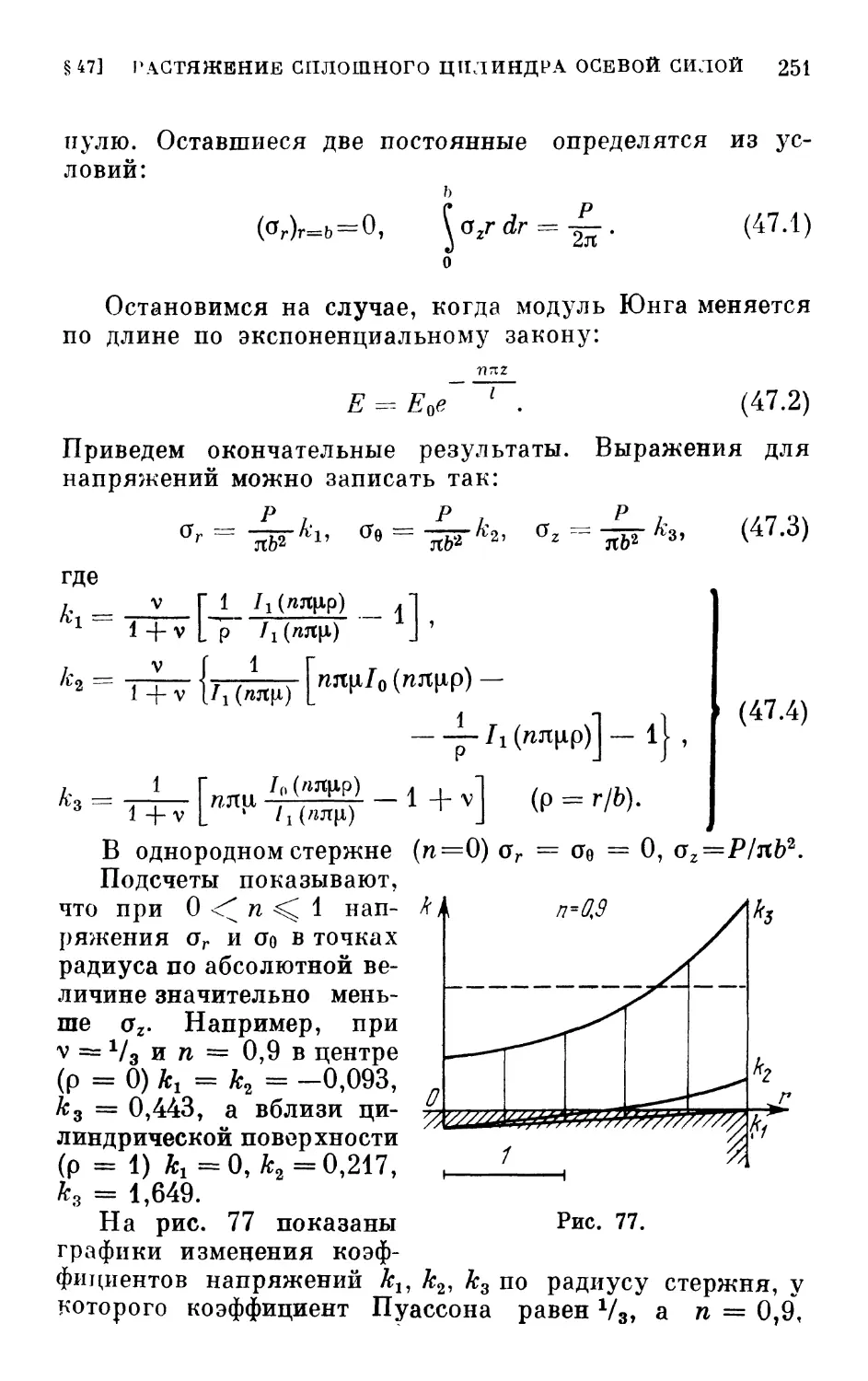
§ 47. Растяжение сплошного цилиндра с модулем, ме-
меняющимся только по длине, осевой силой .... 250
§ 48. Изгиб плоского кривого бруса моментами и силой,
приложенными на концах ... - 252
Глава 6. Обобщенное кручение и кручение стержней .... 258
§ 49. Обобщенное кручение однородных стержней с пря-
прямолинейной анизотропией 258
§ 50. Совместное действие скручивающих и изгибающих
моментов 263
§ 51. Простое или чистое кручение однородного стерж-
стержня 266
§ 52. Связь напряжений и перемещений с функцией ус-
усложненной комплексной переменной 269
§ 53. Упругое равновесие стержня эллиптического сече-
сечения под действием скручивающих и изгибающих
моментов 272
§ 54. Чистое кручение однородного ортотропного стерж-
стержня эллиптического или кругового сечения .... 275
ОГЛАВЛЕНИЕ
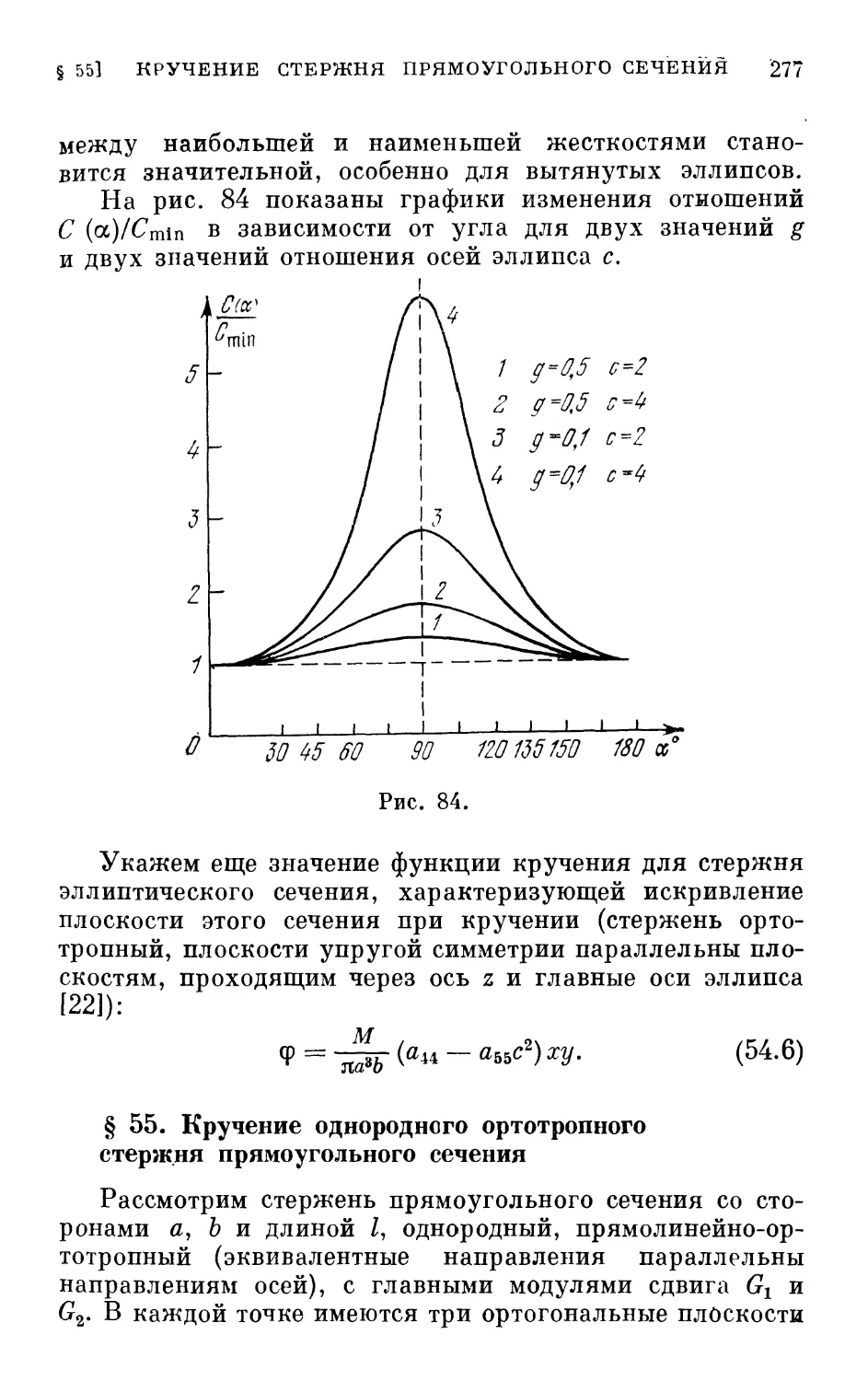
§ 55. Кручение однородного ортотропного стержня пря-
прямоугольного сечения 277
§ 56. Приближенные методы решения задач о кручении 282
§ 57. Кручение непрерывно-неоднородного стержня с
прямолинейной анизотропией 287
§ 58. Кручение ортотропного стержня прямоугольного
сечения с переменными модулями сдвига .... 290
§ 59. Некоторые другие случаи неоднородного ортотроп-
ортотропного стержня прямоугольного сечения 295
§ 60. Кручение цилиндрического или призматического
стержня, обладающего цилиндрической анизотро-
анизотропией 299
§ 61. Кручение неоднородного полого кругового цилинд-
цилиндра, обладающего цилиндрической анизотропией. . 302
Глава 7. Равновесие анизотропной консоли под действием из-
изгибающей нагрузки простейшего вида 308
§ 62. Обобщенный изгиб однородной консоли под дей-
действием поперечной силы 308
§ 63. Общие выражения для функций напряжений, со-
составляющих напряжений и проекций перемещения.
Граничные условия 314
§ 64. Изгиб однородной прямолинейно-анизотропной
консоли поперечной силой 317
§ 65. Распределение напряжений в однородной консоли
эллиптического и кругового сечения 322
§ 66. Изгиб однородной ортотропной консоли прямоу-
прямоугольного сечения 324
§ 67. Приближенные методы решения задачи об изгибе
консоли поперечной силой 328
§ 68. Изгиб неоднородной ортотропной консоли .... 330
§ 69. Изгиб неоднородной ортотропной консоли прямо-
прямоугольного сечения 334
§ 70. Равновесие консоли, обладающей цилиндрической
анизотропией, под действием поперечной силы . . 337
§ 71. Распределение напряжений в консоли, имеющей
форму полого или сплошного цилиндра 341
Глава 8. Кручение тел вращения . » » 345
§ 72. Общие уравнения теории кручения пепрерывно-не-
однородных тел вращения, обладающих цилиндри-
цилиндрической анизотропией 345
§ 73. Кручение однородного тела вращения 350
§ 74. Кручение криволинейно-анизотропного конуса . . 352
§ 75. Влияние сферического и сфероидального включения
и полости на распределение напряжений в скручен-
скрученном стержне 356
§ 76. Точное решение задачи о кручении кругового ци-
цилиндра 362
§ 77. Кручение цилиндра, у которого модули сдвига меня-
меняются пропорционально степени расстояния г (точ-
(точное решение) 365
ОГЛАВЛЕНИЕ
Глава 9. Осесимметричная деформация трансверсально-изо-
тропного тела вращения 368
§ 78. Общие уравнения осесимметричной деформации.
Функция напряжений 368
§ 79. Общие выражения для напряжений и перемещений
через две функции. Общий случай деформации
трансверсально-изотропного тела 375
§ 80. Распределение напряжений в цилиндре под дейст-
действием произвольной осесимметричной нагрузки . . 379
§ 81. Распределение напряжений в тяжелом массиве с
вертикальной полостью 383
§ 82. Распределение напряжений в упругом полупрост-
полупространстве под действием осесимметричной нормальной
нагрузки 385
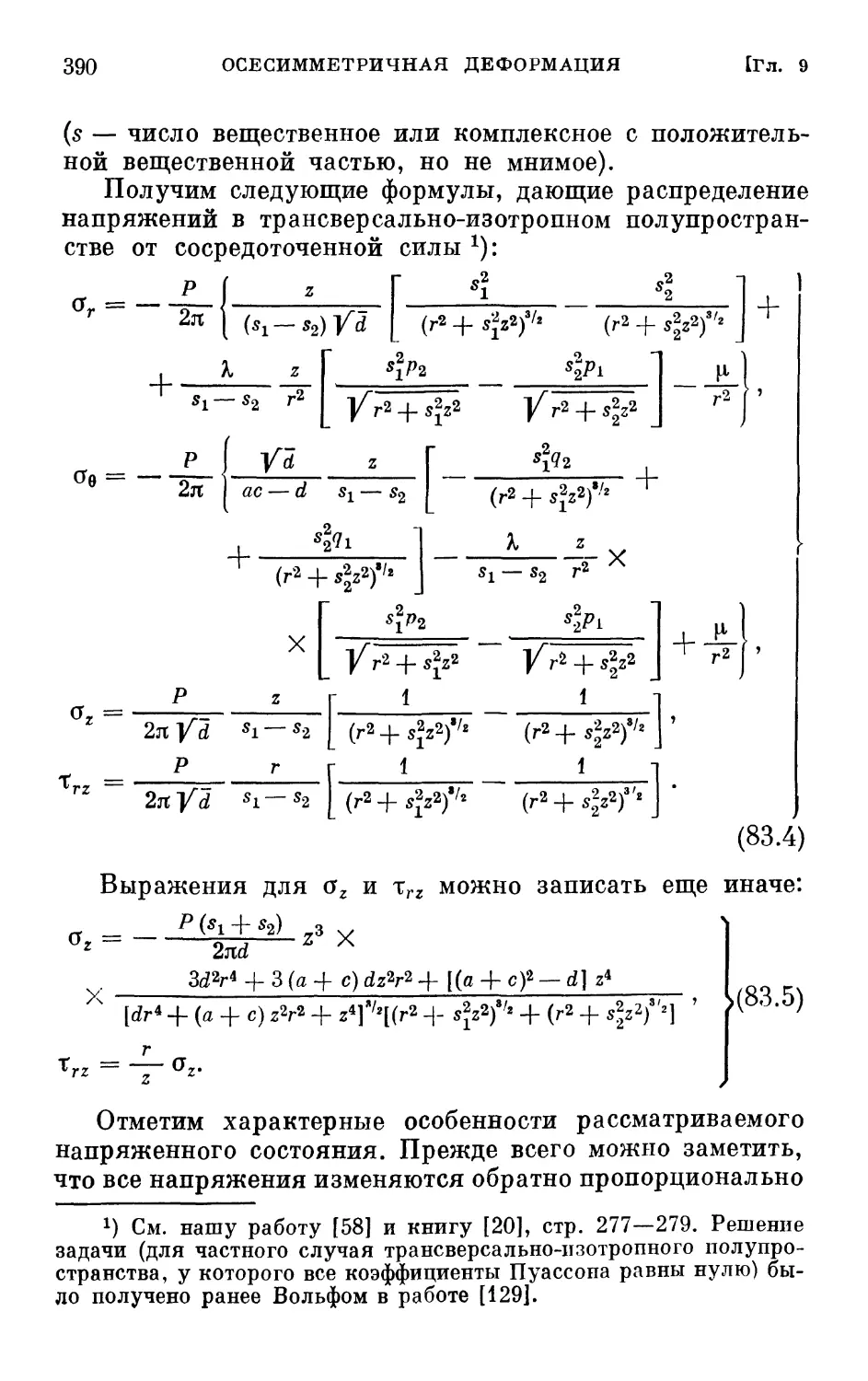
§ 83. Распределение напряжений в полупространстве под
действием сосредоточенной силы и произвольной
нормальной нагрузки 389
§ 84. Растяжение упругого конуса 393
§ 85. Распределение напряжений вблизи эллипсоидаль-
эллипсоидального и сферического включения или полости при
одностороннем и всестороннем растяжении . . . 396
§ 86. Распределение напряжений в стенке сферического
сосуда под действием внутреннего и наружного
давлений 403
Литература 408
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Первое издание книги «Теория упругости анизотроп-
анизотропного тела» вышло в свет в 1950 г. За время, прошедшее с
1950 г., теория упругости анизотропного тела непрерывно
развивалась и пополнялась все новыми и новыми исследо-
исследованиями как серьезных проблем общего характера, так и
частных задач, относящихся к этим проблемам. Так, под-
подведена строгая научная база под общую теорию и установ-
установлен ряд закономерностей, благодаря чему эта теория, раз-
разработанная впервые Сен-Венаном и П. Бехтеревым, если
можно так выразиться, испытала свое второе рождение.
Разработано множество частных проблем из области обоб-
обобщенных плоской деформации, кручения, изгиба и решено
очень большое количество частных задач, относящихся к
этим проблемам. Рассмотрены и решены новые задачи о
кручении и изгибе тел вращения, концентрации напряже-
напряжений в пространственных системах — в строгой постановке
и т. д. Весьма существенно, что разработано и сконструи-
сконструировано много совершенно новых анизотропных материалов,
обладающих рядом преимуществ перед известными до сих
пор (например, армированные стеклопластики). Таким
образом, за четверть века данная отрасль науки значи-
значительно шагнула вперед как в теоретическом отношении,
так и в чисто практическом, по части конструирования
новых анизотропных материалов. Тем не менее, то, что
было сделано по теории упругости анизотропного тела до
1950 г., не потеряло своего значения и в наше время G0-е
годы XX века) и, как нам кажется, нуждается в повторе-
повторении (частично в новой редакции) и во втором издании
книги.
Разумеется, нет никакой возможности отразить в не-
небольшой книге все, что сделано в данной области нового за
четверть века. Поэтому мы сразу же оговоримся, что при-
приводимый здесь материал не является исчерпывающим.
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ 9
Более того, некоторых проблем и задач мы вовсе не рас-
рассматриваем, а приводим такие решения, которые пред-
представляются нам наиболее важными и интересными для
практики (среди них есть и ряд новых). По-прежнему, как
и в первом издании, мы рассматриваем анизотропные тела,
испытывающие только малые упругие деформации и сле-
следующие обобщенному закону Гука. Так же как и в первом
издании, мы совершенно не рассматриваем неупругих де-
деформаций анизотропного тела, а из конкретных проблем и
задач исключаем из рассмотрения задачи об устойчивости
пластинок (тонких плит) и оболочек, задачи динамики и
общие задачи трех измерений1). Из новых задач упомянем
о некоторых задачах об изгибе, кручении и других дефор-
деформациях неоднородных тел, а также укажем несколько за-
задач, решаемых в строгой постановке.
В целом объем второго, переработанного издания не-
несколько больше объема первого издания, хотя мы сочли
возможным некоторые параграфы, входящие в первое из-
издание, исключить, как менее важные.
Во втором издании книги — девять глав, охватываю-
охватывающих шесть проблем: 1) общие положения и уравнения;
2) простейшие задачи; 3) упругое равновесие тела, ограни-
ограниченного цилиндрической поверхностью, в котором напря-
напряжения не меняются вдоль образующей (обобщенная плос-
плоская деформация, обобщенное кручение, плоская задача,
чистое кручение— главы 3—6); 4) равновесие анизотропной
консоли; 5) кручение тел вращения и 6) осесимметричная
деформация тел вращения.
В конце книги приложен перечень литературы, содер-
содержащий названия работ, непосредственно использованных в
тексте, а также других работ по теории упругости анизо-
анизотропного тела (монографий и статей), которые представля-
представляются нам важными и интересными. Сюда же включены не-
некоторые основные курсы теории упругости и несколько
справочников, использованных при выводе ряда формул.
Ссылаясь на литературу в тексте, мы указываем в квадрат-
квадратных скобках номер работы по списку. Перечень литературы
отнюдь не претендует на исчерпывающую полноту. По-
Попытка отразить всю известную литературу по Еопросам,
рассмотренным в книге и смежным, привела бы к весьма
1) Впрочем, решений таких задач до сих пор известно еще мало.
10 ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
объемистому списку и мы от этого отказались, рассчитывая,
что более полные списки литературы будут даны в соот-
соответствующих обзорных статьях и библиографических ука-
указателях. В настоящее время опубликованы такие указате-
указатели для неоднородных тел, изотропных и анизотропных,
составленные Г. Б. Колчиным и Э. А. Фаверманом [14],
охватывающие работы, опубликованные с 1923 по 1973 год
включительно (более 2600 названий).
С. Г. Лехницкий
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
В современных конструкциях наряду с материалами,
обычно при расчетах принимаемыми за однородные и изо-
изотропные, используются для изготовления деталей и ани-
анизотропные материалы, у которых наблюдается резкое раз-
различие в упругих свойствах для разных направлений.
Примером таких материалов может служить натураль-
натуральная древесина; общеизвестно, что модуль упругости древе-
древесины при растяжении вдоль волокон значительно больше
соответствующего модуля при растяжении поперек волокон
и что упругие постоянные ее зависят от направления по
отношению к древесным волокнам. Анизотропными (и при-
притом неоднородными) являются синтетические материалы,
применяемые в самолетостроении: дельта-древесина, авиа-
авиафанера, текстолит и др. Анизотропией упругих свойств
обладают кристаллы и некоторые горные породы. Разными
авторами отмечалась и исследовалась анизотропия бетона.
Кроме деталей, изготовленных из материалов, облада-
обладающих анизотропией, зависящей от внутреннего строения
(«естественной» анизотропией), в современных конструк-
конструкциях используются элементы с так называемой конструк-
конструктивной или искусственной анизотропией. К последним от-
относятся пластинки и оболочки из изотропного материала,
которым придана волнистость путем гофрирования или
усиленные часто поставленными ребрами.
Для того чтобы иметь возможность рассчитывать на
прочность анизотропные детали, испытывающие упругие
деформации, необходимо уметь определять напряжения и
деформации в анизотропных телах теоретическим путем,
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ Ц
т. е. решать задачи теории упругости анизотропного тела.
Как известно, число независимых упругих постоянных в
изотропном теле равно двум (модуль Юнга и коэффи-
коэффициент Пуассона). В случае анизотропного однородного тела
число независимых упругих постоянных может быть значи-
значительно больше — достигать 21 в общем случае анизотро-
анизотропии. Для решения задач о распределении напряжений и
деформаций в анизотропном теле нужно исходить из урав-
уравнений теории упругости, учитывающих различие упругих
свойств для разных направлений и содержащих в соответ-
соответствии с этим более двух упругих постоянных. С подобными
задачами может встретиться конструктор, а также специа-
специалист горного дела и физик, работающий с кристаллами.
В настоящее время теория упругости изотропного тела
весьма полно и всесторонне разработана (благодаря трудам
главный образом советских ученых — Г. В. Колосова,
Н. И. Мусхелишвили, Б. Г. Галеркина, П. Ф. Папковича
и многих других). Теория упругости анизотропного тела
разработана менее полно, однако и в этой области уже на-
накопился довольно большой материал в виде ряда статей,
опубликованных в различных журналах и сборниках и
нескольких монографиях. Наиболее изученными являются
вопросы напряженного состояния и устойчивости анизо-
анизотропных пластинок (изложение их дано, например, в нашей
книге «Анизотропные пластинки»), другие же проблемы
еще не получили достаточно полного систематического ос-
освещения.
Мы полагаем, что в настоящее время уже назрела необ-
необходимость собрать воедино накопленный, но еще не систе-
систематизированный материал, привести его в порядок и опуб-
опубликовать в виде отдельной монографии. Она помогла бы
конструкторам и другим специалистам, которым приходит-
приходится сталкиваться с вопросами упругости анизотропных тел,
ориентироваться в этих вопросах и использовать приведен-
приведенные результаты исследований для решения своих задач.
Такой монографией и является настоящая книга, содер-
содержащая как собственные исследования автора (занимающие
большую ее часть), так и результаты, полученные другими
учеными.
В книге освещены следующие темы: общие уравнения
теории упругости анизотропного тела (глава 1); простей-
простейшие случаи упругого равновесия (глава 2); напряженное
12 из предисловия к первому изданию
состояние анизотропного тела, ограниченного цилинд-
цилиндрической поверхностью, при котором^ напряжения не
меняются вдоль образующей (главы 3 и 4); напряженное со-
состояние анизотропной консоли постоянного сечения, дефор-
деформируемой поперечной силой (глава 5); симметричная де-
деформация и кручение тел вращения (глава 6).
Из этого перечня видно, что книга не претендует на
освещение всех вопросов теории упругости анизотропного
тела, а излагает только некоторые, наиболее изученные,
но еще не приведенные в систему. В ней не содержится ис-
исследований по изгибу и устойчивости анизотропных плас-
пластинок, так как эти вопросы достаточно полно разработаны
в нашей книге ^Анизотропные пластинки». Задача о плос-
плоской деформации и обобщенном плоском напряженном со-
состоянии изложена сжато (в связи с более общей задачей),
причем из частных случаев рассмотрены только наиболее
важные. В книге не затронуты проблемы равновесия и ус-
устойчивости анизотропных оболочек, а также динамики
упругого тела (за исключением общих уравнений движе-
движения). Во всех случаях предполагается, что деформации
являются упругими и малыми, а материал следует обоб-
обобщенному закону Гука. В конце имеется перечень литера-
литературы, куда, кроме работ, излагающих специальные вопро-
вопросы, включены также некоторые основные курсы теории
упругости.
С. Г. Лехницкий
Глава 1
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ
УПРУГОСТИ АНИЗОТРОПНОГО ТЕЛА
Настоящая глава носит вводный характер. В ней мы
напоминаем основные положения теории упругости и об-
общие уравнения, которые в дальнейшем используются для
построения решений конкретных задач теории упругости
анизотропного тела.
§ 1. Напряженное и деформированное состояния
сплошного тела
Изучая напряженное и деформированное состояния
анизотропных тел, вызванные какой-либо внешней нагруз-
нагрузкой, мы примем ряд предположений и ограничений. Важ-
Важнейшие из них сводятся к следующему:
1. Тело является сплошным (сплошной средой), причем
напряжения на любой площадке внутри и на поверхности
являются силами, отнесенными к единице площади. Иначе
говоря, моментными напряжениями, которые вводятся в
ряде современных работ, мы пренебрегаем, как это делается
в классической теории упругости.
2. Связь между компонентами деформации и проекция-
проекциями перемещения и их первыми производными по коорди-
координатам является линейной, т. е. мы рассматриваем только
малые деформации.
3. Между компонентами напряжений и деформаций су-
существуют линейные зависимости, т. е. материал следует
обобщенному закону Гука, причем коэффициенты этих ли-
линейных зависимостей могут быть как постоянными (одно-
(однородное тело), так и переменными функциями координат,
непрерывными или прерывными (в случае неоднородного
тела).
14 ОБЩИЕ УРАВНЕНИЯ ТЕОРИЙ УПРУГОСТИ [Гл. 1
4. Начальных, т. е. существующих без внешней нагруз-
нагрузки, напряжений, в том числе и температурных, не учитыва-
учитываем; конкретных задач динамики не рассматриваем.
Таким образом, мы подходим к теории упругости ани-
анизотропного тела с позиций классической линейной теории
упругости однородного или неоднородного тела. При этом,
конечно, из нашего поля зрения выпадают динамические
задачи, задачи об устойчивости и колебаниях, о больших
деформациях и некоторые другие и задачи для неупругого
анизотропного тела.
Рассматривая конкретные задачи, мы будем пользовать-
пользоваться главным образом декартовыми или цилиндрическими
ортогональными координатами и лишь в отдельных случа-
случаях сферическими.
Укажем прежде всего важнейшие обозначения, кото-
которыми мы пользуемся *).
Координаты точек в трехмерном пространстве будем
обозначать для разных систем координат так: х, у, z —
декартовы, г, 9, z — цилиндрические, р, 9, ф — сфериче-
сферические.
Этими же буквами обозначаем координатные направ-
направления.
На площадках, нормальных к координатным направ-
направлениям, действуют напряжения, каждое из которых мы
раскладываем на три составляющие — нормальную (нор-
(нормальное напряжение) и две касательные (касательные на-
напряжения). Нормальные напряжения обозначаем буквой а
с одним индексом, указывающим направление нормали к
площадке (и напряжения). Касательные напряжения обо-
обозначаем буквой т с двумя индексами (направление нормали
к площадке и направление напряжения). На площадках,
нормальных к осям декартовой системы координат, имеем
составляющие напряжений:
Составляющие напряжений образуют тензор напряже-
напряжений; он часто записывается в виде матрицы, которая из
соображений равновесия бесконечно малого элемента тела
г) Основных формул и уравнений механики сплошной среды,
лежащих в основе теории упругости, мы не выводим, так как их
можно найти в курсах теории упругости (см., например, курсы
А. Лява [24], В. В. Новожилова [27], Л. С. Лейбензона [18] и др.).
§1]
НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЯ
15
оказывается симметричной (а тензор, следовательно, ока-
оказывается симметричным):
Xxv Xxz I
Ранг тензора — второй.
Выражения для тензоров напряжения в цилиндриче-
цилиндрической и сферической системах запишутся таким образом:
1г9
a.
На рис. 1 показаны площадки, нормальные к коорди-
координатным направлениям х, г/, z и г, 6, z декартовой и ци-
цилиндрической систем координат, и составляющие напряже-
напряжений на них, которые мы все принимаем положительными.
Z )
Рис. 1.
Зная составляющие напряжений в точке (из которых
независимых будет, следовательно, только шесть) на трех
взаимно перпендикулярных площадках, проходящих через
какую-нибудь точку тела, мы можем определить напряже-
напряжения на любой четвертой нлощадке, проходящей через ту же
точку. Обозначая через п нормаль к четвертой площадке и
16 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
через Хп, Yn, Zn проекции напряжения, действующего на
эту площадку, на оси х, г/, z, имеем три формулы, по кото-
которым и определим искомые проекции:
Xh = Ox COS (П, X) + Хху COS (П, у) + Xxz COS (П, z), л
Уп = *ху WS (п, X)+ Оу COS (П, у)+ Tyz COS (n,z), A.1)
Zn = *xz cos (n, x) -f xyz cos (n, y) + az cos (n, z). )
Аналогичные формулы можно записать в цилиндриче-
цилиндрических, сферических и других криволинейных координатах.
Кроме декартовых, у нас встретятся только цилиндриче-
цилиндрические и сферические координаты.
В этой же главе при выводе некоторых теоретических
положений мы используем и другие обозначения для со-
составляющих напряжений: вц (i = 1, 2, 3) — нормальные
напряжения, о^ (i Ф /, i, / = 1, 2, 3) — касательные на-
напряжения.
Проекции перемещения точки на оси координат — де-
декартовых, цилиндрических и сферических — обозначим
следующим образом:
и, v, w — декартовы,
иг, щ, w — цилиндрические,
Щ, мв, мф — сферические.
Деформация тела в окрестности данной точки характе-
характеризуется составляющими деформации — тремя относитель-
относительными удлинениями и тремя относительными сдвигами.
Первые три мы будем обозначать буквой г с индексом,
указывающим первоначальное направление отрезка, кото-
который удлиняется или укорачивается, вторые — буквой у с
двумя индексами, указывающими первоначальные перпен-
перпендикулярные направления (например, гх и гу — относитель-
относительные удлинения отрезков, первоначально параллельных х
и У * Уху — изменение угла между отрезками, первоначаль-
первоначальные направления которых были х и у).
Составляющие деформации et и 1/а уц образуют сим-
симметричный тензор'второго ранга. Будучи записанным с по-
помощью матрицы, он для декартовой системы я, г/, z имеет
вид
§1]
НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЯ
17
Для других ортогональных систем координат эта
матрица запишется аналогично и мы приводить ее не
будем.
Укажем далее связь между составляющими деформации
(в отдельных случаях мы будем обозначать их Ец, е^-) и
проекциями перемещения в трех системах координат.
1) Декартова система:
dv
дх '
A.2)
p —
ьх
V —
Yyz
2)
Ye2
Yre
du
дх
dv
dz
» У
, dw
1 ду - Тхг-
Цилиндрическая
дг ' Су г
<Ч 1 Эш
^2 ' Г 06
г dQ дг
dv
ду '
система:
» Yrz
г
ди
dz '
Ur
Г '
dw
дг
1
*\у —
Yxy
8Z
dw
dz
du
dy
dw
dz
A.3)
3) Сферическая система:
-2-.
Если деформации не являются мальэди, то относитель-
относительные удлинения и сдвиги eh уи связан^ ^^рШЩвтна
18
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
нелинейными соотношениями. Приведем для примера за-
зависимости для декартовой системы координат:
sin уху =
ди дУ
дх
ди ди
дх ду
dv dv
dw dw
дх ду
A-5)
Остальные три компонента ez, yyz, yxz мы найдем из
A.5) путем круговой перестановки индексов.
Наконец, что нам будет необходимо в дальнейшем,
это — дифференциальные уравнения равновесия и движе-
движения сплошной среды (не обязательно упругой). Уравнения
равновесия запишем следующим образом, обозначая через
X, Y, Z и соответственно Я, в, Z и Р, В, Ф проекции объ-
объемных сил на координатные направления (отнесенных к
единице объема).
1) Декартова система координат:
if
дх
дг
дх до, дт„
~дх~ h ду "*" ^ "*" ~ '
dz
дх
ду
¦ +
dz
4- Z = 0.
A.6)
2) Цилиндрическая система:
дг
49
дг
дг ^ г
dz
¦+ я =
2тг9
г
rz
A.7)
§ 2] ПРЕОБРАЗОВАНИЕ СОСТАВЛЯЮЩИХ НАПРЯЖЕНИЙ 19
3) Сферическая система:
¦ 1 **рф
~Г _ „:п о я„ Т"
1
dp ' р dQ ~ р Sin 6
+ -|[- Bар - а„ - <уф + трв ctg9) + Р = О,
р #6 р sin 6 <3ф "•"
A.8)
+ -J- t(^e - аф) ctg 9 + Зтре] + в = О,
^трф , 1 дЧ, 1 ^Ф
ар "^~ р д9 "т" psin0 5ф •"
+ -L Bт9ф ctg е + Зтрф) + ф = о.
Из уравнений равновесия легко получить уравнения
движения, добавляя к объемным силам инерционные чле-
члены. Инерционные члены равны плотности р, умноженной
на проекции ускорения с обратным знаком, которые обыч-
обычно выражают через проекции перемещения. Так, например,
для декартовой системы координат при малых деформациях
к функциям X, У, Z нужно добавить:
- дЧ - дЧ - d*w
~~P~~W' ~~P~W' ~~P~W~
(перемещения — функции координат точек тела до дефор-
деформации и времени t). В дальнейшем на протяжении этой
книги нам другие уравнения движения не понадобятся,
а поэтому мы сказанным и ограничимся.
§ 2. Преобразование составляющих напряжений
к новым осям
На практике часто могут встретиться случаи, когда
известны составляющие напряжений, отнесенные к одной
системе координат х, у, z («старой»), а требуется опреде-
определить их для другой системы х', у', z («новой»). Предпо-
Предполагается, что обе системы ортогональны, но необязательно
декартовы.
Сохраняя для составляющих напряжений, отнесенных
к системе х, у, z, прежние обозначения и отмечая составля-
составляющие в новой системе х\ у', z' штрихом, мы получим иско-
искомые формулы преобразования, используя выражения для
20
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[Гл. 1
Таблица 1
Косинусы
проекций напряжений на площадке с произвольно направ-
направленной нормалью A.1). Зададим косинусы углов между
осями старой и новой систем координат в виде таблицы 1.
Так, например, l±1 = cos (х\ х),
l23 = cos (г/', z) и т. д.
Рассмотрим площадку с нор-
нормалью х' и [напряжения на ней с
проекциями Хх>, Yx>, Zx- на старые
оси. Проектируя напряжения на
направления осей новой системы,
получим
<?х = ХХ>11Х + YX>112 + ZX'Z13
Хху = Хх>1ъ\ + Yxd22 + Zx'l-25
fXz = Xx'lsi "t" Yxd^ H~ 2/Х'&зз
B.1)
Подставляя сюда выражения A.1), где п = х', получим
три составляющие напряжения в виде однородных квадра-
квадратичных функций косинусов 1г]. Затем рассматриваем на-
напряжения на площадках с нормалями г/', z .
Приводим две окончательные формулы:
Xyz = Oxl2i
х'
у'
z'
X
In
hi
hi
У
la
hi
*J2
z
lv»
k»
xl2ihi
tyz (^22^33 + '23^32) + txz (^21^33 4"
Xyz
C2 + ^22^3l)-
Остальные четыре составляющие а', г' найдем путем
круговой перестановки индексов у Zf7-.
Аналогичным путем получим формулы обратного пере-
перехода — от напряжений а', т' к напряжениям а и т. Приво-
Приводим две из них:
(^22^33 + ^23^32) + txz (^12^33 +
I 2] ПРЕОБРАЗОВАНИЕ СОСТАВЛЯЮЩИХ НАПРЯЖЕНИЙ 2i
Формулы преобразования напряжений к новым осям
можно записать очень просто, если воспользоваться сокра-
сокращенными тензорными обозначениями [25], но для этого
придется изменить, как было указано выше, и сами обозна-
обозначения для составляющих напряжения. Будем обозначать
(временно) все составляющие напряжения одной буквой а
с двумя индексами — одинаковыми для нормальных со-
составляющих ^различными для касательных (о^). Таким
образом, о1г = ох, а23 = xVz и т. д. Тогда все шесть^формул
преобразования составляющих напряжения к новым осям
запишутся в виде одной:
B.4)
В такой системе обозначений обычно знаки суммиро-
суммирования отбрасывают и вместо B.4) пишут:
Таблица 2
Косинусы
В этой формуле к, I — фиксированные, a i и / — ин-
индексы, по которым производится суммирование от 1 до 3.
Аналогично запишутся формулы
перехода] от а^* к а^-:
Oij = Oklkik- B-6)
Здесь фиксированными явля-
являются индексы г, /', а суммирова-
суммирование производится по к и Z.
Приведем формулы перехода
от напряжений в декартовой си-
системе координат к напряжениям
в цилиндрической системе г,
6, z (оси z обеих систем совпада-
совпадают). Таблица 1 для косинусов
принимает вид таблицы 2. Окон-
Окончательные формулы запишутся следующим образом:
ar = ox cos2 6 + о у sin2 6 + 2тл1У sin 6 cos 6,
ае = ох sin2 Q + Oy cos2 6 — 2xxy sin 6 cos 6,
tre = (Oy — ox) sin 6cos 6 + xxy (cos2 6 — sin2 6), К B.7)
xrz = xxz cos 6 -j- xyz sin 0,
tez = — xxz sin 6 + xyzcos 6, oz = az.
x'
v'
z'
X
cos 9
sin6
0
У
—sine
cose
0
z
0
0
1
22 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
Такой же вид имеют формулы преобразования поворота,
т. е. перехода от напряжений ох, оу, . . . , тху к напряже-
напряжениям gx, ау, . . . , Тху, отнесенным к системе координат х',
у', z , полученной путем поворота первой системы на угол
Ф вокруг оси z F = ф).
Преобразование составляющих деформации к новым
осям производится по формулам, весьма схожим с B.5) —
B.7), так как эти составляющие образуют тензор, анало-
аналогичный тензору напряжений. Сопоставляя эти два тензора,
мы видим, что нормальному напряжению а соответствует
относительное удлинение 8, а касательному напряжению
т — половина одноименного сдвига г/% у. Следовательно,
формулы для составляющих деформации, отнесенных к
новым осям, мы получим из B.3), подставляя в них 8
вместо а и V2 у вместо т.
§ 3. Обобщенный закон Гука
Приведенные ранее формулы и уравнения верны для
любой сплошной среды, независимо от ее физических
свойств. Переходя к упругому телу, мы должны выбрать
модель, отражающую упругие свойства, и получить, в до-
дополнение к уравнениям §§ 1 и 2, зависимости между со-
составляющими деформации и составляющими напряжений.
Так как мы рассматриваем только малые деформации, то
примем за упомянутую модель — сплошное тело, следую-
следующее обобщенному закону Гука. Иначе говоря, мы будем
рассматривать только такие среды и тела, в которых со-
составляющие деформации являются линейными функциями
составляющих напряжений. Эти функции должны быть
однородными, так как предполагается, что при отсутствии
напряжений составляющие деформации также равны ну-
нулю, и наоборот: если е = y = О» то и а = т = 0.
Тела, подчиняющиеся обобщенному закону Гука, могут
быть различными, а поэтому следует дать их классифика-
классификацию, отражающую хотя бы приближенно их особенности.
В отношении упругих свойств все тела можно разделить,
с одной стороны, на однородные и неоднородные, и с другой
стороны, на изотропные и анизотропные. Под однородным в
отношении упругих свойств будем подразумевать тело, у ко-
которого упругие свойства одинаковы в разных его точках;
§ 3] ОБОБЩЕННЫЙ ЗАКОН ГУКА 23
неоднородным назовем тело с упругими свойствами, раз-
различными в разных точках. Если упругие характеристики,
например, модули упругости (см. ниже), меняются при
переходе от точки к точке непрерывно, то и неоднородность
можно назвать «непрерывной»; если же упругие характе-
характеристики при переходе от точки к точке испытывают разры-
разрывы непрерывности, например, меняются скачками, то не-
неоднородность мы будем называть «прерывной» или «диск-
«дискретной». Скачкообразное изменение имеет место в телах,
составленных из нескольких частей с различными упруги-
упругими свойствами (из различных материалов).
Изотропным в отношении упругих свойств называется
тело, у которого эти свойства (упругое сопротивление)
одинаковы для всех направлений, проведенных через дан-
данную точку; анизотропным называется тело с упругими
свойствами, вообще различными для разных направлений,
проведенных через данную точку. Направления, для ко-
которых упругие свойства (упругое сопротивление) одина-
одинаковы, называют^ упруго-эквивалентными. У изотропного
тела упруго-эквивалентными являются все направления,
проведенные через данную точку, а у анизотропного — не
все, а только некоторые. В зависимости от структуры тело
может быть изотропным или анизотропным и одновременно
однородным или неоднородным. Заметим еще, что в разных
средах можно различить два основных типа анизотропии:
1) прямолинейную и 2) криволинейную. О прямолинейной
анизотропии будет сказано уже в этом параграфе, а о кри-
криволинейной — ниже, в § 10.
В общем случае анизотропии каждая составляющая де-
деформации является линейной функцией всех шести состав-
составляющих напряжений. Рассмотрим однородное тело, обла-
обладающее анизотропией самого общего вида. Отнеся его к
декартовой системе координат, положение которой пока
уточнять не будем, запишем уравнения обобщенного зако-
закона Гука для этой системы (с очевидными сокращениями):
ех = а1гох + а12оу + a^oz -f auxyz + а1ЪхХ2
гу = а21ох + а22оу + . . .
C.1)
24 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
В общем случае C.1) уравнения содержат 36 коэффици-
коэффициентов аи, но в действительности их всегда меньше, как это
будет показано далее.
Предположим, что определитель шестого порядка из
коэффициентов а^-, записанных по порядку, не равен ну-
нулю, а следовательно, уравнения C.1) разрешимы относи-
относительно а и т. Получим уравнения обобщенного закона Гука
для общего случая в другой, эквивалентной форме:
А12гу + А13гх + A14yyz + Albyx
(Ту = А21гх
C.2)
Пусть тело, для которого верны уравнения C.1) и C.2),
растягивается постоянными усилиями р, параллельными
одной из осей координат, например, оси х. Тогда ох = р, а
остальные пять составляющих напряжений равны нулю.
Из уравнений C.1) находим составляющие деформации,
постоянные для любой точки:
гу = а21р, гг = а31р, |
Vvz = a4i/>> Vxz = акр. Уху = аР I
Очевидно, что малые отрезки, проходящие через раз-
разные точки и параллельные оси х, удлиняются одинаково,
и вообще все отрезки, параллельные одному и тому же на-
направлению п, проведенные через разные точки, испытыва-
испытывают одинаковые удлинения (зависящие от констант atj и
пропорциональные р). Это дает основание называть анизо-
анизотропию рассматриваемого однородного тела — прямо-
прямолинейной, а само тело — прямолинейно-анизотропным.
У такого тела все параллельные направления являются
упруго-эквивалентными. Из формул C.3) следует, что эле-
элементы одинаковых размеров в виде прямоугольных парал-
параллелепипедов с соответственно параллельными сторонами
при простом (или двух- и трехстороннем) растяжении де-
деформируются одинаково, независимо от того, где они вы-
выделены, но превращаются, вообще говоря, в косоугольные
параллелепипеды, не имеющие ни одного прямого угла
между гранями.
§ 3J ОБОБЩЕННЫЙ ЗАКОН ГУКА 25
Заметим, что условно, исключительно для простоты
изложения, мы можем называть «прямолинейно-анизотроп-
«прямолинейно-анизотропным» и неоднородное тело, если уравнения обобщенного
закона Гука для него задаются в декартовой системе коор-
координат (ctij, Atj — заданные функции х, у, z).
Вернемся к однородному телу. В однородном теле коэф-
коэффициенты atj и А и из уравнений C.1) и C.2) будем назы-
называть упругими постоянными. В неоднородном теле, когда
эти коэффициенты — функции координат, мы будем назы-
называть их упругими характеристиками. Рассматривая atj
и A tj раздельно, мы, следуя П. Бехтереву, будем называть
atj коэффициентами деформации, аЛ^ — модулями упру-
упругости [8, 48]. В литературе существует еще ряд названий
и обозначений для этих величин. Например, в книге Фойг-
та [38] вместо atj и Аг]- употребляются обозначения stj,
с.ц\ А. К. Малмейстер вместо коэффициентов деформации
и модулей упругости использует термины «константы по-
податливости» и «константы упругости» ([25], гл. II, § 21).
Уравнения C.1) и C.2) показывают, что в каждом теле
число упругих п&стоянных равно 36. На самом деле это
не так даже в самом общем случае^если существует упру-
упругий потенциал (что мы всегда и будем предполагать), рав-
равный потенциальной энергии деформации, отнесенной к
единице объема. Это имеет место, когда изменения тела при
деформировании происходят изотермически или адиаба-
адиабатически. Рассматривая только вопросы равновесия, мы
будем полагать, что изменения при деформации происхо-
происходят изотермически, т. е. температура каждого элемента ос-
остается постоянной. В уравнениях C.1) и C.2) под atj и Atj
будем подразумевать изотермические упругие постоянные,
которые вообще отличаются от адиабатических (см. [17],
стр. 66—67, или [24], стр. 106; см. также [20], гл. 1, § 2).
В этом случае имеют место равенства:
<**=Т^> "»=¦!?¦,•••,f« = ^. C-4)
Продифференцируем составляющие напряжения по со-
составляющим деформации:
х у х ху /о г\
—; ==г . ~х = : • (О О)
<78 с)& ду dz \ ' /
И Т. Д.
26
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[ГЛ. 1
Из равенств C.5) и C.2) следует
и вообще
Л„=Лл(*,/ = 1,2, ..., 6). C.6)
Решив уравнения C.2) относительно 8 и у, мы получим
шесть выражений для 8 и у, у которых коэффициенты пра-
правых частей также будут симметричны:
аи = ап (г, / = 1,2, . . . , 6). C.7)
Теперь мы можем записать уравнения обобщенного за-
закона Гука в общем случае так:
ся = апох + айву + • • • + 016**1/
C.8)
Уху = аиах + а26оу f . . . + л6втаУ,
или так:
+
4- . . - +
C.9)
Интегрируя шесть уравнений C.4), мы получим выра-
выражение упругого потенциала в виде однородной квадратич-
квадратичной функции деформаций:
л
У 4? + ^ 4" • • • + М&хУхг + АиРхУху +
+ ^
4- • • •
4-
4-
-у-ЛбУхг +
4"
Разбивая C.10) на шесть групп по шесть слагаемых
V = -у(АХ1гх + ... 4- А1вухУ) вх+...
... 4- 4"
C.11)
§ 3] ОБОБЩЕННЫЙ ЗАКОН ГУКА 27
и подставляя выражения ох, оу, . . . , rxyj мы получим
очень простую и удобозапоминаемую формулу для упру-
упругого потенциала:
V = -g- (охгх + оугу + ... + ххуухУ). C.12)
Если подставить в эту формулу выражения для со-
составляющих деформации C.8), то мы получим V как одно-
однородную квадратичную функцию напряжений. Выражение
для V построено так же, как и C.10), только вместо е, у
будут а и т с соответствующими индексами и вместо Ац —
коэА&ициенты деформации а^:
C.13)
В общем случае анизотропии число упругих постоянных
А и, dij равно 21, однако из них независимых по-
постоянных меньше. Как сказано в книге В. В. Новожилова
«Теория упругости»: «С точки зрения геометрической все
системы координат равноценны, тем не менее с точки зре-
зрения упругих и вообще физических свойств даже в наиболее
общем случае может быть подмечена некоторая симмет-
симметрия» 1). Следовательно, число независимых упругих кон-
констант равно даже в самом общем случае не 21, а меньше —
18. В курсе В. В. Новожилова (§ 19 и 20) рекомендуется
при исследовании напряжений пользоваться так называе-
называемыми инвариантными константами и указывается, как их
определять по константам аг]-, отнесенным к произвольной
системе координат. В дальнейшем мы этот вопрос под-
подробно разбирать не будем, а будем в каждом случае счи-
считать, что дана система координат х, г/, z (или криволиней-
криволинейная) и отнесенные к ней константы аг]- и Ац. Впрочем, для
тел с развитой упругой симметрией можно сразу же ука-
указать оси, для которых константы аи, Аи будут инвариант-
х) В. В. Новожилов. Теория упругости. Судпромгиз,
1958, [27]. См. также [16], [98].
28 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
ными (например, для ортотропного и трансверсально-
изотропного тела; см. § 4).
В уравнениях обобщенного закона Гука C.8) и C.9)
упругие константы (или характеристики) занимают не-
одинаковое'положение и следует их как-то классифициро-
классифицировать. Один из^принципов классификации в общем случае
предложен П. Бехтеревым, разбившим все коэффициенты
dij (и соответственно A tj) на шесть групп [8]. В этой работе
весьма обстоятельно исследуются" (теоретическим путем)
уравнения обобщенного закона Гука.
Другие авторы, как, например, Н. Г. Ченцов [100],
Я. И. Секерж-Зенькович [92], в частных случаях ани-
анизотропии вместо постоянных ацъ Atj вводят так называе-
называемые «технические константы» —гмодули Юнга и сдвига,
коэффициенты Пуассона и другие. А. Л. Рабинович пред-
предложил развернутую систему технических констант и для
самого общего случая однородного анизотропного тела
[85]. Пусть тело отнесено к какой-то фиксированной сис-
системе координат. Тогда, вводя вместо atj новые обозначе-
обозначения, мы можем, следуя А. Л. Рабиновичу, записать урав-
уравнения C.8) таким образом:
1 , '
*>z = -g— (— vX2crx — v^ + (Тг +
22
?1У2 = * (Лх,, yz°x + Лгу, tjz^iy + Лг, yzaz +
1/2
+ lyz + Vzx, yz*xz + Pxy, yz*xv),
\
Vxz = ~c (Лх, zx^ + Л1/, z.v0?; + Лг, zxaz +
ryz, zx^yz \ Tx2 ~T Гхгу, zxxxyA
Уху = 7^ (Л.г, .пЛл- + Л?/, xw^V + Лг, xy<*z +
'л 7
~T~ И'Уг, xy^yz \ \^zx, xy^xz \ ~xy)'
C.14)
§ 3] ОБОБЩЕННЫЙ ЗАКОН ГУКА 29
Здесь Ехх, Еуу, Ezz — модули Юнга при растяжении —
сжатии в направлениях осей х, у, z\ Gyz, GXZ1 Gxy — модули
сдвига для плоскостей, параллельных координатным;
vVx» vzx, . . . , vyz — коэффициенты Пуассона, характери-
характеризующие сокращение в направлении одной оси при растя-
жении в направлении другой (например, vyx — коэффи-
коэффициент, характеризующий сокращение в направлении оси
х при растяжении в направлении оси у). Эти постоянные
соответствуют хорошо известным модулю Юнга, сдвига и
коэффициенту Пуассона для изотропного тела. Остальные
постоянные являются новыми для упругого тела и у изот-
изотропного тела равны "нулю.
Коэффициенты r \izx, yz, . . ., \izx, xy названы коэффи-
коэффициентами Ченцова; они характеризуют сдвиги в плоскос-
плоскостях, параллельных координатным, вызванные касатель-
касательными'напряжениями, действующими 'в 'других плоскос-
плоскостях, параллельных координатным. Постоянные %г, х,
Лгх, у, • • . * fW zi п0 А. Л. Рабиновичу,— коэффициенты
взаимного влияния первого рода; они характеризуют уд-
удлинения в направлениях осей координат, вызванные каса-
касательными напряжениями, действующими в координатных
плоскостях. Наконец, r\Xi yz, т)у? yz, . . . , v\z,xy выражают
сдвиги в координатных плоскостях от нормальных напря-
напряжений, геттствующих в направлении осей координат; они
названы коэффициентами взаимного влияния второго
рода d).
Все уравнения C.14) записаны только для данной сис-
системы координат; для других систем значения коэффициен-
коэффициентов изменяются, но общее число независимых упругих
постоянных по-прежнему будет равно 18.
Решая конкретные задачи, мы будем пользоваться в
основном обозначениями at7- и А г]-; «технические константы»
будем вводить в случаях, когда тело обладает хорошо раз-
развитой упругой симметрией, т. е. является^ортотропным
или трансверсалыю-изотропным.
Наконец, отметим, что, изменяя обозначения упругих
постоянных и составляющих напряжений, мы можем
х) Нам кажется, что нет необходимости обозначать модули
Юнга с помощью двух индексов; достаточно одного. Индексы у
коэффициентов Пуассона следовало бы переставить, чтобы обозна-
обозначения согласовались с введенными другими авторами ранее.
30 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
записать уравнения обобщенного закона Гука чрезвычайно
просто. Обозначим1 упругие постоянные буквой а (или со-
соответственно А) не с двумя, а с четырьмя индексами, по-
положив:
1) atj = атпы, если г, / = 1, 2, 3 (всевозможные слу-
случаи, когда / = i, не исключаются);
2) dij = 2 amnw, если какой-нибудь из двух индексов,
i или /, равен 4, 5, 6 и
3) atj = 4 атпы, если оба индекса i, j = 4, 5, 6.
Тогда шесть уравнений C.8) запишутся в виде одного
[25]:
&и = аиывы (i, h к, l = *» 2> 3)- C-15)
Знаки, обозначающие суммирование в каждом из шести
равенств C.15) по к и по Z, в такой системе записи обычно
отбрасываются. Число всех констант а^ш с четырьмя ин-
индексами равно 81, но, группируясь, они сводятся к кон-
константам, число которых равно 21 (из них независимых 18).
Уравнения обобщенного закона Гука, решенные относи-
относительно составляющих напряжения, имеют вид
Оц = А1Шгк1. C.16)
Впрочем, обозначениями упругих постоянных с по-
помощью букв а и А с четырьмя индексами и уравнениями
C.15), C.16) мы воспользуемся на протяжении данной
книги только еще один раз, в § 5. Поэтому развивать этот
вопрос подробно мы не будем, а отошлем интересующихся
к книге А. К. Малмейстера, В. П. Тамужа и Г. А. Тетерса
[25] (гл. II, § 21).
§ 4. Основные случаи упругой симметрии
Если структура анизотропного тела обладает симметри-
симметрией какого-нибудь рода, то и в упругих свойствах обнаружи-
обнаруживается симметрия. Упругая симметрия (так ее принято
называть) проявляется в том, что в каждой точке обнару-
обнаруживаются симметричные направления, эквивалентные в
отношении упругих свойств.
Для кристаллов связь между симметрией структуры и
упругой симметрией устанавливается принципом Ф. Ней-
Неймана, который можно сформулировать следующим обра-
§ 4] ОСНОВНЫЕ СЛУЧАИ УПРУГОЙ СИММЕТРИИ 31
зом: материал в отношении своих физических свойств
(в том числе упругих) обнаруживает симметрию того же ро-
рода, что и его кристаллографическая форма, или более совер-
совершенную (см. [24], стр. 167). Принцип распространяется и
на тела, не являющиеся кристаллами, но обладающие
симметрией структуры (древесина, фанера, стеклопла-
стеклопластики).
Если анизотропное тело обладает симметрией упругих
свойств (упругой симметрией), то уравнения обобщенного
закона Гука для него упрощаются, так как некоторые из
коэффициентов ац оказываются равными нулю, тогда как
между другими появляются линейные зависимости. Эти
упрощения можно вывести, применяя следующий метод.
Отнесем тело к системе координат х, у, z, а затем ко вто-
второй — х\ у', z', симметричной с первой, в соответствии с
тем видом симметрии, какая наблюдается в теле. Направ-
Направления осей х, у, z и х', у', z' одинакового наименования
будут направлениями, эквивалентными в отношении упру-
упругих свойств, а поэтому уравнения обобщенного закона
Гука для симметричных систем координат запишутся оди-
одинаково. Записав эти уравнения в системе х, у, z и в системе
х', у', zr, далее переходим к одной из них, выражая, ска-
скажем, х', у', zr через ху у, z. Сравнивая получившиеся одно-
одноименные уравнения, мы находим зависимости между atj
или Atj. Вместо уравнений обобщенного закона Гука мож-
можно взять выражение упругого потенциала, записанное в
основной системе х, у, z и симметричной х\ yf, z'. Пе-
Переходя во втором выражении к системе х, у, z и прирав-
приравнивая упругие потенциалы, приходим к тем же резуль-
результатам.
Не останавливаясь на выводе, который можно найти,
например в книге Лява [24], в гл. 6, приведем уравнения
обобщенного закона Гука и схемы выражений упругого
потенциала в виде треугольных матриц, соответствующих
формуле для У, выраженной через напряжения. Сначала
рассмотрим однородные тела, а затем сделаем несколько
замечаний по поводу неоднородных тел.
Важнейшими являются четыре случая упругой симмет-
симметрии, которые мы и разберем.
1. Плоскость упругой симметрии. Предположим, что
через каждую точку тела проходит плоскость, обладающая
следующим свойством: любые два направления, симметрич-
32 общие Уравнения теории упругости [гл. i
ные по отношению к этой плоскости, являются эквивалент-
эквивалентными в отношении упругих свойств *). Будем называть на-
направление, нормальное к плоскости упругой симметрии,—
главным направлением упругости (или просто главным на-
направлением, если одновременно не рассматриваются другие
главные направления — тензоров напряжений и деформа-
деформаций). В данном случае через точку тела проходит лишь
одно главное направление.
Направляя ось % нормально к плоскости упругой сим-
симметрии, а две другие в этой плоскости, заключаем, что
восемь упругих постоянных должны быть равны нулю:
пЫ = ^24 = #34 = #46 = #15 = аЪЬ = пЪЬ ~ а5б = 0, ^
\ \ \ v \ """
и число упругих постоянных dij сведется к 13. Уравнения
обобщенного закона Гука будут иметь такой вид:
гу = а12ох
е = diz^xi wza^y i waavz i wao vxyi
D.1)
yxz =
УхУ^
Схема выражения упругого потенциала (половины на диа-
диагонали, соответствующие членам вх, ву* . . . > ^у, отбро-
отброшены):
D.2)
LPenmB уравнения D.1) относительно ст, т, мы получим
уравнения, отличающиеся от D.1) только заменой ст, т на
соответствующие е, у и ац на Atj. При произвольных на-
направлениях осей эти уравнения содержат 13 ничем явно
х) ДРУгие пары симметричных направлений вообще не эквива-
эквивалентны направлениям первой пары.
«13
«23
«33
0
0
0
«44
0
0
0
«46
«66
«161
«26 1
<ы\
0 1
о
§4]
ОСНОВНЫЕ СЛУЧАИ УПРУГОЙ СИММЕТРИИ
33
не связанных коэффициентов деформации ац. Тем не менее
независимых постоянных в D.1) и D.2) не 13, а 12, и, зная
пи, мы имеем принципиальную возможность найти их
(§ 3).
Рассмотрим элемент тела в виде прямоугольного парал-
параллелепипеда, у которого две пары граней направлены про-
произвольно, а плоскости остальных двух являются плоскос-
плоскостями упругой симметрии. Пусть по этим двум граням рас-
распределены равномерно нормальные усилия, равносильные
напряжениям az (рис. 2). Из уравнений D.1) находим сос-
составляющие деформации:
гх =
Ъг =
гу =
ez =
D.3)
Отсюда видно, что при растяжении — сжатии в направ-
направлении, перпендикулярном к плоскости упругой симмет-
симметрии, углы между отрезками,
нормальными к плоскости
упругой симметрии и лежащими
в ней, остаются прямыми. Пря-
Прямоугольный параллелепипед пе-
переходит в прямой параллеле-
параллелепипед: боковые грани его оста-
остаются прямоугольными, а осно-
основания превращаются в парал-
параллелограммы.
2. Три плоскости упругой
симметрии (ортотропное тело).
Если через каждую точку тела
проходят три взаимно перпен-
перпендикулярные (ортогональные)
плоскости упругой симметрии,
причем одноименные плоскости упругой симметрии па-
параллельны во всех точках, то, направляя оси координат
нормально к плоскостям упругой симметрии (по главным
направлениям), получим, что, кроме восьми упругих по-
постоянных предыдущего'случая, равны нулю еще четыре:
«16 = «26 = «36 = «45 = 0.
Уравнения обобщенного закона Гука и схема упруго-
упругого потенциала в константах ац принимают следующий
Рис. 2.
2 С. Г. Лехницкий
34
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[Гл. 1
вид
«У
ч
yz
= a12ax
= ai3<?x
«11
+ ^22^y ~
;> i л
«12
«i2
"z =
«13
«23
«S3
Ь^2
Ms
0
0
0
au
'XZf
0
0
0
0
«55
Y*y
0
0
0
0
0
«66
D.4)
D.5)
Введем технические константы Eti Gtj, vtj, причем вмес-
вместо буквенных индексов будем писать численные. Тогда
уравнения D.4) запишутся так:
Vl2
JV J7 UZ>
= -^^-->aw
lx]/'
D.6)
Тело, обладающее тремя ортогональными плоскостями
упругой симметрии в каждой точке (или, что то же, тремя
взаимно перпендикулярными главными направлениями),
называется ортогонально-анизотропным или, короче, ор-
тотропным. Главные направления в данной точке могут
быть и неравноценными, не эквивалентными. Из 12 упру-
упругих постоянных, входящих в уравнения D.6), только де-
девять являются независимыми, так как в силу симметрии
матрицы правой части уравнений обобщенного закона Гука
всегда
i?iv2i = E2v12, E2v32 = E3v23i E3vls = Exv3l. D.7)
Оси координат, нормальные к плоскостям упругой симмет-
симметрии, называют главными осями координат.
Существенно отметить, что дальнейшего сокращения
числа упругих постоянных здесь уже не будет/так как пц
§ 4] ОСНОВНЫЕ СЛУЧАИ УПРУГОЙ СИММЕТРИИ л 35
из уравнений D.4) или Еи Gih vtj из уравнений D.6), в
противоположность случаю одной плоскости упругой сим-
симметрии, сами являются инвариантными константами. Ина-
Иначе их называют главными константами (в отличие от кон-
констант из уравнений, записанных для произвольной системы
х, у, z). Заметим, что элемент, изображенный на рис. 2, с
гранями, параллельными плоскостям упругой симметрии,
будучи растянут, останется прямоугольным параллеле-
параллелепипедом, только изменит свои размеры.
3. Плоскость изотропии (ось симметрии вращения).
Трансверсалъно-изотропное тело. Рассмотрим тело, обла-
обладающее следующими свойствами: через все точки проходят
параллельные плоскости упругой симметрии, в которых
все направления являются упруго-эквивалентными (плос-
(плоскости изотропии). Иначе говоря, в каждой точке имеется
одно главное направление и бесконечное множество глав-
главных направлений в плоскости, нормальной к первому.
Можно такое тело еще рассматривать как тело, через каж-
каждую точку которого проходит ось упругой симметрии бес-\
конечно высокого порядка — ось вращения. Тело с такими
свойствами называется трансверсально-изотропным ([24],
стр. 172).
Направим ось % нормально к плоскости изотропии, а
оси х и у произвольно в этой плоскости. Тогда уравнения
обобщенного закона Гука запишутся так:
гх = апох
Еу = а12ох + anov
+ av)
Ухг = ^4Лг> Уху = ^
D.8)
Число независимых упругих констант равно пяти.
Введем технические константы: Е, Е' — модули Юнга
для растяжения — сжатия в направлении плоскости изот-
изотропии и нормальном к ней, v — коэффициент Пуассона,
характеризующий поперечное сжатие в плоскости изотро-
изотропии при растяжении в этой плоскости, v' — то же, при
растяжении в направлении, нормальном к плоскости
изотропии, G = Е1[2 A + v)], G' — модули сдвига для
плоскости изотропии и любой перпендикулярной к ней.
36
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[Гл 1
Уравнения D.8) перепишутся так *):
гх = -g- К — vtfy) — -~ в„ yvz = -^ tVZf
ву = -g" (— w* + сгу) — -^г cr2, v« = ТГ rxz,
vr 1 1
8 (<* + °) + ° Y Г
D.9)
В некоторых работах трансверсально-изотропный ма-
материал называется сокращенно транстропным
(см., например, [6]).
4. Изотропное тело. Если в теле все направления явля-
являются упруго-эквивалентными и главными, то, полагая в
МЫ ПОЛУЧИМ
E
D.9)? = ?, v = v, G = G= 2(i+v) ,
хорошо известные уравнения обобщенного закона Гука
для изотропного1 тела с модулем Юнга Е, коэффициен-
коэффициентом Пуассона v и модулем сдвига G:
?х = -g- 1<*х — v (Оу + стг)], 7У2 = -^
1
oz%
1
E l z v x
D.10)
Кроме четырех основных случаев упругой симметрии,
существует еще целый ряд других. Типичными здесь явля-
являются виды симметрии монокристаллов различных элемен-
элементов и соединений. Доказано, что существует всего 32 вида
геометрической симметрии кристаллов. Однако число клас-
классов упругой симметрии кристаллов значительно меньше
(равно девяти), так как одна и та же форма уравнений
обобщенного закона Гука кристаллов имеет место для не-
нескольких случаев геометрической симметрии их (от двух
до семи). Мы не будем приводить результатов исследования
этого вопроса, а отошлем интересующихся к книге
А. Лява [24] (гл. 6) и к нашей книге [20], § 4, где имеются
и ссылки на литературу.
г) В работах [65] и [22] приводятся уравнения обобщенного
закона Гука для трансверсально-изотропного тела в другой, экви-
эквивалентной форме.
§ 5] ПРЕОБРАЗОВАНИЕ УПРУГИХ ПОСТОЯННЫХ 37
§ 5. Преобразование упругих постоянных
при переходе к новой системе координат
Решая конкретную задачу теории упругости, нам при-
приходится использовать уравнения обобщенного закона Гука,
в которые входят упругие постоянные а^ или Atj. Эти
величины в случае анизотропного тела зависят от направле-
направлений осей координатной системы, и если направления осей
изменить, то изменятся и, значения упругих постоянных.
Исключение составляет изотропное тело, у которого урав-
уравнения обобщенного закона Гука сохраняют свой вид в
любой ортогональной системе координат, а соответствую-
соответствующие упругие постоянные остаются неизменными (инва-
(инвариантными). При изучении напряженного состояния часто
может возникнуть вопрос: известны
постоянные ац и Atj для координат-
координатной системы х, у, z, но удобнее поль-
пользоваться другой ортогональной си-
системой х', у', %' (рис.3). Требуется
найти постоянные а\.,А\. для второй
системы. Прежде всего нужно за-
задать таблицу косинусов углов меж-
между новыми и старыми направления-
направлениями осей координат (см. таблицу 1). с*
Применим следующий метод. Рассмотрим выражения
упругого потенциала в первой системе («старой») и во
второй («новой») и приравняем их. Получим равенство, в
левую часть которого входят составляющие напряжений
или деформации, отнесенные к системе х, г/, z, а в правую —
те же величины для системы хг, у', zr. Затем выразим
составляющие напряжений или деформаций, отнесенные к
старой системе координат, через составляющие напряже-
напряжений или, соответственно, деформаций, для новой системы.
Сравнивая коэффициенты при квадратах и произведе-
произведениях составляющих напряжений или деформаций, отнесен-
отнесенных к новой системе, в левой и правой частях равенства,
мы получим искомые формулы для новых упругих по-
постоянных — выражения a{j через atj или Ац через Ац.
Пусть atj — коэффициенты деформации в уравнениях
обобщенного закона Гука для системы х, у, z и требуется
определить ац для ортогональной системы координат х\
y\zf'. В общем случае, когда элементы упругой симметрии
38
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[Гл. 1
отсутствуют, уравнения обобщенного закона Гука, отне-
отнесенные к старой системе, будут иметь вид C.8), а упругий
потенциал определится по формуле C.13). Для системы
координат х', у', г' имеем уравнения и выражение *):
гх = апох + а12оу
yyz =
E.1)
V = — CLnGx
Y a22av + • • • 4" fl2e°ryt3cy 4
, 1 ' '«
• • • +— aMXxy
E.2)
Приравнивая два выражения для F, получим равенство
— Meetly =
— ЯЦ0Х +
= -g" fln^x +
•••+
Подставим в левую часть вместо су, х их выражения
через а', т' (формулы B.3) записываем сокращенно); по-
получим
z = ^12^13 4" Gyhzhd 4" • • • 4" Xxy (^12^23 +
E.4)
Приравнивая коэффициенты при квадратах и произве-
произведениях напряжений со штрихами, получим искомые фор-
формулы преобразования. В равенства войдут ац как линей-
линейные функции atj и однородные функции четвертой степени
относительно косинусов ltj. Записанные в развернутом ви-
*) Из уравнений обобщенного закона Гука записываем только
два, пропуская ряд членов; в выражении для V также пропускаем
некоторые слагаемые (ср. C.8) и C.10)),
51
ПРЕОБРАЗОВАНИЕ УПРУГИХ ПОСТОЯННЫХ
39
де формулы получаются довольно громоздкими, но можно
записать их очень просто, введя условные и сокращенные
обозначения qtj, заданные таблицей 3.
Таблица 3
Символы qtj к формулам преобразования коэффициентов ai?.
1
2
3
4
5
6
1
&
<31
2^31^21
212,1ц
2
&
2/32^22
2^32^12
21м1я
3
'I.
2^33^23
2^зз^1з
2^13^23
4
Wl3
*28*22
We2
*33*22 + *32*23
Wl2 + ^32^13
^13^22 + ^ 12*23
5
^13^11
^33^21 + ^31^23
hshi + ^31^13
^13^21 4" ^11^23
6
Wll
/22 21
^31^22 + ^32^21
^31^12 + ^11
*11^22+ ^12*21
В символах qtj первый индекс указывает номер строки
таблицы 3, а второй — номер столбца 4). Например,
С помощью этих выражений, зависящих от ltj, все фор-
формулы преобразования можно записать в виде одной:
в в
j 22 mnQimQjn
m=i n=i
или, отбрасывая знаки сумм, получим
E.5)
E.6)
) В первом издании книги «Теория упругости анизотропного
тела» [20] таблица 2, соответствующая таблице 3, построена
несколько иначе, что в конечном итоге роли не играет. Кроме того,
мы сочли более удобным изменить обозначения для косинусов.
40 ОБЩИЕ УРАВНЕНИЯ ТЕОЬЙИ УПРУГОСТИ [Гл. 1
(г, / = 1, 2, . . . , 6; суммирование производится по ин-
индексам тип). Также легко записать и формулы преобра-
преобразования модулей упругости Atj- к новым осям, которые мы
получим, используя выражение F как функцию г ж у. При-
Приводим без вывода эти формулы; они все получаются из
одной:
Aij = Amnqimqjn. E.7)
Здесь символы qtj берутся из таблицы, которая отлича-
отличается от таблицы 3 только тем, что в клетках на пересечении
строк 1, 2, 3 и столбцов 4, 5, 6 перед произведениями ко-
косинусов ltj стоят коэффициенты 2, тогда как на пересечении
строк 4, 5, 6 со столбцами 1, 2, 3 стоят произведения ко-
косинусов без коэффициента 2 (см. [25], стр. 82 и 83).
Формулы E.6), E.7) и таблица 3 дают возможность
определить модуль Юнга для любого направления п, если
известны упругие постоянные пц для данной фиксирован-
фиксированной системы координат х, у, z. Приводим в развернутом
виде выражение для постоянной a'w обратной модулю Еп:
п
+ «55) ^13
2/12/13 \(аы + а56) l2n
+ 2lnl12 [aul2n + a26l2l2 + (а34 + ai5) /?3]. E.8)
Здесь „
х' = п, 1п = cos (п, х), /12 = cos (ai, у), ZJ3 = cos (п, z).
Формулы преобразования коэффициентов деформации
можно записать и иначе, если обозначать эти коэффициен-
коэффициенты буквой а не с двумя, а с четырьмя индексами и исполь-
использовать сокращенную запись уравнений обобщенного закона
Гука. Приводим без вывода эти формулы, которые все со-
содержатся в одной, взятые из книги, неоднократно упоми-
упоминавшейся ([25], стр. 71):
Суммирование при данных г, /\ к, I производится по
индексам т, п, s, р, принимающим значения 1, 2, 3. По
§ 6] ПРЕОБРАЗОВАНИЕ ПОСТОЯННЫХ ПРИ ПОВОРОТЕ 41
формуле E.9) преобразуются к новым осям компоненты
тензора четвертого ранга; следовательно, константы atjki
образуют тензор четвертого ранга (или, что то же, являют-
являются его компонентами) *). Разумеется, формулы преобразо-
преобразования E.9) не противоречат ранее приведенным формулам
преобразования E.5)—E.6), а находятся с последними в
полном соответствии.
В связи с преобразованием коэффициентов деформации
к новым осям обнаруживается ряд инвариантных зависи-
зависимостей между dijM. Этот вопрос освещен в работе Е. К. Аш-
кенази и Э. В. Ганова [6].
§ 6. Преобразование упругих постоянных
при повороте координатной системы
Рассмотрим частный случай, когда новая система коор-
координат х\ у\ z' получена из старой х, у, z путем поворота
на некоторый угол ср вокруг общей оси z — zr (рис. 4). Во
все формулы преобразования упругих постоянных войдут
косинусы ltj, которые в
данном случае задаются
таблицей 4.
1. Преобразование коэф-
коэффициентов деформации atj.
Пусть тело обладает ани-
анизотропией общего вида У
B1 или, точнее, 18 инва-
инвариантных упругих кон-
констант). Обозначим, как и
раньше, через аи упругие ПС*
постоянные, отнесенные к
старой системе координат х, //, z, и через а\. — постоян-
постоянные, отнесенные к новой, повернутой системе х', у', zf.
Формулы для а'~ мы получим как частные случаи E.5) —
E.6), только в данном случае символы qtj должны быть
взяты из таблицы 5, которую мы получим из таблицы 3,
подставив в нее значения косинусов 1и (см. [25], стр. 84).
*) А. Л. Рабиновичем в работе [85] предложена другая интер-
интерпретация коэффициентов деформации: a{j можно рассматривать
как^компоненты симметричного тензора второго ранга вшестимерном
42
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
Напоминаем, что qtj обозначает число или выражение,
находящееся на месте пересечения i-ik строки и /-го столб-
столбца в таблице 5.
Таблица 4
Косинусы
х'
?/
z'
X
COS ф
—sin ф
0
У
sin ф
COS ф
0
z
0
0
1
Приводим выражения упругих постоянных, получен-
полученных по формуле E.5) с использованием данных таблицы 5,
подробно, без сокращений:
ап = an cos4 ф
Bа12 + aee) sin2 ф cos2 ф + а22 sin4 ф +
+ 2 (а1в cos2 ф + а2в sin2 ф) sin ф cos ф,
#22 —
авв =
а16 =
а2в =
ф + B^12 + авв)81
— 2 (а1в sin2 ф + а2& cos2 ф) sin ф cos ф,
(ап + а22 — 2а12 — авв) sin2 ф cos2 Ф + а12 +
+ (^ie — а2в) (cos2 ф — sin2 ф) sin ф cos ф,
4 (аи + ^22 ~ 2а12 — авв) sin2 cp cos2 ср + а6в —
— 4 (а1в — а2в) (cos2 ф — sin2 ф) sin ф cos ф,
[2а22 sin2 ф — 2an cos2 ф +
+ Bа12 + «ее) (cos2 ср — sin2 ф)] sin ф cos ф +
-\-а1в cos2 ф (cos2 ф — 3 sin2 ф) +
+ #2e sin2 ф Ccos2 ф — sin2 ф),
[2я22 cos2 ф — 2пц sin2 ф —
— Bа12 -f- а6в) (cos2 <p — sin2 ф)] sin ф cos ф +
+ ^le sin2 ф C cos2 ф — sin2 ф) +
+ «2в cos2 ф (cos2 ф — 3 sin2 ф);
F.1)
§ 63 ПРЕОБРАЗОВАНИЕ ПОСТОЯННЫХ ПРИ ПОВОРОТЕ 43
Таблица 5
Символы qtj к формулам преобразования коэффициентов
"Х^
1
2
3
4
5
6
1
COS2 ф
sin2 ф
0
0
0
—2sin ф cos ф
2
sin2 ф
COS2 ф
0
0
0
2sin ф cos ф
3
0
0
1
0
0
0
Таблица 5 (продолжение)
х^
1
2
3
4
5
6
4
0
0
0
COS ф
sin ф
0
5
0
0
0
—sin ф
СОЭф
0
6
sin ф cos ф
—sin ф cos ф
0
0
0
соз*' ф — sin2 ф
44 ОБЩИЕ УРАВНЕНИЯ ТЕОРИЙ УПРУГОСТИ [Гл 1
«44 = «44 cos2 ф — 2«4б sin ф cos ф + «55 sin2 ф,
«45 = («44 — «5б) sin ф COS ф + «45r(C0S2 ф — Sin2 ф),
«55 = «44 sin2 ф + 2«4б sin ф cos ф + «5б cos2 ф;
«14 = «14 cos3 ф + («4б — ап) sin ф cos2 ф +
+ («24 — «5б) S^n2 Ф COS ф — «25 SUl3 ф,
«24 = «21 COS3 ф — («4в + «25) Sin ф COS2 ф +
+ («14 + «5в) sin2 Ф cos Ф — «15 sin3 ф,
«46 = «46 c°s3 ф + (— 2«14 + 2«24 — «56) sin ф cos2 ф +
+ B«]5 — 2«25 — «46) sin2 ф cos ф + «5б sin3 <р,
«is = «15 cos3 ф + («14 + «5б) sin ф cos2 ф +
+ («25 + «4б) Sin2 ф COS ф + «24 Sin3 ф,
«25 = «25 COS3 ф + («21 — «5в) Sin ф COS2 ф +
+ («15 — «4е) sin2 ф cos ф + «14 sin3 ф,
«56 = «5в cos3 Ф + (— 2«15 + 2«25 + «4в) sin ф cos2 ф +
+ (— 2«14 + 2«24 — «бе) sin2 ф cos ф — «4в sin3 ф; t
F.2)
F.3)
F.4)
«13 = «13 cos2 ф + «36 sin ф cos ф + «2з sin2 ф,
«зб = 2 («23 — «1з) sin ф cos ф + «зб (cos2 ф — sin2 ф),
а23 = а13 sin2 ф — «3e sin ф cos ф + «2з cos2 ф,
«зз — «зз»
«34 = «31 cos ф — «35 sin ф,
«35 = «34 Sin ф + «35 COS ф.
Если тело ортотропно и старые оси х, у, z являются
главными осями упругости, т. е. нормальны к плоскостям
упругой симметрии, то в формулах преобразования упру-
упругих констант F.1)—F.4) нужно положить
«14 ^ «15 = «16 = «24 = «25 = «26 = «34 = «35 = «36 =
= «45 = «46 = «56 = 0.
Очевидно,
«14 = «24 = «46 = «15 = «25 = «36 = «34 = «35 = 0, F.5)
но «16, «26, «se, «45 вообще говоря, не равны нулю.
§ 6] ПРЕОБРАЗОВАНИЕ ПОСТОЯННЫХ ПРИ ПОВОРОТЕ 45
На практике может возникнуть следующий вопрос.
Пусть мы имеем какие-то основания считать тело ортот-
ропным, но нам известны только направление одной глав-
главной оси, принятой за ось z координатной системы х, у, z и
упругие постоянные atj для этой системы. Спрашивается:
как определить направления двух других плоскостей уп-
упругой симметрии, или, что то же, угол ф, образованный
главной осью хг с осью х? Ответ на этот вопрос следует
непосредственно из формул F.1), F.2) и F.4): угол ф най-
найдется как наименьшее по модулю решение четырех урав-
уравнений:
«16 (ф) = «26 (ф) = 0, F.6)
«36 (ф) = «45 (ф) = 0. F.7)
Уравнения F.6) после несложных преобразований при-
принимают такой вид:
tg4Ф = 2 , fll6~fl26 , tg2y= fll6 + fl26 , F.8)
ё Y «11 + 022—2О12 —flee & ^ «И—«22 V }
а условие существования у них общих (т. е. одинаковых)
решений запишется таким образом:
(«16 — «2б) [(«И — «22) 2 — («16 + «2б) 21 = («16 + «2б) X
X («и — «i2) («и + «22 — 2 «12 — «6б). F.9)
Кроме того, угол ф должен удовлетворять уравнениям
F.7) или
tg29=—^ , tg 2Ф = 2fl45 , F.10)
Д^з — ^23 ^55 — ^44
а следовательно, должно быть
ai6 + fl2e = а-2— = 2а" . F.11)
^11 ~~~ ^22 ^13 ^23 ^55 ~~ ^44
Если хотя бы одно условие F.9) и F.11) не выполняется, то
это значит, что тело не является ортотропным.
Существенно отметить, что, рассматривая плоскую
задачу, которая подробно разбирается ниже, в главе
4, мы можем не обращать внимания на уравнения F.10)
просто потому, что в уравнения и формулы азв и а4Ъ не
входят. Уравнения F.8) определят положение осей х\ у\
которые хотя, строго говоря, и не являются главными
46 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
(азе и а46 не равны нулю), но в плоской задаче играют роль
главных, так как в системе х\ у\ zr все уравнения плоской
задачи ничем не отличаются от уравнений для ортотроп-
ортотропного тела.
Рассмотрим элементарный пример. Пусть для данной
системы координат я, г/, z получено
а45 < 0.
Тогда четыре уравнения F.8) и F.10) принимают вид
tg 4ф = 0, tg 2ф = оо. F.12)
тг г\ Л Я 3jt
Из первого уравнения находим ф = U, -т-, -^-, -^-, . . . , а из
jt Зя тт
второго ф = -j-, -т—, ... Наименьшее по модулю ф, удовле-
удовлетворяющее обоим уравнениям, равно ф = я/4. Тело орто-
тропное; две плоскости упругой симметрии наклонены к
координатным под углом 45 и 135°.
Формулы упругих постоянных ортотропного тела ста-
становятся более наглядными, если ввести технические упру-
упругие постоянные Еи Gih vu. Тогда вместо F.1), F.2) и F.4)
будем иметь
cos4 Ф , / 1 2v12 \ . о si sin4 Ф
= -ЁГ + fc - -ёг) sm ч»cos ф + -ЕГ'
1 , 2Vio
Ж +
4
1 , 2Vi
2Vi2 1 \ . 2 о , 1
"if - TO Sm Ф C°S Ф+ ^Г '
sins ф cos2jp \
+ G=; 2^М(со82ф — sin2 ф) в
\ Cr12 bY I J
cos ф,
cos2 ф sin2
—щ Ё
— (-q -^-J (cos2 ф — sin2 ф) sin ф cos ф;
2 ф \
ЁГ)-
F.13)
6]
ПРЕОБРАЗОВАНИЕ ПОСТОЯННЫХ ПГИ ПОВОРОТЕ
47
«44 =
cos2 ф . sin2 ф
/1 1 .
«45 =( "г ~r S1T1 Ф C0S Ф»
\ ^23 <>13 /
' _ s*n2 Ф J_ cos2 Ф
«55 — 7» I "n »
^23 ^13
F.14)
a13 = _ J-^LSin2(p + ^cos2
«23 = — (-f^ cos2 ф + -^- sin2 ф) ,
\ ^2 ^l / *•
' __ i
«33 — ~^ >
азв = Z -~ rr- sin ф cos ф.
\ У-1 fi3 / J
F.15)
Прочие а', равны нулю.
Укажем некоторые инварианты для ортотропного тела,
т. е. величины, не меняющиеся при повороте координатной
системы вокруг общей оси z:
' __ !_ . ^ 2vla
= «и + «22
/а =
«ее— '
«44 +
«13 +
«55 =
4v12
^23
/»' /" Vl3 _u Л'23 \
V3i
F.16)
Вопросы, связанные с преобразованием упругих по-
постоянных ортотропного тела при повороте осей координат,
изучались II. Г. Ченцовым; формулы F.3) и F.4) выведе-
выведены в его работе [100] (обозначения Н. Г. Ченцова несколь-
несколько отличаются от наших). Эти же вопросы нашли свое осве-
освещение в «Справочнике» Е. К. Ашкенази и Э. В. Ганова
[6] и в книге [7].
2. Преобразование приведенных упругих постоянных рг-7«.
Как будет показано далее, при изучении упругого равно-
равновесия анизотропного тела, ограниченного какой-нибудь
цилиндрической поверхностью, нам придется иметь дело в
основном не с постоянными а^, а с их нелинейными
48 ОБВДИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
комбинациями:
Рг; = аи - -^ (г, / = 1, 2, 4, 5, 6). F.17)
Эти выражения названы приведенными упругими по-
постоянными. При отыскании решений разных задач может
возникнуть следующий вопрос: известны приведенные по-
постоянные ргу для некоторой системы координат х, у, z с
осью z, параллельной образующей цилиндрической поверх-
поверхности, и требуется определить эти постоянные для другой
системы хг, г/', z', повернутой относительно х, у, z вокруг
общей оси z' = z на угол ф.
Укажем без вывода, что формулы преобразования при-
приведенных постоянных мы получим из F.1) — F.3), за-
заменяя пц на Р;;- с теми же индексами, аа!. — на р!.. Таким
образом, мы получим 15 формул для всех пятнадцати р^.;
ввиду очевидности мы их выписывать не будем *).
Если старые оси х, у, z были главными, то
Pl4 = Pl5 = Pl6 = Р24 = Р25 = Р26 = Р45 = ?4б = Р*6 = 0>
вследствие чего Ри = р^ = $\6 = Pj5 - Р^ = Р^в = 0.
§ 7. Преобразование комплексных параметров
при повороте координатной системы
Все рассмотренные в книге задачи для однородного тела
в декартовых координатах, за исключением простейших,
сводятся к отысканию неизвестных функций U (х, у),
удовлетворяющих дифференциальным уравнениям второго,
четвертого или шестого порядков вида
.. о и , _ о и , , _ аи х/„ „л /п л\
a>o-rwr+ fli . am.!. +••• + а2т —2тг =f(*,y)- С7-1)
дх дх ду ду
Здесь т = 1, 2 или 3; а0, ах, . . . , а2т — заданные по-
постоянные, зависящие от упругих констант, а / (х, у) —
заданная (обычно непрерывная) функция координат х. у.
г) Формулы преобразования fcj и краткий их вывод имеются
первом издании книги [20] (стр. 43—44),
§ 71 ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНЫХ ПАРАМЕТ1 OB 49
С уравнением G.1) связано алгебраическое (характери-
(характеристическое) уравнение степени 2 т:
a2m\i2m + ^m-iH2™-1 + ...+flo = O. G.2)
Корни |Lifc, \xk этого уравнения, как будет показано в
главе 3, для всякого идеально-упругого тела — числа
комплексные или чисто мнимые; они называются комплекс-
комплексными параметрами анизотропного материала *). При реше-
решении разных задач часто приходится переходить от одной
системы координат х, г/, z, где z — ось, нормальная к
плоскости упругой симметрии, к другой системе х', у', z',
повернутой на угол ф относительно общей оси z' = z.
При этом комплексные параметры меняются. Требуется
найти формулы перехода для комплексных параметров при
повороте осей.
Для решения этой задачи разобьем левую часть урав-
уравнения G.1) на 2т линейных дифференциальных операто-
операторов первого порядка, т. е. представим его в виде
D.D, ... DJBJS^ ... DmU = / (х, у), G.3)
где
°^-ду~-^^Г' D« = ^7j—1**-аГ (А = 1,2,...,»»).
G.4)
Перейдя от системы х, у, z к новой, получим
х' = х cos ф + у sin ф, у' = — х sin ф + у cos ф, G.5)
д д
G-6)
Подставляя эти выражения в G.3), мы получим
D[D'2 ... DmD[B[ ... DmU = fx (x\ у'), G.7)
где
д Ц^соэф — sin ф Q Q ' д
ду' cos Ф + И-fcsm ф дх' ду' ^ дх' '
/ ^ |Л> COS ф — Sin ф Q Q —г Q
ду' cos ф + \iK sin ф дх' ду' ^ дх' '
G-8)
х) См. [21], § 10. Чертой сверху мы обозначаем, как обычно,
комплексные сопряженные величины.
50 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
а А (#'» У') — заданная функция f и г/'. Сопоставляя G.8)
и G.4), находим формулы комплексных параметров для
новой системы координат:
\ik cos ф — sin ф _, [Г^созф — sin ф
^к ' ' '
^к cos ф + H-fcsin ф ' ^к cos ф + (Jfc sin ф
Рассматривая формулы преобразования G.9), можно
подметить следующее:
1) если параметры \ik, \in являются комплексными для
одной системы координат, то они остаются комплексными
или чисто мнимыми и для любой другой системы, повер-
повернутой на угол ф вокруг общей оси z\ наоборот, если бы для
какого-нибудь материала или системы координат получи-
получились iifc, \*к вещественными, то они останутся веществен-
вещественными и в любой (декартовой, повернутой) системе коор-
координат;
2) если среди комплексных параметров есть равные
(^т = МгО> то соответствующие комплексные параметры
^т, \\п также будут равными;
3) если один из комплексных параметров для какой-
нибудь системы координат равен i или — i (i = Y—1)»
то и для всякой другой системы, повернутой по отношению
к первой, соответствующий параметр будет равен i или,
соответственно, — i (случай изотропного тела).
§ 8. Поверхности и кривые, изображающие
изменение упругих постоянных с изменением
направления
Как было показано, упругие постоянные для одной и
той же точки зависят от величин, характеризующих на-
направление — от ltj или, в частном случае, от ф. Были пред-
предложены различные геометрические построения, наглядно
иллюстрирующие изменение упругой постоянной данного
наименования для разных направлений, проведенных через
точку О. Для одного и того же материала можно предло-
предложить несколько методов таких построений. Мы остановим-
остановимся на основных методах, не указывая пока, для какого ма-
материала проводится геометрическое построение, а обращая
внимание на то, как строятся соответствующие геометри-
геометрические изображения. Вопрос о конкретных упругих цо-
§ 8] НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ УПРУГИХ ПОСТОЯННЫХ 51
стоянных и геометрических построениях для них разбира-
разбирается в § 8.
1. Направляющие поверхности и кривые. Как было по-
показано, упругие постоянные, преобразованные к новым
осям, являются однородными полиномами четвертой сте-
степени относительно направляющих косинусов. Уместно
вспомнить также, что в теории напряжений нормальное
напряжение является квадратичной функцией направля-
направляющих косинусов нормали к площадке, на которую оно
действует. По формуле для нормального напряжения мож-
можно построить так называемую направляющую поверхность
Коши, которая дает (по крайней мере до некоторой степени)
возможность судить об изменении нормальных напряже-
напряжений на площадках, проведенных через данную точку.
Аналогичным путем можно построить поверхности, ха-
характеризующие изменение модуля Юнга Еп для разных
направлений (см. работу Сен-Венана [123]) и других упру-
упругих постоянных. Будем откладывать по направлениям п
от произвольно выбранной точки, принятой за начало
координат О некоторой фиксированной системы х, у, z,
отрезки, длины которых связаны с модулем зависимостью
г = /с4/^. (8.1)
Здесь к —- масштабный коэффициент, который можно, на-
например, принять равным 1/ \f Ег, где Ех — модуль Юнга
для направления оси х.
Обратимся к формуле E.8). Выражая косинусы Zn, Z12,
113 через координаты по формулам
hi = — , ^2 = — » кз = у (8.2)
и откладывая по разным направлениям, исходящим из
начала, отрезки, равные
(8.3)
заключаем, что концы отрезков г опишут поверхность чет-
четвертого порядка, которая и называется направляющей по-
поверхностью для постоянных ап или для модуля Юнга.
52 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
Уравнение этой поверхности имеет вид
+ Bа13 + аьь) z2x2 + Bau + а66) х2у2 +
+ 2yz [{аи + а5в) ж2 + a2iy2 + auz2] +
+ 2zx [а1ьх2 + (а2б + а4в) i/2 + а35^2] +
+ 2ху [a1Qx2 + a2fiy2 +
+ Kg + 046) 221 = «и- (8.4)
Линии пересечения этой поверхности с плоскостями,
проходящими через начало координат, называются на-
направляющими кривыми модуля Юнга А). Уравнения упро-
упрощаются, если тело является ортотропыым. Направляя оси
х, г/, z нормально к плоскостям упругой симметрии, мы
получим уравнение направляющей поверхности:
?l . (8.5)
Уравнение направляющей кривой на плоскости ху имеет
вид
Хх4 + 2 Вх2у2 + г/4 = X, (8.6)
где
X = -^ , В = -^2- — v2i. (8.6а)
На рис. 5 показаны направляющие кривые модуля Юн-
Юнга для двух значений параметров: а) X = 0,5, В = 10 и
б) X = 0,5, В = 0,05. В частных случаях направляющие
кривые могут выродиться в эллипсы или окружности.
Несколько примеров рассмотрено в работе Сеи-Венана
[123], но мы их здесь разбирать не будем.
2. Поверхности коэффициентов растяжения. Нагляд-
Наглядное представление о сопротивлении материала растяжению
и сжатию мы можем получить, откладывая от данной точки
по разным направлениям отрезки, длина которых пропор-
пропорциональна постоянной ап:
г = kan (8.7)
х) Названия «направляющая поверхность» и «направляющая
кривая» упругой постоянной предложены впервые, по-видимому,
А. Л. Рабиновичем ([85], стр. 19—20).
§ 8] НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ УЙРУГЙХ ПОСТОЯННЫХ 53
(или, что то же, обратно пропорциональна модулю Юнга
для данного направления). Концы таких отрезков опишут
поверхность, называемую «поверхностью коэффициентов
растяжения».
В-0Ж1=0,5
';л-0,5
Рис. 5.
На рис. 6 показан вид поверхности коэффициентов рас-
растяжения для материала, обладающего симметрией, как у
кубического кристалла (ап = а22 = а33, а23 = а13 = а12,
Рис, 6.
Рис. 7.
а44 — а55 = Яве; прочие atj = 0). Поворот фигуры на
а = 2л/4 = 90° приводит к совмещениям всех ее точек.
Такая поверхность получится, например, у монокристалла
альфа-желега. Поверхность отсекает на трех осях симмет-
54
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[Гл. i
рии (главных осях упругости) одинаковые отрезки. На
рис. 7 показан общий характер поверхности растяжения
для ортотропного материала. Оси координат — главные,
т. е. нормальны к плоскостям упругой симметрии г).
3. Диаграммы анизотропии. Существуют еще способы
построения поверхностей, характеризующих изменение
упругих постоянных.
Мы остановимся на так называемых диаграммах ани-
анизотропии, которые представляют собой пространственные
фигуры, но достаточно наглядно изображаются на плос-
плоскости. Для построения используется декартова система
координат.
Ряд преимуществ перед другими имеет такой способ
построения: берется система координат х, у, z и система х ,
у', z с общим началом О,
но так, чтобы оси у и у'
оставались в плоскости ху
(начальной; рис. 8). Угол
между осями у' и у прини-
принимается за одну координату
Ф, а угол между х' и пло-
плоскостью ху — за другую, 0.
Таким образом, упругая
постоянная, изменение ко-
которой мы исследуем, пред-
представляется в виде функции
двух переменных: ф (лежит
в плоскости ху) и 9 (в пло-
плоскости, перпендикулярной
к ху). Затем берется про-
пространственная координатная сетка (первый октант); по
оси абсцисс откладываются значения ф от 0 до 90°, по
оси ординат — углы 0 и по оси z — абсолютные значе-
значения упругой постоянной. Значения упругой постоянной
откладываются от точек с координатами ф, 0 по вертика-
вертикалям, без искажения. Сначала строятся кривые изменения
константы при ф = ф0 = 0 для значений 0,- взятых через
равные промежутки (например, через 15°, или при более
точном построении через 5° и т. д.). Затем строятся кривые
для ф = ф! и 0, меняющихся от 0 до 90°. При этом исполь-
г) Рис. 7 и 8 взяты из первого издания книги [20], стр. 52,
где указаны также в качестве первоисточников работы [85] и [104].
Рис. 8.
§ 8] НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ УПРУГИХ ПОСТОЯННЫХ
55
зуются средства современной вычислительной техники,
на которых мы останавливаться не будем. Когда все кривые
будут построены, то они будут изображать сечения некото-
некоторой поверхности. Удобство такой диаграммы состоит глав-
главным образом в том, что она хотя и представляет собой изоб-
изображение поверхности в косоугольной проекции, но значе-
значения упругой постоянной откладываются без искажения по
вертикали и всегда могут быть определены по графику для
любой пары углов ф и 0. На рис. 9 показан вид диаграммы
для модуля Юнга одного из современных материалов —
стеклопластиков, взятой из книги [7]. Существуют и другие
способы построения диаграмм (поверхностей) анизотропии,
в частности, в полярных координатах. Этот вопрос доста-
точно^нолпо освещен в работах Е. К. Ашкенази и Э. В. Га-
нова [6] н Е. К. Ашкенази и др. [7].
56 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
§ 9. Некоторые анизотропные упругие материалы
Из реальных анизотропных тел в первую очередь сле-
следует назвать монокристаллы различных веществ, а также
стержни и пластинки, вырезанные из монокристаллов.
Доказано, что существует всего 32 вида геометрической
симметрии кристаллов, объединенных в семь сингоний, но-
носящих названия: 1) триклинная, 2) моноклинная, 3) ром-
ромбическая, 4) тетрагональная, 5) тригональная, 6) гексаго-
гексагональная и 7) кубическая. Всякий натуральный кристалл
обладает одним из 32-х видов симметрии и может быть от-
отнесен к одной из семи сингоний [33]. Что касается классов
упругой симметрии, то их значительно меньше, так
как одна и та же форма уравнений обобщенного закона Гу-
Гука имеет место для нескольких видов геометрической сим-
симметрии. По упругим свойствам все кристаллы могут быть
разбиты только на девять классов или групп. Выражения
упругого потенциала (а следовательно, и уравнений обоб-
обобщенного закона Гука) для этих девяти классов можно най-
найти, например, в курсе А. Лява [24] (гл. 6, п. 109) и в ряде
работ, упоминающихся ниже, а поэтому мы, не занимаясь
специально упругостью кристаллов, можем их не приво-
приводить. Отметим только, что упругие постоянные кристал-
кристаллических веществ — монокристаллов, минералов и горных
пород, определялись экспериментальным путем многими
исследователями. В первую очередь нужно назвать клас-
классические исследования Фойгта, изложенные в его курсе
кристаллофизики [38]. Приводим найденные Фойгтом зна-
значения упругих постоянных кварца (горного хрусталя),
образующего кристаллы тригональной сингоний A2 не-
неравных нулю постоянных atj (ось z направлена по оси сим-
симметрии третьего порядка, ось х — по оси второго порядка):
ап = а22 = 12,73.10, а33 = 9,71 • 10'7,
а12 = - 3,67.10-7, а13 = а2д = - 1,49-10-',
аи - аъъ = 19,66.10^, ав6 = 2 (ап - а12),
«5в = «и = — «24 = — 4,23-10,
«15 = «25 = «35 = «45 = «16 = «26 = «36 = «46 = «34 = 0
(в см*/кгс)?).
(9.1)
*
2) кгс — килограмм-сила, в отличие от кг — килограмм-масса.
i 9] НЕКОТОРЫЕ АНИЗОТРОПНЫЕ МАТЕРИАЛЫ 57
Численные значения упругих постоянных для ряда мо-
монокристаллов и минералов приведены в работе Ауэрбаха
[104]. Литература по этому вопросу указана также в статье
Гекелера [117]. В обзорной статье К. С. Александрова и
Т. В. Рыжовой [40] приведены упругие постоянные более
двухсот веществ, образующих кристаллы различных син-
гоний, дан большой список литературы и указаны различ-
различные методы определения упругих постоянных (см. также
[95]).
Известны также упругие постоянные ряда горных по-
пород, в частности, мелкозернистых и тонкослоистых. Бла-
Благодаря слоистости эти породы в первом приближении
можно рассматривать как однородные и трансверсально-
изотропные. Приведем численные значения упругих по-
постоянных для одной из таких пород — для алевролита
крупного темно-серого.Это тонкослоистая, плотно сцемен-
сцементированная осадочная порода, состоящая на 60—70% из
обломков кварца и полевого шпата. Цементирующий мате-
материал в количестве 40—30% всего состава — глинистый,
с примесью мусковита и кальцита. Толщина слоев порядка
1—4 мм.
Направляя ось z нормально к плоскостям слоев,
которые в первом приближении рассматриваются как пло-
плоскости изотропии, имеем для этого материала уравнения
обобщенного закона Гука D.9). Экспериментальным путем
найдены следующие значения модулей Юнга и сдвига и
коэффициентов Пуассона (см. [65]):
? = 6,2Ы05, Я'= 5,68-10*, С = 2,29-10* (в кгс/см2); )
G = 2,55, v = 0,22, v' = 0,24 J
(9.2)
(последние три величины менее точны, чем первые, так как
найдены не экспериментальным путем, а на основании
вычислений).
Несмотря на заметное различие между упругими по-
постоянными Е и ?", G и С, v и v', алевролит следует при-
признать слабо анизотропным, так как параметры, позволя-
позволяющие судить о степени анизотропии, у него близки к пара-
параметрам изотропного тела. В конкретных случаях задания
формы тела, изготовленного из алевролита, и усилий на-
напряжения будут мало отличаться от напряжений в изотроп-
58 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ 1Гл. 1
ном теле той же формы и также нагруженном. Упругие по-
постоянные для многих анизотропных минералов и горных
пород имеются в справочнике [31].
В связи с вопросом об упругих свойствах горных пород
представляет интерес работа Батугина С. А. и Нирен-
бург Р. К. [47]. В ней собраны численные значения всех
технических упругих констант для сорока семи различных
горных пород, которые в первом приближении можно рас-
рассматривать, как трансверсально-изотропные (алевролиты,
филлиты, сланцы, песчаники, известняки, граниты, грано-
диориты и др.)- Численные значения констант взяты из
экспериментальных исследований разных авторов. Анализ
этих данных позволил прийти к следующему выводу.
Хотя модуль сдвига G' для плоскостей, нормальных к
плоскости изотропии, строго говоря, является независи-
независимой константой и никак не связан с остальными упругими
постоянными, тем не менее для сорока пяти пород (из 47)
можно указать приближенную формулу, связывающую G'
с главными модулями Юнга и коэффициентами Пуассона.
В наших обозначениях (см. уравнения D.9)) эта прибли-
приближенная формула имеет вид
В случае изотропного тела она переходит в точную
формулу для модуля сдвига: G = Е/[2 A + v)]. Таким
образом, для сорока пяти обследованных пород можно с до-
достаточной для практики точностью считать, что число неза-
независимых упругих констант равно не пяти, а четырем. Как
будет показано в главе 4, степень (или интенсивность) ани-
анизотропии в случае двухмерной (плоской) задачи характе-
характеризуется двумя величинами. Анизотропию же указанных
выше пород можно характеризовать только одной величи-
величиной и за эту величину авторы предлагают принимать
отношение главных модулей: р = EIE'.
Из некристаллических анизотропных материалов
можно указать на древесину разных пород дерева с пра-
правильными годичными слоями. Строго говоря, древесина —
материал неоднородный, но если пренебречь кривизной
слоев и неоднородностью, то брусок из древесины можно
в первом приближении рассматривать как однородное те-
тело. В нем можно различить три ортогональные плоскости
§ 9]
НЕКОТОРЫЕ АНИЗОТРОПНЫЕ МАТЕРИАЛЫ
59
симметрии структуры, которые одновременно являются
и плоскостями упругой симметрии: первая, yz, нормальна
к древесным волокнам, вторая (тангенциальная), ху,
параллельна годичным слоям и третья (радиальная) xz
ортогональна к первым двум (рис. 10). Все плоскости,
параллельные z/z, xz и ху,
также будут плоскостями
упругой симметрии (ра-
(разумеется, при достаточно
правильной структуре,ког-
структуре,когда отсутствуют трещины,
сучки и другие пороки
древесины). Уравнения
обобщенного закона Гука,
отнесенные к указанной
системе координат, будут
иметь вид D.4) и D.6) и в
них ' войдут девять неза-
независимых (и инвариант-
инвариантных) упругих постоянных.
Иногда пользуются упрощенной моделью древесины —
рассматривают ее, как трансверсально-изотропный ма-
материал, т. е. пренебрегают различием упругих свойств
для разных направлений в плоскостях, нормальных к
волокнам.
Приведем зпачения некоторых упругих постоянных и
графики для сосны^ используя работы [79] и [85] (Еи Е2 —
модули Юнга для растяжения и сжатия в направлениях
вдоль волокон и тангенциальных):
Рис. 40.
?!=»1.10», Я2 = 0,042 -105, л
¦M = 0,01, A, =-§2. = 0,042,
?ia = 0,075 • 105 (в кгс/см2);
v21=0,27.
(9.4)
j
Величины Ег, Е2, v2i получены непосредственно из экспе-
эксперимента, а модуль сдвига вычислен по формуле преобра-
преобразования упругих постоянных на основании данных экс-
эксперимента. На рис. И показана кривая зависимости мо-
модуля Юнга от направления сжатия, взятая из работы
60
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[Гл. 1
А. Л. Рабиновича, в которой имеется и ряд других гра-
графиков для упругих постоянных (см. [85]). На рис. 12 —
направляющая кривая модуля Юнга сосны.
Рис. 11.
—»
д=0,27;Лш0№2
к
s
а,г
В неоднократно упоминавшейся книге Е. К. Ашкена-
зи и Э. В. Ганова [6] имеются подробные таблицы числен-
численных значений всех девяти постоянных древесины двенад-
двенадцати различных пород дерева
(стр. 54—57 и 60—79).
ДРУГИМ примером анизот-
ровного материала может
служить фанера. Лист фане-
0,2 s^— ры обычно изготовляется из
нечетного числа слоев древе-
сины (шпона), расположен-
ных симметрично относитель-
относительно среднего и склеенных по
поверхностям контакта тем
или иным связующим; у боль-
большинства марок фанеры направления волокон соседних
слоев взаимно перпендикулярны. Лист фанеры представ-
представляет собой неоднородное тело, но если размеры велики по
сравнению с толщиной слоев, то в первом приближении
его можно рассматривать как однородную и ортотропную
пластинку, т. е. пренебречь неоднородностью. Плоскости
упругой симметрии нормальны к древесным волокнам.
Пусть рассматривается обобщенное плоское напря-
напряженное состояние фанерной пластинки, т. е. напряжен-
напряженное состояние, вызванное усилиями, действующими в ее
Рис. 12.
НЕКОТОРЫЕ АНИЗОТРОПНЫЕ МАТЕРИАЛЫ
срединной плоскости. Примем срединную плоскость всего
листа фанеры за плоскость ху и'направим оси хну парал-
параллельно и перпендикулярно
волокнам наружных слоев
(см. рис. 13, где показан
элемент трехслойной фане-
фанеры). Тогда, вводя в рас-
рассмотрение средние по тол-
толщине значения составляю-
составляющих напряжения и дефор-
деформации, параллельных сре-
срединной плоскости дх, бу,
ъХу, ?х, еу, уху и пренебре-
пренебрегая средним az, мы запишем три уравнения обоб-
обобщенного закона Гука таким образом:
1 -
х Ei х
Рис. 13.
Уху — Г Та
(9.5)
Здесь Ely E2, G, v2, v2 — осредненные технические
упругие постоянные для всей пластинки в целом (они за-
зависят от упругих констант слоев, их числа и толщин).
Мы приведем численные значения упругих постоянных
для четырех видов фанеры:
1) Трехслойная березовая фанера, склеенная бакели-
бакелитовой пленкой. Эта фанера представляет собой материал
с резко выраженной анизотропией, который очень удобен
для иллюстрации теоретических исследований по плоской
задаче, в частности, по вопросу о концентрации напря-
напряжений вблизи отверстий. Почти все наши исследования
мы иллюстрировали именно на этом материале; сопостав-
сопоставление графиков напряжений в пластинке из березовой
фанеры и в изотропной пластинке очень наглядно пока-
показывает, как влияет анизотропия на распределение напря-
напряжений. Значения упругих постоянных имеются в наших
книгах [20]—[22]. В настоящей работе, исследуя распре-
распределение напряжений в пластинках с отверстиями, мы
также приводим графики напряжений в пластинке из бе-
березовой фанеры и такой же изотропной.
62
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[Гл. 1
2) Клееная фанера БС-1, 1 сорт; семь слоев шпона, тол-
толщина листа — 8 мм.
3) Бакелизированная фанера БФС; семь слоев шпона,
толщина листа — 7 мм.
4) Фанера повышенной водостойкости ФСФ; толщина
листа — 10 мм.
Упругие постоянные фанеры 2), 3) и 4) (из уравнений
(9.5)) мы берем из справочника Е. К. АшкеназииЭ. В. Га-
нова [6] (стр. 84).
В таблице 6 приводятся численные значения упругих
постоянных всех четырех видов фанеры, а именно: модули
Еи Е2 для растяжения вдоль главных направлений (вдоль
волокон рубашки и поперек волокон), а также модули Е'
для растяжения под углом 45° к волокнам; модули сдвига
G и коэффициенты Пуассона vx и v2.
Таблица 6
Упругие постоянные фанеры (четыре вида)
Обозначения упру-
упругих постоянных
.EVICT5 (в кгс/см2)
Е2Л0-* »
#'.1СГ* »
(МО-6 »
Vi
v2
Наименование или марка фанеры
березовая
фанера
1,2
0,6
0,24
0,07
0,071
0,036
БС-1,
1 сорт
1,10
0,85
0,30
0,09
0,076
0,06
БФС
1,48
1,00
0,44
0,135
0,088
0,062
ФСФ
1,09
0,87
0,28
0,079
0,174
0,038
Заметим, что в справочнике [6] модуль сдвига G для
фанеры ФСФ не дан, но его можно вычислить, зная
Еъ Ег, Е\ Vi и v2 (что и сделано).
Говоря об анизотропных материалах, необходимо
хотя бы кратко остановиться на современных компози-
композиционных материалах, получивших к настоящему времени
широкое распространение в современной технике бла-
благодаря их ценным прочностным, упругим и другим свой-
свойствам. Такие материалы состоят из армирующих элемен-
элементов высокой прочности и жесткости и из менее прочного
и жесткого связующего, обеспечивающего монолитность
композиции. Большое распространение получили стек-
НЕКОТОРЫЕ АНИЗОТРОПНЫЕ МАТЕРИАЛЫ 63
лопластики, состоящие из пластмассы, армированной
очень тонкими стеклянными волокнами, нитями (прядя-
(прядями), скрученными жгутами из 100—200 волокон или
стеклотканями различного переплетения. Одни стекло-
стеклопластики создаются путем контактного формирования
при холодном отверждении связующего, другие — путем
намотки стеклянных нитей, жгутов, лент и горячего
прессования и с помощью других технологических про-
процессов. Сведения о стеклопластиках — о том, какие виды
их применяются в технике, как они изготовляются, их
марки и т. д. можно найти в книгах [6] (глава 1) и [7]
(также глава 1). Там же подробно излагаются вопросы
о прочностных и упругих свойствах стеклопластиков, о
величинах, характеризующих эти свойства и о методике
определения прочностных и упругих характеристик (см.
также монографию Кинциса Т. Я., Розе А. В. и Жигу-
на И. Г. [12]). Одной из первых работ по вопросу о стек-
стеклопластиках (вида СВАМ) была работа Бурова А. К. и
Андреевской Г. Д. [9].
Армированный материал можно с некоторым приб-
приближением рассматривать как однородную и анизотроп-
анизотропную упругую среду, обладающую, в зависимости от
структуры армирования, тем или иным видом структур-
структурной симметрии, которая влечет за собой упругую симмет-
симметрию. Одни стеклопластики можно рассматривать как орто-
тропные упругие среды (разумеется, лишь в тех пределах,
в каких деформации под действием внешней нагруз-
нагрузки можно считать упругими); другие — как трансвер-
сальпо-изотропные и даже как изотропные среды. Воп-
Вопрос о том, как теоретически определять упругие харак-
характеристики армированного материала, подробно изучен
в статье В. В. Болотина [49]. Из многочисленных стек-
стеклопластиков мы рассмотрим три вида, имеющие важное
значение для судостроения. Этим стеклопластикам пос-
посвящены две статьи — шести авторов [44] и Ашкенази Е. К.
и Морозова А. С. [43], которые содержат исчерпывающие
сведения об этих материалах. Кроме того, рассмотрим еще
один стеклопластик, сведения о котором имеются в спра-
справочнике [6]. Перечислим все эти материалы.
1. Однонаправленный намоточный стеклопластик.
Состоит из связующего, армированного параллельными
стеклянными волокнами. По сравнению со стеклопласти-
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[Гл. 1
ками другой структуры обнаруживают наибольшую проч-
прочность и жесткость в направлении армирования. Может
рассматриваться как трансверсально-изотропное тело с
плоскостями изотропии, нормальными к волокнам. Нап-
Направив ось z вдоль волокон, мы будем иметь для такого
тела уравнения обобщенного закона Гука в форме D.8)
и D.9).
2. Слоистый стеклопластик ортогонального армиро-
армирования. В основе его — несколько слоев параллельных
нитей, причем слои с волокнами, направленными опре-
определенным образом, чередуются со слоями, у которых нити
перпендикулярны к нитям первого слоя (например, слой
1-го рода — слой 2-го рода — слой 1-го рода и т. д., что
обозначается как 1 : 1 или два слоя первого рода — слой
2-го рода — два слоя 1-го рода и т. д.; обозначается 2 : 1
и т. д.). Этот материал можно рассматривать как ортот-
ропный, у которого одна плоскость упругой симметрии
нормальна к волокнам 1-го рода, другая — нормальна
к волокнам 2-го рода и третья параллельна слоям (орто-
(ортогональна к первым двум). Для этого материала и двух
остальных C) и 4)) справедливы уравнения обобщенного
закона Гука D.6).
3. Тканевый стеклопластик горячего прессования
СТЭТ,
Таблица 7
Упругие постоянные стеклопластиков (четыре вида)
Обозначения упру-
упругих постоянных
?г10-5 (вкгс/см*)
?2.10-5 »
#3-10-5 »
G12.10~5 »
G.23-10 »
G31-10-* »
Vl2
V23
V31
Наименования или марки стеклопластиков
намоточный
однонаправ-
однонаправленный
5,70
1,40
1,40
0,57
0,50
0,57
0,277
0,400
0,068
ортогональ-
но-армиро-
но-армированный 2 : 1
3,68
2,68
1,10
0,50
0,41
0,45
0,105
0,431
0,405
стэт
3,59
2,93
1,83
0,76
0,63
0,66
0,177
0,371
0,157
АСТТ(б)-С2-0
и ПН-3
1,79
1,31
0,43
0,28
0,24
0,24
0,15
0,31
0,08
§ 10] КРИВОЛИНЕЙНАЯ АНИЗОТРОПИЯ 65
4. Стеклопластик на основе стеклоткани марки АСТТ
(б)-С2-0 и полиэфирной смолы марки ПН-3 (АСТТ(б)-С2-0
и ПН-3).
Для четырех указанных материалов получены все
упругие постоянные; значения их приведены в таб-
таблице 7 1).
§ 10. Криволинейная анизотропия
У однородного тела с прямолинейной анизотропией
все параллельные направления эквивалентны в отноше-
отношении упругих свойств, а все элементы в виде одинаковых
прямоугольных параллелепипедов с соответственно па-
параллельными гранями обладают одинаковыми упругими
свойствами. Но у однородных тел, кроме прямолинейной,
возможна анизотропия другого рода — криволинейная.
Криволинейная анизотропия однородного тела характе-
характеризуется тем, что для разных его точек эквивалентными
являются направления не параллельные, а подчиненные
каким-то другим закономерностям. Если выбрать систему
криволинейных ортогональных координат так, чтобы
координатные направления ее в каждой точке совпадали
с эквивалентными направлениями (в отношении упругих
свойств), то бесконечно малые элементы, выделенные тре-
тремя парами координатных поверхностей, будут обладать
одинаковыми упругими свойствами. Наоборот, элемен-
элементы, образованные тремя парами ортогональных плоско-
плоскостей, будут иметь, вообще говоря, различные упругие
свойства.
Пусть тело является однородным криволинейно-ани-
криволинейно-анизотропным и следует обобщенному закону Гука, т. е. сос-
составляющие деформации являются линейными функциями
составляющих напряжения, и наоборот. Обозначим че-
через ?, т|, ? координатные направления упомянутой
криволинейной системы координат. Тогда, предпола-
предполагая, что существует упругий потенциал, можем записать
уравнения обобщенного закона Гука для однородного
2) Мы несколько изменили обозначения работ [43], [44] и [6].
Во всех случаях предполагается, что направление оси х соответству-
соответствует направлению, для которого модуль Е = Е\ наибольший.
66 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
криволинейно-анизотропного тела так:
A0.1)
Уравнения в общем случае содержат 21 упругую посто-
постоянную, но из них независимых, инвариантных, будет,
как и для прямолинейно-анизотропного тела, только 18
констант. Можно, конечно, записать и в этом случае урав-
уравнения обобщенного закона Гука в ортогональной декар-
декартовой системе координат, но тогда в уравнениях обобщен-
обобщенного закона Гука коэффициенты ац уже не будут постоян-
постоянными и будут меняться от точки к точке в связи с
изменением координатных направлений.
Уравнения A0.1) упростятся, если тело обладает
упругой симметрией и эти упрощения будут такими же,
как и в случае прямолинейной анизотропии. Так, можно
говорить о криволинейно-ортотропном теле, о теле, тран-
сверсально-изотропном относительно какого-нибудь из
направлений ?, т), ? и т. д. С другой стороны, понятие
криволинейной анизотропии можно обобщить и рассмат-
рассматривать криволинейно-анизотропные неоднородные тела,
у которых коэффициенты atj из уравнений A0.1) будут за-
зависеть от координат точки.
Из различных видов криволинейной анизотропии наи-
наибольший практический интерес представляют два вида,
рассмотренные еще Сен-Венаном: 1) цилиндрическая
анизотропия и 2) сферическая анизотропия (см. работу
Сен-Венана [124]).
1. Цилиндрическая анизотропия. Пусть с телом не-
неподвижно связана некоторая прямая g-осъ анизотропии,
которая может проходить как внутри тела, так и вне его
(например, в полости) или по поверхности. Все направле-
направления, параллельные g, проходящие через разные точки,
между собой эквивалентны; все направления, пересекаю-
пересекающие g под прямым углом (радиальные), также эквивален-
эквивалентны и все направления, ортогональные к первым двум
(тангенциальные), эквивалентны. Эквивалентными или
§ Ю] КРИВОЛИНЕЙНАЯ АНИЗОТРОПИЯ 67
идентичными будут бесконечно малые элементы, огра-
ограниченные тремя парами поверхностей: двумя плоскостя-
плоскостями, нормальными к g, двумя плоскостями, проходящими
через g, и двумя поверхностями цилиндров с общей осью
у. Приняв ось анизотропии g за ось z цилиндрической си-
системы координат г, 9, z и направляя ось х, от которой
отсчитываются углы G, произвольно, запишем в общем
случае цилиндрической анизотропии уравнения обобщен-
обобщенного закона Гука так:
= апаг +
+ а22сг9 + + «26 tre,
7r0 =
A0.2)
Если тело неоднородное, коэффициенты аг;- будут
функциями цилиндрических координат.
Здесь необходимо сделать очень важное замечание.
Если ось анизотропии проходит вне тела (например, вну-
внутри полости), то уравнения A0.2) сомнений не вызывают.
Но если ось анизотропии проходит по телу, то между
разными аи в однородном теле непременно должны быть
зависимости. В самом деле, на оси z, совпадающей с g,
нет никакой разницы между направлениями г и 9 и все
радиальные направления г должны быть эквивалентными
не только между собой, но и между всеми тангенциаль-
тангенциальными 9. Поэтому уравнения A0.2) мы можем записать
иначе. Переставляя сами уравнения, запишем систему
A0.2) таким образом:
,^q o\
8Г = а22сгг + а12сг0
80 = а12аг +
Сопоставляя системы, получим очевидные равенства:
«22 -«11, «23- 13, «55 -«44, «26 - «16, I
«85 = «34, «66 = «46, «24 = «15, «25 = «14, J
3*
68 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. 1
а всего восемь зависимостей. Если в каждой точке имеется
одна плоскость упругой симметрии, перпендикулярная
к оси z (или g), то
а14 = а24 = а34 = «46 = 0, ,
AU.O)
«15 = «25 = «35 = «56 = 0;
«22 = «11» «23 — «13> «26 = «16» «55 = «44- (Ю.6)
У ортотропного тела с плоскостями симметрии, про-
проходящими через ось анизотропии, радиальной и танген-
тангенциальной, в дополнение к указанным зависимостям имеем
«16 = «26 = «36 = «45 = 0, A0.7)
а неравные нулю коэффициенты связаны тремя равенст-
равенствами
«22 = «П» «23 = «13» «55 = «44- A0.8)
Все эти равенства A0.4) — A0.8) имеют место и в
неоднородном теле. В неоднородном теле равенства A0.4),
A0.6), A0.8) могут быть выполнены за счет того, что
соответствующие atj являются функциями г (а также, мо-
может быть, и других переменных — 0, z) и на самой оси ста-
становятся равными нулю или бесконечности. В однородном
же теле, у которого ось анизотропии пересекает тело,
atj постоянны и анизотропия общего вида невозможна,
так как всегда доляшы выполняться равенства A0.4),
A0.6) или A0.8). На это обратил внимание еще Фойгт в
работе [128].
В случае ортотропного тела с цилиндрической анизот-
анизотропией иногда бывает удобнее иметь дело с техническими
константами или упругими характеристиками — моду-
модулями Юнга и сдвига и коэффициентами Пуассона. Введя
эти обозначения (с буквенными индексами), запишем
уравнения A0.2) таким образом:
6r = -и- <Jr в~ "9 E— °z, 7. — 7,— Tez,
A0.9)
§ ю]
КРИВОЛИНЕЙНАЯ АНИЗОТРОПИЯ
69
Если структура тела такова, что его пересекает ось
анизотропии, не находящаяся внутри сквозной полости,
то тогда непременно должно быть
E» = Er, v20 = v0z, GQz = Grz. A0.10)
Можно уравнения A0.9) записать и иначе, введя коэф-
коэффициенты деформации с числовыми индексами atj (?, j =
= г, 0, z). В уравнениях A0.9)
Е^н = Ем. A0.11)
Примером тела, обладающего цилиндрической анизо-
анизотропией, может служить деревянный брусок с правильны-
правильными цилиндрическими годичными
слоями. В случае, показанном на
рис. 14, уже нельзя пренебречь
кривизной годичных слоев и его
можно рассматривать как однород-
однородное тело с цилиндрической анизот-
анизотропией (в первом приближении,
конечно). Ось анизотропии g сов-
совпадает с осью сердцевины. Если
бы эта ось, находясь внутри брус-
бруска, была идеальной прямой, то
можно было бы записать уравне-
уравнения обобщенного закона Гука в
виде A0.9) с соблюдением условий
A0.10), но на самом деле сердцевина отличается от ос-,
тальных частей бруска еще тем, что часто она является
линией, где сходятся радиальные трещины и, следова-
следовательно, нарушается сплошность. Вопрос оказывается
сложнее, чем кажется с первого взгляда, и древесину с
сердцевиной в пределах образца рассматривать как ци-
цилиндрически-анизотропное тело можно только в первом
приближении и даже условно.
Цилиндрическая анизотропия может появиться в ме-
металлических изделиях в результате соответствующих тех-
технологических процессов (например, при изготовлении
труб, протяжке проволоки и др.). Моделью тела, обладаю-
обладающего в первом приближении цилиндрической анизотро-
анизотропией, может служить свод, построенный из достаточно
большого числа однородных элементов («кирпичиков»),
без зазоров. Каждый элемент обладает прямолинейной
Рис. 14.
70
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[Гл. 1
анизотропией, но главные оси упругости элементов об-
образуют углы, так что свод в целом будет вести себя как
цилиндрически-анизотропное тело (рис. 15).
Рис. 15.
2. Сферическая анизотропия. Криволинейная анизот-
анизотропия этого вида характеризуется следующим. С однород-
однородным телом неподвижно связана точка О (центр анизотро-
анизотропии) и прямая g (ось анизотропии), проходящая через
центр. Направления всех лучей, исходящих из центра,
между собой эквивалентны; кро-
кроме того, направления касатель-
касательных к меридианам всех сфери-
сферических поверхностей с общим
центром О, проходящих через
точки пересечения поверхностей
с g, между собой эквивалентны,
и направления, касательные к
параллелям всех сферических
поверхностей, тоже между со-
собой эквивалентны (рис. 16).
Принимая эквивалентные нап-
направления за координатные нап-
направления сферической системы
р, 9, ф, мы будем иметь для
такого тела уравнения обобщенного закона Гука A0.1),
где нужно положить ? = р, т) = 9, ? = ф. Если центр
анизотропии О лежит вне тела или в полости тела, то
рет никаких осцований ожидать, что между аи сущест-
Рис. 16.
§ Ц] ОБЩИЕ УРАВНЕНИЯ И ПОСТАНОВКА ЗАДАЧ ?1
вуют какие-либо зависимости вроде A0.4). Но если центр
анизотропии совпадает с точкой, принадлежащей телу,
то очевидно, нет никакой разницы между направлениями
р, 6, ф, т. е. все три направления должны быть эквива-
эквивалентными. Записывая уравнения обобщенного закона
Гука и учитывая эквивалентность всех направлений р,
6, ф, мы получим ряд зависимостей между а и, которых
приводить не будем; они нам в дальнейшем не пона-
понадобятся.
Можно еще сказать, что у неоднородного криволиней-
криволинейно-анизотропного тела могут быть элементы упругой сим-
симметрии в зависимости от его структуры.- Важнейшим яв-
является случай, когда через каждую точку проходят три
взаимно перпендикулярные плоскости упругой симметрии
(ортотропное тело). Для тела с цилиндрической анизот-
анизотропией наиболее важным является такой случай ортотро-
пии, когда одна из плоскостей упругой симметрии нормаль-
нормальна к оси анизотропии, другая проходит через эту ось и
третья нормальна к первым двум.
Если для криволинейно-анизотропного тела упругие
характеристики ац или Et, Gtj, vtj являются функциями
координат, то его уместно назвать криволинейно-анизот-
криволинейно-анизотропным и неоднородным. Обобщенный закон Гука для
такого тела при соответствующем выборе координатных
направлений запишется так же, как для соответствующе-
соответствующего тела с прямолинейной анизотропией, но только харак-
характеристики аи будут функциями координат.
§ 11. Общие уравнения теории упругости
и постановка основных задач.
Важнейшие вариационные принципы
Напряженное состояние упругого тела можно считать
известным, если известны составляющие напряжений в
любой его точке (и в любой момент времени, если рассмат-
рассматривается движение тела). Деформированное состояние
определяется составляющими деформации, которые зави-
зависят от трех проекций перемещения на координатные нап-
направления. Таким образом, для полного суждения о нап-
напряженно-деформированном состоянии тела, находящегося
под действием внешних сил, нам нужно определить девять
функций: шесть составляющих напряжения и три проек-
72 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ tm. 1
ции смещения. В частности, если мы пользуемся декарто-
декартовыми координатами, переменными независимыми являют-
являются координаты х, у, z и время.
Полную систему уравнений для определения шести
составляющих напряжения и трех проекций перемещения
мы получим, взяв три уравнения равновесия или движе-
движения сплошной среды и добавив к ним шесть уравнений
обобщенного закона Гука. Такая система, содержащая
все неизвестные функции и состоящая из девяти незави-
независимых уравнений (три уравнения равновесия или движе-
движения сплошной среды и шесть уравнений обобщенного за-
закона Гука), называется основной системой уравнений
равновесия или движения упругого тела ([26], [20]).
Остановимся на случае, когда мы пользуемся декарто-
декартовыми координатами (х, у, z; t). Основная система урав-
уравнений равновесия для тела, не имеющего элементов упру-
упругой симметрии, запишется так:
дх ду
ex = anax + a12oy + aX3az + auxyz + а1Ъххг + a16rxyi
ey = a12ox -
A1.1)
Уху =
где в случае малых деформаций 6<Л, гу, . . . , уху связаны
с перемещениями формулами A.2); X, У, Z — проекции
объемных сил на единицу объема.
Если рассматривается движение, то уравнения движе-
движения отличаются от уравнений равновесия только тем, что
в первых трех уравнениях A1.1), в правых частях, должны
стоять не нули, а члены, пропорциональные вторым про-
- O'hi -дЧ - d*w
изводным от перемещения по времени: р-^2~> Р^' Рц^Г
(р — плотность, т. е. масса единицы объема вещества).
Остальные уравнения записываются так же, как A1.1).
Система A1.1) может быть заменена эквивалентной.
Можно уравнения обобщенного закона Гука взять в фор-
форме, решенной относительно а и т (они будут содержать
модули Аи), или исключить из системы A1.1) напряжения
или перемещения (первое значительно легче) и т. д. За-
?11] ОБЩИЕ УРАВНЕНИЯ И ПОСТАНОВКА ЗАДАЧ 73
дача об упругом равновесии анизотропного тела сводится
к определению девяти указанных функций, удовлетворяю-
удовлетворяющих системе A1.1) (или ей эквивалентной) и условиям на
поверхности.
В зависимости от того, что именно задается на поверх-
поверхности, различают три основные задачи статики упругого
тела: первую, вторую и смешанную (см. [26], стр. 70—72).
Первая основная задача. На всей поверхности задаются
внешние усилия; требуется определить напряжения и
перемещения в любой точке внутри тела и на поверхности.
Можно задать на поверхности три составляющие внешних
усилий — проекции их на три несовпадающие направле-
направления, например, нормальную составляющую о и две про-
проекции касательных усилий на два ортогональных нап-
направления. Чаще всего задают три проекции усилий на
направления координатных осей — Хп, Yn, Zn (n — нап-
направление внешней нормали к поверхности; составляющие
усилий относятся к единице площади).
Граничные условия запишутся следующим образом: •
ах cos (w, x) -f- тху cos (п, у) + rxz cos (/г, z)' = Xn, )
XxyCOS(n, Я) + (Ту COS (Л, lj) + TyzCOS(n, Z) = Уп, A1.2)
Xxz cos (n, x) -4- xuz cos (n, y) 4- &zcos {n-> z) = %n- '
Вторая основная задача. На всей поверхности задают-
задаются проекции перемещения на три несовпадающих нап-
направления; например, проекции и*, v*, w* на оси декар-
декартовой прямоугольной системы координат. Граничные
условия будут иметь вид
и = и*, v — у*, w = w*. A1-3)
(^мешанная задача. На части поверхности задаются
усилия, а на другой части перемещения. Граничные ус-
условия на первой части поверхности запишутся в виде
A1.2), а на второй — в виде A1.3). К смешанным же
нужно отнести и такие задачи, когда на поверхности за-
задаются: одна составляющая усилий (например, нормаль-
нормальная) и две составляющие перемещения, или одна состав-
составляющая перемещения и две составляющие усилий и т. д.
В зависимости от формы тела и распределения усилий час-
часто бывает удобнее пользоваться не декартовой, а подходя-
подходящей криволинейной системой координат.
74
ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[Гл. 1
Исключая из системы A1.1) составляющие напряже-
напряжения, получим три уравнения, содержащие только проек-
проекции перемещения. Для случая ортотропного тела, движу-
движущегося под действием внешних усилий или испытывающего
свободные колебания, уравнения движения в проекциях
перемещения имеют такой вид:
д Г/ л л \ ди .
\diol
- Аьъ) -^ +
д2и> , . d2w . л
+А + А
+
I а
(А
23
. v - д2и
+ Х = р-щ-
12 + А„)Ж
+ Г = р^з
ди .
з— Лв) gjJ + Z - р -
A1.4)
(в задаче о свободных колебаниях X = У = Z = 0).
Единственность решения уравнений равновесия одно-
однородного тела, испытывающего малые деформации, когда
составляющие деформации являются линейными функ-
функциями производных от перемещений по координатам,
устанавливается теоремой Кирхгофа х).
Если отыскание точного решения задач о равновесии
упругого тела встречает затруднения (а с такими случая-
случаями часто приходится встречаться на практике), можно для
определения приближенных решений использовать вариа-
вариационные методы, подробно изложенные в книге Л. С. Лей-
бензона [17] и в [18]. Основой этих методов являются
принцип возможных перемещений и принцип наимень-
наименьшей работы.
Принцип возможных перемещений.
Возможными или виртуальными мы будем называть такие
перемещения в упругом теле, при которых оно остается
сплошным, а граничные условия на частях поверхности
деформированных заданным образом или закрепленных
х) См., например, [18], § 118, стр. 309—311. Вопрос об един-
единственности решения уравнений равновесия неоднородного тела еще
недостаточно изучен.
§ Ц] ОВЩИЁ УРАВНЕНИЯ Й ПОСТАЙОВКА ЗАДАЧ 75
(т. е. на тех, где заданы перемещения), удовлетворяются.
Иначе говоря, это — перемещения, допускаемые геомет-
геометрическими связями, наложенными на упругое тело.
Пусть Хп, Уп, Zn — проекции внешних поверхностных
сил (на единицу площади), X, У, Z — проекции объемных
сил (на единицу объема), V — потенциальная энергия де-
деформации всего тела, выраженная через составляющие
перемещения, и 8и, Sv, 8w — вариации перемещений, до-
допускаемые геометрическими связями.
Согласно принципу возможных перемещений при уп-
упругом равновесии тела мы будем иметь
{Хди + Y8u + Z8w) dco +
+ Ц (Хп6и + Yn6u + Zn6u>) dS-8V = 0. A1.5)
Это уравнение называется вариационным уравнением
Лагранжа; в нем dco — дифференциал объема, dS — диф-
дифференциал поверхности, 8V — вариация потенциальной
энергии деформации, соответствующая вариациям пере-
перемещений. Тройной интеграл берется по всему объему тела,
а двойной (поверхностный) — по той части поверхности, где
заданы усилия. Отсюда, преобразуя A1.5), приходим к
выводу, что перемещения, имеющие место в действитель-
действительном состоянии равновесия, отличаются от всех возмож-
возможных тем, что они сообщают минимальное значение выра-
выражению (см. [17], стр. 141, или [18], стр. 314—317)
Э = J5J Vdio - §5 (Хм + Yv + Zw) dco -
+ yni; + Znii;)AS. A1.6)
Принцип наименьшей работы. Рас-
Рассмотрим наряду с действительными напряжениями ал,
ау, . . ., чху, имеющими место в упругом теле, нахо-
находящемся в равновесии под действием внешних сил, еще
статически возможные, т. е. удовлетворяющие уравнениям
равновесия сплошной среды и условиям на тех частях
поверхности, где заданы усилия. Обозначим эти возмож-
возможные напряжения так:
ах + &(УХ, оу + 6оу, ...,Тху + 8хху.
Напряжения ох + бах, . . ., тху + бтху удовлетворя-
удовлетворяют так же, как и ал, . . ., тху, уравнениям равновесия
76 ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [Гл. i
сплошной среды и условиям на поверхности, где заданы
усилия. Следовательно, вариации напряжений удовлет-
удовлетворяют однородным уравнениям равновесия сплошной
среды (X = Y = Z = 0) и условиям на поверхности:
8вх cos (п, .г) + бтяу cos (п, у) + &rxz cos (n, z) = 8ХШ
у cos (п, х) -f доу cos (п, у) + 8xyzcos (n, z) = 8Yn,
cos (n, x) + 6ryz cos (п, у) + 6(TZ cos (дг, z) = 6Zn,
(Ц.7)
причем 6Xn = 8Yn = 6Zn =0на той части поверхности,
где заданы усилия. Аналитическим выражением принципа
наименьшей работы является вариационная формула
Кастилиано:
§ dS. A1.8)
Здесь V — потенциальная энергия деформации, как
функция составляющих напряжения, a 8V — ее вариа-
вариация, соответствующая вариациям этих составляющих.
После преобразования заключаем, что напряжения, соот-
соответствующие действительному состоянию равновесия,
отличаются от всех статически возможных тем, что они
сообщают минимальное значение выражению (см. [17],
стр. 19 и [18], стр. 317-322):
u + Ynv + Znw)dS. A1.9)
В книге Л. С. Лейбензона [17] рассмотрены многочислен-
многочисленные задачи теории упругости, решенные с помощью раз-
различных вариантов вариационных методов (см. также [19]).
Глава 2
ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО
РАВНОВЕСИЯ
В этой главе рассматриваются наиболее простые слу-
случаи распределения напряжений в анизотропных телах,
преимущественно в стержнях и пластинках. Формулы для
составляющих напряжений и перемещения мы приводим
без вывода, так как они получаются элементарным путем.
Во всех случаях, рассмотренных в этой главе (а также и
в последующих), принимается во внимание известный
принцип Сен-Венана, позволяющий значительно упрос-
упростить в ряде случаев постановку задач 1).
§ 12. Растяжение стержня под действием
осевой силы и собственного веса
Простейшей задачей теории упругости является зада-
задача о растяжении стержня осевой силой, приложенной к
концу. Эта задача была рассмотрена еще Фойгтом ([38],
стр. 631) и более подробно А. Л. Рабиновичем [85]. Рас-
Рассмотрим цилиндрический или призматический стержень,
изготовленный из однородного материала, обладающего
анизотропией (прямолинейной) самого общего вида.
Пусть один конец его закреплен, а к другому приложены
усилия, приводящиеся к равнодействующей Р, направ-
направленной вдоль оси стержня. Поместим начало координат в
центре тяжести закрепленного сечения, ось z направим по
оси стержня, а оси х и у направим произвольно (рис. 17).
Обозначим через I и S длину и площадь поперечного сече-
сечения недеформированного стержня и через atj — упру-
См., например, курс Л. С. Лейбензона [18], § 49, стр. 104—105.
78
ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО РАВНОВЕСИЯ
[Гл. 2
гие постоянные (коэффициенты деформации) из уравнений,
выражающих обобщенный закон Гука, которые в этом об-
общем случае будут иметь вид C.8). Собственный вес пока
не будем принимать во внимание.
Если допустить, что усилия по нижнему концу и реакции
по верхнему концу распределены равномерно и нормаль-
нормальны к плоскостям крайних сечений, то
z j составляющие напряжений и деформа-
деформации, удовлетворяющие уравнениям рав-
равновесия упругого тела A1.1) и услови-
условиям на поверхности, определятся по
формулам
p
= xyz = rxz = rxy = 0;
JL - JL
p p
p p
~j~ ^зз? Yxy == ~?~ ^36*
A2.1)
A2.2)
Определяя перемещения путем интегрирования, по-
получим
Р
S
Р
и = -^- (а13г + a362/ + «35^) + «2z — W32/ + ^о,
+ Щх —
i;
г^;;
Р
—
— щх + гг;0.
A2.3)
Здесь ©!, со2, (о3, и0, v0, w0 — постоянные, характери-
характеризующие «жесткое» перемещение тела в пространстве, не
сопровождаемое деформацией; первые три характеризуют
перемещения при повороте вокруг осей координат, а вто-
вторые три — поступательные перемещения вдоль осей. Эти
постоянные мы определим из условий закрепления стерж-
стержня. Считая закрепленным бесконечно малый элемент на
оси z около начала координат, имеем при х = у = z = 0
§12]
РАСТЯЖЕНИЕ СТЕРЖНЯ
79
условия:
и = v = w — О
ди dv dv ди
dz dz dx dy
Удовлетворяя им, получим
A2.4)
Р
и = -я- {апх + 0,
Р
= -г- @,5a3er + awy),
,A2.5)
w =
^z? yz
Em
«35 =
\l2.6)
Формулы A2.2) показывают, что в общем случае анизо-
анизотропии стержень не только удлиня-
удлиняется в направлении силы и сокра- ^
щается в поперечных направлени-
направлениях, но еще испытывает сдвиги во
всех плоскостях, параллельных
координатным. Эти сдвиги харак-
характеризуются коэффициентами а34,
азь и а36, которые выражаются
через модули Юнга или сдвига и ко-
коэффициенты взаимного влияния пер-
первого и второго рода:
/
Р
г
Рис. 18.
Поперечные сечения остаются плоскими, но вследствие
сдвигов наклоняются к линии действия силы. Стержень,
который имеет форму прямоугольного параллелепипеда,
деформируясь, станет косоугольным параллелепипедом
(рис. 18). Абсолютное удлинение стержня (точнее, его
оси), равно:
__ Pla,3 __ PI M?7v
Если в каждой точке имеется плоскость упругой сим-
симметрии, нормальная к оси, то а34 = азъ = 0 и уп -— yxz = 0;
80 ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО РАВНОВЕСИЯ [Гл. 2
у стержня в виде прямоугольного параллелепипеда
боковые грани останутся прямоугольными, а углы попе-
поперечного сечения изменятся. Наконец, если стержень яв-
является ортотропным, т. е. имеет еще плоскости упругой
симметрии, параллельные оси, то удлинение не будет со-
сопровождаться сдвигами и углы граней параллелепипеда
не исказятся.
Все формулы справедливы, строго говоря, только для
одного специального случая распределения усилий и ре-
реакций. Но на основании принципа Сен-Венана ими можно
пользоваться и в случае усилий, приводящихся к силам
Р, распределенным по концам произвольно; нужно толь-
только исключить из рассмотрения узкие области около кон-
концов, где основная картина напряжений и деформаций
будет искажена вследствие местных напряжений и дефор-
деформаций, зависящих от закона распределения усилий и от
способа закрепления. Это замечание относится и к другим
случаям деформации стержней, а также и пластинок.
Если стержень, изображенный на рис. 17 (закреплен-
(закрепленный в вертикальном положении), деформируется только под
действием собственного веса, то мы получим ([38], § 331)
X = Y = 0, Z = y, A2.8)
tfz = V (I — z), ax = oy = xyz --= rxz = xxV = 0, A2.9)
где у — удельный вес материала.
Принимая, что верхний конец закреплен так же, как
и у стержня, растягиваемого силой, т. е. перемещения
удовлетворяют условиям A2.4), получим
и = у \— 0,5tf35z2 + {а13х + О,5азв2/) A — *)],
= У I— 0,5a34z2 + (а2з2/ + 0,5а36.г) (I — z)],
A2.10)
w = у [0,5 (anx2 + а2ъу2 + (hsxy) +
Отсюда видно, что поперечные сечения не остаются пло-
плоскими, а принимают форму поверхности второго порядка.
В общем случае анизотропии ось искривляется и уравне-
уравнение изогнутой оси будет
х' = -0,5ya3bz2, у' = -0,5уя34з2. A2.11)
При этом центр нижнего конца перемещается не только
вдоль оси г, но и в стороны, и проекции перемещения его
§ 131 СДВИГ 81
на оси координат определяются по формулам
Ez
A2.12)
Если же стержень закреплен так, что центр нижней по-
поверхности остается на вертикали, то перемещение его по
вертикали будет прежним (см. третью формулу A2.12)),
а ось стержня примет форму кривой
х' = 0,5уазъ(Ь — z2), у' = 0,5ya3^{lz — z2). A2.13)
Искривления оси не будет только в том случае, когда пос-
постоянные а34 и азъ равны нулю (например, когда имеется
плоскость упругой симметрии, нормальная к оси).
Как показывают формулы A2.1) и A2.9), распределе-
распределение напряжений в растянутом анизотропном стержне
совпадает с распределением в таком же стержне из изот-
изотропного материала, т. е. не зависит от упругих свойств.
Влияние анизотропии сказывается лишь на деформациях.
Это относится не только к случаю растяжения, но и ко
всем другим случаям, рассмотренным в настоящей главе.
§ 13. Сдвиг
Однородное тело в форме прямоугольного параллеле-
параллелепипеда находится в равновесии под действием касательных
усилий, распределенных равномерно по четырем его граням.
Пусть /, 6, h — длины ребер до деформации и t — уси-
усилие, отнесенное к единице площади. Направим оси коор-
координат параллельно ребрам, как на рис. 19, где показана
проекция на плоскость yz. В общем случае анизотропии
составляющие напряжений и деформации определятся по
формулам ([85], стр. 9—10):
ryz = t, Gx = oy = az = xxz = xxy = 0; A3.1)
ex = tau, yyz = taUj
e = ta2u yV9 = *045, [ A3.2)
e2 = ?a«34, у =¦ ta±Q,
82 ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО РАВНОВЕСИЯ [Гл. 2
Предполагая, что закреплен элемент оси z около нача-
начала координат, получим выражения для перемещений,
удовлетворяющие условиям A2.4):
и = t (аих + 0,5а462/),
и = t @,5а4вя +
w = t
У\
A3.3)
t/
В общем случае все грани и
плоские сечения остаются пло-
плоскими, но углы всех граней
1 искажаются, так что тело при-
\ нимает форму косоугольного
^_ ^.— ^ ^__ | параллелепипеда. Одновремен-
! *" i i i^t но с этим изменяются и рассто-
11 яния между гранями, т. е. ка-
Рис 19. сательные усилия вызывают не
только сдвиг граней, но и удли-
удлинения ребер. Полное удлинение в направлении оси z равно
f2 = tla3i = tl lJ? z = tl 4z'vz . A3.4)
z Vz
Объемное расширение 6, т. е. изменение единицы
объема, зависит от коэффициентов взаимного влияния и
определится по формулам
Э = гх + бу + е* = t {аи + а24 + а34), A3.5)
или
Изменение объема всего тела До равно
Дсо = tlbh (аи + аы + а84). A3.7)
Если в каждой точке имеется плоскость упругой сим-
симметрии, нормальная к нагруженным граням (т. е. к оси
z), то аи = а24 = «34 = 0; касательные усилия t не вы-
вызовут удлинений в направлении ребер, и объем тела не
изменится х).
2) Точнее, изменение объема будет величиной высшего поряд-
порядка малости по сравнению с yyz, yxz, yxyy которая не учитывается
линейной теорией упругости,
§ 14]
ВСЕСТОРОННЕЕ СЖАТИЕ
83
14. Всестороннее сжатие
Упругое однородное тело, ограниченное произвольной
замкнутой поверхностью и не имеющее внутренних поло-
полостей, деформируется нормальными усилиями, равномерно
распределенными по всей поверхности (рис. 20).
Отнесем тело к системе координат х, у, z, для которой
известны упругие постоянные из уравнений обобщенного
закона Гука C.8) или C.9). В этом случае ([38], § 281,
или [85], стр. 6—8)
A4.1)
ах = av = az = — Pi xvz = xxz = xxy =
еу = — pS2i yxz = — pSb,
ez=~ pSs, yxy = - pS&.
A4.2)
Здесь р — давление на единицу площади, а
Sk = а1к + а2к + азк (к = 1,2, . . ., 6). A4.3)
Объемное расширение равно
9 = _ р (Sx + S2 + S3), A4.4)
а изменение объема всего тела
До = __рсо (^ + S2 + S3), A4.5)
84 ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО РАВНОВЕСИЯ 1Гл. 2
где со — первоначальный объем. Очевидно, при всесто-
всестороннем сжатии объем тела не может увеличиться; всегда
Дсо <^ 0. Знак равенства имеет место для тела, абсолют-
абсолютно несжимаемого. Отсюда следует, что упругие постоянные
всякого однородного анизотропного тела удовлетворяют
условию
Si + S2 + S3 > 0 A4.6)
или
«и + «22 + «зз + 2 (а23 + а13 + а12) > 0. A4.7)
Выражая atj через коэффициенты Пуассона и модули Юн-
Юнга, после несложных преобразований получим условие,
которому удовлетворяют коэффициенты Пуассона, отне-
отнесенные к произвольной системе х, г/, z ([85], стр. 7):
vyz + v,x + v^<|-. A4.8)
В частности, для изотропного тела всегда v ^ V2, причем
везде знак равенства соответствует абсолютно несжимае-
несжимаемому телу.
Из формул A4.1) следует, что на любой площадке с
произвольно направленной нормалью п касательное нап-
напряжение отсутствует, а нормальное напряжение равно по
величине внешнему давлению:
On = -р, хп = 0. A4.9)
Такое распределение напряжений, подобное распределе-
распределению давлений в невесомой жидкости, заключенной в зам-
замкнутом сосуде, можно назвать гидростатическим.
Распределение деформаций в анизотропном теле будет
более сложным. Формулы A4.2) показывают, что выделен-
выделенный из тела элемент в виде прямоугольного параллелепи-
параллелепипеда, деформируясь, превращается в косоугольный парал-
параллелепипед. Но, как известно, в каждой точке сплошного
тела всегда существуют такие взаимно перпендикулярные
направления, углы между которыми не искажаются. Эти
направления главных осей деформации х', у , z легко
определить, если известны составляющие деформации,
отнесенные к произвольной ортогональной системе коор-
координат х, г/, z1).
См., например, курс Л. С. Лейбензона [18], § б, стр. 22.
§ 141
ВСЕСТОРОННЕЕ СЖАТИЕ
85
Введем обозначения: ац — коэффициенты деформации,
т|' с соответствующими индексами — коэффициенты вза-
взаимного влияния и e.v, е?у, . . ., уху, ох, ау, . . ., хху —
составляющие деформации и напряжения, отнесенные к
главным осям х', у , z\ а также
S'k = a'iK + a* + %к (к = 1,2,..., 6). A4.10)
Так как yyz = 7^ = 7^ = 0. то SA = S5 = Se = 0.
Это даст нам три условия, которым должны удовлетворять
коэффициенты взаимного влияния, отнесенные к главным
осям деформации:
¦JC,
A4.11)
Элемент А' в виде прямоугольного параллелепипеда
с ребрами, параллельными главным осям деформации
(рис. 20), остается прямоугольным параллелепипедом.
Легко показать, что он не изменит своего объема под дей-
действием касательных усилий tx, t2, t3, приложенных к гра-
граням. Если выделить из тела этот элемент А' и, освободив
его грани от давлений, нагрузить их касательными уси-
усилиями, то на основании сказанного в § 13 мы получим
распределение напряжений и деформаций:
.= *!,
XXZ =
*~. =
A4.12)
т,у =
A4.13)
Объемное расширение определится по формуле
в - е'1 + гу + вг = ^^4 + ^ + t3S'b, A4.14)
а так как S^ S5 и 5в равны нулю, то и 8 = 0.
86 ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО РАВНОВЕСИЯ 1Гл. t
В связи с этим рассмотрим деформацию анизотропного
тела, при которой относительные удлинения по всем нап-
направлениям одинаковы, а относительные сдвиги равны ну-
нулю, т. е. для системы координат х, у, z с произвольно на-
направленными осями:
е* = еУ = Ч = - е, yyz = yxz = уху = 0. A4.15)
В этом случае на гранях элемента А (рис. 20) будут
действовать и нормальные и касательные напряжения:
A4.16)
где
Ск - Л1к + А,к + Азк (к = 1, 2, . . ., 6) A4.17)
(см. уравнения B.5)).
Но, как известно, всегда существуют такие площадки,
на которых будут действовать только нормальные напря-
напряжения (площадки, нормальные к главным осям напря-
напряжений).
Пусть х", у", z" — главные оси напряжений, а в"х,
Оу, . . ., тХу, Aij — составляющие напряжений и упру-
упругие постоянные, отнесенные к ним, и
d = А[к + Afr + Alx (к = 1, 2,..., 6). A4.18)
Для этой системы координат имеем
а^ — _ ес" х'z = 0, 1
Оу = — 6^2, ТХ2 = О,
az = — еС3, хху — О,
С = Съ = С'6 = 0.
Мы приходим к следующему заключению: в анизотроп-
анизотропном теле всегда существуют три взаимно перпендикуляр-
перпендикулярных направления, х", у", z", для которых равны нулю сум-
суммы следующих модулей упругости:
А\ъ + л; + А"зъ = 0, A4.20)
А6 4- А"м + А"ав = 0. J
A4.19)
15]
ИЗГИБ СТЕРЖНЯ МОМЕНТАМИ
87
Эти направления определятся как направления глав-
главных осей напряженного состояния тела, подвергнутого
деформации вида A4.15).
§ 15. Изгиб стержня моментами, приложенными
к концам
Однородный стержень в виде цилиндра или призмы
произвольного сечения деформируется усилиями, распре-
распределенными по концам и приво-
приводящимися к изгибающим мо-
моментам, действующим в главной
плоскости yz (т. е. в плоскости,
проходящей через ось стержня z
и одну из главных осей инерции
у поперечного сечения; рис. 21).
Обозначая через Мг величи-
величину изгибающего момента и через
I и 1г — длину стержня и мо-
момент инерции его сечения отно-
относительно главной оси х, полу-
получим распределение напряжений
и деформаций в случае анизотропии (прямолинейной) об-
общего вида ([38], § 314):
oz=^~y, °х = ву = bz = т„ - т,у = 0; A5.1)
рпс
Л/,
= — Я1з!Л
= АЛ д ?
Mi
Л
Г
A5.2)
Из уравнений A5.2) найдем путем интегрирования
перемещения и, и, w; произвольные постоянные, которые
войдут в полученные выражения, мы определим из усло-
условий закрепления концов. Рассмотрим два случая.
1. Консоль. Один конец стержня, z = I (см. рис. 21),
закреплен, другой, z = 0, свободен. Предполагая, что
закреплен неподвижно элемент на оси вблизи защемлен-
защемленного сечения, мы должны удовлетворить при х = у = О,
88 ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО РАВНОВЕСИЯ [Гл. 2
2 =
1 условиям:
и = v =
du dv
dz dz
В результате получим
и =
V ==
w =
Мх
w + W-
-flis^ + a^2-
itPy + «342/2 —
= w = 0,
_ 5y
«352/ (^ -
-азз(^-
2а.ШA-
ду
— 2I
— Z)
l
+ a35x(l — z)],
A5.4)
Третья формула A5.4) показывает, что поперечные
сечения при изгибе вообще искривляются, принимая
форму поверхностей второго порядка; искривление зави-
зависит от коэффициентов ам и азъ (или, что то же, от коэффи-
коэффициентов взаимного влияния t]7/z, z и "Hzx, z)- Сечения останут-
останутся плоскими, если а34 = я35 = ^, а это будет иметь место,
например, в том случае, когда имеются плоскости упру-
упругой симметрии, нормальные к оси. Изогнутая ось стержня
имеет форму плоской кривой (параболы):
y'=--^aS3(l-z)\ A5.5)
которую при малых деформациях можно принять за
дугу окружности.
Одно из основных уравнений элементарной теории из-
изгиба, связывающее кривизну изогнутой оси с изгибающим
моментом, сохраняет свою силу и для стержня с анизотро-
анизотропией самого общего вида, только вместо модуля Юнга Е,
одинакового для всех направлений в изотропной балке,
будет стоять модуль Ez для растяжения — сжатия в
направлении оси стержня:
Наибольший по величине прогиб (на свободном конце)
равен
§ 15]
ИЗГИБ СТЕРЖНЯ МОМЕНТАМИ
Если коэффициент азъ не равен нулю, то изгиб сопро-
сопровождается закручиванием; угол -закручивания на единицу
длины равен
) A58)
2. Балка на двух опорах. Если на концах стержня име-
имеются шарнирные опоры (рис. 22), то перемещения должны
з?-
I
Рис. 22.
удовлетворять при х = у = 0, z = 0 и при х = у = О,
z = Z условиям
| и = V = ц; = 0. A5.9)
Этих условий недостаточно для определения всех пос-
постоянных. Потребуем, кроме того, чтобы элемент оси около
одной из опор не мог вращаться, т. е. добавим к условиям
A5.9) при х = у = z = 0 еще одно:
Тогда получим
dv ди _ ~
дх ду
и = 4
v = 4т- [—
Z/i
И? = -§J" [«35^2/ + Л342/2 + «332/ B2 — /)].
В этом случае уравнение изогнутой оси
A5.10)
A5.11)
а наибольший прогиб (в середине пролета)
/у ~ g# / •
A5.12)
A5.13)
00 Простейшие случаи упругого равновесий [гл. 2
Формулы для кривизны изогнутой оси и угла Ф оста-
останутся прежними — A5.6) и A5.8).
Если на концах стержня приложены моменты, дейст-
действующие в другой главной плоскости, xz, то мы получим
распределение напряжений:
oz = -j2-x, Gx = oy = xyz = xxz = xxy = 0. A5.14)
В этом случае
-1157*34. A5.15)
При совместном действии моментов Мх и М2 закручи-
закручивание вокруг оси определяется величиной
# = -у [ 77 аз5 + if пъЧ ' A5.16)
Очевидно, можно избавиться от закручивания при из-
изгибе, если подобрать моменты так, чтобы они удовлетво-
удовлетворяли условию
Мхаъь1г = M2a3Jv A5.17)
§ 16. Изгиб прямоугольной пластинки
моментами, распределенными равномерно
по сторонам
Прямоугольная пластинка постоянной толщины, изго-
изготовленная из однородного материала с анизотропией
общего вида, деформируется усилиями, распределенными
по сторонам; при этом на каждом элементе края с высотой,
равной толщине пластинки, усилия приводятся к изги-
изгибающим и крутящим моментам, которые не меняются
по длине стороны.
Примем срединную плоскость пластинки за плоскость
ху и направим оси хи у вдоль осей симметрии прямоуголь-
прямоугольника (рис. 23). Введем обозначения: а, Ъ — длины сторон,
h — толщина, Мг, Н — изгибающие и крутящие моменты
на двух противоположных сторонах, М2, Н — моменты
на двух других сторонах (отнесенные к единице длины).
Допуская, что внешние усилия меняются по толщине
пластинки по линейному закону, получим распределение
напряжений, такое же, как и в соответствующей изотроп-
§ 16] ИЗГИБ ПРЯМОУГОЛЬНОЙ ПЛАСТИНКИ МОМЕНТАМИ 91
ной пластинке (тонкой плите):
0L. =
hS "> "V —
h3
. 19
_ 12Я
~ Дз 2»
A6.1)
Из уравнений B.4) найдем составляющие деформации,
а по ним — проекции перемещения. Предположим, для
определенности, что закреплен элемент срединной поверх-
поверхности в центре пластинки. Тогда условия для перемещений
при х = у = z = О будут иметь вид
и = и = w = 0 \
J^i— dw___ dv__^ ди _ ^ \ A6.2)
дх " ду ~ ~дх ~ду~ ~ J
Для перемещений получим выражения:
и = -rg- [Mi (aibz2 + flie2/z -f- 2anxz) + M2 (а2б2:2 +
2a12a:z) J,- Я (а6б22+ a6Qyz + 2auxz)],
- .W2 (#24Z2 +
w = jta
2a22yz + a2%xz) + H (a4ez2
anx2— a22y2—
A6.3)
92 ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО РАВНОВЕСИЯ [Гл. 2
Прогиб срединной поверхности W = w (х, у, 0) равен:
j + аиху) + М2 (а12х*
H (aux2 + a26y2 +
)
J
. J
Формулы A6.3) показывают, что гипотеза прямых нор-
нормалей в общем случае не соответствует действительности.
Прямолинейные отрезки, до деформации нормальные к
срединной плоскости, при деформации искривляются, о
чем свидетельствуют члены с z2 в выражениях для и и v;
искривления зависят от коэффициентов деформации а14,
#24» ai6» #25* а4в и а6б и исчезают, если эти упругие постоян-
постоянные равны нулю (а это, например, будет в случае, когда
имеются плоскости упругой симметрии, параллельные
срединной).
Несмотря на это, для пластинки с анизотропией общего
вида, изгибаемой равномерно распределенными момен-
моментами, сохраняют силу формулы приближенной теории из-
изгиба тонких плит, основанной на гипотезе прямых нор-
нормалей, а именно:
М
A6.5)
Здесь МХ1 Му, Нху — изгибающие и крутящие моменты
внутри пластинки, действующие на линейные элементы
срединной поверхности, параллельные осям х и у (в дан-
данном случае Мх = Мг, Му = М2, Нху = Я), а Dtj — же-
жесткости анизотропной пластинки, определяемые по фор-
мулам ([21], § 38)
В частном случае, когда пластинка ортотропна
= а2& = 0), нагружена только изгибающими момента-
моментами (Н = 0) и оперта по углам, прогиб ее срединной
§ 17] СТЕРЖЕНЬ С ЦИЛИНДРИЧЕСКОЙ АНИЗОТРОПИЕЙ 93
поверхности равен:
М2агг) (-? - ^)] . A6.7)
Наибольший прогиб (в центре) определится по формуле
/ = ^ КМфп + М2ап) а2 + (Мха12 + М2а22) Ь2], A6.8)
или, иначе,
§ 17. Растяжение и изгиб стержня,
обладающего цилиндрической анизотропией
Рассмотрим стержень в виде цилиндра или призмы
произвольного сечения, изоготовленный из упругого ма-
материала, обладающего цилиндрической анизотропией.
Предположим, что ось анизотропии параллельна оси стер-
стержня и проходит внутри его, вне или по поверхности. Пусть
этот стержень растягивается осевой силой и собственным
весом (рис. 17) или деформируется моментами, приложен-
приложенными на концах (рис. 21).
Для того чтобы найти распределение напряжений и
деформаций, нужно определить шесть составляющих на-
напряжений и три проекции смещения, удовлетворяющие ос-
основной системе уравнений равновесия упругого тела и
граничным условиям. В данном случае удобнее всего
пользоваться цилиндрическими координатами, принимая
ось анизотропии за ось z, и тогда основная система при-
принимает вид
? + !^г + ^+^ + « = °.
ег =
?гв =
A7.1)
ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО РАВНОВЕСИЯ [Гл. 2
где atj — упругие постоянные, а ег, ее, . . ., Угв связаны
с проекциями'перемещения иг, щ, w зависимостями A.3).
Возникает естественный вопрос: будут ли распределе-
распределения напряжений в растягиваемом или изгибаемом стержне
с цилиндрической анизотропией совпадать с теми про-
простыми распределениями, какие получаются в однородном
анизотропном или изотропном стержне? На этот вопрос
в общем случае приходится ответить отрицательно.
Остановимся на случае растяжения осевой силой Р
без учета собственного веса (рис. 17). В стержне с прямо-
прямолинейной анизотропией или изотропном получается эле-
элементарное распределение напряжений:
oz = -^, аг = (те = T6z = хтг = тг9 = 0 A7.2)
(S — площадь'поперечного сечения). Уравнения равнове-
равновесия и граничные условия, очевидно, удовлетворены, а
из уравнений обобщенного закона Гука должны опреде-
определиться перемещения иг, щ, w. Находя по этим напряжениям
перемещения путем интегрирования последних шести
уравнений системы A7.1), мы убеждаемся, что это можно
сделать только в том случае, когда постоянная а34 Равна
нулю; если же аи Ф 0, то уравнения оказываются несов-
несовместными. Но предположим, что условие совместности
ам = О выполнено. Тогда получим
Р
иг = -я- а13г + (оJ cos 9 — (Ox sin 6) z -f- и0 sin 6 + и0 cos 9,
Щ = -j- [(a23 — fli3) гд + a^r In r] — (co2 sin 9 +
+ o)x cos Q)z + v0 cos 9 — u0 sin 9 + co3r,
P
w = -7Г- (a35r + a33z) + ((Ox sin 9 -— co2 cos 9) r + н;0.
3
Здесь (uv oJ» ^з» uo> yo» wo — постоянные, выражающие
жесткие смещения.
Перемещение щ содержит член, пропорциональный
углу 9. Это значит, что оно будет многозначной функцией
координат, если а13 Ф а2з» и ось анизотропии проходит
внутри тела (по телу или в полости), так как при обходе
по замкнутому контуру, окружающему ось анизотропии,
щ получит приращение Р2пг (а23 — a13)/S. Многознач-
Многозначности не будет, если а19 = а23 или ось анизотропии про-
§ 17] СТЕРЖЕНЬ С ЦИЛИНДРИЧЕСКОЙ АНИЗОТРОПИЕЙ 9Г>
ходит вне тела или по поверхности, так как тогда ее нель-
нельзя окружить замкнутым контуром, лежащим целиком
внутри стержня. Многозначность перемещений указывает
на непригодность решения A7.2); перемещения всегда
должны быть однозначными функциями координат.
Таким образом, мы приходим к следующему выводу.
Элементарное распределение напряжений A7.2) может
получиться в стержне с цилиндрической анизотропией толь-
только в двух частных случаях: 1) ось анизотропии проходит
вне стержня или по образующей боковой поверхности и
аы = 0; 2) ось анизотропии проходит внутри стержня и
упругие постоянные удовлетворяют условиям
а34 = 0, а13 = а23. A7.4)
Второе из этих условий можно сформулировать таким
образом: коэффициенты Пуассона, характеризующие
сжатие в радиальных и тангенциальных направлениях
г и Э, при растяжении в осевом направлении z должны
быть равны.
Если стержень, обладающий цилиндрической анизо-
анизотропией, растягивается под действием собственного веса,
то элементарное распределение напряжений A1.9) имеет
место только в том случае, когда упругие постоянные
удовлетворяют условиям:
аз4 = азь = Язе = 0, а13 = а23, A7.5)
независимо от того, где проходит ось анизотропии, так
как A7.5) являются условиями совместности системы урав-
уравнений, определяющих перемещения.
Это же можно сказать и относительно изгиба стержня
моментами М1 и М2. Распределение напряжений в стержне
с цилиндрической анизотропией будет таким же, как в од-
однородном анизотропном или изотропном стержне только
при выполнении условий A7.5) (также независимо от того,
где проходит ось анизотропии).
Исследованию упругого равновесия стержней с ци-
цилиндрической анизотропией более общего вида посвящена
глава 5 этой книги.
Глава 3
УПРУГОЕ РАВНОВЕСИЕ ТЕЛА,
ОГРАНИЧЕННОГО ЦИЛИНДРИЧЕСКОЙ
ПОВЕРХНОСТЬЮ, В КОТОРОМ НАПРЯЖЕНИЯ
НЕ МЕНЯЮТСЯ ВДОЛЬ ОБРАЗУЮЩЕЙ
В главе 3 рассматривается названная общая задача
для однородного тела, обладающего анизотропией общего
вида, прямолинейной или цилиндрической [уравнения
C.8) или A0.2), где atj — величины постоянные]. В по-
последующих главах 4—6 рассматриваются задачи, являю-
являющиеся частными случаями общей задачи об обобщенной
плоской деформации, плоской деформации, обобщенном
плоском напряженном состоянии, и родственные им зада-
задачи об обобщенном и чистом кручении цилиндрических и
призматических тел.
§ 18. Распределение напряжений
в однородном теле с прямолинейной
анизотропией, зависящее только
от двух координат
Поставим задачу следующим образом. Рассматривает-
Рассматривается упругое равновесие однородного тела, ограниченного
цилиндрической поверхностью (или плоскостями), обла-
обладающего анизотропией самого общего вида, под действием
усилий, распределенных по поверхности, и объемных
сил. Область поперечного сечения может быть конечной
или бесконечной, односвязной или многосвязной; длина
тела может быть конечной или бесконечной. Предполагаем,
что усилия, распределенные по боковой поверхности, и
объемные силы действуют в плоскостях, нормальных к об-
образующей и не меняются по длине. Кроме того, на торцах
18]
НАПРЯЖЕНИЯ, ЗАВИСЯЩИЕ ОТ ДВУХ КООРДИНАТ
97
цилиндра конечной длины или полубесконечного дейст-
действуют усилия, приводящиеся к изгибающим моментам,
скручивающим моментам и осевым (продольным) силам;
начальные напряжения отсутствуют 1).
Отнесем тело к декартовой системе координат х, у, z,
у которой ось z параллельна образующей, а плоскость
ху, следовательно, совпадает с плоскостью какого-нибудь
поперечного сечения (например, торцевого); оси х, у
направлены так, как это представляется наиболее удобным,
учитывая форму сечения.
Если область сечения конечная, то удобно поместить
начало координат в центре тяжести и направить оси х, у
по главным осям инерции сечения.
Будем считать, что тело следует обобщенному закону
Гука, уравнения которого имеют вид C.8), причем все
коэффициенты деформации atj, вообще говоря, не равны
нулю. Деформации малы.
Проекции усилий, распределенных по боковой поверх-
поверхности (на единицу площади) обозначаем через Хп, Yn,
где п — нормаль к боковой
поверхности. Проекции объ-
объемных сил (на единицу объе-
объема) обозначаем через X, У,
причем считаем^ что они име- /ЯШ// / I ///
ют потенциал U (х, у), т. е.
ди у. dif
~~ дх ' " ду
A8.1)
Последнее ограничение не
является существенным, но
упрощает выкладки. Силу и
моменты, к которым при-
приводятся усилия, действую-
действующие на торцах, обозначаем
через Pz, Mly M2, Mt (осевая сила, изгибающие моменты,
скручивающий момент; рис. 24).
Представляется очевидным, что составляющие напря-
напряжений в данном теле, нагруженном указанным образом,
Рис. 24.
х) Под «начальными» подразумеваются напряжения, которые
могут быть в теле при отсутствии внешних усилий и тепловых воздей-
воздействий.
08
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл. 3
являются функциями только двух координат х, у. Поста-
Поставим своей задачей вывести общие уравнения, определяю-
определяющие напряженное и деформированное состояния, и усло-
условия на боковой поверхности и на торцах. Впервые эта за-
задача для однородного тела была поставлена Сомильяна в
работе [125]. Дальнейшее развитие она получила в нашей
книге [20], откуда мы и берем (с небольшими изменения-
изменениями) §§ 17—21 (стр. 87—105 книги); см. также работу [56].
Основная система уравнений равновесия для данного
упругого тела будет иметь следующий вид:
дх v
дх
"~дх~
дх_
¦ + ¦
= 0;
дх ' ду
ех = апах + а12ау
8У -= а12ах + а22ау
A8.2)
аы тл1/,
*ху
Введем обозначение:
D =
A8.3)
Отсюда
D 1 .
Gz = — (ai3^x- -
Уравнения A8.3) перепишутся так:
gj = Pll^x + Pl2^y + . • • + PietffV + "J^ Д>
хУ
A8.4)
у). A8.5)
dv . dw
A8.6)
§ 18] НАПРЯЖЕНИЯ, ЗАВИСЯЩИЕ ОТ ДВУХ КООРДИНАТ
99
Из этих уравнений определим перемещения путем
интегрирования, причем здесь и в дальнейшем будем
придерживаться определенного порядка: вначале проинтег-
проинтегрируем уравнения третье, четвертое и пятое, а затем по-
потребуем, чтобы найденные перемещения, содержащие неоп-
неопределенные функции интегрирования Ux(x, у), Vx (x, у) и
Wi(x, у), удовлетворяли остальным уравнениям A8.6) —
первому, второму и шестому. Интегрируя третье, четвер-
четвертое и пятое уравнения, находим:
w = zD + Wx (x, у),
z2 3D ,
и = —
0D
д\Ул
дх
U1(x,y)-
A8.7)
Введем в рассмотрение «жесткие» перемещения — ли-
линейные функции координат, выражающие перемещения
тела как целого, без деформации:
A8.8)
U о,
v1 = ю3.г — ом + г0,
м/ = щу — оJ.х + w0,
где (о1? оJ, оK — произвольные постоянные — компонен-
компоненты поворота тела вокруг трех осей координат х, у, ъ\ и0,
i;0, w0 — произвольные постоянные — поступательные
перемещения вдоль осей.
Далее введем вместо U1, Vx, Wx новые функции U, V,
W, положив
Ui = U — оо3у + и0,
= V + соз* + v0,
A8.9)
w0.
Подставляя выражения A8.7) в левые части первого,
второго и шестого уравнений A8.6) и приравнивая коэф-
100
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл. 3
фициенты при 22, z и свободные члены в левых и правых
частях, получим три уравнения для D и две системы урав-
уравнений для W и U, V:
дЮ
¦fo" ( Pl6ax
дхду
= 0;
а33
0|
A8.10)
A8.11)
ди
dV
«33
HSL D,
«33
«33
A8.12)
Из A8.10) следует, что D есть линейная функция^
и у с произвольными коэффициентами Л, В, С:
D = Ах + By + С,
A8.13)
а следовательно, нормальное напряжение в поперечных
сечениях равно [см. A8.5)]:
- A8.14)
§ 18] НАПРЯЖЕНИЯ, ЗАВИСЯЩИЕ ОТ ДВУХ КООРДИНАТ Ю1
Интегрируя первые два уравнения A8.11) и удовлет-
удовлетворяя третьему, получим уравнения для W:
О f? r\ I Q - I I Q , I
дх
Здесь
A8.15)
Pij = O'xi —
f,/ = 1,2,4,5,6) A8.16)
— величины, названные приведенными коэффициентами
деформации [56]. Исключая U, V и W из A8.12) и A8.16)
(путем дифференцирования, сложения и вычитания),
получим два уравнения для а и т:
+
1/ + • • • +
+ M» + • • • + РвЛу) = 0; A8.17)
-^-(Pi »ff* + P»ff „ + ••• +
дх~
Ааы —
A8.18)
Окончательные выражения для перемещений запишутся
так:
u = --^-z2-$yz + U(x, у) + w/,
A8.19)
у = ^-z2 + #xz +V(x,y) + v\
w - (Ax + By + C)z + W(x,y) + w'.
Эти выражения содержат всего 10 постоянных. Форму-
Формулы A8.19) показывают, что члены с множителем д равны
102
ЦИЛИНДРИЧЕСКОЕ Т ЛО
[Гл. 3
соответствующим членам перемещений при простом кру-
кручении ([22], стр. 39); м', i/, w' — жесткие перемещения
A8.7).
Постоянные А, В, С, ft найдутся из условий равнове-
равновесия на торцах (или в поперечном сечении в случае стерж-
стержня бесконечной длины). Постоянные, входящие в состав
жестких перемещений, определятся из условий закреп-
закрепления торцов. Заметим, что этих условий должно быть
ровно шесть, а не больше и не меньше. Следовательно,
этим методом мы не сможем решить задачу, закрепляя
торцы произвольным образом. В случае конечного сече-
сечения мы будем считать закрепленным неподвижно центр
тяжести сечения и бесконечно малую площадку около не-
него, или элемент оси, проходящий через центр. Для того
чтобы решцть задачу при произвольном закреплении тор-
торцов, необходим более строгий подход (или метод), кото-
которого мы здесь касаться не будем.
§ 19. Функции напряжений
Составляющие напряжений можно выразить через две
функции F (х, у), \р (х, у) двух переменных х, у так, чтобы
уравнения равновесия сплошной среды A.6) или A8.2)
удовлетворялись тождественно. Положим:
а,. =
ду*
0,
дхду*
A9.1)
Шестая составляющая az определится по формуле
18.14). Далее возьмем два уравнения A8.17) и A8.18) и вы-
выразим напряжения через F и if> (функции напряжений), ^о
лучим систему двух уравнений для функций напряжений,
которая сокращенно запишется так:
LAF
Р22)
даР
Pie + Рге)
2ft + —
/ft 1 ft \
- (P11 + P12)
д2°
«33
A9.2)
19]
ФУНКЦИИ НАПРЯЖЕНИЙ
Здесь L4, L3, L2 — дифференциальные операторы^ чет-
четвертого, третьего и второго порядков, имеющие такой вид
= Р22 ^i
Ри-^х»
A9.3)
ft д2
= Р44 -^г —
Напряжения и перемещения, соответствующие функ-
функциям напряжений F и г|), должны быть непрерывными и
однозначными внутри тела. На боковой (цилиндрической)
поверхности должны быть выполнены граничные условия.
Если там задаются внешние усилия Zn = 0, Хп, Уп, как
функций координат точек контура сечения (первая основ-
основная задача), то условия на поверхности или, что то же, на
контуре поперечного сечения, будут иметь вид
ах cos (п, х) + хху cos (л, у) - Хп,
хху cos (л, х) + ву cos (л, г/) = Уп,
xxz cos (л, ж) + тУ2 cos (п, у)= 0.
A9.4)
Здесь п — внешняя нормаль к контуру поперечного
сечения, уравнение которого удобно задать в параметри-
параметрическом виде: х = х (s), у = у (s). За параметр s часто бе-
берут длину дуги контура, отсчитываемую от точки, приня-
принятой за начальную, в положительном направлении. За по-
положительное направление отсчета дуг мы примем такое,
при котором контур (как внешний, так и внутренний,
т. е. контур выреза в случае многосвязной области) об-
обходится против часовой стрелки. Тогда для внешнего
контура области сечения будем иметь
cos (n, х) = -g- , cos (n, y) = -^-
A9.5)
104
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл 3
и для внутреннего г)
dx
cos (л, x) = — -rf-, cos (л, у) = -т— .
A9.6)
Интегрируя A9.4) по дуге контура от начальной его
точки О до переменной точки s, перепишем условия A9.4)
таким образом:
A9.7)
Верхние знаки нужно поставить для наружного кон-
контура, нижние — для внутреннего. Постоянные сг, с2, с3
можно зафиксировать произвольно на одном из контуров,
ограничивающих сечение; в частности, для конечной од-
носвязной области можно принять ct = 0.
Если на боковой поверхности (контуре сеченА) зада-
заданы проекции перемещения и*, у*, w* (вторая основная
задача), то мы имеем там условия:
и = w* (s), v = v* (s), w = w* (s).
A9.8)
Условия на торцах или в поперечном сечении, где дей-
действуют усилия, приводящиеся к равнодействующей Pz и
к изгибающим и скручивающему моментам, первоначаль-
первоначально запишутся так:
A9.9)
Здесь и далее (гл. 3—7) двойные интегралы берутся по
обдасти поперечного сечения цилиндрического тела.
xzdx dy = 0, 55 а*У dx dV = мь
55 ryzdx dy = 0, 55 °гх dx dy = М2,
55 vzdx dy = P2, 55 (rvzx — Х
г) Н. И. Мусхелишвили ([26], стр. 140) за положительное на-
направление обхода по контуру берет такое, при котором область
остается слева.
§ 19] ФУНКЦИИ НАПРЯЖЕНИЙ 105
Сила Р2 и моменты Мх, М2, Mt могут быть как задан-
заданными, так и подлежащими определению (реактивными), в
зависимости от условий закрепления торцов.
Если в теле имеются плоскости упругой симметрии,
нормальные к оси z,
^34 = «35 = 0> Pl4 = Pl5 = Р24 = 025 = Р*6 = Р&6 = О,
и система A9.2) распадается на два независимых уравне-
уравнения — одно для F и другое для гр.
В соответствии с этим и задача распадается на две —
на задачу о плоской деформации и задачу о кручении, ко-
которые и нужно будет решать самостоятельно. Подробнее о
плоской задаче и о кручении будет сказано в главах 4—6.
Остановимся на случае, когда область поперечного се-
сечения конечна и односвязна. Поместим начало координат
в центре тяжести сечения, а оси х, у направим по главным
осям инерции. Преобразуем условия на торцах A9.9).
Прежде всего убеждаемся, что первые два условия
A9.9) удовлетворяются тождественно.
Имеем:
A9.10)
tv zdx dy = \\ -r~ dx dy = \ if cos (л, ?/) ds = 0,
v
ty2ai ay = — \ \ -^- ax dy =
— — \ г|з cos (л, r/:) ds — 0
v
(простой интеграл берется по всему контуру у сечения).
Эти интегралы тождественно равны нулю, так как на кон-
контуре \|) = const. Остальные четыре условия A9.9) содер-
содержат в общей сложности 17 интегралов от напряжений и
напряжений, умноженных на линейные функции (х и у).
Можно убедиться в том, что еще два интеграла равны ну-
нулю, а два выражаются через скручивающий момент Mt.
Имеем
й
?¦
f f2
= \ "o- [Ttz cos (ni x) + ТУ2cos (ra> y)] a5 = 0. A9.11)
106 ЦИЛИНДРИЧЕСКОЕ ТЕЛО [Гл. 3
Аналогично
\\xyzydxdy = O. A9.12)
Условия на торцах принимают такой вид:
CS — \ \ (#13сгд1-|- #23^ ~Ь ^зв^ху) dx dy = Pza33i
bli — \\ (^13^д: + 0>23ву + ^Зб^г + ^Зв^д^) У пХ пу =
A9.13)
y)xdxdy=
txzy) dx dy = Mx. A9.14)
Здесь S — площадь поперечного сечения, /ь /2 — его
главные моменты инерции (относительно осей х и у).
Интегралы от напряжений по площади поперечного се-
сечения и от напряжений, умноженных на х или у, можно
выразить через заданные величины — поверхностные и
объемные силы. Для того чтобы выполнить это преобразо-
преобразование, подведем под знаки интегралов выражения, равные
пулю — левые части уравнений равновесия сплошной
среды A8.2) или левые части уравнений, умноженные на
степени или произведения х и у. Затем двойные интегралы
преобразуем в интегралы по контуру поперечного сечения
у, учитывая граничные условия A9.4). В данных случаях
мы не будем вводить в рассмотрение потенциал объемных
сил, так как удобнее обозначать объемные силы просто
через X, Y. Не приводя всех преобразований, укажем
лишь окончательные результаты 4):
г) Те же интегралы, но при отсутствии объемных сил и сил,
приложенных к боковой поверхности, приведены у Фойгта ([38],
§306), которого интересовали главным образом вопросы кручения и
изгиба.
193
ФУНКЦИИ НАПРЯЖЕНИЙ
107
\\ ах dxdy = \ хХп ds + \\ хХ dx dy,
у
а у dx dy=\^ yYn ds + ^ yY dx dy,
у
tT2 dz dy = 0,
алj/ dr dy =
= 0,5
d^ di/ = 0;
0,5
- 0,5 J y2Xn ds + 0,5 Ц 2/2X dx dy,
v
zy dx dy = 0, Ц xxzy dxdy = — 0,
(T^ dx dy = 0,5 J x2Xn ds + 0,5 Ц я2
v
oyx dxdy = \^ (xyYn ~ 0,5у2Хп) ds +
У
A9.15)
(xyY - 0,5y2X) dx dy,
dy,
^ d^ dy = 0,5 J ж2Уп ds + 0,5
у
\\ ry?o: dj1 dy = 0,5Mf, \\ xxzx dx dy = 0.
A9.17)
В условиях на торцах можно перейти к проекциям по-
поверхностных и объемных сил и тогда вместо A9.13) —
108 ЦИЛИНДРИЧЕСКОЕ ТЕЛО [Гл. 3
A9.14) получим:
CS - J [(а1Ъх + ОзвУ) Хп + a2byYn\ ds -
а36у) X + a23yY] dx dy = Р2а33; A9.18)
5азвУа) ^n + 0,5 (аазуа - а1Эж2) Fn] d5 -
v
- Ц [(агзху + 0,5азву2) X + 0,5 (а23у2 - а13х2) F] dx dy +
+ 0,5аз61^ = A/xOss; A9.19)
Ah - \ [0,5 (а13х2 - a^if) Xa + (a23xy + 0,5a36.r2) Yn] ds -
v
- Ц [0,5 (a13;/;2 - a23y2) X + (a^nj + 0,5азв/2) Y\ dx dy -
- 0f5fl34A/, = Л/аа33. A9.20)
Из уравнений A9.18) — A9.20) определяются одно-
однозначно коэффициенты А, В, С, входящие в формулу для
напряжения az A8.14). Постоянная д найдется из по-
последнего (шестого) условия A9.9). В случае односвязной
конечной области это условие легко упростить, выразив
интеграл в левой части шестого уравнения A9.9) и преоб-
преобразовав его. Будем иметь:
*!/= с - т,гу) dx dy=-\\ [-?- W) + ± B/г|))] d^ dy +
. A9.21)
Преобразуя двойной интеграл в интеграл по контуру, где
можно принять г|) = 0, получаем уравнение для определе-
определения О:
^ A9.22)
§ 20. Общие выражения для функций
напряжений в однородном
прямолинейно-анизотропном теле
Общее решение системы уравнений A9.2) можно за-
записать в виде
F = FX +F0, яр =ih +%. B0.1)
§ 20] ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ФУНКЦИЙ НАПРЯЖЕНИИ Ю9
Здесь Flt i|)x — общее решение однородной системы
+ 1*Ч>1 = 0,
,-o, I <20-2>
a Fo, 'Фо — какое-нибудь частное решение неоднородной
системы A9.2). Частное решение зависит от правых частей
неоднородных уравнений и если эти правые части неслож-
несложны, например, составлены из элементарных функций, то
и частные решения обычно отыскать нетрудно.
Чтобы получить общее решение однородной системы,
исключим из нее какую-нибудь функцию, например, ipx.
Тогда получим для оставшейся функции уравнение шес-
шестого порядка
(L4L2 - L\) Fx = 0. B0.3)
Такое же уравнение получим и для другой функции. Опе-
Оператор шестого порядка LAL2 — L\ можно разложить на
шесть линейных операторов первого порядка Dk и урав-
уравнение B0.3) представится в виде
D,DbD^D^DllD1F1 = 0. B0.4)
Здесь
Dk = — \iK , B0.5)
a [ik — корни алгебраического (характеристического)
уравнения шестой степени, соответствующего дифферен-
дифференциальному B0.3):
h (V) к (V) - К (V) = 0, B0.6)
где обозначено:
/4 (|i) - рп1х4 - 2р1б1х3 + Bр12 + Рее) Ц2 -
- (Pi4 +;Р6б) К2 + (Р2б + Р4в) I* ~ hi B0Л)
Интегрирование линейного уравнения шестого поряд-
порядка можно свести к последовательному интегрированию
шести уравнений первого порядка. Предположим, что
НО ЦИЛИНДРИЧЕСКОЕ ТЕЛО [Гл. 3
среди корней (Х/е нет, кратных. Обозначим:
#1^1 = ф2,
- ф6, #5Фб = фб- J
Функция фв удовлетворяет уравнению
= 0; B0.9)
общий интеграл его равен произвольной функции ар-
аргумента х + [a6z/, которую для удобства мы обозначим
как производную пятого порядка некоторой функции
/в (х + \кву):
Фе = /eV (х + |ie»). B0.10)
Функция фб удовлетворяет неоднородному уравнению
?5Фб = fa (x +|ie»), B0.11)
которое легко интегрируется. В результате получается
B0.12)
Так последовательно из B0.8) мы определим ф4, ф3, ф2
и наконец Fv Изменив обозначения произвольных функ-
функций, получим общие выражения для Fx и tyx:
Fi = 2 Fit (* + НУ), *i = 2 *» (•« + НУ)- B0.13)
Функции Ftf и ifife удовлетворяют не только уравне-
уравнению B0.3), но, кроме того, и системе уравнений B0.2).
Отсюда следует, что между ними должна быть связь, ко-
которая легко устанавливается совершенно элементарным
путем. В результате получаем
F'lK {х + ^у) + пк(х + ^у) + к B0'
Здесь ак, Ък — произвольные постоянные; штрихом
обозначена производная по всему аргументу х + \ЛкУ-
Этот способ решения не годится, очевидно, если среди
корней есть равные. Но и в этом случае отыскание не
представляет большого труда и мы на этом вопросе оста-
останавливаться не будем.
§20] ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ФУНКЦИЙ НАПРЯЖЕНИЙ Ц1
Общее выражение для функции напряжений F может
быть получено и несколько иначе. Будем искать частное
решение уравнения B0.3) в виде
Fi=f(*+ 140- B0.15)
Подставляя в B0.3) и сокращая на /VI (ибо уравнение
содержит производные только шестого порядка), получим
алгебраическое уравнение шестой степени относительно (х,
имеющее шесть корней. Если среди корней нет кратных,
то общее выражение для Fx мы получим в виде суммы
шести функций Д (х + \i;-y) (к = 1, 2, . . ., 6). В случае
наличия кратных корней задача немного усложняется,
но и при корнях любой кратности решение легко может
быть найдено.
Далее остановимся на четырех теоремах, весьма важ-
важных для всей теории равновесия тела, ограниченного ци-
цилиндрической поверхностью ([56], стр. 351—353 и [20],
§ 19). При доказательстве мы исходим из двух основных
положений: 1) любые шесть вещественных чисел можно
принять за значения составляющих напряжений в данной
точке упругого анизотропного тела; 2) потенциальная
энергия деформации V, отнесенная к единице объема, есть
величина положительная при любых значениях составля-
составляющих напряжений (вещественных и не равных нулю од-
одновременно).
Теорема 1. Уравнение /4 (\х) — 0 не может иметь
вещественных корней.
Однородное тело с анизотропией общего вида испыты-
испытывает заведомо упругие деформации и находится в устой-
устойчивом равновесии, если все составляющие напряжений
не превосходят по абсолютной величине некоторого чис-
числа 8 > 0.
Зададим в данной точке напряжения:
а (Уa
B0.16)
где k и N — вещественные числа; тогда в этой точке
?=-щ-Ш- B0.17)
112
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл. 3
Придавая к всевозможные вещественные значения,
будем всякий раз подбирать N так, чтобы все составляю-
составляющие напряжений по абсолютной величине были меньше 8.
При всяких значениях напряжений, заданных указан-
указанным образом, V у> 0, а отсюда /4 (к) ^> 0 при веществен-
вещественных к; следовательно, уравнение lA (l1) = 0 не имеет ве-
вещественных корней.
Теорема 2. Уравнение 1г (ц,) = 0 не может иметь
вещественных корней.
Доказательство проводится аналогичным путем. За-
Задавая значения напряжений:
к
"Ж
имеем
B0.18)
B0.19)
а следовательно, 12 (к) ^> 0 при всех вещественных к.
Теорема 3. Уравнение lA (\i) l2 (\i) — l\ (ц,) = 0 не
может иметь вещественных корней.
Чтобы доказать эту теорему, зададим напряжения в
точке таким образом:
1 к
1 , ,_* , _ , . , , _ ,,., Bа20)
где X = —Z3 (k)/l2 (A) — величина конечная, в частности,
нуль.
Получим выражение упругого потенциала в точке:
и'
1Ж
что и доказывает теорему.
§ 20] ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ФУНКЦИЙ НАПРЯЖЕНИЙ ?13
Т е о р е м а 4. Уравнение
^llM1 — ?#ie[l -f- \?а±2 -f- ^6б)|Ы — 2#2бЦ- Н~ #22 == О
B0.22)
«е может иметь вещественных корней.
Доказывается так же, как теорема 1, только в данном
случае нужно положить
- — а — — k
х ~ У ' у ~~ N '
$z = X\iz = Txz = °-
Для уточнения заметим, что при доказательстве всех
четырех теорем мы заранее исключаем из рассмотрения
такие случаи, когда свободные члены уравнений равны
нулю. Это — особые случаи, которые, впрочем, для нас
большого интереса не представляют.
Совершенно очевидно, что если |322, р44, а22 или посто-
постоянное слагаемое более сложного уравнения /4/2 — ll = 0
будут равны нулю, то соответствующие теоремы теряют
силу, так как один корень уравнения непременно будет
вещественным— равным нулю. Но тогда каждое из урав-
уравнений становится уравнением нечетной степени и, следо-
следовательно, имеет еще по крайней мере один вещественный
корень, а всего не менее двух.
Уравнения
B0.24)
и соответствующие B0.22), левые части которых построе-
построены так же, как левые части рассмотренных уравнений,
только с заменой коэффициентов atj модулями Atji так-
также не могут, за исключением особых случаев, иметь веще-
вещественных корней. Это утверждение не нуждается в дока-
доказательстве, а непосредственно вытекает из уравнений
обобщенного закона Гука, согласно которому atj одно-
однозначно выражаются через Atj и наоборот.
На основании теоремы 3 мы можем утверждать, что
числа \хк — всегда комплексные или чисто мнимые, при-
причем три из них^являются сопряженными с тремя други-
другими. Мы будем называть \ik комплексными параметрами
114 ЦИЛИНД1ИЧЕСК0Е ТЕЛО [Гл. 3
данной проблемы и обозначать таким образом:
M-i = «1 + Фь Н = а2 + ф2, № = а3 + фз,
25
(здесь i — ]/~—1; fik условимся всегда считать положи-
положительными). Далее введем обозначения и названия:
zk = х -f \iky — усложненные или обобщенные ком-
комплексные переменные (к = 1\ 2, 3);
zk = х -f- Jl^y — сопряженные усложненные или обоб-
обобщенные комплексные переменные;
Х2==~1ЖГ' Яз = ~ТТЙГ- B0'26)
Будем обозначать, как обычно, символом Re — веще-
вещественную часть комплексного выражения. Мы можем за-
записать общие выражения для функций напряжений, куда
войдут вещественные части трех функций усложненных
комплексных переменных:
F = 2 Re [Fn (zx) V Fl2 (z2) + F13 (z8)J + Fo,
ip = 2 Re h
B0.27)
(штрихом обозначены производные первого порядка по zk).
§ 21. Общие формулы для составляющих
напряжений и проекций перемещения;
граничные условия
Введем новые функции усложненных или обобщенных
комплексных переменных zk:
(Л = 1,2); ФзЫ=-^-^3Ы; B1.1)
производные от Ф^ (zk) no zk будем обозначать через
(k)
С помощью этих новых функций, которые мы назовем
комплексными потенциалами, можем записать
выражения для первых производных от F по х и у и для
§ 21] ОБЩИЕ ФОРМУЛЫ ДЛЯ СОСТАВЛЯЮЩИХ НАПРЯЖЕНИЙ 115
» таким образом:
-|?- = 2Нв[Ф
2L = 2 Re [\хг
ib = 2 Re ГХ,'
Ф2
Ф3
B1.2)
По формулам A9.1) на основании B1.2) получаем общие
выражения для составляющих напряжений:
ох = 2 Re [цМ>;
- 2
: — 2 Re [\лхф[
- 2 Re [XjOl -
2 Re [[хАхФ! -\
(Ax + By
B1.3)
+
)- B1.4)
Подставляя B1.3) в уравнения A8.12) и A8.15), полу-
получим после интегрирования ([56], стр. 354—355):
U = 2 Re
/о,
B1.5)
116
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл 3
Здесь
обозначено:
Л = Pnf4 +
ft = Pi*» +
r*=Pl4|**H-
Pia -
¦fe"
- Pl*k
- Ри
— ?46
(A- = 1,
Из
2);
T
@45 -
) + P*.
— Pl4),
r24 \
B1.6)
B1.7)
f^o» ^o» W^o — решения уравнений A8.12) и A8.15), со-
соответствующие функциям FQ, г|H, С? и линейным функциям
Ла: -f ?1/ + С, Од:, Oi/, содержащие постоянные Л, 5, С, О.
В случае первой основной задачи, когда заданы уси-
усилия ХП1 Yn, граничные условия или условия на контуре
поперечного сечения принимают такой вид:
2 Re [<2>i + Ф2 + ^зФз] •= /i (s) — -^ +
2 Re [jixOi + (Л2Ф2 + |13^зФз] = /2 («) — %f- + «
2 Re [^Фх + Х2Ф2 + Ф3] = - % + c3>
где
B1.8)
B1.9)
а сх, с2, с3 — постоянные, которые можно зафиксировать
произвольно на одном из контуров, ограничивающих
область поперечного сечения; верхние знаки соответствуют
внешнему контуру, нижние — контуру отверстия (выреза).
В случае второй основной задачи, когда на цилиндри-
g 211 ОБЩИЕ ФОРМУЛЫ ДЛЯ СОСТАВЛЯЮЩИХ НАПРЯЖЕНИЙ Ц7
ческой поверхности задаются перемещения
и* = az2 — ft*yz + U* (s) + az,
v* = bz2 + ft*xz + V* (s) + pz,
w* = - 2(ax + by + c)z +W*(s),
B1.10)
получаем граничные условия в виде
з
2 Re
- м0>
2 Re
2 Re 2 •
= - ^о + V* - (о3х -
W* -
B1.11)
причем
А = — 2а, В - - 26, С - - 2с;
# = ф*, (Ох = — Р, @2 = а.
B1.12)
Рассматриваемая задача о равновесии тела, ограничен-
ограниченного цилиндрической поверхностью, сводится к определе-
определению комплексных потенциалов — трех функций Ф^ (zk)
трех различных комплексных переменных zk = х + \iky
в области S поперечного сечения. Эти функции дол-
должны быть такими, чтобы определяемые ими напряже-
напряжения и перемещения были однозначными функциями коор-
координат х и у и непрерывными вплоть до контура. На конту-
контуре области Ф^ должны удовлетворять условиям B1.8)
или B1.10) (первая и вторая основные задачи). Иначе
говоря, на контуре задаются три комбинации Фк и сопря-
сопряженных функций.
Функции Ф^ можно рассматривать и с другой точки зре-
зрения: как функции обычных комплексных переменных
Ч = %н + iy*, гДе
(к = 1,2,3). B1.13)
Но если стать на эту точку зрения, то комплексные
потенциалы Ф2, Ф2, Ф3 должны быть определены не в об-
области поперечного сечения S, а в областях Su 52, S3,
полученных из S путем аффинного преобразования B1.13).
Прилагаемый рис. 25 дает представление о том, как об-
области SK (к = 1,2, 3) получаются из S.
118
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл. 3
Точки Аи А2, А3 (z1? z2, z3) на контурах областей
Su S2, S3 должны быть аффинно-соответственными по от-
отношению к данной точке А контура S, определяемой ду-
дугой s. Эти особенности математической стороны рассматри-
рассматриваемой задачи теории упругости затрудняют отыскание
ее точного эффективного решения. Только для некоторых,
немногих областей Sk решение удалось довести до конца,
У
Рис. 25.
т. е. до точных формул, определяющих функции Ф^ или F
и г|) в явном виде и дающих возможность подсчитать на-
напряжения и перемещения. В подавляющем большинстве
случаев областей пока приходится довольствоваться при-
приближенным решением, используя тот или иной прибли-
приближенный метод.
§ 22. Распределение напряжений в непрерывно-
неоднородном прямолинейно-анизотропном теле,
зависящее от двух координат
Рассмотрим непрерывно-неоднородное тело бесконечной
или конечной длины, ограниченное какой-нибудь цилинд-
цилиндрической поверхностью или плоскостями, на которое дей-
действуют поверхностные и объемные силы, нормальные к об-
образующей и не меняющиеся по длине, как в § 18 (рис. 24).
Пусть коэффициенты atj являются непрерывными, одно-
однозначными и дифференцируемыми функциями координат
х и у, а по длине не меняются. Усилия на торцах тела ко-
конечной длины приводятся к продольным силам и изги-
изгибающим и скручивающим моментам. Очевидно, напря-
§ 22] НЕОДНОРОДНОЕ ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО Ц9
жения и в случае такого неоднородного тела не будут
зависеть от z.
Основная система уравнений равновесия такого тела
имеет вид A8.2) — A8.3), но в них а^ не постоянные вели-
величины, а функции (непрерывные, дифференцируемые) пере-
переменных хну. В этом параграфе мы приведем уравнения
для непрерывно-неоднородного прямолинейно-анизотроп-
прямолинейно-анизотропного тела, имеющего в каждой точке плоскость упругой
симметрии, нормальную к образующей A3 fl2] независи-
независимых коэффициентов atj).
Порядок вывода общих уравнений для неоднородного
тела точно такой же, как и для однородного, а поэтому мы
можем все промежуточные выкладки пропустить и приве-
привести только окончательные формулы и уравнения. Они
имеют следующий вид:
1) выражения для перемещений совпадают по форме
с выражениями для однородного тела:
и == — -^- z1 — byz + U (х, у) + и',
*>---§¦ z3 + bvz + V (х, у) + v\
B2Л)
w = (Ax + By + C) z -f- W (x, y) -f- ^',
где u', у', i/;' — жесткие перемещения A8.8);
2) функции С/, У, И7 удовлетворяют уравнениям:
##"
ох
h —= 1
dW
dx
dW
Р-2бтх?/ +
С);
B2.2)
B2.3)
120
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл. 3
где
Pij = aV -
(«,/=1,2,6),
Рб5 = аЪЪ
B2.4)
— функции х и у;
3) составляющие напряжения выражаются через две
функции напряжений (так же, как в однородном теле):
*+?7 * |?+
Хху - дхду '
1x2 ~~ ду ' lyz ~ ~
(О — потенциал объемных сил);
B2.5)
az = —- (Ar
й33
С) — —-
а3з
a3Qxxy);
B2.6)
4) функции /" и т|) удовлетворяют двум уравнениям (для
каждой функции — свое уравнение):
^ /ft d*F ft
12
п
ду* Pl6 дхду )~~
дхду
nd*F А
Pie -7ь/г - Р
дЧ
ее
дхду lVM
\ i д I д^>
B2.7)
B2.8)
5) функции F и тр удовлетворяют при заданных уси-
усилиях условиям A9.7). При заданных перемещениях дол-
должны быть выполнены условия A9.8). Постоянные Л, В, С,
Ф определятся из условий на торцах A9.9).
§ 23] ОДНОРОДНОЕ ЦИЛИНДРЙЧЁСКЙ-АНЙЗОТГОПНОЕ ТЕЛО 121
Граничные условия в случае первой основной задачи
формально не отличаются от условий для F и г|) в случае
однородного тела. Условия на торцах также не отличаются
от условий для однородного тела A9.9). В рассматривае-
рассматриваемом случае анизотропии неоднородного тела поставленная
задача, как и в случае однородного тела, имеющего по
крайней мере одну плоскость упругой симметрии, распа-
распадается на две самостоятельные задачи: 1) определение че-
четырех напряжений ох, оу, тхУ, az (по функции F); 2) оп-
определение двух напряжений ryz, xxz (по функции \р).
§ 23. Распределение напряжений
в однородном теле, обладающем
цилиндрической анизотропией, зависящее
от двух координат г, 6
Рассмотрим теперь упругое равновесие однородного те-
тела, обладающего цилиндрической анизотропией общего
вида. Предполагается, что тело ограничено какой-нибудь
цилиндрической поверхностью и плоскостями торцов или
является бесконечным или полубесконечным; с телом свя-
связана прямая g, ось анизотропии, параллельная образую-
образующей, проходящая вне его или внутри полости (если та-
таковая имеется), или же проходящая по телу или по его
поверхности *). Если принять g за ось z цилиндрической
системы координат и направить ось х, от которой отсчиты-
ваются полярные углы 8, параллельно одной из главных
осей инерции, то уравнения обобщенного закона Гука за-
запишутся в виде A0.2), где atj — величины постоянные.
Обозначим через О' центр тяжести торца и рассмотрим
вторую систему координат х', у', z с осью z , параллель-
параллельной g и осями х', у , совпадающими с главными осями
инерции. На тело действуют усилия, поверхностные, рас-
распределенные по цилиндрической поверхности и нормаль-
нормальные к оси анизотропии, и объемные силы; и те, и другие не
г) В последних двух случаях необходимо вспомнить сказанное
в § 10 о равенстве некоторых коэффициентов деформации а,ц и других
упругих постоянных и при выводе общих уравнений учесть это.
В этом параграфе мы будем все время говорить о теле с конечной
областью поперечного сечения.
122
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл. 3
меняются вдоль образующей (т. е. по длине). Кроме того,
по торцам распределены усилия, приводящиеся к осевой
силе Рх, изгибающим моментам с составляющими Мг,
М2 относительно осей #', у' и скручивающему моменту Mt
(рис. 26).
Обозначим проекции внешних поверхностных усилий
через Rn, вл (Zn = 0) и проекции объемных сил через
Рис. 26.
R и в (Z — 0). Будем считать, что объемные силы имеют
потенциал О (г, 0), т. е.
i за
B3.1)
Нам нужно определить в области тела девять неизвестных
функций — шесть составляющих напряжений а2, а0, . . .
. . ., Тге и три проекции перемещения иг, щ, w. Для этих
функций мы как раз имеем девять независимых уравне-
уравнений. Основная система, так же как в теле с прямолинейной
анизотропией, складывается из трех уравнений равновесия
сплошной среды и из шести уравнений обобщенного
§ 23] ОДНОРОДНОЕ ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО 123
закона Гука; выпишем часть этих уравнений:
дг ~ ;
6)9
г <эе
= 0,
= 0;
B3.2)
ег =
а1баг
B3.3)
Общие уравнения данной проблемы выводятся в таком
же порядке, как и для тела с прямолинейной анизотро-
анизотропией; меняются только исходные уравнения в соответствии
с видом анизотропии и окончательные результаты. Сразу
же введем обозначение:
a3bxrz + а36тге, B3.4;
D = а13аг +
откуда
°
B3.5
После подстановки в B3.3) и введения приведенных коэф-
коэффициентов деформации
Ри = «и - ^ («,/==1,2,4, 5, 6) B3.6)
переписываем уравнения B3.3) в виде
B3.7)
124
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл. 3
x „a/ . диЪ R ,
"Г" "To" + ~HT" = Pl*ar +
Т~ Ж
+ . . .
^2 ~ dr
¦¦¦+ Р5вТг9 + ^
аз
B3.7)
Интегрируем третье, четвертое и пятое уравнения B3.7)
и получаем перемещения, содержащие три новые функции
U (г, 0), V (г, 0), W (г, 0). Далее, удовлетворяя уравнениям
первому, второму и шестому из B3.7), получаем, как и
раньше, D как линейную функцию координат х и у:
D = Ar cos 0 + Вт sin 0 + С.
B3.8)
После элементарных преобразований далее получаем си-
систему трех уравнений для U, V и систему двух уравнений
для W:
г
о 1
1 аТ7
7" IT
B3.9)
^ +
+ • • • +
+ J^34_
B3.10)
§ 23] ОДНОРОДНОЕ ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО 125
Исключая U, V, W из уравнений B3.9) и B3.10), полу-
получим систему двух уравнений, содержащих только напря-
напряжения. Исключение функций U, V из B3.9) произведем,
используя тождество х):
(ж-ri)е? + '¦?¦<"*> -як
<23-н>
Исключение W из B3.10) производится элементарно, путем
простого дифференцирования и вычитания. В результате
вместо B3.9) и B3.10) получаются очевидные уравнения
для напряжений, которые мы выписывать не будем.
Когда функции С/, F, W будут найдены, то проекции
перемещения определятся по формулам
щ = — -%-(А cos 9 + В sin Э) + U + иГ1
к
w = z (Ar cos 0 -
Сюда включены «жесткие» перемещения, обозначаемые
штрихами, которые в развернутом виде запишутся так:
иг = z (оJ cos 0 — (Oi sin 0) + и0 cos 0 -\- v0 sin 0,
uQ = — z (co2 sin Э + cox cos 0) + co3r —
— wosin0 + i;ocos0,
wf = — г (co2 cos 0 — 0)! sin 0) + w0.
Введем две функции напряжений. В цилиндрической
системе координат эти функции будут связаны с состав-
составляющими напряжений зависимостями:
^23
1 dF
B3.14)
На основании B3.9) — B3.11) и B3.14) получим си-
систему уравнений, которой удовлетворяют названные две
г) В справедливости этого равенства можно убедиться простой
подстановкой.
126
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл. 3
функции. Эта система запишется таким образом:
L\F + Ljty = -i— I— амА + (а13 — а23) В] ^_ _j-
«33 г
+ j- [(а„ - а2з) А + аиВ] ^ -
«33 Г
/ft _i_ R \ дЮ /ft _L ft \ j a2?7 JL
— (Pi2 + P22) -jpr — (Pn + P12) 7Г ^2" +
1 ^^7
n — 2p32 — P12) — -Qf + (Pie + Ргв) — -щ- >
= — Ba3i^4 - a3bB) cos в
a33
-f- ЫА + 2a3lB) sin 0 + С -^- -
a33 ¦ r
/ft _u ft \ / w 0 \ m
(Pi4 + P2O ^ rJ - (Pis
ft ^ i d0
Pas) — -дв- •
B3.15)
Под Lt, L3, L3 и L2 подразумеваются дифференциальные
операторы четвертого, третьего и второго порядков:
Li = Р22 -gp - 2p2e — ^
+ Bри + Рее) тг -^щг - 2Pie —
1 д4
X
1 a3 _
- 2p16 4-
1
Х
— P11 — ~№ — 2 (Pie + Ргб) 7г
-^-^г + Рп4" -И"
—
+ 2(Pie+P2e)~i
= - Р24-5РГ + (Р25 + Р4в)— ^2^-
Id8
— (Pl4 + Рбв) — + ?
Id3
(Pu — 2pa4) — -jp- + (P« — Pie) тгат
B3.16)
23] ОДНОРОДНОЕ ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО 127
дЪ _i_ /ft L ft \ 1 дЪ
^Г + (Р25 + Р4б) — "^^0 -
— (Ри +
1 д2 Л- /R П1
~Г !h* + VP15 — Р4б) —
-щ + Р46 та- -go"
дгдв
Р65
B3.16)
При заданных внешних усилиях условия на цичинд-
рической поверхности, т. е. на контуре сечения, можяо за-
записать в виде
ar cos (и, г) + tre cos (n, 0) =-• Rn,
tre cos (л, r) + a9 cos (n, 0) = вп, B3.17)
xrz cos (дг, r) + x9z cos (w, 0) = 0,
где n — направление внешней нормали, Rn, &n — про-
проекции усилий, распределенных по боковой поверхности,
на направления осей г и 0 (на единицу площади). Так же
как и в случае тела с прямолинейной анизотропией, усло-
условия B3.17) можно преобразовать путем интегрирования
по дуге контура сечения и тогда они сведутся к следующе-
следующему: на контуре задаются производные dF/dr и dF/dQ,
как функции дуги s (или полярного 4ггла 0, что удобнее
в случаях, когда тело ограничено поверхностями коак-
коаксиальных цилиндров). Граничное условие для г|) очень
просто: -ф = const.
Удовлетворив условиям на боковой поверхности, мы
должны еще определить постоянные А, В, С, Ь из условий
на торцах. Для тела с конечной областью поперечного се-
сечения на торцах (и в любом поперечном сечении) усилия
должны приводиться к силе Рик моменту с тремя состав-
составляющими Ми М2, Mt. После некоторых преобразований
получаем уравнения для постоянных А, В, С, Ф в систе-
системе координат х, у, z:
Z + B
B3.18)
128 ЦИЛИНДРИЧЕСКОЕ ТЕЛО [Гл. 3
(а13сгг + . . . + ЯзвТге) (г sin В — i]) &S ^ MxaXi,
B3.19)
AI2 — \^ (^1зсгг + • • • + ^зв^ге) (г cos 0 — ?) dS = Л/2#зз»
B3.20)
^Mt. B3.21)
Здесь ?, т] — координаты центра тяжести в системе
координат х, у, z, у которой ось z совпадает с осью анизо-
анизотропии, S — площадь поперечного сечения, 1и /2 —
моменты инерции относительно главных осей х', у'.
Решив какую-нибудь задачу рассматриваемого типа,
мы получим функции напряжений, удовлетворяющие си-
системе уравнений B3.15) — B3.16) и условиям на конту-
контуре; они будут содержать постоянные А, В, С, Ф, которые
в одних случаях можно считать заранее известными, а в
других нужно определить из уравнений B3.18) — B3.21).
§ 24. Распределение напряжений
в непрерывно-неоднородном теле,
обладающем цилиндрической анизотропией,
зависящее от двух координат
Поставим задачу так же, как это было сделано в пре-
предыдущем параграфе, но только будем предполагать, что
тело является непрерывно-неоднородным, обладает ци-
цилиндрической анизотропией и является ортотропным. Оно
ограничено поверхностью какого-то цилиндра и, вообще
говоря, плоскостями торцов; внутри могут быть цилинд-
цилиндрические полости. Ось анизотропии g параллельна обра-
образующим внешней поверхности и поверхностям полостей
и принимается за ось z цилиндрической системы г, 0, z,
На тело действуют усилия: поверхностные Rn, Bn (Zn ==
= 0) и объемные R, в (Z = 0), имеющие потенциал U.
На торцах (и в поперечных сечениях) усилия приводятся
к осевой силе Pz и к моменту с тремя составляющими
(рис. 26). Все упругие характеристики — а^ и «техниче-
«технические» Еь Gtj, vtj — считаем непрерывными, однозначными,
дифференцируемыми функциями двух координат г, 9.
§24] НЕОДНО1 ОДНОСТЬ. ЦИЛИНДРИЧЕСКАЯ АНИЗОТРОПИЯ 129
Уравнения обобщенного закона Гуна запишутся так:
8r =z 0>цОг -\- di2^Q \ «13^2»
-[- flooffQ 4- Лоо(Т_. I \^'Ч
Уравнения равновесия сплошной среды и условия на
боковой поверхности и на торцах не будут отличаться от
уравнений и условий для однородного тела, обладающего
цилиндрической анизотропией B3.2), B3.17) и B3.18) —
B3.21). Поэтому мы можем не повторять вывода, а при-
привести готовые результаты, которые сводятся к следую-
следующему:
1. Выражения для перемещений по форме не отличают-
отличаются от B3.12).
2. Входящие в B3.12) функции С/, F, W удовлетворяют
уравнениям типа B3.9) и B3.10), где
D = Ar cos 9 + Вт sin 9 + С, B4.2)
где А, В, С — постоянные,
fo = *u--^ («,/ = 1,2,6), B4.3)
а все коэффициенты $и, atj, кроме ри, р12, р22, р66, а1и
«22т #33» а44» вБ6, Й66» «12» «13» «23» раВНЫ НуЛЮ.
3. Составляющие напряжений ar, ae, тг9, т02, тГ2 вы-
выражаются через две функции напряжений F и \|э по фор-
формулам B3.14);
crz = Ez(Ar cos 9 + 5г sin 9 + С) + v2ro> + v2eae.
B4.4)
4. Функции напряжений F и ^|) удовлетворяют двум
уравнениям с переменными коэффициентами (для каждой
функции — свое уравнение):
W ~ т IF/ ("Т1" "Г + 7Г"р"
5 С Г. Лехницкий
130
ЦИЛИНДРИЧЕСКОЕ ТЕЛО
[Гл. 3
Приведенные коэффициенты j3i7- (г, Э) выражаются че-
через модули упругости и коэффициенты Пуассона таким
образом:
P
11 =
Pl2 =
vr0 ~ yrz z
p66 = -p— •
B5.7)
5. Удовлетворив условиям на боковой поверхности,
получим F ия|), содержащие четыре постоянные Л, В, С,
О, которые должны быть найдены из условий на торцах
(или в поперечных сечениях) типа B3.18) — B3.21).
Глава 4
ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
И ПЛОСКАЯ ЗАДАЧА ДЛЯ ТЕЛА
С ПРЯМОЛИНЕЙНОЙ АНИЗОТРОПИЕЙ
В настоящей главе рассматриваются частные случаи
упругого равновесия тела с прямолинейной анизотропией,
ограниченного цилиндрической поверхностью, на кото-
которое действуют поверхностные и объемные усилия, нормаль-
нормальные к образующей и не меняющиеся по длине. Если коэф-
коэффициенты atj, Atj также не меняются по длине и плоскости
поперечных сечений совпадают с плоскостями упругой
симметрии, то эти сечения остаются плоскими и после
деформации и напряженно-деформированное состояние из-
известно под названием плоской деформации. В более об-
общих случаях анизотропии, когда плоскости упругой сим-
симметрии пересекают геометрическую ось под углом не рав-
равным 90°, или параллельны ей, или совсем отсутствуют,
то деформацию уже нельзя назвать плоской; ее можно
назвать «обобщенной плоской деформацией». В главе 4
исследование ведется в декартовой системе координат,
т. е. предполагается, что обобщенный закон Гука выра-
выражается уравнениями A8.3), где atj — постоянные. Рассмот-
Рассмотрен также случай прямолинейно-ортотропного неоднород-
неоднородного тела и ряд частных задач.
§ 25. Обобщенная плоская деформация
однородного прямолинейно-анизотропного тела
Рассмотрим однородное тело, обладающее прямоли-
прямолинейной анизотропией общего вида (уравнения A8.3)),
ограниченное какой-либо цилиндрической поверхно-
поверхностью.
132
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
Пусть тело нагружено усилиями, поверхностными и объ-
объемными, действующими в плоскостях поперечных сечений,
т. е. нормально к образующей, и не меняющимися по дли-
длине. Сначала длину мы будем считать бесконечной, а область
поперечного сечения произвольной — конечной или
бесконечной, односвязной или многосвязной. Поместим
начало координат в произвольной точке какого-нибудь по-
поперечного сечения и направим ось z параллельно образую-
образующей, а оси х, у — как удоб-
удобнее, в зависимости от фор-
формы сечения (рис. 27).
Представляется очевид-
очевидным, что в бесконечно длин-
длинном теле под влиянием задан-
заданной указанным образом наг-
нагрузки, все поперечные сече-
сечения находятся в одинаковых
условиях, а поэтому напря-
напряжения и перемещения (если
не считать «жестких» смеще-
смещений) в нем не меняются вдоль
образующей, т. е. зависят
только от двух координат х
и г/. В теле изотропном или в анизотропном, у которого
в каждой точке существует плоскость упругой симметрии,
нормальная к образующей, поперечные сечения остаются
плоскими, или, иначе, деформация является плоской.
Если же плоскости упругой симметрии имеются, но среди
них нет параллельных ху, и тем более в общем случае
анизотропии, деформация уже не будет плоской (так как
нельзя удовлетворить всем уравнениям и условиям теории
упругости, приняв w = 0); поперечные сечения будут ис-
искривляться, но все одинаково. Такого рода деформацию, в
отличие от плоской (или чисто-плоской), мы называем
«обобщенной плоской».
Рассмотрим сначала обобщенную плоскую деформа-
деформацию однородного тела.
Так как составляющие напряжения и проекции пере-
перемещения не зависят от z [см. A8.19)], то, следовательно,
в формулах и уравнениях § 18—19 нужно положить
Рис. 27.
А = В = С = # = 0,
= со2 = 0. B5.1)
251
ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
133
Перемещения определятся по формулам
U = U(x,y)
Z7, F,
B5.2)
w = W(x,y) + w0,
связаны с напряжениями уравнениями
P^
dW
dW
Напряжение az определится по формуле
+
+
+
+
B5.3)
B5.4)
- B5.5)
Далее поступаем так же, как в общем случае, рассмот-
рассмотренном в предыдущей главе 3: вводим функции напряже-
напряжений F и if
B5.6)
(U — потенциал объемных сил) и получаем уравнения
¦-= — (Pl2 + p22)-^2" +
+ (Pie + Р2б)
/о I о \ ^2^
— (Pii + РЫТья" »
= (Pli + P2l) -^- — (Pl6 + Р25) -Щ- •
B5.7)
Здесь L4, L3, L2 — операторы, уже использованные в § 19
(формулы A9.3)).
Граничные условия имеют вид A9.7) (первая основная
задача) или A9.8) (вторая основная задача).
134 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
Остановимся коротко на случае, когда объемные силы
отсутствуют. В этом случае выражения для производных
F и для я]), напряжений и перемещений через комплексные
потенциалы Фк (zfr) и граничные условия для них мы полу-
получим из B1.2), B1.3), B1.5) - B1.9), полагая в них
U = Fo = г|H = О, U0 = Vo = 0. B5.8)
Не будем выписывать все эти выражения и условия,
а приведем без доказательства результаты исследований
функций Фк, которые достаточно подробно выполнены в ра-
работе [56].
1. Если область сечения S имеет вырез (тело имеет про-
продольную цилиндрическую полость) и на контуре его дей-
действуют усилия, приводящиеся к главному вектору с проек-
проекциями Рх, Ру (на единицу длины в осевом направлении)
и к главному моменту, то каждая из функций Фк состоит
из непрерывной и однозначной части и из многозначной
части, получающей при обходе по контуру у, окружаю-
окружающему отверстие, постоянное (не зависящее от zfr) прира-
приращение Ак. Приращения функций Ф^ и сопряженных
функций Ф^ (обозначаемые здесь Дй), определяются из
системы шести уравнений:
^ - - Рх,
А3 = 0, B5.9)
PiAi + р2А2 + /?зА3 + PiAi + Д2Д2 + р3А3 = 0,
^iAi 4- q2A2 + 9зДз +9iAi + ^A2 + ^зА3 = 0,
ГхДх + ^2А2 + г3А3 + г^х + г2А2 + г3А3 = 0.
2. Если область S имеет п отверстий (вырезов), т. е.
тело имеет п продольных параллельных полостей, и на
контуре каждого из них усилия приводятся к главному
вектору с проекциями Pxi, Pyi (? = 1,2,..., п)ик глав-
главному моменту, то уравнения, определяющие приращения
многозначных частей функций Фк, будут справедливы для
каждого из контуров yh окружающих одно отверстие.
§ 25], ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ 135
Иначе говоря, мы получим п систем уравнений, подоб-
подобных B5.9), куда вместо Дк, Ак нужно подставить соот-
соответственно AKi и Дк1- — приращения функций Ф^ и Фк
при обходе по контуру yt и Pxh Pyi вместо Рх, Ру. Всего
мы будем иметь п систем, каждая из которых содержит
шесть неизвестных (приращений).
3. Если область S имеет отверстия (вырезы), но на каж-
каждом из них действует уравновешенная система усилий или
усилия приводятся только к главному моменту, то все
уравнения вида B5.9) будут однородными. Определитель
каждой системы не равен нулю, а следовательно, все
приращения Дл, Д& равны нулю, все три функции Фк
будут голоморфными и однозначными (в своих областях
Sk). To же будет и в случае области S без выреза.
Для тела конечной длины деформация, вообще говоря,
не будет обобщенной плоской, так как перемещения будут
зависеть от третьей переменной z. Для такого тела формулы,
выведенные для бесконечного цилиндра, будут справед-
справедливы, строго говоря, только тогда, когда на торцах дей-
действуют усилия, распределенные так же, как напряжения
txz, tyZ, oz в поперечных сечениях бесконечного цилиндра.
Но на основании принципа Сен-Веиана мы можем ут-
утверждать, что распределение напряжений, в первом при-
приближении, будет в теле конечной длины таким же, как
и в бесконечном, если торцы его закреплены; при этом
нужно исключить из рассмотрения зоны местных напря-
напряжений вблизи торцов.
Если торцы тела конечной длины свободны от усилий
и не закреплены, то на них должны быть выполнены точ-
точные условия:
Тд-z = туг = az = О, B5.10)
которые мы можем заменить приближенными, потребовав,
чтобы главный вектор и главный момент усилий на торцах
были равны нулю. Для того чтобы решить эту задачу, нуж
но вернуться к уравнениям § 21, не полагая заранее по-
постоянные Л, В, С, О равными нулю. Определив F, г|з или
Фк, удовлетворяющие нужным условиям на боковой по-
поверхности (или на контуре поперечного сечения), мы най-
найдем затем эти постоянныеизуравнений A9.13), A9.14) или
A9.18), A9.20), где нужно положить Рг = Мх = Мо =
М0
136 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ TEJlO [Гл. 4
§ 26. Плоская деформация и обобщенное
плоское напряженное состояние
Предположим, что рассмотренное в предыдущем пара-
параграфе тело в виде цилиндра бесконечной длины (см.
рис. 27) имеет в каждой точке плоскость упругой симмет-
симметрии, нормальную к образующей, т. е. к оси z. В этом слу-
случае мы будем иметь дело с чистой плоской деформацией,
так как всем уравнениям теории упругости можно удов-
удовлетворить, полагая w = w0 = const и считая перемещения
и, v функциями только двух переменных х, у. Тогда yxz =
— Уух ~ $z ~ О И напряжения определятся по формулам
rxz — tyz = О,
о z = — — (а13ах + а2зОу + а36хху)) I ^
33
Функция F удовлетворяет уравнению
(Pa. + Ы 2?щ - (P« + Р„) -^ • B6.3)
Общее выражение для функции F зависит от комплекс-
комплексных параметров \ik — корней алгебраического уравнения
h (И') ~ О (СМ- § 20). В случае неравных комплексных па-
параметров
F - 2 Re [Fn (Zl) + F12 (z2)] + Fo, B6.4)
где F1X (zO, F12 (z2) — произвольные аналитические
функции обобщенных (усложненных) комплексных пере-
переменных
Zi = х + fiji/, z2 = х + \i2yy B6.5)
a Fo — частное решение неоднородного уравнения B6.3).
В случае попарно равных корней (^ = [д,2, u.x = \i2)
F = 2 Re fi^, (zx) + F12 («i)l + FQ. B6.6)
Если (Л! = |i2 = a + P^ то Zi = #x + и/х, где ^ = л;
+ P
§ 26] ПЛОСКАЯ ЗАДАЧА 137
Для определения напряжений и перемещений нужно
найти две функции F^ fa), F12 fa) обычной комплексной
переменной zx = хг + Ч/i, т. е. решить плоскую задачу
для изотропного тела, но не для области сечения S, а для
области #!, полученной из заданной путем аффинного
преобразования (см. рис. 25). Вопрос о плоской задаче
и о методах ее решения весьма подробно изучен в книге
Н. И. Мусхелишвили [26] х). Не останавливаясь на слу-
случае равных комплексных параметров \хг и ц,2, мы в даль-
дальнейшем будем считать их неравными.
Введем комплексные потенциалы:
<Г>1 fa) = F'n fa), Ф2 (z2) = F'12 (z2) B6.7)
(буквой со штрихом обозначены производные от функций
по усложненной комплексной переменной), получим общие
выражения для первых производных F и для составляю-
составляющих напряжений и проекций перемещения при отсутствии
объемных сил:
8F
ау = 2 Re [ф[ + Ф^, B6.9)
)
и = 2 Re [рхФ! fa) + р2Ф2 (z2)] — щу + щ,
v = 2 Re [дхФх (zx) + ^Фг fe)] + %^ + v0
(сохранены «жесткие» смещения для плоскостей, парал-
параллельных ху). В этих формулах
Ih =- PnlA? + Pi2 —
Pl2 —
B6.11)
1) Напоминаем, что Н. И. Мусхелпшвили рассматривал только
изотроп ные тела. Тем не менее его методы могут быть с успехом при-
применены и при исследовании некоторых случаев упругого равновесия
анизотропных тел.
138 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
Задача сводится к определению двух комплексных по-
потенциалов Фх и Ф2, удовлетворяющих граничным условиям
на контуре области поперечного сечения S. Граничные
условия при заданных на контуре усилиях Хп, Yn имеют
такой вид:
2Пе(Ф!
B6.12)
2 Re (^Фх + ц2Ф2) = ± jj Xnds + сг
О
(для внешнего контура в правых частях B6.12) нужно
взять верхние знаки, для внутреннего, т. е. контура вы-
выреза,— нижние; с1, с2 — постоянные, которые можно за-
зафиксировать произвольно на одном из контуров, ограни-
ограничивающих область). При заданных перемещениях w*,
v* граничные условия имеют следующий вид:
2 Re (д1Фг + ?2Ф2) = у* - соз* - IV J ( '
Рассматривая Фх (z2), Ф2 (z2) как функции обычных ком-
комплексных переменных zk = хк + и/к (/с = 1, 2), мы дол-
должны определить их в областях Su S2, находящихся в
аффинном соответствии с областью поперечного сечения S
(см. § 21).
Условия, которым должны удовлетворять эти функции
внутри области поперечного сечения или в своих облас-
областях Si, S2, получаются из условий более сложной задачи
и достаточно подробно нами исследованы (см. § 25 или ра-
работу [56]).
Все формулы для бесконечного цилиндра можно, учи-
учитывая принцип Сен-Венана, применить к телу конечной
длины с закрепленными концами. В случае свободных
и ненагруженных концов осевые усилия Pz и изгибающие
моменты Mi, M2, получающиеся на концах, можно снять,
накладывая на распределение напряжений в бесконечном
цилиндре элементарное распределение:
S ~~У /2 *' | B6.14)
vz 0
ах -sz av = xvz — rxz ¦= тлу = 0.
§ 26]
ПЛОСКАЯ ЗАДАЧА
139
К задаче о плоской деформации очень близка задача об
обобщенном плоском напряженном состоянии.
Рассмотрим упругое равновесие плоской пластинки по-
постоянной толщины h из однородного анизотропного ма-
материала, имеющей в каждой точке плоскость упругой сим-
симметрии, параллельную срединной. Предположим, что по-
Рис. 28.
верхностные усилия распределены по краю, а объемные
силы — по пластинке, симметричны относительно сре-
срединной плоскости и мало меняются по толщине. Прини-
Принимая срединную плоскость за координатную плоскость
ху и направляя оси х, у как удобнее (рис. 28), будем
рассматривать не истинные напряжения и перемещения,
а средние значения по толщине напряжений и переме-
перемещений, параллельных плоскости ху:
-If
ох = — ^ oxdz,
Ь/2
If
= -у \
-/1/2
-.<?«
Tr7/ =
—h/1
h/2
h /2
a = —г- \ a dz, г; = —r- \ V dz.
—Я/2
B6.15)
Для этих средних значений из уравнений A8.2), A8.3)
получим уравнения, которым удовлетворяют дх, ду, "хху,
п, v (средним значением az, т. е. az, пренебрегаем по срав-
сравнению с ах, ду, гЛ1/). Получаем такие же уравнения для
средних напряжений, что и в случае плоской деформации
B6.2). Функция F удовлетворяет уравнению B6.3), в
140 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО 1гл. 4
котором приведенные коэффициенты деформации C^- дол-
должны быть заменены соответствующими коэффициента-
коэффициентами аи'.
^ • B6.16)
Граничные условия не отличаются от B6.12) или B6.13),
только в них комплексные параметры \iu (л2, jTj, \12 —
это корни уравнения:
Дп[л4 — 2а]6(г3 + Bа12 + а66) (л2 — 2а26И' + а22 = 0.
B6.17)
Поэтому решение, найденное для какого-нибудь случая
плоской деформации, будет решением и для соответствую-
соответствующего случая обобщенного плоского напряженного состоя-
состояния. Очевидно, при замене рг</- на пц структура функций
Фи Ф2 и формул для напряжений и перемещений не изме-
изменится; изменятся лишь коэффициенты в формулах.
Задачи о плоской деформации и об обобщенном плос-
плоском напряженном состоянии объединяются под общим наз-
названием плоская задача теории упругости.
Вопросы существования и единственности решения
плоской задачи для анизотропного тела достаточно хоро-
хорошо изучены. Они нашли свое освещение в работах С. Г.
Михлина [80], Г. Н. Савина [87] и Д. И. Шермана [102],
где плоская задача сводится к интегральным уравнениям.
§ 27. Плоская задача для непрерывно-
неоднородного прямолинейно-ортотропного тела.
Растяжение и изгиб моментами
На основании изложенного в § 22 мы можем получить,
как частные случаи, уравнения и граничные условия плос-
плоской задачи и родственной ей задачи о растяжении осевой
силой и изгибе моментами непрерывно-неоднородного ци-
цилиндра (задачи Сен-Венана).
Пусть имеется тело в виде какого-нибудь цилиндра ко-
конечной или бесконечной длины с коэффициентами дефор-
§ 27] ПЛОСКАЯ ЗАДАЧА ДЛЯ НЕОДНОРОДНОГО TEJlA 141
мации atj, не меняющимися по длине и зависящими of двух
координат. Для простоты мы рассмотрим только ортотроп-
ное тело, у которого через каждую точку проходят три
плоскости упругой симметрии — нормальная к образую-
образующей и две ортогональные и параллельные образующей,
причем эти плоскости в разных точках соответственно
параллельны. Поместим начало координат в центре тяже-
тяжести поперечного сечения и направим ось z параллельно
образующей, а оси х и у — нормально к плоскостям уп-
упругой симметрии; они вообще не совпадают с главными
осями инерции сечения.
1. Плоская деформация. Пусть тело, длина которого
бесконечна, находится в равновесии под действием уси-
усилий, распределенных по боковой поверхности, нор-
нормальных к образующей и не меняющихся по длине. Так
же, как и в случае однородного тела, полагаем
w = wQ = const, и = и (х, у), и = и (х, у), 1 27
A=B=C=ft=0 }
и получаем
^xz = ^Vz — 0, tfz = ^310Я. + V320j/. B7.3)
Функция F удовлетворяет уравнению:
-дхТ + Р" -дуг) + -дТд-у [р™ дТГу)
01
? --%-? [фп + р18) О]. B7.4)
Граничные условия в случае первой основной задачи
сводятся к заданию на контуре первых производных F
(с точностью до постоянных слагаемых). Коэффициенты
Ро- связаны с «техническими» упругими характеристиками
зависимости B2.4^.
2. Обобщенное плоское напряженное состояние. В этом
случае рассматриваются только средние по толщине нап-
напряжения и перемещения ах, ау, тху, п, v.
Напряжения выражаются через функцию напряжений
по формулам B7.2). Функция F удовлетворяет уравнению
142
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл.
B7.4), где fiij нужно заменить коэффициентами atj. Пос-
Последние связаны с «техническими» характеристиками так:
fll2 = ~ "/77 ^ ~ Ж"'
1
X
1
\
B7.5)
3. Растяжение осевой
силой и изгиб моментами.
Если длина тела и область
Рис. 29. поперечного сечения конеч-
конечны и нагрузка распределе-
распределена только по торцам так, что на каждом из них приводит-
приводится к осевой силе Р (приложенной в центре тяжести, при-
принятом за начало координат) и к моментам Ми М2 отно-
относительно осей х, у (рис. 29), то в уравнениях § 22 нельзя
заранее полагать w = const и тогда мы получаем форму-
формулы для напряжений
°х = И ' °У = И". хху = - Ртг i B7.6)
ду* и ох* у их ду v '
ХхХ = УГЛ 1 я , г, , , | B7.7)
gz = Ез (Ах -f- By + С) + V3iCTx -\- Vs2Gy )
Функция напряжений удовлетворяет уравнению:
д1 U дЧ ft дЧ \ , ^2 /Л (92/ , п дЧ
\ -tt + Р12 -л
и граничным условиям на контуре поперечного сечения
ду
_
~ Съ
= с2.
B7.9)
Функция jP, удовлетворяющая уравнению B7.8) и усло-
условиям B7.9), будет содержать три постоянные — Л, В, С,
28] УПРУГОЕ ОДНОРОДНОЕ ПОЛУПРОСТРАНСТВО 143
которые найдутся из условий на торцах (и в любом
поперечном сечении):
\\
Р, §zyy ъ
ozxdxdy =
Заметим попутно, что каждое из уравнений B7.10) содер-
содержит, вообще говоря, все три неизвестные А, В, С, если
оси х и у не совпадают с главными осями инерции сечения.
Задача имеет элементарное решение, если коэффициент
Пуассона v31 зависит только от х, a v32 — только от у
или оба коэффициента Пуассона — величины постоянные.
Тогда общий характер распределения напряжений будет
таким же, как в однородном брусе:
= Еъ (Ах + Ву + С), )
П У ' B7.11)
Единственная из шести составляющих напряжений,
не равная нулю, может быть нелинейной функцией х и у,
в зависимости от Е3 (х, у).
§ 28. Распределение напряжений в упругом
однородном полупространстве под действием усилий,
приложенных к ограничивающей плоскости
Из частных задач обобщенной плоской деформации од-
одной из простейших является задача о распределении на-
напряжений в упругом однород-
однородном полупространстве под дей- уд /
ствием усилии, приложенных к
ограничивающей плоскости и
зависящих только от одной ко- » /N
/
VL
'/////у////////.
ординаты. у,
Рассмотрим упругое равно-
равновесие полубесконечного одно- >{ i
родного тела, ограниченного
плоскостью (упругое полупро- Рис. 30.
странство), в состоянии обоб-
обобщенной плоской деформации под действием усилий, при-
приложенных к ограничивающей плоскости.
Примем эту плоскость за плоскость xz и направим ось
у наружу, а прочие оси так, как показано на рис. 30,
144 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
Предположим, что: 1) материал обладает прямолинейной
анизотропией самого общего вида; 2) усилия действуют
в плоскостях, нормальных к оси z и не меняются вдоль этой
оси; 3) главный вектор усилий, распределенных по любо-
любому участку полосы, параллельной х, конечен и стремится
к определенному пределу, когда концы участка уходят
на бесконечность.
Область сечения S в данном случае есть полуплоскость
(«нижняя» — у <^ 0); области изменения функций Ф1?
Ф2, Ф3, т. е. Sx, S2, S3 — также полуплоскости. Если уси-
усилия удовлетворяют указанным условиям, то естественно
предположить, что на бесконечности напряжения равны
нулю, а это будет иметь место, когда Фк (оо) =0 (к =
= 1,2,3.
Н. И. Мусхелишвили получено решение задачи для
изотропной упругой полуплоскости, основанное на не-
некоторых свойствах интегралов типа Коши, взятых по
прямой [26]. Метод Н. И. Мусхелишвили можно с успе
хом применить и для решения задачи об упругом равно-
равновесии анизотропного полупространства. Напом-
Напомним две необходимые формулы. Пусть / (z)— функция
комплексного переменного z = х + iy, голоморфная в
нижней полуплоскости ^0 и непрерывная вплоть до
границы, причем / (оо) = 0. Тогда, если z — точка в ниж-
нижней полуплоскости, а ? — точка границы (абсцисса),
имеют место следующие равенства:
^J^L* —,<„.
B8-1)
Обозначим через N (?), Т (?) — нормальную и каса-
касательную составляющие внешних усилий (на единицу пло-
площади). Граничные условия при у = 0 запишем таким
образом:
ov = N (I), тху = Т (?), т1/2 = 0. B8.2)
Предположим, что все три комплексных параметра \ik
не равны между собой.
§ 28] УПРУГОЕ ОДНОРОДНОЕ ПОЛУПРОСТРАНСТВО 145
Отсюда получаем условия для функций Ф», Фн (см.
[20], стр. И6):
( ¦ ^
'г (I) + Ф.' (I) + ^зФ; (I) = N (I),
= о.
[ (I)
(I)
Умножим обе части этого равенства на ¦»—г y^—'
где z — точка внутри области S, и проинтегрируем их в
пределах (— оо, оо). Тогда на основании B8.1) получим
\~r
Т
КФ[ + КФг + Фз = 0.
Решая эти уравнения, находим
B8.4)
!«.
B8.5)
Здесь
Д = Ц2 - f*l + &Л (fij - (Х3) + ^Я3 (fi3 - (ia) B8.6)
— определитель системы B8.4). Относительно этой вели-
величины мы всегда будем предполагать, что она не равна
нулю. Она обратится в нуль при равных комплексных
параметрах, но этот случай, как было указано, мы здесь
146
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
не рассматриваем. Может ли обратиться А в нуль при не-
неравных комплексных параметрах — всех трех или двух
равных, остается открытым.
При у = О, х = I комплексные переменные — основ-
основная z и усложненные z2, z2, z3, принимают одно и то же
значение Е- (вещественное); следовательно ([20], стр. 117):
B8.7)
Если существуют плоскости упругой симметрии, нор-
нормальные к оси z, то из формул B8.7) мы получаем решение
плоской задачи (плоская деформация) и для нее формулы
B8.7) принимают вид
J
L-[x2 2m-
B8.8)
А
/
Ф3ы = о.
Вторая основная задача решается аналогично.
Метод Н. И. Мусхелишви-
ли дает возможность полу-
получить решение и для более
сложного случая, когда уп-
упругое полупространство огра-
ограничено сверху не плоскостью,
а вогнутой поверхностью
параболического цилиндра
(рис. 31):
B8.9)
Рис. 31.
у = ах*
и находится в состоянии обобщенной плоской деформации
§ 29] СЛУЧАЙ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ ПО ПРЯМОЙ 147
под действием внешних поверхностных сил Хп, Yn (Zn =
= 0). Предварительно нужно отобразить конформно об-
области S и Sk на нижнюю полуплоскость. В данном случае
можно сделать так, что каждой точке на границе области
S будут отвечать точки границ областей Sl9 S2, S3, нахо-
находящиеся между собой в аффинном соответствии, а всем
четырем аффинно-соответственным точкам — одна и толь-
только одна точка на границе полуплоскости. Подробнее эта
задача рассмотрена в нашей работе [57], а поэтому мы
на ней не останавливаемся, а приводим только окончатель-
окончательные формулы для функций Ф&:
х \ -
— оо
ФП*2) =
'з-И>2) + ^п(Я,2Я,з—1)
5-CiBi)
1 1
X
? YJ^-^K*
X
X
¦/1 +
d%.
B8.10)
Здесь
— функции, принимающие при у = ах2 одно и то же зна-
значение х.
§ 29. Случай нагрузки, распределенной
равномерно по прямой
Рассмотрим частный случай: нормальная нагрузка
распределена равномерно по бесконечной прямой х = 0,
у = 0. Предполагается, что полупространство однород-
однородно, но обладает анизотропией общего вида. Для того,
148
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
чтобы получить решение этой задачи, рассмотрим пред-
предварительно случай, когда нормальные усилия р/Bе)
распределены равномерно по полосе шириной 2е (рис. 32).
В этом случае все интегралы B8.5) легко берутся и мы на-
находим функции Ф/с, содержащие е как параметр. Устрем-
Устремляя затем е к нулю, получаем
(Zl) =
— И-2
р v-i ~
B9.1)
Также легко получаются формулы и для полупространства,
нагруженного касательными усилиями, распределенными
равномерно по прямой; соответствующих выражений Ф^
мы приводить не будем.
Для определения напряже-
напряжений нужно функции B9.1) (или
функции для касательных уси-
усилий) подставить в формулы
B1.3), B1.4) и отделить вещест-
вещественные части.
В случае нагрузки, распре-
распределенной равномерно по пря-
прямой у = 0 (оси z) удобнее поль-
пользоваться цилиндрической систе-
системой координат г, 0, z, отсчиты-
отсчитывая координату г от оси z и
0 — от продолжения оси у
(рис. 32). Тогда получим фор-
Рис. 32.
мулы для случая нормальной нагрузки:
—?44-
(cos 6 + И-! sin бJ
sinе-^чcose
lB9-2)
§ 29] СЛУЧАЙ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ ПО ПРЯМОЙ 149
X
ч cos 6 -
sin e-ti, сове
cos е
cos 6 + Цз sin 6
B9.2)
<?о = тв2 — tr0 — 0.
Составляющая 0*2 найдется из B5.5).
Таким образом, из шести составляющих напряжений
в цилиндрических координатах только три не равны
нулю; для общего случая анизотропии после отделения
вещественных частей получаются довольно громоздкие
выражения, которые мы выписывать не будем.
Отметим, что все составляющие напряжений обратно
пропорциональны расстоянию от загруженной линии
(оси z). Точки, в которых напряжение аг на цилиндричес-
цилиндрической поверхности г = const имеет наибольшую величину,
находятся, вообще говоря, не на линии действия усилий
G = 0, а точки, где ог = 0, не лежат на ограничивающей
плоскости.
Рассмотрим более подробно плоскую задачу (которая,
как было ранее указано, имеет два варианта) для ортотроп-
ноготела. В случае плоской деформации мы имеем упругое
полупространство, нагруженное усилиями, распределен-
распределенными равномерно по бесконечной прямой на ограничиваю-
ограничивающей плоскости. Предполагается, что в каждой точке
имеются три плоскости упругой симметрии, параллель-
параллельные координатным, из которых одна параллельна огра-
ограничивающей плоскости; линия, по которой распределена
нагрузка (ось z), нормальна ко второй плоскости упругой
симметрии. В случае обобщенного плоского напряженного
состояния рассматривается полубесконечная ортотроп-
ная пластинка, нагруженная по краю. В том и в другом
случае область тела (на плоскости ху) есть полуплоскость.
В соответствии с этим мы будем называть исследуемое те-
тело «упругой полуплоскостью», как это делается в случае
изотропной среды (см., например, [26]).
Сначала рассмотрим действие нормальной силы р,
приложенной к границе полуплоскости. В случае орто-
150 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО (Гл. 4
тропии формулы B9.2) чрезвычайно упрощаются и, после
отделения вещественной части, принимают вид:
— р t л. \ \rR ft" cose \
Л. r^ (U) I (Zv.o)
I
a0 = tr9 = t9z = rrz = 0. j
Здесь
# (9) = Pu sin49 + Bpia + p66) sin2 6 cos2 6 +
+ p22 cos4 6 B9.4)
— величина положительная, не равная нулю при всех зна-
значениях G; иг, и2 — корни уравнения
Pii - Bр1а + р6б) и* + р22 - 0. B9.5)
Эти корни связаны с корнями уравнения /4((х) = 0 зави-
зависимостями иг = — i\iv и2 = — i(i2» а следовательно, мо-
могут быть только вещественными или комплексными сопря-
сопряженными числами; поэтому их + и2 — всегда вещественное
число. В случае плоской деформации pf7- — приведенные
коэффициенты деформации р/7- = (atj — ai3uj3)la33\ в дру-
другом случае плоской задачи pf7- должны быть заменены со-
соответствующими коэффициентами а,ц. Заметим еще, что
X (G) равно приведенной упругой постоянной ргг для ради-
радиального направления г:
= Ргг B9.6)
или, если рассматривается обобщенное плоское напряжен-
напряженное состояние, то X — это величина, обратная модулю
Юнга для радиального направления:
Формулы B9.3) показывают, что в упругой полуплоско-
полуплоскости под действием нормальной силы получается распреде-
распределение напряжений, которое можно назвать радиальным
или лучеобразным: на всех площадках, нормальных к ра-
радиус-вектору г, проведенному в плоскости ху из точки
приложения силы, действует напряжение, направленное
по г, а на площадках, проходящих через радиус-вектор
(и нормальных к ху), никаких напряжений не действует.
Напряжение аг является главным, обратно пропорцио-
пропорционально расстоянию г, а при заданном г = const меняется
§ 29] СЛУЧАЙ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ ПО ПРЯМОЙ 151
в зависимости от 0 по довольно сложному закону; напря-
напряжения (Те и тг9 равны нулю.
В случае плоской деформации имеется еще вторая со-
составляющая напряжений — az; она действует на площад-
площадках, нормальных к загруженной линии (т. е. в плоскостях,
параллельных ху) и по величине равна
oz = — ar— (a13 cos2 G + а23 sin2 9). B9.8)
Точки, в которых напряжение аг одинаково — равно
какой-то величине а0, располагаются на кривой четверто-
четвертого порядка. Уравнение семейства этих кривых имеет вид:
Bр12 + р6б) х*у*
У№*(х2 + У2)У = в- B9.9)
Все эти кривые замкнутые, симметричны относитель-
относительно линии действия силы и касаются границы полуплоско-
полуплоскости в точке приложения силы О. В случае нормальной
сжимающей силы все кривые, расположенные в полуплос-
полуплоскости, соответствуют отрицательным а0 и только на гра-
границе G0 — 0; в этом случае их можно назвать изобарами —
линиями одинакового давления. Материал полуплоско-
полуплоскости под действием сжимающей силы будет сжат; граница,
за исключением точки приложения силы О, являющейся
особой, играет роль нейтральной линии — в каждой точ-
точке (за исключением одной О) все напряжения равны нулю.
Форма линий одинаковых напряжений аг зависит от
соотношения между приведенными или истинными коэф-
коэффициентами деформации. Можно отметить три основных ти-
типа кривых.
1. Если упругие постоянные удовлетворяют условиям
или
если
2Pl2 -
2Pia
66 =
1
f 1
,5
(Зев > 1
Р22» ?
l>5 p22,
Ф11 —
3p22 ^
0,
B9
B9
.10)
.11)
то кривые имеют вид овалов, у которых линия действия
силы служит осью симметрии (рис. 33). Напряжение аг
достигает наибольшего по величине значения на линии
действия силы.
152
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
2. Если, кроме условий B9.10) или B9.11), выполняют-
выполняются условия
2pi2 + Рее> 4Рп,
BPia + Рее - 4РПJ - 4рп Dр12 + 2|Зб6 - Зр22) > 0,
то кривые аг = (Уо имеют симметричные боковые выступы
и в зависимости от их длины напряжение может достиг-
достигнуть наибольшего по величине значения не под силой,
а на осях выступов (рис. 34).
Рис. 34.
3. Если имеет место соотношение
или
2|3
12
2р12 +Рбб<1,5р22,
р66 = 1,5 ра2, 8рп - 3
B9.13)
0, B9.14)
то общий характер кривых аг = а0 изменится и они будут
иметь вид, как на рис. 35. Очевидно, напряжение аг до-
достигнет наибольшей величины не под силой, а на двух
симметричных лучах.
При некоторых соотношениях между постоянными кри-
кривые могут выродиться в эллипсы, у которых большая или
малая ось направлены по линии действия силы. Если
полуплоскость изотропна, то у нее
Ри = р22 = 0,5 Bр12 + рм), щ - i/2 = 1, B9.15)
и мы получаем классическое решение задачи Фламана
§ 29] СЛУЧАЙ НАГРУЗКИ, РАС1П ЕДЕЛЕННОЙ ПО ПРЯМОЙ 153
[32]:
2р cos 0
= Т Г9 = 0.
B9.16)
Линии одинаковых напряжений превращаются в окруж-
окружности (рис. 36).
Воспользовавшись формулами B8.8), где N = 0, мы
легко определим напряжения в полупространстве от ка-
касательных усилий t (на единицу длины), перпендикуляр-
перпендикулярных к оси z и распределенных равномерно вдоль этой оси.
Рис. 35.
Рис. 36.
Опуская элементарные промежуточные выкладки, при-
приводим формулы для ортотропного полупространства в ци-
цилиндрических координатах:
= tr9 = 0.
B9.17)
Путем наложения решений B9.3) и B9.17) получим
распределение напряжений в ортотропном пространстве
или в соответствующей пластинке от силы/?, действующей
в плоскости упругой симметрии ху и образующей с осью
у какой-то угол со (рис. 37):
X (CO5
cos (о cos G
у ^- sin о) sin ej , ae = tre = 0.
B9.18)
154 ПРЯМОЛИНЕЙНО-АНИЗОТГОПНОЕ ТЕЛО [Гл. 4
В случае наклонной силы внутри полуплоскости про-
проходит нейтральная линия — прямая, на которой все
напряжения равны нулю. Эта прямая перпендикулярна
к линии действия силы, если pu = р22; в противном слу-
случае она пересекает ли-
линию действия силы под
острым или тупым углом
О . (см. рис. 37).
7777777772
7^^477777777777777, у Есди ПОЛУПЛОСКОСТЬ
7 \ ортотропна, но одна из
плоскостей упругой сим-
симметрии пересекает гра-
\ ницу под произвольным
\ углом или она не явля-
^ ется ортотропной, то ре-
решение и для этих случа-
Рис< 37. ев также легко полу-
получается с помощью мето-
метода Н. И. Мусхелишвили (см. B8.8)). Случай неорто-
тропной полуплоскости был исследован Е. Моссаковским
в работе [120]. Приведем без вывода основные результаты
для полупространства или пластинки, у которых в
каждой точке имеются не три, а только одна плос-
плоскость упругой симметрии, параллельная ху. Моссаковский
направляет ось х по границе, а ось у внутрь области,
т. е. рассматривает не «нижнюю», а «верхнюю» полуплос-
полуплоскость. Мы не будем менять направлений осей и расположим
их так же, как в работе [120]. Пусть
jit! = а + р*\ fx2 = у + б* (Р > 0, б > 0)
— комплексные параметры — корни уравнения /4 (м<) = 0
(§ 20) и \кг, [Г2 — сопряженные величины. Введем обозна-
обозначения:
а = аб + yP, Ъ = (а2 + Р2)б + (у2 + б2) Р; B9.19)
X F) = рп cos4 6 + 2pi6 sin 6 cos3 9 +
+ BPi2 + Pee) sin29 cos29 + 2p26 sin3 9 cos 9 + p22 sin49
B9.20)
(смысл этой величины такой же, как и в случае
ортотропного тела — см. формулы B9.6) и B9.7); угол 9
отсчитывается от оси у).
§ 29] СЛУЧАЙ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ ПО ПРЯМОЙ 155
Если сила нормальна к границе, то напряжения опре-
определятся по формулам
ае = тг9 = 0. B9.21)
Через область тела проходит, вообще говоря, нейт-
нейтральная линия (прямая):
tg6-- i-. B9.22)
В случае касательной силы (направленной по границе)
„ __ 'Рп (Р + б)sine+ лсоя8 ^ _т _а
Угол наклона нейтральной линии получим, приравняв
числитель B9.23) нулю.
В работе [120] рассмотрен конкретный пример и пост-
построены семейства кривых одинаковых напряжений для
материала со следующими значениями отношений р,-/
(или atj):
— = 0,6, —1\ — = 0,35, -—- = — 0,731,
Рп Рп Рп
Ь* =0,751; Цх = l,l + l,0i, ^2 = -0,5 +0,3/.
ll
B9.24)
На рис. 38 даны кривые для случая нормальной силы,
на рис. 39 — то же для касательной силы.
Формулы B9.21) и B9.23) показывают, что качествен-
качественная картина распределения напряжений остается такой
же, как и в случае ортотропной полуплоскости: распре-
распределение налряжений на площадках, нормальных плоско-
плоскости ху, является «радиальным» или «лучеобразным» и
единственное напряжение а,, обратно пропорционально рас-
расстоянию от точки приложения силы1). Кривые одинаковых
напряжений аг = о0 получаются сложнее, чем для орто-
ортотропной полуплоскости и, вообще говоря, лишены какой-
либо симметрии.
х) В случае полупространства (плоская деформация) имеется
еще составляющая oz на площадках, параллельных ху, пропорцио-
пропорциональная о>.
156 ПРЯМОЛИНБЙНО-АНИЗОТ1 ОПНОЕ ТЕЛО [Гл. 4
}30]
ПОЛОСТЬ В ВИДЕ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА
157
§ 30. Распределение напряжений в упругом
однородном пространстве с полостью
в виде эллиптического цилиндра
Рассмотрим бесконечное упругое пространство, запол-
заполненное однородным материалом с анизотропией общего
вида, имеющее полость в виде бесконечного цилиндра
эллиптического сечения. Пусть по поверхности полости
распределены усилия, нормальные к образующей цилинд-
цилиндра и не меняющиеся вдоль
образующей, а объемные си-
силы отсутствуют.
Отнесем тело к системе
координат х, у, z, у которой
начало помещено в центре -
какого-нибудь поперечного
сечения полости, ось z нап-
направлена вдоль ее оси и оси
х, у по главным осям эллипса
(рис. 40).
Обозначим через Хп, Yn
проекции внешних усилий,
отнесенных к единице площади. В общем случае эти уси-
усилия приведутся к главному вектору с проекциями Рх,
Ру и к главному моменту М (на единицу длины образую-
образующей).
В сечении плоскостью ху мы имеем область S в виде
бесконечной плоскости с эллиптическим вырезом; уравне-
уравнение контура ее имеет вид
Рис. 40.
4
Ь1
ИЛИ
х = a cos Ф, у = Ъ sin
C0.1)
C0.2)
Bа, 26 — главные оси эллипса, О — параметр, меняю-
меняющийся при полном обходе по контуру от 0 до 2л). Области
^i» $2> $з также будут плоскостями с эллиптическими вы-
вырезами, контуры которых представятся уравнениями
х]: = a cos fl1 -f ak b sin Ф, 1
yk - p*bsinO (к = 1, 2, 3). J
C0.3)
158 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
Усилия Хп, Yn будут функциями параметра ft, перио-
периодическими с периодом 2л; мы будем считать их представ-
представленными рядами Фурье по cos mft и sin mft. При задан-
заданных усилиях граничные условия будут содержать интег-
интегралы по дуге от Хп, Yn, куда войдут периодические
функции ft и члены, пропорциональные ft. Представляя
тригонометрические ряды в комплексной форме, запишем
условия для функций Ф/f (zk) таким образом:
m=l
2 Re (ргФг + р2Ф2 + \
P
C0.4)
(am, 6m и сопряженные величины — известные постоян-
постоянные; а0, 60, с0 — произвольные постоянные, которые в
рассматриваемом случае можно положить равными ну-
нулю. На бесконечности напряжения должны равняться ну-
нулю, а для этого необходимо, чтобы производные Фк (zjx)
стремились к нулю при zK ->oo.
Задача решается следующим образом. Отобразим все
четыре области S, Sx, S2, S3 на внешность единичного кру-
га | ? | > 1. В данном случае, когда области Sk являются
внешностями эллипсов, находящихся в аффинном соответ-
соответствии, указанное отображение можно осуществить так,
что четырем точкам на контурах областей S и Sk отвечает
одна и та же точка на контуре единичного круга ? = еы,
и это свойство сохраняется для любого значения ft.
На основании этого свойства мы можем решать самые
разнообразные задачи для бесконечной плоскости с эллип-
эллиптическим вырезом — как первую основную задачу, так
и вторую, как задачу об обобщенной плоской деформации,
так и плоскую задачу.
Отобразим конформно области S и Sk на внешность
единичного круга. Отображающие функции имеют вид
a -A- b v . а — Ъ 1 /пл г\
z = —— С + —2— X' ( *
§ 3>] ПОЛОСТЬ В ВИДЕ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА 159
€i-\
(А; 1, 2, ii). (;К).6)
Функции, обратные C0.5) — C0.6), будут:
а - i\ikb
C0.7)
C0.8)
Когда хиу пробегают по контуру эллипса S, принимая
значения C0.2), тогда C0*7) и C0.8) принимают значение
С = Ci = С» = Сз = е*1-
Будем искать выражения для Ф^ в виде
C0.9)
= 1, 2, 3). C0.10)
Коэффициенты Ahm определим из граничных условий
C0.4), а Ак — из граничных условий и условий одно-
однозначности перемещений (каждое из перемещений должно
быть однозначной, или, что то же, периодической функци-
функцией'©). Получаем окончательные выражения:
~1] Вт]
4"
5m]
C0.11)
Здесь
А = LU —
— |А2)
(ц, — fi2); C0.12)
160
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
А±, А2, Л3 — коэффициенты, которые найдутся из урав-
уравнений
А2 +
— - Р
- Ах -А2 - Ms = -2JT '
ргАх + р2А2 + рл/\:) -
Г, — Г>2
~
Л 2
Л;
-о,
Рх
!ш
¦0,
f C0.13)
7-2 Т-2 —
-- 0,
- .vt, - о. J
В этих уравнениях рк, дк, гк — пос янные, входящие
в формулы для перемещений [см. B1.5) — B1.7)], рк, qk1
гк — сопряженные величины. Выражений для коэффи-
коэффициентов Аг, А2, А3 ввиду их громоздкости мы приводить не
будем, а укажем только, что если главный вектор усилий
равен нулю, то и все эти коэффициенты равны нулю:
Аг = А2 = А3 = 0, Л± = А2 = Л3 = 0.
Производные функций Ф^ (zk) определятся по форму-
формулам:
X
т X
Н~ (^2^3 — 1) Ьт]
I л" > т X
X
X
- |i2^) a
г - X2) b
C0Л4)
При наличии плоскостей упругой симметрии, нормаль-
нормальных к образующей, тело будет испытывать плоскую
I 30] ПОЛОСТЬ В ЁЙДЕ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА 161
деформацию и мы получим вместо C0.11)
оо
= Ах 1П ?х + * V Em — Mm) ?Г\
Ф2 (Z2) = ^2 In ?2 - ^i
m=l
C0.15)
После несложных преобразований получаем уравнения
для коэффициентов Аг, А2 и сопряженных:
Ах + А2 - Л, - Аг = -^ .
Pl2
И-2
C0.16)
= Р^2 х _L P26 ^1/
р22 2Л1 ^ р22 2ni '
Определитель этой системы равен:
^а + У) [(«" V)" + (Р - бJ1 [(« - YJ + (Р + 6)*].
C0.17)
При неравных комплексных параметрах всегда d ^> 0,
а следовательно, коэффициенты Л2, Л2 и сопряженные
определятся из системы C0.16) однозначно. При попарно
равных параметрах \ix = ц2, ^ = jl2, d = 0, но тогда
и уравнения C0.16) теряют смысл, так как при решении
задачи нужно исходить из выражения для функции F не
в форме B6.4), а в форме B6.6). На этом случае мы оста-
останавливаться не будем.
Приводим значения коэффициентов ат, Ът для несколь-
нескольких частных случаев нагрузки. Во всех случаях Аг =
= Л2 = А3 = 0, а каждая функция Ф^ представляется
только одним членом ряда (см. [20], гл. 3).
6 С. Г. Лехницкий
162
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. А
1. Нормальное давление, распределенное равномерно
по поверхности полости (рис. 41):
flm = 5W = 0 для m = 2, 3, 4,...
— давление на единицу площади).
Як
В
C0.18)
2. Касательные усилия, распределенные равномерно по
поверхности полости и действующие в плоскостях, па-
параллельных ху (рис. 42):
- __ tbi Л — — )
п1~~> 01- - 2 ' C0.19)
я™ = 5т = 0 для т = 2, 3, 4,... j
(^ — усилие на единицу площади).
§ 30] ПОЛОСТЬ В ВИДЕ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА
163
В следующих трех случаях, когда поверхность поло-
полости не нагружена, а усилия приложены на большом рас-
расстоянии от нее (в теории — на бесконечности) составляю-
составляющие напряжения определятся по формулам:
+ т'ху. C0.20)
ау,
., хуу =
Первые слагаемые (с нуликами) — напряжения, выз-
вызванные теми же усилиями в пространстве сплошном, без
Рис. 43.
полости; вторые слагаемые (со штрихами) — напряже-
напряжения, определяемые функциями C0.11) или C0.15) (во всех
этих случаях Рх = Ру = 0, Аг = А2 = А3 = 0).
3. Растяжение. На большом расстоянии от полости
действуют растягивающие усилия, направленные под уг-
углом ф к оси эллипса 2а (рис. 43).
В этом случае:
сг" = р cos2 ф, о
у
р sin2
о\ = — (а13 cos2
3
+ агъ sin2 ф + а36 sin <p cos ф);
ах — ~ sin ф (a sin ф — ib cos ф),
— ~- cos ф (a sin ф — ^6 cos ф),
= 5т = 0 (т=2,3,...)
C0.21)
C0.22)
C0.23)
б*
164
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
(p — растягивающее усилие на единицу площади,
а > Ъ или а < Ь).
В частности, при растяжении в направлении оси дли-
длиной 2а (ф = 0)
0 _,0 ^0 г\ 0 0 гл. /Qi"\ O/\
о» = _pi"; C0.25)
ах = 0, bt. = Ц-. C0.26)
4. Сдвиг. На большом расстоянии от полости действу-
действуют касательные усилия, параллельные главным осям
\
+ /
f
г
й О
а
t
It*
« t
эллипса (рис. 44):
Рис. 44.
r^ = а^ = 0,
0 -г0 П»
_ __ ^&t r ta
am = 5m = 0 для m = 2, 3,
C0.27)
C0.28)
C0.29)
Здесь / — усилие на единицу площади.
f5. Чистый изгиб. На большом расстоянии от поло-
полости приложены нормальные усилия, меняющиеся по
§ 31] ПЛАСТИНКА С ЭЛЛИПТИЧЕСКИМ ОТВЕРСТИЕМ 165
линейному закону (рис. 4 ):
(У°х = ку, ol = х°ху
rl = т°2 = 0;
0 7~ а13
C0.30)
C0.31)
C0.32)
ат = Ът =¦ 0 для т — 3, 4, 5,...
Вторая основная задача может быть решена тем же
методом, что и первая, с помощью функций Фк вида
Рис.3,45.
30.11). Для определенности необходимо задать главный
вектор усилий (Рх, Ру). Постоянные Ак определятся из
уравнений C0.13), а в случае плоской задачи — из C0.16);
постоянные Акт — из граничных условий.
§ 31. Растяжение однородной ортотропной
пластинки с эллиптическим отверстием
Рассмотрим более подробно упругое равновесие орто-
ортотропной пластинки с эллиптическим отверстием, распо-
расположенным вдали от края, которая растягивается равно-
равномерно распределенными усилиями в одном направлении.
166
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
Мы будем предполагать, что 1) одна из плоскостей упругой
симметрии параллельна срединной; 2) направления глав-
главных осей эллипса х, у не совпадают с главными направле-
направлениями упругости g, rj; 3) усилия действуют под произволь-
произвольным углом к главным осям отверстия, причем край его не
нагружен и не закреплен. Пластинка рассматривается,
как бесконечная и усилия
считаются приложенными
на бесконечности. Решение
этой задачи получено нами
совместно с В. В. Солдато-
вым в работе [64].
^Изложим решение этой
задачи, схема которой ука-
указана на рис. 46. Введем
следующие обозначения:
2а, 26 — главные оси эл-
эллипса,] с = a/b, p — уси-
усилие на!"единицу площади,
Ф — угол наклона усилий
к главной оси 2а эллипса, г|э — угол между направлени-
направлениями главной оси эллипса 2а и главной оси упругости ?.
Введем технические константы: модули Юнга Ег, Е2 для
главных направлений ?, т|, коэффициенты Пуассона v1? v2
и модуль сдвига G для плоскости |т). Далее введем обо-
обозначения: atj — коэффициенты деформации из уравнений
обобщенного закона Гука, записанных для системы ко-
координат ху (не главной) и величины т, /с, п:
Рис. 46.
^. C1.1)
Так как т выражается через п (т = п2 — 2к) и наоборот,
то у нас намечаются два независимых параметра, которые
войдут в формулы для напряжений в ортотропнои плас-
пластинке; мы назовем кип вещественными параметрами обоб-
обобщенного плоского напряженного состояния анизотропной
(точнее, ортотропнои) пластинки. Вещественные параметры
плоской деформации ортотропнои среды выражаются че-
через отношения соответствующих приведенных коэффициен-
коэффициентов
m =
+
Рп
C1.2)
§ 31] ПЛАСТИНКА С ЭЛЛИПТИЧЕСКИМ ОТВЕРСТИЕМ
167
В случае изотропной среды к = 1, п = 2; в случае
ортотропной вообще к Ф 1 и п Ф 2. Это дает нам основа-
основание утверждать, что пара чисел (/с, п) как-то характери-
характеризует отклонение среды от изотропной, т. е. является своего
рода мерой анизотропии (в случае плоской задачи для
ортотропной среды). В следующем параграфе мы еще вер-
вернемся к этому вопросу.
Введем еще обозначения:
C1.3)
L = 0,5га [1 + к + A — к) cos
М = 0,5 [1 — к2 + A + к2 — т) cos 2-ф] sin 2г|>,
jV = 0,25 A + к2 — т) sin2 2ф — А,
Р = 0,125 [3 + т + ЗА2 + 4A - /с2) cos 2ф +
Уравнения обобщенного закона Гука для главных на-
направлений ?, т], связывающие составляющие деформации
и напряжения (средние по толщине), запишутся так:
_ 1 V2_ ___ Vj_ I _L _ 1
V.4)
То же для направлений х, у:
гх = апах + а12ау + аитху,
Ъу = а12Рх + «22^1/ + a2^xyi C1.5)
Коэффициенты aVj выражаются через главные (техни-
(технические) упругие постоянные на основании общих формул
преобразования упругих постоянных следующим обра-
зом:
*И = ^" > «22 = ^Щ- [Р + (к2 - 1)COS 2tp],
«12 = 4" I— vi + °>25A + ^2 — /w) sin2 2я|>],
«ее = 4г["^" + A + ^a - ^) sin2 2ipl ,
aie = ~2E~ t1 — *2 + A + ^2 — rri)cos 2ф] sin 2i|>,
1
«2в = -sg- [1 — Л2 — A + A2 — m) cos 2ij;] sin 2ij;.
C1.6)
J68 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО trri.
Беря уравнение контура в параметрическом виде, т.е.
полагая
х = a cos й, у = Ъ sin ft (a > 6), C1.7)
введем еще обозначения для функций, зависящих от пара-
параметра д:
I2 = с2 sin2'» + cos2'», C1.8)
S = Ех [auc4 sin4 Ъ — 2a16cs sin3 # cos ft +
+ Be12 + a66) c2 sin2 ft cos2 # — 2a26c sin ft cos3 # +
+ a22cos4#]. C1.9)
Нас будет интересовать только напряжение у края от-
отверстия — сг&, где, как показывает ряд решенных различ-
различных задач, оно получается наибольшим. В предыдущем
параграфе есть все необходимое, чтобы вывести формулу
для напряжения о& у края отверстия. Опуская промежу-
промежуточные выкладки, приведем окончательную формулу для
напряжения у самого края отверстия, действующего на
площадки, нормальные к этому краю:
в& = -^г- ({Nc sin2 ф + (К + Me) sin cp cos cp +
+ (L + Рс) cos2 ф} с sin2 $—l{lMNi+\K {L +„Рс
+\[М\(К + Мс) +]Lc (L]+ PcY-\LN] sin> cos Ф
+ {[K[{K\+Mc) + N (N - Lc)\ sin2 cp +
n^ cos> +*PN cos2 Ф}
C1.10)
Отсюда, прифи \|) равных нулю или л/2, получаем вы-
выражения для напряжений для четырех основных случаев,
когда отверстие вырезано так, что направления большой
и малой осей эллипса совпадают с главными осями упру-
упругости, а растяжение производится в направлении боль-
большой или малой оси эллипса. В частности, при растяжении
в направлении малой оси (ф = тс/2) имеем
в» = -^- к [- с2 sin2 # + (к + en) cos2 Щ (г|5 = 0) C1.11)
311 ПЛАСТИНКА С ЭЛЛИПТИЧЕСКИМ ОТВЕРСТИЕМ 169
или
а _; -pl2 [ — кс1 sin2 ft + A + en) cos2 ft]
Естественно ожидать, что при с ^> 1 наибольшее нап-
напряжение получится на концах большой оси и определится
по одной из двух формул:
или
Ы*-о - P(l+cn) (я|з - --) . C1.14)
Однако следует заметить, что это утверждение при не-
некоторых значениях параметров кип может оказаться не-
неверным и напряжение получится наибольшим по величине
на концах малой оси, а небольшой; оно будет сжимающим
и найдется по одной из формул:
(<У*)а=_-71/з = — рк* C1.15)
Заметим, что на концентрацию напряжений около от-
отверстия большое влияние оказывает модуль сдвига G,
входящий в состав выражения для параметра п.
Приведем некоторые результаты вычислений для пла-
пластинки с упругими постоянными, как у березовой фанеры
(см. таблицу 6). Мы будем такую пластинку для кратко-
краткости называть просто «фанерной». Если направление оси х
совпадает с направлением наибольшего модуля Юнга,
то для нее получаются следующие значения комплексных
и вещественных параметров:
к =/2 = 1,414, п = 4,453. J {Л1Л1)
Если же направление оси х совпадает с направлением наи-
наименьшего модуля Юнга, то для той же фанерной пластин-
пластинки получается:
Их = 0,243г, ц2 = 2,91/, |
к = 0,707, п = 3,149. j C1Л8)
170
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
Таблица 8
Наибольшие растягивающие напряжения &тах/Р в фанерной
пластинке
ф°
0
30
45
60
90
ф° = 0
3,23
3,10
3,85
5,58
7,20
30
2,76
4,92
5,55
5,47
5,77
45
2,67
4,64
5,84
6,52
5,52
60
2,21
4,96
6,93
8,20
7,72
90
2,57
2,55
6,19
7,55
9,91
120
2,21
3,80
4,28
4,24
7,72
135
2,67
4,00
4,98
5,33
5,52
150
2,76
3,76
5,18
6,14
5,77
180
3,23
3,10
3,85
5,58
7,20
Таблица 9
Наибольшие [сжимающие напряжения <f'max/P в фанерной
пластинке
ф°
0
30
45
60
90
Ф° = 0
0,71
0,98
1,41
1,60
1,41
30
0,94
0,77
0,76
0,89
1,29
45
1,18
0,79
0,46
0,63
1,13
60
1,38
1,24
1,09
1,11
0,92
90
1,41
1,24
1,16
1,13
0,71
120
1,38
1,54
1,38
1,24
0,92
135
1,18
1,80
1,57
1,37
1,13
150
0,94
1,83
1,82
1,53
1,29
180
0,71
0,98
1,41
1,60
1,41
В таблицах 8 и 9 приведены значения наибольшего рас-
растягивающего напряжения аШак и величины наибольшего
сжимающего напряжения аШах на контуре отверстия в фа-
фанерной пластинке. Отношение полуосей эллипса взято
равным с = 2. Рассмотрено пять случаев ориентации уси-
усилий по отношению к большой оси эллипса и восемь слу-
случаев ориентации главных направлений упругости. Сохране-
Сохранено по два знака после запятой; вычисления с большей точ-
точностью едва ли целесообразны, принимая во внима-
внимание приближенный характер исходных данных (таблица
6), а также то, что нас интересует главным образом ка-
качественная картина распределения напряжений.
§ 31] ПЛАСТИНКА С ЭЛЛИПТИЧЕСКИМ 0ТВЕ1СТИЕМ 171
Приводим величины наибольших растягивающих на-
напряжений в изотропной пластинке (таблица 10);
Таблица 10
Наибольшие растягивающие напря-
напряжения в изотропной пластинке
0
2,00
30
2,80
45
3,54
60
4,29
90
5,00
Для изотропной пластинки во всех случаях (ТШах = р.
На рис. 47—50 изображены графики распределения
напряжения (То по контуру отверстия для четырех
случаев:
1) Ф = Ф = 0,
2) Ф = 90°, ф = 0,
3) ф = 90°, i|> = 45°,
4) ф = 3(f, i|) = 60°.
Величины напряжений отложены от контура отверстия
на продолжениях лучей, проведенных из центра через
данные точки контура; положительные напряжения изо-
изображены стрелками, направленными из центра к перифе-
периферии, отрицательные — стрелками, направленными к цент-
центру. На каждом графике показана схема нагрузки. Для
сравнения пунктиром показаны графики для изотропной
пластинкш
На рис. 51 показано изменение (Ушах//? (кривая 1) и
<*тах/р (кривая 2) в зависимости от г|) при растяжении вдоль
малой оси отверстия. На рис. 52 дано изменение отъх/р
в зависимости от угла наклона усилий к большой оси для
^ = 0° (кривая 1) и для г|) = 90° (кривая 2).
Анализируя полученные результаты, можно сделать
следующие выводы для фанерной пластинки, которые дают
основание судить и о том, как распределяются напряжения
по контуру отверстия в пластинке, у которой к > 1,
п > 2.
Как видно из графиков на рис. 47—50, контур отвер-
отверстия разбивается на четыре симметричных участка, где
действуют попеременно растягивающие и сжимающие
172 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
Рис. 47.
tttti
tttt
киши
Рис. 48.
31] ПЛАСТИНКА1;С1[ЭЛЛИПТИЧЕСКИМ ОТВЕРСТИЕМ 173
ншин
р
Рис. 49.
Рис, 50
174
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
напряжения; при этом во всех случаях наибольшие растя-
растягивающие напряжения значительно превышают величины
наибольших сжимающих. В анизотропной пластинке наи-
наибольшее растягивающее напряжение получается больше,
чем в такой же изотропной пластинке. Как показывает
таблица 8, наибольшее из всех возможных растягивающих
)
(Г
—
60 120 180
Р
Рис. 51.
1
У
г
А
V
0 60° 120° 180°
P
Рис. 52.
напряжений получается в случае, когда отверстие выре-
вырезано так, что направление его малой оси совпадает с нап-
направлением, для которого модуль Юнга является наиболь-
наибольшим и растяжение производится в направлении малой оси
отверстия. В этом случае огтах = 9,91 р. Из других рас-
рассмотренных случаев, приведенных в таблицах, «невыгодны-
«невыгодными» (в смысле наибольших растягивающих напряжений)
оказываются следующие:
1) 1|> = 60°, ф = 60°, (Гтах = 8,20 /?,
2) я|) = 60°, Ф = 90*\ <w = 7,72 /?,
3) я|) - 90°, ф - 60°, огшах = 7,55 р.
Наиболее напряженными местами будут области, на-
находящиеся вблизи концов большой оси (угловое расстоя-
расстояние от оси х не превышает 8°).
При растяжении в направлении малой оси эллипти-
эллиптического отверстия в разобранных случаях наименьшее
значение максимального растягивающего напряжения рав-
равно (Гтах = 5,52 р и получается в том случае, когда оси
отверстия направлены под углом 45° к главным направле-
направлениям упругости.
§ 32] ОГТОТРОПНАЯ ПЛАСТИНКА. КРУГОВОЕ ОТВЕГСТИЕ 175
Как показывает таблица 9, наибольшие по величине
сжимающие напряжения получаются при следующих уг-
углах гр и ф:
1) г|) - 135°, Ф = 30°, сгтах = 1,80 р,
2) о|) = 150°, ф = 30°, а™* = 1,83 р,
3) ар-150°, Ф = 45Р, <w = l,82p.
Как видно из той же таблицы, наименьшие по величи-
величине сжимающие напряжения равны сгШах = 0,71 р и полу-
получатся при гр = 0° и яр = 180°, ф = 0° и при 1|з = 9(У°,
Ф = 90*.
Наибольшие по величине сжимающие напряжения во
всех рассмотренных случаях значительно меньше мак-
максимальных растягивающих напряжений.
А. С. Космодамианским и его учениками изучено боль-
большое число случаев анизотропной пластинки, ослабленной
многими эллиптическими и круговыми отверстиями, а так-
также даны приближенные решения для случаев отверстий
иной формы, края которых свободны или подкреплены
см. работу [15а], где имеется также большой список ли-
ературы).
§ 32. Некоторые случаи распределения
напряжений в ортотропной пластинке
с круговым отверстием
Приведем решения нескольких частных случаев плос-
плоской задачи однородного ортотропного тела для бесконеч-
бесконечной плоскости с круговым вырезом, представляющим прак-
практический интерес. Для определенности мы рассматриваем
пластинку, т. е. обобщенное плоское напряженное со-
состояние, для которой и даем результаты вычислений (хотя
все формулы с соответствующими изменениями остаются
верными и для случаев плоской деформации). Все необ-
необходимое для решения рассмотренных задач имеется в § 30.
Одна из плоскостей упругой симметрии параллельна сре-
срединной ху, оси х, у направлены нормально к остальным
двум. Используем обозначения предыдущего § 31.
Всего рассмотрено шесть различных случаев упругого
равновесия бесконечной пластинки с круговым отверстием;
все они изложены в наших книгах [20] и [21]. Для каж-
каждого случая приводятся формулы для напряжений Се
176 Ш'ЯМОЛИНЕЙНОАНИЗОТ! ОПНОЕ ТЕЛО [Гл. 4
на радиальных площадках в любой точке и в наиболее
важных точках контура отверстия. Для четырех случаев
мы даем таблицы численных значений коэффициентов мак-
максимальных и минимальных напряжений для восьми ма-
материалов — четырех видов фанеры и четырех видов или
марок стеклопластиков, упругие постоянные которых при-
приведены в § 9, и графики распределения напряжений по кон-
контуру отверстия в пластинке из березовой фанеры и для
сравнения — графики для изотропной пластинки, нахо-
находящейся в тех же условиях. Отрезки, изображающие ве-
величины напряжений <Ге, откладываются на продолжениях
радиусов; положительные напряжения изображаются
стрелками, направленными от центра к периферии, от-
отрицательные — стрелками, направленными к центру *).
В правом верхнем углу изображаются схемы нагрузок.
В остальных двух случаях мы ограничиваемся только не-
некоторыми результатами для пластинки из березовой фа-
фанеры.
Все формулы для напряжений содержат множитель
Ъ где Ео — модуль Юнга для направлений, каса-
касательных к контуру отверстия. Эти функции определяются
по формулам:
K }
Прежде всего, приведем таблицу 11 значений вещест-
вещественных параметров кип для восьми анизотропных мате-
материалов, указанных в § 9, с тремя цифрами после запятой.
Для каждого материала рассмотрены два случая: 1)
направление оси .г совпадает ^направлением, для'которого
модуль Юнга наибольший (Ег = Ет&х) и 2) направление х
соответствует^направлению, для которого модуль Юнга
наименьший (Ег — 2?min). Если обозначить параметры
для первого случая через к и тг,а для второго через к' и п\
г) Такой способ построения графиков прпдает последним на-
наглядность; если откладывать отрезки, изображающие отрицательные
orQ, внутрь окружности, то наглядность может быть утрачена.
§ 32] ОРТОТРОПНАЯ ПЛАСТИНКА. КРУГОВОЕ ОТВЕРСТИЕ 177
то легко показать, что
к' =
п = -г- = пк .
C2.3)
У изотропной среды, как было уже сказано, к = 1
и п = 2.
Таблица 11
Вещественные параметры для анизотропных материалов
к
п
' 1 min
к'
п'
Фанера
к
с*
W
«
о)
О
1,414
4,453
0,707
3,149
G-1
W
1,138
3,788
0,879
3,330
о
е
1,217
3,636
0,822
2,988
е
о
е
1,119
3,943
0,894
3,524
Стеклопластики
о
я
о .
|а
X В
2,018
3,672
0,496
1,819
J3 g
X s
ртого
o-apiv
С X
1,172
3,081
0,853
2,629
тэт
и
1,107
2,566
0,903
2,318
о
j
1з§
1,169
2,904
0,856
2,484
Как показывает таблица 11, отличие анизотропного
материала от изотропного более всего для березовой фа-
фанеры и стеклопластика намоточного однонаправленного
(особенно при Е± = ЕПШК). Стеклопластики СТЭТ и
АСТТ (б)--Г2 О и ПН-3 по величине вещественных парамет-
параметров сравнительно мало отличаются от изотропного мате-
материала.
Перейдем к рассмотрению частных случаев.
1. Нормальное давление, распределенное равномерно
по краю отверстия (рис. 53).
Обозначив через q давление на единицу площади, за-
запишем выражение для напряжения Ов на радиальных пло-
площадках вблизи контура в виде произведения
do = qf @). C2.4)
Здесь / @) — безразмерная функция угла 0, отсчитывае-
178
П1 ЯМОЛИНЕЙНО-АНИЗОТГОПНОЕ ТЕЛО
[Гл. 4
мого от оси х, и вещественных параметров кип:
/ (9) = ^1 {п - к + п (к - 1) cos2 Э +
+ [(к + IJ - п2] sin2 9 cos2 0}. C2.5)
Направление оси х соответствует направлению, для кото-
которого модуль Юнга наибольший (Е± = Ет&х).
Рис. 53.
В изотропной пластинке / = 1, сГе = ?.
В точках пересечения контура отверстия с главными
осями упругости А, А1и Ву Вг имеем
со = g/л, <*е = д/в, C2.6)
где
C2.7)
/а и /в характеризуют концентрацию напряжений и их
можно назвать коэффициентами концентрации. Значения
ja, /б, коэффициента наименьшего напряжения /min и
угла 0min в первом квадранте, определяющего точку, где
напряжение наименьшее (с точностью до 1°), приведены
в таблице 12.
§ 32] ОРТОТРОПНАЯ ПЛАСТИНКА. КРУГОВОЕ ОТВЕРСТИЕ 179
Таблица 12
Коэффициенты концентрации и коэффициенты наименьших
напряжений для анизотропных материалов при равномерно
распределенном давлении
/a
1в
Jmin
Фанера
к
березова
2,44
3,04
0,08
49°
6
и
2,45
2,65
0,13
46°
БФС
2,17
2,42
0,22
47°
ФСФ
2,63
2,82
0,08
46°
• »
О Св
aft
намоточ
однонап
1,32
1,65
—0,11
53°
Стеклопластик?
А «
5а
ортогон
но-арми
1,78
1,91
0,41
46°
СТЭТ
1,41
1,46
0,64
46°
АСТТ(б)
И ПН-3
1,63
1,74
0,49
47°
Таблица показывает, что фанеры всех четырех марок
ведут себя как материалы с сильно выраженной анизотро-
анизотропией, так как наибольшие напряжения и особенно наи-
наименьшие сильно отличаются от напряжения в изотропной
пластинке, равного q. У стеклопластиков это отличие зна-
значительно меньше, но следует отметить особенность намо-
намоточного однонаправленного стеклопластика, для которого
качественная картина распределения напряжений отли-
отличается от таковой для остальных семи материалов: вблизи
биссектрис углов между осями появляются на контуре
участки, где напряжение ае не растягивающее, а сжи-
сжимающее.
Деформируясь под действием равномерно распреде-
распределенных усилий #, край отверстия становится эллиптичес-
эллиптическим; величины главных полуосей эллипса равны
C2.8)
V =a[l - ^-(А - Ат
На рис. 53 показано распределение напряжений по
краю отверстия в пластинке из березовой фанеры (сплош-
(сплошная линия) и в изотропной (пунктир). Графики рис. 53
180 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
весьма убедительно показывают, как влияет анизотропия
на распределение напряжений.
2. Касательные усилия, распределенные равномерно по
краю отверстия. Пусть по всему контуру распределены
равномерно усилия t, эквивалентные моменту, вращаю-
вращающему против часовой стрелки. Напряжение ае вблизи
края отверстия равно
ore = tf(Q), C2.9)
где
lut{ik--iHk-n + i) +
+ [(k + If - пг] cos 20} sin 20. C2.10)
В случае изотропной пластинки/ = сге = 0; на ради-
радиальных площадках вблизи края отверстия действуют толь-
только касательные напряжения тго — t. В случае же орто-
тропной пластинки напряжение в$ распределено по краю
по довольно сложному закону — весь контур отверстия
разбивается на восемь участков, где действуют поперемен-
попеременно растягивающие и сжимающие напряжения; в точках
на границах участков о0 = 0. Наибольшее напряжение
сттах может превысить величину касательных усилий,
вызвавших его. В частности, для пластинки из березовой
фанеры наибольшее нормальное напряжение равно при-
приблизительно 1,5 t1).
3. Растяжение под углом к главному направлению.
Пусть пластинка с круговым отверстием растягивается
усилиями р (на единицу площади), приложенными на
большом расстоянии от отверстия, равномерно распре-
распределенными и действующими под углом ф к главному нап-
направлению. Как обычно, рассматриваем пластинку как бес-
бесконечную и усилия относим на бесконечность (рис. 54).
В этом случае напряжение вблизи контура отверстия
0„ = р/(О), (o2.ll)
где
f (9) = -JL {__ [cos2 <p + (k + n) sin2 <p] k cos2 0 +
+ [A + n) cos2 ф — k sin2 ф] sin2 0 —
— n A + k + n) sin ф cos ф sin 0 cos 0}. C2.12)
2) Более подробно этот случай разобран в книгах [20] и [21],
где приведены графики распределения напряжений в фанерной
пластинке.
§ 32] ОРТОТРОПНАЯ ПЛАСТИНКА. КРУГОВОЕ ОТВЕРСТИЕ 181
В изотропной пластинке, работающей в тех же усло-
условиях,
ае = р [i_2 cos 2 (9 - ф)]. C2.13)
Наибольшее напряжение в изотропной пластинке рав-
равно 3 р и получается на концах диаметра, перпендикуляр-
перпендикулярного к растягивающим усилиям. В ортотропной пластин-
пластинке распределение напряжения о% по контуру отверстия
Рис. 54.
не является симметричным относительно линии действия
усилий; оно симметрично только относительно центра
отверстия.
На рис. 54 показано распределение напряжения сге
в пластинке из березовой фанеры, растягиваемой под уг-
углом 45^ к одному из главных направлений упругости х.
Наибольшее напряжение в фанерной пластинке, работаю-
работающей в этих условиях, мало отличается от наибольшего
напряжения в изотропной пластинке; оно равно сгтак =
=¦= 3,3 р. Точки, где Со = 0, определяются углами 0 =
= 13°, 82°, 193° и 262°.
182
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
4. Растяжение в главном направлении. Пусть усилия р
направлены параллельно главному направлению упруго-
упругости х7 т. е. ф = 0 (рис. 55). Тогда напряжение Се У края
отверстия определится по формуле C2.11), где
г»
/(в)= -^M--
C2.14)
Распределение напряжений симметрично относительно
главных направлений упругости. В точках А и Ль на кон-
концах диаметра, параллельного
усилиям, и в точках В и В\ на
концах диаметра, перпенди-
перпендикулярного к усилиям, имеем
/а = — —, /д = 1 + п.
C2.15)
Одно из этих значений
будет наибольшим для всей
пластинки, другое — наи-
наименьшим, причем в пластин-
пластинке с сильно выраженной ани-
анизотропией наибольшим может
оказаться не /в, а | /а |. Без-
Безразмерные величины }в и ) /л )
называют коэффициентами
концентрации напряжений
(растягивающего и сжимаю-
сжимающего). В таблице 13 приведе-
приведены значения | /а | и /в для
восьми ортотропных пласти-
пластинок, рассмотренных выше,
при растяжении в направ-
направлении большего модуля Юнга и меньшего модуля.
Как видно из таблицы, коэффициент концентрации
растягивающих напряжений для всех восьми материалов
получается больше, если пластинка растягивается в
направлении наибольшего модуля Юнга, причем во всех
случаях/в X /а !• У четырех рассмотренных стеклопласти-
стеклопластиков коэффициенты концентрации растягивающих напря-
напряжений меньше, чем у четырех видов фанеры.
Рис. 55.
32] ОРТОТРОПНАЯ ПЛАСТИНКА. КРУГОВОЕ ОТВЕГСТИЕ 183
Таблица 13
Коэффициенты концентрации напряжений для анизотропных
материалов при растяжении в главном направлении
i) *~jW
/в
o\ E» — rp
I/aI
/b
Фанера
резовая
ю
0,707
5,453
1,414
4,149
с
и
0,879
4,788
1,138
4,330
о
и
0,822
4,636
1,217
3,989
е
с
е
0,894
4,943
1,119
4,524
(
t?
'. ее
tog.
О ее
н И
о о
^g
Кс?
0,496
4,672
2,018
2,819
Стеклопластики
. »
э тогональ
-армирова
°s
0,853
4,081
1,172
3,629
и
0,903
3,566
1,107
3,318
о
и
Осе
Ш
0,855
3,904
1,169
3,484
На рис. 55 даны графики распределения о*е по краю
отверстия в пластинке, изготовленной из березовой фа-
фанеры, при растяжении усилиями в направлении, для ко-
которого модуль Юнга наибольший (в направлении волокон
рубашки). График напряжений при растяжении в нап-
направлении меньшего модуля Юнга мало отличается по
характеру от представленного на рис. 55. Очевидно, что
если нужно пластинку с круговым отверстием растягивать
в главном направлении, то выгоднее это делать так, чтобы
направления усилий были параллельны направлению, для
которого модуль Юнга имеет наименьшее значение. За-
Заметим, что при растяжении под углом 45° к главному нап-
направлению наибольшие растягивающие напряжения полу-
получились еще меньше C,3 р). В связи с этим намечается ряд
задач об установлении оптимального направления уси-
усилий, при котором получается наименьшая из возможных
для данной пластинки концентрация напряжений; этими
вопросами мы здесь заниматься не будем.
5. Сдвиг усилиями, произвольно ориентированными по
отношению к главным направлениям упругости. Пусть
имеется прямоугольная пластинка с малым круговым от-
184 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
верстием в центре, у которой одно из главных направле-
направлений упругости образует углы ф и л/2 — ф со сторонами.
По краям распределены равномерно уравновешенные ка-
касательные усилия интенсивности ?, действующие, следо-
следовательно, под углами ф и я/2 — ф с главными направле-
направлениями; контур отверстия не загружен и не закреплен.
Рассматриваем пластинку как бесконечную, и относим
усилия на бесконечность. В этом случае вблизи контура
(Ге = */(в), C2.16)
где
/ (9) = J± A + к + п) { - п cos 2ф sin 20 +
+ [(к + 1) cos 20 + к — 1] sin 2Ф}. C2.17)
Для изотропной пластинки
/ @) = 4 sin 2 @ - ф). C2.18)
В частности, если усилия действуют под углами 45
и 135° к главным направлениям, то формула C2.17)
принимает вид
/ @) = --J- A + к + п) [(к + 1) cos 20 + к - 1]. C2.19)
В этом случае наибольшее напряжение в ортотропной
пластинке должно получиться в точках пересечения глав-
главных направлений с окружностью — А9 Аг и 5, В1у для
которых
fA=* i + hk + n, /в = -A+ * + »). C2.20)
В таблице 14 приведены значения коэффициентов кон-
концентрации напряжений /а, | /б | для восьми ортотропных
материалов. Ось х совпадает с направлением, для которого
модуль Юнга наибольший. Там же дается угол Оо в пер-
первом квадранте, определяющий точку, где (Те = 0.
Здесь также наибольшая концентрация напряжений
получается в пластинке из березовой фанеры; график
распределения напряжений в такой пластинке показан
на рис. 56.
6. Сдвиг усилиями, параллельными главным направле-
направлениям. Предположим, что прямоугольная пластинка с от-
отверстием вырезана из ортотропного листа так, что стороны
§ 32] ОРТОТРОПНАЯ ПЛАСТИНКА. КРУГОВОЕ ОТВЕРСТИЕ 185
Таблица 14
Коэффициенты
углом 45(
/а
во
концентрации напряясений при
Фанера
§
03
;резо
to
4,856
6,867
50°
и
м
5,209
5,926
47°
и
е
и
2,811
5,853
47°
8
е
5,418
6,062
46°
сдвиге под
Стеклопластик!
и а
i§
СТЗ (-Г
к§
3,315
6,690
55°
ё|
«5
§|
о В
4,488
5,253
47°
S
и
4,221
4,673
46°
г
и
ОСО
СТТ(
ПН-
<я
4,339
5,073
47°
ее параллельны главным направлениям упругости и по
этим сторонам равномерно распределены касательные
Рис. 56.
усилия интенсивности t. Полагая пластинку бесконечной
и относя усилия на бесконечность, получим, полагая
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
в C2.17) ф = 0:
/(8)=-
n) sin 20. C2.21)
Очевидно, что напряжение принимает значение, равное
нулю, в четырех точках окружности и в каких-то симмет-
симметричных точках четырех квадрантов достигает наибольшего
по величине значения:
tfmax ~ ^/так- C2.22)
Коэффициент концентрации /шах для изотропной пла-
пластинки равен четырем, а для восьми ортотропных мате-
материалов найдется из таблицы 15,
Таблица 15
Коэффициенты концентрации при сдвиге усилиями, парал-
параллельными главным направлениям
мпах
а
Фанера
§
о
3,94
75°
и
и
3,53
71°
3,58
69°
е
и
е
3,55
72°
Стэклоп ластики
«а
НД
2 °
к о
4,36
69°
is и
5К
§§.
IS
о X
3,53
61°
н
и
3,66
50°
о
'я
О со
3,61
61°
где указаны также углы а в первом квадранте, которым
соответствуют наибольшие по величине напряжения
(с точностью до 1°). Ось х параллельна направлению наи-
наибольшего Е.
В противоположность случаю 5 здесь коэффициенты
концентрации незначительно отличаются от коэффициен-
коэффициента для изотропной пластинки (/max = 4). Наибольшим
из восьми коэффициентов получается /тах для намоточ-
намоточного однонаправленного стеклопластика и далее — для
березовой фанеры. Заслуживает внимания то обстоятель-
обстоятельство, что для семи материалов из восьми коэффициент
/max получается меньше коэффициента концентрации для
§ 32] ОРТОТРОПНАЯ ПЛАСТИНКА. КРУГОВОЕ ОТВЕРСТИЕ 187
изотропной пластинки. Отсюда следует очевидный вывод:
вырезать пластинку нужно так, чтобы касательные уси-
усилия были параллельны главным направлениям упру-
упругости.
На рис. 57 показан график распределения напряже-
напряжений в пластинке из березовой фанеры.
Приведенные выше формулы для напряжения о*о вбли-
вблизи края отверстия показывают, что это напряжение опре-
определяется с помощью различных комбинаций двух незави-
независимых параметров кип. Первый выражается через отно-
отношение главных модулей Юнга, а второй зависит также от
модуля сдвига и играет большую роль в определении кон-
концентрации напряжений. Для данной пластинки может
оказаться, что главные модули Юнга равны (Ег = Е2), и
тем не менее, благодаря модулю сдвига параметр п зна-
значительно отличается от двух, что и вызывает в любом рас-
рассмотренном случае^очень большую концентрацию напря-
188 прямолинейно-анизотропное тело [гл. 4
жений. Следовательно, анизотропия однородного анизо-
анизотропного тела, работающего в условиях плоской задачи,
характеризуется не одним, а двумя параметрами или по-
показателями анизотропии 1). Правда, пара чисел (к, п) еще
не позволяет дать количественную оценку степени анизо-
анизотропии, так как может случиться, что напряжения в ани-
анизотропном теле окажутся по величине точно такими же,
как и в изотропном, несмотря на то, что кип значительно
отличаются от единицы и двух (например, в случаях рас-
растяжения, сдвига и чистого изгиба пластинки без отвер-
отверстия). Поэтому желательно выбрать показатели анизотро-
анизотропии так, чтобы они давали возможность оценивать сте-
степень или интенсивность анизотропии разных тел. Здесь
возможен различный выбор параметров или показателей
анизотропии.
Говоря только о плоской задаче для однородного
прямолинейно-анизотропного тела, можно исходить из
простейшего случая упругого равновесия бесконечной
пластинки с отверстием — одностороннего растяжения.
Примем за первый показатель анизотропии аг отношение
наибольшего нормального напряжения, возможного для
пластинки с круговым отверстием, к наибольшему напря-
напряжению в изотропной пластинке, работающей в тех же усло-
условиях. За второй показатель а2 примем отношение наимень-
наименьшего напряжения в указанной анизотропной пластинке
к наименьшему напряжению в изотропной пластинке.
Если анизотропная пластинка с круговым отверстием
растягивается под углом ф к фиксированной оси х, то на-
напряжение на контуре отверстия представится формулой
tfe = Pf (8; ф). C2.23)
Если менять угол ф, то будут меняться как максималь-
максимальное, так и минимальное напряжения (см. рис. 54 и 55) и
при некоторых значениях ф они достигнут наибольшего
и наименьшего из всех возможных для данной пластинки
значений. Показатели анизотропии определятся по фор-
формулам
Ц aa = |/|mIn. C2.24)
х) Исключением являются горные породы, псследованные в
работе С, А. Ватутина и Р. К. Ниренбург [47].
§ 33] ПЛАСТИНКА С ЭЛЛИПТИЧЕСКИМ ЯДРОМ 189
В частности, для ортотрогшой пластинки
к, C2.25)
причем эти максимальное и минимальное значения дости-
достигаются, когда пластинка растягивается в направлении х,
для которого модуль Юнга наибольший.
Для березовой фанеры получаем
аг = 2,151, а2 = 0,707.
Для стеклопластика АСТТ(б)-С2-0 и ПН-3:
аг = 1,6357 а2 = 0,855.
Для изотропного тела а± = аг — d. Березовую фане-
фанеру и указанный стеклопластик следует признать материа-
материалами с достаточно сильно выраженной анизотропией.
Выражение коэффициента / @; ф) для неортотропной
пластинки, растягиваемой под углом ср к оси х, можно
получить на основании данных §^30 и мы его приводить
не будем.
Заметим, что в других случаях упругого равновесия
(кручение, изгиб, деформации тел вращения и т. д.) пока-
показатели анизотропии должны быть выбраны иначе, но мы
этого вопроса рассматривать не будем.
§ 33. Определение напряжений в однородной
пластинке с эллиптическим и круглым ядром
Пусть имеется анизотропная пластинка произвольно-
произвольного очертания с эллиптическим отверстием, малым по срав-
сравнению с размерами пластинки и расположенным далеко
от края, в которое впаяно без зазора и предварительного
натяжения ядро из другого материала той же толщины.
По краю пластинки распределены, вообще говоря, произ-
произвольные усилия, действующие в ее плоскости; к ядру
внешних сил, кроме контактных, усилий, действующих со
стороны пластинки, не приложено. Объемные силы от-
отсутствуют.
Мы будем рассматривать, как и раньше, область плас-
пластинки как бесконечную плоскость с эллиптическим выре-
вырезом и считать, что внешние усилия приложены на беско-
бесконечности.
190
ШЯМОЛИНЕЙНОАНИЗОТГОПНОЕ ТЕЛО
[Гл. 4
Приняв центр эллипса за начало координат, направим
оси х, у по его главным осям (рис. 58). Уравнение эллип-
эллипса зададим в параметрическом виде:
х = a cos Ф, у = Ъ sin
C3.1)
Все величины для ядра — напряжения, перемещения,
деформации, коэффициенты деформации, в отличие от тех
же величин для пластинки,
мы будем отмечать штриха-
штрихами.
Если пластинка не явля-
является ортотропной, но имеет
в каждой точке плоскость уп-
упругой симметрии, параллель-
параллельную срединной, то уравне-
уравнения обобщенного закона Гука
для нее, связывающие сред-
средние по толщине значения
компонент деформации и на-
напряжений, запишутся следу-
следующим образом (черты над ах, Оу, txy, и, v, обозначающие
осреднение, опускаем):
ех = апох
Рис. 58.
a12oy
¦ Л22а«
#26^я?/»
Ухи =
C3.2)
Такие же уравнения для ядра (у которого также име-
имеется плоскость упругой симметрии, параллельная средин-
срединной) имеют вид:
еу .=
Уху =
C3.3)
Полагая, как и во всех предыдущих случаях, деформа-
деформации малыми, будем решать задачу приближенно, путем
наложения напряжений в пластинке конечных размеров,
без ядра и напряжений в бесконечной пластинке с эллип-
эллиптическим отверстием, нагруженным по краю внешними
усилиями; последние будем подбирать так, чтобы на по-
ПЛАСТИНКА С ЭЛЛИПТИЧЕСКИМ ЯДРОМ
101
верхности контакта ядра и пластинки выполнялись нуж-
нужные условия.
Обозначим через F0, в°х, сг°, тху, и0, v° — функцию на-
пряжений, составляющие напряжений и проекции переме-
перемещений в пластинке без ядра, Фх (%), Ф2 (z2) — функции
усложненных комплексных переменных в пластинке с от-
отверстием. Тогда формулы для напряжений и перемещений
в пластинке с ядром можно представить в таком виде:
- 2Re [ц?Ф', (zx) -
ах =
2Re
v =
Здесь
2Re
2Re
Ф2],
(z2)] —
uOj
а22
— «26,
C3.4)
C3.5)
C3.6)
(* = 1,2),
ю, щ, v0 — постоянные, характеризующие жесткие сме-
смещения в плоскости ху, \1ц — комплексные параметры —
корни уравнения v
а4 - 2а1вц3 +
Bаи + а66)|л2 —
+ а22 - 0, C3.7)
предполагаемые неравными.
Напряжения в упругом
ядре определятся через функ- О
цию F' или через две функ- Рис 59
ции переменных z[ = х + \*>[ У>
2^ = х + |и2г/, где |i|, \i2 — комплексные параметры мате-
материала ядра.
Условия в точке на поверхности контакта запишутся
так (рис. 59):
Ап = —An, * п
U =
17 =
192
ЙРЙМОЛЙНЕЙНО-АЙИЗОТРОПНОЕ ТЕЛО
(Гл. 4
Преобразуя первые два условия путем интегрирования
по дуге контура, получим уравнения, из которых должны
быть определены функции Фг и Ф2:
2Re[
2Re|
2He[
с2,
C3.9)
= U — Uq -f- i
+ ^Фг] = v' — v0 — (ox — y0. >
Ход решения такой же, как в случае бесконечной плас-
пластинки с отверстием, край которого нагружен заданными
усилиями. В общем случае нагрузки вид комплексных по-
потенциалов Фх, Ф2 известен:
• 2i Am?m,
7П=1
Ф2
C3.10)
где
(ft = 1, 2). C3.11)
Простейшими будут случаи, когда нагрузки (нормаль-
(нормальная и касательная) распределены по внешнему краю рав-
равномерно. Рассмотрим их. При принятых упрощениях
имеем
Ох = р, cjy = q, Xx\j = t C3.12)
(известные постоянные);
F° = 4- Qx* — tzy+4r РУ2- C3.13)
Исследование показывает, что мы сможем удовлетворить
условиям C3.8) только тогда, когда распределение напря-
напряжений в ядре также будет равномерным:
в'х = А, в'у=В, %'ху = С C3.14)
(неизвестные постоянные);
F = 4" Вхг -
Ау\
C3.15)
§ 33]
ПЛАСТИНКА С ЭЛЛИПТИЧЕСКИМ ЯДРОМ
193
Добавочные напряжения в пластинке, выражающие
влияние ядра, определятся с помощью функций вида
Ф1 («О =
~~ Р) Ы ~ {В ~
L—[(A-p)bi-
±,
C3.16)
Три неизвестные А, В, С (напряжения в ядре) и чет-
четвертую — разность вращений со' — со — мы найдем из че-
четырех уравнений C3.9). Подробно выписывать эти урав-
уравнения мы не будем, равно как и получившиеся выражения
Ф1э Ф2, которые довольно громоздки.
Эти уравнения в развернутом виде имеются в нашей
работе [61] и книге [21] (стр. 176) и мы можем для случая
неортотропного тела их не выписывать, отсылая интере-
интересующихся к указанным работам. В случае же, когда плас-
пластинка и ядро ортотропны (а16 = а2е = a1Q = а2в = 0), си-
система четырех уравнений C3.9) распадается на две
элементарные системы, которые мы приводим:
А (п + апс) —
а12 — а'12)
\-B(nc — >
= P + q{nc + к),
С (п + к -(- а12) jp— = t (nc + к + а12),
С [с + n + kc(yl2 + v'ee)] + -?- К - со) =
Здесь обозначено:
C3.17)
с =
C3.18)
7 С. Г. Лемипний
194 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
кип — вещественные параметры пластинки (см. §§ 31,
32). Несколько сложнее решается задача в случаях, ког-
когда ядро впаяно или вогнано в отверстие с натяжением.
Задача значительно усложняется, если ядро вложено
в отверстие и контакт иа некоторых участках контура мо-
может нарушаться.
§ 34. Растяжение ортотропной пластинки
с круговым ядром
В виде примера рассмотрим прямоугольную ортотроп-
ную пластинку с круговым отверстием, в которое впаяно
или вклеено без натяжения круговое ядро того же диамет-
диаметра из другого ортотропного материала, упругого или аб-
абсолютно жесткого (недеформируемого). Предполагается,
что главные направления пластинки и упругого ядра па-
параллельны сторонам пла-
пластинки. По двум противопо-
противоположным сторонам равномер-
равномерно распределены нормальные
усилия, приводящиеся на
каждой из нагруженных
сторон к растягивающей си-
силе (рис. 60).
Для нас представляют
Рис. 60. интерес только случаи, когда
модули упругости ядра не рав-
равны модулям упругости плас-
пластинки. Таких случаев может быть практически неограни-
неограниченное количество и изучить их все нет никакой возмож-
возможности.
Мы ограничимся исследованием только частного
случая, когда коэффициенты деформации ядра вдвое боль-
больше одноименных коэффициентов пластинки (а^ = 2atj),
сопоставляя полученные результаты с результатами для
абсолютно жесткого ядра (а^ = 0, ац Ф 0) и для плас-
пластинки с отверстием, ничем не заполненным (ац = оо, atj
конечны). Как и в ранее решенных задачах, мы будем
считать упругие постоянные пластинки равными упругим
постоянным березовой фанеры, а область пластинки рас-
рассматривать как бесконечную плоскость с вырезом, относя
§ 34] РАСТЯЖЕНИЕ ПЛАСТИНКИ С КРУГОВЫМ ЯДРОМ
195
растягивающие усилия на бесконечность. Решение задачи
имеется в работах [62] и [21] (стр. 179).'
При равномерном растяжении в главных направле-
направлениях напряжения в ядре равны
</я = Л, а:1 = В, т'хи = С. C4.1)
Определив постоянные А и В из уравнений C3.17) (С =
= со' —. о) = 0), мы после элементарных преобразований
получим формулы для напряжений в ядре:
n) —1],
C4.2)
Здесь р — интенсивность усилий в кгс/см*, vx = v12, v2 =
= v21 и
A = n2 + 2n A + Щ + 3ft - vx B + v2ft). C4.3)
Определив напряжения в пластинке и перейдя к ци-
цилиндрическим координатам, получим после преобразова-
преобразований на поверхности контакта:
= Р-7ГГ {(* + 4-)sin60 + [п2- 2к +
sin49cos20
(l+n)bt 1
X sin29cos4 9 + -J- ?• cos6 0| . C4.5)
Здесь обозначено:
bi = n2 — к -\- vx + B — ViV2) kn,
fe3 = n _ v, + B —
64 =- [vi (n2 + n - &) + 2 - vxv2]
определяется по формуле C2.2) (§ 32).
196
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
Если ядро абсолютно жесткое (недеформируемое), то
формулы для напряжений в ортотропной пластинке мы
получим, определив коэффициенты А, В из уравнений
C3.17), где нужно положить а^ = а'ц = у'у = 0. Напря-
Напряжения на поверхности контакта определятся по прежним
формулам C4.4) и C4.5), но только коэффициенты Ьг и де-
делитель А будут выражены иначе:
h — — (n2 — к + Vi + ViV2/cw), '
= — (n — Vi + v
= v2 (rc2 + гг — к
C4.7)
Д = n2 __ k A + vxv2) + 2vx. C4.8)
Получим напряжения crr и тГ9 на поверхности контакта:
+ [^г2 + п — /с + v2 — 1
tro = — -^- [л2 + л — А; +
v2fc A + п)] cos 29),
v2k A + n)] sin 29.
C4.9)
Для сто получается более сложная формула и мы ее выпи-
выписывать не будем, а укажем еще выражения для напряже-
напряжений в точках пересечения линии контура отверстия и глав-
главных осей упругости А, Аг, В, Вх (см. рис. 60):
Юа - -f (п2 + п - к + Vl), (сте)л = v2 (сгг)А; C4.10)
Юв = -f-ll - v2ft(l f n)], (ав)в = V! (аг)в. C4.11)
В таблице 16 даны численные значения всех трех на-
напряжений на контуре отверстия в пластинке из березовой
фанеры с круглым жестким ядром и с упругим ядром, у
которого ац = 2atj [62]. Для сравнения в последнем столб-
столбце приведены значения напряжений сто в фанерной плас-
пластинке с круглым отверстием, ничем не заполненным. Рас-
Растяжение производится в направлении, для которого мо-
модуль Юнга наибольший.
§34]
РАСТЯЖЕНИЕ ПЛАСТИНКИ С КРУГОВЫМ ЯДРОМ
197
Таблица 16
Напряжения на контуре отверстия в фанерной пластинке
с жестким и упругим ядрами и без ядра при одностороннем
растяжении
е°
0
15
30
45
60
75
90
Жесткое ядро
1,237
1,156
0,937
0,698
0,338
0,119
0,039
0
-0,299
—0,519
—0,599
—0,519
—0,299
0
0,044
0,093
0,270
0,516
0,699
0,564
0,003
Упругое ядро (a^j =
0,841
0,784
0,627
0,413
0,198
0,041
-0,016
•*гв'р
0
-0,214
-0,371
-0,429
—0,371
—0,214
0
aQ'V
—0,0G2
0,031
0,231
0,488
0,784
1,186
1,084
Ядро
отсутствует
—0,707
-0,340
0,069
0,404
0,964
2,571
5,453
На рис. 61 показаны (в виде полярных диаграмм) гра-
графики распределения напряжения аг по краю отверстия
-упругое ядро
-жесткое ядро
- —.
%
Рис. 61.
в пластинке из березовой фанеры. Сплошная кривая —
распределение напряжений в пластинке с упругим ядром
(ац = 2аи), пунктирная — то же в случае абсолютно жест-
жесткого ядра. На рис. 62 — графики напряжения (Ге^для
С
др ри. 6 графики напряжения (Ге^для
такой же пластинки. Сплошная кривая показывает распре-
198
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 4
деление напряжений в пластинке с упругим ядром, у ко-
которого ciij = 2atj, пунктирные кривые — графики напря-
напряжений в пластинке с жестким ядром и в пластинке без
ядра.
Если ядро жесткое, то наибольшим из трех является
напряжение аг на концах диаметра, параллельного
11¦'
ft/.
у пру г се ядро
жестш^ ядро
Рис. 62.
растягивающим усилиям; оно райно а = 1,237/?. При от-
сутствиы ядра наибольшим является напряжение сгэ; оно
равно ere = 5,453/J и получается на концах диаметра, пер-
34!
РАСТЯЖЕНИЕ ПЛАСТИНКИ С КРУГОВЫМ ЯДРОМ
199
пендикулярного к направлению растягивающих усилий.
В данном частном случае упругого ядра (ац = 2аи) ве-
величина наибольшего нормального напряжения находит-
находится между указанными двумя; оно равно сг0 = 1,684/>
д.
/
( иЧ'
\
\
\
\
ч
\ <
\ **-
Ук
ч
\ f
Ч t j
*^
К у / ^
/ _ упругое ядро
1 жесткое ядро
/ ядро отсутстдует
Рис. 63.
и получается на концах диаметра, нормального к направ-
направлению усилий.
При растяжении пластинки в направлении, для кото-
которого модуль Ег является наименьшим, качественная кар-
картина распределения напряжений не меняется; изменятся
только величины напряжений в отдельных точках.
В пластинке без ядра (cro)max: = 4,153/?, а в пластинке с
упругим ядром (а'ц = 2яо)(сге)тах = 1,603р. Отсюда мож-
можно заключить, что выгоднее пластинку вырезать из листа
фанеры так, чтобы растяжение производилось в направ-
направлении, для которого модуль Юнга является наименьшим.
Так же просто решается задача для всех случаев, когда
а'ц = каи (X ф 2).
200
прямолинейно-анизотропное тело
[Гл. 4
Приведем без вывода основные результаты для беско-
бесконечной фанерной пластинки с круговым ядром, растяги
ваемой равномерно по всем направлениям нормальными
усилиями — таблицу значений напряжения вв на кон-
контуре (таблица 17) и графики (рис. 63).
Таблица 17
Напряжения на контуре отверстия в
фанерной пластинке при всестороннем
растяжении
0
15
30
45
60
75
90
60IV
Жесткое
ядро
0,047
0,460
0,896
0,960
0,927
0,646
0,098
Упругое
ядро
1,541
1,307
1,092
1,022
1,043
1,218
1,557
Ядро
отсутствует
3,422
2,383
1,411
1,092
1,226
2,178
4,039
Остальные две составляющие аг и тге в общей картине
напряженного состояния играют второстепенную роль.
Нормальное напряжение распределено по контуру жест-
жесткого ядра почти равномерно, а касательное мало (не боль-
больше 0,03 р).
§ 35. Замечания относительно решения плоской
задачи и задачи обобщенной плоской деформации
для бесконечной плоскости с вырезом
Изложенные в §§ 30—34 решения задач для бесконеч-
бесконечной плоскости с эллиптическим или круговым вырезом
(пустым или заполненным) являются точными. Они полу-
получаются очень просто — методом Н. И. Мусхелишвили,
основанном на применении конформного отображения
и степенных рядов. Не менее просто получаются решения,
если вместо степенных рядов использовать аппарат ин-
интегралов типа Коши (см. [21], гл. VI, § 37).
Гораздо сложнее решить плоскую и обобщенную плос-
плоскую задачу для бесконечной плоскости с замкнутым вы-
вырезом иной формы, не эллиптическим и не круговым. По-
§ 35 НЕКОТОРЫЕ ЗАМЕЧАНИЯ 201
ка удалось получить только эффективные приближенные
решения двумя путями: 1) рассматривая контур выреза,
как мало отличающийся от кругового или эллиптического
и 2) рассматривая тело, как слабо анизотропное. В том
и в другом случае вводятся параметры, характеризующие
отклонение выреза от эллиптического или кругового, ли-
либо параметры, характеризующие отклонение тела от изо-
изотропного, и функции комплексных переменных или функ-
функции напряжений разыскиваются в виде рядов, располо-
расположенных по степеням этих параметров. Таким образом,
задача сводится либо к ряду задач для бесконечной плос-
плоскости с эллиптическим вырезом, либо к ряду задач для
изотропной среды (в зависимости от того, какой путь из-
избрать). В процессе решения степени или произведения па-
параметров отбрасываются, начиная со 2-го, 3-го, 4-го и
т. д. порядков.
Целый ряд приближенных решений, найденных как
первым путем, так и вторым, имеется в нашей книге [211
(гл. VII и VIII) и работах [61] и [63], причем приводятся
результаты подсчета напряжений в важнейших точках
для пластинки с заданными упругими постоянными и со-
сопоставления величин последовательных приближений.
Пока еще сходимость таких процессов математически стро-
строго не обоснована.
Легкость решения задачи для плоскости с эллиптиче-
эллиптическим или круговым вырезом объясняется тем, что три,
четыре и даже сколько угодно областей — S (заданную)
и S]i (к = 1, 2, 3...) — вспомогательные, полученные из S
путем аффинного преобразования, можно одновременно
отобразить на внешность единичного круга, и притом так,
что точкам А и Ак на контурах областей S и 5ft, находя-
находящимся между собой в аффинном соответствии, отвечает
одна и та же "''точка сгна контуре единичного
круга. Таким образом, граничные значения функций Ф^
удается выразить через одну переменную а. Этим же свой-
свойством обладают бесконечные области, ограниченные кри-
кривой второго порядка — параболой или гиперболой'(и ко-
конечно, прямой).
Если вырез в бесконечной плоскости не является эл-
эллиптическим или круговым, то одновременное отображе-
отображение областей S и 5к на внешность единичного круга при
непременном соблюдении указанного условия аффинного
202
ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО
[Гл 4
соответствия становится невозможным: точкам А и Ак,
находящимся в аффинном соответствии, будут отвечать
разные точки на контуре единичного круга — аи
tffc, которые могут совпасть лишь для отдельных точек
контура области S. Это значительно усложняет задачу,
так как граничные.значения Фк в аффинно-соответствен-
ных точках не удается достаточно просто выразить через
одну переменную а; если Фк ищутся в виде рядов, то для
коэффициентов их получатся бесконечные, достаточно
сложные системы.
§ 36. Радиальное распределение напряжений
в непрерывно-неоднородной упругой полуплоскости
В § 29 было исследовано распределение напряжений
в упругой однородной ортотропной полуплоскости под
действием сосредоточенной силы, приложенной к грани-
границе, и отмечены характерные особенности этого распреде-
распределения: оно является радиальным, причем (в плоскости по-
поперечного сечения) нормальное напряжение обратно про-
пропорционально расстоянию г от точки приложения силы.
Посмотрим, как обстоит дело в непрерывно-неоднород-
непрерывно-неоднородной полуплоскости.
Имеется упругое непрерывно-неоднородное полупрост-
полупространство, находящееся в состоянии плоской деформации
под действием усилий, рав-
равномерно распределенных
вдоль прямой на ограни-
ограничивающей плоскости или
плоскопараллельная пла-
пластинка под действием со-
сосредоточенной силы. В том
и другом случае мы будем
иметь в сечении упругую
полуплоскость, которую
примем за координатную
Рис. 64. плоскость ху\ в данном
случае удобнее направлять
ось у внутрь полуплоскости, а полярный угол 9 отсчиты-
отсчитывать от этой оси. В точке границы, принятой за начало
координат, приложена сосредоточенная сила под произ-
произвольным углом со к оси у (рис. 64). Поставим задачу еле-
§ 36] НЕОДНОРОДНАЯ ПОЛУПЛОСКОСТЬ 203
дующим образом: определим, какими функцияхми должны
быть упругие характеристики, чтобы распределение на-
напряжений было радиальным, и найдем это распределение.
Даже в такой узкой постановке вопрос оказывается
достаточно объемистым в случае анизотропной среды, а
поэтому мы еще более сузим задачу: рассмотрим только
изотропную полуплоскость [66].
Полагая, что из трех составляющих напряжений плос-
плоской задачи только одна аг не равна нулю, а о"е = тге = 0,
запишем основную систему уравнений равновесия упру-
упругого тела таким образом:
¦^-Ь —= 0; C6.1)
= ~пТ О~г,
дг " Е'
1 duQ ur \i
1 диг дщ ив ^
C6.2)
Здесь в случае обобщенного плоского напряженного
состояния Е' = Е, \х = v — модуль Юнга и коэффициент
Пуассона, в случае же плоской деформации
Я' = Т^5-' f^T^V- C6.3)
Из уравнения C6.1) получаем
or = -^- , C6.4)
где / @) — функция, которую нужно определить на осно-
основании уравнений C6.2). Исключая из них перемещения
(путем дифференцирований и вычитания, см. § 23) получим
окончательно уравнение:
Распределение напряжений будет радиальным, если
функция и переменные упругие характеристики удовлет-
удовлетворяют уравнению C6.5).
204 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
Рассмотрим более подробно частный случай: коэффи-
коэффициент Пуассона — величина постоянная, а модуль Е' есть
произведение функции полярной координаты г на функ-
функцию координаты 0:
Е' - Er (r)EQ (9). C6.6)
Подставляя C6.6) в уравнение C6.5) и разделяя пере-
переменные (что оказывается возможным), получим уравнения
для функции 1/Ег переменной г и для функции f/Ев пере-
переменной 6:
Ш+иЧ=0' C6-8)
где
n =/A-а)A + ^а), C6.9)
a — произвольная постоянная (вещественная). Интегри-
Интегрируя C6.7) и C6.8), получаем
^; C6.10)
-L- = AcosnO + В sin тгв. C6.11)
Таким образом мы находим модуль Е\ обеспечиваю*
щий радиальное распределение напряжений:
где Сг, С2 — произвольные (заданные) постоянные, не
равные одновременно нулю, EQ — произвольная функция
угла, но при этом выражение C6.12) только тогда имеет
физический смысл, когда оно положительно. Напряже-
Напряжение аг при п вещественном определится по формуле
ar = -^ (A cosne+ BsinnQ); C6.13)
это будет иметь место, когда подкоренное выражение
C6.9) положительно. Постоянные А ж В определятся из
условий равновесия полукруга, вырезанного из полуплос-
36l НЕОДНОРОДНАЯ ПОЛУПЛОСКОСТЬ 205
кости произвольным радиусом г:
я/2
\ ar sin QrdQ-\-p sin со = 0,
~п/2 I C6.14)
71'2
\ ar cos Qr dQ -\- p cos ш = 0.
—7t2
Если га окажется чисто мнимым (так как а может быть лю-
любым вещественным числом), то в формуле C6.13) косинус и
синус должны быть заменены соответствующими гипер-
гиперболическими косинусом и синусом. Наконец, если а = 1
или а = —1/[х, то п = 0, и вместо C6.13) имеем формулу
<гг = -^!D6 + #). C6.15)
Остановимся на случае, когда модуль Е' меняется про-
пропорционально какой-нибудь степени т расстояния у от
границы полуплоскости:
Е = Етут - Emrm cosm G (fim = const). C6.16)
Такую зависимость мы получим, полагая в C6.12) Сг = 1,
С2= 0, а = —т и Ед = Ет cosm0.
Напряжение определится по формуле:
аг = cosr ° (Л cos ^9 + В sin ив), C6.17)
где
Y C6.18)
Пусть модуль Е' меняется пропорционально расстоя-
расстоянию от границы (Е1 = Егу), на которую действует нормаль-
нормальная сила р, а материал — несжимаем (v = 0,5). В случае
обобщенного плоского напряженного состояния т = 1,
[г = 0,5, тг=1. Окончательная формула для напряжения
имеет вид:
^-. C6.19)
Линии одинаковых напряжений (изобары) будут иметь
каплеобразную форму (рис. 65).
206
ШЯМОЛШ1ЕЙНОАНИЗОТ1 ОШЮЕ ТЕЛО
[Гл. 4
Если модуль меняется обратно пропорционально рас-
расстоянию от границы (?" = Е-г/у) и сила приложена нор-
нормально к границе, то получается совсем другая картина:
напряжение определяется по формуле
<*г - - -~ , C6.20)
а линии одинаковых напряжений будут незамкнутыми, а
именно, прямыми, параллель-
параллельными границе.
Содержание настоящего па-
параграфа, где рассмотрено всего
несколько случаев, дает пред-
представление о том, насколько об-
обширна рассматриваемая область
науки и насколько разнообраз-
разнообразными могут быть распределения
напряжений в непрерывно-не-
непрерывно-неоднородной среде. Практически
число различных случаев рас-
распределений неограниченно ве-
велико, как неограниченно велико
число всевозможных заданий
упругих характеристик, как
функций координат. То же са-
самое можно высказать и по поводу следующей задачи
для неоднородного тела, разбираемой в § 37.
Н. А. Ростовцев дал общее решение задачи о радиаль-
радиальном распределении напряжений, используя методы сов-
современной математики, из которого все решения этого па-
параграфа получаются как частные случаи. К сожалению,
за недостатком места мы не можем изложить здесь эти в
высшей степени интересные результаты и вынуждены ото-
отослать читателя к работе [86].
§ 37. Растяжение и изгиб моментами
прямоугольной пластинки
Задача о растяжении осевой силой и изгибе момента-
моментами однородного стержня с прямолинейной анизотропией
имеет совершенно элементарное решение (гл. 2). Но эта же
задача может значительно усложниться, если стержень
§ 37] РАСТЯЖЕНИЕ И ИЗГИБ МОМЕНТАМИ ПЛАСТИНКИ 207
является непрерывно-неоднородным. Рассмотрим вкрат-
вкратце один из простейших случаев неоднородного стержня.
Пусть имеется стержень в виде прямоугольной плас-
пластинки с сечением в виде узкого прямоугольника, упругий
и непрерывно-неоднородный, у которого длинные сторо-
.р
Рис. 66.
ны свободны от усилий и закреплений, а короткие (тор-
(торцы) нагружены одинаковыми усилиями, приводящимися
к осевой силе Р и моменту М, действующими в срединной
плоскости, принимаемой за плоскость ху. Будем считать
стержень ортотропным, с упругими характеристиками, не
меняющимися по толщине; один торец предполагаем за-
закрепленным (рис. 66).
Длину, толщину и высоту обозначаем через Z, /г, Ь;
силу Р и момент М относим к единице толщины. В рассмат-
рассматриваемом случае можно считать, что напряженное со-
состояние — обобщенное плоское; черточки над составляю-
составляющими напряжений и перемещений, обозначающие осред-
осреднение по толщине, будем всюду отбрасывать.
Предположим, что в неоднородном стержне, так же
как и в однородном, только одна составляющая ох не рав-
равна нулю, a of,, = тГу = 0; ах будет функцией только у.
Уравнения обобщенного закона Гука дают три уравнения
для средних перемещений и напряжений:
дх - Ег ' ду " ех °х> ду ^"д^ - и' \61Л>
Из первых двух следует *)
у^ - щ + и0, v = - ^^2. dy + сот + i;0. C7.2)
х) Здесь мы сразу вводим жесткие перемещения со, u0, vOi ко-
юрые, строго говоря, появляются, когда мы удовлетворяем треть-
третьему уравнению C7.1).
208 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
Третье уравнение, после дифференцирования по х и у,
дает уравнение, связывающее модуль Юнга, коэффициент
Пуассона и напряжение
д2 I v \
H- C7-3)
Если условие C7.3) выполнено, то распределение на-
напряжений будет одноосным (ах Ф 0, ау = хху = 0). Ес-
Если Еи vx заданы (другие упругие характеристики — #2,
G и т. д. могут быть какими угодно), то напряжение ах
определится из уравнения C7.3); последнее может быть
проинтегрировано в общем виде только при частных за-
заданиях упругих характеристик (например, если E1nv1 —
функции только у).
Исследуем случай, когда и модуль Юнга и коэффици-
коэффициент Пуассона являются произведениями функций только
х на функции только г/, т. е.:
Ег = Ех {х)Еу (у), v-l = vlx (x)vly (у). C7.4)
Подставляя в C7.3) и разделяя переменные, получим
два уравнения:
Здесь п — любое постоянное вещественное, чисто мни-
мнимое число или нуль. Обозначим Хг (х, п), Х2 (х, п) — ли-
линейно-независимые решения уравнения C7.5), Yx (у, п),
Y% {У, п) — то же Для C7.6) и выпишем окончательные
результаты (см. [68]).
1. Выражение для модуля имеет структуру:
Е = "C77)
где Еу — произвольная функция у и Сь С2 — произволь-
произвольные постоянные. Эти три произвольные величины — пере-
переменная Еу и две постоянные Сь С2, разумеется, имеют фи-
физический смысл только тогда, когда Ег > 0. Кроме того,
§ 37] РАСТЯЖЕНИЕ И ИЗГИБ МОМЕНТАМИ ПЛАСТИНКИ 209
на функцию Еу должны быть наложены некоторые огра-
ограничения, так как она входит в уравнение C7.6).
2. Произведение функций vlx и vly должно быть поло-
положительным и меньшим единицы, а в остальном эти функ-
функции могут быть произвольными [если не считать ограни-
ограничений, связанных с тем, что они входят в состав уравнений
C7.5) и C7.6)].
3. Напряжение определяется по формуле
огу = Еу {AYX + BY2). C7.8)
Постоянные А и В найдутся из условий на нагружен-
нагруженном торце и в любом поперечном сечении:
Ь/2 Ъ'2
\ axdy~P, \ oxydy = М. C7.9)
—Ь/2 —Ь/2
Отсюда получаем систему двух уравнений для А и В:
Ь/2 Ь/2
A I EyYidy + B J EyY2dy= P,
—Ь/2 —Ь'2
Ь/2 Ь/2
A $ EyYiydy + B J EyY2ydy= M.
—Ь/2 -Ь/2
4. Перемещения найдутся по формулам C7.2), кото-
которые после подстановки ах, Ег и v2 примут такой вид:
и = (AYX + BY2) ^ (СЛ + С2Х2) dx — ay + u0,
и = — (CiXi + С2Х2) vix \ (AYx+BY^Viy dy + ш -f-1;0;
C7.10)
C7.11)
постоянные со, w0, v0 определятся из условий закрепления
элемента оси стержня на торце х = 0.
Случай п = 0 также является одним из возможных;
ему соответствуют модуль и напряжение:
C7.12)
+ ^2 "У
) C7.13)
210 ПРЯМОЛИНЕЙНО-АНИЗОТРОПНОЕ ТЕЛО [Гл. 4
Наконец, заметим, что при постоянном коэффициенте
Пуассона Vi и п вещественном, не равном нулю, формулы
C7.7) и C7.8) принимают вид
Е = Ъ. C7.14)
пх fix ' ч
С1 ch — + С2 sh —
^Lj C7.15)
Если п — число мнимое, то гиперболические косинус
и синус должны быть заменены косинусом и синусом.
Мы привели здесь решение только одной простейшей
задачи об упругом равновесии неоднородной плоской бал-
балки-полосы. Большое число задач для балок, нагруженных
различными усилиями, решено Г. Б. Колчиным, который
получил распределения напряжений, применяя разные
методы, и сделал ряд выводов, интересных и важных для
практики. Решения Г. Б. Колчина изложены в его рабо-
работе [13] и других (см. также Библиографический указатель
[14]).
Глава 5
ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ,
ПЛОСКАЯ ЗАДАЧА И РОДСТВЕННЫЕ
ЗАДАЧИ ДЛЯ ОДНОРОДНОГО
И НЕПРЕРЫВНО-НЕОДНОРОДНОГО ТЕЛ,
ОБЛАДАЮЩИХ ЦИЛИНДРИЧЕСКОЙ
АНИЗОТРОПИЕЙ
В главе 5 мы рассматриваем задачи, которые изучались
в предыдущей главе, но для тела, обладающего цилинд-
цилиндрической анизотропией — об обобщенной плоской дефор-
деформации, плоской деформации, обобщенном плоском напря-
напряженном состоянии, а также сходные задачи, характерные
именно для криволинейной анизотропии и для непрерыв-
непрерывно-неоднородного тела. Это — задачи о растяжении —
сжатии осевой силой и об изгибе моментом; и ту, и другую
нужно представлять себе как обобщенную, так как рас-
распределение напряжений при растяжении — сжатии и при
изгибе оказываются значительно сложнее распределения
в однородном прямолинейно-анизотропном теле. Некото-
Некоторые наиболее важные частные задачи доведены нами до
явных формул для напряжений.
§ 38. Обобщенная плоская деформация
в однородном теле, обладающем
цилиндрической анизотропией
В третьей главе нашей книги был рассмотрен общий
случай упругого равновесия нагруженного цилиндра,
однородного и обладающего цилиндрической анизотропи-
анизотропией, характеризующийся тем, что все составляющие на-
напряжений не меняются вдоль образующей и зависят, сле-
следовательно, только от двух координат (§ 23). В этом и
212 Щтлйнд! ipiECKii-AimrioTForiHOE теЛс) [гл. 5
последующих параграфах мы изучим частные случаи
упругого равновесия указанного типа, представляющие
практический интерес. Начнем со случая, который был ра-
ранее, в главе 4, назван обобщенной плоской деформацией.
Поставим задачу следующим образом. Имеется тело
бесконечной длины, ограниченное поверхностью произ-
произвольного цилиндра (в частности, эта поверхность может
иметь бесконечно длинные плоские участки и даже быть
не криволинейной, а плоской — бесконечный слой, беско-
бесконечное полупространство и т. п.). Тело является однород-
однородным и обладает цилиндрической анизотропией самого об-
общего вида, с осью анизотропии g, параллельной образую-
образующей. Действуют поверхностные силы, распределенные по
цилиндрической поверхности, и объемные силы, причем
и те, и другие действуют в плоскостях, нормальных к об-
образующей и не меняются вдоль образующей, а объемные
силы, кроме того, имеют потенциал 1).
Область поперечного сечения может быть какой угод-
угодно — конечной, бесконечной, односвязной или многосвяз-
многосвязной. Примем плоскость какого-нибудь поперечного сече-
сечения за координатную плоскость г0 или ху, за начало коор-
координат возьмем точку О, в которой ось g пересекает данное
сечение; ось z направим по оси анизотропии, а оси х и у
направим произвольно, если область бесконечна, или па-
параллельно главным осям инерции сечения, если эта об-
область конечна. Ось х одновременно будем считать и поляр-
полярной осью цилиндрической системы координат и от нее бу-
будем отсчитывать полярные углы 0 (расстояние г отсчиты-
вается, как всегда, от начала координат О). При решении
некоторых вопросов для случая, когда область сечения
конечна, мы будем пользоваться еще системой координат
(декартовых) О1', х'\ у'\ z'', у которой начало О' совпадает
с центром тяжести сечения, а оси х', у1 направлены по его
главным осям инерции. Координаты центра тяжести О'
в системе О, х, у, z будем обозначать через ? и г\ (рис. 67).
Проекции поверхностных усилий на координатные
направления г, 0 условимся обозначать через Rn, @n;
х) Последнее ограничение не является существенным и общие
уравнения легко могут быть составлены и без него; если имеется
потенциал, то эти уравнения несколько упрощаются, становятся
более симметричными.
§ 38]
обобщенная Плоская деформация
213
проекции объемных сил (отнесенных к единице объема) —
через R, в, причем
где ?? (г, 0) — потенциал объемных сил (Zn = Z = 0).
Выпишем (с очевидными сокращениями) уравнения
обобщенного закона Гука для общего случая цилиндриче-
цилиндрической анизотропии, используя коэффициенты деформа-
деформации CLij\
гт = anar
ее =
-f*
C8.2)
В этих уравнениях, самое большее, 21 коэффициент,
но по В. В. Новожилову, рассуждения которого можно
перенести и на случай
цилиндрической анизотро-
анизотропии, независимых (инвари-
(инвариантных) коэффициентов в
общем случае будет 18 [27].
Напомним одно важное об-
обстоятельство, о котором
уже говорилось в § 10. Если
ось g проходит вне тела
или внутри цилиндриче-
цилиндрической полости, то никаких
дополнительных ограниче-
ограничений на atj можно не накла-
накладывать; коэффициенты мо- Рис- 67#
гут быть какими угодно.
Но если ось g проходит не в полости, а по телу, тогда
непременно atj должны быть связаны добавочными зави-
зависимостями, подробно разобранными в главе 1 (§ 10); в про-
противном случае задача не будет иметь физического смысла,
так как решается на основании уравнений, заключающих
в себе противоречия.
Так как длина тела бесконечна и усилия не зависят от
z, то все поперечные сечения находятся в одинаковых
условиях, а следовательно, и напряжения, и перемещения
214
ЦИЛИНДРИЧЕСКИ-АНИ30Т1 ОПНОЕ ТЕЛО
[Гл. 5
не зависят от z. Обращаясь к выражениям для перемеще-
перемещений в общем случае B3.12), мы видим, что это условие
будет выполнено, если положить
4=Д = С=Ф = 0, со! - со2 - 0, C8.3)
и тогда
иг = U (г, 0) + и0 cos 0 + и0 sin 0,
= V(г, 0) — и0 sin 0 + ^о cos 0 + coy, C8.4)
(u0, v0, co3 — коэффициенты «жестких» перемещений в
плоскости сечения, w0 — «жесткое» смещение в продоль-
продольном направлении).
Функции U, У, W удовлетворяют уравнениям B3.9) —
B3.10):
dU
1 dV
1 dU
~
V
C8.5)
1 dW
C8.6)
В C8.5) и C8.6) , как известно (§ 23), Р^ — приведен-
приведенные упругие постоянные:
6,, = ai} - ^^ (I, / = 1, 2,4,5,6). C8.7)
Далее, как и в общем случае, вводим две функции на-
напряжений, F и i|), и получаем выражения для пяти состав-
составляющих, такие же, как и в общем случае (§ 23):
г г дг г* дк)л
1 dip
C8.8)
38]
ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
215
Нормальное напряжение в поперечных сечениях выража-
выражается через все остальные:
oz = (^дз^г + Я2з<?е + a34Tez + Нь^тг + Язе^ге). C8.9)
Функции F и i|) удовлетворяют системе двух уравне-
уравнений:
Ь (Pi. + Р26) ±?щ ~ (Ра + Ри) -3"
(Pll ^P22 Pl2/~Z 37~ "I (Pie
= (р14 + р24) (^- -f) -
C8.10)
— (Р1Б + Р25)- QQ-
L4, Z/3, Z/3 и L2 — дифференциальные операторы четвер-
четвертого, третьего и второго порядков, содержащие 13, 7, 8 и 4
слагаемых. Мы не будем приводить их выражений, так
как они имеются в главе 3, § 23 (см. B3.16)). Граничные
условия на цилиндрической поверхности не отличаются
от условий B3.17) общего случая:
ar cos (п, г) + тге cos (п, 0) = Лп,
тге cos (п, г) + ае cos (и, 0) = 0П, C8.11)
хтг cos (п, г) + tez cos (n, 0) = 0.
Задача сводится к определению двух функций напря-
напряжений, удовлетворяющих условиям C8.11) или, иначе ,
к граничной задаче для системы C8.10), вообще неодно-
неоднородной, с известными правыми частями [20]. Найденные
напряжения в каждом поперечном сечении приведутся к
продольной силе Р, к изгибающим моментам с составляю-
составляющими Мг, М2 и к скручивающему моменту Mt. Эти четыре
величины, одинаковые для всех сечений, определятся из
равенств B3.18)—B3.21), где нужно положить А = В =
= С = О = 0 (см. также рис. 26).
Если в каждой точке нет плоскостей упругой симмет-
симметрии, нормальных к образующей, то поперечные сечения
не остаются плоскими после деформации, а искривляются
216 ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО [Гл. 5
и притом одинаково; искривление зависит от функции W
C-я формула C8.4)). Деформация не является плоской
(в общепринятом смысле) и ее можно назвать обобщенной
плоской.
Если тело имеет конечную длину и торцевые сечения
закреплены, так что расстояние между ними не может
изменяться, то, учитывая принцип Сен-Венана, мы можем
считать, что напряжения будут такими же, как в теле бес-
бесконечной длины во всех точках, удаленных от торцов.
Вблизи торцов образуются зоны местных напряжений, но
как там распределятся напряжения, мы судить не можем,
так как для этого у нас недостаточно данных, а принцип
Сен-Венана их не дает, так как носит только чисто качест-
качественный характер.
Несколько сложнее обстоит дело в том случае, когда
тело, нагруженное указанным образом по цилиндрической
поверхности, имеет конечную длину и торцы, свободные
от нагрузки. Приближенное решение для конечной об-
области сечения мы получим, если решим краевую задачу
для системы B3.15), более сложной по сравнению с C8.10)
и содержащей четыре неизвестные постоянные А, В, С, д.
Удовлетворив точно условиям на боковой поверхности
C8.11), мы сможем удовлетворить условиям на свобод-
свободных торцах только приближенно, потребовав, чтобы были
выполнены условия B3.18)—B3.21), где Р = Мг = М2 =
= Mt = 0. Так мы получим систему уравнений для
четырех неизвестных постоянных, а решив ее, найдем
распределение напряжений в теле, при котором главный
вектор и главный момент усилий на торцах будут равны
нулю. Формулы для перемещений в этом случае B3.12)
показывают, что усилия, распределенные по цилиндриче-
цилиндрической поверхности, будут вызывать искривление сечений,
закручивание, растяжение и изгиб оси.
§ 39. Задача о плоской деформации тела
с цилиндрической анизотропией
и родственные задачи
Рассмотренная в предыдущем параграфе задача очень
упрощается, если плоскость поперечного сечения тела
является плоскостью упругой симметрии [20]. Сохраняя
расположение осей координат, как на рис. 67, в этом
§ 39] ПЛОСКАЯ ДЕФОРМАЦИЯ И РОДСТВЕННЫЕ ЗАДАЧИ 217
случае имеем
аы = а24 = я34 = а*6 = п1Ъ = а25 = азь = абв = 0,1
Pl4 = Р24 = ^46 = Pl6 = р25 = Рбв = О- J
Система C8.10) распадается на два уравнения, из ко-
рых одно содержит только функцию F, а другое — толь-
только функцию г|), а задача распадается на две: 1) определение
функции F и соответствующих напряжений и 2) определе-
определение функции г|? (не связанное с нахождением F) и соответ-
соответствующих напряжений, характерных для деформации
чистого кручения. Оставляя пока в стороне вторую зада-
задачу (о кручении, которой мы специально займемся в сле-
следующей главе), рассмотрим различные варианты первой
задачи.
1. Плоская деформация [201. Предположим, что одно-
однородное тело с цилиндрической анизотропией вида C9.1)
является бесконечно длинным и нагружено поверхност-
поверхностными усилиями и объемными силами. И те, и другие дей-
действуют в плоскостях, нормальных к образующей и не ме-
меняются вдоль образующей. Тогда, обращаясь к § 23, мы
видим, что постоянные А, В, С, Ф равны нулю, так как все
поперечные сечения деформируются одинаково, переме-
перемещения же U, V и W удовлетворяют уравнениям:
л/т
C9.2)
i аи , av v
Отсюда заключаем, что общие выражения для переме-
перемещений имеют вид
ur = U (г, 0) + щ cos 0 + v0 sill 0, |
щ = V (г, 0) — щ sin 0 + v0 cos 0 + оKг, C9.4)
w = w0, j
а следовательно, поперечные сечения не искривляются и
деформация будет плоской. Так как функция г|) удовлет-
218 ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО LTn. 5
воряет однородному уравнению и однородным граничным
условиям, то, следовательно, я|) = 0 в любой точке и хтг =
- т02 = 0.
Для остальных напряжений получаем формулы:
- * dF _1~ 1 d*F А^ГТ
C9.5)
az = j— @i3<Jr + Л23СГ9 + a36tre). C9.6)
Функция jF удовлетворяет уравнению:
= — (Pia + P22) -gpr + (Pie + Pse) —
— (Pll + Pl2) 7Г ^gr + (Pll — 2P22 — Pl2) — faT +
+ (Pi6 + P26)^^. C9.7)
Здесь L4 — оператор четвертого порядка, уже встре-
встречавшийся раньше в главе 3 (см. B3.16)). Граничные усло-
условия имеют вид
ar cos (n, г) + тг9 cos (n, 9) = Дя, j
Tr9 cos (тг, г) + aG cos (тг, 0) = вя. J
Деформация будет плоской и в случае тела конечной
длины с закрепленными торцами, расстояние между ко-
которыми не может изменяться. В этом случае нужно исклю-
исключить из рассмотрения зоны местных напряжений вблизи
торцов, где распределение напряжений и деформаций ис-
используемым методом мы найти не можем, но вне этих
зон на основании принципа Сен-Венана деформация будет
плоской и распределение напряжений — такое, как при
плоской деформации.
Если тело имеет конечную длину и конечную область
поперечного сечения и нагружено так, как указано выше,
а торцы его не нагружены и не закреплены, то прибли-
приближенное решение задачи можно получить, используя
?39] ПЛОСКАЯ ДЕФОРМАЦИЯ И РОДСТВЕННЫЕ ЗАДАЧИ
219
уравнение:
L'tF = -?-[- (h«A + (a« - a23) B]
+ ^-[(«13-
dty
sin 9
— (Pl2 + P22)
— (P11 + Pi2)-72"
1 80
C9.9)
Для этого уравнения нужно решить краевую задачу,
удовлетворив условиям C9.8). Неизвестные постоянные
А, В, С, входящие в уравнение C9.9) и в состав выражения
для напряжений crz:
Dc0 + 5sin0 + С) —
— —- (a13ar + a23ae
^33
C9.10)
определим из условий на торцах, потребовав, чтобы там
главный вектор и главный момент усилий были равны
нулю:
C9.11)
— i]) dS == 0,
oz (r cos 9 — 1) dS = 0 (dS = rdr dG).
Из условий C9.11) получаем систему трех уравнений
для трех неизвестных — А, В, С.
Для перемещений получаются следующие общие фор-
формулы:
ur = —±- (A cos 6 + В sin 0) + U +
+ z (oJ cos б — сох sin 6) + м0 cos 8 + u0 sin 8,
( ^i
— z (co2 sin 8 + o)i cos 8) — щ sin 8 + u0 cos 8,
^ = z (^rcosS + 5rsmG + C) +
+ r (— oJ cos 8 +^a)! sin G) + wOi
C9.12)
220
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО
[Гл.
где соь щ, v0, w0 — шесть постоянных, характеризующих
«жесткие» смещения. Функции С/, V определятся из си-
системы трех уравнений:
— = Pll<*r + Pl2<*9 + Pie^rO +
+ а13 (Ar cos 9 + Br sin 0 + С),
— -щ- + —
+ a23 (Ar cos 0 + Br sin 8 + C),
1 dU . dV V
, (Ar cos 0 + Br sin 0 + C).
C9.13)
Найдя неизвестные постоянные и функции U я V, мы
можем заключить из выражений для перемещений C9.12),
что тело со свободными торцами деформируется так, что
ось его изгибается и испытывает продольное растяжение —
сжатие, но не закручивается, а поперечные сечения оста-
остаются плоскими.
2. Равновесие стержня под действием осевой силы и из-
изгибающих моментов [20]. Если боковая поверхность ци-
цилиндра, у которого область поперечного сечения конечна,
свободна от внешних усилий, а на концах действуют си-
сила Р,направленная по гео-
геометрической оси z, и изги-
изгибающий момент с составля-
составляющими Мг, М2 относитель-
относительно главных осей инерции
х, у сечения, то в однород-
однородном цилиндре с прямоли-
прямолинейной анизотропией полу-
получается элементарное рас-
распределение напряжений,
как в однородном изотроп-
изотропном цилиндре. Иначе об-
обстоит дело, если цилиндр
обладает криволинейной и,
в частности, цилиндриче-
цилиндрической анизотропией с осью анизотропии, параллельной об-
образующей (рис. 68). Составляющие напряжений тГ2 и т9г
равны нулю, а сгг, (Те, тге выражаются через функцию
Рис. 68.
§ 39] ПЛОСКАЯ ДЕФОРМАЦИЯ И РОДСТВЕННЫЕ ЗАДАЧИ 221
напряжений F (формулы C9.5)). Функция напряжений
удовлетворяет уравнению C9.9), а шестая составляющая
напряжений определится по формуле C9.10).
Граничные условия в данном случае] будут однород-
однородными:
ar cos (n, г) + тг9 cos (тг, 6) = 0, ]
.9)= 0, C9Л4)
а уравнение для функции напряжений F C9.9) — неодно-
неоднородным. При отсутствии объемных сил условия на цилинд-
цилиндрической поверхности C9.14) весьма упрощаются и при-
приводятся (в случае односвязной области сечения) к следую-
следующим:
-? = 0, -? = 0. C9.15)
Таким образом, задача о растяжении — сжатии осе-
осевой силой и изгибе моментами стержня, обладающего ци-
цилиндрической анизотропией, оказывается родственной за-
задаче о плоской деформации и примерно одинаковой ей
по трудности. Растягивающая сила и изгибающие моменты
вызывают не только нормальное напряжение в попереч-
поперечных сечениях azi но также и напряжения ar, tfo, Ъв, ха-
характерные для плоской деформации.
Задача чрезвычайно упрощается, если между упруги-
упругими постоянными существуют зависимости
a2Z = fll3, «36 = 0 C9.10)
(а это будет, например, в ортотропном теле, у которого
ось анизотропии проходит не в полости, а по телу) и объем-
объемные силы отсутствуют. Уравнение для функции напряже-
напряжения становится однородным: LXF = 0. Учитывая гранич-
граничные условия, можно принять F = 0, чему соответствует
распределение напряжений
C9.17)
ar = a9 = тгв = rrz = t02 = 0, J
где S — площадь поперечного сечения и Ти /2 — момен-
моменты инерции его относительно главных осей инерции х', у'.
3. Обобщенное плоское напряженное состояние. Зада-
Задаче о плоской деформации родственна также и задача об
222
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 5
обобщенном плоском напряженном состоянии плоскопа-
плоскопараллельной пластинки постоянной толщины h [20]. Пусть
имеется такая пластинка произвольного очертания, об-
обладающая цилиндрической анизотропией, с осью анизо-
анизотропии, нормальной к средин-
срединной плоскости, причем эта
плоскость и ей параллельные
являются плоскостями упру-
упругой симметрии. Принимая
ось анизотропии за ось z
цилиндрической системы ко-
координат г, 0, z с началом О
в точке срединной плоскости
(рис. 69), рассмотрим упру-
упругое равновесие под действием
усилий, распределенных по
Рис. 69.
краю симметрично относительно срединной плоскости
и мало меняющихся по толщине.
Достаточно ясное представление о напряженно-дефор-
напряженно-деформированном состоянии пластинки дадут средние_по_тол-
щине значения составляющих напряжения аг, а0, тго и
проекций перемещения:
h/2 h/2
1 Г , _ 1
—h'2 —h'2
1
h'2
fre = -т- \ rr9 dz,
—h'2
h'2
h'2 h'2
1 Г Л l f
Ur = ",— \ Ur UZ, Wq == ~T"~ \
h J n j
—/г/2 —Л/2
C9.18)
-/1/2
Введем в рассмотрение также средние по толщине объ-
объемные силы и их потенциал С/; имеем
= --^. «=--^-S- C9-19)
Так же как и в случае тела с прямолинейной анизотро-
анизотропией, средние напряжения можно выразить через функ-
функцию напряжений (формулы C9.5)). Пренебрегая средним
напряжением az по сравнению с 5Г, 5е и тгв, в результате
§ 40) ПЛОСКАЯ ЗАДАЧА ДЛЯ НЕОДНОРОДНОГО ТЕЛА 223
получим для функции F уравнение
L\F = — (^12 + Я22) ~1Р" + (ttl6 + а26) Т '
JL_ig_ f C9.20)
где ?4 — оператор, полученный из L4 (первая формула
B3.16)) путем замены приведенных коэффициентов р^7-
на соответствующие коэффициенты деформации atj. Сред-
Средние перемещения, на основании уравнений обобщенного
закона Гука, определятся из уравнений:
C9.21)
1 дп* . К
——ае~ ~т~~
+
Граничные условия, т. е. условия на контуре области
пластинки (на срединной плоскости) по форме не отлича-
отличаются от условий на контуре поперечного сечения в случае
плоской деформации.
§ 40, Плоская задача
для непрерывно-неоднородного тела,
обладающего цилиндрической анизотропией
Все общие уравнения, выведенные для однородного те-
тела с цилиндрической анизотропией, можно обобщить и
на случай тела непрерывно-неоднородного с анизотропией
такого же типа [20]. Последовательность вывода такая же,
как и для однородного тела. Ввиду этого мы можем не-
некоторые промежуточные выкладки опустить, а кроме
того, ограничиться только телом с анизотропией частно-
частного вида — ортотропным.
Мы рассмотрим только случай плоской деформации,
так как сходные два случая, как показано в § 39, иссле-
исследуются совершенно аналогичным путем.
224
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 5
Пусть дано тело бесконечной длины, ограниченное
произвольной цилиндрической поверхностью, обладающее
цилиндрической анизотропией и притом ортотропное (ось
анизотропии параллельна образующей, одна из трех плос-
плоскостей упругой симметрии нормальна в каждой точке к
оси анизотропии g, т. е. совпадает с плоскостью попереч-
поперечного сечения). Примем ось g за ось z, а плоскость какого-
нибудь поперечного сечения — за плоскость ху или гб
(рис. 67).
Предположим, что действуют усилия, поверхностные
и объемные, нормальные к образующей и не меняющиеся
вдоль нее; последние усилия имеют потенциал
Л==-^Г' 0 = -—-ж- D0Л)
В случае ортотропного тела удобнее пользоваться тех-
техническими упругими характеристиками, которые мы обоз-
обозначим, как и в § 10: Ет, i?e, Ez — модули Юнга, vr9, ver ,. . •
• . ., vzr — коэффициенты Пуассона, G>e, Goz, Grz — моду-
модули сдвига. Приведенные упругие характеристики выра-
выразятся так (см. B4.5)):
Ри = —Щ
Р*а= —ж
vr9+"
Е
D0.2)
(прочие Pi; или равны нулю, или в формулы плоской де-
деформации не войдут).
Приведем только окончательные результаты, получен-
полученные таким же путем, как и для однородного тела.
Перемещения иГ1 щ, w определятся по тем же форму-
формулам C9.4), что и для однородного тела, а функции U, V
определятся из уравнений:
— = рпаг
1 dU , V
— "go" + — =
P22O9,
1 dU
dV
D0.3)
§ 40] ПЛОСКАЯ ЗАДАЧА ДЛЯ НЕОДНОРОДНОГО ТЕЛА 225
где fiij не постоянные, как в уравнениях C9.2), а функции
г и 0 (так как технические характеристики E,v,G — функ-
функции г и 0).
Из шести напряжений два равны нулю: xrz = Tez = 0,
три выражаются через функцию напряжений:
1 8F
D0.4)
d2F
F \
~Г) '
а шестое, последнее, зависит от tfr и Oq:
az = vzror + vze0e. D0.5)
Функция напряжений удовлетворяет уравнению с
переменными коэффициентами, неоднородному, если
действуют объемные силы, которое мы запишем таким
образом:
V д№ ~Г дг ) \ г дг ^ г* д№ ^ Pl2 дг*
("f)] = - (A ~r-±r) KPn + М G]-
-г ¦%*&$* +fa) О]. D0.6)
При заданных усилиях граничные условия имеют вид
C9.8).
Если цилиндр имеет конечную длину и конечную об-
область поперечного сечения, то, принимая во внимание
принцип Сен-Венана, теорию можно считать верной для
всех его частей, за исключением зон местных напряже-
напряжений вблизи концов, где этим методом напряжения найти
нельзя. Наконец, заметим, что мы можем получить на ос-
основании предложенной теории и приближенное решение
для тела конечной длины со свободными торцами. В этом
случае напряжение az содержит три неизвестные посто-
постоянные:
az = Ez (Ar cos 0 + Br sin 6 + C) + vzrcrr + vretfo,
D0.7)
8 С. Г. Лехницкий
226 ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО [Гл. 5
а функция напряжений удовлетворяет уравнению B4.5),
где ?7-0:
JL - rJL\ (IilIL д. 1r.^!L о. ft
08* Г Or ) \ Г дг "^ Г* 502 "t" Pl2
LQ ^2 / z1
L Рб6 згае U
= (Ж ~ Г^г) \Угт (АГ COS 9 + Br Sill G + C)] +
+ r2-^- [vz9 (^ cos 9 + Br sin 9 + C)]. D0.8)
Постоянные А, В, С определим из условий на торцах,
где мы можем потребовать, чтобы главный вектор и глав-
главный момент усилий были равны нулю. Для этого нужно
сначала найти напряжения tfr, (to, cfz, а после этого опре-
определить А, В, С.
В случае обобщенного плоского напряженного состоя-
состояния все приведенные коэффициенты C^ должны быть за-
заменены коэффициентами atj. Из всех записанных выше
уравнений остаются только D0.3), D0.4) и D0.6).
§ 41. Осесимметричное распределение
напряжений в однородном полом цилиндре,
обладающем цилиндрической анизотропией
Перейдем к изучению конкретных частных задач и
прежде всего остановимся на теле в виде полого кругового
цилиндра с осью анизотропии, совпадающей с геометриче-
геометрической осью цилиндра.
Сначала рассмотрим упругое равновесие тела в виде
полого цилиндра (трубы) конечной длины, изготовленно-
изготовленного из однородного материала, обладающего цилиндриче-
цилиндрической анизотропией самого общего вида, находящегося под
действием усилий, распределенных по боковой поверх-
поверхности и по торцам. Предположим, что: 1) усилия на ци-
цилиндрических поверхностях нормальны и распределены
равномерно и 2) усилия на торцах распределены одинако-
§ 41] ОСЕСИММЕТРИЧНОЕ РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ 227
во по обеим поверхностям и приводятся к равным и про-
противоположно направленным
осевым силам и к скручиваю-
скручивающим моментам.
Примем ось тела за ось z
цилиндрической системы ко-
координат, направим полярную
ось х произвольно в плос-
плоскости одного из крайних се-
сечений и введем обозначения:
а, Ъ — внутренний и внеш-
внешний радиусы сечения; р, q —
внутреннее и наружное дав-
давление на единицу площади;
Р — осевая сила и1- скру-
скручивающий момент (рис. 70).
Введем далее обозначения
для коэффициентов, зависящих от E^-, которые войдут
в формулы для напряжений:
.. _ Pi* —
D1.1)
Pll —
4 — а34 (Pi4 — P24)
Р22Р44 — Р24 — (Р11Р44 — Р24)
fl13 — <?2з) (Р]4 + Р24) — «34 (Рп — Р22) .
Pl4+P24
D1.2)
Можно утверждать, что даже в общем случае анизот-
анизотропии осесимметричное распределение внешних усилий
вызывает напряжения, одинаковые во всех поперечных
сечениях и зависящие только от расстояния г от оси. Мы
можем в системе B3.15) положить А = В = V = 0 и
228
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 5
искать решение полученных уравнений в виде функций
только одной переменной г:
F = F (г), г|> = -ф (г). D1.3)
Тогда для напряжений получим выражения:
*гг = 0» Т9г = — Ф'; ^
oz = С — -— (а13(тг + а2з(Т9 + a34te2). D1.5)
3
Система уравнений для F и г|э принимает такой вид:
IV , лг \ . л / г .г
D1.6)
)-^ + P44 (*• + -f) =
= ?«34 _
Условия на цилиндрических поверхностях:
при г =
при
Условия на торцах сводятся к двум:
r = a or = — p, |
r = 6 o-r == — g. J
D1.7)
D1.8)
Общее решение системы D1.6) имеет следующий вид:
¦ г1"* +
1 1 —к
+ С4 + ^1гз,
= Co lnr
D1.9)
§ 41] ОСЕСИММЕТРИЧНОБ РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ 229
Из шести произвольных постоянных Сг две можно по-
положить равными нулю, так как им соответствуют напря-
напряжения, равные нулю, а именно: С4 = Сь = 0. Составляю-
Составляющие напряжений, выраженные по формулам D1.4) через
постоянные, пока еще не найденные, будут иметь такой
вид:
от = Со -сг~ ~z—\~ ?¦ 1
Р44 Г
(Те = Ci -
= - Со 4- - С g - Clgl -
Определив по напряжениям D1.10) перемещения (пу-
(путем интегрирования уравнений обобщенного закона Гу-
ка B3.7) и B3.8)), мы заключаем, что при произвольных
Со, Сх, С2, С3 в состав выражений для перемещений вой-
войдут непериодические функции угла 9, т. е. перемещения
вообще будут многозначными. Для того чтобы сделать их
однозначными, нужно положить
Со = 0 и Сг = Сщ.
D1.11)
Введем еще обозначения: отношение радиусов сече-
сечения и отношение переменного расстояния к наружному
радиусу
С = ТГ' Р = ТГ (с<!' С<Р<!)- D1.12)
Удовлетворяя условиям на цилиндрических поверх-
поверхностях, получим выражения С2 и С3 через С и три форму-
формулы для трех напряжений (четвертую см. D1.5)):
1-е
,2ft
A -^+2 л
D1.13)
230
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО [Гл. 5
1 -С
,2k L
/ 1 __ М1
A + Ьк*
1 — ск
1 - с
,2^
+
D1.13)
Оставшиеся неопределенными постоянные С и 'ft долж-
должны быть найдены из двух условий на торцах D1.8). Для
того чтобы их получить, нужно проделать совершенно эле-
элементарные, но громоздкие выкладки, которые приведут
к довольно сложным выражениям для коэффициентов С
иФ. Ввиду сказанного мы ни выкладок, ни окончательных
результатов выписывать не будем.
§ 42. Распределение напряжении в полом
однородном цилиндре под действием
внутреннего и наружного давлений
^Если полый цилиндр, рассмотренный в предыдущем
параграфе, закреплен неподвижно по концам и деформи-
деформируется давлениями ряд, распределенными равномерно
по внутренней и наружной поверхностям г = а и г = Ь,
то он будет находиться в состоянии обобщенной плоской
деформации (рис. 71).
Решение задачи для трубы из материала с цилиндриче-
цилиндрической анизотропией частного вида было получено Сен-Ве-
наном [124] и Фойгтом [128] А). Формулы для напряже-
г) А. Н. Митинский рассмотрел напряжения в деревянной свер-
сверленой трубе, как в теле, обладающем цилиндрической анизотропией
[78] и [79]. '
$ 421 ПОЛЫЙ ОДНОЮДНЫЙ?ЦИЛИНДР ИОД ДАВЛЕНИЕМ 23J
ний в общем случае анизотропии мы найдем из D1.13),
полагая, что С = ft = 0, т. е. что внешняя осевая сила и
скручивающий момент, приложенный извне, равны ну-
нулю. Получим (обозначения взяты из § 41):
(У о ---
пс*1—
C*~L
1 - с2*
-0;
1-е2
D2.1)
ХТг = 0,
.53 |_ 1 С
1 -с2
D2.2)
Напряжения огг на концах (и в любом поперечном сечении)
приведутся к осевой силе Р, а То2 — к скручивающему
232
ЦЙДИНДРЙЧЕСКИ-АНЙЗОТРОЙНОЕ ТЕЛО [Гл. 5
моменту М, которые равны:
X
а13 + /сд2з ~
1+Л
• — (gcfc-! — р) A — с*-1) с2 X
X '
1 —к
М = — •
2 + /с
D2.3
Напряжения вблизи внутренней поверхности г = а
равны:
ае =
1-е2
D2.4)
вблизи наружной поверхности г = Ъ
, 2cft+1 . 1 + с2*
1 —с2
D2.5)
В общем случае анизотропии напряжения сгг, ае со-
сопровождаются напряжением, характерным для кручения.
Поперечные сечения искривляются, так как W Ф 0; ра-
радиусы тоже искривляются (У Ф 0).
Если в каждой точке имеется плоскость упругой сим-
симметрии, нормальная к оси трубы, то а34 = Pi4 = ^24 —
^ ?к — ё-к = 0 и касательное напряжение Тв2 становит-
становится равным нулю. Нормальные напряжения определяются
по прежним формулам (первая и вторая формулы D2.1)),
только теперь в них к будет иметь другое значение:
А =
D2.6)
§ 43] ДЕЙСТВИЕ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА 233
Поперечные сечения искривляться не будут и дефор-
деформация будет плоской. Радиусы искривляться не будут
только в том случае, когда всякая радиальная плоскость
есть плоскость упругой симметрии, так как искривление
их зависит от аи и а2в. Если между упругими постоянными
существуют соотношения
Piifru — PL = P22P44 — Ph, D2.7)
то к = 1 и распределение напряжений tfr, tfe будет таким
же, как в трубе из изотропного однородного материала:
__ pc2 ¦— g , (g -— p) c2 l
°r — 1_C2 + j _ C2 p2
pC2 — q (g — p) c2 1
1—C2 T=^2 ^2
D2.8)
Если торцы свободны от усилий, то нужно воспользо-
воспользоваться формулами D1.13) (где к Ф 1 или в только что рас-
рассмотренном случае к = 1) и подобрать Сий так, чтобы
осевая сила и скручивающий момент Р и М были равны
нулю. В общем случае цилиндрической анизотропии обе
постоянные будут отличны от нуля и труба под действием
нормального давления будет не только изменять радиусы
поперечных сечений, но и изменять свою длину и закру-
закручиваться. Закручивания не будет (Ф = 0), если имеются
плоскости упругой симметрии, нормальные к оси.
§ 43. Распределение напряжений в полом
однородном цилиндре под действием
осевой силы и изгибающего момента
Рассмотрим упругое равновесие трубы из однородного
материала с цилиндрической анизотропией, которая имеет
конечную длину и деформируется усилиями, распределен-
распределенными по торцам. Как именно распределены усилия, по
какому закону,— не задается, но известно, что на каж-
каждом торце они приводятся к силе, величина которой равна
Р, направленной по оси в ту или в другую сторону. Один
торец может быть закрепленным и на нем возникает ре-
реакция, равная силе Р на другом торце и направленная в
противоположную сторону (рис. 72).
234
БИЛИНДРИЧЕСКП-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 5
Распределение напряжений мы получим по формулам
D1.13), положив в них р = q — 0 и определив постоянные
С и# из условий на торцах D1.8), где М = 0. Так как ход
решения для трубы с произвольной цилиндрической ани-
анизотропией совершенно ясен, но
приводит к довольно громоздким
формулам, то мы рассмотрим толь-
только частный случай анизотропии,
.когда имеются плоскости упругой
симметрии, нормальные к геомет-
геометрической оси z (которая, напом-
напомним, является одновременно и осью
анизотропии g).
Результаты сводятся к следу-
следующему. Обозначения те же, что
'в § 41 и 42, и, кроме того,
Рис. 72.
P22 РП "- Р22
Напряжения определяются по формулам (см. [60] и [20]):
Ph
D3.2)
р рд г
Здесь
- с2)
1 — с2
1 — с2
(а13 —
-Н
D3.3)
_ A __ С*+1 J
^ (а13
_ A __ с*-1 J
При этом во всех формулах предполагается, что (Зп
Р22 и? значит, к Ф 1.
i 43l
ДЕЙСТВИЕ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА
235
гПри неравных^коэффициентах а13 и а23 напряжение
az распределяется*^ поперечному сечению неравномерно
и сопровождается напряжениями tfr, сге в продольных се-
сечениях, характерными для трубы, находящейся под дав-
давлением. На внутренней и внешней поверхностях получа-
получаем: при г = а огг = О,
Ph 1 + к - 2кс*~1 + (А - 1) c2h
2Л 1 -\ к - 2кс
к-\
- (А- — I) с-
„2/Г
(«.5)
при г ~ Ъ ог — О
Ph 1 — А' Ч- 2Acfr+1 — (Л-
D3.6)
Если анизотропия цилиндра такова, что а22 = ап, а23 =
= а13, то, следовательно, (Зп = р.22 и А = 1. Получаем
совсем простое, элементарное распределение напряжений:
аг =
ггт: ^'^ ~г 1'»
(Ш)
У/
как в изотропном растянутом полом стержне с радиу-
радиусами а и Ъ.
Рассмотрим теперь такой же
полый цилиндр, но деформиру-
деформируемый усилиями, распределен-
распределенными по торцам и приводящи-
приводящимися к изгибающему моменту
М на каждом торце. Так же
как и в случае силы, закон рас-
распределения усилий не задается;
задается только М, действую-
действующий в плоскости, проходящей
через геометрическую ось
(рис. 73). Геометрическая ось со-
совпадает с осью цилиндриче-
цилиндрической анизотропии, причем рассматривается не самый
общий случай анизотропии, а случай ортотропного тела,
Рис. 73.
236
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО
[Гл.5
у которого через каждую точку проходят три плоскости
упругой симметрии — нормальная к образующей, т. е.
совпадающая с плоскостью поперечного сечения, прохо-
проходящая через ось и ортогональная к этим двум.
Будем считать, что объемные силы отсутствуют. В
уравнении C9.9) положим U = a3Q = 0, а также А = О,
и тогда оно запишется подробно следующим образом [60]:
ft
22
+
L2 +
d*F
Г2 дг2 #02 ' ^U Г4 дб4
I d*F
i /9ft I 9ft l ft \ * d'2f l ft i dF
+ Bpn + 2p12 + pee) -^ -gp- 4- pn — _ ==
^ 2(a18 — д23) в sine да g^
Будем искать решение этого уравнения в виде:
F = / (г) sin 6. D3.9)
Получим для / уравнение четвертого порядка и проин-
проинтегрировав его,— выражение для / и F:
D3.10)
Здесь Съ С2, С3, С4, 5 — произвольные постоянные,
~, _л/a
Р
8~~
Напряжения определим по формулам:
1 dF
~~дг
1 dF 1 дЧ
^Г == ~ яГ П ^2~ ЯЙ2 '
' tr0 ~ ¦"'ЗГаГ1"^");
oz = Вт sin 0 (fli3°v + Я2з<*е) = crz (r) sin 9.
Постоянные найдем из граничных условий:
при г = а и г = b )
ог = tr9 = 0, J
D3.11)
D3.12)
D3.13)
D3.14)
§ 431 ДЕЙСТВИЕ СИЛЫ Й ИЗГИБАЮЩЕГО МОМЕНТА 23?
и из условий на торцах:
2« Ъ
azr2sinQdrdQ = М,
o2r2
О а
D3.15)
Окончательные формулы для напряжений будут иметь
такой вид:
а:
1-е1
.Т71-2
1-е1
,2т
cm+2p-m-
1 j sin 8
>i
С
1
- m) P" sin e-
J
1
1 si
J
cm+2
1-е
,т-2
02 = "X r sin 9 "~
2т- г "^cosB;
)р-
D3.16)
^т+2
1-е2
1 —с
m—2
1-е'
,2m
+ A — m) a23] p-m-i| sin 8. D3.17)
Здесь обозначения сир — как в § 41 (формула D1.12)):
т + 2
С2т
т — 2
^1 . D3.18)
238 ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ TEJtO [Гл. 5
Формулы чрезвычайно упрощаются, если коэффициен-
коэффициенты Пуассона, выражающие сокращение в радиальном нап-
направлении и в тангенциальном направлении при растяже-
растяжении в осевом направлении, одинаковы: а13 = а23, и при-
принимают такой же вид, как для изотропной трубы при
чистом изгибе моментами:
<т2 = -^j- r sin9, orr = а9 = туе = т„ = т92 = 0 D3.19)
11 = —^ A — с4) — момент инерции кольца относительно
диаметра).
§ 44. Распределение напряжений
в непрерывно-неоднородном полом цилиндре
под действием давления
Более сложной, по сравнению с рассмотренной в § 42,
будет задача об упругом равновесии непрерывно-неодно-
непрерывно-неоднородного полого цилиндра, обладающего цилиндрической
анизотропией и ортотропного, нагруженного по внутрен-
внутренней и наружной цилиндрическим поверхностям равномер-
равномерно распределенными нормальными давлениями р и q
(на единицу площади). Мы рассмотрим плоскую деформа-
деформацию полого цилиндра для частного случая, когда ось ани-
анизотропии совпадает с геометрической осью z. Цилиндр
является ортотропным, а коэффициенты деформации зави-
зависят только от г; объемные силы отсутствуют. Схема зада-
задачи такая же, как на рис. 71. Длина цилиндра предполага-
предполагается бесконечной или конечной, но торцы закрепленными.
Примем плоскость любого сечения (для стержня бес-
бесконечной длины) или плоскость торцевого сечения (для
стержня конечной длины) за координатную плоскость гб,
направив ось z по оси анизотропии (геометрической оси),
а полярную ось х — по произвольному радиусу.
Очевидно, в данном случае картина распределения нап-
напряжений будет обладать симметрией вращения, т. е. со-
составляющие напряжений не будут зависеть от г, и мы по-
получим ее, считая, что функция напряжений зависит толь-
только от г *).
г) Это условие является достаточным, но не необходимым»
так как существуют функции F, зависящие от 6, которым соответ-
соответствуют напряжения, не зависящие от 6 (например, F = С6).
§ 44] ПОЛЫЙ НЕОДНОРОДНЫЙ ЦИЛИНДР ПОД ДАВЛЕНИЕМ 239
Полагая, что F — F (г) и обозначая F' (г) через ср (г),
получим формулы для напряжений и уравнения для пере-
перемещения иг (щ = 0):
or = -у-, a9 = ф\ rr0 = О,
ur = Pn —r—г Р12Ф » I
-р22гф'. J
D4.1)
D4.2)
Исключая из D4.2) функцию ur, находим уравнение
для функции ф:
(IW + Pirt>)' - Pii -f - Р12ф' = 0. D4.3)
Общий интеграл этого линейного уравнения с пере-
переменными коэффициентами имеет вид
Ф = С1ф1 (г) + С2ф2 (г). D4.4)
Для того чтобы найти линейио-независимые решения,
нужно задать C^- как функции г. Постоянные Съ С2 оп-
определятся из граничных условий, которые в данном слу-
случае запишутся так:
при г = а аг = — р, )
, D4.5)
при г = о ог = — q. ) v '
Задачи данного рода, связанные с уравнением D4.3)
и более сложным для неортотропного цилиндра, рассмат-
рассматривали Берт [105] и Е. Собс [126] (см. также [71] и Биб-
Библиографический указатель [14]).
Проще всего решить задачу в случаях, когда коэффи-
коэффициенты аи пропорциональны какой-либо степени расстоя-
расстояния г; некоторые решения были найдены П. Н. Житко-
Житковым [52] и М. М. Плотниковым [84].
Пусть коэффициенты деформации заданы таким об-
образом:
D4.6)
May- "" J" ¦"""" " "~'b "
240
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 5
— заданные постоянные и п — любое постоянное ве-
вещественное число). При таких заданиях уравнение D4.3)
становится элементарным:
где
Vll
Получаем общий интеграл D4.7) в виде
ф = C^r* + C2rf.
Здесь
J) = 0,5(п±fTF
D4.7)
D4.8)
D4.9)
D4.10)
Подставляя выражение D4.9) в формулы D4.1) и оп-
определяя постоянные Ск из граничных условий D4.5),
Таблица 18
Значения напряжений для материала D4.12) в некоторых
точках диаметра трубы
п
г
рг=т
0,5
0,6
0,7
0,8
0,9
1,0
—1
—1,000
—0,548
-0,299
—0,152
—0,060
0
ое/р
2,100
1,410
1,013
0,763
0,597
0,487
0
-1,000
—0,603
-0,357
-0,194
-0,081
0
°е/р
1,554
1,230
1,021
0,879
0,771
0,694
0,5
<ур
—1,000
-0,637
—0,407
—0,223
—0,097
0
*9/Р
1,225
1,108
1,053
0,250
0,897
0,848
п
г
P=ST
0,5
0,6
0,7
0,8
0,9
1,0
1
<ур
—1,000
—0,662
—0,425
—0,249
-0,110
0
°8/Р
1,190
1,122
1,000
1,074
1,070
1,068
2
—1,000
—0,698
—0,472
—0,286
—0,141
0
°е/Р
0,768
0,840
0,935
1,030
1,210
1,280
3
—1,000
—0,733
—0,523
—0,337
—0,168
0
<VP
0,523
0,661
0,845
1,070
1,344
1,650
§ 45] СЛУЧАЙ ОСЕВОЙ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА 241
находим окончательные выражения для напряжений:
с'-с'
= -pc-
D4.11)
В работах [83] и [84] даны таблицы численных значе-
значений напряжений по диаметру кольца, нагруженного толь-
только по внутреннему контуру (q = 0) для материала, у ко-
которого
Ег = 2-10брп кгс1см2,
?9 = 0,95.105рп кгс/см\
Vr9 = О,
D4.12)
а п может быть различным.
Указано, что эти значения
получены для древесины ду-
дуба. В таблице 18 приведены
численные значения напря-
напряжений, взятые из названных
работ (с = 0,5), а на рис. 74—
график распределения (Те по диаметру для с — 0,1 и 3 из
[84] (с некоторыми несущественными изменениями). В наз-
названной работе даны также графики огг для п = 0, 1, 3,
но мы их не приводим.
1,0 0,8 0,6 0
Рис. 74.
§ 45. Распределение напряжений в круговом
неоднородном цилиндре, обладающем
цилиндрической анизотропией, под действием
осевой силы и изгибающего момента
Решения задач, полученных в §43 для однородного по-
полого цилиндра, обладающего цилиндрической анизот-
анизотропией, легко могут быть обобщены и на случай непрерыв-
непрерывно-неоднородного цилиндра с анизотропией такого же
типа. Эти решения получил Е. Соос [126] и [105] (см.
же [71]).
242 ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО [Гл. 5
Для того чтобы избежать громоздких выкладок, мы бу-
будем считать неоднородный цилиндр ортотропным, с осью
анизотропии, совпадающей с геометрической осью; впро-
впрочем, задача легко может быть решена и для цилиндра с
какой угодно цилиндрической анизотропией и осью ани-
анизотропии, совпадающей с геометрической осью, только
формулы для напряжений в конечном счете получатся
значительно сложнее. Предполагаем, что нагрузка рас-
распределена по торцам, причем закон распределения ее не
задан, а заданы главный вектор и главный момент, к ко-
которым она приводится на каждом торце. Мы рассмотрим
два основных случая.
1. Усилия на торце приводятся к силе Р, направленной
по оси g (которую мы, как и раньше, принимаем за ось z;
рис. 72).
Очевидно, распределение напряжений будет обладать
симметрией вращения (если, конечно, ао- зависят только
от г, что мы и будем предполагать). Введем новую функ-
функцию от г: « м -Щ ?
Ф = § . D5.1)
Обращаясь к уравнениям § 40 и полагая в них А — В =
= ft = U = 0, мы получим формулы для напряжений:
Gr = ^r, ств = ф\ тге = 0, D5.2)
Те* = тГ2 - 0, )
С 1 / ф , ,\
D5.3)
и уравнения для определения составляющей перемеще-
перемещения иг (щ можно положить равным нулю):
D5.4)
Здесь $ц выражаются через технические упругие ха-
характеристики по формулам D0.2), a als/ass = —vzr,
W = —v*»- Исключая иг из D5.4), получим уравнение
? 45] СЛУЧАЙ ОСЕВОЙ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА 243
для ф:
' + Риф)' - р1аФ' - ри-?- - С [^ - (fit)'] . D5.5)
Общий интеграл этого неоднородного уравнения вто-
второго порядка запишется так:
Ф = С1ф1 (г) + С2ф2 (г) + Сщ (г). D5.6)
Частное решение неоднородного уравнения ф0 зависит
от того, как заданы я13, а23 и а33 или коэффициенты Пуас-
Пуассона vzr, vz0. Три неизвестные постоянные С2, С2, С, вхо-
входящие в состав D5.6), определятся из условий на цилинд-
цилиндрических поверхностях и на торцах:
при г = а я г = b
ar = 0, D5.7)
Ь
[osdr^^ D5.8)
а
при z = 0 и z — I.
В частности, если коэффициенты atj, а следовательно
и Р;у, пропорциональны какой-нибудь степени г, т. е.
, piy = vyr-n, D5.9)
то уравнение D5.5) принимает вид
Ф" + -Ц12- Ф' - -J- Ф = <^r"-i, D5.10)
где
Общий интеграл его равен
ф = drs + C2r* + Стпгп+\ D5.12)
Здесь обозначено:
D5.13)
+ и — J
Подставляя выражение D5.12) в формулы D5.2), по-
получим выражения для напряжений аг и о>е, содержащие
244 ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО [Гл. 5
три постоянные, Сг, С2, С, которые все определятся из
условий D5.7) и D5.8).
[Окончательных выражений or мы приводить не будем.
Заметим лишь, что в цилиндре, у которого а23 = а13
(в частности, в изотропном) ог = ае = 0 и только ez не
равно нулю; в зависимости от а33 (г) это напряжение мо-
может распределяться по сечению неравномерно.
2. Усилия на торцах приводятся к изгибающему мо-
моменту М (см. рис. 73), а на цилиндрических поверхностях
усилия, так же как и объемные силы, отсутствуют; коэф-
коэффициенты $и по-прежнему зависят только от одной пере-
переменной г.
В этом случае нужно исходить из уравнения D0.8).
Зафиксировав определенным образом ось х в плоскос-
плоскости торца, будем отсчитывать от нее полярный угол и по-
положив А = С = 0, разыскивать решение уравнения D0.8)
в виде
F = f(r) sin 9. D5.14)
Для функции / получим неоднородное уравнение
f _!_ ft i* P12 i\ /ft i" _L_ P11 /' P11 A'
Ы + P12/ jrJ] — ^Pl2/ + — / pT /) "~
1 /ft f
!iL f Pn Л ! (о ^ Pee
± 1Ж) . D5.15)
«зз / ^ \ «33 / J V '
Составляющие напряжения должны удовлетворять ус-
условиям на цилиндрических поверхностях:
аг = тг0 = 0 при г = а и г — Ъ D5.16)
и на торцах, где усилия должны приводиться к моменту:
2* Ъ
\ 5jazsin9r2drde = M D5.17)
О а
При 2 = 0, Z = I.
Как и в случае осевой силы, уравнение D5.15) сводит-
сводится к легко интегрируемому уравнению Эйлера — Лапла-
Лапласа, если все коэффициенты деформации пропорциональны
одной и той же степени г:
аг1 = ацГ". D5.18)
§ 461 1УПРУГЙЕ ХАРАКТЕРИСТИКИ, МЕНЯЮЩИЕСЯ ПО ДЛИНЕ 245
Подставляя в D5.15), получаем уравнение:
г»-1, D5.19)
где
' а = га -г У12 у* -гч-г гее /45 20)
L Y22 ' v • /
Общий интеграл этого уравнения запишется так:
/ = Сугх + С2г^ + С3г1+П + САг + В1п (п + 2) гп+3. D5.21)
Здесь
— a)
D5.22)
D5.23)
[По формулам D0.4) и D0.5) найдем выражения для
напряжений, а далее удовлетворяем условиям D5.16) и
D5.17).
Постоянная С4 не входит в состав напряжений. Пос-
Постоянной С3 соответствуют многозначные перемещения (про-
(пропорциональные функции 8 cos 8) и нужно положить С3 =
= 0. Остальные три постоянные Сг, С2, В определятся из
условий на боковых поверхностях и на торцах. Этими за-
замечаниями мы и ограничимся.
§j46. Осесимметричное распределение
напряжений в круговом цилиндре
с упругими характеристиками,
меняющимися вдоль радиуса и по длине
До сих пор, рассматривая упругое равновесие полого
кругового цилиндра, мы предполагали, что упругие
характеристики неоднородного цилиндра (коэффициенты
деформации) зависели только от одной переменной г. За-
Задачи усложняются, если коэффициенты деформации за-
зависят не только от г, но и от z, отсчитываемой параллель-
параллельно образующей [72].
246
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 5
Пусть имеется упругий неоднородный круговой по-
полый цилиндр конечной длины Z, нагруженный по цилинд-
цилиндрическим поверхностям г = а и г = Ъ равномерно рас-
распределенными усилиями ^ и q на единицу площади, а по
торцам — усилиями, приводящимися к силам Р, направ-
направленным по геометрической оси. В общем случае мы будем
считать тело обладающим цилиндрической анизотропией
и ортотропным, причем ось анизотропии будем считать
Рис. 75.
направленной по геометрической оси. Направления осей
координат и усилий показаны на рис. 75.
Мы не будем решать задачу во всей ее широте и разра-
разрабатывать общую теорию, которая отвечала бы на вопросы:
даны упругие характеристики, как заданные функции
координат г, z и внешние усилия; требуется в каждом
данном случае определить напряжения. Взамен этой мы
рассмотрим только обратную задачу: установить, как
должны меняться упругие характеристики в зависимости
от г и z, чтобы качественная картина распределения напря-
напряжений была такой же, как в однородном цилиндре (те2 =-
= тГ2= тГ9 = 0, о>г, бе, oz — функции только г) и найти
эти напряжения. Ограничимся только частным случаем:
будем считать, что все коэффициенты деформации являются
произведениями функций только переменной г на функ-
функцию только переменной z, одинаковую для всех коэффи-
коэффициентов:
ао- = Мг)Я(*). D6.1)
§ 46] УПРУГИЕ ХАРАКТЕРИСТИКИ, МЕНЯЮЩИЕСЯ ПО ДЛИНЕ 247
Уравнения обобщенного закона Гука будут иметь такой
вид:
*?г = [Ьц (г) ог + Ь12 (г) сг9 + й13 (г) аг] Z (z),
Z (z),
Чгг = 0.
Так как напряжения зависят только от г (как в задаче
Л яме и задаче о растяжении силой), то из первых трех
уравнений следует *)
ur = Ur(r)Z(z), w = Wr(r)\Z(z)dz + w0(r). D6.3)
Уравнения D6.2) принимают вид по сокращении на Z (z):
U г = Ьпаг + b12a9 + b13ez,
Wr = b13or + ЬиОв + Ь33а2, D6.4)
Ur(r)Z'(z) + W'r(r)lzdz + wo(r) = O.
Четвертому уравнению D6.4) можно удовлетворить,
только положив:
w0 = const; D6.6)
f/r = --J-; D6.7)
a — произвольное вещественное или чисто мнимое число.
Значению a = 0 соответствует однородное тело. Ком-
Комплексным а быть не может, так как в этом случае переме-
перемещение иг получится комплексным, а кроме того, множи-
множитель Z — всегда вещественная величина (если Ьц —
вещественные). Постоянная м?0, выражающая «жесткие»
смещения вдоль оси, может быть какой угодно, если
торцы не закреплены.
Дифференцируя D6.5) по z и интегрируя получившееся
элементарное уравнение второго порядка, мы получим:
х) Значок г у Ur н Wr показывает, что эти величины являются
функциями только переменной г.
248
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 5
1) при вещественном а
Z = A ch az + В sh az, D6.8)
*и = btj (r)(A ch az + S sh az). D6.9)
2) при чисто мнимом а = iax
Z = A cos axz + 5 sin axz, D6.10)
erf; = btj (r)(A cos axz + В sin axz). D6.11)
Здесь А, В — вещественные постоянные, которые, од
нако, совершенно произвольными быть не могут, так как
на dij накладываются некоторые ограничения.
В рассматриваемом случае лучше оперировать с урав-
уравнениями обобщенного закона Гука, решенными относи-
относительно составляющих напряжений, а не наоборот; тогда
все напряжения будут выражены через одну функцию
Wr, для которой из уравнения равновесия сплошной сре-
среды получится уравнение третьего порядка. В самом деле,
решая D6.4) относительно сг и выражая (из D6.7)) Ur че-
через Wr, получим:
w" w'
00= — Л12 ¦—= #22 -ГоТ"
к
-JL
B33W
33 ™ г
D6.12)
(tj коэффициенты, обратные 6fj, которые мы получим,
решая уравнения D6.4) относительно or).
Подставляя D6.12) в уравнение
D6.13)
получим уравнение, которому должно удовлетворять Wr:
г = 0. D6.14)
Три произвольные постоянные, входящие в состав обще-
общего интеграла этого уравнения, полностью определятся
§ 4б] Упругие Характеристики, меняющиеся По длине 249
из условий на цилиндрических поверхностях и на торцах
и тогда задача будет решена до конца. Однако, за неиме-
неимением места, мы не будем исследовать ортотропного тела
с произвольной ортотропией, а ограничимся лишь приме-
примером, когда неоднородное тело изотропно, причем модуль
Юнга его Е (z) зависит только от одной переменной z,
а коэффициент Пуассона v есть величина постоянная.
При вещественном а
при чисто мнимом а — aj
Е - -л ^> . D6.16)
В этом случае связь между составляющими напряжений
и осевыми перемещениями D6.12) и уравнение для пере-
перемещений D6.14) принимают следующий вид:
D6.17)
-f + J-Wr - (ti2a2 + -L)w'r = 0. D6.18)
Здесь введены обозначения: Р, |х — постоянные, свя-
связанные с коэффициентом Пуассона зависимостями
Общий интеграл уравнения D6.18) выражается при
а вещественном через модифицированные функции Бес-
Бесселя и Ганкеля первого порядка х):
W'r = CJX (a\ir) + С2Кг (ayr). D6.20)
х) См., например, Г. Корн и Т. Корн, Справочник по мате-
математике для научных работников и инженеров, «Наука», 1968,
стр. 660 и 670 [15].
250 ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО [Гл. 5
При а = а^ чисто мнимом будем вместо D6.20) иметь
W'r = CJ, (ai|ir) + C2NX (alfir). D6-21)
где Jx — функция Бесселя, N± — функция Неймана.
По функции Wr определим W, напряжения и переме-
перемещения. Три постоянные, которые войдут в выражения для
перемещений, найдем из условий на боковой поверхности
(точных) и на торцах (приближенных). Этими замечаниями
мы в общем случае и ограничимся. Отметим только, что
плоская деформация в цилиндре с модулем, меняющимся
по длине, под действием усилий рид, оказывается невоз-
невозможной.
В самом деле, положив w = Wr = 0, получим из
D6.3)—D6.7) Ur = и = 0, а следовательно, из уравнений
обобщенного закона Гука ar = ore = oz = 0. Допустив,
что w = 0 (при Z, не равной постоянной величине), полу-
получим противоречивый результат.
§ 47. Растяжение сплошного цилиндра
с модулем, меняющимся только по длине,
осевой силой
Рассмотрим пример [72]. Пусть имеется круговой изо-
изотропный неоднородный цилиндр, сплошной, без полости,
у которого коэффициент Пуассона — величина постоян-
постоянная, а модуль Юнга Е ме-
меняется по длине. По одно-
одному торцу, плоскость кото-
которого принимается за плос-
плоскость ху или г8 (рис. 76),
распределены усилия; за-
закон распределения не за-
задается, а задается лишь
осевая сила Р, к которой
Рис 7б они приводятся. Другой
торец, 2 —Z, как-то закреп-
закреплен. Боковая поверхность не нагружена и объемные
силы отсутствуют.
В данном случае в выражениях для напряжений D6.17)
нужно отбросить все слагаемые, неограниченно возра-
возрастающие по мере приближения к геометрической оси z,
а для этого одну из трех постоянных нужно приравнять
§47] РАСТЯЖЕНИЕ СПЛОШНОГО ЦИЛИНДРА ОСЕВОЙ СИЛОЙ 251
нулю. Оставшиеся две постоянные определятся из ус-
условий:
(orr)r=b = 0,
D7.1)
Остановимся на случае, когда модуль Юнга меняется
по длине по экспоненциальному закону:
Е = Еое~~. D7.2)
Приведем окончательные результаты. Выражения для
напряжений можно записать так:
Р , Р , _ Р , //7оч
ЗТо Ли ТСи
где
; v Г 1 /j (пщхр) м "I
1 + v L p h (пл\1) J
; v Г 1 Г
/t2 = -—— ^7-7 nn\ilo (
1 1 1 D7.4)
— —/i(nn|ip)J— 1J ,
В однородном стержне (п=0) ог = ае = 0, oz=P/nb2.
Подсчеты показывают,
что при 0 <^ п <^ 1 нап-
напряжения аг и ао в точках
радиуса по абсолютной ве-
величине значительно мень-
меньше oy Например, при
v = V3 и п = 0,9 в центре
(р = 0) *! = к2 = -0,093,
^з = 0,443, а вблизи ци-
цилиндрической поверхности
(р = 1) ^=0,^=0,217,
к3 = 1,649.
На рис. 77 показаны Рис. 77.
графики изменения коэф-
коэффициентов напряжений ки к2, к3 по радиусу стержня, у
которого коэффициент Пуассона равен V3, a n = ОД
252 ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО [Гл. 5
Пунктиром показана прямая, соответствующая такому
же однородному стержню (п = 0, к3 = 1). Как видно из
рис. 77, 'при данных v и п напряжение oz распределено
по сечению весьма неравномерно и сопровождается на-
напряжениями аг, бе, сжимающими на всем сечении и на
большей его части.
§ 48. Изгиб плоского кривого бруса
моментами и силой, приложенными на концах
С задачей об упругом равновесии неоднородного ци-
цилиндра под действием силы и момента сходна задача об
изгибе плоского кривого бруса моментами и силой, дей-
действующими в срединной плоскости.
Пусть имеется плоский брус постоянной толщины А,
обладающий цилиндрической анизотропией, и неоднород-
неоднородный, ограниченный в плане двумя концентрическими ок-
окружностями радиусов а и Ь и двумя радиальными отрез-
отрезками, образующими произвольный Гугол а ^ я/2. Мы
не будем'в общем случае предполагать брус ортотропным,
но будем считать, что срединная плоскость совпадает с пло-
плоскостью упругой симметрии, а ось анизотропии проходит
нормально к этой плоскости через общий центр окружно-
окружностей. Ось анизотропии принимаем за ось z цилиндрической
системы координат, а ось х, от которой отсчитываются по-
полярные углы 0, направляем как удобнее в зависимости
от нагрузки, которую считаем действующей в плоскостях,
параллельных срединной и симметричных относительно
нее. ц*
Рассматриваем средние по толщине напряжения, де-
деформации и перемещения. Коэффициенты деформации пц
из уравнений обобщенного закона Гука полагаем произ-
произвольными функциями переменной г и четными функциями
координаты z и от 8 не зависящими. Уравнения обобщен-
обобщенного закона Гука, связывающие средние по толщине вы-
выражения для напряжений и перемещений, в случае неор-
тотропного тела запишем так (горизонтальные черты, вы-
выражающие осредненные величины напряжений, деформа-
деформаций и коэффициентов ац, отбрасываем):
ег = апаг
б9 = а12аг + а22а9 + а2вггв, \ D8.1)
§ 48]
ИЗГИБ ПЛОСКОГО КРИВОГО БРУСА
253
Три средние составляющие напряжений выражаются
через функцию напряжений
1 3F , 1 &lF d2F a2 / F \
°г = "Г ~dF + 72" 152"' ав=?2"' тн>= ~ "^ae" \~/
D8.2)
(объемные силы считаем отсутствующими). Тогда для
функции F, после исключения перемещений щ и щ из
D8.1), получаем уравнение, более общее по сравнению
с D4.4), с заменой р^ на*аг7-:
/ аа а \ г / 1 3F , 1 аз/1 \ ьчл
-^)j = 0, D8.3)
и соответствующие условия для средних по толщине нап-
напряжений.
Рассмотрим отдельно два простейших случая изги-
изгиба [70].
1. Чистый изгиб моментами. Дан кривой плоский брус,
о котором говорилось вы-
выше. Криволинейные сто-
стороны г = а и г = b ничем
не нагружены и не закреп-
закреплены; [торцевые поверхно-
поверхности нагружены усилиями,
на каждом торце приводя-
приводящимися к моментам М, на-
напр авленным в противопо-
противоположные стороны. Для оп-
определенности один торец
можем считать закреплен-
закрепленным, другой—свободным.
Направим ось х по оси симметрии фигуры (рис. 78).
На криволинейных сторонах составляющие напряжений
(Тг, тг0 равны нулю, на прямолинейных приводятся к мо-
Рис. 78.
254 ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО [Гл. 5
ментам М. Так же как и в случае однородного бруса с по-
постоянными dij, решение получается с помощью функции
напряжений, зависящей только от одной переменной г.
Полагая
<p = dF(r)/dr, D8.4)
имеем
аг - ф/г, (Т9 = ф\ тге = 0. D8.5)
Уравнение для ф на основании D8.3) можно запи-
записать так:
С D8.6)
Входящие в состав общего интеграла этого уравнения
второго порядка постоянные найдутся из условий на кри-
криволинейных сторонах и из интегральных условий приводи-
приводимости на прямолинейных сторонах. На прямолинейных
сторонах условия совпадают, так что всегда у нас будут
три условия. Столько же мы имеем и произвольных по-
постоянных — с, си с2.
При произвольной зависимости коэффициентов аи от г
решение уравнения D8.6) затруднительно; можно гово-
говорить лишь о решении для частных случаев задания а^,
в том числе о тех, какие рассмотрел М. М. Плотников,
изучая напряженное состояние трубы с различного типа
неоднородностью (§ 44). Наиболее простым является слу-
случай, когда все ац пропорциональны одной и той же сте-
степени расстояния г:
a{j = щГ\ D8.7)
Введем обозначения § 44, заменив всюду ytj на atj [см.
формулы D4.8) и D4.10)]:
с = а/b > 1, р = г]Ь, уп = Fсп+"<*12)/а22,
D8.8)
Тогда, раскрыв скобки, перепишем D8.6) так *):
Ф' + 1^± Ф' - ? Ф = 4г г™. D8.9)
г) Мы можем воспользоваться и интегралом уравнения D5.5)
в форме D5.12); конечный результат не изменится.
§ 48] ИЗГИБ ПЛОСКОГО КРИВОГО БРУСА 255
Общий интеграл равен:
<р - (Vs + C2rl + Cor™ [Со = С/а22 A + п - Yn)]. D8.10)
Удовлетворяя всем трем условиям, получим выражения
для напряжений:
00 ЬЩ I с*-с1 ' с*-с
тг9 - 0.
D8.11)
Здесь знаменатель g представляет собой выражение:
(с1 - см)A-ем) s
_^ D8.12)
Нормальные напряжения ае в поперечном сечении у
внутреннего и внешнего края равны:
((Те)г=а
__ М (n+1—s) сл+я — (/г + 1 - /) сп+/ + (* - 0 g8+'
D8.13)
М (п + 1 — t) cs - (п + 1 — s) с1 - (s - t) cn+l
Щ —j
D8.14)
В однородном брусе все коэффициенты а-^ постоянные и
п = 0, уп = Y^ = Л. D8.15)
Составляющие напряжения равны [21]:
- TT?s-p Т37^ с +1р
Л/ Г. 1— с . . ,
[1 Ар
тг9 = 0.
D8.16)
256
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНОЕ ТЕЛО
[Гл. 5
Здесь в этом случае:
1_С2 к A_(
( Г
* + 1 1-,
-1 1-е
2*
2. Изгиб силой. Пусть плоский брус закреплен одним
концом, а по другому концу распределены усилия, приво-
приводящиеся к силе Р, действующей в срединной плоскости
и образующей с радиусом
угол со (рис. 79). Чтобы не
перегружать выражения
для напряжений формула-
формулами и выкладками, рассмот-
рассмотрим в данном случае уп-
упрощенный случай — орто-
тропное тело, у которого
одна из плоскостей упру-
упругой симметрии совпадает
со срединной, другие идут
по радиусам и третьи орто-
ортогональны к каждой паре
79- первых двух плоскостей.
В этом случае также по-
полагаем, что все коэффициенты пропорциональны одной и
той же степени г, т. е. заданы формулами D8.7).
Функцию напряжений нужно искать в виде
F = U (r) cos 0 + /2 (г) sin 0,
как и в случае однородного бруса.
Введем обозначения:
(Л —
л + 2) + ац + «е
D8.18)
D8.19)
далее — X и ц, определяемые по формуле D5.23), в кото-
которой все ytj нужно заменить соответствующими а^;
(е* _ сП+1) A -
-с*) 1
и»
1
—
¦ 1 '
1 -сп
п
D8.20)
; 48]
ИЗГИБ ПЛОСКОГО КРИВОГО БРУСА
257
Для функций /х и /2 получаются уравнения:
Отсюда
/. = Atr* + Btr^ + CtrUn +Dtr (i = 1,2). D8.22)
Все постоянные определяются из условий на криволи-
криволинейных сторонах и на загруженном конце, причем D± =
= D2 = 0, так как им соответствуют части функции F,
пропорциональные х и у, и следовательно, напряжения,
равные нулю.
Окончательные выражения для напряжений равны:
- с
с — с
,п+1
pn)si
" sin@
D8.23)
Нормальные напряжения достигают наибольших зна-
значений в радиальных сечениях, перпендикулярных к линии
действия силы (где синус равен ±1), или в заделанном
сечении, касательные — на линии действия силы. Зна-
Значения Go в радиальном сечении 9 = 90 у внутреннего
и внешнего края определяются по формулам D8.13)
и D8.14), в которые вместо s> t нужно подставить
X, |i, а коэффициент— 2 заменить соответственно на
и
2
sin (Go
со).
9 С. Г. Лехницкий
Глава б
ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ
СТЕРЖНЕЙ
В настоящей главе изложены основные общие поло-
положения и частные случаи упругого равновесия, которые
названы обобщенным кручением и при развитой упругой
симметрии переходят в обычное или «чистое» кручение
стержней с прямолинейной осью. Теория обобщенного
кручения впервые разработана Фойгтом [38], строгая тео-
теория чистого кручения — Сен-Венаном [121]. По теории
простого или чистого кручения известно очень много ра-
работ и среди них — большая монография Н. X. Арутю-
няна и Б. Л. Абрамяна [4]. В этой монографии указана
обширная литература по кручению, собранная в анноти-
аннотированные списки. Есть и у нас монография, посвященная
кручению [22].
§ 49. Обобщенное кручение однородных
стержней с прямолинейной анизотропией
Рассмотрим однородный цилиндрический или призма-
призматический стержень с прямолинейной анизотропией самого
общего вида B1 или 18 упругих постоянных), находя-
находящийся в равновесии под действием усилий, распределен-
распределенных по торцам и приводящихся к скручивающим момен-
моментам. Боковая поверхность свободна от внешних усилий;
объемные силы отсутствуют. Область сечения предпола-
предполагается конечной (односвязной или многосвязной). Поме-
Поместив начало координат в центре тяжести торцевого сече-
сечения, направим ось z параллельно образующей (по геомет-
геометрической оси стержня), оси х и у по главным осям инерции
сечения (рис. 80). Для такого тела верны уравнения обоб-
обобщенного закона Гука C.8).
§ 49] ОБОБЩЕННОЕ КРУЧЕНИЕ ОДНОРОДНЫХ СТЕРЖНЕЙ 259
Если плоскости поперечных сечений являются плоско-
плоскостями упругой симметрии, то стержень будет испытывать
деформацию кручения, основной особенностью которой
будет поворот одного сечения относительно другого вок-
вокруг оси z при одновременном (за исключением кругового
и кольцеобразного сечения) искривлении сечений, причем
все сечения искривляются . :
одинаково. Напряженное со-
состояние характеризуется тем,
что из шести составляющих
напряжения только два не
равны нулю.
Вопрос значительно ус-
усложняется, если плоскость
поперечного сечения не явля-
является плоскостью упругой сим-
симметрии. Деформация, выз-
вызванная скручивающими мо-
моментами, и напряженное со-
состояние будут более сложными и этот случай упругого
равновесия назван «обобщенным кручением» [56], [22].
Для того чтобы получить общие уравнения обобщен-
обобщенного кручения, обратимся к уравнениям для сГщего слу-
случая упругого равновесия, при котором составляющие
напряжения не меняются по длине (см. §§ 18, 19), и поло-
положим
U = Р = Мг = М2
Получим
дЧ дЧ
Рис. 80.
D9.1)
Из?
дх ду
ду ' у*
D9.2)
—
?;). D9.3)
Функции F и г|) удовлетворяют уравнениям A9.2) и
A9.3) и граничным условиям:
Q*
260 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
В случае односвязной области постоянные ct можно по-
положить равными нулю, так что граничные условия запи-
запишутся совсем просто: первые производные F и сама функ-
функция г|) на контуре должны быть равны нулю. Кроме того,
напряжения на торцах удовлетворяют условиям A9.9),
которые в данном случае сведутся к следующим:
§ ххг dx dy = 0, § агУ dxdy^O,
yZ dx dy = 0, 55 ezx dx dy = 0,
55 ez dx dy = 0, 55 (V ~~ Х^У)dx dy = Mt-
D9.5)
В случае односвязной области трет^ ^. условие D9.5) при-
принимает вит
= Mt. D9.6)
Из условий D9.5) мы выразим постоянные А, В, С, $ че-
через скручивающий момент. Так как боковая поверхность
тела не нагружена и объемные силы отсутствуют, то из
уравнений D9.5) и D9.6), учитывая зависимости A9.18) —
A9.20) получим
(Л» ^2 — главные моменты инерции сечения).
Для составляющей oz будем иметь формулу
^ а39хху). D9.8)
Функции напряжений удовлетворяют системе уравнений
UF + ?„Ч> = 0, ]
D9.9)
Здесь L4, Z/3, L2 — дифференциальные операторы, выра-
выражения которых указаны в § 19 [см. A9.3)].
§49] ОБОБЩЕННОЕ КРУЧЕНИЕ ОДНОРОДНЫХ СТЕРЖНЕЙ 261
Перемещения определятся по формулам [см. A8.19)]:
v = -jj- azbz
— fryz + U (х, у) + и\
V
> D9.10)
Здесь и', v', w' — «жесткие» смещения, содержащие шесть
постоянных и определяемые по формулам A8.8).
Составляющие напряжений можно выразить через три
функции Фц (zfe) комплексных переменных z^ = х +
(комплексные потенциалы):
ох = 2 Re
(Zl) + \х1ф'2 (z2) +
(z,)],
xxy = — 2 Re [)х1Ф1 -
xxz = 2 Re [fiAiOi 4
tyz = — 2 Re [AaOJ + ^2^2 + Фз]«
Граничные условия для Ф^ будут иметь вид
2 Re [Фх + Ф2 + Х3Ф3] - сь
2 Re [[ХхФх + |',Ф2 + [Хз^зФз] = с2,
D9.11)
2 Re [%1Ф1 +
+ Ф3] = с, -
D9.12)
Здесь о|H — частное решение неоднородной системы
D9.9). Так как эта часть постоянна, то можно взять грв
в очень простом виде, например, в виде полинома 2-й сте-
степени относительно х и у:
-^ + — )\
Функции F, г|) и
жителя
D9.13)
определятся с точностью до мно-
мно•-¦?(&+?)•
262 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
В частности,
Неизвестная постоянная ft найдется из уравнения
dxdy = Mt. D9.16)
Введем в рассмотрение новую величину ?, которую
определим как жесткость при кручении изотропного
стержня
C=2§ydzdy. D9.17)
Тогда из уравнения D9.16) получим
¦*-+?(?+?)]-3- <49Л8>
Отсюда следует:
D9.19)
В последнем выражении коэффициенты деформации вы-
выражены через коэффициенты Ченцова. Величину Ct на-
назовем жесткостью при обобщенном кручении. Очевидно,
С<< С.
Выражения для составляющих перемещения D9.10)
показывают, что при обобщенном кручении ось стержня
под действием скручивающих моментов изгибается, не
остается прямой. Если обозначить через I первоначальную
длину стержня и считать заделанным конец z = /, то про-
проекции изогнутой оси на ['плоскости xz и yz представятся
формулами:
г! = ^J-<2ai (I — z\2. I
D9.20)
50J
СКРУЧИВАЮЩИЕ И ИЗГИБАЮЩИЕ МОМЕНТЫ
263
Перемещения центра незакрепленного сечения выра-
выражаются формулами:
fx =
ТГ
ТГ
¦#35 =
х. 2
D9.21)
§ 50. Совместное действие скручивающих
и изгибающих моментов
Рассмотрим некоторые случаи равновесия стержня, на
оба конца которого действуют как скручивающие М\, так
и изгибающие (в главных плоскостях) моменты Мг и М2-
Оси координат расположим как на рис. 81; оси х и у
направим по главным осям инерции одного из торцов [20].
Если материал тела изотропен и деформации малы, то дей-
действие скручивающих и изги-
изгибающих моментов можно
рассматривать независимо
друг от друга: скручивающие
моменты вызывают кручение,
а изгибающие — изгиб в
главных плоскостях.
В анизотропном стержне,
обладающем анизотропией
общего вида, этого не будет:
скручивающие моменты вы-
вызывают кручение и изгиб, а
изгибающие — изгиб, сопро-
Рис. 81.
вождающиися закручивани-
закручиванием. В случае, когда боковая
поверхность не нагружена и не закреплена, в стержне с
прямолинейной анизотропией и однородном имеем
Хп = Yn = X = Y =- О = 0,
В -
Mt I Mi
7 Г "Г—'
у1 ^1
О-
E0.1)
1
<*33
264 обобщенное;*;*учение и крУченйе стержней [Гл. Ь
Остальные пять составляющих напряжений опреде-
определятся по формулам D9.2). Функции напряжений удовлет-
удовлетворяют уравнениям A9.2), куда нужно подставить значе-
значения постоянных А, В, С и О = 0.
Определив составляющие напряжений, найдем переме-
перемещения, в которых постоянные сог-, и0, v0, w0 определятся
из условий закрепления. В частности, если жестко закреп-
закреплен элемент оси, проходящий через центр сечения z = I,
получим выражения для перемещений:
и = —
1
2i;
ТГ (м»°»з + 0,5Mta3l) (I - zf +
- zf -
w = —
W-(WH.
E0.3)
Функции U, F, W удовлетворяют системе уравнений
A8.12), A8.15); величины, отмеченные нуликами,— зна-
значения функций переменных х, у при х = у = 0. В ре-
результате для функции г|) получаем выражение вида
E0.4)
где о|5 — функция такая же, как в случае обобщенного кру-
кручения, зависящая от формы и размеров поперечного сече-
сечения и от упругих постоянных. Из уравнения D9.16) опре-
определяем относительный угол закручивания:
— ~7^ о7~" ^35
2/,
E0.5)
§ 50] СКРУЧИВАЮЩИЕ И ИЗГИБАЮЩИЕ МОМЕНТЫ 265
Проекции изогнутой оси на плоскости xz и yz равны:
х'=--±- (Л/аа3з +
7
E0.6)
r / 71 /f" Г\ f 71 /f \/7 \О I
Эти формулы показывают, что при произвольных Мг,
М2, Мх стержень изгибается и закручивается. Однако мо-
моменты можно подобрать так, что не будет либо изгиба, либо
закручивания.
1. Кручение без изгиба. Подберем моменты следующим
образом:
Mi = Mt -—^- , М2 = — Mt -p±-. E0.7)
Тогда х' = 0, у' = 0, т. е. ось стержня останется прямо-
прямолинейной и будет происходить только кручение. Относи-
Относительный угол закручивания равен:
Mt
Ь = -~- . E0.8)
Жесткость при кручении € будет, очевидно, больше
жесткости при обобщенном кручении.
2. Изгиб без закручивания. Подбирая моменты, мы мо-
можем добиться того, что стержень будет изгибаться в одной
из главных плоскостей (например, yz) и изгиб не будет соп-
сопровождаться закручиванием. Полагая х' — 0 и Ф = 0
и решая получившиеся уравнения относительно М2 и Mt1
находим
х 4а33 /х
' + ХГ-Г-
a35 С
1 +4^777
E0.9)
Уравнение изогнутой оси (в плоскости yz) будет
иметь вид
35 о
„..*?, «-» , E0.,0)
35
266 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
Для такого же стержня, изгибаемого только моментом
Ми получим уравнение изогнутой оси: у' — f (z) или,
подробно:
_, = _^рз_(/_^2# E0.11)
Сопоставление этих двух уравнений показывает, что
если к стержню приложить моменты М2 и Mt, препят-
препятствующие его закручиванию, то жесткость^ изгиба его
увеличивается: она будет равна не величине В = IJa^ =
= EZIU а определится по формуле
В= В + 0,25 f-^-V С = В + 0,25гь2х ZC. E0.12)
\ бзз /
В этом случае напряженное состояние будет сложным:
составляющие напряжения определятся с помощью функ-
функций F, я|) или Фк (zk) и в общем случае все отличны от нуля.
§ 51. Простое или чистое кручение
однородного стержня
Предположим, что однородный стержень, изображен-
изображенный на рис. 80, обладает прямолинейной анизотропией
частного вида: в каждой точке имеется плоскость упру-
упругой симметрии, нормальная к образующей (т. е. совпа-
совпадающая с плоскостью поперечного сечения), причем уси-
усилия распределены по торцам и на каждом из них приво-
приводятся к скручивающему моменту Mt. В этом случае вся
теория очень упрощается. Вместо системы D9.9) мы будем
иметь только одно уравнение для функции я)), так как
функцию F можно, принимая во внимание уравнения
D9.9) и граничные условия и условия на торцах, поло-
положить равной нулю. Кроме того, А = В = С = 0
Т Т Т/ Г\ Г\ \
^Za,7 ' Р*! = а!1= ' р55 = «55. ! E1Л)
Из шести составляющих напряжений четыре равны
нулю,
ах = а = xxlJ = az = 0, E1.2)
а остальные связаны с функцией я)):
т« = -жг, ти = ~аг- E1-3>
§ 51] ЧИСТОЕ КРУЧЕНИЕ ОДНОРОДНОГО СТЕРЖНЯ 267
Функция я)) удовлетворяет уравнению второго порядка
и в развернутом виде (не сокращенно) оно запишется так:
+ ^55-^ = *. E1.4)
На контуре поперечного сечения
я|) = с3, E1.5)
причем в случае односвязной области сечения можно
принять с3 = 0.
Функция г|) и напряжения определятся с точностью до
множителя О
ij>=<hjT(*,y). E1.6)
Неизвестный относительный угол закручивания (крут-
(крутку) найдем из условий на торцах или, что то же, из усло-
условий равновесия в плоскости поперечного сечения, из урав-
уравнения:
2§ydxdy = M, E1.7)
откуда
* = 1Г . E1-8)
Здесь С — жесткость при простом или чистом кручении
dxdy. E1.9)
Полный угол закручивания стержня длиной I равен
#/ - MUC.
Введем вместо W новую функцию ф (х, у), положив
W = Фср. E1.10)
Эту функцию, характеризующую искривление плоскости
поперечного сечения, называют функцией кручения или
функцией перемещения, в противоположность я)), которая
называется функцией напряжений при кручении 1).
Функция ф удовлетворяет уравнениям
д(р \
\иу ) ~- - -- —
х) См., например, [24], стр. 327 и [4], стр. 36—38.
268 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ 1Гл. 6
Наконец, проекции перемещений будут иметь вид
и = —byz + u\ v = ftxz + v\ E1.12)
и; =с тЭ'ф (#, ^) -f- Wj
что вытекает непосредственно из выражений D9.10) и
значений E1.1).
Можно указать два основных способа решения задач
о кручении. Первый способ — за неизвестную функцию
берется функция напряжений при кручении. Эта функция
удовлетворяет уравнению E1.4) и на контуре поперечного
сечения принимает постоянное значение (в частности,
равна нулю).
Второй способ — за неизвестную функцию принима-
принимается функция кручения ф. Выразив через нее напряжения,
получим:
Здесь
А g55 А 9 g45 Л __ aU \
Аи - -д- . A45J- — -д- , А** А" • I E1-14)
А = а44аб5 ~" а4б. >
Требуя, чтобы напряжения удовлетворяли единствен-
единственному уравнению равновесия сплошной среды,
*% 0, E1.15)
дх ду
получим уравнение, которому удовлетворяет ф:
fA4-|S-=0, E1.16)
ИЛИ
Граничное условие получим из равенства
txz cos (n, x) + туг cos (n, у) = 0. E1.18)
I 52J КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ 269
Оно будет для функции ф сложнее, чем для я)), а по-
поэтому второй способ менее удобен для решения конкретных
задач, чем первый. Во всех случаях мы будем предпочитать
первый способ.
§ 52. Связь напряжений и перемещений
с функцией усложненной комплексной
переменной
Функцию напряжений, удовлетворяющую уравнению
E1.4), и напряжения и перемещения можно выразить че-
через одну функцию усложненной комплексной перемен-
переменной z3 — комплексный потенциал. В самом деле, разы-
разыскивая решение однородного уравнения E1.4) (при -б1 = 0)
в виде
E2.1)
мы заключаем, что коэффициент [i должен удовлетворять
уравнению
а44 = 0. E2.2)
Теорема 2, доказанная в главе 3, § 20, показывает, что
при любых коэффициентах j3i7- корни уравнения E2.2)
будут чисто мнимыми или комплексными (если только
C44 или Рб5 не равны нулю). Совершенно так же, только
заменив E17- на а17-, мы докажем отсутствие вещественных
корней у уравнения E2.2) (если, конечно, один или
оба крайние коэффициенты а44 или аъъ не равны нулю; в
противном случае корни уравнения будут веществен-
вещественными), у
Таким образом, во всех случаях, исключая упомяну-
упомянутые особые, имеем
я|) = 2 Re [Ф, (z3)] + г|H, E2.3)
где
z3 = х + \i3y E2.4)
и Мз = «з + Фз» Гз = аз — Фз (Рз > 0) — комплексный
параметр кручения и сопряженная величина (ср. § 49), а
^о — частное решение неоднородного уравнения E1.4).
Составляющие напряжения и перемещение выражаются
270 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. б
через функцию Ф3 (z3) следующим образом:
т«= 2Re[jx3O;(z3)]+^r
Ф= §- Re [(a46 - -g-) Ф. (z3)]. E2.6)
Граничное условие для комплексного потенциала име-
имеет вид
2 Re[(D3] = c3 -i|v E2.7)
Задача о кручении анизотропного стержня с областью
сечения S сводится к такой же задаче для изотропного
стержня, у которого область поперечного сечения S3
получается из заданной путем аффинного преобразования
E2.8)
О том, как из S получается ?3, Дает представление
рис. 25 для случая плоской задачи, где приходится иметь
дело с двумя преобразованными областями S^ S2 (а в слу-
случае обобщенной плоской деформации и кручения — даже
с тремя — #!, 52, ?3).
Решив уравнения E2.8) относительно х, у, получим:
Если контур сечения S анизотропного стержня задан
уравнением / (ж, у) = 0, то задача сводится к задаче
о кручении изотропного стержня, контур сечения кото-
которого задан уравнением
-^-2/з, -?¦&) = 0, E2.10)
Остановимся коротко на случае ортотропного стерж-
стержня. Направляя оси х и у нормально к плоскостям упругой
симметрии, запишем уравнения обобщенного закона Гу-
ка так:
Ъг =--а[ГУг, Ухх = -G7T*z E2.11)
(Gj, G2 — модули сдвига для плоскостей yz и xz\ Gx = —,
§ 53] РАВНОВЕСИЕ СТЕРЖНЯ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ 271
Go = — , (i±*> = 0). Подставляя значения коэффициентов
а5Ъ
ац в уравнение E1.4) и вводя обозначение
получим вместо E1.4)
Ь Я-г 2 I А. #2 ~~
E2.12)
E2.13)
Задачу о кручении ортотропного стержня легко свести
к задаче для изотропного стержня несколькрши способами,
вводя в E2.13) замену переменных. Одна из замен такова:
х =
E2.14)
Другие замены указаны в работах Сен-Венана [121],
Л. С. Лейбензона [17, 19], А. Ш. Локшина [75] и в книге
Лява [24].
§ 53. Упругое равновесие стержня эллиптического
сечения под действием скручивающих
и изгибающих моментов
Рассмотрим упругое равновесие цилиндра эллипти-
эллиптического сечения, обладающего прямолинейной анизотро-
анизотропией общего вида B1 или 18 упругих констант), у кото-
которого один торец закреплен, а
на другом действуют усилия,
приводящиеся к скручиваю-
скручивающему моменту и к изгибаю-
изгибающим моментам в плоскостях,
проходящих через геометри-
геометрическую ось и главные оси
эллипса. Поместим начало
координат в центре незакреп-
незакрепленного сечения, ось z нап-
направим по геометрической оси,
а оси х и у — по главным
осям эллипса (рис. 82). Вве-
Введем обозначения: I — длина
стержня, а, Ъ —длины глав-
главных полуосей эллипса, Mt — скручивающий момент, Ми
М% — изгибающие моменты в главных плоскостях yz, x%.
Рис. 82.
272 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
Решение задачи о кручении ортотропного стержня было
найдено Сен-Венаном [121]. Более общая задача о неор-
тотропном однородном стержне, который скручивается,
а кроме того, изгибается моментами, решена Фойгтом
[38]. Мы остановимся на основных случаях равновесия,
рассмотренных Фойгтом при различных комбинациях
моментов.
1. Обобщенное кручение. Пусть действуют только скру-
скручивающие моменты Mt, а изгибающие отсутствуют (Мг =
—М2 = 0). Две функции напряжений удовлетворяют трем
очень простым граничным условиям:
дх
ду
E3.1)
Решение также будет очень простым;
Mt / fl34 fl35 \
-ф — ^33 * * — A ^
В этом случае
^44 Р5Б
Л2 "Г А2
I*
E3.2)
яаЬ3
E3.3)
Жесткость при обобщенном кручении найдем по формуле
<53-4>
Функция напряжений и напряжения, выраженные че-
через момент Mt, представятся таким образом:
_^_ Л __
^ шЪ \ а2 Ь2
*" ' E3.6)
E3.5)
Формулы E3.6) показывают, что при заданном моменте
распределение напряжений не зависит от упругих постоян-
§53]
РАВНОВЕСИЕ СТЕРЖНЯ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ 273
ных и совпадает с распределением в таком же изотроп-
изотропном теле. Общий характер напряженного состояния также
будет таким же, как в изотропном теле (из шести состав-
составляющих напряжений четыре равны нулю). Жесткость
Ct будет такой же, как при кручении ортотропного тела,
у которого главные модули сдвига равны 1/а44 и 1/а5Ъ.
Перемещения, удовлетворяющие нужным условиям на
закрепленном конце z = I, определятся по формулам:
Mf
anb2x2 — 2а1Ъа2ху —
аъва2) у2],
M
v =
(I — zf — (aub2 + аъъа2)A — z) x
+ alba2) x2 + 2а2ф2ху - a^
M
w =
- a2!/2)
аьъа2)ху]. 4
E3.7)
Ось стержня изгибается под действием момента Mt и
принимает форму кривой:
х = ~-^ка^1 - *J> У' = lJrb(l - z)\ E3.8)
Если имеются плоскости упругой симметрии, нор-
нормальные к оси, то ось останется прямолинейной; переме-
перемещения E3.7) также очень упрощаются.
2. Кручение, не сопровождающееся изгибом. Ось стер-
стержня остается прямолинейной даже в случае, когда ани-
анизотропия является общей, если к скручивающему моменту
добавляются изгибающие, подобранные следующим об-
образом:
"Йг = 0>5^Ъ
E3.9)
В этом случае жесткость при обобщенном кручении
равна С, т. е.
С, = С =
E3.10)
274 ОБОБЩЕННОЕ Kb УЧЕНИЕ И Kl УЧЕНИЕ GTEi ИСНЕЙ [Гл. 6
Касательные напряжения тХ2, ъ>2 определяются по
прежним формулам E3.6), ох, оу, тху равны нулю, а в по-
поперечных сечениях, кроме касательных, действуют еще
нормальные напряжения:
1 ' " ¦ 22/) =
у). E3.11)
3. Изгиб в главной плоскости, не сопровождающийся
закручиванием. Для того чтобы моменты, скручивающие
и изгибающие, приложенные на концах, вызывали только
изгиб в плоскости yz без закручивания, их нужно подо-
подобрать так, чтобы между ними были зависимости E0.9).
Эти зависимости для стержня эллиптического сечения
принимают вид
М2 = - М
аЬ5 +
Mt - Мх 2я35 -
'
E3.12)
Уравнение изогнутой оси (на плоскости yz) будет
yf = _ -^-A — zf, E3.13)
где В — жесткость при изгибе:
„2
1. 7 +Р«
Очевидно, В^> В, где 5 = яяЬ3/Dа33) жесткость при
изгибе только изгибающими моментами Л/2. Касательные
напряжения в этом случае определятся по формулам
E3.6). В поперечных сечениях появляются нормальные
напряжения, равные:
4 / Мл , Мо
/ГО Л С\
таг (тг у +sr *) • E3-15)
Все формулы этого параграфа сохраняют свою силу и
для случая стержня кругового сечения. В этом случае
нужно всюду положить Ь = а.
§ 54] КРУЧЕНИЕ СТЕРЖНЯ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ 2?5
§ 54. Чистое кручение однородного
ортотроиного стержня эллиптического
или кругового сечения
Рассмотрим ортотропный стержень эллиптического се-
сечения, у которого одна из плоскостей упругой симметрии
нормальна к оси z или образующей, а две другие парал-
параллельны оси. Эти две плоскости необязательно в данной
точке пересекают плоскость сечения по линиям, парал-
параллельным главным осям эллипса; линия пересечения одной
из этих двух плоскостей упругой симметрии с главной
осью эллипса 2а образует
угол а, не равный 0° и 90°
(рис. 83).
Обозначим через а44, а45,
аьъ коэффициенты деформа-
деформации для направлений глав-
главных осей эллипса х, у и че-
через a, b — длины главных
полуосей эллипса. Рассмат-
Рассматривая простое или чистое
кручение, мы будем обозна-
обозначать скручивающий момент
и жесткость при кручении—
М и С (без индекса t). В данном случае формулы для фун-
функций напряжений, жесткости при кручении, напряжений и
перемещений мы определим совершенно элементарным пу-
путем на основании §§ 51, 53 и получим, как при совместном
действии изгибающих и скручивающих моментов (при
Мг = М2 = 0),
Рис. 83.
Q __
2М
2М
X.
E4.1)
E4.2)
Составляющие напряжений не зависят от упругих по-
постоянных. Жесткость является функцией пц и угла а,
который образует главное направление упругости с нап-
направлением главной оси 2а эллипса (рис. 83).
Обозначим через G± и G2 модули сдвига для главных
направлений упругости Е, rj; g, с — отношения главных
1276 ОБОБЩЁННОЕ Kl УЧЕНИЕ Й КРУЧЕНЙЁ СТЁРНШЕЙ [Гл.
Таблица 19
Значения отношения C(a)/Cmin для эллиптического сечения
а0
0
15
30
45
60
75
90
? = 0,5
с = 1,5
1
1,015
1,060
1.128
1,205
1.269
1,294
2
1
1,023
1,091
1,200
1,333
1,451
1,500
3
1
1,029
1,118
1,267
1,462
1,647
1,727
4
1
1.031
1.128
1.294
1,517
1,737
1,833
5
1
1,033
1,133
1,308
1,545
1,783
1,889
g = 0,1
с = 1,5
1
1,033
1,136
1,315
1,560
1,807
1,918
2
1
1,046
1,197
1,491
1,976
2,533
2,929
3
1
1,056
1,246
1,655
2,460
3,821
4,791
4
1
1,059
1,265
1,722
2,695
4,194
6,192
5
1
1,060
1,274
1,755
2,823
5,087
7,200
модулей и осей эллипса: g = G2/Gu с = alb
ния для atj и жесткости запишутся так:
sin2 a
Я55 =¦
sin4 a
+
cos2 a
A + g) A + c2) + (g - 1) A - c2) cos 2a
1. Выраже-
ВыражеE4.3)
E4.4)
Жесткость будет наибольшей, если плоскость упругой
симметрии с наибольшим модулем сдвига проходит через
большую ось 2а сечения (а = ±90°), и наименьшей, если
эта плоскость проходит через малую ось эллипса (а = 0 и
а = 180°). Эти наибольшая и наименьшая жесткости рав-
равны (см. [29], стр. 57—59):
C С E4.5)
, gC2
,
В таблице 19 приведены численные значения отноше-
отношения С (a)/Cmin при различных а для двух значений отно-
отношения главных модулей сдвига: g = 0,5 и g = ОД и пя-
пяти значений отношения главных осей эллипса с = 1,5; 2;
3; 4; 5.
Из таблицы видно, что при g = 0,5 отношение жестко-
стей невелико (не больше двух), однако при большой раз-
разнице между модулями сдвига, т.е. при малом g, разница
§ 55] КРУЧЕНИЕ СТЕРЖНЯ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ 277
между наибольшей и наименьшей жесткостями стано-
становится значительной, особенно для вытянутых эллипсов.
На рис. 84 показаны графики изменения отношений
С (a)/Cmin в зависимости от угла для двух значений g
и двух значений отношения осей эллипса с.
>
5
3
2
1
dec
j
I I
/
/
/
/
V
\
\
\
3
Z
/
2
\ 3
V
х
i
9
f
9
9
\
i
=0,5
-0,5
,1
-0,1
•
0=2
с=Ь
с =2
с =4
30 45 60 90 110135150 180
Рис. 84.
Укажем еще значение функции кручения для стержня
эллиптического сечения, характеризующей искривление
плоскости этого сечения при кручении (стержень орто-
тропный, плоскости упругой симметрии параллельны пло-
плоскостям, проходящим через ось z и главные оси эллипса
[22]):
М I 24 /К/ СЧ
ф = —гг- (п\\ — а^с)ху. (о4.Ь)
§ 55. Кручение однородного ортотропного
стержня прямоугольного сечения
Рассмотрим стержень прямоугольного сечения со сто-
сторонами а, Ь и длиной Z, однородный, прямолинейно-ор-
тотропный (эквивалентные направления параллельны
направлениям осей), с главными модулями сдвига Gx и
G2. В каждой точке имеются три ортогональные плоскости
278 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
упругой симметрии, параллельные граням параллелепи-
параллелепипеда. Один конец закреплен, по другому распределены
усилия, приводящиеся к скручивающему моменту М\
других усилий извне не приложено и объемные силы от-
отсутствуют.
В данном случае удобнее за начало координат принять
середину короткой стороны торцевого свободного попереч-
поперечного сечения, если они не
одной и той же длины (ес-
ли же сечение квадратное,
то середину одной из четы-
рех сторон), ось у напра-
вить по короткой стороне,
а ось х — параллельно
длинной; ось z, следова-
следовательно, будет направлена
параллельно ребрам от
Рис- 85. свободного торца к закреп-
закрепленному (рис. 85).
Функция напряжений гр должна обращаться в нуль на
всех четырех сторонах поперечного сечения: х — О, х = а,
у = dhb/2. Мы будем искать решение, т. е. функцию г|),
в виде простого ряда, потребовав, чтобы эта функция
заранее обращалась в нуль на двух противоположных
сторонах сечения; неизвестные постоянные определим из
условий на двух других сторонах, подобно тому как ре-
решается задача о кручении изотропного стержня прямо-
прямоугольного сечения ([20] или [22]).
Разложив правую часть уравнения E2.13) в ряд Фурье
по синусам, перепишем его следующим образом:
у k
v
/
/
/ Sf
a
A
^тт + тт^ У —sin . (э5.1)
т=1,з,5,...
Здесь обоз1тачсио:
g = G2/Gv E5.2)
Разыскиваем решение этого уравнения в виде ряда,
заранее удовлетворяющего условиям на сторонах х = 0
и х = а:
2j jE5.3)
гл=1,3,5, ...
§ 55] КРУЧЕНИЕ СТЕРЖНЯ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ 279
Подставляя if» в левую часть E5.1) и сравнивая коэф-
коэффициенты при синусах одинаковых аргументов в левой
и правой частях, получим для Ym обыкновенное урав-
уравнение
(У^± E5.4)
Общий интеграл этого уравнения имеет вид
Определяя постоянные ^4m и 5m из условий на сто-
сторонах у = ±6/2, получим окончательное выражение для
функции напряжений:
_mjtML
1 sin (с = а/
\ /?ut|Ji I а v '
m=i,3,5,... \ ch~2^/
E5.6)
По формулам E1.3) находим составляющие напряже-
напряжений также в виде рядов
ТХ7 "
2-J W2
Я2 Z-l W2
w=i,3,5,... ch
2с
cos ¦
ch —;
E5.7)
Далее введем новый параметр, зависящий от отношения
модулей упругости и от отношения сторон:
и коэффициенты р, &х, к2 — функции этого параметра,
280 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
заданные в виде рядов
Р =—г~ V -V(l — th4^; E5.9)
m-i
( \\ 2
~ th^-; E5.10)
m=l,3,5, ...
тл )
m=i,3,5,... W СП 2^
С помощью этих коэффициентов мы можем записать
очень простые формулы для жесткости при кручении С,
крутки и наибольшего касательного напряжения. Имеем:
С = G2ab*$; E5.12)
* = TWT- <55ЛЗ>
Касательное напряжение в изотропном стержне полу-
получается наибольшим на серединах длинных сторон (см.,
например, [32], стр. 317). В ортотропном стержне точки
с наибольшим касательным напряжением могут оказать-
оказаться на серединах как длинных, так и коротких сторон, в за-
зависимости от d. Таким образом, наибольшее из напряжений
определится по одной из двух формул:
Ттах = ~^Гк1 E5.14)
(в точках В и В±; см. рис. 83) или
Т„,ах = -^ *2 E5.15)
(в точках О и А).
В таблице 20 приведены численные значения коэффи-
коэффициентов р, к1У к2, вычисленные по формулам E5.9) —
E5.11), для некоторых значений параметра d. После за-
запятой удержано по три знака :).
г) В таблице 3 книги [20] имеются опечатки,
55] Кручение стержня прямоугольного сечения 281
Таблица 20
Значения коэффициентов р, кг и А-.-, из формул
E5.9)—E5.11)
d
1
1,25
1,5
1,75
2
2,5
0,141
0,172
0,196
0,214
0,229
0,249
/и
4,803
4,545
4,329
4,184
4,065
3,882
Иг
4,803
4,141
3,718
3,431
3,232
2,970
d
3
4
5
10
20
ОС
3
0,263
0,281
0,291
0,312
0,323
0,333
/и
3,742
3,550
3,430
3,202
3,098
3,000
2,820
2,644
2,548
2,379
2,274
—
Таблица 20 получена в результате обработки более под-
подробных таблиц Сен-Венана [121]. В ней указаны значения
коэффициентов только для d, больших или равных единице,
т. е. для отношений сторон с ^> у g. Но ее можно ис-
использовать и в случаях, когда с < ]/g; нужно только так
выбрать обозначения сторон, чтобы было выполнено ус-
условие с > Yg, а это всегда можно сделать. Пусть, напри-
например, длины сторон равны 4 и 3 см, а модули сдвига для пло-
плоскостей упругой симметрии, параллельных сторонам,
равны соответственно 1 • 10 кгс/см2 и 9 • 10 кгс/см2. В этом слу-
случае нужно положить а = 4, 6 = 3, Gx = 9• 105, G2 =
= 1-Ю5 и тогда g = 1/9, \х ¦= 1/3, d = 4; по таблице на-
находим:
C = 0,281, кх - 3,550, К - 2,644.
Наибольшее напряжение получится в точках на се-
серединах сторон Ъ (коротких); по формуле E5.15)
Тшах - = 0,220 А/.
В точках на серединах длинных сторон а получаем:
т - 0,099 М.
Можно получить решение задачи о кручении стержня
прямоугольного сечения, ортотропного и однородного,
и в другой форме — в виде двойного тригонометрического
ряда. В этом случае поместим начало координат в одном
из углов сечения и направим оси х и у по сторонам. Разло-
Разложив правую часть уравнения E2.13) в двойной ряд Фурье
282 ОБОБЩЕННОЕ Ki УЧЕНИЕ И К УЧЕНИЕ СТЕi ЖНЕЙ [Гл. 6
по синусам и разыскивая выражение гр также в виде двой-
двойного ряда, расположенного по синусам, получим
L
m=lt'S,b,...
1
ma
П1ЛХ
sin a
¦sin -
плу
и
32d6V*2 \H
<»h - ^ Ж
m=L,'3,b,... m=i,3,6,...
E5.16)
Очевидно, что эта функция обращается в нуль на всех
четырех сторонах сечения. Несмотря на свою крайнюю
простоту, эта форма решения менее удобна, чем форма
E6.6) по той простой причине, что члены ряда E5.16)
убывают значительно медленнее по сравнению с членами
ряда E5.6). Поэтому формула E5.16) представляет теоре
тический интерес, но для использования на практике зна-
значительно удобнее функция гр в виде простого ряда.
Заметим, что решение для неортотропного стержня
хотя и было получено (оно равносильно решению для стер-
стержня с сечением в виде параллелограмма, найденному
Р. С. Минасяном [76]), но практически реализовать его
значительно труднее, чем решение для ортотропного
стержня.
§ 56. Приближенные методы решения
задач о кручении
Известно довольно много приближенных методов ре-
решения задач о кручении, которые можно применить в тех
случаях, когда отыскание точного решения сопряжено
с большими математическими трудностями. Такие труд-
трудности могут встретиться, например, в случае, когда контур
сечения ограничен какой-либо сложной кривой, отрез-
отрезками кривых и прямых, или область сечения многосвязна,
когда модули меняются по площади сечения (неоднород-
(неоднородный стержень) и так далее. В основах этих методов заложе-
заложены разные принципы, как чисто теоретические, так и
экспериментальные. Мы остановимся коротко только на наи-
наиболее распространенном методе — энергетическом, имею-
имеющем несколько вариантов, и покажем, как с его помощью
решаются сравнительно несложные задачи.
Общая идея метода заключается в следующем. Вместо
того чтобы решать краевую задачу для дифференциального
§ 56] ПРИБЛИЖЕННЫЕ МЕТОДЫ ?83
уравнения второго порядка, к которой сводится задача
о кручении, решают равносильную ей (с математической
стороны) вариационную задачу об отыскании минимума
интеграла, и притом делают это приближенно. Задаются
выражением для функции напряжений при кручении,
удовлетворяющей нужным условиям на контуре сечения
и внутри и содержащей неизвестные постоянные (коэф-
(коэффициенты) и функции. Затем используют принцип наи-
наименьшей работы, о котором говорилось в § 11 главы 1,
разыскивают минимум интеграла и получают уравнения
для неизвестных постоянных или дифференциальные
уравнения для неизвестных функций. При чистом круче-
кручении однородного неортотропного стержня нужно восполь-
воспользоваться формулой Кастилиано и задача сведется к оты-
отысканию функции г|), сообщающей минимальное значение
интегралу:
E6.1)
Самый простой способ решения заключается в сле-
следующем. Задаются семейством функций %j (х, у) двух
переменных х, у, зависящих от двух целочисленных па-
параметров к, Z, обращающихся в нуль на контуре одно-
связной области (ipfrj = 0). Функиия ty ищется в виде
суммы
К L
*= S %Aktfkl(x,y). E6.2)
После подстановки в выражение E6.1) и интегриро-
интегрирования по области сечения это выражение становится
функцией А1;1. Далее разыскиваются переменные Аки
сообщающие функции U (А^г) минимальное значение. Если
\|) задается в виде E6.2), то для Ак1 получается система
уравнений первой степени, неоднородная, которую и
нужно решить.
В других случаях за неизвестную функцию удобнее
брать не гр, а функцию кручения ср; разумеется, тогда при-
придется искать минимум не интеграла E6.1), а другого, вы-
вытекающего из принципа возможных перемещений.
284 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
Рассмотрим пример. Область сечения имеет одну ось
симметрии; контур ее образован двумя кривыми,
E6.3)
пересекающимися на оси симметрии, где а — постоянный
коэффициент и
(яг, р, q — положительные числа — целые, дробные или
нули).
При разных значениях т, р, q контур, естественно,
имеет разную форму; например, при т = q = 0,5, р =
= 1 — это эллипс, при дру-
других же значениях области
в общем похожи — они име-
имеют каплеобразную форму
(рис. 86). Для таких областей
решено довольно много за-
задач теории упругости, осо-
особенно в работах Л. С. Лей-
бензона [17] и [18] и др. ав-
авторов *). Приближенные ре-
ис* шения с помощью функции гр
мы будем строить, задавшись семейством функций
a*-y-i E6.5)
0
(Л
и
у/ 1
«2?
L 1
>1
(к = 1,2,3 Z = 1,2,3, ...)
и разыскивая я|) в виде сумм E6.2), где коэффициенты Ап
должны сообщать интегралу E6.1) минимальное значение.
Желая построить решение только в первом приближе-
приближении, возьмем только первый член суммы E6.2), отбросив
остальные, т. е. положим
- а* [/ (f
E6.6)
!) Л. С. Лейбензон в своих работах называл фигуру, симметрич-
симметричную или несимметричную, ограниченную двумя кривыми типа
E6.3), —«авиационным профилем».
§ 56] ПРИБЛИЖЕННЫЕ МЕТОДЫ 285
Подставляя в E6.1) и интегрируя, получим U, как по-
полином второй степени относительно 4И и далее ищем его
минимум. Не приводя выкладок, достаточно элементар-
элементарных, приведем выражение для жесткости, найденное
в первом приближении для произвольных ^параметров.
При ПРОИЗВОЛЬНЫХ 771, р, q
с = -§-№•-ye—™^. E6.7)
Здесь g = G2/Gi,
Г (a) = 5 e~xxa-xdx E6.9)
о
бета-функция и гамма-функция *), е — коэффициент, за-
зависящий от значений бета-функции:
)
3m+l
УВ1—р
+
, E6.10)
В частности, для значений параметров т — 0,5, р —
= q = 1, когда сечение ограничено дугами двух полукуби-
полукубических парабол
E6.12)
получим [19] Зе = 11/13,
3465 И
Если воспользоваться принципом возможных переме-
перемещений, то в первом приближении можно взять совсем
г) См., например, Г. К о р н и Т. Корн, Справочник по
математике для научных работников, «Наука», 1970, стр. 633—638.
286 ОБОБЩЕННОЕ Ю УЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
простую функцию ф, характеризующую искривление
плоскости поперечного сечения стержня в виде эллипти-
эллиптического цилиндра:
Ф = Ап ху + А01у. E6.13)
Для стержня с сечением, ограниченным двумя дугами
полукубических парабол E6.И), получаем выражение
для жесткости при кручении:
п п 256 Ьа3 га . /ч
с = G <5614)
жъ Г71Л
1 + ТГ б \ ъ
Формула E6.12) дает преуменьшенное значение же
сткости, ее нижний предел, а E6.14) — преувеличенное
значение, верхний предел. Иначе говоря, истинная вели-
величина жесткости рассматриваемого стержня (с сечением,
ограниченным двумя дугами полукубических парабол)
находится между величинами, определяемыми по фор-
формулам E6.12) и E6.14). Уточнения этой величины С мы
произведем, беря в сумме E6.2) и соответствующей сумме
для ф большее число членов и определяя постоянные из
условий минимума соответствующих интегралов. Но мы
дальше развивать эту тему не будем, а сошлемся на рабо-
работы Л. С. Лейбензона [17] и [19] и многочисленную указан-
указанную литературу.
Отметим только работы Н. X. Арутюняна [41], [42],
посвященные вопросу кручения стержня с сечением, ог-
ограниченным двумя подобными (несофокусными) эллип-
эллипсами и двумя лучами (в частности, эллиптическое разре-
разрезанное кольцо, полукольцо и эллиптический сектор).
Помимо подробного изложения с использованием одного
варианта энергетического метода в работах самого ав-
автора, краткое изложение имеется в наших книгах [20]
и [22].
Другого рода приближенный метод решения задач
о кручении основан на введении в уравнения кручения
малого параметра и в пренебрежении степенями этого
параметра, начиная с некоторой, в процессе решения.
Такой метод или способ предложен В. С. Саркисяном
для решения задачи о кручении стержня с сечением,
которое представляет собой фигуру, вытянутую в
§ 57] Кручение нёш ерывно-неодно1 одного стержня 287
одном направлении («удлиненный профиль», [29], [88],
[90]).
Для получения приближенных решений задач о кру-
кручении можно использовать и различные аналогии в теории
кручения. Сущность этих аналогий заключается в том, что
основное уравнение теории кручения (уравнение для
функции напряжений гр или уравнение для функции кру-
кручения ф) совпадает, с точностью до постоянных коэффици-
коэффициентов, с уравнениями для других задач механики и фи-
физики, которые легче решить, полностью или частично при-
применяя эксперимент. Наиболее важной остается аналогия
Прандтля (мембранная аналогия). Этими замечаниями
мы и ограничимся, сославшись на книгу по кручению
Н. X. Арутюняна и Б. Л. Абрамяна [4], где вопрос об
аналогиях разобран достаточно подробно и где дана
литература.
Других приближенных методов, например, метод се-
сеток, метод конечных элементов и т. д. мы за недостатком
места разбирать не будем и сказанным выше по этому
вопросу ограничимся.
§ 57. Кручение непрерывно-неоднородного
стержня с прямолинейной анизотропией
Из общих уравнений, изложенных в главе 3, легко по-
получить, как частный случай, уравнения кручения непре
рывно-неоднородных стержней.
Пусть дан стержень постоянного сечения, непре-
непрерывно-неоднородный, имеющий в каждой точке плоскость
упругой симметрии, нормальную к образующей, но во-
вообще неортотропный. Один конец предполагается закреп-
закрепленным, на другом конце (торце) действуют усилия, приво-
приводящиеся к скручивающему моменту М. Боковая поверх-
поверхность свободна от внешних усилий и не закреплена; на
закрепленном торце усилия, следовательно, приведутся
к тому же самому, но противоположно направленному
моменту М (рис. 80). Объемные силы считаем отсутствую-
отсутствующими.
Поместим начало координат в точке одного из торцов,
направив ось z параллельно образующей, а оси х и у так,
как это представляется удобным, учитывая форму сече-
сечения. Уравнения обобщенного закона Гука запишутся
288 ОЁОБЩЁННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл.
в заданной координатной системе х, у, z в виде
ех = Лцал + a12oy + а13аг + а16тху,
8У = а12ах + а22ау + а2гог + а26тху,
+ + а33а2 +
E7.1)
причем пи предполагаются непрерывными дифференци-
дифференцируемыми функциями двух координат х, у.
В случае однородного стержня, имеющего одну пло-
плоскость упругой симметрии, нормальную к образующей,
и скручиваемого моментами, из шести составляющих
напряжений только две не равны нулю, остальные же от-
отсутствуют:
or* = огу = хху = az - 0. E7.2)
Предположим, что и в стержне с рассматриваемой не-
неоднородностью качественная картина распределения нап-
напряжений не отличается от картины в случае однородного
тела E7.2), т. е. из шести напряжений только два не
равны нулю, в любой точке,— ххг и ту2, а удовлетворяют
уравнению
дх
дх„
дх
= 0.
E7.3)
Для разнообразия мы выведем уравнения кручения та-
такого стержня не из общих уравнений главы 3, а незави-
независимо.
Основная система уравнений равновесия упругого тела
в данном случае состоит из уравнения E7.3) и уравне-
уравнений E7.1), которые примут вид:
-о. w-°- ? =
dv
dw
ди
ди
дх
dw
~df = auXyz
ди
E7.4)
§ 57] КРУЧЕНИЕ НЕПРЕРЫВНО-НЕОДНОРОДНОГО СТЕРЖНЯ 289
Проинтегрировав эти уравнения в неоднократно ис-
использованном порядке, мы получим выражения для пе-
перемещений:
и = —$yz + u', v = $xz + v', w = % (я, у) + w\ E7.5)
где Ф — относительный угол закручивания, ф — так на-
называемая функция кручения, характеризующая искрив-
искривление сечений ли',v',w' — «жесткие» смещения (см. A8.8)).
Неизвестными функциями у нас будут две составляющие
напряжений ххг {х, у), xyz (х, у) и функция кручения
Ф (я, у). Эти функции удовлетворяют уравнению E7.3)
и уравнениям
Разница между этими двумя уравнениями и уравнениями
для однородного тела с такой же упругой симметрией
заключается лишь в том, что в E7.6) atj — функции т,
у, тогда как у однородного тела они постоянны. Приняв
за основную неизвестную — функцию напряжений г|),
связанную с составляющими напряжений очевидными ра-
равенствами
получим из уравнения E7.6) путем исключения ф — урав-
уравнение для г|):
д I д\р д\Ь \ д
дх \ дх ду I ду
E7.8)
Граничное условие запишется очень просто: на контуре
поперечного сечения гр = const (или гр = 0, если область
сечения односвязна).
Можно принять за основную неизвестную функцию ф
и выразив напряжения через ее производные, воспользо-
воспользоваться уравнением E7.3). Тогда мы получим уравнение для
Ф, второго порядка, с переменными коэффициентами.
Граничное условие запишется сложнее, а поэтому мы этим
способом решения задач о кручении пользоваться не бу-
будем и уравнение и условие приводить также не будем.
290 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
§ 58. Кручение ортотропного стержня
прямоугольного сечения
с переменными модулями сдвига
Из различных случаев непрерывно-неоднородных стер-
стержней с переменными модулями одним из простейших яв-
является случай ортотропного стержня прямоугольного се-
сечения, у которого модули сдвига зависят только от одной
координаты х или у.
Пусть стержень прямоугольного сечения, изображен-
изображенный на рис. 85, является непрерывно-неоднородным,
причем модули сдвига его — функции кординаты у {Gx и
G2 не меняются вдоль стороны длиной, равной а). Функ-
Функции предполагаются непрерывными, однозначными и диф-
дифференцируемыми по своему аргументу у. Вводя модули
сдвига, нужно в уравнении E7.8) положить
_ 1 _ п _ 1
#44 — "ТГ~ » #45 — ", #55 — ~7Г~ »
и тогда оно примет вид:
Напряжения определятся по прежним формулам E7.7).
Метод решения задачи — такой же, как и соответ-
соответствующей задачи о кручении однородного стержня. Разло-
Разложим правую часть E8.1) в ряд Фурье по синусам и ищем вы-
выражение для г|), заранее удовлетворяющее условиям на
двух сторонах х = 0 и х = а.
Уравнение E8.1) перепишется таким образом:
д Г 1
[ ду\
у
я / i т
m=i, з, 5,...
Полагая
^ E8-3)
m=l, 5, 5,...
подставляя в уравнение E8.2) и сравнивая коэффициенты
при одинаковых синусах в левой и правой частях,
? 58] КРУЧЕНИЕ СТЕРЖНЯ С ПЕРЕМЕННЫМИ МОДУЛЯМИ 291
получим уравнения для неизвестных функций Ym (у):
E8.4)
Это уравнение — линейное, с переменными коэффи-
коэффициентами.
Обозначив через Yml, Ym2 линейно-независимые ре-
решения однородного уравнения, соответствующие данному
т и через Ym0 — частное решение неоднородного уравне-
уравнения с тем же индексом т, запишем при любом задании G±
и G2 общий интеграл E8.4):
Ym = AmYml + BmYm2 + Yn0. E8.5)
Функция напряжений запишется в виде
^. E8.6)
т-=\, з, б,...
Граничные условия на сторонах х = О, х = а удов-
удовлетворяются. Требуя, чтобы граничные условия удовлет-
удовлетворялись и на двух других сторонах у = +6/2, мы полу-
получим для каждой пары коэффициентов Ат, Вт систему
уравнений, из которой и определим неизвестные коэффици-
коэффициенты, если найдены Ymv Ym2, Ym0. Эти частные решения
можно найти не для любых значений функций Gl9 G2,
а лишь для некоторых частных заданий их, число которых,
по-видимому, не очень мало. Некоторые случаи мы рассмот-
рассмотрим. По-видимому, простейшим будет случай, когда мо-
модули 'сдвига являются экспоненциальными функциями
г/, т. е.
плу п-у
Сг-gie ь , G2^g2e ь . E8.7)
Здесь gl7 g2 — постоянные, имеющие размерность мо-
модуля сдвига (или что то же, напряжения), п — любая ве-
вещественная безразмерная постоянная величина, неравная
нулю — положительная, отрицательная, целая, дробная,
иррациональная и т. д.
10*
292 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
Введем обозначения:
c = 4-t d = ^. E8.8)
Ут =
sm = 0,5 (п + уп), *ш - 0,5 (п - 7т). E8.10)
В дальнейшем значки т у ут, sm, tm мы для простоты
будем отбрасывать.
Общее выражение для функции напряжений я|) с неопре-
неопределенными коэффициентами Ат, Вт запишется следую-
следующим образом:
т—1, 3, 5,...
-f-e^-Lsin-™". E8.11)
Определив коэффициенты из условий на сторонах у =
zfc^/2, получим окончательно:
X
1
m3
-sin
•я
тлх
a
г=1, з, 5,...
E8.12)
В первую очередь нам следует найти жесткость С и
выразить через нее скручивающий момент Af, относи-
относительный угол закручиванияФ (крутку) и определить напря-
напряжения в любой точке и в узловых точках — на серединах
сторон. Жесткость определяется по формуле E1.9):
С = -тг-\ ytydx dy. E1.9)
Произведя интегрирование по площади прямоуголь-
прямоугольника а х Ъ, перейдя к g2 и просуммировав часть ряда,
воспользовавшись формулой ([111, стр. 21):
7П=1, 3, б,.„
E8.13)
§ 58] КРУЧЕНИЕ СТЕРЖНЯ С ПЕРЕМЕННЫМИ МОДУЛЯМИ 293
получим формулу для жесткости:
С = g2ab* p.
Здесь
оо
V4 7 — schtn -\-
пп
jt5
m=i, 3, б,...
m6 sh
я—
E8.14)
E8.15)
(см. E8.10)).
Дальнейших преобразований этой формулы мы произ-
производить не будем, приняв ее за окончательную. Относитель-
Относительный угол закручивания равен
м E8.16)
Полный угол закручивания сотах для всего стержня,
длина которого I, равен:
<W = <M = ^?sr. E8-17)
По формулам E7.7) находим, дифференцируя функ-
функцию напряжений E8.12), сами напряжения в любой точ-
точке х, у:
М &d^ Ч 1
= ab2 Л2Р { i
пе
ъ —
П=1, 3, 5,...
sh
— / sh -g- e
1 . тпх
—г-Sin
т3 а
sny
tny
sh-^-e
7Я
sh ~2~
COS
E8.18)
Как показывают исследования и вычисления, наиболь-
наибольшее во всем стержне напряжение цолучается посредине
294 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ ?Гл. 6
Таблица 21
Значения коэффициентов жесткости Р и коэффициентов
наибольшего напряжения к1 и к2
п
0,1
0,5
d
0,5
1
2
3
5
0,5
1
2
3
5
3
0,05728
0,1407
0,2287
0,2632
0,2911
0,06005
0,1434
0,2282
0,2611
0,2875
кх
7,359
5,385
4,520
4,154
3,806
11,855
8,311
6,796
6,219
5,705
тс»
8,117
4,797
3,230
2,817
2,547
7,714
4,638
3,167
2,778
2,523
п
1
2
d
0,5
1
2
3
5
0,5
1
2
3
5
0,06932
0,1532
0,2304
0,2592
0,2824
0,1174
0,2101
0,2762
0,2991
0,3174
19,786
13,653
11,009
10,079
9,309
43,796
31,671
26,149
24,321
22,975
кг
6,606
4,165
2,956
2,632
2,416
3,744
2,669
2,090
1,931
1,819
одной из сторон, длинной или короткой, и опреде-
определяется по одной из формул:
М
/>ъ
М
1и.
E8.19)
Структура коэффициентов к1 и /с2 ясна из формул E8.18).
В таблице 21 приведены численные значения коэффи-
коэффициента жесткости и коэффициентов наибольшего напря-
напряжения C, кг и к2 для стержня прямоугольного сечения
с модулям E8.7) для ряда численных значений п и d. Со-
Сохранено по 4 — 5 значащих цифр.
При данных значениях п и d наибольшее напряжение,
очевидно, нужно определять по первой формуле E8.19),
а не по второй (за исключением п = 0,1, d = 0,5). При
других значениях параметров, не указанных в таблице
24, наибольшее напряжение определится по второй фор-
формуле E8.19) (к2/У g^> кх). Разумеется, таблица 21 может
служить только для иллюстрации теории, а не для расче-
расчетов всевозможных стержней данного типа, так как она
содержит коэффициенты для слишком малого числа зна-
значений параметров п, d%
59]
НЕК0Т01ЫЕ ДРУГИЕ СЛУЧАИ НЕОДНОРОДНОСТИ 295
§ 59. Некоторые другие случаи
неоднородного ортотропдеого стержня
прямоугольного сечения
Кроме экспоненциальной зависимости модулей сдвига
от z/, можно указать еще целый ряд зависимостей Gx и G2
от у, при которых частные решения Yml, Ym2 и Ym0 урав-
уравнения для функции напряжений E8.4) можно получить в
явном виде, а следовательно, удовлетворить условиям
на сторонах х — О, х =а , у — +6/2 и тем самым найти
Рис. 87.
решение задачи о кручении в явном виде. Прежде всего
нужно указать Gx и (?2, являющиеся степенными функци-
функциями расстояния у (см. [69] и [22]).
Пусть рис. 87 изображает поперечное сечение стержня,
размеры и расположение осей; у0 — расстояние заданной
прямой, параллельной стороне а, от оси х. Пусть далее,
модули заданы в виде функций:
С-«.
E9.1)
сдвига (или,
вещественное
п характер
казан на рис.
ние кривой G
цательном п
кривой Gt.
множители
что то же,
число. При
изменения
87 справа.
проходит
— прямая
имеющие размерность модуля
напряжений), п — произвольное
положительном и отрицательном
модулей вдоль стороны Ъ по-
При положительном п продолже-
через точку у = — у0; при отри-
у = —у0 является асимптотой
296 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. С
Введем обозначения:
//1 = У + ?/о, 11 = -f-, Ло = -f1,
Л1 = Ло ~ 0,5, т]2 = т]о + 0,5,
a = —
и + 1
E9.2)
Разыскивая выражение для функции яр в виде ряда
E8.3), получим для Ym обыкновенное уравнение, где
штрихами обозначены производные по уг:
у" JLV
E9.3)
Частные решения однородного уравнения зависят от п
и выражаются через функции Бесселя порядка JV(cm. [11],
стр. 670). Если п не является целым числом, то
У mi =
= г/Г V-i
E9.4)
где //v, /-xV — функции Бесселя первого рода.
При N целом функция /_лг должна быть заменена
функцией Бесселя второго рода того же аргумента. В на-
нашем случае аргумент у функций Бесселя — чисто мни-
мнимый, а поэтому они должны быть заменены модифициро-
модифицированными функциями. Имеем
Yml - j/I*/* (yi/i), Ym2 = y?I_N (ууг) E9.5)
(N не является целым числом) или
Yml --= yTlN (Wi), Ym* = U~iaKN(vj/i) E9.6)
(TV — целое число; iiT/v — функция Макдональда).
Частное решение Ym0 неоднородного уравнения E9.3)
найдем с помощью квадратур, зная Ymv и получим
°52 у
пО тгМ™ ml
Ymld!h) dyx. E9.7)
Приведем частные решения однородного уравнения для
нескольких случаев задания модулей.
59] НЕКОТОРЫЕ ДРУГИЕ СЛУЧАИ НЕОДНОРОДНОСТИ 297
1. Линейная зависимость
Gt = ft (Ц + tjo), n = 1, a = -1, N = 1, E9.8)
E9-9)
2. Обратная пропорциональность расстоянию:
Gt == ft (t| + rio)-1, л = -1, a = 0, N = 0, E9.10)
3. Обратная пропорциональность квадрату расстоя-
расстояния:
Gi = gi(Tl + T]o)-2, n = -2, a = -|-' tf = -T« E9Л2)
sh -j-(T| + T|o) ch—(т|+тH)
У ' E9ЛЗ)
В третьем случае частные решения выражаются через
элементарные функции. Это же будет и в четвертом слу-
случае, наиболее простом в смысле выкладок и подсчетов:
4. Квадратичная зависимость от расстояния:
d = gi (r| -f ЛоJ» ть = 2, а = y , N = -7т- . E9.14)
В этом случае получим:
У mi = ch -2р (у] + %) — —- (г) + Ло) sh ^j~ (Л + Ло),
Гт2 = sh ^— (л + Ло) — -^ (Л + Ло) ch -^- (л + %),
E9.15)
Выражения для функции напряжений, удовлетворя-
удовлетворяющей условиям на контуре сечения, мы приводить не бу-
будем, так как далее нигде его не используем и жесткости
и напряжений для данного случая не вычисляем *).
Функция г|) приведена в книге [22] (гл. 3, § 1!*).
298 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
Задача о кручении легко решается и в тех случаях, ког-
когда модули сдвига пропорциональны различным, а не оди-
одинаковым степеням сумм т] + Ло» т. е. *):
Gi = gi (Л + ЧоГ. G2 = g2 (t) + тьГ (m ?= я). E9.16)
Особенно простым будет случай, когда т = п -\- 2
(п — любое вещественное число); функция напряжений
выражается через степенные функции суммы г\ + Ло-
о
Рис. 88.
Задача о кручении легко решается и в том случае,
когда одна сторона сечения значительно длиннее другой
(стержень с сечением в виде узкого прямоугольника).
Поместив начало координат на одной из осей стержня
вдали от короткой части контура (рис. 88) и рассматривая
только случаи, когда главный модуль сдвига G2 для пло-
плоскостей, параллельных длинным сторонам, зависит толь-
только от у, а другой — произвольная непрерывная функция
х и у, мы можем считать функцию г|э зависящей только от
у. Тогда, очевидно, эта функция удовлетворяет уравне-
уравнению
(¦?)' =-2*. E9-17)
откуда получаем самую функцию г|э с двумя произвольны-
произвольными постоянными, выражение которой запишем следующим
образом:
а|) = -20 А (у) + Af0 (у) + В. E9.18)
Здесь обозначено:
G2ydy, U(y) = ^G2dy. E9.19)
Постоянные А и В определим, требуя, чтобы функция
напряжений была равна нулю на поверхностях у=+Ь/2.
См. книгу [22] (гл. 3). Решение следующей задачи см. там же*
§ 60] ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНЫЙ СТЕРЖЕНЬ 299
§ 60. Кручение цилиндрического
или призматического стержня,
обладающего цилиндрической анизотропией
Пусть имеется цилиндрический или призматический
стержень произвольного сечения, обладающий цилиндри-
цилиндрической анизотропией, с осью анизотропии, параллельной
образующей. Боковая поверхность свободна от внешних
усилий и закреплений, объемных сил нет, а по торцам
распределены усилия, приводящиеся к скручивающим
моментам М противоположного направления.
Мы рассмотрим чистое кручение непрерывно-неодно-
непрерывно-неоднородного стержня, у которого в каждой точке имеется пло-
плоскость упругой симметрии, нормальная к образующей,
а коэффициенты аг}- по длине не меняются. Уравнения
теории кручения мы выведем не пользуясь материалом
главы 3, а непосредственно. Предположим, что только две
составляющие напряжения не равны нулю и не зависят
от продольной координаты z, а остальные четыре равны
нулю. Приняв какую-нибудь точку на торце за начало
координат и направив ось z параллельно образующей
цилиндра, запишем основную систему уравнений в цилин-
цилиндрических координатах следующим образом:
с, = О, = 0,-тя,О,%+^-%. + Ь. = О; F0.1)
1 dw
диг , диВ
дд ~*~ дг
F0.2)
Далее из уравнений F0.2) определяем перемещения,
используя их в обычном порядке: 3, 4, 5—1, 2, 6. В ре-
результате получим следующие формулы для перемещений:
иг = и*, щ = drz +щ, w = Фф (г, 9) + м>\ F0.3)
Здесь иг, щ, w' — «жесткие» перемещения, зависящие
300 ОБОБЩЕННОЕ К1 УЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
от шести постоянных — ipex вращений сог- и трех посту-
па1ельных перемещений (см. B3.13) ); Ф — относительный
угол закручивания (крутка) и ф (г, 9) — так называемая
функция кручения. Неизвестные функции переменных г,
9 — тГ2, т02, Ф — два напряжения и функция кручения —
удовлетворяют уравнениям
4 +
+ #55?rz = # -fo-
-foil уравнению равновесия сплошной среды F0.1).
Заметим, что в состав уравнений F0.4) входят только
три коэффициента деформации — а44, #45, аЪ5, а прочие
коэффициенты могут быть любыми (по крайней мере не-
непрерывными) функциями всех трех переменных г, 9, z. На
боковой поверхности напряжения должны удовлетворять
условию
тГ2 cos (п, г) + Tez cos (w, 9) = 0, F0.5)
а на торцах — также по одному условию:
t0zr2 dr dQ = М F0.6)
(на разных торцах моменты имеют противоположные
направления вращения). Из уравнения F0.6) определится
крутка Ф или жесткость, так какФС = М.
Так же как в случае прямолинейно-анизотропного
стержня, можно предложить два способа решения задачи
о кручении, в зависимости от того, что принять за основ-
основную неизвестную функцию.
Способ 1. За неизвестную функцию примем функцию
напряжений при кручении гр:
@0.7)
Исключая ф из F0.4), получим уравнение
!ага
На контуре поперечного сечения
ур = с = const. F0.9)
g 60] ЦИЛИНДРИЧЕСКИ-АНИЗОТГОПНЫЙ СТЕРЖЕНЬ 30]
В случае односвязной области, когда можно принять с = 0,
жесткость определится по формуле
С - -^[[^rdrdQ. (G0.10)
В частности, для ортотропного стержня с плоскостями
упругой симметрии, направленными нормально к коор-
координатным направлениям г, Э, z, вместо F0.8) будем иметь
Г аг J + did \ rG2 <99
где G2 (г, Э), 6?! (г, 6) — модули сдвига для плоскостей,
проходящих через ось z, параллельную оси анизотро-
анизотропии, и параллельных z. Для однородного ортотропного
стержня F0.11) принимает вид
^f =!^. F0.13)
Способ 2. За неизвестную функцию берется функция
кручения ф (г, 0), через которую нужно выразить на-
напряжения и затем найти ее на основании условия на кон-
контуре сечения F0.5).
Имеем
<6ОЛ4)
где Atj — коэффициенты, которые мы получим, решив
уравнения F0.4) относительно составляющих напряже-
напряжений. Подставляя F0.14) в F0.1), получим уравнение для ф.
В частности, для однородного тела оно будет ьметь вид:
Аъъ \~№+~~dF) +2^5ТЖ+ А~7
) ?
F0.15)
Второй способ менее удобен, так как граничное условие
получается сложнее условия F0.9). Это же самое наблюда-
наблюдалось и в случае прямолинейно-анизотропного тела(§ 51).
302 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЫ СТЕРЖНЕЙ [Гл. 6
§ 61. Кручение неоднородного полого
кругового цилиндра, обладающего
цилиндрической анизотропией
Рассмотрим тело в виде полого кругового цилиндра,
обладающего цилиндрической анизотропией и закручи-
закручиваемого моментами, приложенными к торцам (см. работу
[22], гл. 3, § 24). Предполагается, что данное тело ограни-
ограничено поверхностями соосных круговых цилиндров с ра-
радиусами а, Ъ и длиной I (b ^> а). Один торец можно считать
закрепленным неподвижно, а другой находящимся под
действием усилий, приводящихся к скручивающему момен-
моменту М. Анизотропия цилиндра считается цилиндрической,
причем ось анизотропии совпадает с геометрической осью
и принимается за ось z\ начало О помещается на незакреп-
незакрепленном торце. Анизотропию мы не будем полагать самой
общей, а наложим на нее следующие ограничения: 1) уп-
упругие свойства таковы, что относительные удлинения
8г, 8о, е2 не зависят от напряжения Т02, а следовательно,
в уравнениях обобщенно-
обобщенного закона Гука A0.2) ко-
коэффициенты аы, а24 и а34
равны нулю; 2) коэффици-
коэффициенты а44, а45, аъъ зависят
только от расстояния г от
центра поперечного сече-
сечения и не зависят от z и от
угла 9, который отсчитьтва-
ется от оси х, направлен-
направленной по произвольному фик-
фиксированному радиусу сече-
сечения (рис. 89); 3) остальные
коэффициенты могут быть
произвольными функция-
функциями трех координат г, Э, z
и на распределение напряжений не оказывают влияния.
Если цилиндр удовлетворяет всем этим условиям, то
нет надобности использовать общие уравнения типа при-
приведенных в главе 3, а проще общие уравнения для нап-
напряжений и перемещений вывести независимо, приняв за
основу только самые общие уравнения равновесия произ-
произвольного упругого тела. Всем этим уравнениям можно
Рис. 89.
§ 61] НЕОДНОРОДНЫЙ ПОЛЫЙ ЦИЛИНДР 303
удовлетворить, предположив, что из шести составляю-
составляющих напряжений только одна xoz не равна нулю, а из трех
проекций перемещения не равны нулю только две:
ov = Се — Тго = crz = Тгэ — 0, иг — 0. F1.1)
Напряжение Tez зависит только от г (если распреде-
распределение усилий по торцу не дается, а задается только скру-
скручивающий момент М) *), а уравнения обобщенного закона
Гука принимают вид
д"о n dw A I dw , d"e
F1.2)
dw "м- и- v
Интегрируя эти элементарные уравнения, получим
F1.3)
F1.4)
Здесь Ф, как и раньше, относительный угол закручива-
закручивания. Из постоянных, характеризующих жесткие переме-
перемещения, сохранены только две: поступательное переме-
перемещение в осевом направлении wQ и поворот в плоскости
поперечного сечения со3; эти постоянные мы определим из
уравнений на закрепленном торце, полагая там неподвиж-
неподвижной окружность заданного радиуса '¦?.
Жесткость определим по формуле:
F1.5)
а отсюда на основании F1.3)
ъ
-?-йг. F1.6)
х) Еслп распределение касательных усилий по торцу задано
н зависит от 0, тогда, разумеется, и напряжения зависят от 0.
3 Ц ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
Следовательно,
#=—, F1.7)
Полный угол закручивания равен
(О,„ах = ^-. F1.9)
Формулы для перемещений F1.4) показывают, что:
1) поперечные сечения будут искривляться, если а45 не
равен нулю, и останутся плоскими, если а45 == 0; 2) про-
проекции радиусов на плоскость поперечного сечения будут
искривляться, если а46 ф 0:, они останутся прямолиней-
прямолинейными, если aiQ = 0. Если стержень является ортотропным,
то поперечные сечения останутся плоскими и радиусы
при кручении останутся прямолинейными (не будут ис-
искривляться).
Так как на напряжение оказывает влияние только
коэффициент деформации а44 или модуль сдвига Gx (г) =
=¦"= Gqz, to это означает, что в неоднородном изотропном
стержне с модулем сдвига G1 (r) напряжения получаются
точно такими же, как и в неоднородном криволинейно-
анизотропном, у которого я44 = 1/GV Частный случай
исследуемой задачи был рассмотрен еще В. Фойгтом в ра-
работе [128], более общий — в нашей книге [20] (гл. 4, § 44).
Рассмотрим частный случай, когда модуль сдвига
Gez или G1 меняется по радиусу по степенному закону —
пропорционален какой-то степени расстояния г от цен-
центра, т. е.
где п — какое-либо вещественное число. Во всех этих
случаях мы получим
С = -j^(l — с4+п)Ь4, F1.11)
где с = alb.
§ 61] НЕОДНОРОДНЫЙ ПОЛЫЙ ЦИЛИНДР 3Г)Г)
Если модуль сдвига меняется вдоль радиуса пропор-
пропорционально п-й степени расстояния от центра г, то напря-
напряжение меняется также пропорционально степени г, но на
единицу большей. При п положительных, а также отри-
отрицательных, но больших, чем—1, наибольшее напряжение
получается вблизи наружной поверхности:
х-щ*Т^- F1ЛЗ)
При отрицательных же п, меньших минус единицы,
наибольшее напряжение получается на внутренней по-
поверхности, т. е. на поверхности полости, а если полости
нет, то напряжения стремятся по мере приближения к оси
неограниченно возрастать (около оси как бы происходит
концентрация напряжений). В цилиндре из однородного
материала п = 0 и
F1.14)
2/1/ г М /ал .г\
х°* = -шт=^ = х г' F1Л5)
где /0 — яб4 A — с4)/2 — момент инерции относительно
центра сечения цилиндра (полярный).
Необходимо отметить особый случай: п = —4. При
таком п жесткость и напряжение принимают неопреде-
неопределенный вид 0 : 0. Раскрывая неопределенности по пра-
правилу Лопиталя, вместо F1.11) и F1.12) получим *):
С = -гя^ЬсЬ4, F1.16)
М In с /ал . гуч
О характере изменения напряжения по диаметру при
положительных и отрицательных п дают представление
рис. 90 и 91; пунктирные прямые — графики изменения
напряжений по диаметру в однородном стержне тех же
размеров.
Задача усложняется, если коэффициент аи (или мо-
модуль сдвига 6ге2) задается как функция двух координат
г и z, т. е. меняется не только по радиусу, но и по длине.
с < 1; lnc < 0.
306 ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ [Гл. 6
Можно отметить частные случаи, когда и эта задача ре-
решается элементарным путем. Укажем один из них (см. [22]).
' Рис. 90.
Рис. 91.
Пусть цилиндр является ортотропным и коэффициент
деформации его равен произведению функции только г
на функцию только z:
a« = bu(r)Z(z), F1.18)
остальные восемь коэффици-
коэффициентов — произвольные функ-
функции координат. В этом слу-
случае перемещения равны
ur = w = 0, щ = flr \ Z dzy
Рис. 92.
F1.19;
а жесткость и напряжение
определяются по формулам F1.6) и F1.8), куда вместо
а44 нужно подставить ?44-
Представляет интерес задача о кручении неоднород-
неоднородного цилиндрического стержня, составленного из опре-
определенного числа N полых цилиндров (трубок), соеди-
соединенных жестко по поверхностям контакта путем склейки
или спайки (рис. 92). Мы остановимся на случае, когда
каждый слой является цилиндрически-анизотропным и
однородным и в каждой точке имеется плоскость упругой
симметрии, нормальная к геометрической оси (она же яв-
является плоскостью упругой симметрии не только для всего
стержня, но и для всех слоев); при этом слои соединены
§ 61] НЕОДНОРОДНЫЙ ПОЛЫЙ ЦИЛИНДР 307
без предварительного натяжения, т. е. начальные напря-
напряжения отсутствуют. Обозначим через at — расстояния
от центра до поверхности контакта слоев с номерами i и
i + 1, причем aQ = a, un = Ь (внутренний и внешний ра-
радиусы).
В
у)
Вводя обозначения а{и, а*5 и
F1.20)
и удовлетворяя очевидным условиям на внутренней и на-
наружной поверхностях и на поверхностях контакта, полу-
получим после элементарных преобразований следующие
окончательные формулы (верхние индексы всюду — но-
номера слоев):
и\ = -Ъ (I - z) г, и\ = 0, (i = I, 2, ..., N);
F1.21)
a2 (r2 - a\)} + wQ,
- a2 (al — a\) -f- . . . + щ (r2 — a^)] + ^o,
(i = 1, 2,... , Af);
F1.22)
te* - -T-=-5--r , F1.23)
fl44 a44
N 4_ 4 N
c'=-4-L^r=!> F1'24)
(Cj- — жесткость слоя номер г).
Анизотропия и в этих случаях не влияет на жесткость
и напряжения; они получаются такими же, как и у изо-
изотропного многослойного стержня с модулями сдвига
Gl = ilau. При переходе от слоя к слою напряжение
вдоль радиуса меняется скачкообразно, как это показано
на рис. 92, где взят трехслойный стержень, у которого
G2 < G1 < G3.
Глава 7
РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛП
ПОД ДЕЙСТВИЕМ ИЗГИБАЮЩЕЙ
НАГРУЗКИ ПРОСТЕЙШЕГО ВИДА
В настоящей главе исследуется упругое равновесие
консоли, закрепленной одним концом и деформируемой
силой, приложенной к другому концу. При наличии упру-
упругой симметрии, в частности, для ортотропного тела, уп-
упругое равновесие будет такого же типа, как у изотроп-
изотропного тела и деформации, с качественной стороны, будут
мало отличаться от деформаций изотропного тела. Если
же упругая симметрия мало развита или совсем отсут-
отсутствует, мы получаем значительно более сложную деформа-
деформацию и соответствующее напряженное состояние. С изу-
изучения этого напряженного состояния мы и начнем.
§ 62. Обобщенный изгиб однородной консоли
под действием поперечной силы
Поставим задачу следующим образом. Имеется цилин-
цилиндрическое или призматическое тело, однородное и прямо-
прямолинейно-анизотропное, у которого плоскости упругой
симметрии в разных точках не совпадают с плоскостями
поперечных сечений или совсем отсутствуют. Один торец
тела закреплен неподвижно, а на другом действуют уси-
усилия, приводящиеся к силе Р, приложенной в плоскости
торца. Считая области торцов конечными, полагаем, что
направление силы совпадает с направлением одной из
главных осей инерции сечения. Боковая поверхность не
нагружена и не закреплена; объемные силы отсутствуют.
Примем центр тяжести незакрепленного торца за на-
начало координат и направим ось z параллельно образующей,
а оси х и у в плоскости торца по главным осям инерции
$ 02] ОБОБЩЕННЫЙ ИЗГИБ ПОПЕРЕЧНОЙ СИЛОЙ 309
сечения (рис. 93). Напряженное состояние изотропного
тела, нагруженного и закрепленного указанным образом,
характеризуется тем, что в поперечных сечениях z = z0
@ < z0 <. /, где / — длина тела) будут действовать нор-
нормальные напряжения
oz = --j-zy, F2.1)
пропорциональные изги-
изгибающему моменту — Pz
(в обычном понимании со-
сопротивления материалов) \ч^ fy ty+f^^ л
и обратно пропорциональ-
пропорциональные моменту инерции
/ = /х, меняющиеся по
высоте по линейному за- Рис дз.
кону и касательные напря-
напряжения Тяг, ту2; в продольных сечениях х = х0 и у = у0
действуют только касательные напряжения. Такого же
типа будет напряженное состояние тела при развитой уп-
упругой симметрии, когда имеются плоскости упругой сим-
симметрии, совпадающие с плоскостями поперечных сечений;
упругое равновесие в этих случаях называют изгибом
поперечной силой.
Если же плоскости упругой симметрии не совпадают
с плоскостями поперечных сечений или совсем отсутству-
отсутствуют, то распределение напряжений и деформаций будет
значительно сложнее — сходно с состоянием при обобщен-
обобщенной плоской деформации. В этом случае мы будем назы-
называть напряженное и деформированное состояние тела
не изгибом, а обобщенным изгибом поперечной силой.
Само тело в дальнейшем будем называть консолью. Зада-
Задача об обобщенном изгибе была впервые поставлена
Фойгтом [38]; более подробно она изучена в нашей работе
[59] (см. также книгу [20]).
Выведем общие уравнения обобщенного изгиба одно-
однородной консоли. Так как при изгибе поперечной силой
нормальное напряжение в поперечных сечениях опреде-
определяется по формуле F2.1\ то мы предположим, что при обоб-
обобщенном изгибе
р
tfz = — — Zy + CTz (Ж, У), F2.2)
310
РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ
[Гл. 7
а все остальные составляющие напряжений не равны нулю
и не зависят от z. Основная система уравнений примет вид
дх ^ ду
дх ~ ду ~ '
дх ^ ду 1 J'
F2.3)
= аио^ + а12оу
~Т
р
F2.4)
Введем новое обозначение:
т~\ 0 . I / /^ О Г" \
Отсюда следует:
0 D 1
F2.6)
Уравнения обобщенного закона Гука F2.4) перепи-
перепишутся таким образом:
D-Z.
Vxy =
~D — — a3Gzy.
rt33 ^
F2.7)
Из третьего, четвертого, пятого уравнений F2.7) оп-
определяем перемещениям, v, и (с точностью до функций W,
V, U), а затем удовлетворяем остальным уравнениям.
В результате мы получим уравнения и формулы, сходные
§ 62]
ОБОБЩЕННЫЙ ИЗГИБ ПОПЕРЕЧНОЙ СИЛОЙ
311
с уравнениями и формулами для случая, когда напряже-
напряжения в теле не зависят от z с добавлением полиномов, про-
пропорциональных силе Р. Окончательные выражения для
D, az и перемещений будут иметь вид:
D = Ах + By + С — -gy (аъьху + аиу2);
F2.8)
-j-zy+ — I
1 a33
1
a33
-кг—
61 а33
-f
a36tTl/), F2.9)
и = —
W |W2 - a23i/2) z + -^z2] -
p
auy4)
W+w'. t
F2.10)
Здесь u', г?', w'—«жесткие» перемещения A8.8), содер-
содержащие шесть постоянных (ov со2, со3, u0, v0, w0 (их мы най-
найдем из условий на закрепленном торце), А, В, С, Ф —
постоянные, определяемые из условий равновесия части
консоли, U, V, W —функции, удовлетворяющие пяти
уравнениям:
J?L (Ax + By + C) -
a3
^l (Ax + By + C) -
dV
dx
•-^(Ax + By + C) —
Pa*
(a35r?/ +
+
F2.11)
312
РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ
[Гл. 7
дх
= Pi 5^
(а,ьху
^ (Лх + By + С) -
_p_
и
F2.12)
?33
J
(/,/=1,2,4,5,6). A8.16)
Уравнениям равновесия сплошной среды F2.3) мы удов-
удовлетворим с помощью двух функций напряжений F и гр,
полагая:
ду*
ау = ~дхТ
дхду '
Ш
F2.13)
где т1? т2 — какое-нибудь частное решение третьего урав-
уравнения F2.3). Исключая [/и7из F2.11) путем двукратного
дифференцирования и W из F2.12) путем дифференциро-
дифференцирования по х и у, приходим к заключению, что F игр удовлет-
удовлетворяют неоднородной системе уравнений:
Т Z7 , Т . Р
LXF + Lrf = ^т-
^2" (Р24Т2 + Р25Т1)
2Мо
+ (а34а35 - 2а33азв) .V] - 2* + /1^"^-^ +
Здесь L4, L3, L2 — операторы A9.3).
F2.14)
§ 02] ОБОБЩЕННЫЙ ИЗГИБ ПОПЕ1 ЕЧНОЙ СИЛОЙ 313
Условия на боковой поверхности, которая не нагру-
нагружена, или, что то же, иа контуре поперечного сечения, мы
упростим и приведем к такому виду:
s
IF" == с* * = \ (r°-d<r "" Ti ЛУ) + с*- F2-15)
Если область сечения одыосвязна, то можно положить
на контуре с\ = О, с2 = 0. Третье условие F2.15) упро-
упрощается, если частные решения тх, т2 можно подобрать
так, чтобы на контуре выражение i2dx — ixdy было равно
нулю. Тогда третье условие F2.15) запишется так: гр = с3
или, в случае односвязной области сечения, гр = 0.
Напряжения в поперечных сечениях должны удов-
удовлетворять условиям равновесия:
§rxzdcdy = 0, §azydr.dy = — Pz,
§xyzdxdy = — Р, §azxdxdy = 0,
az dx dy = 0, ^ (rVzx — xxzy) d.r dy = 0.
F2.16)
Первые два равенства F2.17) представляют собой тож-
тождества, в чем легко убедиться, преобразуя интеграл по
площади в интеграл по контуру и используя уравнения
равновесия сплошной среды. В самом деле:
\\
ж - -г
р се
-f tV2cos(w, у)] ds ^-\\a:yda'di/ = 0
F2.17)
(так как интеграл от произведения ху равен центробеж-
центробежному моменту относительно главных осей);
= -P. F2.18)
314 РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ [Гл. 7
Остальные условия послужат для определения посто-
постоянных А,В,С,$. В нашем случае Хп = Yn = X =Y = О,
следовательно, интегральные формулы § 19 значительно
упрощаются.
Из уравнений F2.16) находим
А = В = О, С = —4о— F2.19)
2S а33 v '
(S — площадь сечения). Постоянную О мы определим из
шестого уравнения F2.16).
Под действием поперечной силы Р консоль, обладаю-
обладающая анизотропией общего вида, испытывает деформацию
более сложную, чем изотропная консоль тех же размеров,
а именно: 1) к напряжениям txz, tVz, orz, характерным
для изгиба силой, добавляются напряжения ох, ау, тху,
характерные для плоской деформации; 2) поперечные
сечения не остаются плоскими, а как показывает третья
формула F2.10), искривляются; искривление зависит от
функции W (х, у); 3) изгиб сопровождается закручива-
закручиванием. Но даже в общем случае анизотропии изогнутая
ось будет плоской кривой:
у' = ^р BZ3 - Ъ1Ч + z3). F2.20)
Это уравнение тождественно с уравнением изогнутой
оси изотропной консоли, у которой жесткость равна
^/«зз = Ег1, где Е3 — модуль Юнга для растяжения
сжатия вдоль оси ъ. Формула элементарной теории изги-
изгиба, связывающая кривизну изогнутой оси 1/р с изгибаю-
изгибающим моментом, оказывается и в этом случае верной:
¦Т---ЕТ-Ш- F2-21)
§ 63. Общие выражения для функций напряжений,
составляющих напряжений и проекций перемещения.
Граничные условия
Система уравнений для функций F и -ф F2.14) отлича-
отличается от системы A9.2) в главе 3 только правыми частями.
Понятно, что это дает возможность записать общие выра-
выражения для производных F и для г|), составляющих напря-
§ 63] ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ФУНКЦИЙ НАПРЯЖЕНИЙ 315
жений и проекций перемещения через три функции комп-
комплексных переменных zk = х + цкг/ (к = 1, 2, 3), где
М* = ак + Фк — корни алгебраического уравнения (см.
§ 20):
Ми) Ji M - ? (и) = о. F3.1)
Используя далее обозначения_§ 20, будем иметь в случае
неравных корней ци \i2, \i3, \аи ц2» ц3 уравнения F3.1):
-^- = 2Re[0>ii
-J- = 2Re[|XiC
-ф - 2Re[M
a^=2Re[|iiOi(:
ay = 2Re [ф[ -
xxv = - 2Re
ххг = 2Re
ty2 = -2Re|
Ф2 (г,)
(Wl +-^r »
F3.2)
Ф3] - ф-
t2;
F3.3)
= 2Re
3
3
= 2Re
F3.4)
Здесь Fq» *Фо — какое-нибудь частное решение системы
уравнений F2.14), где нужно положить А = В = 0 (см.
F2.10)), U, V, W ~ части перемещений и, у, м;, завися-
зависящие только от х и у; ?/0, Fo, VF0 — частные решения урав-
уравнений F2.11) и F2.12). Все эти функции (частные реше-
решения) будут содержать слагаемые, пропорциональные
крутке Ф и пропорциональные силе Р,
316
РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ
[Гл. 7
Комплексные потенциалы Фк удовлетворяют гранич-
граничным условиям, которые имеют такой же вид, что и в слу-
случае обобщенной плоской деформации или обобщенного
кручения; разница будет только в правых частях:
2Re [Ф_ + Ф2
2Re
r2 dx — ti dy).
F3.5)
Таким образом, в общем случае анизотропии задача об
обобщенном изгибе консоли поперечной силой по трудности
оказывается такой же, как задачи об обобщенных плоской
деформации и кручении. Поэтому три задачи о равновесии
тела, ограниченного цилиндрической поверхностью, столь
различные для изотропного тела, для тела с анизотропией
общего вида сводятся к одной и той же математической
задаче—граничной задаче для трех функций Ф^(^) трех раз-
различных комплексных переменных (комплексных потенциа-
потенциалов), которые должны быть голоморфны и однозначны
в своих областях Sk (см. [59]).
Частные решения т_, т2 можно выбирать по-разному.
Так, например, для симметричного сечения, ограни-
ограниченного кривыми
у = ± VTW (бз.б)
или этими кривыми и одной или двумя прямыми, парал-
параллельными оси у, можно положить:
Р
—< г\ /у* _____ Го/ _— / /^у*\ 1 ^fi^ 7\
Тогда на контуре сечения i2dx — xxdy = 0. Уравнения
F2.14) примут вид
= — [gl + 0,50,4/* (x)},
- 0,5p44/' (x)\ - 20,
= -j- [g%x
F3.8)
64] ИЗГИБ КОНСОЛИ ПОПЕРЕЧНОЙ СИЛОЙ 317
где
о
_ 2^13^34 Д356 _ ^35 О
F3.9)
Функция ф на контуре должна обращаться в нуль.
Определив функции F и ф, удовлетворяющие уравне-
уравнениям F2.14) и граничным условиям, мы получим для них
выражения вида:
F = ^-Fx (*, у) + #F0 (х, у), ф = -у- T|h (х, 2/) + ЭДо (*' У)-
F3.10)
Последний этап в решении задачи об обобщенном из-
изгибе поперечной силой — определение постоянной д, ко-
которая найдется из шестого условия равновесия F2.16).
§ 64. Изгиб однородной прямолинейно-анизотропной
консоли поперечной силой
Если у консоли плоскость поперечного сечения явля-
является плоскостью упругой симметрии, то задача изгиба ее
поперечной силой значительно упрощается. Значительно
упростится картина напряженно-деформированного со-
состояния и, по существу, будет мало отличаться от таковой
в изотропной консоли; упрощаются и все общие уравне-
уравнения и методы их решения. В противоположность консоли
с анизотропией общего вида, в данном частном случае на-
напряженно-деформированное состояние можно назвать «из-
«изгибом консоли поперечной силой» или «простым изгибом
поперечной силой». Задача об изгибе консоли изотропной
и обладающей анизотропией частного вида была изучена
Сен-Венаном [122]. Дальнейшие исследования этого воп-
вопроса имеются в работах Л. С. Лейбензона [17] и [19] и др.
В данном случае ряд постоянных (коэффициентов де-
деформации ац) равен нулю:
аи = а24 = аз\ = #46 = 0. ^\ь = ачь = аъь = аьъ = 0- F4.1)
Всем уравнениям F2.10), F2.11) и F2.14) мы удовлетво-
удовлетворим, положив U = F — V = 0, С = 0,
о* = °у = т*у = °z = 0. F4.2)
318
РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ
[Гл. 7
Получим
p
hi tyz == —
F4.3)
F4.4)
где, как и раньше, т2, т2 — частное решение уравнения
равновесия сплошной среды
дх
ду
1
F4.5)
которое в зависимости от вида сечения можно взять в фор-
форме F3.7) или иначе. Функцию ф будем называть функцией
напряжений при изгибе (поперечной силой).
На контуре поперечного сечения должно быть выпол-
выполнено условие третье из F2.15)
F4.6)
•ф = § (та dx —
(в случае односвязной области сечения можно принять
с3 = 0). Кроме того, должны быть выполнены условия на
торцах, которые сводятся к одному:
Txzy)dxdy = O; F4.7)
оно послужит для определения постоянной д — крутки.
Перемещения удовлетворяют условию на закреплен-
закрепленном торце, где мы условимся считать неподвижным линей-
линейный элемент, проходящий через центр тяжести. Эти усло-
условия имеют вид: при х = у = 0, z = I
А ди dv dv ди п
' dz dz dr ду
Удовлетворив этим условиям, получим:
и - — -?- (а1Ъху + 0,5азв2/2) z + О (I — z) у,
F4.8)
F4.9)
§ 04] ИЗГИБ КОНСОЛИ ПОПЕРЕЧНОЙ СИЛОЙ 319
Функция W (х, у) определится из уравнений:
dW P
^yZltZZ+T^-^-^' 1F4Л0)
Отсюда на основании F4.4) получаем уравнение для ф:
дЩ> 0 а2ф , дЦ> Р
- 20 + А (а44т2 + а^О - -^ (а4бт2 + aeeti). F4.11)
В этом случае ф, rA.z, тУ2 и И7 выражаются через одну
функцию Фз(^з) комплексного переменного z3 = х + Н'З^/^
где |я3 = а3+^Рз и сопряженная величина Ji3~ oc3— ip3—
корни уравнения
к (Ц) = «5б^2 - 2a45ji + a44 = 0, F4.12)
которые всегда получаются комплексными или чисто мни-
мнимыми (см. § 20). Из третьей формулы F3.2), в которой
в данном случае %г = К2 = 0> следует
iff = 2Re№3(z3)] +*o, F4.13)
где г|50 — частное решение уравнения F4.11). Выражения
для напряжений имеют вид (см. F4.4))
xxz = 2Re
F4.14)
Задача сводится к определению комплексного потен-
потенциала Ф3 (z3) в области 53, полученной из области попе-
поперечного сечения S путем аффинного преобразования
х3 = х + а3у, у3 = р3у (z8 = х* + гуз)- F4.15)
Условия для Ф3 на контуре области S3 запишется в виде
з
2Re [Ф3] = с3 - % + \ (т, Ах - хх dy). F4.16)
0
Здесь за основную неизвестную функцию принята
функция напряжений при изгибе я|э. Так же как в теории
320
РАВНОВЕСИЕ АНИЗОТ1 ОПНОЙ КОНСОЛИ
[Гл. 7
кручения, можно было бы за основную принять функцию ср;
для нее также получилось Гы уравнение второго по-
порядка (не совпадающее с F4.11)) и граничное условие.
Но этот способ решения менее удобен, а поэтому мы в даль-
дальнейшем будем предпочитать первый, т. е. будем иметь дело
с функцией напряжений г|).
Задача еще более упрощается в случае, когда материал
консоли является ортотропным или изотропным. В случае
ортотропной консоли, у которой одна из трех плоскостей
упругой симметрии совпадает с плоскостью поперечного се-
сечения, а сила действует во второй плоскости упругой сим-
симметрии (z/z), удобнее ввести технические упругие посто-
постоянные, положив азв = аи = 0> ^44 = 1/Gi, аб5 = 1/С2,
#1з = — v3i/Z?3, ^23 = — v32/#3 и обозначив
g
e =
Тогда для г[) вместо F4.11) получим уравнение:
F4.17)
F4.18)
и граничное условие о|з = 0. Частное решение тх, т2 взято
в форме F3.7). Перемещения определятся по формулам:
Pv
и= -~xyz + ^(l ~z)y,
-QV-Z) -Г,
w =
F4.19)
В некоторых случаях изгиба ортотропной консоли
(особенно при исследовании приближенными методами)
бывает удобно разбить функцию W на три слагаемых:
^х^у - -^V) , F4.20)
W = *<р (х, у) + Ф (х,
где ф — функция, соответствующая кручению (пропор-
(пропорциональная W в теории кручения), удовлетворяющая
§ 04] ИЗГИБ КОНСОЛИ ПОПЕРЕЧНОЙ СИЛОЙ 321
уравнению
sS + l^0' F4-21>
а Ф — так называемая функция изгиба *), удовлетворяю-
удовлетворяющая неоднородному уравнению
2^. 4- ?21 = * (l _ 2e) у. F4.22)
Введя новые функции, можем записать общие формулы
для напряжений таким образом:
дФ , 2Р G2v3i
F4.23)
Для изотропного тела
v3i = v32 = v, Е3 = 5, d = G2 = -2A+v)', «Г = 1,
и уравнения F4.18), F4.21) и F4.22) принимают такой
вид:
V2cp = 0, F4.25
,l^y. F4.26)
Изгибающая сила, проходящая через центр тяжести
торца и действующая в главной плоскости, не совпадаю-
совпадающей с плоскостью упругой симметрии, вызывает не только
изгиб в главной плоскости, но и закручивание вокруг оси z,
которое характеризуется постоянной д. Закручивания
можно избежать, если направить силу эксцентрично по
отношению к центру тяжести. Для сечения произвольной
формы всегда существует точка С, обладающая следующим
свойством: любая поперечная сила, у которой линия дей-
действия проходит через С, вызывает изгиб в главных
х) См. книгу Л. С. Лейбензона [17], стр. 283 или работу [55].
У Лейбензона Ф называется «новой функцией изгиба», а Сен-Венан
пользуется другой функцией изгиба % [122].
11 С. Г. Лехницкий
322
РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ
[Гл. 7
плоскостях, не сопровождающийся закручиванием. Эта
точка носит название центра изгиба ([17], стр. 196)х).
Если поперечная сила направлена по оси геомет-
геометрической симметрии, совпадающей с осью упругой
симметрии, то можно заранее положить Ф = 0.
§ 65. Распределение напряжений в однородной
консоли эллиптического и кругового сечения
В качестве первого примера изгиба однородной консоли
рассмотрим консоль эллиптического сечения. Пусть кон-
консоль с сечением в виде эллипса с полуосями а, Ъ изгибает-
изгибается силой Р, направленной по одной из главных осей
(рис. 95). Для изотропной и ортотропной консоли решение
было найдено Сен-Венаном [122]; мы рассмотрим самый
общий случай однородного материала, когда число коэффи-
коэффициентов деформации ац равно 21A8). Один торец
z = I закреплен, на другом,
z = 0, действует сила Р, нап-
направленная по оси у. Уравнение
P\J0ft/ /////%fc контура сечения имеет вид:
-5 + -8Г-1- F5-1)
Для построения решения
воспользуемся частным ре-
решением уравнения F4.5) в виде
F3.7), где
Рис. 94.
Выражения составляющих напряжения через функции на-
напряжений F и if» в общем случае анизотропии имеют вид*
дх*
дхду '
т*2 =
F5.3)
х) В работах Альманси [103], Мичелла [119], Космодамианского
А. С. [54], Джанелидзе Г. Ю. [51], Хатиашвили Г. М. [96], [97],
Узда лева А. И. [94], иследован изгиб консоли разделенной на-
нагрузкой.
§ 65] КОНСОЛЬ ЭЛЛИПТИЧЕСКОГО И КРУГОВОГО СЕЧЕНИЯ 323
Р Р а** Р
F5.4)
Система уравнений для F и -ф F2.14) запишется так:
Р ,
gzy] -
F5.5)
где gl4 g2, gs— коэффициенты F3,9), а с = alb — отно-
отношение главных полуосей эллипса. Здесь можно заранее по-
положить Ь = 0, так как уравнение F4.7) тождественно
удовлетворяется при Ф = 0.
Граничные условия для F и *ф будут
^ = — = г|) = 0. F5.6)
ох ду v '
Этим условиям мы удовлетворим, взяв элементарные
функции в виде полиномов:
F5.7)
Постоянные р, q, r найдены из уравнений:
рББ) -
F5.8)
Решения этой элементарной системы приводить не будем,
324 РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ [Гл. 7
отметим только, что в общем случае прямолинейной
анизотропии все шесть составляющих напряжений не
равны нулю и распределяются по площади поперечных се-
сечений по квадратичному закону.
Для ортотропной консоли с плоскостями упругой сим-
симметрии, нормальными к оси ее и параллельными плоско-
плоскостям симметрии эллиптического цилиндра, формулы уп-
упрощаются, так как а4Б = а3в = 0 и г = 0. Получаем
АР пмС2 — 2а13
F5.9)
Наибольшей величины касательное напряжение дости-
достигает в центре сечения, где оно равно:
г _2Р 2а«# + а»+2пъ 2Р
Гтах - 1ЙЬ
1
В частности, для изотропной консоли
Формул для напряжений в консоли кругового сечения
мы давать не будем, так как все они получаются из при-
приведенных выше, если положить с = 1. Что каса-
касается нормальных напряжений oz, то места, где они
достигают наибольших по величине значений в слу-
случаях, когда плоскости поперечных сечений являются
плоскостями упругой симметрии, находятся на заделан-
заделанном торце (где z — наибольшее) в точках, где у имеет наи-
наибольшее по величине значение (на концах оси длиной
2 Ъ заделанного торца).
§ 66. Изгиб однородной ортотропной
консоли прямоугольного сечения
С решением задачи о кручении стержня прямоуголь-
прямоугольного сечения, однородного и ортотропного, сходно реше-
решение для такой же консоли, изгибаемой поперечной силой
(рис. 95). Расположим оси, как указано на рис. 95, где
66]
ИЗГИБ КОНСОЛИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
325
плоскости упругой симметрии нормальны к осям ху у, z
или параллельны граням прямоугольного параллелепи-
параллелепипеда. Решение этой задачи также получено Сен-Венаном
в работе [122, 30]; мы выведем его методом, примененным
ранее для решения соответству-
соответствующей задачи о кручении (§ 56).
Выражая напряжения через
функцию напряжений (форму-
(формулы F4.4)), возьмем частное ре-
решение уравнения F4.5) в виде
tx = 0, та = — -ту
F6.1)
Эти напряжения обращают-
обращаются в нуль на сторонах у = ±6/2;
на двух других сторонах х =
= ± а/2 имеем dx = 0. Формулы для напряжений прини-
принимают вид
F6.2)
Рис. 95.
Vz ~" ~~ дх
2/ \ 4
где / = аЬ3/12, а уравнение для г|) будет
F6.3)
так как постоянную Ф можно сразу же принять равной
нулю. Задача сводится к определению функции напряже-
напряжений i|), которая обращается в нуль на всех четырех сторо-
сторонах прямоугольника: х = ± а/2, у = ± Ь/2.
Разложим правую часть уравнения F6.3) в ряд Фурье
на интервале (-— а/2, а/2); ряд будет содержать только си-
синусы и уравнение F6.3) перепишется так:
2Ра V4-1)
~яГе
¦sin-
Ъпш
F6.4)
Ищем решение в виде ряда, удовлетворяющего услови-
условиям на двух сторонах х = ± а/2:
F6.5)
326
РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ [Гл. 7
Подставляя г|) в F6.4), получаем для Ym обыкновенное
уравнение,
'Vm = -^e-bl?-, F6.6)
общий интеграл которого будет
где
Р 3 - / 4\
Ш1 ^~ ' F6'7)
F6.8)
Произвольные постоянные определим из условий на
сторонах у = ± Ь/2, требуя, чтобы там функция напря-
напряжений была равна нулю. В результате получим:
(-if
1-
ch
sinf^x, F6.9)
7П=1
Тл_ = — ¦
/тгя
ch~r
¦ Q 1 ТЛ _
Pa2 J_ Y1
Я2/ Т 2j
(-1)"
/ггя
COS X
7П=1
(л-7Г-т)
F6.10)
Касательные напряжения в центре сечения х = 0,
I/ = 0 и в точках _4 и _4X на серединах сторон, параллель-
параллельных силе (х ='± л/2, г/ = 0), определим по формулам:
в центре
§ 6б1 ИЗГИБ КОНСОЛИ ПРЯМОУГОЛЬНОГО
327
в точках А и Ах
3
Коэффициенты р0 и рд — функции отношения
заданные рядами
F6.12)
F6ЛЗ)
=i />?2 ch
гал
Значения коэффициентов р0 и Ра для четырех отношений г/,
полученные на основании вычислений Сен-Венана, приве-
приведены в таблице 22.
Таблица 22
Коэффициенты (?0 и Рл
d
2
1
0
0
,09
,30
За
0,17
0,63
d
о,
0,
5
25
0
0
,72
,98
1
4
,98
,94
Наибольшее касательное напряжение получится в точ-
точках А и Ах.
По элементарной теории изгиба касательное напряже-
напряжение не меняется по ширине сечения и на оси симметрии,
нормальной к линии действия силы, получается наиболь-
наибольшим:
2 аб
F6.15)
Формула F6.12) вместе с F6.14) дает поправочный ко-
коэффициент, на который нужно умножить ттах, чтобы полу-
32§ РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ 1Гл. 7
чить наибольшее касательное напряжение тшах в орто-
тройной консоли. При больших d коэффициенты ро и fiA
малы и Тщах близко по величине к напряжению, которое
получается по элементарной теории (как в консоли с сече-
сечением в виде узкого прямоугольника). Поправочные коэф-
коэффициенты возрастают с уменьшением d итщх при малых d
будет значительно отличаться от "Ттах, но в этих случаях
касательные напряжения играют второстепенную роль,
так как величина их мала по сравнению с наибольшим нор-
нормальным напряжением атах- Малым отношениям d соответ-
соответствуют случаи изотропной консоли, изгибаемой силами,
нормальными к длинным сторонам прямоугольника.
§ 67. Приближенные методы решения задачи
об изгибе консоли поперечной силой
Уравнения теории изгиба поперечной силой сходны
с уравнениями теории кручения, а поэтому для отыскания
приближенных решений задач об изгибе можно приме-
применить методы, сходные с изложенными в § 56. Остановим-
Остановимся коротко на вариационных методах, причем рассмотрим
только частный случай, когда цилиндр, изгибаемый силой
Р, является однородным, прямолинейно-анизотропным
и ортотропным и изгибается без закручивания (заранее
можно положить Ф = 0).
В зависимости от того, какая именно функция (if> или
Ф) принимается за основную, можно использовать методы,
вытекающие из вариационной формулы Кастилиано или
из вариационного уравнения Лагранжа (см. гл. 1, § 11).
Укажем без вывода основные общие результаты *).
Пусть сечение ограничено кривыми
, F7.1)
или этими кривыми и одной или двумя прямыми, парал-
параллельными оси у. Принимая за основную функцию напря-
напряжений а|), имеем (см. § 64):
г) Вывод имеется в работе Л. С. Лейбензона [17], [19], гл. XII
и в книге [20].
§ 67] ПРИБЛИЖЕННЫЕ МЕТОДЫ 329
Функция г|) удовлетворяет уравнению F4.18) и на контуре
должна быть равна нулю. Задача равносильна задаче об
отыскании функции, сообщающей минимальное значение
интегралу
xdy F7.3)
(причем на контуре \|) = 0). Решая задачу приближенно,
задаемся семейством функций tymn (x, у), зависящих от
двух целочисленных параметров т и п и обращающихся
на контуре в нуль. Приближенное решение ищем в виде
суммы
М N
ч> = 2 2^mntiw FV.4)
m=l n=i
Подставляя F7.4) в F7.3), получаем Ux в виде квад-
квадратичной функции коэффициентов Атп. Затем ищем ми-
минимум иг и получаем систему неоднородных уравнений
первой степени для Атп:
-^ = 0 (т = 1,2, ...,Л/; п = 1, 2, ..., N). F7.5)
Если за основную принять функцию изгиба Ф, то мы
получим
^G F76)
Задача сводится к определению функции Ф (я, у), прида-
придающей минимальное значение интегралу
<в7'7)
Приближенное решение получим, задавая семейство
функцией Фтп (х, у) и разыскивая Ф в виде суммы
Ф = 3 2 ^пФт„- F7.8)
m=l n -1
330 РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ [Гл. 7
Коэффициенты Втп определяются из уравнений
^L = 0 (m = l, 2, ..,М; п = 1,2, ..., АО- F7.9)
тп
Кроме двух указанных, известны и другие приближен-
приближенные методы решения задач об изгибе и кручении стержней.
С одной стороны, имеются разновидности вариационных
методов, а с другой стороны, разработан ряд методов, ко-
которые нельзя назвать вариационными. К числу последних
относятся так называемые методы малого параметра, сущ-
сущность которых заключается в следующем. Если, например,
один размер сечения значительно превышает другой или
модули (или коэффициенты упругости atj) значительно от-
отличаются друг от друга, то вводится малый параметр, ха-
характеризующий это различие. Неизвестная функция
(г|) или Ф) разыскивается в виде ряда, расположенного по
степеням малого параметра; в процессе решения зада-
задачи высшие степени параметра, начиная, например, со
второй, отбрасываются, как величины высшего порядка
малости.
Мы здесь не будем приводить решений частных задач;
некоторые из них, относящиеся к родственной проблеме
кручения, были даны в § 56. Отметим лишь, что много
частных случаев рассмотрено в работах Л. С. Лейбензона
[17] и [55], а также в монографии В. С. Саркисяна [29].
Частный случай — «удлиненное сечение», когда ширина
сечения значительно больше его высоты (или толщины)
рассмотрен и в нашей книге [20].
§ 68. Изгиб неоднородной ортотропной консоли
Если консоль является непрерывно-неоднородной, но
неортотропной, то распределение напряжений в ней будет
сложнее, чем в однородной: из составляющих напряжений
все шесть не равны нулю и уравнения, определяющие их,
будут значительно сложнее. Мы рассмотрим консоль с ани-
анизотропией и неоднородностью частного вида: она орто-
тропна, причем из трех плоскостей упругой симметрии,
проходящих через каждую точку, одна параллельна
плоскости поперечного сечения, а две другие парал-
параллельны оси консоли или, что то же, ее образующей;
одноименные плоскости упругой симметрии между собой
§ 68] ИЗГИБ НЕОДНОРОДНОЙ ОРТОТРОПНОЙ КОНСОЛИ 331
параллельны, т. е. тело является прямолинейно-анизо-
прямолинейно-анизотропным (см. [74]).
Примем центр тяжести 0 незакрепленного сечения за
начало координат и направим ось z параллельно обра-
образующей, а оси х и у нормально к плоскостям упругой сим-
симметрии (рис. 94). Область поперечного сечения полагаем
конечной — односвязной или многосвязной, но при этом
считаем, что оси х и у вообще не совпадают с главными
осями инерции, а сила Р приложена в точке 0 и направлена
произвольно в плоскости ху\ составляющие ее в направле-
направлении осей х и у обозначаем через Рг и Р2. Объемные силы
отсутствуют. В данном случае удобнее использовать на-
наряду с приведенными еще и технические упругие характе-
характеристики — модули Юнга и сдвига и коэффициенты Пуас-
Пуассона — Et, Gtj, vtj. Все эти величины мы будем считать
функциями двух переменных х, у, непрерывными, одно-
однозначными и дифференцируемыми.
Очевидно, что
р-а = -
о = _ vta + V13V32
pi = * - *bvf' ' F8Л)
ft * ft * ft 1
Рб6 = 7J7' Р44==7' Р56^"^-
Всем уравнениям теории упругости, граничным усло-
условиям и условиям равновесия можно удовлетворить, пола-
полагая, что %xz, iyz — функции только х, у, а прочие состав-
составляющие пропорциональны z:
Gx = ZOi, Gy = ZG2, Gz = ZG3, Txy = ZT. F8.2)
Введем обозначение
Di = -g- (a3 — ГзхСГ! — v32a2). F8.3)
Отсюда
gz = z {ESDX + v31g± + v32g2). F8.4)
Основная система равновесия рассматриваемого тела
332
РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ
Гл. 7
запишется так:
дх "" а?/ ' дх ~*~ ду ~~ '
дх
дх
ду
дх ~*~ ду 3 1
B.v = - (Pll°l + Pl2CT2 —
v32cr2 = 0;
т..
.rz
с •
F8.5)
F8.6)
Дальнейший ход решения такой же, как и в случае
однородной консоли. Не останавливаясь на промежуточ-
промежуточных выкладках, приведем окончательные формулы и урав-
уравнения.
1. D, = Ахх + Вгу + Сх. F8.7)
2. Напряжения выражаются через две функции на-
напряжений 1\ и г|?:
д 2 »
_
F8.8)
где Ti, т2 — частное решение третьего уравнения F8.5).
3. Первая функция напряжений Fx удовлетворяет
линейному неоднородному уравнению четвертого порядка
с переменными коэффициентами:
=-- -У [vM (i4i« + Д1У + С,)] + -^ [V3i (A& + Б1У + Сг)},
F8.9)
и граничным условиям на контуре поперечного сечения:
Ч± = сг, ^ = с%. F8.10)
дх ду v '
В случае конечной односвязной области сг = с2 = 0.
§68] ИЗГИБ НЕОДНОРОДНОЙ ОРТОТРОПНОЙ КОНСОЛИ 333
4. Вторая функция напряжений я|) удовлетворяет урав-
уравнению
dy\G2 ду
x ~
Ci) dx+-k \
- -2; \ Ф12Р1 + P22O2) dy + r) (y) +1 (x) - 2*. F8.11)
Здесь Т) (у) и ^ (x) — слагаемые выражения
d) da;-
F8.12)
зависящие только от у и только от я.
Граничное условие для г|) имеет вид
с F8.13)
о
(s — дуга контура и с — постоянная, которую можно за-
зафиксировать произвольно на одном из контуров, ограни-
ограничивающих сечение).
5. Кроме условий на боковой поверхности, должны
быть выполнены условия равновесия в каждом поперечном
сечении, имеющие такой вид:
F8.14)
xxzdx dy «= — Pu ^ Gzy dxdy = — P2z,
xyzdx dy = — P2, \\ огх dxdy = — Pxz,
7zdx dy = 0, \\ (xyzx — xxzy) dx dy = 0.
Можно показать, что этих уравнений как раз достаточ-
достаточно для определения четырех неизвестных постоянных Аи
#1, Сь t>.
В частном случае, когда v3i зависит только от х, a v32—
только от г/, задача очень упрощается, так как тогда
ох = оу = хху =. 0, Fx = 0,
334 РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ 1Гл. 7
Для остальных напряжений остаются верными форму-
формулы F8.8), где тх, т2 — по-прежнему частное решение
уравнения F8.5), в котором аг = а2 = 0.
Функция напряжений ty удовлетворяет уравнению:
dx\G1 дх I "" ду \ G2 ~ду
F8.16)
Нормальное напряжение по-прежнему пропорцио-
пропорционально расстоянию от незакрепленного торца, но является
вообще нелинейной функцией координат х и у,в зависимо-
зависимости от того, как задан модуль Е3 {х, у). Задача упрощается
также и в том случае, когда главные оси инерции сече-
сечения х и у нормальны к плоскостям упругой симметрии и
сила направлена по одной из этих осей.
§ 69. Изгиб неоднородной ортотропной
консоли прямоугольного сечения
Наметим ход решения одной из самых простых задач
об изгибе неоднородной консоли поперечной силой [74].
Пусть имеется консоль прямоугольного сечения, с разме-
размерами а, 6, /(/ — длина), ортотропная, с плоскостями упру-
упругой симметрии, параллельным граням параллелепипеда.
Направим оси х, у, z, как показано на рис. 95 и предпо-
предположим, что модули C?i, С?2» Е3 зависят только от г/, а коэф-
коэффициенты Пуассона v31 и v32 постоянны. На основании
изложенного в предыдущем параграфе три составляющих
напряжения равны нулю:
ох = оу = тхУ = 0. F9.1)
Нормальное напряжение в поперечном сечении равно:
az = Е3 (Агх + Вгу + Сг) z, F9.2)
но из первого уравнения равновесия F8.5) следует, что
Аг = 0 и
az = Е3 {Вгу + Сг) z. F9.3)
Можно считать очевидным, что сила Р не вызовет за-
закручивания и, следовательно, Ф = 0. Постоянные Вг и Сх
§ 69] НЕОДНОРОДНАЯ КОНСОЛЬ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ 335
определятся из уравнений равновесия F8.14) в зависимо-
зависимости от того, как задано Е3; для них получаются два урав-
уравнения, которых мы выписывать не будем. Третье уравне-
уравнение равновесия сплошной среды F8.5) имеет вид
^ ^ C1) = 0. F9.4)
Будем считать Вг и Сг известными (определенными по
заданному модулю Е3(у)) и возьмем решение F9.4) в форме
хг = - Е3 (Бгу + С,) х, т2 = 0. F9.5)
Оставшиеся два напряжения определяются по формулам
где функция напряжений \р удовлетворяет в данном слу-
случае уравнению
JL/JL^\ 4-JL/JLi
дх \ Gx дх ) "" ду \ G2 ду
=xw[%{BlV + Cl)]"xBlVn- F9>7)
Далее задача решается по такому же плану, как и за-
задача об однородной консоли. Раскладываем правую часть
уравнения F9.7) в ряд Фурье на интервале (—а/2, а/2)
и вместо F9.7), после элементарных преобразований, по-
получаем уравнение
_^2^ ^ MY** _
Gx дх* "Г" dp ^ 2\G2) ду ""
?!=^йп«=х. F9.8)
тп=1
Разыскиваем выражение для г|? также в виде ряда
^ F9.9)
тп=1
Получаем уравнение для Ym:
v" G2 vr /2тя\2 G2 v _
m ~~G m V a / ~G~ —
F9.10)
336 РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛ^ [Гл. 7
общий интеграл которого имеет вид
Ym = AmYml + BmYm2 + Ym0. F9.11)
Для функции напряжений получаем выражение, сходное
с выражением для функции напряжений при кручении
неоднородного ортотропного стержня (см. E8.6)):
t|> = ? (AmYml + BmYm2 + Ym0) sin ^ x. F9.12)
m=l
Дальнейшая работа по отысканию решения задачи об
изгибе консоли сводится, с одной стороны, к определению
частных решений Yml, Ym2, Ym0 уравнения F9.10), соот-
соответствующих заданным Gu G2, E3 (функций переменной у),
и, с другой стороны,— к определению постоянных Ат и
Вт из граничных условий на сторонах у = ± 6/2 (условия
на двух других сторонах, очевидно, удовлетворены).
Укажем частные решения для случая, когда модули
являются экспоненциальными функциями координаты у.
Пусть
ппу ппу ппу
Gx = gie~, G2 = g2e~ , Еъ = еъе~, F9.13)
где п — любое вещественное число, не равное нулю.
Тогда линейно-независимые решения однородного урав-
уравнения, соответствующего F9.10), и частное решение неод-
неоднородного уравнения будут иметь следующий вид:
fny hny
Yml = e» , Гта=е" , F9.14)
m0
В (^)V lK^' F9.15)
Здесь, кроме введенных ранее, имеются новые обоз-
обозначения:
F9.16)
§ 70] ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНАЯ КОНСОЛЬ 337
Этими замечаниями мы и ограничимся, помня, что за-
задача об изгибе неоднородной ортотропной консоли очень
близка к задаче о кручении такого же стержня, рассмот-
рассмотренной более подробно в § 58 и 59.
§ 70, Равновесие консоли, обладающей
цилиндрической анизотропией,
под действием поперечной силы
Рассмотрим также напряженное состояние однородной
консоли, материал которой обладает цилиндрической ани-
анизотропией, выведем уравнения для определения напря-
напряжений и перемещений и дадим конкретный пример. Мы
будем считать консоль цилиндрически-ортотропнои; обоб-
обобщение решения на случай, когда имеется только одна плос-
плоскость упругой симметрии или когда они отсутствуют, не
составляет большого труда, только уравнения несколько
усложнятся г).
Пусть имеется консоль, ограниченная поверхностью
произвольного цилиндра. Внутри данного тела, по по-
поверхности или снаружи проходит ось анизотропии, кото-
которую мы примем за ось z цилиндрической системы коорди-
координат; во всех случаях она параллельна образующей.
Через каждую точку проходят три плоскости упругой сим-
симметрии: нормальная к оси анизотропии, проходящая че-
через ось и ортогональная к этим двум. Один торец консоди
закреплен, а к другому приложена изгибающая сила Р,
линия действия которой проходит через центр тяжести
О' и совпадает с одной из главных осей инерции области
поперечного сечения (последняя предполагается конеч-
конечной). Отнесем тело к двум системам координат: 1) х', у',
ъ', у которой ось z' параллельна образующей, но вообще
не совпадает с осью анизотропии, а х', у' направлены по
главным осям инерции сечения; 2) х, у, z, у которой ось
z совпадает с осью анизотропии, а х, у параллельны осям
х' и у'.
От оси х будем отсчитывать полярный угол 0, а от на-
начала О — полярную координату г. Координаты точки О'
в системе я, у обозначим через |, т) (рис. 96).
*) Случай одной плоской упругой симметрии рассмотрен в
книге [20],
338
РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ
[Гл. 7
В консоли изотропной или анизотропной,и однородной
с плоскостью упругой симметрии, нормальной к оси, по-
получается распределение напряжений, которое, как уже
было отмечено выше, характеризуется следующим: на-
напряжение а2 пропорционально изгибающему моменту:
oz = - -f zy' = - ~(r sinG - т,), G0.1)
составляющие тГ2, Те2 не зависят от z, а остальные, сгг,
tfe, тг0, равны нулю. Легко
показать, что такое распреде-
распределение возможно лишь в слу-
случае ортотропного тела, у ко-
которого
а13 = а23. G0.2)
Если условие G0.2) не
выполнено, то для того, что-
чтобы получить уравнения и ре-
решение задачи, нужно исхо-
исходить из более общих [пред-
[предположений. Предположим,
что все шесть составляющих
напряжений не равны нулю, но из них две, тГ2, то2, не за-
зависят от z, а остальные пропорциональны z:
Рис. 96.
ar = zan, сге Bl,
tre = zTrfi, az = zazl. G0.3)
Тогда основная система уравнений теории упругости
для рассматриваемого тела запишется так:
до
G0.4)
G0.5)
70]
ЦИЛИНДРИЧЕСКИ-АНИЗОТРОПНАЯ КОНСОЛЬ
339
Так как консоль предполагается однородной, то все
ац — постоянные.
С этой системой поступим так же, как с системами,
рассмотренными раньше при исследовании других про-
проблем: интегрируя уравнения третье, четвертое, пятое (из
G0.5)), получаем выражения для перемещений, содержа-
содержащие произвольные функции переменных г, Э. Далее удов-
удовлетворяем уравнениям первому, второму и шестому и
вводим функции напряжений, тождественно удовлетво-
удовлетворяющие уравнениям G0.4). В результате получаем все
уравнения, необходимые для определения напряжений и
перемещений. После преобразований приходим к следую-
следующим результатам.
Перемещения определятся по формулам:
Ur = — ¦
x cos 0
= !-'(— ^isin6
Lsin 0) -f zUi + u'r,
Вг cos 8) + zVi + щ,
w = 4" И^ cos 6 + 5xr sin Q + CJ + W + w'.
G0.6)
Здесь Av Вl9 Сг — постоянные, которые определятся
из условий равновесия части консоли произвольной длины
z, а иг, Щ, w' — «жесткие» смещения, определяемые по
формулам B3.13); они содержат шесть постоянных, кото-
которые должны быть найдены из условий закрепления.
Функции Uv Vv W удовлетворяют уравнениям
G0.7)
-02- (Air cos 9 + Bxr sin 9 + d),
cos 9
1 dUx , дУг Vx 33
"Г'Ж+'Тг ~ =
+ U °Ы f
^*r. G0.8)
340 РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ [Гл. 7
В уравнениях G0.7) pi7- — приведенные Коэффициенты
деформации:
fa = aij ^^- (i, 7 = 1,2, 6; a16 = a26 = a36 = 0).
G0.9)
Исключая C/2, Vt из G0.7) и If из G0.8) путем диффе-
дифференцирования и вычитания, мы получим два уравнения,
связывающие компоненты напряжения. Вводим затем
две функции напряжений Fi (г, 6) и г|? (г, 0), как в задачах
о плоской деформации и о кручении:
__ я* (J'A _ 1 а^ i
дг
G0.10)
(^i> T2 — какое-нибудь частное решение третьего уравнения
равновесия G0.4)). Для напряжения сг2 получаем формулу:
сг2 = -^— (i4xr cos О Н- Ь\г sin 0 + С}) —
G0.11)
Из уравнений, полученных путем исключения J72, F2
из G0.7) иИ^из G0.8), найдем уравнения, которым удов-
удовлетворяют функции напряжений *):
а2^ , 1 дг|> V 1
-а* + — IF I + пъь 7^
G0.13)
На боковой поверхности должны выполняться условия,
которые в случае односвязной области сечения после
2) Здесь L4 — дифференциальный оператор B3.16).
§ 71] ЦИЛИНДРИЧЕСКАЯ КОНСОЛЬ 341
интегрирования по дуге контура принимают вид
s
^ = ==0 ^
- с. G0.14)
Постоянные Аг, Bv Сг и ft определятся, как было ска-
сказано, из условий равновесия. В цилиндрических коорди-
координатах эти условия будут иметь такой вид:
{А& + В^ + С\) S \\ (ai30rriH-^23°rei) dS = 0,
азз JJ
-бхД \\ (^i3^ri Н~ а23^01 )(^* sin 6 —т]) d^= —/^,
«зз Л G0.15)
Лх/2 — -i- ^ (a13ari + а23а01) (г cos 0 — g) dS = 0,
Здесь S — площадь поперечного сечения, Iv /2 — момен-
моменты инерции относительно главных осей х' и у'; интегралы
берутся по площади поперечного сечения.
Напряжения сг2, тГ21 тог, характерные для изгиба, со-
сопровождаются напряжениями ап сге, тго, характерными для
плоской задачи; разделить эти системы напряжений ока-
оказывается возможным в ортотропном теле, у которого
Ход решения таков. Сначала определяем функцию Fx,
т. е. решаем задачу о плоской деформации; найденная
функция будет содержать три постоянные, Av Bv Cv кото-
которые мы определим из трех первых уравнений G0.15).
Определив напряжения ar, tfe, тге, далее из уравнений
G0.7) находим функции U1 и Vl9 входящие в уравнение
G0.13), которому удовлетворяет г|).
Постоянная О найдется из четвертого условия G0.15).
§ 71. Распределение напряжений в консоли,
имеющей форму полого или сплошного цилиндра
В виде примера рассмотрим консоль, ограниченную
двумя поверхностями коаксиальных круговых цилиндров
(рис. 97). Предполагается, что ось анизотропии совпадает
с геометрической осью z и что в каждой точке имеются
342
РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ
1Гл. 7
Р
три плоскости упругой симметрии — перпендикулярная к
оси z, радиальная и ортогональная к этим двум (см.
[20], § 53).
Условия на цилиндрических
поверхностях, внутренней и на-
наружной, запишем в таком виде:
при г = аи г = b
<Jr-=Tr» = rrz = 0. G1.1)
Рассмотрим сначала случай,
когда упругие постоянные
удовлетворяют условию
%з = аъз> G1.2)
Рис. 97.
а затем выскажем соображения
относительно распределения напряжений в случаях, когда
условие G1.2) не выполнено.
Если коэффициенты деформации удовлетворяют усло-
условию G1.2), то функция Рг удовлетворяет однородному урав-
уравнению L±F\= 0 и условиям G0.14) (первому и второму),
а поэтому можно считать, что
аг = а6= тг9 = 0,
^rz — „ да ~Т~ ^1»
Р
G1.3)
G1.4)
Здесь
/="(&*_««)
(момент инерции относительно диаметра), a xlf т2 — ка-
какое-нибудь частное решение уравнения
G1.5)
Можно, например, принять
= 0, т2 = j- г2 cos 6.
G1.6)
§ 71]
ЦИЛИНДРИЧЕСКАЯ КОНСОЛЬ
343
Тогда уравнение для яр G0.13) примет вид
аъъ
G1.7)
Ищем решение этого уравнения в форме:
г|э = / (г) cos 9. G1.8)
Неизвестная функция / (г) удовлетворяет уравнению
Отсюда
где обозначено:
+ 2a13)r. G1.9)
cosB, G1.10)
к =¦
2а,
3—¦
I — «55
0 —
G1.11)
Здесь Gez» Grz — модули сдвига для тангенциальной и
радиальной плоскостей, Ez — модуль Юнга для осевого на-
направления z и v2r — коэффициент Пуассона, характеризу-
характеризующий деформацию в радиальном направлении при растя-
растяжении в направлении оси z.
Определив постоянные М и N из граничных условий
G1.1), получим следующие окончательные формулы для
касательных напряжений:
тгг =
sin в,
G1.12)
344 РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ [Гл. 7
Здесь обозначено:
Напряжения в точках диаметра, перпендикулярного
к силе, около внутренней и наружной поверхностей
равны:
в точке А (р = с)
(^; G1.14)
\ 1 — С г /
в точке В (р == 1)
Тег -=— ЬЧЗХ-1-Xix ___I_j. G1.15)
Одно из этих значений является наибольшим для всей
консоли. Например, при X = (х = 1, с = 0,5,
Тшах=^-1,75 G1.16)
и получается около внутренней поверхности, тогда как
около наружной поверхности
tez =-^-0,5. G1.17)
Глава 8
КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ
Последние две главы, восьмая и девятая, посвящены
исследованию упругого равновесия анизотропных тел
вращения, которые деформируются под действием внешних
усилий, но при этом остаются телами вращения. Такого
рода деформации возможны лишь для частных случаев
анизотропии и для частных случаев распределения на-
нагрузки. Можно различить два вида напряженно-деформи-
напряженно-деформированного состояния, при котором тело вращения перехо-
переходит в тело вращения: 1) кручение и 2) осесимметричная
деформация. В данной главе мы выводим общие уравнения
теории кручения тел вращения и даем решения несколь-
нескольких задач, представляющих практический интерес.
§ 72. Общие уравнения теории кручения
непрерывно-неоднородных тел вращения,
обладающих цилиндрической анизотропией
Рассмотрим упругое тело вращения (например, стер-
стержень переменного сечения), обладающее цилиндрической
анизотропией с осью анизотропии, совпадающей с осью
вращения z и непрерывно-неоднородное, с упругими ха-
характеристиками atj, зависящими только от двух коорди-
координат. Для определенности будем считать, что оди& торец
закреплен неподвижно (жестко), а по другому распреде-
распределены касательные усилия, приводящиеся к скручивающе-
скручивающему моменту; по боковой поверхности распределены усилия
tn, касательные к контуру поперечного сечения и не ме-
меняющиеся вдоль этого контура. Деформируясь, тело оста-
останется телом вращения, если плоскости меридиональных
сечений являются плоскостями упругой симметрии; если
S46 Кручение тел вращения (Vn.t
это условие не выполняется, то деформированное тело, во-
вообще говоря, уже не будет телом вращения. Отнесем тело
к цилиндрической системе координат (рис. 98). Уравне-
Уравнения обобщенного закона Гука для тела, имеющего в каж-
каждой точке плоскость упругой симметрии, проходящую
Рис. 98.
ег — anor
ее = а12ог + а2209
ez = aisor +
а25тГ2,
Yrz ^ ^16^ + ^25^9 + ^35^2 +
Yr9 = +
через ось вращения z (т. е. меридиональную), имеют сле-
следующий вид:
G2.1)
В этих уравнениях мы можем считать коэффициенты
#44» а*б, «ее произвольными непрерывными дифференциру-
дифференцируемыми функциями двух переменных, г и z; остальные ко-
коэффициенты atj могут быть какими угодно функциями
всех трех переменных г, 0, z, так как в уравнения теории
кручения не войдут 1).
При выводе общих уравнений мы будем исходить из
тех же предположений, которые лежат в основе теории
кручения однородного изотропного тела вращения. Имен-
Именно, поперечные сечения не искривляются и перемещения
в радиальных направлениях отсутствуют, т. е. каждое
поперечное сечение поворачивается вокруг оси вращения,
х) Вопрос о том, существуют ли еще другие типы анизотропии
[выходящие за рамки схемы G2.1)], при которых скрученное тело
остается телом вращения, требует специального исследования.
§ 72] ОБЩИЕ УРАВНЕНИЯ 347
не изменяя своего диаметра 1). Иначе говоря, будем исхо-
исходить из следующих основных положений:
ur = w = 0, щ = v (г, z). G2.2)
Тогда, очевидно
ег = ее = е2 = Чп = 0» 1
3v dv v \ G2-3)
Полагая, как обычно, что уравнения G2.1) однозначно
разрешимы относительно составляющих напряжений, по-
получим
or = eB = oz = orz = 0; G2.4)
На боковой поверхности должны быть выполнены ус-
условия:
tez cos (я, z) + тг9 cos (д,г) = tn. G2.6)
Если усилия на торцах не заданы, а известен только
скручивающий момент в любом поперечном сечении на
расстоянии z от свободного торца —М (z), то в этом сече-
сечении должно быть выполнено условие:
G2.7)
тдесь R (z) — наружный радиус тела на расстоянии z от
Зорца z = 0, a Ro (z) — радиус соосной полости, если она
имеется; если же тело сплошное, без полостей, то Ro = 0.
При z = 0 и z = / из G2.7) получим условия на торцах.
Можно указать два основных способа решения задачи
о кручении, в зависимости от того, что принимается за ос-
основную функцию, определяющую напряжения и переме-
перемещения.
*) См. работу [58] и книгу [20] (гл. 6, §54). См. также [22], [67]
348 КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ 1Гл. 8
Способ 1. За основную функцию принимается функция
напряжений яр (г, z), которая вводится так, чтобы первое
из уравнений G2.5) удовлетворялось тождественно. По-
Положим
—
/70 ft\
Исключая v из остальных двух уравнений G2.5), по-
получим уравнение, которому удовлетворяет функция на-
напряжений:
д Г 1 / dip дгЬ Л 1 5 Г dtb dtbi A
G2.9)
Задача сводится к отысканию функции яр (г, z) в области
половины меридионального сечения, т. е. ограниченного
осью z, двумя прямолинейными отрезками, нормальными
к оси z (торцы) и образующей. Если имеется сквозная
соосная полость, то половина меридионального сечения
ограничена двумя прямолинейными отрезками и двумя
кривыми. Условие G2.6) можно преобразовать путем
интегрирования по дуге s образующей, принимая во внима-
внимание, что
cos (/г, z) = - ijj-, cos (/г, г) = -jji . G2.10)
Получим вместо G2.6) условие
*ds + c, G2.11)
т. е. на боковой поверхности и поверхности полости (или,
точнее, на их образующих) можно считать заданной с точ-
точностью до постоянной функцию напряжений. Эта функ-
функция, кроме того, должна удовлетворять условию
G2.12)
Условие G2.11) упрощается, если внешние усилия (и ре-
реакции) распределены только по торцам. Тогда на обра-
образующих боковой поверхности функция я|) равна постоян-
постоянной, которую в случае сплошного тела можно положить
равной нулю.
§ 72] ОБЩИЕ УРАВНЕНИЯ 349
Если тело является неоднородным и ортотропным, то
уравнения обобщенного закона Гука D-е и 6-е из G2.1))
запишутся так:
Yez = 7t9z' Vre = 7 Тг9' G2.13)
где G1! = Gqz, G3 = Gre — модули сдвига — функции г
и z. Вместо G2.9) будем иметь более простое уравнение:
<7гЛ4>
Способ 2. За основную функцию принимается переме-
перемещение v (г, z). Решив второе и третье уравнения G2.5)
тносительно т, получим
Здесь
Подставляя G2.15) в первое уравнение системы G2.5), по-
получим уравнение, которому удовлетворяет перемещение
v = щ:
ta-A.— +Aa r'iL-JL
ТГ9 — /±4в Я, "Г лвв ( Яг г
fl46
—
—, ^46 - —, л66 - -?- , G2.16)
А % J
Граничные условия вытекают из уравнений G2.15)
и условия G2.6); они будут сложнее, чем в случае,
когда за основную функцию принимается г|). Второй спо-
способ удобен тогда, когда на поверхности задается переме-
перемещение V.
В случае ортотропного тела
^44 = #1» ^46 = 0, Авв = G3
и уравнение G2.17) принимает вид
350 КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ [Гл. 8
Если тело обладает анизотропией более общего вида,
когда меридиональные плоскости не являются плоскостя-
плоскостями упругой симметрии, то задача усложняется. В этих
случаях деформацию уместно назвать не кручением, а
обобщенным кручением тела вращения.
§ 73. Кручение однородного тела вращения
В случае однородного тела, обладающего цилиндриче-
цилиндрической анизотропией, а^, Gv G3 — постоянные величины и
соответствующие дифференциальные уравнения будут
уравнениями с постоянными коэффициентами [22].
В общем случае будем иметь вместо G2.9) и G2.17):
В случае ортотропного тела:
||+g||_J_jJL = O; G3.3)
1 dv v ^
Здесь введено обозначение:
В случае изотропного однородного тела g = 1. Задача
о кручении однородного анизотропного тела вращения
с областью S может быть сведена к такой же задаче для
изотропного тела, но с измененной областью Sv путем
простой замены переменных. Для ортотропного тела эта
замена имеет вид
Г1 = г, za = -!=-. G3.6)
731
КРУЧЕНИЕ ОДНОРОДНОГО ТЕЛА ВРАЩЕНИЯ
351
О том, как область S± получается из данной, дает пред-
представление рис. 99.
Иногда, в зависимости от упругих свойств и формы се-
сечения, удобнее пользоваться криволинейными координа-
координатами, в частности, сферическими. Приводим основные
формулы и уравнения кручения для однородного тела,
О
Рис. 99.
обладающего сферической анизотропией, в сферических
координатах.
Сферическими координатами какой-нибудь точки
будут р, ф, 9 — расстояние точки
от начала координат или полюса,
угол, образуемый радиус-векто-
радиус-вектором с осью z и угол, образуемый
проекцией радиус-вектора на
плоскость ху с полярной осью х
(рис. 100). Между сферическими
и цилиндрическими координата-
координатами имеется связь:
г = р sin ф, z = p cos ф, 9 = 0.
G3.7)
Единственную не равную ну-
нулю компоненту перемещения обоз-
обозначим по-прежнему через г; (р, ф). Рис iqq
В уравнения войдут напря-
напряжения на площадках, нормальных к координат-
координатным направлениям р, ф, 0; не равны нулю только две
ЗГJ КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ [Гл. 8
составляющие — т^ и трэ. Принимая это во внимание, вы-
выпишем выражения для составляющих деформаций и урав-
уравнение равновесия сплошной среды, взятые из книги
А. Лява [24] (стр. 68, 102):
8р = 8ф = 80 = Ypcp = 0, |
dv v I dv . v \ G3.8)
G3.9)
, — аф — (Tg — Трф = 0.
Обобщенный закон Гука для сферически-анизотроп-
сферически-анизотропного ортотропного тела представится уравнениями
Тре = СгрйУрв, Тф9 = бгфеУсрд. G о. 10)
Подставляя эти выражения в G3.9), получим уравнение
для v:
Здесь через ^5 обозначено отношение модулей сдвига:
«Г.-Iй-- G3.12)
Уравнение длягр приводить не будем; оно далее не исполь-
используется.
§ 74. Кручение криволинейно-анизотропного конуса
Вопрос о кручении однородного изотропного тела в ви-
виде усеченного конуса, сплошного и полого, подробно иссле-
исследован в книге Н. X. Арутюняна и Б. Л.Абрамяна [4].
Кручение анизотропного конуса (с анизотропией част-
частного вида) под действием скручивающего момента, при-
приложенного к вершине, рассмотрено в наших работах [58],
[20], [22].
Укажем, как выводится решение задачи для однород-
однородного тела. Относительно решения для неоднородного тела
мы ограничимся некоторыми замечаниями.
74 КРУЧЕНИЕ КРИВОЛИНЕЙНО-АНИЗОТРОПНОГО КОНУСА ЗГK
Пусть дано упругое тело длиной Z, ограниченное сна-
снаружи и внутри поверхностями круговых конусов с общей
осью и с общей вершиной (конический полый стержень, не
обязательно тонкий), и двумя плоскими торцевыми по-
поверхностями, нормальными к оси. Тело обладает анизо-
анизотропией частного вида: в каждой точке имеется плоскость
упругой симметрии, нормальная к оси вращения (или па-
параллельная плоскостям поперечных сечений). Примем
общую вершину конических поверхностей за начало коор-
координат и направим ось ъ цилиндрической системы коорди-
координат по общей оси конических поверхностей, а г — как
угодно (нормально к z; рис. 101). Уравнения обобщенного
Рис. 101.
закона Гука для такого тела будут иметь вид G2.1); они
содержат 13 A2) упругих постоянных аи. Будем считать,
что один торец (например, имеющий большую площадь)
как-то закреплен, а по другому распределены внешние
усилия. Закон распределения усилий не задается, а зада-
задается скручивающий момент Л/, к которому они приводятся.
Если решать задачу с помощью функции напряжений яр,
то эта функция должна удовлетворять уравнению G3.1),
граничным условиям:
при г = z tg а яЬ = сх = const, _ _ л
(/4.1)
при г = ztga0 t = c2 = const,
и условию в любом поперечном сечении и на торцах:
м
i|>(ztga, z) — ij)(ztga0, z) =¦«—.
G4.2)
Здесь а и а0 — углы наклона образующих наружной
12 С. Г. Лехницкий
354
КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ
[Гл. 8
и внутренней поверхности к оси z (а0 < а); скручиваю-
скручивающий момент М — величина постоянная. Условиям G4.1)
и G4.2) мы удовлетворим, если найдем решение уравне-
уравнения G2.1) в виде функции отношения t = r/z:
У =f(t). G4.3)
Подставляя G4.3) в уравнение G2.1), получим обыкновен-
обыкновенное уравнение, легко разрешимое:
A + 2mt + пН*) /" @ + ( ~ - т + 2/Л) /' (/) = 0 G4.4)
Общий интеграл G4.4) представится формулой
2nU
Удовлетворяя условию G4.2), которое примет вид
получаем
G4.5)
G4.6)
М (п* — тгJ
2J г2
где
Л/ — 1 + ^ tg a
A + mtgaf __ 1 + т tg a0
G4.8)
(l+"ttgaoK
G4.9)
3K30
К =
n2tg2a0.
qq — постоянная, не влияющая на напряжения и дефор-
деформации; ее можно положить равной нулю.
Перемещение v мы найдем, интегрируя второе и третье
уравнения G2.5). Произвольную постоянную, получен-
полученную в результате интегрирования, мы найдем, уточняя
^ ^41 КРУЧЕНИЕ КРИВОЛИНЕЙНО-АНИЗОТРОПНОГО КОНУСА 355
условия закрепления. Если принять, что закреплена вне-
внешняя окружность широкого конца г = (Z + l0) tg а, то,
определив постоянную, мы получим выражение для угла
поворота радиуса г сечения, находящегося на расстоянии
z от вершины конусов:
?f Г 1 1 1 /7/ ,,,
G4Л1)
Так как о есть функция двух переменных, г и z, то нуж-
нужно условиться, что подразумевать под полным углом за-
закручивания. Можно, например, считать, что полный
угол закручивания (отах — это угол, на который повер-
повернется внешняя окружность незакрепленного конца (ради-
(радиус ее равен /0 tg а). Получим
(Ото* = •—¦—5—^-—~ "Ц ¦ ;г • G4.12)
6шУ /03(/ + /0J К* У }
Для сплошного неортотропного конуса а0 = О, Ко = 1
N == 1 + mtga _ A + mtgaK __ _2_ ,?4 ^
В случае ортотропного конуса нужно всюду положить
т = 0, п = Уg, а следовательно,
G4.14)
Полагая во всех формулах т =0, п ~ 1, g — 1, по-
получим известное решение для изотропного тела.
Если конус обладает цилиндрической анизотропией,
но является непрерывно-неоднородным, т. е. модули сдви-
сдвига его — непрерывные дифференцируемые функции коор-
координат г и z, то можно указать ряд случаев, когда решение
задачи о кручении находится сравнительно просто. При-
Приведем два таких случая (решения для них имеются в на-
нашей книге [22]):
1) модули сдвига — произвольные функции отноше-
отношения t = r/z; в частности,
G1 = g1tn, G3 = ^n, G4.15)
где п — любое вещественное число;
356 КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ [Гл. 8
2) модули сдвига заданы в виде выражений:
(р, q — вещественные числа).
Заметим, что для конуса, обладающего сферической
анизотропией и однородного, у которого начало коорди-
координат находится в вершине конической поверхности, а ось
z направлена по геометрической оси, получается совер-
совершенно элементарное решение:
. хР» = С^1, G4.17)
а остальные составляющие равны нулю. С определяется
из условия равновесия.
§ 75. Влияние сферического и сфероидального
включения и полости на распределение
напряжений в скрученном стержне
Как было показано раньше, в главе 4, круговое или
эллиптическое включение из другого материала в пластин-
пластинке, находящейся в плоском напряженном состоянии под
действием заданных усилий, искажает поле напряжений.
Это же явление наблюдается и в случае, когда в пластинке
имеется не включение, а отверстие; вблизи отверстия
получаются напряжения больше, чем в сплошной пла-
пластинке, находящейся под действием тех же усилий или,
иначе, происходит концентрация напряжений. Искаже-
Искажение поля напряжений наблюдается и в теле, находящемся
в пространственном напряженном состоянии и содержа-
содержащем включения из другого материала или полости в виде
тел трех измерений.
Мы рассмотрим простейшие случаи кругового цилин-
цилиндра радиуса R, имеющего на оси вращения сферическое
включение или полость и находящегося в упругом равно-
равновесии под действием скручивающих моментов М, прило-
приложенных к торцам. Все задачи этого рода будем решать
приближенно: цилиндр рассматриваем как беско-
бесконечное упругое пространство с включением или полостью,
а напряжения разыскиваем так, чтобы они точно удов-
удовлетворяли условиям на поверхности включения или поло-
§ 75] ВЛИЯНИЕ СФЕРОИДАЛЬНОГО ВКЛЮЧЕНИЯ 357
сти и стремились бы по мере удаления от них к напряже-
напряжениям в цилиндре, который скручивается моментами М.
Простейшим будет случай анизотропного цилиндра
со сферическим включением на оси, изготовленным из ма-
материала со сферической анизотропией и притом ортотроп-
ным. Центр сферы примем за начало сферической системы
координат р, ф, Э, связанной с цилиндрической г, 0, z,
у которой ось g направлена по геометрической оси цилинд-
цилиндра (см. рис. 100). Напряжения и перемещения в цилиндре
будем отмечать верхним индексом A), во включении —
верхним индексом B). Радиус включения обозначим через
а, модули сдвига его, отнесенные к сферической системе
координат, через G^e, GP9 и модуль сдвига цилиндра —
через G. Найдем приближенное решение (см. [114]).
В сплошном цилиндре имеем напряжения
и перемещение и относительный угол закручивания Ф:
Ц G5.2)
(с точностью до жесткого перемещения — вращения во-
вокруг оси z). Для включения справедливы уравнения
обобщенного закона Гука:
B) ,B) Х2) г B) /7С О\
Ype ^ф9 = wsYo Gb.6)
и уравнение для перемещения (см. G3.10) и G3.11))
Условия на поверхности контакта включения и полости
имеют вид (для случая, когда проскальзывание по по-
поверхностям контакта полости и ядра невозможно)
vm = vw, т(РУ = т(рУ. G5.5)
Внутри включения напряжения должны быть конеч-
конечными, а по мере удаления от него перемещения должны
358
КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ
[Гл. S
стремиться к перемещениям в сплошном цилиндре:
i/1)—^ftzr = -s-p2sin 2ф. G5.6)
Принимая во внимание условие G5.6), будем разыски-
разыскивать решение уравнения G5.4) в виде
in 2Ф. G5.7)
Получим совершенно элементарную функцию:
у(а) - (Л2рп-°'5 + ?2p-n-°>5) sin 2ф, G5.8)
где
G5.9)
Постоянную 52 нужно отбросить, иначе напряжения
в Центре включения будут иметь особенность. Следова-
Следовательно,
sin 2ф; G5.10)
= —2G9Qpn-1>* sin2
G5.11)
Перемещения и напряжения в изотропном цилиндре
мы получим из G5.8) — G5.9), полагая gs = 1. Тогда
г*1> = (AlP2 + Btf-3 )sin 2Ф; G5.12)
G5.13)
Постоянные А19 В1 и А2 определим из условий G5.5)
и G5.6). Получим окончательные формулы:
5М g2,5-npn-0.5 л
Л2)_ ЪМ
-81п2ф,
ЮЛ/
G5.14)
G5.15)
75]
ВЛИЯНИЕ СФЕРОИДАЛЬНОГО ВКЛЮЧЕНИЯ 359
Здесь использованы обозначения:
—1.5) •
<75-">
G5-18)
%$
Наибольшее значение %$ получается у поверхности
включения в точках ф = я/4, а наибольшее значение
T^V — на экваторе, в точках ф = я/2:
ЪМа (n — l,
10Л/Д
(ТФе)тах =
Решение для случая кручения цилиндра со сферической
полостью мы получим из G5.17), полагая g2 = 0:
A)
CD
т9
M
'25 ^jsin ф'
G5.21)
Из последней формулы получим наибольшее значение
напряжения в цилиндре
1,25.
G5.22)
Сравнивая это выражение с G5.1), получим коэффициент
концентрации напряжений в изотропном цилиндре со
сферической полостью на оси, при кручении:
к = 1,25.
Из G5.16) — G5.18), полагая g2 = оо, мы получим
распределение напряжений и в изотропном цилиндре
360
КL1 УЧЕНИЕ ТЕЛ Bl А1ДЕНИЯ
[Гл.
с абсолютно жестким сферическим включением на оси:
CD
х
G5.23)
На поверхности жесткого включения
Трв)р=а = 2,5—7^-sin29, (Тфо)Р==а = 0; (/5.24)
— ^Ма 9 s /7Г) ^5^
Максимальное напряжение в цилиндре с абсолют-
абсолютно жестким сферическим включением получается вдвое
М
Pirc. 102.
больше, чем в таком же цилиндре со сферической поло-
полостью на оси.
С. Ч. Дас [112] решил задачу о кручении изотропного
вала с включением в виде вытянутого эллипсоида враще-
вращения (рис. 102, а), сферы и сплющенного эллипсоида вра-
вращения (рис. 102, б). Как частные случаи, найдены решения
75]
ВЛИЯНИЕ СФЕРОИДАЛЬНОГО ВКЛЮЧЕНИЯ
361
для цилиндров с жесткими включениями. Подсчитаны
коэффициенты концентрации, т. е. отношения наибольшего
напряжения на поверхности контакта к напряжению
в тех же точках цилиндра без включения для не-
нескольких отношений полуосей Ыа и модуля сдвига вклю-
включения G' к модулю сдвига вала. Приводим таблицу, взя-
взятую из указанной работы (таблица 23).
Таблица 23
Значения коэффициента концентрации напряже-
напряжений в изотропном цилиндре с изотропным вклю-
включением
G7G
Вытянутый эллипсоид, с? = 0,866
Сфера, d ~ 1
Сплющенный эллипсоид,
d = l,15
0,25
0,28
0,3
0,36
4
2,8
2,5
1,8
оо
7,0
5,0
2,5
Из этой краткой таблицы все же можно подметить, что
коэффициент концентрации возрастает с возрастанием
жесткости кручения, т. е. отношения G /G, и уменьшается
с возрастанием отношения полуосей d = Ыа эллипсоида.
Задачи этого рода решены также и для некоторых част-
частных случаев анизотропии цилиндра и включения. Пере-
Перечислим некоторые из них:
С. Босе [108] и [109] (Трансверсально-изотропный
вал и изотропное включение в виде сферы или эллипсоида
вращения);
С. Босе [110] (Трансверсально-изотропный вал и сфе-
сферическое включение из материала со сферической анизо-
анизотропией);
С. К. Боумик [106], Р. Субраманиан [127] (Изотроп-
(Изотропный вал с упругим включением, обладающим криволиней-
криволинейной анизотропией специального вида);
П. П. Чаттаржи [111] (Трансверсально-изотропный
вал с жестким сферическим включением);
С. К. Боумик [107] (Трансверсально-изотропный ци-
цилиндр, эллипсоидальное включение).
Известны и еще работы на ту же тему, но мы о них
упоминать здесь не будем (см. [22]).
362
КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ
[Гл. 8
§ 76. Точное решение задачи о кручении
кругового цилиндра
Рассмотренные в главе 6 задачи о кручении стержней
все были решены приближенно: на боковой поверхности
граничные условия удовлетворялись точно, а на торцах —
приближенно. На торцевых поверхностях усилия не за-
задавались, а задавались скручивающие моменты, к кото-
которым и должны были приводиться касательные усилия.
Но для кругового цилиндра конечной длины, полого или
сплошного, однородного или неоднородного, можно полу-
получить и точное решение (по крайней мере, для частных
случаев анизотропии и неоднородности), т. е. найти напря-
напряжения, соответствующие касательным скручивающим
усилиям, распределенным по торцам по заданному закону,
при незагруженной или закрепленной боковой поверхно-
поверхности и поверхности полости (если она имеется).
Выведем это решение. Пусть дан круговой цилиндр ко-
конечной длины, вообще полый, обладающий цилиндриче-
цилиндрической анизотропией, с осью, направленной по геометриче-
геометрической оси. Мы будем считать цилиндр ортотропным, но
неоднородным; модули сдвига его G$z = Gx (г), Gre =
== ^з (r) — функции одной координаты г — расстояния
от данной точки до геоме-
геометрической оси. Отнесем тело
к цилиндрической системе
координат, примем центр од-
одного из торцов за начало,
а геометрическую ось — за
ось z и обозначим через I—
длину, 6, а—радиусы попе-
поперечного сечения (внешний и
радиус полости). Из различ-
различных случаев нагрузки оста-
остановимся на двух:1) оба торца
нагружены одинаковыми ка-
касательными усилиями,нор-
усилиями,нормальными к радиусам и за-
заданными как функции г (оче-
(очевидно, такие усилия на каждом торце приводятся к скру-
скручивающим моментам, которые направлены в разные сто-
стороны и взаимно уравновешиваются); 2) один торец за-
Рис. 103.
§ 761 ТОЧНОЕ РЕШЕНИЕ ЗАДАЧИ О КРУЧЕНИИ ЦИЛИНДРА 363
креплен неподвижно (так, что каждая точка его остается
неподвижной), а другой нагружен касательными усилия-
усилиями, приводящимися к скручивающему моменту, задан-
заданными как функции г (рис. 103).
В случае неоднородного ортотропного тела напряже-
напряжения выражаются через функцию напряжений \р, которая
удовлетворяет уравнению второго порядка с переменными
коэффициентами (переписываем G2.8) и G2.14)):
<76-2»
Укажем ход решения задачи. Разыскиваем решение
уравнения G6.2), которое даст возможность удовлетво-
удовлетворить условиям на цилиндрических поверхностях:
при г = Ъ и г = а
тг9 = 0, G6.3)
в виде произведения
•ф = R (г) Z {?). G6.4)
Подставляя G6.4) в G6.2) и разделяя переменные, полу-
получим
Г R'jr)
Z(z) " И (г)
Отсюда получаем два уравнения (обыкновенные):
= 0; G6.6)
^°- «76-7)
В уравнении G6.5) g — положительная постоянная,
которую можно задать произвольно, а А, — другая посто-
постоянная, которую нужно определить. Общие решения урав-
уравнений G6.6) и G6.7) имеют вид (при А, Ф 0):
Z= A ch-^ + 5sh-^-; G6.8)
R = Cii?! (г; 1) + C2R2 (r, X). G6.9)
364 КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ [Гл. 8
При X = О
Z = Az + Я, G6.10)
R= djG^dr + Ca. G6.11)
Линейно-независимые решения Лг и i?2 для X Ф 0 мы
можем найти в явном виде, разумеется, только задавая
функции Gx (г) и G3 (г).
Предположим, что функции Gx и G3 заданы, а Дь Д2
определены. Потребуем, чтобы каждое решение G6.4)
удовлетворяло условиям G6.3) на свободных поверхно-
поверхностях (или условию v = 0 на закрепленных неподвижно).
Тогда для постоянных Сх и С2 получим систему однород-
однородных уравнений первой степени; приравнивая нулю ее
определитель, получим уравнение, которому удовлетво-
удовлетворяет А, : А (к) = 0. Отсюда получаем собственные значе-
значения X — Ях, А,2, . . ., Ят, . . ., которым соответствуют соб-
собственные функции Нт; они определятся с точностью до
постоянного множителя. Постоянный множитель мы мо-
можем отнести за счет А и В или, что то же, приравнять
единице. Тогда выражение для я|? запишется в виде
суммы:
оо
$ = Rq(Aqz + BQ) + 2 Rm(r)(Anchamz + Bnshanz),
m=l
G6.12)
где
Чтобы удовлетворить условиям на торцах, нагружен-
нагруженных одинаковыми усилиями, нужно эти заданные усилия
представить в виде ряда
=4г' Я™= dr у
G6.14)
Если это удастся, то тогда из условий на торцах мы по-
получим по два неоднородных уравнения (для каждого т),
§ 77] КРУЧЕНИЕ НЕОДНОРОДНОГО ЦИЛИНДРА 305
которым удовлетворяют Ат и Вт, и определим функцию
напряжений и сами напряжения в виде рядов.
Если цилиндр не имеет полости, т. е. является сплош-
сплошным, то нужно постараться в выражениях G6.9) и G6.11)
отбросить члены, которые неограниченно возрастают по
мере приближения к оси.
Таким же путем решается и задача, когда на наружной
поверхности и на поверхности полости задано перемеще-
перемещение (равное нулю) или на одной цилиндрической поверх-
поверхности задано напряжение, а на другой перемещение. Ра-
Разумеется, и в том, и в другом случае должно быть найдено
перемещение v, соответствующее функции напряжений ty
(путем интегрирования уравнений G2.13)).
§ 77. Кручение цилиндра, у которого
модули сдвига меняются пропорционально
степени расстояния г (точное решение)
Одним из наиболее простых будет случай, когда модули
сдвига меняются по сечению пропорционально какой-либо
степени расстояния, а по длине не меняются. В этом слу-
случае удается найти общий интеграл уравнения G6.7) в яв-
явном виде.
Рассмотрим сплошной цилиндр, у которого модули
сдвига заданы в виде функций:
Gx = ftp", G3 = g3p\ G7.1)
где #!, g3 — множители, имеющие размерность модуля
сдвига, п — какое-нибудь вещественное число и р = rib.
Уравнение G6.7) имеет общий интеграл, выражающийся
через функции Бесселя. Положим g равным отношению
модулей сдвига (g = gjg3) и введем обозначение а =
= 1 + 0,5тг. Отбросим в выражении ty G6.12) функции, даю-
дающие особенности в центре сечения, и тогда получим для
сплошного цилиндра (без полости):
2(а + 1
С»
Y ch а">г + Вт sh а™*У>
366
КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ
[Гл. 8
z + Bm sh amz),
m=l
X
v =
co3r
у—
X
sh am z
sh a
tchamz);
G7.3)
Постоянная ca3 определится из условия в среднем попе-
поперечном сечении или на закрепленном торце.
Рассмотрим два основных случая.
Случай 1. Оба торца нагружены одинаковыми скручи-
скручивающими касательными усилиями т (р), распределенными
по радиусу по заданному закону. Условия на торцах бу-
будут иметь вид
при z = 0, z = I
tez = t(p). G7.5)
Умножим это равенство на р1-а и разложим функцию
трх-а в ряд Дини — Бесселя. Получим
m=l
G7.6)
где Xm — последовательные корни функции Бесселя пер-
первого рода порядка a + 1, т. е. /a+i (x). Коэффициенты aQj
ат определяются по формулам *):
2Х2
Тр/а
G7.7)
См., например, книгу Г. Н. Ватсона [10], стр. 768.
§ 77]
КРУЧЕНИЕ НЕОДНОРОДНОГО ЦИЛИНДРА
367
Следовательно, при z = О, z = I
оо
тв2 = «оР20 + Р"-1 S amJa (Kmp).
т=1
G7.8)
Удовлетворяя граничным условиям G7.5), определяем
постоянные Ат, Вт, а по формулам G7.3) — G7.4) — на-
напряжения и перемещение v:
A cha (г — 0,51)
oo
m=l
*тР) ch0>5amr
sham(s-O,5Z)
ch O,5
G7.9)
m=l
Здесь
sh am (z — 0,5/)
' chO,5am/
G7.10)
G7.11)
Среднее сечение можно считать неподвижным; из этого ус-
условия определена постоянная со3.
Случай 2. Один торец, z = 0, нагружен заданными уси-
усилиями, другой, z = I, полностью закреплен (перемещение
каждой его точки равно нулю). Формулы для напряжений
и перемещения мы получим из G7.9) и G7.10), заменив
всюду I на 21.
Полагая всюду п — 0, получим формулы для однород-
однородного цилиндра, с постоянными модулями Gx, G3. В этом
случае А,т будут корнями функции Бесселя второго по-
порядка /2 (я). Напряжение Те* и перемещение v предста-
представятся рядами, расположенными по функциям Бесселя
первого порядка, и тГ9 — по функциям Бесселя второго
порядка.
Решения для однородного ортотропного цилиндра
можно получить и из решения для изотропного цилиндра
(подробнее см. [22], § 47).
Глава 9
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ
ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО
ТЕЛА ВРАЩЕНИЯ
В последней, девятой главе рассматривается второй
вид напряженно-деформированного состояния, при ко-
котором тело вращения, деформируясь, остается телом вра-
вращения; в этом случае говорят об осесимметричной дефор-
деформации. Теория осесимметричной деформации разработана
со всей полнотой только для тела изотропного и тела, об-
обладающего анизотропией частного вида — трансверсаль-
ио-изотропного. В этой главе мы всегда будем предпола-
предполагать, что рассматриваемое тело является трансверсально-
изотропным; из формул для него получаются формулы
jjjih изотропного тела как частные случаи.
§ 78. Общие уравнения осесимметричной
деформации. Функция напряжений
Представим себе тело из упругого однородного транс-
версально-изотропного материала, ограниченное одной
или несколькими коаксиальными поверхностями враще-
вращения, находящееся в равновесии под действием внешних
усилий, поверхностных и объемных. Предположим, что
плоскости изотропии, проходящие через каждую точку
тела, нормальны к геометрической оси его (оси вращения),
а распределение усилий обладает симметрией вращения
относительно той же оси.
Отнесем тело к цилиндрической системе координат г,
6, z, поместив начало координат в какой-нибудь точке
на геометрической оси (например, в центре крайнего се-
сечения) и направив ось z по этой оси, а полярную ось х —
§ 78] ОБЩИЕ УРАВНЕНИЯ ОСЕСИММЕТРИЧНОЙ ДЕФОРМАЦИИ 369
произвольно в плоскости поперечного сечения (рис. 104).
Обозначим через Rn, Zn — проекции поверхностных уси-
усилий на координатные направления г, z и через R, Z —
проекции объемных сил (вп = 6 = 0). Как обычно,
поверхностные силы относим к единице площади, а объем-
объемные — к единице объема. Уравне-
Уравнения обобщенного закона Гука за-
запишутся так же, как и в декарто-
декартовой системе (см. D.8)):
а12а0
80
a13ez,
гг = а13 (аг + а9)
G8.1)
yr0 = 2 (an — a12) тг9.
Рис. 104.
Всего мы имеем пять незави-
независимых упругих постоянных. Решив G8.1) относительно
составляющих напряжений, получим уравнения обобщен-
обобщенного закона Гука в другой форме:
G8.2)
а, = Апгг -
Оо = А\2гг -
о2 = А13 (ег + ев) 4
гг0 = у (Ап — А12) уг0.
Выражая коэффициенты Ац через atj, имеем:
2
А ___ аП«33~ «13
1
fl3_
(ап — а12) J
Здесь
«и — а12
G8.3)
= («
G8.4)
Коэффициенты деформации ац и модули упругости
370
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ
[Гл. 9
можно выразить и через технические константы (см. D.9)):
1 v J_
Е' '
ян = "Tf,
р~ » ^33 =
V
2(ап
V
~Е
1
#44 ~ Г' '
2A+ v)
G
G8.5)
где Е, Е' — модули Юнга для растяжения и сжатия в
плоскости изотропии и в направлении, перпендикулярном
к ней, v — коэффициент Пуассона, характеризующий со-
сокращение в плоскости изотропии при растяжении в той же
плоскости, v' — коэффициент Пуассона, характеризую-
характеризующий сокращение в направлении, нормальном к плоско-
плоскости изотропии при растяжении в этой плоскости,
G = Е/[2 A + v)], G' — модули сдвига для плоскостей
изотропии и перпендикулярных (радиальных). Выраже-
Выражений Atj через Е, G, v мы приводить не будем.
В силу симметрии в распределении усилий и упругой
симметрии радиальные сечения останутся плоскими и тело
останется телом вращения и в деформированном состоя-
состоянии, т. е.
иг = иг (г, z), щ = 0, w = w (г, z). G8.6)
Отсюда следует, что у$2 = угв = 0 и те2 = тге = 0;
остальные составляющие деформации не будут зависеть
от 0, причем
8Г =
дг
г
dw
dz
Четыре составляющие напряжений, не равные нулю,
удовлетворяют двум уравнениям равновесия:
дг
dz
дг
G8.8)
(третье уравнение превращается в тождество).
Присоединяя сюда первое, второе, третье и пятое урав-
уравнения обобщенного закона Гука G8.1) или G8.2), получим
систему шести независимых уравнений для определения
шести неизвестных функций аг, ае, az, trz, мг, w.
§ 78] ОБЩИЕ УРАВНЕНИЯ ОСЕСИММЕТРИЧНОЙ ДЕФОРМАЦИИ 371
Остановимся на случае отсутствия объемных сил,
т. е. примем R = Z = 0. Исключая перемещения ur, w
из выражений для составляющих деформации G8.7),
получим зависимости:
ег-—(п>9) =0,
дг
drdz
= 0.
G8.9)
Подставляя сюда выражения для деформаций из урав-
уравнений G8.1), получим
апог + а12сте + a13oz — — [г (а12ог
дг
rz = 0.
G8.10)
Присоединяя сюда G8.8), будем иметь четыре урав-
уравнения для четырех неизвестных — составляющих напря-
напряжений.
Первому уравнению равновесия (при R = 0) и урав-
уравнениям G8.10) мы можем удовлетворить, введя функцию
напряжений ф (г, z), которая является обобщением функ-
функции напряжений для изотропного тела х). Для транс-
версально-изотропного тела выражения напряжений че-
через ф имеют вид:
д I д2ф Ъ дф д2ф \
г dz \ дг2 ' г дг ' 5z2 / '
I L т^ I СУVI/ - С/ Ц/ \
= "яг!0 ~ал~ "Т т ^ г а ~лл~)
г дг
*rz =
а /
+7
G8.11)
2) См., например, курс Лява [24], стр. 288.
372 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ [Гл. 9
где
a\S (al\ — а1ъ) + flUa44 i
12 • ° —
G8.12)
Из второго уравнения равновесия G8.8) (при Z ~ О
получаем уравнение для функции напряжений:
/а2 1 э и а^ф | 1 ^
\ дг2 "*" г 'аГ/
С дифференциальным уравнением четвертого порядка
G8.13) связано алгебраическое уравнение
ds* ~(a + ф2 + 1=0, G8.14)
корни которого равны
«1,3 = ±
:V2 — 4d
«2,4= ±" '" ¦ ' ' '" ¦
G8.15)
Введя дифференциальные операторы
V2 д2 . 1 д . 1 д2 .. л п\ /но ла\
i-^ + T-d^-JlJJ (г = !.2). G8-16)
s
можно записать уравнение G8.13) очень просто (см. [20],
стр. 259 и [58]):
v;v;<p - о. G8.17)
Операторы Vi и V2 можно переставлять, так как
легко убедиться, что V\^l <р = V2 V\ ф.
Относительно чисел s± и s2, зависящих от упругих по-
постоянных dij, можно доказать следующую теорему.
Теорема. Числа s2 и s2 для любого трансверсаяъно-
изоТпропного упругого тела могут быть только веществен-
§ 78] ОБЩИЕ УРАВНЕНИЯ ОСЕСИММЕТРИЧНОЙ ДЕФОРМАЦИИ 373
ними или комплексными (с вещественной частью, неравной
нулю), но не могут быть чисто мнимыми.
Доказывается эта теорема тем же методом, что и теоре-
теоремы 1—4, рассмотренные в § 20. Выражение упругого потен-
потенциала для трансверсально-изотропного тела запишется
так:
У' = ~2 1аи (°г + ае) + 2апагав + аъъа\ +
+ 2a13(ar + ao)az + a4ltr22]. G8.18)
Задавая значения напряжений в виде
/с'2 __ 1 __ к
G8.19)
где к и N — произвольные вещественные числа и N Ф 0,
получим
V = aU23ffl3u^3 t^ + (а + О А* + И- G8-20)
При всяких вещественных А: и N имеем: V ^> 0. Так как
всегда ап > 0, апа33 — а\3 > 0 (см. [8], ч. I, или [47]),
то мы получаем
d№ + (а + с)к2 + 1 > 0 G8.21)
при всяких вещественных &, а следовательно, уравнение
d|x4 + (а + c)ii2 + 1=0 G8.22)
не может иметь вещественных корней. Но параметры s±
и s2 связаны с корнями уравнения G8.22) [д,х и щ соотно-
соотношениями:
52 = — i\iu s2 = —ф2, G8.23)
в чем можно убедиться, решив уравнение G8.22) и сопо-
сопоставив решение с G8.15), а следовательно, они не могут
быть чисто мнимыми. Квадраты параметров s\ и корней
jli2 могут быть вещественными или комплексными числами.
Это следует из формул G8.23); они могут быть и чисто мни-
мнимыми (если вещественная часть \it равна по абсолютной
величине мнимой).
374 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ [Гл. 9
Граничные условия в случае заданных на боковой
поверхности усилий Rn и Zn сводятся к условиям на ме-
меридиане поверхности вращения и имеют вид
ar cos (п, г) + тГ2 cos (п. z) = Rn. }
xrz cos (n, r) -f az cos (n, z) = Zn. J
При заданных на поверхности перемещениях g± E),
g2 (s) имеем условия:
ur = ft E), w = g2 (s). G8.25)
В том и другом случае заданные усилия или переме-
перемещения можно считать функциями дуги s меридиана ра-
радиального сечения или какого-нибудь другого параметра,
определяющего положение точки на этой кривой.
Из приведенных уравнений и формул для трансвер-
сально-изотропного тела, как частный случай, получаются
уравнения и формулы для изотропного тела. В случае
изотропного тела с модулем Юнга Е и коэффициентом
Пуассона v имеем:
а = о = — -; , с = -; , а = 1,
l_v i_v G8.26)
Введя новую функцию
1 = т^— . G8.27)
получим из G8.11) известные формулы:
G8.28)
dz* J '
где
v2 = JL.+- -#- + -?т . G8-29)
аг^ г or oz^
Функция х удовлетворяет уравнению
V*V2x = 0, G8.30)
т. е. является бигармоническои (см. [24], стр. 288).
§ 79] ВЫРАЖЕНИЯ ДЛЯ НАПРЯЖЕНИЙ И ПЕРЕМЕЩЕНИЙ 375
§ 79. Общие выражения для напряжений
и перемещений через две функции. Общий случай
деформации трансверсально-изотропного тела
Кроме общего представления напряжений и переме-
перемещений с помощью одной функции ф (г, z), удовлетворяю-
удовлетворяющей уравнению четвертого порядка, можно указать и
другое представление — с помощью двух функций, удо-
удовлетворяющих уравнениям второго порядка.
Общие формулы этого рода были предложены Эллиот-
Эллиоттом в работе [115]; они использовались далее разными
авторами, решавшими конкретные задачи, например,
А. А. Баблояном (работы [45], [46]) и другими.
Введем в рассмотрение две функции ф2 (г, z) и
Фг (Г> z)i удовлетворяющие уравнениям
^?ф1 = 0, ^2ф2 = 0, G9.1)
где V? — операторы G8.16). Полагая
^- = ф1+ф2, G9.2)
и используя равенство -z-4tVtq> = -j~ V2V^p, убеждаемся,
что уравнение G8.17) будет удовлетворено, т. е. сумма
ф1 + ф2 является его решением.
Приводим без вывода формулы для перемещений и на-
напряжений (см. [115], [45], [46]):
д / ¦ ч д
аг = —
Ur =
Лп-А
w =
G9.3)
12
¦^г(ф1 + Фг) —
Ф1
г) Фг),
= Aii ~Wdz
>G9.4)
376 0СЕСИММЕТ1 ИЧНАЯ ДЕФОГМАЦИЯ [Гл. 9
Здесь обозначено: Х\, XI — квадраты корней уравнения
А А № Л- \ А (А 4- 9А } А А IJ -I А А О
G9.5)
предполагаемых неравными,
кг = A^+a^ (^^!'2) G9.6)
и Atj — упругие постоянные из уравнений обобщенного
закона Гука G8.2), решенных относительно составляю-
составляющих напряжений г).
Заметим, что уравнение G9.5) может быть записано
проще, а именно — в виде
Xй - (а + с)Х2 + d = 0, G9.7)
где а, с, d определяются по формулам G8.12). Нетрудно
подменить и связь между корнями уравнений G8.22),
G9.7) и параметрами st:
/wj , /V2 ~~~""" . V ' "'<J;
Отсюда следует, что корни Хи Х2 могут быть веществен-
вещественными или комплексными, но не могут быть чисто мнимыми,
а квадраты их Х\, Xl — вещественные или комплексные
числа. Не исключается и случай, когда Xf получаются
чисто мнимыми (если вещественная часть \it равна по
абсолютной величине мнимой).
В работе [99], которую мы рассмотрим ниже, в § 85,
Чен несколько изменяет общие формулы G9.3) и G9.4),
вводя новые переменные
Z Z
Zi = -г- , Z2 = -т— ,
и потенциальные функции Фх (г, zx) и Ф2 (г, z2) вместо
фх (г, z) и ф2 (г, z). Эти общие формулы [преобразованные
1) В упомянутых работах используются несколько иные обозна-
обозначения: упругие постоянные и корни уравнения G9.5) обозначены
через c\j и \\. Мы изменили эти обозначения в соответствии с при-
принятыми в нашей книге.
§ 79] ВЫРАЖЕНИЯ ДЛЯ НАШ ЯЖЕНИЙ И ПЕРЕМЕЩЕНИЙ 377
формулы G9.3) и G9.4)] имеют следующий вид:
G9.9)
dz2 '
= - (Лп - Л1а) -gr (Фх -I- Ф3)
¦*Г 1N
G9.10)
Функции Ф^ (г, zt) являются гармоническими функция-
функциями переменных г и zt, т. е. удовлетворяют уравнению
дф.
Преимущества общего представления G9.9), G9.10)
заключаются в том, что мы имеем дело с гармоническими
функциями Ф2 и Ф2, которые и нужно определить на осно-
основании условий на поверхности. Недостаток же это-
этого представления в том, что у функций — различные
аргументы: Фх есть функция г и zu а Ф2 — функция
Г И 22.
Рассмотрим теперь трансверсально-изотропное тело,
которое деформируется усилиями, вызывающими дефор-
деформацию общего вида, зависящую от всех трех координат.
Ху Хай-чаном и В. Новацким показано, что перемещения
и напряжения можно выразить через функцию, удовле-
удовлетворяющую уравнению четвертого порядка, а также через
378 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ [Гл. 9
функции, удовлетворяющие уравнению второго поряд-
порядка 1).
Отнесем тело к декартовой системе координат, напра-
направив ось нормально к плоскостям изотропии. Приводим
формулы для перемещений, взятые из работы [118]:
*
дх dz ду ' dydz~T дх
Здесь
Y = А At\ G9.13)
А и — упругие постоянные из уравнений D.8) или G8.2).
Функции ф и я|) удовлетворяют уравнениям
ViV»q> = 0, G9.14)
V& = 0. G9.15)
Здесь
V? = ^L + -IV + 4-4t (i = 0,1,2), G9.16)
OX" Oil 2 OZ
i
su s2 — параметры, введенные ранее, определяемые по
формулам G8.15) и G8.12), а
*о2=4^. G9Л7)
Составляющие напряжений мы определим из уравне-
уравнений обобщенного закона Гука D.8), подставив в них
выражения для перемещений. Мы не будем их приводить.
Если пользоваться цилиндрической системой г, 0, z
с осью 2, направленной нормально к плоскости изотро-
изотропии, то выражения для перемещений примут такой вид:
~W
G9.18)
х) См. работы Ху Хай-чана [118] и В. Новацкого [82]; в первой
из них вместо ф и \|? используются обозначения ^иф.
§ 80] ПРОИЗВОЛЬНАЯ ОСЕСИММЕТРИЧНАЯ НАГРУЗКА 379
Для функций ф и if остаются верными уравнения
G9.14) и G9.15), где
vi==-^ + 7T + 72"'aP" + l2"'^" G9.19)
Выражения для напряжений через ф и if получим из урав-
уравнений G8.2). Здесь также вместо функции ф можно ввести
две функции ф2 и ф2 переменных х, у, z, или г, 0, z, удовле-
удовлетворяющие уравнениям (см. работу Эллиотта [115])
Vfo = 0, У*ф2 = 0, G9.20)
где операторы V? имеют вид G9.16) и G9.19).
С помощью представлений, указанных в этом парагра-
параграфе и предыдущем, решено много задач. Так, Ху Чай-чан
в работе [118] исследовал изгиб конуса поперечной си-
силой, приложенной к вершине, В. Новацкий рассмотрел
напряженное состояние полупространства и тонкой
плиты (работа [82]), А. А. Баблоян решил нетривиальную
задачу об упругом равновесии кругового цилиндра конеч-
конечной длины (работы [45], [46]) и т. д.
§ 80. Распределение напряжений в цилиндре
под действием произвольной
осесимметричной нагрузки
Рассмотрим цилиндр, нагруженный по боковой по-
поверхности произвольными осесимметричными усилиями
N (z) и Т (z). Примем только одно ограничение: усилия,
как функции z, удовлетворяют условиям Дирихле, а сле-
следовательно, могут быть представлены рядами Фурье.
В этом случае нужно искать решение уравнения G8.17)
также в виде ряда, расположенного по синусам или ко-
косинусам аргументов —-,— (ш = 1, 2, 3, . . .). Предваритель-
Предварительно определим решение уравнения G8.17) в виде произве-
произведения:
Фт = /т(г)8т-^, (80.1)
где пг — целое число, или в соответствующей форме с ко-
косинусом. Подставляя (80.1) в G8.17), получим для fm
380
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ
[Гл. 9
уравнение четвертого порядка
-J/m] = o,
(80.2)
которое приводится к двум уравнениям Бесселя. Общий
интеграл этого уравнения выражается через функции Бес-
селя и Вебера нулевого порядка аргументов —j— г и —т-г,
вообще комплексных. Если эг и s2 вещественные числа,
то /т и фт выражаются через модифицированные функции
Бесселя и функции Макдональда. Для определенности мы
будем рассматривать только случай вещественных неравных
sx и s2. Окончательное выражение для функции фт имеет
вид
Фт
тп
гая
гаЯ
A Isin-
1
(80.3)
Такой же вид имеет функция фт в виде произведения
fm (г) cos —— .
Наметим ход решения сле-
следующей задачи. Дан сплошной,
не имеющий полости, круговой
цилиндр, нагруженный по бо-
боковой поверхности нормальны-
нормальными усилиями N, распределен-
распределенными симметрично относительно
среднего поперечного сечения
(рис. 105). Поместим начало
координат в центре среднего
сечения и обозначим длину
через 2Z. Разложим функцию N (z) в ряд Фурье, который
будет содержать только косинусы и постоянное слагаемое.
Условия на боковой поверхности запишутся так:
при z = R
J
%
o\
7'
ft
Щ
Рис. 105.
or = — N = — <^o —
cos-
mnz
= 0. (80.4)
m=-x
§ 80] ПРОИЗВОЛЬНАЯ ОСЕСИММЕТРИЧНАЯ НАГРУЗКА 381
Требуя, чтобы равнодействующая усилий на торцах была
равна нулю, добавим еще условие:
при z = ±1
в
\ azrdr = 0. • (80.5)
Функция Ко при г = 0 имеет особенность; следова-
следовательно, в выражении для ф нужно коэффициенты при Ко
положить равными нулю.
Окончательное выражение для ф будет
Ф =
со
BmI0 (—-rjjsin-p-. (80.6)
m=i
Далее определяем напряжения по формулам G8.11)
и удовлетворяем граничным условиям (80.4). Получаем
два уравнения для Аш и Вш и одно уравнение для В30
и В32- Недостающее уравнение получим из условия на тор-
торцах (80.5). Напряжение xrz будет на торцах обращаться
в нуль, что и требуется. Этими общими замечаниями мы
и ограничимся.
В настоящее время известно и точное решение для кру-
кругового цилиндра, удовлетворяющее как условиям на боко-
боковой поверхности, так и на торцах. Оно было найдено
А. А. Баблояном в работах [45] (частный случай) и [46]
(более общий случай). Не останавливаясь на этих реше-
решениях подробно, укажем только общий ход решения задачи,
рассмотренной в работе [46].
Предполагается, что на боковой поверхности сплошно-
сплошного цилиндра длиной 21 и с радиусом R заданы усилия,
представленные в виде рядов Фурье:
С» (X)
N = Vo + 2j Ym cos-7~' T = 2 T sm
m=i m=i
а на торцах — усилия, представленные рядами:
m=i
382 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ [Гл. 9
Напряжения и перемещения удовлетворяют условиям:
or(R,z) = N, rrz(R,z) = T; (80.9)
oz(r,l) = Nl9 ггг(г,/) = Гь (80.10)
и, кроме того, условиям
Функции фх, ф2 разыскиваются в виде х):
Фг = W + bt f-4 77-)+ У. Amh ( r^-г) COS-^^ +
ТП=1
(80.12)
(здесь и выше \х,т — корни уравнения J1 (х) = 0,
±^2 — корни уравнения G9.5), предполагаемые нерав-
неравными). После удовлетворения части условий постоянные
Am, Cm, Am, Cm оказываются выраженными через новые
постоянные Хт, Ymi причем получается, что Вт =
= 5^ = 0.
Далее задача сводится к определению неизвестных по-
постоянных Zm, Ym. Для них получается бесконечная си-
система уравнений, которая, как показано в работах, яв-
является регулярной. Коэффициенты bv b2 определяются
однозначно, а
а. = -^4-, (80.13)
где кг, к2 находятся по формуле G9.6). Этим кратким
обзором мы и ограничимся, отсылая желающих более
подробно ознакомиться с вопросом к упомянутым работам
А. А. Баблояна.
2) См. формулы и уравнения G9.3)—G9.7). Мы несколько из-
изменили обозначения А. А. Баблояна, в соответствии с принятыми в
этой книге. Начало координат помещено в центре среднего сечения.
§ 81]
ТЯЖЕЛЫЙ MVGGITB С ПОЛОСТЬЮ
383
§ 81. Распределение напряжений в тяжелом
массиве с вертикальной полостью
Задаче о равновесии цилиндра родственна следующая
задача, представляющая некоторый интерес для горного
дела.
Имеется однородный трансверсально-изотропный мас-
массив, ограниченный горизонтальной плоскостью (полупро-
(полупространство); все плоскости изотропии параллельны огра-
ограничивающей. От этой плоскости внутрь идет вертикальная
полость в виде кругового цилиндра радиуса i?0. Требуется
определить напряжения вблизи полости от собственного
веса.
В теории мы сначала будем полагать массив бесконеч-
бесконечным и длину полости бесконечной. Начало координат
поместим на ограничивающей
плоскости в центре сечения по-
полости, а ось z направим верти-
вертикально вниз (рис. 106). Задача
решается элементарно (см. ра-
работы [58] и [20], стр. 268-270).
Определим предварительно
напряжения и перемещения от
собственного веса в сплошном
массиве, без полости; мы бу-
будем отмечать их нуликами. По- Рис* 106*
лагая u? = i$ = 0, w° = w° (z),
из уравнения обобщенного закона Гука G8.1) находим
(81.1)
Интегрируя второе уравнение равновесия G8.8), где
R = 0, Z = у (у — удельный вес) и удовлетворяя усло-
условию на свободной поверхности z = 0, где должно быть
0*2 = 0, будем иметь
о°г = о? =
¦ «12
o°z =
и°г = ul = 0,
2 («и + «12)
(с — произвольная постоянная).
¦ yz2 + с
(81.2)
384 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ [гл. 9
Распределение напряжений в полупространстве с по-
полостью получим путем наложения напряжений (81.2) и
напряжений, определяемых по формулам G8.11), соответ-
соответствующих функции напряжений:
Ф = (C2Oz2 + С22г2Iпг; (81.3)
последние стремятся к нулю при неограниченном возра-
возрастании г.
Если на поверхности полости никаких внешних уси-
усилий не приложено, то там должны выполняться условия:
при г — /?0
ar = %rz = 0. (81.4)
Кроме того, на плоскости z ~ 0
oz = xrz = 0. (81.5)
Определяя постоянные С20 и С22 из этих условий, получим
= 0,
(81.6)
__ (flu —fl!2)fll8 ... #0
Ur — ; VZ
a + a2 r г
Напряжение о*е в радиальных сечениях у поверхности
полости определится по формуле:
Это напряжение будет вдвое больше напряжения
в сплошном массиве на том же расстоянии z от ограничи-
ограничивающей плоскости. Выражения для перемещений пока-
показывают, что край отверстия деформированного массива,
рассматриваемого с позиций классической теории упруго-
упругости, должен приподниматься.
Если на поверхность полости действует давление qz,
меняющееся пропорционально расстоянию z, то к напря-
§ 82] НАПРЯЖЕНИЯ В УПРУГОМ ПОЛУПРОСТРАНСТВЕ 385
жениям (81.6) добавятся следующие:
аг=-^г, o^^f-z, ez = rrz = 0. (81.9)
Это будет иметь место, когда полость доверху запол-
заполнена жидкостью.
Гораздо сложнее задача о распределении напряжений
в упруго^ тяжелом массиве с вертикальной полостью
конечной длины, т. е. имеющей плоское дно. Эта задача
решалась В. 3. Васильевым для случая изотропного мас-
массива (см. [50]). Задача свелась к системе трех интег-
интегральных уравнений, которая решалась приближенно. В
результате получены формулы, позволяющие провести
подсчет напряжений в нулевом и в первом приближении.
§ 82. Распределение напряжений
в упругом полупространстве под действием
осесимметричной нормальной нагрузки
Поставим задачу следующим образом. Дано упругое
однородное трансверсально-изотропное полупространство,
ограниченное бесконечной плоскостью с плоскостями
изотропии, параллельными ограничивающей. На этой
ограничивающей плоскости по площади некоторого круга
распределены нормальные уси-
усилия, обладающие симметрией ^-4—i-i-4^j
вращения относительно норма- '
ли, проведенной через центр ПО
круга, принимаемый за начало vl
О цилиндрической системы ко-
координат (ось z направлена нор- *у I
мально к границе внутрь). IZ
Обозначая через р (г) интен-
интенсивность нагрузки (рис. 107) Рис- 10/*
мы будем предполагать, что эта
функция удовлетворяет условиям: 1) она конечна при
всяком г; 2) в любом конечном интервале г ^> 0 число то-
точек разрыва непрерывности и экстремальных точек конеч-
оо
но и 3) интеграл ^ pYrdr абсолютно сходится, т. е.
о
главный вектор нагрузки конечен или равен нулю. Эти
1Я С. Г Лехнипкий
386 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ [Гл. 9
довольно общие ограничения дают возможность предста-
представить нагрузку, как функцию г, интегралом Фурье—Бес-
Фурье—Бесселя, т. е. в виде
(82.1)
О
где
со
(82.2)
Jo — функция Бесселя нулевого порядка вещественного
аргумента.
Условия на поверхности запишутся так:
при z = О
о* = — Р (г) = - § Ч> (*) tJo (*r) dt, xrz = 0. (82.3)
0
Естественно предположить, что на бесконечности все
напряжения равны нулю:
при z -»- оо
ог = а9 = az = xrz = 0. (82.4)
Сначала будем искать выражение для ф в виде произ-
произведения
Ф - Z (tz)J0 (tr). (82.5)
Подставляя в уравнение G8.13), получим уравнение для Z:
dZ*v - {а + c)Z" + Z = 0 (82.6)
(производные берутся по аргументу tz), которому соответ-
соответствует характеристическое уравнение:
ds4 _ (а + C)S2 + 1=0. (82.7)
Это уравнение уже встречалось (в § 78); корни его ±$15
zt52 всегда вещественные или комплексные числа, но не
могут быть чисто мнимыми. Выражение (82.5) имеет вид
при неравных st и s2:
ф = (Ае*и + Be**iz + Ce-**tz + De-°*tz) Jo (tr), (82.8)
а при sx = s2 = s
ф = [(A + Btz)estz + (C + Dtz)e-stz)J0 (tr). (82.9)
82]
НАПРЯЖЕНИЯ В УПРУГОМ ПОЛУПРОСТРАНСТВЕ
387
Потребуем, чтобы напряжения, найденные по функ-
функции ф, удовлетворяли условиям на бесконечности (82.4);
для этого, очевидно, нужно положить А = В = 0.
Функция ф, полученная путем интегрирования по t
выражений (82.8) или (82.9), также является (по крайней
мере формально) решением уравнения G8.17). Считая,
что sx =г*= 52, примем в качестве функции ф выражение:
*tz) /0 (tr) dt,
(82.10)
где С и D зависят от параметра t. Соответствующие напря-
напряжения, найденные по формулам G8.11), также представят-
представятся в виде интегралов; в частности,
(Т2 *= — $ [Cs1 (ds\ — с) e-**tz +Ds2 (ds\ — с) e~**tz] t*J0 (tr) dt,
тГ2 = - $ [C{as\ — 1) e-**tz + D (asl — \)e~^z\ t*Jx {dr) dt
о
(82.11)
(•^i — функция Бесселя первого порядка). Удовлетворяя
условиям (82.3), получим уравнения
Отсюда
С = —-
Csx (ds\ ~с) + Ds2 (ds\ - с) =
C(asl-1)+ D(as%—l) = 0.
(82.12)
A — л^у-
c— d)
82.13)
Введем для сокращения записи обозначения:
Pi = 1 — as?, gi = F — ast) A — a^),
P2 = 1 — «S2, #2 = (Ь — ^j) A — i
ac — d
ac — d
(82.14)
388 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ [Гл. 9
и тогда окончательные формулы для напряжений примут
вид (см. работу [58], стр. 49—50 и [20], стр. 274—277):
1 X
о
1 "'¦ •- " (tr)dt,
7
0
~ Sie~"tZ) tJ°(/r) dt'
(«1—*2)M
(82.15)
Для того чтобы определить напряжения, нужно
прежде всего найти функцию г|) (?), соответствующую дан-
данной нагрузке, по формуле (82.2). При простых распреде-
распределениях усилий р (г) вычисление интегралов, входящих
в (82.15), не представит большого труда.
На случае равных корней мы останавливаться не
будем, так как формулы для него при заданной на-
нагрузке мы получим путем предельного перехода при
Таким методом мы можем получить и решения задач
для случаев, когда на границе, кроме нормальных, за-
задаются касательные симетрично распределенные усилия
trz (ri 0)> или осесимметричные перемещения щ (г, 0),
w (г, 0), а также решения смешанных задач (задаются
одна составляющая перемещения и одна составляющая
напряжений).
§ 83] СОСРЕДОТОЧЕННАЯ СИЛА И НОРМАЛЬНАЯ НАГРУЗКА 389
§ 83. Распределение напряжений в полупространстве
под действием сосредоточенной силы и произвольной
нормальной нагрузки
Пусть в точке О на ограничивающей плоскости к
полупространству приложена сосредоточенная сила Р
(рис. 108). Чтобы получить напряжения, вызванные ею,
рассмотрим предварительно нормальную нагрузку ин-
интенсивности р = Р/(яе2), распределенную равномерно по
площади круга бесконечно малого радиуса 8. Для такой
нагрузки
(83.1)
О
Р
net
Подставим это выражение в
формулы (86.15), а затем устре-
устремим радиус 8 к • нулю. При
е->-0 выражения, стоящие под
знаками интегралов, стремятся
к определенным пределам, так
как
lira -
/е
(83.2)
Все интегралы, входящие в формулы для напряжений,
сводятся к четырем различным, выражения которых из-
известны; приводим их (см. [11], стр. 721 и 726).
оо
[ e-sUJ0 (tr) dt =
ОО
\ e-st4J1(tr)dt =
(83.3)
390
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ
[Гл. 9
(s — число вещественное или комплексное с положитель-
положительной вещественной частью, но не мнимое).
Получим следующие формулы, дающие распределение
напряжений в трансверсально-изотропном полупростран-
полупространстве от сосредоточенной силы 1):
р ( * Г *? ,; 1 1
Г *\ 1
(83.4)
Выражения для oz и xrz можно записать еще иначе:
= -1 ^ 2; z3 X
2nd
X
з (а + с) dzV2 + [(а + cf — d] z*
(Г2 + ф
Г —
*Г7
а,.
.(83.5)
Отметим характерные особенности рассматриваемого
напряженного состояния. Прежде всего можно заметить,
что все напряжения изменяются обратно пропорционально
х) См. нашу работу [58] и книгу [20], стр. 277—279. Решение
задачи (для частного случая трансверсально-изотропного полупро-
полупространства, у которого все коэффициенты Пуассопа равны нулю) бы-
было получено ранее Вольфом в работе [129].
§ 83] СОСРЕДОТОЧЕННАЯ СИЛА It НОРМАЛЬНАЯ НАГРУЗКА 391
квадрату расстояния р от точки приложения силы, т. е.
убывают довольно быстро. На площадках, нормальных
к силе, действует напряжение tz с составляющими в2 и xrz.
Величина полного напряжения на этих площадках равна
tz = |/^Т^Г = ! oz ||/(l + -^J, (83.6)
а направление его совпадает с направлением радиус-
вектора, проведенного из точки приложения силы в дан-
данную точку или обратно направлению этого радиус-вектора
(рис. 108). Точки, где напряжение имеет заданную посто-
постоянную величину tz = t0, располагаются на поверхности
вращения, проходящей через начало координат; уравне-
уравнение этой поверхности будет:
X
X
•3(a + c)dzW + [(я + cJ — d] z*
. CJ 22Г2 _)_ 24^2 ^r2 _(_ 52Z2K'2 _|_ (r2 + s]
Распределение напряжений в изотропном полупрост-
полупространстве найдем путем предельного перехода. Полагая
в формулах (83.4) sx = s2 = 1, v' = v, и раскрывая не-
неопределенности, получаем *):
3zr2 , 1_2^
р Г
~ in L
(83.8)
Здесь p = ]/~r2 -f- z2 — расстояние от точки приложения
силы до данной точки. Поверхности одинаковых напря-
напряжений tz = г0 становятся сферическими, проходящими
через точку приложения силы, с центром на линии дей-
действия силы.
От сосредоточенной силы легко перейти к нормальной
нагрузке, распределенной как угодно по ограничивающей
См., например, [32], стр. 403.
392
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ
[Гл.
плоскости. Исследование в этом случае удобнее вести,
пользуясь системой декартовых координат, у которой плос-
плоскость ху совпадает с ограничивающей плоскостью полу-
полупространства.
Предварительно нужно найти напряжения от силы
Р, приложенной не в начале координат, а в произ-
произвольной точке О' с коорди-
координатами ?, т] (рис. 109). Зная
напряжения <тг, <те, сг2, тГ2
для цилиндрической систе-
системы координат с осью z',
zt Y.:f
Рис. 109.
Рис. 110.
направленной по линии действия силы, найдем состав-
составляющие напряжений в декартовой системе х, уу z
^J —(у —ЛJ
-f (cTr-<re)
1
1
(83.9)
Здесь <тг, 0e, 02, т/2 определяются по формулам (83.4),
в которых нужно заменить г на У(х — ?J + (у — г\J.
Пусть нагрузка распределена по некоторому участ-
участку S ограничивающей плоскости и является нормаль-
нормальной и заданной функцией х и у — р (х, у) (рис. 110).
84]
РАСТЯЖЕНИЕ УПРУГОГО КОНУСА
393
На элемент загруженного участка d^dr) приходится на-
нагрузка р dl dr\, которую мы рассматриваем как сосре-
сосредоточенную силу. Напряжения аХУ ау,. .., %ш мы получим
путем суммирования напряжений, вызванных бесконечно
малыми силами, т. е. путем интегрирования по \ и г) в
пределах области S. Всех формул мы приводить не будем,
а укажем только выражение для а2:
1
2л
- s2)
dldr). (83.10)
§ 84. Растяжение упругого конуса
Теория осесимметричной деформации трансверсально-
изотропного тела дает возможность определить напряже-
напряжения в коническом стержне, растягиваемом осевой силой Р
(рис. 111).
Предполагается, что в исследуемом конусе (вообще
усеченном) плоскости изотропии нормальны к геометри-
геометрической оси. Иначе говоря, рассматривается упругое рав-
равновесие тела, ограниченного поверхностью кругового
Рис. 111.
конуса и двумя торцевыми плоскостями, нормальными
к геометрической оси конуса. Один торец предполагается
как-то закрепленным (например, широкий торец), а дру-
другой — нагруженным усилиями, приводящимися к силе Р.
Примем вершину конической поверхности за начало коор-
координат цилиндрической системы и направим ось z по геоме-
394 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ [Гл. 9
трической оси. Угол при вершине обозначим через 2а,
длину стержня — через I и расстояния от вершины до
узкого и широкого торцов — через 10 и 10 + I-
Граничные условия на боковой поверхности запишутся
таким образом:
при г = z tg a
or cos а — xrz sin а = 0, 1
(84.1)
xrz cos а — а2 sin а = 0. J v '
Рассекая тело плоскостью, нормальной к оси z, доба-
добавим к условиям (84.1) условие равновесия
z tea
\ a>rdr=-W' (84-2)
о
оно, очевидно, должно выполняться при любом расстоя-
расстоянии z от вершины, а в том числе и на торцах z = /0 и
z = 10 + /. Кроме того, напряжения должны быть конеч-
конечными в любой точке, кроме вершины (если рассматривает-
рассматривается равновесие полного конуса), а по мере удаления от
вершины должны стремиться к нулю.
Пусть параметры s± и s2 неравны. Тогда функцию ср
можно представить в виде суммы
Ф = Ах [S& In (sxz + Vr2 + s[z2) — sxz In r—Vr2 + s\z2] +
+ A2 (s2z In (s2z + Vr2 + s\z2) - s2z In r — Vr2 + s\z2} +
+ Bz\\\r. (84.3)
При таком выборе ф можно удовлетворить всем усло-
условиям, как точным на боковой поверхности (84.1), так и
условиям равновесия (84.2). Соответствующие напряже-
напряжения определим по формулам G8.11)—G8.12); они будут
зависеть от трех постоянных — Аг, А2 и В.
Для того чтобы напряжения были конечными (за ис-
исключением вершины, если тело имеет форму полного ко-
конуса), необходимо положить
В =AlSl +A2s2. (84.4)
Тогда выражения для напряжений, определенные по
§ 84]
РАСТЯЖЕНИЕ УПРУГОГО КОНУСА
395
функции ф по формулам G8.11), запишутся так:
ог =
Ь— 1
K/s
Здесь введены обозначения:
^. = 1 — as\, rx = Ъ — as],
р2 = 1 —
г2 = Ь —
(84.5)
(84.6)
Наконец, удовлетворяя условиям (84.11) и (84.2), на-
находим выражения для постоянных Ах и А2:
• *1 clg a)
ctg2a (Vl + 52 ctg2a
•s2ctga)-
где
+ 52 ctg2 a + rl5l ctg a
/l + 52ctg^ a - s2 /l + si ctg* a
(84.7)
(84.8)
Формулы (84.5) вместе с (84.7), (84.8) вполне опре-
определяют напряжения в упругом усеченном конусе при
396 ОСЁСИММЕТРЙЧНАЙ ДЕФОРМАЦИЯ Ьл. д
любом угле 2а <; л; мы не будем их дальше преобразо-
преобразовывать, а примем за окончательные. Длина I и расстоя-
расстояние /0 в них не входят, а следовательно, распределение
(84.5)—(84.8) имеет место при любых значениях I и /0.
Распределение напряжений в конусе обладает теми же
особенностями, что и распределение напряжений в полу-
полупространстве иод действием нормальной силы. Напряже-
Напряжения меняются обратно пропорционально квадрату расстоя-
расстояния от вершины. Полное напряжение tz на площадках,
нормальных к оси, направлено по радиус-векторам (или
в противоположную сторону).
Путем предельного перехода при sx = s2 = 1, v' = v
приходим к известным формулам для изотропного конуса,
растягиваемого осевой силой Р *).
§ 85. Распределение напряжений вблизи
эллипсоидального и сферического включения
или полости при одностороннем
и всестороннем растяжении
Как известно (гл. 4), задача о распределении напря-
напряжений в анизотропном теле вблизи цилиндрического вы-
выреза эллиптического или кругового сечения решена срав-
сравнительно простым методом, с помощью конформного ото-
отображения и рядов. Получено решение для тела, находя-
находящегося в условиях обобщенной плоской деформации и
плоской задачи, для нагрузки общего вида, и доведены
до конца решения частных задач. Для выреза с сечением
в виде эллипса или круга найдено строгое решение, а для
вырезов иной формы — приближенное, если вырез можно
рассматривать, как мало отличающийся в сечении от
эллиптического или кругового или в случаях, когда
анизотропию можно считать слабой (см. [21], гл. 7, 8).
Решено уже довольно большое число задач о кручении
тела с включением или вырезом (см. [21], гл. 8, § 76).
Большой интерес представляют также задачи о распре-
распределении напряжений вблизи включений в виде эллипсои-
эллипсоида вращения или сферы в теле, находящемся в условиях
осесимметричной деформации, однако, эти задачи оказы-
оказываются значительно труднее вышеупомянутых. В работе
г) См., например, курс Лява [24], стр. 212—214.
§ 85]
ВЛИЯНИЕ ЭЛЛИПСОИДАЛЬНОГО ВКЛЮЧЕНИЯ
397
Чена [99] с достаточной полнотой дается решение одной
частной задачи этого рода и его анализ; эту работу мы
вкратце и изложим *).
Пусть дано тело в виде кругового цилиндра, у которого
на оси имеется включение из другого материала или полость
в форме эллипсоида вращения или сферы. Одна из осей
эллипсоида, ось вращения, направлена по геометрической
оси цилиндра; центр эллипсоида или сферы принимается
за начало О цилиндрической системы координат, а ось z
направляется по оси цилиндра. Тело и упругое включение
являются трансверсально-изотропными и имеют плоскости
изотропии, нормальные к
оси цилиндра. Нагрузка за-
задается в виде нормальных
усилий рг (на единицу площа-
площади), распределенных равно-
равномерно по цилиндрической
поверхности, и нормальных
усилий рг (также на единицу
площади), распределенных
равномерно по торцам
(рис. 112).
Уравнение поверхности
включения имеет вид
4+-5—1. (85.1)
Считаем, что размеры
включения а и Ъ малы по
сравнению с радиусом и длиной цилиндра; это дает ос-
основание рассматривать цилиндр как бесконечное прост-
пространство с эллипсоидальной полостью, заполненной дру-
другим материалом или пустой. Центр полости принят за
начало координат; на бесконечности задается поле на-
напряжений вида
00 0 ооо П /Я.К 9\
Ог = Oq = pr, Oz — рг, Tnz = Trz = T"g — u< {OO.6)
Для построения решения используется теория осесим-
метричной деформации трансверсально-изотропного тела.
*) Мы изменяем некоторые обозначения Чена в связи с приня-
принятыми нами. Решение для изотропной среды имеется в курсе
А. И. Лурье [23], гл. V, § 5.
Рис 112>
398 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ [Гл. 9
Все величины (напряжения, перемещения, упругие посто-
постоянные) для цилиндра (упругого пространства) обозна-
обозначаются, как обычно, а для упругого включения отмеча-
отмечаются штрихами. Перемещения и напряжения выражаются
через две потенциальные функции Фх (г, zx) и Ф2 (г, z2)
(см. формулы G9.9) и G9.10)), которые и нужно опреде-
определить, учитывая, что они являются гармоническими функ-
функциями переменных г и zh т. е. удовлетворяют уравнениям
о?
0ф.
* dz* ^ ' (85.3)
и что напряжения и перемещения удовлетворяют условиям
на поверхностях контакта включения и пространства
(матрицы, по терминологии Чена), а также условиям на
бесконечности. Предполагается, что проскальзывание ма-
материала включения по поверхности полости в простран-
пространстве невозможно.
Условия на поверхностях контакта запишутся так:
Rn = Rn, Z'n = Zn (85.4)
(усилия на поверхности включения и пространства дол-
должны быть равными) и
ur = uri w' = w (85.5)
(перемещения точек поверхностей включения и полости
должны быть одинаковыми). Условия (85.4) можно запи-
записать и иначе, используя выражения для проекций усилий
(см. G8.24)):
(оу — ar) cos (n, г) + (тг2 — xrz) cos (n, z) = 0,
(trz — tr2) cos (n, r) + (o'z — az) cos (n, z) = 0.
(85.6)
Условия на бесконечно большом расстоянии от центра
включения запишутся следующим образом:
or = pr, a9 = Pr, ®z = Pz, ^rz = 0. (85.7)
Весьма существенно знать характер распределения на-
напряжений внутри упругого включения. Ссылаясь на рабо-
работу Эшелби [116], Чен полагает, что там напряжения
постоянны, а перемещения, следовательно, линейные
i 85]
ВЛИЯНИЕ ЭЛЛИПСОИДАЛЬНОГО ВКЛЮЧЕНИЯ
399
функции гиг, т. е.:
щ = Bir, w' = B2z,
o'r = OQ = (An + Л[2)
o'z = 2A[3B1 + AS3B2.
A13B2,
(85.8)
В пространстве (матрице) напряжения складываются
из двух частей — из напряжений в сплошном простран-
пространстве, без включения, деформируемом заданными усилия-
усилиями, и из добавочных напряжений, стремящихся к нулю
по мере удаления от центра включения; последние обо-
обозначаются с помощью индекса А. Таким образом,
Ог = рг + Ог ,
= Pr
^rz —' trz*
ur = vrr
т^? w = vzz + wA,
(85.9)
Здесь
ur = -
Al2)pz~2Al3pr
(85.10)
m = ^33 (Ли — A12) — 2Л13.
Далее вводится функция q (r, z), связанная с г и z
зависимостью:
"Г
и функции <7i, определяемые из уравнения
Здесь
(85.11)
(85.12)
(85.13)
Аг — корни уравнения G9.7). Кроме того, вводятся посто-
постоянные
(85.14)
400 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ [Гл. 9
Если положить qt = ри то два уравнения (85.12)
перейдут в уравнение поверхности эллипсоида (85.1) и
это обстоятельство играет существенную роль при построе-
построении решения.
По Чену, функции, дающие решение рассматриваемой
задачи, имеют вид:
Здесь Ац А2 — постоянные, которые нужно определить
из условий (85.5), (85.6) и условий на бесконечности и
Я (г, z) = 4" l*N>i (?) + *|>2 (?) ~ *Чо (в)]. (85.16)
Здесь
q-\ '
to) 0,25 In-f^f + 0,5 -5^-
(85.17)
Далее нужно подставить значения Фх, Ф2 в общие
формулы для перемещений и напряжений G9.9), G9.10).
Получатся довольно громоздкие формулы, которых мы
приводить не будем, отсылая интересующихся к той же
работе Чена [99] (стр. 162). Отметим лишь, что выра-
выражения левых частей равенств (85.6) на поверхности
полости (включения) принимают очень простой вид,
что и дает возможность определить все постоянные —
-^1» ^2» **И **2'
В случае упругого включения из условий непрерывно-
непрерывности перемещений (85.5) получаем уравнения
АгУ* (pi) + Л'Фг Ы — Вх - — vr,
Ахкх , t ч , А2к2 , . ч D > (85.18)
-Jr-*i (Л) + i^1 (ft) - ^ = - i; J v ;
а из условий непрерывности усилий (85.4) или (85.6) —
$85]
ВЛИЯНИЕ ЭЛЛИПСОИДАЛЬНОГО ВКЛЮЧЕНИЯ
401
уравнения
(ft)
kt)
= р2,
AJA
2 ^44"
(85.19)
+ (Ап — A12) -ф2 (;
i (P2) + (An — Ли)
L Л2
-f- B\ (An — -^.12) ~h ^2^13 == Pr
(kx и к2 определяются по формуле G9.6)).
Уравнения (85.18) и (85.19) дают систему, из которой
определяются все четыре неизвестные постоянные.
Если включение является абсолютно жестким, недефор-
мируемым, то нужно положить Вг = В2 = 0; постоянные
Аг и А2 определятся из системы
.(л)
(85.20)
В случае сфероидальной (имеющей форму эллипсоида
вращения) полости, ничем не заполненной, также нужно
положить Вх = Вг = 0; для оставшихся постоянных
Ах и А2 на основании двух условий для усилий (85.6)
получим уравнения (85.19), из которых вычеркнуты сла-
слагаемые, содержащие Вх и В2.
В работе [99] подробно рассмотрен случай сферической
полости, ничем не заполненной. Для этого случая а = bf
(85-21)
i|>o(ft) = ln( j- -J,
(Pi) = 0,
W
L - In
. (85.22)
402
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ
[Гл. 9
Напряжения в пространстве у поверхности полости
равны:
в точках экватора
/^i (Pi) +Л2{1 + к2)^ (ра) + р2;
(85.23)
у полюсов
z=0 = Аг
q=p
@г)г=о = Ах [-f A + к,) -
+ Л [JL A + л,) -
+
(85-24)
В работе Чена даны две таблицы значений напряжений
у экватора и у полюса сферической полости для несколь-
нескольких веществ, кристаллизующихся в гексагональной си-
системе (уравнения и формулы для них будут такими же,
как и для трансверсально-изотропного тела). Рассмотрены
два случая нагрузки: 1) одностороннее растяжение в на-
направлении, нормальном к плоскостям изотропии (рг = 0,
pz ^> 0) и 2) всестороннее растяжение (рг = рг = р).
Приводим две таблицы, взятые из работы Чена 1).
Таблица 24
Напряжения у поверхности полости при односто-
одностороннем растяжении
Материал
Изотропный материал
Цинк
Магний
р-кварц
Кадмий
Кобальт
Титанат бария (керамика)
Напряжения
у экватора
2,046
1,626
2,129
2,027
1,791
2,306
2,080
у полюсов
—0,682
—1,019
—0,638
—0,490
—1,090
—0,635
—0,654
х) Численные значения упругих постоянных взяты из работы
Хантингтона [95].
186]
НАПРЯЖЕНИЯ В СТЕНКЕ СФЕРИЧЕСКОГО СООУДА
403
Таблица 26
Напряжения у поверхности полости при всесто-
всестороннем растяжении
Материал
Цинк
Магний
Р-кварц
Кадмий
Кобальт
Титанат бария (керамика)
Напряжения
у экватора
oz'V
1,403
1,559
1,603
1,524
1,626
1,450
у полюсов
0,654
1,695
1,323
0,855
2,093
1,639
Анализируя данные таблиц 24 и 25, мы можем отме-
отметить, что у рассмотренных материалов напряжения в об-
общем мало отличаются от напряжений в соответствующих
точках у поверхности полости, так что рассмотренные ма-
материалы можно назвать слабо-анизотропными. Разумеется,
из этого отнюдь не следует, что все материалы являются
слабо-анизотропными.
При одностороннем растяжении наибольшие по вели-
величине напряжения получаются на экваторе полости. При
всестороннем растяжении наибольшие по величине напря-
напряжения могут получиться на экваторе, но для дру-
других материалов могут получиться и вблизи полюса
(см. табл. 25).
§ 86. Распределение напряжений в стенке
сферического сосуда под действием
внутреннего и наружного давлений
В заключение рассмотрим упругое тело в форме полой
сферы (сферический сосуд), на которое действует внутрен-
внутреннее давление р, равномерно распределенное по поверхно-
поверхности и наружное давление q, также распределенное равно-
равномерно.
Задача об упругом равновесии изотропной сферы, по-
полой или сплошной, довольно хорошо изучена *). Если же
г) См., например, курсы: А. Лява [24], гл. 11, п А. И. Лурье
[23], гл. 5.
404
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ
1Гл. 9
сфера неизотропна, то для нее число изученных случаев
значительно меньше. Мы рассмотрим лишь самую простую
задачу для анизотропной полой сферы, решенную еще
Сен-Венаном [124]. Именно, мы будем считать, что мате-
материал данного тела обладает трансверсальной изотропией
относительно любого радиус-вектора, проведенного из об-
общего центра сфер в данную точку.
Исследование удобнее всего вести, пользуясь сфе-
сферической системой координат р, 0, ф с началом в центре
сфер. Оси х и z, от которых
отсчитываются углы 0 и ф,
направлены произвольно, об-
образуя друг с другом прямой
угол (рис. 113). Введем обо-
обозначения: R,R0—внешний и
внутренний радиусы; сгР, (Те,
СФ, Тер, тРФ, тРо — состав-
составляющие напряжений на пло-
площадках, нормальных к коор-
координатным направлениям р, Э,
ф; ер> ее, еФ, 7вФ, Yw» Tp9 —
относительные удлинения и
сдвиги для координатных
направлений.
Уравнения обобщенного закона Гука в сферической
системе координат можно записать по-разному. Если
ввести технические константы, то уравнения примут вид
a(а + а)
Рис. ИЗ.
89 = ~~
("~ va<p
2A+v)
Е
(86.1)
Здесь Е' и Е — модули Юнга для растяжения вдоль
радиус-вектора р и в направлении, перпендикулярном
к нему; v' — коэффициент Пуассона, характеризующий
НАПРЯЖЕНИЙ В СТЕНКЕ СФЕРИЧЕСКОГО СОСУДА
405
поперечное сокращение в направлениях, перпендикуляр-
перпендикулярных к р при растяжении в направлении р; v — коэффи-
коэффициент Пуассона, характеризующий сокращение в плос-
плоскости, нормальной к радиус-вектору при растяжении
в той же плоскости, G, G' — модули сдвига для плоско-
плоскостей, нормальных к р и для плоскостей, проходящих че-
через центр (диаметральных). Уравнения обобщенного за-
закона Гука, решенные относительно составляющих на-
напряжений, имеют такой вид:
4i2 (е, + ев),
а0 =
(86.2)
Модули упругости А и связаны с Е, G, v следующим обра-
образом:
л ff'(l-v)
Л11
Л44
где
f v)m
-^512 ===
Е
2 A + v) '
т = 1 — v — 2V2 -^т- •
(86.3)
(86.4)
Очевидно, что распределение напряжений и деформа-
деформаций при указанных упругих свойствах будет зависеть
только от одной переменной р, а все точки будут переме-
перемещаться при деформации только в радиальных направлени-
направлениях *). Обозначив единственную составляющую переме-
перемещения (радиальную) через и (р), имеем составляющие де-
деформации, отнесенные к сферическим координатам:
6Р = -jf- > «ер = е0 = -~ , 7оф = Тр* = 7р9 -= О- (86.5)
х) Разумеется, если отбросить возможные «жесткие» перемеще-
перемещения тела как целого (без деформации).
406
ОСЕСЙММЕТРЙЧНАЯ ДЕФОРМАЦИЯ
[Гл. 9
Так как все сдвиги равны нулю, то и пропорциональные
им касательные напряжения будут равны нулю: т^ =
= тРФ = тР9 = 0, а о? = Со. Из уравнений равновесия
сплошного тела, отнесенных к сферической системе коор-
координат, остается только одно:
Условия на поверхностях
будут:
при р = R
при р = До
— аф) = 0. (86.6)
наружной и внутренней —
<*р = — 9,
— p.
(86.7)
В данной задаче удобнее использовать не функции на-
напряжений, а принять за основную функцию перемеще-
перемещение и. Подставляя первые три выражения для напряжений
из уравнений обобщенного закона Гука (86.2) в (86.6),
получим уравнение для перемещения:
^ _2
dp2 ' р
du
учения
л/ [
9 ^22
:
-А23 +
АЛ1
J22 "Г ^
— А
^;я —
In
12 и
Р2
^12
+Ли(/г —0,5)
Общий интеграл уравнения (86.8) имеет вид
и = Лрп-°'5 + -#р~п~°'5.
(86.9)
(86.10)
(86.11)
Подставляя в (86.2) и определяя постоянные А и В
из условий на поверхностях (86.7), находим
Л,Ь-п
(86.12)
J.5) '
§86]
НАПРЯЖЕНИЯ В СТЕНКЕ СФЕРИЧЕСКОГО СОСУДА
407
Получаем формулы для составляющей напряжений:
1— сг
тг-1,5
С2п
П-1,5
п+1,5
)
(86.13)
Наибольших значений напряжение достигает на пло-
площадках, проходящих через радиус-вектор, у внутренней
или у наружной поверхности. Обозначая отношение радиу-
сов через с = ~б~ » имеем:
у поверхности полости р — Ro
„271
>г-1,5 .
1-е
.271
(86.14)
у наружной поверхности р = R
r>n+l,5 .
!_С2П
1 - с
5Г1-- (86-15)
Какая из двух величин, стоящих в правых частях ра-
равенств (86.14) и (86.15), больше (по абсолютной величине)
и какая меньше, заранее сказать невозможно.
В случае изотропного материала п = 1,5 и формулы
(86.13) дают известное решение *):
1 — сз
рс3—д
д-р съ (JLK
-с3 V Р /
(86.16)
См. первую сноску в начале этого параграфа.
ЛИТЕРАТУРА1)
А. КНИГИ
1. Амбарцумян С. А., Теория анизотропных оболочек.
Физматгиз, М., 1961.
2. Амбарцумян С. А., Теория анизотропных пластин.
Физматгиз, М., 1967.
3. Амбарцумян С. А., Общая теория анизотропных обо-
оболочек. «Наука», М., 1974.
4. Арутюнян Н. X., Абрамян Б. Л., Кручение упругих
тел. Физматгиз, М., 1963.
5. АшкеназиЕ. К., Анизотропия машиностроительных ма-
материалов. «Машиностроение», Л., 1969.
6. А ш к е н а з и Е. К., Г а н о в Э. В., Анизотропия конструк-
конструкционных материалов. Справочник. «Машиностроение», Л., 1972.
7. Ашкенази Е.К.,Го л ьфман И.Б.,Рожков Л.П.,
Сидоров Н.П., Детали из стеклопластика в судовом маши-
машиностроении. «Судостроение», Л., 1974.
8. Бехтерев П., Аналитическое исследование обобщенного
закона Гука. Ч. 1, 2. Изд. автора (литограф). Л., 1925.
9. Буров А. К., Андреевская Г. Д., Высокопрочные
стеклопластики СВАМ. Изд. АН СССР, М., 1958.
10. В а т с о н Г. Н., Теория бесселевых функций, часть 1 (перевод
с англ.). ИЛ, М., 1949.
11. Градштейн И. С, Рыжик И.М., Таблицы интегралов,
сумм, рядов и произведений. Изд. 5, М., 1971.
12. Кинцис Т. Я., Розе А. В., ЖигунИ. Г., Методы стати-
статических испытаний армированных пластиков. «Зинатне», Рига,
1972.
13. К о л ч и н Г., Расчет элементов конструкций из упругих
неоднородных материалов. «Картя молдовеняска», Кишинев,
1971.
13а. Колчин Г. Б., Плоские задачи теории упругости неодно-
неоднородных тел. «Штиинца», Кишинев, 1977.
х) Сокращения: АН — Академия наук, ОТН — Отделение тех-
технических наук, ф.-м.н.—физико-математические науки, ДАН —
Доклады Академии наук, ИзвАН — Известия Академии наук,
Инж. сб.—Инженерный сборник, Инж. ж.— Инженерный журнал,
ПММ — Прикладная математика и механика, ПМ — Прикладная
механика, МТТ — Механика твердого тела, Тр.— труды.
ЛИТЕРАТУРА 409
14. К о л ч и н Г. Б., Фавор м а н Э. Л., Теория упругости
неоднородных тел. Библиографический указатель отечествен-
отечественной и иностранной литературы. «Штиинца», Кишинев, 1972 и
1977.
15. Корн Г., К о р н Т., Справочник по математике для науч-
научных работников и инженеров (перевод с англ.). «Наука», М.,
1968.
15а. Космодамианский А. С, Напряженное состояние
анизотропных сред с отверстиями или полостями. «Влща школа»,
Киев—Донецк, 1976.
16. JI а н д а у JI. Д., Лифшиц Е. М., Механика сплошных
сред. Гостехиздат, М., 1953.
17. Л ейбе нзон Л. С, Вариационные методы решения задач
теории упругости. Гостехиздат, М., 1943.
18. Л е й б е н з о н Л. С, Курс теории упругости. Гостехиздат,
М., 1947.
19. Л е й б е н з о н Л. С, Собрание трудов, т. I. Теория упругости.
Изд. АН СССР, М., 1951.
20. Л е х н и ц к и й С. Г., Теория упругости анизотропного тела.
Гостехиздат, М., 1950.
21. Л е х н и ц к и й С. Г., Анизотропные пластинки, изд. 2. Гостех-
Гостехиздат, М., 1957.
22. Л е х н и ц к и й С. Г., Кручение анизотропных и неоднород-
неоднородных стержней. «Наука», М., 1971.
23. Л у р ь е А. И., Теория упругости. «Наука», М., 1970.
24. Л я в А., Математическая теория упругости (перевод с англ.),
ОНТИ, М. -Л., 1935.
25. Малмеистер А. К., Т а м у ж В. П., Т е т е р с Г. А.,
Сопротивление жестких полимерных материалов. Изд. 2, «Зи-
натне», Рига, 1972.
26. Мусхелишвили Н. И., Некоторые основные задачи
математической теории упругости. Изд. 5, «Наука», М., 1966.
27. Новожилов В. В., Теория упругости. Судпромгиз, Л.,
1958.
28. С а в и н Г. Н., Распределение напряжений около отверстий.
«Наукова думка», Киев, 1968.
29. Саркисян В. С, Некоторые задачи математической теории
упругости анизотропного тела. Изд. Ереванского ун-та, Ере-
Ереван, 1976.
30. Сен-Венан Б., Мемуар о кручении призм. Мемуар об
изгибе призм (перевод с франц. под ред. Г. Ю. Джанелидзе).
Физматгиз, М., 1961.
31. Справочник физических констант горных пород (под
редакцией С. Кларка-мл.), «Мир», М., 1969.
32. Тимошенко С. П., Гудьер Дж., Теория упругости.
(Перевод с англ. под ред. Г. С. Шапиро.) «Наука», М., 1975.
33. Флинт Е. Е., Практическое руководство по геометрической
кристаллографии. Изд. 3, Госгеолтехиздат, М., 1956.
34. Bors С. J., Teoria elasticitatii corpurilor anizotrope. Ed.
Acad. republ. soc. Romania, Bucuresti, 1970.
35. G г e e n A. E., Zerna W., Theoretical elasticity. «Oxford
University Press», London, 1954.
410 ЛИТЕРАТУРА
36. Landolt*—Bornstein., Zahlenwcrte und Funktio-
nen aus Physik, Chemio, Astronomie, Geophysik und Technik.,
t. 4., Technik, B. 1 (Springer), Berlin, 1955.
37. N e u m a n n F., Vorlesungen iiber die Thcorie der Elastizitat
(Teubner), Leipzig, 1885.
38. Voigt W., Lehrbuch der Kristallphysik (Teubner), Leipzig —
Berlin, 1928.
Б. СТАТЬИ
39. Абрамян Б. Л,, Баблоян А. А., Кручение анизотроп-
анизотропного цилиндра. ДАН Арм. ССР 27, № 5, 1958, 269—275.
40. А л е к с а н д р о в К. С, Рыжова Т. В., Упругие свой-
свойства кристаллов. Обзор. Кристаллография 6, вып. 2, 1961,
289-314.
41. Арутюнян Н. X., О кручении эллиптического кольцевого
сектора. ПММ 11, вып. 5, 1947, 543—546.
42. Арутюнян Н. X., Приближенное решение некоторых за-
задач о кручении анизотропных стержней. Сообщения Ин-та
математики и механики АН Арм.ССР, вып. 2, 1948, 41—55.
43. А ш к е н а з и Е. К., Морозов А. С, Методика экспери-
экспериментального исследования упругих свойств композиционных
материалов. Заводская лаборатория, № 6, 1976, 731—735.
44. А ш к е н а з и Е. К., Г е р ш б е р г М. В., ГотлибЦ. А.,
Сборовский А. К., Чумакова Р. Ю., Никифо-
Никифоров Н. Н., Влияние схем армирования и технологии изго-
изготовления на анизотропию упругих свойств и прочности судовых
стеклопластиков при сжатии. Сб. «Вопросы судостроения»,
сер. «Технология судостроения», Изд. ЦНИИ «Румб», вып. 12,
Л., 1976.
45. Баблоян А. А., Об одной задаче осесимметричнон де-
деформации круглого цилиндра конечной длины из трансвер-
салыю-изотропного материала. ДАН Арм.ССР 32, № 4,1961,
189-195.
46. Б а б л о я н А. А., К задаче осеснмметрпчной деформации
круглого цилиндра конечной длины из трансверсально-изо-
тропного материала. Изв. АН Арм.ССР, ф.-м.н. 14, №4, 1961,
61-70.
47. Б а т у г и н С. А., Н и р е н б у р г Р. К., Приближенная
зависимость между упругими константами горных пород и па-
параметры анизотропии. Физико-технические проблемы разработ-
разработки полезных ископаемых 7, № 1, 1972, 7—11.
48. Бехтерев П., Аналитическое исследование обобщенного
закона Гука. Журнал Русского физ.-хим. общества, а) 57,
вып. 3—4, 1925, 359—392; б) 58, вып. 3, 1926, 415—446.
49. Болотин В. В., Плоская задача теории упругости для
деталей из армированных материалов. Расчеты на прочность.
Сборник статей, вып. 12, «Машиностроение», М., 1966, 3—31.
50. Васильев В. 3., Напряжения в упругом изотропном по-
полупространстве вблизи торца вертикальной цилиндрической
выемки. ПМ (Киев) 3, вып. 7, 1967, 109—117.
ЛИТЕРАТУРА 411
51. Джанелидзе Г. Ю., Задачи теории упругости анизо-
анизотропной среды, приводящиеся к плоским. В сб. «Проблемы
механики сплошной среды» (к семидесятилетию академика
Н. И. Мусхелишвили). Изд. АН СССР М., 1961, 145—151.
52. Житков П. Н., Плоская задача теориии упругости неод-
неоднородного ортотропного тела в полярных координатах. Тр.
Воронежского гос. ун-та 27, 1954, 20—29.
53. К о с м о д а м и а н с к и й А. С, Изгиб анизотропной балки
под действием равномерной нагрузки. Ученые записки Ростов-
Ростовского гос. ун-та 32, № 4, 1955, 75—94.
54. Космодамианский А. С, Изгиб анизотропной балки
под действием распределенной нагрузки. Инж. сб. (Ин-т меха-
механики АН СССР) 24, 1956, 114-126.
55. Лейбензон Л. С, Некоторые задачи об изгибе и кручении
анизотропных призм. Ученые записки Московского гос. ун-та,
вып. 46, Механика, 1940, 139—160.
56. Л е х н и ц к и й С. Г., Некоторые случаи упругого равно-
равновесия однородного цилиндра с произвольной анизотропией.
ПММ 2, вып. 3, 1939, 345—367.
57. Лехницкий С. Г., Обобщенная плоская деформация в
бесконечном упругом анизотропном полупространстве, огра-
ограниченном поверхностью параболического цилиндра. ДАН СССР
25, № 3, 1939, 182 —185.
58. Л е х н и ц к и й С. Г., Симметричная деформация и кручение
тела вращения с анизотропией частного вида. ПММ 4, вып. 3,
1940, 43-60.
59. Л е х н и ц к и й С. Г., О равновесии анизотропной консоль-
консольной балки. ПММ 6, вып. 1, 1942, 3—18.
60. Лехницкий С. Г., Распределение напряжений в упру-
упругом стержне с криволинейной анизотропией под действием
растягивающей силы и изгибающих моментов. ПММ 13, вып. 3,
1949, 307—316.
61. Л е х н и ц к и й С. Г., Приближенный метод определения
напряжений в упругой анизотропной пластинке вблизи отвер-
отверстия, мало отличающегося от кругового. Инж. сб. (Ин-т меха-
механики АН СССР) 17, 1953, 3-28.
62. Л е х н и ц к и й С. Г., Распределение напряжений в анизот-
анизотропной пластинке с эллиптическим упругим ядром (плоская
задача). Инж. сб. (Ин-т механики АН СССР) 19, 1954, 83—106.
63. Л е х н п ц к и й С. Г., Некоторые случаи упругого равно-
равновесия анизотропной пластпнкп с некруглым отверстием (плос-
(плоская задача). Инж. сб. (Ин-т механики АН СССР) 22, 1955,
160-187.
64. Лехницкий С. Г., С о л д а т о в В. В., Влияние поло-
положения эллиптического отверстия на концентрацию напряжений
в растягиваемой ортотропной пластинке. Изв. АН СССР, ОТН,
Механика и машиностроение, № 1, 1961, 3—8.
65. Лехнпцкий С. Г., Теоретическое исследование напряже-
напряжений в упругом анизотропном массиве вблизи подземной выра-
выработки эллиптического сеченпя. В НИМИ, Тр. по вопросам гор-
горного давления, сдвижения горных пород и методики маркшей-
маркшейдерских работ. Сб. 45, Л., 1962, 155—179,
412 ЛИТЕРАТУРА
66. Л е х н и ц к и й С. Г., Радиальное распределение напряжений
в клине и полуплоскости с переменными модулями упругости.
ПММ 26, вып. 1, 1962, 146-151.
67. Л е х н и ц к и й С. Г., Кручение анизотропного тела вращения
с переменными модулями упругости. ПММ 28, вып. 6, 1964,
1112-1116.
68. Л е х н и ц к и й С. Г,, Одноосное напряженное состояние
ортотропного стержня с переменными модулями упругости.
Изв. АН СССР, Механика и машиностроение, № 1, 1964, 27—32.
69. Л е х н и ц к и й С. Г., Некоторые случаи кручения стерж-
стержней с переменными модулями упругости. Исследования по
упругости и пластичности, сб. 4. Изд. ЛГУ, Л., 1965, 72—85.
70. Лехницкий С. Г., Плоская задача теории упругости для
среды, обладающей цилиндрической анизотропией, с перемен-
переменными модулями упругости. Инж. ж., МТТ, № 1,1967,84—87.
71. Лехницкий С. Г., Элементарные решения двух частных
задач о равновесии анизотропного неоднородного цилиндра.
Исследования по упругости и пластичности, сб. 6, Изд. ЛГУ,
Л., 1967, 3-9.
72. Лехницкий С. Г., Об одном частном случае осесимметрич-
ной деформации цилиндра с модулями упругости, меняющимися
по длине. Исследования по упругости и пластичности, сб. 7.
Изд. ЛГУ, Л., 1968, 3-12.
73. Л е х н и ц к и й С. Г., Кручение неоднородного анизотропно-
анизотропного цилиндра касательными усилиями, распределенными по
торцам. Изв. АН СССР, МТТ, вып. 5, 1970, 100—104.
74. Лехницкий С. Г., Задача Сен-Венана для непрерывно-
неоднородного анизотропного бруса. В сб. «Механика сплошной
среды и родственные проблемы анализа» (к восьмидесяти-
восьмидесятилетию академика Н. И. Мусхелишвили), «Наука», М., 1972,
273-279.
75. Л о к ш и н А. Ш., К кручению анизотропных призм, а) За-
Записки Днепропетровского ин-та народного образования, 1927,
53—59, б) Тр. Всероссийского съезда математиков в Москве,
Госиздат, М., Л., 1928, 271—272.
76. М и н а с я н Р. С, О кручении и изгибе анизотропных приз-
призматических стержней с поперечным сечением в виде параллело-
параллелограмма. Изв. АН Арм. ССР, ф.-м.н. 11, № 3, 1958, 41—62.
77. М и н ч е в И. Т., О трехмерном напряженном и деформиро-
деформированном состоянии сплошных слоистых сред. «Механика сплош-
сплошных сред». Сб. материалов Международной конференции по
механике сплошных сред (Варна, 1966). София, 1968.
78. Митинский А. Н., К вопросу об определении напряжений
в деревянной сверленой трубе, подверженной действию внут-
внутреннего давления. Вестник инженеров и техников, № 5, 1936,
300—301.
79. М и т и н с к и й А. Н., Напряжения в толстостенной анизо-
анизотропной трубе под действием наружного и внутреннего давления.
Сб. Лининградского ин-та инженеров ж.-д. транспорта,
вып. 136, (теоретический), 1947, 55—78.
80. М и х л и н С. Г., Плоская деформация в анизотропной среде.
Тр. Сейсмологического ин-та АН СССР, № 76, 1936, 1—19.
ЛИТЕРАТУРА 413
81. Моссаковская С, Функции напряжений для упругих
тел, обладающих трехосной ортотропией. Бюллетень Польской
АН, (отд. 4) 3, № 1, 1955, 3-6.
82. Новацкий В., Функция напряжений в пространственных
проблемах упругого тела с трансверсальной изотропией. Бюл-
Бюллетень Польской АН (отд. 4) 2, № 1, 1954.
83. Плотников М. М., О напряжениях в толстостенной
неоднородной анизотропной трубе. Известия вузов. Машино-
Машиностроение, № 8, 1959, 21—26.
84. Плотников М. М., К расчету толстостенной неоднородной
трубы. Изв. вузов. Машиностроение, № 12, 1960, 104—109.
85. Р а б и н о в и ч А. Л., Об упругих постоянных и проч-
прочности авиационных материалов. Тр. ЦАГИ, № 582, 1946,
1-56.
86. Ростовцев Н. А., К теории упругости неоднородной
среды. ПММ 28, вып. 4, 1964, 601—611.
87. С а в и н Г. Н., Основная плоская статическая задача теории
упругости для анизотропной среды.Тр. Института строительной
механики АН УССР, № 32, 1938, 1—55.
88. С а р к и с я н В. С, Кручение анизотропных призматических
стержней с сечением в виде удлиненного авиационного профиля.
Изв. АН Арм.ССР, Физ.-матем. науки 14, № 2, 1961, 45—70.
89. С а р к и с я н В. С, Изгиб анизотропных призматических
стержней удлиненных симметричных профилей. Изв. АН
Арм.ССР, Физ.-матем. науки 14, № 4, 1961, 70—86.
90. С а р к и с я н В. С, Кручение анизотропных призматических
стержней с удлиненным профилем, изготовленных из ортотроп-
ного материала. Изв. АН Арм.ССР, Физ.-матем. науки 14,
№ 5, 1961, 59-70.
91. Саркисян В. С, О центре изгиба анизотропного стержня
с удлиненным симметричным авиационным профилем, изго-
изготовленного из ортотропного материала. Изв. АН Арм.ССР 15,
№ 4, 1962, 25-47.
92. Секерж-Зенькович Я. И., К расчету на устойчивость
листа фанеры, как анизотропной пластинки. Тр. ЦАГИ, № 76,
1931, 3—26.
93. Тер-Мкртичьян Л. Н., Некоторые задачи теории
упругости неоднородных упругих сред. ПММ 25, вып. 6, 1961,
1120—1125.
94. У з д а л е в А. И., Упругое равновесие стержня, обладаю-
обладающего цилиндрической анизотропией, под действием нагрузки,
равномерно распределенной по длине. Инж. сб. (Ин-т механики
АН СССР) 26, 1958, 148-160.
95. Хантингтон Г., Упругие постоянные кристаллов. Успе-
Успехи физических наук 74, а) вып. 2, б) вып. 3, 1961, 303—352,
461—520.
96. X а т и а ш в и л и Г. М., Упругое равновесие однородного
ортотропного цилиндрического бруса с нагруженной боковой по-
поверхностью. Тр. В. Ц. АН Груз.ССР 2, 1961, 123—142.
97. X а т и а ш в и л и Г. М., Задача Альманси—Мичелла для од-
однородного анизотропного цилиндрического бруса. Тр. ВЦ
АН Груз.ССР 3, 1963, 141—160.
414 ЛИТЕРАТУРА
98. X а т к е в и ч А. Г., Об упругих константах кристаллов.
Кристаллография 6, вып. 5, 1961, 700—703.
99. Чен (W. Т. Chen), Осеспмметричное поле напряжений вокруг
сфероидальных включений и полости в трансверсально-изотроп-
ном материале (перевод «Transaction ASME», ser. Е), ПМ № 4,
1968, 160-164.
100. Ч е н ц о в Н. Г., Исследование фанеры, как анизотропной
пластинки. Технические заметки ЦАГИ, № 91, 1936, 1—27.
101. Шармазанашвили А. X., Расчет анизотропных
толстостенных сферических оболочек. Вестник инженеров и
техников, № 7, 1938., 35—37.
102. Шерман Д. И., Плоская задача теории упругости для
анизотропной среды. Тр. Сейсмологического ин-та АН СССР,
№ 86, 1938,51-78.
103. Almansi Е., Sopra la deformazione dei cilindri sollecitate
lateralmente. Rendic. Accad. Lincei. Roma, ser. 5, 10, 1901,
333-338.
104. A u e r b а с h F., Elastizitat der Kristalle. Handbuch der
physikalische und technische Mechanik, B. 3, Leipzig, 1927,
239-282.
105. Bert С W., Displacements in a polar-ortotropic disk of
varying thickness. Zeitschr. angew. Mathemat. und Phys. 14,
№ 2, 1963, 101-111.
106. Bhowmick Smriti Kana, Stress due to spheroidal
inclusion of material having curvilinear aeolotropy on the axis
of a large twisted isotropic cylinder. Archiwum mech. stosowanei,
13, № 3, 1961, 321-325.
107. Bhowmick Smriti Kana, Stress concentrations
around a small rigid spheroidal inclusion on the axis of a trans-
transversely isotropic cylinder under torsion. AIAA Journal 1, № 5,
1963, 1219-1220.
108. В о s e S. C, On the torsion of a circular cylinder of transversely
isotropic material having a spherical inclusion of spherically
isotropic material on its axis. Indian Journ. theoret. phys. 12,
№ 2, 1964, 29-38.
109. В о s e S. C, Torsion of an aeolotropic cylinder having a sphe-
spheroidal inclusion on its axis. AIAA Journal 3, № 7, 1965,
1352-1354.
НО. В о s e S. C, On the torsion of a transversely isotropic circular
cylinder having a small spherical elastic inclusion of an isotropic
material. Zeitschrift. f. angew. Math, und Mech. 45, H. 2/3,
1965, 133-135.
111. Chattarji P. P., Torsion of a circular cylinder having
a rigid spherical inclusion Bull. Calcutta math. soc. 49, № 4,
1957, 199-205.
112. D a s S. C, Stress concentration around a small spherical and
spheroidal inclusion on the axis of a circular cylinder in torsion.
Journ. appl. mech. (Trans. ASME, ser. E) 21, № 1, 1954, 83—87.
113. Deutsch E., Torsion of a transversely isotropic semiinfinite
body. Archiwum mech. stosowanej 15, № 4, 1963, 517—533.
114. p u 11 S. В., Stress concentrations around a small spherically
isotropic spherical inclusion on the axis of an isotropic circular
ЛИТЕРАТУРА
cylinder on torsion. Journ. of technology (Calcutta) 3, № 1,
1958, 13—17.
115. Elliott H. A., Three-dimensional strees distributions in
hexagonal aeolotropic crystals. Proc. of the Cambridge philos.
soc. 44, part 4, 1948, 522—533.
116. E shelby J. D., Elastic inclusions and inhomogeneities.
Progrees in Solid Mechanics, North Holland, Amsterdam, 11,
1961, 89-140.
117. Geckeler J. W., Elastizitatstheorie anisotroper Korper
(Kristallelastizitat). Handbuch der Physik, B. 6, Berlin, 1928,
404—427.
118. H u H a i - с h a n g ., On the three-dimensional probleme
of the theory of elasticity of a transversely isotropic body. Acta
physica sinica (Chiness journal of physics) 9, № 2, 1953,
130-147.
119. M i с h о 11 J. H., The theory of uniformly loaded beam. Quart.
Jounrn. of Math. 32, 1901, 28—42.
120. Mossakowski J., The Michell problem for anisotropic
semi-infinite plate. Archiwum mech. stosowanej 8, № 4, 1956,
539—548.
121. Saint-Venant В., Memoire sur la torsion des prismes.
Memoires presented par divers savants a l'academie des sciences.
Sciences math, et phys. 14, Paris, 1856, 233—560.
122. Saint-Venant В., Memoire sur la flexion des prismes.
Journal de math, pures et appl. (Liouville), ser. 2, 1, 1856,
89—189.
123. Sain t-V e n a n t В., Memoire sur la distribution d'elasti-
cites. Journal de math, pures et appl. (Liouville), ser. 2, 8,
Paris, 1863, 257-295, 353-430.
124. Saint-VenantB., Memoire sur les divers genres d'homoge-
neite des corps solides. Journal de math, pures et appl.
(Liouville) 10, 1865, 297—349.
125. Somigliana C, Ricerche sulla deformazione ed i fenomeni
piezoelettrici in un cilindro cristallino. Annali di math, pura ed
appl., ser. 2.20, Milano, 1892, 61—99.
126. S о 6 s E., Sur le probleme de Saint-Venant dans le cas de barres
heterogenes avec anisotropie cilindrique. Bull. Math. Soc. Sci.
Math, et Phys. RPR 7, № 1—2, 1963, 61—75.
127. Subramanian R., Stress concentration around a small
anisotropic spheroidal inclusion on the axis of circular cylinder
in torsion. Archiwum mech. stosowanej 20, № 1, 1968.
128. Voigt W., Ueber die Elasticitatsverhaltnisse cylindrisch
aufgebauter Korper. Nachrichten. v. d. Konigl. Geselsch. der
Wissenschaft. und der Georg-Augustin Universitat zu Gottingen,
№ 6, 1886, 505—514.
129. Wolf K., Ausbreitung der Kraft in der Halbebene und im Hal-
hraum bei anisotropem Material. Zeitschrift f. angew. Math, und
Mech., B. 15, H. 5, 1935, 249-254.
Сергей Георгиевич Лехницкай
ТЕОРИЯ УПРУГОСТИ
АНИЗОТРОПНОГО ТЕЛА
М., 1977 г., 416 стр. с илл.
Редакторы Я. Я. Васипа, В. Л. Добровольский
Технический редактор В. Я. Кондакова
Корректоры Е. А. Белицкая, М. Л. Медведская
Сдано в набор 20/IV 1977 г.
Подписано к печати 8'1Х-1977 г. Бумага 84xiO8V32.
Физ. печ. л. 13. Условн. печ. л. 21,84.
Уч.-изд. л. 21,54. Тираж 5000 экз. Т-16416.
Цена книги 1 р. 60 к. Зак:\з № 2484.
Издательство «Наука»
Главная редакция физико-математической
литературы
117071, Москва, В-71, Ленинский проспект, 15
2-я типография издательства «Наука»
121099, Москва, Г-99, Шубинский пер., 10