Author: Иванов Н.М.
Tags: техника средств транспорта астрономия космические аппараты космонавтика
Year: 1977
Text
Н. М. Иванов
А. И. Мартынов
УПРАВЛЕНИЕ
ДВИЖЕНИЕМ
КОСМИЧЕСКОГО
АППАРАТА
В АТМОСФЕРЕ
МАРСА
МЕХАНИКА
КОСМИЧЕСКОГО
ПОЛЕТА
ИЗДАТЕЛЬСТВО «ПАУКА»
ГЛАСНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
НОС К I! л 19 7 7
Н. М. ИВАНОВ, А. И. МАРТЫНОВ
УПРАВЛЕНИЕ ДВИЖЕНИЕМ
КОСМИЧЕСКОГО
АППАРАТА
В АТМОСФЕРЕ МАРСА
ИВДА ТЕJIЬСТВО «IIАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
Ф] \ ЛИ КО-МА ТЕ Л Г Л ТЯ Я ЕС К* ОЙ Л ИТЕРА ТУР I ,Т
МОСКВА 1977
6.Т5.2
И 20
УДК 029.1514
Управление движением космического аппарата в атмо¬
сфере Марса. Иванов П. М., М а р т ы и о в А. II.
Главная редакция фт т з и к о -м а тсм ат и ч е с к о i г литературы изда¬
тельства «Наука», М., 1977, 416 стр.
Монография посвящена проблеме управления движени¬
ем КА в атмосфере Марса при спуске на поверхность планеты
и при выходе па орбиту искусственного спутника.
Приводится общая постановка и методика решения основ¬
ных баллистико-навигационных задач торможения в атмо¬
сфере Марса из условия доставки максимума полезной на¬
грузки на поверхность планеты ттли на орбиту спутника.
Формулируются критерии оптимальности. Определяется опти¬
мальное управление движением КА скользящего и плани¬
рующего типов. Проводится анализ оптимальных траекторий
для различных проектно-баллистических параметров КА и
широкого диапазона начальных условий. Синтезируются
алгоритмы управления. Выводы проиллюстрированы мно¬
гочисленными числовыми примерами.
Табл. 28, илл. 109, библ. 111.
Николай Михайлович Иванов, Александр Иванович Мартынов
Управление движением космического аппарата в атмосфере Марса
М., 1977 г., 416 стр. с плл.-
Редактор О. Э. Цыикова
Техн. редактор И. Ш. Аксельрод
Корректор Я. Д. Дорохова
Сдано в набор 8/YIIT 1977 г. Подписано к печати 29/XI 1977 г.
Бумага 84 хЮЗГзг- Фив. печ. л. 13. Услови. печ. л. 21,84. Уч-изд. л. 21,95.
Тираж 1470 ок:з. Т-20758. Цена книги 2 р. 50 к. Заказ J\° 2749
И здате л ьство <•■ II ау к а»
Главная редакция физико-математическом литературы
117071, Москва. В-71, Ленинский проспект. 15
2-я типография издательства «Наука».
Москва. ПТубипскпп пер., д. 10
91901-Л 70
И 053(02)^77 158-78
(С) Главная редакция
физико-математической литературы
издательства «Наука»,*1977
ОГЛАВЛЕНИЕ
Предисловие . . . 8
Введение 11
РАЗДЕЛ 1
ОБЩАЯ ПОСТАНОВКА ПРОБЛЕМЫ УПРАВЛЕНИЯ
ДВИЖЕНИЕМ В АТМОСФЕРЕ МАРСА
Глава 1. Планета Марс 19
§ 1.1. Общие сведения 19
§ 1.2. Поверхность планеты и со рельеф 20
§ 1.3. Атмосфера Марса 22
§ 1.4. Ветры в нижней атмосфере 24
§ 1.5. Облака 25
§ 1.6. Некоторые результаты исследований Марса с по¬
мощью КА «Викинг» 26
Глава 2. Основные проблемы управления движением в
атмосфере Марса 31
§ 2.1. Условия подлета КА к плотным слоям атмосферы 31
§ 2.2. Модели атмосферы 37
§ 2.3. Анализ траекторий КА в атмосфере Марса ... 41
§ 2.4. Особенности движения КА в атмосфере Марса . 51
Глава 3. Постановка задачи мягкой посадки .... 59
§ 3.1. Основные проблемы задачи оптимизации .... 59
§ 3.2. Выбор критерия оптимальности 61
§ 3.3. Классификация систем мягкой посадки 79
§ 3.4. Математическая модель движения КА 83
§ 3.5. Упрощение основной задачи оптимизации ... 87
1’ А 3 Д Е Л 2
СПУСК НА ПОВЕРХНОСТЬ МАРСА
Глав а 4. Реактивная система мягкой посадки .... 90
§ 4.1. Исходные предпосылки 90
ь 4.2. Оптимальное управление КА на участке реактивного
торможения ...... , 94
6
ОГЛАВЛЕНИЕ
§ 4.3. Выбор оптимальной тяговооруженности 100
§ 4.4. Влияние начальных условий на массу реактивной
СМИ 106
Г лава 5. Паранпотно-рсактивная система мягкой посадки 109
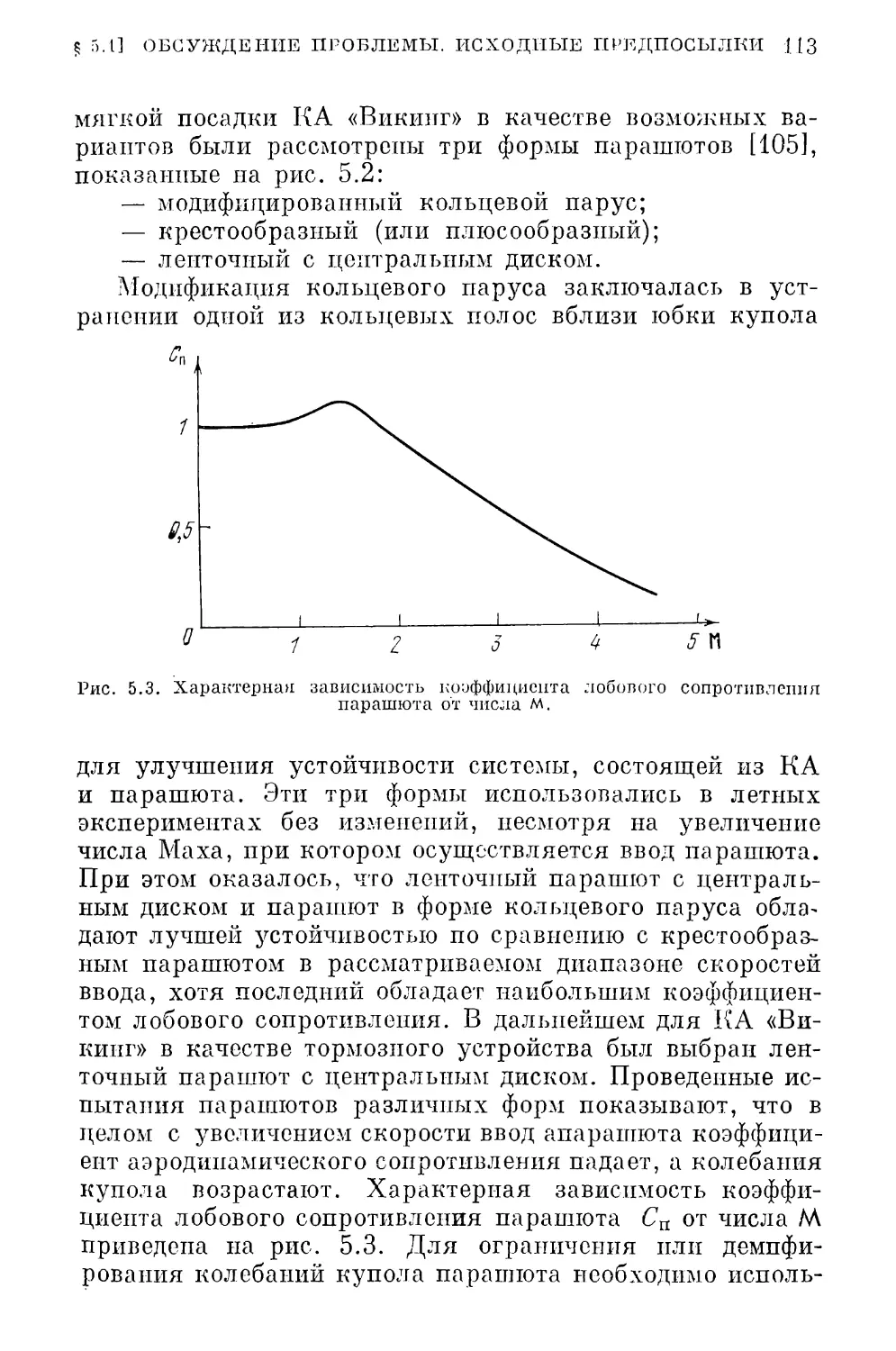
§ 5.1. Обсуждение проблемы. Исходные предпосылки 109
§ 5.2. Выбор основных проектно-баллистических пара¬
метров парашютно-реактивной системы 120
§ 5.3. Требования к участку аэродинамического тормо¬
жения 129
§ 5.4. Система мягкой посадки спускаемого аппарата
«Марс-6» 134
§ 5.5. Система мягкой посадки КА «Викинг» 138
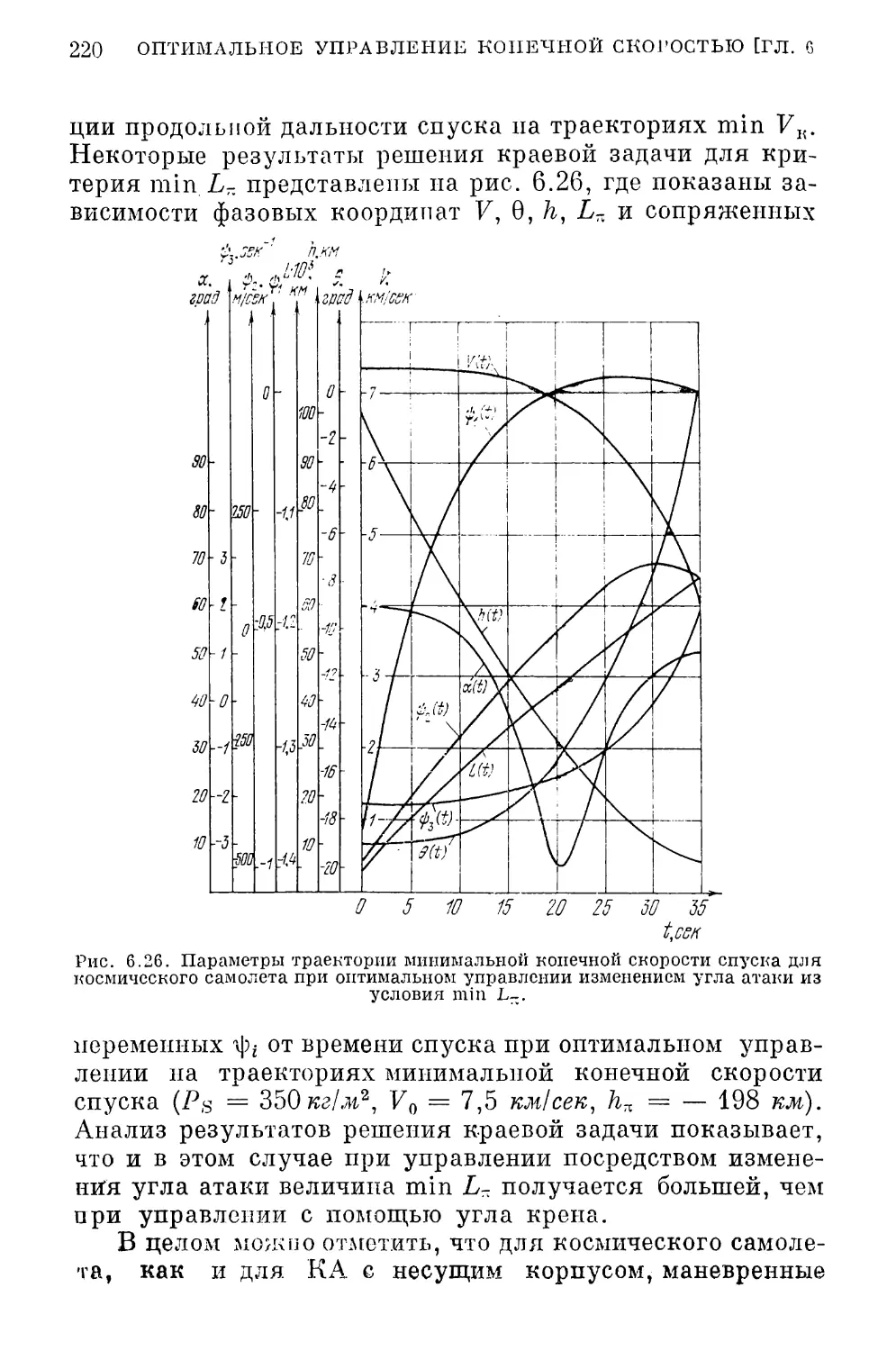
Глава 6. Оптимальное управление конечной скоростью
спуска КА на участке основного аэродинамического тормо¬
жения 1-19
§ 6.J. Установившееся движение КА в атмосфере ... 119
§ 6.2. Постановка задачи. Необходимые условия оптималь¬
ности . . 153
§ 6.3. Общин анализ оптимальных траекторий 159
§ 6.4. Ачадпз численных результатов 169
§ 6.5. Дополнительные задачи оптимального управления
КА па траекториях минимальной конечной скорости 176
§ 6.6. Об эффективности использования оптимального уп¬
равления 181
§ 6.7. О границах применимости критерия минимума
конечной скорости 189
§ 6.8. Оптимальнее управление конечной скоростью спу¬
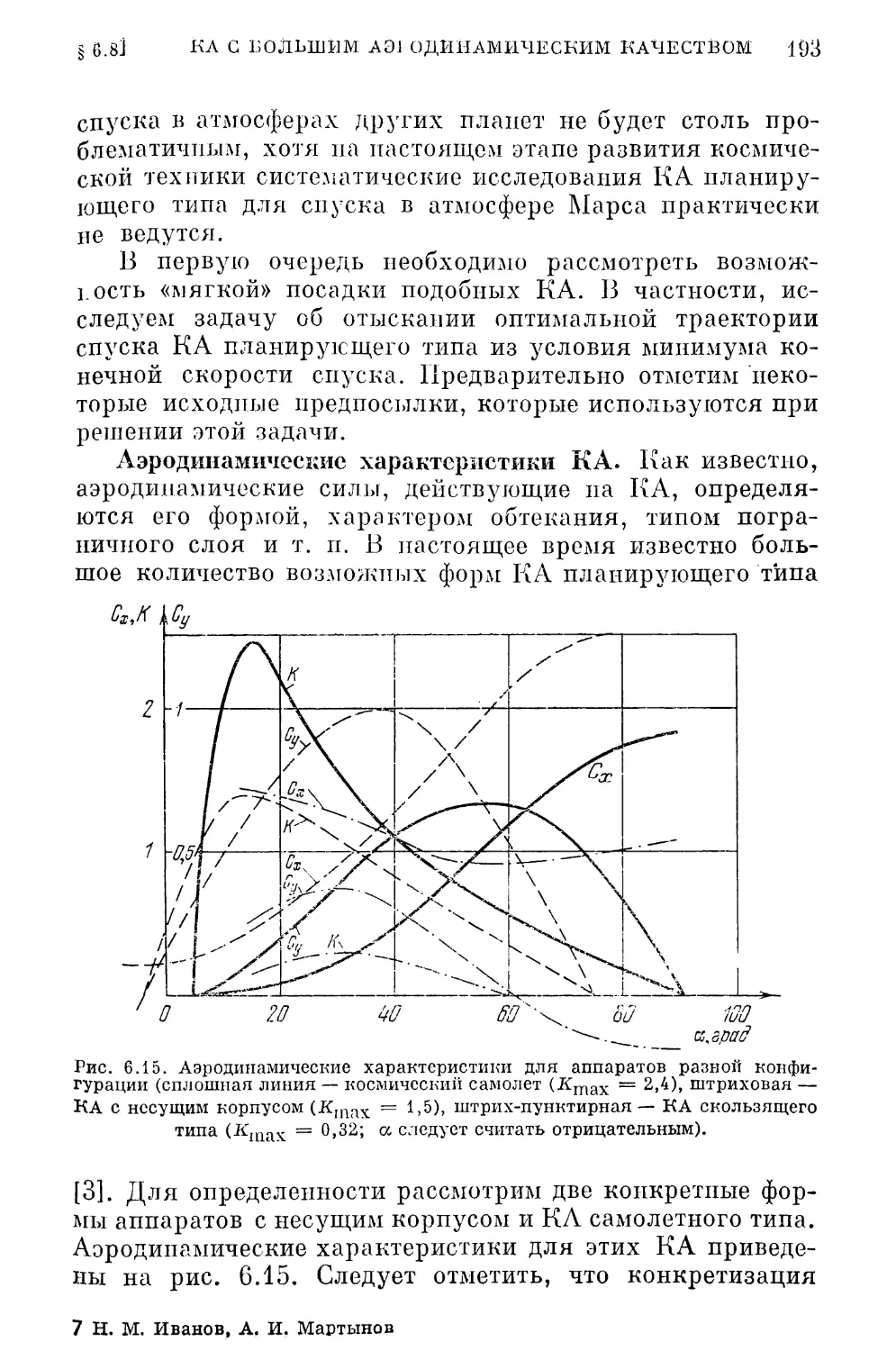
ска ГОЛ с большим аэродинамическим качеством . 192
Постановка .чадами ( 92). Минимизация конечной скорости
спуска (197).Минимизация времени спуска и максимально !
перегрузки на траекториях минимальной конечной скоро¬
сти (200).
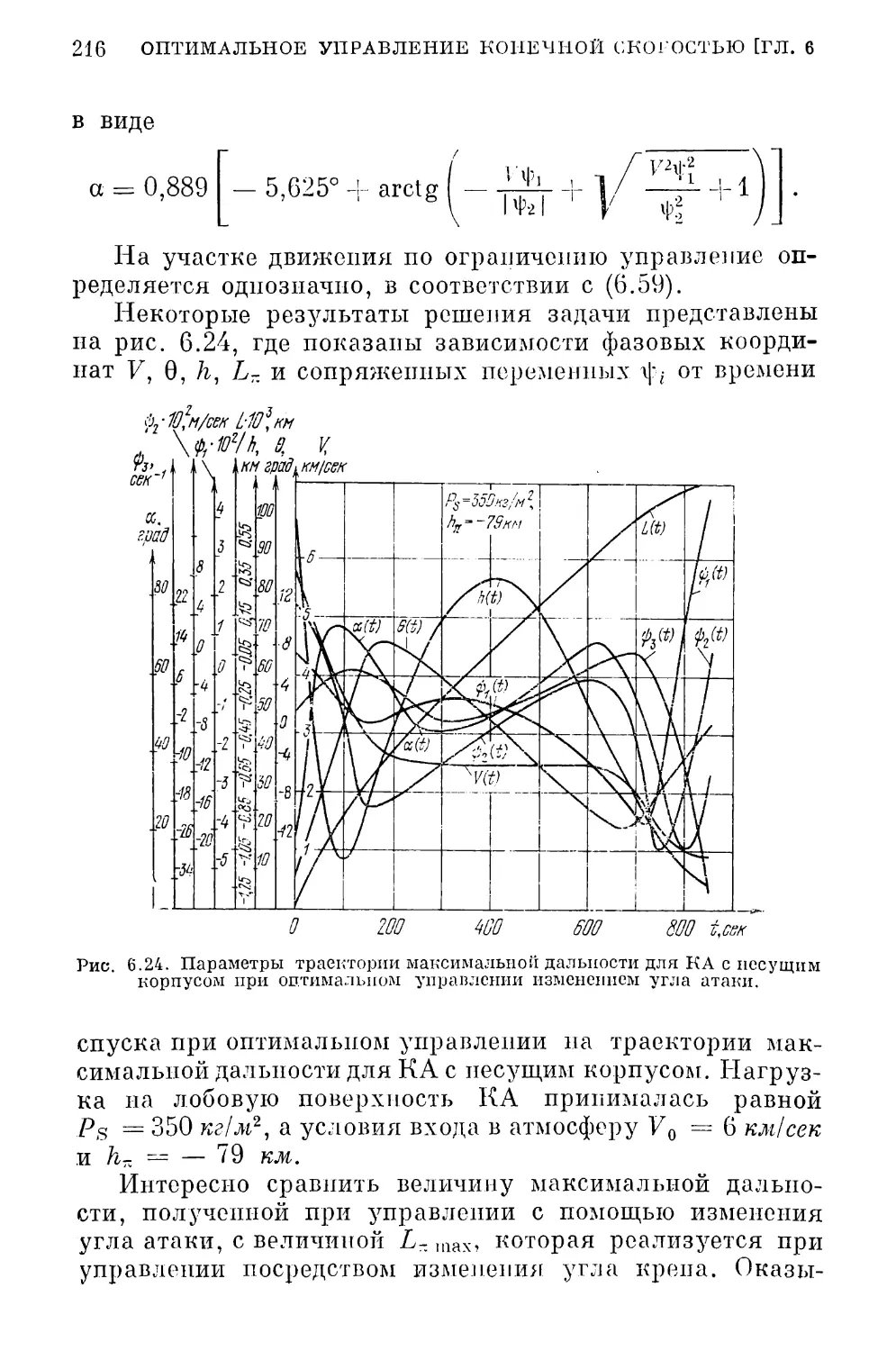
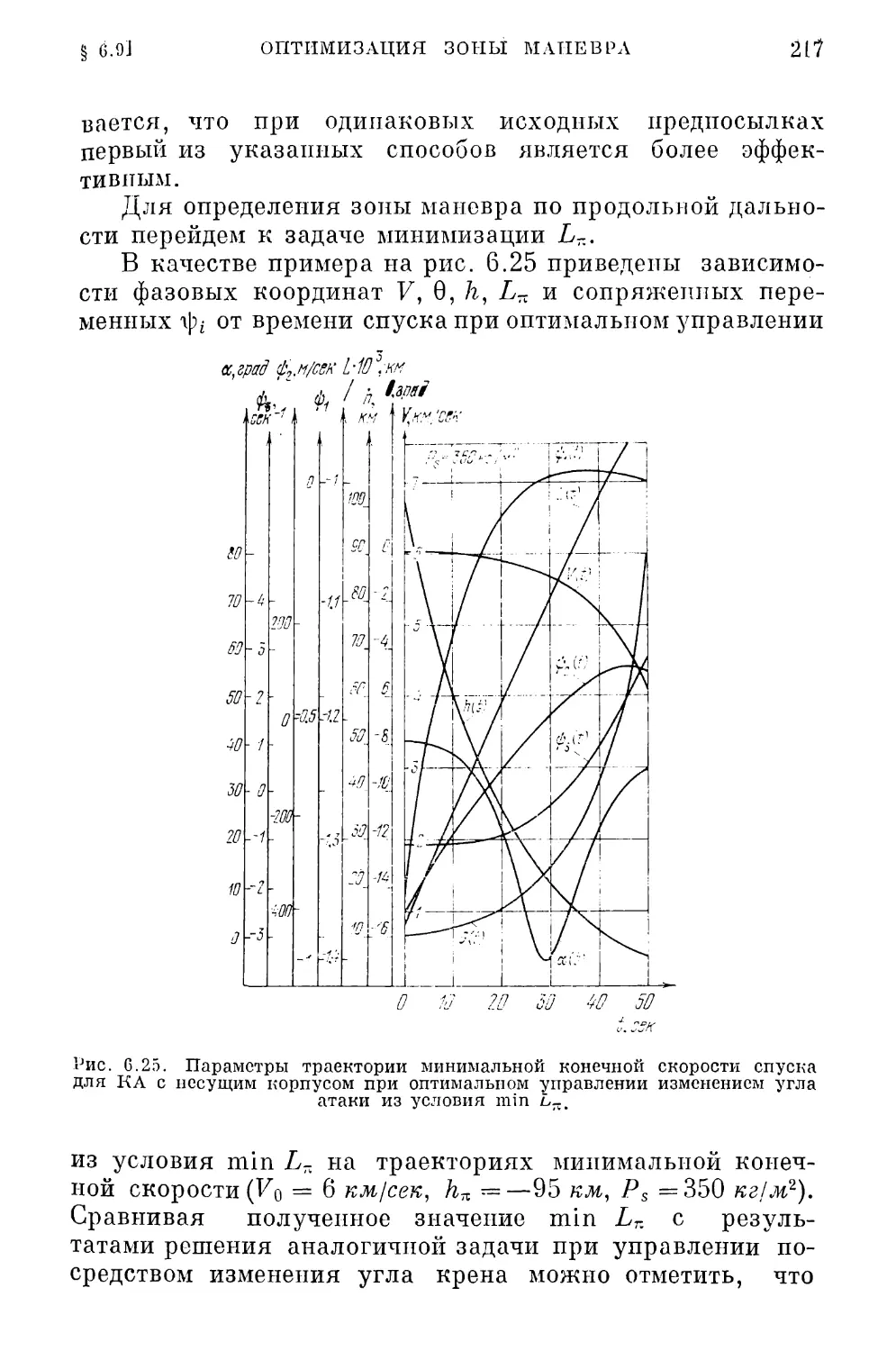
§ 6.9. Оптимизация зоны маневра КА на траекториях
минимальной конечной скорости спуска .... 213
Оптимизация продольной дальности спуска (214). Макси¬
мизация боковой дальности спуска (224).
Глава .7. Некоторые задачи баллистического проектиро¬
вания 238
§ 7.1. Краткая характеристика основных направлений
проектирования КА 238
§ 7.2. Выбор способа управления 243
§ 7.3. Область применимости КА различных типов . . . 217
§ 7.4. Выбор основных проектно-баллистических пара¬
метров К Л 251
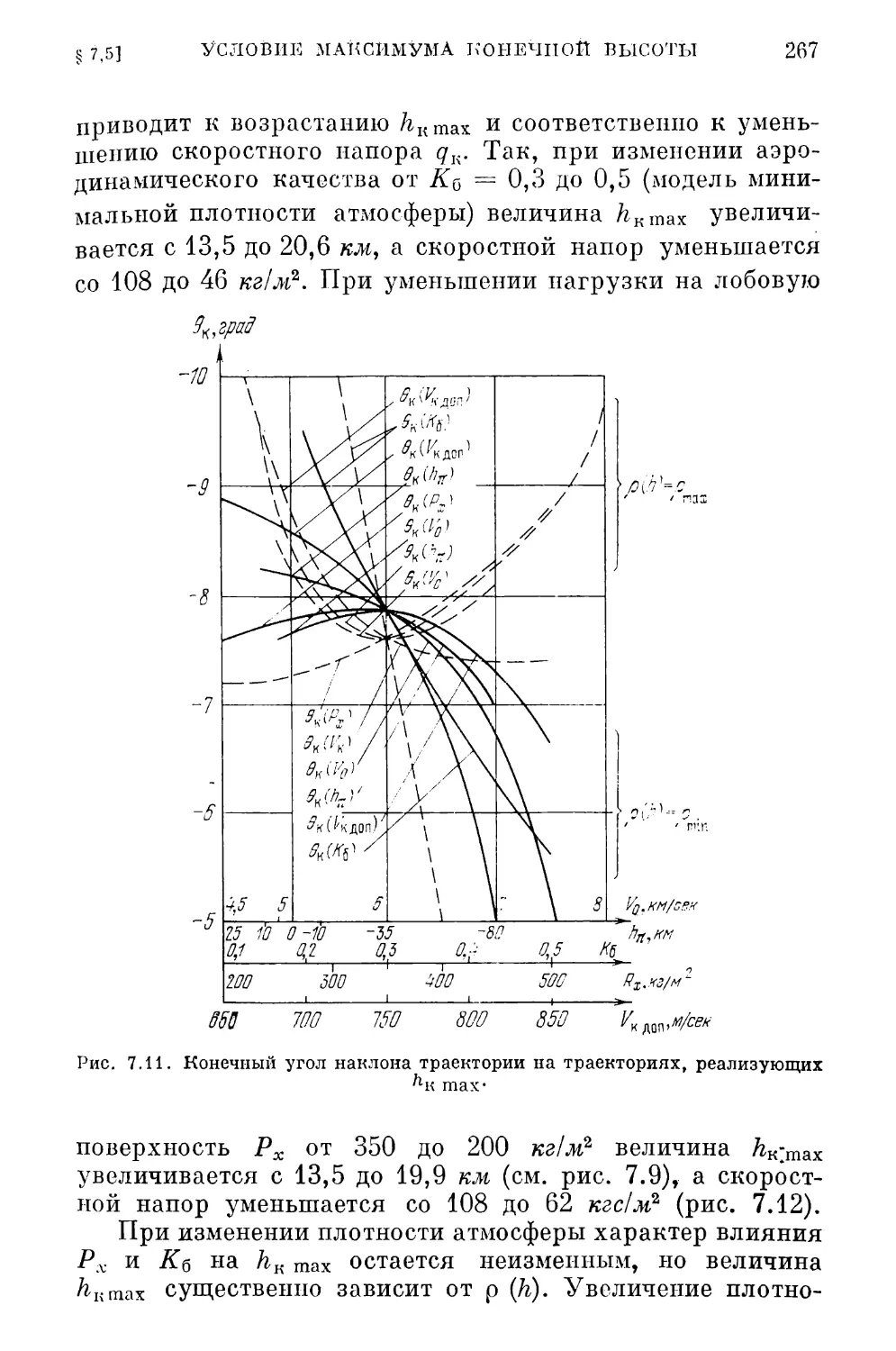
§ 7.5. Оптимальное управление КА из условия максимума
конечной высоты 258
Об эквивалентности задач максимизации конечной высоты
и минимизации конечной скорости спуска (27.9). Анализ
(птимальпых траекторий (261).
ОГЛАВЛЕНИЕ
7
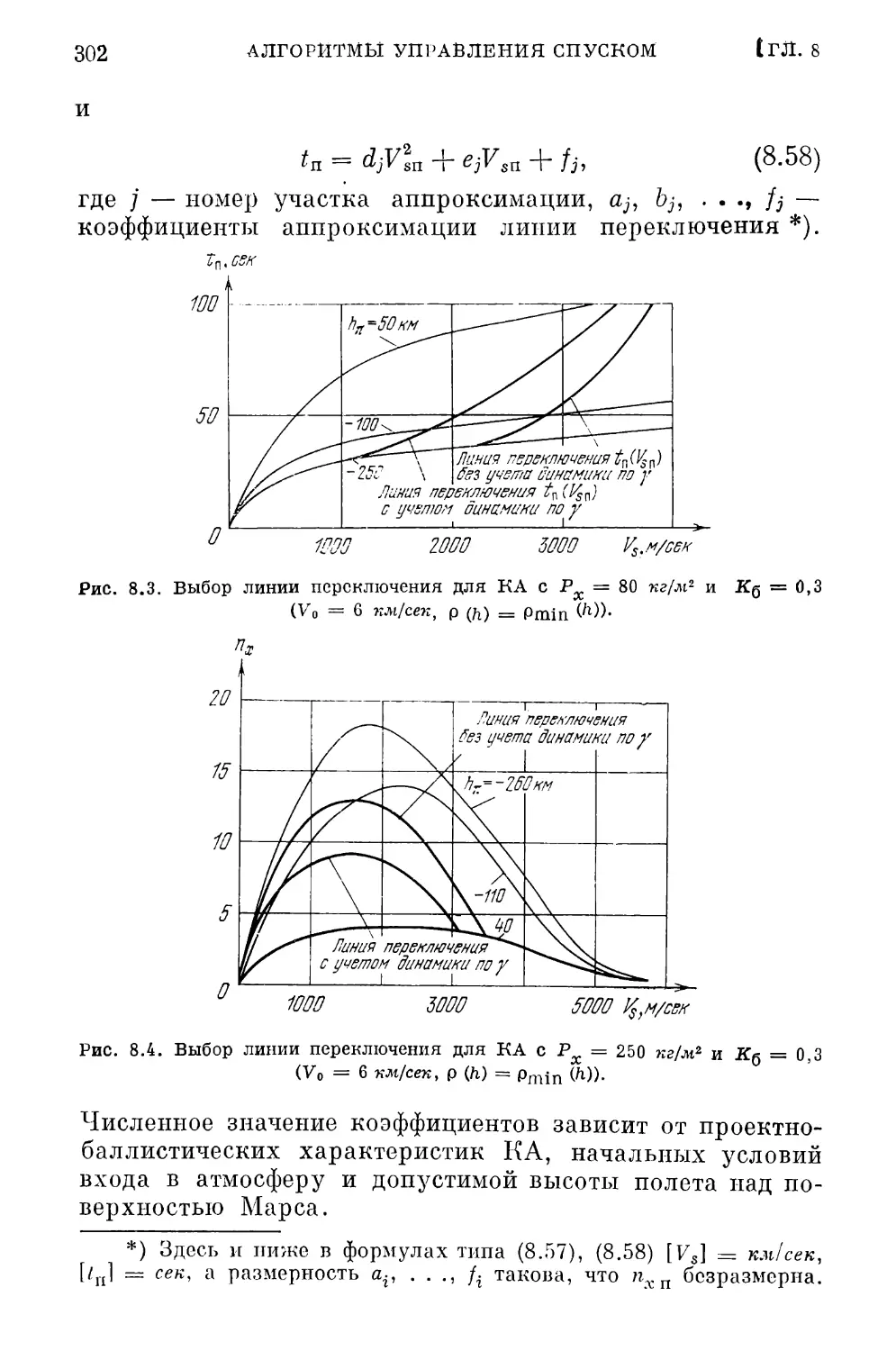
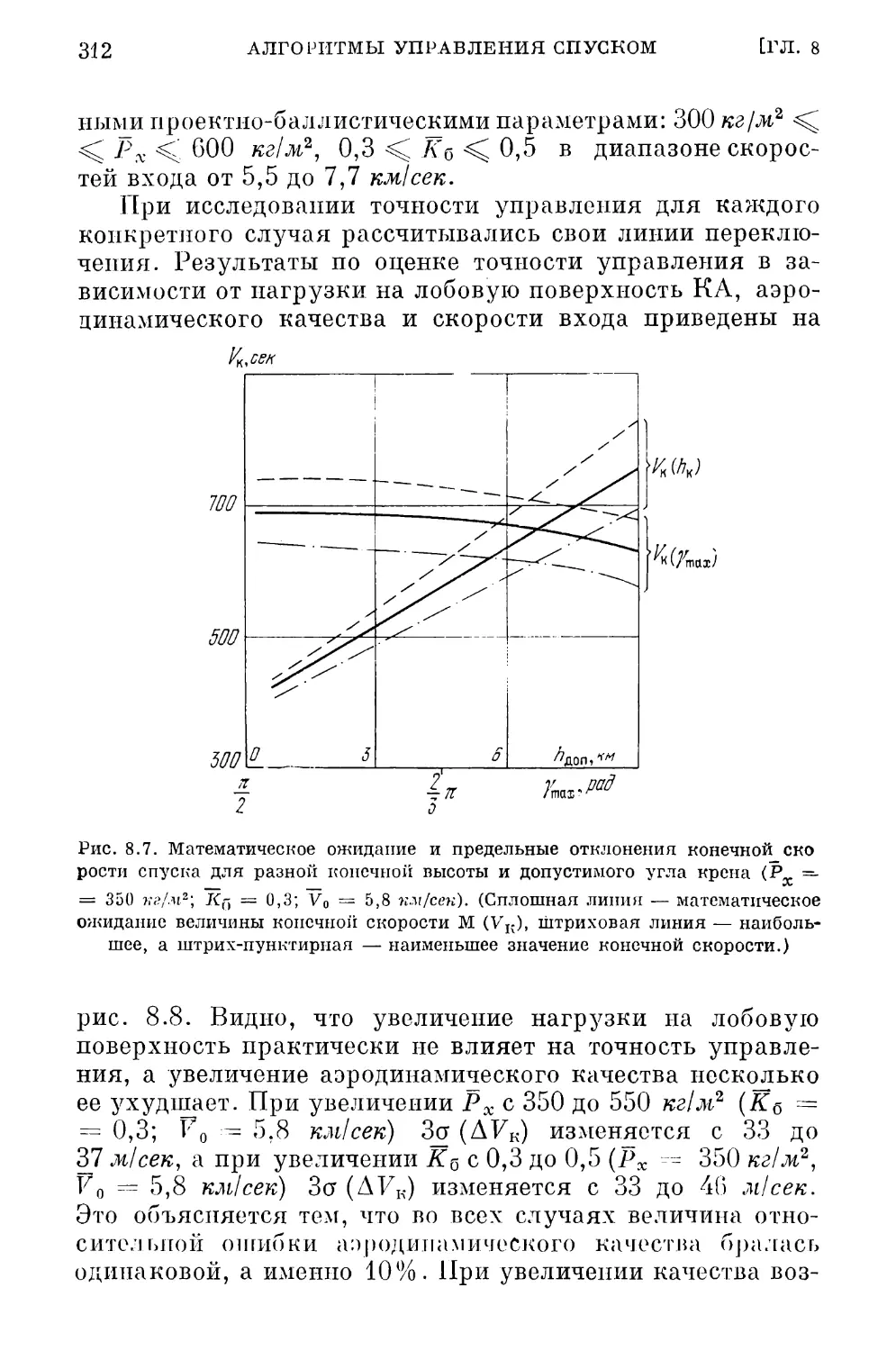
Глава 8. Алгоритмы управления спуском 270
§ 8.1. Постановка задачи. Принцип гарантирующего уп¬
равления 270
§ 8.2. Синтез дискретных алгоритмов управления конеч¬
ной скоростью спуска КА 286
Синтез линейного алгоритма управления (286). Синтез алго¬
ритмов управления с упрощенной логикой (299).
§ 8.3. Алгоритмы управления относительно опорной тра¬
ектории 314
§ 8.4. Адаптивный алгоритм управления конечной ско¬
ростью спуска 321
Алгоритм с использованием прогнозирования конечных ус¬
ловий (323). Алгоритм с использованием опорной траекто¬
рии (849).
РА 3ДЕЛ 3
ОРБИТАЛЬНО-ДЕСАНТНАЯ СХЕМА СПУСКА
Глава 9. Оптимальное управление при выведении КА на
орбиту ИСМ с использованием аэродинамического тормо¬
жения 355
§ 9.1. Обсуждение проблемы 355
§ 9.2. Оптимальное управление КА на участке аэроди¬
намического торможения 357
§ 9.3. Анализ численных результатов 360
§ 9.4. Выбор основных проектно-баллистических харак¬
теристик КА 364
Глава 10. Синтез алгоритмов управления при выведении
КА на орбиту ИСМ 370
§ 10.1. Постановка задачи 370
§ 10.2. Адаптивный алгоритм управления КА на атмос¬
ферном участке полета . 372
§ 10.3. Алгоритм предварительного формирования орбиты
ИСМ на участке ракотодпнамичсского маневра 382
§ 10.4. О некоторых путях совершенствования алгоритма
управления 386
Глава 11. Спуск КА с орбиты ИСМ 389
§ 11.1. Постановка задачи и способы ее решения . . . 389
§ 11.2. О возможном классе орбит ИСМ 391
§ 11.3. Внеатмосферный участок спуска 393
§ 11.4. Участок аэродинамического торможения и мягкой
посадки КА 397
§ 11.5. Определение оптимальных условий входа КА в
атмосферу 399
Литература 408
Основные обозначения 415
ПРЕДИСЛОВИЕ
Изучение Вселенной и прежде всего планет Солнечной
системы направлено на решение ряда фундаментальных
проблем возникновения и развития Земли и в целом Сол¬
нечной системы, строения материи, возникновения и
эволюции жизни и т. д. Не представляется возможным
добиться успеха в решении этих проблем без проведения
исследований с использованием космических аппаратов,
которые могут быть доставлены в окрестность планеты
назначения и способны совершить посадку на ее поверх¬
ность.
При реализации космических полетов наряду со мно¬
гими другими следует решить сложную и ответственную
задачу торможения, под которой понимается задача гаше¬
ния всей энергии космического аппарата при организации
его мягкой посадки на планету назначения или некоторой
ее части — при переведении аппарата с гиперболической
траектории па орбиту искусственного спутника. При
наличии у планеты атмосферы первая задача наиболее
эффективно решается с использованием аэродинамичес¬
кого, т. е. пассивного, торможения. Вторая задача принци¬
пиально может быть решена как активным путем (с ис¬
пользованием тяги двигателя), так и комбинированным —
с предварительным подтормаживанием в атмосфере и с
последующим сообщением небольшого разгонного импуль¬
са для окончательного формирования заданной орбиты.
Качество решения этих задач в значительной степени
ПРЕДИСЛОВИЕ
9
определяет эффективность полета космического аппарата,
ибо чем меньше затраты его массы на организацию тормо¬
шения, тем больше в общем случае масса полезной нагруз¬
ки, в состав которой входит и исследовательская аппара¬
тура.
Предлагаемая вниманию читателя книга посвящена
рассмотрению основных задач торможения в атмосфере
Марса. С изучением этой планеты связываются большие
надежды, и исследования Марса занимают важное место
в советских и американских космических программах.
Характерной особенностью Марса является наличие раз¬
реженной атмосферы, плотность которой почти на два
порядка меньше плотности земной атмосферы. Это пред¬
определяет основные трудности аэродинамического сйо-
соба торможения. Как показал опыт создания советских
и американских космических аппаратов типа «Марс» и
«Викинг», решение задачи мягкой посадки на Марс требу¬
ет полной мобилизации всех возможностей современной
космической техники.
В настоящее время в литературе отсутствуют книги,
содержащие систематическое изложение основных задач
торможения космического аппарата в атмосфере Марса.
Авторы попытались в некоторой степени восполнить суще¬
ствующий пробел. Основное содержание книги посвящено
изложению баллистико-навигациоиных проблем торможе¬
ния в разреженной атмосфере Марса. Эти проблемы явля¬
ются главными в решении задачи мягкой посадки или вы¬
ведения космического аппарата па орбиту искусственного
спутника. Они позволяют получить исходные данные для
решения других сопутствующих задач и в целом для соз¬
дания космического аппарата. В основу книги положены
результаты многолетних исследований авторов. Для пол¬
ноты изложения были использованы материалы имеющих¬
ся публикаций, однако приводимый список литературы не
претендует па библиографическую полноту.
10
ПРЕДИСЛОВИЕ
Книга предназначена для научных работников и инже¬
неров, занимающихся вопросами проектирования космичес¬
ких аппаратов. Она может быть полезна преподавателям,
аспирантам и студентам старших курсов соответствующих
специальностей. Несмотря на специфику операций в ат¬
мосфере Марса, излагаемый в книге подход к решению
основных задач торможения космического аппарата явля¬
ется достаточно общим и может быть использован при ана¬
лизе вопросов управляемого движения космических
аппаратов в малоизученных атмосферах других планет
(Венера, Юпитер, Сатурн).
Авторы считают своим долгом поблагодарить JI. Г. Ан¬
типенко, В. Д. Белых, А. С. Жукова, Н. JI. Соколова за
их помощь при проведении численных расчетов по отдель¬
ным вопросам рассматриваемой проблемы, а также
Г. М. Дорда, Р. И. Тохтуеву, Т. А. Махалкипу и Т. А. Ива¬
нову за большую помощь, оказанную при оформлении
рукописи.
Авторы пользуются возможностью высказать свою
признательность Ю. Г. Сихарулидзе и О. М. Марину,
взявшим на себя труд по предварительному просмотру
рукописи и сделавшим ряд ценных замечаний, которые
были учтены при окончательной доработке книги.
ВВЕДЕНИЕ
Исключительно сложные условия спуска космическо¬
го аппарата (КА) в разреженной атмосфере Марса приво¬
дят к тому, что сам факт посадки на поверхность планеты
является большим техническим достижением; каждая
реализация «мягкой» посадки па планету не только обо¬
гащает паши знания о пей, по и позволяет проверить на
практике во многом гипотетические исходные данные и
методики, которые применялись при проектировании
первых космических аппаратов.
К проблемам торможения КА в атмосфере относится
комплекс вопросов, связанных с организацией подхода
КА к атмосфере планеты, безопасным прохождением ее
плотных слоев и обеспечением, в зависимости от цели
полета, либо мягкой посадки КА в заданном районе поверх¬
ности планеты, либо выведения на заданную орбиту ис¬
кусственного спутника Марса (ИСМ).
В дальнейшем способ выведения КА на орбиту ИСМ,
предполагающий использование предварительного
аэродинамического торможения для гашения избытка
скорости (от начальной гиперболической до околокру го-
вой) и с последующим приложением небольшого разгон¬
ного импульса, формирующего требуемую орбиту спут¬
ника, будем называть для краткости выведением с пред¬
варительным аэродинамическим торможением.
Предметом исследований в дальнейшем будут балли-
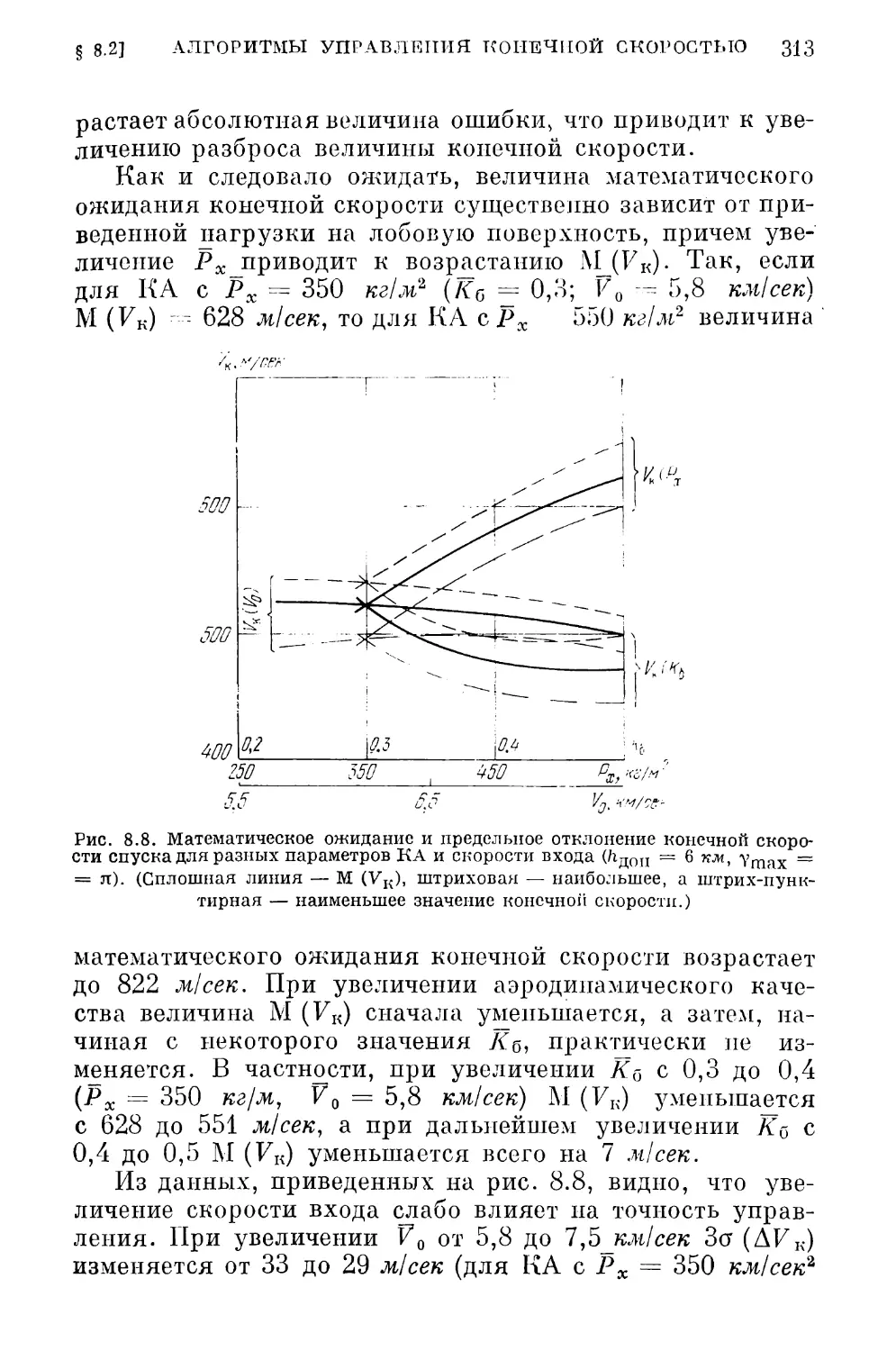
стико-навигациопные задачи, возникающие при решении
указанных двух проблем. Участок же подхода КА к плот¬
ным слоям атмосферы подробно не будет рассматривать¬
ся. Мы ограничимся лишь его краткой характеристикой
и описанием основных особенностей, влияющих на после¬
дующее движение в атмосфере.
Перечислим основные б аллистико-навигационные проб¬
лемы спуска.
12
ВВЕДЕНИЕ
1. Выбор способа посадки (прямой спуск КА; спуск с
орбиты искусственного спутника планеты).
2. Синтез траекторий спуска («короткие», «протяжен¬
ные», оптималыше и т. п.).
3. Определение вида спуска (управляемый, неуправ¬
ляемый и др.)«
4. Выбор способа управления (управление эффектив¬
ным качеством, двухканальное управление, управление
баллистическим параметром).
5. Определение основных проектно-баллистических
характеристик КА (располагаемое аэродинамическое
качество, баллистический параметр).
6. Разработка алгоритмов навигации и управления.
7. Анализ систем мягкой посадки (реактивная, пара¬
шютная, самолетная и др.).
8. Задачи баллистико-павигациоиного управления
полетом (включая задачи предполетного и послеполетного
анализа).
Каждая из названных проблем в свою очередь объ¬
единяет большое число сложных задач, общее решение
которых требует огромного количества времени, и при
этом бессистемный подход не гарантирует получения
рационального решения, ибо зачастую даже оптимальное
решение различных задач в отрыве их друг от друга не
приводит к хорошему результату в целом. Все задачи
должны быть взаимно увязаны, по каждому вопросу не¬
обходимо иметь исчерпывающее решение или по крайней
мере ряд частных решений, которые можно использовать
при комплексном анализе. Окончательное решение тре¬
бует участия специалистов разного профиля, что также
увеличивает общие трудности, так как формализация
задач зачастую невозможна. В силу этого, для получения
удовлетворительного комплексного решения необходимо
придерживаться при проведении исследований опреде¬
ленной последовательности.
На первом этапе исследований с учетом имеющегося
практического опыта, теоретических и экспериментальных
исследований определяются главнейшие направления и
соответственно основные задачи, требующие первоочеред¬
ного решения. На следующем этапе с использованием
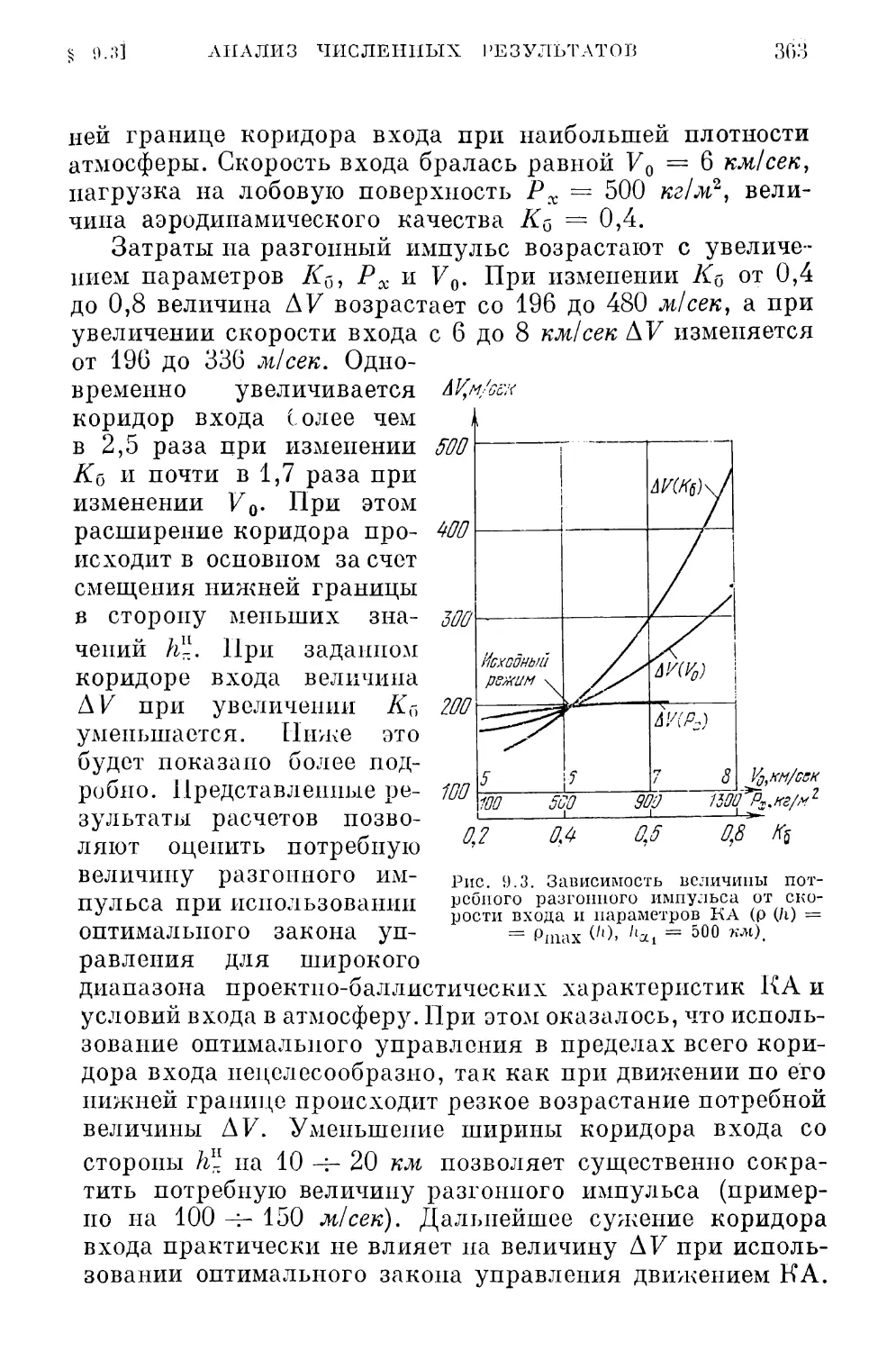
приближенных и оптимальных методов или путем парамет¬
рических расчетов проводится решение основных задач.
ВВЕДЕНИЕ
13
Поело того как определены основные особенности и труд¬
ности, выявлены целесообразные пути преодоления этих
трудностей, следует приступать к определению основных
проектно-баллистических характеристик КА, затем про¬
водить исследование возмущенного движения и синтези¬
ровать алгоритмы управления, реализующие полет по выб¬
ранным траекториям. Естественно, результаты исследо¬
ваний каждого последующего этапа используются для
уточнения предыдущих решений. Кроме того, по мере
накопления информации осуществляется комплексное
согласование найденных решений с учетом поставленных
целей и технических возможностей.
13 соответствии со сказанным в книге будет использо¬
ваться следующая последовательность расчетов и исследо¬
ваний:
— исследование класса возможных траекторий движе¬
ния в атмосфере;
— выбор основных проектно-баллистических характе¬
ристик КА;
— анализ возмущенных траекторий и определение
алгоритмов управления, реализующих спуск по заранее
выбранным или формируемым па борту траекториям.
Указанный подход и выделенные задачи исследований
являются общими при организации спуска КА в атмосфере
любой планеты. Однако специфические особенности
каждой планеты (прежде всего различные характеристики
их атмосфер) не позволяют получить универсального ре¬
шения перечисленных выше основных баллистико-иавига-
Цйоппых проблем спуска, которое было бы пригодно для
осуществления спуска КА в атмосфере любой планеты.
В предлагаемой вниманию читателей книге рассмотре¬
ны возможные пути решения основных баллистико-нави-
гациоипых задач торможения в атмосфере Марса. 11 глав
книги тематически разбиваются па 3 раздела. Первый
раздел, состоящий из трех глав, посвящен выявлению
основных особенностей движения КА в атмосфере Марса
и содержит общую постановку задач торможения. Глава
1 носит вспомогательный характер, в ней приводятся
краткие сведения о планете, ее атмосфере, поверхности и
рельефе.
Вторая глава начинается с рассмотрения схем полета
КА для выявления условий входа и возможных видов
14
ВВЕДЕНИЕ
движения в атмосфере. 13 дальнейшем изучаются три ос¬
новных случая торможения:
— прямой спуск с траектории гиперболического пере¬
лета;
— выведение КА на орбиту ИСМ с предварительным
аэродинамическим торможением в атмосфере;
— спуск с орбиты ИСМ.
Проведенный анализ траекторий показал, что основ¬
ные особенности спуска определяются разреженностью
атмосферы Марса, благодаря чему оказывается невозмож-
ным полностью погасить энергию КА пассивным путем,
в отличие от спуска в атмосфере Земли и тем более Венеры.
Это приводит к необходимости организации движения по
таким траекториям, на которых работа сил аэродинами¬
ческого торможения максимальна.
Большой интерес представляет способ выведения КА
на орбиту ИСМ с предварительным аэродинамическим
торможением. Во многих случаях этот способ имеет боль¬
шие энергетические преимущества по сравнению с приме¬
нявшимся до сих пор активным способом торможения
(КА типа «Марс», «Викинг»), но требует решения ряда
сложных задач:
— обеспечение высокоточного входа в плотные слои
атмосферы;
— создание КА, который должен функционировать в
течение длительного времени после прохождения плотных
слоев атмосферы;
— разработка совершенной системы управления КА,
которая должна функционировать па участке подлета к
планете, прохождения плотных слоев атмосферы и на
внеатмосферном участке с целью формирования орбиты
ИСМ.
Глава 3 посвящена исследованию траекторий невоз¬
мущенного движения. Ее решение начинается с выбора
критерия оптимальности. Приведенные материалы пока¬
зывают, что в качестве основного критерия оптимальности
при решении задачи спуска следует принимать условие
минимума массовых затрат на систему мягкой посадки.
Необходимость комплексного анализа траектории на уча¬
стке основного аэродинамического торможения и мягкой
посадки приводит к большим математическим и вычисли¬
тельным трудностям при синтезе оптимальных траекторий.
ВВЕДЕНИЕ
15
]3 главе приводятся описание возможных систем мягкой
посадки (СМИ), математическая модель движения КА и
предполагаемый путь решения поставленной задачи, кото¬
рый заключается в следующем. Сначала анализируется
участок работы СМП с целыо выработки требований к
участку основного аэродинамического торможения. Затем
проводится поиск оптимального управления на участке
аэродинамического торможения, удовлетворяющего най¬
денным условиям.
Раздел 2 (главы 4—8) определяет основное содержание
книги и посвящен рассмотрению проблем прямого спуска
КА па поверхность Марса. Материал в разделе компону¬
ется следующим образом. В главах 4 и 5 проводится
решение основных задач, возникающих на участке мягкой
посадки. Для двух типов СМГ1 — реактивной и парашют¬
но-реактивной — исследуются оптимальные режимы
снижения, определяется рациональный диапазон харак¬
теристик и анализируется влияние начальных условий
на массу СМП.
Проведенные исследования показали, что масса реак¬
тивной СМП тем меньше, чем меньше скорость и величина
угла наклона траектории к моменту начала ее работы, а в
случае парашютно-реактивной СМП — чем больше, при
заданной скорости, высота, на которой включается систе¬
ма посадки. Полученные результаты позволяют существен¬
но упростить задачу синтеза оптимальных траекторий
спуска в атмосфере Марса, так как ее решение можно про¬
водить только на участке основного аэродинамического
торможения с использованием простых критериев опти¬
мальности без специального рассмотрения участка мягкой
посадки.
В главе 6 приводятся результаты решения задачи опти¬
мизации траекторий спуска тга участке основного аэроди¬
намического торможения из условия минимума конечной
скорости; для К А различных типов: скользящего (с ве¬
личиной аэродинамического качества Кишх 0,7), с
несущим корпусом (А1|1;1Х 1,5) и космического самолета
(^тах ~ 2,4). При этом рассматриваются различные
способы управления КА: углом крена, углом атаки и
путем совместного изменения угла крена и угла атаки.
Проводится сравнение эффективности каждого из рассмат¬
риваемых способов управления для всех указанных ти-
16
ВВЕДЕНИЕ
нов КА. Задачи решаются с использованием принципа
максимума Понтрягииа. Анализ необходимых условий
оптимальности позволяет выявить очень важное свойство
траекторий минимальной конечной скорости, заключа¬
ющееся в неединственности оптимального управления.
Это позволяет в рамках критерия минимальной конечной
скорости проводить улучшение траекторий по дополни¬
тельным критериям. В частности, приводится решение за¬
дач максимизации зоны маневра КА, минимизации време¬
ни спуска и максимальной перегрузки на траекториях
минимальной конечной скорости спуска.
Для оценки эффективности найденных законов управ¬
ления осуществляется их сравнение с более простыми
программами спуска КА.
Глава 7 посвящена выбору типа КА и определению его
основных проектно-баллистических параметров. В ней
дается краткий анализ основных направлений, определя¬
ющих облик КА. Приводится решение некоторых задач
баллистического проектирования КА на основе анализа
оптимальных траекторий. Это задачи выбора способа уп¬
равления КА и определения границ применимости КА раз¬
личных типов. Показывается, в частности, что, в силу
особой связи между приведенной нагрузкой на лобовую
поверхность и аэродинамическим качеством, при решении
задачи о минимуме конечной скорости не всегда выбор КА
с большим значением аэродинамического качества являет¬
ся иаилучшим.
В заключении главы 7 рассмотрена экстремальная за¬
дача по отысканию оптимального управления КА из усло¬
вия максимума конечной высоты. Показано, что задачи
максимизации конечной высоты и минимизации конечной
скорости спуска КА эквивалентны по структуре оптималь¬
ного управления и по методам решения. Это существенно
облегчает построение оптимальных траекторий. Матери¬
алы исследований, содержащиеся в главах 6 и 7, дают
достаточно полное представление об оптимальных траек¬
ториях спуска КА с различными значениями проектно-
баллистических параметров.
1В соответствии с изложенной методологией приводятся
материалы следующего этапа исследований, заключающе¬
гося в анализе возмущенного движения и синтезе алго¬
ритмов управления спуском. Рассмотрению этих задач
■ПВЕДЕННЕ
17
посвящена глава 8. Для решения поставленных задач
авторами сформулирован принцип гарантирующего управ¬
ления. Введение специального термина продиктовано тем,
что при спуске па планету необходимо обеспечить гаранти¬
рованную мягкую посадку даже в случае неблагоприятных
предельных значений возмущающих факторов, а ограни¬
чение, которому должен удовлетворять функционал, носит
односторонний характер, т. е. конкретная величина
функционала управления, реализующаяся в процессе
спуска, не играет принципиальной роли. С использовани¬
ем этого принципа в главе проведен синтез как простых
алгоритмов управления, предполагающих применение
простых измерительных и вычислительных средств, так
и достаточно сложных адаптивных алгоритмов с примене¬
нием бортовой ЦВМ и инерциальпой системы навигации.
При этом рассматриваются непрерывные и дискретные
алгоритмы управления. Наибольшее внимание уделяется
управлению конечной скоростью спуска КА. Вместе с тем
приводятся примеры использования принципа гарантиру¬
ющего управления конечной высотой.
Третий раздел книги (главы 9 — 11) посвящен изуче¬
нию проблем торможения КА в атмосфере при реализации
орбитально-десантной схемы спуска. Методы исследова¬
ний используются те же, что и при анализе прямого спуска
КА. В главе 9 приводятся результаты решения экстре¬
мальной задачи по определению оптимального закона уп¬
равления КА при выведении его на орбиту ИСМ с предва¬
рительным аэродинамическим торможением. При этом в
результате обсуждения проблемы выявляется достаточно
простой критерий оптимизации траектории движения в
атмосфере — максимум скорости КА в апоцентре заданной
орбиты. Задача решается с использованием принципа
максимума Понтрягина. Проводится анализ оптимальных
траекторий и формулируются требования к основным
проектно-баллистическим характеристикам КА в зависи¬
мости от ширины навигационного коридора входа. В главе
10 рассмотрена задача синтеза алгоритма управления
КА на участке аэродинамического торможения и ракетно-
динамического маневра с целыо формирования пред¬
варительной орбиты ИСМ. Результаты моделирования
предлагаемых алгоритмов управления КА показывают
принципиальную возможность реализации при совремсп-
18
ВВЕДЕНИЕ
ном уровне развития космической техники способа фор¬
мирования орбиты ИСМ с предварительным аэродинами¬
ческим торможением.
И наконец, в главе 11 рассмотрены вопросы спуска КА
с орбиты ИСМ. Этот способ является более сложным по
сравнению с прямым спуском, однако его использование
имеет ряд преимуществ, которые оказывают заметное влия¬
ние па успешное решение задачи мягкой посадки. При
реализации этого способа оказывается возможным учесть
ряд факторов, которые не принимаются во внимание при
прямой посадке, что в свою очередь позволяет осуществить
более гибкий выбор рациональной траектории спуска.
Кроме того, в этом случае заметно облегчается работа си¬
стемы управления спуском КА, включая решение задачи
точной посадки в заданном районе поверхности планеты.
Спуск с орбиты ИСМ выдвигает ряд новых требований к
оптимизируемому функционалу, заключающихся в том,
что необходимо в комплексе учитывать затраты на систему
мягкой посадки и па сообщение тормозного импульса при
сходе с орбиты. В главе 11 излагается способ решения этой
задачи и определяются оптимальные условия входа КА
в атмосферу, обеспечивающие доставку на поверхность
максимальной массы: полезного груза.
Таким образом, представленные в книге материалы
затрагивают весь комплекс основных баллистико-павига-
циониых задач движения КА в разреженной атмосфере
Марса, показывают принципиальную возможность орга¬
низации аэродинамического торможения КА для его мяг¬
кой посадки на поверхность или выведения па орбиту
ИСМ. Этот материал является исходным для решения в
целом проблемы торможения КА в атмосфере Марса, для
проектирования и создания КА, предназначенных для
спуска па поверхность этой планеты или выведения на ор¬
биту с использованием предварительного аэродинамичес¬
кого торможения.
РАЗДЕЛ 1
ОБЩАЯ ПОСТАНОВКА ПРОБЛЕМЫ
УПРАВЛЕНИЯ ДВИЖЕНИЕМ
В АТМОСФЕРЕ МАРСА
ГЛАВА 1
ПЛАНЕТА МАРС
§ 1.1. ОБЩИЕ СВЕДЕНИЯ
Приведем некоторые общие сведения о планете Марс,
ее атмосфере, поверхности, рельефе и т. д. с тем, чтобы
понять, в каких условиях происходит спуск КА, выявить
основные особенности и правильно сформулировать тре¬
бования и ограничения в постановке решаемых задач.
Марс относится к планетам земной группы и является
первой внешней планетой относительно Земли. Полный
оборот вокруг Солнца Марс совершает за 1 год и 11 меся¬
цев. Он движется в ту же сторону, что и Земля, и через
каждые 2 года 50 дней Земля обгоняет Марс на целый
оборот. Расстояние от Земли во время противостояний
составляет от 56 до 102 млн. километров. Противостояния
наиболее удобны для наблюдений, так как в это время
Марс не только близок к Земле, но и виден всю ночь в
отраженных лучах Солнца.
Ось вращения планеты наклонена к плоскости орбиты
почти так же, как земная, поэтому па Марсе, как и на
Земле, происходит смена времен года, только их продолжи¬
тельность вдвое больше земных. Марсианские сутки лишь
па 37 мин превышают земные. Масса планеты прибли¬
зительно в 10 раз меньше земной; гравитационный пара¬
метр Марса равен ц =42 828,48 км?/сек1. Экваториальный
радиус Марса составляет R,)K =3400 км, полярный ради¬
ус 7?,, = 3373 км, средний радиус принимается равным
Я =3395 км. Коэффициент геометрического сжатия
оц = 0,08; коэффициент динамического сжатия с1 =
=—0,002013. Угловая скорость вращения Марса со =
=0,708821766-10-4 секГЕ Первая и вторая космические
скорости соответственно равны V\ = 3,55 км!сек, Vц =
=5,06 км/сек. Ускорение силы тяжести на поверхности
g'o — 3,72 м/сек1.
2о
ПЛАНЕТА МАРС
[гл. i
Физическая поверхность Марса может бj»rrь энпроксп-
мирована трехосным эллипсоидом с полуосями Аф —
—3400,12 км, Вф —3394,19 км, Сф —3372,45 км. Эта по¬
верхность не является эквипотенциальной. Уровню дав¬
ления атмосферы у поверхности приблизительно в
6,1 мбар соответствует трехосный эллипсоид с полуосями
Л! =3396,67 км, В1 =3395,23 км, Сг =3377,22 км.
Небесные экваториальные координаты северного по¬
люса Марса, задающие положение оси вращения планеты,
определяются формулами
а - 316°50'38",4-'г 2351",88-Тс,
б = 53°00'32",4 + 1275", 12- Те,
где а — прямое восхождение, б — склонение, Т(1 — вре¬
мя в тропических столетиях:
(J. IX) — 2433282,4234
1 е 36524,22
J. D.—текущая юлианская дата; (J. D.)o =2433282,4234
(1 января, полночь 1950 г.—начальная эпоха); 36524,22 —
число эфемеридных суток в тропическом столетии.
Наклонение экватора Марса к плоскости его орбиты:
/ =25°,19969.
§ 1.2. ПОВЕРХНОСТЬ ПЛАНЕТЫ И ЕЕ РЕЛЬЕФ
На поверхности Марса различают области трех основ¬
ных цветов [59]:
— оранжево-желтые, окружающие темные пятна и
названные «материками» («континентами»);
— темные области, получившие название «морей»,
«озер» и т. п.;
— белые образования у полюсов планеты — «полярные
шапки».
Очертания светлых и темных областей в общем устой¬
чивы, что позволяет составлять карты поверхности Марса
в ареографических (марсианских) координатах.
Открытые водоемы на Марсе не обнаружены (водоем
диаметром более 300мдавал бы заметные блики от Солнца).
Материки имеют постоянную светлую окраску, они зани¬
мают 2/3 площади поверхности планеты.
ПОВЕРХНОСТЬ ПЛАНЕТЫ И ЕЕ РЕЛЬЕФ
21
Данные радиолокационных наблюдений и исследований
в инфракрасных лучах согласуются с предположением о
том, что в состав вещества светлых областей в качестве
основной компоненты входит очень топкая и рыхлая квар¬
цевая пыль, образующая покров, который достигает в
некоторых районах глубины порядка нескольких метров*
Темные области со сменой марсианских времен года
периодически меняют свою окраску. Весной и летом они
темнеют, приобретая более ясные очертания и зелено-голу¬
бой оттенок, причем темная окраска распространяется
со стороны «тающей» полярной шапки по определенным
направлениям, а осенью и зимой блекнут, окрашиваются
в желто-коричневые тона, и границы их становятся рас¬
плывчатыми. Отдельные темные участки иногда на про-
тяжеиии нескольких месяцев или лет изменяют свои очер¬
тания.
Средняя температура поверхности планеты 220 + 10 9К.
Эта величина относится к среднему расстоянию планеты
от Солнца. В перигелии средняя температура возрастает
приблизительно на 20°, в афелии на столько же уменьшает¬
ся. Температура поверхности по планете меняется в диа¬
пазоне от 300 °К на экваторе до 150 °К в полярных шапках.
Рельеф марсианской поверхности имеет несколько ти¬
пичных образований, различных по своей топографии:
—кратерная местность;
--слабо расчлененные равнины;
—территории с хаотическим рельефом и изломами;
—в ул к а иичес кие образов ания;
—каналы и каньоны.
Поверхность первого типа характеризуется различной
формой кратеров и различной плотностью насыщения ими.
Области «высокой плотности», как правило, покрыты силь¬
но разрушенными, примыкающими друг к другу кратера¬
ми. Области «средней плотности» образованы сильно разне¬
сенными кратерами с волнистой поверхностью меящу ними.
Для этих равнин характерны кратеры со средней сохран¬
ностью, диаметром до 100 км. Меячкратерные равнины за¬
частую пересечены хребтами с сильно изрезанными скло¬
нами. Кроме того, имеется еще один вид образований,
представляющий из себя большие эллиптические впадины,
окруженные приподнятыми валами отложений грубой
структуры.
22
ПЛАНЕТА МА! С
[ГЛ. 1
Второй тип поверхности — слабо расчлененные рав¬
нины — содержит обычно малое число структурных де¬
талей. Эти равнины располагаются чаще всею в обширных
низменностях неправильной формы.
Территории с хаотическим рельефом и изломами ха¬
рактеризуются сложной мозаикой изломанных блоков и
плит и располагаются обычно ниже поверхности окружа¬
ющих геологических структур.
Вулканические образования по своему виду условно
делятся на щиты, купола и конусы. Вулканические щиты
имеют неровные вогнутые склоны, завершающиеся каль¬
дерами. Они достигают в диаметре ООО км и по высотам до
10 км. Вулканические купола по размеру меньше щитов.
Их диаметр более 100 км. Они имеют сглаженные выпук¬
лые склоны и вершинные кальдеры с плоским дном и кру¬
тыми стенками. Вулканические конусы представляют из
себя низкие широкие образования с ровной поверхностью
склонов, па вершинах конусов обычно имеются плоскодон¬
ные кратеры большого размера.
Важным элементом марсианской поверхности являют¬
ся каналы и каньоны. Каналы представляют собой волни¬
стые структуры, высеченные в поверхности. Они образуют
сложный переплетенный узор. Вдоль линии простирания
каналов иногда встречаются террасы.
Каньоны состоят из ряда почти параллельных линей¬
ных депрессий. Они имеют крутые стенки. Глубина кань¬
онов достигает 1 — 3 км при средней ширине 100 — 150 км
и длине до 2500 км. От стен каньонов часто тянутся
большие овраги и ущелья, напоминающие земные, раз¬
мытые текущей водой. Параллельно главным каньонам
иногда располагаются цепочки углублений, не имеющие
окружающих валов.
Отметим, что от типа рельефа существенно зависят ук¬
лоны поверхности Марса. Наибольшие уклоны характер¬
ны для хаотического и каньояного типов. Средние уклоны
па базе 50 км составляют около 1°.
§ 1.3. АТМОСФЕРА МАРСА
Хиушческий состав. Анализ сведений о химическом
составе атмосферы, полученных различными методами
(прямые измерения с КА «Марс-6», инфракрасная спектро¬
скопия с гюмощыо наземных и космических средств, ульт-
АТМОСФЕРА МАРСА
23
рафиолетовая спектроскопия па американском спутнике
«Орбитальная Астрономическая Обсерватория» и т. п.),
показал, что основной составляющей атмосферы является
углекислый газ С02. Остальная часть атмосферы состоит
из аргона и других малых примесей: кислорода, воды и
окиси углерода. Содержание азота не превышает 5%
[40, 47].'
Полное давление у поверхности. Наиболее достоверны¬
ми результатами оценки величины полного давления па
среднем уровне поверхности планеты считаются данные,
полученные при радиорефракциошшх измерениях во
время радиозатмения КА «Маринер-9». Согласно этим дан¬
ным среднесезонное среднесуточное давление составляет
р0 = 5,4 + 0,1 мбар. Следует отметить, что при обработке
результатов этих измерений принималась гипотеза о
100 %-м содержании углекислого газа в атмосфере Majpc-a.
Прямые измерения давления марсианской атмосферы
с помощью КА «Марс-6» [1, 42] подтвердили оценки,
полученные ранее радиорефракциопиыми и спектроско¬
пическими методами. Давление у поверхности в районе
посадки оценивается приблизительно в 6 мбар.
Максимальное отклонение давления на среднем уровне
за счет суточных колебаний оценивается в +0,2 мбар.
Причем наибольшее давление у поверхности имеет место
около 15 часов местного времени, наименьшее — около
6 часов.
Температура атмосферы у поверхности планеты сильно
зависит от широты и сезона. Средняя по сезонам и широтам
температура атмосферы у поверхности по данным назем¬
ных спектроскопических и радиорефракциошшх измерений
составляет 210 °К. Эта температура должна рассматривать¬
ся как результат экстраполяции к поверхности тропосфер¬
ного температурного профиля, имеющего место на высотах
более 2 — 3 км. Суточные колебания этой экстраполирован¬
ной температуры невелики (примерно +10°), в то время
как температура самой поверхности и непосредственно
прилегающих к пей слоев атмосферы колеблется в течение
суток в экваториальных и средних широтах примерно на
100°. В экваториальном поясе температура атмосферы у
поверхности планеты принимается в среднем равной 220 °К
(летом 2«>0 °К и зимой 190 °К). В период пылевой бури тем¬
пература атмосферы возрастает до 260 °К.
24
ПЛАНЕТА МАРС
[ГЛ. 1
§ 1.4. ВЕТРЫ В Ш1ЖШШ АТМОСФЕРЕ
Известные в настоящее время экспериментальные дан¬
ные о динамике процессов нижней атмосферы Марса,
полученные по наблюдениям с Земли и при помощи авто¬
матических КА, тте позволяют составить достоверной
картины нолей основных метеорологических элементов —
температуры, давления и скорости ветра. Поэтому многие
важные для целей инженерного проектирования характе¬
ристики выведены из анализа основных динамических и
термодинамических соотношений в атмосфере и результа¬
тов численного моделирования общей циркуляции.
Проведенный анализ показал, что для северного лета
вблизи поверхности имеется хорошо выраженный поток
через экватор с юга на север, а на больших высотах — в
обратном направлении. Максимум средней величины ме¬
ридиональной компоненты скорости достигает порядка
10 м/сек в районе экватора на высоте 15 км.
Наличие меридиональных потоков согласуется с пере¬
носом массы от тающей северной полярной шапки к уве¬
личивающейся южной. С Земли в этот период наблюдается
перемещение тонкой белой мглы от полюса к полюсу.,
Средний поток в летнем (северном) полушарии устойчив
и почти невозмущен. Поток в зимней полусфере неустой¬
чив и образует циклопические волны. Максимальные зна¬
чения скорости ветра вблизи поверхности следует ожидать
в южных широтах (~20° ю. ш.).
Исключительно сильные западные ветры могут наблю¬
даться на больших высотах. На высоте 15 км значение
скорости для 40° ю. ш. достигает 70 м/сек. Среднее значе¬
ние скорости ветра составляет 0,2 -к- 0,3 от максималь¬
ного. С вероятностью 0,8 --к- 0,9 скорость ветра не пре¬
вышает максимальной величины.
Следует отметить, что указанные значения скоростей
ветра могут быть увеличины в 2—3 раза за счет локальных
ветровых систем, порождаемых в протяженных впадинах,
горных системах, длинных склонах и крупных кратерах.
В атмосфере Марса должны быть четко выражены суточ¬
ные изменения скорости ветра, объясняемые резким темпе¬
ратурным различием между дневной и ночной сторонами
планеты. Суточные вариации скорости ветра могут дости¬
гать амплитуды порядка 20 м/сек,
ОЬЛАТчА
25
§ 1.5. ОБЛАКА
Облака обычно имеют от 300 до 2000 км в поперечнике.
Они наблюдаются сравнительно редко (в среднем 2—4
раза в год). Облачные образования в атмосфере Марса
разделяются по цвету па желтые, синие и белые.
Желтые облака и помутнения, порождаемые вероятнее
всего пылевыми бурями, наблюдались как образования
с самыми различными пространственными масштабами в
видимом и инфракрасном диапазонах спектра по всему
диску. Они появляются в нижних слоях атмосферы, на
высоте примерно 5 км и ниже. Максимальное их число
наблюдается при прохождении Марсом перигелия и мини¬
мальное в афелии. Это объясняется большим потоком
солнечной радиации в перигелии и связанным с этим
увеличением температурных градиентов, что приводит к
развитию мощных ветровых систем, способствующих
поднятию песка и пыли.
Облака состоят, ио-видимому, из мелкой пыли, напри¬
мер, из частиц гидрата окиси железа размером в несколько
микрон. Особенно сильные помутнения наблюдались во
время великого противостояния в 1956 г., когда коэффи¬
циент прозрачности атмосферы уменьшился в 3 раза и было
отмечено даже полное исчезновение южной полярной шап¬
ки на период с 15 августа по 15 сентября. Скорость пере¬
мещения желтых облаков колеблется от 6 до 130 м/сек.
Синие облака, видимые в фиолетовых и ультрафиоле¬
товых лучах, возникают в высоких слоях атмосферы во
время понижения ее температуры и поэтому наблюдаются
вблизи линии терминатора. Эти облака обычно интерпре¬
тируют как местное уплотнение фиолетового слоя (фиоле¬
товой дымки), лежащего на тех же высотах и состоящего,
вероятно, из мелких кристалликов льда. Этот слой не
пропускает коротковолнового излучения, но иногда в нем
происходят кратковременные прояснения, и тогда поверх¬
ность Марса можно наблюдать в синих лучах.
Белые облака наблюдаются в видимых и инфракрасных
лучах. Они имеют, по-видимому, ту же природу, что и
синие облака, но состоят из более крупных кристалликов
льда. Основная масса белых облаков концентрируется в
полосе от 20° ю. ш. до 25° с. ш. Скорость их перемещения
меняется от 2 до 15 м/сек. Большая часть их движется
26
ПЛАНЕТА МАРС
[ГЛ. 1
со скоростями, меньшими, чем 10 м!сек. Преимуществен¬
ное движение этих облаков происходит в широтном направ¬
лении. Количество белых облаков уменьшается по мере
приближения Марса к афелию.
§ 1.6. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ МАРСА
С ПОМОЩЬЮ КА «ВИКИНГ»
В период подготовки рукописи книги появился ряд
публикаций по первым результатам исследования Марса
с помощью КА «Викинг-1, 2», которые углубляют наши
знания об этой планете и ее атмосфере *). Кратко изложим
некоторые из этих результатов.
КА «Викинг-1» и «Викинг-2» были запущены к Марсу
20 августа и 9 сентября 1975 г. Соответственно через 10 и
11 месяцев полета они достигли окрестности планеты и
вышли па орбиту спутников, а 20 июля и 3 сентября 1976 г.
спускаемые аппараты отделились от орбитальных и совер¬
шили мягкую посадку на поверхность Марса.
Посадочный аппарат КА «Викинг-1» опустился в районе
равнины Хриса (Cliryse) с координатами 22,5° с. ш. и
48° з. д. Дно котловины оказалось довольно плоским,
и отклонение аппарата от местной вертикали составило
менее 3°.
Посадочный аппарат КА «Викииг-2» достиг поверхности
в районе равнины Утопия (Utopia) в 6400 км к северо-вос¬
току от «Викинга-1». Координаты точки посадки 47,97°
с. ш. и 225,7° в. д. Посадочный аппарат на грунте наклонен
на 8,2° в западном направлении вследствие того, что под
опору шасси попал камень. Это, однако, не помешало
проведению экспериментов и, в частности, ие препятство¬
вало нормальной работе грунтозаборника.
Рельеф планеты. Преобладающие формы рельефа
области Хриса — равнины, усеянные кратерами и пере¬
сеченные горными грядами. Эти равнины напоминают
моря на Луне. Предполагается, что марсианские равнины,
как и лунные моря, образованы потоками лавы, обладав¬
шей относительно малой вязкостью в диапазоне темпера¬
тур плавления. По составу грунта они, очевидно, близки
*) Sky and Telescope, 1976, v. 52, № 3; Science News, 1976,
v. 110, №,\<j 8, 17, 18; Aviation Week and Space Technology, 1976, v.
105, №№ 7, 11, 13. См. также обзор [58].
§ 1.6] ИССЛЕДОВАНИЯ МАССА С ПОМОЩЬЮ КА «ВИКИНГ»
27
к базальтам. В этой же области встречаются отдельные
плато, возвышающиеся над равниной.
На южной и западной границах бассейна Хриса обна¬
ружены многочисленные детали, которые американские
ученые интерпретируют как признаки катастрофических
наводнений, однако посредине бассейна не обнаружено
никаких признаков накопления толстого слоя отложений.
Съемки поверхности Марса со спутника выявили не¬
которые неизвестные ранее типы ландшафтов. Например,
в области Хриса обнаружены разнообразных форм трещи¬
ны, расположенные на расстоянии нескольких километ¬
ров друг от друга. Они намного протяженнее трещин, ко¬
торые обычно возникают при остывании лавы. Подобные
трещины на Земле наблюдаются в Арктике и Антарктиде,
где они вызываются сезонным таянием и образованием
льда.
В свете новых данных ряд ученых выдвигает новые
гипотезы о полярных областях, считая их состоящими из
водяного льда.
Снимки полярной шапки показали чередующиеся
слои льда и пыли, нанесенной ветром. В некоторых слу¬
чаях видно, как верхний слой опускается, проникая
через нижележащие слои, а в самом этом верхнем слое
формируются новые слои. Полагают, что изучение слоев
может позволить получить представление о климатичес¬
ких изменениях на Марсе.
По мнению ряда ученых, в полярных областях нет пос¬
тоянных резервуаров углекислоты. Полярные области
представляют собой временные резервуары углекислоты:
в зимний сезон температура падает, и водяные пары кон¬
денсируются из атмосферы в шапках. Температура пони¬
жается и в некоторый момент становится достаточно низ¬
кой для конденсации С02 из атмосферы. С повышением
температуры летом С02 сублимирует в атмосферу, остав¬
ляя остаточную шапку водяного льда, которая полностью
не тает.
Поверхность планеты. Поверхность Марса в месте
посадки «Викинга-1» покрыта многочисленными мелкими
камнями и крупными валунами, между которыми находит¬
ся мелкозернистая порода, возможно, песок — продукт
эрозии вулканических пород. Многие камни имеют оспи¬
ны, как лава па Земле. На снимках, сделанных через
28
ПЛАНЕТА МАРС
[ГЛ. 1
светофильтры, поверхность Марса имеет красноватый цвет.
Это считают следствием процесса окисления железа при
высоком содержании кислорода в прошлые эпохи или при
современном низком его содержании под длительным воз¬
действием ультрафиолетового излучения. Наиболее веро¬
ятным минералом, ответственным за красноватый цвет,
считают лимонит. У камней и валунов наблюдается зеле¬
новатый оттенок, что может быть как собственным свойством
материала поверхности, так и результатом выветривания.
По мнению американских ученых, марсианский ландшафт
в определенной степени напоминает ландшафт пустынь
в западной части США.
Поверхность в месте посадки КА «Викинг-2» оказалась
в основном аналогичной.
Весьма интересны данные по исследованию состава
марсианского грунта. Оказалось, что основным элементом
марсианского грунта, так же как земного и лунного,
является кислород (примерно 50%), затем идет кремний
(15 -ж 30%), третьим же по распространенности элементом
является железо (12 -ж 16%), а не алюминий, как па Зем¬
ле. Содержание алюминия в марсианском грунте равно
2-ж 7%. Кроме того, обнаружены фосфор, сера, хлор,
калий, кальций, титан, ванадий, хром, магний, кобальт,
никель, медь, цинк, галлий, мышьяк, селен, бром, ру¬
бидий, стронций, итрий, цирконий, ниобий, молибден
и другие.
Атмосфера Марса. Снимки Марса, полученные с около-
марсианской орбиты, а также исследования с помощью
инфракрасных спектрометров позволили получить ряд
интересных фактов об атмосфере. В частности, над райо¬
ном Тарсис (Tharsis) наблюдались сравнительно плотные
белые облака, скорость перемещения которых в северном
полушарии не превышала 10 м/сек, а в экваториальной
зоне —15 -ж 45 м/сек.
Оказалось, что содержание паров воды в марсианской
атмосфере резко различается в зависимости от широты:
от меттее 0,1 мкм осажденной воды на крайнем юге до при¬
мерно 100 мкм вблизи северной полярной шапки, т. е.
в высоких широтах с е в ер по гоПт о л у ша р ия в летний период
содержание паров воды резко возрастает. Например, из¬
мерения вдоль 180-го меридиана показали, что на экваторе
ато содержание составляет 6 мкм осажденной воды,wна
§ 1.6] ИССЛЕДОВАНИЯ МАРСА С ПОМОЩЬЮ КА «ВИКИНГ» 29
30° с. ш.— 15 мкм, па 00° с. in. — 40 мкм и достигает мак¬
симума (почти 80 мк) на 75° с. пт., у края полярной шапки.
13 полностью покрытых льдом районах содержание па¬
ров падает до 30 -г- 40 мкм (по некоторым данным возра¬
стает до 100 мкм). Содержание паров зависит также от
времени суток и высоты места относительно среднего уров¬
ня Марса. Суточные изменения объясняются испарением
поверхностного льда с восходом Солнца и появлением ту¬
мана. Низменные области характеризуются наиболее вы¬
соким содержанием паров, возвышенные области — низ¬
ким содержанием.
Полученные «Википгом-1» средние значения давления,
температуры и температурного градиента в тропосфере
и стратосфере хорошо согласуются с данными измерений
J i L
0 Z Ь 6 DMOJD
1нс. 1.1. Данные по температуре в градусах Кельвина («Марс-6» и «Викинг-1»)
и но плотности, («Марс-СД-
от высоты 80 км до поверхности, переданными в 1974 г.
спускаемым аппаратом советской межпланетной станции
«Марс-6» (рис. 1.1). На высотах от 90 до 25 км температу¬
ра Изменяется от 165 до 120 °К, локальные максимумы
температуры отмечаются на высотах около 65 и 30 км.
Средний температурный градиент в тропосфере равен 3,7°
па 1 км. В месте посадки КА «Викинг-!» максимальная тем-
п е р а т ура с о с т а в л я л a 2W 7 К 7 д i и и т: л г а л ъ н а я температура.
30
ПЛАНЕТА МАГС
[ГЛ. 1
188 °К. Непосредственно после посадки КА «Викинг-1» бы¬
ло зарегистрировано атмосферное давление у поверхности
7,7 мбар, которое через 85 марсианских суток упало до
6,5 мбар.
В месте посадки «Викинга-2» средняя максимальная
температура составляет 242,5 °К, минимальная темпера¬
тура 192 °К.
Средняя скорость ветра в области Утопия составляет
4,3 ж!сек, минимальная 1,1 м/сек, максимальная 7,2 м/сек.
Направление ветра в течение суток регулярно смещается
по часовой стрелке. Атмосферное давление у поверхности
в первые сутки после посадки было 7,74 мбар, а через 53
марсианских суток упало до 7,4 мбар.
Исследование состава атмосферы у поверхности Марса
в месте посадки «Викштга-1» показало, что атмосфера
состоит из углекислого газа (95%), азота (2 л- 3%),
аргона (1 -ч-2%) и кислорода (0,3%), т. е. подтвердилось
содержание азота в марсианской атмосфере и уточнилось
содержание аргона, количество которого предполагалось
значите л ьн о бол ыиим.
Из приведенных в настоящей главе материалов видно,
что решение задачи управления движением КА в атмосфе¬
ре Марса сопряжено со многими трудностями, вытекаю¬
щими из особенностей поверхности планеты и окружающей
среды. В частности, из-за исключительной разрежен¬
ности атмосферы возможности аэродинамического тормо¬
жения ограничены. Сложный рельеф поверхности с пере¬
падом высот в 10 и более километров приводит к постановке
специальной задачи — выбора районов посадки, кото¬
рые должны быть по возможности ровными и вместе с тем
находиться ниже среднего уровня поверхности. При этом
проблема мягкой посадки осложняется наличием большого
количества камней на поверхности планеты. Наличие
сильных ветров, пылевых бурь также относится к объек¬
тивным- факторам, существенно затрудняющим реализацию
спуска КА. Все это должно обязательно учитываться при
выборе схемы полета, разработке различных проблем
спуска, включая прежде всего проектирование КА.
Ip ABA 2
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ
В АТМОСФЕРЕ МАРСА
§ 2.1. УСЛОВИЯ ПОДЛЕТА КА К ПЛОТНЫМ СЛОЯМ
АТМОСФЕРЫ
Номинальные условия входа КА в плотные слои атмо¬
сферы полностью определяются параметрами подлетной
траектории, которые позволяют в общем случае рассчитать
вектор состояния х, рассматриваемый па некоторой высо¬
те /га — условной границе плотных слоев атмосферы:-
х = (*0; .т0; у о; 20; Vx0] Vy0; V z0),
где t0 — момент входа КА в плотные слои атмосферы;
• •> Ую — соответственно координаты и проекции
вектора скорости на оси выбранной системы координат.
В качестве условной границы плотных слоев атмос¬
феры принимается то максимальное значение высоты над
поверхностью планеты, на которой аэродинамичес¬
кая сила торможения КА становится соизмеримой (по¬
рядка нескольких процентов) с силой притяжения пла¬
неты.
Как известно, аэродинамическая сила Ra равна
Ла = Сл-?£-ЛИ,- (2.1)
где Cr — коэффициент аэродинамической силы, р — плот¬
ность атмосферы на высоте h, V — скорость полета, SM —
площадь миделя КА.
Из выражения (2.1) следует, что величина i?a, помимо
плотности, зависит от параметров спускаемого КА и ско¬
рости его движения. Отсюда ясно, что в каждом конкрет¬
ном случае одно и то же значение Rа для различных КА
будет достигаться на разных высотах ha. Это неудобно для
проведения исследований, и обычно во всех случаях вы¬
сота условной границы атмосферы Марса принимается
32
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ I ГЛ. 2
постоянной и равной 100 км. Внесенные этим допущением
погрешности в реальном полете оказываются весьма не¬
значительными. При полете КА выше условной грани¬
цы атмосферы в задачах спуска считается, что аэроди¬
намическая сила не оказывает влияния на движение аппа¬
рата.
Для проведения качественного анализа, выявления ос¬
новных особенностей и общих закономерностей движения
нет необходимости рассматривать пространственное дви¬
жение, привязываться к конкретной точке входа, что дает
знание компонент вектора состояния, а достаточно рас¬
сматривать лишь продольное движение в плоскости под¬
летной орбиты. В последнем случае за начальные условия
принимаются скорость входа V0 и так называемый угол
входа 0О — наклонение вектора скорости к местному гори¬
зонту на границе плотных слоев атмосферы.. За начальную
высоту принимается /г0 — /га.
Во мыогих случаях вместо угла 0О более удобно исполь¬
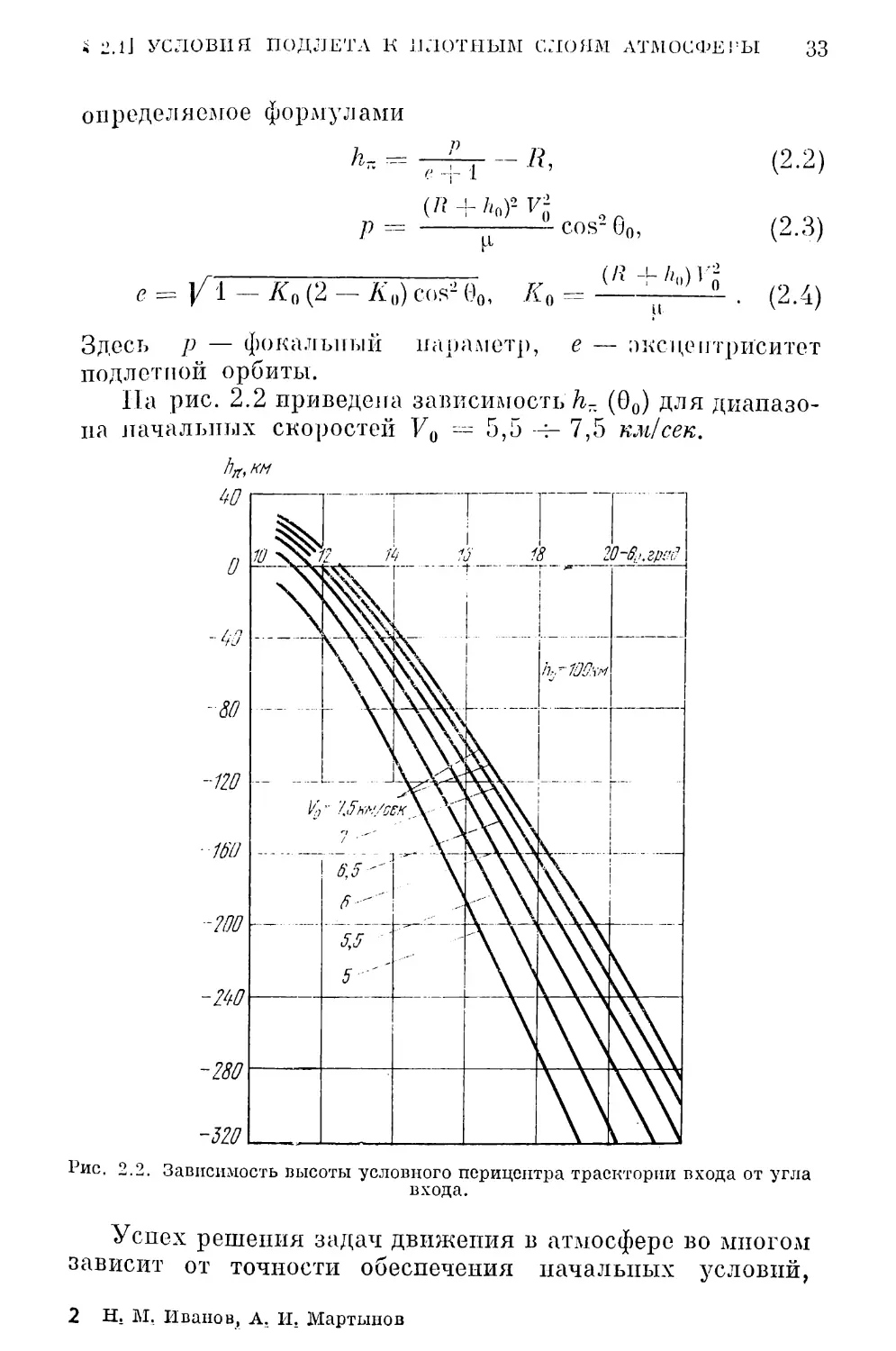
зовать высоту условного перицентра траектории входа h-
(рис. 2.1). Это то минимальное расстояние от поверхности
Местный йслобная границе атмосферы
планеты, на котором прошла бы траектория при отсутствии
атмосферы, т. е. высота перицентра оскулирующей под¬
летной гиперболической траектории. Между высотой
условного перицентра h~ и углом входа 0О для каждой
скорости входа существует однозначное соответствие,
4 2.1 J УСЛОВИЯ ПОДЛЕТА К ПЛОТНЫМ СЛОЯМ АТМОСФЕРЫ 33
определяемое формулами
h- = ]- R
е + 1 -П’
(л + Кf v\
р = -
1 и
COS2 0О,
(2.2)
(2-3)
e=fl-Ко (2 - А'о) cos4 Go, А0 = Sl±h)Vo . (2.4)
Здесь р — фокальный параметр, е — зксцеитриситет
подлетной орбиты.
На рис. 2.2 приведена зависимость h- (0О) для диапазо¬
на начальных скоростей V0 — 5,5 -л- 7,5 км/сек.
hrttKM
Вис. 2.2. Зависимость высоты условного перицентра траектории входа от угла
входа.
Успех решения задач движения в атмосфере во многом
зависит от точности обеспечеиия начальных условий,
2 Н. М. Иванов, А, И. Мартынов
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ [ГЛ.2
формирование которых начинается еще при отлете КА с
околоземной орбиты, когда выбирается и реализуется та
или иная межпланетная траектория полета. Последующи¬
ми коррекциями этой траектории и добиваются требуемых
условий входа. При этом скорость входа почти полностью
определяется выбранной схемой полета. Точность обес¬
печения; расчетного значения V0 достаточно высока и со¬
ставляет величину порядка нескольких метров в секун¬
ду. Такая погрешность обычно не оказывает существен¬
ного влияния на траекторию спуска.
Схемы полета. В настоящее время известно большое
число схем полета КА к планетам. Все они могут суще¬
ственно различаться по решаемым задачам, по сложно¬
сти реализации и баллистическим характеристикам. Обыч¬
но для их классификации используют следующие основные
признаки [2, 88]:
— сложность маршрута полета;
— возвращение или невозвращение КА к Земле;
— конструктивно-целевое назначение КА;
— баллистические характеристики схем и траектории
полета.
По сложности маршрута схемы полета КА к планетам
можно разбить на две группы:
— к одной планете (без возвращения к Земле);
— к нескольким планетам (как с возвращением, так
и без возвращения к Земле), например, схемы полета к
Марсу с возвращением к Земле (полет к двум планетам)
или полета к Марсу через Венеру с возвращением к Зем¬
ле (полет к трем планетам).
По конструктивно-целевым признакам можно выделить
следующие схемы полета межпланетных КА:
— пролетные (пролет у планеты для ее предваритель¬
ного изучения);
— десантные (посадка на поверхность планеты);
— орбитальные (вывод КА на орбиту искусствен¬
ного спутника планеты);
— комбинированные (различные комбинации перечи¬
сленных выше схем).
Для задач оптимизации траекторий перелета КА опре¬
деляющим является число импульсов, т. е. число активных
участков (участков включения двигательной установки)
для изменения скорости полета КА на траектории полета.
2.1] УСЛОВИЯ ПОДЛЕТА К ПЛОТНЫМ СЛОЯМ АТМОСФЕРЫ 35
Среди многочисленных схем полета к Марсу будем рас¬
сматривать только такие, которые предусматривают полет
КА в его атмосфере. Во всех случаях предполагается, что
КА стартует с орбиты ИСЗ на гиперболическую относи¬
тельно Земли траекторию.
Параметры стартовой гиперболической траектории
обеспечивают полет по переходной, эллиптической отно¬
сительно Солнца траектории между орбитами Земли и
планеты назначения. В сфере действия планеты КА дви¬
жется по гиперболической траектории. В прямых десант¬
ных схемах осуществляется затем непосредственный
спуск на поверхность Марса. Орбитально-десантные
схемы отличаются от прямых десантных тем, что КА с гипер¬
болической траектории сначала переводится на орбиту
ИСМ, а затем на поверхность планеты десантируется спус¬
каемый аппарат (СА).
В настоящее время обе схемы реализованы: полеты
советских КА «Марс» осуществлялись по прямой десант¬
ной схеме, а американских КА «Викинг» — по орбиталь¬
но-десантной схеме. Формирование орбиты ИСМ в послед¬
нем случае осуществлялось активным образом, т. е. путем
приложения тормозного импульса для гашения избытка
скорости.
В зависимости от величины импульса, сообщаемого
на орбите ИСЗ, полет КА к планете назначения будет
проходить либо по энергетически оптимальным, но дли¬
тельным по времени, либо по так называемым «ускорен¬
ным» траекториям. Достоинством последних является сок¬
ращение времени перелета. Вместе с тем в этом случае
существенно возрастают скорости входа КА в атмосферу:
У о ~ 7,5 -т- 10 км/сек по сравнению с У0 ~ 5,5 -= 7 км/сек
для энергетически оптимальных траекторий. Баллисти¬
ческие характеристики «ускоренных» схем могут быть в не¬
которых случаях существенно улучшены за счет попут¬
ного пролета Венеры: суммарная потребная характерис¬
тическая скорость КА для большинства циклов полета
уменьшается на 1 -г- 1,5 км/сек, а скорость входа до У0 =
= 7-:-8 км/сек.
Таким образом, в зависимости от схемы перелета к Мар-'
су возможны три вида движения КА в плотных слоях ат¬
мосферы:
— прямой спуск с гиперболической траектории;
2*
36
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ [ГЛ. 2
— переведение КА па орбиту ИСМ с использованием
предварительного торможения в атмосфере;
— спуск с орбиты ИСМ.
Диапазон возможных скоростей входа V0 в первых
двух случаях от 5,5 до 10 км/сек,а при спуске с орбиты ИСМ
от 3,5 до 4,7 км/сек.
При этом, как отмечалось выше, в каждой конкретной
реализации начальная скорость известна с высокой точ¬
ностью. Иначе обстоит дело с другим начальным пара¬
метром — высотой условного перицентра (или углом вхо¬
да 0О). Посредством небольших по энергетике коррекций
траектории КА па завершающем участке перелета можно
обеспечить практически любое значение h- независимо
от выбранной схемы полета. В силу этого вводят понятие
прицельной или номинальной высоты условного перицент¬
ра /А1’ (соответственно номинального угла входа 0« р).
Это то желаемое значение высоты условного перицентра
(или угла входа), которое выбирается из ряда определен¬
ных соображений, удовлетворяющих условиям поставлен¬
ной задачи. Точность обеспечения номинального значения
h~" (соответственно 0qр) оказывает большое влияние на
режим движения КА в атмосфере, и поэтому желательно
иметь минимальный разброс Ah- (соответственно Д0О).
Величина Ah- зависит от выбранной системы коррекции
и навигации КА па межпланетном и припланетном участ¬
ках полета. Уменьшение ее связано с усложнением и соот¬
ветственным утяжелением этих систем.
Учитывая сказанное, а также возможности управления
аппаратом в атмосфере, в каждом конкретном случае фор¬
мулируются требования к так называемому навигацион¬
ному коридору входа, который определяется точностью
работы систем навигации и коррекции КА па подлетном
участке траектории и характеризует ошибки входа КА
в плотные слои атмосферы: Л/А"11 или ДОо". Величины
Д/А;Ш или Д0Г зависят от типа и точности навигацион¬
ных измерений, используемых для определения траекто¬
рии полета, от распределения измерений па навигацион¬
ных участках, от выбора типа и момента проведения кор¬
рекции, от точности решения навигационных задач, от
точности исполнения коррекций, от точности знания эфе¬
мерид планеты и других астрономических постоянных.
§ 2.2]
МОДЕЛИ АТМОСФЕРЫ
37
Наземные навигационные комплексы обеспечивают
сравнительно невысокую точность наведения КА при по¬
лете к планетам Солнечной системы. Так, при полете
к Марсу разброс по высоте условного перицентра может
составлять Ah]~XB ± 50 —г- ± 80 км [2, 6, 11].
Использование автономных или комбинированных си¬
стем навигации, особенно на участке подлета к планете
назначения, позволяет существенно уменьшить навига¬
ционный коридор входа. В частности, применительно
к Марсу можно говорить о навигационных коридорах по¬
рядка ±10 -- ± 30 км [2, 11].
Другие начальные параметры — время подлета к плот¬
ным слоям атмосферы, координаты: точки входа — не
играют столь существенной роли в исследовании общих
закономерностей движения КА в атмосфере. Они имеют
большое значение только при решении специальных задач
{например, точная посадка в заданном районе поверхно¬
сти) и при конкретных реализациях.
§ 2.2. МОДЕЛИ АТМОСФЕРЫ
Анализ проблем, возникающих па подлетном участке
траектории, представляет собой очень важный и ответ¬
ственный этап, ибо от них в значительной степени зави¬
сят условия движения КА в атмосфере. Очевидно, что
выбранное па этом участке конкретное решение поставлен¬
ных задач коренным образом влияет на другие участки.
И все же прохождение плотных слоев атмосферы является
решающим участком спуска, так как именно здесь аппа¬
рат испытывает воздействие мощных физических факто¬
ров. Участок спуска определяет требования не только
к подлетному участку, но и к выбору всей схемы и траек¬
тории перелета.
Действительно, возможности использования атмо¬
сферного торможения предопределяют требования к под¬
летному участку и навигационному коридору входа, а это
в свою очередь означает выбор траектории перелета,
стратегии ее корректирования, состава бортовой аппара¬
туры, наземного измерительного комплекса и др.
Анализ участка аэродинамического торможения не
может проводиться без предварительного построения до¬
стоверных моделей атмосферы. Под моделью атмосферы
38 ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ [ГЛ. 2
понимается закон изменепия плотности, температуры и
давления по высоте, а также газовый состав атмосферы.
Знание этих параметров необходимо для расчета аэроди¬
намических, динамических, тепловых нагрузок и для рас¬
четов на прочность КА. Построение модели атмосферы
является самостоятельной задачей, объективно влияющей
на выбор схемы полета, траектории спуска и в целом на
конфигурацию КА. С ее изучения начинается анализ проб¬
лемы торможения КА в плотных слоях атмосферы. Для
решения этой задачи используются теоретические оценки,
а также вся имеющаяся косвенная информация об атмо¬
сфере, полученная с помощью радиоастрономических на¬
блюдений. Первоначально анализ этих данных давал сред¬
нюю температуру па поверхности Марса 250 °К с разбро¬
сом порядка =Ь 70°. Давление атмосферы у поверхности
оценивалось в пределах 5 20 мбар.
Дальнейшее существенное уточнение параметров атмо¬
сферы возможно при использовании межпланетных ав¬
томатических аппаратов путем проведения:
— экспериментов на КА, пролетающих вблизи пла¬
неты (КА типа «Маринер»);
— экспериментов на КА, выведенных на орбиту ИСМ
(КА типа «Маринер», «Марс», «Викинг»);
— прямых измерений с КА, осуществляющих посадку
па поверхность («Марс-3, 6», «Викинг-1, 2»).
Совершенно очевидно, что наибольшую достоверность
результатов дает третье направление. Однако получаемые
при этом данные соответствуют одному профилю на траек¬
тории спуска. Их трудно экстраполировать на всю пла¬
нету и на все времена года. Поэтому для создания досто¬
верной инженерной модели нужно применять комплекс¬
ный подход, учитывающий данные как прямых, так и
косвенных измерений параметров атмосферы.
Первые космические аппараты проектировались в пред¬
положении самых неблагоприятных (энергоемких) ус¬
ловий спуска. В силу этого в качестве расчетной модели
атмосферы была принята наиболее разреженная (по ре¬
зультатам наземных измерений) атмосфера. Полеты со¬
ветских и американских автоматических станций к Марсу
позв-олили уточнить параметры атмосферы, ив настоящее
время при проектировании КА можно рассматривать более
точные модели атмосферы.
МОДЕЛИ АТМОСФЕ ГЫ
39
Очевидно, модели атмосферы по самой своей природе
требуют периодического пересмотра и обновления, с тем
чтобы своевременно учитывать изменения как в наших
знаниях о планете, так и в требованиях технического ха¬
рактера, предъявляемых к модели. Рассматриваемый ниже
вариант модели учитывает информацию, имевшуюся на
начало 1975 г. 11, 40, 42, 47, 59, 00].
Б зависимости от характера изменения температуры но
высоте атмосферу Марса можно разделить па два слоя:
конвективную тропосферу и изотермическую атмосферу.
Из наблюдений и теоретических расчетов следует, что
температурный режим в атмосфере Марса близок к режи¬
му лучистого равновесия, вертикальный температурный
градиент мал. Прямые измерения температуры, проведен¬
ные на КА «Марс-0» во время снижения па парашюте,
а также комплексный анализ измерений перегрузок при
торможении в атмосфере и доплеровских скоростей со¬
гласуются с этими утверждениями. Оказалось, что в об¬
ласти высот от 0 до 25—30 км температура монотонно
падает с увеличением высоты. Средняя скорость измене¬
ния температуры с высотой (градиент) составляет пример¬
но 2,5 град/км.
Летом в экваториальной зоне градиент возрастает до
3 град!км. В средних широтах зимой и в полярных райо¬
нах градиент уменьшается до 1,2 град!км. Малый градиент
(1 град!км) наблюдается также во время пылевых бурь
при высоких температурах атмосферы. Выше тропопаузы
атмосфера изотермична и имеет температуру порядка
150 100 °К. Анализ температурного режима в атмосфере
Марса по последним данным позволяет пересмотреть и об¬
новить наши представления об очень важной характери¬
стике атмосферы — законе изменения плотности атмосфе¬
ры по высоте р (h). При составлении моделей атмосферы
Марса обычно рассматривают три температурных профи¬
ля: основной, минимальный и максимальный [59]. Для того
чтобы оценить диапазон возможных изменений плотности
р (h), максимальные давления комбинируются с минималь¬
ными температурами, и наоборот. Зависимость плотности
от высоты для трех моделей (кривые 2, 3, 4) дана на
рис. 2.3. Следует, однако, отметить, что основные расчеты
траекторий спуска КА, результаты которых нашли от¬
ражение в предлагаемой вниманию читателей книге,
40
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ [ГЛ. 2
проводились в период 1972—1975 гг., когда использова¬
лись иные модели, составленные на основании имеющихся
представлений об атмосфере именно в эти и предшествую¬
щие годы. Зависимость плотности от высоты принималась
экспоненциальной и имеющей вид
р = p0erP/f, (2.5)
где р0 = 0,013 кг!ж', (3 ~ 0,09 км~1 — для наиболее раз¬
реженной атмосферы (кривая 1 на рис. 2.3) и р0 ~
= 0,019 кг!ж\ р — 0,07 клГ1 — для наиболее плотной
(кривая 5 на рис. 2.3).
р,кг/мъ
Рис. 2.3. Зависимость плотности от высоты для различных моделей атмосферы
Марса.
Сравнение использованных авторами моделей (кривые
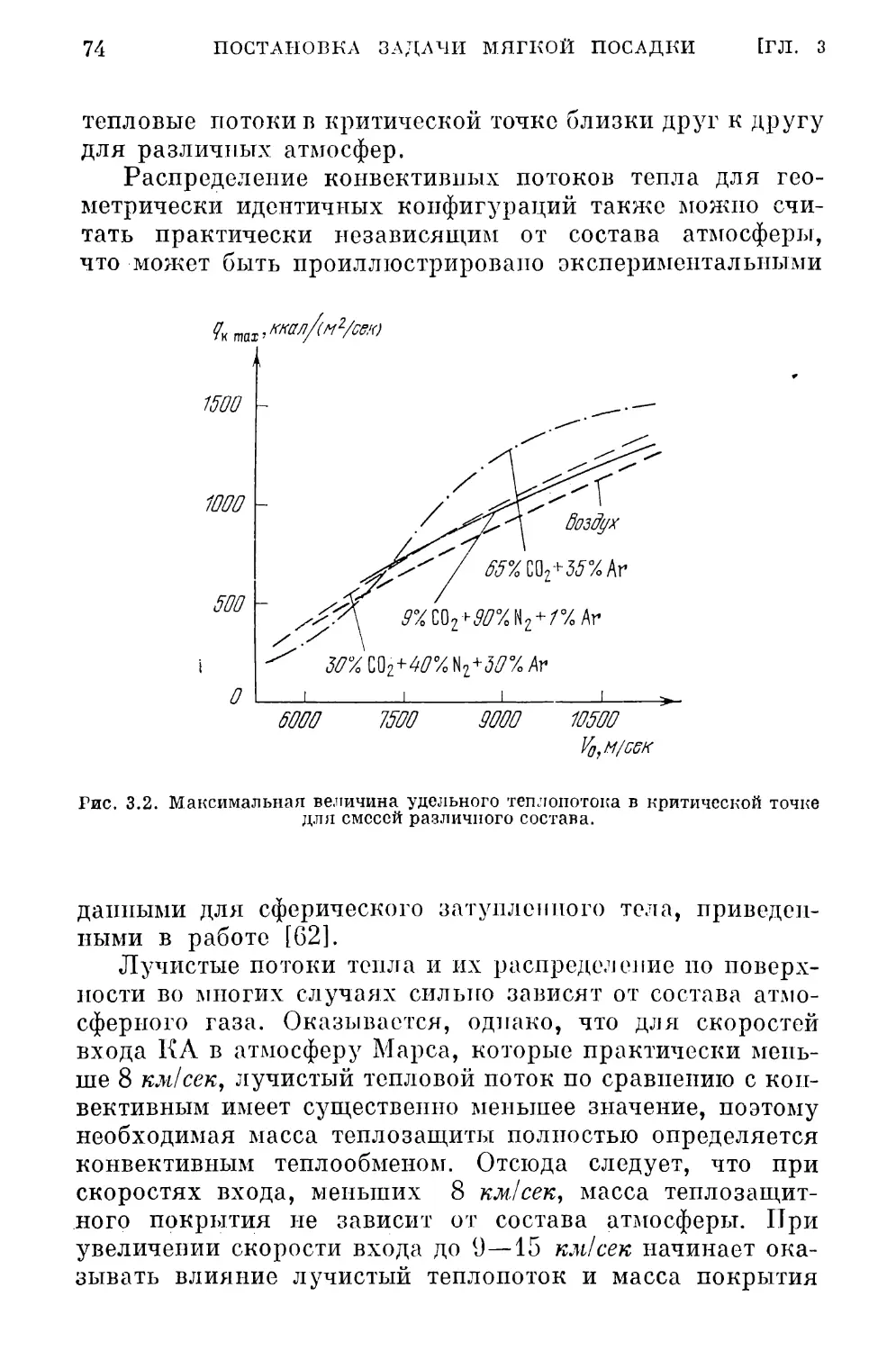
1 и 5) с рассматриваемыми в настоящее время (кривые 2,
3 ж 4 на рис. 2.3) показывает, что за последние годы про-
и зоитло незначительное уточнение (отличие в пределах 3-4
ч-5%), которое не оказывает заметного влияния на каче¬
ственные и количественные результаты исследований.
Лишь при синтезе траекторий конкретных КА появляет¬
ся необходимость в проведении расчетов с использовани¬
ем новых моделей.
$ 2.3]
АНАЛИЗ ТРАЕКТОРИЙ В АТМОСФЕРЕ МАРСА
41
§ 2.3. АНАЛИЗ ТРАЕКТОРИЙ КА В АТМОСФЕРЕ МАРСА
Б настоящее время способ гашения энергии КА с ис¬
пользованием аэродинамического торможения при спуске
на поверхность планеты, окруженной атмосферой, как
энергетически оптимальный, находится вне конкуренции
с другими способами, и именно таким образом осущест¬
влялись посадки всех КА па поверхность Земли, Венеры
и Марса. Однако использование его для торможения мар¬
сианских КА сильно затруднено, прежде всего, из-за
разреженности атмосферы планеты. Это приводит к тому,
что организация мягкой посадки на Марс находится на
грани возможностей современной космической техники.
Для выявления основных особенностей движения КА
Тис. 2.4. Зависимость максимальной перегрузки (штрих-пунктирная линия)
и конечной скорости (сплошная и штриховая линии) от угла входа.
в атмосфере Марса будем рассматривать два основных
типа траекторий — баллистического и планирующего
спуска.
Баллистический спуск. Так называется спуск без ис¬
пользования подъемной силы, когда аэродинамическое
качество равно нулю (К — 0).
На рис. 2.4 приведены зависимости характерных пара¬
метров траектории спуска — максимальной перегрузки
42
ОСНОВНЫЕ И ГОБЛ К МЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ [ГЛ. 2
(^х max) и скорости в конце участка аэродинамического тор¬
можения Ук (конечная высота принималась равной 5 км)
от угла входа для аппаратов баллистического типа, имею¬
щих различные значения приведенной нагрузки на лобо¬
вую поверхность. Видно, что величина 7ivinax существенно
зависит от угла входа, при этом с уменьшением 10О |
происходит уменьшение 7гтШах. Так, при V0 = 6 км/сек
и | 0О | = 90° максимальная перегрузка составляет 50 -г-
—т- 70. При более пологом входе эта перегрузка умень¬
шается вплоть до 10 -Е- 12 вблизи границы захвата.
Под границей захвата будем понимать то максимальное
значение высоты условного перицентра h™ (соответственно
минимальное значение модуля угла входа ]0о|), при
входе с которым КА не вылетает за пределы плотных сло¬
ев атмосферы.
Рассмотрение зависимостей, приведенных на рис. 2.4,
показывает также, что с уменьшением модуля угла входа
величина Ук уменьшается. Так, при крутом входе КА
в атмосферу Марса с углом | 0О | = 80° и скоростью входа
V0 = б км/сек аппарат с величиной Рх = 250 кг/м2 тор¬
мозится до скорости порядка 5,1 км/сек. Уменьшение мо¬
дуля угла входа до 20° позволяет затормозить аппарат
до 3,2 км/сек. Анализ зависимостей рис. 2.4 показывает
также, что даже при достаточно точном входе вблизи гра¬
ницы захвата можно затормозить до скорости Ук 500 -е-
700 м/сек только те аппараты баллистического типа, ко¬
торые имеют нагрузку на лобовую поверхность не более
Рх = 50 -ч- 70 кг/м2 (КА. типа «Марс-3, С»). Это чрезвы¬
чайно малая величина. Создание таких аппаратов пред¬
ставляет собой достаточно сложную задачу. В результате
это приводит к тому, что масса полезной нагрузки, до¬
ставляемой па поверхность планеты, у аппаратов с малой
величиной Рх существенно меньше, чем у аппаратов с
большим значением (при одной и той же начальной мас¬
се КА). Отметим, что спускаемые аппараты кораблей типа
«Союз» имеют нагрузку на лобовую поверхность порядка
500 -г- 600 кг/м2, а спускаемые аппараты станций «Вене-
ра-9, 10» — порядка 400 кг/м2.
Итак, из анализа траекторий баллистического спуска
следует, что максимальная эффективность аэродинами¬
ческого способа торможения достигается при использо¬
вании КА с малыми нагрузками на лобовую поверхность
§ 2.3]
АНАЛИЗ ТРАЕКТОРИЙ В АТМОСФЕТЕ МАРСА
43
(Рх ^ 50 ^ 70 кг/м2), входящих в атмосферу Марса
вблизи границы захвата. При этом конечная скорость
КА в конце участка аэродинамического торможения до¬
статочно высока (составляет величину порядка VK =
— 500 -г- 700 м/сек, максимальная перегрузка /гхтах .=
=.- 12 -г- 15) и существенно превышает скорость звука,
составляющую для Марса примерно 185 -н 200 м/сек
в зависимости от плотности атмосферы.
Планирующий спуск. Так называется спуск при учас¬
тии подъемных сил, когда аэродинамическое качество не
равно нулю (К Ф 0). Следует отметить, что КА плани¬
рующего типа с большим значением аэродинамического
качества (К 1) пока не находят широкого применения
в космической технике. (В настоящее время в США проек¬
тируется КА подобного типа с величиной аэродинамичес¬
кого качества КШ1ЛХ ^ 2,2.)
Остановимся на особом классе аппаратов планирую¬
щего типа, нашедших широкое распространение в косми¬
ческой технике и получивших специальное название —
космических аппаратов скользящего типа. Недостатки
КА баллистического типа — большие максимальные пе¬
регрузки, малые допустимые коридоры входа, отсутствие
управления па траектории снижения — могут быть
в значительной степени устранены путем создания подъем¬
ной силы Y = CvSyl pV2/2 (где Си — коэффициент аэро¬
динамической подъемной силы) и использования ее для
целей управления. Вместе с тем разработанные КА балли¬
стического типа имеют ряд существенных преимуществ —
простота реализации, максимальное значение коэффициен¬
та лобового сопротивления, что приводит к уменьшению
нагрузки на лобовую поверхность и облегчению теплового
режима, и т. д. В силу этого велись поиски таких форм
аппаратов, которые сохраняли бы основные преимущест¬
ва КА баллистического типа и одновременно имели повое
качество — подъемную силу на траектории снижения.
В результате появились аппараты скользящего типа,
которые при достаточно большом коэффициенте аэроди¬
намической подъемной силы (Си ф 0,3 -4- 0,5) имеют не¬
большое значение аэродинамического качества (К --
Си/Сх ж 0,2 -г- 0,5) в силу больших значений Сх.
11а рис. 2.5 схематически изображен, аппарат сег¬
ментно-конической формы, представляющий собой тело
44
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ [ГЛ. 2
вращения с сегментной лобовой поверхностью и конической
задней. При симметричном обтекании КА подобной фор¬
мы (при угле атаки а = 0) подъемная сила будет отсут¬
ствовать, т. е. спуск в этом случае будет баллистическим.
При несимметричном обтекании (а Ф 0) появляется вер¬
тикальная составляющая аэродинамической силы —
подъемная сила {К ф 0). Режим спуска аппарата такой
Рис. 2.5. Схема сил, действующих на КА сегментно-конической формы при
управлении посредством изменения угла крена. У — скорости набегающего
потока.
формы с а Ф 0 можно обеспечить приложением реактив¬
ных управляющих сил, создающих необходимую вели¬
чину угла атаки на траектории снижения (управление
с помощью изменения угла атаки). Однако такой способ
сопряжен с большими расходами рабочего тела для ре¬
активного управления, так как момент инерции относи¬
тельно поперечной оси аппарата сегментно-конической
формы достаточно велик. Но существует другой путь.
Пусть центр масс КА окажется смещенных! вверх от оси
симметрии. Тогда спуск такого аппарата будет проходить
с некоторым балансировочным углом атаки а — осо ф 0,
благодаря появлению момента относительно центра масс
от силы лобового сопротивления, который для перехода,
в режим устойчивого полета будет уравновешиваться
моментом от подъемной силы (см. рис. 2.5). Для удержа¬
ния аппарата в полете па ао не требуется специального ре¬
активного управления. Реактивное управление для ста¬
билизации по углу атаки может понадобиться только для
парирования разного рода возмущений.
Необходимо отметить один важный момент: вектор
подъемной силы всегда лежит в одной плоскости — плос¬
кости симметрии аппарата, проходящей через центр масс
§ 2.3]
АНАЛИЗ ТРАЕКТОРИЙ В АТМОСФЕРЕ МАРСА
45
и ось симметрии аппарата. В силу этого, при развороте
аппарата на угол крепа у относительно оси «ц.м. — ц.д.»
будет изменяться проекция подъемной силы Уб =
= СиС)$MpF2 2 па вертикальную плоскость симметрии КА
(здесь С „о — значение коэффициента аэродинамической
подъемной сил i»i при а ап). Значение подъемной силы
при полете на балансировочном угле атаки а -- ао и при
угле крепа у = 0 обозначим Уб. Тогда вертикальная со¬
ставляющая Уп при у = 0 равна Уи = У о cos у. и соот¬
ветственно горизонтальная Уг = Yо sin у. Таким обра¬
зом, появляется возможность не только получить подъем¬
ную силу Ув, по и изменять ее в полете от Ун --- Уб до
У„ = —У<1 посредством изменения угла крепа.
В силу того, что К Л. статически нейтрален: при враще¬
нии относительно оси крепа «ц.м. — ц.д.», потребная ре¬
активная сила для его поворота на некоторый угол у
незначительна. Величина реактивного момента зависит
в основном от ожидаемой величины возмущающего аэ¬
родинамического момента, определяемого коэффициентом
тх0. Возмущающий момент может возникать из-за пе-
симметрии аппарата, неравномерного уноса массы при
обгаре тепловой защиты и т. д. Управление с помощью
изменения угла крепа имеет большие преимущества из-за
экономичности и простоты.
Необходимо отметить, что спуск аппаратов скользя¬
щего типа па основном: участке траектории (при числах
М )> 5 Е- 6) протекает практически с постоянным про¬
странственным углом атаки ocg ~ const. В силу этого до¬
статочно обосновано допущение о постоянстве коэффици¬
ентов лобового сопротивления Схо и аэродинамической
подъемной силы Суо, а следовательно, и аэродинамиче¬
ского качества Ко = Сио/Схо. Поэтому аппараты скользя¬
щего типа удобно характеризовать баллистическим пара¬
метром ах = 11РХ (или Рх) и располагаемым значением
аэродинамического качества Красп, за которое принимает¬
ся значение качества при полете с углом атаки а = а(п,
т- е. АраоЛ[ = Ко- Вертикальная составляющая аэроди¬
намического качества, называемая эффективной, зави¬
сит от угла крепа у, а именно: Упфф = У о cosy; соот¬
ветственно Кяф = Ко cosy = КХУЛ?,и cos у.
В соответствии с этим; говорят об у правлении с помощью
изменения угла крена или эффективного качества. Нетрудно
40
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ [ГЛ. 2
видеть, что ЛГЭф может принимать любое значение от
Кэф = к6 (у = 0) до Кэф = -Ко (у = 180°).
В дальнейшем режим мгновенного перехода с 7 = 0
на полет 07 = 180° (или наоборот) будем называть пере¬
ключением управляющего параметра с -\-Ко на —Ко
(или с —Ко на -\-Ко). Случаи, когда учитывается ди¬
намика разворота КА по углу крена, будут оговаривать¬
ся особо.
Проведем анализ траекторий скользящего типа. Рас¬
смотрим неуправляемый спуск с постоянным положитель¬
ным значением аэродинамического качества — наиболее
простой вид снижения с аэродинамической подъемной
силой, для реализации которого требуется лишь стабили¬
зация аппарата по крену. При достаточно крутом входе
(|0о|>4О°) траектории аппаратов скользящего типа не¬
существенно отличаются от баллистических траекторий
спуска при прочих равных условиях. Так, при | 0О | = 403
VK = 4,38 км/сек для КА с Рх = 250 кг/м2 и Ко = 0
и VK = 4,12 км/сек для аппарата с тем же Рх, но с Ко =
= 0,3 (рис. 2.4).
При пологом входе в ограниченный коридор конечная
скорость аппаратов с Ко ф 0 существенно меньше, чем
соответствующая скорость аппаратов баллистического ти¬
па. Для приведенного выше примера уменьшение |0О|
до 20° приводит к существенному уменьшению конечной
скорости аппаратов скользящего типа: VK = 0,492 км/сек
(при Ко = 0,3; Рх = 250 кг/м2) и Кк = 3,18 км/сек
(при Ко = 0; Рх = 250 кг!м2). Отмеченная скорость имеет
место лишь в небольшом диапазоне углов входа, вблизи
границы захвата (рис. 2.4). Следует, однако, отметить,
что при входе КА в атмосферу под малым углом режим по¬
лета с К = const на всей траектории спуска может оказать¬
ся недопустимым из-за возникающей опасности вылета
КА за пределы атмосферы. Для того чтобы избежать ри-
конгетировапия КА и вылета за пределы атмосферы при
входе по пологим траекториям и в то же время осущест¬
влять полет па возможно больших высотах, необходимо
организовать специальным образом управление КА. Это
позволяет существенно сместить границу захвата КА
атмосферой в сторону меньших значений модуля угла
входа (выигрыш составляет примерно 1 -г- 2°), расширяет
возможности управляемого спуска КА и увеличивает
АНАЛИЗ ТРАЕКТОРИЙ В АТМОСФЕРЕ МАРСА
47
эффект использования аэродинамических подъемных сил
по сравнению с баллистическим спуском.
Итак, использование КА с аэродинамическим качест¬
вом имеет большие преимущества по сравнению с аппара¬
тами баллистического типа с точки зрения эффективности
аэродинамического способа торможения КА в разреженной
атмосфере Марса. При этом, однако, оказалось, что как
в случае баллистического спуска, так и в случае управляе¬
мого недостаточно навести КА па диск планеты, а нужно
организовать сравнительно точный вход в плотные слои
атмосферы по крайней мере с разбросом но высоте услов¬
ного перицентра, не превышающим Д/г”;ш ж ±80 -т-
-г- ±100 км (Д0оав = ±3 -ь- 3,5°).
Выведение КА на орбиту ИСМ с использованием аэро¬
динамического торможения. Используемый в настоящее
время способ выведения КА па орбиту ИСМ посредством
реактивного торможе¬
ния с помощью двига¬
тельной установки тре¬
бует больших энергети¬
ческих затрат. Так, при
организации перехода
с траектории межпла¬
нетного перелета на су¬
точную орбиту ИСМ
советских КА «Марс»
и американских КА
«Викинг» потребная ве¬
личина тормозного им¬
пульса составила при¬
мерно 900—1000 м/сек.
Следует учесть, что тор-
можепиекаждых Юм/сек
скорости на аппара¬
те с начальной массой
5л-8 71 требует пример¬
но 15 —- 20 кг дополнительной массы КА (масса топлива
и конструктивных элементов двигательной установки).
Поэтому выведение КА на орбиту ИСМ с предваритель¬
ным аэродинамическим торможением во многих случаях
Должно привести и к существенному энергетическому
выигрышу. Это подтверждается рис. 2.0, где показана
muJ
Рис. 2.G. Масса полезного груза па ор¬
бите ИСМ(2 — при торможении с помощью
двигательной установки, 1 — с использо¬
ванием торможения в атмосфере).
4S
ОСНОВНЫЕ ПРОБЛЕМЫ У1Т С А В Л Е НИ Я ДВИЖЕНИЕМ [ГЛ. 2
зависимость массы полезного груза, выводимого на орбиту
ИСМ, от начальной массы КА, подлетающего к планете при
использовании «активного» способа и с предварительным
азродипамическим торможепием.
На рис. 2.7 представлены основные этапы схемы вы¬
ведения на орбиту ИСМ с предварительным аэродинами¬
ческим торможением. КА входит в плотные слои атмосферы:
(точка с) со скоростью V0
под углом 0о. После а зро¬
ди i iaмическо.го торможе¬
ния (участок сЪ) он выле¬
тает из плотных слоев атмо¬
сферы и осуществляет дви¬
жение по переходному
эллипсу с высотой апоцент¬
ра h-jx и высотой перицент¬
ра h-\. Из геометрических
соображений ясно, что 7г-L
должно быть меньше высо¬
ты условной границы атмо¬
сферы (h-i <. /га).
При выведении КА на
орбиту с использованием
предварительпого аэроди-
11 а л I ич е с к о г о то р л i о ж е ни я
си л а а з р о д и и а м ич е ск о г о
сопротивления оказывается вполне достаточной для умень¬
шения скорости от начальной гиперболической до око-
локруговой. Однако формирование окончательной орби¬
ты с апоцентром высотой /га2 и перицентром высотой
/г-2 возможно только активным путем с использованием
двигательной установки. В общем случае, если апоцентр
окончательной орбиты обеспечивается соответствующим
управлением на участке аэродинамического торможения,
то потребные энергетические затраты на формирование
орбиты ИСМ будут тем меньше, чем меньше разница
между 1г-л и /г-2, т. е. чем больше будет скорость КА в апо¬
центре переходного эллипса.
Проведенный анализ аэродинамического способа фор¬
мирования орбиты ИСМ показывает, что для этой цели
11 е в о з м о ж п о и с п о /1 ь з о в а т ь i г е у и р a i s л я е ^ г ы е а п и а р а ты б а л л и-
стичсского типа. Дело в том, что даже при точном знании
Условная границе атмосферы
>&V
Гнс. 2.7. Основные этапы выведении
КА на орбиту ИСМ с предварительным
аэродинамическим торможением.
АНАЛИЗ ТРАЕКТОРИЙ 3 АТМОСФЕРЕ МАРС V
49
параметров атмосферы Марса выход КА баллистического
типа на заданную высоту апоцентра переходной орбиты
^ }гУ2 возможен по единственной траектории при
входе КА в атмосферу с вполне определенным значением
угла 0О. Ясно, что даже в этих идеальных условиях потреб¬
ный коридор входа КА в атмосферу будет близок к пулю.
Отклонение плотности атмосферы от расчетной и погреш¬
ности проектно-баллистических характеристик КА не¬
избежно приводят к существенным: ошибкам, полностью
исключающим этот способ выведения КА па орбиту ИСМ.
Возможность управления траекторией снижения КА
с помощью аэродинамических сил позволяет парировать
возмущения па атмосферном участке и достаточно точно
вывести КА па заданную высоту апоцентра кил. При этом
такое выведение возможно не для одного значения вы¬
соты условного перицентра траектории входа /Ар, а для
некоторого диапазона, называемого в дальнейшем кори¬
дором входа. Коридором входа называется такой диапазон
высот Ah- условных перицентров траекторий, при входе
в любую точку которого КА с заданными параметрами и
при идеальной работе системы управления может быть
обеспечено выполнение поставленных условий. Так, в за¬
даче выведения КА па орбиту ИСМ границы коридора
входа определяются минимальной и максимальной вы¬
сотой условных перицентров траекторий входа, когда еще
обеспечивается достижение аппаратом требуемой высоты
апоцентра /га1 = hx2. Иными словами, при фиксированных
параметрах аппарата и атмосферы для каждой скорости
входа можно указать минимальное (/А) и максимальное
(hr:) значения высот, при которых реализуются требуе¬
мые высоты апоцентра hy{ при граничном управлении
(у 0° и у --- 180° соответственно для /А и /А).
Па рис. 2.8 представлены зависимости верхней /А
и нижней /А границ коридора входа от величины аэроди¬
намического качества Ко для различных скоростей входа
К0 и значений приведенной нагрузки на лобовую поверх¬
ность Рх. Их рассмотрение показывает, что при отсутствии
ограничений па величину максимально допустимой пере-
гРУзки и глубину погружения в атмосферу ширина кори¬
дора входа увеличивается с ростом нагрузки па лобовую
п° в ер х I гость, располагаемого качества и скорости входа.
50
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ [ГЛ. 2
При этом в последних двух случаях расширение кори¬
дора достигается за счет сдвига нижней границы услов¬
ного перицентра /г", в то время как верхняя граница прак¬
тически не зависит от величины Ко и V0.
4-.км Рх = 100 кг /м 1
для различных значений Ко и Рх (сплошная линия — при У0 = 6 км/сек,
штриховая лишне — при V'0 = 8 км/сек).
На рис. 2.9 показаны зависимости минимальной вы¬
соты пролета КА над поверхностью Марса (/гГш„) от вели¬
чины располагаемого качества для разных значений V0
и Рх. Эти зависимости получены для предельных условий
движения: КА входит по нижней границе коридора и дви¬
жется в самой разреженной атмосфере. Видно, что hm-m
возрастает с уменьшением Ко, Рх и V0. При этом для
Ко > 8 км!сек, Рх > 500 кг/м2 и Ко > 0,3 величина /ггпin <
< 10 -г- 12 км, т. е. в некоторых случаях в силу исклю¬
чительной разреженности атмосферы Марса движение
КА может происходить па достаточно низких высотах.
Из-за особенностей рельефа Марса это может привести
к жесткой посадке КА на поверхность. Уменьшить ве¬
роятность подобного события можно путем сдвига нижней
границы в сторону больших значений высоты условного
перицентра. Однако в этом случае величина умень¬
шается, что вызывает ужесточение требований к нави¬
гационному коридору входа.
ОСОБЕННОСТИ ДВИЖЕНИИ В АТМОСФЕРЕ МАРСА 51
Приведенные результаты (см. рис. 2.8 и 2.9) показы¬
вают, что для достаточно широкого диапазона параметров
КА принципиально возможно реализовать рассмат¬
риваемый способ выведения, хотя это и сопряжено с
Рг =
400кг/м2
500
Рис. 2.9. Минимальная высота пролета КА над поверхностью Марса (сплош¬
ная линия — при У0 = 6 км/сек, штриховая — при У0 = 8 пм/сек, штрих-
пунктирная — при У0 = 10 км/сеп, линия с крестиками — при У0 = 12 7см'сеп).
необходимостью решения многих сложных задач — органи¬
зации точного входа, использования совершенных систем
управления, создания тепловой защиты и многих других.
Однако во многих случаях здесь можно ожидать суще¬
ственного энергетического выигрыша (см. рис. 2.6).
§ 2.4. ОСОБЕННОСТИ ДВИЖЕНИЯ КА В АТМОСФЕРЕ МАРСА
При спуске КА на Землю или Венеру не возникало
сомнений в достаточности тормозящих способностей ат¬
мосферы этих планет. Поэтому основные усилия были на¬
давлены на такую организацию аэродинамического тор¬
можения, поиск таких траекторий движения, чтобы
минимизировать массу теплозащитного покрытия КА, вели¬
чину максимальной перегрузки и т. п. При спуске КА
52
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЯ
[ГЛ. 2
в атхмосфере Марса основные трудности связаны с орга¬
низацией мягкой посадки при возможно меньших затра¬
тах энергии, что приводит к ряду специфических требо¬
ваний при управлении КА.
1. Необходимость точного входа КА в плотные слои
атмосферы приводит к задаче максимизации коридора
входа (средствами управления на атмосферном участке
движения). Дело в том, что система внеатмосферной на¬
вигации и коррекции получается тем проще, надежней
и легче, чем меньшую точность она должна обеспечить,
т. е. чем больше допустимый навигационный коридор. Для
атмосферного участка, наоборот, чем точнее вход, тем про¬
ще организовать оптимальные или близкие к ним режимы
снижения. В таких условиях возможен следующий ком¬
промиссный подход: решается задача максимизации кори¬
дора входа (max Ah-) и, исходя из полученных резул ьтатов
и практических возможностей, выдвигаются требования
к величине навигационного коридора. При этом ока¬
зывается, что задача максимизации коридора входа ради¬
кально может быть решена только при использовании КА
с большим значением аэродинамического качества, а это
влечет за собой дополнительный комплекс сложных проб¬
лем. В случае решения задачи более простыми способами
(па аппаратах скользящего или баллистического типа)
расширение коридора возможно в основном за счет уве¬
личения массы системы мягкой посадки КА, что в целом
нежелательно.
Еще большую остроту проблема расширения коридора
входа имеет при выведении КА па орбиту ИСМ' с пред¬
варительным аэродинамическим торможением. Достаточ¬
но сказать, что если для практического решения задачи
спуска КА на Марс необходимо обеспечить ширину на¬
вигационного коридора входа по высотам условного пе¬
рицентра Д/г“‘ш = ± (50 ы- 80) км, то для выведения на
к орбиту ИСМ с предварительным аэродинамическим тор¬
можением необходим навигационный коридор не более
Д/Дыв = + (25 -у- 30) км. А это выдвигает большие до¬
полнительные трудности при построении системы меж-
плане т 11 о й 11 а в иг ации.
2. Необходимо максимально уменьшить возможность
«жесткой» посадки КА (т. е. встречи с поверхностью до
введения СМИ) и увеличить вероятность благополучной
§ 2.4] ОСОБЕННОСТИ ДВИЖЕНИЯ В АТМОСФЕ1 Е МА1 С А
53
мягкой посадки. Это выдвигает требование ограничить
максимальную глубину погружения в плотные слои атмо¬
сферы, а также ставит проблему выбора места посадки.
Разреженность атмосферы Марса вызывает стремление
организовать движение КА в ее нижних, приповерхност¬
ных слоях, где плотность наибольшая, чтобы максималь¬
ным образом: увеличить эффективность ее тормозящих
свойств. Однако это стремление входит в противоре¬
чие с имеющейся большой неопределенностью в знании
рельефа поверхности Марса: возможный перепад высот
может достигать 5 10 км и более. Чтобы исключить
вероятность жесткой посадки КА, при организации дви¬
жения в нижних слоях атмосферы для гашения избытка
скорости необходимо накладывать ограничение по ми¬
нимально допустимой высоте полета над поверхностью
(/zmin /Щоп)- Как отмечалось, чем меньше величина hROily
тем больше возможностей у КА эффективно использовать
тормозящие свойства атмосферы. Поэтому рациональная
величина ДД(Ш является очень важной характеристикой,
во многом определяющей решение проблемы мягкой по¬
садки. Выбору Адои должен предшествовать достаточно
тщательный анализ рельефа поверхности планеты по
трассе снижения КА, а также в районе посадки.
Важность и ответственность выбора района посадки
можно проиллюстрировать па примере решения этой
задачи для КА «Викинг». Предварительный и тщательный
выбор районов посадки для аппаратов «Викинг» произво¬
дился в основном по телевизионным изображениям и ре¬
зультатам зондирования поверхности Марса, полученным
в 1972 г. от КА «Мари.пер-9», выведенного на орбиту ИСМ,
а также учитывалась представленная советскими учены¬
ми информация с А М. С «Марс» [83].
Выбирались районы, удовлетворяющие сл с-д ующим
требованиям:
1) Достаточно низкий уровень поверхности, что обус¬
ловливает сравнительно высокое атмосферное давление
и повышает эффективность аэродинамического торможе¬
ния посадочных блоков, а также увеличивает вероятность
наличия воды в жидкой фазе.
2) Отсуа гствис сильных ветров, поскольку СМИ поса¬
дочных аппаратов «Викинга» эффективна лишь при ско¬
рости ветра до 67 м/сек.
54
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ [ГЛ. 2
3) Небольшая пересеченность и отсутствие крутых
склонов, поскольку клиренс посадочного аппарата «Ви¬
кинга» составляет всего 23 см.
4) Достаточная несущая способность грунта для удер¬
жания аппарата и в то же время не слишком высокая его
твердость, чтобы грунтозаборник мог брать пробы.
5) Местоположение между 25° ю. ш. и 75° с. ш., что
предопределено баллистическими требованиями.
В качестве возможных мест посадки рассматривались
22 района Марса: 11 — вблизи экватора, 7 — в средних
широтах и 4 — в северном полярном районе (между 63
и 73° с. ш.). В конечном счете для каждого из двух поса¬
дочных аппаратов были выбраны один основной и один
запасной районы посадки, каждый из которых представ¬
ляет собой эллипс размером 77 X 580 км. На этом реше¬
ние задачи не считалось законченным, и в целях гаранти¬
рованного обеспечения мягкой посадки была разработана
соответствующая схема полета, предполагающая пер¬
воначальное выведение КА на орбиту ИСМ, дополни¬
тельное изучение района посадки, включая и метеоб-
становку. Лишь в случае подтверждения правильности
ранее принятых решений разрешается спуск посадочного
аппарата. Предполагаемый интервал между моментом
выхода КА на ареоцентрическую орбиту и моментом
посадки составлял около трех недель, но он мог быть уве¬
личен и до 50 суток, если бы это потребовалось для луч¬
шего изучения заранее выбранных районов посадки или
выбора новых, если бы выяснилась непригодность пред¬
полагаемого места посадки.
Американские специалисты надеялись, что посадка
на поверхность Марса будет совершена 4 июля 1976 г.
f в день 200-летттей годовщины США, по это оказалось
невозможным. КА «Викинг-1» был выведен на орбиту ИСМ
19 июня 1976 г., 21 июня КА был переведен на синхрон¬
ную орбиту с периодом 24 ч 37 мин. и начал изучение райо¬
на посадки. Выяснилось, что намеченный район не благо¬
приятен для посадки и 8 июля была проведена коррекция
КА с целыо создания наиболее благоприятных условий
для съемки нового района приземления. И лишь 20 ию¬
ля 1976 г. был проведен успешный спуск посадочного
блока в район равнины Хриса. Аналогичная картина на¬
блюдалась и во время полета КА «Википг-2», который
§ 2.4] ОСОБЕННОСТИ ДВИЖЕНИИ В АТМОСФЕРЕ МАРСА
7 августа 1976 г. был выведен на орбиту ИСМ, причем
только 4 сентября был осуществлен спуск посадочного
аппарата в районе равнины Утопия.
3. Необходима комплексная увязка всех участков траек¬
тории спуска. При спуске в разреженной атмосфере Мар¬
са значительно возрастает роль участка мягкой посадки
КА. Из-за существующей связи участков аэродинамичес¬
кого торможения и мягкой посадки возникает необходи¬
мость комплексной увязки этих участков на траектории
снижения КА. Условно можно выделить два взаимосвя¬
занных этапа:
— синтез номинальных траекторий (задача комплекс¬
ной траекторией оптимизации);
— синтез возмущенных траекторий (на уровне разра¬
ботки автономных алгоритмов управления).
Комплексная оптимизация траекторий спуска — это
необходимый первоочередной этап всестороннего иссле¬
дования проблемы мягкой посадки КА на Марс, позво¬
ляющего в конечном итоге наиболее эффективно решить
рассматриваемую проблему. Значение математической тео¬
рии оптимизации трудно переоценить. Во-первых, она
позволяет устранить эмпирический подход в решении
различных частных задач. Во-вторых, полученные при
оптимальном управлении численные результаты опреде¬
ляют тот теоретический предел, к которому надо стре¬
миться при практическом построении той или иной си¬
стемы. Вместе с тем не всегда и не везде целесообразно
применять эти методы. Для хорошо изученных систем,
проверенных практически, методы оптимизации дают,
как правило, небольшой выигрыш, так как из опыта удает¬
ся обычно определить решения, близкие к оптимальным.
Но для перспективных комплексных задач, примером од¬
ной из которых является спуск в атмосфере Марса, ис¬
пользование методов оптимизации весьма целесообразно.
Комплексная увязка номинальных траекторий на обо¬
их участках спуска показывает принципиальную воз¬
можность решения задачи спуска КА на поверхность
Марса. О реализуемости мягкой посадки КА можно су¬
дить лишь после комплексного анализа возмущенных
траекторий и оценки возможности создания автономных
алгоритмов управления КА, способных эффективно спра-
вляться с действующими возмущениями на всех участках
56
ОСНОВНЫЕ ПГОКЛКМЫ VI И*А В. 1 IvJ 1ПН ДВИЖЕНИЕМ [ГЛ. 2
снижения КА и обеспечить мягкую посадку на поверх¬
ность (либо выведение на орбиту ИСМ) при в.ыполнении
всех поставленных ограничений и условий.
Задача синтеза оптимального управления на борту
КА при действии значительных атмосферных возмуще¬
ний, ошибках в начальных условиях входа, возможных
отклонениях проектно-баллистических характеристик КА
и других приобретает исключительно важное значение.
Специфика управления траекторией как при спуске,
так и при выведении па орбиту ИСМ заключается в том,
что погрешности алгоритма управления должны компен¬
сироваться за счет дополнительных затрат массы КА либо
на торможение КА (при спуске), либо па формирование
требуемых элементов орбиты (при выходе на орбиту ИСМ).
Поэтому точность управления возмущенной траекторией
спуска должна быть очень высокой, чтобы эти дополни¬
тельные затраты были но возможности минимальными.
При спуске первых КА на поверхность Марса организа¬
ция точной посадки не является первостепенной задачей,
в то время как для выведения КА па орбиту ИСМ задача
управления КА должна решаться чрезвычайно точно. Это
накладывает свои специфические особенности па синтез
автономных алгоритмов управления КА при выведении
на заданную орбиту ИСМ с использованием предваритель¬
ного а э р о д и 11 а л i ич е с к о г о т о р м о ж с п и > г.
В соответствии с имеющимися тенденциями развития
космической техники комплексное исследование автоном¬
ных алгоритмов управления, марсианских КА ведется
в двух направлениях:
— построение простых алгоритмов управления, когда
используется сравнительно легкодоступная для измере¬
ний информация и предполагается ее обработка в про¬
стейших вымпелител ьпых устройствах;
— построение более совершенных алгоритмов управ¬
ления с использованием' бортовых ЦВМ.
При использовании алгоритмов первого типа постав¬
ленная задача решается, как правило, с существенными
методическими ошибками, по тем не менее достигаемая
в этом случае точность управления обычно удовлетворяет
требованиям. Простота алгоритмов обеспечивает создание
достаточно надежной системы управления при минималь¬
ной ее массе.
§ 2.Л1
ОСОБЕННОСТИ ДВИЖЕНИЯ Б АТМОСФЕРЕ МЛ PC Л
57
Качественно новью 'возможности сиптоза автономных
алгоритмов появились в связи с разработкой компактных
и высокоэффективных бортовых ЦВМ. Оказалось возмож¬
ным проводить па борту КА выбор требуемого управле¬
ния и определять в ходе полета оптимальную стратегию
управления. В настоящее время все перспективные и мно¬
гие из современных разработок алгоритмов управления
рассчитаны исключительно па применение бортовых ЦВМ.
Хотя возможности системы управления с бортовой
ЦВМ существенно расширяются, однако они все же огра¬
ничены характеристиками вычислительной машины. По¬
этому среди всех возможных алгоритмов следует рассмат¬
ривать только те, которые требуют для своей реализа¬
ции бортовой ЦВМ с приемлемым быстродействием и
памятью (оперативной и долговременной) при прочих рав¬
ных условиях. В дальнейшем будет рассмотрено несколь¬
ко возможных путей синтеза автономных алгоритмов уп¬
равления движением КА в атмосфере Марса как с помо¬
щью простых бортовых вычислительных устройств, так
и при использовании бортовых ЦВМ. При построении
алгоритмов будут учитываться выявленные особенности
решения задач комплексной программной оптимизации
траекторий снижения КА в атмосфере Марса.
4. Необходим взаимосвязанный выбор проектно-бал¬
листических характеристик КА. Под основными проект-
но-баллистическими характеристнками КА скользящего
типа подразумевается прежде всего располагаемое аэро¬
динамическое качество КХГЛСП, а также баллистический
параметр crv (или обратная величина — приведенная на¬
грузка на лобовую поверхность Рх). Известно, что для ап¬
паратов, управляемых по крену и осуществляющих по¬
садку па планеты с более плотной атмосферой (например,
па Землю), решают,ее значение имеет величина Арасп,
а абсолютная величина Рх не играет принципиальной ро¬
ли по крайней мере с баллистической точки зрения. Ина¬
че обстоит дело при рассмотрении задачи спуска в атмо¬
сфере Марса. Здесь одинаково важное значение имеют
оба рассматриваемых параметра.
Эффективность управления в общем случае зависит
от возможного диапазона изменения управляющего пара¬
метра, в качестве которого используется аэродинамичес¬
кое качество. Как известно, величину К о <С 1 можно реа¬
58
ОСНОВНЫЕ ПРОБЛЕМЫ УПРАВЛГСПТТЯ ДВИЖЕНИЕМ [ГЛ. 2
лизовать на бескрылых аппаратах, имеющих простые
аэродинамические формы; реализация значений аэроди¬
намического качества, близких к максимальному для вы¬
бранной формы КА, сопряжена с большими трудностями
в отношении компоновки и тепловой защиты, обеспечении
динамической и статической устойчивости и т. д. Поэ¬
тому прежде всего необходимо решить задачу определе¬
ния минимального значения располагаемого качества,
потребного для решения поставленной задачи.
В отношении второго проектно-баллистического пара¬
метра Рх можно отметить следующее. С увеличением Рх
уменьшается эффективность использования тормозных
свойств атмосферы Марса для гашения избытка скорости
спуска КА (см. рис. 2.4). В этом смысле желательно иметь
возможно меньшее значение Рх. Однако последнее тре¬
бование связано с рядом существенных ограничений,
которые имеют место при создании КА: определенная
величина диаметра миделевого сечения головного обте¬
кателя ракеты-носителя, возможная величина выводимого
полезного груза, конструктивные особенности проекти¬
рования КА и ряд других. Все это требует дополнитель¬
ных комплексных исследований, выходящих за рамки
получения исходных предпосылок на проектирование
КА. Главным является то, что при спуске в атмосфере
Марса задачу о минимальном потребном значении К1Уасп
нельзя решать в отрыве от возможной нагрузки на лобо¬
вую поверхность. Если известны масса КА и возможный
диаметр миделя, то с баллистической точки зрения сле¬
дует выбирать такую фдрму, которая обеспечивает мак¬
симальное значение коэффициента лобового сопротивле¬
ния при прочих равных условиях.
В силу отмеченных факторов задача определения
проектно-баллистических характеристик КА, предназна¬
ченного для спуска в разреженной атмосфере Марса,
оказывается существенно сложнее, чем для КА, осуще¬
ствляющих спуск на планеты, которые имеют более плот¬
ную атмосферу (Земля, Венера), и указанная задача тре¬
бует комплексного решения.
ГЛАВА 3
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ
§ 3.1. ОСНОВНЫЕ ПРОБЛЕМЫ ЗАДАЧИ ОПТИМИЗАЦИИ
После того как получены общие понятия о характер¬
ных особенностях движения КА в атмосфере Марса и
сформирован круг задач, требующих первоочередного ис¬
следования, можно перейти к следующему этапу — поис¬
ку оптимальных траекторий и оптимальных параметров
КА, позволяющих реализовать оптимальные режимы-
снижения.
Оптимальным режимом спуска считается такой, при
котором достигается экстремум некоторого числового по¬
казателя — критерия оптимальности. Если нам изве¬
стен объект оптимизации, который каким-то определен¬
ным образом описан, метод оптимизации и параметры
управления, то с использованием этого метода осущест¬
вляем направленное воздействие на систему с целью до¬
стижения экстремума 1 = 1*. Последний зависит как от
заданных характеристик объекта, которые не подвергают¬
ся процедуре оптимизации,— некоторый вектор р =
= {р1У р2,. . ., рт}, так и от вектора управления и =
= (А, щ,. . ип):
I =1 (р, и). (3.1)
В зависимости от управления и критерий / может быть
как функционалом, когда гь — функция, так и критери¬
альной функцией, если гь описывается совокупностью кон¬
стант.
В процессе оптимизации необходимо обеспечить
/* = I [р. ц*) = extr/ (/?, гь),
г«=и
где гь* — оптимальное управление, принадлежащее об¬
ласти допустимых управлений U.
GO
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ
[ГЛ. 3
При постановке и решении задачи оптимизации иссле¬
дователи сталкиваются по крайней мере с тремя пробле¬
мами [7(5].
а) Определение критерия оптимальности. Необходи¬
мо сформулировать и сформировать некоторые условия,
которые отражают основное назначение системы и ха¬
рактеризуют эффективность выполнения поставлен л ых
перед пей задач.
Исследователи сталкиваются с большими трудностями
ф о р л 1 а л ь т I о г о п р еде т а в л спи я к р и т е р и я о п ти д i а л ь но с ти
для таких сложных систем, как космический аппарат, ра¬
бота которых характеризуется различными, зачастую
противоречивыми показателями качества. При этом
необходимо подчеркнуть, что практическая ценность кри¬
терия целиком зависит от того, насколько полно он
соответствует i;азiгачепию объекта.
б) Проблема идентификации, т. с. формального пред¬
ставления объекта оптимизации, составления его мате¬
матической модели. В общем случае оптимизируемый
объект может быть описан разными математическими мо¬
делями. Это в значительной степени определяется поста¬
новкой задачи, в соответствии с которой разрабатывается
модель, отражающая наиболее важные для изучения
свойства объекта. Исследователю приходится, как пра¬
вило, идти на компромисс между ожидаемой точностью
результатов и сложностью модели. Здесь очень важен опыт
и квалификация исследователя.
в) Выбор метода решения задачи. После того как по¬
строена математическая модель изучаемого объекта и
сформулирован критерий оптимальности, следует присту¬
пать к процедуре оптимизации с привлечением определен¬
ного математического аппарата. Можно указать различ¬
ные методы решения. Но в каждом конкретном случае4
требуется найти метод, который, с одной стороны, давал
бы искомое решение задачи, а с другой — являлся бы
наиболее рациональным с точки зрения его применимости,
корректности и потребных ресурсов ЭВМ. А. это в свою
очередь определяется свойствами рассматриваемой мате¬
матической модели и зависит от сложности оптимизируе¬
мых параметров, накладываемых ограничений и т. д. При¬
емлемых рекомендаций в этом направлении, как правило,
не оказывается.
ВЫБОР КРИТЕРИЯ ОПТИМАЛЬНОСТИ
GI
Указанные проблемы в той или иной степени присут¬
ствуют в любой задаче оптимизации, и в зависимости от
характера сложности конкретной решаемой задачи па
первый план выходит та или иная из них.
Перейдем к более подробному рассмотрению указан¬
ных проблем применительно к рассматриваемой задаче
мягкой посадки иа поверхность Марса.
§ 3.2. ВЫБОР КРИТЕРИЯ ОПТИМАЛЬНОСТИ
Надежность и корректность решения задачи зави¬
сят от правильного выбора критерия оптимальности.
Основной принцип выбора критерия заключается
в строгом соответствии избранного критерия той цели,
которая должна быть достигнута в результате функцио¬
нирования объекта. Формулировка в то го принципа до¬
статочно проста, однако при его применении в конкрет¬
ных задачах возникают существенные трудности, которые
видны из следующих соображений. Во-первых, к крите¬
риям предъявляются, как правило, противоречивые тре¬
бования. С одной стороны, критерий должен быть про-'
стым, физичным, легко вычисляться, по с другой —
учитывать все существенные особенности работы систе¬
мы в данном окружении, среде. Кроме того, критерий
должен заметным образом реагировать па изменение па¬
раметров. Во-вторых, в сложных системах из-за неяс¬
ности в оценке наилучшего результата критерий может
принимать векторную форму, по которой трудно оценить
эффективность системы (проблема многокритериалъно-
спги). И наконец, в силу иерархической структуры боль¬
шинства систем трудно, а иногда и невозможно, оцепить
степень соответствия частных задач эффективности под¬
систем общей задаче эффективности глобальной системы.
Указанные трудности преодолеваются прежде всего
Путем предварительного анализа системы, выявления
наиболее существенных факторов и отбрасывания второ¬
степенных. Подобная процедура может быть основана па
анализе чувствительности критериальной функции. Ос¬
новным направлением в преодолении второй и третьей из
Указанных здесь групп трудностей является синтез не¬
которого глобального критерия на базе нескольких част¬
ных критериев. Следует отметить, что наиболее простой,
62
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ [ГЛ. Л
однокритериальиый подход, заключающийся в осмыслен¬
ном, направленном выборе наиболее важного критерия
и в переводе остальных критериев в разряд ограничений,
обладает известной ограниченностью, иногда не позво¬
ляющей корректно решить поставленную задачу, особенно
с учетом требований системного подхода.
Многокритериальная задача наиболее сложна в поста¬
новке и решении, по ее необходимо рассматривать в тех
случаях, когда
— оценивается эффективность совместно действую¬
щих нескольких систем, каждая из которых определяете;!
своим показателем эффективности;
— эффективность системы оценивается для различных
условий и для каждого вводится отдельный критерий;
— производится одновременная оценка системы с не¬
скольких точек зрения.
В общем виде задача оптимального проектирования
оценивается скалярными критериями /1? /2,..., 7S, обра¬
зующими вектор эффективности I. В процессе проекти¬
рования могут быть найдены различные варианты реше¬
ний /г, определенные в допустимой области решений Хх,
образованной соответствующими ограничениями. Необ¬
ходимо найти решение /*, принадлежащее области Тх
и обеспечивающее оптимальное значение вектора эффек¬
тивности.
Рассматриваемый подход является наиболее общим,
а путь решения наиболее трудоемким. При этом возни¬
кают следующие основные проблемы:
а) Выбор принципа оптимальности, определяющего
отношение порядка между компонентами вектора эффек¬
тивности.
б) Нормализация, т. е. приведение к одному масштабу
измерений компонент вектора эффективности.
в) Учет приоритета, степени важности компонент, оп¬
ределяющего значимость достижения совершенства по от¬
дельным компонентам.
Для принятия решения, оптимального в смысле век¬
торного критерия, в первую очередь выделяется область
компромиссов, или область решений, оптимальных по
Парето [53]. Эту область можно определить как некоторое
подмножество, принадлежащее множеству допустимых
решений и обладающее тем свойством, что внутри этой
ВЫБО Р К РИТЕ IЧ1Я ОПТИМАЛЬНОСТИ
63
области одна компонента вектора эффективности не может
быть улучшена без ухудшения хотя бы одной другой
компоненты. Задача нахождения области Парето сводит¬
ся к задаче нахождения глобальности экстремума линей¬
ной формы, справедливого для выпуклого допустимого мно¬
жества, при отсутствии выпуклости производится опре¬
деление всех локальных экстремумов и их проверка по
условиям доминирования. Выделение области Парето
существенно сужает области поиска оптимальных реше¬
ний и тем самым ускоряет процесс оптимизации. После
выделения этой области выбор оптимального решения
производится на основе какой-либо схемы компромисса,
имеющей общие принципы.
Пусть все компоненты вектора эффективности равноцен¬
ны; тогда справедливым будет такой компромисс, при кото¬
ром относительный уровень снижения качества по одной
из компонент не превосходит аналогичной величины по
остальным компонентам. Этот подход называют принци¬
пом справедливого компромисса. Существенным недостат¬
ком этого принципа является неприменимость его в слу¬
чае различной важности компонент вектора эффектив¬
ности. Этот недостаток можно устранить введением век¬
тора распределения важности критериев
Ф = {фи- • •, фу}*
в соответствии с компонентами которого изменяются коэф¬
фициенты. Однако при этом возникают трудности в аргу¬
ментированном построении вектора ф. Поэтому вводятся
другие принципы компромиссов, например принципы гиб¬
кого и жесткого приоритетов. При использовании прин¬
ципа жесткого приоритета компоненты располагаются по
важности в ряд предпочтения
111 ^21 liji
на основе которого проводится последовательная оптими¬
зация. При этом недопустимым считается повышение уров¬
ня менее важных компонент, если это приводит к любому
уменьшению уровня более важных компонент. В этом
случае оптимизация сводится к последовательному отыс¬
канию локальных оптимумов и при практическом приме¬
нении приводит к одиокритериальной оптимизации по
наиболее важному критерию.
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ
[ГЛ. 3
Применение принципа гибкого приоритета предпо¬
лагает задание коэффициентов важности компонент, об¬
разующих вектор распределения <р. Соответствующие
компоненты вектора ф учитываются при проведении нор¬
мализации компонент. Таким образом, производится двой¬
ная нормализация критериев — по масштабу и по важ¬
ности. Этот принцип аналогичен принципу справедливо¬
го компромисса с корректировкой критериев по важности.
Одним, из широко распространенных методов много¬
критериальной оптимизации является метод априорного
ранжирования, являющийся достаточно точным инстру¬
ментом при необходимости выбора одного из многих ва¬
риантов принципиально различающихся решений [20J.
Метод сводится к выбору компонент векторного критерия
эффективности, ранжированию этих компонент по важ¬
ности путем введения весовых коэффициентов и опреде¬
лению числовых значений каждой компоненты (как по
объективным, так и по субъективным факторам). После
этого осуществляется свертывание векторного критерия
в скаляр и выбирается вариант с наибольшим (или наи¬
меньшим) значением этого скаляра. Последнее приводит
во многих случаях к существенному упрощению задачи.
Следует отметить, что под свертыванием (или объедине¬
нием) векторного критерия оптимальности понимается
процесс образования скалярной функции I = Ф [/1? /2, . . .
. . ., 7J, являющейся обобщенным критерием для задачи
многокритериальной оптимизации. Вопросам построе¬
ния обобщенных критериев оптимальности и сведению мно¬
гокритериальных задач к однокритериальным посвяще¬
но много работ (см., например [14, 15, 17, 76]). Ниже
кратко остановимся лишь на нескольких наиболее распро¬
страненных и характерных способах свертывания.
1. Самым простым способом свертывания векторного
критерия в скаляр является суммирование компонент
с соответствующими весовыми коэффициентами, т. е.
строится обобщенный критерий качества в аддитивной
форме:
/-Ус т„ (3.2)
где Is — критерий эффективности s-й операции, fs — ве¬
совой коэффициент s-й операции.
ВЫБОР К ГИТЕ I ЛЯ ОПТИМАЛЬНОСТИ
Подобный способ может быть применен в задачах
проектирования при оценке эффективности системы по
критериям веса (или стоимости), когда суммарный вес
(стоимость) аддитивно включает веса (стоимости) подси¬
стем.
2. Другим способом свертывания векторного крите¬
рия в скаляр является последовательное достижение
частных целей. При этом компоненты располагаются
в некоторой последовательности и оптимизация по .s-ii
очередной компоненте начинается после выполнения оп¬
тимизации предыдущих компонент. Математически это
вы р а жа е тся со о тпошением
3-1
I* = 1} + S sup /;,
где snp It — верхняя граница возможных критериев эф¬
фективности.
Данный способ приемлем при оценке эффективности
объекта (подсистемы) в иерархической структуре.
3. Во многих случаях удается выделить какой-либо
основной показатель (например, Д), к экстремальному
значению которого и следует стремиться, в то время как
другие компоненты удовлетворяют. неравенствам, полу¬
ченным, например, на основании тактико-технических
требований,
/2 /*2тр) Iз ^Зтр И Т- П.
4. При наличии в системе случайных возмущений за
обобщенный критерий оптимальности рекомендуется при¬
нять максимум вероятности И удовлетворения всем тех¬
ническим требованиям (3.1):
/ = П [/i ^ ^Ггр? ^*2 ^ -^2Тр? /3 ^ ^ЗТр? • • •]•
Кроме этих способов, возможны также другие, осно¬
ванные па получении компромиссных решений. Приведен¬
ные сведения и имеющиеся в литературе другие рекомен¬
дации тем не менее не позволяют при решении конкретной
практической задачи однозначно к правильно выбрать
критерий оптимальности. По существу вопроса следует
сделать ряд принципиальных замечаний [76].
1. При любом представлении критерия оптимальности
присутствуют элементы субъективизма, проявляющиеся
3 Н. М. Ивановг А. И. Мартынов
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ [ГЛ. 3
либо при оценке отдельных показателей, либо при фор¬
мулировке требований и т. н. Только хорошее знание
условий работы системы и состояния техники в ближайшей
перспективе может уменьшить эффект субъективизма.
2. Свертывание многокритериальной задачи фор¬
мально производится достаточно просто. Но далеко не
всегда удается оптимизация по такому критерию. Причи¬
на заключается в отсутствии однозначной зависимости
искомого оптимального управления и* от множества част¬
ных показателей, которые становятся зачастую очевид¬
ными лишь после реализации системы.
3. Возможен случай, когда максимум искомого функ¬
ционала достигается в результате компенсации положи¬
тельных свойств системы отрицательными, так как
весовые коэффициенты fs в (3.2) могут быть и положитель¬
ными, и отрицательными. В силу этого необходимо ана¬
лизировать характер изменения отдельных компонент
в процессе оптимизации.
Сделанные замечания в значительной степени оправды¬
вают распространенный практический подход при выборе
критериев оптимизации, заключающийся в том, что сна¬
чала используются наиболее простые и очевидные кри¬
терии, включающие лишь принципиальные требования
к системе, а удовлетворение остальным проверяется после
проведения оптимизации. Система дорабатывается лишь
в том случае, когда полностью не удовлетворяются вспо¬
могательные требования или ограничения.
Сформулируем теперь критерий оптимальности для
рассматриваемой технической задачи. При проектирова¬
нии КА, осуществляющих посадку на поверхность какой-
либо планеты, в качестве основного критерия, характери¬
зующего оптимальность того или иного варианта решения,
часто используется критерий максимума полезной наг¬
рузки, доставляемой па поверхность
С-К:.’: шах т1П1. (3.3)
Обычно полезная нагрузка включает научную аппа¬
ратуру, отсеки с оборудованием, используемые для ра¬
боты на планете, планетоход или ракету возвращения
и т. п.
Выбор критерия (3.3) в качестве основного опреде¬
ляется огромной стоимостью доставки 1 кг массы груза
§ 3.2]
ВЫБОР КРИТЕРИЯ ОПТИМАЛЬНОСТИ
67
на поверхность планеты, но одновременно и новыми науч¬
ными данными, которые могут быть получены с помощью
аппаратуры, стоящей на КА. В этом смысле указанный
критерий универсален, так как сочетает в себе элементы
стоимостного показателя эффективности и величину науч¬
ной отдачи.
Начальная масса КА, входящего в атмосферу (//гка),
определяется энергетическими возможностями ракеты-
носителя и выбранной схемой полета. Масса полезного
груза, являющегося составной частью /??кА, зависит от
массы остальных систем , обеспечивающих его
При заданной массе тпкамаксимум полезной нагруз¬
ки соответствует условию
Укрупненно можно выделить четыре основные состав¬
ляющие суммы (3.4), образующие массу остальных систем
(табл. 3.1):
— конструкция КА;
— система тепловой защиты КА;
— система мягкой посадки'(СМП).
К четвертой составляющей отнесем систему управления
спуском КА и все приборы и агрегаты, обеспечивающие
нормальное функционирование и контроль за система¬
ми, входящими в полезную нагрузку КА (система термо¬
регулирования, телеметрические датчики, радиоаппарату¬
ра и т. п.).
Усилия исследователей на выполнение условия (3.4)
направлены по двум путям. Во-первых, стремятся наи¬
лучшим образом решить все специальные задачи, возни¬
кающие при разработке указанных выше систем, т. е.
всячески совершенствуют конструкцию КА и его тепло¬
вую защиту, СМП и систему управления и т. п. Во-вто¬
рых, проводят комплексную оптимизацию, чтобы в рам¬
ках возможных технических решений и возникающих
доставку на поверхность:
тШ1 = Шкл — S тг-
min mi-
(3.4)
з*
68 ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ [ГЛ. 3
Таблица 3.1
Участок
спуска
Система
Физический
фактор
Характеристики КА,
от которых занизит
уронень ноздейстния
сГ
Конструкция КА
Аэродинамиче¬
ские и инерци¬
онные нагруз¬
ки (перегруз¬
ки)
Гсометрия формы
КА, распределе¬
ние массы
н
о
о
а:
о
Теплозащита
Нагрев и дав¬
ление
Конфигурация, ха¬
рактеристика теп¬
лозащитного мате¬
риала
R
о
<
Система управле¬
ния и стабилиза¬
ции, приборы, дат¬
чики и т. д.
Динамические
нагрузки, на¬
грев
Компоновка и рас¬
пределение массы
а
Конструкция сис¬
темы мягкой по¬
садки
Аэродинамиче¬
ские и инер¬
ционные на¬
грузки, нагрев
Тип системы мяг¬
кой посадки
s=C
а
о
о
«
03
Сч
Система управле¬
ния и стабилиза¬
ции (включая мас¬
су топлива при ис¬
пользовании ТДУ)
Динамические
нагрузки
Тип системы мяг¬
кой посадки
Конструкция по¬
садочной платфор¬
мы и шасси
Перегрузка в
момент кон¬
такта с по¬
верхностью
Вид амортизирую¬
щего устройства
противоречивых требований найти компромисс в создании
отдельных систем, приводящий в итоге к наилучшему
удовлетворению условия (3.4).
Одно из центральных мест в разработке отдельных си¬
стем и в проектировании КА в целом занимает оптимиза¬
ция траектории. Действительно, семейство траекторий
ВЫБОР КРИТЕРИЯ ОПТИМАЛЬНОСТИ
69
спуска в сочетании с некоторыми внешними факторами
(характеристики окружающей среды и т. д.) практически
полностью определяют все нагрузки и условия снижения
КА. Задача оптимизации траектории, как и любая ва¬
риационная задача, также начинается с выбора критерия
оптимизации. И здесь мы сталкиваемся с большими труд¬
ностями. Обращаясь к опыту создания КА, спускаемых
на Землю, мы обнаруживаем большое количество крите¬
риев, выдвигаемых при решении различных оптимальных
задач: минимизация массы тепловой защиты, максимиза¬
ция коридора входа, минимизация максимальных пе¬
регрузок и многие другие. При этом в каждой конкретной
задаче в качестве основного выдвигалось то или иное ус¬
ловие, а другие выступали в качестве ограничения. Так
как задача мягкой посадки на поверхность Марса являет¬
ся многокритериальной задачей оптимального проекти¬
рования, то без детального анализа условий спуска в
атмосфере Марса трудно отдать предпочтение тому или
иному требованию, опираясь только на опыт посадки на
Землю.
Для формирования достаточно удобного и физически
оправданного критерия оптимальности, а также с целью
упрощения общей задачи оптимизации сформулируем и по¬
пытаемся решить следующие две задачи:
1. Определить для марсианского КА основную состав-
i
ляющую суммы 2 ти минимизация которой способст-
г=1
вует наилучшему выполнению условия (3.4) и соответствен¬
но условия (3.3).
2. С целью обеспечения максимальной эффективности
оптимизации траектории определить некоторые усло¬
вия, удовлетворение которым приводит к максимуму
массы полезиой нагрузки.
В формальной постановке это означает, что мы пы¬
таемся выделить основную компоненту векторного крите¬
рия оптимальности, а остальные переводим, например,
в разряд ограничивающих условий, т. е. в этом случае
объединение частных критериев проводится посредством
введения наиболее важного критерия, который миними¬
зируется при некоторых «пороговых» значениях осталь¬
ных частных критериев [9].
70
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ
[ГД 3
Для решения первой из сформулированных задач про-
I
анализируем каждую из составляющих 21 miK, опираясь
г=1
на опыт создания земных КА, попытаемся определить их
место в рассматриваемой проблеме.
Обратимся опять к табл. 3.1, где, помимо основных
г-4
составляющих 21 ть на каждом из участков спуска КА
г=1
в атмосфере Марса приведены и основные физические фак¬
торы, которые обуславливают воздействие внешней сре¬
ды на их массу. Видно, что факторы, определяющие
массу каждой из обслуживающих систем, не зависят от
задач конкретной экспедиции. Поэтому при методологи¬
ческом решении вопроса о выявлении основной составляю-
i
щей 21 тг можно отвлечься от целевых задач и исследо-
г=1
вать этот вопрос параметрически. В общем случае для
этого нужно проводить достаточно сложный и громоздкий
объем исследований и расчетов, требующий большого
числа экспериментов и натурных испытаний, возможные
комбинации которых должны обеспечивать в модельных
условиях величины нагрузок, нагрева и других характе¬
ристик режима, которые ожидаются при спуске КА в ат¬
мосфере Марса и определяют условия работы конструк¬
ции, теплозащиты, системы мягкой посадки и т. д.
Однако, учитывая тот факт, что нет необходимости
в точной количественной оценке массы рассматриваемых
систем и достаточно дать лишь их сравнительный анализ,
поставленная задача может быть существенно упрощена.
Идея заключается в следующем. Основной состав средств,
обеспечивающих доставку полезной массы на поверхность,
остается примерно одинаковым при спуске КА в атмосфе¬
ре любой планеты (см. табл. 3.1). Сравнивая режимы спус¬
ка КА в атмосферах разных планет, можно сделать каче¬
ственный вывод об определяющем влиянии массы какой-
либо системы, если для одной из этих планет имеется
отработанный КА. В качестве эталонных КА могут рассмат¬
риваться, например, земные аппараты, ибо именно здесь
имеется наибольшее количество методических разработок,
подтвержденных многочисленными запусками КА.
ВЫБОР КРИТЕРИЯ ОПТИМАЛЬНОСТИ
71
Конструкция КА. При использовании КА одинаковой
формы и геометрии масса конструкции зависит от величи¬
ны аэродинамической и инерционной нагрузки, действую¬
щей на спускаемый КА при прочих равных условиях.
Исследования показали (см., например, [62]), что величина
аэродинамических сил, действующих па КА, практически
не зависит от имеющегося различия в газовом составе
атмосфер Земли и Марса при прочих равных условиях.
Мерой влияния состава газа на аэродинамические силы
могут служить, например, отношения коэффициентов
лобового сопротивления (Сх) и подъемной силы (Су) при
спуске в атмосфере Марса к соответствующим величинам
(СхЛ и Суг) в земной атмосфере. Полагая, что распределе¬
ние давления по поверхности КА при гииерзвуковых чис¬
лах Маха описывается формулой Ныотоиа
Р^2 • q
Р = Pup-L2-sm'»>
где ft — угол между направлением потока и касательной
к телу, рпр — приведенное давление в критической точ¬
ке, можно показать, что имеют место тождества
СX Су Лф /О пл
5-3 ^ Суз -ftipi ■ ( }
На рис. 3.1 в качестве примера показано изменение
величины /?пр для атмосферы Марса (100% С02) и Земли
Aip .1
_ (0у)$\г
А"
I!
Ар при 100°/о со2
1,90
-V
s'
Ар Оля Зоздуха
т
1,88
0
-1,0 /
/
0,9 , X’
^ i . i 1 1 >.
1 2 4
0 8 10 11 V0iKM/cm
Вис. 3.1. Влияние состава атмосферы на коэффициенты аэродинамических
сил и величину приведенного давления в критической точке (Рцр).
при спуске аппаратов, имеющих форму затупленных тел
малого удлинения. Видно, что величина рпр для воздуха
и С02 незначительно изменяется в зависимости от скоро¬
сти, а отношения коэффициентов лобового сопротивления
72
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ
[гл. з
практически постоянны и в рассматриваемом диапазоне
скоростей близки к единице. (Коэффициенты для С02
при этом лишь примерно на 3% больше, чем для воздуха.
С уменьшением содержания С02 в атмосфере Марса раз¬
личие этих коэффициентов еще более уменьшается.)
Отмеченное свойство практической независимости аэ¬
родинамических сил от газового состава атмосфер Марса
и Земли позволяет легко проводить сравнительный ана¬
лиз массы конструкции КА. Действительно, при прочих
равных условиях можно считать, что величина аэродина¬
мической силы, а следовательно, и масса конструкции КА
в первом приближении, достаточном для сравнительных
оценок, зависят лишь от скорости полета и плотности ат¬
мосферы (см. главу 2). Поскольку скорость и плотность
входят в выражение (2.1) в виде произведения, то оказы¬
вается, что масса конструкции КА зависит от безотно¬
сительной к атмосфере любой планеты характеристики —
величины перегрузки, испытываемой КА на траектории
снижения. Проведенные исследования показали, что
спуск КА на поверхность Марса можно обеспечить с пе¬
регрузками, несущественно превышающими перегрузки,
действующие на КА, возвращаемые на Землю. Это поз¬
воляет предположить, что доля массы конструкции ос¬
тается примерно одинаковой при спуске КА как на Марс,
так и на Землю.
Как известно, задача уменьшения максимальной пере¬
грузки является чрезвычайно актуальной при спуске
пилотируемых КА. Возможный в этом случае выигрыш
даже в несколько единиц птах может существенно улуч¬
шить комфортабельность условий для человеческого ор¬
ганизма, и в силу этого может быть оправдана постановка
задачи с использованием критерия min 7imax* При этом
достигаемое улучшение режима спуска (очень важное
с точки зрения безопасности человека) практически не
оказывает влияния на массу конструкции КА. При ис¬
следовании Марса в ближайшем будущем целесообразно
рассматривать лишь автоматические КА и выдвижение
подобного критерия было бы оправдано лишь в случае
значительного уменьшения нагрузок на КА, приводяще¬
го к существенному выигрышу в массе конструкции. Од¬
нако ничего подобного не наблюдается. Действительно,
в главе 2 было показано, что даже при баллистическом спус-
§ 3.2]
ВЫБОР КРИТЕРИЯ ОПТИМАЛЬНОСТИ
73
кс КА с использованием аэродинамического торможения
максимальные перегрузки сравнительно невелики и не
превышают 15 -— 18. Введение подъемной силы не позво¬
ляет существенно снизить 71шах, особенно если учесть все
возможное семейство возмущенных траекторий. В си¬
лу этого критерий min птах не эффективен с позиций
уменьшения нагрузок на КА и уменьшения соответствен¬
но массы конструкции. Единственным путем остается со¬
вершенствование конструкции путем введения оригиналь¬
ных конструктивных решений, улучшения технологии
и качества применяемых материалов.
Теплозащита КА. Составляющими суммарного тепло-
потока к поверхности спускаемого КА являются конвек¬
тивный тепловой поток, равновесное и неравновесное из¬
лучение и излучение продуктов абляции теплозащитного
покрытия. Последнее может быть существенным в зави¬
симости от материала покрытия, режима движения и со¬
става атмосферы. Если влиянием внешней среды на излу¬
чение продуктов абляции можно пренебречь, то при оцен¬
ках тепловых режимов эту составляющую теплоподвода
можно считать практически одинаковой при спуске КА
как в атмосфере Земли, так и в атмосфере Марса в случае
одинаковых геометрических параметров КА и материала
теплозащитного покрытия.
Влияние состава атмосферы на внешний теплообмен
КА (конвективный нагрев) исследовалось эксперимен¬
тально и теоретически и обсуждалось многими авторами
(например, [2, 3, 62]). При этом результаты и выводы
количественно и качественно ограничены рамками ис¬
ходных предположений, упрощениями моделей явлений
или связаны со спецификой конкретного эксперименталь¬
ного оборудования. В работе [62] оценивалось в ударной
трубе влияние состава атмосферы на конвективный тепло-
поток в передней критической точке на моделях со сфери¬
ческим затуплением. Использовались различные комби¬
нации газов С02, N2, Аг. На рис. 3.2 представлены осред-
ненные результаты измерений для смесей газов различ¬
ного состава. По оси ординат отложена максимальная
величина удельного ламинарного конвективного тегшо-
потока qkmax, а по оси абсцисс скорость входа КА в атмо¬
сферу. Из представленного рисунка видно, что при скоро¬
стях V0 ^ 7,6 км/сек ионизация еще несущественна и
74
ПОСТАНОВКА ЗА7ЦАЧИ МЯГКОЙ ПОСАДКИ [ГЛ. 3
тепловые потоки в критической точке близки друг к другу
для различных атмосфер.
Распределение конвективных потоков тепла для гео¬
метрически идентичных конфигураций также можно счи¬
тать практически независящим от состава атмосферы,
что может быть проиллюстрировано экспериментальными
шх^ал/м^/свю
О I I I I =►
6000 7600 9000 10500
V0, м/сек
Вис. 3.2. Максимальная величина удельного теплопотока в критической точке
для смесей различного состава.
данными для сферического затупленного тела, приведен¬
ными в работе [02].
Лучистые потоки тепла и их распределение по поверх¬
ности во многих случаях сильно зависят от состава атмо¬
сферного газа. Оказывается, однако, что для скоростей
входа КА в атмосферу Марса, которые практически мень¬
ше 8 км/сек, лучистый тепловой поток по сравнению с кон¬
вективным имеет существенно меньшее значение, поэтому
необходимая масса теплозащиты полностью определяется
конвективным теплообменом. Отсюда следует, что при
скоростях входа, меньших 8 км,/сек, масса теплозащит¬
ного покрытия не зависит от состава атмосферы. При
увеличении скорости входа до 9—15 км/сек начинает ока¬
зывать влияние лучистый теплопоток и масса покрытия
ВЫБОР КРИТЕРИЯ ОПТИМАЛЬНОСТИ
75
начинает зависеть от газового состава атмосферы. Этот
случай нуждается в специальном исследовании.
Как известно, для КА, совершающих спуск в атмо¬
сфере Земли, при скоростях входа, меньших 8-Н-9 км/сек,
необходимая масса тепловой защиты составляет 5 -т- 10%
от суммарной массы КА [2, 111]. В силу вышесказанного
эти значения характерны и для марсианских КА.
При больших скоростях входа (F0 = 10 н- 15 км/сек)
КА в атмосферу Марса необходимая масса теплозащиты
спускаемого КА может достигать 20—25% от его полной
массы и существенно зависит от выбранной схемы спуска
и формы аппарата.
Как отмечалось в главе 2, повышенные скорости входа
(V0 ^> 8 км/сек) характерны прежде всего для ускоренных
схем полета, применения которых в ближайшем будущем
не следует ожидать. Дополнительно к этому следует‘отме¬
тить, что эффект оптимизации траектории сказывается
на массе теплозащитного покрытия лишь в случае входа
в атмосферу Марса с высокой точностью по высоте услов¬
ного перицентра, по крайней мере с Д/г"ав = +(3 ч- 5) км
и при хорошем знании характеристик атмосферы. Точ¬
ность, обеспечиваемая современными средствами нави¬
гации, почти на порядок хуже (см. главу 2). Поскольку
наибольшее тепловое нагружение КА испытывает при
движении по одной из границ навигационного коридора,
где управление, как правило, близко к граничному и вы¬
бирается из соображений, не связанных с оптимизацией
траектории, то и возможность какого-либо варьирования
и управления на траектории снижения из условия мини¬
мизации массы теплозащитного покрытия практически
отсутствует.
Независимость массы теплозащитного покрытия от
газового состава атмосферы, а также существенно мень¬
шая длительность спуска марсианских КА и соответ¬
ственно уменьшенная в несколько раз по сравнению
с земными условиями суммарная величина теплопотока
позволяют сделать вывод, что для современных аппаратов,
осуществляющих спуск в атмосфере Марса, степень теп-
лопапряженности различных траекторий спуска, вообще
говоря, не является определяющим фактором. В связи
с этим при решении задач оптимизации траекторий спус¬
ка не обязательно для каждой траектории одновременно
76
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ [ГЛ. 3
рассчитывать тепловые нагрузки и массу теплозащиты.
Они определяются после выбора траектории из условия
удовлетворения некоторым другим критериям оптималь¬
ности.
Система управления. Масса системы управления КА
зависит от многих факторов, основными из которых яв¬
ляются:
— динамические нагрузки, испытываемые спускаю¬
щимся КА;
— выбранный критерий оптимизации траектории;
— эффект реализации выбранного критерия гс по¬
мощью системы управления.
Величина динамических нагрузок и теплового нагрева
определяется геометрией выбранной формы и распределе¬
нием массы внутри КА. Эти факторы, как было показано,
не зависят от газового состава атмосфер, а их величины при
спуске КА в атмосфере Марса не превышают получающих¬
ся в земной атмосфере при прочих равных условиях.
Тогда чрезвычайно возрастает роль последних двух фак¬
торов.
Действительно, масса системы управления существен¬
ным образом зависит от критерия оптимизации траек¬
тории и эффекта его реализации. Наилучшее удовлетво¬
рение выбранному критерию возможно лишь при исполь¬
зовании более совершенных, как правило, усложненных
систем управления, а это неизбежно приводит к возраста¬
нию их массы. Поэтому в каждом конкретном случае не¬
обходимо проводить сравнительную оценку выигрыша
в массе, который может получиться в результате оптими¬
зации траектории по выбранному критерию с учетом за¬
трат массы на реализацию системы управления. Таким
образом, масса системы управления не может служить са¬
мостоятельным оптимизируемым критерием.
Система мягкой посадки. Сравнение масс СМП аппа¬
ратов, совершающих спуски в атмосферах Земли и Марса,
представляет существенно более сложную задачу, чем
обсужденные выше, так как условия ввода в действие
СМП в атмосфере Марса значительно отличаются от зем¬
ных условий (для определенности предполагаем, что в
обоих случаях используется парашютно-реактивная си¬
стема мягкой посадки). Эти условия можно характеризо¬
вать двумя параметрами для начального момента ввода
§ 3.2J
ВЫБОР КРИТЕРИЯ ОПТИМАЛЬНОСТИ
77
в действие парашютной системы: числом Маха М, опреде¬
ляющим аэродинамическую картину обтекания парашю¬
та, и скоростным напором q — количественной характери¬
стикой потока, от которой зависят нагрузки па тормозное
устройство. Они определяют конструкцию и массу пара¬
шютно-реактивной СМ II.
На рис. 3.3 в координатах. (М, q) представлены типич¬
ные условия ввода в действие парашютной системы для
КА [62], осуществляющих спуск в атмосферах Земли и
Марса. Видно, что харак¬
терной особенностью спус¬
ка в атмосфере Земли яв¬
ляется ввод парашютов
при числах М 1, в то
время как q изменяется
в широких пределах (150 —=—
-г- 1000 кгс/м2, включая
нештатные ситуации). Рас¬
ширение области приме¬
нения дозвуковых пара¬
шютов в земных условиях
может быть вызвано, на¬
пример, значительным увеличением приведенной нагрузки
на лобовую поверхность либо необходимостью стабилиза¬
ции и торможения КА на больших высотах. В нижней части
рис. 3.3 показана область типичных условий ввода пара¬
шютов в марсианской атмосфере. Видно, что, в отличие от
земных КА, ввод парашютов осуществляется при доста¬
точно малых значениях скоростного напора (q 100 -г-
150 кгс/м2), но при числах М, значительно превышаю¬
щих скорость звука (М ж 2,5 -г- 3,5). Отсюда возникает
необходимость разработки качественно новых видов си¬
стем мягкой посадки, способных нормально функциони¬
ровать в столь необычных условиях.
Можно указать два основных направления оптимиза¬
ции СМП:
— выбор рационального типа СМП;
— оптимизация траектории для создания наилучших
условий при вводе в действие СМП.
Оптимизация СМП по указанным направлениям долж¬
на осуществляться с точки зрения минимума ее массы,
так как именно она служит основной минимизируемой
кгс/мг
Гис. 3.3. Характерные условия ввода
в действие парашютов для земных (J)
и марсианских (2), КА.
78
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ [ГЛ. 3
I
составляющей массы 2 при посадке на Марс. Действи-
г=1
тельно, при тех условиях ввода в действие парашютно¬
реактивной системы, которые представлены на рис. 3.3,
для достижения пулевой скорости в момент контакта КА
с поверхностью Марса необходимо использовать парашю¬
ты, площадь которых в несколько десятков раз превы¬
шает площадь парашютов, обеспечивающих мягкую по¬
садку в земных условиях, или в несколько раз увеличить
массу топлива на активное торможение. Это объясняется
не только большими скоростями, сопровождающими ввод
в действие СМИ, по и большей разреженностью марсиан¬
ской атмосферы по сравнению с земной. Из сказанного
вытекает существенное увеличение массы СМИ. Отсюда
следует, что оптимизация траекторий спуска на поверх¬
ность Марса должна проводиться из условия минимума
массы СМИ.
Итак, проведенный анализ позволяет выделить осиов-
i
ную составляющую 2J в задаче мягкой посадки КА
г—1
на поверхность Марса и соответственно сформулировать
критерий оптимальности в виде
min 77iCMn. (3.6)
Другие составляющие должны учитываться как ограни¬
чивающие факторы и после решения задачи из условия
(3.6) еще раз анализироваться. Если окажется, что по
какой-то из составляющих нет удовлетворительного ре¬
шения, то полученные данные пересматриваются, т. е.
система дорабатывается.
На этом заканчивается общее рассмотрение задачи вы¬
бора критерия оптимальности, но со следующей оговор¬
кой. Критерий (3.6), как видно, не дает прямого ответа
на поставленную задачу 2 § 3.2, т. е. не сформулирован
критерий оптимальности для синтеза траекторий спуска
на участке основного аэродинамического торможения.
Эта задача будет рассмотрена ниже, после анализа участ¬
ка .мягкой посадки согласно условию (3.6).
Рассмотрим основные типы систем мягкой посадки и
приведем расчетные формулы для оценки их массы.
§ 3.3] КЛАССИФИКАЦИЯ СИСТЕМ МЯГКОЙ ПОСАДКИ
70
§ 3.3. КЛАССИФИКАЦИЯ СИСТЕМ МЯГКОЙ ПОСАДКИ
Проведенный анализ траекторий спуска на участке
аэродинамического торможения показал, что при посадке
КА на Марс необходимо создавать качественно новый
тип СМП, способной функционировать па сверхзвуковых
скоростях полета (М ^ 2,0 3,5). Это обстоятельство
и малая плотность атмосферы препятствуют применению
разработанных для земных условий систем посадки КА,
к которым можно отнести систему посадки самолетного
типа, роторную систему посадки, гибкое крыло Рогалло
(парапланер) и др. Новые условия применения требуют
проверки и пересмотра многих прежних представлений и
выработки новых конструктивных решений.
В основном при спуске КА на поверхность Марса рас¬
сматриваются три типа систем мягкой посадки:
— пассивная тормозная система с амортизацией;
— активная тормозная система;
— комбинированная СМП, предполагающая последо¬
вательное использование пассивного и активного тормо¬
жения.
Наиболее простым типом СМП является пассивная тор¬
мозная система (без двигателей мягкой посадки). Ее кон¬
структивное исполнение может быть различным. К ней
относятся парашютные системы, так называемые тормоз¬
ные зонтичные устройства, парабалоштые системы и т. д.
Благодаря конструктивной простоте, высокому лобовому
сопротивлению при относительно небольшой массе и ком¬
поновочном объеме наиболее эффективным тормозным
устройством является парашют. В случае использования
парашюта для достижения допустимых перегрузок при
контакте с поверхностью необходимо применение аморти¬
зирующих устройств (надувные мешки, колесное или лыж¬
ное шасси с амортизацией и пр.). Система посадки полу¬
чается достаточно легкой и простой, однако при реальных
величинах'хода"7амортизатора*ударные перегрузкищоста-
точно велики (nmiXX > 50). Кроме того, следует отметить,
что посадка на шасси (амортизаторы) при боковом сносе
под действием ветра (простая амортизация в виде"балло¬
нов) может привести к опрокидыванию КА. Применение
же систем с амортизаторами самолетного типа (стойкиТц
пята-лыжа) приводит к их усложнению. В целом сущест¬
80
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ
[ГЛ. 3
вует ряд достоинств паратттютттых систем, по они в зна¬
чительной степени перечеркиваются некоторыми недостат¬
ками этих систем, особенно проявляющимися при спуске
в разрежен пой и неспокойной атмосфере Марса. Пер¬
вый из них заключается в трудностях управления процес¬
сом спуска КА па парашюте. Второй недостаток опреде¬
ляется тем обстоятельством, что потребная масса парашю¬
та обратно пропорциональна скорости парашютирования.
Это приводит к тому, что, начиная с некоторого значения
скорости парашютирования, масса парашюта резко воз¬
растает, что делает его практически непригодным. Третий
недостаток заключается в том, что при торможении в раз¬
реженной атмосфере Марса с увеличением массы спускае¬
мого КА резко возрастает площадь парашюта. В силу
зтого парашютная система (с амортизаторами) может быть
применена только для простейших автоматических аппа¬
ратов лгал ой массы с аппаратурой, выдерживающей боль¬
шие ударные перегрузки при посадке.
Обеспечить комфортабельные условия спуска, снизив
перегрузки практически до пуля («мягкая» посадка), мож¬
но при использовании реактивной системы мягкой посад¬
ки. Для этой цели возможно использование жидкостных
или твердотопливных ракетных двигателей. Отметим, что
можно построить реактивную СМИ и с комбинацией дви¬
гателей: твердотопливного — для основного участка тор¬
можения, а жидкостного — для участка предпосадочного
маневра и посадки.
Исследования, проведенные в процессе разработки КА
«Марс-3, 6» и «Викинг-1, 2», показали, что одним из наи¬
более рациональных вариантов является парашютно-ре¬
активная система мягкой посадки. Основной составляющей
массы такой системы является масса топлива. Предвари¬
тельное торможение КА парашютом позволяет сущест¬
венно снизить потребные затраты топлива, а следовательно,
и массу СМП. Это обстоятельство, однако, тте дает нра¬
ва сделать однозначный выбор в пользу СМП парашютно¬
реактивного типа для любых марсианских КА, ибо, по-
лгимо массы, нужно учитывать и другие факторы, которые
могут заметно повлиять на выбор системы посадки. Так,
при сравнительно большой массе КА (?Щ;\ Э> 8 10 т)
использование парашюттто-реактивпой СМП может ока¬
заться недостаточно падежным, хотя и выигрышным в
^ 3.3] КЛАССИФИКАЦИЯ СИСТЕМ МЯГКОЙ ПОСАДКИ 81
массовом отношении. Это объясняется тем, что с увеличе¬
нием начальной массы КА заметно возрастает площадь па¬
рашюта, что влечет за собой большие трудности по обеспе¬
чению устойчивой и безопасной работы СМИ этого типа.
Поэтому в дальнейшем проводится исследование про-,
блемы спуска КА, использующих как реактивную, так
и парантютно-реактивпую СМИ. Приведем основные рас¬
четные формулы по оценке массы каждого из указанных
типов систем.
Реактивная система посадки. Масса реактивной СМП
(mvз) определяется совокупностью масс топлива, двига¬
телей, аппаратуры, оборудования, топливных баков и
может быть выражена следующей зависимостью [23]:
Щрс = тпкл (1 -Г ао) (1 — е ) + тКАуяв, (3.7)
где — коэффициент совершенства топливных баков,
Тдн — удельная масса конструкции двигателей, Руд —
удельная тяга двигателя, Кхар — величина характерис¬
тической скорости, равная
Гхар - Го + Ат;д + ДУ*Ш - AVt (3.8)
Здесь К* — скорость КА в момент включения двигателя,
Л Киот — величина гравитационных потерь при работе
двигателя, AK*an — запас характеристической скорости
на возможные отклонения от принятых режимов спуска,
А Ка — торможение КА за счет воздействия аэродинами¬
ческого сопротивления на участке работы двигателя.
Здесь и далее звездочкой будут обозначаться парамет¬
ры, которые соответствуют участку мягкой посадки.
Из (3.7) и (3.8) следует, что масса тормозной двига¬
тельной установки (ТДУ) является функцией следующих,
параметров:
а) начальных условий: K<j\ 0О*\ 1ц (в соответствии с ра¬
нее принятыми обозначениями параметры конца траекто¬
рии па участке аэродинамического торможения К/с, 0fe, hк
являются начальными для участка мягкой посадки, т. е.
К, = Ко*, 0й == 0*, hk = /г*);
б) параметров КА: массы тка, площади миделя SM,
коэффициента лобового сопротивления Сх\
82
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ
[ГЛ. 3
в) параметров ТДУ: удельной тяги Руд и тяговоору-
женности Р, расхода массы, массы ТДУ вместе с топлив¬
ными баками.
В общем случае для уменьшения массы системы посад¬
ки желательно иметь возможно меньшую скорость на вы-
высоте включения ТДУ, использовать топлива, обладаю¬
щие высоким удельным импульсом, и, кроме того, выбрать
оптимальную тяговооруженность и оптимальную прог¬
рамму управления вектором тяги двигателя.
Парашютно-реактивная система посадки. Полная мас¬
са парашютно-реактивной СМП складывается ^из массы
парашютной системы 7?гпси массы реактивной системы т[12:
т-прс = Шцс +Щс- (3.9)
Поскольку формулы для расчета массы реактивной
системы аналогичны представленным выше, здесь приве¬
дем лишь формулы для оценки массы парашютной систе¬
мы. Будем рассматривать однокаскадные парашютные
системы с рифлением купола.
Масса парашютной системы определяется по формуле
[23] _
тт = ancRmax (Dha + 0,2 ЦFu) pIICFn. (3.10)
Здесь /?щах — нагрузка на парашют; /?кл — диаметр
спускаемого КА; апс = 0,0003 и |Зас = 0,26 — коэффици¬
енты, характеризующие свойства материала и конструк¬
ции парашюта; Fn — площадь купола парашюта (при вы¬
воде формулы принималось, что длина строп равна 8£>ка).
При раскрытии зарифованиого парашюта нагрузка рас¬
считывается по формуле [23]
Я|П« 1 = Х?* FnC„, (3.11)
где &Д1 = 2,0 — коэффициент динамичности; Сп = 0,9 X
X Ср-См — коэффициент сопротивления парашюта, при¬
чем С р — коэффициент рифления; См — коэффициент,
учитывающий зависимость коэффициента сопротивления
от числа М.
При разрифлении нагрузка определяется по формуле,
аналогичной (3.11),
■^щах 2 х ^*д2FnCnQp'i
§ 3.4] МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ КА
83
при этом А:Д2 = 1,8; qp — значение скоростного напора в
момент разрифления парашюта t = £*.
Анализ представленных расчетных формул позволяет
выделить основные параметры и факторы, от которых за¬
висит //iripc:
а) начальные условия по высоте, углу наклона траек¬
тории, скорости (или скоростному напору): Aq, 0*, Vt (или
qо — qK), а также все необходимые характеристики сни¬
жающегося КА: шца, Сх, См, Du а;
б) параметры парашютной системы: площадь купола
парашюта Fu, коэффициент лобового сопротивления Сп,
коэффициент рифления Ср;
в) параметры реактивной системы, аналогичные при¬
веденным выше для активной СМП.
Таким образом, при использовании рассматриваемых
типов СМИ задача минимизации их массы является комп¬
лексной, зависящей от обоих участков спуска (аэродина¬
мического торможения и мягкой посадки). Ниже дана
общая постановка этой задачи.
§ 3.4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ КА
Математические модели движения КА на отдельных
участках спуска требуют включения различного числа
переменных состояния и различных управляющих пара¬
метров. В общем виде динамика движения КА описыва¬
ется обыкновенным дифференциальным уравнением, кото¬
рое в нормальной форме Коши имеет вид
х = f (х, а, а, г), (3.12)
где
xeRn, weUm, а ЕЕ Аг, (3.13)
х — вектор состояния, и — вектор управления, а —
вектор проектных параметров, t — время, Rn — /г-мер-
ная допустимая область изменения значений переменных
состояния, Um — /^-мерная допустимая область измене¬
ния значений управляющих переменных, АГ — /-мерная
допустимая область изменения значений параметров объ¬
екта управления.
В зависимости от типа используемой системы мягкой
посадки формулы расчета ее массы могут быть различными
84
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ
[ГЛ. 3
(см. формулы (3.8) — (3.11)). Запишем оптимизируемый
функционал в общем виде:
/ = Ф(х(*)), t е [t0, Л, (3.14)
где t0 — начальный момент времени, Т — момент окон¬
чания управления.
Будем полагать, что в начальный момент времени t0
состояние системы (3.12) известно: x\t=t0 = х0, а состоя¬
ние системы в конечный момент времени определяется
некоторой гиперповерхностью X пространства (х, t):
X (х (Г), Т) = 0. (3.15)
При выборе математической модели всегда необходимо
учитывать ограничения (3.13) на параметры состояния,
на управление и т. д., существующие в реальной задаче.
Будем предполагать, что класс допустимых управлений
и состоит из кусочно-непрерывных ограниченных функ¬
ций. Обычно они также непрерывно дифференцируемы
по всем аргументам ас, и, t по крайней мере до второго
порядка включительно.
С учетом принятых обозначений задача оптимального
управления может быть сформулирована следующим об¬
разом: определишь управление и* ЕЕ Um, доставляющее ми¬
нимум функционалу (3.14) при дифференциальных связях
(3.12), имеющихся ограничениях (3.13) и граничных усло¬
виях (3.15).
Рассмотрим задачу минимизации т?гсмп в предположе¬
нии использования парашютно-реактивного типа СМП.
Будем считать, что движение КА на участках аэродинами¬
ческого торможения и мягкой посадки осуществляется
соответственно па отрезках времени В0, tl{] и [$, Т]. При¬
нимается, что момент времени окончания участка аэро¬
динамического торможения совпадает с моментом време¬
ни начала работы СМП: tK = £*• Внутри второго интерва¬
ла имеются следующие характерные точки, достигаемые
в моменты времени: — окончание процесса наполнения
купола зарифоваиного парашюта, £* = t* — разрифовка
парашютов, £* — сброс их, £* — окончание задержки пос¬
ле сброса парашюта, t* — включение ТДУ.
Раскроем смысл используемого параметра управле¬
ния и на всех участках спуска КА. Как отмечалось выше,
§ 3.4]
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ КА
85
на атмосферном участке снижения КА широко использу¬
ется управление эффективным качеством путем изменения
угла крена:
и —- Къф = cos у. (3.16)
При этом величина эффективного качества может изме¬
няться в пределах
-#б<Аоф<Яб. (3.17)
Этот способ управления общепринят для КА скользяще¬
го спуска и ему уделяется основное внимание. При рас¬
смотрении КА с большим значением аэродинамического
качества (К 1) требуется анализировать и двухка¬
нальное управление по углу крена и атаки.
На участке работы парашютно-реактивной системы
КА совершает сначала пассивный неуправляемый спуск
на парашюте на отрезке времени U* -г- £*], а затем управ¬
ляемый полет с использованием ТДУ — на отрезке [tl -н Т].
При этом в качестве управления Р (t) используются два
параметра: величина тяги двигателя, варьируемая в диа¬
пазоне
и угол тангажа
о < р (О
О <тЭ' (t) < 2я.
(3.18)
(3.19)
В предположении, что поле тяготения Марса цен¬
тральное и атмосфера не вращается, уравнения плоского
движения центра масс КА имеют вид [2]
ir Р (h) V2 /и\ • о I Р cos (Ф ~ 6)
У = — -Чгтт g (h) si n 0 -\ -
ф-
2 Р
8(h)
cos О
h =. V sin 0, А = — с,
Д3
8 (h) = g0
(l{ + hj■■ ’
КА
V cos О
R + h
+
P sin (ft — 0)
(3.20)
lKA
86
ПОСТАНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ
[ГЛ. 3
и
Рх = 1 Р = П при (3.21)
Р = 0 при £<*<£; (3.22)
п п
Рх = /ЛА , р = о при <*<«<<*; (3.23)
^иг п
/\. = />tT{A~”l"° ~Шт{Л* , /> = р (t) фо, о = д (/) (3-24)
'.V1 м
при *>**,
где Сп, Ап — коэффициент лобового сопротивления и пло¬
щадь зарифованиого парашюта; Сп, Fn — то же для раз-
рифованного парашюта; тас — масса парашютной сис¬
темы; шка — секундный расход массы, принимаемый по¬
стоянным и равным — с.
Следует отметить, что при расчете траекторий спуска
на участке мягкой посадки второе уравнение системы
(3.20) может быть несколько упрощено за счет преиебре-
V cos 0
жения членом R ^ ■ , величина которого чрезвычайно
мала и практически не оказывает влияния па точность ре¬
шения задачи.
Приведем основные ограничения, накладываемые на
траекторию спуска КА. Одним из наиболее важных яв¬
ляется ограничение на минимально допустимую высоту
пролета КА над поверхностью Марса:
v (t) = Адоп - h (t) < 0. (3.25)
Ограничение (3.25) учитывает возможные колебания
рельефа поверхности Марса (см. главу 1) и исключает
возможность жесткой посадки КА при полете его в низ¬
ких слоях атмосферы. Как уже отмечалось выше, харак¬
терной особенностью работы СМП в условиях разреженной
атмосферы Марса являются большие начальные скорости,
при которых осуществляется ввод системы в действие.
Так как прочностные и теплозащитные свойства парашю¬
тов ограничены и при больших начальных скоростях воз¬
можно их разрушение, необходимо учитывать ограничение
§ 3.5] УПРОЩЕНИЕ ОСНОВНОЙ ЗАДАЧИ ОПТИМИЗАЦИИ
87
на скоростной напор
£(^) = ?доп-?|^*>0> (3.26)
1—]го
и на скорость, при которой вводится в действие парашют¬
ная система,
е(^) = УДоп-У(^)>0, (3.27)
где q (t) — текущее значение скоростного напора; г/Д(Ш —
его максимальная величина, допустимая для парашютной
системы; КД()П — максимальная величина скорости, до¬
пустимая для ввода в действие этой системы.
§ 3.5. УПРОЩЕНИЕ ОСНОВНОЙ ЗАДАЧИ ОПТИМИЗАЦИИ
Сформулируем теперь следующую задачу оптимиза¬
ции: определить программу изменения управляющих пара¬
метров Къф (£)» Р №» б (t), минимизирующую функцио¬
нал (3.9) при ограничениях на управление (3.17) — (3.19)
и на фазовые координаты (3.25)—(3.27), при дифференци¬
альных связях (3.20) — (3.24) и краевых условиях:
при t = l0 V = V09 0 = 0О, h = h0; (3.28)
при t = T V = 0, е = — А- , h = 0. (3.29)
Следует отметить, что в случае использования на ко¬
нечном участке торможения реактивной СМП постановка
задачи и ее формулировка остаются такими же, исключая
уравнения (3.22), (3.23) и ограничения (3.26), (3.27).
> | Характерной особенностью поставленной задачи ком¬
плексной оптимизации траектории спуска является нали¬
чие скачков в правых частях дифференциальных уравне¬
ний (3.20) в моменты раскрытия парашюта (£{;), снятия
рифления (/* = £*)» сброса парашютной системы (£*) и
включения ТДУ (£*). Как известно, в настоящее время тео¬
рия решения разрывных вариационных задач для нели¬
нейных систем дифференциальных уравнений развита не¬
достаточно, а предлагаемые в ней пути решения громозд¬
ки и приводят к возрастанию порядка краевой задачи.
Кроме того, необходимость оптимизации траектории
сразу по трем параметрам управления К^ф (£), Р (t)
и 6 (t) также усложняет задачу, и ее решение в полной
S8
ГЮСТЛНОВКА ЗАДАЧИ МЯГКОЙ ПОСАДКИ
[ГЛ. 3
постановке без использования каких-либо специальных
приемов затруднитсяьпо.
Обсудим выбор рационального метода решения. Чис¬
ленным и аналитическим методам решения вариационных
задач посвящено много работ [9, 37, 76, 103]. Естествен¬
но, аналитические методы очень привлекательны, так как
в некоторых случаях удается получить решение в замк¬
нутой форме. Однако в подавляющем большинстве слу¬
чаев для наиболее актуальных и сложных задач выводятся
только аналитические условия (признаки) оптимальности
и совсем не указываются способы нахождения искомого
оптимального режима. В других случаях для получения
решения приходится вводить ряд принципиальных огра¬
ничений, которые приводят к модельной задаче, значи-*
тельно отличающейся от первоначальной. Поэтому часто
отдается предпочтение алгоритмическим, машинным ме¬
тодам, которые не связаны с необходимостью полного опи¬
сания задачи в аналитическом виде [9, 67]. Иногда исполь¬
зуются элементы формально-эвристических методов [37,
103], которые позволяют получить ответ на поставленную
задачу, хотя и не совсем точный, но зато вычисленный
при минимальных затратах машинного времени. Приме¬
нение численных методов оказывается достаточно эффек¬
тивным и в тех случаях, когда известна структура оп¬
тимального управления. В этом случае существенно
упрощается получение данных. Хорошие результаты
обычно достигаются при решении задачи в интерактивном
режиме, предполагающем оперативное взаимодействие
исследователя с ЭВМ.
Вернемся к сформулированной задаче и попробуем ее
упростить. Для этого необходимо учесть то обстоятель¬
ство, что при спуске КА на поверхность участку работы
СМП предшествует участок основного аэродинамического
торможения. Рассмотрим сначала участок работы СМП
независимо от участка аэродинамического торможения.
Найдем оптимальный режим движения КА, минимизи¬
рующий функционал (3.9). Затем для этого режима (или
близкого к нему) исследуем влияние начальных условий
Vq у б*, А? на массу СМП и определим требования к конеч¬
ным значениям параметров траектории участка основно¬
го аэродинамического торможения. После этого на участ¬
S 3.5]
УПГОЩЕНИЕ ОСНОВНОЙ ЗАДАЧИ ОПТИМИЗАЦИИ
89
ке основного аэродинамического торможения найдем та¬
кой закон управления Клф (t), который обеспечивает
попадание КА в найденную область фазовых координат.
В результате предлагаемого подхода комплексная за¬
дача оптимизации траектории снижения КА в атмосфере
Марса из условия минимума массы СМП сводится к реше¬
нию последовательно двух более простых задач — снача-.
ла на участке мягкой посадки, а затем на участке основ¬
ного аэродинамического торможения. Это позволяет из¬
бавиться от разрывов правых частей в сформулированной
задаче и существенно ее упростить без нарушения общ¬
ности.
Кроме того, в результате решения первой задачи, как
будет показано ниже, удается сформулировать достаточ¬
но простые критерии оптимальности для участка основ¬
ного аэродинамического торможения.
В следующих двух главах исследуется решение пер¬
вой задачи для двух типов СМП — реактивной и парашют¬
но-реактивной.
РАЗДЕЛ 2
СПУСК НА ПОВЕРХНОСТЬ МАРСА
ГЛАВА 4
РЕАКТИВНАЯ СИСТЕМА МЯГКОЙ ПОСАДКИ
§ 4.1. ИСХОДНЫЕ ПРЕДПОСЫЛКИ
Проектирование активной системы мягкой посадки и
организация движения на этом участке является большой
самостоятельной областью космической техники, имею¬
щей свою специфику и свои проблемы, разработка которых
требует специальных методик и соответствующего матема¬
тического аппарата [38, 39, 104—108]. В настоящей главе
изучение участка реактивного торможения проводится в
ограниченном объеме — только в плане проектно-баллис¬
тического анализа, целью которого является выработка
требований к участку аэродинамического торможения. Бу¬
дем считать, что траектории аэродинамического торможе¬
ния удовлетворяют всем поставленным условиям (см. гла¬
ву 3), если обеспечивается выведение КА в некоторую
точку фазового пространства, из которой путем реактив¬
ного торможения можно произвести с минимальными энер¬
гетическими затратами мягкую посадку на поверхность
планеты.
Как отмечалось, участок работы СМП можно рассмат¬
ривать сначала независимо от предшествующего ему
участка аэродинамического торможения. В этом случае
задача анализа участка мягкой посадки сводится к поис¬
ку такого сочетания начальных условий ввода реактив¬
ной СМП— скорости У*, угла 0* наклона траектории к
местному горизонту и высоты ho, которые создают наилуч¬
шие предпосылки для осуществления мягкой посадки с
наименьшими затратами массы. Решение этой задачи за¬
висит от ряда факторов, основными из которых являются
(см. § 3.3):
— выбор оптимальной программы управления векто¬
ром тяги двигателя;
4.1]
ИСХОДНЫЕ ПРЕДПОСЫЛКИ
9i
— выбор оптимальных проектных характеристик ТДУ
(тяговооруженность, удельный импульс топлива);
— выбор типа используемой ТДУ.
Ниже будут рассмотрены все указанные факторы и
показана их роль в формировании требований к участку
аэродинамического торможения.
Диапазон начальных условий. Если не принимать во
внимание участок аэродинамического торможения, пред¬
шествующий участку работы СМГ1, то диапазон варьируе¬
мых начальных условий следует рассматривать очень ши¬
роким:
Понятно, что задача сравнительного анализа потреб¬
ной массы СМП для различных сочетаний начальных ус¬
ловий ее ввода внутри диапазона (4.1) даже при извест¬
ной программе управления величиной и направлением
тяги двигателя требует очень больших затрат машинного
времени. Кроме того, найденное наивыгоднейшее сочета¬
ние начальных условий У*, 0*, h* может оказаться нере¬
ализуемым на участке аэродинамического торможения.
Поэтому задача выбора разумных границ диапазона варьи¬
рования начальных условий ввода СМП является важным
этапом исследования участка мягкой посадки КА с реак¬
тивной СМП. Представляется целесообразным ориентиро¬
ваться на значения параметров в конце участка основ¬
ного аэродинамического торможения Ук, 0К, hKi реали¬
зуемые на траекториях спуска с постоянным значением
аэродинамического качества. Проведенные численные ис¬
следования показали (глава 2), что в зависимости от
проектно-баллистических характеристик КА (Рх и Аб),
условий входа в атмосферу (У0 и /гя), величины ограниче¬
ния по высоте (3.25) и плотности атмосферы (р (/г)) зна¬
чения конечной скорости, угла наклона траектории и вы¬
соты лежат в диапазонах
(4.1)
(4.2)
92
РЕАКТИВНАЯ СИСТЕМА МЯГКОЙ ПОСАДКИ
[ГЛ. 4
Диапазон параметров движения (4.2) определен при
рассмотрении характеристик КА (Рх и К о) и начальных
условий входа в атмосферу, представляющих наибольший
практический интерес. Так, нагрузка на лобовую поверх¬
ность и аэродинамическое качество варьировались в пре¬
делах 50 кг/м1 ^ Рх 800 кг/м2, 0,15 ^ КС) <1 0,7, а на¬
чальная скорость входа и угол наклона траектории
к местному горизонту изменялись в соответствии с требова¬
ниями к траектории межпланетного перелета, изложен¬
ными в главе 2.
Требования к заключительному участку траектории
реактивного торможения. Основной задачей СМП явля¬
ется обеспечение сохранности полезной нагрузки, обору¬
дования или экипажа (в случае пилотируемой экспедиции).
Для удовлетворения этого требования достаточно, чтобы
максимальная перегрузка при контакте с поверхностью
не превышала 40 50 для автоматических КА и 8 10
для пилотируемых КА [92].
В общем случае возможны два вида посадки КА па
поверхность — вертикальная посадка и так называемая
самолетная посадка. В первом случае траектория ре¬
активного торможения на конечном участке должна быть
близка к вертикали, т. е. угол наклона к местному гори¬
зонту 0* ^ —90°. Для обеспечения требуемых значений
перегрузки при наличии обычных посадочных устройств
(см. главу 3) в конце участка вертикальной посадки систе¬
ма управления КА должна гарантировать к моменту кон¬
такта КА с поверхностью планеты уменьшение скорости
снижения КА примерно до 10 -т- 12 м/сек. Горизонталь¬
ная составляющая' посадочной скорости должна быть
небольшой по сравнению с вертикальной, чтобы при небла¬
гоприятных условиях (наличие неровностей, крутых скло¬
нов или сыпучих грунтов в месте посадки) КА не мог
опрокинуться. Вертикальную посадку наиболее целесооб¬
разно применять на первых этапах исследования планеты
Марс при использовании аппаратов баллистического и
скользящего типа, когда поверхность в районе посадки
известна недостаточно хорошо. Именно так осуществляли
посадку советские автоматические аппараты «Марс-3, 6»
и американские КА «Викинг-1, 2».
Существенно более сложной является самолетная по¬
садка КА. Она может быть произведена лишь на специ¬
§ 4.1]
ИСХОДНЫЕ I ГРЕДПОС ЫЛКН
93
ально выбранную достаточно ровную площадку. В этом
случае часть горизонтальной составляющей скорости КА
снимается в процессе движения по поверхности этой пло¬
щадки. Кроме того, чтобы совершить такую посадку, КА
должен иметь особую аэродинамическую форму с разви¬
той несущей поверхностью. При этом КА па конечном
участке должен двигаться почти горизонтально. В момент
касания с поверхностью вертикальная составляющая ско¬
рости не должна превышать 1-4-2 м/сек, а горизонталь¬
ная составляющая должна быть не более 60 -4- 70 м/сек
[92]. Использование самолетного способа посадкиfна по¬
верхность Марса в ближайшем будущем представляется
весьма проблематичным.
В дальнейшем будем считать, что конечный участок
траектории близок к вертикальному и в момент каса¬
ния КА с поверхностью Марса должны выполняться ус¬
ловия
Во многих случаях с целью выбора места посадки и бо¬
лее точного выдерживания условий (4.3) следует предус¬
матривать режим прецизионного торможения КА, кото¬
рый реализуется либо путем глубокого дросселирования
основного двигателя, либо с использованием дополни¬
тельных двигателей небольшой тяги. Однако такой учас¬
ток не обязателен, и во многих случаях им можно пренеб¬
речь.
Как правило, СМП является сложной системой, вклю¬
чающей в себя двигатель (либо связку двигателей), топ¬
ливные баки с топливом, автоматику управления ТДУ
(в частности, счетно-решающее устройство, допплеровские
измерители высоты, которые обеспечивают включение ТДУ
в нужный момент, и т. д.). При исследовании СМП будем
рассматривать только ТДУ (массу конструкции и тягу),
топливо (массу и удельный импульс) и массу конструк¬
ции баков, а остальные элементы будем считать выбран¬
ными оптимальным образом. В зависимости от вида топ¬
лива величина удельного импульса может варьироваться
в пределах [46]
2 '
(4.3)
230 сек gC Руд ^ 320 сек.
(4.4)
94
ГЕАКТИВНАЯ СИСТЕМА МЯГКОЙ ПОСАДКИ [ГЛ. 4
Максимальная тяга варьируется в диапазоне
ткА (Ф ga < Рmax < 5mKA (ф ga Для ЖРД, (4.5)
^KA(^o)?3<^max<15mKA(t*)g-:i для РДТТ. (4.6)
Считается, что двигатель жестко связан: с корпусом
аппарата и направление тяги совпадает с направлением
его продольной оси. Рассматривается общий случай уп¬
равления вектором тяги, который предполагает измене¬
ние величины Р (t) и угла наклона тяги к местному гори¬
зонту — угла тангажа # (t). Поскольку при моделирова¬
нии траектории реактивного торможения используется
запись уравнений движения центра масс КА в скоростной
системе координат (3.20), (3.24), то в дальнейшем будем
пользоваться углом атаки, однозначно связанным с уг¬
лом тангажа Ф через угол наклона траектории
а = О - 0. (4.7)
Предполагается, что переключение тяги и угла атаки
с одного значения па другое осуществляется мгновенно,
а на величину изменения угла атаки никаких ограниче¬
ний не накладывается.
Учитывая изложенные требования и исходные пред¬
посылки, рассмотрим задачу об отыскании оптимального
закона управления КА на участке реактивного торможе¬
ния из условия min /псмп. Следует отметить, что масса
СМП при заданных проектных характеристиках ТДУ
и начальных условиях однозначно определяется массой
топлива ттгг, потребного для организации мягкой посадки
КА (см. (3.6)). Поэтому в дальнейшем в качестве миними¬
зируемого функционала выберем критерий min тТ.
§ ;4.2.ГОПГИМАЛЬНОЕ УПРАВЛЕНИЕ КА
НА У'ЧАСТКЕЦРЕАКТИВНОГО ТОРМОЖЕНИЯ
Рассмотрим сначала управление КА с использовани¬
ем двух управляющих параметров Р (t) и a (t). В этом
случае задача формулируется следующим образом: для
процессов, описываемых системой дифференциальных урав¬
нений (3.20), требуется определить закон управления
Р (t) и a (t), обеспечивающий минимум расхода топлива
или, что одно и то же, максимум конечной массы КА:
max 77i к д. (Т) (4.8)
§ 4.2]
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
95
при ограничении на управление (3.18) и граничных условиях
t = t*: V (f J) = V*, 0 (г*) = 0O*, h (£) = ho,
rni;A (tK) = mKA (tt) = m*; (4.9)
t = /* = 7’: V (T) = 0, 0 (71) = - , h(T) = 0,
T свободно. (4.10)
Необходимые условия оптимальности. Решение сфор¬
мулированной задачи можно получить, используя прин¬
цип максимума [79]. Введем в рассмотрение функцию
Гамильтона
II = фхГ -ЬФгО -\- фз^- Ф- Ф^ка
или, в развернутом виде,
II
(4.11)
Р Р
cos афх -1 sin аф2 —
/1КА 771 к а
С У oF*
КА
g sin 0^1 -f 4j)3V sin 0 -f-
1 2 ni
В этом выражении ф* (г)
определяемые уравнениями
КА
• фа - ‘
Фа- (4.12)
сопряженные переменные,
Ф1 =
011
0V
+
КА
-^ЭфС.АмР
2 пг
КА
g cos 0
W~
* — тт-О
-(
КА
g COS и —
КА
sin 0
КА
7 sin ф2 — ф3 sin0,
>in фх —
Ф2 — Уфз cos 0,
Ь = ТйГ =
= ~~~ От,
ОН
Oh
ОН
Ъп
КА
КА
-W3
КА
2/7гКА
+ •
КА
•COS
а)
Ф1 +
+
U
'uAV
K^CSnV
sma + ~^hT~]b-
(4.13)
9G
[ К А КТ Я ВIIЛ Я СИСТЕМА МЯГКОЙ ПОСАДКИ
[ГЛ. 4
Из условий трансверсальности получим граничные
Принимая во внимание, что система уравнений (3.20)
автономна и время Т свободно, получим
Тогда, учитывая (4.10) и (4.14), из уравнения (4.15) полу¬
чим
В соответствии с принципом максимума Понтрягина
необходимым условием максимума функционала I =
= и^КА {Т) является условие минимума функции II
как функции управления.
Представим функцию Гамильтона в виде
От параметров управления Р (t) и a (t) зависит только
второе слагаемое в функции /7, т. е. функция В2. Функ¬
цию В2 будем называть функцией переключения. Запишем
условие минимума функции В2 по а в виде
II {Г) - 0.
(4.15)
С ) — V sin 0
(4.16)
II = В1 -|- Вг,
(4.17)
где
С 6’ PFa
— ^ si n бар! ^ tyL, (4.18)
НА
(4.19)
§ 4.2]
ОПТИМАЛЬНОЕ УПДАВЛЕНИЕ
97
Используя (4.20), получим
lg а
V4>i
sin а = —
ф.
(4-21)
(4.22)
(4.23)
Условия (4.22) и (4.23) определяют направление тяги на
оп тимал ьиой траектории.
С учетом соотношений (4.22) и (4.23) получим следую¬
щие уравнения оптимального движения КА:
■у X М‘
2 т
КА
— g (К) sin0 ■
PV^X
0
g (h) COS 0
2 т
КА
тКА Yv'^l + ф* ’
"'КA Yv'^l + l|>* ’
h = V sin 0,
7*1 К а = — С,
CSrjV
ф! =-*Г—4V
},1КА
2т
КА
V2
Рфо
= /
I
g COS 0 -
/ g sin 0
wI{AV*K^+^
P'pl
wk.\ ^ + 'I52
Pi1)1
CA^
Ь = —^ tl 57Г- t2,
-)% — A|33sui0,
Ф1 —
4>-2 — Н’з cos 0,
2/Uj-a
<pi =
сАмОЛ!
2"lK.A
P I4h
ti
2/nKA
Рфо Э ID
,mlAV Vv^l+^l 2m*5A
4 H. М. Иванов, А. И. Мартынов
'Фг-
(4.24)
98
РЕАКТИВНАЯ СИСТЕМА МЯГКОЙ ПОСАДКИ
[ГЛ. 4
Функция В2 на оптимальной траектории может быть
записана следующим образом:
в,—г(—** +—^, -+^У
\ '"КА У+ ^2 '"КА У V^1 + ^2 /
(4.25)
Из рассмотрения (4.19) и (4.25) видно, что минимум
функции В2 (а следовательно, и гамильтониана В) по ве¬
личине тяги Р достигается при граничных значениях
Р = Ршах, если Вау О, (4.26)
Р = 0, если £„<0. (4.27)
Итак, на оптимальной траектории управление по ве¬
личине тяги релейно, а пареключение двигателя с одного
Рис. 4.1. Пример оптимального управления на траектории реактивного тор¬
можения.
режима на другой должно происходить в те моменты вре¬
мени, когда функция переключения меняет знак. Коли¬
чество переключений тяги двигателя определяется числом
нулей функции Ва и выявляется лишь в результате чис¬
ленного решения краевой задачи для системы (4.24) и
условий (4.9), (4.10), (4.14), (4.16).
Структура оптимальной траектории. Для решения кра¬
евой задачи использовался метод последовательных при¬
ближений [49]. На рис. 4.1 и 4.2 в качестве примера пред¬
§ 4.2]
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
99
ставлены зависимости фазовых координат, угла б = Ф +
+ 180° и величины тяги от времени спуска на оптимальной
траектории реактивного торможения для КА с начальной
массой ягкд/= 4,5 г, начальной скоростью Vo = 515 м/сек,
углом наклона траектории 0q = —15° и высотой
/го = 6 км. При этом рассматривалась ТДУ типа ЖРД и
Рис. 4.2. Изменение сопряженных переменных при оптимальном управлении.
топливная смесь с величиной удельного импульса Руд =
= 230 сек [46]. Анализ оптимальных траекторий показы¬
вает, что функция переключения Ва имеет только один
нуль и соответственно величина тяги на всей траектории
переключается только один раз с минимального значения
Р — 0 на максимальное Р = Ртах.
Исследования траекторий реактивного торможения
показали также, что структура оптимального управления
P0[)t (t) и aopt {l) остается неизменной для всего рассмат¬
риваемого диапазона варьируемых параметров F*, 0о\
7??кЛ, Руд и РШах• величина тяги Popt (t) имеет одно
переключение с минимального значения па максималь¬
ное, а угол атаки монотонно убывает с некоторого малого
значения —10-: 12° при t = £3: до а ^ 0 при
/[• = Т. Найденный оптимальный закон управления век¬
тором тяги ТДУ позволяет оцепить предельные возможно¬
сти по управлению ТДУ с точки зрения минимизации рас¬
хода топлива на торможение КА.
100
РЕАКТИВНАЯ СИСТЕМА МЯГКОЙ ПОСАДКИ
[ГЛ. 4
С практической точки зрения представляется интерес¬
ным сравнить оптимальные траектории реактивного тор¬
можения с так называемыми траекториями гравитацион¬
ного разворота, при полете по которым вектор тяги все
время направлен против вектора скорости (а = 0), а ве¬
личина тяги максимальна. Проведенные исследования по¬
казали, что использование программы гравитационного
разворота приводит к незначительным дополнительным
затратам топлива (увеличение тТ составляет ~ 2%) по
сравнению с оптимальным законом управления ТДУ.
Учитывая этот факт, в дальнейшем при анализе участка
мягкой посадки будем пользоваться более простой про¬
граммой гравитационного разворота.
§ 4.3. ВЫБОР ОПТИМАЛЬНОЙ ТЯГОВООРУЖЕННОСТИ
Основная составляющая массы реактивной СМП мо¬
жет быть представлена в виде суммы
/?грз = тТ -|- т() -|- /?гк, (4.28)
где 7пТ —масса топлива, т$ —масса баков и пгк —мас¬
са конструкции ТДУ.
Предварительно оценим влияние величины удельного
импульса РУд и тяговооружениости
Р = Р"мх (4.29)
£аш'кл
на массу реактивной СМП. Потребная для реактивного
торможения масса топлива, как известно, уменьшается
с увеличением удельного импульса (рис. 4.3). С этой точки
зрения для уменьшения суммы (4.28) желательно исполь¬
зовать топливо с высоким удельным импульсом. Однако
высококалорийные топлива с большой величиной Руд мо¬
гут иметь весьма низкую плотность и требуют особых ус¬
ловий для хранения [46], что ведет к увеличению потреб¬
ного объема и соответственно «сухом» массы топливных
баков, а значит, к возрастанию суммарной массы реактив¬
ной СМП. Результирующий эффект этих противоположных
факторов не всегда может быть в пользу топлива с высо¬
ким значением удельного импульса, и в каждом конкрет¬
ном случае требуется специальное исследование. В даль-
§ 4.3] ВЫБОР ОПТИМАЛЬНОЙ ТЯГОВООРУШЕННОСТИ
101
нейшем при анализе траекторий реактивного торможе¬
ния, предполагающих использование ТДУ типа ЖРД,
будем ориентироваться на величину удельной тяги
Руд = 275 сек [46, 88].
Другим важным фактором, влияющим на суммарную
массу реактивной СМП, является рациональный выбор
величины тягобооруженности Р. Величина Р по-рэзному'
влияет на каждую из составляющих суммарной массы
тТ,т
Рис. 4.3. Масса топлива, необходимая для торможения при различных зна¬
чениях удельного импульса (7ig = 6 км, QJj = — 15°; сплошная линия — при
у* = 300 м/сек, штриховая — при Vq = 500 м/сек, штрих-пунктирная —
при Vq = 700 м/сек).
(4.28). Так, малое значение тяговооруженности ведет к
большему времени работы ТДУ, соответственно к боль¬
шим гравитационным потерям и в целом к увеличению
потребного запаса массы топлива. Для минимизации гра¬
витационных потерь желательно величину тяговоору¬
женности иметь достаточно большой. Однако это предъяв¬
ляет повышенные требования к прочности конструктивных
элементов ТДУ и приводит к увеличению массы конструк¬
ции ТДУ, которая пропорциональна величине тяги:
ти = удвР max- (4.30)
Каждый конкретный тип ТДУ характеризуется своим
значением величины удельной массы конструкции [46].
102
РЕАКТИВНАЯ СИСТЕМА МЯГКОЙ ПОСАДКИ [ГЛ. 4
В частности, для ТДУ типа ЖРД с величиной максималь¬
ной тяги Ртах = 5 -г- 10 т можно принять удв = 0,04.
Рис. 4.4 иллюстрирует типичные зависимости трех основ¬
ных составляющих (тк, тГ), тТ), а также суммарной мас¬
сы ТДУ (тпрС) от тяговооруженпости для КА с начальной
массой тт1*А = 5 т. Видно, что кривая m[)Cj (.Р) имеет
минимум, который соответствует оптимальной величине
тяговооруженпости. Оптимум по тяговооруженпости для
рассматриваемого примера
составляет величину Р х
ж 1,5. Проведенные иссле¬
дования показали, что ве¬
личина оптимальной тяго-
вооруженности остается
практически неизменной
в широком диапазоне изме¬
нения начальной массы
КА, удельного импульса
топлива и других харак¬
теристик ТДУ. Поэтому
в последующих расчетах
при торможении с помощью
ЖРД величина тяговоору-
женности принималась рав¬
ной Р = 1,5.
На рис. 4.3 представлена оценка суммарных массовых
затрат, необходимых для осуществления мягкой посадки
КА, в зависимости от начальной массы при различ¬
ных значениях удельного импульса ЖРД и начальной
скорости. Видно, что масса СМП линейно возрастает с
увеличением 7тгКл* Отношение массы СМП к начальной
массе КА для фиксированного значения удельного импуль¬
са остается практически неизменным и в зависимости от
его величины составляет 0,2 -г- 0,25 (У* = 500 м/сек).
При этом большие числа соответствуют меньшим значе¬
ниям удельного импульса. Так, при изменении Руп от
275 до 320 сек величина /тгрс уменьшается от 1,27 до 1,1 т
(для КА с начальной массой 5 m и при У0 = 500 м/сек).
Проанализируем комбинированную С А /77, соспгоягиую
из РДТТ и ЖРД. Постановка такой задачи возникает
в силу того, что твердотопливные ТДУ могут развивать
большую тягу по сравнен и го с ЖРД при одной и той же
7!, Т
I ! !
С
Рис. 4.4. Суммарная масса реактивной
СМП и ее составляющих при различных
величинах тяговооруженпости.
§ 4.3] ВЫБОР ОПТИМАЛЬНОЙ ТЯГОВООРУШЕННОСТИ
103
массе конструкции. Комбинацию двигателей можно ис¬
пользовать для некоторого снижения гравитационных
потерь при спуске. Соответственно увеличивается mmi и
уменьшается величина перепада высот, на которую сни¬
жается КА во время работы ТДУ. Кроме того, примене¬
ние РДТТ позволяет гораздо быстрее приблизить траек¬
торию реактивного торможения к вертикальной, что в
целом создает более благоприятные условия для работы
системы управления КА на заключительном этапе мягкой
Vo =709м/сен
50$
}м
J 5 7 9 гп*к.т
Рис. 4.5. Оценка массы реактивной СМП при Р — 1,5.
посадки. Однако использование только твердотопливных
ТДУ для организации мягкой посадки в настоящее вре¬
мя затруднительно в первую очередь из-за сложности
организации приемлемого по точности управления тягой
ТДУ на заключительном участке траектории. Для устра¬
нения указанного нежелательного эффекта и рассматри¬
вается комбинация РДТТ и ЖРД в качестве тормозной
двигательной установки. Схема посадки выглядит сле¬
дующим образом. Сначала КА осуществляет пассивный
полет от высоты h$ до некоторой высоты h{ ^ на ко¬
торой происходит включение РДТТ. Во время работы
РДТТ скорость спуска гасится до некоторой промежу-
i04
РЕАКТИВНАЯ СИСТЕМА МЯГКОЙ ПОСАДКИ
[ГЛ. 4
точной величины Vu. Соображения, из которых исходят
при выборе этой величины, будут обсуждены ниже. Бла¬
годаря большой тяговооруженности РДТТ (Р = 10 -ч- 15)
гашение скорости КА осуществляется сравнительно быст¬
ро, что позволяет улучшить баллистические характерис¬
тики траектории реактивного торможения. При достиже¬
нии аппаратом скорости V = Vn твердотопливная ТДУ
отключается и КА в течение некоторого времени осущест¬
вляет пассивный полет. В конце участка пассивного дви¬
жения на высоте, обеспечивающей выполнение конечных
условий, включается ЖРД и работает вплоть до момента
контакта КА с поверхностью. Управление на обоих участ¬
ках работы тормозной двигательной установки можно
осуществлять по программе гравитационного разворота.
При анализе работы СМП комбинированного типа вво¬
дились следующие предположения:
— на параметры траектории КА в момент окончания
работы РДТТ не накладываются никакие ограничения;
— после выгорания топлива РДТТ корпус двигателя
может отделяться или нет;
— значения удельного импульса топлива и тяговоо¬
руженности составляют:
Руд = 300 сек, Р = 10 (для РДТТ),
Руд = 275 сек, Р = 1,5 (для ЖРД);
— масса конструкции ЖРД вычисляется по формуле
(4.30), а масса РДТТ принималась равной тк = 100 кг.
Важным вопросом является рациональный выбор ско¬
рости Vn в момент окончания работы РДТТ. Эта скорость
должна выбираться по возможности малой для получе¬
ния наилучших баллистических характеристик траекто¬
рии снижения без увеличения массы: СМП, т. е. уменьше¬
ние высоты участка торможения и увеличения крутизны
траектории в момент включения ЖРД (| 0О |). Например,
при Vn = 150 м/сек угол наклона траектории КА в момент
включения ЖРД составляет величину порядка 55 -г- 57°,
а при Vn = 50 м/сек — | 0О | ^ 78 -г- 81° (в зависимости
от начальной скорости и массы КА). Изменение высоты за
время активного торможения КА при Vn = 50 м/сек не¬
значительно и составляет на участке работы РДТТ вели¬
чину порядка 0,1 ~ 0,3 км, а на участке работы ЖРД
§ 4.3]
ВЫБОР ОПТИМАЛЬНОЙ ТЯГОВООРУЖЕНИОСТП
105
0,6 -л- 0,8 км (для КА с А ~ 4 6 т и Vq = 300 -л-
-л- 600 м/сек).
При проведении дальнейших исследований будем ори¬
ентироваться на величину Vn = 50 м/сек. Для этого слу¬
чая на рис. 4.6 представлена зависимость суммарной мас¬
сы комбинированной СМП от начальной массы КА при
Рис. 4.6. Суммарная масса комбинированной СМП (ЖРД и РДТТ).
различных значениях начальной скорости. Увеличение
7?1ка приводит к возрастанию суммарной массы СМП. Так,
при Vq = 500 м/сек увеличение начальной массы КА от
^ка == 3 т до иг&А = 9 т приводит к возрастанию сум¬
марной массы СМП от т[гг = 0,9 т до mvz = 2,52 т.
В целом можно отметить, что система мягкой посадки,
предполагающая совместное использование РДТТ и ЖРД
при прочих равных условиях, требует больших затрат
массы на организацию реактивного торможения, чем при
использовании одного ЖРД. Из сравнения зависимостей,
представленных на рис. 4.5 и 4.6, следует, что при одина¬
ковых начальных условиях (высота ввода Ji'q = 6 км)
СМП, использующая ЖРД, примерно на 10% легче ком¬
бинированной СМП. Эта разница может быть существенно
106
РЕАКТИВНАЯ СИСТЕМА МЯГКОЙ ПОСАДКИ
[ГЛ. 4
уменьшена, если высоту включения РДТТ подбирать оп¬
тимальным образом. При уменьшении начальной высоты
Рис. 4.7. Суммарная масса ком¬
бинированной СМП в зависимости от
начальной скорости (0О* = —15°).
Рис. 4.8. Суммарная масса системы
мягкой посадки с ЖРД в зависимости
от V0* (Go* = —15°, ho* = 6 км, р = 1,5;
сплошная линия — при Руд = 275 сек,
штриховая—при Руд = 300 сек, штрих-
пунктирная — при Руд = 320 сек).
с Щ = б км до Щ = 2 км масса обоих типов реактивной
СМП становится приблизительно одинаковой (рис. 4.7, 4.8).
§ 4.4. ВЛИЯНИЕ НАЧАЛЬНЫХ УСЛОВИЙ
НА МАССУ РЕАКТИВНОЙ СМП
Определим требования к конечным значениям пара¬
метров траектории аэродинамического торможения. На
рис. 4.8, 4.9 показана потребная масса реактивной систе¬
мы мягкой посадки при различных начальных условиях
включения ЖРД по скорости Vq и углу наклона траекто¬
рии к местному горизонту Qq (А* = 6 км). Варьируются
начальная масса ткх и величина удельного импульса
Руд. Аналогичные зависимости имеют место для всего
рассматриваемого диапазона начальных высот 1ц от 3 до
9 км. С увеличением начальной скорости Vq происходит
возрастание суммарных затрат массы на систему торможе¬
ния. Так, при увеличении начальной скорости от Vq =
= 300 м/сек до Vq = 700 м/сек происходит возрастание
§ 4.4] 1ВЛИЯНИЕ НАЧАЛЬНЫХ УСЛОВИЙ НА МАССУ СМП Ю7
суммарной массы СМ11 от трс = 0,98 т до /?грс ==» 1,5 т.
С уменьшением по модулю угла [ Qq | величина суммар¬
ных затрат массы уменьшается. Например, при измене¬
нии | Qq | от 25 до 0° величина трс уменьшается от 1,64
до 1,4 т. Если величина скорости Vq уменьшается, то за¬
висимость трс от 0Q становится более слабой и при V* ^
1,0
1,1
'50 -5 _ ^
* 1
V0 -700м/а
500
?/е
L 700
300 —
— 500 - -
500
.. ппп
ГПП
dUU
500
%,грпд о -15 ~50 ~ 05 $0.гц§
Рис. 4.9. Суммарная масса системы
мягкой посадки с Жь’Д при раз¬
личных условиях включения дви¬
гателя (h0* = 6 7гм, Р = 1,5, Ру д =
== 275 сек’, сплошная линия — при
у0* = 700 м/сек, штриховая — при
W = 500 м/сек, штрих-пунктир¬
ная — при У0* = 300 м/сек).
Рис. 4.10. Суммарная масса комбини¬
рованной системы мягкой посадки при
различных условиях ввода системы в
действие (h0* = 6 ш).
300 м/сек суммарные затраты массы на реактивное тор¬
можение практически не зависят от начального угла 0О*.
Указанный характер зависимостей трс от Vq и 0О^ со¬
храняется для всего рассматриваемого диапазона началь¬
ной массы тк\ и удельных импульсов Руд.
На рис. 4.7 и 4.10 представлены аналогичные данные,
показывающие влияние начальной скорости Vq и угла
Qq на суммарную массу комбинированной СМП. Характер
изменения зависимостей трс (У0) и трс (0О') при исполь¬
зовании комбинированных СМП такой же, как и при ис¬
пользовании торможения с помощью ЖРД, причем
от 0Q зависит очень слабо.
108 РЕАКТИВНАЯ СИСТЕМА МЯГКОЙ ПОСАДКИ [ГЛ. 4
Таким образом, учитывая, что Vq = VK и Qq = 0К,
можно отметить, что независимо от типа рассматриваемой
реактивной системы мягкой посадки для уменьшения энер¬
гетических затрат на активное торможение КА при ра¬
боте СМП необходимо стремиться к получению в конце
участка аэродинамического торможения (на заданной ко¬
нечной высоте) минимальных значений скорости VK и
угла наклона траектории к местному горизонту | 0К |:
minFK, min|0K|, hK задано. (4.31)
При этом для | 0К | в принципе можно требовать миниму¬
ма, равного нулю (это не противоречит физическому
смыслу). Тогда условие (4.31) можно записать следующим
образом:
min Ук, 0К = 0, hK задано. (4.32)
Полученный критерий оптимальности полностью
удовлетворяет общему функционалу (3.6) и может быть
принят для дальнейшего анализа.
ГЛАВА 5
ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА
МЯГКОЙ ПОСАДКИ
§ 5.1. ОБСУЖДЕНИЕ ПРОБЛЕМЫ. ИСХОДНЫЕ ПРЕДПОСЫЛКИ
Использование парашютно-реактивных систем (ПРС)
является одним из наиболее доступных и эффективных
способов осуществления мягкой посадки КА на планеты,
имеющие атмосферу достаточной плотности (Земля, Ве¬
нера). Разреженность атмосферы Марса выдвигает ряд
специфических требований к системе мягкой посадки это¬
го типа. Здесь в первую очередь следует отметить слож¬
ность ввода в работу ПРС в условиях больших начальных
скоростей спуска (М 1) при сравнительно малых ско¬
ростных напорах (д* ~ 50-г-100 кгс!м2), сложность иссле¬
дования динамики системы, состоящей из КА и парашю¬
та, и т. п. Сказанное в сочетании с обычным требованием
создания СМП минимальной массы делает задачу очень
трудоемкой. Использовать без изменения опыт создания
парашютов для спуска в земной атмосфере невозможно.
Проектирование IIPC для марсианских КА является
большим самостоятельным разделом современной косми¬
ческой техники. Мы рассмотрим здесь кратко лишь состоя¬
ние некоторых характерных проблем разработки ПРС.
Будет проведен также проектно-баллистический анализ,
чтобы выработать требования к участку основного аэро¬
динамического торможения. Как и в случае реактивной
СМП, ставится задача переведения КА из начальной
точки, определенной параметрами Fq , 0О\ 1ц, в конечную
точку с 7к = 0, 0к = —я/2 и А* — 0 при выполнении
условия min 77гПрс-
Диапазон начальных условий ввода ПРС. В отличие
от рассмотренного ранее участка мягкой посадки с реак¬
тивной СМП, на область возможного варьирования на¬
чальных условий ввода ПРС накладываются дополни¬
тельные ограничения, которые объясняются спецификой
110
ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
конструкций систем. Это в первую очередь ограничения
на скорость F* и высоту /г()\ связанные с теплостойкостью
и прочностью материала парашютов. Необходимость вво¬
да парашюта при больших числах Маха приводит к зна¬
чительному нагреву материала парашюта. Повреждение
парашюта от действия аэродинамического нагрева для ис¬
пользуемых в настоящее время материалов начинается при
числах Маха порядка 3,3 -г- 3,5. Таким образом, чтобы
предотвратить разрушение парашюта от теплового нагре¬
ва, начальная скорость ввода не должна превышать не¬
которой допустимой величины:
Vt<Vo-AOn. (5.1)
С другой стороны, разрушение купола парашюта может
произойти и в том случае, если величина действующей на
пего нагрузки превысит не¬
которые допустимые пределы,
откуда вытекает ограничение
на допустимую величину ско¬
ростного напора д0г:
Qo ^ (Яо доп)пщх* (5*-)
Оно в свою очередь опреде¬
ляет допустимые значения
фазовых координат Vq и h'd ,
так как
Ьп.км
Qo =
Р (К) уТ
2
(5.3)
Гис. 5.1. Допустимая
варьирования начальных
ввода парашюта.
ооласть
условий
На рис. 5.1 для различных
значений допустимой величи¬
ны скоростного напора пока¬
зана область варьирования
начальной скорости Vq и вы¬
соты ht, учитывающая огра¬
ничения (5.1) (прямая 1) и (5.2) (прямые 2). Следует рас¬
сматривать величины Vq и /iq, лежащие левее заштрихо¬
ванных прямых 2. Например, для доп = 70 кгс/м2 до¬
пустимая область изменения Vq и Iiq лежит левее ломаной
abc. С увеличением допустимой величины скоростного па-
§ 5.1] ОБСУЖДЕНИЕ ПРОБЛЕМЫ. ИСХОДНЫЕ ПРЕДПОСЫЛКИ Щ
пора область возможных начальных условий расширяется,
однако, начиная с некоторого значения ду*д0п> вступает в
силу ограничение (5.1) на начальную скорость У0*\
Ограничения на начальную скорость Уу и Kq зависят
от теплостойкости материала парашюта и его прочностных
характеристик. При выборе материала, представляющем
одну из важнейших проблем, пеобходимо также учиты¬
вать воздействия, которым будет подвергаться парашют-
пая система в процессе подготовки к запуску, во время
запуска, межпланетного полета и работы в атмосфере
Марса. К ним относятся: стерилизация всех элементов
КА, осуществляющего спуск на поверхность планеты;
длительное нахождение материала парашюта в вакууме
во время перелета от Земли до Марса; тепловой нагрев
КА во время прохождения плотных слоев атмосферы Мар¬
са и т. п.
Принятый в настоящее время способ стерилизации
заключается в нагреве элементов КА до температуры по¬
рядка 150 °С и выдерживании их при такой температуре
в течение длительного времени. В настоящее время при¬
нимается, что нагрев КА в целях стерилизации приводит
к уменьшению прочности материала парашюта на 10%.
При выборе материала для купола парашюта американ¬
ского КА «Викинг» было установлено, что наименее под¬
вержены вредному влиянию нагрева материалы типа «дак¬
рон» и «иомекс». Предпочтение было отдано «дакрону»,
поскольку он имеет большую прочность при комнатной
температуре, более высокую относительную прочность
после длительного выдерживания при температуре 142 °С,
на 30% легче и дешевле в изготовлении [109].
Помимо рассмотренных выше ограничений, наклады¬
ваемых па начальную скорость Vq и высоту h* прочност¬
ными и теплостойкими характеристиками материала па¬
рашюта, немаловажным фактором, влияющим на диапа¬
зон возможных начальных условий по Т7^ и , является
ограничение, накладываемое па скоростной напор q% из
условия наполняемости купола парашюта:
^7о ((7о доп)мпа- (5-4)
Величина (7?дгщ)тт составляет приблизительно 18 -г-
20 met ж2 [105]. На рис. 5.1 (прямая 3) показано, что
112 ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
выполнение условия (5.4) приводит к дополнительному ог¬
раничению на диапазон возможных значений скорости
Vq и высоты h*. Например, при (^о дои)max = 150 кгс/м2,
(#одоп)т1п = 20 кгс/м2 и значении Vq , соответствующем
числу М = 3,5, начальная высота может изменяться в
диапазоне от 8 до 1G км.
Проведенный анализ позволил выявить диапазон на¬
чальных условий ввода ПРС — скорости Vq и высоты
Iiq\ На начальное значение третьей фазовой координа¬
ты — угол наклона траектории 0^ — никаких ограни¬
чений не накладывается, и поэтому величина 0* варьиру¬
ется в пределах от 0 до я/2.
Прежде чем перейти непосредственно к проектно-бал¬
листическому анализу СМП, рассмотрим некоторые про¬
блемы создания ПРС, решение которых в значительной
степени влияет на траекторию участка мягкой посадки.
Выбор формы парашюта. При выборе формы парашюта
необходимо обеспечить, во-первых, высокий коэффици¬
ент аэродинамического сопротивления, что позволяет
Рис. 5.2. Формы парашютов, рассмотренные при выборе системы мягкой по¬
садки КА «Викинг»: а) крестообразиыйпараипот; б) ленточный парашют с цен¬
тральным диском; е) модифицированный кольцевой парус.
уменьшить массу системы посадки при заданной началь¬
ной массе КА. Во-вторых, важно обеспечить хорошую
устойчивость снижения и не допустить сильных колеба¬
ний парашюта в процессе спуска, которые могут нару¬
шить работу систем измерения и управления.
При выборе возможных вариантов формы сверхзвуко¬
вого парашюта ориентируются jia опыт разработки дозву¬
ковых парашютов [105, 107]. Так, при разработке системы
^ 5.1] ОБСУЖДЕНИЕ ПРОБЛЕМЫ. ИСХОДНЫЕ ПРЕДПОСЫЛКИ ИЗ
мягкой посадки КА «Викинг» в качестве возможных ва¬
риантов были рассмотрены три формы парашютов [105],
показанные на рис. 5.2:
— модифицированный кольцевой парус;
— крестообразный (или плюсообразный);
— ленточный с центральным диском.
Модификация кольцевого паруса заключалась в уст¬
ранении одной из кольцевых полос вблизи юбки купола
Рис. 5.3. Характерная зависимость коэффициента лобового сопротивления
парашюта от числа м.
для улучшения устойчивости системы, состоящей из КА
и парашюта. Эти три формы использовались в летных
экспериментах без изменений, несмотря на увеличение
числа Маха, при котором осуществляется ввод парашюта.
При этом оказалось, что ленточный парашют с централь¬
ным диском и парашют в форме кольцевого паруса обла¬
дают лучшей устойчивостью по сравнению с крестообраз¬
ным парашютом в рассматриваемом диапазоне скоростей
ввода, хотя последний обладает наибольшим коэффициен¬
том лобового сопротивления. В дальнейшем для КА «Ви¬
кинг» в качестве тормозного устройства был выбран лен¬
точный парашют с центральным диском. Проведенные ис¬
пытания парашютов различных форм показывают, что в
целом с увеличением скорости ввод апараппота коэффици¬
ент аэродинамического сопротивления падает, а колебания
купола возрастают. Характерная зависимость коэффи¬
циента лобового сопротивления парашюта Сп от числа М
приведена на рис. 5.3. Для ограничения или демпфи¬
рования колебаний купола парашюта необходимо исполь¬
114 ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. b
зовать устройства, поглощающие энергию колебаний ку¬
пола парашюта. В частности, одно из таких устройств,
разработанное и испытанное для ленточного парашюта
с центральным диском, позволяет поглощать энергию
колебаний за счет удлинения элементов, изготовленных
из поливинилхлоридного материала [105]. Летные испыта¬
ния, проведенные в условиях ввода парашюта при М =
= 3-м 3,1, подтвердили высокую эффективность этого
устройства.
Уменьшение коэффициента аэродинамического сопро¬
тивления парашюта и увеличение колебаний купола при
больших числах Маха приводят к необходимости рассмот¬
рения дополнительных иаддуваемых тормозных систем.
Эти устройства позволяют обеспечить хорошую устойчи¬
вость и высокий коэффициент аэродинамического сопро¬
тивления при сверхзвуковых скоростях. Однако при до¬
звуковых скоростях коэффициент аэродинамического соп¬
ротивления этих устройств существенно меньше, чем у
парашюта. Такое устройство может служить первой сту¬
пенью тормозной системы, в которой парашют использу¬
ется только при дозвуковых скоростях.
Выбор длины строп оказывает заметное влияние на ха¬
рактеристики парашюта. Увеличение длины строп приво¬
дит к увеличению площади купола парашюта после на¬
полнения и соответственно к существенному увеличению
силы лобового сопротивления. Однако это сопровождается
значительным нерегулярным изменением формы купола
парашюта, в результате чего возможны большие поперечные
колебания. Кроме того, при выборе длины строп следует
учитывать влияние спутной струи в следе КА на характе¬
ристики парашюта и условия но его наполнению. Поэто¬
му в каждом конкретном случае необходимо проводить
специальное исследование с целью оптимального выбора
длины строп. В настоящее время считается, что длина
строп должна быть не менее чем в 6—9 раз больше диамет¬
ра КА.
Исследование процесса раскрытия парашюта. Боль¬
шой интерес представляет исследование двух факторов:
динамического удара при раскрытии купола парашюта
и времени его наполнения. Величина динамического уда¬
ра определяет требуемые прочностные характеристики
материала купола парашюта, поскольку наибольшие на¬
§ 5.1'J ОБСУЖДЕНИЕ ПРОБЛЕМЫ. ИСХОДНЫЕ ПРЕДПОСЫЛКИ
115
пряжения в конструкции парашютных систем возникают
на этапе наполнения купола. Тем самым величина динами¬
ческого удара влияет на массу всей СМП этого типа. Время
наполнения купола определяет величину пути, прохо-
димого аппаратом в процессе раскрытия парашюта, и за¬
метно влияет на схему спуска КА с парашютно-реактив¬
ной системой мягкой посадки. Исследование динамики
раскрытия парашютов является исключительно сложной
задачей. Действительно, парашют представляет собой гео¬
метрически изменяемое устройство нежесткой конфигура¬
ции. Поток в окрестности наполняющегося парашюта не
поддается теоретическому описанию. Поэтому невозможно
установить теоретически характер изменения геометри¬
ческой формы парашюта, распределения давления на ку¬
пол и стропы в процессе ввода парашюта и наполнения
купола. Проблема исследования динамики раскрытия
парашюта еще больше осложняется необходимостью од¬
новременного учета динамических, аэродинамических,
массовых и других характеристик текстильного материа¬
ла, эффектов его взаимодействия с ударными волнами при
сверхзвуковом обтекании. Основные усилия в этой облас¬
ти направляются на разработку численных методов анали¬
за процесса наполнения парашюта и определения динами¬
ческих нагрузок применительно к парашютным системам
и КА любой формы, поскольку в настоящее время одним
из основных при изучении динамики раскрытия парашю¬
та является метод модельных испытаний в аэродинамиче¬
ских трубах и натурных испытаний парашютов в атмосфе¬
ре Земли с имитацией марсианских условий ввода. Эти
испытания, в частности, показали, что для КА с началь¬
ной массой mf\A 3 ч- 9 т и парашютов с рассмотренны¬
ми выше конфигурациями время наполнения купола может
составлять от долей секунды до нескольких секунд в за¬
висимости от конкретных условий ввода. Динамическая
нагрузка в момент раскрытия купола может достигать
Десятков топи. Поскольку величина этого удара пропор¬
циональна площади купола парашюта, то целесообразно
Для уменьшения нагрузки на купол осуществлять ввод
парашютов по этапам, используя систему рифления ку¬
пола.
Одна из возможных схем рифления купола парашюта
приведена в работе [62]. Натяжение двух строп, соединен¬
116
ПАРАШЮТНО-1'ЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. э
ных с рифующим шнуром на юбке купола, приводит к
уменьшению его входного отверстия. Вследствие этого
нагрузка на купол существенно уменьшается. Спустя не¬
которое время, в течение которого скорость КА заметно
снижается, осуществляется разрифлепие купола парашю¬
та без заметного динамического удара.
Влияние спутной струи на процесс наполнения и ха¬
рактеристики парашюта. Выбор парашюта для аэродина¬
мического торможения требует хорошего знания структу¬
ры поля течения в спутной струе за КА. Эта информация
является основной при оценке коэффициента лобового
сопротивления и устойчивости парашюта в процессе
его наполнения и последующего полета. Влияние спут¬
ной струи особенно сильно проявляется при раскрытии
парашюта в сверхзвуковом набегающем потоке. В связи
с тем, что очень трудно аналитически моделировать поле те¬
чения за телами, особенно за затупленными, обычно при¬
ходится использовать данные экспериментов. Как показа¬
но в работах [105, 107], при вводе парашюта в сверхзву¬
ковой набегающий поток спутная струя за КА может
быть разделена вблизи парашюта на два участка: внут¬
ренний участок повышенной вязкости и наружный учас¬
ток пониженной вязкости. Внутренний участок образует¬
ся главным образом за счет отделения пограничного слоя
КА и характеризуется значительными градиентами дав¬
ления скорости. Наружный участок образуется потоком,
проникающим через головной скачок. Параметры спутной
струи по мере удаления от ее оси приближаются к пара¬
метрам набегающего потока. Поскольку диаметр напол¬
ненного купола парашюта примерно в 3-4 раза превышает
диаметр КА, то спутпая струя будет находиться в створе
купола.
Проведенные исследования показывают, что наиболь¬
шее отличие в значениях скоростных напоров в спутной
струе (дл) и в набегающем потоке (q^) наблюдается в цент¬
ральной части струи при x!D к \ — 1 (где х — расстояние
между куполом парашюта и КА, a DКА —диаметр КА).
С увеличением параметра x/Dk V различие между q± и q^
уменьшается. Центральная часть струи определяется как
геометрическое место точек, где наблюдается минимальное
значение скоростного напора. Центр струи совпадает с
продольной осью аппарата для случая пулевого угла ата¬
5 5.11 ОБСУЖДЕНИЕ ПРОБЛЕМЫ. ИСХОДНЫЕ ПРЕДПОСЫЛКИ 117
ки. При дозвуковых скоростях увеличение числа Маха
приводит к соответствующему уменьшению величины
qjq<x> во всей спутной струе. Увеличение числа АЛ при сверх¬
звуковых скоростях приводит сначала к увеличению
gi/'goc, а затем к уменьшению qi/q^ при числах АЛ )>2 (рис. 5.4).
4i/<L
Рис. 5.4. Относительный скоростной напор на осевой линии спутной струи.
В общем случае точно не установлено, каким образом
спутиая струя влияет на процесс наполнения и характе¬
ристики парашюта. Вопрос осложняется также необходн
мостыо учета влияния угла атаки КА на спутную струю,
особенно в процессе наполнения купола. Для исследова¬
ния этих проблем в каждом конкретном случае необходи¬
мо проводить испытания в аэродинамической трубе и на¬
турное моделирование.
Приведенные на рис. 5.4 результаты исследования па¬
раметров спутной струи получены для КА «Викинг» [105,
107]. Испытания проводились в сверхзвуковых, транс¬
звуковых и дозвуковых аэродинамических трубах. Из
рассмотрения представленных зависимостей видно, что
проблема анализа влияния спутной струи иа характерис¬
тики парашюта находится в тесной взаимосвязи с пробле¬
мой оптимального выбора длины строп. С точки зрения
влияния спутной струи па характеристики парашюта же¬
лательно иметь длину строи как можно большей, посколь¬
118 ПАРАШЮТНО-РЕАКТИБНЛЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
ку с увеличением xlD^^ потери в скоростном напоре
уменьшаются. Например, при трансзвуковых скоростях
для xlDKа = 5 величина скоростного напора состав¬
ляет 1/3 от его значения при дозвуковых или сверх¬
звуковых скоростях. При дальнейшем увеличении рас¬
стояния от КА до купола парашюта, когда яАОкд />
7, потери скоростного напора при трансзвуковых ско¬
ростях становятся значительно меньше. На основании
этих экспериментов, а также с учетом ряда других отме¬
ченных выше факторов и была выбрана оптимальная дли¬
на строп парашюта, обеспечивающая относительное рас¬
стояние между куполом и КА «Викинг», равное 8,5.
Мы далеко не исчерпали проблем, которые возникают
при проектировании парашютов для посадки КА на Марс.
В частности, не были рассмотрены динамика пространст¬
венного движения системы, включающей КА и парашю¬
ты, стабилизация парашюта и КА при действии возмуще¬
ний, расчет конструкции устройства, осуществляющего
ввод парашюта в сверхзвуковой поток, проблема отработ¬
ки парашютов в аэродинамических установках и при на¬
турных испытаниях и многие другие.
Что касается двигательной установки, начинающей
действовать после сброса парашютной системы, то возни¬
кающие проблемы в значительной части были рассмотре¬
ны в главе 4. Отметим лишь, что при анализе Г1РС двига¬
тель предполагается недросселируемым, с постоянной тя¬
гой; включение двигателя однократное, тяга постоянно
направлена против вектора скорости. Условия включения
ТДУ выбираются такими, чтобы в момент достижения
поверхности Марса {h'l = 0) конечная скорость равнялась
пулю. Никаких предпосадочных маневров, а соответствен¬
но и затрат на них не предполагается. Двигатель предпо¬
лагается жестко связанным с корпусом КА, а его тяга
направленной по оси аппарата.
Схема спуска. В табл. 5.1 представлена классификация
типов ПРС и указана область их применения. При прове¬
дении последующего проектно-баллистического анализа
участка мягкой посадки будем ориентироваться на наи¬
более простые типы 5 и 6 построения ПРС. При этом тип 5
является более общим по сравнению с типом 6, отличаясь
от него дополнительным этапом — участком полета с за-
рифованпым парашютом. В этом случае спуск КА на участ-
§ 5.1] ОБСУЖДЕНИЕ ПРОБЛЕМЫ. ИСХОДНЫЕ ПРЕДПОСЫЛКИ 119
Таблица 5.1
п/п
Тип ПРС
Область
применения
1
Надувное устройство типа «ВаПЩе» + тормоз¬
ной парашют + зарифоваиный основной + раз-
рифованпый основной + двигатель
М<4
2
Тормозной парашют + зарифоваиный основ¬
ной + разрифоваиный основной + двигатель
М <3,5
3
Стабилизирующий вытяжной парашют + за-
рифоваиный основной -f- разрифоваиный ос¬
новной + двигатель
м<з
4
Стабилизирующий вытяжной парашют + раз-
рифованный основной + двигатель
М<3
5
Зарифоваиный основной (катапультируемый из
«пушки») парашют + разрифоваиный основ¬
ной + двигатель
М<3
6
Разрифоваиный основной парашют + двига¬
тель
М<3 .
ке мягкой посадки рационально осуществлять по схеме,
основные этапы которой представлены на рис. 5.5.
Предполагается, что введение парашюта в поток про¬
исходит в некоторый момент времени t$. До момента t\
происходит наддув зарифованного парашюта. На участке
от t* до t-2 происходит торможение с использованием за-
рифоваиного парашюта. Промежуток времени Д£* =
= t* — t'l достаточно мал, но тем не менее эффективность
торможения здесь велика. В момент времени t* происхо¬
дит разрифовка парашюта и в течение следующего времен¬
ного интервала (существенно болео продолжительного)
осуществляется полет КА с разрифовапным парашютом,
в процессе которого может быть достигнут установив¬
шийся режим снижения. Для простоты исследований
будем считать, что переходные процессы присходят мгно¬
венно.
После достижения КА некоторой достаточно малой
скорости в момент времени происходит сброс парашюта.
Для надежности выполнения этой операции выделяется
некоторый интервал времени (так называемая гарантиро¬
ванная задержка Atr3 — t'l —Ц), в течение которого за¬
прещается включение ТДУ. Через некоторый момент вре¬
мени t$ — t*, выбираемый из условия осуществления мяг¬
кой посадки КА, происходит включение ТДУ. Двигатель,
120 ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
как уже говорилось, работает с постоянной максимальной
тягой, вектор которой на протяжении всего активного
участка направлен против вектора скорости КА (программа
гравитационного разворота) до момента контакта КА с
поверхностью (/£ = Т).
§ 5.2. ВЫБОР ОСНОВНЫХ ПРОЕКТНО-БАЛЛИСТИЧЕСКИХ
ПАРАМЕТРОВ ПАРАШЮТНО-РЕАКТИВНОЙ СИСТЕМЫ
Используя описанную схему полета КА на участке
мягкой посадки, проведем оптимизацию основных пара¬
метров парашютно-реактивной СМП из условия миниму¬
ма ее массы. В общей постановке это сложная многопара¬
метрическая задача, включающая ряд неизвестных вели¬
чин, ограничения и дополнительные условия,
§ 5.2'j ВЫБОР ПРОЕКТНО-БАЛЛИСТИЧЕСКИХ ПАI’AMETPOB
121
Полная масса ПРС складывается из массы парашют¬
ной системы (тпс) и массы реактивной системы (шрс).
Следовательно, минимальное значение оптимизируемого
функционала определяется минимумом суммы двух со¬
ставляющих:
minmllp3 = mi.n(mJ[C + шро). (5-5)
В отношении функционала (5.5) следует сделать два за¬
мечания.
С одной стороны, необходимо проводить независимую
оптимизацию параметров как парашютной, так и реак¬
тивной систем. В частности, материал парашюта должен
быть как можно легче, прочнее и с наибольшей теплостой¬
костью, желательно также иметь наиболее совершенную
конструкцию парашюта и его автоматики. Подобные тре¬
бования предъявляются и к ТДУ. Желательно иметь ‘бо¬
лее легкий и совершенный двигатель, позволяющий осу¬
ществлять, например, глубокое дросселирование, следует
стремиться к более совершенной конструкции баков и
иметь высокоэффективное топливо и т. п. Удовлетворе¬
ние этим требованиям, естественно, приводит к уменьше¬
нию суммарной массы СМП.
С другой стороны, выбранные параметры парашютной
системы непосредственно влияют па характеристики ТДУ,
и наоборот. Например, площадь купола парашюта, время
спуска на парашюте и высота его последующего сброса
определяют начальную скорость, при которой начинает
работать двигатель. От этого будет зависеть требуемая
величина тяги ТДУ, масса ТДУ и масса топлива. Но ес¬
ли характеристики ТДУ заданы, то они однозначно опре¬
деляют условия включения ТДУ, а последние формируют¬
ся при спуске на парашюте. Отсюда возникают требова¬
ния к характеристикам парашюта.
В дальнейшем предполагается, что конструкции пара¬
шюта, автоматических систем и ТДУ выбраны оптималь¬
ными, а решение задачи проводится путем варьирования
проектно-баллистических характеристик парашютной и
реактивной систем с целыо поиска их паилучшей комбина¬
ции, удовлетворяющей условию (5.5).
Как было показано в главе 3, масса парашютно-реак¬
тивной системы зависит от целого ряда факторов, основ¬
ными из которых являются: начальные условия ввода
122 ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
системы (Vq, 0Q, ho), параметры КА (пг?-А, SM, Сх и др.)» па¬
раметры парашютной системы (Fa, Сп, CD и др.) и пара¬
метры реактивной системы (Руд, Р, ш^А, тн, тв и др.).
В случае решения оптимальной задачи все указанные
параметры должны .варьироваться с целью определения
их наилучшей комбинации. Кроме того, варьируются вы¬
сота отстреливания парашюта (А3) и время гарантирован¬
ной задержки Д£гз.
Итак, в общем случае масса ПРС является функцией
по крайней мере десяти основных параметров
Wnpc = f{hа, 00, Vo. Fn, h3, Atr3, Cp, P, Руя, тпка). (5.6)
Для упрощения решения поставленной задачи прове¬
дем поэтапный анализ влияния указанных параметров
на тпрс. Первоначально зафиксируем начальные условия
ввода ПРС (Vq, Go и h3) и массу КА (mf{A). Кроме того,
воспользуемся результатами исследований активной СМП
и примем параметры ТДУ (р, Руд) также постоянными.
Тем самым на первом этапе будет проведена замена боль¬
шой части параметров постоянными величинами. Такая
операция не приводит к искажению общей качественной
картины и позволяет существенно упростить задачу оп¬
тимизации основных параметров ПРС. В частности, при
проведении исследований, результаты которых представ¬
лены в настоящем разделе, предполагалось, что раскры¬
тие парашюта происходит на высоте h* = 9 км при ско¬
рости Vq = 750 м/сек и угле наклона траектории 0ОЧ =
= —20°. На активном участке торможения используется
ЖРД с величиной удельного импульса топлива Руд =
= 230 сек и тяговооруженностыо Р ^ 1,5. Рассматрива¬
ется КА с начальной массой mi<A = 4500 кг.
При сделанных допущениях и предположениях число
варьируемых параметров задачи существенно снижается
и искомый функционал принимает следующий вид:
и^прз — / II? Аз, А^гз, Ср). (5-7)
Параметры, входящие в функционал (5.7), варьиро¬
вались в следующих пределах:
100 ж2 </^<800 л*2, 0,4<СР<1, |
1 км ^ А3 5 км, 5 сек Д£гз 15 сек. J
§ 5.2] ВЫБОР ПРОЕКТНО-БАЛЛИСТИЧЕСКИХ ПАРАМЕТРОВ
123
В качестве исходных принимались следующие значе¬
ния варьируемых параметров:
/г«ом = 300 ж2, Ср0М = 0,4, А£ом = 2,5 км,
Д£3ОМ = 10 сек. (5.9)
Необходимо отметить, что для исследований бралась
наиболее разреженная атмосфера и, кроме того, считалось,
что изменение коэффициента лобового сопротивления ку¬
пола парашюта от числа Маха соответствует зависимости,
представленной на рис. 5.3.
При сделанных исходных допущениях задача оптими¬
зации параметров ПРС решалась методом покоординат¬
ной оптимизации. Приведем некоторые качественные ре¬
зультаты ее решения.
Выбор площади купола парашюта. Важным фактором,
от которого существенно зависит масса ПРС, является ра¬
циональный выбор площади Fn
купола парашюта. Этот пара¬
метр оказывает влияние на обе
составляющие суммарной массы
^прс (5.5). Увеличение площади
купола парашюта, как это сле¬
дует из соотношения (3.10),
приводит, с одной стороны, к воз¬
растанию массы парашютной
системы, а с другой — к умень¬
шению установившейся скоро¬
сти снижения КА и тем самым
к уменьшению потребных запа¬
сов топлива на активное тормо¬
жение с помощью ТДУ. Влия¬
ние параметра Fu на обе основ¬
ные составляющие суммарной
массы 77inpc приводит к тому, что
зависимость тЩ)С от площади Fn
имеет явно выраженный мини¬
мум. Данные, представленные па рис. 5.6, подтверждают
зтот вывод. Видно, что для КА. с начальной массой А =
^ 4500 кг оптимал ытое значение площади купола пара¬
шюта, обеспечивающее mi и составляет величину
~ 150 -а- 200 м2. Увеличение скоростного напора <7о
//7Прс; !<3
кт
Тис. 5.6. Влияние площади
парашюта на массу параппотио-
реактивной системы посадки
(К0* = 715 м/сек, ()0* = —15°,
тК V = /ja00 пе).
124
ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
в момент ввода ПРС приводит к возрастанию оптимальной
площади купола парашюта. Так, при изменении величи¬
ны (/о с 70 до 150 кгс!м2 величина 7^nPt возрастает со 153
до 194 м2 (см. рис. 5.6).
Существенное влияние на оптимальную величину пло¬
щади купола парашюта оказывает начальная масса КА.
На рис. 5.7 представлены
зависимости величины F,0Ipt от
начальной массы КА для раз¬
личных значений начальной
высоты Д0\ Видно, что с уве¬
личением начальной массы
КА величина оптимальной
площади купола парашюта
возрастает. Например, при
изменении массы КА от 4,5
до 9 т оптимальная площадь
парашюта FnVt увеличивается
со 180 до 310 м2 (/г0: = 9 км).
Выбор коэффициента риф¬
ления купола парашюта.
Анализ зависимостей (3.10) и
(3.11) показывает, что умень¬
шение коэффициента рифле¬
ния купола парашюта оказы¬
вается выгодным с точки зрения уменьшения массы пара¬
шютной системы. Поскольку момент разрифовки парашюта
определяется условием равенства максимальной иаг^
рузки на купол для зарифованного и разрифованпого па¬
рашютов (Rnuxl = Лппх-?)» то может оказаться, что при
недостаточном запасе по высоте полное раскрытие купола
парашюта при малой величине произойдет слишком
поздно и КА не успеет затормозиться до установившейся
скорости снижения к моменту сброса парашюта перед
включением двигателя. В этом случае потребная масса
топлива для активного торможения возрастает и в целом
масса всей ПРС может увеличиться при уменьшении ко¬
эффициента С;), несмотря на уменьшение массы парашют¬
ной системы. Данные, представленные в табл. 5.2, позво¬
ляют оценить величины параметров траектории спуска
в момент разрпфления купола (К2*\ А?) и сброса парашюта
Ml ,м
Гис. 5.7. Оптимальная величина
площади купола парашюта (У0:: =
= 715 м/сек, 0О* = —15°).
Оценка параметров траектории спуска на участке работы ПРС
§ 5.2] ВЫБОР ПРОЕКТНО-БАЛЛИСТИЧЕСКИХ ПАРАМЕТРОВ 125
Параметр »i троектории
г; моменту окончания
задержки
Ж.Ч ‘А'1/
сз
L' ' -О 03 00 LO N 05 Ю (М 05 СМ С- 05 ГО
05 Ю CM CM СС го О —i СГ> СО КО Ю —• v-н со vO о Ю 'У
С о з О - ЭД С СО -ГЧ sf Г-: О СМ О О М О 03 -н
pud г САи
Ю
■О4 05 СО 05 00 Ю 05 05 — I СМ
03 СО С"- 00 05 05 v-ч 1.0 СО СО СО СМ СО СМ Ю Ю КО СМ СО
Ю 05 СО СЗ —i —100005050^—iCMCM О r-i СМ О
Тт Т Т Т Т 7 Т 5" t Т Т Т Т Т Т X Т Т
чдэ,ж ‘
СО СО 00 ОЛ СМ 1>* СО 1-0 О со СМ СМ С- -ч 00 СМ СМ СО см
СО С 05 N LO 50 L'- 05 00 to 05 Ю К- О СО Ю Ю Ю
изо ‘е‘л?у
ООООООООО~к0ЮООООООО
гН -т-i -ттЧ ч-Ч -чЧ -тЧ ч-i -Н -Ч чЧ 'Г—: ч-i чЧ чЧ чЧ чЧ чЧ чЧ
г.ч ‘опги
v* СМ СО КО 05 СО С73 СЗ 05 СЗ 05 03 СО Ю СМ СО Ю КО СО
00 00 СО СМ СО КО СО 00 00 СО СО СО 05 00 Ю СЗ 00 Ю 05
чч —iCM—iH-ri-i-< чч -ч -ч —(^тчн-н
Параметр м траекто¬
рии спуска к момен¬
ту сброса
ж и 1^ц
ко Ю ко 1-0 ко Ю Ю 00 00 СО ко ко КО ко ко ко КО
СМ СМ СМ СМ СМ СМ СМ со -0 со со со см см см см см см см
QVdS ‘;::Е0
05 V-1 СО СО СО
СО 1"- со 05 О СМ ко СМ 05 05 05 со со
СО СО 10 СО СО 05 V- СО Ю СО СО СО чч СО —:1ОГ0М"
О GO X С5 О С О N СО ОС 00 О тч CM С5 О -н 05
Т7 Т Т17 5 °\ 11Т777 7 7 Т 7 Т
ыдэ,ж ‘*ЕА
СМ ^ ) О Vf СО О со СМ СМ СМ СМ СМ 1-0 СО 05 00 СМ 05
О Ю 05 to 'О1 со VT СО Ю СО СО СО СО vp ко СО Vf КО
СМ-Н-Ч^Ч’Н-ЧгЧ-,-тЧ'гЧгЧ^Ч'гЧ'г1’гЧгНтгЧгЧгЧ
? 2
2 £>«
III
V, «= а
жи ‘ .-?ц
'О см ос ь h-14* о ю ю к- to
СО 05 Ю х? CM СО CM CM CM CM CM CM VO О СМ чч 00 СО
ко СМ 05 sj4 ко о: КО ко ко ко 1.0 Ю СО 00 Он СО N Ю гч
СО 10 СО КО СО t— COcOCOCOCOCOKOOO-T-ixft^OOvt4
gvde V'O
С5 05 СО О" СО чч СО СО СО СО СО СО СО —1 CM Ю СО СМ
ко СО 03 СМ К- Ю Ю io Ю К- К- to 10 СМ 0 05 О- СО СО
СО 1-0 КО .О vp< vp! vpl vr v-Ч vp V-. vp —i —-1 CM ■vr Vt1 ко tO
ООО o' o' о о o' о" о o' о" оГ сГ o' o' o' о" o'
1 И 1 1 1 M 1 M 1 1 II 1 1 1 1
2/ 0 J/ Ж ‘*ЕД
со ОС ч-ч о Ю 10 to to Ю to to to CO CM CM 05 to CM
О - - CM CM CM CM (M м w CM CM О V [> ГЧ -■ tv
CM CM CM CM CM CM CM CM CM CM CM CM 44 CM CM ЧЧ CM CM ч-ч
О н
4 2
Р з
р
2 ^
о с?
л K
жи ‘*°г/
03 05 05 05 05 05 05 05 05 05 05 05 CO 05 CM CO 05 CM CO
gtd2 \А0
ООООООООООООООООООЮ
CM CM CM CM CM CM CM CM CM CM CM сл CM CM CM CO
1 M 1 II i 1 II II 1 II 1
;.ж,ог21 ‘ *°0
см см см см см см см см см см см <?л to ^ lO lX jcl (O о
И о.:,Ж ', °а
1.0 iO 1-0 1-0 КО' ко ко ко ко Ю КО ко v- СО vO v-ч о О О
К- to- О О О О О О Ю to to О vp lO СО v"o LO CO o-
г,ге 41Ч/
c 5 о о о о 1 о i-О >о ю lO Со Со о io Со ко ю Со
СМ СМ СМ со V- со v- V-. V-: vp О V- о s? s-f о чч о
?м ‘ VМ ш
0 СМ ко КО Ю Ю Ю Ю Ю 1 О lO Ю ко Ю ко io 1-0 1.0 ко
1 О СО v- V- s'- vO v- v- V- V- V- v4 s- о- о о О О М1
Параметры троекто- Параметры троекто- Параметры траектории
.ачальные условия 1)ИИ к моменту раз- рии спуска к момеп- к моменту окончания
ввода парашюта рифления ту сброса задержки
126
ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
evds ‘/О
изо, ж VA
изо ‘CJjy
гн ‘оиш
wu V*/
Qvdd Ve
uoojж Va
жн Vty
Qvds Vo
иоо,ж ‘ :^А
дЫг ‘*°0
гЖК2Я ‘ :°Ъ
U.00, ИГ ‘ ::.°А
гн *VMl«
>0 000 СООЭСОХХ1>-СОСДСОХХСОСОО
О ^ vt! LO о 'чг1 со о СМ СД СО vri v-r I— О СО СД -н О 00
СО Ю Г— С-^Г-СДХсОСОСОЮЮСССОЮ
Ю-ООЭ <М О N СО -н 00 С С С N О CD СО N М О
^СДОСДСДОООООО^СДСДО'т-гнОО-гнО
TH^O^riOririOrHOrlri-HOriTHOHTHO
I II I I I I I II I I I II I I I I I I
О О 00 OcDOM^OO^NO^CDMv?
I> СО Ю О 1> 00 О 00 *н LO l> l> С N l>
J ■*—( I i I I I ЛЛ —j I — ■ - I
гн\^ rHtO
00 00 00 00
ooooooooooooooooooooo
Ю 00 CO CD —! 00 v-4 —I о о СД Ю CO CO Ю О СД Ю СО О
000000000050000000001>00000 0с)00 05
'гН-^нСД-т-'СДСД'гнСДСДСДСДСД—i—^СД-^-i—(СД-тН^н-г-!
LO ю Ю LO Ю Ю Ю Ю Ю 1-0 ю >о Ю Ю Ю Ю Ю Ю Ю Ю 00
сд сд сд сд сд сд сд сд сд сд сд сд сд сд сд сд сд сд сд сд со
ЮС— ^ЮОСДСДОХСОС-СДСДО Г— Г— 00
ЮсаЮ-нО1>С0ОС0500^-нС:М0М>ЮС0СДс0
Or-iC-H^OOOCOCOCOCDrH^OOOOCOCiCN
(OOOOOOO^-riOO-r-iOo'-r-iO
I I II I I I I II I I I II I II I I I
CD CD v* ю СД О О -О со О О СО Ю СД > О 00 О СД СО 00 00
Ю Ю СО sf Ю Ю О 0 N h С О s? Ю v? v* Ю СО СО СО СО
СД
СО vr
со с—
^ ^ —i х со
D —! СД ГН сом ч^'НООСОСДСТ)СДОООгч
00 СО 00 V? О СО vf ю С- 00 С— О Ю Ю -О С- Ю Ю О
>0 00'H^COCiCOs?t>lOOO'H'C!CCt>COlOlOCD
СД V? СО СО СО СО СО С5 СО СО сососо 00
СД СО о Ю N о о с >о N о: М О 1> са >н sf N
t- С- r-.ri I VC NjH V* C- L— CO -rH -ГН СД x? stf ю C- IT- C- xjH
ООО
I I I
> о о о о
II I I
О О О О С
СД Г— СО СО Ю О Ю СО —■: СО
— ■ (—yj f-v-\ /-"■* ГЛ ЛчЧ
СД СД СД СД
3 СД сд ;
-- —' ю t— хт
— - N, - V _• Ю ~
сд сд хг; сд сд сд
СД СД ТТ-: СД СД СД
ОСДСООСДсООгМсОСОСДОСОСДОСОСДсОСОСД о
Ю Ю О1 о о о о о ю ю ю о :
СО СО сд сд сд со со со
I I
i I I I II I
О V* Ю OMCCN Ю О I' >-0 О —■ Ю СО —: Ю СО О
СО L— СО —■< Э0 СО —■ 00 СО — X О — ■ СД С75 < СД СЭ -г- СД —I
Ю СО СО X О СО СО О СО X ОС ю L— X Ю I- X ю L— X X
§ 5.2] ВЫБОР ПРОЕКТНО-БАЛЛИСТИЧЕСКИХ ПАРАМЕТРОВ 127
(Vз, tit). При этом бралось наименьшее из рассматривае¬
мых значений коэффициента рифления, равное Cv = 0,4.
Из приведенных данных следует, что высота, при достиже¬
нии которой осуществляется разрифление купола пара¬
шюта, существенно зависит от начальной массы КА. С
увеличением т$А высота /г| уменьшается. Например, при
изменении яг'к\ от 3,3 до 5,8 т высота /г2: уменьшается от
5,3 до 2,56 км (Щ = 9 км). Как
и следовало ожидать, увели¬
чение площади купола пара¬
шюта приводит к увеличению
потребной высоты его раз-
рифления: при изменении
величины Fn от 200 до 600 м2
высота Щ увеличивается от
3,95 до 7,06 км.
На рис. 5.8 построены за¬
висимости суммарной массы
ПРС и ее составляющих (мас¬
сы парашютной системы и
массы ТДУ) от коэффициен¬
та рифления Ср для КА с на¬
чальной массой т'хх = 4,5 т
и начальной высотой ввода
ПРС h,Q = 10 км. С уменьше¬
нием коэффициента рифле¬
ния купола масса парашютной системы уменьшается. Для
парашюта площадью Fn = 180 м2 при изменении коэффи¬
циента Ср от 0,9 до 0,4 масса тпс уменьшается от 175 до
83 кг. Указанный характер зависимости (Ср) ^остает¬
ся неизменным для всего г рассматриваемого! диапазона
изменения площади парашюта. Однако с уменьшением
площади парашюта кривые 7тгпс (Ср) становятся более^по-
логими, т. е. зависимость массы парашютной системы
от коэффициента рифления купола становится менее за¬
метной.
Изменение коэффициента рифления купола парашю¬
та оказывает противоположное воздействие на массу ре¬
активной системы (трс): с уменьшением коэффициента Ср
масса реактивной системы увеличивается. В частности,
при уменьшении коэффициента Ср от 0,9 до 0,4 масса трс
увеличивается от 565 до 600 кг (Щ = 10 км и Fn = 180 м2).
т,кг
Рис. 5.8. Зависимость суммарно^
массы Пес и ес составляющих
от коэффициента рифления (т\^ А =
= 4,5 га, /i0* = 10 V0* =
=715 м/сек^00* = —15°, Fa = 180 м2).
128 ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
Несмотря па различное влияние, которое оказывает
изменение коэффициента Ср на массу парашютной систе¬
мы и ТДУ, суммарная масса ПРС уменьшается при умень¬
шении коэффициента рифления Ср купола парашюта до
определенных пределов. Объясняется это тем, что с умень¬
шением величины Ср масса парашютной системы уменьша¬
ется при одновременном увеличении скорости КА в мо¬
мент отстрела парашюта и соответственно общей массы
реактивной системы. Однако проигрыш в величине ягрз
значительно меньше, чем выигрыш, вызванный снижени¬
ем массы парашютной системы, поэтому величина 7тгпрз
при уменьшении коэффициента Ср от 1 до 0,4 уменьша¬
ется.
Следует отметить, что минимум 7тгпрз достигается при
значении Ср ж 0,4 и дальнейшее уменьшение коэффици¬
ента Ср приводит к возрастанию иг1{рс. Поэтому для рас¬
сматриваемого диапазона основных варьируемых пара¬
метров (5.2) величина коэффи¬
циента рифления купола может
быть принята равной Ср = 0,4.
Выбор оптимальной высоты
сброса парашютной системы.
В общем случае достаточно оче¬
виден тот факт, что уменьше¬
ние высоты сброса парашютной
системы (Щ) должно приводить
к снижению массы ПРС. Это
подтверждается данными, пред¬
ставленными в табл. 5.2. При
уменьшении Щ скорость КА
в момент сброса парашютной
системы и, соответственно, в мо¬
мент включения реактивной
системы уменьшается. Поэтому
масса системы реактивного
торможения КА снижается. Этот вывод иллюстрируется
рис. 5.9, на котором показаны зависимости суммарной
массы ПРС и ее составляющих от высоты сброса парашют¬
ной системы для КА с начальной массой т?{А = 4500 кг
и площадью купола Fn = 180 м2. Изменение высоты сбро¬
са влияет только на одну составляющую ПРС — массу
реактивной системы, а вторая составляющая — масса па¬
т,к2
600 ‘
400
200
О
^прс
/77рс
н
*1
Щъ
2-2,5 з #о,5
Рис. 5.9. Влияние высоты сбро¬
са парашюта на суммарную мас¬
су Пь-С и се составляющие
(?nK \ = /а>5 т, hо* = 9 км, Vo* =
= 715 м/сек, 0О* = —15°, Еп =
= 180 ж2).
ё 3.3J
УЧЛО ГОК АЭГОД1ШЛ МПЧ.ГССКОГО ТОР.МОЖЕЫ и я
129
рашютной системы от величины 1ц практически не зави¬
сит. Поэтому и общая суммарная масса IIPC при измене¬
нии величины 1ц ведет себя аналогично изменению массы
реактивной системы, а именно: с уменьшением высоты
сброса суммарная масса ПРС уменьшается. Итак, опти¬
мальной высотой сброса, обеспечивающей минимум сум¬
марной массы ПРС, в каждой конкретной задаче является
такая наименьшая высота, при которой после гарантиро¬
ванной временной задержки торможение с использова¬
нием реактивной системы реализует заданное конечное ус¬
ловие Vk — 0 на высоте h£ = 0. Следует отметить, что для
рассматриваемого диапазона основных варьируемых пара¬
метров (5.11) оптимальная высота отстрела парашюта
составляет величину 1ц ^ 3 -у- 4 км.
Влияние времени гарантированной задержки на мас¬
су 1IPC. Изменение времени гарантированной задержки
приводит к смещению оптимального момента сброса , па¬
рашюта. Поэтому величина Atv3 оказывает на массу ПРС
и ее составляющие влияние, обратное действию высоты
сброса парашюта. С увеличением времени гарантирован¬
ной задержки происходит возрастание суммарной массы
ПРС. Из практических соображений (основным, из кото¬
рых является условие обеспечения стабилизации КА
после сброса) время гарантированной задержки выбира¬
ется не больше 10 -у 15 сек.
Итак, представленные данные позволяют в каждом
конкретном случае осуществить рациональный выбор та¬
ких параметров ПРС, как площадь парашюта, коэффици¬
ент рифления купола парашюта, высоту отстрела парашю¬
та и время гарантированной задержки. Для КА с началь¬
ной массой /тгкл ~ 4 ^ б т параметры составляют:
Fn ж 150 -у- 250 м2, Ср 0,4, h% ^ 3 -у 4 км и
Д£гз ^ 10 -у- 15 сек при тяговооружеппости Р ^ 1,5.
§ 5.3. ТРЕБОВАНИЯ К УЧАСТКУ
АЭРОДИНАМИЧЕСКОГО ТОРМОЖЕНИЯ
Проведем анализ участка мягкой посадки с целью вы¬
явления требований к траектории аэродинамического тор¬
можения. Для этого необходимо оцепить влияние началь¬
ных условий на массу ПРС для принятой схемы спуска
КА на участке мягкой посадки. Будем считать, что
5 Н. М. Иванов, А. И. Мартынов
130 ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
основные проектные характеристики ПРС выбраны наи¬
более рациональным образом в соответствии с данными,
представленными в предыдущем разделе.
Влияние начальной скорости на массу ПРС. Влияние
величины У* на суммарную массу ПРС и ее составляющие
иллюстрируется зависимостя¬
ми , приведенными на рис .5.10.
Увеличение начальной ско¬
рости ввода ПРС приводит
к незначительному увеличе¬
нию тпс: при изменении ско¬
рости ввода парашюта от 500
до 800 м!сек масса парашют¬
ной системы увеличивается
всего лишь на 3 %. Этот факт
объясняется тем противоречи¬
вым влиянием, которое ока¬
зывает изменение величины
500 600 700 800 Т/*
Vо на массу парашютной си-
V0,м/сек п ил и» у
стемы. Как следует из фор-
Рис. 5.10. Зависимость суммарной Мул (3.10) И (3.11), Величина
мас“а?мио*%к°^я^х °т «ю прямо пропорциональна
^ квадрату начальной скорос¬
ти У0 и, казалось бы, изменение величины VI должно
приводить к заметному изменению тпс. Однако этого не
происходит, поскольку масса тас зависит от коэффициен¬
та лобового сопротивления парашюта. Этот параметр
в свою очередь зависит от скорости Vq (см. рис. 5.3), при¬
чем влияние скорости Vq на коэффициент Сп таково, что
приводит к компенсации возможного изменения массы
шпс за счет изменения Vq. В результате величина шас
практически не изменяется при варьировании Уд*.
Более существенно влияет скорость Vq на вторую со¬
ставляющую суммарной массы ПРС — на ш9С. При из¬
менении Vq от 500 до 800 м/сек масса ТДУ возрастает на
15%. Это предопределяет и общий характер зависимости
^прс (Уо): с увеличением Vq происходит возрастание мас¬
сы яг-прс- Вывод оказывается справедливым для широкого
класса КА с различными значениями начальной массы
и для парашютов различной формы.
§ 5.3] УЧАСТОК АЭ1ЮДИНАМИЧЕСКОГО ТОРМОШЕНИЯ 131
Влияние начальной высоты на массу ПРС. Рассмотре¬
ние данных, представленных в табл. 5.2 и на рис. 5.11,
показывает, что увеличение начальной высоты Jiq приво¬
дит к заметному уменьшению массы ПРС. Объясняется это
тем, что при возрастании hо из-
за разреженности атмосферы
Марса уменьшается скоростной
напор и соответственно умень¬
шается масса парашютной сис¬
темы (см. (3.10)). С другой сто¬
роны, изменение начальной вы¬
соты ht практически не влияет
на параметры траектории спус¬
ка, которые имеют место к мо¬
менту включения ТДУ (см.
табл. 5.2). Поэтому масса ТДУ
не зависит от изменения вы¬
соты h0.
На рис. 5.12 в качестве примера приведены зависимо¬
сти суммарной массы ПРС от скоростного напора qо для
300
700
600
50 100 150 q* < кг с/м2
Рис. 5.12. Зависимость суммарной массы ПРС от величины скоростного напора
в момент ввода ПРС.
различных скоростей ввода парашютной системы и вели¬
чин площади купола парашюта. Увеличение скоростного
напора приводит к возрастанию суммарной массы ПРС.
Такой результат следовало ожидать, ибо большим зпаче-
5*
Гнс. 5.11. Суммарная масса
ПРС для разных начальных вы¬
сот торможения.
132 ПАРАШЮТИО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
ниям q% при фиксированной скорое .г и ввода Vq соответ¬
ствуют меньшие величины h*.
Проведенные оценки влияния начального угла накло¬
на траектории 0О па массу ПРС показали, что величина
тщ-)с практически не зависит от значения угла 0q.
Влияние начальной массы КА на суммарную массу
ПРС. Представленные выше результаты расчета участка
мягкой посадки при использовании ПРС соответствуют в
основном КА с начальной массой = 4,5 т. Однако
выявленные закономерности остаются в силе и для КА
с другими величинами на-
чальпой массы. На основе
полученных выше результа¬
тов была проведена оценка
влияния начальной массы КА
на массу ПРС. Некоторые
данные представлены на рис.
5.13, где показана зависи¬
мость суммарной массы ПРС
от начальной массы КА. Как
и следовало ожидать, увели¬
чение начальной массы КА
приводит к возрастанию сум¬
марной массы ПРС. Напри¬
мер, при увеличении т'^А от
3500 до 6000 кг масса ПРС
возросла с 460 до 770 кг.
Итак, масса ПРС в основ¬
ном зависит от начальной вы¬
соты ввода Щ (соответствен¬
но от до ПРИ фиксированном
Vq) и практически не зависит от двух остальных парамет¬
ров (Fq и 6о )• В этом случае можно сформулировать впол¬
не определенные требования к конечным параметрам
у ча стк а а э р од и на мическ ог о тор м ож ени я.
а) Если задана высота раскрытия парашютной системы
(/гк = h*), то программа управления на траектории аэро¬
динамического торможения должна обеспечивать минимум
скорости (min FK — F0r') к моменту достижения 1ц = йь:.
б) В общем. случае минимум массы ПРС при прочих
равных условиях достигается в том случае, когда высота
Гис. 5ЛЗ. Связь суммарной массы
ШС с начальной массой КА
(Vo* = 715 м/сек, /г0* ~ 9 км, 0о* =
= -20», F ГГ — V'/'S-
§ 5.3]
УЧАСТОК АЭРОДИНАМИЧЕСКОГО ТОРМОШЕНИЯ 133
включения системы максимальна, т. е.
та xhK = Щ. (5.10)
Следует отметить, что последний случай является бо¬
лее характерным для ПРС. Таким образом, на основании
проведенных исследований сформулирован простой и
наглядный критерий оптимальности для решения задачи
оптимизации траектории на участке аэродинамического
торможения в случае использования парашютно-реак¬
тивной системы мягкой посадки.
Выбранные критерии (4.32) и (5.10) позволяют присту¬
пить к исследованию первого, основного участка траек¬
тории спуска КА. Но прежде чем этим заняться, проведем
краткое проектно-баллистическое сравнение двух типов
СМП, а затем (в следующем параграфе) дадим описание
систем мягкой посадки, которые использовались на .КА
«Марс-3, 6» и «Викинг-1, 2».
Как следует из проведенного анализа, при одинаковых
исходных предпосылках масса ПРС в 1,5 ч- 2 раза меньше
массы реактивной CM1I. Например, для КА с mf^A = 5 т
величина ттгрс ж 1500 кг, а т?гП!)3 ^ 700 кг, т. е. по отно¬
шению к начальной массе КА масса СМП составляет для
реактивной системы приблизительно 30% от т*1А, а для
ПРС — 14% от нгкА. Следовательно, применение пара¬
шютно-реактивной СМП является более выгодным с
точки зрения экономии массы.
С другой стороны, уже отмечалась целесообразность
быстрейшего перехода к вертикальному участку спуска
и желательность минимального изменения высоты полета
за время активного торможения, что существенно повыша¬
ет надежность посадки КА. Комбинированная реактивная
СМП, использующая РДТТ и ЖРД, позволяет значитель¬
но улучшить баллистические характеристики траектории
по сравнению с использованием только ЖРД. Еще боль¬
ший эффект достигается при использовании парашютно¬
реактивной СМП. Например, если для комбинированной
реактивной СМП угол наклона траектории к местному го¬
ризонту в момент включения ЖРД составляет величину
порядка — 78 -к —81°, то для ПРС этот угол уменьшает¬
ся до — 88v 89°.
Таким образом, применение ПРС имеет преимущество
перед реактивной СМП не только по характеристикам
134 ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
экономии массы, но и в целом повышает с баллистической
точки зрения надежность реализации мягкой посадки.
Следует, однако, отметить, что выигрыш в массе ПРС во
многих случаях не столь однозначен, а выбор того или ино¬
го типа СМП для организации мягкой посадки КА на
Марс — задача далеко не очевидная. Дело в том, что до¬
полнительные затраты массы могут потребоваться при ре¬
шении проблем управления движением КА на парашюте.
Кроме того, при посадке очень тяжелых КА площадь па¬
рашюта может достигать больших величин (см. рис. 5.7)
и в результате всестороннего рассмотрения предпочтение
может быть отдано реактивной СМП.
§ 5.4. СИСТЕМА МЯГКОЙ ПОСАДКИ
СПУСКАЕМОГО АППАРАТА «МАРС-5»
Советская автоматическая межпланетная станция
«Марс-6», запущенная в августе 1973 г., достигла окрест¬
ности Марса в марте 1974 г. При подходе к Марсу на
расстоянии 46 ООО км от планеты произошло отделение
спускаемого ат парата, который при помощи двигателя
был переведен на траекторию сближения с Марсом. При
этом орбитальный аппарат продолжал полет по пролет¬
ной траектории с минимальным расстоянием от поверхно¬
сти планеты около 1600 км [87]. Спускаемый аппарат во¬
шел в атмосферу Марса со скоростью 5600 м/сек. После
аэродинамического торможения по достижении скорости
менее 600 м/сек была введена в действие парашютная си¬
стема. Спускаемый аппарат достиг поверхности Марса
в районе с координатами 23,9° ю. ш. и 19,5° з. д. Весь
участок спуска проходил в соответствии с программой и
продолжался 5,2 мин. На участке движения до входа
в атмосферу и при движении в атмосфере планеты Марс
радиотелеметрическими системами передавалась информа¬
ция, которая транслировалась непосредственно на Землю.
С момента ввода парашютной системы до конца полета
работал радиокомплекс спускаемого аппарата. Передача
сигнала прекратилась примерно через 150 сек с момента
включения радиокомплекса (вблизи поверхности). Во вре¬
мя спуска были получены данные о перегрузках на участке
аэродинамического торможения, давления, температуре
атмосферы и высоте над поверхностью при движении на
§ 5.4] СИСТЕМА МЯГКОЙ ПОСАДКИ АППАРАТА «МАРС-.6» 135
парашюте; были проведены также допплеровские изме¬
рения скорости спускаемого аппарата относительно орби¬
тального аппарата на участке движения после отделения
и до конца полета [1].
Описание спускаемого аппарата. Спускаемый аппарат
(рис. 5.14) оборудован системами и устройствами, обеспе¬
чивающими отделение аппарата от орбитального отсека,
Рис. 5.14. Спускаемый аппарат «Марс-6»: 1 —двигатель увода спускаемого
аппарата; 2 — двигатель ввода вытяжного парашюта; з — антенны связи
с орбитальной станцией; 4— парашютный контейнер; 5 — аптснна радиовысото¬
мера; 6 — аэродинамический тормозной конус; 7 — приборы и аппаратура
системы автоматического управления; 8 — основной парашют; 9 — автомати¬
ческая марсианская станция.
а также мягкую'"'посадку на] поверхность Марса. Кон¬
структивно аппарат объединяет автоматическую марси¬
анскую станцию (9), приборно-парашютный контей¬
нер (4) и аэродинамический тормозной конус (6). В верхней
части аппарата располоя^ена соединительная рама, сты¬
кующая спускаемый аппарат с орбитальным отсеком.
На раме размещены двигательная установка для увода
спускаемого аппарата (1) и агрегаты ряда систем.
Приборно-парашютный контейнер установлен непо¬
средственно на верхнюю часть марсианской станции.
В нем размещены вытяжной и основной парашюты, дви¬
136
ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ
[ГЛ. 5
гатель ввода вытяжного парашюта и тормозная двигатель¬
ная установка мягкой посадки, антенны радиовысотомера,
антенны связи с орбитальным аппаратом и часть научной
аппаратуры. Посадочный аппарат представляет собой гер¬
метичный приборный отсек, в котором находятся блоки
бортовых систем аппарата (радиотелеметрического ком¬
плекса, систем управления, системы терморегулирования,
энергопитания) и блоки научных приборов. Снаружи
установлены научные приборы с механизмами их выноса,
антенны радиокомплекса, система приведения станции
в рабочее положение после посадки.
К нижней части станции крепится аэродинамический
тормозной конус, служащий для гашения скорости при
входе в атмосферу и защиты аппарата от аэродинамических
и тепловых нагрузок при торможении. На кольцевом
шпангоуте основания конуса установлены двигатели за¬
крутки аппарата для его стабилизации до входа в атмосфе¬
ру и двигатели останова закрутки при входе в атмосферу.
Необходимая последовательность работы систем спу¬
скаемого аппарата обеспечивается программно-времен¬
ным устройством. Конструкции аэродинамического кону¬
са, парашютов и двигателя мягкой посадки выбраны из
условия минимальной массы и их падежной работы в ши¬
роком диапазоне возможных условий спуска и характери¬
стик марсианской атмосферы.
Бортовой радиотехнический комплекс аппарата сов¬
местно с соответствующей аппаратурой на орбитальном
аппарате станции «Марс-6» позволяет осуществлять
прием и ретрансляцию на Землю научной и телеметриче¬
ской информации при парашютном спуске, а также ин¬
формации о работе бортовых систем и движении спускае¬
мого аппарата па всем участке полета от момента разде¬
ления до посадки.
Схема функционирования системы мягкой посадки
аппарата приведена па рис. 5.15. При входе в атмосферу
и на протяжении всего участка аэродинамического тормо¬
жения аппарат совершает баллистический спуск, осуще¬
ствляя торможение при помощи лобового экрана (конуса).
При достижении продольной перегрузки пх ж 2 ± 0,5
прекращается закрутка аппарата (при помощи двигате¬
лей). Одновременно подается питание на радиовысото¬
меры, запоминающее устройство измерителя перегрузок,
§ 3.4]
СИСТЕМА МЯГКОЙ ПОСАДКИ АППАРАТА «МАРС-6» 137
дублируется включение радиотелеметрической системы
контроля движения, включается датчик, вырабатываю¬
щий в дальнейшем сигнал на ввод парашютной системы.
После прохождения пикового значения перегрузки при
срабатывании датчика вводится в действие каскадная
парашютная система (вытяжной, а затем основной, вна¬
чале зарифованный парашюты). В это время включаются
Рис. 5.15. Схема спуска КА «Марс-6»: 1 — отделение спускаемого аппарата
(СА); 2 — включение РДТТ; 3 — программный разворот СА; 4 — закрутка
СА; 5 — отделение фермы; 6 — прекращение закрутки, подача питания на ра¬
диовысотомер; 7 — начало ввода парашютной системы; 8 — введение основного
парашюта; 9 — разрифовка парашюта, отделение аэродинамического конуса,
включение радиовысотомера; 10 — расчековка крепления ТДУ, перецепка па¬
рашютной системы; 11 — включение ТДУ.
научные приборы и программно-временное устройство
системы управления посадкой.
Расчетная высота введения парашютной системы в за¬
висимости от угла входа в атмосферу лежит в диапазоне
Л* ^ 5 -г- 10 км (для наиболее разреженной модели атмо¬
сферы). Угол наклона траектории в этот момент составляет
0* ж —20 18°. Дальнейшее функционирование си¬
стем на участке парашютирования осуществляется по ко¬
мандам программно-временного механизма вплоть до
включения двигателя мягкой посадки. После введения
парашютной системы происходит гравитационный раз¬
ворот траектории. Скорость снижения на парашюте
к моменту включения двигателя мягкой посадки с учетом
разбросов всех исходных характеристик лежит в диапа¬
138
ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ
[ГЛ. 5
зоне Fnc = 55-4-70 м/сек. Включение двигателя мягкой
посадки происходит по команде радиодатчика малых вы¬
сот непосредственно у поверхности. Расцепка двигателя
с автоматической марсианской станцией АМС происходит
при достижении нормальной скорости снижения Красц =
= —6,5 ± 1,7 м/сек. Увод отделяемых частей осущест¬
вляется двигателем мягкой посадки.
Автоматическая марсианская станция после расцепки
совершает свободное падение с высоты /грасц = 1,5 -4— 7 м
на поверхность планеты. Скорость соударения аппарата
с поверхностью (по нормали к поверхности) не превышает
12 м/сек. Эта скорость при посадке гасится амортизацион¬
ными устройствами. Данные допплеровских измерений
показывают, что общее время спуска КА «Марс-6» состави¬
ло 312 сек. Расчетное время спуска с учетом возможных
разбросов угла входа (А0О ~ ±1,5°) для исходной мини¬
мальной модели атмосферы составляет ~270 -4- 350 сек [87].
Телеметрическая информация, полученная с участка спус¬
ка на парашюте, шла в течение 149,2 сек. Общее время
спуска на парашюте, начиная с момента подачи сигнала
на ввод парашютной системы, равно 151,6 сек. Сравне¬
ние экспериментального времени спуска на парашюте
с расчетным показывает, что посадка аппарата произо¬
шла на поверхность ниже расчетного нулевого уровня на
Ah ^ 750 -ч- 2000 м. Указанные значения, полученные
по измерениям допплеровской системы и телеметрической
информации с парашютного участка, подтверждаются
показаниями радиовысотомера больших высот.
Комплексный анализ всей информации, полученной со
спускаемого аппарата, позволил сделать важные выводы
о характере траектории спуска и параметрах атмосферы
Марса'.
§ 5.5. СИСТЕМА МЯГКОЙ ПОСАДКИ КА «ВИКИНГ»
Краткие сведения о КА «Викинг». В августе 1975 г.
в сторону Марса были запущены два американских КА
«Викинг», схема полета которых характеризуется следую¬
щей последовательностью операций. Последняя ступень
ракеты-носителя «Титап-ЗЕ» выводит КА «Викинг» на
промежуточную геоцентрическую орбиту высотой 185 км.
5} 5.5J СИСТЕМА МЯГКОЙ ПОСАДКИ АППАРАТА «ВИКИНГ» 139
После 30 мин полета по этой орбите производится повтор¬
ное включение двигательной установки, которая выводит
КА па траекторию перелета к Марсу. После этого КА
отделяется от ракетной ступени. На траектории перелета
к Марсу предусматривается возможность проведения не¬
скольких коррекций, обеспечиваемых за счет включения
корректирующей двигательной установки на орбитальном
отсеке [93]. Эта установка переводит «Викинг» па арео-
центрическую орбиту с расчетной высотой в перицентре
1500 км и расчетной высотой в апоцентре 33 ООО км. Период
обращения КА по такой орбите составляет 24 ч 3'7 мин
и близок к периоду вращения Марса вокруг его оси.
Согласно программе полета в течение 20 -л- 50 суток
нахождения КА «Викинг» на ареоцсятрической орбите
проводится детальная разведка поверхности Марса
с целыо выбора пригодного участка для посадки. Далее
осуществляется отделение спускаемого аппарата от орби¬
тального и его торможение для перевода на траекторию
аэродинамического торможения и посадки. После про¬
хождения участка основного аэродинамического торможе¬
ния на высоте около G км раскрывается парашют и сбра¬
сывается лобовой экран. Па высоте около 1,6 км отделя¬
ется парашют и включаются три многокамерных ЖРД
для торможения на конечном участке, которые работают
5 -л- 10 мин и обеспечивают мягкую посадку КА.
Этапы полета спускаемого аппарата «Викинг» приве¬
дены на рис. 5.16. Моменты начала и конца работы пара¬
шютной системы торможения определяются по данным
радиовысотомера, с помощью которого измеряется рас¬
стояние до поверхности планеты.
Спускаемый аппарат автоматической станции «Викинг»
имеет жесткий корпус, внутри которого располагается
посадочный аппарат. Корпус КА состоит из двух частей:
нижнего конического обтекателя с большим углом конус¬
ности и верхней крышки двойной конусности. Диаметр
спускаемого аппарата составляет 3,52 м, высота 1,7 м,
масса в момент входа в атмосферу 850 кг. После раскры¬
тия парашюта масса аппарата за счет сгорания пороха
и уноса абляционного покрытия теплозащитного экрана
уменьшается до 845 кг, а после сброса обтекателя —
до 695 кг. Масса посадочного аппарата 606 кг. Его центр
масс располагается на расстоянии 35 мм от продольной
140 ПАР А НПОТ IT О - Р Е АК ТИ ВIIА Я СИСТЕМА^ПОСАДКИ [ГЛ. 5
оси лобового экрана, что обуславливает появление подъ¬
емной силы при входе в атмосферу.
На посадочном аппарате КА «Викинг» (рис. 5.17)
установлены научные приборы общей массой приблизи¬
тельно 90 кг [93]. При помощи этих приборов были про¬
ведены исследования состава и физических характеристик
атмосферы как на участке аэродинамического торможе¬
ния, так и после посадки на поверхность планеты. Кроме
Отделе Hus посадочного аппарата cm * осдаталснссс лесу л я
того, после посадки проводились фототелевизионная
съемка, молекулярный анализ грунта и биологические
исследования с целыо поиска каких-либо форм жизни,
метеорологические исследования, изучение физических
свойств грунта, определение химического состава грунта
и атмосферы, а также сейсмическое зондирование к изме¬
рение магнитного поля у поверхности.
Парашютно-реактивная СМИ. В результате проведен¬
ных комплексных исследований, направленных на поиск
оптимального варианта марсианской СМП, были выяв¬
лены следующие требования, которым должна удовлетво¬
рять СМИ «Викинг>:
— диапазон начальных скоростей составляет от
168 м/сек (число Маха М — 0,76) до 430 м/сек (М = 2,2);
— диапазон величин скоростного напора от 24,4 до
49,3 кге/м2;
,/
Сход с сода ты
Гис. 5.16. Этапы полета спускаемого аппарата «Викинг».
§ 5.5] СИСТЕМА МЯГКОЙ ПОСАДКИ АППАРАТА «ВИКИНГ» 141
— высота пад поверхностью планеты 5280 м, высота
над средним уровнем поверхности от 2230 до 8420 м (при
допуске на высоту рельефа от среднего уровня поверхно¬
сти 3050 ль);
Тис. 5.17. Посадочный аппарат «Викинг»: 1 — остронаправленная антенна;
2 — сейсмометр; 3 — антенна; 4 — приемная антенна; 5 — ЖьД на кор е
посадочного блока (всего 6); 6 — топливный бак; 7 — радиолокатор, обеспе¬
чивающий посадку; 8 — антенна радиовысотомера; 9 — один из трех 18-сопло-
вых верньерных двигателей; 10 — грунтозаборник; 11 —штанга грунтозабор-
ника; 12 — приемное устройство; 13 — опора посадочного шасси; 14 — тем¬
пературный датчик; 15 — метеорологические приборы; 16 — фототелевизион¬
ная установка.
— скорость снижения в момент отделения посадочного
аппарата от [30,5 до 87,2 м!сек\
— высота в момент отделения посадочного аппарата
1450 м)
— угол наклона траектории полета в момент отделе¬
ния посадочного аппарата от —70 до —90°;
142
ПАРAILIIOTIIO-PEАТСГ1ТШ1ЛЯ СПС’ПЙМЛ IЮСЛДКП
| 171. 5
— парашют должен полностью раскрываться при чис¬
ле Маха М - 2 и скоростном напоре примерно 43 кгс';м2,
цричем максимальная величина нагрузки в процессе рас¬
крытия не должна превышать (>800 кг]
— парашют должен наполняться при скоростном на¬
поре £o*min = 19,8 кгс\м2;
— размеры парашюта должны быть достаточными,
чтобы обеспечить отход обтекателя па 15 м через 3 сек
после его сброса;
— максимальный угол между осями парашюта и поса¬
дочного аппарата не должен превышать ±25°, а угловая
скорость должна быть не более 30 град/сек]
— полное время работы парашютной системы от 15 до
90 сек;
— максимальная масса парашютной системы с пиро¬
техническим устройством ввода 45 кг\
— максимальные размеры в уложенном состоянии:
диаметр 382 мм, длина (504 мм;
— плотность укладки от 570 до 650 кг!м6\
— максимальная сила отдачи при срабатывании пиро¬
технического устройства ввода 3520 кг.
Кроме того, система должна удовлетворительно рабо¬
тать после стерилизации в течение 114 часов при темпера¬
туре 127 СС после пребывания в условиях, близких к ва¬
кууму, во время межпланетного полета продолжитель¬
ностью от 365 до 415 cytn, после воздействия ударов и
вибраций во время запуска и входа аппарата в атмосферу
и возможного воздействия экстремальных температур при
вводе в действие парашюта в атмосфере Марса,
Выбор типа парашютной системы осуществлялся в не¬
сколько этапов. Вначале, исходя из условий баллисти¬
ческого входа аппарата в атмосферу и допуска по высоте
рельефа от ср е/дне го уровня поверхности Марса +610 м,
предполагалась двухступенчатая парашютная система,
состоящая из тормозного конуса, вводимого при числе
Маха М = 4, и парашюта с кольцевой щечыо, раскрываю¬
щегося при М = 2. Дальнейшие исследования показали,
что торможение и извлечение основного парашюта может
осуществляться посредством тормозного парашюта, рас¬
крывающегося при максимальном числе Маха М 2,7.
Однако, поскольку тормозной парашют имел небольшую
продолжительность времени работы (менее 1 сек), было
§5.5] СИСТЕМА МЯГКОЙ ПОСАДКИ АППАРАТА «ВИКИНГ» 143
решено использовать его только в качестве вытяжного.
В дальнейшем, в связи с уточнением модели Марса и его
атмосферы, допуск по высоте рельефа от среднего уровня
поверхности планеты был расширен до ±3050 м. В связи
с этим в конструкцию были внесены изменения для обес¬
печения входа в атмосферу с использованием аэродинами¬
ческой подъемной силы. Поскольку в этом случае нагруз¬
ки, действующие па парашют, быстро уменьшаются,
предусматривавшийся ранее этап рифления купола пара¬
шюта при М 2,5 был исключен и основной парашют
должен был раскрываться с помощью вытяжного при
М 2,1. В окончательном варианте выстреливание пара¬
шюта было решено осуществлять с помощью пиротехни¬
ческого устройства («пушки») при М 2,1. Купол пара¬
шюта с кольцевой щелыо (см. рис. 5.2) имеет расчетный
поминальный диаметр Dn ж 17,7 м. В наполтгеинрм со¬
стоянии он отстоит от плоскости отделения обтекателя на
расстоянии, равном 8,5 диаметрам посадочного аппарата.
В этом случае давление спутной струи не оказывает
сильного отрицательного влияния на характеристики
парашюта, особенно при сверхзвуковом снижении. На¬
личие так называемого вертлюга исключает возможность
перекручивания строп во время или после наполнения
к у п о л а п а р а ш юта.
Ствол «пушки» одновременно служит контейнером для
размещения парашюта, уложенного в чехол. Камера вы¬
сокого давления казенника и ствол разделены перегород¬
кой с отверстиями, что позволяет уменьшить максималь¬
ную силу отдачи при выстреливании парашюта. Основные
размеры «пушки»: общая длина 665 мм, общий диаметр
384 мм, длина казенника 77 мм, диаметр канала ствола
378 мм, длина ствола 510 мм.
При проектировании ПРС для КА «Викинг» предпо¬
лагалось, что срабатывание «пушки» осуществляется на
высоте 5280 м. Выход пакета парашюта происходит
в течение 1,65 сек. Через 2 сек осуществляется полное
раскрытие купола, а через 7 сек — сброс обтекателя спу¬
скаемого аппарата. Па высоте 1450 м происходит вклю¬
чение ТДУ, а после этого через 2 сек осуществляется отде¬
ление парашютов.
С целью проверки возможностей выбранной парашют¬
ной системы торможения была проведена серия испытаний
144
IIA P A III 10 T110 - Р Е А К Т11В11А И СИСТЕМА ПОСАДКИ
LFЛ- 5
в аэродинамической трубе па гибких и жестких масштаб¬
ных моделях, испытания на сброс натурной системы и
высотные испытания натурного макета аппарата с по¬
мощью ракет в условиях, приближенных к реальным ус¬
ловиям работы парашютной системы.
Реактивное торможение. После сброса парашюта
окончательное торможение КА осуществляется с помощью
реактивной двигательной установки. Подробный обзор,
освещающий эволюцию проектно-баллистических и кон¬
структивных решений в процессе разработки реактивной
системы торможения КА «Викинг», представлен в рабо¬
те [110]. Приведем схему работы системы реактивного
торможения КА «Викинг» и рассмотрим один из возмож¬
ных вариантов управления КА при работающей двига¬
тельной установке.
Основной задачей управления КА на траектории ре¬
активного торможения является обеспечение близкой
к нулю скорости (порядка 2 м- 5 м/сек) на почти нулевой
высоте (2 -р- 5 м) при минимальных затратах топлива,
т. е. решается типичная задача терминального управле¬
ния. Продолжительность процесса посадки является сво¬
бодным параметром. Следует отметить, что при организа¬
ции первых спусков КА на поверхность Марса никаких
ограничений на величину дальности не накладывается.
Таким образом, рассматривается только управление вели¬
чиной скорости посадочного аппарата. В большинстве
случаев при этом предполагается, что управление ори¬
ентацией КА осуществляется отдельно от контура управ¬
ления скоростью спуска.
Для достижения требуемого качества управления на
борту КА производятся измерения дальности и доппле¬
ровской скорости. Кроме того, имеются показания аксе¬
лерометров, измеряющих продольное кажущееся ускоре¬
ние аппарата, обусловленное негравитациопными силами
(сопротивление атмосферы и тяга двигателя).
Динамические уравнения, описывающие спуск КА,
являются нелинейными и исследуются без линеаризации.
Метод"терминалъного~наведения и управления базируется
на разделении задач последовательной оценки состояния
и управления. Результаты, полученные для двух отдельно
рассмотренных задач, затем объединяются в общей схеме,
основой которой является двойной алгоритм интегриро-
§ Г).5] СИСТЕМА МЯГКОЙ ПОСАДКИ АППАРАТА «ВИКИНГ» 145
валия. Один алгоритхМ функционирует как последователь¬
ный фильтр, вырабатывающий скорректированные оценки
параметров атмосферы и переменных состояния, в то время
как другой алгоритм работает в итеративно-логическом
режиме и выдает сигналы для управления положением
регулятора тяги двигателя. В предположении, что пара¬
метры атмосферы известны и возмущения отсутствуют,
сформулированная задача терминального управления мо¬
жет первоначально рассматриваться в детерминированной
постановке. В этом случае закон управления двигательной
установкой представляет собой релейное переключение
тяги с нулевого уровня па максимальный (программа
гравитационного разворота).
Объединенная схема оценки параметров КА и управ¬
ления. Задачей объединенной схемы оценки параметров
и управления КА является компенсация погрешностей зна¬
ния параметров атмосферы и начальных значений перемен¬
ных состояния, конечные значения которых должны быть
достигнуты за счет управления. Управление должно осу¬
ществляться с высокой эффективностью использования
топлива. Преждевременное включение тормозного дви¬
гателя приведет к перерасходу топлива, а чрезмерное
затягивание момента включения может явиться причи¬
ной «жесткой» посадки. Рассматриваемая объединенная
схема оценки параметров и управления предполагает
использование бортового вычислителя сравнительно с не¬
высокими характеристиками, который обрабатывает ре¬
зультаты измерений высоты, скорости и ускорения.
Один из путей реализации управления двигательной уста¬
новкой возможен с помощью двойного алгоритма инте¬
грирования на основе результатов частного решения
задач. Первый алгоритм интегрирования (АИ-1) осуще¬
ствляет последовательную оценку переменных состояния
и параметров атмосферы, а второй алгоритм интегрирова¬
ния (АИ-П) вычисляет] значение управления и {t)\=\P(t).
Управлением является величина тяги, которая за счет
изменения секундного расхода топлива принимает три
значения — максимальное, среднее и минимальное:
Р max? Р ср? Р mi ii-
АлГОрИТМ интегрирования АИ-П определяет уровень
тяги и время включения двигателя. Переключение с одного
146 ПАРАШЮТНО-РЕАКТИВНАЯ СИСТЕМА ПОСАДКИ [ГЛ. 5
уровня тяги на другой производится с программной за¬
держкой At. Для КА «Викинг» было принято Д£ = 5 сек,
т. е. вычисленная коррекция тяги будет реализована
не ранее чем после 5 сек действия текущего уровня тяги.
Очевидно, что это по предполагает переключения с одного
уровня тяги па другой каждые 5 сек. Ожидалось, что за
время посадки будет иметь место наибольшее число пере¬
ключений (обычно 2-3), если априорные значения пере¬
менных состояния будут достаточно хорошими, а значи¬
тельных внешних возмущений за счет атмосферы (ветер)
и изменения параметров тормозного двигателя в период
посадки не будет. Однако в «наихудшем» случае в течение
50 сек активной посадки возможно до десяти переклю¬
чений на один из трех постоянных уровней тяги. Алго¬
ритм интегрирования АИ-I начинает функционировать до
поминального момента начала торможения для того, чтобы
имелось достаточно времени для выработки установив¬
шихся значений оценок переменных состояния и параме¬
тров атмосферы. Величина упреждения составляет 15 —
20 сек. Используя вычисленные в АИ-I оценки, АИ-П
начинает вычислять необходимое время включения дви¬
гателя tt при условии движения со средней тягой Рср.
Такой начальный режим торможения выбран в связи
с возможными ошибками предварительной оценки пара¬
метров и наличием возмущения па этапе торможения.
После начала торможения АИ-I продолжает опреде¬
лять последовательные оценки переменных состояния и
параметров атмосферы с учетом действующей силы тяги.
После начала работы двигателя характеристика фильтра
улучшается, так как фильтр использует более точные
динамические входные сигналы, обусловленные действи¬
ем тяги. Навигационные вычисления, реализуемые АИ-Н,
заключаются в интегрировании уравнений движения
с использованием метода численного интегрирования
Рунге — Кутта третьего порядка. Логическая схема АИ-П
следующая: для заданного (или предварительно вычис¬
ленного) уровня тяги Р0 с использованием информации
от АИ-I, обновляемой каждые две секунды, на борту
КА интегрируются уравнения движения с целью вычис¬
ления конечного промаха по высоте и выбора такой кор¬
рекции тяги АР, которая обеспечивает значительное
уменьшение этой ошибки. (Определение величины кор¬
§ 5.5] СИСТЕМА МЯГКОЙ ПОСАДКИ АППАРАТА «ВИКИНГ
147
рекции основано на простых кинематических соотноше¬
ниях.) Возможны два значения коррекции тяги: АР —
— Лф — Рmax < о, АР ■-= Рср — Рпйч > 0. После ТОГО
как сделано первое переключение с режима РС{), в после¬
дующих циклах работы AM-11 возможно только одно
значение коррекции АР текущего уровня тяги Р. Естест¬
венно, что время включения коррекции является допол¬
нительной степенью свободы решающей логики АИ-11.
В заключение алгоритм AM-11 вырабатывает команду
на выключение двигателя при достижении заданного тер¬
минального состояния. В течение, например, 50-секунд¬
ного интервала работы тормозного двигателя алгоритм
АИ-11 может 25 раз вычислить команды па переключение
уровня тяги, так как оценка параметров производится
в алгоритме АИ-1 с периодом 2 сек.
Система выбора места посадки. Для непилотируемых
космических полетов к дальним планетам, помимо системы
управления мягкой посадкой, также желательно иметь
автономную систему, которая в реальном масштабе вре¬
мени осуществляла бы наблюдение поверхности планеты,
чтобы обеспечить возможность посадки на представляющие
интерес в геологическом отношении и сложные по рельефу
места поверхности этих планет [109].
Работа системы выбора места посадки па поверхность
планеты начинается после сбрасывания парашюта на ко¬
нечном участке спуска. Рабочий диапазон изменения
высоты для этой системы составляет от 1200 до 33 м,
длительность ее работы 30 ~г- 40 сек.
Одним из наиболее интересных мест посадки КА явля¬
ются районы разломов (трещин), связанные с вулкани¬
ческой активностью, а также каналы, которые напоми¬
нают русла водных потоков. Поэтому основной задачей
является создание работающей в реальном масштабе
времени автономной системы, которая могла бы осущест¬
влять обзор поверхности планеты, анализировать полу¬
чаемую информацию и вырабатывать критерий для манев¬
рирования посадочного аппарата для приближения к под¬
ходящему месту посадки. Система должна быть совме¬
стима с посадочным аппаратом КА «Викинг» в смысле
поставленной задачи, динамики посадочного аппарата,
взаимосвязей с другими системами и условий окружаю¬
щей среды. Она также должна обнаруживать препятствия
148 ПЛРЛ1П10ТН0-ГЕАКТИВНАЯ СИСТЕМА ПОСАДКИ
[ГЛ. 5
на местности размером 0,22 .м и избегать их в процессе
последней стадии снижения.
Работа системы иллюстрируется на рис. 5.18. Система
включается вскоре после сбрасывания парашюта (пример¬
но на высоте 1200 м). Координаты прогнозируемой точки
попадания, выработанные в вычислительном устройстве,
вводятся в систему с целью
должной ориентации (элек¬
тронным способом) луча
сечением 12 X 12° относи¬
тельно прогнозируемой
точки посадки в пределах
зоны обзора 60 X 60°, обес¬
печиваемой системой элек¬
тронного сканирования.
Это необходимо для того,
чтобы обеспечить обзор
точки посадки, несмотря
на угловые эволюции по¬
садочного аппарата на эта¬
пе терминального сниже¬
ния. Использование электронного способа управления
ориентацией луча устраняет необходимость значительной
обработки информации, поступающей со всей обозримой
площади поверхности, а также необходимость механи¬
ческих подвесов и переориентации посадочного аппарата
с целью обзора окрестностей. Фиксированное поле зре¬
ния размером 12° обеспечивает соответствие между пло¬
щадкой на поверхности и возможностями маневрирования
посадочного аппарата; при снижении оно уменьшается,
тогда как разрешающая способность улучшается. По окон¬
чании процесса сканирования поверхности происходит
обработка видеоинформации и осуществляется выбор
новой точки попадания в месте с наименьшей контраст¬
ностью. Реализация этой операции обеспечивается управ¬
ляющей командой смещения, которая вводится в вычис¬
лительное устройство посадочного аппарата и обуславли¬
вает его маневр для приближения к желаемому месту по¬
садки. Последовательность операций повторяется через
интервалы в 1 сек до тех пор, пока посадочный аппарат
не снизится до высоты 33 м над поверхностью места по¬
садки.
Новая точка
падения
Прогнозируемая точки
посадки
ис. 5.18. Схема работы системы выбора
места посадки КА «Викинг».
ГЛАВА 6
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
КОНЕЧНОЙ СКОРОСТЬЮ СПУСКА КА
НА УЧАСТКЕ ОСНОВНОГО
АЭРОДИНАМИЧЕСКОГО ТОРМОЖЕНИЯ
§ 6.1. УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ КА В АТМОСФЕРЕ
Под установившимся движением летательного аппарата
обычно понимают такой полет, при котором все основные
параметры — скорость, высота, угол наклона траектории,
угол атаки и т. п.— остаются неизменными [64]. Если рас¬
сматривать заключительный участок аэродинамического
торможения (текущая скорость V <^ V\) в течение доста¬
точно малого промежутка времени, за который высота
полета не успевает измениться существенным образом,
то все параметры, характеризующие атмосферу, можно
считать приблизительно неизменными. В этом случае
снижение КА с известной степенью приближения можно
рассматривать как установившееся.
Изучение установившегося движения КА представляет
определенный интерес по крайней мере в двух аспектах.
Во-первых, установившееся движение можно рассма¬
тривать для получения оценки предельных возможностей
КА. Характеристики движения па таких установившихся
равновесных режимах полета могут служить критерием
оценки летных качеств КА. При спуске в атмосфере
Марса, как уже отмечалось (см. главу 4), требуется найти
такое управление pi соответственно такую траекторию
снижения КА, на которой обеспечивается максимальная
эффективность аэродинамического торможения с тем,
чтобы скорость в конце участка аэродинамического тор-
можения па заданной высоте была минимальна и угол
наклона траектории к местному горизонту был равен
нулю:
Vu минимальна, 0Н = 0. (6-1)
150 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. б
Из общих соображений вытекает, что скорость VK па за¬
данной высоте hK при спуске в разреженной атмосфере
Марса в лучшем случае будет равна или несколько меньше
установившегося значения скорости FyCT, определенной
для КА с заданными параметрами.
Во-вторых, при исследовании последнего этапа аэро¬
динамического торможения КА, па котором с течением
времени кинематические параметры движения меняются
сравнительно медленно, можно без большой погрешности
пользоваться уравнениями установившегося движения.
Практический смысл изучения подобных режимов под¬
крепляется и следующими соображениями. В соответствии
с гипотезой стационарности обтекания величина аэроди¬
намических сил, действующих на снижающийся КА,
полностью определяется кинематическими параметрами
движения в данный момент времени. Поэтому величины
подъемной силы и лобового сопротивления получаются
одинаковыми при установившемся и неустановившемся
движении.
Мгновенному установившемуся состоянию соответству¬
ет условие
V = 0, 0 - 0. (0.2)
Используя условия (0.2) и уравнения движения КА
(3.20), получим
Из-за переменности р (/г) можно говорить о совокуп¬
ности мгновенных установившихся состояний, соответ¬
ствующих весьма малым последовательным промежуткам
времени At, где допустимо принять условия р (h) ■= const.
В результате получим зависимость Куст(/г).
Пренебрегая последним членом во втором уравнении
системы (б.З) (в силу его малости на конечном участке
торможения), после незначительных преобразований по¬
лучим, считая g = const, для планирующего спуска,
когда Ф 0, следующие аналитические выражения
(6.3)
§ 6.1] УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ КА В АТМОСФЕРЕ 151
для установившейся скорости и угла 0уст:
Оуст = — arctg -g
(6.4)
(6.5)
эф
Для баллистического спуска (Кб — 0) получим]
(6.6)
Г) б ^
Оуст — ~2~ •
(6.7)
Из рассмотрения выражения (6.4) видно, что величина
установившейся скорости снижения КА на заданной вы¬
соте не зависит от угла наклона траектории к местному
горизонту как при баллистическом, так и планирующем
спуске, а определяется лишь проектно-баллистическими
характеристиками КА, а именно: с увеличением величины
приведенной нагрузки на лобовую поверхность для обоих
видов спуска наблюдается возрастание величины устано¬
вившейся скорости. К аналогичному эффекту приводит
уменьшение величины располагаемого качества для аппа¬
ратов скользящего типа. Относительно угла наклона тра¬
ектории к местному горизонту можно отметить, что при
баллистическом спуске величина 0уст не зависит от Рх,
постоянна и равна 0уст = —л/2. При использовании же
аппаратов скользящего типа угол наклона траектории
к местному горизонту зависит только от величины распо¬
лагаемого качества и возрастает по модулю с его умень¬
шением. Эти выводы подтверждаются результатами
численных расчетов по формулам (6.4) — (6.7), представлен¬
ными на рис. 6.1. Видно, что для КА со средним значе¬
нием величины приведенной нагрузки па лобовую поверх¬
ность Рх ^ 200 -т- 400 кг!м2 и Ко = 0,3 величина Куст
на высоте hK = 6 км составляет 430 -f- 620 м/сек и сущест¬
венно превышает скорость звука, а угол наклона траек¬
тории к местному горизонту 0у(.т ~ —73 68°. Опре¬
делим условия, когда после достижения Куст в результате
последующего торможения скорость становится меньше
установившийся. Для этого необходимо выполнение
152 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. G
неравенства
Пусть
уст V \ ч р
(6.3) и (3.20) получим
dV ^
dh ^ dh
= pne~fih,
(6.8)
g = const. Тогда из
(6.9)
dh = V sin 0 ' 2p;pr3-gshi0). (6.10)
С учетом соотношений (6.9) и (6.10) неравенство (6.8)
можно привести к виду
=4-р>
dh
dV
2 г' У'т,
1 / 1
sin 0 —
PJP +
2f?
vL
(6.11)
Выполнение неравенства (6.11) является условием ДОСТИ¬
ЧЬ &IJCT,
'/йзи град
500
600
400
100
-7^\ч
к*-о,з
-70
д\к~
^^дз
-да
. 0,5
-50 ^
0,1
03
0,4
О £00 400 Рх,кг/мг
Рис. 6.1. Параметры установившегося движения (сплошная линия — случай
/гк = 6 км, штриховая — случай hK = 9 км).
жения в некоторый момент времени величины скорости,
которая меньше установившейся (6.4).
§ 6.2'j ПОСТАНОВКА ЗАДАЧИ. УСЛОВИЯ ОПТИМАЛЬНОСТИ
153
Введя обозначение
sin 0уст = Р(\;-ч- , (6.12)
\ г уст /
ПОЛУЧИЛ!
|0|<|0уст|. (6.13)
Отсюда видно, что участок траектории спуска, на котором
величина скорости достигает значения, меньшего устано¬
вившейся скорости, должен быть более пологим, чем при
полете с установившейся скоростью.
Таким образом, рассмотрение установившихся режи¬
мов спуска КА в атмосфере Марса показывает, что для
КА скользящего типа величина скорости в конце участка
аэродинамического торможения существенно зависит от
проектно-баллистических характеристик КА (Рх*и Kq)
и конечной высоты полета hK. Полученные соотношения
(6.4), (6.5), (6.13) позволяют оценить диапазон возможных
значений конечных параметров траектории, на которые
можно ориентироваться при решении экстремальной
задачи.
§ 6.2. ПОСТАНОВКА ЗАДАЧИ.
НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ
При использовании реактивной системы торможения
на участке мягкой посадки КА для уменьшения энерге¬
тических затрат следует стремиться в конце участка
аэродинамического торможения получить наименьшее зна¬
чение скорости и модуля угла наклона траектории к мест¬
ному горизонту. Наиболее существенным параметром,
влияющим на массу СМИ, является величина скорости
в конце участка аэродинамического торможения (FK),
а влияние угла 0К не столь важно (см. главу 4). Учиты¬
вая этот факт, задачу об отыскании оптимального управ¬
ления КА на участке аэродинамического торможения
можно решать поэтапно. Сначала будем рассматривать
задачу минимизации скорости (min Ук), не ограничивая
угол 0К. Используя результаты решения этой задачи, про¬
ведем затем анализ траекторий и выбор оптимального
управления из условия (6.1).
154 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
Итак, на участке основного аэродинамического тормо¬
жения требуется определить программу управления
Kdjfr(t), минимизирующую функционал
при ограничении на управление (3.17) и на фазовые пере¬
менные (3.25), при условиях (3.28) и конечных зна¬
чениях параметров /гк, 0К, tK. При этом 0К свободно,
hK задано, а время tK соответствует моменту достиже¬
ния высоты h = hKy когда управление не может обеспечить
движение с h > 0.
Необходимые условия оптимальности. Предположим,
что оптимальная траектория содержит единственный ин¬
тервал движения по ограничению (3.25). Обозначим №
момент выхода КА на ограничение, а — момент схода
с ограничения.
С помощью гамильтониана
запишем уравнения сопряженных переменных при v (0<^ [4]
(6.14)
+ Фг ~~yS 9 + ФзК sin 0 (6.15)
dtyi dli гртрТ^
~df ~ dV ~~
Необходимым условием минимума функционала (6.14)
является условие максимума функции Н как функции
управления Къф.
§ 6.2] ПОСТАНОВКА ЗАДАЧИ. УСЛОВИЯ ОПТИМАЛЬНОСТИ 155
Согласно гамильтониану оптимальное управление на
участке движения внутри допустимой области фазовых
координат является граничным:
/С)ф ^ КС) sign ф2 при ф2 ф 0. (6.17)
Необходимые и достаточные условия прохождения
экстремали вдоль границы допустимых значений фазовых
координат имеют вид [4]
dr
- 0
(к = 0,1,... , п),
(6.18)
где п — порядок производной функции v (3.25), которая
содержит в явном виде управление В нашем
случае п = 2. Тогда получим управление на участке
движения по ограничению (изовысотный участок полета):
Я-пф —
2 Рх
Р()Гр ( ^ “Ь ^доп)
'ДОН/
4--1
V2
(6.19)
ГДе F — -у- , р0Гр — р (^доп)*
Уравнения сопряженных переменных приу = 0 запишут¬
ся следующим образом:
5/7
— _ Ж- L
dt ~~ ~ dV ^
dt
dfl
~Ж~
d\p°rP
dt
где
dll
dk
^эф 5cp ?vri
5cp dV “
prp
дКвф
dTI
дК»ф д<р
5ср 50
дК,
эф
1|'0гргт ihorp pV 1Ь0грТ/
% S — T2 9-73 Тз V ,
2 Px
dir
дЫ ^j.orp Ф2 p
5cp
~dK~
:>ф
dii
dm
~Ir
21\
(6.20)
d.~v
dt-
(6.21)
156 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
В момент выхода на ограничение v = /гдоп — h = О
должно быть выполнено условие касания
-|rU,<.> = <rsi,lB) u» = °-
Сопряженные переменные в точке № скачком меняют
свою величину:
(*Ш) - Фг (^(1)) = Pi -ТГтГ + |Х2
dv
dV
dv
~W
= 0,
'ф2ГР (t^) — ф2 (£Ш) — Pi -^q- + P-2 -^q- — P2V,
^3ГР (^) ~ Фз (^) = Pi -£■ + H* ^ = [*b
(6.22)
где |лЬ2 = const.
Поскольку v и v от времени явно не зависят, то соглас¬
но [4]
Н (**> + 0) = Я - 0). (6.23)
Окончание горизонтального полета определяется мо¬
ментом свободного выбора управления: при ср2гр < 0
максимизация гамильтониана требует Кэф = — Ко, а это
недопустимо из-за ограничения h /&д0П; вместе с тем
при ср°‘ р 0 получим из условия максимума гамиль¬
тониана
я8ф = + кб>к^\
Таким образом, момент схода с ограничения опреде¬
ляется условием а|)2Г|> (£) = 0. В силу того, что функция II
явно не зависит от времени, а конечный момент времени
не задан, имеет место первый интеграл
II = 0. , (6.24)
В этом случае из условий трансверсальности и (6.24),
а также в силу произвола вариаций б У и 60 в конце тра¬
ектории получим
^1И = — 1, ^2К = 0,
■фзп —
А'оф^Р.Тк (Л + К? Ч - 2Ц cos 0К + VK cos 0К (R+h„) VK
2 (It + AK)2 V*t sin 0„
(6.25)
§ 6.2] ПОСТАНОВКА ЗАДАЧИ. УСЛОВИЯ ОПТИМАЛЬНОСТИ 157
Для систем (3.20), (6.16), (6.20) заданы начальные
условия К0, /?,п, 0О. В конце траектории имеем h —
Фш» Фаю Фок- Если задать ф10 и ф20, то из условия /7 = 0
можно определить ф30 и число контролируемых в конце
траектории функций ф, к и ф2к совпадает с числом параме¬
тров, задаваемых в начальной точке. Таким образом,
поставленная экстремальная задача сводится к краевой
задаче для системы обыкновенных дифференциальных
уравнений (3.20), (6.16), (6.20).
Краевая задача. В качестве вычислительного метода
для решения краевой задачи использовался метод после¬
довательных приближений [49, 50], который состоит
в следующем. В качестве начального приближения управ¬
ления (t) задается некоторое допустимое управление,
при выборе которого обычно используются различные,фи¬
зические соображения. Метод состоит из последователь¬
ных итераций; l-я итерация (Z = 1, 2, . . ., i) заключается
в следующем:
1) решая задачу Коши для системы уравнений (3.20)
с управлением гь = u(l) (t), определяем траекторию
х = х<1) (t) па интервале [Z0, £,.];
2) решая задачу Коши (6.16) «справа налево» от момен¬
та t = tu до t = £0ири и = и^1) (£), х = х(0 (£), определяем
сопряженные переменные ф^> (t) па интервале [Z0, £1;];
3) определяем управление (t) на интервале [Z0, ZK]
из условия (6.17).
После этого переходим к следующей итерации. Процесс
последовательных приближений продолжаем до тех пор,
пока последующие приближения не будут отличаться друг
от друга в пределах заданной точности. Полученное реше¬
ние будет удовлетворять принципу максимума.
Этот метод сравнительно прост с вычислительной сто¬
роны, так как на каждом шаге требует лишь решения
двух задач Коши: «слева направо» для системы (3.20)
и «справа палево» для системы (6.16), (6.20). Он не тре¬
бует большой памяти машины. Его использование удобно
также из-за того, что тта каждой итерации приближение
к оптимальному управлению осуществляется в классе
разрывных граничных (или релейных) управлений.
Для улучшения сходимости метода использовался один
из способов, предложенный в работе [50]. Он состоит
в том, что в систему (3.20) вводится некоторый параметр г
158 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
в виде коэффициента при управляющем параметре
так, чтобы при е = 1 получалась исходная система,
а при е-^0 итерационный процесс быстро сходился.
При этом система (3.20) становится слабо управляемой,
и поэтому итерационный процесс будет быстро сходиться.
Получив сходимость при некотором е, постепенно увели¬
чиваем его, беря каждый раз в качестве начального при¬
ближения для итерационного процесса оптимальное управ¬
ление для предыдущего значения 8. Дойдя таким образом
до значения е = 1, получаем решение исходной задачи.
Отметим, что этот способ улучшения сходимости исполь¬
зуется при решении краевых задач только в тех случаях,
когда простейший вариант метода последовательных при¬
ближений расходится или сходится медленно.
Для сходимости итерационного процесса большую роль
играет выбор первого приближения. При решении по¬
ставленной вариационной задачи об отыскании оптималь¬
ного закона управления из условия минимума конечной
скорости спуска выбор первого приближения осуществля¬
ется на основе следующего предположения. Если система
(3.20) зависит от некоторого параметра X и при X = Х0
найдено оптимальное управление, то его можно брать
в качестве первого приближения для значений X, близ¬
ких Х0. Для сформулированной выше краевой задачи в ка¬
честве параметра X может быть использована минимально
допустимая высота полета /гдоп. В этом случае первое
приближение ищется следующим образом. В момент
t = tK задается некоторое значение конечной скорости,
при выборе которого можно, например, ориентироваться
на скорость установившегося полета VK = Еуст-
Далее, подбором значений 0К из области, ограничен¬
ной условием (6.10), решается задача Коши для систем
(3.20), (6.16) и (6.20) «справа налево» при начальных усло¬
виях (6.25) с целыо удовлетворения условий (3.28) при сво¬
бодном параметре /гдоп. При этом управление эффективным
качеством осуществляется в соответствии с (6.17), (6.19)
и будет оптимальным после решения указанной одпопара-
метрической краевой задачи для некоторого значения /гдоп-
Ото управление можтто использовать в качестве началь¬
ного приближения. Решение краевой задачи методом
последовательных приближений показало, что такой
способ определения начального управления имеет высокую
§ 6Лi ОБЩИЙ АНАЛИЗ ОПТИМАЛЬНЫХ ТРАЕКТОРИЙ 159
эффективность: для рассматриваемой краевой задачи точ¬
ное решение обеспечивалось во втором приближении.
Объяснить факт быстрой сходимости можно тем, что
структура оптимальной траектории остается неизменной
для достаточно широкого класса КА и условий входа.
Проведенные исследования подтвердили это предполо¬
жение.
§ 6.3. ОБЩИЙ АНАЛИЗ ОПТИМАЛЬНЫХ ТРАЕКТОРИЙ
Решение сформулированной вариационной задачи в об¬
щем случае представляет известную трудность, обуслов¬
ленную разрывностью сопряженной системы дифферен¬
циальных уравнений и необходимостью решения двухто¬
чечной краевой задачи. При этом отметим, что возможный
выход на ограничение приводит к появлению допол¬
нительных параметров в краевой задаче и порядок ее
существенно возрастает. В связи с этим, прежде чем не¬
посредственно приступить к численному решению постав¬
ленной задачи, целесообразно провести предварительный
качественный анализ траекторий с целью выявления их
структуры. Знание структуры оптимальных траекторий
существенно облегчает решение задачи в целом.
Под структурой оптимальных траекторий будем
понимать качественный характер изменения основных
траекторпых параметров КА и управляющей функции К0ф
по времени спуска. Допустимая область изменения V и h
ограничена снизу величиной hmiL и сверху начальными
условиями h0 и V0.
Пусть для некоторых начальных условий минимум
конечной скорости (min VK) достигается на высоте h = hK
при 0К ^ 0. Из общих соображений можно предположить
существование четырех типов оптимальных траекторий
(рис. 6.2):
— оптимальная траектория содержит участки выхода,
движения по ограничению и последующего схода с огра¬
ничения внутрь допустимой области фазовых координат
(кривая 1 на рис. 6.2; значение скорости при t = № и
и t = № обозначим соответственно через FW и F(2));
— оптимальная траектория целиком лежит внутри
допустимой области фазовых координат (кривая 2);
160 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
— оптимальная траектория касается ограничения
^ — ^доп (кривая 3);
— оптимальная траектория состоит из двух участков—
выхода на ограничение и движения по нему (кривая 4).
При движении внутри допустимой области фазовых
координат для любого типа оптимальных траекторий эф¬
фективное качество может принимать только граничные
Рис.' G.2. Возможные типы оптимальных траектории.
значения Кт\) = —Ко или К^ф ~ -|~ Ко (см. (6. 17)). Коли¬
чество переключений К эф с одного граничного значения
на другое определяется числом нулей функции ф2, и каче¬
ственный анализ структуры оптимального управления
Кэф (t) сводится к изучению поведения функции ф2 (t).
Оптимальные траектории первого типа. При движении
КА по ограничению закон управления эффективным ка¬
чеством Аэфр определяется однозначно согласно выра¬
жению (6.19). С целыо определения закона управления
КЭф (t) при движении внутри допустимой области фазовых
координат проанализируем характер изменения функции
ф2 (t) на участке выхода на ограничение и схода с огра-
§ 0.3J ОБЩИЙ ЛИЛ ЛИЗ ОПТИМАЛЬНЫХ ТРАЕКТОРИИ
ничеиия. Для этого необходимо провести решение крае¬
вой задачи, что представляет известные трудности. К су¬
щественному упрощению решения приводит выявленное
свойство неединственности оптимальных траекторий пер¬
вого типа (и соответственно неединственности управле¬
ния) на участке выведения на ограничение. Это следует
из рассмотрения выражений (0.16), (0.20) и (0.22), которые
показывают, что при выходе на ограничение касание
траектории возможно только при КЛф - : А'о- В точке
касания выполняется неравенство ф^ > 0. Случай ф2 >0
соответствует оптимальной траектории третьего типа, и
его пока рассматривать не будем. В нашем сл учае ф2 = 0.
Тогда из равенства (0.23) в силу непрерывности р, F, 0
при t = № имеем соотношения
фГ = Фь
Поскольку | ф2гр | < оо, 0 |/=/(i)_0 =f= 0, 0огр = 0, то
получаем дополнительное условие ф2 |/=/(d_0 = 0, но тогда
ф°гр = 0 и ф£гр = const.
Если ТА1) Fi, то, как следует из анализа сопряжен¬
ной системы [22, 97], единственный при ф^ Ф 0 нуль
функции ф2 при t < £(1) должен совпадать с £В) и тогда
КЭф = const, а условия v = v = 0, вообще говоря, не¬
выполнимы одновременно.
Если ф.^ = 0, то на участке t <С t{1) получаем един¬
ственное тривиальное решение % = 0, указывающее на
независимость функционала FK от управления КЭф (t) при
t «< t{1). Если F(1) < Fi, то вопрос о существовании ре¬
шений, соответствующих фз° = 0, приходится решать
численно. В принципе, выбирая ф;(}г), можно получить ре¬
шение ф.^, определяющее релейную функцию Кдф (t),
для которой каждому сочетанию F0, h0, 0О соответствует
свой момент переключения Кдф (t) при t <С £(1), т. е.
такое решение может существовать наряду с тривиаль¬
ным. Если считать, что при t < t^l) управление гранично
(ф; = 0), то для выполнения v>0 и перехода на режим
v = 0 требуется Коф — 0) = + Кв, т. е. ф2 \1Ыц)_0 > 0,
6 Н. М. Иванов, А. И. Мартынов
|f)2 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
поэтому при численном решении задачи надо искать
,< 0.
■фз|,=,(!)_„> 0, чтобы было
f=i(D
Проведенное численное исследование показало, что
нельзя подобрать такое значение я|41} 0, при котором
существовал бы нуль функции ф2 (t) на интервале
*о < * < ^(1) ПРИ V(1) <
Итак, во всех случаях при l0 << t <С № сопряженные
nepe.MCiuii.ie ф< = 0, т. е. оптимальная траектория спуска,
содержащая изовысотный участок движения, не зависит
от участка траектории, выводящей КА на этот режим
полета. Следует, однако, отметить, что независимость
оптимальных траекторий первого типа от участка выве¬
дения наблюдается в известных пределах. Дело в том, что
семейство траекторий этого типа может существовать лишь
в некоторой допустимой области фазовых координат, огра¬
ниченной, с одной стороны, траекторией, у которой выход
на ограничение осуществляется с максимально возможной
скоростью V(l) = F,nax, а с другой стороны — траекторией,
лишь касающейся ограничения h = h^0п при скорости
у<Л) = }/(2). в случае движения КА по любой траектории,
лежащей вне этого семейства, решение поставленной
задачи с использованием критерия min FK при соблюде¬
нии всех условий не представляется возможным. Действи¬
тельно, если траектория спуска КА или ее часть на участке
выведения проходит правее заштрихованной области
(рис. 6.2), то для получения min FK она неизбежно должна
пересечь прямую /г = 1ьщт с величиной F(U > Fm-lx и
0(1' < 0, т. е. пройти ниже этой прямой. Тем самым нару¬
шается одно из условий поставленной задачи (3.25).
Если траектория проходит правее допустимой области
(F, h) и выход траектории на ограничение осуществляется
при скорости, меньшей F(2), то в этом случае дальнейшее
движение КА после схода с ограничения с F < F про¬
исходит по траектории, отличной от оптимальной, и вели¬
чина конечной скорости будет больше FK min- Таким об¬
разом, семейство оптимальных траекторий первого типа
на участке выведения ограничено двумя предельными тра¬
екториями, и при исследовании этого участка главным
является определение законов управления Къф на этих
траекториях.
ОБЩИЙ АНАЛИЗ ОПТИМАЛЬНЫХ ТРАЕКТОРИЙ
163
Для анализа предельной траектории, ограничивающей
область неединственности слева (траектория тина 7а),
необходимо решить следующую вспомогательную экстре¬
мальную задачу: при заданных начальных условиях (8.28)
определить программу управления К:)ф (/), максимизи¬
рующую функционал I = У_(1) при ограничении на управ¬
ление (3.17) и граничных условиях
/г(1) = /&доп» б(1) = 0, свободно. (6.27)
Оптимальное управление определяется из условия мини¬
мума гамильтониана (6.15):
— —Къ sign ф2.
При t = t{l) должно быть выполнено условие \|^и = —1;
при этом гр21) и свободны, так как заданы конечный
угол 0(1} и конечная высота Поставленная вспомо¬
гательная экстремальная задача сводится к краевой задаче
для системы обыкновенных дифференциальных урав¬
нений (3.20) и (6.16), численное решение которой пока¬
зало, что оптимальной программой управления на пре¬
дельной траектории, осуществляющей выход па ограни¬
чение С V{1) = Fmax, является программа одноразового
переключения управления с минимального значения
КЭф = —Kq на максимальное Кэф = -- Kq. При этом
оказалось, что найденный закон оптимального управле¬
ния остается неизменным для всего класса КА, осущест¬
вляющих спуск по траекториям первого типа, и не зависит
от проектно-баллистических характеристик КА (Рх и Кб),
начальных условий входа (У0, hr) и допустимой высоты
рикошетирования КА (^доп)- При численном решении
указанные параметры варьировались в пределах
200 кг/м2 Рх 650 кг/м2, hI1 ^ /г- ^ h~, )
0,2^ Кб <^0,5, 4,7 км/сек <Д7 0 <^8 км/сек, i (6.28)
2,5 км /гдоп 9 км. )
В качестве исходных принимались следующие поминаль¬
ные значения параметров:
РГ1 = 350 кг/м2, КТм - 0,3, /г"ом == - 45 км] (629)
Vо = 6 км/сек, h-mi — 6 км. )
6*
IGi ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
Анализ численных материалов исследования другой
предельной траектории (кривая 16, ограничивающая за¬
штрихованную область рис. 6.2 справа) показал, что
во всем диапазоне рассматриваемых параметров (6.28)
выход на ограничение при скорости V(1) = F(2) осуще¬
ствляется при использовании программы двухразового
переключения эффективного качества:
Кзф = + * о, - * о, + Кб. (6.30)
Внутри области неединственности движение КА может
быть реализовано по различным траекториям и с исполь¬
зованием различных законов управления К3ф. В част¬
ности, можно отметить, что выход КА на ограничение
с промежуточным значением скорости (F(2) ^ F(1) ^ Fmax)
возможен при использовании программы двухразового
переключения К3ф (6.30). Эта программа по структуре
совпадает с оптимальным законом управления для предель¬
ной траектории 16, но отличается выбором моментов
переключения К3ф- А именно, если для предельной траекто¬
рии, реализующей F(1) = V(2), суммарная длительность
полета КА с максимальной величиной К3ф = + Ко наи¬
большая, то при увеличении F(1) она уменьшается, а дли¬
тельность участка спуска с К3ф = — К б возрастает.
При этом уменьшение времени полета с положительным
значением аэродинамического качества осуществляется
в основном за счет более раннего момента первого переклю¬
чения Кдф. В пределе при F(1) = Fmax время первого пере¬
ключения К3ф становится равным нулю и программа
двухразового переключения К3ф вырождается в про¬
грамму одноразового переключения
К3ф = —Ко, + Ко,
а траектория спуска совпадает со второй предельной тра¬
екторией, ограничивающей область неединственности
слева.
Обратимся теперь к рассмотрению другого участка
оптимальной траектории первого типа, который, собствен¬
но, и определяет минимальное значение конечной скоро¬
сти — участка схода с ограничения внутрь допустимой
области фазовых координат с h (t) = h^0п- В этом слу¬
чае граничные условия для левого конца траектории
§ 6.3]
ОБЩИЙ АНАЛИЗ ОПТИМАЛЬНЫХ ТРАЕКТОРИЙ
165
запишутся в виде
F(1) свободно, 0(1) = 0, h{l) = Лдоп,
t{1) свободно, г|)1Гр = 0.
Условия (6.31) определяют совместно с условиями (6.25)
двухпараметрическую двухточечную краевую задачу. Как
уже отмечалось, оптимальное управление КА на участке
схода с ограничения является граничным, а количество
переключений К»ф определяется количеством нулей функ¬
ции ф2. Численное решение краевой задачи на этом участке
проводилось для широкого класса КА с различными про¬
ектно-баллистическими характеристиками и для различ¬
ных значений /гдоп. При этом оказалось, что если варьи¬
руемые параметры Рх, Kq и /гдоп лежат в наиболее инте¬
ресном с практической точки зрения диапазоне (6.28), то
функция ф2 после схода траектории с ограничения1 оста¬
ется положительной на всем интервале движения внутри
допустимой области фазовых координат, а следовательно,
оптимальной программой управления КА на этом участке
является программа, предусматривающая полет КА с не¬
изменным максимальным значением эффективного каче¬
ства Кэф = +Kq. Использование этой программы управ¬
ления приводит к тому, что характерной особенностью
оптимальных траекторий первого типа является наличие
после схода с ограничения маневра типа «горки», т. е.
такого режима полета, при котором высота полета в за¬
висимости от времени сначала возрастает, достигая в не¬
который момент максимума, а затем уменьшается до до¬
стижения h = hK. Поскольку программа управления
на этом участке неизменна для различных КА, то макси¬
мальная высота при осуществлении маневра типа «горки»
определяется лишь проектно-баллистическими характе¬
ристиками КА и величиной /&доп.
Между поведением функции сопряженных перемен¬
ных ф2 и высотой полета КА на участке схода с ограни¬
чения наблюдается вполне определенная взаимозависи¬
мость: характер изменения максимумов величины ф2 и h
при варьировании проектно-баллистических параметров
КА и минимально допустимой высоты полета ^догт анало¬
гичен. С возрастанием \р2 тах при соответствующем изме¬
нении величин Рх, Аб, йдоп происходит возрастание
(6.31)
1GG ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
1гтах и, наоборот, с уменьшением ф2 max величина h{пах также
уменьшается. Проведенные численные исследования пока¬
зали, что можно подобрать такие предельные значения
приведенной нагрузки на лобовую поверхность Р^ред>
7 Пред
а также соответствующую величину h^on , при стрем¬
лении к которым максимальное значение функции ф2
и тем самым максимальная высота «горки» становятся
Апазо Аъ *к,
нм сен град
Рис. 6.3. Параметры движения при маневре типа «горна».
сколь угодно близкими к нулю, а по достижении каким-
либо из параметров предельного значения функция ф2
становится равной нулю, и маневр типа «горки» вообще
отсутствует. В этом случае оптимальная траектория пер¬
вого типа совпадает с оптимальной траекторией четвертого
типа (см. рис. 6.2).
На рис. 6.3 представлены зависимости максимальной
высоты «горки», скорости схода КА с ограничения, вре¬
мени полета КА на участке схода с ограничения, а также
угла наклона траектории 0К от величины приведенной на¬
грузки на лобовую поверхность КА. Из их рассмотрения
видно, что маневр типа «горки» вырождается при очень
больших значениях Рх. Таким образом, рассмотрение
класса траекторий четвертого тина не представляет прак¬
тического интереса и приводится лишь для общности.
§ g.3] ОБЩИЙ АНАЛИЗ ОПТИМАЛЬНЫХ ТРАЕКТОРИЙ
Интересно проследить, к какому эффекту может при¬
вести уменьшение параметров Рх и Ко. Как было пока¬
зано, па участке выхода траектории па ограничение
происходит сужение области неединственности решения
при уменьшении величин Рх и KG. При этом оказалось,
что существуют такие значения Рх = Рх-Гд Ко = /^б1)ед,
для которых область неединственности па участке выхода
па ограничение вообще отсутствует. Этому случаю соот¬
ветствует единственная оптимальная траектория первого
типа, которая касается ограничения по высоте (3.25) при
максимальной скорости шах |A1}, а затем оказывается
внутри допустимой области для фазовых координат.
Дальнейшее уменьшение величин Рх и Ко приводит к то¬
му, что оптимальной траекторией, реализующей минимум
конечной скорости спуска, является траектория второго
типа, целиком проходящая внутри допустимой области
фазового пространства. Таким образом, уменьшение зна¬
чений основных проектно-баллистических характеристик
также приводит к качественному изменению типа опти¬
мальных траекторий спуска: сначала к траектории треть¬
его типа (касающейся ограничения h = hmn), а затем
и к траектории второго типа.
Оптимальные траектории второго типа. Для опреде¬
ления оптимальной программы управления на траектори¬
ях второго типа необходимо знать число нулей функции
сопряженных переменных ф2 (£), которое определяет число
переключений эффективного качества с одного граничного
значения на другое. Характер поведения функции ф2 (t)
выявляется из решения двухпараметрической краевой за¬
дачи для системы обыкновенных дифференциальных урав¬
нений (3.20) и (6.16). Расчеты показывают, что функция
сопряженных переменных ф2 на оптимальных траекториях
второго типа имеет всего лишь один нуль и, следователь¬
но, оптимальная программа управления имеет одно пере¬
ключение с .минимального значения (поскольку функция
ф2 при t = t0 отрицательна) па максимальное. Такой вид
оптимального закона управления остается неизменным
для любых значений Рх и Ко, если оптимальная траекто¬
рия спуска лежит внутри допустимой области фазовых
координат.
Следует отметить, что на траекториях второго типа
также имеется маневр типа «горки» на заключительном
У%> 4>1
ns h, 0 К
KMOtrnd M/GGX
0,02*
-0,008
0,5
0,1
-0,4 -
•14 -
о-
-
-- -0,1т
■ 120-
-0,1 -
-10 -
--0,5-
- 80-
-о -
-5 -
—0,9-
- 40-
—0,1 -
-2 ~
-тз
0 0 ~
SO .Л£>$в 150 200 ■ 250
О
-0,3
*(t)
50
r_ir
L_
t,DGK
_L_
_L_
J
100 150 200 250
i,cex
Рис. 6.4. Изменение основных характеристик оптимальных траекторий пер¬
вого типа.
t,uGK
Рис. 6.5. Изменение основных характеристик оптимальных траекторий вто¬
рого типа.
АНАЛИЗ ЧИСЛЕННЫХ I ЕЗУЛЬТАТОВ
169
участке спуска. Наличие этого маневра еще раз подчер¬
кивает условность деления траектории на типы. Действи¬
тельно, если накладывается ограничение Ад0П > Amin,
то траектория выходит на это ограничение и вырождается
в траекторию первого типа.
Мы рассмотрели все возможные случаи оптимальных
траекторий спуска. Оказалось, что могут иметь место
траектории всех четырех отмеченных типов. При этом
траектории третьего и четвертого типов являются частным
случаем оптимальных траекторий второго типа. Учитывая
это, в дальнейшем будем рассматривать в качестве основ¬
ных только первый и второй типы траекторий.
В качестве примера на рис. 6.4 и 6.5 приведено изме¬
нение параметров траектории V, 0, А и сопряженных
переменных ф* в зависимости от времени спуска для аппа¬
рата с Рх = 250 кг/м2 и Kq = 0,3 (первый тип управ¬
ления), Рх = 80 кг/м2 и Kq = 0,3 (второй тип управ¬
ления).
§ 6.4. АНАЛИЗ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ
Общая процедура численного решения задачи о мини¬
муме конечной скорости. Поскольку структура опти¬
мального управления в зависимости от типа траекторий
может быть различной, то при решении задачи о минимуме
конечной скорости в каждом конкретном случае необхо¬
димо придерживаться определенной последовательности
операций, существенно упрощающей процедуру решения
задачи в целом и заключающейся в следующем. Сначала
ограничение на минимально допустимую высоту полета
КА не учитывается. Решается однопараметрическая крае¬
вая задача по определению оптимального момента пере¬
ключения эффективного аэродинамического качества
с КЭф = —Ко на Кдф = -f Kq из условия минимума
конечной скорости спуска. На полученной траектории
второго типа определяется минимальная высота пролета
КА над поверхностью планеты Атт, которая сравнивает¬
ся с величиной Адоп- Если оказывается, что Amin АД0Пт
то решение задачи на этом прекращается, поскольку иско¬
мая оптимальная траектория уже определена и принад¬
лежит ко второму типу.
170 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
Если /^nlin 'С ft длю то необходимо переходить к иссле¬
дованию оптимальных траекторий первого типа. В атом
случае первоначально рассматривается участок схода
траектории с ограничения, на котором определяется оп¬
тимальная скорость в момент схода F(2), обеспечивающая
минимум конечной скорости при полете с /+ф = В Ко.
Затем решается задача по определению предельной тра¬
ектории спуска, реализующей максимальную скорость
при выходе траектории на ограничение Ff^, после чего
осуществляется сравнение величии F,naX и F('+ Если
оказывается, что FmaX +- F(2), то оптимальной является
траектория первого типа, в противном случае — второго
типа. Согласно предложенной процедуре решения задачи
оптимизации, одним из основных косвенных признаков,
на основании которого можно проводить предваритель¬
ную классификацию оптимальных траекторий спуска,
является сравнение в каждом конкретном случае величин
максимальной скорости Fmlx при выходе па ограничение
и оптимальной скорости при сходе F(2). Поэтому представ¬
ляется интересным оценить частное влияние основных
варьируемых параметров (6.30) на Fmax и ЕЕ На рис. 6.6
представлены зависимости этих величин от проектно-
баллистических параметров КА (Рх и Ко), начальных
условий входа (F0 и ft*) и минимально допустимой высоты
полета (/гдоп). Видно, что величина F^ax возрастает
с увеличением Рх, Ко, F0, /&Д(Ш и с уменьшением /гп. Так,
например, при изменении Рх с 200 до 650 кг /м2 величина
скорости F^x. возрастает от 1570 до 3040 м/сек, при возра¬
стании Ко с 0,2 до 0,5 скорость F^?1X изменяется от 1880
до 2800 м/сек, при увеличении F0 от 5 до 8 км/сек скорость
Вшах увеличивается от 2000 до 3130 м/сек, при изменении
ft до п с 3 до 9 км величина V\}^x возрастает от 1980 до
2730 м/сек, а при уменьшении /г- от +45 до —145 км
максимальная скорость увеличивается от 1840 до
2490 м/сек.
Зависимости V\nlx (F0), F^L (ft доп ), EnL(tfo) ЯВЛЯ-
ются практически линейными, а зависимости FtO(/+) и
Птах (ft—) — существенно нелинейными. Это и предопре¬
деляет различную чувствительность изменения величины
Bliax к изменению рассматриваемых параметров.
АНАЛИЗ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ
171
Из рассмотрения рис. 6.6 видно также, что величина
скорости при сходе с ограничения не зависит от началь¬
ных условий входа, что, впрочем, и следовало ожидать,
и с увеличением Рх, /гдоп и уменьшением К а происходит
увеличение Так, при возрастании Рх с 200 до
650 кг/м2 величина V^ изменяется с 1640 до 2160 м/сек,
при увеличении /гдоп с 3 до 9 км величина V^2) возрастает
vJiy(zWcBK
зооо
2500
2000
1500
Vmz Mj>
1
i
Kmx (,Dz)
vZmx-
'\ Knar
Кпах (^on)
Vl2> (hm)
'yn)JPxK^
/ \
' / \
l^\
vm (Уа)х
' (/W
\ \
\1
.. vl2>(W
-145 -05 55 155
5 5 7 8
0,2 0,5 t),0 0,5
100 550 500 550
1— 1 1
Ьк,км
Vo, км/сек
КЬ ?
Р&кг/м
5 5 9 12 Ьт,км
Рис. G.G. Парциальное влияние параметров КА (Рх, К$), начальных условии
входа (V0, h-) и минимально допустимой высоты полета (/1Д0П) на VjJiaX и у(2)*.
с 1800 до 1965 м/сек и при уменьшении с 0,5 до 0,3
происходит увеличение V^2) с 1380 до 2460 м/сек.
По данным рис. 6.6 для частных значений варьируе¬
мых параметров легко установить граничное значение
каждого из них, при котором происходит нарушение
условия
Wax > VE (6.32)
J 72 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
Например, при Рх ^ 220 кг/м2 или КС) <С 0,25 и про¬
чих параметрах, равных номинальным (6.29), выполне¬
ние условия (6.32) невозможно; при этом единственная
оптимальная траектория спуска, реализующая минимум
конечной скорости, лежит целиком внутри допустимой
области фазового пространства. Изложенная процедура
позволяет достаточно просто получить численные мате¬
риалы, показывающие влияние основных параметров
V0, h-, Рх, Ка на конечную скорость при оптимальном
управлении.
Влияние начальных условий входа на минимальную
конечную скорость VK. В дальнейшем будем для крат¬
кости называть величину FK, полученную при оптималь¬
ном управлении, минимальной конечной скоростью FKmm.
Ьп,км
Рис, G.7. Нижняя и верхняя границы оперативного коридора входа в зави¬
симости от рх, Ка, ^доп» до¬
будем рассматривать семейство оптимальных траекто¬
рий, лежащих внутри всего коридора входа А/г- =/г“ —/г,".
АНАЛИЗ ЧИСЛЕННЫХ 1 ЕЗУЛЬТАТОВ
173
Верхняя граница этого коридора (hi) определяется из
условия захвата КА атмосферой, а нижняя граница —
минимальной высотой условного перицентра hi, при ко¬
торой еще возможно с управлением — -\-Кq выпол¬
нение ограничения (3.25). Следует отметить, что нижняя
граница hi существенно зависит от основных рассматри¬
ваемых параметров Рх, КС), VQ, h:mu причем hi возрастает
при увеличении Рх, /щои, V0 и при уменьшении KCi
(рис. 6.7). В силу этого в каждом конкретном случае
рассматривается движение КА в соответствующем коридо¬
ре входа. Так, например, при номинальных значениях
всех варьируемых параметров (6.29) hi = —170 км,
a hi ~ + 45 км.
Влияние высоты условного перицентра на величину
Vк mill* Анализ численных результатов показал (рио. 6.8),
что внутри коридора входа тип управления в некоторых
случаях может меняться и существует такое граничное
значение hi высоты условного перицентра, лежащее
в диапазоне hi h~ hi, с которым при входе в атмо-
сферу реализуется предельная оптимальная траектория
первого типа 16 (касающаяся ограничения).
При значениях h- имеет место второй тип
управления, при h* <1 hi — соответственно первый тип
управления. Различие управлений внутри оперативного
коридора входа отражается на величине минимальной
конечной скорости и характере ее зависимости от h-\
— при изменении hr. от hi до hi величина VK т[п
непрерывно уменьшается. При этом наибольшее значение
min соответствует входу с h- = hi (см. рис. 6.8);
— при дальнейшем уменьшении h- от hi до hi величи¬
на К к mill остается неизменной, что предопределено
свойством неединственности.
Влияние начальной скорости V0 на величину FKmin-
Будем предполагать, что при каждой конкретной реали¬
зации вход КА осуществляется в середине коридора.
В этом случае для всего диапазона начальных скоростей
входа, соответствующих траекториям прямого перелета
Земля—Марс (см. главу 2), реализуются оптимальные
траектории первого типа и величина конечной скорости
спуска не зависит от величины VQ (см. рис. 6.8).
174 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
Таким образом, проведенные численные исследования
показывают, что для достаточно широкого диапазона
значений параметров КА величина конечной скорости
спуска при оптимальном управлении не зависит от началь¬
ных условий входа. Этот вывод очень важен, так как по¬
зволяет при выборе баллистической схемы полета к Марсу
Kmn,v/W<
Рис. G.8. Величина конечной скорости при оптимальном управлении (сплош¬
ная линия — первый тин управления, штриховая — второй).
участок межпланетного перелета в определенных пре¬
делах считать независимым от участка спуска КА в ат¬
мосфере, а имеющийся произвол может быть использован
для независимой дополнительной оптимизации каждого
из этих участков движения.
Влияние основных проектно-баллистических характе¬
ристик на VK „пп. На рис. 6.8 представлены также зави¬
симости влияния аэродинамического качества Kq и при¬
веденной нагрузки Рх на VK шт. Из их рассмотрения
видно, что с увеличением аэродинамического качества
§ 6.4]
АIIА ЛII3 411С Л ЕIIIIЫ X Г Е 3 У Л ЬТД Т О В
:175
для оптимальных траекторий первого типа (сплошная
часть кривой) и второго типа (штриховая часть кривой)
величина конечной скорости спуска уменьшается, а зави¬
симость VK {Кq) близка к линейной. Так, например, при
возрастании Ко от 0,3 до 0,5 величина конечной скорости
уменьшается с 568 до 500 м/сек. Следует отметить, что
наклон кривой V}. {Ко) мало меняется при широких
вариациях остальных параметров (6.30). Частная произ¬
водная дУи/дКоВ среднем равна 350 - 380м/сек. Другими
словами, при изменении качества па 0,1 конечная скорость
на оптимальной траектории изменится па 34 л- 38 м/сек.
Иначе влияет на VK тш приведенная нагрузка на лобовую
поверхность: увеличение Рх ведет к возрастанию VK ти\-
Так, при изменении Рх с 350 до 650 кг/м2 величина конеч¬
ной скорости увеличивается с 568 до 810 м/сек.
Отмеченная особенность противоположного влияния
Рх и Ко на величину ИКП1]11 оказывается существенной
для выбора рациональной формы КЛ, осуществляющего
спуск в атмосфере Марса.
Влияние минимально допустимой высоты полета и
конечной высоты на F"Kinjn. Введение ограничения на
минимально допустимую высоту полета КА сужает
область допустимых фазовых координат, внутри которых
может проходить оптимальная траектория спуска, и,
естественно, приводит к увеличению конечной скорости
спуска в случае, если высота /гдоп больше минимальной
высоты полета hm\n на оптимальной траектории, построен¬
ной при отсутствии этого ограничения. Как и следовало
ожидать, с возрастанием /гдоп величина Vu т\п увеличи¬
вается (см. рис. 6.8). В частности, при изменении ^доп с 6
до 9 км конечная скорость возрастает с 568 до 675 м/сек.
Следует отметить, что с увеличением Рх чувствительность
функционала V1{ min к изменению /гдоп возрастает. Влия¬
ние конечной высоты hк на FK т\п аналогично влиянию
высоты /гдоп, я именно, с увеличением /гк величина min
возрастает. Это объясняется тем, что задача оптимального
управления из условия min VK решалась в предположе¬
нии, что hK = Лдоп. Необходимо подчеркнуть, что ука¬
занная зависимость сохраняется и для случая /? н Ф hu дотт-
Сравнение величины минимальной конечной скорости
со скоростью установившегося полета. Сопоставим полу¬
ченные результаты решения экстремальной задачи по
176 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
величине скорости FK т[П с соответствующими значениями
установившейся скорости (см. рис. 6.1 и 6.8). Оказывает¬
ся, что величина минимальной конечной скорости при оп¬
тимальном управлении К-Лф меньше установившейся ско¬
рости во всем диапазоне изменения рассматриваемых
параметров. Однако разница AF -- FycT — 7НП1(П не¬
значительна и составляет в среднем 20 л- 25 м/сек.
Последнее обстоятельство позволяет утверждать, что
для достаточно широкого класса КА, осуществляющих
спуск в атмосфере Марса по оптимальным траекториям
из условия min I7,., для исследования участка аэродинамиче¬
ского торможения в первом приближении нет необходи¬
мости в строгом решении оптимальной задачи (что в ряде
случаев связано с определенными вычислительными труд¬
ностями и большими затратами машинного времени).
Достаточно провести расчет величины FyCT по форму¬
ле (6.3) и принять эту величину за то значение скорости,
которое необходимо погасить с помощью ТДУ на участке
активного торможения. Погрешность в этом случае бу¬
дет составлять 2-3%, что вполне допустимо на этапе
проведения общих проектно-баллистических исследо¬
ваний.
Следует также отметить, что хотя на величину угла 0К
не накладывалось ограничение при постановке экстре¬
мальной задачи, однако этот параметр являлся наблюдае¬
мым в процессе ее решения. При этом оказалось, что ве¬
личина угла | 0К |, полученная при оптимальном управ¬
лении из условия min FK, существенно меньше угла | 0угт |.
Так, для КА с Рх = 350 кг/м2 и Кб = 0,3 величина | 0К |
при оптимальном управлении составляет 13°12', а при
установившемся движении | 0уст | = 73°20'. Это лишний
раз подтверждает справедливость выводов, сделанных
ранее из анализа формулы (6.13).
§ 6.5. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ КА НА ТРАЕКТОРИЯХ
МИНИМАЛЬНОЙ КОНЕЧНОЙ СКОРОСТИ
Решение задачи оптимизации по критерию min FK
является важным результатом в проблеме обеспечения
мягкой посадки КА на поверхность Марса с минимальны¬
ми суммарными затратами энергетики. Вместе с тем су¬
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ УПРАВЛЕНИЯ
177
ществует ряд других, не менее важных задач, практиче¬
ское решение которых также необходимо на определенном
этапе исследования планеты Марс. Это прежде всего зада¬
ча обеспечения точной посадки в заданном районе поверх¬
ности, задача минимизации максимальных перегрузок
и т. д.
Известно, что введение дополнительных условий и
критериев обычно ведет к ухудшению результатов по ос¬
новному критерию оптимальности. Однако, как было уже
установлено, оптимизация траекторий спуска в отношении
других критериев в некоторых случаях и в определенных
пределах возможна без ухудшения результатов по ос¬
новному критерию min VK. Это объясняется тем, что для
достаточно широкого диапазона изменения параметров КА
спуск с min VK может происходить по одной из траекто¬
рий, принадлежащих некоторому семейству и имеющих
одинаковый конечный участок схода с ограничения по
высоте. Это и позволяет рассматривать некоторые допол¬
нительные задачи оптимального управления КА на тра¬
екториях минимальной конечной скорости.
Оптимизация зоны маневра КА. Одним из основных
условий обеспечения точной посадки КА в заданном
районе поверхности планеты является его способность
к маневрированию: чем шире зона маневра, тем проще
решение задачи при прочих равных условиях. В силу
этого и рассмотрим задачу максимизации зоны манев¬
ра КА.
Под зоной маневра будем понимать диапазон дости¬
жимых дальностей полета, от минимальной до максималь¬
ной, при соблюдении условия минимизации конечной
скорости min Vu.
Для траекторий минимальной конечной скорости опре¬
делим такой закон управления углом крепа (или АЭф),
который обеспечивает максимальную (или минимальную)
дальность спуска при ограничении на высоту полета.
Дополним уравнения движения (3.20) соотношением
для расчета дальности полета, измеряемой по поверхности
планеты:
L R• (6'33)
Имеем следующие краевые условия для параметров
178 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
движения:
t = : Т7 (^о) = К0, 0 (^о) = 6о> А (^о) — А(н L (t0) = Z/q,
(6.34)
* = <(2): F (Р2)) = F'F, 0 (tm) = 0, h (t(i) = /гдо„. (6.35)
В соответствии с результатами исследований, приведенных
в главе 5, условия при t = t^2) обеспечивают минимиза¬
цию конечной скорости min Гк.
Запишем функцию Гамильтона
dt
dt
Ь-^г- (6-36)
Вспомогательные переменные фх (£) на участке движения
КА внутри допустимой области определяются уравне¬
ниями
dl
dt
dll , pF
= '
dv
g(lR2 cos 0
cos 0
Ф-2
К1>фР
r2[/2
3/7
с'о
— фз sin0 — ф4
R cos 0
= Ф]
g,R1 cos 0
Ф-2
g{)R2 sin 0
sin 0
4'3F cos 0 -I- i|>4
I'-'V
VII sin 0
d ф, dll
■=~ж=^
dt
dt
p-
sin 0
+ Ф'2
К
pi
2 Px ^
V cos 0
[ (6-37)
2я„/?2 cos 0
T
+
VR cos 0
d/l
0L
0.
На участке движения вдоль ограничения (3.25) получим
d\|)°r Р a rr nElh01'^ Т,
dt
dll
dV
4_ л = ?V}Sfl
д V
■фдГР А
d^T'V __ _ дИ_ _L , Зф
dt <90 1 <90
2Р,
4>SrpF,
(6.38)
§ 6.5]
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ УПРАВЛЕНИЯ
179
d\[%VV __ Ш_ . дф
~~ТС дк Ж ~~
dt
где
эф
Из уравнений (6.37) и (6.38) видно, что ф4 = const
на всей траектории спуска.
Условия разрыва сопряженных переменных в точке
выхода экстремали на ограничение запишутся так же,
как и ранее (см. § 6.2), с добавлением уравнения
Поскольку фазовые координаты фиксированы при t =
остается потребовать
^гр (ги)) = - 1 при минимизации L(№), 1
^огр (^С2)) __ | прИ максимизации £,(№). J ^ ^
Решение краевой задачи для систем уравнений (6.37),
(6.38), (3.20), (6.33) с граничными условиями (6.34), (6.35)
и (6.40) после анализа условий скачка сводится к поиску
решения на отрезке [t0, №].
Оптимальной программой управления, обеспечивающей
минимальную дальность траекторий, удовлетворяющих
условиям касания в точке t = t^l\ является программа
с одноразовым переключением К{)ф при t ^ № (с —К<$
на -\-Kq).
При № t <1 (движение на граничной высоте)
управление определяется однозначно в соответствии
с (6.19). На траекториях, обеспечивающих максимальную
дальность при FKmin, участок движения по ограничению
отсутствует (Д1) = №) и оптимальным законом управ¬
ления является программа двухразового переключения
Ф*1 Р (h) — Ф4 (*i) = На -Qjp- + И'-г -qpp — 0. (6.39)
Т^эф — “Ъ 7^6, — А'б, -f- К§.
180 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
На рис. 6.9 показана зависимость L- mill и I- шах
(индекс я означает, что дальность спуска отсчитывается
от условного перицентра траекторий входа) от параметров
аппарата (Рх и Кв), условий входа (hn и F0) и минимально
допустимой высоты полета (/&д0П). Видно, что при возра¬
стании /г- зона маневра КА несколько увеличивается,
Ц,км
О
■200
-ООО
-ООО
-800
-1000
0000
/Г
'Le(hn)
Шь)
rj—
/
/
/
1
/
Ln(Vo) /
Ln(Px)
|\
/
/у
/
У
-245
-105
-05
55 tiff, км
0,1 O.t
50 20,
^
? о,
0 '55
^
1 0,
0 50
1
Кб
0 Рх,кг/мг
5000
5000
7000 м/сек
Гис. 6.9. Парциальное влияние параметров Рх, К$, V0, h- на ширину зоны
маневра КА на траекториях минимальной конечной скорости (сплошная ли¬
ния — min штриховая — max L~).
достигая максимума вблизи середины коридора входа,
а затем снова уменьшается. Увеличение параметров Рх,
Ка, V0 приводит к расширению зоны маневра КА на тра¬
екториях минимальной конечной скорости.
Минимизация максимальной перегрузки. В ряде слу¬
чаев при анализе траекторий управляемого торможения
КА в атмосфере Марса может представлять интерес до-
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ УПРАВЛЕНИЯ
181
полнителыюе требование снижения величины максималь¬
ной перегрузки min (пх шах) при сохранении условия
min FK.
Эта задача приобретает особую актуальность для КА,
подлетающих к Марсу по ускоренным траекториям и
имеющих увеличенную скорость входа (F0 х 8 -л-
-г- Ю км/сек). Максимальные перегрузки пхпшх при входе
с увеличенными скоростями в 2-3 раза больше, чем для
аппаратов, подлетающих но энергетически оптимальным
траекториям (F0 ^ (5 км/сек). Увеличение максимальной
перегрузки на траектории снижения КА в свою очередь
требует пересмотра прочностных характеристик элемен¬
тов конструкции КА и, как правило, приводит к их утя¬
желению.
Рассмотрим задачу минимизации максимальной пере¬
грузки на траекториях минимальной конечной скорости
min FK. Для типичных значений Рх, Кб,1г~, F0,/гдоп (6.28)
максимум продольной перегрузки при граничном управ¬
лении (КЭф = +Ао) наступает всегда до момента вырав¬
нивания траектории (0 =0). Если t < tr, максимум
единствен. Было показано [97], что если F(1) больше пер¬
вой космической скорости, то под влиянием граничных
условий при t = № минимальное значение максимальной
перегрузки будет обеспечиваться при двухразовой пере¬
кладке эффективного качества:
А^эф — +АГб, —АГо, -\-Кц.
Из численного анализа следует, что структура оптималь¬
ного управления сохраняется и при меньших значе¬
ниях F^4).
Для сравнения были получены оценки наибольших
значений перегрузок, возможных при выполнении усло¬
вий касания при t = № и достигаемых при одноразовом
переключении:
АГЭф “ +АГб, —Kq.
Результаты расчетов приведены на рис. 6.10, где показано
парциальное влияние параметров РХ1 Kq, hn, F0, Адоп на
min (пх 1Пах) и max (гс* max) при найденных законах
управления. Видно, что при увеличении F0, а также
при уменьшении Kq, Рх, h* происходит увеличение
min (пх 1Пах) и max (Агхтах)- Наибольший эффект введе¬
ния управления, минимизирующего ихШах на траекто¬
182 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. G
риях Vu min, достигается при скоростях входа, соответ¬
ствующих ускоренным схемам перелета КА. Если при
скорости входа Р0 -- G км/сек величина пхпглх может быть
mc£i
Гис. 6Л0. Предельные значения максимально!! перегрузки (сплошная ли¬
ния (пх rnax^miii’ штриховая (пх пшх+ач)*
уменьшена на 3-4 единицы по сравнению с max (ra^max),
то при V0 = 8,5 км/сек перегрузки снижаются на 10—
12 единиц при входе в коридор Ah- х +50 км.
Минимизация времени спуска. Рассмотрение этой за
дачи представляет большой интерес в силу следующих
причин. Результаты многочисленных исследований пока¬
зывают, что для наиболее употребительного в настоящее
время способа тепловой защиты КА с помощью сублими¬
рующих покрытий минимум массы системы тепловой
защиты гатш всегда обеспечивается па траекториях ми¬
нимального времени спуска min tC[l (здесь tcn — полное
время спуска на участке основного аэродинамического
торможения). Выявленная закономерность позволяет во
многих случаях существенно упростить решение задачи
выбора траекторий из условия минимальной массы тепло¬
защиты, ибо взаимосвязь минимизируемого функциона¬
ла ттш и параметров траектории спуска имеет достаточно
§ 6.Г’]
ДО ПОЛ II ИТ H ЛЬ IIЫЕ ЗАДАМИ У! ПЛАВЛЕНИЯ
183
сложный вид и, кролге того, для каждого типа теплоза¬
щитного материала оказывается различной. Это сущест¬
венно затрудняет форлгализацию задачи и требует громозд¬
ких вычислений при ее решении. Кроме того, при
использовании прямого критерия min ттдП затруднен
сравнительный анализ эффективности различных видов
теплозащитных материалов. Эти трудности во многом уст¬
раняются при использовании существенно более простого
критерия min £сп, эквивалентного критерию min ттзп.
Использование условия min /(.п позволяет сущест¬
венно упростить решение задачи об отыскании оптималь¬
ного закона управления КА и согласовать эту задачу
с баллистико-навигационпыми требованиями к траекто¬
рии снижения КА в атмосфере Марса.
Итак, требуется определить программу управления
(/), минимизирующую функционал / = при огра¬
ничениях на фазовые координаты (3.25), управление (3.17)
и краевых условиях
V(t0) = V о, 0(/0) 0(), h(t0) = h0i |
V (ti;) = V’k .„in, h(tft) = hK, 0K свободно. J 'l
В силу отмеченного выше свойства неединственности
траекторий минимальной конечной скорости функцио¬
нал / - = и условия (6.41) на правом конце примут вид
/ = /(1\ /г(^°) = hu, 0 (*(1)) = О, V (t^) и t^l) свободны.
Решение краевой задачи показало, что оптимальной
программой управления, обеспечивающей минимальное
время спуска КА па участке выхода па ограничение, яв¬
ляется программа одноразовой перекладки эффективного
качества: = —Аж, -1-А7,. На рис. 6.11 показана зави¬
симость min tcn от условий входа (F0, h~) и от параметров
КА (Рт, К с). Видно, что при увеличении приведенной на¬
грузки на лобовую поверхность, высоты условного пери¬
центра и аэродинамического качества происходит увели¬
чение min tcn.
Для сравнения была рассмотрена задача максимизации
времени спуска КА на траекториях FK inin- Программой
управления в этом случае на участке выхода на ограни¬
чение является программа двухразового переключения
эффективного качества: Кдф ; У\о, —/аД, -рАф.
184 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ 6
Результаты решения задачи о минимальном времени
спуска показывают, что для рассматриваемых диапазонов
условий входа и параметров КА выигрыш во времени
спуска (а следовательно, в массе тепловой защиты) на
траекториях минимальной конечной скорости незначи¬
телен и в лучшем случае составляет 10 -ч- 15 сек. В то же
время разница во времени спуска при движении по верх¬
ней и нижней границам коридора входа составляет вели¬
чину порядка 45—50 сек. Отсюда видна неэффективность
HT..CGK
Гис. 6.11. Минимальное время спуска на траекториях минимальной конечной
скорости.
оптимизации траекторий минимальной конечной скоро¬
сти по критерию минимальной массы теплозащиты — по
крайней мере для рассматриваемых условий и парамет¬
ров КА.
Отметим также, что на траекториях, минимизирующих
*сп» реализуется максимально возможная перегрузка
max а это часто нежелательно.
§ 6.6. ОБ ЭФФЕКТИВНОСТИ ИСПОЛЬЗОВАНИЯ
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
В рассматриваемой задаче эффективность использова¬
ния оптимального управления аэродинамическим качест¬
вом для спуска КА в атмосфере Марса можно определять
величиной конечной скорости, до которой тормозится ап¬
§ 6.6] ОБ ЭФФЕКТИВНОСТИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ 185
парат [28]. Чтобы оценить, в какой степени оптимизация
траекторий позволяет уменьшить скорость FK, целесооб¬
разно рассмотреть некоторые упрощенные законы управ¬
ления КА на траектории. Величина разности конечных ско¬
ростей
6F„ = F„-F„min, (6.42)
которые достигаются при использовании соответственно
простой и оптимальной программ управления КА,
м/сек
№
800
100
600
Гис. 6 12. Конечная скорость при полете с постоянным аэродинамическим
качеством.
позволяет судить о том, какой из них отдать предпочтение
в каждом конкретном случае.
Самым простым для реализации видом управления КА
с подъемной силой является спуск с постоянным значением
эффективного качества (КЭф = const). Рис. 6.12 иллюстри-
ISO ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. о
р у е т влияние п р о е к т и о - б а л л и с т и ч е с к и х и а р а м с т ров К А
(Рх, К о) и высоты условного перицентра (h-) па величину
конечной скорости при снижении с Кдф = + Аб. Варьи¬
рование указанных параметров (за исключением 1гт) осу¬
ществлялось в диапазоне (6.28). Что касается величины
h~, то для каждой программы управления А;)1) существует
различный допустимый интервал Ah-, внутри которого
может рассматриваться изменение отого параметра. При
этом положение одной или обеих границ коридора входа
может быть различным в зависимости от используемой про¬
граммы управления. Наибольшая ширина коридора входа
достигается при использовании оптимальной программы
управления. В случае применения любой другой, не опти¬
мальной программы происходит уменьшение Ah-. Имея
этот факт в виду, для удобства сравнения эффективности
различных программ управления КА будем пользоваться
понятием коридора входа, определенного для случая ис¬
пользования оптимальной программы управления.
Рассмотрим зависимости, представленные па рис. 6.12.
Видно, что величина конечной скорости существенно за¬
висит от высоты условного перицентра траектории входа.
Наименьшее значение величины VK достигается при дви¬
жении КА по нижней границе коридора входа. С увели¬
чением высоты условного перицентра величина конечной
скорости заметно возрастает, достигая максимума вблизи
середины коридора входа, а при дальнейшем увеличении
hK величина FK незначительно уменьшается. Максималь¬
ный разброс величины конечной скорости при движении
внутри коридора входа с К.0ф ----- КС) достаточно велик и
составляет 120 -н 150 м/сек. Например, для рассматривае¬
мых номинальных значений параметров (6.29) при /г” -=
~ —170 км имеем FK - 625 м/сек, а при увеличении 1ьл
до —70 км конечная скорость возрастает до максималь¬
ного значения FK --- 760 м/сек. Как и следовало ожидать,
увеличение нагрузки па лобовую поверхность Рх приводит
к увеличению конечной скорости при использовании про¬
граммы управления К^ф = -\-Kq. Получающаяся зави¬
симость FK (Рх) практически не отличается от линейной.
Если Рх увеличивается от 350 до 650 кг/м2, величина конеч¬
ной скорости возрастает с 760 до 980 м/сек.
Интересно отметить, что при увеличении от нуля до
некоторого значения происходит уменьшение FK, а за-
§ 0.6] ОБ ЭФФЕКТИВНОСТИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ 187
нем при дальнейшем возрастании КС) конечная скорость
увеличивается. Подобный эффект влияния на конечную
скорость легко объясняется, если рассмотреть характер
изменения параметров V и h па траектории спуска.
Оказывается, что при спуске КА с постоянным значе¬
нием аэродинамического качества, как и при оптималь¬
ном управлении, наблюдается маневр типа «горки».
Причем с увеличением аэродинамического качества К0
минимальная высота рикошета траектории /г1Пш и макси¬
мальная высота «горки» hnuxx возрастают. В этом случае
на величину конечной скорости оказывают противополож¬
ное влияние два фактора:
— увеличение V1{ за счет движения КА в верхних,
более разреженных слоях атмосферы;
— уменьшение VK за счет большей длительности по¬
лета в целом.
В случае Ко < Ко второй фактор оказывает решаю¬
щее влияние на Vи, а при Ко у> Ко — первый фактор.
Этим и объясняется отмеченный выше характер зависимо¬
сти VK(K6).
Анализ траекторий спуска с Кдф — const позволяет оце¬
нить эффективность оптимального управления. Сравни¬
вая зависимости, представленные на рис. 6.8 и 6.12, легко
видеть, что для КА с заданными характеристиками наи¬
больший эффект достигается в случае полета КА вблизи
середины коридора входа, а наименьший — при движе¬
нии вблизи нижней границы. Эффект использования опти¬
мального управления возрастает с ростом Аб, увеличение
же Рх слабо влияет на величину вариаций конечной ско¬
рости. Программа полета КА с Кэ$ = + 7^ используемая
для сравнения с оптимальным управлением, обладает
несомненным достоинством простоты, однако дает очень
большой разброс по сравнению с оптимальным управле¬
нием. Для уменьшения разброса целесообразно рассмот¬
реть возможности использования других программ управ¬
ления, также достаточно простых по структуре.
Проведенные исследования показали, что в качестве
такой программы управления может быть использована
Программа, предполагающая одно переключение эффектив¬
ного качества. На рис. 6.13 представлены зависимости
Конечной скорости от нагрузки на лобовую поверхность
188 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. О
в случае оптимального управления и при использовании
программы одного переключения. Сравнение этих данных
с приведенными на рис. 6.12 показывает, что программа
одноразового переключения позволяет весьма существен-
но снизить величину VK. Так, для рассмотренного выше
примера КА с Рх = 350 кг/м2, Kq = 0,3 и hma = 6 км
величина конечной скорости может быть уменьшена по
Ук, м/сск
Рис. 6.13. Конечная скорость при оптимальном управлении и использовании
программы с одним переключением эффективного качества (/iK = 6 км).
сравнению с программой Кэф —- const дополнительно еще
на 43 м/сек.
Необходимо отметить, что программа одноразового пе¬
реключения для аппаратов с малыми значениями Рх и
является оптимальной и реализует абсолютный минимум
конечной скорости. При увеличении Рх и использова¬
ние этой программы не дает оптимального решения. В каж¬
дом конкретном случае необходимо оценить массу СМП
и массу системы управления спуском, а также надежность
работы этих систем, прежде чем отдать предпочтение про¬
стому или сложному алгоритму управления спуском.
Сопоставляя результаты, полученные для субопти-
мальных и оптимальных траекторий при различных зна¬
чениях Рх, можно утверждать, что выбор рациональной
схемы спуска существенным образом зависит от значений
Рх. При малых Рх (Рх <С 150 кг/м2) можно использовать
траектории с постоянным углом крена, при средних зна-
О ГРАНИЦАХ ГН ИМЕНИМОСТИ Kl ИТЕ I ИЯ min У,-
189
нениях Рх (от 150 до 300 кг/м2) — траектории спуска
с одним переключением К[}ф, а при больших Рх (Рх
300 кг/м2) следует применять траектории с оптималь¬
ным управлением (два переключения К0ф).
§ 6.7. О ГРАНИЦАХ ПРИМЕНИМОСТИ КРИТЕРИЯ
МИНИМУМА КОНЕЧНОЙ СКОРОСТИ
Оптимальное управление, полученное в результате
решения задачи из условия min VK при свободном 0И,
обеспечивает абсолютный минимум конечной скорости
V^m/csh
!7'
\\
V \ >«.
\
//
/у
^ Г71
\ X.
'г/м1 // 1
/
/\ Л
у V1
1
г
О -10 -20 -30
В0,граО
Гис. 6.14. Величина спорости в конце участка аэродинамического торможе¬
ния (/iK = 6 км) и затраты характеристической скорости для обеспечения мяг¬
кой посадки (/Гк = 0). (Сплошные линии — зависимость Ук (0К); штриховые —
зависимость УХар (^к^ кривые 1 — КА с Kq = 0,3; кривые 2 — КА с
Ко - 0,5.)
для КА с заданными параметрами. Этот важный вывод
необходимо иметь в виду при дальнейшем анализе, ибо
априори ясно, что введение дополнительного условия по
конечному значению 9К должно привести к увеличению
FK при прочих равных условиях [34]. Рассмотрим рис. 6.14,
190 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. Г,
где для аппаратов с величиной аэродинамического качества
Ко = 0,3 и 0,5 представлены зависимости минимальной
конечной скорости спуска VK Ш[[Х от угла 0Н наклона траек¬
тории к местному горизонту на конечной высоте hu = 6 км
для различных значений приведенной нагрузки на лобо¬
вую поверхность Рх. Заметим, что для КА с другими зна¬
чениями Kq и hu качественная картина остается без изме¬
нения. Для удобства анализа выделим два класса КА в
зависимости от нагрузки на лобовую поверхность: 1-й
класс Рх 2000 кг/м2,2-й класс РХ^С 2000 кг/м2.
Выше было показано, что с увеличением Рх конечная
скорость VK увеличивается, а угол 0К асимптотически
приближается к нулю, достигая его для аппаратов с боль¬
шим значением приведенной нагрузки на лобовую поверх¬
ность Рх.
Таким образом, для КА с Рх'^>2000 кг/м2 доказа¬
тельство соответствия критерия min V1{ условию (0.1)
достаточно тривиально, ибо оптимальное управление
по этому критерию одновременно обеспечивает и
нулевые значения угла наклона траектории к местно¬
му горизонту в конце полета, т. е. полное выполнение
условия (6.1).
Рассмотрим теперь второй случай, когда Рх
^ 2000 кг/м2. Данные, представленные в главе 4, а также
на рис. 6.3, показывают, что условие min FK обеспечивает¬
ся для аппаратов второго типа только при 0К << 0. Это
объясняется структурой оптимального управления и ха¬
рактером соответствующих оптимальных траекторий, от¬
личающихся тем, что КА после достижения некоторой
глубины погружения либо сразу осуществляет маневр
схода внутрь допустимой области фазовых координат, либо
сначала движется по ограничению (изовысотный участок
полета), а в некоторый, строго определенный момент вре¬
мени осуществляет сход с ограничения внутрь допустимой
области фазовых координат. От момента схода с ограниче¬
ния аппарат движется с максимальным значением аэроди¬
намического качества (т. е. осуществляет маневр типа
«горки»). Для удовлетворения второго из условий (6.1),
т. е. для уменьшения угла | 0,. |, следует с момента выхода
на ограничение осуществлять изовысотный полет или
стремиться оттянуть момент схода, т. е. срезать «горку»
и тем самым уменьшить |0К'|. Однако такие действия при¬
О ГРАНИЦАХ П1 НМГЛШМОСТИ K1I1TEI ИЯ min Ук
191
водят к увеличению конечной скорости Ук, и следует
искать компромиссное решение между Уи и 0К, чтобы до¬
биться наилучших результатов по минимуму массы систе¬
мы мягкой посадки.
Рассмотрим второй предельный случай, когда необхо¬
димо обеспечить в первую очередь условие 0К = 0 при
произвольном значении Ук. Согласно представленным на
рис. 0.14 зависимостям Ук (0к), в этом случае резко воз¬
растает величина конечной скорости Ук, что полностью
уничтожает эффект уменьшения |0К|. Следовательно, с
точки зрения выполнения критерия min трс не сущест¬
вует никакого промежуточного решения по Ук, отличаю¬
щейся от У к „пп и | 0К |, ведущего к выигрышу в потребной
массе СМП.
Сделанный вывод полностью подтверждается резуль¬
татами решения задачи определения оптимального управ¬
ления КА из условия минимума характеристической ско¬
рости КА. Как отмечалось в главе 4, величина характери¬
стической скорости однозначно определяет потребные за¬
пасы топлива, а следовательно, и массу реактивной СМП.
Именно поэтому и представляет интерес сравнить резуль¬
таты исследований оптимальных траекторий по критерию
min Ук и минимизации характеристической скорости, по¬
требной для окончательного торможения, т. е. обеспече¬
ния мягкой посадки КА (min Vx). Постановка последней
задачи аналогична; изложенной в работе [84] и поэтому
подробно здесь не рассматривается. Приведены лишь чис¬
ленные результаты, полученные при тех же исходных дан¬
ных и ограничениях, как и в случае использования кри¬
терия min Ук (см. рис. 6.14). Сравнение зависимостей
Vх (9 к) и Vк (9 к) показывает почти полное совпадение их
минимальных значений. Зависимость характеристической
скорости Vх от угла наклона 0К траектории к местному
горизонту на высоте hu имеет более пологий, т. е. менее
выраженный экстремум. Последнее объясняется зависи¬
мостью потребной энергетики па активное торможение
не только от Ук, но и от 0К.
Таким образом, показано, что удовлетворение крите¬
рия min VK на участке аэродинамического торможения
обеспечивает минимальную массу реактивной СМП.
В этом смысле указанный критерий является универсаль¬
ным для данного типа СМП.
192 ОПТИМАЛЬНО]: УПРАВЛЕНИЕ конечной СКОРОСТЬЮ [ГЛ. 6
§ 6.8. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
КОНЕЧНОЙ СКОРОСТЬЮ СПУСКА КА
С БОЛЬШИМ АЭРОДИНАМИЧЕСКИМ КАЧЕСТВОМ
Постановка задачи
По мере усложеиия целей и задач космических по¬
летов к Марсу будут, очевидно, изменяться требования
к схеме и конструкции спускаемых КА. В связи с этим
представляет интерес изучение проблемы мягкой посадки
на поверхность Марса КА планирующего типа, обладаю¬
щих аэродинамическим качеством Ктлх ^>0,7. Здесь в
первую очередь имеются в виду КА с несущим корпусом,
у которых величина Ктах не превышает 1,5, и аппараты
самолетной формы, имеющие гиперзвуковое аэродинами¬
ческое качество порядка 2,5.
Основные преимущества КА планирующего типа обще¬
известны. Это прежде всего:
— возможность максимального облегчения режима
перегрузки (максимальная «комфортабельность» спуска);
— большие маневренные возможности не только в про¬
дольном, но и в боковом направлении;
— возможность выбора траектории с целыо уменьше¬
ния интенсивности нагрева КА;
— возможность в широких пределах выбирать точку
посадки на поверхности Марса при нерасчетных условиях
входа в атмосферу;
— расширение коридора входа;
— возможность реализации разного рода оптимальных
траекторий и многие другие.
Вместе с тем известны и огромные трудности создания
КА подобного типа (часть из которых указана в главе 3),
преодоление которых требует принципиально новых ре¬
шений в различных областях науки и техники и больших
материальных затрат [12, 35, 43—45, 54, 77, 82, 91, 96,
98-100].
В ближайшем будущем КА планирующего типа будут
реализованы для земных транспортных космических си¬
стем, но их применение экономически будет оправдано
лишь в случае многоразового использования [77, 100].
Логично предположить, что после того, как будут созданы
подобные КА для посадки на Землю, применение их для
§ 6.8J КЛ С БОЛЬШИМ АЭРОДИНАМИЧЕСКИМ КАЧЕСТВОМ 193
спуска в атмосферах других планет не будет столь про¬
блематичным, хотя на настоящем этапе развития космиче¬
ской техники систематические исследования КА планиру¬
ющего типа для спуска в атмосфере Марса практически
не ведутся.
В первую очередь необходимо рассмотреть возмож¬
ность «мягкой» посадки подобных КА. В частности, ис¬
следуем задачу об отыскании оптимальной траектории
спуска КА планирующего типа из условия минимума ко¬
нечной скорости спуска. Предварительно отметим неко¬
торые исходные предпосылки, которые используются при
решении этой задачи.
Аэродинамические характеристики КА. Как известно,
аэродинамические силы, действующие па КА, определя¬
ются его формой, характером обтекания, типом погра¬
ничного слоя и т. п. В настоящее время известно боль¬
шое количество возможных форм КА планирующего типа
№
к
у
А
/
1
£с
^3?
X /
\/
А
/ \—
V /
\ /
/у
//] А
\
\ \
А
\
i>A 1
О 20 00 00 \ 60 100
^ сс.зраО
Рис. 6.15. Аэродинамические характеристики для аппаратов разной конфи¬
гурации (сплошная линия — космический самолет (Ктах = 2,4), штриховая —
КА с несущим корпусом (Кшах = 1,5), штрих-пунктирная — КА скользящего
типа (Кшах = 0,32; а следует считать отрицательным).
[3]. Для определенности рассмотрим две конкретные фор¬
мы аппаратов с несущим корпусом и КА самолетного типа.
Аэродинамические характеристики для этих КА приведе¬
ны на рис. 6.15. Следует отметить, что конкретизация
7 Н. М. Иванов, А. И. Мартынов
194 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
аэродинамических характеристик для других форм КА
не влияет на качественные выводы при решении задачи
мягкой посадки КА, а приводит лишь к некоторому изме¬
нению количественных характеристик.
1.1 ри анализе вопросов динамики спуска КА планиру¬
ющего типа желательно иметь аналитические выражения
зависимостей аэродинамических коэффициентов С х и Су
от угла атаки а. В работе [3] отмечается, что при малых
углах атаки (ос ^ 15 ч- 20°) для КА планирующего типа
с большой величиной аэродинамического качества зависи¬
мости Сх (а) и Су (а) могут быть приближенно представ¬
лены в виде
где т = 2, п = 3/2.
При больших углах атаки вместо выражений (6.43) и
(6.44) следует использовать соотношения
Конкретные значения коэффициентов Сх0, Сау, В, Аг,
Вг в зависимости от числа Маха можно найти, например,
в работе [3].
Представление зависимостей аэродинамических харак¬
теристик КА от угла атаки в виде четырех аналитических
соотношений типа (6.43) — (6.46) не совсем удобно при
решении задач динамики спуска КА. Проведенные иссле¬
дования показали, что для рассматриваемых форм аппа¬
ратов аэродинамические характеристики с достаточной
степенью точности могут быть аппроксимированы следую¬
щими двумя аналитическими зависимостями:
Сх (а) - 0,2 + 2,3 sin2 (1,125 а + 5,625°), (6.47)
Су (а) = - 0,1 + 2,3 sin (1,125 а + 5,625°) х
(6.43)
(6.44)
Сх — Схо -1- Вх sin3 а,
Су = Ai sin2 a cos а.
(6.45)
(6.46)
xcos (1,125 а + 5,625°) (6.48)
для КА типа несущий корпус и
Сх (а) - 1,8 sin2 (а - 5°), (6.49)
Су (°0 = 1)3 sin (а — 5°) cos (а —- 5°) (6.50)
5 6.8] КЛ С БОЛЬШИМ АЭРОДИНАМИЧЕСКИМ КАЧЕСТВОМ
195
для космического самолета. Здесь а — угол атаки в гра¬
дусах.
Способ управления. Возможны три способа управле¬
ния КА планирующего типа при спуске в атмосфере:
— с помощью изменения угла крена у ~ var при по¬
лете с постоянным значением угла атаки а = аб;
— с помощью изменения угла атаки а = var при по¬
лете с постоянным значением угла крена;
— совместным из' енеыием угла крена и угла атаки.
Для КА скользящего типа был рассмотрен первый из
указанных способов управления и определены оптималь¬
ные законы управления углом крена при решении ряда
задач оптимизации траекторий, в том числе и задачи о ми¬
нимуме конечной скорости спуска. Найденные законы уп¬
равления остаются справедливыми и для планирующих
аппаратов типа несущий корпус или космический самолет.
Поэтому основное внимание будет уделено анализу опти¬
мальных траекторий спуска, на которых управление КА
осуществляется либо с помощью угла атаки, либо совмест¬
ным изменением углов кретта и атаки.
При анализе траекторий спуска КА, управляемых из¬
менением угла атаки, принимается, что величина угла
крена имеет постоянное значение уПост- Из опыта решения
баллистико-навигапионных задач для типичных аппара¬
тов, управляемых путем изменения угла атаки (например,
управление самолетом), а также из результатов решения
задачи о FK min для КА, управляемых изменением угла кре¬
на, можно установить, что постоянный угол крепа це¬
лесообразно принять равным нулю (уПОст = 0).
л нализ траекторий спуска КА с большим значением
яэго^инамического качества, управляемых только изме¬
нением угла крена, следует проводить в предположении
постоянства угла атаки (а^ = const). При этом выбор кон¬
кретного значения аб в каждом отдельном случае должен
осуществляться путем проведения специальных исследо¬
ваний.
При исследовании баллистико-навигационных проб¬
лем спуска КА, управляемых изменением угла крена,
в качестве основных проектных параметров рассматри¬
ваются^ "аэродинамическое качество КГ) и приведенная
нагрузка на лобовую поверхность Рх — тк\/(СXSM), отно¬
сительно которых делается предположение об их иосто-
7
196 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. G
янстве на траектории спуска. При управлении измене¬
нием угла атаки такое допущение невозможно и целесооб¬
разно в качестве проектно-баллистических характеристик
КА использовать максимальное аэродинамическое ка¬
чество Ктах и нагрузку на лобовую поверхность Рg
—
Так, для КА с несущим корпусом величина Ашах =
= 1,5, а для космического самолета КПГ()Х — 2,4.
Необходимо сделать следующее замечание. Для КА
скользящего типа и КА с несущим корпусом в качестве
характерной площади обычно берется площадь миделе-
вого сечения, а для КА самолетной формы — площадь
аппарата в плане (или площадь крыла). Эти параметры
наиболее полно отражают несущие свойства соответству¬
ющих форм КА. Для удобства исследований сделано ус¬
ловное предположение о равенстве площади миделевого
сечения для КА всех форм. Это следует иметь в виду при
рассмотрении КА самолетной формы (Атах ^ 2,4), для
которого отношение площади крыла к площади миделя
в рассматриваемом примере (см. рис. 6.15) равно 6,5.
Граничные условия и ограничения. Как и ранее, бу¬
дем предполагать, что КА осуществляет вход в атмосферу
Марса с заданными начальными условиями
t = to, V(t0)=--Vо, е (t{}) ^ 6Q, h (t0) — h0. (6.51)
В конце траектории спуска фазовые координаты в об¬
щем случае должны удовлетворять следующим условиям:
* tK, VK минимальна, h 0 (1К) свободно. (6.52)
Для выявления наибольших возможностей по аэроди¬
намическому торможению аппаратов планирующего типа
будем считать, что ограничения па величину аэродинами¬
ческого нагрева и перегрузку отсутствую г, а действует
лишь одно ограничение на фазовые координаты КА — по
высоте полета" КА (3.25). Будем, ташке предполагать*
юо углы крена и атаки могут изменяться в диапазонах
О < у.у; 180"'.
1?’, i si 'Ю. О. ' (Цгпу ■
(с.. г»:?)
(0.51)
^ 6.8] КА С БОЛЬШИМ АЭРОДИНАМИЧЕСКИМ КАЧЕСТВОМ
197
где 06min == — 5°, атчх = ^5° для КА с несущим корпусом;
amin = 5°, amax = 90° для космического самолета. Пере¬
ключение величин углов крепа и атаки с одного значения
на другое будем полагать мгновенным.
Формулировка задачи. Для КА, движение которого
описывается системой дифференциальных уравнений (3.20),
требуется определить такой закон управления измене¬
нием, угла атаки (или совместного изменения углов крена
и атаки), который обеспечивает минимум функционалу
j ук при выполнении условий (6.51), (6.52) и ограниче¬
ний (3.25), (6.53) и (6.54).
Минимизация конечной скорости спуска
Решение экстремальных задач для КА, управляемых
‘ изменением угла атаки, имеет ту особенность, что найден¬
ные оптимальные законы управления для какого-либо КА
с конкретными аэродинамическими характеристиками не
являются универсальными в том смысле, что они не могут
быть использованы для других КА, имеющих отличаю¬
щиеся аэродинамические характеристики. Именно поэто¬
му для каждого КА необходимо решать экстремальную
задачу заново. Учитывая это, рассмотрим отдельно задачи
об отыскании оптимального закона управления измене¬
нием угла атаки из условия min У,, для КА с несущим
корпусом (А"тах = 1,5) и для космического самолета
{Кт;х = 2,4).
а) Оптимальное управление конечной скоростью спуска
КА с несущим корпусом (А1Пах = 1,5).
Необходимые условия оптимальности. Составим га¬
мильтониан
тт I (IV . , d0 . , dh /£?г'сг\
11 = ^ -ЛГ + ИГ + ^ ИГ • (6-°5)
Учитывая (3.20), преобразуем выражение (6.55) к
виду
У пТ/2 X OF
Я ^ _ -ф! — сх — U’lg' sin 0 - ф2 — Су cos V —
ZmK\ -П1хл\
I Я COS 0 . . Vcn.sO , . т7 • П ,п
— ^-у г ^2-R— -г +«V SU1 0. (6.об)
198 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. О
Запишем уравнения сопряженных переменных при
V (t) < О
_ дН VCx(a)PSw
dt
dv
КА
СУ (“) р^м cos v COS
Ч?2 —
2т
КА
фх -
А
Ф-2-
Фз — sin 0ф3,
R + h
g COS 0
d\\>2 dll n ,
-JT = -^ = SC0S^h
d\pz
dQ
g sin 0
V sin 0 . Tr n .
„„. ih2 _ v cos 0ф3,
дН
Oh
CJa) V*Sy
£кл
Робе-^'ф! +
I v
°v («) cos v
2пг
KA
РоР^р,,Фа +
V cos 0
(R + hf
2д sin 0
(Л'-!-/?.)®1*''1 7(Л + Л)3
Необходимым условием минимума функционала V (tK)
является условие максимума функции II по управлению
[791. Учитывая (6.47) и (6.56), запишем необходимое ус¬
ловие экстремума в виде
^-=_2,3siii(2,25а + 11,25°).1,125 |^.фх +
РVS" cos у
+ 2,59 cos (2,25а -|- 11,25°) “ к ф2 = 0.
2ц cos 0
Ч-2-
(6.57)
Отсюда следует
КА
а =
5,625° + arctg ( -
+ 1
• 0,889.
(6.58)
Определим закон управления углом атаки при полете на
постоянной высоте. Учитывая (6.19), получим
Г l,74/?iT-^
11 “
^ = 0,44 — 11,25'
arcsm
j ?VSM ~
х (4т- -jX-r-) Ф 0.087]) .
V к и -i- /я /
(6.59)
§ 6.8] КА С БОЛЬШИМ АЭРОДИНАМИЧЕСКИМ КАЧЕСТВОМ
199
Уравнения сопряженных переменных при движении
во изовысоте имеют вид
где
#?'
1-огр
dt
С
dty0/р
dt
л =
dt
dll
да
дН I А дф
— dV 'r dV ’
— - _ 1'IL _i_ л
аб i' ае ’
_ дН , А дф
dh ^ дк ’
Эф
да
d*h
dv
^ dt2 dt2
(6.60)
С учетом соотношений
v = /гдоп — h, v = h = V sin (
определим
ф != v = —
"*ЧКА
cvPV2Sm cos v
—о sin 0 — g sin2 0 +
2nir ° 1
+ •
2т
КА
cos 0 — g cos2 0
V2
Я + /г
COS2 0,
(6.61)
откуда
Эф
IV = '
Эф
~Ж ~~ '
Эф
“э/Г
vcx?sK
mKA
• sin0 +
2m-
COS (
vcy?SM cos у
mKA
CyPV2SM cos У
К A
2m
COS (
Sill (
2mKA” Shl 0poe'PhP + TF+ A)'»
К A
2ц,
Эф
Эа
ЭЯ
Эа
pW
2m
cos V
2F
Я + h
V*
R + h
cos'
sin 20,
F2COS2 0
KA
dCx pFV
sin0-^- + •£ ^cosf
2mKA COS0Poe~phP (Д + Л)г ’
Эа
2m
Эа 2m
к A
■4>i +
dCn,
KA
P™*
dC
у
да
да 2m
К A
■фа-
200 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. П
Учитывая, что на изовысотном участке 0 = 0
_5ф_ _ 'VCypSм cos у 2V
oV “ тКА R + h ’
5Ф _
50 ~~ 2тКА ’
_ С/^»со8У Btlfi , 2р
d/i ~ 2 тк № I (« + /1)з
V2
(« + Л)2
5Ф _ Р^и 3G
V
да 2/?гк ^ 5а ’
\ - / _Ё£_ — _ ЭС*
~ да I да — dCy F ’
л cos V 5CX >ь
A 3F - 2ткд дСу ^
_ ^ + 2
« + h дСу Y 1 тк\ «-j~/i
л_3ф. = ^* lb C»P^M <?>.?„
50 dCy 2mK v 2//ika ^2’
5<n ^ r cos 7 dC,
л4т - г.,;А “
С.ДЛУ., cos 7 2li
- -JS4rL **** - wfw *7 * +
2p x|>, V- дСх V
; (II hf F (It h)~ OCy^1 (U + lifV*
Учитывая (6.62) и (6.63), получим при v = 0
<rp VCxPSa >ь0гр CyPSM cosY>b0pp
Л - ,»|{д —
_ ^ГР __ X th^P _ ГГ»рЛ” C0S Y дСх ,horp _
Н -r h V* 2/«ка дСу
W t‘*V 6>^мС0зу 2 огр
л + л асу^ т ^ т-ТГ+Г^ ’
получим
г (6-62)
[ (6.63)
f (6.64)
s 6 g] КА С БОЛЬШИМ АЭРОДИНАМИЧЕСКИМ КАЧЕСТВОМ 201
rfCP
~ЯГ
dt
^ dCu
CJ'2S.
tfrp
2 m
К A
CoVS^
X ■ M
, Ol'p
2/?г
К A
f'o,6e-p4iH’P -\~
CVS„ cos v „
• Poe-P'42 1 +
F
2m
KA
(Д + /г)2
zV*
orp
2jx
F(fl + /Ц3
c,ySMcos v
I U
l|.V
C,y2S cos V
2m,
2mKA
+
2|л
KA
p0e‘P,lP^2rp —
-ф?гр
-Po?
2u
dCv
,°rp_
TL
(Д /г)3 F
dCx
(R-\-hf dCy
F2 dCx^„
фг +
(R + h)2 ac
F
(Д + Л)*
(6.64)
В момент выхода на ограничение сопряженные перемен¬
ные скачком меняют свою величину в соответствии с
(6.22).
Анализ уравнений (6.60) — (6.64) показывает, что вы¬
ведение КА па режим горизонтального полета может про¬
ходить по различным траекториям без нарушения за¬
данной цели управления, т. е. при минимальном значении
конечной скорости спуска. Следовательно, как и при упра¬
влении посредством изменения угла крена, имеет место
свойство неединственности оптимальных траекторий.
В этом случае решение задачи из условия min VK доста¬
точно проводить лишь на участке движения КА внутри
допустимой области фазовых координат после схода с ог¬
раничения. Тогда граничные условия для левого конца
траектории запишутся в виде
V (£j) свободно, 0 (£]) — 0, h (ti) — h;lоп, ----- 0, (6.65)
а для правого в виде
h(tK) = hK, V (*к) и
4ч (1к)
0(£к) свободны, (6.66)
- 1, ф2 (tu) — 0, ф3 (tu) свободно. (6.67)
202 ОПТИМАЛЬНОЕ. УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. G
Условия (6.65)—(6.67) определяют совместно с (3.20),
(6.57) двухпараметрическую двухточечную краевую задачу.
Численные результаты. Существенное упрощение по¬
ставленной задачи, связанное с учетом свойства неедин¬
ственности оптимальных траекторий, приводит к тому,
что краевая задача быстро сходится даже при использова¬
нии обычного метода последовательного перебора. Для
t,G9K
Рис. 6.1G. Параметры оптимальной траектории спуска при Управлении по¬
средством изменения угла атаки (у = 0).
примера на рис. 6.16—6.18 представлены зависимости из¬
менения фазовых координат, сопряженных переменных и
угла атаки от времени спуска при оптимальном управле¬
нии для КА с различными значениями нагрузки на ло
бовую поверхность Р$ = 350 кг! ж2, 800 кг!ж? и 1200 кг!ж2
на участке схода с ограничения. Видно, что во всех слу¬
чаях характер изменения угла атаки от времени спуска
аналогичен, а именно угол а монотонно возрастает после
схода с ограничения и достигает максимума в конце тра¬
ектории спуска. При этом оказывается, что изменение
угла атаки происходит в ограниченном диапазоне: от ami„,
соответствующего Су тах, до а, отвечающего условию К = 0
(независимо от величины Ps). В частности, для КА Vне¬
сущим корпусом (Ктлх = 1,5) управление углом атаки
на оптимальных траекториях начинается с а ^ 35° и за¬
канчивается при а ^ 75°.
§ 6.8] НА С БОЛЬШИМ АЭРОДИНАМИЧЕСКИМ КАЧЕСТВОМ
203
б) Оптимальное управление конечной скоростью спус¬
ка космического самолета (Ктах = 2,4). Приведем резуль¬
таты решения экстремальной задачи определения оптималь¬
ного закона управления посредством изменения угла ата¬
ки для космического самолета.
Уравнения оптимального движения были получены
аналогично тому, как это делалось для КА с несущим кор¬
пусом.
t.DBK
Тис.£.6.17. Парамзтры оптимальной траектории спуска при равлеи.хи по¬
средством изменения угла атаки {у = 0).
Оптимальный закон управления углом атаки при дви-
жении|КА внутри допустимой области фазовых координат
имеет вид
а = 5° + arctg I - 1,39-^ + ^1,9 + 1 j , (6.68)
а на участке движения по ограничению
аогР = 5° + 0,5 arcsin
3 т
КА
R + h,
)]• (6.69)
Как и в предыдущем случае, оптимальные траектории, ре¬
ализующие min Ук для аппарата с величиной аэродина¬
мического качества Кmax = 2,4, обладают свойством не¬
единственности. Поэтому для получения численных
204 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. b
значений минимальной конечной скорости достаточно
решить краевую задачу на участке схода траектории КА
после ограничения.
Численные результаты решения краевой задачи пока¬
зали, что характер изменения угла атаки при оптимальном
управлении космическим самолетом (Атах = 2,4) анало¬
гичен рассмотренному случаю для КА с несущим корпу¬
сом (Атах = 1,5). А именно, с увеличением времени полета
К К ААп-А А А=1200 кг/м2
t,CBK
Рис. 6.18. Параметры оптимальной траектории спуска при управлении по¬
средством изменения угла атаки (у = 0).
после схода с ограничения происходит возрастание угла
атаки, причем ашах = 90° при t = tK. Изменение а начи¬
нается с величины а = amiQ ж 50° и соответствует Су тах
(см. рис. 6.15).
Итак, результаты решения поставленной экстремаль¬
ной задачи для КА двух типов (несущий корпус и косми¬
ческий самолет) позволяют выявить структуру оптималь¬
ных законов управления углом атаки. При этом ока¬
залось, что, в отличие от КА, управляемых посредством
изменения угла крена, знание структуры оптимального
закона управления изменением угла атаки а не столь суще¬
ственно облегчает процедуру нахождения численных зна¬
чений min VK и в каждом конкретном случае (имеются в
виду соответствующие значения нагрузки на лобовую по¬
верхность Ps) необходимо решать свою краевую задачу.
(* 8] КА С БОЛЬШИМ АЭРОДИНАМИЧЕСКИМ КАЧЕСТВОМ 203
Очевидно, при проведении широких проектно-баллистичес¬
ких исследований, требующих анализа большого количес¬
тва оптимальных траекторий, могут возникнуть трудности,
связанные с большими затратами машинного времени.
В этом случае представляется целесообразным проведе¬
ние исследований с целью отыскания более простых зако¬
нов управления КА, позволяющих, с одной стороны, по¬
лучить результаты, близкие к оптимальным, а с другой —
существенно уменьшить время расчета траекторий спуска
VK,M/C8K
У(2\м/сек
1нс. 6.19. Конечная скорость при квазиоптимальном релейном управлении
посредством изменения угла атаки (Кшах - 1,5; Pg = 350 кг/м1).
На рис. 6.19 представлены некоторые результаты исследо¬
вания квазиоптималытых траекторий спуска при управле¬
нии посредством изменения угла атаки. Исследования
проводились в классе релейных программ управления из¬
менением угла атаки. При этом оказалось, что наилучшее
приближение к оптимальной программе управления неза¬
висимо от величины Ps дает программа одноразового
переключения с на а2 (максимальная погрешность в
206 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ.
величине конечной скорости составляет ДУК ; 5 -ч-
-4- 7 м/сек). Так, для КА с несущим корпусом = 50',
а2 = 75°, а для космического самолета а1 ■ Go", а2 -- 90".
Двухкаиальное управление. При управлении КА пу¬
тем совместного изменения углов крена и атаки задача об
отыскании оптимальной траектории из условия min Vк
решалась с использованием необходимых условий прин¬
ципа максимума. Проведенные исследования показали,
что при таком способе управления выход на ограничение
возможен не единственным образом и поэтому минимум ко¬
нечной скорости определяется только участком движения
внутри допустимой области фазовых координат после
схода с ограничения.
Уравнения для сопряженных переменных и гамильто¬
ниан остаются без изменений и имеют вид (6.56), (6.57),
(6.62). Оптимальный закон управления посредством изме¬
нения а описывается зависимостями (6.58) для аппарата
с Атах = 1,5 и (6.68) для аппарата с Ашах = 2,4, а закон
управления изменением угла крена имеет вид
cosy = sing^2- (6.70)
Численное решение краевой задачи показало следую¬
щее: если оптимальная траектория содержит участок
схода с ограничения, то функция ф2 (0 на этом участке ос¬
тается все время положительной независимо от типа и
характеристик КА, что соответствует режиму спуске
с углом крена у — 0. В этом случае оптимальное двух¬
канальное управление а — var, у var из условия
min VK полностью совпадает с рассмотренным выше управ¬
лением при использовании одного изменяющегося пара¬
метра — угла атаки, а КА во все время полета должен
сохранять постоянный угол крена у — 0.
Минимизация времени спуска
и максимальной перегрузки
на траекториях минимальной
конечно и скорости
Для двух рассматриваемых типов КА, обладающих
большим значением аэродинамического качества, прове¬
дем исследование, аналогичное приведенному в § 6.5 для
КА скользящего типа. Учитывая свойство неединствен-
^ 6.8] I'A С БОЛЬШИМ АЭРОДИНАМИЧЕСКИМ КАЧЕСТВОМ 207
пости оптимальных траекторий, рассмотрим задачи о мас¬
се тепловой защиты КА и о максимальной перегрузке на
траекториях min Уь..
Первая из этих задач особенно важна для КА с боль¬
шим аэродинамическим качеством, так как при их исполь¬
зовании значительно возрастает длительность полета в ат¬
мосфере и поэтому аэродинамический нагрев КА может
оказаться существенным ограничивающим фактором.
Как известно [3], полное и достаточно точное исследо¬
вание тепловых режимов по всей поверхности обшивки
КА является весьма сложной задачей. Поэтому обычно
при задании ограничений на траекторию спуска по аэро
динамическому нагреву и выявлении требований к систе¬
мам теплозащиты используются приближенные соотно¬
шения, с помощью которых оценивается интенсивность
теплового нагрева для некоторых характерных участков
поверхности аппарата. Но даже приближенные соотноше¬
ния имеют достаточно громоздкий вид и неудобны для
анализа оптимальных траекторий спуска. Вместе с тем
на первом этапе исследований нет необходимости в коли¬
чественной оценке величины аэродинамического нагрева
КА и достаточно использовать наиболее простой крите¬
рий — время спуска КА в атмосфере.
Учитывая свойство неединственности оптимальных тра¬
екторий, задачу дополнительной оптимизации траекто¬
рий min Ук будем рассматривать только на участке вы¬
хода на ограничение, а участок схода с ограничения бу¬
дем считать неизменным и обеспечивающим выполнение
критерия min Ук.
Управление эффективным качеством. Оптимальная тра¬
ектория, минимизирующая время спуска при выполнении
условия min Уь., для КА, управляемых изменением угла
крена (см. § 6.5), состоит из трех участков:
— участка выхода на ограничение, на котором управ¬
ление осуществляется путем одноразового переключения
эффективного качества с минимального значения на мак¬
симальное (/у:)ф — К С), ! Кб);
— участка движения по ограничению, на котором уп¬
равление осуществляется однозначно в соответствии
с (6.19);
— участка схода с ограничения, на котором полет осу¬
ществляется с постоянным значением Клт,
208 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. (5
При исследовании траекторий, обеспечивающих мини¬
мальное время спуска, будем предполагать, что баланси¬
ровка КА может осуществляться па любом угле атаки в диа¬
пазоне . amin а б ^ ctmax. Время полета КА на каждом
из участков, а соответственно и суммарное время спуска
будет существенно зависеть от величины аб. Учитывая
это, проведем анализ каждого из участков оптимальной
траектории спуска, обозначив при этом At(i\ 1}^ время и
дальность полета на участке выхода па ограничение,
Д/<2), AfJ2) — время и дальность полета па изовысотпом
участке, At(3), AL'3> — время и дальность полета на участ¬
ке схода с ограничения, t'2 = A1п) -j- Ati2) + А/'3), L^L) —
суммарное время и дальность полета КА и tn — время пе¬
реключения.
Таблица 6.1
Характерные параметры оптимальных траекторий спуска
из условия min Д£(В (КА с несущим корпусом)
&
с\з
гГ
к
!И
ct
о
<
а
О
О
Jf
>
§
С-1-
о
о
сэ
<
у(’2), км'сеп
о
сек
со
ч
с: ^
о
k - 3
53
о
С-Г
-0
10
58
10
70
4,6
—601
201
1 ,4
1 12
1 66
02
0,04
437
—487
20
57,5
14
68
4
—714
114
1 ,0
108
151
84
0,71
333
—522
30
57,0
16,4
68
3,2
—720
00
0,0
82
137
70
0,52
271
-568
40
57,6
18,5
70
2,5
-725
41
1.0
55
130
67
0,49
241
—003
50
58
17,5
80
1,8
-711
14
1,25
15
120
72
0,34
223
-624
В табл. 6.1 приведены некоторые численные результа¬
ты исследования оптимальных траекторий спуска из ус¬
ловия min А^1) для КА с несущим корпусом. Рассматри¬
валась балансировка КА на различных углах атаки а(->.
Из представленных в таблице данных видно, что мини¬
мальное время спуска КА на участке выхода на ограниче¬
ние может составлять 68 80 сек. Как и следовало ожи¬
дать, время спуска А^^ существенно зависит от балан¬
сировочного угла атаки. При увеличении осб происходит
сначала убывание времени Atil) и при некотором аб = а-
функция Д^1) (ас) достигает минимума. Дальнейшее уве-
§ 6.8] КЛ С БОЛЬШИМ АЭРОДИНАМИЧЕСКИМ КАЧЕСТВОМ
209
личеиие аз приводит к непрерывному возрастанию вре¬
мени Д£(1). Так, увеличение а-, с 5 до аз = 25° приводит
к уменьшению времени At'1- с 71 до 68 сек, а при увеличе¬
нии аз с 25 до 60° время At(1) увеличивается с 68 до 99 сек.
Время движения по ограничению (А/(2)) также сущест¬
венно зависит от балансировочного угла атаки, причем
меньшим углам атаки соответствует большая длитель¬
ность полета КА на изовысоте. Например, для рассмат¬
риваемого случая (см. табл. 6.1) при а г, = 50° время дви¬
жения по ограничению составляет Д= 14 сек, а при
аз = Ю° величина Д№ возрастает до 201 сек.
В табл. 6.1 приведены также данные по 3-му участку
оптимальной траектории. Зависимость времени спуска на
третьем участке (Д£(3)) от угла атаки аз аналогична зави¬
симости Д^2) (аз) для случая движения по ограничению,
а именно, уменьшение аз приво¬
дит к возрастанию величины
Дt3). Например, при уменьше¬
нии аз с 50 до 10° величина Д.£3)
возрастает со 129 до 166 сек.
Итак, численный анализ всех
участков оптимальной траекто¬
рии показывает, что величина
балансировочного угла атаки
оказывает различное влияние на
время полета КА на каждом
участке. Чтобы иметь возмож¬
ность оценить эффективность КА
с точки зрения дополнительного
улучшения траекторий мини¬
мальной конечной скорости спу¬
ска по критерию времени, необ¬
ходимо рассматривать зависи¬
мость суммарного времени
от балансировочного угла ата¬
ки. Подобные зависимости при¬
ведены па рис. 6.20 для двух
типов рассматриваемых КА. Из их рассмотрения сле¬
дует, что с увеличением аз суммарное время спуска умень¬
шается, причем для КА с несущим корпусом величина
£,nj., при любом значении аз примерно па 150 сек меньше,
чем для космического самолета,!
t^cBK Vq~6 нм/сбк
Гис. 6.20. Минимальное и мак¬
симальное суммарные времена
спуска па траекториях мини¬
мальной конечной скорости
(Р8 = 350 кг/м2).
210 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. (5
Для сравнения на рис. 6.20 приведены зависимости мак¬
симального суммарного времени полета от угла атаки на
траекториях min VK. Отличие этих траекторий от рассмот¬
ренных выше заключается в том, что на участке выхода
па ограничение управление КА осуществляется путем
двухразового переключения при этом выход на ог¬
раничение происходит при скорости F(1) = V(2\ т. е. уча¬
сток движения по ограничению отсутствует. Наибольший
возможный выигрыш во времени спуска достигается при
полете на малых значениях угла атаки. Так, для КА
с несущим корпусом величина A= fmax — £min состав¬
ляет примерно 85 сек при аб = 60° и ~510 сек при аб = 10°,
а для космического самолета Д^ 500 сек при аС) = 60°
и 1120 сек при as = 20° (см. рис. 6.20).
Рассмотрим теперь задачу минимизации максимальной
перегрузки на траекториях min Vl{. Минимальное значе¬
ние лх max реализуется при использовании программы двух¬
разового переключения КЭф на участке выведения КА на
режим горизонтального поле¬
та (см. § 6.5). Некоторые ре¬
зультаты решения этой зада¬
чи для КА с несущим корпу¬
сом и космического самолета
представлены на рис. 6.21.
Оказалось, что минимальное
значе ттие* п х max существенно
зависит от балансировочного
угла атаки, причем для обо¬
их типов КА увеличение аб
приводит к возрастанию
^ятяу.
Можно также отметить,
что при использовании КА
с большей величиной Кт^: на
траектории спуска реализу¬
ются меньшие значения .
В частности, при ап = 60°
для КА с несущим корпусом минимальное значение ?гг тпх
составляет 10,2, а для космического самолета 7,5. Для
сравнения на рис. 6.21 представлены зависимости наиболь¬
шего значения пхтах от балансировочного угла атаки.
]ЗиДПО, ЧТО раЗНИЦа Д/2^ 1ПаХ — (jlx in.ax)max iP'x max)miп МИНИ-
^xmx
Рис. 6.21. Минимальное и макси¬
мальное значении максимально1”!
перегрузки на траекториях мини¬
мальной конечной скорости Р$ ==
= 350 кг/м2, У о — 6 7 ;м/сек, li~ —
= —79 км).
С (5.8j IU С Б0ЛЫШ1М Л О РОДИИ АМН ЧЕСК11М КАЧЕСТВОМ
малыш при наибольших и наименьших значениях угла
атаки и максимальна при углах атаки, соответствующих
шах Си (см. рис. 0.15). Для КА с несущим корпусом Алх :11ах
составляет о,75; 12,2; 5,5 при а3 -- 10", 40и, 00° соот¬
ветственно, а для космического самолета имеем
ДМя.пах ~ 1В,5; 8 при а; — 25°, 00°, 80" соответ¬
ственно.
Таким образом, для двух типов КА с одинаковой ве¬
личиной 1\б при одних и тех же условиях входа (К0 и /г..)
в атмосферу исследована возможность улучшения траекто¬
рий минимальной конечной скорости с точки зрения удов¬
летворения дополнительным критериям минимизации вре¬
мени спуска и максимальной перегрузки при управлении
посредством изменения угла крепа. Многочисленные рас¬
четы показали, что качественные выводы, характерные
для рассматриваемого случая, остаются в силе и при дру¬
гих значениях 7Д, VQ и 1гл.
Управление с помощью угла атаки. Решение экстре¬
мальной задачи для КА, управляемых посредством изме¬
нения угла атаки, па участке выхода на ограничение по¬
казало (табл. 6.2), что эффект улучшения траекторий ми¬
нимальной конечной скорости с точки зрения дополни¬
тельной минимизации максимальной перегрузки меньше,
чем при управлении с помощью изменения угла крена.
Так, для рассматриваемых условий входа в атмосферу и
нагрузки на лобовую поверхность при одинаковых значе¬
ниях РК11нЛ минимальная величина пх плх составляет 7,2
для КА с несущим корпусом и 4,9 для космического само¬
лета. Видно, что по сравнению с управлением с помощью
изменения угла крена минимальная величина пх шах воз¬
росла на 3,8 для КА с несущим корпусом и па 1,2 для кос¬
мического самолета. То же самое можно сказать и в отно¬
шении другого дополнительного критерия — времени спу¬
ска. А именно, при использовании для управления угла
атаки величина Спш незначительно возрастает по сравнению
с рассмотренным выше способом управления путем изме¬
нения угла крена. Так, для КА с несущим корпусом вели¬
чина tmuv — 229 сек, а для космического самолета QAi —
= 257 сек. Сравнивая эти цифры с полученными ранее
данными для КА, управляемых изменением угла крена,
легко видеть, что величина Сши практически не изменилась
212 ОПТИМАЛЬНОЕ УНТ А БЛЕ 11И Е КОНЕЧНОЙ СКОГОСТЫО 1ГЛ. ii
Т а б л и ц а 6.2
Оценка эффективности различных способов управления КА
Мипимиппр уем1:1 ii
Тип КА
Способ управления
фушлрлопал iia
участке исхода
КА па огранп-
чение
L^. cn:
,}x max
-г
li
.р
i!
I11
22 5
17,5
у = var, а6 -- 10°
а - - var, у - 0
Пх ша х;
1207
3,9
КА с
несущим
i ^
229
13,4
корпу¬
сом
а = var, у = 0
11 х шах
у 292
7,2
у = var, а = var
224.
17,8
у ^ var, а = var
пх max
1207
3,9
у var, = 70°
r:
239
16
у = var, я0 = 20°
nx max
1296
3,7
Косми¬
a =: var, у = 0
257
12,1
ческий
самолет
a=var, у —0
>l'x max
326
4,9
у — \ ar, а — var
t"
227
•16,7
1!
sc
li
SLx max
1296
3,7
для КА с несущим корпусом (увеличение tnlin соста¬
вило 2 сек) и возросла на 18 сек для космического самолета.
Минимизация времени спуска и максимальной пере¬
грузки для КА, управляемых изменением углов^крена и
атаки. Использование совместного управления изменени¬
ем углов крепа и атаки позволяет существенно умень¬
шить время спуска и максимальную перегрузку на траек¬
ториях минимальной конечной скорости по сравнению
с любым из рассмотренных выше способов одиопараметри-
ческого управления КА. Приведенные в табл. 6.2 данные
позволяют оценить эффективность использования двух-
каналыюго управления по сравнению с одноканальным
с точки зрения получения минимальных значений t1] и
Пх пах. При двухканалыюм управлении величина при¬
близительно на 15 -л- 20% меньше, чем при управлении с
помощью изменения угла крена или только изменения угла
атаки для КА с несущим корпусом и примерно па
ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА
213
18-.-27% —для космического самолета. Величина мак¬
симальной перегрузки уменьшается па 27—30% по срав¬
нению с одпокапальпым способом управления для КА с
несущим корпусом и па 24—28% — для космического,
самолета.
§ 6.9. ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА КА
НА ТРАЕКТОРИЯХ МИНИМАЛЬНОЙ
КОНЕЧНОЙ СКОРОСТИ СПУСКА
Одним из достоинств КА с большим значением аэроди¬
намического качества являются достаточно широкие ма¬
невренные возможности, что, в частности, позволяет ста¬
вить задачу высокоточной посадки в заданный район.
Ниже рассмотрим задачу о максимизации полной зоны
маневра (в продольном и боковом направлениях) и полу¬
чим численные результаты для КА рассматриваемых ти¬
пов. Специфические условия спуска в атмосфере Марса
не позволяют в полной мере воспользоваться многочис¬
ленными результатами (см., например, [98]) для решения
аналогичной задачи для спуска на поверхность Земли.
Необходимо учесть особенности, накладываемые условия¬
ми мягкой посадки и ограничениями на траектории спус¬
ка. Как и ранее, будем предполагать, что в конце участка
аэродинамического торможения траектория спуска должна
удовлетворять условию min FK, причем конечный угол
0К наклона траектории не ограничен и существует ограни¬
чение на минимально допустимую высоту полета КА.
/(ля оценки предельных маневренных возможностей
КА используем критерии максимума продольной и боковой
дальности, которые реализуются при выполнении ус¬
ловия min Т%. В этом случае для построения достижимой
области (зоны маневра) при заданных начальных условиях
входа КА в атмосферу достаточно максимизировать боко-.
вую дальность спуска при различных фиксированных зна¬
чениях продольной дальности от = L-m[n до L- ==
= inmix- Геометрическое место точек посадки полученных
траекторий определит па поверхности планеты границу
искомой области.
Рассмотрим три основные экстремальные задачи на
траекториях F,. 1Пш с критериями оптимальности: min Ln,
max LK и max L6 при LK =■- const с учетом исходных пред¬
посылок (см. § 6.8).
214 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОГОСТЬЮ [ГЛ. 6
Оптимизация продольной дальности спуска
Управление эффективным качеством. Оптимальная
программа управления, реализующая минимум (или мак¬
симум) продольной дальности спуска на траекториях ми¬
нимальной конечной скорости
для КА, управляемых по
углу крена, была опреде¬
лена выше в § 6.5. Исполь¬
зуя эти программы, про¬
ведем анализ маневренных
возможностей р ассматри -
ваемых КА.
На рис. 6.22 представ¬
лены зависимости мини¬
мальной и максимальной
дальности спуска от ба¬
лансировочного угла атаки
для КА обоих типов при,*
входе их в атмосферу Мар¬
са со скоростью У 0 =
= 6 км!сек, hn — — 79 км
и величине нагрузки на
лобовую поверхность Ps =
= 350 кг/м2. Из рассмот¬
рения представленных за¬
висимостей видно, что для
КА обоих типов уменьше¬
ние балансировочного угла
атаки приводит к возраста¬
нию как минимальной, так
и максимальной дальностей спуска. Так, для КА с несу¬
щим корпусом изменение балансировочного угла атаки от
60 до 10° J приводит к возрастанию L~ min от —640 до
—490 км, а Ьл max — ОТ —540до 1450 км. Для космического
самолета при изменении otg от 70 до 20° величина L^min
увеличивается с —750 до —650 км, a L- max — с —495 до
1680 км.
В целом можно отметить, что интенсивность изменения
минимальной дальности спуска при увеличении угла ата¬
ки меньше, чем для максимальной дальности. Это приво¬
дит к тому, что наибольшими маневренными возможностя¬
ми в продольном направлении КА обоих типов обладают
го
оо
60 ос $, град
1 ис. U.22. Минимальная и максималь¬
ная дальности спуска на траекториях
минимальной конечной скорости спуска
(Р<3 = 25U кг/ai2, У0 = 0 пм/сек, —
= —79 7;м).
ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА
215
при малых углах атаки (рис. 6.23). Например, для КА
типа несущий корпус при рассматриваемых выше услови¬
ях входа в атмосферу величина
А А- ~ J-j-r. max L-x min
составляет 100 км при — 60° и 1940 км при ао = 10°,
а для космического самолета
ДА- = 265 км при осб — 70° ^Ln=LnnwjT Lmm^M
и 2330 км при ад = 20°.
Отметим, что оценка сравни¬
тельной эффективности способов
управления КА по млтевреттным
возможпостям рассматривается
при одинаковых исходных пред¬
посылках на величину конеч¬
ной скорости. Принимается, что
величина конечной скорости
должна быть наименьшей для
данного типа КА. В этом слу¬
чае для КА, управляемых изме¬
нением угла крепа, необходимо
рассматривать величину ДL-,-
соответствующую такому значе¬
нию балансировочного угла
атаки осп, при полете с которым
величина конечной скорости на¬
именьшая. Как было показано
в § 6.8, для КА с несущим кор¬
пусом осб = 50°, а для космиче¬
ского самолета а$ =70°. Из
рис. 6.22 и 6.23 видно, что зона
ДА^ маневра КА в продольном
направлении составляет для этих значений 260 км в слу¬
чае КА с несущим корпусом и 255 км в случае космиче¬
ского самолета. Именно на такие значенияинужно ориен¬
тироваться при сравнении указанного способа управле¬
ния КА с любым другим.
Управление с помощью изменения угла атаки. Прежде
всего рассмотрим задачу максимизации продольной даль¬
ности для К А. с несущим корпусом.
Используя необходимые условия оптимальности [4],
получим оптимальный закон управления углом атаки
Риз. 6.23. Диапазон продольном
м шевренности на траекториях
минимальной конечной скоро¬
сти (PS = 350 кг/м2, Vo =
= fi км.'сек. /i_ = —79 км).
216 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
в виде
а = 0,889
— 5,625° arctg —
Пт
I I
V
Ha участке движения по ограничению управление оп¬
ределяется однозначно, в соответствии с (6.59).
Некоторые результаты решения задачи представлены
на рис. 6.24, где показаны зависимости фазовых коорди¬
нат V, 0, h, L- и сопряженных переменных \|з от времени
Рис. 6.24. Параметры траектории максимальной дальности для КА с несущим
корпусом при оптимальном управлении изменением угла атаки.
спуска при оптимальном управлении на траектории мак¬
симальной дальности для КА с несущим корпусом. Нагруз¬
ка на лобовую поверхность КА принималась равной
ps = 350 кг/м2, а условия входа в атмосферу У0 = 6 км/сек
и = — 79 км.
Интересно сравнить величину максимальной дально¬
сти, полученной при управлении с помощью изменения
угла атаки, с величиной L- шах, которая реализуется при
управлении посредством изменения угла крена. Оказы¬
ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА
21?
вается, что при одинаковых исходных предпосылках
первый из указанных способов является более эффек¬
тивным.
Для определения зоны маневра по продольной дально¬
сти перейдем к задаче минимизации L-.
В качестве примера на рис. 6.25 приведены зависимо¬
сти фазовых координат V, 0, /г, L-, и сопряженных пере¬
менных Ф; от времени спуска при оптимальном управлении
Рис. G.25. Параметры траектории минимальной конечной скорости спуска
для КА с несущим корпусом при оптимальном управлении изменением угла
атаки из условия min ь-.
из условия min L- на траекториях минимальной конеч¬
ной скорости (F0 = 6 км/сек, hn =—95 км, Ps =350 кг/м2).
Сравнивая полученное значение min ЬГ, с резуль¬
татами решения аналогичной задачи при управлении по¬
средством изменения угла крена можно отметить, что
218 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
при одинаковых исходных предпосылках некоторое
преимущество имеет способ управления путем изменения
угла крепа. А именно, при управлении КА путем из¬
менения угла атаки величина продольной дальности сос¬
тавляет L-„а,! = —938 км, что па 40 км больше, чем
для случая управления КА с помощью изменения угла
крепа.
Сопоставляя результаты решения экстремальной за¬
дачи о максимизации продольной зоны маневра при ис¬
пользовании двух различных способов управления —
посредством изменения угла крена или угла атаки, —
легко видеть, что маневренные возможности космическо¬
го аппарата в продольном направлении во втором случае
шире.
В табл. 6.3 приведены результаты исследований неко¬
торых квазиоптимальных алгоритмов управления углом
атаки (Си = 6 км/сек, h- = —79 км, 1\ — 350 кг/ж2).
Исследования велись с целью отыскания простых
релейных законов управления по а, обеспечивающих ре¬
зультаты, близкие к оптимальным для критериев min Lr.
и птах Ьл при сохранении условия min FK. Участок траек¬
тории спуска после схода с ограничения предполагался
неизменным и совпадающим с траекторией минимальной
конечной скорости. Из рассмотрения приведенных мате¬
риалов видно, что результаты, наиболее близкие к опти¬
мальным (разница не превышает 40 -е- 45 км) для крите¬
рия шах Ьл, дает программа двухразового переключения
по а (а1? а2, аД, а для критерия min — одноразового
переключения (ах, а2). При этом значения аг и а2 соответ-
ствуют экстремальным точкам на зависимостях аэродина¬
мических коэффициентов от угла атаки. А именно, в пер¬
вом случае соответствует максимальному значению аэро¬
динамического качества, а а2 — максимальному значению
коэффициента лобового сопротивления. Во втором случае
соответствует Сяшах, а а2 — Сутах.
Рассмотрим экстремальную задачу об отыскании опти¬
мального управления углом атаки космического самолета
по критерию птах L- на траекториях min FK.
Методика исследований полностью аналогична рас¬
смотренной выше и отличается при записи условий опти¬
мальности только из-за различного представления аэро¬
динамических характеристик КА.
ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА
219
Результаты решения задачи показывают, что способ
управления космическим самолетом путем изменения угла
атаки оказывается, как и для КА с несущим корпусом,
Таблица 6.3
Параметры траектории при релейном изменении угла атаки
Программа
управления:
изменение а
Критерий
оптималь¬
ности
/0),
сек
nx max
l(D,
KM
Примечание'
35°-^ 75°—> 35°
max L_
129
6,5
722
n p
у max xjnax1
—max
15°-*75°->15°
max Ln
174
7,2
815
^ max ““* Ox max ~*
~* ^max *
5°-> 75°-^ 5°
max L_
153
12,4
796
c . С -»
x min .x max
r
x min
о
Ю
СО
t
о
О
1>-
min L„
109
12,1
—654
Ox max-* ^y max
0
о
1
сл
min Lr
108
12,1 .
—653
С К
x max max
70°—> 10°
min L_
108
12,1
—619
С ' Г
^'x max ' x min
70°—» 5°
min L_
108
12,1
—642
С —* С
x max x min
*<1
0
о
1
Сл
О
о
min L_
111
12,1.
—652
Ov max-* Oxi
75°—>35°
min Lr
90
13,4
—683
Ox max ^y max
более эффективным но сравнению с ранее рассмотренным
способом управления КА путем изменения угла крена
с точки зрения получения max L- при одинаковых зна¬
чениях min V]{. Так, для КА с Ps = 350 кг/м2 при V0 =
= 6 км/сек Ji~—— 79 км в случае управления посредством
изменения угла крена величина L- max =—495 км, а при
управлении посредством изменения угла атаки L- тах =
= 2350 км, т. е. увеличивается нац2845*кж.
Обратимся теперь к з-даче об отыскании оптимального
управления углом атаки космического?самолета из усло¬
вия min L- на траекториях минимальной конечной ско¬
рости спуска. Из необходимых условий!оптимальности
следует, что в этом случае уравнения оптимального дви¬
жения имеют такой же ви;ц как и для задачи о максимива-
220 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. G
ции продольной дальности спуска на траекториях min V1{.
Некоторые результаты решения краевой задачи для кри¬
терия min L- представлены на рис. 6.26, где показаны за¬
висимости фазовых координат V, 0, h, LT, и сопряженных
Рис. 6.26. Параметры траектории минимальной конечной скорости спуска для
космического самолета при оптимальном управлении изменением угла атаки из
условия min L_.
переменных ф* от времени спуска при оптимальном управ¬
лении на траекториях минимальной конечной скорости
спуска (Ps = 350 кг/ль2, V0 = 7,5 км/сек, hn = — 198 км).
Анализ результатов решения краевой задачи показывает,
что и в этом случае при управлении посредством измене¬
ния угла атаки величина min L- получается большей, чем
при управлении с помощью угла крена.
В целом можно отметить, что для космического самоле¬
та, как и для КА с несущим корпусом, маневренные
Т а б л и ц а
Параметры траектории при релейном изменении угла атаки для различных значений 7П0(
$ 6.9] ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА 221
У.и ‘(jbj
1 1 i II
Mill
296
293
287
281
| 269
CD
t—
l>-
t—
L-
CO
I-
00
СО
CO
CM
CO
об
i о
CM
CO
CM
со
CD
;■<<).), ж.ч
‘(1)Л
_■
—Г
—Г
CM
со
СО
L—
3'
S?
VO
vr;
О
l>-
lo
1.
1^
LO
1
t'-
’!
CD
Го
I
CM
i.
LO
CM
LO
!
LO
CM
7
CM
CM
Ю
!
О
CM
LO
1
LO
LO
1
oo
CM
CM
) о
CM
CM
CM
о
LO
см
CD
OO
О
CM
t'-
со
WU ‘(,;)7V
CM
00
CM
00
CM
CO
CM
CO
CM
00
CO
CO
со
со
OO
CO
CO
co¬
co
CO
CO
со
CO
СО
со
со
СО
со
о
Wlt *(s)r/v
CM
CM
о
CM
со
oo
o
CD
CO
со
СО
со
CM
СП
CM
о
о
о
о
о
о
** ‘('7V
CO
00
CD
1
CO
r—
CD
1
CM
l>-
CD
1
CD
CD
1
VO
CD
CD
1
LO
CD
1
LO
CD
1
v-*
CD
1
CO
CO
CD
1
00
CD
1
LO
00
CM
CM
со
CM
LO
о
см
СО
СО
СО
о
СО
XVMU ха
vC
CO
CO
L"-
--
CD
o
CO
о
CM
v-H
см
CO
CM
CM
33
CO
CM
CM
3
о
V?
Ю
loT
CD.
M ЭЭ lr~]
CM
CM
00
CM
CM
oo
Cl
Cl
oo
CM
3
CM
CD
LO
CM
CD
CM
LO
CM
CD
CM
CD
CM
CD
CD
CO
со
CO
oo
vf
CM
со
CD
СО
СМ
о
см
изо
00
00
00
00
CO
LO
CO’ •
CO
LO
CO
LO
CO
об
LO
CO
LO
CO
LO
со
1-0
СО
об
\z)W
CO
OD
CD
CM
О
CD
CM
CM
CM
CO
°
о
-
О
-
■Hd.) ‘(1 )?v
о
CM
CO
CO
О
CM
LO
CO
I"-
со
о
[>•
О
CO
CM
со
CM
CM
со
00
3
о
4i)?> 1
iulu) (jn с1г
-
£
CO
ю
§
О
LO
со
V"
CD
о
LO
о
со
LO
о
CD
~L о ^ £
Г LO
о CO
l2 li
i
* о
1 LO
CO
5 I!
il ^
J
ii
t о
О LO
LO —1
7 1!
-м ?Т
?5 .
>-
I
«
1
?T
т
1
6 5 " ~
>1
с
Я
с
01
X
c
5
:B
H
:В
н
Я
с
£;
fS
я
о
о
о
и
%
я
о
222 ОПТИМАЛЬНОЕ УПИЛЬЛЕТШЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. П
возможности КА в продольном направлении при управле¬
нии с помощью изменения угла атаки значительно расши¬
ряются по сравнению со способом управления путем изме¬
нения угла крена. Так, при входе космического самолета
в атмосферу со скоростью VQ = 6 км/сек и h- — —79 км
величина AL- — L- max — L- тщ составляет ALn = 2895 км
при управлении углом атаки и AL- = 255 км при управ¬
лении углом крена.
Все рассмотренные выше программы управления по
углу атаки для КА обоих типов исследовались в предпо¬
ложении постоянства угла крена, причем величина угла
крена принималась равной нулю (у = уПорт = 0). Просле¬
дим, как изменяются параметры траектории при управле¬
нии по углу атаки, если величина уппст принимает ненуле¬
вое значение. В табл. 6.4 приведены некоторые результа-
ты^исследовапия траекторий спуска КА, управляемых
по углу атаки, иа"участке"выхода па ограничение для раз¬
личных" значений угго-г. На траекториях, обеспечивающих
min L-, изменение величины уц0-т в достаточно широких
пределах (от 0 до 60°) практически не влияет на парамет¬
ры траектории спуска, а на траекториях, обеспечиваю¬
щих max’l/п, ото влияние более заметно.
Т а б л и ц а 6.5
Опенка эффективности различных способов управления КА
Способ
управления
'Гии К А
max*
^-min* r'M
ЛТ,~, h\M
у — var
огб —'50°]
с несущим
корпусом
—380
—640
260
у = var
аб-70°
космический
самолет
—495
—750
255
а = лиг
у — 0
с несущим
корпусом
922
-583
1505
7 = л аг
Т -- 0
космическ ий
самолет
2350
-545
2895
а = var
у г— var
с несущим
корпусом
1820
-670
2490
а = var
Космический
2180
-795
3270
у — var
самолет
ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА
223
Совместное управление с ^помощью изменения углов
крена и атаки. Использование совместного управления
с помощью углов крена и атаки позволяет значительно
улучшить маневренные возможности КА в продольном на¬
правлении. В табл. 6.5 приведены данные (случай входа
КА с VQ = 6 км/сек и /г- =—79 км), которые позволяют
оценить эффективность двухканального управления по
сравнению с однокаиальным. В рассматриваемом примере
при использовании способа управления КА, предполагаю¬
щего совместное изменение углов крена и атаки, величина
Д£* существенно возрастает (в 10—15 раз для КА с несу¬
щим корпусом й в 15 — 30 раз для космического самолета)
по сравнению с любым из рассмотренных выше способов
одноканального управления КА.
tfBK
Рис. 6.27. Параметры траектории минимальной конечнойfскорости спуска
для космического самолета при оптимальном управлении из условия max Ln.
В .’качестве примера яа рис. 6.27 приведены зависимо¬
сти фазовых координат, сопряженных переменных и уп¬
равляющих параметров а и у от времени спуска при оп¬
тимальном управлении из условия max Ьл>
224 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. G
Максимизация боковой дальности спуска
При осуществлении бокового маневра продольная
дальность горизонтального полета заведомо уменьшается,
причем величина L- изменяется в диапазоне
Lr. Ь-ц1Лх.
Будем предполагать, что при исследовании задач, свя¬
занных с максимизацией боковой дальности, управление
КА может производиться посредством изменения как угла
крена, так углов крена и атаки совместно. Рассмотрим
последовательно для каждого из указанных способов уп¬
равления задачу о максимизации Lо на траекториях ми¬
нимальной конечной скорости спуска при ограниченной
продольной дальности.
Управление КА путем совместного изменения углов
крена и атаки. Упрощенные уравнения пространственного
движения КА имеют вид
dV Ма)р^м .
1Г = 2ni7. ^Sm0’
dt
КА
Су (а) рРАлг g cos 0 V п.
C0Sy _ + _^cos0,
2"гкл
clh T7 . л
—- = V sin 0,
at
dL _ VR cos s cos 0
dt R Г- h
de, Сy (а) р!7У f 8[п у
dt
dL*
2"1i;a
VR
cos 0
dt
R
COS 0 sin 8,
V COS 0 cos 8 tg y~p~
ITfTi
(6.71)
где 8 — угол между плоскостью подлетной траектории
и текущей плоскостью движения, Ьу — боковая даль¬
ность.
Запишем необходимые условия оптимальности при
движении КА с несущим корпусом. Внутри допустимой
§ 6.9]
ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА
225
области фазовых координат гамильтониан имеет следую¬
щий вид:
rr t dV , , сШ . dh dL
н = ^ Фз—+Ф4-
' dt
dt
dt
-Ф#
dt
de
Сопряженные переменные на участке движения внутри
допустимой области фазовых координат имеют вид
— — —
dt “ dV
cos 0
VC oS
w
К A
■4>i
CvpSM cos у
2 m
KA
“Фа
-Tf+r*»-
COS 8 COS 0 R
4Z\^+h
g cos 0 , . n .
- ~уГ ■ Фа — sin 0ф3 —
COS
№
^г/Р^м sin у
R
R + h
cos 0 sin ефб —
2m
KA
cos 0
(LA
COS 0 COS 8 tg I —5Г /
Фе +
^2
dt
dH n , g sin 0 , .
g cos ефх — i|?a +
. V sin 0 , Tr A .
+ Trrts — v cos 0фз
+
R + h
VR
R + h
VR cos 8 sin 0
R + h
(A
sine sin0Tp5
Cy?VSM sin у sin 0
2m
KA
COS2 0
(L o'
Фв —
dt
эн
Cjns„
dh
, CvVSmcosV
2 m-
2m
KA
V cos 8 tg (-7f)
7Г+7, shl 0Ф'«
• poPe-P'1^! +
+
KA
2ji sin 0
“7R~+W
V cos 8 cos 0 R
Р.Р«-ИЧ>а + -^5|т%
№)-
V (R + hf
, . RV cos 0 sin e , ■ ,
-ФН-—77ГТ-МГ-Ф5 +
!(Л + hf-
8 H. М. Иванов, А. И. Мартынов
(R + hf
(6.73)
226 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
+
sin у
2mKA cos®
Poe_phP4,6 —
V cos 0 cos е tg
(Д + h)‘l
= —= const,
dt dL
d\|)5 dll ___
~df ~~ dL. ~~~
VR
R + h
cos 8 cos 0 sin
(4f)
cos2 (if)
+
*7Г^4 +
V COS 0 COS 8
(R + h) cos2
dty6
dt
dl-I
de
VR cos 0 sin 8
№
-Фб
R
R + h
•(£)
^4 —
cos
VR
cos 0 cos ефб
V cos 0
/U
R -\- h ““то R + h
Получим гамильтониан в виде
Я = -
2 т
КА
Cxtyl +
2 т
+
-cos yip2
КА
gyP^M sin V
2wka
COS 0
Кб i
(6.73)
sin ei|v,.
A*.
(6.74)
A:i — сумма членов гамильтониана, не зависящих от уп¬
равления. Из условия максимума гамильтониана (6.74),
учитывая (6.47) и (6.48), получим закон оптимального
управления по углам атаки и крена:
а = — 5° + 0,89 arctg / —
% cos у -
sin у
cos 0 X^G
+
ущ>1
sin у
саз + -^0- Ч>.
■ + 1
у = arctg
1)52 cos 9
(6.75)
(6.76)
§ 6.9]
ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА
227
Сопряженные переменные в точке tx скачком меняют ве¬
личину:
tfrp(f
cp(?
Ч Г" (t
СЦ*
, ч дд - dq
Фг (^l) — Ил ~$уг "Т И2 Qy
О,
- (*i) = Hi Jg- + На || = ИзЕ
. ,, v дд д(]
- Чз (М = Hi ад + Ра ад - Чь
- i|),4 (^i) = Hi “air + Иг "ах" =
- 4-5 (*i) = Hi -йг + На -Щ = °.
- ым = hi ч- ч2^ = о,
где [1± и |т2 = const.
Определим законы управления а и у при движении
КА по изовысоте:
г|^Р
уо^р = arctg
^rpcos0 Г
a°ip __ — 5° + 0,44 arcsin
V
R + /г
1,74
КА
Р™м
1
arctg
г6гр
■фОГР
(*-
- + 0,087j
(6.77)
(6.78)
Уравнения сопряженных переменных с учетом (6.77) и
(6.78) при h = /гогр имеют вид
228 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ ГЛ. G
X
Ь°п> \ 1
arctg'
COS 8 I " I -44- j
R 4- h
+ +JL L
• V \ V ft
orp
I ОГ1)
“Фз •
2V .
R h
Ф‘ГР tg Qt +
ft ■: h
+—+-
^ V \ V
R -I -h
tg
arc Iff
<L'P
2 ЛГР
lb°rp
ГП Tfi
R-\-h Yb Я|)0гр ’
clг|)°гр
clt
= Л11,-ЛГ’ +
+ [0.2 + 2,3 sill2 (0,50,)] -
9 ^ м . orp
-[0,2 +2,3 siir (0,5001
2 m
К A
Vs *V .ornCP
- [0,2 + 2,3 sin2 (0,50,)] -£JL- ^*rp 3
К A
V*s„
d\borp
+- = - [0,2 + 2,3 sin2 (0,5Q,)] ^_2L pp^P
К A
1 1 V R i -li
orp
+
V
(R i /0
b"rp _
2Ц
К (Л I - hf
VR
FT
VR
(R |-/t)2^'4 / L
COS
b()|,p
R
^ (ft -j- Ilf SlUe^ H y-y R I, J фШ-р
V
,|,nrp
+1ЛГ-
Lr
V cos 6 tg \~ft"
( R I- kf
X Fptg Qtf'r
CP -!- (-p-
V
•Г
(6.79)
§6.9]
ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА
229
2ц
-tg +
2ц
€ГР
(R + hf
+ тттгй 4l’irp —
(R + hf V
Ь°ГР .
+
V
+
(R + hf
Ь_ _
V
2|л
р
(R +hf
4'2
<р +
R + h
4>огр ^огр
-фогр
(R + /г)3 V
= Const,
d*cr
€гр
V
(R + hf
orp
dt
VR
R + h
sin
cose-
(40
+
R cos!
V cos e
R 4- h
040
-<p +
R coS'
(40
Ж
orp
<rp
dt
VR
R + h
VR
(40
orp
COS бф5
orp
V sin e tg
(40
R + ,
Ч’б
orp
где
Q1 =
=arcsm
1 74 _KA (JL_
A’ A 1 "
V
R 4- h
)-
arctg
(6.79)
tr_\
Ч’Г’ j
0,087
]•
Из условия трансверсальности в конце траектории
спуска (точка схода с ограничения) получим
^51! ^ 1, ^(!K == 0. (6.80)
Остальные сопряженные переменные не определены.
Таким образом, поставленная задача сводится к четырех¬
параметрической краевой задаче для систем дифференци¬
альных уравнений (6.71), (6.73) и (6.79).
230 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
Некоторые результаты решения краевой задачи при¬
ведены на рис. 6.28, где показаны зависимости боковой
дальности от продольной при оптимальном управлении.
Начальные условия входа V0 = 6 км/сек, hn = — 79 км,
а величина нагрузки на лобовую поверхность Ps ==
= 350 кг/м2. Сформулированная задача решалась в пред¬
положении, что на последнем участке при оптимальном
Рис. 6.28. Зоны маневра при оптимальном (из условия max L6) управлении
посредством изменения углов крена и атаки для КА с несущим корпусом
(Vo = 6 км/сек, h~ = —79 км, Pg = 350 кг/м2).
управлении из условия VK = FK mjn) боковой маневр от¬
сутствует (у=0 на всем участке полета). Очевидно, ослаб¬
ление требований к величине скорости в конце траектории
спуска позволит расширить возможную зону маневра КА
при оптимальном управлении. Данные, представленные
на рис. 6.28, подтверждают этот вывод. Для рассмотрен¬
ного выше примера максимальная величина Lq увеличи¬
вается на 76 км при увеличении конечной скорости на
30 м/сек. (Величина Ьл берется во всех случаях одной и
той же: L- = 150 км.)
§ fi-9j
ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА
Рассмотрим задачу о максимизации боковой дальности
СПуСКа При фиксированной ПРОДОЛЬНОЙ И При VK = FKmiH
для космического самолета при совместном управлении
с помощью изменений углов крена и атаки. Необходимые
условия оптимальности записываются таким же образом,
как для КА с несущим корпусом, и исходная экстремаль¬
ная задача сводится к четырехпараметрической двухто¬
чечной краевой задаче. Некоторые численные результаты
решения этой задачи приведены на рис. 6.29.
Ц.км
Рис. 6.29. Зоны маневра при оптимальном (из условия max L6) управлении
посредством изменения углов крена и атаки для космического самолета (V0 —
— 6 км/сек, /г - = —79 км, Р$ = 350 кг/м2).
Рассмотрим задачу о максимизации боковой дальности
при фиксированной продольной дальности КА, управляе¬
мого с помощью угла крена, на траекториях минималь¬
ной конечной скорости спуска.
РТекоторые результаты решения этой задачи приведе¬
ны на рис. 6.30 и 6.31, где показаны зависимости боковой
дальности от продольной при оптимальном управлении
КА с несущим корпусом (рис. 6.30) и космического само¬
лета (рис. 6.31) с помощью изменения угла крена для раз¬
личных значений балансировочного угла атаки и величи¬
ны конечной скорости.
232 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
Видно, что управление КА только с помощью крена
заметно снижает маневренные возможности КА в боко¬
вом направлении по сравнению с двухканальным управ¬
лением с помощью углов крена и атаки. Так, для КА
с несущим корпусом (рис. 6.30) (Рх = 350 кг/м2), осущест¬
вляющего вход в атмосферу Марса с начальной скоростью
V0 = 6 км/сек и 1гп = — 79 км, максимальная боковая
Ц,км
Рис. 6.30. Зоны маневра для КА с несущим корпусом при оптимальном управ¬
лении посредством изменения угла крена для различных значений балансиро¬
вочного угла атаки (У0 = 6 км/сек, h- = —79 км, Pg = 350 кг/м2).
дальность при L* =150 км составляет: AL6 = 205 км
в случае управления только посредством угла крена,
ALq = 260 км в случае совместного управления с помо¬
щью углов крена и атаки. Видно также, что использова¬
ние аппаратов с большим значением максимального аэро¬
динамического качества позволяет получить и большую
зону маневра.
Для сравнения в табл. 6.6 и 6.7 приведены результаты
исследования упрощенного алгоритма управления про¬
странственным движением КА, который заключается в сле¬
дующем. Полет КА происходит с постоянным значением
аз = const. Обеспечение заданной продольной дальности
полета КА осуществляется
Основные характеристики траектории при использовании упрощенного алгоритма
пространственного движения для КА с несущим корпусом
ОПТИМИЗАЦИЯ ЗОНЫ МАНЕВРА
233
CD
3
и
Wit
Qrj
3)
12
С-
>>
о
иэо
‘зг
й
иэо
‘(s)?
о
и
о
а)
ж и ‘
Qrj
(8)Z
° ни
О К
И м
кем ‘
Urj
(8)7
а
£ S
н я
<v а,
§ё
<не
С о
О
н
о
Л
МЭЭ/W
‘ИЛ
tr
>»
0юйг *хоопЛ
«
Н о
г<ээ
‘(г)»
tc D
$ к
я S
S гг
и
WH
So
н g
О 2*
о О
WU
‘ Url
(z)J
Й с
£ "
Ud'JiWU 1
‘(S)A
й
(V
02
Я F-
щ О
к Я
о
WK
\т)7
гг ^
о
as
хи
11
2? 2
нээ
‘(I)?
и |
8 §*
2<ЭЭ/жи
(I)A
О tH
Гг
(>г,йг ‘-т
doit л
«О
Ю
t—
Ю
00
02
in
in
ю
Г-
00
CO
CO
vt4
in
О
CD
CD
00
00
00
02
S-H
CO
02
in
CD
tr-
vT4
tc-
CM
I'-
02
02
t>-
02
LO
vt4
1
i
CO
1
CO
1
7
ОС
1
t—
1
см
1
02
1
CM
1
00
CD
02
г-
О
О
о
СО
о
00
02
О
02
со
00
00
ш
V4
r-
CM
CM
CO
CO
СО
vt4
Sf
со
СО
см
t-
Г—
Г-
СМ
см
CM
in
in
CO
CO
CO
со
со
СО
CO
см
СМ
02
^ГЧ
00
00
00
00
V}4
vt4
OO
ч*гЧ
см
см
О
О
О
о
СО
со
CO
"О
V*4
о
t-
С—
I>*
Г—
t-
с-
[—•
1--
с—*
CD
'H
ЧЧ
-ч
1П
in
in
1П
in
t-
с-
t-
Г-"
СО
СО
CO
см
см"
CM
7
7
7
7
чЧ
1
7
ЧгЧ
1
7
—1
1
7
^r4
V*4
V*4
00
vl4
vf
v?4
VJ4
4J4
CD
o'
о"
o'
о"
o'
О
o'
о"
о"
О
Ю
in
in
in
о
О
О
in
in
О
СО
СО
CO
VH
CD
00
о
02
00
О
Vй
о
О
CD
m
in
СО
со
Ю
CO
00
о
CD
in
О
“О4
о
О
t-
CM
Г—
о
Г-
in
о
00
о
о
[>-
t-
CD
v*4
со
in
02
02
02
02
02
02
02
02
02
О
о
О
o'
о"
o'
о"
о"
о"
CM
CD
02
о
02
CD
_ц
0
CD
о
T—1
CM
ю
00
v*
in
CD
CD
о-
CD
02
in
00
02
t-
<м
СО
CD
CM
oo
о
02
O
in
СО
t-
CD
1
in
1
in
1
Т—i
1
СО
1
CM
1
тгЧ
1
со
1
7
со
1 ,
CO
CO
CO
со
t2—
t-
СО
со
in
in
in
1п
m"
in
in"
CD
CD
С—
о
о
CD
о
00
00
02
02
о
CM
CD
CD
CO
vf4
02
и-Ч
С—
СМ
чЧ
CM
CM
СМ
ч-1
in
12-
in
CM
02
С—*
CD
02
^О4
02
02
СМ^
CM
cm"
' о"
тгН
о"
о"
о"
in
Ю
»n
ю
о
р
ю
in
о
CO
ГО
vT4
vf4
CD
Продолжение табл. 6.6
234 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ. 6
2
5
и
и
л
ИГ 24
(s9)7
О 05 00 се 00 °0
СОЮО(М^СЧ
t— 00 05 СО Г— 05 00
СМ ^ 'ТЧ СО СО со VT
дам
(З)7
Ю С— О 00 СО 00
N <н О Ю О ^
см см со vf со ю
1 1 1 м 1
[>N00 Ю СО -Ч
00 СО СМ ч? СО тч СМ
V— io tO t О t-О СО СО
1 1 II 1 1 1
£
О
24ээ
О О ^ (М CD
Ю Ю СО О IN Ю
СО СО СО СМ СО чч
СМ 00 ^ t> С СМ чч
05 СО vf СО vf1 тч —-ч
-ч СМ СМ СМ СМ чч чч
ей
И
2490
‘(К)?
г— t— ю со со см
см см см см см см
120 iO >20 sen sc4 CM CM
CM CM CM CM CM CM CM
И
О
<и
ИГ 24
‘ Qrj
(ег
120 Ю СМ СМ СМ 00
т-ч СМ СМ см
120 120 120 чЧ ——i Г— 05
чч -H —i CM
о
О к
R В
^ в
ИГ 24
1 (в)7
—J с-- о. 00
t— 12— С— t— t— 00
CM CM CM V* ч-t CO 05
C— L— 12— t— L— [— 00
*< 0J
К Е
ей К
Н ей
R с-i
(оюйг ‘»0
Ю Ю 00 s?
CM CM t—i ■^—i чч гч
1 1 1 1 II
чч CM
О О О 05 05 00 t-
cq см см чч тч тч -ч
1 1 1 1 1 1 1
о
о
н
о
ей
2490'ИГ ‘ЯА
CO CO t—• 05 05 CM
СО СО СО 00 CO VF
о" о о о о* сГ
i О 1-0 Ю со со L—
СО СО СО СО СО СО v-ч
о о о о о о о
>>
о
О
II
ю щ о ю ю о
чгН тн СО vjt ^Ct1 со
о
О
ю
II
120 120 120 о О 1 о о
чч чч чч СО СО VT: СО
5
и 2
24 00
‘(г)?
II
to
е
со о о о о о
II
Ю
<о
о о о о о о о
a 5
К S3
5 50
3 S
IAIM
‘(^7
т-1 о о о о о
о о о о о о о
К В
S
о a
н fe
о о
ИГ 24
*(з)7
СО о о о о о
о о о о о о о
S2
24 00, ИГ.4
‘U)A
05 05 05 СМ -гч СО
о o' о" - —Г т-Г
CM CM ч-: СМ О О О
А на режим
полета
ИГ 24
‘(О7
vfvf: СО СО СО 00
to Ю 05 см см см
12— СО v~ lO СО 05 СО
СМ чч чч CM CM СО
ИГ 24
‘(I)7
СМ 00 1— 00 С 00
С 00 N LO V- VT
СО М СО SP LQ
II II 1 1
I4— 05 О Vй 05 СО чч
СО О 05 тч О т-ч СМ
V4 СО 120 СО СО СО СО
1 1 1 1 1 II
^ ?
5 S
S и
хи
Ю Ю 05 СО СО со
СО СО СО 12- О- 00
СО СО 05 со
00 00 00 00 СО 00 05
Я 5
к ч
<D £
Я ~
2400
‘(D*
о со СО СМ 00 СО
СМ СМ О О 05 ю
СМ СМ СМ СМ -ч -ГЧ
см со со со со см чч
Ц
й
^ t-i
24ЭО/ИГ24 ‘(Т)А
тн 05 05 t— чч 05
т-Г о o' o'т-Г o'
СО СМ ~ СМ О 05 05
С гч ч гч гч С О
о
>>
(0?2Ct3 ‘-ЬЭО^Л
120 120 О 1-0 t-О о
-ТЧ СО Ntf N? со
120 to 120 С2 о Ю О
—I -ч -ч СО СО VT СО
Основные характеристики траектории при использовании упрощенного алгоритма
пространственного движения для космического самолета
§ 1>, 9]
ОПТИМИЗАЦИЯ ЗОНЫ МЛНЁ13РЛ
235
02
й
о
Wf\4
Qrj
(sr
^ГН^СО
чч со Ю ст.
СО СО со СО
00 Vf 0 02
О О СМ СО
'ТЧ см см см
t4
M
1870
1668
1628
1410
чн 00 О CM
^ vj< 02 чч
NOIOlO
>>
О
«ЭО ‘К7
ЮЮМСО
00 02 05
СО СО СО СО
M1 CM гн О
Vf LO Ю v4
CO CO CO CO
о
2<ЭЭ
‘(e)*
О О 'г' О
Ю С" 00 00
ЧЧ Ч-Н чЧ чЧ
02 vj-- О гч
^ CDI> t>
X
о
о
WJt
‘ Qrj
(V)1
ONOO'H
-гч СМ СО
02 CO CM t>-
CM CO LO
о м
С £
<! 5
U1
(e)7
02 с- ^ 02
СО CD 00 02
ttH — 1 О
О см СО V-
Ь cL
gs
pncfe ‘у1о
см 00 02
V" ю ю ю
1 1 1 1
>0
Ю 00 02 02
00 02 02 02
II 1 1
^ о
с
МЭЭ/ИСН
‘HA
00 СМ 00
оо оо
o' o' О ^ч
t— CM CO* CO
LO CO CO t>-
0 o' o' 0
(шсГг ‘^зои^
0
0
CO
ю О LO о
СО VT1 СО
о
О
>0 О 1-0 0
чч CO XT CO
§2
H9D
(o)?
II
10 '
«
1-0 — — С'-
СМ СМ СМ чч
II
О
CD СО О th
00 00 CO t>*
g S
YCU
‘ Qrj
(z)J
О СО СО чч
СО СМ СМ ГЧ
CM О N CO
СО СО Ю ^
й В
р
WU 1
w7
ю 0 О W
*4 02 CO CO
ч-ч О О 00
2 о
>> м
иэо!жн ‘
:(г)Л
чч СМ СО СО
О чч CM iO
чЧ чЧ чч чч
на режим
юл ста
WU
< Ory
dr
чч 00 С"* СО
СО ОС ^
СМ чЧ чЧ СМ
t>- ЧЧ ч—1 *<f
СО CM СО СО
WH 1
'(I)7
О !>• L—
00 Ю 02 00
LO СО СМ О
СО СМ СО чч
СМ -и 10 00
L.O чч со СМ
^ -1
^ р
хи
^ОЗМ<^
OlOCON
СО чч L''- v4
Ю СО L" 00
р й
й R
О Р
7190
‘(Т)?
HOOt4
02 02 02 00
02 m —! ос
О О О 02
Я ГС
£ р
hoj’wu '
‘(Т)Л
Ю vf О СО
СО Ю чс? 00
см см см см
о ^
£
gods l'L0011^
о о ю о
чч СО *<4 со
LO О LO О
чч СО vr СО
Продолжение табл. 6.7
236 ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНЕЧНОЙ СКОРОСТЬЮ [ГЛ Л
05 5
?s
‘(я)7
1ГК —T
МЭО ‘(e)?
(s)7
wu
(e)
udolwn ‘HA
«
S
к 2
щ s
Й s
Я e>
и tr
HS
s ^
cr
I»
нээ ‘(z)}
WM ‘(5>
‘(Z)A
*“ a®7
ХЭЭ ‘
(I)?
хдЭ/Wx ‘(x)A
guctg *хсоил
s? CD 05 I P
CO CD 05 CO
СО О Ю 05
(N ST CD
CO CO CO CO
00 CD чг-i CM
00 00 CD CD
04 CM CM CM
05 tr-i CO 05
C4 M ST M
l> 00 CM
COOOs^M1
CM CD
XT vr LO CD
LO о Ю О
^COsrCD
l> s? см CM
LO CD 00 О
ST' ST V Ю
00 CM 05 00
CO 00
t> CDsr CO
00 C"— CD LO
v? 00 t> CO
05 05 О
sj^lDlOCD
COC'HO
CD CD CM CM
CM CM т—i t—I
CD CD 05
r-i rH CO
CD CM CM 05
CD t> l> l>
CM CD 'ri
'Р^ЮЮ
ю о ю о
тч СО vr CD
I I
LO CD CM 05
^СМ^Ю
05 ^г-i t>* CO
00 05 05 О
LO LO LO CD
I I
CO 05 v?
00 00 05
CO CM 05 00
«ч-T ^-T o' o'
01 :т Т И М И 3 А Ц И Я т 3 О Н Ы М А Ы Е В Р А
237
— по программе двухразового переключения эффек¬
тивного качества на участке выхода на ограничение
К$-+К$-+К(вI (6.81)
ГДе 4ф = Ко COS (Vinin “Ь Упоет)> Уф = Ко COS (у max У пост)
Я Yiniu — О? Ymax =
— на участке движения по ограничению управление
осуществляется в соответствии с (6.19);
Ц,км
атаки (Уо = и км/сек, /г- = —7У км, Pg = 35U кг/м1),
— на участке движения после схода с ограничения
полет протекает с постоянным значением эффективного
качества К0ф = Ко cosyi1uot.
Величина бокового маневра для рассматриваемой прог¬
раммы управления, как видно из табл. 6.6 и 6.7, сущест¬
венно зависит от величины у1Ю^- Каждому значению L-6aд
соответствует вполне определенная величина у^ост, обеспе¬
чивающая для рассматриваемого алгоритма управления
максимальный боковой маневр. Предлагаемая программа
управления при значении ушх.т = у2оСТ позволяет получить
результаты, весьма близкие к оптимальным. При использо¬
вании этой программы уменьшение боковой дальности по
сравнению с оптимальным управлением составляет всего
5-г-7%.
ГЛАВА 7
НЕКОТОРЫЕ ЗАДАЧИ
БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ
§ 7.1. КРАТКАЯ ХАРАКТЕРИСТИКА ОСНОВНЫХ
НАПРАВЛЕНИЙ ПРОЕКТИРОВАНИЯ КА
Выбор окончательного варианта КА означает заверше¬
ние напряженного труда большого числа специалистов из
различных областей науки и техники [10, 29, 32, 33, 35, 86].
Перечислим главные моменты, от которых зависит
облик проектируемого космического аппарата (см. также
рис. 7.1).
Рис. 7.1. Общая схема проектирования КА.
1. Основные направления, определяющие компонов¬
ку КА:
— баллистическое проектирование (определение ос¬
новных проектно-баллистических характеристик КА —
■^расп -И Рs) 1
— аэрогазодинамическое проектирование;
— поиск оптимальной (рациональной) аэродинамиче¬
ской формы КА;
— выбор системы тепловой защиты, включая теплоза-
щи т н ы е м а т е р и а л ы;
§ 7.1] ОСНОВНЫЕ НАПРАВЛЕНИЯ ПРОЕКТИРОВАНИЯ КА 239
— разработка конструкции и выбор конструкцион¬
ных материалов;
— определение системы мягкой посадки;
— разработка системы управления;
— разработка, выбор прочих систем (система термо¬
регулирования, бортовой радиокомплекс, телеметриче¬
ская система и прочие).
2. Специфические условия работы:
— малая плотность атмосферы;
— большая неопределенность характеристик атмо¬
сферы;
— разброс условий входа в атмосферу;
— неопределенность условий па планете.
3. Общие требования к КА:
— максимум полезной нагрузки;
— мягкая посадка;
— статическая и динамическая устойчивость * КА;
— необходимая надежность КА и его систем.
4. Факторы, ограничивающие принятие решения:
— срок создания КА;
— вид полезной нагрузки;
— предельно допустимая масса КА;
— предельные габариты, определяемые особенностя¬
ми ракеты-носителя;
— допустимые перегрузки на участке спуска и по¬
садки;
— возможность отработки КА и его систем в условиях,
близких к натурным;
— общее состояние технологии, материаловедения,
приборостроения и т. п.;
— стоимость создания КА.
5. Дополнительные требования:
— точность посадки;
— маневр для посадки в заданном районе;
— предпосадочный маневр для выбора удобного места
посадки;
— ограничения по перегрузкам, угловым скоростям,
ускорениям, включая частотные характеристики.
Очевидно, создание КА возможно лишь на основе ком¬
плексного анализа результатов исследований по всей со¬
вокупности составляющих задач с учетом дополнительных
условий и ограничений. Хотя не все направления равно¬
240
ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ [ГЛ. 7
значны, но по каждому должен проводиться обширный
комплекс исследований, не связанных с выбором какого-
либо конкретного КА. Это очень важно, так как, присту¬
пая к решению той или иной задачи, приходится зада¬
ваться определенными предпосылками относительно не¬
достающих данных и эти предпосылки тем справедливее,
чем глубже проведены исследования по смежным обла¬
стям. В силу этого следует говорить об оптимальном
или по крайней мере рациональном решении различных
задач по каждому из указанных направлений. Получение
же наилучшего варианта КА, как указывалось выше, воз¬
можно лишь в результате комплексной оптимизации, при¬
бегая во многих случаях к компромиссу, ибо частные
оптимальные решения зачастую выдвигают противополож¬
ные требования.
С точки зрения проектирования КА отправным пунк¬
том является выбор основных проектно-баллистических
характеристик — это прежде всего потребная величина
аэродинамического качества Кпаоп и допустимая нагрузка
на лобовую поверхность Ря- Выбор указанных парамет¬
ров во многом предопределяет тип КА и, следовательпо,
направления дальнейших исследований. Вместе с тем по¬
нятно, что определение диапазона приемлемых значений
для ЛГрасп и Ря невозможно без принятия определенных
предположений по другим направлениям проектирования.
В силу отмеченного следует говорить о проектно-бал¬
листических аспектах исследований, выходными парамет¬
рами которых являются значения величины аэродинами¬
ческого качества (ЙГПагп) и допустимой нагрузки на лобо¬
вую поверхность, а также ряд сопутствующих факторов.
Найденные значения Крагп и Ря в сочетании с условия¬
ми входа и характеристиками атмосферы позволяют опре¬
делить конкретную траекторию снижения КА, что вносит
достаточную ясность в другие направления и позволяет
рассчитать многие характеристики спуска. Действитель¬
но, теперь представляется возможным определить тепло¬
вой и перегрузочный режимы спуска КА, условия радио¬
связи, условия работы системы управления и других си¬
стем КА (в частности, системы терморегулирования и т. п.).
В результате можно приступать к решению задачи тепло¬
защиты КА," выбору конструкции, управления; можно ис¬
кать оптимальную форму КА, удовлетворяющую требуе¬
§ 7.1] ОСНОВНЫЕ НАПРАВЛЕНИЯ ПРОЕКТИРОВАНИЯ КА 241
мым значениям 75Грасп и Ps; проводить исследования по
уточнению аэродинамических характеристик (как стати¬
ческих, так и динамических) и т. п. Одним словом, есть все
необходимые условия для проведения первой итерации по
выбору КА, которая, в частности, может показать, что
выбранные величины Ps и Kvаеп не удовлетворяют рацио¬
нальному решению в целом. Например, в силу некоторых
обстоятельств приходится принять определенное решение
по системе мягкой посадки. Это может коренным образом
повлиять на требуемые значения Ps и ifpaCn и в целом на
форму КА.
Другим важным направлением, определяющим выбор
КА, являются исследования по аэр о газодинамике. Это на¬
правление включает теоретические изыскания, экспери¬
ментальные, модельные (макетные) и натурные испыта¬
ния и т. д. Для решения задач аэрогазодинамического про¬
ектирования привлекаются все современные средства, от
ЭВМ и аэрогазодинамических труб до испытаний с исполь¬
зованием самолетов, вертолетов и ракет-носителей. Специ¬
фика проектных работ приводит к необходимости проведе¬
ния исследований в два этапа.
Главной задачей первого этапа является получение
максимального количества данных по аэрогазодинами-
ческим характеристикам большого числа разнообразных
форм аппаратов, которые используются при системном
анализе задачи проектирования и создания КА. В ре¬
зультате исследований определяются принципиальные
возможности различных типов КА в отношении прежде
всего величины аэродинамического качества и других
статических характеристик.
Второй этап связан с конкретизацией формы КА вы¬
бранного типа и уточнением всего спектра аэродинамиче¬
ских характеристик, как статических, так и динамиче¬
ских. В этом случае необходима глубокая детализация и
тщательная проработка всех возникающих задач. Как пра¬
вило, по материальным и людским затратам исследования
второго этапа существенно превышают первый. Действи¬
тельно, если на первом этапе во многих случаях возмож¬
ны теоретические расчеты, а сравнительно незначительные
эксперименты ставятся лишь с целью подтверждения тео¬
ретических выводов, причем основной объем эксперимен¬
тов проводится на имеющихся установках, то на втором
242 ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ [ГЛ. 7
этапе уровень выдвигаемых требований по точности аэро-
газодинамических характеристик чрезвычайно высок, что
в подавляющем большинстве случаев требует всесторон¬
них натурных испытаний и уникальных экспериментов.
Второй этап является решающим, так как получаемые
результаты в некоторых случаях могут заставить отка¬
заться от намечаемой формы КА и искать приемлемый
вариант.
Третьим важным направлением, определяющим облик
КА, является выбор типа и аэродинамической формы ап¬
парата. Сложность проблемы состоит в том, что ее реше¬
ние зависит от целого ряда факторов: от условий входа,
выбранной схемы спуска и параметров атмосферы; от
принятой системы управления, теплозащиты, способа по¬
садки; от характера полезного груза, особенностей ком¬
поновки и многих других. При этом необходимо отме¬
тить многообразие вариантов по возможным формам КА,
в целом удовлетворяющих определенным исходным
данным.
Предположим, что выбран КА скользящего типа и име¬
ются данные по потребным значениям аэродинамического
качества У^расп и нагрузки на лобовую поверхность Р$. На
основании имеющегося опыта эксплуатации КА скользя¬
щего типа остановимся на управлении эффективным каче¬
ством. Обеспечить заданные величины Кхтса и Р$ можно
при самых разнообразных формах лобовых экранов: сег¬
ментной (с разным радиусом сегмента), конической (с раз¬
ными углами конуса) и т. д. Балансировка аппарата па
определенном балансировочном угле а о может быль до¬
стигнута за счет смещения центра масс или лобового экра¬
на относительно продольной оси симметрии, созданием
разного рода несимметричных лобовых щитов и т. д.
Столь же многообразны и варианты хвостовой части КА.
Из всего этого многообразия необходимо выбрать един¬
ственную рациональную (еще лучше — оптимальную)
форму, удовлетворяющую всем основным требованиям.
Объем исследований несоизмеримо возрастает в случае
необходимости сравнительного анализа различных ти¬
пов форм КА с целыо выбора наилучшего.
Ниже будут рассмотрены некоторые задачи баллисти¬
ческого проектирования как основополагающего направ¬
ления при разработке КА, в результате которого следует
ВЫБОР СПОСОБА УПРАВЛЕНИЯ
243
определить область применения различных типов КА и
сформулировать требования к основным проектно-балли¬
стическим параметрам КА, оцепив их влияние па основные
характеристики траекторий спуска.
§ 7.2. ВЫБОР СПОСОБА УПРАВЛЕНИЯ
В качестве главной задачи будем рассматривать задачу
обеспечения мягкой посадки КА с минимальными энерге¬
тическими затратами, что в итоге должно обеспечить
максимальную массу доставляемой на поверхность Марса
полезной нагрузки (max /яИ11). Никаких дополнительных
ограничений и требований но перегрузке и тепловому
режиму, по маневру и точной посадке в заданном райо¬
не и т. п. не выдвигается. Исследуется прямой вход КА
в плотные слои атмосферы с гиперболических подлетных
траекторий. Движение КА происходит внутри коридора
входа, ширина которого не превышает zh 70 км, а при¬
цельная высота условного перицентра h™9 выбирается из
условия наилучшего выполнения основной задачи. Чис¬
ленные материалы получены в основном для модели, со¬
ответствующей наиболее разреженной атмосфере. Возмож¬
ное увеличение плотности в реальном полете будет способ¬
ствовать лишь облегчению выполнения задачи спуска и
посадки. Как обычно, па траекторию спуска накладывает¬
ся ограничение по минимальной высоте пролета над по¬
верхностью планеты (в случае рикошетировапия h > ^доп).
Как было показано в главах 4 и Г), требуемые условия
в конце участка аэродинамического торможения сущест¬
венно зависят от вида СМП. Однако качественная картина
не изменится, если задачи баллистического проектиро¬
вания будут решаться для какого-либо одного типа СМП.
Для определенности будем полагать использование реак¬
тивной системы мягкой посадки, т. е. эффективность тор¬
можения на основном участке снижения будем оценивать
по достигаемой конечной скорости, имея в виду, что полу¬
чение min VK обеспечивает минимум массы CMII. За мак¬
симально допустимое значение скорости в конце участка
аэродинамического торможения примем VK ^ 700 ч-
—- 750 м/сек (соответственно 3 -г- 3,5 М). Будем полагать,
что на протяжении спуска нагрузка па лобовую поверх¬
ность Ps = const. В реальном полете за счет уноса тепло¬
244 ЗАДАМИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ [ГЛ. 7
защитного покрытия и выработки рабочего топлива на
управление величина Ps к концу участка основного аэро¬
динамического торможения несколько уменьшается (на
несколько процентов), но это не оказывает существенного
влияния на конечные результаты.
В случае использования КА, обладающих аэродинами¬
ческим качеством, предполагаем оптимальное управле¬
ние этим качеством из условия minFK. Если для КА
скользящего типа способ управления эффективным каче¬
ством (с использованием угла крена) в настоящее время
общепризнан и проверен на практике, то для КА с боль¬
шим значением аэродинамического качества (КА с несу¬
щим корпусом или космический самолет, для которых
i^max 1) рациональный способ управления не столь оче¬
виден. Рассмотрим этот вопрос несколько подробнее.
Выбор способа управления КА планирующего типа
с использованием критерия оптимальности min FK. Если
известны характер и структура оптимального управления
любого из рассматриваемых способов управления (см.
главу 6), то не представляет особых трудностей получение
численных результатов по FK min, достигаемых для КА раз¬
личных типов, отличающихся проектно-баллистическими
характеристиками. Численные результаты исследования
получены для КА трех типов, аэродинамические характе¬
ристики которых представлены на рис. 6.15 и которые
имеют значения Атах, равные 0,32 (КА скользящего ти¬
па), 1,5 (КА с несущим корпусом) и 2,4 (космический са¬
молет) .
При исследовании управления путем изменения угла
крена используем результаты решения вариационной
задачи об отыскании оптимального управления углом
крена из условия min FK, представленные в главе 6. Бу¬
дем предполагать, что для КА заданной конкретной фор¬
мы возможна балансировка на любом значении угла атаки
внутри Диапазона G^min О&б ОЬщах? где O&min 6?
О&тах ^ ^0 .
В этом случае, задаваясь последовательно различными
значениями а^, можно для каждого конкретного значе¬
ния осо -- а* определить минимальную конечную скорость
Fк min при использовании программы оптимального управ¬
ления углом крена. Очевидно, каждому значению а* соот¬
ветствует своя, вполне определенная величина Kq и Рх
ВЫБОР СПОСОБА УПРАВЛЕНИЯ
245
и, следовательно, свое винчение минимальной конечной
скорости.
На рис. 7.2 в качестве примера представлены зависи¬
мости минимальной конечной скорости от угла о&о для
трех рассматриваемых типов КА. Из их рассмотрения вид¬
но, что вначале с увеличением ао от аб — amin, примерно
соответствующего максимальному аэродинамическому
Рис. 7.2. Минимальная конечная скорость при оптимальном управлении с по¬
мощью изменения угла крена (Pg = 350 кг/м2, /гдоп = 6 км). (Для КА с Ктах =
= 0,32 ag следует считать отрицательным).
качеству Ктах, минимальная конечная скорость заметно
уменьшается. Например, для КА с несущим корпусом
(Tfmax = 1,5) увеличение а& от 15 до 35° (или соответствен¬
но уменьшение К о от К§ = Атах = 1,5 до 0,95) приводит
к уменьшению конечной скорости при оптимальном управ¬
лении от 530 до 355 м/сек. При дальнейшем увеличении
угла атаки до ао = aoptвариация FKmin заметно снижается
и для широкого диапазона ао наблюдается достаточно по¬
логий минимум функции Fк min (а?0- Так, для того же КА
дальнейшее увеличение ао от 35° до aopt ^ 52° приводит
к изменению Fj-min от 355 до 344 м/сек. При дальнейшем
увеличении угла атаки происходит сначала незначитель¬
ное, а при ас > 65° резкое возрастание конечной скорости
FK. Аналогичная зависимость FKmiU (ao), как видно из
рис. 7.2, при управлении эффективным качеством наблю¬
дается также для КА скользящего и самолетного типа.
Итак, при! управлении с использованием угла крена для
достижения минимальной конечной скорости нет необ¬
ходимости стремиться к увеличению аэродинамического
246
ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ [ГЛ. 7
качества и, более того, режим полета с углом атаки, соот¬
ветствующим ifтах» в рамках поставленной задачи оказы¬
вается невыгодным.
В дальнейшем будем предполагать, что при управлении
эффективным качеством КА балансируется на оптималь¬
ном (из условия min FK) угле атаки = a(6Pt. Целесооб¬
разно отметить, что оптимальные значения o&6Pt соответ¬
ствуют достаточно малым значениям аэродинамического
качества 0,3 -т-0,5) при сравнительно большом зна¬
чении коэффициента лобового сопротивления независимо
от типа КА (табл. 7.1).
Таблица 7.1
Оценка эффективности различных способов управлении К V
Управление
углом атаки
■^тах
а при К = Х1П.1Х ,
град
Сх при К = Кшах
VK [|lin. M'ro;
0,32
1,5
2,4
31
14
16
1,24
0,43
0,05 (X0,5 *))
530
320
111
g Управление
НК» углом крена
о _
opt
зс0 , град
opt
К при y.Q — y.Q
Г.х при ag = agpt j VK miu. Mice,:
27
52
70
Отношение
оставляет t
0,285
0,5
0,36
площади крыла к пл(
j ,5.
1,3
1,7
1,5 (X6,5*))
ощади миделя космиж
540
335
150
некого само-
Данные табл. 7.1 позволяют сравнить эффективность
применения различных способов управления для КА рас¬
сматриваемых типов. В частности, приведены значения
минимальных скоростей в конце участка аэродинамическо¬
го торможения при управлении эффективным качеством,
а также с использованием угла атаки и угла крена. Ре¬
зультаты получены при одинаковых исходных предпосыл¬
ках и условиях на управление, т. е. во всех случаях рас-
матривалось оптимальное управление аэродинамическим
качеством.
При рассмотрении двухкапального управления посред¬
ством углов атаки и крепа воспользуемся результатами
§ 7.3] ОБЛАСТЬ ПРИМЕНИМОСТИ КА РАЗЛИЧНЫХ ТИПОВ 247
решения соответствующей оптимальной задачи в главе 6-
В этом случае величина скорости в конце участка основ¬
ного аэродинамического торможения несколько меньше,
чем при управлении эффективным качеством, однако раз¬
ница по FKmin чрезвычайно мала и не превышает З-л-4%
от величины VK (15 -л- 20 м/сек). Эти результаты справед¬
ливы для широкого диапазона изменения нагрузки на
Kmin^A^
Рис. 7.3. Минимальная конечная скорость при оптимальном управлении
изменением угла крена (сплошная линия) и угла атаки (штриховая линия).
(7 — КА с Ашах = 0,32; 2 "Кщах = Е5; 3 -^тпах = 2,4.)
лобовую поверхность и при различных ограничениях по
/&доп, что подтверждается, например, зависимостями, при¬
веденными на рис. 7.3.
Таким образом, оптимальное {по min VK) управление
с помощью изменения углов атаки и крена не имеет сущест¬
венных преимуществ по сравнению с управлением посредст¬
вом одного лишь угла крена. Это важный результат, ибо
при решении задачи о выборе типа КА можно рассмат¬
ривать только управление эффективным качеством, что
существенно проще с точки зрения получения численных
результатов для различных конкретных форм КА.
§ 7.3. ОБЛАСТЬ ПРИМЕНИМОСТИ КА РАЗЛИЧНЫХ ТИПОВ
Общая тенденция развития космической техники, со¬
стоит в том, что реализация того или иного проекта с ис¬
пользованием принципиально новых технических средств
целесообразна лишь тогда, когда старые средства не удов¬
248
ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ
[ГЛ. 7
летворяют новым условиям и требованиям, и если воз-
можны альтернативные варианты решения одной и той же
задачи, то в большинстве случаев предпочтение отдается
более простому, надежному и отработанному, хотя этому
и предшествует всесторонний сравнительный анализ.
Отмеченные соображения следует иметь в виду при оконча¬
тельном выборе конкретного типа КА.
КА баллистического спуска. Это самый простой вид
спуска, реализуемый, как правило, на простых и хорошо
изученных аэродинамических формах, не требующих
сложных и громоздких систем управления. Но как было
показано в главе 2, посадка на поверхность Марса КА
баллистического типа возможна лишь при ограниченных
значениях нагрузки на лобовую поверхность. Так, при обе¬
спечении самых благоприятных условий баллистические
КА в состоянии погасить энергию за счет аэродинамиче¬
ского торможения лишь до скоростей У,. ^ 600 -г-
-ч- 750 м/сек (что соответствует числам Маха М ^ 2,5 -ч- 3,5)
при РХ<С 70 -ж 80 кг/м2. Такая малая нагрузка на лобо¬
вую поверхность далека от оптимального значения, оию-
шение /ппн//^ка получается существенно меньше, чем у КА
с большими значениями Рх. Увеличение массы полезного
груза, который требуется доставить на поверхность
Марса, приводит к принципиальным трудностям в созда¬
нии КА с малыми значениями Рх (и, следовательно, Ps).
Как известно, площадь миделя КА прямо связана с пло¬
щадью миделя ракеты-носителя, и, начиная с некоторого
значения Ps, единственным путем увеличения площади
миделя с целыо уменьшения Ps является создание всякого
рода раскрывающихся конструкций. Этот путь решения
задачи принципиально возможен, но при очень больших
массах КА становится нерациональным и требует перехо¬
да к КА, обладающим аэродинамической подъемной силой.
КА планирующего типа. Использование планирующих
КА позволяет удовлетворить многим условиям и требова¬
ниям, которые даже не рассматриваются при баллистиче¬
ском спуске. При этом эффективность их применения
в общем случае зависит от величины располагаемого аэро¬
динамического качества, которое используется для управ¬
ления.
Выше было выделено три характерных типа КА плани¬
рующего спуска: КА скользящего спуска, с несущим кор¬
§ 7.3] ОБЛАСТЬ ПРИМЕНИМОСТИ КА РАЗЛИЧНЫХ ТИПОВ 249
пусом и космический самолет. Каждый из них обладает
своими преимуществами и недостатками, различной сте¬
пенью экспериментальной и летной отработки и соответ¬
ственно различной сложностью реализации. Пока не су¬
ществует общих критериев сравнения таких аппаратов, и
заранее трудно отдать предпочтение какому-либо типу.
Определим границы применимости указанных типов
КА с точки зрения возможного диапазона реализуемых
нагрузок на лобовую поверхность. Для этого используем
данные, представленные на рис. 7.3 и 7.4. На рис. 7.3 по¬
казано влияние нагрузки на лобовую поверхность Ps и
Рис. 7.4, Зависимость минимальной конечной скорости и допустимой нагруз¬
ки на лобовую поверхность от максимального аэродинамического качества при
оптимальном управлении посредством изменения углов крена (сплошная ли¬
ния) и атаки (штриховая линия).
ограничения на глубину погружения КА /гдоп на скорость
в конце участка основного аэродинамического торможения
при оптимальном управлении по углу атаки и по углу кре¬
на. На рис. 7.4 приведены зависимости минимальной ко¬
нечной скорости VK min и допустимой нагрузки на лобовую
поверхность Р<$°п от величины располагаемого аэродинами¬
ческого качества при соответствующих ограничениях.
Величина Vl{ mjn увеличивается почти линейно с ростом Ps
и hR0U. При этом кривизна соответствующих кривых су¬
щественно увеличивается при переходе от КА самолет¬
ных форм к КА скользящего спуска. Например, при
ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТ!!! ОВАИИЯ 1ГЛ.
увеличении Ps с 200 до 800 кг/м2 FK1niu возрастает при¬
мерно на 260 м/сек для КА с А1ТШХ = 2,4 и на 500 м/сек
для КА с Арпах ~ 0,32. Характер зависимостей VKmia(Ps)u
Fк min (^доп) практически одинаков для обоих способов уп¬
равления.
Приведенные данные определяют однозначную зависи¬
мость между потребной величиной аэродинамического
качества, поставленными условиями по конечной скорости
FK и глубиной погружения /гдоп• Они позволяют, но край¬
ней мере в первом приближении, определить требуемый
тип КА. Рассмотрим этот вопрос подробнее.
Наибольший интерес представляет определение границ
применимости КА скользящего типа. Достоинства подоб¬
ных КА общепризнаиы, они находят широкое практиче¬
ское применение (КА типа «Союз», «Аполлон), «Викинг»),
по ним имеется большой объем теоретических и экспери¬
ментальных данных, а также накоплены результаты на¬
земных и летных испытаний. Однако реализовать спуск
тяжелых КА скользящего типа при больших нагрузках
на лобовую поверхность чрезвычайно затруднительно: при
оговоренных выше исходных условиях по конечной скоро¬
сти (FK< 600ч- 700 м/сек) область применения этого
типа аппаратов ограничена нагрузками на лобовую по¬
верхность порядка 500 ч- 600 кг/м2, (рис. 7.2, 7.4). Выдер¬
живание Ps в требуемых пределах для КА скользящего
типа в случае возрастания массы КА возможно, так же
как и для баллистических КА, путем создания разного
рода раскрывающихся устройств для увеличения площади
миделя SM, компенсирующего увеличение тк\- Это нелег¬
кая задача, и ее практическое решение может оказаться по
затратам и потребному объему отработки эквивалентным
разработке более перспективного типа КА с большим зна¬
чением аэродинамического качества (AIIlax > 1), па кото¬
рых существенно проще компонуются грузы большой .мас¬
сы и которые обладают новыми возможностями решения
других задач, помимо задачи мягкой посадки (см. гла¬
ву 6). Использование аппаратов с несущим корпусом уве¬
личивает область допустимых нагрузок па лобовую по¬
верхность (Р£оп), до 1000-.- 1100 кг/м2, а космические
самолеты расширяют диапазон Р§°П до 2000 2200 кг/ль2.
Особенно интересно рассмотреть применение различ¬
ных типов КА в зависимости от Ps, когда необходимо га-
§ 7.4] ВЫПОР ПРОЕКТПО-Г» АЛЛИСТИЧЕСКПХ ПАРАМЕТРОВ 251
хттеттие энергии па основном участке аэродинамического
торможения до дозвуковых скоростей (FK < 200 м/сек).
Данные рис. 7.3, 7.4 показывают, что это можно реализо¬
вать па КА скользящего типа при Р^т < 80 кг/м2; ко¬
смический самолет увеличивает Ря°п до 300 л- 400 кг/м2.
Следует иметь в виду, что представленные па рис. 6.15
аэродинамические характеристики справедливы только
для гипсрзвукового диапазона скоростей полета; при
уменьшении числа Маха аэродинамические характери¬
стики резко изменяются, особенно в районе критических
скоростей полета. 13 этом случае для КА с Ктах 1 ха¬
рактерно существенное возрастание величины аэродина¬
мического качества (до нескольких единиц). Однако
общий вид зависимостей, представленных на рис. 7.3, 7.4,
принципально не изменяется.
Хотя в некоторых случаях тип КА определяется одно¬
значно, часто он может быть выявлен лишь в результате
тщательного сравнительного анализа разных аппаратов,
способных обеспечить решение целевой задачи.
% 7.4. ВЫБОР ОСНОВНЫХ ПРОЕКТНО-БАЛЛИСТИЧЕСКИХ
ПАРАМЕТРОВ КА
Предположим, что тип КА известен. Даже при этом
условии задача выбора конкретной аэродинамической фор¬
мы чрезвычайно сложна. Чтобы приступить к ее решению,
необходимо задаться определенными предпосылками в от¬
ношении основных проектно-баллистических характери¬
стик, прежде всего по требуемой величине располагаемого
аэродинамического качества’ 7Грасп и нагрузке на лобовую
поверхность Р$. Чем больше у КА величина располагае¬
мого качества при прочих равных условиях, тем больше
возможностей реализовать оптимальную траекторию сни¬
жения и поэтому меньше затраты па организацию мягкой
посадки. Однако это пожелание реализовать очень слож¬
но. Наибольший интерес представляет задача определения
минимально необходимого значения аэродинамического
качества (Kvacn)min, позволяющего обеспечить приемлемое
решение целевой задачи с учетом всех ограничений и не¬
обходимых предпосылок. В рассматриваемом случае —
это обеспечение необходимой скорости в конце участка
252 ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ [ГЛ.
основного аэродинамического торможения. При оконча
тельном выборе аэродинамической формы КА, позволяю
щей реализовать то или иное значение i£pacn, решают
целый комплекс дополнительных задач, куда входят тепло
вые, компоновочные, динамические и многие другие воп¬
росы. Но (Z£pacn)min является той основной характери-
стикой, которая всегда принимается во внимание. Обычно
(i£pacn)mm не превышает максимального значения аэроди¬
намического качества, которое можно получить при вы¬
бранной форме КА. Это особенно характерно для КА, уп¬
равляемых эффективным качеством, когда соответствую¬
щей балансировкой на угле атаки а = ао обеспечивают
Кб = ( K.tq асп) mi п •
Прежде чем перейти к описанию методики выбора
(A’pacn)min, остановимся кратко на втором основном про¬
ектно-баллистическом параметре — нагрузке на лобовую
поверхность Ps. При спуске в атмосфере Земли абсолют¬
ная величина Ps не играет, по крайней мере с баллисти¬
ческой точки зрения, особого значения. Иначе обстоит
дело при рассмотрении задачи спуска в атмосфере Марса.
С увеличением Ps возрастает конечная скорость Ук при
прочих равных условиях. В этом смысле желательно иметь
возможно меньшее значение Ps- Однако последнее требо¬
вание, как уже отмечалось, связано с рядом существенных
ограничений, которые имеют место при создании КА: оп¬
ределенная величина диаметра миделевого сечения КА,
возможная величина выводимого полезного груза, конст¬
руктивные возможности проектирования КА и ряд других.
Все это требует дополнительных комплексных исследо¬
ваний, выходящих за рамки получения исходных пред¬
посылок для проектирования КА. Главным является то,
что при спуске в атмосфере Марса задачу о минимальном
потребном значении (К])1ХСП)т[]Х нельзя решать в отрыве от
возможной нагрузки па лобовую поверхность. При этом,
если известна масса КА и возможный диаметр миделе¬
вого сечения, то с баллистической точки зрения следует
выбирать такую форму, которая обеспечивает максималь¬
ное значение коэффициента лобового сопротивления при
прочих равных условиях.
Проведенные исследования показывают, что при фик¬
сированном значении приведенной нагрузки на лобовую
поверхность (РА) увеличение аэродинамического каче¬
§ 7.4] ВЫБОР ШЮЕКТЫО-БАЛЛИСТИЧЕСКИХ ПАРАМЕТРОВ 253
ства ведет к уменьшению величины конечной скорости Ук.
С другой стороны, при фиксированном значении рас¬
полагаемого качества уменьшение Рх ведет также к
уменьшению VK. Такая зависимость У,. от Рх и Kvacn на¬
водит на мысль о существовании некоторого оптимального
сочетания величин Рх и Kvacn для аппарата определенной
формы при заданной массе и площади миделевого сечения.
Очевидно, что при определенном значении Ps оптимальное
сочетание следует определять для Сх и Къ. Численные
исследования позволили выявить указанные закономер¬
ности. В результате была определена (рис. 7.5) расчетная
. лтеор
L>x
Рис. 7.5. Теоретическая зависимость между приведенным коэффициентом
лобового сопротивления С^00^ и величиной аэродинамического качества Хд60р
обеспечивающая равные значения конечной скорости Ук для КА с одинако¬
выми значениями Рх и при прочих равных условиях (управление с изменением
угла крена; /гДОп = 6 км> ^к = 6 км).
зависимость между величиной располагаемого качества
и коэффициентом лобового сопротивления K}fov(C™°v),
соответствующая равным скоростям Ук для КА с одина¬
ковыми значениями Ps и при прочих равных условиях.
Построена она следующим образом. За исходное значе¬
ние аэродинамического качества берется величина ЛГоо°Р =
= 0,3; значение коэффициента лобового сопротивления Сх
254 ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ [ГЛ. 7
можно принять любой величины. Для простоты рассужде¬
ний примем Схо°р = 1. Увеличивая или уменьшая К1°(ц\
определяем значение СхРор из условия сохранения неизмен¬
ной величины конечной скорости У,., достигнутой при ис¬
ходных значениях Къо°р = 0,3 и СДо'01* = 1. Как и следовало
ожидать, при увеличении КГ)Сор выполнение этого условии
достигается уменьшением СД001\ и наоборот. Например, при
увеличении Kl°ov до 0,5 требуется уменьшение СДоор при¬
мерно до 0,82. Необходимо отметить, что указанная за¬
висимость K™°v (СГР) слабо зависит от нагрузки на ло¬
бовую поверхность в диапазоне Ps = 200 -f- 500 кг/м2,
а также от ограничения по ^доп и от высоты окончания
участка основного аэродинамического торможения hK.
Для дальнейших исследований можно принять некоторую
среднюю расчетную зависимость. При этом будем рассмат¬
ривать не конкретное значение СДор, соответствующее
взятому /£ое°р, а отношение коэффициента лобового сопро¬
тивления при выбранном значении Ag°°p к значению СД0при
Кб о = 0,3, которое обозначим через £Деор. Это удобно
для проведения сравнительного анализа различных аэро¬
динамических форм.
Перейдем к анализу подобных зависимостей для КА
некоторых форм (рис. 7.6). С баллистической точки зре¬
ния уменьшать или увеличивать располагаемое значение
качества сверх 0,3__целесообразно только в том случае,
если зависимость Сх (К<-,) для данного КА лежит выше
соответствующей расчетной зависимости, так как в этом
случае может быть уменьшена величина F,.. Вывод спра¬
ведлив для любых КА, управляемых но углу крепа и осу¬
ществляющих спуск в разреженной атмосфере Марса.
В результате анализа зависимостей С... (Кб) для боль¬
шого числа возможных аэродинамических форм, по каж¬
дому из рассматриваемых типов КА, выявлены сле¬
дующие основные закономерности (см. рис. 7.6 и табл. 7.1):
— практически для всех реальных форм: КА скользя¬
щего типа фактическая кривая Сл. (Кс) лежит ниже рас¬
четной зависимости СДеор (АТ°Р), очень незначительно от¬
личаясь от нее в диапазоне Кб = 0,2 -г- 0,4, в котором и
следует искать реализуемое оптимальное значение;
§ 7.4] ВЫБОР ПРОЕКТНО-БАЛЛИСТИЧЕСКИХ ПАРАМЕТРОВ
255
— для любых форм КА с большим значением аэроди¬
намического качества (Amax 1) только в диапазоне
Кб » 0,3 -г- 0,6 кривые С х (Кб) проходят несколько вы¬
ше расчетной кривой, а при Кб 0,5 -г- 0,6 расположены
ниже, резко расходясь с пей при Кб 0,6 ч- 0,8.
Отсюда вытекает целесообразность поиска рациональ¬
ного значения (Kvacn)min, обеспечивающего посадку КА без
C.xz
к
О 0,0 0,8 1,1 ю /Г5
Рис. 7.6. Приведенный коэффициент лобового сопротивления для реальных
аэродинамических форм КА (управление эффективным качеством). (1 — сред¬
няя теоретическая кривая С*"0'1 (.К(зс0р); 2 — плоская пластина; з — космиче¬
ский самолет (КШах = 2>4); 4 — КА с несущим корпусом (Жтах = 1,5). Лобо¬
вой экран в виде: 5 — сегмента с углом 60°; в — конуса с углом 60°; 7 — сег¬
мента с углом 70°; 8 — конуса с углом 70°.)
ущерба в достижении целевой задачи. Особенно актуаль¬
ное значение этот вопрос приобретает для КА скользя¬
щего типа, так как для них проще всего реализовать мини¬
мальные значения аэродинамического качества при балан¬
сировке КА любым возможным способом. Действительно,
при балансировке за счет несимметрии массы требуется
минимальная величина смещения центра масс КА отно¬
сительно продольной оси, при аэродинамической балан¬
сировке — минимальный угол разворота лобового экра¬
на. Например, величина Кб = 0,2 реализуется при ба¬
лансировке КА па угле ао = —18°, а Кб = 0,3 — на
256 ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ ГГЛ. 7
а = —28° (см. рис. 6.15), или соответственно разворотом
лобового экрана на угол 2 -ч- 6° для Kq = 0,2 и 5 --г- 10°
для К§ = 0,3 (рис. 7.7).
Проведем сравнение двух аппаратов одинаковой массы,
габаритов и форм, отличающихся величиной располагае¬
мого аэродинамического качества: Кб = Kvасп = 0,2 и
Кб = 0,3. Будем предполагать, что аэродинамическое
h
^pacn)min
7]. град
Рис. 7.7. Балансировочное значение аэродинамического качества при разных
углах г) разворота лобового экрана и требуемое минимальное значение каче¬
ства в зависимости от приведенной нагрузки на лобовую поверхность.
качество обеспечивается разворотом лобового экрана на
соответствующий угол т) (см. рис. 7.7). Для 60-градусного
конического (или сегментного) лобового экрана уменьше¬
ние Кб до 0,2 вызывает уменьшение приведенной на¬
грузки на лобовую поверхность (Px)Kq==0>2 == 0,91
(А,кб=0,3. Уменьшение качества до 0,2 приводит к увели¬
чению конечной скорости приблизительно на 10 м!сек.
Для гашения этой избыточной скорости активным путем
требуется 30 -ч- 50 кг топлива при ttzka ~ Ю т. Вместе
с тем уменьшение аэродинамического качества приводит
к уменьшению времени спуска и соответственно потребной
массы тепловой защиты. Действительно, для КА массой
10 т и диаметром миделя Dka ~ 5,0 м уменьшение каче¬
§ 7.4] ВЫБОР ПРОК КТ И О - Г. А Л ЛИ С, ТIIЧ F.CKIIX ПАРАМЕТРОВ 257
ства с 0,3 до 0,2 ведет к уменьшению потребного веса теп¬
ловой защиты более чем па 50 кг. Таким образом, полезная
масса па спускаемом КА остается без изменения, проис¬
ходит только перераспределение массы топлива для ак¬
тивного торможения и массы тепловой защиты,
В результате анализа представленного материала мож¬
но для КА скользящего типа ставить задачу о выборе ми¬
нимально необходимого значения аэродинамического ка¬
чества только из условия обеспечения заданного коридо¬
ра входа. И это значение будет близким к оптимальному
для каждой рассматриваемой формы. На рис. 7.7 приве¬
дена зависимость (ApaCn)mm от нагрузки на лобовую по¬
верхность при разной ширине коридоров входа. В частно¬
сти, при Ah~ ~ ±70 км необходимы следующие величины
располагаемого аэродинамического качества (/гдо п =
= hK = б км):
(^pacn)min > 0.2 при Рх > 300 -к- 359 кг/м2,
(Kvacn)min > ОД 7 при Рх > 150 ~~ 200 кг/м2.
Для аппаратов с большим значением максимального
аэродинамического качества (КА с несущим корпусом,
космический самолет) задача об определении (ifpacn)rnin
имеет определенную специфику. Дело заключается в том,
что при управлении по крепу подобные КА целесообразно
балансировать на углах атаки, превышающих углы, на
которых достигается Kmtlx. Это однозначно следует из
рассмотрения рис. 6.15 и 7.2, а объясняется тем, что при
меньших углах атаки (ао < (ас)ктлх) коэффициенты ло¬
бового сопротивления КА рассматриваемых форм имеют
сравнительно малые значения и оптимальное сочетание
и Сх обеспечивается при аб (ао)кшах» где значе¬
ния Сх достаточно велики при относительно малых значе¬
ниях Ко (см. табл. 7.1). Складывается такая ситуация, что
требование уменьшения ао приводит к увеличению Ко при
одновременном уменьшении Сх. При этом эффект влияния
Сх сказывается существеннее, что проявляется в увели¬
чении конечной скорости (см. рис. 7.2). Однако следует
иметь в виду два важных факта. Во-первых, для КА с
Ачпах 1 конечная скорость сравнительно слабо зависит
от а о в достаточно широком диапазоне его изменения
(рис. 7.2). Так, для КА с Kmflx — 2,4 изменение аб от 70
9 Н. М. Иванов, А. И. Мартынов
258 ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ [ГЛ. 7
до 50° приводит к возрастанию конечной скорости менее
чем на 40 м/сек. Во-вторых, и это очень существенно для
КА с Кта^^> 1, менее остро (по сравнению с КА сколь¬
зящего тина) стоит задача балансировки на больших уг¬
лах атаки, ибо появляется возможность использования
для этих целей всякого рода щитков и закрылков. Поэтому
для КА с большим значением аэродинамического качества
балансировочный угол атаки можно выбирать, исходя в ос¬
новном из требований устойчивости и компоновки КА.
§ 7.5. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КА
ИЗ УСЛОВИЯ МАКСИМУМА КОНЕЧНОЙ ВЫСОТЫ
Как было показано, использование парашютно-реак¬
тивной системы мягкой посадки КА предъявляет специ¬
фические требования к траектории спуска на участке аэро¬
динамического торможения. Особенность здесь состоит
в том, что главной целью при выборе управления на тра¬
ектории спуска является не уменьшение скорости до ми¬
нимального значения на некоторой конечной высоте (как
это требуется для системы активного торможения), а мак¬
симизация высоты hK, на которой скорость снижения не
должна превышать некоторого допустимого значения
Vк дои •
hj. максимальна (7-1)
при условии
Fk< Кндоп. (7.2)
Обеспечение (7.1) при условии (7.2) позволяет умень¬
шить потребные затраты массы на ПРС и создать наибо¬
лее благоприятные условия для ввода ее в работу (см.
главу 6).
Величина Ркд0п соответствует предельно допустимой
скорости ввода ПРС и определяется в основном теплофи¬
зическими свойствами материала, из которого изготов¬
ляется купол парашюта, а также условием наполняемости
купола и устойчивости системы аппарат-парашют. В на¬
стоящее время предельно допустимым значением скорости
раскрытия парашютной системы считается скорость FK Д0П)
соответствующая числу М ^ 3,5 [62]. На эту величину
Vк доц будем ориентироваться при анализе траекторий аэ¬
§ 7.5J
УСЛОВИЕ МАКСИМУМА КОНЕЧНОЙ ВЫСОТЫ
259
родинамического торможения КА с последующим исполь¬
зованием ПРС.
Итак, сформулируем следующую задачу: при заданных
начальных условиях (3.28), ограничениях на управление
(3.17) и фазовые координаты (3.25) требуется определить
такой закон управления эффективным качеством, при
котором функционал
I = h„ (7.3)
достигает максимума. На правом конце (tK = Т) парамет¬
ры траектории удовлетворяют следующим требованиям:
Vu = VK доп, 0К свободно, tK свободно. (7.4)
Сформулированная задача полностью эквивалентна
(по виду функционала, ограничениям на фазовые коорди¬
наты и управление, а также по уравнениям связи) задаче
о минимуме конечной скорости, рассмотренной в главе 6.
Для ее решения в принципе может быть использован тог
же подход и методика, что и для задачи об отыскании
оптимального управления из условия min VK.
Проведенные исследования показали, что задача о
min V1{ при hK /гдоп и задача о max hu при У,. — Укдоп
являются не только однотипными по форме их записи, но
и эквивалентными по структуре оптимального управления.
Остановимся на этом вопросе несколько подробнее.
Об эквивалентности задач максимизации
конечной высоты и минимизации конечной
скорости спуска
Численный анализ результатов решения задачи о ми¬
нимуме конечной скорости спуска показал (см. главу 6),
что для аппаратов с различными значениями аэродинами¬
ческого качества и приведенной нагрузки на лобовую по¬
верхность, а также для различных условий входа с увели¬
чением конечной высоты минимальная скорость спуска
монотонно увеличивается. Этим обстоятельством можно
воспользоваться для доказательства эквивалентности за¬
дач максимизации конечной высоты при ограничении
Т7!-£^УнДП1Т и минимизации конечной скорости при ог¬
раничении hn /?,. До,1*
Действительно, задаваясь последовательно различны^
ми значениями конечной высоты и решая задачу о миыг-
260
ЗАДАЧИ БАЛЛИСТИЧЕСКОГО П1 ОЕКТИГОВАШШ [ГЛ. 7
муме Ук, можно найти такую высоту на которой вели¬
чина минимальной конечной скорости спуска будет равна
допустимой скорости ввода ПРС: Ук mm = Укдоп. Учи¬
тывая характер зависимостей Ук шт (йн), можно утвер¬
ждать, что не существует никакой другой высоты hK ^> /г*,
на которой Ук min Ук доп- Отсюда следует, что /г* и есть
та искомая максимальная высота, на которой еще воз¬
можен ввод ПРС при ограничении на скорость ввода Ук ^
^ У к доп-
Итак, любая траектория максимальной конечной вы¬
соты может быть найдена в классе траекторий минималь¬
ной скорости спуска, что и доказывает эквивалентность обе¬
их задач. В этом случае становится ясной структура опти¬
мального управления. Как и для траекторий минимальной
конечной скорости, оптимальное управление может быть
двух типов: в
— одноразовое переключение эффективного качества
с .минимального значения Kt)ф —Ко на максимальное
Кэф - ] Ко (второй тип управления); в этом случае тра¬
ектория спуска, реализующая максимум конечной высоты,
лежит целиком внутри допустимой фазовой области, ог¬
раниченной минимально допустимой высотой пролета КА
над поверхностью Марс-а;
— одноразовое или двухразовое переключение К»ф на
участке выхода на ограничение, изменение К-Уф в соответ¬
ствии с (6.19) при движении по ограничению и сход с огра¬
ничения с максимальным положительным значением К
до получения конечной скорости Ун = Укдои (первый тип
управления).
В соответствии с отмеченным свойством неединствен¬
ности (см. главу 6) управление на участке выхода КА
на ограничение может отличаться от указанного выше.
Таким образом, как ив задаче min У,., траектории .мак¬
симальной конечной высоты, содержащие участок гори¬
зонтального полета, обладают свойством неединственно¬
сти, а величина максимальной высоты определяется .лишь
скоростью при сходе с ограничения.
Знание структуры оптимального управления КА сво¬
дит поставленную задачу оптимизации с критерием (7.1)
к достаточ но простой одно параметрической к раевой за¬
даче для системы дифференциальных уравнений (3.20),
УСЛОВИЕ МАКСИМУМА КОНЕЧНОЙ ВЫСОТЫ
261
решение которой заключается либо в определении момента
переключения эффективного качества с минимального
значения на максимальное (второй тип управления), либо
в определении оптимальной скорости при сходе с ограни¬
чения (первый тип управления).
Тип оптимального управления, как и для рассматри¬
вавшихся ранее траекторий минимальной конечной ско¬
рости, зависит от проектно-баллистических параметров
КА, начальных условий входа, минимально допустимой
высоты полета над поверхностью и от величины предель¬
ной скорости ввода ПРС.
Анализ оптимальных траекторий
Исследуем методом численного интегрирования4 опти¬
мальные траектории спуска, реализующие максимальную
высоту к моменту достижения заданной скорости ввода
парашютной системы. Будем рассматривать прежний диа¬
пазон (6.28) основных варьируемых параметров: V0, hn,
Рх, K<j. Величина скорости при вводепараппотпоисистемы
находится в пределах
500 м/сек ^ VK доп <1 850 м/сек,
и учитывается ограничение на максимальную глубину
погружения КА в атмосферу h йдоп-
Существенным этапом решения поставленной задачи
является предварительный анализ траекторий спуска
с целью определения возможного типа оптимального уп¬
равления. Признаком, но которому можно провести по¬
добную классификацию оптимальных траекторий, являет¬
ся сравнение минимальной высоты рикошета (/гтт) при
использовании программы одноразового переключения
Кэф без учета ограничения (3.25) с допустимой высотой
полета hKOn. Если 1гт-ил ;> /гДОп, то оптимальным является
второй тип управления; если же hmux <L hKon, то опти¬
мальным является первый тип управления. Проведение
такого предварительного анализа существенно упрощает
процедуру решения поставленной задачи в целом.
На рис. 7.8 представлены зависимости, показывающие
частное влияние каждого из варьируемых параметров
V0, /г-, Рх, Kq, Кдоп на глубину погружения КА в атмос¬
феру femin при использовании программы одноразового
262 ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ [ГЛ. 7
переключения КЭф с —Кб на JrKб. При этом рассматрива¬
лось движение iL4 как в наиболее разреженной атмосфере
(Р (h) = pmin)» так и в наиболее плотной (р (/7) = ртах).
Изменение любого из варьируемых параметров приводит
практически к линейному изменению величины hmin-
Aun 7км
Рис. 7.8. Минимальная высота пролета КА над поверхностью Марса при
использовании программы одноразового переключения.
С возрастанием скорости входа, приведенной нагрузки;
на лобовую поверхность, аэродинамического качества
и с уменьшением высоты условного перицентра, а также
с уменьшением допустимой скорости ввода парашютной
системы происходит уменьшение минимальной высоты,
В целом можно отметить, что даже при полети КА в на¬
иболее разреженной атмосфере минимальная высота /гш1г.
УСЛОВИЕ МАКСИМУМА КОНЕЧНОЙ ВЫСОТЫ
263
почти во всех случаях оказывается выше 2—3 км, Наи¬
большее влияние на величину /imin оказывают приведен¬
ная нагрузка на лобовую поверхность и аэродинамическое
качество КА, а наименьшее — высота условного пери¬
центра траектории входа и допустимая скорость ввода
парашютной системы.
Увеличение плотности атмосферы, как и следовало
ожидать, приводит к заметному увеличению hmin, но при
этом характер зависимости Amm от варьируемых парамет¬
ров остается таким же, как и для наиболее разреженной
атмосферы. Практически происходит только параллельное
смещение соответствующих кривых (см. рис. 7.8). В сред¬
нем возрастание минимальной высоты за счет перехода от
модели атмосферы с минимальной плотностью к модели
с максимальной плотностью составляет величину порядка
10—11 км.
Представленные данные позволяют легко определить
в каждом конкретном случае тип оптимальных траекторий
при заданной величине Адоп- В отличие от рассмотренной
ранее задачи минимизации конечной скорости спуска,
второй тип управления имеет более широкое распростра¬
нение на траекториях максимальной конечной высоты
и охватывает больший диапазон проектно-баллистических
параметров и начальных условий входа КА в атмосферу.
Весьма существенное влияние на выбор требуемого типа
оптимального управления оказывает величина принятого
ограничения на минимально допустимую высоту полета
КА. Так, для Адоп = 6 км при спуске КА, имеющего
Рх ^ 350 кг/м2 иЯб< 0,3, реализуется второй тип опти¬
мального управления (одноразовое переключение).
С уменьшением высоты Адоп до 2 км этот тип управления
возможен практически во всем диапазоне варьируемых
параметров (6.28).
Отметим, что поставленная экстремальная задача ре¬
шалась без учета ограничений, таких, как максимальная
перегрузка и угол наклона траектории к местному гори¬
зонту в конце участка аэродинамического торможения. Та¬
кой подход допустим, поскольку величина пх шах практи¬
чески не влияет на массу системы мягкой посадки, а величи¬
на 0К оказывает несущественное влияние на тЩ)с в опре¬
деленном диапазоне ее изменения (см. главу 5). Однако
знание этих параметров является весьма важным по другим
2G4
ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТ!!РОБАШШ [ГЛ. 7
причинам. Величина максимальной перегрузки определяет,
в частности, характеристики прочности конструкции КА,
а величина 0К оказывает существенное влияние на участок
мягкой посадки при использовании ПРС. В последнем
случае имеется в виду перепад высот за время введения
парашютной системы.
Следует отметить, что, кроме nxinixx и 0К, на выбор ха¬
рактеристик прочности парашюта большое влияние оказы¬
вает скоростной напор, который действует па КА в момент
раскрытия парашюта. При заданной скорости введения
парашютной системы траектория максимальной конеч¬
ной высоты обеспечивает минимальный скоростной на¬
пор min gK.
Рассмотрим влияние основных варьируемых парамет¬
ров (6.28) на величину максимальной конечной высоты,
обращая при этом внимание па характерные параметры
траектории пхmax, 0К, ql{. При этом будем считать, что
^доп = 6 КМ.
Влияние начальных условий входа КА. В дальнейшем,
для сокращения, величину конечной высоты, полученной
при оптимальном управлении из условия (7.1), будем обоз¬
начать через hK max- Величина максимальной конечной
высоты мало зависит от высоты условного перицентра тра¬
ектории входа: с увеличением 1г- внутри оперативного ко¬
ридора входа происходит незначительное уменьшение
шах (рис. 7.9). Увеличение начальной скорости входа
приводит к незначительному возрастанию /гкшах. Харак¬
тер зависимостей hl{ max (hT) и /г-к max(F0) остается неизмен¬
ным для разных моделей плотности атмосферы, по сама
величина hKinах существенно зависит от модели.
Сравнение величины /гк шах, рассчитанной для двух
предельных моделей атмосферы при оптимальном управ¬
лении, показывает, что увеличение плотности от мини¬
мальной до максимальной приводит к возрастанию hK шах
в среднем на 8-9 км. В целом можно отметить, что для рас¬
сматриваемого диапазона изменения V0 и h- максималь¬
ная высота лежит выше 12 км при минимальной плот¬
ности и выше 20 км при максимальной.
Данные рис. 7.10 показывают зависимость максималь¬
ной перегрузки от начальных условий входа па траекто¬
риях, реализующих hKmах. Видно, что с уменьшением 1гл
происходит незначительное возрастание максимальной
§ 7.5]
УСЛОВИЕ МАКСИМУМА КОПЕЙНОЙ ВЫСОТЫ
265
перегрузки. Так, при движении КА вблизи верхней гра¬
ницы коридора входа величина пхтах ^ 8, а вблизи
нижней ТЬХ щах 10. Изменение скорости входа оказы¬
вает существенное влияние на пх тах. В частности, воз¬
растание скорости входа от 5 до 8 км/сек приводит к
A шах»км
Атах^А^
'А гтшх(Адоп)
А шъ^Уо)
A max (К$)
A max (Адоп)
A max Уо)
A max
V0, км/сек
hfcKM
AL
Рх,кг/м2
550 700 m BOO 853 м/сек
Рис. 7.9. Максимальная конечная высота при оптимальном управлении.
увеличению максимальной перегрузки от 6,2 до 17,8 при
минимальной плотности атмосферы.
Частное влияние начальных условий входа (V0 и hT) на
величину (),. показано на рис. 7.11. Видно, что зависи¬
мости 0К (F0) и 0,. (h-) имеют явно выраженный нелиней¬
ный характер. При увеличении скорости входа до V0 ж
6 км!сек происходит незначительное возрастание
| 0К |, а при дальнейшем увеличении скорости входа угол
О,, уменьшается по абсолютной величине. Вариация h-
приводит к однозначному изменению 0Н — с увеличением
h- конечный угол по модулю возрастает, В целом можно
66
ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ
ГГЛ. 7
отметить, что для всего рассматриваемого диапазона У0 и
hn величина 0К мала и составляет примерно —5 -4 9°.
Таким образом, начальные условия оказывают несу¬
щественное влияние на основные параметры оптимальной
Ях mix
Рис. 7.10. Максимальная перегрузка на траекториях, реализующих hl{ тах.
траектории с критерием hl<maxj за исключением зависимо-
СТИ Пх max (F0).
Влияние основных проектно-баллистических характе¬
ристик КА. Заметное влияние на максимальную конечную
высоту оказывает изменение величины приведенной на¬
грузки на лобовую поверхность и аэродинамического ка¬
чества КА. При этом увеличение Ко (и уменьшение Р^)
УСЛОВИЕ МАКСИМУМА КОНЕЧНОЙ ВЫСОТЫ
267
приводит к возрастанию /гктах и соответственно к умень¬
шению скоростного напора <7К. Так, при изменении аэро¬
динамического качества от Кб = 0,3 до 0,5 (модель мини¬
мальной плотности атмосферы) величина /гктах увеличи¬
вается с 13,5 до 20,6 км, а скоростной напор уменьшается
со 108 до 46 кг/м2. При уменьшении нагрузки на лобову7о
$к,град
Рис. 7.11. Конечный угол наклона траектории на траекториях, реализующих
max-
ПОВерХНОСТЬ Рх от 350 до 200 кг/м2 величина Ак:шах
увеличивается с 13,5 до 19,9 км (см. рис. 7.9), а скорост¬
ной напор уменьшается со 108 до 62 кгс/м2 (рис. 7.12).
При изменении плотности атмосферы характер влияния
Рх и Kq на hK шах остается неизменным, но величина
max существенно зависит от р (h). Увеличение плотно¬
268 ЗАДАЧИ БАЛЛИСТИЧЕСКОГО ПРОЕКТИРОВАНИЯ [ГЛ. 7
сти от р (h) = pmiii до р (h) = ртах приводит к возраста-
нию hK шах на 10 ч- 15 км (рис. 7.9).
Влияние параметров Рх и Кб на характеристики тра¬
ектории спуска 71 хmax и 0К проявляется менее заметно.
Так, при варьировании Рх и Кб в диапазоне (6.28) макси¬
мальная перегрузка изменяется в пределах 7,5 ч- 10,5,
Ск,кгс/у2
Рис. 7.12. Скоростной напор на траекториях, реализующих 7iK max. (Сплош¬
ная линия — р = Pmjm штриховая — р = Pjnax-)
а конечный угол наклона траектории составляет | 0Г | ^
ж 5,5 ч- 9,6°.
Влияние допустимой скорости введения парашютной
системы (Пкдоп). При увеличении 7кД0п происходит
возрастание hKmах и уменьшение wvmaxH| 0К | (рис. 7.9—
7.12). Интересно отметить, что величина скоростного на¬
пора в котщс траектории максимальной конечной высоты
УСЛОВИИ МАКСИМУМА КОНЕЧНОЙ ВЫСОТЫ
практически не зависит от изменения конечной скорости
у Д()Г1. Это объясняется тем, что с увеличением скорости
Гкдоп одновременно происходит возрастание максималь¬
ной высоты. Поэтому ожидаемое увеличение скоростного
напора за счет возрастания КкД(Ш компенсируется его
уменьшением, вызванным возрастанием
Представленные численные результаты расчетов оп¬
тимальных траекторий по критерию max /гк показыва¬
ют, что во всем диапазоне варьируемых параметров (6.28)
имеет место достаточный запас по высотам для работы IIPC
при сравнительно небольших значениях скоростного на¬
пора. Действительно, даже для наиболее разреженной ат¬
мосферы /гк Ш,1Х ^ 7 л- 8 км, a qK </ 120 -л 150 кгс/м1.
Максимальная перегрузка не превышает /гЛ1П1Х = 15 л
18, а величина конечного угла наклона траектории
к местному горизонту .мала и составляет примерно —5 л
л 9°. Последнее обстоятельство очень важно/ ибо
отсюда следует, что найденные оптимальные траектории
из условия max /гк одновременно в значительной степени
удовлетворяют и другому важному условию — миними¬
зации модуля угла наклона траектории к местному гори¬
зонту, что позволяет получить некоторый выигрыш в массе
СМП и, кроме того, уменьшить величину перепада высот
но траектории в процессе раскрытия парашютной системы.
ГЛАВА 8
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
§ 8.1. ПОСТАНОВКА ЗАДАЧИ. ПРИНЦИП
ГАРАНТИРУЮЩЕГО УПРАВЛЕНИЯ
Обсуждение проблемы. Первоочередная задача управ¬
ления на участке основного аэродинамического торможе¬
ния заключается в обеспечении наилучших условий рабо¬
ты СМП с минимальными затратами массы.
Техническую проблему конструирования оптималь¬
ного (или по крайней мере рационального) управления КА
обычно решают в два этапа. На первом этапе выбирается
номинальная (расчетная) траектория, удовлетворяю¬
щая поставленным требованиям, и определяется соответ¬
ствующее управление. На втором этапе осуществляется
синтез алгоритма управления, использование которого поз¬
воляет парировать действия возмущений и обеспечивать
движение вблизи расчетной траектории.
При выборе номинальных траекторий руководствуются
самыми различными соображениями (простота и рациональ¬
ность, оптимальность и возможность реализации и т. п.).
Естественно, наиболее желательными являются оптималь¬
ные номинальные траектории. В предыдущих главах
было найдено оптимальное управление спуском КА из
условия минимума массы СМП. Для решения этой задачи
принимался ряд упрощающих предположений: аэродина¬
мические силы, действующие на КА, считались известны¬
ми и вполне определенными функциями фазовых коорди¬
нат КА (скорости и высоты полета); начальные значения
фазовых координат принимались строго фиксированными;
масса и размеры КА считались заданными и неизменными
величинами и т. д. Кроме того, определенные допущения
вносились и в схему движения: не принимались во вни¬
мание малые силы, а также не учитывались некоторые сте¬
пени свободы.
£ 8.1] ПРИНЦИП ГАРАНТИРУЮЩЕГО УПРАВЛЕНИЯ 271
Подобные упрощения невозможны на втором этапе син¬
теза управления. Реальное движение КА обычно про¬
исходит в условиях, существенно отличающихся от тех,
которые были приняты при расчете номинального движе¬
ния. В общем случае КА, совершающий спуск в атмосфере,
не будет двигаться вдоль расчетной оптимальной траек¬
тории. И если не совершать коррекции номинального уп¬
равления, то реальное движение может заметно отличать¬
ся от расчетного и цель управления не будет достигнута.
Так возникает проблема синтеза алгоритмов управления,
использование которых в системе управления спуском при
определенном уровне возмущающих воздействий обеспе¬
чивало бы достижение поставленной цели управления —
безопасной мягкой посадки на поверхность планеты.
Предположим, что номинальная (и при этом опти¬
мальная) траектория спуска КА задана, но в силу каких-
то причин (например, действующих на КА возмущений)
траектория спуска оказалась отличающейся от расчетной.
Принципиально возможны два основных способа управ¬
ления движением КА:
— управление относительно номинальной траектории,
в результате которого устраняются текущие отклонения
параметров траектории от расчетных;
— управление конечным состоянием (терминальное
управление), направленное на устранение отклонений от
требуемого состояния только в конечной точке траектории
^ При этом выбор конкретного способа управления опре¬
деляется физическими особенностями оптимальной тра¬
ектории снижения КА, конечной целью управления и
технической реализуемостью предлагаемой схемы управ¬
ления. Существует много различных методов и приемов
конструирования алгоритмов, которые можно классифи¬
цировать по некоторым общим признакам. Прежде всего
рассмотрим общую схему функционирования системы
управления спуском (рис. 8.1), в состав которой входят
в общем случае чувствительные элементы, преобразую¬
щие устройства и исполнительные органы.
С помощью чувствительных элементов вырабатывается
информация о векторе состояния КА. В зависимости от
способа установки чувствительных элементов на борту КА
различают алгоритмы управления, использующие по¬
казания датчиков, определенным образом ориентирован¬
272
АЛГОРИТМЫ УП 1»А 13ЛГЛТИЯ СПУСКОМ
[ГЛ. 8
ных в инерциальном пространстве, или, напротив, жестко
связанных с корпусом КА.
В первом случае могут быть использованы показания
акселерометров, установленных на гиростабилизирован-
ной платформе таким образом, чтобы их оси чувствитель¬
ности образовывали прямоугольную систему координат,
сохраняющую заданное положение в инерциальном про¬
странстве во время движения КА. При этом точность ори¬
ентации осей чувствительности акселерометров может
Гис. 8.1. Общая схема системы управления спуском.
быть достаточно высокой и определяется в основном ско¬
ростью ухода гироскопов.
Во втором случае наиболее доступным средством по¬
лучения информации является измерение перегрузки (со¬
ответственно интегралов от перегрузки и производных)
с помощью акселерометра, жестко связанного с корпу¬
сом КА.
Преобразующие устройства в соответствии с выдавае¬
мой чувствительными элементами информацией и исполь¬
зуемым алгоритмом управления вырабатывают командное
управление.
Сигналы управления, вырабатываемые в преобразую¬
щих устройствах, поступают па устройства управления
исполнительными органами. Па современных КА сколь¬
зящего типа в качестве исполнительных органов исполь¬
зуются реактивные двигатели, осуществляющие угловой
разворот КА в пространстве для управления величиной
и направлением эффективной составляющей аэродинами¬
ческой силы. В зависимости от того, каким образом осу¬
ществляется реализация опорной траектории (запоии
5 S.1I ПРИНЦИП ГАРАНТИРУЮЩЕГО УПРАВЛЕНИЯ 273
пасмой на борту КА или прогнозируемой), различают
а л гор ит мы, предполагаю щи е:
— непрерывное управление относительно расчетной
траектории;
— дискретное корректирование траектории в некото¬
рых характерных точках.
В настоящее время имеется большое количество работ,
посвященных синтезу автономных алгоритмов управления
спуском КА в атмосфере Земли. Подробный обзор совре¬
менного состояния этой проблемы можно найти в книге
Д. Е. Охоцимского, 10. Ф. Голубева и Ю. Г. Сихарулид¬
зе [701. Опыт, накопленный при разработке алгоритмов
управления КА, осуществляющих спуск в атмосфере Зем¬
ли, бесспорно, облегчает задачу синтеза алгоритмов уп¬
равления спуском КА в атмосфере Марса, хотя приме¬
нение разработанных алгоритмов без соответствующих
изменений, конечно, невозможно в подавляющем боль¬
шинстве случаев из-за специфических марсианских ус¬
ловий.
Используемая модель возмущений. Основные возмуще¬
ния, действующие на КА в процессе спуска, можно разбить
па четыре основные группы.
1. Возмущения по начальным условиям входа: ошибки
определения высоты условного перицентра (или соответ¬
ственно угла входа), скорости входа, координат начальной
точки, времени входа.
2. Возмущения, вызванные неточным знанием аэроди¬
намических и конструктивных параметров КА: коорди¬
нат положения центра масс, аэродинамических коэффици¬
ентов Сх и Су, площади миделевого сечения Sм, массы КА
и т. д.
3. Возмущения, возникающие в результате неточного
знания характеристик атмосферы и в первую очередь не¬
точного знания зависимости плотности от высоты, турбу¬
лентности атмосферы и др.
4. Приборные ошибки: погрешности чувствительных
элементов, средств обработки информации, исполнитель¬
ных органов и т. п.
Как обычно, при синтезе алгоритмов стремятся полу¬
чить как можно более точную информацию о возможном
характере и диапазоне изменения возмущающих воздей¬
ствий. Для этого необходимо иметь достаточно ясное
274 АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ [ГЛ. 8
представление об их физической природе, что позволяет
во многих случаях построить определенную модель воз¬
мущений.
Возмущения по начальным условиям входа опреде¬
ляются точностью работы систем наземной или авто¬
номной навигации (см. главу 2). При проведении исследо¬
ваний можно принимать предельные ошибки по высоте ус¬
ловного перицентра не превышающими + (50 70) км,
по скорости входа порядка 3 -г 5 м/сек и по времени
подлета к плотным слоям атмосферы Марса At ^ 60 л-
-f- 100 сек при нормальном законе распределения этих
параметров. Использование систем автономной навига¬
ции позволяет увеличить точность определения началь¬
ных условий входа и прежде всего А/г"ав в несколько
раз [6]. Возмущения, вызванные неточным знанием
аэродинамических и конструктивных параметров КА,
для упрощения методики их моделирования целесо¬
образно привести к возмущениям двух основных проект¬
но-баллистических характеристик КА — приведенной
нагрузки на лобовую поверхность и аэродинамичес¬
кого качества. При этом считается, что отклонения па¬
раметров Рх и Kq от номинального значения носят случай¬
ный характер с нормальным законом распределения и они
статистически независимы. Максимальная величина от¬
клонений Рх и Къ не превышает 20%.
Из всех атмосферных возмущений, влияющих на ди¬
намику спуска, в первую очередь учитываются отклоне¬
ния плотности атмосферы от расчетных значений и ветер.
Они имеют случайный и неопределенный характер. Если
для Земли удалось построить достаточно верную матема¬
тическую модель вариаций плотности атмосферы и ветра
[70], в основу которой положены данные многолетних
исследований атмосферы с помощью высотного зондиро¬
вания ракетами и на основе результатов обработки тра¬
екторий спуска КА, то для атмосферы Марса подобных
данных в настоящее время пет. Существуют только оцен¬
ки предельных границ возможных отклонений парамет¬
ров атмосферы от некоторого номинального значения.
Характер поведения параметров атмосферы между этими
границами неизвестен. В силу этого в качестве примера
использовался предельный способ задания атмосферных
возмущений плотности в виде периодических скачков
$8<1] ПРИНЦИП ГАРАНТИРУЮЩЕГО УПРАВЛЕНИЯ
между максимальной и минимальной величиной (так на-
зываехмая «змейка»). Частота скачков плотности опреде¬
ляется шагом по времени Д/.ш, который в свою очередь
варьируется в пределах от 15 до 120 сек.
Приборные ошибки определяются главным образом
ошибками элементов системы управления спуском, приво¬
дящими к отклонению управляющей аэродинамической
подъемной силы от расчетного значения. В соответствии
с описанной выше структурой построения системы (см.
рис. 8.1) к ним будем относить: ошибки чувствительных
элементов, преобразующих устройств и исполнитель¬
ных органов. Анализ причин возникновения этих оши¬
бок достаточно подробно рассмотрен, например, в ра¬
боте [78].
Подавляющее большинство возмущений носит случай¬
ный характер. Вместе с тем их статистические характери¬
стики не всегда известны достаточно полно (особенно это
относится к атмосферным возмущениям), что заставляет
делать дополнительные предположения о характере недо¬
стающих данных. В различных исследованиях исполь¬
зуется та или иная методика задания возмущений [78, 54,
55]. Наиболее общее представление возмущений дости¬
гается при использовании канонических разложений. Ис¬
пользуя каноническое представление случайной функции,
в качестве которой следует рассматривать действующее
возмущение, можно записать для нее следующее выраже¬
ние [80]:
.г/) ,гы) ..(/). (8.1)
Здесь A* (t) —математическое ожидание случайной
функции A(t); а,} —некоррелированные случайные ве¬
личины, математические ожидания которых равны нулю,
называемые коэффициентами канонического разложения;
A.j (t) — некоторые (не случайные) функции, называемые
координатными функциями канонического разложения;
t — выбранный аргумент. Отдельные слагаемые вида
(t) представляют собой некоррелированные элемен¬
тарные случайные функции. В общем случае канонические
разложения дают бесконечный ряд. При практическом
исследовании число членов этого ряда ограничивают
конечным числом.
276
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
Во многих случаях исследования ведутся при еще более
упрощенных схемах задания возмущений. В частности,
в настоящих исследованиях моделирование движения КА
проводилось при следующих представлениях возмущений
(кроме возмущения по плотности):
где Аь —номинальное значение параметра (здесь и далее
в настоящей главе чертой обозначаются поминальные зна¬
чения параметров), ДЛгшах —максимальная величина
ожидаемого отклонения соответствующего параметра от
номинального значения, ах — случайная величина с оп¬
ределенным законом распределения и нулевым матема¬
тическим ожиданием, р — число возмущений. Принима¬
ется допущение о независимости действия возмущений,
т. е. величин ах.
Обычно описание случайного процесса А (I) основы¬
вается на экспериментальных данных и сведениях, ко¬
торые не всегда являются вполне достоверными. И все же
указанное представление возмущений в виде (8.2) оказы¬
вается достаточным для синтеза падежной системы уп¬
равления спуском, что подтверждают результаты летных
испытаний КА типа «Союз», «Зонд», «Аполлон» и др. Вме¬
сте с тем это приводит к тому, что в правые части диффе¬
ренциальных уравнений движения возмущения войдут
в виде случайных величин (а не функций), и это суще¬
ственно упрощает исследование. В этом случае уравнения
возмущенного движения КА в атмосфере можно записать
в следующем общем виде:
(0 = f i (К • • • 1 ^T>ni ^1?* • • йАг> А\^А^» • • , Ар),
ГДе £ij £2» • • •> £п — координаты фазового вектора £;
Щу • • •> ип — координаты вектора управления и;
А и А21 . . ., Ар — координаты вектора возмущения А ;
t — аргумент, в качестве которого можно использовать
любой удобный параметр траектории (например, время,
высоту, кажущуюся скорость, их комбинацию и т. д.).
Особенности спуска КА в атмосфере Марса. Анализ
оптимальных траекторий спуска КА в атмосфере Марса
показал (глава 6), что независимо от вида СМП, исполь¬
I max
(I = 1,2, . . р), (8.2)
ПI И11ЦИП ГА I ’AITTIT. V V ЮЩГ.ГО УП ГАПЛ EI111 Я
зуемой для окончательного гашения скорости спуска КА
после прохождения участка основного аэродинамического
торможения, структура оптимальных траекторий спуска
в атмосфере имеет одинаковый вид. Это позволяет при
управлении конечной скоростью и конечной высотой при¬
менять одинаковые принципы построения алгоритмов.
Для определенности, в дальнейшем основное внимание
будет уделено синтезу алгоритмов управления конечной
скоростью спуска КА. Без каких-либо принципиальных
изменений они могут быть использованы при синтезе ал¬
горитмов управления конечной высотой.
Отметим некоторые] особенности, которые необходимо
учитывать при синтезе алгоритмов управления спуском
КА в разреженной атмосфере Марса. Первая особенность
заключается в том, что нормальная работа реактивной
СМП будет обеспечена только в том случае, если после
прохождения основного участка аэродинамического тор¬
можения на определенной высоте (/гк) аппарат будет иметь
скорость (17к), не превышающую заданного значения
(Vк ;!ад), на гашение которой рассчитывается СМП:
Гк<БНЗад, (8.4)
т. е. скорость в конце участка основного аэродинамического
торможения ограничивается только сверху. Конечная
скорость не может превышать Ук лад, так как это привело
бы к невозможности обеспечения мягкой посадки. С Дру¬
гой стороны, если в силу каких-то причин окажется, что
Ук Ук зад, то это не даст какого-либо ощутимого вы¬
игрыша. Действительно, можно предположить такую си¬
туацию, что в каком-то единичном конкретном случае
требуемая масса тсш[ существенно меньше заложенной
в реализацию (из расчета Ук = УКгтд)- Практическое
использование образовавшихся излишков массы топ¬
лива представляется проблематичным, ибо все расчеты
делаются в предположении возможного случая Ук =
^ VK зад. (Еще более убедительно это рассуждение вы¬
глядит для парашютно-реактивной системы.)
Итак, конкретная величина Ук лад в значительной сте¬
пени определяет массу СМП, и в силу этого весьма важным
является выбор ее значения.
Как известно, наихудшие условия при гашении энер¬
гии КА с помощью аэродинамических сил соответствуют
278
АЛГОI'll!МЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
случаю спуска в наиболее разреженной атмосфере (мини¬
мальная модель плотности атмосферы). Наименьшая воз¬
можная для этой атмосферы скорость спуска (V’i'-min) Д-J я
КА с заданными характеристиками будет обеспечена,
естественно, при оптимальном управлении (см. главу 6).
Если расчет системы посадки производится из условия
обеспечения мягкой посадки даже в самой неблагоприят¬
ной ситуации, то задаваемая величина конечной скорости
(V к зад) должна быть больше или по крайней мере равна
Иктш- Будем исходить из необходимости обеспечения
посадки в самой разреженной атмосфере и ориентироваться
на величину конечной скорости (У* min)» полученной
в этих условиях:
V — У* •
V к зад — У к min*
Выше было показано, что оптимальной траекторией
спуска, реализующей Ук т-пи является траектория рико¬
шетирующего типа, причем с уменьшением минимально
допустимой высоты начала рикошета (^доп), как правило,
происходит уменьшение Ук injn. Этим обстоятельством
можно было бы воспользоваться для уменьшения Ук min
и соответственно массы СМИ, однако оно вступает в про¬
тиворечие с требованием обеспечения наибольшей безо¬
пасности полета КА, поскольку имеется большая неопре¬
деленность в знании рельефа поверхности Марса.
С учетом этих противоречивых требований определяет¬
ся компромиссное значение Лдоп и соответственно У* min,
т. е. Ук зад- Для повышения безопасности спуска управ-
ление конечной скоростью должно быть организовано так,
чтобы высота начала рикошета траектории над поверх¬
ностью Марса была максимальна:
max hiahl (8.5)
при выполнении условия (8.4).
Таким образом, одна из основных особенностей, кото¬
рую необходимо учитывать при синтезе алгоритма управ¬
ления конечной скоростью, заключается в том, что при
снижении КА в атмосфере алгоритм управления должен
обеспечивать величину конечной скорости, не превышаю¬
щую заданного значения Ук УКЗад пРи максимально
возможном значении hinia.
^ 8>1J ПРИНЦИП ГАРАНТИРУЮЩЕГО УПРАВЛЕНИЯ 279
Второй особенностью, которую необходимо учитывать
при синтезе алгоритмов управления, является тот факт,
что среди всех рассмотренных возмущений имеется но
крайней мере один вид случайных возмущений — вариа¬
ции плотности атмосферы — отличающийся своей неопре¬
деленностью.
Принцип гарантирующего управления. Можно ука¬
зать два наиболее целесообразных пути решения рассмат¬
риваемой задачи. Один из них связан с идеей адаптации.
Во время движения КА в атмосфере Марса можно получить
некоторую информацию о структуре случайного процесса,
выявить основные возмущения, прежде всего атмосфер¬
ные. Таким образом, априорная информация о возмуще¬
ниях, полученная в результате предварительных теорети¬
ческих и экспериментальных исследований, уточняется на
борту КА в процессе его спуска в атмосфере. Эта инфор¬
мация может быть использована в алгоритме управления,
тем самым осуществляется адаптация управления к ок¬
ружающим условиям.
Идея адаптации в настоящее время очень популярна и
находит все большее применение в теории управления
движением КА [70, 78, 90]. В случае полной адаптации
(что обычно предполагает наличие полной информации
о параметрах КА и атмосферы) и при использовании соот¬
ветствующих алгоритмов можно получить наилучшее
решение. Поставим задачу обеспечения мягкой посадки
даже при спуске в самой разреженной атмосфере, т. е.
определим величину Кк зад min, полученную для
этих условий. Как отмечалось выше, стремление получить
в некоторых реализациях конечную скорость меньше miM
не приводит к должному эффекту, и поэтому представ¬
ляется целесообразным использовать при построении ал¬
горитма управления другой способ принятия решений —
способ гарантирующих стратегий [48, 61].
Предположим, например, что
A fE Gf, (8.6)
где Gf — некоторое заданное множество.
Пусть в качестве критерия фигурирует минимизируе¬
мый функционал вида
/ = $ (*ь:). (8.7)
280
АЛГОРИТМЫ УПРАВЛЯЛИ Я СПУСКОМ
[•М. *
Значения этого функционала зависят от управления ц
и реализации случайного процесса А, т. е.
1 = 1 (и, А). (8.8)
Поскольку никакие статистические характеристики
процесса А неизвестны, то в качестве критерия для оценки
алгоритма управления в этом случае естественно принять
функционал
I* (и) = max /(if, А). (8.0)
A<=_CxF
/* — это наихудшее из возможных значений функционала
при выбранном управлении и. Из двух управляющих
функций iij и и2 считается лучшей та, которая обеспечи¬
вает меньшее значение функционалу /*. Тогда оптималь¬
ным алгоритмом управления будем называть такой, ко¬
торый реализует
Ш1п/*(гс) = min max I (и, Л ). (8.10)
и Az=G]7
Чтобы не путать это понятие с оптимальным управлени¬
ем, которое было рассмотрено в предыдущих главах, уп¬
равление и, реализующее минимум функционала (8.9),
в дальнейшем будем называть гарантирующим управле¬
нием.
Применительно к задаче мягкой посадки КА на Марс
принцип гарантирующего управления в зависимости от
вида CM1I формулируется следующим образом: алго¬
ритм управления спуском должен обеспечивать наимень¬
шее из возможных значений конечной скорости VK т-1П =
— VK (или наибольшее значение конечной высоты) при
наихудших атмосферных условиях, а во всех остальные
случаях величина конечной скорости не должна превышать
величину VK зад (соответственно величина конечной высоты
должна быть не меньше hK 1ПЛХ = /гк ,Т1Д). Проведенные ис¬
следования показали, что наихудшее из возможных зна¬
чений Ук и hK достигается при одной и той же структуре
управления в случае движения КА в наиболее разрежен¬
ной атмосфере Марса. Любое увеличение плотности ат¬
мосферы приводит лишь к улучшению результата как по
Ук, так и по /гк.
Отметим, что принцип гарантирующего управления
и адаптивный подход при синтезе алгоритмов управле-
fg1j HI 111111Ш1 ГАРАПТШ’УЮтг.ГО УПРЛВЛКШШ 281
имя К A, снижающегося в атмосфере Марса, не являются
взаимоисключающими. Более того, как это будет показано
ниже, они могут в значительной степени дополнять друг
друга.
формулировка задачи синтеза алгоритма управления.
Рассмотрим задачу управления КА, динамика которого
описывается системой нелинейных дифференциальных
уравнений (8.3). Поскольку ее правая часть содержит
вектор случайных возмущений А, то вектор £ также будет
случайной функцией времени. Следовательно, любая
детерминированная характеристика Е (£) фазовой тра¬
ектории будет также некоторой случайной величиной.
Поэтому в качестве функционалов, характеризующих уп¬
равление, следует рассматривать математическое ожида¬
ние этих величин. При спуске КА в атмосфере Марса нас
интересует значение функции Е [£ (tK)]. Тогда в качестве
критерия оптимальности примем математическое ожида¬
ние этой функции:
/ (а) = м {№ [£ (*к)]}. (8.11)
В процессе спуска КА па вектор управления обычно
накладываются определенные ограничения, которые мо¬
гут быть записаны в виде
и еЕ U. (8.12)
При синтезе алгоритма управления приходится учи¬
тывать также дополнительные ограничения на текущие
значения фазовых координат, вытекающие из постановки
задачи:
м [<?„ (£, и)] < Сп (п = 1,2,..., 7), (8.13)
гДе Qn (£> — известные функции векторов £ и и, Сп —
заданные постоянные величины, j — число ограничений.
Величина математического ожидания в (8.13) определяет¬
ся по всем реализациям случайного процесса, описывае¬
мого системой уравнений (8.3) и вызванного случайными
отклонениями фазовых координат и случайными возму¬
щениями. Необходимо также учитывать ограничения,
которые могут накладываться на отклонение конечных
282
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[гл. S
значений фазовых координат *):|
О2 (*к) = <£rn (*к)> < Dm (т = 1, 2, i), (8.14)
где а2 (£к) — дисперсия, £т (tK) — отклонение конечных
значений фазовых координат, Dm —допустимое значе¬
ние дисперсии по /-й компоненте вектора £т. В общем
виде задача синтеза алгоритма управления в рамках прин¬
ципа гарантирующих стратегий формулируется следую¬
щим образом: определить вектор и, доставляющий мини¬
мальное значение функционалу
I* (и) = max М [Е (£ (*„))] (8.15)
a^gf
при ограничениях (8.12) — (8.14) и условиях связи (8.3).
Сформулированная задача по своей постановке кажет¬
ся аналогичной задачам оптимизации, рассмотренным
в главах 6 и 7. То обстоятельство, что функционал (8.11)
и ограничения (8.12) — (8.14) записаны в форме матема¬
тического ожидания, на первый взгляд не меняет дела.
Однако техническое и математическое содержание этих
задач существенно разное [54, 61, 78]. В задачах оптими¬
зации искомое управление разыскивается как функция
времени и начального состояния: гь — и (£0, t). Начальное
состояние объекта является случайной функцией. Кроме
того, функция и должна зависеть от вектора £. В простей¬
шем случае гс может быть функцией фазовых координат
£ и времени t:
а = и (£, £). (8.16)
Этот случай обычно и рассматривается. Задачу оты¬
скания функции и (£, t), минимизирующей функционал
/* (и), принято называть задачей синтеза оптимального
управления. Поиск оптимального управления в виде (8.16)
означает, что ставится задача синтеза оптимального ал¬
горитма управления КА, действующего по принципу об¬
ратной связи. При этом считается, что в каждый момент
времени измерению доступен вектор фазовых коорди¬
нат, т. е. имеется информация о состоянии объекта.
Рассмотрим задачу синтеза оптимального управления
движением КА, когда не все координаты могут быть из¬
*) Угловыми скобками < > обозначена операция усреднения.
ШЧШЦИП ГЛРАПТИГУЮЩГГО УПРАВЛЕНИЯ
283
мерены и управление должно выбираться как функция
только тех координат, относительно которых имеется ин¬
формация. Это означает, что решение на борту КА при вы¬
боре управления гь (£, t) должно приниматься по неполной
информации о поведении управляемого объекта — спус¬
каемого КА.
В качестве критерия оптимальности выбранного ал¬
горитма управления будем по-прежнему рассматривать
функционал вида (8.15). Пусть измерению доступен неко¬
торый вектор ft, причем измерения его компонент проис¬
ходят с ошибками. Вектор наблюдений ft является вектор-
функцией вектора £ измеряемых фазовых координат и
случайного вектора т|, характеризующего ошибки изме¬
рения [54]:
Ъ = Р (Б, л). (8.17)
Соотношение (8.17) можно рассматривать как уравнение
безынерционного измерительного устройства [54]. Иско¬
мый алгоритм управления может быть представлен в виде
и = и (ft, t). (8.18)
Таким образом, наряду с описанием модели движения
КА необходимо описать процесс поступления и обработки
информации. Формирование обратной связи при синтезе
алгоритмов управления, помимо отмеченной выше задачи
оценки состояния текущего вектора возмущенного движе¬
ния КА, связано также с проблемой определения динами¬
ческих характеристик КА и его управляющих возможно¬
стей. В теории разработки систем управления КА эта за¬
дача идентификации (т. е. задача получения необходимой
информации об управляемом объекте) является одной из
Центральных, и ее постановка вызвана тем, что при про¬
ектировании системы управления КА отсутствует до¬
статочная априорная информация о возмо жных отличиях
геометрических, массовых и аэродинамических характери¬
стик КА от расчетных значений. В настоящее время тео¬
рия и методы идентификации получили интенсивное раз¬
витие (см., например, обзор [631), однако, несмотря на это,
отработка алгоритма определения характеристик КА
в процессе спуска продолжает оставаться исключительно
сложной задачей, требующей выполнения большого объ¬
ема вычислительных операций,
284
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
Рассмотрим теперь ряд конкретных задач синтеза ал¬
горитмов управления КА. В первую очередь исследуем
задачу управления конечной скоростью спуска КА и ко¬
нечной высотой. При этом будет использован принцип
стохастической эквивалентности (принцип разделения)
[13], в соответствии с которым общая задача управления
КА разделяется на задачи а) формирования оптимального
закона управления, б) определения вектора фазовых ко¬
ординат КА, в) идентификации характеристик КА и г) по¬
строения алгоритма управления КА на основе получен¬
ных оценок. Каждой из указанных задач посвящено боль¬
шое число работ [13, 26, 48, 54, 55, 56, 61, 63, 70, 78], но при
этом отсутствуют какие-либо общие стандартные методы
их решения для КА, движение которых описывается си¬
стемой нелинейных дифференциальных уравнений (8.3),
и поэтому проблему нельзя считать исчерпанной.
Метод решения задачи синтеза управления движением
спускаемого на Марс КА в большой степени зависит от
состава измерительных и вычислительных средств, кото¬
рые имеются на борту КА. Ниже будут рассмотрены два
возможных пути синтеза алгоритмов управления КА:
— с использованием простых измерительных и вычис¬
лительных средств и обладающих небольшой массой, но
достаточно грубых по точности систем управления спу¬
ском [7, 31];
— с использованием бортовой ЦВМ и высокоточных
алгоритмов управления траекторией снижения [16, 24].
В целях наиболее надежного решения задачи мягкой
посадки на Марс следует, вообще говоря, стремиться к мак¬
симальной простоте алгоритма. Однако в ряде случаев
эффективность аэродинамического торможения при ис¬
пользовании простых алгоритмов может оказаться на¬
столько низкой по сравнению с оптимальным управле¬
нием, что это приводит к существенному утяжелению
СМП. В таких случаях, особенно для тяжелых КА, це¬
лесообразнее применять более совершенные алгоритмы,
предполагающие использование бортовых ЦВМ. Часть сэко¬
номленной массы, потребной для работы СМП, можно
использовать для повышения надежности работы системы
у гг р а в л стт и я ей ус к о м.
Будем считать, что на фазовые координаты траектории
спуска накладывается единственное ограничение: мате-
§3.1]
11Г И НЦ1Ш Г А Р АНТ IT Р У ЮТЦЕ ГО У11Р Л В ЛЕII11Я
285
^атическое ожидание высоты пролета КА над поверхно¬
стью планеты М (К) при движении по рикошетирующей
траектории не должно быть меньше некоторой минималь¬
но допустимой высоты
Имея в виду автоматические КА, можно не учитывать ог¬
раничения в отношении перегрузок, а также массы тепло¬
защитного покрытия.
При синтезе алгоритмов будем предполагать, что уп¬
равление осуществляется с помощью эффективного ка¬
чества. Вращательное движение КА будет учитываться
в наиболее простом виде:
где у — угол поворота КА относительно оси крена,
Ут\п'С) — его необходимое значение, Myirp — управляю¬
щий, а Л/1ШШ — возмущающий аэродинамический мо¬
мент относительно этой оси, J — момент инерции КА от-
н о сн г с л ь I т о нее, /ь ^2 — постоянные. Задача стабили¬
зации вращательного движения КА является отдельной
задачей управления. Во многих случаях при исследова¬
нии алгоритмов управления движением центра масс КА
оказывается допустимым учитывать движение относи¬
тельно центра масс в виде (8.20). Анализ проблемы стаби¬
лизации углового движения КА был дан в работах
Д. К. Охоцимского и Ю. Г. Сихарулидзе [70—74], где
были показаны различные пути усовершенствования ал¬
горитмов стабилизации КА с целыо уменьшения потреб¬
ных затрат топлива и улучшения процесса стабилизации
(улучшение устойчивости переходного процесса, умень¬
шение рассогласования по углу крена и угловой скорости
н конце заданного временного интервала и т. д.). Предло¬
женные для спуска в земной атмосфере идеи и методы
М (h) -йдоп>0.
(8.19)
(8.20)
а - Ад Ду ! - А:2у, Ду у — утреб,
СЦад COHSt,
286
АЛГСН 11ТМЫ УПРАВЛЕНИЯ СПУСКОМ
[PJJ. 8
могут быть использованы при создании совершенных (с при¬
менением бортовых ЦВМ) систем стабилизации КА, осу¬
ществляющих спуск в атмосфере Марса.
При рассмотрении алгоритмов управления спуском
КА в атмосфере Марса основное внимание будем уделять
дискретным алгоритмам. Это объясняется тем, что системы
с бортовыми ЦВМ по своей природе дискретны, а также
тем, что оптимальное управление на траектории спуска
может быть реализовано дискретным образом путем одного
или двух переключений Къф. При использовании бор¬
товой ЦВМ коррекция траектории может осуществлять¬
ся достаточно часто (с интервалом в несколько секунд или
долей секунды), в то время как простые системы управле¬
ния целесообразно строить в предположении одного или
двухразового переключения управляющего параметра.
Ниже наибольшее внимание уделяется проблеме уп¬
равления конечной скоростью спуска КА, по вместе
с тем приводятся примеры использования принципа га¬
рантирующего управления конечной высотой.
§ 8.2. СИНТЕЗ ДИСКРЕТНЫХ АЛГОРИТМОВ
УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ СПУСКА КА
Синтез линейного алгоритма управления
Выше было показано, что минимум конечной скоро¬
сти (или максимум конечной высоты) может быть достиг¬
нут при использовании программы одноразового или двух¬
разового переключения аэродинамического качества. Ис¬
ходя из этого, вполне логично для синтеза алгоритмов
управления использовать предположение о существовании
в общем случае т моментов времени tx, t2, tm, в ок¬
рестности которых управляющая функция (аэродинамиче¬
ское качество К) испытывает разрывы первого рода и ко¬
торые можно назвать моментами переключения управляю¬
щей функции. В этом случае изменение параметров
траектории определенным образом зависит от моментов
времени t2) * * tm, и можно решать задачу об исполь¬
зовании сдвигов моментов переключений для коррекции
траект ий с целью достижения определенных результа¬
тов [5
§ 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ 287
Рассмотрим синтез дискретного алгоритма управления
из условия постоянства скорости в конце участка основ¬
ного аэродинамического торможения на поминальной и
возмущенной траекториях VK = VK (Т) при удовлетво¬
рении ограничения по глубине погружения h = йдоп.
(Без принципиальных изменений в качестве функции для
синтеза алгоритма управления можно рассматривать вы¬
соту в конце участка аэродинамического торможения hK —
= hK(T) при дополнительном ограничении VK ^ НКЗад.)
Значение функции Ук зависит как от действующих воз¬
мущений, так и от выбора моментов переключений управ¬
ляющих функций:
У к = У (Аи А2, • . ., Ai\ ^2 ? • • •» h) (8.21)
{1 = 1, 2, . . ., р; i = 1, 2, . . /?г).
Ставится задача о нахождении такой системы коррекций,
при которой влияние этих факторов на величину функции
VK возможно более полно компенсировали бы друг друга.
Математические условия, на основании которых будет
проводиться синтез дискретного алгоритма управления,
запишутся следующим образом:
dV
" _ =0 = (8.22)
К
dA,
Величины производных, входящих в условия (8.22), опре¬
деляются зависимостью функции Ук, от параметров
А1ч А2, . . Av и зависимостью моментов переключений
управляющих функций от этих же параметров, которая
определяется системой управления.
В случае удовлетворения условиям (8.22) путем сдвига
моментов переключений управляющих функций можно
в линейном приближении полностью скомпенсировать влия¬
ние возмущений на величину скорости в конце участка ос¬
новного аэродинамического торможения. Понятно, что
с увеличением числа р параметров Аь характеризующих
расчетную модель возмущений, усложняется алгоритм
определения коррекций. Поэтому из всей совокупности
А2, . . ., Ар следует выбирать только наиболее суще¬
ственные возмущения.
Для синтеза автономной системы управления необхо¬
димо, чтобы в процессе снижения на борту КА происхо-
28В
АЛГОРИТМЫ УПРАБЛГЛ III И С И'УС ком
[IM. *
дило измерение некоторых параметров х1? х2, . . х(/,
которые зависят от действующих возмущений и, следо¬
вательно, дают некоторые представления о последних.
Введем понятие корректирующей функции S. При
решении задачи считается, что она известна и представ-
ляет собой некоторую функцию от измеряемых парамет¬
ров и времени:
5 - S (х1? х2, . . . , xry, t). (8.23)
Номинальное значение корректирующей функции рав¬
но S (t). Предполагается, что корректирующая функция
зависит от времени как явно, так и через изменение изме¬
ряемых функций. Вычисляя значения этой функции при
номинальных значениях моментов переключения tt ■
получим пг констант, задающих номинальную траекторию:
S (1;) -= Si (i == 1,2, . . . ,т).
Очевидно, что возмущенное значение S (t) Ф S (t).
Моменты переключений управления будем определять,
исходя из равенств
S (U) ---- К {ц) (I 1,2, . . ., т). (8.24)
Здесь (ti) подлежит определению и является по су¬
ществу функцией переключения. Итак, предполагается,
что в окрестности значений t tt происходит сравнение
функций S (t) и A; (I) и в момент их совпадения следует
команда па переключение управления. При этом для реа¬
лизации поминальной траектории необходимо, чтобы
К (ti) Si (i = 1,2,..., т). (8.25)
Синтез алгоритма управления будем проводить в линейной
постановке, т. е. считаем, что А±, А2, . . ., Ар на возмущен¬
ных траекториях мало отличаются от номинальных зна¬
чений Ях, А2, . . Ар. В этом случае функции S (t) и
S (t) также будут мало отличаться одна от другой и пе¬
ресечение функций S (t) и Xi(t) будет иметь место на линей¬
ном участке функции Xt (t), расположенном в окрестности
t = ti. Тогда эту функцию можно искать в виде
Xi (t) - Si + Z, (t- ti) (i -- 1,2, . . .. m), (8.26)
где Zt — константы, подлежащие определению. Следует
§ 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ 289
отметить, что пересечение корректирующей функции и
функции! переключения на линейном участке функции пе¬
реключения возможно лишь при
dS.
— = Zi (i = 1,2,... ,т).
Итак, синтез дискретного алгоритма управления пред¬
полагает решение следующих четырех основных задач:
— определение параметров функции переключения.
В частности, при решении задачи в линейном приближе¬
нии — это определение коэффициентов управления
— определение зависимости корректирующей функ¬
ции S от измеряемых параметров. В частности, если S
представляет собой линейную комбинацию измеряемых
параметров, то необходимо определить постоянные или
переменные коэффициенты этой комбинации;
— определение потребного числа измеряемых пара¬
метров, достаточного для осуществления компенсации
влияния по крайней мере выбранных расчетных возмуще¬
ний. Здесь же необходимо выработать требования к виду
измеряемых параметров (или функций);
— определение числа т переключений управления на
номинальной траектории, удовлетворяющего поставлен¬
ным условиям.
Определение параметров функции переключения. При
действии возмущений между значениями корректирующей
функции на возмущенной и номинальной траекториях по¬
явится некоторое рассогласование, которое и является
основой для формирования корректирующих поправок
к моментам времени переключения управления. Обозна^
чим через AS приращение корректирующей функции при
переходе от поминальных значений при t = t-x к значениям
ее на возмущенной траектории:
ASt - Si (£ = 1,2,..., т). (8.27)
Приращение ASt определяется приращениями всех
параметров, характеризующих возмущения А1, А2, . . .
. . .,АР, смещением всех моментов переключений £1? t2, . . .
. . ., £*_i, предшествующих моменту t = tt и смещением
Ю Н. М. Иванов, А. И. Мартынов
2П0
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
момента последнего переключения t = tt\
AS, = ^LAt1+^Ah + ... + +
+ ^At,+ Yj^-AA, = (8-28)
2 1=1 1
Все производные, входящие в (8.28), вычисляются для ус¬
ловий номинального режима полета, т. е. при t = tt
(i = 1,2,.. т) и A, (I = 1, 2, . . ., />).
Имея в виду (8.26) и (8.27), получаем
AS* = ZiAti (1 = 1,2,.. ., т) (8.29)
и, учитывая (8.28), приходим к следующим уравнениям:
-^4(, + ■ ■ • + «,4«, - - 44, (8.30)
г 2—1 7—1
(i = 1,2,... ,?тг),
где
(i = l,2,...,m). (8.31)
Эти уравнения имеют треугольную матрицу коэффициен¬
тов, и из них могут быть последовательно определены
приращения Д^, At2, . . Afm, если только Nt = 0. Сог¬
ласно условиям задачи, искомые коэффициенты управле¬
ния Zi (или АТj) и корректирующая функция S должны
быть определены таким образом, чтобы выполнялись усло¬
вия (8.22). Для этого необходимо провести совместное ис¬
следование уравнений управления (8.29) и условий (8.22).
Прежде чем перейти к преобразованию и решению ука¬
занных уравнений, отметим следующее. Корректирующая
функция в общем случае записывается в виде (8.23).
С другой стороны, ее величина в каждом конкретном слу¬
чае зависит от действующих возмущений и текущих зна¬
чений управляющей функции, т. е. от моментов времени
переключения управления:
Si — Si (i4i, Л2, . . Ai\ t1j t2J . . ., ti) (8.32)
(i = 1,2,..., m; I = 1, 2, . . p).
§ 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ 291
Текущее потребное время переключения управления
также зависит от действующих возмущений и времени
перекладок, предшествующих моменту t ~ t^.
ti (или Mt) = ti (Аг, Л2, . . ., Ар; tl9 U, . . t^) (8.33)
(i = 1, 2, . . т).
От тех же параметров Ар и зависит и функция VK.
Итак, для решения уравнений (8.29) и (8 22) располагаем
явным соотношением (8.23), позволяющим вычислять на
борту КА в процессе снижения корректирующую функ¬
цию S, и неявными (в указанном смысле) соотношениями
(8.21), (8.32), (8.33).
Приступим к преобразованию и решению уравнений
управления (8.29) и условий (8.22). Перейдем к матрич¬
ной форме записи. Для этого введем в рассмотрение век¬
тор смещения времени переключения управления [At),
вектор приращения корректирующей функции (AS) и
матрицу коэффициентов управления (Z):
At =
Д«!
AS1
At 2
II
ъ
<
&s2
, z =
А*т
m
m
Zi
0
0
. . .
0
0
z2
0
. . .
0
0
0
0
0
0
0
. . .
2
Уравнение (8.29) перепишем в следующем виде:
AS = ZAt. (8.34)
Используя линейные приближения и обозначая еди¬
ничную матрицу через JE, можно записать после некоторых
преобразований:
At = (Е -Q)'1 DA А, (8.35)
AS = BAA +CAt. (8.36)
Здесь
ААг
AA =
A A,
A A3
A A„
— вектор возмущении,
10*
292
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
dt,
~dfx
0
0
. . 0
dh
dtx
01*
dt,
0
0
dt
т
d*m
dtm
dt
m
dtx
dt.
dta
dtm-i
dtx
dt x
dt,
~dA
d/U * •
■ dAv
dt.
dt.
dt.
) r=
dA~x
dA,
Щ
dt
m
dt
m
dAx
Ja
d,,p
1 0
0
0
0
ds,
p77
0
0
0
0S:i
oti
dS3
dt.
0
0
\dS
m
ds
m
dS
m
dS
m
dt1
dt.
dtz *
‘ ' dtm
-1
dSi
dSx
dSx
dAx
~dA,
dA,
dS2
dS,
ds.
dA
dA7
Щ
dS
dS
ds
m
m
m
dAx
dA
dA[
Подставляя в (8.36) значение At из (8.35), получаем
окончательное выражение для приращения корректи¬
рующей функции
AS ВАЛ + С (Е - Q)~XDAA. (8.37)
Подставляя выражения (8.35) и (8.37) в уравнение
(8.34) и сокращая на А А Ф 0, окончательно получим
(Z - С) (-Е - Q)~lD = В. (8.38)
§ 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ 293
Итак, (8.38) является преобразованным уравнением (8.34)
и оно должно решаться совместно с уравнением (8.22).
С учетом выражения для конечной скорости после неко¬
торых преобразований условия (8.22) запишем в следую¬
щем виде:
V [{Е — Q)"1 D = —VA.
(8.39)
Здесь
(W*
[ dh
dVK dVK
dt,
dV
dh
dV„
dt,
dV,
,dVK dVK dVK dVK \
A [ dAx ЗА, dA3 • • * dAp)
При каждом фиксированном p уравнения (8.38) и (8.39)
представляют собой систему т -j- 1 уравнений (т уравне¬
ний, содеряшщихся в (8.38), и одно уравнение (8.39)), куда
входят пг величин dti/dAv (матрица D), относительно ко¬
торых разрешим систему. Как известно [51], для нахож¬
дения совместного решения системы уравнений (8.38) и
(8.39) необходимо, чтобы ранг матрицы
Г
(Z-C) (E-Q)-i
V. (Е - 0)-i
(8.40)
равнялся рангу расширенной матрицы
[(Z-C)(E-Q)-i] в
[Vt(E-Q)^] -VA
Y*
т. е. ранг Г — ранг Г*.
Ранг матрицы Г равен т. Действительно,
(E-Q)
-г.
(8.41)
1
0
0
. • .
0
0
dt,
~di~
1
0
. . .
0
0
( dh dt, . dh \
\ dt, dtx dli )
dh
dt.
1
. . .
0
0
dt
m
1
* •
dtw~X
проставляет соооп невырожденную квадратную патрицу.
294
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
Ранг матрицы
(Z-C) =
Zi
0
0
0
0
dSt
7
0 . .
0
0
dtx
dS3
dS3
7
0
0
dti
dt2
«^3
dS™
m
dSm
m
m
dSm
dt-^
dt.
~ dt3
равен 77?, так как определитель этой матрицы равен произ¬
ведению коэффициентов Zu Z2, . . Zm, которые по усло¬
виям задачи не должны быть равны нулю. Ранг квадратной
матрицы (Z — С) (Е — Q)”1 также будет равен 7?г [51], а
отсюда следует, что ранг Г равен т. Тогда для удовлетво¬
рения условиям совместимости уравнений (8.38), (8.39) тре¬
буем равенства нулю определителя расширенной матрицы
или
(Z-C)
0.
= 0, (8.42)
(8.43)
t 'А 4 1
Известно [51], что определитель га-го порядка тогда
и только тогда равен нулю, если между его строками су¬
ществует линейная зависимость. В силу того, что на кор¬
ректирующую функцию S и на коэффициенты Zt (i =
= 1,2, . . ., т) не были наложены какие-либо ограниче¬
ния, решение уравнения (8.43) может быть получено в удоб¬
ном виде. Так, для разрешимости уравнения (8.43) по¬
требуем равенства нулю векторов-столбцов. В результате
получаем следующие соотношения:
у дУ”
Zm-i +
dVu
dS.
m—l
m
dS™
m
dtm-1
dS
dt„
dt„
= o,
= 0,
= 0,
7 , as,
1 ‘ ** *
dS
/71—1
du
as
m
' dtx
= o,
(8.44)
5 S.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ 295
И
dVK / дйг . ds, , , '
*Ai \3-4* ^ dAi ~г"* ' dAi +
(2 = 1.2,.. .,р).
Уравнения (8.44) дают возможность вычислять коэф-
фициеяты для определения параметров переключения уп¬
равления, если известна корректирующая функция S.
Вид же корректирующей функции определяется системой
уравнений (8.45).
В сокращенной записи (8.44) и (8.45) перепишутся
с учетом (8.31) следующим образом:!
771
Nt + (8.46)
1 2=1
771
d7r{V*-YjSi) = 0 (2 = 1.2,-...m; 2 = 1,2,...*, р).
(8.47)
Определение зависимости корректирующей функции от
измеряемых функций. Эта задача в значительной сте¬
пени не связана с предыдущей и в силу этого может иссле¬
доваться самостоятельно. Рассмотрим один из практи¬
ческих важных случаев, когда корректирующая функция
представляет собой линейную комбинацию измеряемых
функций с переменными коэффициентами [52]:
5- 2 (8*48)
.;=i
В этом случае соотношения (8.45) или (8.47) позволяют
получить систему уравнений для определения значений
коэффициентов pj (t) (/-=1,2, . . ., q) при t = t1, . . .
• . ., t tm.
Обозначим Pj (ti) через pfJ- и будем считать, что в окре¬
стности t = ?!, . . ., t = tm значения коэффициентов
Рj(t) и pfJ- совпадают. Соответственно выражения для
St ---- S (t£) (£ = 1,2,..., in) — значений корректирую¬
щей функции в окрестности номинальных значений мо¬
ментов переключения — можно будет записать в виде
^=SMi(2i) (i = l,2,...,m). (8.49)
j=l
296
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
Подстановка (8.49) в (8.45) дает систему уравнений для
определения qm констант (30- (i 1, 2, .. га;/ = 1,2,
В результате мы получили систему линейных алгебраи¬
ческих уравнений. При этом, если р ^ qm, то число
уравнений не превышает числа неизвестных и уравнениям
(8.50) можно удовлетворить при более или менее произ¬
вольных измеряемых функциях. Например, если предпо¬
лагается проведение двух коррекций (число переключений
управления т = 2), а число произвольных измеряемых
функций q = 3, то максимальное число возмущений, ко¬
торое можно скомпенсировать выбранной системой кор¬
рекций, не должно превышать шести (р ^ 6).
Для разрешимости уравнений (8.50) необходимо, что-
дх-
бы определитель, составленный из производных -f- (t\)
dAi
(/ = 1,2, . . ., q; I ~ 1,2, . . ., p), был отличен от нуля.
Отсюда вытекают некоторые необходимые требования, ко¬
торым должны удовлетворять измеряемые функции:
а) в различные моменты времени (?17 ?2, . . ., tm) одни
и те же измеряемые функции должны изменяться различ¬
ным образом при одних и тех же возмущениях;
б) в одни и те же моменты времени различные измеряе¬
мые функции должны изменяться различным образом при
одних и тех же возмущениях;
в) при различных возмущениях измеряемые функции
должны изменяться различным образом.
Невыполнение любого из этих условий приводит к об¬
ращению в нуль определителя системы (8.50). Необходи¬
мые и достаточные условия для разрешимости уравнений
(8.50) даются известной теоремой Кроиекера — Капелли
[51], согласно которой для разрешимости уравнений
(8.50)
(I = 1,2,.. ., р).
§ 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ
297
должны быть равны ранги обычной матрицы
F =
дкг (г,)
dKq (Fi)
дУ- (FJ
д\ (ij
д Ау
дА1
дАл
дАх
дкх (Fj)
dxq (fx)
dKi Cj
д*Ч С,п>
дАр •
'• дАр •
• ' ЭАр •
•• дАр
(8.51)
и расширенной матрицы
jF* =
дА±
F
(8.52)
Из условия равенств рангов матриц F и F* можно полу¬
чить в каждом конкретном случае вполне строгие требо¬
вания к измеряемым функциям.
Следует отметить, что в рамках линеаризованной те¬
ории важно знать значения переменных коэффициентов
Рj (t) лишь при номинальных значениях переключения
управляющих функций. Вне окрестности этих моментов
времени поведение переменных коэффициентов корректи¬
рующей функции оказывается несущественным. Вслед¬
ствие этого в алгоритме коррекции необходимо иметь лишь
набор констант (i = 1,2, . . т\ /--1,2, . . ., q),
N; (i 1,2, . . т).
Переключение управления следует производить в мо¬
мент времени, когда в силу соотношений (8.24), (8.26),
(8.27) и (8.49) выполняется равенство
S Ри [*; СО — *з СО! = Ni Ci — ti) (t = 1,2, • • •, m).
i=i
(8.53)
После того как i-e переключение произошло, констан¬
ты, соответствующие t = tt в этом равенстве, должны быть
заменены константами, соответствующими моменту вре¬
мени t — t-i ^т, и т. д.
Таким образом, если система строится на базе более или
менее произвольных измеряемых функций, то для осуще¬
298
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
ствления коррекции число возмущений должно быть
меньше qm. Но в случае специального выбора функций
уравнениям (8.45) или (8.47) можно удовлетворить и при
р > qm. В частности, это имеет место при
В этом случае уравнения (8.47) удовлетворяются тожде¬
ственно, а формулы для Nu . . Nm дают
Эти результаты на основании равенств (8.24) — (8.26)
позволяют заключить, что при таком выборе измеряемых
функций моменты времени £1? t2, . . ., tm^1 могут быть оп¬
ределены произвольно, а коррекция осуществляется путем
сдвига моментов времени tm в соответствии с равенством
Определение моментов времени £1? t2, . . ., tm^1 можно
производить, исходя из каких-либо условий, например,
таким образом, чтобы в процессе движения возмущенные
траектории проходили бы возможно ближе к номинальной
и т. д. Для осуществления последнего переключешш в со¬
ответствии с равенством (8.56), очевидно, должна иметься
весьма полная информация о движении. В действительно¬
сти равенства (8.54) можно реализовать лишь прибли¬
женно.
Рассмотрим случай одноразового переключения уп¬
равляющей функции (лтг = 1). В этом случае записыва¬
ются:
— условия переключения
— уравнения для определения коэффициентов р1?
(8.54)
(8.55)
Vк (^ъ ^2» • • • > 4li, А%, . • . , Ар) — S. (8.56)
Pi [^1 Он) — К C?l)] + • • • + Pri [Kq (Д) — (7L)] = Ni(tx t\)\
(I = 1, 2, . . . ,p);
— выражение для N±
§ 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ 299
С помощью одного переключения можно скомпенси¬
ровать действие любых возмущений, которые имеют место
до некоторого момента времени tQ, предшествующего
номинальному значению момента переключения ti- Дей¬
ствие любых возмущений при t ^ t0 приведет к изменению
фазовых координат при t = t0. Тогда значения фазовых
координат при t = t0 можно записать в виде
*^г |/=/о ~ |^эг ~ 1 (£=1,2,..., Tl).
Отличия ^ от единицы говорят об истории возмущенного
движения. Таким образом, имеет место ^-параметрическая
система возмущений, на которую в соответствии с изло¬
женной теорией нетрудно настроить алгоритм коррекции.
При плоском движении в общем случае имеем п~- 4, т. е.
должны быть четыре независимые измеряемые функции.
При числе коррекций более единицы в некоторых слу¬
чаях последнее переключение целесообразно проводить
так, чтобы оно компенсировало все накопившиеся ошибки
в фазовых координатах, подобно тому, как изложено выше.
Итак, рассмотрены и две последние задачи синтеза
алгоритма дискретного управления, связанные с выбором
потребного числа измеряемых параметров и числом пере¬
ключений управления. При решении этих задач дополни¬
тельно должны быть учтены вопросы реализуемости и
требования по допустимой точности управления.
Синтез алгоритмов управления с упрощенной
логикой
Рассмотрим простой вариант реализации дискретного
алгоритма управления с использованием наиболее простых
измерительных и вычислительных средств, имея в виду при
этом опыт создания систем управления для КА, осуще¬
ствляющих спуск в атмосфере Земли. Прежде всего рас¬
смотрим случай одноразового или двухразового переклю¬
чения /£Эф, теоретически позволяющего при наличии пол¬
ной информации об условиях входа, о параметрах КА и
окружающей среды и т. д. реализовать оптимальное уп¬
равление.
Определение потребного числа измеряемых парамет¬
ров, Основными факторами, влияющими на выбор точек
переключения,! являются разброс проектно-баллистиче¬
300
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[гл. 8
ских параметров КА (Д Рх и ДА о), условий входа (ДК0 и
ДА,), большая иеопределенность в знании параметров ат¬
мосферы (Др). Все возмущения (за исключением атмо¬
сферных) предполагаются независимыми, имеющими нор¬
мальный закон распределения с нулевым математическим
ожиданием.
В общем случае семейству возмущенных траекторий
входа соответствует некоторая поверхность точек пере¬
ключения в области фазовых координат V, 0, h. Запом¬
нить такую поверхность достаточно сложно, а для ее
использования необходимо иметь ЦВМ на борту КА. При¬
меним широко используемый прием — переход от пара¬
метров V, 0, h к параметрам, более доступным для изме¬
рения бортовыми средствами. Простым эквивалентом этих
параметров являются измерения кажущейся скорости
t.
(v&= g'6\nxdt)i перегрузки (пх) и производной от пере-
' о '
грузки по времени (я*). При этом предполагается, что
акселерометр (или система акселерометров) жестко связан
с корпусом КА. Поскольку получение пх сопряжено с
определенными трудностями, первоначально будем рас¬
сматривать только два параметра Vs и пх. В этом случае
трехмерная поверхность точек переключения вырождает¬
ся в некоторую двумерную область параметров измере¬
ния Vs и пх. Для уменьшения ошибок измерений вместо
параметра пх во многих случаях удобнее и целесообраз¬
нее использовать время £, отсчитываемое от некоторого
фиксированного значения К*- Дальнейшее построение
системы будем вести в предположении наличия только
указанных измерений.
Используя датчик случайных чисел, можно путем чис¬
ленного моделирования построить семейство точек пере¬
ключения, каждая из которых будет пол учена при различ¬
ных случайных комбинациях возмущений, действующих
на КА. Оказалось, что точки переключения занимают
обширную область в плоскости (пх и Vs) или (t и Fs),
имеющую форму вытянутого эллипса, и поставленная за¬
дача не упрощается существенно но сравнению с простран¬
ственным представлением поверхности точек переключения.
Чтобы систематизировать и упростить полученную ин¬
формацию, определим точки переключения с использова¬
§ 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ 3(j[
нием следующей процедуры. Будем варьировать только
один из каких-либо возмущающих параметров, считая
все другие номинальными. В этом случае для каждого из
параметров получаются линии переключения (рис. 8.2).
При этом оказывается, что наиболее характерной является
линия переключения, полученная при варьировании вы¬
соты условного перицентра, ибо
она практически совпадает с боль¬
шой осыо полного эллипса точек
переключения. Поэтому в даль¬
нейшем линию переключения
tt.vit(Cn) или *u('Csn), соответ-
ствующую этому случаю, и будем
использовать при построении про¬
стого дискретного алгоритма управ¬
ления конечной скоростью спуска.
При синтезе алгоритма, пред¬
полагающего двухразовое пере¬
ключение эффективного качества,
линии переключения строятся сле¬
дующим образом. Сначала по изло¬
женной выше методике строится
первая линия переключения в
предположении, что вторая точка переключения выби¬
рается оптимальным образом из условия min Vl{. Затем
с учетом построенной первой линии переключения осущест¬
вляется построение второй, что позволяет частично ком¬
пенсировать ошибки аппроксимации первой линии пере¬
ключения. Следует отметить, что расчеты проводились
в предположении мгновенного переключения К0ф. В об¬
щем случае необходимо учитывать динамику вращения
вокруг оси крепа. Перестроение линий переключения
в этом случае не представляет больших затруднений.
В качестве примера на рис. 8.3—8.6 приведены линии
переключения для КА с различными значениями приве¬
денной нагрузки на лобовую поверхность и аэродинами¬
ческого качества. Исследования показали, что они могут
быть с достаточной степенью точности аппроксимированы
простыми линейными или квадратичными зависимостями
перегрузки пх п или времени tn от кажущейся скорости:
Лхп
2000 5000 то
Рис. 8.2. Семейство линий
переключения для КА с
Рх = 80 к г 1м2 п Kq — 0,3.
7Ь\-1т -- &jKlS1[ | bjVgii | Cj,
(8.57)
302
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
1гЛ. 8
tn = djV2sn + ejVs п + /j, (8.58)
где j — номер участка аппроксимации, Ъj, . . /j —
коэффициенты аппроксимации линии переключения *).
Гп, CSK
Рис. 8.3. Выбор линии переключения для КА с Р = 80 кг/м2 и Kq = 0,3
(Уо = 6 км/сек, р (h) = Pmin
Рис. 8.4. Выбор линии переключения для КА с Рх = 250 кг/м2 и Jfg = 0,3
(Vo = 6 км/сек, р (Л) == pmin (Л)).
Численное значение коэффициентов зависит от проектно¬
баллистических характеристик КА, начальных условий
входа в атмосферу и допустимой высоты полета над по¬
верхностью Марса.
*) Здесь и ниже в формулах типа (8.57), (8.58) [Vs] = км/сек,
[/п] = сек, а размерность av ...,/. такова, что пх п безразмерна.
8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ
303
пх
fi~- ~150нм
\
I
. Лини
у\ без уча»
я л арак;;?оч.
та динамик
7
яки;;
и а у
/-100
к/0
' К \
I
i
\\ i
/ у'
7 >
V
\Ч
л
7
/ 7
У
/
/ -
Линия /
; с цчегяом
I ^ I
i
креключения
динамики не
ч
i\
0 /ООО 1000 о ООО 0000 ОООО У^м/сик
Рис. 8.5. Выбор линии переключения для КА с Р% = 80 кг/м2 и '= 0,3
(У0 = 6 км/сек). (Сплошная линия — Pmin, штрих-пунктирная — Ртах*)
Рис. 8.6. Линии переключения для КА с Рх = 350 кгГм2 и Kq— 0,3 и различ¬
ными значениями /1д0Н и утях (У0 = 5,8 км/сек). (Сплошная линия —
штриховая — пхп (VS|t).)
304
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
Алгоритм] управления. На борту КА в память ЦВМ
закладываются коэффициенты а$, bj, . . /у и с исполь¬
зованием этих коэффициентов производится расчет пере¬
грузки /г?спСЧ или времени г£а0,1 в функции измеренной (те¬
кущей) кажущейся скорости FSTeK:
л£Г = «Лк +bjVsreK + cjt (8.59)
С 1 = djVsren + + /;• (8.60)
Одновременно осуществляется измерение перегрузки
Пх6К или времени tTei<. Переход в полете с одного значе¬
ния на другое происходит в момент, когда текущее значение
перегрузки или времени станет равно расчетному:
Ил-тек = п'х ;Г\ (8.61)
ИЛИ
Цек - СГЧ. (8.62)
Следует отметить, что равенство (8.61) может выпол¬
няться на траектории спуска дважды: один раз на восхо¬
дящей ветви зависимости тг^ (Fs) и один раз на нисходя¬
щей после прохождения максимума перегрузок. Это об¬
стоятельство необходимо учитывать при синтезе простых
алгоритмов управления конечной скоростью спуска,
а именно для каждого КА необходимо вводить в логику ал¬
горитма управления признак, указывающий, на какой
ветви зависимости пх (Fs.) необходимо осуществлять пере¬
ключение /<эф.
В случае двухразового переключения KDф расчет пере¬
грузки или времени в обоих случаях производится по
тем же формулам (8.59) и (8.60) с соответствующей заменой
коэффициентов о,-, bj ,. . ., /;-. Следует отметить также, что
начальное положение осей КА перед входом в атмосферу
различно в зависимости от того, предусматривается одно¬
разовое или двухразовое переключение Кдф. В случае,
когда т — 1, КА входит в плотные слои атмосферы
с минимальным значением эффективного качества KDф =
“ Amiri (Y ~ Ymax)-
Сигнал «атмосфера» выдается при достижении задан¬
ного малого значения перегрузки пх = п* или кажущейся
скорости ТС Ffi в момент выполнения условия (8.01)
или (8.62) следует команда на режим полета с максим а ль-
5 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ 305
ным значением Къф. Следует подчеркнуть, что по кон¬
структивным ограничениям величины утах и утт могут
быть не равны соответственно 180° и 0°. В случае т — 2
КА подходит к атмосфере с Kt)ф К
mnx и соответствен¬
но осуществляется переход на Ктш в момент первой кор¬
рекции и на Атах в момент второй. Для повышения надеж¬
ности работы системы управления команды на переклю¬
чение АЭф во всех случаях подаются с некоторой задерж-.
кой, в течение которой осуществляется проверка условий
(8.61) и (8.62).
Отметим следующее важное обстоятельство. В соот¬
ветствии с изложенной выше стратегией гарантирующего
управления предлагаемый простой дискретный алгоритм
должен обеспечивать наименьшее значение функционала
/* = max М (FK) (8.63)
pmin^P^pmax
при спуске в наихудших атмосферных условиях — наи¬
более разреженной атмосфере: р (h) = pmm (h). Для
всех остальных значений р (/г) величина математического
ожидания конечной скорости при возможном суммарном
действии всех возмущений не должна превышать
min /* — min max М (FK)- (8.64)
*эф
Проведенные исследования показали, что предлагае¬
мый алгоритм управления удовлетворяет сформулирован¬
ным требованиям, если функция переключения, закла¬
дываемая в алгоритм бортовой ЦВМ, рассчитывается для
минимальной модели атмосферы. В частности, линии пере¬
ключения, представленные на рис. 8.3, 8.4 и 8.6, по¬
строены при Р (/?) ~ Pm in (h).
Следует также отметить, что при синтезе рассмотрен¬
ного дискретного алгоритма управления конечной
скоростью не рассматривался ряд важных задач,
отмеченных в § 8.1. Здесь имеются в виду задачи уточне¬
ния вектора состояния КА в процессе спуска и идентифи¬
кации параметров КА и окружающей среды (плотности
атмосферы). Это было сделано преднамеренно, с целыо
максимального, упрощения "алгоритма управления, а так¬
же с целью выявления предельных возможностей ал¬
горитма, предполагающего использование априорных
306
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
сведений об этих параметрах. Строго говоря, косвенное уто¬
чнение одного из начальных условий в алгоритме управле¬
ния осуществляется и используется при его работе. Дей¬
ствительно, основным возмущением, на которое настра¬
иваются коэффициенты функции переключения (8.57) или
(8.58), является разброс высоты условного перицентра
траектории входа. А это позволяет при возможном от¬
сутствии всех остальных возмущений уточнить при жела¬
нии параметр hn по времени или величине перегрузки,
рассчитываемой по формуле (8.59) или (8.60) на борту КА.
Оценка эффективности алгоритма одноразового пере¬
ключения К9ф. Такая оценка проводилась для двух ти¬
пов КА_с одинаковым значением аэродинамического ка¬
чества АТз 0,3, но с различными значениями приведен¬
ной нагрузки на лобовую поверхность Рх — 80 кг/м2
и Рх = 250 кг/м2*). Максимальная величина угла крена
принималась равной уШах _= 180° для КА с Рх = 80 кг/м2
и ушах = 135° для КА с Рх — 250 кг/м2. Рассматривался
прямой вход в атмосферу Марса со скоростью V0 —
= 6 км/сек. Минимально допустимая высота полета КА
над поверхностью Марса варьировалась в диапазоне от
2 до 9 км. Моделирование движения КА (с учетом динами¬
ки разворота по крену и алгоритма управления) осуществ¬
лялось на универсальной ЭВМ. Точность управления ве¬
личиной конечной скорости оценивалась с использова¬
нием методики, предложенной Б. Г. Доступовым [41].
При этом определялась величина математического ожи¬
дания М (FK) и утроенное среднеквадратичное отклоне¬
ние конечной скорости За (АРК) при работающей системе
управления и при суммарном действии всех возмущений.
Влияние возмущений на величину конечной скорости
оценивалось для двух вариантов алгоритма управления,
первый из которых использует линию переключения в ви¬
де зависимости, nxn(Vsn), а второй — в виде tn(VsU).
В первом случае линия переключения с достаточной
степенью точности аппроксимируется для КА с Рх ~
= 80 кг/м2 прямой
И'яп = Vtn “Ь 12,5,
*) Здесь и в дальнейшем номинальные значения параметров,
которые используются при моделировании алгоритмов управления,
•^означаются под чертой.
§ 8.21 АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ 307
а для КА с Рх = 250 кг/м2 квадратным трехчленом
пх п = 1,1 Fln + ll,lFsn — 3,5.
Во втором случае линию переключения целесообраз¬
но аппроксимировать для КА с Рх — 80 кг/м2 двумя пря¬
мыми!
при Vs 1,88 км/сек tn = 18,9Fsn + 20,79;
рри Vs +>1,88 км/сек ta = 23,6Fsn + 0,2.
Величина конечной скорости, которой достигает ап¬
парат на заданной конечной высоте /гк при действии раз¬
ного рода возмущающих факторов в случае управляемого
спуска с применением изложенного алгоритма, представ¬
лена в табл. 8.1.
В результате численного моделирования получены
следующие значения математического ожидания М (FK)
и утроенного среднеквадратичного отклонения конечной
скорости За (AFK) в случае совместного действия всех
возмущений.
Для алгоритма с линией переключения по времени
tn (Vsn) при hK = 3,5 км, Рх = 80 кг/м2 оказалось
М (FK) = 234 м/сек и За (AFK) = 30 м/сек; при hK = 2 км
М (FK) — 206 м/сек, За (AFK) = 28 м/сек; при hK = 5 км
и Рх — 250 кг/м2 оказалось М (FK) = 441 м/сек,
За (AFK) = 32 м/сек.
Для алгоритма с линией переключения по перегрузке
72хП (Fsn) при /гк — 3,5 км и Рх = 80 кг/м2 оказалось
М 0+) — 231 м/сек, За (AFK) 32 м/сек; при /гк = 2 км
и Рх ■-= 80 кг/м2 оказалось М (FK) - 201 м/сек, За (AFK)
--- 26 м/сек.
Сравнивая работу алгоритма управления при моде¬
лировании динамики переворота КА и действия различного
рода возмущений с идеализированным алгоритмом в пред¬
положении мгновенного переворота КА и оптимальной для
каждой конкретной траектории точки переключения, мож¬
но отметить, что ошибки (За) из-за неучета реальных ус¬
ловий работы алгоритма управления конечной скоростью
могут достигать следующих величин. __
Для аппарата с Рх = 80 кг/м2 и Kq = 0,3 в случае
переключения по времени при kK = 3,5 км За (AFK) =
= 51 м/сек, а при hK = 2 км За (AFK) — 37 м/сек; в
Оценка эффективности алгоритма управления с одной линией переключения
308
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[гл. s
VO
гг!
N
\>
з 55
: к
к
с
со
с
|3s
!>
и
Я
PQ
о
о
см
со
1-0
о
О
СМ
Ю>
о
ю>
см
ю
00
V?
СО
Г-
со
о
мг
СО
СМ
ю
v-h
ю
ю
см
см
см
о
о
NT1
см
со
о
ю
СО
о
см
00
L-6
ю
[.'t-
СО
о*
00
—н
VT1
С4]
СО
см
vr
V?
1-0
ю
см
СО
со
1-0
ю
о
со
о
ю
о
LO
о
О'
ю
ю>
1-0
СО
L—
ю
см
СО
ю
vr
V-H
VT
СО
V*
Vf
VT1
VC
t--
гг-1
СО
ю>
оо
1-0
о
ю
см
сз
т-Н
05
со
05
05
со
Г"
см
см
см
см
о
со
t'-
ю>
Ю
ю
ю
LO
ю
о
СП
05
00
О
VT1
СО
ГГ-1
см
см
ТН
СМ
см
rrs
см
см
1-0
о
СО
ОО
ю
1-0
Ю)
00
00
со
см
см
см
V?
[>•
см
см
СМ
см
см
см
СМ
см
СМ
см
см
СО
о
СО
00
LO
СМ
о
О
о
L'-
см
LO
см
см
05
1-0
L'-
см
со
СМ
см
см
см
тн
см
см
см
см
см
о
05
t-
со
о
о
LO
см
со
со
тгН
см
00
1
1
СО
ю
I'-
оо
о
О
1
О-
о.
6 . s
§ 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ
309
случае переключения но перегрузке при /гк 3,5 км
3о (AFK) = 49 м/сек, а при /г[{ 2 км За (AFI;) — 37 м/сек.
Для аппарата с Рх = 250 км1м2 и К§ -- 0,3 в случае
переключения по времени при hK = 5 км За (AFK) —
= 41 м/сек.
Для сравнения в табл. 8.1 представлены данные для
случая, когда вместо линии переключения используется
единственная точка переключения, соответствующая вхо¬
ду по центру коридора. Видно, что в этом случае невоз¬
можно осуществить надежный спуск КА на поверхность
планеты с приемлемыми затратами топлива на торможение.
Представленные данные показывают, что эффективность
предлагаемого алгоритма практически не зависит от спо¬
соба задания линии переключения в виде пхП (FS1I) или
UFsn). Максимальный разброс величины конечной ско¬
рости уменьшается при снижении конечной высоты hK,
на которой осуществляется введение системы мягкой по¬
садки. Методическая ошибка составляет величину по¬
рядка 50 м/сек.
Оценка эффективности алгоритма двухразового пере¬
ключения К эф. Программа управления с одноразовым пере¬
ключением Къф имеет ограниченное применение, так как
ее эффективность падает с увеличением Рх и В этом
смысле программа двухразового переключения является
более универсальной. В качестве примера рассмотрим
алгоритм двухразового переключения для управления ко¬
нечной скоростью спуска КА с Рх = 350 кг/м2 и К§ = 0,3.
Линии переключения для этого случая представлены на
рис. 8.6 в виде зависимостей перегрузки и времени от
кажущейся скорости: пхП (Fsn) и tn(Vsn). Видно, что
линии переключения tn (Fsn) имеют более простой вид,
чем пхП (Fsn), и соответственно их легче аппроксимиро¬
вать. Учитывая этот факт, а также то, что способ задания
линий переключения практически не влияет на величину
FK, в дальнейшем будем предполагать, что они заданы на
борту КА в виде tn ( Fsn).
Линии переключения на рис. 8.6 могут быть аппрок¬
симированы следующим образом:
— для первого момента переключения — одной прямой:
tni = axV s + Ь1?
где ах —11,111 сек2/км, Ьл = 101,666 сек;
310
Алгоритмы управления спуском
[ГЛ. 8
— для второго момента переключения — тремя пря¬
мыми:
^П21 “ ^21 ^S + Ь21 (Fs si)»
где а21 = —113,4 сек2!км, Ь21 = 481,9 сек, FS1 =
= 3,45 км!сек;
^□22 = ^22 Т 522 (Fsi ^ Vs "Д УS2) »
где а22 = — 925 сек2!км, Ь22 = 3191 сея, Fs2 = 3,47 км/сек]
^П23 ~ a23^s А- Ь23 (Fs Fs2),
где а23 = 100 сек2!км, Ъ23 - —275 сек.
Длительность интервала времени At между двумя
моментами переключения 7Ауф для каждого типа КА су¬
щественно зависит от высоты условного перицентра
траектории входа h-. Так, при движении рассматриваемо¬
го КА вблизи верхней границы коридора At имеет наиболь¬
шее значение и составляет примерно 70 сек. Уменьшение
hK приводит соответственно к уменьшению интервала
времени между двумя переключениями К^ф вплоть до
полного его исчезновения при движении КА по нижней
границе коридора входа /гА В последнем случае аппарат
движется на всей траектории спуска с неизменным зна¬
чением КЭф = +/£g-
В табл. 8.2 приведены результаты оценки эффектив¬
ности работы алгоритма. Видно, что использование пред¬
лагаемого алгоритма позволяет достаточно хорошо от¬
рабатывать все возмущения. Математическое ожидание
М (FK) и утроенное среднеквадратичное отклонение ко¬
нечной скорости За (AFK), определенные при возможном
совместном действии всех возмущений по методу Б. Г. До-
ступова, составляют соответственно М (FK) = 028 ж! сек
и За (AFK) = 33 ж!сек.
Возможная погрешность алгоритма управления ко¬
нечной скоростью не превышает 50 м/сек по сравнению с
«идеальным») управлением (мгновенная перекладка КА
по крену, отсутствие приборных ошибок и т. д.) и 95 м/сек
по сравнению с оптимальным управлением.
Необходимо отметить, что минимальная высота полета
КА на возмущенной траектории может принимать зна¬
чения, отличающиеся от заданного /гдоп: величина мате¬
матического ожидания минимальной высоты полета при
§ 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ ЗЦ
Таблица 8.2
Оценка эффективности алгоритма управления с двумя
линиями переключения
(Рх = 350 кг/м*\ Ттах = 180°, Кб = 0,3, hK =6 км, hn = -70 км,
V ) = 5,8 км/сек, VK = 590 м/сек)
Вид возмущения
Величина возмущения
Ук ,Mjcert
Д hn
-[-70 км
621
—70 км
595
AF0
+10 м/сек
596
—10 м/сек
597
Д^Рх
+35 кг/мг
670
—35 иг pvt2
604
ДКб
+0,03
633
—0,03
675 ‘
возможном суммарном действии всех возмущений состав¬
ляет М (Amin) = 6,2 км, а величина утроенного средне¬
квадратичного отклонения За (А/г1Пт) — 0,88 км.
Расслготрим теперь, как влияет на точность алгоритма
управления изменение максимальной величины угла крена
у max и минимально допустимой высоты полета над по¬
верхностью Марса. Как видно из рис. 8.7, уменьшение
Ушах (при соответствующем изменении линий переключе¬
ния, см. рис. 8.6) приводит к увеличению М (FK), вели¬
чина За (AFK) при этом остается практически неизменной.
Например, при изменении у max от 180 до 90° величина
М (FI{) возрастает с 628 до 686 м/сек, а За (AFK) с 33 до
38 м/сек. Увеличение минимально допустимой высоты по¬
лета приводит к увеличению М (FK) и За (AFK). Так, при
изменении АдПП с 3 до 9 км (линии переключения для этих
случаев представлены на рис. 8.6) величина М (FK) воз¬
растает с 508 до 742 м/сек, а За (AFK) с 18 до 46 м/сек.
Представленные результаты свидетельствуют о достаточно
высокой эффективности алгоритма с двумя линиями пере¬
ключения для КА с Рх -- 350 кг/м2 и Ко = 0,3.
Рассмотрим теперь возможность использования ал¬
горитма двухразовой перекладки КЭф для КА с различ¬
312
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
ными проектно-баллистическими параметрами: 300 кг/м2
^ Рх ^.600 кг/м2, 0,3 < ти < 0,5 в диапазоне скорос¬
тей входа от 5,5 до 7,7 км/сек.
При исследовании точности управления для каждого
конкретного случая рассчитывались свои линии переклю¬
чения. Результаты по оценке точности управления в за¬
висимости от нагрузки на лобовую поверхность КА, аэро¬
динамического качества и скорости входа приведены на
У^сек
'УЖ)
У* (Утх)
/7 2 ~ у рад
— — 77 /тъ'н
2 о
Рис. 8.7. Математическое ожидание и предельные отклонения конечной ско
рости спуска для разной конечной высоты и допустимого угла крена (Р —
= 350 7?г/мг\ Ко = 0,3; V0 = 5,8 км/сек). (Сплошная линия — математическое
ожидание величины конечной скорости М (Ук), штриховая линия — наиболь¬
шее, а штрих-пунктирная — наименьшее значение конечной скорости.)
рис. 8.8. Видно, что увеличение нагрузки на лобовую
поверхность практически не влияет на точность управле¬
ния, а увеличение аэродинамического качества несколько
ее ухудшает. При увеличении Рх с 350 до 550 кг/м2 (Ко =
= 0,3; F0 — 5,8 км/сек) 3_а (AFK) изменяется с 33 до
37 м/сек, а при увеличении Ко с 0,3 до 0,5 (Рх ----- 350 кг/м2,
V0 = 5,8 км/сек) Зет (AFK) изменяется с 33 до 46 м/сек.
Это объясняется тем, что во всех случаях величина отно¬
сительной ошибки аэродинамического качества бралась
одинаковой, а именно 10%. При увеличении качества воз¬
§ 8.2] АЛГОРИТМЫ УПРАВЛЕНИЯ КОНЕЧНОЙ СКОРОСТЬЮ 313
растает абсолютная величина ошибки, что приводит к уве¬
личению разброса величины конечной скорости.
Как и следовало ожидать, величина математического
ожидания конечной скорости существенно зависит от при¬
веденной нагрузки на лобовую поверхность, причем уве¬
личение Рх приводит к возрастанию MJFK)* Так, если
для КА с Рх — 350 кг/м2 (Ко = 0,3; V0 -- 5,8 км/сек)
М (VK) ----- 628 м/сек, то для КА с Рх 550 кг/м2 величина
Ук.у/пек
Рис. 8.8. Математическое ожидание и предельное отклонение конечной скоро¬
сти спуска для разных параметров КА и скорости входа (/гдои = 6 км, утах =
= л). (Сплошная линия — М (VK), штриховая — наибольшее, а штрих-пунк¬
тирная — наименьшее значение конечной скорости.)
математического ожидания конечной скорости возрастает
до 822 м/сек. При увеличении аэродинамического каче¬
ства величина М (FK) сначала уменьшается, а затем, на¬
чиная с некоторого значения Ко, практически не из¬
меняется. В частности, при увеличении Ко с 0,3 до 0,4
(Рх = 350 кг/м, V0 = 5,8 км/сек) М (VK) уменьшается
с 628 до 551 м/сек, а при дальнейшем увеличении К о с
0,4 до 0,5 М (FK) уменьшается всего на 7 м/сек.
Из данных, приведенных на рис. 8.8, видно, что уве¬
личение скорости входа слабо влияет на точность управ¬
ления. При увеличении V0 от 5,8 до 7,5 км/сек За (AFK)
изменяется от 33 до 29 м/сек (для КА с Рх = 350 км/сек2
314
АЛГОРИТМЫ УПРАВ ЛГИ III Я СПУСКОМ
[ГЛ. N
я Kq = 0,3). Видно также, что при увеличении скорости
входа величина математического ожидания конечной ско¬
рости несколько уменьшается. Например, при изменении
скорости входа от 5,8 до 7,5 км/сек М (Ёк) уменьшается
от 628 до 596 м/сек.
Таким образом, дискретный алгоритм управления, ис¬
пользующий линии переключения, может быть применен
при построении систем управления конечной скоростью
спуска для широкого класса КА и при различных скорос¬
тях входа. Величина математического ожидания М(ЕК)
всего на 60 м/сек превышает значение конечной скорости,
полученное при оптимальном управлении, а разброс от¬
носительно математического ожидания не превышает
50 м/сек; максимальные потери но сравнению с оптималь¬
ным управлением могут достигать приблизительно
100 м/сек.
Мы рассмотрели наиболее простой вариант дискретно¬
го управления. Это следует из принятого состава изме¬
рительных средств и необходимости использования про¬
стого вычислителя для выполнения арифметических и
логических операций (расчет по формулам (8.59), (8.60)).
Настройка системы управления осуществляется простым
пересчетом коэффициентов, аппроксимирующих линии
переключения и запоминаемых бортовьш вычислителем.
| 8.3. АЛГОРИТМЫ УПРАВЛЕНИЯ
ОТНОСИТЕЛЬНО ОПОРНОЙ ТРАЕКТОРИИ
Принцип гарантирующего управления траекторий сни¬
жения КА в атмосфере Марса может быть использован
и при синтезе другого, достаточно распространенного
класса алгоритмов 118], предполагающих отслеживание
опорной траектории, которая выбирается заранее или фор¬
мируется на борту КА в процессе полета. Основная идея
заключаемся в тОхМ, что выбор опорной траектории, отно¬
сительно которой осуществляется управление движением
КА в атмосфере Марса, производится для наиболее раз¬
реженной атмосферы р (h) = p,nia (h). Тогда отклонение
плотности атхмосферы может происходить лишь в сторо¬
ну ее увеличения. Если управляющее воздействие (эф¬
фективное аэродинамическое качество) окажется не¬
достаточным для парирования возмущения по плотности,
5 8.3] УПРАВЛЕНИЕ ОТНОСИТЕЛЬНО ОПОРНОЙ ТРАЕКТОРИИ 315
то конечные значения параметров траектории будут от¬
личаться от расчетных. Однако увеличение плотности
атмосферы оказывает положительное влияние на функцио¬
нал управления при организации мягкой посадки КА на
поверхность Марса (величина конечной скорости умень¬
шается при использовании реактивной СМП, а величина
конечной высоты увеличивается при использовании ПРС).
Поэтому погрешность управления будет компенсироваться
и величина функционала управления в результате долж¬
на оказаться не хуже требуемой.
В связи с этим рассмотрим одно из возможных направ¬
лений построения алгоритма управления траекторией
снижения КА относительно опорной траектории, пред¬
полагающее непрерывное изменение АЭф при отслеживании
опорной траектории.
В качестве функционала управления может быть ис¬
пользован либо Критерий Вк С зад, Либо Ак>Акзад
в зависимости от типа используемой СМП. Ниже для при¬
мера рассмотрим алгоритм управления величиной конеч¬
ной высоты.
При выборе измеряемых на борту КА параметров бу¬
дем исходить из наиболее простого варианта, который в
то же время обеспечивает приемлемую точность решения
задачи. А именно, будем предполагать возможность авто¬
номного измерения на борту КА перегрузки пх или вре¬
мени полета t и вычисления кажущейся скорости Vs.
Выбор опорной траектории. В качестве опорной траек¬
тории целесообразно рассматривать оптимальную траек¬
торию, реализующую максимум конечной высоты при
заданном значении конечной скорости (см. главу 0).
В табл. (S.3 для КА с величиной приведенной нагрузки на
лобовую поверхность Рх --- 350 кг/м2 и Кь — 0,3 пред¬
ставлены данные, показывающие зависимость максималь¬
ной конечной высоты hK max от высоты условного перицен¬
тра траектории входа при оптимальном управлении. Вид¬
но, что величина hKmRX практически не зависит от hr, в
достаточно широком диапазоне изменения hn. Поэтому
с точки зрения обеспечения наибольшего значения hK mSLX
в качестве опорной может быть использована оптимальная
траектория, рассчитанная для любого значения /г- внутри
коридора входа. Проведем исследование алгоритма управ¬
ления, предполагающего использование одной опорной
316
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. Я
Таблица 8.3
Оценка влияния высоты условного перицентра на конечную
высоту при оптимальном управлении
0о, град
/)_, км
/п, сек
п х max
Anin.’ км
^max> км
" ■ 1
,гкшах<
км
-8,5
42,100
139
5,984
8,533
13,928
11,103
-9
35,113
111
7,249
8,530
13,215
11,749
-9,5
27,735
96
8,274
7,624
13,914
12,102
-10
19,964
85
9,112
7,041
13,852
12,408
—10,5
11,8024
75
9,657
7,305
15,321
12,697
-11
3,2512
69
10,306
6,811
15,038
12,933
—11,5
— 5,6885
63
10,816
6,61
15,267
13,110
—12
—15,0155
58
11,281
6,436
15,425
13,245
—12,5
—24,728
54
■11,765
6,078
15,111
13,430
—13
-34,826
50
12.035
6,180
15,743
13,480
—13,5
—45,306
46
12,094
6,610
17,048
12,907
—14
—55,168
43
12,333
6,560
17,235
12,961
-14,5
—67,410
40
12,781
6,043
16,333
13,603
-15
-79,030
37
12,794
6,316
17,148
13,235
—15,5
—91,027
35
13,060
6,065
16,768
13,543
-16
— 103,399
31
12,979
6,368
17,563
12,984
—16,5
—116,144
29
13,196
6,153
17,201
13,323
траектории. Выберем ее для случая движения КА в се¬
редине коридора входа. Для приведенного выше примера
это соответствует высоте условного перицентра hn =
= —45 км.
Алгоритм управления должен отслеживать опор¬
ную траекторию согласно закону управления
ДйГэф - aAt(Vs), (8.65)
где а — коэффициент усиления. At --- tTeK (Vs) —
— ton (Vs), *тск (V,) текущее время, ton (Vs) — время,
соответствующее опорной траектории, выбранной для
номинальной высоты условного перицентра.
Проведенные исследования показали, что подобный
алгоритм управления оказывается очень чувствительным
к действию одного из основных возмущений — отклоне¬
нию высоты условного перицентра траектории входа.
Данные, приведенные в табл. 8.4, показывают, что при
Ah- 10 7- 15 км использование алгоритма, нредпо-
§ 8.3] УПРАВЛЕНИЕ ОТНОСИТЕЛЬНО ОПОРНОЙ ТРАЕКТОРИИ 817
Таблица 8.4
Оценка эффективности алгоритма при отслеживании заданной
опорной траектории
1гп, км
пШ:\х
^min» пм
^тах* км
hK, км
0К, град
ql{, кгс!м2
—15,015
—24,73
—34,826
-45,306
-56,168
7,779
8,885
10,177
11,758
11,3845
6,63
7,26
35,98
29,08
21,82
16,026
18,34
1,93
3,43
7,92
13,17
11,78
— 1,4,5
—17
—16,7
— 8,8
—12,9
311
272,5
182,2
113,67
128,7
латающего отслеживание одной жестко заданной опор¬
ной траектории, неэффективно (конечная высота умень¬
шается па 6 -г- 8 км).
Для более эффективной компенсации возмущения по
hr. целесообразно использовать настройку опорной тра¬
ектории на это возмущение. На рис. 8.9 приведено се¬
мейство опорных траекторий в виде зависимости ton (Fs),
построенных для различных значений высоты условного
перицентра траектории входа. Эти зависимости практи¬
чески параллельны в значительном диапазоне изменения
кажущейся скорости. Этим обстоятельством можно вос¬
пользоваться для организации гибкой настройки опорной
траектории, которая формируется в зависимости от вы¬
соты hr. согласно соотношению
ton (Fe, hr) = ton (Vs) + AT (A*), (8.66)
где A77 (hr) — величина поправки. Для определения ве¬
личины А Т (hr) возникает необходимость в уточнении вы¬
соты условного перицентра траектории входа hr.. Это
можно сделать косвенным образом, например, используя
информацию о темпе изменения кажущейся скорости.
Тогда
ДГ(А„) -/(**), (8.67)
где t* — время достижения фиксированного значения
кажущейся скорости Vs -- V'.
Если величину F* принять равной 100 м/сек, то для
рассматриваемого примера зависимость (8.67) примет
318
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
ВИД
[ #11* + bi при t* 20,3 сек,
(Ьл) j ^ при ^ 20?3 сек,
где % = 4,04, Ьх = —90,84 сек, а2 = 4,38, Ь2 =
= —97,73 сек.
Результаты моделирования алгоритма управления ко¬
нечной высотой с гибкой настройкой опорной траектории
Рис. 8.9. Семейство опорных траекторий fon (V ) для различных значений
высоты условного перицентра /г-.
представлены в табл. 8.5—8.7. Алгоритм управления до¬
вольно успешно парирует все действующие возмущения,
в том числе колебательные возмущения плотности. Вели¬
чина математического ожидания конечной высоты при
возможном суммарном действии всех возмущений, оп¬
ределенная по методу Б. Г. Доступова, составляет
Моделирование алгоритма управления конечной высотой с гибкой настройкой опорной траектории
§ 8.3] УПРАВЛЕНИЕ ОТНОСИТЕЛЬНО ОПОРНОЙ ТРАЕКТОРИИ 319
05
О
232
229
223
219
209
о
т—1
СМ
217
204
СО
Ю
м
CD
см
Ю
с-^
LO
со
СО
00
[>•
СО
о
СМ
оо
СО
со
ЧЧ
ю
чЧ
о
со
—-I
05
00
00
СО
ю
СО
г-н
чч
чЧ
о
о
о
о
О
см
со
с.
г-1
ЧЧ
чч
чч
-Ч
тЧ
-ч
чч
ЧН
ЧЧ
с?
1
(О
00
t>.
СМ
05
СО
СО
СО
СО
05
Оо"
00
00
1>-
со
оо
СО
сГ
О
1
1
1
1
1
т
1
1
1
1
сГ
1
00
со
05
_
00
00
О
Ю
vf
О
СМ
).Ь
о
со
ю
О*
СО
СМ
V?
ю
L'—
[>■
05
CD
к
СО
СО
СО
со
СО
СО
СО
СО
СМ
ЧЧ
л;
чЧ
чч
чЧ
5
05
Ю
см
СМ
СМ
05
см
оо
со
СО
см
L—
I'-
СО
и
05
05
00
!>■
см
LO
см
ЧЧ
ей
ю
Ю
ю
ю
Ю~
LO
СО
LO*
см
,_7
S
ЧЧ
—ч
5С
00
О
ю
о
СО
см
LO
см
V*
о
ю
Vjl
00
V?
С
ю
со
чЧ
05
00
со
•s
CD
СО
СО
СО
IO
ю
юГ
Ю~
со"
СО
СО
и
СМ
со
ю
СО
Ю
V*
г>
СМ
см
00
о
V*
О
СМ
Ю
Ю
О
1
ю
СО
см
ю
00
05
со
со
00
S
,_4
_Г
см
CM
см
см
СО
S
чч
'т-1
о.
II
СО
СО
00
о
L"-
со
^сг
II
см
О
СО
■^ч
со
СМ
05
со
vf
O'
00
СО
чн
о
CD
СО
см
L'-
1гГ
СО
!>•
05
СО~
СО
05
CM
й
со
ю
СО
05
О
тН
см
о
-с:
1
1
1
1
1
|
ГЧ
«
1
1
1
1
н
г,
о
сз
со
ю
ю
ю
LO
ю
С2
со*
СО
СО
vr
ю
LO
СО
со
t—
X
чЧ
чЧ
Ч-ч
чЧ
сЗ
1
I
1
1
1
1
1
1
1
I
н
о
1
|
1
1
|
]
05
о
1
1
1
О
&
£
со
С—
ю
05
СО
со
СО
РЗ
со
t-
см
_Г
СМ
О
05
05
05
00
05
см
см
см
см
см
чЧ
ЧЧ
S
5
LO
ей
со
ю
1^
LO
05
см
05
05
СО
00
LO
ю
см
g
О
со
05
р,
СО
СО
00
О
CM
СО
|Ч
Еч“
СО
o'
1
1
1
1
ЧЧ
ч-ч
■чч
К
<1
1
1
1
1
1
1
1
1
320
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
Т а б л и да 8.6
Моделирование алгоритма управления конечной высотой
с гибкой настройкой опорной траектории
о
S*
Ъ
с\Г
н
Он
CJ
£
«с
£
У,
<х.
В
si
£
s
й
а
В
►сГ
5
а
со
К
о
§
с
со
*«й
Q0
0,27
350
6
12/163
5,158
11,1
10,875
—2,5
140,1
174
0,30
350
6
12,575
5,754
15,27
13,704
-6,7
108,4
209
0,33
350
6
12,678
6,301
20,03
12,55
-14
120,2
265
0,3
315
6
12,399
7,384
17,53
14,688
-8,9
99,38
223,8
0,3
385
6
12,575
5,754
15,269
13,704
—6,6
108,37
209
0,3
350
5,99
12,522
5,785
15,295
13,699
—6,7
108,5
210
0,3
350
6,01
12,604
5,776
15,368
13,737
—6,8
108,2
210
Примечание: в расчетах принято p(h) = pm\n(h).
Таблица 8.7
Моделирование алгоритма управления конечной высотой
с гибкой настройкой опорной траектории
ю
*
%
К
я
Он
о
и
л
в
е
-
S
х;
й
к
к
СО
в
Рн
го
О
5
"о
со
£
К
Сг1
о
0,33
385
6
12,739
5,06
18,452
12,18
—13
124,5
256
0,3
315
5,99
12,372
7,36
17,42
14,67
-8,8
99,3
223
0,3
385
5,99
12,456
4,84
14,456
12,59
-7,3
119,11
213
0,27
315
5,99
12,281
6,727
13,052
12,566
—3,7
120,16
182
0,33
315
5,99
12,478
6,876
22,27
12,311
—15,6
122,8
280
0,33
385
5,99
12,709
5,04
18,35
12,274
—11,6
123,3
255
0,33
350
6,01
12,730
6,266
20
12,67
—13,8
119,16
263
0,3
385
6,01
12,537
4,828
14,528
12,625
-7,3
119,48
213,5
0,33
385
6,01
12,64
5,374
19,34
10,99
—14,6
138,3
270
Примечание: в расчетах принято
р(/0 = 1
Piiiax(^0*
1
^ 8.4] АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ 321
М(йк)= 13,4 км, а утроенное среднеквадратичное отклоне¬
ние За (йк) = 2,8 км. Из сопоставления этих результатов
с данными, приведенными в табл. 8.3, видно, что по срав¬
нению с оптимальным управлением максимально возмож¬
ное уменьшение конечной высоты составляет
АЙитах = Й'ктпах [М (^к) Зог (Й-к)] = 616 Ж,
где йк шах — максимальное значение конечной высоты,
полученной при оптимальном управлении траекторией
спуска.
§ 8.4. АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
КОНЕЧНОЙ СКОРОСТЬЮ СПУСКА
Основным недостатком рассмотренных выше алгорит¬
мов является то, что они построены в предположении
известного характера действия возмущений и не мог;ут
адаптироваться к изменению условий движения. Система
управления настраивается на определенную модель воз¬
мущений и тем эффективнее, чем достовернее эта модель.
Кроме того, после проведения последней коррекции имеет¬
ся достаточно продолжительный участок фактически не¬
управляемого полета, что приводит к ухудшению точ¬
ности.
Точность и надежность управления могут быть сущест¬
венно повышены, если в рамках ранее изложенной стра¬
тегии гарантирующего управления использовать адап¬
тивный подход. Для этого на борту КА должны находиться
более совершенные измерительные средства и ЦВМ; тогда
появляется возможность синтеза алгоритмов управления,
способных эффективно функционировать в неопределен¬
ных условиях, заранее неизвестных, и адаптироваться
к ним.
Кроме того, на борту КА необходимо иметь инерциаль-
ную систему отсчета. Она может быть получена двумя
способами:
— с помощью гиростабилизированной платформы;
— с помощью бесплатформенной системы автоном¬
ной навигации.
В первом случае платформа позволяет обеспечить оп¬
ределенную пространственную ориентацию системы аксе¬
лерометров (например, по трем взаимно ортогональным
11 Н, М. Иванов, А. И. Мартынов
322
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. S
направлениям). Измеряемые компоненты перегрузки ис¬
пользуются для определения текущих координат и ком¬
понент вектора скорости, а гиростабилизированная пла¬
тформа позволяет получить параметры пространственном
ориентации КА.
Во втором случае инерциальная система получаете}]
расчетным путем и хранится в памяти бортовой ЦВМ.
Все неинерциальиые измерения приводятся к ней путем
пересчета. Количество чувствительных элементов подби¬
рается таким образом, чтобы обеспечивалось получение
информации о векторе аэродинамического ускорения и век¬
торе абсолютной угловой скорости КА. При этом требо¬
вания к бортовой ЦВМ значительно возрастают, ибо для
определения фазовых координат на борту КА необходимо
проводить значительно больший объем вычислений, чем
в случае использования гиростабилизированной плат¬
формы.
Рассмотрим задачу синтеза адаптивного алгоритма
управления конечной скоростью спуска при наличии гиро-
стабилизироваиной платформы с установленными на ней
акселерометрами и бортовой ЦВМ в системе управления.
При ее решении ставится условие гарантированного
обеспечения конечной скорости F* 1П-М1 при мини¬
мально возможной глубине погружения КА в атмос¬
феру, что соответствует условию максимизации мини¬
мальной высоты пролета над поверхностью /гт[П —> max.
Кроме того, алгоритм управления должен обеспечивать:
максимальную ширину коридора входа, который реализу¬
ется с помощью конкретной системы управления спуском
с принятой логикой управления, ограничениями, мето¬
дическими и исполнительными ошибками, а также оши¬
бками измерений; возможность быстрой и минимальной
перенастройки параметров системы управления при из¬
менении скорости входа КА в атмосферу, параметров
КА (величины приведенной нагрузки на лобовую по¬
верхность и аэродинамического качества) и величины
заданного ограничения на высоту полета над поверхносг
тыо Марса.
Изменение со временем требуемого значения угла
крена должно быть достаточно плавным, чтобы система
угловой стабилизации КА могла легко и с наименьшими
ошибками его отрабатывать.
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
323
Алгоритм с использованием прогнозирования
конечных условии
Общий методический подход. Идея синтеза алгоритма
управления заключается в том, что в начале траектории
спуска определяется зависимость Кэф (t) эффективного
аэродинамического качества от времени, которая при от¬
сутствии начальных ошибок и возмущений обеспечивает
выполнение конечных условий и ограничений, в том числе
(8.4). В результате действия возмущений на траектории
спуска значения фазовых координат КА будут отличаться
от расчетных. Поэтому через некоторое время после нача¬
ла движения необходимо уточнить зависимость Кэф(£)
с новыми начальными условиями, соответствующими реа¬
лизовавшимся значениям фазовых координат КА. Про¬
цедура уточнения этой зависимости должна периодически
повторяться до тех пор, пока не будет выполнено условие
(8.4).
Синтез адаптивного алгоритма управления можно про¬
вести следующим образом [5, 66]. Пусть с использованием
некоторого алгоритма управления КА осуществляется
построение последовательности приближений оптимального
управления и0 (t) и соответствующей траектории х0 (t),
начинающейся в фазовой точке х0 (t0). В текущий момент
времени t вычисляется упрежденное на шаг At положение
фазового вектора КА х (t0 + At), которое принимается
для исполнения в течение следующего промежутка вре¬
мени [t0 + At, t0 г 2At], а система управления в это
время готовит управление для предполагаемого положения
х (£0 + 2At) и т. д. В результате движение КА будет
осуществляться по участкам траекторий, которые являют¬
ся приближениями оптимальных траекторий для после¬
довательности предсказываемых положений КА.
Итак, пусть имеем некоторый класс траекторий
х (t, и, х0), t > 0, х (0, и, х0) = х0. (8.68)
Предположим, что вектор-функция х (t, и, х0) непре¬
рывна по совокупности (t, х0) и допускает сдвиг по време¬
ни начальной точки:
х (t, и, х0) = х (t — т, и, х (т, и, х0)), (8.69)
где т > 0.
11*
324
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
Предположим также, что для каждой точки х0 су¬
ществует оптимальное управление и0, которое обеспечи¬
вает минимум функционал у I (щ, х0). Кроме того, будем
считать, что некоторый алгоритм позволяет для любой
точки х0 ЕЕ В строить последовательность управлений
и(х0) ЕЕ U (здесь В — область управляемости, огра¬
ничивающая множество точек х0; U — область, ограни¬
чивающая некоторый класс управлений и). В этом слу¬
чае выполняются соотношения
x{t(V(x0), и<*)(Хо). ЭСо}->0, 1
/<« (Хо) -> / (ЗСо) при I —> ос. | (б-/и)
В силу (8.70) для любого произвольного числа е —> 0
существует номер i (г, х0) такой, что при i > i (в, х0)
разность правых и левых величин в соотношениях (8.70)
меньше е [5].
Задаваясь числом Дt Е> 0, можно составить синтези¬
руемую траекторию из участков вида (8.70):
х (т, 8, М) х^ (т), т е [/АС (/ + 1) Д*] (/ - 0,1, 2, . . .).
(8.71)
Здесь
эсб) (т) = х(т — jAt, Uj, x{i~l) (At)), ttj =■■= nli (x^-v (At)),
ij = i (ej, xO-D (Дг)), x~l (t) = x0, Ej > 0.
Эта траектория будет сколь угодно близка к оптималь¬
ной в том смысле, что
I (х0, е, At) -*■ I (х0) при е -> 0, At 0.
Следует отметить, что для нелинейных систем нет в
настоящее время каких-либо общих рекомендаций отно¬
сительно алгоритма построения последовательности уп¬
равлений и^ (х0). Сложность задачи приводит к неиз¬
бежности использования эвристических приемов. При
этом очень важным элементом, влияющим на вид синте¬
зируемой траектории, является учет особенностей струк¬
туры номинального движения КА (оптимальных траекто¬
рий).
Проблема синтеза адаптивных алгоритмов управления
па основе итеративных методов для КА, осуществляющих
спуск в атмосфере Земли, была рассмотрена в работах
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
325
Д. Е. Охоцимского, Ю. Ф. Голубева, 10. Г. Сихарулидзе
и Др. [65—70], предложивших метод многошагового ал¬
горитма управления движением КА, к которому близок
рассмотренный выше метод синтеза адаптивного алгорит¬
ма ш
Ниже обсуждается один из возможных путей синтеза
адаптивного алгоритма гарантирующего управления ко¬
нечной скоростью спуска КА в атмосфере Марса. Пред¬
полагается, что на борту КА имеются измерительные и
вычислительные средства, позволяющие определять те¬
кущие фазовые координаты аппарата, уточнять его харак¬
теристики и прогнозировать траекторию путем интегри¬
рования уравнений движения для выбора программы
управления.
Алгоритм управления предполагает решение следую¬
щих основных задач:
— прогноз движения КА и решение краевой задачи;
— выбор стратегии управления как функции теку¬
щего фазового состояния;
— определение фазовых координат движения КА (за¬
дача навигации);
— определение характеристик КА (задача идентифика¬
ции).
Выбор стратегии управления. Будем рассматривать
класс аппаратов, для которых оптимальным оказывается
управление первого типа (см. главу 6). Для таких траек¬
торий характерным является наличие изовысотного участ¬
ка движения КА. Величина конечной скорости определя¬
ется только скоростью схода с ограничения (Т^2)) и не
зависит от траектории выведения на режим горизонталь¬
ного полета при условии, если
> V&\ (8.72)
где V(1) — скорость при выходе па ограничение.
Неединственность траекторий минимальной конечной
скорости можно использовать для их оптимизации по
другим критериям. Так, в главе 6 была рассмотрена ва¬
риационная задача по определению закона управления
эффективным качеством, который обеспечивает минималь¬
ное (дг[Пах)min или максималыюе (пШ1ХХ) 1Пах значение макси¬
мальной перегрузки па траекториях минимальной конеч¬
ной скорости. Величина (щт1х)тчх реализуется при одно¬
3243
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
разовом переключении Кдф с минимального значения
Коф = — Кб на максимальное Кдф = +Аб на участке
до выхода на ограничение, a (ftmax)miri — при двухразовом
переключении К0ф = + К б, —К б, -\-К q. При исполь¬
зовании этих двух программ управления для КА с Рх~
^ 200 -г- 500 кг!м* и Аб = 0,3 -г- 0,5 разность
Д^тах == (п max) max (^max)min
может составлять 3 -г- 4 при одинаковых условиях входа.
На любой траектории спуска, удовлетворяющей условию
(^max)max ^ ^max ^ (^max)min> (8.73)
можно обеспечить неизменное значение VK = YKmin =
= У к зад- Используя эту особенность, траекторию спуска
можно разбить на два участка: от момента входа до до¬
стижения птах и от пт.лх До конца траектории. На первом
участке алгоритм управления должен обеспечить только
попадание КА в допустимую область максимальных пере¬
грузок (8.73). На втором участке обеспечиваются тре¬
буемые конечные условия при одновременной максимиза¬
ции hmUl.
Такое разделение траектории спуска на два участка
позволяет существенно упростить решение задачи. Дей¬
ствительно, на первом участке можно применить упро¬
щенное управление и лишь только на втором участке —
точное управление с использованием прогнозирования ко¬
нечных условий.
Обеспечение выведения КА в допустимую по 7гтах об¬
ласть можно осуществлять при разных номинальных про¬
граммах управления эффективным качеством, из которых
наиболее простой является программа полета с постоян¬
ным значением К»ф. Эту программу и рассмотрим в первую
очередь. Численные исследования показали, что существует
диапазон высот \ перицентров траекторий входа, при
движении внутри которого с КЭф = const возможно
выведение КА в допустимую по перегрузке область
(8.73).
С другой стороны, на первом участке управления имеет¬
ся некоторая свобода в выборе постоянного значения
А именно, каждой величине внутри коридора
входа соответствует некоторый набор значений КЪф из
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
327
диапазона
(8.74)
которые обеспечивают приведение КА в область допусти¬
мых перегрузок. Этот некоторый произвол в выборе Кэф
можно использовать для создания наилучших условий
при управлении на втором участке.
Опишем стратегию управления на первом участке
спуска. КА входит в плотные слои атмосферы со значе¬
нием эффективного качества Кдф = + Аб, с которым
продолжает движение до Vs = 7*. Вход в атмосферу
фиксируется при достижении порогового значения пере¬
грузки (720) или кажущейся скорости (У50). В момент
достижения Vs = У* = 100 ж!сек происходит поворот
КА на такой угол крена у0, с которым КА осуществляет
выход на требуемое значение тгтах. При этом величина
угла у0 зависит от времени t* достижения заданного зна¬
чения кажущейся скорости У*:
Построение зависимости (8.75) производится из усло¬
вия наведения КА в область допустимых перегрузок (8.73)
таким образом, чтобы создавались наиболее благоприят¬
ные условия для решения задачи управления на втором
участке при полете в самой разреженной атмосфере.
Время движения от момента ?г0 до /гтах отводится на ре¬
шение навигационной задачи, уточнение параметров ат¬
мосферы и некоторых характеристик КА.
Решив задачу наведения в заданный диапазон /гшах,
следует приступить к обеспечению значения Ук ^ Ук зад
при одновременном выполнении условия максимизации
hmin. Как уже отмечалось, для получения 7К = Ук min
управление полетом достаточно организовать таким обра¬
зом, чтобы обеспечивалось выведение КА в точку с фазо¬
выми координатами У = У^2), /г = /гдоп и 0 - 0. Даль¬
нейшее движение КА осуществляется с неизменным мак¬
симальным значением Кэ ф = + К$. Для упрощения
алгоритма управления и уменьшения необходимого быстро¬
действия и памяти бортовой ЦВМ при выведении КА в
эту точку будем использовать программу с Кэф = const.
То = / (**)•
(8.75)
328
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
Перейдем к стратегии управления на втором участке.
После достижения /гтах решается краевая задача по оп¬
ределению такого постоянного угла крена, при полете
с которым от текущей точки коррекции до момента вы¬
равнивания траектории (hmin) с последующим переходом
па полет с у — 0 (т. е. Кэф — Ко) в конце траекто¬
рии спуска обеспечивается VK Ккзад. Найденный
угол крепа выдерживается до следующей коррекции.
В связи с изменением реальных условий спуска, неточ¬
ным знанием начального положения, наличием возму¬
щений и т. д. необходимо периодически решать краевую
задачу для коррекции управления. В момент достиже-
ния hm[n устанавливается угол крена у — 0. Даль¬
нейший полет протекает с неизменным значением у — 0
до конца траектории спуска.
Навигационная задача. В настоящее время разработан
ряд методов решения навигационной задачи при спуске
КА в атмосфере [13, 54, 70]. Опишем кратко их суть.
Один из возможных подходов состоит в уточнении не¬
обходимых параметров на некотором начальном этапе
входа в атмосферу. Затем осуществляется интегрирование
навигационной системы дифференциальных уравнений.
Этот подход имеет недостатки, существенно влияющие на
точность решения навигационных задач, которые свя¬
заны с тем, что длительность начального участка входа
в атмосферу ограничена.
В работе [70] рассмотрен один из методов навигации,
который заключается в определении уточняемого на бор¬
ту КА параметра (высоты условного перицентра траекто¬
рии входа) с помощью измерений вблизи начальной точки
входа. В этом случае можно считать, что сопротивление
атмосферы еще не успело оказать заметного влияния на
траекторию спуска, и для расчета ожидаемого значения
модуля аэродинамического ускорения можно использо¬
вать формулы кеплеровского движения. Сравнивая вы¬
численное и измеренное значения модуля аэродинамиче¬
ского ускорения, можно найти то значение hni при котором
они совпадают.
Для уменьшения погрешности определения h- же¬
лательно увеличивать мерный интервал. Однако из-за
применения приближенных формул, осуществляющих
пересчет фазовых координат точки входа в фазовые
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
329
координаты точки текущего положения КА, длительность
мерного интервала ограничена. Поэтому в работе [70]
развит новый подход к решению навигационной задачи,
который позволяет уточнять фазовые координаты движе¬
ния центра масс КА на протяжении всей траектории
спуска параллельно с определением потребного управле¬
ния. Разработанный метод параметрического семейства
заключается в следующем. Пусть требуется определить
один параметр — высоту условного перицентра траекто¬
рии входа h~. В процессе движения интегрируются две
траектории, соответствующие двум различным значениям
высоты условного перицентра /г^0) и В правых частях
уравнений этих траекторий используется одно и то же
значение аэродинамического ускорения, определяемое па
основе показаний акселерометров. Эти траектории
принадлежат однопараметрическому по h- семейству,
включающему и траекторию с искомым значением h~.
Искомое значение h- определяется путем использования
формул линейной интерполяции параметров движения КА
по радиусу-вектору и скорости для двух опорных тра¬
екторий: r(W, r(1\ К(0), Показано, что для КА, осу¬
ществляющих спуск в атмосфере Земли, эти формулы
справедливы в любой момент времени и могут быть ис¬
пользованы па всей траектории спуска. При этом наблю¬
дается высокая точность линейного приближения по h-.
Аналогичным образом: можно определить и начальную вы¬
соту входа КА в атмосферу. Метод параметрического се¬
мейства применим также в более общем случае, когда тре¬
буется определять не один, а несколько параметров на¬
вигации.
В работе [54] рассмотрен один из методов определения
оптимальных оценок компонент обобщенного вектора
состояния для КА, осуществляющих спуск в атмосфере
Земли. В целях улучшения сходимости оценок при
решении задачи навигации предлагается использовать ме¬
тодику обработки информации с помощью модифициро¬
ванного дискретного фильтра Калматта. Приводится соот¬
ветствующий алгоритм обработки информации. Возможно¬
сти модифицированного фильтра применительно к оценке
скорости полета V, угла 0 наклона траектории к мест¬
ному горизонту и высоты h проверяются статистическим
моделированием и свидетельствуют о высокой эффектив¬
330
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
ности предлагаемого алгоритма навигации для спуска
КА в атмосфере Земли. Представленные материалы о пос¬
ледовательности обработки информации, а также об из¬
менении дисперсии оценок для типичной реализации по¬
казывают, что точность оценки угла 0 за 4 сек измерений
не хуже 0,02°, а точность оценки скорости спуска за те же
4 сек не хуже 0,35 ж!сек. Если мерный интервал увеличи¬
вается до 8 сек, точность определения параметров воз¬
растает до 0,005° и 0,1 м/сек.
В работе [13] рассмотрены вопросы использования
фильтров Калмана для оценки параметров траекторий
спуска КА в атмосфере Венеры. В качестве измеритель¬
ной информации предполагается использование сигналов
двух акселерометров, жестко закрепленных на борту КА.
Для оптимальной обработки измерений применяются ал¬
горитмы линейного фильтра Калмана — Шмидта. Ре¬
зультаты моделирования демонстрируют высокую эффек¬
тивность этих алгоритмов. В частности, через 30 сек
измерений точность оценки] величины скорости КА со¬
ставляет 0,03 м/сек.
Проведенные исследования показали, что большая
часть из предлагаемых алгоритмов с соответствующей
доработкой может быть использована для решения на¬
вигационной задачи при спуске КА в атмосфере Марса.
Однако особенности спуска КА в атмосфере этой планеты
позволяют построить более простые алгоритмы навигации
[25]. Обсудим один из возможных путей построения та¬
кого алгоритма автономной навигации.
Рассмотренный ранее адаптивный алгоритм управле¬
ния конечной скоростью спуска, предполагающий раз¬
биение траектории на два участка, использует известные
начальные данные для интегрирования уравнений дви¬
жения. Тогда решение навигационной задачи сводится
к построению во время движения одной интегральной
кривой навигационных уравнений с известными началь¬
ными условиями. Однако в действительности начальные
условия входа КА в атмосферу Марса известны с большой
неопределенностью:
— возможный разброс по высоте условного перицент¬
ра составляет несколько километров;)
— разброс в начальной скорости входа составляет
несколько метров в секунду,
§ 8.4] АДАПТИВНЫЙ АЛГОРИТМ _ УПРАВЛЕНИЯ 331
Кроме того отсутствует точная привязка начальной
высоты точки входа КА в плотные слои атмосферы. В си¬
лу этого неизбежны навигационные ошибки, которые
могут привести к недопустимому увеличению конечной
скорости спуска относительно заданного значения или
к существенному уменьшению высоты начала рикошети-
рования. Оценка влияния ошибок в знании начальных
условий А70иаБ, Дfo£aB и /г”ав на определение величин-
FK и ^min показала *), что предлагаемый адаптивный
алгоритм обеспечивает успешную работу системы управ¬
ления, если погрешности начальных условий входа не
превышают:
— по высоте условного перицентра Дhl™B — ЧЬ 5 км;
— по начальной высоте Д/&оав = ± 0,8 км;
— по скорости входа AFoiaB = dt 10 м/сек.
В настоящее время автономные средства наведения
на участке подлета КА к плотным слоям атмосферы Марса
не позволяют обеспечить вход с указанной точностью до
и h0. Следовательно, эти два параметра должны опреде¬
ляться в первую очередь на атмосферном участке спуска.
Если каким-то образом удается осуществить точную
привязку текущей высоты КА, то высота условного пери¬
центра hK может быть определена автономно любым из
известных способов [13, 54, 70]. Проведенные исследования
показали [24, 27], что можно построить аппроксимируе¬
мые полиномами невысокой степени простые зависимости,
которые позволяют легко определить h- на начальном
участке входа по времени t* достижения фиксирован¬
ного значения кажущейся скорости Vs — Fs\ Такой под¬
ход использует различную эффективность торможения
КА при изменении условий входа. В качестве примера на
рис. 8.10 приведена зависимость hn при F* =
— 100 м/сек для КА с Рх = 350 кг/м2 и К о = 0,3. Она
может быть аппроксимирована тремя прямыми:
-/?£ав = а^* + bi при t* ti,
h"dB = a2t* + Ь2 при t'i </ t* </t2,
hr*B — a3t* -j- b3 при t* ^t2.
*) В дальнейшем индексом «пав» будем обозначать навигацион¬
ные параметры.
332
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
1ТЛ. 8
Здесь % — 25,81 км/сек, а2 = 15,48 км/сек, а3
= 2,93 км/сек, Ьх = —683,86 км, Ь2 = —442,23 км, Ъ3 =
— —109,72 «ж, £* — 23,4 сек, t2 — 26,5 сея.
При построении этой зависимости предполагалась
минимальная модель плотности атмосферы, а угол крена
на начальном участке входа у0 = 0. Одним из основных
возмущающих факто¬
ров, которые ухудшают
точность определения h-
по такому методу, яв¬
ляется возможное зна¬
чительное отклонение
параметров атмосферы
Марса от расчетной мо¬
дели. Из-за того, что
в расчетах использует¬
ся модель атмосферы
с минимальной плотно¬
стью, отклонение изме¬
ряемой величины плот¬
ности возможно только
в сторону ее увеличения
по сравнению с расчет¬
ной. Это обстоятельство позволяет, с одной стороны, исклю¬
чить плотность из параметров, подлежащих уточнению на
борту КА, и, с другой стороны, использовать описанный
метод уточнения h- для совместной работы алгоритмов
управления конечной скоростью спуска КА и навигации.
Действительно, при увеличении плотности атмосферы по¬
является погрешность в h~, которая ухудшает точность
управления, но вместе с тем это приводит к существен¬
ному уменьшению величины конечной скорости по срав¬
нению с заданным значением при одновременном уве¬
личении высоты начала рикошетироваиия траектории.
Последние эффекты проявляются сильнее и в целом по¬
зволяют нейтрализовать влияние ошибки в определении
h- при возмущениях атмосферы.
Приведенные выше результаты справедливы в пред¬
положении, что известно точное значение начальной вы¬
соты входа. Поскольку точное определение высоты при
подлете КА к плотным слоям атмосферы Марса связано
со значительными трудностями из-за неточного знания
го 22 20 26 28
Рис. 8.10. Связь высоты условного пери¬
центра траектории входа с временем дости¬
жения фиксированного значения кажущей¬
ся скорости.
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЕ
333
физических параметров планеты и условий в районе по¬
садки, то приходится прибегать к косвенным методам.
Так, например, можно считать, что при входе КА в ат¬
мосферу некоторому фиксированному значению перегруз¬
ки /г* или кажущейся скорости F* соответствует вполне
определенное значение начальной высоты h0l вычисляе¬
мое для принятого расчетного закона распределения
плотности по высоте. Эту высоту целесообразно опреде¬
лять для минимальной модели атмосферы.
Идентификация параметров КА и характеристик атмо¬
сферы. Одной из центральных задач создания высоко¬
точных адаптивных алгоритмов управления движением
КА является задача идентификации, связанная с полу¬
чением необходимой информации об управляемом объек¬
те и о характеристиках окружающей среды. Несмотря на
интенсивное развитие теории и методов идентификации
[63], их применение к задачам спуска КА в атмосфере
еще не нашло широкого распространения. Можно ука¬
зать на один из известных методов идентификации, кото¬
рый основан на использовании алгоритма с параметриче¬
ской адаптивной эталонной моделью. В работе [63]
показано, что этот метод является одним из наиболее про¬
стых и гибких. Суть его заключается в том, что заданный
сигнал одновременно поступает на вход как неизвестной
системы, так и ее модели. Параметры модели непрерывно
изменяются с целью уменьшения ошибки между выход¬
ными сигналами системы и модели. В этом случае пара¬
метры модели асимптотически стремятся к параметрам
неизвестной системы. Алгоритмы настройки параметров
модели могут быть построены с использованием различных
методов: прямого'метода Ляпунова, методов, основанных на
использовании квадратичного критерия качества, функ¬
ций чувствительности и т. д. Использование метода Ля¬
пунова имеет некоторое преимущество перед остальными
(в основном базирующимися на градиентном подходе),
поскольку гарантирует глобальную устойчивость и обес¬
печивает хорошую скорость сходимости. В работе [63]
отмечается, что для идентификациии аэродинамических
коэффициентов КА могут быть использованы градиентные
алгоритмы, которые более просты в вычислительном от¬
ношении и позволяют осуществлять идентификацию пара¬
метров КА в реальном масштабе времени.
334
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
Ьгл. 8
В работе 170] предлагается один из возможных спосо¬
бов прогнозирования величины аэродинамического ка¬
чества для будущих моментов времени. Он основан, па
предположении, что при движении в атмосфере КА оди¬
накового типа происходят подобные физические процес¬
сы. В силу этого искомая функция Ао (t) принимается
подобной в среднем некоторой эталонной функции А^ (/)
согласно соотношению
Кб (t) = ^{t)Kl(t),
где ф (t) — некоторая функция, характеризующая подо¬
бие. Рассмотрены различные способы задания указан¬
ных функций. Представлены результаты исследования вли¬
яния различного рода ошибок на вычисление этих функ¬
ций. Показано, что в оценках погрешности важно не точное
значение величины отклонения истинного аэродинами¬
ческого качества от расчетного, а та минимальная грани¬
ца, которую отклонение не может превзойти.
Основными параметрами, которые в общем случае
требуется определять на борту КА при синтезе адаптив¬
ного алгоритма управления конечной скоростью спуска,
являются аэродинамическое качество (Ао) и приведенная
нагрузка на лобовую поверхность (Рх), знание которых
определяет эффективность прогноза и в целом управления
конечной скоростью спуска. Прежде чем решать задачу
идентификации, рассмотрим влияние вариации параметров
Рх и Kq на точность управления.
Предположим, чо задача идентификации решена на
борту КА. Пусть при этом имеется погрешность опреде¬
ления параметров ДР* и ДА".
Рассмотрим следующие возможные случаи на приме¬
ре спуска КА с номинальными значениями параметров
Рх = 350 кг/м2, АГ) = 0,3.
К Р1> Рх, гДе Рх — истинное значение параметра.
В этом случае увеличение погрешности приводит к умень¬
шению конечной скорости относительно заданного значе¬
ния и к уменьшению минимальной высоты (табл. 8.8).
Если величина ДРх составляет +35 кг/м2, то конечная
скорость уменьшается на 26 м/сек, а минимальная высо¬
та — на 0,63 км.
g 8.4] АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ 335
Таблица 8.8
Оценка влияния вариаций параметров Р” и Кна точность
управления
Кб - 0,3
Рх — 350 кг'м2
K8/JH2
%iin- пм
, ж'сек
к*
о
Vj., м'сек
315
6,54
608
0,27
6,29
592
330
6,36
509
0,28
6,26
593
340
6,21
502
0,29
6,17
588
360
5,01
578
0,31
5,97
582
370
5,73
570
0,32
5,91
578
385
5,37
564
0,33
5,82
575
2. Рх <С Рх- В :тш случае величина Vu возрастает
при одновременном увеличении hm[U. Если АРх
= —35 кг/м2, то конечная скорость возрастает па 18 м./сек,
а минимальная высота на 0,54 км.
3. Кь < КГ>. Уменьшение К£ относительно реального
значения практически не изменяет величину конечной
скорости и приводит к некоторому увеличению минималь¬
ной высоты. Так, уменьшение на 0,03 приводит все¬
го лишь к увеличению FK на 2 м/сек и femin на 0,29 км.
4. К § ]> К б. В этом случае увеличение К% приводит
к уменьшению VK и незначительному уменьшению hm[n.
Например, увеличение Kq на 0,03 (т. е. действительное
значение качества Кб = 0,3) приводит к уменьшению
VK на 15 м/сек и hmin на 0,18 км.
Качественная картина не изменяется при рассмотре¬
нии КА с любыми исходными параметрами, а меняются
только количественные результаты. Итак, если на борту
КА не осуществлять уточнения параметров Рх и Кп и в
правые части уравнений прогноза подставлять номиналь¬
ные значения характеристик КА независимо от их действи¬
тельных значений, то максимальные величины погреш¬
ностей получения и hm\n составляют соответственно
ДУК 3% и А/г inin ~ 10% при точности задания величии
Рх и А'п порядка 10%. Следует, однако, отметить, что
336
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
погрешности управления могут быть существенно умень¬
шены, если воспользоваться отмеченным свойством про¬
тивоположного влияния величин Рх и К б на параметры
Ук и hmin. Действительно, если прогнозирование дви¬
жения с целью выработки управления вести с использо¬
ванием наибольшего значения Рх == Рх + АРх и наимень¬
шего значения — К о — AKq независимо от их дей¬
ствительных значений, то величины погрешностей ДАб
и Afemin могут быть существенно снижены до величии
~ 0,7% и ~2% соответственно при изменении значений
Рх и Ко в диапазоне Рх = Рх ± АРх и КG = Ко ± АКо.
Отсюда можно сделать важный вывод о том, что вместо
решения полной задачи идентификации на первом этапе
можно использовать в правых частях дифференциальных
уравнений прогноза определенным образом выбранные зна¬
чения параметров КА Рх — 7^ max и Ко = Agmin-
Перейдем к задаче идентификации параметров окру¬
жающей среды. Как уже отмечалось, наибольший интерес
представляет уточнение закона изменения плотности ат¬
мосферы р (К), который также влияет на качество про¬
гноза и управления конечной скоростью спуска. Нетрудно
показать, что использование в уравнениях прогноза мини¬
мальной модели плотности атмосферы позволяет синте¬
зировать алгоритмы управления, обеспечивающие выпол¬
нение условия (8.4) без специального решения задачи
идентификации параметров атмосферы на борту КА. Дей¬
ствительно, если истинное значение плотности атмосферы
больше принятого для прогноза, то это приведет к улуч¬
шению тормозящих свойств атмосферы и соответственно
к уменьшению Ук.
Результаты исследования алгоритма на устойчивость
по отношению к вариациям плотности атмосферы при¬
ведены в табл. 8.9 и 8.10. Алгоритм, построенный в пред¬
положении рп (h) = pmin (К), оказался достаточно эф¬
фективным. Если плотность атмосферы окажется наи¬
большей, то Ук уменьшается примерно на 20-^-25%
при одновременном возрастании hm\a на 28 -ч-30%. При
действии других возмущений и р (h) — pmax (К) алгоритм
обеспечивает выведение КА на заданную конечную вы¬
соту: при скорости Vк Vк зад величина hmin превы¬
шает поминальную на 2-3 км.
§ 8.4] АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ 337
Таблица 8.9
Оценка эффективности алгоритма
Возмущения
км
кг, м2
У0, км/сек
—16,0
-1С6
-150
0,33
0,27
385
315
6,01
5,99
VK, м/сек
455
452
477
455
459
519
434
536
462
итах
11,0
10,7
11,4
10,7
10,7
10,7
10,4
11,1
10,6
Чпах> км
19,1
18,9
19,4
19,03
19,0
17,6
21,5
17,8
10,2
/lmin> км
9,2
8,3
10,0
9,20
7,68
6,3
12,1
5,8
20,2
Примечание: в
расчетах принято p(/i)
' — РтахОО,
рп =
pmin00-
Таблиц а ‘8.10
Оценка эффективности алгоритма при действии атмосферных
возмущений типа «змейки»
Хараьтер вариаций
ПЛОТНОСТИ p(/l)
х
й
а
п
сГ
с
67
п
х
а
67
X
сГ
ti
с
67
£
67
п
X
67
й
CL
п
с
67
67
п
я
67
X
л
67
ti
с
67
At3M, сек
120
120
60
60
30
30
15
VK, м/сек
459
590
463
474
485
585
590
,гтах
11,3
10,7
11,3
4,87
19,8
13,5
13,1
h , км
nmax
11,8
18,9
11,9
20,3
17,0
21,9
18,5
^lmi п5 км
6,12
8,12
6,8
5,6
6,88
12,2
10,7
Примечание: и рючетах принято р|/() — Pmin^O-
Рассмотрим теперь устойчивость алгоритма управле¬
ния к атмосферным возмущениям типа знакопеременных
вариаций плотности. Они представляют собой периоди¬
ческое кусочно-постоянное изменение плотности в зависи¬
мости от времени в пределах минимально и максимально
возможных значений. Результаты исследования устойчи¬
338
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. ь
вости алгоритма управления при таких возмущениях плот¬
ности приведены в табл. 8.10. Чередование максимальной
и минимальной плотности на траектории спуска задава¬
лось с различным периодом: А£зм = 120, 60, 30 и 15 сек.
Алгоритм управления эффективно функционирует и при
таких возмущениях плотности: приведение КА на конеч¬
ную высоту осуществляется со скоростью VK VK зад
практически без потерь в величине hm\n и даже во многих
случаях с некоторым ее увеличением относительно
Задача прогноза движения. Решение задачи прогноза
сводится к выбору системы уравнений движения и метода
интегрирования [70, 94, 95]. При решении этих проблем
необходимо исходить из того, что все расчеты, осуществ¬
ляемые в бортовой ЦВМ, должны быть выполнены за огра¬
ниченное время At. Кроме того, вычислительная програм¬
ма, реализующая алгоритм, должна занимать как можно
меньше места в памяти бортовой ЦВМ.
Как справедливо отмечается в работе [70], использо¬
вание на первый взгляд привлекательных в смысле быстро¬
действия конечных формул для прогнозирования движе¬
ния КА оказывается не совсем удобным. Объясняется
это тем, что известные аналитические решения уравнений
движения найдены для случая полета с у const при
некоторых частных условиях движения КА в атмосфере.
Чтобы получить решение уравнений в общем случае и с
переменным значением у (t), необходимо воспользоваться
численным интегрированием.
При выборе системы уравнений движения предпочте¬
ние следует отдавать той из них, которая позволяет при
одинаковой точности осуществлять интегрирование с
большей величиной шага. Если же совпадают и величины
шага, то в качестве критерия принимается количество
операций для вычисления правых частей. Достаточно
подробный сравнительный анализ различных систем диф¬
ференциальных уравнений, используемых при решении
задачи прогноза, представлен в упомянутой работе [70].
Отмечается, что система дифференциальных уравнений,
записанная в скоростной системе координат, предпочти¬
тельнее для осуществления прогноза, чем уравнения дви¬
жения относительно неподвижной прямоугольной системы
координат с началом в центре планеты. Вместе с тем ис¬
пользование уравнений движения, записанных в скорост¬
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
339
ной системе координат, влечет за собой заметное увели¬
чение количества арифметических операций.
Именно поэтому предлагается рассматривать уравне¬
ния прогноза, записанные в так называемой присоединенной
системе координатные. 8.11).
Оси этой системы координат
О^е^е^ расположены следу¬
ющим образом. Начало си¬
стемы координат (точка Ог)
лежит на проекции rv вектора
v на плоскость Оеге3. Ось
Огс^ направлена вдоль век¬
тора г.р, а ось Оге3 перпенди¬
кулярна этому вектору в пло¬
скости О ере3. Оси Оге^ и Ое\
образуют угол ср, отсчиты¬
ваемый по направлению ча¬
совой стрелки, если смотреть
с конца единичного вектора
е2. Ось Оге2 направлена па¬
раллельно е2. Полученные
в [70] уравнения движения
в присоединенной системе координат удобны для прогноза
при малых значениях аэродинамического качества и име¬
ют вид
Рис.
8 Л1. Присоединенная сис¬
тема осей координат.
Ц =--
Г2 =
СО =
7Г Ф + Л) + ‘°2 Ф + Л) +
рг Г2 ~Т~ О'Ъ
— 2ощ г
Ь -г Л
(8.76)
где со = 1]1'А ?ъ°1 , ср = arcsin—, rj и г2 — координаты
?'р гр
центра масс, отсчитываемые вдоль осей Охе[ и Охе2 соот¬
ветственно; г) = гр — Ь, ц = ll?1- ' ъ'б7'л , Ъ — длина отрез-
1 v
ка, соединяющего центр неподвижной системы координат
О и присоединенной Op, aTi, а2, а? — проекции вектора
340
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
аэродинамического ускорения а на оси O^i, О^2, Оге™,
г = У (Ь + г])2 + г'1
Проекции аг„ а2, а^ определяются равенствами
a-D xpF [ — УГ| (1 -f К2) + VtJKx], \
ч = хрУ [- V^K, - У^(1 + К2)у (8.77)
си = хрУ [— Vo -] - /ГУр sin. у], J
в которых
V„ = Vvl + Ft, =
P P
а через У^, У2, V^ обозначены проекции на присоединен¬
ные оси вектора скорости относительно набегающего по¬
тока.
В работе [70] проводится сравнение систем дифферен¬
циальных уравнений прогноза в навигационной системе
координат Ое^е^е3, в скоростной системе координат и в
присоединенной Оле[е\ез для алгоритмов управления КА,
осуществляющих спуск в атмосфере Земли. Сравнение
проводилось по количеству арифметических операций,
необходимых для счета правых частей, начальных данных
и решения краевой задачи. Однако этих давных в общем
случае оказывается недостаточно, и вывод о целесообраз¬
ности применения той или иной системы уравнений может
быть сделан лишь после учета особенностей реализации
алгоритма в системе команд конкретной бортовой ЦВМ.
Все же необходимо отметить, что использование системы
дифференциальных уравнений в присоединенной системе
координат имеет некоторое преимущество по сравнению
с системой уравнений, записанной в скоростной системе
координат. В дальнейшем при решении задачи прогноза
использовалась система уравнений (8.76).
Быстродействие алгоритма управления во многом за¬
висит от используемого метода интегрирования уравне¬
ний прогноза. В работе [70] рассмотрены некоторые прос¬
тые методы численного интегрирования дифференциальных
уравнений прогноза, требующие небольшого количества
арифметических операций и малого объема оперативной
памяти бортовой ЦВМ. Учитывая необходимость сокра¬
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
341
щения арифметических операций, рассмотрены два ме¬
тода, в которых на каждом шаге интегрирования достаточ¬
но произвести одноразовый расчет правых частей диффе¬
ренциальных уравнений: метод Эйлера — Коши и метод
Адамса. Показано, что, несмотря па несколько большую
сложность формул, метод Адамса более предпочтителен
по сравнению с методом Эйлера — Коши, так как позво¬
ляет выбирать больший шаг интегрирования.
Построение алгоритма управления. Конечным резуль¬
татом функционирования алгоритма управления на каж¬
дом шаге коррекции является выбор значения аэродинами¬
ческого качества К3ф, с которым должно осуществляться
дальнейшее движение КА. Это значение определяется в
результате решения краевой задачи. Известен ряд чис¬
ленных методов решения краевых задач (см., например,
[81]). Было показано [27], что для рассматриваемого адап¬
тивного алгоритма управления конечной скоростью
спуска задача выбора требуемого значения угла крена
решается удовлетворительно даже при использовании
метода последовательного перебора с постоянным шагом
по углу крена Ду„ТРр.
В каждой точке коррекции расчет первой прогнозируе¬
мой траектории производится с минимальным значением
угла крена у0 = 0 (Аэф = -\-К{,) от точки предполагаемой
коррекции до конца траектории. Если оказывается, что
Vn ^ Vn зад, то решение задачи на этом заканчивается. Если
же Vn^> Vn зад, то осуществляется новое интегрирование
уравнений движения со значением yt = у0 + /ДуИтер, где
/ — номер итерации. Итерации продолжаются до тех пор,
пока не будет подобрано значение угла крена, удовлетво¬
ряющее условию Vn ^ VK зад- При решении задачи вы¬
бора управления на одном временном интервале между
коррекциями важно уменьшить число итераций /. Для
описанного выше способа число итераций определяется
величиной поправки ДуИТер; с увеличением ДуИтер про¬
исходит уменьшение /. На рис. 8.12 в качестве примера
для КА с величиной приведенной нагрузки на лобовую
поверхность Рх = 350 кг/м* и аэродинамического ка¬
чества = 0,3 приведены зависимости максимального
числа итераций /шах из множества коррекций на интерва-
ле (Wax* *nmin) и величины hmui от ДуИТСр для трех зна¬
чений высот условного перицентра траекторий входа
342
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
Рис. 8.
'max Anin ?км
6,5-
65
5,9
/>*= -Ш
4N
1
чг h
\
\
\
\
\
' \
max
О Ю 20 50 50 Sy,zDdd
^max ^т^им
L2. Зависимость коэффициента /тах и минимальной высоты /imjn
от величины AVpITep-
§ 8.4]
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
343
hn = —16,6; —106; —150 км при скорости входа КА в
атмосферу V0 —■ 6 км/сек.
Существуют определенные значения АуИтер, обеспе¬
чивающие решение задачи о выборе управления при мини¬
мальном числе итераций. Так, при hn = —16,6 км
А У ит ер может приниматься в пределах от 25 до 45°; при
1г- = —106 км — от 30 до 50°, а при h* = —150 км —
от 35 до 50°. Во всех этих случаях число итераций не пре¬
вышает двух. Следует отметить, что при / = 2 ве¬
личина hmin несколько изменяется в зависимости от
А Унтер» а именно: с увеличением ДуИТер происходит
незначительное уменьшение минимальной высоты пролета
над поверхностью. Так, для /г- = —16,6 км при увеличе¬
нии Дуитер от 25 до 45° величина 1гт\п уменьшается всего
с 6,17 до 5,8 км; для 1ги = —106 км при изменении АуИТер
от 30 до 50° величина /гШт уменьшается с 6,24 до 5,74 км,
а для hn = —150 км увеличение ДуИтер от 35 до 5*0° при¬
водит к уменьшению /г1Тпп с 6,32 до 5,95 км.
Таким образом, описанный выше алгоритм решения
краевой задачи позволяет при помощи не более чем двух¬
разового интегрирования уравнений движения от точки
коррекции до конца траектории находить требуемое зна¬
чение угла крепа. Причем величина поправки АуИТер
может быть выбрана одинаковой для всех hu внутри кори¬
дора входа, так как при этом потери в femin будут прием¬
лемы.
Следует также отметить, что по мере погружения в ат¬
мосферу длительность прогнозируемого участка траек¬
тории сокращается и соответственно уменьшается время
решения задачи прогноза. Этим обстоятельством целе¬
сообразно воспользоваться для более точного решения
задачи выбора управления Клф: в связи с сокращением
оставшегося участка полета количество итераций на од¬
ном временном интервале может быть увеличено, что
позволит более точно решить краевую задачу.
Моделирование алгоритма управления. Математиче¬
ское моделирование алгоритма проводилось па ЭВМ с
использованием двух систем уравнений типа (8.76) [70].
Первая система служит для расчета траекторий, определе¬
ния фактических величин VK и 1гт\„ и для решения задачи
прогноза и выбора управления па борту КА. Вторая систе¬
ма уравнений с использованием ускорений а, получаемых
344
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
из решения первой системы и моделирующих показа¬
ния акселерометров, позволяет определять текущий ра¬
диус-вектор КА /Л1Ш.
Эффективность алгоритма управления проверялась
для КА с величиной приведенной нагрузки на лобовую
поверхность Рх = 350 кг/м2 и аэродинамического качест¬
ва К б = 0,3. Рассматривался случай входа КА в атмос¬
феру Марса со скоростью У0 — 6 км/сек. Номинальное
значение минимально допустимой высоты пролета КА над
поверхностью планеты принималось равным /гдоп =
= 6,7 км, а конечная высота hK = 6 км. Величина ко¬
нечной скорости Ук зад предполагалась равной Ук min при
оптимальном управлении в наиболее разреженной ат¬
мосфере. Для рассматриваемых параметров КА и /гДШ1 =
= 6,7 КМ будет Ук min = У к зад = 590 м/сек.
На первом этапе моделирования исследовались прин¬
ципиальные возможности алгоритма с целыо оценки
границ его применимости. При этом были сделаны сле¬
дующие предположения:
— к моменту начала проведения коррекций (дости¬
жение пт^х) текущие фазовые координаты и вектор ско¬
рости КА известны точно, т. е. г = гпм\ у =
— никакие ограничения на характеристики бортовой
ЦВМ не накладываются;
— проектно-баллистические параметры КА (приведен¬
ная нагрузка на лобовую поверхность Рх и аэродинами¬
ческое качество К§) и плотность р известны точно.
Результаты этого этапа моделирования представлены
в табл. 8.11. Алгоритм достаточно эффективно функцио¬
нирует при всех рассмотренных возмущениях. Он поз¬
воляет реализовать заданное значение конечной скорости
спуска Ук = 590 м/сек даже для наихудших атмосферных
условий при небольших потерях в минимальной высоте
полета КА.
На втором этапе моделирования оценивалась эффек¬
тивность совместной работы алгоритмов управления и на¬
вигации при действии разного рода возмущений, в том
числе и инструментальных. Основные результаты сов¬
местного моделирования алгоритмов навигации и управ¬
ления при условии точной привязки h0 представлены в
табл. 8.12 и 8.13. Применение рассмотренного выше мето¬
да определения hn обеспечивает получение значения
§ 8.4]
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
345
Таблица 8.11
Оценка эффективности алгоритма на первом этапе
моделирования
Варьируемые п а р ам е т р ы
nmax
hy, , k.u
"тпах
/1;П iQ, KM
Vj■, м/сек
/г^ = —10,6 км
7,95
13,0
6,26
572
hn =: —106 км
11,3
11,9
6,12
587
hn = —150 км
12,6
11,3
6,18
590
к6 = 0,33
11,2
12,3
6,37
585
=0,27
11,4
11,6
5,74
583
Рх = 385 кг/м2
11,3
10,8
4,64
590
Рх = 315 кг/м2
11,3
13,0
7,53
589
V0 = 6,01 км/сек
11,5
11,4
5,5
577
V0 = 5,99 км/сек
11,1
12,4
6,6
588
Таблица 8.12
Оценка эффективности алгоритма на втором этапе моделирования
Варьируемые
параметры
Модель минималыюй
плотности атмосферы
Модель максималь¬
ной плотности
атмосферы
^min,
км
/7ЬШВ
min’
км
м/сек
у на в
к ’
м'сек
км
/Т1ав
mm»
км
VK.
Mi се к
/?__ = —60 км
6,26
6,10
573
571
8,30
—52,0
420
hn = —106 км
6,12
6,04
587
585
8,70
—4,9
422
hл — —150 км
6,18
6,07
590
589
10,00
25,3
427
Кб =0,27
5,81
5,49
584
590
7,98
21,4
457
Кб = 0,33
6,26
—
595
572
8,71
22,8
410
Рх — 315 кг/м2
7,47
7,57
580
578
11,80
22,7
411
Рх = 385 кг/м2
4,32
4,87
583
572
7,05
21,4
450
F0 = 5,99 км/сек
6,10
6,37
585
564
8,36
22,3
423
F0 = 6,01 км/сек
6,12
6,07
587
603
8,27
21,9
424
Ук <5 Ук зад при действии всех основных возмущений
даже в случае наихудших вариаций плотности атмосферы.
Увеличение плотности приводит к существенному улуч¬
шению результатов: величина конечной скорости оказы¬
вается на 100 -г- 130 м!сек меньше заданной при одновре-
346
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. S
Т^аблиц[а 8.13
Оценка эффективности алгоритма на втором этапе моделирования
Варьируемые
параметры
Характер вариаций
плотности
сек
^min,
км
, пав
М11П ’
км
VK,
MtceK
hn = —60 км
Pmin Ршах
120
6,05
5,94
459
iT
II
1
О
Ртах Pmin
120
8,27
21,30
578
hn = —150 км
Pmin Ршах
60
6,77
6,69
463
К б = 0,27
Ртах Pmin
60
4,75
18,60
467
кб = 0,33
Pmin Ртах
30
6,88
6,74
485
Рх = 315 кг/м*
Ртах Pinin
30
5,77
19,30
469
Рх = 385 кг/м'1
Ртах «— Pinin
сс
8,70
—4,90
422
менном увеличении ыа 2 -г- 3 км относительно /&доп мини¬
мальной высоты полета КА над поверхностью Марса.
Обсудим теперь результаты расчетов при действии
знакопеременных вариаций плотности атмосферы. Чере¬
дование максимальной и минимальной плотности на тра¬
ектории спуска задавалось с полупериодом Д £зм = 120,
60 и 30 сек. Система управления справляется и с этими
возмущениями (табл. 8.13). Лишь в отдельных случаях
(например, при Д£зм = 60 сек) наблюдается уменьшение
минимальной высоты полета на 1-2 км относительно рас¬
четного значения. Конечная скорость во всех случаях не
превышает VK злп = 590 ль/сек.
Таким образом, оценка эффективности совместной ра¬
боты алгоритмов определения h- и управления показала,
что даже при действии возмущений осуществляется устой¬
чивое приведение КА на заданную высоту со скоростью
VK < VK зад и max hmin.
В табл. 8.14 и 8.15 представлены результаты оценки
эффективности совместной работы алгоритмов навигации
и управления в случае, когда определяется начальная
высота h0. Использование предложенного способа оцен¬
ки h0 обеспечивает практически те же значения контро¬
лируемых параметров, что и в случае точного знания
начальной высоты.
В качестве примера па рис. 8.13 приведено изменение
скорости V, угла 0 наклона траектории к местному гори¬
§ в.4]
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
347
зонту, высоты hj дальности Lr. спуска, отсчитываемой
от условного перицентра, и перегрузки в зависимости от
времени спуска для р (h) = рШ\п (h) (Рх — 350 кг!м2,
Кь = 0,3, li- — —106 км). Там же представлены зависи¬
мости, демонстрирующие качество управления; программ¬
ное изменение угла крена по времени спуска упр (t) и
К 9 Ln, К
км/сек град км км
м
-дО
18
1100
900-00
- 5
100-
18
500
20
0
60
у, граб
60
80
0
-15
50 150 250 %свк
Рис. 8.13. Изменение параметров траектории при управляемом спуске.
текущее значение утек (£)• Длительность шага коррекции
принималась равной 5 сек.
В заключение приведем некоторые оценки характерис¬
тик бортовой ЦВМ, необходимых для реализации адап¬
тивного алгоритма управления конечной скоростью спус¬
ка. Одноадресная машина с плавающей запятой долж¬
на располагать оперативной памятью порядка 120 ячеек;
постоянной памятью 760 ячеек; средним быстродействием
/
/
\V">
348
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. N
Таблица 8.14
Оценка эффективности алгоритмов навигации и управления
Варьируемые
параметры
Модель минимальной
и л от ности ат мое фер ы
Модель максималь¬
ной плотности
атмосферы
h, км
/нав
min’
КМ
м/сек
у нав
К ’
м 'се к
^min-
км
, нав
min’
км
vK.
Mi сек
h_ ----- —60 км
6,26
6,10
573
571
8,30
—24,20
420
1гп = —106 км
6,12
6,04
587
585
8,70
1
DO
СО
422
/?ч = —150 км
6,18
6,07
590
589
10,40
0,49
430
к 5 = 0,27
5,88
4,78
586
607
8,14
—4,61
454
К0= 0,33
6,36
5,93
589
595
9,47
—2,90
416
Рх = 315 кг/м2
7,74
5,56
593
629
12,30
—3,60
416
Рх = 385 кг/м2
4,40
4,88
584
574
7,40
—3,42
445
V0 = 5,99 км/сек
6,21
5,57
592
586
8,70
—3,70
422
Ц0 = 6,01 км/сек
6,24
5,26
593
625
8,70
—4,02
422
Таблица 8.15
Оценка эффективности алгоритмов навигации и управления
Варьируемые
параметры
Характер вариаций
плотности
сек
,linin>
км
hHa.B
ПИП’
км
*”к.
м 'се к
hr ■— —60 км
Р mi и Ртах
120
6,05
5,94
459
/ц = —106 км
Ртах ,1— Pinin
120
8,70
—17,60
578
h —150 км
Pinin *— Ртах
60
6,77
6,69
463
К $ =0,27
Ртах -г— Pinin
60
5,71
—20,60
477
кб ----- 0,33
Pinin Ртах
30
6,88
6,74
485
Рх —- 315 кг/м- ’
Ртах *— Pmi п
30
7,14
—19,20
489
Рх = 385 кг/м'-
Ртах Pmi п
г>о
8,70
1
to
СО
422
20 ООО операций в секунду; достаточна длина разрядной
сетки в 14 — 16 двоичных разрядов. Эта характеристики
являются вполне приемлемыми. Как известно [89], совре¬
менная типовая одноадресная бортовая ЦВМ параллель¬
ного действия с плавающей запятой использует 75 команд,
§ 8.4]
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
349
имеет время сложения 1 мксек, умножения —8 мксек,
деления — 10 мксек, объем оперативного запоминаю¬
щего устройства составляет 4096 32-разрядиых слова.
Алгоритм с использованием опорной
траек тории
Одним из возможных методов управления траекторией
спуска КА в атмосфере Марса является метод управ¬
ления с использованием опорной траектории.
После уточнения подлетной траектории в коридоре
входа опорная траектория вычисляется или выбирается
из семейства этих траекторий, хранящихся в памяти бор¬
товой ЦВМ. При выборе опорной траектории необходимо
выполнить условия по захвату КА атмосферой и ограни¬
чение на минимальную высоту пролета КА над поверх¬
ностью Марса. В общем случае при этом требуется реали¬
зовать программное изменение эффективного аэродинами¬
ческого качества.
Эффективный способ управления траекторией спуска
может быть получен на основе применения второго метода
Ляпунова [8, 57]. Получающийся закон управления обес¬
печивает асимптотическую устойчивость программного
движения в силу нелинейных исходных дифференциаль¬
ных уравнений движения. Переменные, используемые для
задания программной траектории, должны удовлетворять
следующим условиям:
— измерение их на борту может производиться с при¬
емлемой точностью;
— отслеживание выбранных переменных должно обес¬
печивать приведение КА в заданную точку фазового про¬
странства.
Будем предполагать, что на борту КА установлены ак¬
селерометры, измеряющие ускорения по трем взаимно
перпендикулярным и неподвижным в инерциальном про¬
странстве направлениям. С помощью акселерометров мож¬
но определить составляющие аэродинамического уско¬
рения ах, а2, а3, а затем и вычислить компоненты скорости
Fi, F2, V3 и радиуса-вектора г1? г2, г3. В качестве перемен¬
ных для задания программной траектории можно выбрать
скорость полета
V ■ V п + VI + (8.78)
350
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
производную от высоты по времени
h = r'Vl + rf-+ rzVs°': (8.79)
и производную от скорости по времени
V = + + -g-~. (8.80)
Здесь
r-VifЙТ+7;, * =
Для получения уравнений возмущенного движения ис¬
пользуем уравнения движения КА в атмосфере в скорост¬
ной'системе координат.
Введем обозначения:
Х± = Лv = v* — v, 22 = AV = V*-V, \
„ = Ак = к*-&, I <8-81»
где У, У, h — значения переменных на опорной траекто¬
рии, запоминаемые в бортовой ЦВМ; У*, У*, Д* — зна¬
чения переменных на возмущенной траектории, вычисляе¬
мые в ЦВМ по уравнениям (8.78) — (8.80). Уравнения воз¬
мущенного движения можно записать в виде
dxx
dt —
- = Cl-2lX± -г Я'22^2 "У a23X3i
dxi'
~df~ = a3lXl Jr a32X2 4“ a 33X3 Jr till,
(8.82)
где я21» a22 >• • •> азз ~ некоторые коэффициенты урав¬
нений, В — коэффициент при управляющей функции.
Для того чтобы управление входило в уравнения воз¬
мущенного движения линейно, управление и следует
представить как разность
и = Д cos у = cos у* — cos у. (8.83)
Будем задавать управление и в виде
и = Jcixi + k2x2*-\J к3х3. (8.84)
§ 8.4]
АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ
351
Примем следующие допущения:
R
cos (0 -f- Д0) ~ cos 0 ^ 1,
li + h
dt
(g sin 0) ^ 0.
(8.85)
Пренебрежем изменением ускорения силы тяжести с
высотой. Тогда коэффициенты atj и В запишутся следую¬
щим образом:
о h 2F*
«21 — goP т/т/* т/т/*
2gJiV (F + F*)
61о-2 — 2
FF* FF*
V + F*
VW**
V* | ("“ Р + ~р§г)^
/г + h* / д 2£(
«31 = '
р*
^0/гА'0 cos у
"W*
о_
р* 2
-Р +
V + F* F к
jR т/т/л
VV*
азз = у*Кб cos у,
1
«33 = -Щ (V* — ^ogo cos y),
itK6gn
В =
P*
V*Kq-.
(8.86)
Как показывают проведенные расчеты, можно без ухуд¬
шения точности положить в этих формулах а21 = 0.
Выберем функцию Ляпунова W (х) в виде квадратич¬
ной формы:
2ех2х3. (8.87)
W = x\Jr cixl 2Ъххх2 -|- схз + 2dxxx3
Чтобы функция W была определенно-положительной,
необходимо выполнение неравенств Сильвестра, которые
запишутся в следующем виде:
а — 62 > 0, (8.88)
(а - Ъ2) (с - d2) > (Ы - е)\ (8.89)
Из условия теоремы Ляпунова иевозмущенное движе¬
ние хх = х2 = х3 = 0 будет асимптотически устойчивым,
если полная производная от функции Wпо времени в силу
352
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
уравнений возмущенного движения будет определенно¬
отрицательной [57]:
где
сп = d (а 31 + Вкг),
с12 = 1 -f- Ъа22 + d (а 32 -|- Вк2) + е (а31 -f- Вкх),
с22 = е (а32 + Вк2) -\- b + аа22,
с13 = 6а2а + с (а31 Вк±) + d (а33 -f- 7?&3),
с23 = аа2з -f- с (а32 + Вк2) е (а33 -[- Вк3) d -f- еа22,
^зз = ^ (азз Вк3) -f- еи2з|
где к±1 к2, к3 — некоторые коэффициенты.
Условия определенной отрицательности квадратичной
формы (8.87) будут
Из первенства (8.91) получаем граничное значение
для коэффициента кг\
Отсюда следует, что коэффициент к± можно взять в
виде
где п 1 — постоянный коэффициент, введенный для
создания определенного запаса устойчивости. Из нера¬
венств (8.92) и (8.93), решая соответствующие квадратные
си <С о?
(8.91)
1
Сп 2 °12
>о,
(8.92)
1 1
Си 2 °12 2 Cl3
(8.93)
1 1
2 ci3 2 с'13 Сзэ
(8.94)
(8.95)
АДАПТИВНЫЙ АЛ ГО РИТМ УПРАВ ЛТ2 НИИ
уравнения, найдем средние значения коэффициентов к.2
и к3:
/, _ (1 — п) — 1 — ba,, — cla3, /Q псч
/Ь2“ М ’
/„ ея31 (1 Л) + &Я.2з ~Ь ^я33 /Q П7\
А3= • МО
Если для простоты принять искомые коэффициенты к2
и к3 равными средним значениям, то из (8.92) и (8.93) по¬
лучим дополнительно следующие неравенства:
d [е — bd + а22 (be — ad)] ^>0, (8.98)
4а23 (be — de) [е — bd + а22 (be — ad)]
^>[d2 — с a22 (de — be) j- a23 (ad — be)]2. (8.99)
Неравенства (8.88), (8.89), (8.99) определяют достаточные
условия устойчивости невозмущонпого движения и слу¬
жат для вычислений коэффициентов функции Ляпунова.
После выбора коэффициентов функции Ляпунова в
плоскости переменных (kh t) (i = 1,2, 3) можно построить
допустимые области изменения величии АдЦ), k2(t),
k3(t). Необходихмо выполнить при этом ограничение
(к±х± + к2х2 + к3х3) < Д. Выбор конкретных значений
Ад, к2У к3 внутри этих областей устойчивости следует под¬
чинять требованиям качества переходного процесса.
Результаты моделирования алгоритма. Моделирование
алгоригша управления проводилось для КА с величиной
приведенной нагрузки на лобовую поверхность Рх =
= 350 кг/м2 и аэродинамического качества К§ = 0,3
при скорости входа V0 = 6 км/сек.
В качестве опорной была взята оптимальная траекто¬
рия, содержащая участок движения по ограничению (траек¬
тория первого типа, Схм. главу 6). Предполагалось, что
в бортовой ЦВМ хранятся зависимости V (£), V (t), h(t),
рассчитанные для случая движения КА в наиболее разре¬
женной атмосфере р (h) = pmin (h). Уточнение высоты
условного перицентра и начальной высоты траектории
входа осуществлялось в соответствии с методикой, изло¬
женной в § 8.4.1. Оценка точности совместной работы ал¬
горитмов навигации и управления показала достаточно
высокую эффективность применения метода Ляпунова к уп¬
равлению конечной скоростью спуска. С учетом движе-
12 Н. М. Иванов, А. И. Мартынов
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ
[ГЛ. 8
ния относительно центра масс увеличение конечной ско¬
рости по сравнению с заданным значением (Ун зад —
= 590 м/сек) при действии всех возмущений не превышает
10 -г- 15 м/сек, а максимальная погрешность в величине
минимальной высоты пролета КА над поверхностью пла¬
неты не превышает примерно 220 м в сторону уменьшения
^min*
Отметим преимущества и недостатки данного алгорит¬
ма. Его положительные стороны:
— для реализации алгоритма на борту КА требуется
бортовая ЦВМ с достаточно малым быстродействием;
— система управления с использованием этого алго¬
ритма обеспечивает высокую точность наведения при
спуске в различных условиях;
— алгоритм управления не требует уточнения началь¬
ных условий входа в достаточно широких пределах, что
следует из результатов численных расчетов;
— использование алгоритма позволяет с приемлемой
точностью выдерживать выбранную опорную траекто¬
рию.
К недостаткам алгоритма можно отнести следующее:
— для его реализации требуется бортовая ЦВМ с до¬
статочно большим объемом памяти для запоминания про¬
граммных зависимостей;
— по сравнению с адаптивным алгоритмом, предпо¬
лагающим прогнозирование конечных условий, имеются
некоторые трудности в перенастройке на разные требуемые
условия спуска, так как для каждого случая необходимы
свои программные зависимости; система управления, ис¬
пользующая этот алгоритм менее гибка и менее универ¬
сальна.
РАЗДЕЛ 3
ОРБИТАЛЬНО-ДЕСАНТНАЯ СХЕМА СПУСКА
ГЛАВА 9
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПРИ ВЫВЕДЕНИИ КА
НА ОРБИТУ ИСМ С ИСПОЛЬЗОВАНИЕМ
АЭРОДИНАМИЧЕСКОГО ТОРМОЖЕНИЯ
§ 9.1. ОБСУЖДЕНИЕ ПРОБЛЕМЫ
Помимо схемы посадки непосредственно с подлетной
траектории, может быть совершена посадка КА па поверх¬
ность Марса с использованием орбитально-десантной схе¬
мы (так, в частности, организована схема полета КА
«Викинг»). В этом случае КА первоначально выводится
на орбиту ИСМ с использованием тормозной двигательной
установки или с использованием комбинированного ма¬
невра, включающего предварительное аэродинамическое
торможение в атмосфере и доразгон с помощью двигатель¬
ной установки для выхода на орбиту. Затем весь КА или
его часть (спускаемый аппарат) совершает спуск с орбиты
на поверхность планеты. Описанный маневр имеет и само¬
стоятельное значение, если конечной целью является толь¬
ко выведение КА на орбиту ИСМ (без последующего спус¬
ка на поверхность).
В главе 2 мы указывали на высокую экономичность
формирования орбиты ИСМ с использованием предвари¬
тельного аэродинамического торможения по сравнению
с активным способом.
Напомним схему движения КА при реализации аэро¬
динамического способа выведения на орбиту ИСМ (см.
рис. 2.7):
— вход в верхние слои атмосферы Марса с начальными
условиями h0, F0, Q0;
— аэродинамическое торможение в атмосфере;
— вылет из атмосферы с начальными параметрами
новой траектории Ып\ 1АВ), 0(в) и полет но переходной
орбите, имеющей требуемое значение высоты апоцентра
hxl (высота перицентра 1ггл зависит от программы управ¬
ления КА на участке аэродинамического торможения);
12*
356
УПРАВЛЕНИЕ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ
[ГЛ. 9
— формирование с помощью двигательной установки
требуемой орбиты ИСМ с апоцентром йа2 и перицентром
Для формирования орбиты ИСМ указанным способом
приходится решать ряд новых сложных технических
задач, из которых в первую очередь можно указать сле¬
дующие.
1. Обеспечение высокой точности навигации на под¬
летном участке с целыо организации точного входа КА
в требуемый коридор по высоте условного перицентра.
Дело в том, что даже при использовании управляемого
спуска ширина коридора входа в атмосферу Марса мала.
2. Создание КА, который должен функционировать
в течение длительного времени после прохождения плот¬
ных слоев атмосферы. Это требует обеспечения на¬
дежной теплозащиты, соответствующего выбора проектно-
баллистических характеристик КА, обеспечения сохран¬
ности радиоантенн (создание убирающихся или складыва¬
ющихся антенн, разработка теплозащитного покрытия для
них, ввод в действие нового комплекта антенн после вы¬
хода КА из плотных слоев атмосферы и т. д.). Существен¬
ные трудности возникают и при компоновке такого КА.
3. Разработка совершенной системы управления КА,
которая должна функционировать на участках подлета
к планете, прохождения плотных слоев атмосферы и тга
внеатмосферном ^участке с целыо" формирования орбиты
ИСМ. Такая система должна быть полностью автономной
и быть комбинированной, т. е. способной функционировать
как на участке, где в качестве основной управляющей
силы используется пассивная аэродинамическая сила,
так и на участке ракетодинастического маневра, где г. ка¬
честве активной управляющей силы используется тяга
двигательной установки.
Рассмотрим последовательность операций, осуществ¬
ляемых системой управления. Сначала с использованием
наземных и автономных средств определяется место¬
положение КА, осуществляется его ориентация в про¬
странстве и строится на борту КА иттертщальпая система
координат. Затем при подлете к плотным слоям атмосфе¬
ры производятся все необходимые развороты для ориен¬
тированного входа КА в атмосферу. Как отмечалось в гла¬
ве 2, при выведении КА на орбиту ИСМ за счет аэродина¬
§ 9.2] УЧАСТОК АЭРОДИНАМИЧЕСКОГО ТОРМОЖЕНИЯ 357
мического сопротивления можно погасить скорость КА
от начальной гиперболической до околокруговой. Пери¬
центр переходной орбиты hnl всегда оказывается меньше
перицентра заданной орбиты кП2У но потребные энерге¬
тические затраты на формирование орбиты ИСМ будут
тем меньше, чем меньше разница между Ая1 и hn2 при за¬
данном значении Аа1, т. е. чем больше скорость КА в
апоцентре переходного эллипса [36]. Поэтому на атмос¬
ферном участке система управления должна обеспечить
такое аэродинамическое торможение, чтобы в апоцентре
переходной орбиты КА имел максимальную скорость
УУЛ. После вылета из атмосфеты осуществляются программ¬
ные развороты аппарата, стабилизация его осей в нуж¬
ном направлении и ему сообщается разгонный импульс
для формирования заданной орбиты ИСМ. Для практи¬
чески важных случаев наиболее выгодно по энергетике
включение двигательной установки в апоцентре* [86].
При этом сначала формируется промежуточная орбита,
а затем с помощью повторных включений двигателя оп¬
тимальным образом^осуществляется выведение на оконча¬
тельную орбиту ИСМ.
Возможность решения перечисленных задач пред¬
определяет реализуемость рассматриваемой схемы вы¬
ведения КА на орбиту. Ниже мы исследуем проблемы:
— отыскания оптимального закона управления на
участке аэродинамического торможения при использо¬
вании критерия шах Уча1 при hxl = йа3ад;
— определения требуемых проектно-баллистических
характеристик КА в зависимости от ширины навигацион¬
ного коридора входа;
— синтеза комбинированной системы управления, ра¬
ботающей на участках аэродинамического торможения
и ракетодинамического маневра.
§ 9.2. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КА НА УЧАСТКЕ
АЭРОДИНАМИЧЕСКОГО ТОРМОЖЕНИЯ
Рассмотрим задачу об отыскании оптимального закона
управления КА на участке аэродинамического торможе¬
ния.при использовании критерия max Fal. Эта задача ис¬
следовалась в работах А. А. Шилова, Н. А. Эйсмонта и др.
[30, 101]. Приведем некоторые результаты.
358
УПРАВЛЕНИЕ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ
[ГЛ. О
Перепишем уравнения движения КА (3.20) в виде
рУ2 р
V =
2 Рх (« + Л.)*й1п6,
рУ* , (!_
эф 21>х~ V RJrh (H-'rhf
h = vsjll0
cos 0
(9.1)
(9.2)
(9.3)
Введем дополнительные упрощения [1021. Предпола¬
гая малость угла 0, линеаризуем уравнения (9.1) — (9.3)
относительно 0. В правой части уравнения (9.1) положим
второй член равным нулю, пренебрегая его величиной
по сравнению с первым членом. Считаем также, что
У2 11 V2 |1
(9.4)
Исключая время t из системы уравнений (9.1)
(9.3), получим
dh_ _ 0/^
dv ,
dQ
dV
эф I
рУ2 ш
уз
иА>
R
(9.5)
(9.6)
Итак, имеем систему с двумя фазовыми переменными
h, 0, независимой переменной V и управлением ф.
При заданной величине hxl минимальная величина им¬
пульса скорости, увеличивающего высоту перицентра h-x
до заданной величины h-2, имеет место при максимальной
скорости на выходе из атмосферы. Поэтому задача об
отыскании оптимального управления может быть сфор¬
мулирована следующим образом: в интервале — К$
К0 ф ^ + К о определить закон изменения К^ф = (F),
переводящий КА из начального положения (/г0, 0О, F0)
в положение (/гв, 0й) при условии FB) = F,(^x.
Угол наклона траектории к местному горизонту в
момент вылета КА из атмосферы связан со скоростью
FB) конечным соотношением
0'в) =
— arccos
Л Г {я 4
sl/
V (Я Ч-
ад) ^
/Чв)ут.
; (П -)"
R JrlK -,т/
2~ГП^2'
§ 0.2]
УЧАСТОК АЭРОДИНАМИЧЕСКОГО ТОРМОЖЕНИЯ 359
Это ограничение на величину 0(в> необходимо учитывать,
чтобы удовлетворить условию hxl = hx зад.
Для решения задачи используехМ принцип максимума
Понтрягина 179]. Запишем функцию Гамильтона
тг , dh , d0 п
H = -*4v-V*d7 ’ М
где фц и ф2 — решение сопряженной системы уравнений
d'tyi d[j | / [Г V2 \ dp ф-2-Ух: /п о\
dV'l~ V dk р* -\- }1д)'2 R + kA)dh p'2V3 ’• '}
^Ф? ФА /д д\
dV pV Vе/
Оптимальное управление, доставляющее максимум га¬
мильтониану (9.7), имеет вид
к,Зф = Kq sign ф2- (9.10)
Отсюда следует, что число переключений управления
равно числу нулей функции ф2 на интервале 1АВ) < V <
<< V0. Исключая фд из уравнений (9.8) и (9.9), получим
уравнения второго порядка для ф2
^Ф-2 , J_ ( v1 _ __iL_\ in _ о /о i i ч
dV> ^ F dV 1 \rt + /tA (« + hAyl J dll p2F3 ‘ l /
Используя подстановку
У
^2 (F) = Z (F) exp -i- ^ ,
Vo
приведем уравнение (9.11) к виду
^L+B(V)z = 0, (9.12)
где
в = 1 , / Г2 р \ dp р~
4^ ^ I Л + /*л (Я + /*А)а ) dh
Функции ф2 (F) и z (V) обращаются в нуль одновре¬
менно. Если функция В (У), определенная при 0 < е ^ V
< оо, удовлетворяет неравенству В (V) 0,25У2, то лю¬
бое нетривиальное решение уравнения (9.12) имеет не
более одного нуля [102]. Поскольку dp/dh <С 0, то
3(50
УПРАВЛЕНИЕ LIPII ВЫВЕДЕНИИ НА ОРБИТУ [ГЛ. 9
В < 0,25Г2 при V2/{R + hA) - \x/(R + hAf > 0. Отсюда
следует, что оптимальный закон управления при выведе¬
нии КА на орбиту ИСМ имеет не более одного переключе¬
ния, если скорость в конце торможения не менее круговой.
Проведенные исследования показали [102], что подобная
структура управления остается и в том случае, если ко¬
нечная скорость меньше круговой.
Численное решение краевой задачи, к которой сводит¬
ся поставленная экстремальная задача, показало, что
функция ф2 в начальной точке положительна, затем в про¬
цессе полета она уменьшается до нуля и остается отрица¬
тельной до конца траектории выведения. Это означает в
соответствии с (9.10), что КА осуществляет вход в плотные
слои атмосферы с максимальной величиной подъемной си¬
лы (Кэф = -\-Kq). Затем в процессе полета осуществляет¬
ся переключение эффективного качества с Кдф = -\~КС)
на Кдф = — Kq для обеспечения требуемых условий на
выходе КА из атмосферы.
Следует отметить, что существуют два таких значения
высоты условного перицентра траектории (/А1 и /&!!), при
входе с которыми в атмосферу Марса оптимальная програм¬
ма управления вырождается в программу полета с посто¬
янными граничными значениями эффективного качества
КЭф = +Ао и К0ф = —К($. При отсутствии каких-либо
дополнительных ограничений на траекторию движения и
при заданных параметрах КА, скорости входа и точном
знании атмосферы Марса эти значения определяют нижнюю
(h*) и верхнюю (h/t) границы коридора входа.
§ 9.3. АНАЛИЗ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ
Численное решение поставленной задачи проводилось
при следующих исходных предпосылках:
— начальная скорость входа варьировалась в диапа¬
зоне 6 км/сек У о 8 км/сек;
— величина аэродинамического качества изменялась
в пределах 0,3 Кб 0,8;
—величина приведенной нагрузки на лобовую поверх¬
ность бралась в диапазоне 100 кг/м2 ^ Рх <; 1000 кг/м2;
— движение КА рассматривалось внутри всего кори¬
дора входа (см. главу 2).
5 9.3]
АНАЛИЗ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ
361
Рис. 9.1 показывает влияние высоты условного пери¬
центра траектории входа па величину разгонного импуль¬
са АР при формировании соответствующей круговой ор¬
биты с оптимальным управлением. Характерной особен¬
ностью оптимального управления является наличие гори¬
зонтального участка у графика зависимости АР (h-), когда
величина потребного разгонного импульса практически
AV, м/сек
к
\
\
500
ч
Полет
с const
3h-
Ь^ЮООкм
/
V
[200
__
\
_ ЛА
Х7Я7
100 ^ '
Оптимально,
управление
е
/
!
-10 О Z0 АО 50 80
h-г.км
I ис. 9.1. Величины потребного импульса ДУ при оптимальном управлении
КА и при полете с постоянным значением К;кт} (У0 = 6 км/сек, Рх = 350 кг/-\12,
К о = 0,5, р (/i) = Р|плх
остается неизменной в значительной части коридора вхо¬
да (70 ч-75% от величины коридора); только вблизи ниж¬
ней границы происходит резкое возрастание величины
АР, которая достигает максимума при входе КА с h- =
Так, при изменении высоты условного перицентра от
= 76 км до h- — 10 км величина АР изменяется с
91 до 105 м/сек (hal = 500 км, Рх = 350 кг/м2, = 0,5,
у0 = 6 км/сек, р (h) = ртах Ш • Дальнейшее уменьшение
fo, от 10 км до /4П) = —15 «жприводит к увеличению АР
от 105 до 275 м/сек, т. е. более чем в 2,5 раза. Увеличение
высоты апоцентра переходной орбиты hyl (см. рис. 9.1)
приводит к тому, что в целом энергетические затраты для
выведения КА па орбиту ИСМ возрастают.
362
УПРАВЛЕНИЕ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ [ГЛ. 9
Таблица 9.1
Оценка влияния плотности атмосферы на потребную величину
разгонного импульса
hn, км
p(7i) — Pmin(^)
Р(Ь) = Pmax(,l>
Уа1, м'сек
ДУ, м'сек
Уа1, м'сек
ДУ, Mi сек
40
3206,57
96,94
321:1,79
91 ,62
30
3206,54
96,96
3211,48
91,93
15
3206,16
97,23
3208,71
94,70
0
3204,00
99,39
3187,22
116,19
— 5
3201,22
102,22
3165,62
137,79
—13
3188,89
114,55
3093,53
209,88
В табл. 9.1 преставлеиы результаты оценки влияния
плотности атмосферы (р (h)) на потребную величину раз¬
гонного импульса (АУ) при оптимальном управлении по
углу крена. В случае увеличения р (К) от pmiu (h) до
Ртах О*) происходит незна-
чительиое уменьшение по¬
требного импульса А У при¬
мерно на 5 -г-10 м/сек вбли¬
зи верхней границы кори¬
дора входа и увеличение
АУ на 30 ч- 40 м/сек вбли¬
зи нижней.
На рис. 9.2 и 9.3 по¬
казаны частные зависимо¬
сти скорости Van на высоте
h = hal и потребного раз¬
гонного импульса А У от
скорости входа У0, нагруз-
Vq км/сек Ки Иа лобовую ПОВСрХПОСТЬ
Рх и аэродинамического
качества Ко. При оценке
влияния каждого из пере¬
численных параметров на
величину Val и А У в каче¬
стве исходных брались сле¬
дующие условия движения КА. Вход КА в атмосферу
для каждого расчетного случая осуществляется по нюц-
Рис. 9.2. Влияние скорости входа и
параметров КА на скорость в апоцен¬
тре (р (h) = ртах (/г), /га = 500 км).
§ 9.3]
АНАЛИЗ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ
363
АКм/осх
ней границе коридора входа при наибольшей плотности
атхмосферы. Скорость входа бралась равной У0 = 6 км/сек,
нагрузка на лобовую поверхность Рх = 500 кг/м2, вели¬
чина аэродинамического качества К о = 0,4.
Затраты на разгонный импульс возрастают с увеличе¬
нием параметров К$, Рх и V0. При изменении Кб от 0,4
до 0,8 величина AV возрастает со 196 до 480 м/сек, а при
увеличении скорости входа с 6 до 8 км/сек AV изменяется
от 196 до 336 м/сек. Одно¬
временно увеличивается
коридор входа Солее чем
в 2,5 раза цри изменении
Къ и почти в 1,7 раза при
изменении VQ. При этом
расширение коридора про¬
исходит в основном за счет
смещения нижней границы
в сторону меньших зна¬
чений /А1. При заданном
коридоре входа величина
AV при увеличении Ко
уменьшается. Ниже это
будет показано более под¬
робно. Представленные ре¬
зультаты расчетов позво¬
ляют оценить потребную
величину разгонного им¬
пульса при использовании
оптимального закона уп¬
равления для широкого
диапазона проектно-баллистических характеристик КА и
условий входа в атмосферу. При этом оказалось, что исполь¬
зование оптимального управления в пределах всего кори¬
дора входа нецелесообразно, так как при движении по его
нижней границе происходит резкое возрастание потребной
величины AV. Уменьшение ширины коридора входа со
стороны /А на 10 -г- 20 км позволяет существенно сокра¬
тить потребную величину разгонного импульса (пример¬
но на 100 150 м/сек). Дальнейшее сужение коридора
входа практически не влияет на величину AV при исполь¬
зовании оптимального закона управления движением КА.
Vq,km/gck
1
Рис. 9.3. Зависимость величины пот¬
ребного разгонного импульса от ско¬
рости входа и параметров КА (р (h) =
= Ртах ^6, 1 = ^00 км).
364
УПРАВЛЕНИЕ ПРИ ВЫВЕДЕРШИ И А ОРБИТУ
[ГЛ. 9
§ 9.4. ВЫБОР ОСНОВНЫХ ПРОЕКТНО-БАЛЛИСТИЧЕСКИХ
ХАРАКТЕРИСТИК КА
Одной из важных задач в проблеме выведения КА на
орбиту ИСМ с использованием аэродинамического тормо¬
жения является выбор основных проектно-баллистичес¬
ких характеристик КА — аэродинамического качества и
приведенной нагрузки на лобовую поверхность. Основ¬
ным критерием при выборе параметров Рх и служит
потребная ширина коридора входа. Использование этого
критерия необходимо при рассмотрении участка аэроди¬
намического торможения КА и при анализе возможностей
системы навигации на участке подлета КА к плотным сло¬
ям атмосферы. Для упрощения задачи управления КА
на атмосферном участке желательно, чтобы навигацион¬
ный коридор входа был минимален. Это дает возможность
реализовать с высокой степенью точности оптимальное
движение КА в атмосфере и снижает требования к проект¬
но-баллистическим характеристикам КА.
Для создания простой и легкой системы управления,
работающей на участке подлета к атмосфере планеты,
желательно, чтобы величина требуемого навигационного
коридора входа была максимальной, т. е. КА должен рас¬
полагать большими возможностями управления на атмос¬
ферном участке. Проанализируем прежде всего факторы,
влияющие на ширину оперативного коридора входа,
и изучим возможности ее максимизации с целыо выработки
разумных требований к навигационному коридору и основ¬
ным проектно-баллистическим характеристикам КА.
Влияние скорости входа КА в атмосферу на ширину
оперативного коридора входа. В общем случае скорость
входа КА в атмосферу Марса определяется выбранной
схемой перелета, датой старта КА к Марсу, располагаемы¬
ми энергетическими возможностями и т. д. (см. главу 2).
Увеличение скорости входа КА в атмосферу может быть
достигнуто, например, при увеличении скорости старта
КА с промежуточной околоземной орбиты.
На рис. 9.4 представлены зависимости верхней (h*)
и нижней (hll) границ коридора входа от скорости входа
F0. При увеличении скорости входа коридор расширяет¬
ся в основном за счет снижения нижней границы h~.
Верхняя граница коридора входа (h£) практически ос¬
§ 9.4]
ГПЮЕКТНО-БАЛЛИСТИЧЕСКИР, X А PAKTEPHCTIIKII 303
100
50
тается неизменной. Действительно, если при увеличении
скорости входа с 6 до 7 км/сек верхняя граница опера¬
тивного коридора входа уменьшается с 81 до 71) км (Рх =
= 350 кг/м2, Ко — 0,5, р (h) = ршах (h)), то величина
h1* уменьшается (т. е. ширина коридора увеличивается)
с —10 до —42 км при тех же условиях. Для расширения
коридора входа на 10 -ч- ,
-г- 12 км необходимо уве-
личить скорость входа при¬
мерно на 500 м/сек. Это
э к вив а л е нтн о ув ел ич е и ию
затрат массы топлива КА
при старте с околоземной
орбиты примерно на 1 % от
массы КА, подлетающего
к планете, что ставит под
сомнение эффективн ость
такого способа расширения
оперативного коридора
входа.
Влияние неопределен¬
ности в знании параметров
атмосферы Марса на ши¬
рину коридора входа. Как
уже говорилось в главе 2,
имеющиеся сведения о за¬
коне распределения плот¬
ности атмосферы Марса по
высоте р (h) не позволяют
построить достаточно точ¬
ную модель. При расчетах
обычно используется модель, которая представляет собой
некоторое семейство зависимостей плотности атмосферы
от высоты, ограниченное с двух сторон наиболее разре¬
женной (Pmi и (Щ и наиболее плотной (р1Ш1Х (Щ атмо¬
сферой. Наличие двух равновероятных граничных зави¬
симостей плотности от высоты приводит к сужению
коридора входа. Действительно, если разброс по плот¬
ности отсутствует, т. е. pmill (К) = р11ШХ (А), то ширина
коридора входа максимальна. Если жерПц;1 (/г) ршах (/г),
то при расчете верхней (/Д) и нижней (/г") границ
-50
-100
\bUv0)
1-Vt—-
&
1
1000
Л
4 (bcv)
6 I
c.
' \
i i
' \
'\%\KM/CSK
\
-V"
ЫОы)
1
к%)
<
I ис. 9.4. Верхняя и нижняя границы
коридора входа при вариации скорости
входа в атмосферу и высоты апоцен¬
тра переходной орбиты (Рх — 350 кг/м'1,
jfff) --- 0,5). (Сплошная линия —
р(Ю — РmIX (/l), штриховая —pmiri (/i).)
3()(i УПРАВЛЕНИЕ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ [ГЛ. О
коридора входа следует исходить из наихудшего слу¬
чая. В частности, при оценке величины й" необ¬
ходимо использовать наиболее разреженную атмосфе¬
ру, а при расчете й” — наиболее плотную. Используя
данные рис. 9.4, можно проследить зависимость верх¬
ней и нижней границ коридора входа от высоты йа1 апо¬
центра переходной орбиты в случаях «точного» и «неточ¬
ного» знания параметров атмосферы Марса. (В качестве
«точной» зависимости р (h) была взята наиболее плотная
атмосфера.) При этом рассматривался КА с Рх = 350 кг/м2,
и = 0,5. Скорость входа в атмосферу бралась равной
F0 = 6 км/сек. Видно, что ширина коридора за счет «не¬
точного» знания параметров атмосферы существенно су¬
жается. Если при «точном» знании закона изменения
плотности по высоте ширина коридора входа составляет
94 км (йа1 = 500 км), то при «неточном» она равна Ahn =
= 68 км. Уточнение параметров атмосферы внутри рас¬
смотренных моделей приводит к расширению коридора
входа на 20 -у- 25 км. Однако этот фактор при современ¬
ном уровне знаний атмосферы Марса, очевидно, не может
быть использован для максимизации коридора входа.
Влияние на ширину коридора входа высоты апоцентра за¬
данной орбиты. Рассмотрим: теперь влияние выбора задан¬
ной высоты апоцентра переходной орбиты на ширину
коридора входа. Зависимости, представленные на рис. 9.4,
показывают, что с увеличением высоты апоцентра 1гал
ширина коридора входа в целом уменьшается. Так, па-
пример, при увеличении йа1 с 500 до 1000 нм Ай- изменяет¬
ся с 68 до 56 км. Сужение коридора входа с увеличением
йя1 происходит в основном за счет смещения нижней гра¬
ницы й“, а верхняя граница й” практически остается не¬
изменной. Этим обстоятельством можно воспользоваться
для расширения коридора входа. Действительно, если до¬
пустить, что КА после вылета из атмосферы может вы¬
водиться не на заданную высоту апоцентра йа1, а в некото¬
рый диапазон h7l йа1 ^ hfl, то нижняя граница ко¬
ридора входа будет определяться из условия выведения
КА на высоту йяУ и снижаться, а верхняя при выведении
на любое значение йа1 из указанного диапазона практичес¬
ки остается неизменной. В целом это приводит к расшире¬
нию коридора входа.
§ 9.4] ПРОЕКТНО-БАЛЛИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ 367
На рис. 9.5 представлены зависимости верхней и ниж¬
ней границ коридора входа от величины аэродинамического
качества при выведении КА на высоту апоцентра йа1 =
= 500 км и в диапазон высот йа1 от 250 до 500 км. Видно,
что с увеличением аэродинамического качества эффект рас¬
ширения коридора входа при выведении КА в диапазон
высот апоцентра возрастает. Ели при Ко = 0,5 ширина
Ьп,км
Рис. 9.5. Зависимость верхней и нижней границ коридора входа от аэродина¬
мического качества для КА, осуществляющего выход на орбиту ИСМ.
коридора входа увеличивается на 15 км по сравнению с
выведением КА на заданную высоту йл1, то при Ко = 0,6
величина Ah- возрастает на 30 км. Таким образом, за¬
метное расширение коридора входа может быть достиг¬
нуто при ухудшении точности выведения КА на высоту
hxl примерно на 200 -н 300 км. Следует отметить, что ис¬
пользование такого способа расширения Ah- приводит к
дополнительным затратам, необходимым для окончатель¬
ного формирования требуемой орбиты ИСМ после прохо¬
ждения КА плотных слоев атмосферы.
Влияние основных проектно-баллистических характе¬
ристик КА на ширину коридора входа. При выявлении
основных проблем выведения КА на орбиту ИСМ с исполь¬
зованием аэродинамического торможения были приведе¬
ны зависимости верхней и нижней границ коридора вхо¬
да от величины аэродинамического качества для различ¬
308
УПРАВЛЕНИЕ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ
[ГЛ. 9
ных скоростей входа и значений приведенной нагрузки
на лобовую поверхность (см. рис. 2.8). Рассматривался ко¬
ридор входа, полученный с учетом возможных колебаний
плотности атмосферы в пределах р (К) = prnin (h) и р (К) =
= Рппх Ф)- Для этого при расчете верхней границы ко¬
ридора входа использовалась наиболее разреженная ат¬
мосфера, а при расчете нижней — наиболее плотная.
Анализ представленных на рис. 2.8 зависимостей показыва¬
ет следующее:
— геличина коридора входа практически не зависит
от нагрузки на лобовую поверхность;
— с ростом располагаемого аэродинамического качест¬
ва величина коридора входа увеличивается.
Расширение коридора достигается за счет снижения
его нижней границы (уменьшения высоты hll условного
перицентра), в то время как верхняя граница практически
не зависит от величины аэродинамического качества. На¬
пример, для КА с величиной Рх = 500 кг/м2, входящего
в атмосферу Марса с начальной скоростью V0 = 6 км!сек,
увеличение аэродинамического качества с 0,3 до 0,5 при¬
водит к расширению Ah- с + 20 до + 40 км. Проведенный
анализ позволяет сделать вывод о том, что основным
фактором, позволяющим увеличить Ah-, является изме¬
нение проектно-баллистических характеристик КА и пре¬
жде всего увеличение располагаемого качества.
Для аппаратов скользящего спуска величина Ко мо¬
жет быть порядка 0,5 -ь- 0,7. В этом случае требуемый
навигационный коридор достаточно велик и составляет
величину порядка +35 -ь- +40 км. Это свидетельствует
о возможности практического решения задачи выведения
КА на орбиту ИСМ с использованием предварительного
аэродинамического торможения, так как предъявляемые
к характеристикам КА и навигационному коридору
входа требования могут быть удовлетворены на сов¬
ременном уровне развития космической техники.
К дальнейшему расширению коридора входа может
привести использование других типов КА. Так, например,
при использовании КА с несущим корпусом, имеющим
максимальное аэродинамическое качество Кт*х = 1,5 и
нагрузку на лобовую поверхность Ps = 350 кг!м2, ширина
коридора входа возрастает приблизительно тта 80 ь- 100 км
по сравнению с КА скользящего типа (F0 = G км!сек).
ГГ Р О Е КТ IIО - Г. Л Л л IIС ТIIЧК С I? 1Г Е X А Р А К ТЕ Р11С ТIIКII
369
Для КА разных типов на величину Ah- могут оказывать
влияние различные ограничения. В первую очередь это
относится к случаю движения КА по нижней границе ко¬
ридора. Здесь общим для всех типов КА является ограни¬
чение на минимально допустимую высоту пролета КА над
поверхностью планеты. Это ограничивает возможность
расширения коридора входа за счет увеличения Кг}. Для
КА скользящего типа изменение femjn при вариации па¬
раметров аппарата и скорости входа не настолько велико,
чтобы ограничивать ширину коридора входа (см. рис. 2.9).
Действительно, для скоростей входа V0 8 км!сек и
величины аэродинамического качества К§ 0,7 мини¬
мальная высота превышает 15 км при Рх = 500 кг!м2 и
превышает 30 км при Рх = 100 кг/м2. При переходе к
другому классу КА, имеющих большее значение аэродина¬
мического качества, необходимо учитывать ограничение
на минимально допустимую высоту полета (hmin). Так,
например, для КА с несущим корпусом (Ктлх = 1,5) ши¬
рина коридора входа составляет Ah- = ±130 км при
отсутствии ограничения на femin и Ah- = ±80 км при
/гдоц = 6 км.
Следует отметить, что при полете КА с несущим корпу¬
сом и космического самолета вблизи нижней границы ко¬
ридора входа могут возникнуть недопустимые перегрузки.
Учет этого обстоятельства может также привести к сужению
коридора входа. Действительно, для рассмотренного выше
примера при выведении на орбиту КА с несущим корпусом
величина 7гГПах = 13,6 (при /гдоп — 6 км). Уменьшение до¬
пустимого значения максимальной перегрузки до тг]Ш1Х =
= 8 приводит к сужению коридора с Ah- = ±80 км до
Ah- = ±45 км.
ГЛАВА 10
СИНТЕЗ АЛГОРИТМОВ УПРАВЛЕНИЯ
ПРИ ВЫВЕДЕНИИ КА НА ОРБИТУ ИСМ
§ 10.1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим задачу синтеза алгоритма управления,
обеспечивающего выведение КА на орбиту ИСМ с исполь¬
зованием предварительного аэродинамического торможе¬
ния в атмосфере. Решение ее будем проводить поэтапно.
На первом этапе осуществляется построение алгоррггма
па атмосферном участке в предположении идеального ис¬
полнения маневра одноразовой коррекции в апоцентре
переходной орбиты ИСМ. Задачей управления КА при
этом является обеспечение режима, наиболее близкого к
оптимальному, т. е. к такому, при котором скорость в
апоцентре переходной орбиты максимальна (критерий
max Val).
На втором этапе синтезируется алгоритм управления
КА на участке ракетодинамического маневра с целыо
формирования предварительной орбиты ИСМ из условия
минимума величины разгонного импульса (min А У) с уче¬
том результатов управления КА иа участке аэродинами¬
ческого торможения.
Участок аэродинамического торможения. Основной за¬
дачей управления па участке аэродинамического тормо¬
жения является обеспечение максимальной скорости в
апоцентре переходной орбиты. Используем результаты
решения экстремальной задачи (см. главу 9), определяю¬
щие теоретический предел, к которому необходимо стре¬
миться при реализации управления, ибо отступление в
сторону уменьшения от оптимального значения Уацпах
требует существенных дополнительных затрат топлива
па разгонный импульс (Д???т). В частности, для КА с
/гакл = 10 т иа каждые 10 м/сек дополнительно необ¬
ходимо АтТ ж 30 -= 40 кг.
Синтез адаптивного алгоритма управления будем про¬
водить в предположении, что па борту КА имеется инер-
§ in.i]
П О С Т Л I1011К Л 3 Л Д А 411
циальная система навигации и ЦВМ, позволяющие оп¬
ределять составляющие скорости и координаты КА в
каждый момент времени и решать основные задачи (ука¬
занные в главе 8), которые возникают при синтезе адап¬
тивных алгоритмов управления.
Как уже отмечалось, ширина коридора входа для КА
скользящего типа мала. Это предопределяет жесткие тре¬
бования к величине потребного навигационного коридора
входа. Поэтому на первом этапе построение алгоритмов
управления будем проводить в предположении использо¬
вания всего возможного коридора для каждого типа КА.
Это обстоятельство накладывает определенные особен¬
ности на выбор структуры алгоритма управления, способ
решения задачи прогноза движения КА и увеличивает
потребную энергетику на величину разгонного импульса
(см. рис. 9.1).
В соответствии с принципом гарантирующего управ¬
ления необходимо при движении в пределах всего коридо¬
ра обеспечить выведение КА на заданную высоту апо¬
центра /га1 = зад со скоростью
КатЖ.зад. (Ю.1)
Величина Уа:>ад выбирается из условия
Ка зад < V*a,
где У а —значение скорости, достигаемое при оптимальном
управлении в случае движения КА по нижней границе
коридора при максимальной плотности атмосферы.
Участок ракетодинамического маневра. После прохож¬
дения КА плотных слоев атмосферы для предварительного
формирования орбиты ИСМ используется одноразовая
коррекция траектории в апоцентре переходной орбиты с
направлением корректирующего импульса по вектору ско¬
рости КА. .Несмотря па принципиальную простоту этого
маневра, реализация автономного управления в этом
случае представляет довольно сложную задачу, так как
после прохождения КА плотных слоев атмосферы пере¬
ходная орбита реализуется не единственным образом.
Имеется семейство переходных орбит, каждой из которых
соответствуют свои оптимальные значения величины и вре¬
мени сообщения разгонного импульса, позволяющие под¬
нять перицентр переходной орбиты до требуемого значе-
372 СИНТЕЗ АЛГОРИТМОВ ПРИ ВЫВЕДЕНИИ 11 л ОРБИТУ [ГЛ. и,
ни я h-2. Поэтому для проведения коррекции на борту КД
необходимо определять время включения двигательной
установки, направление и величину потребного разгонно¬
го импульса для каждой конкретной траектории движе¬
ния КА на внеатмосферном участке, что усложняет задачу,
§ 10.2. АДАПТИВНЫЙ АЛГОРИТМ УПРАВЛЕНИЯ КА
НА АТМОСФЕРНОМ УЧАСТКЕ ПОЛЕТА
Выбор стратегии управления. Было показано, что оп¬
тимальным законом управления в атмосфере, обеспечива¬
ющим выведение КА на орбиту ИСМ с заданной высотой
hxl апоцентра переходной орбиты и с максимальной ско¬
ростью Па1таХ5является программа одноразового переклю¬
чения эффективного аэродинамического качества с мак¬
симального значения А0ф = +Ао на минимальное Аоф =
= —Ко* Этот закон управления в целом является до¬
статочно простым и его можно было бы использовать при
построении адаптивного алгоритма управления углом кре¬
на. Однако в этом нет необходимости, если учесть требова¬
ние о работоспособности алгоритма внутри всего коридо¬
ра входа. Действительно, из рассмотрения зависимостей
на рис. 9.1 видно, что при использовании всего диапазона
высот коридора входа на его границах величины Fal для
обоих законов управления совпадают, так как снижение
с оптимальным управлением вырождается в спуск с пре¬
дельными значениями управления:
К эф = + Ко (h- = hi) или К эф = — Ко (hr. = hi).
Поскольку наименьшая величина Fal (т. е. max AF), оп¬
ределяющая Fa:Jafl» соответствует случаю движения КА
по нижней границе коридора входа, то при использовании
программы полета с Аоф = const для других значений
hr. hi оказывается возможным выведение КА па задан¬
ную высоту апоцентра переходной орбиты со скоростью
Vа 1 Ка3ад* Исходя из этого и представляется целесо¬
образным при построении адаптивного алгоритма управ¬
ления углом крена использовать программу К0ф = const.
Стратегия управления заключается в том, что в процессе
спуска в атмосфере на каждом шаге коррекции пеобхо-
§ 10.2] АДАПТИВНЫЙ АЛГОРИТМ НА АТМОСФЕРНОМ УЧАСТКЕ 373
димо определять новое значение K^l = const (i — номер
коррекции), при котором выполняется условие кл1 = hX3ад.
Общая структура управления. КА входит в плотные
слои атмосферы со значением эффективного качества
К.,ф = +Аг» {у = 0), с которым и осуществляется полет
до момента достижения значения кажущейся скорости
I*
V* = \ nxdt, где — время полета КА от момента до-
0
стижения на траектории некоторого малого порогового
значения перегрузки пх0 (или кажущейся скорости Vs0)
до момента Vs = Vf- Этот промежуток времени отводится
на уточнение начальных условий, параметров атмосферы
и некоторых характеристик КА. Затем (при Vs V*)
осуществляется периодическая коррекция угла крена у.
Каждый раз выбирается такой угол крена, при полете с
которым от точки коррекции до вылета из атмосферы ре¬
ализуется требуемая высота апоцентра переходной орби¬
ты, если не окажется возмущающих воздействий. Найден¬
ное значение угла крена выдерживается до следующей
коррекции. В связи с отклонением реальных условий
полета от прогнозируемых, неточным знанием начального
вектора положения и т. д. необходимо корректировать
угол крена через некоторый интервал времени (шаг коррек¬
ции) .
Навигация. Начальная скорость V0 обычно известна
с достаточно высокой точностью до входа КА в плотные
слои атмосферы, и ее можно не уточнять. Параметры h- и
/г0 необходимо уточнять в процессе полета в атмосфере
для приемлемого решения навигационной задачи. Рас¬
смотрим два возможных способа решения этой задачи.
В основе первого способа лежит идея определения па¬
раметра hjr в предположении, что начальная высота h0
фиксируется с удовлетворительной точностью с помощью
радиовысотомера. В этом случае можно построить простые
зависимости, аппроксимируемые полиномами невысокой
степени, которые позволяют определить h- в зависимо¬
сти от времени t* или перегрузки в момент достижения ка¬
жущейся скоростью значения К/. На рис. 10.1 в качестве
примера приведены зависимости при V* = 100 м/сек
для КА с Рх = 350 кг/м2 и /йг, =0,5 для плотной и
374 СИНТЕЗ АЛГОРИТМОВ ПРИ ВЫВЕДЕНИИ ПА ОРБИТУ [ГЛ. И>
разреженной моделей атмосферы Марса. Неопределенность
в знании закона распределения плотности атмосферы по
высоте оказывает существенное влияние на зависимость
й"пм (**)•
При решении задачи в соответствии со стратегией га¬
рантирующего управления целесообразно использовать за¬
висимость h~iUi (£*), рассчитанную для р (/г) = ршах (К). Со¬
ответствующая кривая может быть аппроксимирована в
виде
h^iU = aLt* Jr bi при **<*?, I
* (Ю.2)
= a2t* + b2 при t* > t[, J
где ax — 4,55 км/сек,
= 1,73 км/сек, Ьг = — 152,2 км,
b2 = —42,5 км, t'[ = 39 сек.
Второй способ является бо¬
лее общим, так как в число
уточняемых параметров добав¬
ляется и высота h oIdB. В этом
случае уточнение навигацион¬
ных параметров может также
осуществляться с использовани¬
ем указанного приема. А имен¬
но, для наиболее плотной модели
атмосферы рассчитываются за¬
висимости /&11ав (£*) и (£*),
с помощью которых И ПрОВО’
дится уточнение выбранных на¬
вигационных параметров.
Задача идентификации ха¬
рактеристик КА и параметров
атмосферы на первом этапе не
рассматривается. Как и при
спуске па поверхность, для рас¬
чета уравнений прогноза дви¬
жения КА используются неко¬
торые априорно заданные значе¬
ния параметров: аэродинамиче¬
ское качество и нагрузку на лобовую поверхность можно
принимать номинальными, а плотность атмосферы —мини¬
мальной. Однако в этом случае, чтобы обеспечить необходи¬
мую точность выведения, структура алгоритма управления
Рис. 10.1. Определение высоты
условного перицентра но вре¬
мени достижения заданного зна¬
чения кажущейся скорости
(V* = 100 м/сек, Рх =J3d0k2/m2,
Кб = 0,5).
§ 10.2] АДАПТИВНЫЙ АЛГОРИТМ НА'АТМОСФЕРНОМ УЧАСТКЕ 375
должна несколько измениться. В частности, величину
уп, необходимую для выхода па орбиту ИСМ, целесообраз¬
но брать не постоянной, а изменять в соответствии со
складывающейся ситуацией. Будем определять уп по фор¬
муле:
Vn = ТтР + Ду. (Ю.З)
Значение первого слагаемого в правой части уравнеция
(10.3) получается в результате решения задачи прогноза.
Второе слагаемое Ду служит для создания запаса регули¬
рования на основе прогноза ситуации. Примем
ДТ = /(**)-^ (Ю.4)
а.
где / (£*) — неотрицательная функция времени, величина
которой определяется па момент Vs = 100 м/сек и харак¬
теризует погрешность в знании закона распределения плот¬
ности; а — суммарное аэродинамическое ускорение, из¬
меряемое акселерометрами; апав — суммарное аэродина¬
мическое ускорение, вычисляемое при решении краевой
задачи для принятой расчетной модели атмосферы. По¬
правка Ду вводится в том случае, если выполняется сле¬
дующее условие:
(М-5)
где б (£*) — зона ошибок' измерений и вычислений, ве¬
личина которой определяется па момент Пч = 100 м/сек.
Следует отметить, что поправка Ду возникает лишь при
обнаружении отклонения в плотности атмосферы от рас¬
четного значения. При большой величине этого отклонения
поправка Ду может быть значительной и оказывать сильное
влияние па процесс регулирования. При малой величине
отклонения плотности величина Ду мала и влияние ее
почти не сказывается. В частном случае, когда реальное
распределение плотности совпадает с расчетным, поправ¬
ка Ду исчезает.
Пара .метры фу нкций / (/ *) и б (t*) подбираются эк¬
спериментально по результатам численного моделирования
из условия наилучшего удовлетворения всем требовани¬
ям к процессу регулирования. Приведенный вариант ме¬
тода изменения уп тте является, конечно, единственно
37С) СИНТЕЗ АЛГОРИТМОВ Hi II ВЫВЕДЕНИИ НА 014.',ПТУ [ГЛ. 10
возможным. Он представляет собой лишь пример исполь¬
зования подобного приема для увеличения стойкости ал¬
горитма по отношению к вариациям плотности.
Задача прогноза. Эта задача связана с выбором метода
и шага интегрирования дифференциальных уравнений,
используемых для прогноза движения КА, выбором систе¬
мы координат и соответственно видом записи правых
частей дифференциальных уравнений, выбором метода ре¬
шения краевой задачи при определении требуемого уп¬
равления. Отличие решения перечисленных задач от рас¬
смотренных ранее при управлении прямым спуском за¬
ключается в наличии участка внеатмосферного движения,
на котором целесообразно использовать простые формулы
невозмущенного движения. Как и ранее, выбор требуемо¬
го значения угла крена осуществляется путем прямого
интегрирования уравнений движения до конечного момен¬
та времени при выходе на орбиту. Для ее решения оказы¬
вается достаточным использовать метод последовательного
перебора.
Процедура решения состоит в следующем. Предполо¬
жим, что в момент проводится коррекция угла крена
и дальнейшее движение осуществляется с у = уг_г до
момента проведения следующей коррекции в момент tt.
За промежуток времени, равный шагу коррекции A t =
= ti — tt-i, необходимо выбрать управление для прове¬
дения следующей коррекции. Первый расчет уравнений
прогноза движения КА осуществляется с текущим зна¬
чением угла крена 7И. Если точность управления не удов¬
летворяет заданной точности Ah, то возможны два
случая.
1. Аа1<йазпд— Ah. В этом случае осуществляется
повторное интегрирование уравнений движения со зна¬
чением
7 г ~ 7г-1 /Ауитпр»
где yt — искомое значение угла крена на момент i-й кор¬
рекции, / — 1, 2 — номера итераций, /\уИТер — шаг ите¬
рационного процесса. Величина АуИТер выбирается по
результатам численного моделирования алгоритма уп¬
равления. В частности, для рассмотренного примера
(Рх = 350 кг/м2, К о = 0,5, Ьл = 500^ГАуИТор* = Ю°.
Такой итерационный процесс продолжается до тех пор,
§ 10.2] АДАПТИВНЫЙ АЛГОРИТМ НА АТМОСФЕРНОМ УЧАСТКЕ 377
пока не выполнится условие !> йа3ад — Ah. Если ока¬
зывается, что величина ЬьуЛ лежит в пределах заданной
точности, то решение краевой задачи на этом заканчи¬
вается. В противном случае происходит уменьшение Дуитер
вдвое, вчетверо и т. п., пока не выполнится условие на¬
ведения КА в заданный диапазон А/г.
2. /&а\ Аазад + Ah. В этом случае интегрирование
уравнений движения производится с углом крека
Vi = Yi-l -t- MYm-ep •
Решение краевой задачи с заданной величиной Дуитер
продолжается до тех пор, пока не выполнится условие:
hlZi /^азад + Ah. В дальнейшем решение краевой за¬
дачи прекращается, если точность управления удовлет¬
воряет условию наведения в диапазон Ah, а в противном
случае продолжается согласно вышеизложенной процеду¬
ре с дроблением величины Ау,птр до тех пор, пока точность
не окажется удовлетворительной.
Очень важным является вопрос о выборе числа итера¬
ций, которое в значительной степени определяет потребное
быстродействие бортовой ЦВМ. Общий анализ, подтверж¬
денный результатами численного моделирования, показал,
что потребное число итераций переменно в зависимости
от участка движения на траектории. Условно можно вы¬
делить три участка:
— начального входа в атмосферу (до пхх 1);
— основного аэродинамического торможения;
— конечного вылета из атмосферы (2 -т- 3 пх 0).
На участке входа в атмосферу возможности управле¬
ния с помощью подъемной силы ограничены, и поэтому
целесообразно рассматривать его как подготовительный,
обеспечивающий условия для успешного управления на
последующих участках. Решение краевой задачи здесь не
проводится.
Эффективность управления на участке основного аэро¬
динамического торможения столь велика, что даже неболь¬
шое изменение угла крена вызывает резкое изменение вы¬
соты апоцентра переходной орбиты. Перерегулирование
на этом участке во многих случаях не может быть ском¬
пенсировано последующим управлением. В силу этого
378 СИНТЕЗ АЛГОРИТМОВ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ [ГЛ. 10
число итераций должно быть достаточным для выбора
такого значения у (£), которое гарантирует выполнение
целевой задачи при дальнейшем управлении на третьем
участке траектории.
Участок вылета из атмосферы характеризуется посте¬
пенным убыванием плотности и уменьшением эффективно¬
сти управления. Но этот участок предъявляет повышенные
требования к выбору управления, ибо здесь оконча¬
тельно формируются конечные условия. В связи с умень¬
шением эффективности управления уменьшается и чув¬
ствительность к ошибкам. Длительность заключительного
участка траектории движения в атмосфере невелика. По¬
этому количество итераций при выборе управления не
будет предъявлять требований к быстродействию бортовой
ЦВМ.
Моделирование алгоритма управления на атмосферном
участке. Это моделирование проводилось в предположении
идеальной работы системы управления на внеатмосферном
участке.
На первом этапе использовались следующие
предположения:
— шаг коррекции принимался равным 5 сек;
— к моменту начала коррекций текущие фазовые ко¬
ординаты и вектор скорости КА известны точно, т. е.
Ф — ^,нав у — у пав.
— при учете вращения КА относительно оси крена
зона нечувствительности принималась равной 1°;
— управляющее угловое ускорение относительно оси
крена составляло 0,1 рад/сек2;
— ограничения на характеристики бортовой ЦВМ не
накладывались.
В качестве номинальных значений параметров траек¬
тории и КА были_ приняты следующие: скорость входа
КА в атмосферу F0 = 6 км/сек; высота условного пери¬
центра hn = 10 км; аэродинамическое качество Ко 0,5;
приведенная нагрузка на лобовую поверхность Рх =
= 350 кг/м2; высота апоцентра переходной орбиты йа1 —
= 500 км. Для этих условий при оптимальном управлении
и р (й) = рГпах (й) имеем Faf1 = 3,217 км/сек, а потреб¬
ная величина разгонного импульса для перевода КА на
круговую орбиту с высотой йкр = 500 км составляет
AF = 99 м/сек. Величина Faaaa, выбираемая из условия
§ 10.2] АДАПТИВНЫЙ АЛГОРИТМ НА АТМОСФЕРНОМ УЧАСТКЕ 379
движения КА по нижней границе коридора, составляет
Ка зад = Ка = 3,07 км/сек; при этом потребная величина
импульса для перехода КА на круговую орбиту ИСМ до¬
стигает А К = 246 м/сек.
Численные результаты моделирования алгоритма уп¬
равления при максимальном действии каждого из рас¬
сматриваемых возмущений (см. главу 8) представлены
в табл. 10.1. Видно, что во всех случаях алгоритм
управления осуществляет выведение КА на заданную вы¬
соту апоцентра переходной орбиты с точностью не хуже
А/га1 = ±10 км, а скорость в апоцентре переходной ор¬
биты при действии максимального значения любого из
возмущений не меньше Ка зад- Оценка эффективности
предлагаемого алгоритма управления при возможном сум¬
марном действии всех возмущений проводилась с исполь¬
зованием метода Б. Г. Доступова [41]. Математическое
ожидание величины скорости в апоцентре орбиты составляет
М (Kai) = 3,130 км/сек, а утроенное среднеквадратичное
отклонение Зет (Kai) = 61 м/сек. Результаты моделирова¬
ния свидетельствуют о том, что предложенный алгоритм
управления углом крена успешно справляется со всеми
возмущениями при условии точного решения навигацион¬
ной задачи. При этом математическое ожидание величины
потребного разгонного импульса, необходимого для пере¬
вода КА на орбиту ИСМ, составляет М (АКа1) = 186 м/сек.
Максимальная величина потребного импульса с уче¬
том предельного разброса по скорости составляет
247 м/сек.
Следует отметить, что на участке аэродинамического
торможения при выборе управления допускалось не бо¬
лее четырех итераций, а па участке вылета ограничений
на число итераций не накладывалось (при численном
моделировании оказалось, что оно не превышает
шести).
На втором этапе осуществлялось совместное мо¬
делирование алгоритмов навигации (в предположении
точного знания параметра 1цлп и управления). Из рассмот¬
рений данных, приведенных в табл. 10.1, видно, что ал¬
горитм обеспечивает выведение КА в апоцентр переход¬
ной орбиты со скоростью TY, Д> Казал, однако точность
выведения па заданную высоту апоцентра существенно
ухудшается до сравнению с результатами, полученными
Результаты моделирования алгоритма управления
380 СИНТЕЗ АЛГОРИТМОВ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ [ГЛ. 10
III этап моделировшия
(алгоритм о п реде лепил
Сш и СВ)
W.7 ‘^"1/
^ Q ^ н CNl C2 C5 h N II
О СО СО СО о о о lo 11
Cl СО СО W О !М V-4 00 N ^
1 1 1 II II II §«
ж к ‘тгу
ОО 1" СМ N СО СО О О Ю
О СО LO с М ^ со Н -
о
иээ/жи ‘^ГА
^ со СО О с\1 °
S5
СО.СОСОСОСОСОСОСОСО''
<LD
QVd2 ‘(g^0
LO LO II
о Г- О to 00 — LO с
CD 00 СО О 1> С 1> О* sT ^
UdQ.WU ‘(g) А
3,53
3,32
3.48
3.49
3,3В
3,52
3,47
3,28
3,6
L00 км\
II этап моделирования (алго¬
ритм определения
/г“ав при точном знании /г^ав)
ЖН ‘I-Ц
О '—I СМ СО LO со ОТ со СО „
'Н СО Ч-4 00 N О С С1 СО 1|
Г— СЧ1 О! СО LO ^ о
1 ! 1 1 1 II 1 w
ЖН ‘ir^
ю
СМ N СО М О со CD —1 с-Г
01 Ю О LO СО 00 СО СЧ1 СЧ1
Ю СО Ю чО LO 4f ю со ю И
Н93/ЖН ‘Г»д
3,2
3,09
3.14
3.16
3.15
3,14
3.17
3.17
3.18
at2;
ende ‘(a)o
3.04
8,23
6.05
6,07
4,03
6,31
4,13
6,37
4.06
350 кг'
U9D,WH ‘(g)A
CO VO оо О СО —i 00 о Г' 1!
ю со Ю Ю Ю Ю Ю 40 LO ^
сососососососососо"
I этап моделирования (точное
решение навигационной
задачи)
Ж It
ОГ-^ГМОООО^^н
LO vt1 N о о со о г- со
HiOMMNMlNNH ^
1 1 1 ! 1 1 1 1 1 ^
ЖН
504
490
502
498
504
501
505
594
505
■) = рщ
) км-
идэ'жи ‘^-ЮА
N О ч^ чч СО ^ ч-н со N Ч”
-H0rST-i>r!rlT-lrHrH [|
сососососососососо д к
О <
QVd2 ‘(g)0
са & •-
«НО^СОЮМСОСОО QJ к
LO 00 СО СО CD СО СО СО vf % Ч
Си ^
нэо,жн ‘(a-)A
СН СО Ч? со М О ^ 5с
LO ч^ СО СМ М С] (М (М Ю з
ьО^ЮЮЮЮЮЮЮ с-
СОСОСОСОСОСОСОСОСО S со
Вид возмущения
« ^ -«II
С.' С_> .. ^г
о о N ^ rt 3
S s"s =? Л 5 “
S 8 * »■ 5 's'*
2 LO ^ СО 1П W ю А
* -Г-н О О ю £g Lr^ vF Д . -
g 1 J g §
II 1! I! II II II II II I 1 *
ИСИЙйИИдП и
л *д £ ’й -с й 5 -о а. ^ г-
В»; ©О кию© II ^ со’
^ ^ ^ ^ О, ^ CL „
§10 2] ' АДАПТИВНЫЙ АЛГОРИТМ НА АТМОСФЕРНОМ УЧАСТКЕ 381
на первом этапе моделирования, когда предполагалось
точное решение навигационной задачи. В частности, при
совместной работе алгоритмов навигации и управления
оценка точности, полученная с учетом действия всех
возмущений по методу Б. Г. Доступова, показала, что
при выведении КА на орбиту ИСМ с /&азад = 500 км мате¬
матическое ожидание высоты апоцентра переходной орби¬
ты составляет М (feal) — 431 км, а утроенное среднеквад¬
ратичное отклонение 3a (h*Ц = ±130 км. При этом мате¬
матическое ожидание значения скорости в апоцентре
переходной орбиты составляет М (Fai) = 3,144 км/сек,
а предельный разброс по скорости За (Fal) = 65 м/сек.
Сравнивая результаты 1-го и 2-го этапов моделирования,
мы видим, что при незначительном увеличении М (Fai)
во втором случае резко ухудшается точность выведения
по высоте /га1. Последнее приводит к существенному уве¬
личению скорости, потребной для формирования заданной
орбиты.
Результаты третьего этапа моделирования
алгоритма навигации, предполагающего уточнение двух
параметров /^1ав и /zq:IB, совместно с алгоритмом управле¬
ния показали, что точность управления КА при выведе¬
нии на орбиту ИСМ несколько ухудшается но сравнению
с предыдущим этапом. Математическое ожидание высоты
апоцентра переходной орбиты становится равным М (/&ai) =
= 426 км, а предельный разброс по высоте апоцентра
3a (/?ai) = 197 км. Математическое ожидание значения
скорости КА в апоцентре орбиты составляет М (Fai) =
= 3,128 км/сек, а ее предельный разброс 3a (Fal) =
= 80 м/сек. Соответственно максимальная величина
импульса, потребного для перевода КА па круговую
орбиту ИСМ с 7гкр = 500 км, увеличивается примерно до
450 м/сек.
На основании результатов численного моделирования
можно сделать вывод, что рассмотренный адаптивный
алгоритм управления позволяет в целом справляться
с воздействием основных возмущений на участке аэроди¬
намического торможения КА. Характеристики ЦВМ,
которые необходимы для реализации такого алгоритма
управления, удовлетворяют параметрам типичной ЦВМ
(см. главу 8).
382 СИНТЕЗ АЛГОРИТМОВ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ [ГЛ. 10
§ 10.3. АЛГОРИТМ ПРЕДВАРИТЕЛЬНОГО ФОРМИРОВАНИЯ
ОРБИТЫ ИСМ НА УЧАСТКЕ
РАКЕТОДИНАМИЧЕСКОГО МАНЕВРА
Для выполнения ракетодинамического маневра после
аэродинамического торможения в атмосфере требуется
определенная ориентация вектора тяги двигательной
установки. Обозначим через х угол между номинальным
направлением вектора тяги и требуемым для каждой реали¬
зуемой траектории, через тВкЛ — оптимальное время вклю¬
чения двигателя, через А 7 — величину разгонного им¬
пульса. Задачей системы управления КА на участке полета
по переходной орбите является определение параметров
Твкл» 4F, х и последующая их реализация.
Алгоритм управления КА. Поставленная задача может
быть решена в наиболее простом варианте с использова¬
нием легко определяемого параметра taTM — промежутка
времени, отсчитываемого от момента достижения пере¬
грузки ОД на нисходящей ветви траектории до момента,
достижения той же перегрузки на восходящей ветви.
Так как определение трех параметров твкл» АУ и х,
необходимых для осуществления реактивного маневра,
проводится с использованием только одного параметра
tатм, эта задача может быть решена только приближенно.
Построение зависимостей твкл (£атм)» А V (taTм) и х (taTM)
можно выполнить следующим образом. С использованием
датчика случайных чисел, задающих различные комбинации
возмущений на участке аэродинамического торможения,
при функционирующем алгоритме управления на атмо¬
сферном участке определяются требуемые значения твнл,
AF и х в предположении идеальной работы системы уп¬
равления на внеатмосферном участке. Обрабатывая ре¬
зультаты статистических испытаний с использованием
метода наименьших квадратов, можно построить функции
Твкл (*атм), А7 (£атм) и х (^атм)- Затем эти функции аппрок-
симируются в следующем виде:
Твкл ^ afM ~Г ~ О^атм “У ^ атм /п (Ю.8)
где i — 1, 2, 3, . . ., тп, . . ., п, . . ^ р — номер участка
аппроксимации; т, л, р — количество участков аппрок¬
симации функций Твкл» А7 и х соответственно; аи bif Си
§ 10.3] УЧАСТОК РАКЕТОД1ШАМИЧЕСКОГО МАНЁВРА 383
dt, eiy fi — коэффициенты, определяемые эксперименталь¬
но по результатам численного моделирования.
Алгоритм управления работой двигательной установки.
После вылета КА из атмосферы по зависимостям (10.8)
определяются параметры твкл, AF их. Затем осуществля¬
ется разворот КА на требуемый угол и последующая его
стабилизация, чтобы к моменту включения ось двигателя
была направлена соответствующим образом. По достижению
вычисленного момента времени твкл включается двигатель
и отрабатывается импульс величиной AF.
В результате проведения указанных маневров получа¬
ется предварительная орбита, высота условного перицен¬
тра которой гарантированно должна быть больше h0. При
этом желательно, чтобы все остальные параметры были близ¬
ки к требуемой орбите ИСМ. Далее, с использованием ав¬
тономных или наземных средств осуществляется уточне¬
ние параметров полученной орбиты и последующая ее
коррекция с целью формирования окончательной орбиты.
Моделирование работы алгоритма управления при пред¬
варительном формировании орбиты ИСМ в предположе¬
нии импульсной коррекции скорости проводилось для
трех различных случаев:
а) величины всех трех параметров твкл, AF, х прини¬
маются постоянными и заданными заранее;
б) время включения двигательной установки вычис¬
ляется в соответствии с зависимостью (10.8), а парамет¬
ры AF и х принимаются постоянными;
в) параметры тВК1, AF и х вычисляются в соответствии
с (10.8).
Обсудим каждый из перечисленных случаев.
а) Величины твкл = const, AF = const и х = const
вычисляются для случая входа КА в центр коридора в
предположении отсутствия возмущений (F0 = 6 км!сек,
Нъ = 10 км, Рх = 350 кг/м2, Ко = 0,5, р (h) = ршах Ф)\-
Это наиболее простое решение, поскольку используемая
информация является априорной и не зависит от возму¬
щающих факторов при движении КА в плотных слоях
атмосферы.
В табл. 10.2 представлены результаты моделирования
алгоритма предварительного формирования орбиты ИСМ
совместно с алгоритмом управления на атмосферном участ¬
ке в предположении использования радиовысотомера для
384 СИНТЕЗ АЛГОРИТМОВ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ [ГЛ. \и
Таблица 10.2
Моделирование алгоритма предварительного формирования
орбиты ИСМ совместно с алгоритмом управления на атмосферном
участке
Вид возмущения
ТВКЛ»
X == const
Ык
AV,
л — var,
x = const
ТВКЛ’
x = var
CD
sf
Cl
8
>
Cl
8
Cl
e
CD
о
S
Cl
8
>
Cl
8
as
se
Cl
Ji
о
Sj
Cl
>
л
Cl
Ji
Cl
\i
/^_ ;— Зо км
3,02
994
409
3,17
738
434
3,31
529
521
К. min= ~15 км
3,13
527
—250
3,22
383
— 151
3,33
412
273
V0 max= 6>01 KMjctK
3,31
532
496
3,31
499
403
3,31
491
409
Fomin=5-99 км1сек
3,31
502
415
3,31
519
497
3,31
526
488
Pxmin= 315 K*/;,‘3
3,11
844
458
3,16
764
465
3,17
756
478
Рх max= 385^г/,,Г-
3,31
504
426
3,3
505
413
3,31
497
419
■^б max=
3,1
856
445
3,17
677
300
3,24
638
506
min = 0И5
3,2
505
— 16
3,2
507
— 12
3,3
543
471
Р Pmin
3,18
742
603
3,23
610
471
3,26
559
388
определения начальной высоты входа при выведении КА
на орбиту с высотой апоцентра Аа зад — 500 км. Видно,
что для рассматриваемого случая оказывается невозможным
формирование орбиты ИСМ с приемлемым значением hЛ2.
При движении КА по нижней границе коридора входа
(h* = —15 км) высота перицентра сформированной ор¬
биты составляет hr2 = —250 км вместо требуемого зна¬
чения hK2 = 500 км.
б) Величины AF и к принимаются постоянными,
а время включения определяется по формуле (10.8). Коэф¬
фициенты аппроксимации имеют следующие значения:
ах == 567,38, = — 124 940 сек при £атм ^ 222 сек,
а± = 14,27, Ьх = — 2150 сек при 222
<^273 сек,
ах = 6,46, £>1 = — 22,8 сек при £атд1 273 сек.
§10.3] УЧАСТОК ГЛКЕТОДШГЛМИЧКСТч’ОГО МАНЕВРА 3s;i
Как и и первом случае, точность решения задачи ока¬
залась неудовлетворительной, хотя и произошло некоторое
улучшение параметров формируемой орбиты (см. табл. 10.2).
в) Коэффициенты аппроксимирующих зависимостей
(10.8) для Твкл аналогичны предыдущему случаю, а для
параметров А У и х имеют следующие значения:
cL = —0,000542 м/сек, dL = 0,833 м/сек при tlYm >
>272 сек,
сх = — 0,0023 м/сек, Д ~ 0,813 м/сек при 222 сек >
Ом <272 сек,
щ = — 0,208 м/сек, сД = 46,4 м/сек при £атм <
< 222 сек,
eL — — 0,00608 1 /сек, Д — 1,707 при Д1ТМ > 272 сек,
ех = — 0,0127 i/сек, Д = 3,257 при 222 сек < £атм <
2/2 се К)
ех = — 0,508 1/сек, Д = 1113,44 при /атм<Д222‘ сеи.
Результаты моделирования совместной работы алго¬
ритмов навигации и управления на атмосферном и вне¬
атмосферном участках полета свидетельствуют (см. табл.
10.2), что в этом случае использование алгоритма предва¬
рительного формирования орбиты ИСМ позволяет довольно
успешно справляться с действием различных возмуще¬
ний. При суммарном действии всех возмущений получа¬
ются следующие статистические характеристики основных
элементов предварительной орбиты:
М(<2) = 532,25 км, За «>) = 221,4 км,
М(/гк2) = 473 км, За (/г< = 181,7 км,
М(Уа2) = 3,265 км/сек, За(Уа2) = 93 м/сек.
Максимальная величина разгонного импульса не пре¬
вышает ДУ = 340 м/сек. Представленные материалы под¬
тверждают вывод (см. главу 9) о возможности технической
реализации способа формирования орбиты ИСМ, преду¬
сматривающего предварительное аэродинамическое тор¬
можение. Для КА с величиной приведенной нагрузки на
лобовую поверхность Рх — 350 кг/м2 и аэродинамического
качества /Д = 0,5 точность выведения КА на круговую
орбиту ИСМ с высотой /гкр — 500 км составляет +250 км
1 3 II. М. Иванов, А. И. Мартынов
386 СИНТЕЗ АЛГОРИТМОВ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ [ГЛ. 10
при величине разгонного импульса А Г -- 340 м/сек. Дли
устранения разбросов в величине /г-2 и Ла2 необходимо
проведение нескольких коррекций, что потребует допол¬
нительных затрат характеристической скорости ДУКор ~
ж 140 -4-150 м/сек, т. е. суммарные затраты на формиро¬
вание круговой орбиты в рассматриваемом примере
составляют ~480 м/сек. При этом система автономной на¬
вигации должна обеспечить вход КА в атмосферу с раз¬
бросом по высоте условного перицентра не более чем
Д/г*ав — ±30 км.
§ 10.4. О НЕКОТОРЫХ ПУТЯХ СОВЕРШЕНСТВОВАНИЯ
АЛГОРИТМА УПРАВЛЕНИЯ
Проведенное моделирование показало возможность ре¬
ализации способа выведения КА на орбиту ИСМ с предва¬
рительным аэродинамическим торможением. Поставлен¬
ная задача может быть решена с использованием достаточ¬
но простого алгоритма управления. Однако потребная
величина разгонного импульса получается достаточно боль¬
шой. В рассматриваемом примере (выведение на круговую
орбиту КА с К о 0,5 и Рх ^ 350 кг/м2) требуется сум¬
марная величина импульса AV ^ 480 м/сек. Для срав¬
нения отметим, что эта цифра в несколько раз превышает
величину разгонного импульса, потребную для форми¬
рования заданной орбиты ИСМ при идеальном управ¬
лении КА.
Обсудим возможности снижения потребных энерге¬
тических затрат.
Один из путей связан с изменением характеристик
КА (увеличение располагаемого аэродинамического ка¬
чества) и уточнением параметров атмосферы. Этот путь
является наиболее общим и понятным, поэтому не будем
на нем особо останавливаться.
Второй путь, который будет рассмотрен более подроб¬
но, заключается в совершенствовании системы управле¬
ния. Предположим, что в результате повышения характе¬
ристик точности системы управления на участке подлета
к плотным слоям атмосферы обеспечивается ширина нави¬
гационного коридора А/Дшв ±20 км. В этом случае для
рассматриваемого примера при соответствующем смещении
номинального значения Тг- возможно увеличить 17а:зад ДО
^ 10.43 СОВЕРШЕНСТВОВАНИЕ АЛ ГО РИТМА УПРАВЛЕНИЯ
387
3,18 м/сек (против Казад = 3,07 м/сек в §10.3) и соответ¬
ственно уменьшить величину разгонного импульса
(см. рис. 9.1). Одновременно необходимо синтезировать
более совершенные алгоритмы управления на всех^ эта¬
пах выведения КА на орбиту.
На атмосферном участке полета следует использовать
оптимальный закон управления ЛГ0ф — +АГо,— Kq. Алго¬
ритм несколько усложнится, так как точка переключения
очень чувствительна к возмущениям. Поэтому требуется
существенно более высокая точность решения краевой за¬
дачи, а также задачи идентификации параметров КА и
атмосферы. Для упрощения выбора управления можно
использовать специальный прием, суть которого состоит
в том, что при решении краевой задачи проводится только
одна итерация. Это достигается следующим образом.
Пусть КА осуществляет вход в атмосферу с величиной
КЭф —- и летит до некоторого момента времени tt с
этим значением К я ф. Будем считать также, что время рас¬
чета одной итерации равно At. Проводим прогноз дви¬
жения в предположении, что на участке tt + At ~ ti+i КА
движется со значением КПф = +АТ, в с момента ti+1
осуществляется переход на полет с К^ф = —К§. Если
оказывается, что а) прогнозируемая траектория пересека¬
ет поверхность планеты или б) после вылета из плотных
слоев атмосферы hal <С йазад, то дальнейший полет КА
па участке ti+1 + Дt проходит с К^ф Действи¬
тельный переход на К^ф = —К б осуществляется в том
случае, если величина /г71 лежит в требуемом диапазоне
по hai = йазад ± А/г. Величина Ah зависит от длитель¬
ности шага коррекции At и стремится в пределе к нулю при
Точность выведения КА в апоцентр переходной ор¬
биты зависит от многих возмущающих факторов, влияющих
на траекторию полета КА. Действие возмущений может
быть парировано выбором момента переключения. Однако
для этого надо уметь тоатто прогнозировать возмущения,
что невозможно. Тогда для создания запаса по управлению
следует после переключения управления осуществлять
полет с КЭф *>• —-Kq, Кроме того, при прогнозе движения
после переворота необходимо предполагать минимальную
плотность атмосферы рп (/;.) - ргл[,л (А),
388 СИНТЕЗ АЛГОРИТМОВ ПРИ ВЫВЕДЕНИИ НА ОРБИТУ [ГЛ. 10
Совершенствование алгоритма управления на внеат¬
мосферном участке полета состоит в том, что параметры
тВкл и AF рассчитываются по результатам прогноза тра¬
ектории на внеатмосферном участке. Это стало возможным
благодаря повышению точности решения задачи навигации
и идентификации после введения указанных мероприятий.
Правда, оказалось необходимым иметь более высокую
точность априорного знания параметров атмосферы (ми¬
нимальная плотность может отличаться от максимальной
не более чем па 25%). Использование полученных в усо¬
вершенствованном алгоритме величин тпкл и AF в сочета¬
нии с параметром /атм позволяет уточнить и третий па¬
раметр — угол х.
Предварительные результаты моделирования усовер¬
шенствованного алгоритма показали возможность реали¬
зации движения КА, близкого к оптимальному. Действи¬
тельно, для рассматриваемого выше примера точность вы¬
ведения на круговую орбиту ИСМ составляет Ah
= ±45 км, а максимальная величина импульса скорости,
потребная для формирования заданной орбиты, не пре¬
вышает 160 180 .м/сек.
ГЛАВА 11
СПУСК КА С ОРБИТЫ ИСМ
§ 11.1. ПОСТАНОВКА ЗАДАЧИ И СПОСОБЫ ЕЕ РЕШЕНИЯ
Организация посадки на поверхность Марса с предва¬
рительным выведением КА на орбиту ИСМ является бо¬
лее сложной задачей по сравнению с прямой посадкой, но
в то же время обеспечивает ряд преимуществ. В их числе:
— возможность выбора района посадки и времени
спуска с орбиты, что очень важно в условиях частых]мар¬
сианских пылевых бурь и сильных ветров;
— меньшие начальные скорости входа в атмосферу;
— возможность организации существенно более точ¬
ного входа КА в атмосферу (А0оав ~ ±10' -т-+15') по
сравнению с прямым входом.
Последнее обстоятельство оказывает заметное влияние
на решение проблемы мягкой посадки КА; позволяет при
выборе траектории спуска учесть ряд факторов, которые
не принимались во внимание при прямой посадке, и тем
самым осуществить более гибкий выбор рщиональной
траектории спуска; заметно облегчает работу системы
управления спуском КА, включая решение задачи точ¬
ной посадки в заданном районе поверхности планеты.
Спуск с орбиты спутника начинается с момента вклю¬
чения тормозной двигательной установки для переведения
КА на траекторию снижения, которую условно можно
разделить па три участка: 1) работы ТДУ; 2) внеатмос¬
ферного полета по переходному эллипсу; 3) движения в
плотных слоях атмосферы, включая участок работы СМП.
В этом заключается основное отличие спуска с орбиты
от прямого спуска с межпланетной траектории перелета,
который содержит лишь третий участок.
’Наличие трех участков при спуске аппарата с орбиты
выдвигает новые требования к оптимизируемому функ¬
ционалу [19]. Известно, что начальные условия входа КА
890
СПУСК КА С ОРБИТЫ ИСМ
[гл. I 1
в плотные слои атмосферы при известных параметрах ор¬
биты спутника полностью определяются величиной тор¬
мозного импульса ит и его направлением Хт, а также вре¬
менем включения ТДУ tm{n. Величина щ может достигать
600 -ч- 800 м/сек при спуске с достаточно низких орбит.
Эта особенность спуска КА с -орбиты ИСМ объясняется
разреженностью атмосферы Марса. Для захвата КА
атмосферой необходимо осуществлять вход с достаточно
большими (по модулю) начальными углами. Если при
спуске с орбиты ИСЗ угол входа, при котором осуществля¬
ется захват КА земной атмосферой, близок к нулю (0J ^
^ —0,5°), то при спуске с орбиты ИСМ 0В ~ —3,5—5°.
Итак, с одной стороны, имеется возможность выбором
величин ит, ^т, £внл обеспечить с высокой точностью тре¬
буемые начальные условия входа, наиболее благоприятные
для спуска в плотных слоях атмосферы. Но вместе с тем
спуск связан с существенными затратами энергетики.
Отсюда ясно, что если при прямом спуске в качестве ос¬
новного критерия оптимальности достаточно рассматри¬
вать минимум массы СМП (min тсми), то при посадке с
орбиты ИСМ необходимо рассматривать функционал, со¬
стоящий из двух частей:
min / = min (тсх -[- ?псма), (11.1)
где тск — массовые затраты, потребные для схода КА с
орбиты и обеспечения требуемых начальных условий входа.
Обеспечить условия (11.1) простой минимизацией каж¬
дого его слагаемого не удается из-за существования связи
между ними. Действительно, масса mcs монотонно увели¬
чивается с увеличением угла входа j 0О |. Масса 7??смптакже за¬
висит от начальных условий (0О и У0), причем зависимость
оказывается существенно нелинейной. Минимум функ¬
ционала (11.1) достигается при определенной комбинаций
иТ, %г, Тикл и начальных условий ввода в действие СМИ.
Отсюда видна сложность нахождения общего решения за¬
дачи при использовании критерия оптимальности (11.1)*
Воспользуемся способом поэтапного решения задачи•
что ведет к существенному ее упрощению. Такой путь
исследования оказывается возможным тГсилу особенностей
траекторий спуска КА с орбиты, Дейетвителыю, влияние
первого участка траектории на третий проявляется толк
§ 11.2] О ВОЗМОЖНОМ КЛАССЕ ОРБИТ ИСМ 391
ко через начальные условия входа в плотные слои атмосфе¬
ры. Второй участок (пассивный полет) практически не
оказывает никакого влияния па величину функционала
(11.1). Траектория на этом участке полностью определяет¬
ся значениями кинематических параметров в конце участ¬
ка работы ТДУ и для ее расчета можно применить ко¬
нечные формулы невозмущенного кеплер овского дви¬
жения.
Сказанное позволяет рассчитать зависимость начальных
условий входа КА в атмосферу от величины, направления
тормозного импульса и времени включения ТДУ, провес¬
ти анализ первого участка и получить зависимость потреб¬
ной массы тсх от начальных условий входа. Затем про¬
водится анализ траекторий спуска в атмосфере из условия
min пгсут при определенных выше начальных условиях.
Все ограничения, исходные предпосылки и метод исследо¬
вания остаются такими же, как при прямом спуске с
межпланетных траекторий.
После этого осуществляется сопряжение всех рассмат¬
риваемых участков траектории спуска, которое заключа¬
ется в том, что по результатам исследования каждого из
них определяются начальные условия входа КА в атмосфе¬
ру Марса, обеспечивающие минимум функционала (11.1).
Найденная точка фазового пространства является общей
для сопрягаемых участков, поэтому можно утверждать,
что траектория спуска, проходящая через эту точку, и
есть искомая оптимальная траектория. Таков предлага¬
емый метод исследования оптимальных траекторий спус¬
ка КА с орбиты ИСМ.
§ 11.2. О ВОЗМОЖНОМ КЛАССЕ ОТ БИТ ИСМ
Величина функционала (11.1) зависит от многих фак¬
торов, включая параметры КА, его системы управления,
системы мягкой посадки и т. д., а также зависит от па¬
раметров орбиты ИСМ. Поэтому предварительно рассмот¬
рим вопрос о возможном классе орбит ИСМ.
Будем предполагать орбиту ИСМ лежащей в плоскости
подлетной гиперболы, так как некомплаиарный маневр
обычно связан с большими энергетическими затратами.
Движение КА по орбите зависит от ее параметров /га и
h~, которые определяются на основе анализа энергетичес¬
392
СПУСК КА С ОРБИТЫ ИСМ
[ГЛ. 11
ких затрат, потребных для выхода на орбиту ИСМ, оцен¬
ки затрат для обеспечения спуска КА и, при необходимос¬
ти, возвращения взлетной ступени па орбиту ожидания
простоты и точности выполнения космических операции
разрешающей способности аппаратуры, возможности ра¬
диосвязи с Землей, времени существования КА на орбите
ИСМ, районов посадки КА па планете и т. д. Из-за слож¬
ности задачи остановимся только на некоторых требова¬
ниях, позволяющих выбрать рациональные параметры ор¬
биты ИСМ.
Как известно, энергетически оптимальная орбита ИСМ
должна иметь минимально допустимую высоту пери¬
центра к- и максимально допустимую высоту апо¬
центра кх. (При этом под энергетически оптимальной
понимается такая орбита, для формирования которой тре¬
буются минимальные энергетические затраты при перехо¬
де с подлетной гиперболической траектории иа эллипти¬
ческую орбиту ИСМ.) Высота перицентра к- определяется
из условия потребного времени существования КА па
орбите ИСМ и точности наведения па межпланетной тра¬
ектории. Обычно к- лежит в пределах от 500 до 3000 км.
Максимально допустимая высота апоцентра кх при задан¬
ной высоте перицентра может определяться из потребного
периода Т обращения КА по орбите спутника. При выборе
величины Т, кратной периоду обращения планеты, КА
будет перемещаться по одним и тем же трассам на поверх¬
ности планеты, что может противоречить требованиям
картографирования Марса. Выбор периода Т, кратного
земным суткам, обеспечивает сеансы связи с КА в одно и то
же время. Из этого условия обычно и выбирают высоту апо¬
центра орбиты ИСМ. Как правило, кх лежит в пределах
от 20 000 до 40 000 км и более.
В качестве примера приведем параметры орбиты КА
«Марс-5», который осуществил выход па орбиту ИСМ
12 февраля 1974 г.: период Т = 24 ч 52 мин 50 сек, накло¬
нение i — 35° 20', большая полуось а ^ 20 550 км, экс¬
центриситет е — 0,74974, расстояние до центра планеты
в перицентре г- = 5150 км, в апоцентре тх = 35 950 км.
Эта орбита близка к синхронной, т. е. период обращения
КА на орбите примерно совпадает с периодом вращения
Марса (Тпл ~ 24 ч 37 мин). На синхронные орбиты вы¬
водились и КА «Викинг».
§ И.я]
В 11 К ЛТ М ОСФК 1 ’ ПЫЙ УЧАСТОIX С ПУС К V
393
Существенным достоинством орбит с большим эксцен¬
триситетом является сравнительная малость энергети¬
ческих затрат па их формирование.
Другой характерный класс — это круговые орбиты.
Такие орбиты с минимальной высотой значительно уп¬
рощают операцию спуска КА на Марс и возвращение
па орбиту ИСМ, а также имеют целый ряд других досто¬
инств.
При формировании низких круговых (или эллиптичес¬
ких) орбит наиболее полно проявляются достоинства ме¬
тода выведения с предварительным аэродинамическим тор¬
можением.
Учитывая вышеизложенное, будем проводить исследо¬
вание траекторий спуска для двух орбит:
— низкой круговой с /с1ф = 500 км;
— эллиптической с h- = 500 км и /га = 20 000 км.
Указанным орбитам соответствуют скорости входа КА в
атмосферу VQ ^ 3,6 км/сек (круговая орбита ИСМ) и
V0 5,05 км/сек (эллиптическая орбита ИСМ).
§ 11.3. ВНЕАТМОСФЕРНЫЙ УЧАСТОК СПУСКА
Для спуска КА с орбиты спутника необходимо сообщить
ему тормозной импульс с помощью двигательной установ¬
ки. Схема полета КА но траектории спуска с орбиты по¬
каз апа на рис. 11.1. Прежде всего осуществляется задан¬
ная ориентация аппарата на орбите. Затем в заранее рас¬
считанное время включается ТДУ, которая работает в
течение времени, обеспечивающего переход КА па траек¬
торию спуска.
Расчетные формулы. Для проектировочных расчетов
можно пренебречь длительностью участка реактивного
торможения, т. е. предположить, что тормозной импульс
прикладывается мгновенно. Если известны требуемые ус-,
ловия входа на высоте условной границы атмосферы
(величина скорости V0, угол наклона траектории 0О, ра¬
диус-вектор из центра планеты 7*0, аргумент широты
со о), то этим самым определены параметры переходного
эллипса и ориентация его линии апсид. При известных
параметрах орбиты ИСМ (радиус перицентра г-, радиус
апоцентра га и аргумент широты перицентра со-) точка
пересечения этой орбиты с переходным- эллипсом опреде¬
394
СПУСК КЛ С ОРБИТЫ ИСМ
[гл. Ц
Местный горизонт
А
Орвита
ИСМ
ляет (см. рис. 11.1) момент импульсной коррекции скорос¬
ти тБКЛ, величину тормозного импульса щ и его направ¬
ление КТ относительно векторач?орбиталыюй скорости, вре¬
мя "спуска tcn и дальность спускает места коррекции скоро¬
сти до входа в атмосферу. Формулы для~расчета указанных
величин следуют из уравне¬
ний невозмущеппого (кепле-
ровского) движения.
Решим задачу определе¬
ния условий входа в атмосфе-
РУ (Б>, 0о. го, Щ, т0) в за-
висимости от момента кор¬
рекции скорости тВкл» вели¬
чины тормозного импульса иТ
и его направления Хт. Пара¬
метры орбиты в момент кор¬
рекции скорости предпола¬
гаются известными: скорость
Р"и к л ’ угол наклона траекто¬
рии 0пклч радиус-вектор КА
7’вкл ’
Условная
граница
аргумент широты сош<л.
Тогда величина скорости
КА после коррекции Т^т.ч
и угол 0ВКЛ наклона траекто¬
рии определяются но известным формулам [2]:
Центр плана
Рис. 11.1. Схема спуска КА с ор¬
биты ИСМ.
^ вил — Т i вил Г и'\' 21 икл^т COS (Хт Овил)
0вкл — 0вь*л I arcs ill
:— I DKJI UT COS (Хт 0вкл)»
It.r sin (/\т - 0БКЛ)
Т/вь-л + “т C0S (К - °пкл)
' 0вкл ~1 у (Хт 0цкл)-
вкл
Параметры входа Р0, 0О, со0 определяются при фиксирован¬
ном г0: j
Т^о = Т/2 - ±- , 0О = arctg
f 1 о аЛ
С.)0 = СО* + tfo, Твкл = Г
г1г0 sm -On
Pi
ВКЛ Т“
§ li.oj
в ii к л тм о с фу i н ы У\ у ч л ст с- у п i ус к л
Здесь
г у2 ?'
_ ВКЛ д г ВКЛ ВКЛ
Ch - 2 -ЛГВКЛ ’ "вкл - jl *
ei = VУ — Л'вкл)2 -|- Л^вкл(2 — Л/вкл) sin4 0цКЛ,
Pi = а-1 (1 — el),
Pi ,
L A^. „ cos2 0_.._ — 1
(\ '0 л ^ ^ acl вьл вьл
COS Oq = “ » ^OS в к л — ~ i
C1 cl
G>75 = (0ВКЛ 'Й'вкл?
A* = 4- l{E’o — eL sill Eq) — (Евкл — eL sin £Ш{Л)],
71
У-г=уУ|t«%.
где р — фокальный параметр, е — эксцентриситет, а —
большая полуось эллипса, с — постоянная интеграла
площадей, й — истинная аномалия, со — аргумент ши¬
роты (sin со = sin ср/sin i, i — наклонение орбиты, ср —
географическая широта), Е — эксцентрическая аномалия,
ii — средняя угловая скорость движения КА по орбите,
т — время, отсчитываемое от момента прохождения пе¬
рицентра (индекс 1 и штрих относятся к параметрам
переходного эллипса).
Анализ условий входа КА в атмосферу. Рассмотрим
спуск с круговой орбиты. Положение точки схода в этом
случае не влияет на условия входа в атмосферу. Близкая
к минимальной величина тормозного импульса, необходи¬
мая для получения заданного угла входа, достигается при
направлении тяги тормозной двигательной установки,
противоположном вектору орбитальной скорости, т. е.
X = 180° [85]. Для этого случая на рис. 11.2 показаны за¬
висимости потребного тормозного импульса ит от угла
входа 0О. Как и следовало ожидать, с уменьшением
| 0О | величина ит уменьшается и при 0О = 0 достигает
своего минимального значения.
Рассмотрим спуск с элиптической орбиты (h- =
= 500 км, hx = 20 000 км). В этом случае условия входа
396
СПУСК КА С ОРБИТЫ ИСМ
[ГЛ. 11
существенно зависят от величины истинной аномалии в
момент схода КА с орбиты. На рис. 11.2 показаны также
зависимости величины тормозного импульса щ от истин¬
ной аномалии точки схода с эллиптической орбиты при
фиксированном угле входа КА в атмосферу. Видно, что
требуемые углы входа в атмосферу обеспечиваются при
ит,м/сек
Рис. 11.2. Величина тормозного импульса для разных условий торможе¬
ния и входа. (Сплошная линия — спуск с круговой орбиты (/iKp = 500 км),
штриховая линия — спуск с эллиптической орбиты (/il4-p - 500 км,
Пу. = 20 000 км).)
минимальных энергетических затратах в случае включения
ТДУ в апоцентре орбиты (Фцнл = 180°) и при Xopt = 180°
[85]. При этом с уменьшением по модулю угла входа
КА в атмосферу величина тормозного импульса умень¬
шается, как и при спуске с круговой орбиты.
• 11.4] ЛЭГЮДШГАМ ПОИСКОВ ГО ГМ О/К RUHR It ПОСАДКА
397
Сравнивая величины тормозных импульсов, потребных
для организации спуска КА соотвественно с низкой кру¬
говой и эллиптической орбит с большим эксцентрисите¬
том, следует отметить, что для одинаковых углов входа
в атмосферу во втором случае величина иг примерно на
порядок меньше, чем в первом. Например, чтобы обеспе¬
чить вход КА в атмосферу с углом 0о • —8 величина
потребного импульса составляет ит 38 м/сек при спус¬
ке с эллиптической орбиты и иг 250 м/сек при спуске
с круговой орбиты.
§ 11.4. УЧАСТОК ЛОР ОДП НЛМИЧ ЕСКОГО ТОРМОЖЕНИЯ
И МЯГКОЙ ПОСАДКИ КА
Задача минимизации тс:,т при спуске КА с орбиты
ИСМ аналогична подобной задаче при прямом спуске.
Только в первом случае необходимо построить зави¬
симость игСШ1 от угла входа 0О, а затем, используя зави¬
симость тск от 0О, найти минимум функционала (11.1)
и определить оптимальные углы входа в атмосферу. Вос¬
пользуемся найденным оптимальным законом управления
движением КА (см. главы 6,7) для анализа траекторий спу-
ка КА с орбиты ИСМ. Будем предполагать, что после про¬
хождения участка аэродинамического торможения исполь¬
зуется либо реактивная, либо парашютно-реактивная CM 11.
В этом случае для обеспечения минимума массы СМИ па
участке аэродинамического торможения необходимо осу¬
ществлять спуск либо по траектории минимальной конеч¬
ной скорости для активной СМИ, либо по траектории мак¬
симальной конечной высоты (для парашютно-реактивной
CMI1). Кроме того, предполагается, что движение КА про¬
исходит внутри всего коридора входа (см. главу 6). Иа
рис. 11.3 в качестве примера представлены зависимости
минимальной конечной скорости (Кнтт) и максималь¬
ной конечной высоты (/гкт.х) от угла входа для аппарата
с величиной приведенной нагрузки на лобовую поверхность
Рх - 350 кг 1м- и аэродинамического качества К о — 0,3.
При спуске с эллиптической орбиты величина конечной
скорости сначала уменьшается с увеличением угла вхо¬
да до некоторого значения 0О, а затем при дальнейшем
увеличении | 0О | в некотором интервале конечная скорость
остается неизменной. Это объясняется тем, что, начиная
308
СПУСК КА С ОРБИТЫ ИСМ
[ГЛ. 11
с некоторого 0О = 0О, осуществляется переход от второго
тина управления (одноразовое переключение /С.ф) к пер¬
вому (управление с выходом КА на ограничение) на оп¬
тимальной траектории спуска. При таком управлении
величина VK не зависит от начальных условий входа в
рассмотренном диапазоне углов входа.
При спуске с круговой орбиты в достаточно широком
диапазоне углов входа (примерно до — 20°) оптимальной
h V •
"к max* 'к min*
НМ М/СБН
Рис. 11.3. Влияние угла входа в атмосферу на минимальную конечную ско¬
рость и максимальную, конечную высоту (Р — 350 иг/м-, = 0,3, р (/1) =»
“-Pmm ^-доп = 6 км).
является программа второго типа. По мере увеличения угла
входа 0О происходит сначала уменьшение конечной ско¬
рости до некоторого минимального значения, затем вели¬
чина конечной скорости монотонно возрастает.
Па оптимальных траекториях спуска, реализующих
шах /гк, характер зависимости величины hl{ Ш1Х от угла
входа несколько иной. При спуске с эллиптической и с
круговой орбит с увеличением угла входа наблюдается
сначала возрастание а затем после достижения
максимума происходит резкое уменьшение конечной вы¬
соты.
Отмеченный характер зависимости FK mm и /^к Ш;1Х, от
угла входа 0О остается таким же и для других значений
Рх и Kq из диапазона (6.28). Зная характер изменения
^ 11.5]
ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ УСЛОВИЙ ВХОДА 399
Vк min и кктлх от угла 0О, можно получить требуемую за¬
висимость тслш (0О). Для примера на рис. 11.4 приведены
такие зависимости для аппарата с начальной массой ткА =
= 5 т. Как и следовало ожидать, изменение массы реак¬
тивной системы торможения т[)С (0О) аналогично поведению
кривой КК1|1ш (0О), а зависимость массы парашютно-реак¬
тивной системы 771Прс от угла 0О носит иной характер, чем
mj
Рис. 11.4. Зависимость массы системы мягкой посадки и массы ?псх от угла
входа в атмосферу (т[ч- у = 5 т).
Ли шах (0О). С увеличением | 0О | происходит сначала умень¬
шение тпрс, а затем, после достижения минимума при
угле входа, соответствующем max /гк, наблюдается замет¬
ное увеличение массы mavc с последующим ростом | 0О |.
Качественный характер зависимостей тсмп (0О) ос¬
тается неизменным для широкого диапазона изменения на¬
чальной массы ттгкл. Количественная же оценка зависит
от многих факторов, подробный анализ которых дан в
главах 4 и 5.
§ 11.5. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ УСЛОВИИ
ВХОДА КА В АТМОСФЕРУ
Имея оценки потребной массы для организации тор¬
можения на каждом участке спуска, можно определить
оптимальную траекторию спуска путем сопряжения вне¬
атмосферного и атмосферного участков полета. Это сопря¬
жение заключается в выборе такого угла входа КА в
СПУСК КА С ОРБИТЫ ИСМ
[ГЛ. 11
атмосферу, при котором обеспечивается минимум функци¬
онала (11.1). В дальнейшем будем для краткости называть
этот угол оптимальным углом входа и обозначать 0qp1.
Произведя перестроение кривых ит (00), hf{mxx(Q0) и
Vk mill (0О.) в виде пгсх (0О) и тсмп (0О) для конкретных
двигательных установок, характеристик топлива и пара¬
шютов и проведя сложение величии шсх (0О) и тсш1 (0О),
получим результирующую кривую (0О).
Возможны два случая.
1. Зависимость т^ (0О) имеет явно выраженный мини¬
мум. Угол входа, при котором достигается т% mill, будет
соответствовать оптимальному углу входа 0QPt.
При практической реализации может выдвигаться ряд
дополнительных условий и требований — по перегрузкам,
режиму радиосвязи с объектом и т. п., удовлетворение ко¬
торым может привести к некоторому смещению угла вхо¬
да относительно выбранного значения 0Upt. На этапе
предварительных исследований при решении задачи о
выборе 0opL не принимается во внимание зависимость
массы теплозащитного покрытия и конструкции КА от
угла входа. Эти составляющие могут быть учтены па эта¬
пе окончательного выбора угла входа, когда при необхо¬
димости вводится ряд дополнительных условий.
2. Зависимость тб (0о) не содержит минимума, и сум¬
марная масса монотонно увеличивается с ростом | 0О |.
В этом случае
Как и в первом случае, при наличии дополнительных
требований и ограничений величина | 0°pt | может изме¬
няться.
Определим OoPt для некоторых конкретных случаев.
Реактивная система мягкой посадки. Определение
0^pt в первом приближении можно проводить без анализа
зависимостей тсу (0О) и тсмп (0О). Действительно, для
КА с заданной начальной массой значения тсх (0О) и
темп (во) однозначно определяются величиной скорости
торможения иГ и конечной скоростью, которую необхо¬
димо погасить с помощью ТДУ. Величина IT (0„) ~
£ 11.о] ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ УСЛОВИЙ ВХОДА /Д)|
= ит (0О) + Vl{ (0О) в общем случае не равна суммарной
характеристической скорости, потребной для обеспечения
мягкой посадки, так как не учитывает затрат на преодо¬
ление сил притяжения и предпосадочный маневр. Однако
минимумы ТА и тя обычно достигаются при одном и
том же значении угла входа 0o1)l. На рис. 11.5 приведены
Ъ, я*,
Рис. 11.5. Суммарные затраты характеристической скорости и масса системы
торможения (??г[ч-д = е т)•
зависимости Vц (0О) для КА с тн\ = 5 т. Характер кри¬
вых ТА (0О) в зависимости от типа орбиты ИСМ различен.
Так, при спуске с низкой круговой орбиты увеличение
по модулю угла входа приводит к монотонному возрастанию
величины ТА;. Это объясняется существенным влиянием на
воличиу ТА (0О) составляющей щ (0О), которая при спус¬
ке с круговой орбиты ИСМ в несколько раз больше, чем
при спуске с высокой эллиптической орбиты. Поскольку
402
СПУСК КЛ С ОРБИТЫ ИСМ
[ГЛ. и.
изменение угла входа приводит к малозаметному измене¬
нию величины FK (0О) и к существенному изменению
ит (0О), то последняя составляющая и определяет вид
кривой Fl (0о).
При спуске с эллиптической орбиты тормозной им¬
пульс невелик и характер зависимости Fs (0О) определя¬
ется составляющей FK (0О). Это подтверждается сопостав¬
лением зависимостей Ук (0О) и Fs (0О), приведенных на
рис. 11.3 и 11.5. Видно, что с увеличением по модулю угла
входа 0О сначала происходит уменьшение Fs, а затем,
после некоторого угла 0О, величина Fs начинает монотон¬
но возрастать. Как и следовало ожидать, суммарные за¬
траты Fs при спуске с круговой орбиты существенно пре¬
вышают аналогичные затраты при спуске с эллиптической
орбиты. Для приведенного на рис. 11.5 примера величина
Fv при спуске с круговой орбиты составляет 800-г- 1000м/сек
в зависимости от угла входа, а при спуске с эллиптиче¬
ской орбиты 630 -г- 680 м/сек. Зависимости (0О) отслежи¬
вают изменение FS(0O)- Оптимальные значения угла’входа
0оор\ обеспечивающие min Fs, соответственно обспечивают
минимум функционалу тs. Анализируя представленные
на рис. 11.5 зависимости, можно в целом отметить, что
в случае использования реактивной системы мягкой
посадки оптимальные углы входа КА в атмосферу со¬
ставляют:
— при'спуске КА с круговой орбиты 0QPt ~ —3,5 —
4,5°;
— при спуске КА с эллиптической орбиты 0QPt ^
ж -8,5 -г- -10,5°.
На одну из составляющих Fs, а именно на FKinin, су¬
щественное влияние оказывает выбор проектно-баллисти¬
ческих характеристик КА — величины приведенной на¬
грузки на лобовую поверхность и аэродинамического ка¬
чества. Проведенные исследования, однако, показали, что
изменение величины Рх или в диапазоне (6.28) ведет в
основном к количествепному'изменепиго конечной скорости
FH при сохранении характера кривой Fs (0О). Поэтому
величина 0qp1 не меняется. Потребные минимальные за¬
траты массы wv на организацию спуска КА с орбиты
ИСМ в зависимости от проектно-баллистических характе¬
ристик КА составляют величину порядка 1,65 -г- 2 т (от
§ 11.Г)] ОШШДКЛ КШ1 К ОПТИМАЛЬНЫХ УСЛОВИЙ ВХОДА
33% до 41% тК\) при спуске с круговой орбиты и ягЕ ж
^ 1,5 -д 1,95 т при спуске с эллиптической орбиты
(рис. 11.6). Увеличение Рх и уменьшение Ко приводит к
возрастанию пг^.
Помимо анализа изменения потребной для торможения
массы от условий входа и параметров КА, интересно про¬
следить за изменением характерных параметров траектории
Списк
я круговой
орбиты
: С
Спуск
о эллиптической
орбиты
ООО км,
. -20G00 км)
в
1
“V
\\ ЛгЩ)
\т
Щ(Р*)
(СМП типа ПРС)
200
{СМП типа ПРС)
500
И-Д
тг(°х)
{активная СМП)
ООО 500
Рх,кг/м
02
43
он
Гис. И.О. Суммарные затраты характеристической скорости и массы систем
торможения (»4\A. -- bin).
спуска па участке аэродинамического торможения: мак¬
симальной перегрузки, конечной скорости и конечного
угла наклона траектории к местному горизонту. Макси¬
мальные перегрузки на траектории спуска при варьиро¬
вании величины Рх и в диапазоне (6.28) не превышают
8 -х- 9 единиц, а углы наклона траектории 0К составляют
величину порядка —8 л 15°. Величина конечной скорости
VK существенно зависит от приведенной нагрузки на лобо¬
вую поверхность и аэродинамического качества, поэтому
диапазон ее возможных значений достаточно широк —
от 400 до 800 ль!сек (рис. 11.7 —11.9).
404
СПУСК КЛ С ОГГ.ИТЫ ИСМ
[ГЛ. 1i
В целом можно отметить, что по сравнению с прямы
спуском (см. главы 6 и 7) величина максимальной перегруз-
ки уменьшается на 7 -л- 8 единиц, а модуль конечного
угла наклона траектории также уменьшается в среднем
на 10 -л- 15°. Величина конечной скорости при переходе
8к/брад
Г’ис. 11.7. Влияние параметров КА на конечный угол наклона траектории
для парашютно-реактивной (кривые 1 и 2) и реактивной (кривые з и 4) СМП.
(Сплошная линия — спуск с круговой орбиты (/ТКр = 500 км), штриховая —
с эллиптической орбиты (/1_ = 500 км, hy = 20 0С0 км).)
от прямого спуска к спуску с орбиты ИСМ практически
остается неизменной.
Парашютно-реактивная СМП. Для этой системы оп¬
тимальный угол входа 0Г определяется из анализа за¬
висимостей (0О). В качестве примера на рис. 11.5 приве¬
дены зависимости т v (0О) для КА с начальной массой тк\^
§ 11.5]
ОПРЕДЕЛЕНЕН ОПТИМАЛЬНЫХ УСЛОВИЙ ВХОДА 405
= 5 т. Характеристики парашютно-реактивной системы
брались оптимальными в соответствии с результатами ис¬
следований, представленными в главе 5. Характер зави-
гках
Рис. 11.8. Максимальная перегрузка при использовании парашютно-реактив¬
ной (кривые 1 и 2) и реактивной (кривые з и 4) CM1I. (Сплошная линия — спуск
с круговой орбиты (йкр = 500 ш), штриховая линия — спуск* с эллиптической
орбиты (к- = 500 км, ку = 20 000 км).)
симостей т* (0О) аналогичен рассмотренному выше слу¬
чаю спуска с использованием активной СМП. Величина
Q(0)pt при спуске с круговой орбиты в обоих случаях оди¬
накова и находится в диапазоне от —2,5 до —4,5°. При
4.00
СПУСК КА С ОРБИТЫ ИСМ.
[ГЛ. 11
спуске с эллиптической орбиты величина 0Qpt несколько
смещается в сторону больших (по модулю) углов входа:
е;н* ~ _Ц _13°.
Как и при использовании активной СМИ, изменение
проектно-баллистических характеристик КА практиче-
h V ■
"к max > mm»
Рис. 11.9. Зависимость максимальной конечной высоты и минимальной ко¬
нечной скорости от основных параметров КА. (Сплошная линия — спуск
с круговой орбиты (/ij-р = 500 км), штриховая линия — спуск с эллиптической
орбиты (/i- = 500 к л, hy — 20 000 км).)
ски не влияет на характер кривой тs (0О) соответственно на
величину 0Qpt. Увеличение Рх и уменьшение К§ в диапа¬
зоне (6.28) приводит к возрастанию т%. В целом видно
(см. рис. 11.6), что для широкого класса КА при спуске
с круговой и с эллиптической орбит использование пара¬
шютно-реактивной СМП дает существенный выигрыш в
§11.5] ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ УСЛОВИЙ ВХОДА 407
потребной массе по сравнению с активной СМП. Так, для
КА с ткА = 5 т при использовании активной СМП по¬
требная суммарная масса на организацию спуска с
орбиты ИСМ, как уже отмечалось, составляет величину
1,65 л- 2 т, а при использовании парашютио-реактивиой
системы она уменьшается до 0,9 -д- 1,1 т. т. е. выигрыш
составляет около одной тонны (18—20% от шка).
Из проведенного сравнения двух схем спуска следует,
что прямой спуск обеспечивает некоторую экономию по¬
требной массы для организации мягкой посадки КА.
Однако этот вывод сделан на основе только проектно-бал¬
листического анализа номинальных траекторий. При уче¬
те способности систем управления спуском справляться с
действующими па КА возмущениями и погрешностями в
начальных условиях входа может произойти некоторое
перераспределение затрат массы на организацию посадки
КА для двух рассмотренных схем.
ЛИТЕРАТУРА
1. Л в д у с в с к п й В. С., А к и м Э. Л., А л е тн и н В. И.
и др., Атмосфера Марса в районе посадки спускаемого аппара¬
та «Марс-6» (предварительные результаты). Космические ис¬
следования, 1975, т. XIII, вып. 1.
2. А в д у с в с к и и В. С., А и т о и о в Б. М., А и ф п-
м о в II. А. и др., Основы тГорни полета космических аппара¬
тов. «Машиностроение», 1972.
3». А н д р е с в с к и и В. 13., Динамика спуска космических
аппаратов на Землю. «Машиностроение», 1970.
3. А II о р о в В. П., Принцип максимума для процессов с огра¬
ничениями общего вида. Автоматика и телемеханика, 1967,
№№ 3, 4.
5. Бабкин А. Г., Кирин II. Б., О синтезе управления
па основе итеративных методов. Автоматика и телемеханика,
1975, № 10.
6. Б а ж и п о в И. К., А л е ш и и В. И., И о ч у к а е в В. И.,
11 о л я к о в В. С., Космическая навигация. «Машинострое¬
ние», 1975.
7. Б а ж и н о в И. К'., II в а и о в II. М., М а р т ы-
н о в А. П., Дискретны]! алгоритм управления конечной
скоростью спуска космических аппаратов в атмосфере Марса.
Ученые записки ЦАГИ, 1972, т. III, № 4.
8. Б а ж и п о в И. К., Иванов Н. М., Йогов О. А.,
Яковлев О. С., Некоторые адаптивные алгоритмы управле¬
ния спуском в атмосфере Земли КА, возвращающихся от планет.
В сб. статен: «Информационные матери злы. Проблемы авиа¬
ционной и космической кибернетики», под ред. Петрова Б. И.,
АП СССР, ВИНИТИ, 1972, вып. 6.
9. Б а т и щ е в Д. И., Поисковые методы оптимального проек¬
тирования. «Советское радио», 1975.
К). Б о й ко А. (У, II в а п о в II. М., К а р я г и и 13. П.,
К р е м и ев Р. (У, М а р т ьг н о в А. И., И и ч х а-
дзе К. М., О некоторых особенностях выбора основных про-
сктпо-баллистичсскнх характеристик аппаратов, спускаемых
на Марс. Космические исследования, 1976, т. XIV, вып. 2.
11. Бсттин Р., Паведсппе в космосе. «Машиностроение»,
1966.
12. Б то ш гене Г. С., Студией Р. П., Динамика прост¬
ранственного движения самолета. «Машиностроение», 1967.
ЛИТЕРАТУРА
409
13. Б а с п л ь с в Б. Б., Методы о i пм i м а л .biioii фильтрации в сис¬
темах управления космических аппаратов. Б сб.: «Вопросы
управления космическими аппаратами», под род. Петрова Б. П.,
«Мир», 1975.
14. В е и т ц ель Е. С., Исследование операции. «Советское ра¬
дио», 1972.
15. В о с к о в и ч В. Л., Методы принятия решения по множе¬
ству критериев оптимальности (обзор). В кн.: «Сложные сис¬
темы управления», вып. 1, ИК A11 УССР, 1968.
16. Г е л о в а II и В. А., Голубев ТО. Ф., Многошаговый
алгоритм управления спуском в атмосфере Марса. Препринт
№ 9, ИПМ АН СССР, 1974.
17. Г е р м с и с р 10. Б., Введение в теорию исследования опе¬
раций. «Наука», 1971.
18. Глазков А. Г., И б р а г и м о в ТС 3., К л и м и н А. В.,
Т р у н о в 10. В., Хаза и М. A., X и т р и к М . С.,
Яро ш с в с к и и В. А., Управление космическим аппа¬
ратом при входе в атмосферу. Космические исследования, 1969,
т. VII, вып. 2.
19. Голубцов В. Г., М и т р о ш и н Э. II., К задаче после¬
довательного аэродинамического и реактивного торможения
космических аппаратов в атмосфере Марса. Космические ис¬
следования, 1974, т. XII, вып. 5.
20. Д п к с о п Д., Проектирование систем. «Мир», 1973.
21. Д м и т ]) о ч с н к о Л. А., Л о и а т и и В. П., Особенно¬
сти алгоритмов бесилатформенных инерцпалытых навигацион¬
ных систем. В сб. статей: «Вопросы управления космическими
аппаратами», под ред. Петрова Б. ТТ., «Мир», 1975.
22. Ж е л и и и 10. П., Ш и л о в А. А., Траектории минималь¬
ной дальности при входе космического аппарата в атмосферу
Земли со свсрхкруговой скоростью. Ученые записки ЦАГИ,
1970, т. I, № 1.
23. И в а и о в II. М., К о т о в Б. Б., М а р т ы н о в А. И.,
Синтез оптимальных траекторий спуска КА в атмосфере Марса
при использовании параппотпо-рсактпвной системы мягкой
посадки. Космические исследования, 1977, т. XV, вып. 3.
24. И в а и о в II. М., М а р т ы нов А. II., Адаптивный алго¬
ритм управления конечной скоростью спуска космических
аппаратов в атмосфере Марса. Космические исследования,
1973, т. XI, вып. 5.
25. И в а и о в Н. М., М а р т ы н о в А. П., Алгоритм авто¬
номной навигации при управлении конечной скоростью спуска
КА в атмосфере Марса. Космические исследования, 1976,
т. XIV, вып. 1.
26. И в а и о в II. М., М а р т ы и о в А. II., Об одном алгорит¬
ме управления конечной скоростью спуска автоматических
аппаратов в атмосфере Марса. Ученые записки ЦАГИ, 1971,
т. II, Х° 5.
27. И в а и о в II. М., М а р т ы нов А. П., Об особенностях
моделирования адаптивного алгоритма управления конечной
скоростью спуска космических аппаратов в атмосфере Марса.
Ученые записки ЦАГИ, 1973, т. IV, вып. 2.
410
ЛИТЕРАТУРА
28. II в а и о в II. М., М а р т ы и он А. И., Об эффективности
использования аэродинамической подъемной силы при спус¬
ке в атмосфере Марса. Ученые записки ЦАГИ, 1972, т. III,
№ 3.
29. Иванов Н. М., М а р т ы и о в А. И., О максимально
допустимой нагрузке на лобовую поверхность аппаратов, осу¬
ществляющих аэродинамический спуск в атмосфере Марса.
Ученые записки ЦАГИ, 1971, т. II, № 3.
30. И в а и о в II. М., Мартынов А. И., Ш и л о в А. А.,
О переведении космического аппарата с гиперболической тра¬
ектории на орбиту искусственного спутника планеты с исполь¬
зованием аэродинамического торможения в атмосфере. Косми¬
ческие исследования, 1975, т. XIII, выл. 4.
31. Иванов II. М., Мартынов А. И., Оптимальное упра¬
вление конечной скоростью космических аппаратов, соверша¬
ющих спуск в атмосфере Марса. Космические исследования,
1972, т. X, вып. 2.
32. И в а н о в II. М., Мартынов А. И., Проблема спуска
космических аппаратов в атмосферах планет. «Знание», 1972.
33. И в а н о в Н. М., Мартынов А. И., Управление меж¬
планетными космическими аппаратами. В сб. статей: «Вопросы
управления космическими аппаратами» под ред. Б. II. Петро¬
ва, «Мир», 1975.
34. И в а и о в II. М., Мартынов А. И., Белых В. Д.,
Об эффективности использования критерия минимума конеч¬
ной скорости при синтезе траекторий спуска КА на поверх¬
ность Марса. Космические исследования, 1976, т. XIV, вып. 4.
35. II в а и о в II. М., М а р т ы н о в А. И., Соколов II. JI.,
О выборе основных проектно-баллистических характеристик
и способа управления КА планирующего типа, предназначен¬
ных для спуска на поверхность Марса. Космические исследо¬
вания, 1977, т. XV, вып. 1.
36. И в а и о в II. М., М а р т ы н о в А. И., III и л о в А. А.,
Некоторые задачи оптимального управления траекторией кос¬
мического аппарата в атмосфере Марса. Космические исследо¬
вания, 1973, т. XI, вып. 1.
37. Ивахненко А. Г., Зайченко 10. П., Димит¬
ров В. Д., Принятие решений на основе самоорганизации.
«Советское радио», 1976.
38. Исаев В. К., Принцип максимума JI. С. Понтрягина и оп¬
тимальное программирование тяги ракет. Автоматика и теле¬
механика, 1961, т. XXII, № 8.
39. Исаев В.К., Давидсон Б.Х., Оптимальная посадка
космического аппарата на поверхность Луны. Космические ис¬
следования, 1969, т. VII, вып. 3.
40. Истомин В. Г., Гречнев К. В., Озеров Л. II.
и др., Эксперимент по измерению состава атмосферы Марса
на спускаемом аппарате космической станции «Марс-6». Кос¬
мические исследования, 1975, т. XIII, вып. 1.
41. Казаков И. Е., Доступов Б. Г., Статистическая
динамика нелинейных автоматических систем. Физматгиз,
1962.
ЛИТЕРАТУРА
42. Колосов М. А., Яковлев О. И., Яковлева Г. Д.
и др., Результаты исследований атмосферы Марса методом ра¬
диопросвечивания с помощью аппаратов «Марс-2,4,6». Косми¬
ческие исследования, 1975, т. XIII, вып. 1.
43. К о н я с в В. Г., Оптимальное использование аэродинами¬
ческих сил для маневра летательного аппарата. Космические
исследования, 1967, т. V, вып. 2.
44. Коняев В. Г., Об одном классе траекторий квазистацио-
нарного планирования. Ученые записки ЦАРИ, 1970, вып. 1.
45. Коп п и п 10. М., Об уравнениях пространственного движе¬
ния спутника, использующего аэродинамическую подъемную
силу. Космические исследования, 1968, т. VI, вып. 3.
46. Космическая техника. Под ред. Сейферта. «Наука», 1964.
47. К р а с н о п о л ь с к и й В. А., К р ы с ь к о А. А., Ро¬
гачев В. II., Озон в атмосфере пл анеты по измерениям с бор¬
та АМС «Марс-5». Космич. исследования, 1975, т. XIII,bltii. I.
48. К р а с о в с к и й Н. И., Игровые задачи о встрече движе¬
ний. «Наука», 1970.
49. Крылов И. А., Ч е р н о у с ь к о Ф. Л., О методе после¬
довательных приближений для решения задач оптимального
управления. Журнал вычислительной математики и матема¬
тической физики, 1972, т. XII, № 1.
50. К р ы л о в И. А., Ч с р н о у с ь к о Ф. Л., Алгоритм мето¬
да последовательных приближений для задач оптимального
управления. Журнал вычислительной математики и математи¬
ческой физики, 1972, т. XII, № 1.
51. К у р о in А. Г., Курс высшей алгебры. «Наука», 1971.
52. К у з м а к Г. К., Теория одного класса дискретных самокор¬
ректирующихся систем. Доклады АН СССР, 1964, т. 155, № 5.
53. Л а и г е О., Оптимальные решения, нерев. с польского. «Про¬
гресс», 1967.
54. Лебедев А. А., К р а с и л ь щ и к о в М. II., М а л ы-
ш ев 13. П., Оптимальное управление движением космичес¬
ких летательных аппаратов. «Машиностроение», 1974.
55. Л е т о в А. М., Динамика полета и управление. «Наука»,
1969.
56. Л и Р., Оптимальные оценки, определение характеристик
и управление. «Наука», 1966.
57. Ляпунов А. М., Общая задача об устойчивости движения.
Гостехиздат, 1951
58. М а ]) о в М. Я., Повое о Марсе и Юпитере. Земля и Вселен¬
ная, № 2, 1977.
59. М о р о з В. П., Физика планет. «Паука», 1967.
60. М о р о з В. П., II а д ж пи А. П.. Предварительные ре¬
зультаты измерений содержания водяного пара в атмосфере
планет},] по измерениям с борта АМС «Марс-5», Космические
исследования, 1975, т. XIJI, выи. 1.
61. Моисеев Н. П., Племепты теории оптимальных систем.
«Паука», 1975.
62. Некоторые проблемы создания и отработки космических айна
ратов, предназначенных для входа в атмосферы ттлчиет.-
ВИНИТИ, 1975 >
412
ЛИТЕРАТУРА
63. Н и к о л а е б 10. Д., Некоторые методы параметрической
индентификанни линейных систем управления. В сб.: «Вопро¬
сы управления космическими аппаратами», под ред. Петро¬
ва Б. Н., «Мир», 1975.
64. О с т о с л а в с к и и И. В., Стражева И. В., Дина¬
мика полета. Траектории летательных аппаратов. «Машино¬
строение», 1969.
65. О х о ц и м с к и ii Д. Е., Б е л ь ч а н с к и и Г. И., Б у-
х а р к и и а А. П., Голубев ТО. Ф., Золотухи¬
на И. И., Иванов 10. II., Оптимальное управление при
входе в атмосферу. Космические исследования, 1968, т. VI,
вып. 1.
66. О х о ц и м с к к й Д. Е., Б у х а р к и и а А. П., Го л у-
б е в 10. Ф., Алгоритм автономного управления приведением
космического-аппарата в заданную точку посадки. Космичес¬
кие исследования, 1970, т. VIII, вып. 2.
67. О х о ц и м с к и й Д. Е., Кухаркина А. П., Г о л у-
б с в 10. Ф., Прогнозирование при управлении входом в ат¬
мосферу. Космические исследования, 1972, т. X, вып. 3.
68. О х о ц и м с к и й Д. Е., Б у х а р к и и а А. П., Го л у-
б е в 10. Ф., Управление движением при входов атмосферу.
Космические исследования, 1969, т. VII, вып. 2.
69. О х о ц и м с к и it Д. Е., Голубев 10. Ф., Б у х а р-
к и и а А. П., Филипов и ч И.В., Ше л у хина В. К.,
Управление при входе в атмосферу Марса с целью выведения
на орбиту ИСМ. Препринт № 1, ИПМ АН СССР, 1976.
70. О х о ц и м с к и ii Д. Е., Голубев 10. Ф., С и х а р у-
л и д з с 10. Г., Алгоритмы управления космическим аппара¬
том при входе в атмосферу. «Наука», 1975.
71. О х о ц и м с к и ii Д. Е., Сихарулидзе 10. Г., Адап¬
тивный алгоритм стабилизации космического аппарата при
входе в атмосферу. Изв. АН СССР. Техническая кибернетика,
1973, № 2.
72. О х о ц и м с к и ii Д. Е., Сихарулидзе 10. Г., Алго¬
ритм управления угловым движением космического аппарата
на траектории спуска в атмосфере. Препринт ИПМ АП СССР,
1971.
73. О х о ц и м с к и й Д. Е., Сихарулидзе 10. Г., Одно-
параметричсский многошаговый алгоритм стабилизации при
входе космического аппарата в атмосферу. Космические ис¬
следования, 1971, т. IX, вып. 5.
74. О х о ц и м с к и й Д. Е., Сихарулидзе 10. Г., Трех-
параметрпческип многошаговый алгоритм стабилизации косми¬
ческого аппарата на траектории спуска в атмосфере. Косми¬
ческие исследования, 1972, т. X, вып. 5.
75. О х о ц п м с к и й Д. Е., Э п с с в Т. М., Некоторые вариа¬
ционные задачи, связанные с запуском искусственного спутни¬
ка Земли. УФН, т. 63, вып. 1а, 1957.
76. П ашкоев С. Д. гг др., Машинные методы оптимизации
в технике связи. «Связь», 1976.
77. Пономарев А. Н., Пилотируемые космические корабли.
Воениздат, 1968,
ЛИТЕРАТУРА
413
78. Пономарев В. П., Теория управления движением косми¬
ческих аппаратов. «Наука», 1965.
79. П о и т р я г и н Л. С., Б о л т я и с к и й В. Г., Г а м-
к р е л и д з е Р. В., Мищенко Е. Ф., Математическая
теория оптимальных процессов. «Наука», 1969.
80. Пугачев B.C., Теория случайных функций и ее приме¬
нение к задачам автоматического управления. Физматгиз,
1960.
81. П in е li и ч п ы й Б. П., Д а и и л и и ТО. М., Численные
методы в экстремальных задачах. «Паука». 1975.
82. Ра б и и о в и ч Б. II., Вариационные режимы полета кры¬
латых летательных аппаратов. «Машиностроение», .1969.
83. Семенов В. В., С о л о д о в н и к о в В. В., Спект¬
ральная теория нестационарных систем управления. «Паука»,
1974.
84. Семенов В. В., К о л о к о л ь н и ков А. В., Г рис¬
ков И. А., Траектории аэродинамического торможения
в атмосфере Марса, обеспечивающие минимум характеристи¬
ческой скорости на участке гравитационного разворота. Кос¬
мические исследования, 1975, т. XIII, вып. 4.
85. Сихарулидзе ТО. Г., Оптимальное импульсное тормо¬
жение при входе в атмосферу. Космические исследования, 1970,
т. VIII, вып. 2.
86. Современное состояние механики космического полета. Сб. ста¬
тен под ред. Ричардса И. Б.. «Наука», 1969.
87. С о"к о л о в С. С., Ф о к и и В. Г., Б у рдев В. ГГ. и др.,
Функционирование спускаемою аппарата AM С «Марс-6» в ат¬
мосфере Марса. Космические исследования, 1975, т. XIII,
вып. 1.
88 Соловье в Ц В., Тарасов Е. В., Прогнозирование
межпланетных полетев. «Матптшостроонпс», 1973.
89. Т е р я е в Е. Д., III а м р и к о в Б. М., Сергеев Э. А.,
Перспективы применения Б ЦВМ в комплексно-автоматизи¬
рованных адаптивных системах управления летательных ап¬
паратов. В сб. статей: «Информационные материалы. Пробле¬
мы авиационной и космической кибернетики», под ред. Петро¬
ва Б. П., АН СССР. ВИНИТИ, 1972, вып. 6.
90. Уколов И. С., Процессы адаптации в системах управления
летательных аппаратов, В сб. статей: «Информационные мате¬
риалы. Проблемы авиационной и космической кибернетики»,
под ред. Петрова Б. П.. АН СССР, 1972, вып. 6.
91. У о л л о с Р. А , Г р с й В. А., Минимальное аэродинами¬
ческое качество, необходимое для приземления аппарата в лю¬
бой точке земного шара. Ракетная техника и космонавтика,
1963, .У 11.
92. Управление космическими летательными аппаратами. Перевод
с английского, под ред. Лебедева А. А. «Машиностроение»,
1967.
93. Хроника Космических исследовании. Вкспресс-пнформацпя
«Астронавтика и ракетодпнамика», Да 24, ВПИШИ, 1975.
94. Ч а р и ы li В. П., О двух методах интегрирования уравнений
движения. Космические нс'лто/ипшшщ к VIII, вып, 5, 1970.
414
ЛИТКРЛТУРЛ
95. Ч а р н ы й В. И., Б it р з г а л А. Г1., Борисе п-
к о В. И., С в и щ е в А. Г., О применении прямых методов
в алгоритмах управления спуском аппарата в атмосфере. Кос¬
мические исследования, 1969, т. VII, вып. 6,
96. Шаповалов Е. П., Кубы ш к и и В. В., Оптималь¬
ные траектории движения спускаемых аппаратов с двумерным
управлением в атмосфере Марса. Космические исследования,
1976, т. XII, вып. 6.
97. III и л о в Л. А., Ж е л н и н 10. II., О минимуме максималь¬
но]'! перегрузки при торможении аппарата в атмосфере. Кос¬
мические исследования, 1966, т. IV, вып. 4.
98. III к а д о в Л.М., Бух а нова Р. С., Илларио¬
нов В. Ф., Плохих В. П., Механика оптимального
пространственного движения летательных аппаратов в атмос¬
фере. «Машиностроение», 1972.
99. Ш к а д о в Л.М., Илларионов В. Ф., Поворот плос¬
кости круговой орбиты спутника. ПММ, 1962, т. XXVI, вып. 1.
100. Ш у н е йк о И. И., Крылатые космические корабли. ВИНИТИ.
1966.
101. Э й с м опт II. А., Использование аэродинамического тор¬
можения для перевода спутника планеты с орбиты с большим
эксцентриситетом на почти круговую. Космические исследо¬
вания, 1972, т. X, вып. 2.
102. Э й с м о и т Н. А., Оптимальное управление космическим
аппаратом, переводимым с гиперболической траектории па ор¬
биту спутника планеты торможением в атмосфере. Космичес¬
кие исследования, 1972, т. X, вып. 2.
103. Ю д и и Д. Б., Математические методы управления в услови¬
ях неполной информации. «Советское радио», 1974.
104. Campbell J. F., Brown С. A., Experimental ware
flaw properties of a Viking 75 entry Vehicle. .T. Space and Rock.,
1974, v. 11, № l.
105. G i 1 1 i s E., The Viking deceleration system an overview.
AIAA Paper, № 442, 1973.
106. L a u R. A., The Hussong J. C., The Viking Mars lander de¬
celeration system. AIAA Paper, N® 1162, 1970.
107. M о о g R. D., Bendura R. J., Timmons .1. D.,
L a u R. A., Qualification fligh tests of the Viking decelerati¬
on system. AIAA Paper, № 457, 1973.
Ю8. Ruari P., Feedback arqnment ober Mars landing sites bub.
Scientist, v. 58, Л® 847, 1973.
109. S с h a p p e 1 R. Т., J о n s о n R. G., Experimental and
simulation stady results on the development of a planetary lan¬
ding site selection sisiem (Guidance and Flight Control Confe¬
rence, August, 14, 16, 1972). AiAA Paper, vV 868, 1972.
110. Steinberg S., S i e m e г s P. М., S 1 a u p m a n R. G.*
AIAA Paper № 73, 454, AIAA 4th Aerodynamic Deceleration
Systems ConE, Palm Springs, Calif., May 21—23, 1973.
111. E о i n e f II. N0 F r e n ch С. E., H о w a г d D. A., A new
approach to performance optimization nf the 1976 Mars Viking;
Bunder, AIA A Paper- A® 869, 1973,
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
c=mKA—секундный расход массы;
Сх — коэффициент лобового сопротивления;
Су — коэффициент аэродинамической подъемной силы;
Fn — площадь купола парашюта;
h — высота условной границы плотных слоев атмосферы;
h — высота апоцентра переходной орбиты;
h7li — высота перицентра переходной орбиты;
h , h~2 — высота соответственно апоцентра и перицентра тре¬
буемой орбиты ИСМ;
hn — высота условного перицентра траектории входа;
h^v — прицельная высота условного перицентра;
hK — высота круговой орбиты;
i — наклонение орбиты;
К — аэродинамическое качество;
Ьп — дальность спуска, отсчитываемая от условного пери¬
центра;
М — число Маха,
М—математическое ожидание;
пх—перегрузка в направлении, противоположном скорости;
Р — тяга двигателя;
Р — тяговооружеиность;
Руд — удельная тяга;
Рх — приведенная нагрузка на лобовую поверхность;
Ps — нагрузка на лобовую поверхность;
q — скоростной напор;
г — радиус-вектор КА;
гп, га — расстояние в перицентре и апоцентре орбиты до центра
планеты;
S — корректирующая функция;
Ам — площадь миделя КА;
t — время (см. нижние индексы, а также рис. 5.5);
и — управление;
ит — величина тормозного импульса;
V — скорость полета;
1Д, Уц — первая и вторая космические скорости;
Vs — кажущаяся скорость;
416
ОСНОВ II ЫЕ ОБО 3IIА Ч EIIИ >1
Y — подъемная сила;
Уг, YB — горизонтальная и вертикальная составляющие подъ-
емпой силы;
а — прямое восхождение, угол атаки;
у — угол крена;
8 — угол между плоскостью подлетной траектории и текущей
плоскостью д в и жени я;
Ф — истинная аномалия; угол тангажа;
0 — угол наклона траектории к местному горизонту;
Ат — угол между местным горизонтом и вектором тормозной
скорости;
\х — гравитационный параметр Марса;
р0 — плотность атмосферы у поверхности Марса;
р (/г) — плотность атмосферы иа высоте /г;
ох — баллистический параметр.
Верхние индексы
opt — оптимальное значение;
в — верхнее значение;
нав — навигационные параметры;
тек — текущее значение;
(1) — значение коэффициентов в момент выхода космического
аппарата на ограниченно;
(2) — значение параметров в момент схода КА с ограничения;'
* — соответствует участку работы СМП.
Нижние индексы
б — балансировочный; бак;
бок — боковой;
гз — гарантированная задержка;
дон — допустимое значение;
з — земное;
к — конечное значение параметра;
оп — опорное значение;
п — переключение; парашют;
пр — программное значение;
прс — парашютно-реактивная система;
пс — парашютная система;
пн — полезная нагрузка;
р — разрифлеште;
расп — располагаемое значение;
рс—реактивная система;
т—топливо; торможение;
тек — текущее значение;
эф — эффективное значение;
О — соответствует начальным значениям параметров на каж¬
дом из участков спуска (аэродинамическом и мягкой посадки) или
значению у поверхности планеты;
а—апоцентр;
п — перицентр.