Author: Иванов М. Ушаков В. Сергиенко А.
Tags: электротехника общая радиотехника электроника радиотехника сигналы электрические цепи
ISBN: 978-5-496-00503-6
Year: 2014
Text
ЧЕБНИК
ДЛЯ ВУЗОВ
ПИТЕР'
СТАНДАРТ ТРЕТЬЕГО ПОКОЛЕНИЯ
м. Иванов А. Сергиенко В. Ушаков
Радиотехнические
цепи и сигналы
Направление «Радиотехника»
Специальность «Радиоэлектронные системы и комплексы»
РЕКОМЕНДОВАНО
УЧЕБНО-МЕТОДИЧЕСКИМ ОБЪЕДИНЕНИЕМ
УЧЕБНИК
й
ДЛЯ ВУЗОВ
СТАНДАРТ ТРЕТЬЕГО ПОКОЛЕНИЯ
М. Иванов А. Сергиенко В. Ушаков
Радиотехнические
цепи и сигналы
Рекомендовано Учебно-методическим объединением вузов Российской
федераоии по образованию в области радиотехники, электроники,
биомедицинской техники и автоматизации в качестве учебника
для студентов высших учебных заведений, обучающихся
по направлению 210400 «Радиотехника»
Сканировал
strelok_hunter@mail.ru
Г^ППТЕР
Москва • Санкт-Петербург • Нижний Новгород Воронеж
Ростов-на-Дону • Екатеринбург Самара Новосибирск
Киев • Харьк' i- Минск
2014
ББК 32.841 я7
УДК 621.37(075)
Р15
Авторский коллектив:
Михаил Тимофеевич Иванов, Александр Борисович Сергиенко, Виктор Николаевич Ушаков
Рецензент:
завкафедрой электроники и оптической связи ГУАП
д. т. н., профессор С. В. Кулаков
Р15 Радиотехнические цепи и сигналы: Учебник для вузов. Стандарт третьего
поколения / Под ред. В. Н. Ушакова — СПб.: Питер, 2014. — 336 с.: ил. — (Се-
рия «Учебник для вузов»),
ISBN 978-5-496-00503-6
В учебнике изложены основы теории детерминированных и случайных сигналов, линейных
и нелинейных цепей с постоянными параметрами, оптимальной и дискретной фильтрации сигна-
лов, а также автогенераторов. Помимо теоретического материала приводятся контрольные вопро-
сы, подробно рассмотренные примеры решения задач, а также задачи для самостоятельного реше-
ния (с ответами).
Рекомендовано Учебно-методическим объединением вузов Российской Федерации по образова-
нию в области радиотехники, электроники, биомедицинской техники и автоматизации в качестве
учебника для студентов высших учебных заведений, обучающихся по направлению 210400 «Ра-
диотехника».
ББК 32.841 я7
УДК 621.37(075)
Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было фор-
ме без письменного разрешения владельцев авторских прав.
Информация, содержащаяся в данной книге, получена из источников, рассматриваемых издательством как
надежные. Тем не менее, имея в виду возможные человеческие или технические ошибки, издательство не
может гарантировать абсолютную точность и полноту приводимых сведений и не несет ответственности за
возможные ошибки, связанные с использованием книги.
ISBN 978-5-496-00503-6
© ООО Издательство -Питер», 2014
Оглавление
Поедисловие ................................................... 7
1. Основные характеристики детерминированных
сигналов .................................................. 8
1.1. Сигналы. модели сигналов ..............................8
1.2. Обобщенный ряд Фурье .................................11
1.3. Тригонометрический ряд Фурье .........................14
1.4. Спектры некоторых периодических сигналов..............17
1.5. Преобразование Фурье и его свойст ва .............21
1.6. Преобразование Фурье некоторых сигналов ..............24
1.7. Теоремы о спектрах ...................................30
1.8. Спектральные функции произведения и свертки сигналов .32
1.9. Преобразование ферье некоторых неинтегрируемых
абсолютно сигналов....................................33
1.10. Энергетические соотношения в спектральном анализе.....38
1.11. Корреляционный анализ детерминированных с игналов ....40
1.12. Свертка сигналов......................................44
1.13. Корреляционно-спектральный анализ
детерминированных сигналов ...........................47
Контрольные вопросы и задания ..............................48
Задачи......................................................49
2. Модулированные радиосигналы.................................54
2.1. Модуляция. Основные понятия ..........................54
2.2. Радиосигналы с амплитудной модуляцией ................55
2.3. Радиосигналы с угловой модуляцией.....................62
2.4. Фурье-анализ модулированных радиосигналов ............66
2.5. Амплитудно-импульсная модуляция ......................68
2.6. Внутриимпульсная модуляция............................72
2.7. Комплексная огибающая радиосигнала. Взаимная
корреляционная функция модулированных сигналов .......73
2.8. Аналитический сигнал и преобразование Гильберта ......76
4
Оглавление
Контрольные вопросы и задания...........................83
Задачи..................................................84
3. Основы теории случайных процессов ......................86
3.1. Ансамбль реализаций...............................86
3.2. Вероятностные характеристики случайных процессов..89
3.3. Корреляционные функции случайных процессов .......94
3.4. Стационарные и эргодические случайные процессы ...98
3.5. Спектральные характеристики случайных процессов..104
3.6. Теорема Винера—Хинчина...........................106
3.7. Узкополосный случайный процесс...................110
Контрольные вопросы и задания..........................116
Задачи.................................................117
4. Линейные цепи с постоянными параметрами ...............120
4.1. Частотные и временные характеристики линейных цепей
Методы анализа прохождения детерминированных
сигнатов ........................................... 120
4.2. Расчет переходной и импульсной характеристик
линейной цепи ........................................125
4.3. Преобразование характеристик случайного процесса
в линейной цепи .....................................127
4.4. 7?С-фильтры нижних и верхних частот
и их характеристики................................. 130
4.5. Прохождение сигналов через простейшие /?С-цепи ..135
4.6. Одиночный колебательный контур и его основные
характеристики ......................................138
4.7. Линейные цепи с обратной связью..................148
4.8. Условия устойчивости линейной цепи ..............153
Контрольные вопросы и задания..........................155
Задачи.................................................156
5. Принципы оптимальной линейной фильтрации сигналов
на фоне помех ............................................160
5.1. Согласованная фильтрация детерминированных сигналов .. ..160
5.2. Отношение «сигнал/шум» на входе и выходе
согласованного фильтра ...............................163
5.3. Применение согласованных фильтров ................166
Оглавление
5
5.4. Оптимальная фильтрация при небелом шуме.............172
5.5. Квазпоптимальная фильтрация детерминированных
сигналов .............................................174
5.6. Оптимальная фильтрация случайных сигналов ..........179
Контрольные вопросы и задания.............................184
Задачи....................................................185
6. Основы дискретной фильтрации сигналов.....................188
6.1. Аналоговые, дискретные и цифровые сигналы ..........188
6.2. Шумы квантования ...................................190
6.3. Теорема Котельникова ...............................192
6.4. Спектр дискретизированного сигнала..................197
6.5. Дискретное преобразование Фурье ....................203
6.6. Быстрое преобразование Фурье .......................208
6.7. Метод z преобразования .............................211
6.8. Алгоритм дискретной фильтрации......................215
6.9. Системная функция дискретного Фильтра...............218
6.10. Рекурсивные и нерекурсивные дискретные фильтры .....220
6.11. Формы реализации цифровых фильтров..................223
6.12. Методы синтеза дискретных фильтров..................228
6.13. Примеры синтеза цифровых фильтров...................230
6.14. Дискретные случайные сигналы .......................235
Контрольные вопросы и задания.............................237
Задачи....................................................238
7. Преобразования радиосигналов в нелинейных
радиотехнических цепях.......................................240
7.1. Нелинейные элементы ..............................240
7.2. Аппроксимация нелинейных характ еристик ..........241
7.3. Воздействие гармонического сигнала на безынерционный
нелинейный элемент ....................................244
7.4. Би и полигармоническое воздействие на безынерционный
нелинейный элемент. Преобразование частоты сигнала....248
7.5. Нелинейное резонансное усиление и умножение частоты.251
7.6. Получение амплитудно-модулированных колебаний ....254
7.7. Амплитудное детектирование .......................255
6
Оглавление
7.8. Частотное и фазовое детектирование.................261
7.9. Воздействие случайного стационарного сигнала
на безынерционный нелинейный элемент....................263
Контрольные вопросы и задания ..........................270
Задачи..................................................271
8. Генерирование гармонических колебаний...................274
8.1. Автоколебательная система..........................274
8.2. Баланс амплитуд и баланс фаз.......................277
8.3. Возникновение колебаний в автогенераторе ..........278
8.4. Стационарный режим работы автогенератора ..........280
8.5. Мягкий и жесткий режимы самовозбуждения............282
8.6. Нелинейное уравнение автогенератора ...............287
8.7. Анализ схем LC-автогенераторов ....................289
8.8. .RC-автогенераторы и автогенераторы с внутренней
обратной связью.........................................296
Контрольные вопросы и задания...........................301
Задачи..................................................302
Приложение. Ответы к задачам ...............................305
Ответы к задачам главы 1 ...............................305
Ответы к задачам главы 2................................307
Ответы к задачам главы 3................................310
Ответы к задачам главы 4................................312
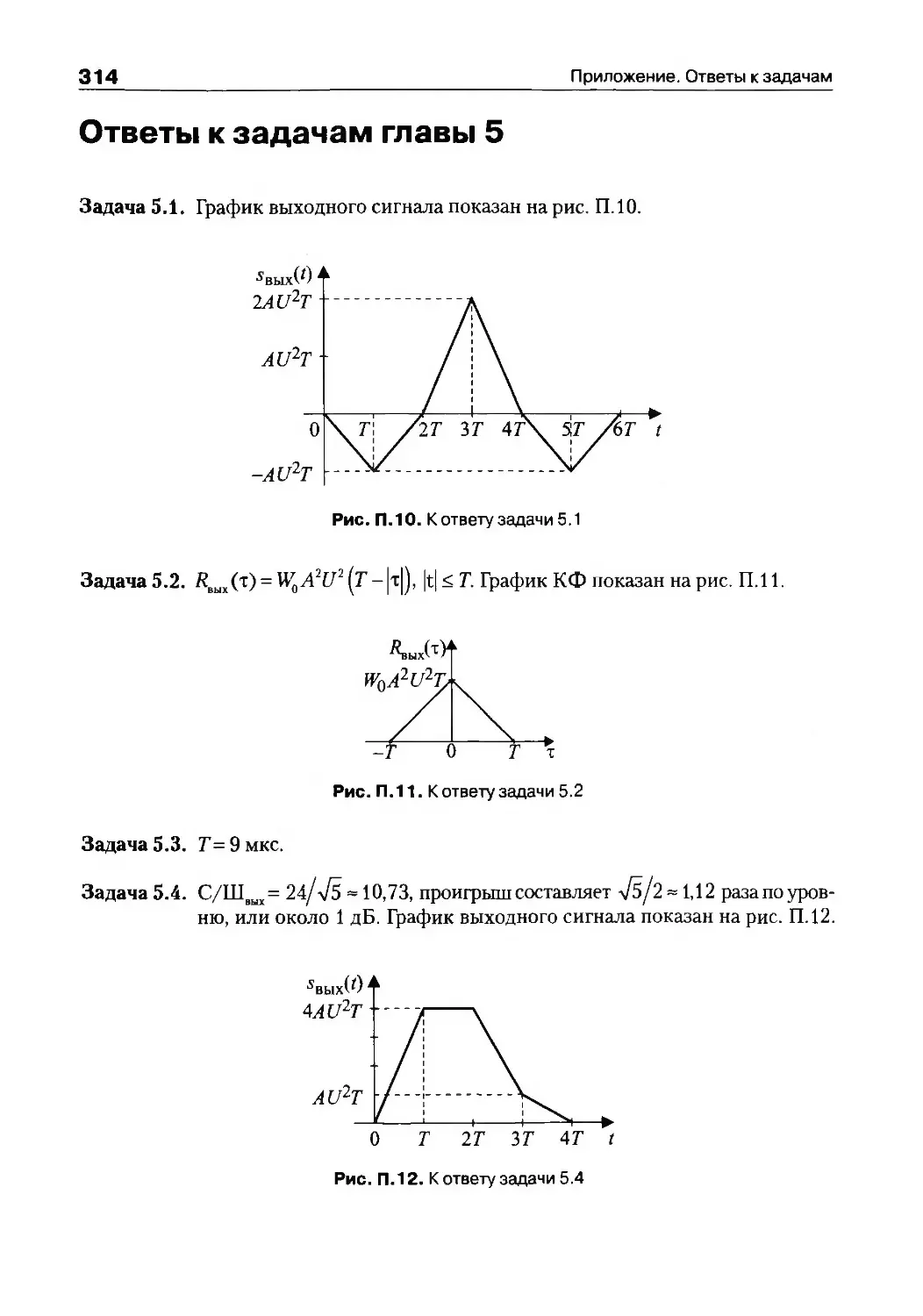
Ответы к задачам главы 5................................314
Ответы к задачам главы 6................................316
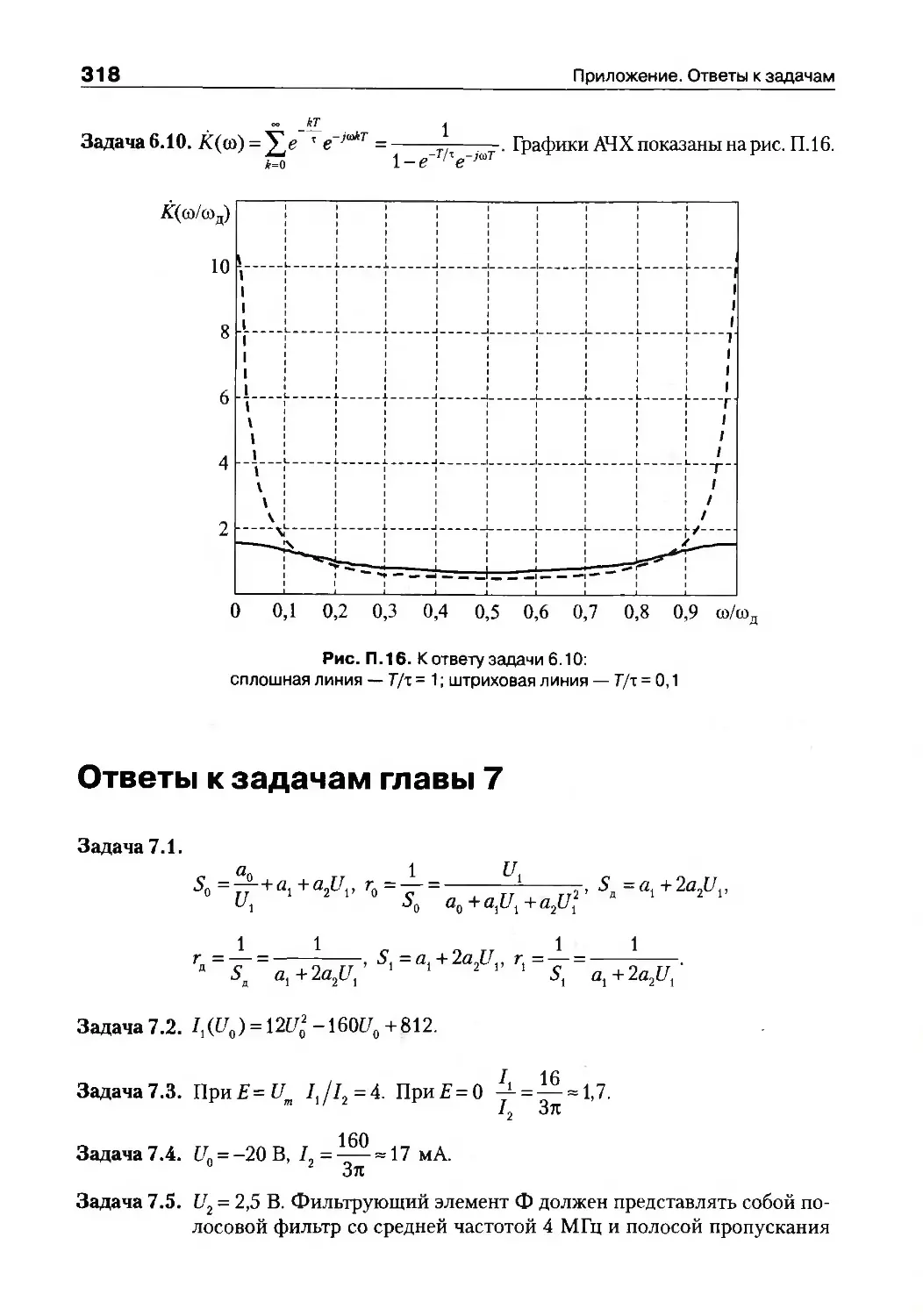
Ответы к задачам главы 7................................318
Ответы к задачам главы 8................................319
Список литературы..........................................320
Алфавитный указатель .......................................321
Предисловие
Матерна.’! настоящего учебника базируется на курсе лекций по дисциплине «Радио-
технические цепи и сигналы», который в течение многих лет читают студентам
факультета радиотехники и телекоммуникаций Санкт-Петербургского государ-
ственного электротехнического университета «ЛЭТИ» им. В. И. Ульянова (Лени-
на), обучающимся по программе подготовки бакалавров техники и технологии по
направлению «Радиотехника».
Содержание книги полностью соответствует требованиям Федерального государ-
ственного образовательного стандарта нового (третьего) поколения, отраженным в
примерной программе дисциплины «Радиотехнические цепи и сигналы», входящей
в образовательные программы подготовки бакалавров по направлению «Радиотех-
ника» и инженеров по специальности «Радиоэлектронные системы и комплексы».
Учебник также может быть полезен студентам бакалавриата в рамках направлений
«Инфокоммуникационные технологии и системы связи» и «Конструирование
и технология электронных средств».
Включенный в учебник материал по существу является базовым для подготов-
ки специалистов в области современной радиотехники. Его успешное изучение
предполагает хорошее знание таких дисциплин, как математика, физика, основы
теории электрических цепей, и служит необходимым фундаментом для освоения
циклов специальных дисциплин соответствующих магистерских и инженерных
образовательных программ.
В работе над настоящим учебником авторы учитывали свой опыт, полученный
при подготовке к изданию и многолетнем использовании в учебном процессе посо-
бия «Теоретические основы радиотехники» [1,2], а также с гремились использовать
достоинства классических учебников [3, 4] и задачников [5-7] по дисциплине
«Радиотехнические цепи и сигналы» в части методических подходов к изложению
материала. Наличие контрольных вопросов, примеров решения и дополнительного
списка задач в содержании каждой главы, по мнению авторов, существенно повы-
сило методическую ценность книги. Многолетний опыт чтения лекций по данному
курсу позволил, как нам представляется, соблюсти труднодостижимый баланс
между объемным содержанием примерной программы дисциплины и ее лаконич-
ным изложением.
Авторы признательны рецензенту книги за полезные критические замечания
и с благодарностью примут их от заинтересованного читателя
От издательства
Ваши замечания, предложения, вопросы отправляйте по адресу электронной почты
comp@piter.com (издательство «Питер», компьютерная редакция).
Мы будем рады узнать ваше мнение!
На веб-сайте издательства www.piter.com вы найдете подробную информацию
о наших книгах.
1, Основные характеристики
детерминированных сигналов
В технике под термином «сигнал» подразумевают величину, каким-либо образом
отражающую состояние физической системы. В радиотехнике сигналом называют
функцию времени s(t), описывающую изменение напряжения (чаиде всего) или тока.
В данной главе рассматриваются основы спектрального и корреляционного
анализа детерминированных, то есть полностью известных, сигналов.
1.1. Сигналы, модели сигналов
Заданная аналитически (детерминированная, определенная в любой момент вре-
мени), функция s(t) становится абстрактной математической моделью сигнала, не
свя данной с его физическим характером и удобной для изучения.
Примеры математических моделей детерминированных радиотехнических
сигналов.
□ Непрерывный сигнал (гармоническое колебание):
s(l) = (7cosco0/, s(t) = (7 sin и0/. (1.1)
Область определения гармонического сигнала t е (-°°, =»).
□ Непрерывный сигнал (гауссов импульс):
s(t) = Ue~a2'2, t.e(—°°,°°). (1.2)
□ Непрерывный сигнал (экспоненциальный импульс):
zx Ue^, ie[0,oo),
s(f)= о. ,<o. <L3>
□ Финитный, то есть принимающий отличные от нуля значения на ограниченном
интервале времени, сигнал (прямоугольный видеоимпульс):
ге[-Т/2,Т/2],
[О, п[-Т/2,Т/2].
(1.4)
1.1. Сигналы, модели сигналов
9
Заметим, что термин «eucteo» в этом контексте совсем не подразумевает отноше-
ния сигнала именно к телевизионной технике. Смысл термина будет разъяснен
в ходе дальнейшего изложения
□ Финитный сигнал (треугольный видеоимпульс):
х(0 =
у^-О-
0,
Ге[О,Т],
(«[О.П.
(1.5)
□ Периодический сигнал:
5гЙ)= У- ^~kT),k = Q,±l,±2...,
(1-6)
где г(0 — финитный на интервале Т(периоде последовательности) сигнал; ино-
гда говорят о «представительном» сигнале последовательности.
□ Дискретный сигнал, являющийся последовательностью отсчетов (чисел):
s{kT) = e~°JlT,k = Q, 1,2...
(1.7)
Тестовые сигналы. Особое место среди математических моделей сигналов
занимают модели тестовых, испытательных или пробных сигналов. Они широко
используются в теоретических исследованиях, а приближенно отвечающие им фи-
зические (радиотехнические) сигналы — в экспериментальной радиотехнической
и радионзмерительной практике.
Известным тестовым сигналом является единичная ступенчатая функция,
функция включения, или функция Хевисайда'.
о(0 = 1(0 =
1,
О,
г>о,
Г<0.
(1.8)
Важнейшим тестовым радиотехническим сигналом является дельта-функция,
или функция Дирака 8(0, которая определяется соотношениями
О 8(0 =
t = 0,
t 0;
2) 8(t)r7t = l (площадь 8-функнии).
(1-9)
Из первой части определения (1.9) следует, что 8(0 существует лишь при аргу-
менте t = 0, поэтому справедливо:
О 8(г-го) =
7 — ^0’
t^t0;
(1.10)
2) j8(f-f0)J( = l.
Из второй части определения (1.9) следует, что размерность 8(0 обратна раз-
мерности аргумента t. Отметим также важное соотношение, определяющее филь-
трующее свойство 8-функции,
10
1. Основные характеристики детерминированных сигналов
J /(Г)З(Г -10 )dt = f(t0) J 8(Г -10)dt = /(Го) , (1.11)
то есть то, что определенный интеграл, подынтегральная функция которого име-
ет вид f -t0), равен значению функции f(t) с аргументом t = t0, при котором
S-фцнкция не равна нулю
Функция 3(г) относится к так называемым обобщенным, символическим функ-
циям. С ее помощью, мапример, определяют не существующую в классическом
смысле производную функции Хевисайда
-°(Q=3(o- <112>
dt
В свою очередь, функция Хевисайда (1.8) может быть на основании (1.12)
определена как
а(?) = j 5(Х)Л (1.13)
Тестовыми являются гармонический сигнал (1 1) и гармоническая (квазигармо-
ническая) функция включения s(r) = (7 cos co0t, t> О, которую, используя функцию
Хевисайда, можно записать как s(t) = Uo(t) cos сооЛ
Радиосигнал. Так называют сигнал, модель которого удобно представлять
в форме
м(0 = t/(f)cos{a>0r + <p(t) + <р0} = 17(t)cos\|/(t) •
(1.14)
Выделяют огибающую U(t), полную фазу радиосигнала y(t) и фазовую функ-
цию <р(0. Частоту о>0 = 2л/0 называют несущей частотой. Используя модель (1.14),
обычно предполагают, что огибающая U(f) и фазовая функция <р(1) изменяются за
время То = 2л/со0 (период несущей частоты) незначительно (если это предположение
не выполняется, то может оказаться удобнее иная форма представления сигнала).
Очевидно, что представления многих сигналов могут рассматриваться как частные
случаи выражения (1.14), например, при U(t) = U = const, или при о>0 - 0, или при
<p(t) = 0 и т. д. В последнем случае <р0 называют начальной фазой.
Простейшим радиосигналом является гармоническая функция (1.1).
Если огибающая U(f) — финитная функция, то радиосигнал (1.14) называют
радиоимпульсом, огибающую U(t) — соответствующим ему видеоимпульсом, а со„ —
частотой заполнения радиоимпульса (при ф(г) = <р0). Выбрав в качестве огибающей
прямоугольный видеоимпульс (1.4) и приняв <p(t) = <р0 = 0, получим радиосигнал
в виде прямоугольного радиоимпульса
U cosco„f,
s(r)- о.
Ге1-Т/2,Т/2],
te[-T/2,T/2],
(1.15)
Если огибающая U(t) — непрерывная функция, определенная на интервалах
t е (—о», оо) или t е (0, °°), то ее иногда называют видеосигналом, соответствующим
радиосигналу (1.14).
1.2. Обобщенный ряд Фурье
11
1.2. Обобщенный ряд Фурье
Для анализа сигналов очень важны методы представления математической модели
сигнала в виде разложения ее в функциональный ряд. Разложения по линейно не-
зависимым и ортогональным системам функций (базисам) широко используются
при решении многих задач физики и математики.
Бесконечная (в общем случае) система (последовательность) непрерывных на
интервале Тфункций {<р, (/*), i = 0,1, 2,...} является ортогональной на Т, если
/ф,(Оф,(О<* =
т
О,
kll2-
г j,
i = j-
d-16)
где величина
||ф,|| = lf<$(t)dt*O (1.17)
V г
называется нормой системы функций I <р, (7)}, при этом никакая из функций системы
не равна тождественно нулю (неравенство в соотношении (1.17), определяющем
Ik II)-
Представление произвольной кусочно-непрерывной модели сигнала s(t), удо-
влетворяющей условию
J |x(t)|2 dt <~ , (1.18)
в виде линейной комбинации взвешенных функций {<р, (7)}
х(0 = С0<р0 (О + С, <р! (7) +... + С (р. (О + • • = Xе. Ф, (о (1 19)
i=0
называется разложением в обобщенный ряд Фурье. Линейная независимость си-
стемы {<Р, (0 } обеспечивает единственность разложения (1.19).
Умножив обе части уравнения (1.19) на <р, (0 и интегрируя по интервалу Т,
получим соотношение, в котором справа (с учетом (1.16)) стоит единственный
отличный от нуля член:
J5(0<Р; (t)dt = JC,<p, (t)<р, (t)dt = С, 1|2,
т т
откуда следует выражение для i-ro коэффициента обобщенного ряда Фурье:
(1-20)
Ik IIт
Совокупность коэффициентов С называется спектром сигнала s(t) в системе
{Ф, (7)} и полностью определяет сигнал.
12
1. Основные характеристики детерминированных сигналов
ЗАМЕЧАНИЕ 1.1 ----------------------------------------------------
Проще всего коэффициенты С рассчитываются в том случае, когда система
функций {ср (/,)} является не только ортогональной, но и ортонормиро-
ванием то есть подчиняется следующим условиям:
<р,(0<р (Г)Л = Л’ .
1 1, г=7
(1.21)
Однако в ортонормированную может быть преобразована любая система
линейно независимых функций, поэтому условие (1.21) никак не влияет
на область применимости разложения (1.19).
Неравенство Бесселя. Разложение сигнала в обобщенный ряд Фурье по
ортогональной системе функций обладает важным свойством: если нужно полу-
чить приближенное представление сигнала в виде линейной комбинации конечного
числа п взвешенных базисных функций {ср, (/)}, то невязка (ошибка представления
сигнала) Дх, которую определяют как
дх=П х(г)-Ха(р,(0
Т \ i=0
dt,
(1.22)
будет минимальной, если коэффициенты такого разложения совпадают с коэффи-
циентами обобщенного ряда Фурье, рассчитанными по формуле (1.20):
а, = С,,
то есть усеченный ряд Фурье обеспечивает минимальную ошибку представления
сигнала в так называемом конечном базисе.
Покажем это. Для этого раскроем квадрат разности в (1.22), преобразуем квадрат
суммы в двойную сумму и поменяем местами суммирование и интегрирование:
Дх = j x2(O-2x(t)^a<p,(O+ 1а,Ф,(О
dt =
i=0
1=0
= js2(t)^-2j х(£)£а,ф,(О р+f 1°,ф,(0 =
т Л
4f-2Z| a,J5(o<p,(o^ 1+ II: |ф,(0ф,(О^ I,
1=0
t=0
(1.23)
1=0
Т
2
т
т
где по аналогии с (1.17) интеграл J s\t)dt = ||х||2 есть квадрат нормы модели сиг-
нала s(f).
Учтя в (1.23) соотношения (1.20) и (1.16), получаем:
Дх = ||xf - 21«С,||<р,||2 + £< ||<р ,||2 = И - К ||<р, f+ 1(С,-«)2||<Р,||2.
1=0 1=0 1=0 1=0
1.2 Обобщенный ряд Фурье
13
Отсюда видно, что при at = С; невязка минимальна и равна
1=0
(1-24)
Поскольку невязка, согласно ее определению (1.22), неотрицательна, из (1.24)
следует неравенство Бесселя
J=O
(1-25)
справедливое для любой линейно независимой и ортогональной системы функций
!<Р,(')}.
Система (<р, И)} называется полной, если, увеличивая число членов усеченного
ряда, невязку Asmin можно сделать сколь угодно малой.
Обобщенный ряд Фурье в комплексном базисе. Если функции системы
1Ф,(0) принимают комплексные значения, приведенные определения могут быть
обобщены
□ ортогональность системы функций:
/ф,(Оф,(О^ = -
О, i # j,
lid2-
□ вычисление коэффициентов ряда Фурье:
С, =
11ф,|| Т
(1-26)
где <р* (f) есть функция, комплексно-сопряженная ср, (/*).
ЗАМЕЧАНИЕ 1.2--------------------------------------------
Разложение модели сигнала (или другой функции) в функциональный ряд
в радиотехнике проводят при решении разнообразных задач, основными из
которых являются либо спектральный анализ функции, либо оптимальная
по определенным критериям аппроксимация функции
Спектральный анализ чаще всего проводят на базе ортогональных
систем, образованных основными тригонометрическими функциями.
В главе 6 рассматривается своеобразная ортогональная система базисных
функций для разложения в так называемый ряд Котельникова.
Вторая задача ассоциируется, как правило, с так называемыми нели-
нейными преобразованиями сигналов (глава 7) либо с задачами синтеза
сигналов и цепей.
14
1. Основные характеристики детерминированных сигналов
1.3. Тригонометрический ряд Фурье
Тригонометрический, гармонический ряд, который чаще всего называют просто
рядом Фурье, среди радиотехнических приложений функциональных рядов
занимает особое место: важность разложения сигнала по ортогональной гармо-
нической системе функций определяется, в частности тем характером преоб-
разования, которое претерпевает сигнал при прохождении через стационарную
линейную цепь.
Выходным сигналом в этом с тучае является гармонический сигнал с той же кру-
говой частотой со, отличающийся от входного амплитудой и фазовым сдвигом. Если
разложение входного сигнала по системе тригонометрических функций известно,
то выходной сигнал может быть получен как сумма независимо преобразованных
цепью входных гармоник. Кроме этого обеспечивается возможность использования
в расчетах так называемого символического метода (метода комплексных амплитуд),
хорошо известного из курса теории цепей.
Тригонометрическая форма ряда Фурье. Будем считать известным [3],
что периодический сигнал sr(t) = , ±2 ..., определенный на бес-
k=-~
конечном интервале t е (—°°, °°), может быть представлен в виде ряда Фуръе
s, (0 = ~+X(fl*cos kt£>xt + bksm £со/), (1.27)
где СО; = 2яь/Т = 2л/р = \/Т и k = 1,2...
Установлено, что разложение существует, если г(г) на периоде Т удовлетворяет
условиям Дирихле:
□ не имеет разрывов 2-го рода (с уходящими в бесконечность ветвями функции);
□ имеет конечное число разрывов 1-го рода;
□ имеет конечное число экстремумов.
Коэффициенты ak (включая а0) и bk определяются формулами
2 2 7
ak=- | r(f)cos ka{t dt, =—jr(()sin k&tt dt. (1.28)
T rj о
Иногда удобнее вычислять a^/2 не по общему выражению для ak, полученному
в результате интегрирования, а приняв k = 0 непосредственно в (1.28):
^ = |jr(O^. (1.29)
2 ‘о
В радиотехнической практике часто оказывается удобнее иное представление
ряда.
1.3. Тригонометрический ряд Фурье
15
Проделав элементарные преобразования
ак cos&n/ + bk sin^co/ = ^a2 + bk
a, , b,
. —COSKCOT + , . .
9 ♦ О 1 /О
sin&iOjt =
= y]a2k +Ьгк (cos<pt cosko)tt - sin<p* sin^co^) =
= cos(&(D/+ <pj,
где tg <pt = , Ak = yja2k + b2 , получим представление сигнала sr(t) в виде ряда
ak
Фурье в вещественной форме:
а 00
\ (О = V + X A COSTCO/ + (р J.
*=1
(1.30)
Часто используется обозначение (Ок = &С0, = 2nkfl = 2itk/T. Совокупность |о0|/2
и коэффициентов Ak в (1.30) образует амплитудный, а совокупность — фазовый
спектры периодического сигнала sr(t). Возможный их вид показан на рис. 1.1, а, б
соответственно.
Рис. 1.1. Возможный вид спектра периодического сигнала:
а — амплитудный спектр; б — фазовый спектр
Комплексная форма ряда Фурье. Воспользовавшись формулами Эйлера
cosa = — (е’а +е •'“), sina = X(e^“ -e~Ja),
2 j2
ряд (1.27) можно записать в виде
=1+Й(°‘ +Й<“‘
(1.31)
16
1. Основные характеристики детерминированных сигналов
Введем комплексные амплитуды
1 1
-(a*-;A)=G- 2(a*+A)=^-*=G‘ 0-32)
и «отрицательные» частоты со_k = -ko, = -cot, то есть включим в область изменения
k значения k < 0. и запишем (1.27) в виде
Если дополнительно ввести обозначение Со =С0 = а0/2 , получим лаконичное
представление, называемое комплекс ной формой ряда Фурье:
(1.33)
Целесообразность введения комплексной формы ряда Фурье обусловлена
удобством выполнения математических преобразований и уже упоминавшейся
возможностью использования совместно с Фурье-анализом метода комплексных
амплитуд (символического метода).
Коэффициенты ряда Ск образуют дискретный комплексный спекгр периодиче-
ского сигнала $,(t), определенный на всех частотах оо*, k = 0, ±1 ±2..., вместе с ам-
плитудным |cj и фазовым ф* =arg Ck спектрами. На рис. 1.2 приведен возможный
вид амплитудного спектра С* .
IQlf
Рис. 1.2. Амплитудный спектр пеоиодического сигнала
при использовании комплексной формы ряда Фурье
Очевидно, что |cj = |С_*| = Ск = Akj2. Рассмотрим ряд (1.33) подробнее.
s (Г) = £ Ckew =... + Сke-^‘ +... + Со +... + Ckejka'' +...;
преобразуем, вновь используя формулы Эйлера, сумму
’*Ш|' + Cke,ku>'' = 2Ckcoscp* cosZ?o>,r-2Cksin<ptsin tao.t =
= ak cos^co/ + bk sin Цо t = 2Ck cos^co,? + <pj.
1.4. Спектры некоторых периодических сигналов
17
Следовательно, a. = 2C.cos<p., b, =-2Csin<p,.
Сопоставив выражения (1.28) и (1.32), замечаем, что
Ck=^[ak-jbk) =
= — r(t)cosk w/dt - j—j"r(r)sin со(?<Уг = — p (r)f <-/r. (1.34)
T о Tо
Формула (1.34) используется для непосредственного вычисления Ck, k = 0, ±1,
±2...
ЗАМЕЧАНИЕ 1.3-----------------------------------------------------------
Пределы интегрирования в выражениях (1.28) и (1.34) могут быть из-
менены, существенно лишь то, что интегрировать следует по интервалу,
равному полному периоду, например от -Т/2 до Т/2 или от -Т до 0 и т. д.
Это связано с тем, что для периодической с периодом Т функции f(t)
значение определенного интеграла
л+Т
J
нс зависит от X. Это соображение иногда оказывается полезным при
практических вычислениях. Например, рассматривая функцию при сим
метричныл пределах интегрирования от-Т/2 до Т/2, легко видеть, что ряд
будет содержать в случае четности функции s/f) лишь косинусоидальные
члены с коэффициентами а4; в случае нечетности функции s/t) — лишь
синусоидальные члены с коэффициентами bk независимо от того, какие
пределы интегрирования будут реально выбраны при вычислении коэф-
фициентов ак и bk.
ЗАМЕЧАНИЕ 1.4--------------------------------------------------
Подчеркнем эквидистантность спектра Фурье: частоты, на которых
расположены коэффициенты ряда, образуют эквидистантную последо-
вательность (... -2сОр —со,, 0, (Ор 2(0р 3(0р..), непременно содержащую со = 0
и имеющую шаг со, = 2п/Т. Сами же коэффициенты могут принимать
любые, в том числе нулевые значения.
1.4. Спектры некоторых
периодических сигналов
Последовательность прямоугольных видеоимпульсов. Рассмотрим спектр
сигнала, изображенного на рис. 1.3. Такой сигнал часто используется в различных
радиотехнических приложениях, а его модель — в теоретической радиотехнике.
18
1 Основные характеристики детерминированных сигналов
Рис. 1.3. Последовательность прямоугольных видеоимпульсов
Аналитическое представление сигнала на интервале Т (представительный сиг-
нал на периоде):
, . (Г, Ге[-т/2,т/2].
r<t) = l0, J4|-,/2.,/2|.
(1 35)
Введено обозначение длительности прямоугольного импульса т. Воспользуемся
комплексной формой ряда Фурье (1.33):
1 1 т'2 и х'2
С, =- [r(Oe->*“'f^ = - f Ue~^'dt =------------— f e,ha’d(-jk(dyt) =
t/2 с л ika. - - ikto. —
U и 2U e 2-e '2
--------e 1 =-----------(e 2 -e 2 > =--------------------------------
lk(f>.T _ jkocT [ J kta.T j2
or, - - Sin&CO,- , sm&— Я
2C7 . , т т >? ггт т
-----sm&co, — = U-----------— = U--------—
kto.T *2 T , т T ,x
1 k - Я
T
r
. k
U SmqK
q *я
<7
(1.36)
Вместо пределов интегрирования 0 и Г использовано обозначение (Г), ука-
зывающее на необходимость интегрирования по интервату Т (см. замечание 1.3).
Удобные для вычислений пределы интегрирования появляются при подстановке
в подынтегральное выражение конкретного г(Т).
. k
sin-я
Так как lim ^— = \, Со= — = U—. Численно Со и остальные ко )ффициен-
° - я Я Т
q
ты Ск определяются по формуле (1.36) при задании конкретного значения отноше-
ния Т/т = q, которое называют скважностью последовательности. Коэффициенты
с номерами к = q, 2q, 3q... равны 0. Анализируя поведение амплитудного спектра,
kn
(заменяя дискретный аргумент синуса —
U sinx
<7 х
непрерывным аргументом х) как огибающую щскретного амплитудного спектра \Ск
Огибающая (пунктирная тиния) и спектр |Ct | для q = 6 и U= 1 приведены на рис. 1 4.
удобно рассматривать функцию
1.4. Спектры некоторых периодических сигналов
19
Рис. 1.4. Амплитудный спектр последовательности
прямоугольных видеоимпульсов (q = 6)
При q = 2 коэффициенты разложения последовательности прямоугольных ви-
деоимпульсов в ряд Фурье в комплексной форме приобретают значения
,, sink—
______2
2 , л
к—
2
(1.37)
так что г = £, г = —, С,
О п 1
Z 71
= о, С3=-—, С5= —
Зя 5л
Разложение представляется следующим образом:
5 +Ие^' + lL+^Le^' (t38)
' ' 7 5л Зл л 2 л Зл
Каждая пара составляющих вида ~^~(е
Эйлера: kjl
kji'
-—cosktn t,
kn
преобразуется по формуле
и ряд (1.38) может быть записан в виде
/ \ 2П л 1 1 1
s f =—( — -i-coscn.t—cos3co с +—cos5co,i—cos7co,f + ...
' 1 л 14 1 3 1 5 1 7 1
(1.39)
Так как последовательность, приведенная на рис. 1.3, является четным сигналом,
представление (1.39) можно рассматривать и как ряд Фурье в форме (1.27) с коэф-
фициентами Ьк = 0 , и как ряд Фурье в форме (1.30). В последнем случае фазовый
спектр (pt «обеспечивает» соответствующие знаки перед гармониками разложения,
поэтому принимают <р, = 0, <р3 = -л, <р5 = -2л, <р7 = -Зл ., так что
z ч 2U л 1 х
s (t) = —( — + cos со, Г+ -cos ЗсоТ-л
л л [4 1 3 ' 1 7
^cos(5®/-2л) + ...>.
20
1. Основные характеристики детерминированных сигналов
В качестве упражнения читателю рекомендуется самостоятельно найти разложе-
ние в ряд Фурье для сигнала, изображенного на рис. 1.5. Такой сигнал также часто
используется в различных радиотехнических приложениях и называется .меандром
-ЗТ/4
-774
774
3774
Рис. 1.5. Меандр
Аналитически формирующий меандр sr(t) представительный сигнал последо-
вательности г(7) на интервале Т может быть записан так:
г(Г) =
[-U/2,
te[-T/4,T/4],
£*{Г/4,ЗТ/4].
Легко видеть, что рассмотренная последовательность прямоугольных видео-
импульсов получается суммированием меандра с постоянной составляющей U/2,
которой обязан своим появлением в разложении (1.38) член Со = U/2.
Заметим, что значения коэффициентов разложения последовательности прямо-
угольных видеоимпульсов (при q = 2) и меандра убывают по закону 1/k
Последовательность треугольных видеоимпульсов. Рассмотрим пери-
одический сигнал, состоящий из треугольных видеоимпульсов (рис. 1.6). Аналити-
ческое выражение для импульса последовательности.
к|е[0,т/2],
О, И«[о. т/2].
(140)
Рис. 1.6. Последовательность треугольных видеоимпульсов
2
1.5. Преобразование Ф^оье и его свойства
21
Вновь обратившись к ряду Фурье в комплексной форме (1.33), запишем вы-
ражение для коэффициентов Ck:
После вычисления интегралов и несложных, но громоздких выкладок (которые
читателю предлагается проделать самостоятельно), получим
. k(O.T 2 '’ЯТ 2 k it 2
С -Ux sin —L- 4 Ut sin — 2Г и sin q 2 (1-41)
k 2Т kat ' 2T A’7TT 2(? k Л
. 4 2T -?2
Приняв (?=1, чтобы длительность треугольного видеоимпульса (1.40) «по ос-
нованию» т совпадала с периодом последовательности Т, получим выражение для
коэффициентов ряда (1.33):
ck = u-
к 2
sin k Л
2
k-
Обнаруживается связь между спектрами сигналов (1.35) и (1.40), но значения
коэффициентов разложения последовательное ги треугольных видеоимпульсов
(1.40), определенных, по аналогии с (1.39), суммированием соответствующих пар
составляющих ряда Фурье в комплексной форме,
sr(0 =—
Я
— + < os со, t +—cos Зю, t +—cos 5(0. t + - -cos 7(o.t +...
4 1 32 1 52 1 72 1
убывают по закону 1 /k2, то есть существенно быстрее коэффициентов разложе-
ния (1.39). Это связано с формой треугольного видеоимпульса: в нем отсутствуют
«скачки» или разрывы 1-го рода.
1.5. Преобразование Фурье и его свойства
В основе спектрального анализа сигналов лежат прямое
F{s(0} = 5((0)= J s(r)e’^(/r
(1.42)
22
1. Основные характеристики детерминированных сигналов
и обратное
F~l { 5(со)} = s(t) = j 5(со)?“ Дсо (1.43)
преобразования Фурье. 5(со) называют спектральной функцией (иногда говорят
«спектральная плотность» или просто «спектр») сигнала s(f). Установлено, что
преобразования (1.42) и (1.43) существуют, если сигнал s(t) на любом интервале
конечной длительности удов летворяет условиям Дирихле (по аналогии с сигналом
r(f) на периоде, см. раздел 1.3), а также является абсолютно интегрируемым.
J |s(t)|</r <оо.
Спектральная функция S ( <г ) в общем случае является функцией комплексной
и с учетом формулы Эйлера e±ia = cos а ± у sin а может быть представлена как
5(G)) = j s(t)cos(i>tdt - j j s(t)sino3tdt =
= Re5(co) + jIm5(co) = A(co)- /B(co). (1.44)
Определенный интеграл от нечетной функции в симметричных пределах равен
нулю. Представляя в (1.44) сигнал s(t) в виде суммы четной и нечетной функций
(.s(f) = $чет(£) + 5He4eT(t)), легко видеть, что косинусоидальное преобразование Фурье
А(со) определяется четной, а синусоидальное преобразование Фурье В(со) — нечетной
частями сигнала s(t). Отсюда следует полезный для практики вывод: преобразование
Фурье четной функции s(t) всегда вещественная нечетной функции s(f) — всегда
мнимая функции частоты со.
Далее, рассматривая обратное преобразование Фурье F'1 i 4(со) - jB(со)}, можно
ноказать, что А(со) — четная, а В(со) — не четная функции частоты со:
Л(со) = А(-со), В(со) = -В(-со).
Доказательство читателю предлагается выполнить самостоятельно (следует
учесть, что обратное Фурье-преобразование 5(со) должно быть вещественной
функцией времени).
Отсюда вытекает еще одно важное свойство 5 (со):
5*(со) = {а(со)-;В(со)} =
= Д(со) + ;В(со) = Л(-со)- ;В(-со) = 5(-со), (1-45)
то есть для нахождения функции, комплексно сопряженной исходной спектральной,
достаточно поменять знак аргумента со.
Спектральную функцию можно представить в показательной форме:
5(со) = '5(со)|ехр/ср(со). (1.46)
1.5. Преобразование Фурье и его свойства
23
Здесь
|5(«>)| = 7л2(со) + В2(со) > О
есть амплитудная спектральная функция (часто, несмотря на неточность термина,
говорят «амплитудный спектр»), а
ср(а>) = arg 5(ш) = arctg ? '
Re5(co)
есть фазовая спектральная функция (фазовый спектр или спектр начальных, то есть
соответствующих моменту ( = О, фаз). Очевидно, что амплитудный спектр |.5'(<х>)|
является четной, а фазовый спектр <р(ш) — нечетной функциями со. Принимая это
во внимание и подставляя (1 46) в (1.43), получим соотношение
s(() = ^~] |5((о)|е7’’<ш)е''шгб/а> = j- ^cos[co( + <р(со)]da, (1-47)
иллюстрирующее «физический смысл» спектральной функции: сигнал s(t) пред-
ставляется в виде суммы бесконечно большого числа гармонических составляющих
х |5(со)|Ло
с бесконечно малыми амплитудами I I , непрерывно заполняющих интервал
п
частот от 0 до Начальные фазы этих составляющих заданы функцией <р(со),
а частотная зависимость «плотности» бесконечно малых амплитуд описывается
функцией 5(со)|. Второй интеграл в соотношении (1.47) поясняет смысл «от-
рицательных» частот, существование которых прямо предполагает выражение
(1 43) (см. пределы интегрирования в упомянутой формуле): их появление связано
с характером прямого и обратного преобразований Фурье как математических опе-
раций и физически нереально. Эти соображения полезно сравнить с результатами,
полученными в разделах 1.3 и 1.4.
Размерность спектральной функции 5(со) есть размерность сигнала, умножен-
ная на время, так что, если размерность s(t) — вольты, то [ 5(о>) ] = [В с] = [В/Гц].
Симметрия преобразований Фурье. Пусть четному сигналу $(0 соответ-
ствует вещественный с пектр S(a) = 5(со), который, в свою очередь, будет являться
четной функцией частоты со; тогда сигналу 5(f) должен соответствовать спектр
2тг5(ш). Именно «взаимозаменяемость» аргументов со и t, входящих в ядро exp(±jcof).
и подразумевают, говоря о симметрии пары интегральных преобразований (1.42)
и (1.43). Симметрия ( гановится очевидной, если в рассмотрение введены ком-
плексные сигналы.
Связь спектра периодической последовательности и спектральной
функции одиночного импульса. Сравнивая выражение (1.34) для коэффици-
ентов ряда Фурье в комплексной форме
Ck =^r(t)e~j^dt
1 о
24
1. Основные характеристики детерминированных сигналов
и формулу (1.42) прямого преобразования Фурье или спектральной функции пред-
ставительного импульса периодической последовательности /(0
/?(со) = j r(t)e dt
устанавливаем простое и часто используемое соотношение
Ck =^R(kal).
(1.48)
1.6. Преобразование Фурье
некоторых сигналов
Рассмотрим преобразование Фурье некоторых часто используемых моделей ви-
део- и радиосигналов.
Функция Дирака. Воспользуемся фильтрующим свойством 5-функции (1.11)
и будем искать ее спектр:
5(со)= j5(Oe->,A = e''<o0=l.
(1.49)
Во всем частотном диапазоне модуль спектра 5-функции постоянен, фазовый
спектр равен нулю
Естест венным является предположение о существовании представления 5(0
в виде обратного преобразования Ф'щье найденной спектральной функции S (ш | = 1:
5(0 = — f 1 eia,d& = — Г e^dto.
2л J 2л J
Из последней формулы следует, что
2л5(О = J e±}Md(f> = J ''os cotd(o ± j j sin (£>tda> = j cos cotdco,
(1.50)
а также, в силу отмеченной в разделе 1 5 симметрии преобразования Фурье от-
носительно переменных t и со,
2лб(со) = j e±iaxdt = j cosoxdt
(1.51)
Преобразование Фурье функции 5(t-/0):
5(со)= |5(^-г0)е->шгЛ = е !м°.
(1.52)
1.6. Преобразование Фурье некоторых сигналов
25
Амплитудный спек гр сдвинутой во времени 6-функции не изменяется, фазо-
вый спектр приобретает дополнительное слагаемое Принятое графическое
обозначение 6(? - £0), а также ее амплитудный и фазовый спектры показаны на
рис. 1.7, а и б.
|6(/-/0)
О t0 t
а
Рис. 1.7. Функция Дирака: а — временное представление; б — спектр
Прямоугольный видеоимпульс. При практическом вычислении интеграта
(1.42) пределы интегрирования определяются интервалом (интервалами) суше
ствования отличных от нуля значений сигнала.
Для сигнала (1.4)
5(со) = [Ue~ja'dt=-— \ e-ia'd(-ja>t) = -—(e-jaT2-eJ,,,T2) =
7® г 2 7®
2L/е?шГ'2-е'7“г/2 2U . саТ
------------------= — sin — =
со j2 ft 2
t Tsin(ojr,2)
co Г/2
ит„т((йТ'2)
олТ/2
(1.53)
Как и следовало ожидать, Ф\ рье-преобразование четной функции оказалось
вещественной функцией со. Показательная форма 5(со) удобна для анализа и гра-
фического построения. На рис. 1.8, а и б приведены графики модуля и фазы спек-
тральной функции прямоугольного видеоимпульса. Здесь
5(0) = limS(co) = 6T,
со—>0
координаты «нулей» модуля определяют при k = ±1, ±2... из уравнения соГ/2 = kit.
Полезно сравнить полученный результат и ряд Фурье последовательности прямо-
угольных импульсов, рассмотренный в разделе 1.4.
Фазовый спектр ср(со) в рассматриваемом случае своеобразен: мнимая часть
спектральной функции тождественно равна нулю, но именно ехр /ср(со) является
множителем, который при записи в форме (1.53) отражает знакопеременный ха-
рактер вещественной функции 5(со). Поэтому принимают:
□ для интервала частот со е [-4л/Г, -2л/Г]: ср(со) = л;
□ для интервала частот со е [-2л/Г, 2л/Г]: <р( со) = 0;
□ для интервала частот со е [2л/Г, 4л/Г]: ср(со) = -л и т. д.
26
1. Основные характеристики детерминированных сигналов
Рис. 1.8. Спектры прямоугольного видеоимпульса: а — амплитудный; б — фазовый
Прямоугольный радиоимпульс (радиосигнал). Длч радиосигнала (1.15)
получим:
7’.2 722 +Р
5(со) = J = J --------------------£>-,шг* =
-Т/2 -Т/2
. (® + ®о)Г . (®-®о)Г
, sin2--------— sm2-------
- ит\- ---\ +—--------\-----
2 (co + cojT (to-cojT
2 2
(1.54)
График модуля выражения (1.54) приведен на рис. 1.9. Оказывается, что ум-
ножение видеоимпульса на гармоническую функцию cos со0г в спектральной об-
ласти приводит к смещению спектра видеои мпулъса влево и вправо по оси частот
на величину ±со0.
Рис. 1.9. Амплитудный спектр прямоугольного радиоимпульса
|S(w)|f
-----1<
Лфэф
Г'Лпах со
о
1.6. Преобразование Фурье некоторых сигналов
27
Назовем спектральную функцию (1.53) спектром огибающей, введем обозначение
. иГ
sin---
2
и используем его, переписав выражение (1.54) в виде
5(со)Ц{5у(ю + ®^ + 5д(й)-(О0)}, (1.55)
подчеркивающем найденную связь спектров радиосигнала и его огибающей.
ЗАМЕЧАНИЕ 1.5
Поведение спектральной функции (1.54) на всей частотной оси (со е (-®0,00))
определяют оба слагаемых в фигурных скобках, хотя в окрестностях ча-
стот ±ю0 доминируют компоненты S,. (со - ю0) и Sv (со + со0) соответст венно.
Значения максимумов модуля спектра в точках ±со0
5(±со0) = М1 +
sin2cooT 1
2сооГ |
и степень взаимного влияния компонент 5 (со - со0) и Sv (со + со0) оценивает-
ся величиной |sin(2co07’)/(2co0r)| = |sinc(2co0T)| < 1, или, другими словами,
соотношением частоты заполнения со0 и длительности сигнала Т. Так, чем
больше значение соо при фиксированном Т, тем незначительнее влияние
компоненты Sv (со + со0) на поведение спектральной функции (1.54) в об-
ласти положительных частот и т. д.
Эффективная ширина и максимальная (граничная) частота спектраль-
ной функции. Амплитудные спектры рассмотренных видео- и радиоимпульсного
финитных сигналов оказываются бесконечно широкими, хотя и убывают с ростом |со|.
В связи с этим обычно ставят вопрос о «практической», эффективной ширине спек-
тра сигнала. Критерии для определения этой величины могут быть различными.
При «лепестковой» структуре амплитудного спектра, как в рассмотренных случаях,
за эффективную иногда принимают ширину «главного» лепестка спектра. При
этом становится актуальным уже затрагивавшийся вопрос о физической реаль-
ности отрицательных частот: так, за эффективную ширину амплитудного спектра
прямоугольного видеоимпульса принимают интервал со е [0, 2л/7] и
Используя аналогичный критерий, интервал о) е [со0 - 2л/Г, <и0 + 2л/Г] прини-
мают за эффективную ширину амплитудного спектра соответствующего прямо-
угольного радиоимпульса. Это значение оказывается в два раза больше-.
28
1. Основные характеристики детерминированных сигналов
Длительность сигнала и эффективная ширина ею спектра связаны обратно
пропорциональной зависимостью: чем короче сигнал, тем шире его спектр. Это
общее, справедливое для сигналов любой формы положение обычно фиксируют
эвристически, анализируя конкретные сигналы.
С эффективной шириной спектра тесно связано понятие максимальной (гранич-
ной ) частоты спектральной функции. Спектр видеосигнала всегда концентрируется
в области нулевой и низкие частот («низкочастотный спектр»), его максимальная
частота совпадает (при использовании единого критерия) со значением Д<фф,.:
со = Дсо , .
max г эф г
Максимальная частота спектра соответствующего радиосигнала, концентриру-
ющегося в области несущей частоты со0 («полосовой спектр»), как легко видеть из
рис. 1.9 связана с эффективной шириной спектра соотношениями
со = со.-г Дсо. = со,, +-Дсо. •
max г 0 эф г ° 2 э<*>г
База сигнала. Этим термином обозначают произведение длительности сигнала
на эффективную ширину его спектра. Для рассматриваемого видеосигнала база
ТДсо>ф - 2л, или ГД/ ф ~ 1. Такой порядок значений базы характерен для видеоим-
пульсов. База с оответствующего радиосигнала вдвое больше. Иногда, по аналогии
с известными результатами квантовой механики, эти соотношения называют соот-
ношениями неопределенности теории сигналов. Их часто используют для грубой
оценки эффективной ширины спектра сигналов различной формы.
ЗАМЕЧАНИЕ 1.6--------------------------------------------------------
О сигналах, база которых существенно больше единицы, речь пойдет в раз-
деле 5.3 при обсуждении областей применения согласованных фильтров.
Сигналы в виде прямоугольных видео- и радиоимпульсов широко используются
в радиотехнике; к ним часто обращаются в теоретических исследованиях и подробно
рассматривают в учебной литературе.
Гауссов импульс. Спектральная функция с лепестковой структурой чаще
всего соответствует финитным моделям сигналов с разрывами, резкими скачками.
В других случаях спектр может оказаться гладкой функцией частоты. Приведем
без вывода, например, спектральную функцию сигнала (1.2):
оо / ( 2 \
5(со) = 5(со) = \Ue-a^e-^dt = U—exp —, (1.56)
£ а 4а J
которая оказывается вещественной и тоже гауссовой функцией частоты. Ампли-
тудный спектр бесконечно широкого гауссова видеоимпульса также бесконечно
широк, фазовый спектр равен нулю. Эффективную ширину и максимальную частоту
спектра (1.56) сопах = Дсо,,t> иногда определяют по уровню 5(сошах) = U^-e~‘2, тогда
1.6. Преобоазование Фуоье некоторых сигналов
29
®тах = Аналогично по уровням Uе~,/2 определяют эффективную длительность
сигнала (1.2), которая оказывается равной 7^ = V2 сс [3]. Таким образом, по пред-
ложенному критерию база гауссова видеоимпульса = 2.
Экспоненциальный импульс. Гладкой функцией частоты оказывается
спектральная функция сигнала (1.3)
О
е-(“+;шЦ-(а + 7ю)г} =
U U -jarctg—
---------= — -е а
а + 7® >/а2 +со2
(1.57)
Амплитудный спектр экспоненциального импульса бесконечно широк. Чита-
телю предлагается самостоятельно построить графики амплитудного и фазового
спектров сигнала (1.3) и рассчитать его базу. В качестве критерия для определения
эффективной длительности сигнала можно выбрать уровень 1/е от значения
и принять о>тах = а.
ЗАМЕЧАНИЕ 1.7--------------------------------------------
Вернемся к вопросу о симметрии преобразований Фурье (см. раздел 1.5)
и покажем, какое практическое значение могут иногда иметь приведен-
ные там соображения. При вычислении спектральной функции прямо-
угольного видеоимпульса выяснилось, что финитному, ограниченному
во времени сигналу соот ветствует бесконечно широкий, неограниченный
по частоте спектр. Рассмотрим финитную вещественную прямоугольную
спектральную функиию
2лА, о>е
5(со) = 5((о) = "
О, сой
Асо Ао>
V’T"
Асо Асо
Т’ПГ
и применим к ней обратное преобразование Фурье (1.43). Результатом
оказывается бесконечно протяженный во времени (то есть физически
нереальный) сигнал:
. Acof
sm------
2
s(f) = ААсо
re(-oo,oo).
\<£>t
2
На основании этого можно сделать вывод (не вполне строгий, разумеется)
о физической нереальности сигналов с финитным спектром.
30
1. Основные характеристики детерминированных сигналов
1.7. Теоремы о спею рах
«Площадь» сигнала. Приняв в соотношении (1.42) со = О, получим:
5(0) = j s(t)dt.
Значение 5(0) численно равно «площади» сигнала в системе координат «вре-
мя — сигнал». Полезно сравнить этот общий результат с результатом вычисления
спектральной функции (1.54) прямоугольного видеоимпульса.
Сумма сигналов (линейность преобразования Фурье). Пусть
— его налы со спектральными функциями f(co), G(co) , (со)... соответственно.
Тогда сигналу 5(f) = f(t) + g(f) + соответствует преобразование Фурье в виде
5(®) = Л®) + С(со) + Н(со)
Доказательство предоставляется читателю выполнить самому.
Сдвиг сигнала во времени. Пусть сигналу 5(f) соответствует спектральная
функция 5(со). Найдем преобразование Фурье сдвинутого во времени сигнала.
5(f ± Го):
j 5(r±t0)e-;“fA = e-7“'" J 5(i±t0)e’7“(f±r"W±t0) =
= 5(со)е±7ШГ» =|5((о)|ИФ(ш)±Ч (1.58)
При сдвиге сигнала на временной интервал ±t0 амплитудный спектр сигнала не
изменяется, в фазовом спектре сигнала появляется дополнительная компонента
Множитель expjiof0 называют оператором задержки сигнала.
Пример 1.1. Спектральная функция задержанного, то есть сдвинутого по оси
абсцисс на время Т/2 видеоимпульса (1.4),
5(Г) =
и,
О,
(1.59)
UT
<оТ
expj
(1.60)
fe|_0,r
' ёГ0,Т
2
Полезно сравнить этот результат и формулу (1.58). В качестве <р(со) в формуле
(1.60) выступает фазовый спектр рассмотренного ранее прямоугольного видео-
импульса (1 4). График фазового спектра сигнала (1.59) показан на рис. 1.8, б,
штриховой линией.
1.7. Теоремы о спектрах
31
Изменение масштаба оси времени Найдем преобразование Фурье для
сигнала с измененным по времени масштабом, s(at), а > 0:
s(at)e lwdt = — [ 5(а0ехр| -j—at jd(at) = — s(—
аД у й 7 а \а
При а < 0 аналогичным образом получим:
Объединение обоих результатов дает формулу
|а| (а)
Сжатию (растяжению) сигнала во времени отвечает растяжение (сжатие) спек-
тральной функции по оси частот.
Дифференцирование сигнала (спектральная функция производной).
Пусть сигналу g(t) соответствует спектральная функция 6(со). Будем искать спек-
тральную функцию сигната s(t) = dg/dt. Воспользуемся определением производной
и применим преобразование Фурье непосредственно к выражению для предела,
принимая во внимание теоремы о сумме сигналов и о сдвиге сигнала во времени
1 _ . 1 _ е
S (со) = lim---G (со) = G (со) lim--= jcoG (со). (161)
1 - е'7°”
Здесь lim------= jco (по правилу Лопиталя).
т->0
Говорят, что множитель zco есть оператор дифференцирование в частотной об-
ласти. При дифференцировании происходит относительный подъем амплитудного
спектра сигнала в области верхних частот.
Интегрирование сигнала (спектральная функция интеграла). Пусть
сигнал представлен в виде интеграла с переменным верхним пределом:
40=
Исходя из (1.61), формально запишем:
5(со) = —Г(со).
усо
(1.62)
32
1. Основные характеристики детерминированных сигналов
Соотношение (1.62) справедливо [3] только для сигналов/(?), отвечающих
условию
F(0)=j/(O^ = 0 (1.63)
(сигналы с «нулевой площадью»).
ЗАМЕЧАНИЕ 1.8---------------------------------------------------------
В [3] показано, что если условие (1.63) не выполняется, то спектральную
функцию сигнала s(t~) следует записывать в виде
5(co) = nF(0)8(co) +—F(co). (1.64)
;со
Множитель 1 /(/со) называют оператором интегрирования в частотной области.
При интегрировании происходит относительный подъем амплитудного спектра
сигнала в области нижних частот.
1.8. Спектральные функции произведения
и свертки сигналов
Сверткой функций /(f) и g(t) называют интеграл вида
5(*) =
(1.65)
Интегральное преобразование (1.65) весьма часто используется в теоретической
радиотехнике 13,4, 8]. В рамках настоящего учебника операция свертки подробно
рассматривается и анализируется в разделах 1.12 и 4.1.
Спектр произведения сигналов (теорема о свертке спектров). Пусть
/(f)ng(f)-сигналы со спектральными функциями /(со) и G(co) соответственно.
Тогда сигналу s(t) =f(t)g(t) соответствует спектральная функция
5((0)= j/(Og(Oe-^r = ;1 Г
1 r • Л?
= 7 ~P'(® ) Jg(O<?
7Г f (F(a')e^'da'dt =
271 ' J
dt >da)' = -^- j F(co')G'((o-co'X®,« (1.66)
-j(w-to')r
центральная функция произведения сигналов есть свертка их спектральных
функций (с коэффициентом 1/(2п)).
Теорема Рэлея. При со = 0 из выражения (1.66) следует теорема Рэлея.
00 1 00
J/(f)g(f)c/f = — р(со')С (co')c/co' = 2-j/-(ro)G-(co)6/co. (1.67)
1.9. Преобразование Фурье некоторых неинтегрируемых абсолютно сигналов
33
Здесь учтено соотношение (1.45) G' (со) = G(-co).
Равенство Парсеваля. При /(?) = g(t) = s(t) из теоремы Рэлея следует ра-
венство Парсеваля
1X1 1 °° 1 °0 2 1 00
Гs\t)dt = — f 5(со)5’(со)с/со = —f |S(co)| da>~ — P5(a>)|2 da. (1.68)
Д 2л Д 2л Д1 1 л'1 1
Спектр свертки сигналов. Пусть f(f) ng(t) — сигналы со спектральными
функциями -F(co) и G(co) соответственно. Будем иска! ь спектральную функцию
свертки (1.65) этих сигналов, для чего представим функцию g( Г) как обратное пре-
образование Фурье (1.43) спектральной функции G(co):
g(O = ^jG(®)e^®,
g(r-C) = -~- ?С(со)е7' 'с/со = — j G(co) e’we dm.
2 я J 2 л J
Таким образом,
5(0= j f(t')g(t-t')dt' =
= j G(co)| j /(О) e-jat dt' -e^da =-£- j G(co) F(co) ejMda =
= — f S(o3)e^do3.
2л J
Показано (изменением не влияющего на результат порядка интегрирования
в двойном интеграле), что спектральная функция свертки сигналов есть произ-
ведение их спектральных функций'.
5(co) = G(co)F(co). (1.69)
Это важнейшее для дальнейшего изложения соотношение, связывающее, в част-
ности, временной и спектральный подходы к анализу преобразований сигналов
в линейных цепях.
1.9. Преобразование Фурье некоторых
неинтегрируемых абсолютно сигналов
Математические модели некоторых широко используемых в теоретической радио-
технике сигналов не удовлетворяют условию абсолютной интегрируемости (1.44).
Следовательно, преобразование Фурье в обычном виде к ним неприменимо.
2 № 675
34
1. Основные характеристики детерминированных сигналов
Распространить методы преобразования Фчрье на сигналы такого рода позво-
ляет использование функции Дирака 5(t), спектральная характеристика которой
была определена в разделе 1.6.
Спектральная функция постоянного во времени сигнала. Воспользуем-
ся результатом (1.50) и запишем спектральную функцию постоянного во времени
(очевидно, абсолютно неинтегрируемого) сигнала s(t) =U,te (-«>, °о):
5(«>) = J Ue'^dt = 2лС5(со).
(1.70)
Физический смысл этого результата очевиден — постоянном} во времени сиг-
налу соответствует спектр, состоящий из единственной составляющей на нулевой
частоте — 2тг t7S(a>).
Преобразование Фурье функции Хевисайда График функции Хевисайда
(1.8) показан на рис. 1.10.
ст(г)
1
0
Рис. 1.10. Функция Хевисайда
Согласно (1.12), производной функции Хевисайда является 5-функция, спектр
которой в соответствии с (1.49) оказывается равным единице:
f 1^(01 =1
[ dt J
Тогда спектральная функция a(t) в силу соотношений (1.9) и (1.64) есть
5(со) = л5(со) + —.
(1-71)
Спектр сдвинутой во времени функции Хевисайда <s(t ± t0) формально следует
записывать как
5(ю) = л5(со)+— е±7Ш,°,
I j&J
но так как 5(со) отлична от нуля лишь при со = 0, спектр а(Г х t0) представляют в виде
5(<о) = тг5(со) + — е-1^. (1.72)
Преобразование Фурье гармонического сигнала. Гармонический
сигнал (1.1) также является неинтегрируемой абсолютно функцией, Введем на-
1.9. Преобразование Фурье некоторых неинтегрируемых абсолютно сигналов
35
чальную фазу ф0 и будем с учетом (1.51) искать спектральную функцию сигнала
х(Г)= Gcos(co0£ +ф0):
5(со) = П | cos(coor+ <р0)е‘'ш,б?г = у j{e'<mo+’,o> +е‘я“»+ф»)|е“>ш,<7г =
= у*'Ф” J * J e^^dt =
= лГг|е7ф"8(со-со0) + е ;ф"8(ш + со0)}. (1.73)
Гармоническому колебанию с конечной амплитудой соответствует спектраль-
ная функция с 8-особенностями в точках ±со0 частотной оси. Приняв в (1.73) со0 = 0
и ф„ = 0. как частный случай получим уже известный результат (1.70) — спектр
постоянного во времени сигнала.
Продемонс трпровано использование 8-функции при формальном примене-
нии преобразования Фурье к простейшим неинтегрпруемым абсолютно сигналам
(в частности, периодическому) и тем самым показана принципиальная возмож-
ность единого подхода к спектральному анализу периодических и непериодических
сигналов.
ЗАМЕЧАНИЕ 1.9--------------------------------------------
Изложенное в некоторых случаях позволяет заметно упростить вычис-
ления. Рассмотрим, например, сигнал представленный как произведение
двух функций, каким, по существу, является радиосигнал (114)
w(O = U (0cos{coor + ф(О + Фо} -
Спектральная функция произведения сигналов рассматривалась в разде-
ле 1.8. Обозначим как 5г(со) спектр огибающей U(f), примем ф(О = 0, вос-
пользуемся формулами (1.73) для спектра 5(со) гармонической функции
cos(co0f+ ф(|) при U= 1 и ф0 = 0 и подставим эти спектры в формулу (1.66),
полагая F(co) = 5,. (со) и G(co) = 5пк(со). Тогда спектр радиосигнала u(t)
5(со)= Г u(t)e-,wdt=-^- J =
1 ”
= — f Sv (со'){л8(со - со0 - со') + л8(со + со0 - со')}с/со' =
л Д
= |{5, (со-со0) + 5,.(со-со0)}.
Использовано фильтрующее свойство 8-функции (1.11). Аргументами,
при которых существуют 8(со - соп - со ) и 8(со + со0 - со'), здесь являются
со = со - со0 и со' = со + со0 соответственно.
продолжение, с/
36
1. Основные характеристики детерминированных сигналов
На функцию U(t') не накладывалось никаких ограничений, в то же
время полученное выражение в точности совпадает с результатом (1.55),
приобретающим, таким образом, общее значение.
О вычислении спектра сигнала, представленного кусочно-полино-
миальной функцией. Если модель финитного сигнала представлена кусочно
(на отдельных интервалах) или полностью только функциями вида
х(Г) = ап + a.t + a.t? + ... + a F+ ..., t е [£., £,],
' z U 1 1 П * 1
то для вычисления его спектральной функции целесообразно применение процеду-
ры (и + 1 )-кратного дифференцирования s(t) с последующим определением спектра
производной s^n+1)(t) и с использованием оператора интегрирования в частотной
области I/O®)"’1 — собственно спектра chi нала.
Пример 1.2. Возьмем прямоугольный видеоимпульс (1.59), являющийся на
интервале [О, Г] полиномом степени п = 0.
Производная сигнала (1.59):
5'(Г) = (/{5(О-8(Г-Т)}
(заметим, что сигнал (1.59) можно трактовать как сумму двух функций Хевисайда,
s(t) = U{cs(t) - cs(t- Т)}). Спектральная функция первой производной
5(1)((О) = П(1-е--'“7'),
спектральная функция сигнала
U /
S((o) = — (1-е’7“г
. (оТ
sin —
____2_
соТ
2
Проще было бы сразу обратиться к формулам (1.71) и (1.72), но здесь речь
идет о демонстрации универсального и практически весьма полезного приема,
основанного на использовании результатов (1.49) и (1.52) и теорем о спектрах
производной и интеграла с переменным верхним пределом от сигнала, изложен-
ных в разделе 1 6.
Так как сигнал является первообразной функцией для своей производной, «пло-
щадь» под графиком производной финитного сигнала оказывается равной нулю:
J s\t}dt = s(°°) - s(-oo) = 0-0 = 0.
То же справедливо и для производных более высоких порядков Таким образом,
условие (1.63) всегда выполняется.
1.9. Преобразование Фурье некоторых неинтегрируемых абсолютно сигналов
37
Сигнал s(t) дифференцируют до тех пор, пока его производная не станет пред-
ставлять собой последовательность 5-функций и производных5-функций. Процесс
дифференцирования удобно сопровождать соответс твующими рисунками.
Пример 1.3. Вычислим спектральную функцию сигната (1.5), представленного
на интервате [О, Г] полиномом степени п = 1. Сигнат, его первая и вторая произ-
водные показаны на рис. 1.11 a-в. Выражение
5"(O = ^8'(O-y8(t) + ^5G-T)
позволяет сразу записать спек тральную функцию второй производной:
5,2)(<о) = — г->шТ.
Рис. 1.11. Вычисление спектра треугольного импульса
методом дифференцирования: а — исходный сигнал;
б — первая производная; в — вторая производная
ЗАМЕЧАНИЕ 1.10 ------------------------------------------
Производная 5'(0, как и производные 5(0 более высоких порядков, — по-
нятие физически бессодержательное и его следует воспринимать здесь
формально', спектром н-й производной 5-функции является (/со)".
Далее, дважды используя оператор интегрирования в частотной области, полу-
чаем спектральную функцию сигната $(0:
5(со) =
1
О)2
jaU- — +—е]шТ
Т Т
Преобразование полученного для 5(a)) выражения в показательную форму
(1.47) и его анализ читателю предлагается выполнить самостоятельно.
38
1. Основные характеристики детерминированных сигналов
1.10. Энергетические соотношения
в спектральном анализе
Удельная энергия сигнала. Энергетические параметры сигнала вводят, опираясь
на следующие положения:
□ пусть s(t) есть напряжение или ток, тогда мгновенная мощность сигнала [Вт]
определяется как
, . u2(t) . ,
p t)= S =й , :
□ напряжение действует на активном сопротивлении R = I Ом, ток проходит через
активное сопротивление R = 1 Ом, тогда мгновенная удельная (приходящаяся
на 1 Ом) мощность сигнала | Вт] численно определяется как
рУ«(<)=“2(0=г‘2(0=52(0-
а удельная энергия сигнала [Дж] — как
070
вне зависимости от размерности ([В] или [А]) сигнала s(t), что очень удобно. В даль-
нейшем при всяком упоминании термина «мощность» или «энергия» определение
«удельная», как и индекс «уд», опускается, но (если нет специальных оговорок)
подразумевается, так что [В2], [А2] непос редственно определяют мощность, а [В2с],
[А2-с] — энергию.
Энергетический спектр детерминированного сигнала. Обратившись
к равенству Парсева тя (1.68), немедленно получаем выражение для энергии сигнала:
Е - j s2 (t)dt = j 5(со)5’ (со)Ло = у- j |5(«>)| da> =
= -^-Jg(co)c/co = ^JG(co)c/co. (175)
Квадрат модуля спектральной функции
5(со)5’ (со) = 15( со)|2 = G(co) (1.76)
называют энергетическим спектром сигнала s(t). Энергетический спектр не зависит
от фазового спектра сигната и явтяется вещественной неотрицательной (G( со) > 0)
и четной (G(co) = G(-co)) функцией частоты. Размерность энергетического спектра
[G(co)] — [В2/Гц2 = В2-с/Гц]. Энергетический спектр, или «спектральная плотность
энергии», описывает распределение энергии сигнала по частоте Это позволяет
в частности, оценивать долю энергии сигнала, приходящуюся на тот или иной
частотный интерват.
1.10. Энергетические соотношения в спектральном анализе
39
Пример 1.4. Полная энергия радиоимпульса (1.15)
2 , ..2fl + cos2a>.i , U2T U2\ n
E - JU2 cos2 cooZ dt = U‘ J- dt------+—Jcos2co0fcZf =
о о 2 2 2 0
U2t(4 sin2a> T 1
—---- 1 н--------.
2 2cooT J
Если длительность радиоимпульса T много больше периода частоты запол-
нения То, Т » То = 2л/а>0, то интеграл j cos2co0tc/zl« Т , или, что то же самое,
sin2a>0T/(2со0Г) « 1. и полная энергия радиоимпульса Е - 1РТ/2,то есть в Эва раза
меньше энергии соответствующего видеоимпульса (см. замечание 1.6).
Удельная мощность непрерывного и периодического сигналов. Опре-
делим полную удельную энергию непрерывного сигнала (1.2), существующего при
t е (—<*>, ©о):
Е = J U2e-2a2t
dt = 2U2 f е’2“2'2dt = U2 —.
Использован табличный интеграл [9] Оказывается, модель (1.2) — это модель
непрерывною и существующего на бесконечном временном интервале сигнала
с ограниченной, конечной энергией. Но чаще встречаются модели неограниченно
протяженных во времени (например, периодических) сигналов, энергия которых
бесконечно велика. Энергетическую оценку моделей таких сигналов проводят,
вводя среднюю удельную мощность
1 т . Т/2
Р = lim—Js2 (t)dt или P = lim— j s2(^)Jr. (1-77)
0 T~>°“ -7/8
где T— произвольный временной интервал.
Для периодических сигналов, энергия которых бесконечно велика по опреде-
лению, усреднение удобно проводить по периоду Т:
P = ±]s2(t)dt. (1.78)
‘ о
Средняя удельная мощность гармонического сигнала (1.1) Р= 1Р/2. Применяя
формулу (1.78) к периодическому сигналу представленному в форме (1.27)
или (1.30) ряда Фурье, и принимая во внимание условия ортогональности (1.16),
для средней мощности Р такого сигнала получим:
(1.79)
Полная средняя мощность периодического сигнала равна сумме средних мощ-
ностей сос гавляюших сигнал гармоник включая, естественно, мощность постоянной
составляющей (нулевой гармоники).
40
1. Основные характеристики детерминированных сигналов
ЗАМЕЧАНИЕ 1.11 -------------------------------------------------------
Иногда используют так называемый односторонний энергетический спектр
ЛД/), аргументом которого выступает линейная частота/. Односторонний
N(f) существует только при/> 0, и вводят его так, чтобы энергия сигнала
в полосе частот [0,/inlx] определялась простым соотношением
£= j N(f)df.
О
Для определения связи между N(f) и G(w) рассмотрим пример: задан
сигнал с энергетическим спектром G((o) = Go, существующим в интервале
круговых частот со е [-2л, 2л]. В соответствии с (1.75) полная (удельная)
энергия этого сигнала [Дж]
£ = ^- Jo^--fc;f>=2G0.
ziTt л 7Т «
-2 л О
Если используется соответствующий односторонний спектр Лт0, то
О
так как 2л рад/с = 1 Гц. Следовательно, численная связь между М/) и G(w)
определяется соотношением N(f) = 2G(co) = 2С(2л/).
Например, если N(f) = N0 = 2 В2с2/Гц, то G(a>) = Go = 1 В2с2/рад.
1.11. Корреляционный анализ
детерминированных сигналов
В теории сигналов наряду со спектральным широко используется корреляционный
анализ.
Корреляционная функция детерминированного сигнала $(£) определяется вы-
ражением
В(т)= j s(t)s(t-x)dt, (1.80)
где т — временной сдвиг копии сигнала s(0.
При вычислении корреляционной (иногда говорят автокорреляционной) функ-
ции финитных сигналов бесконечные пределы интегрирования в (1.80) заменяют
конечными, определяемыми интервалом времени, на котором подынтегральная
функция s(zj s(t - т) отлична от нуля.
Пример 1.5. Корреляционная функция (КФ) прямоугольного видеоимпульса.
На рис 1.12 показано взаимное расположение сигнала (1.59) и его сдвинутой на
время т копии s(t- т) при положительных (рис. 1.12, а) и отрицательных (рис. 1.12, б)
1.11. корреляционный анализ детерминированных сигналов
41
Рис. 1.12. Вычисление корреляционной функции
прямоугольного видеоимпульса: а — т>О;б — т<0
значениях т. Область существования отличного от нуля произведения s(t) s(t - т)
заштрихована.
□ Для 0 < т < Т
т
В(т) = |{/2Л = {/2(7'-т).
т
□ Для-Т<т < О
т-Н
В(т) = j U2dt = U2(T-\x\).
О
Полученные выражения можно объединить и записать КФ в виде
В(т) = U2(T-|т|), т е [-Г, Г]. (1.81)
Аргументом КФ является т — временной сдвиг копии относительно сигнала s(t).
Легко увидеть, что корреляционная функция сигнала (рис. 1.13) не зависит от поло-
жения s(t) на временной оси: вычисление КФ прямоугольного видеоимпульса (1.4)
вновь приведет к результату (1.81).
Рис. 1.13. Корреляционная функция прямоугольного видеоимпульса
Свойства КФ сигналов с ограниченной энергией
1. В( 0) = | s2 (t) dt = Е, то есть при т = 0 значение КФ численно равно полной удель-
ной энергии сигнала. Размерность КФ сигнала с конечной энергией [В( г)] —
[В2 с].
2. В(0) > |В(т)|, то есть КФ имеет максимум при т = 0. Для доказательства запишем
очевидное неравенство
j {s(£)±s(£-t)}2<#>0
42
1. Основные характеристики детерминированных сигналов
и преобразуем его:
J {s(t)±s(t-x)}2 dt = j s2(t)dt + J 25(05(Г-т)г/г+ j s?(r-T)</f =
= J s2(t)dt + 2 j s(t)s(t-x)dt + j s2 (£ - x)d(t - x) =
= 2 j s2(t)dt±2 j s(t)s(t -x)dt >0.
Следовательно,
s2(t)dt> js(t)s(t-x~)dt
или B(0)> |B(t)| .
3. B(-t) = J s(t)s(t + x)dt = J s(t)s(t - x)dt = В(т), to есть КФ является четной
функцией аргумента х (доказывается заменой переменной).
4. limB(T) = 0 (без доказательства).
Взаимная корреляционная функция (ВКФ) сигналов с ограниченной энергией
(и финитных) 5t(0 и х2(Г) определяется выражениями
В12<т)= p,(Os2(£-t)A, В21(т)= J5,(гг-t)s2(O^- (1-82)
Корреляционная функция является частным случаем ВКФ при хДГ) = s2(f) = s(t).
Пример 1.6. ВКФ прямоугольного (1.47) и треугольного импульсов. Пусть
51(0 =
Ге [0,7’]
<£[0,Г]
К
И 52(0 = ( Т
о,
Ге [ОТ],
4 g [ОТ].
Взаимное расположение сигналов х,(г) и s2(t - т) для х > 0 и т < 0 показано па
рис. 1.14, а, б.
Рис. 1.14. Вычиспение ВКФ прямоугольного
и треугольного импульсов: а — т>0;б — т<0
1.11. Корреляционный анализ детерминированных сигналов
43
После выполнения соответствующих расчетов получаем следующий результат:
□ для 0 < т < Т
□ для -Т< т < О
7'+т тт2 тг2
Д,^) = I Y^~^dr=2T^T2~X^'
График ВКФ прямоугольного и треугольного импульсов приведен на рис. 1.15.
В12(т)4
и2т^-
О Г т
Рис. 1.15. В КФ прямоугольного и треугольного импульсов
Свойства ВКФ сигналов с ограниченной энергией
1. В12(0) не обязательно является максимальным значением В12(т). В качестве
примера рекомендуется самостоятельно рассмотреть ВКФ сигналов (1.59)
и (1.5).
2. |в1?(т)|<дё; , где Е2 — энергии сигналов st(f) и s2(t) соответственно.
3. При перемене порядка индексации в обозначении ВКФ и соблюдении формы
записи, указанной в выражении (1.82), происходит инверсия графика ВКФ от-
носительно оси ординат т = 0:
Д2(-т) = j s^tys^t + ^dt = j s1(r-T)52(O</f = B21(T) .
Рекомендуется проверить это положение для сигналов из примера 1.6 непо-
средственно.
4. lim В12(т) = 0 (как и для КФ).
ВКФ является своеобразной мерой «похожести», соответс твия, коррелирован-
ности двух сигналов при различном их взаимном расположении. КФ отражает
корреляцию сигнала с собственной копией-, говорят об автокорреляционных свой-
ствах сигнала. Неравенство В(0) > |В(т)|, то есть непременный максимум КФ при
т = 0 в этом контексте может трактоваться как свидетельство полной корреляции
всякого сигнала с самим собой. Уменьшающиеся (пусть немонотонно) значения
В(т) характеризуют меру коррелированности, связи сигнала со своей копией при
различных т Ф 0.
44
1. Основные характеристики детерминированных сигналов
Корреляционная функция сигналов с неограниченной энергией.
Определение (1.80) для вычисления КФ указанных сигналов, вообще говоря, не
используют по отмечавшимся в разделе 1.10 причинам (энергия сигнала, то есть
В(0), может оказаться бесконечно большой). КФ непрерывного и периодического
сигнала определяют как
. Т/2
В(т) = Нт— [ s(t~)s(t -T.)dt, (1.83)
-Т/2
усредняя по интервалу времени Г—»
Пример 1.7. Корреляционная функция гармонического сигнала (1.1):
В(т) = 1пп— J cosco0fcos<B0(^-T)A = —costt>0Tlim— J dt =—cosco0t. (1.84)
T _T/2 2 т->-р_t/2 2
В отличие от КФ и ВКФ финитных сигналов, КФ периодического сигнала
сама является периодической функцией и имеет размерность мощности. Значения
аргумента т, для которых В(т) = 0, определяют временные сдвиги сигнала и его ко-
пии, при которых корреляция отсутствует. Значение В(0) периодического сигнала
численно равно мощности сигнала; для гармонического сигнала (1.1) В(0) = U2/2.
ЗАМЕЧАНИЕ 1.12 --------------------------------------------------------
Обоснованность требования ограниченности энергии сигналов, КФ
и ВКФ которых определяются по соотношениям (1.80) и (1.82). становится
очевидной после обсуждения корреляционных свойств моделей сигналов
с бесконечно большой энергией. Следует обратить внимание на то об-
стоятельство, что удовлетворяющие условиям Дирихле (см. раздел 1.3)
финитные сигналы всегда являются сигналами с ограниченной энергией.
ЗАМЕЧАНИЕ 1.13 ------------------------------------------------------
Без доказательства, основываясь на рассмотренных примерах, сформу-
лируем еще одно общее характерное свойство КФ и ВКФ: если исходная
(КФ) или одна из исходных (ВКФ) функций не содержит 5-особенностей,
то КФ и ВКФ не содержат скачков (разрывов 1-го рода).
1.12. Свертка сигналов
Свертка сигналов f(t) и g(r) определяется интегралом свертки (1.65)
40 = ]
Интеграл свертки используется, в частности, для определения сигнала на вы-
ходе четырехполюсника. Существуют различные формы представления интеграла
1.12. Свертка сигналов
45
свертки; в электро- и радиотехнической литературе интегра i (1.65) иногда называют
также интегралом наложения или интегралом Дюамеля. Техника вычисления этого
интеграла аналогична технике вычисления КФ и ВКФ (см. раздел 1.11). Однако
следует обратить внимание на весьма существенное различие: переменная, по
которой ведется интегрирование, в сомножители подынтегральной функции ин-
теграла (1.65) входит с различными, а интеграла (1.80) — с одинаковыми знаками.
Технику вычисления интеграла свертки удобнее всего пояснять на конкретных
примерах.
Пример 1.8. Возьмем в качестве сигнала f(t) прямоугольный видеоимпульс
(1.59). а в качестве сигнала g(t) — финитный сигнал (1.5).
Как следует из выражения (1.65), интеграл вычисляется по вспомогательной
переменной t'. Аргумент свертки t выступает в качестве параметра. На рис. 1.16, а
(в системе координат «Л' - сигнал») показано взаимное расположение функций,
произведение которых образует подынтегральное выражение в (1.65) при t = 0,
в частности, инвертированная относительно оси ординат функция g(t - t'). Здесь
g(r-A) = y(T-r+ f'), при t = 0 имеем g(-t') = ^(T + t'). На рис 1.16, б показано
тоже, но для 0 < t < Т, на рис. 1.16, в — для Т< t < 2Т.
Рис. 1.16. Вычисление свертки прямоугольного и треугольного импульсов:
a — х = 0; б — 0<t<T; в — T<t<2T
Интегрирование в (1.65) ведется по интервалу, соответствующему области су-
ществования отличного от нуля произведения f(t')g(t-t'). Именно протяженность
и расположение этой области в каждом конкретном случае определяет пределы
интегрирования в (1.65). В рассматриваемом случае:
□ для 0 < t < Т
{ rr2 тт2 f л.2
□ для Т < t < 2 Т
s(t) = J -(T-t + t')dt'^—(2T2-2Tt + —
v 7 (JT T ’ T 2)
Очевидно, что для 7>2Ги?<0 свертка s(t) = 0. График свертки приведен на
рис. 1.17. Вычисление свертки ведется по «участкам», что характерно для фи-
нитных или кусочно-заданных функций. Если f(t) и g(t) не содержат аддитивно
8-функций (1.9), то значения свертки в точках соединения (стыках) отдельных
участков должны совпадать; в рассматриваемом примере s(T) = U2T/2.
46
1. Основные характеристики детерминированных сигналов
ДО 4
Ц2Т
2
О Т 2Т t
Рис. 1.17. Свертка прямоугольного и треугольного импульсов
Читателю рекомендуется сравнить полученный здесь результат и результат
вычисления ВКФ (см. пример 1.6).
Заменой переменной показывают (это предоставляется читателю), что интеграл
(1.65) можно также записать в виде
(1.85)
Результаты вычислений по формулам (1.65) и (1.85) совпадают; выбор той или
иной формы записи определяется соображениями упрощения вычислений.
Разумеется, может вычисляться свертка не только финитных функций, но
и функций, определенных на любых, в том числе бесконечных, интервалах.
Пример 1.9. В качестве сигнала/(£) вновь возьмем прямоугольный видеоимпульс
(1.59), а в качестве сигнала g(0 — экспоненту (1.3).
Рисунок, отражающий взаимное положение функций g(r - (') и f(t'~) в системе
координат «t' — сигнал», читателю предлагается выполнить самостоятельно. Ин-
теграл свертки записывается следующим образом:
□ для 0 < t < Т
s(t) = f U2 = — е"1 [ем dot' = — (1 - е~ш);
Jo “ о а
□ для Т< t < оо
При t < 0 свертка s(f) = 0.
Пример 1.10. Рассмотрим, наконец, свертку произволпного сигнала/(() с функци-
ей Дирака 8(Г). Следуя формулам (1.65) и (1.85) и учитывая фильтрующее свойство
(1.11) 8-функции, запишем:
5(0 = J f(t')8(t-t')dt'= j /(r-C)8(C)t/C = /(0.
Сверткой произвольной функции с функцией Дирака является сама произ-
вольная функция.
1.13. Корреляционно-спектральный анализ детерминированных сигналов
47
1.13. Корреляционно-спектральный анализ
детерминированных сигналов
Особенно важным вопросом является связь корреляционных и спект ральных
характеристик детерминированных сигналов.
Корреляционная функция и энергетический спектр. Поставим в соот-
ветствие двум финитным сит на там х,(?) и s2(r) спектральные функции 5, (со) и S2 (со).
Обратимся к определению ВКФ (1.82) и, последовательно воспользовавшись тео-
ремой о спектре сдвинутого во времени сигнала (1.58) и теоремой Рэлея (1.67),
представим
ОО . <ж> .00
Si2<T) = f \(r)s2(t-x)dt = — J 5, (to)52 (со) e,,mda = — Г G12 (со) d(o. (1.86)
Комплексная в общем случае функция
G12(co) = 5’1(co)5‘(co)
(1.87)
называется взаимным энергетическим спектром сигналов x/t) и s2(t).
Но выражение (1.86) является обратным преобразованием Фурье (1.43) с ядром
ехр(усот), примененным к взаимному энергетическому спектру G12(co), следователь-
но, существует соответствующее прямое преобразование Фурье
G12(co)= /В12(г)с--с/т.
(1.88)
Соотношения (1.86-1.88) являются основой корреляционно-спектрального
анализа детерминированных сигналов. В частности, определение (1.86) позволяет
глубже осмыслить уже обсуждавшееся понятие ВКФ. В самом деле, при непере-
крывающихся (концентрирующихся в различных частотных интервалах) спектрах
5/w) и 52(со) произведение S/co)/’(со) = 0. Следовательно, и В12(т) = 0, то есть эти
сигналы оказываются абсолютно некоррелированнычи
Приняв в (1.86) s/t) = s2(t) = s(t), получим соотношения, связывающие КФ
I I2
сигнала с его энергетическим спектром G(co) = 5(<о)5 (со) = 5(<в) , введенным вы-
ражением (1.75):
В(т) = j G((i))e’md(i), G(co) = j B^e'^di:. (1.89)
Эти соотношения, используя четность и вещественность функций В(т) и G(<o),
часто представляют в виде
В(т) = — jG(co)coscoT</(o, G(co) = 2jB( t)cos(OTc/x (1.90)
71 о о
48
1. Основные характеристики детерминированных сигналов
ЗАМЕЧАНИЕ 1.14
В(т), как и G(co) = |S(a))| , не зависит от фазовой спектральной функции
сигнала s(t). Но форма сигнала s(t) при заданной спектральной функции
амплитуд |S(to)| существенно зависит от фазового спектра <р(со), поэтому
можно утверждать, что различные по форме, но обладающие одинаковыми
амплитуоными < пектпрами сигналы имеют одинаковые КФ.
Контрольные вопросы и задания
1. Запишите формулы представления сигнала в виде ряда Фурье в вещественной
и комплексной формах.
2. Что такое амплитудный и фазовый спектры периодического сигнала?
3. Комплексный коэффициент Сп на некоторой положительной частоте соп равен
1,5 ехр(ул/4). Какой физический смысл имеют коэффициенты 1,5 и л/4?
4. Запишите выражения для спектральной функции 5(со) одиночного импульса
и комплексной амплитуды Сп (через Ап и <рп) ряда Фурье, описывающего пери-
одическую последовательность, составленную из таких импульсов. Как связаны
между собой 5(со) и Сп ?
5. У периодического сигнала изменилась полярность. Что произойдет с его ам-
плитудным и фазовым спектрами?
6. Если сигнал является периодическим, то его спектр дискретен. Справедливо ли
обратное утверждение? Почему?
7. Какие соображения определяют выбор системы базисных функций при раз-
ложении chi налов в обобщенный ряд Фурье?
8. Какое важное свойство коэффициентов разложения сигнала в обобщенный ряд
Фурье вам известно?
9. Приведите формулы прямого и обратного преобразования Фурье. При каких
условиях можно пользоваться формулой прямого преобразования Фурье?
10. Какой физический смысл имеют модуль и аргумент спектральной функции
непериодического сигнала?
11. Спектральная функция 5(<в) непериодического сигнала на некоторой по-
ложительной частоте со равна 1,5 ехр(7'л/4). Какой физический смысл имеют
коэффициенты 1,5 и л/4?
12. Как изменяется спектральная функция 5(<в) при умножении сигнала s(t) на
cos со0£ ? (Привести формулу.)
Задачи
49
13. Как изменяются амплитудный и фазовый спектры сигнала при его запаздыва-
нии?
14. Чему равна спектральная функция произведения двух ф\ нкций, если известны
спектральные плотности сомножителей? (Привести формулу.)
15. В чем заключается фильтрующее свойство 5-фуикции? (Привести формулу.)
16. Дайте определение и перечислите основные свойства корреляционной функции
детерминированного сигнала. Как опа связана со спектром сигнала?
17. Зависит ли форма корреляционной функции детерминированного сигнала от
фазового спектра этого сигнала? Почему?
18. Перечислите особенности корреляционной функции периодического сигнала.
19. Как определяются мгновенная мощность, энергия и средняя мощность сигнала
s(t) на интервале времени [£,, t2]?
Задачи
Задача 1.1
Найти энергию за период и среднюю мощность сигнала, представляющего собой
периодическое повторение экспоненциальных фрагментов (рис 1.18):
s(t) = Ае~а(-‘~кТ}, kT<t<(k+V)T, ~^<k<oo.
Рис. 1.18. Сигнал для задач 1.1 и 1.2
Задача 1.2
Рассчитать коэффициенты ряда Фурье для сигнала из задачи 1.1.
Задача 1.3
Рассчитать коэффициенты ряда Фд рье для периодической последовательности
треугольных импульсов (рис. 1.19).
Задача 1.4
Найти спектральную функцию треугольного импульса (рис. 1.20).
50
1. Основные характеристики детерминированных сигналов
Рис. 1.20. Сигнал для задачи 1.4
Задача 1.5
Найти спектральную функцию одиночного экспоненциального импульса конечной
длительности (рис. 1.21):
s(t) = Ae ,0<t<T.
Рис. 1.21. Сигнал для задачи 1.5
Задача 1.6
Найти сигнал s(t), спектральная функция которого равна 0,5 • 10-3 В • с в диапазоне
частот-1 кГц...1 кГц.
Задача 1.7
Воспользовавшись свойствами преобразования Фурье и результатом решения за-
дачи 1.4, найти спектральную функцию сигнала, показанного на рис. 1.22.
Задача 1.8
Воспользовавшись свойствами преобразования Фурье и результатом решения за-
дачи 1.5, найти спектральную функцию сигнала, показанного на рис. 1.23.
Задачи
51
Рис. 1.22. Сигнал для задачи 1.7
Рис. 1.23. Сигнал для задачи 1.8
Задача 1.9
Воспользовавшись свойствами преобразования Фурье и считая что спектральная
функция сигнала s0(t) равна 50(со), найти спектральную функцию следующего
сигнала (рис. 1.24):
s(t) = ^aksQ(t-kT),O<a<l.
4=0
Задача 1.10
Определить комплексный спектр 5(о>) сигнала s(t) = cos2 (<в0/), -оо < t < оо. Задачу
решить двумя способами-
а) путем сведения данного сигнапа к сумме двух сигналов с известными спектрами;
б) с помощью теоремы о спектре произведения двух функций.
52
1. Основные характеристики детерминированных сигналов
Задача 1.11
т,
I т I I т
Сигнал задан в виде s(t) = А 5 £ + -т- - 8 £ - -~-
I v \ ,
характеристику Как изменятся форма сигнала и его спектр при интегри-
. Определить его спектральную
ровании?
2
Задача 1.12
Используя теорему о свертке спектральных плотностей и считая известными спек-
тральные плотности гармонического колебания и прямоугольного видеоимпульса,
найти спектральную плотность радиоимпульса с прямоугольной огибающей:
5(Г) = -
О,
Ccos(w0o, |г| <у,
г
2'
Задача 1.13
Сигнал s(f) представляет собой треугольный видеоимпульс изображенный на
рис 1.25. Получите формулу, описывающую корреляционную функцию данного
сигнала. Пос гройте график.
Рис. 1.25. Сигнал для задачи 1.13
Задача 1.14
Найти взаимную корреляционную функцию В12(т) прямоугольных импульсов
с параметрами Ц = 1 мВ, Tt = 1 мс, U2 = 2 мВ, Т2 = 0,5 мс (рис. 1.26).
51,2(0“
С2 ------------
С,-------------------
0 Т2 тх t
Рис. 1.26. Сигналы для задачи 1.14
Задачи
53
Задача 1.15
Для двух сигналов s,(0 = At exp(-att) и s2(t) = А2 exp(-a2f), существующих при t> О,
рассчитать:
а) взаимную корреляционную функцию;
б) свертку (отдельно рассмотреть случай, когда а, = а2 = а).
Задача 1.16
Найдите аналитическое выражение и постройте график взаимной корреляционной
функции сигналов st(t) и s2(t), изображенных на рис. 1.27.
Рис. 1.27. Сигналы для задачи 1.16
2. Модулированные
радиосигналы
При создании радиотехнических систем передачи информации часто оказывается,
что спектр сигнала, подлежащего передаче, сосредоточен в одной области частот,
а имеющийся канал связи позволяет эффек гиьно передавать другие частоты. Из-
за этого приходится использовать некоторое обратимое преобразование сигнала
для согласования его свойств со свойствами канала связи. Таким преобразованием
служит модуляция, сущность которой заключается в том, что передаваемый сигнал
управляет параметрами несущего колебания (чаще всего гармонического).
В данной главе рассматриваются свойства сигналов, получающихся при ис-
пользовании наиболее распрос граненных видов модуляции.
2.1. Модуляция. Основные понятия
Радиосигнал (1.14)u(t) = /7(0cos{<not + <р(0 + <р0} = U(t)cosу(0 описывает при
/7(0 = U= const, <р(t) = 0 простое гармоническое колебание, не содержащее инфор-
мации (характерное свойство любого детерминированного сигнала, то есть сигнала,
все параметры которого известны).
Пусть s(t) — подлежащий передаче и содержащий, несущий информацию (и сле-
довательно, случайный), или информационный, сигнал. Если реализуется какая-либо
функциональная связь между s(t) и параметрами радиосигнала (1.14), например
[7(0 = &(0,
где k — коэффициент пропорциональности, то радиосигнал
u(t) = /7(0 cos(<»0t + tp0) = ks(t) cos(w0t + фо) (2.1)
называется модулированным радиосигналом. Он содержит информацию о сигна-
ле s(0 и гармоническим уже не является. Сигнал (2.1) может быть сформирован
устройством, структурная схема которого приведена на рис. 2.1.
Устройство, осуществляющее модуляцию, называется модулятором', в рассма-
триваемом примере модулятор перемножает два сигнала и реализует амплитуд-
ную модуляцию (AM) несущего колебания cos{to0t + <р0}. Если при /7(0 = U= const
реализуется некоторая функциональная связь между s(t) и полной фазой сигнала
(1.14) у(0, то говорят об угловой модуляции.
2.2. Радиосигналы с амплитудной модуляцией
55
Рис. 2.1. Формирование модулированного радиосигнала
Используются и такие виды модуляции, при которых информационный сигнал
s(f) функционально связан с U(t) и у(г) одновременно.
Необходимость применения для передачи информации модулированных
радиосигналов связана с двумя основными обстоятельствами. Во первых, при
радиопередаче следует использовать сигнал, эффективно излучаемый антенной.
Но эффективное излучение происходит лишь тогда, когда геометрические разме-
ры антенны соизмеримы с длиной волны X = c/f (с — скорость света) излучаемого
колебания. Это положение диктует целесообразность использования в качестве
несущего колебания относительно высокочастотного гармонического сигнала.
Во-вторых, для неискаженной передачи (прохождения) радиосигнала через
радиотехнические цепи и антенно-фидерное устройство необходимо, чтобы эф-
фективная ширина спектра (см. раздел 1.6) передаваемого радиосигнала была
мала по сравнению с частотой несущего колебания, Асоэфг« <в0. Последнее условие
узкополосности радиосигнала часто записывают в форме
А<Вэфг _ А4фГ .
®о Л
2.2. Радиосигналы с амплитудной
модуляцией
Для выделения из принимаемого приемником высокочастотного АМ-колебания
информационного (модулирующего) сигнала s(t) или, с точностью до постоянного
множителя, ks(t) используют амплитудный детектор (детектор огибающей). По-
этому «классический» AM-сигнал не формируют, реализуя алгоритм (2.1) непосред-
ственно, то есть полагая U(t) = ks(t). Если 5(f) принимает отрицательные значения
(рис. 2.2, а), то огибающая, выделяемая амплитудным детектором, уже не будет
соответствовать 5(f) (рис. 2.2, б). Модулирующий множитель представляется в виде
U(t) = Ua +fo(f), Uo >|^5(t)|,
и AM-сигнал формируют как
5лм (О = м(0 = {иа + fe(0}cos (co0f + <р0).
Детектор огибающей выделяет (рис. 2.2, в) сигнал U(t), соответствующий
информационному с точностью до постоянной составляющей и постоянного
множителя.
56
2. Модулированные радиосигналы
в
Рис. 2.2. Формирование AM-сигнала: а — двуполярный модулирующий сигнал;
б — результат его непосредственного умножения на несущее колебание (огибающая
искажена)' в — к модулирующему сигналу добавлена постоянная составляющая (получена
неискаженная огибающая)
Спектральный состав радиосигнала с гармонической (тональной) AM.
Как отмечалось в разделе 2.1, реальный информационный (модулирующий) сигнал
s(t) детерминированным быть не может. Но для изучения основных особенностей
модулированных сигналов в качестве x(t) используют модели детерминированных
chi налов. Простейшей моделью AM-сигнала является колебание с гармонически.»
модулирующим сигналом
U(t) = Ug + AZ7 cos (Q£ + <pQ0),
где Д/7 = const, <pn0 — начальная фаза сигнала модуляции. В этом случае
u(t) = [Uo + Д/7 cos (Qt + (p£10)}cos(io0t + <р0) =
= Ug {1 + mcos (Qt + <pno )}cos(®0£ + <p0) =
zntA r ,
= Un cos (co0t + <p0 ) + -— cos [(w0 + Q)t + <p0 + <pn0} +
mUn r. 1
+ -y-cos {(O)0 - Q)t + <p0 - <pn0},
(2-3)
где m = &U/U() — коэффициент амплитудной модуляции, 0<m< 1. Формула (2.3)
определяет модель и спектральный состав AM -сит нала с гармонической модуля-
цией (иногда говорят «сигнал, модулированный чистым тоном» или «сигнал с то-
нальной модуляцией»). Принято называть со0 несущей, <оп + Q — верхней боковой,
<о0 - Q — нижней боковой частотами.
Амплитудная и фазовая спектральные характеристики радиосигнала с гармо-
нической AM изображены на рис. 2.3, анб. осциллограмма сигнала приведена на
рис. 2.4.
Тональный AM-сигнал часто используется в лабораторной практике, при на-
стройке радиоаппаратуры и т. п.
2.2. Радиосигналы с амплитудной модуляцией
57
А
cog - Q cog coq + Q со
Ф0 + ФП0
Фо
Фо _ Фпо Т
(Oq - Q (Oq (Oq + ®
Рис. 2.3. Спектры радиосигнала с гармонической амплитудной модуляцией:
а — амплитудный; б — фазовый
Рис. 2.4. Радиосигнал с гармонической амплитудной модуляцией
Эффективная ширина спектра радиосигнала с тональной AM опреде-
ляется очевидным соотношением
Дю .... =2Q. о л\
эф AM .4)
Векторная диаграмма радиосигнала с тональной AM. Диаграмма по-
ясняет процесс формирования AM-сигнала. Построение связано с использованием
хорошо известного из курса теоретической электротехники символического метода,
или метода комплексных амплитуд, сущность которого состоит в ппедставлении
гармонического сигнала в виде вещественной части комплексной функции
s(0 = Uo cos (ю0£ + <р0) = К«{[/Ое7(ш°г+Ф” ’} =
= Ке{с/0е7ф,'Ош"'} = Re{droe/cu<'r} = Re{s(O},
где 5(0 = и^е1^' — комплексный сигнал, Оо = Uoe,4’° — комплексная амплитуда сигна-
ла 5(t), содержащая информацию об амплитуде Uo и начальной фазе <р0 сигнала 5(0;
ее изображают вектором на комплексной плоскости.
58
2. Модулированные радиосигналы
Представим таким образом радиосигнал (2.3):
u(t) = Re
рЛФ.+Ф.,,,)| О С'СФ„-Ф„„)С-;^
2 2
= Re[nAM(r>w].
Комплексная амплитуда радиосигнала с тональной AM оказывается функцией
времени', ее называют комплексной огибающей AM-сигнала. Векторная диаграмма
радиосигнала с гармонической амплитудной модуляцией показана на рис. 2.5. Век-
тор Г/дм(0) представлен на комплексной плоскости как сумма векторов Йо = бгое;ф",
IL ЛтиУ’^и U.
о+ 2 о
=—mUneliv" Ф11"), помещенных в систему координат, вра-
щающуюся против часовой стрелки с угловой скоростью (круговой частотой) со0.
В этой системе координат вектор UQ неподвижен. Векторы боковых составляющих
t/6+ и U6_ всегда расположены симметрично относительно вектора Uo и вращаются
в соответствующих направлениях с угловыми скоростями ±Q. При этом вектор
t/AM(f) ’ модуль которого изменяется по закону
Л\М ) = Ц> {1 + т cos (Q/ + Ф™)} >
всегда коллинеарен J70. Проекция на вещественную ось вращающейся
системы координат, или ReFt/AM(r)l, совпадает с u(t).
Рис. 2.5. Векторная диаграмма радиосигнала
с гармонической амплитудной модуляцией
Радиосигнал с многотональнои Если в модулируюптии множитель
входит сумма косинусоид
= ип р + cos(Q/ + <рП10) + т2 cos(Q/ + (р^0) +...Jcos(<o0t + <р0),
то кроме несущей частоты в спектральном составе сигнала появится ряд боко-
вых частот: соо ± Qp со0 ± Q2... Все сказанное о тональном AM-сигнале верно и для
2.2. Радиосигналы с амплитудной модуляцией
59
AM-сигнала с многотональной модуляцией. Легко построить и соответствующую
векторную диаграмму. На парциальные коэффициенты модуляции mv т2,..., тк не-
обходимо наложить условие Полоса частот, занимаемая спектром радио-
k
сигнала с многотональной AM, определяется соотношением
А^эфлм
(2-5)
где Qmax — максимальная частота дискретного спектра модулирующего сигнала.
Спектр AM-радиосигнала в общем случае. Б реальной ситуации слу-
чайной модулирующей функции соответствует Фурье-преобразование, в которое
могут входить как дискретные 5-составляющие, так и континуальная (сплошная)
часть (смешанный спектр).
Характер спектра AM-радиосигнала в этом случае можно представить себе каче-
ственно, опираясь на выражение (1.55) и рис. 1.9. Разумеется, форма спектральной
функции AM- радиосигнала будет определяться видом конкретного модулирующего
сшнала s(t) и может радикально отличаться от спектра прямоугольного радиоим-
пульса, изображенного на рис. 1.9.
Пример спектра AM-радиосигнала приведен на рис. 2.6, а.
Рис. 2.6. Амплитудные спектры разновидностей АМ-сигналов:
а — классическая AM; б — балансная AM; в — SSB с частично подавленной несущей;
г — SSB с полностью подавленной несущей
Полоса частот, занимаемая AM-сигналом при произвольном законе модуля
ции, определяется соотношением (2.5), где Qllax — максимальная (по некоторому
избранному критерию, см. раздел 1.6) частота спектральной функции модулиру-
ющего сигнала.
60
2. Модулированные радиосигналы
Корреляционная функция AM-радиосигнала. В формулу (1.83), опреде-
ляющую КФ сигнала с неограниченной энергией,
j г/2
В(т) = Йт— f s(t)s(t-P)dt
Т —J
1 -Т/2
подставим выражение (2.1) для AM-сигнала u(t) - U(t) cos(co0f + <р0), примем <р0 = О
и вычислим интеграл:
т
! т/2
B(x) = lim— f [7(r)cosco0tt/(t-T)cosco0(?-T)^ =
Т—»ос Т J
* -Т'2
* 7'2
= lim— j U(t)U(t-T)cosa>0xdt +
2Т т/2
! Т/2
+ lim— Г [/(t)/7(i-T)cos(2coor-<B0T)6?r.
г->«> 27 •'
1 -Т 2
Можно показать, что с учетом медленного изменения огибающей АМ-сигнала
[7(0 второй интеграл равен нулю как интеграл от быстроосциллирующей функции.
Вынося за знак первого интеграла cos со0т, получаем:
B(t) = |cosco0t ИпД J U(t)U(t-x)dr = ^B„(t)cosw0t, (2.6)
2 ^'Г-7'2 2
1 f7'2
где В,.(т) = рту] г2(7(7)(/(7-т)Д7 есть корреляционная функция огибающей
АМ-сигнала. Но ^cosco0t есть корреляционная функция (1.84) гармоники cos co0t;
тем самым показано, что корреляционная функция радиосигнала с AM есть произ-
ведение КФ огибающей и КФ несущего колебания.
Распределение мощности в спектре AM-радиосигнала. В соответствии
с представлением (2.3) и результатом (1.78), полученным в разделе 1.10, средняя
мощность радиосигнала с тональной AM определяется суммой средних мощностей
его гармонических (несущей, нижней и верхней боковых) составляющих:
„ о п U2 m2U2 m2U2 U2 m2U2
Р — Р + /1 + Р — Р 4- Р. —-------------1--------1------—------1-------
нес бок. в бок н нес бок 2 8 8 2 4
Этот простой результат показывает, что часть мощности АМ-радиосигната (2.3),
расходуемая на передачу собственно информационной составляющей спектра (КПД
амплитудной модуляции), относительно невелика:
Пам Р 2 + т2
и даже при практически никогда не используемом коэффициенте модуляции т = 1
составляет около 33 %. Исторически AM была первым применяемым методом
2.2. Радиосигналы с амплитудной модуляцией
61
модуляции, и небольшое значение Т|АМ в числе многих (в том числе более важных)
обстоятельств явилось стимулом для поисков альтернативных видов модуляции.
Балансная амплитудная модуляция (БАМ) явилась первым и очевидным
шагом в этом направлении. Для более эффективного использования мощности
передатчика решили формировать сигнал с подавленным несущим колебанием
(рис. 2.6, б). Модель сигнала с гармонической БАМ можно записать, отталкиваясь
от выражения (2.3), так:
ыбам(О = U0mcos(Qi + <pno)cos(co0t + <р0) =
mU. r
= ^cos {(“о + + <Ро + <Роо} +
mU
+-^cos{(co0-Q)r + <p0-<pno}. (2.7)
Сигнал (2.7) представляет собой биения двух гармонических колебаний с близ-
кими ( Асо = 2Q ) частотами и одинаковыми амплитудами mt/0/2. На осциллограмме
этих биений (рис. 2.7) можно видеть участки сигнала с квазичастотой со0, однако
в спектре сигнала с БАМ этой гармоники нет. Дело в том, что на интервалах времени
порядка половины периода модулирующего колебания сигнал (2.7) претерпевает
180-градусный скачок фазы, что и вызывает отмеченный эффект.
Рис. 2.7. Сигнал с гармонической балансной AM
Отсутствие информации о фазе и частоте несущего колебания затрудняет де-
модуляцию принятого сигнала, поэтому иногда используют неполное подавление
несущей, передавая так называемый пилот-сигнал. Однако БАМ, несмотря на
энергетическую эффективность, широкого применения не нашла.
Однополосная амплитудная модуляция (сигнал с одной боковой полосой
(ОБП), или SSB (Single SideBand)-cnnian), напротив, самым широким образом ис-
пользуется в системах связи и в настоящее время. Как видно из названия, здесь речь
идет о подавлении одной боковой полосы (см. рис. 2.6, в и г), ведь верхняя и нижняя
62
2. Модулированные радиосигналы
боковые полосы идентичны (являясь зеркальным отражением друг друга), и пере-
даваемая информация при таком подавлении, вообще говоря, не теряется.
Несущее колебание в данном случае может отсутствовать (см. рис. 2.6, г) либо
полностью или частично сохраняться (см. рис. 2.6, в).
Модель SSB-сигнала с тональной модуляцией и подавленной, например, нижней
боковой полосой можно записать в виде суммы
г 1
ussb (О = иоcos (<М + Фо) + -^~cos Ж + Q) * + Фо + ФйО } =
777 67.,
= Uo cos (щ01 + <р0) + —^-cos(Qt + <pQ0 )cos(w0t + <p0) -
77717
----—sin(Qr + <pno)sm(®ot + <p0) =
= Uo j1 + у cos(Qt + <pfl0 ) j- cos(co0t + <p0) -
777 t/n
----^-sin(Qr + <pno )sin(co0r + <PO).
(2.8)
Проделанные преобразования позволяют рассматривать выражение (2.8) как
сумму произведений пары быстро- и медленно меняющихся функций Так как «бы-
стрые» cos(co0t + <p0) и sin(co0i + <р0) находятся в квадратурах, вычислим огибающую:
[7ssb(0 = ^oa 1 + ^-соз^г + Фоо) +—sinTQr ыр120)
V 2 4
т2
=и° v+т + т C0S(Qf+Фп0 )-
(2.9)
Выражение (2.9) показывает, что детектирование SSB-сигнала в режиме, анало-
гичном режиму детектирования классического AM-сигнала (см. главу 7), приведет
к искажению информации — SSB-сигнал следует детектировать иначе. Выигрыш,
получаемый при использовании SSB, сопровождается некоторым усложнением
приемной аппаратуры, тем не менее двукратное сокращение занимаемой сигналом
полосы частот является полезным.
2.3. Радиосигналы с угловой модуляцией
Приняв в выражении (1.14) U(f) = U= const, получим модель радиосигнала с угловой
модуляцией (УМ):
syM(t) = u{t) = Ucos[(t>Qt + <p(t) + <p0} = U cos y(t) (2.Ю)
В гармоническом сигнале (1.1) частота со0 есть не что иное, как скорость изме-
нения полной фазы. Распространяя это определение на произвольный радиосиг-
2.3. Радиосигналы с угловой модуляцией
63
нал, вводят понятие мгновенной частоты как производной (скорости изменения)
полной фазы:
®(O = 4v(O = w0+^-<p(t). (2.11)
at at
Тогда полную фазу как аргумент тригонометрической функции в модели радио-
сигнала (1.14) можно определить как
у(0 = /ш(0Л = юоГ + ф(£) + фо. (2.12)
Напомним, что полная фаза произвольного радиосигнала содержит линейную
часть co0t (линейный набег фазы за время t), фазовую функцию ф(г) и ф0 = const,
которая при ф(Г) = 0 называется начальной фазой (см. раздел 1.1).
Фазовая модуляция (ФМ). Пусть, как и в разделе 2.1, информационный (мо-
дулирующий) сигнал есть s(t) или, с точностью до постоянного множителя, ks(t).
Тогда, приняв ф0 - 0, получим для полной фазы (2.12) выражение \|/(t) = co0t + ks(t),
а для сигнала с фазовой модуляцией
wOM(0 = Hcos{co()r + WO}- (2.13)
Частотная модуляция (ЧМ). Пусть мгновенная частота co(t) = соо + Aco(t), где
Aco(t) = ks(t), тогда при частотной модуляции полная фаза
\|/(t) = J a>(t)dt = coot + k j s(t)dt,
сигнал с ЧМ записывается как
мчм (t) = U cos |co0r + k j s(t) dt}. (2.14)
Сравнивая частотную и фазовую модуляции, легко заметить что эти виды угло-
вой модуляции в силу соотношений (2.11) и (2.12) тесно связаны. А именно: если
модулирующая функция представлена как ks(t), то ЧМ при Aco(t) = ks(t) = dy(t)/dt
соответствует ФМ по закону <p(t) = k|s(t )dt; ФМ при <p(t) = ks(t) соответствует
ЧМ по закону Aco(t) = kds(t)/dt.
Гармоническая угловая модуляция (УМ). Установленная связь особенно
очевидна при выборе гармонического модулирующего сигнала s(t) = cos Qt. Тогда
ФМ-сигнал можно записать как
MOM(t) = t/c°s(cOor +AcpcosQt), (2.15)
где Аф — девиация фазы.
Для ЧМ-сигнала од г) = со0 + Асо cos Qt с полной фазой
V(t) = co0t + k j s(t)dt = co0t + -^sin + Фо-
Здесь Асо — девиация частоты, и ЧМ-сигнал можно записать как
M4M(t) = f/cos co0t +—sinQr + ф, ]• (216)
64
2. Модулированные радиосигналы
Вводят индекс гармонической угловой модуляции р, под которым при частотной
модуляции подразумевают отношение Д<о/£2, а при фазовой мод> ляции - девиацию
фазы Дф, и анализируют сигнал
"фм(О = и cos (ф/ + Psin Ш + Фо) <2'17)
Спектральный состав радиосигнала при гармонической УМ. Восполь-
зуемся известным разложением
e'₽s,n' = £ /Ж
где Jk — функция Бесселя 1-го рода порядка k от вещественного аргумента.
ЗАМЕЧАНИЕ 2.1 --------------------------------------------------------
Функции Бесселя, являющиеся решением дифференциального уравнения
Бесселя, табулированы [10]. Примерный вид графиков первых четырех
функцийJ/Р) показан на рис. 2.8.
Рис. 2.8. Функции Бесселя
Перепишем (2.17) в виде
«ум(0 = Re £ Jk$)e^> = U £ J* (P)cos [(<о0 + Ш)Г+ ф0]. (2-18)
I J k—
На рис. 2.9 представлен амплитудный спектральный состав радиосигнала с УМ.
Особенностями этой спектрограммы являются бесконечное количество гармоник
и необязательно монотонный характер убывания коэффициентов U |/4(Р)|, что
связано с колебательным характером поведения функций Бесселя.
Рис. 2.9. Амплитудный спектр радиосигнала
с гармонической угловой модуляцией
2.3. Радиосигналы с угловой модуляцией
65
Структура выражения (2.18) говорит о потенциально большем, чем при AM,
КПД угловой модуляции, т]ум > Т|АМ. Из графиков, приведенных на рис. 2.8, напри-
мер, видно, что при некоторых значениях Р в разложении (2.18) вообще не бу dew
компоненты на несущей частоте о>0.
Спектральный состав радиосигнала с гармонической УМ при р « 1.
При этом условии можно принять cos(P sin Qi) = 1, sin(P sin Qi) = P sin Qi и пред-
ставить сигнал (2.17) в виде
w(i) = [/cos(PsinQi)cos(co0i + <р0) -t/sin(PsinQr)sin((not + <р0) =
~ U cos(co0t + <р0) - pt7 sin Qi sin(co0i + <p0) =
= U cos(co0r + <p0) + ^-cos[(co0 +
Q)i + <p0]-
-^c°s[(wo-^X + <Po]-
(2.19)
С груктуры амплитудных спектральных характеристик радиосигналов с гар-
монической угловой при Р « 1 и с гармонической амплитудной модуляцией (см.
рис. 2.3, а) аналогичны. На рис. 2.10 приведена соответствующая радиосигналу
с гармонической УМ при Р « 1 векторная диаграмма, по< троенная так же, как
векторная диаграмма радиосигнала с тональной AM (см. рис. 2.5). Отрицательный
знак перед компонентой ip[/cos(w0 -Q)t (180° — фазовый сдвиг) обусловливает
изменение направления вектора UyM относительно вектора U во времени, что харак-
терно для угловой модуляции. Заметим, что в соответствии с рис. 2.10 меняется во
времени и модуль вектора (7ум, хотя амплитуда радиосигнала с УМ должна быть
постоянной. Это следствие довольно грубого приближения, на основании которого
записано выражение (2.19). Впрочем, с учетом условия Р « 1 эти изменения, как
и изменения направления UyM, весьма малы.
Рис. 2.10. Векторная диаграмма радиосигнала с гармонической УМ
при малом индексе модуляции
3 №675
66
2. Модулированные радиосигналы
Эффективная ширина спектра сигнала с гармонической УМ. При
k > Р величина |/Л(Р)| быстро убывает. Поэтому в разложении (2.18) принимают в
расчет все гармоники с номерами k < Р + 1, а остальными пренебрегают. Тогда по-
лоса частот, занимаемая спектром сигнала с гармонической угловой модуляцией,
определяется как
Д®эфум=2й(Р + 1). (220)
При Р » 1 эффективная ширина спектра сигнала с гармонической УМ равня-
ется удвоенной девиации частоты:
Дсо . VM = 20Q = 2—Q = 2Дсо.
эф ум '
При р « 1 эффективная ширина спектра сигнала с гармонической УМ равня-
ется удвоенной частоте модуляции:
А^эфум ~ 2^-
2.4. Фурье-анализ модулированных
радиосигналов
Анализ спектрального состава сигналов с AM и УМ в разделах 2.2 и 2.3 проводился
на основании разложений (2.3) и (2.18), полученных с помощью элементарных
тригонометрических преобразований и представляющих соответствующие сигналы
в виде суммы гармоник; аппарат преобразования Фурье или рядов Фурье, пред-
назначенный для спектрального анализа сигналов, не использовался (за исключе-
нием обсуждения спектра AM-сигнала в общем случае). Это объясняется тем, что
указанные разложения в общем случае не являются рядами Фурье, содержащими
компоненты спектра на последовательности эквидистантно расположенных частот
0, со,, (см. замечание 1.4).
Такая последовательность в рассматриваемых случаях возникает лишь тогда, ког-
да отношение <oo/Q принадлежит множеству рациональных чисел (иными словами,
необходимо существование такой частоты со(, для которой отношения co0/cOj и Q/co1
являются целыми числами). Следовательно, в общем случае рассматривавшиеся
модели сигналов периодическими функциями не являются и разложению в ряд
Фурье подвергаться не могут.
Тем не менее разложения (2.3) и (2.18) являются дискретными гармоническими
рядами (но не рядами Фурье). Отсюда следует полезный общий вывод: непериоди -
ческая функция может иметь дискретный спектр (в подобных случаях математики
говорят о «почти периодических» функциях).
Что касается преобразования Фурье (1.42), то оно с использованием
8-формализма может быть применено для отыскания спектральных функций мо-
дулированных радиосигналов. Использовав соотношение (1.73), можно получить
(читателю рекомендуется проделать это самостоятельно) для любого сигнала, пред-
ставленного в разделах 2.2 и 2.3 в виде суммы гармоник, спектральную функцию,
2.4. Фурье-анализ модулированных радиосигналов
67
являющуюся суммой 8(со)-функций с соответствующими коэффициентами, рас-
положенных в точках ±со0, ±(со0 ± Q), ±(соо ± 2Q)... частотной оси. Но эта полезная
как упражнение операция че добавит ничего нового к уже полученным сведениям
о спектральном составе модулированных радиосигналов.
Узкополосность радиосигнала с AM. Рассмотрим условие узкополосности
AM-радиосигнала подробнее. Так, в разделе 1.6 при анализе спектра прямоуголь-
ного радиоимпульса выяснилось, что умножение видеоимпульса на гармониче-
скую функцию cos ®ог в спектральной области приводит к смещению спектра
видеоимпульса влево и вправо по оси частот на величину ±со0 (см. рис. 1.9). Если
спектральная функция информационного сигнала U(t) = ks(t), который являет-
ся, как следует из выражения (2.1), огибающей амплитудно-модулированного
радиосигнала, есть Sv (со), то спектр AM-радиосигнала может быть представлен
выражением (1.55)
•?(®) = |{Л (со + со0) + 5,,(со-со0)},
универсальность (независимость от вида огибающей) которого показана в разде-
ле 1.9 при рассмотрении преобоазования Фурье гармонического сигнала.
Следовательно, вопрос выполнения требования (2.2) есть вопрос выбора соо при
заданной величине Асо^ спектра информационного (модулирующего) сигнала,
который, в свою очередь, зависит от параметров s(t). В подавляющем большинстве
радиотехнических приложений спектр модулирующего сигнала концен грируется
в области нулевой и низких частот (видеосигнал, характеризуемый «низкочастот-
ным спектром», см. раздел 1.6), и тогда его максимальная частота совпадает со
значением Аш. :
эф V
со = Асо . .
max г эф г
Эффективная ширина амплитудного спектра соответствующего радиосигнала
в два раза больше-.
Доз = 2Дсо . = 2со
эф г эф v max v
При изучении радиосигналов (в том числе модулированных) традиционно и для
упрощения записи максимальную частоту спектра огибающей радиосигнала обо-
значают QmaK = соп1ах и условие узкополосности радиосигнала (2.2) записывают как
2Q 2F
—щх = —(2 21)
“о /о
Узкополосность радиосигнала с УМ. Преобразуем выражение (2.10), при-
няв ср0 = 0:
u(t) = U cos {со01 + ср(Г )} = U cos <р(Г ) cos co0f - V sin ср(Г) sin o)0t. (2.22)
Радиосигнал с УМ можно трактовать как сумму двух радиосигналов с AM. Несу-
щая частота этих AM-радиосигналов со0, в качестве огибающих выступают функции
Ucos <р(г) и Usin ф(?). Следовательно, условие узкополосности (2.21), гдесравнива-
68
2. Модулированные радиосигналы
ются максимальная частота спектра огибающей Qraax и несущая частота радиосигна-
ла <о0, сохраняет силу и для радиосигналов с УМ, но вместо максимальной частоты
спектра огибающей нужно рассматривать максимальную частоту спектральной
функции cos <p(t). Своеобразие угловой модуляции проявляется, таким образом,
в том, что максимальную частоту спектра модулирующего сигнала определяют
косвенно по соотношению (2.20) как
йтв=Я(Р + 1)-
Представление узкополосного радиосигнала в форме (2.22) иногда называют
квадратурным.
Пример 2.1. Максимальная частота спектра воспринимаемых человеком
звуковых сигналов не превосходит 20 кГц (а практически существенно меньше),
и поэтому радиовещательные станции, используя в качестве несущих частоты
порядка 150 кГц и выше, работают уже с узкополосным радиосигналом. Эффек-
тивная ширина спектра телевизионного радиосигнала составляет около 6,5 МГц,
и поэтому самый низкочастотный телеканал использует несущую частоту порядка
50...60 МГц, при этом отношение 2Fmax//0 = 0,1, что с инженерной точки зрения еще
удовлетворяет неравенствам (2.2) и (2.21). Для того же телесигната, передаваемого
в дециметровом диапазоне, отношение ‘2Fm^/f(i оказывается ветичиной порядка
0,01 и менее.
ЗАМЕЧАНИЕ 2.2-----------------------------------------------------
Указание об относительной медленности изменения огибающей, которое
было сделано при введении понятия радиосигнала в разделе 1.1, прямо
связано с представлением о радиосигнале как о сигнале узкополосном.
Не останавливаясь на строгом определении понятия огибающей (огиба-
ющая узкополосного AM-радиосигнала очевидна на рис. 2.2, в), заметим,
что при рассмотрении графика или осциллограммы радиосигнала (2.1),
у которого FmaK = /0, явно выделить огибающую такого сигнала было бы
невозможно.
ЗАМЕЧАНИЕ 2.3---------------------------------------------------
Гармоническая функция (1.1) является простейшим и предельно узко-
полосным радиосигналом с огибающей U = const. В используемых нами
обозначениях для сигнала (1.1) Fraax = 0 (спектром огибающей является
8-функция, существующая при со = 0), Дсо^;, = 0 и отношение 2Fm^/f() = 0.
2.5. Амплитудно-импульсная модуляция
Наряду с рассмотренными в современной радиотехнике широко используются
разнообразные виды импульсной модуляции (ИМ). В этом случае в качестве моду-
2.5. Амплитудно-импульсная модуляция
69
лирующего несущее колебание сигнала выступает предварительно подвергнутая
так называемой предмодуляции (иногда говорят «взвешенная») непрерывным
информационным сигналом s(f) последовательность видеоимпульсов, обычно
прямоугольных. Часто используется периодическая последовательность, например
сигнал (1.6) r(t-kT), k = 0, ±1,±2...
Рассмотрим конкретную модель радиосигнала с амплитудно-импульсной моду-
ляцией — АИМ-радиосигнал (рис. 2.11):
cosw0i,
(2.23)
где U{ 1 + и cos — характерный для однотональной AM (см. раздел 2.2) множи-
тель, в рассматриваемом случае модель информационного сигнала s(t).
Рис. 2.11. Радиосигнал с амплитудно-импульсной модуляцией
Сумма r(t-kT) — периодическая (с периодом Т) последовательность
видеоимпульсов (1.6), имеющих единичную амплитуду, длительность т и чаще
всего прямоугольную огибающую. Впрочем, при непосредственной реализации
«АИМ(?) по алгоритму (2.23) форма (вершина) видеоимпульсов будет искажена, но
если длительность импульсов последовательности существенно меньше периода
модулирующей функции (т « 1/(2лО)), этой деформацией можно пренебречь.
С учетом соображений, приведенных в разделе 2.4 о Фурье-анализе модулированных
радиосигналов, очевидно, что рассматриваемый сигнал в общем случае периодиче-
ским не является, поэтому следует говорить не о спектре Фурье, но о спектральном
составе АИМ-сигнала (2.23).
Однако для последовательности -kT) ряд Фурье существует. Ис-
пользуем представление ряда Фурье в вещественной форме (1.30):
\ (О = V + Е A cos(fao/ + <р J.
*=1
70
2. Модулированные радиосигналы
Тогда для последовательности радиоимпульсов
k=
У, r(t-kT) cosco0t = ^-cosw0r + -£Aicos{(co0±^co1X±(pJ =
u—. J 4
fln A fz
= — cos coni +—cos 1 (co„
2 2 u
-co1)t-<p1} +
—cos
2
{(со0 + w1)t + <p1} + ^-cos{(co0 - 2с0] )t -<р2} +
{(й)0+2й)]У + ф2}-1-...
(2.24)
+—cos
2
Здесь CO] = 2it/T. Последовательность (2.24) есть простейший вид АИМ-радио-
сигнала, который называют амплитудно-манипулированным (АМн). Амплитудный
спектр этого сигнала приведен на рис. 2.12, а.
a
Рис. 2.12. Спектры: a — амплитудно-манипулированного сигнала;
б — соответствующего ему радиосигнала с АИМ
ЗАМЕЧАНИЕ 2.4-------------------------------------------
При получении разложения (2.24) вновь встречаемся со смещением
комплексной спектральной функции видеосигнала по оси частот на
величину си0. Здесь рассматривается дискретный спектр и использована
вещественная форма ряда Фурпе — отрицательных частот, как и в (1.30),
нет. поэтому спектр видеопоследовательности смещен на величину со0
вправо. Сопоставляя (1.30) и (2.24), следует еще раз обратить внимание
на удвоение эффективной ширины спектра радиосигнала относительно
спектра соответст вующего видеосигнала (огибающей); каждой &-й ком-
2.5 Амплитудно-импульсная модуляция
71
поненте исходного спектра с амплитудой А к в правой части соотношения
(2.24) соответствует пара компонент
А А
у cos{(co0 -&С0, У - <р J + -^cos{((D0 + kto')t + <р J.
Заметим, что уже АМн-радиосигнал не является в общем случае пе-
риодическим
Далее, подставляя (2.24) в исходное для АИМ-радиосигнала выражение (2.23),
мы получим сумму произведений вида
anU
МАИм(О _
mcosil" -cos«»0t +
2
л U
{1 + mcosQf}cos{(co0 - ©j )i - (р1} +...
(2.25)
Но каждое входящее в (2.25) слагаемое будет не чем иным, как классическим
представлением радиосигнала с тональной AM, и может быть преобразовано по
формуле (2.3), например:
{1 -ь zncosQf}cosco0t =
aJJ manU , .
= -=—cos аг/ +—— cos a>„ +Q t +
2 0 4 v ° ’
maQU
4
cos(co0 -Q)t.
Следовательно, в спектре АИМ-радиосигнала около каждой составляющей,
соответствующей спектру АМн-радиосигнала (2.24) на частотах со0, со0 ± Юр.., по-
явится пара боковых компонент на частотах ш0 ± Q, a>0 ± Wj ± Q... соответственно
(см. рис. 2.12, б).
ЗАМЕЧАНИЕ 2.5-------------------------------------------------------
Огибающей действительных, существующих в области о) > 0 дискретных
амплитудных спектров АМн- и АИМ-радиосигналов (см. рис. 2.12, a
и б), является с точностью до постоянного множителя и положения на
частотной оси (сдвиг вправо на соо) модуль спектра представительного
импульса видеопоследовательности r(t), что следует из выражения (1.48)
Ct=^(kco,).
С учетом использованных при записи (2.23) обозначений это функция
2
где т — длительность видеоимпульса r(t).
72
2. Модулированные радиосигналы
2.6. Внутриимпульсная модуляция
Для многих радиотехнических приложений большой интерес представляют им-
пульсные радиосигналы, частота заполнения которых изменяется по некоторому
закону. Рассмотрим радиоимпульс с линейной частотной модуляцией (ЛЧМ-сигнал):
частота заполнения радиоимпульса с длительностью Т и прямоугольной огибаю-
щей (1.4) меняется по закону а>(£) = соо+ yt, |t| < Т/2. Полная фаза в соответствии с
выражением (2.12) есть (при <р0 = 0)
V(0 = J w(O dt = ю0Г + <р(Г) = щ0Г + Ц-,
гак что ЛЧМ-сигнал представляется выражением
Г
5(£) = Hcos wot + ^4, |t|<7/2. (2.26)
Примерный график ЛЧМ-сигнала, законы изменения частоты и фазы показаны
на рис. 2.13.
Рис. 2.13. Сигнал с линейной частотной модуляцией
Особенностью ЛЧМ-сигнала является, в частности, возможность управлять его
базой Т Д^ф (введенным в разделе 1.6 параметром), при постоянной длительности
импульса регулируя девиацию частоты. При значениях базы Т Д/^ >100 спектр
ЛЧМ-радиоимпульса хорошо аппроксимируется [3] финитной функцией частоты
с прямоугольной огибающей:
= сое
Д<о . До>
эф :
а>„-------,соп + —
0 2 0 2
а Дсо^ радиоимпульса при этом значении базы совпадает с диапазоном изменения
мгновенной частоты (удвоенной девиацией частоты) уТ.
2.7. Комплексная огибающая радиосигнала
73
ЗАМЕЧАНИЕ 2.6-----------------------------------------------------
В силу этого свойства сигнал с ЛЧМ играет особую роль в радиоизмери-
тельной технике: он используется в таких важных приборах, как измери-
тели амплитудно-частотных характеристик (АЧХ) и анализаторы спектра.
Корреляционная функция ЛЧМ-сигнала. Энергетический спектр сигнала
(2.26) определяется как
। • i2 nV2 Дсо . Дсо .
^(®) = |^4M<®)| = “е “о------2^’,С°о + —Г- '
Обратимся к соотношению (1.89) и вычислим корреляционную функцию ЛЧМ-
сигнала:
. (уТ А
1 " ТгГ/2 шо+ГГ/2 -.27,510! Т I
В(т) = — j Wr(co)e7“TJco =--- j coscotJco =----------A-—-coso>0t. (2.27)
2K- 2y ^--rT/2 2 ILT
2
Читателю рекомендуется самостоятельно обосновать выбор пределов интегри-
рования в (2.27). Из этого выражения следует важный вывод: ширина главного
лепестка КФ обратно пропорциональна девиации частоты сигната. Следовательно,
при заданной девиации можно, увеличивая длительность (а следовательно, и энер-
гию) сигнала (2.26), получить узкий главный лепесток КФ с большим значением
В(0) = Е. Говорят о хороших корреляционных свойствах ЛЧМ-сигчала. Такими
свойствами обладают также некоторые радиоимпульсные сигналы с фазовой ма-
нипуляцией (речь о них пойдет в разделе 5.3 главы 5, посвященной оптимальной
фильтрации сигналов).
ЗАМЕЧАНИЕ 2.7----------------------------------------------------
Сигналы этого типа были предложены и изучались в основном для ис
пользования в сфере радиолокационных приложений, но в настоящее
время они находят все более широкое применение в телекоммуникаци-
онных системах при решении задачи повышения помехоустойчивости
радиоканалов.
2.7. Комплексная огибающая радиосигнала.
Взаимная корреляционная функция
модулированных сигналов
При построении векторной диаграммы радиосигнала с гармонической ампли-
тудной модуляцией в разделе 2.2 было введено понятие комплексной огибающей
радиосигнала.
74
2. Модулированные радиосигналы
Поставим в соответствие общему выражению для радиосигнала (1.14)
u(t) = U (i)cos {со0Г + tp(O + <₽„} = ^(Ocos у (Г)
комплексный сигнал
и(Г) = [/(Ое7{ш“'+ч><',+’'п} =[/(Г)е;{ф('>+ф"}е7Ш»' = Г, (г>'“»',
где U= — комплексная огибающая радиосигнала.
Очевидно, что |17m(t)| = U(t) и arg Um(t) = <р(£) + Фо. Вещественный сигнал u(t)
определяется как
n(O = Re{«(O} = Re{nm(t>w}.
Предполагается, что u(t) удовлетворяет условию узкополосности (2.2).
ЗАМЕЧАНИЕ 2.8--------------------------------------------------------
В настоящем разделе и разделе 2.8 будем полагать огибающую радиосигна-
ла [7(f) > 0, относя возможные отрицательные значения U(t) к поведению
полной фазы радиосигнала.
ВКФ модулированных сигналов. Рассмотрим взаимную корреляционную
функцию двух финитных узкополосных радиосигналов (1.14) с ограниченной
энергией
Н;(0 = Ц(0 cos + Ф1 (0}> I е [0- Г],
ц2(Г)=П2(Г)со5{(ОоГ + <р2(0},Гб [О, Г].
Взаимная корреляционная функция сигналов с ограниченной энергией (1.82)
была введена в разделе 1.11:
В12(т) = j (7, (r)cos {©/ + <Pj (t)}(72 (Г - t)cos {co0(t - t) + <p2 (t - i)]dt =
= ±] Ut(t)U2(t - T)cos{2w0r - co0t + cp/t) + <р2(Г - t)}dt +
j Ut(t)U2(t - t)cos {wot + ф,(t) -<p2(t- t)}dt.
Интеграл, содержащий быстроосциллирующий множитель
cos{2<a0r - со0т + ф, (Г) + ф2(Г - т)},
может быть принят равным нулю. Это следует из условия узкополосности сигналов
п,(г) и u2(t) (см. раздел 2.1).
2.7. Комплексная огибающая радиосигнала
75
Поскольку
cos
рассмотрим второй интеграл
{со0т + Ф, (Г) - ф2 (Г - т)} = Re(exp Дсоот + (О - <р2 (f - т)}),
В12(т) = |ке- j Ui(t)K2(t-T)eJ<fl(r)e ^‘^e^dt =
= lRe^J[71(t|^
=|Re Н^М’иа-^р“’т
z [V—’ 7
•>'(,’[72(t ?“»x
= ^Ке{Д2га(т)^"'},
(2.28)
где H2m(t) — комплексные огибающие сигналов u\t) и zz2(t),
a B12ra (t) = j Uim (t)U'2m (t - x)dt — ВКФ комплексных огибающих.
Интегрирование в выражении (2.28) ведут по интервалу, на котором подынте-
гральное выражение отлично от нуля
Пример 2.2. Определим КФ радиоимпульса с прямоугольной огибающей (1.59):
t/COS((D(/ + ф0), t е [О, Г],
О, ££[0,Л-
w(t) =
КФ — это частный случай ВКФ (см. раздел 1.11). КФ комплексной огибающей
радиоимпульса
Вт(х) = $U(t)e^U(t-T)e "’dt = [72(Т-|т|), те [-Г,Т].
В(т) = -Ке|Вт(т)е;“’х| — корреляционная функция вещественного радиосиг-
нала, равная в данном случае B(t) = ^-(T-|t|]coso)0t, те [-Г, Т] (внеуказанного
интервала В(т) = 0). График В(т) приведен на рис. 2.14. Получили уже известный
результат (2.6): корреляционная функция радиосигнала равна произведению КФ
огибающей и КФ высокочастотного заполнения. Отметим, что В(т) не зависит от
начальной фазы радиоимпульса ф0.
Рис. 2.14. Корреляционная функция радиоимпульса с прямоугольной огибающей
76
2. Модулированные радиосигналы
2.8. Аналитический сигнал
и преобразование Гильберта
Понятие комплексной огибающей, введенное в разделе 2.2 и рассматривавшееся
в разделе 2.7, тесно связано с понятием комплексного сигнала
u(t) = Um(t)eja"‘ = = U(t)eJV(,\ (2.29)
где y(t) — полная фаза.
В представлении комплексного сигнала (2.29)
M(i) = H(r)cosy(f) + jU(t)sin y(f) (2.30)
в виде суммы вещественной, совпадающей с исходным сигналом
u(t) = U(£)cosу(0 = U(t)cos {co0t + <p(Z) + <р0}, (2.31)
и мнимой, [/(t)sin *Р(£) = £/(£) sin{co0£ + <p(f) + <p0}, частей, в частности, различают
(см. раздел 1.1) огибающую U(t), фазовую функцию <p(t) и несущую частоту со0
радиосигнала w(t).
Дальнейшим обобщением понятия комплексного сигнала, соответствующего
вещественному сигналу u(t), является представление
Z(t) = u(t) + ju(t). (2.32)
Здесь u(t) — некоторый сигнал, определенным образом связанный {сопряжен-
ный) с исходным сигналом u(t).
Для сигнала (2.32) вводят физическую огибающую
|Z(O| = 7«2(0+»2(O- <А33>
полную фазу
T(r) = arctg^|| (2.34)
u(t)
и мгновенную частоту
= ^(0 = H\t)u{t)-u(t)u'(t) (2 35)
dt u2(t) + u2(t)
Сигнал Z(t) может быть представлен и в показательной форме:
Z(0 = Zm(t)e;“<, (2.36)
где Zm(t) — комплексная огибающая Z(t), a o>z — «несущая» частота.
2.8. Аналитический сигнал и преобразование Гильберта
77
При сравнении выражений (2.30) и (2.32) выясняется, что представление (2.30)
удовлетворяет условиям (2.33-2.35) в том смысле, что огибающая комплексного
сигнала совпадает с физической огибающей сигнала u(t),
[/(r) = |Z(r)|,
полная фаза и мгновенная частота Z(r) также совпадают с соответствующими
параметрами w(f).
Однако в представлении (2.36) комплексная огибающая Zm(t) не обязательно
совпадает с комплексной огибающей Um (t). Вид Zm (t) зависит от выбора часто-
ты Действительно, выражение (2.29) можно записать и так:
u(r) = [/m(r)ew = t7m(z>K“-+A“)r =
= Umi(t)eJa,t =иа)е^щ^мУш1, (2.37)
где = U(t)eJ^(,)+^1'1 — «новая» комплексная огибающая й(£), а со, — «новая»
несущая частота. Соотношение (2.37) демонстрирует зависимость комплексной
огибающей Zm(f) от выбора частоты coz.
Если вещественный сигнал u(t), для которого ищут комплексное представление
Z(t), представлен «естественным» образом в форме (2.31), где явным образом вы-
делена его несущая частота со0, и (р(Г) не содержит линейной составляющей фазы
со0Г, то проблема выбора a>z для записи (2.36) решается просто: со0 = (0z, и огибающая
?(t)| = U(t). При этом гарантируется выполнение обеспечивающих использование
в качестве физической огибающей и полной фазы сигнала s(f) требований к функ-
циям U(t) и ЧДГ) соответственно.
Эти требования [11] таковы:
1. Абсолютное значение сигнала u(f) не превышает значений огибающей U(t):
2. Касательные, проведенные к графикам U(t) и u(t) в тех точках, где предыдущее
неравенство превращается в равенство, совпадают, что означает если U(t) - \и( Г)|,
dU(t) Jlu(t)|
то---------=-----—.
dt dt
3. Малым вариациям u(t) соответствуют малые вариации U(t) и 'P(t).
4. Необходимо, в частности, чтобы для простого гармонического колебания
u(t) = U cos (co0t + <р0) выполнялось
№=U
и полная фаза искомого Z(t) была равна
Т(Г) = со/ + <р0.
5. Полная фаза и мгновенная частота не должны зависеть от мощности сигнала.
78
2. Модулированные радиосигналы
Эти требования выполняются, когда мы ставим в соответствие вещественному
узкополосному сигналу u(t) = Ucos {co0t+ <p(t)} комплексный сигнал
Z(t) = u(t) + jH(t) = U cos {coo£ + <p(0} + jU sin{co0t + <p(t)},
так что
w(t) = U sin {co0t + <p(t)}.
Установлено, что при формировании комплексного сигнала Z(t) для любого ве-
щественного сигнала u(t). не обязательно представленного в виде (2.31), требова-
ния 1-5 выполняются, если мнимую часть комплексного си] нала Z(t) определяют,
используя соотношение
<(t) = l = (2.38)
n£t-t'
которое называется преобразованием Гильберта Нетрудно заметить, что соотноше-
ние (2.38) можно трактовать как свертку сигнала u(t) и функции 1/(лГ), а результат
преобразования Гильберта (2.38) — как реакцию цепи с импульсной характеристи-
кой l/(nt) (рис. 2.15) при подаче на ее вход сигнала u(t).
Рис. 2.15. Преобразование Гильберта
На рис. 2.16 показан график h(t) = \ (nt). Очевидно, что четырехполюсник с та-
кой импульсной характеристикой физически нереализуем, так как h(t) * 0 при t < 0.
Рис. 2.16. Импульсная характеристика, соответствующая
преобразованию Гильберта
Тем не менее формально найдем комплексный коэффициент передачи такого
четырехполюсника:
7 1 , 17 coscot 17 sin cot, 17sincot,
Х(со) = f —e:dt = - [-------dt-j- [-------dt = -j- [-----dt, (2.39)
Д nt n Д t n Д t n Д t
так как интеграл от нечетной функции cos(cot)/t в симметричных пределах равен
нулю. Интеграл (2.39) принимает слетующие значения:
2.8. Аналитический сигнал и преобразование Гильбеота
79
следовательно,
sincof ,
------dt = О,
t
я,
со < О,
<о = 0,
со > О,
Л
К(со) = < О,
со < О,
со = 0,
со>0.
(2.40)
Графики К(ю) и фазочастотной характеристики <р(со) показаны на рис. 2.17.
1ВД|.
Г”
---------------►
О и
а
<р(со)
------► тс/2
б со
-тс/2 И--------
б
Рис. 2.17. Графики: а — АЧХ; б — ФЧХ цепи, осуществляющей
преобразование Гильберта
ЗАМЕЧАНИЕ 2.9----------------------------------------------------
При обсуждении некоторых проблем преобразования Гильберта при-
шлось привлечь уже известные учащимся из курсов теоретических основ
электротехники или теории электрических цепей, но еще не введенные в
настоящем курсе понятия импульсной реакции и коэффициента передачи
четырехполюсника. Они подробно рассматриваются в главе 4.
Пример 2.3. Найдем, опираясь на соотношение (2.40), функцию, сопряженную
по Гильберту с гармоническим колебанием w(t) = U cos (co0t + <р0):
w(t) = U cos
it
°V + <Po-2
= C7sin(co0t + <p0).
Как видно, преобразование Гильберта обеспечивает необходимый выбор мнимой
части комплексного сигнала для гармонического п(Г) (см. требование 4 к функциям
огибающей и полной фазы, приведенное ранее в этом разделе). Операция (2.39)
сдвигает все гармонические составляющие сигнала по фазе на ±л/2 и уничтожает
постоянную составляющую сигнала.
80
2. Модулированные радиосигналы
Вводят также обратное преобразование Гильберта
тгJ t-t
(2.41)
Преобразование (2.41) является сверткой сигнала й(г) и импульсной реакции
й(0 = -4=А(-0-
(2.42)
Комплексный коэффициент передачи, соответствующий четырехполюснику
с импульсной реакцией (2.42), есть функция
K(®) = W,
со < О,
со = О,
j, со > 0.
Свойства преобразования Гильберта
1. Прямое и обратное преобразования Гильберта линейны, в чем можно убедиться
непосредственно: Н[ ри{ (t) + qu2 (£)] = /?Н[ (t)] + ^Н[м2 (Г)].
2. Ядро преобразования Гильберта 1 /(л£) есть нечетная функция, поэтому сигнал,
сопряженный по Гильберту с постоянным во времени сигналом, тождественно
равен 0.
3. Если при каком-либо значении t сигнал u(t) достигает экстремума, то в окрест-
ности этого значения t сигнал u(t) проходит через 0 (простейшей иллюс тра-
цией этого положения является рассмотренный пример преобразования по
Гильберту гармонического сигнала). Аналогичное преобразование функции
U sin (co0i + <р0):
Н{Usin (со0£ + ср0)} = —Ucos (cooi + ср0).
ЗАМЕЧАНИЕ 2.10 ------------------------------------------
Очевидно, что вычисления интегралов по формулам (2.38) и (2.41), как
правило, не могут не вызывать затруднений, так как интервал интегриро-
вания содержит точку t = tв которой подынтегральное выражение может
с гремиться к бесконечности; то есть чаще всего речь идет о несобствен-
ном интеграле. В таких случаях вычисляют главное значение интеграла
в смысле Коши [12], а именно: пусть задана функция g(x), такая, что
limg(x) —> оо, а < b < с. Тогда главным значением интеграла будет
х->й
с й-е с
fg(x)dx = lim- j g(x)dx + j g(x)dx •, e>0.
£—>0
Й+Е
Некоторые примеры преобразования Гильберта приведены в табл. 2.1.
2.8. Аналитический сигнал и преобразование Гильберта
81
Таблица 2.1. Примеры преобразования Гильберта
u(t) = H-‘[w(r)] = -- f ^-dt' n^t-t w(0 = H[«(0]=-[—e/r л Д t-t
H<r/2- > [0, |t|> T/2 u, In л t-T/2
t + T/2
1 1 + f4 t 1 + t2
cosT Sint
sin Г -cost
sint t 2 . 2 -sin t (t 1 —cost t
5(0
1
тгГ
Аналитический сигнал. Комплексный сигнал (2.32) Z(t), сформированный
для вещественного сигнала u(t) с помощью преобразования Гильберта, называ-
ется аналитическим сигналом. Для него справедливы соотношения (2.33-2.35).
Смысл термина «аналитический» состоит в том, что при замене аргумента t
аргументом £ + /Т], то есть при переходе к комплексной переменной, и(^ + ;т|) как
функция комплексной переменной оказывается функцией аналитической (при
всех т| > 0) [3].
Следовательно, аналитический сигнал, соответствующий видеоимпульсу (1.4),
записывается так:
1(0=
l-j—In
л
t-T/2
t + T/2
И< Т/2,
\t\>T/2.
При исследовании радиосигналов полная фаза T(t) в расчетах по формуле (2.34)
представляется в виде
4/(t) = co0t + (p(t),
где <р(0 не содержит слагаемого типа ДюГ, линейно зависящего от времени. Тем
самым произвол в выборе несущей частоты устраняется.
ЗАМЕЧАНИЕ 2.11 -------------------------------------------------
Комплексное представление гармонического сигнала Ucos (.<+>,{ + <р0),
сформированное с помощью преобразования Гильберта, совпадает с его
представлением в рамках метода комплексных амплитуд.
82
2. Модулированные радиосигналы
Сформулируем важное правило: при произвольных U(t) и 'V(t) комплексный
сигнал вида
u(t) = U(t)e^
совпадает с аналитическим (сформированным по Гильберту) с тем большей точ-
ностью, чем более этот сигнал узкополосен. В случае предельно узкополосного
(гармонического) сигнала наблюдается полное совпадение.
ЗАМЕЧАНИЕ 2.12 ---------------------------------------------------
Произвольный комплексный сигнал Z(i), сформированный по Гильберту,
аналитичен вне зависимое ги от своей широкополосности.
Спектральная функция аналитического сигнала. Пусть сигналу u(t)
соответствует преобразование Фурье 5(со). Для определенности примем 5(0) = 0
и воспользуемся результатами (2.40). Тогда при со > 0 5(со) = -;5(со); при со < 0
5(со) = у'5(со).
В силу линейности преобразования Фурье Sz (со) = 5(со) + j'5(co) и
5^(со) =
5(co) + j(-j)5(co) = 25(co),
S(a) + jjS(a) = 0,
со>0,
со<0.
Спектральная функция аналитического сигнала существует (отлична от нуля)
только на положительных частотах. Примерный вид графиков |5(со)| и |5z(co)|
показан на рис. 2.18.
Рис. 2.18. Спектр вещественного сигнала (верху) и соответствующего ему
аналитического сигнала(внизу)
Будем искать спектральную функцию комплексной огибающей аналитического
сигнала Zm(t). Поскольку
Z(t) = Zm(t)e'a°',
Zm(t) = Z(t)e^‘,
Контрольные вопросы и задания
83
спектральная функция Zm(t)
St (со) = J Z(t)e-}a°'e-)a,dt = J /(г)е'Лш+Ш|,,'<й = 4(со + со0).
Возможный вид модулей спектральных функций 5Z (ю) и ^(<й) показан на
рис. 2.19. Особо следует отметить, что модуль спектральной функции 5^ (со) не
обязательно симметричен относительно оси со = 0. Если |5(со)| несимметричен от-
носительно со = со0, что характерно для сигналов со смешанной амплитудно-угловой
модуляцией, то и 5Z (со) несимметричен относительно со = 0.
Рис. 2.19. Спектры аналитического сигнала (вверху)
и его комплексной огибающей (внизу)
Во всяком случае, спектральная функция Sz (со) отлична от нуля в области
отрицательных частот. Следовательно, комплекс гая огибающая аналитического
сигнала аналитической функцией не является и вещественная и мнимая части
Zm (t) не сопряжены по Гильберту.
Ряд преимуществ такой формы представления сигналов при исследованиях
стимулировал введение аналитического сигнала в круг методов теоретической
радиотехники.
Контрольные вопросы и задания
1. Запишите общее выражение для колебания с гармонической амплитудной мо-
дуляцией, изобразите графики его амплитудного и фазового спектров.
2. Изобразите векторную диаграмму AM-колебания для случая гармонической
модуляции.
3. Запишите общее выражение для колебания с угловой модуляцией. Какими со-
отношениями связаны полная фаза и мгновенная частота колебания?
4. Дайте определения понятий частотной и фазовой модуляции. В чем состоит
взаимос вязь между ними?
84
2. Модулированные радиосигналы
5. Какой физический смысл имеют понятия «девиация фазы» и «девиация час готы»
при угловой модуляции? Как рассчитывается индекс гармонической угловой
модуляции р?
6. Запишите общую формулу для оценки эффективной ширипы спектра колебания
с гармонической угловой модуляцией и ее приближенные варианты для случаев
Р « 1 и р » 1.
7. Чем различаются спектральные и векторные диаграммы AM- и ЧМ-колебаний
при малой глубине модуляции?
8. Приведите графики амплитудных спектров периодических последовательностей
прямоугольных видео- и радиоимпульсов.
9. Запишите выражения, соответствующие прямому и обратному преобразованиям
Гильберта. Что должны представлять собой цепи, реализующие данные преоб-
разования9
10. Как связаны спектры видео- и радиосигналов при импульсной AM?
11. Запишите выражение для комплексной огибающей ЛЧМ-сигнала.
Задачи
Задача 2.1
На приведенных далее рисунках показаны осциллограммы AM-сигналов с одно-
тональной модуляцией при т < 1 (рис. 2.20, вверху) и т > 1 (рис. 2.20, внизу).
Получите для этих случаев формулы для расчета коэффициента модуляции т по
результатам измерений значений амплитуд и f/max.
Задача 2.2
Радиопередающее устройство с амплитудной модуляцией в режиме «молчания»,
то есть при отсутствии модулирующего сигнала, излучает мощность Ро = 4 кВт.
Найдите среднюю Рср и пиковую Ртзх мощность излучаемого AM-сигнала, если ко-
эффициент модуляции т = 80 %. (Пиковая мощность — это максимальное значение
мгновенной мощности сигнала.)
Задача 2.3
На рис. 2.21 показан график модулирующего сигнала su(t). Построить зависимости
от времени для мгновенной частоты, фазовой функции и полной фазы:
а) для частотной модуляции:
б) для фазовой модуляции.
Задача 2.4
Получите приближенное спектральное представление сигнала с угловой модуля-
цией
s(O = 8 cos( 106f + 0,06 sin 1040.
85
Задачи
Рис. 2.20. Сигналы для задачи 2.1
Рис. 2.21. Сигнал для задачи 2.3
Задача 2.5
Однотональный ЧМ-сигнал имеет девиацию частоты Дю = 6 104 с *. Найдите наи-
большее из возможных значений частоты модулирующего сигнала Qn . при котором
в спектре сигнала будет отсутствовать составляющая с несущей частотой.
3. Основы теории
случайных процессов
В отличие от значений детерминированных сигналов, которые мы знаем точно
мгновенные значения случайных сигналов заранее неизвестны и могут быть пред-
сказаны лишь с некоторой вероятностью, меньшей единицы. Характеристики таких
сигналов являются статистическими, то есть имеют вероятностный вид.
В радиотехнике существует два основных класса сигналов, нуждающихся
в вероятностных описаниях. Во-первых, это шумы — хаотически изменяющиеся
во времени электромагнитные колебания, возникающие в разнообразных физи-
ческих системах из-за беспорядочного движения носителей заряда. Во- вторых,
случайными являются все сигналы, несущие информацию, поэтому для описания
закономерностей, присущих осмысленным сообщениям, также прибегают к веро-
ятностным моделям.
В данной главе рассматриваются основные способы математического описания
и анализа случайных сигналов.
3.1. Ансамбль реализаций
Математическая модель изменяющегося во времени случайного сигнала называется
случайным процессом. По определению случайный процесс X{t) — это функция
особого вида, характеризующаяся тем, что значения, принимаемые ею в любой
момент времени t, являются случайными величинами.
ЗАМЕЧАНИЕ 3.1 --------------------------------------------
В радиотехнической литературе термины «случайный сигнал» и «случай-
ный процесс» часто используются как синонимы.
До регистрации (приема) случайный сигнал следует рассматривать именно как
случайный процесс, представляющий собой совокупность {ансамбль) функций
времени х (t), подчиняющихся некоторой общей статистической закономерности.
Одна из этих функций, ставшая полностью известной после приема сообщения,
называется реализацией случайного процесса. Эта реализация является уже не
случайной, а детерминированной функцией времени На рис 3.1 приведен пример
нескольких реализаций случайного процесса.
3.1. Ансамбль реализаций
87
Рис. 3.1. Реализации случайного процесса
Для анализа свойств и характеристик случайного процесса, а также различных
его преобразований необходимо задать .чатечатическую модель случайного про
цесса. Такая модель может представлять собой описание возможных реализаций
случайного процесса в сочетании с указанием относительной частоты их появ ления.
Приведем несколько примеров моделей случайных процессов, задаваемых таким
образом.
Пример 3.1. Гармонический сигнал со случайной начальной фазой. Во многих
практических задачах используется модель случайного процесса, реализации ко-
торого представляют собой гармонические колебания с известными (детерминиро-
ванными) амплитудой п частотой, но случайной начальной фазой. Таким образом,
реализация рассматриваемого случайного процесса может быть записана как
д(Г) = Л cos(copr + <р),
где Л — амплитуда (детерминированная), со0 — частота (детерминированная), (р —
случайная начальная фаза, которая в большинстве интересных для практического
использования случаев может считаться равномерно распределенной па интервале
О...2тг. то есть имеющей следующую плотность вероятности:
—, 0<ф<2л,
2л
О во всех остальных случаях.
Графики нескольких реализаций данного случайного процесса, представляющие
собой смещенные друг относительно друга по временной оси синусоиды, показаны
на рис. 3.2.
ЗАМЕЧАНИЕ 3.2---------------------------------------------------------
Случайные процессы, конкретный вид реализаций которых определяется
значениями конечного числа параметров (случайных величин), иногда
называют квазидетерчинированнычи случайными процесса чи.
РФ(ф) =
88
3. Основы теории случайных процессов
Рис. 3.2. Реализации гармонического сигнала со случайной начальной фазой
Как видим, конкретный вид реализации процесса в данном случае определяется
значением всего одной случайной величины — начальной фазы.
Пример3.2. Сигналеамплитудно-импулъснои модуляцией. При использовании
амплитудно-импульсной модуляции (АИМ) сигнал представляет собой сумму
сдвинутых по времени импульсов известной формы s0(r). амплитуды которых ak
являются случайными и определяют передаваемую полезную информацию:
л(0= X akso(t-kT'>’ (31>
где Т — временной сдвиг между последовательными импульсами (рис. 3.3).
Рис. 3.3. Реализация АИМ-сигнала (слева) и формирующий импульс (справа)
ЗАМЕЧАНИЕ 3.3------------------------------------------------------
На рис. 3.3 для большей наглядности импульсы изображены непере-
крывающимися. В реальных системах связи отдельные импульсы могут
перекрываться. Кроме того, множители ak могут быть в том числе и отри-
цательными так что использование в данном случае термина «амплитуда»
является условным.
В данном примере реализация задается в общем слунае бесконечным, но сметным
множеством случайных ве шчин ak.
ЗАМЕЧАНИЕ 3.4----------------------------------------------------
Сами коэффициенты ak образуют дискретный случайный процесс. Речь
о таких процессах пойдет в разделе 6.14.
3.2. Вероятностные характеристики случайных процессов
89
Пример 3.3. Случайный телеграфный сигнал [13]. Таким сигналом называют
случайный процесс, реализации которого принимают значения +1 и -1, причем
перепады уровня происходят в случайные моменты времени и число У перепадов
уровня, происходящих за время т, является случайной величиной с дискретным
распределением вероятности, подчиняющимся закону Пуассона:
(3.2)
где X — неотрицательный параметр, определяющий среднюю частоту возникнове-
ния перепадов уровня.
С качки уровня происходят в случайные моменты времени поэтому аналити-
чески записать формулу для отдельной реализации данного случайного процесса
оказывается весьма затруднительно, а изобразить ее график можно лишь условно
(рис 3.4).
В данном случае, как и в предыдущем, конкретная реализация задается беско-
нечным множеством случайных величин — моментов перепадов уровня t., а харак-
теристики случайного процесса определяются статистическими свойствами этих
случайных величин.
Итак, полное описание случайного процесса дает его ансамбль реализаций.
Однако для решения практических задач зачастую достаточно более простых ха-
рактеристик, выражающихся в виде числовых параметров и детерминированных
функций. Об этом пойдет речь в следующих разделах данной главы.
3.2. Вероятностные характеристики
случайных процессов
Пусть Х(1) — случайный процесс, заданный ансамблем реализаций {х^Г), x2(t),
xk(tВыбрав произвольный момент времени tv зафиксируем значения, принима-
емые всеми реализациями: {x^t^,x2(t^, ...,xk(t^..} (см. рис. 3.1). Совокупность этих
значений образует одномерное сечение случайного процесса и представляет собой
случайную величину Х(с,). Напомним кратко основные характеоистики случайных
величин, отметив при этом, что для одномерных сечений случайных процессов они
в общем случае зависят от выбранного момента времени tv
90
3 Основы теории случайных процессов
Функция распределения вероятности F(x, Г,) равна вероятности того, что в мо-
мент времени Г, значение случайного процесса не превосходит .г:
F(.r,ri)=P(X(r,)<.r).
F(x, i() является неубывающей функцией, значения которой лежат в диапазоне
О < F(.r, < 1. Для предельных значений хвыполняются следующие соотношения:
Д(-оо Г1) = 0и£(ооД1) = 1.
Вероятность попадания значения случайного процесса в интервал (а, Ь\ равна
разности значений функции распределения на концах этого интервала:
Р(а < X(F) <b) = F(b, Г,) - F(a, £,).
Одномерная плотность вероятности р(х, Г,) представляет собой производную
от функции распределения:
Произведение р(х, Q dx представляет собой вероятность попадания значе-
ния случайного процесса ЛГ(Л,) в бесконечно малый интерва. i шириной dx в окрест-
ности х
p(x,tt)dx = у < X(t}) < х + y-'j,
откуда следует, что плотность вероятности является неотрицательной функцией:
р(х. L) > 0. Чтобы рассчитать вероя гность попадания значения X(tt) в произвольный
интервал [а, 6], необходимо вычислить следующий интеграл:
Л
Р(а < X(t{) < b) = j р(х,tl)dx\
а
Так как случайная величина обязательно принимает какое-нибудь значение,
должно выполняться условие нормировки
J p(x,Qdx = Р(-~<Х^Х ~) = 1. (3.3)
Зная плотность вероятности, можно рассчитать и функцию распределения:
F(x-,tl)= p(x-.tl)dx (3.4)
Математическое ожидание и дисперсия. Знание одномерной плотности
вероятности р(х, Г() позволяет произвести статистическое усреднение как самой
величины X(t}), так и любой функции от нее. Под статистическим усреднением
3.2. Вероятностные характеристики случайных процессов
91
подразумевается усреднение по множеству (ансамблю реализаций) в каком-либо
сечении процесса, то есть в фиксированный момент времени.
Для практических приложений наибольшее значение имеют следующие пара-
метры случайного процесса:
□ математическое ожидание, которое служит теоретической оценкой среднего
взвешенного значения случайного процесса в момент времени t:
тх (t) = М{X (Г)} = j xp(x.,t)dx;
(3.5)
Во многих практических задачах приходится вычислять математическое
ожидание некоторой функции /от случайной величины .г, имеющей плот-
ность вероятности р/х). Такое вычисление выполняется по следующей
несложной формуле:
Af{/(x)} = J f(x)px (x)dx.
(3.6)
Формула для математического ожидания (3.5) является частным
случаем (3.6) при /(.г) = х.
□ дисперсия, характеризующая среднюю мощность отклонений случайного про-
цесса от его среднего значения пр(г), называемых ф чуктуасргями:
D (Г) = м{[А'(Г)-т/0]2} = Л/{А'2(0}-^(0= j х2р(х,Г)Ж (3.7)
□ среднее квадратическое отклонение, представляющее собой квадратный корень
из дисперсии и служащее амплитудной мерой разброса значений случайного
процесса в момент времени t относительно математического ожидания:
(О = {[*(0 - тх (г)]2} = ^Л/{а2(г)}-п?2 (Г). (3.8)
ЗАМЕЧАНИЕ 3.6---------------------------------------------------------
Дисперсия случайной величины X часто обозначается а2.
Вот еще два параметра, связанные с одномерной плотностью вероятности
и встречающиеся в некоторых задачах:
□ мода представ тяет собой наивероятнейшее значение случайного процесса в мо-
мент времени t, то есть значение, при котором достигается максимум плотности
вероятности;
92
3. Основы теории случайных процессов
□ медиана представляет собой такое значение случайного процесса в момент вре-
мени t отклонения от которого в любую сторону равновероятны. Математически
это можно записать следующим образом:
Р X(t) < med(A(r))] = P[A'(t) > med(A(r))J = 1/2
или
F nied(A'(f)),r] = 1/2.
(3.9)
Пример 3.4. Проиллюстрируем вычисление различных параметров связан-
ных с одномерной плотностью вероятности случайной величины, на простом
примере.
Пусть случайная величина X имеет плотность вероятности треугольного вида
при 0 <л < 1 (рис. 3.5, а). Условие нормировки (3.3) приводит к очевидному выводу:
р( 1) = 2. Ф<)рмулу для плотное ги вероятности можно, таким образом, записать в виде
(2.г 0<л<1,
р(.г) = ^
И 7 [0, л <0, л >1.
Функция распределения, согласно (3.4), равна интегралу от плотности вероят-
ности (рис. 3.5, б)'.
Рис. 3.5. Характеристики случайной величины: а — плотность вероятности (отмечены
также числовые параметры случайной величины); б — функция распределения
(3.10)
Рассчитаем параметры такой случайной величины. Математическое ожидание,
согласно (3.5), равно
т
~ 9 г* 3
= j vp(x)dx = J.v 2xdx = J2л dx = ——
— 0 0 3 0
2
— = 0,67
3
3.2. Вероятностные характеристики случайных процессов
93
Дисперсия согласно (3.7), равна
п г 2 . 2 h 3 , 4 2.Г4 1 4 1 4 1 nn_„
D = л pi Ойл - m = 2л ax— =------- —=---------= — -0,056,
® Д 'I 9 4 o 9 2 9 18
а квадратный корень из полученного числа дает среднее квадратическое отклоне-
ние (3.8):
о = Jd~ = J1718 = Ц= = 0,24.
v 3V2
Мода рассматриваемой случайной величины, очевидно, равна 1, так как именно
в этой точке плотность вероятности максимальна.
Для нахождения медианы, согласно (3.9) и (3.10), необходимо решить уравнение
[med(X)]2=|,
отсюда получаем med(X) = 1/^2 ~ 0,707.
Чтобы проиллюстрировать разницу между понятиями математического ожида-
ния, моды и медианы, покажем соответствующие значения на графике плотности
вероятности (см. рис. 3.5, а).
ЗАМЕЧАНИЕ 3.7
Если плотность вероятности имеет симметричный вид, то значения
математического ожидания и медианы совпадают с центром симметрии.
ЗАМЕЧАНИЕ 3.8----------------- - ------------------------------------
Если модель случайного процесса представляет собой описание ансамбля
реализаций, подобное примерам, приведенным в разделе 3.1, то расчет
одномерной плотности вероятности случайного процесса сводится к рас-
смотрению нелинейного преобразования случайных величин-параметров,
определяющих вид конкретных реализаций. Нелинейным преобразовани-
ям сигналов в радиотехнических цепях будет посвяшена глава 7 данного
учебного пособия, а речь о нелинейных преобразованиях плотностей
вероятности пойдет в разделе 7.9.
Одномерная плотност ь вероятности и связанные с ней числовые характеристики
позволяют получить важную информацию о свойс гвах случайного процесса. Однако
для решения многих задач таких сведений недостаточно, так как они дают веро-
ятностное представление о случайном процессе X(t) только в отдельные моменты
и ничего не говорят о том, как он изменяется во времени.
94
3. Основы теории случайных процессов
3.3. Корреляционные функции
случайных процессов
Как отмечалось в разделе 3.2, одномерной плотности вероятности недостаточно для
описания поведения случайного процесса во времени. Гораздо бо. [ьше сведений
можно получить, располагая двумя сечениями случайного процесса в произвольные
моменты времени и t2 (см. рис. 3.1). Совокупность этих двух сечений образует
двумерную случайную величину' {А’(Г1), которая описывается двумерной
плотностью вероятности p(xi, х2, tv t2). Произведениеp(xv л2, Гр t^)dx{dx2 представ-
ляет собой вероятность того, что реализация случайного процесса Х(г) в момент
времени t{ попадает в бесконечно малый интервал шириной dx. в окрестности .г,, а в
момент времени t2 — в бесконечно малый интервал шириной dx2 в окрестности х2:
р(х,, х.,, £,, t2 )dx,dx2 = Р ) - Л- | < ^1, |X(f2) - x21 < .
Естественным обобщением является п-мерное сечение слу чайного процесса,
приводящее к «-.мерной плотности вероятности p(xvx2, tv t2,..., Q. При n —> °°
такая функция является исчерпывающей вероятностной характеристикой случай-
ного процесса.
По аналогии с одномерным случаем можно ввести многомерную функцию
распределения F(.r1, х2, ..., хл, tv t2.t ), равную вероятности того, что значения
случайного процесса А'(г) во все моменты времени Г не превосходят .у:
F(.r1,.r2,...,.c,,ri,r2,...,tn) = P(X(ri)<.r1,X(r2)<x2,...,X(y)<.rJ.
Многомерная функция распределения может быть найдена интегрированием
плотности вероятности:
F(xt,xv...,xn ,tl,t2,...,tn) = |.../х^Л2.^„,tl,t2,...,t„)d^2...d^.
Так же, как и одномерная, многомерная плотность вероятности должна быть
неотрицательна, а условие нормировки приобретает следующий вид:
J ... jp(x1,.v2,...,xn,^,^2...tn)dxidx1...dxn =1.
Зная «-мерную плотность, всегда можно найти m-мерную плотность при tn < п
путем интегрирования по «лишним» координатам:
р(х,,х9,...,х„„)= I ... f р(х.,х,,..., v )dx ....dx .
* х 1 ’ 2 1 т’ 1 ’ 1 ' т ' J 2 п 1’2' п' т -*-1 п
Описание свойств случайных процессов с помощью многомерных плотностей
вероятности высокой размерности может быть весьма подробным, однако на этом
3.3. Корреляционные функции случайных процессов
95
пути часто встречаются серьезные математические трудности. К счастью, многие
задачи, связанные с описанием случайных сигналов, удается решить на основе
двумерной плотности вероятности.
В частности, задание двумерной плотности вероятности р(.гр х2, tv t2) позволяет
определить важную характеристику случайного процесса — его ковариационную
функцию
Согласно этому определению, ковариационная функция случайного процесса
Х(р) представляет собой статистически усредненное произведение значений слу-
чайной функции X(f) в моменты времени и t2.
Для каждой реализации случайного процесса произведение г(£Д x(t2) является
некоторым числом. Совокупность реализаций образует множество случайных чи-
сел, распределение которых характеризуется двумерной плотностью вероятности
р(лр х2, 0 t2). Если эта плотность вероятности известна, операция усреднения по
множеству осуществляется по формуле
j jx{x2p(x{,x2,tvt2)dx.dx2.
Часто при анализе случайных процессов основной интерес представляет их
фл} ктуационная составляющая. В таких случаях применяется корреляционная
функиия, представляющая собой статистически усредненное произведение зна-
чений центрированной случайной функции A'(t) - z»v(i) в моменты времени t{ и
R (f,, t2) = М{[ А(;,)-тх(t,)][Х(Г2)- mr(t2)]} =
= Ak.(ri,r2)-mv(r1)OTi.(r2).
Корреляционная функция характеризует степень статистической связи тех
значений случайного процесса, которые наблюдаются при t = и t = t2. При
= t2 = Г последнее выражение соответствует определению дисперсии случайного
процесса А(Г). Следовательно, при совмещении сечений функция корреляции
равна дисперсии:
Д С,г) = К (г,= .0.(0. (3.11)
ЗАМЕЧАНИЕ 3.9--------------------------------------------------------------
Так сложилось, что в иностранной литературе используется обратная
терминология. t2) называется корреляционной, а RXtlt Г2) — ковариа-
ционной функцией. Во избежание недоразумений об этом следует помнить
в процессе работы с зарубежными источниками.
96
3. Основы теории случайных процессов
Пример 3.5. Рассчитаем корреляционную функцию гармонического сигнала со
случайной равномерно распределенной начальной фазой (см. пример 3.1).
Можно легко убедиться в том, что данный случайный процесс является центри-
рованным то есть его математическое ожидание не зависит от времени и равно нулю:
т,(0= |л(Орф(Ф)<Лр = J/lcos((o0t + (p)y-(/(p = 0. (3.12)
Поэтому ковариационная и корреляционная функции данного процесса совпа-
дают и могут быть найдены следующим образом (поскольку реализации данного
случайного процесса представляют собой функции, зависящие от одной случайной
величины, для усреднения произведения нет нужды прибегать к двумерной плот-
ности вероятности — достаточно воспользоваться формулой (3.6), позволяющей
произвести усреднение произвольной функции от случайной величины):
Я «,г2) = (tvt2) = J x(i,)x(42)^^p)«((p =
2к 1
- | Лсо5(со0^ + <р)Асоз(со0г +<р)—dq> =
i 2я
A2 f2л 1 2я 1 '
= — J -cos(co0(ri + f,) + 2<р)Лр + J -со»(со0(^ -t2)) г/ср
Z7t ( о 0 >
Здесь в первом слагаемом интегрирование производится по двум периодам
функции cos, поэтому данный интеграл равен нулю. Во втором слагаемом подын-
тегральная функция не зависит от переменной интегрирования <р, так что результат
интегрирования равен произведению подынтегрального выражения и длины про-
межутка интегрирования, равной 2л Окончательно получаем:
А2
/?jai,r2) = Ki(t1,t2) =—cos(co0(ri -f2)). (3.13)
Как видите, корреляционная функция данного случайного процесса гармони-
чески зависит от расстояния между анализируемыми моментами времени. При
совпадении моментов времени и Г2 получаем величину дисперсии случайного
процесса
А2
(3.14)
Пример 3.6. Рассчитаем корреляционную функцию АПМ-сигнала (см. при-
мер 3.2). Характеристики такого случайного процесса определяются как формой
несущего импульса sn(f), так и статистическими связями между амплитудами ak.
Часто эти амплитуды считаются статистически независимыми и имеющими иден-
тичные вероятностные характеристики. Именно этот случай и будет рассмотрен
в данном примере. Будем также считать, что эти амплитудные множители имеют
3.3. Корреляционные функции случайных процессов
97
нулевое математическое ожидание. При этом математическое ожидание самого
случайного процесса также будет нулевым:
т^) = М\ X ^0(4-#T)U X M{ak}so{t-kT) = O. (3 15)
Таким образом, в данном случае ковариационная и корреляционная функции
процесса также совпадают. Рассчитаем их согласно определению:
r (г,,г2) = к (Г, Д2) = м {*(r;)X(f2)} = м X а^> (?1 - *г) L ал (f2 -*г)
Л1=-
Преобразуем произведение сумм в двойную сумму и перенесем операцию ста-
тистического усреднения внутрь этой двойной суммы:
Д(Г1Д2) = Х\(Г1,Г2)= £ V Af{ats0(t,-^T)ams0(t2-тТ)}.
£=—*
Случайными здесь являются только амплитуды ak и ат, поэтому и усреднение
должно применяться только к ним:
Л (Г1Д2) = Х\(Г1>Г2)= £ £ M{akam}s0(ti -kT)s0(t2 -тТ).
Однако согласно условиям примера эти амп титулы являются статистически
независимыми и имеют нулевые средние значения. Поэтому
<
О,
k = т,
т.
где оа2 — дисперсия случайных величин аь. Таким образом,
Д(Г,,Г2) = К/г1,г2) = аа £ 50(^ -kT)s0(t2-kT).
(3.16)
Как видите корреляционная функция данного процесса определяется формой
импульса ,s0(f) и дисперсией амплитуд этих импульсов оа2. Рассчитаем дисперсию
случайного процесса:
Л (t)=R (v) = <r Д>02(с-£О
(3.17)
Взаимная корреляционная функция. Подобно тому как корреляционная
функция показывает статистическую связь значений одного случайного процесса
в различные моменты времени, взаи иная корреляционная функция (ВКФ) делает
это для двух случайных процессов. Математически она определяется следующим
образом:
Л12(Г1,Г2) = Л/{Л-1(Г1)А’2(Г2)}.
4 №675
98
3. Основы теории случайных процессов
Некоррелированность и статистическая независимость. Если совместно
рассматривать две случайные величины А^ и А’,, между ними может существовать
либо не существовать статист аческая связь. Отсутствие такой связи означает,
что плотность вероятности одной случайной величины не зависит от того, какое
значение принимает другая случайная величина. Двумерная плотность вероятности
при этом представляет собой произведение одномерных плотностей:
Это условие называется условием статистической независимости.
При наличии статистической связи между случайными величинами статистиче-
ские свойства каждой из них зависят от значения, принимаемого другой случайной
величиной. Эта связь может быть сильной или слабой, линейной или нелинейной.
Мерой линейной статистической связи между случайными величинами является
коэффициент корреляции'.
М{Х.Х2}-М{Х }М{Х,}
^D{X}}D{X2}
(3.18)
Можно показать, что |r]2| < 1. П седельные значения ±1 достигаются, если реали-
зации случайных величин жестко связаны линейным соотношением х2 = а.х\ + Ь, где
а и b — некоторые константы. Знак коэффициента корреляции при этом совпадает
со знаком множителя а.
Равенство коэффициента корреляции нулю свидетельствует об отсутствии
линейной статистической связи между случайными величинами (при этом говорят
об их некоррелированности). Как видно из (3.18), при этом математическое ожи-
дание произведения случайных величин равно произведению их математических
ожиданий:
М{Х[Х._} = М{Х[}М{Х2}.
Легко показать, что из|статистической независимости следует некоррелирован-
ность случайных величин. Обратное утверждение в общем случае неверно — не-
коррелированные случайные величины могут быть зависимыми.
ЗАМЕЧАНИЕ 3.10 -------------------------------------------------
Классическим примером этого явления является пара случайных величин
г = cos ф и х2 = sin ф, где ф — случайная величина, равномерно распреде-
ленная на интервале О...2тг. Очевидно, что .г, и х2 зависят друг от друга,
однако их коэффициент корреляции оказывается равным нулю.
3.4. Стационарные и эргодические
случайные процессы
Стационарные случайные процессы. Так принято называть случайные про-
цессы, статистические характеристики которых одинаковы во всех временных
сечениях.
3.4. Стационарные и эргодические случайные процессы
99
Говорят, что случайный процесс строго стационарен (или стационарен в узком
смысле), если его многомерная плотность вероятности p(xv х2,..., х , tv t2,.... t_) про-
извольной размерности п не изменяется при одновременном сдвиге всех временных
сечений Гр t2,..., Гп вдоль оси времени на одинаковую величину т:
Р(ЛР х2,..., хп, tv t2,..., tn) = p(xt, ,r2,..., л;, t, + т t2 + I,..., t„ + t)
при любом т.
Если же ограничить требования тем, чтобы от временного сдвига не зависели
лишь о хномерная и двумерная плотности вероятности, то такой случайный про-
цесс будет стационарен в широком смысле Понятно, что из стационарности в узком
смысле следует стационарность в широком смысле, но не наоборот.
Для стационарного случайного процесса математическое ожидание и дисперсия
не зависят от времени, а корреляционная функция зависит не от самих моментов
времени, а только от интервала между ними т = t2 -1,:
R,(tt,t2) = Rjj2-t{) = RJf).
По этой причине при записи статистических параметров стационарного случай-
ного процесса можно опускать обозначения фиксированных моментов времени:
те D , К\т) Rf(r).
Легко убедиться, что корреляционная функция стационарного случайного про-
цесса является четной:
Я(-т) = Я(т).
Кроме того, абсолютные значения этой функции при любых т не превышают
ее значения при т = 0 (напомним, что это значение равно дисперсии случайного
процесса):
|Я(т)|<Я(0) = Я.
Часто удобно использовать коэффициент корреляции (его также называют
нормированной корреляционной функцией)
/ ч « (т)
D
Л
Для коэффициента корреляции выполняются соотношения г (0) = 1 и |Г.(т)| < 1.
Функции /?д(т) и г.(т) характеризуют связь (корреляцию) между значения-
ми А’(Г), разделенными промежутком т. Чем медленнее убывают эти функции
с ростом абсолютного значения т, тем больше промежуток, в течение которого
наблюдается статистическая связь межд\ мгновенными значениями случайного
процесса, и тем медленнее, плавнее изменяются во времени его реализации.
ЗАМ ЕЧ АН И Е 3.11 ----------------------------------------------------
Если ВКФ случайных процессов А'^Г) и А',(г) зависит только от разности
моментов времени, то есть Rt2(tt, t2) = — эти случайные процессы
называются стационарно связанными.
100
3. Основы теории случайных процессов
Пример 3.7. Легко увидеть что гармонический случайный процесс со случай
ной начальной фазой (см. пример 3.1 и вычисление характеристик этого процесса
в примере 3.5) является стационарным в широком смысле. Действительно, за-
висящие от одномерной плотности вероятности математическое ожидание (3.12)
и дисперсия (3.14) не зависят от времени, а корреляционная функция (3.13), за-
висящая от двумерной плотности вероятности зависит лишь от интервала между
рассматриваемыми моментами времени:
А2
R Сс) = А\(т) = —cos(co0t). (3.19)
Коэффициент корреляции такого случайного процесса
/;(т) = -^—= cos(co0t).
л
ЗАМЕЧАНИЕ 3.12 -------------------------------------------------------
Здесь следует отметить, что стационарным будет любой случайный
процесс, реализации которого являются периодическими функциями
идентичными по форме и различающимися лишь «начальной фазой»,
то есть положением начала отсчета времени в пределах периода. При
этом принципиальной является равномерность распределения началь-
ной фразы в пределах периода. Действительно, пусть у гармонического
процесса начальная фаза равномерно распределена в пределах половины
окружности — на интервале 0...Л. Математическое ожидание процесса
в этом случае будет равно
7 , г 1 , 23sin(oV)
отл(-г)= J .т(Орф(ф)</ф = ]3cos(co„/+(p)- dq =---.
Результат вычислений показывает, что математическое ожидание про-
цесса зависит от времени следовательно, он не является стационарным.
Пример 3.8. АИМ-сигнал (см. пример 3.2 и вычисление характеристик этого
процесса в примере 3.6), очевидно, не является стационарным, поскольку’ его дис-
персия (3.17) зависит от времени, а корреляционная функция (3.16) зависит не от
расстояния между моментами времени, а от двух моментов времени по отдельности.
Пример 3.9. Причиной нестационарноеги случайного процесса из предыдущего
примера является жесткая привязка положения импульсов к временной оси в фор-
муле (3.1). Можно усложнить модель случайного процесса, введя в нее случайный
временной сдвиг. Формула (3.1) при этом принимает следующий вид:
х(0 = 11аЛ(г-^7'-го)-
где tb — случайная величина, равномерно распределенная на интервале 0...Т.
3.4. Стационарные и эргодические случайные процессы
101
Покажем, что такой случайный процесс является стационарным в широком
смысле. Формула (3.16) с учетом произведенной модификации принимает вид
Л (r],r2) = X\(ri,r2) = Ai ст £s0(ri-^7’-?0)s0(r2-A>T-r0)k
I J
Усреднение здесь выполняется по случайному параметру tQ. Произведем его
в соответствии с формулой (3.6):
а2 т *
R^(tvt2) = Kil(г1,г2) = -^-| Y -kT-t0)dtg.
Поменяем местами суммирование и интегрирование и выполним замену пере-
менной t = Г; - kT- Го:
с2 „ Т
R С,Д2) = к, (Г,,t-) = -Г X ]\(г, -kT-г„)50(г2 -kT-tn)dt0 =
1 k=^ о
a2 -
= fl J sg(t)s0(t-(^-t2))dt. (3.20)
* *=—f, tr г
Интеграл в (3.20) представляет собой фрагмент корреляционного интеграла
(1.80), вычисляемый по временному интервалу длительностью Г. а суммирование
в этой формуле объединяет такие фрагменты, что в итоге эквивалентно интегри-
рованию вдоль всей временной оси:
Я (W = к.(г,,t2) = ф- j50(х>0(г-(|-r2))Л = во(г,-t2), (3.21)
где В (f] -f2) — корреляционная функция детерминированного импульса $0(Г),
определяемая по формуле (1.80). Дисперсия случайного процесса
о2
д =7?1(Г,о = й(0) = _±£ , (3.22)
где £s — энергия импульса s0(t).
Таким образом, данный случайный процесс является стационарным в широком
смысле, так как его математическое ожидание (3.15) и дисперсия (3.22) не зависят
от времени, а корреляционная функция (3.21) зависит только от интервала между
рассматриваемыми моментами времени.
Эргодические случайные процессы. Дальнейшее упрощение анализа слу-
чайных процессов достигается при использовании условия эргодичнос?пи процесса.
Стационарный случайный процесс называется эргодическим, если при определении
тюбых его статистических характерце гик усреднение по множеству (ансамблю)
реализаций эквивалентно усреднению по времени одной, теоретически бесконечно
длинной, реализации.
102
3. Основы теории случайных процессов
Обозначив усреднение по времени угловыми скобками, можно записать следу-
ющие выражения, позволяющие вычислить важнейшие статистические характери-
стики эргодического случайного процесса по его единст венной реализации х(Г) (еще
раз обращаем внимание на то, что эргодический случайный процесс обязательно
является и стационарным, но не наоборот):
т, =(.т(0) = 1пгД j x(t)dt, (3.23)
-Т 2
I 9\ 1 Т 2
=([v(r)= lim — J x\t)dt-m2, (3.24)
\ / T 2
(t) = ([x(0- w, ][x(r - t) - mx ]) = (x(t)x(t - t)) - nr =
| T f
= lim— f v(t)x(t - x)dt - m (3.25)
T —/ J
1 2
Математическое ожидание эргодического случайного процесса равно постоянной
составляющей любой его реализации а дисперсия имеет наглядный физический
смысл мощности флуктуационного компонента.
Достаточным условием эргодичности по математическому ожиданию случай-
ного процесса, стационарного в широком смысле, является затухание его функции
корреляции с ростом временного сдвига т (см., например, [8]):
1ппЛ! (т) = 0. (3.26)
При экспериментальном исследовании случайных процессов доступно, как пра-
вило, наблюдение одной реализации сигнала, а не всего ансамбля Если изучаемый
процесс является эргодическим, то его реализация достаточной длины является
типичным представителем статистического ансамбля. Согласно приве зенным ранее
формулам, по этой единственной реализации можно определить математическое
ожидание, дисперсию и корреляционную функцию эргодического случайного про-
цесса. На практике интегрирование выполняется, естественно, не в бесконечных
пределах, а на конечном интервале Т, длина которого должна быть тем больше, чем
выше требования к точности результатов измерения.
Пример 3.10. Провесим эргодичность гармонического процесса со случайной
начальной фазой (стационарность такого процесса была проверена ранее). Его
корреляционная функция (3.19) с рос гом т не стремится к нулю, так что условие
(3.26) не выполняется. Однако это лишь достаточное, но не необходимое условие,
поэтому его невыполнение еще не означает неэргодичности процесса. Проверим
эргодичность согласно определению, вычислив усредненные по времени параметры
(3.23-3.25):
со
(х(0) = — j Acos(co0^+(р)Л = 0 = 7Пг,
-л. О)о
3.4. Стационарные и эргодические случайные процессы
103
^.r(r)-mj2^ = |^ J Л2соз2(соог + ф)^ =
А2
— = D ,
2
(В
][х(Г-Т)-т = J Л'СО5((В0Г + ф)сО5(И0(Г-Т) + (р)Л =
Л2
= —cos(co0T) = /?i(r).
ЗАМЕЧАНИЕ 3.13 ----------------------------------------------------
Тот факт, что реализации рассматриваемого процесса яв тяются периодиче-
скими функциями, позволяет упростить вычисления, заменив усреднение
по бесконечному (в пределе) промежутку времени усреднением по одному
периоду, равному в данном случае 2л/<вп.
Итак, параметры, вычисленные усреднением по времени, совпади с параметрами,
полученными ранее путем статистического усреднения Следовательно, гармони-
ческий случайный процесс со случайной начатьной фазой является эргодическим.
ЗАМЕЧАНИЕ 3.14 -----------------------------------------------------
Здесь также следует отметить, что любой случайный процесс, реализации
которого являются периодическими функциями, идентичными по форме
и различающимися лишь «начатьной фазой», будет не только стационар-
ным, но и эргодическим.
Нормальный случайный процесс. Нормальный (гауссовский) закон рас-
пределения случайных величин очень удобен для анализа и часто ы тречается на
практике, особенно он характерен для шумов в радиотехнических устройствах.
Одномерная плотность вероятности стационарного нормального процесса опре-
деляется выражением
X-i) =
(3.27)
где т и о 2 — соответственно, математическое ожидание и дисперсия процесса.
На рис. 3.6 приведен график плотности вероятности нормальной случайной
величины, построенный согласно (3.27) при т = 0 и ох = 1.
Широкое распространение нормального закона распределения в природе объ-
ясняется тем, что при суммировании достаточно большого числа равномощных ста
тистпчески независимых случайных величин имеющих произвольные плотности
распределения вероятности, плотность распределения суммы стремится к нормаль-
ной. Это положение носит название центральной предельной теоремы
Весьма полезным для математического анализа свойством нормального рас-
пределения является то что из некоррелированности гауссовых случайных величин
104
3. Основы теории случайных процессов
Рис. 3.6. Плотность вероятности случайной величины с нормальным распределением
следует их статистическая независимость (о разнице между этими понятиями
говорилось в разделе 3.3).
ЗАМЕЧАНИЕ 3.15 ---------------------------------------------------
Следует обратить внимание на то. что данные о распределении вероятно-
сти не дают никаких с ведений о поведении случайного процесса во време-
ни Для описания его временных характеристик необходимо использовать
корреляционную функцию или привлечь для этого спектральные харак-
теристики случайного процесса, которые рассматриваются в разделе 3.5.
3.5. Спектральные характеристики
случайных процессов
Каж тая отдельно взятая реализация случайного процесса представляет собой де-
терминированную функцию и к ней можно применить преобразование Фурье. При
этом различные реализации будут, естественно, иметь различные спектры. Нас же
интересуют статистически усредненные характеристики случайных процессов.
Попытаемся найти среднее значение спектральной плотности случайного iiponec
са (горизонтальной чертой здесь и далее обозначается операция статистического
усреднения по ансамблю реализаций):
5x(to) = j x(t)e ,aXdt- jx(t)e iwtdt= J mx(f)e '“dt.
Как видно из формулы, усредненная спектральная плотность случайного про-
цесса представляет собой спектр его детерминированной составляющей (матема-
тического ожидания). Для центрированных процессов mx(t) = 0 и 5х((в) = 0. Таким
образом, усредненное значение спектральной плотности не несет никакой инфор-
мации о флуктуационной, то есть собственно случайной, составляющей случайного
процесса. Это говорит о том, что фазы спектральных составляющих в различных
реализациях процесса случайны и независимы.
3.5. Спектоальные характеристики случайных процессов
105
Можно, однако, рассмотреть спектральную плотность мощности случайного
процесса, поскольку мощность не зависит от соотношения фаз спектралоных со-
ставляющих.
Рассмотрим стационарный центрированный случайный процесс и выделим из
его ансамбля какую-либо реализацию x(i), ограничив ее длительность конечным
интервалом времени [-7/2; Г/2]. Применив затем к этой реализации прямое пре-
образование Фурье, найдем ее спектральную плотность ХДсо). Энергию ^рас-
сматриваемого отрезка реализации, согласно равенству Парсеваля (1.68), можно
вычислить как
Т/2 . о»
ЕТ= J x2(t)dt = —J|xr((n)|2J(o.
-Т/2 П - .
Разделив эту энергию на Т, получим среднюю мощность Рт реализации на дан-
ном временном интервале:
При увеличении длительности промежутка времени Т энер! ия отрезка реа-
лизации неограниченно возрастает, а средняя мощность стремится к некоторому
пределу. Произведя усреднение по ансамблю реализаций и совершив предельный
переход 7’-» «>, получим:
<7со = — I W'(co)d(o,
2л J
где функция
Хг(со)2
(3.28)
W) = lim
у
представляет собой спектральную плотность средней мощности рассматриваемой
реализации.
ЗАМЕЧАНИЕ 3.16 ------------------------------------------------
Часто говорят «спею ральная плотность мощности» (СПМ) или «спектр
мощности».
ЗАМЕЧАНИЕ 3.17---------------------------------------------------
Может показаться, что в случае эргодического процесса усреднение по
ансамблю реализаций в формуле (3.28) не является обязательным, по-
тому что один и тот же результат будет получен при рассмотрении любой
отдельно взятой реализации. Однако в литературе по статистической
продолжение
106
3. Основы теории случайных процессов
радиотехнике (см., например, |8]) показано, что без статистического
усреднения предел ч правей части (3 28) просто не существует.
Статистически усредненная средняя мощность реализаций с тучайного процесса,
очевидно, равна его дисперсии: (х2(0/ = Dx. Таким образом,
UX®) — вещественная функция, она не содержит информации о фазах спектраль-
ных составляющих и не позволяет восстановить отдельные реализации случайного
процесса. Кроме того, из определения спектральной плотности (3.28) очевидно, что
UX®) является неотрицательной и четной функцией частоты.
ЗАМЕЧАНИЕ 3.18 --------------------------------------------------
Мы не приводим здесь примеров расчета спектра случайного процесса
согласно приведенному определению, поскольку такого рода расчет редко
необходим на практике. Как правило, вычисление спектра случайного про-
цесса производится на основе его корреляционной функции с помощью
теоремы Винера—Хинчина, речь о которой пойдет в следующем разделе
3.6. Теорема Винера—Хинчина
Как распоеделение спектральной плотности мощности, так и вид корреляционной
функции связаны со скоростью изменения случайного процесса во времени. Найдем
связь между этими двумя характеристиками.
Корреляционная функция детерминированного сигнала связана преобразовани-
ем Фурье с его энергетическим спектром (см. раздел 1.13). Применим это свойство
к отрезку реализации случайного процесса длительностью Г:
Т/2 1 °°
j x(t)x(t-T.)dt- — j|xr((B)| e^da.
-Т/2
Применим к обеим частям этого равенства усреднение по ансамблю реализаций,
разделим обе части равенства на Т и устремим Т к бесконечности:
, 1 Т------------- 1 г ^г(ю)
lirn - J x(t)x(t-T)dt= — Jlim--—
e^dm.
(3.29)
В левой части последнего равенства получается корреляционная функиия слу-
чайного процесса, а в правой части под интегралом содержится выражение (3.28)
для спектральной плотности мощности этого процесса.
3.6. Теорема Винера—Хинчина
107
С учетом этого
7?(т) = ^ jw)e;“Tdco.
Таким образом, корреляционная функция случайного процесса и его спектраль-
ная плотность мощности связаны друг с другом преобразованием Фурье. Это со-
отношение носит название теоремы Винера—Хитина.
Так как и 7?(т), и являются четными вещественными функциями, можно
отказаться от комплексной формы записи преобразования Фурье и перейти к по-
лубесконечным пределам интегрирования:
R(t) =—j W(<n)cos((OT)</a>,
WYcd) = 2j 7?(t)cos(cbt)</t.
0
Очень часто используемая модель случайного процесса оказывается такова, что
воспользоват ься непосредственно определением (3.28) для расчета спектральной
плотности мощности не представляется возможным. Если при этом удается вычис-
лить корреляционную функцию, получить спектральную информацию позволяет
теорема Винера—Хинчина.
Пример 3.11. В качестве примера рассмотрим случайный телеграфный сигнал
(см. пример 3.3). Поскольку скачки уровня происходят в случайные моменты
времени для данного случайного процесса затруднительно даже изобразить гра-
фик отдельной реализации, не говоря уже о расчете спектра ее ограниченного во
времени фрагмента.
Однако рассчитать корреляционную функцию для данного процесса оказыва-
ется совсем несложно. Действительно, произведение разнесенных во времени на
т значений случайного процесса может быть равно +1 (если эти значения имеют
одинаковый знак) или -1 (если знаки противоположны). Но совпадение знаков
означает что за интервал т произошло четное количество перепадов уровня, а несо-
впадение знаков соответствует нечетному количеству перепадов. Итак, чтобы найти
вероятности для двух возможных значений произведения x(f)x(t - т), нужно про-
суммировать значения.. [аваемые формулой (3.2), отдельно для чегных и нечетных N:
P(x(t)x(t - т) = 1) = р(й,| ТI) = =
k=o k=a
=l(ew+e-^)e-^=l+L&-^i
2 2 2
Р(х(Г)х(Г - т) = -1) = ±P(2k +1,| т I) = =
= - (ex|T|-
7 2 2
108
3. Основы теории случайных процессов
Полученные результаты позволяют рассчитать среднее значение произведения
x(t)x(t-x)\
R (т) = 1. [ 1 + 1е~2^ 1 + (-l)f- --e’2XW = е’2Х|Т|.
1,2 2 ) v \2 2 )
Итак, корреляционная функция данного случайного процесса экспоненциально
затухает с ростом абсолютного значения т. Теперь с помощью теоремы Винера —
Хинчина можно найти спектральную плотность мощности:
W (<о) = [ R (т)е’;тх</т= [ e~2Z|V;mJT= ,4Х
Д Д 4Х + (О
Интервал корреляции. Случайные процессы, изучаемые в радиотехнике,
часто обладают следующим свойством: их функция корреляции стремится к нулю с
увеличением временного сдвига т (напомним, что это яв тяется дос гаточным усло-
вием эргодичности процесса по математическому ожиданию). Чем быстрее убывает
функция 7?(т), тем слабее оказывается статист ическая связь между мгновенными
значениями случайного сигнала в два несовпадающих момента времени.
Числовой характеристикой, служащей для оценки протяженности корреляци-
онной функции, является интервал корреляции тк. Общепринятого способа рас-
чета данного параметра не существует, один из возможных вариантов предс гавлен
следующей формулой:
Если известна информация о поведении какой-либо реализации случайного
процесса «в прошлом», то возможен вероятностный прогноз случайного процесса
на время порядка тк.
Эффективная ширина спектра. Пусть исследуемый случайный процесс ха-
рактеризуется спектральной плотностью мощности W(co), имеющей максимальное
значение Заменим мысленно данный случайный процесс другим, у которого
спектральная плотность мощности постоянна и равна в пределах некоторой
полосы частот, выбираемой из условия равенства средних мощностей обоих про-
цессов. Ширина этой полосы частот называется эффективной шириной спектра
случайного процесса:
Д®^ = J 1Г(ш)J®, Лс% = j«W®
q max О
Эффективную шиоину спектра случайного процесса можно определить и дру-
гими способами, например исходя из условия уменьшения значений спектра мощ-
ности на границе этого частотного интервала до уровня 0,1 Wmax. В любом случае
величины тк и Д®^ связаны известным из свойств преобразования Фурье соот-
ношением неопределенности
Д® ,т ~2л.
эф к
3.6 Теорема Винера—Хинчина
109
Правая часть данной формулы показывает лишь порядок величины, конкретное
значение зависит от испотьзованных способов определения тк и Лсо^.
Для иллюстрации этого соотношения на рис. 3.7 в центре приведены примеры
реализаций двух случайных процессов, слева — корреляционные функции этих
процессов, а справа — их спектральные плотности средней мощности.
Рис. 3.7. Взаимосвязь между видом оеализаций случайных процессов (в центре),
их корреляционными функции (слева) и спектрами (справа)
Белый шум. В радиотехнике так называют стационарный случайный процесс,
спектральная плотность мошности которого постоянна на всех частотах:
ИД со) = Wo = const.
Согласно теореме Винера—Хинчина, корреляционная функция белого шума
представляет собой дельта-функцию:
ИЛ °°
R(T) = ^\e^d(a = W05(T).
то есть равна нулю всюду, кроме точки т = 0. Дисперсия белого шума бесконечно
велика.
В несовпадающие моменты времени значения белого шума некоррелированы —
как бы ни был мал интервал т, сигнал за это время может измениться на любую
величину
Белый шум является абстрактной математической моделью и физически суще-
ствовать не может. Это объясняется, прежде всего, бесконечностью его дисперсии
(то есть средней мощности). Однако в тех случаях, когда полоса пропускания ис-
следуемой цепи существенно уже эффективной ширины спектра шума, который на
нее воздейс гвует, можно для упрощения анализа приближенно заменить реальный
случайный процесс белым шумом.
110
3. Основы теории случайных процессов
ЗАМЕЧАНИЕ 3.19 -----------------------------------------
Отметим еше раз, что вероятностные и корреляционные (или спектраль-
ные) характеристики случайного процесса — это совершенно различные
и не связанные между собой функции. Так, например, нормальный случай-
ный процесс может иметь самую разнообразную спектральную плотность
мощности, а белый шум — произвольную функцию распределения. Един-
ственная «точка соприкосновения» вероятностных и корреляционных
характеристик — это возможность расчета дисперсии случайного процесса
как на основе одномерной плотности вероятности (формула (3.7)), так
и исходя из корреляционной функции (Формула (3.11)).
3.7. Узкополосный случайный процесс
Важную роль в радиотехнике играет особый класс случайных процессов, спектр
которых сосредоточен в относительно узкой полосе вблизи некоторой частоты со0.
Рассмотрим статистичес кие свойства таких процессов.
Итак, пусть x(t) — случайный процесс, СПМ которого 1Р(й) имеет узкополосный
характер (рис. 3.8). Будем также считать этот случайный процесс стационарным,
нормальным и цен грированным.
Со1ласно теореме Винера—Хинчина (см. раздел 3.6), корреляционная функция
и СПМ случайного процесса связаны друг с другом преобразованием Фурье. Уз-
кополосный характер спектра 1У((о) говорит о том, что корреляционная функция
7?х(т) имеет вид узкополосного радиосигнала:
Я (т) = Я0(т) cos [®от + Фо< 0L
где 7?0(т) и ф0(т) — медленно (по сравнению с cos (со0т)) меняющиеся функции.
Рис. 3.8. СПМ узкополосного случайного процесса
Узкополосный спектр и осциллирующий характер корреляционной функции
означают, что отдельные реализации узкополосного случайного процесса пред-
ставляют собой квазигармонические колебания-.
x(t) = A(t) cos [co0t + ip(0],
у которых как огибающая A(t), так и фазовая функция ф(£) являются случайными
фvнкциями, медленно (по сравнению с cos (<flof)) изменяющимися во времени
3.7. Узкополосный случайный процесс
111
Чтобы определить статистические параметры огибающей и фазовой функции,
поставим в соответствие вещественному случайному процессу x(t) комплексный
случайный процесс Z(t) следующим образом:
Z(t) = x(t) + jx(t),
где x(t) — сопряженный случайный процесс, реализации которого связаны с реа-
лизациями процесса x(t) преобразованием Гильберта (см. раздел 2.8):
1 00
x(O = -f
л J
t-t'
(3.30)
Также в разделе 2.8 было показано, что с помощью сопряженного сигнала можно
определить мгновенные значения огибающей и полной фазы узкополосного сигнала:
A(t) = |Z(r)| = 7^2(i) + x2(r),
<р(Г) = argZ(i) = •
arctg[x(t)/r(O],
arctg [x(r) / x(r)] + л,
x(f) > 0,
x(t) < 0.
Рассмотрим статистические свойства сопряженного процесса. Вначале опреде-
лим его математическое ожидание, применив усреднение к формуле (3.30) и затем
поменяв усреднение и интегрирование местами:
------- dt'=Q,
t-t
так как процесс x(t) является центрированным.
Далее, поскольку процесс x(t) нормальный, а преобразование Гильберта является
линейным интегральным преобразованием, то нормальным будет и сопряженный
процесс x(t).
Из свойств преобразования Гильберта (см. раздел 2.8, формула (2.40)) следует,
что спектры конкретных реализаций процессов x(t) и х(Х) связаны следующим
образом:
5,(со) = ]о,
-Д (®),
А (со),
со > 0,
<о = 0,
со < 0,
откуда видно, что энергетические спектры реализаций процессов х(Г) и х(£) со-
впадают, а следовательно, совпадают и СПМ этих процессов: (со) = (со). Кор-
реляционные функции связаны с СПМ обратным преобразованием Фурье, поэтому
они тоже одинаковы Ri (т) = R, (т).
Нам осталось выяснить, имеется ли статистическая связь между процессами
x(t) иx(t). Ограничимся при этом расчетом взаимной корреляции между ними
в совпадающие моменты времени, то есть вычислим Rti (0):
112
3. Оснос ы теории случайных npoueccut
1 7 x(t)x{t')dt,
t-t'
^(0) = ЛГ {x(t)x(0} = M x(t)- j ^-^dt' = - f
1 J Tt J t — t It J
Далее, как и прежде, внесем операцию статистического усреднения под знак
интеграла, а затем используем замену переменной x = t-f:
= 1 J *{*040} л.__ I j л.= _1 j *£>.Л .0.
nJ t-t' 71 J t-t' 71 J T
Результат интегрирования равен нулю так как 7?х(т) является четной функцией,
а все подынтегральное выражение, следовательно, — нечетной. Таким образом, про-
цессы x(t) и x(t) в совпадающие моменты времени некоррелированы Поскольку
они, кроме того, являются нормальными, то из некоррелированности следует ста-
тистическая независимость.
ЗАМЕЧАНИЕ 3.20 -----------------------------------------
Если вычислить полную ВКФ процессов x(t) и x(t), окажется, что она
связана с корреляционной функцией /?г(т) преобразованием Гильберта:
тс J т-т
Огибающая и полная фаза узкополосного случайного процесса.
Мгновенное значение комплексного случайного процесса Z(t) можно графически
изобразить в виде вектора на комплексной плоскости (рис. 3.9) Проекции этого
вектора на оси Re и Im равны мгновенным значениям процессов x(t) и x(t) соот-
ветственно. Эти мгновенные значения статистически независимы и имеют нормаль-
ные распределения с нулевым средним и одинаковыми дисперсиями (равенс гво
дисперсий следует из равенства корреляционных функций). Поэтому совместная
плотность вероятности процессов х(С) и x(t) равна произведению их одномерных
плотностей вероятности, каждая из которых имеет вид (3.27):
Рис. 3.9. Комплексный случайный процесс
в виде вектора на комплексной плоскости
(3.31)
3.7. Узкополосный случайный процесс
113
Для определения статистических свойств огибающей и фазы необходимо
перейти в выражении (3.31) от декартовой (х,х) к потярной системе координат
(А, ф) (см. рис. 3.9) и определить совместную плотность вероя гности р4ф(А, ф).
Связь между этими двумя координатными системами выражается следующими
формулами:
х = A cos ф,
х = Asin ф.
Кроме того, вероятность попадания в бесконечно малую область в окрестностях
каждой точки комплексной плоскости при смене системы координат должна, оче-
видно, остаться неизменной. Площадь такой бесконечно малой области в декартовых
координатах выражается как dxdx, а в полярных — как AdAdty (рис. 3.10). Таким
образом, получаем:
/^(х.х^гДг = /^(Acos ф,А5Шф)АДАб/ф = рЛф(А,ф)г/Аб/ф.
Рис. 3.10. Переход от декартовой системы координат к полярной
Отсюда видно, что искомая плотность вероятности выражается как
Л»(АФ) = АРп (Асозф, Asin Ф) =
А
2ло2
ехр
(3.32)
Чтобы найти одномерные плотности вероятности для огибающей и фа »ы, нужно
проинтегрировать двумерную плотность (3.32) по «лишним» координатам:
2п
р/л) = J РяфСЛфШ
о
Рф(Ф) = |Раф(Аф)</А.
о
Так как двумерная плотность (3.32) не зависит от фазы ф, плотность вероятности
амплитуды рассчитывается совершенно элементарно:
(л. 2r А f А2 | , 2кА ( А2 ] А | А2 |
</ф=^ехр =^ехр • <3-33)
0 2лсх 2ох J 2ЛОХ у 2ОХ 7 У )
114
3. Основы теории случайных процессов
Целесообразно перейти к безразмерной переменной z = А/Ъх, относительно
которой
p(z) = zexp
L J
(3.34)
Плотность вероятности, описываемая законом (3.33) или (3.34), носит название
закона Рэлея. График этого распределения, соответствующий формуле (3.34), при-
веден на рис. 3.11. Из графика видно, что наиболее вероятны некоторые средние
(порядка ох) значения огибающей. В то же время маловероятно, чтобы огибающая
принимала значения как близкие к пулю, так и значительно превосходящие средне-
квадратичный уровень бх узкополосного процесса.
Рис. 3.11. Плотность вероятности огибающей
узкополосного случайного процесса (закон Рэлея)
Формула (3.33) позволяет известным образом (см. раздел 3.1) вычислить среднее
значение и дисперсию огибающей:
Л/{Л} = jApA (A)dA = j^-exp
О О °х V
ах =1,253о
= м{л2}-М2{л} = [—ехр----- dA-^-c2
11 о I 2g2 J 2
(2--V = 0,429g2.
I 2 J х
Чтобы найти плотность вероятности фазы, необходимо проинтегрировать вы-
ражение (3.32) по Л:
"? л Г л2 1
= J-—гехР -у-т dA = —, (3.35)
' 2ло2 2ло2 J 2л
то есть фаза имеет равномерное распределение на интервале [0, 2л]. Физически
это означает отсутствие какого-либо преимущественного значения полной фазы
у отдельных реализаций узкополосного случайного процесса.
Из (3.32, 3.33) и (3.35) видно, что
РлФ(Л’ф) = Рл(Л)Рф(ф)>
3.7. Узкополосный случайный процесс
115
следовательно, амплитуда и полная фаза узкополосного случайного процесса в один
и тот же момент времени являются статистически независимыми.
Узкополосный случайный процесс при наличии детерминированной
составляющей. Рассмотрим теперь ситуацию, когда к узкополосному шуму до-
бавлен узкополосный же детерминированный сигнал. Комплексный случайный
процесс в данном случае будет иметь следующий вид:
Z(r) = s(r) + js(t) + x(t)+jx(t).
Изображение мгновенного значения Z(t) на комплексной плоскости будет от-
личаться от рис. 3.9 наличием детерминированного вектора s(t) (рис. 3.12).
s(t) z(t) Re
Рис. 3.12. Комплексный случайный процесс в виде вектора на комплексной плоскости
при наличии детерминированной составляющей
Совместная плотность вероятности вещественной и мнимой частей этого
комплексного процесса будет отличаться от (3.31) наличием смещений для х и х,
равных s(f) и s(t) соответственно:
(x-s(O)2+(x-s(O)2
2°х
х ,
Pxi(x,x) = px(x')pi(x) = -—- exp
2тсог
Переход от декартовой системы координат к полярной, аналогичный рассмо-
тренному ранее (см. (3.32)), дает следующее:
Лф(л-Ф) = АР^А cos Ф-Л sin ф) =
А
ГехР
2 ЯСУ
(A cos <р - s(f))2 + (Л sin (р - s(f))2
•* J
Интегрирование этой двумерной плотности по фазе <р дает одномерную плот-
ность вероятности для амплитуды данного случайного процесса (промежуточные
выкладки опущены):
2? . Л Г Л2+52>| (AS
РзИ)=1Рз(р(Аф)^Ф = — ехР > (336)
где Sm = s2(t)+s2(t) — амплитудная огибающая детерминированного сигнала
в данный момент времени. Плотность вероятности (3.36) носит название закона
116
3. Основы теории случайных процессов
распределения Рэлея—Райса. На рис. 3.13 показаны графики данной плотности
вероятности, соответствующие разным отношениям сигнал/шум, то есть разным
значениям SПри Sm = 0 из (3.36) получается плотность вероятности, соот-
ветствующая закону Рэлея (3.34) При » 1, как видно из графиков, рас-
пределение огибающей приблиз сается к нормальному закону с математическим
ожиданием Sm и дисперсией а2.
Рис. 3.13. Плотность вероятности огибающей узкополосного случайного процесса
при наличии детерминированной составляющей (закон Рэлея—Райса)
Контрольные вопросы и задания
1. Какие сигналы называются случайными? Что является наиболее полной ха-
рактеристикой случайного сигнала? Можно ли считать реализацию случайного
нрочесса случайным сигналом? Почему?
2. Запишите выражения для расчета статистических характеристик случайного
процесса, связанных с одномерной плотностью вероятности.
3. Перечислите основные свойства плотности вероятности и функции распреде-
ления вероятностей случайной величины.
4. Что такое ковариационная и корреляционная функции случайного процесса?
Как они связаны между собой?
5. Какие из графиков, приведенных на рис. 3.14, могут изображать корреляционную
функцию случайного пооцесса? Почему?
6. Дайте определения случайных процессов, стационарных в узком и широком
смыслах.
7. На рис. 3.15 приведены графики двух характерных реализаций случайного про-
цесса. Может ли этот процесс быгь стационарным в широком смысле?
8. Что такое эргодический случайный процесс?
9. Запишите выражение для плотности вероятности стационарного нормального
случайного процесса. Поивелите формулировку центральной предельной тео-
ремы.
Задачи
117
г
Рис. 3.14. Графики для контрольного вопроса 5
в
е
I
Рис. 3.15. Графики для контрольного вопроса?
10. Что такое интервал корреляции случайного процесса? Как он вычисляется?
В какой связи он находится с эффективной шириной спектра?
11. Почему понятие комплексного спектра не используют в отношении случайного
процесса?
12. Что такое спектральная плотность мощности случайного процесса? Какова ее
размерность? Сформулируйте теорему Винера—Хинчина.
13. Что такое бе тый шум? Каковы его дисперсия и функция корреляции9 Реализуем
ли в действительности сигнал такого вида? Почему?
Задачи
Задача 3.1
Случайная величина X принимает дискретные значения X' с указанными в табл. 3.1
вероятностями Р(Х). Найти математическое ожидание, дисперсию, срсднеквадра-
тическое отклонение, функцию распределения данной случайной величины.
118
3. Основы теории случайных процессов
Таблица 3.1. Данные для задачи 3.1
xt 0,5 0,8 1,3
Р(Х) 0,35 0,45 0,2
Задача 3.2
Случайная величина X имеет непрерывную плотность вероятности р(х) следую-
щего вида:
х>0,
= L а
О, х < 0.
Найти математическое ожидание, дисперсию, среднеквадратическое отклонение,
функцию распределения вероятности данной случайной величины.
Задача 3.3
Случайная величина X, имеющая равномерное распределение на интервале О...л/2,
подвергается нелинейному преобразованию у = 5 cos х + 12 cos 2х. Наити матема-
тическое ожидание и дисперсию случайной величины Y.
Задача 3.4
Усилитель состоит из трех последовательно соединенных каскадов, коэффициенты
усиления которых являются независимыми случайными величинами, имеющими
средние значения цр ц2, ц3 и дисперсии Dt, D2, D3.1 [айти математическое ожидание
и дисперсию общего коэффициента усиления.
Задача 3.5
Найти и построить графики функции распределения и одномерной плотности
вероятности случайного процесса, реализации которого представляют собой пе-
риодические последовательности трапециевидных импульсов со случайной разно-
вероятной начальной фазой (рис 3.16). Найти среднее и среднеквадратическое
значения этого сигнала.
Рис. 3.16. Сигнал для задачи 3.5
Задача 3.6
Случайная величина X, имеющая равномерное распределение на интервале 0...1,
подвергается нелинейному преобразованию у = х(1 - х). Найти математическое
ожидание и дисперсию случайной величины Y.
Задачи
119
Задача 3.7
Установить, стационарен ли в широком смысле случайный процесс
x(t) = A cos(w0t + ф), где соо — известная величина, ф — случайная начальная фаза
с равномерным распределением на интервале от -я до я, А — случайная амплитуда,
не зависящая от ф.
Задача 3.8
Является ли процесс х(£), описанный в задаче 3.7, эргодическим?
Задача 3.9
Найти корреляционную функцию суммы и произведения двух независимых цен-
трированных случайных процессов, корреляционные фчнкции которых равны
и 7?2(т) соответственно.
Задача 3.10
Спектральная плотность мощности случайного процесса изображена на рис. 3.17.
Найти корреляционную функцию этого процесса.
-сов 0 юв и
Рис. 3.17. Спектральная плотность мощности для задачи 3.10
Задача 3.11
Случайный процесс имеет двустороннюю спектральную плотность мощности, рав-
ную Wo в полосах частот ±ю0 ± (Дю/2) (рис. 3.18). Найти корреляционную функцию
этого случайного процесса
Дю
1Г(ю)'
Ио
Дю
-ю0
0
ю
ю0
Рис. 3.18. Спектральная плотность мощности для задачи 3.11
Задача 3.12
Найти интервал корреляции, спектральную плотность мощности и эффективную
ширину спектра для случайного процесса с функцией корреляции вида
й(т) = о2(1 + а|т|)ехр(-а|т|), а>0.
4. Линейные цепи
с постоянными параметрами
Цепи, применяемые для преобразования сигналов, ве< ьма разнообразны по физи-
ческим принципам своей работы, внутреннему устройству и внешним характери-
стикам. В данной главе будет анализироваться прохождение детерминированных
и случайных сигналов через линейные стационарные цепи.
Важнейший принцип классификации цепей основан на том, что различные
цепи по-разному ведут себя при подаче на вход суммы нескольких сигналов. Цепь
называется линейной, если для нее выполняется принцип суперпозиции, то есть
выходной отклик на сумму сигналов представляет собой сумму откликов на эти
сигналы, поданные на вход цепи по отдельности. Математически это можно вы-
разить следующим образом. Если входной сигнал ивх1Ц) производит выходной
отклик мвых1(£)> а сигналу uex2(t), поданному на вход, соответствует выходной сиг-
нал uBwx2(f), то Для линейной цепи поданная на вход комбинация сигналов в виде
awBx|(f) + Pubx2(£) создаст выходной отклик, выражающийся как апвых1(£) + Рмвых2(0,
где а и Р — произвольные числа. Если принцип суперпозиции не выполняется, то
говорят, что цепь является нелинейной.
Цепь называется стационарной, если вид ее выходной реакции не зависит от того,
в какой момент времени поступает входной сигнал. Иначе говоря, если входному
сигналу uBX(i) соответствует выходной сигнал «вых(0- т0 сдвинутый во времени
входной сигнал wBX(t - т) будет создавать на столько же сдвинутый выходной сигнал
М||ых(Г - т) при любом значении временного сдвига т. Стационарные цепи называют
также цепями с постоянными во времени параметрами.
Если же свойства цепи не инвариантны относительно выбора начала отсчета
времени, такую цепь называют нестационарной (а также цепью с переменными во
времени параметрами или пара метрической цепью).
4.1. Частотные и временные характеристики
линейных цепей. Методы анализа
прохождения детерминированных
сигналов
Свойства линейности и стационарности позволяют рассчитать выходной сигнал
цепи для тюбого входного воздействия, зная лишь реакцию цепи на элементарный
4.1. Частотные и временные характеристики линейных цепей
121
входной импульс — дельта-функцию. Такая реакция является важнейшей харак-
теристикой линейной цепи, она называется импульсной характеристикой и обо-
значается h(t). То есть если uBX(t) = 5(t), то пвь1Х(£) =
Знание импульсной характеристики цепи позволяет найти ее реакцию на про-
извольный входной сигнал.
Для уяснения сути этого метода поступим следующим образом. Разобьем
произвольный сигнал uBx(f) на элементарные импульсы, как показано на рис. 4.1,
и найдем отклик цепи в момент времени 10 на элементарный импульс, действую-
щий на входе в момент tЕсли бы площадь этого импульса равнялась единице,
его можно было бы рассматривать как дельта-функцию, возникшую в момент t'.
При импульсной характеристике цепи h(t) отклик в момент t0 был бы, очевидно,
равен -t'). Поскольку, однако, заштрихованная на рис. 4.1 площадь импульса
равна wBx(t')Af' (а не единице), отклик в момент t0 будет wBX(t')A(t0 - Г')ДГ'. Для опре-
деления полного значения выходного сигнала в момент t0 нужно просуммировать
действие всех импульсов. При Д£’-> О суммирование сводится к интегрированию,
следовательно,
«вых(0 = j u^(t')h(t-t')dt'. (4.1)
Рис. 4.1. Формирование выходной реакции цепи
Эта формула называется интегралом Дюамеля и представляет собой интеграл
свертки.
Итак, если известна импульсная характеристика линейной цепи h(t), то можно
найти ее реакцию на произвольный входной сигнал.
Условие физической реализуемости. Вне зависимости от конкретного
вида импульсной характеристики физически осуществимой цепи всегда должен
выполняться важнейший принцип причинности’, выходной сигнал, отвечающий
импульсному входному воздействию, не может возникнуть до момента появления
импульса на входе. Отсюда вытекает очень простое ограничение на вид допустимых
импульсных характеристик: h(t) = 0 при t < 0.
Легко видеть, что для физически реализуемой системы верхний предел в (4.1)
может быть заменен текущим значением времени.
Г
(4.2)
122
4. Линейные цепи с постоянными параметрами
Формула (4.2) имеет ясный физический смысл: линейная стационарная цепь,
выполняя обработку поступающего на вход сигнала, проводит операцию взвешен-
ного суммирования всех его мгновенных значений, существовавших «в прошлом».
Принципиально важно, что физически реализуемая система ни при каких обсто-
ятельствах не способна оперировать «будущими» значениями входного сигнала
ЗАМЕЧАНИЕ 4.1 -----------------------------------------------------
Под физической реализуемостью здесь понимается только выполнение
рассмотренного ранее условия причинности, а не возможность реализовать
устройство с данной импульсной характеристикой в виде цепи с сосредо-
точенными параметрами или в каком-либо ином виде.
Переходная характеристика. Пусть на вход линейной стационарной цепи
воздействует сигнал в виде единичного скачка c(t) (см. раздел 1.1). Выходную реак-
цию цепи на такой сигнал называют переходной характеристикой и обозначают g(t).
Так же как и импульсная, переходная характеристика физически реализуемой цепи
должна быть равна нулю при t < 0.
Функция единичного скачка представляет собой интеграл от дельта-функции.
Интегрирование является линейной операцией, поэтому между импульсной и пере-
ходной характеристиками существует простая связь
/,(/) = ^, g(0=fW'. (4-3)
dt _•
ЗАМЕЧАНИЕ 4.2-----------------------------------------------------
Если входной сигнал удается представить в виде линейной комбинации
функций, результаты прохождения которых чеоез рассматриваемую цепь
уже известны, свойства линейности и стационарности позволяют силь-
но упростить расчет выходного сигнала. В частности, прямоугольный
импульс с амплитудой U, занимающий временной интервал от t, до t2,
можно представить как умноженную на U разность двух должным образом
сдвинутых по времени функций единичного скачка:
$м(0 = U(c(t-Q - o(f- Q).
Отсюда сразу же следует, что выходной сигнал, то есть реакция произ-
вольной цепи на прямоугольный импульс, представляет собой разность
сдвинутых по времени переходных характеристик:
5„ых<0 = Uigit-Q
Комплексный коэффициент передачи. Из свойств преобразования Фу-
рье известно, что спектр свертки двух сигналов представляет собой произведение
4.1. Частотные и временные характеристики линейных цепей
123
спектров этих сигналов. Таким образом, спектры входного и выходного сигналов
линейной цепи связаны друг с другом следующим образом:
где Л? (со) = Jh(t)e~ia‘dt — преобразование Фурье импульсной характеристики цепи.
Функция Х(со) называется комплексным коэффициентом передачи цепи и имеет
простую физическую интерпретацию: если на вход цепи поступает гармонический
сигнал с частотой со и комплексной амплитудой Авх, то комплексная амплитуда вы-
ходного сигнала рассчитывается следующим образом: Авых = Х(со)Авх.Часто пользу-
ются представ гением комплексного коэффициента передачи в показательной форме:
К(ю) = |Х(ш)|ехр[;фк(ш)].
Обе входящие сюда вещественные функции имеют специальные названия:
|К(ш)| — амплитудно-частотная характеристика (АЧХ), фк(со) — фагочастотная
характеристика (ФЧХ).
ЗАМЕЧАНИЕ 4.3----------------------------------------------------------
Можно наглядно пояснить связь между импульсной характеристикой
и комплексным коэффициентом передачи цепи следующим образом.
Пусть на вход цепи подан сигнал в виде дельта-функции, тогда выходная
реакция будет иметь форму импульсной характеристики. Комплексный
коэффициент передачи определяется как отношение выходного и входного
спектров, но спектр дельта-функции (см. формулу (1.49)) равен единице.
Отсюда получаем, что комплексный коэффициент передачи равен спек-
тральной функции импульсной характеристики цепи.
Так как импульсная характеристика цепи является, очевидно, вещественной
функцией, значения коэффициента передачи для противоположных частот пред-
ставляют собой комплексно-сопряженные числа:
Х(-со) = К' (со).
Из этого следует, что АЧХ цепи представляет собой четную функцию частоты,
а ФЧХ — нечетную:
|к(-со)| = |Х((о)|,
<рк(-щ) = -фк(со).
ЗАМЕЧАНИЕ 4.4-----------------------------------------------------------
Из формул, приведенных в этом разделе, видно, что для цепи, входной
и выходной сигналы которой имеют одинаковую размерность, переходная
продолжение &
124
4. Линейные цепи с постоянными параметрами
характеристика и комплексный коэффициент передачи являются безраз-
мерными функциями, а импульсная характеристика (как и дельта-функция
временного аргумента) имеет размерность частоты.
Фазовая и групповая задержка. С ФЧХ связаны две важные характери-
стики, описывающие задержку, приобретаемую сигналами при прохождении через
линейную стационарную цепь.
Фазовая задержка — это задержка, приобретаемая гармоническим сигналом:
если входной сигнал цепи
5вх(0 = Лсо5(аи+<р0),
то выходной сигнал
(О = А |/С(со)| cos (сог + <р* (со) + Фо) =
= |х((о)| A cos^co^f + + фр =
= I (* - SM’
где тф (со) = - фк ((о)/(о — вносимая цепью фазовая задержка.
Поскольку фазовый сдвиг на величину, кратную 2л радиан, неразличим, фазовая
задержка может быть определена только с точностпю до периода гармонического
сигнала, равного 2л/(0.
Групповая задержка (синонимы - групповое время запаздывания, групповое время
прохождения) на частоте (О — это задержка, приобретаемая комплексной огибающей
узкополосного сигнала, спектр которого сосредоточен в окрестностях частоты со.
Рассчитать ее значение проще всего, если воспользоваться понятием аналитиче-
ского сигнала, введенным в разделе 2.8. Пусть входной сигнал представляет собой
узкополосное колебание вида
(О = и G)cos(ro0t + ф(0),
причем медленно меняющиеся амплитудная огибающая U(t) и фазовая функция
ф(£) определены с использованием преобразования Гильберта (см. раздел 2.8). Тогда
соответствующий аналитический сигнал с односторонним спектром будет иметь вид
<ЛО = ^кх“’г+ф<0)-
Пусть спектральная функция этого аналитического сигнала равна Zbx (со) и со-
средоточена в малой окрестности частоты со0. Так как рассматриваемый сигнал
является узкополосным, комплексный коэффициент передачи цепи в пределах
полосы частот, занимаемой сигналом, меняется мало и в области положительных
частот может быть аппроксимирован следующим образом (АЧХ считается посто-
янной, а ФЧХ — линейно зависящей от частоты):
4.2. Расчет переходной и импульсной характеристик линейной цепи
125
где
(4.4)
В соответствии со сделанным приближением спектральная функция выходного
аналитического сигнала
Согласно свойствам преобразования Фурье, касающимся линейности и сдвига
сигнала во времени (см. раздел 1.7), спектру (4.5) соответствует аналитический
сигнал
Наконец, выходной сигнал цепи равен вещественной части аналитического
сигнала (4.6):
5вых(0 = Н^Ь1Х(0) =
= |*(Ч)\Uf - тпМ))cos(“o (l ~ ТФ(“о)) + <₽(f - Гр (юо)))'
(4.7)
Из полученной формулы видно, что комплексная огибающая сигнала, опреде-
ляемая функциями U(t) и <р(Г), приобрела задержку т,т(®0), определяемую выра-
жением (4.4), а высокочастотное заполнение получило временной сдвиг, равный
фазовой задержке на центральной частоте сигнала, тф(со0).
Чем узкополоснее проходящий через цепь сигнал, тем более точным является
приближенное равенство (4.7).
4.2. Расчет переходной и импульсной
характеристик линейной цепи
Дифференциальное уравнение цепи. Классическим методом анализа по-
ведения линейной 7?£С-цепи под воздейс гвием того или иного сигнала является
решение описывающего цепь неоднородного линейного дифференциального
уравнения k-ro порядка с постоянными коэффициентами. Этот метод изложен во
многих руководствах, например в учебнике [14], к которому и следует обращаться
за более подробными разъяснениями.
126
4. Линейные цепи с постоянными параметрами
Решение (относительно функции y(t)) неоднородного линейного дифференци-
ального уравнения k-ro порядка
dky dk~'y dy
akdir + ak-'~dFr + '" + a,~dt+aoy = g(t)' (48)
где g(t) — возмущающая функция, ищут в виде суммы свободной составляющей
yCB(t) — решения однородного дифференциального уравнения
dky dk~'y п
a^ + a^^r + -- + aod = O (4.9)
at at
и вынужденной составляющей yBblll(t) — частного решения уравнения (4.8):
y(t) = yJt) + yBJf).
Решение уравнения (4.9) записывают в виде
= (4.Ю)
П=1
где Ап — произвольные постоянные интегрирования, рп — корни характеристиче-
ского (алгебраического) уравнения
акрк +ak-iPk~' +-.- + alp + a0 =0. (4.11)
Если характеристическое уравнение имеет кратный корень pt кратности т, то
решение уравнения (4.9) записывается в виде
= Z Апе”"‘- (4.12)
^n=l J п=т+\
Для получения единственного решения уравнения (4.8) k произвольных по-
стоянных Ап определяют, задавая k начальных условий в момент t=0. Что касается
частного решения, то при выборе в качестве g(t) функции Хевисайда (1.8), то есть
g(t) = const при t > 0, все производные dkg/dtk равны нулю и вынужденная состав-
ляющая определяется предельно просто.
Располагая найденной таким образом переходной характеристикой цепи, на
основании соотношений (4.3) определяют импульсную характеристику и решают
задачу определения реакции цепи на произвольный сигнал с помощью интеграла
Дюамеля (4.1).
Для составления дифференциального уравнения используются известные ме-
тоды теории цепей и соотношения, связывающие токи и напряжения в элементах:
= uL(t) = L<^^-, uR(t) = RiR{t).
dt dt
Расчет комплексного коэффициента передачи. Чтобы найти комплекс-
ный коэффициент передачи цепи, в общем случае следует воспользоваться мето-
4.3. Преобразование характеристик случайного процесса в линейной цепи
127
дом узловых напряжений или контурных токов [14] или же, если это возможно,
рассмотреть цепь как делитель напряжения, подчас весьма сложный. При этом
следует использовать комплексные сопротивления (импедансы) й!£С-элементов,
определяемые следующим образом:
ZB = R, Z= j<oL, Zr = —.
R L J c jnC
4.3. Преобразование характеристик
случайного процесса в линейной цепи
Пусть на вход линейной стационарной цепи с комплексным коэффициентом пере-
дачи К((й) и импульсной характеристикой h(f) воздействует случайный процесс
хта(0. Совокупность реализаций этого процесса, прошедших через цепь и преоб-
разованных ею, образуют выходной случайный процесс хви(0-
Каждая конкретная реализация входного случайного процесса является детерми-
нированным сигналом и ее прохождение через линейную стационарную цепь можно
анализировать, используя методы, описанные в разделе 4.1. Здесь же нас будет
интересовать, как при этом изменяются статистические параметры случайного
процесса, а именно: корреляционная функция, спектральная плотность мощности
и плотность вероятности. Рассматривать будем лишь стационарные в широком
смысле случайные процессы с нулевым средним значением.
Начнем с нахождения спектральной плотности мощности выходного с тучай-
ного процесса. Эта задача легко решается с помощью рассуждений, аналогичных
тем, которые использовались в разделе 3.5 при выводе формулы (3.28). Умножив
спектральную плотность ХвхГ(го) «усеченной» по времени реализации процесса
xBX(t) на комплексный коэффициент передачи цепиК(го), получим спектральную
плотность этой же реализации на выходе:
ХвыхГ(®) = ^т(®)ВД-
Спектр мощности выходного сигнала может быть найден как
W (го) = lim
вых' /
х т(ю)2
выхГ \ 7
т
1хвхГ«оЖ(®)|2
lim---------------
г->~ f
= lim
|х(ш)|2=и;х(го)|к(го)|2
Таким образом, спектральная плотное гь мощности выходного случайного про-
цесса записывается как
(4.13)
128
4. Линейные цепи с постоянными параметрами
Теорема Винера—Хинчина (см. раздел 3.6) позволяет определить и корреляци-
онную функцию выходного случайного процесса:
J я 00
Л-(т) = 5- J = — J И;,(о))|К(Ш)|>^Ш. (4.14)
Обратное преобразование Фурье произведения спектров представляет собой
свертку соответствующих временных функций (см. раздел 1.8). Спектральная
плотность мощности входного случайного процесса 1Твх(ю) является спектром его
корреляционной функции Двх(т). Квадрат модуля комплексного коэффициента
передачи |К(<в)| связан преобразованием Фурье с корреляционной функцией
импульсной характеристики цепи (см. раздел 1.13 и формулу (1.89)).
Таким образом,
i R.AWT-t)dt,
(4.15)
где (т) = J - t)dt — вышеупомянутая корреляционная функция импульс-
ной характеристики цепи.
Дисперсия выходного случайного процесса может быть найдена с помощью
формул (4.14) или (4.15) путем подстановки в них значения т = 0:
-Лвых(0) = ^ JТКх(ш)|Х((о)рсо= JRJt)Bh(t)dt. (4.16)
ВКФ выходного и входного сигналов можно вычислить непосредственно во
временной области:
R (т) = х (f)x (Г-т) =
вых-вхv ' ВЫХ V ' ВХ ' 7
XBx(t')/z(f-£')<#' *BV(t-T).
Введем лвх(£ - т) внутрь интеграла и перенесем операцию статистического ус-
реднения на случайную часть подынтегрального выражения:
Л.ьП-вх(т) = jxx(t-T)xBx(i')/z(t-i')J^
Усреднение дает корреляционную функцию входного сигнала
^x^-TXx(^) = ^BX(i'-i + T).
После замены переменной т' = t' -1 + т окончательно получаем:
ЛВых.вх<т)= Rx(tW-tW (4.17)
4.3. Преобразование характеристик случайного процесса в линейной цепи
129
Итак, ВКФ выходного и входного случайных процессов определяется как
свертка корреляционной функции входного сигнала и импульсной характери-
стики цепи.
Пример 4.1. Преобразование белого шума. Пусть на вход линейной цепи с им-
пульсной характеристикой h(t) и соответствующим ей комплексным коэффици-
ентом передачи К(со) поступает белый шум с двусторонней спектральной плотно-
стью мощности Wo. Тогда форма корреляционных функций и спектра выходного
случайного процесса определяются лишь характерце тиками цепи. Действительно,
из (4.13,4.15) и (4.17) легко получить:
WMX(®) = W0|K(®)|2, (4.18)
= (4.19)
Для рассматриваемого случая формула (4.16), дающая значение дисперсии,
несколько упоощается:
d^ = WoBh(O) = Wojh2(t)dt = WoEh. (4.20)
Итак, определение спектральных и корреляционных характеристик стацио-
нарного случайного процесса на выходе линейной цепи не связано с какими-либо
трудностями. Иначе обстоит дело с определением плотности вероятности выходного
случайного процесса. В общем случае, при произвольном законе распределения
случайного процесса на входе это представляет собой весьма сложную задачу. Лишь
при нормальном распределении входного процесса задача упрошае гея, так как при
любых линейных операциях с гауссовским процессом его распределение остается
нормальным, изменяются лишь функции Д(т) и IV(w).
Итак, если на вход линейной стационарной цепи воздействует нормальный
случайный процесс с нулевым средним, то математическое ожидание выходного
случайного процесс а будет также нулевым, а его дисперсия может быть найдена
с помощью формулы (4.16).
ЗАМЕЧАНИЕ 4.5---------------------------------------------------------
Если эффективная длительность импульсной характеристики цепи
существенно превосходит интервал корреляции входного случайного
процесса, то вычисление интеграла свертки (4.1) можно приближенно
представить как суммирование большого числа некоррелированных друг
с другом вкладов от разных фрагментов сигнала xBX(t). В соответствии с
центральной предельной теоремой (см. раздел 3.4) это означает, что рас-
пределение вероятности выходного случайного процесса нормализуется,
то есть приближается к гауссову независимо от закона распределения
хвх(О [3,4].
5 Ns 675
130
4. Линейные цепи с постоянными параметрами
4.4. КС-фильтры нижних и верхних частот
и их характеристики
Прос гейшие цепи, состоящие из резисторов и конденсаторов, широко применяются
в радиотехнике для преобразования формы ко. [ебаний. Рассмотрим свойства двух
основных цепей этого типа.
Интегрирующая ЯС-цепь. Рассмотрим схему, представляющую собой по-
следовательное соединение резистора и конденсатора; выходной сигнал снимается
с конденсатора (рис. 4.2).
Рис. 4.2. Интегрирующая ЯС-цепь
Комплексный коэффициент передачи такой цепи проще всего найти, рассмотрев
ее как делитель напряжения:
1
К(со) = 7ЮС =-----------= —-—, (4.21)
1 D 1 + jtoRC 1 + /сот
где т = RC — постоянная времени цепи. Амплитудно- и фазочастотная характери-
стики интегрирующей /?С-цепи имеют следующий вид:
1
К(ю) = -===, <pK(co) = -arctg(coT).
V1 + C0 т
Графики этих функций представлены на рис. 4.3, а и б.
Рис. 4.3. Частотные характеристики интегрирующей ЯС-цепи: а — АЧХ, б — ФЧХ
4.4. RC-фильтры нижних и верхних частот и их характеристики
131
Из графика АЧХ видно, что такая цепь пропускает низкие частоты, задержи-
вая высокие, то есть является фильтром нижних частот (ФНЧ). Частота среза
фильтра, на которой модуль коэффициента передачи составляет 1/^2= 0,707 от
максимального значения, определяется как
со =- = —. (4.22)
с т RC
Чтобы найти временные характеристики этой цепи, запишем вначале диффе-
ренциальное уравнение, связывающее входной и выходной сигналы. Ток, протека-
ющий через конденсатор, пропорционален производной по времени от выходного
напряжения цепи:
ic<t) = C
dt
(4.23)
Но тот же ток протекает и через резистор, создавая на нем падение напряжения,
равное разности входного и выходного напряжений цепи:
г (0=Цвх(0~Цвых(0. (4.24)
R R
Приравнивая друг к другу (4.23) и (4.24), получим дифференциальное уравнение
интегрирующей ДС-цепи:
du (t)
Мв/0 = Т^к2 + ^(°- (425)
Если параметры цепи и сигнала таковы, что
du (t)
ВЫХ X '
dt
dU (t) z X 1 Г Z ,
то MBx(t) = т——, или ивых(Г) » - J w„x(t )dt.
Таким образом, выходной сигнал примерно пропорционален интегралу по вре-
мени от входного сигнала, поэтому такая ДС-цепь и называется интегрирующей.
Приближенное интегрирование выполняется тем точнее, чем больше относительная
доля высокочастотных составляющих в спектре входного сигнала. Действитель-
но, согласно свойствам преобразования Фурье, при интегрировании сигнала его
спектр умножается на l/(jco). Согласно формуле (4.21), приближенное равенство
Х(со) ~ 1/(/сот), обе< печивающее интегрирующее свойство цепи, будет справедливо
при сод » 1, где сон — нижняя граничная частота спектра сигнала.
Рассчитаем импульсную и переходную характеристики цепи. Начнем с переход-
ной характеристики, воспользовавшись для этого дифференциальным уравнением
(4.25), подставив в него в качестве ugx(t) единичную ступенчатую функцию (то есть
Мв,(0 = 1 ПРИ { > °)-
132
4. Линейные цепи с постоянными параметрами
Таким образом, для нахождения переходной характеристики необходимо решить
дифференциальное уравнение
dt
и (0 = 1
ВЫХ V /
при начальном условии ?2BbIX(0) = 0.
Общее решение этого линейного неоднородного дифференциального уравнения
имеет вид
Начальное условие мвых(0) = 0 позволяет найти константу С: С= -1. Итак, пере
ходная характеристика интегрирующей Д С-цепи имеет следующий вид (рис. 4.4, а):
g(t) =
t>0,
t <0.
(4.26)
Импульсную характеристику можно найти дифференцированием переходной
характеристики (рис. 4.4, б):
h(t) =
dg(t) =
dt
(4.27)
Рис. 4.4. Временные характеристики интегрирующей RC-цепи:
а — переходная, б — импульсная
Дифференцирующая ЯС-цепь. Диаметрально противоположными свой-
ствами обладает цепь, также состоящая из последовательно соединенных резистора
и конденсатора, но в случае снятия выходного сигнала с резистора (рис. 4.5).
Ubx(0 Нвых(0
Рис. 4.5. Дифференцирующая RC-цепь
4.4. RC-фильтры нижних и верхних частот и их характеристики
133
Комплексный коэффициент передачи найдем, рассмотрев цепь как делитель
напряжения:
К(м). я , >йс
д ! 1 1+J&RC 1 + JCOT
jmC
(4.28)
где т = RC — как и раньше, постоянная времени цепи. Амплитудно- и фазочастотная
характеристики цепи имеют следующий вид:
К(о>) =
сот
>/1 + со2т2
фх((0) =
П , X
— - arctg (сот),
-|-arctg (сот),
со>0,
(о<0.
Графики этих функций представлены на рис. 4.6, а и б.
Из графика АЧХ видно, что такая цепь пропускает высокие частоты, задерживая
низкие, то есть является фильтром верхних частот (ФВЧ). Частота среза фильтра,
на которой модуль коэффициента передачи составляет 1/72 = 0,707 от максималь-
ного значения, определяется Формулой (4.22).
Рис. 4.6. Частотные характеристики дифференцирующей ЯС-цепи: а — АЧХ, б — ФЧХ
Составим дифференциальное уравнение для этой цепи. Напряжение на кон-
денсаторе равно разности входного и выходного напряжений цепи, поэтому ток,
протекающий через него,
гс(О = С
dt dt J
Но этот же ток, протекая затем через резистор, создает выходное напряжение
«.ьоХО = R
134
4. Линейные цепи с постоянными параметрами
Таким образом, дифференциальное уравнение цепи имеет вид
du (t) du (t)
at at
Если постоянная времени т настолько мала, что в любой момент времени
т
du (t)
вых X /
dt
du (t)
то будет выполняться приближенное равенство пвых(£) - т——•
Такая ДС-цепь выполняет операцию приближенного дифференцирования сиг-
нала. Дифференцирование выполняется тем точнее, чем больше относительная
доля низкочастотных составляющих в спектре сигнала. Действительно, согласно
свойствам преобразования Фурье, дифференцирование сигнала приводит к ум-
ножению его спектра наусо. Согласно формуле (4.28), приближенное равенство
/С(ш) “ /сот, обеспечивающее дифференцирующие свойства цепи, будет справедливо
при совт « 1, где сов — верхняя граничная частота спектра сигнала.
Чтобы найти импульсную и переходную характеристики этой схемы, обра-
тимся к результату, уже полученному для интегрирующей 7?С-цепи. Различие
состоит лишь в том, откуда снимается выходной сигнал — с резистора или кон-
денсатора, а так как uR(t) + wc(t) = для переходной характеристики получим
(рис. 4.7, а):
g(0=
1-(1-е“'/т) = е
О,
(4-29)
Рис. 4.7. Временные характеристики дифференцирующей НС-цепи:
а — переходная, б — импульсная
Импульсную характеристику получим дифференцированием переходной ха-
рактеристики (рис. 4.7, б)
dg(t) = , t>0,
dt 0, t < 0.
(4.30)
4.5. Прохождение сигналов через простейшие RC-цепи
135
ЗАМЕЧАНИЕ 4.6-------------------------------------------------------
Легко убедиться, что аналогичными фильтрующими возможностями
обладают двухэлементные цепи, состоящие из сопротивления и индук-
тивности (7?£-цепи). Интегрирующими свойствами обладает 2?£-цепь,
выходное напряжение которой снимается с сопротивления, а диффе-
ренцирующими — 7?£-цепь, выходное напряжение которой снимается
с индуктивност!1. Постоянная времени таких цепей рассчитывается как
т = L/R, а все частотные и временные характеристики полностью совпа-
дают с приведенными в данном разделе для соответствующих .RС-цепей.
4.5. Прохождение сигналов
через простейшие ЯС-цепи
В данном разделе приводится несколько примеров анализа прохождения несложных
сигналов через рассмотренные ранее дифференцирующую и интегрирующую RC-
цепи. В первых двух примерах входным сигналом является прямоугольный импульс:
(и, 0<t<T,
S“W=[0, t<0, t>T.
(4.31)
В разделе 4.1 было указано, что выходная реакция произвольной цепи на пря-
моугольный импульс представляет собой разность двух сдвинутых по времени
переходных харакя еристик, умноженную на амплитуду входного импульса. Поэтому
для прямоугольного импульса (4.31) выходной сигнал будет записываться как
sain(t) = U(g(t)-g(t-T)).
(4.32)
Пример 4.2. Преобразование пря наугольного импульса интегрируюиц и RC-цепью.
Воспользуемся для расчета формулой (4.32) и полученной ранее переходной ха-
рактеристикой интегрирующей 7?С-цепи (4.26):
О,
U(\-e-T^e^\
£ < О,
0<t<T,
t>T.
(4.33)
График выходного сигнала (4.33) приведен на рис. 4.8.
Пример 4.3. Преобразование прямоугольного импульса дифференцирующей RC-
цепью. Воспользуемся для расчета формулой (4.32) и полученной ранее переходной
характеристикой дифференцирующей 7?С-цепи (4.29):
0,
5 (t) = < Ue ,
ВЫХ У '
U(l-eTh)e^\
t <0,
0 < t < Т,
t>T.
(4.34)
136
4. Линейные цепи с постоянными параметрами
Рис. 4.8. Результат преобразования
прямоугольного импульса интегрирующей НС-цепью
Рис. 4.9. Результат преобразования прямоугольного импульса
дифференцирующей ЯС-цепью: сплошная линия — Т~ т. пунктирная линия — Т » т
Выходной сигнал (4.34), показанный на рис. 4.9, имеет разрывы первого рода
при t = 0 и t = Т, что харак герно для линейной цепи, в импульсную характеристику
которой аддитивно входит 8-функция (см. (4.30)).
ЗАМЕЧАНИЕ 4.7------------------------------------------------
Для данной цепи Х(0) = 0, вследствие чего в ее выходном сигнале всегда
будет отсутствовать постоянная составляющая:
/^(0^=0.
Пример 4.4. Прохождение экспоненциального импульса через интегрирующую
RC-цепь. Входной сигнал в данном примере имеет следующий вид:
Ue~M
«
о,
i>0,
t < 0.
Простота сигнала и цепи позволяет оперировать как во временной, так и в частот-
ной областях. Начнем с расчета во временной области. При этом нам необходимо
знать импульсную характеристику цепи. Эта характеристика рассматривалась в
предыдущем разделе, она определяется формулой (4.27). Подставим выражения
для сигнала и импульсной характеристики в формулу свертки (4.1), учитывая при
4.5. Прохождение сигналов через простейшие RC-цепи
137
этом область ненулевого значения подынтегрального выражения соответствующим
выбором пределов интегрирования:
' г . 1 ~ и ‘г 4»--к
звых(0 = ]s^(t')h(t-t')dt'= jUe at -e ’ dt' =—e t/xje 1 dt'.
о о T T 0
Здесь следует обратить внимание на особый случай, когда а = 1/т и под интегра-
лом вместо экспоненты оказывается константа. С учетом этого получаем:
«вых (О
U
1-ат
U-te~‘
. т
1
а*—,
т
1
а .
т
Следует обратить внимание на то, что формула для особого случая может быть
получена из общей формулы при предельном переходе а -> 1/т. Графики выходного
сигнала для случаев а = 1/(2т), а = 1/т и а = 2/т приведены на рис. 4.10.
Рис. 4.10. Результат прохождения экспоненциального импульса
через интегрирующую ЯС-цепь
Теперь выполним аналогичный расчет в частотной области. Для этого прежде
всего необходимо получить спектральную функцию входного сигнала:
5х(<о) = )Mdr
о
Ue~ale~J(M
-(а + »0
U
a + ja
Комплексный коэффициент передачи интегрирующей ЯС-цепи, полученный
в предыдущем разделе (см. (4.21)), позволяет сразу же рассчитать спектр выход-
ного сигнала:
•Lx(®)=-U®)*(«>)=
и
(a +jw)(l +уют)
Чтобы получить выходной сигнал как функцию времени, необходимо подверг-
нуть это выражение обратному преобразованию Фурье. Однако в данном случае
138
4. Линейные цепи с постоянными параметрами
можно избежать вычисления интеграла Фурье, представив спектр выходного сиг-
нала в виде суммы простых дробей:
и и
S = = (—-----------1
вых a + jut 1 + jcot l-ax^a + jco l/x + jwJ
Каждое из двух слагаемых имеет вид, соответствующий преобразованию Фурье
одностороннего экспоненциального импульса (см. раздел 1.6 и формулу (1.57)).
Таким образом, выходной сигнал во временной области будет представлять собой
разность двух экспонент:
5 = t>0.
выЛ 7 1-ат '
Как видно из формулы, данный результат совпадает с полученным ранее.
ЗАМЕЧАНИЕ 4.8---------------------------------------------------
При расчете в частотной области тоже необходимо отдельно рассматривать
особый случай а = 1/т, поскольку использованный метод разложения на
простые дроби предполагает отсутствие кратных корней у знаменателя.
4.6. Одиночный колебательный контур
и его основные характеристики
Простейшей цепью, позволяющей выделить или задержать определенную полосу
частот, является одиночный колебательный контур.
Последовательный колебательный контур. Рассмотрим цепь, состоящую
из последовательно включенных катушки индуктивности L, конденсатора С и рези-
стора г (рис. 4.11). Входным сигналом будем считать напряжение между концами
цепи, а выходным — ток в ней. Комплексным коэффициентом передачи, таким
образом, будет являться величина, обратная комплексному сопротивлению цепи:
К(со) = Д^ = ^—.
(7(a>) Z(w)
Рис. 4.11. Последовательный колебательный контур
4.6. Одиночный колебательный контур и его основные характеристики
139
Рассмотрим зависимость этого комплексного сопротивления Z от частоты:
Z(co) = г + ;со£ +--= г + j\ mL------
ja>C v (£>C
= r + j
. co2£C-l
(4-35)
Частота co0 = 1 / VZc называется резонансной частотой контура. С учетом этого
обозначения (4.35) можно переписать в виде
Z(w) = r + j^— = r + j
(йС
ю2~юо = г + . (to + to0)(o-Юр)
со2®С со2соС
(4.36)
Приведенные ранее выражения для Z(co) были получены без каких-либо при-
ближений, они справе щивы для любой час готы со и для любых параметров контура.
Далее рассмотрим приближенное поведение комплексного сопротивления контура
вблизи его резонансной частоты со„. 11ри этом можно считать со + со0 ~ 2со0 в числителе
формулы (4.36) и принять со2со = со’ в ее знаменателе. Получим:
Z(co) = r + ;
2со0(со-сРр)
со2С
1 + ;2
I
и-(Ор
“о
1
со0гС
= г
Безразмерная величина е = (со - co0)/cd0 характеризует отклонение частоты
от резонансной и называется относительной расстройкой. Безразмерная ве-
личина
1 _ (Dpi _ y]b / С _ р
ГСОрС г г г’
(4-37)
где р = y/L/C — характеристическое сопротивление контура, называется доброт-
ностью контура и характеризует его способность поддерживать незатухающие
свободные колебания.
Таким образом, с учетом введенных обозначений комплексное сопротивление
последовательного колебательного контура вблизи его резонансной частоты можно
записать как
Z(co) = r(l + ;2Qe).
(4.38)
Модуль и фаза этого сопротивления равны
|Z(co)| = rJl + 4Q2£2,
argZ(co) = arctg(2QE).
Поведение функций |Z(®)| и argZ(co) в окрестностях резонансной частоты со0
представлено на рис. 4.12 а и б.
140
4. Линейные цепи с постоянными параметрами
Рис. 4.12. Комплексное сопротивление последовательного колебательного контура
в окрестностях резонансной частоты. Частотная зависимость: а — модуля; б — фазы
Резонансной характеристикой последовательного контура называется зависи-
мость комплексной амплитуды тока в нем от частоты, нормированная к резонанс-
ному значению тока:
К (Ю) = AM = £М =----------г_---=-----1---. (4.39)
Р /и(®о) ад r(l + j2Q£) l + ;2Qe
Модуль резонансной характеристики имеет вид
I 1 ,7' <4-40’
1 1 71+42е
его график представлен на рис. 4.13.
Определим полосу пропускания контура по уровню 1/72 = 0,707. Как видно из
(4.24), модуль резонансной характеристики принимав т такое значение при 4Q2e2 = 1,
отсюда e = ±l/(2Q).
Рис. 4.13. Модуль резонансной характеристики колебательного контура
в окрестностях резонансной частоты
4.6. Одиночный колебательный контур и его основные характеристики
141
Подставив сюда выражение, определяющее относительную расстройку £, полу-
чим:
М-Гор =± 1
“о b-Q
COn
и, следовательно, со = со0 ±——. Это соотношение определяет граничные часто-
2(2
ты полосы пропускания контура. Ширина полосы пропускания будет, очевидно,
равна
Д“о.7О7=-^- (441)
Отсюда следует еще одно определение добротности, удобное для ее экспери-
ментального измерения:
Q = ю° = ^— (4.42)
^^0,707 АЛ),707
Последовательный колебательный контур как четырехполюсник.
Рассмотрим теперь последовательный контур как делитель напряжения, выход-
ное напряжение которого снимается с одного из реактивных элементов, например
емкости (рис. 4.14).
«вх(0
мвых(0
Рис. 4.14. Последовательный колебательный контур,
включенный в виде четырехполюсника
Расчет коэффициента передачи по напряжению для такой цепи не представляет
сложностей:
1
Л-(со)= - -----= ----- , (4.43)
1 . т 1 - соLC + ititrC .со . со г
——+/со£ + г 7 1---- + j----
J®c (О2п «о Р
где параметры со0 и р имеют тот же смысл, что и раньше.
Произведя упрощения, аналогичные сделанным ранее, можно получить при-
ближенное выражение для коэффициента передачи в окрестностях резонансной
частоты со0:
К(Дсо) =
~jQ
l + j2Q—
“о
где Дсо = со - со0.
(4.44)
142
4. Линейные цепи с постоянными параметрами
Из полученной формулы видно, что форма АЧХ совпадает с графиком резонанс-
ной характеристики, показанным на рис. 4.13, а модуль коэффициента передачи
данной цепи на резонансной частоте равен Q. Фазовый сдвиг, вносимый цепью на
резонансной частоте, равен -90°.
ЗАМЕЧАНИЕ 4.9--------------------------------------------
На резонансной частоте, то есть при Дсо = 0, формула (4.44) дает точное
значение коэффициента передачи. Однако при анализе точной формулы
(4.43) оказывается, что максимальное значение модуля коэффициента
передачи достигается не на резонансной частоте контура, а в стороне от
нее, при смещении на со0/(2Q* * 2) вниз (если выходное напряжение снима-
ется с конденсатора) или вверх (если выходное напряжение снимается
с катушки индуктивности) от резонанса. Модуль коэффициента передачи
при этом равен
Из формул видно, что на практике эти отклонения могут стать заметными
только для контуров с очень низкой добротностью
Чтобы продемонстрировать альтернативный способ расчета временных характе-
ристик, получим их для данной цепи не с помощью дифференциального уравнения,
как было сделано ранее для ЯС-цепей, а через обратное преобразование Фурье
комплексного коэффициента передачи (4.43). Для этого прежде всего следует
представить эту формулу в виде суммы прос тейших дробей:
к(<й)=—--------
, (О . со г
1--2+ ]--
“о “о р
“о L 1
7С0 + —z-+ 7СО„ 1-------
J 2Q J °\| 4Q2
мо
1
,2
_______________
Y “о h
юо
;2 1—1—
N 4Q
17
2
со,
Д1-
со0 . Г, 1 юо L
7СО + -—— — 7CDr, 1-- 7СО + —-+ 7СО„,1-
2<2 V 4Q2 2Q °V 4Q
Теперь, зная, что спектральная функция вида 1/(а +усо) соответствует одно-
стороннему экспоненциальному импульсу exp(-at), существующему при t > 0
4.6. Одиночный колебательный контур и его основные характеристики
143
(см. раздел 1.6 и формулу (1.57)), можно сразу же записать импульсную харак-
теристику:
Л(0 =
юо
у 2 11—1—
N 4Q2
юо
1/1
I C0n . 1 . 1
exp------5-t+;co0t 1------7 -exp т-г-усо0г 1--------------
2Q V 4Q2 J I 2Q V 4Q2
2Q
4<2:
4Q
co 1 1
exp _5n427'sin
4Q
®Р
ехр —
I 2Q
—t jsin (O0t 1------Ц-
2Q J I N 4Q2
1
Для случая контура с высокой добротностью (Q » 1) полученное выражение
может быть приближенно представлено в следующем виде:
соп 1
Л(г) = со,. ехр --*-t sm(co0t).
\ )
ехр (2Qcos(“oO + sin(coo0) =
Чтобы получить переходную характеристику, проинтегрируем полученное вы-
ражение и учтем сделанное предположение о величине Q.
, X 4О2 2(2
1 + 4Q 1+4Q
7 со у)
= l-expl-^-jcos(a)o0.
Графики переходной и импульсной характеристик колебательного контура по-
казаны на рис. 4.15.
g(Of
А(П%
Рис. 4.15. Временные характеристики колебательного контура:
а — переходная, б — импульсная
144
4. Линейные цепи с постоянными параметрами
Параллельный колебательный контур. Эта цепь представляет собой
параллельное соединение тех же элементов, что и ранее: катушки индуктивности,
конденсатора и резистора (рис. 4.16). Входной сигнал в данном случае создается
источником тока, а выходным сигналом будем считать напряжение на элементах
этой параллельной цепи. Таким образом, коэффициентом передачи будет являться
величина, обратная комплексной проводимости цепи:
U
= = ---.
4 W
1
Рис. 4.16. Параллельный колебательный контур
Выкладки, аналогичные приведенным при рассмотрении последовательного
контура, приводят к такому результату:
y((0) = |(l+j2Q£).
К
Относительная расстройка е определяется здесь так же, как и раньше, а доброт-
ность для параллельного контура рассчитывается по-другому:
л ос R R
О-«)
Резонансная характеристика в данном случае определяется как зависимость
напряжения на элементах контура от частоты, нормированная к резонансному
значению. Она записывается так же, как и для последовательного контура (см.
(4.39) и (4.40)). Формулы (4.41) и (4.42), показывающие связь между частотными
параметрами контура и его добротностью, также сохраняют силу.
Пример 4.5. Воздействие амплитудно-модулированного сигнала на колебатель-
ный контур. Пусть на последовательный колебательный контур с параметрами г,
L, С (см. рис. 4.11) подано напряжение в виде AM-сигнала с однотональной мо-
дуляцией (несущая частота со0, частота модулирующего сигнала Q, коэффициент
модуляции т — см. раздел 2.2 и формулу (2.3)). причем несущая частота совпадает
с резонансной частотой контура. Проанализируем ток, который будет протекать
в контуре.
Прежде всего убедимся в том, что этот ток тоже будет представлять собой
AM-сигнал с однотональной модуляцией. Как было показано в главе 2 (см. (2.3)
4.6. Одиночный колебательный контур и его основные характеристики
145
и рис. 2.3), спектр такого сигнала содержит три гармонические составляющие на
частотах о)0 и m(l ± Q. Каждой из них соответствует гармоническая составляющая
тока на той же частоте, комплексная амплитуда которой связана с комплексной
амплитудой напряжения согласно закону Ома:
im=um/z^.
Комплексное сопротивление последовательного контура на интересующих нас
частотах легко находится из формулы (4.38) с учетом того, что на резонансной
частоте относительная расстройка е равна нулю, а на боковых частотах она со-
ставляет Q/co0:
Z((D0) = ?-,
Q
Z(a>n+Q) = r 1+/2Q— •
a>n
На рис. 4.17 показаны спектрограммы напряжения и тока в колебательном
контуре, полученные с учетом приведенных соотношений.
Как видно из рисунка, амплитудный и фазовый спектры тока, протекающего
через последовательный колебательный контур, сохраняют симметрию, а это го-
ворит о том, что ток в данном случае тоже является AM-сигналом с однотональной
модуляцией.
Теперь найдем коэффициент амплитудной модуляции тока. Прежде всего за-
метим, что этот коэффициент при однотональной модуляции равен удвоенному
отношению амплитуды любой из боковых спектральных составляющих к амплитуде
составляющей с несущей частотой (это видно из графика рис 4.17 или из форму-
лы (2.3)). Применим это соотношение к спектру тока:
Наконец, перепишем последнюю формулу, выразив результат через параметры
элементов контура, воспользовавшись для этого выражением для резонансной
частоты и формулой (4.37):
Следует обратить внимание на то, что полученный результат не зависит от ем-
кости конденсатора колебательного контура.
146
4. Линейные цепи с постоянными параметрами
Рис. 4.17. Спектры тока и напряжения при воздействии на последовательный
колебательный контур АМ-сигнала с однотональной модуляцией
ф-Ф-arctg——
“от
Ф
. 200
ф + Ф + arctg ——
Т “о
ш0- Q со0 со0+ Q со
ЗАМЕЧАНИЕ 4.10 ------------------------------------------------
Столь простым результат анализа получается благодаря совпадению
несущей частоты АМ-сигнала с резонансной частотой контура. При на-
личии расстройки между этими двумя частотами спектр тока оказывается
несимметричным, что говорит о наличии как амплитудной, так и угловой
модуляции.
Пример 4.6. Входное сопротивление параллельного контура с частичным включе-
нием. Пусть в параллельном колебательном контуре сделан отвод от индуктивной
ветви (рис. 4.18). Коэффициент включения (доля общей индуктивности контура,
к которой производится подключение) обозначен а. Найдем входное сопротивление
этого двухполюсника на резонансной частоте о>0.
Прежде всего заметим, что формула (4.45) позволяет записать реактивные
сопротивления индуктивности и емкости контура на резонансной частоте в виде
со0А =
1 _R
^0C~Q'
(4.46)
4.6. Одиночный колебательный контур и его основные характеристики
147
(l-a)Z
aL
Рис. 4.18. Частичное включение параллельного колебательного контура
Рассматриваемый двухполюсник можно представить как параллельное со-
единение индуктивности aL и ветви, состоящей из последовательно включенных
индуктивности (1 - a)L и параллельной ЯС-цепи.
В соответствии с этим искомое входное сопротивление можно записать следу-
ющим образом:
7 >0al(>0 (1 - a)£ + ZRC (<о0))
>oi + ^c(®o)
(4-47)
где ZRC(к>0) — сопротивление параллельной /?С-цепи на частоте cn0. С учетом со-
отношений (4.46) это сопротивление
R^c
R+J^c
R —
jQ _ R
1 R+*
jQ
(4.48)
Подставив (4.48) и (4.46) в (4.47), получаем:
. R( ... .7? R
ja— j(l-a)— +-------
JQ jQ + 1
R
. RI ...
v п
. Л
JQ jQ + i
Упрощение этого выражения дает окончательный результат:
ZM=^2R+J^^-R-
При высокой добротности контура (Q » 1) вторым слагаемым можно пре-
небречь:
zj^y^R.
Итак, при частичном включении контура его сопротивление на резонансной
частоте уменьшается пропорционально квадрату коэффициента включения.
148
4. Линейные цепи с постоянными параметрами
4.7. Линейные цепи с обратной связью
Существует целый класс радиотехчичес ких цепей, в которых выходной сигнал или
некоторая его часть снова подается на вход. Такие цепи называют цепями с обрат-
ной связью. Введение обратной связи (ОС) в ряде случаев позволяет существенно
улучшить рабочие характеристики цепей. Однако при определенных условиях
такие цепи становятся неустойчивыми и в них возникают автоколебания. На этом
принципе построены различные автоколебательные системы, прежде всего, гене-
раторы гармонических колебаний, которые являютс я неотъемлемыми элементами
любого радиопередающего устройства.
Обратная связь может вводиться в схему преднамеренно с целью изменения
характеристик последней. В этом случае она является полезной. Однако иногда
обратная связь возникает вопреки намерениям разработчика устройства из-за не-
учтенных электромагнитных связей между входными и выходными цепями. Такая
обратная связь называется папазитной.
Обобщенная схема устройства с обратной связью представлена на рис. 4.19.
Здесь канал прямой передачи (КПП) имеет комплексный коэффициент передачи
К(со) и, как правило, является активным звеном (усилителем). Канал обратной
связи (КОС) обычно представляет собой пассивный четырехполюсник, его коэф-
фициент передачи обозначен P(w).
Рис. 4.19. Устройство с обратной связью
В теории систем с обратной связью предполагается, что КПП и КОС являются
однонаправленными, то есть в данных устройствах отсутствует передача сигнала
с выхода на вход.
Коэффициент передачи схемы с обратной связью. Выясним, как связан
комплексный коэффициент передачи цепи, охваченной обратной связью, с коэффи-
циентами передачи трактов прямой и обратной передачи. Для этого обозначим $,(£)
сигнал на входе КПП (то есть после суммирующего ус гройства) и s2(£) — сигнал
на выходе КОС (см. рис. 4.19).
Спектры сш налов в различных точках схемы связаны друг с другом очевидным
образом:
51(«) = Пх(со) + 52(ш),
Й „(«>) = 5,
(4.49)
(4.50)
4.7. Линейные цепи с обратной связью
149
Ш = ^ы/«>)0(“)- (451)
Чтобы найти коэф&ициент передачи цепи с обратной связью
^) = Сых(от)/Сх(ш),
нужно исключить из системы уравнений (4.49-4.51) спектры сигналов s,(t) и s2(t).
Подставим сначала выражение (4.51) в формулу (4.49):
51({й) = Пвх(со) + Сых (<о)р(ш),
а полученный результат — в формулу (4.50):
йвых (“) = (“№) + (со)р(со)к(ю).
Отсюда можно получить выражение для искомого коэффициента передачи:
U (со) К(ы)
К '(со) = - 7 =-------------. (а 521
Пвх(0)) 1-К(ю)Р(со)
При выводе соотношения (4.52) рассматривалась схема обшего вида, в которой
не конкретизировался вид входного сигнала: это может быть как ток, так и на-
пряжение.
Классификация. Рассмотрим структуру К'(со) подробнее. Обозначим, в част-
ности, К{(£>) = K((o)eiVkM и Р((о) = Р(со)е;фр<“). С учетом этого
К == Х(ш)
1-р(со)е;фр<ш’Х(ш)е7Фк<ш) 1-р(щ)К(щ)е;[фрГ“)+Фк<ш)|
Полученное соотношение служит основой для приводимой далее классифика-
ции видов обратной связи. Физическую основу этой классификации составляет
различие фазовых соотношений между суммирующимися входным сигналом
и сигналом обратной связи.
Положительная обратная связь. Если <рр(со) + <рк(со) = 2itk, где k = 0, ±1,
±2..., то сигнал обратной связи и входной сигнал складываются синфазно, при этом
|*»|= >Х(со)
1 1 l-P(w)X(w)
и обоатная связь называется положительной (ПОС), причем при Р(щ)К((о) -э 1
имеем K'(w) -э и цепь с обратной связью приближается к границе устойчиво-
сти При Р(со)2С(со) > 1 цепь неустойчива, то есть в ней возникают незатухающие
колебания и схема работает как генератор.
ЗАМЕЧАНИЕ 4.11 --------------------------------------------------------
Данный режим работы цепей будет подробно рассмотрен в главе 8, цели-
ком посвященной автогенераторам.
150
4. Линейные цепи с постоянными параметрами
Отрицательная обратная связь. Если <рр(со) + <рА( о>) = 2nk + п, где k = 0, ±1,
±2... , то сигнал обратной связи и входной сигнал складываются в противофазе,
при этом
|*'((о)| = х<К^ <453)
1 1 1 + Р(о>)АГ(о>)
и обратная связь называется отрицательной (ООС), причем при Р(щ)Х(со) -» °°
получается, что
то есть коэффициент передачи цепи с обратной связью в данных условиях опреде-
ляется практически лишь четырехполюсником обратной связи.
ЗАМЕЧАНИЕ 4.12 --------------------------------------------------
В данной ситуации говорят о сильной ООС. Она часто используется при
построении разнообразных схем на операционных усилителях.
Реактивная и комплексная обратная связь. Если <рр(ш) + <рк(со) = 2nk ± л/2,
где k = 0, ±1, ±2..., то обратная связь называется реактивной (при этом фазовый
сдвиг между входным сигналом и сигналом обратной связи составляет ±90°),
а в остальных, не перечисленных случаях — комплексной.
ЗАМЕЧАНИЕ 4.13 ----------------------------------------------------
В реальных устройствах фазы коэффициентов передачи каналов прямой
и обратной связи неизбежно зависят от частоты. Поэтому зависящим от
частоты оказывается и характер обратной связи: на одних частотах она
может быть отрицательной, а на других — положительной.
Влияние ООС на характеристики усилителя. Отрицательная обратная
связь широко используется в радиотехнике. Ее применение позволяет, в част-
ности, за счет снижения общего коэффициента передачи улучшить такие важ-
ные параметры устройства, как стабильность коэффициента усиления и частотная
характеристика, а также уменьшить искажения. Рассмотрим эти эффекты под-
робнее.
Стабильность коэффициента усиления. Пусть канал прямой передачи
на некоторой частоте имеет средний коэффициент усиления Ко, а нестабильность
этого коэффициента составляет А/<0. Относительная нестабильность равна, таким
образом, ДХ0/Х0. Рассчитаем нестабильность коэффициента передачи для уси-
лителя, охваченного ООС. Среднее значение коэффициента передачи согласно
(4.53) будет
К>=
° 1 + ₽<Л>
4.7. Линейные цепи с обратной связью
151
а нестабильность, вызванная изменением коэффициента усиления тракта прямой
передачи на АК(), составит
==... 1
° <ж0 " (i+p.V (1+P.V °
Относительная нестабильность коэффициента передачи для усилителя с ООС,
таким образом, оказывается
AX0'_(1 + P0X0)2 °_ 1 ДКд
К' Ко 1+Р0Х0 к0 •
1+₽<Л
(4-54)
Из формулы (4.54) видно, что за счет использования ООС нестабильности, вы-
званные изменением температуры, разбросом параметров элементов схемы и т. п.,
уменьшаются в (1 + PqKq) раз.
Коррекция частотной характеристики. Изменение коэффициента пере-
дачи Ко в зависимости от частоты также можно рассматривать как его нестабиль-
ность. Следовательно, применение ООС позволит при тех же изменениях час готы
уменьшить относительное изменение коэффициента усиления в (1 + fV<0) раз.
Таким образом, произойдет расширение АЧХ усилителя.
Рассмотрим простейший пример — инвертирующий усилитель с резистив-
но-емкостной нагрузкой (рис. 4.20, а), имеющий комплексный коэффициент
передачи
Х(со) = -
1 + jafi’
где т = RC.
Рис. 4.20. Усилитель с ЯС-нагрузкой: а — исходная схема;
б — введение отрицательной обратной связи
um(t)
Граничная частота такого усилителя, определяемая по спаду АЧХ до уровня 0,707,
очевидно, равна 1/т. Охватим усилитель петлей частотно-независимой обратной
связи с коэффициентом передачи P(w) = Ро.
152
4. Линейные цепи с постоянными параметрами
В результате согласно (4.52) получим:
Ко
К 7(0) = = ~К° = ~К° 1
1,в к« 1+РоА;+;ол i+Po*o1+/(0^—
Ро1+7ол 1+рол;
Отсюда видно, что граничная частота усилителя с ОС равна (1 + Р0Х0)/т, то есть
увеличивается в (1 + Р0К0) раз. Достигается это за счет уменьшения во столько же
раз коэффициента усиления, который теперь составляет Kq/{ 1 + РД<0). На рис. 4.21
приведены графики АЧХ рассмотренного усилителя при различных значениях
произведения Р0Х0.
Рис. 4.21. Влияние отрицательной обратной связи на АЧХ усилителя
ЗАМЕЧАНИЕ 4.14 -----------------------------------------------
Реализовать отрицательную обратную связь в данной схеме можно, до-
бавив в цепь эмиттера дополнительный резистор (см. рис. 4.20, б).
Протекающий через него ток пропорционален выходному напряжению
усилителя, в результате входное напряжение транзистора формируется
как разность наппяжения входного сигнала и напряжения обратной
связи.
Уменьшение искажений. Использование ООС дает возможность уменьшить
возникающие в усилителе искажения сигнала — фон, вн\ гренние шумы, высшие
гармоники и т. и. Такие искажения можно представить как добав тение к выходному
сигналу канала прямой передачи внешней помехи un(t) (рис. 4.22). В отсутствие
4.8. Условия устойчивости линейной цепи
153
ОС такой паразитный сигнал беспрепятственно попадает на выход устройства,
но при введении в схему отрицательной ОС ситуация меняется. Теперь сигнал
помехи, пройдя по петле обратной связи, приобретает фазовый сдвиг, равный
180°, и суммируется сам с собой в противофазе, уменьшая уровень помехи на вы-
ходе. Действительно, коэффициент передачи для помехи можно легко рассчитать,
если заметить, что сигнал *п(£) попадает на выход через охваченную ООС схему,
в которой усиление в канале прямой передачи отсутствует (то есть коэффициент
передачи КПП равен 1), а коэффициент передачи цепи ОС равен Р0К0. Согласно
(4.53) коэффициент передачи для помехи
п 1+Р<Л>’
то есть в (1 + Р0К0) раз меньше, чем при отсутст вии ООС. Такой способ уменьшения
искажений широко используется на практике.
«п(0
Рис. 4.22. Структурная схема устройства с обратной связью
с учетом воздействия внешних помех
4.8. Условия устойчивости линейной цепи
Линейная цепь с постоянными параметрами описывается неоднородным линейным
дифференциальным уравнением вида
Jm,, SJm-2,,
, а и , а и , а и
= Ь —s^ + b ---------— + b --------
т dtm т~‘ dim~{ т~2 dtn~2
+ b^ + b^'
где а. и b — постоянные вещественные коэффициенты и п > т.
Решение этого неоднородного дифференциального уравнения в самой общей
форме складывается из общего решения соответствующего однородного уравнения
и частного решения неоднородного уравнения. Частное решение неоднородного
уравнения связано со входным воздействием MBX(t) и представляет собой вынуж-
денные колебания, тогда как общее решение однородного уравнения соответствует
свободным колебаниям цепи.
154
4. Линейные цепи с постоянными параметрами
При отсутствии входного сигнала в цепи существуют лишь свободные колеба-
ния, подчиняющиеся однородному линейному дифференциальному уравнению
d"u d"~'u dn~2u du
a ----!2S- + a ,--+ a ,--------^- + ... + a.— +ая =0.
" dt" dt"-1 2 dt"-2 1 dt 0 вых
Цепь называется устойчивой, если свободные колебания при любых начальных
условиях являются затухающими, то есть если справедливо соотношение
limw (t) = 0.
Общее решение однородного линейного дифференциального уравнения при
отсутствии кратных корней имеет вид
ивых(0 = ^Аел',
i=l
где А. — вещественные постоянные, ад — корни характеристического уравнения
а„р" + ап_у1 + ап_2р"~2 +... + alP + а0 = 0.
Для устойчивости цепи необходимо, чтобы входящие в решение однородного
уравнения экспоненты были затухающими. А это, в свою очередь, означает, что кор-
ни pvp2, ...,рп характеристического уравнения должны быть либо отрицательными
действительными числами, либо комплексными величинами с отрицательными
действительными частями. Из этих простых физических представлений вытекает
следующий фундаментальный критерий устойчивости любых линейных систем:
система устойчива, если действительные части всех корней ее характеристического
уравнения отрицательны.
ЗАМЕЧАНИЕ 4.15 ----------------------------------------------------
При наличии у характеристического уравнения кратных корней в фор-
муле, описывающей общее решение однородного дифференциального
уравнения, появляются слагаемые вида At*-1 exp(pir), где k — целые числа
в диапазоне от единицы до степени кратности корня р.. Такие слагаемые
также являются затухающими при Re(p.) < 0, так что приведенные ранее
рассуждения сохраняют силу.
Заметим, что левая час ть характеристического уравнения представляет < обой
знаменатель передаточной функции цепи, записанной в операторной форме:
b рт +b .рт~' +... + b.p + bn
К(р) = —------—-----------——5-, п > т.
а„рп +ап_1рл~' +... + alP + a0
Таким образом, корни характеристического уравнения являются полюсами
передаточной функции К(р) этой цепи Отсюда следует, что сформулированные
условия отрицательности действительных частей корней равное ильны следующе-
Контрольные вопросы и задания
155
му положению: для устойчивости цепи необходимо, чтобы полюсы передаточной
функции К(р) лежали в левой полуплоскости комплексной переменной р.
Возникновение нарастающих собственных колебаний в электрических цепях
возможно лишь тогда, когда в составе цепи помимо пассивных элементов L, С, R
содержатся активные элементы, передающие в цепь часть энергии от внешних ис-
точников. Распространенной моделью такого активного элемента служит резистор
с отрицательным сопротивлением. Система, содержащая такой элемент, может
самопроизвольно возбуждаться, если отрицательное сопротивление элемента пре-
восходит (по модулю) некоторое критическое значение.
ЗАМЕЧАНИЕ 4.16 ------------------------------------------------------
Речь об использовании элементов с отрицательным дифференциальным
сопротивлением для генерации гармонических колебаний пойдет при
анализе общих энергетических соотношений в автоколебательной системе
в разделе 8.1 и при обсуждении авто! енераторов с внутренней обратной
связью в разделе 8.8.
Контрольные вопросы и задания
1. Каковы основные характеристики линейной цепи во временной и спектральной
областях? Как они связаны между собой? Почему?
2. Как связаны детерминированные сигналы на входе и выходе линейной цепи во
временной области?
3. Как связаны энергетические спектры случайных процессов на входе и выходе
линейной цепи?
4. Какую характеристику случайного процесса на выходе линейной цепи и как
находят при временном подходе?
5. Может ли интервал корреляции случайного процесса на выходе линейной цепи
быть:
1) больше, чем на входе;
2) таким же, как на входе;
3) меньше, чем на входе?
6. Изобразите схемы и частотные характеристики простейших ЛС-фильтров ниж-
них и верхних частот.
7. Изобразите схемы, переходные и импульсные характеристики простейших RC-
фильтров нижних и верхних частот.
8. Запишите выражение для входного сопротивления последовательного колеба-
тельного контура вблизи резонансной частоты. Изобразите графики частотных
зависимостей его модуля и фазы.
156
4. Линейные цепи с постоянными параметрами
9. Запишите выражение для комплексного коэффициента передачи линейной цепи
с обратной связью и дайте определения видов обратной связи.
10. Какие характеристики усилителя и как улучшаются при использовании в нем
отрицательной обратной связи?
11. Какая линейная цепь называется устойчивой? Какие вам известны критерии
устойчивости?
Задачи
Задача 4.1
На вход цепи, изображенной на рис. 4.23 (Rt = R2 = 1 кОм; С = 0,2 мкФ), подается
прямоугольный импульс с амплитудой 20 В и длительностью 100 мкс. Рассчитать
импульсную и переходную характеристики цепи, определить ее комплексный ко-
эффициент передачи, найти сигнал на выходе цепи.
Рис. 4.23. Цепь для задачи 4.1
Задача 4.2
На цепь, представленную на рис 4.24, в момент t=0 подается импу тьс e(f) = Е exp(-af)
при Г> 0. Определить в общей форме ток Какие размерности имеют комплекс-
ный коэффициент передачи, импульсная и переходная характеристики этой цепи?
Рис. 4.24. Цепь для задачи 4.2
Задача 4.3
Найти коэффициенты передачи и импульсные характеристики цепей, показанных
на рис, 4.25 (7?С = т):
а) интегрирующая и дифференцирующая 7?С-цепи включены друг за другом;
б) между интегрирующей и дифференцирующей Я С-цепями включен идеальный
усилитель с единичным коэффициентом усиления.
Задачи
157
Рис. 4.25. Цепи для задачи 4.3
Задача 4.4
Коэффициент амплитудной модуляции напряжения, приложенного к последова-
тельному колебательному контуру, равен 100 %, коэффициент модуляции тока в кон-
туре — 71 %. Контур настроен в резонанс с несущей частотой и имеет следующие
параметры: L = 2 мГн; С = 500 пФ; г = 20 Ом. Определить модулирующую частоту.
Задача 4.5
На последовательный колебательный контур подано напряжение в виде одното-
нального AM-сигнала (рис. 4.26). Частота несущего колебания/0 = 1 МГц совпа-
дает с резонансной частотой контура, частота модулирующего сигнала F= 1 кГц,
коэффициент модуляции тпи = 50 %, индуктивность контура L = 50 мкГн. Найти
добротность контура Q, емкость конденсатора С и сопротивление потерь г, если
известно, что коэффициент модуляции тока в контуре mt = 20 %.
Рис. 4.26. Сигнал и цепь для задачи 4.5
Задача 4.6
Некоторая линейная система преобразует входной сигнал x(t) таким образом, что
выходной сигнал y(t) = — где Т — постоянный параметр с размерностью
времени. На вход системы подается напряжение, имеющее вид белого шума с дву-
сторонней спектральной плотностью мощности Wo = 1012 В2 с. Найти время Гр за
которое среднеквадратический уровень напряжения на выходе системы достигнет
0,2 В, если Т= 1 мкс.
Задача 4.7
Линейная система имеет частотный коэффициент передачи А (со) = —(1 - е~^т),
/соv ’
где А > 0, Т> 0 — постоянные величины. На вход системы поступает белый шум
158
4. Линейные цепи с постоянными параметрами
со спектральной плотностью мощности УУ0. Найти корреляционную функцию
сигнала на выходе.
Задача 4.8
На вход цепи, показанной на рис. 4.27 ( R = у] L/C, усилитель считать идеальным),
поступает белый шум с двусторонней спектральной плотностью мощности IV0.
Найти спектральную плотность мощности шума на выходе, его корреляционную
функцию и дисперсию.
Рис. 4.27. Цепь для задачи 4.8
Задача 4.9
Какой сигнал нужно подать на вход интегрирующей ЯС-цепи, чтобы на ее выходе
получить идеальный треугольный импульс (рис. 4.28)? Параметры цепи выбраны
так, что RC = Т.
Рис. 4.28. Цепь и сигнал для задачи 4.9
Задача 4.10
В параллельном колебательном контуре сопротивление потерь включено в индук-
тивную ветвь (рис. 4.29).
1. Чему равно сопротивление этого двухполюсника на частоте й0 = 1/у/LC ?
2. На какой частоте достигается резонанс, то есть сопротивление двухполюсника
становится чисто вещественным?
3. Чему равно сопротивление двухполюсника на частоте резонанса?
4. Чему равна добротность колебательного контура (считать, что сопротивление
потерь мало, так что г « JL/С)?
Задачи
159
Рис. 4.29. Цепь для задачи 4.10
Задача 4.11
На рис. 4.30 показана схема усилительного каскада с общим эмиттером (без цепей
смещения). Определить комплексный коэффициент передачи данной цепи, по-
казать, что она может рассматриваться как цепь с обратной связью, и определить
комплексные коэффициенты передачи канала прямой передачи к(т) и цепи об-
ратной связи Р(со). Считать, что коллекторный ток транзистора пропорционален
разности напряжений между его базой и эмиттером: IK - S U6_3, где S — крутизна
проходной характеристики транзистора.
Мвх(Г)
Рис. 4.30. Цепь для задачи 4.11
5. Принципы оптимальной
линейной фильтрации сигналов
на фоне помех
Выделение сигнала из помех является одной из важнейших задач, которые не-
обходимо решить при разработке практически любой системы передачи инфор-
мации. Критерий качества такого выделения сильно варьиреется в зависимости
от назначения системы. Так, при передаче аудио- или видеосигнала важно обе-
спечить минимально возможное искажение его формы, а в радиолокационной
аппаратуре — установить факт наличия отраженного сигнала и определить
момент его прихода.
Помимо критериев качества различными являются также наши знания
о структуре полезных сигналов и шумов и, соответственно, используемые для
их представления математические модели. Поэтому не существует единственно
оптимального устройства, во всех случаях обрабатывающего сигнал наилучшим
образом. Понятие оптимальности имеет смысл только в связи с постановкой кон-
кретной задачи, то есть для конкретной комбинации критерия качества, моделей
сигналов и шумов.
В данной главе рассматриваются некоторые классические задачи обработки
сигналов и соответствующие оптимальные фильтры.
5.1. Согласованная фильтрация
детерминированных сигналов
Пусть форма обрабатываемого сигнала заранее известна и нам нужно определить
лишь факт присутствия сигнала на фоне шумов. В этом случае фильтр должен
вместо сохранения формы сигнала обеспечить его максимальный (по сравнению с
шумом) уровень на выходе. Критерием качества обработки в данном случае может
служить отношение «сигнал/шум», определяемое как
С/Ш
о
где |s(?)|max — максимальное абсолютное значение сигнала, о — среднеквадратиче-
ское значение шума.
М Lax
5.1. Согласованная фильтрация детерминированных сигналов
161
Итак, теперь мы можем сформулировать задачу об оптимальной фильтрации
детерминированного (полностью известного) сигнала. Пусть на вход фильтра по-
ступает аддитивная смесь сигнала и шума:
5вх(0=51(0 + «1(0,
где st(t) — детерминированный сигнал, который нужно обнаружить, — стаци-
онарный нормальный центрированный белый шум с двусторонней спектральной
плотностью мощности Wo. На выходе линейного фильтра также будет присутство-
вать аддитивная смесь сигнала s2(t) и шума n2(t):
= 52<0 + Чг(г)-
Требуется найти такой линейный фильтр, который обеспечит в некоторый момент
времени Го максимальное отношение «сигнал/шум» на выходе:
С/Швых=ЬШ^^тах. (5.2)
СТ2
Как было показано в разделе 4.1, детерминированная составляющая выходного
сигнала фильтра в момент г0 может быть рассчитана по следующей формуле:
52<ro)= (5.3)
где h(t) — импульсная характеристика фильтра.
В курсе математики доказывается неравенство, носящее имя Коши—Буняков-
ского, согласно которому
\f(x)g(x)dx < \f2(x>dx jg2(.ryZr .
(5.4)
причем максимум левой части (равенство) достигается только в том случае, если
функции /(х) ng(r) пропорциональны друг другу:
g(r) = £/(*)•
(5.5)
Применив неравенство (5.4) к правой части формулы (5.3), получим
р,(т)/г(Г0 -т)</т
< js*(i:)di:fh2(t0-T)dT.
Равенство, согласно (5.5), будет достигаться, если
Л(Г0-т) = Л5,(т), (5.6)
где А — постоянный коэффициент, имеющий размерность [В'с1 = Гц/В] (ведь
импульсная характеристика имеет размерность частоты, то есть 1 /с). Выполнив
замену переменной t = t(l - т, формулу (5.6) можно переписать в виде
(5-7)
6 №675
162
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
Фильтр, обладающий такой импульсной характеристикой, называется согласо-
ванным фильтром для сигнала s,(r). Как видно из (5.7), импульсная характеристика
согласованного фильтра представляв г собой зеркально перевернутую и сдвинутую
на f0 во времени копню входного сигнала (рис. 5.1).
Рис. 5.1. Сигнал (слева) и импульсная характеристика
согласованного с ним фильтра (справа)
Если входной шум и((т) является белым, то согласованный фильтр оказывается
также оптимальным, то есть реализующим условие (5.2). С доказательством этого
факта можно ознакомиться, например, в [3, гл. 13].
Поскольку импульсная характеристика физически реализуемой цепи должна
равняться нулю при г < 0, значение t0 не может быть меньше длительности вход-
ного сигнала, а так как t0 соответствует максимальному выходному сигналу, этот
максимум достигается после окончания воздействия полезного сигнала st(t) на
вход фильтра, то есть для обеспечения максимального от клика фильгр должен об-
работать весь входной сигнал. По этой причине согласованный фильтр может быть
реализован только для сигналов конечной длительности.
Получим выражение для комплексного коэффициента передачи согласованного
фильтра. Преобразование Фурье импульсной характеристики (5.7) дает
К(т)- j -t)e~luxdt.
Используем замену переменной t'= t0 -1. С учетом этого
К(ю) = = j sx(t’)e’w dt'.
Получившийся интеграл представляет собой спектральную функцию сиг-
нала $,(?) на частоте -со. Но согласно свойс гвам спектра вещественного сигнала
5, (-со) = 5’ (со), поэтому окончательно для коэффициента передачи согласованного
фильтра получаем:
K((p) = AS\(tP)e~1M'>. (5-8)
Полученной формуле можно дать наглядную физическую трактовку. Рассмо-
трим, какие преобразования производит согласованный фильтр с фазовым спектром
сигната. Пусть фазовый спектр входного сигнала равен ф^со):
argS,(со) -ф,(со).
5.2. Отношение «сигнал/шум» на входе и выходе согласованного фильтра
163
Согласно (5.8) фаза коэффициента передачи согласованного фильтра может
быть представлена как
Фх(<в) = -9,(10) - сог0.
Таким образом, фазовый спектр выходного сигнала будет иметь вид
<р2(со) = 9,(10) + 9к(со) = -<ot0,
а это означает, что в момент Го все спектральные составляющие сигнала складыва-
ются на выходе синфазно, образуя пик выходного отклика. Это называется ком-
пенсацией начальных фаз. Механизм компенсации начальных фаз иллюстрируется
на рис. 5.2.
Рис. 5.2. Механизм компенсации начальных фаз
при согласованной фильтрации
Модуль коэффициента передачи, как следует из (5.8), повторяет форму модуля
спектральной плотности сигнала 5, (t):
|К((О)| = Л|51(И)|.
Таким образом, коэффициент передачи велик на тех частотах, где сосредоточена
основная часть энергии полезного сигнала, и мал там, где мала спектральная плот-
ность. Сочетание компенсации начальных фаз с увеличением амплитуды сильных
спектральных составляющих сигнала и обеспечивает оптимальность согласованного
фильтра для регистрации сигнала на фоне белого шума.
5.2. Отношение «сигнал/шум» на входе
и выходе согласованного фильтра
Определим отношение «сигнал/шум» на входе и выходе согласованного фильтра,
воспользовавшись определением (5.1). В качестве модели для n,(t) мы использовали
белый шум, дисперсия которого бесконечно велика, поэтому о, —> °° и
с/швх
о.
164
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
Для того чтобы найти выходное отношение «сигнал/шум», необходимо предва-
рительно определить вид полезного выходного сигнала. Сигнал на выходе линейной
стационарной цепи с импульсной характеристикой h(t) определяется как
s2(t) = j -t'ydt'.
Подставим сюда выражение (5.7) для импульсной характеристики:
s2(t) = j 5,(Го -1 + t')dt' = A j s,(t')As,(t'-(t-t0))dt' = ABS
где Bs (t)= j s, (t)s}(t - x)dt — корреляционная функция сигнала s/f).
Таким образом, выходной сигнал согласованного фильтра представляет со-
бой (с точностью до масштабного множителя А) сдвинутую во времени на t0
корреляционную функцию сигнала s^t). Как известно, максимальное значение
корреляционной функции детерминированного сигнала достигается при т = 0 и
равно его энергии:
ВДт) =ВД0) = £.,
где £j = j s2(t)dt — энергия сигнала Итак, максима льное значение сигната на
выходе согласованного фильтра достигается при t = t0 и равно АЕ,.
Теперь необходимо определить свойства шума на выходе. Согласно формулам
(4.18-4.20), приведенным в разделе 4.3 для случая прохождения белого шума через
линейную пепь с постоянными параметрами, получаем, что СПМ, корреляционная
функция и дисперсия выходного шума равны соответственно,
ВД=w;|x(®)|2 = iv0a2|51((o)|2,
R2(x) = WQBh(x) = W0A2Bs(i.),
o22 = W0Eh = WilA2El.
Полученные результаты показывают, что СПМ и корреляционная функция вы-
ходного шума совпадают по форме с энергетическим спектром и корреляционной
функцией полезного сигнала соответственно.
Теперь мы можем получить выходное отношение «сигнал/шум»:
С/Ш = Л£| = £. (5.9)
" №
Итак, отношение «сигнал/шум» на выходе согласованного фильтра не зависит от
формы обрабатываемого сигнала, а определяется лишь его энергией и спектральной
плотностью мощности входного белого шума.
5.2. Отношение «сигнал/шум» на входе и выходе согласованного фильтра
165
Пример 5.1. Сигнал в виде несимметричного трапециевидного импульса
(рис. 5.3, а) обрабатывается с помощью согласованного фильтра. Спектральная
плотность мощности белого шума равна Wo = 3-10“12 В2-с, половина длительности
сигнала Т= 9 мкс. Определим, при какой амплитуде импульса U на выходе фильтра
будет достигнуто отношение «сигнал/шум», равное 10.
Рис. 5.3. Согласованная фильтрация трапециевидного импульса: a — обрабатываемый
сигнал; б — импульсная характеристика согласованного с ним фильтра
Для решения данной задачи прежде всего необходимо определить энергию об-
рабатываемого сигнала, а это, в свою очередь, требует аналитической записи сигнала:
Ut/T,
0 < t < т,
T<t<2T,
в остальных случаях.
Теперь можно рассчитать интересующую нас энергию:
£=х = = dt+ = +U4^ =
0\ J / т 1 л о
_ и2т {U2T_4u2t
3 3
Чтобы получить выходное отношение «сигнал/шум», воспользуемся форму-
лой (5.9):
С/Ш = p^=2U — .
вь,х \W0 \3W0
Осталось лишь выразить искомую амплитуду Uчерез исходные данные задачи:
Г,с/Шцх ю
2 7 I 910^с
ри/ Уз-зю-12в2-с
= 5 мВ.
Итак, для получения требуемого отношения «сигнал/шум» на выходе амплитуда
входного импульса должна быть равна 5 мВ. На рис. 5.3, б показана импульсная
характеристика фильтра, согласованного с данным сигналом.
166
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
5.3. Применение согласованных фильтров
Рассмотрев идею согласованной фильтрации детерминированных сигналов, об-
судим возможные области применения таких фильтров и некоторые связанные
с этим вопросы.
Повышение разрешения по дальности в локационных системах. На-
помним вкратце принцип действия радиолокационных систем. Передатчик излу-
чает зондирующий импульс, он доходит до цели, отражается от нее и, многократно
ослабленный, в смеси с шумом поступает на вход приемника.
Для обнаружения цели нужно зафиксировать факт присутствия отраженного
сигнала на входе, а для определения расстояния до цели — измерить задержку
между зондирующим и отраженным импульсами
Так как форма излучаемого импульса известна, для обнаружения отраженного
сигнала нужно использовать согласованный фильтр, позволяющий максимизиро-
вать отношение «сигнал/шум» на выходе.
Если имеются две близко расположенные цели, для их разрешения необходимо,
чтобы два отраженных сигнала воспринимались раз 1ельно. Поэтому желательно
иметь выходной сигнал согласованного фильтра в виде как можно более узкого
пика Этого можно достичь, уменьшая длительность излучаемого импульса, но при
этом падает его энергия и, следовательно, отношение «сигнал/шум» при приеме.
Чтобы энергия не уменьшалась, необходимо одновременно с укорочением импульса
увеличивать его амплитуду. Однако это нельзя делать бесконечно — электрическая
прочность элементов выходного каскада передатчика имеет предел.
Но существует и иной путь решения проблемы. Вспомним, что выходной сигнал
согласованного фильтра по форме совпадает с корреляционной функцией обнару-
живаемого сигнала, а последняя, в свою очередь, связана преобразованием Фурье
с энергетическим спектром. Таким образом, для получения узкого пика на выходе
согласованного фильтра необходимо расширять спектр сигнала. Как известно,
эффективная ширина спектра сигнала и его длительность связаны соотношением
неопределенности (см. раздел 1.6)
<510>
Сигналы, для которых соотношение неопределенности (5.10) близко к равенству,
называются простыми. Однако, поскольку ширина спектра определяется внутриим-
пульсной структурой сигнала, существуют сигналы с той же энергией, для которых
ДГ . Д/. » 1.
Эф J эф
Такие сигналы называют сложными. Само произведение эффективных значений
ширины спектра и длительности называют базой сигнала:
^ДЦДДф.
Соответственно, простые сигналы называют также сигналами с малой базой,
а сложные — сигналами с большой базой.
Сложные сигналы. Таким образом, можно увеличить разрешение по дальности,
не уменьшая длительности сигнала, за счет введения внутриимпульсной модуляции.
5.3. Применение согласованных фильтров
167
Из-за расширения спектра корреляционная функция (которая по форме совпадает
с выходным сигналом согласованного фильтра) сужается.
Сложным сигналом является рассмотренный в разделе 2.6 ЛЧМ-радиоимпульс.
Другими примерами сложных сигналов могут служить, в частности, коды Баркера.
График сигнала, манипулированного 13-элементным кодом Баркера, показан на
рис. 5.4, а, а его корреляционная функция — на рис. 5.4, б. Пунктиром на рис. 5.4, б
изображен график корреляционной функции прямоугольного импульса с такими
же длительностью и энергией.
Рис. 5.4. Сложный сигнал: а — сигнал, манипулированный 13-элементным кодом Баркера,
б — его корреляционная функция
Из рисунка видно, что корреляционная функция представляет собой узкий пик,
окруженный боковыми лепестками малого уровня. Коды Баркера обеспечивают
минимально возможный относительный уровень боковых лепестков, равный 1/У,
где N — число элементов кода. К сожалению, такие коды существуют лишь для
длин 2, 3, 4, 5, 7, 9, 11 и 13 элементов.
Есть и другие классы сигналов с «хорошими» корреляционными функциями.
Скрытная передача сигналов. Тот факт, что отношение «сигнал/шум»
на выходе согласованного фильтра определяется лишь энергией полезного сиг-
нала и не зависит от его формы, позволяет замаскировать сигнал, «спрятав» его
в шумах.
Действительно, если сильно уменьшить амплитуду полезного сигнала, соответ-
ственно увеличив при этом его длительность, чтобы сохранить энергию постоянной,
сигнал перестанет визуально выделяться на фоне шумов (рис. 5.5. а). Так как энер-
гия сигнала не изменилась, отношение «сигнал/шум» на выходе согласованного
фильтра останется прежним.
Однако если сигнал имеет простую форму, то есть небольшую базу, такая маски-
ровка во временной области приведет к сильному сужению спектра сигнала. Так как
энергия остается неизменной, на тех частотах, где сосредоточен спектр сигнала, его
спек грачьная плотность будет значительно превышать (по модулю) спектральную
168
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
Рис. 5.5. Сигналы с малой базой: маскировка во временной области приводит
к легкому обнаружению в частотной области, и наоборот
Рис. 5.6. Сигнал с большой базой может быть замаскирован
одновременно во временной и частотной областях
Рис. 5.7. Сложные сигналы с различными законами изменения частоты
5(т).
Рис. 5.8. Корреляционная функция сигнала с линейной частотной модуляцией
5.3. Применение согласованных фильтров
169
плотность шума (рис. 5.5, б). Такой сигнал замаскирован во временной области, но
легко обнаруживается в спектральной области.
Если одновременно с удлинением сигнала ввести внутриимпульсную моду-
ляцию, можно избежать сужения спектра и «скрыть» сигнал под шумами как во
временной, так и в спектральной области (рис. 5.6, а, б).
К применяемым на практике сложным радиосигналам относятся:
□ частотно-модулированные (ЧМ) радиосигналы;
□ фазоманипулированные (ФМн) радиосигналы.
Для ЧМ-сигналов наиболее распространены следующие законы изменения
частоты:
□ квадратичная ЧМ;
□ линейная ЧМ (ЛЧМ);
□ V-образная ЧМ.
Соответствующие этим законам графики зависимое ги мгновенной частоты
от времени показаны на рис. 5.7, а, а графики самих сигналов — на рис. 5.7, б. На
рис. 5.8 показан вид корреляционной функции сигнала с линейной частотной
модуляцией.
В качестве примера ФМн-радиосигнала на рис. 5.9 показан сигнал, манипули-
рованный по фазе 13-элементным кодом Баркера.
s(ty1
Рис. 5.9. Радиосигнал, манипулированный по фазе 13-элементным кодом Баркера
(вверху), и его корреляционная функция (внизу)
170
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
Коррелятор. В случае применения согласованного фильтра для обнаружения
сигнала приемная система должна выглядеть гак, как показано на рис. 5.10. Сиг-
нал, получаемый на выходе согласованного фильтра, сравнивается с некоторым
порогом, в случае превышения порога принимается решение о наличии полезного
сигнала на входе.
Рис. 5.10. Обнаружитель детерминированного сигнала на основе согласованного фильтра
Однако при использовании сигналов сложной формы согласованный фильтр
реализовать трудно. В этом случае можно использовать показанное на рис. 5.11
устройство, называемое корре тятором.
Рис. 5.11. Коррелятор
Оно включает в себя перемножитель, на один вход которого подается прини-
маемый сигнал s(t) + «(t), а на другой — сформированный в приемном устройстве
опорный сигнал s(t-т), форма которого повторяем форму обнаруживаемого сигнала.
После цикла интсг рирования на выходе получим:
т т
\ых (Г) = Л f(5(0 + - ^)dt = АВ. (т) + A J -t)di, (5.11)
о о
где А — некоторая константа.
Если задержка между принимаемым и опорным сигналами отсутствует (т = 0),
а время интегрирования Травно длительности сигнала s(t), то получим.
т т т
хвых(Т) = j s2(t)dt + A J 5(t)n(r)r/t = АЕ + а| s(t)n(t)dt.
0 0 о
Легко убедиться, что это совпадает с выходным сигналом согласованного фильтра
в момент окончания полезного сигнала на входе.
Таким образом, коррелятор может давать на выходе то же, что и согласованный
фильтр, и, следовательно, его заменять. Однако при этом необходимо знать время
прихода полезного сигнала на вход, что невозможно (если время прихода сигнала
известно, незачем его и обнаруживать).
5.3. Применение согласованных фильтров
171
ЗАМЕЧАНИЕ 5.1 -------------------------------------------
Говорят, что согласованный фильтр инвариантен к моменту прихода
входного сигнала, а коррелятор неинвариантен к моменту прихода вход-
ного сигнала.
Решить эту проблему можно, построив многоканальную схему и подавая в разные
каналы опорный сигнал с разной задержкой по времени (рис. 5.12).
Рис. 5.12. Многоканальный коррелятор
На выходах корреляторов разных каналов, согласно (5.11), будут формироваться
отсчеты корреляционной функции Bs (т) для разных значений т. При наличии по-
лезного сигнала на входе выходной сигнал того канала, опорный сигнал которого
имеет минимальную задержку относительно принимаемого, будет максимален.
Поэтому для обнаружения сигнала необходимо после выполнения цикла интегри-
рования сравнить между собой выходные сигналы всех каналов, выбрать из них
максимальный и сравнить его с порогом (см. рис. 5.12). В случае превышения по-
рога принимается решение о наличии полезного сигнала на входе, а номер канала,
соответствующий максимуму, дает оценку времени его прихода.
Для сложных сигналов реализовать схему, показанную на рис. 5.12, часто ока-
зывается проще, чем согласованный фильтр (см. рис. 5.10).
Необходимое число каналов и временной сдвиг опорного сигнала между
соседними каналами определяются формой корреляционной функции обнару-
живаемого сигнала и общими требованиями к системе (возможным диапазоном
времени прихода принимаемого сигнала и необходимой точностью измерения
этого времени).
172
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
ЗАМЕЧАНИЕ 5.2---------------------------------------------------
Для радиосигналов, имеющих быстроосциллирующее внутреннее заполне-
ние, такая система сильно усложняется, так как временной сдвиг опорного
сигнала между соседними каналами в данном случае будет определяться
именно периодом этого заполнения, что приведет к резкому увеличению
необходимого числа каналов.
ЗАМЕЧАНИЕ 5.3-----------------------------------------------------
В системах цифровой связи корреляторы могут использоваться вместо
согласованных фильтров и без необходимости построения многоканальной
структуры. Поскольку импульсы, несущие передаваемую информацию,
следуют друг за другом с равными интервалами, после первоначального
достижения вре ценной синхронизации временное положение пос чедующих
импульсов является известным.
5.4. Оптимальная фильтрация
при небелом шуме
В разделе 5.1 был рассмотрен согласованный фильтр, осуществляющий оптималь-
ную обработку детерминированного сигнала в том случае, если шум является белым.
Теперь рассмотрим более общий случай, когда шумовой случайный процесс имеет
произвольную спектральную плотность мощности
Простейшее и само собой напрашивающееся решение состоит в том, чтобы пред-
варительно «обелить» шум с помощью фильтра, коэффициент передачи которого
К, (to) выбран так, чтобы компенсировать неравномерность спектра входного шума
(рис. 5.13):
Жо = W»|x»|2
и, следовательно,
(5-12)
где Жо — произвольная константа.
Рис. 5.13. Структура оптимального фильтра для детерминированного сигнала
в случае небелого шума
5.4. Оптимальная фильтрация при небелом шуме
173
Полезный сигнал s'(t) на выходе этого фильтра будет, очевидно, иметь спек-
тральную плотность, равную
5'1'(ог) = 51(со)Х1(со). (5.13)
Итак, на выходе «обеляющего» фильтра мы имеем белый шум со спектральной
плотностью мощности ',V0 и измененный полезный сигнал s'(t). Так как шум белый,
мы можем использовать рассмотренный в разделе 5.1 фильтр, согласованный с сиг-
налом комплексный коэффициент передачи которого, согласно (5.8), равен
к2 (ю)=as;’ (ю)<^ = as\ (ю)х; (сок74,
где t't — длительность сигнала s'(t) на выходе первого фильтра, t' > t0 (t0 — дли-
тельность входного сигнала).
Общий коэффициент передачи полученной таким образом системы
k(co) = К, (со)к2(ю) = Х1(ш)А51* ((о)К; (ш)е’м = А$',‘ (io)]#, (со)|2 е^.
Воспользовавшись (5.12), окончательно получим
<514>
Фильтр /С2(со), безусловно, оптимален для обнаружения сигнала s'^t) в белом
шуме, но еше неизвестно, является ли полученная таким путем составная схема в
целом оптимальной для решения первоначально поставленной задачи, то есть для
обнаружения сигнала $/£) в шуме со спектром ^(ю). Докажем оптимальность
схемы рис. 5.13 методом от противного.
Предположим, что существует фильтр с коэффициентом передачи К(а>),
обеспечивающий при подаче на вход аддитивной смеси сигнала s((£) и шума со
спектральной плотностью W^co) большее выходное отношение «сигнал/шум»,
чем схема на рис. 5.13. Представим коэффициент передачи такого фильтра в виде
Пусть к{ (со) является коэффициентом передачи «обеляюшего» фильтра, то есть
удовлетворяет условию (5.12). На выходе этого фильтра будут получены сигнал
s'(t) и белый шум со спектральной плотностью Wo, то есть те же условия, что и на
выходе первого фильтра на рис. 5.13.
Так как отношение «сигнал/шум» на выходе, согласно сделанному предположе-
нию, должно быть больше, чем для рассмотренной схемы (рис. 5 13), то фильтр с
комплексным коэффициентом передачи к(а>)/ обеспечивает при подаче на
вход аддитивной смеси сигнала $'(£) и белого шума большее отношение «сигнал/
шум», чем фильтр, согласованный с сигналом s'(t), что невозможно. Полученное
противоречие доказывает, что схема на рис. 5.13, имеющая коэффициент передачи
К(а>)
к^У
174
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
(5.14), действительно является оптимальной для обнаружения детерминированного
сигнала в шуме с известной спектральной плотностью мощности.
Рассчитаем для данного случая выходное отношение «сигнал/шум». Так как
второй фильтр согласован с сигналом s'(t), то согласно (5.9) это отношение может
быть представлено как
С/Ш.„=Д, (5.15)
где Е' = j s'2(t)dt — энергия сигнала s'(t), а Жо — спектральная плотность белого
шума после «обеляющего» фильтра.
Согласно равенству Парсеваля энер1 ия сигнала s'(t) может быть рассчитана
и в спектральной области:
Ж'Н
Подставив сюда выражения (5.13) для спектра S/co) и (5.12) для коэффициента
передачи ^(со), получим:
Е' = — ] |5, (со)|2 к (ю)|2 d(O = — j
1 2л!1 1 1 1 1 1 2л1 1Т(оэ)
Подставив этот результат в (5.15), окончательно получаем:
1 7 5. (со)2
С/Ш = . —[ —--------dm. (5.16)
ВЬ1Х W/co)
Таким образом, в общем случае выходное отношение «сигнал/шум» определяется
«взвешенной» в частотной области энергией обрабатываемого полезного сигнала,
весовая функция нри этом обратно пропорциональна спектральной плотности
мощности шума.
ЗАМЕЧАНИЕ 5.4-------------------------------------------------------
Легко увидеть, что при W/co) = const формула (5.16) превращается в полу-
ченное ранее для случая белого шума выражение (5.9).
5.5. Квазиоптимальная фильтрация
детерминированных сигналов
Во многих случаях точная реализация согласованного фильтра оказывается слож-
ной, а подчас и неразрешимой задачей. В таких ситуациях можно использовать
следующий подход: выбрать относительно узкий класс физически и конструктивно
5.5. Квазиоптимальная фильтрация детерминированных сигналов
175
реализуемых фильтров и отыскать в пределах этого класса такие значения пара-
метров фильтра, которые обеспечивают максимальное отношение «сигнал/шум»
на выходе. Это отношение «сигнал/шум», разумеется, окажется заведомо хуже,
чем при использовании согласованного фильтра. Однако при обработке сигналов
поостой формы проигрыш может быть невелик. Выбранный указанным образом
фильтр называется квазиоптималоным.
Рассмотрим конкретный пример — отыщем квазиоптимальный фильтр для об-
работки прямоугольного импульса (рис. 5.14). Класс рассматриваемых фильтров
ограничим простейшими интегрирующими /?С-цепями (см. рис. 4.2 в главе 4). У та-
кой цепи имеется единственный параметр — по< тоянная времени т = RC, которую
нам и нужно оптимизировать, чтобы добиться максимального отношения «сигнал/
шум» на выходе, определяемого согласно (5.1).
Рис. 5.14. Прохождение прямоугольного импульса
через интегрирующую RC-цепь
Импульсная характеристика интегрир} юшей ЯС-цепи была получена в раз-
деле 4.4 (см. формулу (4.27)), а прохождение через такую цепь прямоугольного
видеоимпульса было проанализировано в разделе 4.5 (см. пример 4.7 и формулу
(4.33)). Выходной сигнал цепи показан на рис. 5.14 пунктиром.
Легко увидеть, что максимальное значение выходного сигнала достигается
в момент t = Т:
Теперь необходимо рассчитать среднеквадратическое значение выходного шума.
Это проще сделать, ис пользуя спектральный метод.
Комплексный коэффициент передачи интегрирующей 7?С-цепи с постоянной
времени т (см. раздел 4.4)
К(щ) = —.
1 + /сот
При подаче на вход белого шума с двусторонней спектральной плотностью
мощности Wo выходной случайный процесс будет иметь спектральную плотность
мощности, рассчитываемую как
। ,2 Щ.
« = »> =7Т7Ь- (517)
1 1 + (О т
176
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
Дисперсия выходного шума, согласно теореме Винера—Хинчина, пропорцио-
нальна интегралу от спектральной плотности мощности (5.17):
о2 = R (0) = —((0)^ = Л 7 d(O
вых Bb,xV / вых к ) 2л £1 + СО2Т2
Произведем замену переменной х - сот и учтем, что j(l + x2) ’<£r = arctgx:
2 "г dx №0 “ №0 (л ( TtYl
вых 2ktj1 + x2 2лт & 2лт^2 2)J 2т
Итак, искомое среднеквадратическое отклонение выходного шума составляет
о =Ж. (5.18)
вых у 2т
Теперь мы можем записать выражение для отношения «.сигнал/шум»:
Для получения квазиоптимального фильтра нам необходимо отыскать то зна-
чение постоянной времени т, при котором выходное отношение «сигнал/шум»
максимально. Перепишем (5.19) в следующем виде:
<5.20)
Величина А2Травна энергии входного прямоугольного импульса, поэтому пер-
вый множитель в (5.20) представляет собой, согласно (5.9), отношение «сигнал/
шум» на выходе согласованного фильтра. Следовательно, оставшаяся часть (5.20)
является безразмерным множителем, характеризующим проигрыш квазиоптималь-
ного фильтра согласованному. Как видно из (5.20), этот проигрыш зависит от соот-
ношения т/Т между постоянной времени ДС-цепочки и длительностью импульса.
Обозначим это отношение буквой х. С учетом сказанного нам необходимо найти
максимум следующей функции:
/(х) = 727(1-е’1Л). <5-21)
К сожалению, приравнивание к нулю производной функции (5.21) приводит
к трансцендентному уравнению, не имеющему аналитического решения График
функции/(х) приведен на рис. 5.15. Использование численных методов решения
уравнений позволяет определить, что максимальное значение функции /(х) до-
стигается при х = 0,7959 и равно 0,9025.
Итак, для получения максимального отношения «сигнал/шум» на выходе при
обработке смеси прямоугольного импульса и белого шума постоянная времени ин-
тегрирующей ДС-цепи должна составлять примерно 0,8 от длительности импульса.
Проигрыш согласованному фильтру составляет при этом около 10 %.
5.5. Квазиоптимальная фильтрация детерминированных сигналов
177
Рис. 5.15. Зависимость проигрыша интегрирующей RC-цепи согласованному фильтру
от соотношения между постоянной времени цепи и длительностью обрабатываемого
прямоугольного импульса
Как отмечалось в разделе 5.1, форма импульсной характеристики согласованного
фильтра повторяет форму обрабатываемого сигнала, перевернутого во времени.
Поэтому разумно предположить, что для получения лучших результатов форма
импульсной характеристики квазиоптимального фильтра должна быть «похожа»
на форму обрабатываемого сигнала. Таким образом, можно ожидать, что от инте-
грирующей .RC-цепи можно получить меньший проигрыш согласованному филь-
тру при обработке не прямоугольного, а треугольного несимметричного импульса
(на рис. 5.16 приведены графики такого импульса и импульсной характеристики
7?С-цепи). Проверим это.
ис. 5.16. Входной треугольный импульс и импульсная характеристика
интегрирующей RC-цепи
Поскольку на входе действует все тот же белый шум, мы можем воспользоваться
уже полученным результатом (5.18) для среднеквадратического значения выходного
шума. Заново необходимо рассчитан ь лишь пиковое значение выходного сигнала.
На интервале времени от 0 до Г выходной сигнал рассчитывается как
5
вых
й) = '[£t ’1 'dt' = — - — (1 - е*).
J Т т ТТ
При t> Т выходной сигнал равен
5вых(0= t'-e <r 'v'dt'= и[ ет>'- — ет' +—
вых х ' J j-, rj-t j
(5.22)
(5.23)
178
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
Рис. 5.17. Прохождение треугольного импульса через интегрирующую RC-цепь
Графики входного и выходного сигналов приведены на рис. 5.17. Максималь-
ное значение выходного сигнала, так же как и в случае прямоугольного импульса,
достигается при t=T. Согласно (5.22) и (5.23), это максимальное значение равно
1$ (al =cf i--(i-e-r/I) I.
| вых X /|max I J'v 7 I
Теперь можно рассчитать выходное отношение «сигнал/шум»:
С/Ш
ВЫХ
С7^1-у(1-е-г/т)
Л/<2т)
(5.24)
Перепишем (5.24) таким образом, чтобы выделить в нем множитель, равный
отношению «сигнал/шум» на выходе согласованного фильтра. Прежде всего за-
метим, что энергия нашего треугольного импульса составляет
гГпгУ. и2т
С учетом этого можно записать (5.24) в следующем виде:
с/ш = EG-S(i-e-r/x)\
вых \3W0VT{ г
(5.25)
Первый множитель в (5.25) представляет собой отношение «сигнал/шум» на
выходе согласованного фильтра, а оставшаяся часть характеризует проигрыш ква-
зиоптимального фильтра согласованному, зависящий от отношения т/Г. Обозначив
это отношение буквой х, запишем функцию проигрыша:
/(х) = >/бх(1- х(1-е 1/I)j.
(5.26)
Как и в случае прямоугольного импульса, максимум выражения (5.26) невоз-
можно найти аналитически. График этой функции приведен на рис. 5.18. Численное
решение уравнения f\x) = 0 показывает, что максимум достигается прих= 0,4653
и равен 0,9841.
5.6. Оптимальная фильтрация случайных сигналов
179
Рис. 5.18. Зависимость проигрыша интегрирующей RC-цепи согласованному фильтру
от соотношения между постоянной времени цепи и длительностью обрабатываемого
треугольного импульса
Итак, для квазиоптимальной фильтрации треугольного импульса постоянная
времени интегрирующей .RC-цепи должна составлять 0,47 от длительности импуль-
са. Проигрыш согласованному фильтру при этом равен 1,6 %.
Благодаря тому что импульсная характеристика интегрирующей RC-цепи ближе
по форме к треугольному импульсу, чем к прямоугольному, в случае треугольного
сигнала мы получили лучшее приближение к согласованному фильтру (проигрыш
составил 1,6 % вместо 10 %).
В заключение отметим, что столь малый проигрыш согласованному фильтру
в рассмотренных примерах был получен лишь благодаря простой форме обрабаты-
ваемых сигналов. Для сложных сигналов реализовать квазиоптимальные фильтры
в виде прос гых цепей и обеспечить при этом малый проигрыш согласованному
фильтру не представ тяется возможным.
5.6. Оптимальная фильтрация
случайных сигналов
Рассмотрим теперь другую задачу обработки сигналов. Пусть случайным является
не только шум, но и полезный сигнал. Такая ситуация встречается часто, поскольку,
строго говоря, любой сигнал, несущий какую-то информацию, является случайным.
Входной сигнал в этом случае можно записать следующим образом:
V0 = 5(0 + "(0-
где ^(Г) — полезный случайный сигнал, a n(t) — шум. Оба случайных процесса будем
считать нормальными, стационарными, центрированными (M{^(t)} = - 0) и
статистически независимыми друг от друга. Двусторонние спектральные плотности
мощности процессов ^(4) и n(t) равны соответственно 1Т.(со) и VP^cd).
Изменим также критерий качества обработки — пусть нам нужно по возможно-
сти очистить полезный сигнал ^(t) от шумов. Тогда мерой качества может служить
ошибка воспроизведения полезного сигнала на выходе:
е(0 = ^(0-5(0-
180
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
Так как предполагается, что рассматриваемый фильтр является линейной цепью
с постоянными параметрами, то выходной сигнал $вых(0 и сигнал ошибки e(t) так-
же будут стационарными случайными процессами. Поэтому логично требовать
минимальной дисперсии ошибки:
Z>{e} -> min.
Дисперсия процесса e(t) связана с его математическим ожиданием и средним
квадратом следующим образом:
D{e} = M{e2}-M2{e}.
Ясно, что М{е} = 0, так как ЛД$вьк} = 0 (линейная цепь не нарушает центрирован-
ности процесса) и ЛД£,} = 0. Поэтому
D{e} = М{е2} = ДДО) = A- J We (co)J(o,
/Я
где Де(т) — корреляционная функция сигна ia ошибки e(t), а ИДсо) — его спектраль-
ная плотность мощности.
Так как We(co) > 0, то стремление минимизировать D{e} означает необходимость
минимизировать площадь под кривой We(co).
Рис. 5.19. Формирование сигнала ошибки при фильтрации случайного процесса
На рис. 5.19 приведена структурная схема, демонстрирующая формирование
сигнала ошибки e(t). Эта схема линейна, поэтому коэффициенты передачи для сиг-
нала ^(i) и шума n(t) можно легко определить, представив, что один из случайных
процессов на входе отсутствует.
1. Пусть n(t) = 0 (шум на входе отсутствчет); для полезного сигнала £,(£) коэффи-
циент передачи равен К(а)-1.
2. Пусть ^(t) = 0 (полезный сигнал на входе отсутствует); для пгума n(f) коэффи-
циент передачи равен К (а).
Вследствие статистической независимости процессов ^(i) и n(t) их прохожде-
ние через линейную цепь (и, следовательно, вклады их спектров в спектр сигнала
ошибки) можно рассматривать по отдельности, объединив затем результаты со-
гласно принципу суперпозиции.
Спектральная плотность мощности вклада от полезного сигнала
U7(w) = W. ((o)|k(co)-l|2.
5.6. Оптимальная фильтрация случайных сигналов
181
Спектральная плотность мощности вклада от шума
wn'(®)=w;(Co)|x((o)l2.
Согласно принципу суперпозиции, спектральная плотность мощности сигнала
ошибки составляет
ИДсо) = FF'(co) 4- РКДсо) = FK (со)|/С(со) -1|2 + (оз) | AT(<o)|2 =
= Wn (со) |X(co)f + (К (со)(Х(со) -1)( К‘ (со) -1) =
= Wn (со) |Х(со)|‘ + W.. (со) (К(а)к‘ (со) - Х(со) - К‘ (со) +1).
Записав Х(со) в виде Х(со) = Х(со)е;ф''<ш), получаем:
W;(со) = IV (со)Х2(со) + W,(co)(X’2(co) - 2X(co)cos срА.(со) + 1). (5.27)
Дисперсия ошибки пропорциональна интегралу от IV(co) по частоте, поэтому
для уменьшения этой дисперсии нам нужно стремиться уменьшить значение IV (со)
на всех частотах.
Рассмотрим сначала фазовый спектр срДсо). Согласно (5.27) спектральная плот-
ность мощности сигнала ошибки IV (со) будет минимальна, если cos срА(со) - 1, то
есть при <рА(со) = 2nk k = 0,1,2... Таким образом, фильтр не должен вносить задержки
сигнала. С учетом этого
IV (со) = IV (со)Х2(со) + IV,(co)(X(co) - I)2.
(5.28)
Продифференцируем (5.28) по Х(со) для фиксированной частоты со и прирав-
няем производную к нулю:
2IV (со)Х(со) + 2W^(co)(X(m) - 1) = 0.
Решив это уравнение относительно Х(со), находим точку экстремума (несложно
убедиться, что этот экстремум является минимумом):
X(co)(IV(co) + IV (со)) = Н'(со),
откуда
IV (со)
IV. (со) + IV (со)
(5.29)
Полученное выражение для Х(со) обеспечивает минимальную спектральную
плотность мощности сигнала ошибки на всех частотах со, а следовательно, и его
минимальную дисперсию.
Фильтр с коэффициентом передачи (5.29) называют оптимальным фильтром
для случайного сигнала, или фильтром Винера
Фазочастотная характеристика фильтра нулевая, следовательно, нет задержки
по времени и сохраняются фазовые соотношения, имевшиеся во входном сигнале.
В области частот, где полезный сигнал намного сильнее шума, имеем
11-Дсо) » IV (со) и коэффициент передачи Х(со) = 1. Там же, где сигнал слабый,
182
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
ll^(co) « Wn((o) и коэффициент передачи К((о) ~ 0. Если на какой-то частоте
спектральные плотности мощности сигнала и шума одинаковы, то коэффициент
передачи на этой частоте равен 0,5.
Таким образом, оптимальный фильтр пропускает те частоты, на которых сигнал
сильнее шума, и подавляет те, где он слабее. Отсутствие фазовых сдвигов обеспе
чивает лучшее сохранение формы полезного сигнала.
ЗАМЕЧАНИЕ 5.5--------------------------------------------------------
Разумеется, степень сохранения формы полезного сигнала не изменится,
а значит, оптимальность фильтра не нарушится, если ввести произвольную
(но одинаковую для всех частот) задержку tQ. Фазочастотная характери-
стика фильтра в этом случае
Фк(со) = -со£0.
ЗАМЕЧАНИЕ 5.6-------------------------------------------------------
При выводе формулы для частотной характеристики винеровского филь-
тра не накладывалось требование физической реализуемости получаемого
фильтра. Поэтому в болыпинс гве практических задач использование
формулы (5.29) даст нереализуемый фильтр, имеющий бесконечно про-
тяженную в обе стороны импульсную характеристику.
Определим, чему равна дисперсия ошибки воспроизведения полезного сигнала
для оптимального фильтра. Подставив (5.29) в (5.28), получим спектральную плот-
ность мощности сигнала ошибки:
IV (со) = (со)(Х(со) -1)2 + IV (со)К2(со) =
IV2 (со) Ж2 (со)
= IV (со)--------п—----------- + Wn (со)--------------------
(lV;(co) + IV(co)) (lV5(co) + IV(co))
_ W.. (co)IV2 (co) + IV (co)W* (co) _ W' (co)Wn (co)
(lV;(co) + IV (co))2 WL(co) + IV„(co)’
Дисперсия, равная значению корреляционной функции при т = 0, может быть
рассчитана с помощью теоремы Винера—Хинчина:
= — j IV (co)Jco = — j
2л J ' 7 2л J
а
2
IV;(co)IV (со)
—----------------асо.
IV. (co) + IV (co)
(5.30)
ЗАМЕЧАНИЕ 5.7------- ------------------------ - -----------------
Как указано ранее, использование формулы (5.29), как правило, дает ча-
стотную характеристику, соответствующую физически нереализуемому
фильтру. Вследствие этого значение дисперсии ошибки воспроизведения
5.6. Оптимальная фильтрация случайных сигналов
183
полезного сигнала, даваемое формулой (5.30), также не может быть до-
стигнуто на практике.
Переход от круговой частоты (со) к обычной (f- со/2л) позволяет избавиться
от множителя перед интегралом:
2 ~ W^2nf)Wn(2nf)
CTf l^(2n/) + VF(2n/) Л
Пример 5.2. Полезный случайный сигнал имеет спектральную плотность мощ-
ности вида
и;(со) =
1 + (со/<о0)2
где IFj = 16-10~12 В2с и со0 = 3-108 рад/с, а шум является белым и имеет спектраль-
ную плотность мощности Wo = 210’12 В2 с (рис. 5.20, а). Найдем характеристики
оптимального фильтра и рассчитаем дисперсию ошибки воспроизведения полез-
ного сигнала.
Рис. 5.20. Пример оптимальной фильтрации случайного сигнала: а — спектры полезного
сигнала и шума; б — АЧХ оптимального фильтра
Коэффициент передачи оптимального фильтра рассчитывается согласно (5.29):
VF1+IVo+IV0((o/®0)2
i
Wo , / \2
-----у—(со/соЛ
(5.31)
184
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
С учетом численных данных задачи можно записать:
ВД = |------------.
9 1 + (со/Зсо0)
График полученной АЧХ приведен на рис. 5.20, б. Пунктирные линии на рис. 5.20
иллюстрируют, что, как указывалось ранее, на той частоте, где IV.(co) = Wn(co) (в дан-
ном примере эта частота примерно равна 8-108 рад/с), К((й) = 0,5.
ЗАМЕЧАНИЕ 5.8----------------------------------------------------
Обратное преобразование Фурье, примененное к формуле (5.31), дает
импульсную характеристику оптимального фильтра:
g(0 =
—t ‘ ° =ехр
2>O(1V1+IVO)
lw1+w0
Id
-оо < t < оо.
Импульсная характеристика оказывается бесконечно протяженной во
времени и, таким образом, соответствует физически нереализуемому
фильтру, что согласуется со сделанным ранее замечанием.
Теперь рассчитаем ошибку воспроизведения полезного сигнала, воспользоьав-
шись для этого формулой (5.30):
W
--------W
z ч2 о
со |
J
W
— + VT
/ \2 о
2л 1
W1+lVo+IVo
1+ —
1 w-л I
2л W.+Wj
-----у</(0 =
(О
“о )
\2
(О
1 WVV
Jco = —-2^-
2л wj+w;
W1+Wo
—-----СО„Л =
W 0
2л J
1
^0
tf.+wucoj
Подстановка численных данных дает сГ = 8-10 4 В2.
Контрольные вопросы и задания
1. Какова постановка задачи о согласованной фильтрации детерминированного
сигнала?
Задачи
185
2. Приведите формулы, связывающие комплексный коэффициент передачи
и импульсную реакцию согласованного фильтра с характеристиками исходного
сигнала.
3. Поясните механизм компенсации начальных фаз гармонических составляющих
в спектре обрабатываемого сигнала при согласованной фильтрации.
4. Какой параметр служит количественной характеристикой соотношения сигнала
и шума в их аддитивной смеси? Как он вычисляется?
5. Чему равно отношение С/Ш на входе и выходе согласованного фильтра при
обработке детерминированного сигнала на фоне аддитивного белого шума?
6. Какие сигналы называются сложными? Приведите примеры сложных видео-
и радиосигналов (с изображением временной структуры). Где и с какой целью
сложные сигналы находят применение?
7. Каким образом в локационной системе добиваются сочетания большой даль-
ности действия с высоким разрешением по дальности?
8. Поясните сущность принципа скрытной передачи сигналов.
9. Изобразите структурную схему одноканального коррелятора. В чем состоят
сходст во и различие коррелятора и согласованного фильтра?
10. Чему равен комплексный коэффициент передачи согласованного фильтра при
небелом шуме?
11. Какова постановка задачи об оптимальной фильтрации случайного сигнала?
12. Как вычисляется комплексный коэффициент передачи фильтра, осуществля-
ющего оптимальную фильтрацию случайного сигнала?
Задачи
Задача 5.1
На вход согласованного фильтра подается трехэлементный код Баркера (рис. 5.21).
Найти отклик фильтра, если максимальное значение отклика наступает при t0 = ЗТ.
0
---!-►
ЗТ t
Рис. 5.21. Сигнал для задачи 5.1
186
5. Принципы оптимальной линейной фильтрации сигналов на фоне помех
Задача 5.2
Фильтр согласован с сигналом s(t) = |g' g На вход фильтра поступает
белый шум со спектральной плотностью мощности Wo. Найти корреляционную
функцию шума на выходе такого фильтра.
Задача 5.3
Полезный сигнал, график которого показан на рис. 5.22, поступает на вход согла-
сованного фильтра в аддитивной смеси с белым шумом, имеющим двустороннюю
спектральную плотность мощности Wo. Определить значение параметра Т, если
[/= 4 мВ, Wo = 5-10~12 В2 с, С/Швых = 12.
2U -
U--------------
I
I
I
I
---------I-----—►
О Т 2Т t
Рис. 5.22. Сигнал для задачи 5.3
Задача 5.4
Сигнал и шум из задачи 5.3 поступают на вход фильтра, импульсная характеристика
которого повторяет форму сигнала: h(t) = As(t). Определить форму выходного по-
лезного сигнала, рассчитать максимальное выходное отношение «сигнал/шум». Во
сколько раз данный фильтр проигрывает согласованному фильтру из задачи 5.3?
Задача 5.5
На вход интегрирующей 7?С-цепи поступает аддитивная смесь гармонического
сигнала с амплитудой А и частотой со0 и белого шума, двусторонняя спектральная
плотность мощности которого равна IV0. Определить оптимальную постоянную
времени 7?С-цепи т, при которой достигается максимальное отношение «сигнал/
шум» на выходе. Найти его значение.
Примечание. Выходное отношение «сигнал/шум» рассчитывается как отношение
амплитуды гармонического сигнала к среднему квадратическому значению шума
на выходе цепи.
Задача 5.6
Полезный сигнал представляет собой экспоненциальный импульс конечной дли-
тельности: s(t)=A ехр(-а t) при 0 < t < Т. Шум представляет собой экспоненциально
коррелированный случайный процесс: Лп(т) = ст,2 ехр(-р |т|). Найти комплексный
коэффициент передачи фильтра, который будет оптимальным для обнаружения дан-
ного сигнала в данном шуме, и отношение «сигнал/ шум» на выходе этого фильтра.
Задачи 187
Задача 5.7
Односторонняя спектральная плотность мощности полезного случайного сигнала
равна 5 10 6 В2/Гц в полосе частот 1...3 кГц и 0 — на остальных частотах. Одно-
сторонняя спектральная плотность мощности шума равна 2,5-10-6 В2/Гц в полосе
частот 2...4 кГц и 0 — на остальных частотах. Определить коэффициент передачи
оптимального фильтра и дисперсию ошибки воспроизведения полезного сигнала
на выходе.
Задача 5.8
Полезный сигнал x(i) и шум «(i) представляют собой экспоненциально коррелиро-
ванные случайные процессы: 7?х(т)=ах2 ехр(—а |т|), R„(^) = а2 ехр(-Л |т|). Определить
коэффициент передачи оптимального фильтра и дисперсию ошибки воспроизве-
дения полезного сигнала на выходе.
6. Основы дискретной
фильтрации сигналов
В настоящее время благодаря бурному развитию микропроцессорной техники
получила широкое распространение цифровая обработка сигналов. При этом физи-
ческий сигнал (напряжение, ток и т. д.) преобразуется в последовательность чисел,
которая затем подвергается математическим преобразованиям в вычислительном
устройстве. Трансформированный цифровой сигнал (последовательность чисел)
может быть преобразован обратно в напряжение или ток. В данной главе будут
рассмотрены принципы математического описания цифровых сигналов, а также
теоретические основы построения ус гройств для их обработки.
6.1. Аналоговые, дискретные
и цифровые сигналы
Исходный физический сигнал является непрерывной функцией времени. Такие
сигналы, определенные во все моменты времени, называют аналоговыми. После-
довательность чисел, представляющая сигнал при цифровой обработке, является
дискретным рядом и не может полностью соответствовать аналоговому сигналу.
Числа, составляющие последовательность, являются значениями сигнала в от-
дельные (дискретные) моменты времени и называются отсчетами сигнала. Как
правило, отсчеты берутся через равные промежутки времени Т, называемые пери-
одом дискретизации (или интервалом, шагом дискретизации}. Величина, обратная
периоду дискретизации, называется частотой дискретизации'. /Т.
Ясно, что в общем случае представление сигната набором дискретных отсчетов
приводит к потере информации, так как мы ничего не знаем о поведении сигнала
в промежутках между отсчетами. Однако, как будет показано далее, существует
класс аналоговых сигналов, для которых такой потери информации не происхо-
дит и которые могут быть точно восстановлены по значениям своих дискретных
отсчетов.
Процесс преобразования аналогового сигнала в последовательность отсчетов
называется дискретизацией, а результат такого преобразования — дискретным
сигналом.
При обработке сигнала в вычислительных устройствах его отсчеты представля-
ются в виде двоичных чисел, имеющих ограниченное число разрядов. Вследствие
этого отсчеты могут принимать лишь конечное множество значений, и следователь-
6.1. Аналоговые, дискретные и цифровые сигналы
189
но, при представлении сигнала происходит его округление. Процесс преобразования
отсчетов сигнала в числа называется квантованием по уровню, а возникающие при
этом ошибки округления — ошибками (или шумами) квантовании
Сигнал, дискретный во времени, но неквантованный по уровню, называется
дискретным сигналом. Сигнал, дискретный во времени и квантованный по уровню,
называют цифровым сигналом. Сигналы, квантованные по уровню, но непрерывные
во времени, на практике встречаются редко. Разницу между аналоговыми, дискрет-
ными и цифровыми сигналами иллюстрирует рис. 6.1.
5
4
3
2
1
О
-2 0 2 4 6 8 10
Рис. 6.1. Аналоговый (слева), дискретный (в центре) и цифровой (справа) сигналы
Вычислительные устройства, предназначенные для обработки сигналов, могут
оперировать только цифровыми сигналами. Существуют также устройства, по-
строенные в основном на базе аналоговой схемотехники, которые работают с дис-
кретными сигналами, представленными в виде импульсов различной амплитуды
или длительности. Чтобы подчеркнуть отсутствие квантования по уровню, такие
ус гройства иногда называют дискретно-аналоговыми (ДАУ).
ЗАМЕЧАНИЕ 6.1 -------------------------------------------------------
В данной главе термины «цифровой фильтр» и «дискретный фильтр»
будут использоваться как синонимы, хотя, строго говоря, речь пойдет
о дискретнъа' сигналах и фильтрах, поскольку эффекты, связанные
с квантованием, в большинстве случаев не будут приниматься во внима-
ние — о них лишь кратко будет сказано в разделе 6.2.
Обобщенная структура системы цифровой обработки сигналов приведена на
рис. 6.2. На вход поступает аналоговый сигнал $вх(£)- Его временная дискретиза-
ция и квантование по уровню производятся в аналого-цифровом преобразователе
(АЦП). (Вообще эти два процесса — дискретизация и квантование — являются
независимыми друг от друга, но они, как правило, выполняются внутри одного
блока.) Выходным сигналом АЦП является последовательность чисел, пос гупаю-
щая в цифровой процессор ЦП, выполняющий требуемую обработку. Процессор
осуществляет над входными отсчетами различные математические операции; ранее
полученные отсчеты и промежуточные результаты могут сохраняться в памяти
процессора для использования в последующих вычислениях Результатом работы
процессора является новая последовательность чисел, представляющих собой от-
счеты выходного сигнала. Аналоговый выходной сигнал звьи(0 восстанавливается
190
6. Основы дискретной фильтрации сигналов
по этой последовательности чисел с помощью цифроаналогового преобразователя
(ЦАП). Напряжение на выходе ЦАП имеет ступенчатую форму (см. рис. 6.2), при
необходимости оно может быть преобразовано в плавно меняющийся выходной
сигнал с помощью сглаживающего фильтра Ф.
{хь,Х|,х2...} {уо,У1,у2---}
Рис. 6.2. Структурная схема системы цифровой обработки сигналов
Устройства, реализуемые с помощью структуры наподобие изображенной на
рис. 6.2, могут иметь самый разнообразный характер. В цифровой форме можно
создавать фильтры, анализаторы спектра, нелинейные преобразователи сигналов
и многое другое.
ЗАМЕЧАНИЕ 6.2---------------------------------------------------------
Следует отметить, что использование входных и выходных сигналов
в аналоговой форме (и, следовательно, наличие АЦП и ЦАП) не всегда
необходимо. Так, при реализации цифрового генератора сигналов не нужен
входной аналоговый сигнал, а ЦАП может отсутствовать, если конечный
результат необходимо получить в цифровой форме.
К достоинствам цифровой обработки сигналов относятся высокая гибкость
и точность выполнения преобразований сигнала. Основным недостатком являет-
ся ограниченное быстродействие; впрочем, по мере развития технологии рабочие
частоты цифровых устройств постоянно возрастают.
6.2. Шумы квантования
Как было отмечено в разделе 6.1, при представлении отсчетов дискретного сигнала
в виде чисел с ограниченной разрядностью происходит их округление. Разность
между исходным и округленным значениями называется шумом квантования.
Анализ вопросов, связанных с шумами квантования и ошибками округления
в цифровых системах обработки сигналов, весьма сложен (см., например, [15]).
В данном разделе будут представлены лишь несколько положений общего ха-
рактера.
В качестве иллюстрации процесса квантования на рис. 6.3 показаны (без дис-
кретизации по времени) гармонический сигнал s(t), результат его квантования sK(i)
и возникающий при этом шум e(t) = s(t) - sK(t).
6.2. Шумы квантования
191
Очевидно, что значения шума квантования лежат в следующих пределах:
2 v 2
где Д — расстояние между соседними уровнями квантования, то есть разность между
ближайшими возможными значениями квантованного сигнала.
В большинстве случаев можно считать e(t) случайным процессом, имеющим
равномерное распределение вероятности в указанных пределах. Такой случайный
процесс имеет нулевое среднее значение и дисперсию, равную Д2/12.
Рис. 6.3. Процесс квантования гармонического сигнала
ЗАМЕЧАНИЕ 6.3-------------------------------------------------------
На рис. 6.3 предполагалось, что при квантовании производится округление
значений уровня сигнала. В реальных АЦП вместо этого может использо-
ваться усечение, то есть округление в сторону меньшего значения. В этом
случае шум квантования лежит в диапазоне 0...Д, его среднее значение
равно Д/2, а дисперсия, как и в случае округления, составляет Д2/12.
После дискретизации шум квантования представляет собой последовательность
чисел e(kT), образующую дискретный случайный процесс. Во многих случаях от-
счеты этой последовательности можно считать некоррелированными друг с другом.
ЗАМЕЧАНИЕ 6.4-------------------------------------------------------
О дискретных случайных процессах речь пойдет в разделе 6.14.
192
6. Основы дискретной фильтрации сигналов
Пример 6.1. Отношение «сигнал/шум» при квантовании гармонического сигнала.
Пусть квантованию подвергается гармонический сигнал с амплитудой А. Опреде-
лим отношение «сигнал/шум», разделив эту амплитуду на среднее квадратическое
значение шума квантования:
С/Ш = А = = лц/з,
7^712 А
гдеN=2A/A — число уровней квантования, укладывающихся в размахе сигнала.
АЦП, имеющий q двоичных разрядов, обеспечивает N = 2’ уровней квантова-
ния. Если размах сигнала соответствует полному рабочему диапазону АЦП, то
отношение «сигнал/шум»
С/Ш = 2'?у/3.
Если выразить этот результат в децибелах, получится простая формула, пока-
зывающая связь между числом двоичных разрядов, используемых для представ-
ления отсчетов сигналов, и максимально достижимым в этом случае отношением
«сигнал/шум»:
С/ШдБ= 20 lg(2"л/з) = 20/ylg2 +101g3 = 6<? + 4,77 дБ.
ЗАМЕЧАНИЕ 6.5--------- — ----------------------------------------
Шум квантования — не единственная проблема, связанная с конечной
разрядностью используемых чисел. Так. неизбежное округление раз-
нообразных коэффициентов, используемых в алгоритмах цифровой
обработки сигналов, приводит к тому, что параметры фильтров и других
устройств отличаются от желаемых, причем возможны ситуации, когда
эти отличия весьма существенны. Кроме того, из-за округления проме-
жуточных результатов может происходить накопление вычислительных
погрешностей, также искажающих конечный результат.
6.3. Теорема Котельникова
Замена непрерывного сигнала последовательностью его дискретных отсчетов в об-
щем случае неизбежно ведет к потерям информации, ведь при этом ничего нельзя
сказать о поведении сигнала в промежутках между отсчетами. Однако существует
класс непрерывных сш налов, которые могут быть точно восстановлены по своим
дискретным отсчетам. Рассмотрим этот вопрос подробнее, для чего докажем теоре-
му Котельникова, которая гласит: любой сигнал s(t), спектр которого не содержит
составляющих с частотами выше некоторого значения сов = 2л /в, может быть без
потери информации представлен своими дискретными отсчетами {s(kT)}, взятыми
с интервалом, удовлетворяющим следующему неравенству:
7'<Цг = —.
2/ со
J в в
(6-1)
6.3. Теорема Котельникова
193
Восстановление исходного непрерывного сигнала s(t) по набору его дискретных
отсчетов {s(kT)} производится следующим образом:
sin| -(t-kT) |
s(t) = £ s(kr>—Z------£ (6.2)
Y(t~kT)
Формула (6.2) представляет собой разложение сигнала s(t) в обобщенный ряд
Фурье (см. раздел 1.2) по системе функций {<рЛ(0}> называемой базисом Котель-
никова-.
sinf — (t-k7) |
<рдо=——---------}-=4>0(t-kT). (6.3)
л
График функции <р0(£) показан на рис. 6.4. Остальные функции базиса отличают-
ся от Ф0(О сдвигом по времени на величину kT. Функция <р,(t) показана на рис. 6.4
пунктиром. Видно, что в момент времени t=kTфункция <pt(0 достигает максимума,
равного единице, тогда как все остальные функции базиса равны нулю.
Рис. 6.4. Базис Котельникова
Для доказательства теоремы Котельникова необходимо подробнее исследовать
разложение сигнала в ряд по функциям {ф/0}.
Прежде всего обратим внимание на то, что спектральная плотность 50(о)) функ-
ции <р0(£) имеет прямоугольную форму (рис. 6.5):
5о(со) = -
О,
(6.4)
|5o(co)|f
Т
-п/Т 0 к/Т СО
Рис. 6.5. Амплитудный спектр базисных функций базиса Котельникова
7 Ns 675
194
6. Основы дискретной фильтрации сигналов
Спектральная плотность остальных функций базиса, согласно свойствам пре-
образования Фурье (см. раздел 1.7 и формулу (1.58)). отличается от 50(со) лишь
дополнительным фазовым множителем:
5Д®) = 50(<»)е^г.
Теперь докажем ортогональность базиса {ф/0}. Для этого необходимо вычислить
значение интеграла (1.16):
.. sin y(i-i^T) sinly(t-nT)
J ФДОФ„ W = J------------------------dt.
(6.5)
Для вычисления проще всего воспользоваться теоремой Рэлея, связывающей
интеграл от произведения сигналов и s2(t) с интегралом от произведения их
спектральных плотностей S/cd) и 52(со) (см. раздел 1.8 и формулу (1.67)):
] 5,(052(0* = ^-|51(со)5'(со)</со.
J ZJt *
(6.6)
Применив соотношение (6.6) к формуле (6.5), получим:
j ФД0ФД0Л = = /- j |5о«о)|2 e'^-^da.
_оа Jv £ Jv
Теперь примем во внимание вид функции S0(a>) (см. (6.4) и рис. 6.5). С учетом
этого
J<p^)<pn(0jf = J-r J (6.7)
-п/Т
При п = k получаем:
[ф2(0<* = — Т2 f <йо = —Т2 —= Т.
Г‘ 2л J/Т 2л Т
При п k можно вычислить интеграл (6.7) обычным образом:
( Ф*(Оф„(О^ = —-----------=----------------I-----С-лц-) _ем*-л)\ =
_ 2n-j(^-n)T 1-я/г -j2n(k-ny
= ---r(-27sin(7t('t - ”>)) = J sin(n(fe - и)).
-у2п(я-и)х ' Tt(k-n)
Поскольку kun — целые числа, то sin n{k - n) = 0, а значит, нулевым является
и результат вычисления интеграла.
6.3. Теорема Котельникова
195
[Г, k = n,
[О, k*n.
Итак,
J<P*(O<P„(OA =
Таким образом, система функций {ф/f)} является ортогональной, но не нор-
мированной (их норма равна >/г ). Поэтому коэффициенты разложения сигнала в
базисе Котельникова рассчитываются следующим образом (см. формулу (1.20)):
G=y р(О<Р*(О<Й
Снова воспользуемся свойством (6.6):
/Л/
Учитывая вид функции 50(со) (см. (6.4) и рис. 6.5), получим:
. я/7
Ck=— f S(a)e^Tda. (6.8)
-ь'т
Так как спектр сигнала, согласно условию (6.1) применимости теоремы Ко-
тельникова, ограничен частотой <вв < л/Г, пределы интегрирования в (6.8) можно
заменить на бесконечные:
С4=^р(о))Л).
Этот интеграл предс гавляет собой обратное преобразование Фурье для момента
времени t = kT. Таким образом, окончательно получаем:
Ck = s(kT).
Итак, сигнал с ограниченным по частоте спектром может быть восстановлен по
значениям своих дискретных отсиетов. Тем самым теорема Котельникова доказана.
Ошибка аппроксимации. Если условие (6.1) не выполняется, коэффициенты
разложения сигнала в базисе Котельникова, не будут совпадать с отсчетами исход-
ного сигнала. Из формулы (6.8) следует, что в общем случае эти коэффициенты
равны отсчетам сигнала, предварительно пропущенного через идеальный ФНЧ
с частотой среза п/Т. Формула (6.2) при этом принимает вид
(л
sin —(t
°° I тх
Y(t-
196
6. Основы дискретной фильтрации сигналов
Коэффициенты ряда Ck в этом случае рассчитываются по формуле (6.8), а ре-
зультатом расчетов является некий восстановленный сигнал s^t), не совпадающий
с исходным сигналом s(t). Разность между исходным и восстановленным сигналами
дает ошибку аппроксимации soul(t):
5ОШ(0 = 5(0-5^(0-
Восстановленный сигнал $вос(0 — эт0 исходный сигнал, подвергнутый идеаль-
ной низкочастотной фильтрации. Поэтому сигнал ошибки — это высокочастотные
составляющие си] нала s(t), частоты которых превышают п/Т.
= J S(^da.
Сигналы х (0 и 3^(0 являются ортогональными, так как их спектры не пере-
крываются (см. раздел 1.13). Поэтому их энергии суммируются, так что
Е =Е +Е .
S S.u. 5ош
Энергию сигнала ошибки легче всего вычислить в частотной области согласно
равенству Парсеваля (1.68):
£.ш=^Жш|2</<й=^ I |М2</со-
271 — 271 )<о|>«/7-
Эта энергия показывает абсолютную величину ошибки аппроксимации. Мож-
но вычислить безразмерную относительную ошибку, пронормировав результат
к энергии исходного сигнала:
J |S(w)|2Jco
5ош _ 1ШНГ_______
j |5((О)|2 dot
Пример 6.2. Рассчитаем ошибку аппроксимации рядом Котельникова для одно-
стороннего экспоненциального импульса (1.3):
s(t) = Ue~™, t>0.
Спектральная функция и энергетический спектр сигнала:
о ;<о + а । 1 о/ + от
Энергия сигнала:
6.4. Спектр дискретизированного сигнала
197
Энергия ошибки аппроксимации:
Е = —
s“ 2л
>пТ 71 Вт
[/2 .
%VrctgWU
U2
2 = J
“ +« «"/аГ)
и2
ал
Е2 +
= —arctg
ал
Относительная ошибка:
Е
U2
arctg
ал
2
= —arctg
л
(6.9)
2а
Количественный анализ формулы (6.9) показывает, что, например, для до-
стижения относительной ошибки, не превышающей 1 %, должно выполняться
неравенство аТ < 0,049.
Ряд Котельникова в частотной области. Благодаря симметрии прямого
и обратного преобразования Фурье (см. раздел 1.5) можно сформулировать дуаль-
ный вариант теоремы Котельникова; если сигнал имеет конечную длительность Дт,
то его спектр может быть точно восстановлен по своим дискретным: значениям,
взятым с частотным интервалом Дю, меньшим 2л/Дт. Формула восстановления не-
прерывной спектральной функции по ее дискретным отсчетам получается из (6.2)
заменой временных параметров (t и Т) на соответствующие частотные (<о и Доз).
6.4. Спектр дискретизированного сигнала
Преобразование Фурье позволяет вычислить спектральную плотность сигнала,
представляющего собой функцию (как правило, времени либо пространственных
координат). Дискретный же сигнал является последовательностью чисел, поэтому
для анализа его спектра необходимо сопоставить этой последовательности неко-
торую функцию.
Введем в рассмотрение дискретизированный сигнал в виде последовательности
дельта-функций, «взвешенной» значениями отсчетов s(kT) аналогового сигнала s(t)
(рис. 6.6):
sSt)=^^kT)6(t-kT).
(6.10)
ЗАМЕЧАНИЕ 6.6-----------------------------------------------------
Термин «дискретизированный» в данном контексте подчеркивает, что по-
следовательность отсчетов получена именно в результате дискретизации
аналогового сигнала.
198
6. Основы дискретной фильтрации сигналов
Рис. 6.6. Дискретный сигнал в виде последовательности дельта-функций
Так как функция 8(г - kT) равна нулю всюду, кроме момента t = kT, можно за-
менить ь выражении (6.10) константы s(kT) на исходный непрерывный сигнал x(t):
\(o=^(oZ5(t-«). (G.ii)
Получив математическую модель, мы можем приступить непосредственно к вы-
числению спектра дискретизированного сигнала 5Д(®).
Прежде всего рассмотрим спектр второго множителя, входящего в выражение
(6.11). Обозначим этот множитель y(t):
y(t)=^6(t-kT).
Это периодический сигнал, который можно разложить в ряд Фурье. Коэффи-
циенты этого ряда рассчитываются как
ч тп . %2 .
с„=? J y(.t)e ’^dt = - J 8(t)e-^dt=-. (6.12)
2 -Т/2 * -Т/2 *
В формуле (6.12) было учтено, что в интервал интегрирования (-7/2, Т/2) по-
падает только одна 8-функция, соответствующая k = 0.
Таким образом, периодическая последовательность дельта-функций может быть
представлена в виде ряда Фурье:
<6.13)
где соп = 2тг п/Т. Подставив (6.13) в (6.11), получим:
-* П = ^ * П=-«Х>
Теперь можно вычислить преобразование Фурье дискретизированного сигнала:
5д(ю)= j s^)e-’°*dt = ± J £ = ± £ j s^e^'dl. (6.14)
6.4. Спектр дискретизированного сигнала
199
Интеграл в выражении (6.14) представляет собой преобразование Фурье сиг-
нала s(t), вычисленное на частоте со -
/5(Г)е-Л“-ш’хЛ = 5((в-со„).
Поэтому, учитывая, что соп = 2л п/Т, спектр дискретизированного сигнала можно
окончательно записать как
2пп
со------
Т
(6.15)
Таким образом, спектр дискретизированного сигнала представляет собой бес-
конечный ряд сдвинутых копий спектра исходного непрерывного сигнала s(t)
(рис. 6.7). Расстояние по частоте между соседними копиями спектра равно частоте
дискретизации сод = 2п/Т.
-С0д/2 0 (0д/2 сод со
Рис. 6.7. Спектр дискретизированного сигнала
Следует также отметить, что из-за наличия в формуле (6.15) множителя Х/Т
спектр дискретизированного сигнала имеет размерность, совпадающую с размер-
ностью сигнала (это связано с тем, что функция 3(f) имеет размерность частоты).
Характер спектра дискретизированного сигнала еще раз демонстрирует частот-
но-временную дуальность преобразования Фурье:
□ периодический сигнал дискретный спектр;
□ периодический спектр дискретный сигнал.
Рисунок 6.7 наглядно демонстрирует и способ восстановления непрерывного
сигнала по дискретным отсчетам. Для этого необходимо пропустить дискретный
сигнал через идеальный фильтр нижних частот (ФНЧ) с частотой < реза, равной по-
ловине частоты дискрет изации. АЧХ такого фильтра показана на рис. 6.7 пунктиром.
Очевидно, что точное восстановление сигнала возможно, если сдвинутые копии
спектра не перекрываются. Из рис. 6.7 видно, что для этого необходимо, чтобы
частота дискретизации как минимум в два раза превышала верхнюю граничную
частоту в спектре сигнала:
(оя>2(ов. (6.16)
Это то же самое условие (6.1), которое лежит в основе теоремы Котельникова
(см. раздел 6.3).
200
6. Основы дискретной фильтрации сигналов
ЗАМЕЧАНИЕ 6.7
Если для восстановления сигнала воспользоваться не ФНЧ, а идеатьным
моло< offocw фильтром со средней частотой пйд и шириной полосы пропуска-
ния, равной сод, будет выделена пара сдвинутых копий сгк ктра ±
Из свойств преобразования Фурье (см. формулу (1.55) и раздел 1.9, где
была показана ее универсальность) следует, что такой спектр соответствует
радиосигналу вида 2х(С)соз(по)дг) (предполагается, что условие теоремы
Котельникова выполнено и сдвинутые копии спектра не перекрываются).
Таким образом, с помощью полосового фильтра можно из дискретных
отсчетов виоеосигнала получить аналоговый радиосигнал.
Если условие (6.16) не выполняется, сдвинутые копии спектра будут наклады-
ваться друг на друга, что приведет к неизбежным искажениям при восстановлении
непрерывного сигнала (рис. 6.8). Эти искажения вызваны двумя причинами:
□ не будут восстановлены спектральные составляющие сигнала с частотами, пре-
вышающими сод/2;
□ из-за попадания в полосу пропускания восстанавливающего ФНЧ «хвостов»
соседних сдвинутых копий спектра оказываются искаженными и спектральные
составляющие, лежащие в полосе восстанавливаемых час гот.
Рис. 6.8. Перекрытие сдвинутых копий спектра
при недостаточно высокой частоте дискретизации
Если подлежащий дискретизации сигнал может содержать спектральные состав-
ляющие с частотами, большими <х>д/2, полезно предварительно пропустить его через
ФНЧ с частотой среза, равной 0)д/2 (см. рис. 6.8). Искажения, вызванные первой из
перечисленных ранее причин, сохранятся — избавиться от них можно лишь путем
повышения частоты дискретизации. Однако благодаря отсутствию наложения
«хвостов» сигнал в диапазоне частот 0...сод/2 будет восстановлен без искажений.
Спектр сигнала при произвольной форме дискретизирующих им-
пульсов. Запишем выражение (6.10) в более общей форме, использовав вместо
дельта-функций импульсы s0(t) произвольной формы:
хд(1) = X s(kT)s0(t-kT). (6.17)
k-^
6.4. Спектр дискретизированного сигнала
201
ЗАМЕЧАНИЕ 6.8---------------------------------------------------
Формула (6.17) представляет сигнал с амплитудно-импульсной модуля-
цией, введенный в разделе 3.1 в качестве одного из примеров моделей слу-
чайных процессов. Однако в данном разделе этот сигнал рассматривается
как детерминированный, с амплитудами импульсов, соответствующих
отсчетам s(kT) аналогового сигнала s(t).
Получить выражение для спектральной функции сигнала (6.17) будет проще
всего, ести рассмотреть этот сигнал как результат прохождения последователь-
ности дельта-функций (6.10) через линейную стационарную цепь с импульсной
характеристикой sQ(t). Действительно, при этом каждая из дельта-функций в (6.10)
будет порождать на выходе цепи сигнал s0(t) с соответствующими временной
задержкой и амплитудным множителем, так что в результате получится именно
выражение (6.17).
Из сказанного следует, что спектр сигнала (6.17) будет отличаться от bi [ражения
(6.15) дополнительным множителем — спектром импульса s0(t):
a z ч { 2пп
5(ю) = —- (618)
Итак, отличие формы дискретизирующих импульсов от дельта-функций вы-
зывает мультипликативные искажения спектра дискретного сигнала. Спектраль-
ная функция импульса, имеющего конечную энергию, затухает с ростом частоты,
поэтому возникающие при дискретизации сдвинутые копии спектра сигнала s(f)
оказываются ослабленными.
ЗАМЕЧАНИЕ 6.9------------------------------------------------------
Если в качестве импульса s0(t) взять функцию базиса Котельникова
<p0(t) (см. раздел 6.3 и формулу (6.3)), то выражение (6.17) становится
идентичным формуле (6.2), то есть описывает (во временной области)
процедуру восстановления непрерывного сигнала по его дискретным от-
счетам. Формула (6.18) при этом описывает (в частотной области) ту же
процедуру, сводящуюся (благодаря виду спектральной функции 5о(со),
см. формулу (6.4)) к идеальной низкочастотной фильтрации.
Рассмотрим важный с практической точки зрения случай, когдаs0(t) представ-
ляет собой прямоугольный импульс с единичной амплитудой и длительностью,
равной периоду дискретизации (рис 6.9, а). В данном случае дискретный сигнал
приобретает ступенчатую форму, что характерно для сигнала на выходе ЦАП перед
сглаживающим фильтром (см. рис. 6.2). Искажения спектра при этом описываются
множителем 50(щ) следующего вида:
Ш = rsin(“^2)g-^
соГ/2
202
6. Основы дискретной фильтрации сигналов
График модуля функции 50(со) приведен на рис. 6.9, б. Спад амплитудного
спектра на частоте л/Т, равной половине частоты дискретизации, составляет
= sin(Tt/2) = - = 0,637 » -3,9 дБ.
|5о(О)| л/2 л
Рис. 6.9. Прямоугольный дискретизирующий импульс:
а — временное представление; б — амплитудный спектр
Рис. 6.10. Дискретизация треугольного импульса (слева — сигналы, справа — спектры):
а — исходный аналоговый сигнал; б — дискретный сигнал в виде последовательности
дельта-функций; в — ступенчатый сигнал (пунктирной линией показана форма
амплитудного спектра дискретизирующих импульсов)
6.5. Дискретное преобразование Фурье
203
В качестве примера на рис. 6.10 приведены результаты дискретизации треуголь-
ного импульса дельта-функциями и рассмотренными прямоугольными импульсами.
Из графиков видно, что ЦАП сам по себе является фильтром нижних частот,
однако с весьма невысокой степенью подавления сдвинутых копий спектра.
6.5. Дискретное преобразование Фурье
В разделе 6.4 мы проанализировали явления, происходящие со спектром при дис-
кретизации сигнала. Рассмотрим теперь, что представляет собой спектр дискретного
периодического сигнала.
Итак, пусть последовательность отсчетов {x(k)} является периодической с пе-
риодом N: x(k + N) ~x(k) для любого k. Такая последовательность полностью опи-
сывается конечным набором чисел, в качестве которого можно взять произвольный
фрагмент длиной N, например {x(k), k = 0,1,..., N- 1}. Поставленный в соответствие
этой последовательности импульсный сигнал
s(£) = У, x(k)5(t-kT)
ь— (6.19)
также, разумеется, будет периодическим с минимальным периодом NT.
Поскольку сигнал (6.19) является дискретным, его спектр должен быть перио-
дическим с периодом 2п/Т. Так как этот сигнал является также и периодическим,
его спектр должен быть дискретным с расстоянием между гармониками, равным
2л/(ЛТ).
Итак, периодический дискретный сигнал имеет периодический дискретный
спектр, который также описывается конечным набором из N чисел (один период
2л /2л
спектра содержит — / гармоник).
Рассмотрим процедуру вычисления спектра периодического дискретного сиг-
нала. Так как сигнал периодический, будем раскладывать его в ряд Фурье. Коэф-
фициенты Х(п) этого ряда, согласно общей формуле (1.34), равны
4 4 ЛJ Д' - 1
Х(п) = — J s(t)e~’a"'dt = — J £x(W-kT}e~^’ =
4 N-1 NT 4 ,v-l
= J ^t-kT)e^dt = —-Yx{k)e^T =
M i=0 0 *=0
1 v-* /L4 ( ,2itnk . tcotw
=тт2Л’Я)ехр <6-20>
ATS I X )
Таким образом, формула для вычисления комплексных амплитуд гармоник
представляет собой линейную комбинацию отсчетов сигнала.
В выражении (6.20) реальный мае штаб времени фигурирует только в множите-
ле 1/Тперед оператором суммирования. При рассмотрении дискретных последо-
вательностей обычно оперируют номерами отсчетов и спектральных гармоник без
привязки к действительному масштабу времени и ча< тоты. Поэтому множитель 1/Т
204
6. Основы дискретной фильтрации сигналов
из (6.20) удаляют. Удаляют обычно и множитель 1/N(об этом см. замечание 6.10).
Получившееся выражение называется дш кретным преобразованием Фурье (ДПФ):
Х(п) = 2л(£)ехр -J-г- (6.21)
Существует и обратное дискретное преобразование Фурье. Переход от дис-
кретного спектра к временным отсчетам сигнала выражается следующей формулой:
1 V w \ ( 2лл^’
(6.22)
Это выражение отличается от формулы прямого ДПФ (6.21) лишь знаком в по-
казателе комплексной экспоненты и наличием множителя 1/N перед one ратором
суммирования.
ЗАМЕЧАНИЕ 6.10 ----------------------------------------------------
Относительно размещения множителя 1/2Vb формулах (6.21) и (6.22)
нет полного единства. В большинстве источников, среди которых [3]
и [15], а также в математических пакетах компьютерных программ этот
множитель фигурирует в формуле обратною ДПФ (6.22) (этот же ва-
риант принят и в данном учебнике). В то же время в учебнике [4] этот
множитель включен в формулу прямого ДПФ (6.21). Следует отметить
что в любом из перечисленных случаев обеспечивается взаимная одно-
значность преобразований.
Рассмотрим свойства дискретного преобразования Фурье.
1. Линейность. Из формулы (6.21) очевидно, что ДПФ является линейным,
то есть если последовательностям {%(&)} и {y(k)} с одним и тем же периодом N
соответствуют наборы гармоник {Х(и)} и {У(п)}, то последовательности
{ax(k) + by(k)} будет соответствовать спектр аХ(п) + bY(n)..
обходимо умножить на схр
2. ДПФ задержанной последовательности. Если задержать исходную по-
следовательность на один такт (г/(А) =x(k - 1)), то, согласно (6.21), спектр не-
,2пп
~J~N~
y(«) = X(n)expf-/^-
( N
3. Симметрия (для вещественного сигнала). Как уже отмечалось, спектр
дискретного периодического chi нала является периодическим. Кроме того,
сохраняется свойство симметрии, которым обладает спектр непрерывного ве-
щественного сигнала (S(-co) = 5*(<в)). Поэтому
X(N-п) = Х(-п) = Х’(п).
(6.23)
6.5. Дискретное преобразование Фурье
205
4. Значения при п = 0 и п = N/2. Гармоника с нулевым номером (постоянная
составляющая), как видно из (6.21), представляет собой сумму отсчетов после-
довательности на одном ее периоде-
Х(0) = £х(£). (6.24)
*=0
Если Nчетно, то амплитуда гармоники с номером N/2 является суммой отсчетов
с чередующимися знаками:
У-1
Х(Х/2) = х(0) - х(1) +... + х(Х - 2) - x(N -1) = X С"1)* X*)-
k=0
Согласно (6.23), спектр является «сопряженно-симметричным» относитель-
но N/2. Это наглядно иллюстрирует тот факт, что спектр содержит ровно такое
же количество информации что и сам сигнал. В самом деле, исходная после-
довательность представляется набором из У вещественных чисел. Спектр же
представляется набором из N/2 (вторая половина взаимно однозначно связана
с первой) комплексных чисел, каждое из которых с информационной точки
зрения эквивалентно двум вещественным. Если же исходная последователь-
ное гь {х(£)} не является вещественной, симметрия спектра отсутствует и У
комплексным отсчетам во временной области соотве гствуют N комплексных
отсчетов в спектральной области.
5. ДПФ произведения последовательностей. Возьмем две последователь-
ности отсчетов {xt(k)} и {x.,(k)} одинаковой длины N и вычислим результат их
поэлементного умножения:
y(k)=x\k)x2(k).
Если применить к этой формуле прямое ДПФ, получится следующее выражение:
Г(п) = ^ХХ,(0Х2(п-0. (6.25)
N г=о
ЗАМЕЧАНИЕ 6.11 ------------------------------------------------------
При выполнении вычислений по формуле (6.25) могут понадобиться
значения Х2(г) с номерами г, выходящими за рамки диапазона 0...N- 1.
В этом случае следует воспользоваться свойством периодичности спектра:
X2(i) = X2(i±N).
При п = 0 из (6.25) получается дискретный аналог теоремы Рэлея (см. раздел 1.8
и формулу (1.67)):
У(0) = X *, (k)x2 (k) = 1X х, (f)X2(-i) = -J- x'x, (ox; (0- (6-26)
k=Q N i=0 N 1=0
206
6. Основы дискретной фильтрации сигналов
При выводе формулы (6.26) были использованы соотношения (6.23) и (6.24).
Если, кроме того, последовательности {хД£)} и {х2(&)} совпадают, то есть
х,(А) = x2(k) = x(k) для Bcexk = 0...N- 1, из (6.26) получается дискретный аналог
равенства Парсеваля (см. раздел 1.8 и формулу (1.68)):
Д'-1 < лг-i, ,,
Ё*2(*)=тД*(о|.
*=0 ™ >=0
6. ДПФ круговой свертки последовательностей. Так как мы рассматриваем
периодические последовательности, то и суммирование при вычислении сверт-
ки таких последовательностей следует производить по одному периоду. Такую
операцию называют круговой сверткой'.
y(k) = £ х, (0*2 (^ - 0 = X xi ОХ <(* - 0 mod ДГ) (6.27)
1=0 »=0
(в этой формуле выражение (k - г) mod N означает взятие (k - i) по модулю N,
то есть вычисление остатка от деления (k - г) на N).
Подставив выражение (6.27) в (6.21), легко убедиться, что круговая свертка
периодических временных последовательностей соответствует перемножению
их спектров:
У(п) = Х^Х2(п). (6.28)
ЗАМЕЧАНИЕ 6.12 -----------------------------------------------------
Помимо круговой свертки существует операция линейной свертки, кото-
рая применяется к дискретным последовательностям конечной длины.
Линейная свертка является основой алгоритма дискретной фильтрации,
речь о котором пойдет в разделе 6.8.
Пример 6.3. Чтобы проиллюстрировать периодичность сигнала, подразумева-
емую при использовании ДПФ, рассмотрим результаты применения этого преоб-
разования к дискретному гармоническому сигналу
s(k) = A cos((okT + (р). (6.29)
В первом случае (рис. 6.11, а) анализируемая последовательность содержит целое
число периодов гармонического сигнала (то есть отношение М»Т/(2л) является
целым числом). Подставив (6.29) в формулу ДПФ (6.21), получим следующее:
AN е 2 • к х(п) = <—е 0 ГФ кг , п = N, 2л ’;ф, n = fl-—V 1 2л ) в остальных случаях.
6.5. Дискретное преобразование Фурье
207
Рис. 6.11. Дискретное преобразование Фурье для: а — целого и б — нецелого числа
периодов гармонического сигнала (слева — исходные последовательности,
справа — их амплитудные спектры)
Таким образом, аналогично спектру непрерывного гармонического сигнала,
ДПФ отличается от нуля всего для двух значений п. Однако если отношение
N(oT/(2n) не является целым числом (см. рис. 6.11, б), спектр оказывается значи-
тельно более богатым. Этому можно дать простое объяснение: в данном случае
периодически продолженная последовательность, как показано на рисунке, уже
не может являться набором отсчетов непрерывной синусоиды. Поэтому в полном
соответствии со свойствами преобразования Фурье в спектре появляются допол-
нительные составляющие.
Восстановление непрерывного сигнала с помощью ДПФ. Являясь по
своей сути спектром дискретного периодического сигнала, дискретное преобразо-
вание Фурье позволяет легко восстановить непрерывный периодический сигнал,
занимающий ограниченную полосу частот. Для этого в формуле обратного ДПФ
(6.22) необходимо заменить дискретный параметр (номер отсчета k) на непрерыв-
ный — нормированное время t/T, где Т — период дискретизации:
’('Н
ЛГ/2-1
Z
n=-N 2
( .2imt
Х(и)ехр у——
( NT
(6.30)
208
6. Основы дискретной фильтрации сигналов
Следует обратить внимание на еще одно отличие этого соотношения от форму-
лы (6.22): диапазон индексов суммирования смещен вниз на N/2 (при четном N;
при нечетном Wсуммирование производится от п = - (N- 1 )/2 до (Л'- 1)/2). Это
необходимо, чтобы получить аналоговый сигнал, занимающий полосу частот от О
до п/Т. Коэффициенты Х(п) с отрицательными номерами могут быть получены
из соотношения симметрии (6.23).
Результат восстановления непрерывного периодического сигнала с помощью
ДПФ, разумеется, совпадает с результатами, получаемыми при использовании ряда
Котельникова (6.2). Однако использование ДПФ в данном случае оказывается
более предпочтительным, так как ряд Котельникова для периодического сигнала
содержит бесконечное число слагаемых, а формула (6.30) — конечное.
6.6. Быстрое преобразование Фурье
Для вычисления одного коэффициента ДПФ по формуле (6.21) необходимо вы-
полнить У комплексных умножений и сложений. Таким образом, расчет всего ДПФ,
содержащего Nкоэффициентов, потребует № операций «умножение — сложение».
Число операций возрастает пропорционально квадрату размерности ДПФ. Однако
если N не является простым числом и может быть разложено на множители, процесс
вычислений можно ускорить, разделив анализируемый набор отсчетов на части,
вычислив их ДПФ и объединив результаты. Рассмотрим этот процесс на примере
деления набора отсчетов пополам.
Итак, пусть N — четное число. Выделим в формуле (6.21) два слагаемых, соот-
ветствующих элементам исходной последовательности с четными и нечетными
номерами.
N/2-1 _ 2~2тп Ц/2-i _ 2n(2m+l)n
Х(п) = У, х(2тп)е 1 N + У x(2m + l)e ’ N
m=0 m=0
Введем обозначения y(m) =x(2m) и z(m) =x(2m + 1), а также вынесем из второй
суммы общий множитель e^2m/N:
NJ2-1 Х™" _ 21хл УД-1
Х(и) = X y{rrt)e N/2+e’N £z(m)e . (6.31)
щ-0 т=0
Две суммы в (6.31) представляют собой ДПФ последовательностей {у(т)} (от-
счеты с четными номерами) и {z(m)} (отсчеты с нечетными номерами). Каждое из
этих ДПФ имеет размерность N/2. Таким образом,
.2 ля
X(n) = Y(n) + e^''' Z(n), (6.32)
где У(и) и Z(n) — ДПФ последовательностей отсчетов с четными и нечетными
номерами соответственно:
N/2-1 2птп N/2-i 2птп
Y(n) = X у{т)е N/i, Z(n) = Y z(m)e N/2-
m=0 m=0
6.6. Быстрое преобразование Фурье
209
Так как ДПФ размерности N/2 дает лишь N/2 спектрадьных коэффициентов,
непосредственно использовать формулу (6.32) можно только при 0 < п < N/2. Для
остальных п (N/2 <п < Лг) следует воспользоваться периодичностью спектра дис-
кретного сигнала (и, соответственно, периодичностью результатов ДПФ):
у1п + —j = y(n), zln + — l = Z(«).
С учетом этого при п > N/2 формула (6.32) представляется в виде
( ЛМ N
X(n) = Y п- — +е N Z и-у
Процесс вычисления 8-точечного ДПФ путем разбиения его на два 4-точечных
ДПФ иллюстрируется на рис 6.12.
Оценим количество операций, необходимое для вычисления ДПФ указанным
образом. Каждое из двух ДПФ половинной размерности требует №/4 операций.
Кроме того, при вычислении окончательных результатов каждый спектральный
коэффициент Z(n) умножается на экспоненциальный комплексный множитель.
- a a v/o - тл N W + 1)
Это добавляет еще N/2 операции. Итого получается 2 у- + — = —у—что почти
вдвое меньше, чем при вычислении ДПФ прямым способом.
Если N/2 тоже является четным числом (то есть если 2V делится на 4), можно
продолжить описанную процедуру, выразив результат через четыре ДПФ размер-
ности N/4. Это позволяет еще больше сократить число требуемых вычислительных
операций.
210
6. Основы дискретной фильтрации сигналов
ЗАМЕЧАНИЕ 6.13 ---------------------------------------------------
Делить исходную последовательность можно на любое количес тво ча-
стей. Таким образом, приведенный алгоритм позволяет уменьшить число
операций в случае любого У, не являющегося простым числом. Степень
ускорения вычислений зависит от числа фрагментов последовательности
и является максимальной при делении на две части, как в рассмотренном
примере.
Наибольшая степень ускорения вычислений может быть достигнута при N = 2*,
в этом случае деление последовательностей на две части можно продолжать до
тех пор, пока не получатся двухэлементные последовательности, ДПФ которых
рассчитывается вообще без использования операций умножения (достаточно вы-
числить сумму и разность двух отсчетов). Число требуемых при этом пар операций
«умножение — сложение» можно оценить как N log2(N). Таким образом, вычис
лительные затраты по сравнению с непосредственным использованием формулы
(6.21) уменьшаются в A71og2(A') раз. При больших N это отношение становится
весьма велико (например, 1024/log2( 1024) = 102,4, то есть при N= 1024 достигается
более чем 100-кратное ускорение). Рассмотренный способ вычисления ДПФ на-
зывается быстрым преобразованием Фурье (БПФ) и повсеместно используется
на практике.
ЗАМЕЧАНИЕ 6.14 ------------------------------------------------------
Рассмотренный алгоритм БПФ называется алгоритмом с прореживанием
по времени и не является единственно возможным. Можно, например,
разделить исходную последовательность не на отсчеты с четными и не-
четными номерами, а на две следующих друг за другом половины. Если
после этого провести преобразования, аналогичные рассмотренным ранее,
получится алгоритм БПФ с прореживанием по частоте. Существуют
и другие разновидности алгоритмов БПФ.
Завершая краткое рассмотрение идеи БПФ необходимо отметить следующее-
□ БПФ не является приближенным алгоритмом; при отсутствии вычислительных
погрешностей он даст в точности тот же результат, что и исходная формула ДПФ
(6.21). Ускорение достигается исключительно за счет оптимальной организации
вычислений.
□ Применение БПФ возможно, если число элементов в анализируемой последова-
тельности является степенью числа 2. Как уже отмечалось, некоторое ускорение
вычислений возможно и при разложении N на другие множители, однако это
ускорение не столь велико, как при N = 2*.
□ Алгоритм БПФ предназначен для расчета всех спектральных коэффициентов
Х(п). Если же необходимо получить эти коэффициенты лишь для некоторых п,
прямая формула ДПФ может оказаться предпочтительнее.
6.7. Метод z-преобразования
211
6.7. Метод z-преобразования
Удобным способом анализа дискретных последовательностей является г-преобразо-
вание. Смысл его заключается в том, что последовательности чисел {x(k)} ставится
в соответствие функция комплексной переменной z, определяемая следующим
образом:
X(z)=£x(ty-*.
*—
(6.33)
ЗАМЕЧАНИЕ 6.15 ---------------------------------------------------
Разумеется, функция A’(z) определена только для тех значений z, при
которых ряд (6.33) сходится.
Вычислим z-преобразование для некоторых часто встречающихся на практике
дискретных сигналов.
1. Единичная импульсная функция, представляющая собой одиночный отсчет
с единичным значением:
fl, k = 0,
^0. ( )
Расчет его z-преобразования не представляет сложности:
X0(z)=Y*0(k)z-k=lz^=l.
k=—
Функция A0(z) сходится на всей комплексной плоскости.
2. Единичный скачок
Используя определение 2-преобразования (6.33), получаем:
X(z) = £ r(*X* = (6.35)
. t=0
Ряд (6.35) является суммой бесконечной геометрической прогрессии с первым
членом lz° = 1 и знаменателемzX Как известно, такой ряд сходится при ^’| < 1,
то есть при |z| > 1, и его сумма равна
(6.36)
212
6. Основы дискретной фильтрации сигналов
ЗАМЕЧАНИЕ 6.16--------------------------------------------------
Можно записать результат и в виде X(z) = z/(z - 1), но в теории z-преоб-
разования принято использовать отрицательные степени г.
ЗАМЕЧАНИЕ 6.17 --------------------------------------------------
Единичная импульсная функция и единичный скачок являются дискрет-
ными аналогами рассматривавшихся в разделе 1.1 тестовых сигналов —
дельта-функции Дирака (1.9) и ступенчатой функции Хевисайда (1.8)
соответственно.
3. Дискретная экспоненциальная (показательная) функция
Для вычисления z-преобразования нужно вычислить сумму следующего ряда:
X'(z) = X Х(*Х* =1Х2)’‘-
*=0 *=0
Как и в предыдущем случае, этот ряд представляет собой сумму геометрической
прогрессии. Первый член равен 1, знаменатель равен az ’. Таким образом, ряд
сходится при laz-1! < 1, то есть при |z| > |a|, а его сумма равна
ад=—Ц-. (6.37)
1-az
Дискретное z-преобразование очень простым образом связано с преобразовани-
ями Лапласа и Фурье. Рассмотрим последовательность, определенную при k > О,
и сопоставим ей временной сигнал в виде набора дельта-функций:
s(V)=^x(k)S(t-kT), (6.38)
k=0
где Т — интервал дискретизации. Вычислим преобразование Лапласа для сигнала
(6.38):
S(p) = ls(t)e~p‘dt = JX^(^)5(t -^T)e₽t^r = Xx(^)J 3 * 5(г ~kT)e~p' dt
q 0 k=0 о
Воспользовавшись фильтрующим свойством 8-функции (см. раздел 1.1 и фор-
мулу (1.11)), получим:
5(p) = Xx(^-ptr.
i=0
6.7. Метод z-преобразования
213
Эта формула переходит в формулу (6.33), определяющую z преобразование,
если выполнить подстановку z = ерТ.
Таким образом, взаимное соответствие между z-преобразованием X(z) и преоб-
разованием Лапласа S(p) описывается следующим образом:
X(z) = 5^1nz ,
S(p) = X(f"T).
Похожими формулами описывается и связь z-преобразования X(z) с преобразо-
ванием Фурье 5(со) (заметим, что при рассмотрении этой связи нет необходимости
считать последовательность односторонней):
X(z) = S — In z ,
I. iT J
S((o) = X(ejaT).
(6.39)
Столь тесная связь z-преобразования с преобразованиями Фурье и Лапласа
обусловливает и подобие свойств этих преобразований.
Свойства z-преобразования
1. Линейность, /-преобразование, согласно определению (6.33), является ли-
нейной комбинацией отсчетов последовательности, поэтому оно подчиняется
принципу суперпозиции: если {х/А’)} «-> X,(z) и {х,(£)} «-> X,(z), то {ax,(k) +
+ bx2(k)} aX,(z) + bX2(z).
2. /-преобразование задержанной последовательности. Если z-преоб-
разование последовательности (х(&)} равно X(z), то z-преобразование последо-
вательности, задержанной на k0 тактов (y(k)=x(k - k0)), будет иметь вид
r(z)=X«/(^-‘ = X v(k-k0)z~k =
= z~k" X x(^-^)z-*'^ = z4 £ x(«)z" = X(z)zA.
Таким образом, при задержке последовательности на k0 тактов необходимо
умножить ее ’-преобразование на z Ч
3. Z-преобразование свертки последовательностей. Свертка двух бес-
конечных дискретных последовательностей {х((^)} и {x2(k)} определяется сле-
дующим образом:
У(.Ь)= X
214
6. Основы дискретной фильтрации сигналов
Вычислим 2-преобразование для последовательности {y(k)}:
Y(z)=Y y(k)z~k = £ £ х, (n)x2(k - n)zk
k=~oa
= X2(z)^x1(r!)z-’'=X1(z)X2(z).
Л =—<»
(6.40)
Итак, свертке дискретных последовательностей соответствует произведение
их z-преобразований.
ЗАМЕЧАНИЕ 6.18 -----------------------------------------------------
Рассматриваемая здесь свертка бесконечных дискретных последователь-
ностей называется линейной с вер! кой. Ее не следует путать с круговой
сверткой периодических последовательностей, речь о которой шла при
описании свойств дискретного преобразования Фурье в разделе 6.5.
Обратное z-преобразование. Соответствие между дискретной последова-
тельностью чисел и ее 2-преобразованием является взаимно однозначным. Формула
перехода от 2-преобразования к пос тедовательности чисел называется обратным
z-преобразованием и формально записывается следующим образом:
х(*) = -^Х(2)г‘ ~ldz. (6.41)
Интеграл в (6.41) берется по произвольному замкнутому контуру в области
сходимости функции X(z), охватывающему начало координат.
Практическое вычисление обратного 2-преобразования чаще производится путем
разложения функции X(z) на простые дроби. Поясним это на несложном примере.
Пусть функция X(z) определена при |z| > 1 следующим образом:
х^-~ з
2* +2Z
Разложим X(z) на простые дроби:
X(z) =-----r~~i~
(1-2-1) l-jz-1
2 -1
2
(6.42)
6.8. Алгоритм дискретной фильтрации
215
Из сравнения слагаемых (6.42) с примерами z-преобразований (6.36) и (6.37)
видно, что при данной области определения первое слагаемое соответствует скачку
с амплитудой, равной 2, а второе — дискретной показательной функции -2“*, k > 0.
Итак, искомая последовательность имеет вид
x{k) =
2-2*, k>0,
0, k<0.
ЗАМЕЧАНИЕ 6.19 ----------------------------------------------------
При расчете обратного z-преобразования обязательно должна быть ука-
зана область определения функции X(z), так как одна и та же формула в
сочетании с разными областями определения соответствует различным
последовательностям отсчетов. Например, вот что может дать обратное
z-преобразование формулы (6.36):
□ если |z| > 1, то х(£) = < ’ , ’
1, k > 0;
, f-1, k<0,
□ если|г|< 1,то x(k) = ]
О, к > U,
6.8. Алгоритм дискретной фильтрации
В данном учебном пособии мы рассматриваем линейные стационарные дис-
кретные фильтры. Свойство линейности означает, как обычно, применимость
принципа суперпозиции. Если входные последовательности отсчетов {х((&)}
и {x2(k)} порождают на выходе последовательности {y^k)} и {y2(k)} соответствен-
но, то при подаче на вход сигнала {a x}(k) + р x2(k)} выходной сигнал будет равен
{az/X^ + pz/^)}.
Свойство стационарности означает, что задержка входной последовательности
на п тактов приведет к такой же задержке выходной последовательности: если
{x(k)} {y(k)}, то {x(k - п)} \y(k - и)}.
В случае линейных цепей с постоянными параметрами для анализа прохож-
дения любого сигнала достаточно знать результат прохождения элементарного
импульса в виде дельта-функции. Для дискретных фильтров также можно ввести
в рассмотрение единичную импульсною функциюx0(k) (см. раздел 6.7 и форму-
лу (6.34)).
Выходная реакция на единичный импульс х0(А) называется импульсной харак-
теристикой дискретного фильтра и обозначается h(k).
Как и в случае линейных цепей с постоянными параметрами, знание импульс-
ной характеристики позволяет проанализировать прохождение через дискретный
фильтр любого сигнала. Действительно, прежде всего заметим, что произвольный
216
6. Основы дискретной фильтрации сигналов
сигнал {x(k)} можно представить в виде линейной комбинации единичных от-
счетов:
x(k) = У, x(m)x0(£-m).
Выходной сигнал, исходя из линейности и стационарности рассматриваемого
фильтра, должен представлять собой линейную комбинацию импульсных харак-
теристик:
y(k} = У x(m)h(k-m). (6.43)
Выражение (6.43) называется дискретной сверткой (точнее, дискретной линей-
ной сверткой, которую не следует путать с круговой сверткой, рассматривавшейся
при обсуждении свойств дискретного преобразования Фурье в разделе 6.5). Для
физически реализуемого фильтра h(k) = 0 при k < 0, поэтому верхний предел сум-
мирования в формуле (6.43) можно заменить на k\
y(k)= У x(m)h(k — m).
Это означает, что фильтр при вычислении очередного отсчета может оперировать
только прошлыми значениями входного сигнала и еще ничего не знает о будущих.
Пример вычисления дискретной свертки, подробно иллюстрирующий выпол-
няемые при этом математические операции, приведен на рис. 6.13.
При реализации вычислений могут быть использованы данные двух типов:
□ только что поступивший и некоторое количество предыдущих отсчетов входного
сигнала: x(k), x(k - 1),..., x(k - т);
□ некоторое количество вычисленных ранее отсчетов выходного сигнала: y(k - 1),
y(k - 2),.... y(k - п).
Таким образом, в общем случае очередной выходной отсчет y(k) вычисляется
по формуле
y(k) = a„x(k) + axx(k - 1) + ... + amx(k -m) +
+ b,y(k - 1) + b2y(k - 2) +... +bny(k - n), (6.44)
где ия - вещественные коэффициенты.
Если перегруппировать слагаемые в (6.44) таким образом, чтобы входные от-
счеты были с одной стороны от знака равенства, а выходные — с другой, получим
традиционную форму записи разностного уравнения'.
y{k) -b^k-V)- b2y(k - 2) -... - bny(k -n) =
= aox(k) + a^k - 1) + ... + amx(k - m). (6.45)
Разностное уравнение в форме (6.44) называют еще алгоритмом дискретной
фильтрации.
6.8. Алгоритм дискретной фильтрации
217
Исходные сигналы
т ________>
0 12 к
х(к\. | 1|3|2|
Процедура вычисления
У(О)=1 1 = 1
у(1)= 1'2 + 31 =5
у(2)= 1-3 + 3-2 + 21 = 11
у(3) = 1-4 4-3-3 + 2-2= 17
у(4) = 3-4 + 23 = 18
у(5) = 24 = 8
Результат:
Рис. 6.13. Вычисление дискретной свертки
218
6. Основы дискретной фильтрации сигналов
6.9. Системная функция
дискретного фильтра
Применим рассмотренное ранее z-преобразование к уравнению дискретной филь-
трации (6.43). Так как это уравнение представляет собой дискретную свертку, то,
согласно свойствам z-преобразования (см. раздел 6.7), результатом будет являться
произведение z-преобразований:
T(z)=X(z)H(z). (6.46)
Входящая в (6.46) функция H(z), равная отношению z-преобразований выход-
ного и входного сигналов и представляющая собой z-преобразование импульсной
характеристики фильтра, называется системной функцией дискретного фильтра:
я(2)=-^=£ад2-‘. (ел?)
Л \Z) k=0
Комплексный коэффициент передачи. Чтобы получить комплексный
коэффициент передачи (частотную характеристику) дискретного фильтра, вос-
пользуемся формулой (6.39), описывающей связь z-преобразования и преобразо-
вания Фурье:
K(a) = H(eJaT) = ^h(k)e-^T. (6.48)
Из (6.48) видно, что частотная характеристика дискретного фильтра, так же как
и спектры дискретизированных сигналов (см. раздел 6.4), является периодической
функцией частоты с периодом, равным частоте дискретизации 2л/Т.
Физическая реализуемость. Применив z-преобразование к обеим частям
разностного уравнения (6.45), получим:
K(z)( 1 - btz~l - h^z2 - ... - bnzrn) = X(z)(a0 + а,^1 + а^2 + ... + azm\
Отсюда легко получить вид системной функции:
H(z) =
а0 + a(z 1 + a2z 2 +... + amz т
1 —bjZ-1 -b2z~2 - ,..-bnz~n
(6.49)
Таким образом, системная функция физически реализуемого дискретного фильтра
может быть представлена в виде отношения полиномов по отрицательным степе-
ням переменной z, при этом в полиноме знаменателя свободный член обязательно
должен быть ненулевым.
Устойчивость. При отсутствии входного сигнала в дискретном фильтре могут
существовать свободные колебания. Их вид зависит от начальных условий, то есть
значений, хранящихся в элементах памяти фильтра (линиях задержки) в момент
отключения входного сигнала. Фильтр называется устойчивым, если при любых на-
чальных условиях свободные колебания являются затухающими, то есть ори ,с(&) = О
limz/(£) = 0.
6.9. Системная функция дискретного фильтра
219
Любой сигнал на выходе линейного стационарного фильтра представляет собой
линейную комбинацию его задержанных во времени импульсных характеристик.
Поэтому для затухания свободных колебаний необходимо, чтобы была затухающей
импульсная характеристика фильтра h(k):
lim А(&) = 0.
Теперь выясним, как проверить устойчивость фильтра по его системной функции,
которая, согласно (6.47), является z-преобразованием импульсной характеристики.
Для физически реализуемого фильтра системная функция (6.49) имеет вид отно-
шения двух полиномов и может быть разложена на простые дроби:
H(z)= Г' _,+ Гг- _,++ Г" (6.50)
\-p,z i-p2z l-pnz
где pvp2, ...,р — корни (возможно, комплексные) знаменателя выражения для Н(г),
записанного в форме (6.49). Согласно (6.37), каждой из простых дробей rj(\- pz~')
соответствует слагаемое импульсной характеристики вида
г(Л)". (6.51)
Если/?, — вещественное число, то (6.51) является геометрической прогрессией,
затухающей при |р| < 1. Комплексные корни знаменателя в случае фильтра с веще-
ственной импульсной характеристикой образуют комплексно-сопряженные пары,
и сумма простых дробей
г г'
\-p.zl l-p’z~'
дает в импульсную характеристику вклад вида
* (Л)" + < (X)" = 2Re[r,(p,)’ ] - 2Re[ |г||л|" =
= 2|r||pJ' cos(nargpi +argr). (6.52)
Из (6.52) видно, что данная составляющая импульсной характеристики будет
затухающей при выполнении того же условия: |pj < 1.
Теперь мы можем окончательно сформулировать условие устойчивости: для
устойчивого дискретного фильтра полюсы системной функции должны находиться
внутри круга единичного радиуса на комплексной плоскости.
ЗАМЕЧАНИЕ 6.20 ----------------------------------------------------------
Системная функция может быть представлена в форме (6.50) только при
отсутствии кратных корней у знаменателя. При наличии таких корней
разложение становится сложнее, но приведенное ранее условие устой-
чивости сохраняет силу и в этом случае.
220
6. Основы дискретной фильтрации сигналов
6.10. Рекурсивные и нерекурсивные
дискретные фильтры
Ранее нами было получено уравнение (6.44), в общем виде описывающее процесс
дискретной фильтрации. Рассмотрим структурные схемы устройств, реализующих
данное уравнение.
Нерекурсивные фильтры. Прежде всего следует отметить, что при вычис-
лении очередного выходного отсчета y(k) используется информация двух типов:
некоторое количество отсчетов входного сигнала и некоторое количество предыду-
щих отсчетов выходного сигнала. Ясно, что хотя бы один отсчет входного сигнала
должен участвовать в вычислениях, в противном случае выходной сигнал не будет
зависеть от входного. В противоположность этому предыдущие отсчеты выходного
сигнала могут и не использоваться. Уравнение фильтрации (6.44) в этом случае
приобретает следующий вид:
т
г/(^) = Ха.-г^-г)' (653)
1=0
Количество используемых отсчетов т называется порядком фильтра
ЗАМ ЕЧ АН И Е 6.21 --------------------------------------------
Следует различать понятия порядка и длины дискретного фильтра. Под
длиной понимают общее количество отсчетов, участвующих в вычислениях
(включая текущий), а под порядком — лишь число задержанныл отсчетов.
Поэтому длина фильтра на единицу больше, чем его порядок.
Структурная схема, реализующая алгоритм (6.53), приведена на рис. 6.14. Не-
которое количество предыдущих отсчетов входного сигнала хранится в ячейках
памяти, которые образуют цифровую линию задержки. Эти отсчеты умножаются
на коэффициенты а и суммируются, формируя выходной отсчет г/(&).
Так как при вычислениях не используются предыдущие отсчеты выходного
сигнала, в схеме отсутствуют обратные связи. Поэтому такие фильтры называются
нерекурсивными. Применяется также термин «трансверсальный фильтр» (от англ.
transversal — поперечный).
Импульсная характеристика нерекурсивного фильтра определяется очень просто.
Подставим в уравнение (6.53) единичный импульс xa(k) в качестве входного сигнала:
Л(*) = “О-
1=0
Но отсчет xa(k - г) равен нулю для всех k. кроме k = i, когда этот отсчет равен
единице. Поэтому мы получаем очень простой результат:
Л(^) = at,
то есть коэффициенты а. являются отсчетами импульсной характеристики фильтра.
Это можно наглядно пояснить с помощью рис. 6.14. При подаче на вход единичного
6.10. Рекурсивные и нерекурсивные дискретные фильтры
221
импульса он будет перемещаться по линии задержки, умножаться на коэффици-
енты а0, а,, а2... и проходить на выход устройства (ведь все остальные входные
сигналы сумматора будут равны нулю). Очевидно, что в реальном устройстве
линия задержки содержит конечное число элементов, поэтому импульсная харак-
теристика нерекурсивного фильтра также является конечной по длительности. Это
обусловило еще одно название таких фильтров — фильтры с конечной импульсной
характеристикой (КИХ-фильтры).
Рис. 6.14. Нерекурсивный фильтр
ЗАМЕЧАНИЕ 6.22 ------------------------------------------------
Вследствие отсутствия обратных связей любой нерекурсивный фильтр
является устойчивым, ведь какими бы ни были начальные условия (то
есть отсчеты, хранящиеся в линии задержки), при отсутствии сигнала на
входе (х(&) = 0) выходной сигнал (свободные колебания) будет существо-
вать не более чем т тактов, необходимых для очистки линии задержки.
Простота анализа, синтеза и реализации, а также абсолютная устойчивость
привели к тому, что нерекурсивные фильтры широко применяются на практике.
Однако для получения хороших частотных характеристик (например, полосовых
фильтров с высокой прямоугольностью АЧХ) необходимы нерекурсивные фильтры
высокого порядка — до нескольких сотен и даже тысяч.
Рекурсивные фильтры. Если уравнение фильтрации имеет общий вид (6.44),
то есть содержит как входные, так и выходные отсчеты, для реализации такого
фильтра в схему, приведенную на рис. 6.14, необходимо добавить вторую линию
задержки — для хранения выходных отсчетов y(k - i). Получающаяся при этом
структура показана на рис. 6.15.
222
6. Основы дискретной фильтрации сигналов
Рис. 6.15. Рекурсивный фильтр — прямая реализация
Так как при вычислениях используются предыдущие отсчеты выходного сиг-
нала, в схеме присутствуют обратные связи. Поэтому такие фильтры называют
рекурсивными.
ЗАМЕЧАНИЕ 6.23 ---------------------------------------------------
Количество входных и выходных отсчетов, используемых для вычис-
лений, может не совпадать. В таком случае порядком фильтра считается
максимальное из чисел тип.
Импульсная характеристика рекурсивного фильтра рассчитывается значительно
сложнее, чем характеристика нерекурсивного. Рассмотрим формирование лишь
нескольких первых ее отсчетов. При поступлении на вход единичного импульса
он умножается на а0 и проходит на выход. Таким образом,
/г(0) = а0.
Далее входной единичный импульс попадает во входную линию задержки,
а выходной отсчет, равный а0, — в выходную линию задержки. В результате второй
отсчет импульсной характеристики будет формироваться как
й(1) = aY + bJifQ) = а{ +
Продолжив рассмотрение перемещения входного единичного импульса вдоль
входной линии задержки и заполнения выходными отсчетами выходной линии
задержки, можно получить:
й(2) = а2 + 62й(0) + Ь^(1) = а2 + agb2 + bi(ai + аД) = а2 + + адЬ2 + адЬ^.
6.11. Формы реализации цифровых фильтров
223
Видно, что по мере того, как выходная линия задержки заполняется отсчетами
импульсной характеристики, сложность аналитических формул быстро нарастает.
Наличие в схеме обратных связей позволяет получить бесконечную импульсную
характеристику, поэтому рекурсивные фильтры называют также фильтрами с бес-
конечной импульсной характеристикой (БИХ-фильтрами). По этой же причине
рекурсивные фильтры могут быть неустойчивыми.
6.11. Формы реализации
цифровых фильтров
Структурная схема, показанная на рис. 6.15, называется прямой реализацией
рекурсивного фильтра и не является единственно возможной. Рассмотрим еще
несколько вариантов.
Каноническая форма. Разделим общий сумматор в схеме, приведенной
на рис. 6.15, на два отдельных — для рекурсивной и нерекурсивной частей фильтра
(рис. 6.16, а). В результате получим два последовательно соединенных фильтра,
один из которых является нерекурсивным, а другой, напротив, содержит только
рекурсивную часть. Так как результат последовательного прохождения сигнала
через ряд линейных стационарных устройств не зависит от последовательно-
сти их соединения, мы можем поменят ь местами две «половинки» нашего филь-
тра (рис. 6.16, б). Теперь остается заметить, что в обе линии задержки подается
один и тот же сигнал, поэтому они будут содержать одинаковые наборы отсчетов.
Это позволяет объединить линии задержки. Полученная в результате схема
изображена на рис 6.17 она называется канонической реализацией рекурсивного
фильтра.
С теоретической точки зрения оба варианта эквивалентны. Однако при практи-
ческой реализации необходимо обратить внимание на ряд особенностей, присущих
Рис. 6.16. Перестановка рекурсивной и нерекурсивной частей фильтра —
путь к получению канонической реализации
224
6. Основы дискретной фильтрации сигналов
Рис. 6.17. Рекурсивный фильтр — каноническая реализация
этим схемам. С одной стороны, при канонической реализации используется общая
линия задержки, что уменьшает число необходимых ячеек памяти Однако при
этом абсолютные величины отсчетов, «бегающих» в линии задержки, могут суще-
ственно превосходить амплитуду входного и выходного сигналов. Это приводит
к необходимости увеличивать разрядность представления чисел в линии задерж-
ки по сравнению с разрядностью входного и выходного сигнатов, что усложняет
реализацию устройства. При прямой реализации в линиях задержки хранятся
непосредственно отсчеты входного и выходного сигналов, то есть повышенной
разрядности линий задержки не требуется. Единс гвенным элементом, требующим
повышенной разрядности в данном случае является сумматор, и это учтено в архи-
тектуре микропроцесс оров, специально предназначенных для обработки сигналов
в реальном времени.
Транспонированная форма. Поменяем в схеме рис 6.14 последователь-
ность выполнения операций умножения и задержки, использовав в каждой ветви
отдельную линию задержки на нужное количество тактов. Разделим также общий
сумматор на несколько двухвходовых сумматоров. Получившаяся структура по-
казана на рис. 6.18. Теперь, рассмотрев любую пару соседних сумматоров, можно
заметить, что суммируемые ими сигналы претерпевают некоторую общую задерж-
ку. Это дает возможность поменять местами операции суммирования и задержки.
Получившаяся схема (рис 6.19) называется транспонированной (transposed) реа-
лизацией дискретного фильтра.
ЗАМЕЧАНИЕ 6.24 --------------------------------------------------
Чтобы упростить рисунки, на рис. 6.18 и 6.19 преобразование в транс-
понированную форму произведено для нерекурсивного фильтра, однако
это можно сделать и с рекурсивным фильтром.
6.11. Формы реализации цифровых фильтров
225
Рис. 6.18. Изменение последовательности выполнения операций умножения и задержки —
путь к получению транспонированной реализации фильтра
Рис. 6.19. Транспонированная реализация нерекурсивного фильтра
Транспонированная схема позволяет эффективно распараллелить вычисления
и потому применяется при реализации цифровых фильтров в виде специализиро-
ванных или программируемых логических интегральных схем. Действительно, при
реализации фильтра в форме рис. 6.14 или рис. 6.15 можно одновременно выполнять
все операции умножения, но для получения выходного результата необходимо до-
ждаться окончания выполнения всех операций сложения. В транспонированной же
схеме помимо умножения можно одновременно выполнять и все операции сложения,
поскольку они являются независимыми (то есть не используют в качестве с>мми-
8 №675
226
6. Основы дискретной фильтрации сигналов
руемых величин результаты других сложений). Как видно из схемы, приведенной
на рис. 6.19, собственно для расчета выходного сигнала необходимо выполнить
одно умножение и одно сложение, все остальные операции подготавливают про-
межуточные результаты для вычисления последующих выходных отсчетов.
Последовательная (каскадная) реализация. В разделе 6.9 было показа-
но, что системная функция физически реализуемого дискретного фильтра пред-
ставляет собой отношение полиномов по отрицательным степеням переменной z.
Эти полиномы можно разложить на линейные (относительно г1) множители
(при этом некоторые из них будут иметь комплексные коэффициенты) либо на
линейные и квадратичные множители с вещественными коэффициентами. Таким
образом, системная функция общего вида (6.49) может быть записана в следую-
щей форме
тт/ \ aiO+aitZ а20+Я212
H(Z) =---------;------------
1-Z>tl2 1- b2lz
а,а +aaz 1 +й,2z 2
1 — £>,i-z-bi2z~2
Каждый из сомножителей соответствует рекурсивному фильтру 1-го или 2-го
порядка, а сама операция умножения соответствует последовательному (каскад-
ному) включению этих фильтров
Рассмотрим конкретный пример, задав численные значения коэффициентов
фильтра:
ч 0,0985 + 0,29562-'+0,2956г'2 +0,0985г “3
Н (Z) =-------------;----------5-------------=
1-0,57722-' +0,4218г'2-0,0563г'3
= 0,0985---—-------г-----1 + 2\ +Z-------
1-0,15842'' 1-0,41882“' +0,3554z-2
(6.54)
ЗАМЕЧАНИЕ 6.25 ----------------------------------------------------
Данный фильтр является фильтром Баттерворта 3-го порядка с частотой
среза, равной 1/5 частоты дискретизации, синтезированным методом
билинейного 2-преобразования (см. раздел 6.12).
Стоуктурная схема получившейся последовательной реализации фильтра пред-
ставлена на рис. 6.20.
Последовательная реализация часто используется на практике, поскольку она по-
зволяет ослабить нежелательные эффекты, связанные с ошибками округления [16].
Параллельная реализация. Еще один способ преобразования системной
функции физически реализуемого фильтра — представление ее в виде суммы про-
стейших дробей. Об этом уже шла речь при обсуждении устойчивости дискретных
фильтров (см. раздел 6.9 и формулу (6.50)). Каждое из слагаемых при таком пред-
ставлении соответствует системной функции рекурсивного фильтра 1-го порядка
(возможно, с комплексными коэффициентам) либо 1-го или 2-го порядка (если
используется представление в виде суммы простейших дробей с вещественными
6.11. Формы реализации цифровых фильтров
227
коэффициентами). Сама операция сложения эквивалентна параллельному соеди-
нению этих фильтров с суммированием выходных результатов.
Рис. 6.20. Последовательная реализация дискретного фильтра
Рассмотрим конкретный примео, используя ту же системную функцию (6.54),
что и раньше:
,г/ х 0,0985 + 0,2956z-1+0.2956z“2+0,0985z’3
H(z) =-------------:----------:---------5--=
1-0,5772г’1+0,4218z-2-0,0563z“3
-0,0792 +0,5г’1 0,1777 - 0,2094г’1+0,5z~2
l-0,1584z’‘ + l-0,4188z“*+0,3554z“2 '
Структурная схема получившейся параллельной реализации фильтра пред-
ставлена на рис. 6.21.
-0,0792
Рис. 6.21. Параллельная реализация дискретного фильтра
228
6. Основы дискретной фильтрации сигналов
6.12. Методы синтеза дискретных фильтров
Под синтезом понимают поиск коэффициентов фильтра, при которых достигаются
требуемые характеристики. Методы синтеза дискретных фильтров делятся на две
основные категории:
□ с использованием аналогового фильтра-прототипа;
□ прямые (без фильтра-прототипа).
Методы первой категории широко распространены, поскольку теория синтеза
аналоговых фильтров хорошо разработана. Эта категория, в свою очередь, имеет
две разновидности:
□ синтез на основе импульсной характеристики прототипа;
□ синтез на основе операторного коэффициента передачи прототипа.
В первом случае берут импульсную характеристику аналогового фильтра
и осуществляют ее дискретизацию. Далее с помощью z-преобразования получают
системную функцию H(z) дискретного фильтра (см. раздел 6.7):
H(z) = £^r)z-\
В зависимости от вида импульсной характеристики и требуемой точности ее
воспроизведения реализация фильтра может производиться как в рекурсивной, так
и в нерекурсивной форме. Частотная характеристика фильтра будет представлять
собой периодически повторенную (со сдвигом, кратным частоте дискретизации)
частотную характеристику фильтра-прототипа.
Так как частотная характеристика дискретного фильтра является периодической,
синтез по операторному коэффициенту передачи фильтра-прототипа оказывается
более сложной задачей. Рассмотрим связь между операторным коэффициентом
передачи и системной функцией дискретного фильтра:
z = epT, p = ^nz’ H(z) =/C^ylnz^. (6.55)
Для физически реализуемой аналоговой цепи операторный коэффициент пере-
дачи К( р) является дробно-рациональной функцией. Для реализуемого дискретного
фильтра H(z) — тоже дробно-рациональная функция, поэтому подстановка вида
(6.55) приводит к нереализуемому выражению. Чтобы избежать этого, необходимо
аппроксимировать соотношение (6.55) дробно-рациональной функцией. В качестве
такой аппроксимации часто используется билинейное z-преобразование:
2 2-1
Р-7— <6.56)
Это аппроксимирующее выражение является первым членом разложения функ-
1, г-1
ции —Inz в ряд по степеням---.
Т z + 1
6.12. Методы синтеза дискретных фильтров
229
Использование этой подстановки дает
2 г-1
Т г + 1
Если К(р) является дробно-рациональной функцией, то использование под-
становки (6.56) дает системную функцию Н(г) также в дробно-рациональном, то
есть реализуемом виде Кроме того, если К(р) соответствует устойчивому анало-
говому фильтру, то полученный таким путем дискретный фильтр тоже сохранит
устойчивость.
Рассмотрим трансформацию частотной характеристики прототипа при исполь-
зовании билинейного г-преобразования. Подставим в правую часть (6.56) точное
соотношение (6.55) и учтем, чтор = jw.
. = 2 е,а'г -1 = 2 е7ш//2 -е = 2 2jsin(a>J/2) = . 2
7“а т e;Mj+l Т е!Ш'т/2 Т 2cos(co//2) 7ГД 2 /
где соа и сод — пары значений частот, на которых комплексные коэффициенты пере-
дачи аналогового и дискретного фильтров идентичны.
Таким образом, частоты, на которых комплексные коэффициенты передачи
аналогового К(й)а) и дискретного К((йд ) фильтров совпадают, связаны следующим
образом:
2,
4=ytg
(6.57)
На низких частотах, когда <£>Т/2 « 1, <оа = сод. Однако значение шд = (й/Т соот-
ветствует соа = оо. Связь между АЧХ аналогового прототипа и дискретного фильтра
иллюстрирует рис. 6.22.
Рис. 6.22. Трансформация частотной оси при билинейном г-преобразовании
ЗАМЕЧАНИЕ 6.26 ------------------------------------------
Трансформацию частотной оси необходимо учитывать при разработке
фильтров. Так, для синтеза ФНЧ с частотой среза сод необходимо взять
аналоговый прототип с частотой среза, рассчитанной по формуле (6.57).
продолжение &
230
6. Основы дискретной фильтрации сигналов
Полученная АЧХ будет отличаться по форме от АЧХ прототипа, но иметь
при этом заданную частоту среза.
Бурное развитие вычислительной техники и теории оптимизации позволило
осуществлять поиск экстремумов функций с большим числом переменных (до
нескольких сотен). В результате стала возможной практическая реализация пря-
мых методов синтеза дискретных фильтров. При этом производится поиск набора
коэффициентов фильтра, обеспечивающего максимум или минимум заданной
функции качества.
ЗАМЕЧАНИЕ 6.27 -------------------------------------------------
Подробнее узнать о методах синтеза дискретных фильтров можно, на-
пример, из книги [15].
6.13. Примеры синтеза цифровых фильтров
Чтобы более наглядно пояснить сугь перечисленных в предыдущем разделе методов
синтеза дискретных фильтров по аналоговому прототипу, рассмотрим конкретный
пример — синтез дискретного аналога интегрирующей /?С-цепи (см. раздел 4.4).
Импульсная характеристика аналогового прототипа в данном случае имеет вид
/г(Г) = 1е-'Л, £>0,
т
где т = RC — постоянная времени цепи.
Синтез на основе импульсной характеристики аналогового прототипа.
Синтезируем дискретный аналог интегрирующей ДС-цепи методом дискретизации
импульсной характеристики. Для этого помимо собственно дискретизации над им-
пульсной характеристикой необходимо произвести еще одно преобразование. Как
отмечалось в разделе 4.1, импульсная характеристика аналоговой системы имеет
размерность частоты. В то же время импульсная характеристика дискретной систе-
мы — функция безразмерная. Поэтому импульсную характеристику аналогового
прототипа необходимо умножить на некоторую константу, имеющую размерность
времени. Для того чтобы комплексный коэффициент передачи получающегося
фильтра представлял собой сумму сдвинутых копий частотных характеристик
аналоговою прототипа (без дополнительного множителя), эта константа должна
быть равна периоду дискретизации Т.
Таким образом, импульсная характеристика и системная функция дискретного
фильтра должны выглядеть как
h(n) = -e-Tn/\ и>0, (6.58)
т
H(z) = —(1 + е“ГЛ2“1 + e~^xz"2 +...).
6.13. Примеры синтеза цифровых фильтров
231
Эта импульсная характеристика бесконечна — с ростом п она лишь стремится
к нулю, но не достигает его.
Чтобы реализовать нерекурсивный фильтр (фильтр с конечной импульсной ха-
рактеристикой) порядка N, придется отбросить отсчеты импульсной характеристики
с номерами п > N. В результате мы получим структуру, показанную на рис. 6.23, а
и имеющую импульсную характеристику вида
—е-ЛТЛ
т
—, — е~т/\ —е-2Г/т,
X ’ Т X
Рис. 6.23. Результаты синтеза нерекурсивного фильтра:
а — структурная схема, б — частотные характеристики
Рассмотрим частотную характеристику полученного фильтра. Как указывалось
в разделе 6.9, частотная характеристика получается из системной функции заменой
переменной z = е’шТ. Таким образом, комплексный коэффициент передачи синтези-
рованного фильтра равен
Г
К(а>) = — 1 + е
т
7 т
----J(i)T
27 . NT .
----- jwzT -----j(oNT
+ е т +... + е т
Если воспользоваться формулой для суммы конечной геометрической про-
грессии
°° -1 _
« 1 ч
232
6. Основы дискретной фильтрации сигналов
этот результат можно записать компактнее:
К(®) =
-(Wi-l)f- + ушГ
Т 1-е
(6.59)
Т -Г - усоТ
1-е ’
На рис. 6.23, б приведены графики АЧХ полученного таким образом фильтра
для Т/х = 0,25 и разных значений N. Пунктирной линией показана АЧХ фильтра-
прототипа — интегрирующей ЙС-цепи.
Импульсную характеристику вида (6.59) можно реализовать и при У= •», если
заметить, что системная функция фильтра в этом случае принимает следующий вид
(см. расчет 2-преобразования дискретной экспоненциальной функции в разделе 6.7):
H(2) = ^£e-"z
1
(6.60)
Системная функция, записанная в таком виде, соответствует рекурсивному
фильтру 1-го порядка, структурная схема которого приведена на рис. 6.24, а.
Рис. 6.24. Результаты синтеза рекурсивного фильтра путем дискретизации импульсной
характеристики: а — структурная схема; б — частотная характеристика
Формула для частотной характеристики данного фильтра получается из (6.59)
при использовании предельного перехода N —> •»:
Т 1
Х(®) =---------
Т л —
1-е •
График АЧХ этого фильтра для Т/х = 0,25 показан на рис 6.24, б. Пунктиром,
как и на предыдущем рисунке, показана АЧХ аналогового прототипа.
Из графиков АЧХ, представленных на рис. 6.23 и 6.24, видно, что синтези-
рованный путем дискретизации импульсной характеристики фильтр сохраняет
фильтрующие свойства своего аналогового прототипа (в данном случае является
фильтром нижних частот), но форма АЧХ претерпевает существенные искажения.
6.13. Примеры синтеза цифровых фильтров
233
Так, на нулевой частоте коэффициент передачи не равен единице, АЧХ нигде не
спадает до нуля и частота среза отличается от частоты среза аналогового про-
тотипа. Все это следует иметь в виду при использовании данного метода синтеза
дискретных фильтров.
Синтез на основе билинейного z-преобразования. Синтезируем еще
один дискретный аналог интегрирующей ЙС-цепи, на сей раз методом билинейного
z-преобразования. При использовании этого метода частотная ось претерпевает ис-
кажения, описываемые формулой (6.57), поэтому для получения желаемой частоты
среза параметры фильтра-прототипа необходимо скорректировать. Частота среза
фильтра-прототипа, согласно (6.57), должна быть равна
2 . | “оГ ]
СО =—tR —>
а ср У ° I 2 I
2
где со0 — желаемая частота среза. Частота среза интегрирующей ЙС-цепи (по уровню
0,707) связана с ее постоянной времени соотношением со0т = 1. Поэтому при синтезе
необходимо использовать постоянную времени та:
Г А
2т /
1 Г , .
т = — =—etg —
а со 2 *\2т
а ср V
где т — постоянная времени йС-цепи, дискретный аналог которой мы хотим по-
лучить. Так, если мы, как и в предыдущем примере, возьмем Т/т = 0,25, окажется,
что при синтезе фильтра методом билинейного z-преобразования нужно взять
отношение та/Г равным
- = -ctgO,125 = 3,98.
Т 2
Операторный коэффициент передачи интегрирующей ЙС-цепи
К(р) = -±
Используя билинейное z-преобразование, производим подстановку:
2 z-1
Р = ~--7
Т z + 1
Я(з) =--------= —-—
1 + -—т 1 + 2—
Tz+1 а Т
В результате получаем следующую системную функцию:
1 + 2’1
1 + 2та/Т
В результате синтеза снова получился рекурсивный фильтр 1-го порядка
(рис. 6.25, а), но, в отличие от предыдущего варианта, в нем используется еще и пре-
дыдущий отсчет входного сигнала (слагаемое z 1 в числителе системной функции).
234
6. Основы дискретной фильтрации сигналов
Рис. 6.25. Результаты синтеза дискретного фильтра с помощью билинейного
z-преобразования: а — структурная схема; б — частотная характеристика
Комплексный коэффициент передачи получившегося фильтра
К(ш)=-------
т
1 + 2а-
Т
l + e~jaT
l l 1 ~ с Ж
1 + 2та/Г
График соответствующей АЧХ для Т/х = 1,5 показан на рис. 6.25,6 вместе с АЧХ
аналогового прототипа. Как и при использовании рассмотренных ранее методов
синтеза, дискретный фильтр сохранил фильтрующие свойства аналогового про-
тотипа (фильтр нижних частот). На нулевой частоте коэффициент передачи равен
единице, и АЧХ спадает до нуля на частоте, равной половине частоты дискретизации.
При этом АЧХ сохранила общую форму АЧХ прототипа, претерпев лишь искажения
вдоль горизонтальной (частотной) оси. Кроме того, в данном случае мы получи ди
дискретный фильтр, имеющий в точности ту частоту среза, которая нам нужна
ЗАМЕЧАНИЕ 6.28 ---------------------------------------------------
При построении графика АЧХ на рис. 6.25, б выбрано утрированно большое
значение отношения Г/т. Это сделано намеренно, чтобы показать взаимное
расположение графиков АЧХ цифрового фильтра и аналогового прототи-
па. При меньшем отношении Г/т, более разумном с практической точки
зрения, в области полосы пропускания фильтра графики почти сольются.
Итак, мы рассмотрели несколько методов синтеза дискретного фильтра с ис-
пользованием аналогового прототипа. Подводя итог, можно заметить следующее:
1. При использовании всех рассмотренных методов дискретный фильтр сохраняет
фильтрующие свойства аналогового прототипа.
2. При синтезе нерекурсивного фильтра путем дискретизации импульсной харак-
теристики качество фильтрации оказывается тем выше, чем больше порядок
фильтра.
6.14. Дискретные случайные сигналы
235
3. Использование билинейного z-преобразования гарантирует устойчивость полу-
чаемого рекурсивного фильтра, а также позволяет получить фильтр с заданными
частотами среза.
6.14. Дискретные случайные сигналы
Когда дискретизации подвергается случайный процесс, получающая< я последова-
тельность отсчетов будет зависеть от конкретной реализации дискретизируемого
процесса, и следовательно, ее нужно анализировать статистическими методами.
Что касается одномерной плотности вероятности и связанных с ней статисти-
ческих характеристик, здесь нет никаких отличий от случая аналогового сигна-
ла — просто возможные одномерные сечения случайною процесса соответствуют
моментам дискретизации = kT и поэтому для привязки статистических параметров
ко времени можно использовать номер отсчета. р(х, k), mx(k) и т. д.
Двумерные сечения дискретного случайного процесса также могут браться только
в моменты дискретизации: = kT, t2 = пТ. Поэтому двумерная плотность вероятности
и связанные с ней характеристики случайного процесса зависят от двух номеров
отсчетов k и п- pr(xp х2, k, п), Ry(k, п) и т. д.
В случае стационарного в широком смысле случайного процесса одномерные
характеристики не зависят от момента времени (номера отсчета), а двумерные за-
висят лишь от промежутка между моментами времени (в дискретном случае — от
разности номеров отсчетов Дк = k - и):
рг(.г, k) =рх(х),
m(k) = тх,
Dx(k) = Dx,
рДх,, х2, k. п) - рг(хр х2, Дг),
Rx(k, п) = Rx(Ak).
Таким образом, для стационарного дискретного случайного процесса корреля-
ционная функция является дискретной, то есть представляет собой последователь-
ность чисел {Я (Д£)}.
Для вещественного случайного процесса Rx(k, п) = Rr(n, k), а если процесс еще
и стационарный, то Rt(-k) = R (k).
Дискретный белый шум. Так называется стационарный дискретный случай-
ный процесс, отсчеты которого некоррелированы друг с другом:
\D , Дг = 0,
R. (Д*)= or
Ak 0.
В отличие от случая аналогового белого шума, дисперсия дискретного белого
шума не является бесконечной, а потому такой шум является физически реали-
зуемым.
236
6. Основы дискретной фильтрации сигналов
Прохождение дискретного шума через дискретный фильтр. Пусть
на вход дискретного фильтра с импульсной характеристикой h(k) поступает дис-
кретный стационарный центрированный случайный процесс {х(й)} с корреляцион-
ной функцией Rx(Ak). Найдем корреляционную функцию выходного случайного
процесса. Для этого воспользуемся определением корреляционной функции (см.
раздел 3.3) и формулой (6.43), описывающей преобразование сигнала, осущест-
вляемое фильтром:
Rv(Ak) = y(k)y(k + Ak) = £ x^n^hik-n^ У х(и2)/г(6 + ДА:-п2).
ni=_DO п2=-~
Преобразуем произведение сумм в двойную сумму, воспользуемся линейностью
операции статистического усреднения и заметим, что х(и1)х(«2) = Дх(и2 - иД:
Д/Д^)= £ £ х(п1)х(п2)й(^-п1)Л(^ + М-и2) =
Л, = ~ое Я2 = —оа
= £ £ R^-n^hik-n^hik+Sk-n^. (6.61)
Произведем замену второго индекса суммирования: т = п2 - nv С учетом этого
формула (6.61) принимает вид
* (д*)= t i r (rri)h(k - nx )h(k + Ьк-т-П') =
= У, Rx(m) У h(k-)h(k + &k-m-и,) . (6.62)
W=-oc nt =-oo
Внутренняя сумма в (6.62) представляет собой корреляционную функцию им-
пульсной характеристики фильтра:
У h(k-nx)h(k + t\k-m-n{) = '^ih(n)h(n + Ak-m) = Bh(^k-m).
П{~-оо П = -°°
Таким образом, окончательно получаем, что корреляционная функция случайно-
го сигнала на выходе фильтра представляет собой свертку корреляционной функции
входного шума и корреляционной функции импульсной характеристики фильтра:
* (Л*)= X R (т)В„(М-т). (6.63)
т=-оо
ЗАМЕЧАНИЕ 6.29 -------------------------------------------------------
Полученная формула является дискретным аналогом формулы (4.15)
(см. раздел 4.3), описывающей преобразование корреляционной функции
аналогового шума в линейной цепи.
Контрольные вопросы и задания
237
Дисперсия выходного случайного процесса может быть рассчитана как
В этой формуле учтена четность функции
Если входной случайный процесс является дискретным белым шумом, формула
(6.63) упрощается:
R(Ak) = Dx Bh(Ak).
Дисперсия выходного шума при этом составляет
^=ЦВА(0) = Ц
ьо
Таким образом, при воздействии дискретного белого шума на вход фильтра дис-
персия выходного сигнала пропорциональна сумме квадратов отсчетов импульсной
характеристики фильтра.
Контрольные вопросы и задания
1. Сформулируйте теорему Котельникова и запишите формулу, позволяющую
восстановить аналоговый сигнал по его дискретным отсчетам.
2. Запишите формулу, связывающую спектры аналогового и дискретизированного
сигналов. Почему упомянутые спектры имеют разные размерности?
3. Приведите определение понятий «аналоговый сигнал», «дискретный сигнал»,
«цифровой сигнал».
4. Какие погрешности возникают в процессе квантования сигнала по уровню?
5. Изобразите структурную схему системы цифровой фильтрации сигналов. По-
ясните назначение ее элементов.
6. Перечислите основные источники погрешностей при дискретизации и восста-
новлении непрерывного сигнала. Как с ними борются?
7. Запишите выражение для алгоритма дискретной фильтрации и поясните ис-
пользованные в нем обозначения.
8. Запишите выражение для 2-преобразования дискретного сигнала и перечислите
его основные свойства.
9. Ч го такое системная функция дискретного фильтра? Каковы условия физиче-
ской реализуемости и устойчивости соответствующего фильтра?
10. Изобразите структурные схемы известных вам форм реализации дискретных
фильтров.
И. Кратко изложите сущность метода синтеза дискретных фильтров путем били-
нейного 2-преобразования.
238
6. Основы дискретной фильтрации сигналов
12. Запишите выражения для прямого и обратного дискретного преобразования
Фурье.
13. В чем заключается основная идея быстрого преобразования Фурье? При каком
условии может использоваться этот алгоритм?
Задачи
Задача 6.1
Вычислить z-преобразование X(z) для следующей последовательности отсчетов:
x(k)=А$, —oo<k<oo, |а|< 1.
Задача 6.2
Вычислить z-преобразование X(z) для следующей последовательности отсчетов:
x(k) = A sm(w0Tk), k>0.
Задача 6.3
Найти последовательность отсчетов {x(k)}, z-преобразование которой
*(г)П-0,5гЛо.О^'
Задача 6.4
Найти последовательность отсчетов {х(£)}, z-преобразование которой
x(z)= 2 -2- kl>i-
l-z +z 2
Задача 6.5
Вычислить линейную дискретную свертку следующих последовательностей от-
счетов:
x(k) = {1, 2, 3,4}, y(k) = {1, -1, 2, -2,3, -3}.
Задача 6.6
Найти циклическую свертку последовательностей отсчетов {x}(k)} = {1, 2, 3, 4}
и {x.,(k)} = {1,1, 0, 0} двумя способами:
а) как обратное ДПФ произведения ДПФ этих двух последовательностей;
б) путем непосредственного применения формулы циклической свертки.
Задача 6.7
2
Системная функция дискретного фильтра имеет вид H(z) =-—.
l-2z
1. Записать формулу алгоритма фильтрации.
2. Изобразить структурную схему фильтра.
Задачи
239
3. Определить, является ли данный фильтр устойчивым.
4. Вычислить импульсную характеристику фильтра {h(k)}.
5. Определить выходной сигнал фильтра {y(k)}, если на вход фильтра при нулевых
начальных условиях начинает поступать следующая бесконечная последователь-
ность отсчетов: x(k) = {+1, -1, +1, -1, +1, -1, +1, -1...}.
Задача 6.8
Для обработки сигнала в виде пяти одинаковых отсчетов (дискретный прямо-
угольный импульс) используется согласованный дискретный фильтр. Определить
системную функцию фильтра и алгоритмы фильтрации в нерекурсивном и рекур-
сивном вариантах. Найти сигнал на выходе фильтра.
Задача 6.9
На вход линейною филотра с постоянными параметрами при нулевых начальных
условиях начинает поступать следующая бесконечная последовательность отсче-
тов: x(k) = sin(£n/3), k > 0. На выходе фильтра при этом формируется сигнал вида
y(k) = |sin(£n/3)|, k > 0.
1. Определить системную функцию фильтра H(z).
2. Изобразить структурную схему фильтра.
3. Определить импульсную характеристику фильтра
Задача 6.10
Найти частотную характеристику дискретного фильтра с импульсной реакцией
h(k) = ехр(-1гТ/т), k > 0. Построить график модуля частотной характеристики при
T/i= 1 и Т/т = 0,1.
7. Преобразования радиосигналов
в нелинейных радиотехнических
цепях
Рассматривавшиеся в главе 4 радиотехнические цепи относятся к классу линейных
стационарных цепей. Стационарность означает постоянство параметров цепи во
времени, линейность — справедливость принципа суперпозиции, который в общем
виде математически выражается следующим образом:
Z[5,(i) + 52(t) + ... + 5п(Ц = L [5,(0] + Ф2(0] + • + Ф„(0], (7-1)
где L — оператор, характеризующий преобразование сигнала s(t) цепью.
В данной главе рассматриваются свойства цепей, которые являются стационар-
ными, но нелинейными, то есть соотношение (7.1) для них не выполняется.
7.1. Нелинейные элементы
С гационарная радиотехническая цепь является нелинейной, если в ее состав входят
один или несколько элементов, для которых соотношение (7.1) несправедливо,
то есть параметры которых, а стало быть, и вид оператора L, зависят от уровня
входного сигнала. Примером нелинейного элемента является полупроводниковый
диод, типичная вольт-амперная характеристика (ВАХ) i = f(u) которого показана
на рис. 7.1. Если предположить, что оператор L соотношения (7.1) соответствует
зависимости i = f(u), то очевидно, что соотношение (7.1) не выполняется, а именно:
напряжению и( соответствует ток iv напряжению и2 соответствует ток ь, но соот-
ветствующий напряжению и3 = и, + и2 ток i3 * it + i2.
Неприменимость принципа суперпозиции существенно усложняет анализ
воздействия сигнала на нелинейную цепь, так как выходной сигнал уже не может
быть представлен в виде суммы реакций на элементарные входные сигналы, как
это делается при анализе воздействия сигнала на линейную цепь (заметим, что
процедура поиска спектра выходного сигнала £вых(о>) в виде 5вых(со) = 5вх (со)Х(а>)
или вычисление интеграла Дюамеля являются, по существу, конкретизацией со-
отношения (7.1) для входных сигналов, представленных в виде разложения на
гармонические или 8-составляющие).
Различают резистивные (сопротивления) и реактивные (индуктивности и емко-
сти) нелинейные элементы. Например, упоминавшийся полупроводниковый диод
7.2. Аппроксимация нелинейных характеристик
241
Рис. 7.1. ВАХ нелинейного элемента
при теоретическом анализе часто считают резистивным нелинейным элементом
Здесь существенным является го обстоятельство, что ВАХ г = /(и) не содержит в
явном виде времени. Физически это означает безынерционностъ резистивного не-
линейного элемента, то есть мгновенное, вслед за изменением внешнего входного
воздействия, установление выходной реакции. Кроме диодов к резистивным нели-
нейным элементам при анализе часто относят биполярные и полевые транзисторы,
электровакуумные приборы (лампы) и т. д. Примером нелинейной емкости служит
варикап — специальный полупроводниковый диод, используемый как конденсатор
с электрически управляемой емкостью.
Из курса, в котором изучаются материалы и компоненты радиоэлектроники,
известно, что эквивалентная схема любого полупроводникового или электроваку-
умного элемента содержит так называемые сабс таенные, {паразитные) емкости и
индуктивности. Поэтому безынерционных нелинейных элементов, строго говоря, не
существует. Это представление является моделью, обеспечивающей значительные
удобства для теоретического анализа преобразований радиосигналов в нелинейных
цепях. Адекватность (соответствие свойствам реального элемента) такой модели
определяется частотным диапазоном, в котором будет работать содержащее элемент
анализируемое устройство. Предполагается, что при разработке радиотехнического
устройства входящие в него компоненты выбираются грамотно.
При этих условиях такие радиотехнические преобразования сигналов, как не-
которые виды усиления, модуляцию, детектирование, преобразование частоты,
генерацию, чаще всего считают безынерционными нелинейными. Это определяет
важность изучения таких преобразований в курсе «Радиотехнические цепи и сиг
налы».
7.2. Аппроксимация нелинейных
характеристик
Теоретический анализ позволяет определить лишь общий вид вольт-амперной ха-
рактеристики нелинейного элемента, и практическая ценность таких характеристик
для исследования поведения реальных нелинейных элементов в радиотехнических
схемах невелика; полезные для практического применения ВАХ, как правило,
получают экспериментально.
242
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
Однако эксперимент дает, по существу, табличное представление характери-
стики, в то время как для анализа и расчетов необходимо аналитическое (в виде
формулы) представление ВАХ.
Используются различные способы аппроксимации — замены таблично заданной
характеристики аналитическими функциями, приближенно отражающими пове-
дение реальной ВАХ нелинейного двухполюсника в интересующем исследователя
диапазоне изменения аргумента (поведение аппроксимирующей функции вне
этого диапазона несущественно). К аппроксимирующей функции предъявляют
противоречивые требования: обеспечивая хорошее качество приближения, она
должна быть относительно простой и удобной для дальнейшего использования.
В частности, при выборе аппроксимации целесообразно учитывать вид сигнала,
который подвергается нелинейному преобразованию, а также цель преобразования.
Рассмотрим основные способы аппроксимации нелинейных характеристик,
используемые в радиотехнике.
Полиномиальная аппроксимация. Пусть i = f(u) (рис. 7.1) является гра-
фически заданной (экспериментально снятой) ВАХ. Будем искать представление
этой характеристики в виде ряда Маклорена
i = f(u) = aQ + а,и + а2и2 + a3w3 + a4w4 + ... (7-2)
Ограничиваясь п членами ряда: i = f(u) = aQ + ахи + а2и2 + ... + ап_хип~ \ запишем,
используя график, систему уравнений:
=/(«i) = ао + aiMi + а?и? + - + ап-\иГ'<
i2 =/(«2) = ао + aiM2 + а2и22 + - +
ъ = /(ш) = ап + а,щ + а,и~2 + ... + а и,п~'.
= f(u ) = af + а и + а2и 2 + ... + ап .м"1.
П V 1 Л X Л л-1 л
Решая полученную систему линейных уравнений относительно неизвестных
а0, а,, а2, ..., an_v получим ВАХ полупроводникового диода, аппроксимированную
полиномом л-й степени на участке и е [и,, ип].
В некоторых случаях удобнее оказывается представление в виде ряда Тейлора
i =f(u) = а0 + a,(w - L70) + а2(и - UQ)2 + а3(и - Ц,)3 + a4(u - Ц,)4 + ..., (7.3)
где Uo — так называемая рабочая точка ВАХ. Для представления (7.2), очевидно,
L/o = O.
Иногда полиномом удобно аппроксимировать ВАХ, заданную не таблицей, а не-
которой аналитической функцией. В таком случае коэффициенты ап вычисляются
по известным формулам:
а = 1 [</"/(»)]
" и!1 dun J „
I- 1 u=Un
и, следовательно, зависят от выбора Uo.
7.2. Аппроксимация нелинейных характеристик
243
Как правило, аппроксимация ВАХ полиномом осуществима; поэтому теоре-
тический анализ нелинейных преобразований в радиотехнике часто выполняют,
непосредственно используя общее представление (7.2) или (7.3).
ЗАМЕЧАНИЕ 7.1 ---------------------------------------------------------
Первую производную ВАХ называют дифференциальной крутизной ха-
рактеристики i = f(u)\
di
S = — = a, + 2a,u + 3a,H2 +...
д du 1 2 3
для представления (7.2) или
di
S^= — = ai + 2a2(u- Uo) + За3(и - UQ)2 +...
для представления (7.3). Параметр S- S^U^) = а, называется крутизной
BAX в рабочей точке.
Кусочно-линейная аппроксимация. В некоторых случаях (например, если
и изменяется в довольно больших пределах) ВАХ нелинейного элемента аппрокси-
мируют двумя или более отрезками прямых. Пример чаще всего встречающегося
варианта кусочно-линейной аппроксимации ВАХ показан на рис. 7.2.
Рис. 7.2. Кусочно-линейная аппроксимация нелинейной ВАХ
Аппроксимирующее выражение в данном случае записывается следующим
образом:
|5(М-Пн), и>ии,
10, u<UH.
(7А)
Здесь константа S — крутизна, UH — координата «начала» линейно возрастающей
части ВАХ.
244
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
Экспоненциальная аппроксимация. Иногда для представления ВАХ полу-
проводниковых диодов используют функцию вида
г = А(е““ -1), и > 0. (7.5)
7.3. Воздействие гармонического сигнала
на безынерционный нелинейный
элемент
В качестве простейшей модели узкополосного сигнала используем гармоническое
колебание со «смещением», представляемое выражением
w(t) = L70+Lrnicos(d)/ + (p1). (7.6)
Будем последовательно изучать результат воздействия этого сигнала на нели-
нейный двухполюсник, ВАХ которого аппроксимирована рассмотренными в раз-
деле 7.2 выражениями.
Полиномиальная аппроксимация. В качестве ВАХ возьмем полином (7.3).
Смещение Uo совпадает с координатой положения рабочей точки ВАХ. Ток в цепи
двухполюсника
i(t) = а0 + a,Um cos(o)/ + ф,) + a2Um2 cos2(to/ + ipt) + a3Um3 cos3(o)/ + ф() + ...
после элементарных преобразований с учетом известных формул «кратных дуг»:
, 1
cos а = -(1 + cos2а),
1
cos а = —(3cosa + cos3a),
cos4 а = ^(3 + 4 cos 2а + cos 4а),
cos5 а = ^( L 0 cos а + 5 cos За + cos 5а)
может быть представлен в виде
(13 1
z(f) = ап -I—-I—а,(74 +... +
Г 3 5
+ a,U +—a3Ul +—aJJl +... cos(co,t + <p ) +
lim 3 т g 5 m I v 1 ~ i /
+| -adJ2 +-a.U* + ... |cos2(a> t + <p ) +
। 2 - m g 4 m I 4 J
+1 -а,С3 +—а/75 +... |cos3((o г +ф.) + ...=
I д 3 m 1 g э т i \ 1 т 1 /
= /0 + cos(o)/ + ф,) + /2 cos2(co1t + ф() + /3 0053(0)/ + ф;) +... (7.7)
7.3. Воздействие гармонического сигнала на безынерционный нелинейный элемент 245
Явные выражения для постоянной составляющей тока и амплитуд гармоник
/2, /3... следуют непосредственно из соотношения (7.7).
Отметим следующее:
□ амплитуды гармоник с четными номерами и постоянная составляющая в (7.7)
определяются только четными коэффициентами ряда (7.3);
□ амплитуды гармоник с нечетными номерами определяются только нечетными
коэффициентами ряда (7.3);
□ максимальный номер входящей в представление (7.7) гармоники (количество
гармоник) определяется степенью аппроксимирующего ВАХ полинома;
□ полная начальная фаза и-й гармоники равна пфг
Кусочно-линейная аппроксимация. Для анализа гармонического состава
тока в цепи нелинейного двухполюсника с ВАХ, аппроксимированной выражением
(7.4), обратимся к рис. 7.2, где изображено типичное взаимное расположение ВАХ
и сигнала (7.6), начальную фазу которого без потери общности примем здесь равной
нулю (ф, = 0). Ток в цепи появляется только при и > UK и является периодической
последовательностью импульсов:
г(Г) = -
S(U(+UCOSCO/-Г ) = SU
' и т I н z т
и -ип
cosco/----—-
т
о,
| со/ - 2kit |< 6,
| со/ - 2kit |> 6.
(7-8)
Введенный в выражение (7.8) параме гр 0 называется углом отсечки. Физиче-
ский смысл угла отсечки иллюс грирует рис. 7.2 — очевидно, что по координате со/
(линейная текущая фаза) косинусоидальный импульс тока имеет длительность 20.
При со/ = 2kn ± 0 ток в цепи равен нулю; из уравнения
( и -иЛ
SU COS0-----2---5- =0
т и
следуют часто используемые соотношения
и -ип
cos0 = -2----, (7.9)
т
i(t) = SUm(cos(Oit-cosG), со/е [2&Л-0, 2£л + 0]. (7.10)
Максимального значения 1т импульс тока достигает при со/ = 2kn поэтому
I = SU (l-cos0), SU = —^—. (7.11)
m m m 1-COS0
Используя полученные соотношения, будем искать коэффициенты разложения
периодической (с периодом Т = 2Л/СОД функции (7.10) в ряд Фурье (см. раздел 1.3)
в представлении
62 ж,
?'(Г) = — + COSTCO/ + bk sin&co/).
2 *=i
246
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
Так как функция (7.10) четная, коэффициенты Ьк = 0. Коэффициенты ак вы-
числяются по формуле
2 2 9
ак = — j /(^cos&cpjt dt =---------j i(t)cos^co1t t/(a>j£).
T’ _г/2 -е
Используя четность подынтегрального выражения, формулу (7.11) и соотно-
шение со1Т= 2л, преобразуем последний интеграл:
I 9
= (1— 0) (C0SK>lt ~ ^(®10 •
Коэффициенты ак для k > 0 являются амплитудами гармонических составляю-
щих тока i(t), постоянная составляющая 10 = а()/2. Интегрирование дает формулу
для амплитуды k-й гармоники:
2(sin&0cos0-£cos£0sin0)
k т kR{k2 —1)(1 —COS0)
Приведем явные выражения для амплитуд некоторых гармоник:
, j sin0-0cos0_^ sin0-0cos0
° - т n(l-cos0) ” т л
, 0-sin0cos0 _ 0-sinGcos0
т n(l-COS0) т л
, 2sin30 2 . з
, = I ---------= SU —sin 0.
3n(l-cos0) Зя
(7.12)
(7.13)
(7.14)
Часто используются нормированные к I значения 1к, или коэффициенты Берга
а*(0)=^, Л=а/0)/т,
J т
(7.15)
а также функции Берга
Ь(0) = 77Г- A = V<W.- (716)
т
Коэффициенты и функции Берга связаны друг с другом следующим образом:
у/0) = (1 - cos 0)а/0).
Для ряда значений k коэффициенты и функции Берга табулированы. Графики
а/0) и у/0) для k = 0,1,2,3 приведены на рис. 7.3 и 7.4. Вид графиков указывает на
возможность оптимизации процедуры нелинейного преобразования, так как при
заданной ВАХ (фиксированном /7Н) угол отсечки 0 в соответствии с формулой (7.9)
регулируется выбором амплитуды Um и величины смещения J70.
7.3. Воздействие гармонического сигнала на безынерционный нелинейный элемент 247
Рис. 7.3. Коэффициенты Берга аД0)
Экспоненциальная аппроксимация. Для анализа состава тока в нелиней-
ном двухполюснике с ВАХ, аппроксимированной выражением (7.5), используют
разложение
emcosx = '2 Jk(jm)coskx,
k=l
где Jt(m) ~~ функция Бесселя первого рода k-ro порядка аргумента т [10]. При
использовании указанного разложения и подстановке в выражение (7.5) сигнала
(7.6) получается следующее выражение для тока в цепи:
i(t) = A{j0(jaU())eaU'> -1} + 2Аеа(;”£е 12 J/yal/Jcosfao/ =
k=l
= 1. + У L cosktat.
0 k 1
k=\
(7.17)
248
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
ЗАМЕЧАНИЕ 7.2
Функции Бесселя первого рода с чисто мнимым аргументом дают
модифицированные функции Бесселя, обычно обозначаемые 1к(х\.
Jk(jx) = exp^j—В формуле (7.17) данное обозначение не ис-
пользовалось, чтобы избежать путаницы с амплитудами гармоник тока,
также обозначенными I,.
к
Таким образом, вне зависимости от вида аппроксимирующей функции ток
в цепи нелинейного двухполюсника при узкополосном (гармоническом) воздей-
ствии представляется суммой составляющих: постоянной 10 и гармонических с
амплитудами /2, /3... и частотами (Ор 2®(, Зсо,..., кратными частоте приложенного
напряжения, то есть рядом Фурье.
ЗАМЕЧАНИЕ 7.3--------------------------------------------------------
Из формул (7.7), (7.12-7.17), прямо или косвенно определяющих /0,
следует, что эти величины могут принимать и отрицательные значе-
ния (например, I3 = а3(0)/т при некоторых значениях 0, см. рис 7.3), что
противоречит смыслу понятия «амплитуда». В таких случаях амплитудой
следует считать модуль |7j, а отрицательный знак относить к появлению
у k-ii гармоники дополнительной начальной фазы ±л.
7.4. Би- и полигармоническое воздействие
на безынерционный нелинейный
элемент. Преобразование
частоты сигнала
Пусть на нелинейный двухполюсник с ВАХ, аппроксимированной функцией
i =/(«) = + а2и2, (7-18)
подано напряжение
и(0 = Uo + Umi cos(co,t + ф,) + Um2 cos(co/ + ф2). (7.19)
После подстановки (7.19) в (7.18) и преобразований, аналогичных проводив-
шимся в разделе 7.3, получим для тока в цепи:
/(0 = + a2U2 + ^a2(U2ml + U2m2) +
+ («t + 2a2Uu)Umi cos(co1t + <fe) + (a1 + 2a2/70)t/m2cos(co2t-i-(p2) +
1 1
+ 2 a2Ulx cos 2(°V + Ф1) + 2 a2UL cos2(0)27 + <P2) +
+a2UmPm2 cos[(«! +w2)t + (p, +<p2] + a2l/ml/7m2cos[(o)1 -о)2Х + ф^ф2].
7.4. Би- и полигармоническое воздействие
249
Кроме постоянной и гармонических составляющих на частотах 0, со,, со2, 2(0^
2<о2 в составе тока появились так называемые комбинационные компоненты на
суммарной и разностной частотах C0j + со2 и со, - со2. Частоты возникших в цепи
компонент тока можно определить формулой со = рсо, ± qa)2, где коэффициенты р
и q могут принимать значения:
Р = Ч = Ь
p = q=t
p = 0,q = 2;
p = 2,q = 0.
Суммаp + q = R называется порядком комбинационной частоты; в рассмотренном
примере R принимает значения 0,1, 2.
Не прибегая к громоздким, хотя и элементарным выкладкам, обобщим получен-
ные результаты. Можно утверждать, что при воздействии на нелинейный двухпо-
люсник с ВАХ, аппроксимированной полиномом N-Й степени, напряжения в виде
суммы М гармонических сигналов с различными частотами ток будет содержать
гармоники с частотами
со = ]&,<», + k2a)2 + ... + A^coJ, (7.20)
где k,, k... .... k„ — любые целые числа из диапазона -N...N такие, что У 'W I k I < N.
Комбинационные частоты такого преобпазовання будут иметь порядки R < А.
Общая схема нелинейного преобразования сигналов. Для того чтобы
воспользоваться результатами нелинейного преобразования «напряжение — ток»,
выделив при этом выходное напряжение в виде составляющей на некоторой ча-
стоте (в некотором диапазоне час тот), используют схему, приведенную на рис. 7.5.
Схема содержит нелинейный двухполюсник и линейный фильтр. Фильтром, или
сопротивлением нагрузки Z(co), на котором выделяется выходное напряжение как
правило, является частотно-избирательный пассивный двухполюс ник, например
колебательный контур.
Рис. 7.5. Общая схема нелинейного преобразования сигналов
При этом выходное напряжение нвых(£) приложено к нелинейному двухполюс-
нику (внутреннее сопротивление источника напряжения равно нулю) и, вообще
говоря, влияет на работу схемы. Это в. сияние называют реакцией нагрузки. Реакция
нагрузки может заметно изменить спектральный состав тока цепи.
Это обстоятельство принимают во внимание при анализе и разработке конкрет-
ных радиотехнических устройств. Иногда принимают |«BbB(t)l « l^(t)l и реакцией
250
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
нагрузки пренебрегают. В то же время существуют устройства, в работе которых
реакция нагрузки предусмотрена и очень существенна.
ЗАМЕЧАНИЕ 7.4-------------------------------------------------------
Анализ нелинейного преобразования реального узкополосного сигнала,
содержащего множество расположенных в некотором частотном интер-
вале Дсо = со2 - cOj гармонических составляющих, существенно сложнее
проведенного в разделе 7.3 анализа преобразования гармонического
сигнала. Качественно прогнозировать результаты преобразования можно,
обращаясь к соотношению (7.20); очевидно, например, что спектральные
составляющие второго порядка будут концентрироваться для разност-
ных частот в области со е [0, Дсо], для суммарных частот — в области
со е [2сор 2со2] и т. д.
Гетеродинирование (перенос несущей частоты, или спектра) сигна-
ла. Рассмотрим частный случай нелинейного преобразования суммы гармони-
ческого колебания ur(t) = UT cos(cort + фг) — сигнала гетеродина1 и узкополосного
радиосигнала wp(t), в качестве модели которого возьмем AM-сигнал с тональной
(гармонической) модуляцией
мр (t) - U т (1 + тп cos Q0cos(coot + ф0) =
mU mU
= cos(coor + <p0) + —^-cos[(co0 + Q)£ + cp0] + —^-cos[(co0 - Qy + <p0 J. (7.21)
Для упрощения анализа аппроксимируем ВАХ нелинейного элемента параболой
i = а2и2. Из составляющих тока выделим и рассмотрим следующие гармоники на
суммарных и разностных частотах:
i(t) =. a1UmUr cos[(co0 + й>г )t + <р0 + фг ] +
+-a.mU U cos[(ft)n+ro + ОУ + ф„+ф ] +
2 ТП V 1 ' и Г z ,и 1 Г J
+\aimUmUr cosK^o + “r - Q)i + фо + фг] +
+a2t/mt/r cos[(a>0 -юг)Г + ф0-фг] +
+ 2a2mf/nf;rCOS[((O0 ““г +^У + Фо -Фг] +
+\aimUmUr cos[(co0 -cor -ny + фо -фг] +... =
= ...a2t/m[7r(l+77icosQi)cos[(ft)0 + согУ + ф0 + фг] +
+a2UmUT(1 + 77icosQ^)cos[(to0 -согУ+ф0 -фг]... (7.22)
В составе тока присутствуют компоненты AM-сигналов, аналогичных исходному
сигналу (7.21), но с «перенесенными*, смещенными относительно со0 несущими
Гетеродин — маломощный вспомогательный автогенератор.
7.5. Нелинейное резонансное усиление и умножение частоты
251
частотами ю0 ± сог. Рассмотренное преобразование иллюстрирует рис. 7.6, где вместо
симметричных боковых гармонических составляющих для обобщения и нагляд-
ности условно изображены асимметричные боковые полосы, соответствующие
некоторому реальному сигналу. При переносе «вверх» структура спектра сигнала
сохраняется, при переносе «вниз» результат зависит от соотношения со0 и сог: если
со0 > сог, то структура спектра сохраняется (см. рис. 7.6, а), если о>0 < сог, то верхняя
и нижняя боковые полосы меняются местами, инвертируются (см. рис. 7.6, б), что
в некоторых случаях может иметь значение.
Рис. 7.6. Гетеродинирование
*
со
Существенно, что все компоненты преобразованных AM-сигналов приобретают
одинаковый фазовый сдвиг ±<рг.
Рассмотренное преобразование — гетеродинирование — широко используется
в радиотехнике.
7.5. Нелинейное резонансное усиление
и умножение частоты
Рассмотрим усилительный каскад с коллекторной нагрузкой в виде параллельного
колебательного контура, упрощенная схема которого изображена на рис. 7.7. Ис-
пользуем кусочно-линейную аппроксимацию (см. рис. 7.2) проходной ВАХ, то есть
зависимости тока коллектора от напряжения на базе iK = f(u6) транзистора. Пусть
на входе действует напряжение вида (7.6)
«6(0 = UQ+ C7m cos(co/4- <р,).
Каскад работает с отсечкой, так что коллекторный ток представляется после-
довательное! ью косинусоидальных импульсов (7.8). Без учета реакции нагрузки
(контура) на работу каскада амплитуды гармоник коллекторного тока представ-
ляются формулами (7.16)
L=VtSU .
k *k т
252
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
Рис. 7.7. Нелинейный резонансный усилитель
Рис. 7.8. Нелинейное резонансное усиление
Если контур настроен на частоту первой гармоники Юр то амплитуда выходного
напряжения
U^ = ^)SUR3, (7.23)
где R3 — эквивалентное сопротивление контура.
Для качественного анализа особенностей работы нелинейного резонансного
усилителя обратимся к рис. 7.8, на котором представлены временные зависимости
коллекторного тока первой гармоники коллекторного тока i\t) и выходного
напряжения каскада
и (t) = E-U cos со,7,
где Е — напряжение источника питания каскада. Частотно-избирательная нагрузка
позволяет эффективно использовать нелинейную ВАХ транзистора: амплитуда
выходного напряжения Um вых достигает значений, близких к Е, так что в некото-
7.5. Нелинейное резонансное усиление и умножение частоты
253
рые моменты времени выходное напряжение превосходит напряжение питания1
(пвых(() > Е). Этим обусловлен большой коэффициент усиления нелинейного резо-
нансного усилителя. Как и резистивный усилительный каскад с общим эмиттером
(истоком), нелинейный резонансный усилитель инвертирует (поворачивает на
180°) фазу входного напряжения.
Амплитудная характеристика (7.23) Umвых = /(Um) называется также колебатель-
ной характеристикой нелинейного резонансного усилителя. Очевидным является
требование линейности этой характеристики, особенно прч работе с АМ-сигналами.
Но аргумент функции уД0) связан в соответствии с формулой (7.9) с Um:
и -ип
0 = arccos—2--
ит
и анализируя зависимость (7.23) при заданных L/ и [70, можно лишь указать интервал
допустимых с точки зрения линейности значений U . Оптимальным является вы-
бор UK = Uv так как уДл/2) = 1/2 и функция (7.23) при этом оказывается линейной:
U =-SU R .
т вых 2 т э
Нелинейные резонансные усилители час го используются как выходные каска-
ды мощных радиопередающих устройств, и существенным оказывается их КПД,
под которым подразумевается отношение выделяемой в колебательном контуре
мощности первой гармоники к мощности, потребляемой каскадом от источника
питания. Обычно, как уже указывалось, Um вых ~ Е и
I
у т вых 1 у (0)
Т| = -1------------.
Е10 2уо(0)
(7.24)
При 0 —> 0 КПД Т| —> 1; при 0 = л/2 (с учетом требования линейности колеба-
тельной характеристики)
г) = л/4 = 0,785.
Резонансное умножение частоты. Если в рассмотренной схеме (см. рис. 7.7)
контур нас гроить на частоту иго, — частоту одной из высших гармоник, то нелиней-
ный резонансный усилитель можно использовать в качестве умножителя чей шоты
Потребность в умножи гелях возникает, например, при разработке источников гар-
монических колебаний с высокой стабильностью частоты, если непосредственное
создание такого источника в заданном диапазоне невозможно пли затруднено, но
имеется высокостабильный низкочастотный генератор.
Трудность создания подобных умножителей связана с относительно малыми
значениями функций Берга у^(0) при больших k. Оптимальный для максимизации
амплитуды тока k-Й гармоники при заданном значении Um угол отсечки определя-
ется соотношением 0 = it/k.
При закрытом транзисторе потенциал коллектора определяется напряжением источника питания,
с которым складывается напряжение на заряжающейся (за счет запасенной в инд\ ктивности контура
энергии) емкости С.
254
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
7.6. Получение амплитудно-
модулированных колебаний
Процедура амплитудной модуляции состоит в нелинейном преобразовании суммы
высокочастотного гармонического (со0 — несущая частота) и низкочастотного мо-
дулирующего сигналов. В качестве последнего возьмем гармоническое колебание и
рассмотрим преобразование бигармонического сигнала (7.19), представленного как
u(t) = Un+U cos ant + Un cos at, an» co, (7.25)
в нелинейном двухполюснике с ВАХ
i = atU + a2u2. (7.26)
Интересующие нас составляющие тока
i(t) =..+ 2a2I70(7m)cosco0f + a2UmUa cos(co0 + Q)t + a2UmUa cos(co0 - Q)£ +...
представляют амплитудно-модулированное чистым тоном колебание
1 +------[/„cosQt cosco,/
I «.+2^ n J 0
с коэффициентом модуляции
--------ua
Амплитудный модулятор. При подаче сигнала (7.25) на вход работающей
с отсечкой схемы нелинейного резонансного усилителя последовательность им-
пульсов коллекторного тока оказывается промодулированной по амплитуде (со-
ответствующий график показан на рис. 7.9).
Рис. 7.9. Амплитудная модуляция
7.7. Амплитудное детектирование
255
По аналогии с формулой (7.8) последовательность может быть представлена
выражением
i(t) = S(UQ +Unicosa>0t + UacosQt-UH) =
= SU
U -I7n[ 1 +—cosQt
U
COSCO,/------------------
о rr
где правая часть
отлична от нуля в пределах, определяемых углом отсечки. Но модулирующее
напряжение перемещает в пределах (70 + Ua... Со - UQ рабочую точку, что приво-
дит к периодическому изменению угла отсечки как функции Un. Сравнивая вы-
ражения (7.10) и (7.27), используя формулу (7.24), получим для углов отсечки
U -ип-ип
0 = arccos —--------2-
max
тп
а uH-u0+ua
0min =arccos--------а
тп
и в соответствии с формулой (7.16) для максимального и минимального значений
амплитуды первой гармоники тока
Ать=Т1(^.пЖ-
Если модуляционная характеристика 7, = /(Ua) линейна, то коэффициент мо-
дуляции можно определить по формуле
— Атах Атт
+ 1
Imax tmm
Можно показать, что линейность модуляционной характеристики оказывается
удовлетворительной, если угол отсечки меняется в пределах 40... 140°.
АМ-сигнал выделяется с помощью частотно-избирательной нагрузки каскада.
7.7. Амплитудное детектирование
Операция амплитудного детектирования (демодуляции) противоположна ампли-
тудной модуляции. На входе амплитудного детектора действует АМ-колебание,
которое в общем виде с учетом смещения, определяющего положение рабочей
точки, может быть представлено как
u(t) = U0+ U(t) cos со/. (7.28)
256
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
На выходе идеального детектора должен присутствовать низкочастотный сиг-
нал, пропорциональный U(t). Таким образом, при амплитудном детектировании в
общей схеме нелинейного преобразования (см. рис. 7.5) частотно-избирательной
нагрузкой должен быть НЧ-фильтр, в качестве которого часто используют па-
раллельную АС-цепочку. Частотная зависимость модуля импеданса АС-цепочки
описывается формулой
1М= / R 2-
yJl + (a>RC)2
Квадратичное детектирование. Рассмотрим преобразование сигнала (7.28)
нелинейным двухполюсником с ВАХ (7.26).
В этом случае ток
i(t) = atUQ + a2U% + ^a2U2(t) + (at + 2a,C0)C(?)cosw0?+ -^a2C2(?)cos2co0?
действительно содержит низкочастотную компоненту a2U2(t)/2, которая может быть
выделена НЧ-фильтром; однако имеет место нелинейное (квадратичное) искаже-
ние информационного (модулирующего) сигнала, допустимое только при приеме
простого амплитудно-манипулированного колебания. Необходимо располагать
устройством, выделяющим передаваемый сигнал без искажений.
Линейное детектирование. Пусть на входе амплитудного детектора дей-
ствует AM-колебание, в качестве модели которого примем сигнал, модулированный
чистым тоном:
u(t) = Um( 1 + т cos cot) cos co0t; (7.29)
на выходе необходимо получить низкочастотное колебание
и (t) = U cos £2t.
Рассмотрим схему коллекторного детектора, представляющего собой усили-
тельный каскад с нагрузкой в виде параллельной АС-цепочки (рис. 7.10).
На вход этой схемы поступает сигнал (7.29) со смещением Uo, при этом ампли-
туда Um достаточно велика для того, чтобы можно было воспользоваться кусочно-
линейной аппроксимацией ВАХ. Упрощая рассмотрение, примем UH = Uv так что
угол отсечки 6 = 90° и не зависит от амплитуды входного сигнала. Процессы в кол-
лекторном детекторе иллюстрируются графиками, представленными на рис. 7.11.
Последовательность импульсов коллекторного тока промодулирована по амплиту-
де, при этом постоянная составляющая тока изменяется во времени с частотой Q
70 = SUm (1 + TncosQ7)y0 = 0,318SUm (1 + mcosQt),
а выходное напряжение детектора
и (?) = Е - InR = Е - 0,318 SRU (1 + т cos Q?).
вых ' г v ’ т' '
(7.30)
7.7. Амплитудное детектирование
257
Рис. 7.10. Коллекторный детектор
Рис. 7.11. Амплитудное детектирование (коллекторный детектор)
Введем коэффициент детектирования
д mUm ’ (7.31)
равный отношению размаха (амплитуды) изменения выходного сигнала к размаху
(амплитуде) изменения огибающей входного сигнала:
|{f/m(l + 7H)-[/m(l-«)} = mUm.
В соответствии с формулой (7.31) коэффициент детектирования коллекторного
детектора kR = 0,31857?.
9 №675
258
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
Для эффективной работы детектора необходимо обеспечить выполнение условий
»R»-,
Q С---------т,С
шах и
(7.32)
где Qmax — максимальная частота спектра передаваемого НЧ-сигнала (модулиру-
ющего колебания).
По аналогии с модуляционной характеристикой из раздела 7.6 рассматривают ха-
рактеристику детектирования /0 = f(U ). Очевидно, что при выбранном угле от-
сечки 6 = 90° коллекторный детектор является линейным. Если же условие UH = Uo
не выполнено, то, как и в разделе 7.6, следует определить пределы изменения Um,
для которых характеристика детектирования приближенно является линейной.
Амплитудный линейный диодный детектор. Простой и широко рас-
пространенной является схема диодного детектора, приведенная на рис. 7.12. Для
анализа работы этой схемы сделаем следующие предположения:
□ детектор работает при достаточно большом уровне входного сигнала, так что
используется кусочно-линейная (7.4) аппроксимация ВАХ диода при UH = 0;
□ сопротивление нагрузки детектора R значительно превышает внутреннее сопро-
тивление открытого диода Rt = 1 /5, где S — крутизна ВАХ диода:
RS» R.S=l.
I
(7.33)
Рис. 7.12. Амплитудный диодный линейный детектор
Работу схемы удобно рассматривать, задавая вначале входной сигнал в виде
гармонического колебания Um cos о>0£. Емкость С заряжается при открытом диоде с
постоянной времени R.C, разряжается при закрытом диоде в силу условия (7.33) го-
раздо медленнее, с постоянной времени RC. В течение нескольких периодов входного
сигнала после его подачи напряжение на емкости (выходное напряжение диодного
линейного детектора) достигает значения, близкого к амплитуде выходного сигнала.
Это же напряжение приложено к диоду и запирает его, так что в установившемся
режиме большую часть времени диод закрыт (рис. 7.13). Почти постоянное вы-
ходное напряжение U является напряжением смещения: U= = -Uo.
Коэффициентом детектирования в рассматриваемом случае уместно назвать
отношение UJVm- Учитывая соотношения (7.9) и Un = 0, запишем:
^=[7=/L/m = cos0. (7.34)
7.7. Амплитудное детектирование
259
Рис. 7.13. Установившийся режим в схеме рис. 7.12
при гармоническом воздействии
Выходное напряжение диодного детектора можно определить, привлекая фор-
мулы (7.12) и (7.16) и записывая соотношение
ТТ Т D СЫТ /Ач сыт SiH0-0COS0
-[70 = IqR = SRUmyQ(Q) = SRUm
л
откуда следует уравнение
71
tg0 —0 = —-
RS
(7.35)
В силу малости угла отсечки tg 0 можно разложить в ряд Маклорена и, ограни-
чиваясь двумя первыми членами разложения
tg0=0+—+—
3 15
определить коэффициент детектирования через параметры элементов схемы, ис-
пользуя уравнение (7.35):
Зя , „ /Зя
0 =—, k = cos 0 = cos?—
RS л VRS
(7.36)
Если на вход диодного детектора поступает AM-сигнал, то при правильно
выбранных значениях R и С, то есть при выполнении условий (7.32), выходное
напряжение отслеживает мгновенный уровень амплитуды входного сигнала, тем
самым реализуется линейное детектирование. Возвращаясь к определенному соот-
ношением (7.31) коэффициенту детектирования, заметим, что при детектировании
AM-колебания, модулированного чистым тоном (7.29), размах (амплитуда) изме-
нения напряжения на выходе составит mUm cos 0, следовательно, применительно
к диодному линейному детектору определение (7.34)
U
, m выл _
k =-------= cost)
л mU
m
совпадает с определением (7.31).
260
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
Рассмотренная схема широко используется в радиоизмерительной технике
(«пиковый» детектор). Сочетание нелинейности (например, переход «эмиттер —
база») и НЧ-фильтра в виде параллельной КС-цепочки часто используется в не-
которых радиотехнических схемах (усилительных каскадах, автогенераторах) для
организации автоматического смещения
ЗАМЕЧАНИЕ 7.5------------------------------------------------------
При рассмотрении амплитудного линейного диодного детектора была при-
нята во внимание реакция нагрузки, что усложнило анализ, но позволило
получить уже не качественные, но достаточно строгие и применимые на
практике результаты.
ЗАМЕЧАНИЕ 7.6------------------------------------------------------
Важным параметром амплитудного линейного диодного детектора явля-
ется его входное сопротивление. Очевидно, что входное сопротивление Квх
схемы, работающей с отсечкой, непостоянно, меняется в течение периода
входного напряжения. Под Квх в данном случае понимают некоторую
усредненную величину — отношение амплитуды входного напряжения
к амплитуде первой гармоники входного тока. Используя соотношение
(7.13), можно получить:
Um 1 я
sum^ S71(e) Xisin2eY
I 2 )
а с учетом малости угла отсечки и соотношения (7.36)
л
I 3
ЗлКК
6л5
(7.37)
Аналогичный результат получается, если составить уравнение баланса
мощности, потребляемой детектором от источника сигнала, и мощности,
выделяемой на сопротивлении нагрузки:
U2 U2
т _ =
2Я„ " R
С учетом соотношения UJUm = 1 получаем формулу (7.37).
Синхронное детектирование. Рассмотоим преобразование суммы узкопо-
лосного АМ-сигнала С(0 cos со0г и гармонического колебания
мг(£) = Ur cos(co/ + <рг)
с помощью нелинейного двухполюсника с ВАХ i = а2и2.
7.8. Частотное и фазовое детектирование
261
Воспользуемся аналогией с полученным в разделе 7.4 результатом (7.22), вновь
обратив внимание на компоненты тока на суммарной и разностной частотах:
i(t) -.. ,a2U(t)Ut cos[(co0 + <n r)t + ф0 + фг ] + a2U(t)Ur cos[(co0 - <nr )t + <p0 - <pr ] +...
Приняв юг = <n0, получим, в частности, медленно меняющуюся составляющую тока:
/(с) = ... а2 U(f)Ur cos(<p0 - <pr)...,
совпадающую по форме с огибающей AM-сигнала, которую можно выделить, ис-
пользуя НЧ-фильтр.
Достоинством изложенного метода детект ирования, называемого синхронным,
является возможность повысить качество приема слабых сигналов на фоне шума.
Однако реализация этого метода затруднена необходимостью с высокой точностью
поддерживать соотношения <пг = соо и ф0 = фг = const, то есть синхронизм частот ге-
теродина и принимаемого сигнала.
7.8. Частотное и фазовое детектирование
Информация, передаваемая с помощью высокочастотного колебания с угловой
модуляцией, рассмотренного в разделе 2.3,
w(t) = U cos H'(t) = U cos{a>0t + ф( t)}, (7.38)
содержится в фазовой функции ф(() — компоненте полной фазы 'F(t). На выходе
частотного детектора должно быть напряжение
и (t) = S
° чл dt ’ (7.39)
на выходе фазового детектора
иФд(О = ^фд<р(О, (7.40)
где 5Ч д и 5ф д — крутизна преобразования частотного и фазового детекторов соот-
ветственно.
Рассмотрим нелинейное преобразование сигнала (7.38), для примера предпо-
ложив, что используется гармоническое модулирующее колебание1, то есть приняв
ф(0 = Р sin Qt.
Пусть ВАХ нелинейного двухполюсника аппроксимирована полиномом (7.26).
Оказывается, что ток
z(t) = a,U cos{co0t + psin fit} + a2U2 cos2 {<aot + Psin Qt} =
= ^a2U2 + ap cos{co0t + psinQt} + -^a2t/2cos2{<n0t + psinQt}
не содержит информационной низкочастотной компоненты 17 m sin Qt.
Напомним (см. раздел 2.3), что индекс угловой модуляции Р = Дсо/О, где До> — девиация частоты,
£2 — частота (при гармоническом законе угловой модуляции) модулирующего колебания. При
фазовой модуляции девиация фазы Д<р = р.
262
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
Напомним, что при аналогичном преобразовании AM-колебания соответству-
ющая компонента появляется (с некоторым искажением).
Было установлено, что приводящая к возникновению новых спектральных со-
ставляющих трансформация спектра происходит лишь при нелинейном преобразо-
вании, так что со спектральной точки зрения та или иная процедура детектирования
AM-колебания может быть сведена к переносу спектра ВЧ-сигнала в ооласть низких
частот. При рассмотренном нелинейном преобразовании постоянная составляющая
тока a2U2/2 действительно появляется, но информации о модулирующем сигнале
не содержит.
Это принципиальное положение: для детектирования колебания с угловой мо-
дуляцией только нелинейного относительно амплитуды колебания преобразования
недостаточно. Необходимы дополнительные преобразования. При этом следует
в силу соотношений (7.39) и (7.40) отдельно рассматривать фазовое и частотное
детектирование.
Синхронное детектирование ФМ-сигнала. По аналогии с анализом
синхронного детектирования AM-сигнала рассмотрим преобразование суммы
ФМ-сигнала (7.38) и гармонического колебания
ur(t) = UT cos(co£ + фг)
с помощью нелинейного двухполюсника с ВАХ i = а2иг. Воспользуемся аналогией
с полученным в разделе 7.4 результатом (7.22), обратив внимание на компоненты
тока на суммарной и разностной частотах:
i(t) =... a2UUr cos[(o>0 + йг )Г + <p(t) + <pr ] +
+a2UUr cos[(co0 - co.)t + tp(O - <pr ] +...
Приняв o>r = <n0, получим медленно меняющуюся составляющую тока:
i(t) =. ..a2UUt cos[<p(0 - <pr]... =
= aJJUT [cos tp(f )cos tpr + sin <p(0sin <pr ]...
Если <pr = л/2 и (p(0 изменяется в небольших пределах (sin х ~ х при малых х),
НЧ-фильтр выделит сигнал, пропорциональный модулирующему:
i(t) = ...а2 UUrq>(t)
Как и при синхронном детектировании AM-сигнала, реализация фазового син-
хронного детектора затруднена необходимостью жесткой стабилизации частоты и
фазы опорного генератора (гетеродина). Кроме того, накладывается требование
малого индекса модуляции.
Детектирование ЧМ-сигнала. Частотный детектор можно создать, используя
сочетание избирательной цепи, преобразующей ЧМ в AM, и амплитудного детек-
тора. Схема такого частотного детектора приведена на рис. 7.14. Если резонансная
частота контура отличается от средней частоты ЧМ-сигнала о>0, то амплитуда на-
пряжения на контуре будет (при девиации частоты Аго, не выходящей за пределы
линейного участка ската АЧХ контура) изменяться пропорционально мгновенной
частоте сигнала, то есть соответствовать закону модуляции (рис. 7.15). Получен-
7.9. Воздействие случайного стационарного сигнала
263
ный таким образом ВЧ-сигнал со смешанной амплитудно-частотной модуляцией
поступает на амплитудный линейный диодный детектор, реагирующий только на
изменения амплитуды входного сигнала.
Рис. 7.14. Простейший детектор сигнала с ЧМ
Рис. 7.15. Частотное детектирование
На практике используется много более сложных схем фазовых и частотных
детекторов, работающих на основе рассмотренных принципов или их сочетании.
Заметим также, что соотношения (7.39) и (7.40) указывают на возможность ис-
пользовать для детектирования ФМ-сигнала частотный, а для детектирования
ЧМ-сигнала — фазовый детекторы, применяя, соответственно, дополнительную
интегрирующую или дифференцирующую цепь, корректирующую выходной сигнал.
7.9. Воздействие случайного стационарного
сигнала на безынерционный
нелинейный элемент
Преобразование случайного стационарного сигнала (процесса) в линейной цепи
рассматривалось в разделе 4.3. Отмечалось, что определение корреляционных или
спектральных (что в силу теоремы Винера—Хинчина эквивалентно) характеристик
выходного процесса не связано с какими-либо принципиальными трудностями,
264
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
в то же время определение плотности вероятности выходного процесса представ-
ляет весьма сложную задачу, которая несколько упрощается лишь при нормальном
распределении процесса на входе цепи.
Напротив, анализ преобразования плотности вероятности случайного стацио-
нарного сигнала в безынерционной нелинейной цепи относительно прост. Основ-
ная трудность состоит в нахождении корреляционных характеристик выходного
процесса.
Плотность вероятности случайного стационарного процесса на вы-
ходе нелинейной безынерционной цепи. Как и в предыдущих разделах, при
анализе преобразований случайных процессов в нелинейных цепях под входным
процессом чаще всего подразумевается напряжение, а под выходным — ток, свя-
занные нелинейной ВАХ. Не забывая об этом, воспользуемся в данном разделе
обозначением нелинейного преобразования в общем виде: у = /(х).
В основу метода определения плотности вероятности р(у) процесса у на выходе
преобразователя у = /(х) положено соотношение (дифференциальное уравнение)
p(y)dy=p(x)dx, (7.41)
выражающее совпадение элементарных вероятностей (дифференциалов вероят-
ности) принятия случайными величинами х и у значений в окрестностях точек х
и у, соответствующих их функциональной связи у = f(x).
Из соотношения (7.41) с учетом неотрицательности плотности вероятности
следует:
dx 1
Р(у) = Р(*> — = р{х) (7.42)
dy \dy/dx\
Если зависимость у = /(х) неоднозначна, то формулу (7.42) необходимо запи-
сывать в виде
Р<У} = \Р{х)
dx
dy
„ , dx
+\p(x) —
dy
^2=№)
ИЛИ
(7-43)
где x, = f(y), x2 = /(г/) или у = /,(х), у = /2(х) — однозначные ветви рассматриваемой
функциональной зависимости.
Если в зависимость у = f(x) входит на некотором интервале соотношение
у = г/0 = const, хе [хрх2],
то выражение (7.43) дополняется слагаемым с дельта-функцией А5(у - г/0), учи-
тывающим вероятность пребывания х в интервале [хр х2], которой в соответствии
с формулой (7.41) отвечает вероятность принятия процессом у фиксированного
значения у0.
Методику определения р(у) удобно пояснять на практических примерах.
7.9. Воздействие случайного стационарного сигнала
265
Пример 7.1. Пусть у = ах3, а > 0. Задана равномерная плотность распределения
входного случайного процесса р(х) = ± ,хе [-1,1].
Функциональная зависимость однозначна, поэтому непосредственно исполь-
зуется выражение (7.42):
<«/) = "). ^ । = р(х)—Ц-.
|ау/ах| Зах
Необходимо, однако, чтобы/О) была представлена в виде функции от у явно.
Иногда это подчеркивают, вводя обозначенияру(у),рх(х). Для надлежащего пред-
ставления полученного результата необходимо, записав обратную функцию
х = ^у/а,
подставить ее в выражение для рх(х):
Ъуау
В рассматриваемом примере функция рх\уу / а) = 0,5 постоянна на интервале
[-1, 1], и последняя формула должна быть переписана с учетом интервала опре-
деления ру(у}.
^ау
Вне этого интервала ру(у) = 0.
Полученная функция автоматически удовлетворяет условию нормировки
]py{y)dy = -^=\y~Vidy = \.
Приведенные выкладки иллюстрирует рис. 7.16.
Рис. 7.16. Преобразование плотности вероятности (пример 7.1)
266
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
Функцию р (у) можно использовать для вычисления моментов процесса у.
Однако если ставится задача определения только моментов выходного процесса,
то целесообразно сразу пользоваться известной формулой
mk(y) = J fk(x)p(x)dx,
не обращаясь к вычислению ру(у).
Пример 7.2. Пусть у - ах2, а>0. Процесс х нормально распределен:
f хИ
Ч 2<У2'
р(х) =—/7Г
сг\/2п
(7-44)
С учетом неоднозначности заданного функционального преобразования пред-
ставим обратную функцию xl 2 = +^у/а и модуль производной:
^1,2
du
1
2^ау
Воспользовавшись представлением (7.43), получим:
/х 1 1
Ру(У) = Р. \|- Tj= + P> -\Г Тг
\Уа 2^ау L
или
1
У
2ав2г
----1 ехр _
Ру(У) = ' Gxy]27tay V
О,
2/6(0,°°),
г/й(0,°о).
Процесс у принимает только положительные значения (рис. 7.17).
Рис. 7.17. Преобразование плотности вероятности (пример 7.2)
7.9. Воздействие случайного стационарного сигнала
267
Пример 7.3. Рассмотрим заданное кусочно-линейной функцией (рис. 7.18) пре-
образование, которое можно гаписать следующим образом:
У = Угхе (—°°, х,),
у = О,хе [х„0),
у = ах, хе [0,х2],
г/ = г/2,хе (х2, °°).
Рис. 7.18. Преобразование плотности вероятности (пример 7.3)
На входе преобразователя действует нормальный процесс с распределением
(7.44). Всем значениям процессах из интервала х,) соответствует единственное
значение у = у{, что отражается слагаемым с дельта-функцией:
Д5(г/-г/1) = ^ jp(x)(h Sfo-y,).
Аналогично учитывается присутствие в нелинейном преобразовании участков
у - 0 и у = у2, компонента плотности распределения ри(у), соответствующая интер-
валу значений [0, х2] процессах, определяе гея по уже рассмотренной методике — на
интервале [0, х2] у = ах, поэтому
/ ч 1
Л О’) = -Л
а
1 [ у2
-----= ехр <-----
ааху2т1 ( 2а ох
у е [0, ах2].
Объединяя это выражение с суммой 5-функций'
Ру(У} = А£(у - l/i) + Л,5^) + А25(у - г/2),
получим формулу для полной функции плотности вероятности преобразованного
таким образом процесса (см. рис. 7.18).
Корреляционная функция случайного стационарного процесса на
выходе нелинейной безынерционной цепи. Очевидно, что ковариация,
или ковариапионная функция, случайного стационарного процесса на выходе не-
268
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
линейной цепи с характеристикой у = f(x) не зависит от времени и определяется
(см. разделы 3.3 и 3.4) как математическое ожидание произведения значений у
в моменты времени t и t + т, где t произвольно:
X (т) = M{y{t)y(t + т)} = М(уух) = уух, (7.45)
корреляционная функция
= уух - т\ = уу, - у2. (7А6)
В формулах (7.45) и (7.46) для значений процесса, отстоящих от значений у на
интервал времени т, введено обозначение г/т, усреднение по множеству реализаций
обозначено чертой над усредняемой функцией или выражением (усреднение по
времени, то есть по одной реализации, в главе 3 обозначалось угловыми скобка-
ми). Для непосредственного вычисления корреляционной функции выходного
процесса
= У У. ~У2 = f f f(x)f(xt)p(x,xx;t)dxdxz- j f(x)p(x)dx
(7-47)
необходимо располагать двумерной плотностью вероятности [3, 4] входного про-
цесса р(х, хх; т). Это обстоятельство и математические трудности вычисления
двойного интеграла в выражении (7.47) определяют сложность задачи определе-
ния корреляционной функции процесса на выходе нелинейного преобразователя.
Относительно просто определяется 7?у(т) в том случае, когда входной процесс
распределен нормально.
Приведем без вывода формулу для двумерной плотности вероятности нормаль-
ного стационарного процесса:
р(х,хт ;т) =-- .-----ехр-
2шт2 у/1 - г2
х2 + х2 - 2гхххх
2о2 (1-г2)
где г. = г(т) = 7?Дт)/ст 2 — коэффициент корреляции (нормированная к дисперсии
корреляционная функция) входного процесса [8].
Пример 7.4. Будем искать корреляционную функцию процесса на выходе ква-
дратичного преобразователя у=ах2 при нормально распределенном центрированном
(х = 0) входном процессе:
а2
х2 + х2 - 2г ххх
2СТх(1-^2)
dxdx, =
2ms2
х2 ехр-
•dx. (7.48)
7.9. Воздействие случайного стационарного сигнала
269
Замечая, что х2 -2г ххт = (хт -ггх)2 -гх2х2, и вводя обозначение хт - rx = X,
рассмотрим внутренний интеграл:
Здесь и далее использованы табличные интегралы [9]:
j ехр(-а2х2 )dx = —
о 2а
00 j
|хехр(-а2х2)<7х = -^—р
jх2exp(-a2 х')dx =
о
°° 1
j х3 exp(-a2x2 )dx =
o
Подставляя этот результат в выражение (7.48) и учитывая соотношение
гх(т) = /?х(т)/ст 2, получим окончательно для корреляционной функции выходного
сигнала:
Я (т) = a2o4 + 2а2ах4г2(т) = а2о 4 + 2a2R 2(т). (7.49)
Спектральная функция (спектр мощности) случайного стационарного
процесса на выходе нелинейной безынерционной цепи. Прямое опре-
деление спектра мощности IV(co) на выходе нелинейной безынерционной цепи
невозможно. Единственный способ — это применение прямого преобразования
Винера—Хинчина (см. раздел 3.6) к корреляционной функции выходного процесса:
lV(co) = j Я(т)е ;штс/т = 2|я(т)со5сот</т.
о (7.50)
Пример 7.5. Рассмотрим преобразование спектра мощности нормально рас-
пределенного узкополосного случайного стационарного процесса квадратичным,
у = ал2, преобразователем В качестве модели корреляционной функции входного
сигнала примем (см. раздел 3.7):
Я (г) = ах2гх(т) = ах2рх(т) cos со0т, (751)
где рх(т) — нормированная к дисперсии огибающая корреляционной функции про-
цессах, а со0 — центральная частота спектра мощности IV(co).
270
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
Последовательно подставляя (7.51) в формулу (7.49):
^(т) = а2стг4 + 2а2ог4рг2(т) cos2co0t =
= а2ох4 + а2ст/р12(т) + a2aj4pi2(T) cos 2<вот (7.52)
и (7.52) — в соотношение (7.50), получим выражение для спектра мощности вы-
ходного процесса:
Ц^(со) = 2ла2о45(со) + а2ст4 j р2(т)е';т«/т + а2о4 j р2(т)соз2о)0те“;тЛ,
или
^(®) = w^(co) + Wy нч(») + Wy вч(со) (7.53)
соответственно (рис. 7.19). Компонента W^co) (5-функция на нулевой частоте)
отвечает постоянной составляющей, компонента 1У нч(к>) — низкочастотной со-
ставляющей, компонента IV вч(со), концентрирующаяся вокруг частоты 2<в0, — вы-
сокочастотной составляющей выходного процесса. Сравнивая выражения (7.53)
и (7.7), легко усмотреть аналогию между преобразованием нелинейной цепью
узкополосного (гармонического) детерминированного и случайного сигналов —
появление новых спектральных составляющих, мультипликацию спектра.
ЛИуВч(<£>)
Zcoq <о
Рис. 7.19. Спектр мощности на выходе квадратичного преобразователя
Контрольные вопросы и задания
1. Какие элементы электро- и радиотехнических цепей называются нелинейными?
Чем они отличаются от линейных элементов?
2. Назовите известные вам методы аппроксимации характеристик нелинейных
элементов. В каких случаях их целесообразно использовать?
3. Дайте определение понятия «угол отсечки». Что такое коэффициенты Берга
и функции Берга?
4. Запишите выражение для расчета угла отсечки. В каких пределах он может из-
меняться? Может ли данное выражение использоваться при полиноминальной
аппроксимации характеристики нелинейного элемента? Почему?
5. Изобразите форму тока, протекающего через нелинейный резистор, если зна-
чения угла отсечки равны соответственно, 0; л/2; л.
Задачи
271
6. Изобразите общую схему нелинейного преобразования радиосигналов и по-
ясните назначение ее элементов.
7. Качественно изобразите амплитудную спектрограмму тока нелинейного элемента
с квадратичной характеристикой при воздействии на его вход бигармонического
напряжения.
8. Как можно получить колебание с амплитудной модуляцией? Изобразите прин-
ципиальную схему простейшего амплитудного модулятора.
9. Что такое гетеродинирование? Как оно реализуется с помощью нелинейного
элемента?
10. В чем суть принципа квадратичного детектирования сигналов с амплитудной
модуляцией?
И. В чем суть принципа линейного детектирования амплитудно-модулированных
колебаний?
12. Относится ли линейное детектирование амплитудно-модулированных колебаний
к классу линейных преобразований сигналов? Почему?
13. Изобразите схему амплитудного диодного детектора и объясните принцип его
действия.
14. Как найти плотность вероятности случайного сигнала на выходе нелинейного
безынерционного звена с взаимно однозначной характеристикой?
Задачи
Задача 7.1
Вольт-амперная характеристика (ВАХ) нелинейного элемента представлена пара-
болой i = a0 + а^и + а2п2 при и > 0. Рабочая точка выбрана при Ui=El> 0. На нели-
нейный элемент подано гармоническое напряжение u(f) = Um cos coof, причем Um<Et.
Определить параметры нелинейного элемента: крутизну ВАХ — статическую So,
динамическую 5Д, по первой гармонике 5! и сопротивления — г0, гд и гг
Задача 7.2
ВАХ нелинейного элемента имеет вид i = 2 и3 - 40 и2 + 400 и (напряжение
в вольтах, ток в миллиамперах). На нелинейный элемент подано напряжение
u(£) = Uo + 2 cos(tt>o0. Найти зависимость амплитуды первой гармоники тока от
напряжения смещения Uo.
Задача 7.3
ВАХ нелинейного элемента аппроксимируется зависимостью г - аи2 при и > 0
и i = 0 при и < 0. На вход этого элемента подан сигнал u(t) = Е + Um cos (o0t. Опре-
делить отношение амплитуд токов первой и второй гармоник при значениях
E/Um, равных 0 и 1.
272
7. Преобразования радиосигналов в нелинейных радиотехнических цепях
Задача 7.4
К нелинейному элементу, характеристика которого аппроксимирована ломаной
прямой (1/н = -20 В, 5 = 4 мА/B), приложено напряжение u(t) = Uo + 20 cos co0t.
Определить, при каком смещении Uo амплитуда второй гармоники тока макси-
мальна. Найти ее.
Задача 7.5
Схема модулирующего устройства изображена на рис. 7.20. Зависимость тока
в цепи от напряжения на зажимах АБ задана уравнением i = би + 0,12 и1 (напряже-
ние в вольтах, ток в миллиамперах). Напряжение на зажимах генератора Г, имеет
частоту 4 МГц, напряжение на зажимах Г2 — частоту 300 Гц. Найтг амплитуду на-
пряжения на зажимах генератора Г2, при которой коэффициент модуляции первой
гармоники тока равен 10 %. Какими свойствами должен обладать фильтрующий
элемент Ф, который производит выделение АМ-колебаний?
Рис. 7.20. Схема для задачи 7.5
Задача 7.6
Возможна ли амплитудная модуляция в схеме, содержащей нелинейный элемент,
характеристика которого задана уравнением i=bx + b2u + Ь3и3, причем рабочая точка
соответствует и = 0?
Задача 7.7
ВАХ нелинейного элемента аппроксимирована как i = 2и + 0,1м2 (ток в милли-
амперах, напряжение в вольтах). На нелинейный элемент подается напряжение
u(t) = 5 + 2 cos(2n/0r) + х cos(2nF0t), где/0 = 1 МГц и Fo = 1 кГц. При каком напряже-
нии модулирующего сигнала х коэффициент модуляции тока будет равен 20 %?
Задача 7.8
На нагрузке амплитудного линейного диодного детектора (см. рис. 7.12) необходимо
получить напряжение звуковой частоты с амплитудой 1 В при коэффициенте мо-
дуляции входного напряжения 40 %. Какой должна быть в этом случае амплитуда
несущей АМ-сигнала, поданного на детектор, если для ВАХ диода используется
кусочно-линейная аппроксимация с параметрами UH = 0, S = 2 мА/B, а сопротив-
ление нагрузки R = 500 кОм?
Задачи
273
Задача 7.9
На нелинейный элемент с характеристикой у = ах подан случайный процесс x(t)
с плотностью вероятности
2А’
О,
|х| < А,
|х| > А.
Найти плотность вероятности ру(у) процессаy(t). Построить график ру(у)-
10 №675
Р.(*) =
8. Генерирование гармонических
колебаний
В разделе 4.7 при рассмотрении линейных цепей с обратной связью было показано,
что при наличии положительной обратной связи цепь может стать неустойчивой
и начать генерировать незатухающие колебания. В данной главе этот режим работы
цепей рассматривается более подробно.
8.1. Автоколебательная система
Обобщенная схема ус тройства с обратной связью показана на рис 8.1. Здесь КПП —
канал прямой передачи, являющийся усилителем с комплексным коэффициентом
передачи К(со), КОС — канал обратной связи, обычно представляющий собой
пассивный четырехполюсник с комплексным коэффициентом передачи Р(<о).
Рис. 8.1. Усилитель с цепью обратной связи
Для коэффициента передачи устройства с обратной связью в целом в разделе 4.7
было получено выражение
К'(со) = ____
^внеш (®) 1 - К(со)р(<в) (81)
Если
К(со) = К(со)е'ф‘<% Р(со) = р(ю)е;ф’(“), (82)
то (8.1) можно переписать в форме, удобной для классификации видов обратной
связи:
К'(со) =-----------------------------------е7’’*<ш>
1 - К(со)р(со)ехр|;|фк (ю) + ср^щ)]}
8.1. Автоколебательная система
275
В частности, если ф/о») + <рр(со) = 2for где k = 0, ± 1, ±2..., то есть сигналы обратной
связи и входной складываются синфазно, то
1 1 1-К(го)р(со)
и обратная связь называется положительной (ПОС).
При Х(©)р(со) -> 1 имеем |Х',(со)| -> оо — устройство находится на границе
устойчивости, при Х(со)Р(со) > 1 устройство становится неустойчивым и следует
предположить возможность возникновения в нем колебаний.
При рассмотрении условий устойчивости линейной цепи (см. раздел 4.8) подчер-
кивалось, что возникновение в ней нарастающих собс гвенных колебаний возможно
лишь тогда, когда в составе цепи кроме пассивных R, L, С-элементов содержатся
активные элементы, передающие в цепь часть энергии от внешних источников. Рас-
пространенной моделью способного отдавать энергию активного элемента служит
резистор с отрицательным сопротивлением.
Схема на рис. 8.2, содержащая активный элемент (усилитель) и охваченная по-
ложительной обратной связью (внешний входной сигнал на схему, изображенную
на рис. 8.1, не подается, Йвнсш = 0), является обобщенной схемой автогенератора, то
есть автоколебательной системой; входным сигналом для усилителя КПП служит
выходной сигнал цепи КОС.
Рис. 8.2. Автоколебательная система
В разделе 4.7 анализировалась охваченная обратной связью активная линейная
цепь, что предполагает независимость К (го) от уровня (амплитуды) поступающего
на усилитель сигнала. Приступая к изучению автоколебательных систем, необхо-
димо сразу предположить наличие такой зависимости. В противном случае невоз-
можно ставить вопрос о стационарном режиме работы автоколебательной системы:
возникающие в ней (по тем или иным причинам) при ПОС колебания, очевидно,
должны были бы иметь бесконечно возрастающую амплитуду.
Рассмотрим этот вопрос подробнее, используя в качестве источника энергии
модель резистора с отрицательным сопротивлением. В автоколебательной системе,
находящейся в стационарном режиме, имеет место энергетический баланс: рас-
ходуемая в ней энергия Е должна равняться доставляемой отрицательным сопро-
тивлением энергии Е_. Если £+ > Е_, колебания в системе затухаюл, если Е+ < Е ,
избыток получаемой от отрицательного сопротивления энергии идет на увеличение
амплитуды колебаний.
276
8. Генерирование гармонических колебаний
Пусть система составлена из некоторого колебательного контура с потерями
и отрицательного сопротивления R_ (рис. 8.3). Контур является линейной системой,
и потребляемая им энергия Е+ растет пропорционально квадрату амплитуды тока
контура 1^ (рис. 8.4): Е (1^). В случае линейности R отдаваемая им энергия Е_
также пропорциональна 2^, и в зависимости от соотношения угловых коэффици-
ентов прямых Е+(1^) и Е (1^), может иметь место один из трех случаев:
□ k+ = k_ (баланс Е+ = Е обеспечен при любой амплитуде 2^);
□ k+<k- UnJ. неограниченно возрастает, так как сообщаемая контуру энергия Е_
всегда больше энергии потерь £+);
□ k^>k_ (колебания не возникают).
Рис. 8.3. Колебательный контур с отрицательным сопротивлением R
Рис. 8.4. Энергетический баланс в колебательном контуре с Я
Очевидная неудовлетворительность линейной модели эквивалента источника
энергии приводит к единственно правильному заключению: колебания с устано-
вившейся конечной амплитудой возможны только в нелинейной системе. На рис. 8.4
показан возможный вид кривой Е_ ). Если в начале системы координат k+ < k_,
система должна «самовозбудиться», колебания должны возникать в ней, начиная
с амплитуд практически нулевого, флуктуационного уровня, без внешнего воз-
действия. Установившаяся амплитуда колебаний определяется точкой пересечения
линий Е+ и Е_ (энергетический баланс, стационарный режим). Продолжая рассма-
тривать систему под «энергетическим» углом зрения, заметим, что соответствую-
щая этой точке амплитуда устойчива, поскольку при случайном уменьшении
амплитуды возникает неравенство £_ > Е+, стимулирующее рост 2^, при увеличении
амплитуды возникает неравенство Е+ > Е , стимулирующее снижение Imk.
8.2. Баланс амплитуд и баланс фаз
277
8.2. Баланс амплитуд и баланс фаз
Пусть автоколебательная система (см. рис. 8.2) возбуждена и находится в стацио-
нарном режиме генерации гармонического сигнала на частоте юг; входным сигналом
с комплексной амплитудой Ubx для усилителя КПП служит выходной сигнал цепи
КОС с комплексной амплитудой
К(сог)Р(сог)Йвк=Й.
Следовательно, в стационарном режиме выполняется условие
(8.3)
Из этого условия, используя представление (8.2), получим:
К(юг)р(юг) = 1, (8.4)
<рк(сог) + ФрС0^) = k = 0, ±1, ±2... (8.5)
Соотношения (8.4) и (8.5) определяют так называемые баланс амплитуд и баланс
фаз соО1ВетС1’венно, характеризующие стационарный режим работы автогенератора
с внешней обратной связью: необходимо, чтобы на генерируемой частоте полное
усиление при обходе кольца обратной связи составляло единицу (баланс ампли-
туд), а полный фазовый сдвиг при обходе кольца обратной связи был равен 0 или
кратен 2л (баланс фаз). Полученные результаты соответствуют и выражению для
коэффициента передачи цепи с обратной связью (8.1). В самом деле, если предпо-
лагается существование режима, при котором мвнеш(0 = 0, а uabix(f) * 0, необходимо
принять К'(о>)—>°°, и следовательно, К(со)Р(а>) —> 1, го есть получаются условия
(8.3-8.5).
Коэффициент передачи пассивного четырехполюсника КОС Р не зависит
от амплитуды колебаний, поэтому соотношение (8.4) можно использовать для
определения установившейся амплитуды колебания. Установленная в разделе 8.1
нелинейность автоколебательной системы проявляется здесь снижением модуля
коэффициента передачи K(Uw, сог) (коэффициента усиления), происходящим
параллельно с нарастанием амплитуды колебаний. Когда коэффициент усиления
достигнет значения
дальнейший рост амплитуды колебаний прекратится (рис. 8.5).
K(Um, ®r)f
1/P(cor)
О и'вхО tXx
Рис. 8.5. Баланс амплитуд в автоколебательной системе
278
8. Генерирование гармонических колебаний
П ри подаче питания на схему, то есть в момент, когда 1/вх = 0, самовозбужде-
ние автоколебательной системы может произойти, если К(0, со)Р(ю) > 1. При
К(0, <о)Р(со) < 1 самовозбуждения не будет — нет необходимой компенсации потерь
(рассмотренный в разделе 8.1 случай Е+ > Е ).
8.3. Возникновение колебаний
в автогенераторе
Рассмотрим схему резонансного усилительного каскада на полевом транзисторе
(рис. 8.6). Параллельный колебательный контур — нагрузка каскада — индуктивно
(катушка связи LCB) связан с цепью стока. Выходной сигнал усилителя снимается
с емкости С. При непосредственном соединении выхода каскада с его входом
(затвором транзистора) получается один из возможных вариантов трансформа-
торной схемы LC-автогенератора (рис. 8.7), которую чаще всего используют для
теоретического анализа.
Рис. 8.6. Резонансный усилитель с трансформаторной связью
Рис. 8.7. LC-автогенератор с трансформаторной связью
Выбрав произвольное направление тока колебательного контура гк(Г), запишем
уравнение Кирхгофа:
u + L^ + ri +М^- = 0,
dt к dt
(8.6)
где и = u(t) — напряжение на конденсаторе (затворе транзистора), i = i(t) — ток
стока. Знаки «±» перед слагаемым M(di/dt) отвечают согласному или встречному
включению индуктивностей контура L и катушки связи ZCB соответственно.
8.3. Возникновение колебаний в автогенераторе
279
Используя следующие соотношения:
□ гк = C(du/dt\,
□ i = Su (справедливо при предположении линейности ВАХ транзистора, S — кру-
тизна линейной ВАХ);
□ со0 = 1/4LC (формула Томсона для резонансной час готы контура без потерь),
приведем уравнение (8.6) к виду
d2u
dt2
г + MS^
L~ LC )
du 2 A
Л+“"“=о-
(8.7)
Уравнение (8.7) — линейное однородное дифференциальное уравнение 2-го
порядка с постоянными коэффициентами. Введем обозначение
г MS „
— ±--= 2а
L LC
и для дифференциального уравнения
d2u ~ du 2 а
—- + 2а— + агм = О
dt2 dt 0
(8-8)
(8.9)
запишем характеристическое уравнение
р2 +2а^ + со^ =0.
Заметим, что при анализе пассивного колебательного контура с потерями в его
уравнении состояния, формально совпадающем [4] с уравнением (8.9), параметр
а = г/(2£). Для высокодобротных контуров обычно выполняется условие
_ Q >;> |
г г
или со0» а, поэтому корни характеристического уравнения записывают в виде
Аг = -« ± >7®о-а2 = "« ± >Р = “а ± А >
а общее решение уравнения (8.9) — как
w(t) = Ae"cos(copZ + <p0). (8.10)
Постоянные интегрирования А и <р0 решения (8.10) определяются начальными
условиями.
Для пассивной цепи а = г/(2£) > 0 и (8.10) определяет затухающее колебание.
В рассматриваемом случае условием нарастания (неограниченного) амплитуды
колебаний или условием самовозбуждения автогенератора будет введенное соот-
ношением (8.8) неравенство а < 0:
А^<0,
L LC
280
8. Генерирование гармонических колебаний
что возможно лишь при отрицательном знаке перед MS/(LC). Этот знак опреде-
ляется знаком взаимной индуктивности М, следовательно, для самовозбуждения
автогенератора необходимо встречное включение катушек L и £гв. Условие а < О
удобно представить в виде
MS
(8.И)
С учетом знака а для пассивного контура соотношение (8.11) естественным об-
разом приводит к такой трактовке роли транзистора (активного элемента) в схеме
£С-автогенератора: в контур вносится отрицательное активное сопротивление,
компенсирующее собственные потери контура, что согласуется с качественным
анализом в разделе 8.1.
Предположение о линейности ВАХ транзистора позволяет сформулировать
условие самовозбуждения (8.11), но не дает возможности анализировать стацио-
нарный, установившийся оежим работы автогенератора.
8.4. Стационарный режим работы
автогенератора
Теперь сделаем предположение о нелинейности ВАХ транзистора / = /(w). Вернемся
к уравнениям (8.6) и (8.7) и заменим слагаемое Мdi/dt= MS du/dt на
dt du dt
то есть используем введенную в разделе 7.2 дифференциальную, зависящую от
напряжения на затворе крутизну 5Д = df/du. Тогда уравнение (8.7) преобразуется:
d2u
г М df }du 2 л
--------т~ -г- + а>п« = О.
L LC du dt 0
(8.12)
Уравнение (8.12) — нелинейное однородное дифференциальное уравнение 2-го
порядка, общие методы решения которых неизвестны. В математической физике
решение подобных уравнений ищут, опираясь на физические предпосылки, свя-
занные с особенностями исследуемого объекта.
Метод укороченного уравнения. В рассматриваемом случае исходным
пунктом может быть решение (8.10). u(t) выделяется на высокодобротном контуре,
амплитуда колебаний U(t) медленно (относительно сорГ) изменяется. Это позволяет
представить предполагаемое решение уравнения (8.12) следующим образом:
u(t) = U(t) cos со0Г, (8.13)
пренебрегая несущественной в данном случае начальной фазой и приняв на осно-
вании неравенства (О0» а (см. раздел 8.3) сор ~ со0.
8.4. Стационарный режим работы автогенератора
281
Используя представление (8.13), определим производные:
Ju dU
---=-----COS СО7 - wnU sincont,
dt dt oo
J2u d2U ndU . 2r7
--- =----COSCO, Г - 2—— CO, SinOLt - wJ cos co, t.
dt2 dt2 dt 0 0 0
Учитывая медленность изменения огибающей U(t), запишем неравенство
dU
dt
TJd
U—coswnt
dt
= <oQU
max
и, сделав на основании неравенства приближения
du ТТ . — ~ -OinU sin (07, dt 0 0 (8.14)
du dU 2 r dt2 dt 0 0 0 0 (8.15)
подставим выражения (8.14) и (8.15) в уравнение (8.12):
dU l(r М df\ п
dt 2{L LCdu) (8.16)
Уравнение (8.16) — это так называемое укороченное (Л-го порядка) дифференци-
альное уравнение, описывающее процессы в LC-автогенераторе с высокодобротным
контуром.
Средняя крутизна. Производная dj/du является дифференциальной кру-
тизной 5д нелинейной ВАХ активного элемента (транзистора). В стационарном
режиме при некоторой фиксированной амплитуде Uток стока можно представить
в виде аналога ряда (7.7):
i(t) = f{u(t)} = IQ + Il cos co07 +12 cos 2co0t + ... = /0 + 7, cos co0t (8.17)
(в силу предположения о высокой добротности колебательного контура будем
учитывать только постоянную состав зяющую и первую гармонику). Тогда с учетом
выражений (8.13) и (8 17) производная будет равна
dl^dl /du s
du dt! dt -co0(7sinco0( U д
Дифференциальная крутизна, связывающая амплитуду первой гармоники тока
стока (коллектора, анода и т. д.) и амплитуду напряжения на затворе (базе, сетке)
активного элемента автогенератора, называется средней крутизной ВАХ, или кру-
тизной по первой гармонике'.
(8.18)
282
8. Генерирование гармонических колебаний
Укороченное уравнение (8.16) с учетом формулы (8.18) принимает вид
dU 1[г
dt+2[L LC
-^LSl(U)\u = 0.
(8.19)
Стационарный режим. Стационарный режим характеризуется установив-
шимся, постоянным значением амплитуды UCT = const и dU^/dt = 0.
Следовательно, в стационарном режиме из уравнения (8.19) вытекает соот-
ношение
SX(U ) = 0,
L LC 1 ст'
определяющее среднюю крутизну в рабочей точке:
S(U„) = —
14 ст' м
(8.20)
и (при известной функции i = f(u)) значение (значения) UCT.
8.5. Мягкий и жесткий режимы
самовозбуждения
В зависимости от положения рабочей точки на ВАХ активного элемента автогене-
ратора возможны два варианта поведения функции S^U). Если средняя крутизна
монотонно убывает с увеличением амплитуды управляющего напряжения, то
говорят, что генератор работает в мягком режиме самовозбуждения (рис. 8.8, а).
На этом же рисунке проведена так называемая линия (прямая) обратной связи —
горизонтальная линия с ординатой rC/Mv Единственная точка пересечения кривой
5j(C0 и прямой гС/М{ определяет амплитуду стационарных колебаний {7ст, как
следует из соотношения (8.20).
б
Рис. 8.8. Зависимость средней крутизны ВАХ от амплитуды входного напряжения:
а — при мягком режиме самовозбуждения; б — при жестком режиме самовозбуждения
Если же кривая 5,( U) представляет собой (рис. 8.8, б) немонотонную функцию,
то речь идет о жестком режиме самовозбуждения. В этом случае возможны стаци-
онарные режимы с амплитудами 17ст1 и Uct2.
8.5. Мягкий и жесткий режимы самовозбуждения
283
Устойчивость стационарного режима. Устойчивость стационарного ре-
жима — это способность автоколебательной системы при происходящих по тем
или иным причинам малых отклонениях амплитуды генерируемых колебаний от
значения Urт возвращать амплитуду к этому значению.
Представим амплитуду в виде U = U^ + MJ, где AU — малое изменение амплитуды,
и подставим эту сумму в укороченное уравнение (8.19):
^^ + ll7“7F[5‘(^) + AA(/]!(^+ACZ) = 0' (8'21)
at LC J
Здесь функция St(U) в силу предположения о малости АП аппроксимирована
в окрестности Ц.т отрезком прямой:
где А - dSjdJU\ является угловым коэффициентом касательной к графику St(U)
в точке U = Ur:T.
Используя формулу (8.20), преобразуем уравнение (8.21):
^) + 1[_^дС/{С/ст+(АС/)2} = 0,
at 2^ LC J
откуда, пренебрегая слагаемым (ALT)2, получим:
<7(ДП) AMU^ (8.22)
dt 2LC
Из уравнения (8.22) следует, что если коэффициент А < 0, то при увеличении
U (MJ > 0) производная d(AU)/dt < 0, при уменьшении U (AU < 0) d{^U)/dt > 0,
то есть при любых флюктуациях U автоколебательная система стремится к восста-
новлению значения U = UCT. Иначе говоря, при А < 0 стационарный режим является
устойчивым:
^><0.
dll
Легко убедиться, что при А > 0 имеет место неустойчивый стационарный режим.
Особенности мягкого и жесткого режимов самовозбуждения. Для
подробного анализа режимов самовозбуждения, кроме рис. 8.8, а и б, используем
графики на рис. 8.9, а и б. Здесь приведены введенные в разделе 7.5 колебательные
характеристики' It =f(U) резонансного усилительного каскада (см. рис. 8.6), пре-
вратившегося при введении положительной обратной связи в рассматриваемый
автогенератор. Характеристики I,(U) связаны соотношением (8.18) с функциями
бДСТ). Мягкому режиму самовозбуждения соответствует рис. 8.9, а, жесткому —
рис. 8.9, б.
В разделе 7.5 колебательная характеристика связывала амплитуды входного и выходного напряже-
ний и записывалась в виде U = f(U ).
т вых •> ' т'
284
8. Генерирование гармонических колебаний
а
Рис. 8.9. Зависимость амплитуды первой гармоники тока стока от амплитуды входного
напряжения: а — при мягком режиме самовозбуждения; б — при жестком режиме
самовозбуждения
Линии обратной связи на рис. 8.9, а и б изображаются прямыми с угловым ко-
эффициентом rC/М, проходящими через начало координат:
1 М
Для добротности последовательного колебательного контура, используемого
в рассматриваемой схеме, в разделе 4.6 было приведено соотношение
со0гС
Введем понятие сопротивления обратной связи1 хсв = и представим
rC _ (itfC _ 1
м X„Q’
так что
I =—и = — и.
М хО
св
Напряжение на емкости контура (и на затворе транзистора) в Q раз больше
вводимой в контур ЭД С E=xaIi. Угловой коэффициент 1/(хсв0 линии обратной
связи на графиках (рис. 8.9, а и б) тем меньше, чем сильнее обратная связь. Пере-
сечение линии обратной связи и колебательной характеристики определяет точку
стационарного режима (7ст:
Tqu~=i^
св**-
Напомним, что в курсе теоретической электротехники комплексная амплитуда ЭД С, вносимой в цепь,
индуктивно (коэффициент взаимной индукции М) связанную с цепью с током I, определяется как
U = joMI = jxj.
8.5. Мягкий и жесткий режимы самовозбуждения
285
Условие устойчивости генерации в стационарной точке при анализе с помощью
колебательных характеристик записывается так:
rC 1 dl^U)
М~ xbQ> dU
(8.23)
Заметим, что до сих пор обсуждался режим генерации, соответствующий по-
ложению линии обратной связи при М = Mv
Рассмотрим другие возможные ситуации.
□ Если взаимная индуктивность М = М2 такова, что прямая гС/Мг на рис. 8.8, а
и б не пересекается с кривой S^U), rC/M2 > S}(U), то самовозбуждения нет.
Устойчивым состоянием автоколебательной системы является состояние с U= О
(состояние покоя), что следует и из рис. 8.9, атлб. Здесь [7 = 0 — единственная
точка пересечения, и условие (8.23) выполняется как при мягком, так и при
жестком режимах самовозбуждения.
□ При увеличении М от значения М2, соответствующего состоянию покоя,
в условиях мягкого режима самовозбуждения на графике появляется един-
ственная точка пересечения линии обратной связи гСЩ и кривой S{(U), соот-
ветствующая устойчивому (dS, /dU\ r < 0) стационарному режиму (рис. 8.8, а,
8.9, а). При этом точка U = 0 становится точкой неустойчивого состояния, из
которого система и переходит в состояние с амплитудой U= U^. При да тьнейшем
увеличении М (например, до значения М3) амплитуда колебаний возрастает.
□ При увеличении Мот значения М2, соответствующего состоянию покоя, в усло-
виях жесткого режима самовозбуждения на графиках появляются две (с абсцис-
сами Ucil и Uct2) точки пересечения прямой rC/Mt и кривой S\U) (рис. 8.8, б),
или, что то же самое, прямой I{ = U/(xCBQ) и кривой Ц(и) (рис. 8.9, б). Несмотря
на это, колебания не возникают. Причина этого выясняется при рассмотрении
графика (рис. 8.9, б): самовозбуждение невозможно, так как при М=МХ точка
[/= 0 остается точкой устойчивого состояния. Внешний толчок, возбуждение в
системе с помощью какого-либо внешнего генератора колебаний на резонансной
частоте с амплитудой [7т1 переведет автогенератор в положение неустойчивого
состояния. Амплитуда колебаний будет возрастать до значения Uci2 — точки
устойчивого стационарного режима генерации.
□ При дальнейшем увеличении М до значения М3 в условиях жесткого режима
самовозбуждения автогенератор возбудится-, линия обратной связи (рис. 8.9, б )
займет положение, при котором точка U = 0 станет точкой неустойчивого со-
стояния-.
1 'dl^U)
^Q< du
Амплитуда колебаний при этом будет возрастать от нулевого значения до зна-
чения Un3 — точки устойчивого стационарного режима генерации.
286
8. Генерирование гармонических колебаний
□ При уменьшении М от значения М3 генератор будет продолжать работать, ампли-
туда автоколебаний будет снижаться от значения 17ст3 до некоторого значения U,
удовлетворяющего уравнению
1 dl^U)
dU
Применительно к графику (рис. 8.9, б ) это означает совпадение угловых коэф-
фициентов линии обратной связи и касательной к колебательной характеристике
Ц(и). Применительно к графику (рис. 8.8, б) это означает равенство
л
dU
то есть линия обратной связи rC/М займет положение касательной к кривой
5,(17) в экстремальной точке. При дальнейшем уменьшении М генерация
срывается, амплитуда колебаний скачком паОает до нуля: в автогенераторе с
жестким режимом самовозбуждения колебания возникают и прекращаются при
различных значениях коэффициента обратной связи. Это явление называют
колебательным гистерезисом.
ЗАМЕЧАНИЕ 8.1 ------------------------------------------------------
Полезно сопоставить результаты проведенного анализа с материалом из
раздела 8.1, где тема самовозбуждения и устойчивости стационарного
режима работы автоколебательной системы рассматривалась в самом
общем виде, с «энергетической» точки зрения.
Зависимость режима автогенератора от выбора рабочей точки.
В начале раздела уже отмечалось существование такой зависимости и затем
анализировались мягкий и жесткий режимы самовозбуждения с привлечением,
в частности, графиков средней крутизны 5,(17). Рассмотрим возможное аналити-
ческое представление функции 5,(17): при аппроксимации ВАХ активного эле-
мента автогенератора рядом (7.2) или (7.3) эта функция, введенная в разделе 8.4,
является полиномом
3 5
5, (17) = а, +—a„U2 + — a .U* + ...,
/ 1 4 3 g 5
что вытекает из выражений (7.7) и (8.19).
Ограничиваясь первыми двумя членами полинома
5,(1/) = а,+4аз172 (8.24)
4
и сопоставляя (8.24) с рис. 8.8, аиб, легко усмотреть, что мягкий режим самовоз-
буждения реализуется при а3 < 0, жест кий режим — при а3 > 0.
8.6. Нелинейное уравнение автогенератора
287
Подобный подход можно использовать, связывая характер режима самовоз-
буждения с видом колебательных характеристик на рис. 8.9, а и б:
Ч 5
/, (U) = aU + —a3U3 + -a,U5 +...
14/1 4 3 8
Заметим, что более глубокий и точный ана тиз работы автоколебательных систем
(являющийся обычно предметом Kvpca радиопередающих устройств) часто требует
удержания в аппроксимирующем ВАХ полиноме не менее 3-4 членов ряда.
8.6. Нелинейное уравнение
автогенератора
Подход, использованный в разделе 8.4, где была введена средняя крутизна S^U),
учитывает нелинейность ВАХ транзистора лишь косвенно. Для получения пря-
мого аналитического решения укороченного нелинейного дифференциального
уравнения (8.19) используем приближение (.8.24) при а3 < 0, то есть будем искать
закон изменения во времени амплитуды U(t) в автогенераторе с мягким режимом
самовозбуждения. Уравнение приобретает вид
dU 1 г а}М
~dt+2\T~~LC
3a3MU2'
МС
и=о.
Будем полагать, что
П(О) = По, (8.25)
где Uo — сколь угодно малое, но конечное значение амплитуды колебаний в момент
времени t = 0 (граничное условие).
Введем обозначения:
11 а.М
а = - ——
2l LC L
|)=^<0
8LC
(с учетом условия а3 < 0).
Левую и правую части уравнения dU/dt= (а + $U2)Uумножим на U.
jjdU_=idlP_ = ^ ^2^2
dt 2 dt V P ’
и разделим переменные, в качестве которых выступают t и U'1'.
2(a + pt/2)(72
288
8. Генерирование гармонических колебаний
Представив левую часть полученного уравнения в виде суммы элементарных
дробей:
_ 1 ( f>dU2 _ dU^\ = 1 pH2 _ </(а + рП2)] =
га^а + рп2 U2 )2a[U2 а + pt/2 J ’
запишем решение:
1 1 ATI2
^-{1пП2 - 1п(а + р£72) + InA} = — In—L— = t,
2а 2а а + pt/
(8.26)
где In А — постоянная интегрирования. Определим А, используя граничное условие
(8.25):
—In AUo\=O,
2а а + рп2
откуда
(8.27)
Из (8.26) и (8.27) для U = U(f) следует:
(8.28)
При t —> оо амплитуда автоколебаний U стремится к стационарному значению:
(8.29)
ЗАМЕЧАНИЕ 8.2
В разделе 8.4 было получено соотношение S^U^) = rC/М, позволяющее
определить Z7ct при заданной ВАХ или колебательной характеристике
активного элемента.
Воспользуемся приближением (8.24): 5,([7) = + За3£72/4.
Приравнивая правые части выражений (8.20) и (8.24) при U = U^, сразу
находим значение
IrC/M-^
СТ v Заз
совпадающее с формулой (8.29).
8.7. Анализ схем LC-автогенераторов
289
Можно рассматривать это совпадение как косвенное подтверждение
справедливости результата (8.28).
8.7. Анализ схем LC-автогенераторов
Различают три основные разновидности схем LC-автогенераторов: трансформатор-
ная (рис. 8.7 и 8.10), один из вариантов которой (см. рис. 8.7) подробно обсуждался,
и трехточечные (транзистор подключен к трем точкам контура) индуктивная
(рис. 8.11) и емкостная (рис. 8.12) схемы.
Рис. 8.10. LC-автогенератор с трансформаторной связью
Рис. 8.11. LC-автогенератор (индуктивная трехточечная схема)
Рис. 8.12. LC-автогенератор (емкостная трехточечная схема)
Трехточечные схемы являются основой для разработки практически использу-
емых ZC-автогенераторов.
Несмотря на то что в разделах 8.3-8.6 анализировалась конкретная (см. рис. 8.7)
схема, основные результаты проведенного исследования процессов возникновения и
установления стационарной амплитуды являются общими, характ ерными для всех
290
8. Генерирование гармонических колебаний
ZC-автогенераторов (и не только для них). Под анализом схем в настоящем раз-
деле подразумеваются выяснение соотношения той или иной схемной реализации
автогенератора с общей схемой (см. рис. 8.2), а также формулировка требований
к параметрам элементов автогенератора, обеспечивающих самовозбуждение и вы-
полнение условий (8.4) и (8.5):
Х(шг)₽(Ч) = 1,
(Рк(юг) + (Рр(юг) = 2^л, & = 0, ± 1, ± 2...,
то есть баланса амплитуд и баланса фаз на частоте генерации со..
Резонансный усилительный каскад рассматриваемых схем соответствует КПП
структурной схемы (см. рис. 8.2). Выходное напряжение КПП есть напряжение на
колебательном контуре с комплексной амплитудой {7к. Четырехполюсник КОС в
явной форме не выделяется: напряжение обратной связи (управляющее напря-
жение) снимается либо с части контура (трехточечные схемы), либо с катушки
связи (трансформаторная схема, приведенная на рис. 8.10). Поэтому коэффициент
передачи КОС ищут, записывая отношение комплексных амплитуд напряжения
обратной связи й и напряжения на колебательном контуре U :
к
В ZC-автогенераторе (см. рис. 8.7) напряжение обратной связи совпадает с вы-
ходным (на емкости контура) напряжением КПП; для этой схемы сразу можно
записать p(to) = 1 и срр(о>0) = 0.
Предположим, что влияние на контур входного и выходного импедансов ак-
тивного элемента схемы учтено (активные части импедансов пересчитаны в со-
противления потерь, реактивные части импедансов — в реактивности контура),
иными словами, будем считать, что входное и выходное сопротивления транзистора
бесконечно велики. Тогда предстоящий анализ существенно упрощается и сводится
к расчету совпадающих с частотой генерации резонансных частот колебательных
контуров, а также фазовых и амплитудных соотношений между U и UK, то есть
к определению (3(со0). Необходимо также установить значение комплексного ко-
эффициента усиления (передачи) Х(со0).
Частота генерации. На резонансной частоте в параллельном колебательном
контуре [14] имеет место резонанс токов-, в контуре существует кольцевой ток
с комплексной амплитудой . Реактивные сопротивления ветвей равны по модулю
и противоположны по знаку. Отсюда вытекает извес тная формула
х/сод) + х2(ш0) + х3(со0) = 0, (8.30)
которой удобно пользоваться для определения резонансной частоты сложного ко-
лебательного контура (см. рис. 8.11,8.12). Здесь х*(со0) — реактивное сопротивление
k-ro элемента контура на резонансной частоте.
Воспользовавшись формулой (8.30), получим для резонансных частот:
□ контура схемы, приведенной на рис. 8.11
1
^Ll+L2)C
8.7. Анализ схем LC-автогенераторов
291
□ контура схемы, приведенной на рис. 8.12
Эквивалентная схема колебательной системы [14] автогенератора с транс-
форматорной связью (рис. 8.10) приведена на рис. 8.13. Знаки «плюс» и «минус»,
стоящие перед значением индуктивности М, учитывают установленную в раз-
деле 8.3 необходимость встречного включения катушек индуктивности конту-
ра Л и связи £св. Полная индуктивность контура схемы, показанной на рис. 8.10:
Z3KB = (I + A0 + (-M) = Z.
L + Л/ ^св + М
-м
Рис. 8.13. Колебательная система LC-автогенератора с трансформаторной связью
Следовательно, его резонансная частота
LC
Очевидно, что резонансная частота контура схемы (см. рис. 8.7) определяется
аналогично.
Коэффициент передачи цепи обратной связи
□ Трансформаторная схема (см. рис. 8.10). Управляющее (на индуктивности
£св и затворе транзистора) напряжение в соответствии с эквивалентной схемой
(рис. 8.13) снимается с индуктивности (-М). Присутствие индуктивности
£св + М несущественно в силу предположения о бесконечно большом входном
сопротивлении транзистора.
Ток индуктивной ветви, или кольцевой ток контура
I =
К
A1™ А1’
напряжение на индуктивности (-Л/)
7ш0£ к L
А, \ м т i* / \
^ю°)=-Т=Те ’ фр(1Оо)=л-
292
8. Генерирование гармонических колебаний
□ Индуктивная трехточечная схема (см. рис. 8.11). Кольцевой ток контура
к МД ’
напряжение на индуктивности £2
= (8.31)
j<bo Zj Д
(знак «минус» в (8.31) поставлен с учетом того, что относительно UK направле-
ния кольцевого тока /к в индуктивной и емкостной ветвях контура различны),
Р(«°) = -^ = ^л, <рр(со0) = л.
□ Емкостная трехточечная схема (см. рис. 8.12). Кольцевой ток контура
Д =j%Cfi3,
напряжение на емкости С2
P(«o) = -|L = 7Le,S’ <Мюо) = л-
с2 с2
Коэффициент усиления (передачи) КПП. В соответствии с представле-
нием (8.2)
Модуль коэффициента усиления резонансного усилителя на резонансной частоте
К(со0) определяют, привлекая введенное в разделе 8.4 выражением (8.18) понятие
средней крутизны
5,(Ю = ^
Л 7 LJ
и эквивалентного сопротивления контура Яэ; ток I. и напряжение U* синфазны
и связаны соотношением
Отсюда следует:
К(ш0) = ^ = М^ = 7?5(^) = ^Л- (8.32)
8.7. Анализ схем LC-автогенераторов
293
ЗАМЕЧАНИЕ 8.3-----------------------------------------------------
Формула (8.32) справедлива для всех рассматриваемых схем, однако
определение значения эквивалентного сопротивления контура для
индуктивной (схема Хартли) и емкостной (схема Колпитца) схем трех-
точечных автогенераторов при этом нуждается в уточнении (трансформа-
торная схема автогенератора, показанная на рис. 8.10, называется схемой
Мейснера).
В самом деле, при анализе схем рис. 8.11 и 8.12 необходимо принять во
внимание то обстоите тьство, что колебательный контур включен в схему
частично. Частичное включение параллельного колебательного контура
рассматривалось в разделе 4.6, где было показано, что эквивалентное со-
противление контура R' в этом случае определяется как
R' =a2R =а2рО,
Э Э г
где коэффициент включения а (см. рис. 4.18) есть
L L^+ L2
для схемы Хартли и
С, +С2
для схемы Колпитца.
Поэтому для трехточечных схем коэффициент передачи усилителя (КПП)
на резонансной частоте
К = -SpQa2,
коэффициент передачи канала обратной связи (КОС)
а
а петлевой коэффициент усиления
KP = pQ5a(l-a).
Баланс фаз. Как отмечалось в разделе 7.5, управляющее U и выходное (на сто-
ке транзистора) UK напряжения на резонансной частоте находятся в противофазе,
как в обычном резистивном усилительном каскаде с общим истоком [4]. Поэтому
(p^tOg) = л и для всех рассмотренных схем условие баланса фаз (8.5) выполняется:
Фк(“0) + Фр(«>о) = Зя-
Баланс амплитуд. Используя выражение (8.32) и найденные для модулей
КОС выражения, можно сформулировать требования, обеспечивающие баланс
амплитуд (8.4):
294
8. Генерирование гармонических колебаний
□ трансформаторная схема (см. рис. 8.10):
Х((о0)р((О0) = 517?эу = 1; (8.33)
□ индуктивная трехточечная схема (см. рис. 8.11):
5Д^- = 1; (8.34)
□ емкостная трехточечная схема (см. рис. 8.12):
5Д^ = 1. (8.35)
С2
При использовании полученных выражений следует помнить, что средняя кру-
тизна есть функция управляющего напряжения и баланс амплитуд устанавливается
в автогенераторе при некоторых определенных значениях U- Un и St( U) = 5/ Uct).
Замена знака «равно» знаком «больше» превращав т соотношения (8.33-8.35), как
отмечалось в разделе 8.2, в условия самовозбуждения (если батане фаз обеспечен).
Однако значение 5t при этом будет иным, например: = S/0).
Трансформаторная схема автогенератора (см. рис. 8.7). Здесь, как уже
отмечалось, управляющее напряжение U совпадает с выходным напряжением
Uc, и поэтому
P(to) = l, <Pp(CDo) = O.
Условия баланса амплитуд и баланса фаз для этой автоколебательной системы
обеспечиваются при
Х(ш0) = Х(со0) = 1.
Найдем комплексный коэффициент усиления (передачи) резонансного усили-
теля. схема которого была показана на рис. 8.6:
□ ток стока Д;
□ вносимая в колебательный контур ЭДС Е =
□ ток контура на резонансной частоте /к = jto0 MI/г,
□ напряжение на емкости контура (выходное напряжение усилителя)
j(£>nM I. ML
Ur = J—^---!- =--'- = U.
j(i>f)rC rC
Ток Д и напряжение U = UC синфазны. С учетом этого обстоятельства и фор-
мулы (8.18) получаем:
Х(ш0) = Х(ш0) = 5,^ = 1. (8.36)
гС
8.7. Анализ схем LC-автогенераторов
295
Выполнение этого условия одновременно обеспечивает и баланс амплитуд,
и баланс фаз. Условием самовозбуждения будет неравенство
Полезно сравнить условие (8.36) с выражением (8.20), определяющим стацио-
нарный режим работы аналогичного автогенератора.
Автоматическое смещение в автогенераторе. Обычно используемые
на практике ЛС-автогенераторы для повышения КПД работают с отсечкой тока.
При этом уменьшается постоянная составляющая тока истока (коллектора) и сни-
жается рассеиваемая на транзисторе мощность (аналогичными соображениями
объясняется использование резонансных усилителей мощности, как отмечалось
в разделе 7.5). Для работы с отсечкой необходимо обеспечить соответствующее
постоянное напряжение смещения на затворе, то есть установить рабочую точку
ВАХ. Однако час го оказывается, что оптимальное для повышения КПД смещение
ставит автогенератор в нежелательный режим жесткого самовозбуждения (это
обсуждалось в разделе 8.6).
Рис. 8.14. LC-автогенератор с цепью автоматического смещения
На рис. 8.14 приведен один из возможных вариантов схемы автогенератора
с автоматическим смещением, соответствующий эквивалентной «по переменной
составляющей» трансформаторной схеме (см. рис. 8.10). В цепь затвора включе-
на цепочка R3C3. Непосредственно после подачи питания Еп напряжение между
затвором и истоком близко к нулю, и рабочая точка находится на участке ВАХ
с максимальным значением средней крутизны Sv что соответствует мягкому режиму
самовозбуждения. Амплитуда колебаний возрастает, на затворе появляется управ-
ляющее напряжение и возникает ток затвора, постоянная составляющая которого
заряжает емкость Сз и смещает рабочую точку. Процессы в цепи затвора аналогичны
процессам в амплитудном линейном диодном детекторе, рассматривавшемся в раз-
деле 7.7. Роль диода играет промежуток «исток — затвор транзистора», ЯзС3-цепочка
является нагрузкой детектора. Смещение рабочей точки приводит к снижению 5,
и в итоге — к установлению стационарного режима генерации.
При этом смещении кривая средней крутизны S,(U) автогенератора, как правило,
приобретает вид, соответствующий жесткому (см. рис. 8.8, б) режиму самовозбуж-
дения. Очевидно, однако, что при срыве генерации но какой-либо причине в схеме
296
8. Генерирование гармонических колебаний
с автосмещением рассмотренный цикл самовозбуждения повторится и стационар-
ный режим установится вновь.
Использование автоматического смещения позволяет сочетать условия, благо-
приятные для запуска автогенератора (мягкий режим самовозбуждения), с энерге-
тически выгодным (отсечка тока стока) стационарным режимом.
8.8. ЯС-автогенераторы и автогенераторы
с внутренней обратной связью
Для использования на частотах ниже 103... 105 Гц ЛС-автогенераторы по ряду причин
оказываются неудобными (в частности, колебательный контур получается гро-
моздким и трудно перестраиваемым) На этих частотах широко (особенно в радио-
измерительной технике) используют ЯС-автогенераторы, представляющие собой
комбинацию резистивного усилителя (КПП) и пассивного ЯС-четырехполюсника
обратной связи (КОС).
Рассмотрим наиболее распространенные схемы ЯС-автогенераторов.
ЯС-автогенератор с трехзвенной цепочкой обратной связи. Схема этого
автогенератора приведена на рис. 8.15. Напряжение с комплексной амплитудой Uc
на сопротивлении нагрузки (на стоке транзистора) Rc находится в противофазе с
напряжением U на затворе транзистора (усилительный каскад с общим истоком),
поэтому <рк(©) = л. Следовательно, для выполнения условия баланса фаз ЯС-цепочка
должна обеспечивать 180°-ный фазовый сдвиг на частоте генерации Это требование
является определяющим при расчете параметров цепи обратной связи.
Если цепочка КОС составлена из трех одинаковых (как обычно и делается)
«интегрирующих» ЯС-звеньев (см. рис. 8.15), то ее комплексный коэффициент
передачи записывается в виде
Р(ю) = -г-----—т—р--------;-------т (8-37)
[5(соЯС)2 -1] + у[((оЯС)3 - бсоЯС]
Вывод этой формулы предоставляется читателю1. В соответствии с выражением
(8.37) 180°-ный фазовый сдвиг получается при частоте, отвечающей условию
юЯ0(й)Я02-6] = О.
Произведение (постоянная времени) RC определяет частоту генерации:
(8.38)
r RC
Подставив это значение в выражение (8.37), получим:
р(юг) = |р(юг)| = -^.
Распространенной ошибкой является попытка искать коэффициент передачи в виде р = Р’, где
р] — коэффициент передачи «элементарного» Г-образного ЯС-звена.
8.8. RC-автогенераторы и автогенераторы с внутренней обратной связью
297
В стационарном режиме модуль коэффициента передачи усилителя КПП должен
быть равен (баланс амплитуд):
К(со ) = —!—= 29.
г Р(Ч)
Условием самовозбуждения является неравенство Я(сог) > 29.
В подобном ЯС-автогенераторе можно использовать и цепочку, составленную
из трех «дифференцирующих» ЯС-звеньев. В этом случае частота генерации
ю,"яс7б’
(8.39)
а модуль коэффициента передачи усилителя КПП, обеспечивающий баланс ам
плитуд, не изменяется:
К(ю ) = —*—= 29.
г Р(ф)
Для перестройки генерируемой частоты используют ступенчатое переключение
резисторов и конденсаторов; плавную перестройку в ограниченном диапазоне ча-
стот чаще всего производят с помощью трех конденсаторов КОС, емкости которых
одновременно изменяют.
При определении коэффициента передачи Р(и) предполагают (как и в раз-
деле 8.7), что параметры КПП на работу ЯС-цепочки не влияют. Практически
формулами (8.37-8.39) пользуются, если выполняется неравенство
R » Я„,
где Яс — сопротивление в цепи стока транзистора.
ffC-автогенератор с мостом Вина. Эта распространенная схема
ЯС-автогенератора приведена на рис. 8.16. Баланс фаз здесь реализуется в самом
КПП, который может, например, представлять собой два последовательно вклю-
ченных усилительных каскада, каждый из которых поворачивает фазу на 180°. (На
рис. 8.16 изображена схема генератора на операционном усилителе (ОУ); сигнал
обратной связи поступает на неинвептириющий вход ОУ.) Мост Вина вносит на
частоте генерации нулевой фазовый сдвиг (заметим, что нулевой фазовый сдвиг
имеет место и при непосредственном соединении выхода и входа усилителя КПП,
298
8. Генерирование гармонических колебаний
однако условия баланса фаз соблюдаются при этом в широком диапазоне частот,
что для генератора гармонического колебания неприемлемо). Роль моста Вина
состоит в возможном ограничении диапазона частот, на которых условие баланса
фаз соблюдается.
Рис. 8.16. ЯС-автогенератор с мостом Вина
Если параметры КПП на работу ЯС-цепочки не влияют (или влияют слабо),
комплексный коэффициент передачи моста Вина имеет вид
₽(®) =
+ ; юСЯ-----—
Я «с, я.
X 1 г
Частота, на которой вносится нулевой фазовый сдвиг, определяется из уравнения
(oC2Rt -
1
coCj.R2
= 0,
откуда
1
“г = /
yjRlR2ClC2
Чаще всего используют одинаковые резисторы и конденсаторы: Я, = Я2 = Я,
С1 = С2 = С. Тогда на частоте генерации сог = 1/(ЯС) коэффициент передачи
Р(сог) = 1/3. Отсюда вытекают условия баланса амплитуд и условия самовозбуж-
дения. АЧХ и ФЧХ моста Вина приведены на рис. 8.17.
Преимуществом рассматриваемой схемы автогенератора является меньшее
число перестраиваемых элементов (используют спаренный конденсатор пере-
менной емкости).
В ЯС-автогенераторах фильтрация высших гармоник осуществляется цепью об-
ратной связи. По очевидным причинам эта фильтрация выражена гораздо слабее, чем
в ЯС-автогенераторах, поэтому приходится уделять особое внимание обеспечению
гармонической формы генерируемого сигнала. Простейшим решением оказывается
ограничение уровня генерируемого сигнала, и поэтому ЯС-автогенератор является
маломощным. Мощность выходного сигнала повышают, включая дополнительный
усилитель.
8.8. RC-автогенераторы и автогенераторы с внутренней обратной связью
299
Для автоматического ограничения уровня выходного сигнала в схему RC-авто-
генератора вводят отрицательную обратную связь, для чего часто используют
терморезистор (Rt на рис. 8.16), через который инвертирующий вход ОУ соединен
с общим проводом (шиной). Сопротивление терморезистора растет < ростом его
температуры. Если амплитуда генерируемого сигнала по какой-либо причине воз-
растает, то увеличивается уровень напряжения на инвертирующем входе ОУ, что
приводит к снижению уровня генерируемого сигнала.
Автогенераторы с внутренней обратной связью. В разделе 8.1 использо-
валась модель источника энергии в виде гипотетического «отрицательного сопро-
тивления», компенсирующего потери колебательного контура. В разделе 8.3, где
обсуждался автогенератор с внешней обратной связью, понятие отрицательного
активного сопротивления приобретает более предметный характер, но остается
всего лишь одной из возможных трактовок полученных результатов.
Существуют, однако, электронные приборы с ВАХ i = /(«), имеющей «падаю-
щий» участок, то есть участок, на котором di/du < 0. При этом и du/di < 0, то есть
дифференциальное сопротивление прибора на этом участке отрицательно. Таким
прибором, в частности, является туннельный диод; говорят, что он имеет N-образную
ВАХ (рис. 8.18). При подключении такого прибора к колебательному контуру может
возникнуть генерация.
Рис. 8.18. ВАХ туннельного диода
На рис. 8.19 приведена схема автогенератора с внутренней обратной связью на
туннельном диоде, на рис. 8.20 — эквивалентная ей «по переменному току» схема.
300
8. Генерирование гармонических колебаний
Оказывается, что приведенная на рис. 8.3 схема, которая в разделе 8.1 рассматрива-
лась как иллюстрация к качественному анализу, с добавлением некоторых вспомо-
гательных элементов становится, по существу, используемой на практике схемой.
Рис. 8.19. Автогенератор на туннельном диоде
Рис. 8.20. Эквивалентная схема автогенератора на туннельном диоде
Источник питания Еп устанавливает рабочую точку на участке ВАХ с отрица-
тельным дифференциальным сопротивлением. По отношению к отрицательному
сопротивлению R напряжение на контуре рассматривается как ЭДС, и ток через
диод определяется как i = -u*/R_. Напряжение на контуре и токи связаны очевид-
ными соотношениями
du di,
i = i, + i„ ic =C-f-, и = r i +L—^.
д L c c dt dt
Используя эти формулы, можно получить:
= iL +r^C~h + LC~T^-
L K dt dt2
В то же время,
ГЛ
1
г =——и
д R
J.
R
dt
Сопоставление правых частей этих уравнений приводит к дифференциальному
уравнению
d\ (гк 1 }diL i + T\/R-- n
dt2 CRJdt LC L
Контрольные вопросы и задания
301
Легко провести аналогию между этим уравнением и уравнением (8.7), подроб-
но исследованным в разделе 8.3. Воспользуемся результатами анализа уравнения
(8.7) и сразу сформулируем условие нарастания амплитуды колебаний в контуре:
коэффициент при первой производной должен быть отрицательным. Условием
самовозбуждения оказывается неравенство
г 11
к_____
L С R
\R\<-^ = R,=pQ = -^
или г* 0
(8.40)
Когда соотношение (8.40) перейдет в равенство \R (1/к)| = R,, рост амплитуды
прекратится и в контуре установится стационарное ее значение. Нетрудно провести
аналогию между с ре дней крутизной St(U), рассмотренной в разделах 8.4-8.6, и про-
водимостью 1/|7? ( UK)\; режим оказывается устойчивым, если в точке пересечения
с прямой R3 кривая |7? (UK)\ имеет положительную производную (рис. 8.21).
Рис. 8.21. Стационарная амплитуда колебаний
в автогенераторе на туннельном диоде
Контрольные вопросы и задания
1. Что такое баланс фаз и баланс амплитуд в автогенераторе гармонических коле-
баний? Выполняются ли они в режиме установления колебаний? Почему?
2. Опишите на качественном уровне процесс установления колебаний в автогене-
раторе.
3. Линейным или нелинейным устройством является автогенератор? Почему?
4. Изобразите эквивалентную схему по переменному току для автогенератора
с трансформаторной обратной связью. Запишите выражение для частоты гене-
рации.
5. Каким образом (за счет чего) в схеме автогенератора с трансформаторной об-
ратной связью реализуется баланс фаз?
6. Изобразите полную схему автогенератора с трансформаторной обратной связью.
7. Изобразите емкостную трехточечную схему автогенератора по переменному
току. Запишите выражение для частоты генерации.
8. Изобразите индуктивную трехточечную схему автогенератора с учетом элементов
цепей питания. Запишите выражение для частоты генерации.
302
8. Генерирование гармонических колебаний
9. Изобразите схему 7?С-автогенератора с трехзвенной цепочкой обратной связи.
Как в ней реализуется баланс фаз (обязательно изобразите ФЧХ цепи обратной
связи)?
10. Нарисуйте схему 7?С-автогенератора с мостом Вина. Как в ней реализуется
баланс фаз (обязательно изобразите ФЧХ цепи обратной связи)?
11. Сформулируйте условия самовозбуждения автогенератора на туннельном диоде.
Задачи
Задача 8.1
Найти минимальную взаимную индуктивность М, при которой наступит само-
возбуждение автогенератора, изображенного на рис. 8.22. Параметры контура:
L = 500 мкГн, С = 2000 пФ, г = 50 Ом. Крутизна характеристики транзистора в ра-
бочей точке 5 = 3,3 мА/В.
Рис. 8.22 Схема для задачи 8.1
Задача 8.2
Схема автогенератора показана на рис. 8.23. Частота генерации 400 кГц, коэффи-
циент обратной связи 0,1. Найти параметры элементов контура, если известно, что
на частоте генерации х3 = -2200 Ом.
Рис. 8.23. Схема для задачи 8.2
Задачи
303
Задача 8.3
Индуктивная трехточечная схема собрана на транзисторе с крутизной 5=2 мА/В
(рис. 8.24). Параметры контура: £, = 1 мкГн, Ь2 = 9 мкГн, С= 10 нФ, Q = 80. Может
ли существовагь генерация в этой схеме?
Рис. 8.24. Схема для задачи 8.3
Задача 8.4
Генератор включает в себя RLC- и 7?С-цепи, соединенные в кольцо через два идеаль-
ных усилителя. Коэффициент передачи первого из них К, второго -1 (рис. 8.25).
Резонансная частота RLC -цепи/0 = 1 МГц, ее добротность Q=50. Определить частоту
генерации и минимально необходимый коэффициент усиления К.
Задача 8.5
Определить частоту колебаний, генерируемых кольцевым трехкаскадным RC-
автогенератором, изображенным на рис. 8.26, если RC = 4 мс, R » Rc, Rc « Rgx.
Рис. 8.26. Схема для задачи 8.5
304
8. Генерирование гармонических колебаний
Задача 8.6
Туннельный диод вместе с источником смещения подключен к колеба гельному
контуру (рис. 8.27). Дифференциальная крутизна ВАХ диода в рабочей точ-
ке 5д = -5 мА/B. Резонансное сопротивление контура при полном включении
R3 = 32 кОм. Определить, при каком минимальном значении коэффициента вклю-
чения а активного элемента в контур возникнет самовозбуждение системы.
Рис. 8.27. Схема для задачи 8.6
Приложение.
Ответы к задачам
Ответы к задачам главы 1
А2
Задача 1.1. Энергия за период: Е = —(1 — е
2а '
средняя мощность: Рср = ——- е
,-2аТ
-2аТ
i-e~aT
Задача 1.2. Коэффициенты комплексного ряда Фурье: Ck = А-.—-.
аТ + j Ink
Задача 1.3. В данном случае целесообразно использовать синусно-косинусную
форму записи ряда Фурье, так как сигнал является четной функцией
времени и, следовательно, bk = 0 для всех k. Косинусные коэффици-
енты
k = 0,
k четно и k Ф О,
A,
0,
4Л
.л2*2’
Задача 1.4. S(w) = —e~iaT +—
jco
j _ p-(0+.'°>)r
Задача 1.5. 5(co) = A------------.
a + jut
„ . „ . . sin(2rt -103£) . .
Задача 1.6. s(t) =---------;—- (время в секундах, результат в вольтах).
2л 10 t
Задача 1.7. Если обозначить сигнал из задачи 1.4 как sQ(t), сигнал s(t) можно
связать с ним следующим образом: s(t) - -s0(2t + Т) + s0(T - 2t). Взаи-
co
k нечетно.
,-;шТ
мосвязь соответствующих с пектров: 5(со) = -j Im So
е, ' 2А . 4А
T( id)
. (оТ
sin ----
I 2
, отсюда
.шТ \
Задача 1.8. Если обозначить сигнал из задачи 1.5 при Т —> <» как $0(£), сигнал s(t)
можно связать с ним следующим образом: s(f) = s0(2t) + s0(-t). Взаи-
11 № 675
306
Приложение. Ответы к задачам
2
мосвязь соответствующих спектров: 5(щ) =—50[ — |+50(-0)), отсюда
ЧА 1 2 <2/
5(<о) =
ЗА 1
2а . . о со2
~}2а + 2а*
• 00 S бсо)
Задача 1.9. 5(со) = ^а*50(со)е’7“*г = 0
ь-п 1 — ае
^5(<о-ц
Задача 1.10. 5(со) = л8(щ)+
)+^8((о + ш0).
Задача 1.11. 5(<п) = у2Лзт
, после интегрирования
2
f . ((СО + Шо)^
Sin -----—
ЦТ 2 )
Задача 1.12. 5(со) = —---------—— +
2 ((о + (о0)Г
. Г(<о-ш0)7'Л
sin -----й—
I 2 J
((о-со0)Т
П2Т| 3|т| |т|
Задача 1.13. В(т) = —
э V 27 21 7
|t| < Т. График КФ показан на рис. П.1.
Рис. П. 1. К ответу задачи 1.13
Задача 1.14. График ВКФ показан на рис. П.2.
Рис. П.2. К ответу задачи 1.14
Ответы к задачам главы 2
307
Задача 1.15. т>0,
а) В12(т) = < а, +а2 т<0.
б) С12(т) = - т>0, а * а2-ах' ' ДЛ2те“ат, т>0, ах=а2.
Задача 1.16. График ВКФ показан на рис. П.З.
Рис. П.З. К ответу задачи 1.16
Ответы к задачам главы 2
и -и . и +и .
Задача 2.1. Прит< 1 тп = ——--—, при т > 1 т = ——---—
U +U . U -U
max mm max min
Задача 2.2. Pcp = 5,28 кВт, Pmax = 25,92 кВт.
Задача 2.3. Требуемые зависимости для случая частотной модуляции показаны
на рис. П.4, для случая фазовой модуляции — на рис. П.5.
Задача 2.4. s(t) ~ 8 cos(106t) + 0,24 cos(l,01 106i) - 0,24 cos(0,99 - 106t).
Задача 2.5. Qmaj[ = 2,495 1 04рад/с.
308
Приложение. Ответы к задачам
Фра1 менты парабол
Рис. П.4. К ответу задачи 2.3 (случай частотной модуляции)
Ответы к задачам главы 2
309
-Т 0 774 772 3774 Т t
Рис. П.5. К ответу задачи 2.3 (случай фазовой модуляции)
310
Приложение. Ответы к задачам
Ответы к задачам главы 3
Задача3.1. Х = 0,795, о2х =0,081475, ох =0,285438.
0, х<0,5,
0,35, 0,5 <х <0,8,
Г(х) = ^
0,8, 0,8<х<1,3,
1, х>1,3.
График функции распределения показан на рис. П.6.
ЗадачаЗ.2. Х=^, ох=-^-, ох=р F1(x) = l-e *, х>0.
XX X
График функции распределения показан на рис. П.7.
Рис. П.7. К ответу задачи 3.2
ч о о 10 Ч1ОО1 п 80 169 100
Задача 3.3. Шу =— = 3,1831, Dv =------I--------— = 100.
Л Я 2 7Г
Задача3.4. =(д+ц^)(О2+ц^)(пз
Ответы к задачам главы 3
311
Задача 3.5. x(t) -1 В, x2(t) = 14/9 ~ 1,56 В2. Графики функции распределения
и плотности вероятности показаны на рис. П.8.
Рис. П.8. К ответу задачи 3.5: а — функция распределения; б — плотность вероятности
Задача 3.6. т =—, о2 = ——.
у6 г 180
Задача3.7. X(t) = 0 = const, ox(t) = ±A2 =const, Rx(ti,t2) = ^A2cos(mQ(ti-t2)).
Отсюда следует, что данный случайный процесс является стационар-
ным в широком смысле.
Задача 3.8. Попытка рассчитать дисперсию путем усреднения по времени дает
результат Л2/2, где А — амплитуда рассматриваемой реализации
случайного процесса. Это отличается от формулы, полученной при
решении задачи 3.7, в которой фигурирует статистически усредненный
квадрат амплитуды. Поэтому данный случайный процесс не является
эргодическим.
Задача 3.9. Rx(т) = 7?,(t) + /?2(t), 7?А.х (т) = 7?1(т)/г2(т).
UCto sin(w т)
Задача 3.10. R(j) = -^—^4
л (Овт
W.Acd sin(A<m;/2)
Задача 3.11. R(a) = —-------—cos(co0t).
л Дсот/2
312
Приложение. Ответы к задачам
Ответы к задачам главы 4
Задача4.1. h(t) = — Г>0; g(O = -(l-e’t/T), t>0; Х(со) = -^2-;
2т 2' ’ l + jm
^(0= 10(1-*-'Л),
10(е-1)е^,
t < О,
0<£ <100 мкс,
t> 100 мкс.
Здесь т = RC/2 = 100 мкс.
Задача 4.2. i(f) =-—-(е “ -е t>0. Здесь т = ^—5—Поскольку вход-
fl/l-aT)' ’ R^R?
ным воздействием является напряжение, а выходной реакцией — ток,
комплексный коэффициент передачи и переходная характеристика
имеют размерность [А/В = 1/Ом], а импульсная характеристика
[А/(Вс) = Гц/Ом]
Задача 4.3.
, . . 1 1
; h(t) = —j= —е
а) К(а) =----——
1 + 73®т-(о2т2
2RC 2RC
Здесь Tj =---т2 =-------
1
1
-----е
Т2
, t>0.
б) ОД =-----/ЮТ 2 2; A(0 = -(l--V/\ t>0. Здесь т = ЯС.
l + J2a>T-a> т ту т)
Задача 4.4. £2 = 5 • 103 рад/с, Я» 796 Гц.
Задача 4.5. Q = 1146, С = 507 пФ, г = 0,044 Ом.
Задача 4.6. tl = 40 мс.
Задача4.7. Явьп(т) = WА2(Т0-|т|), |т|<7\
W W ( 1тН W
Задача4.8. 1Гвых(ш) = ° ; Лвых(т) = -^ехр -2^ ; =
t (mRC} т RC) х
1+ ----
I 2 J
d
Задача 4.9. $вх (О = $вых(Г)+RC—sBba (t),
график входного сигнала приведен на рис. П.9.
Ответы к задачам главы 4
313
Задача 4.10.
Р2
a) Z((o0) = y-Jp, где Р = ^--
хч [ г*
о) “ = ®oJ1-^7-
в) Z(®) = 4; = --
гС г
г) Q=p/r.
SRt
Задача 4.11. К '(со) =------------=— --------i + j^C---------
i+>s,cxv 1 ’)
SR, 7?„ ,
отсюда Х((°) = -1 + 7(ОдС и Р(®) = -^-(1 + >7?1С).
314
Приложение. Ответы к задачам
Ответы к задачам главы 5
Задача 5.1. График выходного сигнала показан на рис. П.10.
Задача 5.2. /?вых(т) = WQA2U2 (Т-|т|), |t| < Т. График КФ показан на рис. П.11.
Рис. П.11. К ответу задачи 5.2
Задача 5.3. Г=9мкс.
Задача 5.4. С/Швых= 24/^5 = 10,73, проигрыш составляет >/5/2 = 1,12 раза по уров-
ню, или около 1 дБ. График выходного сигнала показан на рис. П.12.
Рис. П.12. К ответу задачи 5.4
Ответы к задачам главы 5
315
Задача 5.5. топт = 1/<о0; С/Швы1тах
А
(1-е-(а->ш)Г)(й2+®2) .
Задача 5.6. K(ai) = C----------—-------е 1<ato, где С — произвольная константа,
a- jot
tQ — момент достижения максимального значения выходного полез-
ного сигнала. Следует обратить внимание на то, что такой фильтр не
является физически реализуемым, так как его коэффициент передачи с
ростом частоты неограниченно возрастает. С/Швых = <», это объясняется
тем, что спектр шума с ростом частоты затухает быстрее, чем спектр
сигнала.
1, / = 1...2кГц,
2/3, / = 2...3 кГц, , 5 з
Задача 5.7. £(/) = • 0, о2 =-10~3 В2. / = 3...4кГц, ‘ 3
не имеет значения на остальных частотах.
Задача 5.8. К(ш) =
a2aZ>2 +o2a(o2
(о2 6 + a2na)ab + (o2a + c2Z>) co2
2 2
02=O;O
316
Приложение. Ответы к задачам
Ответы к задачам главы 6
Задача 6.1. X(z) =---------------—. Область сходимости представляет собой
-az+(l + a )-az
кольцо с внутренним радиусом |а| и наружным радиусом 1 /\а\.
Задача 6.2. X(z) =----4sin(g>or)z-- область сходимости |z| > 1, то есть
l-2cos(co07')z-1+z-2
вся комплексная плоскость, за исключением круглой области
единичного радиуса с центром в начале координат.
Задача 6.3. x(k') = 3 0,3* - 2 0,2*, k>0.
Задача6.4. x(^) = -y=cos| — k~— |, k>Q.
\ 3 6)
Задача 6.5. {1,1,3,3,1,5, -5,3, -12}.
Задача 6.6. {5, 3, 5, 7}.
Задача 6.7.
a)y(k) = 2x(k) + 2X^-1).
б) Структурная схема фильтра показана на рис. ПЛЗ.
в) Фильтр неустойчив, так как полюс системной функции равен 2,
то есть превосходит по модулю единицу.
г) h(k') = 2k+l,k>0.
2 L 4
Э) ^) = -(-1/+--2‘, k>0.
«Э «J
Рис. ПЛЗ. К ответу задачи 6.7
Задача 6.8. Для получения рекурсивного алгоритма фильтрации можно применить
к системной функции формулу суммы конечной геометрической про-
1-z"5
грессии: H(z) = 1 + z~' + z~2 + z~3 + z~^ =-----—.
Ответы к задачам главы 6
317
Алгоритм фильтрации в нерекурсивной форме:
y(k) =x(k)+x(k - 1) +x(k - 2) +x(k- 3) + x(k- 4).
Алгоритм фильтрации в рекурсивной форме:
y(k) = x(k) - x(k - 5) + y(k - 1).
Структурные схемы фильтра в нерекурсивной и рекурсивной фор-
мах показаны на рис. П.14.
Рис. П. 14. К ответу задачи 6.8: а — нерекурсивная форма; б — рекурсивная форма
Задача 6.9.
1 + z"3
a) =
1-z J
б) Структурная схема фильтра показана на рис. П.15.
в) h(k) = {1, 0, 0, 2, 0, 0, 2, 0, 0, 2, 0, 0, 2...}, в аналитическом виде
Рис. П. 15. К ответу задачи 6.9
318
Приложение. Ответы к задачам
1
оо kT
Задача 6.10. X(w) = ^e ’ ё~’“лт =у—_jmT Графики АЧХ показаны на рис. П. 16.
Рис. П.16. К ответу задачи 6.10:
сплошная линия — Г/т = 1; штриховая линия — Г/т = 0,1
Ответы к задачам главы 7
Задача 7.1.
a. 1 U,
=—+а. + аЛ,, га = — =-1-----S = а. + 2аЛ.
° U, 1 2 1 0 50 а0+аД1+аД2 д 1 21
1 1 „ п гт 1 1
г = — =------, S, = а. + 2аЛ,, г= — =-.
я 5 а,+2аЛ, 11 2 1 5. а.+2аЛ
Д 1 Z 1 llzl
Задача 7.2. Wo) = 12£02 -16О£7о + 812.
Задача7.3. При£=£ I.ll,=i. При£ = 0 — = — = 1,7.
m ' 12 Зя
Задача 7.4. Uo = -20 В, /, = — = 17 мА.
Зя
Задача 7.5. U2 - 2,5 В. Фильтрующий элемент Ф должен представлять собой по-
лосовой фильтр со средней частотой 4 МГц и полосой пропускания
Ответы к задачам главы 8
319
не менее 600 Гц. Ограничение полосы пропускания сверху в данном
случае слабое, так как требуется только подавление второй гармоники
частоты модулирующего сигнала (600 Гц) и второй гармоники несущего
колебания (8 МГц).
Задача 7.6. В спектре тока в данном случае отсутствует набор частот, необходимых
для реализации амплитудной модуляции на несущей частоте о>0. Однако
следует отметить, что AM в данном случае оказывается возможной на
второй гармонике несущей.
Задача 7.7. х = 3 В.
Задача 7.8. 2,56 В.
Задача 7.9. р(у) =—^=, уе(0,аА2).
У 2Ау]ау
Ответы к задачам главы 8
Задача 8.1. М > 30 мкГн.
Задача 8.2. — индуктивность 800 мкГн, х2 — индуктивность 80 мкГн,
х3 — емкость 180 пФ.
Задача 8.3. Баланс амплитуд: Х(о>г)р(®г) = 0,45 < 1, поэтому генерация
не возникнет.
Задача8.4. /г =^^14-1/(2=1,01 МГц, X>^^ = 0,04.
Задача 8.5. со =—^—j= = 144 рад/с, f =----—= = 23 Гц.
ЯСл/З 2jc7?CV3
Задача 8.6. а>—^= = 0,08.
4V10
Список литературы
1. Иванов М. Т., Сергиенко А. Б., Ушаков В. Н. Теоретические основы радиотехники:
Учеб, пособие / Под ред. В. Н. Ушакова. — М.: Высш, шк., 2002.
2. Иванов М. Г, Сергиенко А. Б., Ушаков В. Н. Теоретические основы радиотехники:
Учеб, пособие. — 2-е изд. / Под ред. В. Н. Ушакова. — М.: Высш, шк . 2008.
3. Гоноровский И. С. Радиотехнические цепи и сигналы: Учеб, пособие для вузов —
М.: Дрофа, 2006.
4. Баскаков С. И. Радиотехнические цепи и сигналы: Учеб, для вузов по спец.
«Радиотехтика». — М.: Высш, шк., 2000.
5. Жуков В. П., Карташев В. Г., Николаев А. М. Задачник по курсу «Радиотехниче-
ские цепи и сигналы»: Учеб, пособие для студентов вузов спец. «Радиотехни-
ка». — М.: Высш, шк., 1986.
6. Баскаков С. И. Радиотехнические цепи и сигналы. Руководство к решению задач:
Учеб, пособие для радиотехн. спец, вузов. — М.: Высш, шк., 1987.
7. Радиотехнические цепи и сигналы. Примеры и задачи: Учеб, пособие для вузов /
Под ред. И. С. Гоноровского. — М.: Радио и связь, 1989.
8. Тихонов В. И. Статистическая радиотехника. — М.: Радио и связь, 1982.
9. Двайт Г. Б. Таблицы интегралов и другие математические формулы / Пер. с англ.;
Под ред. К. А. Семендяева. — М.: Наука, 1983.
10. Янке Е., Эмде Ф., Лёш Ф. Специальные функции / Пер. с нем.; Под ред. Л. И. Се-
дова. — М.: Наука, 1968.
11. Финк Л. М. Сигналы, помехи, ошибки... Заметки о некоторых неожиданностях,
парадоксах и заблуждениях в теории связи. — 2-е изд., перераб. и доп. — М.:
Радио и связь, 1984.
12. Тихонов В. И. Нелинейные преобразования случайных процессов. — М.: Радио
и связь, 1986.
13. Френке Л. Теория сигналов / Пер. с англ.; Под ред. Д. Е. Бакмана. — М.: Сов.
радио, 1974.
14. Основы теоретической электротехники: Учеб, для вузов. — 2-е изд. / Ю. А. Быч-
ков, В. М. Золотницкий, Э. П. Чернышев, А. Н. Белянин. — СПб.: Лань, 2009.
15. Сергиенко А. Б. Цифровая обработка сигналов: Учеб, пособие. — 3-е изд. — СПб.:
БХВ-Петербург, 2011.
16. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов / Пер.
с англ.; Под ред. Ю. И. Александрова. — М.: Мир, 1978.
Алфавитный указатель
абсолютно
интегрируемый
сигнал, 22
автогенератор
- £С-схемы
- баланс
амплитуд, 293
- баланс фаз, 293
- коэффициент
обратной связи, 291
- коэффициент
усиления КПП, 292
- трансформаторная,
278, 289, 294
- трехточечные, 289
- частота
генерации, 290
- .RC-схемы, 296
- с мостом Вина, 297
- трехзвенная,296
- автоматическое
смещение, 295
- амплитуда
колебаний, 277
- баланс амплитуд
и фаз, 277
- возникновение
колебаний, 278
- нелинейное
уравнение, 287
- нелинейность, 276
- обобщенная
схема, 275
- самовозбуждение, 283
- жесткий
режим, 282
- мягкий режим, 282,
295
автогенератор
(продолжение)
- с внутренней
обратной связью, 299
- стационарный
режим, 275, 277, 280,
282
- устойчивость, 283
- условие самовозбуж-
дения, 280
- энергетический
баланс, 275
автоколебания,148
автоколебательная
система, 275
автокорреляционная
функция, 40
автоматическое
смещение, 260
- в автогенераторе, 295
АИМ, 69, 88, 96, 100
активный элемент, 155
алгоритм дискретной
фильтрации, 217
AM, 54
АМн, 70
амплитуда
- бесконечно малая, 23
- комплексная, 16, 57,
123
амплитудная
- демодуляция, 255
- манипуляция, 70
- модуляция, 54, 254,
259'
- гармоническая, 250
- спектральная
функция, 23
амплитудное
детектирование, 255
- квадратичное, 256
- линейное, 256
амплитудно-импульсная
модуляция, 69, 88, 96,
100,201
амплитудно-частотная
характеристика, 123
амплитудный
- детектор, 55
- линейный
диодный
детектор, 258
- модулятор, 254
- спектр, 15, 23, 30
анализ
- корреляционно-
спектральный, 47
- корреляционный, 40
аналитический
сигнал, 81, 124
аналоговый
сигнал, 188
аналого-цифровой
преобразователь, 189
ансамбль
реализаций, 86, 89
аппроксимация, 242
- кусочно-
линейная, 243, 245,
251,258
- полиномиальная, 242,
244, 249, 250
- экспоненциальная,
244,247
АЦП, 189
АЧХ, 73, 123
322
Алфавитный указатель
Б
база сигнала, 28, 72, 166
базис, И
- конечный, 12
- Котельникова, 193,
201
- ортогональный, 11,13
~ ортонормирован-
ный, 12
баланс
- амплитуд и фаз, 277
- энергетический, 275
балансная амплитудная
модуляция, 61
БАМ, 61
Баркера код, 167,169
безынерционный
нелинейный
элемент, 241, 264
белый шум, 109,129,161
- дискретный, 235
- преобразование
фильтром, 237
Берга коэффициенты
и функции, 246
бесконечная импульсная
характеристика, 223
бесконечно малая
амплитуда, 23
Бесселя
- неравенство, 12,13
- функция, 64, 247
бигармонический
сигнал, 248, 254
биения, 61
билинейное z-преобразо-
вание, 228
БИХ-фильтры, 223
БПФ, 210
быстрое преобразование
Фурье, 208
- число операций, 210
В
варикап, 241
ВАХ, 240
взаимная
корреляционная
функция, 42
- свойства, 43
- случайных
процессов, 97
взаимный
энергетический
спектр, 47
видеоимпульс, 9,10
- прямоугольный, 8, 17
- спектр, 25
- треугольный, 9,20
видеосигнал,10,67
Винера фильтр, 181
Винера—Хинчина
теорема, 106,128,269
ВКФ, 42, 97, 99,112,128
вольт-амперная
характеристика, 240
восстановление
непрерывного сигнала
с помощью ДПФ, 207
временная
синхронизация, 172
встречное включение
катушек, 280, 291
вынужденная
составляющая, 126
вынужденные
колебания, 153
вычислительные
погрешности, 192
Г
гармоника, 245,249
гармонический ряд
Фурье, 14
гармонический сигнал,
8,10, 96,100,102, 124,
190,192, 244
- дискретный, 206
- спектр, 34
гауссов импульс, 8, 28
гауссово
распределение, 103
- двумерное, 268
генератор, 148, 149
генерация колебаний, 241
геометрическая
прогрессия,211
гетеродин, 250
гетеродинирование, 250,
251
- инверсия спектра, 251
Гильберта
преобразование, 78,
111,124
гистерезис
колебательный, 286
граница
устойчивости, 149
граничная частота
спектральной
функции, 28
групповая задержка, 124
групповое время
запаздывания
(прохождения), 124
д
ДАУ, 189
двумерная
- плотность
вероятности, 94, 235
- случайная
величина, 94
Алфавитный указатель
323
двумерное сечение
случайного
процесса, 94
девиация
- фазы, 63
- частоты, 63, 72
делитель напряжения,
127, 141
дельта-функция, 9,46,
109,121,197, 264
- размерность, 124
- спектр, 24
~ фильтрующее
свойство, 9
демодуляция
амплитудная, 255
детектирование, 241
- амплитудное, 255
~ квадратичное, 256
- линейное, 256
- коэффициент
детектирования, 257,
258
- синхронное
- амплитудное, 260
- фазовое, 262
- характеристика
детектирования,258
детектор
- амплитудный, 55
- диодный
линейный, 258
~ коллекторный, 256
- огибающей, 55
- пиковый, 260
- фазовый, 261
- синхронный, 262
- частотный, 261, 262
детерминированная
составляющая, 104
диод туннельный, 299
диодный детектор, 258
- входное
сопротивление, 260
Дирака функция, 9
- спектр, 24
Дирихле условия, 14, 22
дискретизация, 188
- ошибка
аппроксимации,195
- произвольными
импульсами, 200
дискретизированный
сигнал, 197
- спектр, 198
дискретная
- показательная
функция, 212
- свертка, 217
- экспоненциальная
функция, 212
дискретно-ана лотовые
устройства, 189
дискретное
преобразование
Фурье, 204
- быстрое, 208
- обратное, 204
- свойства, 204
- число операций, 208
дискретный
- белый шум, 235
- преобразование
фильтром, 237
- гармонический
- ряд, 66
- сигнал, 206
- ряд, 188
- сигнал, 9,188, 199
- периодический, 203
- случайный
- процесс, 88,191
- сигнал,235
- спектр, 199
- фильтр, 189
дисперсия, 90, 91
- на выходе цепи, 128
дифференциальная
крутизна, 243
дифференциальное
уравнение, 153, 279,300
- нелинейное, 280, 287
- цепи, 125
дифференцирование
сигнала, 31
- приближенное, 134
дифференцирующая
ЯС-цепь, 132
длина дискретного
фильтра, 220
длительность
- импульса, 18
- эффективная, 29
добротность, 139,144
ДПФ, 204
Дюамеля интеграл, 121
Е
единичная
- импульсная
функция, 211
- ступенчатая
функция, 9
единичный скачок, 122
- дискретный, 211
емкость собственная
(паразитная), 241
задержка
- групповая
и фазовая, 124
- оператор, 30
закон распределения
- гауссовский
(нормальный), 103
- Рэлея,114
- Рэлея—Райса, 116
324
Алфавитный указатель
изменение масштаба оси
времени, 31
ИМ, 68
импеданс, 127
импульс
- видеоимпульс, 9,10
- гауссов, 8, 28
- прямоугольный, 122,
135, 175
- длительность, 18
- радиоимпульс, 10
- треугольный, 177
- экспоненциальный, 8,
29, 136
импульсная
модуляция, 68
импульсная
характеристика, 121
- дискретного
фильтра, 215
- размерность, 124
инвариантность, 171
инверсия спектра, 251
инвертирующий
усилитель, 253
индекс гармонической
угловой
модуляции, 64
индуктивность
собственная
(паразитная), 241
интеграл
- Дюамеля, 45,121
- наложения, 45
- свертки, 44,121
- спектр, 31
интегрирование
сигнала, 31
- приближенное, 131
интегрирующая
7?С-цепь, 130,175
интервал
- дискретизации, 188
- корреляции, 108
- частот, 23
информация, 86
искажения
- мультипликатив-
ные, 201
- при восстановлении
непрерывного
сигнала, 200
источник энергии, 275
каналы прямой передачи
и обратной связи, 148,
274
каноническая реализация
фильтра, 223
каскадная реализация
фильтра, 226
квадратичное
детектирование, 256
квадратурное
представление, 68
квазигармоническая
функция включения, 10
квазигармонические
колебания, 110
квазиоптимальный
фильтр, 175
квантование, 189
- уровни,191
- шум, 190
Кирхгофа уравнение, 278
КИХ-фильтры, 221
ковариационная
функция, 95
код Баркера, 167,169
колебания
- возникновение, 278
колебания {продолжение)
~ вынужденные, 153
- гармонические, 8
- квазигармони-
ческие, 110
- незатухающие, 149
- свободные, 139, 153,
218
колебательная
характеристика, 253,
283
колебательный
гистерезис, 286
колебательный
контур, 249
- параллельный, 144
- частичное
включение, 146, 293
- последовательный,
138, 144
коллекторный
детектор, 256
Колпитца схема, 293
кольцевой ток, 290
комбинационные
частоты, 249
комбинация
линейная, 11,12
компенсация начальных
фаз, 163
комплексная
- амплитуда, 16, 57, 123
- обратная связь, 150
- огибающая, 58, 73, 76,
124
- форма ряда Фурье, 16
комплексное
сопротивление, 127
комплексный
- коэффициент
передачи,122
- дискретного
фильтра, 218
Алфавитный указатель
325
комплексный
{продолжение)
- размерность, 124
- расчет, 126
- сигнал,76
- случайный
процесс, 111
конечная импульсная
характеристика, 221
конечный базис, 12
контур
колебательный, 249
- эквивалентное
сопротивление, 252
контурных токов
метод,127
коррелированность
сигналов, 43
коррелятор, 170
- многоканальный, 171
корреляционная
функция, 95
- взаимная, 42
- комплексных
огибающих, 75
- модулированных
сигналов, 74
- случайных
процессов, 97
- детерминированного
сигнала, 40
- дискретная, 235
- импульсной
характеристики
цепи,128
- нормированная, 99,
268
- преобразование
линейной цепью, 128
- свойства, 41
- связь со спектром
сигнала, 47
- сигналов
с нео1 раниченной
энергией, 44
корреляционная
{продолжение)
- случайного процесса,
267
корреляционно-
спектральный
ана 1из, 47
корреляционный
анализ, 40
корреляция
- интервал, 108
- коэффициент, 98, 99
КОС, 148, 274
Котельникова
- базис, 193, 201
- теорема, 192, 199
Коши—Буняковского
неравенство, 161
коэффициент
- амплитудной
модуляции, 56
- парциальный, 59
- Берга, 246
- включения, 146
- детектирования,257,
258
- корреляции, 98, 99,
268
- передачи
комплексный, 122
- усиления,
стабильность, 150
КПД, 253, 295
КПП, 148, 274
критерий
устойчивости, 154
круговая свертка, 206
крутизна, 243
- дифференциаль-
ная, 243
- по первой
гармонике, 281
- средняя, 281
кусочно-линейная
аппроксимация, 243,
245, 251,258
КФ, 40
Л
Лапласа
преобразование, 212
линейная
- комбинация, И, 12
- свертка, 214, 217
- цепь, 120
- частота, 40
- частотная
модуляция, 72
- корреляционная
функция,169
линейное
детектирование, 256
линейность, 215, 240
- преобразования
Фурье, 30
Лопиталя правило, 31
ЛЧМ, 72,167, 169
М
Маклорена ряд, 242, 259
максимальная частота
спектра, 28
математическая модель
сигнала, 8
математическое
ожидание, 90, 91
мгновенная
- мощность, 38
- частота, 63, 76
меандр, 20
медиана, 92
Мейснера схема, 293
метод
- контурных токов, 127
326
Алфавитный указатель
метод (продолжение)
- узловых
напряжений, 127
- укороченного
уравнения, 280
многомерная функция
распределения,94
мода, 91
модулирующий
сигнал, 55
модулятор, 54
- амплитудный, 254
модуляция, 54,241
- амплитудная, 54, 55,
254, 259
- балансная, 61
- векторная
диаграмма, 57
- гармоническая, 56,
250
- корреляционная
функция
сигнала, 60
- коэффициент
модуляции, 56
- КПД, 60
- многотональная, 58
- однополосная, 61
- однотональная, 144
- распределение
мощности, 60
- спектр сигнала, 56,
59
- тональная, 56
- узкополосность
сигнала, 67
- ширина спектра, 57
- амплитудно-
импульсная, 69, 88,
96,100, 201
~ спектр сигнала, 71
- импульсная, 68
- угловая, 54, 62,146
- векторная
диаграмма, 65
модуляция
(продолжение)
- гармоническая, 63
- индекс, 64
- спектр сигнала, 64
- узкополосность
сигнала, 67
- ширина спектра, 66
- фазовая, 63
- частотная, 63
- линейная, 72
мощность
- мгновенная, 38
- средняя, 39
- удельная, 38
- флуктуационного
компонента, 102
мультипликативные
искажения спектра, 201
Н
нагрузка, 249, 251, 252,
256, 258
- реакция, 249, 260
наложение сдвинутых
копий спектра, 200
начальная фаза, 10, 63
- случайная, 87
невязка, 12
некоррелированность, 98,
103
нелинейная цепь, 120
- преобразование
случайного
процесса, 264
нелинейное
преобразование, общая
схема, 249
нелинейный
- резонансный
усилитель, 251, 254
- элемент, 240
- безынерцион-
ный, 264
неопределенности
соотношение, 108, 166
неравенство
- Бесселя, 12,13
- Коши—Буняковского,
161
нерекурсивный
фильтр, 220
нестационарная цепь, 120
несущая частота, 10, 28,
76, 254
несущее колебание, 54
низкочастотный
спектр, 28
норма, 11
нормализация
распределения
вероятности, 129
нормальный
- закон
распределения, 103
- двумерный, 268
- случайный
процесс, 103, 129
нормированная
корреляционная
функция, 99, 268
обеляющий фильтр, 173
обнаружение
сигнала, 170
обобщенная
функция, 10
обобщенный
ряд Фурье, И, 193
- комплексный, 13
ОБП, 61
обратная связь, 148
- классификация, 149
- комплексная, 150
Алфавитный указатель
327
обратная связь
(продолжение)
- отрицательная, 150
- паразитная, 148
- положительная, 149,
275
- реактивная, 150
огибающая, 10, 67, 76,
110,112
- дискретного
спектра, 18
- комплексная, 58, 73,
76, 124
- спектральная
функция, 82
- спектр, 27
- физическая, 76
одномерная плотность
вероятности,90, 235
одномерное сечение
случайного
процесса, 89
- дискретного, 235
однополосная
амплитудная
модуляция, 61
односторонний
энергетический
спектр, 40
округление, 190,191, 226
ООС, 150
оператор
- дифференциро-
вания, 31
- задержки, 30
- интегрирования,32
операционный
усилитель, 150, 297
опорный сигнал, 170
оптимальная
фильтрация
- детерминированного
сигнала, 161
оптимальная
фильтрация
(продолжение)
- при небелом
шуме, 172
- случайного
сигнала, 179
оптимальный
фильтр, 162
ортогональная система
функций,И, 13
ортонормированная
система функций, 12
ОС, 148
относительная
расстройка, 139
отношение «сигнал/
шум», 160, 192
отрицательная
- обратная связь, 150
- частота, 16, 23
отсечка, 251, 295
- угол, 245
отсчет, 9, 188
ОУ, 297
ошибка
~ аппроксимации, 195
- воспроизведения
полезного
сигнала, 179
- квантования,189
- округления,190, 226
П
паразитные емкости
и индуктивности, 241
паразитный сигнал, 153
параллельная реализация
фильтра, 226
параллельный
колебательный
контур, 144
параметрическая
цепь, 120
Парсеваля равенство, 33,
38,196
- дискретное, 206
пассивный элемент, 155
перенос спектра
по частоте, 250
переходная
характеристика,122
- размерность, 124
период
дискретизации, 188
периодический
- сигнал, 9,14,199
~ спектр, 199
пиковый детектор, 260
пилот-сигнал, 61
плотность
вероятности, 264
- w-мерная, 94
- двумерная, 94
- одномерная, 235
- преобразование
линейной
цепью, 129
площадь под графиком
сигнала, 30
погрешности
вычислительные, 192
полиномиальная
аппроксимация, 242,
244,249, 250
полная ортогональная
система функций, 13
полная фаза, 10, 76,112
положительная обратная
связь, 149, 275
полоса пропускания, 140
полосовой
- спектр, 28
- фильтр, 200
328
Алфавитный указатель
полюс передаточной
функции, 154
порядок
- дискретного
фильтра, 220, 222
~ комбинационной
частоты, 249
ПОС, 149, 275
последовательная
реализация
фильтра, 226
последовательный
колебательный
контур, 138,144
постоянная времени
- 7?С-цепи, 130, 133, 175
- 7?Л-цепи, 135
постоянная
составляющая, 20, 55,
102,249, 256
постоянный сигнал,
его спектр, 34
похожесть сигналов, 43
правило Лопиталя, 31
предмодуляция, 69
представление сигнала
приближенное, 12
преобразование
- z-преобразование, 211
- Гильберта, 78, 111,
124
- свойства, 80
- Лапласа, 212
- Фурье, 21
- быстрое, 208
- дискретное, 204
- косинусоидаль-
ное, 22
- линейность, 30
- свойства, 30
- связь
с z-преобразова-
нием,213
преобразование
(продолжение)
- связь с рядом
Фурье, 24
- симметрия, 23
- синусоидальное, 22
- частоты, 241
приближенное
представление
сигнала, 12
принцип
- причинности, 121
- суперпозиции, 120,
215, 240
причинность, 121
прогрессия
геометрическая, 211
производная,
ее спектр, 31
прореживание
по времени
и частоте, 210
простой сигнал, 166
прямая реализация
фильтра, 223
прямоугольный
видеоимпульс, 8,122,
135,175
- периодическая
последователь-
ность, 17
- спектр, 25
прямоугольный
радиоимпульс,
его спектр, 26
Р
рабочая точка, 242, 244,
286
равенство Парсеваля, 33,
38,196
- дискретное, 206
радиоимпульс
прямоугольный, 10
~ спектр, 26
радиолокация,166
радиосигнал, 10
~ модулированный, 54
размерность
спектральной
функции, 23
разностное
уравнение, 217
разрешение
по дальности, 166
распараллеливание
вычислений, 225
распределение
вероятности
- гауссово
(нормальное), 103
- двумерное, 268
- Пуассона, 89
- равномерное, 87
- Рэлея,114
- Рэлея—Райса, 116
расстройка
относительная, 139
реактивная обратная
связь, 150
реактивный нелинейный
элемент, 240
реакция нагрузки, 249,
260
реализация
случайного
процесса, 86
резистивный
нелинейный
элемент, 240
резистор
с отрицательным
сопротивлением, 155
резонанс токов, 290
Алфавитный указатель
329
резонансная
- характеристика, 140,
144
- частота, 139, 279
резонансное умножение
частоты, 253
рекурсивный фильтр, 221
Рэлея
- закон
распределения,114
- теорема, 32,194
- дискретная, 205
Рэлея—Райса
распределение, 116
ряд
- дискретный, 188
- гармонический, 66
- Котельникова, 193
- в частотной
области, 197
- Маклорена, 242, 259
- Тейлора, 242
- Фурье, 14, 203
- вещественная
форма, 15
- гармонический, 14
- комплексная
форма, 16
- обобщенный, И
- связь
с преобразованием
Фурье, 23
~ тригонометриче-
ская форма, 14
- обобщенный, 193
С
самовозбуждение, 155
свертка, 32, 44, 78, 121
- круговая, 206
- линейная, 214, 217
- спектр, 33
свободная
составляющая, 126
свободные
колебания,139, 153, 218
связь
- обратная, 148
- статистическая, 95, 98
- стационарная, 99
сглаживающий
фильтр, 190
сдвиг
- сигнала
во времени, 30
- спектра, 250
сечение случайного
процесса
- двумерное, 94, 235
- одномерное, 89, 235
сигнал, 8
- абсолютно
интегрируемый, 22
- аналитический, 81,
124
- спектральная
функция, 82
- аналоговый, 188
- база, 28,166
- бигармонический,
248, 254
- видеосигнал, 10
- восстановление
по дискретным
отсчетам, 199
- гармонический, 10,
87, 96, 100,102, 124,
190,192, 244
- дискретный, 206
- детерминирован-
ный, 8
- дискретизирован-
ный, 197
- спектр, 198
- дискретный, 9, 188,
199
- периодический, 203
- случайный, 235
сигнал (продолжение')
- дифференцирова-
ние, 31
- интегрирование, 31
- комплексный, 23, 76
- кусочно
полиномиальный, 36
- модулирующий, 55
- опорный, 170
- паразитный, 153
- периодический, 9, 14,
199
- дискретный, 203
- меандр, 20
- прямоугольные
видеоимпульсы,17
- треугольные
видеоимпульсы, 20
- площадь под
графиком, 30
- простой- 166
- радиосигнал, 10
- сдвиг во времени, 30
- сложный, 166
- случайный, 86, 263
- телеграфный, 107
- с одной боковой
полосой, 61
- сопряженный, 76
- тестовый, 9
- узкополосный, 124
- физический, 188
- физически
нереальный, 29
- финитный. 8
- цифровой, 189
- энергия, 38
- эффективная
длительность, 29
символическая
функция, 10
симметрия
преобразований
Фурье, 23
330
Алфавитный указатель
синтез дискретных
фильтров, 228
- билинейное
z-преобразование, 228
- примеры, 230
- прямые методы, 230
синхронизация
временная, 172
синхронное
детектирование
- амплитудное, 260
- фазовое, 262
система
автоколебательная,275
системная функция, 218
схачок
- единичный, 122
- фазы, 61
скважность, 18
скрытная передача
сигналов, 167
сложный сигнал, 166
случайная величина, 89
- двумерная, 94
случайный процесс, 86,
263
- «-мерное сечение, 94
- ансамбль
реализаций, 89
- гауссов, 103
- двумерное сечение, 94
- дискретный, 88,191,
235
- дисперсия,90,91
- квазидетерминиро-
ванный, 87
- комплексный, 111
- математическая
модель, 87
~ математическое
ожидание, 90, 91
- медиана, 92
- мода, 91
- нормальный, 103,129
случайный процесс
(продолжение)
- одномерная
плотность
вероятности, 90
- одномерное
сечение, 89
- реализация,86
~ сопряженный, 111
- спектральная
плотность
мощности, 105
- среднее
квадратическое
отклонение, 91
- стационарный, 98
- телеграфный
сигнал, 89,107
- узкополосный, 110
- функция
распределения
вероятности, 90
- центрированный, 95,
96
- эргодический, 101
смещение, 256
- автоматическое, 260
собственные емкость
и индуктивность, 241
согласованный
фильтр, 170
- АЧХ, 163
- выходной сигнал, 164
- выходной шум, 164
- импульсная
характеристика, 162
- комплексный
коэффициент
пеоедачи, 162
- отношение «с игнал/
шум»
- входное, 163
- выходное, 164
- применение, 166
~ ФЧХ, 163
соотношение
неопределенности, 28,
108, 166
сопротивление
~ входное, 146
- диодного
детектора 260
- дифференциальное
отрицательное, 299
- отрицательное, 155,
275, 280
- характеристиче
ское, 139
- эквивалентное, 252
сопряженный
- сигнал, 76
- случайный
процесс, 111
составляющая
- вынужденная, 126
- детерминирован-
ная, 104
~ свободная, 126
- флуктуационная, 104
спектр, 22
- амплитудный, 15, 23
- граничная частота, 28
- дискретизированного
сигнала, 198
- дискретный, 16,199
- огибающая, 18
- инверсия, 251
- интеграла, 31
- комплексный, 16
- кусочно-
полиномиального
сигнала, 36
- максимальная
частота, 28
- мощности, 105
- низкочастотный, 28
- обобщенный, 11
~ огибающей, 27
- периодический, 199
- периодического
сигнала, 16
Алфавитный указатель
331
~ полосовой, 28
- произведения
сигналов, 32
~ производной, 31
- свертки сигналов, 33
- случайного
процесса, 269
- фазовый, 15, 23, 38
- эквидистантность, 17
- энергетический, 38
- эффективная
ширина, 27,108
спектральная
плотность, 22
- мощности, 105
- преобразование
линейной
цепью, 127
- средней
мощности, 105
- энергии,38
спектральная
функция, 22
~ интеграла, 31
- постоянного во
времени сигнала, 34
- производной, 31
- размерность, 23
- физический
смысл, 23
СПМ, 105
среднее квадратическое
отклонение, 91
средняя
- крутизна, 281
- удельная
мощность, 39
статистическая
независимость, 104
- и некоррелирован-
ность, 98
статистическая связь, 95,
98
- линейная, 98
статистическое
усреднение, 90
стационарная линейная
цепь, 14,120
стационарно связанные
случайные
процессы, 99
стационарность, 215, 240
- в узком смысле, 99
- в широком
смысле, 99, 235
- строгая, 99
стационарный
- режим, 275
- случайный
процесс, 98
строгая
стационарность, 99
суперпозиции
принцип, 120, 215, 240
схемы Колпитца,
Мейснера, Хартли, 293
Т
Тейлора ряд, 242
теорема
- Винера—Хинчина,
106, 128, 269
- Котельникова, 192,
199
- о свертке спектров, 32
- Рэлея, 32,194
- дискретная, 205
- центральная
предельная, 103, 129
терморезистор, 299
тестовый сигнал, 9
Томсона формула, 279
точка рабочая, 242, 244,
286
трансверсальный
фильтр, 220
транспонированная
реализация
фильтра, 224
треугольный
видеоимпульс, 9, 177
- периодическая
последователь-
ность, 20
тригонометрический
ряд Фурье, 14
туннельный диод, 299
У
угловая модуляция, 54,
62
угол отсечки, 245, 255
удельная мощность
и энергия, 38
узкополосность, 55
узкополосный
- сигнал, 124
- случайный
процесс, 110
узловых напряжений
метод, 127
УМ, 62
умножение частоты, 253
уравнение
- дифференциальное,
153, 279, 300
- нелинейное, 280,
287
- Кирхгофа, 278
- характеристическое,
126,154, 279
уровни квантования, 191
усечение, 191, 241
усилитель, 274
- инвертирующий, 253
- коррекция частотной
характеристики,151
332
Алфавитный указатель
усилитель (продолжение)
- нелинейный
резонансный, 251,
254
- операционный, 150
- с обратной
связью, 150
- уменьшение
искажений, 152
условие
- Дирихле, 14, 22
- статистической
независимости, 98
- узкополосности
радиосигнала, 55
усреднение
- по времени, 101
- статистическое. 90
устойчивое гь, 149, 154,
275
- дискретного
фильтра, 218
- критерий, 154
Ф
фаза
- начальная, 10, 63
- полная, 10, 76,112
фазовая
- задержка, 124
- модуляция, 63
- спектральная
функция, 23
- функция, 10, 63, 76,
110
фазовый
- детектор, 261
- синхронный, 262
- спектр, 15, 23, 30, 38,
48
фазочастотная
характеристика, 123
ФВЧ, 133
физическая
огибающая, 76
физическая
реализуемость
- дискретного
фильтра, 218
физический
- сигнал, 188
- смысл спектральной
функции, 23
физически нереальный
сигнал, 29
фильтр
- верхних частот, 133
- Винера, 181
- дискретный
- алгоритм, 217
- БИХ-фильтр, 223
- длина, 220
- каноническая
реализация, 223
- каскадная
реализация,226
- КИХ-фильтр, 221
- комплексный
коэффициент
передачи, 218
- нерекурсивный, 220
- параллельная
реализация, 226
- порядок, 220, 222
~ последовательная
реализация, 226
- преобразование
дискретного
шума, 236
- прямая
реализация, 223
- рекурсивный, 221
- синтез, 228
- системная
функция, 218
- транспонированная
реализация, 224
- устойчивость, 218
фильтр (продолжение)
- физическая
реализуемость, 218
~ квазиоптималь-
ный, 175
- нижних частот, 131,
199, 200, 203
- обеляющий, 173
~ оптимальный, 162
- полосовой, 200
~ сглаживающий, 190
- согласованный, 162
~ трансверсальный, 220
флуктуации, 91
флуктуационная
составляющая, 104
ФМ,63
ФМн, 169
ФНЧ, 131, 199, 200
формула
- Томсона, 279
- Эйлера, 15, 16, 19, 22
функция
- автокорреляцион-
ная, 40
- Берга, 246
- Бесселя, 64, 247
- включения, 9
- квазигармониче-
ская, 10
- дельта-функция, 9
- Дирака, 9,46
- спектр, 24
- единичная
импульсная, 211
- единичная
ступенчатая, 9
- ковариационная, 95
- корреляционная, 40,
95
- дискретная, 235
- норма, 11
- ортогональность, И,
13
Алфавитный указатель
333
функция
(продолжение)
- ортонормировка, 12
~ показательная
дискретная,212
- распределения
вероятности, 90
- многомерная, 94
- системная, 218
- спектральная, 22
- фазовая, 63, 76
- Хевисайда, 9, 10
- производная, 10
- спектр, 34
- экспоненциальная
дискретная,212
Фурье
- преобразование, 21
- быстрое, 208
- ряд, 203
- гармонический, 14
- обобщенный, 11
- тригонометри-
ческий, 14
ФЧХ, 123
характеристика
- амплитудно-
частотная, 123
- детектирования, 258
- импульсная, 121
- дискретного
фильтра, 215
- колебательная, 253,
283
- переходная, 122
- резонансная, 140, 144
- фазочастотная, 123
характеристическое
- сопротивление, 139
- уравнение, 126,154,
279
Хартли схема, 293
ц
ЦАП, 190, 201
центральная предельная
теорема, 103, 129
центрированная
случайная функция, 95
центрированный
случайный процесс, 96
цепь
- дифференциальное
уравнение, 125
- линейная, 120
- нелинейная, 120, 240
- преобразование
случайного
процесса, 264
- нестационарная, 120
- неустойчивая, 148,
149
- параметрическая, 120
- преобразование
гармонического
сигнала, 123
- преобразование
случайного
процесса, 127
- с обратной
связью, 148, 274
- с постоянными
во времени
параметрами, 120
- стационарная
линейная, 14,120
- условие
физической
реализуемости, 121
- устойчивость, 154
цифроаналоговый
преобразователь, 190,
201
цифровые сигналы
и фильтры, 189
ЦП, 189
Ч
частота
- дискретизации, 188,
199
- заполнения, 10
- линейная, 40
- мгновенная, 63, 76
- несущая, 10, 28, 76,
254
- отрицательная, 16, 23
- резонансная, 139, 279
- среза, 131, 133
- умножение
частоты, 253
частотная модуляция, 63
частотный
детектор, 261, 262
частоты
- комбинационные, 249
- преобразование, 241
- умножитель, 253
ЧМ, 63,169
Ш
шаг дискретизации, 188
шум, 86,103
- белый, 109, 129, 161
- дискретный, 235
- квантования,189, 190
Э
Эйлера формула, 15,16,
19, 22
эквивалентное
сопротивление
контура, 252
эквидистантность
спектра Фурье, 17, 66
экспоненциальная
аппроксимация, 244,
247
334
Алфавитный указатель
экспоненциальный эргодический случайный R
импульс, 8, 29, 136 элемент цепи - активный, 155, 275 ~ ПР 7ТТЛНРЙТ4Ъ.ТЫ процесс, 101 эргодичность по математическому ожиданию, 102 эффективная 7?£-цепь, 135 - дифференциру- ющая, 132
ПСЛИПСНИшН - безынерцион- - интегрирующая, 130, 175
ный, 264 - пассивный, 155 - длительность сигнала, 29 с
энергетический - баланс, 275 - ширина спектра, 27, 108 О SSB.61
- спектр, 38 - взаимный, 47 - односторонний, 40 эффективность излучения, 55 Z
- связь с корреляционной функцией, 47 N «-мерная плотность z-преобразование, 211 - обратное, 214 - свойства, 213
энергия, 38,41 вероятности, 94
Радиотехнические цепи и сигналы: Учебник для вузов
Стандарт третьего поколения
Под ред. В. Н. Ушакова
Заведующий редакцией
Руководитель проекта
Ведущий редактор
Художественный редактор
Корректор
Верстка
А. Кривцов
А. Юрченко
Ю. Сергиенко
С. Заматевская
В. Листова
И. С.марыилева
ООО «Питер Пресс», 192102, Санкт-Петербург, ул. Андреевская (д. Волкова), д. 3. литер А, пом. 7Н.
Налоговая льгота — общероссийский классификатор продукции ОК 005-93, том 2; 95 3005 — литература учебная.
Подписано в печать 05.07.13. Формат 70x100/16. Усл. п. л. 27,090. Тираж 1500. Заказ 675.
Отпечатано по технологии CtP в ООО «Полиграфический комплекс «ЛЕНИЗДАТ».
194044. Санкт-Петербург, ул. Менделеевская. 9. Телефон / факс (812) 495-56-10.