Д. Р. МЕРКИН
ВВЕДЕНИЕ В ТЕОРИЮ
УСТОЙЧИВОСТИ
ДВИЖЕНИЯ
ИЗДАНИЕ ТРЕТЬЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством высшего
и среднего специального образования СССР
в качестве учебного пособия для студентов
высших технических учебных заведений
0
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1987
ББК 531
М 52
УДК 531.1 (075.8)
М е р к и п Д. Р. Введение и теорию устойчииости движения:
Учеб, пособие для вузов.— 3-е изд., перераб. и доп,— М.: Нау-
ка. Гл. ред. физ.-мат. лит., 1987,— 304 с.
Дается изложение основ теории устойчивости движения, ба-
зирующееся на общем курсе высшей математики для втузов. Основ-
ное внимание уделено наиболее эффективным методам исследова-
ния — прямому методу Ляпунова, исследованию устойчивости по
уравнениям первого приближения и частотным методам. Отдельные
главы посвящены исследованию устойчивости движения по струк-
туре действующих сил, устойчивости неавтономных систем, в том
числе систем с периодическими коэффициентами, и систем автома-
тического регулирования.
Для студентов, аспирантов, преподавателей, инженеров и на-
учных работников, изучающих и использующих теорию устойчи-
вости движения в своей работе.
Ил. 74. Библиогр. 60 назв.
Рецензент
член-корреспондент АН СССР В. В. Румянцев
Давид Рахмильевич Меркин
ВВЕДЕНИЕ В ТЕОРИЮ УСТОЙЧИВОСТИ ДВИЖЕНИЯ
Редакторы Н. М. Бокова, А. Г. Мордвиицев
Художественный редактор Т. Н. Кольченко
Технический редактор И. Ш. Аксельрод
Корректоры Л. И. Назарова, Н. Б. Румянцева
ИВ № 32416
Сдано в набор 16.12.86. Подписано к печати 21.05 87. Формат
84x108/32. Бумага книжно-журнальная. Гарнитура обыкновен-
ная. Печать высокая. Усл. печ. л. 15,96. Усл. кр.-отт. 15,96.
Уч.-изд. л. 16,73. Тираж 8100 эка. .Заказ № 17. Йена 85 кон.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
2-я типография издательства «Наука»
121099 Москва Г-99, Шубинскип пер,, 6
1703020000—132
М 053 (02)-87	85-87
© Издательство «Наука».
Главная редакция
физико-математической
литературы, 1976;
с изменениями 1987
ОГЛАВЛЕНИЕ
Предисловие........................................... 6
Введение.............................................. 9
Глава	I. ПОСТАНОВКА ЗАДАЧИ......................... 13
§ 1.1.	Основные определения........................ 13
| 1.2.	Уравнения возмущенного	движения............. 18
§ 1.3. Примеры на составление уравнении возмущенного
движения.......................................... 23
1. Дифференциальные уравнении возмущенного движения
конического маятника (23). 2. Дифференциальные уравне-
ния возмущенного движения центра масс искусственного
спутника Земли (25). 3. Уравнения возмущенного движе-
ния линейных систем (27).
Глава II. ПРЯМОЙ МЕТОД ЛЯПУНОВА (АВТОНОМ-
НЫЕ СИСТЕМЫ) ..................................... 29
§ 2.1.	Функции Ляпунова. Критерий Сильвестра. .	29
§ 2.2.	Теорема Ляпунова об устойчивости движения . .	37
§ 2.3.	Теоремы об асимптотической устойчивости ...	39
§ 2.4.	Теоремы о неустойчивости движения............. 49
§ 2.5.	Методы построения функции Ляпунова ....	53
§ 2.6.	Примеры на применение теоремы Ляпунова об
устойчивости движения................................ 57
1. Устойчивость движения конического маятника (57).
2. Устойчивость стационарного движения центра масс ис-
кусственного спутника Земли (59). 3. Достаточное условие
устойчивости волчка (условие устойчивости вращательного
движения снаряда) (62).
§ 2.7.	Примеры на применение теорем об асимптотиче-
ской устойчивости и неустойчивости движения 67
1. Асимптотическая устойчивость равновесия твердого
тела, находящегося в сопротивляющейся среде (67). 2. Ус-
тойчивость установившихся режимов вольтовой дуги в цепи
с сопротивлением и самоиндукцией (68). 3. Условие устойчи-
вости лампового генератора (72). 4. Устойчивость равнове-
сия системы с одной степенью свободы, находящейся под
действием потенциальной нелинейной силы и силы сопро-
тивления, пропорциональной первой степени скорости (74).
Г л а в а III. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ И СТА-
ЦИОНАРНЫХ ДВИЖЕНИЙ КОНСЕРВАТИВНЫХ
СИСТЕМ......................................... 77
§ 3.1.	Теорема Лагранжа....................... 77
§ 3.2.	Обратимость	теоремы	Лагранжа .......... 81
§ 3.3.	Циклические	координаты.	Преобразование Рауса 82
4
ОГЛАВЛЕНИЕ
§ 3.4.	Стационарное движение и условия его устойчи-
вости ....................................... 86
§ 3.5. Примеры .................................... 89
1.	Устойчивость стационарного движения конического ма-
ятника (89). 2. Устойчивость стационарных движений цент-
ра масс искусственного спутника Земли (90). 3. Устойчи-
вость регулярной прецессии тяжелого гироскопа (92).
4.	Устойчивость равновесного положения оси вращающегося
уравновешенного ротора, установленного в нелинейных
опорах (95).
Г л а в а IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИ-
ЖЕНИЮ .................................................. 97
§ 4.1.	Постановка задачи............................
§ 4.2.	Предварительные замечания....................
§ 4.3.	Основные теоремы об устойчивости по первому
приближению.........................................
§ 4.4.	Критерий Гурвица.............................
§ 4.5.	Примеры .....................................
1.	Условии устойчивости установившихся режимов воль-
товой дуги в цепи с сопротивлением, самоиндукцией и за-
шунтированной емкостью (110). 2. Условие устойчивости
лампового генератора (112). 3. Условие устойчивости уста-
новившегося режима двигателя с центробежным регулятором
(113). 4. Необходимое условие устойчивости волчка (враща-
тельного движения снаряда) (118). 5. Устойчивость стацио-
нарных движений оси вращающегося неуравновешенного
ротора, установленного в нелинейных подшипниках (120).
97
98
101
106
110
Г л а в а V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМ-
НЫХ СИСТЕМ....................................... 124
§ 5.1.	Введение ................................. 124
§ 5.2.	Матрицы и основные действия с ними........ 124
§ 5.3.	Элементарные делители..................... 133
§ 5.4.	Устойчивость линейных автономных систем. Устой-
чивость резонанса. Примеры...................... 142
Г л а в а VI. ВЛИЯНИЕ СТРУКТУРЫ СИЛ НА УСТОЙ-
ЧИВОСТЬ ДВИЖЕНИЯ................................. 150
§ 6.1.	Введение ................................. 150
§ 6.2.	Классификация	сил..................... 151
§ 6.3.	Постановка задачи......................... 163
§ 6.4.	Коэффициенты	устойчивости................. 168
§ 6.5.	Влияние гироскопических и диссипативных сил
на устойчивость	равновесия потенциальной системы 170
§ 6.6.	Примеры на применение теорем Томсона — Те-
та — Четаева	............... 175
1. Устойчивость волчка (175). 2. Устойчивость системы инер-
циальной навигации (176). 3. Гироскопический однорельсо-
вый вагон (180).
§ 6.7. Устойчивость равновесия под действием одних
гироскопических и диссипативных сил. Пример. 183
§ 6.8. Влияние на устойчивость равновесия неконсер-
вативных позиционных сил..................... 191
§ 6.9.	Примеры исследования устойчивости движения
систем с неконсервативными силами.................. 203
1. Модель упругого стержня, находящегося под действием
следящей силы (204). 2. Неустойчивость ротора, вращающе-
гося в аэродинамической среде (207). 3. Гировертикаль с ра-
диальной коррекцией (211).
ОГЛАВЛЕНИЕ
а
Глава VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ
СИСТЕМ .........................................  214
§ 7.1.	Функции Ляпунова для неавтономных систем.
Обобщенный критерий Сильвестра..................... 214
§ 7.2.	Основные теоремы прямого метода для неавто-
номных систем...................................... 219
§ 7.3.	Примеры построения функции Ляпунова для неав-
тономных систем.................................... 222
1.	Устойчивость движения гирогоризонткомпаса (222).
2.	Математический пример (224).
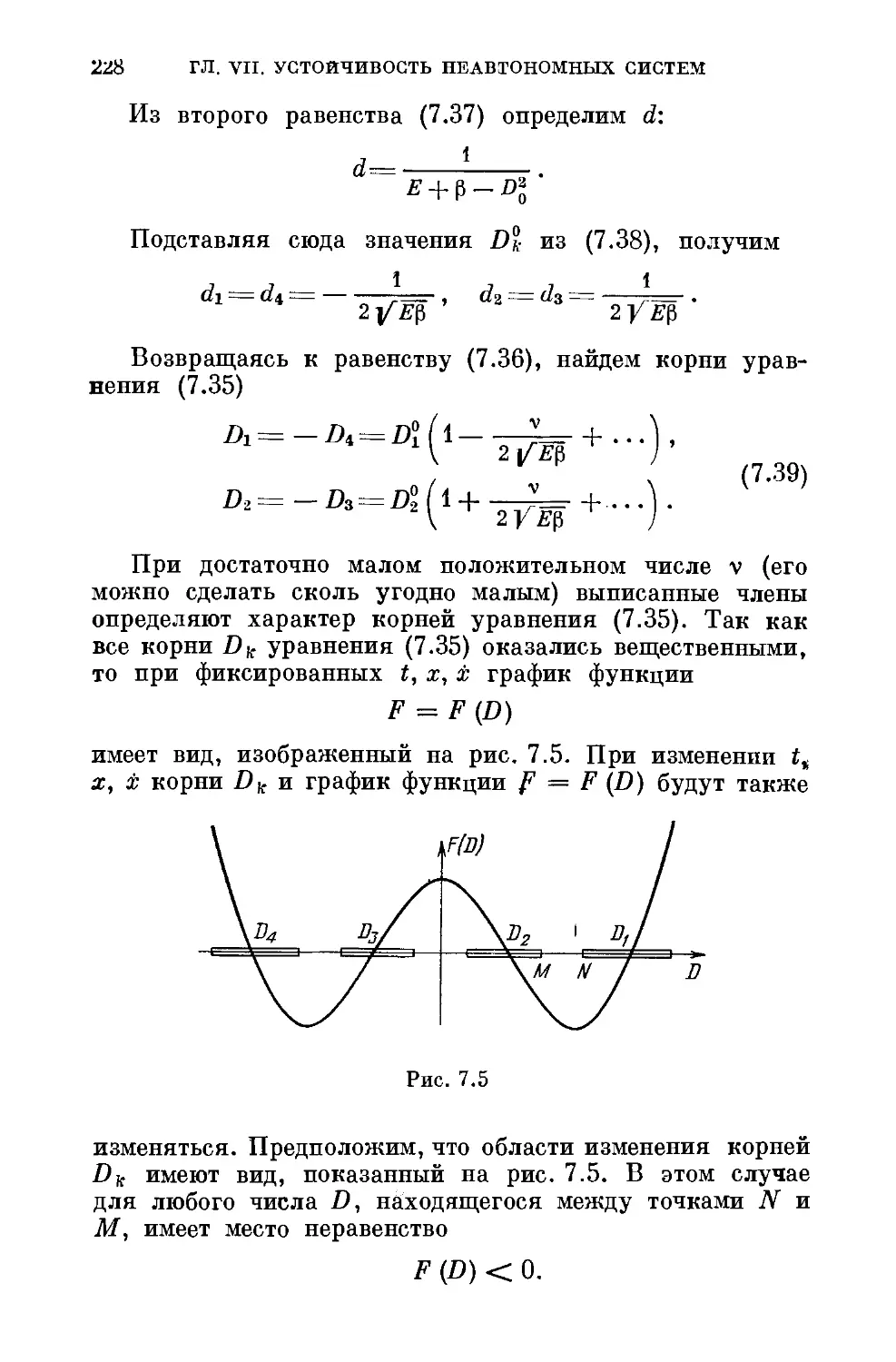
§ 7.4.	Достаточные условия асимптотической устойчи-
вости системы, жесткость и демпфирование ко-
торой нелинейны и зависят явно от времени . .	224
§ 7.5.	Устойчивость линейных систем с периодически-
ми коэффициентами.................................. 231
§ 7.6.	Устойчивость решений уравнений Хилла и Матье 239
§ 7.7. Примеры исследования устойчивости систем с па-
раметрическим возбуждением.......................... 254
1.	Влияние ви'рацпи точки подвеса па устойчивость равно-
весия маятника (2з5). 2. Исследование устойчивости нуле-
вого решения уравнении Хилла при параметрическом виз-
Оуждевии по закону квазиврямоуголыюго синуса (257).
Глава VIII. ПРИМЕНЕНИЕ ПРЯМОГО МЕТОДА
ЛЯПУНОВА К ИССЛЕДОВАН ПО УСТОЙЧИВОСТИ
СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ .	261
§ 8.1.	Введение .	.......................... 261
§ 8.2.	Дифференциальные уравнения возмущенного
движения систем автоматического регулирования 262
§ 8.3. Преобразование уравнений возмущенного дви-
жения системы регулирования к канонической
форме............................................... 266
§ 8.4.	Построение	функции	Ляпунова................. 270
§ 8.5.	Определение	условий	абсолютной устойчивости.
Пример ....................•................... 277
Г л а в а IX. ЧАСТОТНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
УСТОЙЧИВОСТИ ...................................... 286
§ 9.1.	Введение	. 286
§ 9.2.	Передаточные функции и частотные характерис-
тики .............................................. 286
§ 9.3.	Критерий	Найквиста устойчивости линейной сис-
темы 	 290
§ 9.4.	Частотные	критерии абсолютной устойчивости
систем с	непрерывной нелинейностью. 292
§ 9.5.	Примеры	. 296
1.	Математический пример (296). 2. Исследование устойчи-
вости самолета с курсовым автопилотом (297). 3. Непрямое
регулирование двигателя с жесткой обратной связью (299).
Список литературы...................................... 301
ПРЕДИСЛОВИЕ
Предлагаемая читателю книга является одним из по-
собий, выходящих в издательстве «Наука» в качестве до-
полнения к курсу теоретической механики Н. В. Буте-
нипа, Я. Л. Лунда и Д. Р. Меркипа. Издание этих посо-
бий связано с тем, что учащиеся некоторых втузов нуж-
даются в более подробном ознакомлении с рядом важней-
ших проблем, чем это удалось сделать в основном курсе.
Книги, входящие в предлагаемую серию, посвящены имен-
но таким проблемам: аналитической механике, теории
устойчивости движения, теории колебаний, теории гиро-
скопов, теории удара; в будущем этот перечень предпо-
лагается продолжить,
В Советском Союзе издано много книг [5, 6, 8, 16, 18,
21, 27, 28, 29, 35, 37, 49], в которых теория устойчивости
движения излагается с различных точек зрения и с раз-
личной полнотой. Некоторые из этих книг являются не
учебными пособиями, а научными монографиями. Книги
же, построенные как учебные руководства, рассчитаны,
как правило, на студентов математико-механических фа-
культетов университетов, имеющих специальную матема-
тическую подготовку. Для лиц, знающих математику в
объеме высшего технического учебного заведения, эти
книги малодоступны.
Настоящая книга рассчитана в основном на студентов
и преподавателей втузов, а также на инженеров и науч-
ных работников, использующих теорию устойчивости дви-
жения в своей работе, В связи с этим в книге применяется
математический аппарат, не выходящий за рамки курса
ПРЕДИСЛОВИЕ
7
математики, читаемого почти во всех высших технических
учебных заведениях. Необходимые дополнительные све-
дения из курса математики приводятся в книге.
В целях упрощения изложения вначале рассматрива-
ются автономные системы и только в седьмой главе изу-
чается устойчивость движений неавтономных систем.
С этой же целью доказательство некоторых теорем приве-
дено в упрощающих предположениях. Во всех этих слу-
чаях оговаривается, в чем состоит упрощение и где мож-
но найти доказательство, свободное от сделанных огра-
ничений.
Основное внимание в книге уделено наиболее эффектив-
ным методам исследования устойчивости движения —
прямому методу Ляпунова и исследованию устойчивости
по уравнениям первого приближения. Отдельные главы
посвящены исследованию устойчивости движения по струк-
туре действующих сил, устойчивости движения неавто-
номных систем, в том числе систем, возмущенное движе-
ние которых описывается линейными дифференциальны-
ми уравнениями с периодическими коэффициентами.
В восьмой главе излагается применение прямого ме-
тода Ляпунова к исследованию устойчивости систем авто-
матического регулирования и, наконец, последняя, де-
вятая глава посвящена применению частотных методов
к исследованию устойчивости движения.
Учитывая, что лица, впервые изучающие теорию устой-
чивости движения, испытывают обычно затруднения в
применении ее к решению практических задач, в книге
большое внимание уделено подбору и решению примеров,
взятых из различных областей науки и техники; значи-
тельная. часть примеров имеет самостоятельное значение.
В основу настоящего руководства положен курс лек-
ций, читанный в течение ряда лет автором в Ленинград-
ском государственном университете на факультете по-
вышения квалификации преподавателей теоретической
механики. Большое влияние на содержание и характер
8
ПРЕДИСЛОВИЕ
книги оказали многочисленные консультации инженеров
и научных работников научно-исследовательских инсти-
тутов Ленинграда по различным вопросам теории устой-
чивости движения и ее приложений.
В настоящее, третье издание книги (первое издание
вышло в свет в 1971 г., второе — в 1976 г.) добавлены но-
вые примеры, в нем учтены некоторые работы, опублико-
ванные после выхода второго издания, пересмотрен текст
книги, исправлены замеченные опечатки.
При подготовке первого издания книги большую по-
мощь автору оказали чл.-кор. АН СССР А. И. Лурье,
чл.-кор. АН СССР В. В. Румянцев, доценты Б. А. Смоль-
ников и Б. Л. Минцберг. Большая часть девятой главы
написана А. X. Гелигом. Много ценных замечаний сде-
лал по второму и третьему изданиям чл.-кор. АН СССР
В. В. Румянцев. Автор пользуется случаем выразить
всем перечисленным лицам свою искреннюю благодар-
ность.
Д. Р. Меркин
ВВЕДЕНИЕ
Проблемы устойчивости возникли впервые в меха-
нике при изучении равновесных положений системы.
Простое наблюдение показывает, что некоторые положения
равновесия системы устойчивы к небольшим возмущениям,
а другие принципиально возможные равновесные положе-
ния практически пе могут быть реализованы. Так, на-
пример, если маятник занимает пижпее положение, то
небольшие возмущения могут вызвать только колебания
его. Если же после некоторых усилий удастся установить
маятник в верхнем положении, то малейший толчок вы-
зовет его падение. Конечно, в данном примере вопрос об
устойчивости решается элементарно, но в общем случае
далеко пе всегда ясно, при каких условиях равновесное
положение системы будет устойчиво. В 1644 г. критерий
устойчивости равновесия системы тел, находящихся под
действием сил тяжести, в общем виде сформулировал
Е. Торричелли, а в 1788 г. Ж. Лагранж доказал теорему,
определяющую достаточные условия устойчивости равно-
весия произвольной консервативной системы (см. § 3.1).
В середине XIX столетия в науке и технике возникли
проблемы, потребовавшие постановки общей задачи об
устойчивости не только равновесия, но и движения. Ука-
жем на одну из них.
Центробежные регуляторы, установленные на паровых
машинах небольшой мощности, устойчиво сохраняли за-
данные обороты двигателя. С увеличением мощности ма-
шин регуляторы, построенные по тем же схемам, не толь-
ко не обеспечивали надежное регулирование, но даже
разгоняли двигатели, создавая неустойчивый режим ра-
боты (см. пример 3 § 4.5). Это непонятное для инженеров
и техников тех лет явление вызвало серьезный кризис в
двпгателестроении и потребовало усилий ученых многих
стран для решения возникшей проблемы. Исследования
Дж. К. Максвелла (1868 г.), И. А. Вышнеградского
10	ВВЕДЕНИЕ
(1876 —1877 гг.) и других показали, что решение как этой
задачи, так и общее развитие теории регулирования тре-
бует, прежде всего, установления критериев устойчиво-
сти движения.
В конце XIX столетия появились работы, в которых
вопросы устойчивости движения трактовались с общих
позиций. Так, в 1877 —1884 гг. были опубликованы моно-
графии Э. Дж. Рауса 156, 57], а в 1882 г. — докторская
диссертация Н. Е. Жуковского [20], в которых авторы,
пользуясь различными методами, рассмотрели ряд общих
вопросов устойчивости движения. Некоторые результаты
и методы, развитые ими, не утратили своего значения и
в наши дни.
Основной недостаток работ того времени состоял в том,
что при анализе уравнений возмущенного движения авто-
ры исходили из линеаризованных уравнений возмущен-
ного движения и не рассматривали влияния членов выс-
шего порядка. Так, например, если уравнения возмущен-
ного движения имеют вид
dXi	1 лГ 2 I 2
=- — а.г2 4-Ш11 г, + j-2,
I	(*}
~ a.Ti -|- a.r-2 V >'! + а"2,
то, согласно рекомендациям авторов тех лет, их можно
упростить, отбросив нелинейные члены, т. е. заменить
уравнения (*) уравнениями
и судить устойчиво или неустойчиво движение не по урав-
нениям (*), а по уравнениям (**). Между тем вывод об
устойчивости движения, основанный на линейных урав-
нениях (**), ничего общего не имеет с результатом ана-
лиза точных уравнений (*) (см. пример на с. 20—21).
В 1892 г. была опубликована докторская диссертация
А. М. Ляпунова «Общая задача об устойчивости движения».
Эта работа содержит так много плодотворных идей и ре-
зультатов первостепенного значения, что всю историю
теории устойчивости движения не без основания делят па
доляпуновский и послеляпуновский периоды. В кратком
введении невозможно дать обзор всего, что внес А. М. Ля-
ВВЕДЕНИЕ
11
пунов в теорию устойчивости движения. Полностью оце-
нить его работу может только специалист, хорошо знаю-
щий предмет. Поэтому мы ограничимся здесь указанием
на некоторые результаты, принадлежащие А. М. Ляпу-
нову.
Прежде всего А. М. Ляпунов дал строгое определе-
ние устойчивости движения. Отсутствие такого определе-
ния приводило часто к недоразумениям, так как движение
устойчивое в одном смысле может оказаться неустойчивым
в другом понимании этих слов, и наоборот. Определение
А. М. Ляпунова оказалось настолько удачным, что оно
принято как основное всеми учеными.
А. М. Ляпунову принадлежит постановка задачи об
устойчивости движения по уравнениям первого прибли-
жения, когда об устойчивости можно судить по линеари-
зованным уравнениям без необходимости привлечения
к анализу точных уравнений. Он дал полное решение этой
задачи для так называемых установившихся движений,
когда уравнения возмущенного движения не содержат
время t в явной форме, и для большого класса неустано-
вившихся движений, причем особенно подробно им были
изучены периодические движения. А. М. Ляпунов пред-
ложил два основных метода исследования устойчивости
движения, из них второй метод, или, как сейчас принято
называть его, прямой метод, получил наибольшее распро-
странение благодаря своей простоте и эффективности. Он
поставил вопрос об обратимости теоремы Лагранжа и до-
казал ее для двух частных случаев.
После А. М. Ляпунова теория устойчивости движения
развивалась по различным направлениям. Углублялись
методы и уточнялись результаты самого А. М. Ляпунова,
расширялся круг понятий, введенных А. М. Ляпуновым
в теорию устойчивости движения, в частности, усилия
многих ученых были направлены на определение условий
устойчивости при больших начальных и постоянно дей-
ствующих возмущениях, а также на конечном промежутке
времени и при случайных силах. Возникло также направ-
ление, которое условно можно назвать прикладным. Речь
идет не о многочисленных, ежедневно возникающих в на-
уке и технике частных задачах, решаемых с помощью уже
развитой теории, а о создании общих методов исследова-
ния устойчивости движения отдельных, достаточно об-
ширных классов систем (системы автоматического регули-
рования, управляемые системы и т. п.).
12	ВВЕДЕНИЕ
Теория устойчивости движения широко применяется
в физике, астрономии, химии и даже биологии (см., на-
пример, [466]). Особо важное звачение теория устойчи-
вости движения имеет для техники. Корабль, самолет, ра-
кета при своем движении должны устойчиво сохранять за-
данный курс. Турбины, генераторы должны устойчиво
сохранять заданный режим работы. Гироскопический
компас должен устойчиво показывать направление геогра-
фического меридиана и т. п.
В заключение отметим, что теория устойчивости дви-
жения еще далека от завершения. Она продолжает разви-
ваться, охватывая все более широкий круг вопросов. В ее
разработке принимают участие много ученых различных
стран. Перечислить все имена практически невозможно,
некоторые из них будут названы в тексте книги.
ГЛАВА I
ПОСТАНОВКА ЗАДАЧИ
§ 1.1.	Основные определения
Обозначим через yi, . . уп вещественные переменные,
характеризующие состояние механической, электромеха-
нической или какой-нибудь другой системы. Этими пере-
менными могут быть координаты, скорости, токи, напря-
жения, температуры и т. п. или функции этих величин.
Предполагается, что число переменных уг, . . ,,уп конечно
и что движение системы (процесс изменения переменных
Уи . . Уп во времени) описывается обыкновенными диф-
ференциальными уравнениями, которые могут быть ре-
шены относительно производных по времени х)
уЛуг,---, Уп, Л
dl................. (1.1)
Щ == 1 п (У1, • • -, Уп, I).
В этих уравнениях Ylt . . ., Yn — известные функции
переменных уг, . . ., уп и времени t, удовлетворяющие ус-
ловиям существования и единственности решения. Если
все функции Yfr не зависят явно от времени t, то система
называется автономной, в противном случае — неавто-
номной. Заметим, что при решении конкретных задач урав-
нения движения не обязательно приводить к виду (1.1),
в частности, их можно представить как одно или несколько
уравнений высшего порядка.
Некоторое вполне определенное движение системы
подлежащее исследованию на устойчивость, называется
невозмущенным движением. Невозмущенному движению
системы отвечает определенное частное решение
!/1	/1 (/), . . ., ?/„ = /„(<)	(1.2)
*) Формулы нумеруются двумя числами: первое число означает
номер главы, второе — номер формулы в этой главе.
14	ГЛ. I. ПОСТАНОВКА ЗАДАЧИ
дифференциальных уравнений (1.1), удовлетворяющеь
начальным условиям:
при t = t0: у. = /j (f„), . . уп = /п (Zo).	(1.3)
Изменим условия (1.3), дав начальным значениям пе-
ременных уА, . . ., уп небольшие по модулю приращения
е,, . . ., е,(, а именно пусть теперь
при t - t0: уА = (Zo)	уп= fn (Zo) 4- en.
(1.4)
Движение системы, отвечающее измененным начальным
условиям (1.4), называется возмущенным движением, а
величины еп . . ., еп — возмущениями.
Обозначим значения переменных yj в возмущенном
движении через yj(t), а в невозмущенном движении че-
рез /j (Z) и составим разности между ними
XJ = У) (z) — fj (0 (/ = 1, . . ., п).	(1.5)
Переменные xj называются отклонениями или вариациями
величин ур Если все отклонения равны нулю, то есть
ху = 0, х2 = 0, . . ., хп = 0,	(1.6)
то возмущенное движение yj (Z) будет совпадать с невоз-
мущенным движением /у (Z), иначе говоря, невозмущен-
ному движению отвечают нулевые значения переменных Xj.
В дальнейшем для удобства изложения будем пользо-
ваться часто языком геометрии. Совокупность отклоне-
ний Xj, . . хп в тг-мерном пространстве переменных
xt, . . ., хп определяет точку М (она называется изобра-
жающей точкой) ’). В возмущенном движении при из-
менении величин хЛ, . . ., хп изображающая точка М
будет описывать некоторую траекторию у. Невозмущен-
') В обычном трехмерном евклидовом пространстве совокуп-
ность трех чисел xlt х2, х3 определяет точку М. Обобщая это поня-
тие, под точкой М в n-мерном пространстве переменных xlt . . ., хп
понимают совокупность п чисел хг, . . хп. Расстояние г от этой
точки до начала О ортогональной координатной системы Ох,х2 . . . хп
определяется равенством
Продолжая обобщение понятий, существующих в обычном трех-
мерном евклидовом ‘пространстве, говорят, что всякое уравнение
/ (.rj, . . ., хп) = 0 определяет в пространстве п измерений некото-
рую поверхность, в частности, уравнение zj3 . . . + xft ---= г2 оп-
ределяет в га-мерном пространстве сферу радиуса г.
§ 1Л ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ	15
ному движению х, = 0 тпвечает неподвижная точка —
начало координат.
Отклонение возмущенного движения от невозмущен-
ного движения определяется величинами х, (t). Если
все Xj (t) малы по модулю, то будет мала и сумма их
квадратов
п
4" J + • • • 4" ^4	3 -rv	(1-7)
j=i
если же отклонение хотя бы одной координаты будет
велико, то сумма (1.7) будет велика. Обратное утвержде-
ние, очевидно, также справедливо. Поэтому в качестве
меры отклонения возмущенного движения от невозму-
щенного движения можно выбрать величину суммы
(1.7). Так как сумма (1.7) равна квадрату расстояния
от изображающей точки до начала координат, то это
расстояние характеризует отклонение возмущенного
движения от невозмущенного.
Согласно определению возмущенного движения и
равенствам (1.4), (1.5), будем иметь
при t = i0: Xj — xaJ ~ Ej (j = 1, . . .,n), (1.8)
т. e. начальные значения отклонений xaj представляют
возмущения системы.
Примем следующее определение Ляпунова. Если по
любому положительному числу е, как бы оно мало ни было,
можно найти такое положительное число б, что при
всяких возмущениях xOj, удовлетворяющих условию
(1-9)
и при любом t 4-> ta будет выполняться неравенство
Е^<г,	(1.10)
то невозмущенное движение устойчиво, в противном
случае — неустойчиво.
Геометрически это определение означает следующее.
Рассмотрим сферу SzJ = е. Выберем радиус е этой
сферы произвольно малым. Если движение устойчиво,
то для этой сферы должна найтись другая сфера = б
радиуса }^б, обладающая следующим свойством. Изобра-
жающая точка М, начав свое движение из любого поло-
жения Ма, лежащего внутри или на поверхности сферы
[6
ГЛ. Т. ПОСТАНОВКА ЗАДАЧИ
61), при своем дальнейшем движении остается всегда
внутри сферы е, никогда не достигая ее поверхности
(рис. 1.1)2). Если же возмущенное движение неустой-
чиво, то хотя бы одна траектория изображающей точки
М с течением времени пересечет сферу 8 изнутри наружу
Если невозмущенное
при сколь угодно близком поло-
жении точки М к началу коор-
динат.
Практически устойчивость
данного невозмущенного движе-
ния означает, что при достаточ-
но малых начальных возмуще-
ниях возмущенное движение
будет сколь угодно мало отли-
чаться от невозмущенного дви-
жения. Если же невозмущенное
движение неустойчиво, то воз-
мущенное движение будет отхо-
дить от него, как бы малы ни
были начальные возмущения,
движение устойчиво и при этом
любое возмущенное движение при достаточно малых
начальных возмущениях стремится к невозмущенному
движению, т. е. если
lim 3^(i) =0,	(1.11)
то невозмущенное движение называется асимптотически
устойчивым. Заметим, что одного предельного условия
(1.11) недостаточно для асимптотической устойчивости —
необходимо, чтобы помимо этого условия движение
было устойчивым. Геометрически это означает, что при
асимптотической устойчивости изображающая точка
должна неограниченно стремиться к началу координат,
не выходя из сферы 8 (см. пример па с. 20—21).
Кроме пространства отклонений хг, . . ., хп рассмотрим
пространство исходных переменных г/ъ . . ., уп. Сово-
купность значений уъ . . ., уп определяет в этом простран-
стве некоторую точку N. Пусть в невозмущенном движе-
нии (1.2) точка N описывает траекторию I, а в возму-
х) Будем для простоты сферу с радиусом У6 (аналогично Vе)
называть сферой 6 (или сферой е).
2) Для наглядности все рисунки, соответствующие «-мерному
пространству, строятся для п = 2.
§ 1.1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
17
щенном движении — траекторию II (рис. 1.2, а). Возь-
мем на этих траекториях две произвольные точки N
л Л', отвечающие одному и тому же моменту времени t.
Квадрат расстояния г между этими точками равен
г2 = 2 (у, - W = 2^.
При устойчивом движении траектория II близка к
траектории I (г всегда меньше е), а при асимптотической
устойчивости траекто-
рия II неограниченно
стремится к траекто-
рии I (рис. 1.2, б).
Близость траекто-
рий I и II —необходи-
мое условие устойчиво-
сти движения, но оно,
конечно, недостаточно.
Действительно,расстоя-
ние между точками N и
N', отвечающими одно-
му и тому же моменту
времени, может возра-
стать не только для рас-
ходящихся, но и для
близких траекторий
(рис. 1.2, е).
Может оказаться, что движение, устойчивое относи-
тельно одних переменных, неустойчиво относительно
других. Так, можно показать, что движение искусствен-
ного спутника Земли по круговой орбите устойчиво
относительно его радиуса-вектора (орбитальная устой-
чивость) и неустойчиво относительно декартовых коор-
динат. Поэтому, говоря об устойчивости движения,
необходимо всегда оговаривать, относительно каких
величин рассматривается устойчивость.
В тех случаях, когда асимптотическая устойчивость
имеет место при любых возмущениях (не обязательно
малых), невозмущенное движение называется устойчи-
вым в целом.
Иногда устойчивость имеет место не при любых воз-
мущениях, а при возмущениях, подчиненных некоторым
условиям. Такая устойчивость называется условной.
Остановимся на особенностях определения устой-
чивости движения по Ляпунову. Во-первых, преднола-
18	ГЛ. I. ПОСТАНОВКА ЗАДАЧИ
гается, что возмущения налагаются только на начальные
условия, иначе говоря, возмущенное движение проис-
ходит при тех же силах (источниках энергии), что и
невозмущенное движение. Во-вторых, устойчивость
рассматривается на бесконечно большом промежутке
времени. В-третьих, возмущения предполагаются ма-
лыми. Несмотря на эти ограничения, определение Ля-
пунова устойчивости движения является эффективным
и плодотворным в приложениях. Кроме того, методы,
развитые Ляпуновым, очень часто лежат в основе иссле-
дования других видов устойчивости движения х).
§ 1.2.	Уравнения возмущенного движения
В тех случаях, когда известно общее решение диф-
ференциальных уравнений движения (1.1), можно непо-
средственно определить значения переменных yj (7) в
возмущенном движении, составить вариации Xj =
= У] (t) — /; (i) и, исследуя их, решить вопрос об устой-
чивости невозмущенного движения (£).
Однако в подавляющем большинстве случаев общее
решение дифференциальных уравнений движения (1.1)
неизвестно^ поэтому этот метод практически редко может
быть использован. Но даже в тех случаях, когда общее
решение дифференциальных уравнений (1.1) можно
построить, ответ на вопрос — устойчиво ли движение,
целесообразно, как правило, искать не из анализа об-
щего решения, а с помощью методов, специально раз-
работанных в общей теории устойчивости движения.
Эти методы основаны на качественном анализе дифферен-
циальных уравнений возмущенного движения, которым
удовлетворяют отклонения (вариации) Xj.
') Устойчивость движения при постоянно действующих воз-
мущениях излагается в книгах И. Г. Малкина [37], Н. Н. Красов-
ского [27], Е. А. Барбашина [5] и др. В книгах Е. А. Барбашина
[5, 6] и книге Н. Н. Красовского [27] рассматривается устойчивость
в целом (см. § 2.3). Устойчивость движения на конечном интервале
времени и конечных начальных возмущениях излагается в книгах
Н, Г. Четаева [49] и К. А, Карачарова, А, Г, Пплютика [25]; за-
дача об устойчивости движения со случайными параметрами рас-
сматривается в работе И, Я. Каца, Н. Н. Красовского [26] и др.
Устойчивость систем с последействием (с запаздыванием времени)
излагается в книге Н. Н, Красовского [27], Подробные обзоры ра-
бот по исследованию устойчивости методом построения функций Ля-
пунова, устойчивости неголономных систем и устойчивости па ко-
нечном интервале даны в [2а, 46а, 1а] соответственно.
§ 1.2. УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ
19
Для вывода уравнений возмущенного движения
найдем из равенства (1.5) переменные //_, (i):
Uj (0 = h Ю + xi (О-
Внесем эти значения для (i) в дифференциальные урав-
нения движения системы (1.1). Получим
<// <Дс.
~dT + ~dF "= У ’	+ Х1' • • •’ -lri + •г"’ г)'
Разложим правые части этих уравнений в ряды Тейлора
по. степеням xf. ])
dtj , dxi _
dt T" fit
= Y i (fl, . . f „, 0 + ( '7^') X1 +••• + ( ~g~- )	+ Xj,
\	/ 0	\ J о
где X* — совокупность членов, зависящих от отклоне-
ний в степени выше первой.
Учтем теперь, что в невозмущенном движении функ-
ции fj (t) должны удовлетворять уравнениям движения
(1.1), т. е.
df.
_^=Yj(fl,...,fn,t)	(j~l,...,n).
На этом основании будем иметь
+ ... + ajnxn + X* (/=1, ..., п). (1.12)
В этих уравнениях коэффициенты
[
«Д— Ь/	(1ЛЗ)
в общем случае являются функциями времени t, в част-
ности, они могут быть постоянными.
Уравнения (1.12) называются дифференциальными
уравнениями возмущенного движения. Если в этих урав-
нениях отбросить члены X*, то полученные при этом
уравнения
dx 
а,рч Ч «;2.т2 +.•  • +	(] = !,..., п) (1.14)
называются уравнениями первого приближения.
2) Здесь и в дальнейшем предполагается, что функции, разла-
гаемые в ряды, удовлетворяют соответствующим требованиям.
20
ГЛ. I, ПОСТАНОВКА ЗАДАЧИ
Уравнения первого приближения во многих случаях
дают верный ответ на вопрос об устойчивости движения,
но очень часто заключение, которое можно получить
из этих приближенных уравнений, ничего общего не
имеет с решением исходных уравнений.
Приведем пример. Пусть уравнения возмущенного движения
имеют вид (<z = const)
dxi	.	l/~ 2 t 2
—- — — cu2 + axi у a-.;,
dt	_______ (1.15)
= сил + си2 + x22.
Умножим первое уравнение на ад, второе на х2 и сложим по-
членно оба уравнения:
dx, . dx2 , 2 I 2ч3/0
п ~dt~ r2~dta +
или
1 d , 2 .	2\	/ 2 I 2\ э/о
_ _ (^ + г2) = а (х- + х$
Положим X} + х2 = г2, где г — расстояние от начала коорди-
нат до изображающей точки. После перехода к новой переменной г
будем иметь
1 dr2 о
------= аг3
2 dt
или
Это уравнение легко интегрируется, и его общее решение имеет
вид
г = ______1_______,
1 — <zr0 (t — to)
где г0 — значение г при t = t0.
Из этого решения видно, что при а >> 0 расстояние г от изо-
бражающей точки М до начала координат неограниченно возрастает
при t —» t0 + —, т. е. движение неустойчиво. (Заметим, что lim г2 =
<ХГ0	/_оо
= 0, т. е. условие (1.11) выполнено, хотя движение неустойчиво.)
Если же а <; 0, то г монотонно убывает, стремясь к нулю при t —>
оо, т. е. движение асимптотически устойчиво.
Рассмотрим теперь уравнения первого приближения
которые получаются из уравнений (1.15) отбрасыванием членов по-
рядка выше первого.
§ 1.2. УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ
21
Для этих уравнений вместо равенства г = аг- будем иметь
dt
или, интегрируя, г = г0.
Это решение показывает, что изображающая точка М, отвечаю-
щая уравнениям первого приближения, движется по окружности,
радиус которой равен начальному отклонению точки М от начала
координат. Таким образом, и.з уравнений первого приближения сле-
дует устойчивость невозмущенного движения = х2 = 0 при всех а.
Этот вывод ничего общего не имеет с результатом анализа исход-
ных уравнений (1.15), согласно которому при а >• 0 движение не-
устойчиво, а при а < 0 асимптотически устойчиво.
Вернемся к уравнениям возмущенного движения
(1.12). Обозначив все члены, стоящие в правых частях
этих уравнений, символами Х7-, получим для неавтоном-
ных уравнений возмущенного движения
dx-
-^=,Xj^,...,xn,t}	(1.16)
Если уравнения возмущенного движения автономны,
т. е. не содержат время t явно, то будем иметь
dx-
~ Xj(x!,..хп).	(1.17)
В дальнейшем совокупность уравнений возмущенного
движения мы будем называть часто просто системой.
Таким образом, уравнения (1.16) определяют неавто-
номную, а уравнения (1-17) автономную системы (урав-
нений возмущенного движения).
Форма дифференциальных уравнений возмущенного
движения (1.16) или (1.17) называется нормальной, а
движения, определяемые этими уравнениями, называ-
ются неустановившимися и установившимися движениями
соответственно.
В дальнейшем для сокращения записи совокупность
отклонений хи . . ., хп будем часто обозначать одной
буквой х (в главе V этому будет дано смысловое обосно-
вание). В соответствии с этим для автономной Системы
будем иметь
Xj (зд, . . ., X,,} Xj (х),
а для неавтономной системы
X; = Xj (2.J, . . ., Хп, t) = Xj (х, t).
22
ГЛ. I. ПОСТАНОВКА ЗАДАЧИ
Из вывода уравнений возмущенного движения видно,
что при х = 0 (то есть при х1 = х., — . . . = хп = 0)
все функции Xj обращают-
ся в Нуль;
Xj (0,0 = 0.	(1.18)
У'	Нормальная форма диффе-
ренциальных уравнений воз-
Рис. 1.3	мущенного движения допу-
скает простую геометричес-
кую интерпретацию. Действительно, как уже отме-
чалось, в возмущенном движении изображающая точка
М описывает в пространстве хг, . . хп некоторую траек-
торию у. Скорость U движения точки М направлена по
касательной к этой траектории, а ее проекции определя-
ются равенствами J)
*) Если бц . . ., еп — единичные векторы ортогональной систе-
мы Охг, . . ., хп, то разложение любого вектора а по координатным
ортам в re-мерном пространстве имеет вид
а = а1е1 -|- . . . -|- апеп,
где аг, . . ., ап — проекции вектора а на соответствующие оси. Мо-
дуль а вектора а определяется равенством
а = У aj + а* -|- . . . + а*,
производная da/dt вектора я будет
П’
а ее проекции
da
dt
da
__п
dt
Радиус-вектор г изображающей точки М равен
а ее скорость
dr dxi
и — — = —£
dt dt
dx
n ,,
§ 1.3. ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
23
или, пользуясь уравнениями (1.16),
иг =	. ., ип = Хп.	(1.19)
Следовательно, правые части нормальных уравнений
возмущенного движения (1.16) равны проекциям ско-
рости U изображающей точки М (рис. 1.3).
В заключение отметим, что при решении конкретных
задач уравнения возмущенного движения можно не
приводить к нормальной форме (1.16) или к виду
(1.12), в частности, их можно представить как одно или
несколько уравнений высшего порядка.
§ 1.3. Примеры на составление уравнений
возмущенного движения
Поясним общие методы составления дифференциаль-
ных уравнений возмущенного движения на трех при-
мерах.
Пример 1. Дифференциальные уравнения
возмущенного движения конического маят-
ника. Рассмотрим материальную точку М массой т, подвешенную
па невесомой нити ОМ к точке О (сфериче-
ский маятник). Будем считать, что длина нити
равна I. Положение точки М будем опреде-
лять углами ф и 0, значения которых видны
на рис. 1.4 (ось Oz вертикальна, ось х парал-
лельна неподвижной горизонтальной оси х,
прямая MN перпендикулярна оси Oz).
Кинетическая и потенциальная энергии
сферического маятника определяются равен-
ствами
Т = -Lml2 (б3 -ф2 sin3 0),
n = rcgZ(l-СО..0).	(1.20)
Пользуясь уравнениями Лагранжа
d 5Г __ 5Г _ 5П d d£_5T _5П
dt 59 50	50 ’ dt 5ф йф 5ф
mg
Рис. 1.4
составим дифференциальные уравнения движения сферического
маятпика:
ml2Q — т.1г\\12 sin 0 cos 0 -ф- mgl sin 0 — 0,
in22ф sin2 0 + 2пН20ф sin 0 cos 0 ~ 0,
24
ГЛ. I. ПОСТАНОВКА ЗАДАЧИ
или, после очевидных упрощений,
0 = — Я- sin 0 4 ф- sin 0 cos О,
1. . (1-^1)
ф = — 20 ф ctg 0.
Положим
0 = 2/1, 0 = у2, ф = у3.	(1-22)
Теперь уравнения движения сферического маятника принима-
ют вид уравнений (1.1):
Й '= У 2,
Й = — 1-sin У!-1-1/2 sin й cos 1/1,	(1.23)
,’з = — 2у2у3 ctg ух.
Рассмотрим движение маятника по горизонтально располо-
женной окружности с постоянной скоростью (конический маятник).
В этом случае будем иметь
0 - yt — Д (/) — а - - const,
0 =1/2= /2 (0 = °,	(1-24)
ф = Уз = /з (0 = « = const.
Подставив эти значения для ylt у2 и у3 в (1.23), получим из вто-
рого уравнения (первое и третье уравнения обращаются в тождества)
io2 cos а -- у.	(1-26)
Конечно, это условие, которому должны удовлетворять параметры
конического маятника, можно получить из элементарных соображе-
ний, например, применяя принцип Даламбера.
За невозмущенное движение примем движение, определяемое
равенствами (1.24). В соответствии с общей теорией положим
У1 = а + яг1; у2 = х2, Уз = w + х3	(1-26)
и внесем эти значения для г/1; у2 и у3 в уравнения (1.23). У читывая,
что а и со — постоянные, получим дифференциальные уравнения
возмущенного движения в нормальной форме (1.17):
^1 = х2,
±2 = —у sin (а ^1) (со + .т-з)2 sin (а 4- -ri) cos (а 4- ^i), (1’27)
is = — 2х2 (со 13) ctg (а 4- zj).
Легко видеть, что правые части этих уравнений обращаются при
= х2 .г3 = 0 в пули (во втором уравнении пужпо учесть равен-
ство (1.25)), т. е. они удовлетворяют условиям (1.18), Разлагая
правые части в ряды ио степеням хг, х2 и х3 и ограничиваясь чле-
нами первого порядка малости, получим уравнения первого
§ 1.3. ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ
25
приближения
Л = *2,
г2 = —со2 sin2 а -.^1 + w sin 2а-т3
-г3 = —2со ctg а -х2,
(1.28)
при этом учтено равенство (1.25).
В следующем примере будет показано, что при со-
ставлении дифференциальных уравнений возмущенного
движения можно не прибегать к уравнениям движения
системы в форме (1.1).
Пример 2. Дифференциальные уравнения
возмущенного движения центра масс ис-
кусственного спутника Земли. Будем предпола-
гать, что на спутник действуют только силы притяжения Земли,
приводящиеся к одной равнодействующей F, приложенной к центру
масс спутника, причем модуль ее определяется законом всемирного
тяготения:
^ = 1^
т *
(1-29)
Здесь ц = gR2 = fM — гравитационный параметр Земли (R — ее
радиус, g — ускорение силы тяжести иа поверхности Земли, At —
ее масса, / — гравитационная постоянная), г — ОС — расстояние
от центра Земли О до центра масс С спутника, т — его масса.
Ряс. 1.5
Рассмотрим равномерное движение центра масс искусственного
спутника по круговой орбите радиуса г0, лежащей в плоскости л
(рис. 1.5, а). Такое движение называется также стационарным дви-
жением искусственного спутника Земли (см. § 3.4). Параметры, оп-
ределяющие стационарное движение спутника, должны удовлетво-
рять следующему условию, непосредствеиио вытекающему из вто-
рого закона Ньютона (тг0со2 = цт/г^):
= р,	(1.30)
где со = ср = const ~ угловая скорость вращения радиуса-вектора
г0 спутника в стационарном движении.
26
ГЛ. I. ПОСТАНОВКА ЗАДАЧИ
Предположим, что на это движение спутника Земли наложены
некоторые возмущения (это равносильно тому, что при отделении
спутника от последней ступени ракеты незначительно нарушены
условия, которые должны были обеспечить движение искусственно-
го спутника по круговой орбите радиуса г0, лежащей в плоскости л).
В результате наложенных возмущений спутник начнет совер-
шать возмущенное движение, в частности, орбита уже не будет кру-
говой, движение не будет происходить в плоскости л, угловая ско-
рость q> вращения радиуса-вектора не будет равна У р/г®.
Для составления уравнений возмущенного движения спутника
построим систему отсчета Oxyz, координатная плоскость ху которой
совмещена с плоскостью орбиты в стационарном движении, т. о.
с плоскостью л. Положение центра масс С искусственного спутника
в возмущенном движении будем определять сферическими коорди-
натами г, ф, 0 (рис. 1.5, б). Кинетическая Т и потенциальная П энер-
гии спутника определяются равенствами (в сделанных предположе-
ниях вращательное движение спутника не влияет на движение его
центра масс и, следовательно, из рассмотрения может быть исклю-
чено):
7= “ (г2^ Г202 -|- Г2СОо2Оф2), П :—11— .	(1.31)
2	г
Имея в виду изучить устойчивость стационарного движения искус-
ственного спутника относительно величин г, г, 0, О и ф, составим
уравнения возмущенного движения. Для этого воспользуемся урав-
нениями Лагранжа второго рода:
d ВТ ВТ
dt д /. дд.
дП
д<Ь
(9 ;• = Г, 0, ф).
Составим сначала уравнение для координаты г. Имеем
дТ • d дТ " дТ д, .	<> п * <>
— — znr,-------= mr. —~ ттху -4- mr со. 2 (кг2,
dr	d! dr	дт
йП___Цт
~дг W
Внеся полученные выражения в уравнение Лагранжа для координа-
ты г, найдем
mr — mrQ2 — mr cos2 Оф2 = — Н — ,
г2
или, сократив на массу m и положив г-= r0 -|- z и ф-= со -|- у, по-
лучим уравнения возмущенного движения искусственного спутника
(уравнения для 0 и ф получены аналогично)
х — (г0 + z)О2 — (г0 + z) cos2 0-(со + у)2 = — _—Е_— ,
Со Ч
(г0 4- х) 0 -|- 2t() -|- (го + х) cos 0 sin 0 • (со + у)2 = 0,	(1.32)
^-[(го+ Ч cos3 0-(со + у)] =0.
§ 1.3. ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ
27
Прежде чем привести эти три дифференциальных уравнения
возмущенного движения спутника Земли (два из них второго поряд-
ка, а одно — первого) к нормальному виду, введем для общности
йовые обозначения:
X = X — х2, 0 = Л'з, 0 = xt, у — х3.
Внеся эти выражения в уравнения (1.32) и решив их относитель-
но производных, получим дифференциальные уравнения возмущен-
ного движения в нормальной форме:
= (го+ и) + COS2 х3 (со + z5)!]
dx3 _ т
dt
и ;
(г0
(1.33)
= - 2 X2Xi , - (со +z5)2 sin 2хл,
dt	r„	Хг 2
= - 2	(co -J- xj + 2.r4 (co -I- x5) tg x.j.
dt	г о —p
Легко видеть, что правые части этих уравнений обращаются
в нуль при zj = . . . = z5 = 0, т. е. они удовлетворяют условиям
(1.18) (во втором уравнении нужно учесть равенство (1.30)). Разла-
гая правые части в ряды и ограничиваясь членами первого порядка
относительно . . ., z5, получим дифференциальные уравнения
первого приближения возмущенного движения искусственного спут-
ника Земли:
dx^, _ .
~diT 2’
^2. — BigAtj -|- 2ro со.т,,
dt
dx-3
dt
(1.34)
dx$ ____g м x
dt r0
При выводе этих уравнений было принято во внимание равенство
(1.30).
Пример 3. Уравнения возмущенного движе-
ния линейных систем. Рассмотрим важный для прило-
жений случай, когда движение системы описывается неоднородны-
ми линейными дифференциальными уравнениями
•'4	+ Fk (')	(*=“->>2, • • •, «).	О-35)
j= =i
28
ГЛ. I. ПОСТАНОВКА ЗАДАЧИ
где a^j и Fy — заданные функции времени (в частности, они могут
быть постоянными числами).
Предположим, что требуется определить устойчивость какого-
либо движения этой системы (г), . . fn (г). Воспользуемся ра-
венствами (1.5): ук =	+ хк. После подстановки в уравнения
(1.35) получим
4+	+
i
Учитывая, чт	• /],.. ., fn удовлетворяют уравнениям
(1.35), найдем
*К- = S akjxj (fc = l,2,. ,.,и).	(1.36).
Таким образом, уравнения возмущенного движения линейной
неоднородной системы представляют однородную часть уравнений
движения (1.35). Анализ последних и решает вопрос об устойчиво-
сти движения yr =	(г), . . ., уп flt (/).
Г Л AB A II
ПРЯМОЙ МЕТОД ЛЯПУНОВА
(АВТОНОМНЫЕ СИСТЕМЫ)
§ 2.1. Функции Ляпунова. Критерий Сильвестра
Одним из наиболее эффективных методов исследова-
ния устойчивости движения является прямой метод
Ляпунова (очень часто этот метод называется вторым
методом Ляпунова). В этой главе прямой метод будет
изложен для автономных систем (неавтономные системы
рассматриваются в гл. VII).
Изучение прямого метода начнем с рассмотрения
некоторых вещественных функций V (ж) — V (хг, . . ., хп),
определенных в области
(2.1)
где н постоянное положительное число.
Предполагается, что в области (2.1) эти функции
однозначны, непрерывны и обращаются в нуль, когда
все xY, . . ., хп равны нулю, т. е.
V (0) = 0.	(2.2)
Если в области (2.1) функция V кроме нуля может
принимать значения только одного знака, то она назы-
вается знакопостоянной (соответственно положительной
или отрицательной). Если же знакопостоянная функция
обращается в нуль только в том случае, когда все х±, . . .
. . ., хп равны нулю, то функция V называется знакоопре-
деленной (соответственно определенно-положительной или
определенно-отрицательной). Функции, принимающие как
положительные, так и отрицательные значения, назы-
ваются знакопеременными функциями. Введенные таким
образом функции V, используемые для исследования
устойчивости движения, называются функциями Ляпу-
нова.
Рассмотрим два примера.
1.	Функция
V = х^ +
30
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
при Xj и х2, не равных нулю одновременно, принимает положитель-
ные значения и обращается в нуль только при хг = х2 = 0. Следо-
вательно, эта функция определенно-положительна. В пространстве
х1, х2, V поверхность V = х% + 5х\ расположена по одну сторону
от плоскости xj, х2, касаясь ее только в начале координат (рис. 2.1, а).
2.	Функция
V =	— 2хгх2 + х"‘- = (zj — х2)2
не может принимать отрицательные значения, но в нуль она обра-
щается не только в начале координат х1 — х2 — 0, но и на прямой
Рис. 2.1
Xj == х2, V = 0. Следовательно, эта функция положительна, но не
определенно-положительна. В этом случае поверхность V = {хг —
— х2)2 в пространстве xn х2, V также находится по одну сторону
плоскости zj, х2, но касается ее не в одной точке, а по прямой х. =
= х2, V = 0 (рис. 2.1, б).
Из определения и этого примера видно, что положи-
тельную (отрицательную) функцию в указанном смысле
можно назвать также неотрицательной (неположитель-
ной) функцией. Из сделанных определений видно, что
знакоопределенная функция имеет при хк = . . . = хп =
= 0 экстремум {минимум для определенно-положитель-
ной функции и максимум для определенно-отрицатель-
ной функции). Знакопостоянная же функция в начале
координат экстремума не имеет, так как в окрестности
начала координат имеются точки, в которых функция V
принимает значения, равные V (0) = 0 (во втором приме-
ре эти точки расположены на прямой ху = х2, V = С).
Остановимся на признаках, с помощью которых можно
определить характер функции V. Прежде всего заметим,
что знакоопределенная функция V должна содержать
все переменные xlt . . ., ха. Действительно, пусть, на-
§ 2.1. ФУНКЦИИ ЛЯПУНОВА. КРИТЕРИЙ СИЛЬВЕСТРА 31
пример, функция V не содержит переменную х„. Тогда
при х1 = . . . = х,,-! = 0, хп 0 функция V будет
’обращаться в нуль, что недопустимо для знакоопределен-
ных функций.
Пусть знакоопределенная функция V = V (х) непре-
рывна вместе со своими производными. Тогда при
х, = . . . = хп = 0 она будет иметь изолированный
экстремум и, следовательно, все частные производные
первого порядка, вычисленные в этой точке, будут равны
нулю (необходимые условия существования экстремума)
I 9V \	„	...
(J-- 1, . . п).
(2-3)
Разложим функцию V в
ряд Маклорена по степеням
7 =
?? п
Г7 V4 / d*V
о
dxkdxi Jo'
тде точками обозначены члены высшего порядка. Учиты-
вая соотношения (2.2) и (2.3), получим
V 2	Ч- • • •
(2.4)
Здесь постоянные числа c,,j = с^!с определены равенствами
/
(2-5)
\ к- j /о
Из формулы (2.4) видно, что разложение знакоопре-
деленной функции V в ряд по степеням Zj, . . ., хп не
содержит членов первой степени.
Предположим, что квадратичная форма
2 J"1, J"1, cijxk^j
(2-6)
принимает положительные значения и в нуль обращается
только при х} = . . . = хп = 0. Тогда вне зависимости
от членов высшего порядка при достаточно малых по
модулю xj функция V будет принимать также положи-
тельные значения и в нуль она будет обращаться только
при . . . = хп = 0. Таким образом, если квадратич-
32
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
пая форма (2.6) определенно-положительна, то и функция
V будет определенно-положительной.
Рассмотрим матрицу коэффициентов квадратичной
формы (2.6)
	С11	С11	с13	' • • ст
	С21		: с23	• ‘ ‘ С2.п
С —	С31	С32	С33	• ’ ’ С3п
	СП1	СП2,	СпЗ	' * * Спп
(2-7)
и составим
(в матрице
Ах = Гц,
из нее п главных диагональных миноров
(2.7) они окантованы пунктиром)
(2-8)
В линейной алгебре доказывается следующий крите-
рий Сильвестра [9, 14]: для того чтобы квадратичная
форма с вещественными коэффициентами была опреде-
ленно-положительной, необходимо и достаточно, чтобы
все главные диагональные миноры Д1( Д2, . . ., Дп матрицы
ее коэффициентов были положительны, т. е.
Дг> О, Д2> 0, . . Дп> 0.	(2.9)
Из сказанного следует, что критерий Сильвестра (2.9)
для квадратичной части функции V является достаточным
(но не необходимым) условием определенной положи-
тельности самой функции V.
Если функция V определенно-отрицательна, то функ-
ция — V будет определенно-положительной. Поэтому
достаточным условием определенной отрицательности
функции V будет критерий Сильвестра (2.9) для матрицы
—С. Этот критерий имеет вид
Дг<0, Д2>0, Д3<0, ...,	(2.10)
т. е. определители Д7- должны последовательно чередо-
вать знак, причем знак Д2 = сп должен быть отрица-
тельным.
В качестве примера рассмотрим функцию
V = 1 + sin2 — cos — х2).
§ 2.1. ФУНКЦИИ ЛЯПУНОВА. КРИТЕРИЯ СИЛЬВЕСТРА 33
Разложим эту функцию в ряд по степеням хг и х.,. Имеем
Sill2.Z1=J'2 + . . ., COS (^ — г2) = 1 — у (*1 — л:2)2+ . .
где точками обозначены члены, содержащие хг и х2 в степени выше
второй. Внося эти выражения для sin2 хг и cos (л:х — х2) в функцию
V, получим
F=l + ^-l+l-(^-^)2+ ...
или, упрощая,
И = _ (3-г^ — 2xi_x2 х~) + . . .
Составим матрицу коэффициентов квадратичной части функции
V (по главной диагонали стоят коэффициенты при квадратах пере-
менных, элементы с12 и с21 равпы половине коэффициента при про-
изведении ед);
и -ill-
Вычислим теперь главные диагональные миноры:
Д1 = 3, Д3 = Ц -}| = 2.
Отсюда следует, что условие Сильвестра выполнено (все Д, >• 0)
и поэтому рассматриваемая функция V в окрестности нуля опреде-
ленно-положительна. Заметим, что на всей плоскости х±х2 функция
V только положительна, так как при хг = х2 = лп 4= 0 (n = 1,
2, . . .) она обращается в нуль.
Может оказаться, что разложение знакоопределенной
функции V в ряд по степеням ж1, . . ., хп начинается
не с членов второго, а с членов более высокого порядка.
К сожалению, общих приемов исследования функции
на знакоопределенность в этом случае нет, но можно
указать на один необходимый признак: разложение
знакоопределенной функции в ряд по степеням х,, . . ., хп
не может начинаться с членов нечетной степени (для
членов первой степени это было уже показано (см. приме-
чание к формуле (2.4)). Действительно, пусть разло-
жение знакоопределенной функции V в ряд по степеням
xt, . . ., хп начинается с членов (2А + 1)-й степени, где
к — целое положительное число. Положим х2 = . . .
• • • = хп = хг. При этих значениях xi функция V при-
мет вид
V^Axlk+1+ Вх?+2+-..
Здесь А и В постоянные, а точками обозначены члены
порядка выше 2к + 2. При хх, достаточно малом по мо-
2 Д. Р. Меркни
34
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
дулю, знак функции V будет совпадать со знаком первого
члена. Но этот член меняет знак при изменении знака хг.
Следовательно, при А ф 0 функция V будет знакопере-
менной, что доказывает сделанное замечание.
Перейдем к изучению свойств функции V. Покажем
прежде всего, что если функция V знакоопределенная,
то поверхность V (xlt . . ., хп) = с замкнута.
При доказательстве, не нарушая общности, можно
считать, что функция V определенно-положительна.
Возьмем сферу SzJ = р и пусть I — наименьшее зна-
чение функции V на этой сфере, так что на сфере р, функ-
ция V удовлетворяет неравенству
Уц> I.
Число I больше нуля, так как функция V определенно-
положительна и, следовательно, на сфере р она не может
принимать нулевые или отрицательные значения.
Построим поверхность V = с, выбрав число с < I.
Будем двигаться из начала координат О по произвольной
прямой OL до сферы р (рис. 2,2, а). При этом перемеще-
нии функция V будет меняться от нуля до некоторого
числа Уц, большего с (так как Уи > I с). Следовательно,
в силу непрерывности в некоторой промежуточной точке
М функция У принимает значение, равное с, т. е. пря-
мая OL пересекает в этой точке поверхность У = с. Так
как прямая OL произвольна, то эта поверхность замк-
нута.
Заметим, что свойство замкнутости поверхности У = с
справедливо только для знакоопределенных функций.
Для знакопостоянных или знакопеременных функций
поверхности У = с разомкнуты.
§ 2.1. ФУНКЦИИ ЛЯПУНОВА. КРИТЕРИЙ СИЛЬВЕСТРА
35
Из этого доказательства вытекают два следствия:
1, Если | с | ^> | Cj |, то поверхность V = сА находится
внутри поверхности V = с, причем обе поверхности не
имеют общих точек (функции V по определению одно-
значны) (рис. 2.2, б).
2. Если изображающая точка М перемещается в
сторону возрастания определенно-положительной функ-
ции V, то траектория этой точки пересекает поверхности
Рис. 2.3
V =~ с изнутри наружу, а при движении в сторону убы-
вания функции V — снаружи внутрь (для определенно-
отрицательной функции картина обратная). Конечно,
в общем случае все эти свойства справедливы только в
достаточно малой окрестности нуля.
Выберем на поверхности V (х) = с произвольную
точку 71/ и вычислим в этой точке вектор grad V:
, dV dV	dV	1Г) ..
P2 + ... + —en, (2.11)
n
где e2, . . en — орты осей л2, . . xn.
Известно, что вектор grad V направлен по нормали
к поверхности V = с в точке М в сторону возрастания
функции V. Из этого следует, что вектор grad V направ-
лен во внешнюю часть поверхности V = с, если функция
V определенно-положительна (рис. 2.3, а), и внутрь
поверхности V = с, если функция V определенно-отрица-
тельна (рис. 2.3. б).
Одновременно с функцией Е будем рассматривать
ее полную производную V по времени t, взятую в пред-
36
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
положении, что переменные Xj удовлетвиряют дифферен-
циальным уравнениям возмущенного движения (1.17).
Имеем
т> dV dV . , dV . ,	, dV .
И == ~Zj7~ == "л—	П—a #2 + • • • П—о 
at дхл ox*	ox„
или, учитывая уравнения (1.17),
Х1 +	. + 2L xn. (2.12)
Напомним теперь, что величины Х}- равны проекциям
скорости U изображающей точки М, а производные
9 И	j TZ тт
—----проекциям grad V. Поэтому правая часть равенства
(2.12)	равна скалярному произведению векторов U и
grad V Д, т. е.
И = U -grad V.	(2.13)
Знание производной V функции V позволяет наглядно
проследить за движением изображающей точки. Дейст-
вительно, пусть в данный момент времени t изображающая
точка М занимает некоторое положение. Выберем какую-
нибудь определенно-положительную функцию V и постро-
им поверхность V = с, проходящую через точку М.
Затем по формуле (2.12) вычислим в этой точке произ-
водную F функции V. Рассмотрим три возможных случая.
1.	В данном положении точки М производная V
отрицательна
Р = 4г<°-
dt
Из этого следует, что функция V убывает, т. е. точка
М переходит внутрь поверхности V = с (следствие 2,
с. 35). Этот вывод можно получить и из равенства
(2.13). Так как И < 0, то из формулы (2.13) заключаем,
что угол между скоростью U изображающей точки М и
х) Скалярное произведение двух векторов а и b в n-мерном про-
странстве равно, так же как и в обычном трехмерном пространстве,
сумме произведений одноименных проекций
а • b =—	-(- <12^2 Т~ ... -|- вл
Угол между двумя векторами определяется равенством
a-b = ab cos а,
где а и Ь — модули векторов а иЬ. Угол а острый, если а-Ь^> О,
прямой, если а-b = 0, и тупой при а-b < 0.
§ 2.2. ТЕОРЕМА ЛЯПУНОВА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ 37
градиентом функции V тупой. Учитывая, что для опре-
деленно-положительной функции V вектор grad V сов-
падает с внешней нормалью к поверхности V = с, заклю-
чаем, что вектор U направлен внутрь этой поверхности.
Иначе говоря, траектория изображающей точки М пере-
секает поверхность V = с снаружи внутрь (рис. 2.4, а).
Рис. 2.4
2.	В данном положении точки М производная И = 0.
Скалярное произведение fT’-gradF равно нулю, угол
между этими векторами прямой, траектория изображаю-
щей точки касается поверхности V = с (в частности,
она может целиком лежать на этой поверхности).
3.	В данном положении Г > 0. Функция V возраста-
ет, траектория изображающей точки пересекает поверх-
ность V = с изнутри наружу (угол между векторами U
и grad V острый) (рис. 2.4, б).
§ 2.2. Теорема Ляпунова об устойчивости движения
Теорема. Если для дифференциальных уравнений воз-
мущенного движения можно найти знакоопределенную
функцию V, производная которой V в силу этих уравнений
была бы знакопостоянной функцией противоположного
знака с V, или тождественно равна нулю, то невозму-
щенное движение устойчиво.
Доказательство. Выберем произвольное, достаточно
малое положительное число е 0 и построим сферу
Szj = е. Затем построим поверхность V = с, лежащую
внутри сферы е (рис. 2.5). Это можно всегда сделать,
38
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
так как функция V непрерывна и равна нулю в начале
координат. Выберем теперь число б настолько малым,
чтобы сфера Szj = б целиком лежала внутри поверх-
ности V = с, не имея с ней общих точек. Покажем, что
Рис. 2.5
или тождественно равна
очевидного тождества
изображающая точка М, на-
чав движение из сферы б,
никогда не дойдет до сферы е,
что и будет служить доказа-
тельством устойчивости дви-
жения.
Не нарушая общности’,
можно считать, что функция
V определенно-положительна
(если V < 0. то можно взять
функцию -- F). По условию
теоремы ее производная, вы-
численная в силу уравнений
возмущенного движения, бу-
дет отрицательной функцией
нулю, т. е. V «С 0. Тогда из
t
V -Vo^fdt,
ia
(2-14)
где Vo — значение функции V в начальной точке Мо,
будем иметь
V - vu < о
или
Но-
Из этого неравенства следует, что при t t0 изобра-
жающая точка М либо находится на поверхности V =
= Vo = с± (при F == 0), либо находится внутри этой
поверхности (рис. 2.5). Таким образом, изображающая
точка М, начав движение из положения Мо, находя-
щегося внутри или на поверхности сферы б, никогда
не выйдет за пределы поверхности V = с, и тем более
не сможет достигнуть поверхности сферы е. Это доказывает
теорему.
Доказательство теоремы можно проиллюстрировать чисто гео-
метрическими соображениями. Из условия F 0 следует, что траек-
тория изображающей точки М войдет внутрь поверхности V = с,
или будет лежать на этой поверхности (см. окончание § 2.1, рис. 2.4
и 2.5). В дальнейшем траектория изображающей точки Мне сможет
§ 2.3. ТЕОРЕМЫ ОБ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ 39
перейти во внешнюю часть поверхности Г = с1У так как по условию
теоремы производная Г удовлетворяет неравенству Р- О 0 во всех
точках окрестности нуля (для выхода наружу из поверхности V =
= tj нужно, чтобы неравенство V' > 0 выполнялось хотя бы в одной
точке).
Применение основных теорем прямого метода по-
дробно будет рассмотрено в § 2.6 и §2.7, а сейчас приведем
небольшой пример чисто иллюстративного характера.
Пусть уравнения возмущенного движения имеют вид
Tj = — .2Д	З.г;, Х-2 = —^1^2 — *2-
Возьмем определенно-положительную функцию
Г .Г('! ' 'i)
и вычислим ее производпую по времени в силу уравнений возмущен-
ного движения. Имеем
v	.гр-!  h т2г2.
(it
Подставляя вместо и ,т2 их значения из уравнений возмущенного
движения, получим
Г = ЛГ1 (—^ + 3^) + хг (—— лф = —	— ^)2.
Так как функция V определенно-положительна, а ее производ-
ная V — отрицательная функция, то на основании доказанной тео-
ремы Ляпунова можпо утверждать, что невозмущенное движение
= 0, х2 = 0 рассматриваемой системы устойчиво. В § 2.3 (с. 45),
пользуясь другой теоремой, мы докажем более сильное утверждение,
а именно, что это движение не просто, а асимптотически устойчиво.
§ 2.3. Теоремы об асимптотической устойчивости
Теорема Ляпунова об асимптотической устойчивости.
Если для дифференциальных уравнений возмущенного
движения можно найти знакоопределенную функцию К,
производная которой V" в силу этих уравнений была бы
знакоопределенной функцией противоположного знака с V,
то невозмущенное движение асимптотически устойчиво.
Доказательство. Прежде всего заметим, что выполне-
ны все условия теоремы Ляпунова об устойчивости дви-
жения и, следовательно, изображающая точка не выйдет
из поверхности V = сх (рис. 2.5). Однако в теореме об
асимптотической устойчивости условия более сильные —
производная Р не может тождественно равняться нулю
и даже более — н пуль опа обращается только в начале
координат (так как V" знакоопределенная, а не знако-
40
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
постоянная функция). Поэтому изображающая точка М
сразу после начала движения входит внутрь поверх-
ности V = сг.
Не нарушая общности, будем, как и раньше, считать,
что функция V определенно-положительна. По условию
теоремы ее производная F определенно-отрицательная
функция. Из неравенства
и=4г<°
следует, что функция V, оставаясь положительной, моно-
тонно убывает. Это означает, что функция V имеет предел
с2 0. Иначе говоря, изображаю-
щая точка М стремится с внешней
стороны к предельной поверхности
V = с2 (рис. 2.6).
Покажем,-что с2 = 0, т. е. по-
верхность V = с2 вырождается
в точку — начало координат. Пред-
положим, что с2 Ф 0. Тогда в замк-
нутой области, заключенной между
поверхностями V = и V — с3,
функция И по условию теоремы
будет отрицательна. Обозначим че-
рез — I, где I 0, ее точную верхнюю границу в этой
области, причем Z #= 0, так как функция И обращается
в нуль только в начале координат. По определению
точной верхней границы имеем
И < -I.
Воспользуемся теперь тождеством (2.14)
t
V = Vo + frdt.
Учитывая соотношение И	— I, получим неравенство
t
V < Vo — $ I dt
t,
или, интегрируя,
V < Vo - I (t - t0).
Согласно этому неравенству, функция V с течением
времени сделается отрицательной, что невозможно, так
§ 2.3. ТЕОРЕМЫ ОБ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ
41
как по условию теоремы функция V определенно-поло-
жительна. Полученное противоречие возникло из сде-
ланного допущения, что с2 =# 0. Таким образом, с2 = 0
и изображающая точка асимптотически стремится к
началу координат, что доказывает теорему.
Проиллюстрируем теорему небольшим примером. Пусть урав-
нения возмущенного движения имеют вид
3	1	’
= — *2 + Х1Х2 —	х1х2>
±2 = — Зх2 + XjX2 + х^х2— ~2 х1х2-
Возьмем функцию V в следующей форме:
Т = у (3xJ — 2х]Х2 + х|).
Эта функция определенно-положительна (условие Сильвестра для
нее проверялось на с. 33). Вычислим полную производную но вре-
мени от этой функции:
V = (3xj — х2)	— (xj — х2) i2.
Внесем сюда значения Xj и х2 из уравнений возмущенного движения
и сгруппируем члены Р" = —Зх^ + 2х^х2 — 2х^. Составим матрицу
коэффициентов этой функции, считая за переменные xi и х2:
Г< -И-
Имеем
Д1 = —3<0, Д2 = |-3 _1 | = 5>0.
Выполнен критерий (2.10), и, следовательно, производная F — оп-
ределенно-отрицательная функция относительно х^ и х2 (тем самым
и относительно х± и х2). На основании последней теоремы Ляпунова
невозмущенное движение (xj = 0,х2 = 0) асимптотически устойчиво.
Теорема Ляпунова об асимптотической устойчивости
предъявляет очень высокие требования к функции V и
к ее производной К (они должны быть знакоопределен-
ными функциями разных знаков). Н. Н. Красовский
показал, что требования, налагаемые на производную К,
могут быть ослаблены.
Пусть производная К (х) функции V (х), вычисленная
в силу уравнений возмущенного движения (1.17), явля-
ется не знакоопределенной, а только знакопостоянной
функцией переменных х. Обозначим через К многообра-
зие (множество, совокупность) точек из области (2.1),
42
ГЛ. П. ПРЯМОЙ. МЕТОД ЛЯПУНОВА
в котором F = 0, причем в это многообразие не включает-
ся начало координат х = 0, где F = 0 всегда. Многооб-
разие К может представлять поверхность, линию, их ком-
бинацию и т. п.
Теорема Красовского об асимптотической устойчиво-
сти. Если для дифференциальных уравнений возмущен-
ного движения (1.17) можно найти определенно-положи-
тельную в области (2.1) функцию V такую, что ее про-
изводная V удовлетворяет в этой области двум условиям'.
1)	Е<0 вне К,
2)	У = 0 на К,
где К — многообразие точек, не содержащее целых траек-
торий системы при 0 t •< оо, то невозмущенное дви-
жение асимптотически
устойчиво.
Строгое аналитиче-
ское доказательство этой
теоремы можно найти
в книге Н. Н. Красов-
ского [27] и в третьем
дополнении редактора
2-го издания книги
И. Г. Малкина [37]. Мы
же ограничимся нагляд-
ной геометрической ил-
люстрацией теоремы.
Обозначим через М
изображающую точку
дифференциальных ура-
внений (1-17) возмущенного движения. По условию тео-
ремы во всех точках окрестности нуля У О (С < О
вне К и V = 0 на К). Из этого следует, что траекто-
рия у изображающей точки М в области (2.1) не может
пересечь поверхность V = с изнутри наружу (см. с. 35).
Если точка М находится вне многообразия К, то ее
траектория у будет пересекать замкнутые поверхности
V = Cj снаружи внутрь. Действительно, по условию
теоремы функция V определенно-положительна, а вне
К производная V < 0 (рис. 2.7 J)). Предположим теперь,
что при своем движении изображающая точка М попала
на многообразие К. Очевидно, что на этом многообразии
На рис. 2.7 многообразие К имеет условное изображение.
§ 2.3. ТЕОРЕМЫ ОБ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ 43
точка М движется по поверхности V = с2 (на К производ-
ная F = 0). Так как многообразие К не содержит целых
траекторий системы, то точка М должна покинуть это
многообразие, причем в месте схода траектория у, ка-
саясь поверхности V = с2, войдет внутрь нее (ибо вне К
она пересекает эти поверхности снаружи внутрь — см.
рис. 2.7).
В дальнейшем точка М может снова попасть на много-
образие К и будет двигаться по новой поверхности
V (х) = с3, расположенной ближе к началу координат,
Рис. 2.8
чем поверхность V(x) — с2 (с3 < с2, так как после схода
точки М с поверхности V — с2 производная V < 0 и,
следовательно, функция V убывает). Этот процесс может
неоднократно повторяться, причем изображающая точка
М будет неограниченно приближаться к началу коорди-
нат (строгое доказательство теоремы сводится по существу
к аналитическому описанию этого процесса).
Пэ приведенного обоснования теоремы Красовского
видно, и чем состоит отличие в поведении функции V в
условиях его теоремы от поведения этой функции в ус-
ловиях теоремы Ляпунова. Для асимптотической устой-
чивости теорема Ляпунова требует, чтобы при t оо
функция V стремилась к нулю монотонно (рис. 2.8, а);
Красовский ослабил это условие и показал, что для
асимптотической устойчивости функция V может стре-
миться к нулю не монотонно, а ступенчато (на рис. 2.8, б
горизонтальные участки графика функции V соответст-
вуют нахождению изображающей точки М на многооб-
разии К).
Остановимся кратко на определении условий, при вы-
полнении которых многообразие К не будет содержать
целых траекторий дифференциальных уравнений возму-
щенного движения (1.7).
44
ГЛ. И. ПРЯМОЙ МЕТОД ЛЯПУНОВА
Выбрав определенно-положительную функцию V, вы-
числим ее производную F. Предположим, что производная
не определенно-отрицательная, а просто отрицательная
функция, т. е. она может принимать помимо отрицатель-
ных также и нулевые значения. Совокупность тех значе-
ний хх, . . ., хп, при которых производная Г обращается
в нуль (кроме начала координат) определяет многообра-
зие К. На вопрос, содержит или не содержит это многооб-
разие целые траектории
уравнений (1.17), можно
во многих случаях отве-
тить непосредственной
проверкой. Для этого
достаточно внести урав-
нение многообразия (ес-
ли его можно написать
в явном виде) в диффе-
ренциальные уравнения
возмущенного движе-
ния. Если при этом
уравнения обращаются
в тождества, то много-
образие К содержит целые траектории; в противном слу-
чае не содержит.
В тех случаях, когда многообразие К представляет
некоторую поверхность
F fax, • • , хп) = О,
достаточно составить скалярное произведение U-gradF,
где U — скорость изображающей точки М.
Если это произведение тождественно равно нулю, то
скорость U будет все время перпендикулярна к grad F,
т. е. к нормали поверхности F = 0. Это означает, что
траектория у изображающей точки М лежит всеми своими
точками на этой поверхности (рис. 2.9). Таким образом,
для того чтобы целые траектории дифференциальных
уравнений возмущенного движения (1.17) не принад-
лежали поверхности F = 0, достаточно, чтобы скалярное
произведение U -grad F не равнялось нулю тождественно
[37]
Р-8га<1?=^Х,^фО.
3-1	3
(2-15)
§ 2.3. ТЕОРЕМЫ ОБ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ 45
Пример. В § 2.2 были рассмотрены следующие дифференциаль-
ные уравнения возмущенного движения:
хх = •—хх + Зх^, х2 = —xix2 — х2'
Определенно-положительная функция
V =1/2(^ + х*)
имеет в силу уравнений возмущенного движения отрицательную
производную
Г = — (Х1 — х2)2.
Так как производная F не определенпо-отрицательная, а прос-
то отрицательная функция, то теорему Ляпунова об асимптотической
устойчивости применить нельзя. Попытаемся воспользоваться теоре-
мой Красовского. Множество К найдем, приравняв производную Р”
к нулю:
F — х1 — х2 = О
(на плоскости хх, х2 это парабола).
Составим скалярное произведение (2.15)
H.gradF = X1^+X2 ™
UX1	иХ%
или, подставляя соответствующие величины и учитывая, что на К
Xi = х.],
tZ-gradF = (—хх + 3xj)-l + (—ххх2 — х®) (—2х2) = 2х2 + 4х*.
Это выражение не обращается в нуль (точка х = 0, как обычно,
исключается), поэтому многообразие F = хх — х2 = 0 не содержит
целых траекторий. Теперь видно, что выполнены все условия теоре-
мы Красовского об асимптотической устойчивости. Действительно:
1) функция V определенно-положительна; 2) производная И на К
равна нулю, а вне К. она отрицательна; 3) многообразие К не содер-
жит целых траекторий. Следовательно, рассматриваемое движение
асимптотически устойчгго.
Теорема Ляпунова и обобщение Красовского устанав-
ливают достаточные условия асимптотической устойчи-
вости в малом, т. е. при малых начальных возмущениях.
Е. А. Барбашину и Н. Н. Красовскому принадлежит тео-
рема, определяющая достаточные условия асимптотиче-
ской устойчивости при любых начальных возмущениях.
Теорема Барбашина — Красовского. Если для диффе-
ренциальных уравнений возмущенного движения можно
найти определенно-положительную функцию V (х), удов-
летворяющую условию
lim V (х) = оо,	(2.16)
Я-*оо
46
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
производная которой, вычисленная в силу этих уравнений,
удовлетворяет при всех х двум условиям:
1)	V < 0 вне К,
2)	F = 0 на К,
где К — многообразие точек, не содержащее целых траек-
торий системы при 0 t < оо, то невозмущенное дви-
жение х = 0 устойчиво в целом (символ х -> оо в равен-
стве (2.16) означает, что хотя бы одна координата хк
стремится к бесконечности по любому закону).
Не останавливаясь на доказательстве этой теоремы
(см., например, [5, 6, 27]), покажем необходимость усло-
вия (2.16). При доказательстве теоремы Ляпунова об
асимптотической устойчивости решающее значение имеют
два свойства знакоопределенных функций V:
1) в окрестности нуля поверхности V (х) = с замкну-
ты;
2) неограниченное стремление знакоопределенной
функции V (х) к нулю свидетельствует о стремлении изоб-
ражающей точки к началу координат.
При рассмотрении устойчивости в целом необходимо
учитывать, что координаты хк могут принимать большие
по модулю значения (хотя бы в начале движения). Поэто-
му, если условие (2.16) не выполнено, то может оказаться,
что поверхности V (х) = с, замкнутые при достаточно ма-
лых | xjc |, будут разомкнуты при больших | хк | . В ре-
зультате значения функции V (х) могут убывать, а изоб-
ражающая точка не будет стремиться к началу координат.
Не вдаваясь в подробный анализ, поясним сказанное примером,
взятым из [6]. Пусть уравнения возмущенного движения имеют вид
___+ 2у
dt (1 -J- х2)2
.	'	-	(2-17)
dy 	2х	2у
dt~~ (1 + х2)2	(1 + х2)2 ’
Функция
очевидно, определенно-положительна, а ее производная, вычислен-
ная в силу уравнений возмущенного движения,
F = -4 Г_____х-____+_________1
L (1+х2)<	(1 +х2)2 J
определенно-отрицательна на всей плоскости (х, у).
§ 3.3. ТЕОРЕМЫ ОГ, АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ 47
На основании теоремы Ляпунова можно утверждать, что невоз-
мущенное движение х — 0, у = 0 асимптотически устойчиво при
малых начальных возмущениях. Однако теорему Барбашина — Кра-
совского об устойчивости движения в целом применить нельзя, так
как условие (2.16) не выполнено. Действительно, при х —> оо и у =
-= а = const функция V стремится к 1 + а2, а не к бесконечности,
как требует условие (2.16).
Покажем, что система (2.17), асимптотически устойчивая в ма-
лом, не является устойчивой в целом. Для этого рассмотрим поверх-
ности
или, решая относительно у,
Отсюда видно, что при 0 < с < 1 поверхности V (х) --= с будут
замкнуты, а при с '>> 1 — разомкнуты (рис. 2.10).
Рассмотрим теперь кривую
у=2 + ^_	(2.18)
1 х2
и найдем угловой коэффициент касательной к этой кривой
,	<	2х
с ~ у — —___________.
(1-|-.т2)2
На кривой (2.18) дифференциальные уравнения возмущенного
движения (2.17) имеют вид
= __ 2т _,4i.	2
dt (t 4~ х2)2 1	1 1 -|- х2 ’
= _	2л‘	—	1 -L 2 )
dt (t+л-2)2	(If?)2 \ ’ 1 + х2) ‘
48
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
Отсюда найдем угловой коэффициент касательной к траектории
у системы (2.17) в точках кривой (2.18)
1 1	1 / 2 1	1	\
Ь* _ dV _ _ 2х _	х \	1 + х2/
dx '	(l-f-z2)2 д ,	2	_ 2z '
+ 1 + X2 (1 + Z2)2
Сравнивая с выражением для к, получим
lim—= ± <1.
х—»со к	4
Следовательно, найдется такое достаточно большое положитель-
ное число zx, что при всех х xt будет выполняться неравенство
I к* | < | к |
(из выражений для к* и к видно, что при достаточно больших х
оба коэффициента отрицательны).
Рассмотрим далее область G, определенную неравенствами
(рис. 2.10)
1
z>z2>z1, у > 2 + -£	2
где z2 удовлетворяет соотношению
2*2
(1 + ^)2 < ’
(2.19)
Область G имеет следующие свойства.
1. Изображающая точка М системы (2.17), перемещаясь по ин-
тегральной кривой у, не может пересечь кривую (2.18) изнутри
наружу, так как для этого необходимо, чтобы в точке пересечения
угловые коэффициенты удовлетворяли условию | к* | > | к | ,
а при х > xt имеет место неравенство | к* | <( | к | .
2. Изображающая точка М системы (2.17), попав в область G,
удаляется все время вправо от ее левой границы х = z2 (рис. 2.10).
В самом деле, при х > х2 из неравенства (2.19) следует, что
___2^<4
/ I т2\2
(z2 достаточно велико).
Теперь, пользуясь определением области G, из первого уравне-
ния системы (2.17) последовательно получим
dz	2z л	2z , л ,	2	2 п
~dt ~ ~~ (1 Ч- Z2)2 + 2г/ > — (1	х2)2 + 4 + 1 _|_Х2 > 1 _|_х2 > °,
что доказывает возрастание абсциссы х изображающей точки М си-
стемы (2.17).
Из свойств 1 и 2 следует, что если начальная точка Мо находит-
ся в G, то интегральная кривая не выйдет из этой области. Это сви-
детельствует об отсутствии устойчивости в целом.
§ 2.4. ТЕОРЕМЫ О НЕУСТОЙЧИВОСТИ ДВИЖЕНИЯ
49
§ 2.4. Теоремы о неустойчивости движения
Ляпунову принадлежат две теоремы о неустойчивости
движения. В 30-х годах нашего столетия Четаев обобщил
эти теоремы и доказал теорему, из которой как частный
случай вытекают теоремы Ляпунова. Поэтому мы начнем
с изложения теоремы Четаева.
Пусть вещественная непрерывная и однозначная функ-
ция V (х) по-прежнему определена в области (2.1)
34 < и.
где р — постоянное положительное число.
Совокупность значений переменных хг, . . ., хп из
этой области, удовлетворяющих неравенству
V (х) > 0,
называется областью У^>0, а поверхность У — 0 — гра-
ницей области У )>0. Предполагается, как и прежде,
что У (0) = 0, т. е. начало
координат принадлежит гра-
нице области У 0. Так,
например, границей области
У > 0 для функции
У = хг — х%
будет парабола (рис. 2.11)
Если функция У опреде-
ленно-положительна, то об-
ластью У )> 0 будет вся ок-
рестность нуля. Для отрицательных функций У область
У 0 не существует.
Теорема Четаева. Если дифференциальные уравнения
возмущенного движения позволяют найти функцию У (х),
для которой в сколь угодно малой окрестности нуля суще-
ствует область У >• 0, и если производная У функции У,
вычисленная в силу этих уравнений, положительна во всех
точках области У 0, то невозмущенное движение не-
устойчиво.
Доказательство. Возьмем положительное сколь угодно
малое число е и построим сферу Hxf- — е (конечно, е р).
Чтобы обнаружить неустойчивость невозмущенного дви-
жения, достаточно заметить всего одну траекторию изоб-
50
ГЛ, II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
раздающей точки М, выходящую за пределы сферы е. Возь-
мем начальное положение точки М в области V 0,
причем точка Мо может быть сколь угодно близка к нача-
лу координат, но не совпадать с ним. Так как по условию
теоремы в области V )> 0
at
то функция V монотонно возрастает и, следовательно, для
всех t tn будем иметь
v(*)> Vo>O,
где Vo значение функции V в
Изображающая точка М,
своем дальнейшем движении
Рис. 2.12
от t явно, будет при всех t
удовлетворять условию
V 5
точке Мо.
начав движение из Мо, при
не может пересечь границу
области V 0 (на границе
V = 0, а в начальный мо-
мент Vo 0 и V возрастает
монотонно). Предположим,
что при дальнейшем дви-
жении изображающая точ-
ка М не выйдет за пределы
сферы е, т. е. находится все
время внутри замкнутой
области G (рис. 2.12)
S4 < е, V (х) > Уо.
Тогда функция V, как не-
прерывная и не зависящая
 t0 ограничена, т. е. будет
L,
где L — некоторое положительное число.
В замкнутой области G производная В положительна
и также ограничена (положительна по условию теоремы,
ограничена — так как непрерывна и не зависит от t явно).
Поэтому в этой области производная Р имеет точную
нижнюю границу Z, причем I 0. Если предположить,
что изображающая точка М не выходит за пределы сферы
е и, следовательно, все время находится внутри области
G, то при всех t t0 производная F будет удовлетворять
условию
Р > I > 0.
§ 2.4. ТЕОРЕМЫ О НЕУСТОЙЧИВОСТИ ДВИЖЕНИЯ
51
Пользуясь этим неравенством и соотношением (2.14),
уайдем
V > Vo + l(t - f0).
Отсюда следует, что с течением времени функция V
неограниченно возрастает. Противоречивость получен-
ных для V неравенств возникла из сделанного предполо-
жения, что изображающая точка не выйдет за пределы
сферы 8. Таким образом, это предположение неверное, что
доказывает теорему.
Как уже отмечалось, теорема Четаева является обоб-
щением двух теорем Ляпунова о неустойчивости движения.
Приведем одну из них.
Теорема Ляпунова о неустойчивости движения. Если
дифференциальные уравнения возмущенного движения по-
зволяют найти, функцию V, которая обладала бы в силу
этих уравнений знакоопределенной производной К и могла
бы принимать в окрестности нуля значения одного знака
с К, то невозмущенное движение неустойчиво.
Действительно, по условию теоремы Ляпунова произ-
водная К определенно-положительна во всех точках ок-
рестности нуля (не нарушая общности, можно считать, что
К > 0) и, следовательно, она определенно-положительна
и в той области, в которой функция V принимает положи-
тельные значения (область V )> 0). Таким образом, вы-
полнены все условия теоремы Четаева, что служит дока-
зательством теоремы Ляпунова.
Обобщение Четаева состоит в том, что он ослабил ус-
ловия Ляпунова, налагаемые на производную К — дос-
таточно, чтобы опа была определенно-положительной не
во всех точках окрестности нуля, как требует теорема Ля-
пунова, а только в области V 0.
Другое ослабление требований, налагаемых на произ-
водную Г, содержится в следующей теореме.
Теорема Красовского о неустойчивости движения.
Если для дифференциальных уравнений возмущенного дви-
жения (1.17) можно найти функцию V такую, что ее
производная К удовлетворяет условиям'.
1)	К> 0 вне К,
2)	К = 0 на К,
где К — многообразие точек, не содержащее целых траек-
торий при 0 t < оо, и если при этом можно указать
точки, лежащие в произвольной окрестности начала коор-
52
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
динат, такие, что в них V 0, то невозмущенное движе-
ние неустойчиво.
Геометрическое обоснование этой теоремы в значитель-
ной своей части совпадает с аналогичным обоснованием
теоремы Н. Н. Красовского об асимптотической устой-
чивости — см. § 2.3. Действительно, возьмем началь-
ную точку Мо (;г0) такую, чтобы в ней выполнялось ус-
ловие V (х0) >0. Так как в этой точке Го> 0 и F >0
(предполагаем вначале, что Мо не принадлежит многооб-
разию К), то функция V будет возрастать, а изображаю-
щая точка М будет удаляться от начала координат. Ес-
ли при своем движении изображающая точка М попадет
на К, или Мо принадлежит К, то вскоре она должна будет
покинуть это многообразие (оно не содержит целых траек-
торий) и снова начнется удаление точки М от начала ко-
ординат. Строгое доказательство этой теоремы можно
найти в книге Н. Н. Красовского [27].
Рассмотрим небольшой пример. Пусть уравнения возмущенно-
го движения имеют вид
= Х^ ~Г 2х«,	#2 = х1х2’
Покажем, что невозмущенное движение х, = х2 = 0 неустой-
чиво. Для этого возьмем функцию
Г 2	4
= *1 —
Эта функция имеет область V > 0, состоящую из двух частей, ог-
Xi = — х“ (рис. 2.13). Вычислим
производную Р функции V
в силу уравнений возмущенно-
го движения
Р = 2^1?! — 4х2«2
или, внося значения fj и#2 и
упрощая,
Р = 2х’.
Так как эта производная
положительна при всех хг > 0
и любых х2, то в правой части
области V 0 выполнены все
условия теоремы Четаева (ле-
вую часть области можно про-
раниченных параболами хг = х2 и
Рис. 2.13
сто игнорировать) и, следовательно, невозмущенпое движение
Xi = х2 = 0 неустойчиво.
Заметим, что выбранная в этом примере функция V не удов-
летворяет условиям теорем Ляпунова и Красовского (производная
Р меняет знак при изменении знака х,).
§ 2.5. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИИ ЛЯПУНОВА 53
Прежде чем перейти к приложениям, отметим, что из-
-ложенные в § 2.2—2.4 теоремы составляют фундамент
прямого метода Ляпунова. При их доказательстве пред-
полагается, что рассматривается устойчивость относитель-
но всех переменных, входящих в уравнения возмущенно-
го движения. В. В. Румянцев в работе [45] распростра-
нил прямой метод Ляпунова на системы, в которых
изучается устойчивость движения относительно части пе-
ременных.
§ 2.5.	Методы построения функции Ляпунова
Применение основных теорем прямого метода требует
знания функций Ляпунова, удовлетворяющих определен-
ным требованиям. К сожалению, общих методов построе-
ния таких функций нет, но во многих случаях их можно
сконструировать. Не останавливаясь на подробном раз-
боре различных способов построения функций Ляпунова
(см. обзор [2а]), укажем на несколько методов, чаще всего
применяемых при решении практических задач.
1.	Метод преобразования координат. Если для данных
уравнений возмущенного движения трудно найти функцию
Ляпунова, то часто переходом к новым координатам (ко-
нечно, прежде всего следует испробовать линейное преоб-
разование с постоянными коэффициентами) уравнения
удается привести к такой форме, для которой соответствую-
щая функция находится сравнительно просто. Этот метод
неоднократно используется в настоящей книге (§ 4.2, 4.3,
5.4, 6.2 и др.).
2.	Метод неопределенных коэффициентов. Будем искать
функцию Ляпунова в виде квадратичной формы с постоян-
ными коэффициентами
п п
v	=4" У, У, a^xi- (2-2э)
А’=1
Прежде всего подчиним неопределенные коэффициенты
akj критерию Сильвестра (2.9). Тогда функция V будет
определенно-положительной. Так как число коэффициен-
тов a^j равно п (п + 1)/2, то после этого останется еще
п (га — 1)/2 независимых коэффициентов, которыми можно
распорядиться по своему усмотрению.
Предположим теперь, что требуется найти условия, на-
лагаемые на параметры системы, при выполнении которых
54
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
невозмущенпое движение будет асимптотически устойчиво
(в технических положениях этот случай встречается чаще
всего). Тогда постараемся подобрать оставшиеся незави-
симые коэффициенты а-1:] функции V так, чтобы производ-
ная К, вычисленная в силу уравнений возмущенного дви-
жения, была бы функцией определенно-отрицательной или
удовлетворяла условиям теоремы Красовского. Если такие
коэффициенты a^j можно найти, то невозмущенное движе-
ние будет асимптотически устойчиво. Этот метод применим
не всегда, но в некоторых случаях он дает хорошие резуль-
таты. Прежде чем перейти к рассмотрению примера, за-
метим, что от умножения па постоянное положительное
число свойства функции V не изменяются. Поэтому один
коэффициент функции (2.20), например агп, можно поло-
жить равным единице.
Пример. Дапы нелинейные уравнения возмущенного движения
4 = az, + Ъх2. х2 = схтх2 4' ех2.	(2.21
Требуется определить, каким условиям должны удовлетворять па-
раметры системы а, Ь, с и е, чтобы невозмущенное движение х^ =
= х2 = 0 было асимптотически устойчиво.
Будем искать функцию V в форме (2.20)
У = -^(^4-2щг1г24-^),	(2.22)
где 1и|1 пока не определены. Критерий Сильвестра (2.9) для матри-
цы коэффициентов
IIZ И|1
II I1 1 II
имеет вид
=- X > 0,	=- X — р'2 > 0.	(2.23)
Считая, что эти неравенства выполнены, вычислим произ-
водную К
К = (Xxj 4- ,uz2) r1 4- (ЩГ! 4- Z2) .r2.
Внесем сюда значения 4 и 4 из уравнений (2.21), тогда по-
лучим.
К = (Xzj 4- цг2) (azj 4- Ьх2) 4- (fix, ф- х2) (сх,х2 ф- exf)
или, раскрывая скобки и группируя члены,
К — ).ах^ ф- (ХЬ ф- с) Zi-^2 +	+ В + Ъх^ + сх2х2 ф- ех^х^).
При ц 4= 0 эта функция будет знакопеременной. Поэтому, не
нарушая условия (2.23), положим ц = 0. При этом производная К
примет вид квадратичной формы относительно хг и х2:
К = Хаж2 ф- (Х6 ф- с) хгх2 ф- ех\.	(2.24)
g 2.5. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИИ ЛЯПУНОВА
Постараемся подобрать неопределенный множитель А > 0 так,
чтобы эта квадратичная форма была определенно-отрицательной.
Для этого составим главные диагональные миноры матрицы коэффи-
циентов. Имеем
Aj = Аа, Д, = Кае — (Kb + с)2/4.
Для того чтобы квадратичная форма (2.24) относительно хг
и х; была определенно-отрицательной, необходимо и достаточно,
чтобы был выполнен критерий Сильвестра (2.10). В нашем случае
это дает два неравенства:
Ка < 0, Кае — (КЬ + с)2/4 > О.	(2.25)
Для выполнения этих неравенств при К > 0 необходимо потре-
бовать прежде всего, чтобы коэффициенты а и е исходной системы
(2.21) удовлетворяли условию
а<0, е < 0.	(2.26)
Преобразуем теперь второе соотношение (2.25) к виду
Ь2К2 + 2 (6с — 2ае) А + с2 < 0.	(2.27)
Это квадратичное неравенство можно удовлетворить при К > 0,
если оба корня Ах и К2 левой части будут вещественными и положи-
тельными. Действительно, в этом случае для всех К, удовлетворяю-
щих условию Aj < К < А2, будет справедливо неравенство (2.27).
Для этого нужно, чтобы дискриминант трехчлена был положите-
лен, а коэффициент при К в первой степени отрицателен:
(6с — 2ае)2 — 62с2 > 0, 6с — 2ае О 0
или
4ае (ае — be) > 0, 6с О 2ае.
Так как, согласно (2.26), произведение ае положительно, то
оба последние неравенства будут удовлетворены, если
be О ае.	(2.28)
Теперь можно подвести итоги. Если параметры а, 6, сие систе-
мы (2.21) удовлетворяют условиям
а О 0, е < 0, 6с О ае,	(2.29)
то при ц = 0 и Xj < А< А2, где Кг и К2 — корни левой части нера-
венства (2.27), функция V, определенная равенством (2.22), будет
определенно-положительной, а ее полная производная по времени,
вычисленная в силу уравнений возмущенного движения (2.21), бу-
дет функцией определенно-отрицательной. На основании соответ-
ствующей теоремы Ляпунова заключаем, что при выполнении усло-
вий (2.29) невозмущенное движение х2 = х2 = 0 системы (2.21)
асимптотически устойчиво.
Теорема Барбашина — Красовского позволяет сделать
более сильное утверждение: если параметры системы (2.21)
удовлетворяют неравенствам (2.29), то невозмущенное дви-
жение xt = х2 = 0 будет устойчиво в целом. Читатель лег-
ко докажет это самостоятельно.
5(5
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
3.	Построение функции Ляпунова с помощью связки
интегралов. Предположим, что уравнения возмущенного
движения (1.17) допускают интеграл
F (хг, . . ., хп) = h = const,	(2.30)
для которого разность F (х) — F (0) является определен-
но-положительной функцией переменных xlf . . ., хп. Тог-
да в качестве функции Ляпунова можно взять функцию
V = F (xr, ...,xn)-F (0).	(2.31)
Действительно, производная функции V по времени
в силу уравнений возмущенного движения согласно ин-
тегралу (2.30) тождественно равна нулю и, следовательно,
эта функция будет удовлетворять всем условиям теоремы
Ляпунова об устойчивости движения (см. § 2.2).
В некоторых случаях дифференциальные уравнения
возмущенного движения допускают несколько интегралов
^1 (*^1т " • •> ^п) =	•  ч Fщ (^j, . . ., Хп} — hmi (2.32)
где /i1, . . ., hm — постоянные интегрирования, причем
ни один из них не является определенно-положительной
функцией. Для такого случая Н. Г. Четаев [49] предло-
жил искать функцию V в форме связки интегралов (2.32).
В общем виде эта связка имеет вид
V = Xi [Л - Fr (0)] + . . . + Кт [Fm - Fm (0)] +
+ хх - F2 (0)] + .. + xm [Fm - F2m (0)], (2.33)
где X1, . . ., Xm, xx, . . ., xm — неопределенные постоянные.
Если постоянные Ху и Ху удастся подобрать таким обра-
зом, что функция V будет определенно-положительной,
то она будет удовлетворять всем условиям теоремы Ляпу-
нова об устойчивости движения (так как V = const яв-
ляется также интегралом уравнений возмущенного дви-
жения).
Метод Четаева построения функции Ляпунова с по-
мощью связки интегралов весьма эффективен. Прежде
чем проиллюстрировать его на примерах (они будут рас-
смотрены в следующем параграфе), сделаем несколько за-
мечаний:
а)	один из 2m коэффициентов Ху и Ху можно выбрать
произвольно, например, положив Хх — 1;
б)	часто функцию V можно построить с помощью ли-
нейной связки интегралов, положив все Ху = 0. Члены
§ 2.6. ПРИМЕРЫ НА ПРИМЕНЕНИЕ ТЕОРЕМЫ ЛЯПУНОВА 57
с квадратами интегралов следует привлекать только в том
случае, если линейная связка недостаточна;
в)	во многих случаях интегралы уравнений возмущен-
ного движения можно построить из общих соображений
(например, с помощью общих теорем механики), не со-
ставляя самих уравнений. Этим приемом следует широко
пользоваться, избегая лишних преобразований.
Примеры на применение метода связки интегралов
будут рассмотрены в § 2.6. Заметим только, что этот метод
был обобщен и послужил основой для построения вектор-
функции Ляпунова [12а].
§ 2.6. Примеры на применение теоремы Ляпунова
об устойчивости движения
При исследовании устойчивости движения (не асимп-
тотической, а простой устойчивости) одним из наиболее
эффективных методов является метод Четаева построения
связки интегралов. В этом параграфе будут рассмотрены
примеры применения этого метода.
Пример 1. Устойчивость движения кониче-
ского маятника. Рассмотрим стационарноех) движение
материальной точки М массой т, подвешенной на невесомой нити
длиной I и движущейся с постоянной скоростью под действием силы
тяжести по горизонтально распо-
ложенной окружности (кониче-
ский маятник (рис. 2.14, а)). Нить
маятника, закрепленная в точке
О, описывает в стационарном дви-
жении круговой конус; обозначим
угол между нитью и вертикалью
ООг через а, а угловую скорость
вращения нити вокруг вертикали
ООг через со. Между углом а, уг-
ловой скоростью со и длиной маят-
ника I в стационарном движении
существует хорошо известное со-
отношение
со2 cos а = g/l, (2.34)
которое может быть получено,
например, с помощью принципа
Даламбера.
Примем стационарное движение маятника по окружности за
певозмущенное движение. Предположим, что на это движение нало-
жены небольшие возмущения. Обозначим угол между нитью и вер-
Э Термин «стационарное движение» будет более подробно разъ-
яснен в § 3.4.
тд
[al
'О!
М '0.
i/=l since ш
а)
Рис. 2.14
тд
6)
О
О
L
м

58
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
тикалью ООГ в возмущенном движении через 0 (рис. 2.14, б), а уг-
ловую скорость вращения плоскости ООАМ вокруг вертикали ООГ
через ip.
Введем обозначения
О = а -|- ,г1, 0 — .r2, ip in 4~ •Гз-	(2.35)
Будем изучать устойчивость невозмущенного движения отно-
сительно величин 0, 0 и ip. Кинетическая Т и потенциальная П энер-
гии маятника определяются равенствами
ml2 
Т — —2~ (О2	sin2 0’р2), П = —• mgl cos 0.
Так как действующая па маятник сила тяжести потенциальна,
а координата ip циклическая (кинетическая энергия Т зависит от
обобщенной скорости ip, по не зависит от координаты ip, и обобщен-
ная сила, соответствующая этой координате, раИпа пулю:	=
— —<?П/<?1р — 0), то существуют два интеграла движения (А и п —
постоянные):
ml2 .		ml2
Т -J- П = —2~ (О2 4~ sin2 (йр3) — mgl cos 0 -- 2	,
дТ
—г— — ml2 siu2 Оф -- ml2n
dip
(множители ml2/2 и ml2 введены для удобства).
Второе равенство представляет интеграл момента количества
движения маятника относительно вертикали ООГ, и его можно по-
лучить из элементарных соображений.
Пользуясь равенствами (2.35), запишем эти интегралы в следую-
щей форме:
,	2g
Fi (xr, хг. z3)	[.г- + sin2 (а + .и) (ю -J - ,r3)2] — у- cos (а х() -= h,
(2.36)
F2 (zi, z2, z3) = sin2 (a 4” *i) (w 4- *з) = n.
Интегралы (2.36) получены из общих теорем динамики. Конеч-
но, можно было сначала составить дифференциальные уравнения
возмущенного движения (1.27), а затем, комбинируя их, найти ин-
тегралы (2.36). Как уже было отмечено ранее в § 2.5, выбранный
здесь путь является, как правило, более простым х).
Перейдем к исследованию устойчивости стационарного движе-
ния маятника относительно величин 0, 0 и ip. Ни один из найденцых
интегралов не является знакоопределенной функцией относительно
величин х2 и х3. Поэтому составим линейную связку интегралов
(2.36), положив = 1 и = X:
V = F1 — Fi (0) 4- [F2 — F2 (0)] — [z2 sin2 (a 4~ ^i) • (<o 4~ zs)2] —
2g	/	, 2g \
- —j- cos (a 4- zx) — I co2 sin2a — -y- cos a ) 4-
4- X sin2 (a Jj)-(1'" + а’з) — sin2 a-co.
3) Для того чтобы оценить рассмотренный здесь метод, реко-
мендуем читателю получить интегралы (2.36) из уравнений возму-
щенного движения (1.27).
§ 2,0, ПРИМЕРЫ НА ПРИМЕНЕНИЕ ТЕОРЕМЫ ЛЯПУНОВА 59
/	2g \
Члены — ! со2 sin2 а — -у cos а I и —A sin2 а •« внесены для того,
чтобы функция V обращалась в нуль при = л:3 = лг3 = 0. Заме-
ним отношение gft его значением из равенства (2.34) и разложим
функцию V в ряд по степеням л^, х2, х3. Имеем
sin2 (а + лГ1) = sin2 а + sin 2а х1 + cos 2а-ж2 + . .
1
cos (а -j- X,) — cos а — sin а- -у cos а-ж2
где точками обозначены члены высшего порядка,
Внесем эти значения для sin2 (а + хг) и cos (а + хг) в послед-
нее выражение для функции V и сгруппируем члены:
V = « [(А + со) cos 2а + со cos2 а] х^ + л:] + sin2 а -л:2 +
+ со sin 2а -(А + 2со) Xj -f- sin2 а -(А + 2<о) ж3 +
+ sin 2а-(А 4- 2со) л:1.г3 + . .
Для того чтобы функция V была определенно-положительной,
необходимо прежде всего избавиться от членов, содержащих вариа-
ции л?!, х2 и х3 в первой степени (см. примечание к формуле (2.5)).
В данном случае для этого достаточно положить
А = —2со.
При таком значении А функция V примет вид
V — со2 sin2 а-ж2 + х2 + sin2 а-л:2 -|- . . .
Так как квадратичная часть функции V определенно-положи-
тельна относительно xlt л3 и л?3, то при достаточно малых значени-
ях х,, х2 и л?3 вся функция V будет также определенно-положитель-
на. Производная по времени функции V на основании интегралов
(2.36) тождественно равна нулю, и, следовательно, стационарное
движение конического маятника устойчиво относительно 0, 0 и ф.
Этот результат будет получен в примере 1 § 3.5 другим методом.
Пример 2. Устойчивость стационарного движе-
ния центра масс искусственного спутника Зем-
ли. В § 1.3 было показано, что искусственный спутник Земли мо-
жет совершать движение с постоянной скоростью по окружности
радиуса г0. Параметры этого движения удовлетворяют условию
(1.30)
со2г® = ц.	(2.37)
Положение спутника в возмущенном движении будем опреде-
лять сферическими координатами г, ср, 0 (рис. 1.5, б). Кинетическая
Т п потенциальная П энергии спутника определяются выражения-
ми (1.31):
те	.	m
Т -~2~ (г2 -|- г2Э2 -|- г2 cos2 0q>2), П = — ц -у .
Так как действующая на искусственный спутник Земли сила тяготе-
ния потенциальна, а координата q) циклическая, то существуют два
60
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
интеграла движения (h и п — постоянные) 3)
т .	.	т т
Т + П = -Я- (г2 + г202 + г2 cos2 0<р2) —и — = -Я- h,
дТ	.	(2 38)
—— = mr2 cos2 Оф = mn.
дф	т
Будем рассматривать устойчивость стационарного движения спут-
ника по круговой орбите относительно величин г, г, 0, 0 и ф. Вве-
дем обозначения: г = г0 + л^, г = х2, 0 = х3, 0 = х4, ф =
= |со —|- хъ. В сделанных обозначениях найденные интегралы можно
записать в следующей форме:
Fi =	+ (г0 + ла)2 л^ + (г0 + ЛГ1)2 cos2 л:3- (со + л:Б)2 — 2	= h,
Ft — (ro + аа)2 cos2 л:3-(со + л:Б) = n.	(2.39)
Отметим, что, так же как и в первом примере, оба интеграла
дифференциальных уравнений возмущенного движения получены
из общих соображений, без помощи самих уравнений. Конечно, вто-
рой интеграл (2.39) вытекает непосредственно из третьего уравнения
(1.32), а первый интеграл может быть получен путем комбинации
этих уравнений, но этот путь требует не только составления самих
уравнений (1.32) или (1.33), но и умения получить из них необхо-
димые интегралы.
Перейдем к исследованию невозмущенного движения спутника.
Ни один из найденных интегралов не является знакоопределенной
функцией величин xlt х2, х3, х4, xs. Поэтому функцию Ляпунова V
будем искать в форме связки этих интегралов
v = л - Л (0) + X [Fs - F2 (0)] + х [Fl - Fl (0)],
где X и к — постоянные числа.
Внесем в это выражение для V значения интегралов F4 и F2:
V = л^ + (г0 + ЛГ1)2	+ (г0 + Ла)2 COS2 х3- (со + л:Б)2 —
—2 7^	— го'"2 + 2 7^ + М(го + ЛГ1)2 cos2 л:3- (со + л:Б) — г2со] +
+ х [ (г0 + ла)4 cos4 х3. (со + л:Б)2 — г4со2]'.
Разложим правую часть этого равенства в ряд по степеням х4, . . .
. . ., хъ. Имеем
/	л:2	\2
cos2 л:3 = 1 — "у- + • • • J = 1 — Xg + . . . ,
/	я2	х4
cos1 х3 = ^1 —	+ . . . ) = 1 — 2л:2 + . . . ,
И	И	*1 ,	*1 ,
г _i_ г — г — И а+Н ч~ + •  • »
Го -г Ла	Го	г2 го
где точками обозначены члены высшего порядка.
1) Эти интегралы можно получить путем комбинации уравнений
возмущенного движения центра масс искусственного спутника Зем-
ли (1.33).
§2,6. ПРИМЕРЫ НА ПРИМЕНЕНИЕ ТЕОРЕМЫ ЛЯПУНОВА
61
Подставим эти выражения в последнее равенство и учтем, что
в-стационарном движении параметры со и г0 удовлетворяют условию
(2.37). Тогда после очевидных преобразований получим
V = ш (—со + % + 6xr2<o) х2 + Xj — г2<о (со + % + 2хг2ш) Zg +
+ r2z2 + ro (1 + хгц) ^5 + 2госо (2со + % + 2zr2<o) Xj +
+ Гд (2со + % + 2хг2<о) х5 + 2г0 (2со + % + 4xr2<o) xjx6 + . . .
Для того чтобы функция V была знакоопределенной, нужно
прежде всего приравнять нулю коэффициенты при членах, содер-
жащих переменные х, и х5 в первой степени (см. примечание к фор-
муле (2.5)). Таким образом, числа X и х должны удовлетворять со-
отношению
2со + % + 2хг2<о = 0.
Отсюда
% = —2со — 2хг2<о.
Подставляя это значение % в последнее выражение для V, найдем
V = СО2 (4ХГ2 — 3) X* + X* + ГдСО2х| +	+
+ Н) (1 + ХГо) ХЬ + ^ХГдСОХхХд + . . .
Разобьем квадратичные члены на две функции:
vi =	+ ^<о2х| + ф2,
Р2 = со2 (4хг2 — 3) xf + 4хг2<ох1х5 + г2 (1 + хг2) х*.
Функция Pi определенно-положительна относительно величин
х2, х3 и х3. Поэтому для того, чтобы функция V была знакоопреде-
ленной относительно xlt ха, х3, х3, х5, достаточно показать, что
можно найти такое число х, при котором функция V2 будет опреде-
ленно-положительной относительно х1 и хБ. Критерий Сильвестра
для функции Va имеет вид (см. формулы (2.9))
Д1 = со2 (4хгд — 3) > О,
со2 (4хГд — 3) 2хГдС0
2хф г2 (1 + хг2)
= со2г2 (хг2 —3)>0.
Из этих выражений видно, что при х > 3/г2 оба условия будут
выполнены и, следовательно, функция V2 будет определенно-поло-
жительной относительно xlt х5, а функция V — определенно-поло-
жительной относительно xlt х2, х3, xt, х3, что и доказывает устойчи-
вость стационарного движения искусственного спутника Земли от-
носительно величин г, г, 0, 0, <р !).
х) Этот результат получен В. В. Румянцевым [46] другим ме-
тодом (см. пример 2 § 3.5). Там же исследованы на устойчивость
другие стационарные движения искусственного спутника Земли.
62	ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
Прежде чем перейти к следующему примеру, сделаем
одно замечание. Во многих задачах требуется ответить на
вопрос: будет ли рассматриваемое движение устойчиво,
асимптотически устойчиво или неустойчиво? Первые два
примера относились как раз к этой группе задач. Однако,
как уже отмечалось ранее, в технике, как правило, встре-
чаются задачи другого плана, а именно: известно, что при
некоторых значениях параметров системы невозмущенное
движение неустойчиво. Ставится задача: как следует вы-
брать параметры системы, чтобы ее движение сделалось
устойчивым (или асимптотически устойчивым)? Третий
пример относится ко второй группе задач.
Пример 3. Достаточное условие устойчивос-
ти волчка (условно устойчивости враща-
тельного дв и ж е н и я снаряд а). Каждому ребенку
известно, что невращающпйся волчок падает и, для того чтобы его
ось сохраняла вертикальное положение, волчок нужно сильно за-
крутить, т. е. ему нужно сообщить достаточно большую скорость
собственного вращения. Точно так же все артиллеристы знают, что
невращающийся продолговатый снаряд (снаряд, выстреленный из
гладкоствольного орудия) кувыркается. Естественно возникает во-
прос: какую угловую скорость собственного вращения нужно сооб-
щить волчку (снаряду), чтобы он не падал (снаряд не кувыркался)?
Так как вращательное движение продолговатого снаряда, центр
масс которого перемещается по весьма пастильной траектории,
и движение волчка около вертикали описываются совершенно оди-
наковыми дифференциальными уравнениями, то достаточно рассмот-
реть устойчивость движения одного из них, например устойчивость
волчка.
На волчок, угловая скорость собственного вращения которого
равна ф, действуют две внешние силы (силами сопротивления пре-
небрегаем): сила тяжести Р, приложенная к центру масс С волчка,
и реакция Ко опоры О (рис. 2.15, а). Положение оси z симметрии
волчка относительно неподвижных осей gpc (ось £ вертикальна)
будет определяться углами аир (рис. 2.15, б). За невозмущенное
движение волчка примем его равномерное вращение с угловой ско-
ростью ф0 = п вокруг оси симметрии г, совпадающей с неподвижной
вертикальной осью £. В невозмущенном движении
а = 0, а = О, р — О, Р = 0, ф = ф„ = п = const.
В возмущенном движении все эти величины будут меняться.
Введем оси х, у, z (рис. 2.15, б) и обозначим через pI, и г±
проекции угловой скорости СЩ вращения трехгранника xyz относи-
тельно неподвижных осей
Пользуясь рис. 2.15, б, найдем
щ = а, й = Р cos а, = —р sin а.
Проекции р, q,r угловой скорости о) вращения волчка опреде-
ляются равенствами
р = a, q ~ р cos а, г = ф — р sin а.
§ 2.6. ПРИМЕРЫ НА ПРИМЕНЕНИЕ ТЕОРЕМЫ ЛЯПУНОВА
63
Теперь найдем кинетическую энергию волчка
1 1
Т — — ,1Х (а2 Ц- р2 cos2 а)	J, (q1 — р sin а)4.
Здесь Jx Jy — экваториальные, a J, — аксиальный моменты
инерции волчка.
Рис. 2.15
Потенциальная энергия П волчка будет
П = Pl cos a cos р,
где Р — вес волчка, I — расстояние от его центра масс С до опо-
ры О.
В рассматриваемом случае можно, так же как и в первых двух
примерах, не составляя дифференциальных уравнений возмущен-
ного движения, найти три интеграла. Два интеграла определяются
зразу — это интеграл энергии и интеграл, соответствующий цикли-
ческой координате q> (второй интеграл — интеграл моментов коли-
геств движения волчка относительно оси z):
1 1
Т + II —	J х (a2 -L р2 cos2 а) + Jz (ф — р sin а)2 +
+ Pl cos а cos р = h,
дТ
-—Г- == /г (ф — Р а) = 1 Zni-
dq)
Третий интеграл — это интеграл моментов количеств двпже-
гия волчка относительно неподвижной оси £
К-_ = k = const.
64	ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
Для того чтобы написать этот интеграл в явном виде, воспользуем-
ся очевидными равенствами:
Кх — JхР = Jх4, Ку	Juq = JхР cos сс, К2 — Tzr =
= /г (ф — Р sin а),
Kj. = Кх cos (&r) + Ку cos (£у) + Kz cos (£z).
Пользуясь рис. 2.15, б, найдем
cos (£z) = —sin p, cos (ty) = sin a cos p, cos (£z) = cos a cos p.
Следовательно, третий интеграл имеет вид
Jx (—a sin P + P cos a sin a cos P) + /z(q> — Psin a) cos a cosP =k.
Будем изучать устойчивость движения волчка относительно
величин а, й, Р, Р и ф. Введем следующие обозначения:
a = xlt & = х2, р = х3, Р = х4, ф = Фо + х6.
В этих обозначениях найденные интегралы дифференциальных урав-
нений возмущенного движения примут вид
1
Fi = ~2~ Jx (х£ + х\ cos2 xj +
1
+ ~2~ J z (фо + ^5 —	31П х1)2 + Pl cos Х1 COS х3 — h,
F2 = Фо + х5 — xi sin xi = п1,	(2-40)
F3 — Jx (—хз sin хз 4" sin xt cos xt cos x3) +
+ Jz (Фо + хъ — x4 sin xi) cos xi cos x3 — k.
Так как ни один из этих интегралов не является знакоопределенной
функцией, то составим линейную связку интегралов
F = Л - Л (0) + И [F2 - F2 (0)Г + % [F, - F3 (0)],
где ц и X — неопределенные постоянные коэффициенты.
Внесем сюда значения F±, F2 и F3, разложим в ряд по степеням
xlt . . ., х3 и учтем, что фо = п. Тогда после группировки членов
получим
1 1
V = (J zn 4- р. -|- XJZ) х3 — ~2~ (Pl + XJzn) х2 + ~2~ Jхх% —
— ~2~	zra) х3 + ~2~ Xх! + ~2~ zx3 —
— (/z7l 4" Ц 4"	z х) *^1Х4	kJ Хх3х3 4“ . . . ,
где точками обозначены члены высшего порядка.
Для того чтобы функция V была знакоопределенной, необходи-
мо прежде всего приравнять нулю коэффициент при первой степени
х3. Имеем
Jzn 4- Ц + kJz = 0.
s c.o. ПРИМЕРЫ НА ПРИМЕНЕНИЕ ТЕОРЕМЫ ЛЯПУНОВА 65
Теперь функция V примет вид
11 11
У = 2 ах^ 2	4" 2 ахз "Ь 2 хХ4
1
2 Jz*^5	х%2&3 "4“ • • • i
где
а = - (Pl + Vzn).	(2.41)
Разобьем квадратичную часть функции V на три функции:
1	1
Vi = ~2~ах% XJxXjX4 -j" 2
1	1
И2 = 2 аХд — XZхх3х2 -ф- 2 ^хх2г
Функция V3 определенно-положительна относительно х5, а
функции F, и У2 имеют одинаковую структуру. Поэтому, согласно
общей теории для определения условия устойчивости невозму-
щенного движения волчка относительно величин а, а, 0, 0 и ф, до-
статочно определить условие, при
котором функция Pi будет опреде-
ленно-положительной относитель-
но величин х1 и х4 (при этом же
условии функция V2 будет опре-
деленно-положительной относи-
тельно величин х3 и х2).
Напишем условие Сильвестра
для функции У3:
= а >0, А2 =
а
™х
™х
J-
= 7я(а-/ж12)>0.
Пользуясь выражением (2.41), приведем аги неравенства к следую-
щему виду:
Р1
' /(1)=7ж1’ + 7гп1 + Р/<0.	(2.42)
Осталось выяснить условия, при выполнении которых можно по-
добрать число X, удовлетворяющее соотношениям (2.42).
Если дискриминант трехчлена f (X)
D = fy? - UxPl
положителен, то оба корня X, и Х2 уравнения / (X) = 0 будут веще-
ственны и различны. Из графика функции f = f (X) (рис. 2.16) вид-
но, что в этом случае для всех X, удовлетворяющих неравенству
Xi < X < Х2, функция / (X) < 0, т. е. будет выполнено второе ус-
3 Д. Р. Меркин
66
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
ловие (2.42). Заметим, что при п > 0 оба корня отрицательны (слу-
чай, показанный на рис. 2.16), а при п < 0 оба корня Ai и А2 поло-
жительны.
Покажем, что для этих А будет выполнено и первое неравенство
(2.42). Для этого достаточно показать, что при п > 0 этому усло-
вию удовлетворяет больший корень А2. Имеем
I	______________
А2 = -2J- (- Jn + /- iJxPl)
Используя теперь очевидное неравенство
[Л 1 — х <1 — —2~ х,
получим
что доказывает сделанное замечание для п > 0 (при п < 0 нужно
рассмотреть меньший корень А,!).
Итак, если угловая скорость п в невозмущенном движении
волчка удовлетворяет условию D > 0, т. е.
J'zn2>iJxPl,	(2.43)
то для всех А, заключенных между А.х и А2, функция V будет опреде-
ленно-положительной. Ее полная производная по времени в силу
уравнений возмущенного движения на основании интегралов (2.40)
равна нулю. Следовательно, неравенство (2.43) является достаточ-
ным условием устойчивости вертикального положения волчка отно-
сительно величин а, а, 0, 0, ф (для снаряда в условии (2.43) нуж-
но заменить произведение Р1 на модуль момента опрокидывающей
пары х)).
Остается невыясненным вопрос об устойчивости вертикального
положения волчка, когда угловая скорость собственного вращения
его в невозмущенном движении будет меньше граничной величины,
определяемой неравенством (2.43). Этот вопрос будет решен в при-
мере 4 § 4.5.
Прежде чем перейти к примерам на применение теоре-
мы Ляпунова об асимптотической устойчивости, заметим,
что иногда с помощью выбранной связки интегралов
построить знакоопределенную функцию нельзя. В этом
случае нужно испытать другие комбинации интегралов.
Если же все связки интегралов не дают возможности оп-
ределить условия устойчивости движения, то это еще не
') Впервые условие устойчивости (2.43) для вращательного дви-
жения снаряда (оно известно как условие Маниевского — Крылова)
строго доказал Н. Г. Четаев (см. [49]).
§ 2.7. ПРИМЕРЫ НА АСИМПТОТИЧЕСКУЮ УСТОЙЧИВОСТЬ 67
означает, что движение неустойчиво — нужно просто пе-.
рейти к другим методам, с помощью которых можно будет
решить вопрос об устойчивости.
§ 2.7. Примеры на применение теорем
об асимптотической устойчивости
и неустойчивости движения
Пример 1. Асимптотическая устойчивость
равновесия твердого тела, находящего-
ся в сопротивляющейся среде. Рассмотрим сво-
бодное твердое тело, движущееся в соопротивляющейся среде посту-
пательно относительно инерциальной системы отсчета (в частности,
оно может находиться в покое). Это движение тела примем за не-
возмущенное. Дадим телу небольшие возмущения, в результате чего
возникает вращательное движение относительно поступательно пе-
ремещающихся координатных осей	начало которых совпа-
дает с центром масс С тела.
Будем считать, что среда, в которой движется тело, создает мо-
мент сил сопротивления М, пропорциональный некоторой степени
угловой скорости <о тела:
М — — Ws>a	(2-44)
где а» — угловая скорость тела в возмущенном движении, а х и а —
положительные коэффициенты (они могут быть постоянными, но
могут зависеть и от <о, изменяясь в некоторых пределах: 0 < хх
< V, (<о) < х2, 1 < ах < а (<о) < с^).
Кроме того, будем предполагать, что другие силы, действующие
на тело (если они существуют), не создают момента относительно
центра масс. В этих предположениях динамические уравнения Эй-
лера (см., например, [12]) примут вид
Jx ~dT + Ч - Jy>	Ч,
Jy ~dd~ + 4 — Jz> “Л = —	4/’	(2-45)
dm
Jz ~dF + 4 “ Ч = - ZW““4>
где Jx, Jy, Jz — моменты инерции тела относительно главных цент-
ральных осей инерции тела х, у, z, а &у, <oz — проекции угло-
вой скорости тела на те же оси.
Будем рассматривать устойчивость вращательного движения
тела относительно проекций угловой скорости <ож, <oz. Так как
по условию задачи в невозмущенном движении <ож = <о„ = <oz = О
(тело двигалось поступательно пли находилось в покое), то урав-
нения (2.45) будут дифференциальными уравнениями возмущенно-
го движения.
Докажем, что невозмущенное движение тела асимптотически
устойчиво относительно величин <ож, <оь, <oz. Для этого умножим
3*
68
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
первое уравнение (2.45) на <ох, второе на ау, третье на <ог и сложим
все уравнения. После очевидных преобразований получим
da	da	da
~аг +	~sr +	~sr = -XM'X~1 (“x + 4 + “г)-
(2.46)
или, учитывая, что <o = (co2 + cOy +
1 d
T ~di~ <7xwx -b /w“y + Jzaz) = ~y- (°4 4-	+ (0“) 2 .	(2.47)
Функция
1
V = ~n~ (J co5?. — J -I- /.co?)
2 4 X X  у У 1	2 Z>
определенно-положительна, а ее производная в силу уравнений воз-
мущенного движения, согласно равенству (2.47), определенно-от-
рицательна. Следовательно, выполнены все условия соответствую-
щей теоремы Ляпунова и вращательное движение тела в сделанных
предположениях асимптотически устойчиво относительно величин
сох, ау и сог.' Заметим, что из этого не следует устойчивость относи-
тельно угловых перемещений.
Пример 2. Устойчивость установившихся
режимов вольтовой дуги в цепи с сопро-
тивлением и самоиндукцией [4]. Рассмотрим вольто-
ву дугу, включенную в цепь с омическим сопротивлением R, само-
индукцией L и источником энергии, электродижущая сила кото-
рого равна Е (рис. 2.17). Вольтова дуга представляет собой провод-
ник, не подчиняющийся закону Ома. На рис. 2.18 приведен график
статической характеристики вольтовой дуги для установившихся ре-
жимов. В дальнейшем будем считать, что установленная этим гра-
фиком зависимость и = ф (i) между током i и напряжением и в
дуговом промежутке справедлива и для режимов, близких к устано-
вившимся. Это равносильно предположению, что скорость колеба-
тельных процессов в схеме мала по сравнению со скоростями уста-
новления ионных процессов, обусловливающих ток в вольтовой дуге.
Пользуясь вторым законом Кирхгофа, получим в сделанных
предположениях следующее дифференциальное уравнение:
di
£	-|- Hi + ф (i) = Е.	(2.48)
g 2.7. ПРИМЕРЫ НА АСИМПТОТИЧЕСКУЮ УСТОЙЧИВОСТЬ 69
Внося сюда i = I= co'nst, получим уравнение для определения зна-
чений тока, отвечающих установившимся режимам:
RI + 1|? (/) = Е.	(2.49)
Корни этого уравнения легко определяются как абсциссы точек пе-
ресечения графиков функций•
и = ф (j), и = Е — Ri.
В зависимости от значений параметров Е и R уравнение (2.49)
может иметь три, два, один и ни одного вещественного корня.
На рис. 2.19 изображен случай трех корней этого уравнения (при
двух корнях точки мг и М2(или и Af3) сливаются, при одном кор-
не прямая и = Е — Ri пересекает график функции и = ф (/) в одной
точке, при отсутствии корней трафики не пересекаются).
Рассмотрим случай трех различных корней. Это означает, что
теоретически могут существовать три установившихся режима воль-
товой дуги, соответствующих трем значениям тока /2, /3. Оче-
видно, что практически реализуемы только устойчивые режимы,
поэтому необходимо исследовать каждый из этих режимов на устой-
чивость.
За невозмущенное примем установившееся движение i = I.
Обозначим значение тока в возмущенном движении через
I = I + X.
Внося это значение тока в дифференциальное уравнение движения
системы (2.48) и учитывая, что di/dt = 0, получим
, dx
L-dT + RU + d+W + ^E.
Разложим функцию ф (Z + х) в ряд по степеням х
ф (Z + х) = ф (/) + ф' (/) х + . . .,
где точками обозначены члены высшего порядка.
Дифференциальное уравнение движения примет вид
dx
L + RI + Rx + ф (/) + ф' (/) х + . . . = Е,
70	ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
или, учитывая, что значения тока I удовлетворяют уравнению (2.49):
_ dx
£-^г = -(Л+х)х+...,	(2.50)
где для простоты положено и = ф' (/).
Умножим обе части этого дифференциального уравнения воз-
мущенного движения на х. Тогда после очевидных преобразований
получим
d I 1	\
-^г^-г£^--=-(Л + я);£2+...	(2.51)
Функция
1
V = -у Lx2
определенно-положительна относительно х. Ее производная по
времени, вычисленная в силу дифференциального уравнения воз-
мущенного движения (2.50), определяется правой частью равенст-
ва (2.51). Если R + х > 0, то производная V- будет определенно-от-
рицательной функцией х и, следовательно, на основании теоремы
Ляпунова движение будет асимптотически устойчиво. Если же R +
+ х < 0, то производная Р будет определенно-положительной
функцией, и на основании теоремы Ляпунова о неустойчивости ус-
тановишееся движение будет неустойчиво.
Таким образом, имеем
R + х > 0 — установившееся движение асимптотически ус-
тойчиво,
R + х < 0 — установившееся движение неустойчиво.
Из рис. 2.19 видно, что в точках Мг и М3 функция и = ф (i)
возрастает и, следовательно, ее производная ф' = х в этих точках
положительна. На этом основании при i = 11 и i = /3 число R +
+ х больше нуля. Это означает, что установившиеся режимы, соот-
ветствующие значениям i, равным 11 и /3, асимптотически устойчи-
вы относительно тока.
В средней точке М2 функция и = ф (i) убывает, поэтому Xj =
= Ф' (Л) < 0- Кроме того, график этой функции в точке М2 более
крутой, чем прямая и = Е — Ri. Это означает, что модуль углово-
го коэффициента касательной, проведенной к графику функции
и = ф (i) в точке М2, больше модуля углового коэффициента прямой
и = Е — Ri, т. е. | Xj | = | ф' (/2) | > | — R | = R. Учитывая,
что х2 = ф' (/2) < 0, будем иметь 7? + х2 < 0. Следовательно, ус-
тановившийся режим, соответствующий току 12, неустойчив.
При установившемся режиме угловой коэффициент х = ф' (/)
может быть положительным, но может быть и отрицательным. Если
на плоскости (R, х) построить прямую х = —R, то, очевидно, всем
точкам, лежащим выше этой прямой (для них х > — R, или R +
+ х > 0), отвечают асимптотически устойчивые установившиеся
режимы, а для точек, лежащих ниже этой прямой,— неустойчивые
режимы. На рис. 2.20 показана область асимптотической устойчи-
вости на плоскости R, х.
При одной и той же функции v = и = ф (i) число корней урав-
нения (2.49) и их значения зависят от параметров системы — элек-
тродвижущей силы Е и сопротивления R. Меняя один из этих пара-
метров или одновременно оба, можно получить один, два или три
установившихся режима. Рассмотрим для примера зависимость то-
§ 2.7. ПРИМЕРЫ НА АСИМПТОТИЧЕСКУЮ УСТОЙЧИВОСТЬ 71
х
Область .
асимптотической
ка I в установившемся режиме от параметра Е. Для этого построим
на плоскости EI график уравнения (2.49)
Е — RI — ф (7) = О,
считая сопротивление R неизменным (рис. 2.21). Этот график мож-
но построить, например, следующим образом. Задаем определенное
значение Е и определяем с помощью
рис. 2.19 соответствующие значения
тока I, после чего наносим получен-
ные точки (ЕГ) на плоскость EI.
Так, значению Е электродвижущей
силы (рис. 2.19) отвечают три значе-
ния тока 71,12 и 73; точки Aj, N2, А3
рис. 2.21 соответствуют точкам Л7\,
Л73, Л73 рис. 2.19.
Было показано, что крайним зна-
чениям тока 7Х и 73 соответствуют
асимптотически устойчивые режимы
вольтовой дуги, а среднему значе-
нию 12 — неустойчивый режим. Из
этого следует, что точкам кривой
ABCDFH рис. 2.21, лежащим на
участке CD, соответствуют неустойчивые режимы, а токам той же
кривой, лежащим на участках АС и DH — асимптотически устой-
чивые режимы. Точки С и D, разделяющие устойчивые участки от
О
устойчибости R
Рис. 2.20
X=-R
Рис. 2.21
неустойчивых, называются точками бифуркации, а всама кривая
ABCDFH, устанавливающая зависимость координат в установив-
шемся режиме от параметра (в данном примере зависимость тока 7
от электродвижущей силы источника Е), называется кривой равно-
весия !).
х) Теория бифуркаций, созданная А. Пуанкаре, развивалась в
дальнейшем многими учеными, в частности Н. Г. Четаевым,
А- А. Андроновым и др.
72
ГЛ. II, ПРЯМОЙ МЕТОД ЛЯПУНОВА
Кривая равновесия дает возможность наглядно проследить за
состоянием системы при изменении параметра. Так, если медленно
и непрерывно изменять Е, начиная от Е = 0, то, как видно из
рис, 2.21, при значениях Е, меньших Е*, установившихся режимов
Рис. 2.22
не существует и, следовательно, вольтовой дуги не будет. При даль-
нейшем изменении Е от Е* до Е2 мы будем перемещаться по участ-
ку АС кривой равновесия. Возникшей вольтовой дуге будет соот-
ветствовать ток, изменяющийся от 0 до 1С. При переходе электро-
движущей силы Е через значение Е2 ток скачкообразно изменится
от Гс до IF и затем будет непрерывно увеличиваться вместе с увели-
чением Е (рис, 2.22, а). Если теперь уменьшать Е от значений, боль-
ших Е2, до Е1г то ток будет непрерывно уменьшаться до ID. При
прохождении электродвижу-
щей силы Е через Е± ток скач-
кообразно уменьшится от до
и в дальнейшем будет непре-
рывно уменьшаться вместе с
уменьшением Е (рис. 2,22, б).
Аналогично можно пост-
роить кривую равновесия, со-
ответствующую изменению со-
противления R.
Пример 3. Условие
устойчивости лампо-
вого генератора [4].
Рассмотрим простейшую схему
лампового генератора с индук-
тивной обратной связью и коле-
бательным контуром в цепи
сетки (рис. 2.23). Пользуясь
законами Кирхгофа и учитывая направления токов в цепи, а также
положение положительной полярности конденсатора, получим сле-
дующие уравнения (сеточными токами пренебрегаем):
du 1
dT = ~
di	dia
L ~dt~ =
(2.52)
§ 2.7. ПРИМЕРЫ НА АСИМПТОТИЧЕСКУЮ УСТОЙЧИВОСТЬ 73
Член —М dijdt представляет э.д.с. обратной связи, наводи-
мую благодаря воздействию на контур анодного тока, протекающего
по катушке La. Считая, что анодный ток зависит только от сеточ-
ного напряжения ug = и (это достаточно хорошо выполняется для
триодов с большим коэффициентом усиления), будем иметь
dia du о du
~dt~ = Тй ~dT = 5 ~di~ ’
di
где S (и) =	— крутизна характеристики ia лампы (пример-
ная зависимость тока 1а и величины ° от напряжения us = и по-
Рис. 2.24
казаны на рис. 2.24). Теперь дифференциальные уравнения движе-
ния (2.52) примут вид
du i	di	1
-dF=- — ’	= u —	(2.53)
Исследуем устойчивость равновесного состояния и = 0, i =
= 0 относительно напряжения и и тока I. Для этого возьмем функ-
цию- Ляпунова в следующей форме:
V =	(-£- i2 + и2} .	(2754)
Очевидно, что эта функция определенно-положительна. Вычислим
производную Р функции У:
L di du
V =-(Г l~di~ + u~dr ‘	(2>55)
Подставим вместо di/dt и duldt их значения из уравнений (2.53)
L ( и 1	1	/ i \
[тг - Тс ^RC - MS г) + “
или, раскрывая скобки и группируя члены,
1
— [ЛС - MS (u)] i«.	(2.56)
Разложим функцию S (и) в ряд по степеням и:
S (и)= S (0) S' (0) и + . . .,	(2.57)
74	гл. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
и внесем это выражение для S (и) в производную V:
„ 1
V = — -^2- (RC - MS») i* + . . .,	(2.58)
где точками обозначены члены, содержащие и и i в степени выше
второй, а .S'o = S (0).
При достаточно малых по модулю значениях и и I производная У
будет не знакоопределенной, а только знакопостоянной функцией
переменных и и i. Поэтому, пользуясь выбранной фунцией V (2.54),
мы не можем применить теоремы Ляпунова об асимптотической ус-
тойчивости и неустойчивости движения. Неприменима к ней и тео-
рема Четаева о неустойчивости движения. Воспользуемся теорема-
ми Красовского. В качестве многообразия К возьмем совокупность
точек, для которых и =/= 0, i = 0 (на плоскости (i, и) это ось и). По-
кажем, что многообразию К не принадлежат целые траектории си-
стемы. Для этого внесем в уравнение движения (2.53) значения пе-
эеменных i и и, определяющих К. При i = 0 и и =£ 0 эти уравнения
примут вид
du
• .. =0, и — 0,
at 1	’
что невозможно, так как на К и^О.
Рассмотрим теперь два случая:
RC — MSo>0,	(2.59)
RC — A7.S'O < 0.	(2.60)
Если параметры системы удовлетворяют неравенству (2.59), то
будут выполнены все условия теоремы Н. Н. Красовского об
асимптотической устойчивости § 2.3. Действительно, функция V
определенно-положительна, а ее производная Р, согласно равенст-
ву (2.58) и соотношению (2.59), отрицательна вне К и равна нулю
на К (i = 0, и =)= 0). Поэтому равновесное состояние системы i =
= 0, и = 0 будет асимптотически устойчиво относительно тока
i и напряжения и.
Пусть теперь параметры системы удовлетворяют соотношению
(2.60). Тогда будут выполнены все условия теоремы Н. Н. Красов-
ского о неустойчивости движения § 2.4. Действительно, функция V
может принимать положительные значения (она определенно-поло-
жительна), а ее производная У, согласно (2.58) и (2.60), положи-
тельна вне К и равна нулю на К. Следовательно, равновесное со-
стояние системы I = 0, и = 0 неустойчиво.
Таким образом, при выполнении условия (2.59) равновесное со-
стояние системы асимптотически устойчиво относительно тока I
и напряжения и, а при выполнении условия (2.60) равновесное со-
стояние системы неустойчиво. Случай RC = М 8д требует дополни-
тельного исследования, но практического интереса он не представ-
ляет, так как при небольшом нарушении этого условия (что всегда
возможно, ибо все элементы системы изготовляются с определенны-
ми допусками) получится неустойчивая или асимптотически устой-
чивая система. В § 4.5 разобранный здесь пример будет решен дру-
гим, более простым методом.
Пример 4. Устойчивость равновесия си-
стемы с одной степенью свободы, находя-
§ 2.7. ПРИМЕРЫ НА АСИМПТОТИЧЕСКУЮ УСТОЙЧИВОСТЬ 75
щ е й с я под действием потенциальной не-
линейной силы и силы сопротивления,
пропорциональной первой степени • ско-
рости. Обозначим обобщенную координату, отсчитываемую от
положения равновесия, через q. Будем считать, что кинетическая
Т и потенциальная П энергии системы определяются равенствами
1	X
т = Mq*, п =_ —рг gm+1,	(2.61)
где М — приведенная масса системы, предполагаемая постоянной,
х — постоянный коэффициент, a m — положительное целое число,
не меньшее двух (га>2).
Считая, что, помимо потенциальной силы, на систему дейст-
вует сила сопротивления, пропорциональная первой степени ско-
рости, составим уравнение возмущенного движения (за невозмущен-
ное движение принимается состояние покоя, при котором q = О,
? = 0):
d ЭГ	ЭГ	эп
dt dq	dq	dq
где ц — положительная постоянная, характеризующая силу со.
ротивления.
Учитывая значения Т и П, получим
M'q = —— цт.	(2.62)
Положим q = лгц q = х2. В новых переменных уравнение (2.62)
будет эквивалентно системе двух уравнений первого порядка
= Xi,	(2.63)
причем по условию га>2. В качестве функции Ляпунова возьмем
полную механическую энергию
1	X
7=Г + П = -2-Л^+-^-ргд^,
или, в новых переменных,
1	X
=	+	(2-64)
Найдем полную производную по времени
V = Мх1т1 +
Внесем сюда значения и i2 из уравнений возмущенного движения
(2.63):
V = Xi ( —ЦХ1 — кс2т) +
или, после упрощения,
У =	(2.65)
Рассмотрим теперь возможные случаи.
1.	Число х положительно (х>0), а число т нечетное. Для
этого случая V — определенно-положительная функция перемен-
76
ГЛ. II. ПРЯМОЙ МЕТОД ЛЯПУНОВА
ных г, и х2 (т + 1 — число четное), а производная F — отрицатель-
ная функция относительно совокупности переменных лгх и х2. Со-
гласно теореме Ляпунова об устойчивости движения, можно утверж-
дать, что невозмущенное движение устойчиво, но не асимптотиче-
ски. Теорему Ляпунова об асимптотической устойчивости приме-
нить нельзя, так как производная V отрицательная, но не опре-
деленно-отрицательная функция переменных ;гх и х2 (при з-j = О,
,т2 =/= 0 производная F — 0).
Обратимся к теореме Барбашина — Красовского. Прежде все-
го, отметим, что функция V, определенная равенством (2.64), удов-
летворяет условию (2.16)
lim V (xlt х2) = оо.
X—»оо
Многообразие К получим, положив V = —= 0. Это ось х2
(xj = 0, х2 =fe 0). Это многообразие не содержит целых траекторий,
так как на нем уравнения (2.63) принимают вид
—ха:™ = 0,	= 0,
что невозможно (на К переменная х2 =fe 0).
Очевидно, что на К производная' F = 0, а вне К она отрица-
тельна. Таким образом, при сделанных предположениях (х>0,
т — нечетное число), выполнены все условия теоремы Барбаши-
на — Красовского § 2.3 и, следовательно, положение равновесия
xj = 0, х2 = 0 асимптотически устойчиво в целом при любых началь-
ных возмущениях.
2.	Число х положительно (х > 0), а число т четное'. Функцию
V определим теперь следующим образом:
У =	(2.66)
Очевидно, что
При х > 0 и т четном функция V может принимать положи-
тельные значения (например, при хх = 0 и х2 < 0). На прежнем
многообразии К (хх — 0, х2 4= 0) производная F = 0, а вне К про-
изводная V > 0. Кроме того, многообразию К не принадлежат це-
лые траектории системы. Поэтому выполнены все условия теоремы
Н. Н. Красовского § 2.4 и положение равновесия хг = q = 0, х2 =
= q = 0 неустойчиво.
3.	Число х отрицательно (х < 0), а т — любое целое положи-
тельное число, не меньшее двух [т 2).
Функцию V берем в форме (2.66). Прй любом целом га ах<0
функция V может принимать положительные значения (например,
при хх — 0 и < 0). Повторяя доказательство случая б), убеж-
даемся, что при х < 0 положение равновесия неустойчиво.
Таким образом, система асимптотически устойчива относитель-
но q и q при х > 0 и и нечетном. Во всех остальных случаях она не-
устойчива.
Г Л A В A III
УСТОЙЧИВОСТЬ РАВНОВЕСИЯ
И СТАЦИОНАРНЫХ ДВИЖЕНИЙ
КОНСЕРВАТИВНЫХ СИСТЕМ
§3.1. Теорема Лагранжа
Рассмотрим механическую систему с голономными и
стационарными связями, положение которой определяется
s обобщенными незавивимыми координатами дг, . .	q3.
Как известно, в положении равновесия все обобщенные
силы Qx такой системы равны нулю:
<?i = 0.....Q3 = 0.	(3.1)
Если обобщенные силы зависят от координат qs
и скоростей то для определения положений, в которых
система может находиться в равновесии, достаточно вне-
сти в равенство (3.1) значения qj = 0 и решить получен-
ные уравнения относительно q13
Для консервативных сил Qk =
; <1з-
ап гт
-z— , где 11 — потен-
а9)(.
циальная энергия системы, и уравнения (3.1) принимают
вид
a?i	oq
(3-2)
Решая эти уравнения относительно . . ., q3, найдем
те значения обобщенных координат, при которых система
может находиться в равновесии. Таких положений может
оказаться несколько, причем в некоторых из них равно-
весие может быть устойчивым, а в некоторых неустойчи-
вым. Так, например, простой маятник, подвешенный на
стержне, имеет два возможных положения равновесия, из
них в нижнем положении равновесие устойчиво, а в верх-
нем неустойчиво.
Рассмотрим одно из возможных положений равновесия.
Будем считать, что в этом положении потенциальная энер-
гия равна нулю. Это всегда можно сделать, так как потен-
циальная энергия определяется с точностью до аддитивной
постоянной. Кроме того, не нарушая общности, можно
считать, что в этом положении все обобщенные координа-
78
ГЛ. III. УСТОЙЧИВОСТЬ’КОНСЕРВАТИВНЫХ СИСТЕМ
ты qlf . . qs равны нулю (для этого достаточно отсчет
координат вести от этого положения). Будем рассматри-
вать устойчивость равновесия относительно обобщенных
координат (?i, . . qs и обобщенных скоростей г х, . . .
• • Qs.
Тогда уравнения Лагранжа второго рода
d дТ дТ ____________ дП
do,.
ЧГ = С^ (* = *............
будут уравнениями возмущенного движения. Число урав-
нений п = 2s и они допускают интеграл энергии
Т + П = h,	(3.4)
где Т — кинетическая энергия системы.
Лагранжу принадлежит следующая теорема (1788 г.),
определяющая достаточные условия устойчивости равно-
вестия консервативных систем 1).
Теорема; Если в положении изолированного равновесия
консервативной системы с голономными и стационарными
связями потенциальная энергия П имеет минимум, то
в этом положении равновесие устойчиво.
Доказательство. В рассматриваемом положении рав-
новесия потенциальная энергия равна нулю и имеет ми-
нимум. Поэтому по крайней мере в достаточно малой ок-
рестности нуля значения функции П будут положитель-
ны. Это означает, что в этой окрестности потенциальная
энергия П представляет определенно-положительную
функцию переменных q;, а полная энергия системы
F = 71 + П	(3.5)
определенно-положительную функцию обобщенных ко-
ординат qlt . . ., qs и обобщенных скоростей f'x, . . ., (s
(так как кинетическая энергия Т механической системы
с голономными и стационарными связями является оп-
ределенно-положительной квадратичной формой обобщен-
ных скоростей (см., например, [12])).
Полная производная функции V по времени на основа-
нии интеграла (3.4) равна нулю. Следовательно, эта функ-
х) Строгое доказательство теоремы Лагранжа впервые дал Ди-
рихле, поэтому эта теорема часто называется теоремой Лагранжа —
Дирихле. Здесь приводится доказательство Ляпунова, вытекающее
непосредственно из его прямого метода.
§ 3.1. ТЕОРЕМА ЛАГРАНЖА
79
ция удовлетворяет всем условиям теоремы Ляпунова об
устойчивости, что и доказывает теорему Лагранжа.
Теорема Лагранжа широко используется в приложе-
ниях. Как правило, при ее практическом применении
удобнее всего разложить потенциальную энергию в ряд
по степеням qlt . . ., qs, а затем воспользоваться критери-
ем Сильвестра (2.9). В общем виде имеем
;=1	j=l /.-=1
где точками обозначены члены, содержащие qlt . . ., qa
в степени выше второй.
По условию П (0) = 0 (в положении равновесия по-
тенциальная энергия равна нулю); кроме того, в этом по-
ложении должны наполняться равенства (3.2). Поэтому
j=i /;=1
где постоянные коэффициенты
—	— I д2П \
Cm сзк- dq^dq*
Если коэффициенты удовлетворяют критерию Силь-
вестра (2.9), то квадратичная часть равенства (3.6) будет
определенно-положительной квадра-
тичной формой переменных qu . . .,
qs, а вместе с ней будет определенно-
положительна в окрестности нуля и
потенциальная энергия П. Это озна-
чает, что потенциальная энергия П
имеет изолированный минимум и,
следовательно, согласно теореме Лаг-
ранжа, в рассматриваемом положе-
нии равновесие устойчиво.
Пример. Система представляет двойной
маятник; тела Мг и М2 с массами т1 и т2
рассматриваются как материальные точки;
массой стержней, сопротивлением воздуха
и трением в горизонтальных цилиндриче-
ских опорах пренебрегаем; спиральные
пружины' с жесткостями Xj и х.2 при верх-
(3.6)
(3.7)
нем вертикальном положении маятни-
ков находятся в естественном недеформированном состоянии
(рис. 3.1). Считая массы т1 и т2 маятников и их длины и задан-
80
ГЛ. III. УСТОЙЧИВОСТЬ КОНСЕРВАТИВНЫХ СИСТЕМ
ними, определим жесткости пружин хх и х2 так, чтобы в верхнем
вертикальном положении равновесие маятников было устойчивым.
Связи системы идеальны, стационарны и голономны, а актив-
ные силы, действующие на систему, консервативны. Поэтому здесь
применима теорема Лагранжа. Положение маятников будем опре-
делять углами <pj и ф2. Потенциальная энергия П системы склады-
вается из потенциальной энергии Пх пружин и потенциальной энер-
гии П2 сил тяжести
П = Щ + П2.
Имеем
1 , 1
П1 = — ХХф2 + "у Х2 (ф2 — ф!)2,
П2 = .— mjgZj (1 — cos Ф1) — m2g [Zj (1 — cos q>x) -|- Z2 (1 — cos <p2)].
Следовательно,
1	1	о
п = -у Х1Ф1 + -у х-2 (ф2 — 2ф1ф2 4- ф2) —
— (mi 4- m2) gli (1 — cos Ф1) — m2gZ2 (1 — cos <p2).
Пользуясь разложением косинуса в-ряд Маклорена:
z2
COS Z = 1 — -у -|  . . . ,
получим после группировки
1
II = -у {[-Z1 + и2 — (mi + m2) gZJ ф2 —
— 2х2ф!фа + (х2 — m2gZ2) ф2}	,
где точками обозначены члены, содержащие фх и ф2 в степени выше
второй.
Введем обозначения
Си = Xi + х2 — (mi + m2) gllt с12 = c2i = —х2, с22 = х2 — m2gZ2.
Тогда
1
П = -у (Сцф1 + 2с12ф1ф2	С22ф2)
Критерий Сильвестра (2.9) в данном примере имеет вид
Д1 = сц>0, Д2 = IС11	12 | = сцс22 — с2 > 0.
| С21 с23 I
Вместо этих неравенств можно ввести два других, им эквивалент-
ных (они могут быть получены, в частности, из критерия Сильвестра
простой перестановкой индексов):
с22 > О' с11с12	с12 > «.
Пользуясь значениями cgj, получим
%2 — m2gl2 > 0, (х2 — m2gZ2) [Х1 + х2 — (mx + m2)gZi] — х2 > 0.
Решая эти неравенства относительно хх и Ха, легко найдем
х2 > m2gZ2, Xi > XY— m2gZ2 + (nl1 +	g11 ~
§ 3.2. ОБРАТИМОСТЬ ТЕОРЕМЫ ЛАГРАНЖА
81
Положим
А = m2gl2, В = (mj 4- m2) gl±:
Тогда последние неравенства принимают вид
^2 > A,	Х2-
7^2 - 
Преобразуем второе неравенство. Имеем
х^ — А2 -|- А2	А2
*1 > х2 —А Н в - *2 = *з + А +	_ л + £ - х2.
Теперь условие устойчивости принимает вид
*i>	+ А + £’ ^>А-	(3,8)
На рис. 3.2 показана область устойчивости равновесия верти-
кального положения.
А2
Граница области определяется уравнением Xj = --т- + A -f-
Х2 — Л
+ В и неравенством х2 > А.
§ 3.2.	Обратимость теоремы Лагранжа
Теорема Лагранжа определяет только достаточные
условия устойчивости равновесия консервативной си-
стемы: если потенциальная энергия имеет в положении
изолированного равновесия минимум, то равновесие ус-
тойчиво. Ляпунов первый поставил вопрос об обратимо-
ти теоремы Лагранжа, а именно: можно ли утверждать,
что при отсутствии минимума потенциальной энергии
равновесие будет неустойчивым? Ему принадлежат сле-
дующие две теоремы, которые приводятся здесь без дока-
зательств (см. 1351).
1.	Если в положении изолированного равновесия потен-
циальная энергия не имеет минимума и его отсутствие
определяется членами второго порядка малости без необ-
82 ГЛ. III. УСТОЙЧИВОСТЬ КОНСЕРВАТИВНЫХ СИСТЕМ
ходимости рассматривания членов высшего порядка, то
равновесие неустойчиво.
2.	Если в положении изолированного равновесия потен-
циальная энергия имеет максимум, определяемый по чле-
нам наименее высокого порядка, которые действительно
имеются в разложении этой функции, то равновесие не-
устойчиво.
Н. Г. Четаев обобщил эти теоремы Ляпунова и дока-
зал следующую теорему: если в изолированном положении
равновесия потенциальная энергия П, предполагаемая
аналитической функцией qr, . . ., qs, не имеет минимума,
то равновесие неустойчиво (см. [491).
На основании приведенных теорем § 3.2 и 3.1 будем
в дальнейшем считать, что устойчивому положению рав-
новесия потенциальной системы отвечает минимум потен-
циальной энергии. Из этого следует, что устойчивое поло-
жение равновесия потенциальной системы изолировано.
§ 3.3.	Циклические координаты.
Преобразование Рауса
Существует обширный класс механических систем,
для которых некоторые координаты не входят явным об-
разом в кинетическую энергию системы, а обобщенные
силы, соответствующие этим координатам, равны нулю.
Такие координаты называются циклическими, а осталь-
ные координаты системы — позиционными или просто
нециклическими. Так, например, для искусственного
спутника Земли (см. пример 2 § 2.6) координата Ф —
циклическая, а координаты 0 и г — позиционные. Для
конического маятника (пример 1 § 2.6) координата гр —
циклическая, а координата 0 — позиционная. Для волчка
(пример § 3 § 2.6) координаты аир — позиционные,
а координата ф — циклическая.
Пусть дх, . . ., qs — позиционные, а фх, . . ., фт —
циклические координаты системы. Запишем уравнения Ла-
гранжа для циклических координат
d ОТ дТ „	..	.	, /о п\
-щ--------~Л— = (?№ (/ — 1,..., т).	(3.9)
dl dif-	дц х	v	\ /
Кинетическая энергия T системы по определению цикли-
ческих координат не зависит явным образом от фх; поэтому
§ 3.3. ЦИКЛИЧЕСКИЕ КООРДИНАТЫ	83
Кроме того, обобщенные силы Q,f^, соответствующие цик-
лическим координатам, .равны нулю
<?ъ=о.
Следовательно, уравнения Лагранжа (3.9) для цикличе-
ских координат принимают вид
А 4^ = ° (7 = !,•••, т).	(3.10)
dt дф.	w ’	’	/	\	/
Эти уравнения допускают очевидные первые интегралы
(7 = 1, • • •, "*).	(3-И)
показывающие, что обобщенные импульсы, соответствую-
щие циклическим координатам, остаются постоянными
во все время движения.
Первые интегралы (3.11) можно использовать для пре-
образования уравнений Лагранжа для позиционных ко-
ординат. Это преобразование принадлежит Раусу и носит
его имя. Не останавливаясь на выводе (см., например,
[38, 491), приведем только результаты.
Правые части первых интегралов (3.11) содержат цик-
лические скорости ф7- линейно, так как Т — квадратич-
ная функция скоростей. Найдем из т первых интегралов
(3.11) все фу, выразив их через и внесем затем их
в выражение для кинетической энергии и обозначим ре-
зультат подстановки через Т*, после чего составим функ-
цию Рауса по следующей - формуле:
т
Л = Т* — 3 Щ.ф,.	(3.12)
f=i
В этом выражении циклические скорости ф,; должны
быть заменены их значениями, полученными из первых
интегралов (3.11). Уравнения для позиционных коорди-
нат <?у примут вид (предполагается, что силы, действующие
на систему, потенциальны; в противном случае в правой
"ости уравнений будут стоят обобщенные силы Qs)
d dR dR _______ 5П .._______j , zQ 4 o\
= <> = 1..............* <3'131
Функция Рауса не содержит циклических координат
ср и скоростей ф, а зависит только от q* и tft. Поэтому
движение в позиционных координатах qj можно изучать
84
ГЛ. III. УСТОЙЧИВОСТЬ КОНСЕРВАТИВНЫХ СИСТЕМ
по уравнениям (3.13), как бы игнорируя циклические ко-
ординаты (конечно, до тех пор, пока рассматриваются од-
ни уравнения (3.13)). В связи с этим движение в цикличе-
ских координатах называется скрытым движением, а дви-
жение в позиционных координатах — явным движением.
Остановимся подробно на структуре функции Рауса.
В результате всех преобразований, связанных с построе-
нием по формуле (3.12), в функции Рауса R можно выде-
лить слагаемое /?2, содержащее позиционные скорости (j
во второй степени, слагаемое содержащее позицион-
ные скорости q в первой степени, и слагаемое Ro, незави-
сящее от скоростей q:
R = R2 + Ri + Ro,	(3.14)
где
s _s
(3-15)
3=1 1C=1
Ri= 3	(3.16)
3=1
В этих равенствах коэффициенты a^j = a,j, а также
/?0 — функции позиционных координат qu . . ., qs и по-
стоянных интегрирования q, . . ст. Не останавливаясь
на доказательстве (см., например, [38]), отметим, что
квадратичная форма Rz является определенно-положи-
тельной.
Внесем в уравнения (3.13) значение функции Рауса
из формулы (3.14):
д (Т?2 +	Я») __ d (^?2 + Rl + Яо) _ дП
dt	dqi	dq-	~dq7 •
Разбивая на отдельные слагаемые и учитывая, что Ro не
дНа п
зависит от q и, следовательно, = и, получим после
группировки
d dR2 0R2	с?П . ORq ( d dR\ dR\)	. y.
dt dq- dq-	dq- dq- ( dt dq. dq- J '	'
Пользуясь формулой (3.16) для /?j, преобразуем выраже-
ние, стоящее в скобках. Имеем
dR, д V
-у— = У а,(; = а:.
dq}	dq, 3‘~	3
1	1 М
§ 3.3. ЦИКЛИЧЕСКИЕ КООРДИНАТЫ
85
Учитывая, что зависит от времени t сложным образом
через qt, . . qs, получим по правилам дифференцирова-
ния сложной функции
d dRt _ da-   yi .
dt dqi dt	/ i dq,;.
Заменим теперь в формуле (3.16) индекс суммирования j
на к и продифференцируем по qp
dRt d V V1 да* 
% ~ 9q} 2-J ак'(- ~ 2-1 dq- (*к’
3	1 К=1	fc=l 3
Следовательно,
dt dq-	dq-	2-1 \	dq. J	2-1 ^}к ' к’
3	3	fr=i '	33	k=l
где так называемые гироскопические коэффициенты gjk
определены равенствами
да,	da,.
gjk~ dqk	dq
(3.18)
Теперь уравнения (3.17)1 приводятся к следующему
виду:
d dRi dRi dW	.	. ... ,n.
ТГЧ7 =	<' = 1...',>'(ЗЛ9>
3	3	1 k=i
где
W П - Ro.	(3.20)
Уравнениям (3.19) можно отнести некоторую систему
(она называется приведенцой системой), в которой функ-
ции Т?2 и W служат кинетической и потенциальной энер-
гиями; обобщенные силы этой системы определяются равен-
ствами
=	(3.21)
3 ft=l
причем	называются гироскопическими силами. Из
определения гироскопических коэффициентов видно,
что их матрица кососимметричная, т. е.
gjk----------glcj-
(3.22)
86 ГЛ. III. УСТОЙЧИВОСТЬ КОНСЕРВАТИВНЫХ СИСТЕМ
В этом легко убедиться, поменяв в формуле (3.18) места-
ми индексы /си/. Заметим, что при отсутствии гироскопи-
ческих сил (это, как правило, бывает при Rr = 0) систе-
ма называется гироскопически несвязанной. Основное свой-
ство гироскопических сил состоит в том, что сумма их
работ на действительном перемещении равна нулю. Это
свойство лежит в основе их определения, данного Томсоном
и Тетом (см. [58]). Гироскопические силы встречаются не
только в системах с циклическими координатами (част-
ный случай их — системы, содержащие гироскопы), но
и в различных других физических системах (см. примеры
§ 6.7).
Из дифференциальных уравнений (3.19) приведенной
системы легко получить интеграл энергии
Rz + W == Rz + П — Ro = const. (3.23)
Этот интеграл может быть получен формальными метода-
ми, но физически он очевиден — гироскопические силы,
действующие на приведенную систему, не производят
работы и, следовательно, они не могут изменить общий ба-
ланс энергии.
§ 3.4. Стационарное движение
и условия его устойчивости
При некоторых условиях материальная система, име-
ющая т циклических и s позиционных координат, может
совершать стационарное движение, которое состоит в том,
что все позиционные координаты и циклические скорости
сохраняют постоянные значения, равные начальным. Ус-
ловия, при которых осуществляется стационарное дви-
жение, легко получаются из следующих очевидных со-
ображений.
Согласно определению в стационарном движении, все
позиционные координаты сохраняют постоянное значе-
ние:
Чк (С = Чко = const (k = 1, . . ., s).
Это означает, что приведенная система находится
в покое. Но для этого, согласно равенствам (3.1), необходи-
мо и достаточно, чтобы все обобщенные силы (3.21) этой
системы равнялись нулю, т. е.
к 3 'я.
g 3.4. СТАЦИОНАРНОЕ ДВИЖЕНИЕ
87
или, учитывая, что в стационарном движении (равновесии
нриведенной системы) все	= 0:
(тЯ =° У=1...............’>•	<3-24>
' qj 'q.
Принимая во внимание выражение (3.20) для потен-
циальной энергии W приведенной системы, этим услови-
ям можно придать и другой вид, а именно:
Таким образом, для осуществимости стационарного
движения необходимо и достаточно, чтобы начальные зна-
чения позиционных координат qj удовлетворяли х равен-
ствам (3.24) и все начальные значения позиционных ско-
ростей qj равнялись нулю (при q — const и q = 0 все цик-
лические скорости ф будут сохранять постоянные значе-
ния). Отметим, что в функцию Ro входят постоянные Cj
циклических интегралов (3.11), поэтому значения qOj в
стационарном движении зависят от циклических скоростей
ф, содержащихся в с}.
Перейдем теперь к определению условий устойчивости
стационарного движения, которое будем считать за не-
возмущенное движение. Не нарушая общности, можно
считать, что в стационарном движении все позиционные
координаты qj равны нулю. Тогда уравнения движения
(3.19) приведенной системы будут дифференциальными
уравнениями возмущенного движения относительно по-
зиционных координат qj и скоростей qj. Раусу принадле-
жат несколько теорем об устойчивости стационарного дви-
жения. Здесь приводится одна из них, получившая наи-
большее распространение.
Теорема Рауса. Если ц стационарном движении потен-
циальная энергия W = П — Ro приведенной системы име-
ет минимум, то это движение устойчиво относительно
позиционных координат qj и скоростей q}, по крайней мере
для возмущений, не нарушающих значения циклических ин-
тегралов (3.11).
Доказательство. При стационарном движении исход-
ной системы приведенная система находится в покое.
Кроме того, для этой системы имеет место интеграл энер-
гии (3.23). Поэтому для доказательства теоремы Рауса
достаточно повторить доказательство теоремы Лагранжа.
88
ГЛ. III. УСТОЙЧИВОСТЬ КОНСЕРВАТИВНЫХ СИСТЕМ
Теорема Рауса в данной формулировке справедлива,
конечно, для возмущений, при которых не нарушаются
циклические интегралы (3.11) (так как последние входят
в потенциальную энергию приведенной системы через
функцию 7?0). Ляпунову принадлежит существенное до-
полнение к этой теореме, устраняющее этот недостаток.
Ниже приводится без доказательства дополнение Ляпуно-
ва в форме следующей теоремы х).
Теорема. Если потенциальная энергия W приведенной
системы имеет минимум как при данных р] = с j, отве-
чающих рассматриваемому стационарному движению, так
и при всяких достаточно близких к данным значениях р; —
= С) + где ц; малы по модулю, причем значения пере-
менных qk, обращающие ее в минимум, суть непрерывные
функции величин р}, то стационарное движение устойчиво
относительно <-,к и qk.
Примечание. Циклические интегралы (3.11) содержат
позиционные q и циклические ф скорости линейно. По-
этому из устойчивости стационарного движения относи-
тельно величин qk и qk следует устойчивость и относитель-
но циклических скоростей ф (но не координат q>).
Необходимо отметить, что устойчивость стационарного
движения может быть осуществлена и при отсутствии ми-
нимума потенциальной энергии (за счет гироскопических
сил). Поэтому распространить теоремы Ляпунова и Четае-
ва об обратимости теоремы Лагранжа на стационарное
движение нельзя. Однако для гироскопически несвязан-
ной системы справедлива следующая теорема, являющая-
ся перефразировкой теоремы Четаева об обратимости тео-
ремы Лагранжа.
Теорема. Если для изолированного стационарного дви-
жения гироскопически несвязанной системы при фиксиро-
ванных циклических интегралах (3.11) функция W, пред-
полагаемая аналитической функцией переменных q, не име-
ет минимума, то стационарное движение неустойчиво.
В заключение отметим, что для практического приме-
нения теоремы Рауса достаточно заметить, что при выпол-
') А. М. Ляпунов приводит свое дополнение к теореме Рау-
са без доказательства. В. В. Румянцев в работе [46] доказал
это дополнение в предположении непрерывности функции W. В
этой же работе приводится наиболее полное изложение теории
устойчивости стационарных движений; часть результатов принад-
лежит В. В. Румянцеву. В работах [24а, 536, 53в] приводятся
условия обратимости теоремы Рауса и, как следствие условия
обратимости, теоремы Лагранжа — Дирихле.
§ 3.5. ПРИМЕРЫ
89
нении ее условий функция W — Wo будет определенно-
положительной (Wo — значение функции W в стационар-
ном движении). Поэтому здесь рационально использовать
обычный прием разложения этой функции в ряд с после-
дующим применением критерия Сильвестра.
§ 3.5. Примеры
В примерах 1 и 2 § 2.6 устойчивость стационарных дви-
жений конического маятника и ИСЗ была доказана с по-
мощью связки интегралов. Получим теперь эти же резуль-
таты с помощью теоремы Рауса.
Пример 1. Устойчивость стационарного
движения конического маятника. Ранее были
найдены следующие выражения для кинетической Т и потенциаль-
ной П энергий маятника (см. рис. 2.14 и формулы на с. 58):
1
Т =~2 ml2 (02 Ц- ф2 sin2 0), П = — mgl cos 0.
Из этих выражений видно, что координата ф циклическая (она вхо-
дит в кинетическую энергию только через скорость ф и не содержит-
ся в потенциальной энергии), а координата 0 позиционная. Соста-
вим, согласно формуле (3.11), циклический интеграл
р =	= ml2 sin2 0ф = с.
дф
Отсюда найдем ф и внесем его в выражение для кинетической энер-
гии:
. с	1.1с2
= ml2 sin2 0 ’ Т* = ~2 mltQ2 + ~2 ml2 sin2 0 ’
Пользуясь формулой (3.12), составим функцию Рауса
1.1с2	с
R = Т* — сф = у ™Р02 + у mpsina9 — с‘ mZ2sin20
ИЛИ
1	.	1 са
Я = у mZ202 — у sjna 0 •
Отсюда видно, что (см. равенство (3.14))
1	„	„	1с2
/?2 = ymZ202, ^ = 0, 2?0 =	2 mZ2sin20
Так как RT = 0, то система гироскопически не связана. Согласно
общей теории, составим потенциальную энергию W = П — Rn при-
веденной системы:
1 с2
]V = — mgl cos 0 + у mpsina0 •	(3.27)
90 ГЛ. III. УСТОЙЧИВОСТЬ КОНСЕРВАТИВНЫХ СИСТЕМ
Обозначим значение угла 9 в установившемся движении через
а, а значение циклической скорости ip через со. Условие (3.24) осу-
ществимости стационарного движения принимает вид
/tW\	с2 cos а
(-дд-1	= mgl sin а-——„ „ »— = 0	(3.28)
\ ои/6=а	®	mZ2sin3a	'	’
или, после преобразований,
sin4 a	с2
cos a ~ m2gl3 ’
Это равенство определяет однопараметрическое семейство реше-
ний уравнения (3.28), причем соответствующая величина угловой
скорости конического маятника определяется равенством (3.26)
Ф — % = “ = sin2a ’	(3.30)
Исключая из равенств (3.29) и (3.30) параметр с, найдем
, g
со2 cos a =	.
Как уже отмечалось в примере 1 § 2.6, это условие стационар-
ного движения конического маятника может быть получено из эле-
ментарных соображений.
Примем стационарное движение маятника за невозмущенное и
исследуем его устойчивость с помощью теоремы Рауса с дополнением
Ляпунова. Положим 9 = a + х, внесем в выражение (3.27) для
функции W и разложим разность W — Wo в ряд по степеням х:
или, учитывая равенство (3.28),
1 / d2W \
W -Wo=-2-	)0=ах3 + •••’
где точками обозначены члены, содержащие х в степени выше
второй.
Вычисляя производную, найдем
тт7 т.г 1 Г	са sin3 a + 3 cos2 a
W — Tl о = -у I mgl cos a 4-	---- —
sin4 a
Так как множитель при х2 положителен, то функция W имеет
в стационарном движении минимум. Кроме того, для всякого
л
9 = а^=~2- решение (3.29) непрерывно зависит от постоянной с
интеграла (3.26), а циклическая скорость ф = <о непрерывно зависит
от той же постоянной при 9 = a =/= 9. Поэтому на основании тео-
ремы Рауса и дополнения Ляпунова стационарное движение кони-
ческого маятника устойчиво относительно 9, 9 и ф.
Пример 2. Устойчивость стационарных
движений центра масс	искусственного
§ 3.5. ПЕЙМЕРЬ!
91
спутника Земли [46]. В примере 2 § 2.6 были получены
следующие выражения для кинетической Т и потенциальной П
энергий искусственного спутника Земли (см. рис. 1.5 и формулы на
с. 26):
m .	.	.	m
Т =-g—(ra + ra cosa 0<ра + га02), П = —р, —.
Из этих выражений видно, что координата <р циклическая, а
координаты г и 0 позиционные. Циклической координате гр соответ-
ствует интеграл площадей
дТ
р = —cos2 Огр—с.	(3.31)
dip
Из этого равенства найдем производную ф и внесем ее в выражение
для кинетической энергии:
с	m .	.	1 с2
45 = mr2 cos2 0 ’ Т* = ~2~ (г’2 + r202) + ~2 m/2cos20
Пользуясь формулой (3.12), составим функцию Рауса
m .	.	1 с2	с
R = 7'* — cm = -s- (г2 4- г202) 4- -я-»-5-5- — с —$----г-ц
Y 2 ' 1	' 1 2 mr2 cos2 0 mr2 cos2 0
или
m .	.	1 c2
7? = -s- (r2 4- r292) — -9-»--j-д- .
2 '	1	'	2 mr2cos20
Отсюда видно, что (см. равенство (3.14))
m .	1 с2
д2 = _(г2 + г202)1 д1 = 0,	Д() = ______
Так как 7Ц = 0, то система гироскопически не связана.
Согласно общей теории,, составим потенциальную энергию W =
= П — На приведенной системы
m 1 с2
W = — р — + ~2 mr2 cos20 •	(3-32)
Условия (3.24) осуществимости стационарного движения при-
имают вид
dll7 m с2 л	dW	с2 sin 0 л о
~дг~ -=	И 7Т	— тгз C0S2 Q	= °-	"эд- =	тг2 С03з 0	= °- (3-33)
Эти уравнения имеют однопараметрическое семейство решений
с2
Г = r° = |1т2 ’	<3-34)
0 = 0о = 0,	(3.35)
причем соответствующая угловая скорость вращения радиуса-век-
тора центра масс спутника определяется из интеграла (3.31):
ф = <Ро = “ ==—~ .	(3.36)
92 ГЛ. III. УСТОЙЧИВОСТЬ КОНСЕРВАТИВНЫХ СИСТЕМ
Как было уже показано в примере 2 § 2.6, стационарные дви-
жения искусственного спутника представляют собой движения в
плоскости Оху по круговым орбитам радиуса г0 с постоянными угло-
выми скоростями. Исключай из равенств (3.34) и (3.36) параметр с,
найдем
<о2г® = р.
Эта формула была получена ранее из простых физических соображе-
ний (см. равенство (1.30)).
Примем стационарное движение спутника за невозмущенное и
исследуем его устойчивость с помощью теоремы Рауса и дополнения
Ляпунова. Положим г = г0 + х, внесем этд в выражение (3.32) для
функции W и разложим разность W — Wa в ряд по степеням х и 0:
/ dW \	/ dW \
Ж_1Уо=(__)оХ+(__)о0 +
1 {! дг№ \	/ d*W \ I дЧУ \ 1
+ т [\~i372-+ Ц ^ж)ох0 + \~д&) 02 J
или, учитывая равенства (3.33),
Имеем
'WF\	т с2 / d2W \	7д21У\ с2
. дг2/о	г2	mr(*	’	\й^й0;о	’ \ d02/у	тог;
Следовательно,
W -W0 = 4r
Так как, согласно равенству (3.34), в установившемся движе-
нии с2 = цт2г0, то будем иметь
1 т ( 1	\
=	— z2+02 U...
\ О	'
Из этого выражения видно, что функция W имеет в стационар-
ном движении минимум. Кроме того, для всякого г0 =£ 0 решение
(3.34) непрерывно зависит от постоянной с интеграла (3.31). Поэто-
му на основании теоремы Рауса и дополнения Ляпунова стационар-
ное движение спутника устойчиво относительно г, г, 0, 0 и ф.
Пример 3. Устойчивость регулярной пре-
цессии тяжелого гироскопа. Рассмотрим симмет-
ричное твердое тело, имеющее одну неподвижную точку О и движу-
щееся под действием силы тяжести. Положение оси симметрии z
тела будем определять углом прецессии ф и углом нутации 0; угол
собственного вращения обозначим через (р (рис. 3.3). Кинетическая Т
и потенциальная П энергии такого тела определяются равенствами
1 1
т = ~2Jx(ax + «у) + ~2JZ^2Z’ n = W*cos0,
§ 9.5. ПРИМЕРЫ
93
где Jx = Jу и Jz — моменты инерции тела относительно осей Ре-
заля х, у, z, а <ох, ыу, a>z — проекции угловой скорости тела на те
Hte оси, М — масса тела, h — расстояние от его центра тяжести до
точки опоры.
Пользуясь рис. 3.4, легко найдем
ых = — ф sin 0, <£>у = 9, <oz = ф + ф cos 0.
Внося эти выражения для (лу, в кинетическую энергию
Т, получим
Г = -у 7я (02 + sin2 Оф2) + ~2 Jz (Ф + cos 0ф)2.
Так как координаты ф и ф входят в кинетическую энергию Т
только через свои скорости ф иф, а потенциальная энергия П от них
Рис. 3.4
не зависит, то эти координаты циклические, а 0 — позиционная.
Циклическим координатам соответствуют два первых интеграла
дТ
—- = Jz (ф + cos 0ф) = J п,
(3.37)
дТ	...
—г- = J sin2 0ф + Л (ф + cos 0ф) cos 0 = m,
dvp
где Jzn и m — постоянные интегрирования (множитель Jz введен
для удобства).
Эти интегралы выражают постоянство кинетического момента
относительно осей z и £ соответственно. Из равенств (3.37) найдем
циклические скорости
m — J п cos 0	m — Jzn cos 0
= Zxsin20 ’ Ф =л — у* sin2 О cos 9-
Внесем найденные значения ф и ф в кинетическую энергию. Пос-
ле очевидных преобразований получим
j 1	1 (m — Jzn cos 0)2	1
7'* = -2	+ -2 7x'sin20 + Т
94
ГЛ. III. УСТОЙЧИВОСТЬ КОНСЕРВАТИВНЫХ СИСТЕМ
Пользуясь формулой (3.12), составим функцию Рауса (в рас-
сматриваемом случае с2 = Jzn и с2 = т):
'	1	1 (т — J2п cos 0)2
7? = 7 — У2пф — тф =	/ж92 + -g у* sin2 е
Г т — Jzn cos 6 "I т — Z2ncos0
— J 2n\ji — yxSin2 0 cos 0 J — m 7xSin20 ,
или, группируя члены и отбрасывая несущественную постоянную
- Ч^П2,
1	.	1 (т — Jzn cos 0)2
R -= ^JJ? — Jxsin20 •
Сравнивая с равенством (3.14), найдем
1	„	i (т— Jzn cos 0)2
Ri = У 7*02’ Л1 = °’ R« = — "2 7xsin20
Составим далее потенциальную энергию
приведенной системы
IT = П — Ro
W = Mgh cos 0
1 (m — Jzn cos 0)2
+ ~2 Jx sin2 9
и напишем условие осуществимости стационарного движения (3.24):
1/ ь • о , (m~ Ancos0o) (J2n - m cos 0О)
Mgh sln +-------------Jxsin30o---------- = °- <3-38>
Считая известными постоянные т и п, из этого уравнения легко
найти угол 0 = 0О. Для этого достаточно представить данное урав-
нение в следующей форме:
MghJx cos4 0О — (М ghJx -|- Jznm) cos2 0O +
+ (J2n2 -|- m2) cos 0O + MghJx — Jznm = 0. (3.39)
Это уравнение определяет семейство решений, зависящее от
двух параметров тип. Для практических целей удобнее задавать
просто начальные условия
при t = 0: 0 = 0О, 0 = 0, ф = фо, ф = ф0.
Если теперь выразить постоянные интегрирования т и п по
формулам (3.37) через эти*начальные условия, то уравнение (3.39)
легко приводится к виду
Фо (Jx — Jz) cos 0О — ЛФоФо + Mgh = 0.
Это равенство устанавливает связь между начальными условия-
ми движения, при которых осуществляется стационарное движение.
Последнее состоит в том, что гироскоп равномерно вращается с уг-
ловой скоростью ф = ф0 вокруг оси симметрии z, а ось z равномер-
но вращается вокруг вертикальной оси £ с угловой скоростью
Ф = Фо. описывая круговой конус с углом раствора, равным 20о
(см. рис. 3.3). Такое движение называется регулярной прецессией.
Исследуем устойчивость регулярной прецессии. Для этого по-
ложим 0 = Оо х, внесем это в потенциальную энергию W при-
§ 3.5. ПРИМЕРЫ
95
веденной системы и разложим функцию W — Wo в ряд по степеням х:
где точками обозначены члены, содержащие х в степени выше вто-
рой. Первое слагаемое на основании равенства (3.38) выпадает,
а второе после несложных преобразований приводится к виду
г (,“7б2~ ^е=о0 =
1 (т—Jzn cos0o)a sin2 0о + (J zn + Jzn cos2 0O — 2m cos O0)2 e
=27;	sTn®0^	x 
Так как при всех значениях 0О, не равных 0 или л, коэффициент
при х2 положителен, то функция W имеет в стационарном движе-
нии минимум. Кроме того, для всех 0О, не равных 0 или л, решение
уравнения (3.38) непрерывно зависит от постоянных тип интег-
ралов (3.37) (корни алгебраического относительно cos 0О уравне-
ния (3.39) непрерывно зависят от коэффициентов уравнения). По-
этому на основании теоремы Рауса и дополнения Ляпунова регу-
лярная прецессия устойчива относительно 0, 0, ф и ф.
Пример 4. Устойчивость равновесного по-
ложения оси вращающегося уравновешен-
ного ротора, установленного в нелиней-
ных опорах [26а]. Рассмотрим абсолютно жесткий уравно-
вешенный ротор с вертикальной осью вращения, установленный
в жестко укрепленных на неподвиж-
ном основании упругих подшипни-
ках. Будем предполагать, что под-
шипники обладают в общем случае
нелинейной податливостью, в резуль-
тате чего ось ротора может переме-
щаться плоскопараллельно х). Собст-
венное вращение происходит вокруг
оси'материальной симметрии (соот-
ветствующие центробежные моменты
инерции и эксцентриситет е равны
нулю), реакции подшипников при-
водятся к одной равнодействующей
Fo, зависящей от радиального пере-
мещения р оси О ротора и направлен-
ной к точке Ог пересечения плоскости
движения центра масс с осью неде-
формированных подшипников (рис.
3.5 — точки О и С при е = 0 совпадают). Очевидно, что любая ре-
акция Fo (р) должна обращаться в нуль при отсутствии деформации
(р = 0) и в области допустимых деформаций возрастать с увеличе-
нием р, т. е. для любой реакции FQ (р) должны выполняться
!) Этим условиям удовлетворяет также движущийся плоско-
параллельно уравновешенный ротор, укрепленный на безынер-
ционном гибком валу, установленном в жестких вертикальных
опорах.
96
ГЛ. III. УСТОЙЧИВОСТЬ КОНСЕРВАТИВНЫХ СИСТЕМ
условия
7?о(°)=0’ 4г >0 (р>°)’	(з-4°)
кроме того, производная dFBldp должна быть ограничена при р = О,
а производная (PFldp2 — непрерывна в тех же пределах.
Этим условиям удовлетворяют, в частности, линейная реакция
FB = ср, нелинейные жесткие или мягкие реакции вида FB —
= ср + Ьр2 + ар3, реакции FB = aopa (a > 1) и др. Заметим, что
для шариковых подшипников большинство авторов принимает
FB — аора> гДе а = 3/2 (формула Герца).
Очевидно, что потенциальная энергия упругой реакции
Р
П (р) = Fo (р) dp
о
в положении равновесия (р = 0) имеет изолированный минимум
(П (0) = 0 и П (р) > 0 при р > 0).
В сделанных предположениях о материальной симметрии оси
ротора движение центра масс и вращательное движение не зависят
друг от друга и их можно изучать раздельно.
Рассмотрим вопрос об устойчивости равновесного положения
оси вращающегося ротора (р = 0), сделав предварительно одно
тривиальное, но вместе с тем важное замечание: координаты и их
скорости должны быть определены для каждого состояния системы.
При исследовании стационарного движения неуравновешенного
ротора, установленного в нелинейных подшипниках (см. пример 5
§ 4.5), удобно пользоваться полярными координатами. Но в поло-
жении равновесия радиус р центра масс С ротора и его скорость р
равны нулю (р = 0, р = 0), а полярный угол ф и угловая скорость
ф не имеют смысла. Кроме того, в полярных координатах уравнения
движения оси ротора (они являются одновременно и уравнения-
ми возмущенного движения около положения равновесия) имеют вид
...	d .
тр — трф2 = — F (р),	(траф) = 0.
При р = 0 и любом ф эти'уравнения обращаются в тождества, т. е.
они имеют в положении равновесия бесчисленное множество ре-
шений, что нарушает основное требование о единственности реше-
ний уравнений (1.1). Поэтому для анализа устойчивости равновес-
ного положения оси уравновешенного ротора нельзя пользоваться
полярными координатами. В связи с этим введем обычные прямо-
угольные координаты х и у точки О, которые и будут характеризовать
отклонение оси ротора от положения равновесия в йеподвижнои
системе координат) х, у.
Кинетическая и потенциальная энергии определяются равен-
ствами
Р
Т = ~Ym (*2 + г/2). п (*. у) = j f (р) p = Vxa + ya.
о
Так как потенциальная энергия при х = 0, у = 0 имеет изо-
лированный минимум, то на основании теоремы Ляпунова заклю-
чаем, что равновесное положение оси уравновешенного ротора ус-
тойчиво относительно а:, у, -т и у; следовательно, оно устойчиво и от-
носительно р = |/"а:а + У2 и v = у^2 + у2.
ГЛАВА IV
УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
§ 4.1. Постановка задачи
Во многих случаях, особенно в приложениях, устой-
чивость движения исследуется по уравнениям первого при-
ближения. Это объясняется не только простотой метода,
но также и тем, что весьма часто наши знания процессов,
происходящих в реальных системах, позволяют надежно
определить только первые линейные члены. Однако, как
было показано в § 1.2 (см. пример на с. 20—21), уравне-
ния первого приближения могут дать иногда совершенно
неверное заключение об устойчивости движения. Поэтому
естественно возникает вопрос об определении условий,
при выполнении которых уравнения первого приближения
дают правильный ответ об устойчивости движения. В об-
щем виде задача ставится следующим образом.
Даны уравнения возмущенного движения
Х1 — а11х1 + • • • + а1пхп + ^1,
.................................... (4.1)
ХП &П1Х1 “Ь • • • “Ь &ппхп “Ь Хп,
где нелинейные члены . ., Хп содержат хг, . . ., хп
в степени выше первой (в этой главе вместо А* будем пи-
сать просто Xj).
Требуется определить условия, при которых заключе-
ние об устойчивости движения можно составить по урав-
нениям первого приближения
хх ~ апх1 + • • • +
.................................. (4.2)
Хп ^nlxl	аппхц
при любых нелинейных членах . . ., Хп.
Впервые эта задача была поставлена А. М. Ляпуно-
вым. Ему же принадлежит ее полное решение для авто-
номных систем, когда все коэффициенты сц-; — постоянные
числа, а также для многих случаев неавтономных систем
при a^j, зависящих от времени t,
4 д. р. Меркца
98
ГЛ. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
§ 4.2. Предварительные замечания
В этом параграфе, не определяя вида общего решения
уравнений первого приближения, ограничимся напомина-
нием метода построения характеристического уравнения
и некоторыми другими предварительными замечаниями,
которые понадобятся в дальнейшем.
Для автономной системы (см. с. 21) все коэффициенты
a^i уравнений (4.2) — постоянные числа. Частное решение
этих уравнений ищется в форме
хг = Агеи, . . ., хп = Апеу,	(4.3)
где . . ., Ап, к — постоянные числа.
Дифференцируя равенства (4.3) по времени, получим;
хг = AjkeM, . . хп = АпКеи.
Внесем эти выражения для производных ±15 . . ., хп
и выражения для хг, . . хп из равенств (4.3) в уравнения
(4.2) и сократим их на не равный нулю общий множитель
еи. Тогда, после группировки членов, будем иметь
(«и — X) А± + а1242 + . . . + а1пАп = О,
a21^1 + (а22  	42 + . . . +	= 0,	(4.4)
OnMi + ап2^-2 +    + (а-пп — Ап — 0.
Так как эта система линейных однородных алгебраи-
ческих уравнений относительно постоянных Аг, . . ., Ап
должна иметь решение, отличное от нуля (в противном
случае все хк- = 0), то определитель этой системы должен
равняться нулю:
°11	а12	• •  а1п
а21	а22	' а2п
ащ	ап2	• ' ' апп ~
= 0.
(4.5)
Полученное уравнение относительно X называется ха-
рактеристическим уравнением, а соответствующий опре-
делитель — характеристическим определителем.
Характеристическое уравнение содержит неизвестное
число X в степени п. Следовательно, оно имеет п корней
Хц Х2, . . ., Хп.
Если среди корней характеристического уравнения
нет равных (корни простые), то всегда существует такое
§ 4.2. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ	у9
неособенное линейное преобразование
п
ZR—(ic = 1,..., п),	(4.6)
где akj — некоторые постоянные числа, которое приво-
дит уравнения первого приближения (4.2) к виду
Zj — XjZj,
^2 ~ ^2Z2»
.....	(4.7)
zn ^nzn*
Переменные z15 . . ., zn называются каноническими пе-
ременными (общий случай преобразования линейных диф-
ференциальных уравнений к каноническим переменным
при наличии кратных корней характеристического урав-
нения рассматривается в гл. V). Если применить преобра-
зование (4.6) к уравнениям возмущенного движения (4.1),
то получим
Zi — XjZj -|- Zj,
Z2 = ^'“2Z2 “Ь ^2,	(4.8)
Zn ~	4" Zn.
В этих уравнениях Z1, . . ., Zn — нелинейные члены,
содержащие zn . . ., zn в степени, выше первой.
Каждому комплексному корню X = v + ip, характе-
ристического уравнения (4.5) отвечает сопряженный ко-
рень X =- v — ip (v и р — вещественные постоянные чис-
ла); им соответствуют комплексно-сопряженные канони-
ческие переменные z — и + iv и z = и — iv, где и и v —
вещественные функции времени t. Вещественным корням
X характеристического уравнения (4.5) отвечают вещест-
венные канонические переменные z.
Так как коэффициенты а&7- преобразования (4.6) по-
стоянные числа, то из устойчивости (неустойчивости) не-
возмущенного движения относительно переменных сле-
дует устойчивость (неустойчивость) относительно канони-
ческих переменных zk и наоборот.
Предположим теперь, что система линейна, то есть
дифференциальные уравнения возмущенного движения
имеют вид уравнений (4.2) или в канонических перемен-
ных — уравнений (4.7). В сделанных предположениях
(корни характеристического уравнения простые) диффе-
4*
100
ГЛ. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
ренциальные уравнения (4.7) независимы друг от друга.
Они интегрируются элементарно и их общее решение
имеет вид
......................... (4.9)
М
где z01, .. ., zOn—значения переменных zL, . . .,zn при t = 0.
Пусть = v/c + ipifc — корень характеристического
уравнения (если =/= 0 и =/= 0, то корень комплексный,
при vj. = 0 и =/= 0 корень чисто мнимый, при = О
вещественный и при = р* = 0 нулевой). Имеем
|А‘ |=-_	^‘1?^
или, учитывая, что | e^f1 | = 1 при любых pfr и t,
\е^\ = е^.	(4.10)
Из этого равенства следует, что при t ->• оо
|	| —0, если v/£ < 0,
| еЧ‘ | = 1, если = 0,	(4.11)
| Л' | -> оо', если Vfc ~^> 0.
Из общего решения (4.9) и предельных равенств (4.11)
непосредственно вытекают следующие теоремы об устой-
чивости движения линейной автономной системы, имеющей
простые корни характеристического уравнения (случай
кратных корней рассматривается в гл. V):
1.	Если вещественные части всех корней характеристи-
ческого уравнения отрицательны (все < 0), то невоз-
мущенное движение асимптотически устойчиво (все z^ —
->• 0 при t —оо);
2.	Если среди корней характеристического уравнения
имеется хотя бы один, вещественная часть которого по-
ложительна, то невозмущенное движение неустойчиво (хо-
тя бы одно Z]t ->• оо при t —оо);
3.	Если вещественные части некоторых корней харак-
теристического уравнения равны нулю, а вещественные
части остальных корней отрицательны, то невозмущенное
движение устойчиво, но не асимптотически (все zk ограни-
чены, и часть из них стремится к нулю) х).
В следующих параграфах этой главы рассматривается
влияние нелинейных членов.
*) Первые два вывода справедливы и для кратпых корней ха-
рактеристического уравнения.
§ 4.3. ОСНОВНЫЕ ТЕОРЕМЫ
101
§	4.3. Основные теоремы об устойчивости
по первому приближению
Теорема Ляпунова об устойчивости движения по пер-
вому приближению. Если вещественные части всех корней
характеристического уравнения первого приближения от-
рицательны, то невозмущенное движение асимптотиче-
ски устойчиво независимо от членов выше первого порядка
малости.
Доказательство. Сформулированная теорема Ляпунова
справедлива как для случая кратных, так и для случая
простых корней характеристического уравнения (4.5).
Учитывая характер настоящего руководства, мы ограни-
чимся рассмотрением случая простых корней (полное до-
казательство можно найти, например, в книгах А. М. Ля-
пунова, Н. Г. Четаева, И. Г. Малкина (см. [35, 49, 37])).
Итак, будем считать, что все корни характеристического
уравнения простые. Так как вариации xt, . . ., хп связа-
ны с каноническими переменными zlt . . ., zn линейным
преобразованием (4.6) при постоянных то достаточно
доказать, что в условиях теоремы невозмущенное движе-
ние асимптотически устойчиво относительно переменных
ZH . . •, ип.
Пусть часть корней характеристического уравнения
комплексно-сопряженные, а часть вещественные. Для оп-
ределенности будем считать, что имеются две пары комп-
лексно-сопряженных корней. Занумеруем все корни сле-
дующим образом:
комплексно-сопряженные корни
^1 = V1 + ф1’ ^2 = ^1 =	-- ф4,
(4.12)
Х3 — v2 4- i|.i2, ^4 =	= v2 —
вещественные корни
^5,	• • • ,
Комплексно-сопряженным корням Х17 Х2 и Х3, Х4 бу-
дут отвечать комплексно-сопряженные канонические пе-
ременные zlt z2 и z3, z4
z, = ui + iv,, z2 = z, = u, — iv,,
. .	_	.	(4.13)
Z3 — U2 "T" ^2> £4 — ^3 — ^2 — ^2»
(4.15)
102 ГЛ. IV, УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРЙБЛЙЖЕнЙТО
где uv, и2, vlf v2 — вещественные функции времени t. Ве-
щественным корням Х5, Хв, . . ., отвечают вещественные
канонические переменные zB, z6, . . zn.
Составим функцию Ляпунова в следующем виде г):
V = (zjZa + Z3Z4 + zB + zB + • • • 4~ Zn). (4.14)
Отметим прежде всего, что функция V является определен-
но-положительной вещественной функцией переменных
и17 б15 и2, v2, zB, . . ., zn. Это следует из равенств
ziz2 = zizi = (“1 + ivj) («! — ivj) = u’i + v[,
Z3Z4 <= Z3Z3 = (^2 4” ^2) (^2 ^2) ~ ~У~ ^2-
Вычислим производную У функции V
I
F" = ~2~(ZlZ2 + Z1Z2 + Z3Z4 + Z3Z4) + Z5Z5 + . . . + znzn.
Внесем сюда значения zk из уравнений (4.8)
F = -у [(X1Z4 + Zl) Z2 + Z1 (X2Z2 + Z2) + (X3Z3 -J- Z3) Z4 +
+ £3(^434 + Z4)] + Z5 (X5Z5 + Z5) -f- ... + zn ('hnzn -|- Zn)
или, группируя члены,
F" = -у [(A-l + ^2) Z1Z2 + (^3 + ^-4) Z3Z4] +
+ ^5Z& + • • • + ^nZn + Z,
где Z — совокупность членов, содержащих z15 . . ., zn в
степени выше второй. Так как, согласно равенствам (4.12),
Ч" ^2 = 2vlt ^3	^4 = 2v2,
то, учитывая выражения (4.15), получим
= vi (ui 4“ vi) 4“ v2 («2 + P-j) + X5Z5 + . . . + Xnz„ + Z.
(4.16)
Ч Если все корни комплексно-сопряженные, то
1
= ~2 (Z1Z2 4“ гзг« + • • • + гп_4гп),
если все корни вещественные, то
7=1(4+^+... + ^).
§ 4.3. ОСНОВНЫЕ ТЕОРЕМЫ
103
По условию теоремы вещественные части всех корней
характеристического уравнения отрицательны. В приня-
тых обозначениях будем иметь
v4 < 0, v2 < 0, л5 < 0, . . лп < 0.
Из этого следует, что квадратичная часть производной
V будет определенно-отрицательной функцией переменных
u4,	и2, v2, z5, . . ., zn, а вместе с ней при достаточно
малых значениях | zA. | определенно-отрицательной будет
и производная У независимо от членов высшего порядка.
Таким образом, выполнены все условия теоремы Ляпуно-
ва об асимптотической устойчивости (§ 2.3), что доказы-
вает сформулированную теорему.
Теорема Ляпунова о неустойчивости по первому при-
ближению. Если среди корней характеристического урав-
нения найдется хотя бы один с положительной веществен-
ной частью, то невозмущенное движение неустойчиво неза-
висимо от членов выше первого порядка малости.
Доказательство. По условию теоремы хотя бы один
корень характеристического уравнения имеет положи
тельную вещественную часть. Пусть это будет Х4, т. е.
v4 = Re Х4 0. .
Для упрощения доказательства сделаем следующие
предположения:
1)	вещественные части всех корней не равны нулю;
2)	корни Х4, . . .,	— простые (доказательство тео-
ремы, свободное от этих ограничений, можно найти,
например, в книгах А. М. Ляпунова, Н. Г. Четаева,
И. Г. Малкина [35, 49, 37]).
Для определенности будем по-прежнему считать, что
имеются две пары комплексно-сопряженных корней (Х4,
л2 = Х4, Х3, л4 = Х3), а остальные корни Х5, . . ., ве-
щественные. Составим функцию Ляпунова в следующей
'форме:
V = Vi (Z1Z2 + v2z3z,t + X5Z5 + . .. + XnZn). (4.17)
Отметим, что эта вещественная функция может принимать
положительные значения, например, при z3 = z4 = z5 =
= . . . = zn = 0 и z4 =/= 0, z2 =/= 0. Вычислим производную
Р функции V:
{1
-J- [ZjZ2 + ZjZ2 + v2 (Z3Z4 + z3z4)] +
+ ^ftZgZg 4- ... 4. Xnznzn>.
104 ГЛ. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ приближению
Внесем сюда значения производных z!; из уравнений (4.8)
и сгруппируем члены, как это было сделано при доказа-
тельстве первой теоремы:
Р =	[(^1 + ^2)21X2 + v> (Х3 + 2»4)Z3Z4] +
+ ^5Z5 + • •  + ^zn| + z,
где Z — совокупность членов, содержащих zx, . . ., zn в
степени выше второй. Пользуясь равенствами (4.12)
и (4.15), получим
Р = vx {vx (ux + гх) + v2 (на + к2) + XjZj + . ..
• • • + ^riZn} + Z. (4.18)
В сделанных предположениях vx 0 и v2, A.s,  . hn
не равны нулю. Поэтому квадратичная часть производной
V будет определенно-положительной, а вместе с ней при
достаточно малых значениях | z* | определенно-положи-
тельной будет и производная У независимо от членов выс-
шего порядка. Таким образом, выполнены все условия
теоремы Ляпунова о неустойчивости движения (см. § 2.4)
(функция V может принимать положительные значения,
а ее производная V, вычисленная в силу уравнений воз-
мущенного движения, определенно-положительная), что
доказывает сформулированную теорему.
Доказанные две теоремы Ляпунова об устойчивости
по первому приближению решают задачу в двух случаях:
1)	вещественные части всех корней характеристическо-
го уравнения отрицательны;
2)	вещественная часть хотя бы одного корня положи-
тельна.
В обоих случаях уравнения первого приближения пол-
ностью решают задачу об устойчивости движения без не-
обходимости привлечения к анализу нелинейных членов.
Конечно, структура корней характеристического уравне-
ния может быть и другой, а именно: вещественные части
некоторых или всех корней характеристического уравне-
ния могут равняться нулю (в частности, среди корней
могут быть и нулевые), а вещественные части остальных
корней отрицательны. В этих случаях (они называются
особыми или критическими случаями) для определения
характера устойчивости движения одних уравнений пер-
вого приближения недостаточно — необходимо рассмот-
реть влияние нелинейных членов.
§ 4.3. ОСНОВНЫЙ ТЕОРЕМЫ
105
Исследование особых случаев требует, как правило,
применения весьма тонких методов анализа, а также боль-
ших и трудоемких преобразований. Учитывая характер
настоящего руководства, мы ограничимся разбором двух
примеров, показывающих, что в особых случаях уравнения
первого приближения не могут решить задачу об устойчи-
вости движения (подробный разбор особых случаев см. в
книгах А. М. Ляпунова, Н. Г. Четаева, И. Г. Малкина,
А. П. Маркеева [35, 49, 37, 37а[).
Пример 1. Рассмотрим уравнения возмущенного движения,
которые были приведены па с. 20:
*1 — — CW2 + СМД V + Х%,
х2 = axt + az2 У х[ + х%,
где a = const.
Составим уравнения первого приближения:
Ч = —a.r2,
— OLXf
Характеристическое уравнение
Л
— a
= Л2 а2 = О
имеет два корня (Л1;2 = + | a | i), вещественные части которых рав-
ны нулю (Re Ч = Re Л2 = 0). Следовательно, для рассматриваемых
уравнений теоремы Ляпунова об устойчивости по первому прибли-
жению неприменимы. В § 1.2 было показано, что решение полных
уравнений ничего общего не имеет с решением уравнений первого
приближения (см. с. 21).
Пример 2. Рассмотрим устойчивость равновесия системы с од-
ной степенью свободы, находящейся под действием нелинейной по-
тенциальной силы и силы сопротивления, пропорциональной пер-
вой степени скорости (см. пример 4 § 2.7). Уравнения возмущенного
движения в сделанных предположениях имеют вид (см. (2.63))
Mit — — pxj — ух™,
^2 = (m А" 2, р > 0).
Составим уравнения первого приближения
= — pzj,
s2 =
Характеристическое уравнение
I Л/Л -|- u. 0 I
| ___i Л |	"4* И) = 0
имеет один отрицательный вещественный корень (Лх = —ц/М) и
один нулевой корень (Л2 = 0). Согласно теореме 3, приведенной
106
ГЛ. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
на с. 100, невозмущенное движение хг = х2 = 0, соответствующее
уравнениям первого приближения, устойчиво, но не асимптоти-
чески. Так как один корень характеристического уравнения равен
нулю (1.2 = 0), то этот вывод может оказаться ошибочным. Действи-
тельно, анализ нелинейных уравнений (см. пример 4 § 2.7) показы-
вает, что при и> 0 и m нечетном движение асимптотически устой-
чиво в целом, а во всех остальных случаях движение неустойчиво.
§ 4.4. Критерий Гурвица
Раскроем характеристический определитель, сгруппи-
руем члены по степеням X и приведем уравнение (4.5)
к виду
“Ь djKr‘ 1	ип = 0,	(4.19)
причем, не нарушая общности, можно считать, что а0
>01).
Согласно первой теореме § 4.3, для определения устой-
чивости движения по уравнениям первого приближения
нужно знать, когда вещественные части всех корней ха-
рактеристического уравнения будут отрицательны. Естест-
венно, что наибольший интерес представляет решение
этой задачи, не связанное с непосредственным вычислением
корней характеристического уравнения.
Впервые эту задачу в 1868 г. поставил Д. Максвелл;
он же привел решение для п = 3. В общем виде в 1877 г.
решил эту задачу Е. Раус [56]. Его решение носит
алгоритмический характер; в явном виде он дал условия
для п = 4 и п = 5. В 1895 г. А. Гурвиц получил анали-
тическое решение. Алгоритм Рауса и критерий Гурвица
эквивалентны, хотя они и различны по форме. Полезно
отметить, что работы Максвелла были связаны с его иссле-
дованиями регуляторов, а математик Гурвиц занялся этой
проблемой по просьбе проф. А. Стодолы, инженера-ма-
шиностроителя, одного из основоположников теории ре-
гулирования турбин. Работы Д. Максвелла и А. Стодолы
приведены в [13]. Мы рассмотрим условие Гурвица — оно
носит алгебраический характер, более удобно в приложе-
ниях и имеет наибольшее распространение.
!) Если уравнения первого приближения решены относительно
производных у/,-, то коэффициент а0 при старшем члене в уравнении
(4.19) равен (—1)"; при п нечетном умножением всего уравнения на
—1 его можно сделать равным -|-1. В общем случае а0 ф 1, и делить
на этот коэффициент не всегда рационально.
§ 4.4. КРИТЕРИЙ ГУРВИЦА
107
Построим из коэффициентов
{4.19) следующую матрицу:
а0, я1, . . ап уравнения
“1	«з	а5 .	. 0
		at .	. 0
0	«1	а3 .	. 0
0 0 0	... а
п
(4.20)
Эта матрица строится следующим образом: в первой
строке стоят коэффициенты уравнения (4.19) с нечетными
индексами, начиная с аг. Элементы каждой последующей
строки образуются из соответствующих элементов пред-
шествующей строки уменьшением индекса на единицу.
Если в соответствии с этим правилом индекс коэффициен-
та а^, т. е. число к, превосходит степень п уравнения (4.19)
или должен быть отрицательным, то ак заменяется нулем.
В результате такого построения на главной диагонали
должны стоять коэффициенты at, . . ., ап, а в последнем
столбце все элементы, кроме последнего, равны нулю.
Составим из матрицы (4.20) главные диагональные ми-
норы
Д1 Я1, Д2  л ’ ’ ’ ’’	— ®п^п—!•	(^*21)
Gq «2 |
Последнее равенство очевидно, если учесть, что в послед-
нем столбце матрицы (4.20) все элементы, кроме ап, равны
нулю.
Теорема Гурвица. Для того чтобы все корни алгебраи-
ческого уравнения (4.19) с вещественными коэффициентами
и положительным коэффициентом при старшем члене име-
ли отрицательные вещественные части, необходимо и дос-
таточно, чтобы все главные диагональные миноры (4.21)
были положительны'.
Дг > 0, Д2 > 0, . . ., Дп_! > 0, Дп > 0.	(4.22)
Не останавливаясь на доказательстве этой, чисто ал-
гебраической теоремы (см., например, [49]), заметим, что
из теоремы Гурвица и первой теоремы Ляпунова об устой-
чивости по первому приближению можно сделать следую-
щий вывод: если при а0 0 все миноры Гурвица Дь . . .
. . ., Дп положительны, то невозмущенное движение асимп-
тотически устойчиво, независимо от членов выше первого
порядка малости.
Заметим также, что если хотя бы одно из неравенств
(4.22) имеет противоположный смысл, то среди корней
108 гл. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
• • •> уравнения (4.19) имеются такие, вещественные
части которых положительны (это служит признаком не-
устойчивости системы — вторая теорема Ляпунова, § 4.3).
Прежде чем перейти к рассмотрению частных случаев,
остановимся па следствиях, вытекающих непосредственно
из формул Виета:
= --- (^-1 + ^2 + • • • + >-п),
“О
“ = ^1^-г + • • • +	(4.23'
а
-- 1)” ^2 • • ' ^п-
«о
1. Для того чтобы при а0 )> 0 все корни уравнения
(4.19) имели отрицательные вещественные части, необхо-
димо, чтобы все коэффициенты а±, . . ., ап были положи-
тельны
aY 0, а2 0, . . ., ап 4> 0.	(4.24)
Заметим, что эти неравенства (конечно, они только
необходимы, но не достаточны) можно получить из кри-
терия Гурвица.
2. Если при а0 ~^> 0 хотя бы один из коэффициентов
«и . . ., ап отрицателен, то среди корней . . ., Хп урав-
нения (4.19) имеются такие, вещественные части которых
положительны.
Перейдем к рассмотрению частных случаев.
1.	Система первого порядка (и = 1). Характеристиче-
ское уравнение имеет вид
а07. + aY = 0.	(4.25)
Условие асимптотической устойчивости (а0	0)
а± > 0.	(4.26)
2.	Система второго порядка (п = 2):
а0№ 4- aj. + а2 = 0.	(4-27)
Матрица (4.20) и условие Гурвица имеют вид
II 01 0 ||
, Xi — Hi > 0, Д2 = aia2 0.
|| а0 аг II
Отсюда следует условие асимптотической устойчивости
системы второго порядка (а0 4> 0)
0, а2 0	(4.28)
§ 4.4. КРИТЕРИЙ ГУРВИЦА
109
3.	Система третьего порядка (п = 3):
а0л3 4* я^2 + я2Х + аз — 0.	(4-29)
Составим матрицу (4.20) и условие Гурвица:
ai а3 0 II
ао а2 0 1 Дг — ai^>0, А2^Я1Я2— я0я3>0,
0 ai оз ||
Аз = ЯзД2 9.
Пользуясь неравенствами (4.24), сразу получаем условие
асимптотической устойчивости системы третьего порядка
(«о > 0):
0, я2 ^> 0, аз	О, А2 —	— я^я3 (4.30)
4.	Система четвертого порядка (п = 4). В этом случае
я0/.' 4*	4* я2л2 4* я3Х 4* я4 = 0.	(4.31)
Составим матрицу (4.20) и условие Гурвица (4.22):
si »з О О
Gq ^2 ^4 О
О fll <?3 О
О Gq G2 G4
Ai = а1 О, А2 = ava2 — я0я3 _> О,
А3  я3А2 я4я4 О, А4 — Л4А3 0.
При выполнении неравенств (4.24) условие А2 О
становится следствием условия А3 0. Поэтому условие
асимптотической устойчивости системы четвертого поряд-
ка имеет вид (я0	0)
аг > 0, а2 0, а3 0, я4 О,
А3 — яi^z2Лз — а3а3 — я4я4 0	(4.32)
(в А3 внесено значение А2).
Приведем пример, показывающий, что при п > 2 выполнение
одних неравенств (4.24) недостаточно для отрицательности вещест-
венных частей всех корней характеристического уравнения. Рас-
смотрим уравнение третьей степени
X3 + X2 + 4Л + 30 = 0.
Все его коэффициенты положительны, так что условие (4.24) выпол-
нено. Однако два корня этого уравнения,
Xj = 1 + 34, Xj = 1 — 34,
110
ГЛ. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
имеют положительные вещественные части (Re = Re 'к2 — 1),
а корень Л3 = —3 отрицателен. Заметим, что последнее неравен-
ство из (4.30) имеет в этом случае противоположный знак:
Л2 = aia2 — аоаз =	—1-30 = —26 <. 0.
В заключение этого параграфа заметим, что в общем
виде условие Гурвица очень удобно при п 4. В тех слу-
чаях, когда п велико и левая часть характеристического
уравнения имеет форму определителя и не приведена к
многочлену (раскрытие определителя большого порядка
представляет трудоемкую задачу), целесообразно перей-
ти к численным методам с использованием электронных
вычислительных машин. Численные методы с примене-
нием ЭВМ полезны и в тех случаях, когда характеристиче-
ское уравнение задано в форме многочлена.
§ 4.5. Примеры
Пример 1. Условия устойчивости устано-
вившихся режимов вольтовой дуги в це-
пи с сопротивлением, самоиндукцией и
з а ш у нтир ова иной емкостью. В примере 2 § 2.7 бы-
ли рассмотрены условия
устойчивости установив-
шихся режимов вольтовой
дуги в цепи с сопротивле-
нием и самоиндукцией. Рас-
смотрим усложненную схе-
му [4], когда в цепь допол-
нительно включена зашун-
тированная емкость (рис.
4.1). Предполагаем, как и
раньше, что ток, проходя-
щий через дуговой проме-
жуток, является функцией напряжения на дуге, т. е. снова будем
пренебрегать инерцией ионных процессов в дуге. Пользуясь зако-
нами Кирхгофа, легко получим следующие дифференциальные
уравнения процессов, протекающих в схеме:
di	du Е — и
L ~dT = “ ~	С ST = ~R
(4.33)
R этих уравнениях L — самоиндукция, С — емкость конденсатора,
R — омическое сопротивление, Е — электродвижущая сила источ-
ника постоянного тока, ф (i) = v — напряжение на дуге (график
этой функции изображен на рис. 2.18).
Ннося в уравнения i — I = const и и — U = const, получим
уравнения для определения тока I и напряжения U, отвечающих
установившимся режимам:
U — ф (Z) = 0, Е — U — RI = 0,	(4.34)
§ 4.5. ПРИМЕРЫ
111
или, исключая напряяение U,
RI + ф (/) = Е.	(4.35)
Это уравнение совпадает с уравнением (2.49), которое соответ-
ствует схеме без емкости. Из этого следует, что внесение емкости
в схему вольтовой дуги не изменяет значения тока в возможных ус-
тановившихся режимах. При анализе уравнения (2.49) было пока-
зано, что таких режимов принципиально может существовать три,
два, один; при отсутствии вещественных корней уравнения (2.49)
или, что то же самое, (4.35), установившихся режимов не сущест-
вует. В том же примере были установлены условия асимптотической
устойчивости установившихся режимов. Рассмотрим, какие изме-
нения внесет зашунтированная емкость в полученные результаты.
Примем установившийся режим за невозмущенное движение.
Обозначим значение тока i в возмущенном движении через I + х,
а значение напряжения и в этом движении через U + у:
i = I + х, и = U + у.
Внесем эти выражения в уравнения (4.33):
£	= U + у — ф (I -|- х),
„ dy	Е — U — у
С dt	R	—Is.
Разложим функцию ф (/ + х) в ряд по степеням х и воспользуемся
введенным ранее обозначением х = ф' (/).
ф (/ + х) = ф (/) + кх + . . .,
где точками обозначены члены высшего порядка. Подставив это
выражение для функции ф (/ + х) в последние уравнения, полу-
чим
L	= lJ — хх + U — +' ’ ’’
dy у	Е — U
С	=	+	R ~ 1-
Учитывая, что значения тока I и напряжения U в установив
шемся режиме должны удовлетворять равенствам (4.34), найдем
дифференциальные уравнения первого приближения возмущен-
ного движения:
dx	dy	у
L-^- = y—%x, С	х.	(4.36)
Будем искать решение в форме (4.3):
х = Аеи, у = Веи.	(4.37)
Продифференцируем эти выражения по времени, внесем найденные
значения для производных и сами функции в уравнения (4.36)
и сократим их на ё'л. Тогда после очевидных преобразований
получим
(£Х + х)Л — В --0, А ф- (сХ	= 0.	(4.38)
112
ГЛ. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
Приравнивая нулю определитель этой системы, получим характе-
ристическое уравнение
L). + х — 1
1
1 Ск + -д-
^0,
или
/ L \ х
CW + (-д- + хС \к + -д- + 1 = 0.
(4.39)
Согласно критерию Гурвица (4.28), для системы второго поряд-
ка (4.27) установившееся движение i = I, и = U будет асимпто-
тически устойчиво, если коэффициенты аг и а2 этого уравнения по-
ложительны. В рассматриваемом случае будем иметь следующие ус-
ловия асимптотической устойчивости установившегося режима от-
носительно тока i и напряжения и:
L	х
д- + хС>0, д- + 1>0.	(4.40)
В этих неравенствах L,Rti С — положительные параметры системы,
а число х = ф' (/) — угловой коэффициент касательной, проведен-
ной к графику функции v = ф (i) в точках i = I (крутизна харак-
теристики напряжения). Если х > 0, то оба неравенства (4.40) бу-
дут выполнены и, следовательно, соответствующий установивший-
ся^режим асимптотически устойчив. Если же х <( 0, то установив-
шийся режим вольтовой дуги бу-
дет асимптотически устойчив для
тех значений х, которые удовле-
творяют условиям (4.40), или
устойчивости установившихся
L
v‘> — CR '	%> — в-
Если хотя бы одно из нера-
венств будет иметь противополож-
ный смысл, то соответствующий
установившийся режим будет не-
устойчив. Поэтому на плоскости
R, х границей области асимптоти-
ческой устойчивости будут пря-
мая R — 0, гипербола CRv. = —L
и прямая х = —R (рис. 4.2). Вне
этой области установившиеся ре-
жимы неустойчивы. Сравнивая
рис. 2.20 и 4.2, видим, что введе-
ние емкости уменьшает область
режимов вольтовой дуги. Это не
означает, конечно, что введение емкости нерационально для рассмат-
риваемой схемы, так как при этом можно получить качественно
другие переходные процессы.
Пример 2. Условие устойчивости лампово-
го генератора. В примере 3 § 2.7 были получены следую-
щие нелинейные дифференциальные уравнения возмущенного
§'4.5. ^РИМЕРЫ
ИЗ
движения лампового генератора (см. рис. 2.23 и уравнения (2.53)):
du	di	1	. .
С-чг = — г, L - и—[RC— MS(u)]i. (4.41)
(11	CL С	О
Условие асимптотической устойчивости (2.59) было установле-
но непосредственным применением прямого метода Ляпунова.
В этом примере условие (2.59) будет получено с помощью теорем Ля-
пунова об устойчивости по первому приближению.
Воспользуемся разложением (2.57) функции S (и) в ряд по сте-
пеням и;
S (и) = 6’0 + S' (0) и + . . .,
и внесем это выражение для S (и) во второе уравнение (4.41). Огра-
ничиваясь линейными членами, получим дифференциальные урав-
нения первого приближения
du	di	1
С — — I,	= и (RC — MS a) i.
Характеристическое уравнение
Ск	1
легко приводится к виду
CZA2 + (RC — М8й) к + 1 = 0.
Критерий Гурвица (4.28) сводится к одному неравенству (2.59)
RC — MS0 > 0,
при выполнении которого равновесное состояние лампового генера-
тора будет асимптотически устойчиво относительно тока i и напря-
жения и. Если это неравенство будет иметь противоположный смысл,
то равновесное состояние лампового генератора неустойчиво.
При RC — MS0 = 0 корни характеристического уравнения
чисто мнимые и уравнения первого приближения не могут дать обос-
нованного ответа на вопрос об устойчивости движения.
Сравнивая приведенное здесь решение с решением этой задачи
в § 2.7, видим, что применение теорем Ляпунова об устойчивости
по первому приближению может существенно упростить исследо-
вание.
Пример 3. Условие устойчивости устано-
вившегося режима двигателя с центро-
бежным регулятором. Центробежный регулятор
скорости вращения двигателя J), изображенный на рис. 4.3, воз-
действует непосредственно на регулирующий орган (дроссельную
заслонку, регулирующую подачу горючего или пара), поэтому он
относится к классу регуляторов прямого действия.
Проблемы, возникшие в середине XIX столетия в связи с при-
менением регуляторов этого типа к двигателям большой мощности,
х) Центробежный регулятор скорости вращения паровой маши-
ны изобретен Уаттом в 1784 г.
114 гл. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
впервые обратили серьезное внимание инженеров и ученых на зна-
чение теории устойчивости движения для техники.
Прежде всего приведем распространенное в свое время объяс-
нение принципа действия регулятора, изображенного на рис. 4.3.
В установившемся режиме угловая скорость со вращения вала регу-
лятора (она отличается от угловой скорости вращения маховика дви-
гателя на передаточное число) сохраняет постоянное значение со0;
кроме того, в установившемся реяшме стержни, удерживающие ша-
ры, составляют постоянный угол а с осью вращения регулятора.
Муфта М регулятора и дроссельная заслонка неподвижны и зани-
мают вполне определенное положение, соответствующее заданной
угловой скорости со0.
Предположим, что установившийся режим нарушен, например
по каким-либо причинам немного увеличилась угловая скорость
маховика двигателя. В этом случае шары под действием увеличенных
центробежных сил разойдутся на больший угол, муфта М подни-
мется и через систему рычагов опустит дроссельную заслонку,
уменьшив тем самым подачу топлива или пара. Это приведет к умень-
шению угловой скорости, и вся система вернется в установившееся
состояние, соответствующее заданной угловой скорости со0.
В этом распространенном ранее описании принципа действия
центробежного регулятора не учитывались инерционность двига-
теля и силы сопротивления. Более того, предполагалось, что силы
сопротивления могут иметь только отрицательное значение; поэтому
инженеры и механики, занятые изготовлением центробежных регу-
ляторов, принимали все доступные в те времена меры для уменьше-
ния сил сопротивления. Заметим, что изображенный на рис. 4.3
§ 4.5. ПРИМЕРЫ
115
демпфер *) появился только во второй половине XIX столетия, ког-
да десятки тысяч центробежных регуляторов уже использовались
Ь промышленности.
При переходе к двигателям большей мощности обнаружилось,
что регуляторы, изготовленные по этому принципу, не только не
обеспечивают устойчивый режим работы, но даже разгоняют дви-
гатели. Для того чтобы уяснить причины этого явления, составим
дифференциальные уравнения возмущенного движения и опреде-
лим условия устойчивости установившегося режима.
Для простоты выкладок пренебрежем массой муфты и стержней;
кроме того, будем считать шары за материальные точки и предполо-
жим, что в установившемся режиме пружина с жесткостью с нахо-
дится в недеформированном состоянии. Углы а, 0 и расстояние L
муфты М от верхних шарниров, показанные на рис. 4.3, соответ-
ствуют установившемуся режиму. Пусть установившийся режим на-
рушен: муфта М поднялась на величину х, а угол а изменился
на 6.
Имея в виду составить уравнения первого приближения, будем
считать величины х и 6 малыми. Тогда с точностью до членов выс-
шего порядка получим
6 — щг,	(4.42)
•ctgP ,
где Ц = —j— (читатель легко установит эту зависимость самостоя-
тельно).
Обозначим угловую скорость вращения регулятора в неуста-
новившемся режиме через ф, а угол между стержнями шаров и осью
регулятора через <р = а + 6. Так как движение шаров складывает-
ся из переносного движения (вращение вокруг оси регулятора) и
относительного движения (вращение вокруг верхних шарниров на
угол <р), то кинетическая энергия системы будет равна
Т = ml1 2 (<р2 + ф2 sin2 <р) + >/2 Л'2-
Здесь m — масса одного шара, a J — приведенный к оси вала дви-
гателя момент инерции его вращающихся частей с учетом переда-
точного числа (предполагается, что J = const).
Потенциальная энергия силы тяжести шаров и пружины опре-
деляется равенством
1 с
П = 2ml (cos а — cos ф) + "«j" jjy (ф — а)2
(в сделанных предположениях деформация пружины равна х = 6/ц).
Обобщенные силы системы равны
ОТ
Л = “	“ V<₽’ <4=
где — vcp — приведенная к стержням шаров сила жидкостного соп-
ротивления (v = const), создаваемая демпфером или естественны-
ми силами сопротивления, Л/j — движущий момент, М2 — момент
1) Гидравлический демпфер (катаракт) состоит из поршня и
цилиндра, заполненного вязкой жидкостью. При перемещении пор-
шня жидкость протекает через небольшие отверстия (они делаются
в поршне или в обводном канале), создавая силы сопротивления,
пропорциональные первой степени скорости.
116 ГЛ. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
сопротивления двигателя, приведенный к его оси. Можно считать,
что движущий момент Мг зависит от поступающего рабочего тела,
т. е. от положения дросселя, угол поворота которого есть функция
<р, а момент сопротивления М2 зависит от угловой скорости враще-
ния вала ф.
Применяя обычную схему Лагранжа
d дТ	дТ
dt dq	dq ~ ^'1	~
составим уравнения движения системы
..	с
2ml2<p — ml2^2 sin 2<р — — 2mgl sin ср — —2 (cp — a) — vcp,
(4.43)
(J + 2mP sin2 cp) ф + 2ml2 sin 2срсрф = (cp) — M2 (ф).
В установившемся движении ср = a = const, ф = co = const.
Внося эти значения в уравнения (4.43), найдем связь между пара-
метрами системы
со2 cos a = g/l, М\ (a) = М2 (со).	(4.44)
Положим ф=со + гиср = а + рх. Подставив эти значения
для ф и ср в (4.43), получим уравнения возмущенного движения
2тц12х — ml2 (со г)2 sin 2 (a + px) =
с
= — 2mgl sin (a + рх) — х — pvx,
г
[/ + 2ml2 sin2 (a + px)] z -f- 2p ml2 sin 2 (a + px) t (co + z) =
= (a + px) — M2 (co + z).
Разложим нелинейные члены в ряды по степеням х и z. Тогда,
ограничиваясь членами первой степени относительно х и z и учи-
тывая равенства (4.44), получим уравнения первого приближения
возмущенного движения системы около установившегося движения
ср = а и ф = со:
2p2mZ2x + p2vx + (с + 2p2mZ2co2 sin2 a) x — 2pmZ2co sin2a-z,
(J -|- 2ml2 sin2 a) z -|- 2цт12а> sin 2a -x =
I dM1	[ dM2
= И \ dx /x=ox ~ \ dz z-
Для простоты обозначений введем постоянные времени Тг, Т2, Тй
и коэффициенты усиления к0, кг и к2:
тг_________2\k2ml2	__________p2v________
21 с -|- 2p2znZ2co2 sin2 a ’	2 с -ф- 2p2mZ2co2 sin2a ’
„ .	Г [dM-\ l-i	„ UdM.A I"1
Tn = (J + 2ml2 sin2 a) |	. k> — 2и.п;/2со sin 2a | j J ,
2pmi2cosin2a	/ dMt \ Г fdM2\ I-1
к* c -f- 2p2mZ2co2sin2 a ’	—	\ dx /0 L \ dz /0J ’
§ 4.5. ПРИМЕРЫ
117
Теперь уравнения возмущенного движения примут свой окон-
чательный вид
Т^х + T2t + х = AjZ, Tai + z = — кйх — k2t. (4.45)
Здесь необходимо отметить, что производная (dM2ldz)0 положи-
тельна (момент сопротивления М2 возрастает с увеличением угловой
скорости тр, т. е. z), а производная (дМ11дх)й отрицательна, так как
из самого устройства регулятора видно, что с увеличением подъема
муфты М (возрастания х} дроссельная заслонка будет пропускать
меньше рабочего тела (см. рис. 4.3). Из этого следует, что коэффи-
циент усиления кй положителен.
Будем искать решение уравнений (4.45) в форме
х = Ае^1 z = Веи
Найдем отсюда .?, х, z и внесем соответствующие значения
в уравнения (4.45). Произведя очевидные преобразования, получим
обычным путем следующие алгебраические уравнения:
(Т^к’- + Т2к + 1) А — кгВ = О,
(к2к+к0)А +(7\Л.+ 1) В = 0.
Так как эта система однородных уравнений должна иметь
решение относительно А и В, отличное от нуля, то определитель
этой системы равняется пулю:
I Tjk? -]- Т2к 1	— А, |
I к2к + к0 Ток + 1 I = U
или
Т0Т^ + (Т[ + Т0Г2) М + (Г0 + Т2 + ktk2) к + 1 + kokL = 0.
Для большей наглядности учтем, что члены Т2 и кгк2 сущест-
венно меньше То. На этом основании последнее уравнение можно
записать так:
ТоТ^М + (^ + Т0Т2)к* + Tok+i + кокг = 0.
Все коэффициенты этого уравнения положительны, поэтому
критерий Гурвица (4.30) приводится к одному неравенству
Л2 — ^1^2 —
что в нашем случае дает
А3 = То (Т0Т2 — к^к^Т^)	0.	(4.46)
Таково условие асимптотической устойчивости системы двига-..
тель — центробежный регулятор. Все постоянные времени То, Tt,
Т2ъ коэффициенты усиления ка и kv легко вычисляются по парамет-
рам системы, и, для того чтобы успешно осуществлялось регули-
рование, необходимо прежде всего подчинить их неравенству (4.46).
Отметим теперь, что при отсутствии сил сопротивления в ре-
гуляторе постоянная времени Т2 равна нулю и неравенство (4.46)
принимает противоположный смысл:
Аг -- кок^TQT^ 0.
118 гл. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
Это означает, что без сил сопротивления регулирование неосу-
ществимо, так как система неустойчива.
Возникает, естественно, вопрос: почему десятки тысяч центро-
бежных регуляторов, изготовленных до середины XIX столетия,
успешно работали? Объясняется это следующим. Маломощные
двигатели имели большие маховики и легкие регулирующие устрой-
ства, перемещавшиеся с существенным трением, обусловленным гру-
бым выполнением. В этих условиях постоянная Т2 4= 0, а постоян-
ная То очень велика (за счет больших моментов инерции J махо-
виков). В результате неравенство (4.46) выполнялось автоматичес-
ки без заботы об этом конструкторов. При увеличении мощности
двигателя увеличилось число его оборотов и уменьшился момент
инерции J маховика (при большом числе оборотов большие маховики
не выдержат внутренних напряжений). Это привело к уменьшению
постоянной Го, в результате чего естественных сил сопротивления,
характеризуемых постоянной Тг, оказалось недостаточно для выпол-
нения условия устойчивости (4.46). Необходимо было увеличить
силы жидкостного сопротивления, что и было сделано установкой
демпфера. Его основная характеристика — постоянная времени
Т2, лежащая в основе расчетов,— легко определяется при задан-
ных То, Т\, кй и кА из неравенства (4.46). Эти обстоятельства были
впервые установлены И. А. Вышнеградским в работе [13], опубли-
кованной в 1876 г. J).
Пример 4. Необходимое условие устойчи-
вости волчка (вращательно го движения
снаряд а).В примере 3 § 2.6 было получено следующее достаточ-
ное условие устойчивости установившегося движения волчка (вра-
щательного движения снаряда) относительно переменных а, &, 0,
0 и ф:
/У > i/xPl.	(4.47)
Покажем теперь, что при противоположном смысле этого неравен-
ства установившееся движение волчка (вращательное движение
снаряда) будет неустойчиво.
Составим дифференциальные уравнения возмущенного движе-
ния. Выражения для кинетической Т и потенциальной П энергий
волчка были получены в примере 3 § 2.6:
1 1
Т —	Jх (а2 + 02 cos2 а) +	J i (q> — 3 sin а)2,
П = Pl cos а cos 3-
Так как для доказательства неустойчивости движения доста-
точно показать, что хотя бы одна траектория в возмущенном движе-
нии выходит за пределы сферы е, то рассмотрим возмущения (а =
= а0, а = а0, 3 = Зо, 3 = Зо, Ф = Фо = п при t = 0), для
’) В упомянутой статье И. А. Вышнеградского впервые дан под-
робный анализ работы регулятора прямого действия и сделаны прак-
тические выводы, оказавшие глубокое влияние на развитие теории
и практики автоматического регулирования. Не без основания
считается, что эта работа положила основание современной теории
регулирования.
§ 4.5. ПРИМЕРЫ
119
которых интеграл
дТ
—— = J z (ср — р sin а) = Jzn	(4.48)
dtp
сохраняет свое значение.
Чтобы составить уравнения первого приближения, разложим
выражения для кинетической Т и потенциальной П энергий в ряд
по степеням а, а, 0 и 0, сохраняя члены до второго порядка мало-
сти включительно. С точностью до постоянной будем иметь
1 1
Т = з- Jx (аг+ ₽2) + Jz (ф - ₽а)8.
1
П= _-g-PZ(a»+p»),
Пользуясь уравнениями Лагранжа второго рода и интегралом
(4.48), получим дифференциальные уравнения первого приближе-
ния возмущенного движения волчка относительно координат а,
3 и скоростей й и 3
Jxd + J2n3 — Pla = О,
(4.49)
Jx3 - Jzna — PZ0 = О,
Обычным путем составим характеристическое уравнение
I — Pl	Jznk I
I — 7гпА. — Pl I - и’
или
+ (J2n2 — 2JxPl) к2 + P2l2 = 0.	(4.50)
Критерий Гурвица для этого характеристического уравнения
применить нельзя, так как неравенства (4.32) не выполняются
(а1 = 0, а3 = 0, Д3 — 0) и ни одно из них не имеет противополож-
ного смысла. Поэтому исследуем это уравнение обычными методами.
Каждому корню к = v -Ь ц/ уравнения (4.50) отвечает корень
—к = — v 4- цг (неизвестное число к содержится только в чет-
ной степени). Поэтому если вещественная часть хотя бы одного кор-
ня не равна нулю (ReA. = v=4 0), то обязательно будет корень,
вещественная часть которого положительна. Согласно теореме
Ляпунова о неустойчивости по первому приближению (см. § 4.3),
невозмущенное движение в этом случае будет неустойчиво. Из этого
следует, что для устойчивости невозмущенного движения волчка
необходимо, чтобы все корни характеристического уравнения (4.50)
были чисто мнимыми, т. е. имели вид к = цг, а корни относительно
к2 — вещественными отрицательными числами. Но для этого не-
обходимо, чтобы дискриминант D уравнения (4.50) относительно к2
был положительным:
D = (J2zn2 - 2JxPl)2 — iJ2P2l2 = J2zn2 (J2zn2 — iJxPl) > 0.
Отсюда видно, что при противоположном смысле неравенства
(4.47) дискриминант D будет отрицателен и, следовательно, устано-
вившееся движение волчка (вращательное движение снаряда)
сделается неустойчивым.
120
ГЛ. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
Рис. 4.4
Пример 5. Устойчивость стационарных дви-
жений осп вращающегося неуравнове-
шенного ротора, установление го в нели-
нейных подшипниках. Ранее было показано (см.
пример 4 § 3.5), что равновесное положение оси уравновешенного
ротора устойчиво. Однако уравновешенный ротор (е = 0) следует
рассматривать как случайное событие, вероятность которого прак-
тически равна нулю. В реальных условиях всегда имеется хотя бы
небольшой эксцентриситет е, в результате чего в нелинейных, в ча-
стности шариковых, подшипниках возникают большие давления на
опоры, приводящие иногда к раз-
рушению последних. Для приня-
тия соответствующих мер пред-
осторожности необходимо, прежде
всего, определить стационарные
движения оси ротора и их устой-
чивость.
Будем, как и в § 3.5, считать,
что абсолютно твердый ротор мас-
сы т с вертикальной осью вра-
щения установлен в жестко укреп-
ленных на неподвижном основа-
нии упруго податливых подшип-
никах. Предполагается, что ротор,
эксцентриситет которого е = ОС,
движется плоскопараллельно, а
собственное вращение, происходя-
щее вокруг оси О с постоянной ча-
стотой со, осуществляется идеаль-
ным двигателем (двигателем неограниченной мощности). Нелиней-
ные в общем случае реакции опор приводятся к равнодействующей
Fo (Р), удовлетворяющей условиям (3.40). Положение оси ротора от-
носительно неподвижной системы координат Огху будем определять
полярными координатами р и ср (рис. 4.4). В сделанных предполо-
жениях относительно двигателя угол между отрезком ОС и осью х'
с точностью до начальной фазы равен со/ (ось х’ перемещается по-
ступательно, параллельно оси х). Проекции скорости ф0 оси О
ротора на полярные оси координат р0 и ф0, как известно, опреде-
ляются равенствами
vp= Р> % = рф.	(4.51)
Из рис. 4.4 видно, что проекции относительной скорости
центра масс С на те же оси будут равны
VCP = — we sin (tot — <p), up,? = we cos (coi — ф).	(4.52)
Кинетическую энергию найдем по формуле [12]
Т mi,o + mvo’vc + ro-	(4.53)
Здесь т масса ротора, Тг0 — его кинетическая энергия относи-
тельно поступательно перемещающихся осей координат Ох’у'. Оче-
видно, что Tq = JОсо2/2 и в сделанных предположениях Тт0 = const.
§4.5. ПРИМЕРЫ
121
Скалярное произведение	вычислим с помощью равенств
/4.51) и (4.52):
v0 '“°с ~ ае I— Р s*n (“г — Ф) + РФ cos (wt — Ф)Ь
Пользуясь теперь равенством (4.53), найдем с точностью до
постоянной кинетическую энергию ротора
Т = -L m (р2 р2<р2)	тпые [—р sin (coi — ф) + РФ cos (<oi — ф)].
(4.54)
Учитывая силу сопротивления Fc = пропорциональную
первой степени скорости оси О (р — const) и пользуясь вторым ме-
тодом Лагранжа, получим дифференциальные уравнения движения
оси ротора (первое уравнение сокращено на т, второе — на тр)
р — рф2 — со2е cos (at — ф) = — F (р) — рр, F (р) = F0(p)/m,
(4.55)
pip + 2рф — со2е sin (oat — ф) = — ррф.
В установившемся движении р = г = const, ф = и = const,
где постоянные г и у = <л1 — ф удовлетворяют равенствам
гео2 со2е cos у — F (г), есо2 sin у = ргсо, (4.56)
определяющим г и у как функции и.
Амплитудно-частотная характеристика представляет непрерыв-
ную линию, лежащую между двумя разомкнутыми ветвями, отве-
чающими случаю р. = 0. Точки А2 3 пересечения амплитудно-час-
тотной характеристики (4.56) со скелетной кривой (рис. 4.5)
и = х (г), х2 — F (г)/г	(4.57)
определяются равенствами
рг = ех(г), со =-Е. г, у = 2L .	(4.58)
е	2
Так, для реакции Fa = а0Ра будем иметь
г = /?£ е2\1/(3-а) w = р /ао е^\1/(3-а)
р2/	’ е \т р2/	’	2
Дифференцируя равенства (4.56) по со и исключая затем dyldut,
получим
{[х2 (г) — и2] [F" (г) — со2] 4- р2«2} — = — [2F (г) е cos у 4- p2r2J.
dw г
(4.59)
Если коэффициент при drid<s>
а4 = [х2 (') — w2] [F' (г) — со2] -|- р2со2	(4.60)
не имеет вещественных корней г ~ г (со), то амплитудно-частотная
характеристика не будет иметь касательных, параллельных оси г;
в противном случае такие касательные существуют. Для примера
на рис. 4.5 показана амплитудно-частотная характеристика для ре-
акции F = ара при 1 < а < 2. Характеристике 2 отвечает первый
случай (отсутствие вещественных корней а4), а характеристике 3 —
122
ГЛ. IV. УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
второй случай. Очевидно, что при небольших и очень больших со,
коэффициент а4 положителен, а в точках В и С он равен нулю. Учи-
тывая, что а4 представляет непрерывную функцию и, получим на
участках ОВ и CD амплитудно-частотной характеристики а4 > О,
а на участке ВС этот коэффициент отрицателен.
Положив р = г 4- и ф = <о£ — у z2 (zk — вариации коор-
динат), получим из (4.55) уравнения возмущенного движения
*i +	— 2rwz2 + [Г(г) — и2] Z1 — ргиг2 = Zn
4" ргг2 -|- 2a>z1 4- [icozj 4- г [z2 (г) — и2] z2 = Z2.	’ '
Здесь Zj — члены, содержащие z’,: и zjf в степени выше первой.
Характеристическое уравне-
ние системы (4.61) приводится
к виду
V + 2pV + [к2 (г) + F’ (г) +
+ 2и2 + р,2] Л2 + [х2 (г) +
+ F' (г) -ф- 2<о2] X 4- [к2 (г) — со2]*
•[F (г) — со2] 4- |i2co2 = 0. (4.62)
В силу условия (3.40) опре-
делитель Гурвица
А3 = ц2 [х2 (г) - F' (г)]2 4- 2[х2 (г) 4-
4- F' (г)] (4со2 4- И2), (4*63)
и все коэффициенты уравнения
Рис. 4.5	(4.62), кроме последнего, всегда
положительны, поэтому при а4)>0,
где а4 совпадает с (4.60), ста-
ционарное движение будет асимптотически устойчиво относитель-
но р, р, ф и ср, а при а4 < 0 это движение неустойчиво, причем оба
утверждения не зависят от членов высшего порядка. Уравнению
а4 = 0 отвечают точки бифуркации, в которых касательные к ам-
плитудно-частотной характеристике параллельны оси г. Поэтому
для реакции F = ар“ всей характеристике 2 и участкам ОВ и CD
характеристики 3 (рис. 4.5) отвечают асимптотически устойчивые
прецессии, а участку ВС — неустойчивые прецессии. На рис. 4.6
показан характер изменения радиуса орбиты стационарного дви-
жения при медленном увеличении (уменьшении) частоты собствен-
§ 4.5. ПРИМЕРЫ
123
його вращения ротора для мягкой (а) и жесткой (б) упругой подат-
ливости подшипников.
Для нелинейной реакции Fo (р) на восходящей ветви амплитуд-
но-частотной характеристики давление Л' на подшипники может до-
стигнуть значительной величины даже при ничтожно малом эксцент-
риситете. Действительно, при FtJ = a^p’ 2 (закон Герца, принятый
для шариковых подшипников) уравнение скелетной кривой 1
(рис. 4.5) принимает вид г аА/а2 = т2(а*/а2. Так как на участке
ОА3 радиус орбиты г (и, е) > г (о, 0) = пг2и4 */а^, то при любом е =f^
=/= 0 суммарное давление Л' = аог!'1 на подшипники будет удовле-
творять условию
дг>.^!.и6.	(4.64)
ао
Отсюда видно, что при увеличении частоты и собственного вра-
щения ротора давление Л' на участке ОА3 быстро возрастает. Таким
образом, анализ устойчивости объясняет возникновение больших
давлений неуравновешенного ротора, установленного в нелиней-
ных подшипниках 4). Для борьбы с этим нежелательным явлением
в некоторых случаях шариковые подшипники устанавливают в
линейные упругие обоймы [26а].
4) Более подробный разбор устойчивости движения оси неурав-
новешенного ротора, в частности, с учетом ограниченной мощности
двигателя содержится в [40а].
ГЛАВА V
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ
АВТОНОМНЫХ СИСТЕМ
§ 5.1. Введение
В этой главе будет продолжено рассмотрение методов
исследования устойчивости движения линейных автоном-
ных систем. В нормальной форме дифференциальные урав-
нения возмущенного движения имеют вид (см. уравнения
(1-14))
^1 — аи%1 + • • • + dm^ni
• • • ......................... (5-1)
Хп Оп^! “I- • • • “I-
где коэффициенты — постоянные вещественные числа.
Случай, когда характеристическое уравнение системы
(5.1) имеет простые корни, был уже рассмотрен в § 4.2.
В этой главе мы будем изучать устойчивость движения
при любой структуре корней характеристического урав-
нения.
Решение вопроса об устойчивости систем, возмущенное
движение которых описывается уравнениями (5.1), в об-
щем случае требует знания некоторых разделов теории
матриц. Кроме того, вся теория таких уравнений значи-
тельно проще и изящнее излагается в матричной форме.
Поэтому эта глава начинается с изложения основных, а
также некоторых специальных разделов теории матриц.
Читатель, знакомый с элементами матричного исчисления,
может опустить следующий параграф.
§ 5.2. Матрицы и основные действия с ними
а) Основные определения. Всякая си-
стема из п-т чисел, расположенных в форме прямоугольной
таблицы, содержащей п строк и т столбцов, называется
матрицей типа п X т. Числа, составляющие матрицу
(т. е. таблицу), называются элементами матрицы; в об-
щем виде их снабжают индексами внизу (первый индекс
означает помер строки, второй — номер столбца), а сама
§ 5.2. МАТРИЦЫ И ОСНОВНЫЕ ДЕЙСТВИЯ С НИМИ 125
матрица обозначается соответствующей буквой без ипдек-
сов. Так, например, матрицу А типа п X т записывают
следующим образом:
а11 а12 • • • а1т
д __ а21 й22 • • • а2т
ап1 апг •   апт
Сокращенно матрицу можно записать так:
А = || akj || (и х т).
Если число столбцов равно единице (nt = 1}, то получим
матрицу-столбец
(5-2)
Если же число строк равно единице (п = 1), то полу-
чим матрицу-строку
У = II У1 • • • г/m II-	(5.3)
Любой вектор ас с составляющими хи . . ., хп можно
представить как матрицу-столбец ас или матрицу-строку ас.
В связи с этим разложение вектора х по ортам (см. сноску
на с. 22)
ас = XiCi + • •• + хпеп	(5-4)
и представление его в форме матрицы-столбца (5.2) будем
считать эквивалентными.
Если число строк матрицы равно числу ее столбцов,
то матрица называется квадратной, а число ее строк (столб-
цов) называется порядком матрицы.
Определитель, состоящий из элементов некоторых к
строк и к столбцов матрицы, называется минором к-го по-
рядка данной матрицы. Так, например, минорами первого
порядка будут сами элементы матрицы, и их число равно
п-т. Для матрицы
Я11 Я12 я 13
«21 а22	«23
можно составить три существенно различных минора вто-
рого порядка
«11	«12 I	I а11	«13 |	| «12	«13
«21	Я22 |	| «21	Я2з |	| «22	«23
126 гл. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЬТХ АВТОНОМНЫХ СИСТЕМ
Для квадратной матрицы А порядка п минор «-го по-
рядка равен определителю матрицы А, который обозна-
чается символом det А или | А
Две матрицы называются равными, если числа строк
и столбцов их соответственно равны и равны их соответ-
ствующие элементы. Поэтому матричное равенство А — В
эквивалентно п-т скалярным равенствам
а1;1 =	(/с = 1, . .	= 1, . .	т).	(5.5)
Произведением матрицы на число называется новая
матрица, элементы которой равны произведениям соот-
ветствующих элементов исходной матрицы на данное чис-
ло, т. е.
-КА = Х ||М| = || 1а,; ||.	(5.6)
Например,
|1 2 1 0 || _ || 6 3 01|
3|| -1 4 5 — -3 12 15 И •
Матрица, все элементы которой равны нулю, называ-
ется нулевой и обозначается символом 0.
Суммой матриц одного и того же типа называется но-
вая матрица того же типа, элементы которой равны сум-
мам соответствующих элементов слагаемых матриц. На-
пример,
Ц 4 о 5 II + II 5 —3 6 II II 9 —3 И II ’
Из сделанных определений следует (латинские буквы
означают матрицы, греческие — скаляры):
А + (В + С) = (А + В) + С,
А + В = В + А,
А +0 = А,	(5.7)
(а + Р) А = аА + РЛ,
а (А + В) = аА + аВ.
Произведением двух матриц А и В при условии, что
число столбцов первой из них равно числу строк второй,
называется третья матрица С, элементы которой образуют-
ся по следующему правилу:
ТП
§ 5.2. МАТРИЦЫ И ОСНОВНЫЕ ДЕЙСТВИЯ С НИМИ 127
Словами это правило можно прочитать так: элемент
матрицы произведения АВ, стоящий в к-й строке и j-м
столбце, равен сумме произведений элементов к-й строки
первой матрицы А на соответствующие элементы j-го
столбца второй матрицы В. Например,
II а11 а12 || || &11 &12 ^13 ||  
II а21 а22 II II ^21 &22 &23 II
__ ||	+ а12^21	а11&12 + а12^22	а11&13 + а12^23 ||
|| а21&11 + а22&21	а21^12 + а22^22	а21&13 + а22^23 II
Произведение двух матриц, вообще говоря, зависит
от порядка сомножителей, т. е. в общем случае
АВ у= В А.
Пользуясь определением сложения и умножения мат-
риц, легко показать, что
(Л + В) С = АС + ВС.
Кроме того, легко установить, что определитель произ-
ведения двух квадратных матриц равен произведению их
определителей
det (ЛВ) = det Л det В.	(5.9)
Сумма элементов, стоящих на главной диагонали квад-
ратной матрицы, называется следом матрицы. След мат-
рицы обозначается символом Sp. По определению имеем
Sp Л = ап + а22 + . . . + апп. (5.10)
Квадратная матрица, все диагональные элементы ко-
торой равны единице, а остальные нулю, называется еди-
ничной матрицей и обозначается буквой Е-.
1 0 ... 0
0 0 ... 1
Непосредственным вычислением легко установить ра-
венства
АЕ = ЕА=А.	(5.11)
Квадратная матрица, имеющая вид
ах 0 ... 0
0 а2 ... 0
00	... а
п
называется диагональной,
128 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ
Если определитель квадратной матрицы не равен нулю,
то матрица называется неособенной, в противном случае —
особенной. Матрица Л-1 называется обратной к Л, если
произведение Л Л"1 или Л-1Л равно единичной матрице Е,
то есть
ЛЛ"1 = Л’1 Л = Е.	(5Л2)
Легко показать, что всякая неособенная матрица имеет
обратную.
Если в матрице заменить строки, на столбцы и столб-
цы на строки, то получим новую матрицу, которая назы-
вается транспонированной по отношению к данной; обо-
значается транспонированная матрица той же буквой,
но ставится штрих наверху справа. Так, для исходной
матр ицы
А = ||	||
транспонированной матрицей будет
А' = II «ж II-
Операция транспонирования применима к любым ма-
трицам, в частности, если транспонировать матрицу-
столбец
то получим матрицу-строку
х' = || х±, . . ., хп ||.
Непосредственно из определений произведения и тран-
спонирования матриц следует формула
(АВ)'=В'А'.	(5.13)
Аналогичная формула справедлива для обратных ма-
триц:
(АВ)-1 = В-1Л-1.	(5.14)
Так как определитель не меняется от замены его строк
па столбцы и столбцов на строки, то определители транс-
понированной п исходной квадратных матриц равны
det Л' = det Л,
Квадратная матрица называется симметричной, если
ее элементы, расположенное симметрично относительно
§ 5.2. МАТРИЦЫ И ОСНОВНЫЕ ДЕЙСТВИЯ С НИМИ 129
главной диагонали, равны между собой, иначе говоря,
матрица называется симметричной, если ее элементы удо-
влетворяют равенствам
akj = ajk-
Так, например, матрица
5 3—1
3 0	2
— 1 2 — 4
симметрична.
Очевидно, что транспонированная симметричная ма-
трица равна исходной
А' = А.	(5.15)
Квадратная матрица называется кососимметричной,
если ее элементы, стоящие на главной диагонали, равны
нулю, а элементы, расположенные симметрично относи-
тельно главной диагонали, равны по модулю, но противо-
положны по знаку, иначе говоря, матрица А называется
кососимметричной, если ее элементы удовлетворяют ра-
венствам
= djjf.
Так, например, матрица
10-1	4О
1	0 — 3
— 4	3	01|
кососимметричная.
Из сделанных определений следует, что для кососим-
метричной матрицы справедливо равенство
А' = —А.	(5.16)
В высшей алгебре доказывается, что кососимметричный
определитель нечетного порядка тождественно равен ну-
лю, а кососимметричный определитель четного порядка
представляет квадрат целой рациональной функции его
элементов. Таким образом, кососимметричный определи-
тель с вещественными элементами не отрицателен.
Легко показать, что любую квадратную матрицу мож-
но представить как сумму симметричной и кососиммет-
ричной матриц. Действительно, пусть
А = II «м II
5 Д. Р. Меркин
130 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ
— произвольная квадратная матрица. Составим из нее
две другие матрицы:
Л=4-(Л + Л'), B = -i-(A-A').	(5.17)
Очевидно, что матрица А симметрична, а матрица В косо-
симметрична. Равенство
Л = А + В
доказывает сделанное замечание.
Квадратная матрица Л = || akj || называется ортого-
нальной, если ее произведение на транспонированную
матрицу Л' = ||	|| равно единичной матрице
АЛ' = Е.
Из этого определения вытекают несколько следствий,
которым удовлетворяют ортогональные матрицы Л:
1)	транспонированная матрица Л' равна обратной
матрице Л-1:
Л' = Л"1;
2)	определитель ортогональной матрицы равен 4-1:
Д = det Л = ±1;	(5.18)
3)	сумма квадратов элементов любой строки (столбца)
равна единице:
3 — 3 = 1;
з	К
4)	сумма произведений элементов какой-либо строки
(столбца) на соответствующие элементы другой строки
(столбца) равна нулю
= 0 (к=£т).
з	з
Если элементы матрицы зависят от ска лярного пара
метра, например от времени t, то производной матрицы
по параметру называется матрица, элементы которой
равны производным по этому параметру. Таким образом,
если х = || хк] ||, то
dz	II II
dt	I dt ||
или в других обозначениях
£ = II ||.
S 5.2. МАТРИЦЫ И ОСНОВНЫЕ ДЕЙСТВИЯ С НИМИ 131
До сих пор рассматривались матрицы, элементами ко-
торых служили числа. Можно представить себе матрицы,
элементами которых являются не числа, а любые объекты.
Нужно только, чтобы все действия с такими матрицами
были определены и возможны. В частности, можно рас-
сматривать сложные матрицы, элементы которых сами
являются матрицами. Например, матрицу
«и	ац	aj3	Ci	с2
«21	а22	а2з	<Лг
61	62	63	d2i	<^32
можно короче записать так:
где
д ____ «11 «12 «13
I] «21 «22 «23 II
В = 116! 62 6з||,
С =|| С! С2||,
Ц a2i «221|
б) Матричная форма записи систе-
мы дифференциальных уравнений.
Дифференциальные уравнения (5.1) можно записать в
простой и компактной форме с помощью матриц. Дейст-
вительно, введем в рассмотрение две матрицы.
1. Матрицу коэффициентов правой части уравнений (5.1)
«11 «12 • • • «1п
«21	«22 ------ «2П
ап2 * * ’ апп
2. Матрицу-столбец или вектор
Составим матрицу из их произведения. Согласно
(5.8) будем иметь
«Ц^1 + «12^2 + • • • + а1пхп
«21*1 + «22^2 + • • • + а2пХп
формуле
(5.19)
ап1^ + ап^ +   • + «пп*п
5*
132 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ
т. е. произведение квадратной матрицы А на матрицу-
столбец ас равно матрице столбцу, элементы которой рав-
ны правым частям уравнений (5.1). Теперь очевидно, что
эти уравнения могут быть записаны в следующей простой
матричной форме:
х = Лас.	(5.19а)
В этом уравнении ас =	---производная по времени
матрицы-столбца ас.
Столь же просто можно записать в матричной форме
и другие более сложные системы дифференциальных урав-
нений.
В частности, уравнения второго порядка
3	= Xt: (к — 1,... , s) (5.20)
j=i
в матричной форме запишутся следующим образом:
Лас + Вх + Сас = X,	(5.21)
где А = ||	||, В = || Ью ||, С = ||	|| — квадратные
матрицы, а ас и X — матрицы-столбцы с элементами xj
и Xj соответственно.
в) Матричная запись квадратич-
ных форм. Рассмотрим квадратную матрицу А и мат-
рицу-столбец ас. Их произведение определяет матрицу-
столбец (5.19). Ранее отмечалось, что матрица-столбец мо-
жет рассматриваться как вектор. Воспользуемся этим
обстоятельством и будем рассматривать элементы матрицы-
столбца (5.19) и элементы матрицы-столбца ас как состав-
ляющие векторов Ах и ас. Тогда их скалярное произведе-
ние будет равно сумме произведений одноименных проек-
ций (см. сноску на с. 36), т. е.
Л ас-ас = (anX! + а12х2 + . . . -р а1пхп) хг +
+ (^21^1 Н- а22х2 + . . . + ®2пХп) хъ +
-р (anixi -р ®п2-Г2	• • • -Р &ппхп) хп-
Раскрывая скобки и группируя члены, найдем
Ах-х = а1Гх{ +	+ . . . + а^п + (а12 + «21^1^2+
(а13 ~”Ь ^3i) ^з ~”Ь • • • ~”Ь (ап~ 1>п	(5.22)
§ 5.3. ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ
133
или короче
п п
Ах-х — У У akjXkxj.	(5.23)
k=i j—i
Если матрица А симметричная, то akj = ajk и мы полу-
чаем обычную квадратичную форму:
Ах-х = апХ1 + • • • + аппхп +	.
п п
• • • "Ь ^d-n—l, A-l^n — У У	(Alli	(5.24)
fc=l 7=1
Если квадратичная форма Ах-х определенно-положи-
тельна, то для простоты матрица А называется определен-
но-положительной .
Если матрица А кососимметричная, то акк = О,
akj = —aJ)c, т. е. aki + ад- = 0. На основании равенства
(5.22) заключаем, что для кососимметричной матрицы А-
произведение
Ax*Xi=0.	(5.25)
Этим равенством мы воспользуемся в дальнейшем.
§ 5.3. Элементарные дёлители
Рассмотрим квадратную матрицу, элементы которой
fu (X) являются полиномами от некоторого параметра X:

/и (X) ... /1П (X)
Й /„„W
(5.26)
Такие матрицы называются к-матрицами. Обозначим
через Dk (X) (к = 1, . . ., п) общий наибольший делитель
всех миноров к-го порядка матрицы (5.26), причем коэф-
фициент при старшем члене выбираем равным единице.
Легко показать, что многочлен Dk (к) делится на Dk_x (к).
При определении общих наибольших делителей Dk (к)
полезно иметь в виду следующее замечание: если какой-
либо минор Х-го порядка равен постоянной величине, то
Dk =	= . . . =	= 1 (так как этот минор дол-
жен делиться на Dk, a Dk делится на Dk_lt Dk-2, . . ., Dt).
Многочлен, равный отношению
= Ек (к) (к = 1....П-, Do = 1),	(5.27)
134 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ
называется инвариантным множителем матрицы (5.26).
Очевидно, что
(X) = Ег (А)-£2 (А) . . . Е* (А),
a Dn (А) с точностью до постоянного множителя равен
det F (X):
Dn (X) = % det F (A) = Ег (A)-£2 (A) . . . En (A). (5.28)
Разложим каждый инвариантный множитель Е^ (А) на
множители:
Еъ (А) = (А - A/ki (А - А2)е^ ... (А - кр^Р,
где Ах, А2, . . ., Ар — различные корни уравнения
det F (А) = 0.	(5.29)
Очевидно, что
> 0 (А: = 1, . . ., п; г = 1, . . ., р).
Кроме того, ekj е^'р если к < к' (так как Е^ делится
на Е*).
Двучлены (А — Аг) входящие множителями в Е* (А)
и отличные от постоянного числа (т. е. при ekr 0), на-
зываются элементарными делителями A-матрицы. Общее
их число будем обозначать через т, а сами делители через
(А — Ai)6*, . . ., (А — Ага)е,п, причем среди чисел Аг могут
быть и равные (биномы (А — Аг) * могут входить в разные
инвариантные множители Е^).
Рассмотрим пример. Для матрицы
можно составить четыре минора первого порядка:
(А + I)3, (А + I)2, А-1-1, АН-1;
их общий наибольший делитель, очевидно, равен
D, = А+ 1.
Для матрицы (5.30) имеется один минор второго порядка
|(А+1)3 (A + 1PI Х(Х+1)з
I А-|-1 А 4-1 I к ’
с общим наибольшим делителем
D2 = А (А + I)3.
§ 5.3. ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ
135
(5.31)
Пользуясь формулой (5.27), найдем инвариантные множители
£j = £>1 = X-|-l, £г=Я« = Х(Х+1)».
Элементарные делители для рассматриваемой матрицы будут
Х-|- 1, X, (Х-|- I)2
с корнями
Xj = — 1, Х2 = О, Х3 = Х4 = — 1.
Эти же корни являются, конечно, корнями уравнения
det F (X) = О,
ио если для этого уравнения корень X = —1 трехкратный, то этот
же корень для одного элементарного делителя простой, а для дру-
гого двукратный.
Матрица
Et. О ... О
О Е2 ... О
00	...	Е
п
где Ег, Е2, . . ., Еп — инвариантные множители матрицы
(5.26), называется нормальной диагональной формой этой
матрицы. Например, нормальной диагональной формой
для матрицы (5.30) будет матрица
II X + 1	0
II 0	Х(Х+1)2
Элементарными преобразованиями Х-матрицы назы-
ваются следующие операции:
а)	перестановка двух строк или двух столбцов;
б)	умножение всех элементов какой-либо строки (столб-
ца) на один и тот же отличный от нуля постоянный
множитель;
в)	сложение элементов некоторой строки (столбца),
умноженных на один и тот же полином от X, с соответ-
ствующими элементами другой строки (столбца).
Доказывается, что:
а)	элементарные преобразования не изменяют элемен-
тарные делители ^-матрицы;
б)	всякую ^-матрицу конечным числом элементарных
преобразований можно привести к нормальной диагональ-
ной форме (5.31).
Покажем это на примере матрицы (5.30). Переставим в этой
матрице вторую строку иа место первой и второй столбец иа место
первого. Обозначим переход с помощью элементарных преобразо-
136 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ
ваний от одной матрицы к другой стрелкой, получим
II(М-I)3 (*+i)’||_J| * + 1 х + 1 II
II х + 1 х + 1 || ||(х + 1)» (Х + 1)’Г
Вычтем теперь элементы первого столбца из соответствующих эле-
ментов второго:
|| X +1 X +1 || || X 1	0	||
||(Х+1)2 (X-f-l)’|| 11(Х + 1)« Х(Х+1)’||-
Умножим элементы первой строки на X + 1 и вычтем из элементов
второй строки:
|(Х + 1)’ Х(Х+1)«Н o’ Х(Х-|-1)а|"
Полученная матрица является нормальной диагональной для мат-
рицы (5.30).
Заметим, что элементарными преобразованиями часто
пользуются для определения элементарных делителей.
Рассмотрим матрицу порядка е± следующего вида:
Xt 0 0 ..
1 Xt 0 ..
0 1 Хг ..
0 0
0 0
0 0
ООО	... Xj 0
ООО	... 1 Xt
В этой квадратной матрице по главной диагонали стоит
одно и то же число в диагонали под ней стоят единицы,
а остальные элементы равны нулю. Матрица такого вида
называется клеткой Жордана или элементарным ящиком.
Составим Х-матрицу Jr — КЕ (напомним, что Е — единич-
ная матрица):
Х1—X о	о	...	о	о
1 Xj - X	о	...	о	о
О	О	О	...	Xi — X о
0	0	0	...	1	Х1 — X
Вычеркнем из этой матрицы первую строку и последний
столбец и из оставшихся элементов составим минор поряд-
ка ег — 1:
1 Xj - X ... 0
0	1	... 0
0	0	... 1
§ 5.3. ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ
137
Так как этот минор равен единице, то Dr = 1)2 = • • •
. . .=	= 1 (см. с. 133). С другой стороны, единст-
венный минор порядка равен
det (Jx — ХЕ) = (Ах — А)е«,
Следовательно,
Dei = (А — Ч)е*
(в скобках переставлены местами А и Alt так как старший
член в Dei должен иметь коэффициент, равный единице).
Пользуясь формулой (5.27), найдем для матрицы инва-
риантные множители
Ек = 1, Е2 = 1, . . ., Ее^ = 1, Eei = (А — А^.,
Из этого следует, что матрица — ХЕ имеет только один
элементарный делитель, равный (А — А^Ч
Пусть теперь А — произвольная квадратная матрица,
элементы которой постоянные числа akj. Составим А-мат-
рицу А — ХЕ (она называется характеристической для
матрицы А)
	ай — А	а1п	
А — ХЕ-			(5.34)
	ап1		 апп-^	
Найдем элементарные делители этой матрицы
(Х-Х^, (А-А2)Ч . . ., (А-Ага)Х
Каждому корню Xk (k = 1, . . ., т) элементарного дели-
теля соответствует своя клетка Жордана Jk. Нормальной
формой Жордана для данной матрицы А называется ма-
трица, диагональные элементы которой равны клеткам
Жордана, а все прочие элементы нулю:
(5.35)

Очевидно, что элементарные делители матрицы J —
— ХЕ совпадают с элементарными делителями характерис-
тической матрицы. Заметим также, что корни характери-
стического уравнения | А — ХЕ | = 0 совпадают с кор-
нями элементарных делителей.
138 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ
Пример 1.
—2 —1 —1 —1
1—10	0
—4	1 —1 —1
5	12	2
(5.36)
Для того чтобы привести эту матрицу к нормальной форме
Жордана, нужно прежде всего найти элементарные делители харак-
теристической матрицы (5.34):
	-2 -X	—1	—1	—1
	1	—1 —X	0	0
	-4	1	-1 -X	—1
	5	1	2	2-Х
Для этого воспользуемся элементарными преобразованиями. Умно-
жим первую строку на —1, затем умножим последний столбец сна-
чала на —(2 + X) и сложим его с первым столбцом (чтобы получить
в верхнем углу нуль); после этого вычтем из второго и третьего
столбцов последний столбец (чтобы в верхней строке получить еще
два нуля):
0	0	0	1
А — Л.Е — _2 + х
-(1 + Х)
2
1 + X® — (1 — X)
о о
-X -1
X 2-Х
Сложим первую строку с третьей, потом умножим первую строку на
2 — Хи вычтем ее из четвертой; после этого переставим последний
столбец на место первого:
	1	0	0	0
Л — Х£—»	0 0	1 - 2+Х	-(1+Х) 2	0 -X
	0	1 +ха	-(1-Х)	X
Умножим второй столбец на 1 4- X и добавим его к третьему столб-
цу (чтобы получить во второй строке еще один нуль):
	1	0	0	0
	0	1	0	0
Л —Х£—»	0	—24-Х	—Х(1 — X)	-X
	0	1 4-Х2	X (2 4- X 4- Х«)	X
Теперь во втором столбце после единицы можно поставить нули (для
этого достаточно умножить вторую строку сначала на 2 — X и
сложить с третьей строкой, затем умножить вторую строку на
—(1 + X)2 и сложить с четвертой строкой). После этого умножим
четвертый столбец на —(1 — X) и добавим к третьему столбцу:
10	0	0
° 1	0	0
Л-ХЛ-. 0 0	0	.
0 0	X(l-f-X)2	X
§ 5.3. ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ
139
Сложим третью строку с четвертой,
—1 и переставим четвертый столбец
затем умножим эту строку на
на
А — кЕ
1
О
О
О
О
1
О
О
О
О
к
О
место третьего:
О
О
О
к (1 + к)*
(5.37)
Получилась нормальная диагональная форма характеристиче-
ской матрицы А — кЕ. Из нее находим
Ех = \, Е3=\, Е3 = к, Et = А,(*+ I)2-
Следовательно, матрица А — кЕ имеет три элементарных делителя:
к, к, (Л+ I)2,
которым отвечают корни
= О,
Конечно, эти корни
ристического уравнения
Х2 = 0, к3 = kt = —1.
являются одновременно корнями характе-
| А - кЕ | =0.
Отметим существенное для дальнейшего обстоятельство: корни
элементарных делителей и корни характеристического уравнения
всегда совпадают, но их кратность может быть различна. В данном
примере как раз имеет место этот случай: нулевой корень имеет
вторую кратность для характеристического уравнения, но он прос-
той для элементарных делителей (так как двум нулевым корням
отвечают два элементарных делителя). Корни к3 = kt = — 1 име-
ют одинаковую кратность как для характеристического уравнения,
так и для элементарных делителей.
Каждому элементарному делителю отвечает своя клетка Жорда-
на (см. равенство (5.32)) (^ = 0, Cj = 1; к2 = 0, е2 1»	= —1>
е3 = 2):
/1=цо||, /з=цой, /з=|-; _j|.
Теперь легко строится нормальная форма Жордана для рассмат-
риваемой матрицы:
О
О
(5.38)
—1
1
О
—1
причем незаполненные элементы равны
Пример 2.
нулю.
-2
1
-5
6
—1
-1
О
2
—1
о
—2
3
—II
о|
-2 •
3
(5.39)
А -
140 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ
Составим характеристическую матрицу
	—2 —К	—1	—1	—1
	1	—1 —X	0	0
Л -Х£ =	—5	0	—2 — X	—2
	6	2	3	3 -X
Элементарными преобразованиями эта Х-матрица приводится к
нормальной диагональной форме (читатель без труда выполнит са-
мостоятельно необходимые действия):
А — КЕ
1
0
О
О
0	0	О
1	О	О
О	1	О
О	0 Ха(Х+1)а
Из нее находим инвариантные множители:
£4 = 1, Е2 = 1, Е3 =1, £4 = X2 (X + 1)а.
Следовательно, матрица А — ).Е в этом случае имеет только два
элементарных делителя
К1, (Х + 1)а,
которым отвечают корни
Х4 = Х2 = О, Х3 =	= —1.
В данном примере кратность нулевого корня и вещественного
отрицательного корня одинакова как для характеристического
уравнения, так и для элементарных делителей.
Каждому элементарному делителю отвечает своя клетка Жор-
дана (см. равенство (5.32)):
Теперь легко строится нормальная форма Жордана для рассматри-
ваемой матрицы
О 0|
1 0|
-1 О
(5.40)
1 —1
причем незаполненные элементы равны нулю.
Обратим внимание на следующие обстоятельства: характеристи-
ческие уравнения в обоих примерах имеют одинаковые корни:
Х4 = Х2 = О, Х3 = Х4 = —1. Однако нормальные формы Жордана
разные. Это объясняется тем, что в первом примере характеристи-
ческая матрица имеет три элементарных делителя, а во втором при-
мере — только два.
В заключение приведем две теоремы линейной алгеб-
ры, которые нам понадобятся в дальнейшем (см., напри-
мер, [92 14]).
§ 5.3. ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ
141
Теорема 1. Если матрица Л неособенная, то элемен-
тарные делители матриц А — КЕ и ЛАЛ-1 — КЕ оди-
наковы. Обратно, если элементарные делители матриц
А — У.Е и В — КЕ одинаковы, то всегда найдется такая
неособенная матрица А, что
В = ЛАЛ’1.	(5.41)
Некоторые авторы называют эту теорему основной тео-
ремой линейной алгебры.
Теорема 2. Если квадратные матрицы А и С порядка s
симметричны, причем матрица А знакоопределенная, то:
1) все корни характеристического уравнения
det (ЛА. + 0 = 0
вещественны',
2) всегда найдется такая неособенная матрица Л, что
Л'А Л = Е, Л'СЛ = Со,	(5.42)
где Е — единичная, а Со — диагональная матрицы,
0 —	Ci 0 ... 0 0 с2 ... 0	,	(5.43)
	00 ... с 8	
причем с1г с2, . . ., cs равны корням характеристического
уравнения.
Вторая часть теоремы равносильна, очевидно, следую-
щему утверждению: если даны две квадратичные формы
1
Т —~2 Ах-х —
3	3
to=l j=i
1
П — -g- Cx-x =
причем первая из них определенно-положительна, то всег-
да найдется такое преобразование
х — Лг
с неособенной матрицей Л, что в новых переменных обе
квадратичные формы будут равны суммам квадратов:
1	1
r-y®-®=-J-(4 + ..; + 4
1 1
п	+ ... + c,zl),
142 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ автономных систем
причем в первой из них (определенно-положительной) все
коэффициенты равны единице.
Применим ко второму равенству (5.42) формулу (5.9):
det С 0 = det Л'-det С-det Л.
Учитывая, что det Л' = det Л, получим
det Со — A3 det С,
где А = det Л — определитель матрицы преобразования.
Так как матрица Со диагональная, то det Со =
= с,с2 . . .cs. Следовательно,
с,с2 ... cs = A2 det С.
Если матрица преобразования ортогональна, то А =
= +1 (см. (5.18)) и последнее равенство примет вид
сг ... сг = det С.	(5.44)
Кроме того, легко доказывается, что при ортогональ-
ном преобразовании след произвольной квадратной мат-
рицы В равен следу матрицы А'В А, т. е.
Sp В = Sp А'ВА.	(5.45)
§ 5.4. Устойчивость линейных автономных систем.
Устойчивость резонанса. Примеры
Пусть возмущенное движение определяется системой
линейных дифференциальных уравнений с постоянными
коэффициентами. Будем считать, что эти уравнения при-
ведены к нормальной форме:
х = Ах,	(5.46)
где х — матрица-столбец (вектор), а А — квадратная ма-
трица.
С помощью линейного преобразования перейдем от
вектора х к вектору ж (от переменных xltx2, . . ., хп к пе-
ременным Zj, za, . . ., zn)
z = Ах	(5.47)
с неособенной матрицей А =||	||.
Найдем обратное преобразование вектора ж в вектор х.
Для этого умножим слева обе части равенства (5.47) на
матрицу Л-1 (обратная матрица для Л существует, таи
§ 5.4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ 143
как матрица Л неособенная)
Л-1« = Л-1Лас
или, учитывая, что Л-1 А» = (Л-1 Л) ас = Ех = х (см.
(5.12)),
ас = Л-1«.	(5.48)
Продифференцируем это равенство по времени
Л-1® =; х.
Заменим х, согласно уравнению (5.46), на Ах:
Л-1« = Ах\
принимая во внимание обратное преобразование (5.48),
найдем
Л-1« = ЛЛ-1«-
Умножив обе части этого равенства слева на матрицу пре-
образования Л и учтя, что АЛ-1» = Ея = получим
я = Вя,	(5.49)
где матрица В определена равенством
В = ЛАЛ’1.	(5.50)
Таким образом, преобразование (5.47) переводит ма-
тричное уравнение возмущенного движения (5.46) с ис-
комым вектором ас в матричное уравнение (5.49) с иско-
мым вектором я. Очевидно, что если движение устойчиво
(неустойчиво) относительно переменного вектора ж, то
оно будет устойчиво (неустойчиво) относительно пере-
менного вектора ас, и наоборот.
Из равенства (5.50) и сформулированной теоремы ли-
нейной алгебры (см. (5.41)) следует, что элементарные де-
лители матриц А — ХЕ и В — ХЕ имеют одинаковые де-
лители. Пользуясь этим свойством преобразованной си-
стемы (5.49), можно задавать не линейное преобразование
(5.47), а матрицу В, выбрав ее из условия равенства эле-
ментарных делителей характеристических матриц А —
— ХЕ и В — ХЕ.
За новое дифференциальное уравнение (5.49) возьмем
такое, матрица коэффициентов которого является нор-
мальной формой Жордана для матрицы А исходного
144 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ автономных систем
уравнения (5.46):
(5.51)
где
О ... О
... О
К
О О ...А..
К
Переменный вектор ж, входящий в преобразованное
уравнение (5.49) с матрицей коэффициентов (5.51), назы-
вается каноническим вектором, а его элементы zx, za, . . .
. . ., zn — каноническими переменными.
Отметим, что для перехода к каноническим перемен-
ным формула преобразования (5.47) не нужна — нужно
знать только элементарные делители матрицы А — 'КЕ.
Дифференциальные уравнения в канонических пере-
менных разобьются на т независимых друг от друга
групп, каждая из которых соответствует своему элемен-
тарному делителю или своей клетке Жордана В^. Выпи-
шем одну первую группу (остальные имеют аналогичную
структуру):
Zi : Axzx,
Z2 - Z1 -|- AXZ^,
Йз=	Z2 +
(5.52)
Ze, —	Зе,—Х "Ь ^lze,«
Уравнения (5.52) интегрируются элементарно. Дейст-
вительно, из первого уравнения сразу находим
zi =
где z01 — начальное значение zx. Вносим полученное
значение для zx во второе уравнение
za Axza = ZgXC^.
Интегрируя его, получим
z2 = (zo2 + zoi0
§ 5.4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ 145
Продолжая этот процесс, найдем решение уравнений
(5.52):
Zi = z01e^1,
Z2 = (zoa "Ь Z010
2з= fzos + Zgzt	e*-1*,	(5.53)
Ze,— £ Zoe, 4~ Zo.ej-l^ 4“ • • • 4“ Zoi
Аналогичные решения получим для других групп.
Рассмотрим теперь вопрос об устойчивости движения.
Пусть
А-к = Уц 4-
где vjt и — вещественные числа. Тогда
Учтем теперь, что
| | = 1
при любых и t. Следовательно,
I е к = f " .
Из этого равенства следует, что при t—> ос
| | —> 0, если О,
| | —> ос, если у^^>0,
|eXfc< |= 1, если v)I = 0.
Так как показательная функция растет быстрее лю-
бого многочлена f(t), то для произвольного А. = v 4~ рл
будем иметь
О
при v<^0,
lim|/(i)ew|= ос при v^>0,
f-*OO	_	Г\
оо при V = U,
(5.54)
причем в последнем случае предполагается, что / (i)
Ф const.
Из общего решения (5.53) и предельных равенств (5.54)
непосредственно вытекают следующие теоремы об устой-
чивости движения системы, возмущенное движение кото-
рой описывается дифференциальными уравнениями (5.1)
или в матричной форме (5.46).
146 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ
1.	Если вещественные части всех корней характери-
стического уравнения отрицательны, то невозмущенное
движение асимптотически устойчиво.
2.	Если среди корней характеристического уравнения
имеется хотя бы один, вещественная часть которого
положительна, то невозмущенное движение неустойчиво.
3.	Если некоторые корни характеристического урав-
нения имеют нулевые вещественные части, а остальные
корни имеют отрицательные вещественные части, то:
а)	невозмущенное движение будет устойчивым (не
асимптотически), если корням с нулевой вещественной
частью отвечают простые элементарные делители (то
есть соответствующие е* = 1);
б)	невозмущенное движение будет неустойчивым, если
хотя бы один корень с нулевой вещественной частью явля-
ется кратным корнем соответствующего элементарного
делителя (ek Д> 1).
Прежде чем перейти к примерам, сделаем три замеча-
ния.
1.	При исследовании устойчивости линейных стацио-
нарных систем нужно прежде всего определить корни ха-
рактеристического уравнения. Если вещественные части
всех корней отрицательны или имеется хотя бы один
корень, вещественная часть которого положительна, то
вопрос об устойчивости решен и нет смысла исследовать
элементарные делители, т. е. решать задачу более слож-
ную. Точно так же задача сразу решается, если корни
с нулевыми вещественными частями простые (в этом слу-
чае корням с нулевой вещественной частью соответствуют
простые элементарные делители), а остальные крони
имеют отрицательную вещественную часть.
Таким образом, к определению элементарных делите-
лей нужно прибегать только в том случае, если среди кор-
ней характеристического уравнения имеются кратные
корни с нулевой вещественной частью, а вещественные
части остальных корней отрицательны.
2.	В некоторых случаях необходимо ответить не толь-
ко на вопрос об устойчивости движения, но и определить
матрицу преобразования Л переменных х1, х2, . . ., хп
в канонические переменные zx, z2, . . ., zn. Для этого ра-
циональнее всего воспользоваться равенством (5.50), ко-
торое умножением справа на матрицу Л приводится к
виду
В А -= ЛА.
(5.55)
§ 5.4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ 147
Это матричное уравнение относительно А содержит
две известные матрицы (А задана, а В — нормальная фор-
ма Жордана для А и, следовательно, находится по А).
Матричное уравнение (5.55) эквивалентно п2 скалярным
однородным уравнениям относительно akJ-, выражающим
равенство соответствующих элементов. Поэтому имеется
бесчисленное множество матриц преобразования А.
Обратную матрицу А1 можно найти из уравнения
А^В = А А"1,	(5.56)
которое получается умножением равенства (5.50) слева
на А-1.
3.	Очень часто исходные уравнения возмущенного
движения не приведены к нормальной форме и содержат
производные порядка выше первого. Для того, чтобы опре-
делить элементарные делители и решить вопрос об устой-
чивости, нет нужды приводить систему к нормальной фор-
ме — достаточно составить характеристическую л-матри-
цу для исходной системы и исследовать ее. Покажем это
на примере уравнения
Ах + Вх + Сас = О.	(5.57)
Для исследования на устойчивость относительно мат-
риц-столбцов х и х достаточно определить элементарные
делители характеристической А-матрицы
/ (X) = АА2 + ВК + С.	(5.58)
Действительно, перейдем к системе первого порядка,
для чего положим х — у. Тогда уравнение (5.57) заменит-
ся системой двух уравнений первого порядка
Aij= — By — Сх.
Характеристическая матрица этой системы имеет вид
(элементами служат матрицы)
А(Ч=|1Г -АД
Воспользуемся элементарными преобразованиями: умно-
жим второй столбец на А и сложим его с первым, после
чего переставим их
I Е	0
I— 41 — В -ДР — ВЬ-С

148 ГЛ. V. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ автономных систем
Первую строку умножим на А'К + В и сложим со второй,
затем умножим второй столбец на —1:
/х(М-»|0 ЛА13_|_ 5x. + c| = |o /(А.)!’
что доказывает сделанное замечание.
Пример 1. Исследуем устойчивость системы, уравнения возму-
щенного движения которой имеют вид
^1	2х-£ х2 Хд
^2	^1	^2»
*3 = —4x1 + ^2 — х3 — х4,
^4 = 5xi -|- х2 -|- 2х3 -|- 2х4.
В примере 1 § 5.3 было установлено, что характеристическое
уравнение det (А — КЕ) = 0 этой матрицы имеет два нулевых кор-
ня и два корня, равных —1. Последний корень кратный как отно-
сительно характеристического уравнения, так и относительно эле-
ментарного делителя, но он не может испортить устойчивость (так
как он вещественный отрицательный). Что касается нулевого кор-
ня, то хотя он второй кратности для характеристического уравне-
ния, но простой для элементарных делителей. Следовательно, не-
возмущенное движение устойчиво относительно переменных хх, х2,
*^3 ’ *^4 *
Проиллюстрируем этот вывод. Уравнения возмущенного дви-
жения в канонических переменных состоят из трех независимых
между собой групп (см. нормальную форму Жордана (5.38) для
матрицы Л):
41 = 0, z2= 0, 43 =	z3, z4 = z3 — z4
(первая группа — первое уравнение, вторая группа — второе
уравнение, третья группа — последние два уравнения). Напишем
общее решение этих уравнений;
Zi = Z01, z2 — Z02, z3 = Z03e , z3 = (z<J4 -|- ZQ3f)c .
При t —> + оо переменные z3 и z4 стремятся к нулю, a zx и z2
остаются без изменения, и при соответствующих начальных усло-
виях их модули могут быть сделаны сколь угодно малыми. Следо-
вательно, как уже было отмечено, невозмущенное движение устой-
чиво относительно совокупности канонических переменных zx, z2,
z3, z4 и тем самым относительно переменных х2, х3, х4.
Пример 2. Исследуем устойчивость системы, уравнения возму-
щенного движения которой имеют вид
*1 = —2хх — х2 — х3 — х4,
^2 Xi Х2,
х3 = —5х4	2х3 — 2x4,
= 6хх + 2х2 |- Зх3 + Зх4.
Матрица правой части этих уравнений была рассмотрена в
примере 2 § 5.3 (см. матрицу (5.39)). Было установлено, что харак-
теристическое уравнение det (А — ЪЕ) = 0 этой матрицы имеет
два нулевых корня и два корня, равных —1. Оба корня кратные
§ 5.4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОНОМНЫХ СИСТЕМ 149
как относительно характеристического уравнения, так и относи-
тельно элементарных делителей. Так как нулевой корень кратен
относительно элементарного делителя, то невозмущенное движение
неустойчиво относительно хг, х2, х3, х4.
Проиллюстрируем этот вывод. Уравнения возмущенного дви-
жения в канонических переменных состоят из двух независимых
между собой групп (см. нормальную форму Жордана (5.40)):
Zj = 0, Z2 — Z4, Zg = Zg, Z4 Zg Z4
(первая группа состоит из первого и второго уравнений, а вторая —
из третьего и четвертого уравнений). Напишем общее решение этих
уравнений:
Z1 = 20!, Z2 = Zo2 + Zgil, Zg = Zoge"', Z4 = (Z04 4- Zogi)e-(.
Так как z2 —> оо при t —> + оо, то невозмущенное движение
неустойчиво относительно совокупности канонических переменных
zlt z2, z3, z4 и, следовательно, относительно xlt х2, х3, х4.
Пример 3. Устойчивость резонанса. Рассмотрим
простейший линейный колебательный контур, на который действует
возмущение, изменяющееся по
гармоническому закону. Диффе- z
ренциальное уравнение движения
имеет вид
х -j- №х = Н cos (of. (5.59)
Здесь х — координата, определя-
ющая состояние контура (линей-
ное или угловое перемещение, за-
ряд и т. п.), к — частота его соб-
ственных колебаний, <о — частота
возмущающего воздействия, Н=	рис 5 j
= const.
Из элементарного курса физики известно, что при совпадении
частот (к = <о) наступает резонанс, при котором вынужденные ко-
лебания определяются равенством (график этого движения показан
на рис. 5.1)
х = -2L1 sin <о1.	(5.60)
Примем это движение за невозмущенное. Тогда уравнение воз-
мущенного движения будет представлять однородную часть линей-
ного уравнения (5.59) — см. пример 3 § 1.3:
X 4- к2х = 0.
Составим характеристическое уравнение
I2 4- к? = 0.
Так как корни 1 = 4; ki этого уравнения чисто мнимые и раз-
личные, то резонанс (5.60) устойчив, но не асимптотически. Неко-
торым этот результат кажется неожиданным, но следует иметь в
виду, что доказана устойчивость процесса, При котором амплитуды
вынужденных колебаний неограниченно возрастают, иначе говоря,
небольшие возмущения не могут изменить общий характер движе-
ния, изображенного на рис. 5.1.
ГЛАВА VI
ВЛИЯНИЕ СТРУКТУРЫ сил
НА УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
§ 6.1.	Введение
Общие методы исследования устойчивости движения
Ляпунова сильны прежде всего своей универсальностью,
и именно поэтому они не могут содержать анализа различ-
ных физических факторов, влияющих на устойчивость
движения. Между тем во многих случаях такой анализ,
проведенный в достаточно общем виде, может оказаться
весьма полезным. В этой главе мы рассмотрим, как влия-
ют на устойчивость движения различные силы.
Исследование влияния структуры сил на устойчивость
движения началось по существу с работ Томсона и Тета J).
В 1879 г. они дали общее определение гироскопических
сил и доказали четыре теоремы об устойчивости движения.
Это направление не развивалось около семидесяти лет.
По-видимому, это можно объяснить тем, что за эти годы
была создана общая теория устойчивости движения с ее
эффективными методами исследования. Другая причина
состоит в том, что теоремы Томсона и Тета были сформу-
лированы только для линейных автономных систем. На-
конец, эта теория не включала неконсервативные пози-
ционные силы, значение которых для многочисленных тех-
нических приложений прояснилось в полной мере лишь
за последние десятилетия.
В начале пятидесятых годов нашего столетия снова воз-
ник интерес к вопросам исследования устойчивости дви-
жения по структуре действующих сил. Было дано строгое
доказательство теорем Томсона и Тета, затем эти теоремы
были распространены на нелинейные системы и были по-
лучены новые результаты, охватывающие неконсерватив-
ные позиционные силы. Эти результаты позволяют со-
ставить отчетливое физическое представление о влиянии
*) Теорема Лагранжа об устойчивости равновесия (см. § 3.1),
имеющая непосредственное отношение к изучаемому вопросу, до-
казана в годы, когда рассматривались практически только консер-
вативные системы.
§ 6.2. КЛАССИФИКАЦИЯ СИЛ	151
различных сил на устойчивость движения. Поэтому даже
в тех случаях, когда применение их не упрощает чисто
вычислительной части анализа, они могут оказаться по-
лезными для качественной оценки отдельных факторов,
влияющих на устойчивость движения, особенно в процес-
се проектирования на этапе завязки системы (см. пример 3
§ 6.6 и др.).
§ 6.2.	Классификация сил
Будем считать, что положение системы определяется s
обобщенными координатами qlt . . ., qs, а движение ее
описывается уравнениями Лагранжа 2-го рода
d дТ дТ „ .	..	.	.
=	=	(6.1)
В этих уравнениях кинетическая энергия системы
8	8
(6-2)
К=1 >=1
представляет определенно-положительную квадратичную
форму обобщенных скоростей q с коэффициентами инер-
ции ан (q) = a.ft (<?), зависящими от координат q, а обоб-
щенные силы QK являются функциями координат q и ско-
ростей д.
Для большей наглядности введем в рассмотрение s-мер-
ное ортогональное пространство (qx, . . ., qs) и два вектора:
Предполагается, что первый вектор определяет изоб-
ражающую точку М, а второй — силу, приложенную к
этой точке.
Перейдем теперь к характеристике сил.
а.	Линейные силы. Рассмотрим сначала слу-
чай, когда сила Q линейно зависит от радиуса-вектора q
и скорости q изображающей точки
Q = -с15 - В&,	(6.3)
где и Вх — заданные квадратные матрицы порядка
s X s с постоянными элементами.
152
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Разобьем матрицы С\ и на симметричные С и В и
кососимметричные Р и G части, положив (см. (5.15)—
(5.17))
= С + р, Вх = В + G,	(6.4)
где
С = С' = ±-(С1 + СХ), Р=-Р'^1-(С1-С’Х),
1	,	1	(6.5)
В = В' = 4" (5i + 2?1)- G = — G' =-i?-(Bi — Вх).
Теперь сила Q принимает вид
Q= Я +	+ D + Г.	(6.6)
Здесь
K ~Cq. Jt ~ Pq, I> ~B<j, Y = — Gq. (6.7)
Сила К = —Cq с симметричной матрицей С = || ckj ||
называется потенциальной или консервативной, а квадра-
тичная форма
(6.8)
к J
равна потенциальной энергии системы.
Составим с помощью симметричной матрицы В =
— || bkj || квадратичную форму
F^^-Bq-q^^^b^^i.	(6.9)
К }
Если эта функция не отрицательна, то она называется
функцией рассеивания или диссипативной функцией Ре-
лея-, соответствующие силы D = —Bq называются дис-
сипативными силами с положительным сопротивлением
(или просто диссипативными силами). Если квадратичная
форма F определенно-положительна, то диссипация назы-
вается полной, в противном случае — неполной. Наконец,
если функция F может принимать отрицательные значе-
ния, то среди составляющих силы D = —Bq имеются
ускоряющие силы (силы отрицательного сопротивления).
Обычно диссипативные силы с положительным сопротив-
лением возникают естественным образом при движении
тел в сопротивляющейся среде, в электрических цепях при
наличии омического сопротивления и т. п. Ускоряющие
силы (силы отрицательного сопротивления), как правило,
создаются с помощью специальных устройств (см. при-
мер 3 § 6.6).
§ 6.2. КЛАССИФИКАЦИЯ СИЛ
153
Силы Г = —Gq, линейно зависящие от скоростей q
и имеющие кососимметричную матрицу коэффициентов
6 = II gnj II, называются, как уже говорилось в § 3.3, ги-
роскопическими. Чаще всего эти силы встречаются в си-
стемах, содержащих гироскопы, но они могут быть и в
других системах (см. пример § 6.7).
Силы R = —Pq, линейно зависящие от координат
q с кососимметричной матрицей коэффициентов Р = || р*}||,
называются неконсервативными позиционными или просто
неконсервативными силами г). Неконсервативные пози-
ционные силы возникают как естественным образом, так
и с помощью специальных устройств (см. § 6.9).
Рассмотрим пример. Пусть силы и Q2 имеют вид
Qi = —5?1 + 91 — 2д2,
Qi = 211 + 92 SQi 5g2.
Составим матрицы и Bf.
2||,	5i=||	5	°||.
6 51|	11—2 —1||
Найдем транспонированные матрицы и В1 (в матрицах Сг и Вх
переставляем строки и столбцы):
Разложим матрицы С± и на симметричные и кососимметричные
части:
с (G+c;)=
5=1(В1+в;)=
в1=
—1

—211
ОII ’
'Л-
О
2
—1
4
5
—1
*||,	Р = ^(С1-С'1) =
Э ||	л
Zj||. G = 1(^-5;)=
О
—1
х) Неконсервативные позиционные силы не имеют твердо уста-
новившегося названия. Г. Циглер называет эти силы циркуляцион-
ными [59, 60], в теории гироскопических систем их называют силами
радиальной коррекции [38], в теории упругости их называют прос-
то неконсервативными силами [11], некоторые авторы называют их
собственно или существенно неконсервативными силами, псевдо-
гироскопическими силами, силами ограниченного демпфирования
(последний термин распространен в американской научной лите-
ратуре, посвященной космическим исследованиям). Первые два
названия легко оправдать физическими соображениями, но, по-
видимому, термин «неконсервативные позиционные силы» являет-
ся наиболее точным: позиционные, так как они зависят от коорди-
нат системы, неконсервативные, так как работа их зависит от пути
и для них не существует интеграла энергии. Для простоты мы бу-
дем иногда называть неконсервативные позиционные силы просто
неконсервативными силами.
154
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Найдем потенциальную энергию П и функцию Релея F'.
n=V2(-?13 + 8?1?2 + 5?2),
Р =1/2(5<7'J —2^72— 4|).
В данном примере функция Релея F может принимать как по-
ложительные значения (например, при 4= 0 и q2 = 0), так и от-
рицательные значения (например, при <Д = О и ?2=/=0). Поэтому
диссипативная сила —Bq имеет положительные и отрицательные
составляющие. Матрицы-столбцы потенциальных — Cq, неконсер-
вативных —Pq, диссипативных —Bq и гироскопических—Gq сил
соответственно равны:
II 91—4дг||	|| 2д2||	||—57!-|-(М	||—<7г ||
II-4?i- 5?г||’ ||-2?1|| ’ || 7!-М2 Г II 11Г
б.	Нелинейные силы. Приведенная класси-
фикация линейных сил по их математической структуре
очень удобна для линейных систем, особенно при иссле-
довании устойчивости движения. Однако для нелинейных
сил этот метод неприменим. Поэтому для общей характе-
ристики сил воспользуемся их физическими свойствами.
Как известно, работа потенциальной силы К (q) не
зависит от пути перемещения точки приложения силы.
Для этой силы справедливо равенство
К (<?) = —giad П	(6.10)
или для составляющих
=	С6-11)
где П — потенциальная энергия.
Для того чтобы некоторая сила К (<?), зависящая
от положения изображающей точки М, была потенциаль-
ной, необходимо и достаточно, чтобы ее проекции удов-
летворяли равенствам (число их равно числу сочетаний иэ
s по два)
(необходимость этих условий вытекает непосредственно
из (6.11)).
Справедливость формул (6.10)—(6.12) для линейной
силы К — —Cq следует из равенства (6.8).
По определению Томсона и Тета [58] сила Г (q) на-
зывается гироскопической, если мощность (работа) ее
3 8.2. КЛАССИФИКАЦИЯ СИЛ
155
тождественно равна нулю
1Ч=Ш = 0.	(6.13)
Из этого определения следует, что гироскопическая
сила перпендикулярна скорости q изображающей точ-
ки М. Линейная сила Г = —Gq удовлетворяет этому ус-
ловию, так как в силу косой симметрии матрицы G произ-
ведение Г-д' = —Gq • q тождественно равно нулю (см. ра-
венство (5.25)).
Сила D ((), зависящая от скорости q изображающей
точки М, называется диссипативной силой с положитель-
ным или отрицательным сопротивлением, если ее мощ-
ность не равна нулю тождественно. Диссипативным силам
положительного сопротивления отвечает отрицательная
мощность
JV-D-q—. 3	(6.14)
К=1
(знак равенства в этом соотношении не может быть тож-
дественным), а силам отрицательного сопротивления —
положительная мощность. Если мощность N (д) является
определенно-отрицательной функцией скоростей то
диссипацию назовем полной-, если же мощность N (д) —
просто отрицательная функция скоростей д^, то дисси-
пацию назовем неполной или частичной (в дальнейшем
будет показано, что из этих общих определений следуют
соответствующие определения, введенные для линейных
сил сопротивления).
Нам осталось дать общее определение неконсерватив-
ных позиционных сил. Из определения линейной некон-
сервативной силы следует, что она перпендикулярна ра-
диусу-вектору q изображающей точки М (R q = -Pq-
q = 0, так как матрица Р — кососимметричная). Обоб-
щая это свойство, будем называть любую силу И (<?), зави-
сящую от координат системы q\-, неконсервативной по-
зиционной силой, если она ортогональна радиусу-вектору
q изображающей точки
в
3 /?Л = 0.	(6.15)
К=1
Выше было показано, что произвольные силы, линей-
но зависящие от координат и скоростей системы, можно
156	ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
разложить на потенциальные К, неконсервативные по-
зиционные R, гироскопические Г и диссипативные JD си-
лы. Покажем, что аналогичное разложение можно про-
извести для широкого класса нелинейных сил.
Теорема. Любую непрерывную вместе со своими произ-
водными первого порядка силу Q (q), зависящую только
от положения системы, можно разложить на потенци-
альную и неконсервативную позиционную, составляющие
(Ш = - grad П + R (q),	(6.16)
где поле R и потенциальная энергия П подлежат опреде-
лению х).
Доказательство. Умножим обе части равенства (6.16)
скалярно на радиус-вектор изображающей точки q:
Q-q = — (grad П)-q + R-q,	(6.17)
x) Этой теореме можно придать другой, более общий, вид, не
связывая ее с разложением сил [40]. Действительно, назовем для
краткости поле векторов R (q), удовлетворяющее условию ортого-
нальности (6.15), циркуляционным. Тогда будет справедлива следую-
щая теорема: произвольное непрерывное вместе со своими произ-
водными первого порядка векторное поле Q (q) всегда можно раз-
ложить на потенциальное и циркуляционное поля:
Q (д) = -grad П + В (д),
где поле R (д) и потенциал —П подлежат определению.
Заметим здесь же, что линейное циркуляционное поле R (д) =
= Pq, где Р — кососимметричная матрица, будет одновременно и
соленоидальным полем, т. е. полем, для которого дивергенция рав-
на нулю:
(так как в силу косой симметрии матрицы Р проекция R\ вектора R
не содержит координаты gfe и, следовательно, все dR^/dq^ = 0).
В общем нелинейном случае циркуляционное поле не является со-
леноидальным. Так, если Bj = g^g^, В2 = —g^g^, то дивергенция
вектора R
div R = dJh +	= g^ _ 2дЗда=/= 0,
ogi «да
т. е. циркуляционное поле R, для которого R q =	+ В2д2 =
= 0, не является соленоидальным.
Полезно отметить, что практически одновременно, независимо
друг от друга и в совершенно различных формах, аналогичные ре-
зультаты были получены в разных странах при разборе термоди-
намических задач [44а, 53а]. Автор настоящей книги не уверен, что
эта теорема не было доказана еще в прошлом веке.
§ 6.2. КЛАССИФИКАЦИЯ СИЛ	157
или, учитывая равенство (6.15),
Q-q = -(grad ПН.	(6.18)
Левая часть этого равенства представляет известную
функцию координат . ., qs (так как сила Q задана).
Обозначим эту функцию через Н:
H(qi,...,qs)=^Q-q='ZQkqK-	(6.19)
u=i
Если функция Н тождественно равна нулю, то, сог-
ласно равенству (6.15), сила Q будет неконсервативной
позиционной силой и задача разложения силы Q будет
полностью решена при Q = И и П = 0.
Рассмотрим общий случай, когда Н и, следователь-
но, потенциальная энергия не равны нулю. Запишем
равенство (6.18) в скалярной форме, учтя при этом ра-
венство (6.19)
+	+	= ~Н.	(6.20)
В этом равенстве функция Н известна, а функция П
неизвестна. Поэтому равенство (6.20) можно рассматри-
вать как линейное неоднородное дифференциальное урав-
нение в частных производных относительно потенциаль-
ной энергии П. Как известно, решение уравнения (6.20)
сводится к решению следующей системы обыкновенных
дифференциальных уравнений:
dqi __ Ч-i __ d4s _
91	'' ’	9,-1	9,	—Н‘
Из первых s — 1 уравнений найдем
?1 — Ci?,» • • ч ?s-i = ('s—iQsi	(6.21)
где Сг, . . ., Cs-j — произвольные постоянные интегриро-
вания.
Последнее уравнение
d4s _ dll
9, “ -Н
приводится к виду
Н (5), . . . , q )
ЛЬ==-------—------^—dqs.	(6.22)
9«
Заменим в функции Н переменные qlt . . ., q^ на
их значения из (6.21). Тогда эта функция будет зависеть
158
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
только от одной переменной qa и постоянных Clt . . .
. . C8_v Интегрируя обе части равенства (6.22), найдем
(CiQ ..... Со_. о )
—~ "1а 8  dqa + С„
где Са — новая постоянная интегрирования.
Общее решение уравнения в частных производных
(6.20) можно привести теперь к следующей форме:
^l^S1 • • • ’	9») &	, ip ( <71	^3-1	,
<7S	qs T \ 4a ’ ' ’ ’ ’ ?S / ’
где *F — произвольная функция.
Учтем теперь, что при Н = 0 потенциальная энергия
равна нулю (см. примечание к формуле (6.19)). Поэтому,
положив ’F — 0, получим окончательное выражение для
потенциальной энергии
(• Н (С,о , ... ,С. ,о , о )
П = - \----dqs (6.23)
J	Qs
(конечно, после вычисления интеграла входящие в него
постоянные интегрирования Сх, . . ., Cs_x нужно заме-
нить на их значения из (6.21)).
После того как будет найдена потенциальная энергия П
неконсервативная позиционная сила R определится из
равенства (6.16)
R = Q + grad П.	(6.24)
Составляющие потенциальной силы К = — gradn
определятся равенствами (6.11)
Составляющие неконсервативной позиционной силы R
определяются из равенства (6.24)
п „ . дП п , ЗП
7?1 = <?1 + ^r’---’7?5 = <?s + ^T-	(6-26)
Заметим, что первые формулы (6.5) для линейной по-
зиционной силы Q — — можно, конечно, получить из
равенств (6.25) и (6.26), но зто значительно более слож-
ный и трудоемкий путь, к которому следует прибегать
только для нелинейных систем.
§ 6.2. КЛАССИФИКАЦИЯ СИЛ
159
Пример. Даны обобщенные позиционные силы
<?i =	<?2 =	+ 2^-	(6.27)
Требуется разложить эти силы на потенциальные и неконсерва-
тивные позиционные составляющие.
Составим по формуле (6.19) функцию
Н = Qiqi + Q2g2 = gf + 2g*g® + 2g®.
Интеграл (6.21) в нашем случае будет
Qi = С?2-
Внесем это значение для дх в функцию Н:
Н= C*q* + 2С»д| + 2д®.
Вычислим теперь по формуле (6.23) потенциальную энергию
Имеем
J'C<g|+2^ + 2g®
11 = — \ -------------— 0^2»
J	Q2
ИЛИ
II = _lcV2--|c2g|_lg®.
Заменив постоянную С на ее значение qjq^ получим оконча-
тельное выражение для потенциальной энергии
n=-(v?+4^+| ?2)-	<6-28)
Заметим, что при дх = д2 = 0 потенциальная энергия имеет
максимум (так как для переменных д^ и д| выполнен критерий
Сильвестра (2.10): Дх = —1/4 <0, Д2 = 13/300 > 0).
Составляющие потенциальной силы К = —grad П и некон-
сервативной позиционной силы R найдем по формулам (6.25) и
(6.26):
Ki = + 4	*2=4 + Ч <6-29)
J?a = -_Lg*g|.	(6.30)
О	о
Легко проверить, что силы R, и Т?2 удовлетворяют условию
(6.15).
Рассмотрим теперь силу Q (q), зависящую от скорости
q изображающей точки М. Если выделить из этой силы
гироскопическую составляющую Г (силу, не производя-
щую работу), то в соответствии с определениями остав-
шаяся часть будет равна диссипативной силе с положитель-
ным или отрицательным сопротивлением. Таким образом/
160
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
имеем
Q (д) = D (q) 4- Г (д).	(6.31)
Покажем сейчас, что силу сопротивления (q) можно
представить как градиент некоторой скалярной функции
D— grad F.	(6.32)
В этом равенстве grad F определяется в пространстве
скоростей (дь . . ., qs) так, что
ар
D^ = -^r~ (* = l,...,s),	(6.33)
причем должны выполняться равенства
aD. aD.
=	(A,/ = 1,...,S).	(6.34)
Для доказательства сделанного утверждения доста-
точно заметить, что в соответствии с определениями гиро-
скопическая сила Г в пространстве скоростей (qx, . . .
. . qs) и неконсервативная позиционная сила R в про-
странстве координат (дг, . . ., gs) удовлетворяют одинако-
вым условиям ортогональности (6.13) и (6.15). Поэтому,
повторяя почти дословно обоснование возможности раз-
деления позиционных сил, можно доказать следующую
теорему.
Теорема. Любую непрерывную вместе со своими произ-
водными первого порядка силу Q (q), зависящую только от
скоростей системы, можно представить суммой двух сил
Q {q)= - grad F 4- Г,	(6.35)
где Г — гироскопическая сила, а F — некоторая скаляр-
ная функция скоростей q^.
Сравнивая равенства (6.35) и (6.31), получим (6.32).
Функцию F (q) будем называть функцией Релея 1). Заме-
тим, что функция — F (<j) является потенциалом поля сил
сопротивления.
4 Для линейных сил положительного сопротивления диссипа-
тивная функция F введена в 1873 г. Релеем. Определение полной
и частичной диссипации для таких сил дано Четаевым. Здесь при-
ведены обобщения этих понятий на произвольные силы сопротивле-
ния [38].
§ 6.2. КЛАССИФИКАЦИЯ СИЛ
161
Учитывая равенства (6.32) и (6.33), вычислим мощ-
ность силы сопротивления
N(() = D-q = — gradE-# —— У	(6-36)
Если составляющие Dh. силы сопротивления D одно-
родны относительно скоростей и степень их однородности
равна т, то функция F также однородна, причем степень
ее однородности будет, очевидно, т + 1. В этом случае,
пользуясь равенством (6.36), по известной теореме Эйлера
об однородных функциях получим
N = _ (т + 1) F.	(6.37)
В частности, для линейных сил сопротивления N =
= —2F.
Из равенства (6.37) видно, что однородным силам по-
ложительного сопротивления с полной диссипацией от-
вечает определенно-положительная диссипативная функ-
ция F, а при неполной (частичной) диссипации — просто
положительная функция F.
В дальнейшем, если не будет специальной оговорки,
под силой сопротивления D будем понимать силу поло-
жительного сопротивления (диссипативную силу). В тех
редких случаях, когда будут рассматриваться силы от-
рицательного сопротивления, они будут называться уско-
ряющими силами.
До сих пор мы считали, что гироскопические силы Г и
силы сопротивления D зависят только от скорости q. На
практике эти силы очень часто зависят также от положе-
ния системы, т. е. от радиуса-вектора q изображающей
точки М:
Г = Г(<м), D = D(q,g).
Все определения для этих сил сохраняются без вся-
кого изменения, если только радиус-вектор q точки М
рассматривать как параметр. В частности, будем считать,
что силы Г и D обращаются в нуль при q = О
Г (q, 0) = 0, D (q, 0) = 0,	(6.38)
причем предполагается, что при	эти силы не рав-
ны нулю при любых значениях q, расположенных вблизи
точки q = 0.
6 Д. Р. Меркин
162
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Мощность N силы D будет теперь зависеть не только
от скорости q, но и от <7
N (д, О - D (д, () • q.	(6.39)
Определение полной и частичной диссипации остается
почти без изменения: диссипация называется полной (час-
тичной), если мощность N (q, <) силы D является опреде-
ленно-отрицательной (отрицательной) функцией скорости
q при всех значениях q, расположенных вблизи точки
3 = 0.
Пример 1. Сила Г с линейными относительно скоростей сос-
тавляющими
Ti = cos рр, Г2 = —cos P<z
гироскопическая, так как ее мощность
N = Г^а Г2*р = cos PPa + (— cos Р&) р
тождественно равна нулю.
Пример 2. Сила Г с нелинейными относительно скоростей сос-
тавляющими
Г1 = (В С) .^2^з, Г2 = (С — A) Tgfj, Г3 = (Л В)
где А, В и С — произвольные функции координат х15 х2, х3 и ско-
ростей i-ц r2, х3, гироскопическая, так как ее мощность
N — 1А + Г 2Г2 + Г3г з
тождественно равна нулю.
Пример 3. Сила D, составляющие которой определяются ра-
венствами
£>1 = —[1 + cos2 (ft -|- g2)] sign <ц, D2 = —(?2 + ??).
является силой положительного сопротивления с полной диссипа-
цией. Действительно, мощность этой силы
TV = £>А + D2'2 = —{[1 + cos2 (?1 + g2)]j» | 7i | + <?2 + </2}
представляет определенно-отрицательную функцию скоростей
42 при любых qr и q2 (при вычислении N учтено, что ц sign <7i = I Qi |).
Функция Релея для данных сил имеет вид
F = -L I1 + cos2 И' 92)] I 911’ + 4 ’2 + Т ’Г
Эта функция удовлетворяет равенствам (6.33), так как
-^-|'7i|3 = 3|<h|2-£| 711=3)» sign ,!•
d/i	<171
Пример 4. Методом, изложенным на с. 160—161, силы
<?1=-731/2,
!) Символ sign х означает знак х.
в в.З. ПОСТАНОВКА ЗАДАЧИ	1вЗ
можно разложить на гироскопические и диссипативные состав-
ляющие:
Г —	1 I	 I4	_ I3 А	Г	— 1 / -,4	; _л2;3,
41	(	172	1^27*	^2 Tj" ( 1	2	71^27»
п _	_ 2 л352	_ 1	•, -,4	Г) _ _	2 .2-3	1	•,
—	"J- 71 2	"д’	1 2’	~	‘3'71'2	у '<1 2‘
Легко проверить, что гироскопические силы Г\ и Г2 удовле-
творяют условию (6.13), а силы/?! и D2 - условию (6.34). Функция
F в данном примере равна
Так как эта функция определенно-положительна, то имеется
полная диссипация.
§ 6.3. ПостаноЬка задачи
Будем считать, что уравнения возмущенного движения
относительно величин q и < приведены к виду
d ОТ _ дТ
dl ° 'к дЧк
-|2- + о, + г, + п,„
(6.4);
-£=<> <*=1...»•
В этих уравнениях Т — определенно-положительная
квадратичная форма скоростей <
8	8
К=1 ;=1
где akj = a,jk — функции q. Предполагается, что при
q = 0 потенциальная энергия П равна нулю. Кроме то-
го, предполагается, что при q = 0 обращаются в нуль по-
тенциальные и неконсервативные позиционные силы, а
при £ = 0 обращаются в нуль диссипативные и гироско-
пические силы.
Независимо от способа получения уравнений возму-
щенного движения (6.40) функцию Т можно рассматри-
вать как кинетическую энергию приведенной системы,
переменные q^ и < к — как обобщенные координаты и
скорости, а члены, стоящие в правых частях этих урав-
нений,— как потенциальные, диссипативные, гироскопи-
ческие и неконсервативные позиционные силы соответ-
ственно. Относительно сил предполагается только, что
6*
164
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
они удовлетворяют сделанным в § 6.2 определениям и ус-
ловиям существования и единственности решения диффе-
ренциальных уравнений (6.40). Никаких других ограни-
чений на силы не налагается — они могут быть линей-
ными, существенно нелинейными (их разложения по
степеням q и < могут начинаться с членов любого порядка),
наконец, они могут быть неаналитическими функциями
координат q и скоростей cj.
К уравнениям возмущенного движения (6.40) приво-
дятся все задачи на исследование устойчивости равнове-
сия механических систем с голономными и стационарны-
ми связями и многие задачи на исследование устойчивости
установившихся и стационарных движений механи-
ческих, электрических и электромеханических систем..
Не вдаваясь в анализ физической природы координат q
и рассматриваемого явления, будем говорить, что значе-
ниям q = 0 и ( =0 отвечает равновесие системы, а урав-
нения (6.40) описывают возмущенное движение около
положения равновесия. Поэтому, говоря об устойчивости
равновесия системы, нужно помнить условный характер
этого выражения — возможно, что на самом деле речь
идет об устойчивости установившегося движения электро-
механической системы. Точно так же нужно помнить
условный характер употребляемого здесь слова «сила».
В действительности может оказаться, что члены урав-
нений (6.40), которые мы трактуем как силы, не пред-
ставляют реальные силы, а получились в результате не-
которых математических преобразований. Несмотря на
это, все члены правых частей уравнений (6.40) мы будем
называть силами, действующими на систему.
Задача ставится следующим образом: как определить
характер устойчивости равновесия системы по структуре
действующих сил? Примером решения такой задачи
может служить теорема Лагранжа и ее обращение, на
основании которой вопрос об устойчивости равновесия
консервативной системы решается исследованием одной
потенциальной энергии без привлечения анализа левых
частей уравнений (см. § 3.1 и 3.2).
Кроме уравнений возмущенного движения в форме
(6.40), будем рассматривать случай, когда разложения
всех сил по степеням q и < содержат линейные члены. Длв
таких систем уравнения возмущенного движения при-
водятся к виду
Aq + B,q + Ciq = Q<2>.	(6.42)
g в.З. ПОСТАНОВКА ЗАДАЧИ
165
В этом векторно-матричном уравнении А — опреде-
ленно-положительная симметричная матрица, В1 и С1 —
некоторые квадратные матрицы (элементы всех матриц
постоянные числа); составляющие вектора содержат
координаты qi: и скорости дк в степени выше первой.
Воспользуемся формулами (6.4) и (6.5) и разобьем
матрицы BY и С1 на симметричные и кососимметричные
части. Тогда получим
Aq + Bq + Gq + Cq + Pq = Q(2>.	(6.43)
Кинетическая энергия этой системы определяется ра-
венством (6.41), в котором коэффициенты akj следует счи-
тать постоянными числами. Потенциальные, неконсерва-
тивные позиционные, гироскопические и диссипативные
силы определяются равенствами (6.7), потенциальная
энергия — равенством (6.8), диссипативная функция Ре-
лея — равенством (6.9).
Уравнение возмущенного движения (6.43) можно
представить в двух других формах. Для этого перейдем
к новому переменному вектору х по формуле
q -Ах,
где Л — ортогональная матрица преобразования. После
подстановки в уравнение (6.43) получим
А Ах + В Ах + GAx + С Ах РАх Zv
Умножим слева обе части этого уравнения на транспо-
нированную матрицу Л'
А'А Ах + А'В Ах + A'GAx + А’С Ах + А’РАх = Z, (6.44)
где Z = A'Zj — вектор, составляющие которого содер-
жат Zjr и Z;,- в степени выше первой. Учтем теперь, что
матрицы А и С симметричны и, кроме того, матрица А
определенно-положительна. На основании второй тео-
ремы § 5.3 существует такая неособая ортогональная мат-
рица Л, для которой будут справедливы равенства (5.42).
Пусть Л — такая матрица. Тогда
Л'ЛЛ = Е, А’СА = Со,
где Е — единичная, а Со — диагональная матрицы.
Легко видеть, что матрица А'ВА симметричная, а мат-
рицы A'GA и А’РА — кососимметричные. Действитель-
но, на основании правила транспонирования произведения
166
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
матриц (5.13) имеем
(А'ВА)' = (ВЛ)'(Л')' = Л'В'(Л')'.
Из самого определения следует, что дважды транспо-
нированная матрица равна исходной матрице, т. е. (Л')' =
= Л. Кроме того, матрица В симметричная и, следова-
тельно, В' = В (см. (5.15)). Таким образом,
(А'ВА)' = А'ВА,
что на основании той же формулы (5.15) служит доказа-
тельством симметричности матрицы А'ВА.
Если вместо симметричной матрицы В взять кососим-
метричную матрицу G (или Р), то будем иметь
(А'ВА)' = (ВЛ)'(Л')' = Л'В'Л
или, учитывая, что матрица G кососимметричная и для
нее справедлива формула (5.16), на основании которой
G' = - G,
(А'ВА)' = - А'ВА.
Согласно той же формуле (5.16) заключаем, что мат-
рица А'ВА кососимметричная. Аналогичный вывод спра-
ведлив, конечно, и для матрицы А'ВА.
Учитывая сказанное и принимая во внимание, что
Ей = S, уравнение (6.44) можно записать следующим
образом:
£ + Bit Gz + Соз; + Px — Z,	(<оАЬ)
где для простоты симметричная матрица А'ВА и кососим-
метричные матрицы А'ВА и А'ВА обозначены прежними
буквами В, G и Р соответственно.
До сих пор мы применяли теорему § 5.3 к матрицам
А и С уравнения (6.43). Но эту же теорему можно приме-
нить для матриц А и В. Тогда получим еще одну форму
уравнения возмущенного движения
« + Во« + Git + Сг + В« = Z. (6.46)
В уравнениях (6.45) и (6.46) Со и Во — диагональ-
ные матрицы с вещественными элементами (см. вторую
теорему § 5.3):
Со-
Q 0 ... О
О с2 ... О
О 0 ... с
5
§ 6.3. ПОСТАНОВКА ЗАДАЧИ
167
Таким образом, с помощью линейного ортогонального
преобразования q = Л» уравнение (6.43) можно привести
к одной из двух форм (6.45) или (6.46), причем потенци-
альные, диссипативные, гироскопические и неконсерва-
тивные позиционные силы преобразуются в силы той же
структуры. Очевидно, что из устойчивости (неустойчиво-
сти) относительно координат z и скоростей z следует ус-
тойчивость (неустойчивость) относительно координат q
И скоростей ( и наоборот. Поэтому нас не будет интересо-
вать само преобразование q = Л«, приводящее уравнение
(6.43) к одному из уравнений (6.45) или (6.46). Достаточ-
но знать, что такое преобразование существует.
Рассмотрим в уравнении (6.46) силу сопротивления
— Во« более подробно. Если коэффициент > 0, то со-
ставляющая этой силы — bkik будет замедлять движение,
если же Ьк < 0, то эта составляющая будет ускорять
движение. Будем говорить, что диссипативные силы до-
минируют над ускоряющими, если сумма элементов bk
матрицы Вп положительна; если же < 0, то ускоряю-
щие силы доминируют над диссипативными. При отсут-
ствии ускоряющих сил среди элементов b'k матрицы Во
нет отрицательных (но могут быть элементы, равные
нулю), а при полной диссипации все элементы bk положи-
тельны.
Так как след матрицы и ее определитель являются
инвариантами при ортогональном преобразовании, то
будем иметь следующие тождества:
SpB0= 3	= S &„ = SpS = SpS1, (6.48)
fc=i fc==i
сх . . . cs = det C, det (С + P) = det Cx. (6.49)
Из первого тождества следует, что вопрос о домини-
ровании диссипативных и ускоряющих сил решается ис-
ходной системой (6.42).
Кроме системы (6.43), содержащей линейные члены,
будем рассматривать частично линеаризованные системы,
когда некоторые силы могут не содержать линейных чле-
нов. Дифференциальное уравнение таких систем запишем
в следующем виде:
-А_ (Д4) = — grad П — Bq + Г (q, q) Д- R (q). (6.50)
Здесь A (q) — определенно-положительная матрица,
элементы которой зависят от координат системы q, В —
168
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
постоянная симметричная матрица, а все остальные чле-
ны, стоящие в правой части уравнения, представляют со-
ответственно произвольные потенциальные, гироскопи-
ческие и неконсервативные позиционные силы, удовлет-
воряющие самым общим определениям.
§ 6.4. Коэффициенты устойчивости
Пусть на систему действуют только потенциальные
силы, содержащие линейную часть, а все остальные силы
отсутствуют (D = Г = R = 0). Тогда, пользуясь урав-
нением (6.45), получим
а + Сог = Z.
Это векторно-матричное уравнение эквивалентно s
скалярным уравнениям (напомним, что Со — диагональ-
ная матрица)
+ c1zl — Zj,
	 (6.51)
Zs csz5	Zs,
где функции Zh содержат координаты z7 и скорости z7 в
степени выше первой.
Линейная часть каждого уравнения (6.51) содержит
только одну координату (такие координаты называются
нормальными). Характеристические числа /с-го уравнения
этой системы равны ± |/— Отсюда следует, что если
какое-нибудь число ch положительно, то при отсутствии
соответствующего нелинейного члена Z1; движение в нор-
мальной координате zk будет устойчиво. Если же какое-
нибудь число ск < 0, то движение в этой нормальной
координате неустойчиво независимо от членов высшего
порядка (так как из двух характеристических чисел
± У — ск одно будет положительно — см. теорему Ля-
пунова о неустойчивости движения по уравнениям пер-
вого приближения § 4.3). В связи с этим числа ск назы-
ваются коэффициентами устойчивости системы, а число
отрицательных чисел ск — степенью неустойчивости (эти
определения принадлежат Пуанкаре). В дальнейшем бу-
дет иметь значение не число неустойчивых коэффициентов
Сд, а его четность. Пользуясь первым равенством (6.49)
Ci . . . с# = det С,
§ 6.4. КОЭФФИЦИЕНТЫ УСТОЙЧИВОСТИ
169
можно определить четность степени неустойчивости си-
стемы, не прибегая к непосредственному переходу к нор-
мальным координатам (такой переход представляет боль-
шой интерес в теоретических исследованиях, но осущест-
вить его не менее сложно, чем решить исходную систему).
Действительно, если число отрицательных коэффициен-
тов, ск четное, то произведение с± ... сд положительно
(предполагается, что среди коэффициентов устойчивости
нет нулевых). Но тогда из последнего равенства следует,
что det С 0; если же число отрицательных с(- нечетное,
то произведение с, . . . св отрицательно и, следовательно,
det С < 0; обратные утверждения, очевидно, тоже спра-
ведливы. Таким образом, имеем простое правило; если
определитель матрицы С потенциальных сил исходных
уравнений возмущенного движения положителен, то сте-
пень неустойчивости системы четная, если же det С < 0,
то степень неустойчивости системы нечетная.
Для иллюстрации этого правила рассмотрим два простых
примера.
1. Уравнения возмущенного движения имеют вид
91 + 9г + 5?i Т 2д2	0,
91 + 3<7г 4" ^91 9г ~ 0
Система потенциальная, так как матрица коэффициентов сил, ли-
нейно зависящих от координат, симметричная:
С-|2 Л
Определитель этой матрицы det С = —9 отрицателен. Поэтому,
не приводя уравнения к нормальным координатам, можно утверж-
дать, что система имеет нечетную степень неустойчивости. Так как
число координат равно двум, то имеются одна неустойчивая и одна
устойчивая координаты.
2. Уравнения возмущенного движения имеют вид
91 + 91 + 29з = 0, q2 3q2 -|- q3 = 0, q3 -|- 2qx -|- q2 — 93 = 0.
Матрица коэффициентов сил, линейно зависящих от координат,
1 0
0 -3
2 1
2
1
С =
— 1
симметрична. Поэтому система потенциальна. Определитель ц^т-
рицы del С ~ 14 положителен. Не приводя уравнения к нормаль-
ным координатам, можно утверждать, что если система имеет не-
устойчивые координаты, то число их четное. Легко установить, что
неустойчивые координаты имеются и число их равно двум. Дейст-
вительно, составим главные диагональные миноры матрицы С:
Д1--1>0, Д2 - I 1	Д3 т= det С — 14 > 0.
170
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Так как один из определителей Сильвестра (2.8) для матрицы
коэффициентов потенциальной энергии отрицателен, то система не-
устойчива (см. § 3.1), и, следовательно, должны быть неустойчивые
координаты. Но число их должно быть четным, а всего координат
три. Поэтому система имеет две неустойчивые и одну устойчивую
координаты.
§ 6.5. Влияние гироскопических и диссипативных сил
на устойчивость равновесия потенциальной системы
В реальных условиях на потенциальную систему на-
лагаются диссипативные силы, возникающие за счет
сопротивления среды (омического сопротивления) или
в результате действия специально установленных уст-
ройств. Кроме того, очень часто встречаются системы, на
которые действуют не только потенциальные и диссипа-
тивные, но и гироскопические силы.
Предположим сначала, что невозмущенное движение
г = 0, ж = 0 под действием одних потенциальных сил не-
устойчиво. Естественно возникает вопрос: нельзя лй ста-
билизировать неустойчивое движение, присоединив к по-
тенциальным силам гироскопические силы? Простые
примеры показывают, что в некоторых случаях это
осуществимо. Действительно, потенциальная система
2'1 I cizi —
z2 + c2z2 = 0
(6.52)
при отрицательных с, и с2 неустойчива. Присоединим к си-
стеме гироскопические силы — gz2 и gz± соответственно.
Получим
2i + gZ? 4- C,Z, = 0,
..	.	п	(6.53)
z2 — gZ± + ^2^2 — 0.
Составим характеристическое уравнение этой системы
IZ21?	1=+ci++cic^=°-
I —	-f- ^2 I
Так как в этом уравнении X содержится только в четных
степенях, то каждому корню X будет отвечать корень — X.
Поэтому, если вещественная часть хотя бы одного корня
не равна нулю, то найдется корень, вещественная часть
которого положительна. Из этого следует, что устойчи-
вость наступит только в том случае, если все корни ха-
рактеристического уравнения будут чисто мнимыми чис-
лами, а корни относительно X2 — отрицательными веще-
§ 6.5. ВЛИЯНИЕ ГИРОСКОПИЧЕСКИХ СИЛ
171
ственными числами. Для этого необходимо и достаточно,
.чтобы коэффициенты характеристического уравнения
удовлетворяли следующим условиям:
CiC2 >0, g2 + с1 + с2 > 0, (g2 + ct + с2)2 — 4cjC2 > 0.
Эти три неравенства сводятся к одному условию (напом-
ним, что по предположению сг < 0 и с2 < 0)
I g | > V— ci + К— с-2-	(6-54)
Таким образом, если коэффициент g удовлетворяет
этому условию, то неустойчивая потенциальная система
(6.52) будет стабилизирована добавлением гироскопиче-
ских сил — gz2 и gz±.
Вслед за этим возникает другой вопрос: всегда ли
можно стабилизировать неустойчивую потенциальную
систему гироскопическими силами? Одно из необходимых
условий гироскопической стабилизации определяет сле-
дующая теорема (достаточные условия установлены в ра-
ботах [38, 49]).
Первая теорема Томсона — Тета — Четаева. Если не-
устойчивость изолированного положения равновесия сис-
темы при одних потенциальных силах имеет нечетную
степень, то гироскопическая стабилизация равновесия не-
возможна при любых членах, содержащих координаты
и скорости в степени выше первой х).
Доказательство. Пусть потенциальная система
я + Соя = Z	(6.55)
имеет нечетную степень неустойчивости. Присоединив
к системе произвольные гироскопические силы — Gz, по-
лучим
& -|- G% -|- С$я = Z.
Составим характеристическое уравнение, учитывая,
что Со — диагональная, a G — кососимметричная мат-
рицы
№ + Cj g12l ... glsX
gsiX gsA ... A2 + cs
!) Во всех теоремах этой главы при отсутствии специальной
оговорки рассматривается устойчивость относительно координат
и скоростей, причем за невозмущенное движение принимается г =
= 0, z = 0.
172
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
или, раскрывая определитель и группируя члены по сте-
пеням X,
А = Vs + . . . + а2, = 0.
Свободный член этого уравнения равен, очевидно, произ-
ведению Cj . . . cs (чтобы найти его, достаточно в опреде-
лителе А положить X, = 0):
As = Q" •  Cs-
Из условий теоремы следует, что a2s < 0. Действитель-
но, число отрицательных коэффициентов устойчивости ск
нечетное и среди них нет нулевых (так как положение
равновесия изолированное). Поэтому среди корней харак-
теристического уравнения имеется хотя бы один с поло-
жительной вещественной частью (см. пояснение к форму-
лам (4.23)). Доказательство теоремы следует теперь из
теоремы Ляпунова о неустойчивости движения по урав-
нениям первого приближения (см. § 4.3), и того обстоятель-
ства, что свободный член a2s характеристического урав-
нения не зависит от гироскопических сил.
Прежде чем перейти к исследованию влияния гироско-
пических и диссипативных сил на равновесие устойчивой
потенциальной системы, остановимся на одной формуле,
которая нам понадобится в дальнейшем. Пусть в системе
общего вида (6.40) отсутствуют неконсервативныс пози-
ционные силы	(RK — 0)
d	дТ	дТ	<Ш	n г	гй,
-----з— =-----ч----F /А- +	(6.56)
*	dj*	dq.f.	'
Умножим каждое уравнение на и полученные произ-
ведения сложим. Тогда, учитывая равенство (6.13), по-
лучим после несложных преобразований
-^-(Т + П)=АГ,	(6.57)
где N =	— мощность сил сопротивления '). Если
силы сопротивления однородны относительно скоростей,
то, согласно формуле (6.37), будем иметь
_£(7’ + П) = ^(т + 1)А.	(6.58)
Заметим, что для линейных сил сопротивлений m — 1
и правая часть этих равенств будет равна — 2F (именно
2) Вывод можно найти в любом достаточно полном курсе тео-
ретической механики (см., например, [12]).
§ 6.5. ВЛИЯНИЕ ГИРОСКОПИЧЕСКИХ СИЛ
173
для этого случая формула (6.57) приводится в курсах
теоретической механики).
Вторая теорема Томсона — Тета — Четаева. Если
изолированное положение равновесия системы устойчиво
при одних потенциальных силах, то при добавлении про-
извольных гироскопических и диссипативных сил устойчи-
вость равновесия сохранится.
Доказательство. Воспользуемся формулой (6.57). Так
как мощность N диссипативных сил не положительна,
то будем иметь
±(Т + П)<0.
Учтем теперь, что в положении устойчивого равнове-
сия потенциальная энергия П имеет минимум (см. заме-
чания в конце § 3.2). Поэтому функция Т + П будет
определенно-положительной относительно совокупности
координат qi; и скоростей ((см. доказательство теоремы
Лагранжа § 3.1). Доказательство теоремы следует теперь
из теоремы Ляпунова об устойчивости движения (§ 2.2).
Третья теорема Томсона — Тета — Четаева. Если изо-
лированное положение равновесия системы устойчиво при
одних потенциальных силах, то оно становится асимп-
тотически устойчивым при добавлении произвольных гиро-
скопических сил и сил сопротивления с полной диссипацией.
Доказательство. Функция V (q, () = Т + П опре-
деленно-положительна относительно совокупности коор-
динат q* и скоростей (f. (см. теорему 2). Ее полная произ-
водная по времени в силу уравнений возмущенного дви-
жения определяется равенством (6.57)
dV *Tf -X
У (?,<;).
На многообразии К {q =/= 0, q = 0) производная F
равна нулю, а вне этого множества она отрицательна (по
условию теоремы диссипация полная — см. равенство
(6.39)). Покажем, что многообразие К не содержит целых
траекторий системы (6.56). Действительно, при q = 0 ки-
нетическая энергия Т, силы сопротивления I) (q, () и ги-
роскопические силы Г {q, () обращаются в нуль (см. равен-
ства (6.41) и (6.38)). Следовательно, при q = 0 и q'0
уравнения (6.56) принимают вид
=0	(*=!,. ...s),
174
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
что невозможно при изолированном положении равнове-
сия потенциальной системы *). Доказательство теоремы
следует теперь из теоремы II. И. Красовского об асимпто-
тической устойчивости (§ 2.3).
В начале этого параграфа было показано, что в неко-
торых случаях неустойчивую потенциальную систему
можно стабилизировать гироскопическими силами. При
доказательстве мы не учитывали диссипативные силы.
Рассмотрим сейчас, какое значение имеют эти силы для
гироскопической стабилизации.
Четвертая теорема Томсона — Тета — Четаева. Если
в окрестности изолированного неустойчивого положения
равновесия консервативной системы потенциальная энер-
гия может принимать отрицательные значения, то при
добавлении сил сопротивления с полной диссипацией и
произвольных гироскопических сил равновесие останется
неустойчивым.
Доказательство. Запишем равенство (6.57) в следую-
щей форме:
у1^_(7’ + П).
Рассмотрим прежнее многообразие К (q =/= 0, q = 0).
На нем Pj = 0, а вне его Pj 0 (диссипация полная и,
следовательно, N < 0 при с =/= 0). По условию теоремы
в окрестности нуля существуют точки, в которых П < 0.
В этих точках при q = 0 функция VT принимает положи-
тельные значения. Кроме того, многообразие К не содер-
жит целых траекторий системы (6.56) (по тем же сообра-
жениям, что и в предшествующей теореме). Доказатель-
ство теоремы следует теперь из теоремы Н. И. Красов-
ского о неустойчивости движения * 2).
*) В положении равновесия q = 0 потенциальной системы
должны выполняться равенства (3.2)
=.0 tk I,...,«).
Если частные производные равны нулю в окрестности положе-
ния равновесия при q =t= 0, то равновесие ие изолировано.
2) Все теоремы этого параграфа были сформулированы Томсо-
ном и Тетом в 1879 г. [58]. Строгое доказательство этих теорем для
нелинейных систем в некритических случаях принадлежит Н. Г. Че-
таеву [49]. Возможность распространить эти теоремы на нелиней-
ные системы общего вида была доказана в шестидесятых годах на-
шего столетия различными авторами.
§ 6.6. ПРИМЕНЕНИЕ ТЕОРЕМ ТОМСОНА — ТЕТА — ЧЕТАЕВА 175
Из доказанной теоремы следует, что если неустойчи-
вую потенциальную систему стабилизировать гироскопи-
ческими силами (см. начало параграфа), То даже малые
силы сопротивления с полной диссипацией (практически
они всегда существуют) разрушат с течением времени дос-
тигнутую устойчивость. Поэтому устойчивость, сущест-
вующую при одних потенциальных силах, Томсон и Тет
назвали вековой, а устойчивость, полученную с помощью
гироскопических сйл, — временной.
В примере 3 следующего параграфа будет показано,
что если кроме дйссипативных сил имеются ускоряющие
силы, то гироскопическая стабилизация неустойчивой
потенциальной системы может быть осуществлена.
Остановимся еще на физической интерпретации ра-
венств (6.57) и (6.58). Выражение Т + П представляет
полную механическую (электромеханическую) энергию.
При полной диссипации мощность N < 0, а функция Ре-
лея F 0. Поэтому
4(НП)<°-
Отсюда следует, что с течением времени Полная энер-
гия Т + П убывает, рассеивается (разумеется, не исче-
зает, а переходит в другие виды энергии, например в теп-
ловую). Мощность N и функцию Релея F на основании
формул (6.57) и (6.58) можно рассматривать как меру рас-
сеивания полной энергии Т + П. Этим и объясняется
причина, по которой силы положительного сопротивления
называют диссипативными силами, а соответствующую
функцию Релея F — диссипативной функцией (лат. dis-
sipare — рассеивать).
§ 6.6. Примеры на применение теорем
Томеона — Тета — Четаева
Пример 1. Устойчивость волчка. Определяя поло-
жение оси z волчка углами а я Р (см. пример 3 § 2.6 и рис. 2.15),
мы видим, что обё координаты при невращающемся волчке неустой-
чивы (так как центр тяжести С находится выше точки опоры
(рис. 6.1, а)). Таким образом, волчок имеет четное число неустойчивых
координат И неебходимое условие, налагаемое первой теоремой
Томсона и Тета, выполнено. Дифференциальные уравнения первого
приближения возмущенного движения волчка в переменных а и 0
были получены в примере 4 § 4.5 (см. (4.49)):
1ха + J — Pla. = 0,
Z0 = 0.	(6-59>
176
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Эти уравнения можно рассматривать как результат наложения
на неустойчивую потенциальную систему
J — Р1а — О, — Р/р = О
гироскопических сил JznP и —Jzna соответственно.
Уравнения (5.59) совпадают с уравнениями (6.52), если поло-
жить
Условие гироскопической стабилизации (6.54) принимает в
данном примере вид
J2nlJx>2]/HiTx
или
> iPlJx.
Это условие было получено в примере 3 § 2.6 в нелинейной поста-
новке задачи (см. соотношение (2.33)).
Если центр тяжести С будет ниже точки подвеса (гироскопи-
ческий маятник) (см. рис. 6.1, б), то обе координаты а и Р будут
устойчивы. Согласно второй теореме Томсона и Тета, в этом случае
устойчивость будет достигаться при любой угловой скорости п.
На основании четвертой теоремы Томсона — Тета -- Четаева ус-
тойчивость волчка временная, а устойчивость гиромаятника
вековая.
Пример 2. Устойчивость системы инерциаль-
ной навигации. При использовании систем инерциальной
навигации для определения координат движущегося объекта (под-
водной лодки, самолета, космического корабля и т. и.) измеряют
обычно его линейное ускорение и угловую скорость относительно
инерциальной системы отсчета. Для этой цели могут быть ис-
пользованы различные устройства, в частности платформа с тремя
§ 6.6. ПРИМЕНЕНИЕ ТЕОРЕМ ТОМСОНА — ТЕТА — ЧЕТЛЕВЛ 177
гироскопами (они измеряют составляющие абсолютной угловой
скорости) и тремя акселерометрами пх, пу, nz (они называются также
ньютонометрами) (рис. 6.2). Предположим, что в невозмущенном
движении точка О платформы пере-
мещается с постоянной скоростью
по параллели Земли, принимаемой
за правильный шар, причем оси
х, у, z, жестко связанные с плат-
формой, ориентированы географи-
чески (ось х направлена на восток
ось у — на север, а ось z — вер-
тикально вверх). В работа [3] по-
лучены следующие дифференци-
альные уравнения возмущенного
движения точки О в предположе-
нии, что ориентация платформы
не нарушается:
£M + 2g> d<6z) ...
dt2 г dt v dt '
+ (“о ~ “a ~ “Ь Ьх = °’	Рис. 6J2
+ 2ог + (о2 - О)2) бу +	= о, (6.60)
+ шУы^у ~ (2“о + “Ф = °-
В этих уравнениях х, у, z — координаты точки О в невозмущенном
движении в' системе О^у^ (Oj — центр Земли, оси OjXj, Огуг,
O1z1 параллельны осям Ох, Оу, Oz), бх, бу, бг — отклонения соот-
ветствующих координат в возмущенном движении, шу, саг — проек-
ции абсолютной угловой скорости платформы на оси у и z (при
рассматриваемом движении а>ж = 0), о>о = ц/r3, где ц — гравита-
ционная постоянная Земли, г — расстояние от центра Земли до
точки О в невозмущенном движении.
Для удобства изменим масштаб времени, положив
т = COof,	(6.61)
и введем безразмерные положительные параметры
св2 о
“ = Ч1	~4 	(6-62>
“о	("о
Тогда уравнения возмущенного движения (6.60) примут вид
j 1 — 2 Р -|- 2 yf а#з -р (1 — а — Р) - - 0,
х2+2рг^1 + (1-Р).т2+ |Лгфхг3 = 0,	(6.63)
у3 _ 2 У а + |/аР х2 — (2 + а) х3 = 0.
Здесь Xj — бх, х2 — бу, х3 = 6z, точками обозначены произвол
ные п
Исследование устойчивости движения х^ = 0 упрощается, если
применить теоремы Томсона — Тета — Четаева.
178
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Матрица коэффициентов сил, линеййо зависящих от х„, х3,
симметрична. Поэтому уравнения (6.63) можно рассматривать как
результат наложения на потенциальную Систему
.т'1 -I- (1 — а — P)_xt = О,
а:3 -j- (1 — Р) х2 -|- |ЛаР;г3 = 0,	(6.65)
х3 + У— (2 + а)*з ~ °
гироскопических сил
—2 |/р f2 -|- 2 /а х3, 2 У jT.ii, — 2 У а Л
соответственно.
Координата хг нормальная (первое уравнение (6.65) не связано
с Двумя другими). Эта коорди-
ната устойчива, если
“+Р<1,	(6.66)
и неустойчива при
а + Р>1.	(6.67)
На плоскости а, Р область
устойчивости координаты xt
находится в первом квадранте
(а > О, Р > 0) ниже прямой
а + Р = 1; область неустойчи-
вости выше этой прямой
(рис. 6.3).
Перейдем к рассмотрению
последних двух уравнений
(6.65) ч составим матрицу коэффициентов потенциальных сил:
1-Р /йГ II
У “Р	— (2 + а) II
Найдем главные диагональные миноры:
* = 1 - Р, А* = -а + 2Р - 2.	(6.68)
Ниже прямой — а + 2р — 2 = 0 определитель А* < 0, по-
тому средн координат х2 и х3 одна устойчива и одна неустойчива;
выше этой прямой Д2 > 0 и, следовательно, обе координаты не-
устойчивы (так как При этом А* < 0) (рис. 6.3).
Из сказанного следует.
1.	В области I (рис. 6.3) координата хг устойчива, а среди
координат .т2 и х3 одна устойчива и одна неустойчива, т. е. в этой
области имеется всего одна неустойчивая координата.
2.	В области II две координаты неустойчивы (ij и одна Нз х2
и х3).
§ 6.6. ПРИМЕНЕНИЕ ТЕОРЕМ ТОМСОНА — ТЕТА — ЧЕТАЕВА 179
3.	В области III все три координаты неустойчивы.
На основании первой теоремы Томсона и Тета гироскопическая
Стабилизация в областях I и III невозможна. Выясним, можно ли
осуществить гироскопическую стабилизацию в области II. Для
этого составим характеристическое уравнение системы (6.63):
Х2 + (1-а-0)
2 /0А.
— 2 |/+А
— 2 [/0А
+ (К- 0)
1Л“0
2 |/+А
/“0
А2 — (2 + а)
= 0.
(6.69)
Раскрывая определитель и группируя члены, приведем это урав-
нение к виду
<4 А4 + а2А2 + а3 = 0,	(6.70)
где
at = 2 (а + 0), а2 = (а + 0)2 — 3 (1 — а + 20),
а3 = (1 - а - 0)(-а + 20-2).	'
Так как характеристическое уравнение (6.70) содержит А, толь-
ко в четных степенях, то для устойчивости движения необходимо
и достаточно, чтобы все корни этого уравнения были чисто мнимы-
ми. Это означает, что корни относительно А,2 должны быть отрица-
тельны и вещественны. Этим условиям можно удовлетворить, если
подчинить коэффициенты а к критерию Гурвица (4.30)
aj >0, а2 > 0, а3 >0, Д2 = aLa2 — а„а3 > 0	(6.72)
и условию вещественности корней кубического относительно А,2
а1
уравнения (6.70). Для этого с помощью подстановки v — А.2 —
преобразуем уравнение (6.70) к виду
v3 + pv + q = 0
и потребуем, чтобы выполнялось неравенство *)
Выражая с помощью указанной подстановки р и q через коэффи-
циенты ах, а2 и а3, преобразуем последнее неравенство к виду
Q = а] (4а2 — а^) + 27 а3 + 2аха3 (2а^ — 9а2) < 0. (6.73)
Выразим с помощью формул (6.71) условия (6.72) и (6.73) че-
рез параметры а и 0 и выделим в области II ту ее часть, в которой
осуществляется гироскопическая стабилизация. Для этого напом-
ним прежде всего, что параметры а и 0 положительны и, следова-
тельно, неравенство аг >• 0 выполняется автоматически. Кроме
того, в области II коэффициент а3 >• 0, а на прямых 1 и 2
*) Существуют критерии, при выполнении которых все корни
уравнения аохп + а^”"1 + . . . + ап-1х + ап = 0 вещественны
и отрицательны (см., например, [14]).
180
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
(рис. 6.3 и 6.4) а3 = 0. Построим отрезки кривых
а2 (а, 0) = 0,
Д2 (а, р) = 0,
о («, Р) — 0,
находящиеся в области II (вне этой области стабилизация невоз-
можна). При построении полезно отметить, что все эти кривые
пересекают прямые 1 и 2 в одних и тех же точках А (8/9, 1/9) и
В (4/3, 5/3). Действительно, на этих прямых а3 = 0 и функции Д2
и Q обращаются в нуль одновременно с а2 (при а3 = 0 имеем Д2 =
= а2а2, Q = 4а] — а]а]). Легко установить, что левее кривых
а2 — 0 и Д2 = 0 функции а2 и Д2 отрицательны, а правее — поло-
жительны. Кроме того, <2 > 0 левее кривой Q = 0 и Q <; 0 правее
этой кривой. Таким образом, в области II правее кривой <2 = 0
одновременно выполняются все неравенства (6.72) и (6.73) и, сле-
довательно, в этой области осуществляется гироскопическая ста-
билизация (кривые а2 = 0 и Д2 = 0 пересекают область II только
по линиям, изображенным на рис. 6.4; часть кривой <2 = 0, кроме
той, что показана на рисунке, находится в области II, но она рас-
положена левее кривых а2 = 0 и Д2 = 0, где а2< 0 и Д2 </ 0).
Пример 3. Гироскопический однорельсовый
вагон. В первой четверти XX столетия появились опытные
образцы однорельсового вагона и двухколесного автомобиля,
центр тяжести которых был выше рельса (дороги) (рис. 6.5). Вер-
тикальное положение самого вагона (автомобиля) неустойчиво, и
для стабилизации использовался гироскоп Г.
Прежде чем установить количественные соотношения, которым
должны удовлетворять параметры системы для того, чтобы обеспе-
чить стабилизацию вертикального положения вагона, рассмотрим
вопрос с качественной стороны. Центр тяжести G вагона находится
выше рельса, поэтому угол ф, определяющий отклонение вагона
от вертикали, является неустойчивой координатой. По первой тео-
реме Томсона — Тета — Четаева гироскопическую стабилизацию
можно осуществить только при четном числе неустойчивых коог-
§ 6.6. ПРИМЕНЕНИЕ ТЕОРЕМ ТОМСОНА — ТЕТА — ЧЕТАЕВА 181
Рис. 6.5
динат. Из этого следует, что вторая координата системы О (угол
поворота кольца К, в котором установлен гироскоп) должна быть
тоже неустойчивой. Для этой цели к верхней части кольца прикреп-
ляют грузик L. Таким образом, система имеет две неустойчивые
координаты ф и # и гироскопическая стабилизация в принципе
может быть осуществлена.
Учтем теперь силы сопротивления, возникающие при колеба-
ниях вагона и кольца с гироскопом (эти силы возникают за Счет
сопротивления среды и трения в опорах). Согласно четвертой тео-
реме Томсона — Тета — Четаева, эти
силы разрушат гироскопическую ста-
билизацию (так как без гироскопа си-
стема неустойчива). Поэтому для стаби-
лизации необходимо ввести силы другой
природы. С этой целью на оси N — N
вращения кольца К устанавливалось
специальное электромагнитное устрой-
ство (на рисунке оно не показано),
которое создавало ускоряющий момент
/с2Д, действующий в сторону вращения
кольца и пропорциональный угловой
скорости вращения его (в теории коле-
баний такие моменты и силы называ-
ются отрицательным трением).
Установив с помощью теорем Том-
сона и Тета характер сил, которые долж-
ны обеспечить устойчивость однорель-
сового гироскопического вагона, перей-
дем к количественному анализу. Для
этого воспользуемся дифференциальными уравнениями возмущенно-
го движения системы (эти уравнения без труда составит читатель,
воспользовавшись уравнениями Лагранжа II рода или уравнения-
ми моментов (см. также [42])):
где
Ajijj + AjTp — ЯО — стф = Т,
Л2$ — М + Яф — с2Ф = 6,
At = 1 + {М + Мд)а2 + А + Сд,
Аг = Ло + A, ст = Р-с, с2 = р -Ь.
Здесь Ло и Сд — моменты инерции кольца, Мд—его масса,
А — экваториальный момент инерции гироскопа, М — его масса,
J — момент инерции вагона относительно оси рельса, Р — вес
вагона, р — вес добавочного грузика L, Н — кинетический мо-
мент гироскопа,, кг — коэффициент сил сопротивления, действую-
щих на вагон, к2 — крутизна характеристики устройства, создаю-
щего ускоряющую силу кг&, значения постоянных а, Ь и с видны
из рис. 6.5 (G — центр тяжести всей системы, исключая грузик L),
У и 0 — нелинейные члены.
Уравнения (6.74) можно рассматривать как результат наложе-
ния на неустойчивую потенциальную систему
Лтф — стф = О, Аг& — с2й = 0
182
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
гироскопических сил — Яй и Hty, диссипативной силы /схф, уско-
ряющей силы — kJ} и нелинейных сил Тиб соответственно.
Составим характеристическое уравнение
I ЛХА,2 кгк — сх — Нк I
| Нк AV - к.Л - с. I = °
или, раскрывая определитель и группируя члены,
	zZqX4	+ а2№ 4“	-j- (Z4 — 0,	(6.76)
где	а0 — А1-4 2т	— М2 ^2-^1’ tz2 = Н2 — с2А1 — сгА2 — kYk2l	(6.77)
dg ^gCx	dj CxCg.
Воспользуемся критерием Гурвица (4.32) для системы четвер-
того порядка (ао > 0):
dx >
0,
dg
о,
о,
d4
о,
аз >
Дд -- dxdgdg	0.
В нашем случае условия d0 > 0 и d4 > 0 выполняются автомати-
чески, а условие а2 > 0 следует из неравенства Д3 > 0.
Подчиняя с помощью формул (6.77) параметры системы остав-
шимся условиям (dx >0, d3 > 0, Д3 > 0), легко найдем
Сд	Лд
— ^1 < *2 <	*1,
Н2 СдЛх СхЛд к^к2
-Д1-Д-2 (h'Si — kjC.)2 Ч~ cic2 (^i-Дд — ^г-^х)2
(А?дСх — А^хСд) (&x*4g — Ml)
(6.78)
Первое условие устанавливает пределы для крутизны к2 ха-
рактеристики устройства, создающего ускоряющий момент, второе
условие определяет нижнюю границу кинетического момента Я.
Так как при выполнении условий (6.78) все корни характеристи-
ческого уравнения будут иметь отрицательные вещественные части,
то на основании первой теоремы Ляпунова об устойчивости по пер-
вому приближению однорельсовый вагон асимптотически устойчив
независимо от членов высшего порядка ’Гиб.
Из формул (6.77) видно, что при к2 < 0 (вместо ускоряющего
момента имеется обычная сила сопротивления) коэффициент d3
будет отрицателен и система в соответствии с четвертой теоремой
Томсона — Тета — Четаева сделается неустойчивой х).-
х) Во многих вузах имеются модели однорельсового гироско-
пического вагона. При демонстрации необходимо следить за тем,
чтобы грузик кольца занимал верхнее вертикальное положение;
при колебаниях кольца нужно слегка подталкивать его в сторону
движения, имитируя ускоряюш.ее устройство.
§ 6,7. ГИРОСКОПИЧЕСКИЕ И ДИССИПАТИВНЫЕ СИЛЫ 183
§ 6.7.	Устойчивость равновесия под действием
одних гироскопических и диссипативных сил. Пример
До сих пор рассматривались системы, в которых дис-
сипативные и гироскопические силы действовали вместе
с потенциальными силами. Между тем в приложениях
встречаются системы, в которых диссипативные и гиро-
скопические силы действуют без потенциальных сил. Изу-
чению устойчивости таких систем посвящен этот параграф.
а.	Одни гироскопические силы. Рас-
смотрим вначале случай, когда на систему действуют
только гироскопические силы, считая, что уравнения
возмущенного движения приведены к форме
ё + Gz = 0.	(6.79)
Теорема 1. Равновесие системы, на которую действуют
одни гироскопические силы, всегда устойчиво относитель-
но скоростей [38].
Доказательство. Умножим справа обе части уравнения
(6.79) на матрицу z. Тогда, учитывая, что для кососиммет-
ричной матрицы G имеет место равенство Gz-z =0 (см.
формулу (5.25)), получим
Z'Z =0
или, интегрируя,
z • z = -у (ii + ^2 + ... + is) ~ h, (6.8 *)
где h. — постоянная интегрирования.
1
Функция V = -у z • z удовлетворяет всем условиям тео-
ремы Ляпунова об устойчивости движения (она опре-
деленно-положительна и ее полная производная по вре-
мени в силу уравнений возмущенного движения тождест-
венно равна нулю (см. § 2.2)), что доказывает теорему.
Примечаиие. Теорема доказана для линейной автоном-
ной системы, но она справедлива й для линейной неавто-
номной системы, когда гироскопическая матрица G зави-
сит явно от времени (равенство Gz-z — 0, на котором ба-
зируется доказательство теоремы, справедливо для любой
кососимметричной матрицы, зависящей явным образом
от времени), а также для нелинейной системы (см. статью
В. В. Румянцева [45]).
Устойчивость равновесия определяется, конечно, не
только устойчивостью в скоростях, но и устойчивостью
184
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
в координатах. Следующая теорема устанавливает необ-
ходимые и достаточные условия устойчивости системы
(6.51) относительно совокупности координат и скоростей.
Теорема 2. Для того чтобы равновесие линейной авто-
номной системы, находящейся под действием одних гиро-
скопических сил, было устойчивым относительно коорди-
нат, необходимо и достаточно, чтобы определитель
матрицы гироскопических сил не равнялся нулю [38].
Доказательство. Докажем вначале, что если det С?у=О,
то невозмущенное движение z = 0, s = О устойчиво от-
носительно координат » (устойчивость относительно ско-
ростей доказана предыдущей теоремой при любом значе-
нии det G). Проинтегрируем уравнение (6.79) один раз по
времени
# + Gz = D,	(6.81)
где D — постоянная интегрирования матрица-столбец
определена равенством
D = «о Ч- G&o.	(6.82)
Перейдем к новой переменной матрице у по формуле
» = У + G~lD	(6.83)
(так как по условию матрица G неособенная, то обратная
матрица G~l существует). После подстановки в уравне-
ние (6.81) получим
У + Gy + GG4) = D
или, учитывая тождество GGlJ) = ED = D,
у + Gy = 0.	(6.84)
Согласно теореме 1 этого параграфа, движение устой-
чиво относительно скоростей х. Из совпадения форм
уравнений (6.79) и (6.84) следует, что движение устойчиво
относительно у. На основании равенств (6.82) и (6.83)
заключаем, что движение устойчиво относительно коор-
динат » (при достаточно малых по модулю и эле-
менты' матрицы D будут также малы).
Докажем теперь необходимость условия теоремы.
Для этого достаточно показать, что при det G = 0 систе-
ма неустойчива. Составим характеристическое уравнение
§ G.7. ГИРОСКОПИЧЕСКИЕ II ДИССИПАТИВНЫЕ СИЛЫ
185
для дифференциального уравнения (6.79):
д~- det(EA2 + GA) —	A2 gi3A. gaiA А2 .	Si,1	(>.	(6.85)
	gslA gs.,A.	. A2		
Вынесем из каждой строки общий множитель А:		
	А	• .. gls	
A—7s	?21 А . . . g,s	= 0
	^A'l ?S2 * • •	
и разложим полученный определитель по степеням А:
А = А8 (А8 4* .... 4* а5) = 0.
Очевидно, что
0	£12 • • . gls
Ssl gsi-'-V
- detG.
Из условия det G = 0 и последних двух равенств
следует, что уравнение (6.85) имеет не менее s + 1 нуле-
вых корней.
Перейдем теперь к исследованию элементарных дели-
телей характеристической матрицы (см. § 5.3)
A2 gi2A • • . gi5A
g2iA А2 ... g2sA
gslA gs3k . .. А2
Обозначим через D]; общие наибольшие делители всех
миноров к-го порядка. Очевидно, что Dx = A, D2 делится
на A2, D3 делится на А3 и т.д. (так как все элементы этой
матрицы имеют общий множитель А). Поэтому все инва-
риантные множители
Е^у^- (А = 1, 2,..., s; Z>o—1)
делятся на А, т. е. каждый инвариантный множитель
£”к(А) имеет по крайней мере один нулевой корень.
Воспользуемся формулой (5.28):
х det F (А) = Ег (А)	(А) . . . . Ев (А),
186	ГЛ, VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Так как число нулевых корней левой части не менее
s + 1, а в правой части имеется s инвариантных множите-
лей Ех (А), то хотя бы один из них содержит нулевой
корень кратности больше первой. Это доказывает неустой-
чивость системы (см. § 5.4 с. 146).
Следствие. Если на систему действуют только гиро-
скопические силы и она имеет нечетное число координат,
то равновесие такой системы всегда неустойчиво (если s —
нечетное число, то det G тождественно равен нулю (см.
§ 5.2, с. 129)).
Примечание 1. Так как невозмущенное движение устой-
чиво относительно скоростей при любом значении det G,
то из доказательства неустойчивости системы следует,
что при det G = 0 система теряет устойчивость только
в координатах.
Примечание 2. Если det G У= 0, то характеристиче-
ский определитель системы имеет ровно s нулевых корней.
Из устойчивости системы следует, что эти корни простые
для элементарных делителей.
Примечание 3. Уравнение (6.79) во многих случаях
представляет уравнение первого приближения нелинейной
системы, на которую действуют только гироскопические
силы. Конечно, из устойчивости движения при det G =# О,
определяемого уравнением первого приближения, не следует
устойчивость исходной нелинейной системы.
б.	Гироскопические и диссипатив-
ные силы. Прежде чем перейти к исследованию влия-
ния диссипативных сил, приведем один результат теории
определителей, который понадобится нам и в других раз-
делах (доказательство будет приведено в конце параграфа).
Пусть даны две квадратные матрицы одного порядка
s: одна матрица Во — знакоопределенная диагональная и
вторая G — кососимметричная. Составим определитель Д
матрицы Во + (?:
Д = det (Во + (?).
Тогда справедливы следующие утверждения.
1.	Матрица Во + G неособенная, т. е.
Д = det (Во + (?) Ф 0.	(6.86)
2.	Если матрица 50 определенно-положительна, то
Д = det (Бо + (?) > 0.	(6.87)
§ fl.7. ГИРОСКОПИЧЕСКИЕ И ДИССИПАТИВНЫЕ СИЛЫ 187
3.	Если матрица Во определенно-отрицательна, то
при s четном Д = det (Во + G) > 0,	(6.88)
при s нечетном Д = det (Во + G) < 0.	(6.89)
Рассмотрим теперь влияние диссипативных сил.
Теорема 3. Если помимо гироскопических сил действуют
силы полной диссипации, то равновесие системы асимпто-
тически устойчиво относительно скоростей и просто ус-
тойчиво относительно координат [38].
Доказательство. Приведем уравнения возмущенного
движения к виду (6.46), учтя, что по условию теоремы
имеются только гироскопические и диссипативные силы,
« + Во& + Gz — 0.	(6.90)
В атом уравнении G — кососимметричная, а Во — опре-
деленно-положительная диагональная матрицы (так как
диссипация является полной). Умножим обе части этого
уравнения на матрицу
а  ® + Во% -х + Gz •» — о
или, преобразуя первое слагаемое и принимая во внима-
ние, что для кососимметричной матрицы Gz-z =0, будем
иметь
4--^-(«•«)= —5о« •«.
2 at '	’
В развернутой форме это равенство имеет вид
-у у (zx + . . . + Zs) — — (&1Z1 + • • • + ^sZg).
тт 1	.	.	1/.2	«2\
Функция V	4- ... 4- zs) удовлетворяет
всем условиям теоремы Ляпунова об асимптотической
устойчивости — она определенно-положительна относи-
тельно скоростей «jr и ее полная производная по времени в
силу уравнения возмущенного движения (6.90) является
определенно-отрицательной функцией тех же величин zk
(по условию теоремы диссипация полная и, следовательно,
все bk > 0). Таким образом, движение асимптотически
устойчиво относительно скоростей zt.
Перейдем к доказательству второй части теоремы.
Проинтегрируем уравнение (6.90) один раз по времени:
® 4~ (-®о + G)« = D,	(6.91)
188
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
где постоянная матрица D определена равенством
D = 20 + (Во + G)z0.	(6.92)
Согласно равенству (6.86) матрица Во + G неособен-
ная, вследствие чего существует обратная матрица
(Во + G)"1. Введем новую переменную матрицу у, опре-
делив ее равенством
z = у + (Во + G)~lD.	(6.93)
После подстановки в уравнение (6.91) получим
у + (Bo + G) у + (Во + G)~l(B0 + G)D=I)
или, учитывая, что (Во + G)~l (Во + G) D = JJ,
у + (B0 + G)y = 0.	(6.94)
Согласно первой части теоремы, движение асимптоти-
чески устойчиво относительно скоростей z. Из совпадения
форм уравнений (6.90) и (6.94) следует, что движение
асимптотически устойчиво относительно у. На основании
равенств (6.93) и (6.92) заключаем, что движение устой-
чиво (но не асимптотически) относительно координат z.
Примечание. Теорема остается справедливой и в нели-
нейной постановке задачи [36, 38].
Пример. Исследование устойчивости дви-
жения электрона в постоянном магнитном
поле. Если т — масса электрона, е — его заряд, Н — напря-
женность магнитного поля, с — электродинамическая постоянная,
равная скорости света (с = ЗЛО10 см/сек), то уравнение движения
электрона при Н = const будет
dv е
m~dT = х	(6.95)
где v — вектор скорости электрона [48].
Запишем это уравнение через проекции на оси неподвижной
системы координат:
,	i	j	к
dv е
m~dt — ~ ±	У	z - °-
IIX Hv Hz
Отсюда найдем
тх	---— Н2у + — ну = 0,
ту + Н; i	ну -- 0,	(6.96)
.. е	Iе
,nz ~ Т ~ Нхй -- °-
§ 6.7. ГИРОСКОПИЧЕСКИЕ И ДИССИПАТИВНЫЕ СИЛЫ
189
В этих уравнениях матрица сил, линейно зависящих от скорос-
тей ±, у, i, кососимметричная. Следовательно, эти силы гироско-
пические. Так как другие силы отсутствуют, то на основании тео-
ремы 1 этого параграфа заключаем, что невозмущенное движение
электрона устойчиво относительно скоростей х, у, z, а на основании
следствия теоремы 2 оно неустойчиво относительно совокупности
всех координат х, у, z (так как число координат равно трем).
Если ось z направить параллельно вектору И, то Нх = О,
ffv = О, Hz = Н и уравнения (6.96) примут вид
тх
--^Яу = 0,
е
mij + — Hi
m’i
= 0,
= 0.
Рассмотрим первые два уравнения отдельно (они не зависят от
третьего уравнения). Определитель матрицы гироскопических
коэффициентов для этих уравнений
отличен от нуля, поэтому, согласно теореме 2, движение электрона
устойчиво относительно координат х и у. Что же касается коорди-
наты z, то из третьего уравнения имеем z = zot -|- z0, откуда сразу
видна неустойчивость по этой координате.
В заключение этого параграфа докажем соотношения
(6.86)—(6.89).
Введем вспомогательный параметр р и составим определитель
Д (р) = det (рВ0 + G) =
Р*>1 ?12	• • • £Г1в
ё-л рЬ2 ••• g2s
(6.97)
^Si ^2	•••
Очевидно, что искомый определитель Д получается из Д (р) при
р = 1:
(6.98)
Д = Д (1).
Вычислим Д (—р) = det (—рВ0 -|- G). Поменяем в этом опре-
делителе строки на столбцы и наоборот (определитель от этого не
изменится). Эта операция равносильна замене матриц Во и G на
транспонированные:
А (—Р) = det (—рВ0 + G) “ det (—рй' + G').
Учтем теперь, что матрица Во диагональная, a G кососимметричная.
Поэтому
Во — Во, G — —G'.
190
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Внося эти выражения в Д (—р), получим
- |xbt ... - gls
Д (— р) — det (— р_В0 — G) —
-gsl ••• - нь,
Вынесем из каждой строки общий множитель —1:

gii	gJS
git	• • • g2S
gSl g.,2 
или, принимая во внимание равенство (6.97), получим
Д(-р) = (1)Д(р).	(6.99)
Отсюда следует, что при s четном Д (р) содержит р только в
четных степенях, а при s нечетно.л — в нечетных степенях, т. е.
Д (р) = аор + a2ps + . . . + <z.._ р2 + as	(s = 2к),
Д (р) = р (aops-1 + a2ps-:i +... + as_3p2 + а^) (s = 2к + 1),
(6.100)
где ак- — некоторые коэффициенты.
Пользуясь теперь равенством (6.98), ьолучпм
Д = «о + а2 +••• + as-i + ач	(« = 2Л),
Д = а0 + я2 + ••• + аз-з "Ь a.<-i (s ~	+ !)•
Рассмотрим теперь структуру коэффициентов а\. Параметр
р содержится в определителе (6.97) множителем элементов, стоящих
на главной диагонали. Поэтому
а0 = Ъ,Ъ, . . . Ъ..	(6.102)
Перейдем к другим коэффициентам а2, а4 и т. д. Возьмем для
примера аг. Этот коэффициент стоит в равенствах (6.100) множи-
телем при ps-2. Такой множитель может нолучиться в разложении
определителя (6.97), если взять любые s — 2 элемента главной диа-
гонали и умножить их на минор, который получается из матрицы G
вычеркиванием всех строк и столбцов, пересекающихся на выбран-
ных элементах. Так, например, если мы возьмем элементы
Ьг, Ь2, . . ., bs_3, то соответствующий минор будет
^1,2,..., S-3
0	^s-1,
Ss, s-i °
' ^s-1, s’
а для элементов b3, bit . . b„
I 0
0 | - ®12*
дз,’
g.l
Взяв всевозможные сочетания из s элементов главной диаго-
нали по s — 2 элемента и умножив их на соответствующие миноры,
? 6.8. ВЛИЯНИЕ НЕКОНСЕРВАТИВНЫХ СИЛ
191
получим
а., — V Ь„ Ь„ ... Ь„ Д„ „
- z.' 04 аз а3_,, а,,..., ай.„..
Здесь сумма распространена на все сочетания индексов а4,
. . . , а5_, из 1,2,	а Да а — диагональные миноры
матрицы G, получающиеся из нее вычеркиванием строк и столб-
цов с индексами а4, . .	as_2. Эти миноры представляют собой
иососимметрцчные определители второго порядка, и, следователь-
но, ори не отрицательны. Для коэффициентов а4, а* и т. д. получим
аналогичные суммы, в которых соответствующие миноры будут
иметь четвертый, шестой и т. д. порядок.
В общем случае будем иметь (п — четное число)
а, п = у h Ь„ ... Ь„ А„ „ ,	(6.103)
где
Д„ „	>0	(6.104)
(как кососимметричные определители четного порядка).
Пусть теперь все &п 6а, . . ., bs положительны (В„ — опреде-
ленно-положительная матрица). Тогда, принимая во внимание
(6.102)—(6,104), получим
а0 > 0, <zs_n > 0 (п = 2, 4, . . .).
Пользуясь равенствами (6.101), найдем А > 0, что доказывает
соотношение (6.87).
Рассмотрим теперь случай, когда все Ь^ <; 0 (Вв — определен-
но-отрицательная матрица) и s — четное число. Тогда в равенстве
(6,103) число множителей 6^ будет четное, произведение Ъа . . . Ьа
четцого числа отрицательных чисел Ьк будет положительно и все
> 0 (п = 2, 4, . . ., s). Принимая во внимание, что при чет?
HOM s коэффициент яа > 0, из первого равенства (6.101) найдем
А > 0. Это доказывает соотношение (6.88).
Перейдем теперь к последнему случаю, когда Ьг, . . ., bs отри-
цательны и s — нечетное число. Из равенства (6.102) найдем ад < 0
(произведение нечетного числа отрицательных чисел), а из (6.103)
и (6.104) получим as_n < 0 (п = 2, 4, . . ., s — 1). Из второго ра-
венства (6.101) следует А <0, что доказывает соотношение (6.89).
Осталось доказать соотношение (6.86). Но оно следует из толь-
ко что доказанных неравенств (6.87)—(6.89).
§ 6.8.	Влияние на устойчивость равновесия
неконсервативных позиционных сил
а.	Одни неконсервативные позицион-
ные силы. Рассмотрим сначала случай, когда дви-
жение системы происходит под действием одних некон-
сервативных сцл.
Теорема 1. Равновесие системы, находящейся под дей-
ствием одних линейных неконсервативных позиционных
192
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
сил, всегда неустойчиво независимо от членов высшего по-
рядка.
Доказательство. В условиях теоремы уравнения воз-
мущенного движения можно привести к виду (6.45), где
В = G = Сп = 0:
» +	(6.105)
Здесь Р — кососимметричная матрица, Z — матрица-стол-
бец, элементы которой содержат z • и z^ в степени выше
первой, причем они обращаются в нуль, когда все zk и
Zj- равны нулю.
Рассмотрим характеристическое уравнение
А (X) = det (EX2 + Р) = 0.	(6.106)
Из устойчивости системы (6.79) относительно скоростей
следует, что не равные нулю корни уравнения (6.85)
det (EX2 + GK) = V det (EX + G) == 0
будут чисто мнимыми числами. Это означает, что отлич-
ные от нуля корни уравнения
А (X) = det (EX + G) = 0	(6.107)
имеют вид X = Ч- ai, где а — положительное веществен-
ное число *).
Уравнение (6.106) получается из уравнения (6.107)
простой заменой X на X2 (матрица Р, так же как и G, косо-
симметричная). Поэтому не равные нулю корни харак-
теристического уравнения (6.106) относительно X2 имеют
вид
X2 — + ai.
Отсюда
Х = + J-2—(1 ±г).
Таким образом, среди корней характеристического
уравнения (6.106) имеются корпи с положительной веще-
ственной частью. Это доказывает теорему.
*) Легко показать, что A (—X) = (—1)6А (X). Следовательно,
если X — корень уравнения А (X) = 0, то —X тоже корень этого
уравнения- Поэтому, если имеется корень, вещественная часть ко-
торого не равна нулю, то должен быть корень, вещественная часть
которого положительна- Но в этом случае движение будет неустой-
чиво, что противоречит доказанной теореме 1 § 6.7. Из этого следу-
ет, что все отличные от нуля корни уравнения (6.85) — чисто мни-
мые числа.
§ 6.8. ВЛИЯНИЕ НЕКОНСЕРВАТИВНЫХ СИЛ
193
В этой теореме предполагалось, что неконсервативные
позиционные силы линейны. Кроме того, не учитывались
силы сопротивления, которые практически существуют
почти во всех системах. Поэтому рассмотрим теперь
случай произвольных неконсервативных позиционных
сил, считая, что сила В (?) обращается в нуль при q = О
и что эта точка равновесия изолирована, т. е.
В (0) = 0, В (д) #= 0, если q =/= 0.	(6.108)
Кроме того, будем считать, что на систему действуют ли-
нейные диссипативные силы и возмущенное движение опи-
сывается уравнением (6.50).
Тегрема 2. Равновесие системы, находящейся под дей-
ствием произвольных неконсервативных позиционных сил
и линейных диссипативных сил, всегда неустойчиво.
Доказательство. Уравнения возмущенного движения
имеют вид (см. (6.50))
-L(Aq)^B(g)-Bq.	(6.109)
Здесь В (д) — произвольная неконсервативная позицион-
ная сила, В — постоянная неотрицательная, а А (д) —
определенно-положительная матрица (см. § 5.2, б).
Рассмотрим функцию
V = Aq-q + -^-Bq-q.	(6.110)
Вычислим ее полную производную по времени
V=-^(Aq)-q + Aq-q + Bq-q. (6.111)
Пользуясь уравнением возмущенного движения (6.109),
найдем
Р = B-q + Aq-q,
или, принимая во внимание общее определение неконсер-
вативных позиционных сил (6.15),
V = Aq-q.
На множестве К (q = 0, q Ф 0) производная F = 0,
а вне этого множества К > 0. Кроме того, множество К
не содержит целых траекторий, ибо на К уравнение (6.109)
принимает вид
В (?) = 0, q 0,
что невозможно в силу условия (6.108).
7 Д. Р. Меркин
194
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Так как функция V, определенная равенством (6.110),
может принимать положительные значения (например,
при q = q), то доказательство теоремы 2 следует из тео-
ремы Н. Н. Красовского о неустойчивости движения
(см. § 2.4).
Примечание 1. Для доказательства не требуется пол-
ная диссипация, поэтому теорема остается справедливой
и при отсутствии сил сопротивления.
Примечание 2. Теорема 1 в общем случае не является
следствием теоремы 2, так как входящие в правую часть
уравнения (6.105) члены высшего порядка могут быть
образованы другими существенно нелинейными силами.
б.	Неконсервативные и потенциаль-
ные силы. Перейдем теперь к случаю, когда на
систему действуют одновременно потенциальные и некоп-
сервативные позиционные силы. Ограничиваясь пока ли-
нейным случаем, возьмем уравнения возмущенного дви-
жения в форме (6.45):
й + Coz + Рг = 0.	(6.112)
Здесь С(| —диагональная, а Р — кососимметричная мат-
рицы. Составим характеристическое уравнение:
det (£Х2 + Со + Р) = 0.
Так как X содержится в этом определителе только в квад-
ратах, то в развернутой форме будем иметь
А2' Д- d2№s~2 Д' ... Д" ®2s-2^2 Д' n2s ~~ 0.	(6.113)
В этом уравнении
а2 = Ci + . . . Д- cs, a2s = det (С’о -(- Р), (6.114)
где сг, . . ., cs — элементы матрицы С» (см. (6.47)).
Левая часть уравнения (6.113) не изменяется от заме-
ны X на —X, поэтому для устойчивости необходимо, чтобы
все корни этого уравнения относительно X были чисто
мнимыми числами, а относительно X2 — вещественными
отрицательными (в противном случае среди корней урав-
нения (6.113) будут корни с положительной вещественной
частью).
На основании теоремы 1 этого параграфа система без
потенциальных сил (при Со = 0) неустойчива. Поэтому
можно ожидать, что добавление к устойчивой потенциаль-
ной системе неконсервативных сил может в некоторых
случаях разрушить устойчивость. Покажем на примере,
§ 6.8. ВЛИЯНИЕ НЕКОНСЕРВАТИВНЫХ СИЛ
195
тто неконсервативные позиционные силы могут не только
разрушить устойчивость потенциальной системы, но и
стабилизировать неустойчивую потенциальную систему.
Для этого рассмотрим систему с двумя степенями свободы.
Пусть уравнения возмущенного движения приведены к
виду
£ + срс — ру = 0, у + с2у + рх = 0.	(6.115)
Эти уравнения можно рассматривать как результат на-
ложения на потенциальную систему
х + срх = 0, у + с2у = 0	(6.116)
неконсервативных сил ру и — рх с кососимметричной мат-
рицей коэффициентов
Составим характеристическое уравнение системы
(6.115)
I № + С1 — Р I _ П
I Р х2 + с21— ’
или, раскрывая определитель,
V + (С1 + c2)V + С1е2 + р2 = о. (6.117)
Система будет устойчива, если оба корня относительно
X2 будут вещественны и отрицательны. Для этого необ-
ходимо потребовать, чтобы коэффициенты и дискриминант
уравнения (6.117) были положительны:
<\ + с2 > 0, <\с2 + р2>®, (Cj + с2)2 — 4 (сгс2 + р2) > б.
Преобразуя последнее неравенство, приведем условие
устойчивости к виду
С1 + С2 > 0, <\с2 > —р2, I — с2 I > 2 I р |. (6.118)
При р = 0, т. е. при отсутствии неконсервативных по-
зиционных сил, эти условия дают >0, с2 > 0, что
непосредственно следует и из уравнений (6.116). На пло-
скости параметров <\ и с2 область устойчивости потен-
циальной системы (6.116) заполняет весь первый квадрант
(рис. 6.6,а). При р 0 область устойчивости показана на
рис. 6.6, б. Границами этой области служат пря мая
1 (ci + с2 = 0), ветви гиперболы сгс2 = —р2 и прямые 2 и
3 (сх — С2 = + 2р), касающиеся гипербол в их верши-
нах. Из рисунка видно, что значительная часть области
7*
196'
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
устойчивости потенциальной системы (6.116), занимаю-
щая весь первый квадрант (рис. 6,6, а), при добавлении
неконсервативных позиционных сил переходит в область
неустойчивости (коридор между заштрихованными обла-
стями рис. 6.6, б). Одновременно видно, что небольшие
части области устойчивости рассматриваемой системы
(6.115) расположены во втором и четвертом квадрантах,
Рис. 6.6
где одна потенциальная система (6.116) неустойчива. Та-
ким образом, неконсервативные позиционные силы мо-
гут разрушить устойчивость потенциальной системы, но
в некоторых случаях они стабилизируют ее.
На рассмотренном примере (6.115) покажем, как могут
влиять диссипативные силы на устойчивость движения
системы с потенциальными и неконсервативными позици-
онными силами. Для этого присоединим к системе (6.115)
силы —Ьрс и —Ь2у, где Ьг и Ь2 положительны. Тогда
получим
х + Ь,х + с,х — ру = О,
П	(6.119)
У + Ъ2у + с2у + рх = 0.
Составим характеристическое уравнение:
I + Ър. -[- <4	— Р	I  Q
I р X2 + с2 I ’
или, раскрывая определитель,
№ + (^i + Ь2)№ + (сх 4- с2 + &1&2)^2.+ (cib2 + с2Ь1)'к -р
+ <\с2 + р2 = 0.
Напишем для этого уравнения критерий Гурвица (4.32):
Ъг + Ъ2 > 0, Cj + с2 + ЪГЪ2 > 0, сгЪ2.-\- с2Ъг > 0,
cic2 + Р2 > 0, (6.120)
§ 6.8. ВЛИЯНИЕ НЕКОНСЕРВАТИВНЫХ СИЛ	197
А3 = (Ь1 + 62)(cj + С2 + б^Дс^ + ^А) —
-(С163 + с2Ь^ - А + Ь2)2(С1с2 + р2) > 0.
Преобразуем последнее неравенство:
А3 = &J&2 (6Х + 62)(с152 + c2^i) 4~ brb2 (с2 — сх)2 —
-(bi + 62)2р2 > 0. (6.121)
Покажем прежде всего, что диссипативные силы могут
при некоторых условиях стабилизировать неустойчивую
систему (6.115). Действительно, при сх = с2 = с > 0 кри-
терий Гурвица примет вид
-J- 62	0, 2с -|- \Ь2	0,
с (Ь± + Ь2) >0, с2 + р2 > 0,
Аз = (61 + 62)2(5152с - р2) > 0.
Первые четыре условия выполняются автоматически
(по предположению, с > 0, Ъг > 0, Ь2 > 0), а последнее
неравенство будет выполнено, если подчинить диссипа-
тивные силы условию
(6.122)
Таким образом, неустойчивую систему, находящуюся
под действием потенциальных и неконсервативных пози-
ционных сил, можно стабилизировать диссипативными
силами (при сх = с2, р 0 и Ьг = Ь2 = 0 система (6.115)
неустойчива — см. рис. 6.6, б).
Покажем теперь, что диссипативные силы могут раз-
рушить устойчивость системы, находящейся под дейст-
вием потенциальных и неконсервативных сил. Действи-
тельно, пусть выполнены условия (6.118). Тогда система
(6.115) будет устойчива. Присоединим к этой системе дис-
сипативные силы, положив Ъ2 = 0, и br = Ъ > 0. Тогда
условие (6.121)
А3 — —Ь2р2 <. 0
принимает противоположный смысл, что свидетельствует
о неустойчивости движения (см. примечание к условиям
Гурвица (4.32)).
Из рассмотренного примера (6.115) с двумя степенями
свободы видно, что при равенстве коэффициентов устой-
чивости сх и с2 добавление любых неконсервативных
позиционных сил ру и — рх разрушает устойчивость по-
тенциальной системы. Покажем, что это свойство справед-
198	гл. АЛ. ВЛИЯНИЕ СТРУКТУРЫ сил
либо для системы с любым числом степеней свободы. Для
этого рассмотрим устойчивую потенциальную систему с
равными коэффициентами устойчивости
Су = сг = . . . = cs = с.
Напомним, что для устойчивой потенциальной системы
коэффициенты устойчивости равны квадратам частот
собственных колебаний.
Теорема 3. Если в устойчивую потенциальную систему
с равными собственными частотами вводятся линейные
неконсервативные силы, то устойчивость будет разрушена
вне зависимости от нелинейных членов [38].
Доказательство. Уравнение движения системы, на ко-
торую действуют линейные потенциальные и неконсер-
вативные позиционные силы, возьмем в форме (6.45)
is + Cots + Pts — Z.
При равных коэффициентах устойчивости Са = сЕ,
где Е — единичная матрица, и последнее уравнение при-
мет вид
« +	+ Pts - Z.
Составим характеристическое уравнение
det [Е (%2 + с) + 73] = 0.
Это уравнение совпадает с уравнением (6.106), если в по-
следнем заменить X2 на X2 + с. Поэтому не равные нулю
корни последнего уравнения относительно X2 + с будут
X2 + с = + ai.
Отсюда
Наличие корней с положительной вещественной частью
служит доказательством теоремы.
Перейдем к рассмотрению устойчивости равновесия
систем, находящихся под действием произвольных по-
тенциальных и неконсервативных позиционных сил и
линейных диссипативных сил с положительным сопро-
тивлением, считая, что возмущенное движение определяет-
ся уравнением (6.50).
Теорема 4. Если в положении неустойчивого равновесия
консервативной системы потенциальная энергия (д') имеет
6.8 ВЛИЯНИЕ НЕКОНСЕРВАТИВНЫХ СИЛ
199
максимум, определенный наинизшими членами разложения
ее в ряд по степеням q, то при добавлении произвольных
неконсервативных позиционных сил и линейных дисси-
пативных сил равновесие останется неустойчивым [38].
Доказательство. Уравнение возмущенного движения
(6.50) в сделанных предположениях имеет вид
4(^) = -gradn+ R(q)-^Bq.	(6.123)
Здесь R (q) — произвольная неконсервативная позицион-
ная сила, В — постоянная неотрицательная, a A (q) —
определенно-положительная матрицы, П (q) — потенци-
альная энергия системы, имеющая при q = 0 максимум.
Разложим потенциальную энергию в ряд по степеням q:
П (?) = Пт (?) + . . .,	(6.124)
где Пт (?) — однородная форма степени т, а точки оз-
начают совокупность членов, содержащих координаты в
степени выше т. Так как по условию теоремы максимум
потенциальной энергии П (?) определяется наинизшими
членами разложения ее по степеням ?, то однородная
форма Пт (?) должна быть определенно-отрицательной
функцией координат ?, причем число т, конечно, четное.
Возьмем следующую функцию V,
V = Aq-q + -^-Bq-q,
и вычислим ее производную по времени в силу уравнения
возмущенного движения (6.123). Тогда, учитывая равен-
ство (6.15), получим
Р = Aq-q — д'-grad П.
На основании теоремы Эйлера об однородных функциях
и равенства (6.124) будем иметь
S
g-gradll= V ?fc-^b--=rnllm(?) + ...
Следовательно,
Р = Aq-q — тПт (?) + ...
Первое слагаемое в этом выражении представляет опре-
деленно-положительную функцию ; скоростей, а вто-
рое слагаемое — тПт (?) — определенно-положительную
функцию координат. Поэтому в окрестности нуля q = 0,
200
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
4 = 0 производная V функции V будет определенно-поло-
жительной функцией координат и скоростей. Так как сама
функция V может принимать положительные значения
(например, при q — q), то доказательство теоремы явля-
ется прямым следствием теоремы Ляпунова о неустойчи-
вости движения (см. § 2.4).
Заметим, что условие, по которому определяется мак-
симум потенциальной энергии, можно ослабить.
в. Общий случай. Перейдем к рассмотрению
случая, когда на систему действуют линейные потенци-
альные, диссипативные, ускоряющие, гироскопические,
неконсервативные позиционные и нелинейные силы. Урав-
нения возмущенного движения возьмем вначале в форме
(6.46)
« + 5о« +	+ Ра = Z. (6.125)
Составим характеристическое уравнение
А = det (£7? + S0X + G7, + С + Р) = 0 (6.126)
или, более подробно,
X2 -|- Ьр. еп ...	cls -|- pls
Д =
= 0.
"I" Csl + PS1	+
Раскроем определитель и сгруппируем члены по степе-
ням X:
А = X25 + а1Х2,_1 + .... + a2s^ + a2s = 0. (6.127)
Очевидно, что
ai = bi + • • • • + 1>S = Sp В = Sp Br,
a2s = det (С + P) = det Cu	(	’
где В1 и Cr — матрицы исходного непреобразовапного
уравнения (6.42).
Пользуясь этими равенствами, докажем теоремы, оп-
ределяющие необходимые условия устойчивости движения.
Теорема 5. Если ускоряющие силы доминируют над
диссипативными, то система будет неустойчива при лю-
бых других линейных и нелинейных силах.
Доказательство. В соответствии с определением доми-
нирования диссипативных и ускоряющих сил будем иметь
(см. § 6.3, с. 167)
Sp£0 = Sp В = Sp Br < 0.
§ 6.8. ВЛИЯНИЕ НЕКОНСЕРВАТИВНЫХ СИЛ
201
На основании первого равенства (6.128) коэффициент
at характеристического уравнения (6.127) будет отрица-
телен. Из этого следует, что среди корней характеристи-
ческого уравнения имеется хотя бы один, вещественная
часть которого положительна. Это доказывает теорему.
Теорема 6. При отсутствии нелинейных членов (Z = 0)
асимптотическую устойчивость нельзя осуществить без
диссипативных сил.
Доказательство. При отсутствии диссипативных сил
dj = 0 и, следовательно, не выполнен критерий Гурвица,
необходимый для асимптотической устойчивости линейной
автономной системы.
Теорема 7. Если определитель | С\ | = | С + Р | отри-
цателен, то система неустойчива при любых гироско-
пических, диссипативных и ускоряющих силах и вне за-
висимости от нелинейных членов Z.
Доказательство. В условиях теоремы коэффициент <z2s
характеристического уравнения (6.127) отрицателен (см.
второе равенство (6.128)). Из этого следует, что хотя бы
один корень уравнения (6.127) имеет положительную ве-
щественную часть. Это доказывает теорему.
Следствие (см., первую теорему Томсона — Тета —
Четаева § 6.5). Если неустойчивость изолированного поло-
жения равновесия потенциальной системы имеет нечетную
степень, то стабилизировать равновесие нельзя никакими
гироскопическими, диссипативными и ускоряющими
силами.
Действительно, если система потенциальна, то Р = 0
и при изолированном равновесии и нечетной степени не-
устойчивости | С1 | = | С | < 0 (см. § 6.4, с. 169).
Теорема 8. Если линейная система не содержит по-
тенциальных сил, то:
1) при нечетном числе координат асимптотическую
устойчивость нельзя осуществить никакими гироскопи-
ческими, диссипативными и ускоряющими силами',
2) при четном числе координат для осуществления
асимптотической устойчивости необходимо, помимо дис-
сипативных сил, присоединить гироскопические си-
лы [38].
Доказательство. Если отсутствуют потенциальные си-
лы и число координат нечетное, то | С + Р | = | Р | = 0
(как кососимметричный определитель нечетного порядка).
В этом случае, согласно (6.128), свободный член aZs ха-
рактеристического уравнения (6.127) равен нулю, что
202
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
служит признаком отсутствия асимптотической устойчи-
вости (имеется нулевой корень).
Для доказательства второй части теоремы заметим, что
присоединение диссипативных сил необходимо по теоре-
ме 6. Если же отсутствуют гироскопические силы, то си-
стема неустойчива (теорема 2).
Теорема 9. Если потенциальная энергия системы име-
ет максимум, то:
1) при нечетном числе, координат и любых нелинейных
членах систему нельзя стабилизировать никакими гиро-
скопическими, неконсервативно позиционными, ускоряющи-
ми и диссипативными силами;
2) при четном числе координат и при условии, что на
систему действуют силы сопротивления с полной дисси-
пацией, для стабилизации системы необходимо одновре-
менно присоединить гироскопические и неконсервативно
позиционные силы (вне зависимости от нелинейных чле-
нов) [38].
Доказательство. Рассмотрим уравнение возмущенного
движения в форме (6.45). Составим для него характеристи-
ческое уравнение
А = det (ЕМ + ВК + GK + Сй + Р) = 0.
Свободный член этого уравнения равен a2s = det (Со + Р).
При максимуме потенциальной энергии все элементы
ch-, стоящие на главной диагонали матрицы Со, будут от-
рицательны. На основании соотношения (6.89) определи-
тель | С 0 + Р | при нечетном числе координат отрицате-
лен при любой кососимметрической матрице Р. Следова-
тельно, свободный член характеристического уравнения
при нечетном числе координат отрицателен, и система на
основании теоремы 7 неустойчива.
Рассмотрим теперь случай четного числа координат.
Если отсутствуют неконсервативные позиционные силы,
то система будет неустойчива на основании четвертой тео-
ремы Томсона — Тета — Четаева § 6.5. Если же отсутст-
вуют гироскопические силы, то неустойчивость системы
следует из теоремы 4 этого параграфа. Таким образом,
для стабилизации системы с четным числом координат
необходимо присоединить одновременно гироскопические
и неконсервативно позиционные силы. Теорема доказана
полностью.
Проиллюстрируем доказанные теоремы сначала фор-
мальными примерами.
§ 6.9. СИСТЕМЫ С НЕКОНСЕРВАТИВНЫМИ СИЛАМИ 203
Пример 1. Система
Х1 + Ь1±1 + g±i2 + g2*3 + PiX2 + р2х3 —	= Х1;
. Х2 + 52#2 - 81Х1 + 8з"з — Р1Х1 + Рзх3 С2Х2 = ^2,
Х3 + Мз — g2i\ — g3r2 — Р2Х1 Рзх2 С3Х3 ~ ^3
при ел- > 0 неустойчива при любых git, рк, Ь/с > 0 и Хк (так как
потенциальная энергия П = —1/2 (qa^ + с2х2 + с3х3) имеет в по-
ложении равновесия = q2 = q3 = 0 максимум и число коорди-
нат нечетное — теорема 9).
Пример 2. Систему
+ЬА -сЛ = 0 (b)t > о, C)t > 0)
*^2 "Т” ^2 <2	^2*^2
можно стабилизировать только в том случае, если подходящим
образом присоединить одновременно гироскопические и неконсер-
вативно позиционные силы (так как потенциальная энергия П =
= —1/2	+ с2х2) имеет в положении равновесия максимум,
диссипация полная и число координат четное — теорема 9).
Пример 3. Система
91 + <7i + (1 + 91 + 9^) 914 == °’
9г + 9г — (1 + 91 + 9а) 919з == °
неустойчива, так как на нее действуют линейные силы сопротив-
ления и неконсервативно позиционные (нелинейные) силы Р± =
= —(1 + 91 + 9^) 919^ и Р2 = (1 + qf + q22) q2q2 — теорема 2.
Пример 4. Система
5П
91 + 2 71 + 5?2 -Ь + Pi +
••	<Ш , ,
92 + 5?i — 4)2 + Г2 + Р2 -]-	= Q,
неустойчива при любых гироскопических Г^, неконсервативных
позиционных Рх, потенциальных и нелинейных силах так
как след матрицы В отрицателен (Sp В = 2 — 4 = —2) и, сле-
довательно, ускоряющие силы доминируют над диссипативными —
теорема 5.
§ 6.9. Примеры исследования устойчивости
движения систем с неконсервативными силами
Интересные и очень важные для техники задачи на
исследование устойчивости систем с неконсервативными
позиционными силами возникли в теории упругости.
Здесь можно выделить три группы таких задач. Первая
связана с упругими системами, подверженными дейст-
вию так называемых следящих сил, т. е. сил, линия дей-
204
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
ствия которых совпадает с касательной к упругой оси
стержня (см. пример 1). Такие силы могут возникнуть,
в частности, при отделении продуктов сгорания реактив-
ной установки. Е. Л. Николаи [41] в 1928 г., по-видимому,
первый начал исследование таких систем. Вторая группа
имеет дело с устойчивостью вращающихся валов, а тре-
тья — с устойчивостью упругих тел, движущихся в
сопротивляющейся среде *). Пример 2 дает некоторое
представление об этих задачах.
Кроме систем, содержащих упругие тела, существуют
различные устройства, в частности гироскопические (см.
пример 3), в которых неконсервативные силы создаются
с помощью специальных приспособлений (это делается, в
частности, для ускорения переходных процессов).
Учитывая характер настоящей книги, мы можем рас-
смотреть только некоторые, наиболее простые задачи.
Пример 1. Модель упругого стержня, находя-
щегося под действием следящей силы. Рас-
смотрим два однородных стержня длиной 1г и 12, связанных шар-
ниром и спиральной пружиной жесткости с2. Первый стержень
может вращаться вокруг неподвижной опоры О, с которой он свя-
зан другой спиральной пружиной жесткости ct. Обе пружины
находятся в недеформированиом состоянии, когда стержни рас-
положены по одной прямой (оси х — см. рис. 6.7). На второй
стержень действует сила F, направленная всегда вдоль оси стержня
(следящая сила). Эта система может рассматриваться как модель
упругого стержня, находящегося под действием следящей силы.
Составим дифференциальные уравнения возмущенного движе-
ния. Кинетическая энергия системы обычными методами (при
*) См. книгу В. В. Болотина [11]. По первой проблеме подроб-
ный обзор методов и полученных результатов дан в статье Г. Херрма-
на [54].
§ 6.9. СИСТЕМЫ С НЕКОНСЕРВАТИВНЫМИ СИЛАМИ 205
подсчете кинетической энергии второго стержня используется тео-
рема Кёнига) приводится к виду (выписаны члены только второго
порядка малости)
Т = V2 (апФг + 2“12ф1Фз + аззФа).
где
Яц = J1 -J- т21%,	Я12 = Vs ^2^3»	^22 ~ ^2 4" Vl ^2^2*
Здесь /j — момент инерции первого стержня относительно оси
вращения О, т2 — масса второго стержня, J2 — момент инерции
второго стержня относительно его центра тяжести.
Потенциальная энергия пружин Пх определяется равенством
1 > 1
П1=-2-С1ф^ + -2-с2(ф,— фО2.
Найдем обобщенные силы Q± и Q2, отвечающие следящей силе
F. При изменении одного угла ф2 (фх = const) работа силы F равна
нулю. Поэтому
= о-
Дадим теперь приращение 6фх углу фх, оставив угол ф2 без
изменения, и вычислим работу 64' силы F на этом виртуальном
перемещении. Имеем
64' = — Flr sin (ф2 — фх) 6фР
Отсюда для малых углов
<?i = —Fli (Фз — Ф1)-
Полные обобщенные силы, соответствующие углам фх и ф2,
найдем по формуле (для простоты считаем, что вся система рас-
положена на гладкой горизонтальной плоскости, в результате
чего силы тяжести исключены из рассмотрения)
йЩ
Пользуясь найденными выражениями, получим
Q1 — ~е1Ф1 + е2фз, Q2 — С2Ф1 ---- сзф2>
где
= С1 4" с2 - Fill е2 ~ С2 -- Fl^.
Применяя второй метод Лагранжа, составим уравнения воз-
мущенного движения системы около положения равновесия:
“11Ф1 + Я12(р2 + е1ф1 - езфз — Ф1,
а21ф1 4" а22$2 сзф1 4" С2ф2 — Фз-
Здесь «Г»! и Ф2 — неучтенные ранее члены, содержащие фх и ф2
в степени выше первой.
2С6
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
В этих уравнениях матрица коэффициентов
при координатах <рх и <р2 не симметрична. Разбивая ее на симмет-
ричную и кососимметричную части но формулам (6.5), найдем
с ||еИ C12 II р=| 0 Р||
II е21 е22 II ’	|| — Р О II ’
где
Сц = е, — <?1 -ф- с2 — Fllt
d?2 Ч- ^2	1
е12 = е21 = —	2	~ ~2~	' 2Сг), е22 ~ е2>
1 1
Р = — ~2 (е2 — ег) = ~2~ Fh-
Из этих выражений видно, что следящая сила F создает не-
консервативные позиционные силы
1 1
Pi = ~2 FI <Р2,	^2 = — ~2 ^1фь
В потенциальную энергию всей системы
1
П = ~2~ (сцф1! + 2ci2<Pi<P2 + СггФз)
входят слагаемые, зависящие и от следящей силы (см. выражения
Для с/с;).
Составим характеристическое уравнение
I ап'-2 + Cl <Z12V — е2 I _
I «21^-2 — Cs «2:4-2 + е2 I ’
или, раскрывая определитель,
«Л4 -f- Ь/.2 -ф- с0 = О,
где
a = аца22 — Ь = ЯцС2 Ч- «22«1 Ч- «is (е2 Ч- ег)>
Со = с2 («1	С2) = С^.
Рассматриваемая система будет устойчива в нервом прибли-
жении, если все корпи относительно № будут вещественными от-
рицательными числами. Для этого необходимо и достаточно, чтобы
выполнялись условия
Ь > О, Д = Ь2 — 4ас0 > 0	(6.129)
(а > 0 и с0 > 0 при любых значениях следящей силы F). Из этих
неравенств можно найти наименьшее значение следящей силы,
при котором сохраняется устойчивость системы (легко проверить,
что при отсутствии следящей силы система устойчива). Мы ограни-
чимся рассмотрением простейшего случая идентичных стержней
§ 6.9. СИСТЕМЫ С НЕКОНСЕРВАТИВНЫМИ СИЛАМИ
207
И пружин. При т1 = т2 = т, Zj ~ l2 ~ I и Cj = с2 = с получим
а11 = ‘/'З mZ2, а12 = Х/з Ш?!	q22 = х/з mZ2, а = 5/з m2li,
е1 = 2с — FI, е2 = с — Ft.
После подстановки в (6.129) получим
/	5
Ь = ml2 (Зс — -g- Fl \ )> 0,
Г/ 5 V 5	1
а - т211 ( Зс — -g-FZj —4--g-c2 >0.
Отсюда находим, что рассматриваемая система будет устойчива
в первом приближении при
Если модуль следящей силы будет больше этой величины, то
второе неравенство (6.129) приобретает противоположный смысл
и система сделается неустойчивой.
Пример 2. Неустойчивость
ющегося в аэродинамической
показывает опыт, вращающийся в кожухе
трения об аэродинамическую сре-
ду приобретает неустойчивое по-
перечное движение. Это явление,
хорошо иллюстрирующее первую
часть § 6.8, впервые исследовал
П. Л. Капица [24].
На рис. 6.8 изображен ротор 1
массой М, вращающийся с угловой
скоростью со в кольцевом кожухе 2.
Пространство между ротором и ко-
жухом заполнено гидродинамической
средой, например газом. Если центр
Ох ротора совпадает с центром О
кожуха, то трение о газ вызовет
только тормозящий момент, который
не скажется на положении оси ро-
тора. Покажем, что при смещении
оси Oj ротора возникают неконсервативные
объяснением П. Л. Капицы; заметим только, что он не классифи-
цировал силы по их структуре).
Пусть для примера центр Oi ротора сместился вправо вдоль
оси х на величину OOi—x. Газ в кожухе увлекается вращением
ротора и приобретает скорости щ и и2. Так как зазор между кожу-
ротор
с
ротор
а, в р а щ а-
р е д е. Как
при наличии
силы (мы пользуемся
хом и ротором в направлении сдвига становится меньше, а коли-
чество газа в круговом движении постоянно, то и2>щ. Поэтому
трение поверхности ротора о газ пе будет одинаковым с правой
и с левой стороны; очевидно, что оно будет больше в тех частях
его поверхности, где разность между периферийной скоростью
ротора и газа больше. В сделанных предположениях о направле-
нии смещения центра ротора левая его сторона будет испытывать
большее трение о газ, чем правая, в результате чего появится сила
208
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Sy (кроме силы Sy, перпендикулярной смещению, возникают еще
силы в направлении передвижения; эти силы, вызванные явле-
нием Бернулли, малы и для простоты изложения нами не учиты-
ваются).
Вычисление силы Sv произведем в простейших предположе-
ниях, а именно: когда скорость газа велика и его движение можно
принять полностью турбулентным; кроме того, предполагаем, что
трение ротора от вязкости газа в первом приближении пе зависит.
Обозначим величину зазора между ротором и кожухом при сов-
падении их центров через е. Пусть центр ротора сместился по оси
х на величину ООг = х. Проведем из точки Ох прямую О±М под
углом 0 к оси х. Величину зазора КМ при смещенном положении
ротора обозначим через ех (рис. 6.8). Из треугольника ОМОг по
теореме косинусов найдем (радиус кожуха ОМ, очевидно, равен
R + е, где R — радиус ротора)
(Д -|- е)2 = х2 + (7? 4- ех)2 — 2х (R ех) cos (л — 0),
или, раскрывая скобки,
2Re -|- е2 = х2 -j- 27?ех	2Rx cos 0 -ф- 2хех cos 0.
Считая величины х, е и, следовательно, <?х малыми по сравнению
с R, пренебрежем членами второго порядка малости:
2Re — 2Ret -ф- 2Rx cos 0.
Отсюда
ex = e — x cos 0.
Среднюю скорость газа при несмещенном роторе принимают
равной 7?со/2, т. е. половине скорости точек ротора, лежащих на
его периферии. При смещении ротора скорость v газа в зазоре
будет меняться, но количество газа, проходящего через любое
сечение, равняется тому, которое было до перемещения ротора.
Следовательно,
где I — толщина ротора. Пользуясь выражением для ех и сокра-
щая на I, получим
„ /?со
v (е — х cos 0) = —е.	(6.130)
При больших скоростях сила трения dS, действующая на
элемент наружной поверхности ротора RI <70, будет приближенно
пропорциональна квадрату относительной скорости (R со — <л)2
и плотности окружающей среды р. Сила эта направлена по каса-
тельной к ротору (см. рис. 6.8). Проектируя ее на ось у и интег-
рируя по 0 от 0 до 2л, получим
2Л
Sy = — noRl (7?со — с)2 cos 0 <70,
о
где х — коэффициент трения.
§ 6.9. СИСТЕМЫ С НЕКОНСЕРВАТИВНЫМИ СИЛАМИ 209
Найдем скорость v из равенства (6.130) и внесем ее в это выра-
жение для Sy:
2Л
sv = - *РЛЗг“2 П1 - Т z cos о) cos 0 М-
о
Будем считать, что смещение х мало по сравнению с величиной
зазора е. Тогда, разлагая подынтегральное выражение в ряд по
степеням х и ограничиваясь членами первого порядка малости,
получим после очевидных преобразований
лхр Z7?3co2
sy — 2 * е х-
Аналогично получается составляющая -5Ж:
лхр Ш3®2
sx = — 2 ’ е у-
К ротору, кроме сил трения Sx
гости F, проекции которой на оси
и Fy = —су, где с — коэффициент
жесткости вала ротора на изгиб
(на рис. 6.9 изображены силы 5
и F).
Пользуясь теоремой о движении
центра масс, составим дифферен-
циальные уравнения движения то-
чки О±:
Мх = Fx 4- Sx 4- X,
Му — Fy 4- Sy 4- Y.
Здесь X и Y — неучтенные нели-
нейные члены, содержащие х, у
±, у в степени выше первой.
Внесем значения Fx, Fy, Sx
и Sy, приложена сила упру-
координат Г
будут Fx — —сх
и
и
Sy, разделим на массу ротор’а М и
перенесем часть членов в левые части уравнений. Тогда, введя обоз-
начения
с	лхр Z7?3co2
fc2 = ЛГ ’ р = ~Т~ ’ еМ
получим
х 4- к2х — ру = X, у 4- к2у 4- px = Y.
(6.131)
В этих уравнениях слагаемые к2х и к2у, полученные от упру-
гой силы F, представляют потенциальные силы, слагаемые — ру
и рх (проекции главного вектора 5 сил трения, взятые с обратным
знаком и отнесенные к единице массы) — неконсервативные силы,
X и Y — нелинейные члены.
Левые части уравнений (6.131) совпадают с уравнениями
(6.115). Для последних было показано, что при равенстве коэффи-
циентов и с2 (в данном примере ct — с2 — к2), движение неус-
тойчиво при любых значениях р =)= 0 и любых нелинейных членах.
Поэтому при отсутствии демпфирования поперечное движение оси
210
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
ротора, вращающегося в гидродинамической среде, всегда неустой-
чиво.
Ограничиваясь случаем X — Y — 0, рассмотрим характер
неустойчивого движения более подробно. Для этого умножим
второе уравнение (6.131) на i =	—1 и сложим почленно оба урав-
нения:
х + iff + к2 (х iy) -j- р (ix — у) = 0
пли
Z 4- (к2 4- ip) Z = 0,	(6.132)
где комплексная переменная z определена равенством
z = х 4" iy-
Решение уравнения (6.132) будем искать в обычной форме:
, XI
z = Ае ,
трр А — некоторое комплексное число. Внося z = Ае^ в уравне-
ние (6.132), получаем
[V 4 (*24- (»] АеМ = 0.
Отсюда
V — — к2 ip.
Будем считать, что п <«? к2. Тогда, извлекая корень пз комп-
лексного числа —к2 — ip, находим с точностью до р2//с4
1	_Е_ к- 1
Л1 — 2^.. ki, л.2 — — 2/.- ~Ь ki-
Общее решение уравнения (6.132) примет вид
JLt	_V-t
z = Ae2*	2К е™,
где А и В — произвольные постоянные интегрирования.
Второе слагаемое быстро убывает по модулю, поэтому, пре-
небрегая им, получим
V-t
z = Ae2lc e-iM.
По своему определению z является комплексной координатой
точки О±. Связь между полярными координатами г и <р точки О±
и переменной z определяется равенствами
г = | z | , <р = arg z.
Следовательно,
г = | А | с2'' ’ ф — kt.
Такпм образом, точка движется по логарифмической спи-
рали, а положение равновесия центра ротора является неустой-
чивым фокусом. На рис. 6.10 приведена фотография, заимство-
§ 6.9. СИСТЕМЫ С НЕКОПСЕРВАТИВНЫМИ СИЛАМИ
211
ванная из работы [24], на которой воспроизведена траектория
точки Oj, полученная П. Л. Капицей при постановке эксперимента.
Для стабилизации поперечного движения оси ротора уста-
навливается кольцевой демпфер, создающий силы сопротивления,
пропорциональные скоростям с одинаковым коэффициентом демп-
фирования bj = Mb. Уравнения движения (6.131) принимают вид
х 4- Ы + к2х — ру = X,
У + by 4- к2у 4- рх = У.
Пользуясь условием асимптотической устойчивости (6.122),
получим
b > р/к.
Это неравенство определяет основное требование, предъявляе-
мое к демпферу.
Пример 3. Гировертикаль с радиальной кор»
рекцией. В авиации широкое распространение получили гиро-
вертикали с радиальной коррекцией. Прибор устроен следующим
образом. Гироскоп (на рис. 6.11 он не показан) помещен в кожух I.
На кожухе установлены два уровня 1 и 2, заполненных токопро-
водящей жидкостью *). При отклонении оси гироскопа от вертикали
£ в уровнях создается разность потенциалов, которая усиливается
специальным устройством и подается на датчики моментов ДА и
*) Вместо двух линейных уровней, как правило, устанавли-
вают один шаровой уровень. Тот же эффект в конструкциях более
старого выпуска создавался с помощью струй воздуха.
212
ГЛ. VI. ВЛИЯНИЕ СТРУКТУРЫ сил
Д2. Уровень 1 управляет датчиком Дг, а уровень 2 — датчиком Д2.
При повороте внешнего кольца карданова подвеса па угол а дат-
чик Д2 создает момент Lx = —ха (для малых углов), а при пово-
роте кожуха на угол р датчик Д± создает момент 74) = хр, где х —
Рис. 6.11
крутизна характеристики датчиков моментов. Центр тяжести сис-
темы совпадает с точкой пересечения осей карданова подвеса.
Пользуясь теоремой моментов или уравнениями Лагранжа,
легко получить дифференциальные уравнения движения оси гиро-
вертикали (массой подвеса пренебрегаем)
/а + ba - яр - хр = Xlt
/р 4- &р 4- На + ха = Х2.
В этих уравнениях J — экваториальный момент инерции гиро-
скопа, Я — его кинетический момент, Ъ — коэффициент сил со-
противления, Xj и Х2 — члены, содержащие а, р, а и р в степени
выше первой.
Силы —Яр и На — гироскопические, a —хр и ха — некон-
сервативные (в гироскопии их называют силами радиальной кор-
рекций).
Составим характеристическое уравнение системы
|/Л24-ЬЛ —ЯЛ—х|
I ял 4- X УЛ2 4- &л I 0
или, раскрывая определитель,
РЛ4 4- 2/&Л3 4- (Я2 4- &2)Л2 4- 2хЯЛ 4- х2 = 0.
Так как все коэффициенты этого уравнения положительны, то
критерий Гурвица (4.32) сводится к одному неравенству
.	2	2	л
Ад    Д^ДдДд ~~~ ДцДд	д^д^	и.
§ 6.9. СИСТЕМЫ С НЕКОНСЕРВАТИВНЫМИ СИЛАМИ 213
Внесем сюда значения коэффициентов и преобразуем полученное
выражение. Получим
Д3 = 4-/Я (Я2 + Ь2) (ЬН — %J) > 0.	(6.133)
При отсутствии сил сопротивления (Ь = 0) это условие име-
ет противоположный смысл (Д3<0), что свидетельствует о неус-
тойчивости системы. Из неравенства (6.133) найдем значение коэф-
фициента демпфирования, при котором имеет место асимптотиче-
ская устойчивость:
b > V.J/H.
Отметим, что кинетический момент Н гироскопа очень велик
по сравнению с к/. Поэтому нижняя граница для коэффициента
демпфирования очень мала. Практически для асимптотической
устойчивости достаточно естественных сил сопротивления воздуха,
трения в опорах и т. п.
Г Л А В A VII
УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
§ 7.1. Функции Ляпунова для неавтономных систем.
Обобщенный критерий Сильвестра
Прежде чем перейти к определению функций Ляпунова
для неавтономных систем, остановимся кратко на некото-
рых общих вопросах прямого метода.
Об устойчивости движения мы судим по отклонению
в пространстве хг, . . хп изображающей точки М от
начала координат О (см. § 1.1). В свою очередь (см. § 2.1),
в прямом методе Ляпунова для автономных систем бли-
зость изображающей точки М к началу координат опреде-
ляется по модулю знакоопределенной функции V: если
величина | V (х) | мала, то в силу непрерывности функции
V (х) точка М будет близка к началу координат. Картина
изменится, если функция V будет зависеть явно не только
от вариаций xlt . . ., хп, но и от времени t. В этом случае
знакоопределенная функции V (х, t) в обычном понимании
может сделаться достаточно малой по модулю не за счет
близости точки М к началу координат О, а за счет изме-
нения времени t. Действительно, функция
V (х, I) = е~' (xl + х2)
в обычном смысле определенно-положительна: при всех
значениях х± и х2, не обращающихся в нуль одновременно,
она положительна и в нуль обращается только в том слу-
чае, если хг = х2 = 0. Однако судить о близости изобра-
жающей точки М к началу координат по этой функции
нельзя, так как с течением времени t за счет уменьшения
множителя она сделается и в дальнейшем будет оста-
ваться меньше любого наперед заданного положительного
числа е при любых конечных значениях х± и х2. В связи
с этим функции V, зависящие явно от времени t, требуют
дополнительных определений (читателю полезно еще раз
просмотреть § 2.1).
Предполагается, что вещественные функции V (х, t)
определены для всех вещественных значений t и
§ 7.1. ФУНКЦИИ ЛЯПУНОВА ДЛЯ НЕАВТОНОМНЫХ СИСТЕМ 21
#!,..., хп, подчиненных условиям
t	(7-1)
где (ои р, — постоянные (/0 > 0, pi > 0), причем р может
быть мало. Считается, что в области (7.1) эти функции
непрерывны, однозначны и обращаются в пуль, когда все
х* равны нулю:
V (0, t) = 0.	(7.2)
Если при условиях (7.1), при t0 достаточно большом
а р достаточно малом, рассматриваемая функция V при-
нимает кроме нулевых значения только одного знака,
то такую функцию называют знакопостоянной. Если хотят
отметить ее знак, то говорят, что она положительна или
отрицательна.
Функция V, зависящая явно от t, называется опреде-
ленно-положительной, если существует такая не зави-
сящая от t определенно-положительная функция W (х),
что в области (7.1) при достаточно малом р и достаточ-
но большом t0 будет
V (х, t) > W (х),	(7.3)
и называется определенно-отрицательной, если при тех
же условиях будем иметь
—V (х, t)^W (х). .
Из соотношения (7.3) следует, что для определенно-
положительной функции V (х, t) разность V (х, t) — W (х)
представляет функцию положи-
тельную.
Требование существования гра-
ничной функции W (х) для опре-
деленно-положительной функции
V (х, t), зависящей явно от време-
ни t, можно проиллюстрировать
геометрическими соображениями.
В пространстве V, хг, . . ., хп по-
строим поверхность W = W (х)
и при фиксированном значении
времени t поверхность V=V (х, t).
При изменении t поверхность
V (х, t) будет деформироваться, но при этом она не долж-
на «пуститься ниже граничной поверхности W — W (х)
(рис. 7.1).
216
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
Точно так же, если в пространстве хг, . . хп пост-
роить две замкнутые поверхности W (х) — с и V (х, t) =
= с (последняя для фиксированного t), то при изменении t
поверхность V (х, t) — с будет де-
формироваться, но она не должна
выйти наружу поверхности W (х) =
— с (рис. 7.2). Прежде чем перейти
к дальнейшим определениям, рас-
смотрим, по каким признакам можно
в некоторых случаях определить
знакоопределенность функции У(х, t)
в смысле Ляпунова. Предположим,
что функция V (х, t) имеет вид квадратичной формы
п п
7(.г,/)^4^^а,;7.г,.77,	(7.4)
К=1 з= 1
где akj — некоторые функции времени t и переменных хр.
ajrj = a^j (*, t).
Если в области (7.1) при i0 достаточно большом, а р
достаточно малом все главные диагональные миноры ма-
трицы
®ii (х, t) ... aln (х, t)
а„1 (х, t). . . апп (х, t)
удовлетворяют обобщенному условию Сильвестра
аи ... а1п
Д1 — «и 61	0, ..., Дп =
бп>0,
(7-5)

где 61, . . ., 6П — некоторые положительные постоянные,
то функция V (х, t), определяемая равенством (7.4), бу-
дет определенно-положительной в смысле Ляпунова. Дейст-
вительно, так как все миноры Дп . . ., Д„ положительны,
то функция V (х, t) определенно-положительна в обычном
смысле. За ограничивающую функцию W (х) можно вы-
брать, в частности, функцию
Ж (х) = -g- е (х1 -f- х2 -|-... + хп), (7-6)
где е — некоторое положительное число. Покажем, что
число е можно выбрать так, что функция V — W будет
§ 7.1. ФУНКЦИИ ЛЯПУНОВА ДЛЯ НЕАВТОНОМНЫХ СИСТЕМ 217
положительной. Для этого рассмотрим миноры
функции V — W:
схи — е а12 ... аг.
С&31	0*22 — 8 . . . CXj^
°Ч-1 а1с2 • • • ам — е
матрицы
Д*(8)-
При е = 0 все Д* будут совпадать с минорами Д^ и,
следовательно, они положительны (Д* (0) = Afc 6t;	0).
В силу непрерывной зависимости миноров Д* (е) от пара-
метра е можно утверждать, что всегда найдется достаточ-
но малое положительное число е, при котором все Д* (е)
будут также положительны. Из этого следует, что функ-
ция V — W положительна, что свидетельствует о спра-
ведливости обобщенного критерия Сильвестра.
Для определенно-отрицательной функции V, имею-
щей вид квадратичной формы (7.4), обобщенный критерий
Сильвестра имеет вид
Д1 < -8! <0, Д2 > б2 > О, Д3 < -б3 < 0, . . ., (7.7)
где бп б2, . . . — положительные числа.
Поясним обобщенный критерий Сильвестра примерами.
1. Рассмотрим функцию
V (х, t) = t (х^ + х%) — 2 cos t-XjXz-
Составим матрицу коэффициентов
II t —cost II
II — COS t t II
и главные диагональные миноры
Aj = t, Д2 = t2 — cos2 t.
Если положить t0 = 1, то при всех t 1 будем иметь *)
Дх 1 > О, Д2 1 — cos2 1 ж 0,71 > 0.
Обобщенный критерий Сильвестра (7.5) выполнен, следователь-
но, рассматриваемая функция определенно-положительна в смысле
Ляпунова.
2. Матрица коэффициентов для функции
v (*> t) = {1 — a cos [(а-2 + x2)t]}a-2 + 2а sin [(а-2 + xfytfaxg +
	+ {1 + а cos [(^ + ^)£]} х2
!) Имеем d^ldt = 2t + sin 2t > 0, причем знак равенства
имеет место только при t = 0 (так как х > sin х при х > 0). Сле-
довательно, Д2 (t) при t> 0 неограниченно возрастает.
218
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
имеет вид
1 — a cos Ц- d а sin Kxi + -i'i) О
a sin [(х2 4- <) I] 1 + a cos [(г® + z“) t]
Составим главные диагональные миноры
Аг — 1 — a cos [(.г2 + х2);], Д2 = 1 — я2.
Очевидно, что при любых ;,	.г, будем иметь Ах 1 — | а |,
Д2 = 1 — я2. Отсюда следует, что при | а | < 1 рассматривае-
мая функция будет определенно-положительной в смысле Ля-
пунова.
Вернемся к дальнейшим определениям.
Если при условиях (7.1) значения | V | не превосхо-
дят некоторого конечного положительного числа, то
функция V называется ограниченной. При достаточно ма-
лом значении ц такой будет в силу непрерывности всякая
не зависящая от t функция V.
Если ограниченная функция V такова, что для вся-
кого положительного I, как бы мало оно ни было выбрано,
найдется такое отличное от нуля положительное число 6,
что при
t to, 2j	(7.8)
будет выполняться неравенство
I V | < I,	(7.9)
то говорят, что функция V допускает бесконечно малый
высший предел. Грубо говоря, смысл бесконечно малого
высшего предела состоит в том, что модуль функции
V (х, t) можно сделать сколь угодно малым при любом
t tn только за счет уменьшения модулей всех Xj.
В силу непрерывности бесконечно малый высший пре-
дел имеет всякая не зависящая от t функция V. Но функ-
ции, зависящие от t, хотя бы и ограниченные, могут не
иметь его.
В качестве примера рассмотрим три функции:
sin2 [(^ + . . . + г2);]; (л-2 + . . . + x2)sin2 f, t (г2 + лф —
— 2 cos
Первые две функции ограничены и положительны, но только
вторая из них допускает бесконечно малый высший предел. Заме-
тим, что ни одна из этих двух функций не является знакоопределен-
ной (так как при бесчисленных значениях t они могут обратиться
§ 7.2. ОСНОВНЫЕ ТЕОРЕМЫ ПРЯМОГО МЕТОДА	219
в нуль). Третья функция определенно-положительна, но она неог-
раничена и, следовательно, не имеет бесконечно малого высшего
йредела.
В заключение этого параграфа отметим, что полная
производная функции V (х, t) по времени t, взятая в пред-
положении, что переменные Xj удовлетворяют дифферен-
циальным уравнениям возмущенного движения (1.16), вы-
числяется по формуле
У = -^Х1 + ..,. + ^Хп + ^.	(7.10)
3	п
Читателю полезно сравнить это выражение с равен-
ством (2.12).
§ 7.2. Основные теоремы прямого метода
для неавтономных систем
Основные теоремы прямого метода для неавтономных
систем читаются и доказываются почти так же, как и со-
ответствующие теоремы для автономных. систем. Поэтому
мы приведем сразу все основные теоремы и докажем толь-
ко одну из них.
Теорема Ляпунова об устойчивости движения. Если
для дифференциальных уравнений возмущенного движения
можно найти знакоопределенную функцию V, производ-
ная которой V" в силу этих уравнений была бы знакопо-
стоянной функцией противоположного знака с V или то-
ждественно равна нулю, то невозмущенное движение ус-
тойчиво.
Теорема Ляпунова об асимптотической устойчивости.
Если для дифференциальных уравнений возмущенного дви-
жения можно найти знакоопределенную функцию V, до-
пускающую бесконечно малый высший предел, производная
которой V" в силу этих уравнений была бы знакоопределен-
ной функцией противоположного знака с V, то невозмущен-
ное движение асимптотически устойчиво.
Первая теорема Ляпунова о неустойчивости движения.
Если для дифференциальных уравнений возмущенного дви-
жения можно найти функцию V, допускающую бесконечно
малый высший предел, производная которой F в силу этих
уравнений есть функция знакоопределенная, а сама функ-
ция V в окрестности нуля переменных хк и при всех t
to, где t0 сколь угодно велико, может принимать зна-
220
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
чения того же знака, что и производная, то невозмущенное
движение неустойчиво.
Прежде чем перейти к теореме Четаева о неустойчи-
вости движения, необходимо дать дополнительное опре-
деления области V Д> 0 (см. § 2.4). Совокупность значе-
ний переменных хк, удовлетворяющих в области (7.1)
неравенству V (х, t) Д> 0, называется областью V ~^> 0,
а поверхность V (х, t) = 0 — границей последней. Для
функции V (х, t), зависящей явно от i, граница области
V Д> 0 и сама область изменяются с течением времени t.
Может оказаться, что область V (х, i) Д> 0, изменяясь с
течением времени, перестанет существовать.
Функция U (х, t) называется определенно-положитель-
ной в области V Д> 0, если для произвольного положитель-
ного числа е, как бы мало оно ни было выбрано, найдется
такое положительное число I, что при всех хк, удовлетво-
ряющих условию V е, и для всякого t t0 имеет место
неравенство U (х, i) ;> I.
Теорема Четаева о неустойчивости движения. Если
дифференциальные уравнения возмущенного движения та-
ковы, что можно найти функцию V, ограниченную в об-
ласти V Д> 0, существующей в сколь угодно малой окрест-
ности нуля переменных хк при всех t t0, производная
которой V в силу этих уравнений была бы определен-
но-положительной функцией в области V 0, то невоз-
мущенное движение неустойчиво.
Докажем для примера теорему Ляпунова об устой-
чивости движения (доказательство других теорем можно
найти, например, в [35, 49, 371).
Пусть V — определенно-положительная функция, а
F 0. По определению знакоопределенной функции,
найдется такая не зависящая от t определенно-положи-
тельная функция W, что при достаточно большом t0
и достаточно малом ц в области (7.1) будут иметь место
неравенства
Г < 0, V (х, t) > W (х).	(7.11)
Выберем произвольно малое положительное число е
(конечно, е ц). На сфере е пространства хк (рис. 7.3)
34 = е
к
(7-12)
значения функции W (х) отличны от нуля (так как функ-
ция W определенно-положительная и обращается в пуль
§ 7.2. ОСНОВНЫЕ ТЕОРЕМЫ ПРЯМОГО МЕТОДА	221
только в начале координат О). Поэтому точная нижняя
граница I функции W на сфере е положительна и не может
равняться нулю. Согласно определению точной нижней
границы на поверхности сферы е
будет иметь место неравенство
We (х) > I.
Пользуясь теперь вторым ус-
ловием (7.11), найдем, что в лю-
бой точке сферы е функция V (х, t)
не меньше I:
УЕ (х, t) > I. (7.13)
Рассмотрим функцию V (х, t)
при фиксированном значении вре-
мени t=t0, т. е. функцию У (х, t0).
Эта функция не зависит от t и при х = 0 она обращает-
ся в нуль. В силу непрерывности этой функции по чис-
лу I найдется такое число 6	0, что для всех точек,
находящихся внутри или на поверхности сферы 6,

значения функции У (х, t0) будут удовлетворять неравен-
ству
У (х, t0) < I.	(7.14)
Покажем, что изображающая точка М, начав движе-
ние из сферы 6, никогда не дойдет до сферы е. Действи-
тельно, так как начальная точка Мо берется из сферы 6,;
то значение функции У (х0, t0) в этой точке должно удов-
летворять неравенству (7.14):
Уо = V (х0, t0) < I.	(7.15)
Воспользуемся очевидным равенством
t
У — Уо = f Vdt
io
или, принимая во внимание соотношения (7.11) и (7.15),
У < Уо < I.	(7.16)
Это неравенство выполняется в течение всего времени
движения. Следовательно, изображающая точка М, на-
чав движение из положения Мо, находящегося в сфере 6,
222 ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
никогда не дойдет до сферы е (так как на сфере с, соглас-
но неравенству (7.13), функция Ve (х, t)^ I). Теорема
доказана.
Из приведенного доказательства, принадлежащего
А. М. Ляпунову, виден метод, с помощью которого по
выбранному с можно найти число 6. Действительно, зная
е, нужно найти на сфере е точную нижнюю границу I
функции W (х) (если функция V не зависит от времени t
явно, то точную нижнюю границу функции V (z)). Число
6 найдется теперь из неравенства (7.14) (подробнее об этом
см. статью Н. Г. Четаева, перепечатанную в книге [49]).
Закончим изложение общих теорем прямого метода
Ляпунова следующим замечанием. Во всех теоремах этого
метода можно определить характер устойчивости движе-
ния только после того, как найдена функция Ляпунова,
удовлетворяющая определенным условиям. Естественно
возникает вопрос об обратимости этого метода. Иначе
говоря, можно ли утверждать, что для всякого устойчи-
вого (неустойчивого) движения имеется соответствующая
функция Ляпунова. Исследованием этой проблемы зани-
мались многие ученые. Подробное изложение, основные
результаты и историю вопроса можно найти в книге
Н. Н. Красовского [27].
§ 7.3. Примеры построения функции Ляпунова
для неавтономных систем
Пример 1. Устойчивость движения гирого-
ризонткомпаса. Чувствительный элемент гирогоризонт-
компаса состоит из двух идентичных гироскопов 1 и 2, установлен-
ных в сфере и соединенных между собой (рис. 7.4). А. Ю. Ишлин-
ский в своей работе [22] показал, что если на гироскопы подавать
управляющий момент
4S2
N ==-'^’costsin!?’
где е — угол отклонения осей гироскопов от оси S — N гиросферы,
т — ее масса, В — кинетический момент гироскопа, I — расстоя-
ние от точки подвеса О гиросферы до ее центра тяжести, В — ра-
диус Земли, принимаемой за шар, то в установившемся движении
чувствительный элемент будет показывать плоскость горизонта
и плоскость меридиана при любом движении по поверхности Земли
корабля, на котором установлен прибор.
Восточная составляющая V F скорости корабля относительно
Земли при плавании в не очень высоких широтах меньше пере-
носной скорости В V cos <р, где V — угловая скорость вращения
§ 7.3. ПРИМЕРЫ ПОСТРОЕНИЯ ФУНКЦИИ ЛЯПУНОВА
223
Земли, а <р — шпрота места плавания. Поэтому
I	cos ч>-
Уравнения возмущенного движения системы в упрощающих,
но вполне оправданных предположениях имеют вид (вывод можно
найти в упомянутой работе А. 10.
Ишлинского)
d	ia	25 sins
—г.--7=^ — vB — w-------т---о — О,
dt }[gR	ml gR
<7p v
dt }f gR	1
dv	2B sin a
d 25 sins-6	v
dt ml gR	gR	Г
В этих уравнениях a, 0, у,
6 — координаты системы, определяю-
щие ее положение в возмущенном
движении, v (<) — абсолютная скорость точки О, причем
= (5 77 cos ф + VEy + V2n,
(7-17)
(7-19)
где Уд. — северная составляющая скорости точки О относительно
Земли, со (z) — вертикальная составляющая угловой скорости трех-
гранника Дарбу, относительно которого определяется положение
гпросферы, a (Z) — значение угла е в установившемся движении,
v = g/R — частота, соответствующая периоду Шулера, g — ус-
корение силы тяжести. Отметим, что v (t), со (t) и a (z) — заданные
функции времени, причем но своему физическому смыслу a (t)
> a0 = min a > 0.
Умножим первое уравнение (7.18) на га/^ЛgR, второе на 0,
третье па у и четвертое на 25 sin a-f>lml\f gR и сложим почленно
все уравнения. Тогда после очевидных упрощений получим
i’a d на <7(3	<1у 25sins-6 d 25 sins-6
]fgR dt ~]fgR + P + V + ml ]/^R mi = 0
или, интегрируя,
ра n 4B2 sin2 о
F=75K+P+V+ m№gR 62 =const' (7’2°)
Из соотношений (7.17) и (7.19) следует
v2 (t) > (5 U cos ф — max | VE | )2 > 0.
Кроме того, из условия a (t) > a„ > 0 вытекает, что sin2 a (t) >
sin2 a0 > 0. Эти неравенства означают, что выполнен обобщен-
ный критерий Сильвестра (7.5) и, следовательно, функция V явля-
ется определенно-положительной в смысле Ляпунова. Полная
224 ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ систем
производная F функции V по времени на основании интеграла
(7.20) равна нулю. Согласно первой теореме Ляпунова § 7.2,
возмущенное движение гпрогоризонткомпаса устойчиво относи-
тельно а, р, у и 6.
Пример 2 (математический). Пусть уравнения возмущенного
движения имеют вид
*1 =	+ £12 («)*2 + • • • + g1S(t)xs,
......................................... (7.21)
&S ' gsl “Ь £s2 (t)x2 “b * • • “b
где коэффициенты g^j (z) удовлетворяют условию косой симметрии
gkj (t) = gjtt (l).	(7.22)
Составим определенно-положительную функцию
1
•+*:).
Вычислим полную производную от этой функции по времени
V = х^'г^ -|- г2^2 “Ь • • • “Ь
и внесем сюда значения производных из уравнений (7.21). Тогда
учитывая равенства (7.22), получим
Г = bi + b2 (t)x^ + . . . + bs (t)z|.
Если при t to все коэффициенты b^ (z) неположительны
bn (t)< 0 (k = 1, 2, . . ., s),
то производная F будет отрицательной функцией и, следовательно,
невозмущенное движение х^ = 0 будет устойчиво.
Если все Ь); (z) при t to удовлетворяют условиям
Ък (t) < 6fc < 0,
где 6fr — постоянные отрицательные числа, то производная Т
будет определенно-отрицательной функцией в смысле Ляпунова
и, следовательно, певозмущенное движение ц. = 0 будет асимпто-
тически устойчиво.
Наконец, если при t to коэффициенты b;; (z) удовлетворяют
условиям
h (<) > 6* > 0,
где 6* — постоянные положительные числа, то невозмущенное
движение х^ = 0 неустойчиво.
§ 7.4. Достаточные условия асимптотической
устойчивости системы, жесткость и демпфирование
которой нелинейны и зависят явно от времени
Возмущенное движение различных систем очень часто
описывается одним дифференциальным уравнением вто-
рого порядка
х + a (t, х, х)х + Р (t, х, х)х = 0,	(7.23)
§ 7.4. УСЛОВИЯ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ 225
где положительные вещественные функции а и 0 вещест-
венных переменных t, х, £ определены в области
t > t0, х2 + я2 < И	(7-24)
(t0, р, — некоторые положительные постоянные).
Функцию a (t, х, х) можно трактовать как нелиней-
ный, зависящий явно от времени обобщенный коэффициент
демпфирования, а функцию 0 (i, х, х) — как нелинейную,
зависящую явно от времени обобщенную жесткость си-
стемы.
При любых, но постоянных и положительных коэф-
фициентах а и р невозмущенное движение х — 0, х = О
асимптотически устойчиво. Если же эти коэффициенты,
оставаясь положительными, изменяются, то существуют
режимы их изменения, при которых движение становится
неустойчивым. В тех случаях, когда закон изменения
коэффициентов а и р известен, можно применить тот или
иной метод и исследовать устойчивость движения. Одна-
ко в приложениях встречаются случаи, когда характер
функций а и р не определен и известны только границы
их изменения в области (7.24)
а a (t, х, х) А, b 0 (t, х, х) В, (7.25)
где а, А, Ь, В — заданные положительные числа (случай
а = 0 или b = 0 считаем исключенным).
Поэтому представляет интерес определить условия для
а,А,Ь,В, при выполнении которых невозмущенное дви-
жение х = 0, х = 0 будет асимптотически устойчиво при
любых законах изменения функций а и р в заданных гра-
ницах. (Считая, что функции а и 0 изменяются произ-
вольным образом, мы предполагаем, конечно, что для
всех t, х, х из области (7.24) они удовлетворяют услови-
ям существования и единственности решения уравнения
(7.23).)
Заметим прежде всего, что условие а О, b 0 не-
обходимо. Действительно, если, например, b 0, то,
пользуясь произвольностью аир, полагаем а = const,
0 = b 0. При этих значениях а и 0 движение неустой-
чиво при & < 0 и устойчиво, но не асимптотически при
b = 0 и а = const 0.
Перейдем к рассмотрению поставленной задачи С по-
мощью подстановки
х = хи t =~Схг 4- Dx2r	(7.26)
8 Д. Р. Меркин
226 ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ систем
где С и D — некоторые постоянные, которыми мы распо-
рядимся в дальнейшем соответствующим образом, заме-
ним уравнение (7.23) эквивалентной системой
= Схг + Dx2, х2 = ухг + &г2.	(7.27)
В этих уравнениях функции у и 6 определены равенст-
вами
у = - с(к+дС) + Р , б = — (а 4- С).	(7.28)
Очевидно, что из асимптотической устойчивости отно-
сительно переменных хг и х2 следует асимптотическая ус-
тойчивость относительно х и i, и наоборот.
Возьмем функцию V в следующей форме:
V==A-tf + x22).	(7.29)
Полная производная по времени функции V, вычислен-
ная в силу уравнений (7.27), после очевидных преобразо-
ваний приводится к виду
F = Сх2 + (Z? + у)Х1Х2 + 6x1.	(7.30)
Функция V определенно-положительная. Если нам
удастся подобрать такие постоянные два чисда С и D,
при которых производная Е будет определенно-отрица-
тельной функцией в смысле Ляпунова, то невозмущенное
движение будет асимптотически устойчиво. Составим
матрицу коэффициентов функции Е:
С
4- (Д 4- у) 6
и подчиним главные диагональные миноры обобщенному
критерию Сильвестра (7.7)
Д1^С<-г]<0, Д.^Сб--^-(0 4-у)2> v>0, (7.31)
где т] и v — сколь угодно малые положительные постоян-
ные числа.
Положив С = — ах, где ar = const 0, мы выпол-
ним первое условие (7.31), если потребуем, чтобы число
§ 7.4. УСЛОВИЯ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ
227
aj удовлетворяло дополнительному условию
О < л < o-i <. а = inf а.	(7.32)
Пользуясь равенствами (7.28), приведем второе усло-
вие (7.31) к виду
F (D) = Di - 2 (Е + р - 2v)P2 + (Е - Р)2 < 0, (7.33)
где функция
Е {t, х, х) = ах [a (t, х, х) — aj (7-34)
на основании (7.32) принимает только положительные
значения.
Составим уравнение
F (D) = D1 - 2 (Е + р - 2v)D2 + (Е - Р)2 = 0. (7.35)
Постоянное положительное число v во втором условии
(7.31) может быть сколь угодно малым. Поэтому будем
искать корни уравнения (7.35) в виде ряда
D = Do (1 + dv + . . .),	(7.36)
где Do — корень уравнения (7.35) при v = 0, d — неко-
торый коэффициент, а точки означают члены, содержа-
щие число v в степени выше первой. Имеем
D2 = D2 (1 + 2dv + . . .),
Р4 = D* (1 + 4dv + . . . ).
Внесем эти выражения для D2 и Р4 в уравнение (7.35)
и сгруппируем члены. Тогда с принятой точностью будем
иметь
Р4 - 2 (Е + P)Z>oJ + (Е - Р)2 +
+ 4Dq {LE>o - (Е + P)]d + 1} v + . . . -0.
Учитывая, что v — произвольное число, получим
Р4 - 2 (Е + Р)Р' + (Е - Р)2 = 0,
[Р2-(Е + p)]d + 1 = 0.	(7,37)
Из первого равенства найдем корни уравнения (7.35)
при v = 0:
Р" = -Р’ = /р + /Ё, Р“ = -Е^ = /Р-/Ё. (7.38)
8*
228 ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
Из второго равенства (7.37) определим d:
d=----------------------!----.
E + ^-Dl
Подставляя сюда значения D° из (7.38), получим
di = di =---------, d% = d$ =--------—.
2	2
Возвращаясь к равенству (7.36), найдем корни урав-
нения (7.35)
Л2_-Л3_Л^1 + —
При достаточно малом положительном числе v (его
можно сделать сколь угодно малым) выписанные члены
определяют характер корней уравнения (7.35). Так как
все корни Dk уравнения (7.35) оказались вещественными,
то при фиксированных t, х, х график функции
F = F (D)
имеет вид, изображенный на рис. 7.5. При изменении
х, х корни и график функции f = F (D) будут также
Рис. 7.5
изменяться. Предположим, что области изменения корней
имеют вид, показанный на рис. 7.5. В этом случае
для любого числа D, находящегося между точками N и
М, имеет место неравенство
F (D) < 0.
§ 7.4. УСЛОВИЯ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ 229
Это означает, что для случая, изображенного на
рис. 7.5, существует постоянное число D, при котором
выполняется второе обобщенное неравенство Сильвестра
(7.31) и, следовательно, невозмущенное движение будет
асимптотически устойчиво относительно хг и х2 или х
и х.
Из приведенного рассуждения очевиден путь дальней-
ших действий: для получения асимптотической устойчи-
вости достаточно подчинить корни Dk условиям, при ко-
торых области изменения корней Dx и D2, а также
и D3 не сомкнутся. Иначе говоря, для асимптотической
устойчивости достаточно потребовать, чтобы в области
(7.24) выполнялись неравенства
sup D2 <Z inf Dt, sup D3 < inf Dt.
Считая, что при достаточно малом v корни (7.39) урав-
нения (7.35) определяются выписанными членами, приве-
дем последние неравенства к виду
(1 + 8) sup D°2 < (1 - 8) inf Dl
(1 + e) sup D3 < (1 — e) inf Bj,
где число
v
e =------7=r
2.inf
за счет уменьшения параметра v можно сделать сколь
угодно малым.
Согласно (7.38), (7.32) и (7.34), будем иметь
sup D3 = У sup Р — У inf В = У В — У ai (я — Я1),
sup D3 = У sup E — У inf P = У ai (A — fli) — У b,
inf У inf P + У inf E — УЬ + У ai (a — aj.
Теперь условия (7.40) принимают вид
(1 + е) (Ув — У Я1(я — ai)) < (1 — е) (Уb + Уai (а — Я1)),
(1 + е)(Уа!(Л — ai) — У&)<(1 — е)(УЬ + У (а — Я1))
или
ув - уь <2 уа1(а - яг) - бх,
Уя1(Л — ах)— У <ji(a —ai)<2yi —62,
230
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
где положительные числа
бт = е (]Гь + /£), б2 = е (1% (а — ai) + М — а1))
можно сделать за счет уменьшения параметра е сколь
угодно малыми.
Так как все члены, входящие в неравенства (7.41),—
постоянные числа, а параметры и 62 можно выбрать
сколь угодно малыми, то последние можно отбросить и
заменить неравенства (7.41) на следующие *):
2	(4 — ai) — У{а — ai)J
Таким образом, если границы а, А,Ь, В функций
a (t, х, х) и р (t, х, х) удовлетворяют условиям (7.42), то
невозмущенное движение х = 0, х = 0 будет асимпто-
тически устойчиво. Число ах в промежутке (ц, а), где ц
сколь угодно мало, можно выбрать произвольно. Поль-
зуясь этим обстоятельством, условия (7.42) можно уси-
ливать в желаемом направлении. Рассмотрим три частных
случая.
1.	Жесткость системы постоянна
(Р = const). В этом случае В — Ьи оба неравенства (7.42)
будут выполнены, если верхний предел функции a (t, х, х)
конечен. Действительно, первое неравенство (7.42) при
В = b выполняется для всех а 0. Если взять число аг
достаточно малым, то второе неравенство будет также
удовлетворено при любом b 0 и любом конечном А =
= sup a (t, х, х). Таким образом, при постоянной жест-
кости системы (Р = const) невозмущенное движение х — 0
и х = 0 асимптотически устойчиво при любом перемен-
ном, но ограниченном коэффициенте демпфирования
a (t, х, £).
2.	Коэффициент демпфирования по-
стоянен (а = const). В этом случае А = а и второе
условие (7.42) выполняется автоматически. В первом усло-
вии положим аг = а/2 (при ах — а/2 выражение аг (а — ах)
достигает максимума). Тогда первое условие (7.42) при-
водится к виду
a>/F— УК	(7.43)
х) Если два числа а и Ь связаны неравенством а < Ь, то между
ними всегда можно вставить число а 6 такое, что а 6 < Ьили
а < Ь — 6, где 6 > 0.
§ 7.5. СИСТЕМЫ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ 231
Таким образом, невозмущенное движение х = 0, X =
= 0 будет асимптотически устойчиво при любой перемен-
ной жесткости 0 (t, х, х), если только постоянный коэф-
фициент демпфирования а = а удовлетворяет условию
(7.43).
3.	Если считать В и b заданными, то,
пользуясь свободой выбора числа а15 можно установить
нижнюю границу а для a (t, х, х) и соответствующую
верхнюю границу А. Для этого снова полагаем aY = а/2.
Тогда из неравенств (7.42) найдем
а > }Гв - уг, А < 8b + 4a^r .+_±.	(7.44)
Если границы а, А, Ь, В функций a (t, х, х) и 0 (t, х, х)
удовлетворяют неравенствам (7.42) для всех х, х, t t0,
то будут выполнены условия теоремы Барбашина—Кра-
совского т). В этом случае невозмущенное движение х = О
й х = 0 будет асимптотически устойчиво в целом, т. е.
при любых начальных возмущениях х0 и х0 * 2).
§ 7.5. Устойчивость линейных систем
с периодическими коэффициентами
Исследование устойчивости движения многих систем,
встречающихся в различных технических задачах, часто
сводится к анализу линейных дифференциальных уравне-
ний с периодическими коэффициентами. В матричной фор-
ме эти уравнения могут быть записаны так (см. § 5.2,
формула (5.19а)):
зс = Р (t)sc.	(7.45)
В
этом уравнении х — матрица-столбец или вектор
(7.46)
Теорема Барбашина — Красовского сформулирована в
§ 2.3 для автономных систем. При функции V (х), не зависящей явно
от времени t и удовлетворяющей условию (2.16), эта теорема остает-
ся справедливой и в том случае, когда производная Р, завися явно
от времени, является определенно-отрицательной функцией в смыс-
ле Ляпунова.
2) Для случая, когда функции а и 0 зависят только от времени
t, условия (7.44) были получены другим методом В. М. Старжин-
ским [47]. Приведенный здесь вывод опубликован в работе [39].
232
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
а Р (t) — квадратная матрица
ph (0 • • • р1п (О
РЮ-
(/.47)
Рщ W • • • Рпп W
Будем считать, что все элементы (t) матрицы Р (£),
а следовательно, и сама матрица Р являются периодиче-
скими функциями времени t одного и того же периода Т,
так что для любого момента времени t справедливо ра-
венство
р (t + Т) = Р (t).	(7.48)
Для получения критериев устойчивости таких систем
кратко остановимся на некоторых общих вопросах тео-
рии линейных дифференциальных уравнений с периоди-
ческими коэффициентами, принадлежащей OnoKe(Floquet).
Совокупность п линейно независимых решений урав-
нения (7.45)
(7.49)
называется фундаментальной системой решений этого
уравнения, а матрица
X (t) = || хи . . ., гп||	(7.50)
или, что то же самое,
zn г12 ... ,г1п
Х21 ?22 ... х2п
ХП1 ХП1 ' ' ‘ Хпп
(7-51)
называется фундаментальной матрицей. Здесь, как и в
дальнейшем, первый индекс элемента обозначает номер
функции, а второй — номер решения.
Общее решение ас (t) уравнения (7.45) определяется
обычной формулой общего решения линейного однород-
ного дифференциального уравнения:
(7-52)
х (t) — CiXi + CiXi + ... + Спхп,
§ 7.5. СИСТЕМЫ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ 233
.где . ., Сп — произвольные' постоянные, определяе-
мые из начальных условий. В матричной форме общее
решение (7.52) имеет вид
х (£) = X	(7.53)
где С — матрица-столбец
(7.54)
Не нарушая общности, можно считать, что фунда-
ментальная система решений удовлетворяет следующим
начальным условиям:
( 1, * = Л
W°)=[0, k=£j
или в матричной форме
X (0) = Е,	(7.55)
где Е — единичная матрица
1 0 ... 0
И0- - • • • ° •
0 0 ... 1
Обозначим через A (£) определитель фундаментальной
матрицы
A (£) = det X (t).	'’.56)
Пользуясь равенством (7.55), получим
А (0) = det X (0) = det Е = 1.	(7.57)
В теории дифференциальных уравнений доказывается
следующая формула Лиувилля:
t
) (Pn+...+P„„)d«
A (i) = А (0) е»
Учитывая равенство (7.57), найдем, что при t — Т
т
$ (Ри+- +рпп№
Д(Г) —(7.58)
234 гл. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ систем
Если в каком-нибудь решении хк заменить t на t + Т,
то в силу периодичности матрицы Р (t) мы снова получим
решение, так как вектор xl: (t + Т) будет по-прежнему
удовлетворять уравнению (7.45), если ему удовлетворял
вектор х* (t). Полученное решение не будет совпадать
с первоначальным решением х* (t), но, как всякое реше-
ние уравнения (7.45), оно может быть получено из общего
решения (7.53) выбором соответствующей матрицы-столб-
ца С. Обозначив эту матрицу через Ак, найдем
хк (t -f~ Т) = X (t)-AK (к — 1, 2, . . ., п).
Отсюда видно, что фундаментальная матрица X (t + Т)
решений хг (t + Т), x2(t + Т), . . ., хп (t + Т) имеет вид
х (t + Т) = X (t)X,
где А — постоянная матрица:
(7.59)
А — || Ai, ..., Anft =
а11 а12 •
а21	а22 •
(7.60)
По предположению фундаментальная система решений
хт (t), . . ., xn(t) удовлетворяет начальным условиям
(7.55). Поэтому, положив в равенстве (7.59) t = 0, найдем
X (Т) = X (0)Л = ЕА = А.
Следовательно, если известна фундаментальная матри-
ца X (t), то матрица Л определится из последнего равенства:
aru (Г) ... х1п (Т)
А~Х(Т)~
(7-61)
*nl(r) • • •
Покажем далее, что существует решение х (t), удов-
летворяющее следующей зависимости:
х (t + Т) = px (t),
(7.62)
где р — некоторое постоянное число (такое решение на-
зывается нормальным). Действительно, любое решение
уравнения (7.45) можно получить из общего решения
(7.53). Поэтому если нормальное решение существует,
то должна существовать такая постоянная матрица-
§ 7.5. СИСТЕМЫ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ 235
столбец
(7.63)
для которой будет справедливо равенство
х (г) = х (ОР.
Так как по предположению х (t) удовлетворяет равенству
(7.62), то, имея) в виду, что х (t + Т) = X (t + Т) 0,
получим
X (t + Т)0 = Р* (ПР
или, пользуясь равенством (7.59),
х (олр = рХ (i)P.
Группируя члены, найдем
X (I) (А - рЕ)0 = 0.
Учитывая, что это равенство должно выполняться при
всех t, получим
(Л - р£)0 = 0.
Это матричное уравнение, в котором неизвестными
являются матрица-столбец 0 и число р, эквивалентно п
скалярным уравнениям
(«п — р)0! + а1202 +...+ aln07i = 0.
«21Р1 Н” («22	Р)02 Н” • • • Т «2770п = 0,
«771Р1 + «71202 + • • . + («7171 - Р) Рп = 0.
Для того чтобы система п алгебраических однородных
уравнений относительно 0П . . ., 0П имела решение, отлич-
ное от нуля, необходимо и достаточно, чтобы определи-
тель системы равнялся нулю:
det (Л — рЕ) =
ац — р а12	. . .
Я21	а22 — Р • • •
“177
“277
= 0. (7.64)
ап1 ап2
а
пп
— р
Каждому корню р^ этого характеристического урав-
нения (для простоты будем предполагать, что среди корней
нет кратных) отвечает свое решение хк (t), удовлетво-
236
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
ряющее условию (7.62). В результате получим п нормаль-
ных решений х± (t), . . ., хп (t), удовлетворяющих усло-
вию (7.62):
•»i (t + Т) = pi?! (t), . . ., хп (t + Г) = рпхп (0. (7.65)
Эта система решений линейно независима и может
быть принята за фундаментальную систему решений.
Покажем теперь, что нормальные решения имеют вид
х* (t) =	(t) (к = 1, . . ., п),	(7.66)
где ф>,- (t) — периодическая матрица-столбец периода Т
Фис W
фИ0= • • •
(О
фк (I + Т) — фк (t),
(7.67)
a aft — постоянные числа, называемые характеристи-
ческими показателями, вычисляются по формуле т)
—InpR. (k = i.....п).	(7.68)
Действительно, внесем в равенства (7.66) значение t,
равное t + Т. Получим
(t + Т) = ea*(t+T)<pk (t + Г).
Пользуясь равенствами (7.67) и (7.68), последовательно
найдем
«к- (t + Т) =	(t + Т) = еа^е ^Р^Т ф, (t) =
= рй (О»
т. е. равенства (7.65).
Теперь можно перейти к исследованию устойчивости
движения. Будем считать, что за фундаментальную си-
стему решений уравнения (7.45) принята система нормаль-
ных решений xr (t), . . ., хп (t), удовлетворяющих усло-
виям (7.65). Общее решение уравнения (7.45) запишем
в форме (7.52)
Ж(0=3<Д^ (t).	(7.69)
>t=i
х) Напомним определение логарифма комплексного числа (кор-
ни уравнения (7.64) могут быть комплексными числами):
In р = In | р | + i arg р,
где | р | есть модуль р и arg р обозначает аргумент р.
§ 7.5. СИСТЕМЫ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ 237
Вектор ас (t) определяет изображающую точку М,
а слагаемые С^ас^. (t) являются составляющими его. Через
период Т положение изображающей точки М будет оп-
ределяться равенством
п
+ c^it + T).
k=l
Составляющие этого вектора, согласно (7.65), равны
с^а + 7’)=рл®ио-	(7-7°)
Отсюда
I (\яск (t + Т) I = I pk 11(t)
Это равенство показывает, что если все | р/с | < 1,
то через период Т модули всех составляющих вектора
ас (t + Т) уменьшатся и, следовательно, изображающая точ-
ка М приблизится к началу координат; если модуль хотя
бы одного корня рте больше единицы, то через период Т
соответствующая составляющая С^х* (t + Т) вектора
х (t + Т) увеличится по модулю и изображающая точка
М начнет отдаляться от начала координат; наконец, если
среди корней характеристического уравнения имеются
такие, модули которых равны единице, то модули соответ-
ствующих составляющих вектора ас (t + Т) останутся без
изменения.
Из этого вытекают следующие условия устойчивости
системы, возмущенное движение которой описывается ли-
нейными дифференциальными уравнениями с периоди-
ческими коэффициентами.
Если модули всех корней характеристического уравне-
ния (7.64) меньше единицы, то невозмущенное движение
хг = . . . = хп = 0 асимптотически устойчиво.
Если среди корней характеристического уравнения име-
ется хотя бы один, модуль которого больше единицы,
то невозмущенное движение неустойчиво.
Если среди корней характеристического уравнения име-
ются такие, модули которых равны единице, а модули
остальных корней меньше единицы, то невозмущенное дви-
жение устойчиво, хотя и не асимптотически.
Заметим, что первые два вывода справедливы и при
кратных корнях характеристического уравнения, а по-
следний только ппч простых корнях (точнее, при корнях
простых относи ьно элементарных делителей).
238 ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ систем
Раскроем определитель (7.64) и приведем его к виду
pn + nip71-1 + игр71-2 + • •. + ап-ip + лп = 0. (7.71)
Коэффициент ап определяется, очевидно, равенством
ап = (—I)71 det А.
Пользуясь равенствами (7.61), (7.56) и (7.58), найдем
т
a?l = (-iyv	(7.72)
Таким образом, свободный член характеристического
уравнения (7.71) может быть найден по коэффициентам
исходных уравнений (7.45). К сожалению, для опреде-
ления остальных коэффициентов уравнения (7.71) необхо-
димо знать хотя бы одну фундаментальную матрицу X (t)
(легко доказывается, что уравнение (7.71) не зависит от
выбора фундаментальной матрицы). Задача облегчается
тем, что критерии устойчивости носят характер неравенств,
поэтому можно пользоваться численными и приближен-
ными методами.
Один из этих методов состоит в следующем. Задав
начальные условия (7.55), численным интегрированием
уравнения (7.45) определяют значения линейно незави-
симых решений (7.49) в конце периода Т, т. е. матрицу
X (Т) = А. Так как интегрирование нужно производить
на конечном промежутке времени [0, Т], то все вычисле-
ния можно произвести с любой наперед заданной точностью
(для этой цели лучше всего, конечно, использовать элект-
ронно-вычислительные машины). По найденной матрице А
составляется характеристическое уравнение (7.64), после
чего определяются корни рх, р2, . . ., рп. Хорошим конт-
ролем этого метода может служить равенство (7.72), ко-
торое с помощью последней формулы Виета (4.23) при-
водится к виду
т
j (рич—.+рпп)^
р1...р„ = ео
Отметим, что в этом методе заключение об устойчиво-
сти движения на бесконечном промежутке времени дела-
ется на основании результатов интегрирования на конеч-
ном интервале времени [0, Т}.
§ 7.6. РЕШЕНИЯ УРАВНЕНИЙ ХИЛЛА И МАТЬЕ	239
Со вторым приближенным методом (их существует зна-
чительно больше) мы познакомимся в следующем пара-
графе, а сейчас остановимся на случае, когда среди корней
характеристического уравнения имеются корни, равные
+1 или —1.
Предположим, что р = 4-1. Тогда соответствующее
нормальное решение будет удовлетворять равенству (см.
формулу (7.62)) ас (t -f- Т) = ас (£).
Это означает, что уравнение (7.45) имеет периодиче-
ское решение, период которого Т совпадает с периодом
коэффициентов.
Пусть теперь р == —1. Тогда соответствующее нор-
мальное решение будет удовлетворять равенству
ас (Z 4- Т) — —ас (£).
Еще через один период будем иметь
ас (t 4- 2Т) — —ас (t 4- Т) = ас (£).
Из этого следует, что при наличии корня р — —1 урав-
нение (7.45) имеет периодическое решение, период которо-
го 2 Г вдвое больше периода Т коэффициентов исходного
уравнения.
А. М. Ляпунов показал [35], что всякую систему ли-
нейных дифференциальных уравнений с периодическими
коэффициентами можно привести при помощи линейной
подстановки к системе уравнений с постоянными коэф-
фициентами. Подробное исследование систем, которые мо-
гут быть приведены к линейным уравнениям с постоян-
ными коэффициентами, содержится в работе Н. П. Еру-
гина [19].
§ 7.6. Устойчивость решений уравнений
Хилла и Матье
Возмущенное движение многих систем (см. § 7.7) опи-
сывается одним дифференциальным уравнением второго
порядка
^- + p{t)z = Q,	(7.73)
где р (£) — периодическая функция периода Т. Разложим
функцию р (£) в ряд Фурье
оо
р (0 = ^2- 4- У, (л, cos t 4- В, sin f) . (7.74)
k=i
240
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
Теперь уравнение (7.73) принимает вид
d3x , Г 40 , VI 7 . 2nfc . . D . 2лЛ Д 7 п
2“ + / , (A cos — t + 5, Sin -у- fJJ 2 = 0.
A’=l
(7-75)
Уравнение, записанное в такой форме, впервые рас-
сматривалось Г. В. Хиллом (G. W. Hill) при исследова-
нии движения Луны.
Для наших целей уравнение Хилла удобно записать
в следующей форме:
Я2Г
_£± + [6 + eW)M = 0,	(7.76)
где б и е — некоторые параметры, а ф (t) — периодическая
функция периода Т. Функцию ф (t) называют функцией
возбуждения, а ее частоту со = 2л/Т — частотой возбуж-
дения.
Очевидно, что выбором параметров бив невозмущен-
ное движение х = 0, ± = 0 можно сделать устойчивым
и неустойчивым. Так, например, при в = 0 и б /> 0, дви-
жение устойчиво, а при в = 0 и б 0 это движение не-
устойчиво. Поэтому задачу об устойчивости решений урав-
нения Хилла можно поставить следующим образом:
в плоскости параметров бив найти области устойчивости
и неустойчивости невозмущенного движения х =0, х = 0.
Установим прежде всего некоторые общие свойства
решений уравнения Хилла. Положим
х = х2, х = х2.
Тогда одно уравнение (7.76) будет эквивалентно двум
уравнениям первого порядка
х-L = х2, х2 = — [б + Еф хг. (7.77)
Напишем матрицу коэффициентов этой системы (см. (7.47)):
Р(^ = 1 -[6 + еф(0] 0 ||-
Следовательно, рп = р22 = 0- Пользуясь формулой (7.72),
найдем а2 = 1. Согласно равенству (7.71), характеристи-
ческое уравнение запишется в виде
р2 + яр + 1 = 0.	(7.78)
Коэффициент а нам неизвестен и для его определения
необходимо знать фундаментальную матрицу решений.
s 7.6. РЕШЕНИЯ УРАВНЕНИЙ ХИЛЛА И МАТЬЕ	241
Так как найти эту матрицу в замкнутой форме мы не мо-
жем, то для определения области устойчивости в плоскос-
ти параметров 6 и е воспользуемся следующими сообра-
жениями.
Согласно формуле Виета произведение корней рх
и р2 уравнения (7.78) равно единице
Р1*р2 = I-
Решим уравнение (7.78), считая коэффициент а извест-
ным
а , 1 /г а2 .
Р1>2=----2*+ У -4- — !•
Рассмотрим возможные случаи.
1.	| а | 3> 2. Оба корня уравнения (7.78) будут веще-
ственными и различными. Так как их произведение равно
единице, то один из корней будет по модулю меньше еди-
ницы, а второй больше единицы. Из этого следует, что при
| а | 3> 2 движение будет непериодическим и неустойчи-
вым.
2.	| а | < 2. Тогда
а т 1 f л а* .
Р1,з =---2“+ У 1------4- Ь
где i = 'У—1. Корни получились комплексные. Найдем
модуль этих корней:
im=j/ (--гУ + Й’Й-^Р1-
Модули корней оказались равными единице, а сами
корни различны. Поэтому при | а | < 2 движение будет
устойчивым.
3.	а = —2. В этом случае Pi = р2 = +1. Как было
показано в конце § 7.5, одному из этих корней будет от-
вечать периодическое решение периода Т. Можно пока-
зать (мы не будем останавливаться на этом), что второму
корню отвечает возрастающее решение (корни кратные не
только относительно характеристического уравнения, нд
и относительно элементарных делителей). Движение бу-
дет неустойчивым, но существенно, что имеется периоди-
ческое решение периода Т.
4.	а = +2. При этом условии Pi = р2 = —1- Одному
из этих корней будет отвечать периодическое решение
периода 2Т (движение, как и в случае 3, неустойчиво).
9 Д. Р. Меркни
242
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
Таким образом, движение будет устойчиво только при
| а | < 2. Коэффициент а уравнения (7.78) при данном
периоде Т возбуждающей функции ф (£) зависит, в конеч-
ном счете, от параметров 6 и б. Предположим, что коэф-
фициент а = а (6, б) найден. Тогда границей области ус-
тойчивости на плоскости 6, 8 будут служить уравнения
а (6, б) = ±2.	(7.79)
Из случаев 3 и 4 следует, что на границе области ус-
тойчивости, то есть для значений 6 и б, удовлетворяющих
уравнениям (7.79), существуют периодические решения
периода Т и 2Т. Эти выводы дают возможность определить
границы области устойчивости из условия существования
периодических решений уравнения Хилла.
Прежде чем перейти к определению границ области
устойчивости, рассмотрим аналитический вид решений
уравнения Хилла (7.76). Пользуясь формулами (7.66)
и (7.69), запишем общее решение в следующей форме:
х (i) = CieaApi (t) +	(t)-	(7.80)
В этом решении Сг и С2 — произвольные постоянные
интегрирования, <рг (i) и ф2 (t) — некоторые периодические
функции, период которых равен периоду Т возбуждающей
функцииф (i), а аг и а2 — характеристические показатели,
определяемые равенством (7.68):
1 1
«1= — In pi, cta=-y-lnp2,
где р! и р2 — корни уравнения (7.78).
Рассмотрим сначала область неустойчивости, в кото-
рой | а | )> 2. Как было установлено, при этом условии
корни рх и р2 характеристического уравнения (7.78) ве-
щественны и различны. Предположим, что оба корня по-
ложительны (случай, когда рх и р2 отрицательны, не вно-
сит ничего принципиально нового). Обозначим через рх =
= р больший корень. Тогда, учитывая, что произведение
корней равно единице, будем иметь
Pi>l, р2=-^-<1.
Отсюда
1 111
а = ai = -у- In pi > 0, а3 = — In р2 = — In — = — а < 0.
§ 7.6. РЕШЕНИЯ УРАВНЕНИЙ ХИЛЛА И МАТЬЕ	243
Общее решение (7.80) можно записать теперь в следую-
щей форме:
z (t) =	(i) + С2ега\2 (£).	(7.81)
Так как решение х (t) является вещественной функ-
цией, то произвольные постоянные (\ и С2, а также перио-
дические функции ((д (i) и <р2 it) должны быть веществен-
ными величинами. Второе слагаемое в равенстве (7.81)
быстро затухает (а 0) и практически можно ограни-
читься первым членом
х (t) sa C1ecct(p1 (t).	(7.82)
Е13 этого решения видно, что максимальные значения
(амплитуды) функции х (t) возрастают по закону геомет-
рической прогрессии, знаменатель которой равен еаТ =
= р 1. Примерный вид графика решения (7.82) показан
Рис. 7.6
на рис. 7.6 (этот график зависит от вида периодической
функции ф! (£), которая, как правило, нам неизвестна).
Рассмотрим теперь аналитический вид решения урав-
нения Хилла (7.76), отвечающего значениям параметров
е и 6 из области устойчивости. Как было установлено,
в этой области оба корня рх и р2 уравнения (7.78) — комп-
лексно-сопряженные числа, причем | pi | = | р2 I = 1-
На основании определения логарифма комплексного чис-
ла будем иметь (pt = р)
1
«1,2 = — (In I р I ± i arg р)
или, учитывая, что In | р | = In 1 = 0,
= a2 =----------j-i,	(7.83)
9*
244
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
где
к = | arg р |.	(7.84)
Гак как cq и а2 — комплексно-сопряженные числа,
а решение х (Z) является вещественной функцией, то пос-
тоянные интегрирования Сг и С2, а также периодические
функции фх (Z) и ф2 (t) должны быть комплексно-сопряжен-
ными величинами. Представим их в показательной форме
Сг = А- Ае&, С. = 4- Ле-₽‘,
Ф1 (Z) = у (Z) ф2 — у (Z)	(7.85)
Внося выражения для а^, С; и <р j в равенство (7.80), най-
дем
х (t) = -%- Y (t) [ет	' + е	'1
Пользуясь известной формулой
А (е2г + c'zi) = cos z,
получим
x(t) = Ay(t) cos [4 t + v(Z) + p] (7.86)
или
x (t) — p (Z) cos (4 t + p) + Л (0 sin (4 + p) >
где функции p (Z) и ц (Z) определены равенствами
ц (Z) — Ay (Z) cos v (Z), г] (Z) = —Ay (Z) sin v (Z).	(7.88)
В общем решении (7.86) или (7.87), отвечающем облас-
ти устойчивости, постоянные вещественные числа А и р
определяются из начальных условий движения, а у (Z)
и v (Z) или ц (Z) и г] (Z) — вещественные периодические
функции, период Т которых равен периоду возбуждающей
функции ф (Z). Как правило, функции у (Z) и v (Z) (тем са-
мым и функции ц (Z)ht] (Z)), а также число к — | arg р |
определить в замкнутой форме мы не можем, так что ра-
венства (7.86) и (7.87) определяют только форму решения
уравнения Хилла, а не само решение. Однако из этих
равенств мы можем составить общее представление
о характере устойчивых решений уравнения Хилла. Дей-
ствительно, из равенства (7.87) видно, что общее решенш
§ 7.6. РЕШЕНИЯ УРАВНЕНИЙ ХИЛЛА И МАТЬЕ	245
представляет комбинацию периодических функций с пе-
риодами Т\ = Т и Т-i = Т. Если периоды Тг и Т2
несоизмеримы, то устойчивое решение уравнения Хилла
не является периодической функцией времени. Если же
отношение
1\_____к_
Т2 ~ 2л
представляет рациональное число, то устойчивое решение
уравнения Хилла является периодической функцией.
Из равенства (7.86) можно составить и общее представ-
ление о графике устойчивого решения. Для случая, ког-
да Т1 Т2 (к <^_ 2л), примерный график решения (7.86)
Рис. 7.7
изображен на рис. 7.7 (он напоминает график колебаний
при биении). Заметим, что колебания системы, вызванные
возбуждающей функцией, называются параметрически-
ми колебаниями.
Покажем теперь метод определения границы области
устойчивости на частном, по имеющем большое значение
случае, когда разложение (7.74) функции р (t) в ряд Фурье
содержит только два периодических слагаемых самой низ-
кой частоты, т. е.
р (t) = ——Н Ai cos - у t -f- Bi sin - -у- t.
Положим
Ai = A cos y, Br = A sin y,
где А и у — некоторые постоянные. В этих обозначениях
будем иметь
P(^) = 4L + 4cos(-^-f-T) .
246 гл. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
Внеся р (t) в уравнение (7.73), получим
~dF + [— + Лсо^—i-V)jz = O.
Перейдем теперь к безразмерному времени т по фор-
муле
2л ,
— t — у =
Отсюда
Т j
dt — -^— ах
4Л
и последнее уравнение примет свой окончательный вид
+ (б + е cos т) ж = 0,	(7.89)
где
б = <7-90)
4л.2 2	4л2	'	'
Уравнение (7.89) называется уравнением Матье", оно
является, конечно, частным случаем уравнения Хилла
(7.76).
Возбуждающая функция равна cos т, а ее период ра-
вен 2л. В соответствии с примечанием к (7.79) будем ис-
кать те значения 6 и е, при которых существуют периоди-
ческие решения периодов 2л и 4л. Из самой формы урав-
нения (7.89) видно, что если функция х — х (т) есть реше-
ние уравнения (7.89), то функции х = х (—т) и х =
= —х (т) будут также решениями этого уравнения. Из
этого следует, что среди периодических решений уравне-
ния Матье имеются четные и нечетные решения. Четные
периодические решения периода 2л будем искать в форме
ОО
х — -у- + ai: cos кх,	(7-91)
S=1
а нечетные периодические решения того же периода —
в форме
х— ^b^sinkx.	(7.92)
if=i
Периодические решения периода 4л представим аналогич-
ными рядами:
ОО	00
я = -?г +	COS-^-, х=	(7.93;
к=1	h-=i
§ 7.6. РЕШЕНИЯ УРАВНЕНИЙ ХИЛЛА И МАТЬЕ
247
Остановимся более подробно на решении (7.91). Про-
дифференцировав обе части уравнения (7.91) два раза
по времени т, найдем
ОО
-44* = — у1 c°s
ат3 / 1	*
П=1
Внеся это выражение и выражение (7.91) для х в уравне-
ние (7.89), получим
ОО	00
— у1, А2а(. cos кг + (6 + е cos т)	аК cos кх^ = 0.
к=1	к=1
Раскроем скобки и воспользуемся формулой
cos т cos кх = -у [cos (к + 1) т + cos (к — 1) т].
Тогда последнее уравнение примет вид
00
“2" ао + (б — к2) ак cos кт +
h*=i
00
+ -у |ао cos т + у1, ah. [cos (к + 1) т + cos (А: — 1) т]} = 0.
К=1
(7.94)
Преобразуем выражение в фигурных скобках. Имеем
00	00
{...} = ао cost + 3 ai; cos (к + 1) т + 2 ah-cos(k— 1)т =
R=1	К=1
00	00
= ао COS Т + ’ 2 <2 ;—I COS кх + 2 alc+l cos Act.
R=2	к'=0
Слагаемое а0 cos т внесем в первую сумму, а из второй
суммы выделим первое слагаемое, после чего объединим
обе суммы. Тогда получим
00
{...} = ai + 2 («л-1 + ак-+1) cos кх.
1=1
Теперь равенство (7.94) можно записать в следующей
форме:
S е
уао -|—у оц +
00
+	[-у- ^'--1 + (6 — к2) ак +	cos кт = 0.
R=1
248
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
Так как это равенство должно выполняться для всех
значений т, то отсюда следует
6а0 + еах = О,
~2~ ан-1 + (^ — к2)	-|—ац+1 = 0 (к = 1, 2, ...).
Запишем эту систему равенств более подробно, учиты-
вая, что индекс к принимает значения 1,2, . . .
бао + eai = 0,
-у а0 + (6 — l)ai + -^-а. = 0,
-у ai + (6 — 4) ai, + а3 = 0,
(7.95)
Эти линейные однородные уравнения относительно а0,
alt а2, . . . должны иметь решение, отличное от нуля (так
как существует периодическое решение (7.91)). Поэтому
определитель этой системы
	6	е	0
	е _	е
	Т S — 1 "Г
	0 "Г ё~4
	0	°	-у
	0	0	0
должен равняться нулю’
0	0	...		
0	0	...		
к	0	...	= 0.	(7.95)
6-9	“Г • • ‘		
F	6-16 . . .		
Это уравнение, содержащее в левой части определитель
с бесконечным числом строк и столбцов (он называется
определителем Хилла), устанавливает искомую зависи-
мость между 6 и е:
6 = 6 (е),
при которой существует периодическое решение вида
(7.91). В явной форме эту зависимость можно установить
следующим образом. Раскроем определитель (7.96) при
конечном п. Тогда получим обычное алгебраическое
уравнение, из которого найдем приближенное решение
6П = 6П (е)- Точное решение получается при и-> оо (это
решение можно представить в форме сходящихся ря-
дов). График функции 6 = 6 (е) определяет одну из гра-
ниц области устойчивости решений уравнения Матье в
§ 7.6. РЕШЕНИЯ УРАВНЕНИЙ ХИЛЛА И МАТЬЕ
249
пространстве параметров 6 и е (ниже будет дано решение
уравнения (7.96) при |е | <<:!).
Аналогичными методами получаются трп других урав-
нения для периодических решений вида (7.92) и (7.93):
	6-1	е Т	0	0	...			
	е ~2~	6-4	1 » 			
	0	8	6-9	. . .	=4	),	(7.97)
	0	0	8 -у д-16 . . .			
	1-1	8 Т	0	0			
е т		9	1	0	...			
0		8 Т	25	к 6 	 —7-	~Х~	. .	. 4	2		= о,	(7.98)
0		0	е	49 2	4	• ‘ ‘			
»-4-	8 “Т	8 Т	0	0	...			
е "Г			4- о ...			
0		8 т	25	е 6-4	2	...		= 0.	(7.99)
0		0	в	.	49 2	д“ 4	• • •			
Таким путем определяются области устойчивости для
уравнения Матье; результаты приведены на диаграмме
Айнса — Стретта (рис. 7.8), где областям устойчивости
соответствуют заштрихованные поля, а областям неустой-
чивости — белые поля. Диаграмма дана только для
е 0; для е < 0 она получается зеркальным отображе-
нием относительно оси 6. Отдельные области смыкаются
между собой в точках 6 = и2/4 и е = 0, где п — целое
число.
Как видно из диаграммы, область устойчивости суще-
ствует и при отрицательных 6. Очевидно, что аналогич-
250
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
ными методами можно построить соответствующую диа-
грамму и для уравнения Хилла (7.76), разложив предва-
рительно возбуждающую функцию ф (/)' в ряд Фурье.
Проследим за изменением свойств параметрических
колебаний при изменении частоты <о = 2л/Т возбужде-
ния. Пусть частоте оз на диаграмме Айнса — Стретта
Рис. 7.8
отвечает точка М (см. рис. 7.8). Соответствующие значения
параметров 6 и е найдем из формул (7.90):
6 = ^, е = -4.	(7.100)
2сР	со2	'	'
Из этих равенств видно, что при увеличении частоты
возбуждения <о параметры 6 и е будут уменьшаться, а точ-
ка М будет перемещаться по прямой
6 = -^-в,	(7.101)
асимптотически приближаясь к началу координат (на
рис. 7.8 эта прямая показана пунктиром). Из рисунка
видно, что прямая (7.101) пересекает области устойчивости
и неустойчивости. Это означает, что при увеличении часто-
ты возбуждения <о устойчивые и неустойчивые состояния
системы будут чередоваться. Заметим, что в некоторых
случаях (см. пример 1 § 7.7) параметр е может не зависеть
от <о. В этих случаях прямая, показанная на рис. 7.8, будет
параллельна оси 6, однако вывод о чередовании устойчи-
вых и неустойчивых состояний системы при увеличении
частоты возбуждения остается справедливым.
§ 7.6. РЕШЕНИЯ УРАВНЕНИЙ ХИЛЛА И МАТЬЕ	251
Если при данных значениях параметров 6 и е имеет
место неустойчивость, то говорят, что наступает пара-
метрический резунанс. Из приведенных рассуждений вид-
но, что параметрический резонанс имеет место при бес-
численном множестве значений частоты возбуждения со.
При малых е параметрический резонанс наступает вблизи
значений б = н2/4, где п — целое число (см. описание
рис. 7.8).
Между обычным и параметрическим резонансами име-
ются существенные различия. Действительно, если на
систему с линейным упругим элементом действует возму-
щающая сила, изменяющаяся по гармоническому закону,,
то дифференциальное уравнение движения приводится
к виду
х + k2x = Н cos at.
При совпадении частоты возмущающей силы со с ча-
стотой собственных колебаний к частное решение, соответ-
ствующее вынужденным колебаниям, будет
х = ~ъ—t sin at.
2ш
Из этого решения и его графика (рис. 5.1) видно, что
обычный резонанс представляет неограниченное возраста-
ние вынужденных колебаний устойчивой системы (см.
пример 3 § 5.4), возникающих под действием возмущаю-
щей силы. Резонанс появляется только при одной частоте
возмущающей силы со = к и любых, в том числе и нулевых,
начальных условиях *). Амплитуды вынужденных коле-
баний возрастают практически по закону арифметической
прогрессии, разность которой приближенно определяется
равенством d = 77л/(2п>2) (если не считать нескольких
первых колебаний, то это равенство дает очень хорошее
приближение).
Параметрический резонанс — это возрастающие коле-
бания около неустойчивого положения равновесия. Он
возникает не при одном, а при бесчисленном множестве
значений частоты возбуждения в результате появления
неизбежных начальных возмущений (при нулевых началь-
х) При a =f= к частное решение имеет вид
и, следовательно, амплитуды вынужденных колебаний не возрас-
тают.
252
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
ных условиях система находится в состоянии неустойчи-
вого равновесия). Характер движения системы при пара-
метрическом резонансе практически определяется соот-
ношением (7.82) (см. также рис. 7.6)
х (0 Се“‘<р (О,
где а > 0, а <p (t) — периодическая функция, период
которой равен периоду возбуждающей функции Т. Амп-
литуды колебаний при параметрическом резонансе, как
это следует из последней формулы, возрастают по закону
геометрической прогрессии, знаменатель которой (фактор
возрастания) определяется равенством
f = еаТ/2.
Остановимся теперь на вычислении зависимости
б = 6 (е) при условии, что | е |	1.
Ограничимся в бесконечном определителе (7.96) Хил-
ла сначала двумя строками и двумя столбцами
б е
Д2(е) =
6-1
или
Д2(е)=б(б-1)-4 = 0-
Положим е = 0. Тогда
Д(О) = б (б - 1).
Это нулевое приближение имеет два корня
61О) = 0,	б(20) = 1.
Для определения первого приближения положим
б^ = fiW + Я1е2,	= 6<0) + а2е2
или, учитывая значения 6i0) и б20),
б!1’ = a162,	6?’ = 1 + а2е2.
Составим теперь из (7.96) определитель А3:
	б	6	0 — 6-1	—	
Дз(е) =	2	0	1	2 ° 4	= 0.
§ 7.6. РЕШЕНИЯ УРАВНЕНИЙ ХИЛЛА И МАТЬЕ	253
Раскрывая определитель, находим
Дз(е) = б (б — 1) (б — 4) — -J-(36 — 8) = 0.
Внесем сюда сна'чала 6[L) = а^2:
aj.s2 (aie2 — 1) (яте2 — 4)-(3aie2 — 8) = О
или, ограничиваясь членами не выше второго порядка
малости,
4axe2 + 2е2 = 0.
Отсюда находим
Аналогично найдем а2 и б?’:
« = 4’ 6<» = 1 +.А_е>.
Можно показать, что если придерживаться принятой
точности, то вычисления с помощью определителей более
высокого порядка не внесут улучшения в найденные зна-
чения а± и а2. Это следует из очевидного равенства, полу-
чающегося из определителя (7.96) для конечного п при
раскрытии его по элементам последнего столбца или строки:
Д„= [6 - (и -1)2] Дд-1 Д„_2.
Поэтому будем считать, что при малых е два решения
уравнения (7.96) определяются равенствами:
б = --£, 6-1 + -^-е2.	(7.102)
Аналогично получим решения уравнений (7.97) —
(7.99):
б = 1-А-е2, б = ±--|-, 6^-4	(7.103)
причем улучшить эти результаты за счет повышения-по-
рядка определителей нельзя, если только вычисления ве-
сти до первого члена, содержащего е. На рис. 7.9 показа-
ны области устойчивости для малых е.
Если в систему ввести демпфирование, то уравнение
(7.89) примет вид
-g- + 277^ + (6 + ecosT)^ = 0,	(7.104)
где h > 0.
25 i
ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
С помощью подстановки
х = e~hxz	(7.105)
приведем уравнение (7.104) к виду
— + (6 — 7г2 + в cost) z = 0.	(7.106)
Это уравнение совпадает с уравнением Матье (7.89),
если положить
бх = 6 — h2.
Предположим, что при заданных б, h, е уравнение
(7.106) определяет устойчивое движение относительно z.
Тогда, согласно равенству (7.105), движение будет асимп-
тотически устойчиво относительно переменной х.
§ 7.7. Примеры исследования устойчивости систем
с параметрическим возбуждением
Параметрические возбуждения встречаются во многих
системах. Так, например, они возникают в системах, на
которые действуют периодически изменяющиеся силы (см.
пример 1), при периодически изменяющейся жесткости
упругих элементов системы, при качке судов [7], при
вращении валов с различными моментами инерции и т. п.
Большое значение имеют рассмотренные в этой главе ме-
тоды при исследовании устойчивости периодических коле-
баний нелинейных систем.
Мы ограничимся рассмотрением двух простейших при-
меров.
§ 7.7. СИСТЕМЫ С ПАРАМЕТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ 255
Пример 1. Влияние вибрации точки подвеса
на устойчивость равновесия маятника. Пусть
материальная точка М массой т укреплена на конце стержня,
который может вращаться вокруг горизонтальной оси О. Очевидно,
что такой маятник имеет два положения равновесия: нижнее ус-
тойчивое и верхнее неустойчивое. Исследуем влияние колебаний
точки подвеса О на характер равновесия маятника.
Рассмотрим сначала влияние горизонтальных колебаний точки
подвеса О на устойчивость нижнего положения равновесия маят-
ника (рис. 7.10). Присоединим к силе тяжес-
ти маятника mg переносную силу инерции
Фе = —mi, где х = х (t) — закон движения
точки О. Воспользуемся теоремой об измене-
нии момента количества движения относитель-
но оси вращения маятника (массой стержня
пренебрегаем):
d
-& (ml2<p) = — mgl sin <p — mxl cos cp.
Будем считать, что точка подвеса маят-
ника колеблется по гармоническому закону
х = a cos cot. Тогда для малых углов <р
последнее уравнение примет вид
g аш2
ср — <р = —j— cos at.
Это уравнение обычных вынужденных колебаний системы,
находящейся под действием возмущающей силы (aa2/l) cos at.
Резонанс возможен только при совпадении частоты возмущающей
силы с частотой собственных колебаний, равной if g/l, т. е. при
<0 = ifg/l-
Рассмотрим теперь влияние вертикальных колебаний точки
подвеса на устойчивость нижнего равновесного положения маят-
ника (рис. 7.11, а). Присоединим к силе тяжести маятника mg
переносную силу инерции Фе = —т/, где у = a cos at — закон
движения точки О по вертикали, и снова воспользуемся теоремой
об изменении момента количества движения относительно оси
вращения маятника
d
(ml2q) = — т (g — у) I sin <р,
или, считая угол <р малым,
/ g а2 \
<р 4- (— + a -J- cos at) ср = 0.
Для того чтобы привести это уравнение Матье к канонической
форме (7.89), положим
at = т.
256 ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
После очевидных преобразований получим
/ g а \
^“ + b^ + Tc0ST)(p •	(7‘107)
Сравнивая это с уравнением (7.89), находим
6 = g/(Z<o2), в = all.	(7.108)
Параметрический резонанс при малых е наступает вблизи
значений 6 = /са/4, где к — целое положительное число. Поэтому
Рис. 7.11
при частоте вертикальных колебаний точки подвеса, близких к
значениям
о = 2/n gjl (п = 1, 2, 3,...),
устойчивое нижнее положение маятника сделается неустойчивым.
Отметим, что обычный резонанс будет только при частоте <о =
= 1/"g/l, в то время как параметрический резонанс наступает вблизи
частот
2]/7Ti, tfsih
Проведенный анализ показывает, что устойчивость нижнего
положения маятника может быть разрушена вертикальными коле-
баниями точки подвеса.
Рассмотрим теперь, нельзя ли с помощью тех же колебаний
стабилизировать верхнее неустойчивое положение маятника. Для
получения дифференциального уравнения малых колебаний маят-
ника около верхнего положения равновесия достаточно в уравне-
нии (7.107) заменить g на —g'.
d2(f / g а \
"rfr2"” + \ ~ ta2 + Т COS Х) ф °'
§ 7.7. СИСТЕМЫ С ПАРАМЕТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ 257
Теперь
6 = —g/(Z<o2), е = all.
Будем считать, что амплитуда а колебаний точки подвеса мала
по сравнению с длиной маятника I. Тогда е <<; 1, и можно исполь-
зовать диаграмму, изображенную на рис. 7.9.'Из этой диаграммы
видно, что для стабилизации верхнего положения маятника при
отрицательном б точка М с координатами б, е должна находиться
выше параболы б = —е2/2 и ниже прямой б = 1/4 — е/2, т. е.
должны выполняться неравенства
1/2 — 26 > е > /=2б.
Внесем в это двойное неравенство значения б п е:
или, производя
± , 2	—>!/ 2-^-
2 Т Z Z<o2 > I > V 1а2 ’
простейшие преобразования,
~2~ + 2 пГ> аш >
При а <<?. I левая часть неравенства выполняется всегда и
остается только правая часть, которая означает, что верхнее не-
устойчивое положение маятника можно стабилизировать высоко-
частотными колебаниями точки подвеса при условии, что ее макси-
мальная скорость а<о превышает скорость свободного падения маят-
ника с высоты, равной его длине (]/2gZ). Впервые это свойство
было установлено П. Л. Капицей [23].
Пример 2. Исследование устойчивости нуле-
вого решения уравнения Хилла при пара-
метрическом возбуждении по закону к в а-
зипрямоугольного синуса. Рассмотрим простейшую
систему, уравнение возмущенного движения которой описывается
уравнением Хилла (7.76)
х + [б + еф (t)]x = 0	(7.109)
с функцией возбуждения ф (t), изменяющейся по закону квази-
прямоугольного синуса (рис. 7.12). Период Т функции возбужде-
258 гл. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ систем
ния ф (t) складывается из времени Тг, когда функция ф (t) равна
4-1, и времени Т2, когда ф (!) = —1- При = Т2 имеем обычный
прямоугол ьный синус.
К уравнению (7.109) сводится, в частности, изучение систем,
жесткость которых периодически изменяется с помощью релейного
устройства. Для нас эта задача представляет интерес не только
потому, что ее решение может быть использовано для анализа
устойчивости движения конкретных систем, но также потому, что
на ней будет показано построение для одного периода [0, Г] фунда-
ментальной матрицы решений X (t), удовлетворяющей условию
(7.55), построение матрицы А = X (Т), характеристического урав-
нения (7.64) и определение условий устойчивости решейия х =
= 0, х = 0.
В уравнении (7.109) число е равно глубине пульсации, а число
б равно при 6> 0 и е = 0 квадрату частоты к собственных коле-
баний, т. е. б = к2. Совместим начало отсчета времени t с началом
какого-либо периода Т. Тогда для первой части периода 0 <4 t
уравнение (7.109) принимает вид
х 4- (к2 4- е)ж = 0	(0 < t < Л),	(7.110)
а для второй части периода
х 4- (к2 — 8)ж = 0 (TjCfCT).	(7.111)
Рассмотрим сначала уравнение (7.110). Полагая, как и прежде,
х± = х, х2 = х, мы сведем уравнение (7.110) к системе двух урав-
нений первого порядка
#1 = х2, х2 = —k2xt (0 <4 t <4 Т),	(7.112)
где
к2 = к2 4- е.	(7.113
Система (7.112) решается элементарно. Два линейно незави-
симых решения этой системы, удовлетворяющих условиям (7.55),
будут	1 Гц = cos Alt,	х12 =	sin kit,	(7 114) лги =— A] sin Ait, х22 = cos kit
(напомним, что первый индекс означает номер функции, второй —
номер решения).
Таким образом, на первой части периода фундаментальная
матрица решений (7.51) принимает вид
Х(1) =
1
cos Ait	sin kit
— ki sin kit cos Ait
(0< t < Ti).
(7.115)
Очевидно, что X (0) = E (условие (7.55)).
Перейдем ко второй части периода Т\ <4 t <4 Т. Уравнение
(7.111) при прежней подстановке перейдет в систему вида (7.112)
с заменой AJ = к2 4- е на А^ = к2 — е:
#1 = х2, х2 = —к2х±	(7.116)
§ 7.7. СИСТЕМЫ С ПАРАМЕТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ 259
В общем решении этой системы
Xi = cos Аа (t — 1\) + Са sin к2 (t — 7'1),
ха = — к2С\ sin к2 (t — 7\) + к2С2 cos к2 (t — Т\)
(7.117)
подберем постоянные интегрирования Сх и С2 так, чтобы оно оп-
ределяло первое частное решение. Для этого решение (7.117) должно
совпадать с решением zn, ха1 из (7.114) при t = Т1. Имеем
cos к1Т1 = Сх, —к± sin к1Т1 = к2С2.
Подставляя значения Сх и Са из этих равенств в (7.117), найдем
первое частное решение уравнений (7.116) на втором участке пе-
риода 7\ t Т (мы выписываем сразу второе частное линейно
независимое решение, полученное аналогичным образом):
Ai
хц = cos kj\ cos к2 (t — 7\) — sinic17'1 sinica (t — T]),
xaj = — k2 cos кгТу sin k2 (/ — 7’,) — sin k1T1 cos k2 (I — Tj),
1 1
x12 = — sin inT1! cos k2 (t — 7\) 4- cos klT1 sin k2 —	(7.118)
x22 = — — sin AiT1! sin fca (t — Ti) -|- cos ktTt cos ic2 (t — T}).
Эти выражения определяют элементы фундаментальной мат-
рицы X (t) на втором участке периода Т± < t «С Т. Если в (7.118)
положить t = Т, то получим элементы матрицы А = X (Т) —
см. (7.61). Составим характеристическое уравнение (7.64), учиты-
вая, что ajtj = xjtj (Т):
I (Т) — р х12 (Т) I
I xai (Г)	х22 (Г) — р I
Подставляя в это уравнение значения x^j (Т) из (7.118) и учитывая
равенства к‘[ = к2 е, к2 = к2 — е, Т — 7\ = Т2, непосредст-
венными вычислениями найдем
где
ра + ар -г 1 = О,
(7.119)
Г 1
а = 2 г
L V 1 -
р. = е/Ас2 = е/б.
= sin к1Т1 sinк2Т2 — cos кхТ± cos k2T2~j, (7.120)
(7.121)
В этом примере все коэффициенты характеристического урав-
нения получены с помощью непосредственных вычислений. Как
и следует из общей теории уравнения Хилла, свободный член
уравнения (7.119) равен единице (см. (7.78)). Для того чтобы дви-
жение было устойчивым, необходимо и достаточно, чтобы выпол-
нялось неравенство | а | < 2 (см. с. 242). В нашем случае условие
устойчивости (простой, но не асимптотической) принимает вид
I sinA:1711sinA:27’2
I |Л1 — ца
cos к1Т1 cos к2Т2
<1-
(7.122)
260 ГЛ. VII. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
Если все числа 6, 8, 1\ и Т2 заданы, то проверить это условие
не представляет труда. Не останавливаясь на более подробном
анализе неравенства (7.122), установим только условия возникно-
вения параметрического резонанса при р. = е/б 1. Пренебрегая
в (7.122) всеми членами, содержащими р. в степени выше первой
(отметим, что число р входит в к± и к2), и учитывая, что параметри-
ческий резонанс для уравнения Хилла возникает уже на границе
области устойчивости (см. с. 241—242), получим
|cos (^7! +W| = 1.
Отсюда
к1Т1 + к2Т2 = пп (п = 1, 2, 3, . . . ).	(7.123)
Учтем теперь значения кг и к2
к± = |/Л2-|- 8 = к j/1 -р р, k2 = ~\f к2— s = к (/ 1 — р.
При р = e/fc2 = е/б достаточно малом будем иметь
*1 = к (1 + i/г И). к2 = к (1 —1/2 р).
Подставляя эти значения для к± и к2 в (7.123), найдем (Тг -|- Т2 = Т)
кТ + J/2 рЛ (Т2 — 71) = л.п,
или, с точностью до главных членов,
к
<0 = 2— (га = 1, 2, 3,...),	(7.124)
где о = 2л/7 — частота пульсации, а к — |/б — частота собст-
венных колебаний системы при отсутствии параметрического воз-
буждения.
Из выражения (7.124:) видно, что при достаточно малой глу-
бине пульсации s параметрический резонанс наступает при бес-
численных значениях ее частоты <о. Заметим, что выражение (7.124)
для критических значений частоты пульсации при параметрическом
возбуждении по закону квазипрямоугольного синуса не зависит
от соотношения частей периодов 7Х и Т2 и что оно в точности сов-
падает с соответствующими значениями критической частоты при
параметрическом возбуждении но закону обычного синуса (коси-
нуса). Действительно, если уравнение Матье записать в следующей
форме:
х (к2 s cos at)x = О,
где к — частота собственных колебаний системы при отсутствии
параметрического возбуждения, то при переходе к безразмерному
времени по формуле = т мы получим каноническую форму (7.89)
этого уравнения, в котором б = к2/®2. На с. 251 было показано,
что при малом 8 критические точки для б определяются равенством
б — n2/i, или к2/о2 = га2/4, где га = 1, 2, 3, . . . Отсюда получим
о = 2к/п, т. е. формулу (7.124).
В заключение этого примера заметим, что условие устойчивости
(7.122) справедливо и для случая, когда одно из чисел б, 6 + 8 =
= к2> и б — е = к2 или все они отрицательны. Для этого доста-
точно перейти от тригонометрических функций мнимых аргументов
к гиперболическим функциям действительных величин.
ГЛАВА VIII
ПРИМЕНЕНИЕ ПРЯМОГО МЕТОДА ЛЯПУНОВА
К ИССЛЕДОВАНИЮ УСТОЙЧИВОСТИ СИСТЕМ
АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
§ 8.1. Введение
В большинстве случаев системы автоматического регу-
лирования представляют сложные устройства, состоящие
из объекта регулирования и регуляторов. Назначение
последних состоит в том, чтобы непрерывно поддерживать
в объекте регулирования установившийся режим работы
или режим, изменяющийся по заданному закону. Все
отклонения от заданного режима, возникающие в системе
регулирования, должны быть с течением времени сведены
практически к нулю. Иначе говоря, система регулирова-
ния должна быть асимптотически устойчива.
Начиная с работ И. А. Вышнеградского, о которых
рассказывалось во введении и третьем примере § 4.5, при
исследовании устойчивости систем автоматического регу-
лирования применяется метод линеаризации с дальней-
шим использованием различных критериев (Гурвица,
Рауса, Найквиста, Михайлова и др.). Обоснованием этого
метода служат теоремы Ляпунова об устойчивости дви-
жения по уравнениям первого приближения (см. § 4.3).
В 1944 г. появилась небольшая заметка А. И. Лурье
и В. Н. Постникова [34], в которой для исследования
устойчивости движения конкретной системы автоматиче-
ского регулирования был применен прямой метод Ляпунова.
Устойчивость рассматривалась в целом, т. е. при любых
начальных возмущениях и любой нелинейности сервомото-
ра, подчиненной некоторым условиям (такая устойчивость
получила название абсолютной устойчивости).
В дальнейшем А. И. Лурье в ряде работ развил идеи,
заложенные в первой публикации, построил функцию
Ляпунова для общего случая, охватывающего весьма
широкий класс регулируемых систем, и получил систему
алгебраических уравнений, решение которой определяют
достаточные условия абсолютной устойчивости. В моно-
графии [33], опубликованной в 1951 г., А. И. Лурье до-
вел применение прямого метода Ляпунова к исследованию
262 гл. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
абсолютной устойчивости регулируемых систем до хоро-
шо разработанного алгоритма.
Результаты, полученные А. И. Лурье, послужили от-
правной точкой для дальнейших исследований абсолют-
ной устойчивости. В этой работе приняли активное учас-
тие ученые различных стран. Не имея возможности упомя-
нуть всех авторов, отметим прежде всего работы совет-
ских ученых А. М. Летова [31], Е. А. Барбашина [5, 6],
М. А. Айзермана и Ф. Р. Гантмахера [2], В. А. Якубо-
вича [50, 51, 52, 53], работы американских ученых
Р. Э. Калмана [55], Ж. Ла-Салля и С. Лефшеца [29, 32],
румынского ученого В. М. Попова [43]. Последнему при-
надлежит1 введение частотных методов в исследование аб-
солютной устойчивости, позволивших расширить класс
рассматриваемых систем.
Учитывая характер настоящего руководства, в этой
главе мы кратко изложим основные идеи и результаты
А. И. Лурье.
§ 8.2. Дифференциальные уравнения
возмущенного движения систем
автоматического регулирования
Во многих случаях система автоматического регули-
рования состоит из объекта регулирования, чувствитель-
ных элементов (измерителей), суммирующего прибора,
сервомотора и механизма обратной связи. Структурная
схема такой системы изображена на рис. 8.1. Под регуля-
тором понимается совокупность измерителей и суммирую-
щего прибора; иногда в регулятор включают и сервомотор
с механизмом обратной связи.
Параметры, характеризующие состояние объекта ре-
гулирования при нарушении установившегося режима ра-
боты, замеряются чувствительными элементами (измери-
телями), показания которых вместе с сигналом £ меха-
низма обратной связи подаются на суммирующий прибор.
Последний вырабатывает команду ст, управляющую сер-
водвигателем, который в свою очередь устанавливает в
надлежащее положение регулирующий орган объекта
регулирования и воздействует одновременно на механизм
обратной связи.
Обозначим через хъ . . ., хп параметры, характери-
зующие состояние объекта регулирования, а также коор-
динаты и скорости чувствительных элементов.
§ 8.2. УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ	263
Будем считать, что изменение этих величин при ра-
зомкнутой цепи (отключенном серводвигателе) описывает-
ся линейными дифференциальными уравнениями с по-
стоянными коэффициентами
п
= S a*rxj (Лг — 1, • • • , п).
з=1
При замкнутой цепи на изменение величин х±, . . ., хп
будет влиять регулирующий орган. Обозначая через £
Рис. 8.1
параметр, характеризующий положение последнего,
и учитывая предположение о линейности системы, получим
дифференциальные уравнения объекта регулирования и
чувствительных элементов при включенном серводвига-
теле:
= S ацPi + М (/с=1, га). (8.1)
3=1
В конкретных системах некоторые из коэффициентов
a^j и Ь1С будут, конечно, равны нулю, в частности, в урав-
нениях, соответствующих чувствительным элементам, по-
стоянные = 0.
Будем считать, что механизм обратной связи осущест-
вляется с помощью жесткого выключателя. В этом случае
выходная величина £ механизма обратной связи будет
пропорциональна его входной величине
L= К.
(8.2)
264 ГЛ. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Суммирующий прибор, складывая показания чувстви-
тельных элементов, дает на вход сервомотора величину
п
О = 5 CjXj — г%,	(8.3)
j=i
где с; и г — передаточные числа.
Передаточное число г называется коэффициентом об-
ратной связи. В разумно построенной системе регулиро-
вания коэффициент обратной связи положителен, т. е.
г 0. При отсутствии механизма обратной связи г = 0;
кроме того, передаточные числа с}, соответствующие па-
раметрам объекта регулирования, также равны нулю.
Связь между входной величиной о серводвигателя и
его выходной величиной в случае непрямого регулирова-
ния выражается зависимостью
t = / (а),	(8.4)
где функция / (о) называется характеристикой сервомотора.
Характеристика сервомотора может быть линейной, но
значительно чаще она носит нелинейный характер. На
рис. 8.2 показаны некоторые типичные примеры нелиней-
ности функции / (о). Характеристики а и б непрерывны,
а другие две разрывны.
В дальнейшем будем предполагать, что характеристи-
ки / (о) удовлетворяют следующим условиям.
1.	Функция / (о) определена и непрерывна при всех
значениях о;
2.	/ (0). = 0;
§ 8.2. УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ
265
3.	о/ (о)	0 при любых о 0; другими словами,
функция / (ст) имеет тот же знак, что и ст, и в нуль обраща-
ется только в начале координат;
4.	Интегралы
оо	0
/(ст) (Zct, f(a)d<y	(8.t>;
0	— оо
расходятся.
Характеристики типа биг имеют зону нечувствитель-
ности (в промежутке (стх, ст2) значения функции / (ст) равны
нулю при ст 7^ 0). Анализ решений и устойчивости си-
стем, дифференциальные уравнения которых содержат
функции с зоной нечувствительности и разрывной нели-
нейностью, нельзя рассматривать в рамках общей теории.
Они требуют специального исследования, выходящего
за рамки настоящей книги.
Второе и третье условия не требуют пояснения. За-
метим только, что третьему условию не удовлетворяют
характеристики с зоной нечувствительности, так как
произведение ст/ (ст) равно нулю во всем промежутке
(стх, а2)> гДе ° имеет значения, отличные от нуля.
Последнее, четвертое, условие практически всегда
выполняется. Действительно, геометрически это условие
означает, что площадь под характеристикой неограни-
ченно возрастает при ст -» оо.Так как участки характери-
стики, параллельные оси ст, для реальных сервомоторов
неограниченно продолжаются вправо и влево (эти участки
практически образуются за счет того, что орган, управляю-
щий сервомотором, ложится на упоры), то четвертое условие
фактически реализуется всегда. Однако мыслимы и другие
сервомоторы, поэтому это условие следует предусмотреть
(значение его будет объяснено в следующем параграфе).
Функции / (ст), удовлетворяющие перечисленным ус-
ловиям, называются допустимыми характеристиками.
Уравнения (8.1), (8.3) и (8.4) определяют возмущенное
движение системы непрямого регулирования с одним
регулирующим органом и жесткой обратной связью. Вы-
пишем эти уравнения еще раз, собрав их вместе
п
хк — 3 ak jx j +
М
ё-/(а),	(8.6)
п
СТ = У| CjXj — Гс.
3=1
266 ГЛ. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
При прямом регулировании связь между выходной £
и входной о величинами серводвигателя осуществляется
не через производную, а непосредственно:
? = / (о).
Поэтому уравнения возмущенного движения системы пря-
мого регулирования имеют вид
= s ак}х} + Ьк/(о),
J=1 П	(8-7)
O'-CjXj.
j=l
Сформулируем теперь постановку вопроса.
Задача Лурье. Независимо от начального состояния
системы и конкретного выбора допустимой характери-
стики / (о) сервомотора найти необходимые и достаточ-
ные условия устойчивости системы (8.6) в целом. Иначе
говоря, требуется найти условия абсолютной устойчивости
системы (8.6).
§ 8.3. Преобразование уравнений
возмущенного движения системы
регулирования к канонической форме
Прежде чем перейти к определению условий абсолют-
ной устойчивости системы (8.6), займемся преобразова-
нием ее. В матричной форме уравнения (8.6) имеют вид
х=Ах + &S,
а-/(о),	(8.8)
о с'х — г%.
Здесь А = || akj || — квадратная матрица, ас, & и с —
матрицы-столбцы (с' — матрица, транспонированная с с,
т. е. матрица-строка), г, |, п и / (о) имеют прежние зна-
чения.
В уравнениях (8.8) неизвестными функциями времени
являются матрица-столбец х и скалярная величина £.
Перейдем к новым переменным по формулам:
у — Ах + ^,Ь — х,
, t	(8.9)
О== С X — rg.	'
§ 8.3. ПРЕОБРАЗОВАНИЕ К КАНОНИЧЕСКОЙ ФОРМЕ
267
Будем иметь
У = Ах + bl,
а - с'х — rl.
Принимая во внимание уравнения (8.8) и равенства (8.9),
получим
У = Ау + 6/(о),
О = су — г/ (о).
(8.10)
Потребуем, чтобы определитель линейного преобразо-
вания (8.9) был отличен от нуля (см. понятие о сложных
матрицах в § 5.2):
detM NUo
II с — г ||
или более подробно
“11 • • • Л
а
пп
^0.
(8.11)
. . . с — г
п
В этом предположении дифференциальные уравнения
возмущенного движения (8.8) и (8.10) будут взаимно эк-
вивалентны. Это означает, что из абсолютной устойчиво-
сти относительно переменных у и о следует абсолютная
устойчивость относительно переменных х и g и наоборот.
Заметим, что условие (8.11) не является жестким, так
как элементы определителя зависят от параметров систе-
мы, которые всегда можно выбрать так, чтобы это условие
выполнялось.
Условия устойчивости системы (8.10) можно искать
в матричной форме, пользуясь некоторыми матричными со-
отношениями (см. [51, 52]). Если считать эти соотношения
известными, то вывод условий абсолютной устойчивости
будет простым. Однако простота вывода и самих условий
устойчивости является кажущейся, так как доказатель-
ство матричных соотношений, на которые опирается вы-
вод, и их явное выражение через параметры системы до-
статочно сложны. Поэтому остановимся на методе Лурье
[33], состоящем в переходе к каноническим переменным.
Сделаем линейное преобразование
и = Ау
268 гл. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
с неособенной матрицей Л. = || och-^ ||. Будем иметь
у — А^и, у=А~{й.
После подстановки в уравнения (8.10) получим
Л-1й = АЛ"1?* + 6/(о),
о — c'A-1w — г/ (о).
Умножим первое уравнение слева на матрицу Л. Тогда,
учитывая равенства AA-1m = Ей = и, найдем
й -= Ви + Л/ (о),
,, х	(8-12)
о —у и — rf(a),	'	'
где
В = ЛАЛ*1, h = Лб, у = (Л-1)'с.	(8.13)
Будем задавать не матрицу преобразования Л, а ма-
трицу В, считая, что она представляет нормальную форму
Жордана для матрицы А (см. § 5.3). Тогда матрицы Л и
Л-1 могут быть определены из уравнений (5.55) и (5.56):
В А = АЛ, А~1В = АЛ-1, АЛ-1 = Е. (8.14)
Если матрица преобразования А найдена, то обрат-
ную матрицу Л-1 проще всего найти по формуле
Л-i =|| а,;,-1| = ||4^||,	(8.15)
где a'kj — элементы обратной матрицы Л-1, Л^ — ал-
гебраические дополнения элементов ад- матрицы Л,
а А = det Л (следует обратить внимание на расстановку
индексов).
В дальнейшем будем считать, что все корни Хк (Л =
= 1, 2, . . ., п) характеристического уравнения
det (А - ХЕ) = 0	(8.16)
простые и имеют отрицательные вещественные части
Re Xj- < 0,
причем в некоторых случаях будет допускаться один ну-
левой корень.
§ 8.3. ПРЕОБРАЗОВАНИЕ К КАНОНИЧЕСКОЙ ФОРМЕ
269
В сделанных предположениях матрица В имеет вид *)
0 ... О
О . . . О
(8-17)
о о ...
Запишем уравнения (8.12) в скалярной форме
= Хкик + hkf (о) (к = 1, . . ., п),
S g^k — rf(a).	(8.18)
К=1
В этих уравнениях некоторые коэффициенты hk могут
равняться нулю. Введем новые переменные zk, положив
{hkzk, если hk О,
zK, если hk — 0.
(8.19)
Тогда уравнения (8.17) примут свой окончательный вид
эти уравнения называются каноническими уравнениями
истемы регулирования)
2м = h-zK + 6J (о) (к = 1, . . ., п),
й— S ekZK — rf (о),
где множители 8к равны единице или нулю
{1, если hk О,
О, если hk = О,
(8.20)
(8.21)
а коэффициенты ек определяются равенствами
fgiA, если Лк-=#0,
к I если kk — 0.
(8.22)
Отметим, что вещественным корням отвечают веще-
ственные канонические переменные zk и вещественные чи-
сла ек', комплексно-сопряженным корням Кк = Кк+1 от-
вечают комплексно-сопряженные канонические перемен-
ные zk = z.+1 и комплексно-сопряженные числа ек =
= ё,г+1.
2) См. (5.35) и (5.32). В случае простых корней характеристиче-
ского уравнения числа ег = е2 = . . .= еп = 1, поэтому каждая
клетка Jk состоит из одного элемента Хк.
270 гл. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Уравнения (8.20) совпадают по своей форме с урав-
нениями (8.18), но отличие их состоит в том, что в урав-
нениях (8.20) коэффициенты 8К. удовлетворяют соотно-
шениям (8.21).
В заключение этого параграфа отметим, что сущест-
вуют различные методы приведения уравнений систем ав-
томатического регулирования к канонической форме (8.20).
Здесь изложен наиболее общий метод, основанный на
матричных уравнениях (8.14). Практическое применение
этого метода будет разъяснено на примере.
§ 8.4. Построение функции Ляпунова
Пусть имеется s пар комплексно-сопряженных корней
(Xi, Xj), (Х3, Х4), . . ., (A.2S-1, ^2s)>
которым отвечают s пар комплексно-сопряженных коор-
динат
(Zj, Z2), (z3, Z4), . . ., (Z2S-1, Z2S)
и п — 2s вещественных корней
^2S+1, ^2S+2>  •
которым отвечают вещественные координаты
Z2S+1, Z2S+2, • • zn.
Для нахождения достаточных условий абсолютной
устойчивости движения А. И. Лурье предложил исполь-
зовать функцию Ляпунова в следующей форме:
п п	S	n—2S	(Т
F=JEj JEj ч+а — е JEj z2*~iZik г V, ~ dQ-
К=1 j=l	3	К=1	о
(8.23)
Здесь a2s+i> •  -1 ап — вещественные, а а4, а2, • • ,
«2s — попарно-сопряженные комплексные числа, которы-
ми мы распорядимся в дальнейшем соответствующим об-
разом; положительное число е может быть выбрано сколь
угодно малым.
Докажем прежде всего, что функция V определенно-
отрицательна. Действительно, из условия ст/ (ст) /> 0 сле-
дует, что последнее слагаемое представляет определенно-
отрицательную функцию переменной ст. Совокупность
членов, содержащих множитель е, определенно-отрица-
272 ГЛ. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Внесем в это выражение для V значения производных z
и о из уравнений (8.20). Получим
1С=1 j=l к 1
~~ Е 3 {Z3R- [^2IC-1Z2>;-1 + б2ц/(о)] + г3К-_!	+ <53/г/(ст)]} —
К=1
п—28	г п	->
— £ X Z'is+K [^2s! I'22S+K + 62S+Kf (ст)] — /(o)[ S — r/(CT)J
или, группируя члены,
n n	n—2s
F = 2 У У 	a^djZj + г/2 (ст) — e У %23+iZ2SH- —
lf=l j=i * j	K=1
8
--- E 3	Z2'i-lz2k -
lr=l
S	Г	n	a 6
У	[eS-ft +б27-1 — У,
n— 2S	П	6
z , Zjs+ft сбгз+л: + C2s+ir 2a2s+jc У t-------^-~-
fei L	+
Поясним, что при группировке членов, содержащих
произведение функции / (ст) на двойную сумму и на пара-
метры е^, суммирование по к разбито на три суммы.
Займемся теперь преобразованием двойной суммы.
Имеем
Присоединим к двойной сумме слагаемое г/2 (ст) и
272 гл. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Внесем в это выражение для V значения производных з
и о из уравнений (8.20). Получим
к=1 7=1 к 1
-в X {Z2K	+ 62lc-if(o)] +	[A^-z^ + 62t/(o)]} —
Jf=l
n—28	г n	1
~ £ X z^ + 62S+J (a)] — f (о) X e A ~ rf (°) J
или, группируя члены,
n n	n—2s
F = 2 У У-x a^ajZj + rf2 (о) — e У Xmu-zLk —
lf=l j=l k j	K=1
8
— E X (^2K—1 +	Z2V-1Z21T —
K=1
S	" a 6 Ч
+ У z2v-i [e6.ft + e27_! - 2a^ У ” J +
i'=i	j=i	7
n-2S	n afi T)
+	! ^28+/C	4“ ^2S+/C	’ 2й28+1С
Поясним, что при группировке членов, содержащих
произведение функции / (о) на двойную сумму и на пара-
метры ек, суммирование по к разбито на три суммы.
Займемся теперь преобразованием двойной суммы.
Имеем
~ Xj Xj Ч- + \ а1Ла& + X X Ак + Л. a^aizf
К=1 j=l h 1	Tt=! j=l К 1
---d^Z^CljZj-------------- UftZj.
t=l 7=1	1С=1	7=1
К=1
Присоединим к двойной сумме слагаемое rf2 (о) и
§ 8.4. ПОСТРОЕНИЕ ФУНКЦИИ ЛЯПУНОВА	273
представим оба члена в следующей форме:
23 2 + г/2 (ст) = ( 2 akzk)2 + г/2 (о) =
4=1
= [2 akzk + У г/(ст)]2 — 2 УГ/(ст) 2 akzk.
к=1	4=1
Отнесем выделенную здесь группу слагаемых с произве-
дениями zkf (ст) к соответствующим слагаемым в производ-
ной Р”. Тогда получим
akzk + /г/(ст)]“ —
[S	П—28	-
3 (^24-1 + ^к) zzk-iz2k + 2 ^2s+kz2s+k —
4=1	4=1	J
z s г	I n a 6	\ 1
~ I 22,c L66^-1 + б2,с + 2fl2fc V Г “ У A./+A. ) J +
fc=i	j=i	3
+ У [ебз,с +	+ 2a2fr-i (- У V-1+*”) 1+
fc=i	j~i	3
n—28
+ z2s+ic I eSjs+j ejs+j-]-
4=1
+ 20„, (/7-)]}/(„).	(8.24)
Для того чтобы знак производной V" не зависел от функ-
ции / (ст), выберем постоянные числа а1, а2, . . ап так,
чтобы множители при z2fr, z2k-i и z2s+k обратились в нуль,
т. е. подчиним эти числа п условиям;
e^2k-i + еа|с + 2a2S —=0 (/с = 1, .. ,,s),
>=i	3
ебг^ + e24-i + 2a2k-i ^Уг — Ух—J_ji х") = 0 (^ ~ 1, •••>s),
j=i 2|с-1	3
&$2з+к + ^2з+к + ^a2sik Уг —	х 3х =
~0 (к = 1, ...,n-2s). (8.25)
13 Д. Р. Меркин
274 гл. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
При таких аг, а2, . . ап производная Г примет вид
[3 a.z. + /г/(п)]2 —
-- 8 [2	+ ^31,’) Z2fc-1Z3R + 3 \>Sb?rZ2S+fr] •	(8.26)
к=1	lt=l
Первое слагаемое не отрицательно (по условию ком-
плексные слагаемые входят в сумму Xakzk попарно с со-
пряженными, поэтому эта сумма представляет вещест-
венное число). Кроме того, по условию е 0, числа
A<2^-i -j- и Xjs+ic отрицательны (Хг^ = Л,2к--1И Re X;-
< 0), а множители z^^z^ и z^+n — положительные ве-
щественные числа (по условию z2^ =	вещест-
венны). Отсюда следует, что при всех аг, а2, . . ., ап, удо-
влетворяющих уравнениям (8.25), производная Г будет
определенно-положительной функцией переменных zlt . ..
. . ., zn и о независимо от вида допустимой характеристики
/ (о). Кроме того, функция V определенно-отрицательна
и при выполнении условия (8.5) она удовлетворяет всем
требованиям теоремы Барбашина — Красовского (см.
§ 2.3) (квадратичные формы, входящие в функцию (8.23),
стремятся к бесконечности при | z | —> оо, а интеграл
стремится к бесконечности при | о | > оо в силу условия
(8.5)).
Прежде чем перейти к выводам, сделаем одно замеча-
ние относительно уравнений (8.25). Положительное число
е можно выбрать сколь угодно малым. Поэтому в силу
непрерывной зависимости корней уравнения от его коэф-
фициентов наличие числа е не может изменить характера
этих корней. На этом основании слагаемые еб;, можно
просто отбросить и вместо уравнений (8.25) рассматривать
следующие уравнения (при е = 0 все уравнения имеют
одинаковую структуру):
е, + 2а. ( V 7- £	) = 0	= 1, ..., п). (8.27)
;=1
Теперь можно сформулировать теорему.
Теорема Лурье. Если система квадратных уравнений
(8.27) имеет хотя, бы одно решение а±, а2,. . ., ап, в ко-
тором комплексно-сопряженным значениям К. = Xj.-+1 (к =
= 1,3, . . ., 2s — 1) корней характеристического уравне-
§ 8.4. ПОСТРОЕНИЕ ФУНКЦИИ ЛЯПУНОВА	275
ния (8.16) отвечают комплексно-сопряженные числа ак =
-= «);+1 (А = 1, 3, . . ., 2s — 1), а вещественным корням
^2s+ic (Л = 1,. . п — 2s) отвечают вещественные числа
aas+Jt (& = !,..., п — 2s), то система регулирования
(8.20) абсолютно устойчива.
Заметим, что определять корни уравнений (8.27) не
нужно, достаточно найти условия, которым должны удов-
летворять параметры системы, чтобы соответствующее
решение существовало.
До сих пор мы предполагали, что все корни характе-
ристического уравнения (8.16) различны и имеют отрица-
тельные вещественные части. Рассмотрим теперь случай,
когда среди этих корней имеется один нулевой корень,
а остальные корни удовлетворяют прежним условиям.
В этих предположениях уравнения возмущенного движе-
ния (8.20) примут вид (предполагаем, что Кп = 0)
4 = kkzk + (ст) (* = 1,. 	п-1),
zn = / (ст),
"-1	(8.28)
ст= 2j	+ е А — rf (о).
Ic=l
Число бп не должно равняться нулю, так как в против-
ном случае zn — 0 и zn = const, т. е. будет отсутствовать
асимптотическая устойчивость. Поэтому на основании ус-
ловия (8.21) полагаем бп = 1.
Докажем теперь, что коэффициент еп должен быть от-
рицательным. Действительно, рассмотрим линейную ха-
рактеристику
/ (о) = ко,
принадлежащую к классу допустимых характеристик.
Из условия о/ (о) = ко2 > 0 следует, что к 0. Со-
ставим характеристическое уравнение системы (8.28)
при / (о) = ко (напомним, что кп =0, бп = 1):
к —	. . . О 0	— *51
	о .	• •	\i-i 0	k^n-i	= 0.
	о .	0	к — к	
	— .	  - еп-1 - еп Х + кг	
Если раскрыть определитель, то коэффициент при
старшем члене будет равен Д1. Найдем свободный член
10*
276 гл. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
ап = А (0). Имеем
	— Xj .	0	0 — A6i
Яп=-Д(0)=-	0 .		0
	0 .	0	0 - к
	— С1 . .	 -еп-1	— е кг п
Раскрывая этот определитель по элементам предпослед-
ней строки, а полученный при этом минор — по элемен-
там последнего столбца, найдем
ап = —кеп (—. Xn-i.
По условию все вещественные части корней Хп . . ., Xn-i
отрицательны, следовательно, произведение (—1),1^1Х1Х2. . .
. . , Хп—! будет положительно. Учитывая к тому же, что
к 0, найдем, что знак свободного члена характеристиче-
ского уравнения для линейной характеристики совпадает
со знаком — еп. Из условия Гурвица должно быть ап 0,
следовательно, еп < 0, что и доказывает сделанное за-
мечание.
Функцию Ляпунова для этого случая можно взять
в следующей форме (ср. с уравнением (8.23)):
п—1—2*	а
-4- У, ^k + ^-enz2n-^f(a)da. (8.29)
/Г=1	о
При еп < 0 это будет определенно-отрицательная
функция всех п + 1 переменных zn . . ., z^, zn, а. Произ-
водная по времени от функции V, вычисленная в силу
уравнений возмущенного движения (8.28), будет иметь тот
же вид, что и (8.24), если заменить в ней п на п — 1; пе-
ременная же zn в выражение Г не войдет. Поэтому если
подчинить постоянные числа а±, а2, . . ., an-i условиям
(8.27), то производная Г будет знакоопределенной функ-
цией п переменных zn . . ., zn_±, а и знакопостоянной
функцией всех п + 1 переменных z15 . . ., zn-i, zn, о.
Производная Г обращается в нуль при z± = . . .
. . . = zn_! = о = 0, т. е. на оси zn. Так как эта ось не
является целой траекторией возмущенного движения
(функции = ... = zn-! = о = 0 не обращают урав-
§ 8.5. УСЛОВИЯ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
277
нения (8.28) в тождества), то выполнены условия теоремы
Барбашина — Красовского об асимптотической устой-
чивости в целом (см. § 2.3).
Из всего изложенного следует, что при наличии одного
нулевого корня критерии абсолютной устойчивости по-
лучаются из квадратных уравнений (8.27), но с заменой п на
п — 1. Кроме того, нужно потребовать, чтобы коэффи-
циент еп удовлетворял условию
еп < 0.	(8.30)'
В заключение этого параграфа остановимся кратко
на системе прямого регулирования. В канонических
переменных уравнения (8.7) имеют вид
(о),
2i eKzK.	(8.31)
А=1
Функцию Ляпунова для этой системы можно взять
в форме (8.23), только без интеграла. Тогда, повторяя
почти в точности все выкладки, придем к следующей си-
стеме квадратных уравнений для определения постоян-
ных Дц . . ., ап:
" а
-2д,^ ^.аД +еь,==0 (А==1’	П}' (8‘32)
Если существует решение этих уравнений, удовлет-
воряющее вышеупомянутым условиям, то система регу-
лирования (8.31), а вместе с ней и система (8.7) будут аб-
солютно устойчивы.
§ 8.5. Определение условий
абсолютной устойчивости. Пример
В общем случае решение системы квадратных урав-
нений (8.27) представляет значительные трудности. К на-
стоящему времени существуют обозримые решения для
п 6. Мы рассмотрим частный, но имеющий большое
значение для многочисленных приложений случай двух
квадратных уравнений (8.27); при этом будем предпола-
гать, что 6j = 62 = 1 (см. равенства (8.21)). Положив
278 гл. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО регулирования
в уравнениях (8.27) к = 1, а
“1 о г~
~— + 2‘aiVr
+ 2а2/Г —
Л2	г
затем к = 2, получим
а1а2 , „ Л
Т^+б1=0’
(8.33)
Я1Я2 , „ Л
йдг + "!=0-
Требуется определить, каким условиям должны удов-
летворять числа А,!, Х2, е2 и г, чтобы эти уравнения
имели решение указанного ранее вида. Следуя А. И. Лурье
(см. [33]) преобразуем уравнения (8.33). Для этого разде-
лим сначала первое уравнение на а второе на Х2 и по-
лученные результаты сложим почленно. Тогда получим
Третий член, очевидно, равен — 2а1а2/Ъ1'к2. Объединяя его
с первым членом, получим
Это равенство можно записать еще и так:
+ _ДА _	= Г2,	(8.34)
где
Г2=—Д— + ~- + г.	(8.35)
Ai	Ад	7
Если %! и Х2 вещественны, то числа а± и а2 должны быть
тоже вещественными, если же и Х2 комплексно-сопря-
жены, то аг и а2 должны тоже быть комплексно-сопря-
женными числами. Поэтому величина, стоящая в круглых
скобках равенства (8.34), вещественная, а ее квадрат
должен быть положительным числом. На этом основании
правую часть равенства (8.35) необходимо подчинить
условию
Г2 = -К- + -V- + г>°.
А1 Л2
(8.36)
Считая в
ложим Г =
дальнейшем, что это условие выполнено, по-
+ /Г2. Тогда одно квадратное уравнение
§ 8.5. УСЛОВИЯ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
279
(8.34)	распадается на два линейных уравнения
-^- + -£L = r + /F -£- + -р- = -Г+ /7. (8.37)
Л1 Л2
Вычтем теперь почленно из первого уравнения (8.33)
второе уравнение
/а2	а? \	.—
— ( -j---л— ) + 2 У7 (ai — Яг) + — е2 = 0.
Легко видеть, что это равенство можно представить в сле-
дующей форме:
— г — Н" ^2 (Vг —xf”)	Г' + 62 — 61‘
(8.38)
Два линейных уравнения (8.37) и одно квадратное
уравнение (8.38) эквивалентны двум квадратным уравне-
ниям (8.33).
Рассмотрим вначале случай, когда оба корня и Х2 —
комплексно-сопряженные числа. Введем новые перемен-
ные х и у, определив их равенствами
Уг-----^- = х + 1у, У г---^- — x — iy. (8.39)
В новых переменных уравнения (8.37) и (8.38) примут
вид
2х = У г — Г, 2х = У г + Г,
(Х2 —	(х2 — у2) — 2(Хх + xyi = г (Х2 — XJ+ejj — ег.
(8.40)
Разделим третье уравнение на (Х2 —
я2 — Уа + 2кху = г +	,
Л»2 — Л1
где в сделанных предположениях коэффициент
и== м + л2 .	(841)
является вещественным.
Последнее уравнение представим в следующем виде:
(1 +ха).г2 — (их — у)2 —г +	.
Введем еще одну переменную z, положив
их — у = У1 + x2z,
280 гл. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО регулирования
Теперь уравнения (8.40) примут свою окончательную
форму
2х= /г — Г, 2х = /г + Г,	84?
23-х2 = 0,
где вещественное число 0 определено равенством
п__	1	, е2 — е1 \ _ г (Х2 — Х1)2	(е2 — £1) (Х2 — М)
1 + х2 \ Х2 — Xi /	4ХД2
(8.43)
Уравнения (8.42) получены из уравнений (8.33)
в предположении, что корни и л2 комплексно-сопряжен-
ные. Легко видеть, что точно такие же уравнения мы по-
лучим и при вещественных корнях и Х2. Нужно только
в равенствах (8.39) заменить х ± iy на х ± у, в равенстве
(8.41) отбросить число г, а переменную z определить ра-
венством кх + у — ]Лх2 — 1 z. При этом параметр 0
будет по-прежнему определяться выражением (8.43). Та-
ким образом, уравнения (8.42) эквивалентны уравнениям
(8.33) при любой структуре корней и л2 (общие предпо-
ложения о том, что Re < 0 и Re л2 < 0 и что Х2,
остаются в силе).
На основании теоремы Лурье можно сделать следую-
щий вывод: если уравнения, (8.42) имеют хотя бы одно ве-
щественное решение относительно переменной z, то си-
стема регулирования абсолютно устойчива (переменная х,
согласно первым двум уравнениям, принимает только ве-
щественные значения).
Из первых двух уравнений (8.42) найдем
Х = (/г ±г).
Внесем это выражение для х в последнее уравнение и ре-
шим его относительно z2:
z2 = 0 + _1(/;+Г)2.	(8.44)
Из этого равенства видно, что при 0	0 величина z2
будет положительна, a z вещественно. Это означает, что
при 0	0 система регулирования абсолютно устойчива.
Рассмотрим теперь случай 0 < 0. Из равенства
(8.44) видно, что для вещественности переменной z нуж-
но потребовать, чтобы параметры Г и 0 удовлетворяли
§ 8.5. УСЛОВИЯ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
281
условию
е+4 (/;±г)2>°-
Учитывая, что Г 0, достаточно в скобках взять верх
ний знак. Таким образом, при 0 < О система регулиро
вания будет абсолютно устойчива, если параметры систе
мы г, Г и 0 удовлетворяют
условию
(Г + /г)2 >	40. (8.45)
Если вместо параметра Г
ввести новый параметр
¥==Г +	=
то достаточное условие абсолютной устойчивости системы
при 0 < 0 принимает вид
Т2 > —40.	(8.47)
К этому условию необходимо присоединить общее ус-
ловие (8.36).
Область абсолютной устойчивости на плоскости пара-
метров 0 и Т изображена на рис. 8.3.
Пример. Непрямое регулирование двига-
теля с жесткой обратной связью. На рис. 8.4
и 8.5 показаны принципиальная и структурная схемы непрямого
регулирования двигателя с жесткой обратной связью. Отличие от
прямого регулирования (см. пример 3 § 4.5) состоит в том, что
перемещение муфты центробежного устройства (измерителя угло-
вой скорости двигателя) передается на дроссельную заслонку
не прямо, а через золотник (суммирующий прибор) и сервомотор
(гидравлический двигатель). Кроме того, шток серводвигателя,
воздействующий на дроссельную заслонку, связан с рычагом жест-
кой обратной связи.
Перейдем к составлению уравнений возмущенного движения
системы. Уравнение двигателя было получено ранее при рассмот-
рении примера 3 § 4.5. Пренебрегая моментом сопротивления М2 (<о)
и полагая, как и прежде, z = ы — <о0, где <о0 — угловая скорость
двигателя в установившемся движении, будем иметь
dz
Тп ~аГ = ~ кс1~-
Здесь — постоянная времени, характеризующая момент инер-
ции вращающихся частей двигателя.
282 гл. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Напишем уравнение центробежного регулятора вместе с демп-
фером (см. равенство (4.45)):
Т^х -f- T2t -f- х — k^z.
Измеритель
Рис. 8.4
Рис. 8.5
Уравнение золотника (суммирующего прибора) имеет вид
а = х —
а уравнение сервомотора
t - У (а).
Если ввести обозначения —
7’о
,т2 — х, х3 = х, то урав-
нения движения всей системы приводятся к виду (8.6):
^1 — —— aixi 2яг£2 -f- aaxa,
*з = хг, I = У (о), о = xa — g,
§ 8.5. УСЛОВИЯ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
283
где
Мо „ Tt	1_
=	2а2 = -—, аз = -—.	(8.48)
Выпишем матрицы А, Ъ и || 0	0	0 А — Hi 2и2 Из		с. Имеем II- 1		, с =	0 0 1	*
		’ Ь =	0 0			
	II0	10					
Составим уравг	1вние (8.16) -X .0	и найдем 0	его корни:			
det (4 - ХЕ) = Отсюда	2а 2 —	@3 0	1	— X ^1,2 = а2 i V а2 + 0		31	— X р - Хз = 0.	- 2агХ — аз) = 0, (8.49)	
^1 + ^2	— 2в2» ^1^2	= — а3, X	1 —	*2= 21	' и	2 + о3. (8.50)
составим матрицу В:
Пользуясь формулой (8.17),
В =
Xj	О	О	II
О	Х2	0	.
О	0	01|
Вычислим произведения ВЛ и ЛЛ:
II	0	°||	«11	«12	«13
вл= О		0	021	«22	«23
о	0	о|	«31	«32	«33
^i«n	^i«i3	||
^2«21	^“2«22	^“2«23	i
О 0	0
лл =
«11
«21
«31
«12
«22
«32
«13
«23
«33
О
01
О
О
2а2
1
° II
«з
О II
#1«12 2д2«12 -|- «13 ^3«12
#1«22 2о2«22 -|- «23 ^3«22 •
Д1«32 2из«32 -)- (%зз Из«32
Так как матрицы ВЛ. и ЛЛ, согласно (8.14), равны, то должны
быть равны соответствующие элементы:
Х1«ц = П1«12,	^2«21 =	®l«22i	^1«32 = О,
Х1«12 = 2вз«12	4“ «131	^2«22 =	2п2«22	4“ «231 2й2«32	4“ «33 = ®1
^1«13 = ®3«121	^2«23 =	^3«221	®3«32 = О-
Из этих девяти уравнений независимых только шесть (в каж-
дой группе среднее уравнение является следствием верхнего и
нижнего уравнений, а также уравнения (8.49)).
Положим «11 — ^1» «21 — ^ii «з1 — 1» Тогда «12 — Xj, «13 — П3,
«22 = ^2i «23 = a3i «32 = «зз = 0 и, следовательно,
л =
01 ^1 Од ||
01 А,2 а3 .
1 о о в
284 ГЛ. VIII. СИСТЕМЫ АВТОМАТИЧЕСКОГО регулирования
Для вычисления обратной матрицы найдем А = det А и соот-
ветствующие алгебраические дополнения:
Отсюда
А = det Л = а3 (Xj — Xj),
Лц = 0, Л21 = 0, Л31 = а3 (Xj — Х2),
Л12 = е3, Л22 — —а3, Л32 = 0,
A33 =	Х2, Л23 — Xj, Л33 = —а3 (Х3 — Х2).
О
1
Xj -- Xj
. Х2
а3 (Xj — Xj)
О
1
Xj---Х2
^1
а3 (Xj — Xj)
1
О
ai
«з
Непосредственной проверкой убеждаемся, что АЛ-1 = Е. Для
перехода к уравнениям (8.18) найдем по формулам (8.13) матрицы
h Ti д-.
Xj
II	а3 (Xj — Х2)
—Я1	X
Л = Л^ -aj , д — {Е~1)'с—	•
_ —
аз
Теперь можно перейти к уравнениям в переменных ult и2,
и3, а (см. уравнения (8.18)). Имеем
“1 =	+ W (о), й2 = XjU2 + Л2/ (а),
“з = W (а),	& ~ £iui + 8гиг + ёзиз — / (о),
где hit и gif — элементы матриц h ид соответственно. По формулам
(8.19) перейдем к каноническим переменным. Полагаем
Uj = XjZj, u2 ~ X2z2, и3 = h3z3.
После подстановки получим канонические уравнения
Zj = XjZj + / (о), Z2 = X2Zj + f (a), z3 = / (a),
d = ejZj e2z2 + e3z3 — / (a).
В этих уравнениях
,	ajXj
<Я=М1= a3(Xj— Xj) ’
,	ajXj
e2 = Ajg2__ ^(Xj-Xj)"’
aj	XjXo
c3 — h3g3 —	~	„
«з	Io
(8.51)
В рассматриваемом примере n = 3 и один корень нулевой.
В соответствии с общей теорией коэффициент еп = е3 должен
быть отрицательным, что и имеет место в данном примере (с.
примечание к уравнениям (8.28)).
§ 8.5. УСЛОВИЯ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ	285
Для получения достаточных условий абсолютной устойчивости
подчиним прежде всего параметры е± и е2 условию (8.36):
0.
С помощью формул (8.51), (8.50) и (8.49) это условие приводится
к виду
г - р > О,	(8.52)
р = кокгТ 2/ То.
где
Заметим, что при отсутствии обратной связи (г = 0) условие
(8.52) не будет выполнено.
Вычислим по формулам (8.43), (8.51), (8.50) и (8.49) параметр
0. Получим
e = -4(4r-^-v)’
где
v =
Абсолютная устойчивость бу-
дет обеспечена при следующих
условиях (в рассматриваемом
примере г = 1):
1) р < 1, р + 1/v > 4;
2) р< 1, (/Г^1+1)»>
> 4 — р — 1/v.
Первый случай отвечает условиям (8.36) и 0 > 0. Второй
случай отвечает условиям (8.36) и (8.45). Комбинируя эти условия,
можно получить более простые условия абсолютной устойчивости
непрямого регулирования двигателя с жесткой обратной связью:
1)	р<1,	v < 1/2;
2)	р < 1/v — l/4v2, v > 1/2.	(8.53)
Область абсолютной устойчивости показана на рис. 8.6. Ко-
нечно, все выводы справедливы при сделанных предположениях.
ГЛАВА IX
ЧАСТОТНЫЕ МЕТОДЫ
ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
§ 9.1.	Введение
Частотные методы исследования устойчивости линей-
ных и нелинейных систем весьма удобны для инженерных
расчетов, поскольку частотная характеристика инвари-
антна относительно линейного неособенного преобразо-
вания координат и легко определяется как по уравнениям
системы, так и экспериментально. Кроме того, частотные
методы позволяют расширить класс рассматриваемых систем.
Впервые частотный критерий для исследования устой-
чивости линейных систем предложил Найквист в 1932 г.
В 1958 г. румынский ученый В. М. Попов [43] получил
достаточные условия абсолютной устойчивости в частот-
ной форме, т. е. на языке требований, предъявляемых
к частотной характеристике линейной части системы.
В 1962 г. В. А. Якубович [51], а затем в 1963 г. аме-
риканский математик Р. Калман [55] опубликовали ра-
боты, из которых следует эквивалентность методов
А. И. Лурье и В. М. Попова.
В этой главе кратко излагаются основы частотного ме-
тода В. М. Попова для исследования систем с непрерыв-
ными нелинейностями. Анализ систем с разрывными не-
линейностями, скользящим режимом и неединственным
положением равновесия («отрезком покоя») можно найти,
например, в работах [15, 156, 29, 30].
§ 9.2.	Передаточные функции
и частотные характеристики
Рассмотрим линейную неоднородную систему диффе-
ренциальных уравнений
dz VI
= У ,+ ъаи (а=1, ...,п),
п	(9.1)
0=3 CjXj,
§ 9.2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
287
где аа;-, ba, Cj — постоянные коэффициенты, и — неко-
торая заданная функция времени.
Будем называть функцию и «входом» системы, а функ-
цию о «выходом» системы.
Заменив в системе (9.1) формально оператор d/dt на р,
получим соотношения
п
рха=	+ Ьа.и (а=1, . . . , п),
п
О —	। CjXj.
3=1
Исключив из этих равенств переменные х±, . . хп
и выразив о через и, придем к формуле
a = W(p)u,	(9.2)
где
Q (р)
<М)
Здесь Qm (р) и Qn (р) — полиномы относительно р степени
тип соответственно. Очевидно, т < п и Qn (р) является
характеристическим многочленом однородной системы,
получающейся из (9.1) при и = 0.
Рис. 9.1
Дробно-рациональная функция W (р) называется пе-
редаточной функцией системы (9.1) от «входа» и к «выходу»
о. Это название вытекает непосредственно из равенства
(9.2): передаточная функция W (р) передает (преобразует)
«вход» и в «выход» о (рис. 9.1, а).
Заметим, что для определения передаточной функции
не надо предварительно приводить систему к виду (9.1),
разрешенному относительно производных. Если система
содержит производные выше первого порядка, то для
вычисления передаточной функции надо заменить dk7dtk
на pk.
288
ГЛ. IX. ЧАСТОТНЫЕ МЕТОДЫ
Пример 1. Найдем передаточную функцию от «входа» и к
«выходу» х в уравнении ± -]- За- = и. Заменяя t на рх, получим
рх + За- = и. Следовательно, передаточная функция имеет вид
1/(р + 3).
Пример 2. Найдем передаточную функцию от «входа» — / к
«выходу» а в системе
Уф + ф = —
I = /,	(9.4),
а =	+ с2ф — rg,
где Т, к, clt с2, г — постоянные. Делая элементарные выкладки,,
последовательно найдем
(Гр2 + р)ф = —fcg, pg = /, о = (qp + с2)ф — г%.
Отсюда
1	к	к
Ф = — Тр2+р = — р(Тра + р)
Следовательно, искомая передаточная функция имеет вид
т,, ! \ Тгр2 (fcct —|- г) р —}- кс2
и W -- р2(Ур + 1)
(9-5)
Покажем, что передаточная функция не изменяется при
линейном преобразовании системы. Для этого запишем
уравнения (9.1) в матричной форме
dx
= Ах + Ьи, о = с'х,	(9.6)
где А — квадратная постоянная матрица, b — постоянная
матрица-столбец, с' — постоянная матрица-строка,
х (/) — матрица-столбец, и — скалярная функция. Найдем
передаточную функцию от «входа» (—и) к «выходу» о.
Введя оператор р = d/dt и единичную матрицу Е, после-
довательно получим
рх=Ах + Ьи,х = — (А — рЕу^Ъи, о = — с' (А — рЕу1 Ьи.
Следовательно, передаточная функция для системы (9.6)
будет
W (р) = с (А — рЕу^Ь.	(9.7)
Сделав в системе (9.6) линейное преобразование х —
= Лг/, где Л — квадратная неособенная постоянная мат-
рица, получим
Лу = А Ху + Ьи, о = с Ху.
§ 9.2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
289
Отсюда
у = А~'АА.у 4- Л-16и, о = с'Ху.	(9.8)
Полагая у =ру и выполняя последовательно очевид-
ные преобразования, получим
у = — Л-1 (Л — Ер)~1Ьи.
Теперь находим
ст — — с'ЛЛ-1(Л — Ер) лЬи = — с'(А — Ер) хЬи.
Из этого равенства видно, что передаточная функция
преобразованной системы (9.8) равна передаточной
функции W (р) исходной системы, иными словами, пере-
даточная функция инвариантна относительно линейного
преобразования.
Если в передаточную функцию (9.3) подставить р = гео,
где i = У—1, а со — вещественное число, то получим
функцию W(гео), называемую
частотной характеристикой
системы (9.1). Функция ТУ(гю)
имеет простой наглядный
смысл. Действительно, пусть
«вход» и (t) представляет воз-
мущение, изменяющееся по
гармоническому закону.Пред-
ставим его в комплексной
форме и — reia>t, где г — ам-
плитуда возмущения, а	рис 9 2
eia>t — комплексный гармони-
ческий сигнал частоты со. Подставим это значение для и
в равенство (9.2), заменив в нем предварительно р на гео.
Имеем
cr = W (ito)reia>l.
Равенство (9.2) можно рассматривать как дифференци-
альное уравнение, эквивалентное системе (9.1). При гар-
моническом возмущении частное решение этого линейного
уравнения будет определять вынужденное колебание той
же частоты со, но другой амплитуды R при сдвинутой
фазе (предполагается, что знаменатель передаточной функ-
ции (9.3) не имеет корней, равных со). Из этого следует,
что «выход» о можно представить равенством
cr =
290
ГЛ. IX. ЧАСТОТНЫЕ МЕТОДЫ
где ф — сдвиг фазы. Сравнивая полученные два выраже-
ния для «выхода» о и представляя частотную характери-
стику в следующей форме: W (гео) = | W (гео) | е' arsw, по-
лучим
R = | W (г'со) | г, <р — arg W (гео).
Таким образом, модуль частотной характеристики ра-
вен отношению амплитуды вынужденного колебания на
«выходе» системы к амплитуде гармонического возмущаю-
щего воздействия на ее «входе», а аргумент частотной ха-
рактеристики равен сдвигу фазы вынужденного колеба-
ния.
Выделим в W (г'с») вещественную и мнимую части:
W (гео) = и (со) + iv (со).	(9.9)
На плоскости (и, v) при изменении со конец вектора
W (гео) описывает кривую, представляющую собой го-
дограф частотной характеристики (она называется также
амплитудно-фазовой характеристикой системы).
Для примера 1 имеем (с. 288)
1	3 — гео
П (“°) = гео 4" 3 = со2 4-9 •
Поэтому
3	со
“ (“) = со2 4- 9 ’ v (“) = — со2 4-9
и годограф частотной характеристики при изменении со от 0 до
4- оо представляет полуокружность, изображенную на рис. 9.2.
Действительно, исключая из последних равенств параметр со, по-
лучим
/ 1 \2 / 1 \2
§ 9.3. Критерий Найквиста устойчивости
линейной системы
Положив в системе (9.1) и = — ко, где к — постоян-
ная, получим однородную систему
i-a=	— kba 3 CjX} (а = 1, ..., п), (9.10)
3=1	3=1
которую, в отличие от разомкнутой системы (9.1), назы-
вают замкнутой. Если система (9.1) схематично изобра-
жается рис. 9.1, а, то замкнутой системе (9.10) соответ-
ствует рис. 9.1, б.
§ 9.3. КРИТЕРИЙ НАЙКВИСТА
291
Попытаемся выяснить, при каких значениях параметра
к. замкнутая система (9.10) асимптотически устойчива,
т. е. все корни ее характеристического уравнения имеют
отрицательные вещественные части и, следовательно, ле-
жат в левой полуплоскости.
Например, для асимптотической устойчивости урав-
нения
х + Зх = —кх	(9.11)
необходимо и достаточно, чтобы к —3. Действительно,
в этом случае корень —(к + 3) характеристического
уравнения будет отрицательным. Для систем более вы-
сокого порядка поставленный вопрос не тривиален.
Ответ на него и дает критерий Найквиста. Оказывает-
ся, об асимптотической устойчивости замкнутой системы
(9.9) можно судить по поведению частотной характери-
стики W (гео) разомкнутой системы (9.1). Ограничимся
случаем, когда полином Qn (р), стоящий в знаменателе
передаточной функции (9.3), имеет все корни в левой по-
луплоскости, т. е. разомкнутая однородная система асим-
птотически устойчива.
На плоскости и, v построим вектор R, выходящий из
точки (—1/к, 0) и оканчивающийся в точке (и (со), v (со)),
лежащей на годографе частотной характеристики. При
изменении со угол ср между этим вектором и осью абсцисс
будет меняться. Критерий Найквиста утверждает, что для
асимптотической устойчивости замкнутой системы (9.10)
необходимо и достаточно, чтобы приращение Дер угла ср
при изменении а от 0 до -фоо равнялось нулю. На 9.3, а,
очевидно, Дер = 0, а на рис. 9.3, б Дер = 2л.
292
ГЛ. IX. ЧАСТОТНЫЕ МЕТОДЫ
Для частотной характеристики, изображенной на
рис. 9.2, Дф = 0, если точка (—1//с, 0) лежит вне диа-
метра полуокружности, и Дф = л, если эта точка лежит
на интервале (0, 1/3). Таким образом, для асимптотиче-
ской устойчивости уравнения (9.11) необходимо и доста-
точно, чтобы —1/к < 0 либо —1/к '_> 1/3. Отсюда по-
лучаем неравенство к /> —3, установленное ранее из
элементарных соображений. Доказательство сформу-
лированного критерия Найквиста можно найти в книге
Е. П. Попова [44].
То обстоятельство, что устойчивость замкнутой системы
(9.10) определяется по годографу частотной характери-
стики разомкнутой системы (9.1), является сильной сторо-
ной критерия Найквиста. Недостатки этого критерия со-
стоят в том, что он требует реального построения годо-
графа частотной характеристики системы (9.1), что в свою
очередь требует знания численных значений всех коэф-
фициентов передаточной функции. Таким образом, кри-
терий Найквиста дает возможность проверить устойчива
или неустойчива рассматриваемая система при выбранных
численных значениях коэффициентов, но в общем случае
с его помощью нельзя построить область устойчивости в
пространстве коэффициентов.
В следующих параграфах будут рассмотрены частот-
ные методы, применимые не только к линейным, но и к не-
линейным звеньям замыкания и свободные от этих недо-
статков.
§ 9.4. Частотные критерии абсолютной устойчивости
систем с непрерывной нелинейностью
Рассмотрим систему
dx п
=	+ ъ<х.и (а = 1, ..., п),
и — — ф(о),	(9.12)
п
О = S C3XV
3=1
где ф (о) — непрерывная функция, удовлетворяющая при
о 0 условию
0<	+ оо,	(9.13)
а	Cj — постоянные коэффициенты,
§ 9.4. ЧАСТОТНЫЕ КРИТЕРИИ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ 293
Условие (9.13) означает, что на плоскости (о, <р) гра-
фик функции <р = <р (о) должен находиться в секторе, ог-
раниченном осью о и прямой <р = ко (рис. 9.4), причем
закон изменения функции <р = <р (о) может быть любым,
в частности он может иметь вид, изображенный на
рис. 8.2, а.
Как видно, отличие системы (9.12) от (9.10) заклю-
чается в том, что (9.12) получается из системы (9.1) путем
замыкания через ее нелинейное звено
и = — <р (о).
Поэтому критерий Найквиста к системе (9.12) неприменим.
Вместо него для нелинейной системы (9.12) установлен
следующий частотный критерий абсолютной устойчивости.
Обозначим через W (р) передаточную функцию системы
(9.12) от «входа» (—<р) к «выводу» о.
В зависимости от расположения полюсов х) передаточ-
ной функции W (р) различают некритический случай,
когда все полюсы лежат в левой полуплоскости, а также
критические случаи, когда имеются полюсы на мнимой оси.
Приведем без вывода основные теоремы, определяющие
достаточные условия абсолютной устойчивости систем рас-
сматриваемого класса при условии, что нелинейность не-
прерывна (доказательство можно найти в [2, 53]).
Теорема 1 (некритический случай). Пусть выполнены
следующие условия:
1)	нелинейная функция <р (о) удовлетворяет условию
(9.13);
2)	все полюсы W (р) имеют отрицательные веществен-
ные части',
х) То есть корней полинома, стоящего в знаменателе W (р).
294
ГЛ. IX. ЧАСТОТНЫЕ МЕТОДЫ
3)	существует такое вещественное число Ф, что при всех
со 0 выполнено частотное условие
+ Re [(1 + icoft) (ico)] > 9.
(9.14)
Тогда система (9.8) абсолютно устойчива.
Частотный критерий (9.14) допускает наглядную гео-
метрическую интерпретацию. Так как W (гео) = и (со) +
+ iv (со), то условие (9.14) равносильно неравенству
I
+ и (со) — fttoV (со) 0.
(9.15)
Построим видоизмененную частотную характеристику,
изображающая точка которой определяется координатами
Рис. 9.5
и (со), а>и (со). Если ввести новую плоскость иг = и,
щ = сон и на этой плоскости построить годограф видоиз-
мененной частотной характеристики при со 0, то усло-
вие (9.14) означает, что должна существовать прямая
1/к + иЛ — •Qvx = 0, проходящая через точку (—1/к, 0)
и лежащая левее этого видоизмененного годографа
(рис. 9.5).
Частотный критерий (9.14) гарантирует абсолютную
устойчивость системы (9.12) в том смысле, что начало ко-
ординат устойчиво в целом, какова бы ни была непре-
рывная функция ср (о), график которой заключен в сек-
тор (9.13). В частности, будет устойчива в целом любая ли-
нейная система, получающаяся из (9.12) при ср (о) = ho,
0<h<k.
§ 9.4. ЧАСТОТНЫЕ КРИТЕРИИ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ 295
Теорема 2 (критический случай одного нулевого полюса).
Предположим, что выполнены следующие требования'.
1)	нелинейная функция <р (<т) удовлетворяет условию
(9.13);
2)	передаточная функция W (р) имеет один нулевой
полюс, а остальные ее полюсы (если п 1) имеют отрица-
тельные вещественные части',
3)	р = lim pW (р)	0 и существует такое веществен-
р-М»
ное число V, что при всех со 0 выполнено частотное
условие (9.14).
Тогда система (9.12) абсолютно устойчива.
Теорема 3 (критический случай двух нулевых полюсов).
Пусть выполнены следующие условия:
1)	функция ф (о) удовлетворяет неравенству (9.13)
при к = оо1) и соотношению
±00
ф(о)йо=оо;	(9.16)
о
2)	передаточная функция имеет два нулевых полюса,
а остальные ее полюсы (если п^> 2) имеют отрицатель-
ные вещественные части',
3)	а = lim p^W (р)^>0,
р—*о
p = lim-^-[pW(p)]>0,
р—о аР
л (со) = со Im ТУ,(г(о) О при всех <в^>0,
lim л (со) 0.
(й-*оо
Тогда система (9.12) абсолютно устойчива.
Прежде чем перейти к примерам, заметим, что крите-
рии абсолютной устойчивости, установленные теоремами
1—3, носят аналитический характер и для проверки их
не нужно строить годограф передаточной функции И7 (гео)
и не нужно знать численные значения коэффициентов си-
стемы (9.12). Поэтому с их помощью можно строить обла-
сти абсолютной устойчивости, что нельзя сделать, даже
для линейного звена замыкания, применяя критерий
Найквиста.
*) Случай к = оо означает, что сектор, изображенный на
рис. 9.4, образован координатными осями о, ср, т. е. полностью за-
полняет первый и третий квадранты.
206
ГЛ. IX. ЧАСТОТНЫЕ МЕТОДЫ
§ 9.5. Примеры
Пример 1 (математический). Рассмотрим сначала чисто мате-
матическую задачу. Пусть "уравнения возмущенного движения
имеют вид
V1 +	= х3 — ф (х2),
T2t2 + х2 = xi,	(9.17)
^3 ~	*^2’
где Tj > 0 и т2 > 0 — постоянные времени, а функция ф (,г2) не-
прерывна п удовлетворяет условию (9.13) при к = оо.
Найдем передаточную функцию от «входа» (—ф) к «выходу»
в = х2. Для этого введем прежде всего оператор р = d/dt и пере-
пишем систему (9.17) в следующей форме:
[(ИР + l)zr = х3 — ф (х2),
(т2р 4“ 1)з:2 ~ рх3 	х2.
Исключая из этих уравнений xt и х3, найдем
_	______________Р____________
Х2 ~ Т1Т2Р3 -f- (Tj + т2) р2 + р 4- 1 *Р-
Следовательно, передаточная функция для данного примера равна
(напомним, что «вход» равен (—ф))
П ~ ар3 + Рр2 + р + 1 ’
где
СС “ Т2Т2, Р — Т| 4~ т2.
Пусть
Р>а.	(9.18)
Тогда, применяя критерий Гурвица (4.30), найдем, что все полюсы
передаточной функции (корни ее знаменателя) имеют отрицательные
вещественные части и, следовательно, можно воспользоваться тео-
ремой 1.
Составим левую часть условия (9.14). Проведя несложные
преобразования, последовательно получим (по условию к = оо)
Re [(1 + iwft) W (гео)] =
(1 + г<ай) iw	<в2 [(йр — а) <а2 + (1 — й)]
= Re 1 — Ро)2 + Iw (1 — aw2) = (1 — Pw2)2 + w2 (1 — aw2)2 '
Для выполнения неравенства (9.14) при всех w > 0 необхо-
димо и достаточно, чтобы число (I удовлетворяло условиям
— a > 0, 1 — О > 0. Отсюда
Такое й найдется ввиду (9.18). Следовательно, в силу теоремы 1
область абсолютной устойчивости системы (9.17) определяется
неравенством (9.18) или, переходя к исходным коэффициентам,
условием
Гх 4~ т2 > т2т2.
§ 9.5. ПРИМЕРЫ
297
На рис. 9.6 показана область абсолютной устойчивости сис-
темы (9.17) (она ограничена прямыми тх = 0, т2 = 0 и одной ветвью
гиперболы + т2 = TjT2).
Пример 2. Исследование устойчивости само-
лета с курсовым автопилотом. При регулиро-
вании курса самолета (объект регулирования) на нем устанавли-
ваются два чувствительных эле-
мента (Ч.Э.). Первый (Ч.Э.1)
представляет свободный гиро-
скоп — он измеряет отклонение
самолета от курса (угол ф).
Второй чувствительный эле-
мент (Ч.Э.11) представляет ги-
роскопический тахометр — он
измеряет скорость изменения
угла ф, т. е. ф. С помощью по-
тенциометров измеренные вели-
чины (ip и ip) преобразуются
в соответствующие напряже-
ния U\ и U2, которые подаются	р g g
на усилитель (суммирующий
прибор) (рис. 9.7). Усилитель
вырабатывает напряжение U, воздействующее на электродвига-
тель. Последний с помощью редуктора поворачивает руль само-
лета (регулирующее устройство) на угол g, в результате чего вы-
равнивается отклонение самолета от заданного курса. Одновременно
Рис. 9.7
угол g поворота руля регистрируется механизмом обратной связи,
который преобразует сигнал £ в напряжение U3', это напряжение
подается в усилитель — см. [44].
Перейдем к составлению дифференциальных уравнений воз-
мущенного движения всей системы.
Уравнение отклонения самолета от заданного курса в прос-
тейших предположениях имеет вид
Тф 4- ф = — к%.
Здесь Т — постоянная времени самолета, характеризующая его
инерционность, к — постоянный коэффициент, характеризующий
момент сил, создаваемых рулем.
298
ГЛ. IX. ЧАСТОТНЫЕ МЕТОДЫ
Чувствительные элементы (гироскопы с потенциометрами)
практически безынерционны, и вырабатываемые ими напряжения
U1 и U2 пропорциональны измеряемым величинам
= /^ф, U2 = /саф.
Будем считать, что механизм обратной связи жесткий. Это
означает, что вырабатываемое им напряжение U3 пропорционально
углу £ отклонения руля:
U3 = к£.
Усилитель, суммируя входящие в него напряжения, дает на
выходе напряжение U, определяемое равенством
U = kJJi + къи2 - keU3,
где кц, ks и кв — коэффициенты усиления.
Учитывая значения Ut, U2 w U3, получим
U = С1ф + саф — г£,
где
Cj = к2къ, с2 = kjki, г = к3к3.
Электродвигатель с редуктором и рулем, представляют нели-
нейный элемент, уравнение которого имеет вид
Перепишем полученные уравнения в виде системы, заменив
предварительно U на о:
Гф + ф = —
I = f (а),
о = С1Ф + саф — г£.
Передаточную функцию от —f к о для этой системы мы нашли
в § 9.2 (см. (9.4) и (9.5)):
Ггр2 -|- (feet + г) р -|- кс2
W(P}~ р*[Тр + 1)
Она имеет два нулевых полюса, и, следовательно, можно восполь-
зоваться теоремой 3.
Подчиним коэффициенты системы условиям 2, 3 этой теоремы,
После очевидных преобразований получим
а - - limр2И7 (р) = кс2,
Р"*0
d
Р =Iim 77У [P*w (р)] = г + * (ci — с2Т),
P-о аР
, кс2— гТш2 + iw (ксг -I- г) гТш2 -I- г -I- к (<?i — с2Т)
л (w) = w Im _ W2 (i + Tia>) = —	1 +7М2	’
lim л (w) = — г.
(0-»oo
Поэтому условия 2, 3, теоремы 3 выполняются, если
кс2 )> 0, г -|- к (cj — с2Т) )> 0, г > О, (9.19)
§ 9.5. ПРИМЕРЫ
299
устойчивости с методом
Область ^абсолютной
устойчивости
Следовательно, рассматриваемая система абсолютно устойчива
при выполнении неравенств (9.19), если нелинейность удовлетво-
ряет условию 1 теоремы 3.
На плоскости переменных X = (с2Т — сг)к и г последние два
неравенства (9.19) образуют заштрихованную область, изображен-
ную на рис. 9.8 (условие кс2 > 0 выполняется всегда).
Пример 3. Непрямое регулирование двига-
теля с жесткой обратной связью. Сравним частот-
ный метод исследования абсолютной
А. И. Лурье. С этой целью рассмотрим
систему непрямого регулирования дви-
гателя с жесткой обратной связью,
описываемую уравнениями (см. пример
§ 8.5)
Toi = —*0L Т2х + Т2+ + х = k2z,
(9.20)
t = / (а), ст = х — g,
где То, Ti, Т2, к0, кг — положительные
параметры.
Сначала найдем передаточную функцию от (—/) к а. Имеем
Тйрг = — *oL (Т& -j- Т^р + l)z = k2z,
pl = f (»). ст = х — g.
Из первого и третьего уравнения найдем
1	кй	к0
Р f’ Z ~ ~ Тор ~ Top2 h
Согласно второму и четвертому уравнениям, получим
*0*1
Top2(T1P^+T2p+i) }’
____Г__________*0*1_____ 1 1
[т’орЧУ’У 4-^+1) + Р Г
Следовательно, передаточная функция
*0*1	1
(Р) = Top2(T2f + T2p+l) + ~Р
имеет два нулевых полюса. Воспользуемся теоремой 3 и подчиним
коэффициенты системы условиям теоремы. После несложных пре-
образований получим
*0*1
а - lira р2РР (р) — —,
р—о	1 °
d	кок/Г о
р = lim [p2W (р)] = -	+ 1,
p-оаР	1 о
^ZZZZZZZZZZZZZZZZZZZZZZZ
о
Л
Рис. 9.8
300
ГЛ. IX. ЧАСТОТНЫЕ МЕТОДЫ
[kaki	1 "I
7- l -	' '- J
_________kpkiT 2_____
= То [(ту - 1)2 + 7-2(02] “
Согласно теореме 3, для абсолютной устойчивости системы
достаточно, чтобы выполнялись условия
а > 0, р > 0, л. (со) < 0 при всех со .> 0,
lim л (со) < 0.
Ы -*оо
Первое и последнее условия выполняются, очевидно, всегда. Второе
условие р>0 будет выполнено при р < 1, где ц — кок1Т2/То.
Третье условие равносильно неравенству
Т^со2 + (7-2<о2 - I)2 - р> 0.
Если ввести обозначения v =	со2?72 — у, то это нера-
венство приводится к виду
v2y2 + (1 - 2v)y + 1 - р > 0.	(9.21)
Так как условие л (со) < 0 должно выполняться при всех
со > 0, то неравенство (9.21) должно быть справедливо при всех
у > 0. При v -С 1/2 средний коэффициент левой части этого нера-
венства будет неотрицателен при двух положительных других
коэффициентах (р <; 1). Поэтому при v 1/2 неравенство (9.21)
будет справедливо при всех у 0.
Пусть теперь v > 1/2. Корни полинома, стоящего в левой части
(9.21), определяются формулой
2v - 1 ± l<(2v-l)2-4v2(l-p)
1*1,2 -	2v2
Если подкоренное выражение положительно или равно нулю, то
условие (9.21) нарушается при у = уг > 0. В случае отрицатель-
ности подкоренного выражения корни полинома мнимые и, следо-
вательно, (9.21) справедливо при всех у > 0.
Поэтому при v > 1/2 должно выполняться неравенство
(2v — I)2 < 4v2 (1 — р),
которое равносильно следующему:
1 1
9	4v2
Таким образом, согласно теореме 3, область абсолютной устой-
чивости системы (9.20) имеет вид
р < 1	при vCZ1/,,
р < 1/v — l/4v2 при v > 1/2
и совпадает с областью, найденной в предыдущей главе при помощи
метода А. И. Лурье (см. (8.53) и рис. 8.6).
Сравнение двух методов исследования абсолютной устойчи-
вости, проведенное на этом примере, показывает, что частотный
метод, не изменяя области устойчивости, более экономичен с точки
зрения количества необходимых вычислений.
СПИСОК ЛИТЕРАТУРЫ
1.	Абгарян К.А. Устойчивость движения на конечном ин-
тервале И Итоги науки и техники. Сер. Общая механика.— М.:
ВИНИТИ, 1976.— Т. 3.
2.	Айзерман М. А. иГантмахер Ф. Р. Абсолютная
устойчивость регулируемых систем.— М.: АН СССР, 1963.
2а. Анапольский Л. Ю., Иргетов В. Д., Мат-
росов' В. М. Способы построения функций Ляпунова И
Итоги науки и техники. Сер. Общая механика.— М.: ВИНИТИ,
1975,— Т. 2.
3.	Андреев В.Д. Теория инерциальной навигации. Авто-
номные системы.— М.: Наука, 1966.
4.	Андронов А. А., Витт А. А. иХайкин С. Э.
Теория колебаний.— 2-е изд.— М.: Физматгиз, 1959.
5.	Б а р б а ш и н Е. А. Введение в теорию устойчивости дви-
жения.— М.: Наука, 1967.
6.	Б а р б а ш и н Е. А. Функции Ляпунова.— М.: Наука, 1970.
7.	Басин А. М. Качка судов.— М.: Транспорт, 1969.
8.	Веллман Р. Теория устойчивости решений дифференци-
альных уравнений: Пер. с англ.— М.: ИЛ, 1954.
9.	Веллман Р. Введение в теорию матриц: Пер. с англ.— М.:
Наука, 1969.
10.	Болотин В. В. Динамическая устойчивость упругих сис-
тем.— М.: Гостехиздат, 1956.
11.	Болотин В. В. Неконсервативные задачи теории упругой
устойчивости.— М.: Физматгиз, 1961.
12.	Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс
теоретической механики,— Т. 2,— М.: Наука, 1971.
12а.Вектор-функции Ляпунова и их построение/Под ред. В. М. Мат-
росова и Л. Ю. Анапольского.— Новосибирск: Наука, СО,
1980.
13.	Вышнеградский И. А. О регуляторах прямого дей-
ствия // Д. К. Максвелл, И. А. Вышнеградский
и А. Стодола. Теория автоматического регулирования.—
М.: АН СССР, 1949.
14.	Г а н т м а х е р Ф. Р. Теория матриц.— 3-е изд.— М.: Наука,
1967.
15.	Г е л и г А. X. Исследование устойчивости нелинейных раз-
рывных систем автоматического регулирования с неединствен-
ным равновесным состоянием // Автоматика и телемехани-
ка.— 1964.— № 2.
15а.Г е л и г А. X., Комарницкая О. И. Абсолютная
устойчивость нелинейных систем с неединственным положением
302
СПИСОК ЛИТЕРАТУРЫ
равновесия в критических случаях // Автоматика и телеме-
ханика.— 1966.— № 8.
156.Г е л и г А. X., Л е о н о в Г. А., Я к у б о в и ч В. А.
Устойчивость нелинейных систем с неединственным состоянием
равновесия.— М.: Наука, 1978.
16.	Д е м и д о в и ч Б. П. Лекции по математической теории ус-
тойчивости,— М.: Наука, 1967.
17.	ДиментбергФ. М. Изгибные колебания вращающихся
валов.— М.: АН СССР, 1959.
18	Д у б о ш и н Г. Н. Основы теории устойчивости движения.—
М.: МГУ, 1952.
19.	ЕругинН. Н. Приводимые системы.— Минск: Наука и
техника, 1966.
20.	Жуковский Н. Е. О прочности движения // Собр.
соч.— М.: Гостехиздат, 1948.— Т. I.
21.	Зубов В. И. Устойчивость движения.— М.: Высшая шко-
ла, 1973.
22.	И ш л и н с к и й А. 10. К теории гирогоризонткомпаса // ПММ,
1956.— Т. 20, вып. 4.
23.	КапицаП. Л. Динамическая устойчивость маятника при
колеблющейся точке подвеса // ЖЭТФ.— 1951,— Т. 21, вып. 5.
24.	КапицаП. Л. Устойчивость и переход через критические
обороты быстро вращающихся роторов при наличии трения //
ЖТФ,— 1939,— Т. IX, вып. 2.
24а.К а р а п е т я н А. В. Об обращении теоремы Рауса // Вест-
ник МГУ. Математика. Механика.— 1973,— № 5.
25.	КарачаровК. А. иПилютикА. Г. Введение в тех-
ническую теорию устойчивости движения.— М.:Физматгиз, 1962.
26.	КацИ.Я. иКрасовскийН.Н. Об устойчивости систем
со случайными параметрами // ПММ.— 1960.— Т. 24, вып. 5.
26а. К ельзонА. С., Циманский Ю. П., Я к о fl-
ле в В. И. Динамика роторов в упругих опорах.— М.: Наука,
1982.
27.	К р а с о в с к и й Н. Н. Некоторые задачи теории устойчи-
вости движения.— М.: Физматгиз, 1959.
28.	КузьминП. А. Малые колебания и устойчивость движе-
ния.— М.: Наука, 1973.
29.	Ла-СалльЖ. иЛефшецС. Исследование устойчивости
прямым методом Ляпунова: Пер. с англ.— М.: Мир, 1964.
30.	Л е о н о в Г. А. Об устойчивости нелинейных регулируемых
систем с неединственным положением равновесия // Автома-
тика и телемеханика.— 1971.— № 10.
31.	ЛетовА. М. Устойчивость нелинейных регулируемых сис-
тем.— 2-е изд.— М.: Физматгиз, 1962.
32.	Л е ф ш е ц С. Устойчивость нелинейных систем автоматичес-
кого управления: Пер. с англ.— М.: Мир, 1967.
33.	Л у р ь е А. И. Некоторые нелинейные задачи теории автома-
тического регулирования.— М.: Гостехиздат, 1951.
34.	Лурье А. И. иПостниковВ. Н. К теории устойчи-
вости регулируемых систем//ПММ.— 1944.— Т. 8, вып. 3.
35.	Л я п у н о в А. М. Общая задача об устойчивости движе-
ния.— М.: Гостехиздат, 1950.
36.	МатросовВ.М. К вопросу устойчивости гироскопичес-
ких систем с диссипацией//Труды Казанского авиац. ин-та.—
1959.— Вып. 45.
СПИСОК ЛИТЕРАТУРЫ
303
37.	Малкин И. Г. Теория устойчивости движения.—
2-е изд.— М.: Наука, 1966.
37а. МаркеевА. П. Точки либрации в небесной механике и
космонавтике.— М.: Наука, 1978.
38.	М е р к и н Д. Р. Гироскопические системы.— М.: Гостехиз-
дат, 1956; 2-е изд.— М.: Наука, 1974.
39.	М е р к и н Д. Р. Достаточные условия асимптотической устой-
чивости одной нелинейной системы И Уч. зап. Лен. гос. пед.
ин-та им. А. И. Герцена.— 1966.—Т. 125; 1958.— Т. 141.
40.	М е р к и н Д. Р. К вопросу об устойчивости по структуре
сил // ПММ,— 1975,— Т. 39, вып. 5.
40а.М е р к и н Д. Р. Об устойчивости стационарных движений
оси вращающегося ротора, установленного в нелинейных под-
шипниках// ПММ.— 1983.— Т. 47, вып. 3.
41.	Н и к о л а и Е. Л. Об устойчивости прямолинейной формы
равновесия сжатого и скрученного стержня //Николаи Е.Л.
Труды по механике.— М.: Гостехиздат, 1955.
'42. Николаи Е. Л. Теоретическая механика.— М.: ГОНТИ,
1939,— Ч. 3.
43.	П о п о в В. М. Гиперустойчивость автоматических систем: Пер.
с рум.— М.: Наука, 1970.
44.	ПоповЕ.П. Динамика систем автоматического регулиро-
вания.— М.: Гостехиздат,. 1954.
44а,П ресновЕ. В. Потенциальный характер критерия эво-
люции термодинамики необратимых процессов И ЖФХ.—
1973. — Т. 47, № И.
45.	РумянцевВ. В. Об устойчивости движения по отноше-
нию к части переменных//Вестник МГУ.— 1957.— № 4.
46.	РумянцевВ.В. Об устойчивости стационарных движе-
ний спутников И Математические методы в динамике косми-
ческих аппаратов.— М.: ВЦ АН СССР.— 1967.— Вып. 4.
46а.Р умянцев В. В., Карапетян А. В. Устойчивость
движений неголономных систем И Итоги науки и техники.
Сер. Общая механика.— М.: ВИНИТИ, 1976.— Т. 3.
466.С вирежев Ю. М., Логофет Д. О. Устойчивость био-
логических сообществ.— М.: Наука, 1978.
47.	СтаржинскййВ.М. Достаточные условия устойчивос-
ти одной механической системы с одной степенью свободы И
ПММ,— 1952,— Т. 16, вып. 3.
48.	ТаммИ. Е. Основы теории электричества.— 9-е изд.— М.:
Гостехиздат, 1976.
49.	Ч с т а е в Н. Г. Устойчивость движения. Работы по анали-
тической механике.— М.: АН СССР, 1962.
50.	Я к у б о в и ч В. А. О нелинейных дифференциальных урав-
нениях систем автоматического регулирования с одним регули-
рующим органом И Вестник ЛГУ.— 1962.— № 7.
51.	Якубович В. А. Решение некоторых матричных нера-
венств, встречающихся в теории автоматического регулиро-
вания И ДАН СССР,— 1962,— Т. 143, № 6.
52.	Якубович В. А. Метод матричных неравенств в теории
устойчивости нелинейных регулируемых систем. 1. Абсолют-
ная устойчивость вынужденных колебаний И Автоматика и
телемеханика.— 1964.— Т. 25, № 7.
53.	ЯкубовичВ.А. Абсолютная устойчивость нелинейных
регулируемых систем в критических случаях // Автоматика
304
СПИСОК ЛИТЕРАТУРЫ
и телемеханика. — 1963.— Т. 24,	№ 3;	1963.— Т. 24,
№ 6; 1964.— Т. 25,№ 5.
53а.Е d е 1 е n D. G. В. On the characterization of fluxes in non-
linear irreversible thermodynamics// Int. I. Eng. Sei.— 1974.—
№. 12.
536.H agedorn P. Die Umkehrung der Stabilitatssatre von
Lagrange — Dirichlet und Routh // Arch. Rational Meeh, and
Anal.— 1971.— Bd 42, № 4. (Русек, перев.: Хагедорн П.,
Обращение теорем Лагранжа — Дирихле и Рауса // Механи-
ка: Период, сб. переводов ин. ст.— 1972.— № 5.
53в.Н agedorn Р. Uber die Instability konservativer Systeme
mit giroskopischen Kraften// Rational Meeh and Anal.—1975.—
Bd 58, № 1.
54.	Herrman G. Stability of Equilibrium of Elastic Systems Sub-
jested to Nonconservative Forces 11 Applied Mechanics Re-
views.—1967.— V. 20, № 2.
55.	KalmanR.E Liapunov Functions for the Problem of Lurie
in Automatic Controls//Proc. Nat. Acad. Sci. USA. —1963.—
V. 49.
56.	RouthE.J.A treatise on the stabiliteofa given state of mo-
tion.— London, 1877.
57.	RouthE.J. The advanced part of a treatise on the dynamics
of a system of rigid bodies.— London, 1884.
58.	T h о m s о n W. and Tait P. Treatise on Natural Phylo-
sophy.— Cambridge University Press, 1879.— Part I.
59.	Wehrli C., Z i c g 1 e г H. Zur К lassifi Ration von Kraften 11
Schweiz. Bauzeitung. —1966.— V. 84, №48.
60.	Ziegler H. Linear Elastic Stability. A. Critical Analysis
of Methods // ZAMP.— Basel — Zurich, IV, F —2.—1953,