Элементы теории оптимальных систем - Моисеев Н.Н.

Author: Моисеев Н.Н.
Tags: математика
Year: 1975
Similar
Элементы теории оптимальных дискретных процессов
Математическая теория оптимальных процессов
Теория и практика рационального выбора
Введение в теорию оптимального поиска
Text
                    ОПТИМ ИЗАЦИЯ
И ИССЛЕДОВАНИЕ
ОПЕРАЦИИ
Элементы теории
оптимальных
систем


ОПТИМИЗАЦИЯ
И ИССЛЕДОВАНИЕ
ОПЕРАЦИЙ
Редактор серии
Н. Н. МОИСЕЕВ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1975
Н. Н. МОИСЕЕВ
ЭЛЕМЕНТЫ ТЕОРИИ
ОПТИМАЛЬНЫХ
СИСТЕМ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1975
518
М74
УДК 519.95
Элементы теории оптимальных систем.
Моисеев Н. Н., Главная редакция физи-
ко-математической литературы изд-ва «Нау-
ка», 1974.
В первой части дается систематическое
изложение численных методов теории оп-
тимальных управлений. Сначала описыва-
ются методы, использующие необходимые
условия экстремума функционала. Далее
рассматриваются численные методы, исполь-
зующие идеи последовательного анализа ва-
риантов и динамического программирования.
Вторая часть (главы IV, V и VI) по-
священа вопросам синтеза систем управле-
ния объектами, подверженными действшо
внешних возмущений разного типа. Сначала
подробно обсуждается математическое со-
держание проблемы синтеза и приводятся
разнообразные методы синтеза, основанные
на эвристических соображениях. Затем из-
лагаются строгие методы теории линейного
синтеза.
В заключение этой части обсуждается
проблема синтеза в условиях неопределен-
ности и приводится решение простых задач,
иллюстрирующих роль информированности
при построении оператора управления.
В последней главе обсуждается поста-
новка задач теории иерархических систем
управления.
Илл. 39.
20204—044
М -------------
053(02)-75
73-74
© Главная редакция
физико-математической литературы
издательства «Наука», 1975 г.
ОГЛАВЛЕНИЕ
Предисловие.................................................. 7
Глава I. Оптимальные программы (теория оптимального
управления)................................................11
§1.0 постановке задач теории	оптимального	управления	13
§ 2.	Необходимые условия в задачах классического вариа-
ционного исчисления....................................26
§ 3.	Принцип максимума Л.	С.	Понтрягина	....	45
§ 4.	Условия оптимальности в системах с дискретным вре-
менем .................................................79
§ 5.	Задачи оптимального управления на бесконечном ин-
тервале времени........................................89
Глава II. Численные методы расчета оптимальных про-
грамм,.использующие, необходимые условия эк-
стремума .................................................114
§ 1.	Простейшие способы решения краевых задач .	.	115
§ 2.	Задачи оптимального управления, сводящиеся к крае-
вым задачам для систем линейных дифференциальных
уравнений. Перенос граничных условий ....	124
§ 3.	Применение метода переноса граничных условий для
построения итерационных схем..........................140
§ 4.	Методы теории оптимального управления, использую-
щие процедуру решения задач со свободным концом	147
§ 5.	Методы, использующие функции штрафа .	.	.	166
§ 6.	Задачи с нефиксированным временем и задачи на
быстродействие........................................175
§ 7.	Методы теории возмущений. Возможный способ реше-
ния краевых задач.....................................183
Глава III. Прямые методы теории оптимального управления 193
§ 1.	Конечномерные аналоги задач теории оптимального
управления............................................194
§ 2.	Методы нелинейного программирования в задачах оп-
тимального управления.................................210
§ 3.	Последовательный анализ вариантов. Схемы динами-
ческого программирования.........................229
§ 4.	Элементарная операция. Некоторые	примеры	.	.	253
§ 5.	Проблемы устойчивости.......................267
§ 6.	Некоторые задачи для систем	е дискретным	временем	279
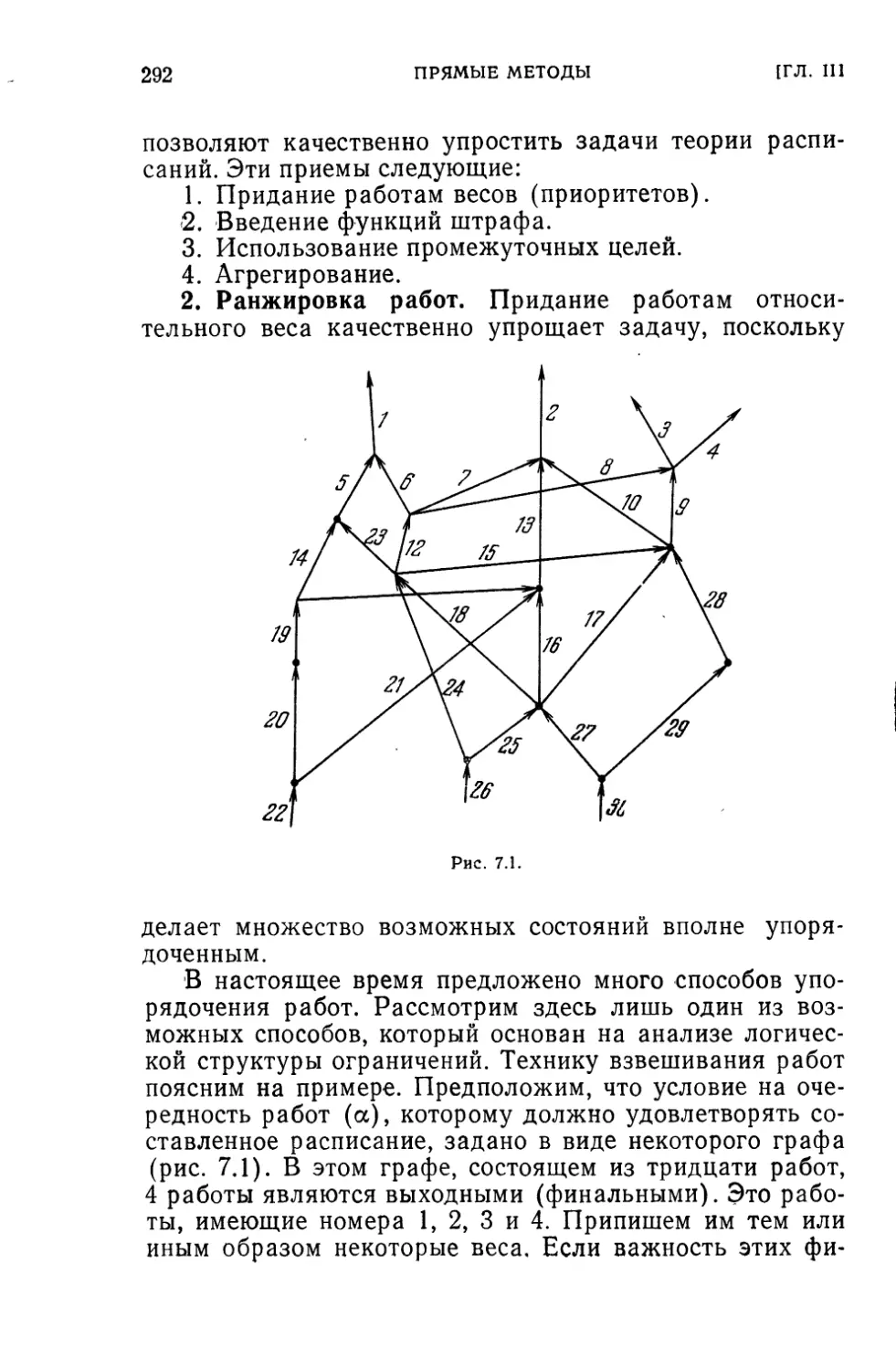
§ 7.	Задачи теории расписаний......................... 290
ОГЛАВЛЕНИЕ
Глава IV. Проблема синтеза оптимальных систем управле-
ния ........................................ ,	.	. .	304
§ 1.	О постановке задач синтеза оптимальных систем
управления..................................	306
§ 2.	Детерминированные задачи синтеза...............323
§ 3.	Применение динамического программирования для
задач синтеза .... ..............................334
§ 4.	Методы динамического программирования в задачах
синтеза с неполной информацией и при наличии оши-
бок измерений.........................................351
Глава V. Задачи синтеза, сводящиеся к задачам оптималь-
ного управления...........................................368
§ »1	.	Задачи линейного синтеза.......................369
§ 2.	Линейный синтез с ограничениями. Принцип макси-
мума .................................................396
Г пава	VI. Проблема разделения задач и игровые постанов-
ки задач синтеза оптимальных систем .	.	.	415
§ 1.	Проблема разделения .........	415
§ 2.	Гарантирующие стратегии и задачи синтеза .	.	.	434
§ 3.	Использование канонических разложений фазового
вектора в задачах линейного синтеза...................446
§ 4.	Статистическая линеаризация и синтез нелинейных си-
стем управления .		455
Глава VII. Иерархические системы управления .	465
§ 1.	Обсуждение некоторых понятий ...... 466
§ 2.	Предварительный анализ...........................474
§ 3.	Динамические системы с двухступенчатой иерархией 490
§ 4.	Один пример трехуровневой системы................503
§ 5.	Заключительные замечания.................. .	.	514
§ 6.	Некоторые новые исследования.....................520
ПРЕДИСЛОВИЕ
«Элементы теории оптимальных систем» написаны на
основе книги «Численные методы в теории оптимальных
систем». Несмотря на то, что со времени ее издания
(1971 г.) прошло сравнительно немного времени, в тео-
рии управления появилось немало новых идей и резуль-
татов, которые потребовали переработки книги и много-
численных дополнений.
Мне кажется, что наиболее значительным из того, что
произошло за эти годы, было возникновение новой боль-
шой главы, посвященной изучению систем, обладающих
иерархической организацией. Это обстоятельство означа-
ет, по существу говоря, постепенное перемещение цент-
ра тяжести интересов теории управления в сторону
изучения действительных сложных систем. По-видимо-
му, все управляемые системы естественно разбить на
простые, которые для достижения своих целей не нуж-
даются в иерархической организации, и сложные,
для которых иерархия управления является необходи-
мостью.
Переход к изучению сложных систем, требующих
иерархической структуры, приведет, вероятно, к значи-
тельному обогащению и пересмотру традиционных идей,
методов и объектов исследования в теории управления.
В частности, он позволит распространить многие из ре-
зультатов, найденных при изучении технических систем,
на задачи управления процессами более общей природы
и, прежде всего, экономическими. Фрагментарному изло-
жению элементов этой теории посвящена новая седьмая
глава.
Таким образом, схема книги приобрела следующий
вид. Первые три главы посвящены тому, что теперь при-
нято называть «теорией оптимального управления», т. е.
вариационному исчислению при дифференциальных свя-
зях и ограничениях на управляющие воздействия. Цент-
ральное место здесь занимают задачи Лагранжа и
8
ПРЕДИСЛОВИЕ
Л. С. Понтрягина. Рассмотрение ограничивается только
кусочно-непрерывными управлениями. Это обстоятельст-
во позволило получить очень простое доказательство
принципа максимума. Помимо традиционного материала
в первую главу книги включена, также задача об асимп-
тотике оптимального управления на бесконечном интер-
вале времени.
Две следующие главы содержат изложение числен-
ных методов теории оптимального управления в той фор-
ме, как они изучались и использовались в Вычислитель-
ном центре Академии наук. Последующие три главы по-
священы проблемам синтеза оптимальных управлений.
Сложность задачи, отсутствие надежного математическо-
го аппарата не позволили дать систематического изложе-
ния теории синтеза. Оно носит фрагментарный характер.
Неизбежность использования эвристических приемов и
апелляции к интуиции заставила автора подробно обсуж-
дать техническое содержание обсуждаемых проблем тео-
рии синтеза и приемы анализа, основанные на интуитив-
ной базе.
Завершается книга, как уже было сказано, главой о
иерархических системах, где любое решение задачи необ-
ходимо носит характер синтеза.
Эта книга ни в коей мере не претендует на роль энцик-
лопедии методов теории оптимальных систем. Она напи-
сана на основе опыта, приобретенного в Вычислительном
центре Академии наук СССР и отражает прежде всего
опыт автора данной монографии и его взгляды на сущест-
во изучаемой проблемы.
Необходимо заметить, что в последние. годы значи-
тельно обогатился не только идейный базис теории
управления, но и ее аппарат. Прежде всего, появился ряд
первоклассных исследований алгоритмов оптимизации.
Новые способы доказательства сходимости, предложен-
ные В. Г. Кармановым, идеи ускорения сходимости
Н. 3. Шора, Б. Н. Пшеничного и их учеников, методы
стохастического программирования Ю. М. Ермольева и
многие другие работы, выполненные в традиционном сти-
ле, составляют, конечно, замечательную новую главу
прикладной математики.
Тем не менее эти результаты не нашли своего места
в книге. И тому много причин.
ПРЕДИСЛОВИЕ
9
Во-первых, их изложение потребовало бы значитель-
ного расширения объема и в какой-то степени дублиро-
вало бы выходящие в данной серии книгу Б. Н. Пшенич-
ного и Ю. М. Данилина и книгу Ю. М. Ермольева.
Во-вторых, как уже говорилось, автор старался вклю-
чить в книгу лишь те разделы, в развитие которых он сам
внес определенную лепту.
Но третье и главное — это стремление сохранить
«физический уровень» строгости и не перегружать книгу
чисто математическими исследованиями. Это стремление
отражено и в заглавии. Сам термин «оптимальные систе-
мы» очень нечеток, и благодаря этому он отражает суще-
ство дела.
Когда речь идет о любой реальной системе техничес-
кой, экономической, военной,— то процесс ее проектиро-
вания никогда не может быть четко сформулирован и
сведен к решению какой-либо одной задачи или даже це-
почки математических задач. Противоречивость требова-
ний к конструкции и наличие ряда других неопределен-
ностей, с которыми неизбежно сталкивается человек, про-
ектирующий систему, приводит к тому, что неформаль-
ный анализ, поиск компромисса занимает значительное
место в процессе проектирования. В результате именно
такого неформального анализа в проектировании и уда-
ется эффективно использовать оптимизационные методы
(как некоторый вспомогательный элемент), дающие пре-
дельные оценки конструкции.
Поэтому в предлагаемой книге автор хотел изложить
не только математическую теорию оптимального управ-
ления, которая, конечно, занимает большое место в кни-
ге, но и показать место оптимизационных задач в проб-
лемах проектирования систем управления.
И, наконец, последнее. В книгах по методам оптими-
зации стало традиционным особенное внимание уделять
проблемам сходимости алгоритмов. Студент, окончив-
ший математический факультет, глубоко убежден в том,
что сходящийся алгоритм — это хороший алгоритм, а
расходящийся — плохой. А строго говоря, свойство схо-
димости алгоритма в общем случае не является ни необ-
ходимым, ни достаточным для того, чтобы его можно
было рекомендовать для окончательной оценки алго-
ритма. Существует много примеров, когда реализация
10
ПРЕДИСЛОВИЕ
сложных вычислений была осуществлена с помощью за-
ведомо расходящихся алгоритмов и, наоборот, устойчи-
вые сходящиеся алгоритмы приводили уже на одной из
первых итераций к машинной бесконечности.
Эти примеры ничего не опровергают. Они просто по-
казывают недостаточность традиционных представлений.
Постепенно начинает возникать понимание того фак-
та, что математика не так уж существенно отличается от
других естественных наук и, во всяком случае, имеет та-
кое же эмпирическое начало. После работ Геделя, изо-
бретения ЭВМ и опыта работы математиков в приклад-
ных областях этот тезис становится все более распрост-
раненным. Как и любое другое знание, любая другая
наука, математика нужна человеку для решения опреде-
ленных практических задач, достижения определенных
целей. И каждый раз требования к этим знаниям, к ана-
лизу должны находиться в определенном соответствии с
этими целями.
При подготовке рукописи я пользовался советами и
помощью многих лиц. Гермейеру Ю. Б., Ермольеву Ю.М.,
Крылову И. А., Ринго Н. И., Пшеничному Б. Н., Шевчен-
ко Е. М. я обязан советами, вниманием и помощью. Вап-
нярский И. Б., Ватель И. А. и Ерешко Ф. И. прочли руко-
пись в черновике и внесли целый ряд изменений, значи-
тельно усовершенствовавших первоначальное изложение.
Всех указанных лиц я прошу принять мою глубокую
благодарность.
ГЛАВА I
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
(ТЕОРИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ)
Даже на фоне общего прогресса естественных и тех-
нических наук теория управления в послевоенные годы
выделялась особым богатством новых- идей и методов.
Расцвет теории управления, подготовленный всей пред-
историей ее развития, тесно связан с появлением элект-
ронно-вычислительной техники, благодаря которой обре-
ло смысл создание сложных алгоритмов управления.
Центральной идеей, определявшей развитие теории
управления в последние десятилетия, безусловно, была
идея оптимизации. Сама эта идея не нова. Уже в пред-
военные годы большое значение стали приобретать рабо-
ты, в которых изучалось качество управления. Основной
задачей теории управления в предвоенный период была,
по общему мнению, задача отыскания устойчивых управ-
лений. Но свойство устойчивости еще не выделяет единст-
венного решения. Поэтому естественно поставить вопрос
о том, как можно воспользоваться произволом, который
мы здесь имеем. Задачи нахождения управления, обла-
дающего в некотором смысле «лучшим качеством», уже
содержали оптимизационную точку зрения. В середине
40-х годов стали актуальными задачи расчета траекто-
рий ракет, решавших проблему достижения заданной вы-
соты или дальности, вывода на орбиту и т. д. при мини-
мальном расходе горючего.
Количество работ, посвященных этим проблемам, в
настоящее время исчисляется десятками. Среди них
я считаю необходимым выделить работу Д. Е. Охоцим-
ского «К теории движения ракет» (ПММ, 10, № 2, 1946).
В этой статье уже содержалась (с точностью до терми-
нологии) современная постановка задач теории опти-
мального управления.
Задачи, возникшие в теории летательных аппаратов,
снабженных ракетными двигателями, значительно отли-
чались от традиционных задач автоматического уп-
равления. В те годы усилия специалистов по теории
12
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
(ГЛ. I
регулирования (синоним автоматического управления)
были главным образом направлены на изучение способов
управления стационарными движениями на бесконечном
интервале времени. Задачи же динамики ракет — это су-,
щественно нестационарные задачи, поскольку время про-'
текания процесса (работы двигателей) относительно ма-
ло. Кроме того, в традиционных задачах теории регулиро-
вания вопрос об отыскании программного движения, кото-
рым мы собираемся управлять, обычно не ставился. Это
движение было либо задано заранее, например, заданная
скорость вращения турбины, либо его определение было
тривиальным. В теории регулирования решалась другая
задача отыскания оператора обратной связи, управления
как функции фазовых координат системы, а не как функ-
ции времени.
Поэтому, несмотря на то, что в динамике ракет изу-
чался один из классов управляемых движений, эта тео-
рия вначале развивалась независимо от теории автома-
тического управления. Слияние обеих теорий произошло
уже в пятидесятые годы, когда оптимизационные поста-
новки задач управления начинают занимать внимание и
специалистов по теории автоматического управления.
Начало этим исследованиям положили работы, посвящен-
ные исследованию быстродействий (А. А. Фельдбаум
и др.). Класс оптимизационных задач, возникших в тео-
рии управления, не сводился к классическим задачам
вариационного исчисления и требовал создания специаль-
ного аппарата. Несмотря на то, что к началу пятидеся-
тых годов целый ряд конкретных задач такого типа был
уже решен, в теории управления еще не был выработан
единообразный подход к их анализу.
Выдающуюся роль в развитии теории оптимального
управления сыграл Л. С. Понтрягин, который сформули-
ровал принцип максимума, позволяющий с помощью
множителей Лагранжа свести задачу оптимального
управления к некоторой специальной краевой задаче для
обыкновенных дифференциальных уравнений.
После работ Л. С. Понтрягина и его школы в теории
оптимального управления произошла та канонизация
методов и языка, которая свидетельствует о появлении
новой дисциплины. Она получила название теории опти-
мального управления.
ПОСТАНОВКА ЗАДАЧ
13
§ И
В настоящее время теория оптимального управления
и оптимизационная идеология глубоко проникли во все
исследования конкретного характера и конструкторские
разработки, и можно сказать без преувеличения, что
язык теории оптимальных процессов сделался общим
языком современной теории управления.
В технике возник термин «оптимальные системы».
Это очень расплывчатое понятие, которое не имеет еще
четкого математического содержания. Однако когда ин-
женеры говорят о конструировании оптимальных систем,
то всем более или менее ясно, что это означает. Это озна-
чает, что на разных этапах конструирования системы вы-
бор ее элементов определяется теми или другими оптими-
зационными соображениями.
Как мы это увидим ниже, одна из особенностей зада-
чи проектирования «оптимальных систем» управления
состоит в том, что систему нельзя охарактеризовать
одним числом — одним критерием. Поэтому процесс кон-
струирования оптимальной системы — это целая цепочка
оптимизационных задач.
В этой главе мы будем рассматривать первую из тех
задач, с которой встречается инженер (или экономист),
проектирующий оптимальную систему управления. Эта
задача носит название задачи расчета оптимальной про-
граммы (или оптимального плана). Мы будем изучать ее
только для динамических систем (эволюция которых опи-
сывается дифференциальными или разностными уравне-
ниями). В этом частном случае задача расчета програм-
мных движений совпадает с задачей теории оптимально-
го управления. Место этой задачи в общем процессе
конструирования системы управления динамическим объ-
ектом будет раскрыто в последующих главах этой книги.
§1.0 постановке задач теории
оптимального управления
1. Обсуждение технического содержания задач рас-
чета программных движений *). Во введении говорилось,
что один из первых вопросов, с которым сталкиваются
*) Ряд дисциплин, занимающихся отысканием оптимальных ре-
шений: линейное программирование, нелинейное программирование,
теория оптимального управления, динамическое программирование
14
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
(ГЛ. I
при разработке системы управления динамическим объ-
ектом,—это вопрос о выборе программного движения.
Поясним содержание этой задачи.
Предположим, что речь идет об объекте, движение
которого описывается некоторой системой дифференци-
альных уравнений. Эту систему будем записывать в век-
торном виде
х — f (х, и, t),	(1.1)
где х, и п f — векторы с компонентами х‘, и* и соответст-
венно, х(/) —называется фазовым вектором (или векто-
ром состояний), он определяет состояние системы в мо-
мент времени —управляющим вектором или управ-
лением. Их размерности могут совпадать или быть
различными. Предполагается, что векторы x(t) и u(t)
могут изменяться лишь в некоторой допустимой области
x(t)sGXl	(1.2)
u(0eG„.	(1.2')
Условие (1.2) называется фазовым ограничением, (1.2') —
ограничением на управление. Gx и Gu—некоторые задан-
ные множества.
Например, если описывается движение ракеты, запус-
каемой в космос, то векторное уравнение (1.1) может
быть представлено в виде системы
у! -• 4гЗ у2 _
/V — Л J Л - /V I
X3 = — (ф1 + u1 cos и2),
т	(11')
х4 — — (ф2 4- u1 sin и2),
т
_______________ т — — F (и1),
и т. д., объединяют обычно одним термином — математическое про-
граммирование. Этот термин неудачный, поскольку математическим
программированием называют одновременно совокупность дисциплин,
связанных с переводом алгоритмов на язык машины (и в том числе
алгоритмические языки). В последнее время вопросы, связанные с
построением оптимальных решений, стали объединять общим терми-
ном— программатика, оставляя за математическим программирова-
нием только вопросы, связанные с процессом трансляции алгоритма
на внутренние языки машины. Согласно этой терминологии первые
главы данной монографии содержат краткое изложение методов про-
грамматики, используемых в теории управления динамическими объ-
ектами.
ПОСТАНОВКА ЗАДАЧ
15
§ 1]
в которой х1, х2—координаты положения, х3, Xs—коор-
динаты скорости, т — масса ракеты, м1— величина тяги,
и2—угол между направлением тяги и осью х1, F(ul) —
секундный расход массы. Кроме силы тяги на ракету
действуют сила тяжести, сопротивление атмосферы и т. д.
Суммарные проекции этих сил на координатные оси обо-
значены через ф1 и ф2.
Для рассматриваемой задачи множество Gx— это
некоторая заданная область пространства, окружающего
Землю. Траектория ракеты не может пересекать поверх-
ность Земли, не должна заходить в зону радиационных
поясов и т. п.
Управление полетом ракеты осуществляется за счет
регулирования величины и направления вектора тяги
двигателя: управляющие функции — это тяга и1 и угол и2.
Тогда множество Gu— это множество всех тех значений
«=(«*, и2), которые допустимы из конструктивных сооб-
ражений.
Движение динамического объекта стеснено некоторы-
ми начальными и конечными условиями, которые мы
будем обозначать следующим образом:
х (/0) <= й’о,
(1-3)
X (Т) €=
Например, могут быть заданы начальное положение, ско-
рость и масса ракеты. В этом случае первое из условий
(1.3) запишется так:
х1 (Q = xj, х2 (Q = Хо,
Х3(/0) = Х3,	Х4(/0) = Хо,
/п (Q = т0,
где xj, х%, х2, х*,тй—фиксированные числа. Предполо-
жим, что ракета должна быть выведена на круговую
орбиту заданного радиуса R. Тогда второе из условий
(1.3) будет таким:
(?(7))*+(?(Т))а = /?,
х3 (Т) х1 (Г) + х4 (Т) х2 (Т) = 0,	(1.3')
(x3(T))2 + (x4(T))2-v«.
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
где va—это скорость соответствующего кругового дви-
жения.
Первое из этих условий означает, что точка с коорди-
натами (х‘, х*) в момент времени t=T находится на ок-
ружности заданного радиуса 7?. Второе условие означает,
что векторы f и г>, имеющие соответственно компоненты
(х1, хг) и (Xs, х4), ортогональны, т. е. скорость точки в мо-
мент t=T направлена по касательной к окружности
заданного радиуса. Из третьего условия следует, что
скорость точки должна равняться скорости движения по
круговой орбите. Условие (1.3') гарантируют, что если
при t=T двигатель будет выключен, то последующее сво-
бодное движение будет движением по окружности.
Второе из условий (1.3) называется целью управле-
ния. Достижение системой (1.1) за заданное время Т не-
которого конечного состояния (например, достижение
аппаратом заданной высоты, или выход аппарата на ор-
биту) может быть реализовано, вообще говоря, бесчис-
ленным множеством способов, каждый из которых име-
нуется программой (или программным движением).
В технических задачах обычно возникает вопрос об оты-
скании наиболее «экономной» программы. Например, в
случае ракеты программа будет тем более экономной,
чем меньшее количество топлива будет израсходовано.
Математическое выражение этого факта, согласно по-
следнему уравнению (1.1')» состоит в том, что управле-
ние u(t) должно быть выбрано из условия минимума
интеграла:
т
Ци)= §F(uP)dl.	(1.4)
г.
Функцию и(0, которая удовлетворяет всем ограничени-
ям, обеспечивает достижение объектом цели управления
и доставляет минимальное значение интегралу (1.4), мы
будем называть оптимальной программой или оптималь-
ным управлением.
Не менее часто встречается и другая постановка зада-
чи. Например, при заданной энергии, которая может
быть израсходована для вывода ракеты, заданном време-
ни вывода и заданном расстоянии до перигея мы должны
так построить программу управления — так выбрать
ПОСТАНОВКА ЗАДАЧ
17
$1]
функцию u(t) и соответствующую ей траекторию x(t), что-
бы расстояние до апогея было максимальным. При соот-
ветствующем выборе переменных эта техническая поста-
новка задачи сводится к отысканию управления, макси-
мизирующего функционал
J(x, и) = х1(Т),	(1.5)
где xi— некоторая компонента вектора х.
Первая из задач называется задачей Лагранжа, вто-
рая— задачей Майера, функционал (1.4) (или (1.5))
часто называют целевой функцией или функцией цели.
Он определяет «стоимость» достижения цели .управления.
2. Математическая формулировка задач определения
оптимальных программ. В предыдущем разделе на при-
мере движения ракеты мы пояснили содержание, задач
отыскания оптимальных программ. Теперь мы дадим ма-
тематическую формулировку тех задач, которые будут
рассматриваться в первых главах этой книги.
В достаточно общем виде задача оптимального управ-
ления может быть сформулирована следующим образом.
Определить вектор-функции x(t)^Rn, u(t)^Rm при
te[/0, TJ, доставляющие минимум (максимум) функцио-
налу
J = J(x,u)	(1.6)
при дифференциальных связях
x = f(_x, и, 0,	(1.7)
ограничениях вдоль траектории
(х, и,	(1.8)
и краевых условиях
(*Л)е=£0,	(1.9)
(х, Т) <= ST.
Будем считать, что функции f непрерывны и дифферен-
цируемы по совокупности переменных х и и. Множество
G — некоторая область пространства /?“Х/?тХ#‘, а мно-
жества ЙГо и ST — некоторые многообразия в /?ПХ₽’.
Конкретизация выражений (1.6) — (1.9) порождает раз-
личные типы задач оптимального управления.
18
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Принятая ниже классификация задач оптимального
управления является весьма условной, однако она помо-
жет читателю ориентироваться в литературе по данному
вопросу.
Типы задач можно разбить на три группы. В каждой
из групп определяющей характеристикой являются спосо-
бы, с помощью которых задаются соответственно
1.	Функционал (1.6).
2.	Ограничения вдоль траектории (1.8).	।
3.	Краевые условия (1.9).
1.	Способы задания функционала.
а)	Интегральный функционал. Задача
Лагранжа. Интегральным функционалом называется
функционал вида
т
J(x,u) = ^F(x,u,t}dt,	(1.10)
^0
где F предполагается дифференцируемой функцией своих
переменных.
В случае отсутствия ограничений (1.8) задача о ми-
нимуме (1.10) при условиях (1.7). и (1.9) традиционно
называется задачей Лагранжа. Она является классиче-
ской задачей вариационного исчисления *).
б)	Задача Майера. В этом случае минимизи-
руемым функционалом является
J (х, и) = Ф (х (Т), Т).	(1.11)	|
Например, для системы (1.1х) можно поставить следую-
щую задачу Майера: определить управление и=(и1,и2)
так, чтобы за заданное время Т достичь максимальной
дальности х1{Т) при условии, что х2(7’)=0, т. е. чтобы
ракета в момент времени t—T оказалась на поверхности
Земли.
Можно также рассматривать задачу Майера, в кото- >
рой функционал зависит от краевых значений фазовых
координат на обоих концах.
*) Мы сформулировали задачу Лагранжа, несколько сузив ее по-
становку по сравнению с классическими курсами вариационного ис-
числения, записав дифференциальные связи (1.7) в нормальной фор-
ме Коши.
ПОСТАНОВКА ЗАДАЧ
19
§ II
Формально задача Майера является более общей, чем
задача Лагранжа: любая задача Лагранжа может рас-
сматриваться как частный случай задачи Майера. В са-
мом деле, рассмотрим задачу Лагранжа (1.7) — (1.10)
и введем новую скалярную переменную хп+‘ при помощи
уравнения
‘xn+1=F(x, и, t).
Введем еще новый фазовый вектор х и вектор /:
х{ — х1, i = 1, 2, ..., п + 1,
j = 1,2, ..., п,
р
Теперь задачу (1.7) — (1-Ю) мы можем переформулиро-
вать следующим образом. Определить вектор-функции
u(t) и x(t), доставляющие минимум функционалу
J (х, и) — хп+1(Т)
при условиях
х =*f (х, и, t).
В некоторых частных случаях задача Майера, в свою оче-
редь, может быть сведена к задаче Лагранжа.
Рассмотрим задачу Майера с функционалом (1.11)
и предположим дополнительно, что левый конец фазовой
траектории фиксирован
Я (Q ~ Хд.
Вместо функционала (1.11) рассмотрим следующий:
А (х, и) = Ф (х (Т), Т) - Ф (х (Q, t0).	(1.12)
Поскольку Ф(х(М, t0) —величина известная, то функции
x(t) и м(0> доставляющие минимум функционалу (1.12),
доставляют также минимум функционалу (1.11) и об-
ратно.
Но нетрудно видеть, что
А (х, и) = f i^dt = J f (х, и, О) + ^-] dt,
^0	^0
20
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
т. е. задача с функционалом (1.12)—это некоторая зада-
ча Лагранжа.
в)	Задача Больца. Функционал смешан-
ного типа. Определить векторы u(t) и х(/), достав-
ляющие минимум функционалу
т
J (х, и) = J F (х, и, /) dt + Ф (х (/0), /0, х (Г), Т) (1.13)
to
при ограничениях (1.7) — (1.9).
Легко видеть, что задача с функционалом (1.13) мо-
жет быть сведена к задаче Майера.
г)	Задачи на быстродействие. Этим тер-
мином объединяются задачи, в которых функционалом
(объектом минимизации) является время. Предположим,
что концы траектории фиксированы. Тогда задача на
быстродействие формулируется следующим образом: оп-
ределить управление, которое переводит систему из со-
стояния х0 в состояние хт за минимум времени. Задачи
на быстродействие являются важным классом задач тео-
рии оптимального управления.
2.	Способы задания ограничений вдоль траектории.
а)	Ограничение на управление. Пусть огра-
ничение (1.8) имеет вид
u(t)<=Gtt(t),	(1.14)
где Gu— некоторое замкнутое множество из Rm. В част-
ном случае, когда GM совпадает со всем пространством
Rm, а функционал задан в виде (1.10), мы получаем зада-
чу Лагранжа.
Задачи с ограничениями на управление типа (1.14)
более адекватны вариационным задачам, возникающим
в технике: возможности управления всегда ограничены.
Например, часто встречаются ограничения типа
|м(0|<а(/). •	(1.15)
Классические методы, развитые для решения задачи Ла-
гранжа, оказываются в общем случае неприменимыми
при наличии ограничений вида (1.14). Для подобных за-
дач в конце 50-х годов был разработан принцип максиму-
ма Л. С. Понтрягина, который будет подробно рассмот-
рен в § 3.
ПОСТАНОВКА ЗАДАЧ
21
§ И
б)	Ограничения на фазовые перемен-
ные. Это ограничения (1.8) в следующей форме:
x(t)<=r(jx(t).	(1.16)
Смысл подобных ограничений был уже пояснен на при-
мере, который мы рассмотрели в начале параграфа.
Применимость того или иного метода решения задач
с ограничениями на фазовые координаты существенно
зависит от вида ограничений (1.16). Обычно здесь разли-
чают ограничения типа равенств
Q1 0=0,	/ = 1, 2...k^n, (1Л7)
и ограничения типа неравенств
<У(х(0,О<О.	(1.18)
в)	Совместные ограничения на управле-
ние и фазовые переменные. Иногда огра-
ничения на управление и на фазовые координаты не
могут быть разделены, и тогда мы сталкиваемся с зада-
чей на «узкие места», в которой ограничения имеют вид
(1.8). Подобные задачи часто встречаются в экономике.
Здесь также различают ограничения в виде равенств
и (О, 0 = 0, / = 1, 2.. k^n + m, (1.19)
и неравенств
o!(x(t), u(0,0<0.	(1.20)
г)	Изопериметрическая задача (задача с
интегральными ограничениями). Определить
минимум функционала (1.6) при следующих ограниче-
ниях:
т
f¥z(x(O, =	/=1,2,	(1.21)
м
где —некоторые скалярные функции, а U—заданные
числа. Название этому классу задач дала следующая
«историческая» задача, изучавшаяся еще в концеXVII ве-
ка: определить кривую данной длины, которая ограничи-
вает максимальную площадь.
Класс изопериметрических задач играет большую
роль как в технике, так и в экономике, когда задан сум-
22
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
марный объем некоторого ресурса, которым мы вправе
распоряжаться. (Например, когда задан запас горючего,
который должен быть использован для управления реак-
тивным аппаратом или самолетом.) Изопериметрическая
задача может быть сведена к задаче Лагранжа увеличе-
нием размерности фазового вектора х. В самом деле, для
этого достаточно ввести новые скалярные переменные
при помощи уравнений
х»+/= ¥(х,и,/), /=1, 2, k.
Функции xn+i(t) должны, кроме того, удовлетворять ус-
ловиям
х"+^о) = О,
х"+/(Т)= //.
Таким образом, изопериметрическая задача сводится
к задаче Лагранжа (или Майера — в зависимости от
структуры исходного функционала), но для векторалграз-
мерности n+k.
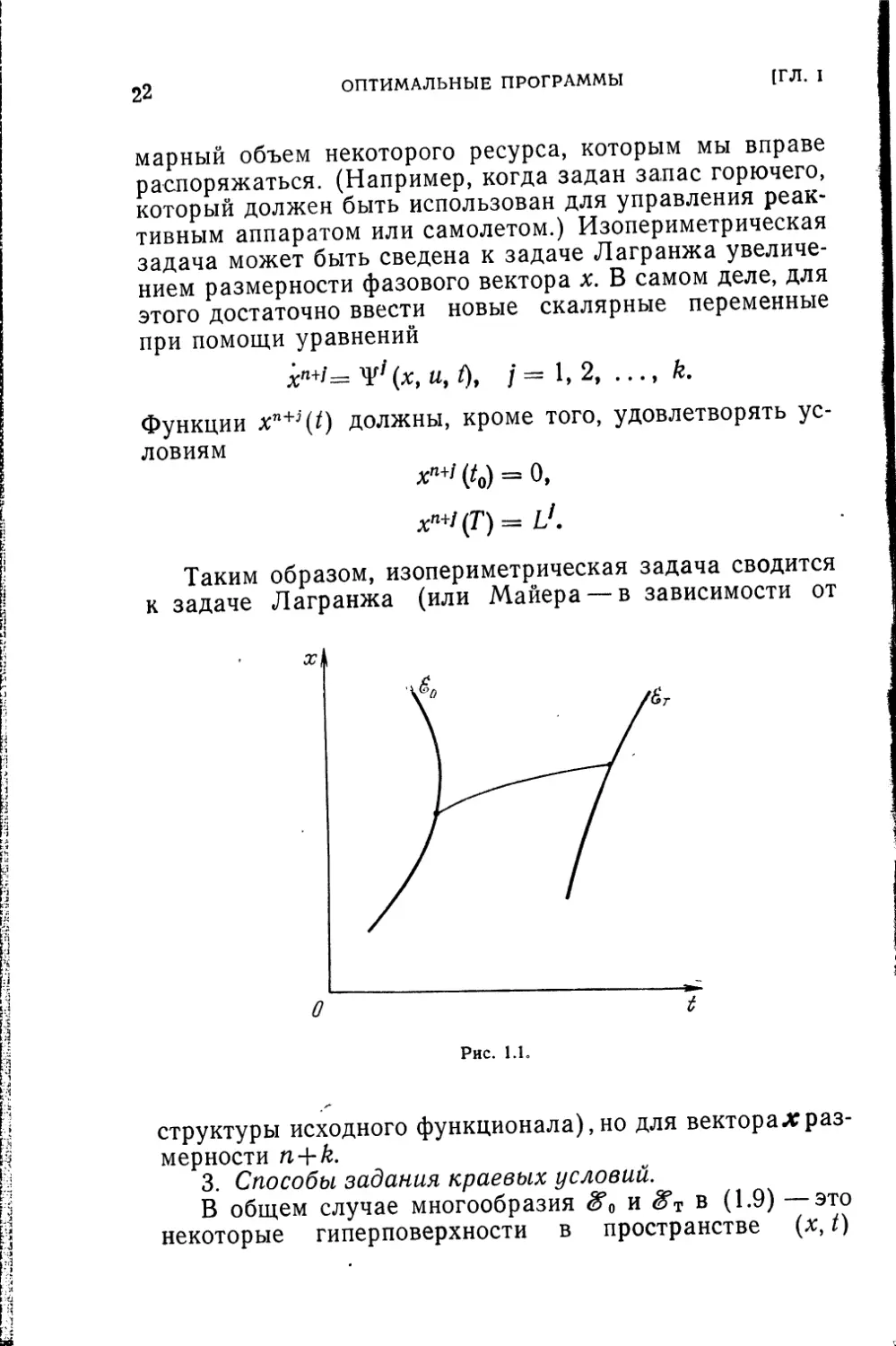
3.	Способы задания краевых условий.
В общем случае многообразия и в (1.9) —это
некоторые гиперповерхности в пространстве (х,t)
ПОСТАНОВКА ЗАДАЧ
23
§ И
(рис. 1.1), задаваемые уравнениями
Xl(x(/0Uo) = 0, 1 = 0,1..s^n,	(-1.22)
Ф/(х(Т), Т) = 0, / = 0, 1, ..4, р^п.	(1.23)
а)	Задача с фиксированными концами.
Этот термин используется в задачах, в которых x(f0) и
х(Т) заданы. Различают также задачи с фиксированным
временем (t0, Т — заданы) и нефиксированным (либо /0,
либо Г не задано).
б)	Задача со свободным концом. Если
х(/0) (или х(Т)) не задано, то мы имеем задачу со сво-
бодным левым (правым) концом. Здесь также различа-
ют задачи с фиксированным и нефиксированным време-
нем. Задачи со свободным концом, как мы увидим ниже,
играют важную роль при построении численных методов.
в)	Задача с подвижными концами. Ес-
ли t0, Т — фиксированы, а векторы x(t0) и х(Т) лежат на
гиперповерхностях, определяемых уравнениями (1.22) и
(1.23), то говорят о задаче с подвижными концами и фик-
сированным временем. Если либо t0, либо Т в (1.22),
(1.23) не фиксировано, то мы получаем задачу с «переме-
щающимся многообразием» на соответствующем конце.
Перечисленные задачи не исчерпывают перечня задач,
которые принято относить к теории оптимального управ-
ления. Существует, например, важный класс задач, в ко-
тором в качестве функционала выступает величина
J (и) = max ф (х (ff), t е [/0 Г].
t
Задача управления — минимизировать эту величину.
Примечание. Эта задача может быть переформу-
лирована, если ввести скаляр у, такой, что
Ф(х(0)<Ш	(*)
Тогда задача с функционалом у(и) сведется к отысканию
управления, которое минимизирует величину у(и) при
фазовом ограничении (*).
3. Задачи с дискретным временем. До сих пор мы го-
ворили о системах с «непрерывным временем», т. е. о
системах, эволюция которых описывается дифференци-
альными уравнениями. Но не менее важное значение
24
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
имеют системы с «дискретным временем». Их роль опре-
деляется не только тем, что при построении вычислитель-
ных процедур мы всегда проводим дискретизацию нашей
задачи—заменяем дифференциальные уравнения конеч-
норазностными. Существует обширный класс технических
и экономических задач, которые являются по существу
дискретными. Это прежде всего многошаговые задачи
принятия решений. Практически всегда развитие эконо-
мической системы описывается конечно-разностными
уравнениями. Шаг дискретизации определяется циклом
экономического процесса. Например, в системах, которые
описывают развитие сельскохозяйственного производст-
ва, таким циклом является год. Поэтому, наряду с дина-
мическими системами типа (1.1), мы будем рассматри-
вать системы конечноразностных уравнений вида
= fn(xn, Un),	(1.24)
где
ДХл — Хп+i Хп,
хп— по-прежнему называется фазовым вектором, ип —
управлением.
Ограничения (1.2) и (1.2') сохраняют свой вид, если
заменить x(t) и u(t) на хп и ип соответственно.
Начальные и конечные условия мы будем записывать
в виде
хое^о, xNf=$N,	(1.25)
где М— число шагов многошагового процесса (1.24).
Мы можем сформулировать аналоги задач Лагранжа
и Майера:
а)	Задача Лагранжа. Определить векторы
«о, Ui,..., uN-i и xit хг,..., хя, доставляющие минимум
(максимум) скалярной функции
N-1
J (х, и) = Fl (xit ut)	(1.26)
Z—О
при условиях (1.24), (1.2), (1.2х) и (1.25).
б)	Задача Майера. Определить векторы и0,...
..., «w-j и %!.xN, доставляющие минимум (максимум)
§ 1]	ПОСТАНОВКА ЗАДАЧ	25
скалярной функции
J(x, u) = <D(xw)	(1.27)
при условиях (1.24), (1.2), (1.2') и (1.25).
Точно так же, как и в случае задач с непрерывным
временем, существует взаимосвязь обеих сформулирован-
ных задач (см. стр. 18). Подобно тому, как мы определи-
ли конечномерые аналоги задач Лагранжа и Майера,
могут быть определены дискретные аналоги всех тех
задач, которые были сформулированы в предыдущем
пункте. Например, изопериметрическими условиями в за-
дачах с дискретным временем мы будем называть усло-
вия вида
N-1
(1.28)
/=о
В этой книге мы будем рассматривать задачи оптими-
зации, возникающие в динамических системах, которые
описываются либо дифференциальными уравнениями
(1.1), либо конечноразностными уравнениями (1.24). Эти
два класса, конечно, далеко не исчерпывают всего мно-
жества задач, которые относятся к программатике.
Примечания.
1.	В экономике часто имеют дело с задачами, в кото-
рых уравнение (1.7') имеет вид
х (0 = f (х (/), и (/ — т), t).	(1.7')
Структура уравнения (1.7) отражает тот факт, что инве-
стиции, вложенные в момент времени т, начинают давать
результат только по прошествии определенного времени.
В самом деле, капитал, вложенный в строительство заво-
да, начнет давать отдачу только тогда, когда он превра-
тится в здания, станки, когда будет налажен технологи-
ческий процесс и т. д.
Таким образом, теория управления динамическими
процессами (1.7') имеет важное значение. К сожалению,
из-за отсутствия места она не может быть включена в
книгу.
2.	Формулируя задачи определения оптимальных про-
грамм, мы выделяли три элемента. Цель управления, ог-
раничения и критерий качества — функционал. Однако
26
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
формально все эти элементы эквивалентны. В самом
деле, второе из условий (1.9) мы можем заменить усло-
вием минимума функционала /*, где
( 0, если (х, Т) е <St,
J* = 4	_
+°о, если (х, Т) е й’т.
Аналогично можно поступить и с остальными ограни-
чивающими условиями, в том числе и с управлением дви-
жения (1.7).
Таким образом, задача, которая формулируется в
данном параграфе есть частный случай следующей зада-
чи: определить функцию y(f), доставляющую минимум
функционалам
Л(Н0) i=l,2, ...
В общем случае подобная задача не имеет решения и
тогда возникает проблема свертывания критерия — заме-
на системы критериев .......Jh другими критериями.
Операция свертывания критериев не является формаль-
ной и мы с ней встретимся в последних главах книги.
Задача оптимального управления может рассматри-
ваться как частный случай задачи со многими критерия-
ми, который допускает решение. Последнее означает,
в частности, что пересечение множеств G^y), состоящее
из элементов, реализующих минимум функционалов
/<(«/), не пусто.
§ 2. Необходимые условия в задачах
классического вариационного исчисления
1.	Задача Лагранжа. В предыдущем параграфе мы
подробно обсудили постановку и терминологию различ-
ных вариационных задач, относящихся к теории опти-
мального управления. Для их эффективного решения мо-
гут быть использованы различные методы. Обширный
класс методов расчета оптимальных программ доставля-
ют методы, опирающиеся на необходимые условия опти-
мальности.
Мы переходим теперь к изложению некоторых усло-
вий такого рода — они будут использованы в дальнейшем
для построения вычислительных методов.
§21	О ЗАДАЧАХ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ	27
В предыдущем параграфе, формулируя задачи, мы
не акцентировали наше внимание на свойствах гладко-
сти, которыми должны обладать искомые функции. По-
этому теперь, прежде чем переходить к отысканию необ-
ходимых условий экстремума, мы несколько уточним
постановку рассматриваемой задачи.
В этом параграфе мы будем изучать следующую зада-
чу Лагранжа:
определить непрерывную вектор-функцию u(f) и диф-
ференцируемую вектор-функцию x(t) со значениями из
Rm и Rn соответственно, доставляющие минимум функ-
ционалу
т
J (х, и) = J F (х, и, t) di,	(2.1)
to
где F — скалярная, непрерывно дифференцируемая функ-
ция своих аргументов, при условиях
x = f(x,u,t),	(2.2)
(x(f0), /0)<=£0,
(x(T),Ds?r;	{ '
f — непрерывно дифференцируемая вектор-функция, <F0
и <ГТ—заданные множества из Rn+l, структура которых
будет уточнена ниже.
Сразу же оговоримся, что развиваемые здесь методы
для задачи Лагранжа могут применяться и для исследо-
вания задач Майера и Больца. Кроме того, мы ограни-
чимся исследованием частного вида ограничений (2.3).
Необходимые условия для задачи Майера и Больца, а
также для случая ограничения (2.3) более общего вида
будут сформулированы и кратко обсуждены в п. 7 этого
параграфа.
Для дальнейшего нам удобно несколько изменить
обозначения. Обозначим Г(х, и, t) =f*(x, и, t) и введем
скалярную величину x°(t), удовлетворяющую уравнению
x°=f°(x, и, i). Тогда функционал (2.1) равен конечному
значению
J (х,. и) = х° (Т).
(2.1') ,
28
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Введем также расширенный фазовый вектор х= (х°, х1*,...
хп\ ss (х°, х) и расширенный вектор правых частей
7= (Г >f‘> ?>•••>	Тогда вектор х будет удов-
летворять уравнению
х =7(х, и, t),	(2.2')
т. е. 7 не зависит от х°.
Теперь задачу (2.1—2.3) мы можем сформулировать
следующим образом: определить непрерывную вектор-
функцию u{t) и дифференцируемую вектор-функцию
x(t) со значениями из Rm и Rn соответственно, доставля-
ющих минимум функционалу (2.1') при условиях (2.2')
и (2.3).
2.	Вспомогательная лемма. Для дальнейшего нам по-
надобится следующая.
Лемма. Пусть f(t) — непрерывная вектор-функция.
Если интеграл
т
I = J(f, фИ
равен нулю для любой непрерывной вектор-функции ф(/),
то необходимо f=0.
Доказательство. Пусть f^O, тогда существует
такая точка ?, что f(f)=#O, и, следовательно, существует
интервал (Г—8, Г + е), где хотя бы одна из компонент
т^о.
Построим функции
I _ [?(*)(!* — 8 — ОТ + 8~О8, если 8,Г+8],
10,	если t е [Г—е, f + 8],
<р/ = 0, если / =7=
Так как произведение ф'(0/г(0 на этом интервале неот-
рицательно и обращается в нуль только на концах, то
интеграл I положителен. Полученное противоречие дока-
зывает утверждение.
3.	Вариации управления и траектории. Сейчас мы
приступаем к выводу необходимых условий. Рассмотре-
ние будем вести для случая фиксированного левого
конца.
О ЗАДАЧАХ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
29
5 2]
Обозначим через й некоторое управление, тогда соот-
ветствующая траектория х определится как решение за-
дачи Коши для уравнения (2.2). Далее обозначим через
8 некоторый скаляр (в может быть как положительным,
так и отрицательным), через би-произвольную непрерыв-
ную функцию и наряду с управлением й рассмотрим
управление и,:
и8 = и + еби.
Через х* обозначим вектор х, который будет удовлет-
ворять уравнению
*8 = 7 (*е. и +g$«, t).
Вариацией вектора х будем называть векторную произвол’
—	/ дх \
ную h = —-	. Вектор-функция h (f) удовлетворяет
X &
уравнению
*=м+м“- м
Поскольку начальное значение вектора х не зависит
от 8, то
ЗД = 0.	(2.4')
В уравнении (2.4) принят^! обозначения fx =	,
II дх1 ||
/„ = -^1, i = 0, 1,2, ..., п, / = 0, 1,2, .... n, 6 =
duk ||
/ fix \
= 1,2, ..., т. Величину h = — будем называть вариа-
X /е=о
цией фазовой траектории, a h°(T), где h°(T) = (— । ,
' ^8 / g=0
— вариацией функционала. Величина h°(t) удовлетворяет
уравнению
ft°=(fU)+(ftt0,6u)'	(2.5)
с начальным условием
/i°(U = 0.
(2.5')
30
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
(ГЛ. I
4. Сопряженные (двойственные) переменные. В даль-
нейшем мы часто будем использовать понятие сопряжен-
ной системы уравнений.
Пусть мы имеем линейное неоднородное уравнение
х — Лх]4- Ь,	(2.6)
где А и b — матрица и вектор, элементы которых at} и
Ь{—заданные функции времени.
Системой, сопряженной (2.6), называется система
Ф = — Л’ф,	(2.7)
где Л*— сопряженная (транспонированная) матрица,
элементы которой получены перестановкой строк и столб-
цов матрицы Л:
aij = ад.
Вектор ф, удовлетворяющий уравнению (2.7), называет-
ся вектором сопряженных или двойственных переменных.
Векторы х и ф обладают следующим важным свой-
ством:
А(ф, х) = (ф.Ь).	(2.8)
at
Справедливость равенства (2.8) устанавливается простой
проверкой:
-А. х) = (ф, х) + (ф, х)« — (Л*ф, х) 4- (ф, Ах + Ь) =
= — (Л’ф, х) + (Л’ф, х) 4- (ф, Ь) = (ф, Ь).
Обозначим теперь через ф=(ф°, ф) вектор, сопряженный
Л, где h удовлетворяет системе (2.4). Тогда
ф=-£ф,	(2.9)
или
ф=-/;ф-г;ф°,	(29,}
— ф° = 0.
Здесь ф— («4-1)-мерный вектор, ф°—скаляр.
Сопряженные переменные ф0, фъ..., ф„ называются
также множителями Лагранжа или импульсами. Заме-
О ЗАДАЧАХ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
31
§ 2]
тим, что в силу однородности уравнения (2.9) определяют
сопряженные переменные с точностью до постоянного
множителя.
Используя сопряженные переменные, можно получить
выражение для вариации функционала в форме, удобной
для составления необходимых условий минимума.
Составим скалярное произведение
М (0 = (ф, й) = (ф, h) + ф°/1°.	(2.10)
В силу свойств (2.8)
(2.11)
at
и, следовательно,
т
М(Т)-М (Q = J (Ф, fu 6м) dt.	(2.12)
^0
5.	Необходимые условия минимума в задаче со
свободным концом. Вывод необходимых условий мы нач-
нем с рассмотрения задачи со свободным правым концом,
поскольку для этого случая можно продемонстрировать
технику вывода, не усложняя ее тонкими рассуждениями,
необходимыми в общем случае.
Итак, рассмотрим задачу со следующими краевыми
условиями:
x(t9)=x0.	(2.13)
На правый конец х(Т) никаких ограничений не наклады-
вается.
Из (2.10) согласно (2.4) и (2.5) при t=ta имеем
М (/0) =0, поэтому из (2.12) получаем
т
М (Г) = (ф, й)|/-г = J (ф, Ju 6u) dt-, (2.14)
to
так как (ф^ й) = (ф, h) + ф°Л°, то
т
Ф°л°=—(ф, /i)L=r + J (ф» 7«6u)dt-
to
32
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Распорядимся вектором сопряженных переменных, под-
чинив значения -ф0(Г) и 'ф(Т) следующим условиям:
гр(Г) = 0,	(2.15)
Фо(Л = -1.	(2-16)
Предположим теперь, что й (I) является оптимальным
управлением. Тогда вариация функционала h°(T) долж-
на обращаться в нуль для любых бы, не стесненных ника-
кими условиями:
Л°(7’)=0.	(2.17)
Отсюда согласно	лемме п. 2 следует,	что для	Т)
2-(^J) = 0.	(2.18)
Если ввести функцию Гамильтона
Н = (ф,7) = (ф,/)-Г,	(2.19)
то условие (2.18) можно записать в виде
= 0.	(2.20)
Итак, мы пришли к следующей теореме:
Теорема. Если функции u(t) и x(t) доставляют
минимум функционалу (2.1) при условиях (2.2) и (2ЛЗ),
то существует такая непрерывная вектор-функция ф(0>
удовлетворяющая уравнению
* =	(2.21)
и условию
ф(Г) = 0, ф0(Л = - 1.	(2-22)
что управление й (I) в каждый момент времени t являет-
ся стационарной точкой функции Гамильтона.
Условие (2.22) представляет собой частный случай
условий трансверсальности, общий вид которых будет
приведен в п. 7.
Сопряженные уравнения (2.21) и условия стационар-
ности (2.20) представляют собой уравнения Эйлера клас-
сического вариационного исчисления.
Итак, функции х (/) и ф(/) необходимо должны быть
решением некоторой краевой задачи для системы диффе-
ренциальных уравнений порядка 2ы, которую мы полу-
S 21
О ЗАДАЧАХ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
33
чим, если определим u(t) из условия стационарности
(2.18)
и=й(х, ф, О
и подставим функцию и в уравнения (2.2) и (2.21):
х == f(x, и (х, ф, /), /) = f (X, ф, О,
ф = —£(*,« (х, ф, t),	(х, и(х, ф', /),/) = ф (X, ф, t).
Порядок этой системы равен 2п, и для отыскания интере-
сующего нас множества решений мы имеем также 2п
условий: на левом конце задано п компонент фазового
вектора x(t0), на правом конце—значения сопряженных
переменных ф (Т) =0.
Примечание. Особенность задачи со свободным
концом состоит, таким образом, в том, что на правом кон-
це траектории полностью определен вектор импульса.
Это обстоятельство (как мы увидим ниже) делает зада-
чу со свободным концом наиболее простой для численно-
го решения среди других задач оптимального управления.
6.	Необходимые условия в задаче с фиксированным
временем и подвижным правым концом. Перейдем теперь
к рассмотрению более
сложной задачи. Время Т
по-прежнему будем счи-
тать фиксированным, но
на правый конец наложим
дополнительное ограниче-
ние типа (2.3): будем счи-
тать, что траектория долж-
на оканчиваться на по-
верхности ф(х)=0, т. е.
должна удовлетворять
граничным условиям
Рис. 2.1.
Х W — Хо>
Ф(х(Т)) = 0,
(2.23)
(2.24)
где Ф — вектор-функция с компонентами Ф*, &=1,2,...
...,р<п, якобиан которой имеет свой максимальный
ранг р.
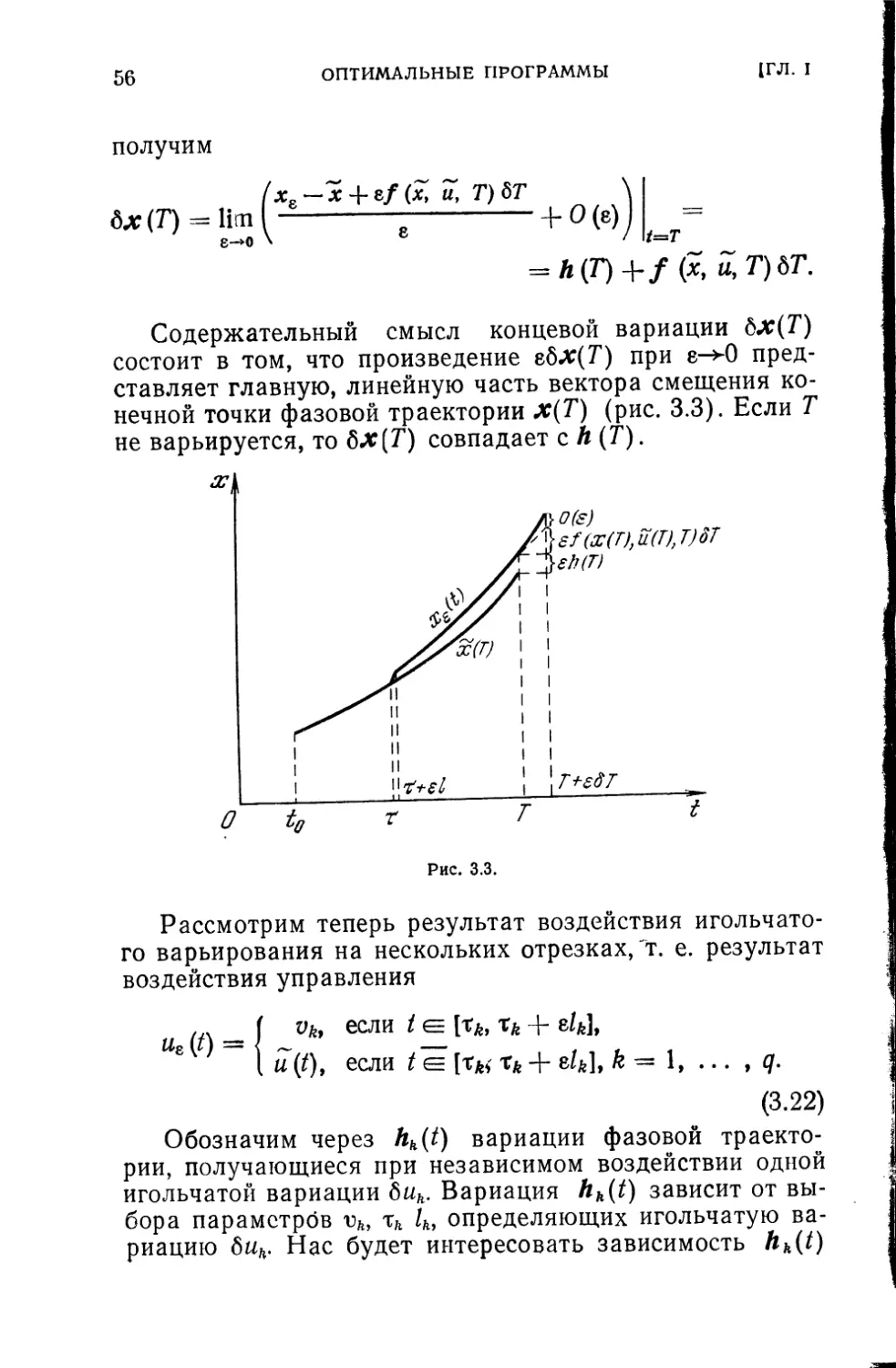
Таким образом, задача состоит в отыскании управле-
ния, которое переводит систему из точки (/0, х») на по-
верхность Ф(х)=0 за заданное время Т —t0 (рис. 2.1).
2 Н. Н. Моисеев
34
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Для изучения этой задачи мы не можем непосредст-
венно применить рассуждения предыдущего параграфа.
В самом деле, эти рассуждения основывались на том, что
функция u(t) реализует экстремум функционала на всем
множестве возможных управлений. Отсюда следовало,
что
/г°(7’)=0,
какие бы ни были вариации бы. В рассматриваемой
задаче, поскольку заданы концевые условия (2.24), ус-
ловие /i°(7’)=0 должно выполняться не для произволь-
ных вариаций 8и, а только для тех из них, которые не
разрушают концевых условий. Поэтому приведенное
доказательство необходимых условий для задачи с под-
вижным концом должно быть заменено другим. Это до-
казательство мы проведем, опираясь на схему рассуж-
дений Блисса *).
Пусть бы< (i= 1,..., р +1)—некоторые заданные
функции, а й — оптимальное управление (решение зада-
чи). Составим новое управление,
р+1
и = и + 2 Ъ1 ^и‘>	(2.25)
ы=1
где е« — параметры, которыми мы можем распоряжаться.
Функция, соответствующая оптимальному управлению,
удовлетворяет условиям (2.24). Функция x(t), определен-
ная управлением (2.25), в общем случае уже не удовлет-
воряет условиям (2.24) при произвольных значениях па-
раметров Зададим некоторое число I и подберем р+1
параметров е,- так, чтобы имели место условия
J (х, и) ~ J (X, и) + I,
(2.26)
ф*(х(Т)) = 0, 6=1.......р.
Эта система имеет решение при /=0. Решением будут
нулевые значения параметров 8,-.
*) См. Г. А. Блисс, Лекции по вариационному исчислению,
ИЛ, 1950.
§ 2]
О ЗАДАЧАХ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
35
Если определитель
д =	dJ d&i дФ1 д&х	dJ д&2 дФ\	dJ	9	(2.27)
			д8р+1 дФх		
			Й6р+1		
	дФр	дФр	дФр		
	д&1	д&1	' Am		
элементы которого вычислены при ef=0, отличен от нуля,
то система (2.26) имеет единственное непрерывное реше-
ние е,(/) (обращающееся в нуль при 1=0) для любых I
в некоторой окрестности 111	|л>0.
Очевидно, что в этом случае u(t) и x(t) не могут быть
оптимальным решением, поскольку может быть построе-
но управление
~ р+1
и = и 2 8/ (0 I О,
i=i
такое, что
J (х, и) = J (х, и) +1,1<0,
Ф(х(Л) = 0,
т. е. функционал может быть уменьшен при сохранении
граничных условий.
Итак, определитель А=0. Заметим, что элементы
этого определителя
где hs находится из уравнения — hs+ — i>us, пол-
дх ди
ностью задаются системой функций 6us. Следовательно, и
2*
36
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
ранг Д определяется этими же функциями. Пусть {&us} —
система функций, доставляющих определителю Д макси-
мальный ранг q<Zp+ 1. В этом случае, в силу линейной
зависимости строк, необходимо должны существовать числа
v0,	, vp, не все равные нулю, такие, что для любо-
го s имеет место равенство
^(T)+^vkd-^- = Q, s= 1,2, ...» р+ 1.
Теперь покажем, что это равенство должно иметь место
для любых ди. В самом деле, пусть найдется вектор-функ-
ция дир+2, для которой оно не имеет места. Тогда, взяв
в качестве новой системы функций совокупность ди2,
д«з, ..., дир+1, дир+ъ (считая для определенности, что стол-
бец, соответствующий диъ есть линейная комбинация
остальных столбцов Д), мы построим определитель Д,
ранг которого будет больше q, что противоречит предпо-
ложению о том, что q есть максимальный ранг Д.
Итак, мы приходим к следующему основному необхо-
димому условию:
Теорема. Если й и х — оптимальные управление и
траектория, то необходимо должны существовать числа
v0, Vi,..., vp, не все равные нулю, и такие, что, какова бы
ни была вариация управления ди, имеет место равенство
р
voh°(T)+^vk^-h^Q.	(2.28)
£==1 dx
Еще раз подчеркнем, что вариация би здесь произ-
вольна; в частности, она может разрушать граничные ус-
ловия на правом конце. При преобразовании условий
(2.28) нам понадобится формула (2.14) для вариации
функционала, которую мы запишем в виде
т
dt,
(2.29)
6
где
н = (ф, Л + ф°/°,	(2.30)
§ 21
О ЗАДАЧАХ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
37
а гр° и ф= {фь ..., ф„} — сопряженные переменные,
удовлетворяющие системе
ф° = О,
{• дН
(2.31)
Положим »!>’=Vo, тогда, подставляя (2.29) в (2.28),
мы приведем необходимое условие оптимальности к виду
= 0. (2.32)
Распорядимся выбором сопряженных функций, подчи-
нив их условиям
«|Т) -2	•	(2.33)
fe=l ОХ ч=т
с тем чтобы внеинтегральное слагаемое в (2.32) равня-
лось нулю для любых вариаций h(T) (в том числе и для
тех, которые приводят к разрушению граничных условий
на правом конце).
Поскольку оставшееся интегральное слагаемое в
(2.32) должно быть равно нулю при любом выборе би, из
леммы п. 2 получаем, что на оптимальной траектории
должно быть выполнено условие стационарности функ-
ции Гамильтона
— = 0.	(2.34)
ди
Итак, мы получили следующую теорему:
Теорема. Если вектор-функции u(t)u x(t) достав-
ляют минимум функционалу (2.1) при условиях (2.2),
(2.23) и (2.24), то существует такая ненулевая, непрерыв-
ная вектор-функция = (ф0, ip), удовлетворяющая систе-
ме (2.31) и условию (2.33), что управление u(t) является
стационарной точкой функции Гамильтона (2.30).
Условие (2.33), наложенное на ip(T), имеет простой
геометрический смысл: вектор гр(/) ортогонален гранич-
ному многообразию Ф(х(Т))=0, т. е. для любых й(Т),
38
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
удовлетворяющих условиям
=0, k=\............р,
\ &Х / |/_7’
выполняется
Ok h) |<=г = 0.
Действительно,
(M)Ur=(s
\£=1 °Х /
Р
= 2 v*
/=Т	Й=1
- 0.
t=T
Условия (2.33) называются условиями трансверсально-
сти. Сопряженные уравнения (2.31) и условия стацио-
нарности (2.34) представляют собой уравнения Эйлера.
7.	Дальнейшее обобщение необходимых условий.
Рассмотрим, какие изменения возникнут в необходимых
условиях оптимальности в случае иного задания гранич-
ных условий. Если конечное время Т не закреплено, тс
для задачи Лагранжа, в которой граничные условия на
правом конце заданы в виде
Ф(х(Т), Т) = 0. k=’a\, ..., р'^п+ 1,
из основного необходимого условия, аналогичного (2.28),
после замены
h (Г) = дх (Г) — f (х (Г), и (Т), Т) дТ
получаем соотношение
т
fI дН . \ ,, . (	, . £
1 I---, бц I dt —1|) + у
J \ ди J \ Г"
/	К~
*0
/ Ч=Т
—)	6Т-0. (2,35)
dt /
р
По-прежнему, выбирая 'ф(Т) в виде (2.33) и рассматри-
вая (2.35) при дГ=О, мы приходим снова к необходимо-
му условию (2.34) стационарности Н по и. Далее, по-
скольку первые два слагаемых в равенстве (2.35) оказы-
ваются равными нулю при любом выборе вариации
О ЗАДАЧАХ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
39
§ 21
а это равенство должно выполняться и при 8Т=£=0, то для
случая нефиксированного конечного времени Т мы полу-
чаем дополнительное необходимое условие
#U=-2v^| .	(2.36)
В случае, если время t не входит явно в граничные
условия и конечное время Т не фиксировано, из (2.36)
получаем условие обращения в нуль функции Гамиль-
тона
Н|/=т = 0.	(2.37)
Для автономной задачи (когда время t не входит яв-
но в функционал, уравнения связи и граничные усло-
вия) при нефиксированном Т применение приведенных
рассуждений для произвольного момента времени т
(ta<_x^T) показывает, что функция Гамильтона равна
нулю на всем отрезке |70, 7]:
Н = const = 0, f е [/0, Т].	(2.38)
Последний результат важен потому, что всякую неав-
тономную задачу с помощью замены
хп+1 = t
и введения дополнительного уравнения связи ----- 1,
dt
xn+1 (/0) = t0 можно свести к автономной задаче, для ко-
торой функция Гамильтона тождественно равна нулю:
Н + фп+i -1 = 0,
откуда
фп+1 = — Н,
и сопряженное уравнение для ф„+1:
принимает вид
.	(2.39)
40
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Таким образом, функция Гамильтона удовлетворяет диф-
ференциальному уравнению (2.39). Это уравнение пона-
добится нам в дальнейшем при выводе условий Эрдма-
на — Вейерштрасса.
До сих пор все рассуждения, с помощью которых были
получены необходимые условия, проводились в предполо-
жении, что оптимальное управление и (/) является непре-
рывной функцией времени. Как будут выглядеть необхо-
димые условия, если оптимальное управление й(0
является кусочно непрерывной функцией (функцией,
имеющей конечное число разрывов первого рода) ?
Если по-прежнему рассматривать непрерывные вариа-
ции управления бм(0, то вариации фазовых координат
h(t) в случае разрывного u(t) останутся непрерывными,
но будут кусочно дифференцируемыми функциями, име-
ющими угловые точки при значениях времени t=r,
соответствующих разрывам й(/). Основное свойство (2.8)
сопряженных переменных также остается справедливым.
При этом ф(/) аналогично h(t) является непрерывной,
кусочно дифференцируемой функцией, так что в точках
t—% разрыва u(t)
фГ) = ф(т+).	(2.40)
Все другие приведенные выше рассуждения дословно
проходят и для случая кусочно непрерывного управле-
ния и (0. Поэтому установленные выше результаты оста-
ются в силе. Используя, в частности, (2.39), мы получаем,
что функция Гамильтона непрерывна в точках /=т раз-
рыва
Я|/==т_ = Я|/=т+.	(2.41)
Условия (2.40), (2.41) называются условиями Эрдмана—
Вейерштрасса. Они требуют непрерывности сопряжен-
ных переменных и функции Гамильтона в точках разры-
ва u(t).
До сих пор мы вели рассмотрение для задачи Лагран-
жа (задачи с интегральным функционалом). Что изме-
нится в полученных результатах, если рассматривается
задача Майера (функционал задан в виде функции конеч-
ного состояния) или задача Больца (смешанный функ-
ционал) ?
Повторение аналогичных рассуждений показывает,
что все необходимые условия, кроме условий трансвер-
О ЗАДАЧАХ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
41
§ 2]
сальности, не изменяют своего вида. При этом функция
Гамильтона для задачи Майера записывается в форме
п
z==l
т. е. включает в себя только правые части дифференци-
альных уравнений.
Условия трансверсальности в задаче Майера с фикси-
рованным конечным временем Т и функционалом
/ = ф»(х(Т))
принимают вид
+	(2.42)
Если в задаче Майера конечное время Т не фиксиро-
вано и функционал задан в виде
J = Ф°(х(Т), Т),
то условия трансверсальности (2.42) дополняются еще
одним соотношением
= -+ 2 v^)l •	(2.43)
\	01	А=1 ot 1 1/=т
Из (2.43) видно, что если время t не входит явно в гра-
ничные условия и функционал, то должно быть
Я|/=г=0.	(2.44)
Для автономной задачи Майера условие (2.44) выполня-
ется тождественно для всех t:
Н — const = 0, t е [/0, Г].
Условия трансверсальности для задачи Больца в точ-
ности совпадают с условиями трансверсальности в зада-
че Майера. Отличие только в виде функции Гамильтона,
имеющей дополнительное слагаемое ф0/°.
В самом общем случае задачи Больца, когда /0 и Т
не фиксированы, а левый и правый концы подвижны, т. е.
42
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
граничные условия заданы в виде
Xs (х (/0), /0) = 0, s = 1, ..., q п + 1,
Ф*(х(Т),Т) = 0, fe=l,...,p, р<п+1,
а функционал
т
J = Ф° (х (Т), Т) — Х° (х (Q, Q + [ /° (х, и, f) dt,
основное необходимое условие (2.28) принимает вид
s	k
и схема рассуждений, аналогичная той, которая была
проведена в п. 6, приводит к условиям трансверсальности
в виде
(2Л5)
«и = -(ч>.^ + 3 + 1>О|		<2-4в)
4	S=1	' '*—*о
’ <2-47>
+	•	(2-48)
k—1
Если t0 или Т закреплены, то из условий (2.45) — (2.48)
исключаются условия (2.46) или (2.48) соответственно.
Сопряженная вектор-функция, для которой сформули-
рованы приведенные необходимые условия, вообще гово-
ря, является неединственной. Во всяком случае, она опре-
делена пока с точностью до произвольного постоянного
множителя.
Выделим класс задач, в котором (после соответствую-
щей нормировки) сопряженная вектор-функция оказыва-
ется единственной. Для этого снова вернемся к выводу
§ 21
о задачах вариационного исчисления
43
основного необходимого условия (2.28), приведенного
в п. 6.
Рассмотрим определитель Д, строки которого суть ва-
риации функционала и граничных условий на выбранном
(р+1) -параметрическом семействе вариаций би3. Если
максимальный ранг матрицы, полученной из (2.27) вы-
черкиванием первой строки, в точности равен своему мак-
симально возможному значению, то будем называть этот
случай нормальным, в противном случае — анормальным.
Для нормального случая первая строка Д есть линей-
ная комбинация остальных строк. Отсюда следует, что
коэффициент Vo отличен от нуля. Поэтому в нормальном
случае систему чисел v0,	, vP можно пронормиро-
вать, разделив все vk на —v0. В результате, переобозна-
чив —vA/vo на vA, получим основное необходимое условие
(2.28) в виде
р
-dJ + 2 vftM)\=r=0.	(2.49)
k=l
Покажем, что в нормальном случае система чисел —1,
V1,..., vp, удовлетворяющая (2.49), является единствен-
ной. В самом деле, если существует другая система чи-
сел— 1, р,!,..., для которой при любых вариациях би (/)
выполняется условие
р
- М + 2 Щ = 0,	(2.50)
k—1
то, вычитая (2.50) из (2.49), мы получим, что существует
ненулевая система чисел
а* = vfc —1, .... р,
для которой
р
2мфЧ=г=о,
k=l
т. е. строки матрицы, составленной из элементов опреде-
лителя Д вычеркиванием первой строки, линейно зависи-
мы, что противоречит определению нормального случая.
Итак, мы установили, что если управление u(t) оптималь-
44
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
If л. i
но, то существует сопряженная вектор-функция такая,
что выполняются условия трансверсальности и условия
стационарности Н по и, причем для большинства практи-
ческих задач (для нормальных случаев) сопряженная
вектор-функция после нормировки оказывается единст-
венной.
Помимо этих необходимых условий оптимальное уп-
равление должно удовлетворять еще одному условию —
необходимому условию Вейерштрасса, требующему непо-
ложительности функции Вейерштрасса
Е = Я —(2.51)
где Н и Й берутся соответственно при произвольном и
оптимальном управлениях «(/) и u(t).
Из (2.51) следует, что в каждый момент времени
функция Гамильтона Н достигает своего максимального
значения на оптимальном управлении м=и (/)*).
Мы не будем специально выводить условие Вейер-
штрасса, поскольку оно содержится в более общем- ре-
зультате—в принципе максимума Л. С. Понтрягина.
В курсах классического вариационного исчисления
устанавливается еще одно необходимое условие — усло-
вие Якоби отсутствия сопряженной точки на исследуемой
траектории. Желающим детально разобрать условие
Якоби мы рекомендуем обратиться к соответствующим
источникам **).
8.	Условия типа равенств. Метод Лагранжа. Предпо-
ложим теперь, что помимо условий (2.2) и (2.3) на выбор
управлений наложены условия вида
V/: <р (х, и, 0 = 0,	(2.52)
где ф(х, и, t)—непрерывно дифференцируемая вектор-
функция своих переменных размерности k<n. Для реше-
*) Нормировка Vo=+'J отличается от Vo=—1 тем, что сопря-
женная вектор-функция (—1, ф1(0, • • • > Фп(0)> соответствующая
v0=—1, умножается на —1. Поэтому при Vo= + 1 знак неравенст-
ва в условии Вейерштрасса (2.51) следует заменить на обратный.
Именно в таком виде условие Вейерштрасса приводится в курсах
классического вариационного исчисления. При выборе коэффициен-
та нормировки Vq=—1 условие Вейерштрасса совпадает по форме с
основным утверждением принципа максимума Л. С. Понтрягина.
**) См., например, Г. А. Б лисе, Лекции по вариационному ис-
числению, ИЛ, 1950.
§ з]
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
45
ния этой задачи можно использовать классический прием
Лагранжа.
Вместо функционала (2.1) рассмотрим функционал
т	т
J = J {/° (х, ц, t) + X, <р (х, и, t)} dt =	(x, u, t) dt, (2.53)
^0	^0
где h(t) —некоторая вектор-функция размерности k.
Повторяя для функционала (2.53) рассуждения пре-
дыдущих параграфов, мы легко придем к следующему
утверждению.
Теорема. П усть вектор-функция ф (t) удовлетворя-
ет уравнению
где Н — функция Гамильтона: Н= (ф, [) — f°— (%, ср).
Тогда, для того чтобы функции x(t) и u(t) доставля-
ли минимум функционалу (2.1) при условиях (2.2) и
(2.53), необходимо, чтобы в любой момент времени функ-
ции u(t) и x(t) удовлетворяли условиям стационарности
f.'i-n -Л<ь) = О,
^7 s Ч> (*, О = О-
ал
(2.54)
Таким образом, множитель Лагранжа Л (0 играет
роль управления: разрешая систему m+k уравнений
(2.54), мы находим функции и=м(ф,х,/), Х=Х(ф,х, f)
и, следовательно, мы снова приходим к краевой задаче
для системы 2п уравнений относительно x(t) и ф(/).
§ 3.	Принцип максимума Л. С. Понтрягина
1.	О постановке задачи Л. С. Понтрягина. В предыду-
щем параграфе мы рассмотрели задачу Лагранжа
и установили необходимое условие оптимальности. Оно
состояло в том, что оптимальное управление должно
быть стационарной точкой функции Гамильтона, т. е.
46
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. 1
удовлетворять векторному уравнению
^. = 0.
ди
Если решение этого уравнения единственно, то мы
может определить управление
и=й(х, ф, /),
и, следовательно, получаем возможность свести вариа-
ционную задачу к решению некоторой краевой задачи
для обыкновенных дифференциальных уравнений.
Основное предположение, сделанное при изучении
задачи Лагранжа, состояло в том, что управление мо-
жет принадлежать всему пространству — на управление
не налагалось ограничений. В практических задачах,
однако, множество допустимых управлений, как правило,
имеет существенно «неклассический» вид: оно ограниче-
но, во многих случаях многосвязно, может не иметь
внутренних точек и т. д. Для таких задач необходимые
условия в том виде, как они установлены выше, естествен-
но, непригодны. Их дальнейшим и существенным расши-
рением является замечательный результат, установлен-
ный Л. С. Понтрягиным *).
Согласно теореме Л. С. Понтрягина, получившей на-
звание «принцип максимума», оптимальное управление
должно доставлять функции Гамильтона максимальное
значение.
Благодаря принципу максимума, редукция вариаци-
онной задачи к краевой получила широкое распростране-
ние и в настоящее время лежит в основе большинства
используемых алгоритмов.
Итак, рассматриваем задачу:
Определить вектор-функции u(t) и х(/), доставляю-
щие минимум функционалу
т
J (х, и) — J /° (х, и, t) dt	(3.1)
*) Л. С. Понтрягин, В. Г. Болтянский, Р. В. Г а м к р е-
л и д з е, Е. Ф. Мищенко, Математическая теория оптимальных
процессов, Физматгиз, 1961.
§ 3]	ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА	47
при условиях
х=/(х, и, t),	(3.2)
и е Gu,	(3.3)
(х(/0),/0)е^0, (х(Т),Т)е=ёт,	(3.4)
где Gu—множество допустимых управлений, и <S?—
заданные многообразия (м+1)-мерного пространства
начальных и конечных условий, структура которых будет
уточнена ниже, а функции f°, f= (fl, f2,..., fn) и их част-
ные производные по х непрерывны по совокупности пере-
менных. Множество Gu может быть весьма общей приро-
ды. В частности, оно может быть замкнутым.
Управление u(t) мы будем разыскивать в классе ку-
сочно непрерывных функций.
Если не считать иных, более слабых предположений
относительно свойств непрерывности функций f°, f, то
единственное внешнее отличие рассматриваемой задачи
от задачи Лагранжа, которая изучалась в предыдущем
параграфе, состоит в появлении нового условия (3.3).
Однако именно это обстоятельство и делает задачу зна-
чительно более трудной. Осложнения, которые возникают
вследствие условия (3.3), связаны с тем, что допустимые
вариации управления должны удовлетворять условию
и — и + е Gu,
т. е. вариации управления теперь не произвольны, они
должны удовлетворять заданным ограничениям.
Исходное утверждение, которое мы использовали для
получения необходимых условий в задаче Лагранжа, со-
стояло в следующем.
Для того чтобы х, и доставляли минимум функциона-
лу J(х, и), необходимо, чтобы б/ (х, и, 8х, 6w)=0 для
любых допустимых *) вариаций бх, би.
Это условие аналогично условию обращения в нуль
линейной части приращения функции <р (х), т. е.
ф' (х) dx = О,
*) То есть таких вариаций 6х и би, которые связаны уравнениями
в вариациях и не нарушают граничных условий исходной задачи.
48
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
которое мы имеем в теории экстремума функции одной
переменной, когда х принадлежит всей числовой оси.
Предположим теперь, что минимум разыскивается на
отрезке [хь х?] (рис. 3.1). Если минимум достигается в
Рис. 3.1.
граничной точке или х2, то в этом случае имеет место
необходимое условие, требующее лишь неотрицатель-
ности линейной части приращения функции
ср' (х) dx > 0.
Так же обстоит дело и в том случае, когда мы имеем
функционал J (х, и), а область допустимых значений
управления Gu замкнута. Если х, и реализуют минимум
J (х, и), то необходимо, чтобы вариация функционала
была неотрицательна
6 J (х», и, 8х, бы) > 0
для любых допустимых вариаций бх, бы.
Примечание. Заметим, что в некоторых случаях
задачу Л. С. Понтрягина можно свести к задаче, рассмот-
ренной в предыдущем параграфе. Например, если управ-
ление и — скалярная величина, удовлетворяющая нера-
венству
|ы|< 1,
то можно либо произвести замену
и = sin а,
§ 3]
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
49
либо дополнить число управлений новой переменной р,
определяемой условием Валентайна
P’ + (u+l)(u-l) = 0.
При этом на а в первом случае и на р во втором — не на-
кладывается ограничений типа неравенств. Далее, рас-
сматривая участки непрерывности управлений, можно,
используя технику предыдущего параграфа и принцип
Вейерштрасса, получить результаты, аналогичные прин-
ципу максимума.
Л. С. Понтрягин предложил иной путь решения постав-
ленной задачи, позволивший получить более сильные
и общие результаты, спра-
ведливые для любых
замкнутых областей уп-
равления, в частности,
для тех, которые нельзя
«раскрыть» с помощью
искусственных приемов
рассмотренного типа.
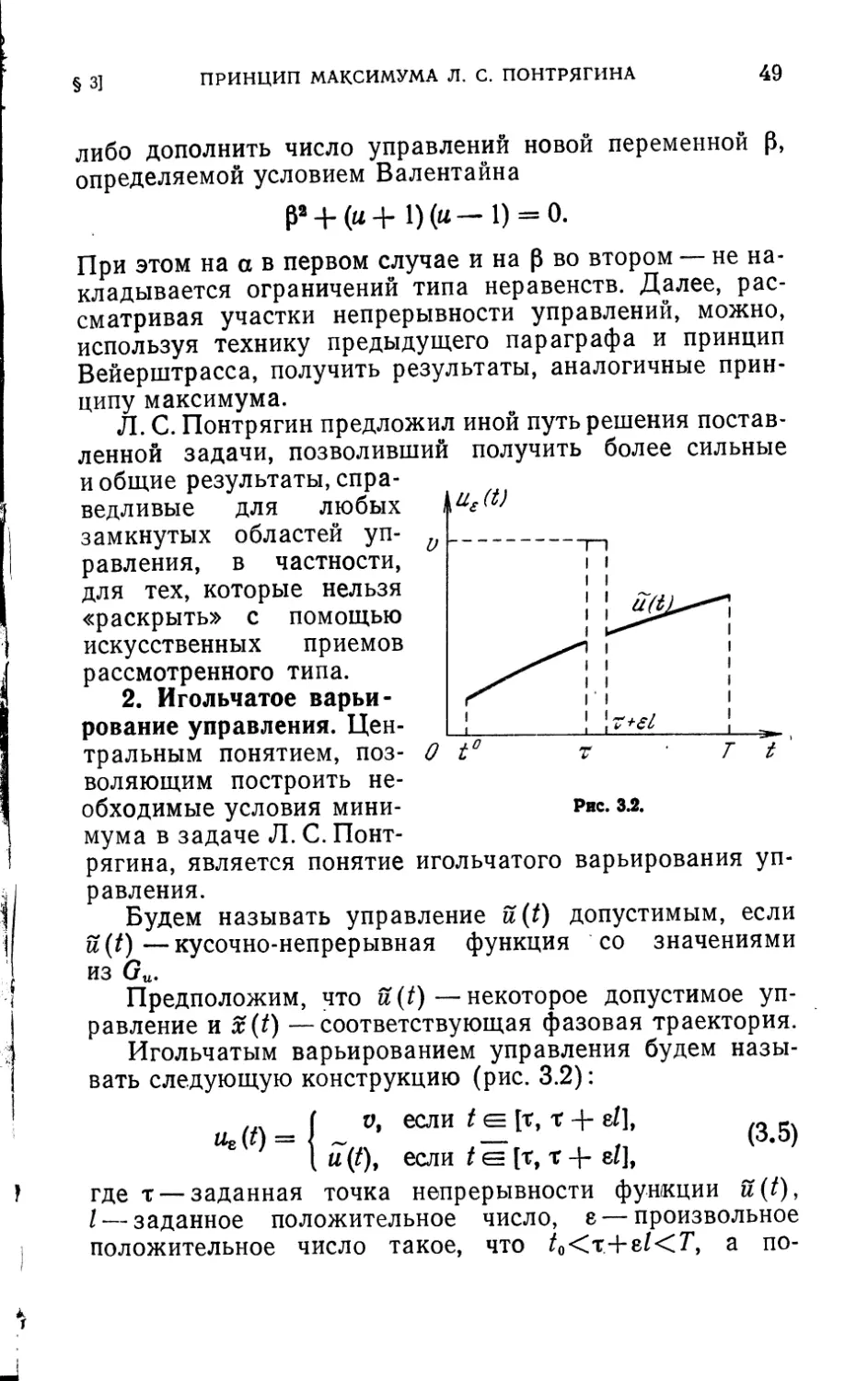
2.	Игольчатое варьи-
рование управления. Цен-
тральным понятием, поз-
воляющим построить не-
обходимые условия мини-
мума в задаче Л. С. Понт-
рягина, является понятие игольчатого варьирования уп-
равления.
Будем называть управление u(t) допустимым, если
u(t)—кусочно-непрерывная функция со значениями
из Gu.
Предположим, что u(t)—некоторое допустимое уп-
равление и x(t) —соответствующая фазовая траектория.
Игольчатым варьированием управления будем назы-
вать следующую конструкцию (рис. 3.2):
если[г. г+ «/1,	(3.5)
( и (Z), если t е [т, т 4- eZ],
где т — заданная точка непрерывности функции u(t),
I — заданное положительное число, 8 — произвольное
положительное число такое, что /о<т+е/<Г, а по-
50
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
стоянная v такова, что v^Gu. Разность ue(t)—u(t) =
— будем называть игольчатой вариацией управ-
ления.
3.	Вариации траектории. Рассмотрим задачу, в кото-
рой левый конец траектории фиксирован, т. е. x(t0)=x0,
/0 задано. Нас будет интересовать результат воздействия
на траекторию игольчатых вариаций управления.
Подобно тому как мы это делали в предыдущем пара-
графе, вместо функционала (3.1) введем эквивалентное
ему уравнение
х° = [°(х, и, t).
Из смысла задачи: х°(0)=0 х"(T)=J(х, и). Введем так-
же расширенный фазовый вектор х= (х°, х1, ..., х") s=
s (х°, х) и расширенный вектор правых частей
Заметим, что уравнение для вектора х имеет вид
х = /(х, u, t), т. е. f не зависит от х°.
Введем, так же как и в предыдущем параграфе, ва
риации фазовых координат.
Обозначим Хе фазовую траекторий, соответствующую
управлению ы8, и определим вариацию фазовой траек-
тории
*eW — x(t)	idxR\
h (0 = lim---------= (— I ,
e->o 8	\ ab /e=o
где ж—траектория, соответствующая рассматриваемому
управлению й.
Содержательный смысл вариации й(£) состоит в том,
что при в—>0 выражение ей(/) является главной ли-
нейной частью приращения фазовой траектории, возни-
кающего вследствие игольчатого варьирования управ-
ления.
Так как .Ге и х удовлетворяют уравнениям связи
•^е — f (
(3.6)
ЛГ = /(х, и, t),
(3.7)
§ з]
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
S1
то
t
Х& = Xq (/о + J f (xe, Ug, t) dt,
io
x (t) = x (t0) + J/(x, u, t) dt.
io
Вычитая из первого равенства второе, деля на е и
переходя к пределу, получим
h (/) = h (/0) + lim С — {/(хе, ие, t) —f(x, u, /)} dt.
8-*0 у s
*o
Из определения ue(t) видно, что для любого /<т
х& (0 — х (0 = о,
и, следовательно,
h (/) — 0, если t <= [/0, т).	(3.8)
При t^x получим
т+е/	_ ~
h (t) = lim £ —{f(x£t tie,f)—f(x, u, t)}dt-\-
E—>0 v 8
T
‘ 1
+ lim i — {/(xe, u, t) —f(x, u, t)} dt.
e-*Q J . 8
t+eZ
Легко видеть, что для любого t^x
|лге(0-л(0| = О(е).	(3.9)
В самом деле, xe(t)—x(t)=0 при t=x. Далее, ле и
х изменяются на интервале [т, т+е/], следуя уравнениям
(3.6) и (3.7), где ив=^=й. Тем не менее, в силу того, что
интервал имеет длину 0(e), мы получаем оценку (3.9)
для /=т+е/. А на интервале [т+в/, Т] изменение
функций х, и х происходит снова согласно одному и тому
же уравнению, и поэтому (3.9) —это следствие теоремы
о непрерывной зависимости решения системы дифферен-
циальных уравнений от начальных данных.
52
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
(ГЛ. J
Используя теорему о конечных приращениях, непре-
рывность f и /*и тот факт, что при ^>т+е/, ие=й,
получаем, что для t>x
h (0 = lim I \f (x (т), v, т) — f(x (т), и (г), т) + О (е)] +
8—>0
xe(t)-x(i)
в
4-0 (в) dt
или, после перехода к пределу,
h (0 = I \f (х (т), v, т) — f (х (т), и (г), т) J +
+ JA(X, u,t)h(t)dt. (3.10)
Из сравнения (3.8) и (3.10) видно, что вариация фазо-
вой траектории h (t) — разрывная функция. При ^^Л<х
h (t) = 0,
а при t^x h (t) удовлетворяет дифференциальному
уравнению
h=fxh	(3.11)
с начальным условием
h (т) = h (т+) = I \f(x (х), v, т)-/(х(т), и (х), т)1, (3.12)
или, в координатной форме,
•	" ad
h,1 — V
hl (т) = Z 0* (х (т), v, т) — (х (т), и (г), т)], i =0, 1,2,..., п.
4.	Сопряженная система. Введем теперь сопряженную
систему
Ф = —/*Ф
или, в координатной форме,
ф/ = — У , i = 0, 1, 2............п.
Йо Эх1
(3.13)
§ 3j гФиНцИП МАКСИМУМА л. с. понтрйгиИа	53
Поскольку уравнение в вариациях (3.11) является одно-
родным, то, согласно (2.8), каково бы ни было решение
h (/) этого уравнения, скалярное произведение М =
= (ф,й) является постоянным:
М = (ф(/), й (/)) = const,	(3.14)
5.	Принцип максимума в задаче со свободным правым
концом и фиксированным временем. Предположим, что
множество <Г0 состоит из единственной точки (^, х0), а
множество St — суть гиперплоскость t=T, иными сло-
вами,
х (/0) = х0, *о> т заданы.	(3.15)
Пусть u(t)—оптимальное управление, a x(t)—соот-
ветствующая оптимальная траектория рассматриваемой
задачи (3.1) — (3.3), (3.15). Из необходимого условия
минимума функционала, состоящего в неотрицательности
его первой вариации, получаем неравенство
й°(Т)>0.	(3.16)
Основная идея дальнейшего вывода принципа макси-
мума состоит в том, что значение вариации функционала
h"(T) с помощью свойства (3.14) связывается с некото-
рым выражением, определенным на траектории. Эта
связь и содержит в себе требуемые необходимые условия
оптимальности.
Распорядимся выбором сопряженной вектор-функции,
подчинив ее следующему условию:
Фо=- 1. ^(Л = 0, /= 1,2...........п, (3.17)
и будем рассматривать ф(£) как решение уравнения
(3.13) при «начальном» условии (3.17)
Подставляя (3.17) в (3.14), получим
fto(7') = —М(Л,
и необходимое условие (3.16) принимает вид
м (Г) = (ф (Т), h (7)) < 0.	(3.18)
Поскольку скалярное произведение (3.14) есть величина
постоянная, то неравенство (3.18) должно выполняться
54
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. 1
и при t = t:
(4(<И(г))<о.
что с учетом выражения (3.12) для Л(т) дает
OP (A	v, т) —/ (х (г), и (т), т)) < 0.
Вводя функцию Гамильтона
п
= 3	(3.19)
i=o
и учитывая, что ф0(0 = const = —1, запишем это нера-
венство в виде
Н(х(г), щ ф (т), т)<Н(х(г), и (т), ф (т), т) (3.20)
или
Н (х (т), и (г), ф (т), т) = max Н (х (т), у, ф (т), т). (3.21)
Итак, мы получили следующую теорему для задачи со
свободным правым концом:
Теорема. Если управление й (t) и траектория x(t)
доставляют минимум функционалу (3.1) при уравне-
ниях связи (3.2), ограничениях на управление (3.3) и
краевых условиях (3.15), то существует такая непрерыв-
ная вектор-функция ф= (ф0, фь ..., фп), удовлетворяющая
сопряженной системе (3.13) и условиям трансверсально-
сти (3.17), что при каждом Т] функция Гамильто-
на H(x(t),	ф(0, 0 (3.19) достигает в точке и(Г)
максимума по всем w=Gu.
В рассматриваемой задаче с фиксированным временем
Т и свободным правым концом х(Т) условия трансвер-
сальности (3.17) требуют, так же как и в задаче Лаг-
гранжа, чтобы при t = T значение нулевой компоненты
фо (Г) было равно —1, а значение остальных компонент
равнялось нулю. Поскольку условия трансверсальности
в задаче Лагранжа и Понтрягина одни и те же, то струк-
тура краевой задачи, которой необходимо должно удов-
летворять оптимальное решение, в обоих случаях оста-
ется одинаковой. Однако системы уравнений могут
быть различными. Рассматривая задачу Лагранжа, мы
§ 3]	ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА	55
выразили управление при помощи условия стационар-
ности
^=0
ди
как функцию от фазовых и сопряженных переменных
u = и (х, ф, t).
В задаче Понтрягина мы проделали ту же процедуру, но
с помощью условия
Н — max Н (х, и, ф, /).
Конечно, в том случае когда Gu совпадает со всем прост-
ранством, а функция Н имеет одну экстремальную точку,
которая при этом является максимумом, оба условия
дадут одну и ту же функцию й (х, ф, t).
Приведенный простой вывод принципа максимума су-
щественно использует тот факт, что правый конец х(Т)
является свободным. В общем случае мы снова сталки-
ваемся с той же трудностью, что и в задаче Лагранжа.
Доказательство усложняется за счет того, что теперь
неравенство, аналогичное (3.16), должно выполняться не
для всех вариаций, а только для тех из них, которые не
нарушают граничных условий.
Доказательство принципа максимума в общем случае
опирается на некоторые предварительные построения.
6.	Конус концевых вариаций. Нас будет интересовать
множество концевых вариаций, получающихся вследст-
вие воздействия нескольких игольчатых вариаций управ-
ления и варьирования конечного времени.
Определим концевую вариацию &Х(Т), получающуюся
при воздействии одной игольчатой вариации управления
и варьировании конечного времени:
хе(Т + едТ)-х(Т)
6х(Т) = lim —--------------,
е-»о	8
где 6Т — произвольное положительное или отрицатель-
ное число. Учитывая, что
Хг (Т + eST) = xs(Г) +f (х (Т), Ц(Г), Г) ебТ + о (е),
56
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
(ГЛ. I
получим
fxE~x + ef(x, и, Т)8Т
&х(Т) = lim --------------------
g-»0 X	8
+ 0(8)
= h (Г) +f (х, и, Т) 8Т.
Содержательный смысл концевой вариации Ъх(Т)
состоит в том, что произведение е8х(Т) при е->0 пред-
ставляет главную, линейную часть вектора смещения ко-
нечной точки фазовой траектории Х(Т) (рис. 3.3). Если Т
не варьируется, то 8х[Т) совпадает с h (Т).
Рассмотрим теперь результат воздействия игольчато-
го варьирования на нескольких отрезках, т. е. результат
воздействия управления
и£ (/) = J Vk’ если 1 е Xk +
в ( и(0, если t е [т*,- т* + e.lk], k = 1, ... , q.
(3.22)
Обозначим через hk(t) вариации фазовой траекто-
рии, получающиеся при независимом воздействии одной
игольчатой вариации 8ик. Вариация hk(t) зависит от вы-
бора параметров v*,	1к, определяющих игольчатую ва-
риацию 8ик. Нас будет интересовать зависимость hk(t)
§ 3]
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
57
только от /*:
hk(t) = hk(t, lk).	(3.23)
Поскольку дифференциальное уравнение (3.11) для
вариации hk линейно, а в начальные условия (3.12) па-
раметр 1к входит как множитель, то зависимость (3.23)
имеет мультипликативный вид
hk(t) = lkhk(t, 1),
где hk(t, 1)—вариация фазовой траектории, соответст-
вующая игольчатому варьированию с параметрами vk,
тк при Z*=l.
Обозначим через суммарную вариацию, получаю-
щуюся при воздействии управления (3.22). На основании
линейности уравнений (3.11) суммарная вариация ft2(Z)
равна сумме вариаций:
М0 = 3 М0 = 3 hhk(t, 1).
k—1	k—1
Окончательно для концевой вариации 8х(Т), получа-
ющейся вследствие воздействия нескольких игольчатых
вариаций управления и вариации конечного момента вре-
мени, имеем выражение
МЛ = 2 hhk (t, 1) + /(х(Т), и(Т), Т)дТ. (3.24)
А—1
Дадим геометрическую интерпретацию множеству
концевых вариаций (3.24). В (п+1)-мерном фазовом
пространстве X переменных х°, х1,..., хп будем рассмат-
ривать множество К, состоящее из точек вида
X. {х(Г) + МЛ}.	(3.25)
иначе говоря, будем откладывать от конечной фазовой
точки х(Т) векторы концевых вариаций (3.24), полу-
чающиеся при всевозможных выборах q, vk, tk, lk, k = \,...
..., q, 8T.
Утверждается — и это один из ключевых моментов
доказательства,— что множество К есть выпуклый конус
58
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. 1
в (п+1)-мерном фазовом пространстве X с вершиной
в точке х(Т), т. е. множество К вместе с каждой точкой
содержит и весь луч, проходящий через вершину, и эту
точку, а вместе с каждыми двумя точками содержит и от-
резок, соединяющий эти две точки.
В самом деле, если дх (Т) есть концевая вариация, то
и адх (Г), а>0, является концевой вариацией; чтобы
убедиться в этом, достаточно, согласно (3.24), взять
lk == alk, = адТ.
Следовательно, вместе с каждой точкой (Т)+6лг(Т)
множество К. содержит и луч
X (Г) 4- abx (Т),	а > О,
исходящий из точки л: (Г) и проходящий через х(Т) +
(Г), т. е. множество К есть конус с вершиной в точ-
ке х(Т}.
Для того чтобы установить выпуклость конуса К,
рассмотрим две произвольные концевые вариации блсДТ)
и ЬХг(Т), и пусть а — произвольное неотрицательное чис-
ло, O^a^l. Мы имеем
«[X (Т) + 6xt (Г)] + (1 - а) [х(Т) + дх2 (Т)] =
= х (Г) + а
+ (1-а)Г § lkihk, (Л 1)+/(х(П«(П.7’)&Л •
L^2=l
(3.26)
Обозначая
l'k = l’k = (1 — a) Zfe2; dT — af>Tt + (1 — a) 6T2,
мы получим, что (3.26) имеет вид (3.24), т. е. входит в
конус К концевых вариаций. Иными словами, вместе со
всякими двумя точками ЛГ(Т)+6Xi(Г) их(Т) +дх2(Т’)
конус К содержит и отрезок (3.26), соединяющий эти точ-
ки, т. е. К — выпуклый конус.
§ 3]
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
59
7.	Принцип максимума в задачах с фиксированным
временем и подвижным правым концом. Основное свой-
ство конуса концевых вариаций. Пусть граничные ус-
ловия имеют следующий вид:
X (Q '—Хо,
фк(х(Т))= О, Л= 1>2, ... , р, р<л, (3.27)
/0, Т заданы,
причем функции Ф* непрерывны и непрерывно дифферен-
цируемы, а якобиан имеет свои максимальный ранг
р (в этом случае говорят, что правый конецх (Т) лринад,-
лежит (п—р)-мерному гладкому многообразию).
Пусть и (t)—оптимальное управление и х (/)—соот-
ветствующая оптимальная траектория задачи (3.1)—
(3.3), (3.27), доставляющие минимум функционалу
J(x, и).
Рассмотрим наряду с конусом К. множество «запре-
щенных концевых вариаций Q, состоящее из таких кон-
цевых вариаций блс (7), у которых нулевая компонента
бх°(7) отрицательна, а остальные компоненты в совокуп-
ности не нарушают граничного условия (3.27) на правом
конце:
Q: {*(7) + 6х(7)},
^(Т)<0,	(3.28)
, fix (Т)j =о, k = 1,2 ... , р. (3.29)
Поскольку дх(Т) удовлетворяет системе линейных
уравнений, а нулевая компонента 8х°(Т) отрицательна,
то множество Q есть (п—р+О-мерная «полугипер-
плоскость» (пересечение гиперплоскости (3.29) с полупро-
странством (3.28)). Очевидно, что всякая полугипер-
плоскость есть в то же время выпуклый конус, поэтому
Q — выпуклый конус.
Теперь мы можем сформулировать основное свойство
конуса К. Оно состоит в том, что пересечение внутрен-
ности конуса концевых вариаций К с конусом «запре-
щенных» вариаций Q пусто.
60
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. 1
В самом деле, если бы это было не так, то существо-
вали бы концевые вариации (и вызывающие их вариации
управления), которые не нарушали бы заданных гранич-
ных условий и в то же время давали бы нулевой компо-
ненте значение ^’(Т) +бх’(Г) меньшее, в силу (3.28), чем
(Г). Отсюда следовало бы, что существует вариация
управления ut(t) и соответствующая проварьированная
траектория xe(t) (е>0), обеспечивающие меньшее зна-
чение функционала при выполнении граничных условий.
Но это противоречит предположению об оптимальности
рассматриваемого решения x(t), U(t).
Приведем более подробное доказательство основного
свойства, конуса К.
Пусть, от противного, имеет место пересечение внут-
ренности конуса концевых вариаций К и конуса «запре-
щенных вариаций Q. Тогда существует луч
L: х(Т) + а$х(Т), а>0,
являющийся общим для конусов К и Q. Поскольку луч
L является внутренним для (п+ 1)-мерного выпуклого
конуса К, то в К можно выбрать п+2 точки 8х((Т), не
лежащие в одной гиперплоскости, такие, что для них
бх (Т) есть линейная выпуклая комбинация
bx(T)^№>Xi(T),	> 0, ^4=1,	(3.30)
z=i	r=i
все коэффициенты которой строго больше нуля. Таким
образом, мы получаем п+2 луча
Li: х (Т) + a&Xi (Т), а>0, i = 1, ... , п+ 2,
для которых луч L является линейной выпуклой комби-
нацией.
Рассмотрим теперь семейство проварьированных уп-
равлений, порождающих векторы смещения ебх.(Т):
и (Q, если t е [т>, Xt + е/J,
Vi, если t е [Т/, т; + е^].
Определим новое семейство ut* (t), получающееся из
последнего равенства заменой 1( . на рЛ, где р.>0,
Ul(t) =
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
61
$ 3]
л+«
Рг = 1. Управлениям и* (/) будут соответствовать конце-
вые вариации е • pfixi (Г).
При е-Ч) «толщина иголок» е-рЛ стремится к нулю.
Составим проварьированное управление
и (t, Р) = и (t) +	(«/* (0 — «(0)-
1=1
Нас будет интересовать конечное состояние х (Т, р)
фазовой траектории, соответствующей управлению
u(t, р). При е->0 имеем
х (Г, Р) = х (Т) + s Р&а (Т)+ о (е).	(3.31)
i=i
Если выбрать то на основании (3.30)
х (t, Р) = х(Т) + в №>Xi (Г) + о (8) ==
Z=0
= х (Г) +• едх (Т) + о (е),
т. е. расстояние отх(Г, р) до луча L будет малой высше-
го порядка по сравнению с 8.
Покажем, что можно подобрать р так, чтобы х(Т, р)
в точности совпадал с направлением луча L, т. е. выпол-
нялись условия
.	П+2
Z=1	~	(3.32)
х(Т, Р) = х(Т) + гЪх(Т).
Систему (3.32) с учетом (3.31) можно представить в виде
П+2
3Pz=l,
П+2
v Р/6ЛЛЛ + — = мл.
1—1	е
(3.33)
62
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Якобиан системы (3.33) по переменным р, при е=0
1	1	. 1
6*1	6*° ..	• бЛ?п+2
в*}	б*£ ..	• б-^п+2
м	6*2 .	
отличен от нуля, поскольку точки Ьх((Т) не лежат на
одной гиперплоскости. Кроме того, система (3.33) имеет
при 8 = 0 решение pf=Xi(i= 1,..., п+2), а при 8>0
вектор р=% с положительными компонентами удовлетво-
ряет (3.33) с точностью до малых высшего порядка по
сравнению с е.
Поэтому для достаточно малых е(е>0) система (3.33)
разрешима, и ее решение есть положительная непрерыв-
ная функция от е, р(=р< (е), р{>0, i=il,..., n-f-2.
Поскольку луч L принадлежит конусу запрещенных
вариаций, то отсюда получается, что при достаточно
малых 8 существует управление u(t, р), не разрушаю-
щее граничных условий и сообщающее функционалу зна-
чение меньшее, чем управление т. е. u(t) не являет-
ся оптимальным. Полученное противоречие доказывает,
что пересечение внутренности конуса концевых вариа-
ций К и конуса «запрещенных» вариаций Q должно быть
пусто.
Это означает, в силу выпуклости конусов К и Q, что
существует разделяющая гиперплоскость, причем по-
скольку Q содержит (п—р) -мерную гиперплоскость
(3.29), то разделяющая гиперплоскость также содержит
(п—р)-мерную гиперплоскость (3.29).
Уравнение разделяющей гиперплоскости имеет вид
п
аг(х‘ —х'(Г)) = О,
1=0
где, по крайней мере, один из коэффициентов щ отличен
от нуля. Это обстоятельство является существенным.
Мы будем считать, изменив, если нужно знаки сц
на обратные, что конус К лежит в отрицательном
§ 3]
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
63
полупространстве
п
ь=о
т. е. для любой концевой вариации
2 а,вхг(Т)<0.	(3.34)
1=0
Для точек конуса «запрещенных» вариаций Q, поскольку
они принадлежат положительному полупространству,
неравенство (3.34) имеет обратный знак. В частности,
это справедливо для точки
(х° (Г) + дх° (Т), х1 (Т).хп (Т)), 6х° (Т) < 0, (Д.35)
отличающейся от конечной точки Ж (Г) только тем, что
у нее уменьшена нулевая компонента. Таким образом,
подставляя (3.35) в (3.34), получаем
а0бх®(7’)>0,
откуда, вследствие 6х°(7’) <0,
а0<0.	(3.36)
Выберем вектор а= (ае, .....ап) в качестве конечно-
го значения для сопряженной вектор-функции
ф (Т) = а.	(3.37)
Тогда ф(Т) =Н=0, и функция ф(г!) есть нетривиальное реше-
ние сопряженной системы (3.13). Отметим, что, в силу
(3.36), для нулевой компоненты ф0 имеем
Фо(Л<0.	(3-38)
Поскольку мы выбираем вектор ф (Т) как направляющий
вектор разделяющей гиперплоскости, а последняя содер-
жит в себе гиперплоскость (3.29), то мы имеем, что для
любых бх(Г), удовлетворяющих проварьированным гра-
ничным условиям (3.29), должно выполняться равенство
(ф(Т), дх (?’)) = 0.	(3.39)
Это и есть условия трансверсальности. Геометрически
они означают, что вектор ф(Т) должен быть ортогонален
64
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
(ГЛ. 1
граничному многообразию
Ф*(х) = 0,	1, ... , р
в точке х—х(Т).
Покажем, что из условий (3.39), (3.29) следуют усло-
вия трансверсальности в виде (2.33), полученные ранее
для задачи Лагранжа
ф<(Л = 3	, i = 1, .... n, (3.40)
i=T
причем система чисел vt,vp определяется по ty(T)
единственным образом.
В самом деле, умножим каждое уравнение (3.29) на
vk, сложим их, а затем результат вычтем из уравнения
(3.39), тогда получим, что на разделяющей гиперплос-
кости
3 (W) - 3 v*	(г) = 0 (3 4
Напомним, что по предположению якобиан |	1
имеет свой максимальный ранг р. Приравнивая нулю
соответствующие р коэффициентов в (3.41), мы получим
систему с ненулевым детерминантом, определяющую
множители v1;..., vp однозначно. Остальные п—р коэф-
фициентов в (3.41) также равны нулю в силу независи-
мости оставшихся вариаций.
Если исключить из р условий трансверсальности
(3.40) р постоянных v1; ..., vp и подставить значения в ос-
тавшиеся соотношения, то мы получим п — р условий
типа равенства, связывающих конечные значения компо-
нент сопряженной вектор-функции.
Условие (3.37) определяет решение сопряженной си-
стемы ф(£). При t—T, согласно (3.34),
3 ф,(Т) • дх'(Т)<0.
/=0
Поскольку мы рассматриваем граничные условия (3.27)
с закрепленным временем Т, то
бхЧТ) = hl(T),
§ з]	ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА	65
так что
п
2 W)-ад<о.
/=0-
(3.42)
Согласно (3.14) выражение Л(0) постоянно. Этот
факт позволяет осуществить перенос неравенства (3.42)
из конечного момента времени t—T в момент времени
/=т, при котором осуществлялось игольчатое варьиро-
вание управления:
п	п
3 Ф<(т) • Л'(т) = 2 ф/(Т) • h‘(T)<0.	(3.43)
i=0	1=0
Подставляя в (3.43) выражение (3.12) для W (т), получа-
ем неравенство
п
2	(т) V1 & (A v>т)—f.‘ (*(*).«(т)» Т)1
/=0
которое, используя функцию Гамильтона (3.19), можно
переписать в виде
Я(х(т), о, ф(т), х)^.Н(х(х), и(х), ф(г), т),
или, окончательно,
Н(х(х), и(х), ф(г), т) = шахЯ(х(т), о, ф(т),т). (3.44)
ое(?„
Итак, мы получили следующую теорему для зада-
чи с фиксированным временем и подвижным правым
концом:
Теорема. Если управление u(t) и траектория x(t)
доставляют минимум функционалу (3.1) при уравне-
ниях связи (3.2), ограничениях на управление (3.3) и
краевых условиях (3.27), то существует такая ненулевая
непрерывная вектор-функция ф=(ф0, ф,,..., фв), фо^О,
удовлетворяющая сопряженной системе (3.13) и услови-
ям трансверсальности (3.40), что при каждом /е[/0, Г]
функция Гамильтона	(3.19) дости-
гает в точке u(i) максимума по всем u^Gu.
3 Н. Н. Моисеев
66
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
(3.45)
Заметим, что в случае свободного правого конца ус-
ловия трансверсальности (3.40) дают
фг(Т) =0, i => 1> ... , п,
и мы получаем теорему из п. 5.
Для полностью закрепленного правого конца
Ф*(х(Т)) = х*(Т) — 4 = 0, fc=l, ...,п,
и из условий трансверсальности получаем
фг(Т) = vit i= 1, ... , п.
Числа ^(Г) определяются в результате решения крае-
вой задачи (см. гл.II).
8. Принцип максимума в задаче с нефиксированным
временем и подвижным правым концом. Пусть теперь
граничные условия имеют вид
х (^о) ~ хо>
Ф*(х (Г)) = 0, k = 1, ... , р, р^п, t0 задано,
отличающийся от (3.27) тем, что время Т не закреплено.
Положим сначала ЬТ—О, тогда, повторяя приведен-
ные рассуждения, мы получим, что необходимые условия
задачи (3.1), (3.3), (3.45) содержат в себе все необходи-
мые условия, установленные для задачи (3.1) — (3.3),
(3.27).
Далее, вернемся к неравенству (3.34). Рассмотрим
концевую вариацию (3.24), получающуюся при q=0
(игольчатые вариации управления отсутствуют) и дТ^О:
6л(Т)=/(х(Т), а(Т), Т)ЬТ.
Подставляя это выражение в (3.34), получим	|
п	~
3 ф/ (Г) г (X (Т), и (Г), Т) ЪТ < 0.	(3.46)
/=0
Поскольку дТ может быть как положительным, так и от-
рицательным, то из (3.46) следует, что
п
3 ^(Т)Г(х(Т),и(Т), Т) = 0,
/=»0
«3]
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
67
т. е. в конечный момент t = T функция Гамильтона
(3.19) должна быть равна нулю
Н (х (Т), и (Т), ф (Г), Т) = 0.	(3.47)
Таким образом, в том случае, когда мы переходим от
граничных условий (3.27) к условиям (3.45), т. е. от фик-
сированного Т к нефиксированному, появляется дополни-
тельное необходимое условие трансверсальности (3.47).
Сформулируем теорему для задачи с нефиксирован-
ным временем и подвижным правым концом:
Теорема. Если управление u(t) и траектория x(t)
доставляют минимум функционалу (3.1) при урав-
нениях связи (3.2), ограничениях на управление (3.3) и
краевых условиях (3;45), то существует такая ненулевая
непрерывная вектор-функция ф = (ф0, фь ...,ф„), фо^0,
удовлетворяющая сопряженной системе (3.13) и услови-
ям трансверсальности (3.40), (3.47), что при каждом /е
о[/0,7] функция Гамильтона	и (/), ф(0,0
(3.19) достигает в точке u(t) максимума по всем и &GU.
9.	Случай «перемещающегося» многообразия на пра-
вом конце. Рассмотрим, наконец, случай, когда точка на
правом конце принадлежит некоторому подвижному
гладкому многообразию, т. е. краевые условия имеют вид
Х(/°)==Х°’	(3.48)
Ф* (х (Т), Т) = 0, k — 1, ... , р, р^.п-\- 1, /0 задано.
Вывод необходимых условий в этом случае проводится
с помощью сведения задачи (3.1) — (3.3),
рассмотренной задаче (3.1) — (3.3), (3.45).
Введем для этого обозначение
х™ = t
и рассмотрим расширенную систему
x=f(x, и, xn+1),
?+1 = 1,
Ф = -/3.
фп+1 = — У •
So ^+1
(3.48) к уже
(3.49)
3*
68
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Условия на правом конце запишем в виде
Ф* (х(Т),	(Г)) = 0, k = 1, ... , р.
Полученная задача, с одной стороны, эквивалентна зада-
че (3.1) — (3.3), (3.48), а с другой стороны, является
частным случаем задачи (3.1) — (3.3), (3.45) (частным
потому, что правые части не зависят от I). Определим
для расширенной задачи функцию Гамильтона
ЗС = Н -}* фп+i • 1
и выпишем необходимые условия оптимальности.
Согласно (3.44) имеем
Н (х (т), и (т) ф (т), xn+1 (т)) + ф„+1 (т) =
= max [Н (х (т), v, ф (г), xn+1 (г)) + ф„+1 (т)], (3.50)
и поскольку слагаемое ф„+1 (т) не зависит от управления,
то (3.50) после обратной замены t—xn+i запишется в
прежнем виде (3.44).
Далее, условия трансверсальности (3.40), (3.47) дают
Н (х (7), и (Т), ф (Г), хп+1 (Г)) + Ф„+1 (Л = 0,
или
ф„и(Л = -#(х(Л» «(ПФ(Л, Л (3.51)
и
ф/ (Л = 2 V* ^(Х(Г)’Г) ,i=l........п, (3.52)
Si
Ф„+х(Л = 3	(3.53)
k—1
Последнее условие, используя (3.51), можно переписать
в виде
Я(Х(Л, «(Л, Ф(Л. Л = -i Vfe^-^r)’r). (3.54)
л=1
Подставляя (3.51) в последнее уравнение системы (3.49),
получим, что функция Гамильтона удовлетворяет
§ 3]	ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА	69
дифференциальному уравнению
— = —.	(3.55)
dt dt
Из (3.55) следует, в частности, что Н является непре-
рывной функцией времени.
Сформулируем теорему для задачи с «перемещаю-
щимся» многообразием на правом конце:
Теорема. Если управление u(t) и траектория x(t)
доставляют минимум функционалу (3.1) при уравне-
ниях связи (3.2), ограничениях на управление (3.3) и
краевых условиях (3.48), то существует такая ненулевая
непрерывная вектор-функция ф = (ф0, фь ..., фп), фо^О,
удовлетворяющая сопряженной системе (3.13) и услови-
ям трансверсальности (3.52), (3.54), что при каждом
е[7о, Г] функция Гамильтона H(x(t), u(t), ф(/), t)
(3.19) достигает в точке u(t) максимума по всем и ^Gu.
До сих пор мы формулировали принцип максимума
для задачи с фиксированным левым концом. Если левый
конец не закреплен, то ко всем приведенным формули-
ровкам добавляются условия трансверсальности на ле-
вом конце, полностью аналогичные по структуре услови-
ям на правом конце.
Итак, мы получили принцип максимума Л. С. Понтря-
гина для задачи Лагранжа при различных способах за-
дания граничных условий. Сравнение с § 2 показывает,
что принцип максимума включает в себя следующие не-
обходимые условия вариационного исчисления:
уравнения Эйлера (сопряженные уравнения и условия
стационарности Н по и в случае, если максимум Н по и
достигается вю внутренней точке Gu);
условия Эрдмана — Вейерштрасса непрерывности
сопряженных переменных и функции Н в точках разры-
ва оптимального управления;
условие Вейерштрасса, требующее максимума функ-
ции Н по и.
Ниже приводятся формулировки принципа максимума
для других постановок задач в соответствии с классифи-
кацией § 1. Эти формулировки даются для случая (3.48),
т. е. для закрепленного левого конца и «перемещающего-
ся» многообразия на правом конце.
70
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ.1
Условия трансверсальности для более частного вида
граничных условий легко получаются из приведенных ус-
ловий.
10.	Задача Майера. В задаче Майера рассматривается
функционал
J = Ф°(х(Т),Т).	(3.56)
Доказательство принципа максимума для задачи Майе-
ра отличается от приведенного доказательства для зада-
чи Лагранжа в непринципиальных деталях, связанных
с изменением вида конуса «запрещенных» вариаций Q.
Поэтому мы его опускаем и формулируем окончательный
результат.
Функция Гамильтона и сопряженная система име-
ют вид
п
1=1
ф/ — —
(3.57)
(3.58)
Теорема. Если управление u(t) и траектория x(t)
доставляют минимум функционалу (3.56) при уравнениях
связи (3.2), ограничениях на управление (3.3) и краевых
условиях (3.48), то существует такая непрерывная век-
тор-функция ip= (ipj, ...,4?n), удовлетворяющая сопряжен-
ной системе (3.58) и условиям трансверсальности (3.59)
ATI	/ M>° , Л
Я|,.г=- v„ —v.—
d®k
t^T
(3.59)

vo<0,
что при каждом	Л функция Гамильтона
u(t), ф(0, 0 (3,57) достигает в точке u(t)
максимума по всем и^.6^
5 3j
ПРИНЦИП МАКСИМУМА л. С. ПОНТРЯГИНА
и
11.	Задача Больца. В задаче Больца требуется мини-
мизировать функционал
т
J = фо (X (Т), Т) + J /° (х, Ц, t) dt.	(3.60)
^0
Избавимся от интегрального члена путем введения до-
полнительной переменной х°(/):
х° = /°(х, и, t), х°(/о)=О.
Тогда функционал (3.60) примет вид
J = х° (Т) + Ф° (х (Г), Г) = Ф° (х (Г), Г),
и задача Больца сведется к задаче Майера для системы
уравнений
х1 — fl (х, и, t), i = 0, 1, ...» л.
Введем функцию
п
Z=0
(3.19)
сопряженную систему (см. (3.13))
• дН Д . df
и выпишем условия трансверсальности
,	( дФ° . Л дФ* \	,qRn
Ф/(Л = *о ~7 + Л vk—-	,	(3.61)
\ дх дх / Z==T
i = 0, 1, ..’. , п.
Из соотношений (3.13) и (3.61) следует
Фо = °> Фо = л’о^°-
Кроме того, условия трансверсальности (3.61) для ф<
(/=1,...,п) полностью совпадают с (3.59). Отсюда мы
получаем теорему.

огтгиМальныё ni’ori’AMMbi
(ГЛ. t
Теорема. Если управление й (() и траектория x(t)
доставляют минимум функционалу (3.60) при уравнени-
ях связи (3.2), ограничениях на управление (3.3) и кра-
евых условиях (3.48), то существует такая ненулевая не-
прерывная вектор-функция Ф = (фо,фь —, Ф«) > фо^О,
удовлетворяющая системе (3.13) и условиям трансвер-
сальности (3.62)
,	/, ЭФ’ . Л ЭФ*\
Ф/(Л = Фо—т + 2 Vk~7	’ i = 1, • • • , п.
UI	л дфо , Л дФ*А
1/=т	I + 3 V* др )	’
\	*=i	/ 1<=т
(3.62)
что при каждом t е [/0* Г] функция Гамильтона (3.19)
п
Я = достигает в точке u(t) максимума по всем
1=0
us Gu.
12.	Задача на быстродействие. В задаче на быстро-
действие (х, и, t) = 1. Выпишем функцию Гамильтона
Ж = tyf1 (X,«, 0 4- Фо • 1 = ^ + Фо- (3.63)
1=1
Сопряженная система (3.13) будет выглядеть следую-
щим образом:
Фо = 0.
; дЖ дН Д . df>
С/Л	(7Л	у__1 ОХ
(3.64)
Условия трансверсальности (3.52), (3.54) не изменяют
своего вида
Р d(J)k
Ф/(Л = ^^-	,
/=г
«I,_, = (« + «!,_г = ~3
§ з]
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
73
Последнее условие в силу фо^О можно записать в
форме неравенства
н|,=г>-3^ . (з.бб)
k=t	Xt=T
Поэтому в окончательной формулировке теоремы сопря-
женную переменную ф0 можно опустить.
Теорема. Если управление u(f) и траектория x(t)
оптимальны по быстродействию при уравнениях связи
(3.2), ограничениях на управление (3.3) и краевых усло-
виях (3.48), то существует такая ненулевая непрерыв-
ная вектор-функция ф = {фь ..., ф„}, удовлетворяющая
системе (3.64), условиям трансверсальности (3.65),
(3.66), что при каждом Т] функция Гамильтона
(3.57) достигает в точке u(t) макси-
мума по всем u^Gu.
13.	Замечание об условиях типа равенств. Применим
метод Лагранжа для анализа того случая, когда управ-
ления и фазовые координаты связаны условием
Ф (х,«• t) = 0.	(3.67)
т
Для этого мы заменим функционал J = J /° (х, и, t) на
^0
функционал
Замена (3.68) позволяет рассмотреть эту задачу в рам-
ках теории Л. С. Понтрягина. Повторяя рассуждения, мы
придем к следующему утверждению:
Теорема. Пусть вектор-функция ф(/) удовлетворя-
ет уравнению
Ф = —	= — £ф + /* + (М <рх).
ОХ
Тогда для того чтобы функции x(t) и u(t) были решени-
ем задачи Л. С. Понтрягина, необходимо, чтобы в любой
момент времени функция u(t) доставляла максимум
функции Гамильтона Н= (ф, f) —— (X, <р), а параметр
74
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
X был ее стационарной точкой:
дН
дК
=s — Ф = 0.
14.	Связь с теоремой Вейерштрасса. Мы уже обраща-
ли внимание читателя на глубокую связь между теоре-
мами Вейерштрасса и Л. С. Понтрягина. Сейчас мы ее
продемонстрируем на примере простейшей задачи вари-
ационного исчисления. Этим термином мы будем назы-
вать задачу отыскания минимума функционала
т
J = ^f°(x,u,t)dt	(3.69)
/о
при ограничении
х° - и,	(3.70)
где х и и — скаляры и их выбор не стеснен никакими ог-
раничениями.
Начальное состояние всегда будем считать фиксиро-
ванным. Если время Т не фиксировано, то
Т+ебТ
J /° (х + и + eSu, t) dt
to
T
= {.fxh -I- /°мб«) dt + f° (x, и, T) 8T.
to
Интегрируя второе слагаемое по частям и принимая во вни-
t
мание, что ^8wit — h(f), получим
to
т
6J = [ (Л - fu] hdt + fuh (Г) + f°8T.
to
Функция Гамильтона для задачи (3.69) — (3.70) будет
такой:
И = — /°,
§ з!
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
75
и, следовательно множитель Лагранжа гр будет удовлет-
ворять уравнению
4’° = -(3.71)
Следовательно, выражению вариации функционала
можем придать вид
мы
т я
W = f 4 ~ hdt + № (л +
J at
to
т
или 6J = (—— hdt + fuh (t) + f0ST. Далее
,	J dt du
to
X /ТЧ r x^(T + ^T)-x(T)
6x (7) = lim------------------=
e-o	6
xe(T) + z’x(DVr-x(T)
= lim---------------------= h (T) + x(T) ST=/i (f)+uST.
г-ю	e
Предположим далее, что мы находимся на оптимальной
dti
траектории; тогда — = 0 и мы имеем
ди
&J —[fuU~f9]6T + f„&x(T).
Используя необходимое условие — = ф — /« = 0, получим
ди
окончательно
6J = Н6Т + /’бх(Т).	(3.72)
Используя эти обозначения, выведем необходимое ус-
ловие Вейерштрасса. Это условие является довольно
простым следствием следующего тривиального утвержде-
ния. Пусть и — оптимальное управление, а х— соответ-
ствующая ему траектория. Пусть далее «’их* — некото-
рые допустимые управление и траектория. Тогда необхо-
димо, чтобы
J(u*,x*)>J(u, х).	(3.73)
Траекторию x*(t) построим следующим образом
(рис. 3.4). Возьмем произвольное u=u*(t) и решим
76
Оптимальные программы
tf Л. i
задачу Коши
х* = и*, х* (/0) = х0
для любого teKo, ^], где tl=t—dt. Мы получим отрезок
траектории, соединяющий точку (х0, to) с точкой
B(x(t)—dx,t — dt). На интервале [f1( t] примем и* =
dx
=	= const, на отрезке [Л, Т] положим и* = й0. Тогда
t-dt	t
t0	t-dt
т_______
+ t\dtt
t
Вычислим разность
J (**, w*) — J (*, a) =
t-dt	t	i
= f /°	u*, t)dt—^ fo (x, u, t) dt + J f° (*’, u\ t) dt.
.	to	) t-dt
Используя формулу (3.72), оценим первое слагаемое
правой части, а ко второму применим теорему о среднем.
В результате получим
/ (х*, и*) — J (х, и) =
= Н dt 4- f°„6x (/) 4- f (х, if, t) dt 4- O(dt). (3.74)
Кроме того, заметим, что bx(t) = —u*dt. Поэтому в силу
(3.74) получим, что необходимо
[Н—«72 4- Л dt 4- О (dt) > О V/.	(3.75)
Заменяя выражение Н через
н=иГи-р,
получим следующее необходимое условие минимума,
справедливое для любых t и и*:
(х,	t) — f° (X,«, t) — («’ — u) f°u (x, и, t) > 0. (3.76)
§ з]
ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
77
Условие (3.76) и есть знаменитое условие Вейерштрасса,
выписанное для простейшей задачи вариационного ис-
числения.
Нетрудно видеть, что его эквивалентной формой бу-
дет следующая:
Н(х,и*,	u,t) Yt,u. (3.77)
Утверждение (3.77) является принципом максимума для
рассматриваемой задачи.
Подобный анализ может
быть проведен и для задач
значительно более общей при-
роды.
15.	Обсуждение. При выво-
де необходимых условий клас-
сического вариационного ис-
числения и принципа максиму-
ма существенным было то, на
каком классе вариаций управ-
ления исследовалась первая ва-
риация функционала.
В классическом вариационном исчислении проварьи-
рованное управление строилось в виде
и (/) = и (t) + 8 •	(/),
где вариация управления du(t)—произвольная непре-
рывная функция. Таким образом, при 8->0 поправка к
управлению равномерно стремилась к нулю на всем от-
резке [/0, Г].
В принципе максимума использовалось игольчатое
варьирование
(0 --
V, если t е [г, г + в/],
и (О, если /е[г, Т + 8/],
при котором поправка к управлению представляла собой
«иголку» высотой
V — u(t)t /е[т, т 4-eZ],
и толщиной, стремящейся к пулю при 8->0,
78
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
(ГЛ. 1
Используя условие максимума (или стационарности)
Н по и, можно выразить управление через переменные х,
ip, t и свести решение задачи оптимального управления
к решению краевой задачи.
Существует класс задач, в которых необходимые ус-
ловия, полученные с использованием «классических» и
«игольчатых» вариаций управления, оказываются слабы-
ми (неполными) и не позволяют непосредственно опре-
делить оптимальное управление. Это задачи со скользя-
щими и особыми оптимальными режимами *).
Для особых оптимальных режимов функция Гамиль-
тона Н не зависит от управления и на некотором отрезке
времени
ау- = 0,	TJ.
ди
Поэтому непосредственно выразить управление через х,
ф, t с помощью принципа максимума или условий стаци-
онарности Н по и на участке (ть т2] нельзя.
Для таких задач оказывается возможным установить
дополнительные необходимые условия, используя новый
класс вариаций управления.
Первое необходимое условие для особого режима (по
одной компоненте управления) было получено Г. Кел-
ли**), который использовал специальные вариации, со-
стоящие из двух примыкающих друг к другу «иголок»
одинаковой толщины, высоты которых равны, но проти-
воположны по знаку. Условие Келли формулируется в
виде некоторого неравенства, которое должно выполнять-
ся на участке оптимального особого режима. В некото-
рых случаях и условие Келли оказывается вырожденным.
Для этих случаев дальнейшие необходимые условия
(также типа неравенства) получили Р. Копп и Г. Мой-
ер ***).
*) Можно показать, что скользящие режимы—это частный
случай особых режимов.
**) Г. Келли, Необходимое условие для особых экстремалей,
основанное на второй вариации, Ракетная техника и космонавтика,
№ 8, 1964.
***) Р. Копп, Г. Мойер, Необходимые условия оптимально-
сти особых экстремалей, Ракетная техника и космонавтика, № 8,
1965.
§ 4J	СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ	79
Для оптимального особого режима, осуществляюще-
гося одновременно по k,k>\, компонентам управления,
обобщение условия Келли привело к установлению необ-
ходимых условий двух типов: типа равенства ---
\ (л
условий) и типа неравенства *).
В целом принцип максимума вместе с дополнитель-
ными необходимыми условиями для скользящих и особых
режимов позволяет определить искомое оптимальное уп-
равление, хотя и ценою усложнения структуры краевой
задачи.
§ 4.	Условия оптимальности
в системах с дискретным временем
1.	Вводные замечания. Условия оптимальности игра-
ют важную роль при построении вычислительных проце-
дур для динамических систем (1.1). Однако, как уже упо-
миналось, при вычислении оптимальных траекторий ис-
пользуется не континуальное описание динамического
процесса, для которого в предыдущих параграфах и были
получены эти условия, а конечномерная аппроксимация.
Поэтому естественно задать вопрос о том, в какой мере
условия оптимальности сохраняют свою силу при замене
дифференциальных уравнений конечноразностными? Кро-
ме того, как мы об этом уже говорили в § 1, нас будут
интересовать также и те динамические процессы с дис-
кретным временем, которые нельзя рассматривать как
конечномерную аппроксимацию процессов с непрерывным
временем. Поэтому поставленный вопрос следует расши-
рить: в какой мере условия оптимальности теории опти-
мального управления системами с непрерывным време-
нем могут быть перенесены на теорию оптимального уп-
равления системами с дискретным временем?
Анализу поставленной задачи и будет посвящен дан-
ный параграф.
*) И. Б. Вапнярский, Теорема существования оптимального
управления в задаче Больца, некоторые ее приложения и необходи-
мые условия оптимальности скользящих и особых режимов, ЖВМ и
МФ 7, 2, 1967,
80
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
2.	Замечание о сопряженных системах. Как мы уже
убедились ранее, в теории оптимального управления
большую роль играют дифференциальные уравнения
х = (0 х>	0 j)
ф = — Л* (t) ф,
где х, ф — векторы размерности п, А — матрица (пХп),
А* — матрица, сопряженная матрице А. Второе из этих
уравнений называется сопряженным к первому (и наобо-
рот) (см. § 2, п. 4).
В силу (2.8) имеем
(ф, х) = const = (ф0, х0).	(4.2)
Рассмотрим теперь конечномерные аналоги этих урав-
нений (здесь и в дальнейшем мы будем использовать
простейшую разностную схему)
Хьн= xk+xA(tk)xk,
фА+i = фл — хА* (tk) Фа, k = 0, 1, ..., Af — 1. (4.3)
Вычисляя произведение (фЛ+1, хк+1), получим
(Фа+1, xk+i) = (Фа» х/г) + О (т2).	(4.4)
Так как xN—O(l), где N — число интервалов, то вместо
равенства (4.2) для конечноразностных уравнений (4.3)
мы получаем следующую оценку:
(фл, xk) = (фо, хо) + ° (х).	(4.5)
3.	Принцип максимума для конечноразностных урав-
нений. Рассмотрим задачу отыскания максимума
J = (с, xN)	(4.6)
при ограничениях
Xk+1 = Xk 4- Xf (xk, uk, tk),	(4.7)
xo = a,	(4.8)
Uk^Gk, fe = 0, 1, ...,	1.	(4.9)
Здесь а и c — некоторые заданные векторы.
§ 4]
СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
81
Пусть uk и xk — оптимальные управления и соответ-
ствующие фазовые векторы. Введем вариации управле-
ний. Положим
Uk =Uk> us — us + du, k=f=s,
где du— некоторый постоянный вектор такой, что us +
+ du<=Gs.
Очевидно, что xk — xk, если k^s. Вычисляя xh для
k>s, имеем
k-i
Xk = Xs -I- т 2 f (xh Щ, ty.
i=s
Введем в рассмотрение величину hk— (хк—хк)1х. Очевид-
но, что /ift=0, если k^s. Для k>s
~	~ ~	fe-1
hk = f(xs, uSt t$) — f (xs, us, ts) -f- 2 [f (xit uh t() — f (x/f uh /,)]
j=S+l
ИЛИ
hk = fts+i + 2 {T hi + ° (t2)} •
/=S+1
Следовательно, вариация фазового вектора удовле-
творяет следующему разностному уравнению:
hk^hk+x-^-hk + Olx*), k = s + 1, ..ЛГ — 1, (4.10)
dxk
hs+i = f (xs, us, is)	f (x$, u$9 /s).	(4.11)
Составим уравнение, сопряженное (4.10):
№+1 = 'I’ft — х IpA, k = S + 1, . . . , 1V — 1.
\dxk)
Тогда, согласно (4.5), для любого k^s
(фб+1> fa+i) — (i|)s+i> hs^.j) 4- О (т).	(4.12)
Составим теперь выражение вариации функционала
V) = (с, hN). (4.13)
\ т /
82
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Выберем -фя так, чтобы
(флг, h^) ~ — &J.	(4.14)
Отсюда следует, что
= —с.	(4.15)
Условие (4.15) есть условие трансверсальности. Исполь-
зуя (4.12), перепишем (4.14) в следующем виде:
6J => (ф$+1, f (-V,	^s)) (фз+l, f ('Vs, Ц>, ^s)) 4“ О (?) =
= H (\|)s+l, *S, tS) H (xps+l, *s, ^s, Q 4“ О (T).
Для того чтобы x и й были оптимальным решением, не-
обходимо, чтобы 6/^0. Отсюда мы получаем, что вдоль
оптимальной траектории
н (фз+1, *s, ts) = max H (фз+1, Xs, us, ts) + О (т). (4.16)
«se<?s
Таким образом, мы пришли к следующему утверж-
дению:
Функция 'Гамильтона вдоль оптимальной траектории
отличается от своего максимального значения на величи-
ну порядка О (т).
Примечание. Этот результат мы получили, рас-
сматривая задачу Майера, и в предположении, что левый
конец траектории фиксирован. Нетрудно, однако, прове-
рить, что теорема остается справедливой в случае произ-
вольной задачи Больца.
Итак, мы установили, что чем меньше шаг разностной
схемы, тем точнее выполняется принцип максимума.
С другой стороны, с увеличением шага т оптимальное
значение функции Гамильтона может все больше и боль-
ше отличаться от своего максимального значения. Следо-
вательно, можно предполагать, что для произвольных
разностных уравнений принцип максимума вообще не
будет иметь места.
4. Произвольные дискретные системы. Уравнения,
описывающие эволюцию управляемой системы с дис-
кретным временем, будем писать в виде
4- fk(Xk, uk\ k 0, 1, ..., N — 1.	(4.17)
§ 41	СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ	83
Функция Гамильтона этой системы в случае задачи
Майера будет
Hk = Н ('фл»4-1> х^ Щг) — (фл+i, fk (Xfa uk)).	(4.18)
В этом случае, когда мы рассматриваем задачу мини-
мизации функционала
2V-1
J=^Fk(xk, uk),	(4.19)
k=0
функцию Гамильтона мы будем писать в виде
Н (фА+1, Xk, Uk) = (фб+1, fk (Xk, Uk)) — Fk (xk, Uk). (4.20)
Выпишем еще сопряженную систему в случае задачи
Майера
=	6—0, J, .... ЛГ-1. (4.21)
\dxk/
В предыдущем пункте мы установили, что на опти-
мальной траектории функция Гамильтона тем больше
может отличаться от своего максимального значения, чем
больше шаг дискретизации. Если дискретная система не
связана с конечномерной аппроксимацией непрерывных
процессов, то у нас вообще нет никаких оснований пред-
полагать справедливость принципа максимума. В под-
тверждение сказанному рассмотрим один пример.
Предположим, что дискретная система описывается
следующими уравнениями:
X/j-i-i = Xk -р Q/Hky
(4.22)
4+1 = Xk — (Xk)2 4- (Uft)2.
Начальное состояние будем считать фиксированным:
4=3,	4 = 0.	(4.23)
Поставим задачу отыскания управления — чисел иа и
«1, доставляющих минимальное значение величине 1=
= —х*. Поскольку число шагов равно двум, мы можем
легко выразить в явном виде значение функционала
и всех фазовых координат через управления. Проводя
64
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. t
очевидные выкладки и используя начальные условия
(4.23), найдем
xj = 3 4- 2м0
х* = — 9 + (и0Д.
xj = 3 4~ 2Ц) 4- St/j,
xl = — 18 — 12и0 — 3 (ы0)2 4- (uj2.
Тогда значение функционала есть
J = 118 4- 12«о 4- 3 (ц,)2] - (и/.	(4.24)
Величину управления подчиним условию |uft|^5, где
£=0,1. Вычислим теперь оптимальное управление:
«о = — 2, «j — ± 5.	(4.25)
Таким образом, мы будем иметь следующие оптималь-
ные значения фазовых переменных и функционала:
х* = — 1, xl = — 5, J = — 19.
Составим теперь сопряженную систему
Фа+i — Фа 4* 2х£фА»
(4.26)
Фа+i — Фа» £ = 0, 1.
Мы видим, что величина ф| не зависит от индекса k. Так
как, согласно условиям трансверсальности (4.15), ф2 = 1, то
и ф? = 1.
Рассмотрим первое уравнение системы (4.26). Так как
фз = 0, то ф! = — 2х} и, следовательно, «оптимальное» зна-
чение ф5 = 2. Рассмотрим теперь функцию Гамильтона вдоль
оптимальной траектории. На первом шаге
Hi — Ф12ц<) 4” Ф1 [ (х0)2 4~ (ио)21 — 4«0 4~ (w#)2 — 9.
На втором шаге
Hz = ф}2их4- Фз I- Й)2 4- («i)2J = («i)2 - 1.
Написанные выражения показывают, что на втором
шаге оптимальное значение функции Гамильтона равня-
4
СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
85
ется ее максимальному. На первом шаге максимальное
значение функции Гамильтона достигается при ц0 = 5.
Оптимальное значение и0= —2. Заметим, что оно дает
минимальное значение функции Гамильтона.
5. Задача Лагранжа со свободным правым концом.
В этом пункте мы рассмотрим задачу отыскания векто-
ров xk и ик, связанных условиями (4.17) и доставляющих
минимум функционалу (4.19) при условии, что на управ-
ление не накладывается никаких ограничений. Для про-
стоты значение х0 будем считать фиксированным, a xN —
свободным. Оптимальное решение рассматриваемой за-
дачи обозначим через хк и йк.
Наряду с оптимальным управлением рассмотрим уп-
равление
и* =Uk + e£uk,	(4.27)
где е — некоторый вещественный параметр.
Величину би*. будем называть вариацией управления,
а вариацией фазовой траектории векторную производную
Перепишем уравнения (4.17):
g (е) = Xk+i — Xk — fh (xk, uk + ебий) = 0.
Это равенство должно выполняться тождественно по
Поэтому
причем Ло = О.
Выпишем теперь вариацию функционала
1 ~ ~ '
6 J = 11Ш — 2 (.Pk (Xk, uk) — Fk (xk, Uk)) =
e-*o 8 r-*
k=Q
86
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
(ГЛ. I
Поскольку на оптимальной траектории 61=0, получаем
Следовательно, какова бы ни была вариация управления
duk и набор будем иметь
*-i[/dFk 1 \ (dFk с \
7. “AM + hA дич +
Z?=o L \ «	'	' *	'
, |	{. и dfk и dfk л '
I	dxk duk J
- 0. (4.28)
Заметим, что
N-l	АГ-1
2 ^+i(^+i— hk)+	— Ф*) hk = ^nIin — фД.
£=o	k=Q
Распорядимся выбором таким образом, чтобы пра-
вая часть этого соотношения обратилась в нуль. Посколь-
ку /го=О, a hN не задано, положим фх=0. Это нам по-
зволяет переписать (4.28) в следующем виде:
dFk	dfk , \
------Фа+1 + — Фл+1 Т~, I 4“
?xk	dxk /
dfb	\
=0. (4.29)
duk	/
Выберем векторы ips так, чтобы имели место равенства
фй — фл+1 4~
Ф*+1
dxk'
(4.30)
Тогда, в силу произвольности векторов 6uh, мы получаем
из (4.29)
dFk / dfk\
hr И>*+1=°-
duk уdukj
Используя выражение (4.20) для функции Гамильтона,
мы можем переписать равенство (4.30) в следующей
§ 4]	СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ	87
форме:
— = 0.	(4.31)
Итак, мы пришли к следующей теореме:
Теорема. Если управление йк и траектория хк до-
ставляют минимум функционалу (4.19) при уравнениях
связи (4.17) и фиксированных начальных условиях, то
существуют такие векторы ф4, удовлетворяющие урав-
нениям (4.30) и граничному условию i|)N=0, что векторы
uk при каждом k являются стационарными точками функ-
ции Гамильтона Hk.
Примечания.
1. Сформулированная теорема была установлена для
того частного случая, когда правый конец траектории не
фиксирован. Не представляет, однако, большого труда,
используя ту же схему доказательства, перенести все
результаты § 2 этой главы на рассматриваемый случай
дискретных систем.
2. Отметим, что при выводе необходимых условий
оптимальности в форме (4.30), (4.31) уравнения для со-
пряженных переменных записаны «справа налево», т. е.
значения ф* определяются через значения фА+1.
Этот факт накладывает определенные ограничения на
использование численных методов расчета оптимальных
программ. Как- мы увидим ниже, форма записи «справа
налево» удобна при реализации метода Крылова — Чер-
ноусько. В тех случаях, когда необходима запись «сле-
ва— направо» (например, в методе Ньютона), уравнения
(4.30) необходимо разрешать относительно ф*+1.
6. Заключение. Итак, мы установили, что оптималь-
ное управление в дискретных задачах обращает произ-
водную функции Гамильтона в нуль, и только. Можно
привести примеры, показывающие, что на оптимальной
траектории функция Гамильтона может иметь и макси-
мум, и минимум, и седловую точку. Пример, рассмотрен-
ный в п. 4 этого параграфа, как раз и демонстрирует эту
особенность систем с дискретным временем. Тем не менее
и условие стационарности функции Гамильтона может
служить источником эффективных численных методов,
особенно в тех случаях, когда уравнение (4.31) имеет
единственное решение.
88
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Благодаря отмеченной особенности задач с дискрет-
ным временем нам удалось получить необходимые усло-
вия. только для того случая, когда ограничения на уп-
равление отсутствуют.
Для изучения общего случая, когда uk<=Ghy где Gk—
множества достаточно произвольного вида (в том числе
и замкнутые), необходимо использовать другие методы,
и прежде всего аппарат нелинейного программирования.
Он позволяет, в частности, установить условия, при вы-
полнении которых принцип максимума имеет место и для
систем управления с дискретным временем. К числу та-
хих условий относится, например, требование выпук-
лости множеств Gh.
В связи с этим имеет смысл обратить внимание чита-
теля на одно обстоятельство, которое до сих пор не по-
лучило достаточно подробного объяснения.
Предположим, что мы имеем некоторую динамическую
управляемую систему
х = f (х, и, f), ueG.	(4.32)
Для этой системы справедлив принцип максимума без
каких-либо условий на структуру множества G. Заменим
теперь систему (4.32) конечноразностной
Xk+i = xk + tf	uk, tk), k = 1, 2 .... N. (4.33)
Если шаг t достаточно велик и множество G не вы-
пуклое, то принцип максимума для системы (4.33) может
не иметь места. Однако, с уменьшением т, т. е. увеличе-
нием размерности задачи (числа N), наступает такой мо-
мент, когда для любого т<т* система (4.33) станет пон-
трягинской, т. е. для нее принцип максимума сделается
справедливым и она будет вести себя так, как если бы
множество G было бы выпуклым.
Следует заметить, что структура ограничений типа
разностных уравнений открывает известные перспек-
тивы для разработки и специальных методов исследо-
вания.
Эти методы основаны на анализе множеств дости-
жимости. Этим термином называют множество значений
хА+1, в которые может перейти изображающая точка х»
I б!
ЁЁСЁОМЁЧМЫй ЙЙТЁЁВАЛ врёмёни
под действием всевозможных управлений из Gk. Мы, од-
нако, не будем заниматься этими вопросами, отсылая
читателя к специальным исследованиям по теории опти-
мального управления дискретными системами *).
§ 5.	Задачи оптимального управления
на бесконечном интервале времени
1.	Предварительные замечания. Все предыдущие рас-
суждения этой главы имели смысл лишь тогда, когда
интервал времени [А>, Г] конечен. Переход к бесконечно-
му времени встречает существенные трудности. Доказан-
ные выше теоремы, в том числе и принцип максимума,
перестают быть справедливыми. Анализ задач при Т-^со
требует привлечение теории, изучающей поведение ре-
шений дифференциальных (или разностных) уравнений
в окрестности особых точек. Это обстоятельство сущест-
венно осложняет теорию оптимизационных задач, и сколь-
нибудь общее ее построение в случае бесконечного ин-
тервала времени сегодня отсутствует. В то же время в
практике такие задачи возникают все чаще и чаще. По-
явление бесконечного интервала времени в оптимизаци-
онных задачах оказывается столь же естественным, как
и в задаче устойчивости.
Кроме того, задачи оптимального управления на бес-
конечном интервале времени интересны и рядом своих
чисто математических особенностей. Нетрудно, напри-
мер, построить примеры задач оптимального управления,
неразрешимых ни для какого конечного интервала време-
ни и разрешимых на бесконечном временном интервале.
Пусть, например, речь идет об отыскании в классе
ограниченных управлений минимума функционала
т
при дифференциальных связях
х == — 4-й
X/2
*) См., например, А. И. Пропой, О принципе максимума для
дискретных систем управления, Автоматика и телемеханика,
т. XXVI, № 7, 1965.
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
ГГЛ. 1
и краевых условиях
% (Q ~^о»	(^*) = О*
Легко убедиться, что эта задача не имеет решения ни
для какого конечного Т. Любое допустимое управление,
переводящее систему в начало координат, стремится к
бесконечности при t—>7\
Однако если Т=оо, то допустимые управления суще-
ствуют (во всяком случае для некоторого множества на-
чальных значений), и величина управления на всем ин-
тервале (70, оо] остается конечной, и значение функциона-
ла также конечно.
Для того чтобы это показать, достаточно построить
одно допустимое управление, которое переводило бы си-
стему из некоторой точки х0 в начало координат.
Положим й—у/7, где v — некоторая постоянная, и бу-
дем искать частное решение х(/) в виде
... (*)
fl '	/2	'	' '
Подставляя ряд (*) в уравнение и сравнивая коэффи-
циенты при одинаковых степенях t, получим Xt=i/v,
X2=llvs и т. д.
Ряд (♦) определяет некоторую допустимую траекто-
рию, поскольку, начиная с некоторого 4>0, он сходит-
ся и удовлетворяет уравнению связи.
Функция и — vjt удовлетворяет всем поставленным усло-
виям. Она является допустимой, т. е. она ограничена при
любом />0и она переводит систему при /~>оо в начало
1 1
координат из точки х0 —------]---. Так как значение
vto Лд
функционала
„	«> л	2
J = \u2(t)dt = —
У	А>
*0
конечно, то оно может служить верхней оценкой для зна-
чения функционала вдоль оптимальной траектории.
2.	Два возможных пути решения задач оптимального
управления на бесконечном интервале времени. Тради-
ционная схема решения задач оптимального управления
состоит в построении необходимых условий в форме урав-
§ 5]	БЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ	91
нений Эйлера или принципа максимума. Используя не-
обходимые условия, мы редуцируем исходную задачу к
некоторой краевой задаче для системы обыкновенных
дифференциальных уравнений. Применение этой схемы
для задачи оптимального управления на бесконечном ин-
тервале времени встречает целый ряд трудностей. Непо-
средственно перенести рассуждения, которые мы исполь-
зовали для конечного интервала времени, на бесконеч-
ный не удается по многим причинам, и главная из них
состоит в том, что мы не знаем характера поведения им-
пульсов (множителей Лагранжа) при t—>оо. Предполо-
жим даже, что нам удалось построить принцип максиму-
ма и, следовательно, свести исходную задачу к краевой.
Но для ее эффективного решения мы необходимо долж-
ны были бы перенести краевые условия из бесконечно
удаленной точки в конечную точку. Для того чтобы со-
вершить подобный перенос, необходимо предварительно
изучить асимптотику решения при t—>оо.
Поэтому естественным кажется сначала провести не-
обходимый асимптотический анализ, заменить исходную
задачу с бесконечным интервалом некоторой «конечной»
задачей, которая давала бы в каком-то смысле асимпто-
тику исходной задачи. Полученную таким способом
«асимптотическую» задачу мы можем затем решать уже
стандартными способами.
Этот путь, однако, тоже содержит ряд значительных
трудностей. Тривиальный перенос условий из бесконечно
удаленной точки в конечную может приводить, как мы
видели, к задаче, решение которой не только не являет-
ся асимптотическим приближением решения исходной
задачи, но и вообще не существует.
В данном параграфе мы рассмотрим несколько клас-
сов задач, в которых удается построить асимптотические
приближения. Однако сначала мы приведем два примера
прикладных задач, иллюстрирующих необходимость по-
строения теории оптимального управления на бесконеч-
ном интервале времени.
3.	Проблема устойчивости систем, обладающих задан-
ным качеством, Рассмотрим управляемую систему
*’= f (х, щ /); ц	(5,1)
где/(0, 0, 0555 О,
92
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
(ГЛ. I
Если множество Gu достаточно «широкое», то выбо-
ром управления u(x0, t) мы можем сделать тривиальное
движение системы (5.1) устойчивым. Более того, возмож-
ный выбор управления, как правило, не единственный,
что позволяет искать управления, удовлетворяющие до-
полнительным условиям. Благодаря этому имеет смысл
следующее определение устойчивости.
Будем называть тривиальное движение /-устойчивым,
если для любого можно найти такое т]>0 и
что каково бы ни было x(t0)=x0t удовлетворяющее
условию ||х0||^т], можно указать такое управление
u(x0, t)QGUf которое переводит систему (5.1) из состоя-
ния х0 в начало координат за любое время T^TQ) причем
так, что положительный функционал
т
J (х0, u, t) = J F (х, и) dt 8,
to
где •F(x0, и) ^0, F(0, 0)s0. Функционал J носит назва-
ние качества управления.
Почти очевидно, что для /-устойчивости решения х=
s0 необходимо, чтобы для любого е>0 можно было ука-
зать такое л^О, что, как только ха удовлетворяет усло-
вию ||х0|| ^Ti-
min J (х0, и, оо) е.
«еои
Таким образом, проверка /-устойчивости сводится к за-
даче отыскания «(/), доставляющего минимум функцио-
налу /(х0, и(^), оо) при ограничениях (5.1) и краевых
условиях
х{^=хй,	х(оо)=0.	(5.2)
4.	Задача экономического роста. В динамических за-
дачах экономики рассматривается следующая задача.
Определить, какую часть производимого продукта сле-
дует использовать на инвестиции, чтобы максимизиро-
вать функцию полезности. Если через x(i) обозначить
суммарный продукт, а через u(t)—инвестиции, то при
известных условиях процесс производства может быть
описан системой (5.1). Множество G„ имеет, как правило,
5 5]	БЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ	93
следующий вид:
(5.3)
В качестве функции полезности чаще всего принимается
линейный функционал вида
J (х0, «) = J (с» *) Р (0 dt,	(5.4)
to
где p(t)—так называемая функция * дисконтирования.
Она показывает, что блага с течением времени обесцени-
ваются. Рубль дохода, который мы можем получить
сегодня, гораздо «дороже» того рубля, который можно
получить через 10 лет. Функция дисконтирования p(t)
выбирается таким образом, чтобы интеграл (5.4) был
сходящимся. Функции x(t) и u(t)—неограниченные.
Подобные задачи оказываются весьма полезными при
изучении перспектив развития экономики, целей прогнози-
рования и составления перспективных планов. Они тесно
связаны с теорией магистралей.
Подобные задачи возникли еще в двадцатых годах.
Они дают косвенный ответ на один из самых трудных во-
просов теории оптимального планирования: «Какие ус-
ловия должны быть сформулированы на правом конце
траектории?» Переход к бесконечному времени и введе-
ние функции дисконтирования позволяет рассматривать
задачу со свободным концом. Этим задачам посвящена
значительная литература, которая, однако, не содержит
законченных результатов математического характера.
5.	О схеме анализа. В обеих задачах, о которых шла
речь, значения функционалов должны быть конечными.
В первом случае это достигается за счет выбора траекто-
рии (т. е. управления). Во втором случае — за счет вы-
бора функции дисконтирования. Благодаря этому харак-
тер задач оказывается существенно различным. Тем не
менее обе задачи аддитивны и это позволяет развить не
которые общие процедуры приближенного анализа.
Будем рассматривать задачу минимизации интеграль-
ного функционала
J (х0? и) = J /° (х, и, t) dt,	(5.5)
94
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
где х и и связаны уравнением (5.1). Начальное значение
 x(t0) фиксировано:	x(to) = xo-	(5.6)
Обозначим	
	хх) = min f f° (x, и, t) dt
при условии х(/1)=х1. Обозначим '
S (/ъ Xi, t2, х2) = min (' /° (х, и, t) dt
и J
при условиях x(tt) =xt, x(t2) =х2.
Функция S (/ъ х4) — это решение исходной задачи и
х(/) должен удовлетворять тем условиям на правом кон-
це, которые мы будем формулировать для этой задачи.
Очевидным является следующее соотношение:
5	*о) = min {S (/0, х0; хг, Т) + S (хт, Т)},	(5.7)
хт
справедливое для любого T>tQ. Решение этой задачи
обозначим через х* и и*. Пусть теперь u=u(t)^Gu—
некоторое управление, такое, что интеграл
J f°(x, и, t)dt,
т
где х удовлетворяет уравнению (5.1) и условию х(Г) =
= хт, конечен. Поскольку й фиксировано, то он будет
функцией только хт. Обозначим его через R(xT).
Вместо (5.7) рассмотрим соотношение
2 (^о. хо) = min {S (t0, х0; хт, Т) + R (хг)}.	(5.7')
*т
Значение хт, реализующее этот минимум, обозначим че-
рез хг. Определение 2 (t0, х0) сводится к следующей за-
даче Больца. Опредлить управление u(t)=u**(t), до-
ставляющее минимум функционалу
т
2 = f (х, и, t)dt±R (хг).	(5.8)
*0
Если |/?(хт) ’^5(Г, хт) >0 при то управление
бесконечный интёёваЛ времени
95
§ 5)
U(t), заданное с помощью соотношения
у ( «"(/), *еР0;П
( u(t),	t(=[T-, оо],
будет аппроксимировать решение исходной задачи ы* в
том смысле, что значение J(U) будет мало отличаться
от оптимального J(U*).
Примечание. Выбор хт в общем случае не произ-
волен. Он должен принадлежать множеству, из которого
достижимо конечное состояние.
6. Дальнейший анализ. Если разность
|/?(хг)—S(T, хт) |—>0 при Т—>-оо,
г
то J— J определяет основной вклад в величину
/о
функционала, поэтому, решив задачу об отыскании ми-
нимума функционала (5.8), мы получаем некоторую
верхнюю оценку, которая тем лучше, чем больше Т.
Реализация обсуждаемой схемы требует эффективно-
го построения возможного (допустимого) управления,
переводящего систему в начало координат или удовлет-
воряющего условию (5.3). Проблема построения допусти-
мых управлений—это самостоятельная и трудная задача,
и в каждом конкретном случае она должна решаться
специальным образом. Заметим, что в задаче устойчи-
вости одно допустимое управление всегда может быть
построено. В самом деле, потребуем, чтобы х(7')=0. Тог-
да допустимым будет управление «=0. В самом деле, в
этом случае в силу свойств функции f(x, и, I)
х==0 Vt>T
и 7?=0. Использование допустимых управлений всегда
дает возможность построить оценку, но она в общем слу-
чае не является асимптотической.
Для построения асимптотических оценок необходимо
наложить определенные условия на поведение управле-
ний в окрестности бесконечно удаленной точки и более
подробно охарактеризовать функционалы.
Рассматривая задачи первого типа с условиями
ограниченности на бесконечности, будем считать, что
96
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ, 1
разложение подынтегральной функции f°(x, и) начи-
нается с членов второго порядка по отношению к х и и:
f°(x, и, t) = (х, R1±x) 4- (х, Т?12и) + («, #21х) -f-
+ (и, R^u) + о (шах {]х||2, ||ыЦ2}). (5.9)
Такому предположению удовлетворяют большинство
функций, с помощью которых обычно оценивается каче-
ство управления.
В задачах устойчивости мы будем считать, что управ-
ление и принадлежит к классу Gx. Это означает, что уп-
равление u(t) допускает в окрестности бесконечно уда-
ленной точки асимптотическое представление вида:
u(t) = A + i -j. ... + ^+o(_LV	(5.9')
v' t t2	\tN I	x '
Если допустимые управления, начиная с достаточно
большого Т,— непрерывные функции времени, то изуче-
ние управлений, удовлетворяющих (5.9), представляет ин-
терес хотя бы потому, что это условие, как мы увидим
ниже, достаточно для сходимости функционала качества.
Однако этот класс, конечно, не исчерпывает те управле-
ния, которые представляют интерес для практического ис-
пользования. Можно рассмотреть, например, релейные
управления вида
I
U =
I o,
где и{ — некоторые постоянные, а — система интерва-
лов, длина которых убывает при т—>оо таким образом,
т
что J f°(x, и, f)dt сходится. Существует еще целый ряд
t
важных для практики классов задач управления, которые
не могут быть непосредственно включены в рассматрива-
емую теорию *).
(5.10)
*) К их числу относятся, например, задачи с функционалом
1 р	1 Р
lim — I F dt. Формально заменой z=— I F dx она сводится к за-
t t J	t J
с 1
даче с функционалом I = j -у (F — z) dt, однако, при этом задача
♦о
перестает быть аддитивной.
§ 5]
БЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ
97
На правые части уравнения (5.1) также должны быть
наложены некоторые условия. Но о них мы скажем ниже.
В задачах экономического роста функция u(t) долж-
на удовлетворять фазовым ограничениям (5. 3). Рассмот-
рим для определенности некоторый частный случай это-
го условия:
для любого i= 1,2, ..., п 0	Х(Х<‘\ (5.11)
где Хг^О — постоянные числа.
Условие (5.11) позволяет вместо u(Z) ввести новое
управление
u(0 = OzX(0.	(5.12)
Функции 0£ удовлетворяют ограничению
Vi 0<ez<Xz.	(5.13)
Равенство (5.12) мы будем записывать в форме
и =	(5.14)
где 0 — диагональная матрица с элементами 0г.
Условимся изучать класс задач, где 0 имеет следую-
щее асимптотическое представление:
0 = ео++	+ _L0„ + o('J_j.	(5.15)
Этот класс мы также будем обозначать через G».
Представление вида (5.15) имеет тесную связь с тео-
рией магистралей. Вдоль магистрали величины б.о будут
либо нулями, либо единицами, и будут соответствовать
управлению, которое обеспечивает максимальные темпы
роста данного линейного функционала. Если эволюция
экономической системы описывается при достаточно боль-
ших t линейным уравнением вида
х = Ах Ви = (A -I- В0) х,	(5.16)
то элементы матрицы 0О определяются из решения сле-
дующей задачи линейного программирования:
(С, Ви) -> шах, 0 sC u(Z)
которая соответствует максимизации скорости возраста-
ния функционала в каждый момент времени. Решение
4 Н. Н. Моисеев
98
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
этой задачи дает крайние значения для управления u{i\
т. е. для элементов матрицы 0О. Поэтому в дальнейшем
величины 0Ог мы будем считать известными.
7. Некоторые факты из теории асимптотических пред-
ставлений решений обыкновенных дифференциальных
уравнений. Рассмотрим линейное дифференциальное
уравнение
х = A(i)x + g(t),	(5.16')
в котором матрица А и вектор g имеют следующий вид:
4 = Ло +	••• + “^	+ 0	>
(5.17)
+ *^"£2 + • • •
, 1	. i \
1----gN + O ------1.
Приведем без доказательства две теоремы.
Теорема 1. (Ху кух а р а, 1934 г.) *). Если все соб-
ственные числа матрицы Ло попарно различны, то любое
частное решение y(s, t) однородного уравнения
x=A(t)x,	(5.16")
соответствующее собственному числу Xs, представимо в
виде
у (s, t) = exp {М + Х“ In t} • {x0 (s) + xt (s) Г1 +
+ ... •+ xN(s)t'N}+o(rN). (5.18)
Опишем процедуру определения неизвестных величин.
Подставляя разложение (5.18) в уравнение (5.16"), по-
лучим следующие уравнения:
(Ло —XsE)x0(s) = 0,	(5.19)
(Ло - Xs£) хх (s) = - (Лх - Х"Е) х0 ($),	(5.20)
(Ло — XSE) х2 (s) = — (Лх — (%® — 1) Е) Xr (s)	— Л2х0 (s),	(5.21)
(Лц hsE) Xg (s) = (Лх (Xs 2) E) Xg (s)	AgXi (s)	ЛзХд (s)
*) Hukuhara М.» Sur les points singuliers des equations dif-
ferentielles liniares. Journ, of the Fac. of Science Hokkaido Imp. Un.,
II, 1934.
БЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ
99
§ 51
и т. д. Ранг определителя | Ао — ksE | равен п — 1, поэтому
уравнение (5.19) определяет x0(s) с точностью до постоянной.
Такой постоянной может быть, например, компонента xj(s).
Тогда
4 =
где az = Ajz/Au, Ду —алгебраическое дополнение элемента я“/.
Рассмотрим уравнение (5.20). Для того чтобы оно
было разрешимо, необходимо и достаточно, чтобы ранг
расширенной матрицы также был равен п— 1, т. е., что-
бы компоненты вектора, стоящего в правой части урав-
нения (5.20), удовлетворяли тому же линейному соот-
ношению, которому удовлетворяют элементы столбцов
матрицы 40—%,Е. Это линейное соотношение мы можем
записать в форме
(</, (Д-^Е)хо(з)) = 0.	(5.22)
Компоненты вектора d пропорциональны алгебраическим
дополнениям элементов какого-либо из столбцов матрицы
До-XsE.
Подставляя в уравнение (5.22) выражение Xo(s) через
xj(s) и сокращая на xj(s), мы получим линейное уравнение
относительно
drfj
ч ! t
Постоянная xj(s) остается неопределенной. Мы ее можем
задать произвольным образом. Если условие (5.22) выпол-
нено, то уравнение (5.20) позволяет определить х± (s) с
точностью до постоянной
Л (s) = М (s).
Рассмотрим теперь уравнение (5.21). Для его разре-
шимости необходимо и достаточно выполнение следую-
щего условия:
(d, (Дх — (Х,° — 1) Е) хг (s) 4- Лах0 (s)) = 0.
100
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. Г
Это—линейное алгебраическое уравнение относительно неиз-
вестной xj(s) и т. д.
Теорема II. Если матрица А и вектор g удовлет-
воряют условиям (5.17), то уравнение (5.16) имеет и при-
том единственное частное решение, представимое с помо-
щью следующего асимптотического разложения:
l4+...+^+4^).	(5-23)
Коэффициенты разложений определяются следующи-
ми формулами:
— gi,
Д0х2 — g2 _ (Лх + Е) х19	(5.24)
ёз (А “Ь 25) х2 А2хг
и т. д.
Заметим, что формулы (5.24) позволяют вычислить
gi по известным хь Если все собственные числа матрицы
40 имеют положительные действительные части, то урав-
нение (5.16) имеет единственное ограниченное частное
решение, удовлетворяющее начальному условию х(Т) =
=хт, и это частное решение представимо в форме (5.23).
Эти результаты распространяются на нелинейные
уравнения вида
х = Ах + g + ср (х, /),
если вектор-функция ф (х, t) имеет вид ф — 211^ Ф2 М	.
/ /2
и если для х, достаточно малых по модулю, ф/ разлагаются
в ряд Тейлора
Ф/ (х) - фйх + Г/2 (х) + .:.,
где Г// — однородные операторы порядка /. Не ограничи-
вая общности, можно принять фй = 0.
Вернемся теперь к исходным уравнениям.
Если управления g и 0 заданы, то мы можем в явном
виде выразить траекторию через управления
х (0	Csy(s, t) +~х = X (Сь .... Cs, 9, g,
§5]
БЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ
101
причем эта функция дает явное выражение траектории
через управление. Если среди К8 нет величины с положи-
тельной действительной частью, то после определения ве-
личин K°s мы всегда можем удержать в разложениях для
у$9 х такое количество членов, чтобы иметь общую
оценку
х(0 = ^csy(s, t) 4- X 4-	=
= Х(СР .... Cs,	4-V
Это утверждение и будет использовано в дальнейшем.
8. Пример использования асимптотических оценок.
Рассмотрим снова уравнение (5.1) и предположим, что
функция f(x, и, t) в этом уравнении имеет вид f(x, и, t) =
=Ах+Ви. Далее будем предполагать, что ограниченная
матрица B(t) такова, что для любых t^T она имеет об-
ратную В~1 (0 (условие а). Предположим, кроме того, что
все собственные числа матрицы Ао имеют положительные
действительные части, т. е. при отсутствии управления
тривиальное решение уравнения (5.1) неустойчиво. В этих
предположениях для уравнения (5.1) рассмотрим задачу
минимизации функционала
J (хт, и) = J /° (х, и, t) dt,	(5.26)
где f° есть А/4-1 раз непрерывно дифференцируемая
функция х и и, удовлетворяющая ограничениям (,5.9)
при условии
х(Т) = хг,	(5.27)
х (оо) = 0.	(5.28)
Условие (а) позволяет ввести новое управление g(t):
Ви = g,	(5.29)
поскольку по найденному g(t) мы всегда можем с помо-
щью (5.29) единственным образом определить управле-
ние u(t).
102
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Предположим наконец, что управление u(t) принад-
лежит к классу GN . В этом случае функция g(t) имеет
представление (5.18) и, следовательно, величины gi=
= Bui будут единственным образом определяться через
Xi с помощью формул (5.24). Поэтому функцию f°(x, и, t)
мы можем представить в виде
/° (х, щ t) = f1 (хх, х2, ..., xN) 4-; О дг) .
Следовательно, интеграл (5.26) будет сходящимся и иметь
порядок о(1/Т) и его можно представить в следующей
форме:
J (хт, и) = z (хн х2,... ,xN)-\-o
Величины xit x2,...,xIf, входящие в выражение (5.30), свя-
заны единственным условием
_ Х1 , хг	XN	7 1 \
Хт =--------------к- ... ------о ------ .
Т [Т2	TN	\TN)
(5.31)
Отбрасывая в выражении (5.31) члены порядка
o(\/TN~l), мы можем определить min z(xI;..., xN)=z(xT)
при условии (5.31) и соответствующее управление и=
— й(хт). Таким образом,
min J (хт, и) — г (хт) + о (——'j.	(5.32)
U	\ypN-lj
Обозначим через x*(t) и и*(0 (^[А>, П) функции, до-
ставляющие минимум функционалу
оо	г
J (хъ и) = J /° (х, и, t)dt = J /° (х, ц, t) dt + J (x-ru),
через x**, и**— величины, реализующие минимум функ-
ционала
т
(х, ц) = f /° (х, и, t)dt-\-z (хт).
§51
ЕЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ
ЮЗ
Поскольку для хт и и имеет место оценка
J (х, и) = J** (х, и) + о(—А ,	(5.33)
I уАГ~11
то справедлива следующая теорема:
Теорема. Если и <=6%, mo управление U
является асимптотическим представлением оптимально-
го управления и* в том смысле, что значение функциона-
ла вдоль траектории, определяемой управлением V, отли-
чается от оптимального на величину о(1/7'к-1) (асимп-
тотическая в слабом смысле).
Примечания.
1. Функция U в точке t—T имеет в общем случае точ-
ку разрыва.
2. В рассматриваемой задаче на вектор хг никаких
ограничений не накладывается.
9.	Пример, когда приведенная схема рассуждений
должна быть уточнена. Условие существования обратной
матрицы В-1 весьма сильное. В прикладных задачах, как
правило, управление входит не во все уравнения задачи,
и его размерность меньше размерности фазового вектора,
а это означает, что матрица В — вырожденная и рассуж-
дения предыдущего пункта должны быть существенным
образом усовершенствованы. Поясним возникшую здесь
ситуацию на простом примере.
Рассмотрим динамическую систему
• (о _ r(i) ,	1 г(«)
А- - А	A j
*	(5.34)
2
где usG^. Оба корня характеристического уравнения си-
стемы (5.34)—положительные: Х12=1±УЗ/2. Следова-
104
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
тельно, отличие рассматриваемой задачи от той, которую
мы изучали в предыдущем разделе, состоит лишь в том,
что управление входит только в одно из уравнений си-
стемы.
Частное решение уравнения (5.34) будем искать в
виде
Связь между величинами х^\ х<2) и «/, которая определя-
ется с помощью системы (5.34), будет следующей:
,(1) иг~ — х(?	— , 2	-V?’	— 24й,
v	v(l) «2 = — Х<? — 4°	,	4“ -	— 24й —4й, (5.35)
v(D „ _	г<2>	9г<г)	3 м-3 —	Ад 	 "^2		 	, 2	г(2) _ АЗ 		— 24й — 442)
и т. д.
Таким образом, и величины щ, определяющие управле-
ния, и векторы xt-2) будут функциями :
щ = Ui (4°, .... х$),
(5,36)
.... А
оо
Следовательно, функционал J (щ) = J /°(х(1), х<2), и) dt будет
т
функцией только величин х^
J (и) = Ф (4°, . • •, 4v)-	(5.37)
§ 5]
БЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ
105
Их определение сведётся к задаче отыскания минимума
X(D X(D	x(i)
функции (5.37) при ограничении х? =	+ • • • + 4;
* *	11“	'рГч
Величина х^ при этом не может быть задана произволь-
ным образом. Она определяется однозначно:
хт = ?
1=1
rpi
Таким образом, хф после решения задачи об отыскании
минимума функции (5.37) будет некоторой функцией хг':
х^^Х(х?).	(5.38)
Следовательно, ограниченное решение системы (5.34)
при фиксированном Т может быть порождено только точ-
ками некоторого одномерного многообразия S1, вдоль ко-
торого компоненты вектора хт связаны соотношением
(5.38).
Следовательно, определение х” и и*" сведётся к опре-
делению минимума функционала
т
J (х, и) =	(х, и, t)dt 2 (Хт)
о
при дополнительном ограничении
• хт е 21.
(5.39)
10.	Общий случай задачи /-устойчивости. Поскольку
в задаче /-устойчивости (х, и, t) в предположении, что
, должно стремиться к нулю при t—>оо, то имеет
смысл рассматривать тот случай, когда для достаточно
больших t уравнение (5.1) представимо в виде
х = Ах 4- Ви ф (х),	(5.40)
где А(/) и ф(х) имеют асимптотические представления
рассмотренного вида. Предположим, что матрица В(/)
также имеет вид (5.18), а вектор и имеет размерность
,п^п. Условимся считать, что ранг п%т матриц В.
106
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
равен ш, ранг Ао равен п, и все ее собственные числа
простые.
Построим частное решение в форме (5.23). Для опре-
деления Xi мы будем иметь следующее уравнение:
Л0Х! = Buv
Поскольку вектор принадлежит к некоторому множе-
ству из Rm, то и его линейное отображение Xi—A^BUi
также принадлежит к некоторому множеству размерно-
сти т. Повторяя рассуждения п. 6, мы определим х как
функцию
х = х (и4,...» uN),
причем вектор х для любого t будет принадлежать неко-
торому множеству размерности т. Обозначим его
через 2™.
Предположим теперь, что среди собственных чисел
К- матрицы До первые г имеют отрицательные действи-
тельные части. Общее решение уравнения (5.40) запи-
шем в форме:
х= ^ctyt(t) + 2 c{yi(t) + ^c-\-o
(=1	i=r+l
где yi(t) —асимптотические представления решений, со-
ответствующих собственным числам и отбросим вели-
чину o(l/TN).
Для того чтобы функция (5.41) была ограничена при
t—>оо, необходимо, чтобы Сг=О, Vf>r. Следовательно,
вектор
хт-х(Т) =	(5.42)
должен принадлежать к некоторому многообразию Q2
размерности Таким образом, вектор х\Т)=хТ не
может быть выбран произвольно.
Если г=0, т. е. все собственные числа матрицы Ао
имеют положительные действительные части, то Q2 стя-
гивается в начало координат. Тогда хг=х(Т), т. е. хт—
произвольный вектор многообразия Sm. Этот случай был
рассмотрен в двух предыдущих пунктах.
Пусть теперь г=1. Это значит, что
Хт = X (Т) +	(Т).
Ы' (541)
J 5]	БЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ
107
Если	и S’"—линейное многообразие, то ничего
нового мы не получаем, множество Й (Т), к которому дол-
жен принадлежать вектор хт, будет по-прежнему совпа-
дать с 2™. Но если то хт может быть любым эле-
ментом некоторого многообразия размерности т+1.
Аналогичная ситуация будет и в общем случае г>1.
Примечание. В каждом конкретном случае не-
трудно определить структуру множества Й(Т’). Заметим
только, что если мы возьмем точку (Г), то она не
может порождать ограниченного решения, т. е. система
(5.42) при заданном х не позволяет определить постоян-
ные Ci.
Рассмотрим теперь интеграл
Jr = и, t)dt.	(5.43)
% *
Если хт<=й(Г), то, заменяя в (5.43) x(t) и u(Z) их асимп-
тотическим представлением. (5.41), находим
со	/	г	\
Jr (и) =	С	I х (t) +	У CzZ/i+ Мт],	2 ~Т	° (_г') ’
Т	\	/=1	v1 7	1	!	)
= f/°М(0 + 2едг’2'т,/Р/‘к	<5-43')
'Г \	t I	\Т /
Вдоль любой допустимой траектории
J (х, и) = J f° (х, и, t) dt = J /° (х, u, t) dt + j* (x, u, t) dt.
Jo	?
Но допустимая траектория необходимо должна про-
ходить через точки множества Q(T), так как другие точ-
ки пространства не порождают ограниченных решений.
Но если точки х(Т)еЙ(Г), то для второго интеграла
справедлива оценка (5.43), и мы будем иметь
оо	Т
J (х, и) = j f° (х, u, t) dt = J f0 (x, u, t) dt +
/0	Jo	,	‘
+	~7’/r/ + 0(‘4r1'|’ <5-44)
T \	1=1 i=i Z J	\ t /
108
ОПТЙМАЛЬНЫЁ ПРОГРАММЫ
(гл. i
и оценка (5 44) справедлива для любых допустимых уп-
равлений, в частности, и для таких щ и с3, которые до-
ставляют минимум второму интегралу. Поэтому, обозна-
чив
°0.	( ~	N и* \
z (хт) = min Г /° х (/, и, ..., uN) +• У Ctyi (t), V р/,
“Г/Т \	7^ J
(5.45)
при условии
х (Т, и,
«лО + 2с‘^(7) =х(Л,
1=1
(5.46)
х(Г)ей(Т),
получим
(Т	/ 1 \
min J (х, и) = min (’ f°(x, и, t) dt 4- z(xr)| 4- о -]
*.*г	хт"-1/ *
(5.47)
Оценка (5.47) позволяет сформулировать следующую
теорему:
Теорема. Если u^G^,, mo управление
F(0Jf *e[0,n
( и, t>T,
где и** — решение задачи Больца о минимуме функционала
т
J [° (х, и, t)dt 4- г (хт),
а й — управление, реализующее минимум функционала
(5.45) при условии (5.46), дает слабую асимптотику оп-
тимального управления и*, т. е.
J(u’)=J(U)+o(l/TN~').
Примечание. Наши рассуждения в этом пункте не
были вполне строгими. Отбрасывая величины o(l/TN), мы
меняем, вообще говоря, структуру множеств допустимо-
сти. Поэтому в том случае, когда множество допустимо-
сти й не совпадает со всем пространством, к числу уело-
§ 5]	БЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ	Ю9
вий необходимо добавить еще условие непрерывности
функции Веллмана.
11.	Задача экономического роста. Рассмотрим теперь
задачу экономического роста — вторую из задач, сфор-
мулированных в начале параграфа.
Для упрощения выкладок рассмотрим частный случай
этой задачи: определить минимум функционала (5.4) при
условиях
х = Ах 4- Ви,	(5.48)
(5.49)
Если kt=O, то отрасль, производящая продукт, соот-
ветствующий индексу i, называется нефондообразующей.
Для фондообразующих отраслей	Следуя об-
щей схеме, введем новое управление 0, и=вх, где 0—
диагональная матрица, элементы которой удовлетворяют
условиям O^Oi^R,-, i= 1, 2,...
Будем рассматривать тот случай, когда матрицы А и
В имеют представление (5.18), a 0eG^.
Уравнение (5.48) можно теперь записать в виде
х = (44-В9)х.	(5.50)
Обозначим через X, собственные числа матрицы (Ао4~
+ Во0о). По предположению, элементарные делители
этой матрицы взаимно простые. Частные решения, соот-
ветствующие Х„ будем обозначать через y(s, t). Заметим,
что величины X, не зависят от управлений, поскольку мат-
рицу 0О мы условились считать известной.
Следуя общей схеме, частные решения системы (5.50)
мы будем разыскивать в следующем виде:
у (s, t) = exp {Kst + Xs° In t} {x0 (s) 4-
4- x. (s) r14- ... 4- xN (s) Г"). (5.51)
Для xf(s) мы получаем следующие уравнения:
(До 4- В090 — XSE) х0 (s) = 0,	(5.52)
(До 4" 5О0О — xr (s) == — (4j 4- В19о 4- ВО0Г 4- XSE) хд
(5.53)
И т. д.
но
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
Так как определитель системы (5.52) равен нулю, а
в силу предположения о том, что ее собственные числа
простые, ранг определителя равен п—1, то уравнение
(5.52) определяет вектор x0(s) с точностью до посто-
янной.
Пусть такой постоянной будет компонента xj ($).
Тогда, отбрасывая первое из уравнений системы (5.51),
мы перепишем оставшуюся систему в следующем виде:
(#22 Х$ 4“ Ьа2%2) ($) 4“ (#23 4~ Ь2з%з) (s) 4~ • • •
• • • 4" (#гп 4- bwfion) Xq (s) =	(#2i 4~ ^21^01) Хо (s), (5.54)
(fln2 4" Xo (s) 4~ • ’ • 4~ (flnn XS 4“ Xo (s) =
=	" iflni 4- bni^oi) Xq (s),
где через а[Г9 Ь\г и 9tr обозначены элементы матрицы Л/,
Bi и 0t- соответственно.
Обозначим через Аи алгебраические дополнения эле-
ментов первой строки определителя системы (5.52). Тог-
да система (5.54) нам дает
4(s) = ^^4(s), fe = 2, 3, п. (5.55)
An (s)
Рассмотрим теперь систему (5.53). Определитель этой
системы равен нулю, а ее ранг равен (п—1). Это
значит, что элементы каждого из столбцов матрицы
(Ло+Во0о—Xs£) связаны между собой одним (и толь-
ко одним) линейным соотношением, которое мы можем
записать в следующем виде:
(#п Xs 4~ Ьп901) (s) 4~ (#2i + ^2i%i) ($) 4“ • • 4“
4~ (#ni 4~ bn-19oi)Cn (s)	0*	(5.56)
Постоянные ct легко вычисляются из разложения опреде-
лителя по элементам первого столбца. Для разрешимости
системы (5.53) необходимо и достаточно, чтобы ранг ее
расширенной матрицы был равен п— 1. Для этого в свою
очередь необходимо, чтобы между компонентами вектора,
стоящего в правой части уравнения (5.53), также имело
§ 5]
БЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ
111
место соотношение (5.56). Оно будет иметь следующий
вид:
2	“Ь bkflij "Ь %о (s) ck (s) = 0,	(5.57)
k, j = 1, 2, ..., n,
где 8kj—символ Кронекера.
С помощью (5.55) мы можем выразить все компоненты
xl (j = 2 ... п) через xj. В результате xl может быть выне-
сен за знак суммы. Так как нас интересуют ненулевые
решения системы (5.52), то полученное выражение мы можем
на него сократить. Итак,
Д • (s)
У (4/ + Ь^о/ + b^i + 8k№	= 0.	(5.58)
A11(s)
Уравнение (5.58)—это линейное уравнение относитель-
но А®. Если условие разрешимости (5.58) выполнено, то
уравнение (5.53) позволяет определить вектор xt также
с точностью до произвольной постоянной.
На следующем шаге из условия разрешимости мы оп-
ределим х] (s), а затем с точностью до постоянной — век-
тор х2 и т. д.
Задавая те или другие значения постоянной xj (s),
мы получаем то или другое частное решение, соответст-
вующее собственному числу Xs.
Дальнейшая схема вполне очевидна. Мы представля-
ем общее решение в виде суммы
х = 2 С*У (s> 0
s=l
и подставляем его в интеграл
J = J (с, 2 С*У (s> 0) Р (0 dx-	(5- 59)
т
Напомним, что y(s, t) в явном виде зависит от управле-
ний Qkh и, следовательно, интеграл (5.59)—это есть
112
ОПТИМАЛЬНЫЕ ПРОГРАММЫ
[ГЛ. I
некоторая функция от cs и 6kj
J = J (clf... ,cN, QkJ).	(5. 59)
Определяя минимум этой функции при условии
S csyJ (s, Т) = Хт,
мы определим функцию z(xT).
12. Заключение. В основе рассмотрений этого пара-
графа была идея предварительной «асимптотической» об-
работки исходной задачи — ее замена некоторой более
простой задачей с конечным интегралом времени. Идея
такого предварительного анализа исходной задачи неод-
нократно использовалась в работах Вычислительного
центра АН СССР. В частности, на ней были основаны
численные методы расчета траекторий, позволившие про-
изводить численное интегрирование с большим шагом
по независимой переменной*), и ряд других задач, в ко-
торых был возможен их предварительный асимптотиче-
ский анализ.
Такой подход к решению задач с особенностями обыч-
но позволяет значительно упростить процедуру построе-
ния их решений. В случае оптимизационных задач он по-
зволил, например, избежать решения трудной вспомога-
тельной задачи построения необходимых условий типа
принципа максимума.
Заметим, что уже после того как мы построили реше-
ние, являющееся асимптотическим приближением к оп-
тимальному, не представляет никакого труда сформули-
ровать условия типа принципа максимума. Так, напри-
мер, функция ц, доставляющая минимум функционалу
т
[ /° (х, щ t)dt + 2 (ХТ)
1°
удовлетворяет следующему принципу максимума: для
любого t она доставляет максимум функции
*) См. Н.. Н. Моисеев, Асимптотические методы нелинейной
механики, «Наука», 1969.
Р(Т)-
§ 5]	БЕСКОНЕЧНЫЙ ИНТЕРВАЛ ВРЕМЕНИ	ИЗ
дЯ**
где Р (/) находятся из уравнений Р =-------и условий
дх
трансверсальности
dz	..
dxT ’
В данном параграфе была изложена общая схема ана-
лиза и, по существу, приведено несколько примеров, ил-
люстрирующих используемую технику. Эта техника мо-
жет быть существенным образом изменена. Вместо разло-
жений по обратным степеням независимой переменной
мы можем непосредственно использовать стандартную
технику асимптотического анализа систем, содержащих
большой параметр. Так, например, полагая t=Tx, мы
приведем уравнение (5.46) к виду
— = Та(т)х + Т₽(т)о-|-Т<р(х),	(5.60)
dx
где
а(т) = 4(Т(т-1));	₽ (т) = В (Г (т - 1));
(5. 61)
у(т) = и(Т(х— 1)).
Если предположить, что Т—>оо, то для исследования
уравнения (5.60) можно использовать представления об-
щего решения уравнения (5.60) в форме рядов, располо-
женных по обратным степеням Т.
Заметим, наконец, что теория, развитая для оптимиза-
ционных задач, на бесконечном интервале времени может
быть использована и для задач с особенностями для ко-
нечных значений времени, например, для задач вида
(5.62)
dt
где &>0, а 6 — фиксированное число. Построение необ-
ходимых условий типа принципа максимума для уравне-
ний (5.62) достаточно трудная задача, а условия, полу-
ченные в конечном счете, вряд ли будут достаточно эф-
фективны для получения численных результатов и все
равно потребуют на следующем этапе асимптотического
анализа. Поэтому кажется разумным сначала с помощью
асимптотических методов редуцировать эти задачи к та-
ким, где необходимые условия уже построены,
ГЛАВА II
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
ОПТИМАЛЬНЫХ ПРОГРАММ, ИСПОЛЬЗУЮЩИЕ
НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА
В этой главе мы переходим к изложению численных
методов теории оптимального управления.
Различные методы отыскания экстремума функции
или функционала f(x) принято разделять на две большие
группы: прямые и непрямые. К первой группе относятся
все методы градиентного спуска. Они основываются на
просмотре окрестности некоторой точки хп, позволяющем
найти другую точку хп+1, в которой значение функции
П*п+1) будет меньше f (хп). Эти методы не используют (во
всяком случае непосредственно) необходимых или доста-
точных условий экстремума.
Непрямые методы направлены на отыскание функции,
непосредственно удовлетворяющей необходимым или
достаточным условиям. Наибольшее значение имеют ме-
тоды, использующие необходимые условия. Задача отыс-
кания минимума функции с помощью необходимых усло-
вий сводится к задаче отыскания корней некоторой функ-
ции, а задача расчета оптимальной программы — к реше-
нию краевой задачи для системы обыкновенных диффе-
ренциальных уравнений. Эти методы в настоящее время
получили широкое распространение. Они просты для про-
граммирования и позволяют использовать простые стан-
дартные программы. В то же время они обладают и це-
лым рядом недостатков. Один из них — это ограниченная
область применимости. Задача становится практически
неразрешимой, если необходимые условия формулируют-
ся относительно сложно (например, в случае фазовых ог-
раничений). Другой недостаток состоит в том, что функ-
ция или точка, удовлетворяющая необходимым условиям,
это всего лишь претендент на право называться реше-
нием.
Для того чтобы убедиться в том, что найденная функ-
ция является искомым решением, надо еще проверить,
удовлетворяет ли она достаточным условиям экстремума.
Поэтому кажется более естественным строить вычисли-
§ 1] ПРОСТЕЙШИЕ СПОСОБЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 115
тельные процедуры, опираясь не на необходимые, а на
достаточные условия. Однако все попытки, которые дела-
лись в этом направлении, не дали еще сколько-нибудь
удовлетворительного результата: несколько задач, ре-
шенных с помощью достаточных условий, демонстрируют
скорее изобретательность авторов, а не возможности ме-
тода. Поэтому в данной монографии мы ограничимся из-
ложением только тех численных методов, которые исполь-
зуют необходимые условия.
Заметим, что разделение вычислительных методов на
прямые и непрямые довольно условно. Практика расче-
тов показывает целесообразность сочетания обоих под-
ходов.
§ 1.	Простейшие способы решения краевых задач
1.	Редукция задачи расчета оптимальных программ
к задаче отыскания корней трансцендентной функции.
В предыдущей главе мы установили, что необходимые ус-
ловия (например, принцип максимума Л. С. Понтрягина)
позволяет нам сформулировать некоторую краевую зада-
чу. Искомая экстремаль должна содержаться среди реше-
ний этой краевой задачи. И проблема расчета оптималь-
ных программ, вероятно, не была бы сложной, если бы мы
умели достаточно хорошо решать краевые задачи для
обыкновенных дифференциальных уравнений. По суще-
ству же мы умеем численно решать только задачу Ко-
ши—определять траекторию по начальным данным. Но
в рассматриваемом случае мы имеем на левом конце все-
го лишь п условий*), хотя система имеет порядок, рав-
ный 2п. Возникает проблема, каким образом, используя
наше умение решать задачу Коши, построить решение
краевой задачи? В этом параграфе мы остановимся на
одной из возможностей решить эту проблему и поясним
ее на примере.
Пусть ставится задача об отыскании управления и(/),
которое переводит систему
х — f (х, и, t)	(1.1)
) Имеется в виду задача с фиксированным левым концом.
116
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЁТА
[ГЛ. II
за время Т —t0 из одного фиксированного состояния х0
в другое фиксированное состояние хт при условии, что
интеграл
J (х, и) = J F (х, щ t) dt	(1. 2)
^0
принимает минимальное значение. Эта задача сводится
к отысканию функций х1, ..., хп, фь ..., фп, удовлетво-
ряющих системе уравнений
х* == fl (х1, ... , хп, и1, ... , um, t),
+ <L3>
/==1
= ф/ (X1, ... , Хп, U1, ... , Um9 t, фь ... , фп),
i = 1, ..., п,
где u = u(x, ф, t) в каждый момент определяется из усло-
вия максимума функции Гамильтона.
Решение системы (1.3) должно удовлетворять 2п
условиям
Х‘ (to) = Хо , xz (Т) — хт,
Для того чтобы построить интегральную кривую си-
стемы (1.3), мы должны тем или иным способом задать
п чисел фг(4)=ам Построив по значениям 4 и а,- тра-
екторию системы (1.3), мы получим при t — T некоторые
значения координат хг(Г). В общем случае, разумеется,
они не будут равны х1т. Введем величины, которые мы
будем называть невязками
х‘ = х1 (Т) -4-.
Очевидно, что невязки будут функциями начальных
значений импульсов
X* = Х‘ (ctj, ct2,, яга),
(1- 5)
i — 1, 2,..., п.
Для того чтобы решить поставленную задачу отыска-
ния оптимальной программы, мы должны найти числа
§ 1] ПРОСТЕЙШИЕ СПОСОБЫ решения краевых задач 117
аь.--, ап, которые обращают функции X1 в нули. Итак, мы
свели исходную вариационную задачу к задаче отыска-
ния нулей функций Хг(ав ап). Заметим, что функцио-
нальная зависимость между величинами № и аг задана
опосредствованно. Для того чтобы по заданным значени
ям «!, ..., ап найти X1, ..., Хп, надо построить численное ре-
шение задачи Коши системы 2п-го порядка (1.3), причем
на каждом шаге численного интегрирования определять
управления и1 (0» •••, ^w(0 из условий максимума функ-
ции Гамильтона, т. е. из решения некоторой вспомога-
тельной задачи нелинейного программирования.
Редукция задачи определения оптимальной програм-
мы к задаче отыскания нулей некоторой системы функ-
ций при другом задании краевых условий для системы
(1.3) проводится совершенно аналогично*).
2.	Метод Ньютона. Для отыскания корней функций
существует много разнообразных методов. Однако для
численного решения конкретных задач наиболее широко
используется метод Ньютона — по-видимому, один из
самых старых способов отыскания нулей трансцендент-
ных функций.
Пусть мы имеем некоторое нулевое приближение —
систему чисел {а0,}. Этой системе чисел соответствуют
величины
Х0 = Х‘ (ctoi, ®02, ••• , «0«)-
Положим
а1/ = ао/ 4“ ^1/»
Считая величины 6^ малыми, примем
Х1 = Х‘(а01 + 6п,...,а0„ + й1п) = Х'+4 d1/f
/=1 \ i / а==а0
I = 1, 2,..., П.
Выберем теперь величины бо- так, чтобы правые части
этих равенств обратились в нуль. Это нам дает п линей-
ных уравнений относительно п величин 6ц, ..., 61Л. Введем
*) Система невязок (1.5) в случае, когда на концах заданы не
все координаты, дополняется соотношениями, получающимися из ус-
ловий трансверсальности после исключения произвольных постоянных.
118
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
матрицу А (а):
л / X (dxi\ I
4(а) = — ,
у I
i,j = 1,..., п.
Будем обозначать А(ак) через Ак. Тогда уравнение от-
носительно вектора 6i= (би, ..., б1п) запишется так:
A06i = Хо,
или	(1-6)
61 = — Ао-1Хо.
Затем в качестве нового приближения принимаем век-
тор «0 4-6,=а, и повторяем процесс. Общая схема итера-
ций будет такой:
6/> = Ak-iXk-i,
(1-7)
ak = ak4 4- 6ft.
На каждом шаге итерации нужно вычислять матрицу А,
причем производные мы должны находить численно. Это
требует решения «4-1 задач Ко-
ши для системы (1.3), порядок
которой равен 2п.
Метод Ньютона иногда на-
зывают методом касательных,
основываясь на следующей его
геометрической интерпретации.
Предположим, что X и а — это
скаляры, и речь идет об отыс-
кании корня функции одной пе-
ременной Х(а). Рассмотрим
рис. 1.1. В точке (а0,-X») прове-
дем к кривой Х(а) касатель-
ную; уравнение касательной
имеет вид
z (а) = X (а0) 4- X' (а0) (а — а0).
Точку пересечения прямой и(а) с осью абсцисс примем
в качестве нового приближения а(. Значение at будет
определяться формулой (1.7), где Ао-‘=1/Х'(ао). Таким
§ 1] ПРОСТЕЙШИЕ СПОСОБЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ Ц9
образом, геометрически процесс вычислений по методу
Ньютона можно представить себе следующим образом.
Задаем а0 и вычисляем Х0 = Х(а0), проводим в этой точ-
ке касательную и точку ее пересечения с осью абсцисс
принимаем в качестве нового значения величины а=а4.
Вычисляем затем Xi = X(ai), проводим касательную и
точку ее пересечения с осью абсцисс принимаем в каче-
стве а2 и т. д.
3.	О сходимости метода Ньютона и его модификациях.
Если начальное приближение а0 выбрано достаточно
близко к значению корня а, то метод Ньютона сходится
очень быстро и удобен для практического использования.
Однако если точка а0 не находится в области «притяже-
ния» корня, то метод Ньютона расходится и в описанном
виде непригоден для практического использования. Очень
легко привести примеры, когда метод Ньютона приводит
к расходящейся последовательности итераций.
На рис. 1.2 дан пример такого расходящегося процес-
са при отыскании корня функции X=arctga; как легко
убедиться, неудачный выбор начального приближения
«о (| а0| <Х) *) приводит к тому, что каждое следующее
значение переменной а отстоит все дальше и дальше от
значения корня.
*) Л — корень уравнения 2a = (1 + a2) arctg a.
120
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
В последние годы было предложено много модифи-
каций метода Ньютона, которые способны преодолеть
указанную трудность. Одна из таких модификаций, по-
видимому, наиболее широко используемая, состоит в
замене первоначальной итерационной схемы (1.7) сле-
дующей:
Ctn+i	1 fan) X fan)>
где хп—некоторый скалярный множитель, не превосхо-
дящий 1. Существуют различные рецепты выбора этого
множителя. Но все они, так или иначе, исходят из требо-
вания, чтобы
|!Х(ап+1)||<||Х(а„)||.
В качестве нормы ||Х|| принимают либо max|Xz|, либо
(W)2)7’.
Рассмотрим рис. 1.3, где изображена та же кривая,
что и на рис. 1.2.
Обозначим через aj значение а, полученное по формуле
(1.7), т. е. по схеме простого метода Ньютона (х0 = 1)-
Как видно из рисунка | X (а*) ] | X (а0) |. Поэтому в качестве
§ 1] ПРОСТЕЙШИЕ СПОСОБЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 121
нового приближения а выберем значение
ai = а0 -j —
' л
1
т. е. положим х0 = —. Мы видим, что а1 находится уже
в окрестности корня, где сходится простой метод Ньютона
(х„ =1, п = 1, 2,...). Таким образом, выбор множителя
х0 ~	, хп = 1, п = 1, 2,... , сделал расходящийся процесс
сходящимся.
Изложенные соображения привели к следующей (ны-
не широко распространенной) процедуре использования
метода Ньютона.
Задаем вектор а0 и вычисляем по формуле 6Х= — Аё1 Хо.
Вычисляем
(хх = а0 A* бх
и
Если окажется, что || Хх ||	|| Хо ||, то принимаем ах =
— а0 + 6Х и делаем следующий шаг (т. е. вычисляем —
— — A^XJ. Если || X* ||	|| Хо ||, то вычисляем
<4 = а0 + —-бх
И
JCi = X fttg -|~ —дД.
\	2 J
Если окажется, что || X* ||	||Х01|, то принимаем
, 1 я
=	+ —Si
А
и делаем следующий шаг.
В противном случае еще раз уменьшаем величину
* 1
т. е. берем ах = а0 4-и т. д.
4
Применение подобной процедуры значительно расши-
ряет возможности использования метода Ньютона, одна-
ко и она не дает в общем случае гарантии сходимости
122
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. 11
метода Ньютона для произвольно выбранного начально-
го приближения а0.
Вероятно, первыми, кто начал широко использовать
эту модификацию метода Ньютона в задачах оптималь-
ного управления, были В. К. Исаев и В. В. Сонин *). В на-
чале 60-х годов целый ряд трудных вариационных задач
динамики космических аппаратов был решен В. Н. Лебе-
девым, который также широко использовал различные
модификации метода Ньютона **).
4. Обсуждение. Несмотря ни на какие модификации,
применение метода Ньютона (или другого метода отыска-
ния корней) невозможно без удовлетворительного перво-
го приближения. Если рассмотреть все задачи, которые
были решены с его помощью, то мы увидим, что успех их
решения определяется в первую очередь удачным первым
приближением. Заметим, что вопрос о первом приближе-
нии обычно бывает достаточно труден, поскольку надо
подобрать начальные значения импульсов, для которых
нет (в общем случае) хорошей динамической интерпрета-
ции. Итак, необходимость предварительного выбора
первого приближения, которое гарантировало бы схо-
димость,— первый недостаток этого подхода, который
связан с редукцией вариационной задачи к краевой и ее
последующим сведением к задаче отыскания нулей
трансцендентной функции.
Вторая трудность, с которой сталкиваются при реа-
лизации изложенной техники, связана с неустойчивостью
«решения». Мы имеем дело с уравнениями, правые части
которых гарантируют непрерывную зависимость решения
от начальных данных. Это значит, что для достаточно
малых а (мы продолжаем пользоваться обозначения-
ми п. 1) с большой степенью точности выполняется
условие
дХ = £6а,
где 6Х и 6а — приращения соответствующих величин.
*) В. К. И с а е в и В. В. С о н и н, Об одной модификации ме-
тода Ньютона численного решения краевых задач, ЖВМ и МФ 3,
6, 1963.
**) В. Н. Лебедев, Расчет движения космического аппарата
с малой тягой, Серия «Математические методы в динамике косми-
ческих аппаратов», выл. 5, ВЦ АН СССР, 1963.
§ 1] ПРОСТЕЙШИЕ СПОСОБЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 123
Коэффициент пропорциональности k зависит, в частности,
от величины интервала интегрирования Т. Если движение
неустойчиво, то при увеличении Т величина k неограни-
ченно возрастает. На практике часто имеет место подоб-
ная ситуация: очень малому значению ба соответствует
машинная бесконечность (т. е. k очень велико). В этом
случае никакие модификации метода Ньютона реализо-
ваны быть не могут.
Проблема сходимости метода Ньютона и его модифи-
каций была предметом многочисленных исследований.
Содержание математических результатов примерно сле-
дующее*). Если начальное приближение выбрано доста-
точно хорошо, то метод Ньютона сходится как геометри-
ческая прогрессия. Однако для реального счета этого еще
мало. Если интервал интегрирования [4, 7] достаточно
велик, то необходимо еще, чтобы решение было устойчи-
вым, т. е. чтобы было возможным реализовать вычисле-
ния невязок. Вот почему метод Ньютона, несмотря на
всю простоту описания, удобство использования и про-
граммирования, не смог сделаться универсальным сред-
ством расчета оптимальных программ для того класса
задач оптимального управления, при решении которых
может использоваться принцип максимума Л. С. Понт-
рягина.
5. Случай задач большой размерности. Применение
метода Ньютона требует на каждом шаге решения систе-
мы линейных уравнений (1.6), которую мы запишем в
виде
Л5 + X = 0.
Если порядок системы достаточно высокий, то вопрос
о выборе способа решения уравнения (1.6) становится
уже существенным с точки зрения построения экономной
схемы расчета.
При реализации метода Ньютона нет необходимости
на каждом шаге решать уравнение (1.6) точно. Поэтому
для его решения имеет смысл использовать итерационные
методы. Среди этих методов выделяется своей простотой
и удобством метод сопряженных градиентов. Без обосно-
*) См., например, М. С. Березин, Н. П. Жидков, Методы
вычислений, «Наука», 1966.
124
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
вания (которое читатель может найти в курсах алгебры)
приведем порядок расчетов *):
1.	Задаем произвольным образом начальное прибли-
жение б0, вычисляем нулевую невязку г0:
—г0 =	-j- X;
выбираем вектор s4:
Si = r0.
2.	Полагаем бх = б0 + ах$х, где скаляр ах определяется
по формуле ах =	.
(si> Л$1)
3.	Вычисляем невязку rt:
—= Лбх + X или rx = ra — AaLslt
и выбираем вектор s2 по формуле s2 = rt -|- bxsx, где &х =
= (n, Л$1)
(slt ‘
4.	Полагаем б2 = бх + a2s2, где а2 = -Г1’ s^-, и т. д.
(s2, Л$2)
Если матрица А симметрична и положительно опре-
деленна, то описанная процедура заканчивается не более
чем через п шагов. Это значит, что обязательно найдется
такое i^n, где п — размерность вектора б, что г«=0.
В процессе проведения расчетов задаются некоторым
числом р, и вычисления прекращаются при достижении
неравенства
Iln-IKP.
§ 2. Задачи оптимального управления, сводящиеся
к краевым задачам для систем
линейных дифференциальных уравнений.
Перенос граничных условий
1.	Предварительные замечания. Методы, которые об-
суждались в предыдущем параграфе, приводили к следу-
ющей схеме расчета: задавая тем или иным способом не-
*) Д. К. Фаддеев, В. Н. Фаддеева, Вычислительные ме-
тоды линейной алгебры, Физматгиз, 1963.
§ 2]	СВЕДЕНИЕ К КРАЕВЫМ ЗАДАЧАМ	125
достающие данные Коши для /7-системы*), мы отыски-
вали точное решение этой системы. Полученные конечные
значения не удовлетворяли краевым условиям. Инфор-
мация о величинах невязок позволяла определить новые
значения недостающих начальных условий и т. д.
К рассматриваемой проблеме можно подойти с иных
позиций, а именно, отыскивать решение среди множества
тех функций, которые удовлетворяют краевым условиям.
Такие решения можно находить методами, основанными
на переносе граничных условий — методами прогонки.
Эта идея высказывалась независимо рядом авторов
(В. Н. Лебедев, Н. Н. Моисеев, Р. П. Федоренко и др.),
и на ее основе были предложены разнообразные схемы
решения вариационных задач.
В этом и в следующем параграфах излагаются мето-
ды решения задач оптимального управления, использую-
щие идеи переноса граничных условий. Приводимая ме-
тодика была разработана в ВЦ АН СССР в начале
60-х годов. Рассмотрение мы начнем с анализа одной из
простейших задач теории оптимального управления.
2.	Линейные задачи с квадратичным функционалом.
Рассмотрим управляемую систему, движение которой
описывается системой дифференциальных уравнений
х = Ах 4- Ви,	(2. 1)
где А и В — матрицы, их элементы — некоторые задан-
ные функции времени.
В скалярном виде система (2.1) запишется так:
п	т
X1 = 2 ацх1 н- 2 bijtiJ.	(2.2)
/=1	/=1
Таким образом, матрица А — это квадратная матрица
(пХп), а матрица В — прямоугольная, имеющая п
строк и т столбцов. На управление и никаких ограниче-
ний не накладывается.
*) Этим термином часто называют систему 2п уравнений, полу-
ченную в результате использования принципа максимума Л. С. Понт-
рягина.
126
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
(ГЛ. II
Пусть начальное состояние системы (2.1) фиксиро-
вано:
х(0) = хо.	(2.3)
Рассмотрим две задачи:
а)	Задача а. Найти управление, переводящее си-
стему (2.1) за время Т из состояния (2.3) в состояние
х(Т) = хг	(2.4)
так, чтобы функционал
т
(2.5)
о i
принимал на оптимальной траектории минимальное зна-
чение.
б)	Задача р. Найти управление, переводящее си-
стему (2.1) за время Т из состояния (2.3) в состояние
(2.4) так, чтобы функционал
т
J = Л Сцх1х1 + 2 ЛцхМ + 2	} dt
о i,i	l.l	i,!
(2.6)
достигал на оптимальной траектории своего наименьше-
го значения.
Функционал (2.5) является, очевидно, частным слу-
чаем функционала (2.6).
Рассмотрим сначала задачу а. Составим для нее
функцию Гамильтона
Н = (Ах, 1|)) + (Ви, чр) — 5 («о2-	(2. 7)
I
Уравнение для импульсов будет иметь следующий вид:
4> = —	(2.8)
Здесь Л* означает транспонированную матрицу.
Заметим, что уравнение (2.8) может быть проинте-
грировано независимо от уравнения (2.1).
§ 21	СВЕДЕНИЕ К КРАЕВЫМ ЗАДАЧАМ	127
Для определения управления вычислим
^- = ЗМ.-2«’ = 0,
откуда us = — 2 bistyi или
2 i
и=±.В^.	(2.9)
Подставляя (2.9) в (2.1), получим
х = Ах-}-	(2.10)
где
в = — вв*.
2 
Итак, задача а свелась к краевой задаче для системы
линейных дифференциальных уравнений (2.8) и (2.10),
порядок которой равен 2п.
Совершенно аналогично рассматривается и общий
случай квадратичного функционала:
Н — (Ах, ф) 4- (Ви, ф) — (х, Сх) — (х, Du) — (и, Ей). (2.11)
С, D и Е — это матрицы, фигурирующие в (2.6).
Для импульса ф мы будем иметь уравнение
ф = —	= — Д’ф + Сх+ Du, (2.12)
гдеС=С+С*, С* — транспонированная матрица.
Управление мы определим из условия
^=В*ф — D*x — Eu = 0,	(2.13)
где Ё=Е+Е*. Отсюда
и = £^1(В’ф — D'x).	(2.14)
Подставляя (2.14) в уравнения (2.1) и (2.12), мы полу-
чим следующую систему 2п-го порядка:
х = Мгх + Л\ф, ф = М$х 4- Уаф, (2.15)
128
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
где
Мх = А — ВЕ~ЧУ, А\ = ВЁ~1В*,
(2. 16)
М2 = С — DE^D*, N2 -= — А* + DE~lB\
Таким образом, и в самом общем случае квадратичного
функционала задача расчета оптимальной программы
для системы (2.1) сводится к краевой задаче для линей-
ной системы (2.15).
3. Одна задача динамики космических аппаратов.
Рассмотрим движение материальной точки в поле одного
притягивающего центра в предположении, что к ней при-
ложена некоторая сила. Уравнения движения имеют вид
их ,
х = — ^ + «1»
(2- 17)
и,у .
# = —^-+“2-
Г3
Здесь х и у — декартовы координаты точки, г=У%2+//а,
ц— гравитационная постоянная, щ и и2— составляющие
ускорения от тяги двигателя. При известных условиях
уравнения (2.17) описывают движение космического
аппарата, снабженного двигателем малой тяги*). Пере-
менные и и2 могут рассматриваться как управляющие
воздействия. Если двигатель идеально-регулируемый, то
оптимальному в смысле энергетики переходу из одного
состояния в другое соответствует минимальное значение
интеграла
т
+	(2.18)
to
Поставим для системы (2.17) задачу коррекции (по-
скольку предполагается, что тяга двигателя мала, то наи-
более естественно использовать подобные двигатели для
исправления малых ошибок). Предположим, что имеется
некоторое иевозмущенное свободное движение аппарата,
*) См. Г. Л. Г р о д з о в с к и й, Ю. Н. И в а н о в, В. В. Т о к а-
р е в, Механика космического полета с малой тягой, «Наука», 1966.
§ 2]	СВЕДЕНИЕ К КРАЕВЫМ ЗАДАЧАМ	129
которое описывается уравнениями
У = ~^	(2.19)
и при t — to удовлетворяет условиям:
х(/0) = х0,
(2-2°)
dx (70) _ ~	dy (Q _ ~
~ ~ Х°’	~ ~ У°-
Пусть в начальный момент реальное состояние системы
отличается от (2.20)
х(4)==х0,	!/(Q = 1/o>
(2.21)
dx (t0) _ ' dy (to) __ •
~~Xot ~~yot
и это отклонение мало, т. е. величины с тильдой мало от-
личаются от величин без тильды.
Для компенсации ошибки включаются двигатели, и
возмущенное движение будет описываться уравнениями
(2-17).
Поставим задачу отыскать такие управления щ. и и2,
чтобы за время Т —t0 была устранена ошибка в началь-
ных условиях.
Считая, что х и у мало отличаются от х и у, линеари-
зуем задачу. Для этого положим
£i = x —х, = — У-	(2-22)
Используя (2.22), (2.17) и (2.19) и отбрасывая величины
порядка ill и более высокого, мы придем к системе
линейных уравнений следующего вида:
ii= ^ii^i + aiaHi + «х»	(2.23)
т]1 = <^21В14" ^aaHi -|-ч2,
где a{j — это некоторые известные функции времени.
. Обозначим еще
1 = U П1 = Па-
5 Н. Н. Моисеев
130
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
(ГЛ. 11
Теперь систему (2.23) можно переписать так:
~	— ЯцВт 4"	4”
(2.24)
Hi = 4а» Па = «2111 + <Wli 4- %
Итак, мы пришли к следующей задаче. Определить
управления и, и и2, переводящие систему за время Т—to
из состояния
IJ; (^«) = Bio» (4) = Вао> Hl (4) = 4io> Ла (^о) = Пао
в начало координат
S1(D = O, &(Т) = 0, Т11Ю = О, г1а(Л = 0
таким образом, чтобы функционал (2.18) достигал ми-
нимального значения.
Задача, к которой мы пришли, является с точностью
до обозначений задачей а.
Можно привести еще много других примеров задач,
возникающих в технике, которые сводятся к линейным
задачам оптимального управления с квадратичным функ-
ционалом. Однако основное значение рассматриваемого
класса задач состоит в том, что он широко используется
при построении разнообразных итерационных способов
решения сложных задач оптимального управления. К это-
му вопросу мы еще вернемся.
4. О переносе граничных условий. Линейные урав-
нения— это единственный класс дифференциальных
уравнений, для которых разработаны регулярные мето-
ды решения краевых задач.
Рассмотрим уравнение
х = Ах 4- f	(2.25)
и предположим, что элементы матрицы А (величины atj)
uf — некоторые функции времени. Методы решения крае-
вых задач для уравнения (2.25) основаны на идее пере-
носа граничных условий из одной точки в другую.
Предположим, что вектор-функция x(t) —решение
уравнения (2.25) — должна удовлетворять условию
(/0, X (t0)) =	lor х{ (to) = а0.	(2.26)
i
j 2]	СВЕДЕНИЕ К КРАЕВЫМ ЗАДАЧАМ	131
Мы будем говорить, что условие (2.26) перенесено из
точки to в точку t, если удастся так определить незави-
симо от х вектор-функцию l(t) и скалярную функцию
a(i), удовлетворяющие условиям
1	=	(2.27)
а (4) = «о,
что для любого момента
(/(0,х(0) = а(0-
Легко убедиться, что для этой цели можно использо-
вать сопряженное уравнение. Этим термином мы услови-
лись называть уравнение
/ = — АП.	(2.28)
Умножим скалярно обе части уравнения (2.25) на I,
а уравнения (2.28) — на х и сложим. Тогда, так как
(Ах,1) ~ (х, А*1),
мы получим
-J- (I, х) = xl 4-- 1х = (/, /),
at
откуда
(i, *)/=/, = (/, x)t==h + J (/, f) dt.
^0
Итак, мы получили следующую теорему:
Теорема. Если l(t) — решение задачи Коши (2.28),
(2.27), а функция а(/) удовлетворяет уравнению
a =	(2.29)
и условию a(Zo)=ao, то вектор-функция x(t) для любых
t удовлетворяет условию
(/(/), х (/)) = a (Z).	(2.30)
Доказанная теорема позволяет любое линейное крае-
вое условие типа (2.26) перенести из точки х0 в любую
5*
132
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
точку. Для этого достаточно решить одну задачу Коши
для сопряженной системы и одну задачу Коши для ска-
лярного уравнения (2.29). Итак, любая краевая задача
для линейных дифференциальных уравнений с условия-
ми (2.26) может быть сведена к задаче Коши: для этого
достаточно перенести все краевые условия в любую из
точек отрезка |70, Т] в том числе и в начальную точку
траектории.
5. Метод А. А. Абрамова. Несмотря на логическую*
простоту результата, изложенного в предыдущем разде-
ле, машинная реализация описанной процедуры может
встретить значительные трудности. Это связано с тем,
что мы можем столкнуться с быстрорастущими решения-
ми исходной или сопряженной системы. В этом можно
убедиться на очень простом примере. Пусть исходное
уравнение скалярное, —ax+f, где а(/)>0; тогда со-
пряженное уравнение l=al будет иметь экспоненциально
растущее решение, и фактически вычислить на машине
функцию l(t) окажется невозможным. В этом случае мы
говорим, что процедура переноса граничных условий
является неустойчивой.
Однако, эта трудность, как показал А. А. Абрамов,
легко преодолима благодаря тому, что аналитические
продолжения l(t) и а(/) заведомо не единственны. Если
это так, то естественно поставить вопрос — нельзя ли так
построить вектор-функцию /(О, чтобы ее модуль был по-
стоянной величиной, равной |/(f0) |?
Умножим равенство (/, х) =а на некоторую функцию
m(Z), т(/, х) — та, и обозначим
где /(7) по-прежнему удовлетворяет сопряженному урав-
нению (2.28).
Составим уравнение, которому удовлетворяет вектор-
функция g(t):
g = ml + Im = ml — тАЧ,
но l—glm, поэтому
•	л*
S = — g— Ag.
Lm
СВЕДЕНИЕ К КРАЕВЫМ ЗАДАЧАМ
133
Выберем m(t) так, чтобы (g, g) = const, т. е. чтобы
(g, g) =0- Это Дает уравнение для m(t):
т =_ (g, A*g) _ (Ag, g) .	(2.31)
m (g,g)	(g<g) '
Поэтому вектор-функция g(0 удовлетворяет уравнению
g=^g-4’g.	(2.32)
(g> g)
Так как, с другой стороны, g(t)=m(t)l(t), то g(M =
= т(£0)/(/0).
Но функция m(t) определяется уравнением (2.31) с
точностью до константы, поэтому мы можем принять,
что w(M = 1- Тогда вектор-функция g(t), определенная
уравнением (2.32), удовлетворяет начальному условию
g(f0) =1<> и, следовательно,
(g (/о), х (/„)) =	(2.33)
Нам осталось определить а(0- Полагаем, как и прежде,
a(0 = (g(0,x(0),	(2.34)
найдем а= (g,, x) + (g, х) и, подставляя g и х из формул
(2.32) и (2.25), получим
a = ^a + (g.f).	(2-35)
Таким образом, перенос граничного условия (2.26) из
точки t0 в точку t совершен по формуле (2.34), где g(t)
определено как решение задачи Коши для уравнения
(2.32) с начальным условием g(tQ)=lOi а функция a(t)
как решение задачи Коши для уравнения (2.35) с началь-
ным условием а(/0) = <х0-
Полученные результаты сформулируем в виде сле-
дующей теоремы:
Теорема (А. А. А б р а м о в) *). Если g(t) — реше-
ние задачи Коши для системы (2.32) с начальным
*) А. А. Абрамов, О переносе граничных условий для систем
линейных обыкновенных дифференциальных уравнений, ЖВМ и МФ
1, № 3, 1961. Аналогичный результат без каких-либо ссылок на ра-
боты А. А. Абрамова опубликован Б. Е. Чупруном в журнале «Ав-
томатика и телемеханика», № 9, 1967.
134	ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА	[ГЛ. II
условием
а функция «(/) удовлетворяет уравнению (2.35) и усло-
вию
«(/о) = «о,
то вектор-функция x(t) для любых t удовлетворяет ус-
ловию
(g(0, х(/)) = а (О,
причем ||g|| = 10 для всех t.
Теорема А. А. Абрамова позволяет избежать трудно-
стей, связанных с существованием быстрорастущих
функций /(0, и сделать процедуру переноса граничных
условий (именуемую иногда прогонкой) устойчивой.
В отличие от того случая, который был рассмотрен
в предыдущем разделе данного параграфа, для переноса
граничных условий нам приходится решать задачу Коши
уже для нелинейных дифференциальных уравнений. За-
метим, однако, что переход от линейных уравнений к не-
линейным практически не усложняет процедуры числен-
ного решения.
6. Решение краевых задач методом переноса гранич-
ных условий. Рассмотрим дифференциальное уравне-
ние (2.25) и поставим для него следующую краевую
задачу:
х‘ (4) = <4, i == 1,2,..., k,
(2.36)
х1 (Г) = (V, i = k + 1,..., n.
Перенесем граничные условия из точки t = ta в точку
i—T, используя метод А. А. Абрамова. Для этого надо
прежде всего ввести векторы (i=l, 2, ..., k). Эти век-
торы удовлетворяют одному и тому же дифференциаль-
ному уравнению (2.32) и следующим граничным усло-
виям:
g‘(/0) = /z(A,),
причем
/ц(/о)
О, если
1, если
!>
i = j-
§21
СВЕДЕНИЕ К КРАЕВЫМ ЗАДАЧАМ
135
Определив векторы gift), мы определим скаляры а1'.
Они удовлетворяют следующей задаче Коши:
* 	ё()	1	/ А-	I Г, \ i
а1 = ------- а‘ + (g6 /), а! (/0) = а0.
(«Гр £?
Определив эти функции, мы можем составить недостаю-
щие условия для функций хг(Т) при t—T (i= 1, 2, ..., k):
п
^gil(T)xl(T) = i = (l,2,...,fe).	(2.37)
/=i
Используя (2.36), равенства (2.37) можно переписать в
следующей форме:
*	п
%gij(T)x}(T) = a‘(T)- 2 gts(T)V,
j=l	s=k-\-i
(2.38)
i — 1,2,..., k.
Разрешив эту систему линейных алгебраических уравне-
ний относительно хДТ) (/=1, 2, ..., k), мы получим пол-
ную систему условий Коши для вектор-функции х при
t = T. Интегрируя теперь систему (2.25) от t = T до t-t*,
мы найдем искомое решение краевой задачи.
Итак, решение краевой задачи (2.36) для системы
n-го порядка сводится к решению ряда задач Коши, об-
щая размерность которых равна kn + k + n. В самом деле,
для того чтобы получйть решение, мы должны проинте-
грировать слева направо от t9 до Т k векторных уравне-
ний (2.32) размерности п и k скалярных уравнений
(2.35), а также одну систему (2.25), порядок которой ра-
вен п справа налево от Т до
Примечание. Мы решали краевую задачу по сле-
дующей схеме. Сначала перегнали все данные Коши с
левого конца траектории на правый конец, и эта проце-
дура всегда устойчива. Далее мы решали задачу Коши
справа налево для системы (2.25). Эта процедура может
оказаться неустойчивой. В таком случае нам следует пе-
регнать сначала все условия Коши справа налево (эта
процедура всегда устойчива, поскольку Hg'll =const, а за-
тем решать задачу Коши для системы (2.25) слева на-
право).
136
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. И
7. Одновременный перенос нескольких граничных ус-
ловий.
Итак, мы видим, что перенос граничных условий воз-
можно организовать так, чтобы задачи Коши, которые
приходится решать в процессе переноса граничных усло-
вий, не имели быстрорастущих решений. Однако на этом
все подводные камни, которые могут встретиться при
эффективной реализации счета, еще не обойдены.
В предыдущем пункте мы рассмотрели одну из ти-
пичных краевых задач и подробно описали процедуру
ее сведения к задаче Коши. Мы видели, что, помимо ре-
шения задач Коши для вектор-функций gi(t) и скаляр-
ных функций а'(0, мы должны еще суметь разрешить
систему линейных алгебраических уравнений (2.38).
Матрица этой системы ||gj| может оказаться плохо
обусловленной, и найти фактическое значение величин
х’(Т) 'без больших ошибок мы не сможем.
Согласно построению векторы gt(ta) (t = l, 2, ..., k)
линейно независимы. Более того, они образуют ортого-
нальную систему векторов. Однако с течением времени
скалярные произведения (gf, gt) могут все более и более
отличаться от нуля. Описанная ситуация является ти- !
личной, и если интервал Т —19 достаточно велик, то мо- j
жет оказаться, что изложенную в предыдущем пункте ’
схему расчета реализовать на ЭВМ будет невозможно. (
С этой трудностью можно справиться, используя ту же
идею, которая нам позволила избежать быстрорастущих .
решений в задаче Коши. '		|
Предположим, что первые из граничных условий |
(2.36) заданы в виде
Q.*x(t0) = ct0;	'	(2.39)
а0 — это некоторый ^-мерный вектор, матрица Р = ||9я1|
(i = l, ..., k, j=l, ..., n) — это прямоугольная (nXfe)-
матрица (n строк и k столбцов), a Q’=||^ || — соот-
ветственно (^Хп)-матрица, причем q^ =дц.	j
Запишем условия (2.39) в скалярном виде:	|
2 Ч*1х1 (4) = “о. i = 1,2,..., k.	(2.40) i
l~i	I
§ 2]
СВЕДЕНИЕ К КРАЕВЫМ ЗАДАЧАМ
137
Первое из условий (2.36) является частным случаем
(2.40), когда матрица Q* имеет вид
1 о ... о ... о
О 1 ... о ... о
k строк.
О о ... 1 ... о
k столбцов,
п столбцов
Предположим, кроме того, что детерминант матрицы
Q*Q—не очень малое число. В частном случае задания
условий в форме (2.36) матрица Q*Q будет единичной.
Будем говорить, что условие (2.39) перенесено из
точки t — to в произвольную точку t=T, если мы можем
независимо от х определить (^Хп)-матрицу G(t) и век-
тор а(0> обращающиеся при i=t9 в Q* и а0 соответствен-
но, так что при t=T вектор-функция x(t) удовлетворяет
условиям
G(T)x(T) = a(T).	(2.41)
Проведем рассуждения, аналогичные тем, которые
были проведены в п. 5. Будем искать матрицу G(t) в
форме
С(0 = Л4(/)Ф(0,	(2.42)
где M(t) —некоторая невырожденная (kxk)-матрица,
которую мы определим ниже, a (kXn)-матрица Ф(/)
удовлетворяет уравнению
ф -j- ФА = 0.	(2.43)
Составим уравнение, которому удовлетворяет матрица
G(t). Дифференцируя (2.42) и используя (2.43), получим
0 = МФ — МФЛ = МИ~1С — GA.	(2.44)
Определим далее матрицу M(t) таким образом, чтобы
A (GG*) = GG* + GG’ = 0.	(2.45)
138
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
Вычислим сначала производную G*. Так как G удовлет-
воряет уравнению (2.44), то
G* = (M.M-1G)* — (GA)’.	(2.46)
Далее, используя формулу
(АВ)’ = В* А*,
преобразуем равенство (2.46):
G* = G* (Й И-1)’— A*G*.	(2.47)
Используя выражения (2.44) и (2.46) для G и G*, а так-
же тот факт, что
(Vf.VTGG* — GAG*)* = (GG*)* (ЙЛГ1)* — (AG*)‘ G* =
= GG’(WVT1)‘ — GA*G*.
перепишем условие (2.45) в таком виде:
М VTlGG’ — GAG* 4- (MATW — GAG*)* = 0.
Отсюда следует, что нам достаточно определить матрицу
M(t) так, чтобы имело место равенство MM~lGG*=
= GAG', откуда AfAf_l = GA G"(GG*)_‘. Возвращаясь к
(2.44), мы найдем дифференциальное уравнение для мат-
рицы G:
G = GAG‘(GG’)-1G —GA;
подчинив G (/) начальным условиям
G(A>) = Q’,	(2.48)
тем самым однозначно определим матрицу G(t).
Аналогично предыдущему определим'вектор а(/) ра-
венством a(t) = G(t)x(t). Составим для него дифферен-
циальное уравнение
а = Gx -г Gx.
Поскольку x(t) удовлетворяет уравнению (2.25)
х =5= Ах + Д
S 21
СВЕДЕНИЕ К КРАЕВЫМ ЗАДАЧАМ

а 0(0 уравнению
G = GAG* (GG*)'1 G — GA,
то
а = GAG* (GG*)~la 4- Gf.	(2.49)
Итак, мы определили правила переноса граничных усло-
вий, гарантирующие не только отсутствие быстрорасту-
щих решений задачи Коши, но и хорошую обусловлен-
ность системы линейных алгебраических уравнений,
которую приходится решать для определения краевых
условий при t = T, если только эта система была хорошо
обусловлена при ( = f0-
Описанную процедуру переноса мы будем называть
процедурой совместного переноса граничных условий.
Она также была предложена А. А. Абрамовым.
В заключение подсчитаем, во что обходится перенос
системы k граничных условий (2.40). Матрица G, так же
как и матрица Q*,— это (&Х ft)-матрица. Следовательно,
матричное уравнение (2.44) эквивалентно #Xft скаляр-
ным уравнениям.
Вектор а имеет размерность, равную k, следователь-
но, уравнение (2.49) эквивалентно k скалярным уравне-
ниям. Таким образом, для переноса k граничных условий
необходимо решить задачу Коши для системы &(«+1)-го
порядка.
Итак, краевая задача для системы, порядок которой
равен п при условии, что мы переносим все условия в
точку t = T, а при / = (0 задано k условий, требует ре-
шения задачи Коши для системы, порядок которой равен
£(/z-|-l) +« *).
Линейные системы дифференциальных уравнений
представляют собой единственный пример систем, для
которых краевые задачи всегда могут быть сведены к за-
дачам Коши, причем эту редукцию можно организовать
таким способом, что соответствующая задача Коши не
будет иметь быстрорастущих решений.
*) Последние п уравнений (2.25) интегрируются независимо от
t—T до /=/».
140	ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА	[ГЛ. II
§ 3. Применение метода переноса граничных условий
для построения итерационных схем
1. Замечание о задаче Майера. В предыдущем пара-
графе мы подробно изучили методы решения задач опти-
мального управления с квадратичным функционалом и
линейными граничными условиями. Фазовые ограниче-
ния и ограничения на управление в этих задачах отсут-
ствовали. Этот класс задач обладал тем замечательным
свойством, что его /7-система является линейной. Это
значит, что расчет оптимальной программы в этом слу-
чае- сводится к стандартной процедуре — решению зада-
чи Коши. Единственная реальная трудность, с которой мы
здесь можем столкнуться,— высокая размерность этой
задачи. Если размерность исходной задачи равна и (раз-
мерность вектора х), то размерность //-системы равна 2п,
причем п условий задано на левом, а п других условий—
на правом конце траектории *). Используя тогда резуль-
таты расчетов, приведенные в конце предыдущего пара-
графа, мы увидим, что задача сведется к решению зада'
чи Коши для системы, порядок которой N равен
Af = п(2л + 1) + 2п = п(2п + 3).	(3.1)
Для системы шестого порядка (динамическая система с
тремя степенями свободы) N=90, причем основной объ-
ем работы связан с интегрированием уравнений для мат-
рицы G. В данном случае эта система имеет порядок
^=2-6-6=72. Эта процедура вполне реализуема на со-
временных ЭВМ. Поэтому использование техники реше-
ния линейных краевых задач открывает определенные
перспективы для численного решения задач оптимально-
го управления.
В начале предыдущего параграфа 'был приведен при-
мер важной технической задачи, которая сводится к рас-
сматриваемой. Количество подобных примеров довольно
велико. Линейные задачи с квадратичным функционалом
имеют значительный интерес, их теории посвящена боль-
шая литература, и в то же время класс задач теории
оптимального управления, которые могут быть непосред-
ственно сведены к краевым задачам для линейных си-
) Имеется в виду задача с фиксированным левым концом.
§ 31
ПОСТРОЕНИЕ ИТЕРАЦИОННЫХ СХЕМ
141
стем, является очень специальным. Линейность исходной
задачи еще никак не гарантирует линейности 77-системы,
и, следовательно, возможности сведения задачи к крае-
вой для линейных дифференциальных уравнений. Так,
например, в этот класс не попадают даже задачи Майера
для линейных систем.
В самом деле, пусть движение управляющего объек-
та описывается системой п линейных уравнений
х = Ах + и,	(3.2)
а функционал задан в следующей форме:
7 = (с, x)t=T.	(3.3)
Тогда уравнения для импульсов имеют вид ф=—
Управление исключается из условия максимума линей-
ной формы
я* = 2
t—1
(3.4)
Задача максимизации линейной формы (3.4) имеет
смысл лишь в том случае, когда величина и ограничена.
Пусть, например, выбор управления стеснен условием:
| и‘ |	Тогда зависимость и? от импульсов будет не-
линейной:
и1 =
если
если
Таким образом, /7-система для задачи (3.2) — (3.3) будет
нелинейной.
2. Задача Лагранжа без ограничений на управле-
ние. Рассмотрим следующую задачу расчета оптималь-
ных программ. Пусть уравнение управляемого объекта
имеет вид
х — f (х> и)>
(3-5)
где х — вектор размерности п, и — вектор размерно-
сти т, а функционал, минимум которого должен быть
142
численные методы расчета
[ГЛ. и
достигнут,— интегральный
т
J (х, u) = J F (х, и) dt,
*0
(3.6)
где F — дважды дифференцируемая функция своих ар-
гументов; никаких ограничений на управление не накла-
дывается.
Предположим, что граничные условия для системы
(3.5) имеют вид
<WO = 0, /=1,2,...,%
(3.7)
Ф‘г(х(Т)) = 0, i= 1,2, ..., sT,
где s0^n, sr^n, n, — размерность вектора х.
Пусть задано некоторое управление uOi которое мы
рассматриваем как «нулевое приближение» к решению,
и некоторое начальное значение х(/0), которое может
не удовлетворять начальному условию. Интегрируя си-
стему (3.5), мы получим некоторую фазовую траекторию
х = х0(/), вдоль которой будет двигаться управляемая
система под действием управления и0. Конечные ус-
ловия в этом приближении могут быть также не вы-
полненными. Для построения следующего приближения
положим
* = х0 + у; и = u0 + V.	(3.8)
Предполагая и и v малыми, удержим в уравнении (3.5)
линейные слагаемые, а в функционале (3.6) — квадратич-
ные. В результате мы придем к уравнению
у = Ay + Bv	(3.9)
и функционалу
т
Ф = f {(а, У) + (Р, 0 + {Су, у) + {Dv, у) + (Ev, и)} dt.
^0
(3.10)
§ 3]
ПОСТРОЕНИЕ ИТЕРАЦИОННЫХ СХЕМ
143
Смысл введенных обозначений очевиден: а и 0 — это
векторы
dF
дх ’
dF
ди
а С, D и £-матрицы
с=-
2
d2F
дх1дх^
d2F I
dxtdd I
d*F
duldu!
.... n;
i — 1, ..., n, j1, ..., tn-,
i, j = 1, ..., tn.
D = -
2
E = -
2
Все эти величины вычислены при x=x9(t) и ы=и0(7).
Линеаризуя условия (3.7), мы найдем, что функции y*(t)
должны удовлетворять следующим условиям:
i yk (Q + Фо' (х0 (70)) = 0, j = 1.........s0,	(3.11)
fe=l
" <ЭФг	t
3 ^^(П + Фг(^о(0) = 0» *=h •••. Sr. (3.12)
Итак, мы пришли к задаче отыскания управления v,
переводящего систему (3.9) из состояния, которое удов-
летворяет условиям (3.11), в состояние (3.12) за время
Т —10 и доставляющего при этих условиях минимум
функционалу (3.10).
77-система для системы (3.9) будет, как мы это уста-
новили, линейной. Краевые условия для нее будут опре-
деляться линейными уравнениями*). Следовательно, мы
можем найти функции у (7) и и (7), применяя аппарат пе-
реноса граничных условий.
В результате мы получим новые управление и фазо-
вую траекторию:
= + Х1 = *о + У-	(3.13)
*) KSi>4-sr краевым условиям (3.11), (3.1Й) добавятся (и—$о) +
+ (п—sT) соотношений, полученных из условий трансверсальности на
левом и правом концах после исключения произвольных постоянных
(см. гл. I).
144
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. П
Вычислим новое значение функционала Л=/(хь щ).
Если окажется, что точность выполнения граничных
условий (3.10) повысилась и /1</(х0, ц0), то решение
(3.13) улучшает исходное приближение, и мы можем
повторить процесс, полагая
и2 = 4- v, х2 = Xj + yt	(3.14)
и т. д. Сходимость такой итерационной схемы не изуче-
на, однако целый ряд решенных задач показывает ее эф-
фективность при условии, что начальное приближение
«достаточно хорошее».
Примечания.
1.	Для улучшения сходимости, так же как и в методе
Ньютона, можно вместо формул (3.13) использовать
следующие:
ц = и0 + kv, х — х0 4- ky,	(3.15)
где k — некоторое положительное число, меньшее 1.
2.	Предложенный Р. Веллманом метод последователь-
ных приближений в задачах оптимизации*), имеет мно-
го общего с вышеизложенным методом. Основное отли-
чие, по-видимому, состоит только в способах решения
краевых задач для линейных уравнений. Р. Веллман не
использует техники переноса граничных условий. Для
отдельных частных случаев он дает анализ сходимости.
3.	Общая схема нелинейной прогонки. Как уже отме-
чалось, метод решения краевых задач, использующий пе-
ренос граничных условий, часто называют методом про-
гонки. Это название соответствует характеру процедуры:
сначала граничные условия переносятся с одного конца
траектории на другой; для этого приходится решать за-
дачу Коши, интегрируя уравнения, например, слева на-
право, потом нам остается решить еще одну задачу Коши,
причем в этом случае мы должны проинтегрировать си-
стему справа налево.
Метод прогонки используется и для решения нелиней-
ных краевых задач. В этом случае строятся итерацион-
ные процедуры, на каждом шаге которых надо решать
краевую задачу для линейных уравнений.
*) Р. Б е л л м а н, Р. К а л а б а, Квазилинеаризация и нелиней-
ные краевые задачи, «Мир», 1968.
§ 3]
ПОСТРОЕНИЕ ИТЕРАЦИОННЫХ СХЕМ
145
Пусть речь идет о нелинейном уравнении
х = ф(х),	(3.16)
и пусть задано некоторое «нулевое приближение» х0.
Тогда уравнение (3.16) мы представляем в виде
х = А (х0) х + L (х, х0),	(3.17)
где L (х, х0) =ф (х) — А (х0) к.
Если ф(х) — дифференцируемая функция, то опера-
тор А —это матрица частных производных:
(Ло)
I, j = 1..............п,
(3.18)
и структура итерационной схемы очевидна:
Хд = Л (Хп-х) xn -J- L (хл_1э хп_х).	(3.19)
Если краевые условия линейны:
7Иох (70) = <х0, Мгх (Т) = ат,
где Мо и Мт — прямоугольные матрицы соответствующих
размерностей, то на каждом шаге задача решается непо-
средственно методом прогонки. Если краевые условия
нелинейны, например, если они имеют вид (3.7), то при-
веденная итерационная процедура должна сочетаться с
итерационным удовлетворением граничных условий, как
это описано в конце предыдущего пункта.
Предположим теперь, что мы имеем некоторую нели-
нейную 77-систему, и пусть управление м=й(х, ф), най-
денное из условия максимума функции Гамильтона Н,
будет дифференцируемой функцией х и ф. Тогда 77-си-
стема может быть представлена в форме (3.16), где
ф(х) — дифференцируемая функция. Следовательно, в
этом случае выбор аппроксимирующего оператора А не
представляет труда, он выполняется по формуле (3.18).
Однако во многих случаях функция й(х, ф) может быть
не только недифференцируемой, но даже разрывной. Тог-
да ф(х) также недифференцируема, и выбор матрицы А—
это всегда некоторая специальная проблема; никакой
общей рецептуры выбора А не существует. Ниже мы рас-
смотрим один подобный пример.
146
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
4.	Одна задача с релейным управлением. В качестве
примера применения методики, которая обсуждалась в
предыдущем пункте, рассмотрим следующую задачу
Майера: пусть уравнения динамической системы линейны
и по фазовой переменной и по управлению:
х=Ах-\-Ви,	(3.20)
где А и В — некоторые заданные матрицы — функции
времени. Будем считать, что краевые условия заданы в
следующем виде:
xl (tQ) = а‘, i = 1, 2, ... , k — 1,
(3.21)
х> (Т) = х'т, j = k,k + 1, ..., п,
и требуется минимизировать функционал
J = (c, х(Т)),	(3.22)
где с — заданный вектор, такой что
Ci = 0, если k.
Стесним выбор управлений и‘ ограничениями вида
|цг|<уг, i = l, 2,..., m	(3.23)
(условие (3.23) мы иногда будем записывать так:
|«|<у).
Имеем
Н = (ф', Ах) + (ф, Ви),	(3.24)
ф = — А*ф.	(3.25)
На правом конце заданы сопряженные переменные
ф*(0 =—«=1,2, ..., k—1.
Системы уравнений (3.20) и (3.25) линейны, но систе-
ма (3.20) содержит еще и управление, которое исключа-
ется из условия максимума Н по и. Максимизация линей-
ной формы (3.24) при условии (3.23) определяет некото-
рую функцию й(ф), вообще говоря, разрывную.
Управление и находится из условия (ф, Ви) =тах при
|и|^у. Например, если уравнение (3.20) и входящее
§ 4] ПРОЦЕДУРА РЕШЕНИЯ ЗАДАЧ СО СВОБОДНЫМ КОНЦОМ 147
в него управление — скалярные, то
-	(+ 7, если Вф>0,
и =	(3.26)
I—у, если Вф<^0.
Таким образом, в общем случае 77-система
| х= Лх + Ви (ф),
1ф = — Л*ф
будет нелинейной. Трудность ее решения в рамках ме-
тода нелинейной прогонки состоит в выборе аппроксими-
рующего линейного оператора, поскольку правые части
этой системы — функции недифференцируемые. Для по-
добных задач использовались разнообразные итерацион-
ные схемы, причем наиболее удачными оказались ите-
рационные схемы следующего вида:
хп = Ахп Вфп И- Bun-i Вфп-ь
фи = — Л*фп.
На каждом шаге управление выбиралось из условия мак-
симума Н, т. е. по формулам типа (3.26).
Никаких результатов, относящихся к проблемам схо-
димости подобных методов, автору неизвестно.
§ 4. Методы теории оптимального управления,
использующие процедуру решения задач
со свободным концом
1. Введение. Задачи теории оптимального управления,
сводящиеся к краевым задачам для линейных систем,
представляют из себя простейший класс задач этой тео-
рии. Чтобы получить их точное решение, достаточно ре-
шить несколько задач Коши. Следующий по трудности
класс задач — это задачи со свободным концом. Для
него мы уже не имеем в общем случае конечной процеду-
ры получения точного решения. Тем не менее для реше-
ния задач со свободным концом разработаны эффектив-
ные приближенные способы. Они используют следующее
замечательное свойство этого класса задач. Для получе-
ния точного решения задачи оптимального управления
динамической системой, если она линейна по фазовой
148	ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА	[ГЛ. It
переменной и на правый конец траектории не наложено
никаких ограничений, достаточно решить две задачи
Коши. Подобно линейным задачам с квадратичным
функционалом, задачи со свободным концом, линейные
относительно фазовой переменной, играют роль основных
элементов для построения итерационных схем расчета
оптимальных программ.
2. Задача Майера для линейной системы. Рассмотрим
динамическую систему, линейную по фазовой переменной
х = A (t)x + ф(^, и),
(4.1)
Х W “ хо*
Размерности векторов х и u^Gu будем считать равными
пит соответственно. Будем искать управление из усло-
вия минимума функционала
J = (c,x(T)).	(4.2)
Составим выражение функции Гамильтона
Н = (ф, Ах) Н- (ф, ф (/, а))	(4.3)
и выпишем уравнение для импульсов:
ф = — Д*ф.	(4.4)
Уравнение (4.4) называется сопряженным к уравнению
(4.1). Мы уже сталкивались с этим уравнением, когда
исследовали возможность переноса граничных условий
из одной точки в другую.
На значения вектора х(Т) никаких ограничений не
накладывается. Поэтому значение импульса на правом
конце задано 2г
ф(Т) = — с.	(4.5)
Условие (4.5) позволяет вычислить вектор импульса ф(£)
независимо от х. Точно так же независимо от х может
быть определено управление u(t). В самом деле, управ-
ление находится из условия максимума скалярного про-
изведения
Я* (и) = (1|) (/), <р(/, «))
(4.6)
§ 4] ПРОЦЕДУРА РЕШЕНИЯ ЗАДАЧ СО СВОБОДНЫМ КОНЦОМ 149
при u^Gu. Задача отыскания «(/)— это некоторая зада-
ча нелинейного программирования, которая может быть
решена, как только будет определен вектор ф(0-
Таким образом, решение задачи Майера для линей-
ной динамической системы сводится к некоторой конеч-
ной процедуре, которая состоит из следующих этапов:
а)	Решение задачи Коши (4.4) — (4.5) для 7].
Эта задача решается справа налево.
б)	Для каждого t решается задача нелинейного про-
граммирования — определяется управление
и = и if).
в)	С найденным управлением решается задача Коши
(4.1). Эта задача решается слева направо.
Примечания.
1.	Значения импульсов запоминать не имеет смысла.
Величины их нам нужны только для расчета управле-
ния. Поэтому, решая численно задачу Коши (4.4) — (4.5),
надо одновременно на каждом шаге определять не толь-
ко импульс, но и управление. Запоминать же следует
только одно управление.
2.	В рассмотренной задаче мы по существу получили
синтез — мы нашли управление, годное для любых на-
чальных условий системы (4.1).
3.	Некоторые вспомогательные формулы. Рассмотрим
линейную систему
у = А у + Bv	(4,7)
и выпишем сопряженную систему	
р = — А*р.	(4.8)
Условимся, что	
0(4>) = о.	(4.9)
Умножая уравнение (4.7) на р, (4.8)	на у, складывая
полученные выражения и принимая во внимание условие
(4.9), мы получим
(р(Т), у (7)) = J (р, Bv) dt.
^0
150
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
(ГЛ. 11
Предположим теперь, что нам задана некоторая линей-
ная форма £= (с, у(Т)). Полагая
р(Т)=-с,	(4.10)
мы можем получить следующее выражение:
т
L = --^{p,Bv)dt.	(4.11)
to
В этой формуле вектор р — это решение задачи Коши
(4.8), (4.10). Один раз определив вектор р, мы можем
затем легко изучить зависимость L от v, не прибегая к
интегрированию системы (4.7). Это важное свойство со-
пряженного уравнения широко используется для построе-
ния различных приближенных методов решения задач
со свободным концом.
Формула (4.11) может быть приведена к следующему
виду:
г
L=\G(t)vdt.	(4.12)
to
Вычислим вектор G(t)-.
~(р, Bv) — — 2 | 2 ЬцР#1] = —3	=	G‘v'’
1=1 \/=1	/	/=1 \i=l J i=l
т. e. G = —B*p.
Формула (4.12) может быть получена, разумеется, и
без использования сопряженного уравнения.
Рассмотрим снова уравнение (4.7) и введем в рассмот-
рение матрицу фундаментальных решений T(t). Она
удовлетворяет следующей задаче Коши:
Г=АГ, Г(/о) = /.
I—	единичная матрица. Тогда решение уравнения (4.7),
которое обращается в нуль при t = t0) можно представить
в виде
t
У Ц) = JT (/) Г"1 (т) В (т) V (т) dr.	(4.13)
to
§ 4] ПРОЦЕДУРА РЕШЕНИЯ ЗАДАЧ СО СВОБОДНЫМ КОНЦОМ 151
Матрица ®(t, т) = ||'уч|| = Г(/)Г-1(т) называется матри-
цей Грина. Вычислим
Т	Т tn
L — (с, у (Т)) = 2 J Ci^bsflidr = J 3 G’vldr, (4.14)
i.s.j h	to /=1
где
G' (r) = S Wis т) ЬУ (T)-
i,s
Этот путь построения формулы (4.12) требует эффек-
тивного построения матрицы Грина, т. е. решения п
различных задач Коши для системы z=Az.
В то же время вывод формулы (4.12) с использова-
нием сопряженного уравнения требует решения лишь
одной задачи Коши для уравнения z=—A*z.
Поэтому использование матрицы Грина приводит к
более громоздкой процедуре, нежели использование со-
пряженного уравнения. Одновременно заметим, что фор-
мула (4.12) дает значительно более частный результат,
нежели формула (4.14), поскольку последняя справедли-
ва для любого t.
4. Метод решения нелинейных задач со свободным
концом, использующий сопряженное уравнение. Будем
рассматривать задачу отыскания управления u(t) и тра-
ектории x(t), связанных условиями
х = /(х, и),	(4.15)
хЦ0) = хй,	(4.16)
usGu	(4.17)
и доставляющих минимум функционалу
/ = Г(х(Т)).	(4.18)
Никаких условий на значения фазовых переменных при
t = T мы накладывать не будем.
Обозначим через х,(/) и «.(Z) некоторое «диспет-
черское решение», т. е. решение, удовлетворяющее урав-
нению (4.15) и условиям (4.16) и (4.17). Рещению (х., ы.)
152
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. If
отвечает некоторое значение функционала
J, = J(x,iU,) = F(x,(T)).
- Введем новые переменные х = х*+у, u = u„ + v и ли-
неаризуем уравнение (4.15):
y = A(t)y + B(t)v,	(4.19)
здесь
матрица А — квадратная, пХп (п — размерность век-
тора х), В — прямоугольная. Она имеет п строк и т
столбцов (т — размерность вектора и).
Вычислим еще 6J — линейную часть разности
F(x(T))-F(x.(T)):
Поскольку x.(Z) удовлетворяет начальному условию
(4.16) и, следовательно, у(А>)=0, то мы можем восполь-
зоваться формулой (4.11), приняв в качестве L величину
т
6J = — j* (р, Во) dt.
/о
(4.21)
Здесь р — вектор, удовлетворяющий сопряженному урав-
нению (4.8) и следующему условию Коши:
р(Л =
ЭМ
дх )х_х
(4.22)
Теперь мы должны выбрать вариацию управления v
таким образом, чтобы максимально уменьшить величину
§ 4] ПРОЦЕДУРА РЕШЕНИЯ ЗАДАН СО СВОБОДНЫМ КОНЦОМ 153
функционала б/. Для этого мы должны выбрать управ-
ление V из условия
max (р, Bv} — Ф (р).	(4.23)
Заметим, что это условие совпадает с принципом максимума
для линеаризованной системы (4.19), если функционал задан
Л \ * Л—*
Таким образом, мы рассматриваем задачу оптималь-
ного управления линейной системой со свободным кон-
цом. Заметим теперь, что задача определения миниму-
ма J, вообще говоря, не тождественна задаче минимиза-
ции 6J. В самом деле, определив v из условия (4.23), мы
найдем новые х и и. Однако из того, что 67 < О, не сле-
дует, что Их*+у, «,+и)</(х., и,). Поэтому в данной
задаче еще возникает некоторая вспомогательная задача
о выборе такого v, чтобы одновременно имели место
неравенства
W < 0 и J (х, 4- у, и, 4- о) < J (х„ и,).
Наличие связи (4.21) позволяет строить разнообраз-
ные варианты спуска. Задача отыскания вектора v (фор-
мула (4.23)) — это задача минимизации линейной формы
— (р, Ви) = —
и
при нелинейных (в общем случае) условиях «,4-це(?и.
Поскольку p(t)— это известная вектор-функция времени,
то решение задачи (4.23) позволит нам определить неко-
торый вектор г>(0, который, в свою очередь, определит
вектор y(t). Если при этом приращение функционала 67
окажется отрицательным и будет иметь место неравен-
ство
J(X, + y,u, + v)<J(Х„ и,),	(4.24)
то мы принимаем v — v. Если неравенство (4.24) не выпол-
няется, то мы проверим вектор v=-^v. Если при v = v
неравенство (4.24) опять не имеет места, то мы продал каем
154
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЁТА
[ЁЛ. П'
уменьшать величину множителя, последовательно проверяя
1 - 1 ~
— У, —V и т. д.
4	8
Задача отыскания вектора v, доставляющего макси-
мум линейной форме (р, Bv) при ограничениях и* +
+ v^GU9 может оказаться достаточно сложной. В этом
случае взамен рассмотренной может быть использована
следующая процедура.
Рассмотрим варицию функционала (4.21). Эту фор-
мулу можно переписать в виде
т
J (В*р, о) dt.
Заметим, что если мы положим
v = kB’p,
(4.25)
где k>0, то вариция будет отрицательна. Выберем. к = кй
так, чтобы v + u,<^Gu. Если при этом неравенство
(4.24) будет иметь место, то мы принимаем ut=«.+
+ у, в противном случае мы берем kt— и проверяем
величину м2=ц«+^1и и т. д.
Введем в рассмотрение конус Ки. возможных направ-
лений относительн множества Gu в точке и,. Будем го-
ворить, что	если можно указать такое А*>0, что
для любого	имеет место ut + Kv^Gu.
Очевидно, что для того, чтобы и. было оптимальным
управлением, необходимо, чтобы для любого t вектор В*р
принадлежал к двойственному конусу К*и (этим терми-
ном мы называем совокупность всех тех векторов с, для
которых
(с, у) О
для любых v^Ku,). В самом деле, предположим, что для
некоторого t—h вектор В'р^Ки.- Тогда, в силу непре-
рывности, найдется некоторый интервал (^—8, Л + е),
на котором вектор В'р^Ки,- На этом интервале сущест-
вует v(t), для которого (В"р, у)>0, т. е. б/<0, и наше
решение не может быть минимумом.
$ 4] ПРОЦЕДУРА РЕШЕНИЯ ЗАДАЧ СО СВОБОДНЫМ КОНЦОМ 155
Покажем, что проверка этого необходимого условия
сводится к некоторой задаче квадратичного программи-
рования.
Введем оператор проектирования вектора а на на-
правление е (рис. 4.1). Через z=Pe а мы будем обозна-
чать такой вектор z=\e (Х^О), на котором достигается
минимум нормы вектора а — z.
Задача определения проекции
сводится к задаче квадратич- S'
ного программирования: опре- s' [
делить	।
min 2 (zz — аг’)2-	Z	е
Рис-41-
Если скалярное произведение (а, е) ^'0, то z = 0. Ана-
логично определяется и проекция вектора на произволь-
ное множество.
Мы установили, что для того, чтобы найденное реше-
ние и* было оптимальным, необходимо, чтобы для лю-
бых имело место условие
(В*р,0<О.	(4.26)
Но для того, чтобы имело место условие (4.26), необхо-
димо и достаточно, чтобы
г = РКи*В*р - 0.	(4.27)
Таким образом, проверка условия (4.26) требует реше-
ния задачи квадратичного программирования (4.27) для
каждого значения t.
Определение v по формуле (4.25) требует выбора k
такого, чтобы v + u^Gu. Если k оказывается очень
малым, то это показывает, что мы уже находимся в ок-
рестности оптимума. Проверку условия (4.26) осущест-
вить легче, чем проверку принципа максимума.
Описанный метод давно вошел в арсенал инженерной
практики. Он очень прост для программирования и по-
зволяет легко уточнить решения, полученные эвристи-
ческим путем. Сейчас трудно назвать имя его автора.
У нас в стране, по-видимому, первыми начали исполь-
156
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
зовать рассуждения подобного рода Л. И. Шатровский *)
и Т. М. Энеев. Изложенная здесь модификация метода
была разработана в Вычислительном центре Академии
наук СССР.
Основной недостаток этого метода состоит в том, что
с его помощью очень трудно получить точный результат.
Поэтому метод сопряженных уравнений следует рассмат-
ривать в первую очередь как метод уточнения диспетчер-
ского решения.
Примечание. Условия сходимости были исследо-
ваны М. Ф. Бейко и И. В. Бейко **).
5. Проблема обеспечения устойчивости счета. Мето-
ды, которые мы рассматривали в предыдущих разделах,
сводились в конечном итоге к решению серии задач Коши
для линейных дифференциальных уравнений. Эта сама
по себе тривиальная процедура может привести к значи-
тельным трудностям вычислительного характера в слу-
чае большого интервала времени или больших положи-
тельных действительных частей собственных чисел мат-
рицы A(t). Поэтому приходится использовать специаль-
ные приемы, позволяющие исключить необходимость
арифметических действий с большими числами. Поясним
их смысл на примере задачи Майера (4.1).
Мы показали, что она сводится к решению задачи
Коши (4.4) — (4.5) и задачи Коши (4.1), в которой управ-
*) Л. И. Шатровский, Об одном численном методе решения
задач оптимального управления, ЖВМ и МФ 2, № 2, 1962. У нас в
стране этот метод часто называют методом Брайсона на том основа-
нии, что он был опубликован А. Брайсоном на 2—3 месяца раньше.
Однако специалистам хорошо известно, что этот метод начал приме-
няться в СССР для решения конкретных задач задолго до его публи-
кации. В частности, в ВЦ АН СССР он вошел в арсенал средств рас-
чета оптимальных траекторий в 1959 г. после доклада Л. И. Шатров-
ского на семинаре по теории оптимального управления в ВЦ АН
СССР. Поскольку изложенный метод был разработан независимо в
СССР Л. И. Шатровским и Т. М. Энеевым и в США А. Брайсоном,
его следовало бы называть методом Шатровского — Брайсона — Эне-
ева. Заметим, что для задач с закрепленным концом методы Брайсо-
на и Шатровского отличаются. Л. И. Шатровский вводит функцию
штрафа, в отличие от Брайсона, который использует идеи проектиро-
вания градиента (см.ниже).
**) М. Ф. Бейко, И. В. Бейко, Об одном новом подходе к
решению нелинейных краевых задач, Украинский матем. журнал
20. № 6. 1968.
§ 4] ПРОЦЕДУРА РЕШЕНИЯ ЗАДАЧ СО СВОБОДНЫМ КОНЦОМ 157
пение считается заданной функцией времени. Предполо-
жим теперь, что хотя бы одно из собственных чисел мат-
рицы А (/) имеет большую положительную действитель-
ную часть. Тогда уравнение х1>=Ах будет иметь
быстрорастущее решение и процесс численного решения
задачи Коши для этого уравнения будет неустойчив. Оче-
видно, что этим же свойством будет обладать и задача
Коши (4.4) — (4.5), поскольку в ней интегрирование про-
водится справа налево.
Не ограничивая общности, положим' х(/)=0 и вос-
пользуемся снова приемом А. А. Абрамова, который был
изложен в предыдущем параграфе.
Вместо уравнения (4.1) рассмотрим такое:
ф = — А*ф + Ф = — А*ф + Ф (Ф) Ф* (4.28)
Мы знаем, что решение этого уравнения — вектор ф—
постоянен по абсолютной величине. Умножая (4.28) на
х, а (4.1) — на ф и складывая, получим
(ф, х) = (Ф (ф) ф, х) + (ф, <р (t, и)).	(4.29)
at
Обозначим /(0=—(Ф(0> х(0)> из основании условия
х(/0) =0 имеем J(Q =0.
Если мы положим ф(Т)=—с, то ЦТ) будет совпа-
дать со значением (4.2). Следовательно, уравнение (4.29)
мы можем переписать в такой форме:
J = ф (/) J — (ф, ф (/, и)).	(4.30)
Напомним, что ф(/)— это известная функция, Ф(/) =
= Ф(Я)(0).
Рассмотрим для уравнения (4.30) задачу отыскания
управления и, доставляющего минимум ЦТ).
Эта вспомогательная задача является задачей Майе-
ра для скалярного уравнения (4.30), причем это уравне-
ние является линейным относительно фазовой перемен-
ной /. Сопряженное уравнение имеет вид
<7 = —Ф(0<7-	(4.31)
158
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
(ГЛ. и
Переменная q(f) удовлетворяет условию q(T) =—1. Та-
ким образом, сформулированная задача сводится к опре-
делению и из условия максимума Н*——<?(ф, <р(/, «))
и интегрированию слева направо уравнения (4.30).
Может оказаться, конечно, что при найденном управ-
лении решение уравнения (4.30) также быстрорастущая
функция. Это будет означать, что значение функционала
I очень велико. В этом случае для изучения уравнения
(4.30) нужны специальные методы. В частности, полагая
Ф(0 =ХФ*(0, где Х=тах|Ф(Г) |, можно воспользоваться
хорошо развитой теорией асимптотических представле-
ний *).
Примечание. Описанный прием является частным
случаем общей схемы анализа подобных задач, основан-
ный на следующем очевидном факте. Положим
Ф = g (Ф) Ф.
где £(ф)— произвольная скалярная функция. Тогда ве-
личины <р, найденные из решения следующих двух задач
max (ф, <р); max (ф, <р)
ф	ф
будут совпадать.
6. Метод И. А. Крылова и Ф. Л. Черноусько. Очень
близок к методу сопряженных уравнений метод решения
задач со свободным концом, предложенный в 1962 году
И. А. Крыловым и Ф. Л. Черноусько**). Он обладает
всеми достоинствами и недостатками метода сопряжен-
ных уравнений, но гораздо удобнее для машинной реали-
зации, поскольку не требует линеаризации и перехода от
системы (4.15) к системе (4.19).
Будем рассматривать задачу отыскания минимума
функционала
J(xtw) = yjc/^(T)	(4.32)
I
при ограничениях (4.15) — (4.17).
*) См., например, Н. Н. Моисеев, Асимптотические методы
нелинейного анализа, «Наука», 1969.
**) И. А. Крылов и Ф. Л. Черноусько, О методе после-
довательных приближений для решения задач оптимального управ-
ления, ЖВМ и МФ 2, № 6, 1962.
$ 41 процедура Решения задач со свободным концом 159
Импульсы	при t = T должны удовлетворять
условиям
фг(Т) = -с/.	(4.33)
Процедура решения этой задачи, предложенная
И. А. Крыловым и Ф. Л. Черноусько, состоит в сле-
дующем:
а)	Пусть нам задано диспетчерское решение Ин-
тегрируя систему (4.15), мы найдем х,.
б)	Составим функцию Гамильтона
н = 2 W1 (*>и)
i
и уравнения для сопряженных переменных
* =	(4-34)
у ил
в)	Проинтегрируем систему (4.34) при краевом усло-
вии (4.33) справа налево от t=T до t = t0. При этом мы
будем считать, что х=х„ u—ut. Одновременно из усло-
вия максимума функции’Гамильтона мы будем опреде-
лять новое управление ut. Поскольку величины х(/) =
= х, и полученные интегрированием системы (4.34),
нам известны, то новое управление будет также извест-
ной функцией времени.
Теперь, используя управление uit мы повторим опера-
ции а) и б), и т. д.
Легко видеть, что для линейной задачи, т. е. если
уравнения (4.15) линейные, оба метода, описанных в этом
параграфе, совершенно эквивалентны и дают точное ре-
шение на втором шаге. Однако метод И. А. Крылова и
Ф. Л. Черноусько более удобен для машинного счета,
поскольку он не требует выполнения трудоемкой опера-
ции линеаризации уравнений на каждом шаге.
В общем случае этот метод расходится. Существует
много способов улучшения его сходимости. Пусть, на-
пример, /(«О>;/(«,). Тогда процедуру а) интегриро-
вания системы (4.15) с управлением мы заменим
160
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. П
интегрированием этой системы с управлением
где k выбирается из условия J (wt) <J («,).
Примечание. Метод, описанный в этом разделе,
удобнее метода, который был изложен выше, не только
потому, что экономится предварительная работа по ли-
неаризации исходной системы. Линеаризованные уравне-
ния обычно оказываются значительно более громоздкими,
чем исходные нелинейные (например, они содержат боль-
ше слагаемых), в силу чего процесс их численного инте-
грирования требует больше машинного времени, чем не-
линейных.
7. Понижение порядка исходной задачи. Формула
(4.12) дает возможность построить процедуру спуска в
задаче с условиями на правом конце. Это обстоятельство
было замечено рядом авторов, которые независимо друг
от друга предложили алгоритмы для решения вариацион-
ных задач с условиями на правом конце (А. Брайсон,
И. О. Мельц и др.). И. О. Мельц показал, что эти алго-
ритмы можно рассматривать в качестве континуального
аналога метода проекции градиента.
Здесь мы изложим алгоритм (который является мо-
дификацией метода Брайсона), предложенный в 1964 году
автором, в связи с обсуждением и сопоставлением мето-
да Л. И. Шатровского и метода И. А. Крылова и
Ф. Л. Черноусько.
Рассмотрим сначала простейшую задачу отыскания
минимума функционала
J (х, «) = ctxl (Т)	(4.35)
«=1
при условиях
х = A(/)x4-B(0u, U£.GO,	(4.36)
х<(/0) = 0, i = 1, ..., п,.„. ”	(4.37)
х«(7) = х?.	(4.38)
$ 4] ПРОЦЕДУРА РЕШЕНИЯ ЗАДАЧ СО СВОБОДНЫМ КОНЦОМ 161
Пусть множество Gu будет многогранником. Введем в
рассмотрение два вектора р, и рф, удовлетворяющие со-
пряженному уравнению
р= — А*р,	(4.39)
но разным условиям на правом конце:
pJ( (Г) = —q, i = 1, 2, ..., и — 1,
Pjn (Л = °.	(4.40)
Рф/(Л = 0,	i=l,2.......п-1,	(4.41)
РФ„(Л=1.
Воспользуемся соотношением (4.12) и выпишем для
функционалов J и <р=х" (Г) следующие формулы:
т
J = — ^{gj, u)dt,	(4.42)
=	(4.43)
где
gj = B*pj, g9 = В’рф.
Заметим еще раз, что векторы р, и pv, а, следователь-
но, и векторы g, и g,, не зависят от управления, посколь-
ку они полностью определяются матрицами А, В и усло-
виями (4.40) и (4.41). Используя формулы (4.42) и
(4.43), мы можем следующим образом переформулиро-
вать задачу (4.35)—(4.38): определить управление u(t),
доставляющее минимум функционалу (4.42) при усло-
вии, что
т
ф = £ (йф, и) di = Хт.	(4.44)
Эта задача уже гораздо проще исходной, посколь-
ку в ней имеется только одна фазовая переменная <р,
6 Н. Н. Моисеев
162
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
удовлетворяющая скалярному уравнению
Ф = (£ф, и)	(4.45)
и условиям на концах <р (/о)=О, ф (7’)=%?. Функция
Гамильтона для этой задачи имеет вид
Н q (g<p, и) + (gj, и)	(4.46)
и, следовательно,
Таким образом, множитель Лагранжа q постоянен.
Если мы тем или иным образом зададим эту величину,
то управление и однозначно определится из условия мак-
симума Н — это некоторая задача линейного програм-
мирования. Решив после этого задачу Коши для уравне-
ния (4.45) с начальным условием <р (/о)=О, мы опреде-
лим величину ф (Т). Следовательно, в этом случае зада-
ча сведется к подбору всего лишь одной постоянной q,
обращающей в нуль разность ф (Т) —х!* .
Итак, использование сопряженного уравнения (а сле-
довательно, формулы (4.12)) позволило исходную зада-
чу размерности п свести к скалярной задаче.
Очевидно, что описанная процедура может быть при-
менена и в том случае, когда при t—T закреплены k
координат, например, х1(Т),..., х* (Г), а функция
J= 2 с{х‘(Т).
/=*+х
Для этого достаточно вместо вектора рф ввести k векто-
ров P<ft(s=l, 2, ...,£), удовлетворяющих уравнению
(4.39) и следующим данным Коши:
р,‘(П= [“•
если i 4= s,
если i = s.
Тогда вектор р} должен удовлетворять следующим усло-
виям:
р7/(Т) = 0, i=l, 2, ...,6,
PJi(T) = —ch i = k+ 1, ..., n.
§ 4] ПРОЦЕДУРА РЕШЕНИЯ ЗАДАЧ СО СВОБОДНЫМ КОНЦОМ 163
Вводя векторы g<fs=B*P<ts > s=l, •••> краевые усло-
вия при t=T мы можем записать в виде
т
<ps(D = $ (g<fs>u)dt = ХТ> S=	(4.47)
7.1
В результате мы приходим к задаче определения мини-
мума функционала (4.42) при дифференциальных связях
<₽s = (£<Ps> “)» s== I, k,
и условиях на концах
<ps(Q = 0, <ps(T) = xr.
Размерность полученной задачи уже равна k<n. По-
добно тому, как решение линейной задачи со свободным
концом было использовано для построения итерационных
схем в нелинейных задачах, изложенный метод может
служить источником для построения итерационных схем
для нелинейных задач с частично закрепленными кон-
цами.
8. Один способ приближенного решения задач с за-
крепленными концами. Рассмотрим снова задачу опре-
деления минимума функционала (4.42) при условии
(4.44).
Для построения приближенного решения заменим
эту задачу другой вариационной задачей.
Предположим, что мы разыскиваем минимум функ-
ционала (4.35), а условие (4.38) отсутствует. Тогда
функция и в каждый момент времени должна доставлять
максимум линейной формы (pj, Ви) = (g}, и) на множе-
стве Gu. Обозначим через v решение этой вспомогатель-
ной задачи.
Положим u=v-j-h и построим вектор-функцию h (/),
наименее уклоняющуюся от нуля, которая гарантирует
выполнение условия (4.38). Уклонение h (t) от нуля
будем понимать в смысле метрики в Ьг:
т

164
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
Тогда задача определения функции h(t) сводится к отыс-
канию минимума функционала
т
U = ^(h,h)dt
to
(4.48)
при условии
т	т	т
4= \(gv,u)dt = ^(g9,v)dt + ^(gv,h)dt == хт. (4.49)
^0	^0	А>
Для решения изопери метрической задачи мы сможем
применить принцип максимума Л. С. Понтрягина. По-
лагая z= (g„, v) + (glf, h), мы составим функцию Га-
мильтона Я = ф((£Ф, v) + (g<„ h)) — (h, h). Так как функ-
ция ф должна удовлетворять уравнению
то ф— это некоторая константа, которая должна быть
определена из условия изопериметричности (4.49).
Условие максимума Н по h позволяет вычислить h;
=	(4.50)
6»
Подставляя это выражение для h в условие (4.49) у мы
найдем
т	т
Хт — (g<f, v)dt = ^ (g9, gv) dt.
t.	2 I
Находя отсюда ф/2 и подставляя в (4.50), получим
(4.51)
§ 4] ПРОЦЕДУРА РЕШЕНИЯ ЗАДАЧ СО СВОБОДНЫМ КОНЦОМ 165
т. е. h=kg<„ где k — скаляр:
т
- j °)
k=------±.
т
J (g<f. gv) dt
t»
Итак, эта процедура нам позволяет определить и в виде
u=v-\-kg4.
Если
u=v+kg^Gu,
то описанная процедура позволяет улучшить приближен-
ное решение V. В противном случае необходимо дробле-
ние множителя k и срезка управления и.
Совершенно аналогично рассматривается задача с m
закрепленными концами, т. е. задача, в которой нало-
жено m условий на значение фазовой переменной в мо-
мент времени t=T.
Примечание. Методы, описанные в последних
пунктах этого параграфа, «хорошо работают» лишь тог-
да, когда решение задачи со свободным концом близко
к решению исходной задачи. В общем случае необходи-
мо действовать более осторожно, определяя управления
v и h из условия постепенного уменьшения функционала
и частичного улучшения граничного условия.
9. Заключение. Как показывает опыт, методы данного
параграфа удобны для получения приближенного реше-
ния задач со свободным концом. Однако получение точ-
ного результата требует относительно большой затраты
машинного времени. Поэтому целесообразно сочетать
изложенные методы с методом Ньютона, который позво-
ляет проводить расчет с любой степенью точности, если
только начальное приближение находится в окрестности
решения. Для того чтобы применять метод Ньютона, мы
должны иметь в своем распоряжении приближенные зна-
чения величин импульсов в начальный момент времени.
Изложенные методы решения задачи со свободным кон-
цом, как мы это видели, обладают требуемым свойством.
166
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
§ 5. Методы, использующие функции штрафа
1. Функции штрафа в задачах об относительном экст-
ремуме. Одновременно с усложнением структуры огра-
ничений резко усложняются необходимые условия эк-
стремума. Соответственно с этим усложняются и методы
расчета, использующие необходимые условия. Поэтому
предлагаются различные приемы преодоления трудно-
стей, вызванных существованием сложных ограничений.
К их числу относится введение функций штрафа, которые
в настоящее время получили широкое распространение в
практических расчетах.
Изучение техники использования функций штрафа
начнем с рассмотрения задачи отыскания максимума
дифференцируемой функции f(x) (хе/?") при ограниче-
нии типа равенств
Ф*(х) = 0, i=l,2, ...» т<^п,	(5.1)
где — также дифференцируемые функции. Идея мето-
да штрафных функций состоит -в замене задачи отыска-
ния относительного максимума задачей отыскания абсо-
лютного максимума функции
т
/(x) = f(x)-^ W(x)]2,	(5.2)
»=i
где А,-— некоторые положительные постоянные.
Выражения Л.[срг(х)]2 называются штрафными функ-
циями. Если условия связи выполнены, то / (х) —[ (х).
Если условия связи не удовлетворены, то второе слагае-
мое в правой части (5.2) характеризует невязку —меру
отклонения точки х от гиперповерхности ф‘(х)=0
(i=l, 2, ..., т). Чем больше будут числа А<, тем боль-
ше будет штраф за нарушение условий связи.
Создание этого метода чаще всего связывают с име-
нем Куранта, который применил его в 1943 году для ре-
шения одной специальной вариационной задачи. Курант
ту принадлежит также первый анализ, позволивший
выяснить соотношение между задачей отыскания относи-
тельного экстремума функции f (х) и абсолютного экстре-
мума функции /(х). Он доказал, что при Л<-»-оо точка
§ 5]	МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ФУНКЦИИ ШТРАФА	167
х* (АО, в которой функция I достигает максимума, стре-
мится к точке х, в которой достигается относительный
максимум функции f (х), и при этом 7(Ж)=/ (Ж).
Метод штрафных функций получает все большее и
большее распространение. Популярность этого метода
объясняется тем, что он дает, вероятно, наиболее простую
схему решения задач на относительный экстремум. В то
же время, как показывает опыт расчетов, получить с его
помощью достаточно точный результат трудно.
Легко понять, почему это происходит. Если величина
min At невелика, то значение вектора х*, реализующего
максимум функции /(х), будет значительно отличаться
от х. Следовательно, при малых А< метод штрафных
функций дает большую погрешность. Если же числа А,-
велики, то значения х* и х будут близки, но в этом слу-
чае при расчетах мы должны оперировать с большими
числами, которые умножаются на малые величины, что в
свою очередь служит источником ошибок. Поэтому ме-
тОд функций штрафа в теории экстремума функций
обычно комбинируют с каким-либо трудоемким методом,
который способен дать точный результат при достаточно
«хорошем» начальном приближении.
2. Теорема Ю. Б; Гермейера. Курант дал обоснование
метода штрафных функций для решения специальных за-
дач, связанных с применением прямых методов к зада-
чам математической физики. Позднее обоснование мето-
да штрафных функций было дано Ю. Б. Гермейером.
Ниже мы приводим это доказательство, показывающее
существование глубокой связи между рассматриваемым
вопросом и теорией максмина.
Рассмотрим задачу отыскания максимума непрерыв-
ной функции f(x), определенной и ограниченной сверху
на некотором ограниченном замкнутом множестве Ее/?"
при условии, что х удовлетворяет равенству <р(х)=0.
Множество точек хеЕ, удовлетворяющее этому равенст-
ву, обозначим через М.
Построим функцию Ф (х):
Ф = О, если хе М,
Ф <С 0, если х <= М.
168
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
(ГЛ. II
Например, в качестве Ф(х) можно взять функцию
т
i—1
Введем в рассмотрение функцию 7(х, X):
/(х, Х) = /(х)4-ХФ(х), Х>0.
Обозначим через х>. точки, ,в которых функция /(х, X)
достигает своего максимального значения на Е при дан-
ном фиксированном X. Обозначим через N множество то-
чек Хх, для которых X изменяется от нуля до оо. В силу
ограниченности множество N компактно, и мы можем
выделить сходящиеся подпоследовательности точек {хх},
обладающие следующим свойством:
lim х>. = хм.
Х-*ОО
Имеет место следующая теорема:
Теорема (Ю. Б. Гермейер*)). Точки хх при-
надлежат множеству М и в этих точках функция f (х) до-
стигает на М своего максимального значения, причем
f (хю) = lim max I (х, X).
Х->оо х^Е
Доказательство теоремы распадается на доказатель-
ство ряда последовательных утверждений.
Лемма 1.
max inf I (х, X) sC lim max I (x, X).	(5.3)
x^M X>o	Z->oo xeE
Доказательство. Так как в точках х&М
Ф(х) =0, то
max inf / (х, X) = max f (х) = f (х),	(5.4)
х^М Х>о	х^М
где х принадлежит N — множеству точек, в которых
f(x) достигает на М своего максимального значения.
*) Ю. Б. Гермейер доказал значительно более общую теорему, от-
носящуюся к теории максмина (см. Ю. Б. Гермейер, Введение в
теорию исследования операций, «Наука», 1971). Из нее как частный
случай следует результат, который мы здесь приводим.
§ 5]
МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ФУНКЦИИ ШТРАФА
169
Величину f (х) формально можно записать так:
/ (х) = lim (f (х) + ХФ (х)),
Х-*оо
поскольку Ф(х) =0. Но
lim (/ (*) +	(х)) lim max I (х, X),	(5.5)
Х->оо	Х-*оо х^Е
что и доказывает лемму.
Лемма 2.
lim хк = х» е М.
X—>оо
Доказательство. Предположим обратное, пусть
х„&М, тогда, в силу замкнутости М, начиная с некото-
рого Х„ все точки последовательности {хх} будут внеш-
ними по отношению к М. Следовательно, для всех
Х>Х, будет иметь место неравенство Ф(хх)<—е<0.
Следовательно,
lim Ф (х>.) < 0.
X—*00
Но тогда
lim (f(xx) 4- ХФ (хх)) = — оо.
Х-*оо
Вспоминая смысл обозначения хх, предыдущее равенство
мы можем записать в виде
lim max I (х, X) = — оо.
Х**оо х&Е
Используя далее лемму 1, мы получим, что
max f (х) sC lim max I (x, X) = — oo.
xeAf	X-*oo x&E
Полученное противоречие доказывает лемму. Итак,
х„еЛ1, т. е. Ф(х„)=0. Первое из утверждений теоремы
доказано.
Л е м м а 3.
lim'max I (х, X) f (x^).
X—*00 х^Е
170
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
Доказательство. Используя обозначение x&,
левую часть этого неравенства можно переписать так:
lim max / (х, X) = lim (/ (х^) + ХФ (х^)).
%->00 х^Е	Х-*оо
Но так как Ф(л\) ^0 для любого конечного %, то
lim max I (х, %) lim f (х^,
X—*оо х^еЕ	Аг”*оо
т. е.
lim max I (х,	(%«).
Х-*оо х&Е
Лемма 3 доказана.
Из леммы 3 и леммы 1 сразу следует второе утверж-
дение теоремы. Действительно,
f (х) lim max I (х, X) <1 f (x»),
X—*oo x^E
T. e. f(xXf(xTO).
Поскольку x принадлежит N — множеству всех точек
максимума функции f(x) на М, то из этого неравенства
следует, что f (х„) =f (х), т. е. х<„ еА и
f (Хо,) = lim max I (х, X).
X->oo х&Е
Теорема доказана полностью.
Примечания.
1.	Очевидно, что в том случае, когда мы разыскива-
ем минимум функции f(x) при условии (5.1), функцию
штрафа следует брать в виде
ф(х)=- мфч*)]2.
Z=1
где А(— положительные числа.
2.	Доказательство теоремы Ю. Б. Гермейера сущест-
венным образом опиралось на предположение о том, что
множество E<=Rn ограничено и замкнуто. Отсюда следо-
вала компактность множества N. Поэтому вместо пред-
положения об ограниченности множества Е можно было
бы включить в формулировку теоремы предположение
§ 5] ‘
МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ФУНКЦИИ ШТРАФА
171
об ограниченности множества точек хк, в которых функ-
ция /(х, %) принимает максимальные значения для фик-
сированных %, когда % пробегает все значения от 0 до оо.
3.	Задачи с ограничениями, наложенными на конец
траектории. Метод штрафных функций в последние годы
начал широко применяться также и в задачах теории
оптимального управления. Впервые он был применен к
решению задач, содержащих ограничения на значения
координат правого конца траектории (конец 50-х годов,
Л. И. Шатровский).
Рассмотрим следующую задачу Майера. Определить
x(t) и доставляющие минимум функции F(x(T))
при ограничениях
x^f(xt	(5.6)
% (Q ~ ^0»
(pf(x(T))==O,	1, 2, ..., £<п,	(5.7)
u^Gu.	(5.8)
В предыдущем параграфе мы изложили метод реше-
ния задач со свободным концом. Для того чтобы его
можно было применять и в рассматриваемом случае,
вместо функционала F(x(T)) вводят такой:
k
J (х, и Д) = F (х (Л) + 3 U [Ф* (х (Т))]2,	(6.9)
i=l
где %i>0, и рассматривают задачу со свободным концом
для функционала J(x, и, %)•
4.	Снятие ограничений на управление. Задачи опти7
мального управления значительно облегчаются, если мы
устраним ограничения на управления таким образом,
чтобы уравнение
определяло управление как дифференцируемую функцию
фазовых координат и импульсов. Тогда оказывается
возможным применять метод нелинейной прогонки.
т
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
|ГЛ. it
Снять ограничения можно с помощью введения функ-
ций штрафа. Предположим, что речь идет об отыскании
минимума функционала J(x, и) при ограничениях (5.8),
которые для определенности мы запишем в виде
i=l, 2......tn. (5.10)
Введем в рассмотрение функцию V (и) следующим. об-
разом:
	2 /=1
¥(«) = 1	iTM з >> 1? о X. «10
если и'>4»
если и{ [d{, dlt], (5.11)
если
и будем решать задачу оптимального управления с
функционалом
т
Ji = J (х, а) + J Т (u) dt,	(5.12)
41
но без ограничений на управление.
Мы привели в качестве примера тот случай, когда ог-
раничения на управления имеют вид (5.10). Разумеется,
описанный способ построения функций штрафа может
быть распространен и на значительно более общий слу-
чай ограничений на управление.
5.	Снятие фазовых ограничений. Фазовыми ограниче-
ниями мы называем ограничения
x(t)e=Gx, t<=[t0,T].	(5.13)
Исследуя необходимые условия, мы ограничились зада-
чами, в которых фазовые ограничения отсутствовали.
Для случая фазовых ограничений также могут быть по-
лучены необходимые условия экстремума. Однако они
оказываются настолько сложными, что их трудно исполь-
зовать для построения эффективных вычислительных
методов. В то же время с помощью метода штрафных
§ 5]
МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ФУНКЦИИ ШТРАФА
173
функций обсуждаемые задачи легко можно свести к
более простым задачам. Предположим, что фазовые огра-
ничения заданы в виде
<pi(0<x'(0<<p/2(0,	(5.14)
Тогда построим функцию Т,(х), аналогичную функции
(5.11):

i
2 К{ (х1 (0 — (О)2, если х1 (0 > (0,
О,	если х1 (0 е [<р( (0, ф, (0],
i
2 h (х' (0 — (О)8. если х{ (0 < <р{ (0,
i=i
и вместо функционала 1(х, и) будем минимизировать
функционал
т
J1 = J(x,u) + JX(x(0)d/.
to
6.	Снятие дифференциальных связей. Схема А. Ф. Ко-
ноненко. Рассмотрим задачу отыскания минимума функ-
ционала
т
J (х,и) = J F (х, и, t) dt	(5.15)
при ограничениях (5.6). Концы фазовой траектории бу-
дем считать фиксированными
х (4) = хо. х (Т) = хт.	(5.16)
Дифференциальные связи не представляют собой какого-
либо исключения, и мы также можем ввести штраф за
их невыполнение. Тогда мы придем к функционалу сле-
дующего вида:
Т	п	1
J (х, и) = С F (х, и, 0 +	Ki (х1 — f (х, и, 0)2l dt.	(5.17)
t9	J
174
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. И
Составим для функционала (5.17) уравнения Эйлера
^--22	0)^ = 0, /==1,2.........tn,
к=1
(5.18)
/=1
+ 2KS — (xs — fs(x, u,t)) = 0, s= 1, 2, ..., n.
dt
Решение этой системы уравнений имеет ту же степень
трудности, что и системы, которую мы получили бы, рас-
сматривая исходную задачу как задачу Лагранжа. Одна-
ко для решения задачи минимизации функционала
(5.17) может быть применена следующая итерационная
процедура, предложенная А. Ф. Кононенко:
 _	п	j
‘ *==1
(5.19)
>п
Un+i —
ди! ’
п
где ап—некоторое малое положительное число, а %•(/) —
выпуклая вверх функция, которая обращается в нуль
на концах интервала, например, %*(t) = (t—tQ) (Т—t).
Схема расчета следующая:
а)	Определяется некоторое начальное приближение—
функция хо(О> удовлетворяющая граничным условиям,
и функция «о (?).
б)	Вдоль траектории х0(/) вычисляются правые части
равенств (5.19) и вычисляются новые приближения x,(t)
и причем условия (5.16) выполняются автоматиче-
ски в силу выбора функции (/).	
Оказывается, что числа ап могут быть подобраны та-
ким образом, чтобы эта итерационная процедура схо-
дилась (если функционал ограничен снизу), причем на
§6]
ЗАДАЧИ С НЕФИКСИРОВАННЫМ ВРЕМЕНЕМ
175
предельной траектории хто(0 значения фигурных скобок
обращаются в нуль, т. е. на предельной траектории вы-
полняются необходимые условия минимума.
А. Ф. Кононенко показал, что описанный метод мож-
но рассматривать в качестве специальной модификации
градиентного метода в функциональном пространстве.
Этот метод не требует решения дифференциальных урав-
нений.
7.	Заключение. Выше мы уже заметили, что методы
штрафных функций не позволяют получать точных ре-
шений. Тем не менее эти методы с каждым годом завое-
вывают все большую й большую популярность. Простота
их реализации — это, вероятно, одно из важнейших
свойств методов, использующих функции штрафа. Кро-
ме того, при расчете оптимальных программ требования
точности бывают обычно не очень высокими. Наконец,
методы штрафных функций сейчас широко используют
для получения первых приближений с последующим ра-
счетом по более точным, но более трудоемким методам.
§ 6. Задачи с нефиксированным временем
и задачи на быстродействие
1.	Структура краевой задачи. Задачи с нефиксиро-
ванным временем, как это следует из результатов гл. 1,
также сводятся к некоторым краевым задачам специаль-
ного вида для /7-системы. Их основная особенность со-
стоит в, том, что для определения времени должно быть
задано еще одно соотношение
Н (х, (/), и (/), ф (/), t)t^T = °-	(6. U
Для того чтобы выяснить некоторые особенности за-
дач с нефиксированным временем, рассмотрим один про-
стой пример. Найти минимум функционала
т
J(x,u,T)~T + у ((и1)2 + (ц2)2) dt
о
при ограничениях
х1 = w1, х2 = и2, х1 (0) — х2 (0) = 0,
xi(T) = 3, х2(Т) = 4.
176
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
Составив функцию Гамильтона Я=ф1и14-ф3м2—(ы‘)г—
— (и2)2—1, мы найдем	1=1,2, где ф,—это неко-
торые постоянные, подлежащие определению. Исполь-
зуя условия при t=T, найдем
Х1(Т) = Т.^ = 3,	=	= А =
&	&	4	1
после чего мы легко найдем выражение для функцио-
нала
/ = Г + ^.	(6.2)
Для того чтобы определить Т, мы можем воспользовать-
ся выражением (6.1), которое в данном случае будет
таким:
Отсюда Т=5. Разумеется, тот же результат мы получим,
если будем разыскивать минимум J(T), вычисляя произ-
водную и приравнивая ее нулю.
На этом простом примере, который позволяет полу-
чить решение в замкнутом виде, мы показали два воз-
можных подхода к решению вариационных задач с не-
фиксированным временем.
Перейдем теперь к рассмотрению общей задачи оты-
скания минимума функционала
т
J = f f (х,и, f) dt	.	(6.3)
•о
при ограничениях
x = f(x,u, t), x(t0) = x0, х(Т) = хт, (6.4)
причем время Т не фиксировано. Составим сопряженную
систему
§ 6]	ЗАДАЧИ С НЕФИКСИРОВАННЫМ ВРЕМЕНЕМ	177
Обозначим -ф (/о) = а. Вектор а нам неизвестен. Введем
далее «невязку» X (а, Т):
X (а, Т) = х (а, Т) — хт.	(6.6)
Векторное равенство (6.6) эквивалентно п скалярным
уравнениям относительно п+1 неизвестной: компонент
вектора а и времени Т. Добавляя к уравнениям (6.6)
уравнение (6.1), которое мы перепишем так:
Н(а, Т) = 0,	(6.7)
мы получаем систему п+1 уравнений относительно
п+1 неизвестных. Для решения этой задачи может быть
использован метод Ньютона.
Однако может оказаться проще другая схема расче-
та. Предположим, что в нашем распоряжении имеется
программа расчета оптимального решения задачи
(6.3) — (6.4) при условии, что время закреплено. Тогда у
нас есть правило для вычисления функционала J (6.3)
как функции от параметра Т. Мы можем теперь оты-
скать минимум этой функции одной переменной любым
из известных методов (алгоритм, использующий числа
Фибоначчи, алгоритм деления отрезка пополам и т. д.).
2.	Применение алгоритмов решения задачи со свобод-
ным концом. Удобство и популярность решения задач со
свободным правым концом привели к появлению ряда
приемов решения задач на быстродействие и задач со
свободным временем, представляющих из себя итераци-
онные процедуры, на каждом шаге которых использует-
ся один из алгоритмов решения задач со свободным кон-
цом (например, алгоритм И. А. Крылова и Ф. Л. Чер-
ноусько) .
Рассмотрим снова задачу (6.3) — (6.4) и введем но-
вую переменную
xn+1 = F (х, и, t)	(6.8)
и новый функционал — «расстояние» до конечной точки
7(х,М) = ((х(0-хг), /?(х(0-хг)),	(6.9)
где R — это некоторая симметричная матрица.
Структура алгоритма следующая. Фиксируем некото-
рое значение переменной х"+1=р() и рассматриваем задачу
178
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
отыскания минимума функционала (6.9) в момент време-
ни, когда
х«”(0 = ₽о.	(6-10)
Отыскание минимума функционала (6.9)—это зада-
ча со свободным концом. Условие (6.10) нам необходи-
мо только для определения момента времени прекраще-
ния счета. Оно ничем не отличается от условия 0О и
для решения обсуждае-
мой задачи изложенные
° fio Pi Рг А Р
методы решения задач со
свободным концом могут
быть использованы без
каких-либо оговорок.
Задав величину
хп+1(/)=р0, мы можем
столкнуться с двумя слу-
чаями. В первом случае
значение р0 больше мини-
мального. Тогда задача —
вырожденная: существу-
ют (в общем случае их
бесконечное множество)
управления, переводящие систему из состояния х0 в со-
стояние хт и доставляющие функционалу 1 значения р0
больше минимального. Этому случаю отвечает нулевое
значение функционала (6.9). Мы должны его отбросить
и добиться, чтобы величина р0 была меньше минимально-
го значения функционала (6.3). В этом случае задача со
свободным концом имеет смысл, и в результате ее реше-
ния мы получаем некоторое конечное значение функцио-
нала (6.9). Затем мы полагаем р4 = р0+Др, причем стре-
мимся выбрать Ар так, чтобы pi была меньше минималь-
ного значения функционала (6.3), и снова решаем задачу
со свободным концом и т. д. Результаты расчетов мы мо-
жем отразить в виде диаграммы, изображенной на рис.
6.1. Заметим, что получить оптимальное значение вели-
чины р = р очень трудно, так как при р = р + е, где s —
сколь угодно малое число, задача уже становится вы-
рожденной. Этот метод многократно использовался в ВЦ
АН СССР, поскольку он опирается на хорошо отработан-
ные стандартные процедуры, а требования точности
$
I
§ 6]
ЗАДАЧИ С НЕФИКСИРОВАННЫМ ВРЕМЕНЕМ
179
в прикладных задачах далеко не всегда бывают вы-
сокими.
Задача на быстродействие является частным случа-
ем рассмотренной задачи, когда Г=1. В этом случае она
будет формулироваться следующим образом. Опреде-
лить решение системы
дН ; дН
X ----, ф =-----— ,
дф	дх
(6.11)
которое переводит фазовую точку х из состояния х„ в со-
стояние хт за минимальное время Т.
Зададим время перехода Т1( меньшее минимального
времени 7”, являющегося решением поставленной зада-
чи. Найдем минимум функционала (6.9) на отрезке
[О, Л]. Затем зададим время 7’2=7’1 + А7’ и повторим из-
ложенную процедуру и т. д. Таким образом мы получим
монотонно возрастающую последовательность 7\, Тг,...,
причем для каждого Т< минимум функционала (6.9)
строго больше нуля. Дальнейшее уточнение решения, на-
чиная с некоторого Т{, достаточно близкого к Т*, Tt<.T*,
становится (как это указано выше) все более трудным.
Однако, если величины Т",—Т( и хт*—xTi невелики, то
для окончательного решения задачи можно воспользо-
ваться методами теории возмущений. Техника примене-
ния методов теории возмущений к решению вариацион-
ных задач будет описана в следующем параграфе.
3.	Существование монотонной переменной. Трудность
построения вычислительных процедур в задачах, где вре-
мя не фиксировано, связана с тем, что неизвестен момент
окончания процесса численного интегрирования. Если
априори известно, что одна из координат изменяется
монотонно, и мы знаем ее конечное значение, то эта
трудность легко преодолевается.
Предположим, например, что условия на правом кон-
це заданы следующим образом:
ф'(х(Т)) = 0,	1, 2, ..., m<n, (6.12)
х" (Г) = х?»
причем заранее известно, что координата xn(t) изменя-
ется монотонно. Для решения этой задачи может быть
180
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
использована стандартная программа метода Ньютона.
Зададим начальные значения импульсам
Ф (70) = а
и будем решать задачу Коши для 77-системы. Процесс
численного, интегрирования мы прекратим в. тот момент,
когда переменная X?! станет’равной хт , и вычислим функ-
ции Ф*(х(7’)). Очевидно, что эти величины будут опреде-
ляться только вектором а:
ф' = ф' (а), i=l,2, .... /п.	(6.13)
Еще п — m условий получатся из условий трансверсаль-
ности после исключения произвольных постоянных. Те-
перь нам надо подобрать
п чисел а1(..., аг, ап таким
образом, чтобы они обра-
щали в нуль полученную
систему п граничных ус-
ловий. Для этой цели мо-
жет быть использована
стандартная процедура
метода Ньютона.
Задачи, в которых од-
на из переменных изменя-
ется монотонно, встреча-
ются не так уже редко.
К их числу относятся, на-
пример, задачи динамики
космического аппарата, совершающего маневр в около-
земном пространстве. В этих маневрах, какая бы ни была
их окончательная цель, полярный угол <р (рис. 6.2) всег-
да изменяется монотонно. Это объясняется тем, что
трансверсальная составляющая скорости о, настолько ве-
лика (она имеет порядок первой космической скорости),
что трудно придумать разумный пример маневра, в ко-
тором эта составляющая должна была бы изменить знак.
В подобных случаях удобно перейти к новой перемен-
ной и свести задачу к обычной задаче Лагранжа. В ка-
честве примера рассмотрим одну простую задачу дина-
мики точки, движущейся в центральном поле сил. Урав-
нение движения этой точки в векторной форме будет
§ 6]
задачи с Нефиксированным временем
181
таким:
— =—(6.14)
dt2 г»	'	’
В уравнении (6.14) приняты следующие обозначения:
г — радиус-вектор точки, ц— гравитационная постоян-
ная, й — вектор управляющих воздействий, г—абсолют-
ная величина радиус-вектора.
Перепишем уравнение (6.14) в проекциях на реи по-
лярной системы координат
^=-4_л+а>,	=	(6.15)
dt г г2	dt г	v '
Здесь
<6Л6>
Для системы уравнений (6.15) — (6.16) поставим следую-
щую задачу. Определить «‘(f) и «2(0, которые за мини-
мум времени переводят точку из состояния <р=0, г=г0,
t»r=t»ro, в состояние ср=2 л, r=r0, ar=0, Уф=Ур./г0.
Итак, маневр состоит в том, чтобы за минимум вре-
мени перевести аппарат на круговую орбиту того же ра-
диуса, причем этот маневр должен совершиться за один
оборот.
В этой задаче полярный угол <р является монотонно
изменяющейся переменной. Естественно выбрать’ именно
эту величину в качестве независимой переменной, тогда
величина Т — общее время маневра выразится квадра-
турой
2Я
Т =Л — d<p.	(6.17)
<Г
Простота численного решения вариационной задачи су-
щественно зависит от выбора переменных. В рассматри-
ваемых задачах, например, в качестве переменных удоб-
но выбрать следующие две величины:
4	_ _ _
w = ~,	h = vx.r.	(6.18)
182
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
(ГЛ. И
Величина h носит название секториальной скорости. Так
как п = arr°+t>ф<р°, где г° и <р°—единичные ортогональные
векторы, то выражению для секториальной скорости
можно придать следующий вид:
Л = г2^ф°х7°.
dt
Так как единичные векторы <р° и г0 ортогональны, то
абсолютная величина секториальной скорости h будет
вычисляться по формуле
h = — —.	(6.19)
w2 dt	4	'
Это позволяет нам представить функционал (6.17) в
форме
2Л
f
J w2h '
(6.20)
Составим теперь уравнения, которым удовлетворяют
величины w и h. Рассмотрим первое из уравнений (6.15).
Заметим прежде всего, что используя (6.19), его можно
представить в виде
— (—') =	— ру2 + и1.	'	(6.21)
dt \dt /
Цалее проделаем следующие вычисления:
dt dtp	dtp /	dtp
d (dr\ d dw\	n (dh dw . t d2w}
dt \dt J dtp\ dtp/	(dtp dtp dtp2)
Используя эти вспомогательные выражения и уравнения
(6.21), получим
d2a> . 1 dw dh	и.	и1	/c oox
—— 4------------P t® ~  --------•	(6.22)
dtp2	h dtp dtp	ft2	u^h2
§ 7]
МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИИ
183
Составим теперь выражение для величины h. Так как
dm <	dr 1 dw
— г— ==wh, vr= — = —h —, то второе из уравне-
dt	dt d(^>
ний системы (6.15) мы можем переписать в таком виде:
A <wh) = ш2Я2 — + и2. Переходя к переменной ср, вычислим
dt	dtp
A (wh) =	шИз этих двух выражений найдем
dh   и2
dtp	w2h
(6.23)
Используя в свою очередь уравнение (6.23), мы можем
dh
исключить из уравнения (6.22) производную . В ре-
зультате получим
dtp2	ft*	dtp teW J	'
Итак, мы пришли к задаче определения минимума
функционала (6.20) при дифференциальных связях
(6.23) и (6.24), которые имеют достаточно простой вид,
и, кроме того, порядок задачи оказался пониженным на
единицу.
Приведенный пример показывает, что в ряде случаев,
используя дополнительную информацию о природе зада-
чи на быстродействие, мы можем свести ее к задаче
Лагранжа, причем в результате мы получим относитель-
но более простую систему дифференциальных связей.
§ 7.	Методы теории возмущений.
Возможный способ решения краевых задач
1.	Обсуждение задачи. Методы теории возмущений
играют важную роль в математической физике. Это объ-
ясняется тем, что часто относительно просто получить
приближенное решение. Имея такое решение, физик
нуждается лишь в некотором его уточнении.
184
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
(ГЛ. И
Аналогичная ситуация типична и в задачах управле-
ния. В этом параграфе мы выясним возможности ана-
лиза, основанного на идеях теории возмущений.
Поскольку решение краевых задач для системы обык-
новенных дифференциальных уравнений занимает цен-
тральное место в теории оптимального управления, мы
сразу рассмотрим эту задачу и продемонстрируем тех-
нику теории возмущений непосредственно на решении
краевой задачи.
Будем рассматривать задачу отыскания траектории
x(f), удовлетворяющей уравнению
х = /(х,0	(7.1)
и граничным условиям
при/ = /0	g(x(to)) = 0,	(7.2)
при t = T	<р (х (Г)) = 0.	(7.3)
Если п — размерность вектора х, а и, и ng размерно-
векторов <р и g, то пФ+п4=п. Соотношения (7.2) и (7.3)
г	определяют в фазовом
пространстве некоторые
Рис. 7.1.	Рис. 7.2.
гиперповерхности, которые мы условимся обозначать
через <Г0 и St. В этих терминах краевую задачу (7.1) —
(7.3) мы можем сформулировать следующим образом
(рис. 7.1).
§ 7]
МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ
185
Определить фазовую траекторию уравнения (7.1),
которая переведет изображающую точку с поверхности
на поверхность за, заданное время Т —10. В том
случае, когда порядок системы уравнений (7.1) равен
двум, а условия на концах имеют вид
xl(t0) = a, х»(Г) = ₽,	(7-4)
задача иллюстрируется рис. 7.2. Задача состоит в отыс-
кании такой кривой из семейства интегральных кривых
уравнения (7.1), соединяющих прямые (7.4), вдоль кото-
рой изображающая точка будет перемещаться заданное
врямя Т — /0.
2.	Задача уточнения начальных условий. Предполо-
жим, что нам известно некоторое решение х уравнения
(7.1), близкое к искомому, которое при t=t0 удовлетво-
ряет условию (7.2). Предположим, кроме того, что при
t=T оно удовлетворяет условию (7.3). Тогда эта кривая,
изображенная на рис. 7.1 пунктиром, пересекает гипер-
поверхность ёт в момент Т=Т — АТ, где Г — заданная
величина. Каким образом, опираясь на эту информацию,
найти требуемое решение? Здесь есть несколько возмож-
ностей. Во-первых, использовать метод Ньютона, подби-
рая на поверхности ёй начальную точку таким образом,
чтобы она определяла траекторию, достигающую поверх-
ности ёт в заданный момент времени. Этот путь решения
задачи и технику его реализации мы изложили в § 1
этой главы. Второй путь решения задачи использует ме-
тод прогонки. Он связан с линеаризацией задачи и со
специальной организацией итерационной процедуры.
Этот путь также был описан в этой главе. Третья воз-
можность «уточнения» решения дается теорией возмуще-
ний и основывается на использовании уравнений в ва-
риациях.
Выпишем уравнение в вариациях для системы (7.1)
при х=х:
z = A(x,t)z,	(7.5)
здесь z(t) =x(t)—x(t),
186
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
Матрицей фундаментальных решений Г(х, t) называ-
ется решение матричного уравнения
— = ЛГ,	(7.6)
dt
удовлетворяющее начальным условиям Г(^)=/, где / —
единичная матрица. Тогда любое решение уравнения
(7.5) мы можем представить в виде
z(t)^T(x(i),t)z(t0).	(7.7) J
Составим выражение для х(t) с учетом .уравнения
(7.5) и проведем линеаризацию	|
х(Т) = х(Т-)-ДТ) + г(Г+ДТ)^х(Г) + хдг+	|
Используя (7.7) и обозначая х0=х^л), хт=х(Т), по-
лучим
хт = х(Т) + Г (х (Г), Т) (х0 - X О + f (х (Г), Т) АГ. (7.8)	;
Добавляя к этому равенству линеаризованную систе-
му уравнений, описывающих	поверхности &0	и	|
^(хг-^(Г)) =	^.(Г(х(Т),Г)(х0-х(/0)))4-	i
OZ	ОХ	I
+ f(x(T),T)&T)	= Q,	I
^(хо-х(/о)) = О,	(L9)	।
ОХ
мы получаем систему 2п уравнений относительно неизве-
стных векторов х0 и хт. Причем система (7.9) позволяет
независимо определить х0.
Эти вычисления очень сильно упрощаются, если при
t = t0 фиксированы некоторые координаты xj, х’, ..., х™,
а при t = ,Т фиксированы оставшиеся п —jn координат.
3.	Пример. В качестве примера рассмотрим систему
второго порядка. Обозначая через уу элементы матрицы
фундаментальных решений, перепишем уравнение (7.8) :
хт = ? (?) 4- уп (xj - х1 (/0)) + Тм (х04 - ? (Q) + f ДТ,
(7.10)
х*т = х8 (Т) + уа (хо1 - х1 (^)) + Yffl № - х^ (/0)) + ^ДГ.
МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИИ
187
§ 7]
Рассмотрим краевые условия (7.4). Так как в этом случае
xi = xl(t0), хт = х2(Т), то уравнения (7.10) упрощаются:
х'т>= х1 (Г) + у12 (х0« - х2 (f0)) + f AT,
(7.11)
0 = Y22(4-x2(Q) + /2AT.
Если Угг^О, то из второго уравнения мы найдем недо-
стающее значение х%. Не интегрируя уравнений, мы при-
ближенно определим хт из первого уравнения системы
(7.П).
Пусть теперь краевые условия заданы для одной и той
же координаты xj = а, хт = 0, тогда система (7.10) прини-
мает вид
х2т^хЦТ) + ую(х1--х\^) + р^Т.
Задача разрешима, если у12(7) =/=().
4.	Задача с нефиксированным временем. Предполо-
жим теперь, что время Т не является фиксированным.
Приближенное решение краевой задачи при некотором
Т=Т в общем случае не удовлетворяет точно краевым
условиям. Возникает ситуация, изображенная на рис. 7.3.
Повторим процедуры предыдущего пункта и составим
выражение (7.8). Используя первое из уравнений (7.9),
получим
Ф (Хт) = ф (X (Т)) +	(х (Т)) (Г (х (Т), Г) (х0 - х (/„)) +
+ /(х(Т), Т)АТ) = 0.
Поскольку ф(х(Т)) т^О, система (7.9) будет иметь сле-
дующий вид:
^(Г(х(Т), Л(х0 —х(/0))+/(х(Т), Т)ДТ)= — ф(х(Т)),
B(*o-*0 = -g(x(Q).	(7.12)
188
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
Система уравнений (7.8) и (7.12)—это система 2п
скалярных уравнений относительно 2м+1 неизвестной:
к неизвестным хт и xQ до-
бавляется еще одна неиз-
вестная величина АТ. Для
ее определения мы долж-
ны в число краевых ус-
ловий включить дополни-
тельное условие и проде-
лать с ним те же преобра-
зования, что с условиями
(7.2), (7.3). Например,
если мы рассматрива-
ем краевую задачу для
77-системы, к условиям
я1 (7.3) добавляется условие
трансверсальности, кото-
Рис. 7.з.	рое (полагая, что х— это
не только фазовый вектор,
но и вектор импульса) мы запишем в виде
Н (хг, Т) = Н (х (Г) + (хг - х (Г)), Т + АТ) = О
или, после линеаризации,
д/ (X (Т), Т) (Г (X (Г), Т) (х0 - х (Q)4- f (х (f), f) &Т) j-
OX
+ д£(х(Т),Т)ЬТ = -Н(x(f), f).	(7.13)
ОТ
Система уравнений (7.8), (7.12) и (7.13)—это систе-
ма 2п+1 линейных уравнений относительно 2п+1 неиз-
вестных.
5.	Переход к пределу. Схемы расчета, описанные в
предыдущих пунктах, являются достаточно типичными
приемами уточнения решения, если, конечно, /7-система
допускает линеаризацию. Известны также и некоторые
обобщения этих схем и возможность их использования
для построения итерационных процедур.
С. А. Пиявский*) предпринял изучение уравнений
(7.8), (7.9) с иной точки зрения. Совершим в этих уравне-
*) См. С. А. Пиявский, Об одном методе решения краевых
задач, ЖВМ и МФ 10, № 4, 1970.
МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИИ
189
§ 7]
ниях переход к пределу при ДТ->-0. Тогда мы получим
некоторые дифференциальные уравнения относительно
х0 и хт:
аТ al
(7.14)
^2. — = 0	— о
дх dT ’ дх dT
Система (7.14)—это система нелинейных дифференци-
альных уравнений относительно хт и х0. В самом деле,
матрица Г определяется уравнением (7.6), где А зависит
от х, т.'е. от х0 и хт; точно так же и f (х, Т) в общем слу-
чае зависит нелинейно от хг.
Система уравнений (7.14) дает определенные воз-
можности для исследования природы краевых задач, а
возможно, и построения численных методов их решения.
Рассмотрим тот случай, когда многобразия и ёт
имеют общие точки (именно этот случай изображен на
рис. 7.1 и 7.2). Тогда уравнения
Ф(х) = 0, g(x) = 0	(7.15)
имеют решение, которое мы обозначим х¥.
В этом случае мы можем (если выполнены некоторые
дополнительные условия) получить решение краевой за-
дачи (7.1) — (7.3), интегрируя нелинейную систему (7.14)
с начальным условием
х0 = хт = х, при Т = /0.	(7.16)
Итак, изложенные соображения позволяют (во вся-
ком случае принципиально) разработать регулярную
процедуру построения решения краевой задачи для не-
линейных дифференциальных уравнений.
6.	Особенности алгоритма. Структура системы урав-
нений (7.14) весьма сложна, поскольку все функциональ-
ные связи заданы с помощью процедур интегрирования
систем дифференциальных уравнений, поэтому для реше-
ния задачи Коши (7.14) — (7.16) еще необходимо указать
вычислительный алгоритм.
190
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. И
Зададим некоторый шаг 8Т по аргументу Т и решим
задачу Коши
X = f (х, t), х = х,.	(7.17)
Решение обозначим через х.(0- Затем вычислим мат-
рицу
<df_ \
/ x=Xf{t)
i, j = 1, ..., п.

Далее вычислим матрицу Г=Г(х#(/), t). После этого
решаем следующую задачу. Определить величины
Хт (А>+67') и х0 (/o-j-бТ), удовлетворяющие уравнениям *)
^ = Г(хД^Л)-^ + Ж(/0), Q,
аТ	аТ
(7Л8)
=	^-^ = 0, хг (Q = х0 (Q = х .
дх dT	дх dT	’	'°7	°'07
Затем мы снова решаем задачу Коши:
х = /(х,0, х(у = х0(дТ).	(7.19)
Решение обозначим через х.»(0- Находим Д(х.»(<), t)
и Г(х.,(^), t), после этого решаем задачу отыскания ус-
ловий хг(^0+26 Т) и х0(£0+26 Т), удовлетворяющих
уравнениям
^ = r(xw(^04-dT)^0 + dT)^4-
+ f(x„(t0 + bT),t0 + dT}, (7.20)
dip	dg dx0 ___ q
dx dT * dx dT
Начальные условия хг(/0 + бГ) и х0(/0 + 67') определены
на предыдущем шаге, и т. д.
*) Описанная процедура на первом шаге избыточна, так как
матрица Г(х(/0), /о) известна — это единичная матрица.
$ 7]
МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИИ
191
Как ни сложна подобная процедура, но если оператор
М =
о
дх j
^-п строк
строк
на каждом шаге описанного процесса оказывается невы-
рожденным, то мы можем получить решение краевой за-
дачи, опираясь на решения задачи Коши.
Примечание. Уравнение для определения
Г(х.(/о+бТ), ^о+бТ) нам надо интегрировать на отрезке
[Аъ М-67], уравнение для определения Г(х..(/0+26Т),
/0+267) на отрезке [4, /о+ЗбТ] и т. д. Таким образом,
вместе с отысканием решения рассматриваемой краевой
задачи мы находим решения целого ряда краевых задач,
для всех t^T^T». Эта дополнительная информация в
ряде конкретных задач может иметь самостоятельную
ценность.
Последнее относится в первую очередь к задачам с
нефиксированным временем, поскольку все методы ре-
шения таких задач связаны, по существу, с анализом (а
иногда и просто с перебором) некоторого множества ре-
шений краевой задачи. Описанный алгоритм как раз и
дает возможность такого анализа.
7.	Случай линейной системы. Рассмотрим теперь тот
частный случай, когда система (7.1) линейна:
х = Ах + Ь.	* (7.21)
В этом случае матрица Г определяется один раз. Для
этого надо решить пг линейных уравнений.
Ограничимся рассмотрением того частного случая,
когда т условий задано слева, а п — т—справа, и эти
условия имеют вид
= х^, 1=1, .... т,
х1 (Т) =хт, i = т 4- 1, ..., п.
192
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
[ГЛ. II
Система уравнений (7.18) тогда примет вид
dxt ”, dxl t
— = V Ytf—+ Д i = 1, 2, .... m,
dT A 11 dT 1	’	’ ’
/«=m+i
(7.22)
"	d4	i
0= 3	+ i=/п+1, n.
. ’	dT
Введем обозначения
у = {*т, Хт...........Хт}, г = {x„m+1, ..., Хо),
И, fn-m^{fm+l, Г),
мт =
Yim+i • • • Ym
Ym+i,m+i • • • Ym+l,n
Afn-m —
Ym,m+i • • • Ymn
Y«,m+1 • • • Ynn
Тогда уравнения (7.22) мы можем переписать в следую-
щей форме:
•— = Mn-mfn-mi
dT
(7.23)
~Г = MmMn-mfn-m 4“ fm*
di
Таким образом, в линейном случае решение краевой
задачи сводится к решению задачи Коши для системы,
порядок которой равен п2+п, т. е. трудоемкость излагае-
мого метода такая же, как и метода прогонки.
Примечание. Реализация таких процедур еще
требует дополнительного анализа. Очень важный во-
прос— это проблема устойчивости систем, поскольку
матрица Г содержит быстрорастущие слагаемые. Заме-
тим, кроме того, что во всех рассуждениях мы считали,
что многообразия и &т имеют общие точки.
ГЛАВА HI
ПРЯМЫЕ МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ
Прямыми методами вариационного исчисления при-
нято называть все те методы расчета экстремалей, кото-
рые непосредственно не используют необходимых усло-
вий. Родоначальником прямых методов (так же как и
непрямых) является Леонард Эйлер. Первым прямым
методом, который известен в литературе, был знаменитый
метод ломаных Эйлера. На грани XIX и XX веков, в свя-
зи с проникновением идей вариационного исчисления в
математическую физику, создается метод Ритца. Его
схема очень проста. Пусть речь идет об отыскании мини-
мума функционала J(х) при х^М, где М — некоторое
множество, например, множество дифференцируемых
функций двух аргументов x{tlt t2), обращающихся в нуль
на кривой Г(/ь t2) =0, которая ограничивает замкнутую
область определения функций x{tlt t2). Тогда решение за-
N
дачи можно искать в виде агрегата х= гДе {XJ—
некоторое подмножество т<=М.
Задача определения постоянных ct сводится к реше-
нию некоторой системы трансцендентных уравнений
^1>Сг, •••.^)==0> f=1>2.........у
дс^
В послевоенные десятилетия прямые методы типа
метода Ритца находят широкое применение в самых
разнообразных областях математической физики и ин-
женерной практики.
Как уже говорилось, разделение вычислительных ме-
тодов на прямые и непрямые довольно условно. Методы,
основанные на идеях поиска, также часто относят к пря-
мым. Появление электронной вычислительной техники
сделало эти методы очень важными с практической точ-
ки зрения, и в последнее время их реализации уделяется
большое внимание. Одновременно развивается и теоре-
7 Н. Н. Моисеев
194
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
тический аспект методов поиска (например, изучение при-
роды градиентных методов в функциональных простран-
ствах).
Данная глава посвящена изложению только тех пря-
мых методов, которые уже нашли свое место в практике
расчета оптимальных программ. Эти методы основыва-
ются на редукции исходной задачи к некоторой конечно-
мерной. Методы, излагаемые в этой главе, будут ис-
пользовать идеи нелинейного программирования и после-
довательного анализа вариантов.
Сначала мы обсудим различные конечномерные ана-
логи задач оптимального управления. Далее рассмотрим
некоторые методы нелинейного программирования, ко-
торые оказываются эффективными в теории оптималь-
ного управления. И, наконец, перейдем к рассмотрению
методов, использующих идеи перебора — последователь-
ного анализа вариантов. В заключение этой главы мы
рассмотрим несколько примеров существенно дискрет-
ных задач, т. е. задач, возникших не в результате дис-
кретизации непрерывных задач, и заметим, что в ряде
случаев конечномерные задачи бывает удобно интерпре-
тировать как конечномерные аналоги динамических за-
дач оптимального управления.
§ 1. Конечномерные аналоги задач
теории оптимального управления
1. Предварительные замечания. Конечномерные ана-
логи задач теории оптимального управления возникают
в двух случаях:
а)	Заменяя дифференциальный оператор конечнораз-
ностным, мы заменяем исходную задачу теории опти-
мального управления некоторой задачей нелинейного
программирования.
За последние 10—15 лет в нелинейном программиро-
вании (имеется в виду нелинейное программирование в
конечномерных пространствах) достигнуты большие ус-
пехи, причем не только в теоретической области. Относи-
тельно большого совершенства достиг и вычислительный
аппарат этой теории. Поэтому понятно стремление ис-
пользовать его и в задачах теории оптимального управ-
ления.
$ 1]	КОНЕЧНОМЕРНЫЕ АНАЛОГИ	195
Следует заметить, что задача нелинейного- програм-
мирования, возникающая при дискретизации задач оп-
тимального программирования, обладает рядом специ-
фических свойств, позволяющих развить специальные
вычислительные процедуры нелинейного программиро-
вания.
б)	Многие задачи линейного и нелинейного програм-
мирования, статические по существу, можно интерпрети-
ровать как многошаговые динамические процессы, в ко-
торых роль дискретного времени играет какая-либо из
монотонно возрастающих переменных (например, ин-
декс). Благодаря этому ограничения в статических зада-
чах приобретают форму конечноразностных уравнений.
Это позволяет, в свою очередь, использовать в задачах
линейного и нелинейного программирования аппарат
теории оптимального управления. Здесь наиболее полез-
ной оказалась идея уточнения «диспетчерских» решений,
которая по существу была изложена в предыдущей главе.
Итак, мы имеем дело с двумя встречными тенденция-
ми. С одной стороны, методы нелинейного программиро-
вания, развитые для решения конечномерных задач, миг-
рируют в задачи оптимизации функционалов. А с дру-
гой стороны, приближенные методы теории оптимальных
управлений начинают с успехом использоваться в ко-
нечномерных задачах. Отмеченное обстоятельство отра-
жает тот факт, что в программатике нет универсальных
алгоритмов — она слишком сложна, чтобы можно было
использовать небольшой набор окончательных рекомен-
даций.
2. Простейший способ сведения задачи оптимального
управления к задаче нелинейного программирования.
В настоящее время разработаны два способа такой ре-
дукции. В первом случае мы получаем в конечном итоге
некоторую функцию от управлений. Во втором случае не-
известными оказываются состояния системы. Каждый из
этих способов имеет свои преимущества и недостатки, и
они не являются взаимно заменяемыми.
Пусть для определенности речь идет об отыскании
минимума функционала
J (х, и) = J F (х, и) dt,	(1.1)
о
7*
196
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
при условии, что векторы х и и связаны дифференциаль-
ным уравнением
х = [(х, и).	(1.2)
В пространстве (х, t) проведем гиперплоскости ~2{:
t ~ ix,
где i = l, 2, ..., N, т — шаг численного интегрирования.
Предположим, что на интервале (гт, (г’4-1)т) управляю-
щая вектор-функция принимает постоянное значение щ.
Заменим тогда уравнение (1.2) разностной схемой
xt+i = Xi 4- xf (хь Ui).	(1.3)
Соответственно с этим, интеграл (1.1) заменится следую-
щей интегральной суммой:
N-1
J (xi, «/) = г F (xlt щ).	(1.4)
Z=o
Примечание. Мы рассмотрели простейшую схему
разностной аппроксимации первого порядка точности.
Вместо схемы (1.3), (1.4) мы могли бы взять любую дру-
гую, в том числе и более высокого порядка точности. Это
не внесло бы никаких принципиальных изменений в ха-
рактер рассуждений.
Итак, в результате конечноразностной аппроксима-
ции мы пришли к следующей задаче теории систем с ди-
скретным временем: определить векторы И/ и Xt, достав-
ляющие минимум сумме (1.4) при связях (1.3) и усло-
виях u^Gi, х^^о, xNe&N, где Gt, и —некоторые
заданные множества.
Эта задача уже является задачей нелинейного про-
граммирования. Ей можно придать несколько иной вид.
Предположим, что начальное состояние системы
(вектор х0) фиксировано, тогда равенство (1.3) позво-
ляет последовательно исключить фазовые векторы
Х1 =	(^о» «о) ~	(“о)»
х2 = Oj (п0) 4- xf (Ф^ (м0), «0 = Ф2 (и0, Ur),
............................................... (1-5)
Xk = Фк-1 («о» • • • . Wfe-s) +
4-	(Ф*_1 (м0...М*_2), Uk-r) = Ф* (Ио, .... Uk-r)
§ 1]	КОНЕЧНОМЕРНЫЕ АНАЛОГИ	197
и т. д. Функционал (1.4) становится функцией только
векторов «о,
N-1
J = 2	иИ>	(1-6)
1=0
где Л (и», «ь .. •, и<) =тГ(Ф<(и0, • • •, «4-1), «О-
Таким образом, задача сведена к минимизации неко-
торой функции конечного числа переменных. При этом
мы получили некоторую специальную задачу, обладаю-
щую рядом особенностей. Одна из них состоит в том, что
функция J — это сумма конечного числа слагаемых Л,
причем Л зависит только от первых i неизвестных. Функ-
ции вида (1.6) будем называть функциями с последова-
тельным включением неизвестных. Эта особенность, как
мы увидим, позволит использовать для отыскания мини-
мума аппарат последовательного анализа вариантов. Ус-
ловие на правом конце также может быть выражено как
функция векторов и0, ..., uN„i. Например, если конечное
значение вектора х (вектор xN) фиксировано, то мы бу-
дем иметь
X~N =	(«О» «1» • • • . UN-l)-	(I-7)
Поскольку xN задан, то (1.7) — это некоторое условие ти-
па равенства, наложенное на искомые величины иа,
..., uN-i. Если мы имеем задачу без фазовых огра-
ничений, то исходная задача Лагранжа формулируется
теперь следующим образом: требуется определить век-
торы «о, «ь «2> • • •, «х-i, доставляющие минимум
функции (1.6) при условии u^Gi и условиях (1.5).
Сформулированная задача уже является некоторой
задачей нелинейного программирования, и для ее реше-
ния могут быть использованы разнообразные методы
этой теории. Выбор конкретного метода численного ре-
шения сформулированной задачи нелинейного програм-
мирования определяется обычно природой функций J (и)
и Ф((«).
Описанная схема решения задачи определения про-
граммного движения довольно широко используется для
198
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
практического решения разнообразных технических за-
дач. Она подробно описана в работах Ю. М. Ермольева,
А. И. Пропоя и многих других*). Для нее получен дис-
кретный аналог принципа максимума, изучены вопросы
сходимости **) и т. д. Соображения, близкие к изложен-
ным, использовались В. А. Поповым, И. О. Мельцем и
другими ***). Возможности этой схемы обсуждались так-
же и в работах сотрудников Вычислительного центра
АН СССР.
В случае, если функции f и F являются выпуклыми
функциями своих аргументов, а области Git и так-
же выпуклые, то для задачи (1.3) — (1.4) справедлив ана-
лог теоремы Куна — Таккера, которая играет роль прин-
ципа максимума в теории оптимального управления ****).
Изложенная схема редукции в некоторых случаях по-
зволяет построить экономные алгоритмы численного рас-
чета оптимального управления. Однако она обладает
также и рядом недостатков; одним из основных недо-
статков описанного подхода является трудность удовлет-
ворения фазовым ограничениям, в том числе и краевым
условиям. Формально они не изменяют природы задачи,
поскольку фазовые ограничения записываются в виде
Xi = Ф; (и0,	U.-1) <= Gx.	(1.8)
Однако при проведении конкретных расчетов добавление
каждого следующего условия типа (1.8) существенно ус-
ложняет задачу.
Вторая трудность, для преодоления которой данный
подход оказывается мало приспособленным, если исполь-
*) Ю. М. Ермольев, В. П. Гуленко, Конечноразност-
ный метод в задачах оптимального управления, Кибернетика, № 3,
1967. А. И. Пропой, Методы возможных направлений в задачах
оптимального дискретного управления, Автоматика и телемеханика,
№ 2, 1967.
**) См., например, Б. М. Будак, Е. М. Беркович,
Е. Н. Соловьева, О разностных аппроксимациях в задачах оп-
тимального управления, Вестник МГУ, № 2, 1968.
***) И. О. Мельц, Учет ограничений в задаче оптимизации
динамических систем в функциональном пространстве на основе ме-
тодов нелинейного программирования, Автоматика и телемеханика,
№ 3, 1968.
****) См. Н. Н. Моисеев, А. Ф. Кононенко, Нелинейное
программирование, Изд-во МФТИ, 1972,
Конечномерные аналоги
499
§ 11
зовать методы спуска,— это резкое усложнение задачи
с увеличением интервала [О, Г].
3. Использование пространства состояний. Второй
способ редукции основан на следующем соображении.
Рассмотрим фазовую траекторию у, которая описывает-
ся системой (1.2) при некотором управлении. Обозна-
чим через Xi точки, в которых фазовая траектория у пере-
секает плоскости Si.
Введем теперь в рассмотрение оператор В(хй Xi+i),
который паре точек хг- и xi+i ставит в соответствие управ-
ление, переводящее систему за время г из состояния х» в
состояние Хг+1, и участок траектории yit i+l, который со-
единяет эти точки. Этот факт мы будем записывать в
следующем виде:
(ty, Yfj’+i) = В (xit Х/+1),	(1.9)
а оператор В будем называть элементарной операцией.
Функционал (1.1) запишем так:
АГ-1 *i+l	АГ-1
J (х, и) = 3 ' J ^(Yz.i+1. Ui)dt = 2	xl+1). (1.10)
1=0 Ц	i=0
Таким образом, если нам дана элементарная опера-
ция, то траектория определяется конечным числом точек
х( — точек пересечения этой траектории с поверхностя-
ми
Понятие элементарной операции может быть расши-
рено. Мы не будем связывать построение дуги <+1 с
отрезком фазовой траектории. Определим операцию
B(xit х<+1) как некоторую процедуру построения вектора
и{ и отрезка у;, ,+1, соединяющего точки xt и х,-+1.
При помощи этой операции мы можем построить ап-
проксимацию исходной фазовой траектории у некоторой
ломаной, состоящей из дуг i+1, и свести исходную зада-
чу оптимального управления к задаче определения мини-
мума функции конечного числа переменных (1.10). Кри-
вую, составленную из этих дуг, мы будем называть лома-
ной Эйлера. Такая терминология, как мы увидим ниже,
оправдывается тем, что в простейшей задаче вариацион-
ного исчисления ломаные, которые мы строим, оказыва-
ются обычными ломаными Эйлера.
266
ПРЯМЫЕ МЕТОДЫ
IM. lit
Вопрос о том, насколько такая задача соответствует
исходной — это трудный вопрос, к обсуждению которого
мы вернемся в § 5.
Заметим, что описанная редукция приводит нас к
функциям весьма специального вида (1.10) —это так на-
зываемые аддитивные функции. Они организованы го-
раздо проще, чем функции с последовательным включе-
нием неизвестных (1.6), полученные в результате стан-
дартной конечноразностной аппроксимации. Это позволит,
как мы увидим ниже, развить некоторые специальные
методы для их исследования. Редукция к задаче (1.6),
(1.5) совершенно тривиальна, в то время как построение
элементарной операции, а следовательно, и редукция к
аддитивной задаче в каждом отдельном случае представ-
ляет собой специальную проблему.
4. Пример: задача о брахистохроне. В предыдущем
пункте мы заметили, что построение элементарной опе-
рации в общем случае не тривиально. Однако легко при-
вести примеры, когда построение этой операции не пред-
ставляет никакого труда. Рассмотрим классическую
Рис. 1.1.
задачу о брахистохроне — задачу, которая изучалась еще
в конце XVII века И. Бернулли и была одной из задач,
положивших начало вариационному исчислению.
Напомним ее постановку (рис. 1.1, а). Определить
траекторию материальной точки, которая, двигаясь под
действием только силы тяжести, переместится из точки
0(0, 0) в точку А(Ь,—а) за минимальное время. В на-
§ 1]
КОНЕЧНОМЕРНЫЕ АНАЛОГИ
201
чальный момент материальная точка находится в состоя-
нии покоя.
Обозначим через ds = dx2 + dy2 элемент дуги кри-
вой. Тогда скорость вдоль кривой определяется форму-
лой v = 4t =	1 + (irT- Но> с ДРУГОЙ стороны,
v = Y — 2gy. Из этих двух равенств находим
^£ — 1/	^~2еу
dt ~ V i.-^(dy[dx)2 *
Из этого соотношения мы можем определить время,
которое будет затрачено материальной точкой на пере-
мещение из состояния О в состояние Л:
61
0 I
Итак, задача свелась к определению и(х) и у(х), до-
ставляющих минимум функционалу
6	______
о
В этой задаче элементарная операция совершенно три-
виальна, она сводится к замене ы.= (У<+1—yi)!x, где т—
шаг интегрирования, и задача о брахистохроне сведет-
ся к отысканию чисел z/,<0, доставляющих минимум
сумме
2 у ---------------- при ограничениях у0 — 0, уы= — а-
В этой классической задаче нет никаких ограничений
на координаты. Как мы увидим, методы, развиваемые в
этой главе, позволяют рассмотреть значительно более
сложные задачи. Например, может быть рассмотрена за-
дача, в которой траектория у(х) не должна пересекать
заштрихованной области (рис. 1.1,6).
До сих пор мы получали системы с дискретным вре-
менем как результат применения конечномерной аппрок-
202
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
симации непрерывных задач. Приведем теперь несколько
примеров существенно дискретных задач, которые при
известных условиях можно рассматривать в качестве ди-
намических систем с дискретным временем.
5. Пример задачи нелинейного программирования,
которая может рассматриваться как задача оптималь-
ного управления с дискретным временем. Рассмотрим
следующую задачу нелинейного программирования: оп-
ределить векторы и2, ..., uN размерности tn, достав-
ляющие максимум скалярной функции
N
.....u„) = 2W (1.11)
1=1
при следующих ограничениях:
ui^Gi,	(1.12)
w
2 ф/(«/)<ь.	(из)
Здесь b и	—векторы размерности п, Gt—некоторые
множества.
Частным случаем задачи (1.11) — (1-13) является рас-
пределительная задача, в которой выражения (1.11) —
(1.13) заменены следующими:
N / т \
j = 2 2<w.	(1-14)
*= \/=»1 /
т
^CifU^c1, 1=1,2, N,	(1.15)
/=х
2W<b\ /= 1, 2, .... п.	(1.16)
1=1
В том частном случае, когда Сц=Ьц=\ и п=т, зада-
ча (1.14) — (1.16) называется транспортной. Она допу-
скает следующую интерпретацию. Пусть —это коли-
чество продукта, которое поступает со склада номера /
потребителю номера i. Запросы потребителя должны
$ 11	Конечномерные аналоги	203
быть удовлетворены:
т
^ui = c‘.	(1.17)
/=1
Но запасы на складе номера j ограничены, следователь-
но, количество продукта, которое взято с данного скла-
да, не должно превышать запасов
N
3	(1.18)
t=i
Наконец, если через а.ц обозначить стоимость перевозки
одной единицы продукта потребителю номера i со склада
номера /, то функция (1.14) —это общая стоимость пе-
ревозки продукта. Таким образом, простейшая из задач
рассматриваемого класса следующая: каким образом
распределить задание на поставку продукта между скла-
дами, чтобы при условиях (1.17) и (1.18) суммарная сто-
имость перевозки э-того продукта была минимальной?
Введем новую переменную
x(s + 1) = 2	*0) = 0> s = 1, 2, ..., Af.
i=i
Это выражение можно переписать следующим образом:
X (S + 1) — X (s) = <Ps (us).	(1.19)
Вектор х условимся называть фазовым вектором, тогда
(1.19) — это некоторое конечноразностное уравнение, ко-
торому должен удовлетворять фазовый вектор. На него
наложены также граничные условия
х (1) = 0, х(М+ 1) = Ь.	(1.20)
Теперь задачу (1.11) — (1-13) мы можем сформулировать
следующим образом: определить вектор-функцию дис-
кретного аргумента и{ и фазовый вектор x(t), доставляю-
щие минимум функционалу
N
J (и)^^ Fi(Ui)
t=i
при условиях (1.19), (1.20) и (1.12).
61>ЯМые мЁТоДЫ
(M. lit
204
Эта задача уже может рассматриваться как обычная
задача оптимального управления (но с дискретным вре-
менем).
Примечания.
1.	Есть одно существенное отличие задач оптималь-
ного управления при дискретизации времени и задач, ко-
торые рассматриваются в этом пункте. В дискретных за-
дачах оптимального управления имеется однозначное
правило упорядоченности моментов времени. Если
то это значит, что и i<.k, т. е. номер момента времени t{
меньше номера момента th. В рассматриваемых задачах
роль времени играет индекс I. Порядок нумерации потре-
бителей в транспортной задаче совершенно произволен.
Изменив эту нумерацию, мы получим, вообще говоря,
другую задачу оптимального управления.
2.	Сведение задач типа распределительных к динами-
ческим задачам имеет смысл лишь в тех случаях, когда
размерность N очень велика, и во всяком случае N^>m.
Если говорить о транспортной задаче, то ее сведение
к динамической целесообразно в тех случаях, когда чис-
ло потребителей гораздо больше числа складов или на-
оборот.
3.	Задачи рассматриваемого класса могут быть све-
дены к аддитивным, т. е. к задачам минимизации функ-
ций (1.10). К этому вопросу мы вернемся в § 6, где бу-
дет обсуждаться применение методов теории оптималь-
ного управления в задачах нелинейного программиро-
вания.
6.	Одна задача теории расписаний. Предположим,
что нам задан список, состоящий из N работ vlf о2,..., vN,
которые должны быть выполнены. Каждая из работ vf
будет выполнена за единицу времени, если на ее выпол-
нение будет выделен ресурс qit например, выделено q\
человек, q*t — специальных машин и т. п. Таким образом,
qf— это некоторый вектор. Суммарный вектор ограничен,
и на каждую единицу времени мы можем выделить
ресурс, равный Q. Следовательно, за данную единицу
времени мы можем выполнять те или другие работы из
нашего перечня работ, но при условии, что
2<7f<Q(2V),	(1.21)
И
$ и	КОНЕЧНОМЕРНЫЕ АНАЛОГИ	205
где сумма распространена по всем тем номерам работ,
которые выполняются в данную единицу времени.
Помимо условия (1.21), ограничивающего выбор ра-
бот, выполнение которых может быть назначено на дан-
ную единицу времени, есть еще одно ограничение на по-
следовательность их выполнения. Физический смысл та-
ких ограничений очевиден: например, для того чтобы
делать крышу дома, необходимо, чтобы был закончен
фундамент и выложены стены. Итак, второе ограниче-
ние будет состоять в следующем. Каждой работе vf по-
ставлена в соответствие некоторая последовательность
работ о41, vi2, ..., o<S}. Работа vt не может начаться рань-
ше, нежели работы o<i,..., vis[ закончатся.
Простейшим примером ограничивающих условий та-
кого типа является условие, что совокупность работ {и.}
должна быть представлена ориентированным графом
(рис; 1.2). На рис. 1.2 показано, в частности, что рабо-
та номера1/ не может начаться, если не закончены рабо-
ты Vi, v„ vn. Это условие будем называть условием а.
Помимо условий подчиненности, в него могут быть
включены и некоторые другие. Например, работа номе-
ра i должна делаться параллельно работе номера /
и т. д.
Мы будем говорить, что расписание работ составле-
но, если каждой единице времени Д/ь Д/2,..., Д/п (усло-
вимся их называть днями) поставлено в соответствие
некоторое множество работ из нашего списка, удовлет-
воряющее ограничениям (1.21) и а. Расписание работ
может быть составлено не единственным образом. По-
ставим задачу составить расписание минимальной дли-
ны, т. е. так распределить работы по дням, чтобы сум-
марное количество дней, затраченных на выполнение
всего списка работ, было минимальным.
Примечание. Условие, что время, необходимое
на выполнение каждой из работ vh равно одному дню,
не очень существенно. Если для выполнения какой-либо
из работ необходимо k дней, то мы эту работу разбиваем
на k работ, которые должны выполняться последователь-
но (на рис. 1.2 показана такая последовательность ра-
бот vit vi+i, vi+2 и v<+3). Таким образом, — это по су-
ществу «дневная порция» работы. Более существенным
20В
ИГ»ЙМЫЕ МЕТОДЫ
[ГЛ. 1й
является услоЬие, состоящее в том, что «дневная пор-
ция» либо выполняется, если для этой работы выделен
полностью весь необходимый ресурс, либо не выполня-
ется, если ресурс может быть выделен не полностью.
Рис. Г.2.
Рассматриваемая задача является простейшей задачей
теории расписаний с ограниченным ресурсом; более
интересен тот случай, когда время выполнения работ
зависит от количества выделенного ресурса. Такой при-
мер рассмотрен в следующем пункте.
Состояние нашего перечня работ на каждый день мы
можем описать двоичным числом, имеющим N разрядов.
Если в 6-м разряде мы имеем 1, то это значит, что ра-
бота номера k выполнена. Если 0, то не выполнена. Это
число мы обозначим через х (t) и будем называть его
$ 1]	КОНЕЧНОМЕРНЫЕ АНАЛОГИ	20
фазовой переменной. Каждое расписание может быть
изображено некоторой фазовой траекторией (рис. 1.3).
В момент начала работ ни одна из работ не выполнена,
следовательно, х(0)=0, и все фазовые траектории исхо-
дят из начала координат. На прямой ^=1 отложим
двоичное число xlt описывающее перечень работ, кото-
рые выполнены к концу первого дня, и соединим эту
точку отрезком с началом координат. На прямой 1=2
отложим двоичное число х2, описывающее перечень ра-
бот, которые выполнены к концу второго дня, и соеди-
ним эту точку отрезком с точкой xt и т. д.
Обозначим через М число дней, затраченных на вы-
полнение всего перечня работ. Тогда фазовая траекто-
рия пересекает прямую t—M в точке (11... 11), в кото-
рой все работы выполнены.
Введем теперь понятие управления. Обозначим через
м(з) ^разрядное двоичное число, описывающее пере-
чень работ, принятых к выполнению в течение дня но-
мера з. Подчиним выбор управления ограничениям «
и (1.21). Тогда уравнение фазовой траектории мы мо-
жем записать в следующей форме:
x(4+1) = x(4)| + |u(s), s — 0, 1, ..., Af—1. (1.22)
В этом уравнении величина x(te+i) получается из вели-
чины x(ts) прибавлением двоичного числа u(s). Однако
это не обычное сложение. Если некоторая работа номе-
ра I, например, выполнена, а в Z-м разряде числа «(з)
тем не менее стоит 1, т. е. на работу номера I выделен
ресурс, то в /-м разряде числа х(^+1) должна стоять 1.
Другими словами, в уравнении (1.22) знак | + | опреде-
ляет нелинейную операцию поразрядного логического
сложения (дизъюнкцию)
0 | + |0 = 0,
0|+|1 = 1,
1| + |1=1.
Задав определенные м(з), мы получим фазовую тра-
екторию, и она при некотором t=M пересечет прямую
х=х». Следовательно, значение t=M будет функцией
и (0), и (1),..., и (М— 1):
М=М(м(0), ..., и(М'— 1)).
208
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
Поставим задачу отыскания величины
М. = min М (и (I)).
и(1)
Итак, мы привели задачу расписаний к такому виду,
что она формально эквивалентна задаче на быстродей-
ствие в теории оптимальных систем дискретного време-
ни: требуется найти такое управление (удовлетворяю-
щее определенным ограничениям), чтобы фазовая траек-
тория достигала точки х, за минимум (дискретного)
времени.
Примечание. Заметим, что кривая х(/;) всегда
является монотонной. Интерпретация задачи теории рас-
писаний как динамической задачи, разумеется, никак
не меняет ее содержания — она продолжает оставаться
одной из труднейших задач дискретного программиро-
вания. Главная трудность рассматриваемой задачи со-
стоит в отсутствии упорядоченности фазовых состояний.
Если мы имеем два числа х,= 10000, х2= 10101, то мы
можем сказать, что х2>хь поскольку число х2 образо-
вано добавлением к х1 числа 00101. Но никаких подоб-
ных суждений относительно двух чисел х,= 10001, х2=
= 10110 мы уже сделать не можем. Тот факт, что мно-
жество возможных состояний {%} не является вполне
упорядоченным, представляет основную трудность для
построения вычислительных алгоритмов*).
7.	Задача расписаний с квантованным ресурсом. Рас-
смотрим следующее обобщение задачи предыдущего
пункта.
Предположим, что ресурс, необходимый, для работы
vf, может выделяться порциями, каждая из которых рав-
на Если ресурс, равный q(, выделяется ежедневно, то
работа v( будет выполняться k дней. Если для выполне-
ния работы выделить k порций ресурса qt, то работа о,-
будет выполнена за 1 день. Если на день начала работы
Vi выделено s(sCk) порций ресурса, то к концу дня ра-
бота будет находиться в состоянии s. Соответственно с
этим работа может находиться в одном из k состояний
0, 1,2,...Д.
*) В. И. Антипов, Решение частной задачи календарного
планирования методом сравнения состояния, Сб. «Системы распре-
деления ресурсов на графах», ВЦ АН СССР, 1970.
КОНЕЧНОМЕРНЫЕ АНАЛОГИ
209
§ 1]
Таким образом, для описания состояния в качестве
фазовой переменной мы применим «&-ичное» число:
х(^) = гхг2 ... rN,
имеющее по-прежнему N разрядов.
Фазовая переменная будет, очевидно, удовлетворять
тому же разностному уравнению (1.22).
Смысл знака | + | также вполне очевиден:
a I + I b — а + Ь, если а 4- b k,
a I + j b — k, если a b > fe.
Ограничение (1.21) будет записано так:
2M/<Q(A0.	(1.23)
tn
где ki — количество «порций» выделенного ресурса для
выполнения работы v{.
Такое видоизменение задачи уже охватывает очень
широкий класс задач теории расписаний с ограничен-
ным ресурсом.
8.	Параметрические задачи. В технике очень часто
встречаются задачи, в которых приходится выбирать не
только управление, но и параметры. Это значит, что
функционал J имеет вид
J = J(x, ы,у),	(1.24)
где х — фазовый вектор, и — управление, а у — постоян-
ный вектор. Задачи такого типа можно рассматривать
одновременно как задачи оптимального управления, по-
скольку в них идет речь об отыскании функции, миними-
зирующей функционал. С другой стороны, величина J
является функцией постоянного вектора у, принадлежа-
щего некоторому множеству С*.
Формально эта задача может быть сведена к зада-
че оптимального управления с фазовыми ограничениями.
Для этого достаточно параметр у включить в число фа-
зовых координат и написать для него уравнение
у — 0, yeGv.	(1.25)
Однако такое видоизменение задачи ничего не меняет
по существу. Поэтому исследование таких задач обычно
210
ПРЯМЫЕ МЕТОДЫ
[ГЛ. Ш
проводится с помощью методов нелинейного програм-
мирования.
Используя ту или другую конечноразностную аппрок-
симацию и повторяя рассуждения п. 3 данного парагра-
фа, мы придем к выражению типа (1.6), которое теперь
будет выглядеть так:
К-1
J = Г 2 Л («0. «1...«/> Y).
i=0
Параметр у оказывается равноправной переменной
задачи нелинейного программирования.
§ 2. Методы нелинейного программирования
в задачах оптимального управления
Методы нелинейного программирования в последние
годы начинают все шире применяться для нахождения
оптимальных управлений и траекторий. Более или менее
полное изложение методов и приемов, использующих
эту теорию, потребовало бы самостоятельной моногра-
фии. Поэтому здесь мы ограничимся лишь самыми про-
стыми вопросами.
1. Метод градиентного спуска в случае простейшей
разностной аппроксимации. В этом параграфе речь бу-
дет идти о конечномерных аналогах задач теории опти-
мального управления, т. е. об оптимизационных задачах
для динамических систем с дискретным временем.
Рассмотрим конечномерную задачу (1.3) — (1.4), счи-
тая для простоты, что левый конец фазовой траектории
фиксирован. Как было показано в предыдущем парагра-
фе, она сводится к минимизации функции (1.6):
N-1
J = 2 Л(«о> ^1» • • • > “О»	(2« 1)
/=0
где и( — это векторы размерности т. Они подлежат оп-
ределению.
Каждый шаг в методе градиентов сводится к расче-
ту очередного приближенного значения векторов щ по
§ 2] МЁТоДы НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 211
следующей формуле:
I	~ N~x dlt
Uj — и/ -~ку> --— Uj — nGj,	(2.2)
W dui
где vij — предыдущее приближение, x>0 называется ша-
гом градиентного спуска.
di.
Напомним, что величины--------это производные ска-
duj
лярной функции по векторному аргументу, т. е. они яв-
ляются векторами с компонентами
dlt д!{	дЦ
ди) ’ ди) ’	’ da”
*	После замены в (2.1) величин us по формулам (2.2),
*	функционал J превратится в функцию скалярной вели-
чины х: У=У(х). Шаг х может быть выбран так, чтобы
4 J (х) было минимальны^, и этот вариант градиентного
спуска условимся называть методом наискорейшего
спуска.
Займемся вычислением векторов G{. Для этого заме-
тим сначала, что функцию J (u+v) можно представить
так:
J(u + v) = J(u) 4- SJ + О(о2),
N-1
где SJ = 2 (pi, vi), Vi — приращение вектора и,-.
/=0
В уравнениях (1.3) положим
Xi = Xi + у{, Ui = Ui + Vi	(2.3)
и, сохраняя линейные члены, будем иметь
yt+i = At+iUi 4- Bi+1vi,	(2.4)
V гдаА., = Я + /«р,	Е-еди-
дх	ди
ничная матрица.
212
ПРЯМЫЁ МЁТОДЫ
|гл. nt
Исключая из (2.4) последовательно фазовые перемен-
ные, мы получим следующие рекуррентные формулы*):
t/s —	4* D,.^ -J- ... -j- Ds,s-i^s~it (2.5)
где D„,i — матрицы:
Ds,о — AsAs_, • • •	(2.6)
Ds,i = 4s4s_j ... A3B2,
Ds,s-i = BS.
Аналогичным образом преобразуем, выражение для
функции б/:
ЛГ-1	N-1
6J (у, о) = 2 (4 yi) 4- 2 (Si>	(2.7)
Зпесь векторы di и g£ вычисляются по формулам
di __ %	----, gi ~ X —------------.
дх	ди
4
Подставляя в равенство (2.7) выражения для у8 по фор-
мулам (2.5), мы получим после очевидных преобразова-
ний следующее выражение:
Ы = % (G£> Vi)t	(2.8)
i=0
где векторы О£ определяются формулами
tf-i
Go = yj DSto ds	gQt
Sz=l
(2.9)
AZ-l
~ ds + gi,
S=2
И т. Д.
*) Поскольку левый конец фазовой траектории фиксирован, то
{/о=О и соответствующее слагаемое в (2.5) не выписывается.
§4
МЕТОДЫ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
213
Таким образом, производные вычисляются по
формулам (2.9). Эффективное вычисление векторов
(2.9) возможно лишь в том случае, если N не очень ве-
лико.
Примечание. Остановимся на том случае, когда
функционал J имеет вид
J,= (С, х (Г)) = (с» xN).
Тогда его вариация будет иметь вид
6J = (с, уы),
и, используя формулы (2.5), мы получим
(N-l	\	N-l	N-1
с, 2 'Dn.Pi ] = 2	v^'	10)
Z=0 J	/	Z=0	1=0
Формула (2.10) является конечномерным аналогом фор-
мулы (4.12) гл. II:
г
= §G(t)vdt.
Для ее построения мы обошлись без явного использова-
ния сопряженного уравнения. Вместо интегрирования
этого уравнения мы вынуждены теперь проводить вы-
числения матриц D,{. Согласно схеме градиентного спус-
ка (2.2) мы имеем
Vi = — hG/	(2.11)
и, следовательно,
б/ = — «2	(2-12)
I
2. Параметрические задачи. Предположим теперь,
что уравнения динамической системы и функционал
имеют вид
Xi+i = х{ 4- т/ (xi, ui, у),	s (2-13)
N-l
J (Xi, Ui, y) = r 2 F (Xi, Ui, y).	(2-14)
i=o
214
ЙИМЫЁ МЁТОДь!
(ГЛ. nt
После замены Xi=xz+//z, ut-=^+^, 7=7 + 67 и линеари-
зации мы получим
yi+l = Ai+iyi Ч" Bi+lPi 4“ ^i+1 Sy,	(2*. 15)
tf-1	W-l	Af-l
SJ {y, v, Sy) = 2 (di' yi} + S Vi^ + 3	6y>’ <2-16)
.	Z=1	i=0	1=0
где L-
где bJ+i — т -	, it = т-----------.
ду	д%
Исключая последовательно из (2.15) фазовые пере-
менные yi, мы получим формулы, аналогичные форму-
лам (2.5)
Us ~ Ds,oVo 4“ Ds, Л 4* • • • 4" Dt,s-iVs-i 4" $Y>
s=l, 2, .... У.	(2.17)
Матрицы Ds,i вычисляются по формулам (2.6). Для
матрицы IFS мы имеем следующую формулу:
U^s —	4* -As^s-i • • • A3L2 4” • • • 4” 4sZ.s-i 4* 7.$.
(2.18)
Теперь для выражения 6J мы можем получить форму-
лу, аналогичную (2.8):
N-1
i>J = 2 (Gt, vi) 4- (Gv. 6Y),	(2.19)
z=o
где для векторов G{ мы имеем формулы (2.9). Вектор
GT определяется следующим выражением:
N-1
Gv = /04-2 (W'sds + ls).	(2.20)
S=1
Имея в своем распоряжении GI и Gv, мы можем реали-
зовать стандартную схему градиентного спуска; для
этого мы должны задаться шагом и и принять vi=
=—«Gf, 6у=—xGv. Линейная часть приращения функ-
ционала 6J будет такой:
/^!	\
SJ == - х I (Gz, Gi) 4- (Gv, GT) I.
V=o	/
5 2]
МЕТОДЫ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
215
Использовать эту процедуру 'можно лишь в том слу-
чае, если выбор v.t и бу не нарушит ограничений ни на
управление, ни на фазовые переменные. Следовательно,
если не вводить никаких модификаций, то метод, изло-
женный в двух последних пунктах, может быть приме-
нен только для решения задач со свободным концом.
Ниже, в одном из последующих пунктов данного па-
раграфа, мы покажем, каким образом изложенная мето-
дика должна быть видоизменена для решения задач с
ограничениями, а сейчас мы перейдем к рассмотрению
градиентного спуска в том случае, когда для построения
разностного оператора используется варьирование в про-
странстве состояний.
3. Градиентный спуск в случае аддитивных задач.
Если в задаче оптимального управления мы будем ис-
ключать управления и рассматривать аддитивную функ-
цию (1.10), то метод градиентного спуска приобретает
ряд особенностей, на которых имеет смысл остановиться.
Итак, мы будем рассматривать задачу минимизации
функции вида
N—1
J(xlt .... xN) =	<р, (хь х/+1).	(2.21)
1=0
Для построения процесса градиентного спуска нам
d(fi
надо вычислить частные производные . Но вектор х,-
(/ == 1, ..., Af— 1) входит только в два слагаемых ф/ и
Ф/_п поэтому
dJ	дф/ . d<pf_t
-----—---------1_ .-----)
dXf	dXj dXj
dJ	дфдг-i
dxN dxN
В том случае, когда мы имеем функцию вида (1.6), вы-
числение производной ^7 требует вычисления произ-
водных N — j слагаемых. В данном случае формула
216
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
типа (2.10) будет иметь вид
N j
М =	(°/> Уд>
1—1
(2.22)
где yt — вариация вектора х{, а вектор Gt имеет вид
д<Ры
дХ{
i = 1...АГ-1,
q__ (d4>N-x
\ dxN J
XN~XN
(2.23)
В процедуре градиентного спуска
N
SJ =	(2.24)
<=i
Xi = х{ — hGi,	(2.25)
где xi — предшествующее приближение. Процесс вычис-
ления прекращается, если все | G{| <е, где е — это не-
которое положительное число, характеризующее точ-
ность решения задачи.
Существует несколько модификаций описанной про-
цедуры.
а)	Предположим, что некоторые из компонент век-
тора G удовлетворяют условию

(2.26)
где е, — некоторое заданное число, не меньшее в (на пер-
вых шагах итераций мы можем принять его равным ke,,
где ^3*1, на последующих шагах мы его уменьшаем).
Тогда в течение нескольких шагов мы не варьируем зна-
чения этих переменных
*1
§2)
МЕТОДЫ ЙЕЛИНЁЙЙОГО ПРОГРАММИРОВАНИЯ
21?
и формулы (2.24) и (2.25) имеют следующий вид:
АГ-1 п
= —x^ (G{.)2,	(2.27)
i=o f=i
Xi= Xi — xG(-,,	(2.28)
причем
, Ci, если |GJ| > ©i,
Сг/ф =
О, если | Gi | ev
Стратегия спуска следующая: задаемся некоторым
приближением и вычисляем векторы G(. Фиксируем все
те координаты х{, для которых выполнены условия
(2.26) и в течение нескольких шагов (в зависимости от
величины е) проводим расчет по формулам (2.28) и
(2.27), используя, например, схемы п. 4 § 4 гл. II. Затем
снова вычисляем полностью векторы Gt и повторяем
процедуру.
Такая модификация градиентного спуска делает его
значительно более экономным с точки зрения расхода
машинного времени, поскольку не тратится время на
вычисления «малых» производных.
б)	Если мы закрепим все переменные, кроме одного
х1, то получится некоторый аналог метода покоординат-
ного спуска. Для данной задачи он особенно удобен, по-
скольку слагаемое ft «сцеплено» только с соседними сла-
гаемыми и в методе покоординатного спуска формула
(2.27) будет такой:
W = — х (G/, Gt).
. Если, кроме того, варьировать последовательно толь-
ко по одной из компонент вектора х/, то мы получим
обычный метод покоординатного спуска. Если, наконец,
фиксировать шаг, то мы получаем метод локальных ва-
риаций, который будет подробно изложен в § 3. В отли-
чие от предыдущей, в данной задаче мы можем легко
учитывать граничные условия. В самом деле, если
х(Т') =хт, где хт — заданный вектор, то в нашей схе-
ме это будет означать, что хя фиксирован и не варьи-
руется.
218
прямые методы
[гл. nt
4. Метод проектирования градиента в задачах с ог-
раничением на правый конец траектории. Метод проек-
тирования градиента — это один из наиболее распрост-
раненных численных методов нелинейного программи-
рования. Он подробно описан во многих публикациях и
монографиях. Поэтому здесь мы рассмотрим лишь не-
сколько примеров его применения в конечноразностных
Рис. 2.1.
задачах оптимального управления. Они помогут пред-
ставить вычислительные возможности этого метода.
Предположим, что на правый конец траектории на-
ложено условие вида
KyN = K	(2.29)
где К—матрица sXn, имеющая s строк и п столбцов,
а X — вектор размерности s (s^n).
Используя представление (2.5), мы перепишем усло-
вие (2.29) в следующей форме:
М-1
2 КА = X,	(2.30)
Z=0
где Ki=K.DN!i.
Введем в рассмотрение пространство управлений
Оно представляет из себя евклидово произведение N
пространствRi,  , размерности т. Следователь-
но, размерность R равна Nm. Если вектор a<=R образо-
ван векторами a^Rt, то векторы сц мы будем называть
векторными компонентами вектора а.
Обозначим через £7 = {й0, иь ..., uN_J начальное уп-
равление (рис. 2.1). Далее задаемся величиной шага х
по направлению градиента функции J. Компонентами
5 2]
МЕТОДЫ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
219
этого вектора являются векторы Gt. Равенство (2.30)
определяет в R некоторую гиперплоскость S. Выберем
новое управление (вектор J7+V) так, чтобы удовле-
творить условию (2.30) и одновременно максимально
продвинутся в направлении антиградиента при задан-
ном шаге. Для этого нам надо спроектировать век-
тор — на S и выбрать V по формуле
+	(2.31)
Здесь h — вектор минимальной длины, соединяющий
точку Р и гиперплоскость S.
Формулу (2.31) перепишем в следующих обозначе-
ниях:
Vi = — kGi + hi,	(2.32)
где Vi и h( — векторные компоненты векторов V и h. За-
дача определения V теперь может быть сформулирована
так: найти векторы ht, минимизирующие функцию
N-1
Л = 3 hl	(2.33)
1=9
при условиях (2.32) и (2.30).
Задача выбора векторов vt может быть сформулиро-
вана и несколько иначе: найти такие vt, наименее отли-
чающиеся от — v,Gt, при которых условия (2.30) оказы-
ваются выполненными. Мера отличия дается функцией
(2.33).
Составим функцию Лагранжа
W-l	/ N-1
hl+ 2 KtVi-K
1=0	\ Z=0
где ц, — множитель Лагранжа. Заменяя v{ по формуле
(2.32), приведем выражение функции Лагранжа к та-
кому виду:
N-1	/ N-1	[W-1
L = hl+ |л, 2	K/Gz- X
z=o	\ i-о	z=o:
N-1 N-i	/	N-1	’	'
= 3 hl (/<;hi} - Hi, к 2 KiGi +%
Z—0 Z—\	0
220
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
Составим необходимые ' условия минимума: -------= 0. От-
dhf
сюда легко получим
hi —----(2.34)
Для вычисления множителя Лагранжа р, восполь-
зуемся условием (2.30):
W-1	.	4	\
1=0	'	'
Отсюда
(N-1	х”1 /	N-1	х
И =-2 Зад’ Х +	.
\ /=0	/ \	1=о	/
Определяя теперь ht по формуле (2.34), мы получим
окончательно
= — xGf + ht = vu + vti,
где
ZW-1	x”1
= 3
\/=o	/
(N-l	X-1W-1
= * Рч 3	3
\S—0	/ Seo
KSGS — Gi
(2.35)
Первое слагаемое мы будем называть компенсационным
составляющим приращения управления, второе — гра-
диентным. Можно показать, что они взаимно ортого-
нальны и vi2 лежит в плоскости S, т. е. не нарушает огра-
ничения (2.30).
Определив теперь
U = U 4- V,
мы переместимся в точку Q. Вычисляя снова в этой точ-
ке вектор — хуЛ мы повторим процесс и т. д. Заметим,
что при этом функционал может возрастать.
§ 2] МЕТОДЫ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 221
5. Случай ограниченных управлений. Предположим
теперь, что кроме ограничений типа равенств (2.30)
движение системы стеснено ограничениями типа нера-
венств, которые накладываются на управление. Пусть
для простоты мы имеем только одно векторное условие
Hi = Hi + ‘С at,	(2.36)
которое эквивалентно т скалярным
(4 —
Предположим сначала, что й( удовлетворяет ограниче-
нию, т. е.
и сделаем пробный шаг, заключающийся в вычислении
градиентной составляющей приращения управления д{2
по второй из формул (2.35). Предположим, что О/2<С0-
Тогда условие (2.36) оставляем без внимания, поскольку
в результате движения в сторону антиградиента мы еще
глубже погружаемся в допустимую область щ <2 сц.
Если t/Z2>0, то существует опасность, что на следующем
шаге мы можем выйти из допустимой области, поэтому
мы зададимся некоторой величиной 6 ,~> 0 ив число огра-
ничений (2.30) включаем условие типа равенства*)
= &. При этом размерность вектора А. повышается на
единицу. Если начальное приближение не удовлетворяет
ограничению, т. е.	то в число ограничений (2.30)
включается такое:
где
а? = а{ — и'.
*) Описываемый подход переносится дословно на более общий
случай задания ограничений (2.36) в виде линейных неравенств
(Ci, Uj) sga.. В случае же (2.36) можно поступить проще: при >
>от брать *4=а/ •
222
ПРЯМЫЕ МЕТОДЫ
[ГЛ, HI
Примечание. Предположим, что мы имеем зада-
чу со свободным концом, тогда выбор vt по формулам
vf=—xGi может вывести управление из допустимой об-
ласти Й. На рис. 2.2 пока-
зана именно такая ситуа-
ция. Тогда величину vt
следует выбрать по фор-
муле v{=— PaK.Gi, где
Ра — оператор проектиро-
вания на допустимую об-
ласть й. Напомним, что
процедура вычисления
оператора проектирования сводится к решению задачи
определения вектора vt, минимизирующего квадратичную
форму
т
min 3 (^ + %$)2-
°<erQ /==1
Если теперь линеаризовать условие о.еГа(Гп—граница
области й), то мы придем к задаче, аналогичной той,
которая рассматривалась
в предыдущем пункте.
6. Ограничения на фа-
зовые координаты. Мето-
ды, которые развивались в
предыдущем параграфе,
были плохо приспособлен-
ными для решения вариа-
ционных задач с фазовы-
ми ограничениями.В рам-
ках излагаемой схемы ка-
кого-либо принципиаль-
ного различия между ог-
раничениями на конец
траектории, ограничениями на управление и фазовыми
ограничениями нет. Рассмотрим, например, условие
F(x, f)<0,
которое ограничивает движение (рис. 2.3). После диск-
ретизации мы получим
Fi(xt)^0,	i=* 1,2, .. N — 1.	(2.37)
§ 2]
МЕТОДЫ НЕЛИНЕЙНОГО программирования
223
Совершаем пробный шаг, как это было описано в
предыдущем пункте, и начинаем принимать во внимание
условия (2.37) лишь в тех случаях, когда возникает
опасность их нарушения на очередном шаге. Тогда мы
поступаем следующим образом.
Полагая х—х+у, перепишем (2.37) в виде
/ dF, \
Ft (х{) + | ——, t/z < 0.
\ &xi J
Теперь в число ограничений (2.30) мы включаем еще и
следующее:
( dF‘	х
—» У1 = —
\ 1
d = Ft Cxi) +
(2.38)
где St — некоторое число. Используя формулы, дающие
связь между yt и vi} мы можем преобразовать условие
(2.38) к виду (2.30).	’ .
7. Задачи на «узкие места». Этим термином обычно
называется класс задач теории оптимального управле-
ния, в котором ограничения имеют вид
F(x,u,t)^0.	(2.39)
После дискретизации задачи условие (2.39) заменяется
условиями
Fi(xi, ui)^0.	(2.40)
Полагая х=х+у и u=u-\-v, мы линеаризуем условия
(2.40):
I dF,
~ ♦ У1
\ /
Исключая уг при помощи формул (2.5), мы приведем
это условие к виду (2.30).
Таким образом, связь между векторами у и v, най-
денная в начале параграфа, позволяет унифицировать
методы анализа основных задач с ограничениями: задач
с ограничениями на концы траектории, с ограничениями
на управление, с ограничениями на фазовые координа-
ты и задач на «узкие места».
224
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
8. Некоторые приемы решения задач большой раз-
мерности. Методы, изложенные в этом параграфе, неиз-
бежно приводят к задачам очень высокой размерности.
Поэтому всякие приемы «улучшения» алгоритма явля-
ются важными.
Первый и наиболее традиционный способ «улучше-
ния» алгоритма — это ускорение его сходимости. Здесь
в последние годы получен целый ряд новых результатов
(Б. Н. Пшеничный, Н. 3. Шор и др.)*). Заслуживает
внимания идея такого локального изменения геометрии,
при котором линии уровня в окрестности предыдущего
приближения имеют форму, близкую к окружностям.
Такое изменение геометрии позволяет значительно уве-
личить шаг градиентного спуска. Другими словами, при
этом достигается значительное ускорение сходимости
метода градиентов. Эта идея, которая впервые была
высказана Т. М. Энеевым еще в 1960 году, яви-
лась основой эффективного метода, разработанного
Н. 3. Шором.
Однако все методы ускорения сходимости, сокращаю-
щие необходимое «количество» итераций, делают более
сложной каждую итерацию. А поскольку каждый вычис-
лительный процесс состоит из конечного числа итераций,
то может оказаться, что количество машинных опера-
ций (а, следовательно, и время счета), требуемое для
получения заданной точности, будет меньше, если поль-
зоваться методом, который сходится медленнее, но зато
для реализации каждой итерации требует меньшей за-
траты машинного времени. Поэтому построение методов
ускоренной сходимости может не дать желаемого резуль-
тата при решении конкретной задачи большой размер-
ности.
Заметим, что на практике, например, очень часто
вместо градиентного спуска используют покоординат-
ный, поскольку расчет одной итерации при покоординат-
ном спуске в п раз (п — размерность пространства)
«дешевле» итерации при градиентном спуске. Более
того, иногда используют несходящиеся схемы теории
*) Б. Н. Пшеничный, Один алгоритм решения общей задачи
математического программирования, Кибернетика, № 5, 1970.
Н. 3. Ш о р, Методы минимизации недифференцируемых функций
и их приложения, Докторская диссертация, Киев, 1970.
§ 2] МЕТОДЫ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ	225
возмущений, поскольку с их помощью можно достаточно
быстро улучшить приближенное «диспетчерское» ре-
шение.
Какие же пути существуют для действительного улуч-
шения алгоритмов спуска в задачах большой размер-
ности?
Заметим прежде всего, что до сих пор не найдена
альтернатива сходимости для оценки качества алгорит-
ма спуска. Проявление существенно дискретной приро-
ды процессов спуска ставит здесь целый ряд вопросов,
решение которых вряд ли возможно в рамках традицион-
ных методов. Поэтому ответ на поставленный вопрос —
указание приемов, ускоряющих счет, носит до сих пор
рецептурный характер, основанный на опыте (причем
ограниченном). В одних случаях предлагаемые рецеп-
ты могут оказаться полезными, в других — нет. Тем не
менее (поскольку существует заведомо не пустое мно-
жество задач, для которых они оказались полезными),
автор счел нужным перечислить некоторые из подобных
рецептов.
а)	Использование метода штрафных функций качест-
венно упрощает задачу, особенно если мы имеем задачу
с ограничениями типа неравенств. Пусть, например, мы
имеем ограничения на управления
- <4 <(/(/,)< at
Тогда мы введем функцию штрафа
.1 I Л I Ws)-«s)2. если
( 0	, если
следующего вида:
I и1 (ts) |	aSt
С помощью функций (2.41) мы сразу получаем возмож-
ность использовать аппарат градиентного спуска, изло-
женный в начале этого параграфа. Однако при этом
всегда остается актуальной проблема точности.
б)	При использовании градиентного спуска мы
df
должны вычислять на каждом шаге производные
(i = 1, 2,...п). Если п велико, то расчет этих величин за-
нимает основное машинное время. В то же время неко-
торые из производных малы и практически не влияют на
Н. Н. Моисеев
226
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
выбор шага. Выше было уже описано, как использовать
это обстоятельство.
в)	Использование методов случайного поиска стано-
вится тем более выгодным, чем выше размерность зада-
чи. В качестве простейшей схемы случайного спуска мо-
жет быть принята следующая:
f(xn^ee)-f(xn)
Xn+i — Хп — Т----------------в,
8
(2.42)
-где т и 8 — заданные числа, е — единичный вектор, вер-
шина которого равномерно распределена по сфере. За-
метим, что выбор достаточно малых т и е всегда может
Рис. 2.4.
сделать схему (2.42) монотонной. Это утверждение де-
монстрируется на рис. 2.4, а и б.
Схемы типа (2.42) с успехом использовались в ВЦ
АН СССР и Институте кибернетики АН УССР*). Каж-
дая итерация рассчитывается очень просто. Однако вся-
кий раз заранее трудно сказать, будет ли эта схема в це-
лом более экономной, чем схема градиентного спуска
или его модификации.
г)	С увеличением размерности задачи возрастает ве-
роятность появления оврагов у поверхности
* = /(*)•
Представим себе, например, что линии уровня этой по-
*) См., например, Ю. М. Ермольев, Стохастические квази-
градиентные методы и их применения, Докторская диссертация,
Киев, 1970.
§ 2J	МЕТОДЫ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ	227
верхности имеют вид, изображенный на рис. 2.5, где че-
рез х* обозначена точка, в которой достигается минимум
функции f(x). Отыскать эту точку методом градиентов,
даже если начальное приближение (точка х0) выбрана
более или менее удачно, очень трудно, поскольку функ-
ция f(x) изменяется быстро в направлении, перпендику-
лярном к оси оврага, и медленно вдоль оси оврага. По-
скольку шаг градиентного спуска всегда ограничен сни-
зу, то градиентная кривая будет переходить с одного
Рис. 2.5.
склона на другой, а движение вдоль оврага, т. е. по на-
правлению минимума, будет крайне медленным. Если к
тому же ось оврага быстро меняет направление, то оты-
скание минимума стандартными способами становится
практически нереализуемым.
Спуск в подпространстве быстрых переменных, опи-
санный в п. б), в данном случае не дает существенной
экономии. При отыскании экстремума функций подобной
природы, даже в случае малой размерности вектора х,
возникают обычно значительные трудности.
Одним из способов преодоления трудностей подобно-
го рода является использование самонастраивающихся
программ. Приведем один пример возможной схемы та-
кой программы.
8*
228
ПРЯМЫЕ МЕТОДЫ
. [ГЛ. III
мл полагаем равными
, мы также полагаем рав-
вычисляем величину
Фиксируем два числа в и N, причем & <С N, и рассмот-
рим два алгоритма А и В.
Алгоритм А — это градиентный спуск в подпростран-
стве быстрых переменных: все производные, которые удо-
I df
влетворяют неравенству уу
нулю.
Алгоритм В — это градиентный спуск в пространстве
медленных переменных: все производные, которые удов-
летворяют неравенству
ными нулю.
Схема работы программы следующая. Задаем- начальное
j
приближение х0. Делаем —М шагов при помощи алго-
2
ритма А и получаем точку хг. Вычисляем- величину
Pai — 2	. Затем делаем — М шагов при помощи
М	2
алгоритма В, получаем точку хг и
р _ 2/W —
B1 м
На этом заканчивается первый
граммы.
Второй этап повторяет первый
Мы делим общее число шагов М в отношении Pai и РВ1
М
и делаем Pai---------- шагов с помощью алгоритма А
РА1 + РВ1
М	г>
шагов при помощи алгоритма В и вы-
алгоритмоз А и
этап работы про-
с одним отличием.
и Pbi
числяем новые веса (или нозую цеяу)
В —числа Рлг и РВ2 и т. д.
Алгоритм А осуществляет спуск по склону оврага.
Алгоритм В вдоль его оси. Ось оврага имеет криволи-
нейный характер. Структура описанного алгоритма по-
зволяет отслеживать изменение ее направления. На
рис. 2.5 показаны две типичные траектории спуска из
точек х.
Исследование подобных самонастраивающихся про-
грамм только начинается, причем оно ограничивается
пока только экспериментированием.
§ 3]	ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ	229
§ 3.	Последовательный анализ вариантов.
Схемы динамического программирования
Истоки динамического программирования лежат в
замечательных исследованиях русского математика
А. А. Маркова по теории «марковских» процессов. Их
основная особенность состоит в том, что последующее
течение процесса зависит только от состояния в данный
момент и не зависит от его предыстории. Она открывает
целый ряд возможностей для эффективного исследова-
ния подобных процессов. В послевоенные годы извест-
ный американский математик Вальд разработал методы
так называемого последовательного анализа, которые в
своем существенном использовали идеи Маркова. Схе-
мы Вальда привели к созданию новых методов решения
оптимизационных задач. В США исследования Вальда
были продолжены Айзексом и Веллманом. Их резуль-
тат — появление динамического программирования.
В СССР идеи Вальда развивались В. С. Михалевичем
и его учениками, создавшими общий формализм после-
довательного анализа вариантов. В этом параграфе мы
ограничимся изложением некоторых алгоритмов для
отыскания экстремума функций конечного числа пере-
менных, причем мы приведем их в том виде, в каком они
были разработаны и использовались в Вычислительном
центре Академии наук СССР.
Заметим, что, по мере расширения возможностей вы-
числительной техники, значение методов, использующих
различные идеи перебора и анализа вариантов, непре-
рывно возрастает.
1.	Аддитивные задачи нелинейного программирова-
ния. Аддитивной функцией векторов xlf ..., xN мы будем
называть функцию, представленную в виде
N-1
f (% ^1> • • • >	= Zj ft (Xi) ^/+1).	(3.1)
Z=0
Задачу нелинейного программирования мы будем назы-
вать аддитивной, если речь идет об отыскании минимума
(максимума) аддитивной функции при ограничениях
вида
Xi (= Gi.
(3.2)
230
ПРЯМЫЕ МЕТОДЫ
[ГЛ. Ill
В § 1 мы уже видели, какая существует связь между
аддитивными задачами нелинейного программирования
и задачами теории оптимального управления.
Аддитивные задачи допускают простую геометри-
ческую интерпретацию, которая нам будет полезна
для последующих исследований (рис. 3.1). В простран-
стве (х, f) построим гиперплоскости : t=ix (i=0,..., N).
2г — это n-мерные векторные пространства. Будем счи-
тать, что х;е2,-.
Рис. 3.1.
Зададим какую-либо совокупность векторов х{: {х0)...
..., Xpi}. Этой совокупности векторов формула (3.1) ставит
в соответствие значение скалярной функции f(x0, xw).
С другой стороны, если соединить точки х. отрезками, то
мы получим некоторую ломаную. В качестве длины от-
резка, соединяющего точки х( и х,+1, примем значение
функции ft(x{, xi+1). Аналогичным образом мы можем
построить границу допустимой области <?=2<?4. На
i
рис. 3.1 запрещенная область заштрихована. Функция
f(xe,...,xK) определяет длину ломаной, проводимой че-
рез точки х(. Теперь нашу исходную задачу мы можем
сформулировать следующим образом: среди всех лома-
§ з)	последовательный анализ вариантов	231
ных, соединяющих плоскости So и и лежащих в допу-
стимой области, найти ту, длина которой наимень-
шая.
Итак, мы имеем некоторое множество вариантов Q,
представляющих множество всех ломаных, соединяющих
2о и 2» и лежащих в допустимой области. Это множе-
ство имеет мощность континуума.
Примечание. Задача с фиксированными конца-
ми траектории является частным случаем рассматривае-
мой. когда множества G. и Gw
состоят только из одной точки.
2.	Алгоритм «киевский ве-
ник». Это один из основных ал-
горитмов, применяющихся для
решения аддитивных задач. Он
был предложен В. С. Михале-
вичем *). Основное содержание
алгоритма состоит в формули-
ровке правил последователь-
ного сжатия множества конку-
рентоспособных вариантов Q.
Алгоритм представляет собой
многошаговый процесс, на каж-
дом шаге (номера s) которого
производится «отметание» не-
Рис. 3.2.
которого множества вариантов
Qs, о котором в процессе работы алгоритма становит-
ся известным, что оно не содержит оптимального ва-
рианта.
Опишем подробно процедуру «отметания».
Рассмотрим точки, лежащие в гиперплоскости St —
точки Расстояние некоторой фиксированной точки Xi
по гиперплоскости So обозначим через l(Xi). Очевидно,
что (рис. 3.2)
/ (хх) = min Д (х0, хх).
xof=Go
*) В. С. Ми х ал ев ич, Последовательные алгоритмы оптими-
зации и их применение, «Кибернетика», №№ 1, 2, 1965. Алгоритм
«киевский веник» был разработан В. С. Михалевичем и Н. 3. Шором
и применен для конкретных расчетов в конце 50-х годов.
232
ПРЯМЫЕ МЕТОДЫ
[ТЛ. lit
Рассмотрим теперь функцию f(x0, х„ ..., xN). Так как
jv-i
min f (х0> xlt , xN} — l (xj + 2 ft (хь x<+i)>
««sfi.	i=i
то и любой вариант, т. е. любая ломаная, не содержа-
щая отрезка /(xj, не может быть претендентом на то,
чтобы считаться решением нашей задачи. Эти ломаные
и образуют множество Йо, которое мы отбрасываем на
нулевом шаге.
Произведем теперь сужение оставшегося множества
й—й0. Для этого рассмотрим точку х2е22. Обозначим
через Z(x2) длину наиболее короткой ломаной, соединяю-
щей точку х2 и гиперплоскость So. Очевидно, что
I (х2) = min (Z (xj) + h (х1( х2)).
Множество вариантов которое мы отбрасываем на
этом шаге, будет состоять из всех ломаных, которые не
содержат ломаной Z(x2).
Пусть теперь каждую из точек мы соединим с
гиперплоскостью 20 ломаной наименьшей длины, кото-
рую мы обозначим через /(%/). Тогда длина наиболее ко-
роткой ломаной, соединяющей точку xt+i и 20, определя-
ется при помощи соотношения
I (xz+1) = min (Z (xz) + fl (xz, xz+1)).	(3.3)
X &3i
Все варианты множества й„ не содержащие ломаной
длины Z(x<+1), мы отбрасываем и т. д.
На последнем шаге каждой точке xNeSN поставлено
в соответствие число l(xN) —длина наиболее короткой
ломаной, соединяющей точку xN с гиперплоскостью So.
Для того чтобы выбрать тот вариант, который нам ну-
жен — наикратчайшую ломаную, соединяющую гипер-
плоскости и Sw, нам осталось совершить еще одну
процедуру минимизации
I = min I (xN).
xn^gn
На этой операции процедура решения задачи заканчи-
вается. Формула (3.3) — это общее рекуррентное соотно-
§ 3]
ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ
233
шение, описывающее многошаговый процесс отыскания
решения.
Изложенный метод позволяет отыскивать глобаль-
ный экстремум.
Найденная оптимальная траектория обладает одним
важным свойством — любой ее отрезок является снова
оптимальной траекторией. Последнее означает, что уча-
сток траектории, соединяющий две ее любые точки и
xk — это некоторая ломаная, которая среди всех лома-
ных, соединяющих эти две точки и удовлетворяющих
ограничениям, имеет наименьшую длину.
Отсюда следует также, что аддитивные задачи удов-
летворяют принципу оптимальности, который может
быть сформулирован следующим образом: выбор траек-
тории, переводящей систему из положения (хг-, Q в по-
ложение (xht 4) (Kk), не зависит от состояния системы
в моменты, предшествующие 4.
Этот принцип получил название принципа Веллмана,
по существу же он выражает общее свойство марковских
процессов.
Примечание. Класс процессов, для которых
справедлив принцип оптимальности Веллмана, имеет
очень большое значение в различных прикладных зада-
чах. Он значительно шире класса процессов, сводящих-
ся к аддитивным задачам (в этом мы убедимся в одном
из последующих параграфов). В свою очередь, процессы,
для которых справедлив принцип оптимальности, обра-
зуют некоторый подкласс задач, для анализа которых
может быть использован общий метод последовательно-
го анализа вариантов.
3.	Численная реализация алгоритма. Для того чтобы
воспользоваться рекуррентным соотношением (3.3), не-
обходимо рассматривать множество £2, которое имеет
мощность континуума. Только в отдельных частных слу-
чаях удается провести аналитическое исследование этой
задачи. При разработке численных методов использу-
ют ее конечномерную аппроксимацию. Для этого в про-
странстве (х, t) строят сетку. Шаг по аргументу t задан,
он равен т. Задаем еще шаг по переменному х — величи-
ну Дх. Узлы сетки обозначим через Ph(i}. Индекс i озна-
чает номер гиперплоскости S<, а индекс k означает
номер узла р гиперплоскости Si. Каждые два узла,
234
ПРЯМЫЕ МЕТОДЫ
[ГЛ. Ill
лежащие на смежных гиперплоскостях Pk(i) и P^i+l),
соединены отрезками, длины этих отрезков мы будем
обозначать через
В результате такой операции мы получим некоторый
граф специального вида (рис. 3.3), в котором роль вер-
шин играют узлы Р; (i), и вместо исходной задачи мы
будем рассматривать задачу отыскания на этом графе
кратчайшего пути, соединяющего гиперплоскости So и
Итак, вместо задачи отыскания решения на множе-
стве Q всех ломаных, соединяющих гиперплоскости So
и мы ищем наикратчайшую ломаную среди конечно-
го множества ломаных Q'eQ. Ломаные из Q' проходят
через узлы Р} (i).
Обозначим через lk (i) ломаную кратчайшей длины
из соединяющую узел Рк (Г) с гиперплоскостью So.
Тогда, повторяя рассуждения предыдущего пункта, мы
снова придем к рекуррентному соотношению (3.3), кото-
рое будет теперь выглядеть так:
+ 1) = min {lk (i) + Iks (0)-	(3>4)
k
Минимум берется по тем номерам k, для которых узлы
лежат в допустимой области и принадлежат гипер-
плоскости 3». Число таких узлов обозначим через
§31
последовательный анализ вариантов
235
Таким образом, на каждом шаге мы совершаем пере-
бор вариантов из множества Mt возможных путей, про-
ходящих через узел Р, (Z+1). Из этого множества по
формуле (3.4) мы выбираем один вариант и его запоми-
"	'	шаге номера i-j-1 мы долж-
Je—з|е
наем. Таким образом, на
ны запомнить Afi+1 чисел
ls (Z+1) ($= 1, <.., Af<+1).
Определение величины
/8 (f-Н) требует вы-
числения Mi функций
A (PJZ),P.(Z+1))=4.(Z),
суммирования их с вели-
чиной Zft(i), хранящейся в
памяти, и сравнения меж-
ду собой полученных
величин. Предположим,
что на это расходуется АГ/
машинных операций. Следовательно, общее число ма-
шинных операций, необходимое для реализации алго-
-эе-
1о
Рис. 3.4.
ритма, равно
N—1
Q = 3 MiMl+1r^MfrN,
Z—О
(3.5)

4—

----Мг

X--
где М = шахАф, N — число шагов.
i
Примечание. В наших расчетах мы сделали пред-
положение, что затраты на вычисление Zs(i+1) пропор-
циональны М{. В самом деле, всегда вычислительную
процедуру можно организовать так, чтобы величина г не
зависела от I. Вычисляем сначала величину и скла-
дываем ее с li(i) *). Полученную величину обозначим
через Z,(Z+1) и запоминаем ее. Вычисляем далее Z2,(i),
складываем ее с Z2(Z) и полученную сумму сравниваем с
Z,(Z+1): из этих двух величин оставляем в памяти толь-
ко одну — наименьшую, и т. д.
4.	Метод «блуждающей трубки». Алгоритм «киев-
ский веник» дает возможность отыскать глобальный
экстремум, причем для функций А произвольного вида.
Никаких предположений о выпуклости функций мы не
*) Здесь предполагается, что нумерация узлов в (3.4) начи-
нается с единицы.
236
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
делали. Однако его реализация требует большой затра-
ты машинного времени и, что может быть еще более
важно,—большой оперативной памяти машины. Число
машинных операций и объем требуемой памяти машины
возрастают пропорционально квадрату числа узлов.
В Вычислительном центре Академии наук СССР ис-
пользовались процедуры, в которых ценой отказа от ре-
шения задачи отыскания глобального минимума удава-
лось значительно сократить число операций. Один из
таких алгоритмов (Н. Я. Багаева, И. А. Крылов,
Н. Н. Моисеев) получил название «блуждающей труб-
ки». Этот алгоритм имеет характер метода последова-
тельных приближений*). Пусть дано некоторое началь-
ное приближение — ломаная Го, которая задана после-
довательностью узлов PM(i) (см. рис. 3.4, где Го показа-
на пунктиром). Задавая Ах, построим сетку So, причем в
каждой из плоскостей мы включаем в сетку So только
по т узлов. (На рис. 3.4 эти узлы отмечены звездочка-
ми). На сетке So реализуем вычислительную схему
алгоритма «киевский веник», рекуррентное соотношение
которого в этом случае будет иметь вид:
Zs(i+1)= min {/*(«)+ ^s(i))-	(3-6)
Определив при помощи соотношения (3.6) новую лома-
ную 1\ (на чертеже она изображена сплошной линией),
мы повторим процедуру и т. д. Таким образом, на каж-
дом шаге мы разыскиваем ломаную на некотором под-
графе Sj.
Оценим число операций, необходимых для отыскания
минимума при помощи алгоритма «блуждающей трубки».
Если ломаная известна, то для отыскания следую-
щего приближения — ломаной Ti+1— нам необходимо
произвести Qj операций, где Q^rm^N. Обозначим че-
рез k общее число итераций. Тогда количество машинных
операций, необходимых для окончания процесса, будет
Q krm2N.
Чем больше число узлов на подграфах S,, т. е. чем
больше число т, тем меньшее число итераций необхо-
*) Н. Н. Моисеев, Методы динамического программирова-
ния в теории оптимальных управлений, ЖВМ и МФ 4, № 3, 1964;
5, № 1, 1965.
§ з)
ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ
237
димо сделать, следовательно, число k зависит от отноше-
ния М1т. Примем, что	Тогда для общего
числа операций мы будем иметь следующую оценку: .
Q^k/MmN,	(3J)
т. е., в отличие от метода «киевского веника», в методе
«блуждающей трубки» число итераций растет линейно с
увеличением числа узлов М.
Оценку (3.7) получил И. А.
Крылов.
5. Метод локальных ва-
риаций. Итак, мы установи-
ли, что чем меньше «объем
блуждающей трубки», тем
меньшее число операций тре-
бует реализация процедуры
поиска решения. Это наво-
дит на мысль о необходимо-
сти на каждом шаге итера-
тивного процесса использо-
вать трубку (подграф), содержащую наименьшее число
узлов. Мы убедились, что при этом, несмотря на возра-
стание общего числа итераций, количество машинных
операций, необходимых для отыскания минимума, будет
наименьшим. Эти наводящие соображения лежат в осно-
ве метода локальных вариаций, предложенного Ф. Л.
Черноусько и разработанного им совместно с И. А. Кры-
ловым *) **).
Пусть снова мы имеем некоторое начальное прибли-
жение’ Го. Наименьшим подграфом So, содержащим Го,
будет, очевидно, тот, который помимо узлов Р0(г)еГл
содержит всего лишь один узел P^i) (рис. 3.5). Длина
звеньев ломаной, соединяющих точку P0(i-\-l) с точ-
кой Ро 0+1), равна
«о = fi-1 (Ро V - 1), Ро (0) + А (Р (0. Р (i + !))• (3.8)
Но на графе So существует еще одна ломаная, соеди-
няющая точки Ро (i—1) и Ро (i-H). На рис. 3.5 она
*) Конечно, эта оценка носит эмпирический характер.
**) И. А. Крылов и Ф. Л. Черноусько, Решение задач
оптимального управления методом локальных вариаций, ЖВМ и
М.Ф 6, № 1, 1966.
238
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
показана пунктиром. Ее длина будет такой:
«1 = А-1 (Л> V -1). Л (0) + А (Л (0. Ро V + 1))- (3.9)
Сравнивая величины (3.8) и (3.9), мы выбираем из них
наименьшую.
Структура сетки позволяет ввести узел P-i (х)—
узел, симметричный Pi (i) относительно Го. В самом
деле, если &х}—шаг по компоненте номера /, то узел
Pi (х) имеет координаты
(0 = Яо (0>
x'l (t) = x’o (i) + Дх/.
Следовательно, узел, координаты которого
Х-i (i) = Xd (i), s =/= j,
(0 = Xo (i) — Ax',
будет симметричен относительно Го; его мы и назовем
P-i (г). Предположим теперь, что имеет место неравенст-
во ао>а!. Тогда в качестве нового приближения (лома-
ной rj мы выбираем ломаную, проходящую через узел
Pi (i). Если a0<cci, то мы проверяем ломаную, которая
проходит через узел P-t (i).
Вычисление величины czi носит название локального
варьирования. Процесс последовательных приближений,
использующий локальное варьирование, сводится, таким
образом, к последовательному «улучшению» положения
узлов, через которые проходит ломаная Г(.
Примечания.
1.	Метод локальных вариаций можно рассматривать
одновременно как метод покоординатного спуска с
фиксированным шагом на фиксированной сетке, задан-
ной в области, определенной ограничениями.
2.	Если подсчитать число операций, необходимых для
реализации метода локальных вариаций, то мы снова по-
лучим оценку типа (3.7), т. е. трудоемкость отыскания
экстремума при помощи схемы локальных вариаций и
схемы «блуждающей трубки» практически одного по-
рядка.
3.	При сравнении методов «блуждающей трубки» и
локальных вариаций может показаться, что мы должны
§ 3]
последовательный анализ вариантов
239
отдать предпочтение последнему, поскольку он требует
I, для отыскания экстремума того же (по порядку) числа
| операций, однако более прост для программирования и
j	требует значительно меньшего объема оперативной па-
’	мяти. Однако такое заключение не всегда верно, по-
скольку метод локальных вариаций обладает также и
рядом недостатков. Наиболее существенный недостаток
состоит в очень большой чувствительности к локальным
экстремумам, которые к тому же часто оказываются
следствием неточностей процесса вычислений. Для ил-
люстрации сказанного приведем пример (рис. 3.6).
। Предположим, что исходное приближение (траекто-
рия Го) проходит через точки Pe(i—1), P9(i), P0(i+l),
Р0(г‘+2). Если мы начнем ее улучшать методом локаль-
ных вариаций, то мы должны сравнить траекторию Го с
траекторией, проходящей через точки Ро(1—1), Pi(i),
।	P0(t+l), с траекторией, проходящей через точки Ро(0,
Pi(i-H), Л>(Н-2) и т. д. Предположим, что при этом ока-
жутся справедливыми следующие неравенства:
А-i (Ро (j- 1), Ро (0) + А (Ро (0; Ро (i + 1)) <
I	< А-1 (ро а -1). Р1 (0) + А (Р1 (0, Ро (I + 1)).
А (Ро (0, Ро V + О) + А« (Ро (i + 1)> Ро (I + 2)) <
I	<А(ЗД, P1(f+1)) + A«(/’1(»+1), Ро(1 + Ъ)
и т. д. Тогда в результате применения метода локальных
вариаций мы должны сделать заключение о том, что ло-
маная Го и есть оптимальное решение. Предположим
I теперь, что ломаная действительно самой короткой дли-
ны проходит через узлы РД0, PJi+l), РДг+2),... Этот
факт методом локальных вариаций никак не может быть
240
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
обнаружен. В то же время он легко обнаруживается,
если мы начнем применять метод «блуждающей трубки».
6.	Стратегия поиска. Алгоритм «киевский веник»
дает возможность отыскать глобальный экстремум адди-
тивной функции. Однако получение -подобного решения
требует значительной затраты машинного времени и воз-
можно только при условии, что в нашем распоряжении
есть машина, обладающая большой оперативной па-
мятью. Методы «блуждающей трубки» и локальных ва-
риаций значительно более экономны, однако они при-
годны для отыскания только локальных экстремумов.
Поэтому, если априори известно, что исследуемая функ-
ция имеет единственный экстремум (например, если
функция выпукла), то следует применять один из этих
методов.
В общем случае используется следующая схема рас-
четов. Сначала с большим шагом Ах0 строим грубую
сетку So и применяем алгоритм «киевского веника».
В результате мы найдем некоторую ломаную Го — самую
короткую из ломаных, удовлетворяющих решению зада-
чи. Далее мы делаем «правдоподобное» предположение,
что ломаная, являющаяся решением задачи, находится
в окрестности Го. В ее окрестности строим новую сетку
Si с меньшим шагом Axj. При этом шаг сетки Axj выби-
рается так, чтобы узлы сетки So были включены в S4, и,
используя затем метод «блуждающей трубки», находим
ломаную Г4. Затем снова дробим шаг, выбираем новый
шаг Ах2, строим новую сетку S2 и т. д.
7.	Задача на быстродействие. Рассмотрим снова ад-
дитивную функцию (3.1)? но число N мы будем считать
неизвестным; тогда
К-1
f (х0, .....х„)	= 2 ft (Xi, xhl) = f* (x0, XN, N).
/=0
Поставим задачу отыскать такие значения переменных
х0, хъ..., xN и число N, которые при минимально возмож-
ном N доставляют функции f* значение f* = c. Величину
х0 будем считать фиксированной.
Так сформулированная задача является естествен-
ным аналогом задач на быстродействие, изучаемых тео-
рией оптимального управления.
§ 3]	ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ	241
Алгоритмы, которые были изложены, могут быть
использованы для их решений. Рассмотрим рекуррент-
ное соотношение (3.3), в котором min заменен на шах *):
I (xi+1) = max {I (xi) + fi (Xi, х,+1)}.	(3.10)
xi^°i
Положим / = 0. Если окажется, что
f l± = max I (xj = max /0 (хс, хх) > с9
x^Gi	x^Gt
то N равно 1, и задача сводится к отысканию корня
уравнения
/о ^1) ==	(3* 11
Если окажется, что /4<с, то для каждого значения Xi
мы должны запомнить значение /(xj. Далее полагаем
i = 1. Если окажется, что
/2 = max I (х2) = max {max (Z (хх) + /i (xi» хг))} > с>
Х2~О2 -tjSGt
то задача снова сводится к отысканию корня х2 уравне-
ния I (Х.) + ft (xt, х2) = с, и т. д.
Для задач на быстродействие также могут быть пост-
роены алгоритмы типа «блуждающей трубки».
8.	Функции с монотонным включением переменных.
Функцией с монотонным включением переменных будем
называть скалярную функцию, имеющую вид
F= F{fN (uN, fa-! (uN.lt f (wj) ...)}.	(3.12)
Здесь щ, u2,..„ uN—это векторы размерностей kt, k2,...
kN соответственно, ft— это однозначные векторные
функции своих аргументов. Выбор и{ стеснен ограниче-
ниями
ui^Gi,	(3.13)
где Gt — некоторые заданные множества.
Мы будем рассматривать задачу отыскания мини-
мума функции F при ограничениях вида (3.13). Функ-
ции вида (3.12) возникают, как мы видели, в резуль-
тате процесса исключения фазовых переменных х, из
*) Полагаем Z(xg) =0.
242
ПРЯМЫЕ МЕТОДЫ
(ГЛ. III
конечноразностных уравнений
xi — fl (Ul> хо) ~ fl (^1)’
Х2 ~ fl (^2» ^1) ~ fz (^2> f 1 («!.))>
(3.14)
XN — ?N (UN> XN-1) = ?N fhl-i (U-N-i, . . . , f (tij)) • • •)•
считать равной п. Зада-
будем называть зада-
чей Майера для системы
(3.14). Используем стан-
дартную геометрическую
интерпретацию подобных
задач. Для этого снова в
(п+1)-мерном простран-
стве (х, t) построим ги-
перплоскости S1; ..., Sx.
Векторы xt будут лежать
в соответствующих гипер-
плоскостях S<.
Совокупность точек х0,
N х^ ..., хк, соединенных от-
резками, образует некото-
Размерность векторов x( будем
чу минимизации функции (3.12)

4 4	4
Рис. з.7.	рую ломаную, которую ес-
тественно назвать фазо-
вой траекторией. Рассматриваемая задача уже не явля-
ется аддитивной и алгоритмы, которые мы рассматрива-
ли в начале параграфа, нельзя непосредственно исполь-
зовать для решения задачи о минимизации функции
(3.12). В самом деле, пусть в точке х,- сходятся две фа-
зовые траектории 1 и 2 (рис. 3.7). Они имеют общее про-
должение 3. При рассмотрении аддитивных задач мы
имели в распоряжении правило отбраковки: из траекто-
рий / и 2 мы выбирали ту, которая дает наименьший
вклад в функцию f. Теперь эти траектории совершенно
равноценны, поскольку значение минимизируемой функ-
ции F определяется только величиной хя, и, следователь-
но, все траектории, удовлетворяющие ограничениям и
достигающие одного и того же конечного состояния, эк-
вивалентны,
5 3]	ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ	243
Для этих задач разработаны специальные методы.
9.	Схема решения задачи Майера. Рассмотрим по-
следний, N-й шаг процесса, описываемого уравнениями
(3.14). Предположим, что наша система находится в со-
стоянии Хх-!, тогда
(3.15)
Следовательно, для того чтобы обеспечить минимум
функции F, нам надо выбрать так вектор uN, чтобы вы-
ражение (3.15) достигло своего минимального значения
на Gn, т. е. для каждого xN^l мы должны определить
число
Fn-i (xjv-1) = min F (fN (uN, хд^)).	(3.16)
uNeGN
Равенство (3.16) определяет некоторую функцию
Fit-iiXjt-i)—то минимальное значение функции F, ко-
торое может быть достигнуто, если система оказалась в
состоянии xw-i. В процессе вычисления величины
мы находим управление — такой вектор мк, зависящий
от xN-i, который доставляет функции F наименьшее зна-
чение.
Итак, одновременно со скалярной функцией FN-t мы
определяем вектор-функцию
Un = Ф# (^аг-1)-	(3.17)
По существу мы уже сформулировали правила отбра-
сывания неконкурентоспособных вариантов. В самом
деле, обозначим через й множество всех последователь-
ностей ия}, удовлетворяющих условиям и^О{.
Каждая из таких (последовательностей определяет лома-
ную {х0, xt..xw}. Поэтому той же буквой й мы будем
обозначать множество ломаных {xt(ut), х2(ив ц2), ...
•^w(Ui, U2, ..., Un-}»
Через мы обозначим подмножество й — совокуп-
ность всех тех последовательностей, у которых
#=Фк(хЛг-1). Очевидно, что оптимальный вариант управ-
ления не может содержаться среди ломаных из <ot.
Итак, на первом шаге нашей вычислительной проце-
дуры мы отбрасываем множество «ц и продолжаем
поиск наилучшего варианта на множестве Й! = Й—©ь
244
ПРЯМЫЕ МЕТОДЫ
|ГЛ. III
Рассмотрим теперь второй шаг. Функцию
мы можем переписать так:
Fn-i (^лг-1) = Fn-i (Av-i (Идг-ц
Следовательно, если мы фиксируем точку xN_2, то наи-
меньшее значение функции F, которое мы можем до-
стичь, определяется только вектором Следователь-
но, на этом шаге мы можем определить функцию
FN-2 (xjv_2) = min F#-! (fw-i (иЛ-1, Хдг_2)). (3.18)
uN-i^gN-i
Функция Fn-2 (3.18) каждому состоянию xN_2 ставит в
соответствие то минимальное значение целевой функции,
которое может быть реализовано в процессе, если в мо-
мент t = N—2 состояние системы определяется вектором
Xjv-2. Одновременно мы находим также функцию
Млг-1 = Флм (Хам).	(3.19)
Итак, если нам известно, что в «момент времени» t =
= N—2 система находится в состоянии xN.2, то для того,
чтобы получить минимальное значение функции F, упра-
вления uN и uN-i следует выбрать по формулам uN-t =
= фк-1(Х2Г-2), =(pw(Xw-i) = фк (fw-i (fpN-i (^к-г), -Vw-г)).
На этом шаге мы исключаем из оставшегося множества
ломаных Q, множество <о2 всех тех ломаных, для которых
^-17^=фл'-1 (Xn-2) •
Продолжая этот процесс, мы на каждом шаге опре-
деляем функцию
Fi (xt) = min Fz+1 (ft+1 (u/+i, xi)),	(3.20)'
“i+ie0/+i
которая состоянию системы x{ в «момент времени» t = i
ставит в соответствие то оптимальное значение функции
F, которое может быть достигнуто из состояния xt. Одно-
временно процедура взятия минимума в (3.20) позволя-
ет определить функцию
ui+i = Ф/+1 (xi).	(3.21)
Функция (3.21) определяет то значение вектора ui+1, с
которым должен развиваться процесс при переходе си-
стемы из состояния х( в состояние xi+1.
§ 3]
ПОСЛЁДОВАТЁЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ

Все те варианты процесса, для которых вектор ut
определяется не по формуле (3.21), отбрасываются и т. д.
Предположим, наконец, что определены функции
F^Xi) и и2 = <р2(Х1). Нам осталось определить только ве-
личину и минимальное значение функции F при за-
данном начальном состоянии х0. Оно определяется по
той же схеме:	.
Ш	х0)),
«1 = Ф1 (*о)'	(3-22)
Задача решена, число F0(x0)—это минимальное значе-
ние функции F на множестве
N
G= U Gb
4=1]
Для реализации этого значения функции F мы должны
построить последовательность векторов
«1 = Ф1 Uo)> =	(*1) = Ф2 (fl («X» Хо)). «3 = Фз W =
= Фз(/2(«2»/1(«1. *0») И Т-Д-
10.	Численная реализация описанной процедуры.
В пространстве (х, t) построим сетку с некоторым шагом
Дх. Узлы сетки будем снова обозначать через На-
помним, что i— это номер гиперплоскости 2,-, a k — но-
мер узла в гиперплоскости 2,.
На первом шаге процесса мы строим функцию Р#.^
Fn-i(xn~i) = min F(/>(«№ Хаг-1)).	(3.16)
uN&iN
Для построения этой функции можно использовать шка-
лу управлений. Для этого мы задаемся еще некоторым
шагом по управлению Ди. Тогда бесконечное множество
G заменяется конечным. Его элементы мы обозначим че-
рез	где i — это снова номер шага по времени, а / —
это номер элемента в Gt. Теперь построение функции
FN_i состоит в построении таблицы ее значений, зави-
сящих от Хи-i, каждое из которых определяется перебо-
ром величин
Pn- 1 (*at-i) = min F (fN (щ (N), x^)).	(3.23)
Кроме того, мы составляем таблицу для функций (3.17).
246
ПРЯМЫЕ МЕТОДЫ
[ГЛ. Ш
Рассмотрим теперь задачу построения функции
FN-t. (xN.t) = min FN-! (fN.t (uN.lt Xjv_s)).
Теперь мы должны построить таблицу для функции FN_2,
но функция FN-i нам задана только таблицей. Следова-
тельно, задав какое-либо из значений из шкалы уп-
равлений, в общем случае мы получим точку Xn-,, кото-
рая не совпадает ни с одним из узлов в гиперплоскости
Sn-ь и, следовательно, ее нет в таблице для функции
Fn-i.
Существуют две возможности преодоления этой труд-
ности:
а)	Переход из заданного состояния xN-2 в заданное
состояние Xn-i возможен лишь в том случае, если суще-
ствует управление которое является корнем век-
торного уравнения
Ajv-i = /jv-i («лг-i, Хдг_2).	(3.24)
Предположим сначала, что размерность вектора uN-i
не меньше размерности вектора х. При фиксированном
xN_2 формула (3.24) дает некоторое отображение множест-
ва GN-l на Sw-!. Этот образ обозначим через Q (GN_b xN-2).
Если некоторый узел Р,(М—l)eQ(GK_1, xN_2), то мы
говорим, что он достижим из точки xN-2, в противном
случае мы говорим, что он не достижим из точки xN-2.
Множество Q(Gn.ь xn_2) мы называем множеством до-
стижимости из точки XN-2.
Элементарной операцией (применительно к данному
случаю) мы называем процедуру отыскания действитель-
ного корня уравнения (3.24). Если xN_1eQ(Gw.1, xN.2),
то мы можем построить функцию
= Фдг-1 (Xjy_j).	(3.25)
Используя элементарную операцию, мы можем построить
таблицу функции FN-2(xN_2) по таблице функции FN_t
(xN_j) и т. д. *).
*) Таким образом, при этом подходе шкала управлений не ис-
пользуется.
§ з]
ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ
247
Процесс вычисления упрощается, если мы умеем за-
ранее устанавливать принадлежность узла xN-i множе-
ству Q(GN_i, Хл-2).
Если размерность вектора и меньше размерности век-
тора х, то ситуация значительно усложняется, так как
размерность множества достижимости в общем случае
оказывается меньшей, нежели размерность пространст-
ва 2я-1. Поясним ситуацию, которая здесь складывает-
ся, на простом примере (рис. 3.8). Пусть размерность
вектора х равна двум, а размерность вектора и равна 1,
и — это скаляр.
Тогда векторное уравнение (3.24) будет эквивалентно
двум скалярным
Хд'-1 = /jV—1 (^-1, Х^-2» *АГ-2),
(3.26)
XN-1 = /#-1	xN-2, xN-b)-
При фиксированном xN_2 равенства (3.26) можно рас-
сматривать как параметрическое задание некоторой кри-
вой в гиперплоскости S^4. Эта кривая в общем случае
минует все узлы. Следовательно, если формально исполь-
зовать приведенные выше рассуждения, то мы должны
сказать, что ни один из узлов в гиперплоскости 2n-i не
достижим из точки xN_2t и, следовательно, все траекто-
рии, входящие в точку xN-2, должны обрываться. Вот по-
чему в этом случае мы должны либо менять структуру
разностной схемы, при помощи которой мы проводим
248
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
дискретизацию задачи, либо элементарную операцию
строить приближенно.
б)	Соображения, которые только что были изложены,
приводят к необходимости ввести следующую важную
модификацию этого процесса.
Каждый узел РД/) мы окружаем некоторым множе
ством, например, мы говорим, что x^R^i), если
В рассматриваемом случае множества R,— это некото
рые параллелепипеды.
Будем теперь относить к числу узлов, достижимых
из точки х^!, все те узлы, окрестности которых имеют с
множеством Q(Git х^) общие точки. Рассмотрим более
подробно, к чему приведет такое расширение множества
допустимых узлов на примере перехода системы из со-
стояния в состояние хг«.
Итак, пусть функция А(*0 построена. Перепишем ее
в виде
Fi (xi) = Ft (ft (ui, xz-i)).
Фиксируем точку x^i (рассматриваем один из узлов
— 1)). Введем понятие шкалы управлений —
заменим множество G, некоторым конечным множеством,
состоящим из точек ui0, uiu ..., uiL. Вычисляем после-
довательно fi(uiQ, Xf-i), хг_4) и т. д. Вычислив, на-
пример, Xi-i), мы должны выяснить, будет ли этот
вектор принадлежать к окрестности одного из узлов в ги-
перплоскости 2/. Если существует такой узел, в окрест-
ность которого входит точкаД(иг7,хг_1),томы запоминаем
uXj и соответствующее ему значение функции fi(uih х^).
Далее мы должны вычислить функцию Fi{fi(uihxi-l) ),
но эта функция нам задана таблицей и мы знаем ее
значения только в узлах сетки. Поэтому точку f^x^)
мы идентифицируем с тем узлом Р5(г), в окрестности
которого она находится, и вместо числа	х^))
мы берем число Fi(Pj(i)).
Теперь функцию Ff(xf) мы определим так:
Fi(Xi) =min Fi(Pj(O),	(3.27)
§ 3)
ПОСЛЁДОВАТЁЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ
249
Продолжая этот процесс, мы найдем некоторую последо-
вательность управляющих векторов и19 uN. По этой
последовательности, используя формулы (3.14), мы мо-
жем построить фазовую траекторию — совокупность то-
чек	xn и, следовательно, вычислить значение
функции Эта про-
цедура тем точнее дает
возможность	вычислить	р /
минимальное	значение	у <
функции F, чем на более
мелкой сетке мы прово-	р
дим вычисления. Но, уве-	0
личение числа узлов при-	рис. з.э.
водит к значительному
увеличению необходимой памяти машины и затрачивае-
мого машинного времени. Поэтому при решении подоб-
ных задач мы вынуждены снова использовать какие-либо
итеративные методы. В предыдущих разделах данного
параграфа мы уже рассматривали некоторые из по-
добных методов, например метод «блуждающей трубки».
Этот метод полностью применим к данной задаче. Пред-
положим, что мы имеем некоторое первое приближение
zz2, Это приближение определяет в каждой из
гиперплоскостей точку хг-. Задаваясь некоторым шагом
Дх, мы построим в каждой из гиперплоскостей некоторые
множества узлов
< = + Дх/,
х{,	— Дх/,
и т. д. На этом множестве узлов мы находим решение на-
шей задачи^— это будет некоторая совокупность управле-
ний uN). Уменьшаем шаг и повторяем процедуру.
Нетрудно провести оценки, показывающие эффект по-
добной модификации исходного метода.
Примечание. Метод локального варьирования к
задаче Майера неприменим. Этот факт очевиден. Пояс-
ним его с помощью рис. 3.9. Траектория Го, которая про-
ходит через узлы, отмеченные кружками, и траектория
Г», проходящая через узел, отмеченный звездочкой,
250
прямые Методы
(ГЛ. ш
реализуют одно и то же значение терминальной
функции.
11.	Метод «бегущей волны» И. А. Вателя и А. Ф. Ко-
ноненко. Напомним, что в рассмотренных выше схемах
перебора в пространстве состояний, предполагалось, что
построена элементарная операция. Это значит, что пост-
роен оператор В(хг-, хг+1), который паре точек и xi+1
на соседних гиперплоскостях 2,- и Si+1 ставит в соответ-
ствие управление, переводящее систему за время т из
состояния Xi в состояние хг+1, и участок траектории yi>i+b
который соединяет эти точки.
Подробно проблема реализации элементарной опера-
ции будет рассмотрена в § 4. Здесь мы только остановим-
ся на одном вопросе, тесно связанном как с проблемой
элементарной операции, так и с проблемой варьирования
фазовой траектории.
Выше мы отмечали, что метод локальных вариаций
можно рассматривать как метод покоординатного спуска
при отыскании минимума аддитивной функции, которая
получена дискретизацией задачи оптимального управ-
ления. Сейчас мы покажем, что эта интерпретация
позволяет нам значительно продвинуться на пути ре-
шения задач оптимального управления прямыми ме-
тодами.
Пусть требуется минимизировать функцию
N-1
F (х0, хи .... xN, и0, ult ..,, uN~i) = г Ft (xt, xhu щ)
i=0
(3.28)
при ограничениях
xi+i = xi + xf (х{, щ),	(3.29)
(= Xtt |
ui e Vi. j
(3.30)
Здесь векторы xit u{ имеют размерность пит соответ-
ственно, а Х{, Vi — заданные области п- и т-мерного
пространства.
Задача (3.28) — (3.30) может описывать какой-либо
дискретный процесс или может быть конечно-разност-
$ з]
ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ
251
ной аппроксимацией континуальной задачи оптимально-
го управления. В последнем случае выражение (3.28)
есть интегральная сумма, заменяющая (1.1), а (3.29) —
конечномерный аналог уравнения (1.2).
Если размерности векторов х и и совпадают, т. е.
т—п, то, найдя из системы (3.29) вектор иг (если эта
система разрешима) и подставив его в (3.28), мы полу-
чим аддитивную задачу с функцией вида (3.1). К этой
задаче применимы все описанные выше схемы перебора
в пространстве состояний. Случай т>п также не вызы-
вает затруднений.
Если же т<_п, что, как правило, встречается в прак-
тических задачах, то такой подход неприменим (систе-
ма (3.29), вообще говоря, переопределена). В этом слу-
чае должны применяться специальные способы построе-
ния элементарной операции. При этом управление и( уже
не будет постоянным на интервале т, и, следовательно,
конечномерный аналог уравнения (1.2) будет иметь
иной вид, нежели (3.29).
В конце шестидесятых годов И. А. Ватель и А. Ф. Ко-
ноненко предложили и начали успешно применять ме-
тод решения*), позволяющий в этих случаях оставаться
в рамках аппроксимации (3.28), (3.29). Схему И. А. Ва-
теля и А. Ф. Кононенко можно трактовать как обобще-
ние метода локальных вариаций.
Пусть задано некоторое начальное приближение к ре-
шению задачи. Будем улучшать его, варьируя траекто-
рию на участке от th до th+p (k+p^.N). При этом векто-
ры хк и хм считаем заданными, а векторы xA+i (Z=
= 1, ..., р—1), uk+4 (7=0, ..., р—1) являются неизвест-
ными.
Общее число неизвестных равно п(р—1)-\-тр. Для их
определения имеем пр уравнений вида (3.29) **). Разни-
ца между число неизвестных и числом уравнений
равна
г = тр — п.	(3.31)
*) И. А. Ватель, А. Ф. Кононенко, Об одной численной
схеме решения задач оптимального управления, ЖВМ и МФ.
№ 1, 1970.
**) Записанных в координатной форме.
252
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
Таким образом, на варьируемом участке имеется г
свободных параметров, которые могут быть использова-
ны для минимизации соответствующего отрезка суммы
(3.28):
fe+p-i
AF = r ’S Ft(Xi,xt+1,ui).	(3.32)
i=k
Естественно выбирать p таким, чтобы г было минималь-
ным положительным числом. Тогда на каждом варьируе-
мом участке минимизируемая функция (3.32) будет за-
висеть от наименьшего числа независимых переменных.
Легко показать, что при этом г^т. Итак, на варьируе-
мом участке (tki tk+P) мы получаем задачу нелинейного
программирования, которая заключается в минимизации
функций (3.32) от рп + r переменных, подчиненных рп
связям (3.29), а также связям (3.30). Для решения этой
задачи можно, как и в методе локальных вариаций, по-
следовательно давать приращения каждой из г неза-
висимых переменных. После этого варьируемый участок
сдвигается на один шаг т, и процесс повторяется. Гео-
метрическая интерпретация предлагаемой процедуры
позволяет назвать ее методом «бегущей волны». Отме-
тим, что «длина волны» р постоянна вдоль всей траекто-
рии, за исключением начального и конечного участка,
где она меняется в зависимости от размерностей началь-
ного и конечного многообразий. Легко видеть, что при
т = п методы бегущей волны и локальных вариаций эк-
вивалентны. Действительно, в этом случае согласно
(3.31) минимальное р>0 равно двум, а г = п.
Подчеркнем, что в качестве варьируемых перемен-
ных могут выбираться любые г компонент векторов х и
и. Существенным является только то, чтобы остальные
пр переменных выражались через них из системы (3.29).
Далее, запоминать в каждой точке достаточно только
т компонент, и только таких, по которым можно восста-
новить остальные компоненты векторов х и и*).
Когда элементарная операция построена, то описан-
ными выше методами перебора мы ищем минимум адди-
тивной функции вида (3.1) в пространстве n(N—1) пе^
*) Например, зная все Ui можно восстановить Xi+i.
§ 4] ЭЛЕМЕНТАРНАЯ ОПЕРАЦИЯ. НЕКОТОРЫЕ ПРИМЕРЫ 253
ременных (если оба конца закреплены). Размерность
этого пространства не зависит от размерности управле-
ния т. Метод «бегущей волны» реализует поиск мини-
мума функции в пространстве mN—п переменных, и так
как	размерность пространства в этом случае
меньше. Специальный вид функции позволяет вести по-
иск минимума также покоординатным спуском, как и в
методе локальных вариаций, но в пространстве размер-
ности г^т.
Недостаток метода «бегущей волны», очевидно, тот
же, что и метода локальных вариаций,— чувствитель-
ность к локальным экстремумам (см. примечание 3 п. 5
этого параграфа). Возможный путь борьбы с этим —
увеличение «длины волны» р.
§ 4. Элементарная операция. Некоторые примеры
Предыдущий параграф был посвящен изложению
алгоритмов динамического программирования. Мы рас-
смотрели два класса дискретных задач, возникающих
при исследовании оптимальных программ с помощью
электронных вычислительных машин. Наиболее простой
оказывалась та форма конечномерной задачи, которую
мы получили из динамической задачи, когда в процессе
дискретизации использовали сетку в пространстве со-
стояний. Однако сама процедура дискретизации требу-
ет при этом построения элементарной операции. Она
представляет определенные трудности. В настоящем па-
раграфе мы рассмотрим серию примеров, иллюстрирую-
щих возможности эффективной реализации элементар-
ной операции.
1. Еще раз о постановке задач. В этом параграфе мы
будем рассматривать задачу Лагранжа, т. е. задачу оп-
ределения минимума функционала
т
J=^F(x,u, t)dt,	(4.1)
^0
при условии, что х и и связаны уравнением
*=/(*, и, t).	(4.2)
Напомним, что элементарной операцией мы назвали
алгоритм, позволяющий по двум заданным состояниям
254
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
х0 и интервалу времени хх определить управление u(Z),
переводящее систему (4.2) из состояния ховххзавремят.
В общем случае может существовать бесчисленное
множество управлений, переводящих за время т систему
из одного состояния в другое. Поэтому элементарная
операция может быть построена не единственным обра-
зом. Используя вид функционала (4.1), имеет смысл не-
сколько сузить наше определение. Обозначим через
/(/0, т) функционал
*0+т
= f F(x,u,t)dt.	(4.3)
Пусть теперь x(t) и u(t) — оптимальная траектория и
управление. Тогда выражение (4.3) — это вклад участка
траектории, заключенного между точками х0 и xt, в об-
щий функционал (4.1).
Итак, в данном случае имеет смысл говорить об опти-
мальном переходе между состояниями х0 и хт, и понятие
элементарной операции мы будем связывать именно с та-
ким переходом. Формально определенная таким образом
элементарная операция требует решения вариационной
задачи той же степени трудности, что и исходная (если
в задаче нет фазовых ограничений). Поэтому обычно го-
ворят о приближенной реализации элементарной опера-
ции. При этом в качестве характеристик точности ее вы-
полнения можно принять разность функционалов (4.3)
на оптимали и на реализуемом участке траектории и
точность, с которой оказываются выполненными условия
x(te) -х0, х(£0+т) =хт.
Рассмотрим теперь пример, иллюстрирующий один
из возможных подходов к построению элементарной
операции.
2. Задача о движении точки в поле центральной си-
лы. Движение точки в поле центральной силы мы будем
описывать следующим образом:
Здесь г — радиус-вектор точки, р, — гравитационная по-
стоянная, и — управляющий вектор. Предположим, что
вектор и — это ускорение от тяги идеально-регулируе-
§ 4]
ЭЛЕМЕНТАРНАЯ ОПЕРАЦИЯ. НЕКОТОРЫЕ ПРИМЕРЫ
255
мого двигателя малой тяги*). Оптимальный переход из
состояния Хо в состояние хх за время т, согласно теории
таких движений, соответствует минимуму функционала
г„+т
J— j (u,u)dt.	(4.5)
Для простоты будем рассматривать плоскую задачу. Ис-
пользуя декартову систему координат, перепишем урав-
нение (4.4) в скалярном виде
х1 = х3, х\— х4, х3 = f1 -J- х4 — f* 4- и3.	(4.6)
Здесь х1 и х2 — составляющие радиус-вектора, х3 и х4—
проекции скорости, f1 и f2— это проекции ньютоновской
силы
п __________н*1	,	________И*2	,
((х1)2 4- (х2)2)3/1 ’	((х1)2 4- (х2)2)3/а ’
и1 и и2 — управления.
Обозначим через х0 и хт два допустимых состояния —
это означает, что они лежат в области, где выполнены
ограничения. Предположим, что оптимальный переход
из состояния х0 в состояние хх происходит вдоль траек-
тории, которая также целиком лежит внутри допусти-
мой области. Следовательно, для решения задачи опти-
мального перехода мы можем использовать принцип
максимума.
Далее, точки х0 и хх близки. В силу этого функции f1
и f2 мы будем считать постоянными величинами, равны-
ми, например, средним значениям компонент напряжен-
ности гравитационного поля. Такое упрощение экви-
валентно тому, что при интегрировании уравнений
мы применяем схему первого порядка точности (схему
Эйлера).
*) См. подробнее Г. Л. Г р о д з о в с к и й, Ю. Н. Иванов,
В. В. Токарев, Механика космического полета с малой тягой,
«Наука», 1966.
256
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
С учетом всего сказанного составим функцию
Гамильтона и уравнения для импульсов
Н = ih*3 + ф2х4 + 4>з (f + U1) + (/2 + и2) — (и1)2 — (и2)2,
*	дН л	।	дН л	tk
ib. =-------— 0, lb, =------------= 0,	(4.7)
41 дх1 ’ Т дх2	4
; йя , t он
Система уравнений (4.7) легко интегрируется, и мы по-
лучаем
Ф1 = С1> Фа ~ ^2> Фз = С3 Ф< “ ^4	(4.8)
где Ci(i=l, 2, 3, 4) — некоторые постоянные, подлежа-
щие определению.
Управления и1 и и2 находятся из условия максимума
функции Н. Так как на величины и* никаких ограниче-
ний не накладывается, то для того, чтобы значения и1 и
и2 доставляли максимум функции Гамильтона, необхо-
димо, чтобы они были корнями системы уравнений
— = 0,	— = 0.	(4.9)
ди1	ди2	v
Система (4.9) в данном случае очень проста, и мы по-
лучаем
(4.Ю)
Подставим теперь найденные значения и1 и и2 в систему
уравнений (4.6). Принимая во внимание, что f1 и f2—
это постоянные, мы легко ее проинтегрируем:
Дх3 = х£— Хо = А + -у С3Т-i-C^2,
(4.И)
Ax^xi-xJ^x’t + ^ + ^-^L.
2*4	12
§ 4] ЭЛЕМЕНТАРНАЯ ОПЕРАЦИЯ. НЕКОТОРЫЕ ПРИМЕРЫ 257
Аналогичная система будет и для переменных х2 и х4.
Система (4.11) — это система двух алгебраических
уравнений относительно двух произвольных постоянных
cL и с3. Разрешая эти уравнения, находим
( 1 1 *1
24 4 Дх1 — xjj? — — /1т2 — — т (Дх3 — /Ч) >
L	z	)
12 /Дх1 — х’т — Ц- /Ч2 —	т (Дх3 — fЧ)
I	2	о
Аналогичные выражения мы получаем также и для с2
и Ci. Таким образом, элементарная операция в данной
задаче может быть выражена явными формулами.
Подобный способ построения элементарной операции
был впервые применен для решения задачи о достиже-
нии второй космической скорости аппаратом, снабжен-
ным двигателем малой тяги при условии, чтобы траекто-
рия аппарата не пересекала поясов радиации *).
3.	Случай, когда размерность управляющего векто-
ра равна размерности фазового вектора. Пример, рас-
смотренный в предыдущем пункте, показывает, что су-
ществуют задачи, в которых элементарная операция мо-
жет быть реализована конечными формулами. Нетрудно
проанализировать точность подобного решения. Мы уви-
дим, что погрешность в вычислении функционала будет
величиной более высокого порядка малости по сравне-
нию с т.
Рассмотрим теперь общую задачу (4.1) — (4.2), пред-
полагая, что размерность векторов х и и совпадает. Для
Построения элементарной операции систему (4.2) заме-
ним такой:
х = f (х, и, 7) = f (и),	(4.12)
где х= (x0+xt)/2, t = t0+ (т/2).
*) N. Bagaeva, N, Moiseev, New Method for Solution of
Problems of Optimal Transfer Theory. Proc, of the XlV-th Internatio-
nal Astronautical Congress, 1963.
9 H. H. Моисеев
258
ПРЯМЫЕ МЕТОДЫ
(ГЛ. ш
Функционал (4.3) мы заменим таким:
J (х9,1) = J F (х, и, t) dt = j F («) dt. (4.13)
to	t0
Функция Гамильтона
Я = (ф, f) —F («)	(4.14)
не содержит фазовых переменных. Поэтому уравнение
для сопряженных переменных имеет вид
Отсюда следует, что вектор ф постоянен. Тогда условие
максимума выражения (4.14) нам даст и=const.
Интегрируя теперь систему (4.12), мы получим
= /(«).	(4.15)
и
Выражение (4.15) — это некоторая трансцендентная си-
стема п скалярных уравнений относительно п компонент
вектора управления. Реализация элементарной операции
сводится, таким образом, к решению трансцендентной
системы уравнений.
Систему (4.15) можно написать и не прибегая к прин-
ципу максимума. Использование необходимых условий
экстремума нам понадобилось только для того, чтобы
убедиться в том, что в задаче с осредненными уравне-
ниями оптимальное управление необходимо должно
быть постоянным вектором.
В проведенных рассуждениях предположение о том,
что размерность векторов х и и совпадает,— существен-
но. В самом деле, если размерность вектора и меньше
размерности вектора х, то уравнение (4.15) в общем слу-
чае не имеет решения.
Однако в технических задачах наиболее типичной яв-
ляется ситуация, когда размерность вектора и меньше
размерности вектора х. Здесь возникают дополнительные
сложности, связанные с выбором разностной схемы.
4.	Об особенностях элементарной операции в тех
случаях, когда размерность вектора управлений меньше
размерности фазового вектора. В задаче предыдущего
пункта управление на каждом шаге длины т было посто-
§4]
ЭЛЕМЕНТАРНАЯ ОПЕРАЦИЯ. НЕКОТОРЫЕ ПРИМЕРЫ
259
янным и для интегрирования уравнения фазовой тра-
ектории могла быть применена разностная схема (4.15).
В общем случае такая простая разностная схема не мо-
жет быть использована. В самом деле, если требовать,
чтобы условия на каждом интервале были точно удов-
летворены, то нетрудно привести пример, когда управ-
ление и нельзя считать постоянным, как бы ни был мал
интервал времени. Пусть, например, компонента не
содержит управления: fl = fl(x, t). Тогда, следуя нашей
схеме,
А (А> + т) = х1 (/0) + /Ч.	(4.16)
Следовательно, значение координаты х1 в момент време-
ни /0 + т вполне определяется формулой (4.16), и ника-
ким выбором управления мы не сможем удовлетворить
краевому условию х1 (/0+т) = Хх. Таким образом, заме-
на исходной системы системой (4.12) сделала ее не-
управляемой. Поэтому любые упрощения, связанные с
реализацией элементарной операции, и в том числе вы-
бор разностной схемы, должны быть такими, чтобы со-
хранить свойство управляемости. Укажем несколько
возможностей для преодоления этой трудности. Все рас-
суждения мы проведем на прцстейшем примере, когда
динамическая система (4.2) и функционал (4.1) имеют
вид
X2 = f2 (х1, X2),
i0+X
J = [ F(u)dt.	(4.13)
/о
5.	Линеаризация относительно фазовых переменных.
Так как интервал т невелик, то естественно систему
(4.17) заменить линейной, положив х*=х1 тогда си-
стема (4.17) заменится такой:
£ - /о1 +	+ Я12£2 + <Р (//),	(4.19)
где /о = f (xj, х^, а,•/ = (X-)
9*
260
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
Величины V должны удовлетворять следующим гра-
ничным условиям:
№ = о, +	(4-20)
Выпишем выражение для функции Н:
Н = tyl (/J +	+ ^12? + Ф (^)) +
+ Фг (/о + ^21^ 4" ^22?) Р (^)-
Условие максимума функции Н позволяет найти управ-
ление u(t), как функцию только одного импульса фр и —
=-и(ф1). Уравнения для сопряженных переменных в этом
случае имеют вид
фх = Ф1 я31ф2,	(4.21)
ф2 =	^1гФ1 ' Я22ф2
и могут быть проинтегрированы в явном виде:
Ф1 = С1^11 + М12>	(4-22)
Фг = С1Ф21 + С2Ф22.
где {ф^}—система фундаментальных решений системы
(4.21),
Если теперь подставить и(ф1), где берется соглас-
но (4.22), в систему (4.19), и проинтегрировать эту си-
стему при нулевых начальных условиях, то мы получим
для V(^o + t) выражения, содержащие две произвольные
постоянные, которыми мы можем распорядиться так,
чтобы удовлетворить последним двум условиям (4.20).
Заметим, что уравнения для импульсов здесь могут
быть проинтегрированы независимо от динамических
уравнений и, следовательно, решение системы (4.19)
всегда может быть представлено в форме квадратур,
содержащих неизвестные произвольные постоянные.
Описанная процедура значительно усложняется, если
не удается выписать решение сопряженной системы в
явном виде, а это будет практически всякий раз, когда
размерность фазового вектора больше четырех*).
*) Более существенное усложнение возникает в том случае, когда
функция <р в (4.17) зависит от х и и.
* 41
ЭЛЕМЕНТАРНАЯ ОПЕРАЦИЯ. НЕКОТОРЫЕ ПРИМЕРЫ
261
6.	Линеаризация относительно фазовых координат
и управлений. В предыдущей главе мы видели, что ли-
нейная задача с квадратичным функционалом всегда мо-
жет быть сведена к задаче Коши и, следовательно, ре-
шена эффективно. Эта особенность линейных задач мо-
жет быть использована для построения элементарной
операции.
Обозначим через х и й фазовый вектор и управление
на предыдущем временном отрезке и положим
х = х +
(4.23)
и = и + •&.
После замены (4.23) динамическое уравнение
X — f (X, U, О
примет вид
ДВ + Bo + fo,	(4.24)
где A—fx, B—fu,	й, t).
Функционал (4.18) заменяем квадратичным
А = J [(а, 0) + (А $)] dt,	(4.25)
^0
где а =
Итак, исходная задача заменена задачей отыскания
минимума функционала (4.25) при переходе системы
из точки £=0 в точку
= %Х
Перенося второе из граничных условий в точку t=t0,
мы сведем построение элементарной операции к задаче
Коши.
Примечания.
1.	Так как интервал т не велик, то проблема устой-
чивости при реализации элементарной операции практи-
чески не возникает.
2.	Задача (4.24) — (4.25) не содержит ограничений
на управления и фазовые координаты. Если найденные
262
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
таким образом управления и траектория х(£) не удовле-
творяют тем ограничениям, которые содержит исходная
задача, то мы считаем точку хх не достижимой из точ-
ки Xq.
3.	Тот факт, что интервал т мал, позволяет внести
целый ряд упрощений в процедуре переноса граничных
условий.
7. Схема дробных шагов. В п. 3 данного параграфа
было установлено, что при известных условиях управле-
ние можно считать постоянным на некотором интервале.
Этот факт следовал из принципа максимума, применен-
ного к системе уравнений, упрощенной в результате
предположения о том, что динамический процесс разви-
вается в течение малого интервала времени т. Однако
такое заключение мы могли сделать только относитель-
но системы, в которой размерности фазового и управ-
ляющего векторов совпадают. Если размерность управ-
ления меньше размерности фазового вектора, то
управление уже нельзя считать постоянным на всем шаге
длины т. Поэтому естественно возникает идея использо-
вать схему дробных шагов. Продемонстрируем содер-
жание этой разностной схемы применительно к задаче
(4.17) — (4.18).
Разобьем шаг т на два и в течение каждого из про-
межутков длины т/2 будем считать управление постоян-
ным, равным Uj и и2 соответственно. Систему (4.17) за-
меним при этом следующими двумя системами:
х1 = f(xj,4) + ф (и?,
X2 = р (xj, Хо),
X1 = fl (xi, х[) + Ф («г),
х2 = /2(х[,х2),
(4.26)
(4.27)
Здесь через х{ обозначены значения переменных в момент
времени t0 + Эти значения заранее не известны.
Системы уравнений (4.26) и (4.27) интегрируются в явном
виде, и для определения постоянных иь и%, х{ и xi мы имеем
ЭЛЕМЕНТАРНАЯ ОПЕРАЦИЯ. НЕКОТОРЫЕ ПРИМЕРЫ
263
§ 4]
следующую систему уравнений:
Хг = х\ + j {f1 (xj, х?) + ф («a/}.,
x* = +	x$,
(4.28)
xl — xj -|- — {f - (xj, Xo) -j- ф (uj),
z
%! = xQ “T“ P (4, xo).
z
Величина x* не зависит от управления и определяет-
ся независимо от других величин. Таким образом, в рас-
сматриваемом случае задача сводится к решению трех
трансцендентных уравнений.
Дальнейшие упрощения в построении этой разностной
схемы связаны с линеаризацией функций, входящих
в (4.28).
Положим xj ~ Хо + й» Хх = *1 + & и линеаризуем
(4.28) относительно этих величин:
Й = Й + V {/J + «11^1 + «12Й + <Р Ш
Z
+	+а21£+а2а&,
- 4
Z
Z
где
/о = f (Л'0> £(>)> ai; ~
\^/ i i
xl=xl
о
Поскольку £1 определяется независимо, то полученная
система — это система трех линейных уравнений относи-
тельно ф(«!), Ф(«а) и gt
264
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
8.	Использование шкалы управлений. Для прибли-
женного построения элементарной операции мы стара-
лись сначала по возможности упростить задачу, но затем
решить эту задачу точно. Возможен и совсем иной под-
ход к этой проблеме. Он использует идею, которую мы
уже применили для построения вычислительной схемы
отыскания минимума функции с последовательным
включением переменных. Пусть построе-
на элементарная операция, реализующая
Ра*!) переход за время т из состояния, харак-
' а теризуемого узлом Ps(t), в состояние
.ж, Л(г+1). Предположим, что за счет упро-
	/ • щения (линеаризация, осреднение внеш-
У них сил и т. д.) мы получим задачу, ко-
торую мы можем решить точно, и пусть
У	— это найденное нами управление.
Оно за время т переводит «упрощенную»
₽ис- систему из состояния Ps (t) в состояние
Но если мы подставим это
управление в уравнение (4.1) и его проинтегрируем, то
в гиперплоскости Si+1 мы получим точку xt, которая не
будет в общем случае совпадать с узлом Pj(i+1) (рис.
4.1), и тем не менее всю процедуру отбора мы проводим
так, как если бы система (4.1) с найденным управлением
действительно оказалась в момент t=t{+x в состоянии
Pi(i+1).
Совершенно тот же результат мы получим, очевидно,
если сразу будем разыскивать управление, которое пере-
водит систему в некоторую окрестность узла jPj(i-{-1).
Техника такой реализации элементарной операции бы-
ла уже описана в предыдущем параграфе. Мы стро-
им шкалу управлений {иг} — дискретное множество по-
стоянных векторов из Gu. Далее задаемся шагом &х‘<
<Дх' и вычисляем вектор хД/.+т), удовлетворяющий
уравнению
хг — f (xr, tlr, t)
и начальному условию
%r (^i) — Ps (О
последовательно для i=l, 2, 3,... То управление иг, при
§ 4] ЭЛЕМЕНТАРНАЯ ОПЕРАЦИЯ. НЕКОТОРЫЕ ПРИМЕРЫ 265
котором хг(/,+т) удовлетворяет неравенству
Р/ (i + 1) — бх» < xkr < Р* (1 + 1) 4- бх»,
мы принимаем в качестве искомого.
Если существует несколько управлений из шкалы
управлений, реализующих переход системы из состояния
Ps(i) в окрестность узла P,(i+1), то мы берем то, для
которого приращение функционала минимально. Если
среди иг нет вектора, переводящего систему в окрест-
ность узла РД1+1), томы говорим, что узел РДг’-Н)
недостижим из состояния Ps(i). Такой способ построе-
ния элементарной операции вполне универсален.
В результате применения одного из алгоритмов ди-
намического программирования мы получим некоторый
набор векторов ы1; ы2, «з, -., где ик определено на интер-
вале [4, /А+т]. Этот набор определяет фазовую траекто-
рию, которая не удовлетворяет условиям на конце тра-
ектории. Мы ее принимаем -в качестве приближенного
решения. В ее окрестности мы строим более мелкую
сетку, уменьшаем одновременно величины бх» и строим
новую «более густую» шкалу управлений.
Рассмотрим теперь построение элементарной опера-
ции на конкретном примере.
9.	Задача о выборе оптимальных путей плавания.
Движение корабля, пересекающего океан, происходит
под действием силы тяги винтов. Одновременно на ко-
рабль оказывают воздействие ветер, волнение, морские
течения и т. д. Давно известной задачей морской нави-
гации является задача о выборе такого пути плавания,
который приведет корабль в порт назначения за крат-
чайшее время или за заданное время с минимальной за-
тратой горючего. Движение корабля описывается систе-
мой дифференциальных уравнений, которой можно при-
дать следующий вид:
х1 = Vcos <р -|- Yj (V, ф, х1, х8),
(4.29)
х8 = V sin ф +	(V, ф, х1, х2).
Здесь х1 и х2 — декартовы координаты, V—абсолютная
величина скорости хода корабля на тихой воде, ф — кур-
совой угол, который составляет направление скорости
266	ПРЯМЫЕ МЕТОДЫ	[ГЛ. Ш
корабля с осью Ох1, функции Т» определяют измене-
ние скорости корабля вследствие перечисленных фак-
торов.
Функции V(t) и ср(О — это управляющие функции.
Если мы ставим задачу о наиболее экономном пути,
то функционал мы запишем так:
т
J(V,<p) = ^Vdt.	(4.30)
о
Если мы стремимся минимизировать время плавания, то
перепишем систему (4.29) в следующем виде:
dx2 _ И sin q +	3
dx1 Vcosq+'lf1 '	{ '
Время T при этом определяется квадратурой
xi
Т
Т= (* ----.	(4.32)
J V cos q: + %,
о
Итак, мы получили следующие две задачи.
Задача а. Найти функции ф(/) и V(t)9 доставляю-
щие минимум функционалу (4.30) при условиях (4.29)
и фиксированных в начале и в конце траектории (порт
отправления и особенно порт прибытия, вероятно, следу-
ет считать заданными).
Задача р. Найти функции <р(х!) и Е(х4), достав-
ляющие минимум функционалу (4.32) при ограничени-
ях (4.39).
Эти вариационные задачи не являются классически-
ми, поскольку помимо сформулированных ограничений
в задачах о плавании корабля всегда существуют фазо-
вые ограничения. Путь корабля не может, например,
пересечь остров. Запретными являются также зоны
туманов, сильных штормов, волнение внутри которых пре-
восходит допустимые пределы. Могут быть и другие
запретные зоны. Например, в Северной Атлантике су-
ществуют в определенные времена года области пла-
вучих льдов, которые корабль должен обходить, и т. д.
Эти задачи были одними из первых задач, решенных
методом «блуждающей трубки» в Вычислительном цент-
.	ПРОБЛЕМЫ УСТОЙЧИВОСТИ	267
3 5J
ре Академии наук. Покажем, как была реализована в
этих задачах элементарная операция.
Задача 0. Сетка строится в пространстве (х‘, х2).
Поверхности 2< —это прямые х*. = ih, где h — это шаг
сетки. Разностный аналог уравнения (4.31) мы записы-
вали в виде
Ах2 _ V sin q +~Уг (V, q)	(4.33)
Ах1 Vcosq+ 4?i(V,q>)
где Yi(V, <p)=4ri(V, <p, x‘, x2), x‘, x2 —это средние зна-
чения координат.
В задаче на быстродействие скорость V естественно
считать постоянной и равной своему максимальному зна-
чению. Таким образом, в рассматриваемой задаче на
быстродействие мы имеем только одну управляющую
функцию — курсовой угол. Поскольку левая часть урав-
нения (4.33)—известная величина, то это уравнение —
некоторое трансцендентное уравнение относительно ф.
В качестве нулевого приближения использовалась функ-
Дх2
ция ф0: ^фо=—х.
§ 5. Проблемы устойчивости
1.	Предварительные замечания. При анализе алго-
ритмов, которые были изложены в предыдущем парагра-
фе, мы сталкиваемся с одним вопросом, носящим прин-
ципиальный характер: в каком соотношении находятся
решения исходной задачи оптимального управления и
задачи, которую мы получали, используя конечномер-
ные аппроксимации, и как это соотношение меняется с
изменением шага разностной сетки. Этот вопрос отно-
сится к общей проблеме устойчивости разностных схем,
которая изучает зависимость решения от характера
дробления шагов разностной схемы. Теория разностных
схем занимается изучением конечномерных аппрокси-
маций уравнений в частных производных. Но любое оп-
тимальное решение определяется частными решениями
уравнения Веллмана, которое является уравнением в
частных производных первого порядка. Следовательно,
вопросы, возникающие при исследовании разностных
268
ПРЯМЫЕ МЕТОДЫ
(ГЛ. III
аппроксимаций теории оптимального управления име-
ют по существу то же содержание, что и классические
задачи устойчивости разностных схем. Однако сущест-
венно нелинейный характер задач теории оптимального
управления делает эти проблемы еще более трудными.
Они только теперь начинают разрабатываться, и резуль-
таты, которые здесь имеются, еще во многом носят пред-
варительный характер.
2.	Уравнение Веллмана. В этом параграфе мы будем
рассматривать задачу определения минимума инте-
грального функционала
J (х, и) = у F (х, и, t) dt
^0
при ограничениях
X = f (х, и, f),
U
хе 0х.
(5.1)
(5.2)
(5.3)
(5-4)
Для решения данной задачи мы можем воспользо-
ваться методом глобального перебора (алгоритм «киев-
ский веник») в пространстве состояний. Покажем, каким
образом, используя рассуждения, лежащие в основе это-
го метода, можно получить уравнение Веллмана.
Рассмотрим некоторую фазовую траекторию x(t),
соединяющую (х0, t0) с точкой (х‘, Г), и управление u(t),
которое ее определяет. Значение функционала вдоль
этой траектории обозначим через /(/0, х0; Г, х*). Пусть
теперь (х1( и (х2, t2)— две произвольные точки (/2>
>/i), и пусть траектория, начинающаяся в точке (х0, ta),
проходит через эти две точки. Тогда в силу аддитивности
функционала
t,
(^о» %о> ^2» ^2) = J Ifot Xg, Xj)	СF (х, и, t) dt,	(5.5)
где интеграл берется вдоль отрезка фазовой траектории,
соединяющей точки (хь t,) и (х2, /2).
ПРОБЛЕМЫ УСТОЙЧИВОСТИ
269
§ 51
Значение функционала J вдоль оптимальной траек-
тории, соединяющей точки (х0, to) и (х*, Г), будем обо-
значать через S(t0, х0; Г, х*). Тогда для любой точки
(х*, Г) имеет место неравенство
5(/0,х0;^х‘)</(/0,х0;Г,х*).
На этом основании
5	(t0, х0; t2, х2) < S (t0, х0; ilt xr) + F (х, и, t) di, (5.6)
б
где х — это оптимальная траектория, проходящая через
точки (хь и (х2, t2), а и — соответствующее оптималь-
ное управление.
Пусть теперь точка (хь t,) лежит на оптимальной
траектории, соединяющей точки (х0, t0) и (х2, t2); тогда
очевидно, что неравенство (5.6) переходит в строгое ра-
венство
^2
S (^0>	(^0> *^0»	^1) ”4"" J (^>	0
л
Итак, для любых t^[t0, /2] и имеем
5 (t0, х0', it, х2) = min S (/0, х0; t, х) +	(х, и, £) Ш .
У	J
u^Gu
(5-7)
Примечания.
1.	Если под точками (х, /) понимать точки (хг, Ъ)
пространства состояний, то равенство (5.7) — это просто
описание метода отыскания оптимальной траектории с
использованием глобального перебора. Множество GX1
по точкам которого производится перебор,— это шкала
состояний, соответствующая моменту времени / = /0-Н’т.
Точка х2 лежит на гиперповерхности
/ t2 — tQ 4- (i 4- 1) т,
где т — шаг по временной переменной.
270
ПРЯМЫЕ МЕТОДЫ
(ГЛ. III
2.	Для того чтобы фазовая траектория x(t) была
оптимальной траекторией, соединяющей точки (х0, /0) и
(х2, U), необходимо и достаточно, чтобы она удовлетво-
ряла уравнению (5.7).
Для дальнейшего равенство (5.7) удобно записать в
следующем виде:
min ! С F (х, и, Q d% — [S (/0, х0; /2, х2) — S (^0, хй\ t, х)] I = 0.
хе°х I /	J
“eg«	(5.8)
Из условия (5.8) следует, что, какова бы ни была точка
(х, I), лежащая на оптимальной траектории, соединяю-
щей точки (х0, /0) и (х2, t2), необходимо, чтобы в этой
точке
min J [F(x(£),u(O^ —
u^Gu I у
^2> ^2)	*5 (^o> ^0»	=	(5*9)
Введем теперь дополнительное предположение: будем
считать, что функция S дифференцируема по всем аргу-
ментам. Тогда, положив х2 = х + Ах, ^2=/ + Д£, получим
*5 (^о>	^2, ^2)	(^ *0>
+ At + f (X, и, t) At + О (ДИ- (5. Ю)
ot ox
Делая в (5.9) замену (5.10), деля на At и переходя к
пределу при AZ->0, получим окончательно
<511)
Уравнение (5.11) носит название уравнения Велл-
мана.
Итак, показано, что оптимальное значение функцио-
нала— функция Веллмана S — удовлетворяет некоторо-
му уравнению в частных производных. Следовательно, при
построении методов, использующих конечноразностные
аппроксимации, мы неизбежно сталкиваемся со всеми
ПРОБЛЕМЫ УСТОЙЧИВОСТИ
271
§ 5]
вопросами, которые уже стали традиционными в теории
разностных схем, развитой для задач математической
физики.
Примечание. Уравнение (5.11) мы вывели в
предположении о дифференцируемости функции S. Не-
трудно привести примеры, показывающие, что это пред-
положение выполняется далеко не всегда. Более того,
во многих задачах функция Веллмана вообще не яв-
ляется непрерывной. Тем не менее содержание проблем
остается тем же. Они только усложняются в силу того
обстоятельства, что вместо классического решения, удов-
летворяющего уравнению (5.11), мы должны рассмат-
ривать обобщенное решение, удовлетворяющее уравне-
нию (5.11) *).
3.	Схема анализа. Для того чтобы наиболее нагляд-
но показать содержание трудностей, которые возникают
при реализации вычислительных процедур, остановимся
на простейшей двухточечной задаче (задача с фиксиро-
ванными концами) и предположим, что ее решение един-
ственно, а элементарная операция реализуется без
ошибок.
Оптимальную траекторию обозначим через x(t).
Введем далее в п+ 1-мерном пространстве (х, /) сет-
ки Qw. Сетка Qm характеризуется шагом тт по времен-
ной переменной и шагами hlm по пространственным пе-
ременным. Последовательность сеток {Qm} обладает тем
свойством, что тт->0 и при т->оо. Обозначим че-
рез наибольшее из чисел Н'т. Каждой сетке Qm мы
можем поставить в соответствие конечное множество
траекторий {х(/, т)}, построенных с помощью элемен-
тарной операции. Эти траектории представляют из себя
ломаные, которые проходят через узлы сетки, и каждый
из отрезков этих ломаных представляет из себя опти-
мальную траекторию, которая соединяет узлы, лежащие
на соседних гиперплоскостях +
*) Заметим еще одно обстоятельство. В математической физике
имеют дело с задачами, размерность которых очень редко бывает
больше трех. В теории оптимального управления мы, как правило,
имеем дело с задачами более высокой размерности, доходящей иногда
до нескольких десятков. Но это уже специальный вопрос, на анализе
котового мы здесь останавливаться не будем.
272
ПРЯМЫЕ МЕТОДЫ
[ГЛ. ГП
На этой сетке, с помощью алгоритма глобального пе-
ребора, мы можем определить ломаную, соединяющую
начальную и конечную точки и имеющую минимальную
«длину». Здесь под длиной понимается величина
т)\ и (/, т)) = J
1=0]^ /0+гт
где Nm= (T—tQ)/xm.
Эту оптимальную ломаную будем обозначать через
z(t, tn). Соответствующее управление будем обозначать
через v(t, т).
Рис. 5.1.
Фиксируем теперь сетку Qm (рис. 5.1). Траекторию
x(f) мы можем аппроксимировать некоторой ломаной из
семейства {х(/, т)}. Эту ломаную мы обозначим через
y(t, т) и через u(t, т) —управление, соответствующее
этой ломаной; тогда будем иметь следующую оценку:
max | х' (0 — у (t, /и) | = О (рт)
для любого ^[f0, Г]. Таким образом, последователь-
ность {y(t, т)} равномерно сходится при т->оо к оп-
тимальной траектории. Обозначим через xt и yt (t, tn)
§ 5]
ПРОБЛЕМЫ УСТОЙЧИВОСТИ
273
точки гиперплоскости t=t0 + ix, через которые проходят
кривые х и у (t, т), к рассмотрим величину
Am — I s (t0, х0; Т, хт) — J (у (t, tn); u (t, tn)) | <
Nm~1
< \S(ti,xi;tl+uxu^ — S(ti,yi(t,m);t^1,yi,l{ttrn))\.{6.\2)
i<=0
Имеет место следующая
Лемма. Если limAOT=0, то последовательность
управлений v(t, tri) сходится слабо (в смысле функцио-
нала J) к оптимальному управлению.
Фиксируем некоторое т. Так как y(t, т) принадле-
жит семейству {x(t, т)}, то
J (у (t, tri); и (/, т))	(г (/, /п); v (t, т)).
Но, с другой стороны, для любого т
J (z (t, tn); v (t, tn)) > S (ta, x0; T, xt).
Но так как по условию Am->-0, то отсюда следует, что
lim J (г (t, tn); о (t, tn)) = S (/0, x0; T, xT).
т—оо
Доказанная лемма сводит задачу исследования сходи-
мости метода глобального перебора к оценке вели-
чины Ат.
Примечание. Мы доказали слабую сходимость
управлений v(t, tn), отбираемых методом перебора на
сетке Qm. Однако сами фазовые траектории при этом
,сходятся равномерно. Этот факт следует из предполо-
жения о единственности решения.
4.	Простейший пример. Приведем два примера, по-
казывающие, каким образом предел (5.12) зависит от
структуры сетки Qm. Рассмотрим сначала простейшую
скалярную задачу. Пусть речь идет об отыскании мини-
мума квадратичного функционала
(5.13)
О
при условии
X = U,
(5.14)
274
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
где х и и — скалярные функции времени. Никаких огра-
ничений на управление u(t) накладывать не будем. Гра-
ничные условия фиксированы.
Решение этой задачи, а, следовательно, и элементар-
ная операция, выписываются в явном виде:
U = ---i------ ?
т
х = Xi + ~ (Xz+i — х‘) V ~е
i = 0,1, ... , N — 1,	(5.15)
S(ti>Xi; tl+1, ,vm) =	.
T
Используя формулу (5.15), вычислим величину Aw:
^tn *^2 '	^*+1’ ^£+1) ~~ (^> У^ ^’+1> Уi+1) I =
г=о
^т~1	~
= S 1	+ yi+i 'у^ (^’+1 yt+1
Т /=о
(5-16)
1
Положим yi = Xi 4- Дхг, так как | Axz | —hm, то
2
Д/n \ —N’mC^rrty	(5.17)
т
где С= max 21 у, — хД. Далее, Nm -= (Г —- Q/xm, и мы
получаем окончательно
Д.<—,	(5.18)
где Cj — некоторая постоянная, не зависящая от т.
Используя доказанную лемму и оценку (5.18), мы
можем сформулировать следующий результат: для схо-
димости метода глобального перебора к точному реше-
§ 5]	ПРОБЛЕМЫ УСТОЙЧИВОСТИ	275
нию задачи (5.13) —(5.14) достаточно, чтобы шаг по
пространственной переменной удовлетворял условию
/1т=ат2^‘, где а и е — произвольные положительные
постоянные *).
5.	Еще один пример. Рассмотрим задачу отыскания
минимума функционала (5.13) при ограничениях
х1 = х2, х2 = и.	(5.19)
Элементарная операция в этой задаче также находится
в явном виде
х1 = х} + х- (t- tj) + .У  {3(х?+1—х,)-т (2х- + х-+1)} +
т2
4------ {— 2 (xj+1 — х?) + т (х2+1 4- я?)}>
х2 = х? + —- {6 (Xf+1 — х-) — т (4х- — 2х*+1)} +
т2
4------3 1 {— 2 (х-+1 — X/) 4- т (х|+1 4- X/)}, t [ti, 6+J»
w(0 =	r(4x* + 2^+1И +
т2
4--------т— {— 2 (x/+l — xf) 4- т (х/+1 4“ ^z)}>
T3
5 (tb Xi\ tiAU xz+1) =	{[6 (x/+1 — xj) — r (4x? 4- 2xz+1)]2 4-
4“ [6 (xz+i — x^ — т (4xz 4“ 2xz+i) [— 12 (xj+1 —• x|) 4-
4- 6т (Xz+i 4- xl)] 4" 12 [—2 (x/+1 xj) 4~ x (xf+1 4- x z)]2}« t
(5.20)
Далее вычислим разность
(ti9 Xi, /z+i, X/+1) S (/z, Уь ti+ii yi+l)*
*) Оценка (5.13) является довольно грубой. Более аккуратный
анализ приводит к более слабому требованию на выбор шага h
(см. п. 5).
276
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
Полагая ///= Х/Ч-Дх/, получим
S (/5 Xi\ xt‘+i) S yi\ ti+u уf+1) =	-j- • • • j &%i+i “b
+	+ • • •'j A*? +	+ •••') A^z+i +
\T3 j	\T2 j
+ №+\^ + O(h\h*).	(5.21)
Здесь точками обозначены члены, которые растут мед-
леннее, чем написанные при т->0.
Таким образом, для величины Д мы получаем оценку
д<АГр^._|.
\ Т3.
bh2 \ (ah1 'bh2 \ .гр . ч
+ ( о)’
где а и Ь — некоторые постоянные.
Итак, мы приходим к следующему результату: для
того чтобы в задаче (5.9) метод глобального перебора
сходился к точному решению, достаточно, чтобы шаги
по пространственным переменным удовлетворяли бы
условиям
= cW, h*m = а24+8‘,	(5.22)
где а1, а2, ei и е2 — произвольные положительные числа.
6. Комментарии. Приведенные примеры показывают
способ построения достаточных условий сходимости ко-
нечноразностных методов. Второй пример показывает, в
частности, что структура сетки существенно зависит от
природы задачи. Шаг по переменной х1 должен быть в
этой задаче малой более высокого порядка, нежели по
переменной хг.
Условия (5.18) и (5.22) являются только достаточ-
ными. Они не являются необходимыми. Более того, они
легко могут быть уточнены. Рассмотрим, например, сно-
ва задачу (5.13) — (5.14). Мы знаем, что
|и| = |хг—х0|/Г=у.
Таким образом,
I xt+1 — xi | = ут.	(5.23)
§ 5]
ПРОБЛЕМЫ УСТОЙЧИВОСТИ
277
Перепишем теперь снова (5.16) в следующем виде:
Wm-l
‘С — I Xi+i Xi 1 “Ь
т .
1=0
или, используя оценку (5.23),
Д^^А^тй + С#),	(5.24)
т2
где Ci и С2 — некоторые постоянные. Отсюда сразу сле-
дует, что для устойчивости достаточно, чтобы шаг h
удовлетворял условию /и=ат^е, где а и 8 — произволь-
ные положительные числа.
Точно так же можно уточнить оценку и во второй из
рассмотренных задач. Уточняя оценку, мы воспользова-
лись дополнительной информацией о свойствах траекто-
рии, поскольку в рассматриваемых задачах в нашем рас-
поряжении было точное решение.
Если априори нам известно, например, что функция
Веллмана S(t0, х0; Г, хТ) удовлетворяет условиям Лип-
шица или Гельдера по фазовым переменным, то нахож-
дение условий устойчивости достаточно элементарно.
Однако извлечь подобную информацию, опираясь только
на свойства правых частей уравнения (5.2) и свойства
функционала, обычно бывает очень трудно. Задача, од-
нако, существенно упрощается, если мы заметим, что
для исследования устойчивости нам достаточно знать
лишь локальные свойства этих функций при малых т. Это
позволяет систему (5.2) заменить такой: x=f(xiy иу /),
tepfc f<+J.
Нам остается найти матрицы — , —— и векторы произ-
dS dS ~
водных — и -----. Однако здесь мы сталкиваемся с новой
трудностью. Если никаких ограничений на управление
не наложено, то определение управления сводится к
анализу корней некоторых функций. Оценки произ-
водных в этом случае получить не очень трудно, исполь-
зуя теоремы о неявных функциях. Если же на величину
управления наложены ограничения типа неравенств, то
278
ПРЯМЫЕ МЕТОДЫ
(ГЛ. Ill
задача качественно усложняется. Один из возможных
путей преодоления этой трудности состоит в использова-
нии методов штрафных функций. Однако такой подход
далеко не универсален, поскольку оценки оказываются
зависимыми от коэффициентов штрафа X, и в условиях
устойчивости надо еще совершить предельный переход
при Х->оо. Такой путь построения условий устойчивости
удалось реализовать только в некоторых примерах.
Другой путь построения условий устойчивости пред-
ложен В. И. Коробовым*). Он состоит в анализе мно-
жеств достижимости. На этом пути ему удалось полу-
чить теорию, позволяющую проводить анализ устойчиво-
сти разностных схем для случая, когда уравнения
(5.2) — линейны.
Возможно, что сочетание обоих этих подходов позво-
лит разработать удовлетворительную схему анализа.
Вопросы, которые обсуждались в этом параграфе,
представляются интересными не только в принципиаль-
ном математическом отношении, поскольку они открыва-
ют перспективу построения общей теории разностных
аппроксимаций широкого круга вариационных задач.
Они важны также и для конкретных расчетов приклад-
ного характера. Дело состоит в том, что разностные ме-
тоды расчета оптимальных программ являются практи-
чески универсальными методами. С их помощью удается
проводить расчеты и тогда, когда мы сталкиваемся со
сложной системой ограничений, и тогда, когда интервал
времени Т—tQ настолько велик, что любая редукция к за-
даче Коши приводит к неустойчивому счету. Наконец,
описанные методы по существу дают возможность реше-
ния ряда задач синтеза. Тем не менее теоретический ана-
лиз устойчивости разностных схем в теории оптимально-
го управления еще очень несовершенен. Однако уже и
то немногое, что мы имеем, позволяет дать определен-
ные рекомендации рецептурного характера. Так, напри-
мер, шаги по пространственноподобным переменным
должны быть малыми более высокого порядка, нежели
шаг по временноподобной переменной. Далее, шаги по
тем пространственноподобным переменным, производные
*) См. В. И. к о р о б о в. О множествах достижимости и об
управляемости линейной системы, ЖВМ и МФ 10, № 4, 1970.
§ 6]	СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ	279
которых явно не зависят от управлений, должны быть
малыми более высокого порядка, нежели шаги по тем
пространственноподобным переменным, производные ко-
торых зависят от управлений, и т. д.
§ 6.	Некоторые задачи для систем
с дискретным временем
1.	Введение. В § 1 этой главы мы подробно обсудили
возможность сведения некоторых классов задач плани-
рования к задачам оптимального управления в конечно-
разностной постановке. Методы, развитые в этой теории,
оказываются иногда весьма удобным средством их реше-
ния. Это относится прежде всего к тем ситуациям, ког-
да требуемая точность невелика. В этом случае иногда
даже задачу линейного программирования большой раз-
мерности оказывается проще решить, рассматривая ее
как динамическую задачу оптимального управления.
Размерность широкого класса задач оптимального
планирования столь велика, что говорить о возможности
точного решения оказывается практически бессмыслен-
ным. Единственный путь, позволяющий надеяться на по-
лучение практически интересных результатов, состоит в
сочетании эвристических приемов, дающих некоторое
«диспетчерское» решение с вычислительными методами,
которые «улучшают» это диспетчерское решение. Мето-
ды оптимального управления, особенно те, которые раз-
виты в этой главе, оказываются весьма удобным средст-
вом уточнения «диспетчерских» решений.
В настоящем параграфе мы остановимся на несколь-
ких примерах подобных задач.
2.	Задача с линейными ограничениями. Рассмотрим
задачу отыскания минимума функции
j («1. • • • , UN) = 2 Fi (Ui)	(6.1)
при следующих ограничениях:
щ > О,
(6.2)
280
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
2	1’^1, ...,АГ,	(6.3)
/=1
N
^b^^b1', btl>0, /=1,...,п.	(6.4)
i=i
Здесь и{ — векторы размерности п.
Задачу (6.1) — (6.4) иногда называют также распре-
делительной задачей. В § 1 этой главы мы дали ее ин-
терпретацию. Индексом / мы обозначили номер склада,
индексом i — номер потребителя; N — означает число
потребителей, п — количество складов.
Функция (6.1) — это затраты на распределение ресур-
са со складов к потребителям.
В линейном программировании рассматривается тот
случай этой задачи, когда функция J — линейная функ-
ция компонент векторов нц
Р/ = 2 ацЖ	(6.5)
/=х
Условие (6.3) означает, что запросы потребителя номе-
ра i должны быть удовлетворены. Условие (6.4) означа-
ет, что емкость склада ограничена.
Важной модификацией этой задачи является задача
с резервными складами неограниченной емкости. В этом
случае условие (6.4) мы перепишем так:
N
bijU}i^.t/, j = 1,2,..., tn<n.	(6.6)
1=1
Представляет известный интерес рассмотреть также и
случай, когда
Такие ограничения могут возникать довольно естест-
венно. Например, если транспортные возможности скла-
да номера j ограничены, то, мы получим дополнительное
ограничение типа (6.6) при той же размерности векто-
ра и.
Следуя § 1, введем новые переменные V, удовлетво-
ряющие уравнениям
(О - xi(/s+1) - xi (ts) = bsiui (ts), s - 1, 2, ... , AT, (6.7)
$ 6]
СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
281
и условиям x,(f1) =0, xJ(fw+1) где i?(Q = t/s. Рас-
смотрим теперь задачу определения минимума функции
J (и (4),«(Q, • • •) - 3 Ft (и	(6.8)
i=i
Сформулированная задача является аддитивной, и ее
решение может быть реализовано стандартной процеду-
рой, изложенной в § 2, если построена элементарная опе-
рация.
3.	Элементарная операция. Рассмотрим сначала про-
стейший случай задачи (6.1) — (6.3), (6.6) при т=п—1
(один резервный склад). Элементарная операция состо-
ит в отыскании управления, которое должно переводить
систему из состояния x(fs) в состояние x(ts+l). Поэтому
величина Дх= (Дх1,..., Дх"-1) при построении элемен-
тарной операции известна, и (6.7) — это уравнения для
определения неизвестных «управлений» г?(4):
ц/ (/s) — А* t j — 1,2,..., n — 1.
6S/
Рассмотрим теперь ограничение (6.3). Если бы оно бы-
ло записано в форме равенства, то уравнение «"(/„) сле-
довало бы находить по формуле
1 Г	П-1
Un = ----- (? — Cs{
Csn L	i=i
(6.9)
(6.10)
csn L /=1	*s/
Поскольку допустимо нестрогое неравенство,
рассмотреть величину 
ДУ = FS(«J,... , w").
то надо
(6.П)
Если в это выражение подставить значения и1 (/,), /=1,
2, п—1, то функция ДУ станет функцией только одно-
го неизвестного:
Д7 = Л‘(«"),
и мы выбираем ц"из условия
min F* (и"),
«" >0, ц" > и",
где и? определяется формулой (6.10).
(6-12)
282
ПРЯМЫЕ МЕТОДЫ
1ГЛ. Ill
В прикладных задачах функция Fs, как правило, -
возрастающая функция своих переменных. Поэтому минимум
Д/ достигается при и” = и".
Точка x(ts+l) считается недостижимой из точки x(t8),
если хотя бы одна из величин uJ(s) оказалась отрица-
тельной.
Рассмотрим теперь ту ситуацию, которая возникает,
когда m<Zn—1 (число резервных складов больше од-
ного).
Пусть, например, т=п—2. Тогда формулы (6.9)
позволяют определить uj(s), если /=1, 2,..., п—2. Для
того чтобы свести эту задачу к рассмотренной, нам до-
статочно ввести новую переменную, удовлетворяющую
разностному уравнению
units').	(6.13)
Таким образом, мы увеличили размерность фазового
вектора на единицу. Поскольку новая переменная отно-
сится к резервному складу неограниченной емкости, ни-
каких условий на значение х97-1^) мы не наклады-
ваем *).
Элементарная операция может быть построена и без
увеличения размерности фазового вектора. В самом де-
ле, пусть f?(^), u2(/s),..., un'2(ts) определены при помощи
формул (6.9). Тогда для оставшихся двух составляю-
щих вектора управления u(ts) мы получаем одно соотно-
шение
.Д%/ (t )
Cs.n-ill”-1 (s) -h Csnun (s) < cs — у 7 s .	(6.14)
Рассмотрим теперь выражение (6.11). После замены
zz1,..., ип~2 по формулам (6.9) мы найдем, что
Д/ = ГГ(и",иГ),	(6.15)
и, следовательно, для определения uns и ип~1 мы полу-
чаем следующую задачу нелинейного программирования:
*) Это значит, что при s=N необходимо будет еще взять мини-
мум функции (6.8) по всем xn~x(tN).
s 6]
СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
283
определить минимум функции (6.15) при условиях (6.2)
и (6.14).
Мы рассмотрели случай, когда т = п—2. Совершен-
но аналогично рассматривается и общий случай k скла-
дов с неограниченной емкостью. Заметим, что случай
т=0 соответствует той ситуации, когда емкость всех
складов неограниченна.
4.	Элементарная операция в случае т = п. Этот слу-
чай более сложный. Он подвергался специальному рас-
смотрению в § 4. Один из методов, который был там
указан — это метод дробных шагов. В рассматриваемой
задаче шаг по «времени» фиксирован. Тем не менее для
построения элементарной операции мы можем рассмот-
реть некоторый аналог изложенной там процедуры.
Будем рассматривать сразу не два, а три значения
дискретного времени ts, ts + 1 И Значения х\ если
—2, мы будем задавать на трех гиперплоскостях t=
= ts, t — ts+i и t = ts+2, а значения хп и хп~1 только при
t’==ts И ^==^s+2’
Введем обозначение
Дхь=х’г(/5+2)—xft(/s),	1, п.
Тогда мы будем иметь следующие два соотношения:
Дх""1 (4+1) + Дх"'1	= Дх"-1,
(6.16)
Ax"(/S+1) +Ax"(/S)= Дх".
Правые части равенств (6.16) заданы. Так как управ-
ления и’(£„) определяются однозначно величинами
Ax'(fs) (см. (6.7)), то выражения (6.16) — это некоторые
уравнения относительно величин и’:
= Ах"-1,
(6.17)
bsnUn (ts) + bs+litlUn (/s+i) — Ax".
Предположим, что в условиях (6.3) стоит знак строго
равенства. Тогда (6.3), выписанное для i=s и »=$+!,
284
ПРЯМЫЕ МЕТОДЫ
[ГЛ. ГП
дает еще два условия для определения ип~* и ип:
cs. п- lU”-1 (4) + csnun (ts) = cs — y	,
/=1 b°l
(6.18)
Cs+i, n-iW”"1 (ts+ 1) H~ Cs+i,nUn (4+1) = Cs+1 —	-~r-- •
U/
Система уравнений (6.17) — (6.18)—это система четырех
линейных неоднородных уравнений относительно четы-
рех неизвестных: ип~*(18)9 un~l(ts+l), un(t8) и un(t8+l).
Для разрешимости этой системы достаточно, чтобы опре-
делитель
^S+l,n-l О О
О 0	bsn bs+i,n
Cs,n-i 0 Csn О
6	£s+i,n-i	0 Cs+i,n
был отличен от нуля.
Итак, когда выполнено условие
Д¥=0,
(6.19)
Элементарная операция состоит в определении управле-
ний, переводящих систему из заданного состояния на
гиперплоскости t—t, в заданное состояние на гиперпло-
скости /=4+2. При этом на промежуточной гиперплоско-
сти / = 4+1 фиксируются только (и—2) компоненты век-
тора состояния.
Изложенная методика может быть распространена и
на общий случай. Кроме того, здесь также применима
схема метода «бегущей волны», изложенная в § 3.
5.	Транспортная задача. Транспортной задачей на-
зывается задача определения величин r?(4), доставляю-
щих минимум линейной форме
N п
§ 6]
СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
285
при ограничениях
и/(^)>0,	(6.21)
2 и! (//) = с1, t = 1,2, ..., АГ, (6.22)
/=1
N
j = \,2, ..., п. (6.23)
i=i
Задача (6.20) — (6.23) — это частный случай задачи
(6.1) — (6.4). Однако она имеет некоторые особенности,
которые заставляют ее рассмотреть специально.
Уравнения (6.7) для фазовых переменных будут в
этой задаче выглядеть так:
j = 1,2,... , п. (6.24)
В этой задаче т=п, и, следовательно, для реализа-
ции элементарной операции мы должны использовать
схему двойного шага, изложенную в предыдущем пунк-
те. Вычислим
	1	1	0	0	
д=	0	0	1	1	= 0.
	1	0	1	0	
	0	1	0	1	
Таким образом, транспортная задача является вы->
рожденной. Поэтому построение элементарной операции
в транспортной задаче требует специального рассмот-
рения.
Система уравнений (6.24) допускает первый инте-
грал. Сложим уравнения (6.24) и воспользуемся усло-
вием (6.22):
2 Дх'(4) = ^ u!(ts) = c\	(6.25)
l-i	i-i
Введем функцию «времени» Ф(^):
/г
Л
$=1
286
ПРЯМЫЕ МЕТОДЫ
[ГЛ. Ill
Эта величина известная. Используя то обстоятельство,
что xJ(/1)=0, получим из (6.25):
п
2 х/(^) = ф(^).	(6.26)
/=1
Равенство (6.26) — это и есть первый интеграл системы
(6.24). Оно позволяет понизить порядок системы (6.24),
исключив из рассмотрения одну из переменных, напри-
мер, хп:
П-1
хп = ф —	х1'.
Итак, мы пришли к задаче, где размерность фазового
вектора и размерность управления совпадают, следова-
тельно, после исключения хп мы можем воспользоваться
схемой построения элементарной операции, изложенной
в п. 4.
6. Некоторые комментарии. Мы рассмотрели не-
сколько задач, в частности, задач линейного программи-
рования, для которых может быть построена элементар-
ная операция и применены методы последовательного
анализа вариантов, например, метод «блуждающей
трубки» или метод локальных вариаций. Некоторые из
этих задач могут быть решены стандартными методами
линейного программирования. Тем не менее изложенные
методы в ряде случаев оказываются вполне конкуренто-
способными методам линейного программирования. Возь-
мем, например, класс задач, где существуют хорошие
диспетчерские решения и где речь идет не о полу-
чении точного решения, а об уточнении решения, полу-
ченного эвристическими методами. В этом случае метод
локальных вариаций, например, оказывается не только
более простым для программирования, но и более эко-
номичным с точки зрения затрат машинного времени,
причем преимущество этого метода будет тем ощутимее,
чем больше число N (точнее, чем больше отношение
ВД*).
*) Метод «блуждающей трубки» дает для двухиндексных задач
линейного программирования процесс, сходящийся к оптимальному
решению. Поэтому в принципе мы можем в качестве нулевого при-
ближения использовать произвольное допустимое решение.
$ 6]
СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
287
Таким образом, использование схем динамического
программирования для решения задач линейного про-
граммирования оказывается оправданным, если матри-
цы задач линейного программирования оказываются
сильно вытянутыми (по строкам или по столбцам).
Примечания.
1.	Подчеркнем еще раз, что описанные методы реше-
ния задач линейного программирования ни в какой ме-
ре не являются альтернативой общим методом линей-
ного программирования. Они могут быть хорошим до-
полнением последних, в особенности в задачах очень
большой размерности. Стандартные методы линейного
программирования позволяют легко сделать первые ша-
ги, выводящие в «окрестность» минимума. Однако по-
следующее продвижение с использованием симплекс-
метода часто бывает затруднено появлением различных
случаев вырождения, резко замедляющих счет.
2.	Мы сравнивали метод последовательного анализа
вариантов и методы линейного программирования. Но
методы линейного программирования — это специфиче-
ский метод решения линейных задач. В то же время ме-
тоды последовательного анализа вариантов могут быть
использованы для решения нелинейных задач.
7.	О переносе граничных условий. В задачах с дис-
кретным временем может быть использована не только
техника динамического программирования, но и другие
методы решения задач теории оптимального управления.
В частности, с успехом могут применяться различные
итеративные схемы, использующие идеи прогонки. Рас-
смотрим произвольную линейную систему
«^п+1 = %п Апхп fnf	(6;27)
где Ап — произвольные матрицы, a fn—произвольные
векторы. Предположим далее, что вектор х0 стеснен ус-
ловием
(х0, Zq) = п0,	(6.28)
где /0 — заданный вектор, а а0 — заданный скаляр.
Мы будем говорить, что условие (6.28) перенесено
в любую точку t=tn, если мы сможем так определить
векторы 1п и скаляры ап независимо от х, чтобы любое
решение системы (6.27), удовлетворяющее условию
288
ПРЯМЫЕ МЕТОДЫ
(ГЛ. III
(6.28), удовлетворяло бы условию
(хл, 1п) = ап.	(6.29)
Будем искать вектор 1п как решение уравнения
— In + Bnlrh	(6.30)
где lQ — заданный вектор.
Вычислим
(Хп+1, ^1+1) — (-'-п» In) 4- (fn> In) 4” (Ai> Bpin) 4- d-n, (6.31)
где величина dn определяется выражением
cfn = (Zn« Апхп) 4* (^n, Bnln) 4" (4дХп> W
Эту величину легко преобразовать к следующему виду:
dn — (Хп> Anin 4” Вп1п 4” AnBnln) — (Хп, Dnln).
Выберем матрицы Da, а следовательно, и Вп так, чтобы
скаляр dn был равен нулю. Тогда мы получим следующее
утверждение:
Если In—решение уравнения (6.30), обращающееся
в заданный вектор при п=0, а а«— это скаляры, кото-
рые определяются как решение уравнения
®п+1 ~ ап 4“ (/п, In) 4” (fn> Bnln)
при условии, что а0 — заданное число, то для любого п
имеет место равенство (6.29).
Матрицы Вп можно определять не единственным спо-
собом. Для наших целей, например, достаточно потребо-
вать, чтобы Dn=0. Это нам дает следующее выражение
для матрицы Ва:
Вп — —Ап(1 4-АлГ1.	(6132)
Доказанная теорема позволяет использовать методы ре-
шения краевых задач, изложенные в §§ 2, 3 гл. II, кото-
рые опираются на способ переноса граничных условий
(метод прогонки).
Примечания.
1.	При фактической реализации этих процедур для
конечноразностных уравнений типа (6.27) мы можем
снова столкнуться с неустойчивостью решения задач Ко-
ши для уравнения (6.30). Эту трудность можно преодо-
§6]
СИСТЕМЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
289
леть, используя неоднозначность определения матрицы
Вп. Метод А. А. Абрамова, изложенный в предыдущей
главе, полностью переносится и на этот случай. Таким
образом, процедура расчета вектора 1п всегда может
быть сделана устойчивой.
2.	Предположим, что речь идет об отыскании реше-
ния задачи Коши для системы (6.27), и эта задача ока-
залась неустойчивой. Тогда, используя изложенную схе-
му переноса граничных условий, мы можем перенести
все условия на правый конец траектории (эта процедура
всегда может быть сделана устойчивой), после чего ре-
шить задачу Коши для системы (6.27) справа налево.
8.	Задача со свободным концом. Подобно тому, как
техника метода прогонки может быть перенесена на за-
дачи для дискретных систем, техника решения задач со
свободным концом также может быть использована в
этой теории.
Рассмотрим общий случай дискретной системы
 Л'А+i = %k 4” fk (х^,	(6.33)
и поставим задачу отыскания экстремума функции
N-1
J = Fi(xhu^	(6.34)
г=о
Начальное состояние будем считать фиксированным,
х0=а, а правый конец свободным. На управление ника-
ких ограничений мы накладывать не будем.
На основании теоремы, доказанной в § 4 гл. I, мы
должны составить уравнение для импульсов (множите-
лей Лагранжа).
Idft \*	dF.
ф/ —	+	I—I фг+i	—
\дх{ /	дх{
(6.35)
и разыскивать решение среди решений краевой задачи
х0=а, i|)w=0 для системы дискретных уравнений (6.33),
(6.35), где управление исключено при помощи уравнения
dF, М. \*
Т1- ^- ^1=°-	(6-36)
dut \dut )	'
10 Н. Н. Моисеев
290
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
Если решение этого уравнения единственно, то для ре-
шения данной задачи может быть применена итерацион-
ная схема И. А. Крылова и Ф. Л. Черноусько.
Предположим, что задано некоторое начальное при-
ближение ик=им. Подставляя его в правую часть урав-
нения (6.33), мы находим последовательно все хк. Таким
образом, все коэффициенты уравнения (6.35) оказыва-
ются определенными, и поскольку ^=0, то, решая эту
систему справа налево, мы можем последовательно оп-
ределить все величины tpj.
Одновременно вычисляем новое управление ик=ик1
из уравнений
— 0 dFN-t / dfN-i \	_ п
duN_2 \duN_2)
Определив новое приближение, повторяем процедуру.
Примечание. Схема И. А. Крылова и Ф. Л. Чер-
ноусько в применении к дискретным задачам имеет це-
лый ряд особенностей. Например, в непрерывных зада-
чах у нас не было необходимости запоминать фазовую
переменную x(t), поскольку мы всегда могли решить
задачу Коши в направлении отрицательного времени
столь же просто, как и в положительном направлении.
В рассматриваемой задаче дело обстоит сложнее, по-
скольку в общем случае разрешить уравнение (6.33) от-
носительно хк, если xk+i задан, мы не можем, не исполь-
зуя сложных итерационных процедур.
§ 7. Задачи теории расписаний
1. Неизбежность использования эвристических мето-
дов. В § 1 этой главы мы сформулировали задачу теории
расписаний, используя язык динамических процессов*).
Согласно сказанному задача теории расписаний сводит-
ся к определению управления u{<=Git при котором вели-
чина х{, удовлетворяющая соотношению (см. (1.22))
х*+1 = х*|+ |«ь	(7.1)
*) Задача составления расписания, задача календарного плани-
рования— часто употребляемые синонимы одной и той же задачи.
ЗАДАЧИ ТЕОРИИ РАСПИСАНИЙ
291
§ 71
достигает заданного значения при наименьшем индексе
i=N.
Предположим, что для решения этой задачи мы ис-
пользовали метод динамического программирования.
Оценим количество машинных операций, которые для
этого необходимы.
Напомним, что х — это целое число, имеющее столь-
ко разрядов, сколько работ находится в нашем исход-
ном списке. Если для описания состояния каждой из ра-
бот мы используем десятичную шкалу, то число возмож-
ных состояний расписания будет М = 10', где I — число
работ. Тогда, согласно оценке трудности схемы динами-
ческого программирования, которую мы получили для
многошаговых процессов в этой главе, число машинных
операций пропорционально величине 102W.
Составление расписания работ, содержащих список
из 1000 работ, это задача довольно обычная и часто
встречающаяся на практике. Легко, однако, подсчи-
тать, что даже имея самые современные машины, нам
для получения точного результата потребуется время,
сравнимое со временем существования нашей га-
лактики.
Обратим внимание на то, что использование даже
сверхбыстродействующей гипотетической техники мало
что изменит в существе вопроса. Время для нахождения
точного решения все равно будет иметь астрономический
порядок. Выход из создавшегося положения один — ис-
пользование эвристических методов. Этим очень неопре-
деленным термином мы называем такие математические
приемы решения задач, для которых отсутствуют при-
вычные для математика обоснования применимости.
Правдоподобные рассуждения, наша интуиция, опыт и
машинный эксперимент — вот пока те оправдания эври-
стики, которыми мы располагаем.
Примечание. Развитие математической мысли
постепенно приводит к такому расширению концепций,
в рамках которых становится понятным место тех или
иных эвристических методов. Тенденции такого процес-
са хорошо видны в теории информации и теории распо-
знавания образов.
В этом параграфе мы ограничимся описанием четы-
рех приемов, носящих эвристический характер, которые
ю*
292
ПРЯМЫЕ МЕТОДЫ
[ГЛ. Ill
позволяют качественно упростить задачи теории распи-
саний. Эти приемы следующие:
1.	Придание работам весов (приоритетов).
2.	Введение функций штрафа.
3.	Использование промежуточных целей.
4.	Агрегирование.
2. Ранжировка работ. Придание работам относи-
тельного веса качественно упрощает задачу, поскольку
делает множество возможных состояний вполне упоря-
доченным.
В настоящее время предложено много способов упо-
рядочения работ. Рассмотрим здесь лишь один из воз-
можных способов, который основан на анализе логичес-
кой структуры ограничений. Технику взвешивания работ
поясним на примере. Предположим, что условие на оче-
редность работ (а), которому должно удовлетворять со-
ставленное расписание, задано в виде некоторого графа
(рис. 7.1). В этом графе, состоящем из тридцати работ,
4 работы являются выходными (финальными). Это рабо-
ты, имеющие номера 1, 2, 3 и 4. Припишем им тем или
иным образом некоторые веса. Если важность этих фи-
ЗАДАЧИ ТЕОРИИ РАСПИСАНИИ
293
§ 71
нальных работ одинакова, то будем считать, например,
что вес каждой из этих работ равен 1. Работа № 5 пред-
шествует одной работе, вес которой равен 1, припишем ей
вес 1 + 1=2. Работа № 8 предшествует двум работам,
каждая из которой имеет вес 1. В качестве веса работы
№ 8 примем число 4=2+1 +1 *). Вес работы № 7 равен 2,
работы № 6 — также 2. Работа № 12 предшествует трем
работам №№ 6, 7 и 8, имеющим веса 2, 2 и 4. Работе
№ 12 мы припишем вес 3 + 2+2+4=11 и т. д. В резуль-
тате мы получим следующую таблицу (в скобках указа-
ны номера работ, которым предшествует данная работа).
В правой колонке указан вес и из чего он складывается.
1 (0) 1
2 (0) 1
3 (0) 1
4 (0) 1
5 (1) 1 + 1=2
6 (1) 1 + 1=2
7 (2) 1 + 1=2
8 (3,4) 2+1 +1=4
9 (3,4) 2+1 + 1=4
10 (2) 1 + 1=2
11 (9, 10) 2+4 + 2 = 8
12 (6,7,8) 3+2 + 2+4 = 11
13 (2) 1 + 1=2
14 (5) 1+2=3
15 (13) 1+2 = 3
16 (13) 1 + 2=3
17 (9, 10) 2+4 + 2 = 8
18 (11, 12, 23) 3+8+11 + 3 = 25
19 (14, 15) 2 + 3 + 3=8
20 (19) 1+8 = 9
21 (13) 1+2 = 3
22 (20,21) 2+9+3=14
23 (5) 1 + 2 = 3
24 (11, 12, 23) 3+8+11 + 3 = 25
25 (16, 17, 18) 3 + 3+8+25=39
26 (24, 25) 2 + 25 + 39=66
*) Число работ, которым предшествует работа № 8, плюс веса
этих работ.
294
ПРЯМЫЕ МЕТОДЫ
(ГЛ. III
27 (16, 17, 18) 3 + 3+8 + 25 = 39
28 (9, 10) 2 + 4 + 2 = 8
29 (28) 1+8=9
30 (27,29) 2 + 39+9 = 50
Итак, все множество работ разбито на двенадцать
групп *):
I.	№ 26.
II.	№ 30.
III.	№№ 25 и 27.
IV.	№№ 18 и 24.
V.	№ 22.
VI.	№ 12.
VII.	№№ 20 и 29.
VIII.	№№ 11, 17, 19, 28.
IX.	№№ 8, 9.
X.	№№ 14, 15, 16, 23, 21.
XI.	№№ 5, 6, 7, 10, 13.
XII.	№№ 1,2, 3,4.
Для того чтобы множество состояний {х} было впол-
не упорядоченным, надо расставить работы в порядке
значимости. Для этого надо еще тем или иным образом
условиться о соотношении работ внутри групп. Тогда
число х будет выглядеть, например, так:
х = • • •
Ранжировка работ вводит на множестве {х} тополо-
гию, следовательно, многие из изложенных способов ите-
ративного решения задач (в частности, метод «блуждаю-
щей трубки») оказываются применимыми, и исходная
задача перестает быть безнадежной.
Примечания.
1.	В уравнении (7.1) стоит знак поразрядного логи-
ческого сложения | + |. Это обстоятельство не вносит ни-
каких принципиальных осложнений, поскольку знак | + |
всего лишь специальная форма записи нелинейности.
2.	Разумеется, результат, который будет получен, за-
висит от введенной топологии. Изменив ранжировку ра-
бот, мы в общем случае получим иное расписание работ
с иным временем завершения всех работ.
*) В соответствии с порядком убывания весов работ.
« 7]
ЗАДАЧИ ТЕОРИИ РАСПИСАНИЙ
295
3.	Другой способ описания задачи. Рассмотрим те-
перь тот случай, когда временной интервал т=/<+1—Л- от-
носительно мал. В этом случае можно использовать язык
дифференциальных уравнений.
Изменение состояния выполнения работы номера i
будем описывать уравнением
рг = М0, 1=1, 2,..., N-,	(7.2)
%((£) —это интенсивность выполнения работы—доля ра-
боты pit которая была бы выполнена в единицу времени,
если бы в течение всего отрезка времени интенсивность
%,- была бы постоянна.
Величина К определяется объемом ресурса, выделен-
ного на выполнение работы номера i. Ограничимся рас-
смотрением простейшей формы зависимости интенсивно-
сти от ресурса. Предположим, что для того, чтобы обес-
печить интенсивность X,-, равную 1, необходимо выделить
сси ресурса первого вида, а» ресурса второго вида и т. д.
Тогда для того, чтобы иметь интенсивность, равную %{,
необходимо выделить Х.-а(1 ресурса первого вида,
второго и т. д. Таким образом, общее количество ресурса
/-го вида, выделенное в данный момент t на выполнение
N
расписания, будет Х,ау. Но эта величина ограничена.
1=1
Таким образом, реализация плана работ будет стеснена
условием
N
/= 1,2,... ,;и,	(7.3)
i=i
где qs— количество /-го ресурса, который может быть вы-
делен на выполнение работ в данный момент.
Начальные и конечные значения величин р,- заданы:
рг(0) = 0, р((Т)=1-	(7.4)
Эволюция системы (7.2) стеснена еще условиями подчи-
ненности. Их можно сформулировать следующим обра-
зом: Pi(t) равны нулю до того момента, пока некоторые
величины Р(«(/)<1- В этих условиях мы можем сформу-
лировать для системы (7.2) задачу на быстродействие.
Такая переформулировка задачи теории расписаний
296
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
открывает определенные перспективы для применения
итерационных методов, разработанных в теории опти-
мальных управлений.
4.	Функции штрафа. Переход от дискретной задачи
теории расписаний к непрерывной задаче теории опти-
мального управления вносит, разумеется, качественные
упрощения. Тем не менее эта задача остается еще очень
сложной. Одна из трудностей связана с выполнением ус-
ловия (а), наложенного на очередность работ. Какой бы
способ решения задачи теории оптимального управления
ни выбран, мы должны для каждого / определить вели-
чины %,-. Но помимо неравенств (7.3) мы должны еще про-
верить условие (а): К{—только тогда отлично от нуля,
когда все работы yit (работы, выполнение которых пред-
шествует началу выполнения работы pt) удовлетворяют
равенству р<в(/) = 1.
Проверка этих условий на каждом шаге требует
большой затраты машинного времени. Преодоление этой
трудности возможно с помощью метода штрафных функ-
ций. Мы будем использовать штрафную функцию следу-
ющего вида:
ф(г) —О, если z^ О,
ф (z) > 0, если z > 0.
Функцию ф(г) удобно строить дифференцируемой.
Для этого достаточно, например, принять
0,
Л
если z<0,
если г > 0.
(7.5)
Вместо функционала Т — общего времени — мы бу-
дем минимизировать функционал
N Г Л
J = т + S f М1 (Pi) 3 ф о — pi»)dt- (7-6)
i=io	S
Функция
Т N
'Fl = J 2 М(pi) 3 фП — Pis)dt	(7-7)
о г* =1	s
определяет норму штрафа за невыполнение ограничений
(а) логического характера. Если условие (а) выполнено
§ 7]
ЗАДАЧИ ТЕОРИИ РАСПИСАНИЙ
297
в любой момент времени, то подынтегральное выражение
в (7.7) тождественно равно нулю. Внутренняя сумма в
(7.7) распространена по всем тем работам, выполнение
которых должно предшествовать началу выполнения ра-
боты номера i.
Заметим, что составить это выражение надо лишь один
раз, и эта работа может быть сделана вручную до реше-
ния задачи.
Начав однажды использовать штрафные функции,
естественно дойти на этом пути до логического конца и
свести с помощью этого метода рассматриваемую задачу
к классической задаче без всяких ограничений (кроме
фиксированного начального состояния).
Для этого введем еще ряд штрафных функций:
^2 = ^	(7.8)
2=1
Функция Т2 определяет величину штрафа за невыполне-
ние граничных условий на конце траектории.
т N
Уз == JS Й(-Р/)Л-	(7.9)
о i—i
Величины pi должны быть неотрицательны. Функция 4%
определяет штраф за невыполнение этого условия.
г N
^4 = J'S	(7.Ю)
О 1=1
Функция аналогична ЧЛ,—она определяет величину
штрафа за невыполнение условия р/^1.
Т m IN	'
^=J2	3 ^/-<7/(0 \dt. (7.11)
o /=i	\Z=1	/
Эта функция определяет норму штрафа за невыполнение
ограничений по ресурсу.
Собирая выражения (7.7) —(7.11), мы придем к функ-
ционалу следующего вида:
/ = Л+^14-Та4-Т3 + ^4-|-Т5.	(7.12)
298
ПРЯМЫЕ МЕТОДЫ
[ГЛ. III
Задача минимизации функционала (7.12)—это класси-
ческая задача с нефиксированным временем и свободным
концом.
Примечания.
1. Описанный способ введения штрафных функций не
единственный. Анализируя конкретную природу задачи,
вероятно, всегда можно придумать форму функций штра-
фа, более удобную для программирования, нежели те,
которые здесь описаны.
2. При и Щ—^°° решение задачи с функционалом
(7.12) будет стремиться к решению задачи, сформулиро-
ванной в предыдущем пункте (соответствующая теорема
для разностного аналога задачи доказана П. А. Непомя-
щим *)). Однако такое обоснование не снимает трудностей
фактического проведения счета: получение точных ре-
зультатов возможно только при больших Ц/ и yf. Но
при этом задача перестает быть устойчивой: приходится
умножать большие величины на очень малые. Потому,
как уже неоднократно отмечалось в данной монографии,
метод функций штрафа не дает возможности проводить
расчеты с высокой точностью. Но задача теории расписа-
ний, как правило, и не требует высокой точности. По
этой причине указанный подход оказывается примени-
мым к широкому классу подобных задач.
5.	Промежуточные цели. В предыдущем пункте мы
сделали еще один шаг, позволяющий внести существен-
ные упрощения в задачи теории расписаний. Но все же
задачи этого типа остаются еще очень сложными и для
организации рациональных вычислительных процедур
необходимы дальнейшие упрощения. В самом деле, вве-
дением штрафных функций мы устранили одну из глав-
ных трудностей — устранили ограничения. Но осталась
вторая трудность — размерность. Еще в начале парагра-
фа мы заметили, что реальные задачи календарного пла-
нирования требуют составления расписания для многих
сотен и тысяч работ. Как бы ни были совершенны и стан-
дартизованы вычислительные методы теории оптималь-
ного управления, они практически бессильны, если идет
*) П. А. Не п ом я щи й, Применение теории оптимального
управления с помощью метода штрафных функций к одной задаче
теории расписания, ЖВМ и МФ 10, № 4, 1970.
$ 7j	ЗАДАЧИ ТЕОРИЙ РАСПИСАНИИ	299
речь о задачах подобной размерности. Одна из идей,
позволяющих упростить подобную задачу, состоит во
введении промежуточных целей, позволяющих одну за-
дачу большой размерности заменить несколькими значи-
тельно более простыми задачами. Промежуточная цель
позволяет заменить составление расписания работ на
весь плановый период Т последовательным составлением
расписания на отрезки меньшей длительности. При этом
мы уже должны работать не со всем списком работ, а
лишь с некоторой частью этого списка. Остановимся на
некоторых особенностях технологии метода промежуточ-
ных целей.
В п. 2 этого параграфа мы описали способ, позволяю-
щий каждой работе pi поставить в соответствие некоторое
число у/, характеризующее относительную значимость ра-
боты pt. Таким образом, величина
•7(0=ЗШ(0	(7.13)
характеризует степень выполнения расписания. Поэтому
в качестве промежуточной цели мы можем использовать
эту величину и поставить следующую оптимизационную
задачу: определить Л/(/) таким образом, чтобы обеспе-
чить минимум функционала
5
-/((о + т) + 2	(7.14)
i ==si
при условиях (7.2) и
Pi (^о) ~ Pi«>	(7.15)
где pio— заданные числа.
Эта задача проще той, которую мы рассматривали в
предыдущем пункте. В самом деле, во-первых, задача
(7.14)—это задача с фиксированным временем, во-вто-
рых, в задаче минимизации функционала (7.14) мы долж-
ны найти фазовую траекторию только на небольшом от-
резке времени [/0, /0+т]. Как ни важны перечисленные
обстоятельства, основное упрощение, которое достигает-
ся введением промежуточных целей, состоит еще не в
этом.
300
ПРЯМЫЕ МЕТОДЫ
[ГЛ. II’
Рассмотрим начальный период производства работ
(длина его равна t<c7). На этот период может быть на-
значена к исполнению лишь небольшая часть работ пер-
воначального списка, удовлетворяющая условию (а).
Поэтому, решая задачу (7.14), нам нет необходимости
рассматривать всю систему уравнений (7.2), а достаточ-
но рассмотреть только часть этой системы. Таким обра-
зом, размерность задачи (7.14) для отрезка (0, т) будет
значительно меньше размерности исходной задачи. Точ-
но так же на следующем интервале (т, 2т) мы должны
исключить из рассмотрения все работы, которые уже вы-
полнены или которые заведомо не будут удовлетворять
условию (а), и т. д.
Возникает вопрос, каким образом назначать список
работ, которые могут быть выполнены в данный отрезок
времени длины т. Для этой цели может быть использова-
на та же самая процедура ранжировки работ, которая
нам позволила назначить функционал (7.13).
В самом деле, предположим, что мы отобрали все ра-
боты pt такие, что соответствующие где L — задан-
ное число. Мы получили некоторый список работ, некото-
рый подграф, все звенья которого удовлетворяют усло-
вию (а). Это обстоятельство позволяет вновь использо-
вать описанный способ ранжировки работ.
Введение штрафных функций позволяет развить при-
ближенные методы расчета. Строгие математические тео-
ремы позволяют понять смысл подобных аппроксимаций
и в некоторых случаях дать оценки. Введение промежу-
точных целей является эвристическим приемом, который
не имеет в настоящее время никакого математического
обоснования. Единственно, что мы знаем, это то, что при
х-+Г (где Т* — решение исходной задачи на быстродей-
ствие) решение задачи (7.14) будет к нему стремиться.
Но эта информация практически бесполезна, поскольку
методы промежуточных целей имеют смысл только при
т«СТ.
При т-Я) метод промежуточных целей позволяет по-
лучить так называемые локально оптимальные управле-
ния, о которых речь будет идти в следующей главе. Для
некоторых классов локально оптимальных управлений
удается понять их природу и доказать соответствующие
теоремы. Что касается немалых т, то обоснование описан-
ЗАДАЧИ ТЕОРИИ РАСПИСАНИЙ
301
§ 71
ных процедур может опираться только на правдоподоб-
ность наших рассуждений и на машинный эксперимент,
относящийся к некоторым задачам, имеющим характер
тестов.
6.	Агрегирование. Метод промежуточных целей, назы-
ваемый иногда методом использования функций прогноза
J(t), дает возможность эффективно построить какое-то
решение, которое мы затем можем уточнить тем или
иным способом. Однако для построения начальных при-
ближений могут быть использованы подходы и совсем
другого типа.
В начале параграфа был изложен способ ранжировки
работ. Он позволяет упорядочить работы по их весам.
Однако если работы р„ и рк имеют одинаковый вес, то
между этими работами нельзя установить соотношения
упорядоченности
Р.<Рк или pk<p.
(знак означает, что одна из работ предшествует дру-
гой) .
Сделаем теперь операцию агрегирования, объединив все
работы одного веса. Эти агрегированные работы будем
обозначать через р*{. Работы {р£*} образуют граф, состоящий
из последовательных работ (рис. 7.2):
рГ-Кр/, если Г</.	(7.16)
Работа р* для своего выполнения требует а£* ресурса пер-
вого вида, а12 ресурса второго вида и т. д., причем
«*/ = 2 “s/’
S
где сумма распространена по всем тем индексам s, для ко-
торых вес работ ys равен весу работы р*.
Построение расписания для графа, изображенного на
рис. 7.2, не представляет никакого труда. Время выполне-
ния работ {р*} по этому расписанию обозначим через Т+
302
ПРЯМЫЕ МЕТОДЫ
(ГЛ. П1
Так как условие (7.16) более жесткое, чем условие (а),
то Г+ дает верхнюю оценку для оптимального директивного
срока Т* < Т°. Хорошо известны разнообразные способы по-
лучения нижних оценок для оптимального времени заверше-
ния работ Г_. Такой оценкой является, например, длина
Ау* г Р»ц .... Рг г А* 
Рис. 7.2.
критического пути *). Разность Т“ — Т_ содержит уже очень
полезную информацию.
Дальнейшее улучшение расписания может быть реа-
лизовано различными способами, выбор которых в значи-
тельной степени связан со структурой графа. Например,
может иметь смысл следующая схема:
Первый шаг. Рассмотрим работы P*N. и P*N,_V
Время, которое занимает их выполнение, обозначим через
tw. и T;w»_r Эти работы представляют собой некоторый
граф Г1( состоящий из небольшого количества работ. Для
него расписание может быть найдено одним из точных
методов. В результате мы найдем некоторое время его
выполнения причем ti^-x^+x^^.
Обозначим через Т\ величину
Т\ — Т\. — Хы* —	Т®.
Мы получим новую верхнюю оценку Т\.
Второй шаг. Рассматриваем работы и Р*ы*-а и
повторяем описанную процедуру. Получаем новую верхнюю
оценку
и т. д.
*) Критическим путем называется самый длинный путь из мно-
жества начальных вершин в множество конечных вершин.
§ 7]	ЗАДАЧИ ТЕОРИИ РАСПИСАНИЙ	303
7.	Заключение. Расчет расписания — это первая, но
отнюдь не единственная задача обсуждаемой теории.
Следующая задача — это задача управления расписани-
ем, возникающая из-за неизбежности помех. Задача
управления расписанием — это задача создания необхо-
димой системы обратной связи. Одним из примеров орга-
низации процедуры управления расписанием дает извест-
ный метод анализа критического пути*). Однако этот
метод не только не является удовлетворительным и уни-
версальным средством управления, но он оказывается в
ряде случаев просто неприменимым. Поэтому конструи-
рование «операторов управления» остается актуальной
проблемой. Как подойти к ее решению? В рамках класси-
ческих методов теории графов не выработано никаких
способов ее решения. Метод критического пути является
удачной и единичной находкой. В то же время в теории
оптимального управления разработаны многочисленные
методы синтеза систем управления. Использование языка
этой теории позволяет и в задачах об управлении распи-
санием разработать методы, позволяющие решить основ-
ные проблемы синтеза: найти оптимальную структуру
обратной связи, решить задачу резервирования, изучить
влияние помех и т. д.
К некоторым из перечисленных вопросов мы вернемся
в следующих главах этой книги, специально посвящен-
ных проблемам синтеза.
В заключение имеет смысл заметить, что те идеи, о
которых речь шла в этом параграфе, послужили источни-
ком целого ряда исследований, в том числе и приклад-
ного характера**). Алгоритмы, основанные на использо-
вании логического ранжирования, оказываются весьма
экономичными. Так, например, составление расписания,
содержащего список из 1500 работ, требует на машине
БЭСМ-6 всего лишь нескольких секунд.
*) См., иапример, С. И. Зуховицкий, И. А. Радчик,
Математические методы сетевого планирования, «Наука», 4965.
**) См., например, И. Н. Зимин и Ю. П. Ива нилов, Ре-
шение задач сетевого планирования сведением их к задачам опти-
мального управления, ЖВМ, т. II, № 3, 1972; И. Н. Зимин, Алго-
ритм расчета сетей при переменных интенсивностях выполнения опе-
раций, Техническая кибернетика, № 6, 1973,
ГЛАВА IV
ПРОБЛЕМА СИНТЕЗА
ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
В предыдущих главах мы. изучали проблему расчета
программных движений — расчета оптимальной програм-
мы. В процессе конструирования оптимальной системы —
это первый и неизбежный этап. Следующий шаг —син-
тез системы управления.
В последние годы появилось много первоклассных ис-
следований в теории синтеза и опубликован ряд моногра-
фий и учебников*). В них, как правило, основное место
уделяется общим концепциям теории синтеза и анализу
примеров конкретных систем. В данной работе внимание
концентрируется на вычислительных аспектах теории.
Общие вопросы обсуждаются лишь постольку, поскольку
мы должны сформулировать возникающие математичес-
кие задачи. Технические приложения, занимающие зна-
чительный объем в монографиях по теории синтеза, вооб-
ще не рассматриваются.
Наиболее важные задачи синтеза — это те, в которых
существенно присутствие случайных возмущений, а функ-
ционал, минимум которого мы разыскиваем, является
математическим ожиданием некоторой случайной вели-
чины.
Основная трудность таких задач состоит в том, что
в общем случае в нашем распоряжении нет аппарата, по-
зволяющего вычислить значение функционала при задан-
ном управлении. Разумеется, мы всегда можем приме-
нить метод Монте-Карло, однако легко себе представить
трудоемкость такого подхода. Известные перспективы
открывает применение методов динамического програм-
*)Т. Той, Optimum design of digital control systems, Academic
Press, 1963.
К. У. M e p p и э м, Теория оптимизации и расчет систем управле-
ния с обратной связью, «Мир», 1967.
ГЛ. IV]
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
305
мирования. Однако, как мы в этом убедимся, и здесь
возможности очень ограничены. Единственный путь, ко-
торый остается в нашем распоряжении—это построение
приближенных методов, причем, как правило, гипотезы,
которые лежат в их основе, носят интуитивный характер
и строгого обоснования не имеют.
Вторая трудность, встречающаяся при реализации вы-
числительных процедур — это необходимость принимать
решения в условиях неопределенности, которые возни-
кают в задачах естественным образом. Мы можем быть
недостаточно информированы о ситуации, в условиях
которой протекает управляемый процесс, мы часто стоим
перед необходимостью строить систему управления, кото-
рая должна управлять набором различных программ, в
экономических и военных задачах мы не знаем стратегию
противника и т. д. Бывают, наконец, ситуации, когда и
цели управления и критерий качества процесса нам не
известны достаточно четко. Все эти обстоятельства при-
водят к тому, что и сами задачи часто оказываются не-
четко сформулированными, в том смысле, что в их фор-
мулировке присутствует элемент неопределенности.
Обсуждение этих вопросов составляет главное содер-
жание глав, посвященных синтезу управлений.
Создание вычислительных методов синтеза представ-
ляется возможным и перспективным направлением вы-
числительной математики и теории управления. Сегодня,
когда электронные вычислительные машины стали есте-
ственным элементом контура управления, значение эф-
фективных алгоритмов отыскания синтезирующих функ-
ций особенно возросло.
Есть еще одно важное приложение методов, об-
суждению которых посвящена данная глава,— это тео-
рия игр.
Игровые постановки начинают все чаще и чаще ис-
пользоваться в разнообразных задачах практики управ-
ляемых систем, причем игровые задачи, как правило,
имеет смысл рассматривать только в рамках синтеза.
Создание эффективных подходов к численному решению
задач синтеза систем управления будет одновременно
очень важным шагом в развитии теории игр и ее исполь-
зовании для решения проблем, возникающих в конкрет-
ной деятельности человека.
306
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
(ГЛ. IV
§1.0 постановке задач синтеза
оптимальных систем управления
1. Предварительное обсуждение. Содержание про-
блем, возникающих при создании оптимальной системы
управления, продемонстрируем на нескольких примерах
технических и экономических задач.
Рассмотрим сначала одну задачу управления косми-
ческой ракетой. Предположим, что цель управления ра-
кетой— выход на заданную орбиту вокруг Земли. Этот
пример выбран из-за своей наглядности, хотя все, что
мы будем говорить в этом параграфе, относится к значи-
тельно более общему классу управляемых систем.
Предположим далее, что задача расчета программно-
го движения решена. Для достижения цели управления
эта программа обеспечивает минимальный расход горю-
чего (или, что то же самое, при заданном запасе горюче-
го обеспечивает вывод на орбиту максимального коли-
чества полезного груза). При расчете программного дви-
жения принимается ряд гипотез: силы, действующие на
ракету, считаются известными и вполне определенными
функциями элементов движения (высоты, скорости
и т. д.); начальное состояние (начальное положение и
скорость) принимается строго фиксированным и т. д.
Кроме того, определенные ограничения вносятся и в саму
схему движения: отбрасываются «малые силы», игнори-
руются некоторые степени свободы. Например, при рас-
чете оптимальной траектории ракеты обычно считают
возможным рассматривать ее как некоторую точку пере-
менной массы. Таким образом, механическая схема дви-
жения, которая принимается при расчете программы,
игнорирует все те степени свободы, которые связаны с
движением ракеты относительно центра инерции.
В то же время реальное движение ракеты происходит
в условиях, существенно отличающихся от тех, которые
были заложены в расчет программного движения. Если
к этому еще добавить, что и само программное управле-
ние реализуется с ошибкой, то станет совершенно очевид-
ным, что ракета никогда не будет двигаться вдоль опти-
мальной траектории. Если ракету не снабдить специаль-
ной системой коррекции, то реальное движение можно
сколь угодно сильно отличаться от расчетного и, следр-
§ 11
О ПОСТАНОВКА ЗАДАЧ СИНТЕЗА
§0?
вательно, цель управления не будет достигнута. Так воз-
никает проблема построения синтеза такой системы
управления, которая при данном уровне помех, обеспечи-
вала бы достижение цели управления или выполнение
программы с максимальной точностью. Мы снова пришли
к некоторой вариационной задаче. Однако, как мы убе-
димся ниже, эта вариационная задача качественно отли-
чается от вариационных задач, которые рассматриваются
при исследовании программного движения.
Иногда говорят не о максимальной точности, а о за-
данной точности. Например, ставят задачу о построении
системы, которая гарантирует, что дисперсия элементов
траектории у цели не будет превосходить некоторой за-
данной величины. В этом случае задача оказывается в
некотором смысле «неопределенной».
В самом деле, предположим, что технические требо-
вания позволяют задать некоторую определенную вели-
чину точности. В этой ситуации мы не будем иметь одно-
значного решения и сможем (в общем случае) создать
несколько систем управления, реализующих заданную
точность. Возникает, естественно, вопрос: какой из этих
систем следует отдать предпочтение. Для того чтобы на
него ответить, мы должны иметь еще один критерий. В ка-
честве такого критерия может быть выбран, например,
вес оборудования, стоимость или энергетика, потребная
для реализации управления, гарантирующего достиже-
ние цели с заданной точностью. Когда такой критерий
будет сформулирован, задача управления снова станет
вариационной задачей, а величина допустимой дисперсии
превратится в ограничение. Итак, мы видим, что проце-
дура синтеза приводит нас к некоторой вариационной
задаче, в которой появляется новый функционал (напри-
мер, дисперсия конечных элементов траектории), отлич-
ный от того функционала, который использовался при
построении программной траектории. Такая ситуация до-
статочно типична, но она не единственно возможная; в
прикладных задачах встречаются и иные постановки за-
дач синтеза. Рассмотрим, например, задачу достижения
ракетой максимальной дальности при заданном расходе
горючего. Рассматривая ракету как материальную точ-
ку, мы найдем программу ^-оптимальную траекторию.
Вследствие причин, о которых говорилось выше, ракета
308
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ [ГЛ. IV
не будет двигаться вдоль расчетной траектории. Какова
в этой ситуации должна быть роль системы управления?
Эта система должна, регистрируя положение аппарата,
обеспечивать цель — достижение максимальной дально-
сти. В такой задаче минимизировать дисперсию смысла
не имеет. Предположим, что, в силу случайных обстоя-
тельств, мы оказались в состоянии достичь большей даль-
ности. Эти возможности нам и следует максимально ис-
пользовать, не заботясь о том, чтобы реальная траекто-
рия мало отличалась от расчетной.
Подобные требования к синтезируемой системе
управления также довольно часто встречаются в практи-
ческих задачах, и не только в тех, которые нам достав-
ляет теория летательных аппаратов. Такие постановки
задач типичны, например, для экономических систем.
Задача, которая наиболее часто встречается в экономи-
ке, формулируется следующим образом: как распоря-
диться заданным количеством ресурса, чтобы получить
к концу периода планирования максимальный выход
продукта? При построении программного решения мы
находим оптимальное распределение ресурса, соответ-
ствующее определенному начальному состоянию эконо-
мической системы. Задача синтеза системы управления
будет состоять в таком перераспределении ресурса, ко-
торое гарантирует максимальный выход продукта, если
становится известным, что состояние экономической си-
стемы в некоторый момент времени отлично от программ-
ного. Это перераспределение ресурса должно произво-
диться с учетом информации о случайных факторах,
влияющих на поведение экономической системы.
Итак, в некоторых случаях при построении системы
управления мы можем использовать тот же самый функ-
ционал, который используется при построении программ-
ной траектории. Однако эта задача, как мы увидим
ниже, будет тем не менее существенно иной, нежели за-
дача программного движения, мы ее можем рассматри-
вать как частный случай общей задачи синтеза, в кото-
ром оба функционала (программного движения и синте-
за) совпадают.
' Подведем теперь некоторый итог нашему обсуждению.
Создание системы управления является, как правило,
многоцелевой задачей. В рассмотренном примере мы
§ и	О ПОСТАНОВКЕ ЗАДАЧ СИНТЕЗА	309
имели два функционала, в соответствии с которыми ис-
ходную задачу мы разделили на две. Сначала мы рас-
считали программу, получили предварительную оценку
траектории, после этого поставили уже другую задачу с
другим функционалом и назвали ее задачей синтеза.
У математика, который сталкивается с подобной ситуа-
цией, естественно возникает вопрос: какой математиче-
ский смысл имеет подобная процедура? Какой матема-
тической модели она отвечает? Эти вопросы не носят
риторического характера: в результате их анализа могут
быть установлены правила, регламентирующие подоб-
ное разделение и последовательное решение задач.
2. Линеаризация. Задачу о построении системы
управления решают обычно при большом числе гипотез.
Одна из наиболее распространенных — гипотеза линеа-
ризации.
Рассмотрим более подробно некоторые особенности
этой гипотезы на том же примере движения ракеты.
Выпишем еще раз систему уравнений, которая рас-
сматривается при исследовании программного движения
ракеты:
d2r	г,/ dr	\	dm	,л	,,
/и— = гг,-,в,	— = р(().	(1.1)
d/2	\ dt	)	dt	'	'	'
Здесь т — масса, г — радиус-вектор центра тяжести ра-
кеты, F — суммарный вектор сил, действующих на ра-
кету:
Р = mg + Rx + Q,
где g — ускорение силы тяжести, Rx(r,—) —сила лобо-
вого сопротивления, Q — реактивная сила (тяга реактив-
ного двигателя). Управлением в этой задаче являются
вектор и, компоненты которого — направляющие косину-
сы вектора тяги, и расход массы p(t).
Компоненты вектора управления определяются в про-
цессе расчета программного движения, и при рассмотре-
нии задач синтеза мы их считаем известными функциями
времени (с точностью до помех).
Полная система уравнений, описывающая движение
ракеты, существенно отличается от системы (1.1). Так, в
первом уравнении сила лобового сопротивления на самом
310
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ [ГЛ. [V
деле зависит от углов атаки и рыскания — аир. Кроме
dr
того, имеется еще подъемная сила Ry=Ry(r, и, а, р)
и т. д.
Наконец, все силы, которые входят в уравнения дви-
жения, определяются всегда с некоторой случайной ошиб-
кой. Следовательно, вектор F в полной системе уравне-
ний будет иметь следующий вид:
р = mg + Rx + Ru + f(f),
где f(t) —некоторая случайная вектор-функция времени.
Этот случайный процесс должен быть тем или иным спо-
собом задан.
Примечание. Обычно описание случайного процес-
са f(t) основывается на экспериментальных данных и
сведениях, не являющихся вполне достоверными. Таким
образом, при исследовании систем управления, мы не
можем игнорировать существование неопределенностей.
Заметим, что эти оба факта — случайность и неопреде-
ленность— имеют совершенно различный смысл и тре-
буют для своего изучения различного аппарата.
Величины а и р, входящие в Rx и Ry, в свою очередь
являются функциями, закон изменения которых описы-
вается сложными дифференциальными уравнениями от-
носительного движения. Поэтому полная система урав-
нений будет иметь следующий вид:
(1-2)
L fa, р, г, —, .. Л = 0,
\ dt )
где L — это некоторый дифференциальный оператор, а
6(/) —случайная флуктуация величины тяги. В послед-
нем из уравнений (1.2) поставлено многоточие. Дело в
том, что изменение углов аир определяется еще целым
рядом величин, которые, в свою очередь, изменяются во
времени, и т. д. Мы не собираемся здесь изучать эти урав-
нения более подробно, и поэтому многоточие в уравне-
ниях обозначает те дополнительные величины, которые
§ 1]	О ПОСТАНОВКЕ ЗАДАЧ СИНТЕЗА	ЗИ
должны быть учтены, чтобы считать эту систему доста-
точно полной для описания процесса движения ракеты.
Обозначим через р и ц выбранное нами решение си-
стемы (1.1) и положим
г = Р + т = ц + т].	(1.3)
Смысл гипотезы линеаризации состоит в том, что вели-
чины g, т], а, 3, ... и составляющие вектора случайных
сил считаются малыми величинами первого порядка ма-
лости 0(e). В соответствии с этим, после подстановки
(1.3), в системе уравнений (1.2) удерживаются только
члены порядка 0(e). Мы придем тогда к системе вида
й-А(Ьч,«. (>,) + №
ч = 5(<).	(14)
а = Л& Г]. «, 0, •• •) + /<» (О,
0 = п. «> 0. ) + №
Здесь Ла, А»—некоторые линейные операторы. Они
известным образом зависят от времени и применяются к
функциям, которые стоят в скобках. Д, fa, fe,— случайные
функции времени. Таким образом, система уравнений
(1.4)—это система линейных неоднородных дифферен-
циальных уравнений.
Другими словами, гипотеза линеаризации состоит в
предположении, что замена системы (1.2) системой (1.4)
приводит к допустимым ошибкам по сравнению с требо-
ваниями точности (т. е. решение системы (1.4) «близко»
к решению системы (1.2)).
Для того чтобы гипотеза линеаризации имела смысл,
недостаточно одного предположения о малости возмуща-
ющих сил Д, fa и Д. В самом деле, пусть, например, слу-
чайные возмущения вообще отсутствуют. Тогда все рав-
но остаются два обстоятельства, которые еще требуют
обсуждения.
а)	Мы проводим линеаризацию относительно про-
граммной траектории, но программное движение в об-
щем случае не является частным решением системы (1.2).
Следовательно, с математической точки зрения (как это
понимается в теории устойчивости), обосновать гипотезу
линеаоизации (в общем случае) нельзя,
312
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
(ГЛ. IV
б)	Система (1.2) имеет более высокий порядок, неже-
ли система (1.1). Поэтому, как бы мало ни отличались
начальные условия, определяющие решения обеих си-
стем, сами решения могут иметь качественные различия.
Вот почему законность описания процесса линейной
системой (1.4) следует считать гипотезой и необходимо
(хотя бы на интуитивном уровне) выяснить законность
ее применения. •
3.	Система замкнутого цикла. Рассмотрим снова си-
стему уравнений (1.4). Вводя в рассмотрение векторную
переменную г, мы можем переписать эту систему в сле-
дующем более компактном виде:
z — Az-}-F(t),	(1.5)
где Д = ||аЛ — матрица, коэффициенты которой являют-
ся заданными функциями времени и зависят от программ-
ного движения, F(t) = {F*’(^)}—случайная вектор-функ-
ция времени, математическое ожидание которой F(t) =O.
Начальные значения компонент вектора z мы не будем
фиксировать, считая их случайными величинами с нуле-
вым математическим ожиданием.
Систему (1.5) естественно назвать системой открыто-
го цикла, поскольку в ней отсутствует управление. Она
описывает процесс движения объекта управления, кото-
рое определяется только начальным состоянием и про-
граммным управлением. Предположим теперь, что в на-
шем распоряжении имеются дополнительные возможно-
сти: вектор w, который мы можем использовать для
изменения величины г.
Если речь идет о самолете или ракете, то эта допол-
нительная сила создается или рулями, или изменением
величины тяги двигателя. Точно так же в динамических
моделях экономики роль вектора w будет играть допол-
нительный ресурс или перераспределение ресурса.
Учитывая эти дополнительные управления, мы заме-
ним уравнение (1.5) следующим:
z = Az -ф w. 4- F (t).	(1.6)
Векторное уравнение (1.6) описывает некоторый управ-
ляемый процесс. Заметим, что для того, чтобы иметь пра-
$ 1]	О ПОСТАНОВКЕ ЗАДАЧ СИНТЕЗА	313
во ввести силы w в правую часть уравнения (1.5), мы
обязаны предположить, что эти управляющие силы так-
же малы, т. е. ускорения, которые они вызывают, имеют
первый порядок малости.
Итак, в системе (1.6) присутствует вектор w, которым
мы можем распорядиться. В частности, мы его можем вы-
брать так, чтобы минимизировать ту или другую харак-
теристику движения.
Систему (1.6), в отличие от (1.5), мы будем называть
системой замкнутого цикла.
Примечание. Подчеркнем еще раз, что ресурс на .
выполнение программы и на дополнительное управление
может быть общим. В этом случае возможность допол-
нительного управления программным движением сущест-
венно зависит от того, какая часть общего ресурса ис-
пользована на выполнение программы. Предположим,
что объект управления — это космический аппарат, ко-
торый должен за минимум времени совершить переход с
одной орбиты на другую. Этот маневр должен совершать-
ся с максимальной тягой. Следовательно, система управ-
ления программой, если это управление осуществляется
с помощью того же двигателя, располагает единственной
возможностью для управления — ориентацией вектора
тяги.
Описанная ситуация порождает новый и очень важ-
ный класс задач, аналогичных проблеме резервирования
в экономике: как надо распределить ресурс между систе-
мами, реализующими программу и ее коррекцию. Этот
вопрос не может быть решен в рамках гипотезы разде-
ления.
4.	Формулировка задачи синтеза оптимальной систе-
мы управления. Будем продолжать изучение системы
(1.6). Поскольку ее правая часть содержит некоторую
случайную функцию времени, то вектор z также будет
случайной функцией времени. Следовательно, любая де-
терминированная характеристика Ф(г) фазовой траекто-
рии будет также некоторой случайной величиной. По-
этому в качестве функционалов, характеризующих управ-
ление, имеет смысл рассматривать математическое ожи-
дание этих величин.
Пусть нас интересует, например, значение функции
Ф(г(Т)). Тогда в качестве оптимизируемого функциона-
314
ПРОБЛЕМЫ СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
может иметь смысл математическое ожидание этого
значения:
/М^£Ф(г(Т)) = ФЖ).	(1,7)
В дальнейшем мы будем не раз иметь дело с функциона-
лами вида
J (w) = г2 (Г),
или
J И = (2, RT)i=Tt	(1.7а)
где R — симметричная положительно определенная мат-
рица. Функционалы вида (1.7а) часто встречаются в при-
кладных задачах, поскольку они характеризуют точность
достижения цели управления. Иногда бывает достаточно
охарактеризовать точность по одной из координат. Тогда
J (w) = (zf)2. Разумеется, могут рассматриваться и другие
характеристики. Например, в экономических задачах
имеют дело с линейными функционалами вида
=	z(T)),	(1.76)
где с — некоторый заданный вектор.
Задачи с функционалами типа (1.7а) и (1.76) по ана-
логии с задачами вариационного исчисления естественно
называть задачами Майера. Имеет смысл рассматривать
также задачи Лагранжа. Этим термином мы будем на-
зывать задачи, в которых функционал, характеризующий
управление,'имеет вид*)
г_____
J (ay) = J <р (г, w) dt.	(1,7в)
О
Рассматривая задачи оптимального управления, мы
не делали различия между задачами Майера и Лагран-
жа, поскольку обе задачи легко сводились одна к другой
введением новой переменной. В данном случае мы также
можем ввести скалярную переменную £=<p(z, w) и свести
*) Интегралы подобного рода для положительных <р характери-
зуют, например, накопление ошибки.
$ 1]	О ПОСТАНОВКЕ ЗАДАЧ СИНТЕЗА	315
задачу (1.7в) к задаче минимизации %(Т). Однако среди
уравнений задачи окажется уравнение, правая часть ко-
торого является математическим ожиданием искомых
величин. Это обстоятельство вносит особенности, требу-
ющие специального изучения.
Итак, мы будем рассматривать следующую вариаци-
онную задачу: определить вектор w, доставляющий ми-
нимальное значение функционалу (1.7) приусловии (1.6),
где F(t) —заданный случайный процесс, z(t0) —началь-
ное значение вектора г — также заданная случайная ве-
личина, причем
Г(0 = 0, <) = 0.	(1.8)
Таким образом, сформулированная задача по своей
постановке кажется аналогичной задаче, рассмотренной
в предыдущих главах. Тот факт, что функционал записы-
вается в форме математического ожидания, на первый
взгляд не меняет дела. Однако и техническое, и матема-
тическое содержание этих задач существенно разное.
В задачах оптимального управления искомое управ-
ление разыскивается как функция времени и начального
состояния w=w(t, г0). Но начальное состояние zQ может
быть случайным и уже это обстоятельство требует до-
полнительных рассмотрений. Но главное в другом. Пред-
положим, например, что начальное состояние фиксиро-
вано, и будем считать, что наша задача, как и раньше,
состоит в отыскании вполне определенной вектор-фупк-
ции w(t), которая минимизирует функционал (1.7). Для
определенности примем, что J(iiy)=z2. Предположим, что
величина z(/o)=O, и мы знаем Г—оператор Грина для
уравнения z=Az + b(t), т. е. мы можем выписать в явном
виде величину z(T).
В случае уравнения (1.6) г=Гк,+ГГ. Мы условились
разыскивать детерминированную функцию времени w\t).
Поэтому, вычисляя величину функционала z2(T), мы
получим
?(Г) = (Г< + (ГЛ5 •	(1.9)
(ГТ7)2—это некоторое известное число, поскольку мы
условились рассматривать только те случайные процес-
316
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
сы, статистическое описание которых нам известно. Вели-
чина (ГТ)2, как это видно из (1.9), не зависит от управ-
ления. Поэтому отыскание минимума величины (1.9)
приводит нас к абсурдному результату: дисперсия эле-
ментов траектории будет минимальна (точность достиже-
ния цели управления максимальна), если w=Q, т. е. если
управление отсутствует.
Итак, мы видим, что стандартная постановка задачи
оптимального управления в рассматриваемом случае
смысла не имеет. Для того чтобы изменить величину дис-
персии, функция w должна изменить оператор Грина, а
для этого она должна сама зависеть от вектора z. В про-
стейшем случае w может быть функцией фазовых коор-
динат z и времени t:
w = w(z, t).	(1.10)
Этот простейший случай обычно и рассматривается в ма-
тематической литературе, и задачу отыскания функции
w(z, /), минимизирующей функционал J(w), принято
называть задачей синтеза оптимального управления.
Инженеры вкладывают в это понятие несколько более
широкий смысл. Задачей синтеза в инженерной литера-
туре называется задача отыскания не функции w(z, t),
а некоторого оператора W. Вообще говоря, управление Т
реализует обратную связь, которая содержит не только
само отклонение z, но и его производные 1, z и т. д., а мо-
жет быть и интегралы от этой функции.
Введем (k -|- 1)-мерное декартово пространство 91,
а#	л	 dz ь
вектор а е эд имеет компоненты а” = г, а1 — —, а* = —.
dt dtk
Пусть теперь И7(а) —некоторая функция от а. Тогда
задача синтеза может быть сформулирована как задача
отыскания такой функции 1Г(а), которая доставляет ми-
нимум функционалу J(w) =J(W(a)). Разумеется, на
класс функций IF(a) могут быть наложены те или иные
ограничения.
Таким образом, формально задача синтеза систе-
мы управления сводится к некоторой задаче нелиней-
ного программирования в функциональных простран-
ствах.
5 П
О ПОСТАНОВКЕ ЗАДАЧ СИНТЕЗА
317
5.	Аппроксимация оптимального оператора управле-
ния. Решение сформулированной выше задачи нелиней-
ного программирования — оператор W(а) — будем на-
зывать оптимальным оператором управления.
Проблема отыскания оператора, реализующего синтез
оптимальной системы управления, является очень труд-
ной и малоисследованной. До настоящего времени изу-
чались только отдельные частные случаи, допускающие
те или другие упрощения. Например, проблема сделается
качественно проще, если нам удастся перейти от сформу-
лированной выше задачи нелинейного программирования
в функциональном пространстве к задаче нелинейного
программирования в конечномерном пространстве или
же к задаче типа оптимального управления.
Такие упрощения возможны, если функцию IF (а)
аппроксимировать конечномерными функциями из неко-
торого класса:
z	Г(а)~Р„(а).
Предположим, например, что Рп—некоторый полином,
Р„(а) =Ata+ (Ага, а) + ... Если At— матрицы, элементы
которых а},— постоянные числа, то функционал / превра-
щается в функцию конечного числа переменных: /=
=/(а'.Д, и задача отыскания оптимального оператора
становится задачей отыскания экстремума функции ко-
нечного числа переменных. Если элементы матрицы Д—
функции времени, то мы приходим к некоторой задаче
оптимального управления.
Таким образом, аппроксимация оператора управле-
ния сводит задачу синтеза к уже рассмотренным оптими-
зационным задачам. Тем не менее аппроксимация опера-
тора управления еще недостаточна для того, чтобы в за-
дачах синтеза стало возможным использовать известные
методы нелинейного программирования и теории опти-
мального управления. Если в задачах оптимального
управления, которые мы рассматривали в предыдущей
главе, у нас никогда не вставал вопрос о вычислении функ-
ционала, то в задачах синтеза этот вопрос перерастает в
большую проблему.
Рассмотрим снова уравнение (1.6). Его мы можем пе-
реписать в виде
z = A? + F(z) + F(0,	(1.6)
318
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
где W(2)—неизвестная функция, о которой мы знаем
заранее лишь то, что она принадлежит к некоторому
классу (например, W — это полином от z и z). Таким об-
разом, в общем случае уравнение (1.6)—нелинейное,
хотя мы и рассматриваем линеаризованные уравнения
движения.
Теперь, имея в распоряжении уравнение (1.6), мы
должны сформировать функционал типа (1.7). Заметим,
что только при заданной реализации случайной функции
F(t) и заданных коэффициентах оператора W(z) мы мо-
жем провести численное интегрирование уравнения (1.6).
Таким образом, в общем случае, только используя метод
Монте-Карло, мы можем заданной совокупности пара-
метров {ajs} поставить в соответствие значение функцио-
нала. При этом количество реализаций должно быть до-
статочно большим, чтобы гарантировать необходимую
точность результата. Сказанного достаточно, чтобы пред-
ставить себе всю необозримую трудоемкость процедуры
нахождения оптимального синтеза системы управления.
Таким образом, то качественное упрощение задачи, на
которое мы пошли, заменив задачу нелинейного програм-
мирования в бесконечномерном пространстве задачей ко-
нечномерной, оставляет ее еще чересчур сложной для
численного решения.
Представим теперь, что тем или иным способом нам
удалось в явном виде (в виде приближенных формул)
выразить фазовый вектор через случайную функцию.
Тогда мы в явном виде можем выписать выражение функ-
ционала и избежать применения метода Монте-Карло.
Этот путь решения задач синтеза интенсивного разра-
батывался В. М. Пономаревым *).
6.	Пример применения схемы В. М. Пономарева. Рас-
смотрим снова уравнение (1.6) и оператор управления
будем искать в виде
Г =	(1.11)
где В — некоторая неизвестная матрица. Эту матрицу
условимся называть матрицей коэффициентов усиления.
*) В. М. Пономарев, Теория управления движением косми-
ческих аппаратов, «Наука», 1965.
5 1]	О ПОСТАНОВКЕ ЗАДАЧ СИНТЕЗА	319
Она подчинена ограничениям вида
bij	i,j=\,...,n.	(1.12)
В частности, для некоторых элементов мы можем принять
by == bi] = 0. Это значит, что компонента zi вектора z не
входит в компоненту управления wl.
Примечание. В реальных задачах далеко не все
координаты могут быть измерены и управление должно
выбираться как функция только тех координат, которые
могут быть «наблюдаемы». На языке теории операций
это означает, что решение в каждый момент времени дол-
жно приниматься по неполной информации о поведении
управляемого объекта.
Уравнение (1.6) примет теперь следующий вид:
z = Az + Bz + F(t).	(1.13)
Обозначим через Г(/, т) матрицу Грина уравнения 2=
= (A + B)z. Тогда решение уравнения (1.13) можно за-
писать в виде
t
z(t) = Г(^O)zo + j Г(/,x)F(x)dx. (1.14)
О
Предположим, что функционал имеет вид
7 = ?(Г).	(1.15)
Используя (1.14) и считая, что начальные возмущения
не зависят от возмущений F(t), мы сможем функционал
(1.15) представить в форме
J = f [ (Г (Т, х) F (т) dx? + (Г (Г, 0) z0, Г (Г, 0) z0) =
\о
= j* [ (Г (Т, F (tJ, Г (7, t2) F (T2)) dXjdxz +
+ (Г(7’,0)го, Г(Г,0)го). (1.16)
Обозначим через у«(/, т) элементы матрицы Г(#, т).
Тогда выражение для функционала можем представить
320
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
в следующем виде:
т т
J = 2 J J Y»/ (Г, Т|)yJS (Г, Tj) kjs (т1( Tg) dXyd.%2 Ц~
+ (Г(Г,О)г0,Г(Г,0)го). (1.17)
Здесь через k}t(xt, т2) обозначены элементы корреляци-
онной матрицы
kjs (И» t2) = F' (Xj) Fs (ta).
Таким образом, если корреляционная матрица слу-
чайного процесса нам известна, то, задав матрицу коэф- «
фициентов усиления В, мы можем вычислить значение j
функционала, не используя метода Монте-Карло. Для |
этого нам необходимо вычислить матрицу Грина, что I
требует решения п задач Коши (п — размерность векто- I
pa z); после этого нам остается вычислить квадратуру Ч
(1.17).	j
Таким образом, J — это некоторая функция коэффи- 1
циентов усиления она задана через решение системы |
линейных уравнений. Для отыскания минимума этой
функции мы можем использовать один из методов нели-
нейного программирования. Заметим, что J(6i}) будет
нелинейной функцией даже в тех простейших случаях,
когда исходная система, описывающая эволюцию объек- i
та управления, будет системой линейных дифференциаль- -
ных уравнений с постоянными коэффициентами.
Возможность выписать в явном виде выражение функ- )
ционала через характеристики функций случайных воз- ь.
мущений — следствие того факта, что в случае линейных
систем мы можем выписать общий интеграл через систе-
му фундаментальных решений. Этот вопрос можно рас-
смотреть и с более общей точки зрения. Представим себе,
что мы тем или иным образом построили приближенное
или точное выражение общего интеграла исходной си-
стемы дифференциальных уравнений, тогда при вычисле-
нии функционала мы всегда можем избежать трудоем-
кой процедуры, связанной с использованием метода Мон-
те-Карло.
§ I]	О ПОСТАНОВКЕ ЗАДАЧ СИНТЕЗА	321
В. М. Пономарев в ряде своих работ *) развиваем ме-
тоды построения приближенного выражения для общего
интеграла и исследуют полученные задачи нелинейного
программирования. Одна из трудностей состоит в том,
что функционалы в этих задачах не являются выпуклы-
ми и содержат много локальных экстремумов. С другой
стороны, в задачах синтеза обычно не возникает высоких
требований к точности. Это обстоятельство имеет реша-
ющее значение при разработке приближенных вычисли-
тельных методов.
7.	Замечание о методе Монте-Карло. Для применения
метода Монте-Карло мы должны многократно выполнить
процедуру численного интегрирования уравнения (1.6).
Рассмотрим простейшую разностную схему
?„+1 = гп + х (Azn + W (zn) + F (/„)).	(1.18)
Выражение (1.18) показывает, что для того, чтобы
провести вычисление одной реализации случайного про-
цесса z(t), нам необходимо задать такое число случай-
ных векторов F(tn), каково число N частичных интерва-
лов N=T/x. При уменьшении т число N растет, увеличи-
вается число случайных векторов и, следовательно, необ-
ходимое число реализаций.
Обозначим через М количество необходимых реали-
заций для каждого из векторов F(tn). Тогда общее коли-
чество реализаций будет пропорционально Таким
образом, при достаточно малом т метод статистических
испытаний становится практически неприменим.
Эту трудность мы можем обойти, если использовать
каноническое представление случайного процесса F(t):
F,(0 = 3^(0,	(1.19)
& j
где |i£— случайные числа, фЛ(0—некоторая система
фундаментальных функций. Предположим далее, что в
*) См. В. М. Пономарев, Методы последовательной опти-
мизации в задачах управления, Техническая кибернетика, № 2,
1967.
В. М. Пономарев, А. И. Птушкин, Последовательная
оптимизация дискретной системы управления, Техническая киберне-
тика, № 3, 1967.
11 Н. Н. Моисеев
322
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ [ГЛ. IV
(1.19) можно ограничиться некоторым конечным числом
слагаемых
i
^(0=2	(1-20)
£=1
где l^N. Аппроксимации типа (1.20) уже вносят каче-
ственные упрощения в процесс статистического модели-
рования и не приводят к трагичным последствиям при
уменьшении шага численного интегрирования.
8.	Некоторые обобщения. Рассматриваемая постанов-
ка задачи синтеза, несмотря на всю ее сложность, явля-
ется тем не менее еще очень простой моделью задач, воз-
никающих в технике и экономике. Заметим несколько об-
стоятельств, которые не были учтены при обсуждении
постановки задачи синтеза:
а)	Мы собираемся разыскивать управление, как функ-
цию координат управляемой системы, которые могут
быть измерены (наблюдаемые координаты). В действи-
тельности же все измерения происходят с ошибкой, и
мы должны разыскивать управление как функцию изме-
ренных значений наблюдаемых координат.
Далее, наблюдаем мы обычно не сами координаты z‘,
а некоторые функции этих величин £*. В простейшем слу-
чае эти величины являются линейными функциями ком-
понент вектора z, g=Lz+ft, где h. — случайная ошибка
измерений, причем матрица L обычно бывает не квадрат-
ной, а прямоугольной: размерность вектора £ меньше
размерности вектора z, и поэтому выразить непосред-
ственно z через £ и h мы не можем. Таким образом, наря-
ду с описанием модели динамической системы, которой
мы управляем, мы должны научиться описывать процесс
поступления и обработки информации.
б)	Внешние возмущающие силы мы рассматриваем
как некоторый случайный процесс с известными стати-
стическими характеристиками. Однако во многих прак-
тических задачах эти свойства нам бывают неизвестны.
В лучшем случае мы можем говорить только о границах,
в которых эти силы могут изменяться. В этом случае
постановка задачи синтеза должна быть иной. Функцио-
налы, которые рассматривались в данном параграфе,
теряют смысл. У нас остается единственная возмож-
5 2]	ДЕТЕРМИНИРОВАННЫЕ ЗАДАЧИ СИНТЕЗА	323
ность: исследовать гарантированные оценки, т. е. мы дол-
жны разыскивать m!in max/ вместо min/.
в) Задача синтеза, которая была сформулирована,
предполагала известной программу (матрица А в урав-
нении (1.6) считалась заданной). Инженерам значитель-
но более интересна другая постановка. Объект управле-
ния, например самолет, может выполнять самые разные
программы. Он может совершать полеты на разных вы-
сотах, на разные дальности и т. д. Но система управле-
ния— автопилот конструируется один раз. Параметры
этой системы должны быть выбраны один раз. Каким
образом в этих условиях следует выбирать эти парамет-
ры? Поставленный вопрос относится уже непосредствен-
но к теории операций, поскольку здесь налицо некоторая
конфликтная ситуация. Очень часто для решения этой
проблемы инженеры используют метод тестов. Некото-
рая программа, выбранная из интуитивных соображений,
объявляется расчетной, и если система управления явля-
ется приемлемой для программы, то она объявляется
приемлемой и для всей совокупности программ, которые
могут быть заданы. Какой смысл имеет метод тестов?
В каких условиях он применим? Эти вопросы оказывают-
ся очень важными, тем более, что легко привести приме-
ры, когда в принципе тестовой программы не существует.
Приведенные здесь обобщения задачи синтеза еще не
исчерпывают всей совокупности возможных постановок
этой технической проблемы. О некоторых из них мы бу-
дем говорить ниже.
§ 2. Детерминированные задачи синтеза
1.	Постановка задачи. Рассмотрим сначала тот класс
задач синтеза, в котором случайные возмущения и ошиб-
ки измерений не учитываются. Тогда функционал J(x, и),
характеризующий качество управления, будет детерми-
нированной величиной, и задачу синтеза мы можем сфор-
мулировать следующим образом: определить функцию
u(x(t0), ta, f), доставляющую функционалу /(х, и) мини-
мальное значение при ограничениях
х = /(х, и, 0,	(2.1)
и (= Gu,	(2.2)
11*
324	ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ [ГЛ. IV
х е GXt	(2.3)
х(Т)е^г.	(2.4)
Так поставленная задача формально совпадает с за-
дачей оптимального управления. Различие заключается в
том, что в задаче синтеза величины х(£0) и ta являются
произвольными. Другими словами, задача синтеза будет
решена, если мы сумеем построить управление — функ-
цию и(х(/0), /о, t), которая переведет за время Т —си-
стему из состояния (х, io) на множество &т (т. е. для
каждой точки (х, /0) мы решим задачу оптимального
управления). Эта функция u(x(f0), ta, t) может быть най-
дена из уравнения Веллмана*). Поскольку в нашем рас-
поряжении нет общих стандартных методов решения
уравнения Веллмана и задач оптимального управления,
то какие-либо общие методы решения задач синтеза так-
же отсутствуют.
2.	О возможных управлениях. Трудности численного
решения задач оптимального управления и необходи-
мость быстро определять величину управляющего воздей-
ствия по сигналу о состоянии управляемой системы при-
водят к отказу от построения строгих оптимальных реше-
ний. Приобретает большое значение задача отыскания
допустимых управлений (т. е. управлений, удовлетворяю-
щих условию (2.2)), которые выводят систему в окрест-
ность заданного состояния. Такие управления мы будем
называть возможными управлениями. Мы уже сталки-
вались с этим понятием в гл. III при рассмотрении раз-
личных конструкций элементарной операции.
Предположим, что программная траектория системы
задана. В силу каких-то причин (внешних возмущений)
состояние системы оказалось отличным от расчетного.
Тогда мы можем представить себе две возможные линии
поведения:
1.	Мы можем постараться немедленно вернуться на
расчетную траекторию.
2.	Мы можем построить новое программное управле-
ние, которое за некоторое время (последнее может быть
*) Об уравнении Веллмана см., например, В. Г. Болтянский,
Математические методы оптимального управления, «Наука», 1969.
5 2]	ДЕТЕРМИНИРОВАННЫЕ ЗАДАЧИ СИНТЕЗА	325
и нефиксированным) приведет нашу систему в окрест-
ность цели управления.
Первый способ поведения мы будем называть коррек-
цией по заданной программе. Второй — коррекцией по
конечному состоянию. Существует много различных спо-
собов конструирования возможных управлений. Выбор
того или другого возможного управления определяется
физическими особенностями управляемой системы и тех-
нической реализуемостью предлагаемой схемы управле-
ния. Поэтому мы ограничимся только демонстрацией не-
скольких примеров.
Если нам удалось построить возможное управление
v(x, t), которое каждой точке (х, t„) ставит в соответ-
ствие вектор-функцию v(x, t), то мы говорим, что «синтез
реализован».
Для того чтобы не путать синтез, построенный с по-
мощью возможных управлений, с решением вариацион-
ной задачи, сформулированной в предыдущем пункте,
будем его называть возможным или виртуальным син-
тезом.
3.	Локально оптимальные управления. Этим терми-
ном мы будем называть управления, которые выбирают-
ся в каждый данный момент времени из условия мини-
мума некоторой скалярной величины. Приведем несколь-
ко примеров таких управлений.
Пусть нам известно программное движение x(t), оп-
ределенное управлением u(t). Введем в рассмотрение
векторы z=x—£(/), v = u—u(t). Первый из этих векто-
ров будем называть вектором траекторного отклонения,
второй — вектором корректирующего управления.
Рассмотрим функцию
F(z) = 4-(z, Яг),	(2.5)
где R— некоторая симметричная положительно опреде-
ленная матрица. Примером локально оптимального уп-
равления будет управление v, которое минимизирует
. dF
величину производной —:
min — = min (—, Rz\.	(2.6)
ceGS1 dt	dt )
326
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
1ГЛ. IV
Функция (2.5) определяет в некотором смысле «рас-
стояние», которое отделяет реальное положение объекта
от его программного значения. Таким образом, управле-
ние v стремится в каждый данный момент «максималь-
но уменьшить» это расстояние. В формуле (2.6) через
Go мы обозначили множество допустимых корректирую-
щих управлений.
Так как
Z — f (х + Z, и 4- v, t) — f (х, и, t),
(2.7)
а выражение (2.6) линейно относительно z, то задача вы-
бора управления сводится к отысканию v^G„, доставля-
ющего минимум функции
*7 (и) = (f (к + z,u + v, t) — f (х, и, t), Rz). (2.8)
Предположим, что G„—открытое множество, тогда
для отыскания управления v нам необходимо решить
уравнение
Управление v, доставляющее минимум выражению (2.8) „
или являющееся корнем уравнения (2.9), будет, очевид-
но, функцией состояния z и времени t, v=v(z, t), и, сле-
довательно, будет реализовать возможный синтез.
Рассматриваемая задача во многих случаях может
быть значительно упрощена. Если ресурс, который мо-
жет быть выделен на корректирующие управления, мал
и отклонения реального движения от программного так-
же малы, то уравнение возмущенного движения (2.7)
можно линеаризовать, и мы будем иметь z=Az+Bv, где
А и В — некоторые матрицы. В этом случае задача по-
строения корректирующего управления сводится к зада-
че отыскания минимума линейной формы
min (Bv, Rz).
t>ec0
Если условия v е Go имеют вид	у1, где сц, у{ —
i
заданные числа, то это обычная задача линейного програм-
мирования.
5 2]	детерминированные задачи синтеза	327
u Рассматриваемый способ управления имеет простой
механический смысл. Пусть нам дана система с одним
управлением:
х1 — х2, х2 — f (х1, х2, и, t),
а функция F взята в виде F— (z‘)2+a(z2)2.
В этой задаче мера отклонения от программной траек-
тории определяется отклонением не только положения,
но и скорости от расчетного значения.
Вычислим
— = 2z& -J- 2az2z2 =•
dt
= 2zlz2 4- 2az2 (f (x14- z1, x2 4- z2, a 4- v, t) — f (x\x2, u, t)).
Первое слагаемое не зависит от управления. Следова-
тельно, условие min требует минимизации второго
слагаемого. Если, начиная с некоторого момента, окажет-
ся, что z2 равно нулю, т. е. скорость объекта управления
равна расчетной, то с этого момента мы лишаемся воз-
можности изменить ситуацию. Очевидно, что такие управ-
ления могут не удовлетворять основному требованию
достижения цели управления: z'sz2=0. Поэтому в тех-
нике должны использоваться более сложные законы
управления. Например, в качестве функции F мы можем
взять следующую;
F(z) = 4-(z, R^ + K-^z.R*),
Л	at
где и R2—положительно определенные квадратичные
формы, а X—некоторый параметр.
Примечание. В автоматическом регулировании
рассматриваются законы управления, имеющие вид
o = Lz,	(2.10)
где L — некоторый дифференциальный оператор. Например,
L=a*^—4~ • • • 4-ai~+ао- Эти законы управления, реали-
зующие виртуальный синтез, также являются локально
оптимальными. Это означает, что для любого оператора L всег-
да мот<но подобрать такую скалярную функцию, зависящую
328
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
от г и ее производных, условие минимума которой реали-
зует выражение (2.10).
Рассмотрим в качестве примера задачу управления
системой
х1 = х2, х2 = V,
и построим управление, приняв в качестве функции F сле-
дующую функцию: F = — (z1)2 = 2z1z2. Тогда
dt
~ = % (ZT + 2z4».
Управление мы найдем из условия minzki.
Если ограничения имеют вид |и|\z11; то
v = — Xz1,
и мы получаем простейший астатический регулятор.
Если ограничения имеют вид | о| с>0, то мы по-
лучаем релейное управление
v = — csignz1.
Если в контуре управления имеется вычислительная
машина, то мы можем делать прогноз на конечное время
вперед, т. е. выбирать управление из условия
min (F (t + М)).
oeGo
Описанные типы возможных управлений могут ис-
пользоваться для коррекции как по заданной программе,
так и по конечному состоянию. Существует целый ряд
специфических методов, пригодных только для одного из
типов коррекции. Например, один из типов коррекции по
заданной программе можно трактовать как следующую
задачу на быстродействие: определить управление v (z, t),
которое за минимум времени возвращает систему на про-
граммную траекторию. Поскольку время возвращения
невелико, то при замене исходной задачи конечно-разно-
стной мы можем взять небольшое число шагов по вре-
мени и получить относительно простую задачу нелиней-
ного программирования.	•
§ 2]	ДЕТЕРМИНИРОВАННЫЕ ЗАДАЧИ СИНТЕЗА	329
4. Коррекция по конечному состоянию. При этом спо-
собе коррекции очень часто возникают задачи со свобод-
ным концом. Простейший случай — это тот, когда сама
исходная задача является задачей со свободным концом.
Приведем один типичный пример. Предположим, что про-
граммное управление для системы (2.1) выбирается из
условия минимума функционала
/»(с,х(Т)).	(2-11)
где с — заданный вектор. Такая ситуация типична, на-
пример, для экономических задач. Полагая z=x—х, v =
= и—и, где х и и — программные траектория и управле-
ние, и линеаризуя (2.1), придем к следующей задаче:
г = Az + Bv,	= (с, z (Т)), z (Q = z0.	(2.12)
В данном случае легко может быть получено точное
решение. Для того чтобы найти управление, нам доста-
точно решить (см. гл. I, § 4) задачу Коши
ф = — Д*ф, ф(Т) =—с
и найти тах(ф, Ву).
Заметим, что полученное этим способом возможное
управление не будет локально-оптимальным по критерию
J(/) = (c, z(T)). Заметим также, что оно не будет зави-
сеть от началыного состояния.
В более сложных случаях можно использовать при-
ближенные методы синтеза. Рассмотрим один пример по-
добной коррекции по конечному состоянию, который сво-
дится к задаче со свободным концом. Задачу корректи-
рующего управления мы можем сформулировать как
задачу достижения минимума функций F(z(T)), где Т —
время достижения цели управления вдоль программной
траектории, F(z(T))—функция, характеризующая от-
клонение z(T) от начала координат. В этом случае мы
можем использовать локально оптимальные управления
с функцией F(z).
Приведем в заключение еще один пример локально
оптимального управления по конечному состоянию. Пред-
положим, что программа реализует решение задачи на
быстродействие для системы (2.1) при начальном состоя-
330	ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ [ГЛ. IV
нии х0 и конечном состоянии хт. Тогда в качестве функ-
ции F мы снова выбираем некоторое расстояние до цели
управления и строим возможные управления с таким
расчетом, чтобы в каждый данный момент максимально
быстро его уменьшать.
5. Об асимптотическом характере локально оптималь-
ных управлений. Итак, мы видим, что локально опти-
мальные управления играют большую роль в задачах
приближенного синтеза, поэтому естественно поставить
вопрос о том, при каких условиях локально оптимальные
управления близки к оптимальным. На этот вопрос уда-
ется ответить для одного специального класса задач.
Рассмотрим задачу Майера — отыскания минимума
функции F(z(T)).
Предположим, что возмущенное (реальное) движе-
ние системы описывается уравнением
z = / (z, во),	(2.13)
где v — корректирующее управление*), а в — малый па-
раметр. Это означает, что мы рассматриваем тот случай,
когда корректирующее управление не может существен-
но изменить траекторию.
Считая, что функция f дифференцируема, перепишем
(2.13) в следующем виде:
z = f (z, 0) + sBv 4- О (&),	(2.14)
где В =	, и отбросим малые второго порядка.
\ ду 1у^
Рассмотрим далее уравнение
* = f(z. 0),
и пусть его полный интеграл имеет вид
z = ¥(/,<?),	(2.15)
где с — произвольная постоянная.
Уравнение (2.15) мы можем рассматривать в каче-
стве формулы замены переменных. Переходя от перемен-
ных z к с, можно заменить управление (2.14) с точностью
*) Здесь, в отличие от п. I, v не предполагается малым,
« 21
ДЕТЕРМИНИРОВАННЫЕ ЗАДАЧИ СИНТЕЗА
331
до величин О(еа) следующим:
•	/ЛИГ \
c = s№-\ Ви.	(2.16)
Выпишем теперь функционал
F (z (Т)) = F (Т (Т, с (Г))) = F* (с (Г)).	(2.17)
Итак, в случае, когда корректирующие управления
малы, задача (если отбросить величины порядка О(еа))
сводится к определению минимума (2.17) при условии
(2.16). Решение этой задачи можно искать в виде
с = с0 + eq О (е2),
где Со—это некоторый постоянный вектор, а с4 удовлет-
воряет уравнению
(2.18)
'	'С=С,
Функционал (2.17) имеет вид
F' (с (7’)) = F* (с0) + (8	, q (Т)] + О (е2).
Отбрасывая малые второго порядка, мы приходим к
задаче минимизации функционала
- «ц-ч
Для этой задачи, учитывая, что сопряженные переменные
ть =— в(—)	» получим функцию Гамильтона
\ /с=Со
Из принципа максимума следует, что управление
должно быть выбрано из условия минимума скалярного
произведения
(Н № в1Л.	(2.19)
\ \ de / с=с0	) с==Со j
332
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ [РЛ. IV
Построим теперь локально оптимальное управление для
системы (2.16). Управление мы будем выбирать из усло-
вия минимума производной
(2-20>
Если отбросить в (2.20) множитель е, то коэффициен-
ты при v в (2.19) и (2.20) будут отличаться на величину
порядка О (в2). Поэтому мы приходим к следующему
утверждению; локально оптимальное управление тем
ближе к оптимальному, чем меньше е, т. е. чем слабее
корректирующее управление.
Этот факт был впервые установлен В. Н. Лебедевым *).
Его строгое доказательство дано Ф. Л. Черноусько**).
Примечание. Количество предлагаемых схем воз-
можного синтеза весьма велико и их систематический
обзор потребовал бы специальной монографии. Из новых
идей автору кажется интересной и многообещающей
схема А. П. Гришина***). Предположим, что задача
управления — перевести систему в заданное состояние хт.
Изменяя управление v(x), мы изменяем тем самым свой-
ства динамической системы, т. е. топологию ее фазового
пространства. А. П. Гришин показывает, что разыскивая
v(x) в форме дробно-линейной функции, при известных
условиях можно так подобрать ее коэффициенты, что все
интегральные кривые из некоторой области необходимо
пройдут через точку хт (в общем случае через терми-
нальное многообразие). Это значит, что точка хт оказы-
вается особой. Показывается, что система переходит в
нее за конечное время.
6. Замечание о задачах устойчивости. Существование
различных синтезирующих управлений v(x, t), с помощью
которых достигается цель управления, требует создания
методов их сравнения и оценки. Таких универсальных
*) В. Н. Лебедев, Расчет движения космического аппарата
е малой тягой, серия «Математические методы в динамике космиче-
ских аппаратов, № 5, ВЦ АН СССР, 1968.
**) Ф. Л. Черноусько, Некоторые задачи оптимального
управления с малым параметром, ПММ 32, Xs 1, 1968.
***) А. П. Г р и ш и н, О синтезе законов терминального управ-
ления, Техническая кибернетика, Xs 6, 1973.
§ 2)	ДЕТЕРМИНИРОВАННЫЕ ЗАДАЧИ СИНТЕЗА	333
методов сравнения нет. Предположим, что мы имеем
некоторое множество технически реализуемых управле-
ний. Какой критерий должен быть положен в основу
выбора? Разумеется, всегда в нашем распоряжении есть
исходный критерий, но поскольку возможные управле-
ния не являются оптимальными, то для одной области
значений (х, /0) одно из управлений может оказаться
лучшим, для другой же области значений (х, /0) лучшим
может оказаться другое управление и т. д.
Для многих процессов возможным критерием оценки
законов управления является устойчивость в смысле
Ляпунова.
Поскольку функция v(z, t) реализует обратную связь
(причем v (0, t) = 0), управление описывающее движение
нашей управляемой системы, мы можем записать в виде
х — ф (х, и, v (х — х, t), t).	(2.21)
Теперь естественно поставить вопрос об устойчивости
того частного решения системы (2.21), которое описыва-
ется уравнением
х =<р(х, и, 0, t), х(0)= х0.	(2.22)
Устойчивость частного решения (2.22) определяется не
только структурой функции o(z), но и особенностями
программного движения, т. е. функций x(t) и u(t). Бла-
годаря этому возникает целый ряд новых задач. Приве-
дем два примера, относящиеся к теории управления дви-
жением.
а)	Корректирующее и программное управление реа-
лизуются различными двигателями и имеют самостоя-
тельный ресурс. В этом случае уравнение возмущенного
движения можно записать так:
х = f (х, и, v, f) = f* (х, vt t),	(2.23)
где й — выбранное программное управление. Структура
уравнения (2.23) определяется выбором й.
Простейшая из проблем, которая возникает в этом
случае,— прямое исследование устойчивости решения
следующей задачи Коши:
х = f * (х, 0, 0, х (0) = х0.	(2.24)
334
ПРОБЛЕМА СИЙТЁЗА ОПТИМАЛЬНЫХ СИСТЕМ (ГЛ. IV
Но можно поставить и более сложную задачу: как в до-
пустимых пределах изменить программное управление,
чтобы решение (2.24) осталось устойчивым?
б)	Корректирующее и программное управление име-
ет общий ресурс. В этом случае выбор программного
управления особенно сильно влияет на устойчивость си-
стемы, поскольку коррекция траектории возможна толь-
ко за счет перераспределения ресурса. Можно привести
примеры, когда оптимальная программная траектория
оказывается практически некорректируемой и, следова-
тельно (в общем случае), неустойчивой.
В большинстве динамических задач экономики имеет
место описанная ситуация — ресурс программного и кор-
ректирующего управления общий. Поэтому исследование
устойчивости в динамических моделях экономики осо-
бенно важно.
Интересная задача, которая здесь возникает, состоит
в следующем: при заданной структуре корректирующего
управления так разделить ресурс между программным
и корректирующим управлениями, чтобы программное
движение было устойчивым. Эта задача аналогична из-
вестной задаче о резервировании.
§ 3. Применение динамического
программирования для задач синтеза
1.	Дискретный аналог задачи синтеза. Рассмотрим
динамическую систему, движение которой описывается
векторным уравнением вида (1.6);
z = Аг 4- w 4- F (t).	(3.1)
Заменим это уравнение разностным:
z*+i = Ф*г* 4- vk 4- fkt & = 0, 1, ... , Af — 1, (3.2)
где N — число интервалов разбиения данного отрезка
[О, Г]. Если мы используем простейшую разностную схе-
му первого порядка точности, то
Ф* = I -4- A т, vk = w (tk) г, fk = F (tk) т,
где x—T/N — шаг по времени, а / — единичная матрица.
Замена дифференциального уравнения разностным в
§ 3] ПРИМЕНЕНИЕ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 335
случае линейных систем может быть реализована и без
применения конечноразностной аппроксимации. Если
нам известна фундаментальная система решений уравне-
ния z=Az, то систему (3.1) всегда можно представить в
форме (3.2), где vk и fh—некоторые функции дискретных
моментов времени, значения которых однозначно опре-
делены заданием величин, входящих в уравнение (3.1),
Это можно сделать, проинтегрировав систему (3.1) на
отрезке [4, 4+1].
Рассмотрим сначала задачу минимизации квадратич-
ного функционала
J = (г(Т), Rz(T)) = \zN,RzN),	(3.3)
где R — симметричная, положительно определенная мат-
рица.
Итак, заменяя дифференциальное уравнение разност-
ным, мы приходим к задаче отыскания векторов о0, »i,...
..., Vjr-i, доставляющих минимум квадратичной форме
(3.3).
В экономических задачах поведение системы, как пра-
вило, описывается конечноразностным уравнением, в ко-
тором шаг по времени задан естественным образом. На-
пример, это цикл производственного процесса (год в
сельскохозяйственном производстве). Поэтому задача
оптимизации (3.2)—(3.3) имеет также и самостоятель-
ный интерес.
Для решения задачи минимизации (3.3) дискретного
многошагового процесса (3.2) естественно в первую оче-
редь выяснить возможности метода динамического про-
граммирования.
2.	Схема динамического программирования. Введем
обозначение
Zv = (zjvi Rzn)	(3.4)
и предположим, что система находится в состоянии zN_t.
С помощью уравнения (3.2) преобразуем квадратичную
форму (3.4)
(Z/V-l, RnZn-i) 4* (UW-1> Dn-iZn~i) + ROtf-i) 4*
4" ^v->zat-x) 4* (fw-it RM 4" 2 (fRvw-i), (3.5)
336
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
где
Rn = ®n-iR®n-i, Dff-.r =	(3.6)
Напомним, что В* означает матрицу, сопряженную В.
Полином второй степени JN является случайной величи-
ной, даже если состояние zN-t мы фиксируем, поскольку
правая часть равенства (3.5) содержит случайный век-
тор fN-t. Обозначим через JN-l(zN-l) условное математи-
ческое ожидание величины при условии, что состоя-
ние zN-i фиксировано:
Jn-1 (Ztf-x) = {Jn/ZN-1) = (2JV-1, RnzN-1) + (OjV-1, DN-iZn~i) 4-
+ (Pn-1,RVN-1) + (fjv.j» RfN-1)-	(3.7)
При выводе равенства (3.7) из (3.5) мы полагали,
что fn-i = 0. Это условие мы будем принимать для всех
векторов A (i=0, 1,..., N—1).
Функция Jn-t—это полином второй степени, завися-
щий от компонент ’вектора Найдем минимум этой
величины. Для этого вычислим
dJ кт -а
—— =^-i2at-i4-27?o^-i-
dvN-i
Приравнивая эту производную нулю, находим управ-
ление
Vn-i —----(3.8)
Итак, на последнем шаге управление является линей-
ной функцией фазовой переменной: Vh-^Bn^Zk-i, где
матрица BN-t определяется формулой
В//-1 = —~~	== — ®n-i-
При подстановке найденного управления в (3.7)
сумма первых трех слагаемых дает нуль, и мы получаем
значение функционала
Jn-i =[(/jv-i,1\RfN-i),
§ 3] ПРИМЕНЕНИЕ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 337
которое, как оказалось, не зависит от значения фазовой
координаты zN-t.
Процесс расчета управления закончен. Мы можем
управлять произвольным образом до момента
В этот момент мы должны измерить фазовые перемен-
ные и принять
Vn-i = —
Тогда
Zn ~ ^N-V
и мы получаем результат, о котором говорилось выше.
Физическое содержание полученного результата оче-
видно, мы рассматриваем систему, в которой нет ника-
ких ограничений на управление. Поэтому если мы хотим
минимизировать отклонение в момент t=tN, то нам до-
статочно в момент компенсировать все накопив-
шиеся отклонения. Так как а>А=Ол/т, то wft-»-oo при т-»-0.
Итак, если управление не стеснено ограничениями, то
оптимальное управление не ограничено.
Если мы рассмотрим реальный случай ограниченных
управлений, то задача определения минимума функции
(3.7) окажется некоторой задачей нелинейного програм-
мирования, в результате решения которой мы снова смо-
жем определить управление как функцию фазовых коор-
динат	Эта функция является сущест-
венно нелинейной и может быть построена только в
форме некоторой таблицы. На следующем шаге метода
динамического программирования, когда мы будем счи-
тать заданным состояние системы в момент времени t=
= tN-2, значение функционала окажется непредстави-
мым в аналитической форме, и мы получим сложную за-
дачу нелинейного программирования. Вычислительные
трудности и объем необходимой памяти с увеличением
числа шагов будут нарастать с такой скоростью, что про-
ведение вычислений окажется невозможным даже в тех
случаях, когда число шагов N весьма невелико.
Поскольку прямое использование динамического про-
граммирования в задачах синтеза с ограниченным управ-
лением неэффективно, можно попытаться использовать
функции штрафа. Для этого вместо функционала (3.3)
338
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
рассмотрим следующий:
________ N-1
J = (zN, RzN) + 2 (oit Rvi),	(3.9)
i—o
где К— некоторая положительно определенная симмет-
ричная матрица. В качестве матрицы К. обычно исполь-
зуют диагональную матрицу
О ‘kn
Выбирая элементы kit kn достаточно большими, мож-
но добиться, чтобы управления v{ удовлетворяли требу-
емым ограничениям.
Функционалы вида (3.9) представляют интерес и са-
ми по себе (вне связи с ограничениями на управление),
поэтому мы рассмотрим более подробно процедуру дина-
мического программирования применительно к таким
функционалам, сохраняя, по возможности, обозначения,
которые были введены ранее. Имеем
at-s
Jn = (гы, Rzn) + (Олт-i, Kv/f-i) + 2 (°л
1=0
N-1
Сумму 2 (v<> мы разбили на два слагаемых, что-
ь-о
бы подчеркнуть, что на данном шаге нам известны не
только значение zN_t, но и управления (i=0, 1, ...
..., N—2). Используя уравнение (3.2), получим
Jn = (zn-i, RmZn-i) + (vn-i, Вы-^ы-д +
+ (VN-i, (R + K)Otf-i) + (fjv.i»	+
Ы-г
+ (fN-t Vn-J +2 (fN-v ^*-1)4- s ^). (3.10)
f=0
где ft# и Ря-i определяются формулами (3.6).
§ з) ПРИМЕНЕНИЕ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 535
Далее мы вычислим Удг-х— условное математическое
ожидание величины считая, что Zjv-i фиксировано, и
найдем минимум JN~i из условия——1 = 0. В результате
^N-l
мы получим следующий аналог формулы (3.8):
^ЛГ-Х = ^N-l^N-u	(3.11)
где
BN-^------+	(3.12)
Управление снова оказывается линейной функцией
фазовой переменной. Подставляя выражение (3.11) в
(3.10), мы можем привести его к следующему виду:
Zv = (ZjV-х» Rn-iZn-i) 4- (Zjf-i, Мл-х/^) +
N-i
+ (Лм«^_1)+3 (vitKvi), (3.13)
^=0
где
Rn-i Rn + Dn-iBn-i 4- Bn-i (R 4- K) Bn-i , (3.14)
Л4лг-1 = Dfo-i 4- 2Bn-iR.
И, наконец, для оптимального значения функционала
Jit-t при условии, что при ^==/к-1 система находится в
состоянии Zit-t, мы получаем следующее выражение:
______________________________________ ы-г
Jn-i(zN-^ = (zjv-i, RN-tZN-i) 4- RfN_t) 4- 2	№<)•
1<=о
(3.15)
На этом первый шаг процедуры динамического про-
граммирования закончен. Мы нашли, что управление яв-
ляется линейной функцией фазовых координат, а значе-
ние функционала зависит не только от величины слу-
чайных воздействий /к-ь но и от состояния системы
zN-i, а, следовательно, и управлений на предшествую-
щих шагах.
Рассмотрим еще один шаг процедуры динамического
программирования. Для этого в выражение (3.13) под-
ставим zw_1=0w-2zN_24-^N-24-fw-2- После пребразований
340
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[1“Л. IV
мы приведем его к следующему виду:
Jn = (?N-2, Rn-iZN-i) -V(Vn-2,Dn-2ZN-2) +
4* Одг-2»	+ (l>AT-2, (Rn~1 4~ R) Vn-2) 4-
+ (UV-2, (Rn-1 4- Rn-1) fN_2) 4- (fN-2' Rn-JN_2) 4-
+ (/jV-P Mn-1^N-^N-2) 4- (y.V-2> ^N-lfN-^) 4-
N-3
4- (fN.2,	4- (fN_lt Rf^) 4- 2	(3-16)
1=0
где введены новые обозначения:
Rn-i — Флг-2^аг-1Фаг-2» Dn-з ~ (Rn-i 4" Rn-i)
Далее, следуя общей схеме, мы должны вычислить
/х-г(^-2)—математическое ожидание величины Jw,
при условии, что состояние zN-2 известно. JN-z будет
квадратичной функцией управления vN-2, оптимальное
0J N—2
управление найдем из условия = 0-
= Bn-IZn-u	(3.17)
где
Bn-2 =* (Rn-i "Ь Rn-i 4” 2TQ 1 Dn-2>	(3.18)
т. е. оптимальное управление на этом участке также яв-
ляется линейной функцией фазовой переменной. Исполь-
зуя (3.17), преобразуем (3.16):
Jn — (zn-ъ, ^-2^-2)+ (zn-29 Mn^n-J +
4" (zn-%9 Mn-zFjy^j) -И (/jv-2» Rw-ifn-z) “i'
N-3
+ (fri-v	+ 3 (Vb
где
Rn-i — Rn-i 4- Dn-JSn-з + Bf/-2 (Rn-i 4- R) Bn-h
R^n-2 — Dn-2 4- Bn-2 (Rn-i 4* Rn-i),
A4w-2 — Bn-2 ^n-i 4* ^n-i^n-!,
Rn = R-
§ 31 ПРИМЁЙЕНИЁ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 341
Оптимальное значение функционала, которого можно
достичь, если система в момент времени t=tN^ находи-
лась в состоянии 2я-2, а предшествующие управления vQ,
.., vN-3 известны, дается формулой
— ------------------------------------
Jn-Z — (Jn/Zn-o) = (Zn-z,Rn-^N-o) + (/Л_2, Ялм/дг-а) +
________________________________ лг-з
+	M-if^) + 3 (% W- (3.19)
1=0
Эту процедуру легко продолжить по индукции, и мы
найдем, что vN-s =BN-szN-s, s— 1,..., N, где
BN-s = — (Rn-s+i 2?Af_s+i + 2/Q-1 Dn-s,
Rn~s — Rn-s+i + D*N-sBN-s + B*N.s (Rn-s+i + K) Bns, (3.20)
Rn-s+i = ®N-sRn-s+i&N-s, Dn-s = (^ЛГ-s+l + Rn-s+1) ®N-s-
Оптимальное значение функционала при условии, что си-
стема в момент t=tKs находится в состоянии zw_s, опре-
деляется следующей формулой *):
JN-s ~~ (&N-s, Rn—sZn-s) “1“	(/N-P ^N-i+lfN—i)
l-l
s s-i  AT-s-1
+ 2 3	3	(^№z),	(3.2i)
i>j /=1	1=0
где матрицы определяются следующими рекуррентны-
ми соотношениями
Л^-s = Dn-s + Bn-s (Rn-s+i -f- Rn-s^1),
Mn-s — Bn-s^N-s+1 4-
^N~s = Bn-sMns+o 4“ ^TV-s Ww-s+a»
Полученные результаты мы можем сформулировать в
виде следующей теоремы:
2V-S-1
♦) В этой формуле член (vi* Kvt) ПРИ s = следует считать
4=0
равным нулю.
342
ПРОБЛЕМА СЙЙТЁЗА ОПТЙМАЛьЙЫХ СЙСТЁМ [ЁЛ. iV
Теорема. Оптимальный синтез управления систе-
мой (3.2) с квадратичным функционалом (3.9) при от-
сутствии ограничений на управление реализует линей-
ная функция фазовых координат
Vi = BiZh i = 0, 1, ... , АГ — 1,	(3.22)
где матрицы Bt определяются по формулам (3.20), а оп-
тимальное значение функционала равно
N ______________
Л) = (20» ^О2») +" 2 (/дм» ^JV-i+1/дм) "+
N N-1 ______
+ 22 Ум	(3-23)
Z=/+l /=1
и определяется исключительно начальным состоянием
системы и статистическими характеристиками случай-
ных возмущений.
Итак, если условия теоремы выполнены, то оптималь-
ный синтез реализуется линейной функцией, причем
матрицы которые мы будем называть матрицами ко-
эффициентов усиления, могут быть рассчитаны по явным
формулам. Реализация машинного счета не встречает
никаких существенных трудностей, даже если система
(3.2) имеет относительно большую размерность.
В результате синтеза мы получаем так называемую
систему переменной структуры, когда обратная связь,
осуществляемая функцией v*=B*z* меняется с течением
времени.	»
Заметим, что все расчеты, связанные с построением
синтеза, могут быть сделаны заранее, кроме расчета са-
мого значения функционала, поскольку в него входит
начальное состояние.
При доказательстве этой теоремы были сделаны сле-
дующие предположения:
1.	На управляющие воздействия никаких ограниче-
ний не накладывается.
2.	Все компоненты вектора z могут быть измерены
(все фазовые координаты наблюдаемы), и мы можем
воздействовать на все фазовые координаты системы.
3.	Фазовые координаты измеряются без ошибок.
§ 3] ПРИМЕНЕНИЕ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 343
Ниже мы увидим, что изложенные методы можно ис-
пользовать иногда и в тех случаях, когда не все фазо-
вые координаты являются наблюдаемыми, не на все фа-
зовые координаты мы можем воздействовать, и измере-
ния производятся с ошибкой.
В реальных задачах коэффициенты усиления — эле-
менты матриц Bt — бывают ограничены. Как следует из
доказательства теоремы, эти матрицы определяются толь-
ко матрицами R, К. и Ф(. Матрица К. находится в нашем
распоряжении — и, как мы уже отмечали, она может ха-
рактеризовать штраф за большие значения управляю-
щих воздействий. Из формул данного раздела видно,
что увеличение элементов К (т. е. увеличение нормы
штрафа) приводит к уменьшению коэффициентов усиле-
ния. Это обстоятельство может быть использовано в ра-
зумных пределах инженером, проектирующим систему
обратной связи, поскольку для всякого значения коэф-
фициентов усиления может быть рассчитано не только
значение функционала (3.9), но и функционала (3.3),
который главным образом и интересует инженера.
Если система (3.2) получена с помощью конечнораз-
ностной аппроксимации системы (3.1), то возникает
важный вопрос о зависимости найденных характеристик
системы управления от шага т. Предположим, что мы
использовали разностную схему первого порядка, тогда
величина управляющего воздействия w(ft) связана с
управлением vt формулой
vi
(3.24)
В непрерывном случае в качестве функции штрафа
мы должны взять величину
Г _	ЛГ-1 ~
[ (эд (0, Kw (0) dt ~ -Г	twb Rwi).
о
В рассмотренной нами дискретной задаче в качестве
функций штрафа мы взяли сумму 2(Vi> Учитывая
связь (3.24), находим #=.£/?. В то же время из формул
(3.20) следует, что ||В{|| = О(||К||-‘), а, следовательно,
|)В(|| = О(т) и1>г=О(т).
344
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ [ГЛ. IV
Таким образом, управляющее воздействие wt имеет
следующий вид: а». = а»<0 + О(т'), 1>0, где wi0 не зависит
от шага т.
Итак, оптимальное управление w, найденное для ди-
скретной системы, стремится к конечному пределу при
неограниченном убывании шага т, и этот предел не за-
висит от характера дробления шага.
3. Случай, когда размерность вектора управления
меньше размерности фазового вектора. Этот случай наи-
более часто встречается в прикладных задачах. Напри-
мер, при управлении динамическими объектами мы мо-
жем непосредственно воздействовать только на величи-
ну ускорений. В этом случае вектор v входит не во все
уравнения системы (3.2).
Тогда мы можем представить вектор z в виде суммы
z=a + Р> где вектор реЕ” имеет размерность т, равную
размерности управляющего вектора, причем управление
входит в каждое из уравнений для компонент z"~m+1, ...
..., zn. Размерность вектора а равна п — т. Он принад-
лежит ортогональному дополнению к Ет. Управление v
не входит ни в одно из уравнений для компонент векто-
ра а. Введем обозначение
л |ф“ ФГ|
ФА = I»
И1 фП
где Ф” и Ф” — квадратные матрицы размерности (га —т)х
X (и — tn) и т х т, ФГ и Ф*1 — размерности (п — т) х
X т и т х (п — tn). С их помощью уравнение (3.2) мож-
но записать в виде
a*+i — ФГ«а + Ф*2?* + Д»»
(3.25)
P*+i = Ф*1«* + фГР» + о* +
k = 1.......N-l,
где f2k—случайные векторы размерности п — т и
т — соответственно. Функционал Jw(zN) мы примем в
виде	•
__________________ М-р
Jn(zn) — (aN, RaN) + (Pai SPaO + (vb K°i), (3.26)
/-0
$ 3] ПРИМЕНЕНИЕ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 345
где R и S — симметричные положительно определенные
матрицы размерности (п — т) X (п — т) и mXm соот-
ветственно.
Попытаемся решить задачу синтеза системы (3.25) с
функционалом (3.26), применяя метод динамического
программирования. Используя обозначения данного па-
раграфа, выпишем
Jn — («№ R^n) 4* (Рдч Spyv) + (Ум-n K^n-i) 4~
+ 2	= (®N-laN-l» R^N-l^N-l) 4"
+ (Фм-1РлГ-Ь #®JV-I0AT-1) 4" 2 (Флг-l^-l, R®N-1$N-1) 4-
4- (fuv-1» Я/1ЛГ-1) 4- 2 R^n-i^n-i) 4-
4" 2 (fjAT-p	4- (®N-1®N-U 5Ф“_1аЛг_1) 4-
4- (ФЙ-хРлг-1,	4- 2 (Ф^-х, ХФ^хРлг-х) +
4" (vn-ь SVfj-i) 4- 2 (Vtf-i, S&N-iaN-i) 4*
4" 2 (vn-ъ S®n-$n-i) 4" (f^N-v SfzN-i) 4-
+ 2 (Zxaz-1. 5Ф”-1«лг-х) 4- 2 (f^.p ЗФЙ-хРаг-х) 4-
4- 2 (Vjv-i, Sf2N_t) +(vn-i, Kvn-i) 4" 2 (°г»
/=0
Выделим ту часть JN, которая после осреднения будет
содержать управление yw_t:
I {on-i) = (Pn-ъ (К 4- S) »w-x) 4*
4- 2 (Олг-х, S (ф^-х 4- Ф“-хРлг-х)). (3.27)
Так как
Zw (глг) __ di
avN-l dvN-l
то оптимальное управление мы найдем из уравнения
-^-=0.
dvN-l
Получаем
Vn-г = (К 4- З^ЗФВ-хах-х 4- (Я 4- 5Г1 ЗФ#-хРаг-х
346
Проблема синтеза оптимальных систем [Гл. iv
или	i
°АГ-Х = ^АГ-1«АГ-1 4"	(3.28)
т. е. и в этом случае управление сохраняет линейный ха-
рактер. Эту процедуру можно продолжить и показать,
что на любом шаге процесса динамического программи-
рования оптимальное управление	будет линейной	функ-	$
цией фазовых координат	J
+	(3.29)	I
Примечание. Система (3.2)	имеет	достаточно
специальный вид. Однако изложенная схема рассужде-
ний остается полностью применимой и к тому случаю,
когда уравнение, описывающее движение управляемого
объекта, имеет вид
z*+x =	4- Cvk 4- fk,
где С — некоторая прямоугольная матрица размерности
пхт
4. Метод динамического программирования в задаче
с линейным функционалом. Рассмотрим снова динами-
ческую систему (3.1), но в качестве оптимизируемого
критерия мы примем теперь линейный функционал
J = (с,г(Т)),	(3.30)
где С — заданный вектор.
Изучение этой задачи проведем с помощью метода
динамического программирования. Для этого перейдем
снова к дискретным уравнениям (3.2) и составим ска-
лярное произведение
«^№ (б, 2дг).	(3.31)
Фиксируя Zjf-ь перепишем (3.31) в виде
/до = (с, Флг-xZv-i) 4* (<4 UN-1) 4- (с» fjy-i)» (3.32)
откуда, сохраняя обозначения предыдущего пункта, по-
лучаем
Jn-1 = Qn/Zn-i) = (с» ®N-lZw-i) 4- (с, Vn-i).
Из этого выражения следует, что задача синтеза си-
стемы с линейным функционалом, если ее состояние в
§ 3] ПРИМЕНЕНИЕ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 347
момент t=tK-i задано, сводится к минимизации линей-
ной формы (с, Uw-i). Эта задача имеет смысл лишь в
том случае, если на управление наложены некоторые
ограничения*). Условимся рассматривать тот простей-
ший случай, когда векторы v{ удовлетворяют ограниче-
ниям:
v?	(3.33)
где Vi и Vi—заданные векторы **).
Обозначим через vN-t решение описанной задачи ли-
нейного программирования. Заметим, что оптимальное
управление не зависит от состояния zN-t и определяется
только ограничениями (3.33) и вектором с.
Пусть теперь нам задано состояние системы zN_2 в
момент t=tN-2. Перепишем выражение (3.32)
JN — (С, Фм_1Фдг_ггм_2) + (<» Фм-Л^-а) + (С, Ом-1) +
+ (ci /м-i + Фм-1/м-а)>
откуда
Jn-2 = (Jn/^N-z) = (с, Фм-х^м-г) (с, Фм-1Фм-2?м-4) 4-
+ (с, Ом-1).-
Следовательно, vN-2 определяется как решение следую-
щей задачи линейного программирования: определить
вектор vN-2, доставляющий минимум линейной форме
L = (с, Фм-10м~2)	(3.34)
при условии (3.33).
Продолжая по индукции, мы легко установим, что
управление vt (i=0, 1, ..., N—1) должно быть решени-
ем задачи линейного программирования для функции Lf:
Lt — (с, Фм-1Фм-8 ... Фг+Л) (3.34)
при ограничениях (3.33).
*) Если не накладывать никаких ограничений на управление, то
можно, используя метод штрафных функций, свести задачу с функ-
ционалом (3.31) к задаче квадратичного программирования, вполне
аналогичной той, которая была рассмотрена в предыдущих пунктах.-
**) Неравенство (3.33) является векторным — это значит, что оно
выполняется для всех компонент вектора Vi.
348
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
Итак, решение задачи синтеза оптимальной системы,
описываемой уравнением (3.2), в том случае, если функ-
ционал— это линейная форма (3.30), не зависит от со-
стояния системы и характера случайного процесса F(t)
и определяется только свойствами объекта (матрицы
Ф() и системой ограничений.
Пр имечание. Рассмотрим задачу оптимального
управления: определить вектор-функцию w (t), удовлет-
воряющую условиям
z = A? + w,	г (0) = 0,	(3.35)
и доставляющую минимум линейной форме (с, z(T)).
Используя принцип максимума, мы найдем, что в
каждый момент времени t вектор-функция w(t) достав-
ляет максимум линейной форме (р, w), где вектор-функ-
ция p(t) —это решение следующей задачи Коши:
р =» — А*р, р(Т) — — с.	(3.36)
Перейдем теперь к дискретному аргументу. Условие
максимума (w, р) мы перепишем в виде max(pz+1, Wi),
а уравнение (3.36) заменим следующей разностной схе-
мой первого порядка точности:
Pt = (I + тД*) pf+i,
тогда wN-i определится из условия:
шах (рх, WM-r) = max {— (с,	= min (с,
WN-1	WH-1	WN-1
Управление u>N-2 определится из условия
max (pv-i, = max {- ((f 4- гЛ*) c, wN^)} =»
= min(c, (I + rA*)*wN^) = min(c,
wN-i
и т. д. Таким образом, управление в задаче (3.35), (3.30)
совпадает с тем, которое мы нашли для задачи (3.2),
(3.30). Это позволяет вычисление произведения матриц
типа Фя-1Фя-2... Фя-ь заменить решением задачи Коши
(3.36).
§ 3] ПРИМЕНЕНИЕ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 349
5. Обсуждение. Итак, мы видим, что методы динами-
ческого программирования дают возможность относи-
тельно просто найти численное решение целого ряда за-
дач синтеза линейных систем. Мы получили три важных
результата:
I.	Если на управляющие воздействия не наложено ни-
каких ограничений, то оптимальное управление при квад-
ратичном критерии качества является линейной функци-
ей фазовых координат w = B(t)z, причем этот вывод
справедлив, каков бы ни был характер случайного про-
цесса F(t).
Если же на величину управляющих воздействий на-
ложены ограничения, то управление становится сложной
нелинейной функцией фазовых координат.
Этот результат имеет важное прикладное значение.
В технических системах очень часто синтезируют линей-
ные системы, используя линейные зависимости управляю-
щих воздействий от фазовых координат. Из результатов
этого параграфа следует, что подобные системы не явля-
ются оптимальными на всем множестве допустимых уп-
равлений.
II.	Система, которую, мы получили в результате син-
теза, является системой «переменной структуры»: матри-
ца обратной связи В изменяется со временем.
Структура матрицы В достаточно сложная (особен-
но в том случае, когда размерность v меньше п), однако
все вычисления мы можем сделать заранее, причем ха-
рактер рекуррентных соотношений позволяет поручить
машине и все формальные (буквенные) преобразования.
III.	Мы установили, что в тех случаях, когда крите-
рий качества является линейным по фазовым координа-
там, оптимальное управление не зависит от фазовых
координат и характера случайного процесса. Оно опреде-
ляется исключительно свойствами самой динамической
системы. Этот факт также имеет некоторые следствия
прикладного характера. Предположим, что мы имеем
линейную динамическую систему
х = Ах ф- и,	(3.37)
например, линейную динамическую модель экономики.
Предположим далее, что управление u(t) выбирается
350
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
из условия минимума целевой функции
7 = (с, х(Г)).	(3.38)
Функция u(t) в экономических моделях определяет
политику в распределении ресурсов. Условимся сначала,
что никаких ограничений на конечное состояние нет.
Предположим, что мы решили эту задачу; функция u(t),
которую мы нашли, согласно терминологии, введенной
в § 1, называется программой.
Рассмотрим теперь движение «реальной» системы,
подверженной действиям случайных сил, и составим
уравнение, описывающее коррекцию. Это уравнение,
очевидно, будет отличаться от уравнения (3.37) только
тем, что в его правой части будет еще одно слагаемое —
вектор случайных возмущений.
Из результатов данного параграфа следует, что скор-
ректированное управление будет совпадать с программ-
ным управлением. Другими словами, никакой коррекции
подобной системе не требуется — политика в распре-
делении ресурсов не зависит от возмущений, которые
вносятся в систему извне.
Таким образом, система обратных связей и измене-
ние в структуре распределения ресурсов необходимы
лишь в том случае, если на конечное состояние системы
наложены определенные ограничения.
Заметим, что вопрос о том, как формулировать огра-
ничения, не является тривиальным. Предположим, на-
пример, что при построении программного управления
мы задались условием
х1(Т) = а,	(3.39)
где а — фиксированная постоянная (в этом случае ком-
понента Ci вектора с в (3.38) должна быть принята рав-
ной нулю).
Под действием случайных возмущений величина
х1(Т) в «реальном движении» будет уже случайной ве-
личиной. Поэтому говорить о строгом выполнении усло-
вия (3.39) не имеет смысла. Вместо этого условия мы
должны наложить какое-либо ограничение статистиче-
ского порядка, например, потребовать, чтобы
(хх(Т) —a)2<av	(3.40)
$ 4)	ЗАДАЧИ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ	^51
Ограничение вида (3.40) существенно изменяет струк-
туру решения, и вывод, который мы сделали о политике
в распределении ресурсов для случая свободного право-
го конца, теперь уже перестанет быть верным.
§ 4. Методы динамического программирования
в задачах синтеза с неполной информацией
и при наличии ошибок измерений
1. О постановке задачи. В предыдущем параграфе
мы рассматривали задачу синтеза системы, поведение
которой описывается уравнением в конечных разностях
(все обозначения предыдущего параграфа будут сохра-
нены) :	’
zfe+i =	+ vk + fk, k = 0, 1, ..., N — 1,	(4.1)
и разыскивали управление о* как функцию фазовых
координат. Тем самым мы предполагали, что все фазовые
координаты в любой момент времени нам известны и
притом абсолютно точно. В реальных задачах мы часто
не можем непосредственно измерить координаты, а из-
меряем некоторые величины у, являющиеся функцией
координат г. Эту функцию в данной работе мы будем
считать линейной
y = Qz.	(4.2)
Размерность у, как правило, меньше размерности г.
Матрица Q — это некоторая прямоугольная матрица
/пХп, причем т^п. Поэтому уравнение (4.2) по задан-
ному у в общем случае еще не определяет вектор z. Кро-
ме того, измерение производится с ошибкой, т. е. вели-
чина у — это некоторая случайная величина. Считая,
что измерения производятся также в дискретные момен-
ты времени f=4, запишем вместо равенства (4.2) сле-
дующее *):
7(^<2г(4).	(4.3)
Из сказанного следует, что мы никогда не будем
знать точно значений фазовых координат, и, следова-
*) Напомним, что у означает математическое ожидание вели-
чины у
352
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ [ГЛ. IV
тельно, управления vK мы должны разыскивать не как
функции фазовых координат, а как функции их стати-
стических оценок. В этом случае возникает еще один
вопрос о выборе статистической гипотезы. Примем про-
стейшее предположение о том, что все ошибки распреде-
лены по нормальному закону. Для построения оценок
будем использовать метод максимального правдопо-
добия.
2. Замечание о методе максимального правдоподо-
бия. Прежде, чем переходить к изложению особенностей
синтеза в системах с неполной информацией, напомним
некоторые факты теории статистических оценок, осно-
ванные на принципе максимального правдоподобия.
Пусть измеряется векторная величина у, a — век-
тор измеренных значений ее компонент. Обозначим че-
рез f(y, —многомерную плотность распределения
случайной величины Ограничимся рассмотрением
того случая, когда распределение ошибки подчиняется
закону Гаусса. Тогда
f (у, & = С ехр	L (у - Ъ, D'1 (у - &))} ,
где с — некоторая константа, выбирающаяся из условия
нормировки, a D — матрица вторых моментов размерно-
сти пХи (в том случае, когда у — скаляр, D — это дис-
персия). Эта матрица всегда положительно определен-
ная и симметричная.
Предположим, что при помощи данного способа из-
мерения произведено k измерений вектора у: gi, g2, ...
• • •, Функцией максимального правдоподобия называ-
ется следующее произведение:
ЦуЛъЪ, ...» ад = f(y, Ш(уЛ) ... 7(г/,ад =
= с*ехр{—(у-$, Я-‘(у-ад)}.
Оценкой максимального правдоподобия величины у
называется то значение у, которое является корнем урав-
нения
k
(4.4)
оу	2 ду
§ 4]	ЗАДАЧИ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ	353
Уравнение (4.4) называется уравнением правдоподобия.
Так как D — положительно определенная матрица, то
этим свойством обладает и матрица Z)”1. Поэтому в ре-
зультате дифференцирования мы получим
k	(	k \
-3	^-3 & =0.
1=1	\	4=1 /
Это уравнение имеет единственное решение, которое
определяется формулой
74 1 k
= <4-5)
к
1=1
т. е. максимально правдоподобным является среднее
арифметическое измеренных значений.
Пусть теперь измеряется не величина у, а некоторая
функция от у, например, Qy, и пусть %(—измеренное
значение величины Qy. Тогда плотность распределения
измеряемой величины будет f(Qy, &), а функция правдо-
подобия примет вид
k
L = П f(Q'y, I).
1=1
Считая по-прежнему закон распределения нормальным,
составим уравнение правдоподобия —L = 0. Это урав-
ду
нение можно записать в следующей форме:
a k
KQy-b),Zr4Qy-b)] = 0,
ОУ .
1=1
где D — матрица вторых моментов размерности kxk.
После очевидных преобразований оно примет вид
a k
j- 3 «У. Q*^Q у) - 2 (у, Q-ZT^) + (&,	= 0
у i=i
или
k
kQ^Qy = Q'D^ &	(4.6)
i=i
12Н. Н. Моисеев
354
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ [ГЛ. IV
Пусть у имеет размерность п, и предположим, что
вектор ^ — Qy имеет ту же размерность. Размерность
матрицы вторых моментов равна пХя. Следовательно,
если матрица Q — невырожденная, т. е. если ее детер-
минант отличен от нуля, то матрица Q*D~lQ — невырож-
денная матрица, и уравнение (4.6) может быть разреше-
но относительно у:
1 k
У ~	2 &	(4.7)
Пусть теперь размерность вектора у равна т, причем
т<п. Тогда Q — прямоугольная матрица размерности
тХп, матрица D будет иметь размерность тхт. Сле-
довательно, матрица Q*Z)_1Q будет иметь размерность
пХм. Однако эта матрица всегда оказывается вырож-
денной *), и, значит, разрешить однозначно уравнение
(4.6) относительно у нельзя. В этом случае мы можем
иметь оценку только для величины Qy (аналогично
(4.5)).
Рассмотрим в заключение этого раздела еще один
случай построения оценки. Предположим, что одновре-
менно измеряются векторы £ и т), связанные с вектором
у равенствами 1, — Qy, r\ = Ry, где Q и R— матрицы раз-
мерностей т^/.п и т2Хп соответственно, причем /п4<;
<.п и m2<n. Плотности распределения вероятностей
измеряемых величин будем обозначать через f(Qy, &) и
ф(#«/. ПО-
Предположим, что производится k измерений величи-
ны g и s измерений величины т]. Функция правдоподобия
для этой ситуации имеет вид -
k	S
L=Uf(Qy, &)П у (Ry, n/).
z=i	i—i
В качестве оценки величины у мы принимаем корень
уравнения
А Г	S
— 2 ln/(Q'/.^) + 'S =0-
ay I	J
(4.8)
*) Так как ранг произведения матриц не выше ранга сомножи-
телей.
? 4]
ЗАДАЧИ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ
355
Будем считать законы распределения величин Qy и
Ry нормальными, а матрицы вторых моментов обозна-
чим через D5 и Dn соответственно; тогда уравнение мак-
симального правдоподобия (4.8) можно переписать в
следующей форме:
а к
-7-3 [(<&-&),	&)] +
+ -гЗ № -	= о
^/-1
или
а
Y- 3 Ку. Q*DixQ У) -2 (у, Q*D^) +	Di^)] +
ду £
а «
+ “гЗ КУ^*^У) —2 (у, R*Dfo}) + (п/. ОлЧ)] = °-
ду i-i
И окончательно
(^*#<2 +sR*D-jR) у = Q*Djx & +/?*D^	т».
i=l	/=1
Если матрица, стоящая в круглых скобках, невырож-
денная, тогда это уравнение можно разрешить относи-
тельно вектора у, и мы получаем следующую формулу
для оценки у:'
(k	S	\
Q*Dgx5J Ъ+R'D^ п/ .
Z—1	Jsssl /
(4.9)
Для этого, в свою очередь, необходимо, чтобы одна из
матриц Q или R была квадратной.
Итак, для некоторых простейших случаев обработки
информации мы получили формулы оценок измеряемых
величин. Здесь приведены только те сведения из теории
максимального правдоподобия, которые нам будут нужны
12*
356
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
для дальнейшего. Более подробно метод максимального
правдоподобия изложен в любом серьезном курсе мате-
матической статистики *).
3. Построение оценок для фазовых переменных. Рас-
смотрим теперь снова систему (4.1) и предположим, что
измеряется величина Qz, причем измерения производят-
ся в моменты времени t—th, fe=0 W—1. Изложим
процедуру построения оценок величины z. Начальное со-
стояние системы будем считать неизвестным.
Пусть go—это результат непосредственного измере-
ния начального состояния. Эту величину мы принимаем
в качестве первоначальной оценки вектора z0. Ошибку
этого измерения будем считать распределенной по нор-
мальному закону с матрицей вторых моментов До и с
плотностью распределения Д:
Д (^о> ^0 = р— (z0 gp, До (?0 U)] •
В момент времени t—tn мы производим, кроме того, из-
мерение у0 (см. (4.2)), ошибки которого распределены
по нормальному закону с матрицей вторых моментов D.
Плотность распределения обозначим через f2(Qz0, у0)'
ft (Qz0» Уо) — ^2 exp	 —- (Qz0 у0, D 1 (Qz0 y0)) .
Используя информацию о первоначальном распреде
лении величины g0 и результат измерения у0, мы можем
с помощью метода правдоподобия получить уточненную
оценку go этой величины. Она будет корнем уравнения
правдоподобия:
4 [(gp - gp), До1 do - У) + ((<& - Уо). D~' (<& - Уо))] = О-
После очевидных преобразований это уравнение при-
мет вид	____
(Др-1 +	= Др"Ъ + Q*D-xJ/p
*) См., например, Б. Л. Ван-дер-Варден, Математическая
статистика, ИЛ, 1960.
$ 41	ЗАДАЧИ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ	357
или, вводя обозначение
F? =	+ Q*Dr4}),
мы можем выписать явное выражение уточненной оцен-
ки |0:
l =	(4.Ю)
Все рассуждения, которые привели нас к формуле (4.10),
остаются справедливыми, какова бы ни была размер-
ность вектора у0, поскольку Д71 —невырожденная ма-
трица размерности пхп.
Величина |0 является случайной. Вычислим матрицу
вторых моментов До вектора £0, имея в виду, что матри-
цы вторых моментов случайных величин и у0 равны До
и D соответственно.
Для дальнейшего нам потребуется следующее утвер-
ждение:
Лемма. Пусть случайные величины г] и f связаны
соотношением
g = Bq + и + f,
где v — детерминированный вектор, а т] и f — независи-
мые случайные векторы*), причем f=0. Тогда матрицы
вторых моментов Db и Df векторов %, ц и f соответст-
венно связаны между собой равенством
D^BD^ + Df.	(4.11)
Доказательство. Так как	то,
обозначая а — £ — |, р = т] — г), находим, что а = ВР + Д
п
Далее вычисляем а/==2 &rsPs + /» ('=1......п, и, ис-
S=1
пользуя независимость векторов т| и f, получаем
___ п ___________ ____
2	+	(4-12)
s.Z=l
*) Векторы 5, т), v, f имеют размерность п.
358
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ
[ГЛ. IV
Так как aW—компоненты матрицы вторых момен-
тов случайной величины а 0'0'—компоненты матрицы
вторых моментов величины т), то, свертывая (4.12), мы
получим формулу (4.11). Лемма доказана.
Используя формулу (4.11), вычислим До—матрицу
вторых моментов величины g0 (4.10) *):
А = (Ро До’1) \ (Fo До’У+О*^1) D
Преобразуем это выражение, используя самосопряжен-
ность матриц Л, До и D:
{До’1 ДоДо-1^ + Q*D'»D (Q*D-1)*F0} =
= Fo {A1 +Q*D-4l} Fo = F„. (4.13)
Используя равенство (4.13), мы можем привести
(4.10) к другому виду, исключив величину До. Для этого
преобразуем (4.10), прибавляя и вычитая величину £»:
S = Во + (А № - Vo1) Во + 3oQ*IF4.	(4.14)
Так как Г»1 = А1 — Q*D~lQ, то (4.14) примет вид
Во = Bo-AQ^QBo + AQ*^-1^
Отсюда окончательно
Во = Во + AQ*^1 (Уо - QBo). (4-15)
Рассмотрим теперь момент времени t—t^. За отрезок
времени [4, система перешла из состояния z0 в со-
стояние z1( причем z^OoZo+fo+fo. Так как для вектора
z0 мы имели уточненную оценку |0, то в качестве оценки
вектора zt мы можем принять величину определяе-
мую равенством
Bi = ФоВо + Ц, +1,	(4.16)
*) В (4.10) v, фигурирующее в лемме, равно нулю, a f=
“FoQW-'yo.
$ 4J	ЗАДАЧИ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ	з&)
где [о — оценка математического ожидания*). Или,
используя (4.15),
= Ф<& + ^o(^o-Q&)) + уо + to, (4.17)
где матрица гР0 определяется формулой
То = Фо = Фо (До"1 +	(4.18)
Формула (4.17) дает связь между начальной оценкой
g0 и оценкой в момент времени t=tt.
В момент времени t=tt производится новое измере-
ние величины y=Qz. Это измерение — величина tji — по-
зволяет получить уточненную оценку g,. Для того чтобы
провести необходимые вычисления, заметим, что ситуа-
ция в момент времени t=tt совершенно аналогична си-
туации в момент времени t=t0: мы снова имеем два из-
мерения. В качестве одного из них мы имеем оценку gb
а в качестве второго yt.
Матрицу вторых моментов ошибок измерения вели-
чин у будем считать по-прежнему равной D (измерения
производятся одними и теми же средствами). Матрицу
вторых моментов Д, случайного вектора g, мы можем
вычислить, используя равенства (4.16) и (4.11):
Дх = Фо ДоФо* + Df -- Фо (Д;1 +Q*D-1Q)-1®; 4- Df. (4.19)
Используя теперь уравнение правдоподобия и повторяя
вычисления начала пункта, мы получим следующий ана-
лог формулы (4.10):
+	(4.20)
где
Л = (Д?1 + Q*D"1Q)*1;
матрица вторых моментов случайного вектора g, будет
*) Имеет смысл рассматривать несколько случаев. Один из них
состоит в том, что мы можем измерять случайный вектор f, и тогда
fo—это оценка с ошибкой, матрица вторых моментов которой равна
Df,. Иная ситуация возникает тогда, когда мы не можем измерять
случайные возмущения, но знаем характеристики распределения. Тог-
да мы можем принять в качестве оценки f математическое ожидание f.
360
ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ [ГЛ. IV
= Повторяя рассуждения, мы запишем аналог
равенства (4.15):
и, наконец, новую оценку для момента t=t2:
Ъ =	(У1 - (&) + А,
где 4fi=01A1Q*Z>-1. Рассуждая далее по индукции, мы
придем к следующему результату, который сформулиру-
ем в форме теоремы:
Теорема. Оценка £(t) фазового вектора z(t), ко-
торый является случайным процессом и описывается
разностным уравнением
Zk+i =	+ ok 4- fk,	(4.1)
при условии, что в моменты t—ik производятся измере-
ния величины yk=Qzk, удовлетворяет разностному урав-
нению
&+» = Ф*& + (yk — Q&) + Ok + fk, (4.21)
где ЧГ*=Ф*(А*1+Q*D_lQ)_‘Q*D_1, D — матрица вторых
моментов случайного вектора у, а матрица А*—матрица
вторых моментов случайного вектора Ik удовлетворяет
разностному уравнению
bk =ФА-1 (Дм +Q*D"1Q)"11>Z-i + DSk^ (4.22)
причем Dtk х означает матрицу вторых моментов случай-
ного вектора fb х.
Данная теорема позволяет по мере поступления ре-
зультатов измерений определять последовательно оцен-
ки go, gj, . . .
Выпишем еще, используя формулы типа (4.20),
(4.16), уравнение для уточненной оценки g*+1:
&>+i = А*+1 АГ+1Фл£л + Аа+! As+iOa 4* А*+1 Afc+j/jt 4-
4-(4.21')
где Ай+1=Ф*А^Фа+^/а- Итак, предположим, мы имеем
оценку g,, для величины zk. Тогда zk должна рассматри-
ЗАДАЧИ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ
361
ваться как случайная величина со следующей плотно-
стью распределения:
f <zk, Ik) = С exp (-[((Q^ — yk), D~l (Qlk — Уь)) 4-
+ ((&-zk),
где yh= Qzh.
Таким образом, значение zk мы можем представить в
виде суммы zft=gk+/ift, где hk—некоторая случайная ве-
личина, плотность распределения которой определяется
формулой
f{hk) = с exp |t \(Qhk, IT'Qhk) + (hk, ДГМ1} •
Мы видим, что /ife=0.
4. Построение синтеза при неполной информации.
Вернемся теперь снова к задаче синтеза управления си-
стемой (4.1) с функционалом (3.9):
__________ АГ-1
J = (ZN, RzN) + (vt, Kvi).
i—0
(3.9)
В предыдущем параграфе мы установили, что оптималь-
ный синтез в том случае, когда мы можем точно изме-
рить величину z, реализуется линейной функцией фазо-
вых координат
Vi = В(2{,	(4.23)
причем матрицы В( определяются формулами (3.20).
Теперь мы рассмотрим тот случай, когда точное значе-
ние zt нам неизвестно. Вместо него мы имеем оценку
или уточненную оценку Следовательно, теперь zt=
= li+h{, где h,— некоторые случайные величины, мате-
матическое ожидание которых, как мы установили в пре-
дыдущем пункте, равно нулю.
Рассмотрим функционал
n-i
J = <zN, Rzn) 4- (Vi, Kvi).	(4.24)
i=so
362
ПРОБЛЕМА- СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ (ГЛ. IV
Делая замену
гАГ = Ф/f-tZjf-i 4“ V/f.t	+ Vn-I + Фм-i,
где Фдг-i = <bN^hN-i 4- fN_lt приведем его к виду
= (&V-1»	+ 2 (<Pw-i, #ФдмВлг-1) 4-
4- 2 (fjv-i, R®n-iIn-i) 4- 2 (флг-i, RUff-t) + (<Pw-i, /?<Pw-i) +
N-2
4- (vn-i, Rvn~i) + (олг-ь Kvn-J 4-	(°i Rvi)- (4-25)
£»0
Это выражение отличается от соответствующего вы-
ражения предыдущего параграфа только тем, что в него
вместо случайного вектора fN-t входит случайный век-
тор фк-ь а вместо zN_4—величина его оценки. Посколь-
ку Vjf-i определяется из условия
57	_
-*— =0 и не зависит
°°N-1
от случайного вектора, то управление oK~i определяется
так же, как и в случае задачи с полной информацией,
если величину z заменить ее оценкой
®N-\ = ВлГ-1$ЛМ,
(4.26)
где определяется так же, как в выражении (4.23),
формулами (3.20):	—(/?4-/0-1/?Фх-1. При помо-
щи (4.26) мы исключим управление Vx-i из выражения
(4.25). Функционал 1 примет вид
N-1
j = / (&V-1, ФАГ-1) + 3 (°«« W (4.27)
£=0
где 1 — полином второй степени от и фк-4.
Затем из выражения (4.27) мы исключим |w_i при
помощи формулы	и, наконец, в полу-
ченном выражении заменим zN-C.
ZN-1 = ®N-2?N-2 4" °N-2 4" fN-2 = Фм-2?М-2 4" ^N-2 4~ ФЛГ-2>
где
%N-2 ~ £v~2 4" hff-2, ФЛГ-2 — Фу-2^ЛГ-2 4- fN-2-
В результате мы приведем / к следующему виду:
J = (рм-г, RN-l°N-2f 4- (aW-2. (Rn-1 4* Rn-1) Фм-а&У-а) 4"
4- (фм-s» (Rn-i 4- Rn-i) ^N-2) 4- (vn-2, Rufir-г) 4- Л» (4.28)
§ 4j	ЗАдачй с нёполйой Информацией	363
где Д, не зависит от aN_2,
Rn-i = Флг-1^Флг-1 + Фы-iRBn-i + Bn-iR^n-i-
_Так как управление vN_t находится из условия
- —- = 0, то мы получаем vN_2 — Bn_2%n-2, где BN_2 сов-
dvN_t
падает с той матрицей Ву-2, которая входит в формулы (4.23):
Bn-* — {Rn-i + Rn-i + 2Л)-1 (Rn-i + Rn-i) Флг-2 (4.29)
и т. д. Повторяя по индукции эту процедуру, мы придем
к следующей теореме:
Теорема. Оптимальный синтез управления линей-
ной системой при квадратичном критерии качества
(3.9) в условиях неполной информации реализуется ли-
нейной функцией
Vi = В&,	(4.30)
где оценка фазовых координат, a Bi определяется
формулой Bt= (Ri^+R^ +2А’)-1(^+<+/?;+1)Ф<.
Итак, оптимальный синтез в условиях неполной ин-
формации реализуется той же линейной функцией, что
и в условиях полной информации, только аргументом
этой функции является не фазовая координата z, а ее
оценка, полученная из метода максимального правдопо-
добия. В этом случае управление не будет зависеть ни
от характера случайного процесса fk, ни от ошибки из-
мерения hk. Значение функционала, разумеется, будет
определяться и управлениями, и этими случайными про-
цессами.
Заметим, что сформулированный результат не зави-
сит от того, какую из оценок g или § мы используем, по-
скольку все различие результатов будет содержаться в
выражении для ошибки h, от которой выбор управления
не зависит, а зависит лишь окончательный результат,
т. е. значение функционала.
Установленный факт играет важное значение в тео-
рии управляемых систем. Он показывает, что задача по-
строения оптимального синтеза, т. е. определение зако-
на управления как функции оценки, и задача оптималь-
ной обработки наблюдения для линейных систем с
§64	ПРОБЛЕМА СИНТЕЗА ОГГГЙМАЛЬНЫХ СИСТЕМ [ГЛ. IV
квадратичным критерием качества могут быть разде-
лены.
В этой книге мы рассмотрели лишь первую задачу.
В результате ее решения мы можем определить значе-
ние качества как функцию оценки 7(g). Но величина
а, следовательно, и J(Jj), зависит от принятой нами ста-
тистической гипотезы. Здесь мы условились рассматри-
вать гипотезу максимального правдоподобия. Но, вооб-
ще говоря, могут быть приняты и другие гипотезы. За-
мена одной гипотезы другой не будет менять найденного
закона управления, но, разумеется, изменит значение
критерия качества. Таким образом, здесь возникает но-
вая оптимизационная задача.
Примечание. Величина оценки, которая входит
в формулы (4.30), определяется теорией, развитой в
предыдущих пунктах данного параграфа. Однако теперь
нам придется несколько уточнить формулы для оценок,
которые мы получили ранее, поскольку при их выводе
мы исходили из уравнения |»+1=Фл|*+»*+Д, где vk пред-
полагался некоторым детерминированным вектором.
В действительности, как мы это установили, vk=Bk^k—
т. е. является случайным вектором. Новые формулы для
оценок мы можем получить, если в старых формулах
положить	Тогда
Ь+1 = Фа& + (.Уь — Q£a) + fk,
= Дб+1 Да+хФа^а + Да+х Да+х/а 4* Да+iQ*^ lyk, (4.31)
Да+х = Ф* ДаФа + Dfk.
Поскольку матрицы В{ могут быть вычислены зара-
нее до реализации процесса (напомним, что они зависят
только от матрицы Ф* и Df), то величины Фк также мо-
гут быть вычислены заранее.
Таким образом, вся структура управления — структу-
ра обратных связей определяется до реализации про-
цесса.
В системе управления должно быть предусмотрено вы-
числительное устройство, задача которого — обработка
измерений ук и вычисление оценок gfe+1.
§ 41	Задачи с нёпОлной инФоёмацйёи	365
5. Комментарии и вопросы.
А. Возможен качественно другой подход к построе-
нию синтеза. Весь процесс эволюции динамической си-
стемы мы можем рассматривать только в рамках урав-
нений для оценок — уравнений (4.21) или (4.21х). Тогда
в качестве характеристики процесса мы должны брать
не дисперсию, а оценку отклонения
ЛЛ-1
<«=0
которая после измерений становится детерминирован-
ной величиной. Такая постановка имеет технический
смысл, однако при ее реализации мы встретимся с од-
ной трудностью. Уравнения типа (4.21) являются стоха-
стическими: их правые части содержат случайные сла-
гаемые, которые становятся известными только после
измерения.
Одно из достоинств процедуры, описанной в этом па-
раграфе, состоит в том, что процесс конструирования си-
стемы обратной связи удается отделить от процесса об-
работки измерений. Это позволяет проделать основные
расчеты в процессе конструирования системы, а в кон-
туре управления иметь весьма простую специализиро-
ванную вычислительную машину. Можно ли при реали-
зации предлагаемого подхода добиться такого же раз-
деления задач построения оценки и матрицы коэффици-
ентов усиления? Этот вопрос требует исследования.
Б. Представляет интерес изучить некоторые асимпто-
тические свойства обсуждаемых решений задачи синте-
за. Предположим, в частности, что измерения величины
у очень точны. Это значит, что дисперсия ошибок изме-
рения этой величины мала. Какие упрощения в проце-
дуру синтеза внесет это предположение? Как осущест-
вить переход к предельному случаю, когда измерения
величины у абсолютно точны?
Другой крайний случай — это тот, когда точность из-
мерения величины у очень мала; но зато количество из-
мерений очень велико.
В. В данном параграфе мы рассматривали задачи
синтеза, предполагая, что каждая из координат — управ-
ляемая в том смысле, что компоненты вектора v входят
S66	ПРОБЛЕМА СИНТЕЗА ОПТИМАЛЬНЫХ СЙСТЁМ [ГЛ. IV
во все уравнения системы (4.1), т. е. предполагая, что
векторы z и v имеют одинаковую размерность. Однако,
как уже указывалось в предыдущем параграфе, типич-
ной является иная ситуация, когда размерность вектора
v меньше размерности вектора z. Она может быть све-
дена к рассматриваемой при дополнительном ограниче-
нии типа
о! = 0, s = 1, 2, ..., п — т. (4.32)
В предыдущем параграфе мы видели, каким образом
можно справиться с этой трудностью. Ограничения типа
(4.32) требуют значительно более громоздких выкладок
при вычислении матрицы обратной связи, однако сохра-
няют в силе основной результат: управление vk является
линейной функцией оценки, причем управление зависит
от оценки так же, как в случае полной информации
управление зависит от фазовых координат.
Для того чтобы избежать осложнений, возникающих
в случае, когда размерность вектора v меньше размер-
ности фазового вектора, можно снова воспользоваться
методом штрафных функций. С целесообразностью их
введения в задачах с ограничениями мы уже встрети-
лись в предыдущем параграфе. Штрафная функция, ко-
торую мы использовали, имела вид
N-1
F(v0, ..., vN) = 2 (Pi, Kvi)
или, если К — диагональная матрица,
JV-1 п
f = S 3	<433>
4=0 S=1
Если, по условию, vl =0, то соответствующий коэф-
фициент k/ должен быть принят очень большим.
Разумеется, в этом случае уже трудно говорить об
оптимальном синтезе в его первоначальной формулиров-
ке. Тем не менее в ряде случаев описанным способом мы
можем получить «хороший» возможный синтез. Заме-
тим, что мы всегда при этом можем оценить качество по-
лученной этим способом системы управления, поскольку
величина отклонения от программы (гя, RzN) всегда мо-
§ 4]	ЗАДАЧИ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ	367
жет быть вычислена, как только управление v = Bz опре-
делено.
6. Еще одно замечание о функциях штрафа. В этой
книге мы не раз подчеркивали значение метода штраф
ных функций в теории оптимального управления. В этой
главе, обсуждая основные вычислительные проблемы
синтеза, мы также были вынуждены использовать функ-
ции штрафа. Однако функции штрафа, которые были
введены ранее, имели совершенно иной характер. На-
помним. что в задаче оптимального управления мы рас-
сматривали наряду с функционалом J(u) «штрафован-
ный» функционал Д(м), который был связан с J (и) ра-
венством
A (u) = J («) + №, (и),
где Л — некоторое положительное число, a Л(м) —функ-
ция штрафа — неотрицательная функция, которая обра-
щается в нуль на множестве допустимых управлений.
Между функционалами Д и J существует одно важ-
ное соотношение. Пусть и* — решение исходной задачи,
ик — «штрафованной задачи». Тогда, очевидно,
А(«%) < А («*) = J (и*) + h (и*),
но /г.(м*) =0, и мы находим
А («х)</(«*)•	. (4.34)
Таким образом, решение «штрафованной» задачи дает
всегда нижнюю оценку. Далее, во многих случаях уда-
ется доказать, что
lim JK (ui) = J («*),
Л—>+oo
т. ё. последовательность nt слабо сходится к и*.
Никакого аналога подобных теорем для функций
штрафа F(v0, ..., t>w), введенных в этой главе, доказать
не удается: функции штрафа F(v0, ..., vN) не обраща-
ются в нуль на допустимых решениях, и даже оценка
(4.34) в общем случае не имеет места.
Глава V
ЗАДАЧИ СИНТЕЗА, СВОДЯЩИЕСЯ
К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Общая задача синтеза, которая обсуждалась в § 1
предыдущей главы, как не раз подчеркивалось, очень
трудна. В настоящее время, обсуждая вычислительные
методы, имеет смысл рассматривать только некоторые
простейшие классы задач этой теории. Наиболее просты-
ми классами задач теории синтеза являются задачи син-
теза линейных систем с квадратичными или линейными
функционалами. Для решения этих задач, как мы в этом
уже убедились, могут быть использованы методы дина-
мического программирования. Однако эти общие и силь-
ные методы оказываются применимыми лишь в некото-
рых исключительных случаях: практическое построение
решения в случае квадратичного функционала оказыва-
ется возможным (если не использовать метод штрафных
функций) лишь при условии отсутствия каких-либо огра-
ничений на фазовые координаты и управления.
В исследованиях предыдущей главы мы не делали
никаких предположений о структуре оператора обрат-
ной связи. Как следствие анализа, оказалось, что опера-
тор управления является линейной функцией фазовых
переменных (или оценок).
Если форму зависимости управления от фазовых ко-
ординат системы задать заранее, то задача качественно
упростится, поскольку в этом случае нам остается опре-
делить лишь некоторые функции времени или парамет-
ра,- Задачи синтеза, в которых форма функциональной
зависимости оператора управления задана, превраща-
ются в некоторые специальные задачи оптимального уп-
равления. Однако, в отличие от задач, которые мы рас-
сматривали в первых главах этой монографии, диффе-
ренциальные связи и ограничения носят стохастический
характер. Это обстоятельство вносит целый ряд особен-
ностей в структуру вычислительных процедур. Анализу
подобных задач (линейных и нелинейных) будет посвя-
щена данная глава.
ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА
369

§ И
§ 1. Задачи линейного синтеза
1. Предмет исследования. В этом параграфе мы про-
должим изучение проблемы синтеза управления в линей-
ной системе с квадратичным функционалом для тех слу-
чаев, когда на управление наложены ограничения.
Возможность продвижения в данном случае достига-
ется ценой сужения множества допустимых решений: мы
будем искать оптимальное управление в классе управле-
ний, являющихся линейными функциями фазовых коор-
динат. Итак, управление мы будем разыскивать в форме
линейного агрегата
W = Cz,	(1.1)
где С=||с«(ОН—искомая матрица. Эту матрицу мы бу-
дем называть матрицей обратной связи. Ее коэффици-
енты условимся называть коэффициентами усиления.
Их значения могут быть стеснены различными условия-
ми, которые мы будем записывать в виде
eeGs-	(1-2)
Наиболее часто мы сталкиваемся с ограничениями вида
сц «С Сц Сц,	(1.3)
где су и су — заданные числа.
В практических задачах не все координаты могут
быть измерены, и поэтому управление W может быть
функцией только некоторых из компонент вектора z. Да-
лее, не на все фазовые координаты мы можем непосред-
ственно воздействовать управлением. Например, мы не
можем непосредственно изменить положение механиче-
ской системы — мы можем изменить лишь скорость си-
стемы. Таким образом, в реальных системах управления
матрица С будет иметь размерность п'Хп", где п' и п"
удовлетворяют неравенствам п'^п и п"^.п, п — размер-
ность фазового вектора. Величины п' и п” должны быть
заданы — это конструктивные характеристики.
Легко видеть, что данная ситуация полностью вкла-
дывается в ограничения вида (1.3). Можно считать, что
многие из элементов матрицы С равны нулю. Эти эле-
менты также удовлетворяют ограничениям вида (1.3),
370
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
где соответствующие им величины с~ и с* равны нулю.
Матрицу C(t), удовлетворяющую условиям вида (1.2) —
(1.3), мы будем называть допустимой. Итак, мы будем
изучать динамические системы, поведение которых опи-
сывается уравнением
г = A(t)z + C(t)z + F(t).	(1.4)
Здесь А (/) =||а«(0 II — заданная матрица, F(t)—слу-
чайный процесс. В этом параграфе мы будем считать,
что F(t) нам задан; либо мы знаем все его корреляцион-
ные функции (мы увидим ниже, что нам достаточно
знать матрицу вторых моментов), либо нам известно ка-
ноническое представление случайного процесса. Не огра-
ничивая общности, мы можем принять, что F(0=0.
Начальное значение вектора z
z(O) = zo	(1.5)
мы будем считать случайной величиной с нулевым мате-
матическим ожиданием zo=O. Как частный случай мы
можем рассмотреть тот, когда начальное состояние нам
известно заранее или измерено в момент начала дви-
жения.
В качестве критерия для выбора функций мы
примем функционал
(1-6)
где /?=||г«|| — заданная матрица. В практических зада-
чах матрица R. всегда симметрична, а квадратичная фор-
ма (1.6)—положительно определенная. Это условие мы
сохраним и в данной работе.
Итак, задача, которая изучается в данном парагра-
фе, состоит в отыскании допустимой матрицы C(t), до-
ставляющей минимум функционалу (1.6). Эту задачу
мы и будем называть задачей о линейном синтезе.
Для дальнейшего нам будет удобно вместо системы
(1.4) рассматривать следующую:
z = Dz + F,	(1.7)
где D—A + C. Матрицу D мы будем считать неизвест-
ной. В силу неравенств (1.3) ее коэффициенты будут
§ 11
ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА
ЗЯ
стеснены условиями
(1.8)
где
dy (0 = ац (0 + су, dh = atj (t) + ctj.
2. Сведение к задаче оптимального управления.
Сформулированная задача может быть сведена к задаче
оптимального управления специального вида. Для того
чтобы это показать, рассмотрим систему уравнений, со-
пряженную системе (1.7):
p = —D*p,	(1.9)
где D* — матрица, сопряженная D. Используя (1.9), нахо-
дим (р, z) = (р, F) или
(р (Т), z (Г)) = (р (0), г (0)) + J(p (0, F (/)) dt.	(1.10)
о
Рассмотрим теперь векторы р«, удовлетворяющие
уравнению (1.9) и следующим условиям при
Р/(Л = ^	(1-11)
где д/ — символ Кронекера. На основании (1.10) мы будем
иметь
z' (Т) = (р/ (0), z (0)) + J (pt (t), F (0) dt, i = 1.n.
0
Составим выражение для функционала (1.6)
п	п ________
^r^(T)zi(T)^ S {П/Ш(0)р?(0) +
/,/=1	Z,/,s,fc=i
Т Т
- • +iirllFs(t1)Fk(tz)psl(t1)p^(tz)dt1dtz}. (1.12)
0 0	'
При выводе выражения (1.12) мы предполагали, что
начальные значения вектора z и случайный процесс F(t}
взаимно не коррелированы.
372 СВЕДЕНИЙ к ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [Г Л. V
Первое слагаемое в выражении (1.12)—это квадра-
тичная форма от начальных значений компонент векто-
ров pt.
Введем обозначения
п ______ п
3 г«Ш(0)Р/(0)= 3 ^Р/(О)Р?(О) =
Z,/,s,&=i	ltifStk=l
где 7’/ = n/ZoZo. Второе слагаемое в выражении (1.12)—это
интеграл от квадратичной формы компонент векторов pt.
Введем обозначения
Т Т п
П 3 n/fs(Q^(^P/(^i)ph4)^^-
6 о ij.s.fal
Т Т п
— J j S r if (4> Q Pi (^i) Pi (fz)	=
О 0 Z,/,S,£=1
Т Т
J J Q ^2» Pi Ui)> Pi (^2)) dti dtfy
о о
где (4Л) = П/П4ИЧ)-
Итак, функционал (1.12) мы можем представить в
виде
т т
J = Р(РАУ, Pi(W) + ИQ(ii, k.	(1.13)
о о
Каждый из векторов Pi <= R" и удовлетворяет уравнению
(1.9). Введем пространство Rn‘ —прямое произведение
евклидовых пространств R" и вектор у <= Rn, векторные
компоненты которого равны pi е R? (i = 1, 2.......п).
Тогда для вектора у мы будем иметь следующее диффе-
ренциальное уравнение:
p = B(dz/(0)P,	•	(1.14)
5 Й
Задачи линейного синтеза
373
где матрица В, зависящая от неизвестных функций </«(/),
размерность которой равна п2, имеет вид
— D*\
: — D*
Компоненты векторов pt и у связаны очевидными со-
отношениями p’ = z/(<_1)n+*. Компоненты вектора у дол-
жны при t=T удовлетворять следующим краевым усло-
виям:
/-1,n+s(T) = dzs.	(1.15)
Соответственно с этим функционал (1.13) мы можем пе-
реписать в таком виде:
т т
J = Р (уq) + J J Q (/lt У (4)> У &)) dtr
о о
где
п	п2
Р(Уо) = 3 ^/Р/(О)Р/(О)= 3	ет1УтУ1~(У,Еу),
п	~	п2
Q- 2	3	^т1УтУ1 = (у, Ф*/).
m,Z=i
Индексы i, j, s, кит, l связаны равенствами
m = (j—l)n + s, l — (i—\)n + k.
Эти равенства однозначно определяют т и I по значени-
ям i, j, s, k. Поскольку i, j, s, fe —целые положительные
числа, не превосходящие п, то при заданных т и I одно-
значно определяются и i, j, s, k. Пусть, например, мы за-
дали числа т^п и 1^п. Тогда из равенства
п
374 Сведение к задачам оптимального управления [М V
следует, что k = l, i=l. Это будет единственное решение,
удовлетворяющее нашим ограничениям.
Аналогично находим s = m, j=l. Если n<Z^2n, то
k=l — п, 1=2 и т. д. Наконец, если п(п—l)<Z<;n2, то
k=l— (п— l)n, i=n.
Используя эти соотношения для индексов и симмет-
рию матрицы и корреляционной матрицы ||, г® z*||, лег-
ко доказать самосопряженность матрицы Е.
Пусть 1^п, т^.п. Вычисляя последовательно emt и
е1т, находим что в первом случае i=l, k = l, j=l, s = m.
Во втором случае Z=l, k = m, j=l, s=l. Таким образом,
- ~ml , ml	„ ~lm ~
6ml — Гц — Гu^o Zo,	в1щ — Гц — Г,
Т. в.
Для полного доказательства нам надо перебрать все
возможные комбинации п</^2п, т^.п\ n<Z^2n, п<
<.т^2п и т. д.
Матрица Ф в общем случае может быть и не самосо-
пряженной, поскольку может оказаться, что F^F^t) =/=
^F^tt^F*^. Используя эти обозначения, функционал
/ можно переписать в следующей форме:
г г
J = (У (0), Еу (0)) + J j (у (Q, Ф (Zn t.) у (tj) dt. dtz. (1.16)
0 0
Итак, мы пришли к утверждению, которое сформули-
руем в виде теоремы:
Теор ем а. Задача линейного синтеза (1.1) — (1.6)
эквивалентна следующей задаче оптимального управле-
ния: определить управления dtj(t) и фазовую траекторию
y(t)^Rn*, удовлетворяющие условиям (1.14) — (1.15) и
доставляющие минимум функционалу (1.16).
Таким образом, задача линейного синтеза сведена к
некоторой специальной задаче теории оптимального уп-
равления. Однако в общем случае эта задача оказыва-
ется еще достаточно сложной. Заметим прежде всего,
что она существенно нелинейна. Далее, ее размерность
может оказаться весьма большой. Если в формировании
функционала участвуют все п составляющих фазового
вектора, то размерность вектора у равна л2. Однако это
не единственная трудность, с которой мы здесь сталкива-
§ и	ЗАДАЧИ линейного синтеза	375
емся. Вторая (и может быть главная трудность) состоит
в том, что функционалы (1.16), с которыми нам прихо-
дится иметь дело, не относятся к тому типу, который
обычно рассматривается в вариационном исчислении и
теории оптимального управления, и для изучения подоб-
ных задач у нас нет готовой теории. Для этой общей за-
дачи, как мы увидим, также может быть сформулирован:
принцип максимума. Однако его трудно использовать
для фактического решения задачи, поскольку уравнения
для множителей Лагранжа (сопряженных переменных)
оказываются интегро-дифференциальными, и вычисле-
ния с их помощью, даже для относительно простых за-
дач, весьма громоздки. Одна из трудностей, с которыми
приходится сталкиваться, состоит еще и в том, что зада-
ча после ее дискретизации оказывается неаддитивной, и
различные эффективные методы уточнения допустимого
решения, использующие свойства аддитивности (метод
блуждающей трубки, метод локальных вариаций), в
этой теории непосредственно не могут быть исполь-
зованы.
3. Градиентные методы. Обсуждение возможных вы-
числительных схем начнем с изложения методов гради-
ентного спуска.
Предположим, что из тех или иных соображений мы
задали матрицу обратной связи S(t). Решая задачу
Коши для системы (1.14), мы найдем значения вектора
соответствующие управлению B(t), а по формуле
(1.16) мы вычислим величину функционала 7. Положим
B = B + dB, y =	(1.17)
Делая замену (1.17) в уравнении (1.14) и отбрасывая
слагаемые, содержащие произведение 8В8у, мы получим
следующее уравнение для by:
6у = В6у + ЪВу.	(1.18)
Функция by(t) при t=T должна удовлетворять следую-
щим данным Коши:
6i/(T) = 0.	(1.19)
Выведем теперь формулу для вариации функционала.
376
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
Делая в (1.16) замену (1.17) и отбрасывая произве-
дение 8В8у, получим
т т
Ы = (8у (0), Е,у (0)) + J j (by (/х), К. Q У &)) dt* (1.20)
О о
где К (/1, Q = Ф (М t2) 4- Ф* (t* /i) Ei = 2Е. Если обозна-
т
чить через k (/) вектор k (/) = [ Д’(t, Q у (/2) dt* то в
6
выражении (1.20) останется только однократный интеграл
т
&J = (Ъу (0), с) + J (Ъу (0 (k (0) dt, (1.21)
О
где с = Еху(0).
Таким образом, если мы задали вариацию управле-
ния 6В, то вариация фазового вектора 8у определится
как решение задачи Коши (1.18), (1.19), а вариация
функционала может быть вычислена по формуле (1.21).
Полученные формулы позволяют поставить следую-
щий вопрос: каким образом выбрать допустимую вариа-
цию 6В, чтобы вариация функционала 6J была мини-
мальна. Ответ дается решением следующей задачи Боль-
ца: определить функции 6В(/) и 8y(t), доставляющие
минимум функционалу (1.21) при дифференциальных
связях (1.18), краевых условиях (1.19) и условии (1.8),
которому должны удовлетворять элементы матрицы
В+бВ.
Эта задача может быть сведена к двум задачам
Коши размерности п2 путем сведения задачи Больца
(1.21) к задаче Лагранжа и применения принципа мак-
симума Понтрягина. Так как
т	т
. бу(О) = — §by(t)dt = — §(Bi>y + 8By)dt,
О	о
то функционал (1.21) можно переписать в следующем
виде:
8J = j [(бг/, (k — В*с)) — (бВу, с)] dt. (1.22)
О
§ 1]	ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА	377
Для задачи (1.18), (1.22) выпишем теперь /7-систему:
6у = ВЬу + Ый,	(1.18)
ф = — B*q + k — В'с.	(1.23)
Функция 6В определяется из условия максимума
функции ff:
Н = (ф + с, дВу) = ЪЬцу1 (ф/ -1- с{)	(1.24)
i.i
при ограничениях
dy^by+bbi^dti.	(1.24')
Так как на значения 6г/(0) не накладывается никаких
условий, то
ф(0) = 0.	(1.25)
Итак, схема расчета 6В и by состоит из следующих
этапов:
а)	Решаем задачу Коши (1.23), (1.25).
б)	Определяем 8В; для этого находим максимум ли-
нейной формы (1.24) при ограничениях (1.24').
а) Решаем задачу Коши (1.18), (1.19).
Выполнив все перечисленные процедуры, мы вычислим
по формулам (1.17) новое значение элементов матрицы
коэффициентов усиления Bt=S+bB и новое значение
вектора у^у+8у.
Описанную процедуру можно использовать для орга-
низации спуска. Прежде всего мы вычисляем новое зна-
чение функционала J(yi). Если при этом окажется, что
(1-26)
то величины yt и Bt мы можем взять в качестве новых
приближений и повторить описанную процедуру, в ре-
зультате которой мы найдем у2, В2 и т. д.
Если неравенство (1.26) не будет иметь места,- и ока-
жется, что
J (У1) > J (у)»
то мы должны в качестве нового управления принять
величину
В = §4-МВ,
378
СВЕДЕНИЕ к ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ (Г Ji. V
где X — положительное число; 0<Х<1. В этом случае
функционал J становится функцией %, и мы выбираем
значение параметра из условия минимума J (X).
4. Случай, когда возмущение является стационарным
марковским процессом. Все расчеты значительно упро-
щаются, если корреляционная функция имеет специ-
альный вид, допускающий переход в выражении (1.16)
к функционалу с однократ-
ными интегралами.
Предположим, что слу-
чайный процесс F (/) в урав-
нении (1.4) является стацио-
нарным марковским процес-
сом с гауссовским законом
распределения. Тогда, со-
гласно теореме Дуба
(Doob)*), корреляционная
матрица случайного процес-
са F(t) имеет вид
где К— симметричная матрица, не зависящая от време-
ни. Число k называется коэффициентом корреляции.
В этом случае матрица Ф(/1( /2), введенная в п. 2,
может быть представлена в виде
где Т — симметричная матрица, не зависящая от време-
ни (доказательство симметрии матрицы Т проводится
аналогично доказательству симметрии матрицы Е в п. 2
настоящего параграфа).
Рассмотрим интеграл в формуле (1.16)
т т
О о
*) Дж, Л. Дуб, ВерЬятностные процессы, ИЛ, 1962.
§ 1]	ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА	379
Здесь G — квадрат (рис. 1.1). Обозначая через Gj и G2
два треугольника, изображенные на этой фигуре, мы
можем написать
1 = JJ	&)• чу lf№ dt* +
+ J (>('.-'«) Ш), 4y(ti))dt1dti,
Gt
поскольку в области G, Z2>Zt, а в области G2 имеет ме-
сто обратное неравенство.
Вычислим
h = JJ (у (Q, Чу (Q) dtt dtz =
Th
=	Vy^dt^.
О о
Заменим в этом выражении на f2, a t2 на tt:
Th
h = f p^)(y(/2), 4y(tl))dtidti,
О о
или, в силу самосопряженности матрицы Т:
т h
/1= J ^^(y^y^dt^.
о о
Отсюда видно, что
/2 = JJ e-k(h-h> (у (tl)f ЧУ (/,)) dta dtr = Zr
Итак, функционал (1.16) может быть переписан в сле-
дующем виде:
т / t	\
J = (у (0), Еу (0)) + 2 J e-ki у (Z), J е^Чу (t) dx dt. (1.27)
о \ о	/
Введем новую векторную переменную g размерности
пг при помощи соотношений
l = d*4y(f), £(0) = 0.	(1-28)
380
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
Теперь мы пришли к следующей задаче: определить век-
тор-функции y(t) и В(0 и управление B(t), доставляю-
щие минимум функционалу
т
(у (0), Еу (0)) + 2 f e~kt (у (t), g (/)) dt. (1.29)
О
Заметим, что скалярное произведение (у(Т), Еу(Т)) —
это известная величина. Поэтому вместо функционала
(1.29) нам достаточно рассмотреть функционал Д:
т
А = J [г* (у (0, | (0) - (ЕУ, Еу)} dt. (1.30)
О
Теперь мы получили уже обычную задачу теории оп-
тимального управления, правда, размерность этой задачи
равна 2п2.
5. Градиентный спуск в случае, когда внешние возму-
щения — стационарный марковский процесс. В п. 3 на-
стоящего параграфа мы рассмотрели метод градиентного
спуска для общего случая. Основная вычислительная
трудность, с которой мы столкнулись, состоит в необходи-
мости вычислять и помнить функцию вида
т
k (t) = J к (t, Г) у (t) dr.
о
В том случае, когда функционал представлен в форме
(1.29), в этом нет необходимости.
Обозначим через В некоторое начальное управление.
Тогда, решая задачи Коши для уравнений (1.14) и (1.28),
мы находим начальное приближение для вектор-функций
у и £. Положим
У=У + &У,	+ в = в + &в.
Подставляя эти выражения в уравнения (1.14), (1.28) и
функционал (1.30) и проводя линеаризацию, получим
Ъу^В6у+ЬВу,	(1.31)
(1.32)
§ 1]
ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА
381
5Л=	+
— [Sy, (ЕВ + В'Е)у — Еу, №у\} dt.
Функция бу обращается в нуль при /=Т, а функция £
обращается в нуль при Z=0. Никаких ограничений на
значения у(0) и £(Т) не накладывается. Поставим снова
задачу отыскания 6В, доставляющего минимум функцио-
налу 6Д. Для этого составим функцию Гамильтона и
уравнения для множителей Лагранжа ф„ и ф?:
И — (ф^, Вбу 4- б By) 4-еы(ф^, Тбу) 4-
4-	(бу, [ЕВ 4- В*Е\у) -ew[(6y,I) 4- (У, 6g)] 4- Ни (1.33)
Ях = —(£у, бВу),
фу = — В*фу—е«Т’ф5 4- e-«f- (ЕВ 4- В*В) у, (1.34)
Фб = <г«у.	(1.35)
Условия трансверсальности нам дают
фД0) = 0,	(1.36)
ih(T) = 0.	(1.37)
Выпишем в заключение общую схему одного шага гра-
диентного спуска:
а)	Решаем задачу Коши (1.35), (1.37) и запоминаем
функцию ф6.
б)	Решаем задачу Коши (1.34), (1.36) и запоминаем
функцию фДО-
в)	Находим 6В из условия максимума функции Я,.
С этой целью мы должны для каждого t решить задачу
линейного программирования.
г)	Положив В=В4-Х6В, определяем минимум Ц(к)
для значений Хе (0, 1].
6. Видоизменение описанной процедуры. Рассматри-
ваемая задача о минимизации функционала (1.30) обла-
дает одной особенностью: на значение векторов у(0) и
g(T) никаких ограничений не накладывается. Это обстоя-
тельство позволяет использовать схему последовательных
приближений, аналогичную схеме Крылова — Черноусько
(см. гл. II, § 4).
382
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
Для задачи (1.14), (1.15), (1.28), (1.30) составим
/7-систему:
/7 = (ф^, By) 4- eV (t|)w Чу) — е-ы (у, I) + (Еу, By),
= — В*^у - W’fc + e~kil — (3*5 + ЕВ) у,	(1.38)
=	(1.39)
Управление B(t) находится из условия максимума:
Нх = (я>₽. By) + (Еу, By).	(1.40)
Схема последовательных приближений выглядит те-
перь следующим образом. Пусть задано управление 3°,
которое мы принимаем за нулевое приближение. По-
скольку, согласно (1.15), у(Т) нам известно и, кроме
того, ф^Г) =0, то мы решаем одновременно задачи Коши
справа налево для уравнений (1.14) и (1.39). В резуль-
тате получаем некоторые функции y°(t) и ф?(/). Значения
этих функций можно не запоминать. Нам достаточно вы-
числить у°(0) и ф( (0). Так как |(0) =0 и ф1((0)=0, то
теперь мы можем решить задачу Коши слева направо для
системы уравнений (1.14), (1.28), (1.38). Одновременно
на каждом шаге процесса численного интегрирования мы
решаем задачу линейного программирования для линей-
ной формы (1.40). В результате находим матрицу ВД/),
которую и запоминаем. Далее повторяем всю описан-
ную процедуру, приняв в качестве матрицы 30 матри-
цу Bt.
Примечание.
1.	Данная схема рассуждений имеет ту же цель, что
и схема градиентного спуска, рассмотренная в предыду-
щем пункте данного параграфа: построить итерационную
схему, последовательно улучшая управления. По сравне-
нию с методом градиентов она требует меньшего объема
оперативной памяти машины.
2.	Для улучшения сходимости метода мы можем всег-
да воспользоваться стандартным приемом: принять в ка-
честве нового управления матрицу
В2 = Во К (Bi Во),
где Ае(0, 1), и подобрать А из условия минимума исход-
ного функционала.
§ 1]	ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА	383
3.	В качестве первого приближения целесообразно
рассматривать постоянную матрицу коэффициентов уси-
ления, коэффициенты которой определяются, например,
с помощью метода В. М. Пономарева. Тогда уже первая
итерация позволит нам оценить эффект, который может
быть получен за счет использования переменных коэф-
фициентов усиления.
7. О релейном характере коэффициентов усиления.
Продолжим изучение задачи оптимизации функционала
(1.6) при условии, что динамический процесс описывается
уравнением (1.7), где элементы матрицы коэффициентов
обратной связи D удовлетворяют ограничениям (1.8).
Функционал J является сложной нелинейной функцией
элементов матрицы D:
. J = J(D).	•	(1.41)
Если воспользоваться формулой Грина, то функция (1.41)
может быть выписана в явном виде, и мы придем к неко-
торой задаче нелинейного программирования. Структура
этой функции окажется весьма сложной, и сделать какие-
либо качественные заключения о природе решения труд-
но. Подход, который развит в этом параграфе, позволяет
с большей полнотой изучить некоторые общие свойства
синтезируемых систем, поскольку он сводит исследова-
ние к стандартной задаче оптимального управления, ко-
торую можно изучать с помощью принципа максимума
Л. С. Понтрягина.
Мы нашли, что исходная задача эквивалентна задаче
отыскания минимума функционала (1.30) при ограниче-
ниях (1.14), (1.15) и (1.28).
В предыдущем пункте мы доказали, что матрица В
необходимо должна доставлять максимальное значение
функций Hi, которую мы можем переписать в следующем
виде:
Hi = (фу + Еу, By) == (С, By), (1.42)
где С—^+Еу. Перепишем (1.42) в скалярном виде
#1 = 3 btfiyi,
t.i
384
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
Эту форму можно представить еще и так:
п2
(1.43)
S=1
где bs — надлежащим образом перенумерованные элемен-
ты Ьц. Так как элементы bs совпадают с элементами di
матрицы D, то они удовлетворяют ограничениям типа
(1.'8), которые мы перепишем так:
bT<bs^bt.	(1.44)
Очевидно, что решение задачи линейного программиро-
вания (1.43) — (1.44) при as# О принимает граничные
значения: bs=b+ при as>0, bs = b~ при a <0. Таким
образом, при as#0 коэффициент усиления является ре-
лейной функцией времени. Это обстоятельство может
быть использовано для построения численных методов.
В некоторых случаях удается показать, что число пере-
ключений не превосходит единицы.
Если на некотором отрезке времени as=0, то имеет
место особый режим *).
8. Анализ специальных случаев.
а) Процесс F (t) сильно коррелирован.
В этом случае в выражении для корреляционной функции
показатель k — величина малая.
Если в уравнениях (1.28), (1.38) и (1.39) положить
fe=0, то они примут следующий вид:
i = Чу,
фу = —	— (В*Е + ЕВ)у, (1.45)
ф5= t/.
Система (1.45) не содержит быстрорастущих множи-
телей и удобнее для численного интегрирования, нежели
*) Возможность существования особых режимов в задачах син-
теза показана в работе: И. А. В а т е л ь, Е. М. Шевченко, Об
одном классе задач линейного синтеза, Автоматика и телемеханика,
№ 10, 1971.

ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА
385
система (1.28), (1.38) и (1.39). Кроме того, эта система
допускает первый интеграл g =Чгф$+С, Так как ^(Т) =
= 0, то постоянная С определяется следующим об-
разом:
т
С=ЦТ)= $4ydt.
о
Это обстоятельство также может служить источником
ряда упрощений для численного счета.
• б) Процесс F(t) слабо коррелирован.
В этом случае k—величина большая. Рассмотрим исход-
ное выражение для функционала (1.16) и выпишем вы-
ражение для двойного интеграла
т т
о о
Т Т
=	Чу (t^)) dt^dt^ —
о о
Т / t	\
= 2 J e~kt у (0, J ekx4y (г) dx dt. (1.46)
о \ о	/
Преобразуем это выражение, вычислив внутренний ин-
теграл по частям:
т
« J	k
о
т	t
— e~kt (у (0, Чу (0) + J е/»Чу (т) dx) dt.
о	о
Повторяя аналогичные выкладки для интеграла Л,
мы убеждаемся в справедливости оценки Л = О(1/&),
и, следовательно, интеграл (1.46) представим в виде
т
1 = 'Т^У {t}'Wy ° dt+ •	(L47)
о
13 H. H. Моисеев
386
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ 1ГЛ. V
(1.49)
Заменяя в выражении (1.16) двойной интеграл его
оценкой (1.47) и отбрасывая величины O(l/fe2), приходим
к задаче со следующим функционалом:
т
J = (У (0), Еу (0)) + -f - J (У (0, Чу (0) dt.	(1.48)
О
Выше мы видели, что
т
(у (0), Еу (0)) = (у (Г), Еу (Г)) - 2 J (Еу, By) dt.
Делая эту замену в интеграле (1.48) и отбрасывая сла-
гаемые, не зависящие от искомых величин, мы придем к
задаче с функционалом
т
A =	4y(t))~(Ey,
О
Легко видеть, что размерность задачи с функциона-
лом (1.49) равняется п2, в то время как размерность
задачи с функционалом общего вида (1.30) равня-
лась 2п*.
Таким образом, в случае слабой корреляции внешних
возмущений вычислительные трудности определения оп-
тимальной матрицы обратной связи значительно умень-
шаются. В предельном случае k=oo система управления
должна компенсировать только начальные возмущения.
Заметим еще, что случай малокоррелированных внешних
возмущений очень часто встречается в практических за-
дачах.
в) Корреляционная функция является
функцией Дирака:
Ф(/1»/я) = Фд(^-/,),
где Ф — некоторая постоянная матрица.
тт	т
J $ (У Pi)» Ф (К, t2) у &)) dtt dt2 = J (у (t), Фу (t)) dt,
0 0	о
J
§ 1]	ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА	387
т. е. в этом случае задача линейного синтеза также сво-
дится к обычной задаче оптимального управления с одно-
кратным интегралом.
9.	Применение канонических разложений. До сих пор
мы все время предполагали, что процесс F(t) задан своей
корреляционной матрицей. В этом случае функционал
содержит двойной интеграл, и задача может быть серьез-
но упрощена только в том случае, когда процесс F(t)
является стационарным и марковским с гауссовским за-
коном распределения. Однако далеко не всякий процесс
можно схематизировать как марковский процесс. Поэто-
му в последние десятилетия при решении инженерных за-
дач все чаще случайный процесс начинают аппроксими-
ровать агрегатом
Г
F(0 = S<W(0>	(1-50)
где аг — взаимно некоррелированные случайные векторы,
а <р*(0—определенным образом подобранные детерми-
нированные функции времени.
Представление (1.50) называется каноническим раз-
ложением случайного процесса*). Если случайный про-
цесс нам задан своим каноническим разложением, то кор-
реляционную матрицу легко вычислить:
К(4, Q - ||Fl(/,)F1 &)|| = 13 (tj <р,(/а)|. (1.51)
Но так как векторы ар и ач независимы, то

Г
3	(^1)	(^2)
<7=1
*) Каноническое представление дает весьма гибкое описание слу-
чайного процесса, удобное для расчетных целей. Заметим, что проце-
дура обработки наблюдений, приводящая к каноническому заданию
случайного процесса, не более трудоемкая, нежели процедуры, при-
водящие к другим описаниям. К некоторым вопросам, относящимся к
теории ,и использованию канонических представлений, мы вернемся в
§' 3 этой главы? ‘ •
13*
388
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
Используя (1.51), преобразуем двойной интеграл в фор-
муле (1.12):
т т ____________
J J riiFs (о Fk	(tj pkt	dt, dt, =
о о
г ______ Т	Т
= 3 гиача9 J Р/ (О Ф<? (О dt J Pi (О Ф« (0 di =
<7=1	О	О
г	Т	Т
= 3 Г/Д J psi (О Ф, (0 dt J pt (О ф, (О dt.
q—1	о	о
Переходя теперь к переменной у, второе слагаемое в
формуле (1.12) мы можем переписать так:
т т
3 П ritFs (Q Fk (t,) psi (О p? (4) dt, dt, =
о о
r n2	T	T
= 23 Smiq J ym (/) ф, (0 dt j у1 (О Ф, (/) dt.
q=l mtl—l о	0
Введем новые векторы:
1 = УФ„ ^(0) = 0.	(1.52)
Тогда окончательно функционал (1.16) мы можем пред-
ставить в следующем виде:
г
j = (У (0), Fy (0)) + 3 (^ (Т), G&, (П).	(1.53)
</=i
Здесь Gq— матрица с элементами gmtq.
Итак, в том случае, когда случайный процесс внешних
возмущений задан своим каноническим разложением, мы
приходим к следующей задаче. Определить вектор-функ-
ции y (i), gg(Z) и управление В (/), доставляющие минимум
функционалу (1.53) при условиях (1.14), (1.15) и (1.52).
Размерность полученной задачи весьма большая —
(г+1)п2. Однако следует иметь в виду два обстоятель-
ства. Во-первых, описанная процедура редукции приме-
нима к задачам линейного синтеза в самом общем слу-
чае, каков бы ни был случайный процесс внешних возму-
щений F(ty Во-вторых, задача оптимального управления,
§ 1]	ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА	389
которую мы получили,— это задача со свободным кон-
цом*). Последнее обстоятельство значительно облегчает
ее численное решение.
10.	Роль ошибок в контуре обратной связи. В этом па-
раграфе мы рассматриваем проблему управления систе-
мой, которая описывается уравнением (1.4). Управление
W (z) при этом мы все время считаем линейной функцией
фазовой переменной
W — C(f)z.	(1.54)
Соотношение (1.54) реализует обратную связь. Значе-
ниям фазовой переменной z оно ставит в соответствие ве-
личину управляющего воздействия, изменяющего состоя-
ние системы.
Возможность представления обратной связи в форме
(1.54) опирается на следующую гипотезу: фазовые коор-
динаты z(t) в любой момент времени могут быть точно
измерены. В действительности мы измеряем эти величины
всегда с некоторой ошибкой. Более того, мы измеряем не
сами величины z(/), а некоторые функции этих величин.
С этим обстоятельством мы уже сталкивались в послед-
нем параграфе предыдущей главы. В результате обработ-
ки измерений мы получаем некоторую оценку величины z.
будем обозначать ее буквой g. Следовательно, вме-
сто (1.54) мы должны искать управление в форме
W = C(t)l	(1.55)
Но величины g и z связаны между собой соотношениями
5(0-г(0 + Л(0,	(1.56)
где /i(0—некоторый случайный процесс. Следователь-
но, уравнение динамической системы будет иметь вид
z = Azh + Cz + Ch 4- F.	(1-57)
Выясним, насколько изменит структуру искомой матри-
цы обратной связи появление в правой части (1.57) сла-
гаемого Ch. Случайные процессы h(t) и F(t) условимся
считать между собой некоррелированными. Такое предпо-
ложение вполне естественно, поскольку оно отражает тот
*) Имеется в виду, что у //(^свободен левый конец, а у %q(t) —
свободен правый.
390 СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
факт, что внешние возмущения (вариации тяги двигате-
лей, порывы ветра и т. д.) не влияют на процессы изме-
рения фазовых координат*).
Коэффициенты матрицы обратной связи будем считать
подчиненными ограничениям (1.3). Поставим задачу оты-
скания матрицы обратной связи С (Г), доставляющей ми-
нимальное значение функционалу (1.6), считая, что h и
F — стационарные марковские случайные процессы с га-
уссовским законом распределения.
Повторим кратко выкладки начала этого параграфа.
Введем снова сопряженные векторы pt (i= 1,2,..., п),
удовлетворяющие уравнению
i>i = — A*pi — C*ph	(1.58)
и подчиним эти векторы условиям pj (Т) = 6/. Введем еще
вектор у размерности п2:
р? = /'1,п+8.
Он будет удовлетворять уравнению у = Му 4- Ny, где
Составим теперь выражение для функционала (1.6).
Повторяя выкладки п. 2 данного параграфа и исполь-
зуя введенные обозначения, мы приведем это выражение
к следующему виду:
т т
j = {У (0), Еу (0)) + j J (у &) Ф (t„ tz) у &)) dt, dt2 +
о о
Т Т
+ И (W &), Фх (!,, У Му (У) dt, dtz. (1.59)
о о
Элементы матрицы Ф, как мы видели, содержат сла-
гаемые ri5F8 (^) Fk (Z2).
Элементы матрицы Ф4 отличаются только тем, что
вместо случайного процесса F(t) в них фигурируют
*) Это предположение не является существенным, но зато прцво.-'
дит к значительному сокращению объема выкладок.
ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА
391
§ 1)
компоненты случайного процесса h(t)-.
rlfha(t.)hk^.
Итак, если мы будем учитывать ошибки измерений,
то придем к задаче отыскания вектор-функции y(t) и
матричной функции N(t) (управления), доставляющих
минимум функционалу (1.59) при условиях (1.58).
Сравнивая функционалы (1.16) и (1.59), мы видим,
что они отличаются одним слагаемым, содержащим мат-
рицу N. Функционал (1.59) зависит не только от фазово-
го вектора y(t), но и от управления N(t). Если ошибки
h(t) достаточно сильно коррелированы, то оптимальное
решение — величина коэффициентов усиления — в реаль-
ном случае может весьма сильно отличаться от идеаль-
ного случая точных измерений, который мы рассмотрели
в начале параграфа. Для иллюстрации сказанного рас-
смотрим простейший пример системы первого порядка.
11.	Иллюстративный пример. Предположим, что ди-
намическая система описывается уравнением первого по-
рядка
г = az 4- с (г 4- h (0) 4- F (t), z (0) == z0.	(1.60)
Здесь z(f), F(t), a(t), c(t) и h(t) —скалярные функции.
Рассмотрим задачу отыскания функций z(t) и с(0,
доставляющих минимум функционалу
J-ЦТУ	, (1.61)
Введем сопряженное уравнение
р = —ар—ср,	(1.62)
где р(Т) = 1. Тогда
т	т
г (Г) = р (0) z (0) 4- f Р (О F (0 dt 4- J р (0 с (0 h (0 dt.
О	о
Составим выражение для функционала (1.61):
т т
J = Цту = ? (0) ?(0) + $ J р (0) р (0) Kf (0, dt. dt2 4-
0 0
T T
+ f f P (0k (0) P (0) C (tj Kb (0, 0) dt. d0. (1.63)
О о
392 СВЕДЕНИЕ к ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
Здесь через К* и K.h обозначены корреляционные функции
процессов F (t) и h(t):

Будем считать эти процессы стационарными марковски-
ми процессами с гауссовским законом распределения.
Тогда
K.F = <*е exp {— kF pj — tz |},
,	(1-64)
Кл = ah exp {— kh | tx — 41}.
Используя выражения (1.64), преобразуем функцио-
нал (1.63):	т
J = (Р2 (Л + 2 J (ар* 4- ср2) dt) г* (0) +
о
г	t
4- 2вр |* в Kpip (t) j еКрХ р (х) dx dt +
О	о
г	*
4* 2<Тй J e~Khtp (t) с (t) J eKf,Xp (x) c (x) dx dt. (1.65)
о	0
Введем еще переменные g и rj:
| = /^р,	цо) = о,	(i.66)
x\—eKhipc, n(0) = 0.	(1.67)
Преобразуем функционал	используя (1.66)
и (1.67), и, кроме того, отбросим в нем величины, не за-
висящие от управления и фазового вектора. В результате
получим
г
4 = J {(ар2 4- ср^^Щ- Ore~KFtpl + <&Кк*рт\с} dt. (1.68)
О
Итак, мы пришли к задаче отыскания минимума функ-
ционала J(p, £, ц, с) при условиях (1.66), (1.67) и (1.62).
Мы видим, что можно пренебречь влиянием ошибки на
выбор коэффициента усиления в двух случаях: а) если
ЗАДАЧИ ЛИНЕЙНОГО СИНТЕЗА
393
§ 1]
дисперсия ошибки пренебрежимо мала и б) если
ошибка очень малокоррелирована, т. е. если Kh— велико.
12. Заключение. В этом параграфе, была изложена
теория, позволяющая для линейных динамических систем
конструировать оператор обратной связи, считая, что он
является линейной функцией фазовых координат. Эта
задача, вероятно, одна из самых распространенных в ин-
женерной теории управления. Однако численные методы
ее решения в случае конечного интервала времени почти
не разработаны.
Впервые оптимизационную трактовку задачи линей-
ного синтеза начал последовательно использовать, по-
видимому, В. М. Пономарев, который развил методы ре-
шения, основанные на ее редукции к задаче нелинейного
программирования. Для этого он использовал различные
приближенные способы построения явной зависимости
фазового вектора ог искомых параметров системы.
Теория, развитая в данном параграфе, основана на
идее редукции задачи линейного синтеза к некоторой спе-
циальной задаче оптимального управления.
Оказалось, что в общем случае функционал содержит
двойной интеграл вида
т т
K(t,x)y(x))dtdx.	(1.69)
О 6
Используя методику рассуждений принципа максиму-
ма (ныне уже ставшую стандартной), нетрудно для функ-
ционалов вида (1.69) получить необходимые условия экс-
тремума. Они будут получены в следующем параграфе.
Однако эти условия оказываются не очень удобными для
построения численных методов. Поэтому при изучении
численных методов мы опустили рассмотрение необходи-
мых условий оптимальности для общего случая и ограни-
чились для функционалов вида (1.69) рассмотрением
только одного метода градиентного спуска.
Анализ возможностей построения вычислительных ме-
тодов, которые предоставляют необходимые условия, мы
проводили, рассматривая, главным образом, простейший
случай, когда внешние возмущения являются стационар-
ным марковским процессом с гауссовским законом рас-
пределения. Полученные задачи уже и в этом случае
394
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ (ГЛ. V
имеют .весьма высокую размерность. Общий случай пред-
ставляет еще большие трудности. В то же время эти труд-
ности не следует и преувеличивать.
В большинстве технических задач расчет оператора
управления производится на стадии проектирования,
когда требования к алгоритмам не содержат жестких ог-
раничений на объем затрачиваемого машинного времени.
Такая же ситуация возникает и в экономических задачах.
Наконец, следует иметь в виду, что требования точности
в задачах синтеза также невелики. Поэтому описанная
методика для широкого круга задач дает приемлемые
способы решения.
Заметим еще, что, сведя задачу синтеза к задаче'
оптимального управления, мы можем использовать для ее
решения не только метод последовательных приближе-
ний, которому было посвящено основное место в работе.
Мы остановили свой выбор на этом методе, поскольку он
оказывается весьма эффективным в задачах со свобод-
ным концом, к числу которых принадлежат рассматри-
ваемые задачи. Для решения полученных задач теории
оптимального управления могут быть с успехом приме-
нены и другие методы. Развитая теория позволяет да-
вать ответы на целый ряд важных вопросов, встающих
перед инженером, проектирующим систему управления.
Одна из основных проблем синтеза, с которой сталки-
вается инженер,—это конструирование оператора обрат-
ной связи. Эта проблема может быть сформулирована на
языке теории матриц, поскольку каждому оператору
управления однозначно соответствует определенная мат-
рица С. Обратно, каждый набор ненулевых элемен-
тов матрицы С определяет оператор управления. Прав-
да, это соответствие уже не является однозначным:
обычно данную систему обратных связей конструк-
тивно можно реализовать несколькими разными спосо-
бами.
Задание данной системы обратных связей означает
задание определенного количества нулевых элементов
матрицы С и системы ограничений на остальные коэф-
фициенты. Используя аппарат, развитый в данном пара-
графе, мы можем выбрать оптимальное значение коэффи-
циентов усиления как функций времени и найти значение
критерия качества.
§ 1]	ЗАДАЧЙ ЛИНЕЙНОГО СИНТЕЗА	395
Следовательно, мы можем сравнивать разные вариан-
ты операторов управления, оценивать роль различных
ограничений и влияние на величину критерия качества
новых обратных связей, т. е. новых ненулевых элементов
в матрице С.
Конструируя оператор управления, инженер подби-
рает значения коэффициентов обратной связи, не поль-
зуясь обычно соображениями оптимальности. Чаще все-
го он их выбирает из условия устойчивости*). Эти же
условия дают иногда и допустимые границы изменения
коэффициентов усиления. Коэффициенты усиления, как
правило, выбираются постоянными.
Когда все параметры системы управления и ограни-
чения уже выбраны, то естественно возникает вопрос
о том, насколько системы с переменной структурой и,
в частности, с переменными коэффициентами усиления
оказываются более «выгодными», т. е. насколько они мо-
гут улучшить качество управления (понизить значение
дисперсии) по сравнению с системами управления, обла-
дающими постоянными коэффициентами усиления. Ответ
на этот вопрос, как мы видели, можно получить, исполь-
зуя приемы теории возмущений. В результате линеариза-
ции мы получаем некоторую линейную задачу теории
оптимального управления со свободным концом, и, сле-
довательно, ответ на поставленный вопрос требует реше-
ния двух задач Коши.
В рамках развитой теории можно решить еще целый
ряд важных инженерных задач. Однако существует, даже
в этом простом случае, целый ряд задач, который требу-
ет существенного усовершенствования используемого ап-
парата.
В §§ 3 и 4 гл. IV мы рассмотрели задачи без ограни-
чений; теперь, сузив класс операторов, среди которых
мы разыскиваем оптимальное управление, мы рассмотре-
ли класс задач, в которых существуют ограничения на
*) Динамический объект, для которого создается система управ-
ления, может быть устойчив или неустойчив — самолет конструиру-
ется устойчивым, а ракета — неустойчивой. Но система — динамиче-
ский объект плюс система управления — всегда конструируется
устойчивой. Если система неустойчива, то даже малые возмущения
могут быстро привести к большим отклонениям от программы.
396
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
величину коэффициентов усиления. Ограничения подоб-
ного рода не исчерпывают класс практически интересных
задач. Во многих случаях мы должны удовлетворять тем
или иным фазовым ограничениям. Наиболее важным слу-
чаем подобных ограничений являются- ограничения на
мощность корректирующего двигателя (энергетические
ограничения). Эти ограничения в частном случае имеют
вид
||Г|| = ||Вг||<6.	(1.70)
Другие типы ограничений имеют вид
р(г‘<с‘)<б	(1.71)
или
тах|?|<(Г	(1.72)
и т. д. Условие (1.71) означает, что вероятность того, что
значение координаты гг меньше фиксированной констан-
ты, ограничена.
Для задач с ограничениями типа (1.70) — (1.72) мето-
ды решения, изложенные в этом параграфе, непосредст-
венно применить нельзя. Для решения задач оптималь-
ного управления с фазовыми ограничениями приходится
обычно отказываться от непосредственного использова-
ния необходимых условий и искать прямые методы реше-
ния, или использовать методы с применением функции
штрафа.
§ 2.	Линейный синтез с ограничениями.
Принцип максимума
В этом параграфе мы рассмотрим необходимые усло-
вия оптимальности, аналогичные принципу максимума
Л. С. Понтрягина. Поскольку задачи линейного синтеза
сводятся к вариационным задачам с двойным интегра-
лом, то принцип максимума для этих задач не является
непосредственным следствием принципа максимума для
классических задач оптимального управления. Однако
применение стандартной техники игольчатых вариаций,
с которой мы познакомились в первой главе; позволяет
довольно просто получить нужные нам теоремы.
§ 2) .
ЛИНЕЙНЫЙ СИНТЕЗ С ОГРАНИЧЕНИЯМИ
39?
1.	Предварительные рассмотрения. До сих пор мы
изучали задачи синтеза без ограничений на правом конце
траектории. Однако представляют определенный интерес
задачи, в которых правый конец траектории подчинен
ряду условий. Наиболее типичное ограничение — это
ограничение на величину дисперсий по одной или не-
скольким фазовым координатам. Например, мы можем
поставить задачу отыскания управления, при котором
(г"-92(Т)^:С;, i = 0, 1,2, ..., fe<n. (2.1)
Остальные координаты свободны и должны быть выбра-
ны из условия минимума функционала
п п
/(г) = 3 3 П^(Т)г/(Т).	(2.2)
1=1 /=х
В этом параграфе мы будем продолжать изучение ли-
нейного синтеза, т. е. будем считать, что эволюция управ-
ляемой системы описывается уравнением
г = Az 4- Cz 4- F,	(2.3)
где A(t)—заданная матрица, C(t)—матрица коэффи-
циентов усиления, которую мы должны разыскать из
условия минимума функционала (2.2) при ограничениях
(2.1) и (1.3).
Условия (2.1) —это то новое, что вносится в рассмот-
рение. Задача с ограничением типа (2.1) весьма сложна.
С другой стороны, во многих практических задачах огра-
ничения выполняются со знаком равенства. Поэтому
вместо задачи с условиями (2.1) будем рассматривать
задачу с ограничением типа равенств
(z"-02(T) = Ci, j = 0, 1, 2, ..., /<п,	(2.4)
что, практически, не сужает класс рассматриваемых при-
кладных задач.
Следуя п. 2 предыдущего параграфа, каждой из пере-
менных z1' (i= 1, 2,..., п) мы поставим в соответствие
вектор pt, удовлетворяющий уравнению (1.9):
pl — — D*pi,	(1.9)
398 Сведение к задачам ОИтИмАльного управления [гЛ. V
где £)=Л + С, a Pt(T) удовлетворяет условию (1.11).
Тогда
т
г' (Т) = (pt (0), г (0)) + J to (0, Р (0) dt, i=l,2, п.
Таким образом, считая случайную величину z(0) и
случайный процесс F(t) независимыми, мы получим сле-
дующие формулы:
Ji = (zn-if(T) = (pn.i(Q), LPn4(0)) 4-
т т
+ J J Pn-{ (^i) К (^i, ^a) Pn-i (^a) dt^dt^.
i = 0, 1, 2,
i,
о 0
где L и К — матрицы: L = ||zU||, K = ||F‘(f1)F/(^a)||.
Введем теперь, следуя предыдущему параграфу, век-
тор У, удовлетворяющий уравнению (1.14). Тогда функ-
ционалы h мы сможем переписать в следующем виде:
т т
Ji (У) = (У (0), ь‘у (0)) + J J У (h) К? (tv у (Q dt.dt,,
(2.5)
о о
где матрица имеет следующую структуру:
0	0	0
0	^11Л12 • • • • • • f^nn	0
0	0	0
(л-£-1)п
п.
In
Матрица L* имеет такую же структуру.
Итак, мы пришли к задаче отыскания функции B(t)
и фазового вектора y(t), связанных уравнением
y = B(t)y	(1.14)
и граничным условием
У(Т)~ут,	(1.15)
§ 2]
ЛИНЕЙНЫЙ СИНТЕЗ С ОГРАНИЧЕНИЯМИ
399
доставляющих минимум функционалу
т т
J (у, В) = (у (0), Еу (0)) + J J (у (О, Ф /8) у (М) dt.dt.
О о
(1.16)
при ограничениях'
Jt(y,B) = Ct,	(2.6)
i = 0, 1,2, .... I.
В целях более подробного изучения задачи с ограниче-
ниями типа (2.6) нам необходимо развить аппарат прин-
ципа максимума для задач оптимального управления, со-
держащих двойные интегралы. Однако для удобства
дальнейших рассуждений мы сначала несколько преоб-
разуем полученную задачу.
2.	Вспомогательное преобразование. Сделав замену
/=—т, мы приведем рассматриваемую задачу к следую-
щему виду: определить функции tji(x) и Bt(T), доставля-
ющие минимум функционалу
j (Уъ = (У1 (0). Еу± (0)) +
+ J j" (У1 (Т1)>	(Ч> ^г) У1 (та)) dx^dx^ (2.7)
-г -г
при ограничениях
^1 = -В1(т)у1,	(2.8)
ат
Л(-Т) = //г,	(2.9)
Л(Л) = (^(0), L^(0)) +
О о
+ J J ({/1 (*i), Ki (tx, Т2) Уг (Т2)) dxtdx2 = Cl,
-т -г
i=0, 1,2, .... I.
(2.10)
При формулировке задачи (2.7) — (2.10) мы исполь-
зовали обозначения <р(—0=ф1(0- Задача (2.7) — (2.10)
400
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
является частным случаем следующей вариационной за-
дачи. Определить функции x(t) и u(t), доставляющие
минимум функционалу
J (х, и) = Ф (х &)) + J J ёй (х &), X &), Bi, У dl^ (2.11)
/° t9	Я
при ограничениях	I
Ji = Ф/ (* &)) + ) gi (х (ВО, х (ВО, , У ^1г	= Cit (2.12)
/о ^0
x = f(x,u, t),	(2.13)	s|
x(U = x0.	(2.14)
В задаче (2.11) — (2.14) фигурируют еще функции Ф„
зависящие от конечного состояния. Нам удобно для даль- ' >
нейшего заменить их однократными интегралами.	g
Прежде всего	|
с АФ,	1
ф< (х (Q) = \~Ч(х,и, Э - ф/ (X (t0)).	I
J ах	Я
Я
Но величины Ф.(х(/0)) —это, согласно условиям, извест-	ч
ные постоянные, которые в выражении функционала мож-	I
но отбросить.	I
Поэтому окончательно мы приходим к следующей за-	*
даче: определить функции x(t) и u (t), доставляющие ми- <
нимум функционалу	?
tt	4 it
J (х, u) = J % (x, и, t) dt -|- j* j" g0 (x (Bi), x (Ba), В1» £2)
^0	^0	j
(2.15) I
при ограничениях	»
x ^-f(x, и, t),	(2.16)	’
(2,17)
X (^q) — Xg,
§ 2]
ЛИНЕЙНЫЙ СИНТЕЗ С ОГРАНИЧЕНИЯМИ
401
jj (х,	(р/ (х, и, t) dt 4- J ( gj (x &), x (&j), у d^d^ =
to	to t0
= Cj, /=1,2, ...Л (2.18)
ueG„.	(2.19)
3.	Вычисление вариаций. Итак, мы будем рассматри-
вать задачу (2.15) — (2.19). Произведем обычным обра-
зом игольчатое варьирование управления и(/) (см.
гл. I, § 3):
«.(o-L” ”Р“'«’ +sl
|u (0 при t е [г, г 4- е].
Постоянная v должна удовлетворять условию aeGu.
Разность 8u(f)=uB(t)—u(t) будем называть игольча-
той вариацией управления.
Следуя общим правилам вариационного исчисления,
введем вариацию фазовой переменной h. Обозначим че-
рез x(t),xB(t) решения уравнений
х = f (х, и, t), хе — f (xg, ие, t),
удовлетворяющие одному и тому же начальному условию
(2.17). Тогда
d& /g=x0
lim
S-H>
xe — x
8
Пусть сначала /<т. Тогда очевидно, что h(t) =0, по-
скольку при t<x управления совпадают, а х„ и х удов-
летворяют одним и тем же начальным условиям. Следо-
вательно, х8(Г) =«(/), Пусть теперь t>x. Тогда по-
скольку при />т+8 имеет место равенство ив — й, то
х (t) = х (т) 4- У f (х, и, I) dl 4- j / (х, и, g) dl,
х	т+е
хе (t) = X (т) 4- ( / (хе, иг, I) dl 4- J / (xs, и, g)
j	Т+6
402
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
и, следовательно,
h (г!) = lim (— f (xe, ue, l) — f (x, u, £)] 4-
e->0 I в J
т
t
+- f m)-/(*.«,	.
8 J	J
T+8
На основании теоремы о конечных приращениях имеем
Л = У [/(*8®, «г, 5) ~f (* ©» « (g),	-
= 8 [/ (хе (т 4- 0хе), и, 14- 01е) —
— f (х(г 4- 0»е), й(х 4- 0ае), т 4- 0ае)],
где 0! и 02 удовлетворяют неравенствам 0^0.^ 1. В силу
непрерывности функций, входящих в это выражение,
f (хе (т 4- 0хе), v, т 4- 0j8) = / (х (г), о, г) 4- О (е),
f (х (т 4- 0ае), и(т 4- 0ав), т 4- 0ае) = f(x (т), и (г), т) 4- О (е).
Используя эти оценки, перепишем выражение для
h(f) в следующей форме:
t
h (0 = hx 4- lim — f ((/*, (x8 — x)) 4- о (| хЁ — x |)J dg, (2.20)
e-*0 8 J
r+e
где
= f(x (t), v, t) — f (x (r), m (t), r).	(2.21)
Заметим, что разность xe—x имеет порядок e. В самом
деле, х8(т)=х(т), а на интервале (т,т4-е) изменение ве-
личин хе и х описывается уравнениями вида (2.16),
правые части которых различны. Но так как длина интер-
вала равна е, то
хе (т 4- е) — х (т 4- е) — О (в).	(2.22)
При />тЧ-8 эти величины описываются одним и тем же
уравнением (2.16). Поэтому в силу теоремы о непрерыв-
§ 2]
ЛИНЕЙНЫЙ СИНТЕЗ С ОГРАНИЧЕНИЯМИ
403
ной зависимости решения от начальных данных оценка
(2.22) сохраняется при любых t, при которых существует
решение задачи Коши для
уравнения (2.16). Поэтому, h
переходя в равенстве (2.20)
к пределу, мы получим окон-
чательно
й(0 = Л1+(2.23)
Рис. 2.1
Таким образом, функция
h{t) разрывна (рис. 2.1).
При t<_x она тождественный нуль. При t>x она является
решением следующей задачи Коши:
h = 8j-h, h (т) = hx.	(2.24)
Рассмотрим теперь первое слагаемое функционала
(2.15)
it
= J<p0(x, u,
и введем новую переменную Р (t), удовлетворяющую сле-
дующей задаче Коши:
~ Фо (х,и, 0, J1(?o) = 0-	(2.25)
at
Определим вариацию этой величины
/ dJ1 \	Р — Л
а (/) = _L	= Нт	,	(2.26)
\ 4е /е_0	г—О	в
где —это значение P(t), вычисленное при u=uz,
х=хе, а Р — значение величины Р на оптимальной тра-
ектории.
Повторяя рассуждения, которые мы только что прове-
ли для величины h, установим, что величина а — разрыв-
ная, при /<т она тождественный нуль, а при />т она
404 СВЕДЕНИЕ к ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
удовлетворяет следующей задаче Коши:
a—а(т) = аь
дх ' ’	1
(2.27)
где
ах = <р0 (х (т), о, т) — <р0 (х, й(х), -г).
(2.28)
Перейдем теперь к анализу второго слагаемого в вы-
ражении (2.15). Обозначим
J2 = J f go &), х (&), & dglt d&.
/о to
Вычислим
ti G
6J2 = lim 1C f {g0 (xe (^), xe (U J-v &) -
e-H) 8 J J
go (% (?1)> * (£2), Ы} —
= j j ^g0 (* Ы, h (lx)) d^ +
to to
+ ( ПФ?о(х(Ы.х(Ы. Ех, Е«), h dlt d&.
Щ дх(&)	I
Меняя обозначения независимых переменных во втором
интеграле, мы приведем это выражение к виду
Я 72 _ С I С dgo(x (11), *(£g)> Е1> Ы !
^х),
(£1) J '
J (J L dx^)
+	**Si) ] jQ h &) d &).
Введем еще одну новую переменную 0(0, которая
удовлетворяет следующему дифференциальному уравне-
нию:

dg0(x(t),x(i), t, g) ago(xq), x(t), £, /)i dl h (t}
dx(t)	dx(t) JS U’
(2.29)
$ 2)
ЛИНЕЙНЫЙ СИНТЕЗ С ОГРАНИЧЕНИЯМИ
405
При t—t0 0(Q=O, и поскольку й(/)=0 при /<т, то
р(/) = о, t^x.	(2.30)
В конечный момент времени
a(Q = SA р(/1) = дЛ
4.	Принцип максимума. Рассмотрим сначала задачу
без ограничений (2.18). Введем сопряженные перемен-
ные: вектор ф и постоянные А.® и Вектор ф подчиним
следующему дифференциальному уравнению;
\дх)	дх
_ хо r,rag»(x(0,xa), /, Е) , ag0(x(E), x(t), g, pi 3
₽J L	dx(t}	dx(t) J s ’ '
^0
и составим скалярное произведение
М(/) = (ф, ft)+^a + ^p.
Легко проверить, что, в силу уравнений (2.24), (2.27),
(2.29) и (2.31),	—0, т. е. величина М постоянна и
М(т) = М(/1).	(2.32)
Распорядимся выбором величин ф(^), подчинив
их следующим условиям:
= - 1, %₽ = —1, ф(4) = 0.	(2.33)
Тогда, имея в виду, что 6/ = а(Л) + P(fi), подставляя
(2.33) в (2.32), получим
6J = — М (г) = — {(ф (т), hj — aj =—(ф (г), / (х (х), v, х)) +
+ Фо (х СО» о, г) + (ф (т), / (х (т), «(г), т)) —
— Фо (х СО» и СО» т) = Я (ф, х, и, т) — Н (ф, х, V, г).
Так как х, и — оптимальные траектория и управление, то
величина 6J должна быть неотрицательной; следователь-
но, на оптимальной траектории в любой момент т должно
иметь место неравенство Я(ф, х, и, т) ^Н(ф, х, v, т), где
v — произвольное допустимое управление. Этот резуль-
40& СВЕДЁНЙЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
тат и составляет содержание принципа максимума, кото-
рый мы сформулируем в виде следующей теоремы:
Теорема. Для того чтобы пара функций u(t) и
x(t) доставляла минимум функционалу (2.15) при усло-
виях (2.16), (2.17), (2.19), необходимо, чтобы управление
u(t) в любой момент времени t доставляло максимум
функции Гамильтона
Н (ф, х, и, f) = (ф, /) — ф0,	(2.34)
где вектор ф удовлетворяет уравнению
:	(df\* . . дфо ।
Ф = — г- Ф+ +
\дх) дх
, С \dgo(x(t), *(£), A g) ,	S, QI
JL dx(t)	dx(t) Is
*0
и условию ф(Л) =0.
5. Условия трансверсальности. Перейдем теперь к за-
даче с интегральными ограничениями (2.18) и построим
вариации функционалов
Л
Л = J ф/ (X, и, t) dt,
*9
6 &
». to
Повторим основные рассуждения п. 3. Сначала введем пере-
менную J] (0, удовлетворяющую условиям
dJj
= ф/ (х, и, 0, Jj (0) = О,
at
и ее вариацию ш = ——	. Она удовлетворяет следую-
\ rfe /е-о
щей задаче Коши:
0,1 =	~ а**	(2.35)
где
ах = Ф/ (х (т), о, т) — Ф/ (х (т), и (т), т).	(2.36)
§ 2]
ЛИНЕЙНЫЙ СИНТЕЗ С ОГРАНИЧЕНИЯМИ
407
Затем вычислим 67/:
, ^/(х(ёг). х(^), g8,gi)
d*(5,) J	S1
и введем переменные ₽J(0, удовлетворяющие уравнениям
+ (2.37)
JL [dx(t)	dx(t) J Ъ w ’
и начальным условиям 0^ (г) = 0. При t = tx а! (^) = 8Jj,
₽'&) = М.
Введем далее сопряженную систему уравнений
;	М\* ,	,/ 5<Р/
Я5 = — г — л ~т~ —
\дхг — дх
/=о
0.x (5). Лё) d8f(x®,x(t),l,ty
dx(t) + dx(i)
ft £•
(2.38)
и составим скалярное произведение
М=($, й) + 2^а'+3^₽'.
/^0	/=0
Снова убеждаемся, что, в силу уравнений задачи,
421-0.
dt
Выбирая величины ty, Ц и Хр так, чтобы бJ = — М, мы
приходим к условиям
Ха=-1, Ь₽=-1,	(2.39)
[СМ) + 2 Ьаа' + 2 4₽'1 =0-
I /=1	/ = 1
408
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
Так как Jj = Ch то б/7=0, поэтому
О'&) + ₽'&) = 0, /=1,2........k.
Тогда предыдущее выражение мы можем переписать в
следующем виде:
k	1
(ф, ft) + 2 Wai W = °-	(2-4°)
/=i	)<=/,
Но величины /г(^) и независимы, поэтому из (2.40)
мы получаем следующие условия трансверсальности:
ф (0 = 0,	(2.41)
U = %' = X'’.	(2.42)
Для вывода принципа максимума мы используем тот
факт, что M(/)=const, и необходимое условие минимума
мы можем записать в такой форме;
SJ = — Д4(г)>0.
Последнее условие мы перепишем в следующем виде:
k
М (т) = (ф (г), /ч)+2^а(<0
Z-=0
или
Н (гр, х, и, т) > Н (гр, х, у, т),
k
где Н (гр, х, щ т) = (гр, f) + ^a<Ps, или, с учетом условия
S—0
к°а = - 1,
k
Н (ф, х, и, Т) = (ф, /) — Фо + 2 kS(P* (2.43)
S=1
Результаты мы сформулируем в виде следующей тео-
ремы:
Теорема. Для того чтобы пара функцийи(£) и x(t)
доставляла минимум функционалу (2.15) при условиях
(2.16) — (2.19), необходимо, чтобы в любой момент време-
ни t управление u(t) доставляло максимум функции Га-

* 2)
ЛИНЕЙНЫЙ СИНТЕЗ С ОГРАНИЧЕНИЯМИ
409
мильтона (2.43), где вектор if удовлетворяет уравнению
(2.38) и граничным условиям (2.41), а постоянные X
Ц связаны условиями (2.39) и (2.42).
6. Принцип максимума в задачах с недостоверной ин-
формацией. В том случае, когда мы не имеем в своем рас-
поряжении достоверной информации о состоянии объек-
та, задача, как мы знаем, несколько усложняется. Задача,
которая при этом возникает, относится к следующему
классу: определить функции u(t) и x(t), доставляющие
минимум функционалу
J (х, и) = J <р (х, и, t) dt +
^0
+ j/ g (х &), и &), х (^), и (У, gr, &	(2.44) '
to Jo
при ограничениях (2.16) и (2.18) *).
Единственное отличие этой задачи от той, которая
была рассмотрена в предыдущих пунктах, состоит в том,
что функция g, стоящая под знаком двойного интеграла,
зависит не только от фазовых переменных, но и от управ-
ления. Однако именно это обстоятельство не позволяет
непосредственно использовать рассуждения, которые при-
вели к формулировке принципа максимума в предыду-
щих разделах, и заставляет нас специально рассмотреть
эту задачу.
Рассмотрим функционал
g (х (li)» и (Bi)> х (&)» u (5г)> ?i> £2)
to to
и ВЫЧИСЛИМ
it h
(>J = lim — C [ (ge — g) d^d^.	(2.45)
E-*0 8 J J
io
Область интегрирования разобьем на 9 частей, как это
*) В данном случае, как.это следует из формулы (1.57), случай-
ный процесс h(t) входит в правую часть уравнения в виде Ch, где
С — искомое управление.
410
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
показано на рис. 2.2. В соответствии с этим выражение
(2.45) мы представим в виде суммы
= 2 м
/=i
и вычислим каждое из слагаемых.
Легко видеть, что 6Jt=0. В самом деле, при
ие = й и х,=х, и подынтегральное выражение в 8Jt будет
равно нулю.
I I
4 \6 । 3
Г
^7
I
I
I
-ч
I
I
I
।
I
I
I
t0 Г	t}
$
Рис. 2.2.
Далее, 6J2 также равно нулю. Этот факт следует из
того, что g — величина конечная. Поэтому
т+е т+8
ДА = J J (^-S)^ = o(82),
т т
и,следовательно,
SJa = lim	= 0.
е-»о в
Вычислим теперь б/3:
б J3 = lim —
£->0	8
T+8 Т+8
Так как при />т+е варьируемое управление совпадает
j f
>2]
ЛИНЕЙНЫЙ СИНТЕЗ С ОГРАНИЧЕНИЯМИ
411
с оптимальным, то
бJs=J J gg£.(5t)>	и^> ь ыh(^)d&ib+
т т
4- С С _.dg(sfa)'“(Ei)> х(Ъ), «(jaXgi, h d^d^ =
J J	дх (£2)
= 6Jj4-6J|. (2.46)
Вычислим б/4-
SJ4 =
= lim С d§2 С {g (х (§х), и (£х), х& (£2), (£г)>	&) g}d%i =
е->о s J J
Т+8 /о
<2-47)
Аналогично,
бл = f М , h &)) d^.	(2.48)
J J \OX (bl/	/
T /о
Объединяя результаты, выраженные формулами
(2.46) — (2.48), получим
Wt+S/; = 5'U'j(^,My)^.
Т	/q
/1 G
бА + б/з= f diA
J J W*(S1)	/
T 4
Или, меняя обозначения независимых переменных, по-
лучим окончательно
87, + 87. + 67, _	{ 8» W0. .-(»««)/?«).-», g). +
. dg(x(i),u(Z),x(t),u(t), .bt) \ h(t}dl
' dx(t)	) V
412
СВЕДЕНИЕ к ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
Вычислим теперь интегралы 6/в и 81а:
+ d/8 = lim — х
8-М) 8
* (у У (Я (-^е (?i)-> ^8 (£i)> % (£г)> и (£2)» li> ^2)	£]	+
Го 1
Ч* У <^2 j* fg (^е (?1)> (?1)>	(?г), И (В2)? > 1г)	•
т+е т
Заметим, что
J ё(хе (£i)> ^8 %е (£2), U (?зХ £1, £2)	==
%
= J g(*8&), М£1)> *(£2), и(У, £1, У ^2 + 0(е2).
т
Поэтому
t1	_
SJ6 4- SJ8 = j [g1 (х (t), u2 (т), x (^з), и (£2)»	§2) g]d%a.
to
(2.49)
Аналогично,
~ ~ ~
8Jj 4- 8Ja = J [g (x (gj), м(^), x(t), Mg(T), gx, t) — g] 4X. (2.50)
Объединяя (2.49) и (2.50), получаем
<Ц>4- dJ7 + 8JS 4- 8Ja = j {(g(x(t), «e(r), x($, u(Q, x, g) -
t
— g(x(x), u(x), x(g), u(g), r, £)] 4-
4- [g (x (I), и (I), x (x), u& (x), I, x) —
— g(x (^), U (I), X (X), й(х), I, t)]} dl.
§2]
ЛИНЕЙНЫЙ СИНТЕЗ С ОГРАНИЧЕНИЯМИ
413
Аналогично тому, как мы это сделали в п. 3 настоя-
щего параграфа, введем новую переменную, удовлетво-
ряющую следующему уравнению:
₽=
i, t7(/), x(g), «(g), Л g)
dx(f)
 dg(x(g),«(g), x(t), и
"T”	dx(t)
Переменную р подчиним начальному условию р(т) =
= 6/в + бЛ + 6/8+бЛ- Тогда очевидно, что
SJ = p(O-
Дальнейшие вычисления дословно повторяют вычис-
ления и. 4, обозначения которого мы полностью сохра-
няем. Сначала мы вводим сопряженное уравнение типа
(2.31)
^3
dg(x(t),	'
J L	dx(t)
»0
, dg(*(E),«(E),x(Q, «(/),£. 0 1
dx(t)
и составляем скалярное произведение М (/) = (if, ti) +
+А.аа+%р-р, где if(^)> мы выбираем так, что-
бы М=—8J. Отсюда мы снова получаем условия транс-
версальности (2.33). Выпишем далее выражение
для М (т):
M(t) = (ip, hj — ах - pj = (if, f(x(x), ие, г)—
— f (х (г), и(г), т)) — (<р (х (т), и£, т) — <р (х (х),~и (г), т)) —
— f {[£(*(*)> «е(г), х M(g), X, g) —
io
— g(x(x), «(t), X(g), U(g), X, g)l +
+ [g(*(I). u(g)i x(x), ue(x), I, x) —
~-g (*(!)» w (I), x(x), u(x), I, t)]}dg.
414
СВЕДЕНИЕ К ЗАДАЧАМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
Введем далее функцию Гамильтона
Я(ф, х, и, т) = (ф, /(х, щ т)) — ф (х, и, г) —
— J [g (х (т), и (т), X (g), и (Э, г, £) +
/о
+ g (х (£), и (g), х (т), и (г), g, т)] dl
Тогда выражение М(х) можно записать в следующем
виде:
М (т) = Hfy, х, ие, т) — Н (г|?, х, и, т).
Для того чтобы и я х были оптимальными, необходи-
мо, чтобы б/=—2И(т)^0. Отсюда следует принцип мак-
симума
Н (ф, х, и, т) > Я(ф, х, ие, г)
для любого допустимого управления иг.
Итак, мы видим, что необходимые условия типа прин-
ципа максимума приводят к сложным интегро-диффе-
ренциальным уравнениям относительно множителей Лаг-
ранжа. В какой мере эти условия смогут быть использо-
ваны для эффективного решения задач синтеза, покажет
будущее.
Заметим, что задача, которая была рассмотрена в
двух параграфах этой главы, представляет определенный
интерес и независимо от задач синтеза. Это относительно
малоизученные вариационные задачи с двойными интег-
ралами. К подобным задачам, в частности, сводится це-
лый ряд оптимизационных задач математической физики.
Г Л А В A VI
ПРОБЛЕМА РАЗДЕЛЕНИЯ ЗАДАЧ
И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ СИНТЕЗА
ОПТИМАЛЬНЫХ СИСТЕМ
При формулировке задач синтеза в гл. IV и V настоя-
щей книги мы опирались на целый ряд гипотез. Две из
этих гипотез имели фундаментальное значение. Первую
из этих гипотез мы назвали гипотезой разделения задач
на задачу программного движения и задачу управления
программным движением. Смысл этой гипотезы мы под-
робно обсуждали в § 1 гл. IV.
Вторую гипотезу, которую мы принимали без обсуж-
дения, естественно было бы назвать гипотезой «полной
определенности». В самом деле, при изучении задач син-
теза программное движение мы считали заданным. Внеш-
ние возмущения мы также считали заданными. Правда,
мы их считали некоторыми случайными функциями вре-
мени. Но все необходимые статистические характеристи-
ки этих случайных процессов мы считали известными.
Другими словами, никаких «неопределенностей» в наших
задачах не было.
В этой небольшой главе мы хотим обсудить содержа-
ние принятых гипотез. Говоря о гипотезе разделения,
естественно попытаться понять, при каких условиях и в
каком смысле мы можем говорить о разделении пробле-
мы проектирования оптимальной системы на задачи про-
ектирования программного движения и управления им.
Рассматривая гипотезу «полной определенности»,
важно отдать себе отчет в содержании тех технических
задач, которые не удовлетворяют этой гипотезе, а также
понять содержание и трудности проблем управления в
условиях неопределенности и возможные пути решения
подобных задач.
§ 1.	Проблема разделения
1.	Предварительные замечания. Мы начали эту работу
с утверждения о том, что техническую проблему кон-
струирования оптимальной системы управления обычно
416
РАЗДЕЛЕНИЯ и ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
решают в два этапа. Первый — это построение програм-
мной траектории. Второй — это синтез управления, кото-
рое должно реализовать программу. В задачах, которые
являются традиционными для автоматического управле-
ния, первой задачи просто нет — ее решение тривиально.
Во многих случаях программа — это заданное движение:
заданное количество оборотов коленчатого вала двига-
теля, заданный установившийся режим полета самолета,
наконец, заданная форма траектории самолета при его
посадке. Однако в последние десятилетия появилось мно-
го задач, в которых проблемы расчета программного дви-
жения приобрели самостоятельный смысл: например, вы-
бор траектории запуска орбитального аппарата, требую-
щий минимума энергии. Все же по традиции инженеры
продолжают рассматривать отдельно обе задачи. Какой
смысл имеет такое последовательное рассмотрение двух
задач управления? Всегда ли оно возможно? Как указать
условия, гарантирующие, что, используя гипотезу разде-
ления, мы будем получать результаты, удовлетворяю-
щие инженеров?
Но преже всего, что означает само утверждение «ре-
зультаты, удовлетворяющие инженеров». Возникновение
задачи расчета программы и проблемы синтеза как са-
мостоятельных этапов проектирования системы управле-
ния отражает тот факт, что качество проекта не может
быть оценено одним показателем. На примере космиче-
ского аппарата мы уже демонстрировали это обстоятель-
ство. Но когда перед инженером стоит задача достижения
различных целей, он неизбежно должен принять некото-
рый компромисс. Максимизируя одни показатели проек-
та, он ухудшает другие и т. д. Поэтому последний вопрос
сводится к назначению правил выбора компромисса.
Число различных задач управления техническими и
экономическими объектами столь велико, и- эти задачи
бывают столь различны по своей математической приро-
де, что указать систему правил рецептурного характера,
дающих ответ на поставленные вопросы, просто не-
возможно.
Поэтому нам остается говорить только об общих прин-
ципах, которые должны лежать в основе подобного ана-
лиза, и ограничиться небольшим числом примеров, иллю-
стрирующих возможности этих принципов.
§ 1)	ПРОБЛЕМЫ РАЗДЕЛЕНИЯ	417
Возможность получения компромисса последователь-
ным решением двух оптимизационных задач отражает
некоторые специальные свойства рассматриваемой про-
блемы. Как мы увидим ниже, с математической точки зре-
ния возможность разделения задачи проектирования —
следствие существования некоторых малых параметров.
Таким образом, анализ проблемы разделения задач
должен проводиться с привлечением той или другой
асимптотической теории.
Наиболее важное значение для изучаемого вопроса
имеют идеи осреднения, лежащие в основе асимптотиче-
ской теории, начало которой положено еще в 30-х годах
работами Н. Н. Боголюбова и Н. М. Крылова. Здесь
мы изложим некоторые факты этой теории в интерпре-
тации, которая нам будет удобна для последующего из-
ложения.
2.	Асимптотические методы осреднения. Предполо-
жим, что речь идет об исследовании системы дифферен-
циальных уравнений, имеющей вид
х = еХ (х, у, е), у = со (х) вУ (х, у, в),	(1.1)
гдех — векторная, а у — скалярная переменная, е — неко-
торый малый 'параметр. Особенность этой системы со-
стоит в том, что часть переменных (компоненты вектора
х) изменяется медленно, их производные имеют порядок
О (б), а величина у изменяется быстро, ее производная
имеет порядок 0(1). Спрашивается, нельзя ли найти та-
кую замену переменных, с помощью которых медленные
движения описывались бы независимо от быстрых?
Эту замену переменных будем искать в следующем
виде:
. х = х + е[/[(х, у, е), y=y+{eV (х, "у, е),	(1.2)
где х и у — новые переменные.
Потребуем, чтобы новые переменные х и у удовлет-
воряли уравнениям, правые части которых не содержали
бы быстрой переменной у, т. е. чтобы уравнения для х и у
имели следующий вид:
А	Д	уч
х = еа (х, в), у = а) (х) + sb (х, в),	(1.3)
14 Н. Н. Моисеев
418
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
где а и b — некоторые функции, которые мы должны
определить.
Подставив выражения (1.3) и (1.2) в систему урав-
нений (1.1) и сокращая на 8, приведем эту систему к
следующему виду:
^7= -Л" {g + eU,y + &V, е) — а(х, в)},
ду а (х)
(1.4)
“7 = —"7" {h (х + 8(7, У + 8^» 8) — Ь (х, в)},
ду <0 (X)
где
„ v ди „ „ди h
g = Л — в —;а — в — Ь,
дх ду
(1.5)
h = ^(х + еи)-^(х) 'У-Ла-Ь^ь.
е	дх ду
Решение системы (1.4) будем разыскивать в классе
функций, ограниченных при г/->оо.
Для эффективного отыскания решения системы (1.4)
используем метод последовательных приближений. Рас-
смотрим сначала первое из уравнений системы (1.4).
В качестве уравнений первого приближения примем сле-
дующее:
“7 = "V {£ СХ> У> 8) — «1 (х, 8)},	(1.6)
ду	<о (х)
где функция g вычислена при а=Ь — О.
Предположим сначала, что g — периодическая функ-
ция быстрой переменной периода Т. Тогда очевидно, что
для ограниченности функции Z7t необходимо и достаточ-
но, чтобы
й+г
(х, 8) = у J g (X, у, 8) dy = g! (X, 8).	(1.7)
§ 1]
ПРОБЛЕМА РАЗДЕЛЕНИЯ
419
Определив а19 мы находим Ui квадратурой
с/х = —U-
1 со (х)
£
у, e^dy — g^x, г) у
Уо
+ const.
(1.8)
В теории асимпотических представлений этого типа
доказывается, что оценка точности не зависит от выбора
постоянной интёгрирования *). Мы всегда можем принять
эту постоянную равной нулю.
Совершенно также определяются и Vt:
Ьх = ~ J h (х, у, е) dy = (х, в),
Уо
(1.9)
Vi-
1
со (х)
У
Jh (х, у, е) dy — hr (х, в) у •,
fo
где hi вычислено при а = b = 0.
Второе приближение будем определять из уравнения
^4 = —^Г Сх + et/i. у + е) — (х, е)}.
ду со (х)
Повторяя рассуждения, найдем
л+т
g(x + &Lfi(x, У,ъ), y + tVi(x, y,e),e)dy =
1
со (х)

= g2(x, 8),
g(x + fdJlt у + &Уъ e)dy — gty.
Уо
и т. д. Заметим, что реализация процесса отыскания
*) См., например, Н. Н. Моисеев, Асимптотические методы
нелинейной механики, «Наука», 1969,
14»
420
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
асимптотического решения не предполагает дифференци-
руемости или даже непрерывности функций X и У.
Описанный процесс последовательных приближений в
общем случае расходится, однако при известных услови-
ях он дает асимптотическое приближение. Например,
если X и У—ограниченные функции своих переменных, то
для функции хп = х + et/n-i, где принято (70 = 0, а х
удовлетворяет уравнению — = еап(х, &), имеет место
dt
следующее утверждение: для любого t из интервала дли-
ной порядка 1/е справедлива оценка |х—хп| =О(еп).
Для функции уп = у + eVn-i оценка будет следующей:
I//—#n| = О(еп~‘).
В настоящее время обоснование асимптотических пред-
ставлений описанного вида получено для весьма широко-
го класса задач. За подробностями мы отсылаем читате-
ля к обзорной статье В. М. Волосова *).
3.	Метод осреднения в тех случаях, когда правые
части не являются периодическими функциями быстрой
переменной. Вернемся снова к уравнению (1.6) и пере-
пишем его в виде
или
, (^Г . . . . '
Ui = —-	g (х, у, е) dy — а± (х, е) Т
(О (х) J
I/O
£/о+Г
U1 = ~^) Т S У' e)d!/ — ai(x> 6)
Уо
(1.10)
Выражение (1.10) показывает, что для ограниченно-
сти Vt при Т—>-оо необходимо, чтобы
ffo+T
а(х, е) = lira f g(x, у, e.)dy. (1.11)
Т—>оо 1 J
Уо
Таким образом, если правые части системы (1.1) не
являются периодическими функциями быстрой перемен-
*) В. М. В о л о с о в, ЖВМ и МФ 3, № 1, 1963. Некоторые виды
расчетов в теории нелинейных колебаний, связанные с усредненным.
ПРОБЛЕМА РАЗДЕЛЕНИЯ
421
§ и
ной, то правые части системы (1.3) находятся как ре-
зультат осреднения по всему бесконечному интервалу
времени.
4.	Один частный случай. Анализ возможности выде-
ления задачи расчета программы (и «правильного» выде-
ления программного движения) опирается не только на
идеи осреднения. Важную роль в этой процедуре играет
также предположение о малости возмущений.
Рассмотрим движение объекта, который содержит
одно колебательное звено. Пусть его движение описы-
вается следующей системой уравнений *):
?=Х(х) + уФ(х),	(1.12)
'у+КЫ(х)у = 0,	(1.13)
где Л — некоторый большой параметр, а <о2(х) а > О
для любых х, х — вектор размерности п, а у — скаляр.
Для системы (1.12) — (1.13) рассмотрим задачу
Коши:
х'(0) = r0, i/(0) = у0, i/(0) = у0.	(1.14)
Согласно схеме, изложенной в §1 гл. IV, решение этой
задачи распадается на два этапа. Сначала мы выделяем
программу. Она определяется как решение задачи Ко-
ши для уравнения
х = Х(х)	(1.15)
при начальном условии х(0) = х<>.
Далее мы полагаем х = х + z и линеаризуем систему
(1.12) — (1.13), считая дополнительную переменную у
(дополнительная степень свободы) также малой. В ре-
зультате мы приходим к системе
z = Аг + уФх (0, У + АА»! (0 У = °.
г(0) = 0, z/(0) = z/0, i/(0) = у0,	(1-16)
(0 = Ф (X (/)), (01 (0 = (X (0).
Естественно возникает вопрос, позволяет ли описан-
ная процедура получить приближенное решение исходной
*) Эта система с помощью специальной замены переменных при-
водится ниже к виду (1.1),
422
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
задачи. Ответ на этот вопрос может быть получен в рам-
ках изложенной теории соединения.
Заметим прежде всего, что одна из особенностей рас-
сматриваемой задачи состоит в том, что изменение пере-
менной у происходит значительно быстрее, нежели изме-
нение компонент вектора х: в течение одного полного
колебания величины у компоненты x(t) изменяются не-
значительно.
В уравнениях (1.12) — (1.13) сделаем замену незави-
симой переменной t = 8Т, 8 = 1/%.
Тогда эта система примет вид
^=6[Х(х) + уФ(х)], ^L = -rf(x)y. (1.17)
'	dy
Далее, вместо переменной у (и переменной вве-
дем две новые скалярные переменные с и if при помощи
равенств *)
у = с cos if, — = — ао (x) sin if.
dx
(1.18)
Равенства (1.18) могут быть переписаны еще и в таком
виде:
fdy \2	dy
= + tg^ = - —•	(1.19)
и* (х)	ыу
Используя (1.19), вычислим и ^в силу уравнений
(1.17):
— = ——sin2 if — (X (х) + с cos if<D (х)],
dx со dx
(1.20)
7^ = (О — — — [X (х) + CCOS 1|)Ф (х)] sin lb cos ib.
dx	in dx
*) Замена переменных (1.18) впервые была предложена Ван*
дер-Полем.
ПРОБЛЕМЫ РАЗДЕЛЕНИЯ
423
$ П
Перепишем еще первое из уравнений системы (1.17)
- = 8 (X (х) + с cos фФ (х)].	(1.21)
dt
Система уравнений (1.20) — (1-21) полностью эквива-
лентна системе (1.17). Но она приведена к такому виду,
который позволяет увидеть, что она содержит одну бы-
струю переменную 11). Эта система принадлежит к виду
(1.1), причем правые части являются периодическими
функциями быстрой переменной ф периода 2л.
Выпишем первые члены асимптотических разложений
х = х, с — с, ф = ф, где х, ф и с удовлетворяют уравне-
ниям
А = вХ(Д А = а_^11х(х),
dt	• dt 2ш dx
(1.22)
— = а» (х).
dt *
Заметим, что два последних уравнения являются
асимптотическим представлением решения уравнения
& + rf(x)-y = Q,	(1.23)
ат2
где х изменяется согласно первому из уравнений (1.22).
Возвращаясь к переменной t, мы получаем следую-
щий результат: асимптотическим представлением реше-
ния задачи Коши для системы (1.12), (1.13) с началь-
ными условиями (1.14) является решение задачи Коши
для системы
А = X (х), & +XW (х) у = О (1.24)
при тех же начальных условиях (1.14).
Первое из уравнений этой системы описывает про-
граммную траекторию, второе — изменение колебатель-
ной переменной у вдоль программной траектории.
Таким образом, если колебания происходят с большой
частотой, то первые члены асимптотических представле-
424
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
ний не содержат слагаемых, отражающих влияние до-
полнительных степеней свободы на программную траек-
торию. В этом смысле выделение программной траекто-
рии в рассматриваемой задаче является'оправданным.
Заметим, что сформулированный результат был полу-
чен без каких-либо предположений о малости у.
Для уточнения результатов расчетов по уравнениям
(1.24) могут быть предложены два пути. Первый путь —
это построение следующих членов асимптотических раз-
ложений. Второй путь — это использование методов тео-
рии возмущений. Однако для этого надо предположить,
что начальные значения г/0 и г/0 достаточно малы, а функ-
ции, входящие в правые части системы (1.1), дифферен-
цируемы по -своим аргументам. В этом случае мы пола-
гаем
х=_х + ?.	(1.25)
Подставляя выражение (1.25) в систему (1.12) и линеа-
ризуя относительно гну, мы придем к следующему
уравнению:
i ^Az + y^ (0,	(1.26)
где
\ах / ~
'	‘ х—х
Схема решения задачи следующая. На первом шаге
мы решаем задачу Коши для системы
£ = *(4	(1.27)
Далее решаем задачу Коши:
^+^(х)^ = 0, у(0) = уо, у(О)=уо (1.28)
и на последнем шаге мы находим поправку г, отыски-
вая решение системы (1.26), удовлетворяющее нулевым
начальным условиям. На основании результатов теории
осреднения и непрерывной зависимости решения от на-
чальных данных мы можем утверждать, что ошибка
ПРОБЛЕМА РАЗДЕЛЕНИЯ
425
§ 11
будет иметь порядок
+ °(тах Уо})-
\ л /
Изложенная схема решения задачи практически без
изменений может быть использована для обоснования ос-
новной гипотезы внешней баллистики, согласно которой
полный расчет траекторий можно разделить на два
этапа.
На первом этапе решается так называемая основная
задача внешней баллистики. Эта задача состоит в расче-
те траектории в предположении, что снаряд представляет
из себя материальную точку.
На втором этапе изучается рассеивание, причем это
изучение ведется с помощью линейных уравнений, полу-
ченных в результате линеаризации относительно траек-
тории, найденной при решении основной задачи внешней
баллистики.
Единственное усложнение задачи внешней баллисти-
ки по сравнению с рассмотренной в этом разделе состоит
в том, что уравнение для у будет содержать комплекс-
ные величины.
5. Система, подверженная внешним возмущениям.
Предположим, что уравнения объекта имеют вид
; = Х(х) + |ф(г)),	(1.29)
где q> (т))—вектор-функция такая, что
т
Ф(пМт] = 0.	(1.30)
т->оо Т J
0
т] — быстрая переменная: она удовлетворяет уравнению
П - Хсо(/),	(1.31)
где % — большой параметр*), £ = £(/)—заданная функ-
ция времени.
В системе (1.29) и (1.30) сделаем замену переменных
/=ет, 8=1/%. В результате мы получим следующую
*) Простым примером рассматриваемой задачи является тот слу-
чай, когда ср(т]) =sin t), a (o=const.
426
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
систему уравнений:
у = 8 (Х(х) +	У = е, =	(1.32)
ах	ах ах
Система (1.32) относится к тому типу, который был рас-
смотрен в начале параграфа, и для ее анализа может
быть применен аппарат асимптотического интегриро-
вания.
Если повторить вычисления, приняв во внимание ус-
ловие (1.30), ограничиться первым приближением и за-
тем вернуться к переменной /, то мы получим следующий
результат: х=%4-о(1/Х), где х удовлетворяет урав-
нению
^ = *(*)•	(1.зз)
Таким образом, программная траектория оказывает-
ся асимптотическим приближением траектории исходной
задачи.
Для того чтобы получить уравнения возмущенного
движения, мы снова должны сделать предположение о
малости HUI, и, используя предположения о дифферен-
цируемости правой части уравнения (1.29), мы можем
составить интересующие нас линейные уравнения
г = ^-г + £р(т]), z(O) = zo. (1.34)
ах
Функция f (/) =|(f) <р(т]), описывающая внешние
возмущения, может считаться случайной функцией вре-
мени. Однако для того, чтобы имело смысл изучать урав-
нение (1.34), считая ||z|| малой, этот случайный процесс
должен обладать определенными свойствами. Мы дока-
зали, например, что для этого достаточно, чтобы процесс
был быстро осциллирующим и удовлетворял условию
(1.30).
Примечание. Если процесс x(t) стационарный,
т. е. Х(х) = 0, то задача качественно упрощается. В этом
случае разложение Фурье функции f (t) не должно со-
держать гармоник, частоты которых соизмеримы дейст-
dX
вительным собственным числам матрицы ~ .
§ 1]	ПРОБЛЕМА РАЗДЕЛЕНИЯ	427
6. Случай управляемых движений. До сих пор мы
рассматривали примеры разделения «неуправляемых
движений». Мы сформулировали условия, выполнение
которых служило гарантией, что разделение исходной
задачи на две последовательные задачи не приведет к
большой ошибке.
Рассмотрим теперь один пример управляемых дви-
жений. Пусть уравнение управляемого объекта описы-
вается системой уравнений
х = X (х, и (0) 4- уч (0 Ф (х),
(1.35)
У -ь А2®2 (х) у = A2S (х, t) 4- At> (t),
где «(/), 6(х, I) и v(t) —некоторые функции времени и
фазовых координат, которыми мы позднее распорядимся,
у — скалярная переменная, X — большой параметр.
Введем еще одну функцию времени — величину у* и
положим у = у* + а. Для величины а мы получим урав-
нение
а + А2®2 (х) а = — [у* + А2®2 (х) у* — A26J + Хо. (1.36)
Определим теперь величину 6(х, t) при помощи ра-
венства
А2д (х, 0 = у* + А2®2 (х) у*	(1.37)
и перепишем (1.36) в следующем виде:
ci 4-А2®2 (х) а = Ао.	(1.38)
Функцию v(t) будем называть корректирующим уп-
равлением. Перепишем еще раз первое уравнение (1.35)
с учетом введенных обозначений:
х = X (х, и) 4- у* (0 и (I) Ф (х) 4- аи (0 Ф (х).	(1.39)
В результате уравнения, описывающие изучаемую дина-
мическую систему, мы привели к виду (1.38) — (1.39).
После замены независимой переменной t — ет, в — 1/А
зта система уравнений будет выглядеть следующим
428
РАЗДЕЛЕНИЯ Й ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ (ГЛ. V!
образом:
— = 8 {X (х, и) + у*иФ (х) + аиФ (х)},
dx
d2a ।	2/ \
— + со2(х)а = 8U,
du2
dt
---- = 8.
dx
Затем введем переменные Ван-дер-Поля
det	, \ .
a = с cos гр,	— == —ссо (х) sin гр
dx
(1-40)
ИЛИ
/da\2	da
C2 = a2+W_, tg>=—
co2 (x)	coct
и вычислим — и — в силу уравнений (1.40). Повторяя с
dx dx
несущественными изменениями выкладки, которые мы про-
делали в п. 5 данного параграфа, мы придем к следующим
уравнениям относительно с и ф:
= —^-{дзшф +	(Х(х, и) + у*иФ(х) +
+ с cos ф «Ф (х)] sin2 ф I,
л	J (1-41)
aib	е (vcostb . rV. , ,	* Л / . ,
—^ == ®----1------- 4---[X (x, u) 4- ц «Ф (x) 4-
dx	<o I c dx
4-c cos ф «Ф (x)j sjn ф COS ф j..
Уравнение для x перепишем так:
— + в {X (x, и) + у*иФ (х) + с cos ф пФ (х)}.	(1.42)
dx .
Для анализа системы (1.41) — (1.42) мы можем при-
менить изложенную выше технику асимптотического ана-
лиза. Ограничиваясь первым приближением, мы найдем
х = х, где
Л 1*	__
— = е {X (х, и) + У*иФ (х)}.	(1.43)
§ 1]	ПРОБЛЕМА РАЗДЕЛЕНИЯ	429
Уравнение (1.43) описывает управляемое программное
движение. Оно является асимптотическим решением ис-
ходной задачи. Как и в предыдущих примерах, дополни-
тельные степени свободы в рамках принятой точности не
оказывают влияния на программное движение.
Функции u(t) и v(t)—это управления, их можно
менять тем или иным способом. Однако асимптотический
характер программной траектории будет сохраняться
лишь в том случае, когда производные этих функций не-
велики. С увеличением производных точность асимпто-
тических представлений будет падать.
После того как программа выделена, мы поступаем
аналогично тому, как мы это делали выше. Считая вели-
чину а малой, мы составляем уравнения для возмущений.
Положив х = х + г, мы придем к следующей системе
уравнений:
z = Az + (шФх (/), а + Х2со2 (х) а = ко (/),	(1.44)
которая описывает движение в окрестности программы.
Матрица А в уравнении (1.44) имеет такой вид:
dx dx
Рассмотренная задача очень близка по своему содер-
жанию к задаче о плоском управляемом движении ра-
кеты, обладающей аэродинамическим качеством. Вектор
х — это вектор, описывающий движение центра массы,
у* (Z) — это установочный угол атаки, определяемый при
расчете программного движения. Соответственно с при-
нятой интерпретацией величины %2б (х, t) — это момент,
создаваемый рулями и обеспечивающий данное значе-
ние установочного (в общем случае, разумеется, пере-
менного во времени) угла атаки у*, отклонение от кото-
рого описывается вторым из уравнений (1.44), u(t) —это
тяга маршевого двигателя, направление которой связа-
но с ракетой, kv(t) —это дополнительный момент рулей,
которым мы можем распоряжаться для коррекции -про-
граммы.
Разумеется, приведенная интерпретация достаточно
условна. Реальная задача оказывается значительно слож-
436
Разделения й игровые Постановки задач [гл. vi
нее. Тем не менее предлагаемый путь исследования впол-
не применим и для анализа реальных движений.
7. О разделении вариационных задач. До сих пор мы
рассматривали только динамические задачи и наметили
методы исследования вопроса о возможности сведения
решения исходной задачи к последовательному решению
двух задач. Последняя из рассматриваемых задач со-
держала управления: свободные функции, которыми мы
могли распоряжаться по своему усмотрению. Однако мы
никак не связывали наше исследование с решением ка-
ких-либо оптимизационных задач.
Предположим теперь, что, занимаясь проектировани-
ем той или другой системы управления, инженер выде-
лил задачу о программном движении, которое описы-
вается уравнением
х = Х(х4«),	(1-45)
и составил уравнения движения объекта управления в
окрестности программного движения:
z = Az + Bv + f.	(1-46)
Уравнения (1.45) и (1.46) содержат произвольные функ-
ции и и V.
Предположим, что разделение задач сделано «пра-
вильно». То есть при заданных и и v вектор х + z, най-
денный из решений соответствующих задач для уравне-
ний (1.45) и (1.46), достаточно точно аппроксимирует
движение объекта управления. Какой следующий шаг
делает инженер?
Поскольку задача разбита на две, то он задает и два
критерия Л и и находит управление и, минимизируя
Л, и управление v, минимизируя /2.
Насколько такая процедура отвечает целям инжене-
ра, проектирующего управляющую систему?
Анализ этого аспекта проблемы разделения требует
уже совсем другого подхода, и аппарат исследования
должен быть совсем иным, нежели тот, с которым мы
имели дело в предыдущих пунктах этого параграфа.
Проблема, которую мы поставили, тесно связана с поня-
тием цели, которую себе ставит инженер. Попробуем по-
казать эту связь на примере орбитального аппарата.
§ 1]	ПРОБЛЕМА РАЗДЕЛЕНИЯ	431
Инженер, создающий конструкцию ракеты и системы
управления, стремится достигнуть многих целей. В дан-
ном случае у него есть по меньшей мере две цели. Во-
первых, он должен обеспечить минимальную затрату
топлива для вывода аппарата на заданную орбиту, а во-
вторых, он должен добиться максимальной точности вы-
вода (минимум дисперсии). Таким образом, используя
основное управление и(/) и корректирующее управле-
ние v(f), он должен добиться минимального значения
двух функционалов: (безразмерная энергия вывода)
и J2 (безразмерная величина дисперсии элементов траек-
тории в момент выключения двигателя), причем оба
функционала зависят, конечно, и от и, и от v: =
=Jt(u, v),	v). Математика не дает инженеру
средств для того, чтобы одновременно минимизировать
два функционала. Поэтому он поступает так, как мы уже
говорили: сначала, используя упрощенные уравнения, он
находит минимум по функционалу Л(м, 0) и оптималь-
ное управление и = u(t). Затем он принимает найденную
траекторию за расчетную и строит синтез, исходя из ус-
ловия минимума hfu, v). Какой смысл имеет эта проце-
дура? Всегда ли она дает инженеру удовлетворительное
решение его задачи? В самом деле, поскольку каждый
из функционалов Д и J2 зависит от обоих управлений,
«основного» и и корректирующего V, априори не очевид-
но, что описанная процедура не приведет нас к таким зна-
чениям Ji и /2, которые никак не смогут удовлетворить
инженера.
Для анализа этой ситуации используем идеи теории
исследования операций, поскольку здесь мы снова стал-
киваемся с неопределенностью (отсутствие однозначной
вполне определенной цели — это тоже неопределенность).
Заметим, что если бы величину одного из функциона-
лов, например Л, мы смогли ограничить, то обсуждае-
мой проблемы не существовало бы. Вместо нее была бы
довольно сложная проблема оптимального синтеза при
ограничениях на энергетику. Однако, как правило, мы
не знаем, насколько уменьшение функционала Ц может
быть компенсировано увеличением функционала J2, и по-
этому инженер, как правило, не может сказать заранее,
какое отклонение от оптимального расхода топлива допу-
432
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
стимо. Таким образом, для выяснения вопроса мы долж-
ны признать существование неопределенности — в дан-
ном случае неопределенности наших стремлений. Тогда,
как нас учит теория операций, мы должны сформировать
новый функционал. Это можно сделать разными спосо-
бами. Для дальнейшего нам удобно ввести функционал
/ =	(и, о) 4- c2J2 (и, v),	(1.47)
где Ci и с2 — некоторые положительные числа, нормиро-
ванные определенным образом, например, ct 4- с2 = 1.
Эти числа нам заранее не известны. Поэтому для пост-
роения управления с функционалом (1.47) мы можем по-
строить только гарантирующую стратегию (и*, и*). Это
будет стратегия, реализующая
J* = min max J (clt c2, и, v).
U,V ClfCi
Предположим теперь, что
а)	Функционал J аналитический по и и v, и корректи-
рующее управление имеет вид v = Bz.
б)	Существует малый параметр е такой, что
Ji = (и, ev).
Замечание. В примере с ракетой малость пара-
метра е означает, что отношение энергии корректирую-
щего управления к энергии, затрачиваемой основным
маршевым двигателем, мало.
в)	Обозначим через GT множество допустимых про-
грамм и пусть yeGT—выбранная тем или иным спосо-
бом программная траектория, а и — управление, реали-
зующее у, й 4- би — управление, реализующее какую-ли-
бо другую программу из множества GT. Пусть, далее,
min max {J2 (u 4- 6u, v) — J2 (и, д)} = О (в).
v и+би
Если условия а), б) и в) выполнены, то
J* = min max {c1J1 (u, 0) 4- c2J2 («» v)} 4- О (e), c2 = О (e),
utv
и, следовательно, в рамках теории возмущений (т. е. с
точностью до величин порядка 0(e)) гарантирующие
стратегии и* и и* совпадают со стратегиями, которые мы
§ 1]	ПРОБЛЕМА РАЗДЕЛЕНИЯ	433
находим из условий
Ji = min (и, 0), J2 = min J2 (u, у).
U	V
Сформулированная теорема дает условия, достаточ-
ные для того, чтобы решения разделенных задач были
близки (в смысле обеих метрик Л и J2) к гарантирую-
щим управлениям для функционала типа (1.47).
Подчеркнем еще раз: наши желания не определены —
мы не знаем относительные веса (относительную значи-
мость) функционалов Ji и J2. Но в данной задаче это
оказывается не существенным. Результат почти не зави-
сит от неопределенности наших желаний. Очевидно, что
именно тогда, когда ситуация обладает подобными -свой-
ствами, задача разделения имеет смысл. Разумеется, не-
трудно привести примеры, когда разделение задач мо-
жет привести к абсурдным результатам. В этом случае
выбор оптимальной программы и синтез системы управ-
ления надо производить одновременно.
8. Заключительные замечания. В этом параграфе мы
изучали проблему, которая с точки зрения инженера
почти беспредметна. Мы пытались понять, при каких
условиях традиционная манера анализа систем управле-
ния -будет достигать -своей цели. Инженер, создающий
систему управления самолетом или ракетой, почти всег-
да безошибочно может ответить на подобные вопросы.
Он наверняка правильно ответит, что быстро осциллиру-
ющими возмущениями можно пренебречь при расчете
программы, и для него не будет проблемой задача, со-
держащая два функционала и две функции, которыми
можно распорядиться «почти независимо» для миними-
зации этих функционалов.
Но с каждым годом жизнь ставит все новые и новые
задачи, сложность которых непрерывно возрастает. С по-
явлением ЭВМ в контуре управления мы начинаем пере-
ходить от проектирования относительно простых систем
управления самолетом, ракетой или спутником к задачам
управления комплексами. Причем эти комплексы — уже
далеко не всегда совокупность технических средств, мно-
голетнее обращение с которыми отточило инженерную
интуицию. Сегодня мы уже реально приступили к разра-
ботке схем управления народнохозяйственными комплек-
434
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
сами глобального масштаба. В задачах такого рода ин-
туиция уже просто не работает — никакого накопленного
опыта практически нет. А принципы управления — струк-
тура обратной связи, проблема синтеза, выделение про-
граммы, управление в условиях неполной или ошибочной
информации и т. д. остаются почти такими же, как и в
«простых задачах» управления космической ракетой.
Поэтому и кажется важным понять математическое со-
держание используемых допущений и приемов и вырабо-
тать методы, которые дают возможность сформулировать
условия, гарантирующие, что эти удобные и апробиро-
ванные в технических системах методы анализа можно
использовать (без больших ошибок) в других задачах.
Мы рассмотрели несколько задач, в которых ответ был
почти очевиден заранее. В каждой из этих задач было
легко привести интуитивно оправданные аргументы. По-
пытка придать этим аргументам математический смысл—
вот цель, к которой стремился автор.
§ 2. Гарантирующие стратегии и задачи синтеза
1. Предварительные замечания. В предыдущих гла-
вах мы рассмотрели несколько способов численного ре-
шения задач синтеза. Эти методы являются достаточно
эффективными при решении некоторых классов задач
теории синтеза. Они возникли как результат формали-
зации инженерных задач, которая, в свою очередь, ос-
новывалась на некоторых гипотезах об уровне наших
знаний характера исследуемых процессов (гипотезах
информированности). Рассмотрим два примера таких
гипотез:
а)	Мы предполагали, что случайные процессы внеш-
них возмущений F(/) и ошибок измерений h(t) нам пол-
ностью известны: либо нам известны корреляционные
функции, либо канонические разложения.
Однако; в подавляющем большинстве практических
задач мы не располагаем такой информацией. Даже ес-
ли инженеры или экономисты полагают, что они могут
предоставить полную информацию, то она на поверку
часто оказывается весьма недостоверной. Во многих слу-
чаях информация, которой мы располагаем, является не-
достаточной для использования аппарата, который был
§ 2j ГАРАНТИРУЮЩИЕ СТРАТЕГИИ И ЗАДАЧИ синтеза 435
изложен. Кроме того, мы можем столкнуться и с други-
ми способами задания процессов F(t) и h{t). Приведем
два типичных примера задания информации о случай-
ных процессах F(t) и h(t) нестатистического характера.
а4) Известно, что функции F(f) и h(t) принадлежат
некоторому классу G, например, значения h по абсолют-
ным величинам не могут превосходить некоторых зна-
чений:
|Й(/)|</1+.
а2) Известно, что корреляционная функция случай-
ного процесса h(t) имеет вид
й (/) h (г) = о2 ехр {— k) t — т |),
т. е. известно, что возмущения представляют из себя
стационарный марковский случайный процесс, но вели-
чины k и о точно не известны. Известно, например, что
k е= [А-, £+].
В обоих примерах, которые мы привели, имеет место
неопределенность — мы должны принять решение — вы-
брать структуру управления (или только коэффициенты
усиления системы) в условиях неопределенности.
В подобной ситуации возможны два пути преодоле-
ния трудностей. Один из этих путей связан с идеологией
адаптации. Во время движения управляемого объекта
мы можем получить определенную информацию о струк-
туре случайного процесса F и h (опираясь снова на опре-
деленные гипотезы типа эргодичности) и построить про-
гноз возмущений. Полученная информация может быть
использована для принятия решения. Идеология адапта-
ции сейчас очень популярна, и она находит все большее
и большее применение. Но может быть использован и
другой способ принятия решения.
Предположим, например, что нам известно то, что
K(/)eGF, где GF— некоторое заданное множество:
например, ||К||^8. Пусть снова в качестве критерия
фигурирует функционал «точности» J=(z(T), Rz(T)).
Значения этого функционала зависят от управления —
матрицы обратной связи B(t) и данной реализации
случайного процесса F(t), т. е. J=J(В(f), F(t)).
Поскольку никаких статистических характеристик про-
цесса F(t) нам неизвестно, то в качестве критерия для
436
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
оценки системы управления в этом случае естественно
принять функционал
Г (В) - max J(B, F),	(2.1)
J+ — это наихудшее из возможных значений функциона-
ла /(В, F) при заданном управлении В(/). Из двух уп-
равляющих функций Bi и В2 мы считаем лучшей ту, ко-
торая обеспечивает меньшее значение функционалу J+.
Тогда оптимальной системой управления мы будем назы-
вать ту, которая реализует
min (В) = min max J (В, F).	(2.2)
В	В FZE-Gp
Для того чтобы не путать это понятие с понятием опти-
мального управления, которое мы рассматривали в
предыдущих параграфах, матрицу B(t), реализующую
минимум функционала (2.1), будем называть нижней га-
рантирующей стратегией (или нижней гарантирующей
оценкой).
Значение функционала, соответствующее этому уп-
равлению, будем называть гарантированным качеством
системы управления.
Функционал (2.1) не является аналитическим, и для
его исследования требуются специальные методы.
Метод построения гарантирующих стратегий и адап-
тивный подход не являются взаимно исключающими.
Более того, они могут в значительной степени дополнить
друг друга. Предположим, например, что устройство,
обрабатывающее информацию, позволяет установить об-
ласть допустимых значений коэффициента корреляции
k <=	k+(i)], причем с течением времени эта инфор-
мация становится все более и более полной, т. е. при
t—>-оо k~—*-k* и k+—Это значит, что множество
допустимых возмущений G(t) сужается. Разумеется, по-
добная информация может и должна быть использована
при построении гарантирующих стратегий.
В данной работе мы не будем изучать методы адап-
тации и остановимся только на некоторых способах по-
строения гарантирующих стратегий.
б)	Во всех рассмотренных задачах мы предполагали
известной программную траекторию. Однако существует
§ 2] ГАРАНТИРУЮЩИЕ СТРАТЁГИИ И ЗАДАЧИ СИНТЕЗА 437
большой класс задач, в которых мы не располагаем по-
добной информацией. В качестве примера рассмотрим
самолет. Сегодня у него одна программа: определенная
скорость и высота, определенный маршрут. Завтра у
него другая программа — он летит по другому маршру-
ту, с другой скоростью и на другой высоте и т. д. Несмот-
ря на то, что программа полетов самолета разная, авто-
пилот во всех случаях используется один и тот же. Как
же поступает инженер, конструирующий автопилот для
нового типа самолета, инженер, который должен один
раз для всех возможных режимов полета самолета выб-
рать коэффициенты усиления в контуре обратной связи
его автопилота? Он задает тест — выбирает типичный
(расчетный) режим, и только для этого режима рассчи-
тывает автопилот. При этом инженер неявно использу-
ет гипотезу о том, что характеристика автопилота очень
мало зависит от программы.
Для самолета эта гипотеза практически всегда оправ-
дывается, и значение функционала, характеризующего
качество системы управления, действительно очень мало
зависит от того, какой из возможных установившихся ре-
жимов мы примем в качестве расчетного. Но если речь
идет об управлении существенно неустановившимся дви-
жением, то законность подобной гипотезы уже становит-
ся сомнительной. Поэтому перед инженером, который
конструирует систему управления, предназначенную для
управления целым пакетом траекторий, встает трудный
вопрос о выборе ее параметров. Здесь он также сталки-
вается с неопределенностью. Но эта неопределенность
будет уже другого типа, нежели та, которая возникла в
предыдущем примере.
Для выбора системы управления в описанной ситуа-
ции также естественно использовать гарантирующие
стратегии, т. е. разыскивать управление, доставляющее
минимум функционалу
Л(В(/))= max J (В, у),	(2.3)
где GT — множество допустимых программных траек-
торий.
Мы привели два примера, в которых естественным об-
разом возникает необходимость построения гарантирую-
438
РАЗДЕЛЕНИЯ Й ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
щих стратегий. Число таких примеров в теории синтеза
очень велико.
2.	Задача проверки качества теста. Предположим, что
конструктор должен выбрать параметры автопилота для
управления некоторым множеством возможных траекто-
рий его ракеты. Траекторию ракеты обозначим через у.
Множество допустимых траекторий обозначим через От.
Как пуступает инженер в этой ситуации? Обычно он на-
зывает некоторую траекторию у расчетной траекторией
или тестом. Каждой программной траектории у отвеча-
ет некоторая матрица Дт(/). Следовательно возмущенное
движение, происходящее в окрестности у, будет описы-
ваться уравнением
z =	+ + f (0-	(2.4)
Далее инженер решает задачу синтеза управления
для системы (2.4), и автопилот, который он построит
этим способом, будет использоваться для всего множе-
ства траекторий GT.
Предположим, что он оценивает качество управления
при помощи функционала
J = (г(П Я* (Л),	(2.5)
а управление он разыскивает в форме v — Bz и пользу-
ется для этого методикой, изложенной в § 1 гл. V.
В этом случае, как мы знаем из предыдущего, задача
сводится к отысканию вектор-функции y(t), удовлетво-
ряющей уравнению
у = (а + $)у,	(2.6)
где
и матрицы B(t), доставляющей минимум функционалу
J = (у (0), Еу (0)) + j f (у (t), Ф (t, т) у (т)) dt dr. (2.7)
О о
§ 2] ГАРАНТИРУЮЩИЕ СТРАТЕГИИ И ЗАДАЧИ СИНТЕЗА 439
Вектор функция y(t) удовлетворяет при t = T условиям
(5.1.15), а Ф(^, т) и Е — матрицы, введенные в предыду-
щей главе. Предположим теперь, что для тестовой
программы мы решили задачу синтеза, т. е. нашли опти-
мальную матрицу В (0- Обозначим Д = Л ~ Ё и у — ве-
личины, относящиеся к тестовой программе и выбранно-
му управлению, тогда
7 = /(Д-,В).
Первый вопрос, который естественно поставить, бу-
дет, вероятно, следующим: насколько изменится значе-
ние функционала /(В), если от расчетной программной
траектории перейти к другим программным траекториям
множества GT? Этому вопросу можно дать другую интер-
претацию. Для данной расчетной траектории построен
автопилот, гарантирующий некоторую «хорошую» точ-
ность. Насколько ухудшится точность выполнения про-
граммы, если мы будет применять наш автопилот для
управления другими допустимыми программными траек-
ториями? Введем в рассмотрение величину
Д/ — max {J (Лт, В) — J (А~, В)}.	(2.8)
veGv	у
Величана Д7 дает ответ на этот вопрос и характеризует
качество теста. Если величина Д7 мала, то это значит,
что тест выбран хорошо и точность выполнения програм-
мы мало зависит от выбора программы из множества GT.
Если Д7 велика, то это значит, что расчетная програм-
ма выбрана плохо.
Может оказаться, что хорошего теста вообще нет.
Множество GT может быть настолько широким, что какую
бы из траекторий yeGT мы ни взяли в качестве теста,
всегда значение Д7 окажется большим. Это значит, что
одним автопилотом нельзя обеспечить достаточно точное
выполнение каждой из программ множества GT. Напри-
мер, один и тот же автопилот не может быть использо-
ван и для управления автоматической посадкой самоле-
та, и для управления равномерным полетом на заданной
высоте.
440
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
Задача определения max J (Ду, В) совершенно аналогична
задаче (2.5) —(2.8) —задаче определения min J (Аг, В).
В самом деле, если матрица Б выбрана, то уравнение,
описывающее динамический объект, будет иметь вид
г =	+• Вг + F	(2.9)
где матрица Б известна, а матрица Д7 является искомой.
Таким образом, в уравнениях (2.4) и (2.9) матрицы В и
А поменялись местами.
3.	Гарантирующее управление в задаче улучшения
теста. Предположим, что множество траекторий GT, для
управления которыми должна быть синтезирована систе-
ма обратной связи, задано. Тогда естественно возникает
вопрос, каким образом выбрать тест — выбрать расчет-
ную траекторию.
Решение этой задачи также может быть получено в
рамках принципа гарантирующих стратегий.
Будем называть гарантирующим управлением, пред-
назначенным для управления множеством программ GT,
управление B(t)^GB, доставляющее минимум функцио-
налу
J+= max J (Ду, В).	(2.10)
VG(?y
Таким образом, задача построения гарантирующей стра-
тегии сводится к определению
J* == min max J (Ду, В).	(2.11)
Функционал J* недифференцируем по В, и задача опре-
деления J* достаточно трудна. В общем случае, для ее
решения нельзя предложить стандартные методы. Вмес-
те с тем она становится почти тривиальной, если пред-
положить, что множества <?т и GB достаточно узкие.
В этом случае для ее решения может быть предложен
алгоритм, основанный на предположении о возможности
линеаризации исходной задачи.
Предположим, что мы выбрали некоторую програм-
му у. Ей соответствует матрица Предположим далее,
s 2]
ГАРАНТИРУЮЩИЕ СТРАТЕГИИ И ЗАДАЧИ СИНТЕЗА
441
что для этой программы мы решили задачу синтеза и на-
шли управление Ё. Этим величинам соответствует вектор
у (/), который удовлетворяет уравнению
*/= (ау + Р) У-	(2.12)
Рассмотрим теперь некоторую окрестность траектории у.
Это множество мы обозначим через G4t. Каждая из тра-
екторий этого семейства определяет матрицу
Лу = Лу + 6Л
и соответственно а? = а~ + ба.
Если множество G6T достаточно узкое (например, если
величина ||у—у|| мала), то величина ||ба|| мала. Предпо-
ложим также, что мы можем только незначительно из-
менять величину управления В, т. е. выбирать B(t) из
некоторой окрестности GiB управления Ё. Тогда, приняв
В — Ё + 6В, 0 = 0 + 60, мы будем считать величину
||б0|| малой. Положим также у = у + 8у. Тогда вариация
8у будет удовлетворять уравнению
Ьу = («у + Р) ^ + (ба + 60) у.	(2.13)
Выпишем теперь вариацию функционала (2.5). В § 1
гл. V мы уже получили необходимую для этого формулу
(5.1.21)
6J = (с, бу(О)) + J (б</(/), К(0И,	(2.14)
о
где К(0—вектор, зависящий от статистических характе-
ристик случайного процесса
Задачу построения гарантирующего управления 8В,
доставляющего
mim max 8J (Лу, В) = бJ",	(2.15)
овеСев 6veG*y
мы будем называть задачей улучшения теста.
Задача улучшения теста может быть сведена к реше-
нию нескольких задач Коши.
442
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
Представим величину 8у в виде суммы бу = 6yi + бу2,
где 8yi и бу2 удовлетворяют уравнениям
= (av + 0) ^У1 + даУ>	(2-16)
^а = («7 + ₽)бу2 + бру.	(2.17)
Используя эти обозначения, перепишем выражение функ-
ционала (2.14)
6J = 6J1(6a) + 6J2(6p),
где
б/, - (с, бух (0)) + J (бух (О, К (/)) dt,
О
6Ja = (с, бу2 (0)) + J (бу2 (0, К (0) dt.
О
Соответственно с этим
&J* •= max 6JX 4- min 6J2.	(2.18)
6veG^ 6BsG6B
Итак, в рассматриваемой задаче определение 6J*
распалось на две независимые задачи — определение
81* и 6J*. Каждая из этих задач является стандартной
линейной задачей теории оптимального управления и
сводится к решению двух задач Коши.
Если В — это решение задачи линейного синтеза для
траектории у, то в результате решения задачи (2.18) мы
можем получить только оценку теста б/’*. Однако опи-
санную процедуру мы можем использовать для построе-
ния, метода последовательных приближений.
В результате решения задачи (2.18) мы находим, во-
первых, некоторую матрицу а во-вторых, матрицу
(т. е. новую программную траекторию). Следователь-
но, мы можем принять эти величины в качестве нового
приближения и повторить процедуру.
По существу описанная схема последовательных при-
ближений имеет много общего с методом последователь-
ных приближений в теории матричных игр — методом
Брауна — Робинсон.
§ 2] ГАРАНТИРУЮЩИЕ СТРАТЕГИИ И ЗАДАЧИ СИНТЕЗА 443
В предыдущем параграфе мы видели, что метод по-
следовательных приближений может быть реализован
без использования линеаризации. Точно так же обстоит
дело и в рассматриваемом случае.
Сначала задается некоторая исходная программа у0
и разыскивается оптимальное управление, доставляю-
щее минимум функционалу = J(AYo, В). Решение этой
задачи обозначим через Во (оно может быть получено
без линеаризации задачи методом, описанным в преды-
дущей главе). На следующем шаге мы находим новую
матрицу доставляющую максимум функционалу
J (Л, Во).
Эту матрицу мы обозначаем через ЛУ1. Эта задача ана-
логична предыдущей. Далее разыскиваем минимум функ-
ционала J3=J (AY1, В) и т. д.
На каждом шаге этого алгоритма мы должны решать
задачу линейного синтеза.
Сходимость метода последовательных приближений,
использующего идею метода Брауна — Робинсон для по-
строения гарантирующих управлений, никем не иссле-
довалась и об условиях его сходимости ничего не изве-
стно. Вполне вероятно, что этот метод расходится, и им
нельзя найти управление (матрицу В), реализующее га-
рантированный синтез. Тем не менее этот метод удобен
для задачи улучшения управления. В самом деле, J2 —
это характеристика теста у0: точность реализации про-
граммы с управлением Во для наихудшей из программ-
ных траекторий данного семейства. Далее мы разыски-
ваем минимум функционала J3. Очевидно, что
И после этого для нового управления Bj определяем
= max J (Av, BJ.
Ay
Если окажется, что /4<Л, то это и значит, что мы улуч-
шили тест.
4.	Еще один пример гарантирующих стратегий. Рас-
смотрим задачу (2.4) — (2.5) и предположим, что слу-
чайный процесс F(t) является стационарным марковским
процессом. Тогда, согласно теореме Дуба, элементы его
444
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
корреляционной матрицы имеют вид
/< = ехр {— ku\t — т|}Ц.
Предположим, дополнительно, что все kl} равны между
собой. Тогда корреляционная матрица этого процесса
имеет вид
K(t, х) ^e-^Q,	(2.19)
где Q— постоянная матрица: Q = ||о«2||. Предположим
теперь, что мы не знаем точно коэффициента корреляции
k. Мы знаем только, что он лежит в пределах
где 8k~ и 8k+ — некоторые положительные числа.
Положим k = % + 8k. Тогда для 8k мы будем иметь
условие
8k <= bk~ < 8k < 8k+.	(2.20)
Решение задачи о гарантирующей стратегии сводится
к отысканию матрицы B(t), доставляющей минималь-
ное значение функционалу
J = max С С (у (0, e~(k+6k)li~xlQy (т) dx dt + (у (0), Еу (0))1,
(2.21)
где у удовлетворяет уравнению (2.6).
Функционал (2.21) неаналитический (по отношению
к г/(О),‘и решить поставленную задачу в общем случае
достаточно трудно. Поэтому предположим, что величи-
ны 8k~ и 8k+ малы, и линеаризируем функционал (2.21)
относительно 8k; обозначим
8J = max — 8k f (у (t), Qy (г)) e~kW\t — х | dx dt. —
о о
= max 81 (8k, В), (2.22)
и задачу определения J* = minJ(B) заменим отысканием
в
8J* = min max 81 (8k, В).
B&Gb
§ 2] ГАРАНТИРУЮЩИЕ СТРАТЕГИИ И ЗАДАЧИ СИНТЕЗА 445
Величина 6/ — это линейная функция 6k, причем 6k удо-
влетворяет ограничениям (2.20). Следовательно, макси-
мум 61 достигается либо при 6k=6k~, либо при 6k=6k+.
Рассмотрим теперь функционал (2.22). Очевидно, что
он равен максимальному из двух чисел:
6ЦВ) = max{5/(5fe+, В); 6!{6k~, В)}.
Выпишем теперь 6J*:
6J* — min<V'(B) = min max {61 (6k*, В); 61 (6k~, В)}.
в	в
Для решения этой задачи мы можем воспользоваться
методами предыдущего параграфа. Зададим некоторое
управление Б и предположим для определенности, что
61(6k*, Б) > 6l(6k~, Б). Для первого из этих функциона-
лов определим управление Б + 6В, доставляющее его ва-
риации минимальное значение. Затем положим В = Б +
+ Х6В, где Ze[0,1]. Тогда оба функционала сделаются
функциями этого параметра:
61 (6k*, В) = Л(Ч 6I(6k~,B)^fz(K).
Обозначим через X = X* е[0,1] значение X, доставля-
ющее минимальное значение А (%). Тогда могут иметь
место два случая:
а) /1(Х*)</2(Г), б) Л(Г)>/2(П
В случае а) управление В + V6B принимаем за новое
управление и повторяем процедуру. В случае б) мы на-
ходим то значение Х=V*, при котором Л (X) =f2(%). В ка-
честве нового управления мы принимаем В = В+%**бВ
и повторяем процедуру, но уже с функционалом
б/(6£- В).
Описанный метод позволяет находить только точки
локального минимума функционала (2.22).
Мы привели несколько примеров из теории синтеза,
показывающих необходимость использования методов
теории игр и исследования операций. Необходимость учи-
тывать факты неопределенности возникает в очень мно-
гих задачах этой теории. Однако последовательное при-
менение принципа гарантирующих стратегий ограничено
446
РАЗДЕЛЕНИЯ и ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
возможностями аппарата: мы не имеем практически ни-
каких общих методов определения экстремумов неана-
литических функционалов.
В этих двух параграфах мы рассмотрели, и притом
очень конспективно, несколько частных вопросов теории
синтеза оптимальных систем. Каждый из этих вопросов
может быть предметом специальных исследований, име-
ющих глубокий прикладной смысл. Центральным вопро-
сом теории синтеза оптимальных систем, по-видимому,
следует считать эффективное построение корректирую-
щих управлений при наличии ограничения на мощность
управляющих воздействий и фазовых координат. Эти уп-
равления будут нелинейными функциями фазовых коор-
динат системы.
Решение этого вопроса упирается, в свою очередь, в
целый ряд труднейших вычислительных проблем. Пер-
вая из этих проблем — это метод эффективного построе-
ния функционала в тех случаях, когда динамическая си-
стема нелинейна. Вторая — это методы отыскания экст-
ремумов неаналитических функционалов вида
min max J (и, о).
и V
Достаточно ограничиться указанием этих двух задач,
чтобы отнести проблему оптимального нелинейного син-
теза к числу безнадежных. Однако автор верит в инту-
ицию инженера, который уже сегодная научился созда-
вать отличные системы управления. По-видимому, если
будет осмыслен опыт происходящего, будут найдены и
пути решения проблемы нелинейного синтеза. Возмож-
но, что решение этих вопросов будет достигнуто не на
формально математическом уровне, а произойдет в ре-
зультате создания новых концепций.
§ 3. Использование канонических разложений
фазового вектора в задачах линейного синтеза
1. О канонических представлениях случайных вектор- ।
функций. В гл. IV и V настоящей монографии мы уже
не раз использовали канонические разложения случай-
ных процессов. Для дальнейшего изложения нам не-
§ 3]
КАНОНИЧЕСКИЕ РАЗЛОЖЕНИЯ ФАЗОВОГО ВЕКТОРА
447
обходимо отметить некоторые особенности этого ап-
парата.
Пусть мы имеем некоторый скалярный случайный про-
цесс f(t). Его каноническим описанием (или каноничес-
ким представлением) называют агрегат
т
(3.1)
1=1
где —некоторые заданные функции, а С,-—незави-
симые случайные величины. Использование представле-
ний (3.1) в ряде случаев оказывается очень удобным как
в задачах обработки информации, так и в задачах дина-
мики и управления. Каноническое описание позволяет в
удобной форме представить целый ряд характеристик
случайного процесса. Например, дисперсия f (t) как функ-
ция времени вычисляется по весьма простой формуле
(Г7?)2 = 3 (Ci-CiY Ф? (0.	(3.2)
Если для случайной вектор-функции f(t) известны ка-
нонические представления ее компонент, то для нее так-
же можно построить каноническое представление вида
(3.2), где ф<(0—заданные вектор-функции, а Q—не-
зависимые скалярные случайные величины. Поясним это
на примере, когда размерность вектора f равна двум.
Пусть для компонент вектора f даны канонические пред-
ставления
Г~с1Ф(0,
Тогда мы можем представить f в виде
где ф1 и фг — вектор-функции, определенные так:
ф5 = ф (0. Фг =0» Фх = 0, Фа = ф (0-
Легко видеть, что и в общем случае, когда скалярные
компоненты f вектор-функции f(t) заданы своими кано-
ническими разложениями, всегда можно для f(i) соста-
вить представление (3.1), где С{ — скалярные независи-
мые случайные величины, а ф;(0—заданные вектор-
функции. Если размерность f(i) равна п, а каждая из
компонент f* аппроксимирована суммой, содержащей I
448
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ (ГЛ. VI
координатных функций, то вектор-функция f(t) будет
аппроксимирована суммой, содержащей не более п х I
векторных слагаемых, каждое из которых имеет размер-
ность, равную п. Заметим, что т = п X I п.
2. Расчет рассеивания. Задачи о рассеивании элемен-
тов траектории, как ее называют в баллистике, или за-
дача о точности системы управления, как ее называют
в теории регулирования, это одна из очень распростра-
ненных технических задач. Ее содержание состоит в сле-
дующем. Предположим, что движение объекта происхо-
дит под действием некоторой системы случайных сил, и
часть параметров, определяющих движение объекта (на-
пример, начальные условия), является случайными ве-
личинами. Тогда говорить об одной-единственной фазо-
вой траектории этого объекта особого смысла не имеет.
Поэтому в подобной ситуации поступают так: выделяет-
ся некоторая «невозмущенная» траектория. В окрестнос-
ти этой траектории уравнения движения линеаризуются
и записываются в виде
г’=Лг + /(0.	(3.3)
Начальное состояние z(Z0)—случайная величина и
f (Z) — случайный процесс внешних возмущений считают-
ся центрированными. Ставится задача: определить эле-
менты матрицы вторых моментов случайного процесса
z(l) в некоторый фиксированный момент t = Т. Для ре-
шения этой задачи удобно использовать канонические
представления случайного процесса z(t), если процесс
f(t) также задан своим каноническим представлением.
Примечание. Очень часто для оценки точности
следящей системы используют обобщенные характерис-
тики вида
J =	(3.4)
где R— симметричная, положительно определенная мат-
рица.
Итак, будем считать, что вектор-функция f(t) задана
своим каноническим представлением
т
=	(3.5)
I § 31 КАНОНИЧЕСКИЕ РАЗЛОЖЕНИЯ ФАЗОВОГО ВЕКТОРА 449
:	где т^п, — вектор-функции размерности п, Ct—
скалярные независимые случайные величины с известны-
ми статистическими характеристиками, причем Ct = 0, а
о начальном состоянии z(t0) известно, что z(4) =0, и,
< кроме того, известны элементы матрицы
Вектор z будем разыскивать в виде суммы
j	z=2CzXz(0,	(3.6)
где fall) — неизвестные вектор-функции.
Функции %<(/) должны быть выбраны так, чтобы урав-
нение (3.3) было удовлетворено для любого t е [/0, 71 и
любых реализаций С{.
Подставим выражение (3.6) в (3.3), после этого урав-
I нение (3.3) примет вид
I	.
3fCz{Xz-^Xz-q)z}=0.	(3.7)
Z=»l
Для того чтобы равенство (3.7) было справедливо для
i любых реализаций С< и любых 7], необходимо и до-
статочно, чтобы величины в фигурных скобках были
равны нулю для любых /е(70, 7]:
	Xz = 4Xz+<pz, i = l, 2...т. (3.8)
Таким образом, функции %г должны удовлетворять
системе дифференциальных уравнений (3.8).
Выясним теперь вопрос о начальных значениях для
• вектор-функций %{(/). Согласно предположению задан-
I ными являются элементы матрицы /С10. Вычислим
______ т т
s—i	/г—i
15 H. H. Моисеев

450
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ (ГЛ. VI
Так как Cs — независимые случайные величины, то это
выражение может быть переписано в виде
?? = 3	(3.9)
S=1
Выражение (3.9) справедливо для любого t. Полагая в
нем t = tQ, мы получаем соотношения, которые связыва-
ют известные величины ау == ^(/о)^(^о) с начальными
значениями компонент вектор-функций %s(t0)'-
a(/ = ^gx'(/0).	(3.10)
s=i
Это уравнения для определения неизвестных величин
(f0) (i=l, 2, ..., п, s=l, 2, ..., т). Так как матрица
вторых моментов симметричная, то число независимых
уравнений в системе (3.10) равно п(п + 1 )/2:
т __
аи = 5] Сз(Х*(/0))2,
3 = 1
т __
а12 = CSXS (/0) Xs (Q>
s=i
(З.П)
т __
a22 = 3C:(Xs2(W
S=1
а13 = 2 C^XS (Q Xs О
s=i
и T. Д.
Число неизвестных равно	n(n-j~l)/2. Поэто-
му часть этих неизвестных мы можем задать по произ-
волу. В зависимости от их задания остальные неизвест-
ные определятся однозначно.
§ з]
КАНОНИЧЕСКИЕ РАЗЛОЖЕНИЯ ФАЗОВОГО ВЕКТОРА
451
Нетрудно видеть, что решение системы (3.11) может
быть дано следующей системой формул:
(3.12)
и т. д. Если начальные значения компонент вектора z(/0)
независимы, то все at; = 0(i =/= j), и, следовательно, в
этом случае х,(^о) = О для всех 1'
После того как мы определили начальные значения
для функций х<, задача расчета рассеивания (точности)
сведется к решению задач Коши для системы (3.8) и вы-
числению характеристик рассеивания типа (3.9).
В заключение данного пункта выведем еще одну
формулу для характеристики точности (3.4), которая
нам будет нужна для последующего изложения:
п  п	tn	tn
rti 2
i,j=l	i,/=l s=l	k— 1
В силу независимости случайных величин С8 получаем
j=з с: г^ (?)	= s с^>	<3-13>
/,/	S
где
Л = (МЛ, /ад».
(3.14)
15*
452
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ (ГЛ. VI
3. Сведение задачи линейного синтеза к задаче Майе-
ра. В предыдущем пункте был описан широко известный
метод расчета точности систем управления. Он сводится
в конечном счете к решению некоторой специальной зада-
чи Коши. Этот же метод может быть использован и в за-
даче линейного синтеза. С его помощью, как мы увидим,
задачу линейного синтеза можно свести к задаче Майера.
Рассмотрим линейную систему
г — Az + со 4- [,	(3.15)
где управление <о разыскивается в виде
<о = В (f) z,
а случайная вектор-функция f(t) задана своим канони-
ческим разложением (3.5). Так же, как и в задаче пре-
дыдущего пункта, мы будем считать, что вектор z(/0) яв-
ляется центрированным случайным вектором с известны-
ми вторыми моментами.
Задача линейного синтеза, как мы это знаем, состоит
в отыскании матрицы В (t), доставляющей минимум функ-
ционалу (3.4). Решение этой задачи снова будет разыс-
кивать в форме агрегата (3.6). Для функций мы полу-
чим тогда систему, аналогичную системе (3.8):
X, = ДХ, + BOQ + q>(-, i = 1, 2.гт. '	(3.16)
В результате этих преобразований задача линейного син-
теза сведется к следующей задаче Майера:
Определить матрицу В (Г) таким образом, чтобы она
доставляла минимум функционалу
/=З^А(Т),/?Х,(Т))	(3.17)
S
при ограничениях (3.16), где вектор-функции х* удовлет-
воряют начальным условиям (3.12), а на элементы мат-
рицы B(f) наложены ограничения вида
B(t)e=G,	(3.18)
где G — некоторое множество.
4. Некоторые комментарии. Итак, аппарат канониче-
ских представлений позволяет, так же как и использова-
ние сопряженных уравнений, свести задачу линейного
§ 3] КАНОНИЧЕСКИЕ РАЗЛОЖЕНИЯ ФАЗОВОГО ВЕКТОРА 453
синтеза к задаче теории оптимального управления. Одна-
ко в этом случае мы получаем задачу значительно боль-
шей размерности, чем та, которая была рассмотрена в
предыдущих параграфах этой главы.
В самом деле, применение техники сопряженных урав-
нений сводит исходную задачу к п2 скалярным уравне-
ниям. Использование канонических разложений нам да-
ет систему, порядок которой п X т, где т > п. В этом
случае, практически, нам приходится работать с систе-
мами размерности порядка 6м2, 8п2 и т. д. Соответствен-
но с этим система для сопряженных переменных будет
иметь порядок 6п2, 8га2 и т. д. Тем не менее рассматривае-
мый подход имеет свои преимущества. Перечислим те
ситуации, когда метод редукции, основанный на исполь-
зовании канонических разложений, оказывается более
эффективным средством анализа.
а) Задача с интегральным функциона-
лом. Предположим, что критерий качества имеет вид
г
J =	(3.19)
to
В этом случае метод сопряженных уравнений не может
быть непосредственно использован. Для метода канони-
ческих разложений этот случай не представляет никаких
затруднений, поскольку функционал (3.19) после заме-
ны (3.6) будет иметь следующий вид:
т m _
J = J 5	dt’ (3.20)
io
т. е. мы имеем стандартную задачу Лагранжа.
б)	П араметрические задачи. Предположим,
что конструируемая схема системы управления не дает
возможности делать коэффициенты усиления переменны-
ми. Тогда задача синтеза превращается в задачу нели-
нейного программирования, поскольку в этом случае
функционал (3.4) становится простой функцией неизве-
стных постоянных величин bts, удовлетворяющих условию
(3.18). Для решения этой задачи мы будем использовать
тот или иной вариант спуска. Поскольку процедура спу-
ска требует многократного вычисления функционала
454
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
(или его производных), а вычисление функционала при
использовании техники, сопряженных уравнений требует
вычисления двойных квадратур, то использование тех-
ники канонических ’разложений может оказаться более
экономным, так как вычисление функционала здесь прак-
тически не требует затраты машинного времени и совер-
шается по конечной формуле (3.17).
в)	«Энергетические» ограничения. До сих
пор мы рассматривали задачи с ограничениями на вели-
чину коэффициентов усиления. На практике чаще всего
встречаются ограничения другого вида. Предположим,
что со* — это угол поворота руля самолета. Величина св4
должна быть функцией его фазовых координат.
=	(3.21)
/
Ограничения, которые здесь возникают естественным об-
разом имеют следующий вид:
1(ог|<а,	(3.22)
где а — некоторое заданное число: руль самолета не мо-
жет отклониться больше, чем на некоторую допустимую
величину. Условия типа (3.22) условимся называть энер-
гетическими. Задача с энергетическими условиями оказы-
зывается уже качественно сложнее, потому что эти ог-
раничения являются фазовыми. Единственный пока (в
задачах большой размерности) реальный способ преодо-
ления трудностей, связанных с фазовыми ограничения-
ми — это метод штрафных функций.
Мы уже вводили функции штрафа для ограничений
типа (3.32). Они имели следующий вид:
т
J1 = х [ф'(/)<#,
h
где
(О, если I со1 К а1,
ф =	,	,	.	.	(3.23)
(© —а)2, если |©‘| >а*.
Но данная задача обладает одной особенностью: вектор
§ 4]
СТАТИСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ
455
z, а, следовательно, и функция со*, которая связана с z
формулой (3.21), является случайной функцией времени,
и возникает еще вопрос, каким образом в рассматривае-
мой задаче следует ввести штрафной функционал?
Так как математическое ожидание а/ = равно
/
нулю, то условие (3.22) можно заменить таким:
(^У2<йа2,	(3.24)
где 6>0. В этом случае штрафной функционал мы можем
принять в виде
т
j[ = ),^l(t)dt,	(3.25)
<0
где
1°, если («/)2<Ы2,
1(сог)2— ka2, если (со')2 ka2.
Если теперь мы сделаем замену (3.6) и перейдем к де-
терминированной задаче для функций %.(0> то выраже-
ние для штрафного функционала мы получим в виде
т	__
J = + X f 2 max (0; ЬцЬцСЫ (/) (0 - dt. (3.26)
t I l,l,s	*
г)	Наконец, использование канонических представле-
ний открывает определенные возможности для построе-
ния синтеза нелинейных систем управления при заданной
структуре нелинейности. Этому вопросу будет посвящен
следующий параграф.
§ 4. Статистическая линеаризация
и синтез нелинейных систем управления
1. Идея статистической линеаризации. В последние
годы идеи статистической линеаризации приобретают все
большее значение в теории оптимальных систем. На их
основе удается развить подход к построению теории син-
456 РАЗДЕЛЕНИЯ и ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ ГГЛ. VI
теза, который является в известном смысле альтернати-
вой той схемы исследования, которая была изложена в
начале § 1.
Статистическая линеаризация сводит рассмотрение
нелинейных систем весьма общего вида к анализу нели-
нейных систем, обладающих рядом специальных свойств,
делающих их уже значительно более удобными для реше-
ния задач синтеза. Статистическая линеаризация откры-
вает (как мы увидим) большие возможности для теоре-
тического и численного анализа. В то же время она
основывается на некоторых гипотезах, априорная про-
верка которых крайне затруднительна. Поэтому методы,
основанные на идеях статистической линеаризации, се-
годня еще нельзя считать вполне строгими. В то же
время с помощью этих идей уже удалось решить целый
ряд важных технических задач, и накапливаемый инже-
нерами опыт показывает, что идеи статистической ли-
неаризации' приводят к методам, точность которых
оказывается вполне приемлемой для технических рас-
четов.
Идею статистической линеаризации поясним сначала
на примере скалярной функции скалярного аргумента *).
Рассмотрим скалярную функцию <р(х) случайной ве-
личины х = х + z, где z — центрированная случайная
величина (т. е. z = 0). Аппроксимируем функцию <р(х)
функцией ф (х):
ф(х) = фо + ф1?,	(4-1)
где фо и ф! — некоторые постоянные, которые мы выбе-
рем из условий
ф (х) = ф(х),	(4.2)
(Ф (х) — ф(х))2 = а = min (ф (х) — ф (х))2.	(4.3)
’i’o.’h
Примечание. В некоторых случаях условие (4.3)
заменяют таким:
(Ф«-<Й< = (Ф«-ф«.	(4.4)
*) Более подробно см. монографию: И. Е. Казаков, Статисти-
ческие методы проектирования систем управления, «Машиностроение»,
1969, где для исследования качества управления последовательно
используются идеи статистической линеаризации..
§ 4]
СТАТИСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ
457
Мы в дальнейшем будем использовать только условие
(4.3).
Если нам известна Ф(х) —функция распределения ве-
личины х, то условия (4.2) и (4.3) нам позволяют опре-
делить и ф1. Так как z, по условию, центрированная
случайная величина, то из (4.2) мы получаем
оо
ф0 = j ф(х)с/Ф(х).
-оо
(4.5)
Преобразуем величину, стоящую в правой части ра-
венства (4.3), учитывая, что z = 0:
(<р(х) — ф(х))2 = ф2(х) + фо —2ф0Ф (х) —
—2фг<р (х) (х — х) + ф2?2. (4.6)
Если функция распределения величины х известна, то
z2 = dx— дисперсия х. Для того чтобы величина (4.6) до-
стигла минимального значения, необходимо, чтобы ф,
было корнем уравнения — {(<р(х)—Ф(х))2}=0- От-
^Ф1
сюда мы получаем
---------——	+СО
= Ф.(х)^-х) = ‘ [ ф W(xX) с/Ф (х).	(4.7)
dx dx J
-эо
Однако метод статистической линеаризации употреб-
ляется для решения задач, в которых величина х, а,
следовательно, и ее закон распределения неизвестны.
Поэтому в методе статистической линеаризации исполь-
зуют еще одну аппроксимацию. Закон распределения ве-
личины х аппроксимируется законом Гаусса, но с неиз-
вестными математическим ожиданием и дисперсией.
В этом случае
4Ф (х) = со (х) dx, где со (х) — —-— exp f————
У 2nd,	(	2d,
458
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
Равенства (4.5) и (4.7) в этом случае примут следующий
вид:

х)ехр
___ (х — х)2 ]
/
dx.
(4-9)
Мы видим, что равенства (4.8) и (4.9) определяют ве-
личины ф0 и как некоторые функции неизвестных х и
dx. Таким образом, аппроксимация (4.1) заменяет одну
нелинейную функцию <р(х) другой нелинейной функцией
ф(х). Однако эта последняя является линейной относи-
тельно центрированной составляющей случайной вели-
чины г.
Последнее обстоятельство и служит источником тех
упрощений, которые удается получить в теории синтеза
с помощью метода статистической линеаризации.
2.	Замечание о вычислении функций ф0 и фь Итак,
формулы (4.8) и (4.9) определяют величины ф0 и ф! как
функции х и dx.
Фо = Фо (*» dx), Ф1 = Ф1 (X, dx). (4.10)
В общем случае функции (4.10)—это сложные транс-
цендентные функции, содержащие интегралы. Однако
дЛя многих нелинейных функций, используемых в техни-
ке, удается получить простые аналитические выражения.
Пусть, например, ф(х)=х3, тогда
оо	_
фо =  1=. f & exp	dx.	(4.11)
дГ 2ndr J ( 2ах J
F * -ОО
Но определенный интеграл (4.11) легко вычисляется —
он является табличным:
^0=3dxx+x3.	(4.12)
Заметим, что получив величину ф0(х, dx), нам нет не-
обходимости для получения ф вычислять еще один интег-
§4]	' СТАТИСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ	459
рал. На основании формул (4.8) и (4.9) мы находим,
что
(4.13)
дх
Используя (4.13), в рассматриваемом примере мы
легко вычислим
ф1==3б/х+3х2.	(4.14)
В цитированной выше монографии И. Е. Казакова *)
дана сводка типичных нелинейных зависимостей, кото-
рые используются на практике и которые допускают про-
стые аналитические представления.
3.	Пример. Для иллюстрации тех возможностей, ко-
торые’открывают идеи статистической линеаризации и
той техники, которая здесь может быть использована,
рассмотрим простейший пример.
Пусть уравнение, описывающее эволюцию управляе-
мого объекта, имеет вид
z = c + f(O,	(4.15)
где z— скалярная величина, f(t)—случайный процесс.
Управление v(z) разыскивается в виде
v = (О 2 + ^2 (0 z3-	(4.16)
Функции kt(t) и kz(?) должны быть выбраны так, чтобы
доставить минимум функционалу
J=z2(T).	(4.17)
Начальные условия z(0) будем считать центрированной
случайной величиной.
Величину zs подвергнем статистической линеари-
зации: г8 — Зг2? + г3+3 (zs +z®)z. Так какг=0, то
z3 —3?z.	(4.18)
Используя (4.18), уравнение, описывающее эволюцию со-
*) И. Е. Казаков, Статистические методы проектирования
систем управления, «Машиностроение», 1969.
460
РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ (ГЛ. VI
стояния объекта управления (4.15), мы перепишем так:
z = kt (0 z 4-36а (0 ?z + f (0.	(4.19)
Уравнение (4.19), как мы видим, остается нелинейным.
. Предположим теперь, что процесс f(f) задан своим
каноническим разложением
f(0 = 3Cs<ps(0.	(4.20)
$=1
Величину z будем разыскивать в виде
z = 2U(0.	.(4.21)
S
Перепишем (4.19), используя (4.20) и (4.21):
2 Cs{Xs - kx (0 (t)-3^(0?Xs(0 -q>s(0} =0,
• S=1
___ m _____
где z2(0 =2 Cjx|(0 = у является детерминированной функ-
s==i
цией. неизвестных величин.
Потребуем, чтобы функции %, (0 удовлетворяли урав-
нениям
Xs = kt (0 Xs +3/г2 (0 yXs + <Ps, s = l,2, .... tn. (4.22)
В начальный момент считаем заданной величину г2(0).
Так как z2 (0) =	(0), TOi положив
S“1
Х2 (0) = Хз (О) = ... = %, (0) = 0,	(4.23)
Xi(0) мы найдем по формуле Xi (0) = Vz2 (0)/Ct
Составим еще уравнение для величины у:
т ___
у = 2 3 Cs’Xs (kt (0 Xs + 362 (/) у Xs 4- <Ps),	(4.24)
s=l
§4]
CtATMCtH4ECKAfl ЛЙНЁАРЙЗАЦЙЯ
4в1
причем
i/(0) = ?(0).	(4.25)
Итак, исходную задачу синтеза мы свели к следующей
стандартной задаче оптимального управления: опреде-
лить управления k^t) и k2(t) и фазовые переменные
Xi, —, Хп» У, удовлетворяющие уравнениям (4.22) и (4.24)
и начальным условиям (4.23) и (4.25) таким образом,
чтобы доставить минимум величине у(Т).
К перечисленным ограничениям должны быть еще до-
бавлены ограничения на управление.
4.	Общий случай. Рассуждения, которые мы исполь-
зовали для анализа простейшего примера, позволяют по-
строить схему синтеза нелинейной системы управления
и в общем случае, если только структура нелинейности
задана. Изложим конспективно схему расчета для сле-
дующего случая: объект линеен, т. е. его уравнение име-
ет вид
z = А(0г-Ь о(г)-Ь(4.26)
управление разыскивается в форме
о* = 2^/ + ^'(г1.........г"),	(4.27)
/=1
где F1— заданные функции своих переменных. Коэф-
фициенты матрицы обратной связи Ьц и коэффициенты
усиления k{(t) должны удовлетворять ограничениям вида
I tty | Ьц, | ki | sC где bij и fe, — заданные числа.
В качестве функционала Мы будем рассматривать снова
функционал типа дисперсий
/=(г(Т),№(Т))	(4.28)
т_____________
или J = {г (7), Rz (Г)) dt.
Первым шагом на пути решения поставленной зада-
чи является статистическая линеаризация функций F\
входящих в выражение (4.27).
I
462
РАЗДЕЛЕНИЯ и ИГрОВЫЁ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
Заменяем /7(х‘,	zn), где 4f=4f0+
п
+	* Полагаем, что плотность распределения вероят-
i=i
ностей гауссова:
® (г* 1, ..., z") = —-  exp (z, D^z),
V 2Vb
где D — матрица вторых моментов, а А — ее опреде-
литель. Тогда величину То находим из условия То=
=F(zl, z2, zn). Условимся рассматривать только функ-
ции F, для которых То=О. Величины Т< мы найдем из
условия минимума выражения
I = (F-2 Tzzz)2 = -2 2	+ 3	+ а,
t—l	i,l=l
где DiS — элементы матрицы D, а величина а не зависит
от Т(.
Величины Т( находим из уравнений
= —2Fzl +2 2 4iD(i =0.	(4.29)
Примечание. Нетрудно заметить, что нам нет не-
обходимости решать систему (4.29), поскольку для функ-
ций Тг мы имеем следующие формулы:
dz^
Итак, в результате статистической линеаризации мы за-
меняем функции F(zl,..., zn) выражениями
Fl(z\ ..., гп) =2 ¥j(D«)?,	(4.30)
/=1
в которых коэффициенты являются функциями вторых
моментов фазовой переменной z.
§ 4)	СТАТИСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ	463
После замены (4.30) система (4.26) принимает вид
п	п	п
az/ (0 / +- 2 Ьц (/) + fez 5} Т) (Dlk) z’ + f, (4.31)
/=i	/=i	/=1
i = 1, 2, ..., п.
Считая, что случайный процесс Задан каноническим разло-
т
жением f = 2 С5ф* (0, будем искать решение в виде
S=1
т
Z‘^Csx‘s(f).
S — 1
Вторые моменты этих величин выражаются формулами
_________________________ т ___
(4.32)
s=i
Повторяя рассуждение предыдущих пунктов этого па-
раграфа для функций %s, получим следующие уравнения:
п	п	т
Хз = 2 a^s + 2 bz/X{ + fez 2 Wj W + <Ps, (4.33)
/=x	/=i	/=i
i = 1, 2...n, s = 1, 2, ..., m.
Система (4.33) имеет порядок n X tn. Начальные зна-
чения для переменных даются формулами (3.12). Си-
стема (4.33) является системой нелинейных уравнений,
поскольку функции зависят, в общем случае, нелиней-
ным образом от величин Dtk, которые определяются фор-
мулами (4.32).
Функционал (4.28), как мы уже знаем, легко вьгра-
жается через функции Xs(T’) и известные дисперсии С2.
Таким образом, рассматриваемая задача нелинейно-
го синтеза с заданной формой нелинейности сведена к
задаче оптимального управления со свободным концом.
5.	Заключение. В этом параграфе мы познакомились
с методом, который позволяет нелинейные задачи син-
теза сводить к задачам оптимального управления и, еле-
464 РАЗДЕЛЕНИЯ И ИГРОВЫЕ ПОСТАНОВКИ ЗАДАЧ [ГЛ. VI
довательно, использовать для их решения хорошо разра-
ботанные методы этой теории.
Заметим еще одно достоинство методов, использую-
щих статистическую линеаризацию: несмотря на нели-
нейный характер рассматриваемой задачи, они дают
возможность вычислить значение функционала, не при-
бегая к методу Монте-Карло.
Однако до сих пор методы статистической линеариза-
ции еще не получили своего строгого обоснования. Без-
условно, они являются асимптотическим приближением
для некоторых классов задач, и вопрос о том, чтобы чет-
ко выделить эти классы и, следовательно, до конца по-
нять содержание методов статистической линеаризации,
является одним из важных и интересных вопросов теории
синтеза.
ГЛАВА VII
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
Эволюция теории управления происходит главным об-
разом в сторону изучения объектов все большей и боль-
шей сложности. Для их описания появились и новые тер-
мины. Большие системы или сложные системы — эти
термины стали уже достаточно широко использоваться,
хотя до сих пор нет их однозначного определения. Дис-
кутируются различные определения, существуют и ак-
тивно обсуждаются различные попытки оценить, ранжи-
ровать сложности систем. Возникают идеи построения
«общей теории систем» и т. д.
Мне не кажутся плодотворными подобные рассужде-
ния общего характера, не содержащие, во всяком случае
сейчас, каких-либо рекомендаций, помогающих при изу-
чении и проектировании конкретных систем. Кажется бо-
лее важным изучение некоторых конкретных классов
систем, обладающих каким-либо общим свойством, ко-
торое позволяет развить специфические методы анализа
(или синтеза). Одним из таких классов являются систе-
мы, обладающие иерархической структурой.
Заметим, что как только система становится «доста-
точно сложной», в ней неизбежно возникает иерархичес-
кая структура. Мы не знаем сколь-нибудь сложных сис-
тем, не обладающих подобной структурой. Это делает
изучение иерархических систем особенно важным не
только с прикладной, но и с теоретической точки зрения.
Эта глава посвящена изучению подобных систем уп-
равления. Основное внимание обращается на два во-
проса.
Первый — зачем вообще нужна в системах управле-
ния иерархическая структура? Как сравниваются раз-
ные структуры, и, в частности, каким образом устано-
вить необходимость введения в системе иерархической
структуры? Ответ на этот вопрос позволит, в частности,
разделить все системы на два класса. Один — это прос-
тые системы, в которых управление полностью центра-
466
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
лизовано, в которых нет необходимости вводить иерар-
хию. Вторые — их естественно назвать сложными,— это
системы с иерархической структурой.
Второй вопрос—это процедуры управления, т. е. про-
цедуры принятия решений в иерархических системах.
§ 1.	Обсуждение некоторых понятий
1.	Принятие решений. В предыдущих главах мы гово-
рили преимущественно о технических системах. Теперь
наряду с техническими мы будем рассматривать систе-
мы экономические, социальные и т. д. Несмотря на это,
мы будем использовать общий язык и вести изложение
по возможности единообразно, не различая эти системы.
Для этого мы должны условиться о смысле понятий, ко-
торые будем использовать в дальнейшем: принятие ре-
шений, иерархическая структура, гипотеза поведения,
качество информации и т. д.
Термин «принятие решения» имеет четкий смысл в
исследовании операций. Он означает выбор некоторого
элемента u^U, где U — допустимое множество. Этот
выбор делается в интересах достижения определенных
целей, он всегда мотивирован. Значит, употребление тер-
мина «принятие решения» всегда предполагает сущест-
вование некоторой цели (или целей), существование це-
левой функции или критерия.
В простейших задачах, когда цель состоит в миними-
зации некоторой скалярной функции F(u), проблема
принятия решения состоит в отыскании такого вектора
и, который доставляет функции F(u) минимальное зна-
чение.
Рассмотрим теперь некоторую управляемую динами-
ческую систему (любой природы), эволюция которой
описывается уравнением
х =	(1.1)
Выбор управления и, в форме программы u=u(t) или
в форме синтеза и = и(х), мы будем также называть
принятием решения. Это выражение мы будем исполь-
зовать в равной степени, как по отношению к техниче-
ским системам, так и по отношению к системам более
§ 11
ОБСУЖДЕНИЕ НЕКОТОЙЫк понятий
467
сложной природы. И мы не будем каждый раз оговари-
вать факт существования целей, т. е. мотивы поведения.
Таким образом, реализация обратной связи в авто-
мате ц = ц(х) и распределение инвестиций — задание
компонент u(t) в экономической системе — будут в на-
шей терминологии некоторыми актами принятия ре-
шений.
2.	Гипотезы информированности и поведения. Как
уже говорилось, принятие решений всегда должно быть
каким-либо образом мотивировано. Если мы знаем эти
мотивы, то мы знаем (во всяком случае принципиально
мы можем знать) и решение, которое будет принято.
Так например, если мы знаем целевую функцию F(u), то
как бы сложна ни была эта функция, мы всегда, в прин-
ципе, можем определить то значение и, которое достав-
ляет минимум этой функции. В этом случае (так же как
и в случае (1.1)) выбор управления и однозначно оп-
ределит как течение динамического процесса, так и
значение целевой функции, т. е. результат принятого
решения.
Может оказаться, однако, что выбор любого u<=U,
т. е. принятие любого решения, не позволяет однозначно
определить результат. Так бывает всякий раз, когда ре-
зультат зависит не только от наших действий. Эту ситу-
ацию будем записывать в форме функции уже двух пе-
ременных F(u, v), где v^V.
Параметр v характеризует неопределенность, имею-
щуюся в операции (задаче). Это могут быть действия
реального противника, отсутствие необходимой инфор-
мации (и, в частности, случайные помехи) или неопре-
деленность наших желаний. На последнее особенно сле-
дует обратить внимание, поскольку к этому случаю сво-
дится, в частности, проблема принятия решения, когда
существует несколько целей.
Каким образом теперь мотивировать выбор wet/ и
превратить проблему принятия решений в условиях не-
определенности в строгую математическую задачу?
Для этого необходимо сделать некоторые дополни-
тельные предположения. Эти предположения я буду на-
зывать гипотезой поведения. В зависимости от характе-
ра этих гипотез мы будем иметь те или другие матема-
тические задачи.
468
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
Подчеркну еще раз следующее тривиальное утверж-
дение. Не делая никаких предположений о процедуре
выбора элемента и и об области его определения, мы не
можем сформулировать никаких мотивов относительно
выбора решения и.
Частным случаем гипотез поведения является пред-
положение о том, что «противник» выбирает v из сооб-
ражений
min F (и, о) = max (— F (и, и)).	(1.2)
Эта гипотеза поведения приводит к теории антагонисти-
ческих игр и их анализу в духе фон Неймана. Одной ги-
потезы поведения еще недостаточно, чтобы полностью
описать действие «противника». Необходима некоторая
гипотеза информированности и порядка ходов. Напри-
мер, можно предположить, что мы делаем «первый ход»
и «противник» будет его знать, т. е. будет знать наш вы-
бор х.
Из этой гипотезы информированности и гипотезы по-
ведения (1.2) сразу следует знаменитый принцип гаран-
тированного результата. Он сводится к тому; что первый
ход делаем мы и «противник» будет знать нашу страте-
гию. Поэтому «противник» строит свое решение в виде
функции v = v(u), которая определяется из ^условия
(1."2). Это означает, что для V u^U функция v(и) до-
ставляет минимум F(u, v):
minF (u, о) = F (и, v (и)) = F* (и).	(1.3)
veV
В этом случае выбор решения и —и сводится к опре-
делению элемента и, доставляющего максимум функции
F* (и). Таким образом,
F* (и) = max min F (и, v).	(1.4)
ueV t>sV
Выбор решения согласно процедуре (1.4) называется
принципом гарантированного результата. В этом случае
выбор решения свелся снова к проблеме оптимизации.
Аналитическая природа функций вида F*(w) обычно бы-
вает очень сложна. Даже если функция F(u, v) —мно-
гократно дифференцируемая, то относительно F’(u) мы
§ Ij	ОБСУЖДЕНИЕ НЕКОТОРЫХ ПОНЯТИЙ	" 469
можем утверждать только дифференцируемость по на-
правлению.
В последнее время к методам отыскания экстрему-
мов функций вида F*(u) привлечено внимание матема-
тиков, и в этой области получено много новых важных,
результатов.
Меняя гипотезу об информированности или гипотезу
поведения, мы будем получать новые типы математиче-
ских задач. Так, например, имеет смысл предположить,,
что «противник» выбирает величину V, зная наш отклик,
на этот выбор, т. е. функцию u=u*(v). В этом случае
«противник», если он следует гипотезе поведения (1.2),
выбирает такой элемент v=v* который доставляет ми-
нимум функции F(u* (и), v):
minF (и* (v), v) = F (и*(о*), и*).	(1.5)
t>SV
Поскольку наши интересы неизменны, то нам остает-
ся только одно. Так выбрать функцию u'(v), чтобы до-
ставить максимум функционалу (1.5). Это решение обо-
значим через «** (и):
F (и** (ц*), v*) = max min F (и"	(1.6)
u*(U) v~V
Задача (1.6) уже совсем иной природы, чем (1.4).
Она сводится к отысканию не элемента и, а некоторой
функции и** (у), т. е. нашего отклика на ход противника.
Пользуясь терминологией теории управления, мы по-
лучили некоторую задачу синтеза.
3.	Об одном классе гипотез поведения, связанном с
теорией игр с непротивоположными интересами. Расши-
рим теперь класс гипотез поведения. Вместо того чтобы
предполагать, что «противник» выбирает свою страте-
гию keV из условия max {—F(u, о)}, предположим, что
oev
он выбирает v из условия
max Ф (м, ц),
где в общем случае
Фф — F.
(1.7)
470
Иерархические системы Управления
[ГЛ. vtt
Такое расширение гипотез поведения приводит к новому
классу игр. Теория, которая здесь возникает, значитель-
но шире теории антагонистических игр. К тому же она
дает язык, удобный для описания многочисленных и
важных приложений *).
Поскольку интересы противника, который распоря-
жается элементом и, не противопоположны нашим, то и
сам термин «противник» мало соответствует существу
дела. Поэтому в дальнейшем вместо слов «мы» и «про-
тивник» будем говорить игрок а и игрок 0. Игрок а кон-
тролирует стратегию и, игрок 0 — стратегию v.
Предположим, что игрок а делает первый ход. Это
значит, что он выбирает значение и и сам сообщает его
игроку 0. (Заметим, что в играх Гермейера одному игро-
ку может оказаться выгодным передавать информацию
другому игроку.) Тогда игрок 0 определяет свою стра-
тегию v = v:
ф (и, v) = max Ф (u, v),
v — это некоторая функция v(и). Теперь игрок а строит
свою гарантированную стратегию из условия достиже-
ния наилучшего гарантированного результата:
max F (u, v (и)) = F (и, v (и)).
Здесь и далее используется предположение об однознач-
ности v(u). Точно так же игрок а может сообщать игро-
ку 0 свой выбор в форме функции u(v). Заметим, что в
данном случае эту функцию можно трактовать как функ-
цию штрафа или поощрения.
Игрок 0 выбирает тогда элемент v* из условия
max Ф (u (v), у) = Ф (и (у*), у*).
иеУ
*) Сейчас теория неантагонистических игр быстро развивается
благодаря работам школы Ю. Б. Гермейера. Основу этой теории се-
годня составляет изучение зависимости окончательного результата от
неформальных моментов — порядка ходов игроков и характера их ин-
формированности. Для этого, чтобы отметить самостоятельное зна-
чение перечисленных вопросов, будем называть эти игры играми
Гермейера, который не только сделал значительный вклад в теорию
игр с непротивоположными интересами, но и показал ее большое
прикладное значение.
§ 1]	ОБСУЖДЕНИЕ НЕКОТОРЫХ ПОНЯТИЙ	471
Заметим, что элемент v* будет теперь уже некоторым
оператором д*=д[и(о)].
Принятие решения для игрока а сведется тогда к вы-
бору такой функции u*(v), которая доставляет макси-
мум функционалу F[u(v'),
Примечание. Мы рассмотрели два случая инфор-
мированности: игрок р знает и, игрок р знает и (у). Име-
ет смысл рассматривать и более сложные игры, где р
знает ы[у(и)1- Все они допускают довольно наглядные
интерпретации. Кажется, что можно наращивать и далее
глубину рекурсии. Однако Н. С. Кукушкин установил
замечательный факт. В случае, когда имеется только
два игрока, возможные типы игр полностью исчерпыва-
ются рассмотренными, все остальные к ним сводятся *).
Этот результат, конечно, не распространяется на случай
многих игроков, где разнообразие типов игр гораздо
богаче.
Я обратил внимание на то, что игры Гермейера обла-
дают рядом новых замечательных особенностей.. Одна
из них состоит в том, что обоим игрокам может оказать-
ся выгоден обмен информацией.
Рассмотрим еще одну особенность.
Предположим сначала, что речь идет об антагонис-
тических играх, т. е. Ф(и, о) =—F(u, v) и t'G V.
Предположим, далее, что игрок а имеет возможность
влиять на структуру ограничений игрока 0 — изменять
его активность, т. е. множество V. Например, он может
заменить V на КеК. Игроку а эта операция выгодна
всегда, так как
V и: min F (и, v) > min F (и, v),
и, следовательно,
max min F (u, v) > max min F (u, v).
и ueVj	и
В играх с непротивоположными интересами этот
факт уже может не иметь места. Если пользоваться язы-
ком теории управления, то может оказаться полезным с
*) Н. С. Кукушкин, Роль взаимной информированности в
играх двух лиц с непротивоположными интересами, ЖВМ и МФ,
№ 4, 1972.
472	ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ 1ГЛ. VII |
точки зрения игрока а расширить множество допусти- I
мых стратегий своего «противника», т. е. игрока 0.
4.	Качество и мера информации. Это понятие исполь-
зуется достаточно часто и ему иногда придается некото-
рый «абсолютный» смысл. В то же время не имеет смыс-
ла говорить о ценности информации самой по себе, без *
указаний целей, для достижения которых она использу- !
ется. Поэтому, оценивая информацию, мы всегда будем
иметь в виду определенный критерий, связанный с целе-
вой функцией задачи. Таким критерием естественно при-
нять меру неопределенности наших знаний о возможных
результатах принятых нами решений.
Предположим, что речь идет о выборе некоторого
процесса а (0, от которого зависит значение нашей це- *
левой функции — функционала
/ = KOI,	(1.8) ;
где КО —некоторый процесс, о котором исследователь
операции не имеет полной информации. В этом случае,
распоряжаясь управлением a(0 для максимизации
функционала (1.8), мы не сможем точно вычислить зна-
чение функционала J и можем дать только некоторую
оценку, зависящую от той информации, которой мы рас- |
полагаем о процессе КО» причем характер этой оценки
будет существенно зависеть от содержания информации.
Дать же какие-либо общие рекомендации здесь вряд ли
возможно.
Пусть, например, о процессе КО известны
верхние и нижние оценки его значений:
'Соответственно рассмотрим два функционала:
Л = /(а.П Л = /(а, Г)
и вычислим
<7+ = max J (а, К), J~ — max J (а, К),
а	а
Тогда величина
только
(1.9)
(1,10)
'§ 1]	ОБСУЖДЕНИЕ НЕКОТОРЫХ ПОНЯТИЙ	473
может служить мерой неопределенности результата при-
нятия решения и, следовательно, оценкой качества ин-
формации о процессе §(/).
Если же процесс g(Q—случайный процесс с матема-
тическим ожиданием £(£), и мы не знаем его конкретной
реализации, тогда естественно выбирать наше управле-
ние а = а из условия
max J (а, |).
а
В этом случае в качестве меры неопределенности, оцени-
вающей качество информации, можно принять диспер-
сию случайной величины J (а (£), £).
Нетрудно привести еще целый ряд аналогичных при-
меров, показывающих целесообразность оценки качест-
ва информации мерой неопределенности наших знаний о
результатах принятых решений.
Примечание. Изложенный взгляд на оценку ка-
чества информации является, по существу, очень близ-
ким к точке зрения Шеннона, которую он развил в сво-
ей знаменитой «математической теории связи». Энтро-
пия Шеннона является именно мерой неопределенности
той информации, которая содержится в передаваемом
сообщении.
5.	Иерархическая структура. Этот термин сейчас
весьма широко распространен. Когда мы употребляем
термин «иерархическая структура» или иерархическая
организация, имеется в виду только то, что наша систе-
ма разбита на отдельные подсистемы или звенья, обла-
дающие самостоятельными правами обработки инфор-
мации и принятия решений.
Это определение будет относиться в равной степени
как к техническим системам, так и к экономическим и
другим системам более сложной природы, если только
вкладывать в понятие «принятие решения» тот смысл, о
котором говорилось в начале параграфа.
Построение теории систем управления, обладающих
иерархической структурой, одна из наиболее актуальных
задач теории управления. Однако ее развитие встречает
целый ряд трудностей принципиального характера.
474
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
Оказывается, например, что анализ (а тем более син-
тез) иерархических систем непосредственно не сводится к
обычной теории оптимальных систем, основы которой
излагались в предыдущих главах. И дело состоит даже не
в том, что во многих случаях функционирование иерар-
хических систем описывается операторами более слож-
ной природы, нежели дифференциальные. В этих систе-
мах изменяется само понятие оптимальности. В самом
деле, что значит оптимальная система, если каждое ее
звено имеет возможность самостоятельно принимать ре-
шения, в частности, максимизировать свой собственный
функционал? Таким образом, иерархическая система —
это принципиально многокритериальная система. И, сле-
довательно, первое требование к любой теории, описыва-
ющей эволюцию управляемой системы, наделенной
иерархической структурой,— найти рациональные мате-
матические постановки задач и вложить разумный смысл
в понятие оптимальности.
§ 2.	Предварительный анализ
1.	Зачем нужна иерархия в системах управления?
Введение в данной динамической управляемой системе
иерархической структуры имеет своим следствим распре-
деление между различными ее звеньями функций обра-
ботки информации и принятия решений по выбору уп-
равляющих воздействий. На первый взгляд может по-
казаться, что создание иерархической структуры — это
просто добавление новых ограничений, т. е. сужение
множества допустимых управлений, которое неизбежно
влечет снижение показателя эффективности системы в
целом. Действительно, может оказаться, что введение
иерархической структуры вредно или бессмысленно, но
возможно и другое—'оказывается, что в известных ус-
ловиях без разделения функций принятия решений си-
стема вообще не сможет функционировать.
Для того чтобы разобраться в этом вопросе и выра-
ботать принципы оценки качества самой структуры, ав-
тору кажется необходимым принять во внимание связь
между критерием качества системы и требованиями к
алгоритмам обработки информации.
§ 2]	ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ	475
Может оказаться, что полностью централизованный
сбор и обработка информации либо технически невоз-
можны, либо приводят к значительному запаздыванию
в принятии решений, т. е. к принятию решений по уста-
релой информации. В обоих случаях это приведет к уве-
личению неопределенности в процедурах принятия ре-
шения, а следовательно, к снижению гарантированных
оценок эффективности системы управления.
Одним из путей преодоления трудностей, вызванных
большим объемом информации или сложностью ее пере-
работки, является «распараллеливание» процедур ее
сбора и обработки. Однако децентрализация процесса
обработки информации неизбежно требует определенно-
го уровня децентрализации также и процедур принятия
решений, т. е. создание самостоятельно функционирую-
щих подсистем.
Появление в системе отдельных звеньев, способных
за приемлемое время (и цену) обработать всю относя-
щуюся к ним информацию, способных учесть все измене-
ния конкретной ситуации и получающих право приня-
тия самостоятельных решений по тем или иным вопро-
сам, и означает появление в системе иерархической
структуры.
Для принятия решений в отдельных звеньях системы
необходим уже значительно меньший объем информа-
ции, который можно быстрее и лучше обработать и, сле-
довательно, принять решение в условиях значительно
меньшей неопределенности.
Таким образом, децентрализация управления при-
водит к уменьшению неопределенности, связанной со
сбором и переработкой информации. Эти утверждения в
равной степени относятся к любым системам техниче-
ским, социальным.
Представим себе какой-либо технологический про-
цесс, например, какое-либо крупное химическое произ-
водство. Существуют некоторые потоки реагентов х(/),
у (/), z(t) и т. д. Течение этих процессов непрерывно кон-
тролируется. Имеется четкая программа процесса и
аппаратура контроля — система датчиков непрерывно
регистрирует возможные отклонения от расчетного ре-
жима, отклонение температуры, качество исходного ма-
териала, скорость движения реагентов и т. д. С точки
476
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
зрения теории оптимального управления следовало бы
всю эту информацию передавать на центральный диспет-
черский пункт и принимать «оптимальное» решение об из-
менении параметров процессов, имея в виду, что все эти
процессы х, у и z связаны между собой. Однако в усло-
виях современного химического производства такая схе-
ма нереализуема в принципе. Размеры производства
требуют совершенной и очень дорогостоящей системы
линий связи, а объем информации столь велик, что его
«оптимальная» обработка и принятие «оптимального»
решения даже на самых быстродействующих ЭВМ тре-
бует времени, значительно большего, чем характерное
время протекания процесса. Иными словами, даже если
будет создана дорогостоящая система связи, если будут
устранены все возможные помехи в процедурах ее пере-
дачи и обработки, решение будет принято тогда, когда
в нем уже не будет никакой необходимости.
Вот почему в реальной системе оказывается необхо-
димым управлять процессами х, у и z независимо, за-
бывая о том, что они связаны между собой, и превра-
щать ее в иерархическую.
Точно такая же картина и в экономических и соци-
альных системах. Однако здесь децентрализация в свою
очередь служит источником новой неопределенности.
В самом деле, как только какая-либо подсистема по-
лучает в свое распоряжение право принятия решений,
она превращается в самостоятельный организм, т. е. не-
избежно приобретает собственные цели, в общем случае
не тождественные интересам других подсистем и систе-
мы в целом.
Таким образом, основная причина неопределенности
в принятии решений, возникающей вместе с образовани-
ем иерархии — неизбежность противоречий между це-
лым и его частями, которые проявляются в первую оче-
редь в нетождественности интересов всей системы и ее
отдельных звеньев.
Вот поэтому можно говорить об оптимальной мере
централизации и децентрализации, об оптимальном рас-
пределении функций принятия решений между различ-
ными уровнями системы.
Такой подход к анализу иерархических систем управ-
ления естественно назвать информационным.
5 21
ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ
477
Для того чтобы развить теорию систем управления,
обладающих иерархической структурой, мы должны от-
ветить на целый ряд вопросов, не имеющих аналогий в
классической теории управления: что такое оптималь-
ность в этих многокритериальных системах, как выби-
рать рациональную (или наилучшую структуру) и т. д.
Изложение будет носить индуктивный характер. Мы
начнем с неформального анализа простейших примеров,
а уже позднее дадим описание тех классов задач, для
которых может использоваться развиваемая теория.
Примечание. Если последовательно использовать
приведенные рассуждения, то мы придем к следующему
выводу: по мере совершенствования техники передачи и
обработки информации уровень централизации должен
расти. Этот вывод справедлив для технических систем и
в известной степени подтверждается практикой для си-
стем более сложной природы. Однако в системах эконо-
мических, социальных, информационный подход недос-
таточен для полного понимания природы иерархических
систем. На характер функционирования таких, систем
влияют различные факторы социальной природы, напри-
мер, уровень самостоятельности.
2.	Рефлекторные системы. Рассмотрим какую-нибудь
техническую систему, функционирование которой описы-
вается уравнением
х — f (х, и,1) = АхЛ-и + 1,	(2.1)
где и — управление, g — случайное возмущение.
Мы условились называть систему иерархической в
том случае, если решения в отдельных звеньях принима-
ются только по информации о состоянии этих звеньев.
В простейшем случае
I? — и1 (х).
Определение оптимальной иерархической структуры в
этом случае вкладывается в общую теорию оптимизации.
В самом деле, пусть
и — В (0 и,
где В — диагональная матрица. Определение оптималь-
ной B{t) сводится, как мы знаем, к задаче оптимального
478
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
управления специального вида. Если матрица В имеет
блочную структуру, то мы говорим о блочной (или есте-
ственной) иерархии. Система распадается на отдельные
блоки и выбор величины управляющих воздействий оп-
ределяется только по значениям фазовых переменных,
входящих в эти блоки.
Рассмотрим теперь несколько более сложный пример.
Структура обратной связи определяется структурой мат-
рицы В, более точно—распределением ее нулевых элемен-
тов. Поэтому мы можем говорить о множестве возмож-
ных структур 91= {В8}, каждая из которых задается
матрицей Bs. В зависимости от выбора В8, приходится об-
рабатывать (в том числе передавать по каналам связи,
перекодировать, делать выборки и т. д.), то или другое
количество информации. На это уходит некоторое
время t(s), и в действительности закон управления име-
ет вид
и (0 = B(s) (/) X (Г- х (s)) ~ B(s)x (/) - х (s) B(s)x (/).
Следовательно, вместо уравнения х=Ах+Ви+% мы при-
ходим к такому:
[B-t(s)B(s)]x-(A + B(s))xH-B.
Используя технику, развитую в предшествующих гла-
вах, мы найдем оптимальное значение функционала J.
Оно будет функцией $:
7 = j(s).
Будем называть оптимальной иерархической струк-
турой тот элемент B(s) множества 91, которому отвечает
min J (s). Таким образом, и в этом случае задача опре-
3
деления оптимальной структуры свелась к решению
задачи теории оптимального управления и отысканию
минимального элемента на конечном множестве.
Оба рассмотренных случая являются примером реф-
лекторных систем, т. е. систем, реакция которых на воз-
мущение вполне однозначна. Изучение рефлекторных
систем сводится к обычным задачам оптимизации и не
требует для своего анализа введения специальных гипо-
тез поведения.
§ 2]
ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ
479
Все технические системы, организованные по иерар-
хической схеме, относятся к числу рефлекторных.
3. Простейший пример нерефлекторной системы. Эко-
номические или социальные системы, обладающие иерар-
хической структурой, уже, как правило, не являются
рефлекторными.
Рассмотрим объединение N промышленных предпри-
ятий (трест, синдикат), выпускающих однотипную про-
дукцию. Это объединение будем называть Центром. Обо-
значим через Pi продукцию, выпускаемую i-м предприя-
тием (Производителем), и для упрощения рассуждений
будем считать величины Р( скалярами. Результат функ-
ционирования Центра определяется результатами функ-
ционирования отдельных Производителей. Оценки этого
результата могут быть самыми разными. Мы не будем
останавливаться на их детализации. Для нас важно
лишь одно — сам Центр не производит никакого продук-
та й его целевая функция однозначно определяется про-
дукцией, которую выпускают Производители
7 = J(PUP2, .... PN).	(2.2)
Центр не имеет права декретировать объем производст-
ва Р^ Он может только влиять на них.
Величина продукта, произведенного i-м Производи-
телем, определяется объемом фондов х( и количеством
рабочей силы L(
Pi ~ fl Li).
Функция fi носит название производственной функции.
Существуют различные способы ее аппроксимации.
В экономической науке широкое распространение полу-,
чила функция Кобба — Дугласа
Pt= dix^L^1, ki^[0, 1],	(2.3)
где dt и ki — некоторые характеристики предприятия.
Доход Производителя Д равен стоимости произве-
денной продукции за вычетом накладных расходов. Ус-
ловимся для простоты, что они состоят только в оплате
рабочей силы. Если мы обозначим через со,- ставку зара-
ботной платы (фиксированную величину), то величины
480
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. vti
будут
Ji^cPi — ViLi.	(2.4)
Если величина фондов х{ фиксирована, то объем выпу-
щенной продукции однозначно определяется количест-
вом рабочей силы Lt. Величина Ц является управляю-
щим параметром, который находится полностью в рас-
поряжении Производителя.
Для того чтобы иметь возможность управлять дейст-
виями Производителей, Центр должен располагать ка-
кими-либо способами воздействия на них. Рассмотрим
простейший — распределение экзогенного ресурса U, ко-
торый полностью находится в распоряжении Центра и
должен расходоваться на инвестиции, на создание основ-
ных фондов Производителей. Следовательно, если i-й
Производитель получит в свое распоряжение ресурс
то в течение года он сможет произвести
Pi — dt (xt 4- ui) 1 Li *.
Значит, задача Центра — задача планирования состоит
в таком распределении ресурса U:
N
U^ui,	(2.5)
/=1
которое доставляет максимум функции (2.2). Однако ре-
зультат этого распределения будет зависеть не только от
действий Центра, но и от того, какие значения парамет-
ров Lt будут выбраны Производителями, т. е. в рассмат-
риваемом случае мы оказываемся как раз в ситуации, о
которой говорилось в предыдущем параграфе, т. е. в ус-
ловиях некоторой игры Гермейера, в которой имеется
N +1 игрок: Центр и N Производителей. Для того чтобы
эффективно произвести планирование, необходимо усло-
виться о «порядке ходов», «гипотезе информированно-
сти» и «гипотезе поведения».
В данной игровой ситуации право первого хода при-
надлежит Центру, и Центр, передавая Производителю
ресурс знает, что Производитель будет знать величи-
ну Ui. Значит, главным здесь является вопрос о гипоте-
зе поведения. Предположим, что Центр знает (или счи-
§ 2]	ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ	4fH
тает, что знает) интересы Производителей. Он уверен,
что они описываются целевой функцией (2.4). Тогда ги-
потеза Центра о поведении Производителя состоит в том,
что он так выберет свое управление чтобы максими-
зировать доход (2.4). пешение этой задачи при фикси-
рованных Xt и и( всегда существует, так как функция
/i(L() выпукла вверх, и его легко получить в явном виде
из условия 5Л/д£(=0:
Li = tt(х{ + щ),	(2.6)
где Ct = (cdt (1 — fez)/coz)1/ft‘.
Гипотеза поведения (2.6) позволяет свести задачу
планирования к стандартной задаче математического
программирования. В силу (2.5)
Pi = Ct kidt (Xi 4- uz) = az -J- pzuz,
и, следовательно,
J (Pt, Pi...Pn) = J (az + ₽i«i, ...» 4n + Pa«a) -
= </*(«!, ц2, ..., uN), (2.7)
и мы приходим к задаче отыскания максимума функции
(2.7) при линейном ограничении (2.5).
Таким образом, гипотеза поведения (2.6) позволила
Центру рассматривать Производителей как обычные ре-
флекторные звенья.
4. Управление с помощью штрафов и поощрений.
В предыдущем примере Производитель получил в свое
распоряжение экзогенный ресурс в строго фиксирован-
ном количестве, не зависящем от способа его использо-
вания и результатов его деятельности.
При таком способе управления Центр не мог влиять
на функцию цели Производителя.
Здесь уместно сделать одно замечание, к обсуждению
которого мы еще не раз будем возвращаться.
Факт существования собственных целей у подсис-
тем— это некоторая объективная реальность. Она опре-
деляется только природой подсистем. Автор этой кни-
ги — сторонник Эшби. Если признается, что некоторый
элемент системы представляет собой самостоятельный
организм, то основная его цель—сохранение гомеостази-
16 Н. Н. Моисеев
482
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
са. В разных условиях для разных организмов выраже-
ния целевых функций могут быть разными. В частности,
если условия функционирования таковы, что стабиль-
ность обеспечивается уровнем дохода Производителя, то
целевая функция может быть представлена в форме
(2.4). Центр не может повлиять на этот факт. Он не мо-
жет изменить общественных отношений, которые в каче-
стве меры стабильности подсистемы определяют функ-
цию (2.4). Но он может повлиять на ее величину, за-
ставляя Производителя действовать в направлении,
нужном Центру. Поэтому рассмотрим теперь пример,
когда Центр имеет возможность непосредственно вли-
ять на целевую функцию, меняя ее значение в зависимо-
сти от того управления, которое выбрал Производитель.
Сохраним условие примера, рассмотренного в пре-
дыдущем разделе, и будем считать, что деятельность
Производителя описывается производственной функцией
Кобба — Дугласа (2.5), причем положим й{=1/2, Z=l,
2, ... АЛ Целевую функцию Производителя мы запишем
в виде
Ji (Li) = cdiX^L^ - (HiLi + Ф/ (Pi).	(2.8)
Здесь 4>i(Pi) — дополнительное вознаграждение (или штраф),
которое выплачивается Центром Производителю в зависи-
мости от результатов его деятельности ф, (Pi) е G$), где
— некоторые множества. Величины Xi будем считать
фиксированными и писать (2.8) в виде
J i = a(LZ’ — (HiLt + Ф/ (Pi).	(2.9)
Гипотезу поведения Производителя оставим старой. Это
значит, что он выбирает свое управление из условия мак-
симума функции (2.9). Следовательно, в интересах Цен-
тра форма штрафа или поощрения должна сообщаться
Производителю заранее, т. е. Производитель должен
быть проинформирован о структуре функции <р((Л).
Условие максимума Ji (Li) позволяет определить значе-
ние Li, доставляющее максимум функции J (Li). Li будет
функционалом — оно будет зависеть' от вида функции
L’ = Lt [ф, (Р;)1 • Точно так же функционалом от ф< будет и
§ 2]	ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ	483
оптимальный объем продукта Pr*, P*i = P*i [<pr (Pi)]. Следова-
тельно, задача определения оптимального управления Цент-
ра — это задача определения таких штрафов <рг- (Л), ко-
торые доставляют экстремальное значение функции цели
Центра J (Р19 Р2, ..., Яу), которую мы теперь перепишем
в виде
J = j [Л (Ф1), ... ^(Ы].	(2.10)
Задача определения экстремумов функционала (2.10)
является сложной и нестандартной задачей оптимиза-
ции, поскольку сами функционалы Л определяются из
решения оптимизационной задачи (2.8). Даже для того
очень простого и частного случая иерархической систе-
мы, который мы рассматриваем, решение задачи эффек-
тивного определения оптимального штрафа требует изо-
бретения специальных методов.
Однако если функция цели Центра явно не зависит
от штрафов и если на величину этих штрафов не накла-
дывается никаких ограничений, то решение этой задачи
не единственно и тривиально.
В самом деле, пусть Ри Р2, ..., Pn — объемы продук-
ции Производителей, которые доставляют максимальное
значение функции цели Центра. Тогда мы можем систе-
му штрафов принять, например, в виде
(Л) = X (Pl - Pl)2 - cdixH'i^ + UiLi, (2.11)
где X ;> 0 — произвольное число. В этом случае Ji^^Pi—Pi)2.
Следовательно, Производитель так будет распоря-
жаться своими ресурсами, чтобы объем его продукции
был равен Р<. Структура штрафа (2.11) делает интере-
сы Производителя не противоположными интересам
Центра.
Легко видеть, что функций вида (2.11), которые де-
лают интересы Производителей совпадающими с инте-
ресами Центра, может быть построено бесчисленное
множество.
Однако неограниченный штраф или поощрение вряд
ли могут представлять какой-либо практический инте-
рес. В задачах, «достаточно реально» поставленных,
16*

ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
(ГЛ. VII
величина штрафа либо ограничена, т. е. удовлетворяет
условию вида
(Ф1, ...» W)eG<₽,	(*)
где — некоторое множество, либо значение функции
] зависит от функций <р(:
J ~ J х» А» • • • • Фо ••• Фа/]»
В том случае, когда на функции наложены ограничения
вида (*) или целевая функция Центра явно зависит от
функций штрафа, задача определения максимального
штрафа становится трудной задачей оптимизации.
Заметим, что основная сложность здесь та же, что и
в задачах синтеза. Необходимо отыскивать функции
<pi(P1). Поэтому, так же как и в задачах синтеза, функ-
ции ф<(/30, по-видимому, следует считать принадлежа-
щими к некоторому достаточно простому классу, эле-
менты которого определяются небольшим числом пара-
метров.
Пусть, например, Pt — объем продукта, который с
точки зрения Центра должен произвести i-й Производи-
тель. Тогда функцию штрафа можно искать в виде
ф<(Л)=--^
Целевая функция Производителя будет согласно (2.9)
такой:
J( = аЛ’/г — со/L/ - фДУ* - А)2,
где а, = (с + в,) d(x.i\ р, = (Цх/*. Управление Производителя
аг
определяется из условия — = 0 в явном виде: Ц =
cJZ..
1/4 + 2^А₽/ \	.
_— -------------- и, следовательно, целевая функция
4 \ со/ + kfif У
Центра будет функцией объемов плановых заданий Pt,
коэффициентов «поощрений» е< и «штрафа» kt. Эти ве-
личины находятся в распоряжении Центра, и последний
может их выбрать так, чтобы максимизировать свою це-
левую функцию. Итак, используя гипотезу поведения,
§ 2]
ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ
485
мы снова задачу управления свели к обычной задаче оп-
тимизации.
Примечание. Выбор класса функций, которому
должны принадлежать штрафы и поощрения,— это спе-
циальная и трудная проблема. Дело в том, что расшире-
ние класса допустимых штрафов и поощрений может су-
щественно изменить значение функционала. Ю. Б. Гер-
мейер указал примеры, показывающие, что включение в
число допустимых штрафов и поощрений разрывных
функций может сколь угодно сильно изменить оконча-
тельный результат.
5. Более тонкое использование экзогенного ресурса.
В третьем разделе этого параграфа мы рассмотрели спо-
соб управления с помощью экзогенного ресурса, причем
непосредственно величину выделяемого ресурса и( мы не
связывали с результатом его использования, т. е. с объе-
мом произведенного продукта.
Вернемся теперь снова к модели, которая была рас-
смотрена в п. 3, но условимся, что величина — некото-
рая функция произведенного продукта
и, = Ut [Р, (и,)],
т. е. и( будет некоторым функционалом от функции
В качестве функции, определяющей гипотезу поведе-
ния Производителя, снова примем предположение о том,
что он максимизирует свой доход
Ji= с (х, 4- Ui \Pi\)k'Ll kl — (b Lt s cPi —
Предположим, что функция u((Pt) задана. Поскольку
никаких ограничений на величину Ц мы не накладыва-
ем, то правило поведения Производителя мы получим из
условия
dJt „ dPi n
—- = с —------------со, = 0.
oLf
Величину производной
-— вычислим, рассматривая равенство
Л-(х, 4-и,	= о,
486
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
(ГЛ. VII
как неявное задание зависимости Pt(Lt)’.
 dPi _ (i-Wf + MP.))*1^	(212)
dL;	А>—1 l-k-
+	b1 ' —
Таким образом, в рассматриваемом случае задача
Центра сводится к следующей задаче: определить неот-
рицательные функции ^г(А), связанные равенством
%Ui(Pi) = U,	(2.13)
доставляющие	максимум функционалу	J	Л?]
при следующих условиях:
с	-<^0.	.	(2.14)
Заметим, что	задача максимизации J	при	условиях
(2.13), (2.14) не является стандартной. Она состоит в оп-
ределении некоторой функции фазовой переменной, т. е.
по терминологии, принятой в этой книге, она относится
к задачам синтеза.
Рациональный способ ее численного решения состо-
ит в том, чтобы разыскивать функции мДЛ) из некото-
рого достаточно простело класса. Обозначая снова че-
рез Pi желаемые выпуски продукта, положим
ui = Uto -I- u-uPi 4- м,-2 (Pt — Pty,
где Mio, Чц и ui2 — величины, которые находятся в распо-
ряжении Центра.
Задача определения величин м<0, м;1, и(г и Pi, достав-
ляющих максимум J(Pt,..., Pn) при ограничениях (2.13)
и (2.14),— это уже некоторая задача математического
программирования.
Способ использования ресурса, рассмотренный в п. 5,
более тонкий, чем в п. 3, и содержит его в себе, посколь-
ку способ п. 3 получается как частный случай, если при-
нять Mil = Ui2=0. Таким образом, если мы обозначим
§ 21	ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ	487
через J(” и /(5) оптимальные значения целевых функций
Центра, которые он может получить, если использовать
способы управления ресурсом, изложенные в пп. 3 и 5
соответственно, то между ними будет очевидная связь
6. Ограничение активности отдельных звеньев. Вер-
немся снова к примеру п. 3 и будем считать, что харак-
теристика производственной функции dt зависит от став-
ки заработной платы
й = <Ш).	(2,15)
Функция (2.15) выпукла вверх и обращается в нуль при
ш,=0 (нулевая производительность труда при нулевой
зарплате). Параметр мы также будем считать управ-
лением Производителя. В распоряжении Центра есть не-
который общий фонд заработной платы Q, который он
распределяет между Производителями, SQf=Q. Тогда
управление Производителей стеснено условием
(2.16)
Формально данный пример может быть включен в схему
п. 3. Мы его выделили для того, чтобы обратить внима-
ние читателя на то, что Центру может оказаться выгод-
ным поощрять одних Производителей и сужать множе-
ство допустимых стратегий других.
7. Цена децентрализации. Итак, мы видим, что выбо{1
управления в иерархической системе сводится к анализу
некоторой игровой и достаточно сложной ситуации. Од-
нако, вводя гипотезу поведения, мы сводим игровую за-
дачу к специальной задаче оптимизации.
Теперь мы можем ввести понятие оптимального уп-
равления иерархической системой как управления, до-
ставляющего экстремальное значение целевой функции
Центра в предположении, что управление Производите-
лей определено на основании гипотезы их поведения.
Оптимальное значение целевой функции Центра обо-
значим через /*. Предположим теперь, что система уп-
равления полностью централизована. Это значит, что
Центр может распоряжаться не только распределением
экзогенного ресурса и фондом заработной платы, назна-
чением штрафов, но и количеством нанимаемых рабочих
и ставкой заработной платы. Оптимальное значение
488
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
ЛГЛ. VII
целевой функции Центра в этом случае обозначим через
J**. Очевидно, что
«/**>/*.	(2.17)
Введем еще величину
Д=	(2.18)
Эту величину естественно назвать ценой децентрали-
зации— это цена, которую платит Центр, и которая ха-
рактеризует уменьшение его дохода вследствие органи-
зации иерархической структуры. Она всегда неотрица-
тельна, т. е. в рассматриваемом примере децентрализа-
ция всегда невыгодна.
Такой вывод мы получили только потому, что мы рас-
сматривали случай полной информированности, когда
Центр располагает всей той информацией, которой рас-
полагает и Производитель. Но введение иерархической
структуры, передача Центром прав о принятии решения
диктуется прежде всего тем, что Центр не имеет в сво-
ем распоряжении (и не может иметь) той информации,
которой располагает Производитель.
- Вернемся снова к нашему первому примеру с распреде-
лением экзогенного ресурса между Производителями. Вместо
производственной функции (2.3) рассмотрим такую:
= (di + x^Li \ & — параметр, который точно известен
Производителю (например, & = 0). Это значит, что Произ-
водитель точно знает свои возможности, т; е. приняв реше-
ние о количестве рабочей силы, которая будет занята на
производстве, он может точно оценить объем продукта,
который он сможет произвести. Центр располагает об этом
значительно меньшей информацией. Пусть, например, Центру
известно, что [gf, ^]. На основании гипотезы поведения
/ dJt	\
—— = 0 Центр может сделать заключение лишь о гра-
\	/
ницах объемов производства. Другими словами, повто-
ряя выкладки п. 3, мы найдем, что целевая функция
Центра зависит не только от характера распределения
ресурсов uit но и от параметров неопределенности g<:
J=J(ul9 и2, ..., uN, gi, ..., gjv). Для того чтобы осущест-
вить планирование, Центр должен задаться еще не-
§ 2]
ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ
489
которой гипотезой о величинах £(. Предположим, напри-
мер, что Центр использует гарантированную стратегию.
Тогда вместо функции J Центр будет использовать функ-
цию I:
I = min </(«!, .........uN, In), (2.19)
которая зависит уже только от величин и{.
Подобно тому как мы это сделали в случае полной
информированности, мы можем ввести величины Г и Г*:
Г = max I («.«а • • • un),
2u(=U
/** = max min J (/\	Pn(unZnLn)).
Su‘=u
Z**—это значение целевой функции Центра в условии
полной централизации.
Теперь уже утверждение (2.17) не имеет места и це-
на децентрализации А может быть любого знака.
8. Заключение. В этом параграфе я хотел на простых
примерах пояснить тот смысл понятий «иерархия», «де-
централизация», которые введены в книге. Существен-
ным является выделение рефлекторных иерархических
систем, где функционирование звеньев точно регламен-
тировано. Это — важный класс иерархических систем,
технических или экономических, которые имеют блоч-
ную структуру. Их исследование возможно с помощью
методов теории оптимального управления. И как бы
сложны ни были эти задачи, тем не менее для их реше-
ния нет необходимости привлекать дополнительные ги-
потезы игрового характера.
Иначе обстоит дело с системами нерефлекторными.
Рассмотренные примеры показывают, что для анализа
их функционирования мы должны принять некоторую
гипотезу поведения. Только в этом случае мы можем
сформулировать какое-либо правило принятия решений
и определить понятие оптимальности.
Однако, коль скоро гипотеза поведения сформулиро-
вана, мы получаем правило, на основании которого дол-
жны действовать отдельные автономные звенья, т. е.
фактически сводим изучение нерефлекторной системы к
рефлекторной.
490
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
Примечание. Существенно, что мы говорим
«должны действовать», а не «действуют», поскольку ги-
потеза не есть строгий закон. Это наше предположение,
на основе которого мы совершаем акты уйравления сис-
темой. В действительности, самостоятельные звенья мо-
гут принимать и иные решения, отличные от тех, кото-
рые им предписывает гипотеза поведения.
Гипотезу поведения мы формулировали, считая из-
вестной целевую функцию. Но определение целевых
функций подсистем — это, по-видимому, наиболее труд-
ная проблема теории иерархических систем. Я думаю,
что она связана с гомеостазисом и требует глубокого
изучения социальных условий функционирования. В ка-
честве целевых функций мы использовали функцию, ко-
торую мы назвали доходом. Но это только правдоподоб-
ное предположение и, изучая иерархические системы,
надо всегда считаться с этим обстоятельством.
В заключение заметим, что для задачи, решаемой
Центром, нет прямой необходимости знать целевые фун-
кции подсистем. По-существу, нам достаточно знать от-
клик, реакцию подсистемы. Вот здесь и возникает цен-
тральная проблема управления иерархическими систе-
мами— сведение, аппроксимация нерефлекторных сис-
тем рефлекторными. Эта редукция требует дополнитель-
ной информации, для которой в статической задаче нет
источника. Однако если мы рассматриваем реальные ди-
намические системы с многократно повторяющимся ак-
том принятия решения, то сведения, которые мы полу-
чаем об эволюции системы, о ее реакции на наше управ-
ление, могут быть использованы для построения некото-
рого адаптационного механизма, с помощью которого
можно осуществлять управление в иерархических сис-
темах.
§ 3. Динамические системы
с двухступенчатой иерархией
1. Пример двуступенчатой иерархической системы.
Перейдем теперь к рассмотрению динамических систем,
ограничиваясь, как и ранее, обсуждением примеров.
Рассмотрим промышленное объединение (фирму),
состоящее из N производственных предприятий (Произ-
§ 3]
ДВУХСТУПЕНЧАТАЯ ИЕРАРХИЯ
491
водителей), которые выпускают продукты Р2 ...,
Обозначим через основные фонды i-ro Производителя.
Предположим, что изменение фондов описывается урав-
нением
Xi = — kiXi + Ui (0 + Vi (0,	(3.1)
k( — коэффициент амортизации,
Ut — инвестиции фирмы (экзогенный ресурс),
vt — внутренние капиталовложения,
и{, Vi — это потоки капиталовложений — вложения в
течение единицы времени,
v<(0 — управляющая функция Производителя,
«,(/) — управляющая функция фирмы.
Процесс производства будем описывать производст-
венной функцией
Pi = <₽/ (Xi, Lt, Yz), i = 1, 2, ..., N. (3.2)
Здесь L{ — количество рабочей силы, у{ — ставки зара-
ботной платы.
Lt и yj также находятся в распоряжении Производи-
теля и подчиняются ограничениям вида
Ь/>£7>0,
Y/>YF>0,	(3.3)
ViLi^Qi.
Смысл первых двух ограничений очевиден. Последнее же
означает, что фонд заработной платы ограничен.
Создав вектор продукта Pi, Производитель реализует
его: сдает на склад фирмы или передает в торговую
сеть. Обозначим через с вектор цен, следовательно, за
реализацию продуктов Производитель получает в еди-
ницу времени сумму (с, Pt). Из этой суммы он дол-
жен заплатить зарплату рабочим сделать вложе-
ния в фонд фирмы Wi(P{), произвести внутренние
капиталовложения v{ и компенсировать текущие зат-
раты R{.
Обозначим через ф, остаток от этих расходов:
Ф« (0 = (С, Pi) - {yiLi 4- Wi (Pi) + Vi (t) + Ri (Xi)}. (3.4)
492
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
Величину условимся называть социальным фондом
предприятия. Эта величина находится в распоряжении
Производителя. Она может расходоваться на поощре-
ния работающих, на социальные нужды и т. д. По свое-
му смыслу эта величина неотрицательна:
V/e[/0) Т] 1М0>0.
Будем считать, что условия гомеостазиса связаны с
объемом социального фонда при дополнительных огра-
ничениях типа Р^Р~. Таким образом, если внешние ин-
вестиции u((t) заданы, если известна функция wt(Pt),
которую естественно назвать функцией поощрения (или
штрафа), если известен фонд заработной платы
то задача t-ro Производителя так распорядиться доба-
вочными инвестициями v{(f), ставкой заработной платы
yf(0 и количеством рабочей силы £<(/), чтобы максими-
зировать свой социальный фонд. Этот функционал мы
обозначим через
Л = Л (о<, Yz, М-	(3.5)
Функционал может иметь самую произвольную при-
роду. Например, естественно принять, что
Ji= min {ipz (/)}.	(3.6)
/е[о,Т]
Максимизация функционала (3.6) означает максимиза-
цию минимального размера социального фонда, созда-
ваемого в единицу времени. Не менее естественно рас-
сматривать функционалы вида
т
(3.7)
О
где Т — плановый период.
Поставленная так задача является стандартной за-
, дачей теории оптимального управления.
Рассмотрим теперь функционирование правления
фирмы, которой подчиняются Производители. По своему
смыслу это организация бюрократическая и сама ника-
ких ценностей не производит. Эффективность ее деятель-
ности оценивается в зависимости от того продукта, ко-
торый производят Производители.
§ 3]
ДВУХСТУПЕНЧАТАЯ ИЕРАРХИЯ
493
Критерий (доход фирмы) мы будем писать в форме
J = J (Ри Р2, Pn, (₽i),	(Р2), • • •,	(Pn)). (3.8)
Примечание. В выражении (3.8) подчеркивается,
что доход фирмы зависит от структуры функций поощре-
ния. Если целевую функцию фирмы принять независимой
от w((Pt), а фонд поощрений неограниченным, то триви-
альной будет следующее утверждение:
Всегда могут быть назначены поощрения (штрафы)
Wi(Pi), w2(P2)......wN(PN) такие, что Производители
будут выбирать свои управления наилучшим способом с
точки зрения интересов фирмы.
В качестве функционала / могут выступать самые
разные величины: точность соблюдения государственного
плана или максимизация числа комплектов оборудова-
ния или, наконец, чистый доход.
Итак, мы пришли к ситуации, о которой говорилось в
первом параграфе.
Существуют «два» игрока — фирма и предприятия,
имеющие свои собственные цели. Здесь нет симметрии:
фирма имеет право первого хода. Задача фирмы так рас-
пределить экзогенный ресурс
N
3 %	(3-9)
^=1
фонд заработной платы
N
=		(3.10)
z=i
и назначить такие поощрения да.-(Л) предприятиям за
выпуск продукции, чтобы максимизировать доход Л
Мы видим, что фирма располагает тремя способами
управления — она может распределять экзогенный
ресурс U, вводить функции штрафов или поощрений
да«(Рг) и ограничивать активность Производителей.
2. Общая схема дифференциальной игры. Приведен-
ный пример показывает, что проблема принятия решений
в иерархической системе, т. е. проблема управления, при-
водит к некоторой дифференциальной игре. Приведем
494
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
теперь формальное описание игры, частным случаем
которой была игра, описанная в предыдущем пункте.
Пусть имеется динамическая система:
Ъ = A (xif uh Vi, t) f = 1, 2, ..., Af. (3.11)
Здесь Xi (t) — вектор-функция времени co значениями из
Ui(t) и Vi(t) — вектор-функции со значениями из Ет.
и Eri соответственно.
На функции %г(0 наложены ограничения
Vt Xi(t)^0,	(3.12)
На управляющие функции Ui(t) наложены ограничения
вида
V/ {и19 и2, ..., uN} <= Gu *).	(3.13)	|
Относительно ограничений на Vi(t) будет сказано ниже. |
С динамической системой (3.11) связывается система
функционалов Л:	'
Ji — Ji \Xi, vit Wi (xi9 01, i— 1,2, ...,Af,	(3.14)
где Wi(Xi, t) — управление типа синтеза co значениями ;
из Eki9 т. е. значение однозначно определяется, как
только мы зафиксировали определенное значение век- >
тора Xi и момент времени t.
На функции Vi Wi и фазовые переменные х» наклады- |
ваются ограничения типа	I
V/Oi(vz, ш/)>0.	(3.15)
Кроме того, вводится понятие генерального функцио-
нала /:
I
J = J (х19 ..., xN, ..., uN, w19 ..., wN, Gu). (3.16)	।
Описание игры. В начальный момент t=0 состояние	I
системы, т. е. векторы хДО), фиксированы. Игрок а I
делает первый ход. Он сообщает игрокам функции ;
u>i(Xi, t) и Ui(t) и множество G«.
Гипотеза поведения игроков Игроки выбирают
функции v.(t) так, чтобы максимизировать функцио-
*) Может быть рассмотрен и более общий случай, когда Ui не
просто функции времени, но зависят еще и от хг. щ [%г («<)].
§ 3]	ДВУХСТУПЕНЧАТАЯ ИЕРАРХИЯ	495'
налы Л. Игрок а имет своей целью так выбрать ui9 wi9
Gu, чтобы максимизировать генеральный функционал Л
Время Г, в течение которого происходит игра, может
быть фиксированным или свободным. То же самое можно
сказать и о значениях х^Т),
Описанный класс задач теории дифференциальных
игр весьма широк. В зависимости от структуры функцио-
налов мы можем получить тот или другой тип игры.
Если Af=l, 7=—|[х||, Jt= ||х||, а Т не фиксировано,
то мы получаем один из вариантов игр преследования.
Какие-либо общие заключения относительно столь
широко поставленной задачи, в том числе и методы
вычислительного характера, вряд ли могут быть пред-
ложены. Для того, чтобы продвинуться дальше, мы
должны сузить рассматриваемую проблему.
Условимся в дальнейшем, что функционалы и J—
интегральные:
т
J = J р (хи ..., xN, и19 uN, w19 ..., шд, Gu) dt,
л
(3.17)
т
Ji = J F{(xit vit wijdt.
0
Следующее упрощение состоит в снятии ограничений.
Это может быть сделано разными способами.
Одним из примеров ограничения (3.15) является
условие ф<(/)^0, где определяется равенством
(3.4). В этом случае мы можем вместо функции vt(t)
ввести новую управляющую функцию yt(t) с помощью
равенства
Vi (0 = — yi (О <(с. Pi) — Yibj — wt (xit t) — Ri (Xi)}.
В этом случае снятие ограничений не вносит какого-
либо изменения в природу задачи. В других случаях мы
будем вводить функции штрафов.
В результате мы заменим исходную задачу другой.
Ее решение будет аппроксимировать решение исходной
задачи, но искомые параметры и функции уже не будут
стеснены ограничениями.
496	ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ [ГЛ. VII
Повторим ее новую формулировку. Игрок а сообщает
игрокам функции Ut(t) и Wi(xb t) таким образом, чтобы
максимизировать функционал
т
J* = (xlt ..., xN, ul9 ..., Uk, wl9 ..., Wk) dt. (3.18)
0
Игроки выбирают свои стратегии vt(t) так, чтобы
максимизировать функционалы
т
J* = ^F'(x{,vitwi)dt.	(3.19)
О
В выражениях (3.18), (3.19) знак * означает, что функ-
ционалы записаны в форме, учитывающей функции
•штрафа, с помощью которых мы сняли ограничения.
Примечание. Применение функций штрафа в эко-
номических задачах целесообразно по ряду причин.
Во-первых, в этих задачах требуемая точность обычно
невелика, а во-вторых, ограничения никогда не бывают
достаточно жесткими.
3. Применение принципа максимума. Для решения
задачи в этой упрощенной постановке может быть
использован принцип максимума.
Рассмотрим сначала задачу для игрока 0(. Введем
функцию Гамильтона Н{:
Hi = (Xf, ft (xt, ub Vi, 0) + Ff (xt, vt, wi).
Поскольку игрок а сообщает игрокам р( заранее функции
ut(t) и wf(xt, t), и поскольку в задаче * на функции uf(t)
никаких ограничений не наложено, то необходимое усло-
вие максимума функции Гамильтона можно записать в
.виде
Это условие мы будем писать в форме
'Г/ (К, Xt, Ui, Vi, t) = 0.	(3.20)
Условие (3.20) — векторное. Оно имеет размерность век-
тор-функции vt(i).
ДВУХСТУПЕНЧАТАЯ ИЕРАРХИЯ
497
§ з]
Множители Лагранжа удовлетворяют следующему
векторному уравнению:
(3.21)
dxt dxt d%i dwi dXi
Поскольку никаких ограничений на правый конец
траектории не наложено, то мы приходим к следующему
результату:
Для того чтобы функция Уг(0 была оптимальной для
игрока р», необходимо, чтобы она удовлетворяла усло-
вию (3.20), где Xi удовлетворяют уравнениям (3.11) и
(3.21) и граничным условиям
хД0) = х,в, %<(Т) = 0,	(3.22)
где xi0—известные векторы.
Написать подобного рода необходимые условия для
игрока а мы не можем, поскольку помимо «стандартной')
управляющей функции «,(0 в распоряжении игрока а
находится выбор функции w((xt, t). Таким образом,
игрок а решает задачу типа синтеза, т. е. он должен
найти управление, зависящее от фазовых координат, для
которой не существует достаточно простых необходимых
условий.
В теории синтеза систем управления синтезирующую
функцию разыскивают обычно в некотором классе
функций.
Будем разыскивать функцию поощрения wt(xh t)
в виде
паг (хг, /) = «о + ch х{ 4- а^х*.	(3.23)
Коэффициентам а*(/) легко дать экономическую интерпре-
тацию. Действительно, представим (3.23) в виде
(xh i) = b^Xi 4- b‘2 (X/ — x*i)2,	(3.24)
где функции b[ (i), b[ (/) и x*i (t) легко определяются через
al0 (/). Функция Xi (t) — это плановое задание предприятию,
b^Xi — поощрение (b{ >0) за выпуск продукции, b{ (х{ —х*)2—
наказание (Ь»^0) за невыполнение плана.
17 Н. Н. Моисеев
498
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
Если мы примем аппроксимацию (3.23), то задача игро-
ка а будет следующей задачей оптимального управления:
определить функции Xi(t) и i= 1, 2, ..., удов-
летворяющие уравнениям (3.11) и (3.21), и функции (t),
Ui (t), а' (0, ai (О и (0» доставляющие максимум функцио-
налу (3.8) и удовлетворяющие ограничениям (3.20) и (3.22).
Задача, которая возникает при использовании необходи-
мых условий, является краевой задачей весьма высокой
размерности. Размерность фазового вектора (х, X) равна
N
2 3 ni> размерность управляющего вектора (и, v, ап, а1г
равна
N	N	N
2 т? + 2 з 2
1—1	1—1	i—i
Высокая размерность задачи делает ее с вычисли-
тельной точки зрения весьма трудной. Облегчающим
обстоятельством является то, что на значения Xi(T) не
наложено никаких ограничений. Оно позволяет исполь-
зовать итерационные методы, на каждом шаге которых
приходится решать только N задач. Размерность каждой
из этих вспомогательных задач равна удвоенной размер-
ности соответствующих фазовых векторов хг*.
4. Динамические задачи с неполной информацией.
Рассмотрим сначала одну вспомогательную задачу.
Пусть эволюция управляемой системы-описывается урав-
нением
	(3.25)
где х— фазовая переменная, « — управление, g — неко-
торый параметр или функция, которая заранее не из-
вестна. Априорная информация о функции g такова:
(3.26)
где — некоторое множество.
Управление u(t)^Gu выбирается из условия
J* — max J (и).	(3.27)
§ 3]	ДВУХСТУПЕНЧАТАЯ ИЕРАРХИЯ	499
Найдем гарантированный результат в условиях
информированноети (3.26). Предположим, что мы вы-
брали некоторое управление u=u(f). Тогда значение
функционала определяется не только управлением и,
но и функцией g(7):
J=/(u, g).
В этих условиях гарантированный результат J (и) будет
/(«)= minj (и, £), и следовательно, выбирая управление
и (/) из условия (3.27), мы можем гарантировать следую-
щий результат, который обозначим J*: 
J* — max min<7 (и, |).	(3.28)
«еб„ geGg
Предположим теперь, что, кроме априорной информации
(3.26), мы знаем заранее, что в каждый момент времени
нам будет известно значение параметра |.
Как использовать эту дополнительную информацию?
В этом случае имеет смысл искать управление не только
как функцию времени, но и возмущения
и = и (g, t).
(Если в момент времени t мне удается иметь | кг дефи-
цитных материалов, или если рыночные цены окажутся
равными |, тогда я найму такое-то количество рабочих
«=«(£, /).) Для того, чтобы найти функцию u(g, t),
будем следовать условию (3.27). Это значит, что мы
найдем значение функционала /*, которое будет зависеть
от
J* (|) = max J (и,
US.GU
т. е. мы сформулировали правило, по которому каждой
функции мы ставим в соответствие значение функцио-
нала J* (£•). Следовательно, результат (доход), который
мы можем гарантировать в этом случае, будет
J’ = min max J (и, £).
u&ju
17*
500
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
Но согласно теореме о минимаксе
(3.29)
Этот результат совершенно тривиален. Он означает, что
если правильно использовать информацию, которой мы
будем располагать, то результат всегда окажется лучше
(или, во всяком случае, не хуже).
Примечания.
а)	Все, что было сказано в этом разделе, может быть
рандомизировано и переписано с помощью языка теории
вероятности.
б)	Рассуждения в данном примере могут быть легко
обобщены на более общие случаи информированности.
Например, вместо гипотезы о том, что в каждый момент
времени будет известно значение параметра g, интересно
и важно рассмотреть гипотезу о том, что в каждый
момент будет известно, что
(3.30)
После этих замечаний вернемся к обсуждению модели
иерархической системы, которая является обобщением
модели п. 2 этого параграфа.
Динамический процесс описывается следующей си-
стемой уравнений:
Х/ = А(хг, «ь (/),/), i= 1, 2, ,..., У. (3.31)
Когда мы пишем f(...	...), то это означает, что
в момент времени t значение f зависит от значения
функции £ в этот же момент времени. Если f является
функционалом (или оператором), то мы будем писать
f(. ..£[/]...) Все остальные обозначения, принятые з
уравнении (3.31), совпадают с ранее введенными.
Для того чтобы придать экономический смысл нашим
рассуждениям, уравнение (3.31) будем называть про-
изводственным процессом i-ro Производителя.
. Новым в уравнении (3.31) по сравнению с уравнением
(3.11) является присутствие функции |4(/). Будем счи-
тать, что Центру (фирме) доступна только некоторая
априорная информация вида

(3.32)
§ 3]	ДВУХСТУПЕНЧАТАЯ ИЕРАРХИЯ	501
Что касается Производителя, то в процессе производства
величина £ (состояние оборудования, качество мате-
риала, производительность труда и т. д.) ему становится
известной.
Мы сохраняем гипотезу о поведении Производителя.
Будем считать, что он стремится максимизировать функ-
ционал (3.14). Сохраним также гипотезу об информиро-
ванности Производителя. Центр делает первый ход,
сообщая Производителям величину экзогенного ресурса
щ(1) и функцию поощрения wf(x(). Получив эту инфор-
мацию, Производитель может реализовать акт составле-
ния плана. Но (и это очень существенно) его план дол-
жен иметь характер синтеза. Это значит, что управляю-
щие воздействия которые находятся в распоряжении
Производителя, должны зависеть не только от времени,
но и от воздействий Центра и параметра неопределен-
ности g:
Vi — Vt (&, и1, Wi, t).	(3:33).
Следовательно, и траектория xt будет некоторым опера-
тором, действующим над множеством этих функций:
Xi = Xi (t, If [/], Ui [/], Wt [X;]).
Следовательно, функционал, характеризующий интересы
Центра, мы также сможем представить в аналогичной
форме:
*7 == .7 [х^ [7, 5р х%	.. Xjy [7,	• • •
...	, uN, ut>lt ..., wN, Gu]. (3.34)
Максимизируя выражение (3.34), мы получаем управ-
ляющие воздействия'Центра также в форме синтеза:
Ui Ui (7, 51» ..., 5vX
Wi^Witf, Xi, &....5w),	(3.35)
Gu^G^t.b........In).
Цоскольку 5i—априори неизвестные факторы, то проб-
лема априорной оценки качества функционирования дан-
ной иерархической системы требует еще дополнитель-
ного обсуждения. Заметим, что априорная оценка — это
основной результат развиваемой теории. Умение ее
502
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
вычислить позволяет сравнивать различные варианты
иерархической организации, создаваемые для решения
одной и той же задачи.
Для построения такой оценки мне кажется естествен-
ным использовать принцип гарантированного результата.
Если в одних и тех же условиях гарантированный
результат системы А больше гарантированного резуль-
тата системы В, то следует предпочесть систему А.
Из процесса построения решения (3.35) следует, что
гарантированным результатом Центра будет число,
вычисленное по следующему правилу:
J**== min max J (хх [/, gx, шх], ..., xN [/,	ux,...
ui»witGu
..., uNt ...» wN, Gu}.
Рассмотрим теперь тот случай, когда управление
динамической системой (3.8) осуществляется из единого
Центра. Это означает, что не только и() w{, Gu, но и vt
находятся в распоряжении Центра и выбираются из
условия максимума функционала J.
Заметим прежде всего, что структура ограничений
Gu перестает быть управляющим воздействием. В инте-
ресах Центра (фирмы) предельно ослабить любые огра-
ничения на выбор управляющих воздествий. Далее,
о параметрах известна априорная информация (3.32)
и никакой другой информации Центр иметь не будет.
Следовательно, гарантированный результат функциони-
рования системы в условиях полной централизации будет
таким:
J — max min J (xv ..., xN, и, ..............ау'дгЬ
u,v,w
Сравнивая J и Г, мы можем оценить качество введен-
ной структуры. Если Д=/—/*>0, то введение иерархии
в системе управления ухудшает качество работы сис-
темы. Если Д<0, то введение иерархической струк-
туры делает экономический механизм более эффек-
тивным.
Примечание. Заранее сравнить величины J и Г,
це решая конкретной задачи, и получить результат (3.29)
§4]
ОДИН ПРИМЕР ТРЕХУРОВНЕВОЙ СИСТЕМЫ
503
в общем случае мы не можем. Проблема проектирования
организации, если мы хотим ее создание поставить на
реальную основу, неизбежно потребует решения задач,
подобных рассмотренной.
§ 4.	Один пример трехуровневой системы
1.	Предварительные замечания. В предыдущих пара-
графах мы рассмотрели несколько моделей функциони-
рования систем, обладающих иерархической структурой.
Эти модели, вероятно, можно было бы назвать моделями
экономических механизмов. Конечно, вряд ли сегодня
кто-нибудь анализирует функционирование фирмы, объ-
единения, корпорации, по схеме, которая была изложена.
Да и задачи, которые здесь возникают, с вычислительной
точки зрения кажутся чрезвычайно сложными. И тем не
менее, в реальных механизмах присутствуют все те эле-
менты, о которых здесь говорится: и существование
несовпадающих целей, и различная информационная
обеспеченность, и право первого хода, и право принимать
самостоятельные решения, и т. д. И решения, которые
принимают управляющий (или правление), объективно
учитывают все эти обстоятельства. Поэтому в преды-
дущих параграфах мы действительно рассмотрели фор-
мализацию некоторых механизмов, реально существую-
щих в нашем реальном мире.
Однако модели экономических механизмов, которые
мы рассматривали в этой главе, были предельно упро-
щены. Вероятно, только в самых простых случаях, когда
объединение можно рассматривать изолированно,
удается свести анализ реальной ситуации к модели,
имеющей два уровня. В самом деле, пусть Центр — это
некоторые Производственные объединения, а Производи-
тели— хозрасчетные предприятия. Мы рассмотрели
функционирование этого множества экономических орга-
низмов как некоторой независимой совокупности, изоли-
рованной от всего остального мира. Но ведь существует
еще Государство, которое имеет юридическое и фактиче-
ское право вмешиваться в деятельность объединений,
ставить им определенные задачи, влиять тем или иным
образом на стратегию Производителей. Частично мы
учли эти возможности, рассматривая экзогенный
504
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
ресурс — капитал, выделяемый Государством в распоря-
жение Центров. Мы назвали его экзогенным ресурсом.
По существу, он имитировал централизованные капи-
таловложения.
Но действительность значительно сложнее. Прежде
всего этот экзогенный ресурс является капиталом, фор-
мируемым в результате действия тех же самых Про-
изводителей. Его формирование — это своеобразный и
сложный механизм, включающий в себя налоги на
фонды, налог на оборот и другие виды отчислений.
Далее, распределение экзогенного ресурса по объедине-
ниям—это еще один механизм—механизм общегосудар-
ственного планирования. Наконец, еще существует банк,
деятельность которого пронизывает все звенья иерархи-
ческой системы. Поэтому даже самая простая модель
общегосударственного механизма должна иметь три
уровня иерархии.
Сделаем теперь еще один шаг в формализации про-
цессов управления экономическим организмом и рас-
смотрим простейшую трехступенчатую иерархическую
модель.
Однако переход к трехуровневой системе качественно
усложняет математическое содержание задачи. Для того
чтобы представить себе функционирование такой системы
и содержание задачи анализа трехступенчатого меха-
низма, рассмотрим условную модель трехступенчатой
иерархической системы, которую назовем «Государ-
ство» — Центры — Производители.
Эта условная модель имитирует функционирование
централизованного народнохозяйственного организма с
высоким уровнем децентрализации в принятии конкрет-
ных решений. Очень часто противопоставляют эти два
понятия, хотя при разумном использовании возможно-
стей управления Производителями, которые есть в рас-
поряжении более высоких уровней, централизация и де-
централизация могут рационально дополнять друг друга.
Централизация управления общегосударственным
народнохозяйственным организмом означает существо-
вание общегосударственных целей и средств управления
(правовых, экономических), могущих обеспечить их
достижение. Что же касается децентрализации, то, как
это следует из предыдущего, существует некоторый уро-
§4]
ОДИН ПРИМЕР ТРЕХУРОВНЕВОЙ системы
505
вень децентрализации, который мы назвали оптималь-
ным и который в наибольшей степени содействует дости-
жению целей верхних уровней и в том числе общегосу-
дарственных целей.
Общегосударственные цели мы будем отождествлять
с некоторой Программой. В этот термин мы будем
вкладывать ограниченное содержание и называть Про-
граммой сформулированный в результате некоторой
неформальной процедуры перечень объемов конечного
продукта.
2.	Модель Программы. Предположим, что в данной
экономической системе, которую мы условно назовем
«Государство» и которая предполагается замкнутой,
вырабатывается М разных продуктов Р1( Р2.........Рм-
Включение в эту модель экспорта-импорта и коньюнк-
туры международного рынка не вносит с математиче-
ской точки зрения качественных усложнений. Все особен-
ности трехуровневой иерархии могут быть прослежены и
на замкнутой модели. Для выполнения программы необ-
ходимо, чтобы эти продукты вырабатывались в течение
планового периода в определенных количествах. Другими
словами, в результате разработки Программы должны
быть определены функции Р* (t). Следовательно, реали-
зация Программы в каждый данный момент характери-
зуется системой показателей rj(t)=Pj(t)IP* (/). По-
скольку P*j (t)—некоторый абсолютно необходимый
норматив, то оценку качества реализации программы
выпуска i-ro продукта в течение планового периода
можно охарактеризовать числом r/=minТогда
te(0,T)
очевидно, что Государство тем лучше выполнит свою
программу, чем больше будет функционал
—	р
J — min г/ = min min—г
/ ‘ i t Pf
Примечание. Вполне реальна такая ситуация,
когда выпуски отдельных продуктов Р\ не равноценны.
В этом случае функционал (4.1) будет заменен таким:
J = minmin(X.-r»(/)),
t I
W
(0
(4.1)
506
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
где Xj — некоторые коэффициенты, соизмеряющие значе-
ния величин Р.
3.	Центры. Предположим, что весь экономический
организм «Государства» состоит из N объединений,
которые мы будем называть Центрами. Каждое r-е объ-
единение состоит из Ni Производителей. Центры выпол-
няют только управленческие (бюрократические) функ-
ции. Они не производят продукт непосредственно. Задача
Центров — распределить капиталовложения, которые
выдаются «Государством». Этот ресурс мы будем обо-
значать Ui (г=1 ,..., N). Этот ресурс выдается «Госу-
дарством» безвозмездно — он моделирует централизован-
ные капиталовложения. Кроме того, «Государство»
выделяет в распоряжение Центра фонд заработной платы
который Центр должен распределить среди Про-
изводителей, входящих в данное объединение. Кроме
того, Центру сообщается его программа P?(t) (i= 1 ,...
..., N, / = 1, ..., Л1) производства.
Примечание. Если r-й Центр производит только
однотипную продукцию, например, Ph то все Р1. =0 для
/=/=/.
Вопрос об определении целевой функции Центров
упирается все в ту же проблему гомеостазиса. Мне
кажется правдоподобным следующее рассуждение. Как
и всякое бюрократическое управленческое учреждение.
Центр заинтересован в наилучшем выполнении про-
граммы. Выполнение распоряжений верхнего уровня
обеспечивает в первую очередь его стабильность. Функ-
ционал, характеризующий благополучие Центра, будем
обозначать через Л. Одна из возможностей описать дей-
ствие Центра — это максимизация функционала
т •	.	Р/«	/у1оч
Jt = min min —-—.	(4.2)
I ‘
Конечно, существуют также полностью хозрасчетные
объединения, которые имеют целевые функции, отличные
от (4.2). Их обсуждение на содержательном уровне нас
увело бы очень далеко от основной нашей задачи —
представить себе особенности математических гипотез,
лежащих в основе функционирования подобного трех-
ступенчатого механизма. Для того чтобы охватить более
§ 4]
ОДИН ПРИМЕР ТРЕХУРОВНЕВОЙ СИСТЕМЫ
507
широкий класс задач, условимся считать, что цели
Центра описываются некоторым функционалом Л, зави-
сящим только от результатов производственной деятель-
ности Производителей, входящих в объединение
=	Рл!).	(4.3)
4.	Банк. В распоряжении «Государства» находится
Банк, который является носителем его интересов. Этим
условным термином мы объединяем как собственно бан-
ковую службу, так и фискальную, налоговую систему.
Через z(0 мы будем обозначать общий объем денег,
находящихся в Банке, т. е. в распоряжении «Госу-
дарства».
В качестве поступлений в Банк мы будем рассматри-
вать следующие составляющие:
а)	Налог на фонды. Фонды k-ro Производителя,
входящего в i-e объединение (Производитель (i, k)),
будем обозначать через xih. Обозначим через некото-
рый числовой коэффициент и будем считать, что Про-
изводитель отчисляет из своей прибыли величину
Обозначим
N- Ni
(4-4>
г=1 k— 1
б)	Налог с оборота. Предположим, что Производитель
(I, k) создал в единицу времени продукт {P[k, Pl2k, . , Р'м}.
Обозначим через Cj рыночную (или оптовую государственную)
цену продукта Р,-. Тогда .«Государству» отчисляется неко-
торая сумма С/, т. е. Производитель получает за продажу
продукта
м
2 (</-М	(4.5)
а «Государству» отчисляется от всех Производителей
n Ni м	м
*₽ = 22 2^ = 2 Л <4-6>
1=1Л=1/=1	/=1
где Р} — суммарный /-й продукт.
508
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
в)	Процент от кредита Центрам. Банк может креди-
товать Центры. Если у(— количество денег, которые
i-й Центр взял в займы у Банка, то он выплачивает
Банку в единицу времени \У1у<. Таким образом, Банк в
форме процента на кредит получает в течение единицы
времени
N
zy ~ 2 У^уг
/=1
(4-7)
г)	Процент от кредита Производителям. В этой
работе речь идет о централизованной экономике, носи-
телем целей которой мы условились называть «Госу-
дарство». Нетождественность интересов всех уровней
иерархии может привести к тому, что «Государству»
выгодно иметь возможность тем или иным способом
непосредственно, минуя Центры, влиять на активность
Производителей. Обозначим через ylk количество денег,
полученных Производителем (i, k) в кредит от Банка
под Xylk процент; тогда Банк в течение единицы времени
получает
A' Ni
^=2 2 ’Ь'унУ1*-
1=1 4=1
(4-8)
Коэффициенты и мы будем называть учетной став-
кой Банка — это некоторые параметры, находящиеся в
распоряжении «Государства».
Общий доход «Государства» расходуется следующим
образом:
а)	Непроизводственные расходы R(t), которые явля-
ются заранее фиксированными функциями времени.
б)	Централизованные капиталовложения Ra. Они
складываются из сумм Ut— средств, безвозмездно вы-
деленных «Государством» Центрам:
N
Ru = 2 Ui-
i=l
(4.9)
§ 4]
ОДИН ПРИМЕР ТРЕХУРОВНЕВОЙ СИСТЕМЫ
509
в)	Фонд заработной платы Q:
N
Q = 2 <2/-
i-1
(4.Ю)
Данный фонд ограничен объемом продуктов, которые
можно приобрести на эти деньги, т. е.
q<2^/.
/
(4.П)
где суммирование распространено по всем тем индек-
сам /, которые отвечают потребительским продуктам
(«рыночный» продукт).
г)	Кредит Центрам Ry. Он складывается из тех
средств, которые в единицу времени объединения берут
^взаймы у Банка:
. N	...
^=2^-	(4-12)
1=1
д)	Кредит Производителям Rvy:
N Ni
^ = 2 2Vik- <4ЛЗ>
1=1 k=l
Кредиты берутся Центрами и Производителями — это
их управления, но максимальный объем кредитов лими-
тируется Банком—это управление «Государства»:
(4.14)
(4.15)
Таким образом, Банк имеет право отказать в кредитах,
причем в общем случае эти управления зависят от
объема капиталов, уже взятых взаймы, и от результатов
функционирования.
Кроме ограничений (4.14) и (4.15) на величину теку-
щих займов, должны быть наложены ограничения и на
общую сумму кредита, находящегося в распоряжении
510
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
кредитуемого:
(4.16)
yik^ytdt).	(4.17)
Теперь изменение общего капитала, находящегося в
распоряжении «Государства — Банка», описывается сле-
дующим скалярным уравнением:
z = zx + zP-[-Zy + Zyy — R — Ru — Q—Ry — Ryy, (4.18)
где величины, входящие в правую часть уравнения,
списываются формулами (4.4), (4.6), (4.7), (4.8), (4.9),
(4.10), (4.12) и (4.13).
Таким образом, задача «Государства» состоит в том, чтобы
так распорядиться управляющими воздействиями 17/ (f),
Qi (0» сь tyh vt> tiki. yt, ytk, чтобы максимизировать
функционал (4.1).
5.  Функционирование Центра. Гипотеза информиро-
ванности предполагает, что «Государство»» (Банк)
сообщит свои решения Центрам и Производителям.
Таким образом, Центр будет располагать некоторым
фондом капитальных затрат кредитом из Банка,
который в пределах, допустимых ограничениями (4.14) и
(4.16), он может взять из Банка. Этот фонд расходуется
на инвестиции Производителей и выплату процентов по
кредиту:
АГ/
Ui + Vt = 2 Ulk + •kyW, V t.	(4.19)
k—1
Строго говоря, здесь должен стоять знак неравенства,
так как объединение должно иметь некоторый резерв:
2 ^ik + ^yi + ty.	(4.19')
k—1
Уг в выражениях (4.19) и (4.19х) определяется урав-
нением
yi =	(4.20)
§ 41	О,ЙЦН ПРИМЕР ТРЕХУРОВНЕВОЙ СИСТЕМЫ	5Ц
Распределение ресурса и выбор размеров кредитов
у Банка — не единственные управляющие воздействия
Центра. Центр распределяет фонд заработной платы
Q/=	+	(4.20)
k=l
где — строго регламентированное число. Оно либо
фиксировано (фонд заработной платы объединения),
либо является однозначной функцией функционала Jt.
Наконец, Центр назначает функцию поощрения Про-
изводителей
-q4(*f) (/=1.2..........М-,	i= 1,..., У;
Функции поощрения (или штрафа) должны быть под-
чинены системе ограничений. Достаточно естественным
является, например, такое:
м Ni
3 2^(Р;‘) + д/ = 0.	(4.21)
/=1 k—1
Здесь 6{ — некоторая регламентированная часть благ,
присваемая Центром. Она может быть поставлена в
зависимость от действий Производителей, например,
так:
М N{
6/= 2	<4-22)
/=i k=i
Выражения (4.22) являются некоторым «внутренним»
налогом с оборота. Равенства (4.21) означают права
Центра в известной степени перераспределить доходы
своих Производителей в зависимости от того, насколько
их активность отвечает целям Центра. Деятельность
Центра состоит в таком выборе своих управляющих
воздействий, который максимизирует функционал (4.2).
6. Производитель. Нижнее звено этой иерархической
системы занимает Производитель. Каждый Производи-
тель (i, k) обладает определенным капиталом (фон-
512	ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ [ГЛ. VII
дами) xik, необходимым для производства продукта Р^.
Развитие фондов описывается уравнением
xik = — ^tkXik + uik + wik,	(4.23)
где — нецентрализованные инвестиции. Производство мы
будем описывать производственными функциями Fjk вида
=	(4.24)
здесь х^ — доля капитала х»*, неиспользуемая для произ-
водства /-го тэззра
м
2	= xtk.	(4.25)
/=i
Стоимость продукции, реализованной Производителем,
будет
м
/=1
Общее количество денег (поток денег), которое получает
Производитель в единицу времени, складывается из сто-
имости реализованной продукции и кредита, получа-
емого из Банка vq. Это количество денег расходуется
следующим образом:
а)	выплачивается Государству налог с оборота
м
б)	выплачивается налог на фонды
n
в)	выплачивается заработная плата = 2 У^Рм> при-
* /“1
чем Q.ik<Q.ik-,
г)	производятся внутренние инвестиции о»»;
д)	выплачивается Центру штраф (или получается поощре-
ние) ср^Р^).
§ 4]
ОДИН ПРИМЕР ТРЕХУРОВНЕВОЙ СИСТЕМЫ
513
Разность
м
Ч* = S (<7 - Q) Plk + Vik - ^Xik -wlk-
l=i
м	м
чШ*)
l=i
представляет собой чистый доход Производителя, кото-
рый он может расходовать по своему усмотрению.
Условимся называть его социальным фондом пред-
приятия.
Условимся, что цель Производителя (f, k)—максими-
зировать интеграл
т
Jik =	(4.27)
Для того чтобы Производитель мог принять решение,
мы должны принять определенную гипотезу о его инфор-
мированности.
Мы будем считать, что до принятия решения Про-
изводителю сообщены и структура функции поощрения
и размер централизованных инвестиций.
7.	Заключение. Для того чтобы данная трехступен-
чатая иерархическая система могла функционировать,
должны быть сформулированы определенные «правила
игры». Прежде всего должен быть определен порядок
ходов. Первый ход делает «Государство»—оно сообщает
Центрам и Производителям значения своих управляю-
щих параметров и функций. После этого задача сведена
к анализу двухступенчатой иерархии. В этой системе
следующий ход делают Центры — они сообщают Про-
изводителям значения своих управляющих воздействий.
Теперь Производитель должен сделать свой ход — при-
нять свои решения, т. е. выбрать значения своих управ-
ляющих функций и параметров. Он их не сообщает
Центрам, Центры принимают решения, исходя из гипотез
Fik поведения Производителя (i, k). Гипотеза Гл состоит
в том, что Производитель максимизирует функционал
(4.27). Его решение — управляющие воздействия Про-
514
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
изводителей— будут функционалами от управляющих
воздействий Центров и «Государства».
Теперь очередь за Центрами. Они принимают реше-
ния и не сообщают их «Государству». Последнее при-
нимает решение, основываясь на гипотезе Fik и гипо-
тезах о поведении Центров. Гипотезы состоят в
максимизации целевых функций Центров. Этого доста-
точно, чтобы принять решение на верхнем уровне —
уровне «Государства», поскольку управляющие функции
Центров будут некоторыми функционалами от управляю-
щих воздействий «Государства». Будем называть план
распределения ресурсов «Государства» и стратегию ис-
пользования бюджета оптимальными, если они доставля-
ют максимальное значение функционалу (4.1) при гипо-
тезах и rik. Аналогично определяются оптимальные
планы Центров и Производителей.
Многое из того, что говорилось в предыдущем пара-
графе о численной реализации оптимальных планов в
двухступенчатой задаче, переносится и на случай трех-
ступенчатой иерархической системы.
§ 5.	Заключительные замечания
1.	Проблема рациональной иерархии — важнейшая
практическая задача. Теории управления. В этой главе
была изложена общая схема формализации и оценки
эффективности иерархической структуры управляемой
системы. Именно схема. Рассмотренные модели были
предельно упрощены. Тем не менее уже эти простые
модели показали, сколь сложными оказываются мате-
матические задачи, возникающие в теории иерархических
систем. Кроме того, автору хотелось (и это главное)
объяснить концепцию иерархической системы, предло-
женной в Вычислительном центре АН СССР. Теорию,
которая здесь обсуждается, правильнее всего назвать
информационной теорией иерархических систем *). Воз-
*) Первая публикация, посвященная этой концепции, дана в сов-
местной статье автора и Ю. Б. Гермейера «О некоторых задачах
теории иерархических систем управления». См. сборник «Проблемы
прикладной математики и механики», Наука, 1971.
§ 51	ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ	515
никновение иерархической структуры я постарался
связать прежде всего со структурой информационных
потоков, техникой передачи и обработки информации.
Если говорить о социальных системах, то введение иерар-
хии неизбежно приводит к появлению у подсистем соб-
ственных целей и это влечет к следствиям, которые
нельзя игнорировать.
Исследование иерархических структур сегодня пред-
ставляется мне одним из важнейших направлений при-
кладной математики, теории управления и экономики.
Это направление представляет не только большой мате-
матический интерес. Развитие производительных сил,
усложнение технологий и все возрастающая роль плано-
вого, не рыночного, начала в распределении приводят к
тенденции усиления роли централизованного управления.
Но централизация, как уже подчеркивалось в предыду-
щем параграфе, ни в коей мере не является альтернати-
вой иерархической организации. Любой достаточно слож-
ный организм* всегда требует определенной иерархиче-
ской организации. И более того, как мы это видели,
имеет смысл говорить о рациональной (а в ряде случаев
и оптимальной) мере децентрализации принятия решений
в централизованной системе.
Этот оптимальный уровень децентрализации в приня-
тии решений зависит от многих причин. В частности, он
зависит от технологии обработки данных и передачи ин-
формации. По мере совершенствования этой технологии
уровень централизации будет, вероятно, возрастать.
Изучение иерархических структур, способов и эффек-
тивности воздействия верхних уровней на деятельность
нижних, по существу, эквивалентно изучению структуры
экономических механизмов.
В социалистических странах с их плановой централи-
зованной экономикой экономические механизмы, обла-
дающие иерархической организацией, имеют очень важ-
ное значение. Воздействуя надлежащим образом на
целевые функции нижних уровней, верхние уровни могут
обеспечить выполнение необходимых плановых показа-
телей, которые возникают при реализации программного
метода управления.
Изучение иерархических структур — это источник
того понимания, которое необходимо для оценки уже
516
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
созданных и проектирования новых организаций. В усло-
виях все увеличивающейся сложности технологий не-
избежно растет и сложность организаций, а следо-
вательно, возрастает необходимость создания теории,
которая могла бы быть основой для практических ре-
шений.
2.	Пути исследования. Мы видели, что задачи, кото-
рые возникают в теории иерархических структур — это,
по существу, задачи теории дифференциальных (или
многошаговых) игр. Сегодня не существует сколько-
нибудь универсальных методов их решения. Отдельные
примеры и теоремы, утверждающие существование аль-
тернатив в задачах теории антагонистических игр — это,
пожалуй, и все, что сегодня может предложить мате-
матика. Я думаю, что и в ближайшие годы ситуация
существенно не изменится. Поэтому теория иерархиче-
ских систем управления будет развиваться в двух направ-
лениях. Прежде всего должны изучаться простейшие
модельные задачи, которые могут быть исследованы до
конца, задачи, подобные тем, которые обсуждались во
втором параграфе. Исследование этих задач должно
помочь интуитивному пониманию тех принципов, кото-
рые составляют фундамент теории. Один из важнейших
вопросов — это сопоставление и оценка разных способов
управления и воздействия верхних уровней на нижние,
структура поощрений, штрафов, определение меры
активности и т. д. Другой — это зависимость окончатель-
ного результата от характера информированности,
порядка ходов, правил поведения, возможности коопе-
рации производителей и т. д. Исследование подобных
вопросов неизбежно должно начинаться с анализа при-
меров, может быть сначала и очень далеких от реальных
задач. Изучение простых примеров должно расставить
вехи, без которых создание эффективного аппарата
теории невозможно. В этой области делается уже до-
вольно много интересного, причем наиболее важные
результаты здесь принадлежат Ю. Б. Гермейеру и его
ученикам *).
*) См., например, Ю. Б. Г е р м е й е р, Игры с непротивополож-
ными интересами (теория принятия решений при неполном единстве),
МГУ, 1972. Н. С. Кукушкин, Роль информированности в играх
§ 5]	ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ	517
Третья из проблем, которая встает при изучении
отдельных примеров — это поиск рациональных числен-
ных схем. Может оказаться, что во многих ситуациях,
близких к реальным, можно на основании анализа
простых примеров сформулировать такие рекомендации
о выборе управляющих воздействий, что окончательный
расчет сведется к грубым схемам типа теории возму-
щений.
Наконец, уже подчеркивалась важность аппрокси-
мации нерефлекторных иерархических систем рефлектор-
ными. Эта аппроксимация качественно упрощает иссле-
дование. Но для этой аппроксимации необходимо еще
разработать некоторый механизм адаптации. По-види-
мому, здесь еще очень далеко до общей теории и только
анализ простых учебных задач может пролить свет на
возможные пути построения подобных механизмов.
Второе направление — это использование техники
имитации, использование имитационных систем.
Термин имитационные системы (Similation sistems)
введен в Вычислительном центре Академии наук СССР,
и он обозначает человеко-машинную диалоговую систему,
которая состоит из системы моделей, описывающих эво-
люцию изучаемого процесса, если все управляющие
воздействия заданы, системы процедур, позволяющей
объединить эти модели с «биологическими» звеньями
этой системы (экспертами) и из специального математи-
ческого обеспечения, необходимого для ее функциониро-
вания. Это математическое обеспечение может включать
в себя и специальные языки общения с машиной - и си-
стему алгоритмов для решения вспомогательных задач,
в том числе и оптимизационных задач.
.Известные модели Форестера и техника, которая им
разработана для описания функционирования динами-
ческих систем (в том числе язык Динамо), являются
достаточно простыми примерами имитационных систем.
Исследования в области имитационных систем начались
в Вычислительном центре АН СССР около 10 лет назад
и сразу приобрели характер, присущий фундаментальным
двух лиц с непротивоположными интересами, ЖВМ и МФ, 12, № 1,
1972. И. А. Ватель и Ф. И. Ерешко, Математика конфликта
и сотрудничества, «Знание», серия математика и кибернетика, № 8,
1973.
518
ИЕРАРХИЧЕСКИЕ СИСТЕМУ УПРАВЛЕНИЯ
(ГЛ. VH
исследованиям. Проблемы принятия решений в раз-
ных звеньях, проблемы осредненного описания функцио-
нирования ансамблей индивидов, структура языков (нам
сразу стала очевидной необходимость проектирования
имитационной системы как некоторой многоязыковой
системы), процедуры последовательного .анализа и от-
браковки вариантов и другие вопросы подобной слож-
ности сразу стали в центре нашего внимания. Очень важ-
ное значение мы придаем технике построения самой
системы моделей, т. е. системе причинно-временных
связей. Следуя методологии, принятой в физике, хочется
выделить связи, носящие характер законов сохранения
и связей типа «уравнений состояния», на которые опира-
ется вся система моделей физики. Однако априори оче-
видно, что, исследуя социально-экономические системы,
нельзя все связи свести к перечисленным. Социально-
экономические системы являются принципиально нереф-
лекторными. Следовательно, большая группа связей
носит характер «гипотез поведения» и определяется
через оператор, описывающий процедуры оптимизации
или вообще не поддающийся формализации. Наконец,
очень часто мы просто не знаем механизмов связи и
вынуждены их формализовать как черный ящик. Но не
просто как систему input — output, которая широко
используется школой Форестера, но связь типа автомата,
когда output — некоторая функция не только input, но и
состояния системы.
Огромную роль играет решение проблемы верифи-
кации и идентификации системы моделей. Особое значе-
ние я придаю методам тестовой диагностики.
Таким образом, каждая имитационная система — это
большой проект, реализация которого требует усилий
большого количества специалистов и глубоких исследо-
ваний фундаментального характера. Однако раз создан-
ная, имитационная система (в особенности, если пред-
усмотрена сменяемость отдельных блоков) превращается
в мощный инструмент анализа.
Важнейшей особенностью имитационной системы
является включение, «биологического» звена, т. е. ее диа-
логовый характер. Именно благодаря этой особенности
имитационные системы позволяют объединять рутинные
расчеты с помощью динамических моделей с неформаль-
§ 5]	ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ	519
ними (или неформализуемыми) процедурами принятия
решений.
Использование имитационных систем в задачах, кото-
рые рассматриваются в этой главе, т. е. в задачах типа
дифференциальных игр, представляется единственной
альтернативой, позволяющей изучать достаточно слож-
ные «реальные» системы, обладающие иерархической
структурой. Варьируя всем арсеналом средств, которые
находятся в распоряжении исследователя, с помощью
метода имитации можно надеяться получать достаточно
удовлетворительные варианты конструкции. В сочетании
с изучением отдельных простых задач, которое может
дать эксперту, исследователю возможность значительно
сузить множество конкурентоспособных вариантов, ими-
тационные системы, по моему мнению, окажутся тем
оружием, которое позволит исследователю пробиться
сквозь барьеры размерности, формальных и неформаль-
ных сложностей.
3.	Возможности коалиций. Описывая иерархические
системы, мы всегда предполагали, что целевая функция
Производителя зависит только от его решений, от его
собственных действий, если, конечно, Центр сообщил ему
свои решения. В действительности, целевая функция
Производителя Л зависит также и от действия других
производителей:
Ji = JI (-^i> • • • ,	• • • >
Следовательно, реальная ситуация значительно более
точно описывается языком теории кооперативных игр.
Действительно, очень часто отдельные предприятия
могут вступать в коалиции, например, совершать взаим-
ные поставки и т. д. И может оказаться, что эта деятель-
ность вполне выгодна с точки зрения Центра и снимает
с него целый ряд обязанностей типа планирования снаб-
жения.
Исследование описанной ситуации представляет зна-
чительный теоретический и прикладной интерес. С чисто
математической точки зрения мы здесь сталкиваемся со
специальной формой кооперативной игры, в которой
также нет равноправия. Существует Центр, который
имеет право первого хода и который имеет право вмеши-
ваться в деятельность Производителей.
520
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
Исследования подобных ситуаций еще не проводи-
лись. Отсутствует и удобная формализация подобны*
задач.
4.	Замечание о задаче синтеза. Под задачей синтеза
в теории управления понимают построение такой управ
ляющей функции, значения которой однозначно опреде-
ляются фазовыми координатами управляемой системы.
Мы эту задачу назвали задачей текущего управления.
По существу, один из вариантов ее постановки приведен
в работе. Функция поощрения как раз и есть синтезирую-
щее управление. Однако приведенная постановка задачи
не является исчерпывающей. Можно привести много
примеров из реальной жизни, в которых четкая регламен-
тация функции поощрения отсутствует. В зависимости
от некоторых внешних причин происходит изменение
стратегии Центра. Другими словами, меняются правила
игры. Это обстоятельство порождает целый класс новых
задач, которые естественно рассматривать под углом
зрения Центра. Можно ли говорить о некоторых опти-
мальных правилах «изменения правил» игры, имея в виду
неизбежную реакцию нижних звеньев, возможности
блефа и т. д.? Интересно проследить на примерах,
к чему приводит отсутствие всяких правил, т. е. анализ
некоторой инфраигры — игры без правил. Можно при-
вести еще целый ряд вопросов и постановок задач,
относящихся к рассматриваемой проблеме.
§ 6.	Некоторые новые исследования
Уже после того, как работа над этой книгой была
закончена, в теории иерархических систем управления и
смежной с ней области теории игр появилось много новых
важных идей и результатов, без информации о которых
у читателя может создаться неправильное представление
о современном уровне развития теории иерархических
систем управления. Краткому изложению некоторых из
этих фактов посвящен данный параграф.
1.	В этой книге мы рассмотрели одну из возможных
схем иерархической .организации, которую мы условно
назвали схемой Центр — Производитель. Эта схема опи-
сывает целый ряд интересных и важных процессов, с ко-
торыми приходится встречаться в практике управления.
§61
НЕКОТОРЫЕ НОВЫЕ ИССЛЕДОВАНИЯ
521
Как мы видели, эта система организации порождает ин-
тересную классификацию игровых ситуаций. Еще раз вер-
немся к этой схеме.
F(x, у) — целевая функция Центра, в распоряжении
которого имеется величина х, и f(x, у)—целевая функция
Производителя, который распоряжается величиной у.
Центр имеет право первого хода.
Ситуация Гр Центр назначает вектор х. Следователь-
но, он может ожидать, что Производитель выберет вектор
у как функцию х из условия / (х, у) =>тах. Следовательно,
выбор х определится Центром из условия
Е(х, у(х))=>шах.
X
Интерпретация — простое распределение ресурсов.
Ситуация Г2: Центр назначает функцию х(у) и имеет
право рассчитывать, что Производитель выберет свое уп-
равление— теперь уже функционал у[х(у)] из условия
l(x(y), y)=>max. Правило выбора Центра
F(x(y), у[х(у)]) ** шах.
Х(у)
Интерпретация — штрафы и поощрения.
Ситуация Г3: Центр назначает функционал х[у(х)] и
ожидает, что Производитель выберет свое управление,,
тоже в форме функционала у [х[г/ (х)]]. Правило принятия
решения Центра
F (х [у (х)\1у [х [у (х)Ц) '=> max.
х[у(х)}
Интерпретация — Центр выделяет ресурс Производителю
в зависимости от способа его использования.
Подобная рекурсия может быть продолжена неогра-
ниченно. Можно определить ситуацию Г4, Г6 ,... и т. д.
Но вот в 1972 году Н. С. Кукушкин (см. стр. 471) пока-
зал, что ситуация Г4 сводится к Гь Г6—к Г2 и т. д. Если
при этом через F* мы обозначим значение целевой функ-
ции Центра в ситуации Гг, то окажется, что F^F^F—
FZ=.F3=F= ..., F3=Fe—Fs= ... и, кроме того:
Fl^F3^F\
Значение этого факта в теории иерархических систем
трудно переоценить. По существу, он позволяет пред- *
ставить, во всяком случае качественно, как основные
522
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
возможности иерархических систем типа
Центр — Производители
2.	Однако схема Центр—Производитель не только не
исчерпывает всех мыслимых форм организации иерархи-
ческих процедур принятия решений, но и является, ве-
роятно, самой простой. Одно из новых направлений в
теории иерархических систем связано, с изучением воз-
можных форм иерархической связанности и их форма-
лизаций. Особого внимания заслуживают, вероятно, так
называемые ромбовидные структуры, которые можно
изобразить следующей схемой:
/ОТРАСЛЬ^
ГОСУДАРСТВО^	ПРОИЗВОДИТЕЛЬ
\ РЕГИОН /
Эта схема отражает тот факт, что принятие решений ди-
ректора завода определяется не только действиями его
непосредственного начальника — отраслью (или объеди-
нением), в которую входит его предприятие, но и регио-
нальными интересами и, в частности, требованиями ре-
гиональных советских и партийных органов.
Ромбовидная структура начала изучаться в связи
именно с региональными проблемами. Однако более вни-
мательный анализ показал, что она достаточно универ-
сальна и может быть использована для описания доста-
точно большого количества практически важных ситуа-
ций. Схема Центр — Производитель является ее простым
частным случаем. Формализация, именуемая «ромбовид-
ной структурой»—это следующий важный этап развития
общей теории.
3.	Развиваемая теория необходимо должна включать
в себя проблемы принятия коллективных решений. Сей-
час уже начат подобный анализ. В центре внимания си-
туация, которую можно было бы назвать «путешествен-
ники в одной лодке». Представим себе, что имеется N
равноправных партнеров, каждый из которых имеет свой
собственный ресурс и свой собственный критерий fit
Но кроме этого «интереса» они связаны некоторым об-,
щим «интересом»—доплыть на лодке до берега. Эту це-
левую функцию мы обозначим через F. Значит, каждый
§ 6]	НЕКОТОРЫЕ .НОВЫЕ ИССЛЕДОВАНИЯ	523
из партнеров должен свой ресурс а, разделить. Часть ре-
сурса Xi он должен выделить на обеспечение своих «лич-
ных» интересов. В результате значение его критерия бу-
дет f(Xt), остальной ресурс у,=а(—xt он выделяет для
достижения общей цели F. Значение целевой функции F
будет, очевидно, зависеть уже от всех участников возник-
шей коалиции:
F=F(yt, у2, ..., yN).
Описанная ситуация также очень типична. К ее анализу
сводится проблема выполнения общих обязательств, тре-
бований руководства, проблема строительства колхозами
общей дороги или овощехранилища, проблема выделения
средств для охраны или восстановления качества окру-
жающей среды, и, наконец, проблема коллективных дей-
ствий суверенных государств и т. д.
Проблема принятия коллективных решений требует
прежде всего формирования некоторого компромисса,
т. е. введения некоторой новой системы целевых функций
<р;, характеризующих цели партнеров. Примем, что
ф/ = min{ft (**); V(ylt	yN)},
где параметр X,- характеризует степень заинтересован-
ности партнера номера i в достижении общей цели.
Такая редукция позволяет свести описанную ситуа-
цию к играм N лиц. В этой игре центральным является
вопрос о том, какие принципы должны быть положены в
основу выбора решения, т. е. величин ylt ..., yN.
Существуют два хорошо известных принципа.
1. Принцип эффективности. Решение у[, ..., у*ы
мы будем называть эффективным,, если не существует ни-
какого другого решения ух, , yN, которое было бы «луч-
шим» хотя бы для одного игрока, т. е. чтобы для всех i
шСуь	Ун)>Vi(y*>	Ун)
и хотя бы для одного /
Ф/(//1> •••> ^)>Ф/(У1,	Ун)- .
2. Принцип устойчивости (состояние равновесия
по Нэшу). Решение ylt ..., у*ц мы условимся называть
равновесным, если отступление от него какого-либо из
524
ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
[ГЛ. VII
партнеров невыгодно прежде всего «отступнику», т. е,
•••> w-i, Уь Ум........=
= тах<р/(г/1,	z//-,, у/, у*+и .... z/лг).
Реальность, однако, состоит в том, что, как правило:
а)	эффективные решения неустойчивы,
б)	устойчивые решения неэффективны.
Так вот, ситуация «путешественники в одной лодке»
обладает одним замечательным свойством. В этой ситуа-
ции состояния равновесия существуют и они эффективны.
Эта теорема доказана И. А. Вателем и Ю. Б. Гермейе-
ром и ей предстоит еще сыграть важную роль в теории
коллективных решений.
Ее авторы установили не только справедливость тео-
ремы, но и дали способ определения ситуации равно-
весия.
Ранжируем всех партнеров (все государства) по прин-
ципу
W1 (а1) > W2 (й2)	Kifn (#п).
Тогда существует такое p^N, что все у г для 1>р равны
нулю, а остальные определяются из решения следующей
системы уравнений:
— у{)=Г(у1г ур, 0, .... 0).
Эта теорема определяет доли участия партнеров в
коллективном решении. Заметим, что часть партнеров
вообще не принимает участия в коллективных мероприя-
тиях. Эти партнеры либо
’ а) не обладают достаточным ресурсом (at мало),
б) либо у них низкая технология (A(zzj) мало),
в) либо у них низка заинтересованность в итогах кол-
лективного решения (%{ мало) *).
4. Исследования последних лет относились не только
к расширению' класса изучаемых моделей и исследова-
нию их общих свойств. Важное место занимала также и
проблема численного анализа.
*) Подробнее см. «Методы системного анализа в проблемах рас-
пределения водных ресурсов», т- I. Изд. JJASA, Вена 1974 ’
5 6]	НЕКОТОРЫЕ НОВЫЕ ИССЛЕДОВАНИЯ	525
Прежде всего был установлен факт некорректности
рассмотренных задач и даны некоторые способы их ре-
гуляризации. Рассмотрим эти свойства на простейшем
примере ситуации Г\*).
Предположим снова, что интересы Центра описывают-
ся функцией F(x, у), Производителя — функцией f(x,y),
вектор х находится в распоряжении Центра, а у — Про-
изводителя. Напомним, что задача определения х сводит-
ся к определению maxF(x, у), где у определяется в свою
X
очередь из решения оптимизационной задачи
f (х, у) => max.
У
Раньше, когда мы обсуждали эту задачу, то приняли
для простоты, что решение задачи f(x, у) =з»тах единст-
венно. Сейчас мы не будем сужать задачу и предполо-
жим, что множество функций у(х), которые реализуют
этот максимум, образует некоторое множество N(x). Не-
корректность определения х здесь почти очевидна. Пред-
положим, что мы неточно вычисляем f(x, у). Обозначим
этот факт так: мы знаем функцию f(x, у, е,). Тогда,
если f — непрерывная функция своих аргументов, то
тах/(х, у, в) и тах/(х, у, 0) при фиксированном х отли-
чаются мало. Но значения yiyt и у2), реализующие этот
максимум, а, следовательно, и значения функции F(x, «/,)
и F(x, z/2), могут отличаться сколь угодно сильно.
Д. А. Молодцовым и В. В. Федоровым дан способ ре-
гуляризации задачи. Он состоит в следующем.
Предположим, что искомое значение F состоит в реа-
лизации следующей процедуры:
U (f) = sup min F (х, у).
х ysNfx)
Введем вместо N(x) множество Na(x) тех значений у, для
которых при фиксированном х
f (х> У) > max f (х> г) ~~ а>
г
и обозначим
t/a(f)=supminF(x, у).
______________ X
*) Изложенные здесь факты установлены Д. А. Молодцовым и
В. В. Федоровым. См., например, диссертацию Д. А. Молодцова,
МГУ, 1974 г.
526	ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ [ГЛ. VII
Тогда доказывается, что
lim Ua=U.
е-»о
а->о
а-2е>о
Этот результат показывает, что в условиях неточною оп-
ределения функции цели Производителя необходимо и
оптимизацию проводить с ошибкой! Если точность опре-
деления цели Производителя стремится к нулю, то точ-
ность расчета плана также должна повышаться и при
этом вполне определенным образом.
Сформулированная теорема открывает возможность
построения рациональных вычислительных процедур и, в
частности (что частично уже сделано), проведение стро-
гого анализа сеточных схем.
Никита Николаевич Моисеев
ЭЛЕМЕНТЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ
М., 1975 г., 528 стр. с илл.
Редактор М. М. Горячая
Техн, редактор Н. В. Кошелева
Корректор И. В. Хорошаева
Сдано в набор 25/Х 1974 г.
Подписано к печати 21/11 1975 г.
Бумаги 84ХЮ81/з2, тип. № 1. Физ. печ. л. 16,5.
Условн. печ. лч27,72. Уч.-изд. л. 26,93.
Тираж 13 000 экз. Т-01956.
Цена книги 1 руб. 96 коп. Заказ № 4329.
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
2-я типография издательства «Наука»,
Москва, Шубинский пер., 10
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ,
Ы7Ю71, Москва, В-71, Ленинский проспект, 15.
ВЫЙДУТ ИЗ ПЕЧАТИ В 1975 ГОДУ В СЕРИИ
«Оптимизация и исследование операций»:
Ермольев Ю. М., Методы стохастического программи-
рования.
Книга посвящена численным методам решения нелинейных
экстремальных задач вероятностной природы. Основное вни-
мание уделяется развитию стохастических процедур поиска
экстремума в задачах с ограничениями, для решения которых
невозможно применить известные методы нелинейного про-
граммирования. Осуждаются приложения к вопросам перспек-
тивного планирования в условиях неопределенности оптими-
зации систем обслуживания, к вопросам складирования, управ-
ления случайными процессами и запасами, к задачам матема-
тической статистики, идентификации.
Книга построена таким образом, что для ее чтения не тре-
буется серьезного знакомства со специальными разделами
высшей математики. Она может быть полезна как специали-
стам-прикладникам, использующим в своей работе теорию оп-
тимизации, так и научным работникам, аспирантам и студен-
там, специализирующимся в этой области.
Пшеничный Б. Н., Данилин Ю. М., Численные
методы в экстремальных задачах.
В книге излагаются методы и алгоритмы численного реше-
ния задач, возникающих в математическом программировании,
экономике, теории оптимального управления и других областях
науки и практики, в которых возникают задачи численного
нахождения экстремума функций и функционалов. Основное
внимание уделено изложению алгоритмов с высокой скоростью
сходимости и практически удобных для реализации на ЭВМ.
Рассматриваются методы минимизации функций как без огра-
ничений на независимые переменные, так и учитывающие та-
кие ограничения.
Книга будет полезной как для специалистов в области ма-
тематического программирования, вычислительной математики
и теории оптимального управления, так и для широкого круга
студентов и инженеров, встречающихся в практике с решением
задач минимизации функций.
Заказы на печатающиеся книги принимаются без ограни-
чения всеми магазинами Книготорга и Академкниги.