Цена 1 p. 13 к.
Книга содержит подробное изло¬
жение теории оптимальных процессов,
основным стержнем которой является
принцип максимума. Этот принцип по¬
зволяет решать ряд задач математи¬
ческого и прикладного характера, ко¬
торые являются вариационными зада¬
чами, но не укладываются в класси¬
ческую схему вариационного исчисле¬
ния. Между тем к задачам именно
такого неклассического типа приводят
многие вопросы техники. Таким обра¬
зом, книга представляет интерес не
только как математическая моногра¬
фия, посвященная изложению новой
теории, но и как руководство, которым
инженер и конструктор могут с успе¬
хом пользоваться в прикладной дея¬
тельности.
Главы первая, третья и четвертая
написаны наиболее элементарно и,
в основном, доступны лицам, знающим
математику в объеме втузовской про¬
граммы. Именноэти главы прежде всего
рекомендуются инженерам, конструк¬
торам, специалистам по автоматическо¬
му управлению. Пятая глава посвящена
сравнению развитых авторами методов
с методами классического вариацион¬
ного исчисления.
Книга может быть использована
специалистами (как математиками,
так и нематематиками), имеющими
дело с обыкновенными дифферен*
циальными уравнениями, вариацион¬
ным исчислением и их применениями,
а также студентами и аспирантами
университетов и втузов.

Л С ПОНТРЯГИН, В. Г. БОЛТЯНСКИМ,
Р.’ в. ГАМКРЕЛИДЗЕ, Е. Ф. МИЩЕНКО
Математическая
теория
оптимальных
процессов
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ fjj1
МОСКВА 196!

ОГЛАВЛЕНИЕ
Введение	 о
Глава 1.	Принцип максимума 	 13
§ 1.	Допустимые управления	 13
§ 2.	Постановка основной задачи	 15
§	3.	Принцип максимума	 23
§ 4.	Обсуждение принципа максимума	 27
§	5.	Примеры. Задача синтеза	 28
§	6.	Задача с подвижными концами и условия	транс¬
версальности 	 53
§	7.	Принцип максимума для неавтономных	систем	68
§	8.	Задачи с закрепленным временем	 76
§ 9.	Связь принципа максимума с методом динами¬
ческого программирования	 80
Глава 2.	Доказательство принципа максимума	 85
§ 10.	Допустимые управления	 85
§ И.	Формулировка принципа максимума для	произ¬
вольного класса допустимых управлений	...	89
§ 12.	Система уравнений в вариациях и сопряжен¬
ная ей система	 93
§ 13.	Вариации управлений и траекторий	 98
§ 14.	Основные леммы	 104
§ 15.	Доказательство принципа максимума	 112
§ 16.	Вывод условии трансверсальности	 122
Глава 3.	Линейные оптимальные	быстродействия ...	130
§ 17.	Теоремы о числе переключений	 130
§ 18.	Теоремы единственности	 139
§ 19.	Теоремы существования	 144
§ 20.	Синтез оптимального управления	 154
§ 21.	Примеры	 159
§ 22.	Моделирование линейных оптимальных быстро¬
действий при помощи релейных схем	 191
§ 23.	Линейные уравнения с переменными коэффици¬
ентами 	 201

ОГЛАВЛЕНИЕ
Глава 4. Разные задачи	 20У
§ 24.	Случаи функционала, заданного несобственным
интегралом	 209
§ 25.	Оптимальные процессы с параметрами	 212
§ 26.	Применение теории оптимальных процессов
к задачам приближения функции	 218
§ 27.	Оптимальные процессы с запаздыванием ....	236
§ 28.	Одна задача преследования	 250
Глава 5. Принцип максимума и вариационное исчисле¬
ние 	 264
§ 29.	Основная задача вариационного исчисления . .	265
§ 30.	Задача Лагранжа	 275
Глава 6. Оптимальные процессы при ограниченных фа¬
зовых координатах	 285
§ 31.	Постановка задачи	 287
§ 32.	Оптимальные траектории, лежащие па границе
области	 293
§ 33.	Доказательство теоремы 22 (основные построе¬
ния) 	 299
§ 34.	Доказательство теоремы 22 (окончание) ....	320
§ 35.	Некоторые обобщения	 328
§ 36.	Условие скачка	 330
§ 37.	Формулировка основного результата. Примеры	341
Г л а в а 7. Одна статистическая задача оптимального уп¬
равления 	 348
§ 38.	Понятие о марковском процессе. Дифференци¬
альное уравнение Колмогорова 	 349
§ 39.	Точная постановка статистической задачи . . .	354
§ 40.	Сведение вычисления функционала J к решению
краевой задачи для уравнения Колмогорова	356
§ 41.	Вычисление функционала J в случае, когда
уравнение Колмогорова имеет постоянные ко¬
эффициенты 	 359
§ 42.	Вычисление функционала J в общем случае . .	383
■ I итература	 389

ВВЕДЕНИЕ
Физические процессы, имеющие место в технике, как
правило у п р а в л я е м ы, т. е. могут осуществляться раз¬
личными способами в зависимости от воли человека. В связи
с этим возникает вопрос о нахождении наилучшего в том или
другохм Схмысле или, как говорят, оптимального управления
процессом. Речь может идти, например, об оптимальности
в смысле быстродействия, т. е. о достижении цели
процесса в кратчайшее время, о достижении этой цели
с минимальной затратой энергии и т. п. Математически
сформулированные, эти вопросы являются задачами в а-
р и а ц и о н н о г о исчисления, которое и обязано им
своим возникновением. В классическом вариационном ис¬
числении нет, однако, решения целого ряда вариацион¬
ных задач, важных для современной техники. Коллективу
авторов этой книги принадлежит излагаемое здесь реше¬
ние значительного числа таких вариационных задач не
классического типа. Решение это в существенных чертах
объединяется одним общим математическим приемом, ко¬
торый мы называем при н ц и п о м макс и м ума. Сле¬
дует заметить, что все основные необходимые условия
классического вариационного исчисления с обыкновен¬
ными производными следуют из принципа максимума
(см. главу 5).
Мы рассматриваем здесь такие управляемые процессы,
каждый из которых может быть описан систехмой обык¬
новенных дифференциальных уравнений
=	 Ur),	г	=	1.	2. .... гг; (1)
здесь х1, . .., хп— величины, характеризующие процесс,

6
ВВЕДЕНИЕ
т. е. фазовые координаты управляемого объекта, опреде¬
ляющие его состояние в каждый момент времени t\
и1, .. ., ит — параметры управления, определяющие ход про¬
цесса, и £ — время. Для того чтобы ход управляемого
процесса (1) был определен на некотором отрезке времени
< * < *1» достаточно, чтобы на этом отрезке времени
были заданы (как функции времени) параметры управле¬
ния и1, .. ., ит\
и1 =	1	= 1,	(2)
Тогда при заданных начальных значениях
\ **(*<>)-4. \ i = i,(3)
решение системы (1) определяется однозначно. Подлежащая
решению вариационная задача, связанная с управляемым
процессом (1), заключается в следующем. Рассматривается
интегральный функционал
Г" h
! / = ^ Р(х\ . ..,хп, и1, ur)dt,	(4)
*0
где /° (х1, . . ., хп, и\ .. ., ит) — заданная функция. Для каж¬
дого управления (2), заданного на некотором отрезке
£0 < t < однозначно определяется ход управляемого про¬
цесса, и интеграл (3) принимает определенное значение.
Допустим, что существуют управления (2), переводящие
управляемый объект из заданного начального фазового
состояния (3) в предписанное конечное фазовое состояние
xi{t1) = x\, I i=l,...,n.	(5)
Требуется отыскать управление
1 ^(t), \	/= 1, . . - , Г, ;	(6)
которое осуществляет переход управляемого объекта из
состояния (3) в состояние (5) таким образом, чтобы функ¬
ционал (4) имел минимальное значение. При этом моменты
времени 10 и t± в рассматриваемой постановке задачи не
фиксируются, а требуется только, чтобы в начальный
момент времени объект находился в состоянии (3), а в
конечный момент —в состоянии (5) и чтобы функционал
(4) достигал минимума. (Случай, когда моменты времени

ВВЕДЕНИЕ
7
tQ9 ьг фиксированы, также представляет интерес; он легко
сводится к задачам, упоминаемым в этом введении, см. § 8.)
В частном случае, когда функция /°(ж1, . .., хп, гг1, .. ., ггг),
определяющая функционал (4), тождественно равна единице,
функционал (4) имеет величину tx —10, и наша вариаци¬
онная задача превращается в оптимальную^ задачу быстро-
действия.	^
В,в!Технических задачах, где параметры управления
гг1, . . ., ггг определяют, например, положение рулей машины,
эти параметры не могут принимать произвольных значе¬
ний, а подчинены некоторым ограничениям. JIo самому
устройству описываемого системой (1) механизма параметр
гг1 может", скажем^ принимать лишь значения,^
щпЩйёГ условию
   Ч и1 i < 1. \	(7)
Или, например, если параметры гг1, гг2 характеризуют
векторную величину на плоскости, модуль которой не
превосходит единицы, а направление произвольно, то эти
параметры подчинены условию
(гг1)2 + (гг2)2<1.	(8)
Вообще следует считать, что точка (гг1, . .., ггг) должна
принадлежать некоторому множеству U пространства с
координатами гг1, . . ., ггг, причем выбор этого множества
U отражает специфику объекта (1). Множество U («область
управления») в математической постановке задачи счи¬
тается произвольным, но для технических ^
важенчу характерен случай замкнутого множества U..
(ср. неравенства (7j, (8)J.T Это"ycSoBB^'T3Ha^aer^ что "для ’
руля допустимы и его крайние положения (значения
гг1 = f 1 в неравенстве (7) или граничные точки круга (8)),
могущие, в частности, давать оптимальное управление.
Именно это обстоятельство делает рассматриваемую вариа¬
ционную задачу неклассической, так как в классическом
вариационном исчислении варьируемые параметры не
могут удовлетворять неравенствам типа (7), (8), включа¬
ющим и равенства.
Особенно ярко демонстрирует неклассический характер
нашей вариационной задачи оптимальная задача по быстро¬
действию для системы (1), правые части которой являются

8
ВВЕДЕНИЕ
л и н е й II ы м и функциями относительно переменных
х1, . .	х]\	и1, .. ., ит с постоянными коэффициентами,
а множество U представляет собой з а м к н уты й вы-
пуклый многогранник, например куб, определяе¬
мы й неравенства ми:
| ^ | < 1,	/	=	1,.. . ., г.
В этом случае оказывается, что оптимальное управление
(6)	осуществляется точкой (w1(/), ..., ur(t)), поочередно
находящейся в различных вершинах многогранника U.
Правила, согласно которым управляющая точка перехо¬
дит скачками из одной вершины в другую, и дают закон
оптимального управления. Эта линейная вариационная за¬
дача, имеющая важные технические приложения, решается
на основе общих методов в главе 3. Классические же ме¬
тоды для решения такой задачи совершенно неприменимы.
Из сказанного о перескоках оптимально управляющей
точки с вершины на вершину многогранника U следует,
что класс допустимых управлений (2) нельзя считать
состоящим из непрерывных функций. Мы предполагаем
обычно, что он состоит из кусочно-непрерывных функций.
Фазовые координаты х1, . .., х11 считаются непрерывными
и кусочно-дифференцируемыми функциями времени. В этих
предположениях необходимые условия оптимальности фор¬
мулируются в виде принципа максимума (ем. главу 1),
который доказывается в главе 2.
Если рассматриваемый объект представляет собой меха¬
ническую систему, то часть х1, . . ., хк фазовых коорди¬
нат описывает се геометрическое состояние, а часть
x/l+1,. . ., x2k (2k = ?г) — се скорость. В некоторых задачах
целью управляемого процесса в этом случае может быть
не попадание объекта в определенную точку (х[, ...,х?)
фазового пространства, а прибытие механической систе¬
мы в определенное пространственное положение
(х|, . . ., хк) при произвольных конечных скоростях. Таким
образом, здесь имеет место вариационная задача об опти¬
мальном переходе объекта из определенной начальной
Точки xj, Г.Т, х™ фазового пространства в произвольную
точку к-мерной плоскости, определяемой уравнениями
х1 = х] .. . ., хк = хк .

ВВЕДЕНИЕ
Мы видим, что ранее сформулированная оптимальная
задача не охватывает ряда важных проблем. Ввиду
этого в § 6 главы 1 разбирается вопрос об оптимальном
переходе объекта с некоторого начального многообразия
Л70 точек фазового пространства на некоторое конечное
многообразие Л/1, причем размерности многообразий MQ
и Mj произвольны (в частности, когда они обе равны
пулю, мы получаем первоначальную задачу).
Совершенно ясно, что не только управляющие пара¬
метры объекта, но и его фазовые координаты, по самому
характеру технической задачи, должны иногда подчинять¬
ся некоторым ограничениям. Если, например, речь идет
о движении самолета и х1 обозначает его высоту над
землей, то должно быть выполнено неравенство'з1 > h > О,
где /^ — минимальная допустимая высота полета. Неравен¬
ство х1 > /г вовсе не вытекает из свойств системы уравне¬
ний (1) и из неравенств, налагаемых на управляющие
параметры, а является совершенно независимым. Задача
об оптимальном управлении объектом, при котором изобра¬
жающая его точка фазового пространства должна все
время оставаться в некоторой замкнутой области G фазо¬
вого пространства, решается в главе 6. Предполагается
при этом, что "область G имеет кусочно-гладкую границу.
Движение объекта в этих условиях протекает частично
внутри области G, подчиняясь там обычному принципу
максимума, частично же по границе области G, подчиняясь
там усложненному принципу максимума. Переходы от
кусков траекторий, проходящих внутри £, к кускам
траекторий, проходящим по границе области G, под¬
чиняются своеобразным правилам, напоминающим зако¬
ны преломления света и в некотором смысле обобща¬
ющим их.
До сих пор речь шла об оптимальном управлении,
приводящем объект в заданную точку или на заданное
подмногообразие фазового пространства. Задачей оптималь¬
ного управления может быть, однако, и задача об опти¬
мальном попадании в д в и ж у щ у ю с я точку фазового
пространства. Допустим, что в фазовом пространстве
имеется движущаяся точка
г1 = 0г (/),	/	=	1	п
(9)

10
ВВЕДЕНИЕ
Тогда возникает задача об оптимальном приведении объ¬
екта (1) в совпадение с движущейся точкой (9). Эта за¬
дача легко сводится к рассмотренной. Достаточно ввести
новые переменные, полошив
=	г	= 1,..л.
В результате этого преобразования управляемая система
(1) превращается в новую, правда, уже не автономную,
а целью управляемого процесса становится приведение
нового объекта (у1, ..., уп) в неподвижную точку (0, .. ., 0)
фазового пространства. Так как основные результаты легко
распространяются и на неавтономные управляемые
процессы (см. § 7), то задача оказывается решенной.
Здесь мы считали, что движение преследуемой точки
(9) определено заранее на протяжении всего рассмат¬
риваемого промежутка времени. Совершенно новый и
практически важный вопрос возникает, когда движение
преследуемого объекта не известно заранее, а сведения
о нем поступают только с течением времени. Для того
чтобы решать такую задачу о преследуемом объекте,
нужно иметь некоторые данные о его поведении. Весьма
важным представляется случай, когда преследуемый объ¬
ект является управляемым, так что его движение описы¬
вается системой уравнений
=	 zn,	i = l,...,n,	(10)
причем движение его происходит в том же фазовом про¬
странстве, что и движение преследующего объекта (1).
Задача заключается в том, чтобы, зная технические воз-
можности преследуемого объекта, т. е. систему уравнений
(10) и его положение в данный момент времени, опреде¬
лить управление преследующего объекта в тот же момент
времени „так, чтобы преследование осуществлялось Тэпти-
_°бразом. В такой постановке задача пока не
решена. В^главе 7 решается другая задача преследования.
Предполагается, что в начальный момент положение пре¬
следуемого объекта известно, а дальнейшее его поведе
ние описывается вероятностным образом, именно процесс
движения его считается марковским. В этих предположе¬
ниях ищется такое управление преследующего объекта (1),

ВВЕДЕНИЕ
11
при котором встреча некоторой малой окрестности объ¬
екта (1) с преследуемым объектом является наиболее
вероятной.
Первоначально мы искали оптимальное управление (6)
при фиксированных начальном (3) и конечном (5)
положениях объекта. Часто, однако, бывает нужно найти
не одно оптимальное управление (6), а общее решение
задачи при произвольных положениях (3) и (5). Будем
для определенности считать, что конечное положение (5)
объекта фиксировано, а начальное (3) является произволь¬
ной точкой пространства. Тогда искомое оптимальное
управление (6) становится функцией не только времени
но и начальной точки
Если х (t) — положение управляемого объекта в момент
времени I при управлении (И), то имеет место очевидное
тождество
выражающее тот факт, что в каждый момент времени t
управлять объектом следует оптимальным образом. По¬
этому вместо функций (11) от п +1 переменных можно
рассматривать функции
от п переменных. Эти функции дают так называемый
синтез оптимального управления. Вопрос о самом сухце-
ствованпи синтезирующего упра в л ения^ТЦ}' ’"^дяется
довольно Сложным’; 'он решён *'по ло>кительно для лиией-
ных систем при Тнек^	-
ниях весьма общего харашгёра~'(с1Г.^
конкретных линейных "систем построено и само синтези¬
рующее управление (12) (см. §§ 5 и 20),
у 	 (/У'^~	у
^0 — •••»•*'<)/>
так что мы имеем оптимальное управление
и> (t, х0), ur(t, х0). |
(11)
Положим
u}(t0, x0) = uj(x0).
и1 (t, x0) = uj (x(t)),	/=	1	г,
в1 (ж), . .иг(х)
(12)

12'
ВВЕДЕНИЕ
Исходя из предположения, что синтезирующее управ¬
ление (12) существует и что соответствующий ему функ¬
ционал (4), являющийся теперь функцией точки х:
/ = /(*;) =/(.г1, . . ха),	(13)
представляет собой непрерывно дифференцируемую функ¬
цию переменных х1, . .., хп, американский математик
Р. Веллман составил для функционала (13) некоторое диф¬
ференциальное уравнение с частными производными. Это
уравнение Веллмана дает другой, отличный от излагаемого
в настоящей книге, но тесно связанный с ним подход
к решению оптимальной задачи управления (см. § 9). Сле¬
дует заметить, что предположение о непрерывной диф¬
ференцируемости функционала (13) не выполняется
в самых простых случаях, так что соображения Веллмана
дают скорее хороший эвристический прием, чем математиче¬
ское решение задачи. Принцип максимума, кроме его
полной математической обоснованности, имеет и то пре¬
имущество, что он приводят к системе обыкновенных
дифференциальных уравнений, в то время как подход
Веллмана требует решения уравнения в частных про¬
изводных.
Наконец, несколько слов о не упоминавшейся ранее
главе четвертой. Здесь собраны некоторые обобщения рас¬
смотренных основных задач и некоторые приложения. В
частности, рассматривается случай, когда в уравнение (1)
входят дополнительно некоторые числовые параметры (ко¬
торые можно выбрать до начала процесса, но нельзя уже
менять в течение процесса), а также случай, когда
уравнение движения объекта осложняется наличием эф¬
фекта запаздывания. Кроме того, приведено применение
принципа максимума к одной задаче теории приближения
функций. В последнем параграфе главы 4 дано решение
одной (довольно частной) задачи преследования.

ГЛАВА 1
ПРИНЦИП МАКСИМУМА
§ 1. Допустимые управления
Мы будем рассматривать поведение объекта, состояние
которого в каждый момент времени характеризуется п
действительными числами х1, .г'2, . . ., хп (например, коор¬
динатами и скоростями). Векторное пространство X век¬
торной переменной х = (х1, . . ., хп) является фазовым
пространством рассматриваемого объекта. Поведение (дви¬
жение) объекта заключается (с математической точки
зрения) в том, что переменные .х1, . . ., х?1 меняются
с течением времени. Предполагается, что движением объ¬
екта можно управлять, т. е. что объект снабжен
некоторыми «рулями», от положения которых зависит
движение объекта. Положения «рулей» характеризуются
точками и некоторой области управления U, которая может
быть любым множеством некоторого /’-мерного эвклидова
пространства Ег\ задание точки и —(и1, и2, ..., ur) £ U
равносильно заданию системы числовых параметров
и1, гг2, . . ., и1'. В приложениях важен случай, когда U
является замкнутой областью пространства Ег. В ча¬
стности, область управления U может быть кубом /’-мер¬
ного пространства переменных гг1, гг2, . . ., иг:
\ I и’1< 1, \	/=1,2,..., г,	(1)
или каким-либо другим замкнутым ограниченным мно¬
жеством этого /’-мерного пространства. Физический смысл
рассмотрения замкнутой и ограниченной (в пространстве
переменных гг1, гг2, . . ., ггг) области управления U ясен:

14
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
управляющими параметрами и1, и2, иг могут служить
количество подаваемого в двигатель топлива, температура,
сила тока, напряжение и т. п., которые не могут при¬
нимать сколь угодно больших значений. Кроме того,
в силу технической конструкции управляющей части
объекта, между управляющими параметрами и1, и2, . . ., иг
могут существовать связи, выражаемые одним или не¬
сколькими уравнениями вида ср (и1, и2, . . ., иг) = 0. В этом
случае область управления U может геометрически иметь
более или менее сложный характер. Если, например,
имеются два управляющих параметра и1, и2, которые
в силу конструкции объекта имеют вид и1 = cos ср, и2 = sin <р,
где ф — некоторый (произвольно задаваемый) угол, то
областью управления будет окружность
(^)2 + 02) 2=1. (2)
В дальнейшем мы просто будем говорить об области
управления U и ее точках u£U и будем представлять
себе U в виде некоторого множества в пространстве пере¬
менных и1, и2, .. ., иг, считая его «точкой» и произволь¬
ную входящую в U систему управляющих параметров
и = (и1, и2, ...,нг) (см., например, (1) или (2)).
Каждую функцию и = и (t), определенную на некото¬
ром отрезке	времени t и принимающую значе¬
ния в области управления U, мы будем называть управ¬
лением• Так как U есть множество в пространстве управ¬
ляющих параметров и\ и2, . . ., иг, то каждое управление
u(t) = {u1{L), иЦ1), . ur(t))
является в е к т о р-ф ункцие й (заданной на отрезке
значения которой лежат в области управле¬
ния U. В дальнейшем, в _заш!сibioст и от характера по¬
ставленной задачи, мы будем накладывать на управле¬
ние u(t) различные условия (кусочной непрерывности,
кусочной дифференцируемости и т. п.). Управления,
удовлетворяющие этим условиям, будем называть допу¬
стимыми управлениями. В этой главе мы будем
считать допустимыми управлениями произвольные ку¬
сочно-непрерывные управления (со значениями
в области управления U), т. е. такие управления u = u(t)y

ПОСТАНОВКА ОСНОВНОЙ ЗАДАЧИ
15
каждое из которых непрерывно для всех , рассматри¬
ваемых t, за исключением лишь конечного числа момен¬
тов времени, где функция и (t) может терпеть разрывы
первого рода. Во избежание недоразумений отметим, что,
по определению разрывов первого рода, в точке разрыва
х предполагается существование конечных пределов
Из этого, в частности, следует, что всякое управление u(t)
ограничено (даже если область Uне является ограниченной).
Значение кусочно-непрерывного управления и (/) в точке
разрыва не играет сколько-нибудь существенной роли
в дальнейшем. Однако _для определенности нам удобно
предполагать, что в каждой-’точке разрыва х значение
управления и (L) равно пределу слева:
и что каждое рассматривавхлюе управление ii(L) непре¬
рывно в концах отрезка £0<£<К> на котором оно задано.
Итак, допустимым управлением мы условимся в этой
главе называть всякую кусочно-непрерывную функцию
и (/),	со значениями в области управления С/,
удовлетворяющую условию (3) в точках разрыва и непре¬
рывную в концах отрезка t0<Ct^Ctv на котором она
задана. Кусочно-непрерывные управления соответствуют
предположению о «безынерционности» рулей, так как
значения функции и (/) могут (в момент разрыва) мгно¬
венно перескакивать из одной точки области управления
в другую. Этот класс допустимых управлений, по-види¬
мому, наиболее интересен для технических применений
развиваемой здесь теории.
Мы будем предполагать, что закон движения объекта
(и закон воздействия «рулей» на это движение) записы¬
вается в виде системы дифференциальных уравнений
и (т — О) = limn(£), н(т +0) = lim и (I).
t-+'г
t< X
и(х) = и( т — 0),
(3)
§ 2. Постановка основной задачи
i = 1, 2, . . ., п,
(4)

ПРИНЦИП МАКСИМУМА
[ГЛ. I
или, в векторной форме,
(5)
где /(х, гг) — вектор с координатами
Z1 (х, и), /2 (.х, гг), . . ., /п (х, гг).
Функции /' определены для любых значений векторной
переменной .х £ X и для значений гг, принадлежащих
области управления U. Они предполагаются непрерыв¬
ными по совокупности переменных х1, х2, ..., хп, и
и непрерывно дифференцируемыми по х1, х2, ..., х'\
Иначе говоря, функции
определены и непрерывны на прямом произведении
IX//.
Заметим, что система (4) автономна, т. е. правые
ее части не зависят явно от времени /. Случай, когда
правые части зависят от /, мы обсудим ниже (см. § 7).
некото¬
рое допустимое управление u = u(t), то уравнение (5) при¬
нимает вид
откуда (при любых начальных условиях х(/0) = х0) одно¬
значно определяется за icon движения объекта х = х (/),
т. е. решение уравнения (6), определенное на некотором
отрезке времени. Именно, если управление u(t) задано на
отрезке £0 < / < С и 0,, 02,	— его точки разрыва
(первого рода), причем t0 < 0, < 02 < • • - < 0/й < tv то мы
рассмотрим сначала уравнение (6) на отрезке
где оно имеет непрерывную правую часть. Обозначим
через x(t) решение этого уравнения с начальным усло¬
вием x(f0) = x0. Если это решение определено на всем
отрезке £0 < £ < 0 г и имеет в точке 6L значение х (02), то
мы можем рассмотреть уравнение (6) на отрезке 0Х < £<02,
воспользовавшись начальным значением х(63). Это ретне-
/'■(х1, х2, ..., хп, гг) и
г, / = 1, 2, . . ., п,
dfl (х1, х2, . . . , хп, и)'
дх!	7
=/(*. «(0).
(6)

ПОСТАНОВКА ОСНОВНОЙ ЗАДАЧИ
17
ние также обозначим через x(t). Таким образом, построен¬
ное решение х (/) непрерывно во всех точках своего опре¬
деления и, в частности, в «точке сопряжения» 0Г Если
теперь решение x(t) определено на всем отрезке £о<£<02
и имеет в точке 02 значение ж(02), то мы можем рас¬
смотреть уравнение (6) на отрезке 02 < £<03, восполь¬
зовавшись начальным значением х (02) и т. д. Получен¬
ное таким образом решение х (t) уравнения (6) является
непрерывным и кусочно-дифференцируемым; именно, во'
всех точках, кроме 0lf 02, . . ., 0/о решение х (t) (там, где оно
определено) является непрерывно дифференцируемым. Пост-
роенное решение x (t) мы будем называть решением систе-
мы Г4) (или уравнения {Ъ))3^огмш^шгщющим-^ргишт\ю
u(t) при начальном условии x(t0) = х0. Это решение
может не быть определено на всем отрезке
задания управления u(t) (оно может уйти в бесконеч¬
ность).
Мы будем говорить, что допустимое управление гг (it),
t0 < £< tlt переводит, фазовую точку из положения х0 в по¬
ложение xv если соответствующее ему решение x(t) урав¬
нения (5) (или, что то же, (6)), удовлетворяющее начальному
условию x(tQ) — x01 определено на всем отрезке
и проходит в момент tx через точку xv т. е. удовлетво¬
ряет также конечному условию x(t1) = x1.
Предположим теперь, что задана еще одна функция
/°(хг, х2, ..., х'\ гг) = /° (х, гг), определенная и непрерывная
 	•	  df°
вместе с частными производными ,г = 1,2, гг,
на всем пространстве X X U, Тогда основная задача
(отыскание оптимальных управлений) может; . быть сфор¬
мулирована следующим образом.
В фазовом пространстве X даны две точки х0 и хг
Сбреди всех допустимых управлений u = u(t), переводящих
фазовую точку из положения xQ в положение хг (если
такие управления существуют), найти такое, для которого
функционал
h	I
J=\f°(x(t),u(t))dt	1	(7)
to
принимает наименьшее возможное значение; здесь
2 Л. С. Понтрягин

18
ПРИЫЦИП МАКСИМ У МА
(.ГЛ. 1
х (t) — решение уравнения (5) с начальным условием
x(t0) = x0, соответствующее управлению u(t), а ^ — момент
прохождения этого решения через точку хг
Отметим, что (при фиксированных х0, хг) верхний
и нижний пределы t0, t1 в интеграле (7) не являются
фиксированными числами, а зависят от выбора управ¬
ления и (t), переводящего фазовую точку из положе¬
ния х0 в положение хг (эти пределы определяются из
соотношений x(t0) = xQ, х (tj) = х2). О решении задачи
для случая закрепленных пределов мы будем говорить
ниже (см, § 8).
Управление и (t), дающее решение поставленной выше
задачи, называется оптимальным управлением, соответ-
ствующим переходу из положения х0 в положение xv
а соответствующая траектория х (t) — оптимальной траек¬
торией. Таким образом, основная задача заключается
в отыскании оптимальных управлений (и соответствую¬
щих оптимальных траекторий).
Важным частным случаем поставленной выше опти¬
мальной задачи является случай, когда /° (х, а) = 1.
В этом случае функционал (7) принимает вид:
и оптимальность управления и (t) означает минималъность
времени перехода из положения х^в положение xv Задачу
отыскания оптимальных управлений (и траекторий) в этом
случае мы будем называть задачей об оптималь¬
ном быстродействии.
Для формулировки и доказательства,необходимого усло¬
вия оптимальности нам будет удобно дать иную форму¬
лировку поставленной выше задачи. Именно, добавим к фа¬
зовым координатам х1,^1, . . ., хп, меняющимся' дб^зако-
ну (4)гетгЩодну координату х°, закон изменения.которой
имеет~'в'ид *	’	'~~ ~	*
где /° — функция, участвующая в определении функцио¬
нала J (см. (7)). Иначе говоря, мы будем рассматривать
J=L — tt
о
(8)

g 2j	ПОСТАНОВКА	ОСНОВНОЙ	ЗАДАЧИ	19
систему дифференциальных уравнений
= /‘ (*i, я2 хп, и1, ..., иг) = /* (*, в),
i = 0, 1, 2, ..п,	(9)
правые части которой не зависят от переменного Вводя
в рассмотрение вектор
х = (х°, х\ х\ . .., Xй) = (х\ х)
(я1)-мерного векторного пространства Х> мы можем
систему (9) переписать в векторной форме
-g£=/(*,B),	(Ю)
где f(x, и) — вектор пространства X, имеющий коорди¬
наты /°(ж, и), ../н(^> м)- Заметим, что вектор f{xy и)
не зависит от координаты х° вектора х.
Пусть теперь и(tj— некоторое допустимое управление,
переводящее х0 в xv а х = х (t) — соответствующее реше¬
ние уравнения (5) с начальным условием x(t0)=x0. Обо¬
значим через (Х0 точку (0, х0), т. е. точку пространства X,
имеющую координаты 0, х\, ..., х™, где х], ..., х™ —
координаты точки х0 в пространстве X. Тогда ясно, что
решение уравнения (10), соответствующее управлению
u(t), с начальным условием x(t0) = x0 определено на всем
отрезке t0 < t < tx и имеет вид
t
х°=^ f°(x(t), u(t))dt,
*0
x = x(t).
В частности, при t^=tx мы получим
<i
Х°= ^ f°(x(t), и (t)) dt = /, x = xlt
to
т. e. решение x(t) уравнения (10) с начальным условием
я(t0) = х0 проходит при t = t± через точку х = (/, хг).
Иначе говоря, обозначив через П прямую линию,
2*

20
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
проходящую в пространстве X через точку х = (0, хг)
параллельно оси щ (эта прямая П образована всеми' точками
(£, я^где число £ произвольно; рис. 1), мы можем сказать,
что решение х (t) проходит в момент t = tx через точку,
лежащую на прямой П и имеющую координату х° = /.
Обратно, если и (t) — такое допустимое управление, что
соответствующее ему решение x(t) уравнения (10) с на¬
чальным условием х (t0) = х0 = (0‘, х0) проходит в некото¬
рый момент ^ через точку хг £ П с координатой х° = J,
то управление u(t) переводит (в пространстве X) фазовую
точку из положения х0 в положение xv причем функцио¬
нал (7) принимает значение J.
Таким образом, мы можем сформулировать поставлен¬
ную выше оптимальную задачу в следующем эквивалент¬
ном виде.
В (п-\- iyмерном *фазовом пространстве X даны точка
хп = (0, х0) и прямая 11~шщШёЖШя~дси ^пттргбТодя-
щая ч^ез’точку[\0, Среди всех допустимыхГуггравле-
нйй ц = и (t), обладающих '^тем^'свойством, что со ответ-
ствующее решение х (£) уравнения (10) с начальным уело-
вием х \Г0У^ хй перебекает 'прямую ТГ, найти такое, для
которого точка пересечения с прямой П имеет наимень¬
шую^ кобрд'шШту'^Т'	~	’
Эту задачу мы и будем решать. Термины «оптималь¬
ное управление» и «оптимальная траектория» мы сохраним
и для задачи в этой новой формулировке.

ПОСТАНОВКА ОСНОВНОЙ ЗАДАЧИ
21
Отметим некоторые простые свойства оптимальных
управлений и траекторий, непосредственно вытекающие
из формулировки основной задачи. Прежде всего, из авто¬
номности системы (9) вытекает, что при сдвиге вдоль
оси~ t (рис. 2) своиствеГ управлений не меняются^ Иначе
говоря, если управление и (£),	переводит	фазо¬
вую точку из положения х0 в положение хг и придает
функционалу (7) значение /, то при любом действитель¬
ном /г управление гг(£ + /г), t0 — h < t <	— h, также
переводит фазовую точку из положения х0 в положение
хх и придает функционалу (7) то же значение /. Это позво¬
ляет перемещать начальную точку t0 отрезка t0 < i< tv на
котором задано управление и (t), в любую точку оси времени.
Далее, если хп, хл, . .., xit — конечная система точек
фазового пространства X и если существует управление
uL(t), переводящее фазовую точку из положения х{_г
в положение xi и придающее функционалу (7) значение
/|, i = 1, . . ., к, то существует управление u (t), переводящее
фазовую точку из положения х0 в положение х-л и при¬
дающее функционалу (7) значение Jx + /2+ .. . +//г
В самом деле, в силу возможности сдвигать управления
вдоль оси времени, мы можем считать, что отрезки, на
которых определены управления ui(t)) непосредственно
примыкают один к другому (рис. 3), т. е. что управление
(t) задано на отрезке < t < ti9 где t0 < tx < . . . < tk.
Обозначим теперь через u(t) управление, заданное на от¬
резке t0 < t < и совпадающее на полуинтервале < t <
с управлением ut (t), т. е. «объединение» всех управлений
ui(t). Непосредственно проверяется, что управление u(t)
переводит фазовую точку из положения х0 в положение

22
ПРИНЦИП МАКСИМУМА
(ГЛ. 1
xk и придает функционалу (7) значение J1 + J2+... +Jft.
Заметим, что указанная операция «объединения» несколь¬
ких управлений была бы невозможна в классе непре¬
рывных управлений (ибо в точках tlt t2i . ..,
построенное управление u(t) может иметь разрывы первого
рода, даже если управления u{(t) были непрерывными;
рис. 3).
Из сказанного выше легко следует, что всякий кусок
оптимальной траектории также является оптимальной
траекторией (и аналогично
х для оптимальных управле-
' ний). Более точно, пусть
u(t),t0<CtK tlt—оптималь¬
ное управление, соответст¬
вующее переходу из поло¬
жения х0 в положение х1}
а х (t) — соответствующая
оптимальная траектория.
Тогда, если^0<т0<т1<^1,
то управление и (t), рассматриваемое на отрезке т0< ^<т2,
является оптимальным управлением, соответствующим пе¬
реходу из положения х(х0) в положение x(x1)i a x(t),
т0 < t < тх, является соответствующей оптимальной траекто¬
рией (рис. 4). В самом деле, обозначим значения интеграла
(7), взятого по отрезкам £0<£<т0,
соответственно через Jv /2, /3. Тогда управление u(t),
переводящее фазовую точку из положения х0
в положение xv придает функционалу (7) значение
/ =	+ /2 + /3. Если бы управление u(t), рассматривае-
Рис. 4.

ПРИНЦИП МАКСИМУМА
23
мое на отрезке x0<t<xv не было оптимальным, то суще¬
ствовало бы некоторое управление v(t), переводящее фа¬
зовую точку из положения х(х0) в положение х(х1) и прида¬
ющее функционалу (7) значение /2 < /2- Но тогда мы по¬
лучили бы управление, переводящее фазовую точку из поло¬
жения х0 в положение хх и придающее функционалу (7)
значение J1 + J'o+Js< J> что противоречит оптимальности
управления u(i), £0<*<К-
§ 3. Принцип максимума
Переходим теперь к формулировке теоремы, дающей
решение поставленной основной задачи. (Доказательство
этой теоремы приведено во второй главе.) Для формули¬
ровки теоремы, кроме основной системы уравнений (9):
^ =р (я, и), £ = 0, 1, 2, ..., п,	(11)
мы рассмотрим еще одну систему уравнений относительно
вспомогательных (дополнительно рассматриваемых) пере¬
менных ф0, фд, . . ., фЛ:
f-ол »■ (12)
а=0
Если мы выбрали некоторое допустимое управление
и(0>	11	имеем соответствующую фазовую траек¬
торию x(t) системы (11) с начальным условием зс(£0) = х*0,
то система (12) принимает вид
'«$- - S »• i *-**	(«)
_ а==0
9та система линейна и однородна; поэтому при любых
начальных условиях для фд она допускает единственное
решение
Ф^(Фо> Ф1> Ф2> •••> Фп)
(определенное на всем отрезке	на котором опре¬
делены управление u(t) и траектория x(t)). Как и ре¬
шение x(t) системы (11), решение системы (13) состоит
из непрерывных функций фд(£), имеющих всюду, кроме

24
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
конечного числа точек (а именно, точек разрыва управ¬
ления u(t)), непрерывные производные по t. Всякое реше-
ние системы (13) (при любых начальных условиях) мы
будем называть решением’ системы (12), соответствую-
г^ШГЛШб“р1МнОТу управлению и (t) и фазовой "траекто¬
рии x(i).
Мы теперь объединим системы (11), (12) одной записью,
для чего рассмотрим следующую функцию перемен¬
ных х1, . . ., х'\ ф0, ф1? . .., фл, и1, . . ., иг:
  	п
S SfC (ч|>. X, и) = (ф, f(x, и)) = 2 %l/“ (ж> и)-
а=0
Непосредственно проверяется, что написанные выше систе¬
мы (11) и (12) могут быть с помощью этой функции т
записаны в виде следующей гамильтоновой системы:
dxl am
dt oti ’
dm
dt	dxi
г = 0, 1, . .., n,	(14)
i = 0, 1, . .., n.	(15)
Итак, взяв произвольное допустимое (т. е. кусочно¬
непрерывное) управление u(t),	и	начальное
условие х(10) — х0, мы можем найти соответствующую
(т. е. удовлетворяющую системе (14)) траекторию ас(/) =
= (х°(1), х1 (/), ...,хп(1)). После этого мы можем нахо¬
дить соответствующие функцшш и(1) и x(t) решения
f =	%(0.	•	•	•>	'l’n(O)
системы (15). Еще раз подчеркнем, что вектор-функции
х (I) и ф(/) непрерывны и всюду, кроме конечного числа
точек, имеют непрерывные производные по t.
При фиксированных (постоянных) значениях ф и х
функция становится функцией параметра и£ U\ точную
верхнюю грань значений этой функции мы обозначим
через м (ф, х):
оЛ1 (ф, х) = sup (ф, X, и),
u£U
Если точная верхняя грань значений непрерывной функ-
цшГ~~е^ Д о стиг а е т с я в некоторой точке области
управления U, то	х)	есть максимум значений функ¬

ПРИНЦИП МАКСИМУМА
25
ции при фиксироваш^ых я^ и х. Поэтому нижеследую-
1цую~ теорему 1 (необходимое условие опт™
главным содержанием'которой является равенство (16),
мы называем п р и нцнп о м мак с и м у м а.
Тендем а '1. Пусть u (t),	— такое допусти-
мое управление, что соответствую'щая ему тпраектория
х(1) (см. (14)), исходящая в момент t0 из точки х0, про¬
ходит в момент /т через некоторую точку прямой П.
Для оптимальности управления и(1) и траектории х(1)
необходимо существование такой ненулевой непрерывной
вектор-функции я|>(*) = (ф0 (t), ^ (*), . .	фп(*))> соответ¬
ствующей функциям u(t) и x(t) (см. (15)), что:
1° при любом t,	функция (\КО» x(t),u)
переменного u^U достигает в точке u — u(t) максимума
р55? Ж0> х(1)’ u(t)) = e$(ty(t), x(t));	(16)
2е в конечный момент выполнены соотношения
^o(<i)<°- мвЬвХ х{Ь)) = ®-	(17)
Оказывается, далее, что если величины г|)(£), x(t), и (t)
удовлетворяют системе (14), (15) и условию 1°, то функ¬
ции ф0(£) и о/Ц (г|э(£), x(t)) переменного t являются посто¬
янными, так что проверку соотношений (17) можно
проводить не обязательно в момент lv а в любой мо¬
мент t,	(Доказательство	теоремы 1 приво¬
дится в гл. 2.)
Выведем теперь из теоремы 1 аналогичное необходимое
условие для оптимальности по быстродействию. Для этого
в теореме 1 следует положить f°(x,u) = l. Функция т
принимает в этом случае вид
71
еЮ =	+	2	15v/v	(х,	и).
v=l
Вводя п-мерный вектор ф = (фд, ф2, . . ., фп) и функцию
71
Я (г|), х, и) = 2 o|\,/v (х, и),
V=1
мы можем записать уравнения (4) и (12) (кроме урав¬
нения (12) для i = 0, которое теперь ненужно) в виде

26
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
гамильтоновой системы
dxi дН
dtyj _	дН
dt ~~	дх1
г=1, 2, .. п,	(18)
i =	2,	. ... тг.	(19)
При фиксированных значениях ф и х функция Н
становится функцией параметра и; верхнюю грань зна¬
чений этой функции мы обозначим через У¥(ф, х):
М (ф, х) = sup Н (ф, х, и).
u£U
В силу соотношения Н(ф, х, и) =	(ф, х, и) — ф0 мы
получаем
М (ф, х) = оМ (ф, х) — ф0,
и потому условия (16) и (17) принимают теперь вид
Я(ф(^), x(t)9	—	x(t))	= — ф0>0.
Таким образом, мы получаем следующую теорему.
Теорема 2. Пусть u(t),	<£г, — допустимое
управление, переводящее фазовую точку из положения х0
в положение xv а х (t) — соответствующая траектория
(см. (18)), так что x(t0) = x0, x(t1) = x1. Для оптималь¬
ности (по быстродействию) управления u(t) и траектории
x(t) необходимо существование такой ненулевой непре¬
рывной вектор-функции ф (t) = (фА (£), ф2 (t), . .., фп (t)),
соответствующей функциям u(t) и x(t) (ель. (19)),
что:
1° для всех t, £()<£<£!, функция #(ф(£), x(t)9 и) пе¬
ременного u£U достигает в точке и= u(t) максимума
#(ф(£), x(t)9 u(t)) = M(ty(t)9 x(t))\	(20)
2° в конечный момент tx выполнено соотношение
М(ф(*х), х(Ь))>0.	(21)
Оказывается, далее, что если величины ф(£)>
удовлетворяют системе (18), (19) и условию 1°, то функ¬
ция .Д/(ф(£), х (t)) переменного t постоянна, так что
проверку соотношения (21) можно проводить не обяза¬
тельно в момент tv а в любой момент t,

4]
ОБСУЖДЕНИЕ ПРИНЦИПА МАКСИМУМА
27
§ 4. Обсуждение принципа максимума*)
Теорема 1 позволяет из всех траекторий, начинаю¬
щихся в точке х0 и кончающихся в некоторой точке
прямой П, и соответствующих им управлений выделить
лишь отдельные, вообще говоря, изолированные траек¬
тории и управления, удовлетворяющие всем сформули¬
рованным условиям. Действительно, мы имеем 2/2 -|- 3
соотношений (14), (15), (16) между 2/2 + 3 переменными**)
яа, фа» и» т* е* имеем «полную систему соотношений» для
определения всех этих переменных. Так как, далее,
соотношение (16) конечное (не дифференциальное), а диф¬
ференциальные уравнения мы имеем в количестве 2/2 + 2
(соотношения (14) и (15)), то решения системы уравне¬
ний (14), (15), (16) зависят, вообще говоря, от 2/2 + 2
параметров (начальных условий). Однако один из этих
параметров является несущественным, так как функции
фа (0 определены лишь с точностью до общего множи¬
теля (ибо функция однородна относительно ф). Кроме
*) Этот параграф имеет своей целью показать «достаточность»
системы соотношений, указанной в теореме 1, для решения
поставленной оптимальной задачи. Приводимые в этом параграфе
рассуждения не претендуют на строгость и нигде в дальнейшем
не используются.
**) Напомним, что «одна» переменная^) может распадаться
на несколько отдельных переменных, например может быть точ¬
кой г-мерного векторного пространства; в__этом случае условие
максимума (16) также можно считать содержащим г отдельных со-
отноше ни й. Е ели, н а прим е р7'И ЛКСим у м'до стй'га е т с я” во’ внутренней
Г6Чкё~7Ямасти управления U (расположенной в г-мерном простран¬
стве переменных и1, ..., мг), то для выполнения условия макси¬
мума (16) необходимо обращение в пуль г частных производных:
д&в (ф (t), х (/), и)
если максимум достигается на (г — 1)-мерной грани области управ¬
ления С/, то должно выполняться условие принадлежности точки
и (t) этой грани (это дает одно соотношение) и должны обра¬
щаться в нуль частные производные функции <^?(ф(0> х (0» и)
по всем направлениям в этой грани (это дает еще г — 1 соотно¬
шений). Аналогичное положение вещей имеет место и на гранях
меньшего числа измерений (или на искривленных частях границы
области управления U). Таким образом, во всех случаях можно
считать, что если область управления U является r-мерной, то
условие максимума (16) содержит г соотношений.

28
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
того, один из параметров связан условием, что в момент
t0 величина
шах зе 0ф (*„), x(t0), и)
иеи
обращается в нуль.
Итак, все многообразие решений системы {14), (15), (16)
зависит от Ъг пар^Те^од. Этими 2п параметрами следует
распорядиться" так, "чтобы траектория x(t) проходила
при заданном t = t0 через точку х0, а при
к а к о м-н и б у д ь t1 > t0 проходила через точку на пря¬
мой П. Число t1 — t0 также является параметром, так
что всего у нас имеется 2п + 1 существенных парамет¬
ров. Условие прохождения траектории через точку х0 и
прямую П дает 2п+ 1 соотношений. Следовательно, можно
ожидать, что имеются лишь отдельные, изолированные
траектории, соединяющие точку х0 с прямой П и удовле¬
творяющие условиям, указанным в теореме 1. Лишь эти
отдельные, изолированные траектории и могут оказаться
оптимальными (ибо указанные в теореме 1 условия н е-
обходимы для оптимальности).
Если, в частности, условиям теоремы 1 удовлетво¬
ряет лишь одна траектория, соединяющая точку х0
с точкой прямой П, а из технических соображений,
приведших к постановке оптимальной задачи, «ясно»,
что оптимальная траектория должна существовать, то
можно надеяться, что найденная траектория как раз
и является оптимальной. Следует, однако, отметить, что
математически вопрос о существовании оптимальной
траектории представляется очень важным и трудным.
В частном случае оптимальности по быстродействию для
линейных систем (4) он решается в третьей главе.
§ 5. Примеры. Задача синтеза
В этом параграфе мы рассмотрим применение прин¬
ципа максимума к решению некоторых простых задач
об оптимальных быстродействиях. Из рассмотрения этих
примеров выясняется новая важная постановка задачи
об оптимальных процессах — задача синтеза оптимальных
управлений.

ПРИМЕРЫ. ЗАДАЧА СИНТЕЗА
29
Пример 1
d2x
Рассмотрим уравнение ^ = и, где и — вещественный
управляющий параметр, подчиненный условию |и|	1.
13 фазовых координатах хг — ху x2=z~jf это уравнение
переписывается в виде следующей системы:
= и.	(22)
dx1	9	dx2
dt ~~ Х ’ dt
Рассмотрим (для фазовой точки, движущейся по за¬
кону (22)) задачу о быстрейшем попадании в начало
координат (0,0) из заданного начального состояния х0.
Иначе говоря, мы будем рассматривать задачу об опти¬
мальном быстродействии в случае, когда конечным
положением служит начало координат: хх = (0, 0).
Функция И в рассматриваемом случае имеет вид
Н =	+ ф2м*	(23)
Далее, для вспомогательных переменных ф15 ф2 мы полу¬
чаем систему уравнений (см. (19), (23))
tfih _ 0	d\р2 _
и -и>	df -	™
откуда фт = с1? ф2 = с2 — cTt (cv с2 — постоянные). Соотно¬
шение (20) дает нам (учитывая (23) и условие
— 1 < и < 1)
и (t) = sign ф2 (t) = sign (с2 — cxt).	(24)
Из (24) следует, что каждое оптимальное управ¬
ление и(1), £0<£<П> является кусочно-постоянной функ¬
цией, принимаюгцей значения f 1 м имеющей не более
двух интервалов постоянства (ибо линейная функция
с2 — сД не более одного раза меняет знак на отрезке
Обратно, любая такая функция u(t) может
быть получена из соотношения (24) при некоторых зна¬
чениях постоянных cv с2.
Для отрезка времени, на котором и = 1, мы имеем
(в силу системы (22))
*2 = t + х1 =	+ s2t + si = i- (t + s2)2 + (sx - (i2)2

30
ПРИНЦИП МАКСИМУМА
[ГЛ. i
(s1,	^	—	постоянные	интегрирования),	откуда получаем
X1 = -i (ж2)2 + s,	(25)
1 ^
где s = s1 — у (s2)2 — постоянная. Таким образом, кусок
фазовой траектории, для которого и=1, представляет
0)
Рис. 5.
собой дугу параболы (25). Семейство парабол (25) пока¬
зано на рис. 5, а).
Аналогично, для отрезка времени, на котором и = — 1,
мы имеем
х2 = — t + s'2,
--у +*'а* + *'1= -4(-* + 6',2)2+("5'1+т (*'2)0.

ПРИМЕРЫ. ЗАДАЧА СИНТЕЗА
31
откуда получаем
Xх = — 2-(ж2)2 + ®'-
(26)
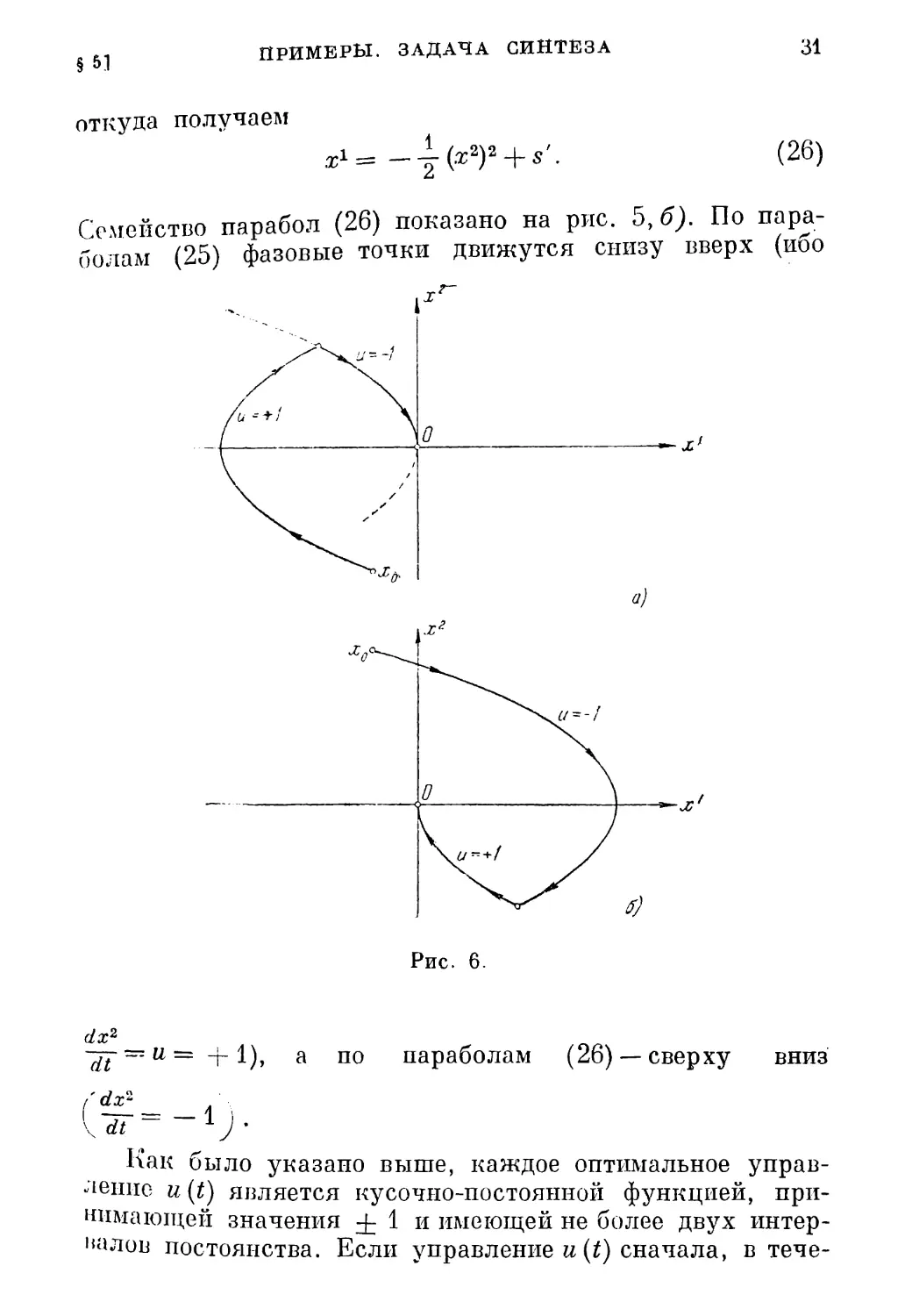
Семейство парабол (26) показано на рис. 5, б). По пара¬
болам (25) фазовые точки движутся снизу вверх (иоо
Рис. 6.
dx2
— —	1), а по параболам (26) —сверху вниз
('*£!_ 1 ,
Kdt ~
Как было указано выше, каждое оптимальное управ¬
ление и (t) является кусочно-постоянной функцией, при¬
нимающей значения f 1 и имеющей не более двух интер¬
валов постоянства. Если управление и (t) сначала, в тече¬

32
ПРИНЦИП МАКСИМУМА
LrJi.!
ние некоторого времени, равно +1, а затем равно — 1,
то фазовая траектория состоит из двух кусков парабол
(рис. 6, а)), примыкающих друг к другу, причем второй
из этих кусков лежит на той из парабол (26), которая
проходит через начало координат (ибо искомая траек¬
тория должна вести в начало координат). Если же,
наоборот, сначала и — — 1, а затем и — +1, то фазовая
кривая заменяется центрально симметричной (рис. 6,6)).
На рис. 6 надписаны на дугах парабол соответствующие
значения управляющего параметра и. На рис. 7 изобра¬
жено все семейство полученных таким образом фазовых
1
траекторий (АО — дуга параболы х1 = -^-(х2)2> располо¬
женная в нижней полуплоскости; ВО — дуга параболы
х1=— — (х2у, расположенная в верхней полуплоскости).
Фазовая точка движется по проходящей через начальную
точку £0 дуге параболы (26), если точка х0 располо¬
жена выше линия ЛОВ и по дуге параболы (25), если
точка х0 расположена ниже этой линии. Иначе говоря,
если начальное положение х0 расположено выше линии
АОВу то фазовая точка должна двигаться под воздей¬
ствием управления и = — 1 до тех пор, пока она не по¬
падет на дугу АО\ в момент попадания на дугу АО

ПРИМЕРЫ. ЗАДАНА СИНТЕЗА
значение и переключается и становится равным +1
вплоть до момента попадания в начало координат. Если
же начальное положение я’0 расположено ниже линии
АО В, то и должно быть равно -f-1 до момента попадания
на дугу ВО, а в момент попадания на дугу ВО значе¬
ние и переключается и становится равным 1.
Итак, согласно теореме 2, только описи иные выше
траектории могут быть оптимальными, причем из про¬
веденного исследования видно, что из каждой точки
фазовой плоскости исходит только одна траектория,
ведущая в начало координат, которая может быть опти¬
мальной (т. е. задание начальной точки х0 однозначно
определяет соответствующую траекторию). Если бы мы
были уверены в том, что оптимальная траектория всегда
(т. е. для любой начальной точки х0) существует,
то могли бы с уверенностью сказать, что все найденные
траектории являются оптимальными. В главе 3 мы
сформулируем теорему существования для линей¬
ных систем оптимального быстродействия, из которой
вытекает, в частности, что в рассматриваемом примере
для любой начальной точки х0 существует оптимальная
траектория (см. стр. 144). Таким образом, найденные
траектории (рис. 7) являются оптимальными, и других
оптимальных траекторий, ведущих в начало координат,
не существует.
Полученное в рассмотренном примере решение опти¬
мальной задачи можно истолковать следующим образом.
Обозначим через v(x\ x2) = v(x) функцию, заданную
на плоскости х1, х2 так:
(+ 1 ниже линии АО В и на дуге АО,
U /дЛ __ г
[ — 1 выше линии АО В и на дуге ВО.
Гогда на каждой оптимальной траектории значение u(t)
управляющего параметра (в произвольный момент t)
равно v(x(t)), т. е. равно значению функции v в той
точке, в которой в момент t находится фазовая точка,
пробегающая оптимальную траекторию:
u(t) = v (х (t)).
Это означает, что, заменив в системе (22) величину я
Л. С. Понтрягин

34
II Р И11Ц Я И М А К С11М У М А
IГЛ. 1
функцией v (х), мы получим систему
dx1 9	л
~di~X ’	}
л г	^	(27)
%-vix1,	х2),	J
решение которой (при произвольном начальном состоя¬
нии xQ) дает оптимальную фазовую траекторию, ведущую
в начало координат. Иначе говоря, система (27) пред¬
ставляет собой систему дифференциальных уравнений
(с разрывной правой частью) для нахождения оптималь¬
ных траекторий, ведущих в начало координат.
Г1 р и мер 2
dH
dt2
d2x
Рассмотрим уравнение j-т + х =	|	и	[	<	1.	Это	урав¬
нение эквивалентно системе
' dx*
■ = х
2
)
dt
) (28)
dx2
~dt
= — X1 + и, j
для которой мы, как и в первом примере, изучим задачу
о быстрейшем попадании в начало координат. Функ¬
ция Н имеет вид
Н =-"ф1ж2 — ty2x1 -f ф2гг.	(29)
Далее, для вспомогательных переменных ф^, ф2 мы полу¬
чаем систему уравнений (см. (19), (29))
)
t=-^ j
откуда ф2 = A sin (t — а0), где А > 0 и а0 —некоторые
постоянные. Соотношение (20) дает нам (учитывая (29)
и условие |и|<1)
и = sign ф2 = sign (A sin (t — а0)) =sign~(sin (t—а0)).	(30)
Отсюда следует, что функция u(t) получается из функ¬
ции sign (sin t), равной поочередно +1 и — 1 на интер¬

§ 53
ПРИМЕРЫ. ЗАДАЧА СИНТЕЗА
35
валах длины л, при помощи сдвига на некоторый отре-
зок а0 (рис. 8).
Для изучения кусков траектории, соответствующих
отрезкам времени, на которых и=1 и и = — 1, мы рас¬
смотрим вспомогательную систему
^ _г2	^
dt	I
^ , ] (31^
—;— =    X
dt	)
(получающуюся из системы (28) при и = 0). Произвольное
решение этой системы может быть записано в виде
хх = — R cos (t + у), х2 = R tin (t Д-у),	(32)
где R и у — постоянные (/?> О,	Таким	обра-
и
1 1 !
1 1 1
0 1 1 1 -
1 *
.... 1 1 !
1 1 1
1 1 1
Рис. 8.
зом, фазовыми траекториями являются окружности с цент¬
ром в начале координат:
(^)2 + (^2)2-i?2	(33)
(рис. 9а). Из (32) видно, что движение фазовой точки
по окружности (33) совершается по часовой стрелке, при¬
чем равномерно, с линейной скоростью 2nR (один оборот
за время 2я). Отметим, в частности, что за промежуток
времени, имеющий длину я, фазовая точка, двигаясь
по часовой стрелке, описывает ровно половину окруж¬
ности (33).
При и = 1 система (28) принимает вид

3b
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
или, иначе,
d (х1	1)	__
dt
w-*)• !
(35)
Вспоминая соотношения (31) и (33), мы находим, что фа¬
зовые траектории системы (35) (или, что то же самое,
системы (34)) представляют собой окружности
(xl_1)2 + (x2)2 = fi2f	(36)
т. е. окружности с центром в точке Ov имеющей коор¬
динаты (1, 0). Эти окружности фазовая точка, движу¬
щаяся по закону (34) (т. е. по закону (28) при и — 1),
пробегает по часовой стрелке, обходя за время я ровно
половину окружности (рис. 96).
Аналогично, при и = — 1 система (28) принимает вид
dx 1

ПРИМЕРЫ. ЗАДАЧА СИНТЕЗА
37

38
ПРИНЦИП МАКСИМУМА
ГГЛ. 1
ее фазовыми траекториями являются окружности
(ж1+1)2 + (я2)2 = Д2	(37)
с центром в точке 0_1, имеющей координаты (—1, 0).
По этим окружностям фазовая точка движется по часовой
стрелке, проходя ровно половину окружности за вре¬
мя я (рис. 9в).
Как было указано выше, каждое оптимальное управ¬
ление п(1) является кусочно-постоянной функцией, полу¬
чающейся из функции sign (sin £), равной поочередно -f 1
и
t0	[сс	\п+ос	]	I	t
	9	4	4	9г	о
I	1	1 	— J\	’
Zn+oc
Рис. 10.
и — 1 на интервалах длины я, при помощи сдвига
на некоторый отрезок а0 (рис. 8). Если оптимальное
управление u(t) имеет вид, показанный на рис. 10,
т. е. поочередно равно -}- 1 и — 1
на интервалах (/0, а), (а, я + а),
(я + а,2я + а),... и, в заключение,
на некотором интервале длины
р<я равно -]-1, то соответст-
х вующая оптимальная траектория
может быть построена следую¬
щим образом.
В течение заключительного
отрезка времени (длины (3) фазо¬
вая точка движется по окруж¬
ности вида (36) (ибо и = 1 на
этом отрезке времени), причем по той из этих окруж¬
ностей/: которая проходит через начало координат (ибо
искомая траектория должна вести в начало координат).
Такой окружностью является окружность радиуса 1 с цен¬
тром в точке Ог (рис. 11а). По этой окружности фазо¬
вая точка попадает в начало координат, проходя дугу,
меньшую половины окружности (ибо Р < я). Таким обра-

5]
11 PI IM К P 1)1	3A A A 4 A	c 1111T E 3 A
30
том обозначив нижнюю полуокружность этой окружности
через Мр, мы найден, что заключительный кусок фазо-
Рис. 116.
вон траектории представляет собой некоторую дугу АО
нолуокружности МгО.
Далее, в положение А фазовая точка попала, дви¬
гаясь в течение отрезка времени, имеющего длину я,

40
L1 МИДИИ МАКСИМУМА
[ГЛ. 1
под воздействием управления и = — 1 (см. рис. 10), т. е.
предыдущий кусок фазовой траектории представляет
собой полуокружность В А с центром в точке 0_л, кон¬
чающуюся в точке А (рис. 116). Так как дуга В А равна
полуокружности, то точка В симметрична А относительно
центра 0_v и потому точка В лежит на полуокружно¬
сти N2N2, симметричной полуокружности ОМг относи¬
тельно центра 0_v Точно так же предшествующая
дуге В А дуга СВ, соответствующая отрезку времени
Рис. 12-
длины я, на котором и — 1, равна полуокружности
с центром Ov и потому точка С лежит на полуокружно¬
сти М2Мг, которая симметрична полуокружности NYN2
относительно центра Ох (рис. 11в), и т. д. Таким обра¬
зом, соответствующая фазовая траектория имеет вид,
показанный на рис. Ив (начальный кусок фазовой ^тра¬
ектории будет меньше половины окружности, если только
0<а — /0<я; см. рис. 10).
Фазовая траектория, соответствующая оптималь¬
ному ^управлению и (t), которое на заключительном отрез-

. гл	ПРИМЕРЫ. ЗАДАЧА СИНТЕЗА	41
s J J
ке длины р равно — 1 (а не +1), получается из
траектории, изображенной на рис. Ив, с помощью
центральной симметрии (рис. 12). Для такой траектории
точки «стыка» дуг окружностей будут лежать на полу¬
окружностях ON^ МгМ2, AyV3, ..., симметричных
(относительно начала координат) полуокружностям ОМ1У
вд,, М2Мз, ...
Объединяя оба эти случая (рис. Ив и 12) вместе,
получаем всю картину поведения фазовых траекторий
(рис. 13). На рис. 12 и 13 надписаны на дугах окруж¬
ностей соответствующие значения управляющего пара¬
метра и. Из рис. 13 видно, что если начальная точка х0
расположена в ы ш е линии . .. М3У1/\М\ON\N\N3 . ..,
составленной из бесконечного числа полуокружностей
Радиуса 1, то фазовая точка должна двигаться под воз¬
действием управления и= — 1 до тех пор, пока она
не попадет на дугу . . . М3М2М\0] в момент попадания
на эту дугу значение и!/ переключается и остается

42
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
равным + 1 (фазовая точка при этом движется ниже ли¬
нии . .. M^M2M1ON1N2Nz • • •) Д° момента попадания
на дугу ONfl^N3 . . .; затем точка снова движется выше
линии ... М3М\М\ON\N'2N3 . .. под воздействием управ¬
ления и= — 1 и т. д. Последний кусок фазовой
траектории (ведущий в начало координат) представляет
собой дугу полуокружности МгО или полуокружно¬
сти NxO. Совершенно аналогично движется точка и в том
случае, если начальная точка х0 расположена ниже
линии ... M3M2M1OAr1N2N3 ... : выше этой линии фа¬
зовая точка движется под воздействием управления и =
= — 1, а ниже этой линии — под воздействием управле¬
ния и = + 1.
Итак, согласно теореме 2, только указанные траекто¬
рии могут быть оптимальными, причем из проведенного
исследования видно, что из каждой точки фазовой пло¬
скости исходит только одна траектория, ведущая в нача¬
ло координат, которая может быть оптимальной. Из тео¬
ремы существования, доказываемой в главе 3, вытекает,
что в рассматриваемом примере для любой начальной
точки х0 существует оптимальная траектория (см. стр. 144).
Таким образом, найденные траектории (рис. 13) явля¬
ются оптимальными, и других оптимальных траекторий,
ведущих в начало координат, не существует.
Как и в первом примере, полученное решение опти¬
мальной задачи можно истолковать следующим образом.
Обозначим через и(хг, x2) = v(x) функцию, заданную
на плоскости х1, х2 соотношениями:
+ 1 ниже линии	.	.	.	MsM2MlON1N2N3	...
и на дуге . .	.	М3М2М10;
v(x)—	_ j Выше линии	...	M3M2M1ON1N2N3	...
и на дуге	ON1N2• • •
Тогда вдоль каждой оптимальной траектории x(t) соот¬
ветствующее оптимальное управление u{t) имеет вид
И (/;) z=v{x (t)).
Это, как и выше, означает, что, заменив в системе (28)

ПРИМЕРЫ. ЗАДАЧА СИНТЕЗА
43
величину и функцией v(x), мы получим систему
dZ1 _ Г2	1
f, '	!	(38)
^ = — x1-\-v(x1t х2)у j
решение которой (при произвольном начальном состоянии
х ) дает оптимальную фазовую траекторию, ведущую
в начало координат. Иначе говоря, система (38) пред¬
ставляет собой систему дифференциальных уравнений
(с разрывной правой частью) для нахождения оптималь¬
ных траекторий, ведущих в начало координат.
Пример 3
Рассмотрим теперь систему с двумя управляющими
параметрами:
dx1 9,1	1
-j-■-*-+!>,	|
*• . . ! <39>
}2
dt	1	J
причем величины гг1, и1 подчиним условиям | гг1 [ ^ 1,
|гг2|<1. Для этой системы мы, как и в двух первых
примерах, изучим задачу о быстрейшем попадании
в начало координат. Выпишем функцию Н
Н = ^1(х2-\-и1) + ^2(-х1 + и2)	(40)
и вспомогательную систему
j
!
Из этой системы мы получаем
ф1 = A sin (t + а),
ф2 = A cos (t + а),
гДе А и а — постоянные; А > 0, 0 < а < 2л Соотношение

44
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
(20) дает нам теперь (учитывая (40) и условия | гг11 ^ 1,
| гг21 < 1)
гг1 = sign = sign (A sin (t -j- а)) = sign (sin (t -+■ а)),
(41)
гг2 = sign ф2 = sign (A cos (t -f- а)) = sign (cos (£-f а)).
Таким образом, в случае оптимального управления каж¬
дый из управляющих параметров гг1, и2 является кусочно-
постоянной функцией, принимающей значения +1 и — 1.
Из рассмотрения системы (39) мы легко заключаем, что
куски фазовых траекторий, соответствующие отрезкам вре¬
мени, на которых гг1 = 1, гг2= 1, представляют собой дуги
окружностей с центром в точке 0Ь1, имеющей коорди¬
наты (1, —1). Аналогично при гг1 = 1, гг2 = — 1 и т. д.,
как это указано в следующей таблице:
Постоянные значения управля¬
ющих параметров на некотором
отрезке времени
Центр окружностей, являющихся соот¬
ветствующими фазовыми траекториями
системы (39)
и1 = 1, и2 = 1
и1 = — 1, и2= 1
и1 = — 1, и2 — — 1
и1=1, и2=— 1
Точка Ох,1 с координатами (1, —1)
Точка 0_1Л с координатами (1, 1)
Точка 0_!,_! с координатами (— 1, 1)
Точка 01} _i с координатами (—1, —1)
Во всех случаях движение по соответствующим фазо¬
вым траекториям (окружностям) совершается по часовой
стрелке, причем равномерно, со скоростью один оборот
зх
за время 2я. В частности, за время, равное -у , фазовая
точка пробегает четверть окружности.
Из (41) следует, что в тот момент, когда аргумент
ТС
t + а проходит через точки /су (к — произвольное це¬
лое число), один из управляющих параметров гг1, гг2
меняет знак (так как в каждой из этих точек либо си¬
нус, либо косинус проходит через нуль). Иначе говоря,
в моменты времени, для которых t + а = к у , происхо¬
дит смена значений управляющих параметров гг1, гг2, т. е.
происходит смена центра окружности, по которой
движется фазовая точка. Такая смена центра происходит

ПРИМЕРЫ. ЗАДАЧА СИНТЕЗА
через каждые
единиц времени,
так что фазовая тра¬
ектория составлена из четвертей окружностей с цент-
рамп 0Ь1) 0_ъ1; 0.и_Ou_v Исключение составляют
только первый и последний куски фазовой траектории:
они могут оказаться меньши¬
ми, чем четверть окружности.
Далее, нетрудно понять,
в каком порядке происходит
смена центров. Если при
возрастании t аргумент t + а
проходит через значение
t-\- а = 2/at (к — целое число),
то непосредственно перед
этим моментом выполнялись
соотношения и1= — 1, и2 =
= +1 (см. (41)), т. е. дви¬
жение происходило по дуге
°-п
»
\
Рис. 14.
с центром
О
а после
; = 1, т. е.
этого момента выполняются соотношения = 1, и2
движение происходит по дуге с центром Ohl. Иначе
говоря, центр 0_Ь1 сменяется центром 0Ь1. Аналогично
Рис. 15.
Центр 01% х сменяется центром [0Xi _г (при прохождении
аргумента £ + а через значение 2to+y (см. (41)), центр
®i,-1 сменяется центром 0_lt-v а центр	— центром
®-i, 1- На рис. 14 стрелки указывают порядок смены
Центров.

4G
ПРИНЦИП МАКСИМУМА
[ГЛ. i
Теперь уже нетрудно предстащггь себе поведение
фазовых траекторий. Для этого мы проведем следующее
вспомогательное построение. Рассмотрим окружность
с центром О j j, проходящую через начало координат,
хг
и обозначим через ОМг дугу этой окружности, располо¬
женную под осыо абсцисс (дуга ОМг равна, очевидно,
четверти окружности). Далее, обозначим через М1М2
дугу, равную ОМг и получающуюся из нее переносом
на отрезок ОМг\ аналогично построим дугу М2М3
и т. д. (рис. 15). Заметим, что абсциссы точек Мг, М2,
М3 . .. равны соответственно 2,	4, 6, . .. Повернув
теперь линию ОМ1М2Мъ . .., составленную из равных чет-
и	^	зт	3	я
вертеи окружностей, на углы — , я, -у- вокруг начала

11 РИМЕРЫ. ЗАДАЧА СИИТЕЗА
47
координат, мы получим изображенные на рис. 16 линии
ON1N2Ns * * • > ОР1Р2Р3 * * •> OQ1Q2Q3 • • •
Теперь начнем строить фазовую траекторию. Возьмем
оптимальное управление (имеющее на некотором конечном
отрезке времени вид (41)) и предположим для определен¬
ности, что на последнем участке постоянства, имею¬
щем длину р <	,	управляющие параметры принимают
значения ^=1, и2= 1. Соответствующий кусок фазовой
траектории (рис. 17, а)) представляет собой некоторую
дугу АО четверти окружности QxO (ибо этот кусок лежит
на окружности с центром 0lt т и оканчивается в начале
координат, а длина этого куска не превосходит четверти
окружности). Согласно сказанному выше, центру Ог л
предшествует центр 0_1} х (рис. 14), и потому участок
фазовой траектории, предшествующий точке А, является
четвертью окружности с центром 0_lt х (дуга ВА
на рис. 17, б)). Управляющие параметры имеют на этом
участке значения и1 = —1, и1 = +1. Так как точка А
находилась на дуге Q-fl, то точка В будет находиться
на дуге, получающейся из QxO поворотом на угол
вокруг точки 0_ltV т. е. на дуге МХМ2.
Далее, центру 0_л л предшествует центр
и потому кусок фазовой траектории, предшествующий
точке В, представлял собой четверть окружности с
центром в точке 0_1г _х (дуга СВ на рис. 17, в)). Управ¬
ляющие параметры имеют значения и1=—1> и2=— 1.
Так как точка В находилась на дуге МХМ2У
то точка С будет находиться на дуге, получающейся
из М1М2 поворотом на угол вокруг точки 0_lt_v
т. е. на дуге N2N3. Продолжая таким образом, можно
вычертить всю фазовую траекторию. На рис. 17, г) пока¬
зана фазовая траектория, составленная из трех дуг, яв¬
ляющихся четвертями окружностей, и двух дуг (на¬
чальной и конечной), каждая из которых меньше чет¬
верти окружности.
Если бы мы предположили, что на последнем уча¬
стке постоянства управляющие параметры принимают
Не значения	п2=	1, а значения и1 = — 1, гг2=1

48
ПРИНЦИП МАКСИМУМА
[ГЛ. I
или значения и1 — 1, а2 — — 1 или, наконец, значения
а1— \у и2 — — 1, то построили бы аналогичные [фазовые
I
О,
о)
б)
Рис. 17.
траектории, получающиеся из траектории, изображен¬
ной на рис. 17, г), поворотом на углы ~, я, — . Четыре

5]
ПРИМЕРЫ. ЗАДАЧА СИНТЕЗА
49
получающиеся таким образом фазовые траектории изобра¬
жены на рис. 18.
Анализируя значения управляющих параметров на
(Л дельных кусках всех получающихся таким образом
фазовых траекторий, мы приходим к следующему выводу.
Линии ОМ1М2М3 ..., ON^N2N^ . .., ОРлР2Р3 .. .,
OQ±Q2Q3... разбивают плоскость на четыре части, четы¬
ре «криволинейных квадранта», которые мы обозначим
римскими цифрами I, II, III, IV (рис. 19). На кусках
фазовых траекторий, расположенных в «квадранте» I,
управляющие параметры принимают значения и1 == — 1,
и2 = —1. Под действием этого управления фазовая точка
Достигает линии ОМгМ2М3 ..., и в момент попадания
* Л. С. Понтрягив

50
ПРИНЦИП МАКСИМУМА
[гл. i
на эту линию значения управляющих параметров пере-
ключаются и становятся равными:	и1 = — 1, гг2= 1.
Под действием этого управления фазовая точка движется
в «квадранте» IV и достигает линии OQ1Q2Q3 . . ., при¬
чем в момент попадания на эту линию управляющие
параметры принимают значения гг1 = 1,	и2=	1	и	т.	д.
Все эти факты собраны в следующей таблице:
в «квадранте» I и на линии ON1N2Ns...
в «квадранте» II и на линии ОРгР2Р3...
в «квадранте» III и на линии OQiQ2Q3...
в «квадранте» IV и на линии [OMiM2M3.
иг= — 1,	и2=	—	1
и1 = + 1, и2= — 1
ui=+l, и2— 4-1
и1= — 1,	и2=	4-1
Итак, согласно теореме 2, только найденные траекто¬
рии могут быть оптимальными, причем из проведенного
исследования видно, что из каждой точкиг фазовой пло¬
скости исходит только одна траектория, ведущая
в начало координат, которая может быть оптимальной.
Из теоремы существования (гл. 3) вытекает, что в рас-

6]
ПРИМЕРЫ. ЗАДАЧА СИНТЕЗА
51
сматриваемом примере для любой начальной точки х0
существует оптимальная траектория (см. стр. 144). 1аким
образом, найденные траектории (рис. 18) являются опти¬
мальными, и других оптимальных траекторий, ведущих
в начало координат, не существует.
Как и в двух первых примерах, полученное решение
оптимальной задачи можно истолковать следующим обра-.
зом. Построим на плоскости х1, х2 две функции и1 (ж1, х2)
и v2{x1, х2):
о1 (а:1, х2) =
v2 (х1, х2) =
+ 1	левее линии ...	QzQzQfiNхN2N3	...
и на дуге ...	QzQzQi°>
— 1	правее линии ...	QzQzQfiN XN 2N 3	...
^и на дуге ...	N3N2N10\
+ 1	ниже линии	...	Р3Р2Р1ОМ1М2М3	..
и на дуге ...	M3M2M-fi,
— 1	выше линии	...	Р3Р2Р1ОМ1М2М3	.
и на дуге ...	Р3Р2РгО.
Тогда вдоль каждой оптимальной траектории х (t) =
= (j:1 (t), х2 (t)) соответствующее оптимальное управление
и (t) = (и1 (t), и2 («)) имеет вид
и1 (0 = у1 (я1 (А «2 (0).	и2(0 = v2	(0.	я2(О)-
Это означает, что, заменив в системе (39) величины и1,
и2 функциями v1(x1, х2), v2{xx, х2), мы получим систему
^ = х2 + V1 (х\ х2),
^-= -x1-j-V2(x1, X2),
(42)
решение которой (при произвольном начальном состоя¬
нии £0) дает оптимальную фазовую траекторию, ведущую
в начало координат. Иначе говоря, система (42) пред¬
ставляет собой систему дифференциальных уравнения
(с разрывными правыми частями) для нахождения опти¬
мальных траекторий, ведущих в начало координат.
4*

52
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
Задача синтеза оптимальных управлений
Рассмотренные выше примеры показывают, что реше¬
ние задачи об оптимальных управлениях естественно
ожидать в следующей форме. Будем решать оптималь¬
ную задачу в обшей постановке (см. (9)), рассматривая
всевозможные начальные состояния ха и каждь11£~раз
предписывая в качестве конечного состояния начало
кбордшат О прпстран’ства,та^г^ТшШ"П(шГ№ТЖко^можно
судиТЬ' но -ртзобрт’Н'НБШ ншше примерам) существует
такая функция v(x)y заданная в фазовом пространстве X
й~ принимающая значения в области, управления U, что
уравнение
\Й‘==К*. »(*))	(43)
(ср. (5)) определяет все оптимальные траектории, веду¬
щие в начало координат. Иначе говоря, оптимальное
управление оказывается естествепн^г искать"56“"^’форме
u = u(t), а в формеТГ= v (х), т. е. искомое оптимальное
управление в каждыи^момёнт зависит'“Л1Шьг“ 0Т ТГОГО,
в ~]кйкои1То^$Нй|Г5с¥р2^^	в данный момент
фазовая точка. "Это й понятно: ведь если мьГ уже^бпали
в фазовую точку х> то и дальнейшее движение (из точки х
в О) должно быть оптимальным (ибо часть оптимальной
траектории сама является оптимальной траекторией,
см. стр. 22). Поэтому значение оптимального управле¬
ния u(t) в момент прохождения фазовой точкой положе¬
ния х зависит только от ж, а не от того, в какой точке
начиналось движение и сколько времени фазовая точка
уже двигалась, прежде чем попала в положение х. Фор¬
мулы (27), (38), (42) как раз и дают решение разбирав¬
шихся оптимальных задач в форме дифференциального
уравнения (43) с разрывной правой частью. (Если
область управления U является множеством г-мерного
пространства переменных гг1, гг2, .. ., ггг, то задание
одной векторной функции v(x) равносильно заданию г
скалярных функций гг1 = V1 (х), ..., ггг = vr (х)\ ср. фор¬
мулы (42).)
Функцию v(х), дающую уравнение оптимальных траек¬
торий вГформе (43), мы будем называть синтезирующей
функцией, а задачу нахождения синтезирующей футтк-

ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
53
дни (если таковая существует хотя бы в достаточно
малой окрестности начала координат) будем называть
задачей синтеза оптимальных управлений. Б разобранных
"выше примерах синтезирующие, ’функции были кусочно-
непрерывными.
Знание синтезирующей функции позволяет считать
задачу оптимального попадания в начало координат
математически решенной до конца. В самом деле,
еслиЛ рассматриваемый технический объект будет снаб¬
жен измерительным прибором, замеряющим фазовые
состояния, и исполнительным механизмом, ставящим рули
в положение и = р (я), где v (х) — синтезирующая функ¬
ция (предполагаемая известной), то интересующий нас
объект будет двигаться оптимально. Если функция v (х)
имеет сложный вид, то для нахождения нужного поло¬
жения рулей u = v(x), по-видимому, целесообразно при¬
менять (универсальные или специализированные) быстро¬
действующие вычислительные устройства. Читателя,
интересующегося этим вопросом, мы отсылаем к обшир¬
ной монографии А. А. Фельдбаума «Вычислительные
устройства в автоматических" системах», Физматгиз,
Москва, 1959^ (см глГ XIII)..
В общем случае задача синтеза (т. е. вопрос о суще¬
ствовании синтезирующей функции и ее отыскании)
не решена. В частном случае линейных систем и опти¬
мальности, понимаемой в смысле быстродействия, эта
задача будет обсуждаться ниже в третьей главе.
§ 6. Задача с подвижными концами и условия
трансверсальности
Для формулировки и решения дальнейших задач об
отыскании оптимальных управлений нам будут необходимы
некоторые геометрические понятия. Для удобства чита¬
теля мы напомним здесь определения этих понятий.
Пусть / (х) = / (ж1, х2у ..., хп) — некоторая действитель¬
ная скалярная функция, заданная в какой-либо обла¬
сти G эвклидова *) пространства X с ортогональными
*) Можно не предполагать пространство X эвклидовым, но
огда вводимый ниже вектор grad / (а?) следует считать повари-

54
ПРИНЦИП МАКСИМУМА
[ГЛ. I
координатами ж1,	.. ., хп. Если функция / имеет
в области G первые частные производные по перемен¬
ным ж1, . . ., хп, то в каждой точке х области G опреде¬
лен вектор
fdj_ df_	jf_\
удх1 ’ дх2’ ‘ дхп ) ’
называемый градиентом функции /(ж) и обозначаемый
символом grad 7 (ж).
Множество S всех точек ж = (ж1, . . ., жп), удовлетво¬
ряющих соотношению	*
j fjx1, х2,	хп) = 0,	(44)
мы будем называть гипеуповеухностъю пространства X,
а соотношение (44) — уравнением этой гиперповерхности.
Будем теперь считать, что левая часть уравнения (44)
имеет непрерывные частные производные по пере¬
менным ж1, ж2, . .., хп. Точка^ж^£б\ у^довлетворяющая
соотношениям	^
Гд№'= df[xf ~
f дх1	дх2 ’ * * дхп	I
(т. е. точка, в которой вектор grad/(ж) обращается
в нуль), называется особой точкой ^нпщщоверхности S.
Прочие точки, принадлежащие гиперповерхности S (т. е.
точки, в которых grad / (ж) Ф 0), называются ее
неособыми точками. Гиперповерхность, определяемая
'уравнением	с	непрерывно	дифференцируемой	левой
частью и не содержащая особых точек, назы¬
вается гладкой^. Все гиперповерх¬
ности, рассматриваемые в дальнейшем, предполагаются
гладкими.
При н = 2./уравнение (44) принимает вид
я2) = 0, ^
и понятие гладкой гиперповерхности сводится в этом
случае к понятию гладкой липши, (тт плоскости перемен¬
ных ж1, ж2). При д=3 уравнение (44) принимает вид
/(ж1, ж2, ж3) = О,

§ 6]
ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
55
и понятие гладкой гиперповерхности сводится в этом
случае к понятию гладкой поверхности (в пространстве
переменных х1, х2, х3).
Если уравнение (44) линейно, т. е. имеет вид
\^арс^~ -}- а2х2 —|- . . . -{- апх -[- b = О, J
то отсутствие особых точек означает, что хотя бы один
из коэффициентов аь отличен от нуля.
В этом случае гиперповерхность, определяемая урав¬
нением (45), на з ы в а ет с я г и п е. ттл о с к о cm ыоя
При п = 2 гиперплоскость представляет собой прямую
линию (на плоскости), а при п = 3 — плоскость (в трех¬
мерном пространстве).
Пусть х0 — произвольная точка гладкой гиперповерх¬
ности S, определяемой уравнением (44). Вектор grad/(^0)
(или любой коллинеарный ему вектор), называется
нормальным вектором_ (или просто нормалью) гиперпо-
верю!ости^	х0.	В случае’ гиперплос¬
кости (см. (45)) нормальные векторы во всех точках
одинаковы, т. е. имеется один единственный
нормальный вектор
(а1У а2, .. ., ип).
Всякая гиперплоскость однозначно определяется заданием
нормального вектора и одной точки, принадлежащей
этой гиперплоскости. Если S — гладкая гиперповерхность
с уравнением (44) и х0— некоторая ее точка, то гипер-
плоск°сть, проходящая через точку х0 и имеющая вектор
graa fJx0J~^ШрШлью Г ’ называется ^''ШсаШльной
гиперплоскостью ' гиперповерхности S в точке х0. Каж¬
дый вектор, начинающийся в точке х0 и лежащий в ка¬
сательной гиперплоскости, называется касательным век-
тороль гиперповерхности S в точке х0. Иначе говоря,
вектор, начинающийся в точке х0, тогда и только тогда
является касательным вектором гиперповерхности 5,
когда он ортогонален вектору grad/(:r0).
Пусть теперь
Sv S2y . . ., Sk
'Гладкие гиперповерхности, заданные в пространстве JC

5ti
ПРИ ИДИ 11 М АКСИМ .V МА
[ГЛ I
соответственно уравнениями
ff1(x1, х2, ..хп) — О,
i /2(ж1, X2,	хп) = О,
	 (46)
(__/,< (ж1, X2, ..жп) = 0.
Пересечение М всех этих гиперповерхностей (т. е. мно-
жество^с~ёх^т5ТеГГж~^“Х, удовлетворяющих одновременно
всем уравнениямназ'ыМ’ётся"(й' — 7с)-мерным (гладким)
ми6гоШражём~в ~Х,' есЖПвыпоЩенсГ следую	:
в каждой точке х^М векторы
grad j\ (х), grad /2 (х),	grad ]k (х)	(47)
линейно независимы. Таким образом, по определению,
fc/J-мерное многообразие в X задается системой п — г урав¬
нений. В частности, (п — 1)-мерное многообразие задается
одним уравнением. Таким образом, (/г — 1)-мерные
многообразия пространства X совпадают с гиперповерх¬
ностями. Одномерные мнотобрадин называются также
линиями. Заметим еще, что условие независимости век¬
торов (47) равносильно требованию, чтобы ранг функ¬
циональной матрицы
fdfi (s)	dfi (*)	Ух (х)\
дх1	дх2 * *’ дхп
df2 (х) df2 (х)	df2 (ж)
дх1	дх2 ’ ’ * дх71	(AQ\
dfb (х) dfk (х)	dfk (х)
^ дх1	дх2	* * * дхп у
был максимальным (т. е. был равен к).
Если „уравнения (46), определяющие (п — /с)-мерное
многообразие ~М9 линейны, то многообразие М' называет-
ся^Я—7с)-мёрной плоскостью пространства X. Иначе
говоря, (п — /с)-мерная плоскость представляет собой
пересечение к гиперплоскостей, нормальные векторы
которых линейно независимы. Одномерные плоскости
называются также прямыми линиями.
Пусть М — гладкое (гг — /ъ)-мерное многообразие,
определенное в пространстве X уравнениями (46), и # —

ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
некоторая его точка. Обозначим через L{ касательную
гиперплоскость к гиперповерхности Д (ж1, ж2, ..., хп) = О
в точке ж (г = 1, 2, ..., /с). Пересечение гиперплоскостей
Ьл, •••> At представляет со§о¥ (п — А]^1ерную^^лос-
'кость, называемую	ост ь/о многообра-
з^'^Тв^очке^.'Бектор, исходящий из точки ж, тогда
и только тогда лежит в касательной плоскости (т. е.
является касательным вектором многообразия 71/ в точ->
ке х), когда он ортогонален всем векторам (47).
Наконец, отметим еще один простой факт, которым
мы будем пользоваться в дальнейшем. Пусть
Дл = ф*(ij, |	г=1,	(49)
— параметрическая запись некоторой линии в простран¬
стве X или' в векторной форме, х = ф (£). Касательный
вектор этой линии в точке, соответствующей значению
£ = £0, имеет вид
Л*фЧЕо) ^Ф2 (So)	^Фп (Ео)Л *Р (5о) i /cm
V dg ’	’	"	”	di J -	*	\	(	}
Если линия (49) лежит целиком на гладком многообра¬
зии М (некоторого числа измерений), то касательный
вектор (50) этой линии является также касательным век¬
тором многообразия М в точке ф(£0). Обратно, если
задан касательный вектор многообразия 71/ в точке ж0£Т1/,
то существует на многообразии М линия, проходящая
через точку х0 и имеющая заданный вектор своим каса¬
тельным вектором. Иначе говоря, вектор, исходящий, из
произвольной точки х0 £ 71/, тогда и только тогда являет¬
ся касательным вектором многообразия М, когда он ка¬
сается некоторой линии, лежащей на 71/.
Перейдем теперь к формулировке задачи оптимального
управления с подвижными концами. Пусть S0 и ^ — глад¬
кие многообразия произвольных (но меньших, чем п)
размерностей r0, rv расположенные в пространстве X.
доставим задачу: найти допустимое управление u(t),
переводит фазовую точку из^ШкдШ^гб^(з1Хра-
энжние хЛ £ t9j 'п~Ър7Гп'~этдм прйдаёт '^функционалу (7)

58
ПРИНЦИП МАКСИМУМА
[ГЛ.
минимальное значение (рис. 20). Эту зайачУ мы и будем
называть"оптимальнои задачей с подвижными концами.
Если оба многообразия SQ, вырождаются в точки, то
задача с. подвижными концами обращается в прежнюю,
уже рассмотренную нами задачу (задачу с закрепленными
концами).
Ясно, что если бы точки х0, хх были известны, то мы
имели'^бь! задачу с закреплеинымй концами". Поэтому
управление и (/), оптимальное в смысле задачи с подвиж¬
ными "концами, оптимально и в прежнем смысле, т. е.
прйнцшГ'Шкси^^	1,^2) остается в силе й' для
задачйЙ5Тс	концами.
~~Однако нужно в этом случае иметь еще соотноше¬
ния, из которых можно было бы определить поло¬
жение точек х0, хг на многообразиях S0, Slt Та¬
кими соотношениями и являются формулируемые в
этом параграфе	L тР^псвврсал ьности. Эти
условия позволяют написать ^0+ri соотноншений,
включающих координаты концевых точек х0 и хг Так
как, с другой стороны, число неизвестных парамет¬
ров (по сравнению с задачей с закрепленными концами)
также увеличилось на г0-\-г1 (ибо положение точки х0 па
г0-мерном многообразии S0 характеризуется г0 параметра¬
ми, а положение точки хх £ характеризуется гг пара¬
метрами), то вместе с принципом максимума условия
трансверсальности образуют «достаточную» систему соотно¬
шений для решения поставленной оптимальной задачи
с подвижными концами.
Приведем теперь формулировку условий трансверсаль¬
ности. Пусть xQ £ SQ, хх £ Sx — некоторые точки, а Т0
и Т1 — касательные плоскости многообразий S0 и Sv про-

ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
50
веденные в этих точках. Плоскости Т0 и 7\ расположены
в пространстве X и имеют размерности соответственно
;-0, rv Пусть, далее, u(t), x(t),	£0< £< tv — решение
оптимальной задачи с закрепленными концами х0 и хг.
Наконец, пусть if (t) — вектор, существование которого
утверждается в теореме 1. Мы будем^говорить, что век¬
тор if(0 удовлетворяет	условию	трансверсальности
^пгралолГ] коэтщ^трашггоршг'
ёсли вектор -ф	,-ТуФп	(Ч))	,0ВТ0,грнахщн
плоскости 1\. ИначеНговоря, условие трансверсальности
означает,Г что для любого	вектора	б = (О1, б2,	бп),
принадлежащего (или параллельного) плоскости Т,, вы¬
полнено соотношение	б) = 0.	Аналогичный	смысл
имеет условие трансверсальности в левом конце
траектории х (t) (нужно лишь заменить tx и ТЛ на t0 и
Т0 соответственно). Ясно, что условие трансверсальности
в правом конце траектории х (t) содержит гЛ независимых
соотШшет^^достаточно
подставвтГ^Г] линейно независимых векторов бг, б2, ...
..., бГ1, расположенных в плоскости Тг. Условие транс¬
версальности __в левом конце содержит rQ независимых
^отношении.				 ^	.
Пользуясь условиями трансверсальности, можно сфор¬
мулировать теперь решение задачи с подвижными кон¬
цами.
Т.е о р е м а 3. Пусть u(t), £0 < £ <	—	допустимое
управление, переводящее фазовую точку из некоторого
положения	в	положение	а	х (t) — соответ¬
ствующая траектория (исходящая из точки х0 = (0, х0)).
Для того чтобы u(t) и x(t) давали решение оптималь¬
ной задачи с подвижными концами,
ществование ненулевой непрерывной вектор-функции if (£),
удовлетворяющей условиям, указанным в теореме 1, и,
кроме того, условию трансверсальности в обоих концах
траектории x(t).
Разумеется, если одно иззногообразий £0, ^„вырож¬
дается в точку, то "услотае . трансверсальности в соответ¬
ствующем конце траектории х[Т) заменяется условием
Для случая оптимальности по быстродействию в фор¬
мулировке теоремы 3 решение x(t) заменяется на x(t),

60
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
а ссылка на теорему 1 заменяется ссылкой на теоре¬
му 2.
Приведем элементарные примеры решения задач с под¬
вижными концами.
Пример. 1
Рассмотрим для точки, движущейся по закону (22)
(с тем же ограничением |к|<1), задачу о быстрейшем
попадании на ось х2 из заданного начального состояния
х0. В этом случае мы имеем
"задачу с подвижным пра¬
вым концом: многообразие
50 вырождается в точку х0,
а многообразием служит
ось х1 = 0. Вектор 0 = (0\02),
касающийся многообразия
51 (в любой его точке),
имеет вид 0 = (0, 02), где
02 Ф 0 и, следовательно, ус¬
ловие трансверсальности
в правом конце записывается
в форме 0 • (I j) + 02ф2 (t L) = 0,
откуда i|)2(^) = 0. Так как по-прежнему функция
ф2(0 линейна (см. стр. 29), то из соотношения
^2(^1) = 0 вытекает, что ф2(0 сохраняет постоянный знак
при £0< £ < tv Таким образом (см. (24)), в этом случае
каждое оптимальное управление и(1) постоянно и
равно -f 1 или — 1, и потому оптимальными могут быть
только движения по параболам (25), (26) (без переключе¬
ний). Предположим сначала, что начальное фазовое состоя¬
ние х0 находится справа от прямой х1 = 0. Согласно
сказанному выше, через точку х0 проходят только две
фазовые траектории, которые могут оказаться оптималь¬
ными: траектория (25), по которой движение происходит
снизу вверх, и траектория (26), по которой движение
происходит сверху вниз (рис. 21). Если точка х0 распо¬
ложена выше линии АО (см. рис. 7), то, двигаясь по
параболе (25), фазовая точка не попадет на ось я1 —0
(рис. 22а), и потому оптимальным может быть только
движение по параболе (26). Если же точка х0 располо¬

ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
61
жена на линии АО или ниже нее, то оба движения (25),
(26) приводят фазовую точку на ось хх = 0 (рис. 226).
Итак, в этом случае имеются две траектории, удовлет¬
воряющие принципу макси¬
мума. Однако легко видеть,
что время движения по этим
траекториям из точки х0 до
оси х1 = 0 различно. Действи¬
тельно, проведя касательные
к параболам (25) и (26) в точ¬
ке х0, мы легко найдем (см.
рис. 23), что QqQ2> QoP2^
= QoPi>QoQv а так как
при и = ± 1 время движения
по дуге параболы равно раз¬
ности ординат (см. второе
уравнение (22)), то движение
по дуге x0Q2 происходит дольше, чем по дуге x0Qv Та¬
ким образом, и в этом случае оптимальным может быть
только движение по траектории (26). Итак, в правой полу¬
плоскости оптимальными могут быть только движения
по параболам (26), т. е. движения, совершающиеся при
и = — 1. Аналогично, слева от оси хг = 0 оптимальными
могут быть только движения по параболам (2Ъ), т. е.

62
ПРИНЦИП МАКСИМУМА
[ГЛ. 1

$ bj
ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
63
движения, совершающиеся при и= -fl. Это и дает син«
тез оптимальных управлений: положив
мы получим совокупность всех оптимальных траекторий
из системы
(ср. (27)). Фазовая картина оптимальных траекторий
изображена на рис. 24.
Уравнения (51) можно, впрочем, считать очевидными
(например, с механической точки зрения).
Рассмотрим для точки, движущейся по закону (28)
(с тем же ограничением | и | < 1), задачу о быстрейшем
попадании на окружность
из заданного начального состояния х0, находящегося вне этой
окружности. В этом случае мы также имеем задачу с под¬
вижным правым концом: многообразием S± служит окруж¬
ность (52). Пусть x1 = (R cos a, R sin а) — произвольная
точка окружности (52). Найдем оптимальную траекторию,
дающую решение поставленной задачи с подвижным пра¬
вым концом и оканчивающуюся в точке хг В качестве
Ф(£]), т. е. вектора, нормального к окружности (52)
в точке хг (в силу условий трансверсальности), мы должны
взять один из двух векторов ( — cos a, —sin а), (cos а, sin а),
первый из которых направлен внутрь окружности, а вто¬
рой—в обратную сторону. Так как искомая оптималь¬
ная траектория должна подходить к точке xv распола¬
гаясь в и е окружности (52), то вектор фазовой скорости
«(г,)) в точке x(ti) = x1 будет направлен либо
внутрь окружности (52), либо по касательной к этой
(51)
.'Пример 2
(я1)2	(х2)2	=	R2
(52)

ПРИНЦИП МАКСИМУМА
LPJ1. 1
окружности в точке хх (рис. 25). Вспоминая теперь, что
скалярное произведение
должно быть неотрицательным (см. теорему 2 и, в част¬
ности, соотношение (21)), мы находим, что в качестве
ф (£j) следует взять вектор ( — cos a, -sin а), направлен¬
ный по радиусу внутрь окружности. (Если вектор фазо¬
вой скорости /(я^), м(^)) окажется направленным по
касательной к окружности, то скалярное произведение (53)
будет равно нулю, и потому в качестве ф (1г) можно взять
как вектор, направленный внутрь окружности, так и про¬
тивоположно направленный вектор; в целях единообразия
мы и в этом случае условимся считать ф(^) направлен¬
ным внутрь окружности.) Итак, мы имеем:
Вспоминая теперь систему уравнений (см. стр. 34)
для нахождения вектор-функции ф(0 = (Ф1(0» Ф2(0)> мы
получаем окончательно
^ (t) = — cos (/ —	—	а),	ф2(0	=	siD	(/	—	1л	~	а).	*0	<	t	<	tr
Рис. 25.
Ф (*i) = ( — cos а, — sin а).

s (3]
ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
05
Соотношение (20) дает нам (учитывая (29) и условие
И<1):
\ и = sign aj52 = sign (sin (I — tl — a)).\	(54)
Если угол а удовлетворяет неравенствам 0<a<n,
то на отрезке тг — (л — a) < t < £х управление u(t) будет,
L
t, t?ct t
-?-?■——
' I
Рис. 26.
в силу (54), равно—1, а перед этим будет попеременно
равно +1 и —1 на отрезках длины я (рис. 26). Таким
образом, последний кусок фазовой траектории (оканчи¬
вающийся в точке хг) представляет собой дугу окруж¬
ности с центром в точке ( — 1, 0), причем эта дуга соот¬
ветствует центральному углу я —а, а предшествующие
^ л. С. Поцтрягин

66
П РИ Н Ц И П М А КС И М У М А
[ГЛ. 1
Рис. 29.

ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
67
куски фазовой траектории являются полуокружностями
попеременно с центрами в точках (1,0) и ( — 1,0). Вид
фазовой траектории показан на рис. 27. Если же угол а
удовлетворяет неравенствам я<а<2я, то траектория,
изображенная на рис. 27, заменяется центрально симме¬
тричной. Легко видеть (см. рис. 28), что при 0<а<л
конец В последней дуги ВЛ рассматриваемой оптималь¬
ной траектории расположен на окружности радиуса 1
с центром в точке ( — R — 1, 0). При изменении а от 0
до л точка В описывает половину N2N1 этой окружности,
расположенную над осыо абсцисс. Далее, предыдущий
кусок СВ оптимальной траектории представляет собой
полуокружность с центром в точке (1, 0), и потому конец С
этой полуокружности лежит па полуокружности М2М3,
которая симметрична А\1У2 относительно центра (1, 0).
Продолжая таким образом, мы и получим всю фазовую
траекторию (рис. 29). Аналогично строится симметричная
траектория. Общее расположение фазовых траекторий
показано на рис. 30.
5*

68
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
Синтез оптимальных управлений осуществляется функ¬
цией v(x1,x2), которая строится, как вытекает из пре¬
дыдущего, следующим образом. К окружности (52) при¬
кладываются справа равные между собой полуокружности
МгМ2, М2М3,... радиуса 1, расположенные под осью
абсцисс. Слева от окружности (52) строятся аналогичные
полуокружности N1N2i N2N3, . . ., расположенные над
осью абсцисс. Функция а (я1, х2) определяется теперь
вне окружности (52) : v(x1J х2) равна +1 ниже
линии . . . N2N1M1M2 ... и равна — 1 выше линии
. . .M2M1N1N2. .. Это и дает синтез оптимальных управ¬
лений:
Idx1 9
dt ~Х '
^ = -*4-о (ж1, я2).
§ 7. Принцип максимума для неавтономных систем
А) Рассмотрим оптимальную задачу такого же вида, как
и (4), (7), но в случае, когда функции /а явно зависят
от времени (область управ лени^^
времени). Таким образом, закон движения
объекта и функционал, минимум которого ищется, прини¬
мают в рассматриваемом случае вид
| !? = /*(*. “.О, ^'=1. 2	/г;
(55)
Время t0 здесь предполагается заданным, а ^ — искомое
врШ^'прохож|ршя''черезточку хх. Введя, как и прежде,
 -■■■-, t
новую координату! х° = ^ /° (х (t), и (/), t) dt,j мы сформу-
L :
лируем рассматриваемую задачу в следующей форме
(ср. § 2).
В (/г+ 1 )-мерном фазовом пространстве X даны точка
ас0 = (0, х0) и прямая П, параллельная оси х° и проходя-

§ 7] ПРИНЦИП МАКСИМУМА ДЛЯ НЕАВТОНОМНЫХ СИСТЕМ 69
щая через точку (0, ху). Среды всех допустимых управле¬
ний и = и (£), обладающих тем свойством, что соответ¬
ствующее решение x(t) системы
= Г {х, и, t), i = 0, 1	(57)
с начальным условием x(t0) = x0 пересекает прямую П,
найти такое, для которого точка пересечения с прямой П
имеет наименьшую координату х°.
Для решения этой задачи введем еще oAH04jBcnojjo.r^-
тельное неизвестное хп+1, изменяющееся по з^кону_
Очевидно, что мы будем иметь xn+*j= L Пространство
переменных х1, х2, . .., хп, х4*1 обозначим через X*.
С помощью неизвестного xll+l система (57) может быть
записана в следующем автономном (т. е. не зависящем
явно от t) виде:
= /г (х, и, xn+1), i = О, 1,... /г,
dxn+i ,
dt ^ *
При этом мы должны найти оптимальную траекторию,
соединяющую в пространстве X* точку	.	.	., хп0, t0)
с некоторой точкой прямой Sv проходящей через точку
(х\, х\, .. ., х™, 0) параллельно оси хп+1 (ибо конечное значе¬
ние переменного хп+1, т. е. момент времени, когда движу¬
щаяся точка приходит в положение xv не является заранее
заданным). Таким образом, мы приходим к обычной опти¬
мальной задаче с закрепленным левым концом и подвиж¬
ным правым концом.
Напишем принцип максимума и условие трансверсаль¬
ности для полученной задачи. Вспомогательная система,
уравнений (12) имеет вид

70	ПРИНЦИП МАКСИМУМА	[ГЛ.	1
Согласно теоремам 1 и 3, для решения рассматриваемой
задачи нужно составить функцию
ф0/°(х, и, хп*л) +ф,/х(х, и, х71*1) + ...
■ ■ ■ -Т^пГ{х< и- жП+1) + ^л+1'1-
Эту функцию мы обозначим через 30* (а не через Цв ■,
как в теореме 1), сохранив обозначение i)C для функции
\	= Фо/° (х> и> 0 + Фх/1 (Х> «,«)+•••+ ФпГ (х> и> 0> ]
с "помощью которой уравнения (57), (58) записываются
в виде гамильтоновой системы
dx{ _ д&е	d\1)| __ _ ш_	■ __ Q	п
dt ~~~ dtyi ’ dt ~~ qxi
Точно	так же максимум по и функции	е%?*	при	фикси¬
рованных х\ ф- мы обозначим через (яр, ж, хп+1) (а не
через оМ, как в теореме 1), сохранив обозначение
оМ (яр, х, I) для максимума (по и) функции $£ (яр, х, t, и)
при фиксированных яр, х, t. Таким образом, учитывая
соотношение хп+1 = /, мы можем иаписать^^* = ' фп+1, \
XgM*~= оМ -f $n+i\ и потому соотношение — <dt* = 0,
твътполняющеесгГ вдоль оптимальной траектории (см. теоре-
. му 1), принимает вид
3e{^(t),x{t), t, и (*)) = <*$ (яр (*), ^(i), t) = —\pn+l(i). (60)
Наконец, условие трансверсальности в правом конце
траектории дает нам, что прямая S± (параллельная оси
zn+1) ортогональна вектору (ф^^), ф2 (*i)> • • • > 'Фп+ЛС))-
Иначе говоря, ярп+1 (/л) = 0. Вместе с соотношениями (60),
'59) это дает нам
Ь*(Ч>(0, x(t), 0=5 S df{x[t\u(t)'
ti a=0
Итак, мы получаем следующую теорему (принцип
максимума для неавтономных систем).	*
Теорема Пусть u(ty, tQ^t ^tv —такое допусти¬
мое управление, что соответствующая ему траектория
х (t) системы (57), исходящая в момент /0 из точки х0, про¬

3 7] ПРИНЦИП ‘ МАКСИМУМА ДЛЯ НЕАВТОНОМНЫХ СИСТЕМ 71
ходит в момент tx через некоторую точку прямой П.
Для оптимальности управления и(1) и траектории х (t)
необходимо существование такой ненулевой непрерывной
вектор-функции ф (t) = (% (t), ^ (I), . . ., фп (/))> соответ¬
ствующей функциям u(t) и x(t) (см. (58)), что:
{\°%для всех t, t0<CtKtv функция ё%/(ф(0> %(t),
переменного и £ £У достигает в точке u = u(t) максимума
(0, t, в (0Р=«« (?(*). x(t),"t)\ i (61).
а> ыполиены соотношения
tl)0 (t) = const < О,
   r..ft      (62)
Uw, хщ, 0 = 5 S дГ{х{1\Дг),})Ы1)^.
\	*1	a=0	J
Оказывается, далее, что если величины ф(£)> x(t), u(t)
удовлетворяют системе (57),	(58) и условию 1°, то
функция ф0(£) переменного t постоянна, а функция
я (г), /) может лишь на константу отличаться
от интеграла, указанного во втором соотношении (62),
так что проверку соотношений (62) достаточно произвести
лишь в какой-либо один момент времени t,
например, вместо (62) достаточно проверить соотно¬
шения
Uo(*i)<6. J ^ (ЧЧО, X («!>, *i) = 0. \	(63)
^ -л.
Б. Если теперь предположить, что точка xv в которую
точка х0 должна переводиться с помощью управления и (£),
не неподвижна, а перемещается, т. е. х1 = х1 (£), то фор¬
мулировка теоремы 4 несколько меняйсяГИменно, пусть
и (0»	^	^ *i> ~ такое допустимое управление, которое
точку х0 в некоторый момент времени t± приводит в точку
хг (tj, и пусть ^	= (g1, д2, ..., qn) —касательный
CLt l=t\
вектор к кривой хг(1) в момент tv Тогда, после введения
вспомогательного переменного xn+1 = t, мы получим, что
многообразие Sx будет уже не прямой, параллельной
оси хп+1, а линией (я}(0), ж, (6), . . ., х^О), 6), где 0 —
параметр. Касательная этой линии в точке 0 = К

72
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
определяется вектором (g1, д2, . . ., gn, 1), и потому
условие трансверсальности принимает вид
п
2	?v+4w(*i)-i	=	o.
v=l
Отсюда, учитывая соотношение (60), получаем
п
Z,) = -\|)n+1(g= 2 ^v(<1)?V.
V=1
Так как, наконец, согласно (60) и (59), функция
еМ (ф (t), x(t), t) является первообразной для
2 <<*«), a(»> t]- гра(0.
а=0
то мы получаем
т)г=-	.
|	i	(64)
J	v=l	l\	a=0	j
Это и есть соотношение, которым необходимо заменить вто¬
рое из равенств^ (62) в формулировке теоремы 4; в связи
с этим соотношения (63) принимают вид
.....	...	?г
•: ^0 (<i) <0, I \<М (1]) (гх), Ж (ij), tj) = 2	(?j) gv.' (65)
(	j *	v=i
В остальном же формулировка теоремы 4 сохраняется.
В.	Наконец, рассмотрим неавтономную оптимальную за¬
дачу с подвижными концами. Ограничимся случаем под¬
вижного правого конца. Пусть Sr (I) — перемещающееся
r-мерное многообразие, дифференцируемым образом зави¬
сящее от t. Задача заключается в отыскании такого до¬
пустимого управления и'(£), £0 < i < tv что точка, двиищу¬
щаяся по закону (5'5)‘‘с' начальным условием х {t0Y='x0,
попадает'" в некоторый момент t2 на многообразие 5!1(t1),
причем осуществляется минимум функционала (56).
Уточним прежде всего понятие «перемещающегося
многообразия». Пусть в (п + 1)-мерном пространстве

7] ПРИНЦИП МАКСИМУМА ДЛЯ НЕАВТОНОМНЫХ СИСТЕМ 73
переменных х1, х2, . . ., хп, t рассматривается (r+ 1)-
мерпое многообразие S*, определяемое системой урав¬
нений
Предполагается далее, что левые части этих уравнений
имеют непрерывные первые производные по х1, х2, . . ., хп, t
точке многообразия S* равен п — г. Рассмотрим теперь
в пространстве X переменных х1, х2, . . ., хп систему
уравнений
получающуюся из (66) при фиксированном значении t = t*.
В силу сделанных предположений, система (67) опреде¬
ляет в пространстве X некоторое г-мерное гладкое много¬
образие, которое мы обозначим через ^(г*). При различ¬
ных значениях t* мы получим целое семейство много¬
образий S (£), меняющих (вообще говоря) свое положение
и форму при изменении t. В этом смысле мы и говорим
о «перемещающемся многообразии S (I)».
Пусть u (t)9 х(1) дают решение поставленной задачи.
Обозначим через 7\ касательную плоскость к многообра¬
зию (0) в точкеЗ!^). Так как множество всех век¬
торов, касательных к многообразию S* в точке (#(£■,), 0)
и имеющих вид (q1, q2, . . ., qn, 0), имеет размерность
а многообразие S* имеет размерность > г, то существуют
такие числа q1, q2, . . ., gn, что вектор (q1, q2, ... у qn, 1)
касается многообразия S* (в точке (ж(0), 0))- Эти числа
Я1* Я2> • • •» Яп Дадут нам возможность написать соотноше¬
ния (64), (65), которым должен удовлетворять вектор ф (/).
Наконец, как и в § 6, будем говорить, что _ вектор
Ф(0 = (ф0 (0> ФЛО» •••. ФЛ0) У
j1{x1y х2у . . ., жп, 0=0.
/2 (ж1, х2, . . ., яп, о = о,
(66)
/п_г (ж1, я2, . . ., я7\ 0 = 0.
и что ранг функциональной матрицы
каждой
f1 (х1, х2, ..., хп, t*) = 0,
/2(^1, я2, . . ., яп, £*) = 0,
(67)
/п_г (ж1, х2, . . ., х11, t*) = 0,

74
ПРИНЦИП МАКСИМУМА
[ГЛ. I
трансверсальности в правом конце t±i если вектор
•••>'!>« (*i)) ортогонален плоскости 7’j
■(т.1 ^."ЧШсТтШЛГОйг Ш10ШВ55ЖЛЯНо1г5'^разйя^|5д_ (tj) в точ¬
ке ./• !рч этих условиях имеется следующее предложе-
нйеП/ооо^щепие теоремы 3 на неавтоиомный_сдзаай);
Теорема 3*. Для того чтобы u(t) и x(t) давали
решение оптимальной неавтономной задачи с подвижным
правым концом, необходимо существование ненулевой
непрерывной вектор-функции	удовлетворяющей
условиям, указанным в теореме 4, с заменой соотноше¬
ний (62), (63) соотношениями (64), (65), и, кроме того,
условию трансверсальности в точке tv
Это утверждение легко вытекает из теоремы 3 после
введения новой переменной xn+1 = t (ср. доказательство
теоремы 4). Отметим, что если многообразие S± непод¬
вижно, то соотношения (64), (65) совпадают с (62), (63),
так как в этом случае вектор (0, 0,	, 0, 1) касается
многообразия S*.
Г. Выведем теперь из теоремы 4 аналогичное необходи¬
мое условие для оптимальности по быстродействию. Иначе
говоря, рассмотрим для точки, движущейся по закону (55),
задачу о быстрейшем переходе из заданного начального
фазового состояния х0 в заданное фазовое состояние xv
Для решения этой задачи в теореме 4 следует положить
f° (x,j^t) = 1. функция принимает в этом случае вид
1 ёв (ф, X, t, и) = ф0 + 2 Wv (х, U, t). \
{    V=1 1
Вводя ?г-мерный вектор ф =	ф2,	.	.., фп) и функцию
|	“	"п ”
| Я (ф, X, t, и) = 2 фу/г’ (х, и, t),	1
I  _	   '-1		  J
мы можем записать уравнения (55) и (58) (кроме урав¬
нения (58) для г = 0, которое теперь не нужно) в виде
гамильтоновой системы
1 dx1 дН

§ 7] ПРИНЦИП МАКСИМУМА ДЛЯ НЕАВТОНОМНЫХ СИСТЕМ 75
При фиксированных значениях ф, ж, t функция II
становится функцией параметра и\ точную верхнюю грань
значений этой функции мы обозначим через М (ф, х, t):
М (ф, х, t) = sup II (ф, х, ty и).\
u£U	j
В силу соотношения II (ф, х, ty и) =	(ф,	ху	t, и) — ф0, мы
получаем
М(ф, х, t) = oM (ф, х, t) — tyо,
и потому условия (61), (62) принимают теперь вид
Я (ф (*), х (0, t; и (t)) = М (ф (/), х (f), 0 =
t п
= М (tf (*), x(t), г)-^0= ^ 2 df (а: (^-“(г)’(0 <^-if0>
/1 V=1
> ^ 2 g/V(*(t^M(0,0 (о л.
*1 v= 1
Таким образом, мы получаем следующую теорему.
Теорема 5. Пусть u{t), £0< t < tly — допустимое
управлешхе^пер^бдягцее фазовую точку из положения х0
в положение xv а х (/) — соответствующая траектория
{ель. (55) или (68)), так что х (£0) = х0, x{t^) = xv Для опти¬
мальности (в смысле быстродействия) управления u(t)
и траектории х (t) необходимо существование такой нену¬
левой непрерывной вектор-функции ф (t) — (фх (t), ф2 (t), . ..
..., ф?г(/))> соответствующей функциям u(t) и x(t)
(см.^ (69)), что:
С.1.5 для всех t, t0<it^.tv функция Я(ф(£), x(t)yt,u)
переменного u£U достигает в точке u = u{t) максимума
  \н (г]? (t), x{t), t, и (t)) М (if (t), X (t), t): j (70)
К^Дыполнено соотношение
Д/(if(г), X(t), t)> \ 2	b-(t)dt\	(71)
.						 <1 v=l ^	^	......	.. ..	*
Оказывается далее, что если величины ф(£), x(t), u(t)
удовлетворяют системе (68), (69) и условию 1°, то раз¬
ность между левой и правой частями соотношения (71)

76
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
постоянна, так что проверку соотношения (71) доста¬
точно произвести лишь в какой-либо один момент вре¬
мени t,	например, вместо (71) достаточно
проверить соотношение
t^WA).s(*i). ^)>0j	(72)
;ГДЛЕсли точка xv в которую точка х0 должна перево¬
диться с помощью управления u(t), не неподвижна,
а перемещается, т. е. x1 = x1(t), то формулировка тео¬
ремы 5 несколько меняется. Именно, пусть гг (г),
f0<	— такое допустимое управление, которое фазо¬
вую точку из положения х0 в некоторый момент времени tx
переводит в положение х1 (£3). Положим
dxx
dt
, , ={q\ q\ .... 9n).
t = t 1
Тогда (ср. (64), (65)) соотношения (71), (72) заменяются
следующими:
М (ф(£)> ж (0> 0>
>2)*v(W + \ %	0	(73)
V= 1	/l V= 1
п
M (tj, х (*,), tj > S	(*i) gv.	(74)
V=1
В остальном же формулировка теоремы 5 сохраняется.
Задача с подвияшым правым концом рассматривается
аналогично (ср. стр. 72 — 74).
§ 8. Задачи с закрепленным временем
А. Предположим теперь, что рассматривается такая же
оптимальная задача, что и в § 2 (или в § 7, т. е. с зави¬
симостью функций /а ог времени), но с условием, что время t0
начала движения точки (из положения х0) и время ее
попадания в точку хЛ заданы заранее, так что
время t1 — t0 закреплено. Решение этой задачи мы легко
получим из предыдущих рассмотрений.

§ 8j	ЗАДАЧИ С ЗАКРЕПЛЕННЫМ ВРЕМЕНЕМ	77
Как и в предыдущем параграфе, добавим к системе
уравнений
~- = f(x,u,t), i = 1	(75)
еще одно уравнение	65
dx^ 1 _ .
dt
с начальным условием xn+1 (t0) = t0. Тогда xn+1 = t, и мы
приходим к следующей оптимальной задаче.
В (п + 1 )-мерном пространстве переменных х1, . .., яп,
хп+1 заданы две точки (х0, £0) гг (а^, Фазовая точка
движется по закону
= fl (х, и, Xй*1), г = 1, ..., га,
dxn+1 ^
dt
Найти управление u(t), гго<9 воздействием которого фазо¬
вая точка переходит (начав движение в момент t0) ггз
положения {xQ, t0) в положение {х±, £х), а функционал
h
J= ^ /° (ж, гг, #n+1)d£	(76)
*0
принимает наименьшее возможное значение. Здесь момент
времени £г попадания в точку (ж15 £2) можно не считать
фиксированным (ибо в силу соотношения хп+1 = t попада¬
ние в точку (xlt £j) может произойти только в момент^),
и потому применима теорема 1.
Согласно теореме 1, мы должны для решения задачи
ввести переменное х°, составить функцию
п
<&е* = з&+^n+i = 2 W“ (х> м>a=n+l) + ^n+i
а=0
и рассмотреть для вспомогательных переменных сле¬
дующую систему уравнений:
_ д&е_	о	1	п	/77л
Л	‘	'	’	’	’	'	'
*Кг±1_ д&е
dt	dt

78
П РИ Н ЦИ Г1 М А К СИ М У М А
[ГЛ. 1
Соотношения (16), (17) теоремы 1 принимают теперь вид
x(t),	+	=	x(t), t) + 'Фп+г (0>
o, з(о» x(0> 0 + ^«*1 (0 = 0,
или, что то же самое, вид
<^?(ф(/), x(l), t, и{1)) = сЛ(Ц(1), x(t), t), %(t0)<0, (78)
аМ (гр (t), х (t), t) + фп+1 (t) = 0.	(79)
Если бы все величины \|?0 (t),	(^), ..., tyn(t) в некото¬
рый момент времени t обращались в нуль, то мы имели бы
ж(0>	и(£)) = 0, и потому tyn+1(t) = 0 (см. (78),
(79)), что невозможно. Таким образом, тр0 (^), ..., фп(£)
есть ненулевое решение системы (77). Это позволяет
нам выбросить из рассмотрения функцию фп+1 (t) и соот¬
ношение (79). Мы получаем, таким образом, следующую
теорему.
Теорем а 6. Пусть u{t), го< t< t1} — допустимое
управление, переводящее фазовую точку из положения х0
в положение xv а х (г) — соответствующая траектория
{см. (75)), так что x(t0) = x0, x{t1) = x1 {моменты вре¬
мени /0, t± фиксированы). Для того чтобы u{t) давало
решение поставленной оптимальной задачи с закрепленным
времен ель, необходимо существование такой ненулевой
непрерывной вектор-функции гр (/) = (ф0 (/),	(t), . . ., фп(0)>
соответствуюгцей функциям и{1) и x(t) {см. (77)), что:
1° для всех ?,	функция	(гр (£), х (0> С м)
переменного u£U достигает в точке u — u{t) максимума
ей?ОФ(0> ж(0»	к(0)	=	<^Ж0> х(1)> 0;
!	2° функция ф0(£) неположительна {что достаточно про¬
верить лишь в какой-либо одной точке отрезка
так как, в силу (77), ф0 = const).
Отметим, что эта теорема в такой же степени решает
задачу с закрепленным временем, в какой теорема 1
решает задачу с незакрепленным временем. Уменьшение
числа условий на одно (а именно, отсутствие, по сравне¬
нию с теоремой 1, условия м (гр (г2), х (^)) = 0) компен¬
сируется здесь тем, что и число неизвестных параметров
уменьшается на единицу, так как время tx прохождения
траектории через точку хЛ теперь задано.

ЗАДАЧИ С ЗАКРЕПЛЕННЫМ ВРЕМЕНЕМ
79
Б. Рассмотрим теперь задачу с закрепленным временем
и подвижными концами жп, хл. Обозначим через 50 и S±
многообразия (в пространстве ж1, жп), на которых
должны выбираться концевые точки ж0, хг Тогда в про¬
странстве переменных ж1, ж2, .. ., жп, x,l+1 мы также полу¬
чаем задачу с подвижными концами. Именно, концы
(х0, t0) и (xv tj искомой траектории должны находиться
соответственно на многообразиях S0 и Sv причем St
состоит из точек вида (ж, tt)f где ж ££., i = 0, 1. Рассма¬
тривая условия трансверсальности (теорема 3) для много¬
образий S0, ^и, как и прежде, отбрасывая координату жп+1,
мы находим, что теорема 3 остается справедливой (в той
же формулировке) и дает решение задачи с подвиж¬
ными концами в случае закрепленного времени. Таким
образом, теоремы 1 и 3 остаются верными и для задачи
с закрепленным временем, если в Формулировке теоремы 1
отбросить второе из соотношений (17).
Обратимся, в частности, к случаю, когда (в задаче
с закрепленным "временем) правый конец совершенно сво¬
боден.
Иначе говоря, рассмотрим задачу: найти такое допу¬
стимое управление u(t), £0<£<£i, чтобы соответствую¬
щая траектория (см. (75)), начинающаяся в момент t0
из начального положения ж0, осуществляла минимум зна¬
чений функционала (76); момент t± фиксирован, положение
точки ж(^) может быть произвольным. Это —задача
с подвижным правым концом, причем многообразие Sx
совпадает со всем пространством X переменных ж1, ж2, . .., жп.
Поэтому любой вектор этого пространства является
касательным к многообразию Slf и условие трансверсаль¬
ности дает нам фх (^) = ф2 (*i) == » • • = фп(М = Из этого
следует, что г])п ф и/ и потому мы можем принять.
фп = — 1. Итак, ф(£х) = ( —1, 0, .. ., 0), и мы получаем
следующую теорему.
Теорема 7. Для того чтобы допустимое управление
u(t),	и соответствующая ей траектория x(t)
(см. (75)) давали решение оптимальной задачи (75), (76)
с закрепленным левым концом ж0 и свободным правым
концом (моменты времени t0, tx заданы), необходимо суще¬
ствование такой ненулевой непрерывной вектор-функции

80
ПРИНЦИП МАКСИМУМА
[ГЛ. 1
<Ф(0 = ('Фо(0» 'МО» •••’ 'МО)’ соответствующей функ-
\ цияжи(1) и x(t)	(см. (77)),	что:
I \£)для всех t,	t0<sCt<tv	функция еМя|)(0>	ж(0»	*»	w)
jпеременного u£U достигает в точке u = u(t) максимума
I ^?(^(0’ ж(0»	m(0) = g^(^ (О* ж(0» 0;
|	©ф(ПН(-1,	0, ..., 0).
■	§ 9. Связь принципа максимума с методом
динамического программирования
В этом параграфе мы вкратце коснемся связи, суще¬
ствующей между	принципом	максимума и	методом дина¬
мического программирования	Р. Веллмана.
Метод динамического программирования был разрабо¬
тан для нужд оптимального управления процессами, имею¬
щими гораздо более общий характер, чем процессы, описы¬
ваемые системами дифференциальных уравнений. Поэтому
метод динамического программирования носит более уни¬
версальный характер, чем принцип максимума. Однако,
в отличие от последнего, этот метод не имеет строгого
логического обоснования во всех тех случаях, когда им
можно с успехом пользоваться как ценным эвристиче¬
ским средством.
Нас, естественно, интересует вопрос о применимости
метода динамического программирования к оптимальной
задаче, сформулированной в § 2. Обоснование метода
динамического программирования, данное Веллманом, пред¬
полагает, что к естественным условиям задачи (см. нашу
теорему 1) добавляется еще одно существенное требова¬
ние — требование дифференцируемости определяемой ниже
функции со (ж). Это предположение не вытекает из поста¬
новки задачи и представляет собой ограничение, которое,
как мы увидим ниже, не выполняется даже в самых
простых примерах.
После того как это предположение сделано, метод
динамического программирования приводит к некоторому
уравнению в частных производных, которое мы будем
называть уравнением Веллмана. Это уравнение (при неко¬
торых дополнительных условиях) эквивалентно гамиль¬
тоновой системе (14), (15) и условию максимума (16), (17).

МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ	81
Здесь мы приведем изложение метода динамического
программирования и покажем его связь с принципом макси¬
мума. Для простоты рассмотрим только задачу об опти¬
мальных быстродействиях.
фиксируем некоторую точку хх пространства X и пусть
а(t), *0<*< tv — оптимальное управление, переводящее,
(в силу закона движения (5)) фазовую точку из некото¬
рого положения х0£Х в положение xv а х (I) — соответ¬
ствующая оптимальная траектория. Время оптимального
перехода t1— /0 из точки х0 в точку хх мы обозначим
через Т(х0). (Точка хг в обозначении времени перехода
не участвует, так как она меняться не будет.) Таким
образом, функция Т (х0) определена на множестве Q всех
тех точек пространства X, из которых возможен оптималь¬
ный переход в точку хг Дополнительное предположение,
обычно используемое для обоснования принципа динамиче¬
ского программирования (и которое мы здесь также при¬
мем), заключается в том, что множество Й открыто
в пространстве X и функция Т (х) имеет непрерывные
частные производные по координатам точки х.
Вместо функции Т (х) обычно вводят функцию
Так как x(t), t0 < t < tv — оптимальная траектория и так
как каждый кусок оптимальной траектории также является
оптимальной траекторией, то для любого t,
имеет место соотношение
Пусть теперь v — произвольная точка области управле¬
ния U. Рассмотрим движение фазовой точки из положе¬
ния х (t) под воздействием постоянного управления, равно¬
го v. Через бесконечно малый промежуток времени Л > О
фазовая точка будет находиться в положении x(t)-\-dx,
^ Л. С. Понтрягин
(О (х) — —Т (х).
© (ж (г))= -T(x0) + t-t0.
Следовательно,
П

82
ПРИНЦИП МАКСИМУМА
[ГЛ.1
где вектор dx = {dx1, . . ., dx11) определяется соотношениями
Если теперь мы из точки x{t)-\-dx будем оптимальным
образом двигаться в точку х19 то затратим на это время,
равное Т (х (t) + dx). Таким образом, общее время, затра¬
ченное при таком способе движения на перемещение из
точки x(t) в точку xv равно Т {x(t)Jrdx)-\- dt. Это время
не может быть меньшим, чем время оптимального пере¬
хода T(x(t))y т. е. выполнено соотношение Т (х (t) + dx) +
+	71	(#	(£)),	или, что то же самое,
со (х (t) + dx) — со (х (£)) < dt.
В силу (81) последнее неравенство переписывается в виде
причем верхняя грань достигается при v = u(t). Так как
через каждую точку х £ Q проходит оптимальная траекто¬
рия, ведущая в точку х19 то мы приходим к выводу, что
функция со (ж) удовлетворяет в области Q следующему
неклассическому уравнению с частными производными,
которое мы назовем уравнением Веллмана'.
при этом верхняя грань достигается для некоторого
u£U {а именно, для значения оптимального управления-
в момент выхода из точки х), а функция со (х) неполо-
жительна и обращается в нуль только в точке хГ 65
Это и есть принцип динамического программирования
в применении к рассматриваемой задаче.
dx1 = /г (х (t)f v) dt,	i = 1, . . ., п.
(81)
П
ИЛИ
n
»)<1. «6 (82)
Соотношения (80) и (82) показывают, что
п
п
(83)

МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ	83
Теперь мы покажем, каким образом из принципа
динамического программирования может быть выведен
принцип максимума; при этом выводе функцию со (х) мы
будем предполагать дважды непрерывно дифференци¬
руемой. В силу этого предположения функция
п
g (X, и) = 2 1а (х, и),	(84)
а=1 Х
стоящая в (83) под знаком верхней грани, имеет непре¬
рывные первые производные по х1, . . ., хп. Из принципа
динамического программирования непосредственно сле¬
дует (см. (80) и (83)), что если и (t) — оптимальное управ¬
ление, переводящее фазовую точку из положения #0 в по¬
ложение х1У а х (t) — соответствующая оптимальная траекто¬
рия, то при фиксированном t, £0<£<£15 функция g (х, u(t))
переменного х£Х достигает в точке х = х (t) максималь¬
ного значения (равного единице). Из этого вытекает, что
9g(x(t),!Lm_ = Q> .= 1	n> f<t<t
дх1
Учитывая вид функции g (х, и) (см. (84)), мы получаем
отсюда соотношения
а=1
+ V	dja	и (L)) = 0) г-=1<	П|	(85)
дха	дх1
а= 1
выполняющиеся вдоль оптимальной траектории. Далее,
мы имеем
a=i
Y	д { дсо (х (t)) Д dxa (t) __ d	/ до) (х (t)) Л
^	дха Ч дх* У dt dt	V Qxi J	»
а=1
и соотношения (85) переписываются в виде
(' do) (х (t)) \	yr\	d)a(x(t),u(t))	da>(x(t))	..
dxi J	dxi	дха ’	’
(1=1
O'

84
ПРИНЦИП МАКСИМУМА
[ГЛ. j
Таким образом, вдоль всякой оптимальной траектории
величины
удовлетворяют линейной системе дифференциальных урав¬
нений
Кроме того, уравнение Веллмана (83) в силу соотно¬
шения (80) записывается в виде
Соотношения (87), (88) совпадают с принципом мак¬
симума, а соотношение (86) указывает в явном виде связь
величин ф|(/) с функцией со (ж). Отметим еще, что, как
следует из (88), оптимальные движения всегда можно
осуществить таким образом, чтобы вдоль оптимальных
траекторий выполнялось равенство
Все эти выводы, напомним, получены при условии дву¬
кратной дифференцируемости функции со (ж). Без этого
дополнительного предположения доказательство соотноше¬
ния (89) теряет силу.
Отметим, что во всех примерах, рассмотренных в § 5,
функция со (я) не имеет первых производных
в точках, лежащих на линиях переключения (это уста¬
навливается непосредственными подсчетами). Так как
при этом каждая оптимальная траектория в течение
некоторого отрезка времени проходит вдоль линии пере¬
ключения, то предположение о дифференцируемости функ¬
ции со (ж) не выполняется ни на одной траектории. Таким
образом, даже в самых простейших примерах предполо¬
жения, необходимые для вывода уравнения Веллмана,
не выполняются.
(86)
П
(0
dt
г|)a(f),	i=l п. (87)
П
П
2	И	(г))	=	sup	2	w)=	1.	(88)
a=l	u£U	a=l
7/(ф(£), x(t), u(t))= 1.
(89)

ГЛАВА 2
ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА
§ 10. Допустимые управления
Здесь мы дадим точное определение класса допусти¬
мых управлений (ср. § 1) и опишем наиболее важные из
этих классов. Область управления U будем представлять
себе произвольным множеством 7-мерного векторного про¬
странства ЕТ*).
Мы будем здесь рассматривать не только кусочно¬
непрерывные, но и значительно более общие управления.
Управление u(t)y £0<£<П (т. е. функция u(t) со зна¬
чениями в области управления U), называется измеримым,
если для любого открытого множества OdEr множество
всех тех значений t, для которых u(t)£0, измеримо
(в смысле обычной лебеговской меры) на отрезке £0< £< tv
Ограниченность понимается в обычном смысле, т. е.
управление u(t),	называется	ограниченным, если
множество всех точек u(t), £0<£<П> имеет в простран¬
стве £г компактное замыкание.
В дальнейшем предполагается, что выбран некоторый
класс D управлений; управления, принадлежащие этому
классу, будут называться допустимыми. От класса D
допустимых управлений требуется только, чтобы он
удовлетворял следующим трем условиям:
*) Приводимые ниже рассуждения проходят без всякого изме¬
нения для случая, когда U представляет собой произвольное под¬
множество некоторого топологического хаусдорфова пространства
со счетной базой. Незначительное изменение доказательства позво¬
ляет снять и требование существования счетной базы. Однако мы
ограничиваемся в тексте случаем подмножества г-мерного вектор¬
ного пространства как наиболее простым и вполне достаточным
для приложений.

86
ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА
[ГЛ. 2
1) Все управления и (t), t0 < t < tv принадлежащие клас¬
су D (т. е. допустимые), измеримы и ограничены.
2) Если и (t), t0 < t < £lf —- допустимое управление
ii если и — произвольная точка множества U, a £', t"—
такие числа, что t0 < t' < t" < tv то управление иг (t),
t0 < £ <	определяемое формулой
j и при £'<£<£",
{ и(£) при	и^"<Г<^,
также является допустимым.
3) Если отрезок	разбит точками деления
на конечное число частичных отрезков, на каждом из
которых управление и (t) допустимо, то это управление
допустимо и на всем отрезке £0<£<£г Допустимое
управление, рассматриваемое на частичном отрезке,
также является допустимым. Управление, получающееся
из допустимого управления и (t), t0*Ct^.tv сдвигом вре¬
мени (т. е. управление их (t) = и (t — a), t0 + а < t < tx -f а),
также является допустимым.
В качестве класса допустимых управлений можно
взять, например, множество всех измеримых огра¬
ниченных управлений. Этот класс допустимых управ¬
лений, очевидно, содержит в себе любой другой класс
допустимых управлений, и потому мы будем обозначать его
СИМВОЛОМ Z?max-
Другим примером может служить множество всех
кусочно-непрерывных управлений, о которых мы
говорили в первой главе.
Наконец, классом допустимых управлений является
множество всех к у с оч н о-п остоянных управлений
(т. е. таких управлений u(t), t0<Ct<Ctv что отрезок
t0 < £ < можно разбить точками деления на конечное чис¬
ло частичных отрезков, внутри каждого из которых
управление u{t) постоянно). Этот класс допустимых управ¬
лений, в силу условий 2) и 3), содержится в любом другом
классе допустимых управлений. Поэтому класс всех ку¬
сочно-постоянных управлений мы будем обозначать симво¬
лом -^min*
В дальнейшем на протяжении всей этой главы мы
будем предполагать, не оговаривая этого специально, что

ДОПУСТИМЫЕ УПРАВЛЕНИЯ
87
раз навсегда фиксирован некоторый класс допустимых
управлений. Этот класс будет обозначаться символом D.
Введение в рассмотрение измеримых (а не только
кусочно-непрерывных) управлений объясняется отнюдь не
стремлением к наибольшей математической общности.
Дело в том, что в главе 3 при доказательстве весьма
важной теоремы существования мы будем вынуж¬
дены пользоваться измеримыми управлениями (несмотря
на то, что в окончательной формулировке теоремы участ¬
вуют лишь кусочно-постоянные управления).
В связи с необходимостью рассматривать измеримые
управления мы отметим здесь некоторые важные для
дальнейшего свойства измеримых функций. Пусть не¬
произвольная измеримая функция, заданная на интервале
а < t < Ъ и принимающая значения в области управле¬
ния U. Точку 0 интервала а < t < Ъ мы будем называть
правильной точкой для функции u(t), если для любой
окрестности OdU точки и (0) выполнено соотношение
Ит mes (ц-i (0)Г)/) = 1.
mes /->0 mes 1
здесь и'1 (О) — множество всех точек t интервала а < t < 6,
для которых и (£) £ О, через / обозначается произвольный
отрезок, содержащий точку 0, а символ mes означает
лебеговскую меру множества. Очевидно, что всякая точка
непрерывности функции u(t) является ее правиль¬
ной точкой (ибо если отрезок /, содержащий точку 0,
достаточно мал, то / CZ гг-1 (О)). Таким образом, если функ¬
ция u(t) кусочно-непрерывна, то все точки интервала
а < t < b, за исключением лишь конечного числа их,
являются правильными точками для функции u(t). Ока¬
зывается*), что в случае произвольной измеримой функции
u(t) множество всех правильных точек имеет на интервале
а < t < b полную меру, т. е. почти все точки интервала
а < t < Ъ являются правильными точками для функции u(t).
*) Это утверждение легко следует из того факта, что почти
все точки произвольного измеримого множества являются его точ¬
ками плотности (см., например, Ф. Рисс и Б. Секефальви-
Н а д ь, Лекции по функциональному анализу, ИЛ, М., 1954, стр. 21;
И. П. Натансон, Теория функций вещественной переменной,
Гостехиздат, М.. 1957, стр. 285).

88	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА	[ГЛ.	2
Далее, пусть g(t, и) — действительная непрерывная
функция пары переменных t£(a, Ъ)у u£U и u(t),
а < £ < Ъу — ограниченная измеримая функция со зна¬
чениями в U. Если 0 — правильная точка для функции и (t),
то имеет место соотношение
0+зе
5 g (t, м («)) dt — z(q — p)g (9, и (0)) + о (е);	(1)
0+ре
здесь р и q — произвольные действительные числа, е —до¬
статочно малое положительное число, а о (е) — бесконечно
малая более высокого порядка, чем е, т. е. lim^) = 0;
е-*0	8
интеграл понимается в смысле Лебега. Соотношение (1)
легко выводится из определения правильной точки. Отме¬
тим, что если функция g непрерывно зависит ещё и от пара¬
метра v, изменяющегося в компактном множестве
N (например, в замкнутом ограниченном множестве неко¬
торого конечномерного векторного пространства), то фор¬
мула (1) сохраняет силу:
0+<№
§ g(t,u(t),v)dt = B(q — p)g(Q,u{Q),v)+o(e,v), v£N, (2)
0+pe
причем величина о(е, v) равномерно по v имеет более
высокий порядок малости, чем е, т. е. отношение
равномерно по v £ N стремится к нулю при е —> 0.
Сделаем еще некоторые замечания о дифференциальных
уравнениях с измеримыми правыми частями *). Рассмотрим
=	zm,	t, и),	1=1, 2, .. ., т. (3)
Правые части уравнений (3) непрерывны по совокупности
переменных z1, z2, . . ., zm, t, и и непрерывно дифференци¬
руемы по z1, z2, ..., zm. Пусть и (t) —произвольная огра¬
ниченная измеримая функция, заданная на отрезке
*0<*<*i и принимающая значения в U. Мы будем рас¬
сматривать абсолютно непрерывные функции
*) См. С. Caratheodory, Vorlesungen iiber reelle Funk-
bionen, Leipzig, 1927, стр. 665; Дж. Санс one, Обыкновенные
дифференциальные уравнения, т. II, ИД, М-. 1954, стр. 120,

§11]
ФОРМУЛИРОВКА ПРИНЦИПА МАКСИМУМА
89
zx(t), •••>	удовлетворяющие	почти всюду на неко¬
торой части отрезка	соотношениям
= hl (z1 (t), . .., z,m (t), t, u(t)), i= 1, 2,	m.
Каждую такую систему функций z1(^),	zm(t)	мы
будем называть решением системы (3), соответствующим
управлению u(t). При таком понимании решений для
системы (3) справедливы (при произвольно заданном
управлении u(t)) все основные факты теории обыкновен¬
ных дифференциальных уравнений и, в частности, теорема
существования и единственности решений. Вообще говоря,
решение системы (3) определяется не на всем отрез¬
ке /0<£<К> на котором задано управление u(t) (и, следо¬
вательно, правые части системы (3)). Однако, если система
(3) линейна относительно z1, ..., zm, то любое реше¬
ние системы (3) определено на всем отрезке
задания управления и (t).
В случае, когда правые части системы (3) непрерывно
зависят ещё и от некоторого параметра ц, имеют место
обычные теоремы о непрерывной зависимости решений от
параметров. В частности, решения системы (3) непрерывно
зависят от начальных значений. Кроме того, «добавки»,
которые получают функции zl при малом изменении
начальных значений, удовлетворяют обычной с и с т е м е
уравнений в вариациях (ср. § 12).
§ 11. Формулировка принципа максимума
для произвольного класса допустимых управлений
Как и в предыдущей главе, мы будем рассматривать
систему дифференциальных уравнений
d т
~dt=f'(xl> х2 Xй, и1, . Цг) = /* (ж, и),	(4)
г' = 1, 2, ..п,
или, в векторной форме,
ж =	“)•	(5)
Функции (г, /=1, 2	п)
f (х\ Х\ . . ., ,г", в) И g/Ж1, г2, •	и)
dxJ

90
ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА
[ГЛ. 2
предполагаются заданными и непрерывными на прямом
произведении X х U, где U — замыкание множества U
в пространстве Ег.
Как и в предыдущей главе, мы введем в рассмотрение
интегральный функционал
h
J = ^ /°(ж(*)> и (t))dt,	(6)
^0
где /° удовлетворяет тем же условиям, что и функции /г,
i= 1, 2, ..., п. Поставим задачу: среди всех допустимых
управлений u = u(t), переводящих фазовую точку из поло¬
жения х0 в положение xv найти такое, для которого
функционал (6) принимает наименьшее возможное значение
(моменты времени t0 и t1 заранее не заданы). Термины
«оптимальное управление» и «оптимальная траектория»
мы сохраним и в этой главе.
Дословно так же, как и в главе 1, поставленная опти¬
мальная задача формулируется в следующем эквивалент¬
ном виде.
В (п	1 )-мерном фазовом пространстве X переменных
х°, х1, . . ., хп даны точка х0 = (0, х0) и прямая П, парал¬
лельная оси х° и проходящая через точку (0, хj). Среди
всех допустимых управлений u = u(t)y обладающих тем
свойством, что соответствующее решение x(t) системы
^ = /‘(®1. .... *п, и). i = 0, 1, П, (7)
с начальным условием x(t0) = x0 пересекает прямую П,
найти такое, для которого точка пересечения с прямой
П имеет наименьшую координату х°.
Для формулировки принципа максимума мы, как
и в главе 1, введем в рассмотрение систему уравнений
TT--S	;=о,	1 л, (8)
а=0
для вспомогательных неизвестных ф0,	..., фп и функ¬
цию
п
х, и) - (г|), /(ж, и))= 2 'Фа/Щ. и)>
а=0

ФОРМУЛИРОВКА ПРИНЦИПА МАКСИМУМА
91
с помощью которой уравнения (7) и (8) записываются
в виде гамильтоновой системы
dxl дзе
dt dtyi
i = О, 1, . . ., н,	(9)
d<h =	i = 0|	(io)
at	Qxi
Взяв произвольное управление и (l), £0<£<Ц, класса
D (т. е. допустимое) и начальное условие x(t0) = xQ, мы
можем найти соответствующую (т. е. удовлетворяющую
системе (9)) траекторию х (t) = (х° (t), х1 (г), . . ., xn(t)).
Предположим, что она определена на всем отрезке
£0<£<Ц- Тогда, подставив функции и(1) и х(1) в пра¬
вые части системы (10), мы получим линейную систему
относительно неизвестных ф0, фр..., фп, коэффициенты
которой определены и непрерывны на всем отрезке
£' < К- Каждое решение
"Ф(г) = (Ч»о(0. Фх(0. • • •> %Л0)
этой системы (оно также определено на всем отрезке
t0 < t < tj) мы будем называть решением системы (10),
соответствующим функциям u(t) и x(t). Подчеркнем,
что вектор-функции x(t) и ф(£) абсолютно непрерывны
(как решения систем дифференциальных уравнений).
При фиксированных (постоянных) значениях ф и х
функция становится функцией параметра u£U; точ¬
ную верхнюю грань значений этой функции мы обозначим
через 00 (Ч>. я):
еМ (1]5, х) = SUp ${> (if, X, U).
иеи
Равенство, выполняющееся почти всюду, мы будем
указывать знаком ( = ). Иначе говоря, если фх(£) и ср2(0
— две функции переменного t, определенные на отрезке
^ * < К’ то запись
Ч>1 (0( = )Фа(0
будет означать, что функции фх и ф2 почти всюду сов¬
падают.
Цель настоящей главы состоит в доказательстве прин¬
ципа максимума (теорема 8) и условий трансверсальности.

92
ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА	[ГЛ
Теорема 8. Пусть и (t), £0<£< tv — такое допусти¬
мое управление, что соответствуюгцая ему траектория
x(t) (см. (9)), исходящая в момент t0 из точки xQy опре¬
делена на всем отрезке	и проходит в момент
tx через некоторую точку прямой Г1. Для оптимальности
управления u(t) и траектории x(t) необходимо сугце-
ствование такой ненулевой абсолютно непрерывной век¬
тор-функции 'ф(г) = (г|)0 (£), ФЛО» •••> Фп(0)> соответ-
ствуюгцей функциям u(t) и x(t) (см. (10)), что:
1° функция	x(t)y и) переменного u£U почти
всюду на отрезке £0< t < tx достигает в точке и = и (t) мак¬
симума
,%ДФ(0> x(t), п(0)( = М(Ф(0>	(11)
2° в конечный момент tx выполнены соотношения
Фо Лт)	^(ф(0)’ х (^i))= 0*	(12)
Оказывается, далее, что если величины Ч>(0. x(t) u(t)
удовлетворяют системе (9), (10) и условию 1°, то функ¬
ции ф0 (t) и оМ (ф (t), х (t)) переменного t являются постоян¬
ными, так что проверку соотношений (12) можно про¬
водить не обязательно в момент tv а в любой момент
t,
Теорема 8 почти дословно совпадает с теоремой 1,
сформулированной в первой главе. Различие заключается
в том, что теорема 8 справедлива для любого класса D
допустимых управлений, в то время как теорема 1 отно¬
сится лишь к классу кусочно-непрерывных управле¬
ний. Далее, условие максимума (11) выполняется лишь
почти всюду, в то время как в теореме 1 оно выпол¬
нялось всюду (см. равенство (16) гл. 1).
Нетрудно понять, что теорема 1 вытекает из теоремы 8.
В самом деле, применим теорему 8 к случаю, когда класс
D совпадает с классом всех кусочно-непрерывных управле¬
ний. Обозначим через N множество тех точек отрезка
£0< tly в которых выполняется условие максимума (И).
Иначе говоря, если t£Ny то
<^?(Ф(0> x(t)9 u(t))> #/?(ф(£), x(t)y v) (13)
для любой точки v£U. Так как множество N имеет на
отрезке t0<Ct<Ct1 полную меру и так как управление

§ 12]	СИСТЕМА	УРАВНЕНИЙ	В ВАРИАЦИЯХ	93
u(t) принадлежит классу D, т. е. непрерывно в концах
отрезка /0 < I < и непрерывно слева в любой точке
разрыва (см. соглашение о значениях в точках разрыва,
стр. 15), то для любой точки т отрезка £0<£<£г суще¬
ствует такая последовательность точек тт, т2, . . ., T/t,...
множества N, сходящаяся к т, что lim и (т,Д = и (т).
к^-со
В силу (13) мы имеем
^Жт,’с).'Ж(та,	ж(тО,	v),	v£U.
Далее, так как ^ — непрерывная функция своих аргумен¬
тов л]?, х, и и так как функции г|э.(£), х (I) непрерывны, то
lim е?6 ("ф СО, x(xk), у) = ЖО х(т), v);
k~>co
точно так же
lim (if (т/;), х(хк), и(тл)) =	ж(т), u(t))
к^оэ
(ибо lim и (т .) = и (т)). Сопоставляя последние три соотно-
шения, мы находим
3&(4>(х)> х(х)> и(т))>^?(г|э(т),	и)
(для любого элемента v£U), т. е.
я(т), и(т)) = 0^ (^(т), ж(т)).
Итак, условие максимума выполнено в любой точке т
отрезка t0 < t < Тем самым теорема 1 доказана (в пред¬
положении, что справедлива теорема 8).
Доказательству теоремы 8 посвящены следующие
четыре параграфа.
§ 12. Система уравнений в вариациях
и сопряженная ей система
В приводимых ниже доказательствах часто будет
встречаться положительный параметр е, который мы будем
считать величиной первого порядка малости. Величины
как векторные, так и скалярные, имеющие более высокий
порядок малости (по е), мы будем обозначать символом
о (г) ( т. е. lim	(Л.	При этом даже для обозначения
V	е->0	6	У

94	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА
[ГЛ. 2
различных величин более высокого порядка мало¬
сти, чем е, мы будем применять один и тот же сим¬
вол о (в) (так что, например, о (в) + о (е) = о (е)).
Пусть и (t) — произвольное допустимое управление,
заданное при /0 < t < tv а х (I) = (х° (£), х1 (/), .. ., хп (/)) =
— (х° (£), х (/,)) — соответствующее этому управлению
решение системы (7) с начальным условием x(t0)=^x0.
Обозначим через у (t) решение, соответствующее тому
же управлению u(t) и исходящее (в тот же момент /0)
из близкой к х0 точки
?Уо = ^о + е|0 + о(е),	(14)
где |0 — постоянный (т. е. не зависящий от параметра в)
вектор пространства X. Решение у (t) имеет вид
У (I) = X (t) + ебх (t) + о (в),	(15)
где 6х (t)-= (Ъх° (t), бх1(/),	6хп(1)) — не зависящий от
в вектор, определяемый следующей системой уравне-
н и й в в а р и а ц и я х:
i = o,
а=0
при начальном условии
Ьх (t0) —|0.
(Суммирование в правой части соотношения (16) можно
было бы производить от 1 до п, так как функции /{(.х, и)
не зависят от х°.)
Замечание 1. Величина о (в) в формуле (15) зави¬
сит, конечно, и от t, т. е. имеет вид о (в, t). Однако она
равномерно по t имеет более высокий порядок мало¬
сти, чем в, т. е. дробь 0 ^ ^ равномерно по /£[/0, С]
стремится к нулю при в—> 0.
Замечание 2. Предположим, что величины |0
и о (в) в формуле (14) непрерывно зависят от параметра v,
изменяющегося в компактном множестве N (т. е.
имеют вид |0(v), о (в, v)) и, кроме того, величина о (в, v)
имеет равномерно по v £ /V более высокий порядок

СИСТЕМА УРАВНЕНИЙ В ВАРИАЦИЯХ
95
малости, чем е f т. е. дробь 0 ^ ^ равномерно по v£N
стремится к нулю при е —> 0 . Тогда формула (15) оста¬
ется справедливой, причем бx(t) зависит теперь и от
параметра vgTV, а величина о(е), зависящая теперьи от v,
т. е. имеющая вид о (е, /, v), имеет равномерно по
v£N, £G[£0»*i] более высокий порядок малости, чем е
/	о	(е,	t, v) А	.	n N
(т. е. £—- —> U равномерно по £, v при е—>0 j.
Уравнения (16) позволяют каждому вектору |0= бx(t0)
поставить в соответствие семейство векторов |, = бх(г)
(для tj больших чем t0). Мы условимся считать = Ьх (t)
связанным вектором, исходящим из точки x(t). Та¬
ким образом, каждый вектор |0, заданный в точке х0,
определяет векторное поле {|f}, заданное вдоль траекто¬
рии x(t). Мы будем говорить, что векторы этого поля
получаются из начального вектора |0 переносом вдоль
траектории x(t).
Обозначим через Xt векторное пространство, получа¬
ющееся из X переносом начала координат в точку x(t),
т. е. пространство связанных векторов, исходящих из точки
х{1). Вектор 1г = бx(t) является элементом этого прост¬
ранства Xt. Обозначим, далее, через At,to преобразова¬
ние пространства Xt0 на пространство Xt, переводящее
каждый вектор |0 пространства Xto в вектор простран¬
ства Xt, получающийся из |0 переносом вдоль траекто¬
рии x(t), Так как система (16) линейна и однородна, то
преобразование Ati iQ линейно и невырожденно. Кроме того,
оно, очевидно, однородно, т. е. переводит начало координат
пространства XtQ в начало координат пространства Xt.
Рассмотрев вместо t0 и t любые другие моменты вре¬
мени t', V (взятые на отрезке, на котором определены
и управление u(t) и решение x(t)), мы аналогичным
образом определим линейное невырожденное однородное
преобразование Ау, у пространства Ху на простран¬
ство Ху. Очевидно, что эти линейные преобразования
обладают следующими свойствами (Е — тождественное
преобразование):
X *у=Е\ Л^,Г.ЛГ, y = At'"ty.	(17)

96
ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА	[ГЛ
Согласно определению преобразований Att to, векторы
Attto(lo) образуют семейство векторов, получающихся из
|0 переносом вдоль траектории x{t), и потому удовле¬
творяют системе (16):
ft <0 ^о)Г = i dfi (х2*и— *»(Ео)Г. (1В)
а—О
1 = 0, 1, . . . , п.
Далее, решение (15) переписывается, очевидно, следую¬
щим образом:
У (0 — ас (i) = eAt< ,0 (|0) + о (е) = Аи <0 [у (г0) - ж (f0)] + о (е).
(19)
Сравним теперь системы (16) и (8). Эти системы ли¬
нейны и однородны, а матрицы их имеют соответственно
вид:
Г др {х (t), и (/)) \	/'	dfa	(х (t), и (0) \
V дха	J ’ V.	dxi	)	*
Иначе говоря, эти матрицы получаются друг из друга
транспонированием и	переменой	знака,	т. е. системы
(16) и (8) — сопряженные. Заметим, что системы (8) и (16)
мы можем рассматривать лишь в том случае, если выб¬
рано управление u(t),	и соответствующая ей
траектория x(t) (т. е. решение системы (7)), ибо функ¬
ции u(t) и x(t) входят в правые части систем (8) и (16).
При этом, в силу линейности систем (8) и (16), решения этих
систем мы можем рассматривать на всем отрезке f0< г< t±,
если решение х (t) определено на всем этом отрезке.
Из	сопряженности	систем	(8)	и	(16)	вытекает,	что
если г]? (t) = (ф0 (t), ipj (f), . . ., ф7г (t)) — произвольное реше¬
ние системы (8), а дх (t) = (дх° (г), dx1(t), . ..,6 xll(t)) —
произвольное решение системы (16), то скалярное произ¬
ведение
п
(-ф(0, 6аг(<))=2 а|)а(1)6ха(г)
а=0
постоянно на всем отрезке	В	самом	деле,

§ 12]
СИСТЕМА УРАВНЕНИЙ В ВАРИАЦИЯХ
97
мы имеем (почти всюду на отрезке
% (t)6xa (<)■+
+ 2 <ыоа/а<,(,У(,)) ьхЦ1)=о:
Пусть, в частности, |0 —произвольный вектор. Тогда
вектор-функция %t = Atit0(|0) является, по определению,
решением системы (16) (см. (18)). Таким образом, спра¬
ведлива следующая лемма.
Лемма 1. Если ■'НО — решение системы (8), а |0 —
произвольный вектор, заданный в точке oc(t0), то на всем
отрезке	выполнено	соотношение
Лемма 1 позволяет дать следующую геометрическую
интерпретацию системы (8). Пусть L0 —некоторая гипер¬
плоскость пространства X, проходящая через точку ас0
(т. е. через начало координат пространства Xto). Линей¬
ное преобразование Ati *0 переводит гиперплоскость Ь0
в некоторую гиперплоскость Lt (проходящую через
точку x(t)). Таким образом, возникает семейство гипер¬
плоскостей {LJ, получающихся, как мы будем говорить,
переносом гиперплоскости Ь0 вдоль траектории x(t).
Уравнение гиперплоскости L, можно записать в виде
где .ха, а = 0, 1, ..., тг, —текущие координаты, взятые
в пространстве Хь а фа (с) — коэффициенты уравнения
этой гиперплоскости (свободный член отсутствует, так
как гиперплоскость Lt проходит через начало координат
пространства Xt). Мы хотим узнать, каковы должны
быть функции фа(0> чтобы уравнение (20) определяло
7 Л. С. Понтрягин
Ж*). Ai, fo(y) = const-
п
2 г|5а (г) .х“ = 0,
(20)

08	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА МАКСИМУМА	[ГЛ.	2
при различных значениях параметра I семейство гипер¬
плоскостей, перенесенных вдоль траектории x(t). Оказы¬
вается, что такие функции фа (£) можно находить из систе¬
мы (8), т. е. если ф (/) = (ф0 (£), ^ (£), . . ., фп (£)) — неко¬
торое решение системы (8), то гиперплоскости (20)
получаются друг из друга переносом вдоль траек¬
тории x(t).
В самом деле, если функции фа(0> а = 0, 1, . . ., п,
удовлетворяют системе (8) и если вектор |0 лежит в гипер-
п
плоскости 2 Фа (£0) яа = О (т. е. скалярное произведение
а=0
(ф(£0), 10) обращается в нуль), то и при любом t ска¬
лярное произведение (г|э(£), ^^«0(10)) обращается в нуль,
т. е. каждый вектор	to	(|0), получающийся из |0
переносом вдоль траектории x(t), лежит в соответствую¬
щей гиперплоскости (20). Так как это справедливо
для любого вектора |0, лежащего в гиперплоскости
п
S •фаСо)ж° = 0. то гиперплоскости (20) получаются друг
а=0
из друга переносом вдоль траектории x(t).
§ 13. Вариации управлений и траекторий
Пусть и (t) — некоторое допустимое управление, опре¬
деленное на отрезке	Выберем	некоторые мо¬
менты времени тх, т2, . . ., ts, т, удовлетворяющие нера¬
венствам tQ < т1<т2< . .. <т3 < т<^ и являющиеся пра¬
вильными точками для управления u(t). Выберем, далее,
произвольные неотрицательные числа б1г, ..., б£3, произ¬
вольное (не обязательно неотрицательное) действительное
число 61 и произвольные (не обязательно различные)
точки vlf v2, . . ., vs области управления U. Определим
теперь зависящие от е полуинтервалы Iv /2, . . ., Is сле¬
дующим образом. Положим
бt — (бth +	.	.	. + бts),	если = т;
- (6ft +	... + 8ts),	если	Tj = xs < т;
- (bt{ +	..	. + 6tj),	если = ritl = ... =
= 4<tm(/<s)>

S i-r l
ВАРИАЦИИ УПРАВЛЕНИЙ И ТРАЕКТОРИЙ	91)
и обозначим через It полуинтервал
xi +	^	xi	+	8	(^i	+	^h)-
Таким образом, если xL = т-+1 = . . . = xj} то полуинтер¬
валы /i5 Ii+V	следуют, примыкая друг к другу,
слева направо; если же к полуинтервалу 1к не примыкает
справа следующий полуинтервал (т. е. если хк < хк+1 или
к = s), то правым концом полуинтервала 1к является
точка хк при хк < т и точка т -j- ебt при хк = т. Длина
полуинтервала /. равна ебtv В случае 6tt = 0 соответст¬
вующий полуинтервал It является «пустым», т. е. отсут¬
ствует.
При достаточно малом е полуинтервалы Iv . . ., Is
попарно не пересекаются и располагаются все на основ¬
ном отрезке t0^t<Ctv причем левее точки т + ебt. Счи¬
тая, что е удовлетворяет этим условиям, мы определим
управление и* (t) на отрезке £0< £<т-{-еб£, положив:
Мы будем говорить, что управление и* (t) получается
варьированием управления и (t). В силу соглашений
о классах допустимых управлений (§ 10), управление
гг* (t) является (при достаточно малом е) допустимым.
Пусть х = | (е),	0 < е < е0 — параметрическая запись
гладкой линии, проходящей при е = 0 через точку х0
Обозначим через x(t), £0<£<£15 траекторию, соответ¬
ствующую (см. (7)) управлению u{t) и исходящую из точки
х0, а через ас* (t) — траекторию, соответствующую про-
варьированному управлению гг* (t) и исходящую из точки
1 (в). (Параметр е в определении проварьированного управ¬
ления и* (t) и в параметрической записи линии 1(e) — один
и тот же.)
Так как управление гг* (£) ограничено и отличается
от u(t) только на множестве меры е (б^+ . . . + &ts), то
из теоремы о непрерывной зависимости решений диффе¬
ренциальных уравнений от начальных значений легко
и (t), если t не принадлежит ни одному
из множеств Iv /2, .. ., /8,
vi9 если
7

100
ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА	[ГЛ.	2
вытекает, что при достаточно малом е решение ас* (t)
определено на всем отрезке £0 < f < т + еб£, на котором
рассматривается управление гг*(£). Нашей ближайшей
целыо является вычисление положения точки ас*(т+ебг).
Именно, мы покажем, что справедлива формула
ас* (х + ебt) = х (т) + гАх, *0 (§0) + еДас + о (е),	(21)
где Ах —не зависящий от е вектор, определяемый равен¬
ством
Ах —f(x (т), и (т)) б£ +
+ 2 Л, т4 [/(ж (Т;), Oj) -/(* (т4), и (т4))] 6f4.	(22)
г=1	1
Доказательство формул (21), (22) мы проведем индук¬
цией по s. Прежде всего, применяя соотношение (1)
к векторной функции g (t,u) = f(x (t), и) (очевидно, непре¬
рывной по совокупности своих аргументов) и полагая
6 = т, р = 0, q = б£, мы получим
т+гбг
^	u(t))dt	= e6t-f(x (т), гг (т)) + о (е),
т
или, так как ас (t) есть решение (абсолютно непрерыв¬
ное!) системы (7),
ас (т + ебзС) = ас (т) + г/(х (т), и (t)) б£ + о(е).	(23)
Далее, если rs < т, то при достаточно малом е отре¬
зок между точками т и т + ебг расположен правее
точки ts, так что на этом отрезке управление гг* (/) сов¬
падает с и (t) и потому
т+ебг
ас* (т + ебг) — ас* (т) = ^ /(я*(0> u*(l))dl =
х
т+еб t
= ^ f(x*(t), u(t))dt. (24)
Т •
Кроме того, как легко видеть (используя теорему о не¬
прерывной зависимости от начальных значений), реше¬
ние ас* (t) равномерно (на всем отрезке t0 < t < т + edt)

[3]	ВАРИАЦИИ	УПРАВЛЕНИЙ	И	ТРАЕКТОРИЙ	Ю1
стремится к oc(t) при е—>0. Поэтому f(x*(t), u(t)) =
= f(x(t), u(t)) + h(t)> где 1Х(<) равномерно (по t) стре¬
мится к нулю при е—>0. Отсюда получаем
т+еб*	т+еб	t
^ f(x*(t), и (t)) dt =	^	f(x(t),	и	(0)	dt	+	о	(е)	=
X	X
= х (х + еб£) — х (т) -f- о (е) = г/(х (т), и (т)) бt-\-o (е)
(см. (23)). Сопоставляя это соотношение с (24), находим
(при т3 < т)
х* (т + ебt) = х* (т) + &f(x (т), и (т)) бt + о (е).	(25)
Наконец, найдем приращение функции x*(t) на полу¬
интервале IТак как на этом полуинтервале
f(x*(t), U*(t))=f(x(t), ^) + 12(0»
где |2(0 равномерно стремится к нулю при е—>0, то для
приращения
х* (tt + е (/. + бу) - х* (tt + elt) = х* \I{
функции х* (t) на полуинтервале It получаем следующее
значение:
h
= \fix (0- vi) dt+o (e) = ef(x (т4),	+	о (e)	(26)
yi
(напомним, что длина полуинтервала 1Ь равна ебti9 при¬
чем при е—>0 этот полуинтервал стягивается к точке т^).
Переходим к индуктивной проверке соотношений (21),
(22). При 5 = 0 мы имеем u*(t) = u(t). Поэтому (см. (14),
(15), (19))
ос* (t) — х (l) + &At) t0 (|0) + о (е).
В частности,
х* (т) - х (т) = еЛТ| ,0 (1о) + о (е).

102	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА
[ГЛ.
Теперь в силу (23) и (25) получаем
х* (т + ебt) — х (т + еб£) = х* (т) — х (т) -f о (е) =
= 8^t, i0 (10) + 0 (е)>
откуда (см. (23))
ас* (х + ебI) = ас (т + ебI) ■+ eAXf 1о (§0) + о(е) =
= х (т) + &f(x (т), и (т)) бI + еЛх ,,0 (|0) + о (е),
и формулы (21), (22) при 5 = 0 установлены.
Предположим теперь, что формулы (21), (22) доказаны
уже для случая, когда число полуинтервалов Iv /2, ...
меньше чем s, и докажем справедливость этих формул
при наличии s полуинтервалов /х, /2, . . ., /s. Обозначим
через к такое целое число, что
*и+1 = *и+2 = • • • = *s и т4 < т3 при i < к
(случай к = 0 не исключается). Заменяя точку т точкой
ts, число б£ числом //1+1, а число 5 меньшим числом к,
мы, в силу индуктивного предположения, получим
из (21), (22)
ж* (ts + е/,£+1) = ж (ts) -f е/(ж (rs), в (ts))4+i + eAts, t0 (10) +
k
+ eS	и(т:4))]6^	+	о(е).	(27)
1=1 6 1
Это есть значение функции ж* (I) в левом конце полу¬
интервала 1к+1. Далее, так как полуинтервалы 1к+1, . .., Is
примыкают один к другому, то, суммируя соотношения
(26) для i=k-1-1, . . ., 5, мы получим приращение функ¬
ции ас* (t) от левого конца полуинтервала 1к+1 до правого
конца полуинтервала /5, т. е. до точки ts +е (Zs+6/.J:
х* (т8 + е (1в + dt')) - ac* (X' + elktl) =
•S
= е Е	Vi)	6fi + o(e).
i-M-i

g j з j	ВАРИАЦИИ	УПРАВЛЕНИЙ	И	ТРАЕКТОРИЙ	ЮЗ
Складывая это соотношение с соотношением (27), найдем
X* (xs + 8 (ls + бу) = х (t8) + е/(х (*„), и (т8)) у! +
+ *ЛХ i (!„) + е S fix (т4), vt) 6 tt +
S °	i=fc	+1
+ 6 2 Л8, Tj [/(* (Tj), t»i) -/(* (Tj), и (ti))]	+	о	(e)	-
i= 1	S 1
= ж (ts) + е/ (ж (т8), M (rs))	+	6i;t+1	+ . . . + бу +
+ &AX , (So) + e S [f(x (tt), Ui) - f{x (т„), и (ts))] Ы- +
&	0	i=fc+l
+ e2 \,xЛ/(*(^). ^)-/(*Ю. w('fi))] 6^ + o(e).
i=l	S 1
Учитывая, что Ax^%i = E при i = /с-)- 1, . .., s (см. (17)),
можем последнее соотношение переписать в виде
х* (т8 + 6 {ls + бу) = х (t8) +
+ гf(x (т8), и (т8)) (1и+1 + б у, + ... + б У +	t0 (Io) +
+ eS Лх , т [fix (tj, v{) - f{x (tj), w (tj)] б^ + о (e). (28)
2=1 6 1
Если xk+1 = xs — x, то, в силу определения чисел Zt, мы
имеем ls + бts = 6t, lk+1 + 6£/i+1 + . . . + 6ZS = St, так что
соотношение (28) совпадает в этом случае с (21), (22).
Если же rs < т, то ls + бts = 0, li+1 + бtk+1 + . . . + 6zs = О,
и соотношение (28) принимает вид
х* (Ts) = X (т„) + еАХа, to do) +
+ еД Л8>т4 [/(ж(у, у-/(ж(t4), и(т.))]б*4 + о(е).	(29)
Так как в этом случае на участке ts < /<т управление
u*(t) совпадает с u(t), то (см. § 12) с точностью до ве¬
личин более высокого порядка малости чем е, векторы
x*(t) — x(t) при ts<£<t получаются друг из друга
переносом вдоль траектории x(t) (см. (19)):
х* it) -x{t) = At, t$ ix* (T8) - x (У) + о (e)	Ц > ts).
Поэтому, применяя к формуле (29) преобразование АХ)

104 ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА	[ГЛ.	2
мы получаем (см. второе из соотношений (17))
ас* (т) — х (t) = eAti ,0 (|0) +
+ eS AXi х [f(x (ti), vi)-f{x(x J, и(т4))]6«4 + о(е).
i= 1	1
Наконец, складывая последнее соотношение с соотноше¬
нием (25), мы и в этом случае (т. е. при т5 < т) полу¬
чаем соотношения (21), (22), чем и заканчивается доказа¬
тельство.
Замечание. Анализируя проведенное доказатель¬
ство, мы заметим, что оно основывается на формуле (1)
и уравнениях в вариациях (формулы (14) — (16)). Поэтому,
учитывая формулу (2) и замечание 2 на стр. 94, мы
приходим к следующему выводу. Если все величины 6tv
6£2, . . ., б£3, 61 зависят непрерывно от некоторого пара¬
метра v, изменяющегося в компактном множестве N, то
формулы (21), (22) сохраняют силу, причем величина
о (е) в формуле (21) (зависящая, конечно, от v) имеет
равномерно по v более высокий порядок малости,
чем е.
§ 14. Основные леммы
Если какое-либо из чисел равно нулю, то его
можно отбросить при определении проварьированного
управления и* (t) вместе с соответствующими точками т.
и иь — от этого управление и* (t) не изменится. Обратно,
добавление новых точек tl, vt, для которых 6^ = 0, не
изменяет управления и* (£). Пользуясь этим, мы можем,
если речь идет о конечно м числе управлений
u*(t), ..., Up(t), получающихся варьированием одного
и того же управления и (t) при одном и том же т, счи¬
тать, что все точки т-, vt при определении управле¬
ний и\ (£), . . ., Up (t) одинаковый взяты в о д и н а к о-
в о м числе, а все различие между этими управлениями
заключается в том, что у них не одинаковы числа б
и бt. Этой возможностью — считать все точки xit vi оди-
наковыми (при рассмотрении конечного числа различ¬
ных вариаций одного и того же управления) — мы бу¬
дем пользоваться в дальнейшем, не оговаривая каж¬
дый раз.

ОСНОВНЫЕ ЛЕММЫ
105
Вектор Дх (см. (22)) не зависит от е, но существенно
зависит, конечно, от выбора точек xif vt, х и чисел bt
и (t = 1, 2, . . ., s). Обозначим совокупность величин
v{, х, btif bt через а:
а = {т;, vt, х, 6/t> 6<},
и будем вектор (22) обозначать далее через Дха, подчер¬
кивая тем самым его зависимость от этих величин.
В этом параграфе мы будем предполагать, что пра¬
вильная точка т управления u(t) зафиксирована
и что все рассматривающиеся вариации этого управления
удовлетворяют условию < тх< х2 . . . <ts<t < tv
Пусть имеется конечное число величин
а' = {xit vt, т, bt[, bt'},
а" = {т4, vit х, bt'i, bt"),
Мы можем считать (см. выше), что все точки xit v,
одинаковы у всех величин а', а", ... (что и преду¬
смотрено обозначениями). Линейную комбинацию к'а' +
+ А/'а" + . • • величин а', а", ... с неотрицательными коэф¬
фициентами к', X", . . . мы определим формулой*)
к'а' + к"а” + ... =
= {хi, viy т, к'bt'i + к”bt'i + . • k'bt' + k"bl” + ...}.
(Неотрицательность коэффициентов к', к", . . . существенна
потому, что в противном случае величины k'bt[-\-к"bt'i + • • •
могли бы оказаться отрицательными, что недопустимо.)
Будем теперь, имея некоторое управление и (t),t0 < t < tv
и соответствующую траекторию x(t), рассматривать
векторы Дх = Дха для различных символов а (х фик¬
сировано). Легко видеть, что имеет место следующая
лемма.
*) Отметим, что, вообще говоря, добавление новых точек т*,
i'i, для которых bti= 0 (благодаря чему все точки Х{, v\ у рас¬
сматриваемого конечного набора величии а', а", ... становятся
одними и теми же), может быть произведено неоднозначно. Вслед¬
ствие этого линейная комбинация A/a'-f-A/'ct" +••• также опреде¬
лена неоднозначно. Однако, как легко видеть, эта неоднозначность
никак не скажется на результатах последующих вычислений.

106
ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА
[ГЛ. 2
Лемма 2. Если а = А/а' + Х"а" + • • • (г^е А/>0,
А/'>0, ...), то соответствующие векторы Ах связаны
такой же линейной зависимостью
Аха = Х'АХа' + К"Аха» + ...
Это непосредственно вытекает из того, что в фор¬
мулу (22) все числа бtv . .., бts, бt входят линейно.
Мы будем считать Ах связанным вектором, исходящим
из точки х(т), т. е. будем считать этот вектор элементом
пространства Хх (см. § 12). Если мы будем брать все¬
возможные символы а (т фиксировано), то векторы Ах=Аха
заполнят некоторое множество Кх в пространстве Хх.
Докажем теперь, что множество Кх является выпуклым
конусом *) векторного пространства Хх.
*) Множество М, лежащее в некотором векторном простран¬
стве, называется выпуклым конусом с вершиной в точке о, если
1) оно является конусом, т. е. вместе с каждой отличной от о
точкой а содержит и весь луч оа, 2) оно выпукло, т. е. вместе
с каждыми двумя точками содержит целиком соединяющий их
отрезок. Заметим, что если выпуклый конус М не заполняет всего
векторного пространства X, в котором он расположен, то суще¬
ствует в пространстве X такая гиперплоскость, проходящая через
вершину конуса о, что весь конус М расположен целиком
в каком-либо одном (замкнутом) полупространстве, определяемом
этой гиперплоскостью. Точка х £ X называется внутренней точкой
выпуклого конуса М CZ X, если некоторая окрестность точки х
в пространстве X целиком содержится в конусе М. Множество
всех внутренних точек конуса М d X называется его внутрен¬
ностью.
Пусть, далее, Мх и М2 —два выпуклых конуса пространства X,
имеющих общую вершину о. Конусы Мг и М2 назовем разделяе¬
мыми в X, если существует разделяющая их гиперплоскость,
т. е. такая гиперплоскость, что конус Mi расположен целиком
в одном (замкнутом) полупространстве, определяемом этой гипер¬
плоскостью, а конус М2 — в другом полупространстве. Для того
чтобы конусы Mi и М2 были разделяемыми, необходимо и доста¬
точно, чтобы выполнялось одно из следующих двух условий:
1) существует гиперплоскость, содержащая оба конуса Mi, М2\
2) не существует точки, которая была бы внутренней точкой
каждого из конусов Мъ М2 относительно его несущей плоскости.
Таким образом, если конусы М± и М2 (с общей вершиной о)
не являются разделяемыми в X, то линейная оболочка их несущих
плоскостей совпадает со всем пространством X, и, кроме того,
существует точка а, являющаяся внутренней точкой каждого
конуса Мъ М2 относительно его несущей плоскости. В этом случае

§ 14]
ОСНОВНЫЕ ЛЕММЫ
107
В самом деле, если а' и а — две точки пространства Хх,
принадлежащие множеству Кх, т. е. если существуют
такие символы а', а", что
а' = Д#а',	а" = ДоСа"»
то для любых неотрицательных А/, А," мы имеем в силу
леммы 2
А/ а -р А* а = А/ ДаСд' -[- А/ ДхЛ" = ДХ(^/Л'_с^"а"р
т. е. точка А/а' + А/'а" также принадлежит множеству Дх.
Это и означает, что ZfT есть выпуклый конус простран¬
ства Хх (или, что то же самое, выпуклый конус про¬
странства X с вершиной в точке х(х)).
Мы будем называть множество Кх копу соль дости¬
жимости.
Докажем теперь две леммы, служащие основой для
применения вышеизложенных конструкций к изучению
оптимальных процессов.
Лемма 3. Пусть х (t0 < т < tx) — правильная точка
управления u(t), х (L) — траектория, соответствующая
управлению и (t) и исходящая из точки х0, а А — некоторая
линия, исходящая из точки х (х)-и имеющая в точке х(х)
касательный луч L. Если луч L принадлежит внутренно¬
сти конуса Кх (т. е. если все точки луча L, кролье его конца,
являются внутренними точками льножества Кх), то суще¬
ствует такое управление u*(t), что соответствующая ему
траектория x%(t), исходящая из той же точки х0, про¬
ходит через некоторую (отличную от х (т)) точку линии А.
Доказательство. Выберем на луче L какую-либо
точку А, отличную от х(т),ииз этой точки А проведем
п векторов еЛ, е2, . . ., еп равной длины г, ортогональных
через точку а можно провести такую плоскость С, ортогональную
прямой оа и пересекающуюся с несущей плоскостью конуса М2
только в точке а, что все точки плоскости С, достаточно близкие
к а, принадлежат конусу А/ь и, кроме того, линейная оболочка
плоскости С и несущей плоскости конуса М2 совпадает с X. Иначе
говоря, шар малого радиуса с центром в точке а дает в пересече¬
нии с плоскостью С «дополнительную площадку» к несущей плос¬
кости конуса М2, причем эта площадка ортогональна прямой оа
и целиком содержится в конусе Мг. Размерность этой «дополни¬
тельной площадки» равна разности размерностей пространства X
и конуса М2.

108	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА	[ГЛ.	2
лучу L и попарно ортогональных между собой. Положим,
далее, /.= — eif i= 1, 2,	. . ., п, причем векторы/,
также будем считать исходящими из точки А. Число
общую длину векторов ev . . ., еп, fv . . ., fn—будем счи¬
тать настолько малым, чтобы концы всех этих векторов
принадлежали конусу Кх (это возможно, так как А есть
внутренняя точка этого конуса). Наконец, через г
обозначим вектор	с началом	в точке х (т) и	концом
в точке А. Так как векторы
С, С Ат е1> С "Г е2> * * • > С ~г ^*п’ С Аг f\, С Art 2' • • • У с Artn
(исходящие из точки х(х)) принадлежат конусу Кх, то
существуют такие символы а0, аА, .. ап, а', . . аА, что
ДХао = с, /±ха1 = c + ev ..., АХап = е + en,
Дяа/= С•••, А ха'п:= ^ Ат fn-
Определим теперь две (очевидно непрерывные и неотрица¬
тельные) функции h+ (q) и /Г (q) действительного пере¬
менного Q, положив:
\ р при	о>0,	[0	при	о>0,
A'te)-| 0 при	«,<0;	*'<«> = { -в	при	SCO.
При (е1)2 + (q2)2 + . . . + (е”)2< 1 формула
a = a(e1 рп) =
i=1	г=1	г	=	1
определяет зависящий от п действительных чисел q1, Qn
символ а(рх, ..., Qn). (Действительно, у нас имеется
конечное число символов a0, at, си, причем все коэф-
п
фициенты /г+(р1), h~(Ql) и 1—|Q1|» как легко видеть,
г=1
неотрицательны.) Вектор Ах, соответствующий символу
a = a(Q1, ..., Q )у имеет, в силу леммы 2 и в силу соот¬
ношений /. = — e-v h+ (q) -f h~ (q) = | Q |, h+ (q) — h~ (q) = q,

§ 14]
следующий вид:
ОСНОВНЫЕ ЛЕММЫ
109
i=1
п	п
+1 2 й+ (Я1) (С + et) +12 Г (Q4) (с + /*) =
г=1	г=1
п
= [j+T2 (-leil + ^(ei) + /r(ei))]c +
i=l
+ |S [At(e,)-A*(ei)K = e + ^fi4-
i= 1	i=l
Следовательно, если точка (q1, . . ., Qn) пробегает в тг-мер-
ном числовом пространстве единичный шар
(Q1)a+... +(Qn)2<l,	(30)
то вектор Аха (точнее, конец этого вектора) также про¬
бегает 7г-мерный шар в пространстве Хх, а именно шар
1
1
А, ортогональный лучу L. При
тех же условиях конец вектора
еДха (все векторы исходят из
точки х(х), т. е. из начала ко¬
ординат пространства Хх) пробе¬
гает 72-мерный шар Ее радиуса
е-—, ортогональный
лучу L]
центр шара Ег расположен в точ¬
ке Ае луча L, находящейся на
расстоянии ed отточки х (т), где
d — длина вектора с (рис. 31).
Так как в нашем рассужде-	рИс.	31.
нии рассматриваются лишь та¬
кие символы а, которые являются линейными комбина¬
циями (с неотрицательными коэффициентами) конеч¬
ного числа символов а0, а{, щ, £=1, 2, ..., п, то
точки Xj, Vp j~ 1, 2, ..., s, входящие в определение

110	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА	[ГЛ	.	2
символа а = а (q1, . . ., q"), одинаковы для всех этих симво¬
лов, т.	е.	не	зависят от q1, . . ., Qn; точка т также фиксиро¬
вана.	Числа	же б^, . . ., бt6 и dt (определяющие проварьи-
рованиое управление и* (£)) зависят, причем непрерывно,
от Q1, . .	q". Поэтому мы будем писать u*(t) и б£а, чтобы
подчеркнуть зависимость величин и* (t) и бt от q1, . .., рп.
Траекторию х* (t), исходящую из точки х0 и соответст¬
вующую управлению и* (t), будем обозначать через x%(t),
так что соотношение (21) (в котором |0 = 0, ибо начальная
точка совпадает с х0 при всех е) даст нам
Ха (т -|- вб£л) = X (т) + еДХа + О (в).	(31)
Отметим,	что траектория x£(t) непрерывно зависит
от параметров Q1, . .., дп; точно так ню, число 6ta не-
п р е р ы в н о зависит от Q1, . . ., Qn.
Поэтому и точка х^ (т + &6ta) н е-
прерывно зависит от Q1, . . ., Qn,
а величина о (в) имеет равномерно
по q1, . . ., q7l более высокий порядок
малости, чем е (см. замечание на
стр. 104). Следовательно, когда
точка (q1,	. . ., qu) описывает
шар (30), точка (31) пробегает (при
любом фиксированном е) некоторый
«диск» F& (т. е. непрерывный образ
шара (30); этот диск может иметь
самопересечения pi т. п.). С точ¬
ностью до малых более высокого порядка, чем е, диск Fe
«совпадает» с шаром Ее (см. (31)); точнее говоря, точки
диска Fe отстоят от соответствующих точек шара Ег
на величину более высокого порядка малости, чем е
(равномерно для всех точек шара Ег). Точка же пере¬
сечения этого шара с линией Л (существующая при доста¬
точно малых в) отстоит от точки х (т) pi от границы
шара Ег на величину порядка в. Следовательно, при
достаточно малом в диск Рг пересекает линию Л
в некоторой точке *) (рис. 32). Выберем такое в. Так как
\
\
V
Рис. 32.
*) Факт существования такой точки пересечения представляется
наглядно «очевидным»; строгое доказательство легко проводится
элементарными средствами топологи и (с помощью понятия

§ J41
ОСНОВНЫЕ ЛЕММЫ
Hi
весь диск F& состоит из точек вида (31), то доказанный факт
пересечения Fe с линией Л означает: существуют такие
q1, Qn (лежащие в шаре (30)), что х* (т + еб£а) £ Л.
Иначе говоря, обозначив величины	Xa{t),	соответ¬
ствующие выбранным значениям g1, ..., gn, через и% (£),
х% (t) и полагая т -|- гЫа = т', мы получим х% (t0) = х0;
х%(х') £ А, и лемма 3 доказана.
Лемма 4. Если управление u(t) и соответствующая
ему траектория x(t),	оптимальны, то для'
любой правильной точки t(f0<T< £3) луч Ьх, исходящий
из точки х (т) и идущий в направлении отрицательной
полуоси х°, не принадлежит внутренности конуса Кх
(т. е. проходит либо вне этого конуса, либо по его
границе).
Доказательство. Допустим, что при некотором т
луч£тпринадлежит внутренности конуса/£т. Применим лем¬
му 3, принимая за линию Л (и за луч L) луч Lx. Тогда мы
получим, что существует такое управление и* (£), для
которого соответствующая траектория х% (t) (исходящая
из той же точки х0) проходит в некоторый момент т' > t0
через точку, лежащую на луче Ьх. Иначе говоря,
Определим на отрезке t0 < t < t± -f- (т' — т) управление
и%% (t), положив
Траектория х%% (£), соответствующая управлению и%% (t)
и исходящая из точки xQ} совпадает, очевидно, на отрезке
индекса пересечения; см., например, В. Г. Болтянский, Гомо¬
топическая теория непрерывных отображений и векторных полей,
Труды Матем. института им. В. А. Стеклова, т. XLYII, 1955; опре¬
деление индекса пересечения «отображенных», т. е. искривленных
цепей дано в п. 5:2 этой книги, а существование при достаточно
малом е точки пересечения диска Fe и линии Л вытекает из
предложения (г) иа стр. 69).
х\ (т') = х1(т), г = 1, 2, .... /г;
4 СО < *° (т).
u%(t)	при	£0<Л<т',
и {t — (т' — т)) при т' < t < tx + (т' — т).

112	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА	[ГЛ.	2
£о<С<т' с траекторией	(t), так что, в частности,
х** (т/) = х% (т)>	i — 1» 2, . . ., п\
xl*{x')<xa(x).
Далее, на отрезке т' < Z< + (т' — т) траектория x%%(t)
имеет вид
X** (t) = x(t — (%' — т)) + ру	(33)
где £? — постоянный вектор
2> = (я£*(т')-ж°(т), 0, 0, ..., 0).
(Это получается непосредственной подстановкой реше¬
ния (33) в уравнения (7) с учетом того факта, что правые
части системы (7) не зависят от t и х°; вектор р опре¬
деляется тем условием, что в точке т' —точке «стыка»
двух кусков траектории x.^(t) — эта траектория должна
быть непрерывна.) При t =	т'—т) получаем
ж** (к + (*' -Х)) = х (tj + р.
Иначе говоря, точка х(£х + (т' — х)) лежит на прямой П,
определенной в § 11 (ибо вектор р параллелен оси ж0), и,
кроме того,
4* (к+-т))=х° (к)+xi* со -х° (т) < х° (к)
(см. (32)). Но это противоречит оптимальности траекто¬
рии x(t) и управления u(t). Таким образом, предположе¬
ние, сделанное е начале доказательства, приводит к про¬
тиворечию, и лемма 4 полностью доказана.
§ 15. Доказательство принципа максимума
В этом параграфе мы будем предполагать, что x(t),
t0 < t < tv—оптимальная траектория (соединяющая точку х0
с некоторой точкой прямой П, см. § И), а и (t) — соответ¬
ствующее оптимальное управление. Пусть т — некоторая
правильная точка управления u(t). Согласно лемме 4,
луч Ьх не принадлежит внутренности конуса Кх, так что
этот конус не заполняет всего пространства X. Поэтому
существует опорная гиперплоскость к конусу Кх в его
вершине, т. е. такая гиперплоскость Г, что весь конус Кх

g 15]	ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА	ИЗ
лежит в одном из двух замкнутых полупространств, опре¬
деляемых гиперплоскостью Г. (Гиперплоскость Г, обла¬
дающая этим свойством, может быть не единственной;
последующие рассуждения справедливы для любой такой
гиперплоскости.) Уравнение гиперплоскости Г (в простран-
п
стве Хх) можно записать в виде 2 аа%а = 0, где
а=0
х°, х1, . . ., хп — текущие координаты. Так как умножение
всех коэффициентов аа на одно и то же отличное от нуля
число не меняет гиперплоскости Г, то мы можем считать
(изменив, если нужно, знаки всех чисел аа на обратные),
что конус Кх лежит в отрицательном полупространст-
п
не ( 2 аа£а<0). Иначе говоря, для любого вектора Ах,
а=0
определяемого формулой (22), выполнено неравенство
(а, Дас)<0 (Ах£Кх),	(34)
где через а обозначен вектор (а0, av . . ., ап) (ибо сово¬
купность векторов (22) и есть конус Кх). Полагая в фор¬
муле (22)	=	bt2 = • • • = bts = 0, мы получим Ах =
= f(x{т), u(x))6t, и, в силу (34),
(.а, f(x(т), и(т))б*)<0.
Так как это неравенство справедливо при любых бt (как
положительных, так и отрицательных), то
(a, f {х (т), к(т))) = 0,
т. е., иначе говоря,
<$?(а, х(т), и(т)) =	0	(35)
(это соотношение	выполняется, если вектор	а	удовлетво¬
ряет условию (34)). Обозначим через
ip(t, a) = (%(t, a),	a).	•••.	^n(*> «))
решение системы уравнений (8) (соответствующее изучае¬
мым оптимальным u(t)) и x(t) с начальным условием
г|э(т, а) = а.	(36)
Решение я|э(£,. а)	определено на всем	отрезке	t0<Ct<Ctv
так как система	(8) линейна.
8 Л. С. Понтрягин

114	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА	[ГЛ.	2
Л с м м а 5. Если вектор а удовлетворяет условию (34),
то во всякой правильной точке управления u(t)> лежащей
на полуинтервале t0 < t < т, выполнено соотношение
«)> x{t), u(t)) = e//i(ty{t, a), x(t)).
Пусть хг — правильная точка управления и (t), расположен¬
ная на полуинтервале t0 < £<т, а ^ — произвольная точка
пространства £/. Рассмотрим символ а (см. § 14) с един¬
ственной точкой хг (т. е. 5=1) и с числами 8tv б£, соот¬
ветственно равными единице и нулю:
a = {Ti, vv х, 1, 0).
Тогда вектор Дас (см. (22)), соответствующий этому сим¬
волу а, будет иметь значение
Ах = Ах> Xjl [f(x (tj),	Vj)	f (x (tj), «(tj))].
В	силу соотношений (34) и	(36)	получаем отсюда
(г|з(т, a), AX)Xj\f{x (tj),	vl) —	f(x( Х «(т^ХО,
и	потому, согласно лемме	1 и	соотношению Ах	? т = Е
(см. (17))
Ж*!' «)./(*(Ti), vx) -/(^(Tj), »(Ti)))<0.
Это соотношение переписывается (в силу определения
функции g%?) в виде
«)> Лт1). yi) — ш (^ (Т1( а), х(тх), BftjjXO,
а так как это неравенство справедливо для любой точки
v1^Ut то мы получаем
('Ф (Х «)> x(Ti)> гг(т1)) = тахХ(гКт1, a), i^), vx) =
vx£U
= е^('ф(Т1> «)» ^(Tl))>
и лемма 5 доказана.
Соотношение, указанное в лемме 5, справедливо и при
£ = х (ибо х — правильная точка):
J{?0|?(т, а), ж(т), и (т)) = ^ (if (т, а), ж(т)).
Поэтому, в силу (35) и (36), мы получаем следующее
утверждение.

§ 15]	ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА	Ц5
Л е м м а 6. Если вектор а удовлетворяет условию (34),
то
М (if (т, а), я(т)) = 0.
Лемма 7. Если абсолютно непрерывная функция if (£)
почти всюду на некотором отрезке I удовлетворяет
уравнениям (8) и соотношению
(if (*), х (I), и (/)) = м (if (t), х (t))9	(37)
то функция G/#(if(0> х (£)) постоянна на всем отрезке I.
Заметим прежде всего, что функция м (if (£), х (I))
полунепрерывна снизу на отрезке I. Действительно, пусть
V — произвольная точка этого отрезка, а е — положитель¬
ное число. В силу определения верхней грани, существует
такая точка и' £ £7, что
{if(*')> ж(г'), и')><м (if (*'), ж (£')) —у.
Далее, в силу непрерывности функции	x(t), и)
по t при фиксированном и = и', существует такое о > 0,
что при 11 — t' | < б имеем
1и') —^(ф(г'), x(t'),u')\
Таким образом, при \ t — V | < б справедливо неравенство
x(£)) = sup J£?(i|)(i), x(t), и) >
u£U
> 36 ('ф (t), X (£), и') > G# (if (*'), X (£')) — 8,
показывающее, что функция qM (if (t), x (£)) полунепре¬
рывна снизу.
Далее, так как управление u(t) допустимо, то образ
отрезка / при отображении и обладает в пространстве
Ег компактным замыканием (см. § 10), т. е. существует
в Ег такое компактное множество Р9 что u(t)£ Р при t £/.
Положим
иг (if, х) = шах $6 (if, х, и).
и£Р
Очевидно, что имеет место неравенство
G#(if, ж) > иг (if, х)9	(38)
8*

116	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА	[ГЛ.	2
справедливое при любых х и ф. Соотношение (37) озна¬
чает, что почти всюду па отрезке I имеет место равенство
ш (ф (£), x(t)) = cMityit), x(t))
(ибо и (t)£P).
Итак,	x(t))	есть	полунепрерывная	снизу функ¬
ция, почти всюду на отрезке / совпадающая с функцией
т (ф (t), х (t)) и связанная с ней соотношением (38).
Из этого следует, что если функция т(ф(£), x(t)) непре¬
рывна, то функция	x{t))	всюду	на	отрезке I
совпадает с ней (и потому также непрерывна). Мы сейчас
покажем, что функция иг(ф-(£), x(t)),— а следовательно,
в силу сказанного, и е#(ф(£), х (£)), — а б с о л ю т н о
непрерывна на отрезке /.
Так как отрезок / компактен, то существует в про¬
странстве переменных ф0, фА, ... ,фп, ж0, ж1,. . ., хп
такое выпуклое ограниченное множество Q, что точка
(ф(£), x(t)) принадлежит множеству Q при ££/. Таким
образом, тройка (ф(£), x(t), и (£)) принадлежит множеству
Q х Р при t б I. Далее, так как частные производные функ¬
ции (ф, х, и) по переменным фа, ха непрерывны по сово¬
купности	переменных	ф,	ж, и (см. условия,	наложенные
на функции	/1 в § И),	то	на компактном	множестве Q х Р
все эти производные ограничены. Отсюда следует сущест¬
вование такой (не зависящей от и) константы К > 0, что
для любых (ф, ж)£ Q, (ф', ас')g Q, и£Р выполнено соотно¬
шение
|е%?(ф, х, и) — 3@(ф', х\ u)\<Kd9	(39)
где я? — наибольшее из чисел |фА —ф£|> \хг — хп\,
г = 0, 1, . . ., п. Пусть (ф, ж) и(ф', ас') —две точки множе¬
ства Q, а и и и' — такие точки множества Р, что
т(ф, х) =	(ф, х, и), т(ф', х') = ей?(ф', х\ и')-
Тогда, очевидно, выполнены неравенства
&е (ф, х} и') <	(ф, х, и),	(ф', х\ и)<$$ (ф', х\ и')у
и потому (учитывая соотношение (39)) мы получаем
— Kd<C&e{ф, х9 и') — Ж (Ф'» х', и')<
<^(ф,	х,	и)-£0(ф', х\	и')	<
<ей?(Ф>	х,	u)—Stf(Ф'» х',	и)	< Kd.

§ 15]
ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА
117
Иначе говоря,
|wi(t|), х) — т('ф', xf) | < Kd,
где d — наибольшее из чисел | фг — фг' |,	| х1 — хп |,
i = О, 1, п. В частности, отсюда получаем
177г (я|5 (^), х (t)) — т (ф (£')> x(t'))\^Kd, t, 2'£/,
где d — наибольшее из чисел |	(t) — фг (t') |, | х1 (t) — х1 (t') |..
Из этого неравенства, в силу абсолютной непрерывности
функций ф(г) и x{t), мы без труда заключаем, что функ¬
ция	x(t))	абсолютно	непрерывна.
Покажем, наконец, что функция т(\|) (г), x(t)) почти
всюду имеет производную, равную нулю. В силу абсо¬
лютной непрерывности функции т(ф(г), x(t)) и опреде¬
ления функций х (t) и ф (t), почти всюду на отрезке / имеют
место следующие обстоятельства: функция т?г(ф(/), x(t))
имеет производную, для функций x(t) и ф(/) выпол¬
нены соотношения (7) и (8), или, что то же самое, (9) и (10),
и, кроме того,
X (t)) = зе (if (t), x(t), и (t)).
Пусть t — т — какая-либо точка, в которой эти обстоятель-
ства имеют место, и t' — произвольная отличная от х точка
отрезка /. Тогда
т(ф(£'), x(t'))> $€ Сф(г'),	и(х))
и потому
т ('Ф (О» я (*')) —т(ф(т), х (т)) >
x{t')> и (т)) — (ф (т), х(х), и(т)).
Будем теперь считать, что t' приближается к т, оста¬
ваясь больше т, так что разность t' — x положительна.
Тогда деление на t' — x не меняет знака неравенства
в последнем соотношении:
т(ф (*'), x(t')) — m(^ (т), х (т))
t' — x	^
^ &G (ф (£')> х (t'), и (т)) — сЩф (т), х (т), и (т)) .
>	t' — x

118
ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА
[ГЛ. 2
Переходя к пределу при >т(2'>т), получаем
отсюда
d
dt
171 СФ (0> $ (0)
n
= 2
(=т> dt
x(t), u(x))
t=x
d&e <*%(*)
dt
«+■2
dm dxa (t)
dxQ-
dt
l=x
= o
a=0	a=0
(здесь производные вычисляются в точке т, где т и, следо¬
вательно, и (т) фиксированы). Аналогично, при V —> т, V < т
получаем обратное неравенство
d
1= X
<0.
Итак, яг(г|э(0, ^(0) [а также и совпадающая с ней
функция оМ (ф (£), #(£))] есть абсолютно непрерывная функ¬
ция, имеющая почти всюду производную, равную нулю.
Следовательно, эта функция постоянна на отрезке I.
Докажем следующее важное свойство конусов Кх.
Лемма 8. Если х и %' — правильные точки управле¬
ния и(/), причем г0<т' < х<г1? то Ах, т/ (KX>)CZKX, где
— отображение пространства Хх> на Хх, определен¬
ное в § 12.
В самом деле, конус Кх> образован векторами, каж¬
дый из которых в силу (22) можно представить в виде
суммы двух векторов:
= f (х (т'), и (т')) бt,
s
Д2ж = 2	[/(ж(^).	Vi)—/(x(xi), и(т4))] btv
г=1
Поэтому нам достаточно показать, что имеют место вклю¬
чения
АХ) xr (Axac) £ Кх,	Ат> т> (Д2ас) £ Др.	(40)
Мы имеем в силу (17):
А.
Г, т,(Д2ас) = 2 Л, Tj	6/;>
г=1
и потому второе из включений (40) имеет место (ибо
тх< .. . <т3<т'<т). Докажем первое из этих включений.
Допустим, что (при некотором бt) вектор Ах> х>(Др#) не при-

§ 15]	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА	Л9
надлежит конусу Кх. Тогда существует гиперплоскость,
разделяющая их, т. е. существуют такие числа а0, av ..., ап,
что конус Кх расположен в отрицательном полупростран-
п
стве 2 аах(Х < 0, а вектор Ах> х> (Агх) — в открытом по-
а=0
ложителыюм полупространстве, т. е.
(■а, Ах> (Д1ас))>0,	(41)
где « — вектор (а0, а1? . . ., ап). Обозначим через ty(t,a) реше¬
ние системы (8) с начальным условием-ф (т, а) = а. Это
решение мы будем рассматривать на отрезке £0<£<т. Так
как конус Кх расположен в отрицательном полупростран¬
стве, т. е. выполнено условие (34), то из лемм 5, 7 и 6
вытекает, что М (г|? (t, а), х (t)) = 0 при t0 < t < т. Так
как, далее, — правильная точка (лежащая на полуинтер¬
вале £0<£<т), то, согласно лемме 5,
(г|) (т', а), х (т'), и(т')) = <з^ (я|з (т', а), ж(т')) = 0,
(•ф(т', а), /(ж(т'), и(т'))) = 0.
Отсюда, согласно лемме 1, мы получаем соотношение
(\j)(T, а), АХуХ, (f(x(т'), и(т'))) = 0,
противоречащее неравенству (41). Полученное противоре¬
чие и доказывает лемму 8.
Пусть теперь т— произвольная правильная точка управ¬
ления n{t), лежащая на интервале tQ<t<.tv Положим
Я(^ = Льт(Ят).
Так как .4/ х есть линейное отображение, то /1^ есть
выпуклый конус пространства Xtv Конусы образуют
возрастающую последовательность:	если
т' < х — правильные точки, то в силу леммы 8 мы имеем
(см. (17))
Я£'> = А,ь (Кх.) = Л1и х (Ах< х. (Кх>)) С= А1и х (Кх) = Е%>.
Поэтому объединение (по всем правильным точкам т интер¬
вала t0<t< tj) всех конусов снова есть выпуклый
конус (возможно не замкнутый) пространства Xtx (с вер¬
шиной в начале). Этот конус мы обозначим через Ktl
и назовем предельным конусом.

120	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА МАКСИМУМА	[ГЛ.	2
Лемма 9. Если управление u(t) и соответствующая
траектория x(t), £0<£<£1? оптимальны, то луч Ltv
исходящий из точки х(1г) в направлении отрицательной
полуоси х°, не принадлежит внутренности конуса Ktl.
В самом деле, пусть луч Ьц принадлежит внутрен¬
ности конуса Кгг. Выберем выпуклый многогранник М,
целиком лежащий в Ktl и содержащий какую-либо точку
I б Ltl внутри себя. Каждая вершина многогранника М при¬
надлежит конусу Жц, т. е. принадлежит некоторому конусу
Ktl\ а так как конусы образуют возрастающую последо¬
вательность, то найдется такая правильная точка т, что
все вершины многогранника М принадлежат конусу Кц\
Следовательно, конус	содержит весь многогранник
М, так что точка I является внутренней точкой конуса
или, что то же самое, луч L/x принадлежит внутренности
конуса К\1\ Но тогда луч х (LfJ принадлежит внут¬
ренности конуса А~г]х (Жц)) = Жс(ибо А~^ х есть линей¬
ное невырожденное, следовательно, гомеоморфное отобра¬
жение). Луч же А\х (Lt±) совпадает с лу чом Lt, исходящим
из точки х (т) в направлении отрицательной полуоси х°. Это
вытекает из того, что система уравнений в вариациях (16)
не содержит в своих правых частях переменного х°,
и потому равные между собой векторы (— 1, 0, 0, . . ., 0),
исходящие из точек кривой х (£), получаются друг из друга
переносом вдоль траектории x(t). Итак, луч Ьх принад¬
лежит внутренности конуса Кх, а это противоречит опти¬
мальности управления и (t) (см. лемму 4).
Переходим к завершению доказательства теоремы 8.
Пусть и (t), t0 < t < tv — оптимальное управление, a x(t) -
соответствующая ему оптимальная траектория. Тогда луч
Ltl не принадлежит внутренности предельного конуса Ktl
(лемма 9), и потому существует разделяющая их гипер¬
плоскость, т. е. существуют такие числа с0, с1У . .., сп,
п
что весь конус К tx лежит в полупространстве ^ са%а < 0,
а=0
п
а луч Lu — в полупространстве	са^а	> 0. Иначе
а=0
говоря, вектор (—1, 0, 0, ..., 0), имеющий направле-

§ 15]	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА	121
иие луча Ь\х лежит в замкнутом полупространстве
п
V. саха> 0, т. е. с0 < 0.
а=0
Обозначим через яр(£) = (% (£), фДО» • • •» Фп(0) реше¬
ние системы (8) с начальным условием я|5(^) = с, где
с — вектор (с0, сг, . ..,сп). Так как система (8) линейна,
то решение гр (£) определено на всем отрезке t0
Покажем, что вектор яр(£) и является тем вектором,
существование, которого утверждается в теореме 8.
Прежде всего, x(t) и i|э(£) удовлетворяют уравнениям
(7)	и (8), или, что то же самое, (9) и (10). Докажем,
что соотношение (11) имеет место во всякой правильной
точке интервала t0 < t < tv Пусть т —правильная точка,
лежащая на этом интервале. Так как весь конус К(г
а следовательно, и конус AtltX(Kx) лежит в отрицатель-
п
ном полупространстве 2 Фа (^i) ха ^ 0» то (совершая пере-
а=0
нос вдоль траектории x(t) из точки x{tr) в точку х(х))
мы получаем, что весь конус AJ^x (Atlt х (^т)) = Кт лежит
п
в полупространстве 2 фа(т)яа<0 (см. § 12). Иначе
а=0
говоря, вектор а = \р(т) удовлетворяет условию (34).
Отсюда вытекает, что для решения xp(t, а) уравнения (8)
с начальным условием яр (г, а) = а — а это решение,
очевидно, совпадает с яр (I) — справедливо утверждение
леммы 5. В частности (в силу того, что т — правильная
точка),
&е (яр (т), X (т), и(т)) = оМ (яр (т), X (т)) = 0
(см. лемму 6).
Итак, условие 1°, указанное в теореме 8, выполняется.
Кроме того, есть точки, в которых функция м (яр (£), х(1))
обращается в нуль (это будет во всякой правильной
точке т), и, далее, ф0 (£г) = с0< 0. Поэтому для проверки
условия 2° теоремы 8 достаточно доказать последнее
утверждение теоремы 8 о постоянстве функций м (яр (г), x(t))
и яр0 (£), если величины яр (£),#(£), u(t) удовлетворяют
системе (9), (10) и выполнено условие 1°. Это непосред¬
ственно вытекает из леммы 7 и того факта, что функции /а

122
ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА	[ГЛ.	2
не зависят от х°, так что первое из уравнений (8) имеет вид
d*o __ Q
dt
Таким образом, теорема 8 полностью доказана. Вместе
с тем доказана теорема 1 первой главы.
§ 16. Вывод условий трансверсальности
Здесь мы докажем сформулированную в первой главе
теорему 3 (она справедлива для произвольного класса D
допустимых управлений).
Пусть и (/), t0 < t < tl9 — некоторое допустимое управле¬
ние, а х (t) — траектория, соответствующая управлению
u(t) и исходящая из точки ас0 = (0, х0). Пусть, далее,
S0 — некоторое гладкое многообразие (в пространстве X)
размерности г0 < п, проходящее через точку .т0, и Т0—каса¬
тельная плоскость многообразия S0 в этой точке. Через 2Г0
обозначим 7’0-мерыую плоскость пространства X, состоя¬
щую из всех точек вида (0, х), где х£Т0. Очевидно, что
плоскость У0 проходит через точку х0. Подвергнув плос¬
кость 2Г0 переносу вдоль траектории x(t) в точку ж (г),
t0<X < tv МЫ получим ПЛОСКОСТЬ АХ} t0(^o)’ проходящую
через точку х(х). Если г —правильная точка управления
u(t), то определен также конус Кх с вершиной в точ¬
ке х(х). Выпуклую оболочку множества АГ, to (.Г о) и я, мы
обозначим через Жх. Очевидно, множество SKX является
выпуклым конусом с вершиной в точке х(х). Докажем
теперь лемму, являющуюся обобщением леммы 3.
JI е м м а 10. Пусть х (t0 < х < ^) — правильная точка
управления и (t), t0 < t < tv a x (t) — траектория, coom-
ветствуюгцая управлению u(t) и исходящая из точки х0.
Пусть, далее, А — некоторое многообразие с краем, имеющее
размерность < п и расположенное в X так, что точка х (т)
лежит на его краю. Обозначим через М касательную
полуплоскость многообразия А в точке х(х). Если конусы
$СХ и М, имеющие общую вершину в точке х(х), не яв¬
ляются разделяемыми, то существуют такое управле¬
ние к* (£) и такая точка x^£S0, что соответствующая
этому управлению траектория x%(t), исходящая из точки

ВЫВОД УСЛОВИЙ ТРАНСВЕРСАЛЬНОСТИ
123
aco = (0, #q), проходит через некоторую точку многообра¬
зия Л, не лежащую на его краю.
Доказательство. Обозначим через л; ортогональ¬
ное проектирование многообразия S0 на плоскость Т0.
Отображение л, рассматриваемое не на всем многообра¬
зии S0, а лишь на некоторой окрестности точки х0, является
гомеоморфизмом, и поэтому определено обратное отобра¬
жение л"1 некоторой окрестности точки х0 в плос¬
кости Т0 на некоторую окрестность точки х0 в много¬
образии S0. Таким образом, если Е, — произвольный век¬
тор, лежащий в плоскости Т0 и исходящий из точки ж0,
то при достаточно малом е > 0 определена точка л-1 (е£) £S0,
т. е. вектор £ определяет линию
ж = л"1 (eg),	0<е < е0,
лежащую на многообразии S0 и исходящую из точки х{).
Эта линия имеет в точке х0 касательный вектор £, т. е.
лГ1 (е|) = а:0 + е£ + о(е).
Из этого следует, что линия (0, л-1(е£)) пространства X
исходит из точки х0 = (0, х0) и имеет в этой точке каса¬
тельный вектор § = (О, £):
(О, л'1 (е£)) = х0 + eg + о (е).	(42)
Пусть теперь a — {xv vt, т, б+ б£} — совокупность вели¬
чин, определяющая варьирование управления u(t) (см.
стр. 105). Обозначим через х\,a(t) траекторию, исходя¬
щую (в момент t0) из точки (0, л-1 (е£)) и соответству¬
ющую проварьированному управлению и* (t) (параметр е
п (42) и в определении управления u*(t) один и тот же).
Из (42) следует, в силу (21), что
Ж|, а (Т + ебг) = х (т) + 8 [AXt ,0 (I) 4- Д05а] + о (г),	(43)
где вектор Дяса определяется формулой (22).
Обозначим через 5+1 размерность многообразия Л
(и размерность полуплоскости М). Так как конусы Жх
и М не являются разделяемыми, то (см. сноску на стр. 106)
существует такая точка а, принадлежащая полуплос¬
кости У¥, но не лежащая на ее краю, и такая плоскость С
размерности тг — 5 > 0, проходящая через точку а, что

ДОКАЗАТЕЛЬСТВО ПРИНЦИПА МАКСИМУМА [ГЛ. 2
шар малого радиуса с центром в точке а дает в пере¬
сечении с плоскостью С «дополнительную площадку»
к полуплоскости М, причем эта «площадка» ортогональна
прямой, проходящей через точки х (т) и а, и целиком
содержится в конусе Жх. Эту «дополнительную площадку»,
являющуюся шаром размерности 72 — я, мы обозначил!
через Е. Пусть ev ..., en_s — взаимно ортогональные
радиусы шара Е\ положим, далее, /{ = — eit 7=1,..., п — s.
Все векторы ev . . ., en_s, fv . . .,/n_s будем считать исхо¬
дящими из точки а. Концы всех этих векторов принад¬
лежат конусу <ЖХ (ибо Еа&х). Наконец, через с обо¬
значим вектор с началом в точке х(%) и концом в точке а.
Так как векторы с, с + е7-, eJrfi(i= 1, . ..,72 —s), исхо¬
дящие из точки х(%), принадлежат конусу с/£*т, а этот
конус образован всевозможными векторами AXi ,0 (|) + Аха,
где £ £ Т0,	Аха	б liT,	то	существуют	в	плоскости Т0
такие векторы £0, glf . . ., gn_s, . . ., g;_s, исходящие
из точки х0, и такие символы а0, av . . ., an_s, а', . . ., ai_s,
что имеют место соотношения
Ar, to (1о) + Аас«о = с, Ах, ,0 (li) + Аха. = С + eit
АТ, to di) + Аха'. = c+/i( г = 1 n — s.
Определим при выполнении условия
(Q1)2+(e2)2+...+(en's)2<i	(44)
символ a	(q1,	. . ., Qn_s) так же, как	и на стр. 108,	только
производя	суммирование по i не от	1 до 72, а от 1	до	72 — s;
положим, далее,
Не1. - ..>епЛ =
n—s	n—s	n—s
= (}-т21еМ)£о+^Е /г* te*) Ь + i 2 А"(е*)
г= 1	г=1	г=1
Тогда мы получим (ср. вычисление на стр. 109):
*0 (1 (б1» * • • > QU S)) + ^Ха (q1, Qn_s) =
n—s
= ^ + ^2еЧ-	(45)
2=1

§ 16]	ВЫВОД	УСЛОВИЙ	ТРАНСВЕРСАЛЬНОСТИ
125
Следовательно, если точка (q1, ..., qu~s) пробегает в (п — s)-
мерном числовом пространстве шар (44), то конец век¬
тора (45) пробегает в пространстве Хх шар Ev получаю¬
щийся из шара Е гомотетией с центром а и коэффи¬
циентом —. При тех же условиях конец вектора
е Ит, to (I (Q1J • • •» en)) + Дха (q1,	Qn_s)]
пробегает (п — я)-мерный шар Е8, получающийся из шара Ег
гомотетией с центром х(х) и коэффициентом е.
При £ = I (q1, .. ., Qn_s), а = а (q1, .. ., Qn_s) траектория
xl a(t) непрерывно зависит от параметров Q1, . . ., Qn_s,
так же как и число бta. Поэтому точка ха (т + ебta) непре¬
рывно зависит от q1, . . ., Qn~s. Следовательно, когда точка
(Q1, . .., Qn s) описывает шар (44), точка х^ а (т -f- еб£а) про¬
бегает (при любом фиксированном е) некоторый «диск» Fe
(непрерывный образ шара (44)), причем с точностью
до малых более высокого порядка, чем е, диск Fe «сов¬
падает» с шаром Ее. Шар Ег и полуплоскость М (точ¬
нее, конечный ее кусок вблизи точки х(х)) являются
цепями (см. сноску на стр. 110) размерностей п — s
и s -f- 1 соответственно, причем индекс пересечения этих
цепей равен ± 1, а расстояние каждой цепи до границы
другой имеет порядок е. Поэтому «диск» Fs (отстоящий
от Ее на величину более высокого порядка малости, чем е)
и многообразие А (касающееся полуплоскости М) также
имеют при достаточно малом е индекс пересечения ± 1,
т. е. при достаточно малом е диск Fe пересекает много¬
образие А в некоторой точке, не лежащей на краю этого
многообразия. Иначе говоря, существует такое е > 0
и такие q1, ...,Qn's, что точка х^ а (т + еб£а) принадле¬
жит многообразию А, но не лежит на его краю. Следо¬
вательно, обозначив величины (t), х^ а (t), соответству¬
ющие выбранным значениям е, q1, ..., Qn_s, через и* (I),	(£),
мы найдем, что траектория x%(t) начинается в точке
(Q = (о, Я-1 (е|)) = (0, х$), где = я"1 (е£) £ S0, и про-
ходит (в момент т' = т + еб£а) через некоторую точку
многообразия А, не лежащую на его краю.
Таким образом, лемма 10 доказана.

126	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА	[ГЛ.	-
Пусть теперь и (t), t0 < t < tv — оптимальное управле¬
ние, а х (t) — оптимальная траектория, дающие решение
поставленной в § 6 задачи с подвижными концами.
Положим x(t0) = x0, x(t1) = x1\ точки х0 и х1 простран¬
ства X определим, как всегда, отбрасывая «нулевую» коор¬
динату у точек х0у xv т. е. х0 = (0, х0), хг — (х° (^), хг).
Обозначим через 1\ касательную плоскость к многообра¬
зию Sx в точке xv а через — плоскость (^-мерную)
пространства X, состоящую из всех точек вида (ж°(^), х),
где х g Tv Проведем через каждую точку плоскости
луч, идущий в направлении отрицательной полуоси х°,
и обозначим множество точек, заполняемое всеми этими
лучами, через Q. Множество Q представляет собой
(тд + 1)-мерную полуплоскость; ее граничными точками
являются точки плоскости У v Обозначения Т0 и У0 вводим
аналогично. Обозначим через <№tl выпуклую оболочку
множества	(J/*0)UТаким образом, конус o/l’t
с вершиной x(t) определен для любой правильной точки t = т
управления u(t), а также для t=tv Если t" > £', то
At", tf (q#V) C q%‘i” (см. лемму 8).
Лемма 11. Конусы o%‘tl и Q, имеющие общую вер¬
шину в точке x(tх), являются разделяемыми.
В самом деле, допустим, что конусы <№ц и Q не яв¬
ляются разделяемыми. Так как конус является объ¬
единением конусов Ailt Х('Ж\), то найдется такая правиль¬
ная точка т управления и (£), что конусы А1ъ х т) и Q
также не являются разделяемыми. Выберем такую точку т.
Обозначим через многообразие с краем, состоящее
из всех точек (х°, х)£Х, для которых х° < ж°(^),
Тогда касательная полуплоскость многообразия Atl в точке
x(t±) совпадает с Q. Для произвольной точки чбАц мы
обозначим через у (t, ц) решение системы (7) с началь¬
ным условием у (tv rj) = тр Мы будем рассматривать это
решение на отрезке тгде т — выбранная пра¬
вильная точка управления u (t). Когда точка ц пробе¬
гает многообразие Atv точка у (т, т]) также пробегает
некоторое многообразие с краем, которое мы обозначим
через Ат. Легко видеть, что касательная полуплоскость
многообразия Ат в точке х(х) совпадает с Aj*tX(Q).
Так как конусы А1ъХфсх) и Q не являются разде¬
ляемыми, то конусы т (Дь т(<ЗД = и AjI% (Q)

§ 16]
ВЫВОД УСЛОВИЙ ТРАНСВЕРСАЛЬНОСТИ
127
также не являются разделяемыми. Но так как т (Q)
есть касательная полуплоскость многообразия Ат, то,
в силу леммы 10, существует такое управление и%(1),
что соответствующая ему траектория x%(t), исходящая
из точки ж* = (0, Xq), где xq£S0, проходит через неко¬
торую точку многообразия Лт, не лежащую на его краю.
Иначе говоря, существуют такое t' > /0 и такая точка
ц £ Atv не лежащая на краю многообразия Aiv что
x*{t') = y(T,\1).	(46)
Определим теперь управление u^(t) на отрезке
— т), положив
и* (0 при £0< £< £',
u(t — (tr — т)) при t' < t < t± + (tf — т).
Траектория	(£), соответствующая управлению и** (t)
и исходящая из точки х%, имеет, очевидно, следующий
вид (ср. (46)):
ж% (г)	при	£0<	t	<	t'y
y(t — (t' — т), г]) при t' < t < (tf — т).
(0
(0 —
В частности, х%*	+ (t' — т)) == у (tv г]) = rj. Но точка г\
принадлежит многообразию Atv т. е. имеет вид Г] = (т]°, rj),
где	Так	как, кроме того, точка ц не лежит на краю
многообразия Atv то т]0<^0(^). Таким образом, управ¬
ление u%*(t) переводит фазовую точку из положения £§
в положение г| £ Sv и для него функционал (6) прини¬
мает значение т]°, меньшее чем для управления u(t).
Но это противоречит тому, что управление и(1) и траек¬
тория x(t) оптимальны. Таким образом, лемма И доказана.
Теперь уже нетрудно закончить доказательство тео¬
ремы 3. Так как конусы и Q являются разделяемыми,
то существуют такие числа с0, cv . .., сп, что конус
(а значит, и KtlCZ^t^) лежит в полупространстве
п
2 са£а<0 (где х°, х1у ..., хп — координаты в прост-
а=0
п
ранстве -ЯГ^), а конус Q — в полупространстве 2 саха^0.
а=0
В частности, луч Ltl (лежащий в полуплоскости Q)

128	ДОКАЗАТЕЛЬСТВО	ПРИНЦИПА	МАКСИМУМА	[ГЛ.	2
71
расположен в полупространстве 2 саха>0. Таким
а=0
образом, числа с0, cv . . ., сп обладают всеми свойствами,
указанными в § 15, и потому решение г|э(£) системы
(8)	с начальным условием (+) = с (где с — вектор
(с0, cv . . ., сп)) удовлетворяет условиям, указанным в
теореме 8 (или в теореме 1).
Покажем, что вектор г|i(t) удовлетворяет условию
трансверсальности в обоих концах траектории х(1).
Плоскость £Гх (содержащаяся в Q) располоядзна целиком
71
в полупространстве 2 саха> 0, и, следовательно, в ги-
а=0
71
перплоскости 2 саха = 0) или» что то же самое, в гипер¬
он о
71
плоскости 2 Фа (*i) ха = 0. Если теперь ц = (ц1, . . ., т]п) --
си=0
произвольный касательный вектор многообразия S±
в точке x(t^)y т. е. вектор, лежащий в плоскости Tv то
вектор rj= (0, ц) пространства X расположен в плоскости S'v
71
и, следовательно, в гиперплоскости 2 Фа (h) х'а = 0- Иначе
а=0
говоря, (г|э (^), т|) = 0. Но так как «нулевая»координата век¬
тора т| равна нулю, то последнее соотношение принимает вид
71
2 флД^Ц^О. Таким образом, вектор-функция я|о (t)
v= 1
удовлетворяет условию трансверсальности в правом конце
траектории х (t).
Далее, плоскость А1ъ <0 (2Г0) С расположена цели-
п
ком в полупространстве 2 сажа< 0, а следовательно, в ги-
а=0
71
иерплоскости 2 саха = 0 или, что то же самое, в гипер-
а=0
п
плоскости 2 Фа(П)яа = 0. Иначе говоря, для любого
а=0

ВЫВОД УСЛОВИЙ ТРАНСВЕРСАЛЬНОСТИ
129
вектора | £ 2Г0 вектор Atlf to (g) лежит в гиперплоскости
п
S 'M<i)£a = 0, т. е.
(4>(*i).4i,to(S)) = 0-
Из этого, в силу леммы 1, вытекает, что (ф (10), |) = 0.
Но любой вектор |£.У0 имеет вид g = (0, g), где
£ = (|1j . . ., gn) — вектор, лежащий в плоскости Т0. Поэтому.
п
соотношение (ф (£0), 1) = 0 принимает вид 2	(£0)	£v = 0*
v=l
Таким образом, вектор-функция ф (£) удовлетворяет усло¬
вию трансверсальности и в левом конце траектории x(t).
Тем самым теорема 3 полностью доказана. Вместе
с тем доказаны и все остальные теоремы первой главы.
Л. С. Понтрягин

ГЛАВА 3
ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ
§ 17. Теоремы о числе переключений
Важными для приложений и хорошо иллюстрирующими
общие результаты примерами являются линейные оптималь¬
ные быстродействияу т. е. оптимальные быстродействия
в случае, когда уравнения, описывающие поведение объ¬
екта, линейны. Рассмотрению таких быстродействий
и посвящена настоящая глава. Здесь мы не только изло¬
жим факты, вытекающие непосредственно из доказанных
выше теорем, но и получим некоторые новые результаты,
в частности докажем теорему существования для линей¬
ных оптимальных быстродействий.
Уточним прежде всего постановку задачи. Мы
будем рассматривать объект, закон движения которого
записывается в виде линейной системы дифференциаль¬
ных уравнений
п	г
-^- = 2 ava;V + 2 ^0м°>	1	= 1,2, и. (1)
v=i	e=i
Мы будем, далее, предполагать, что областью управле¬
ния U является выпуклый замкнутый ограниченный
многогранник *), расположенный в r-мерном векторном
*) Выпуклый замкнутый многогранник в Ег представляет собой
пересечение конечного числа замкнутых полупространств, т. е.
множество точек в Ег, удовлетворяющих конечной системе линей-
г
ных неравенств ^	i=l,	2,	s. Если этот мпого-
k= 1

§ 17]
ТЕОРЕМЫ О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
131
пространстве Ег с координатами и1, . . ., ит. Таким обра¬
зом, управляющий параметр и —{и1,	иг) является
точкой многогранника U.
Наконец, мы будем рассматривать лишь задачу об
оптимальном быстродействии, т. е. задачу о минимиза-
<i
ции времени перехода tx — t0 = ^ dt. Оптимальную зада¬
ло
чу в такой формулировке назовем задачей о линейных
оптимальных быстродействиях.
В векторной форме система (1) . может быть записана
следующим образом:
% = Ах + Ви-,	(2)
здесь А : X—> X и В : Er—> X— линейные операторы, опре¬
деляемые (в координатах х1,	. . ., х11 и и1,	. . .,	и1')
матрицами (ар и (Ь*) соответственно.
Во всех теоремах, доказываемых в этой главе, мы
будем предполагать (не указывая этого каждый раз), что
выполнено следующее условие общности положения,
накладываемое на коэффициенты уравнения (2) и на рас¬
положение многогранника U:
если w — вектор, имеюгций направление одного из ребер
многогранника U, то вектор Bw не принадлежит ни¬
какому истинному подпространству пространства X,
инвариантному относительно оператора А, т. е. векторы
Bw, ABw, . .., An^Bw	(3)
линейно независимы в пространстве X.
Функция Я(ф, х, и) (см. теорему 2) в рассматриваемом
случае имеет вид
Я = (1|), Ах) + (г|з, Ви) = 2	+	2	(4)
М-, V	JLl,	Q
гранник ограничен (и, следовательно, компактен), то он является
выпуклой оболочкой своих вершин; очевидно, что число вершин
конечно.
9*

132 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
а вспомогательная система (см. формулу (19) гл. 1)
записывается в виде
где .4* — оператор, сопряженный к А, т. е. оператор,
определяемый (в той же системе координат) матрицей,
получающейся из матрицы (ар системы (1) транспони¬
рованием.
Очевидно, что функция Я, рассматриваемая как функ¬
ция переменного и £(7, достигает максимума одновременно
с функцией (ф, Ви). Максимум функции (ф, Bu)t рассма¬
триваемой как функция переменного п£[/, мы обозначим
через Р(ф). Из теоремы 2 следует (см. формулу (20)
гл. 1), что если и (£) — оптимальное управление, пере¬
водящее фазовую точку из положения х0 в положение
xv то существует такое решение ф (t) уравнения (5), что
Так как уравнение (5) не содержит неизвестных функ¬
ций x(t) и u(t)y то все решения этого уравнения легко
могут быть найдены, после чего легко могут быть най¬
дены все управления и (£), являющиеся решениями урав¬
нения (6); среди них, очевидно, содержатся все оптималь¬
ные управления для уравнения (2). Вопрос о том,
насколько однозначно условие (6) определяет управле¬
ние u(t) через функцию ф(£)> решается нижеследующей
теоремой.
Теорема 9. Для каждого нетривиального решения
ф(£) уравнения (5) соотношение (6) однозначно*) опреде¬
*) Здесь, как и в главе 1, мы предполагаем, что рассматривае¬
мые управления полунепрерывны слева и непрерывны в концах
отрезка	(ср. стр. 15). Без этого соглашения теорема 9
была бы неточной, а именно значения функции u(t) в точках раз¬
рыва не были бы однозначно определены. Впрочем, ясно, что
значения функции и (t) в точках разрыва не играют никакой роли
в рассматриваемых вопросах.
v=l
или, в векторной форме,
(5)
(6)

§ 17]
ТЕОРЕМЫ О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
133
ляет управляющую функцию u(t); при этом оказывается,
что функция и (t) кусочно-постоянна и ее значениями
являются лишь вершины многогранника V.
Доказательство. Так как функция
(o|>(f), Ви),	(7)
рассматриваемая как функция вектора и, линейна, то она ли¬
бо постоянна, либо достигает своего максимума лишь на
границе многогранника U. Это же соображение применимо
и к каждой грани многогранника U. Таким образом, функ¬
ция (7) достигает своего максимума либо лишь в одной
вершине многогранника /7, либо на целой грани этого
многогранника *). Покажем, что в силу условия общности
положения последнее возможно лишь для конечного числа
значений t.
В самом деле, допустим, что на отрезке £0<£<^
существует бесконечное число таких значений t, для
каждого из которых функция (7) переменного и £ U дости¬
гает своего максимума на некоторой (имеющей положи¬
тельную размерность) грани многогранника U. Так как U
имеет лишь конечное число граней, то мы можем выбрать
бесконечное множество М таких значений £, для каждого
из которых функция (7) достигает своего максимума на
некоторой (одной и той же для всех t £ М) грани Г
многогранника U. Следовательно, для любого t £ М функ¬
ция (7) переменного и постоянна на грани Г. Пусть и0
и их — векторы, идущие из начала координат (простран¬
ства Ег) в концы некоторого ребра грани Г, так что век¬
тор w — их —■ Uq имеет направление этого ребра. Тогда
при t £ М мы имеем (в силу постоянства функции (7) на
грани Г)
(г|5 (<), Bw) = (ty(t), В(и1 — и0)) =
= (о]з (f), Buj) — (if (t), Ви2) = 0.	(8)
Пусть теперь ft1, ft2, ft" — координаты вектора Bw
(величины ft1, ft2,, ft" постоянны, так как да —вполне
определенное ребро многогранника U). Тогда
Сф(0> Bw) = b1ty1(t)+b2ty2(t)+ .. . +ft>n(i).	(9)
*) Сам многогранник U мы также считаем его (несобственной)
гранью,

134 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
Так как функции фг(£),	Фг(0»	•••»	Фп(0 составляют
решение \p(t) уравнения (5) с постоянными коэффициен¬
тами, то они а и а л и т и ч н ы, и потому функция (9)
также является аналитической. Для любого t£M (т. е.
для бесконечного множества значений t) аналитическая
функция (ф(/), Bw) переменного t обращается в нуль
(см. (8)), и потому на всем отрезке	имеет	место
соотношение
(Ф(0, Bw) = 0.	(10)
Последовательно дифференцируя это соотношение по t,
мы получаем (в силу того, что ф (t) есть решение уравне¬
ния (5))
(А*ф(*), Bw) = 0,
(4*2ф(£), Bw) = 0,
(A*n-^(t), Bw) = 0,
или (в силу соотношения (х, Ay) = (A*xf у), справедливого
для любых векторов х, у)
(ф(£)> ABw) = 0,
A2Bw) = о,
(4 (t), An~1Bw) = 0.
Так как, в силу условия общности положения, векторы (3)
образуют базис пространства X, то соотношения (10),
(11)	означают, что при любом t,	вектор ф(£)
ортогонален ко всем векторам некоторого базиса и потому
равен нулю, что, однако, противоречит предположению
о нетривиальности решения ф(0*
Итак, для всех, кроме конечного числа, значений £,
функция (7) достигает (на U) максимума
лишь в одной точке, являющейся вершиной многогран¬
ника U. Отсюда, в силу (6), следует однозначная опре¬
деленность функции u(t) (см. сноску на стр. 132).
Далее, выколов точки неоднозначной разрешимости
уравнения
(И>(0, Яи) = Р(Ч>(*)).	(12)

§ 17]
ТЕОРЕМЫ О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
135
мы разобьем отрезок	на	конечное	число	частей.
Нетрудно видеть, что на каждой из этих частей функ¬
ция u(t) постоянна. В самом деле, пусть / — одна из
этих частей (она может быть интервалом, полуинтервалом
или отрезком). Пусть ev е2У . .., eq — все вершины много¬
гранника U. Обозначим через Мv i= 1, 2, . . ., q, множе¬
ство тех точек t £ /, для которых решением уравнения
(12)	является точка ev Тогда Л/3, М2, . . ., Mq являются,,
согласно сказанному выше, попарно не пересекающимися
множествами, дающими в сумме / (некоторые из этих
множеств могут оказаться пустыми). Мы сейчас покажем,
что каждое из множеств М. открыто на /, откуда (в силу
связности множества /) будет вытекать, что все множе¬
ства Мъ, кроме одного, пусты, так что решение уравне¬
ния (12) постоянно на /. Тем самым теорема 9 будет
полностью доказана.
Пусть ^/ — произвольная точка множества Л/-, так
что (ф(£), Ве|) = /)(ф(^)) и (ф(*), Bej) < Р(ф(0) при 1ф /.
Так как каждая из функций (ф(£), Be;-), / = 1, 2, . .., q,
непрерывна на /, то во всех достаточно близких к t
точках множества / имеет место неравенство (ф(£), Ве{) >
>(ф(£), Bej) при / Ф i. Иначе говоря, все достаточно
близкие к t точки множества / принадлежат множеству
Мiy т. е. Mt открыто на /.
Теорема 9 доказана.
Итак, согласно теореме 9, каждое оптимальное управ¬
ление должно быть кусочно-постоянной функцией со
значениями в вершинах многогранника U. Каждую точку
разрыва оптимального управления мы будем называть
также точкой переключения. Более полно, если t' —
точка разрыва оптимального управления u(t) и если
u(t'— 0) = et, и (£' + 0) == (где е-г и — различные вер¬
шины многогранника £/), то мы будем говорить, что при
t = t' происходит переключение оптимального управления
u(t) из вершины е{ в вершину е-.
Теорему 9 можно теперь кратко охарактеризовать как
теорему о конечности числа переключений. Ясно, что
в каждом конкретном случае число переключений зависит
от значений коэффициентов системы (1), от вида много¬
гранника U и от выбора точек х0, хх. С этой точки зре¬
ния интересно сравнить между собой примеры 1 и 2,

136
ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
приведенные в § 5. В примере 1 при любом начальном поло¬
жении х0 оптимальное управление u(t) имело не более
одного переключения (т. е. имелось не более двух интер¬
валов постоянства управления u(t)), в то время как в при¬
мере 2 число переключений неограниченно увеличивается
при удалении точки х0 от начала координат (хотя для каж¬
дого фиксированного значения х0 число переключе¬
ний конечно). С чем связано это существенное различие
оптимальных управлений в двух указанных примерах?
Как показывает нижеследующая теорема 10, в своем
первоначальном виде принадлежащая А. А. Фельдбауму,
это различие связано с тем, что в примере 1 матрица
системы имеет действительные собственные значе¬
ния, а в примере 2 — к о м п л е к с н ы е.
В теореме 10 мы не будем рассматривать общий слу¬
чай произвольного выпуклого многогранника С/, а ограни¬
чимся лишь следующим случаем, весьма важным в при¬
ложениях. Именно, мы будем считать, что многогран¬
ник U представляет собой параллелепипед, определенный
в пространстве Ет переменных и1, и2, . . . , иг неравенствами
иЯ Pq, q = 1, 2, . . ., г,	(13)
Иначе говоря, мы будем рассматривать случай, когда
каждая из величин и® в уравнениях (1) представляет
собой отдельный управляющий параметр, область измене¬
ния которого не зависит от значений остальных управляю¬
щих параметров и задается неравенством (13). Условие
общности положения (стр. 131) мы по-прежнему будем
предполагать выполненным.
Теорема 10. Предположим, что область управле¬
ния U представляет собой параллелепипед (13) и что
все собственные значения матрицы (а\), составленной из
коэффициентов уравнения (1), действительны. Тогда для
каждого нетривиального решения ф(£) уравнения (5)
соотношение (6) однозначно определяет управляющую
функцию u(t) = (u1(t), u2(t), . . ., ur (t))] при этом оказы¬
вается, что каждая из функций ио (£), Q = 1, . . ., г, кусочно-
постоянна, принимает только значения aQ и PQ (см. (13))
и имеет не более п— 1 переключений (т. е. не более п
интервалов постоянства), где п — порядок системы (1).

ТЕОРЕМЫ о ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
137
Доказательство. Функция (7) в координатной
форме записывается следующим образом (ср. (4)):
Ви)= 2 (у •
Q=1 \JLI=1	J
Для того чтобы эта функция принимала максимальное
значение, необходимо, чтобы.каждая из функций
'2i%(t)bQU.e, е = 1, 2,	(14)
Ц=1
принимала максимальное значение (ибо область измене¬
ния каждой из величин и1, ..., иг не зависит от значе¬
ний остальных). Из этого, как мы сейчас покажем,
и вытекает, что величина uQ принимает только значения
aQ и pQ и имеет не более п— 1 переключений.
Очевидно, что соотношения
иг = аг при i Ф q, aQ < uQ < pQ
определяют одно из ребер параллелепипеда U. Направле¬
ние этого ребра определяется вектором
ш = (0, 0, . .., 1, .. ., 0),
где единица стоит на q-m месте. Таким образом, вектор
Bw имеет вид
Bw = (blQ, Ь\, bnQ),
и потому
(\j)(£), Bw)= У %(t)b%.	(15)
Ц=1
Если бы эта функция тождественно равнялась нулю, то,
как и при доказательстве теоремы 9 (ср. (10), (И)), мы
получили бы ф(г) = 0, что противоречит условию теоремы.
Таким образом, функция (15) при любом q = 1 э 2, . . ., 7-
не равна тождественно нулю и, следовательно, как ана¬
литическая функция, обращается в нуль лишь в конечном
числе точек, а функция (14) получается из функции (15)
умножением на	Так как функция (14) должна
достигать максимума, то величина ив' должна принимать

138 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
значение aQ, если функция (15) отрицательна, и значение
PQ, если функция (15) положительна. Иначе говоря,
точками переключения для управляющего параметра uQ
могут быть только те значения t, в которых функция (15)
обращается в нуль. Таким образом, теорема 10 будет
полностью доказана, если мы установим, что функция (15),
т. е. не равная тождественно нулю линейная комбинация
функций ф1 (t), ф2(0> • • • » Фп№’ имеет не более чем п — 1
действительных корней.
В силу известных теорем о линейных уравнениях
с постоянными коэффициентами, каждая из функций
Фх(0, Ф>2(0> •••> Фп составляющих решение уравне¬
ния (5), имеет вид
+ (16)
где Х1У К2у ..., hm — все попарно различные собственные
значения матрицы — Л*, а Д(0,/2(Д,	/т(£) — много¬
члены, причем степень многочлена Д (t) меньше, чем
кратность собственного значения Следовательно, ли¬
нейная комбинация (15) функций фхД), ф2(0> •••» Фп(0
также имеет вид (16). Все числа Xf, Х2, кт действи¬
тельны (ибо по условию все собственные значения ма¬
трицы Л, а значит и матрицы —А* действительны). Если
мы обозначим кратность собственного значения lki через
i\ (так что гх + г2 + . . . гт = п), то тогда степень мно¬
гочлена ДД) не превосходит числа 1, и потому,
в силу доказываемой ниже леммы, число действительных
корней функции (16) не превосходит числа
(7Ч — 1) + (г2 —!)+•••+ (гт — 1) + т ~~ 1 =
= г1 + г2 + . . . + rrn — 1 -= и — 1.
Тем самым теорема 10 полностью доказана.
Лемма. Пусть Xv к2, ..., \т —действительные по¬
парно различные числа, а ДД), f2(t), ..., fm(t) — много¬
члены с действительными коэффициентами у имеющие
степени kv к2, ..., кт соответственно. Тогда функция
h (0	+ и (0 ** + • • • + /ж (0 ^	(17)
имеет не более чем к1-\- к2 ■+. . . + Дп+7П~1 действи¬
тельных корней.

§ 18]
ТЕ ОРЕМЫ ЕДИНСТВЕННОСТИ
139
Доказательство. При т= 1 лемма, очевидно,
справедлива, ибо функция f1(t)eK^t имеет те же корни,
что и функция Д (t) и потому имеет не более чем кг дей¬
ствительных корней.
Предположим, что лемма уже доказана для случая*
когда в формуле (17) имеется меньше чем т слагаемых,
и докажем ее для случая т слагаемых. Допустим, что
лемма неверна и функция (17) имеет по крайней мере-
кг-\- /с2+ . . . + кт+ш действительных корней. Умножив
функцию (17) на e~%mt (что не изменит ее корней), мы
получим функцию
/i (0	/2 (t)	.
+ (18)
которая также имеет по крайней мере кг + к2 + . . . + кт + т
действительных корней. Так как между каждыми двумя
действительными корнями функции лежит по крайней
мере один корень ее производной, то (/ст+1)-я произ¬
водная функции (18) имеет по крайней мере
(к± + к2 + . . . + кт -f т) — (кт + 1) =
= /«!+...+ кт_ 1 + (т — 1)
действительных корней. Но (/ст + 1)-я производная функ¬
ции (18), как нетрудно видеть, имеет вид
gj (t)	+	g2(t)	_р.	.	_	gm_i	(£) е(Ьт-1-кт) <s (19)
причем числа — Хт, Х2 — Хт, . . ., ^?п_1 — Хт, очевидно,
попарно различны, а степень многочлена g{(t) по-прежне¬
му равна kt. Согласно предположению индукции, функ¬
ция (19) имеет не более кг + к2 + . .. + кт_1 + (пг — 1) — 1
действительных корней, вопреки тому, что было сказано
ранее. Полученное противоречие и завершает индукцию.
Таким образом, лемма доказана.
§ 18. Теоремы единственности
Решим уравнение (2), как неоднородное, методом ва¬
риации постоянных. Для этого обозначим через
<Pi (0> Фг (0> • • • > Фп (0	(20)

140 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
фундаментальную систему решений однородного уравне¬
ния
удовлетворяющую начальным условиям Ф} (£<>) ^ ^'» а
через
^(г), ^2(0,.. .,9"(0
— фундаментальную систему решений однородного урав¬
нения (5), удовлетворяющую начальным условиям
ХР{ (*о)= Легко видеть, что для всех t имеет место
соотношение
(V(0. <Pi(0) = fy *'• /= 1. 2, • • .,П.	(21)
В самом деле, в силу выбора начальных условий это
соотношение выполнено при	далее,
sj(V(0. <Pi (*)) = (-4V(0- 9i(0) + (V(0> 4ф((0) = 0-
Будем искать общее решение уравнения (2) в виде
п
x(t)= S 9v(0cV(0*
V=1
Подставляя это решение в уравнение (2), получим
2 9v(0^=-B«(0;
v=l
умножая последнее соотношение скалярно на (t)
и учитывая соотношение (21), получаем
Таким образом, решение уравнения (2) при произвольном
управлении u(t) и начальном условии x(t0) = x0 =
= (я£,	записывается	в	виде
п	t
*(0=2 9v(0C^+S^v(0. £«№)*)•	(22)
v= t	'

§ 18]
ТЕОРЕМЫ ЕДИНСТВЕННОСТИ
141
Теорема 11. Пусть иг(1) и и2(t) — два оптимальных
управления, заданных соответственно на отрезках
г0< * <	и	11	переводящих	точку	х0	в	одну
и ту dice точку хг Тогда эти управления совпадают
(см. сноску на стр. 132), т. е. t± = t2 и ul(t) = u2(t) на
отрезке £0 < £ < t1.
Доказательство. Прежде всего ясно, что t1—t2y
ибо если бы было, например, l± < t2, то управление
и = и2 (г) не было бы оптимальным.
Так как при t=tx обе траектории, исходящие из
точки х0 и соответствующие управлениям и1(1) и и2(1)}
приходят в одну и ту же точку xv то мы имеем (в си-
лу (22))
П	ti
ж1=2 <PvCi)(zo+ ^ c>v(f),
V=1	t0
П	tl
= 2 4v(h)(xo+ \ 0>v(0< Bu2(t))dtj,
V=1	to
откуда
n	ti	ti
2 4>v Cl) [ ^	('V C)>	Виг (t))	dt — ^	(гр (f),	Bu2	(t)) л]=0.
v=l	/0	*0
Так как	векторы	cpx (£г), ..., срп (^) ’’линейно	независимы,
то из последнего равенства следует, что
tl
^ (фг (t),	(£)) dt = ^ (фг (£),	(£))	i=l,...,	n.	(23)
Оптимальному управлению (г) соответствует вектор-
функция ф (г), удовлетворяющая условию (6) и являю¬
щаяся решением уравнения (3). Начальное значение этой
функции (при t = t0) обозначим через
Фо = (Фю* • • •» Фпо)>
тогда решение ф(£) можно записать в виде
п
ФС) = 2 ^vo^vO-
v= 1

142	ЛИНЕЙНЫЕ	ОПТИМАЛЬНЫЕ	БЫСТРОДЕЙСТВИЯ	[ГЛ.	3
Умножая соотношение (23) на ф|0 и суммируя по г, по¬
лучаем
Но так как, согласно соотношению (6) и определению
величины Р (ф), мы имеем (на отрезке
то из (24) вытекает, что (ф(£), Ви± (£)) — (яр (i), Bu2(t)).
Следовательно, оба управления их(1), и2(1) удовлетворяют
соотношению (6) с одной и той же функцией ф(£), и по¬
тому (в силу теоремы 9) u1(t) = u2(t).
Итак, теорема 11 доказана.
Будем называть управление u(t), £0<£<С, экстре¬
мальным, если оно удовлетворяет условию (6), где ф(£) —
некоторое нетривиальное решение уравнения (5).
Для нахождения оптимального управления, пере¬
водящего фазовую точку из положения х0 в положение хх,
можно найти сперва все экстремальные управления,
переводящие фазовую точку из положения х0 в положе¬
ние хх, а затем выбрать из их числа то (единственное в
силу теоремы И), которое осуществляет этот переход
за кратчайшее время. Возникает вопрос: может ли сущест¬
вовать несколько экстремальных управлений, переводя¬
щих фазовую точку из положения х0 в положение хх?
Вообще говоря, их может существовать несколько. Ниже¬
следующая теорема указывает важный случай единствен¬
ности для экстремальных управлений.
Теорема 12. Предположим, что начало координат
пространства ЕТ является внутренней точкой многогран¬
ника U, и пус?пь iix(t) и u2(t) — два экстремальных управ¬
ления, заданных соответственно на отрезках £0<£<CW
£0 < £ < t2 и переводящих точку х0 в начало координат х± = О
пространства X. Тогда эти управления совпадают, т. е.
tx = t2 и ux(t) ~u2(t) на отрезке £0<£<£г
Доказательство. Обозначим через xx(t) и x2(t)
траектории, соответствующие управлениям ux(t) и u2(t) и
исходящие в момент t0 из точки х0. Согласно условиям
(г|5(г), £и1(0) = 'РС'И0)>('»Иг)> Bu2(t)),

§ 18]	ТЕОРЕМЫ	ЕДИНСТВЕННОСТИ	143
теоремы мы имеем яДК) = x2(t2) — 0, или (в силу (22))
п	Ц
2 фу(«х)(^+ \ (440. Bu1(t))dt) = О,
V=1	to
П	l2
2<Pv(i2)(4 + \ (4V(0. Bu2(t))dt) = 0.
v=l	tl
Отсюда (в силу линейной независимости векторов (20) при
любом t) вытекают равенства (£ =1,2, . . ., п)
11
— 4 = . ^ (4‘ (О-	Ви} (г)) dt =	( (г|51 (г),	Ви2 («)) dt.	(25)
/о	*0
Допустим для определенности,	что t.1>t2i	и	пусть ф(0 —
то решение уравнения (5), для которого на отрезке tQ < t < tx
имеет место соотношение
(Ф(г), Bul{t)) = P{^(t))y
определяющее функцию иДг). Как и при доказательстве
теоремы 11, функцию ф (t) запишем в виде ф (£) =
п
= 2] Ф\-оф%? (0- Умножая соотношение (25) на ф10 и сумми-
v= 1
руя по г, получаем	121
t2
\(4(0. Bu^ifidl^ \	Bu2(t))dt. (26)
to	lQ
Заметим теперь, что для любого решения ф (I) урав¬
нения (5) справедливо неравенство
Р(ф(0)>0.	(27)
В самом деле, так как начало координат пространства Ет
является внутренней точкой выпуклого тела С/, то функция
(ф(/), Ви), как функция переменного и, либо тождествен¬
но равна нулю, либо может принимать как отрицательные,
так и положительные значения.
В силу (27) и (26) мы имеем неравенство
t'2	h
\ (г|з(г), Bul (t)) dt -< ((ф(0- Bu2(t))dt.
Го	to

144
ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИИ [ГЛ. 3
Отсюда так же, как и при доказательстве теоремы И,
получаем
u1(t) = u2(t) на отрезке £0<£<£2-
Учитывая соотношение (26), мы получаем отсюда
Далее, так как равенство P(ty(t)) = 0 может иметь место
только в том случае, если функция (ф(£)» £>и) равна ну¬
лю на всем многограннике С/, т. е. может иметь место
только для конечного числа значений t, то из соотноше¬
ний (27), (28) с необходимостью вытекает, что t1=t2.
Итак, теорема 12 доказана.
Замечание. До сих пор мы использовали только
условие 1°, указанное в теореме 2 (т. е. формулу (20)
гл. 1). Условие же 2° (т. е. соотношение (21) гл. 1)
мы нигде не использовали. Нетрудно видеть, однажо, что
при выполнении предположений теоремы 12 равенство
(21) гл. 1 выполняется автоматически. В самом деле, в силу
соотношений (4),	(6), (27) и соотношения (20) гл. 1,
имеем
Теорема 13. Если для процесса, описываемого урав¬
нением (2), существует хотя бы одно управление, перево-
дягцее фазовую точку из положения х0 в положение xv
то существует и оптимальное управление, переводящее
фазовую точку из положения х0 в положение хГ (Как
всегда, мы предполагаем выполненным условие общности
положения.)
Доказательство. Мы должны предполагать, что
задан некоторый класс D допустимых управлений и что
в классе D существуют управления, переводящие фазо¬
(28)
*(*,)) = # Ж*,), ^ (*х), и (*,)) =
= (г|з(^),	#“(<!))=*
= (г|) (*,), Ас,) + Р (i|) (fj) = Р (ф (*,)) > 0
(ибо ^ = 0).
§ 19. Теоремы существования

§ 19].
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
145
вую точку из положения х0 в положение хг Обозначим
через Апах наибольший класс управлений, т. е. множе¬
ство всех измеримых управлений (со значениями в С/),
а через Anin — наименьший класс управлений, т. е. мно¬
жество всех кусочно-постоянных управлений (со значе¬
ниями в U). Таким образом, Z)max ID D ZD Amn-
Докажем прежде всего, что в классе Апах сущест¬
вует оптимальное управление, переводящее фазовую точку
из положения х0 в положение xv Обозначим через А
совокупность всех управлений класса Апах, переводящих
фазовую точку из положения х0 в положение xv Множество
Д непусто, так как, по предположению, в классе D
(а значит—и в Апах) существуют управления, переводящие
фазовую точку из положения х0 в положение хх. Каждому
управлению и (t) £ А соответствует время перехода (из
положения х0 в положение яД. Нижнюю грань всех таких
времен при и (t) £ А обозначим через t* и докажем, что
существует управление н* (t), переводящее точку х0 в точку
хх за время t*. Ввиду возможности производить сдвиг
времени (см. условие 3) в § 10), мы можем ограничиться
рассмотрением лишь таких управлений, которые заданы
на отрезках вида 0 < t < tv
Выберем из множества А такую бесконечную последо¬
вательность управлений {И/Д£)}» заданных соответственно
на отрезках 0< t < tk (к= 1,2,...), что имеет место ра¬
венство
lim tk = t*.
k-+co
Обозначим через x}l(t) траекторию, соответствующую
управлению uk (t) и исходящую в момент t = 0 из точки
£0; тогда xk(tll) = x1. Мы имеем
п	lh
lim 2 (<Pv(**) - Фу (О) (®Jf + { (\|5V (t), Buh («)) dt) = 0
h-+ со ,	4	J	У
v=l	0
(ибо второй множитель под знаком суммы ограничен,
а первый стремится к нулю); точно так же
н.
lim 2cM<*)Q	Buh(t))dt)j	=	0.
/l"400v=i	t*
Ю Л. С. Понтрягин

146	ЛИНЕЙНЫЕ	ОПТИМАЛЬНЫЕ	БЫСТРОДЕЙСТВИЯ	[ГЛ.	3
Из этих соотношений следует, что
п
<•
lim У, фv(t*)( xv0+ \ Hv(0. Buk{t))dt)
k^co л	Л	J	У
n
k
Рассмотрим теперь гильбертово пространство Ь2 всех
измеримых функций с интегрируемым квадратом, заданных
на отрезке 0<£<£*. Управление u,(t) есть вектор-функ¬
ция; г-ю координату этой вектор-функции обозначим через
гг*(£). Функция	рассматриваемая	на	отрезке 0<£<
< £*, принадлежит пространству L2 (она измерима и ог¬
раничена). Совокупность всех функций ^((), к= 1, 2, ...
при каждом фиксированном i ( = 1, 2, . . ., г), очевидно,
принадлежит некоторому шару пространства Ь2, и потому
из нее можно выбрать слабо сходящуюся подпоследова¬
тельность*). Мы будем просто считать, что сама после¬
довательность
слабо сходится к некоторой функции и1 (£), £ = 1, 2, ..., г.
Докажем теперь, что вектор-функция
почти для всех значений t удовлетворяет условию
гг* (t) £ U. Возьмем какую-либо (г — 1)-мерную грань Г
многогранника U и пусть L (и) = 2	—	такая	линей-
Q= 1
на я форма переменных гг1, гг2, . . ., ггг, что уравнение не¬
сущей плоскости грани Г имеет вид L(u) = b, а сам мно¬
гогранник U расположен в полупространстве L(u)^b.
Пусть, далее, т — множество всех точек t отрезка [0, £*],
*) См., например, Л. А. Лю стерни к и В. И. Соболев,
Элементы функционального анализа, Гостехиздат, М. — Л., 1951,
стр. 194—196.
и\ (0, в* (t), .. ., ul (t), .. .
(30)
в*(0 = (в1(0. и® (0 иг (0)
г

ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
147
для которых L (гг* («)) > by a v(t) — характеристическая
функция множества т. Эта функция измерима и ограни¬
чена (т. е. принадлежит L2) и потому, в силу слабой
сходимости последовательностей (30), мы имеем
t*
lim \ v (l) [L (гг* (0) - L (щ, (t))] dt = 0.
/г->оо J
Так как, далее, L (и* (t)) — L (и; (t)) > 0 на множестве т
(ибо L (и, (£))< Ь), то mes^ = 0. Итак, почти для всех t}
принадлея^ащих отрезку 0<£<£*, точка и* (t) лежит
в том же полупространстве L (и) < Ь, что и многогран¬
ник U. Так как это рассуждение применимо к любой
грани Г многогранника U, то u*(t)£U почти для всех t.
Так как изменение значений функции u* (t) на мно¬
жестве меры нуль не нарушает слабой сходимости после¬
довательностей (30) к функциям и1 (t), i= 1, 2, . . ., г, то
мы можем без ограничения общности считать, что
u*(t)£U при всех ty 0<£<£*.
Из соотношения (29) в силу слабой сходимости после¬
довательностей (30) следует
п	t*
2 фУ(^*)Гжо + 5 (аГ(*)>
v=l	0
Таким образом, и* (t) является измеримым оптималь¬
ным управлением, переводящим фазовую точку из поло¬
жения х0 в положение xv т. е. в классе Dmах существует
оптимальное управление. В силу теоремы 2 (см. также
теорему 8) отсюда вытекает существование такого
нетривиального решения ф(£) уравнения (5), что (см. (6))
почти всюду на отрезке 0 < t < t*
(Ф(г), Bu*{t)) = Pft№
Следовательно, согласно теореме 9, управление гг* (с)
можно считать (изменив его на мноячестве меры нуль —
что не нарушит его оптимальности) кусочно-постоянным.
Таким образом, управление гг* (t) принадлежит классу
Anin» а следовательно, и классу D. Оно осуществляет пере¬
вод фазовой точки из положения х0 в положение х1 за
наименьшее время по сравнению с любыми управлениями
10*

148	ЛИНЕЙНЫЕ	ОПТИМАЛЬНЫЕ	БЫСТРОДЕЙСТВИЯ	[ГЛ.	8
класса Z)max, а потому и по сравнению с любыми управ¬
лениями класса В.
Итак, в классе D существует оптимальное управле¬
ние, и теорема 13 доказана.
Замечание. Если заданный класс D допустимых
управлений совпадает с классом Втах всех измеримых
управлений, то, как видно из доказательства, в форму¬
лировке теоремы 13 можно не требовать выполнения
условия общности положения (это условие требуется липть
в связи со ссылкой на теорему 9).
Теорема 14. Предположим, что в уравнении (2)
оператор А устойчив, т. е. все его собственные значения
имеют отрицательные действительные части, и что на¬
чало координат пространства Ег является внутренней
точкой многогранника £7. (Условие общности положения
по-прежнему предполагается выполненным.) Тогда для
любой точки х0£Х существует оптимальное управление,
переводящее фазовую точку из положения х0 в начало
координат 0 £ X.
Доказательство. Докажем прежде всего, что су¬
ществует окрестность V начала координат 0 пространства
X, каждая точка х0 которой может быть при помощи
некоторого управления переведена в 0. (При доказатель¬
стве этого утверждения устойчивость оператора А не ис¬
пользуется.)
Обозначим через Ф (£) матрицу, столбцами которой
служат координаты векторов фх (£),..., cpn (t) (см. (20)),
т. е. Ф (£) = (ф) (£)). Так как векторы (20) образуют фун¬
даментальную систему решений уравнения
и удовлетворяют условиям ф) (0) = 6j (мы считаем, что
t0 = 0), то имеют место соотношения
™М = АФ((), Ф(0 ) = Е,
откуда получаем
Ф (t) = eiA.
Далее, обозначим через Т* (£) матрицу, строками которой

ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
149
служат координаты векторов я))1 (t), . . ., г|)п (t), т. е.
W (t) = (ify(O)* Соотношение (21) записывается теперь
в виде W (t) Ф (t) = Еу откуда
Полученные выражения для матриц Ф(£) и 4я (t) позво¬
ляют переписать равенство (22) в виде
t
x(t) = etA(x0 + \e~tABu{t)di)\	(31)
4 о	У
здесь х (t) — траектория, соответствующая управлению
u(t) и исходящая в момент £ = 0 из точки х0.
Выберем теперь в U такой вектор v, чтобы вектор — v
также принадлежал U и чтобы вектор
b = Bv
не принадлежал никакому истинному подпространству
пространства X, инвариантному относительно оператора А.
Такой вектор v существует в силу того, что начало ко¬
ординат пространства Ет является внутренней точкой
многогранника U и выполнено условие общности поло¬
жения. При достаточно малом положительном е операто¬
ры А и е~еА имеют совпадающие инвариантные подпро¬
странства *), и потому векторы
е~гАЬу е~2еАЪ, е~пеАЬ	(32)
линейно независимы.
*) Этот факт, относящийся к матричному исчислению, можно
доказать, например, следующим образом. Пусть матрица
М = е~еА — Е\ тогда она представляется в виде сходящегося мат¬
ричного ряда
м=—^А + ^-А* —(*)
Из этого следует, что любая матрица С, представляющаяся в виде
сходящегося степенного матричного ряда
С = а0Е + а1М + а2М2 + а3М3+- • ■,	(**)
перестановочна с матрицей А. Каждое собственное значение мат¬
рицы М имеет вид е~е^—1, где X— собственное значение матрицы Л,
и потому существует такое ев > 0, что при 0 < в < е0 собст-

150 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИИ [ГЛ. 3
Определим, далее, функцию сг(£, т, £) переменного I,
где т и | — действительные параметры, считая ее равной
sign £ на интервале между точками т и т + £ и равной
нулю вне этого интервала. Наконец, определим управле¬
ние u = u(t, .. ., fu), зависящее от н действительных
венные значения матрицы М лежат в единичном круге. Следова¬
тельно (см. Л.С. Понтрягин, Обыкновенные дифференциальные
уравнения, Физматгиз, 1961, стр. 302 — 303), существует такая
матрица С, представимая в виде степенного ряда (**), что
ес = М-\-Е, т. е. ес = е~еЛ. При этом собственные значения мат¬
рицы С можно предполагать как угодно близкими к нулю (при
достаточно малом е0). Так как матрицы А ж С перестановочны,
то из соотношения ес = е~еА вытекает, что ес~^еА = Е, и потому
все собственные значения матрицы С-\-еА имеют вид 2kzti. Так
как, кроме того, они близки к нулю (при малом е0), то все собст¬
венные значения матрицы С-\-гА равны нулю. Пусть S — такая
матрица, что матрица G = S (C-f еЛ) S~l имеет жорданову форму.
•Тогда, умножая соотношение ес~^гЛ = Е слева на S, а справа на
S'1, мы получим eG = E, т. е.
£' = jB,+ G+-|-G2+4-G3+...	(***)
Но так как все собственные значения матрицы G равны нулю, то
все элементы этой матрицы, стоящие на главной диагонали и вы¬
ше нее, равны пулю. Поэтому в матрицах G2, G3, G4, .. . все эле¬
менты, стоящие непосредственно под главной диагональю, также
равны нулю. Тогда из (***) следует, что и в матрице G все
элементы, стоящие непосредственно под главной диагональю,
равны нулю, т. е. G — нулевая матрица (напомним, что G имеет
жорданову форму). Следовательно, и С + еА — нулевая матрица,
т. е. С=—еА.
Из (**) следует теперь, что матрица А представляется в виде
сходящегося степенного ряда
А= —(а0Е + а1М + агМ2 + а3М3+...).	(****)
8
Всякое инвариантное подпространство матрицы А является
в силу (*) инвариантным подпространством и матрицы М. Обратно,
всякое инвариантное подпространство матрицы М является в силу
(****) инвариантным подпространством матрицы А. Таким образом,
матрицы Л и!(а значит также матрицы А и е~гА =М-\-Е) име¬
ют общие инвариантные подпространства (если е настолько мало,
что проведенные рассуждения применимы).

§ 19]
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
151
параметров I1,..., £п, положив
п
и(1,	...,Г)	=	у	Sor(f,	/се,	Iй);
fe=l
это управление мы будем рассматривать на отрезке
О<£<£х, где ^ — фиксированное положительное число,
и при достаточно малых е>0 и .. ., Траектория,
соответствующая управлению u(t, g1, . . ., gn) и исходящая
в момент £ = 0 из некоторой точки ж0, оканчивается (в мо¬
мент t = t1) в точке
Так как при = . . . = |п = 0 сумма, стоящая в (33)
под знаком интеграла, обращается в нуль, то
то, дифференцируя соотношение (33), мы получим
переменных х\, х\у . . ., х* (т. е. координат точки по
переменным £2, . .., £п равен |е^А|-Д, где Д — опре¬
делитель матрицы, составленной из координат векторов
и, кроме того, при достаточно малом е, Д Ф 0 (ибо векторы
xi — xi (хо> &1»	•	•	•» £ ) ""
(см. (31)).
(х0 + \ e~tA b dty
fee
Отсюда вытекает, что якобиан
д (х\, х\, . .	х?)
Б* Бл) &■=&= • • • =£п=о
(35)
(32). Так как определитель матрицы отличен от нуля

152
ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
(32) линейно независимы), то якобиан (35) отличен от
нуля.
Итак, мы можем выбрать в предыдущих построениях
параметр е настолько малым, что якобиан (35) будет от¬
личен от нуля. Кроме того, имеет место соотношение (34).
Из этого, в силу теоремы о неявных функциях, вытекает
разрешимость уравнения
«л*». 51. £2- ....Г) = 0
относительно £2, . . ., |п для всех значений х0, принад¬
лежащих некоторой окрестности V начала координат О £X.
Иначе говоря, для любой точки х0 £ V существует такое
кусочно-постоянное управление и (а именно, управление
u(t, I1, . . ., £п), 0<£<£г, при надлежащим образом вы¬
бранных . . ., £п), которое переводит фазовую точку из
положения х0 в начало координат (за время £2).
Пусть теперь х0 — произвольная точка пространства X.
Заставим фазовую точку сначала двигаться из положения
х0 при управлении u(t) = 0. Так как все собственные
значения оператора А имеют отрицательные действитель¬
ные части, то по истечении некоторого времени движу¬
щаяся точка придет в окрестность У, после чего ее, по
доказанному, можно перевести в начало координат. Отсю¬
да в силу теоремы 13 вытекает существование опти¬
мального управления, переводящего фазовую точку из
положения х0 в начало координат.
Итак, теорема 14 доказана.
Следствие. Предположим, что начало координат
пространства Ег является внутренней точкой многогран¬
ника U. Обозначим через 2 т множество тех точек £0£Х,
которые могут быть (при помощи надлежаще выбранного
управления) переведены в начало координат 0 £Х за вре¬
мя <7" (где Т — некоторое положительное число). Тогда
2 т есть замкнутое выпуклое множество пространства X,
имеющее внутренние точки (т. е. выпуклое тело).
Доказательство. Обратимся к доказательству
теоремы 14, взяв в нем tx = Т. Тогда мы получим такую
окрестность V начала координат Of X, что для любой
точки х0 £ V существует кусочно-постоянное управление,
которое переводит фазовую точку из положения х0 в на¬
чало координат (за время Т). Иначе говоря, Ус2т, т. е.

§ 19]
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
153
начало координат является внутренней точкой мно¬
жества 2т- Замкнутость множества 2т легко следует из
теоремы существования.
Остается доказать, что множество 2т выпукло. Пусть
xi = (xv xv • • •» x1i)	11	Х2	= (х2> х2>	• • • > х2) — Две точки	мно¬
жества	2т, a	u^t)	и	u2(t) — управления,	переводящие
фазовую точку из положений xv х2 в начало коор¬
динат за время < Т. Будем предполагать оба управления
lh(t) заданными на всем отрезке О<£<Г, считая
их равными нулю от момента попадания фазовой точки
в начало координат и до момента Т. Тогда u1{t) и u2(t) —
управления, заданные на отрезке 0 < t < Т и переводящие
за время Т фазовую точку из положений хг и х2 в начало
координат, т. е. в силу (22)
п	т
2 <Pv (Т) (х\ + 5 ('F (0. Вих (0)dt) = 0.	(36)
v=l	О
п	,	т
29v(7’)f^+ ^(xlpv(t),Bu2(t))dt^J = 0.	(37)
v=l	V	О
Пусть теперь ах и а2 — произвольные положительные числа,
удовлетворяющие условию а: + а2 = 1; положим х0 = а1х1 +
+ а2х2, w0 (t) = а1и1 (t) -f а2и2 (t). Тогда точка х0 располо¬
жена на отрезке, соединяющем точки хг и х2> а точка
u0(t) — на отрезке, соединяющем точки Uy(t) и u2(t) (при
любом t, 0 < t < Т), так что u0(t)£U при любом t (ибо
U — выпуклый многогранник). Таким образом, u0(t) —
допустимое управление, заданное на отрезке 0<г<7\
Умножая соотношения (36), (37) соответственно на av а2
и складывая, получаем
п	т
2 Фу (Г) (я* + \ (V(t),Bu0(t))dt) = 0.
v=l	о
Таким образом, управление и0 (t) переводит фазовую
точку из положения х0 в начало координат за время 7\
т. е. £0£2г. Итак, любая точка отрезка, соединяющего
точки Ху и х2, принадлежит множеству 2т, и потому
множество 2т выпукло*

154
ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
§ 20. Синтез оптимального управления
В главе 1 мы рассмотрели на конкретных примерах
задачу синтезирования оптимальных управлений. Эта
задача имеет смысл для произвольного управляемого
процесса (см. формулу (4) в § 2). Однако здесь мы будем
рассматривать лишь линейные системы вида (1), удов¬
летворяющие условиям, указанным в формулировке тео¬
ремы 14 (по поводу условия устойчивости оператора А
см. замечание в конце этого параграфа). Для таких си¬
стем имеют место теоремы существования и единственнос¬
ти (теоремы 14 и 12), благодаря чему задача синтеза
является в принципе решенной. Приводимые здесь сооб¬
ражения дают конструктивный метод решения этой за¬
дачи. Осуществление этого метода в каждом конкретном
случае требует, однако, ряда построений.
Синтезирование оптимального управления линейной
системы (1) было осуществлено ранее (совершенно дру¬
гими методами, т. е. без использования принципа макси¬
мума) лишь для случая одного управляющего параметра
(т. е. при r = 1)—А. А. Фельдбаумом при действительных
корнях оператора А и Д. Бушоу в случае, когда п = 2, а соб¬
ственные значения оператора А комплексны. Использова¬
ние принципа максимума дает возможность значительно
проще получить указанные результаты (см. примеры, из¬
ложенные в § 5). Ниже мы покажем, каким образом с
помощью принципа максимума можно при п = 2 построить
синтез систем оптимального управления с двумя управ¬
ляющими параметрами.
В этом параграфе мы изложим общие соображения о за¬
даче синтеза оптимальных управлений. Мы будем счи¬
тать, что выполнены условия, сформулированные в тео¬
реме 14. Тогда для каждой точки я0 G X существует и
притом только одно оптимальное (кусочно-постоянное)
управление ux^(t), переводящее фазовую точку из точки х0
в начало координат OgX. Единственность имеет место,
конечно, только с точностью до сдвига времени и до значе¬
ний управления uXq (t) в его точках разрыва. Так как в каж¬
дый момент времени нас, естественно, интересует, каким
будет оптимальное управление после этого момента вре¬
мени, то (в отличие от ранее принимавшихся согла¬

§ 20]
СИНТЕЗ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
155
шений — см. стр. 15 и сноску на стр. 132) целесообразнее
всего считать в каждой точке разрыва V управления ux^(t)
его значение равным ux (t'-\- 0). При этом соглашении во
все моменты времени (кроме конечного, когда значение
управления не играет роли) выполняется соотношение
и*о(0 = и*0(* + 0).
благодаря чему устраняется неоднозначность управления
ux^(t) в начальный момент и в точках разрыва.. Величи¬
на uXQ{t0) зависит, таким образом, только от точки х0,
а не от случайно выбранного начала отсчета времени £0,
и потому можно положить
Фо) = %(*(>)'
Пусть х (t) — решение уравнения (2), соответствующее
управлению их^ (£), а t0 < t < tx — промежуток времени,
в течение которого точка, двигаясь при этом управлении,
переходит из положения х0 в начало координат. Так
как для любой точки т, взятой из этого промежутка вре¬
мени, управление их (t), рассматриваемое на отрезке
оптимальным образом переводит фазовую
точку из положения х(х) в начало координат (иначе все
управление в целом не было бы оптимальным), то имеет
место соотношение
иХо(х) = V (х (х)).
Таким образом,
-jfX(t) = Ах (i) + Bv (х (t)),
и мы видим, что решение уравнения
= Ах + Bv (х)
с произвольным начальным условием x{t^) = xQ дает закон
оптимального движения фазовой точки из положения х0
в начало координат. В этом смысле функция v(x) синте¬
зирует оптимальное управление, переводящее фазовую
точку из любой точки х0 в начало (ср. § 5). В нахождении
функции v(x) и заключается решение задачи синтеза
оптимального управления (для линейной системы (2)).

156 ЛИНЕЙНЫЕ оптимальные БЫСТРОДЕЙСТВИЯ [ГЛ. 3
Дадим метод построения функции v(x). Пусть ф(0“~
то (нетривиальное) решение уравнения (5), которое в си¬
лу теоремы 2 соответствует управлению ux^(t)y так что
Пусть, далее, х (t) — решение уравнения (2) с управле¬
нием u — ux^(t)y удовлетворяющее начальному условию
Из теоремы существования и единственности следует,
что существует, и притом только одна (с точностью до
сдвига времени), пара функций wx(£), x(t)y заданных на
отрезке t0 < t < t± и удовлетворяющих условиям (38) — (42).
Ввиду возможности сдвига времени числа t0 и tx этими
условиями не определены однозначно, но число t± —10
определено.
Совершенно не ясно, как искать функции ux^(t)y x{t)y
удовлетворяющие всем условиям (38) —(42), но легко
найти все функции ux^(t)yx(t)y удовлетворяющие лишь
условиям (38), (39), (41), (42). Для этого поступим сле¬
дующим образом. Ввиду возможности произвольного
сдвига времени зафиксируем число tly положив Ьг = 0.
Пусть теперь % = (Xi> %2> •• • > %п) — произвольный вектор,
(38)
(39)
Х (^о) — хо
(40)
и конечному условию
х (£j) = 0,
(41)
так что
*£L = Ax(t) + BuXo(t).
(42)
(43)

СИНТЕЗ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
15?
отличный от нуля, и г|)(£, х) —решение уравнения (38),
удовлетворяющее начальному условию
Ф (°> х) = X
и определенное при г<0. Определим, далее, функцию
u(t, х) из условия
(Ф (*. х)> Ви (*. х)) = р (Ф (*> х))> 1 <
и функцию а:(£, х)> удовлетворяющую начальному условию
ж(0, х) = 0, — из уравнения
X) + B.u(t, х).
Согласно сказанному выше, функция v(x) определится
соотношением
(Ф (*. X). Bv (х (t, х)>) = ^ (Ф (*, X))-	(44)
Из теоремы существования (теорема 14) следует, что
точка x(t, х) описывает все пространство X, когда t
пробегает отрицательные значения, а вектор х меняется
произвольно. Таким образом, соотношение (44) определяет
значение функции v {х) для произвольной точки х простран¬
ства X.
Заметим, что условие устойчивости оператора А ис¬
пользовалось в предшествующих рассуждениях лишь один
раз, а именно в конце предыдущего параграфа, когда
показывалось, что из любой точки пространства X можно
подойти как угодно близко к началу координат. Поэтому
все выводы настоящего параграфа сохраняют свою силу
и в том случае, когда оператор А не является устойчивым,
но за счет выбора надлежащего управления и (t) можно
из любой точки х0 £ X подойти как угодно близко к на¬
чалу координат (см. пример 1 в § 5). Если, однако, и
это условие не выполняется, то синтез все равно воз¬
можен, но не для всего пространства X, а лишь для
некоторой его области. Именно, обозначим через У мно¬
жество тех точек пространства X, из которых можно
(с помощью надлежащего управления) как угодно близко
подойти к началу координат. Тогда функцию v {х) можно
построить (предполагая, что начало координат простран¬
ства Ет — внутренняя точка многогранника U и что

158 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ
[ГЛ 3
выполнено условие общности положения) на множестве У,
что и дает в этом случае решение задачи синтеза. При
этом совсем не нужно заранее проверять, из любой или
не из любой точки можно попасть в начало координат:
если решать задачу синтеза, как указано выше (т. е.
пользуясь «попятными движениями» из начала координат),
то множество всех тех точек пространства X, в которые
мы сможем попасть (на основании формул (38), (39), (41),
(42)), исходя из начала координат, и будет представлять
собой область У, для которой задача синтеза допускает
решение.
Множество У является открыты м, т. е. вместе с каж¬
дой точкой содержит и некоторую ее окрестность. В са¬
мом деле, пусть х0£ У и и (£), t0 < t < tv -- оптимальное
управление, переводящее фазовую точку из положения х0
в начало координат. Пусть, далее, V — такая окрестность
начала координат, из каждой точки которой можно (с по¬
мощью надлежащего управления) попасть в начало коор¬
динат. В силу теоремы о непрерывной зависимости ре¬
шений дифференциальных уравнений от начальных зна¬
чений существует в X такая окрестность W точки х0,
что фазовая траектория, соответствующая тому же управ¬
лению u(t),	и	исходящая в момент tQ из любой
точки у0 £ W, оканчивается в момент t± в некоторой точке
множества V. Следовательно, любая точка у0 £ W может
быть при помощи надлежащего управления переведена
в начало координат, т. е. WciY. Таким образом, мно¬
жество У открыто. Далее, так как из любой точки х0 £ У
можно за конечное время попасть в начало координат,
то (см. следствие из теоремы 14)
со
Y= IJ 2Т,
Т=1
т. е. У представляется в виде объединения возрастающей
последовательности выпуклых множеств и потому само
является выпуклым множеством.
Итак, множество Y всех тех точек пространства X,
из которых можно попасть в начало координат, пред¬
ставляет собой открытое выпуклое множество простран¬
ства X. Внутри этого множества Y задача синтеза опти¬
мальных управлений допускает решение.

§ 21]
ПРИМЕРЫ
159
§ 21. Примеры
Пример 1
(Система второго порядка с двумя управляющими
параметрами и комплексными собственными значениями.)
Рассмотрим систему уравнений
—jj- = а\хх +	+	Ъ\их	-(-	Ь\и2,	)
dx2	о	(	(^)
-j- = а]х1 + а\х2 + Ь\их + Ь\и2	I
в предполоя^ении, что собственные значения матрицы (aj.)
комплексны, т. е. (а\ — а22)2 + ка\а\ < 0. Область управле¬
ния U пусть определяется неравенствами
|и1)<1>	| гг21 < 1.	(46)
Если ранг матрицы (Ь1.) меньше двух, то столбцы этой
матрицы пропорциональны, т. е. b\ = ltb\{i= 1, 2), и потому
система (45) записывается в виде
/7л»1
— = а{хх + а\х2 + Ь\ (и1 + ки2),
= а\х1 + а\х2 + Ь\ (и1 + ки2).
Здесь их-\-ки2 есть величина, которая может принимать
произвольные значения, подчиненные неравенству
| и1 + ки21 < 1 + | к [.
Таким образом, система (45) представляет собой в этом
случае систему с одним управляющим параметром п =
= и1	+ ки2.	Мы исключим	этот случай из	рассмотрения,
т.	е.	будем	предполагать,	что определитель матрицы (6j)
отличен от нуля.
Собственные значения матрицы (а)) обозначим через
^ ± i|i,	где	р, Ф 0; можно считать, что р	>	0.	Все	даль¬
нейшие	рассуящения не зависят от знака	к,	но	для	опре¬
деленности мы будем рассматривать случай к < 0.
Линейным преобразованием переменных
yl=s\x1+sltx*,\
У2 = SjX'1 + s\x2 \

160 линейные оптимальные быстродействия [гл. з
систему (45) можно привести к виду
= Ц1 — W2 + сХ + с\и2,
% = R/1 + ^У2 + сХ+с*и2.
(48)
где коэффициенты с\ очевидным образом выражаются че¬
рез элементы матриц (fej) и (sj). Так как независимое пере¬
менное t (время) не подвергается преобразованию, а фор¬
мулы (47) однородны, то оптимальные траектории системы
(45), ведущие в начало координат, переходят при пре¬
образовании (47) в оптимальные траектории системы (48),
ведущие в начало координат. Ввиду этого мы можем
рассмотреть лишь синтез оптимальных траекторий системы
(48), откладывая переменные у1 и у2 по осям координат.
Получив этот синтез, мы с помощью аффинного преобра¬
зования (47) найдем и синтез оптимальных управлений
для системы (45). Плоскость переменных у1, у2, мы будем
обозначать через я.
Положив
При этом из (49) следует, что точка (и1, гг) при всевоз¬
можных значениях гг1, гг2, удовлетворяющих неравенствам
(46), описывает в плоскости я параллелограмм с
вершинами в точках
(49)
мы сможем записать систему (48) в виде
(50)
Этот параллелограмм мы обозначим через V (рис. 33).
Итак, мы приходим к задаче о синтезе оптимальных
управлений для системы (50), при условии, что точка

21
ПРИМЕРЫ
101
v = (v1, v2) пробегает в плоскости я переменных ?Д у2
некоторый параллелограмм V с центром в начале коор¬
динат. Эту задачу мы и будем рассматривать.
Система (5) принимает в случае управляемого процесса
(Г)0) следующий вид:
— = _
~dt =	2	*	j
Непосредственно находим общее решение этой системы:
л|?х = се~и cos (ц/ + а),
ф2 = се~и sin (fit -f а),
где с>0 и а —постоянные интегрирования. Так как
координаты вектора ф = (фА, ф2) мы рассматриваем лишь
с точностью до общего положительного множителя про¬
порциональности (ибо функция II однородна относительно
величин ф.), то мы можем отбросить положительный
множитель пропорциональности се~и и считать, что
вектор ф задается соотношениями:
ф1 = cos ([it + а), ф2 = sin (М^ + °0-
Иначе говоря, вектор ф=(ф1, ф2) равномерно вращается
(вокруг начала координат) против часовой стрелки с угло¬
вой скоростью ц (напомним, что ц >0).
II Л. С. Поптрягпп

1К2
[ IT Н Е ЙIIЫ Е ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ
[ГЛ. Л
Обозначим теперь вершины параллелограмма V через
rv е2, е3, е4, нумеруя их против часовой стрелки. Далее,
проведем из начала координат прямые, перпендикуляр¬
ные сторонам параллелограмма V, и обозначим образуемые
этими прямыми углы через аг, «2, а3, а4 (рис. 34). Так
как функция Я в рассматриваемом случае имеет вид
Я
(многоточием обозначены члены, не содержащие v1 и и2),
то из рис. 35 ясно, что если вектор ф находится в угле
а{ (г=1, 2, 3, 4), то мак¬
симум функции Я при
v £ V достигается в верши¬
мо и — е-ь. Вспомнив теперь,
что вектор ф равномер¬
но вращается с угловой
скоростью р, мы приходим
к следующему выводу от¬
носительно оптимальных
управлений. В течение вре-
сн
мени управляющий па¬
раметр v имеет значение ei7
затем и «переключается»
в вершину ei+1, где нахо¬
дится в течение времени
Iх
(при i = 4 следует считать, что i-fl = l), после этого
«переключается» в вершину ei+2 и т. д. При этом пер¬
вый и последний отрезки времени могут быть меньше
соответствующих величии ^ , так как в начальный момент
движение могло начаться не в момент «переключения»,
а в конце движение может прекратиться (т. е. фазовая
точка попадет в начало координат) до момента очередного
переключения.
Обозначим теперь через е[ такую точку (а\, at) плоско¬
сти л, координаты которой удовлетворяют соотношениям
Ха-—ца! = — v\, у
рл) + Ха\ = — v\, \
где v\, v1 — координаты вершины параллелограмма V.
(51)

§ 21]
и Р11 М КРЫ
163
Тогда мы получим четыре точки е[, е2, е'ъ, щ, являющиеся
вершинами некоторого параллелограмма V' (ибо соотно¬
шения (51) линейны). Из вида формул (51) легко выте¬
кает, что параллелограмм V' получается из V подобным
преобразованием (с центром в начале) и поворотом
на некоторый угол (рис. 36). Из формул (50), (51) выте¬
кает, что в то время, когда управляющий параметр v.
принимает значение е-, изменение координат у1, у1
описывается уравнениями
dy
-^- = 4^- ai) И" (?/2	а»)>
^ = Iх (у1 - п\) + Ь (?/2 - at)
(при v = ei).\
(52);
(53)
(52)i и (53)
переносом;
i/1
Сравнивая систему (52) с системой
мы видим, что «фазовые портреты» систем
получаются друг из друга параллельным
именно, положение равнове¬
сия системы (52){ расположе¬
но не в начале координат
(как у системы (53), рис. 37),
а в точке е[.
Вспоминая сказанное вы¬
ше о характере оптимальных
управлений, мы получаехМ сле¬
дующее утверждение о струк¬
туре оптимальных траекто¬
рий. В течение времени ^ точ¬
ка описывает дугу фазовой траектории системы (52)., затем
в течение времени ее движение описывается системой
(52).+1, после этого вступает в действие система (52)i+L>
и т. д. (первый и последний отрезки времени могут быть
■меньше, чем соответствующие величины j .
II::

164 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИИ [ГЛ. 3
Теперь уже нетрудно построить на плоскости л
«линии переключения», определяющие синтез оптималь¬
ных управлений. Обозначим через	1,	2,	3,	4)	дугу
траектории системы (52)., оканчивающуюся в точке О
и соответствующую отрезку времени — (рис. 38). Тогда
Р
ясно, что заключительный этап оптимального дви¬
жения фазовой точки происходит по одной из дуг АьО,
причем точка может пройти не всю эту дугу, а лишь
некоторую ее часть Х{0 ^так как последний отрезок вре¬
мени может быть меньше, чем . Далее, так как в точке
Xt произошло «переключение», и фазовая точка после
«переключения» стала двигаться согласно системе (52)р

§21]	ПРИМЕРЫ	165
то перед моментом переключения фазовая точка двига¬
лась по закону (52)i._1. Таким образом, предыдущий отре¬
зок YiXi оптимальной траектории представляет собой
дугу траектории системы (52)^, оканчивающуюся в точке
Х{ и соответствующую отрезку времени . Когда точка
XL пробегает всю дугу
АьО, дуги YiXi указан¬
ного вида заполняют
«криволинейный четы¬
рехугольник» (рис. 39),
одна из «сторон» ко¬
торого совпадает с ду¬
гой А{10 (ибо при
Xt = 0 дуга YiXi сов¬
падает с А^О). Та¬
ким образом, три
вершины рассматриваемого криволинейного четырех-
Тогда дуга В{_ЛАЬ_Х пред¬
ставляет собой геоме¬
трическое место точек
У|, т. е. тех точек оп¬
тимальных траекто¬
рий, в которых про¬
исходит переключе¬
ние (от системы (52)U2
к системе (52)i_1).
Легко понять, что
дуга Bi_1Ai г получа¬
ется из дуги А.р при
помощи подобного
kai-i преобразования с цен¬
тром: e^-i и коэффициентом е ^ и поворота вокруг цент¬
ра 1 на угол а-_1 по часовой стрелке. В самом деле, ре¬
шения системы (53) в полярных координатах (2/1 = pcoscp,
у2 = Q sin ф) имеют вид
угольника находятся в точках Aif су, а{_г; четвертую
вершину обозначим через Вь
q = cekt,
1 де с > 0 и а — постоянные интегрирования. Если точка

166 ЛИНЕЙНЫЕ оптимальные быстродействия [ГЛ. 3
движется по этому закону, то по истечении отрезка вре¬
мени, имеющего длину т, радиус-вектор движущейся
точки увеличивается в еКх раз
и поворачивается на угол р/г.
При т = мы и получаем
требуемое утверждение: век¬
тор, идущий из точки
в точку Xit получается из
вектора, идушдго в точку У;
У' (рис. 40), увеличением дли-
ны в в & раз и поворотом на
угол ai_1 (против часовой
стрелки).
Итак, подобное преобразование с центром \ и коэф-
фициентом е ^ , сопровождаемое поворотом (но часовой
стрелко)1на угол а;_,, переводит дугу ОАх в дугу Ai xBl v
У'
Рис. 41.
на которой происходят «переключения» от системы (52)._2
к системе (52)-_1 (рис. 41).
Перед тем как произошло переключение в точке Y-b,
фазовая точка двигалась но закону (52). 2 в течение

§21]
ПРИМЕРЫ
i(J7
времени (дуга ZiYi на рис. 42). Когда точка
[X
пробегает всю дугу Аь1 Bi v дуги ZiYi указанного вида
заполняют «криволинейный четырехугольник», двумя сто¬
ронами которого являются дуги Аь	и
Четвертую вершину этого четырехугольника мы обозна¬
чим через С._2. Как и выше, устанавливается, что дуга
BL_2CL 2 (геометрическое место предыдущих точек пере¬
ключения) получается из дуги А{ 1В1 ^ при помощи подоб-
Ы\-
i-юго преобразования с центром и коэффициентом е 11
сопровождаемого поворотом (по часовой стрелке)
на угол а-_2 вокруг центра е[~о.
Продолжая таким образом, мы вычертим четыре линии
OAiBiCiDi. . . (г--1, 2, 3,4), исходящие из начала коор¬
динат и представляю1цие в совокупности геометрическое
место точек переключения (рис. 43). Подобное преобразо-
*аг-1
вание с центром и коэффициентом е ^ , сопрово¬
ждаемое поворотом вокруг точки ei_r на угол a- j по часо¬
вой стрелке, переводит линию OAi7?iC';... в линию

лцШ'ЛШык оптимальный иыстгодийотвня 1гл
Ai_1Bi_1Ci	• • (РИ^- 44). Это позволяет последовательно
вычерчивать части линий OAiBiCi. .., зная первые куски
OAv ОЛ2,	(9Л4 этих линий (определение этих кусков
было приведено выше). Остается заметить, что значение е{
управляющий параметр v принимает внутри «угла» между
линиями OAi+1Bi+1Ci+1. . . и OAiBiCi... и на дуге АъО.
Это и дает синтез оптимальных управлений (рис. 45). Вид
оптимальных траекторий показан на рис. 46.

s Zl J
II Р11МКРЫ
Напомним, что рисунки 37 — 46, рассмотренные выше,
относились к случаю, когда X < 0, т. е. когда собствен-
Рис. 44.
Рис. 45.
ные значения матрицы (aj) имеют отрицательные дейст¬
вительные части. В этом случае размеры дуг OAiy Afi^
В{С-, . . . увеличивались, а синтез оптимальных управле¬

170 ЛИ НКЙНЫК ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [гл.
ний осуществляется во всей плоскости л. При К — О
размерь, дуг не меняются (т. е. 0А{--^ В{С ь= . . .,
А{ВL=^( ьОх, . . .); синтез оптимальных управлений по-преж¬
нему осуществляется во всей плоскости л (см. пример 3
в § 5). Наконец, при К > 0 размеры дуг 0А{} ВХС{, . .
а также дуг .4 • Z?•, C-bD-v . . . уменьшаются в геометри¬
ческой прогрессии; синтез оптимальных управлений
осуществляется лишь и ограниченном куске плоскости л
(рис. 47).

S 21]
ПРИМЕРЫ
171
Все сказанное относится к синтезу оптимальных
управлений в плоскости л переменных у1, у2. Переход
к плоскости X исходных переменных х1, х2 осуществ¬
ляется по формулам (47). Картина синтеза оптимальных
управлений при этом аффинно искажается.
Ир и мер 2
(Система второго порядка с двумя управляющими
параметрами и отрицательными собственными значениями.)
Рассмотрим систему (45) в предположении, что соб¬
ственные значения матрицы (ар действительны, отри¬
цательны и различны. Мы по-прежнему будем пред¬
полагать, что область управления U определяется

172
ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ
[ГЛ. 3
неравенствами (46) и что определитель матрицы (bj) отли¬
чен от нуля. Обозначим собственные значения матрицы
(ар через и А,2, причем	<	0. Линейным пре¬
образованием переменных (см. (47)) систему (45) можно
привести к виду
dt
— КУ1 "Ь С1ц1 “Ь С2^2’ |
Чт = К у2 + Ф1 + Ф2.
dt
или, иначе, к виду
sw- ,
dy2
(см. (49)). Как и в первом примере, точка v = (vL,v2)
описывает в плоскости я переменных у1, у2 параллело¬
грамм V (рис. 33).
Система (5) принимает в случае управляемого про¬
цесса (54) следующий вид:
ж -~ *•*'
Ее общее решение:
ty1 = c1e-Kit, ф2 - с2е~к^.
Из этих формул видно, что если одна из постоянных
интегрирования cv с2 равна нулю, то вектор ф=(ф1, ф2)
сохраняет постоянное направление (параллельное одной
из осей координат). Если же оба числа cv с2 отличны
от нуля, то вектор ф монотонно поворачивается (с воз¬
растанием t) от оси абсцисс к оси ординат, оставаясь
все время в одном квадранте (ибо ^	е^~^1—>со
при возрастании t).
Для системы (45) мы предполагаем выполненным
условие общности положения, тогда для системы (54),
получающейся из нее линейным преобразованием, это
условие также выполнено. Иначе говоря, ни одна из

§ 21]
ПРИМЕРЫ
173
сторон параллелограмма V не параллельна ни одной
из осей координат. Проведя из начала координат прямые
lv 12, перпендикулярные сторонам параллелограмма V
(рис. 34; эти прямые отличны от осей координат в силу
сказанного выше), мы, как и прежде, найдем, что если
вектор ф находится в угле а- (i= 1, 2, 3, 4), то максимум
функции Н при v £ V достигается в вершине v = ех (рис. 35).
Обозначим теперь через е[ точку (а-, а\) плоскости я
с координатами
a\=—-£-v\,	а\— —Е vu	(55)
Al	/V2
где v\, v\ — координаты вершины е-ь параллелограмма V.
Тогда мы получим четыре точки е[, е', е', ei'v являющиеся
вершинами некоторого параллелограмма V'. Из формул
(54), (55) вытекает, что в то время, когда управляющий
параметр v принимает значение e.L, изменение координат
у1, у2 описывается уравнениями
% = -«■>. )
dv*	(при	п = е;). J-	(56);
%=KW-<4)	)
«Фазовый портрет» системы (56). получается из «фазово¬
го портрета» системы
dy2 _ 1 п.2
с помощью параллельного переноса; именно, положение
равновесия системы (56); расположено не в начале коор¬
динат (как у системы (57), рис. 48), а в точке е\.
Дальнейшее исследование приведет к существенно
различным результатам в зависимости от того, как рас¬
положены прямые 1г и /2, перпендикулярные к сторонам
параллелограмма У. Мы выделим следующие два случая.
Случай I. Прямые 1г и /2 расположены в различных
квадрантах (т. е. одна в первом и третьем, а другая —
во втором и четвертом квадрантах, рис. 49). Произведем
нумерацию углов а- (определяемых прямыми /, и /2) так,

174
1И11 b П HЫ [■: U11T И i\l A..1 b Li Ы E Б ЫСТРОД EЙ СT В И Я	[Г Л . 3

$21]
ПРИМЕРЬ]
175
как указано на рис. 50. Эта нумерация соответствует
тому, что через е2 п в4 обозначены соответственно верх¬
няя и нижняя вершины
параллелограмма V,
а через и е3 — правая
и левая (рис. 40). Вспо¬
миная сказанное выше
о характере изменения
величин ,ф1 и мы
приходим к следующе¬
му выводу относитель¬
но оптимальных управ¬
лений. Каждое опти¬
мальное управление	PITC
либо совсем не содер¬
жит переключений (т.е.
в течение всего движения параметр v сохраняет постоян¬
ное значение, совпадающее с одной из вершин параллело¬
грамма F), либо содержит толь¬
ко одно переключение, и тогда
до переключения параметр v сов¬
падает с одной из вершин elt
е3, а после переключения — с од¬
ной из вершин е2, е4.
Теперь	нетрудно	построить
на плоскости я «линии пере¬
ключения», определяющие син¬
тез оптимальных управлений.
Обозначим через АО траекторию
системы (5б)2, оканчивающуюся
в начале координат (рис. 51), а
через ВО — аналогичную траек¬
торию системы (56Д. Линии АО
и ВО симметричны относительно
точки О. Если оптимальное
движение	содержит	переклю¬
чение (только одно в силу
заключительный этап движе¬
ния, завершающийся попаданием в начало коорди¬
нат, происходит	в	силу	системы	(56)2 или	(56)4, т. е.
вдоль линии	АО	или	ВО. До этого (т. е. до	попадания
сказанного выше), то

170 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ (.ГЛ. 3
на линию ВОЛ) точка движется в силу системы (56)2
или (56)3. Таким образом, ВО А есть линия переключений,
а две области, на которые плоскость разбивается этой
линией, заполнены Траекториями систем (56)х и (56)3 —
правая область заполнена траекториями системы (56)3,
а левая—траекториями системы (56)г Это и дает синтез
оптимальных управлений (рис. 52).
При переходе от переменных у\ у2 к исходным пере¬
менным ж1, х2 фазовая картина оптимальных траекторий
аффинно искажается.
Случай II. Прямые 1У и /2 расположены в одних
п тех же квадрантах — например в первом и третьем

ПРИМЕРЫ
177
Произведем нумерацию углов аь (определяемых прямыми
и /2) так, как указано на рис. 53; соответствующая
нумерация вершин параллелограмма V показана на
рис. 54. Вспоминая характер изменения величин и г|)2,
мы приходим к следующему выводу относительно опти¬
мальных управлений. Если начальное значение \\>0 векто¬
ра я|э = ('ф1, г|)2) расположено внутри четвертого квадранта
Рис. 54.
'(или на его сторонах), то при дальнейшем своем измене¬
нии вектор г|э не выйдет из этого квадранта, т. е. будет
все время находиться внутри угла аг Следовательно, мы
будем все время иметь v = e1 (без переключений). Этому
управлению соответствует траектория системы (56)х,
оканчивающаяся в начале координат (рис. 55). Анало¬
гично, если начальное значение г|э0 вектора гр находится
12 л. С. Понтрягин

ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫЗТРОДЕЙС ТВИЯ [ГЛ. з
Рис. 55.
внутри или на сторонах второго квадранта, то мы будем
иметь v = e3 в течение всего движения, т. е. получим
траекторию системы (56)3, оканчивающуюся в начале
координат (рис. 56). Все осталь¬
ные оптимальные траектории со¬
ответствуют случаям, когда век-
тор ф0 расположен внутри первого
или третьего квадрантов. Мы
рассмотрим случай, когда ф0 ле¬
жит внутри первого квадранта
(случай третьего квадранта полу¬
чу' чается при помощи симметрии
относительно начала координат).
Итак, пусть вектор ф0 рас¬
положен внутри первого коорди¬
натного угла, но одновременно
лежит в угле аг С течением вре¬
мени вектор ф монотонно по¬
ворачивается против часовой стрелки, приближаясь к оси
ординат. Следовательно, оптимальное управление имеет два
переключения: сначала v = ev за¬
тем, после первого переключения,
v = е2 и, наконец, после второго
переключения, v = е3. Мы сейчас
покажем, что при наличии указан¬
ных двух переключений проме¬
жуток времени, в течение кото¬
рого управляющий параметр v
принимает значение е2, имеет
вполне определенную
длину (независимо от выбора
начальных условий). В самом де¬
ле, обозначим угловые коэффици¬
енты прямых /х и /2 соответ¬
ственно через кг, к2 (где /с, < к2,
см. рис. 53). Так как изменение вектора ф описывается
формулами
ф>1 = c1e~'^t, ф2 = с2е~^1
У’
Рис. 56.
(где сг > 0 и с2 > 0, так как вектор ф расположен в пер¬
вом квадранте), то момент переключения тх из вершины

примеры
179
ег в вершину е2 (т. е. момент перехода вектора i|) через
прямую /х) определяется из соотношения
“**■
Аналогично, момент переключения т2 из вершины е2
в вершину е3 (т. е. момент перехода вектора ip через
прямую /2) определяется из соотношения
с2е
Таким образом,
cie-'x iT2	2
1 т клСг	1	1	^-2^1
4=5 Т2 = 7 г~ In —- ,
Xi — А» 2 с2	^1	— А-2 с2
и потому отрезок времени [тх, т2], в течение которого
управляющий параметр v принимает значение е2, имеет
длину
(58)
Число, стоящее в правой части соотношения (58), не за¬
висит от Cj и с2 (т. е. от начального значения ip0 вектора
ip), и мы обозначим его через Т.
Итак, при изменении вектора ip в первом квадранте
оптимальные управления имеют следующий вид. Управ¬
ляющий параметр v в течение некоторого времени прини¬
мает значение v = ev затем в течение времени Т параметр
v принимает значение v — е2, после чего вплоть до окон¬
чания движения он принимает значение v = е3.
Разумеется, число переключений может оказаться
и меньшим, чем два. Например, мы могли бы начать рассмо¬
трение движения в момент, когда управляющий параметр
v уже принял значение е2. Тогда мы получили бы, что пара¬
метр v в течение времени, не превосходящего Г,
находится в вершине е2, после чего переключается в вер-
шину е3. Точно так же могло бы оказаться, например, что
Движение закончилось (попаданием в начало координат)
До момента переключения из вершины е2 в вершину е3.
Иначе говоря, если управляющий параметр v совершает
меньше двух переключений, то врехмя пребывания его
12*

180	ЛИНЕЙНЫЕ	ОПТИМАЛЬНЫЕ	БЫСТРОДЕЙСТВИЯ	[ГЛ.	3
в вершине е2 не превосходит Т (причем переключе¬
ние может происходить либо из вершины е1 в вершину
е2, либо из е2 в е3).
Теперь уже нетрудно построить на плоскости п «ли¬
нии переключения», определяющие синтез оптимальных
управлений. Наметим сначала
траектории, соответствую¬
щие двум переключениям.
Заключительный этап движе¬
ния на таких траекториях
соответствует значению па¬
раметра v = е3, т. е. движе¬
ние происходит по дуге АО
траектории системы (56)3,
оканчивающейся в начале
координат (рис. 56). Перед
попаданием на линию АО
движение происходило в силу
системы (56)2. Таким обра¬
зом, АО есть линия переклю¬
чения из вершины е2 в вер¬
шину е3. Пусть X — некоторая
точка линии АО. Тогда пред¬
шествующий точке X уча-
рис 57	сток	YX оптимальной траек¬
тории представляет собой
дугу траектории системы
(56)2, соответствующую отрезку времени Т (рис. 57).
Так как решения системы (57) имеют вид у1 = с1ехi*,
у2 = с2ех2*, то в результате движения точки по траектории
этой системы в течение времени Т ее абсцисса умножает¬
ся на е^т, а ордината — на Система же (56)2 отли¬
чается от системы (57) только сдвигом положения равно¬
весия. Таким образом, точки X получаются из соответствую¬
щих точек У (рис. 57) с помощью аффинного преобразования
L, которое в системе координат с началом в точке е'2 (см.
(55)) и осями, параллельными осям г/1, у2, заключается
в умножении абсциссы на eXlT, а ординаты — на ex*T.
Следовательно, геометрическое место точек У представляет
собой линию СВ, переходящую в линию АО при аффин-
ом преобразовании L (рис. 58). Наметив еще линию ВО,

§ 21]
ПРИМЕРЫ
181
представляющую собой дугу траектории системы (5б)2,
оканчивающуюся в начале координат и соответствующую
отрезку времени Т, мы найдем, что вся «полоса» АО ВС за¬
полнена кусками траекторий системы (56)2, начинающимися
на линии СВ, кончающимися
на линии АО и соответствую¬
щими отрезку времени Т.
Итак, геометричсскрш ме¬
стом точек У, в которых
происходит переключение из
вершины ех в вершину е2,
служит линия СВ. До точки
У движение совершалось по
траектории системы (56)г
В результате мы получаем
траектории, соответствую¬
щие двум переключениям
(рис. 59). «Крайняя» траекто¬
рия DBO на рис. 59 соответ¬
ствует одно м у переключе¬
нию — фазовая точка попадает
в начало координат как раз
в тот момент, когда должно
было бы произойти второе
переключение (из вершины е2
в вершину е3).
Рассмотрим теперь траектории, соответствующие одно¬
му переключению из вершины ег в вершину е2. Заклю¬
чительный этап движения происходит в этом случае
по траектории системы (56)2 в течение времени < 71
и оканчивается в начале координат, т. е. происходит по
некоторой части ЪО линии ВО (рис. 60). До точки Z
движение происходило в силу системы (56Д. Когда
точка Z пробегает всю дугу ВО, траектории указанного
вида заполняют «полосу» DBOA' (рис. 61), где А'О —
траектория системы (56)р оканчивающаяся в начале
координат.
Объединяя все полученные оптимальные траектории,
мы находим, что вся часть плоскости слева от линии
АО А1 заполняется ими (рис. 59, 61). Очевидно, что линия
А'О симметрична линии АО относительно начала координат.
Рис. 58.

182 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
Справа от линии АО А' поведение траекторий симмет¬
рично, а переключения происходят из вершины е3 в вер¬
шину ел, а затем в ел. В результате синтез оптимальных
Рис. 60.
управлений осуществляется во всей плоскости (рис. 62).
Вид оптимальных траекторий показан на рис. 63.
При переходе от переменных у1, у2 к переменным х1, х2
картина оптимальных траекторий аффинно искажается.

§ 21]	ПРИМЕРЫ	183
Пример 3
(Случай, когда многогранник U является одномерным,
а собственные значения матрицы (ар действительны.)
Предположим, что в системе (1) г=1, т. е. управляю¬
щий параметр и является действительным числом; пред¬
положим, кроме того, что это число может изме¬
няться в пределах — 1<а<1. Таким образом, мно¬
гогранник U представляет собой в рассматриваемом

184 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
случае отрезок [ — 1, 1] числовой оси, а система (1) при¬
нимает вид
п
^=2 aiv*v+6i“> И<1. i=l. 2,	(59)
V=1
Предположим, наконец, что собственные значения матрицы
Рис. 63.
(aj) действительны. Тогда, согласно теореме 10, оптималь¬
ное управление содержит не более п интервалов постоян¬
ства, причем на этих интервалах поочередно и=1
и и = — 1.

§ 21]
ПРИМЕРЫ
185
Иначе говоря, на каждом интервале постоянства
движение происходит в силу одной из двух следующих
систем:
71
^ = 2	+	Ь*.	1=1, 2, .. ., /г,	(60)+
V= 1
71
^ = 2 а*®* - Ь*.	г = 1, 2, .... /г.	(60),
V=1
Обозначим, через Мп траекторию системы (60)+, окан¬
чивающуюся в начале координат, а через М^ — траекто-
К
Рис. 64.
рию системы (60)_, оканчивающуюся в начале координат.
Вместе М*п и Мп составляют проходящую через начало
координат линию, которую мы обозначим через Мп
Рис. 65.
(рис. 64). В силу сказанного выше о характере оптималь¬
ных управлений ясно, что заключительный этап опти¬
мального движения (завершающийся попаданием в нача¬
ло координат) представляет собой движение по линии
Мп ИЛИ Мп-
Рассмотрим теперь всевозможные траектории системы
(60)+, оканчивающиеся в точках линии Мп (рис. 65). Эти
траектории заполняют некоторую поверхность М^_х, имею¬
щую в качестве своего края линию Мп. Аналогично,

186 линейные оптимальные быстродействия [ГЛ. 3
траектории системы (60)_, оканчивающиеся в точках линии
Мп, заполняют некоторую поверхность М~п_х, имеющую
в качестве своего края линию Мп. Объединив М^_г и Мй_г
вместе, мы получаем поверхность, которую обозначим
через Мп_г (рис. 66). Ясно, что последние два этапа
всякого оптимального движения совершаются по поверх¬
ности Mn_v ибо только по траекториям этой поверхности
можно попасть на линию Мп, по которой совершается
заключительный этап движения.
Рис. 66.
Далее, траектории системы (60)+, оканчивающиеся
в точках поверхности М~п_х, образуют трехмерное много¬
образие Л/*_2, краем которого служит поверхность Mn_v
Траектории системы (60)_, оканчивающиеся в точках
поверхности M^_v образуют трехмерное многообразие
М~п-2 с краем Mn_v Вместе М^_2 и М^_2 образуют трех¬
мерное многообразие Мп_2; в котором совершаются послед¬
ние три этапа всякого оптимального движения.
Продолжая таким образом, мы построим многообразия
МПУ Мп_1У Mv причем многообразие М, имеем раз¬
мерность п — i+1. Многообразие Мi+1 расположено цели¬
ком в многообразии Мх и разбивает это многообразие
на две области Ml и 71/*. При этом область м: образо¬
вана всевозможными траекториями и теш (60)+, оканчи¬
вающимися на Л/гг+ь а область М образована всевоз¬
можными траекториями системы (60оканчивающимися
на М}+1. Последнее многообразие Мг либо совпадает со

ПРИМЕРЫ
187
всем фазовым пространством X, либо представляет собой
некоторую область этого пространства, содержащую нача¬
ло координат. Внутри этой области Мг и осуществляется
синтез оптимальных управлений.
Этот синтез осуществляется следующим образом: во
всех областях М{ управляющий параметр и принимает
значение + 1, а во всех областях Ml он принимает зна¬
чение — 1. Фазовая точка двигается в области Mv при¬
чем к= +1, если она находится в и и= — 1, если
она находится в У1/~. В момент попадания на многообра¬
зие М2 происходит переключение, и все дальнейшее
движение совершается по многообразию М2. Следующий
момент переключения наступает тогда, когда точка,
двигаясь по М2У попадает на многообразие М3. После
этого точка продолжает двигаться по М3 и т. д. Заклю¬
чительный этап движения, завершающийся попаданием
в начало координат, происходит по линии Мп. Таким
образом, всего за время движения происходит п — 1 пе¬
реключений. Разумеется, при некоторых начальных поло¬
жениях фазовой точки число переключений может оказаться
и меньшим, чем п— 1 (например, может оказаться, что
точка х0 расположена на многообразии М2, или же на
многообразии М3 и т. п.).
Пример 1 в § 5 является частным случаем указан¬
ного общего построения.
Пример 4
Поставим следующую задачу. В гс-мерном эвклидовом
пространстве движется управляемая точка, причем «дви¬
гатель» ее может сообщать этой точке ускорение, не пре¬
восходящее по модулю единицы и направленное в любую
сторону. Как следует управлять движением этой точки,
чтобы, имея заданное начальное положение и заданную
начальную скорость, она за кратчайшее время попала
в начало координат (с произвольной конечной ско¬
ростью)?
Для решения этой задачи обозначим координаты дви¬
жущейся точки через х1, х2,	...,	хп, компоненты ее
скорости — через #n+1, .. ., х2'-, а кохмпоненты ускорения —
через и1,	, ип. Массу точки примем равной единице.

188 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
Тогда уравнения движения точки запишутся в виде
dx1
dt
dx2
- = Zn+1,
dt
= Xn+2,
dxn
~dt
dxn* i
= Ж2Л,
dt
dxn+2
dt
dx2n
dt
= W2,
(6i)
Так как ускорение u = (u1, . .., un) должно по модулю
не превосходить единицы, то область управления U опре¬
деляется неравенством
(и1)2 + (и2)2 + . . . + (и11)2 < 1.	(62)
Далее, так как начальное положение и начальная ско¬
рость точки заданы, то в фазовом пространстве X пере¬
менных х1, х2, ..., хп, ..., х2П задано начальное поло¬
жение xQ=(xJ,
х20п). Требование попадания в начало
координат (с произвольной конечной скоростью) означает,
что в конечный момент движения должны быть выполне¬
ны соотношения
х1 = х2= ... =яп = 0,	(63)
а величины хп+1, ..., х2П могут быть произвольными.
Иначе говоря, задача заключается в быстрейшем попа¬
дании объекта, управляемого уравнениями (61), (62), из
начальной точки х0£Х в какую-либо точку многообра¬
зия Sv определяемого в X уравнениями (63). Многооб¬
разие S± представляет собой, очевидно, тг-мерную плос¬
кость.
Функция Н имеет в рассматриваемом случае следую¬
щий вид:
Я =	+	г|)2жт,+2	+	•	■	• + i>nx2nnr
(64)

UPIlMEPbl
189
с помощью этой функции находим систему уравнений
для вспомогательных переменных
^ = 0
dt ’
^2 _п
dt
 q
dt
dtyn+i
dt
^Фп + 2
clt
^2
=
= —“Фа*
dt
-Фп-
Из этой системы вытекает, что в течение всего опти-
мального движения величины фх, ф2, . . ., сохраняют
постоянные значения, и потому величины ф,г+1, фп+2, • • •
. . ., ф2/г являются линейными функциями времени.
Напишем теперь условие трансверсальности в правом
конце оптимальной траектории. Для того чтобы вектор
Ф — (Фи • • • > Фтг> ф/г+1, . .., ф,п) был ортогонален к много¬
образию определяемому уравнениями (63), очевидно,
необходимо и достаточно выполнения условий
^+1 = ,Фп + 2= • •• =^2П = 0-
Таким образом, условие трансверсальности в правом кон¬
це оптимальной траектории имеет вид
(*i) =	(h)	= • • • = 'Фгп di) = 0.	(65)
где tx — момент попадания фазовой точки на многообра¬
зие Sx. Вспоминая теперь, что функции ф,1+1, фд+2> •••> Фгп
линейны, мы находим из (65), что имеют место формулы
■4W = aidi-t)’ =	=	(66)
где dj, а2, . .., ап — постоянные величины. Так как вели¬
чины ф. определены лишь с точностью до общего поло¬
жительного множителя пропорциональности, то мы можем

190 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
при этом предполагать, что вектор а = (av а2, . .., ап)
является единичным, т. е.
(ai)2 + (аг)2 + • • • + (#n)2 = 1*
Подставляя найденные значения (66) в формулу (64),
мы получаем
Н = ... + (tx — t) (аги1 -f- a2u2 + . .. + anun)y
где многоточием обозначены члены, не зависящие от
и1, ..., ип. Так как t1—t'> 0 (ибо —последний
момент движения), то условие максимума функции Н
означает, что в течение всего движения величина
а^и1 ф- а2и2 + .. . + апип = (а, и)
должна быть максимальной, а это, в силу (62), озна¬
чает, что a{t)= а, т. е. что величины и1, и2, . .., ип в тече¬
ние всего движения сохраняют постоянные значения
и1 = ait i = 1, .. ., п.
Итак, в рассматриваемом случае оптимальность дви¬
жения означает, что ускорение и постоянно и вели¬
чина его равна единице. Это позволяет однозначно опре¬
делить искомое ускорение (т. е. найти направление
вектора ускорения и). В самом деле, траектория движе¬
ния точки в рассматриваемом эвклидовом пространстве
представляет собой параболу
X1 = х\ + х*+Ч + и1 Ц, i = i,...,n,
где и = (игу ..., ип) — постоянный вектор ускорения, рав¬
ный по величине единице, т. е. удовлетворяющий условию
(и1)2 + (и2)2 + . . . + (О2 = 1.	(67)
Для того чтобы эта траектория прошла через начало
координат, должны выполняться условия
x\ + x*+it + ul 4г = 0,	1 = 1,..., п.	(68)
Соотношения (67), (68) представляют собой систему из
п + 1 уравнений относительно неизвестных и1, и2, ...,unyt,
причем для t мы должны получить положительное зна¬
чение. В случае, если таких решений окажется несколь¬

§ 22]
МОДЕЛИРОВАНИЕ
191
ко, мы должны взять решение с наименьшим поло¬
жительным значением t (ибо речь идет о быстрейшем
попадании в начало координат). Из (68) мы получаем
2 (яМ-xM-it)
“t==	°-^г-	. 1 = 1,	(69)
и подстановка в соотношение (67) дает уравнение
п
4 2 (хо +	— £4 = 0	(70)
i=l
относительно неизвестного t. При £ = 0 левая часть этого
п
уравнения принимает значение 4 2 (х1)2 > 0 (разумеется,
i=i
мы считаем, что точка (хJ, я2,..., х™) не совпадает с началом
координат, так как в противном случае решение опти¬
мальной задачи очевидно: / = 0). При t—> оо левая часть
уравнения (70) отрицательна. Следовательно, уравнение
(70) имеет хотя бы один положительный корень. Обозна¬
чим через x{xQ) — x(x\, х\, ..., х™, х™+[, ...,х$п) наи¬
меньший положительный корень этого уравнения.
Тогда из (69) мы находим искомые значения компонент
ускорения
2 (4+*”+ч(*0))
1Г =
0(*о))2
Это и дает синтез оптимальных управлений в рассматри¬
ваемом случае. (Функция х (х0), а следовательно, и функ¬
ции и1 кусочно-непрерывны.)
§ 22. Моделирование линейных оптимальных
быстродействий при помощи релейных схем
Возвратимся снова к задаче о линейных оптимальных
быстродействиях, рассмотренной в § 17. В силу теоремы 9
каждая экстремальная траектория (см. стр. 142), исхо¬
дящая в момент t0 из точки х0, определяется начальными
значениями ф(/0) решения ф(/) уравнения (5). Именно,
если задан произвольный отличный от нуля вектор ф0,
то однозначно определено решение ф (t) уравнения (5)

192 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
с начальным условием 'ф(^о) = '11)о* После этого, в силу
теоремы 9, соотношение (6) однозначно определяет соот¬
ветствующее экстремальное управление u(i). Наконец,
зная управление и(1), мы из уравнения (2) находим
и соответствующую траекторию х(1), исходящую из
точки х0. Таким образом, в конечном счете экстремальная
траектория x(t) однозначно определяется выбором на¬
чального значения ф0. Если бы нам удалось найти именно
такое начальное значение ф0, что траектория х (t) про¬
ходит через начало координат О, то управле¬
ние u(t) и траектория x(t), полученные указанным выше
способом, будут оптимальными. В самом деле, получен¬
ная траектория x(t) будет идти в этом случае из точки
х0 в требуемую точку О, и потому оптимальное управле¬
ние существует (теорема 13). Это оптимальное управление
единственно (теорема 11) и удовлетворяет принципу мак¬
симума, т. е. является экстремальным (стр. 142). Но
экстремальное управление, переводящее фазовую точку
из положения х0 в начало координат, также единственно
(теорема 12). Таким образом, экстремальное управление,
переводящее фазовую точку в начало координат, как раз
и является оптимальным управлением.
Следует отметить, что вычисление траектории х (t),
соответствующей начальному значению ф0, является до¬
вольно трудоемким. Действительно, эта задача включает
в себя решение уравнения (5), нахождение функции u(t)
по формуле (6) и, наконец, решение уравнения (2), что
сводится к решению нескольких систем дифферен¬
циальных уравнений с последовательным «припасовыва-
нием» начальных значений (ибо функция u(t) полу¬
чается, вообще говоря, не постоянной, а лишь кусочно¬
постоянной).
Если предположить, что нахождение траектории х (t)
по начальному значению ф0 осуществляется некоторым
прибором, то остается задача поиска начального зна¬
чения ф0, при котором траектория x(t) проходит через О.
В этом параграфе, не касаясь второй задачи (задачи
поиска начальных значений ф0), мы укажем способ
построения моделирующего устройства, позволяющего по
начальному значению ф0 находить соответствующую
экстремальную траекторию х(1). Это моделирующее устрой¬

Моделирование
J УЗ
ство состоит из двух линейных объектов с уравнениями
(2) и (5) и некоторого числа релейных элементов,
количество и схема соединения которых определяются
многогранником U и оператором В.
Переходим к математическому описанию указанного
моделирующего устройства. Рассмотрим линейный объект,
фазовые состояния которого описываются переменными
Фи •••> Ф/г> изменяющимися по закону (5). Этот объект
мы будем условно обозначать так, как показано на рис. 67.
А
Рис. 67.
X/
хг
Ах * Во
х«

Рис. 68.
Задание начальных значений для величин .. ., \\)п
(т. е. задание вектора ф0) однозначно определяет даль¬
нейшее изменение величин ф1, . . ., фп во времени. Исход¬
ный объект (описываемый уравнением (2)) мы будем
ь
Xq
, 1
X*
—►
| и2
Ах + Ви
Хгх
1 :
1 •
■S
1 иг
._j
х”
Рис. 69.
изображать так, как показано на рис. 68. Для того чтобы
однозначно было определено изменение (во времени) вы¬
ходных величин (т. е. фазовых координат) х1, ..., хп,
нужно задать начальное фазовое состояние х0 объекта
и изменение (во времени) входных величин и1, . . ., иг
(т. е. управляющих параметров). Требуемое моделирую¬
щее устройство имеет вид, указанный на рис. 69;
Л. С. Понтрягии

194 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
средний «ящик», помещенный между объектами, изобра¬
женными на рис. 67 и 68, содержит некоторое коли¬
чество релейных элементов. Описанию этого среднего
«ящика» и посвящена остальная часть параграфа.
Прежде всего отметим частные случаи, в кото¬
рых устройство среднего «ящика» особенно просто.
Рассмотрим сначала случай, ког¬
да в уравнение (2) входит только
£	один управляющий параметр и,
А
к
Рис. 70.
Рис. 71.
изменяющийся в пределах — 1<	1	(т. е. случай, когда
многогранник U представляет собой отрезок [—1, 1]).
В этом случае матрица (Ъ)) превращается в столбец
(Ь1, Ъ2, . . ., Ьп), а функция (7) имеет вид
п
2 % (t) ьаи.
а=1
Поэтому уравнение (6) имеет следующее решение:
u	= sign( 2 гА|) (*)).	(71)
а=1	'
Иначе говоря, если мы введем в рассмотрение вспомога¬
тельную величину
(72)
а=1
то решение уравнения (6) будет определяться формулой
и = sign £.	(73)
Переход от величин .. ., фп к величине опреде¬
ляемой формулой (72), осуществляется некоторым сум¬
мирующим устройством, условно изображенным на
рис. 70. На рис. 71 показано условное изображение ре¬
лейного	элемента,	т. е. объекта, выходная	и	входная
величины	которого	связаны соотношением	ц =	sign g.

МОДЕЛИРОВАНИЕ
195
Соединим теперь объекты, изображенные на рис. 67,
68, 70, 71, в одну схему ^(рис. 72). Ясно, что, каков бы
ни был начальный вектор ф0, на выходе первого звена
(в изображенной на рис. 72 схеме) мы получаем вели¬
чины ^(г), ..., фп(0> составляющие решение уравне¬
ния (5). Эти величины в следующем звене (обведенном
пунктиром) преобразуются по формулам (72), (73), так
что на выходе этого звена мы получаем величину (71),
являющуюся решением уравнения (6). Иначе говоря, на
выходе второго звена мы получаем экстремальное
управление u(t), и потому выходные величины
Рис. 72.
xL (t), . . ., хп (t) последнего	звена	будут	давать	соответ¬
ствующую экстремальную	траекторию.	Иначе	говоря,
схема, изображенная на рис. 72, при любых начальных
значениях ф0, х0 осуществляет движение объекта (2)
с фазовыми координатами х1, . . ., хп по соответствую¬
щей экстремальной траектории. Если схема, изображен¬
ная на рис. 72, осуществлена в виде прибора (модели¬
рующего устройства), то при использовании такого при¬
бора остается нерешенной	лишь	задача	поиска	началь¬
ного значения ф0, для которого	(при заданном	началь¬
ном значении х0) получаемая траектория приходит в на¬
чало координат.
Проведенные рассуждения легко обобщаются также
на тот случай, когда область управления U является
г-мерным кубом, т. е. определяется неравенствами
|м{|<1,	£=	1, ..., г.	(74)
13*

196 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
В этом случае функция (7) имеет вид
2 2	(t) Щи*.	(75)
(3=1 а=1
Так как, в силу (74), область изменения каждого из
управляющих параметров и1, . . ., иг не зависит оттого,
какие значения приняли остальные управляющие пара¬
метры, то для того, чтобы функция (75) принимала
максимальное значение, необходимо, чтобы каждое ее
отдельное слагаемое
2 4>а (0
а=1	1
при (3 = 1,	/•	принимало	максимальное значение.
Отсюда получаем
и* = sign ( 2 Vj)a (t) fcp).
a=l
Иначе говоря, если мы введем в рассмотрение вспомога¬
тельные величины
п
2	р = 1,	(76)
а=1
то решение уравнения (6) будет определяться формулами:
KP = sign|p, р=1,...,7\
Переход от величин фд, . .., фп к величинам . . ., £г
осуществляется суммирующим устройством, условно
изображенным на рис. 73. Из сказанного ясно, что
схема, изображенная на рис. 74, вырабатывает на выходе
релейных элементов экстремальное управление
и1^), ...,ur(t), а на выходе последнего звена — соответ¬
ствующую экстремальную траекторию x(t). Отметим, что
число релейных элементов в этой схеме равно числу
у пр а в л я ющи х и а р а ме тро в.
Наконец, перейдем к рассмотрению общего случая,
когда многогранник U произволен. Пусть
wX) w2, . . . , Wy
(77)

§ 22]
МОДЕЛИРОВАНИЕ
197
— попарно неколлинеарные векторы, имеющие направле¬
ние ребер многогранника U (т. с. каждый из векторов
(77) параллелен хотя бы одному ребру многогранника U
и для каждого ребра имеется в системе (77) один
ft,
s/
к
С
t
Рис. 73.
Рис. 74.
параллельный ему вектор). Координаты вектора w-} будем
обозначать через w\, . . ., wr-. Положим
п г
lj = (г|>, BWj) =S2	/'	=	1.	•	•	•. Y- (Щ
a=l q=1	w J
Таким образом, переменные . . ., |Y являются линей¬
ными формами (вообще говоря, линейно зависимыми) от
_ft
Рис. 75.
Рис. 76.
•••> Фп* Переход от переменных ф. к переменным
мы будем обозначать так, как показано на рис. 75. Значе¬
ния величин определяются величинами ф^, но обрат¬
ного воздействия на них не оказывают (это выражено
на рис. 75 направлением стрелок).
Каждую из величин мы подадим на свой релейный
элемент; выходы этих релейных элементов обозначим
1шрез K)v . . ., T|Y (рис. 76):
Т1;-= sign	/	= 1 Y-	(79)

198 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
Пусть теперь ev .. ., е — все вершины многогран¬
ника ’£7. Рассмотрим какую-либо одну вершину еь и пусть
/—одно из чисел 1, 2, . .., у. Если исходящий из вер¬
шины et вектор, равный Wp идет по одному из ребер
многогранника £7, примыкающих к этой вершине, то мы
положим	+1. Если исходящий из вершины ei век¬
тор, равный — Wp идет по одному из ребер многогранни¬
ка £7, примыкающих к этой вершине, то мы положим
= —1. Если же ни один из этих двух случаев места
не имеет, то символ е^- не определяется.
Фиксируем некоторый индекс £( = 1,2, . . ., q) и будем
рассматривать только такие индексы /, для которых
символ определен. Тогда векторы sijwj (рассматри¬
ваемые для указанных индексов /) направлены по ребрам
многогранника Г/, исходящим из вершины ev Пусть
теперь ,ф = ('ф1, ф2> •••> Ф?г) — произвольный отличный от
нуля вектор. Обозначим через B*ty вектор простраы-
п
ства Ег, имеющий £-ю координату 2	г=1,	. . ., г.
а=1
Тогда для любого вектора и пространства Ег, как легко
видеть, имеет место соотношение
(B*ty, и) = (Ф, Вы).	(80)
Проведем теперь в пространстве Ег гиперплоскость Л,
проходящую через точку ei и ортогональную вектору Б*!)),
а вектор	будем считать исходящим из точки е{.
Для того чтобы величина (г|э, Ви), рассматриваемая как
функция точки и £ £7, достигала своего наибольшего зна¬
чения только в одной вершине е., необходимо и достаточно
(в силу (80)), чтобы весь многогранник £7 находился
в том полупространстве, определяемом гиперплоскостью Л,
которое не содержит вектора Б*!)), а для этого, в свою
очередь, необходимо и достаточно, чтобы каждый век¬
тор, исходящий из точки et и направленный по ребру
многогранника £7, составлял с вектором	тупой
угол. Иначе говоря, для того чтобы уравнение
(г|>,Ви) = Р(ф)	(81)
имело единственное решение гг =	, необходимо и

§ 22]
МОДЕЛИРОВАНИЕ
199
достаточно, чтобы все скалярные произведения
(В*% 8uWj)
(соответствующие	индексам /, для	которых	символ etj
определен) были	отрицательными,	или, иначе, чтобы
были выполнены неравенства
еи М>. Bwi) < °-
В силу (78) последнее неравенство принимает вид
8i& < 0.	(82)
Итак, для того чтобы уравнение	(81) имело	единствен¬
ное решение и = ег, необходимо и достаточно, чтобы для
всех / (для которых символ ei;- определен) выполнялось
неравенство (82), или, что то же самое, равенство
8i = -1	(83)
(см. (79)).
Положим теперь
= — 1+ SeiyTlj» z = 1, 2, .. ., д, (84)
з
где — число ребер многогранника U, примыкающих к
вершине ev а суммирование распространено на все значе¬
ния /, для которых символ ем определен (так что в этой
сумме имеется слагаемых). Переход от вели¬
чин т|;- к величинам ^ показан на рис. 77.
Величина!^ принимает значение — 1, если для
всех / выполнено равенство (83), и поло¬
жительное значение, если хотя бы
для одного / выполнено равенство е^-т^:= +1.
(Равенство е1:?т];- = 0, или, что то же самое,
(г|э, Bwj) — 0, см. (78), может, в силу теоремы 9,
выполняться лишь для конечного числа
значений t, которые мы не будем принимать
во внимание). Таким образом, уравнение (81) тогда и
только тогда имеет единственное решение u = ev когда
Ci<0. Подав величины . .., на релейные элементы
и обозначив выходные величины через Xi> • • • > %q (рис. 78),
мы найдем, что уравнение (81) тогда и только тогда
имеет единственное решение u — ev когда выполнено
равенство = —1. Из сказанного ясно, что в любой
момент t (за исключением конечного числа моментов,
7/
с,
Ъ
Ь
С,
Рис.
77.

200 .'ой и ойные оптимал ьные быстродействия [гл
когда хотя бы одна из величин ^ обращается в нуль) одна
из величин принимает значение — 1, а остальные — зна¬
чение + 1.
Пусть теперь
многогранника U. Положим
ei — координаты вершины
«° = У 2 О — Ха) <?а. е = 1.
(85)
а=1
(рис. 79). Из (85) ясно, что точка (и1, ..., иг) совпадает
с вершиной ev если %-ь= — 1, а остальные величины %а
-Ли
х*
Рис. 78.
Рис. 79.
равны +1. Иначе говоря, если уравнение (81) имеет
единственное решение, то этим решением является точка
(гг1, ггг), получаемая по формулам (85).
Соединим теперь объекты, изображенные на рис. 67,
68, 75 — 79, вместе. Мы получим схехму, показанную на
рис. 80. Из сказанного выше ясно, что, каков бы ни был
Рис. 80.
начальный вектор ф0, функции иг(1)у ..., ur (t), получаю¬
щиеся Гна выходе предпоследнего звена, образуют
экстремальное управление (ибо они удовлет¬
воряют уравнению (6)), а на выходе схемы мы полу¬

§ 2 3] УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ 201
чаем величины х1 (£), . .., xn(t), описывающие соответ¬
ствующую экстремальную траекторию.
Итак, схема, изображенная на рис. 80, осуществля¬
ет движение объекта (2) по экстремальной траектории
(при любых начальных значениях ф0, х0).
Остается, как мы отмечали выше, задача поиска такого
начального значения для ф>, при котором (для заданного
начального значения х0) получаемая траектория проходит
через начало координат. Такой поиск можно производить
одним из следующих двух методов: либо, имея фиксиро¬
ванное начальное значение х0, при помощи нескольких
проб найти требуемое начальное значение ф0, либо же,
обратив направление течения времени, вычертить доста¬
точно густую сетку траекторий, исходящих из начала
координат (они все будут оптимальными), после чего,
«запомнив» все точки фазового пространства X, в кото¬
рых происходят переключения, составить «поверхность
переключений» (т. е. произвести синтез оптимальных
управлений).
Следует еще отметить возможность осуществить более
быстрое течение времени в моделирующем устройстве по
сравнению с реальным объектом (за счет подбора пара¬
метров в первом и последнем звеньях схемы). Это может
позволить испробовать на моделирующем устройстве не¬
сколько экстремальных траекторий в течение короткого
времени и получить требуемое оптимальное управление
для исходного объекта.
§ 23. Линейные уравнения с переменными
коэффициентами
Основные факты, установленные в предыдущих пара¬
графах для линейных однородных уравнений с постоян¬
ными коэффициентами (см. (1)), переносятся и на случай
линейных неоднородных уравнений с переменными коэф¬
фициентами. В этом параграфе мы приведем формули¬
ровки получаемых таким образом теорем и укажем те
изменения, которые следует произвести в предыдущих
доказательствах для получения этих теорем.
Уточним прежде всего постановку задачи. Мы
будем рассматривать объект, закон движения которого

202 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
записывается в виде следующей линейной системы диффе¬
ренциальных уравнений:
п	г
-^- = 2av(0®v + S6o(O«o + /‘(O. г = 1, . .., п. (86)
V=1	0=1
Областью управления U по-прежнему будем считать вы¬
пуклый замкнутый многогранник г-мерного пространства
Ег переменных гг1, . . ггг. Как и выше, ограничимся рас¬
смотрением задачи об оптимальных быстродействиях. Отно¬
сительно функций a\(t), blh(t) и fl (t), входящих в систе¬
му (86), мы будем предполагать, что они определены на
некотором интервале а < t < b (возможно, совпадающим
со всей числовой прямой) и имеют на этом интервале
достаточное число непрерывных производных. Именно,
мы будем предполагать, что функции а\ (£) имеют п— 2
непрерывных производных (но не менее одной), функции
blk(t) имеют п— 1 непрерывную производную, а функ¬
ции /г (t) имеют одну непрерывную производную. (Воз¬
можность некоторого ослабления этих ограничений ука¬
зана в замечании, приведенном в конце этого параграфа.)
Все рассматриваемые значения переменного t мы будем
предполагать принадлежащими интервалу а < t < Ъ\ в
частности, всякое допустимое управление будет предпо¬
лагаться заданным на отрезке, являющимся частью
интервала а < t < Ъ.
В векторной форме система (86) может быть записана
следующим образом:
= A(t)x + B(t)u + f(t);	(87)
здесь A (t): X —> X и В (t) : Er—> X — линейные операторы,
определяемые в координатах х1, .. ., хп и гг1, ..., ггг
матрицами (aj. (£)) и (&£(£)) соответственно, а f(t) — вектор
с компонентами
Введем в рассмотрение операторы 51(^), B2(t)} ...
. . ., Bn(t), положив
(t) = В (t), Bj (t)= — A (t)	(t) + d-^dp ,	(88)
/ = 2, ..., n.

§ 23] УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ 203
(Для возможности определения этих операторов необхо¬
димо, чтобы функции blh(t) имели п — 1 производную,
а функции a\(t) имели72—2 производных.) Мы будем гово¬
рить, что в момент времени t выполнено условие общности
положения, если для любого ребра w многогранника U
векторы
Вг (£) w, B2(t)w, . • •, Bn(t)w	(89)
линейно независимы в пространстве X. В этом параграфе
мы будем всюду предполагать, что в любой момент
времени I, а < t < Ъ, выполнено условие\ общности по¬
ложения.
Отметим, что если матрицы (а\ (£)) и (blk(t)) постоянны,
т. е. величины а\ и 7* не зависят от времени, то из (88)
следует, что Bj = ( — iy~1Aj'1B, и потому векторы (89)
совпадают, с точностью до знаков, с векторами (3). Таким
образом, в этом случае сформулированное здесь условие
общности положения совпадает с условием общности поло¬
жения, введенным в § 17.
Функция Н (ф, х, t, и) (см. стр. 74 и теорему 5) в рас¬
сматриваемом случае имеет вид
Я = (i)5, 4(*)a;) + (il>, B(t)u) + (ty, f{t)) =
= S^av(i)a:v+ S 'Mq (*) и° + У 'Фи/м'(0>	(90)
JLl, V	\Х, Q	IX
а вспомогательная система (см. формулу (69) гл. 1)
записывается в виде
= - 2 а) (0 IV, /=1.2, . .п,
V
или, в векторной форме (ср. (5)),
-^=-Л*(г)г1>.	(91)
Очевидно, что функция 7/, рассматриваемая как
функция переменного u£U, достигает максимума одно¬
временно с функцией (ф, B(t)u). Максимум функции
(ф, B(t)u), рассматриваемой как функция переменного
и £ Uу мы обозначим через Р (ф, t). Из теоремы 5 следует

204 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ
[ГЛ. 3
(см. формулу (70) гл.	1), что	если и (t), t0K	tv — опти¬
мальное управление,	переводящее фазовую	точку из
положения т0 в положение xv то существует такое
нетривиальное решение ф(£) уравнения (91), что
=	t)	(92)
для всех t, принадлежащих отрезку 70<£<С-
Некоторую функцию, заданную на интервале а < t < Ъ
или на его части, мы будем называть кусочно-постоянной,
если множество всех	точек	разрыва этой	функции не
имеет предельных точек внутри интервала а < t < Ъ, а
на каждом из интервалов, на которые интервал а < t < Ь
разбивается этими точками разрыва, рассматриваемая
функция постоянна. (Заметим, что точки разрыва могут
накапливаться к концам интервала а < t < b.)
Теорема 15. Для каждого нетривиального решения
ф(£) уравнения (91) соотношение (92) однозначно*) опре¬
деляет управляющую функцию и (t); при этом оказывает¬
ся, что функция и (t) кусочно-постоянна и ее значениями
являются лишь вершины многогранника U.
Это —теорема о «конечности числа переключений» для
линейных уравнений с переменными коэффициентами (ибо
всякое управление и (t) задано на некотором отрезке
*0<t<tv целиком лежащем внутри интервала а < t <
и из теоремы 15 следует, что число точек разрыва функ¬
ции u(t) конечно). В случае постоянных коэффициентов
теорема 15 превращается в теорему 9.
Доказательство теоремы 15 вполне аналогично
доказательству теоремы 9. Укажем лишь те незначитель¬
ные изменения, которые следует произвести в доказатель¬
стве теоремы 9.
Предположим, что множество точек, в которых зна¬
чение управления u(t) не определяется однозначно соот¬
ношением (92), имеет хотя бы одну предельную точку
внутри интервала а < t < Ъ. Тогда, как и выше
(см. формулу (8) и относящийся к ней текст), мы
сможем найти такое ребро w многогранника U и такое
*) Ср. сноску на стр. 132.

§ 23] УРАВНЕНИИ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ 205
множество М, имеющее внутри интервала а < t < Ъ пре¬
дельную точку t, что
(ф(t)yB(t)w)=.0	(93)
при всех t£M.
Формула (9) заменяется соотношением
(г|) (0,5 (0 да) = У o|)v (t) bvQ (t) да®.	(94)
V, О
Так как функции aj. (£) имеют /2 — 2 непрерывных произ¬
водных, то функции	•••>	фп(0’	составляющие ре¬
шение	уравнения	(91), имеют п— 1 непрерывную	произ¬
водную;	функции	ЪЦг) также имеют, по предположению,
/2—1 непрерывную производную. Следовательно, функция
(94) /г—1 раз непрерывно дифференцируема.
Так как т — предельная точка множества М, то, в силу
непрерывности функции (94), из соотношения (93) выте¬
кает, что
(ф(т),5(т)ш) = 0.
Далее, так как между каждыми двумя корнями дифферен¬
цируемой функции содержится хотя бы один корень ее
производной, то производная функции (94) обращается
в нуль в бесконечном множестве точек, имеющем т своей
предельной точкой. Но производная функции (94) имеет
вид
^ (-ф (t),B (t) да) = {-A* (t) (t),B (t) да) + (ф (t), ^ да) =
= (г|>(<). -A(t)B(t)w) +(Ч>(0.
=	B,(t)w)
(см. (88)). Таким образом, в бесконечном множестве точек,
имеющем т своей предельной точкой, выполняется соот¬
ношение
(1|)(0> 52 (t) да) = 0,
и потому (в силу непрерывности)
(гИт), В2(х) да) = 0.

206 ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ [ГЛ. 3
Аналогично, между любыми двумя корнями функции
(ф(£), B2(t)w) содержится хотя бы один корень ее про¬
изводной; из этого с помощью тех же рассуждений по¬
лучаем
(ф(т), B3(x)w) = 0
и т. д. В результате мы получаем соотношения
(ф(т), Bi(x)w) = 0, i = 1, 2, п (95)
(ср. (10), (И)). В силу линейной независимости векторов
(89) из соотношений (95) вытекает, что ф(т) = 0, и потому
решение ф (t) уравнения (91) тривиально. Полученное
протртворечие показывает, что множество точек, в кото¬
рых управление u(t) не определяется однозначно соотно¬
шением (92), не имеет предельных точек внутрр1 интер-
вала а < t < b.
Дальнейшее доказательство не отличается от доказа¬
тельства теоремы 9.
Итак, теорема 15 доказана.
Перейдем теперь к рассмотрению теорем суще¬
ствования и единственности для системы
(86). Как и выше (см. (20)), рассмотрим фундаменталь¬
ную систему решений
Фх (0* •••> Фп(*)
однородного уравнения
удовлетворяющую начальным условиям <pj-(£0) = 6j, и фун¬
даментальную систему решений
г|J1 («),	г)->n{t)
уравнения (91), удовлетворяющую начальным условиям
ф|(^о)== §{• При этом соотношение (21) остается справед¬
ливым. Далее, решение уравнения (87), соответствующее
произвольно выбранному управлению и (£), tQ < t < tlt
можно искать в виде
п
x(t) = 2 <Pv(0 Cv {t)
V=1

§23]
УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ
207
(ср. стр. 140). В результате мы получаем следующую
формулу (ср. (22)):
п	t
*(0 = 2 <pv (о (*о + ^ (г (0. в (t) и (t)+/ (0) dt). (96)
V=1	to
После этого теоремы И и 12 (в дословно тех же форму¬
лировках) переносятся и на рассматриваемый случай.
Сохраняются и доказательства этих теорем —с заменой
соотношения (22) соотношением (96) и вытекающими от¬
сюда очевидными изменениями. Сохраняется и теорема
существования (см. теорему 13).
Теорема 16. Если для процесса, описываемого урав¬
нением (87), существует при заданном t0 хотя бы одно
управление u(t),	переводящее	фазовую точку из
положения х0 в положение xv то существует и опти¬
мальное управление (с тем оке начальным моментом t0),
переводящее фазовую точку из положения х0 в поло¬
жение х1%
Доказательство является дословным повторением
доказательства теоремы 13 (с очевидной заменой ссылок
на формулу (22) ссылками на формулу (96)). Отметим
только, что сдвиг времени, о котором упоминалось на
стр. 145, теперь не может быть применен ввиду того,
что уравнение (87) неавтономно; однако этот сдвиг вре¬
мени теперь и не нужен, так как рассматриваются лишь
управления с начальным моментом t0.
Замечание. Все результаты настоящего параграфа
получены в предположении, что функции а\ (£), blk(t) и
f {t), входящие в систему (86), определены на некотором
интервале а < t < Ъ (возможно, на всей прямой) и функ¬
ции /1 (£) имеют на этом интервале первые непрерывные
производные, а функции a\(t) и blk(t) имеют соответствен¬
ные (/г —2)-е и (п— 1)-е непрерывные производные. (Кро¬
ме того, как всегда, предполагалось выполненным усло¬
вие общности положения.) Нетрудно понять, что все по¬
лученные результаты остаются справедливыми, если функ¬
ции aj.(£), blk(t), /1 (t) непрерывны, а их производные
(в указанном числе) являются лишь к у с о ч н о-н е и р с-
рывными функциями. В самом деле, отметим на

208
ЛИЛЕЙIIЫЕ 011ТИМАЛЫ1ЫЕ БЫСТРОДЕЙСТВ11И
[ГЛ. 3
интервале а < £ < Ъ все точки, в которых хотя бы одна
из указанных производных терпит разрыв непрерывности.
Эти точки разбивают интервал а < t < b на части, на
каждой из которых функции aj.(£), &£(£)> /г (0 имеют тре¬
буемое число непрерывных производных. К каждой из
этих частей в отдельности можно применить теорему 15,
и потому теорема 15 справедлива в применении ко всему
интервалу а < t < Ъ. Очевидно, что остается справедли¬
вой и формула (96), а потому также и теоремы сущест¬
вования и единственности.

ГЛАВА 4
РАЗНЫЕ ЗАДАЧИ
§ 24. Случай функционала, заданного несобственным
интегралом
Рассмотрим следующий вариант оптимальной задачи,
сводящийся к рассмотрению бесконечного интервала ин¬
тегрирования в функционале J.
В фазовом пространстве X дана точка х0. Среда всех
допустимых управлений и (£), tQ < t < + оо, для которых
соответствующая траектория x(t) системы
исходящая из точки х0, определена для всех £>£0 и удов¬
летворяет при t—>00 некоторым (заданным заранее)
предельным условиям, найти такое, для которого
интеграл
сходится и принимает наименьшее возможное значение.
На функции f (х, и) накладываются условия, аналогич¬
ные тем, которые были указаны в гл. 1 — 2: они пред¬
полагаются непрерывными по ж и к и непрерывно диффе¬
ренцируемыми по ж1,	хп на прямом произведении
X X U. Отметим далее, что мы будем понимать здесь под
«допустимыми») управлениями. Функцию u(t), £0<£< со,
принимающую значения в области управления U, мы
^4 Л. С. Понтрягив
оо

210
РАЗНЫЕ^ЗАДАЧИ
[ГЛ. 4
будем считать ограниченной, если множество всех
точек u(t), где t пробегает любой конечный отрезок,
лежащий на промежутке £0<£<оо, имеет в простран¬
стве Ег (содержащем область управления U) компактное
замыкание. Принимая это определение ограниченности
управления (и рассматривая лишь управления, заданные
на промежутках вида £0<£< оо), мыв остальном сохра¬
ним определение класса допустимых управлений, данное
в § 10. В частности, в качестве класса допустимых управ¬
лений можно взять класс всех ограниченных (в указан¬
ном смысле) измеримых управлений, заданных на про¬
межутках вида /0<£<оо, или же класс всех ограни¬
ченных кусочно-непрерывных управлений (кусочная не¬
прерывность понимается в том смысле, что на всяком
конечно м отрезке, содержащемся в промежутке t0 <
<£< оо, управление u(t) имеет лишь конечное число
разрывов первого рода). Наконец, сделаем еще замеча¬
ния относительно «предельных условий на бесконечнос¬
ти», упомянутых в формулировке задачи. Мы предпола¬
гаем, что эти условия имеют вид
lim хх (t) = х[,	(3)
t оо
где x1 = (x\f х\, ..., я™) — заданная точка фазового про¬
странства X. Если для фазовой траектории x(t), соответ¬
ствующей допустимому управлению и (t) и исходящей из
точки х0, выполнены условия (3), то мы будем писать
х(со) = х1 и будем говорить, что управление u(t), £0<
<£ < оо, переводит фазовую точку из положения х0 в по¬
ложение xv
Решение поставленной оптимальной задачи дается тео¬
ремой 1 (или теоремой 8) с очевидной заменой отрезка
^ ^ ^ бесконечным промежутком t0 ^ t <г со и с заме¬
ной условия прохождения траектории через некоторую
точку прямой П предельными условиями на бесконечнос¬
ти. В самом деле, все рассуждения, приведенные в §§13 —
14, были связаны с выбором некоторой правильной точ¬
ки т, удовлетворяющей условию т < tr\ эти рассуждения
дословно, без всяких изменений проходят и в случае
£j= оо. То же относится к формулировке и доказатель-

§ 24]	СЛУЧАИ НЕСОБСТВЕННОГО ИНТЕГРАЛА	211
ству лемм 5 — 8 из § 15. Однако построение предельного
конуса уже не проходит, так как точки /3 (правого кон¬
ца отрезка времени) не существует. Тем не менее, легко
видоизменить конструкцию предельного конуса таким
образом, чтобы ее можно было применить и в рассматри¬
ваемом случае. В самом деле, обозначим через вы¬
пуклый конус AXt\0(Kx). Эти конусы образуют возрастаю¬
щую последовательность:	при	т'	< т (для до¬
казательства этого факта достаточно к включению,
содержащемуся в лемме 8, применить преобразование А^%\0
и воспользоваться формулами (17) гл. 2). Поэтому объеди¬
нение (по всем правильным точкам т) всех конусов
снова есть выпуклый конус (возможно, не замкнутый)
пространства Xt0. Назовем его н а ч а л ь н ы м к о н усом
и обозначим через JKi0. Легко видеть, что (для рассмат¬
ривавшейся в §§ 2, И оптимальной задачи) имеет место
соотношение
Ati,t0 (1Г,0) = Zf(r
Поэтому начальный конус совершенно эквивалентен пре¬
дельному, и можно было завершение доказательства прин¬
ципа максимума (§ 15, после леммы 8) провести с помо¬
щью начального конуса AQ0. При этом лемма 9,
как и ее доказательство, остается в силе (с очевидной
заменой луча Ltl, конз^сов Ktl,	и преобразований
А^х соответственно на L*0, Kt0, к\^ и АХ} /0). После
этого без труда проводятся и заключительные рассужде¬
ния § 15, чем доказательство теоремы 8 (и теоремы 1),
проводимое с помощью начального конуса (вместо
предельного) и завершается. Но такое доказательство до¬
словно (с заменой отрезка t0 < t < tx промежутком t0 < t < oo)
переносится и на случай рассматриваемой оптималь¬
ной задачи (1),	(2). Тем самым наше утверждение
доказано.
Заметим еще, что можно было «сносить» конусы Кх
не в точку ас(£3) или в точку x(t0), а в любую точку
ос (t) рассматриваемой траектории. Поэтому изложенное
доказательство применимо и к случаю, когда промежут¬
ком интегрирования является вся прямая — оо < £< со.
14*

212
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
§ 25. Оптимальные процессы с параметрами
Мы рассмотрим в этом параграфе следующую опти¬
мальную задачу. Функции /°, /\ . ./п зависят от трех
переменных	u£U, w£W, где X и U имеют преж¬
ний смысл, a W — векторное пространство размерности т.
Функции /°, /х, . . ., fn и их частные производные по всем
переменным х1, х2, .. ., хп предполагаются определен¬
ными и непрерывными на всем пространстве X х U X W.
Закон движения объекта задается уравнениями
^ = f(x,u,w),	i = i,2,...,n.	(4)
В пространстве X заданы две точки х0 и xv Требуется
выбрать такую постоянную точку w0 £ W (т. е. до
начала движения подобрать значение параметра w, оста¬
ющееся постоянным в течение всего движения) и такое
допустимое управление u(t), чтобы соответствующая
траектория x(t), исходящая в момент t0 из точки х0,
проходила в некоторый момент через точку хг и чтобы
при этом интеграл
h
•^=^/° (#(£), u(t), w0)dt
to
принимал наименьшее возможное значение. Если функ¬
ции гг(£), х(1) и точка w0 дают решение поставленной
задачи, то величины u(t), x{t)y w0 мы будем называть
оптимальными (для заданных точек х0 и хЛ).
При решении этой задачи мы будем предполагать,
что все допустимые функции к у с о ч н о-н епрерывны,
т. е. что класс D допустимых управлений либо совпадает
с множеством всех кусочно-непрерывных функций (со зна¬
чениями в С/), либо является его подмножеством, удов¬
летворяющим условиям, указанным в § 10.
Отметим некоторую специфику рассматриваемой зада¬
чи, заставляющую ограничиваться лишь кусочно-непре¬
рывными (а не произвольными измеримыми) управления¬
ми. В то время как в оптимальной задаче, сформулиро¬
ванной в § И, каждый кусок оптимальной траектории

§ 25] ОПТИМАЛЬНЫЕ ПРОЦЕССЫ С ПАРАМЕТРАМИ	213
снова является оптимальной траекторией (ибо «улучше¬
ние» куска траектории ведет к «улучшению» всей траек¬
тории. ср. § 2), здесь, в рассматриваемой задаче с пара¬
метрами это уже не так. Ведь оптимальные значения
параметра w для всей траектории и для ее части могут
не совпадать, т. е. если u(t),w0 дают решение поставлен¬
ной в этом параграфе оптимальной задачи, причем управ¬
ление u(t) определено на отрезке £0<£<£1, то на мень¬
шем отрезке за счет изменения параметра
возможно удастся «улучшить» управление u(t). Из ска¬
занного следует, что рассуждения, проведенные при до¬
казательстве леммы 4, неприменимы к рассматривае¬
мой оптимальной задаче. Рассуждения, доказывающие
теорему 8 (или теорему 1), можно, однако, применить
и здесь, считая в лемме 9 точку т совпадающей с кон¬
цевой точкой tx (что делает излишней лемму 4). Но
для этого приходится считать точку правильной
точкой управления и (£), т. е. в качестве допустимых
управлений приходится брать управления, правильные
в правом конце отрезка. При этих условиях наиболее
естественным классом допустимых управлений является
класс кусочно-непрерывных управлений (или какой-либо
его подкласс).
Решение поставленной оптимальной задачи дается сле¬
дующей теоремой, аналогичной теореме 1 (функция <Д6
V
определяется, как и прежде: <Дв = 2 Фа/а)-
а=0
Теорема 17. Пустъ u(t), £0< t< tv — такое допус¬
тимое управление, a w0 = (w1, . .., wm) — такое значение
параметра w, что соответствующая траектория
х (t) = (х° (t), х1 (t), . . ., хп (t)) = (х° (t), х (*))
(т. е. траектория системы (4), пополненной соответ¬
ствующим уравнением для i = 0) удовлетворяет условиям
x(t0) — x0, х° (t0) = 0, x(t1)=x1. Для того чтобы величи¬
ны u(t), x(t), w0 давали решение поставленной опти¬
мальной задачи, необходимо существование такой ненуле¬
вой непрерывной вектор-функции я|э (£) = (ф0 (£),
• • • » 'Фп(О)» Что:

214
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
1° функции x(t), ф(£)> u(t)y wQ удовлетворяют гамиль¬
тоновой системе
dxl _ д&в (if (t)y х (t), и (t), w0)
dt
dtyi __ d&G (i|) (0, x (t), и (t), w0)
dt	dx{
i = 0, 1, . . ., n\
2° функция	%(t),	u, w0) переменного u£U
достигает в точке и— и (t) максимума
->{t),x(t), u(t), w0) = oM x(t), w0)\*)
3° в начальной точке t0 выполнены соотношения
'I’oBoX0-	x(t0),	w0) = 0;
4° имеют место равенства
Wo) dt = 0,	?=1 ш. (5)
а=0	t0
Оказывается, далее, что если величины	x(t),	W0y
u(t) удовлетворяют условиям 1° и 2°, то функции гр0 (^)
и	x(t), до0) переменного t являются постоянны-
миу так что проверку условия 3° можно проводить не
обязательно в момент t0, а в любой момент t> £0<£<£г
Эта теорема отличается от теоремы 1 (или теоремы 8)
наличием условия 4°, которое дает т дополнительных
соотношений, что и дает возможность решать задачу,
так как в эту задачу введено дополнительно т неиз¬
вестных до1, до2, . . ., доте (координаты точки до0 в про¬
странстве W).
Укажем, какие изменения нужно произвести в дока¬
зательстве теоремы 8, чтобы получить доказательство
теоремы 17. Конструкции § 12 сохраняются полностью;
надо только помнить, что они проводятся не только при
фиксированном управлении и (£), но и при фиксированном
значении параметра до0 (меняются только начальные
условия, определяющие решение; см. формулу (14)
гл. 2). Обратимся, далее, к § 13. Правильными точ¬
ками управления и (t) являются все его точки непрерыв¬
ности, т. е. гее точки отрезка	за исключением
*) См, стр. 24.

§ 25] ОПТИМАЛЬНЫЕ ПРОЦЕССЫ С ПАРАМЕТРАМИ	215
конечного числа точек разрыва. Мы продолжим управле¬
ние u(t) несколько дальше, за правый конец отрезка
t0<t<tv полагая u(t) = u(t1— 0) при t > tT. Продолжен¬
ное таким образом управление u (t) непрерывно в точке tl9
так что t1 является правильной точкой. Далее, точку т,
входящую в определение проварьнрованного управления
(стр. 98), мы теперь будем считать совпадающей с tv
т. е. положим t0 <	<	т2	<	...	< xs < т = tv
Основные изменения произойдут во второй полови¬
не § 13. Помимо варьирования управления u(t), мы будем
также «варьировать» параметр w0. Именно, мы выберем
некоторый вектор бw пространства W и через х* (t)
будем обозначать (при достаточно малом е) решение
системы
т. е. траекторию, соответствующую проварьированному
управлению и* (t) и смещенному значению w = w0 + e6w
параметра w. При этом линию | (е) мы будем считать вы¬
родившейся в точку х0, т. е. будем считать, что решение
х* (t) удовлетворяет тому же начальному условию
х* (£0) = х0, что и решение х (t). Мы имеем, очевидно,
/7 т1'
— --=fl(x, u*(t), w0 + ebw), i = О,
Ц -b £6t
to
= aco+ $	“*(*)>	®o)	+
m
m
Q= 1
ti+e6t
= ac0+ \ f(x*(t),u*(t),w0)dt +
Ц+еб* m
to Q=1

216	РАЗНЫЕ ЗАДАЧИ	[ГЛ.	4
*1+е6*
= •"»«+	^	f(x*(t), U*(t), w0)dt-1-
*0
m ti
+ g^ ^yf(X(t),u^t),Wo) ^jtoe + 0(e)_
o=i f0	W
/H-e6f
Так как x0 +	^	f(x*(t), u* (t), wQ) dt есть точка на
to
траектории, соответствующей проварьированному управ¬
лению и* (t), но не изменившемуся значению
параметра w0, то к ней применимы формулы (21), (22)
гл. 2, так что мы в нашем случае получаем
ас* (£х -f еб£) = х (£j) + еДас + ...,
где
3
A x = f(x{t1), и (£,), wa)bt-\-^ А1ъХ.^(х(х{), v{, w0)-
i=1
т	ti
—/(х(т;),	б^-|-2 йа>0	а,°)’	(6)
e=i
Такой вид принимают формулы (21), (22) гл. 2 в рас¬
сматриваемом случае.
Обратимся теперь к § 14. Мы включим вектор боу
в символ а, т. е. будем теперь полагать
а = {т^ vi9 б£., б£, бш}
(мы опустили обозначение точки т, так как теперь т = ^
есть фиксированная точка). Линейная комбинация сим¬
волов а определяется так же, как и раньше, только
с учетом последного аргумента:
А/ {..., боу'} + X" {..., бw"} +	А/бw' + A!'bwn +•••}•
После этого доказательство лемм 2, 3 (прит = ^) про¬
ходит без изменения, а лемма 4 становится просто ненуж¬
ной (ибо т=^). В результате мы получаем конус дости¬
жимости Ktv для которого справедлива лемма 3.

§ 25]
ОПТИМАЛЬНЫЕ ПРОЦЕССЫ С ПАРАМЕТРАМИ 217
Рассуждения § 15 также сохраняются (с заменой т на
а предельный конус становится ненужным, так как
у нас имеется лишь один конус Ktly построенный как
раз в конце x(tj) траектории x(t) (в силу этого лемма 9
не нужна —она просто сводится к лемме 3). Наконец,
рассуждения, приведенные в конце § 15, доказывают
условия 1®, 2°, 3° и заключительную часть теоремы 17.
Остается показать, что для выбранного таким образом
вектора я|) (t) выполняется условие 4®. Положим в фор¬
муле (6) б£ = 6t1 = 6t2 = . . . = 6ts = 0. Мы получим тогда
m	Ц
Ах = у. 6 w° [
^	J	dwQ
6=1	to
Согласно сказанному выше (ср. формулы (34),	(36)
п
гл. 2), мы имеем 2 ^a(*i)A#a<0 для любого век-
а=0
тора (6), и потому
пт	t-[
2 2 % wбдае [ g/a(-r(y>3) dt < о. (?)
а=0 6=1	/о
Так как эти соотношения справедливы при любых дей¬
ствительных значениях параметров бш°, то мы имеем
2	<0	=	0.	е= 1, 2 т,
а=0	t0	W
и теорема 17 полностью доказана.
Заметим в заключение, что если параметр w может
изменяться не во всем пространстве W, а лишь в неко¬
торой замкнутой области И^СГИ7, имеющей кусочно¬
гладкую границу, то условия (5) в формулировке теоре¬
мы 17 заменяются соотношениями
у	С	dia(*M’uM’.?Adt<o,
j	dw
а=0	t0
где производная под знаком интеграла берется по любому
направлению w, исходящему из точки w0 и проходящему

218
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
в области Wv Иначе говоря, для любой дифферен¬
цируемой кривой w(b), исходящей при 0 = 0 из точки w0
и проходящей в области Wv должно быть выполнено
соотношение
£ (У\ *'"<*<■).»<■)..<■)) dt<0.
п(\	Г	0	=	0
а=0	t о
Это утверждение непосредственно вытекает из соотноше¬
ния (7).
§ 26. Применение теории оптимальных процессов
к задачам приближения функций
Пусть F (х, у) — функция, определенная и непрерывная
для всех действительных значений аргументов. Тогда
для любых двух функций x(t), y(t), заданных на отрез¬
ке а < t < b, величина
ъ
J=^F(x(t),y(t))dt	(8)
а
может быть использована для сравнения функций х (t)
и y{t). Например, если F (х, у) = (х — у)2, то интеграл (8)
принимает вид
ь
J = ^ (X (f) - у (*))2 dt	(9)
а
и представляет собой в этом случае квадрат расстояния
между элементами x(t) и у (i) пространства Ь2. (Здесь
и далее в этом параграфе все функции аргумента t будут
рассматриваться на одном и том же фиксированном
отрезке а<г<Ь.)
В настоящем параграфе рассматривается решение
следующей задачи. Заданы функции F (х, у) и y(t).
Кроме того, заданы целое число п> 0 и действительное
число а>0. Среди всех п раз непрерывно дифферен¬
цируемых функций x(t), заданных на отрезке а<£<6
и обладающих тем свойством, что функция xin) (t) удов¬
летворяет условию Липшица с константой а, найти
такую, для которой интеграл (8) принимает наименъ-

§ 26]
ПРИМЕНЕНИЕ К ЗАДАЧАМ ПРИБЛИЖЕНИЯ
219
шее значение. Эту задачу мы будем в дальнейшем назы¬
вать основной задачей.
В частном случае, когда F (х, у) = (х — у)2- (т. е.
вместо функционала (8) рассматривается (9)), а число а
равно нулю, мы приходим к задаче нахождения такого
многочлена п-й степени x(t), который на отрезке а<£<6
имеет наименьшее квадратичное уклонение от заданной
функции у (t), т. е. к классической задаче нахождения
коэффициентов Фурье при разложении функции y(t) по
многочленам Лежандра. Таким образом, рассматриваемая
основная задача является обобщением этой классической
задачи.
Пре жде всего мы покажем, что при некоторых естест¬
венных требованиях, налагаемых на функцию F (х, у),
поставленная основная задача всегда (т. е. для любой
функции y(t)) имеет хотя бы одно решение, а в случае,
когда рассматривается функционал (9), эта задача имеет
(для любой функции у (t)) ровно одно решение.
Далее рассмотрен вопрос о нахождении функции x(t),
являющейся решением основной задачи. Для нахождения
решения используется принцип максимума. В качестве при¬
мера приведена «задача о нахождении профиля дороги».
Вопрос о существовании решения основной
задачи (а в частном случае (9) и вопрос о единственности
решения) рассматривается в нижеследующей теореме.
Теорема 18. Пусть функция F (х, у) определена и не¬
прерывна для всех, действительных значений аргументов
ху у и обладает тем свойством, что при изменении у на лю¬
бом конечном отрезке функция F (х, у) равномерно (по у)
стремится к -j-oo, когда х—> + оо. Тогда основная зада¬
ча имеет хотя бы одно решение для любой непрерывной
функции y(t). Если, в частности, F (х, у) — (х — у)2, то
поставленная задача имеет для любой функции у (t)
ровно одно решение.
Множество всех действительных, п раз непрерывно
дифференцируемых функций x(t), заданных на отрезке
а < t < b и обладающих тем свойством, что их п-е
производные x^(t) удовлетворяют условию Липшица
с константой а, мы обозначим через Qan). Таким обра¬
зом, включение x^Q'™ означает, что функция х (t)

220
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
задана на отрезке [а, Ь], имеет на этом отрезке п
непрерывных производных и удовлетворяет неравенству
| xin) (£') — хт) (t") | (X |	—	t"	\
для любых точек t', t” отрезка [а, Ъ]. Множество Q™,
очевидно, содержится в банаховом пространстве C[0j ъ]
всех непрерывных функций, заданных на отрезке [а, Ь].
Основная лемма. Множество Qan) является
замкнутым выпуклым локально компактным подмножест¬
вом пространства С[а, ьр Любое замкнутое ограниченное
множество, сод ерошащееся в £2ап)» компактно.
Эта лемма известна. Она, например, легко вытекает
из теоремы 3.5.1, приведенной на стр. 127 книги А. Ф. Ти-
мана «Теория приближения функций действительного пере¬
менного», Физматгиз, М., 1960. В самом деле, обозначим
через 2л множество всех функций x£Q(a\ удовлетво¬
ряющих условию ||;г||с</?, а через 2^ — множество всех
функций вида	где x^Xr. Цитированная выше
теорема утверждает, что множества 2л, 2д\ ..., 2л}
«компактны в пространстве	т.	е. замыкания этих
множеств в пространстве	компактны.	Если	не¬
произвольная предельная точка множества 2л, то суще¬
ствует последовательность xv x2f ... элементов множест¬
ва 2л» сходящаяся к х. Переходя, если нужно, к под¬
последовательности, мы можем считать (в силу того, что
замыкание множества 2^ компактно), что последователь¬
ность х[{\ х^\ ... является сходящейся, i— 1, 2, . ..,тг.
Из этого, в силу теоремы об интегрировании равномерно
сходящихся последовательностей, следует, что функция
х (t) имеет непрерывные производные порядков i= 1, 2, ...
. . ., 72, причем хW есть предел последовательности
х^\ х^\ ... В частности, х{Ю (t), как предел последо¬
вательности х™, х^п), ..., удовлетворяет условию Лип¬
шица с константой а, и потому x^Q™. Итак, множест¬
во 2л замкнуто, и, следовательно, компактно. Выпук¬
лость множества	очевидна. Таким образом, основ¬
ная лемма доказана.
Доказательство теоремы 18. Обозначим че¬
рез / отрезок, которому принадлежат значения функ-

8 26]
ПРИМЕНЕНИЕ К ЗАДАЧАМ ПРИБЛИЖЕНИЯ
221
дни y(t) при t£[a, Ь]. Так как при у£1 функция F (х> у)
равномерно по у стремится к + оо, когда я—>±00, то
функция F (х, у) ограничена снизу при y£l и любом х.
Поэтому существует такое неотрицательное число N, что
F (х, г/)> —N при y£l и любом х.	(10)
Выберем произвольные попарно различные точки
а0, av . .., ап, расположенные внутри отрезка [а, Ь], и
обозначим через ф. (£) многочлен степени п, принима¬
ющий значение 1 в точке а. и значение 0 в остальных
точках a,j. Обозначим, далее, через q настолько малое
положительное число, что на интервале It длины q
с центром в точке ai (£ = 0, 1,	многочлен	ф{(£)
принимает значения, большие у, а все остальные много¬
члены ф (t) принимают значения, по модулю меньшие
1
^. Наконец, через А обозначим такое положительное
число, что |фг(^)|<Л при t£[a, Ь], i = 0, 1, ...,/г.
Пусть теперь х (t) — произвольная функция, принадле¬
жащая множеству Q(a \ и ||х\\ = max \x(t)\— ее норма
а<г<ь
в пространстве С[а, ьр Обозначим через ф(£) многочлен
степени /г, удовлетворяющий условиям х^ (а) = ф({) (а),
г = 0, 1, ...,/г. Тогда функция хг (t) = х (t) — ф (t) удов¬
летворяет условиям х{^ (а) = 0, i = 0, 1, . . ., п. Кроме
того, мы имеем
х£"-) (t) = х^ (t) — х(а) =
=	(£)	—	х^п)	(а)]	—	[ф^ (£) — ф(п) (а)] = х(п) (£) —	(а)
(ибо ф<п)(£) есть константа). Так как функция я(7г) (t)
удовлетворяет на отрезке [а, Ъ] условию Липшица с кон¬
стантой а, то при любом t£[ci, b]
[яС”) (t) \ = \x^n)(t) — x^n\a) |< а (£ — а)<а (6 —а).
Разлагая функцию ^(О по формуле Тэйлора, мы найдем
*1(0 = ®1(а)+^р®1 («)+	a?i(a)+	•	•	•
• ■ • + i==75T	1'(а) +	(9)l

222
РАЗНЫЕ ЗАДАЧИ
[ГЛ. k
где 0 — промежуточное значение между а и t. Так как
хг (а) = х[ (а) = .. . = ^п_1) (а) = 0, то при t £ [а, b] мы нахо¬
дим
Выберем теперь такой номер г* = 0, 1,	/г,	что
число |ф(Я|)| является наибольшим среди чисел |ф(а0)1»
| ф (лх) |,	|ф(ап)1*	В	силу интерполяционной формулы
Лагранжа мы имеем
ф (<) = ф ю Фо (0 + Ф («]) Ф1 (*)+•••+ Ф К) Фп (0.
и потому | ф(^)|<(72-(- 1) |ф(а^) | Л при t£[a, Ь], т. е.
Сопоставляя неравенства (12) и (л мы получаем
|ф (t) | = | ф (а0) ф0 (t) + ф(а,) ф, (t) + ... + Ф (а„) фп(0 | >
> I Ф К) Фь (01 - I Ф («о) Фо (0 + • • • + Ф (ai-i) Ф1-1 (() +
+ <P(ai+i)<Pi,i(0+ • • • +ф(а«)фЛ01>
> IФ W | {| ф; (01 - [| Фо № I + • • • +1 Ф1-1 (t) I +
+ I Ф1 + 1 М I + • • • + I Фп (0 |]} >
(b а)п+1
Таким образом, у^ЦСа-	р—, и потому
II ф II = II * -хг II > IIЖ || - II Xl II > IIX II - а геа,)П 1 . (12)
||ф||<(п + 1)|ф(а1)[ А
(13)
На отрезке 1{ выполнены неравенства
ф{ (0 > 4 ’	(0	<	при	i*	г'>
и потому на этом отрезке мы имеем
1 Г
> (»+1)л [
3 п J
3 (ra-f-l) А
[iH—fi-EL].

§ 26]	ПРИМЕНЕНИЕ	К	ЗАДАЧАМ	ПРИБЛИЖЕНИЯ	223
Из этого следует, что на отрезке /.
1Ж (О I = I ф (*) + (О I > I ф (О I -1 *i (О I >
^	1	ГII II	(6—	a)n+l	1	(6-а)»+1	....
>Цп + 1)А	(14)
(см. (И)). Итак, для любой функции x£Q™ найдется
такой номер г = 0, 1, . п, что на отрезке It выполнено
неравенство (14).
Пусть теперь J0 — значение, которое принимает функ¬
ционал (8) для функции x(t) = 0. Пусть, далее, Р — такое
положительное число, что при | х | > Р, у £ / мы имеем
F{x, y)>-J°+Y~tt)
(такое число Р существует в силу указанных в форму¬
лировке теоремы свойств функции F (х, у)). Пусть,
наконец, i? —такое положительное число, что при || х || > R
правая часть соотношения (14) больше чем Р. Тогда для
любой функции x£Q(a\ удовлетворяющей условию
||#||>i?, найдется такой номер г = 0, 1, ..., н, что на
отрезке 1{ выполнено неравенство (14), и потому выпол¬
нено неравенство | х (t) | > Р. Из этого следует, что
F(x(t), y(t))> J«+N^b-a\ при *£/..	(15)
Кроме того, в силу (10),
F(x(t), y(t))>—N при t£[a, Ь].	(16)
Так как длина отрезка Ii равна р, то из неравенств (15)
и (16) мы получаем
ъ
^ (х (0- У (0) dt >
а
>Jo + N(b-a)Q + {_ N) [{b _ д) _ q] > Jo	(1?)
Итак, для любой функции x^QX\ удовлетворяющей
условию ||ж||>/?, выполнено неравенство (17).
Обозначим через множество всех функций x£Q(a\
удовлетворяющих условию \\х\\ < /?, и пусть ,/* — нижняя

224
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
грань значений функционала (8) для функций х£2д.
ь
Очевидно, что	и	потому ^ F(x(t),y(t))dt>J*
а
для любой функции я£~йап): при || х || > R это следует из
доказанного неравенства (17), а при [| х || < R — из опре¬
деления нижней грани. Поэтому для завершения дока¬
зательства первой части теоремы остается установить,
что существует такая функция x£Q(a\ для которой функ¬
ционал (8) принимает значение /*. Это легко вытекает
из компактности множества 2# (см. основную лемму)
и непрерывности интеграла (8), рассматриваемого как
функция от x£Qan)-
Итак, первая часть теоремы (существование решения)
доказана. Так как, в частности, функция F (х, у) = (х — у)2
удовлетворяет указанным в теореме 18 условиям, то
и для функционала (9) поставленная задача всегда имеет
решение. Покажем, что в этом случае решение един¬
ственно. Так как функционал (9) равен d2, где d = d(x> у) —
расстояние между функциями х и у в смысле метрики
пространства L2, и так как величины d и d2 достигают
своего минимума одновременно, то задача сводится к оты¬
сканию такого элемента х £ £2ап\ для которого d (х, у) = min,
т. е. к нахождению ближайшей к у точки x£Qan)-
Пространство C[aj естественно содержится в L2, причем
прямые линии пространства С[а, ь] являются прямыми и в L2.
Поэтому выпуклое в С[а> ь] множество Й2г) (см. основную
лемму) является также выпуклым подмножеством прол
странства L2. Но в пространстве Ь2 (в силу строгой выпук¬
лости его единичной сферы) выпуклое множество не
может содержать более одной ближайшей к у точки.
Поэтому в рассматриваемом случае наша основная задача
имеет только одно решение.
Теорема 18 доказана.
Перейдем теперь кнахождени ю решения с помо¬
щью принципа максимума. Пусть х (t) — произвольная
функция класса Тогда функция x(n) (t) существует на
отрезке [а, Ь] и удовлетворяет условию Липшица с кон¬
стантой а и, следовательно, является абсолютно непре¬
рывной. Поэтому почти всюду существует измеримая

si 26J
11 PJ1 J\] EH JU НИК К ЗАДАЧАМ ll.PPI ЬЛМЖКШ!)!
220
функция и --
■ X
'(t),
причем во всех точках, где функ¬
ция u(t) определена, вьшолнено соотношение | и (t) |< а.
Таким образом, обозначая функции x(t), х/ (t), . . ., хт) (t)
через х1, х2, . . ., хп+1 соответственно, мы найдем, что
выполнены соотношения
dx1	0
dt
dx2
dt
dxn
dt
dxn+i
dt
= x
= u(t),
где | и (t) | < а. Эти соотношения выполняются почти всюду
на отрезке [«, Ь] (первые п соотношений даже всюду).
Нетрудно видеть, что и обратно, если абсолютно непре¬
рывные функции х1, х2, . . ., хп+1 почти всюду на отрезке
[а, Ь] удовлетворяют соотношениям (18), где и (^ — неко¬
торая измеримая функция, удовлетворяющая условию
| и (t) | < а, то функция х (t) — х1 (t) принадлежит классу Qan).
В самом деле, так как функция xl+1(i= 1,2, ..., п)
абсолютно непрерывна и, следовательно, непрерывна., то
dxd’	■	I.
из соотношения =х%+1» имеющего место почти всюду
на отрезке [а, Ь], следует, что абсолютно непрерывная
функция хг является интегралом от н е п р е р ы в н о й функ¬
ции хг+1. Поэтому функция Xх в с ю д у на отрезке [а, b] имеет
непрерывную производную, равную .гг+1(?‘=1, 2, ..., п).
Таким образом, функция х1 (t) илгеет всюду на отрезке [а, Ь]
абсолютно непрерывную п-ю производную, равную xn+1 (t),
dг,г+1
и эта производная, в силу соотношений ——=u(t)\
| и (t) | < а, имеющих место почти всюду, удовлетворяет
условию Липшица с константой а, т. е.
Итак, вместо функций класса QaV мы можем рассма¬
тривать (абсолютно непрерывные) решения системы (18)
при ограничении |гг(£)|<а. Таким образом, основная
задача эквивалентна следующей оптимальной задаче:
Л О Понтрягип

22(\
РЛЗТГЫЕ ЗАДАЧИ
[ГЛ. 4
в классе измеримых управлений и (t), удовлетворяющих
ограничению |гг(£)|<а, найти такое, для которого реше¬
ние системы (18) осуществляет минимум интеграла
ь
./ =
концевые значения х1 (а) и хг (Ь), /’=1,2, . . ., a j 1 произ¬
вольны.
Так как подынтегральная функция интеграла J зави¬
сит явно от t (через заданную функцию у (£)), то
мы введем вспомогательное переменное x"*2=^t, удо¬
влетворяющее, очевидно, дифференциальному уравнению
dxll+2 .
dt =
с начальным условием хп+2(а) — а. Тогда рассматриваемая
оптимальная задача примет следующую форму.
В пространстве X переменных х1, х2, . . ., х11 п, хп+2
задано начальное многообразие S0 с уравнением хп+2 = а
и конечное многообразие	с	уравнением хп+2 — b
(каждое из многообразий имеет размерность п-\-1).
В классе измеримых управлений u(t), удовлетворяющих
ограничению |и(£)|-<а, найти такое, для которого реше¬
ние системы
dx1
dt
dx'1
dt
dx11
~dt~
d: rn+1
~df
dxil+
~~df
--- ut
■= I.
(W)
исходящее в момент tQ — a из некоторой точки много¬
образия $0 и приходящее (в силу последнего уравнения
(19), в момент tx = Ь) на многообразие SL, осуществляет

§ 26]
ПРИМЕ 11ЕПИЕ 1; ЗАДАЧАМ J11ЧШЛИЖЕПИЛ
227
минимум интеграла
11
$ F(x\ у (xn*2))dt.
*0
Эту задачу (эквивалентную нашей основной задаче)
мы и будем решать, для чего воспользуемся теоремами 8
и 3. Функции F (х, у) и y{t) мы будем предполагать
непрерывно дифференцируемыми. Функция для рас¬
сматриваемой оптимальной задачи имеет вид
/г = ^0F (А,' у (хп+2)) + r|),3-2 + iJ)2a:8+ . . .
■ • • +	+	i|W	(20)
С помощью этой функции ift; мы составим систему диф¬
ференциальных уравнений для вспомогательных неиз¬
вестных
i$o=0
dt
сД|д _	д&€
dt	dx1
dx|>2 _	om
dt	dx2
flfrfr з _	dm
dt	dx3
=	д<Ж _lh
dt	dxn+1
(выражение для	мы	не выписываем, так как оно
нам не понадобится).
Пусть x(t) — решение основной задачи. Тогда, согласно
сказанному выше, функции
х1 (t) = х (t), х2 (t) = ж' (t),	xn+1 (t) = *(n) (0, xn*2 = t
дают решение рассмотренной выше оптимальной задачи
(см. (19)). Поэтому существует ненулевое решение ф0,	. . .
• • • > Фп+i» Фп+2 системы (21) (дополненной невыписанным
уравнением для фп+2), удовлетворяющее условиям, кото¬
рые указаны в теоремах 8 и 3. Условие максимума
-Фо-
Фе
-ф2>
dF (х1, у (хп+2))
дх1
(21)

РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
функции Ж дает (почти всюду на отрезке [а, /;]):
max г|>п+1(г)и = г|)п+1(*)ы(0.
—а<и<а
т. е.
n{t)[	если	Ц)п+1 (f) # о,	^
| не определено, если фп+1(£) = 0.
Выпишем теперь условия трансверсальности (теорема 3)*
Так как векторы, идущие вдоль осей х1, х'1, ..., хп+1,
параллельны гиперплоскостям S0 и Slf то условия транс¬
версальности имеют вид
фДа) = 0,	i = 1,	2,	.	.	., 7г+ 1,	(23)
Фг (^) =	^ = 1 >	2,	.	.	., и-т 1.	(24)
В силу первого из уравнений	(21)	мы имеем	ф0 = const,
причем, согласно теореме 8, ф0<0. Нетрудно видеть, что
предположение ф0 = 0 приводит к противоречию. Дей¬
ствительно, если ф0 = 0, то = 0 (см. (21)) и, в силу (23),
ф3 = 0. Из этого получаем = 0 (см. (21)) и, в силу (23),
ф2 = 0 и т. д. Таким образом, мы находим последова¬
тельно ф0 = Ф1 = Ф2 = • • • — Фп+1 — 0- Так как вдоль опти¬
мальной траектории	функция	тождественно	равна
нулю (теорема 8), то отсюда, в силу (20), получаем
фп+2 = 0. Но это противоречит тому, чтоф0, ф1? ф2> . . ., фп+2 —
ненулевое решение. Итак, ф0 < 0, и мы можем счи¬
тать, что ф0 = — 1 (так как все величины ф- определены
лишь с точностью до общего постоянного положительного
множителя пропорциональности). Система (21) теперь
принимает вид (после подстановки xn+2=t):
d\= 9F (х\ у (t))
dt	дх1	’
а?Ф2
dt
’ = - ^1-
dt	^п’

§ 26]	ПРИМЕНЕНИЕ	К	ЗАДАЧАМ	ПРИБЛИЖЕНИИ	229
откуда получаем, учитывая условия трансверсальности (23):
а
г|)2 (t) = - ^	\ дР^^(У.Ю). dt, dt,
а а
,|, (,)=^ Ц, у Л-(■>.»«)’
a (L а
и вообще
xh (0 = ( - О'11 + • + (*+’ dt... dt (к киадратур),
а	а
к = 1, 2, . . /г + 1.
Согласно известной формуле анализа
it	-	i
5 ... $/(*)</* ... а^^+r
<i	а	а
к
мы	дюжем найденное	значение (/) переписать	в	виде
^ (0 =	pCiyr	$ № -	dF{Xlfx[ У(1)) dl,	(25)
a
к = 1, 2, . . . , /2 + 1.
Условия трансверсальности (24) принимают теперь вид
^ W = 7F=IjT \ & - b)k~l dF{Xlfiym dt = °-
a
/£=1,2, . . . , /2+1.
Умножая это	соотношение	на	(/с— 1)! с/г_А и суммируя

2:зо
РАЗНЫЕ ЗАДАЧИ
[ГЛ. /,
по к =1,2, . . ., п + I, получаем
ь
^ [со сг (| — b) + с2 (£ — 6)2 + .. .
...+Cn(£-6)"] ^(xlgt’y(g)) dt; = 0
при любых значениях констант с0, сх, . . ., сп. Так как
co + ci(£"“ + ••• Jrcn(^>-~Wl есть произвольный
многочлен степени < п, то мы можем объединить все
условия трансверсальности (24) одним требованием:
$ Р (s)	dl	= о
а
для любого многочлена Р (£) степени <гс.
Далее, формула (22) переписывается, в силу (25),
в виде
/
(' С /6	,\ jj, йРД®1 (|), 7/(g))
= a sign f \ (£ — t) —-—d^i ^ i ’ если
и (t) {	a
| выражение под знаком sign отлично от нуля;
( не определено, если это выражение равно нулю.
Иначе говоря, почти всюду на отрезке [а, Ь] выполняется
одно из соотношений:
а
и (t) = а sign f ^	-	1)п	д-	(jl fxi—— ' d^> ) ■
а
Наконец, из соотношений (19) мы получаем
«(0 = -^г*х(0
(почти всюду на отрезке [а, 5]). Сопоставляя все сказан¬
ное и обозначая снова xx{t) через x(t), мы получим
следующее предложение.

§ 2G]
II РИМ ЕН ЕШ! Е К ЗАДАЧАМ ПРИ LEI И ЖЕ IIII Я
Теорема 19. Пусть функции F (.г, у) и у(1) имеют
непрерывные первые производные. Для того чтобы функ¬
ция x(t) являлась решением основной задачи, необходимо,
чтобы почти всюду на отрезке [//, Ь] выполнялось одно
из соотношений
и, кроме того, чтобы для любого многочлена Р (/) сте¬
пени -< п выполнялось условие
Пример (задача о нахождении профиля дороги).
Рассматривая функционал (9), мы при п = 0 приходим
к следующей задаче. Даны дифференцируемая на отрезке
[ау b] функция у (/) и число а > 0. Найти такую функ¬
цию x(t), удовлетворяющую условию Липшица с констан¬
той а, для которой интеграл (9) принимает наименьшее
возможное значение. Эту задачу можно интерпретировать
следующим образом. Между двумя пунктами А и />
нужно провести дорогу, причем рельеф местности между
этими пунктами задан (функция ?/(/)), а но условиям
эксплуатации дороги уклон пути в любой точке должен
быть <а, т. е. продольный разрез дороги (профиль ее)
должен описываться функцией, удовлетворяющей условию
Липшица с константой а. Для достижения этой цели
можно либо прокладывать дорогу по местности, либо
сооружать насыпь, либо прорывать траншею для дороги.
Если ж (£)-—проектируемый профиль дороги, то стоимость
земляных работ (сооружение насыпей для участков,
где x(t)>y(t), и траншей для участков, где х (0 <
< у (t)) пусть оценивается интегралом (9). Найти наи¬
более выгодный (в смысле материальных затрат) профиль
дороги.
а
Ь
а

232
РАЗНЫЕ ЗАДАЧИ
[ГЛ. /,
Решение этой задачи существует и единственно (тео¬
рема 18). Для того чтобы функция х (t) являлась искомым
решением, необходимо (в силу теоремы 19), чтобы почти
всюду на отрезке [я, b] выполнялось одно из соотношений
/
$[*(£)-y(S)]dl=0,	(26)
а
I
х' (г) = a sign ( ^ [х (I) - у (I)] d\xj ,	(27)
а
и, кроме того, чтобы было выполнено условие
ь
\[x(t)-y(t))dt = 0.	(28)
а
Если на некотором отрезке, содержащемся внутри
[а, Ь], выполнено соотношение (26), то на этом отрезке
x(t) = y(t), т. е. дорогу следует прокладывать прямо по
местности. Если же на некотором отрезке выполнено
соотношение (27), то в точках этого отрезка x(t)=±:aJ
А	В
так что на этом участке дорога состоит из одного или
нескольких кусков с уклоном а или — а. Таким образом,
общая характеристика дороги заключается в том, что она
состоит из отдельных кусков, проложенных по местности,
и кусков максимально допустимого уклона, идущих по
насыпям или в траншеях.
Пусть, например, пункты А и В расположены на
ровной местности, на которой между пунктами А и В
имеется углубление (скажем, овраг, который дорога
должна пересечь), так что разрез местности по линид АВ
имеет вид, изображенный на рис. 81. Мы будем считать
изображенную на рис. 81 линию графиком функции y(t),

$ 2GJ	ПРИМЕНЕНИЕ	К	ЗАДАЧАМ	ПРИБЛИЖЕНИЯ	233
предполагая, что ось абсцисс совпадает с прямой АВУ
а абсциссы точек А и В равны соответственно а и Ь.
Стенки оврага мы предположим крутыми (имеющими
уклон > а). Функцию, график которой представляет
собой искомый профиль дороги, обозначим, как и выше,
через x(t). Легко видеть, что .х(£)<0 для всех t. Дей¬
ствительно, если х (t') > 0, то, в силу непрерывности
функции х (£), неравенство х (t) > 0 будет иметь место
и в некоторой окрестности точки V. Поэтому, несколько
сместив, если нужно, точку £', мы можем добиться выпол-
v
нения неравенств x(t') > 0, ^ (x(t) — y(t))dt Ф 0. Если
а
имеет место неравенство \ (х (t) — y(t)) dt > 0, то,

2!о4	разные	задачи	[ГЛ.	/,
j j силу	(27),	х	(/)	=	+а	при	(рис.	82),	и	потому
Ь	V	ь
^ О (0 -y(t))dt=^	(X (t)	-	у (t)) dt + ^	(X {t)	- у	(t)) dt	,> О,
a	a	V
что противоречит соотношению (28). Если же имеет место
v
неравенство ^ (х (t) — у (t)) dt < 0, то, в силу (27), х (t) —
а
— — а при t<^t' (рис. 83), а это означает, что х (t) > у (t)
и
при а < t <	—	вопреки	неравенству	\	(х	(t) — y(t))dt< О.
Полученное противоречие показывает, что х (£)<() дли
всех t.
Предположим теперь, что в некоторой точке V
выполнено неравенство x(t')<y(t'). Если при этом
г
^ (х (t) — у (t)) dt < 0, то при t > t' дорога спускается
а
с уклоном а (т. е. х' (t)— — а) до тех пор, пока нера-
t
венство ^ (х (t) — у (t)) dt < 0 не нарушается. При этом
а
графики функций x(t) и у (t) обязательно должны пере¬
сечься при t > t', ибо в противном случае мы имели бы

§ 26]
ПРИМЕНЕНИЕ К ЗАДАЧАМ 1IPH ЕЛ И ЖЕН 11Я
х (0	<	У (О	ПРИ	ьсех	t	>	/'	(рис.	84),	и	потому
ь	г	ь
5	{X(t)-y(t))dt=	^	{x{t)-y(t))dt+\	(x(t)-y(t))dt<0
a	a	t'
вопреки соотношению (28). Аналогично, если выполнены
v
неравенства x(t') < y(t') и ^ (х (t) — у (t)) dt > О, то про
а
а 	   £/
Рис. 85.
t < t' дорога подходит к точке t\ поднимаясь с укло¬
ном а (т. е. #'(£)= + а), причем при t < t' обязательно
имеется точка пересечения графиков х (t) и y(t).
—V
Рис. 80.
Все сказанное позволяет отыскивать функцию х (t)
для различных графиков y(t). Примеры приведены на
рис. 85, 86. При этом для определения точки tx тг зна¬
чения .х (£х) на рис. 85 мы имеем соотношения
н	ь
^ (х (0 - у (t)) dt — 0,	^	(х (0 - у (t)) dt = О,
a	it
а для определения точек ^ и t2 на рис. 86 имеем соот¬
ношения
/,	ь
$ (х (t) - у (I)) dt =	0,	^	(х (I) - у (<)) dt — О.
а	/*2
Разумеется, рассмотренные на приведенных рисунках
случаи очень просты. Они были подробно изучены лишь

230
РАЗНЫЕ ЗАДАЧИ
[ГЛ. U
с единственной целью — показать, что соотношений (26),
(27), (28) (а в общем случае — соотношений, указанных
в теореме 19)* вообще говоря, «достаточно» для нахожде¬
ния искомой функции x(t).
§ 27. Оптимальные процессы с запаздыванием*)
В ряде случаев задача оптимального управления
осложняется эффектом запаздывания. Запаздывание может
возникать в связи с затратой времени на передачу сигнала
или, как это бывает чаще, вызывается упрощающими
явление предположениями, в силу которых считают, что
действие промежуточных и усиливающих звеньев в упра¬
вляемом объекте сводится к передаче сигнала с запазды¬
ванием. Довольно обширный круг технических задач
этого рода укладывается в следующую математическую
схему.
Движение объекта описывается в фазовом простран¬
стве X переменных х1, ..., хп системой уравнений
^ = /i(*1W. •... xn(t), x'it-Q) xn(t- 0), u(t)),
i= 1, . .., n} 0 = const > 0,	(29)
или, в векторной форме,
^ = /(*(0, *(*-6), и(*)).	(30)
Таким образом, запаздывающий аргумент содержится
только в фазовых координатах и отсутствует в управле¬
нии. Функции /г (х1, . . ., хп, у1, . . ., уп, и) предпола¬
гаются непрерывными по совокупности своих аргументов
и непрерывно дифференцируемыми по х1, . . ., хп, у1, ..., уп.
dfi dfi
Иначе говоря, функции /1,	,	—— определены и непре-
dxi ду]
рывны на прямом произведении X х X х U. В качестве
класса D допустимых управлений мы примем класс
всех кусочно-непрерывных управлений со значе¬
ниями в U (или некоторый его подкласс); см. § 10. Как
и прежде, мы будем для определенности предполагать,
*) Результаты этого параграфа принадлежат Г. JI. Харати-
швили.

§ 27] ОПТИМАЛЬНЫЕ ПРОЦЕССЫ С ЗАПАЗДЫВАНИЕМ 237
что рассматриваемые управления в точках разрыва непре¬
рывны слева
Для однозначного определения траектории х (t) урав¬
нения (30) на отрезке t0 < t < необходимо задать не
только допустимое управление u(t),	но
и начальную функцию ср(£) со значениями в X, опреде¬
ленную на отрезке t0 — 0<£<£o. Начальную функцию
ф (t) мы будем предполагать непрерывной на всем отрезке
Функцию ’х (t), заданную на отрезке tQ — 0 < t < t}
и непрерывную на всем этом отрезке, мы будем
называть траекторией уравнения (30), соответствующей
допустимому управлению и (t), t0 < t < tv и задан¬
ной начальной функции ф (£), t0 — 0 < t < t0, если
функция x(t) на отрезке t0^Ct^Ct1 удовлетворяет уравне¬
нию (30), а на отрезке £0 —0<£<£о совпадает с функ¬
цией ф (t).
Перейдем теперь к ф о р м у л и р о в к е оптимальной
задачи, которую мы будем решать в этом параграфе. При
этом мы сразу сформулируем задачу с подвижным правым
концом (которая включает в себя, как частный случай,
и задачу с закрепленным правым концом).
Пусть дана функция /° (.г1, ..., х7\ у1, ..., уп, и),
удовлетворяющая тем же условиям, что и функции /г,
i=l, . . ., п. Пусть, кроме того, в X задано гладкое
к-мерное многообразие Sv 0</с<п—1, и начальная
функция ф(0- Требуется в классе допустимых управле¬
ний выбрать такое управление u(t), £0<£<£г, чтобы
траектория x(t), £о — 0 <£<£], системы (29), соответ¬
ствующая выбранному управлению и (t) и заданной
начальной функции ф (£), удовлетворяла краевому условию
х (£,) £ S} и интеграл
обращался в минимум. Заметим, что пределы интегриро¬
вания в (31) не фиксированы; фиксированы лишь «краевые»
условия: ф (t) и Sj.
a (t) = и (t — 0).
(31)

2;*Ь	РАЗНЫЕ ЗАДАЧ]]	Ц’Л.	h
Если /° = 1, то мы получаем задачу об оптимальных
быстродействиях для систем с запаздыванием.
Если размерность многообразия Sx раина нулю, то
оно превращается в точку, и мы получаем оптимальную
задачу с закрепленным правым концом.
Дадим теперь другую (эквивалентную) формулировку
нашей оптимальной задачи, более удобную для форму¬
лировки и доказательства основного результата.
Введем в рассмотрение (/г+ 1)-мерное фазовое про¬
странство X переменной х = (х°, . . ., хп) = (х°, х) и обо¬
значим через L множество всех точек (я0, х), для
которых х £ S j (т. е. L есть многообразие размерности к-\-1,
являющееся прямым произведением многообразия на
ось х°). Тогда наша оптимальная задача эквивалентна
следующей задаче (ср. стр. 20).
Система уравнений движения фазовой точки x(t) —
— (х° (t), . . ., хп (t)) имеет вид
^ =, /' (X (t), X (t - 0), и (/)), г = 0, 1, ..., п, (32)
или, в векторной форме,
*?VL=f(x(t), х (t — 0), u(t)).	(33)
Требуется выбрать такое допустимое управление гг(£),
чтобы соответствующая этому управлению
и начальной функции ф (/) = (0, ф (/)), t0 — 6 < t < /0,
траектория х (t) = (х° (£), x(t)), t0 <,t<tv системы (32)
удовлетворяла краевому условию х (С) £ L и при этом
координата х° (tj была минимальной.
13сякое допустимое управление u(t) и соответствующую
траекторию x(t), удовлетворяющие сформулированной
задаче, назовем оптимальными.
Для решения поставленной задачи, как и раньше,
введем в рассмотрение вспомогательный вектор \j) =
= (ф0, ..., фп) и составим скалярную функцию
п
■ОС = 2 хМа = (Ч^ /) переменных ф0, . . ., фп, х1, . . ., .г'\
а=0
г/1, ..., у'\ и. Через м (г^, ху у) обозначим верхнюю
грань значений функции <§£ при фиксированных ф, х, у
и при и, меняютцемся на множестве U.

§ 27] ОПТИМАЛЬНЫЙ II РиЦ КИСЫ С 3 All ЛИДЫ НАНН КМ
Введем, далее, в рассмотрение следующие две системы
уравнений для вспомогательных переменных ф0, ф(, . .., фп:
tfifo (I) __ _ дЖ{^(1),х(1),х(1~ 0),а(7)) _
сU ~	Qxi
^(ФО + О). *(« -i-0),g(O, u(tA 0))	, = 0 i n-№)
dy!
"Ф; (l) _ _ № (ф (/), x (I), x (7 — 0), и (I))	^ _ () j .	^
dt	dx\	’	W
А!ы будем говорить, что система непрерывных кусочно-
дифференцируемых на отрезке	функций	г|)0(£),
фДО, ..., фц (/) соответствует фуп гщиям u(t), /0 -, /•	/,,
и ас (О, *о-0 < £ < fj, если на отрезке £0 < t — 0 она
удовлетворяет системе (34), а на отрезке — 0<£<£г —
системе (35).
Теперь мы можем сформулировать н е о б х о д и м о е
условие оптимальности для поставленной задачи (в фор¬
ме принципа максимума).
Теорема 20. Пусть и (£), t0 < t < £д — такое допус¬
тимое управление, ч//?о соответствующая ему траекто¬
рия x(t), t0 — 0<£</д, системы (32) с начальной функ¬
цией ч>(0. £0 — 0</</о, проходит в некоторый момент
tA > /0 через некоторую точку многообразия L. Для
оптимальности управления u(t) и соответствующей
траектории х (t) необходимо существование такой нену¬
левой вектор-функции ф (t) = (ф0 (/), фд (£), . . ., фп (I)), соот¬
ветствующей функциям и(1) и х (t), что:
1° для всех t,	<	tv выполняется условие максимума
н (ф (/), X (t), X(t- 0), и (/)) = сМ (ф (0, т(0> x(t — 0)); (36)
2° в конечный момент /д выполнены соотношения
То (*i) <	^ (Т (*i)> * (*i)>	(*! ~ °)) = 0	(:37)
(заметим, что в силу уравнений (34), (35) мы имеем
Ф0 = const);
3е вектор (Фх(^), ..., ф„ (^)) ортогонален касатель¬
ной плоскости многообразия Sv проведенной в точке
* Cl) = (*4*1), — *“(/,)).
Заметим, что при применении этой теоремы возникает
трудность, связанная с тем обстоятельством, что

24и
РАЗНЫЕ ЗАДАЧИ
неизвестные функции хх(£),	xn{t),	ф2(0> •••> Фм(0
входят в систему (32), (34) как с запаздывающим, так
и с опережающим аргументом. Для линейных систем эта
трудность, очевидно, отсутствует.
В случае оптимальности по быстродействию (/°—1)
п
вместо функции SfC рассматривается функция // = 2 Фа/а
а= 1
переменных фт, ..., фп, х1, ..., хп, у1, . .., уп, и; верх¬
няя грань значений этой функции по и £ U (при фикси¬
рованных ф, х, у) обозначается через М (ф, х, у). Заменяя
в уравнениях (34), (35) функцию ж функцией //, мы
сможем и в этом случае определить функции ф1 (I), . . .
. . ., фп (£), t0 < t < /1, соответствующие функциям и (t),
t0<t<tv и х (.i), t0-b< /<П- После этого для случая
оптимальных быстродействий сохраняется формулировка
теоремы 20 с той только разницей, что функции <$%? и м
заменяются функциями Н и М, а условие 2° заменяется
условием
мт,), х{^)9 х(/1-в))> о.
Иначе говоря, условие оптимальности по быстродействию
вытекает из теоремы 20 совершенно таким же образом,
как теорема 2 получается из теоремы 1.
Доказательство теоремы 20 в общих чертах прово¬
дится по той же схеме, что и доказательство теоремы 1
(или теоремы 8). Мы проведем его, подробно отмечая те
части доказательства, в которых необходимо произвести
некоторые изменения, и опуская построения, ничем
не отличающиеся от изложенных в главе 2.
Пусть х (£) — решение уравнения (33), соответствующее
допустимому управлению u(t),	и начальной
функции ф (t), t0 — 0 <; I < /0. Системой уравнений в вариа¬
циях для системы (32) назовем следующую линейную
систему:
d(&xj (t))_ v fdfi(x(t),x(t — 0), и (t)) я	,
It, “ 2j v	a.^	+
a=0
+ a/i(x(Q,	u(t)) 6жа(/:_е)^ i = o, 1,	(38)
Мы будем рассматривать такие решения системы (38)
на отрезке /0 —	или	на	его	части,	которые	соот-

§ 27] ОПТИМАЛЬНЫЕ ПРОЦЕССЫ С ЗАПАЗДЫВАНИЕМ 241
ветствуют к у с о ч н о-н епрерывны м начальным функ¬
циям; так как мы здесь не исключаем возможности
разрыва решения в начальный момент /0, то для одно¬
значного определения решения системы (38) необходимо
задать (кроме начальной функции) начальное значение
этого решения. Таким образом, если т] (t) — произвольная
кусочно-непрерывная функция, заданная на отрезке
т — 0<£<т, где т£[t0, tj], а | — произвольный вектор
пространства X, то решением системы (38) с начальной
функцией r\(t) и начальным значением § мы будем, назы¬
вать такую функцию бх (I) = (6х° (t), 6x1(t), . ..,б xn(t)),
х —	которая на промежутке х — 0<£<т сов¬
падает с т)(£), на отрезке т<^<^ непрерывна и удов¬
летворяет системе (38) и, кроме того, удовлетворяет соот¬
ношению бх (т) = §. Это решение мы будем обозначать
символом Attx (Ч. I). т-
Мы условимся (при х — 0 < t < £j) считать At,x(4, 1)
связанным вектором, исходящим из точки х (£). Таким
образом, при заданных начальных элементах | и ц (t),
х — 0<£<т, определяется векторное поле AtiX (ц, |),
т — 0<£<£1; мы будем говорить, что векторы At)X(r\, |)
этого поля получаются друг из друга переносом вдоль
траектории x(t).
Отметим следующие легко доказываемые свойства
переноса, которые нам понадобятся в дальнейшем
(ср. формулы (17) гл. 2).
I- А1„. (о On. 1) =1-
II. Положим %(£) = At> х (т|, |), тх— 0<£<т1, где
тогда
At, Ti (%. АХЪ X (Ч> D) = А<, X (Ч> 1). Ь < t < tv
Ш.	-4«,t(Yi4i + Y242. Yi1i + Y212) =
= yiAt, х (Чх> ^i) “Н Y2^<> х (Чг> ^г)> ^ б ^ ^ ^
где у1 и у2 произвольные действительные числа.
IV. Пусть т]1(^) —некоторая кусочно-непрерывная функ¬
ция, заданная на отрезке х — 0 < t<x (где х £ [£0, *J),
Л7—некоторая константа и | — произвольный вектор.
Пусть, далее, полуинтервалы It определяются так же,
как и в § 13, а r\ (t) — функция, определенная на отрезке
16 Л. С. Понтрягин

РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
т— 9<£<т следующим образом:
(" т)(£) = втц (t) + о (г) во всех точках отрезка т — 6<£<т,
<J	не	принадлежащих полуинтервалам I
{ I Ч W I ^	на	полуинтервалах /..
Тогда
Л,т(Ч» е| + о(е)) = ^«,г(еЧ1» е1) + а(е),
Свойства I и II непосредственно вытекают из опреде¬
ления символа At)X(\\, |). Справедливость свойства III
на отрезке £0<£<£0 + 6 вытекает из того, что на этом
отрезке система (38) представляет собой линейную (неод¬
нородную) систему обыкновенных дифференциальных
уравнений. На последующих отрезках длины 0 (вплоть
до г2) свойство III можно доказать совершенно анало¬
гично, воспользовавшись свойством II. Таким же образом
устанавливается и справедливость свойства IV.
Перейдем теперь к вариациям управлений и
траекторий. Пусть и (£), t0 < t < tv — допустимое управ¬
ление, а х (£) — соответствующая ему траектория уравнения
(33)	с начальной функцией ф (г), tQ — 0 < I < £0. Правильны¬
ми точками управления u(t) будут все точки его непрерыв¬
ности, т. е. все, кроме конечного числа, точки отрезка
t0<t^tv Мы условимся всякое управление u(t),
t0<t^Ctv продолжать за точку tv полагая u(t)^=u(tj)
при t > tv Важно отметить, что при этом точка Ц будет
правильной точкой управления u(t). Если х— произволь¬
ная точка непрерывности управления и (t), то, каковы бы
ни были действительные числа р и д, имеет место соот¬
ношение
t-f-ge
^ / (х (£), x(t — 0), и (t)) dt =
т+ре
= е (q — p) f (х (т), ж (т— 0), гг (т)) + о(е) (39)
(ср. формулу (1) гл. 2).
Пусть теперь и (t), t0 < t < tv ■— допустимое управление,
х (t)—соответствующая траектория уравнения (33) с началь¬
ной функцией <р(£), t0 — b<Ct<^,t0, а а —символ, опреде¬
ляющий варьирование управления. Проварьированнос

§ 27] ОПТИМАЛЬНЫЕ ПРОЦЕССЫ С ЗАПАЗДЫВАНИЕМ
управление обозначим через гг* (£), а соответствующую
этому управлению траекторию с той же начальной
функцией ф(£) обозначим через х* (t). (Отметим, что при
любом е>0 траектория х* (t) представляет собой
непрерывную функцию от t в силу определения
решений уравнения (33).) При достаточно малом г траек¬
тория х* (t) определена на всем отрезке	(тео¬
рема о непрерывной зависимости решения от параметров).
Покажем, что для любой точки т непрерывности управ¬
ления и (t) имеет место следующая формула (ср. формулы
(21), (22) гл. 2):
х* (т + еб£).= х (т) + еДх -f о (е),	(40)
где Ах -- не зависящий от е вектор, определяемый фор¬
мулой:
Дх=/(я(т), х(х— б), гг(т))б£ +
+ .2 АГ, Х1 (0, /(x(Tt), а; (т4 - 6), uj-
-f(x(Xi), х (ti - 6), и (tJ)) 6l4.	(41)
Доказательство формул (40),. (41) аналогично выводу
формул (21), (22) в гл. 2. Прежде всего заметим, что
имеют место формулы
х (т + еб£) = х (т) + г/(х(х)} х(х — 0), и (т)) бг.-f- о (е),	(42)
х* (т + гЫ) = х* (т) + е/(х (т), х (х — б), и (т)) бt-{- о (е)	(43)
(при Ts < т).
Эти формулы устанавливаются так же, как и фор¬
мулы (23), (25) гл. 2 (с заменой ссылки на формулу (1)
гл. 2 ссылкой на указанную выше формулу (39)).
Далее, совершенно так же, как и в гл. 2, находится
приращение функции х* (t) на полуинтервале It:
х* |х. = е/(х (т4), х (xi - 0), и4) 6f. + о (е)	(44)
(ср. формулу (26) гл. 2).
Переходим к индуктивной проверке соотношений (40),
(41). При 5 = 0 эти формулы справедливы (см. (42)).
Предположим, что они доказаны для случая, когда число
полуинтервалов /2, ... меньше чем 5, и докажем
справедливость этих формул при наличии s полуинтер¬
16*

244	РАЗНЫЕ	ЗАДАЧИ	[ГЛ. 4
валов Iv /2, . . ., Обозначим через к такое целое
число, что
4*1 = 4*2 = • • • = 4 HTi<Ts при I </с
(случай /с = 0 не исключается). Заменяя точку т точ¬
кой ts, число б£ —числом 4+1> а число 5 — меньшим чис¬
лом /с, мы, в силу индуктивного предположения, получим
из (40), (41)
ас* (т8 + elk+1) = х (т8) + е/(ж (т8), ж (т8 - 6), и (т8)) 1к+1 +
k
+ 8.2^-тг (°’	(Ч)» Х (Ч “ 6)’ °i) "
-f(x (4)> х (Ч - 0)>ц (Ti)))	+ 0 (8)- (45)
Это есть значение функции х* (t) в левом конце полу¬
интервала 1к+1. Далее, так как полуинтервалы 1к+1, . .., Is
примыкают один к другому, то, суммируя соотноше¬
ния (44) для £ = &+!, ...,5 и складывая полученное
соотношение с соотношением (45), найдем
х* (t8 + е (ls + 6Q) = х (т8) +
+ в/(ж (т8), ж (т8 — 0), и (ts))	+ 6i/itl + . •. + bts) +
+ е 2 Ах т (0, /(ж (т4), х (tt - 0), t»t) -
i=1 й 1
-/(«(Tj, aj(Ti-e),B(T1..)))fiti + o(e) (46)
(ср. вывод формулы (28) в гл. 2; при этом ссылка
на первую из формул (17) гл. 2 заменяется ссылкой
на свойство I операции переноса, см. стр. 241). Если
T/i+1 = Ts = T, то соотношение (46) совпадает с (40), (41).
Если же т8 < т, то
h + ^4=	4+i + 64+i + • • • + ^4 = О,
и соотношение (46) принимает вид
X* (т8) = X (t8) + 8 i] Ar , (0, /(ж (ti), Ж (tt - 0), t»i) -
i=1 s г
—f(x(4)> x(4-d)’u(4)))6ti + °(e)	(4<r)-	(47)

§ 27] ОПТИМАЛЬНЫЕ ПРОЦЕССЫ С ЗАПАЗДЫВАНИЕМ 245
Обозначим через r\(t) функцию ас* (£) —x(t), рассматри¬
ваемую на отрезке т3 —0<£<т3. Тогда (так как на от¬
резке т3<г<т управление и* (t) совпадаете u(t)) функ¬
ция ас* (t) — x(t) с точностью до о (е) является на отрезке
т3 — 0 < t < х решением системы уравнений в вариа¬
циях (38) с начальной функцией г](£) и начальным
значением ас*(т3) — ас(т3) (напомним, что обе функции
x(t),	x*(t) непрерывны). Иначе говоря, с точностью
до о(е) векторы, ас* (t) — x(t) получаются друг из друга
(на отрезке т3 — 0<£<т) с помощью переноса:
ас* (t) - ас (t) = AttXs (т|,ас*(т8) — ас(т3)) + о(е),
т3 — 0 < t < т.	(48)
Всюду, кроме конечного числа отрезков /., функция т](£)>
т3 — 0<£<т3, имеет (в силу предположения индукции)
вид
k
•П (t) = ас* (t) - ас (*) = е У А,, х (0, f(x (т4), х (хь - 6), ot) -
i=1	1
Ц^-0), м(т{)))б^ + о(е).
Поэтому, в силу свойства IV (стр. 241—242), мы можем
заменить формулу (48) формулой
x*(t) — x(t) = AttXs(r\v	+ о (e),	(49)
где
k
til (0 = 6 2 At, X j (0, f(x (ti), X (T{ - 6), v{) -
i=1
-/(z(Ti), ж(Г4-6), м(т4)))б^,
It = e S ^,т.(0, /(ж(т4), ж(т4-0), Oj)-
i=l й 1
x (т^	0),	M(tt)))6^
(cm. (47)). В силу свойства III операции переноса
(стр. 241) мы можем формулу (49) переписать в виде

24(i
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
где
Ч(х4)(0 = Аи S (0, f(x (т4), х (т4 - 0), vt) -
-f(x(x-X ж(Tt — 0), и(т4))), ts-0<*<ts, i = l, к,
i(i4) = Л3, Tt (0, /(* (Tt), ж (tj - 0), o4) -
-/(я Ю. ж К - б). u Ю))> i = 1.	• • •, s-
Наконец, в	силу	свойства II операции переноса (стр. 241)
мы получаем
At, xs (п(1{),	1(1{>)	=	At, т4 (0, f{x (т4), х (т4 - 0), Oj) -
-f(x (t4), X (Tt - 0), и (т4))), i = 1,	..., ft,
а в силу свойства I
Si0=/(*(*{), *К-0). wt)-
— /(ЖК). x(xi -6), м(т4)), г = /с+ 1, .. ., 5.
Таким образом, формула (50) принимает вид
S
х* (t) - х (г) = е У т (0, /(ж (т4), ж (т4 - 0), vt) -
г=1	1
*(1ч- 0). в(т4)))8г4+о(е), т8<г<т.
В частности, при £ = т,
s
ж* (т) — х (т) = е ^ Ах, т (0, /(ж (т4), ж (t4 — 0), vt) —
г=1
—/(®(Ti), ж(т4-0), B(t4)))6f4 + o(e).
Складывая это соотношение с соотношением (43), мы
и в этом случае (т. е. при rs < т) получаем соотно¬
шения (40), (41), что и завершает индукцию. Тем самым,
формулы (40), (41) полностью доказаны.
Так как — правильная точка управления u(t), то
формулы (40), (41) применимы, в частности, при т — tx\
х* (t± + ебt) = х (tj) + гАх + о (е),	(51)

§ 27] ОПТИМАЛЬНЫЕ ПРОЦЕССЫ С ЗАПАЗДЫВАНИЕМ 247
где
Ах = /(я (£j), x{tl — 0), и (£-,_)) б£ +
+ 2	(0, /(* (Tj), ® (tt - 6), Oj) -
г=1
-/(*(Ti), ®(т(-0), u{xi)))bti. (52)
Обозначим теперь через К множество всех векто¬
ров (52), исходящих из точки x(t^). Дословно так же,
как в главе 2 (стр. 106 — 111), устанавливается, что К—
выпуклый конус пространства X и что имеет место
лемма 3 (при х = t1). Справедлива также и лемма 4 для
x=tv что следует непосредственно из леммы 3. Таким
образом, если траектория x(t) оптимальна, то конус К
не содержит внутри себя луча Ltl. Поэтому через вер¬
шину x(tx) конуса К можно провести такую гиперплос¬
кость Г, что конус К расположен в одном из двух
замкнутых полупространств, определяемых гиперплоско¬
стью Г, а луч Ltl — в другом. (Конус К здесь заменяет
предельный конус, рассмотренный на стр. 119.) Это позво¬
ляет, как и в главе 2, определить нетривиальное реше¬
ние ф (t) = (ф0 (t), фх (t), . . ., фп (t)) системы уравнений
(34), (35), для которого выполнены соотношения
ф0 = const < 0,	(53)
(ф (£х), Дас) < 0 при Дх£К.	(54)
Докажем, что ф (t) — искомая функция (существо¬
вание которой утверждается в теореме 20). Пусть хг —
произвольная правильная точка, т. е. точка непрерыв¬
ности управления u(t) (t0 <	< t2). Рассмотрим символ а
(см. § 14) с единственной точкой хг (т. е. 5=1) и с чис¬
лами dtv бt, соответственно равными единице и нулю.
Тогда вектор Ах (см. (52)), соответствующий этому сим¬
волу о, будет иметь значение
Ах = Ahi Т1 (0, f(x (tj, х (tj - 0), юг) -
- f(x (tj), Ж (т, - 0), и (г,))).	(55)
Положим
д (t) = AtiXl (0, f{x (тх), х (tj - 0), t)j) -
—f(x(x1), x{xr — 6), м(т,))), x1 — 0<г<*г.

248	РАЗНЫЕ	ЗАДАЧИ	[ГЛ.	4
Тогда, по определению, g(t) = (g°(t), g1^),..., gn(t))
есть решение системы (38), соответствующее начальной
функции, тождественно равной нулю (на отрезке
хг — б < t < хг) и начальному значению
9 (ь) =/(т (Тх), Ж (хг - 0), иг) —f(x (Тх), х(х 1 — 0), и (Тх)). (56)
Кроме того, согласно (55) и (54), мы имеем
Ж*1)> д(Ч))< о.	(57)
Мы сейчас докажем, что имеет место равенство
(Ч> (Тх), д (Тх)) = (t (ix), д (<х)).	(58)
В самом деле, мы имеем (в силу (34), (35) и (38))
ЖУ. д (У) - (ч> (У, д(т2))=	g(t))dt	=
*«)+(*«• ^)]л-
*1
  	 2	^	(t), х (t), х (t 6), и (£)) ^a ^ ^
a=0 tl
d&G (Ч> (* + в)> *(* + в)» *(*). Ц(4-б)) g.a ^ dt—
__ 2	^	д<й?(Ч>(0» x(t), x(t — 6), ц(г))	|
a—0 <i—0
+ 2 )«.WS
a=0 Tj	;'=:0
dfa(x(t), x (t — 0), и (£)) j
+ Ы0 2	*	“	g1 (* - e)) dt =
7Zo	дУ’
— — 2	^	dm	^	^X9).	x	U	+	fl),	X	(t), и (f+9)) aa ^
dy
ff=0

§ 27] ОПТИМАЛЬНЫЕ ПРОЦЕССЫ С ЗАПАЗДЫВАНИЕМ 249
(при вычислении мы использовали определение функ¬
ции	и	тот факт, что g(t) = 0 на интервале
т1 — 0 < t < tj). Таким образом, равенство (58) доказано.
Из (57) и (58) получаем
откуда, согласно (56) и определению функции нахо¬
дим
ж^), х(хг — 0), иДС
<£№[$ я (tj), х (хг - 6), и (tj)).
Так как это неравенство справедливо для всех точек
v1£U, то при t = х равенство (36) выполняется. Итак,
равенство (36) доказано для всех точек непрерывности
управления u(t). Так как функция и (t) в точках раз¬
рыва непрерывна слева, а функции и м непрерывно
зависят от своих аргументов, то соотношение (36) спра¬
ведливо и в точках разрыва управления u(t). Таким
образом, равенство (36) доказано полностью.
Первое из соотношений (37) нами также доказано
(см. (53)). Далее, полагая в формуле (52) б
... = $ts = 0, мы получим
Так как это неравенство справедливо при любых бt
п ti
а—0 х1
д&6 (г|) (t), х (Z), х (t — 0), и (*))
дуа
ga (t — b)dt =
п /1-0
a(gj?(4>(t + 0).«(t + 9).a:(t). И* + 8)) „.a (t) dt +
a=0
n t\ — 0
d&e (г|э (t + ti), X (i + 0), X (t), w(f + 0))
дуй	~
ga (0 dt = 0
a—0 t1— 0
Ax=f(x(t1), x(t1 — 0), u(t.1))6i,
и потому, в силу (54),
x(tj), x(t1— Ъ), и(^))б£< 0.

250
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
(как положительных, так и отрицательных), то
ж(«1 —6), и(^)) = 0,
и второе из соотношений (37) установлено (см. (36)).
Итак, теорема 20 для случая закрепленного
правого конца установлена. Условие трансверсальности
(условие 3° в теореме 20) для задачи с подвижным пра¬
вым концом устанавливается так же, как и в главе 2
(с очевидными изменениями).
Тем самым теорема 20 полностью доказана.
§ 28. Одна задача преследования *)
Предположим, что в п-мерном фазовом пространстве X
движутся две управляемые точки, одну из которых мы
будем называть «преследующей», а другую—«преследуе¬
мой». Движение каждой из этих точек подчиняется своей
собственной системе дифференциальных уравнений со
своим собственным управляющим параметром. Управля¬
ющий параметр, область управления и траекторию дви¬
жения преследующей точки мы будем обозначать соот¬
ветственно через гг, £7, x(t). Для преследуемой точки
будем эти величины обозначать символами у, V, y(t).
Пусть гг (г), v (t) — некоторые допустимые управления,
a x(t), у (t) — соответствующие им траектории с началь¬
ными условиями
х (0) = х0, у (0) = у0.	(59)
Если для некоторого t1 > 0 выполняется равенство x(t1) =
= y(ti)> то число tt мы будем называть моментом встре¬
чи, а сам факт выполнения равенства х (£г) = у (£2) — встре¬
чей, Вообще говоря, если управления u(t) и v(t) выбраны
произвольно, то встречи может не произойти ни при каком
t > 0. Если же встреча происходит, то мы будем говорить,
что u(t) является преследующим управлением (для задан¬
ного управления v(t) и заданных начальных условий
х0, у0). ГГри этом для заданных ж0, у0, v (t) и выбранного
управления u(t) может произойти не одна встреча. Наи¬
*) Результаты этого параграфа принадлежат Д. JI. Келенджо-
ридзе.

§ 28]
ОДНА ЗАДАЧА ПРЕСЛЕДОВАНИЯ
251
меньшее положительное число tv являющееся моментом
встречи, мы будем называть временем преследования,
соответствующим управлениям u(t), v(t). Время пресле¬
дования мы будем обозначать через TU) v. В дальнейшем
начальные условия (59) предполагаются фиксированными
(в связи с чем в обозначение времени преследования
начальные условия х0, у0 не входят).
Мы будем в дальнейшем предполагать, что преследуклцая
точка обладает следующим свойством: для любого задан¬
ного управления v (t) существует (при заданных началь¬
ных условиях (59)) преследующее,управление u{t).
Если управление v(l) преследуемой точки выбрано,
то можно поставить вопрос о нахождении такого пресле¬
дующего управления и (t), чтобы соответствующее время
преследования TU) v принимало минимальное значение. Мы
будем предполагать, что для любого допустимого управ¬
ления v (t) существует допустимое управление u(t),
осуществляющее м и н и м у м времени преследования. Этот
минимум мы будем обозначать через Tv:
Ту = min Ти, V.
и
Мы будем, далее, предполагать, что существует допусти¬
мое управление v (t), осуществляющее макс и м у м вели¬
чины Tv. Этот максимум мы обозначим через Т\
Т = max Tv =• max (min TU) v).	(60)
V	V	и
Задача заключается в том, чтобы выбрать такую пару
допустимых управлений и (t), v (t), что для соответствую¬
щего времени преследования Ти, v выполняется равенство
TUyV=T. Такую пару управлений u(t), v(t) мы будем
называть оптимальной парой управлений, а соответствую¬
щую пару траекторий x(t), y(t) (с начальными значения¬
ми (59)) —оптимальной парой траекторий. Таким
образом, управление и (при любом заданном управ¬
лении v(t)) выбирается таким образом, чтобы по возмож¬
ности ускорить встречу преследующей точки с пресле¬
дуемой; выбор же управления v подчинен задаче макси¬
мально отдалить (во времени) момент встречи. Отметим
еще, что при выборе управления и (t), определяющего

252
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
движение преследующей точки, мы каждый раз предпо¬
лагаем заранее известным управление v(t) для пресле¬
дуемой точки; в соответствии с этим при определении
величины Т сначала берется минимум по всевозможным
управлениям и (t) при некотором фиксированном управле¬
нии v (t), а затем берется максимум по всевозможным
управлениям v(t).
При решении поставленной задачи мы будем предпо¬
лагать, что движение преследующей точки описывается
в пространстве X линейным уравнением (в векторной
форме)
^ = / (х, и) = Ax-j- Ви-\- с,	(61)
для которого выполнено условие общности положения,
а соответствующая область управления U представляет
собой замкнутый выпуклый ограниченный многогранник
в пространстве Ег переменной и = (и1, ...,иг). Движение
преследуемой точки пусть описывается уравнением *)
(векторным)
= (62)
а соответствующая область управления V является мно¬
жеством 5-мерного пространства переменной v = (v1t . .., Vs).
В качестве класса допустимых управлений (как для и,
так и для v) примем множество всех кусочно-непрерыв¬
ных управлений. На координаты векторной функции
g(y, v, t) мы накладываем обычные условия (непрерывность
по переменным у, v, t и непрерывная дифференцируемость
по координатам у1, . . ., уп точки у).
Для решения поставленной задачи мы введем в рас¬
смотрение два вспомогательных вектора
=	....	чЫ.	x	=	(xi.	•••.	Хп)
*) Разумеется, можно было бы ограничиться случаем, когда
правая часть уравнения (62) автономна, т. е. не зависит явно от
времени. Однако проводимые ниже преобразования приводят (даже
в автономном случае) к явному введению переменной t в правую
часть уравнения движения преследуемого объекта. Поэтому ника¬
кого упрощения в случае автономности уравнения (62) не проис¬
ходит.

§ 28]
одна задача преследования
253
и две гамильтоновы функции
п
Н1(г|з, х,и) = 2 'фа/0(ж> «) = (^> /(ж, и)),
a—i
н2 (х. У> и) = 2 %aga (у, V, t) = (х, g (у, V, t)),
a=l
соответствующие преследующему и преследуемому объек¬
там. С помощью функций Н11 Н2 мы напишем следую¬
щие две системы уравнений для вспомогательных неиз¬
вестных и %i:
d^j	дН1
dt	дхi
dXi	дН
2
dt	dyi
i=l,2, .. ., пу	(63)
i— 1,2, . .., п.	(64)
Если заданы функции и (t), х (t), v (t), у (t), то, подставляя их
в правые части систем (63), (64), мы получим линейные
системы относительно неизвестных ф. и Каждое ре¬
шение ф(£), %(t) этих систем мы будем называть соответ¬
ствующим выбранным функциям u(t), x(t), v(t), y(t).
Нижеследующая теорема дает необходимое усло¬
вие оптимальности для рассматриваемой задачи.
Теорема 21. Пусть u(t), v (t) — оптимальная пара
управлений, x(t), у (t) — соответствующая оптимальная
пара траекторий (см. уравнения (61), (62)) и Т — время
преследования. Тогда существуют такие нетривиальные
решения ф(£), % (t) систем (63), (64), соответствующие
функциям u(t), x(t), v(t), y(t), что:
1° для всех t, 0у выполнены	условия максимума
max Нх (ф (£),	х (t),	и) = Нг (ф (£),	x(t),	u(t)),	(65)
u£U
maxH2(%(t),	y(t),	v) = ff2 (x (f),	у (f),	v {t))\	(66)
v£V
2° в момент t = T выполняются условия
Нг (ф (Т), X (Т), и(Т)) > Я 2 (х (Т), у (Т), v (Т)),	(67)
о|)(Л = Х(Н-	(68)

254
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
Доказательство. Пусть и0 — произвольная внут¬
ренняя точка многогранника U. Полошим
и = гг — и0.
Тогда уравнение (61) перепишется в виде
^- = Ах+Ви + (Ви° + с).
Таким образом, перенося начало координат простран¬
ства Ег в точку гг0, мы лишь изменяем свободный член
с в уравнении (61); однако теперь начало координат про¬
странства Ет будет уже внутренней точкой многогранни¬
ка С/. Мы будем предполагать, что такой перенос начала
(если он нужен) уже сделан в уравнении (61), так что
начало координат является внутренней точкой многогран¬
ника U.
Обозначим, далее, через х° (t) решение уравнения (61),
соответствующее управлению и = 0 (это управление допу¬
стимо, так как начало координат принадлежит много¬
граннику U) и начальному значению д:0(0) = ^0 (см. (59)).
Решение х° (t) удовлетворяет уравнению
Щ^ = Ах0(1) + с	(69)
и потому является аналитической функцией от t.
Пусть u1(t), v1{t), 0< £< tv — произвольная допусти¬
мая пара управлений и яД^),	(£) —соответствующие
траектории уравнений (61), (62) с начальными условия¬
ми (59), т. е.
^l = Ax1(t) + Bu1(t) + c,	(70)
^TL = g(yi(t), v^t), t),	(71)
xi (0) = ж0> г/i (°) = г/о-	(72)
Положим
г (г) = ху (г) - х° (г), у (г) = уг (t)
(73)

ОДНА ЗАДАЧА ПРЕСЛЕДОВАНИЯ
255
Тогда, в силу (69), (70), (71), мы имеем
^ = Лх(<) + £М1(г),
= g (у(0 + *° (0. vi (0. 0 - А*0 (0 - с =
= gi (у (0> »Х (0. 0.
где через g,1 обозначена функция
gi {у>	V,	t) = g (у + а;0 (0, V, t) - /1ж° (г) - с
(ср. сноску на	стр.	252).	Итак, функции	x(t),	y(t)	удов¬
летворяют дифференциальным уравнениям
= Ах + Ви,	(74)
= gi {У, о. 0	(75)
(при u = u1(t)y v = v1(t)) и начальным условиям (см. (72))
ж(0) = 0, у(0) = у0-х0.	(76)
Обратно, если функции :r(£),- ?/(£) удовлетворяют уравне¬
ниям (74), (75) и начальным условиям (76), то функции
xi(t), Ух (t), определяемые по формулам (73), удовлетво¬
ряют уравнениям (61), (62) и начальным условиям (59).
Далее, из (73) ясно, что каждый момент встречи траек¬
торий xv у± является также моментом встречи траек¬
торий ху у и обратно (т. е. если x1(t') = y1{t')y то x(t') =
= y(t') и обратно). Поэтому в первоначальной задаче
о преследовании можно заменить уравнения (61), (62)
и начальные условия (59) уравнениями (74), (75) и на¬
чальными условиями (76). Наконец, ясно, что если мы
докажем теорему 21 для задачи (74), (75), (76) и затем
в формулировке теоремы произведем замену (73), то полу¬
чим теорему 21 для задачи (61), (62), (59). Таким обра¬
зом, при доказательстве теоремы 21 мы можем рассматри¬
вать лишь задачу (74), (75), (76). Можно сказать и иначе:
достаточно доказать теорему 21 (в первоначальной форму¬
лировке задачи, см. (61), (62), (59)) для случая, когда
с = 0, х0 = 0	(77)

256
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
и, кроме того, начало координат пространства Ег пере¬
менных гг1, . . ., ггг является внутренней точкой многогран¬
ника U. Переходим к доказательству теоремы 21 при
выполнении этих упрощающих предположений.
Для любого tx > 0 обозначим через 2 ц множество всех
тех точек фазового пространства X, в которые можно
попасть, двигаясь изначала координат в силу системы (74),
за время < t1 (под воздействием надлежащего управле¬
ния). Множество 2 ц является выпуклым ограниченным
множеством пространства X, содержащим внутренние
точки (см. стр. 152). В любую точку множества 2ц можно
попасть и за время, в точности равное tx (ибо перед
началом движения можно в течение любого времени на¬
ходиться в начале координат, считая и ~ 0). Границу
выпуклого тела 2ц обозначим через Stv
Покажем, что во всякую внутреннюю точку множе¬
ства 2ц можно попасть (двигаясь из начала координат в
силу системы (74)) за время, меньшее чем обратно,
если в некоторую точку можно попасть за время, меньнтес
чем tly то она является внутренней точкой тела 2ц.
В самом деле, пусть а — произвольная внутренняя точка
множества 2ц. Пусть, далее, ф*(£) — такое решение урав¬
нения (5) гл. 3, что управление u*(t), определяемое
уравнением (6) гл. 3, переводит фазовую точку из на¬
чала координат в положение я. Обозначим через V
момент времени, когда фазовая точка, движущаяся под
воздействием этого управления, попадает в положение я.
Мы рассмотрим функцию ф* (t), определяемое ею управление
гг*(£) и соответствующую фазовую траекторию х% (t) на
отрезке времени 0<£<Г, где t" > Так как x%(t') = cif
то при £", достаточно близком к £', точка (£") лежит
внутри тела 2ц. Но траектория x*(t), 0<£<Г, является
оптимальной траекторией системы (74) (единственной
в силу теоремы 12), ведущей из начала координат в точ¬
ку х% (£"), и, так как х% (t") £ 2ц, то £"< tv Следовательно,
V < tv Обратно, пусть в точку я можно попасть за время
I' < tx при помощи некоторого управления гг* (t). Рассмот¬
рим множество 2ц_/ц состоящее из точек, в которые можно
попасть (с помощью какого-либо управления) за время
— t'\ оно содержит начало координат внутри себя.
Двигаясь из различных точек множества 2ц_г с помощью

§ 28]
ОДНА ЗАДАЧА ПРЕСЛЕДОВАНИЯ
257
управления w* (t) в течение времени t', мы получим мно¬
жество W, содержащее точку а внутри себя (рис. 87).
В любую точку множества W можно попасть пз начала
за время < t1 (двигаясь сначала в течение времени t1 — t'
внутри множества 2*г_/', а затем в течение времени t' от
множества Яц-г к множеству W), т. е. W CZ%tv Следова¬
тельно, а есть внутренняя точка множества 2*г
Вернемся снова к оптимальным управлениям u(t), v(t)
и оптимальным траекториям х (I), y(t)> упоминаемым в тео¬
реме 21 (при упрощающих предположениях (77)), и покажем,
что точка х(Т) лежит на границе тела 2Т- В самом
деле, допустим, что точка х (Т) является внутренней точ¬
кой этого тела. Тогда в эту точку можно попасть (дви¬
гаясь от начала координат в силу системы (74)) за время
t' < Т. Следовательно, взяв точку tv удовлетворяющую
неравенствам V < tx < Т, мы найдем, что множество 2^ (со¬
стоящее из точек, в которые можно попасть за время tx)
содержит точку х(Т) внутри себя, а следовательно, со¬
держит внутри себя шар некоторого радиуса г с центром
в точке х(Т). При tx < t < Т множество 2; также содер¬
жит внутри себя шар радиуса г с центром в точке х(Т).
Выберем теперь число t (принадлежащее интервалу
tx < t < Т) настолько близким к Т, чтобы расстояние
между точками у(Т) = х(Т) и у (t) было меньше чем г.
Тогда множество 2* содержит внутри себя точку y(t)y
причем £ < 71. Но это означает, что в положение y(t)
преследующая точка может попасть в момент t < Г, т. е.
что (при выбранном управлении v (t) для преследуемой
точки) встреча может произойти в момент t < Т. Однако
И Л. С. Понтрягин

258
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
это противоречит определению числа 7. Тагам образом,
точка х(Т) лежит на границе St множества Sr-
Из этого следует, что и(1), 0<£<7, есть оптималь¬
ное по быстродействию управление, соответствующее пере¬
ходу из начала координат в точку х(Т) (в силу систе¬
мы (74)). Действительно, если бы это управление было не
оптимальным, то в точку х(Т) можно было бы попасть
за время, меньшее чем Г, и тогда точка х(Т) лежала бы
внутри множества St, что не имеет места. В силу сказан¬
ного, управление и (£), рассматриваемое на отрезке 0< £< t±
(где t± < 7), также является оптимальным по быстродей¬
ствию управлением, соответствующим переходу (в силу
системы (74)) из начала координат в точку x(tx). Иначе
говоря, в точку яД^) (0 < Д<7) нельзя попасть быстрее,
чем за время tv и потому точка х (£х) лежит на границе
множества S/r
Обозначим через S объединение всех множеств S*,
t > 0. Ясно, что S —открытое множество пространства Ху
содержащее множество St и, следовательно, точку
х (Т) = у (Т). Поэтому найдется такое число £* < 7, что
y(£)£S при £*<£<7. Для любого £, £*<£<7, мы обо¬
значим через т(/) такое число, что y(t)£SX{i)- Легко
видеть, что x(t) — непрерывная функция переменного t,
£*<£<7. Далее, так как u(t), ^(^-оптимальная
пара управлений и 7 — время преследования, то имеют
место соотношения
В самом деле, если бы для некоторого t < 7 было вы¬
полнено неравенство т (£)<£, то в точку у (t) £ SX(t) Cl S*
преследующая точка могла бы попасть в момент времени
t, т. е. (при выбранном управлении v(t) для преследуемой
точки) была бы возможна встреча в момент t < 7, что
противоречит определению числа 7.
Так как точка y(t) лежит на границе SX(t) выпуклого
тела ST(/), то можно провести в X опорную гиперплоскость
к телу ST(/), проходящую через точку у (t). Эту гипер¬
плоскость (любую из них, если она не единственна) мы
обозначим через Дхц). Единичный вектор, ортогональный
т(7) = 7,
т (t) > t при t < 7.
(78)
(79)

ОДНА ЗАДАЧА ПРЕСЛЕДОВАНИЯ
259
к гиперплоскости Дт щ и идущий из точки у (I) в то полупро¬
странство, которое не содержит множества 2Т (^), мы обозна¬
чим через eX(t)• Так как для любой точки 2Х(0 вектор
x — y(t) направлен в то полупространство, которое содер¬
жит множество 2Х(о, то (x — y(t), ет(О)<0 (при ^g2T(f)).
В частности, из (79) следует, что 2|С2т((), я потому
(;x — y{t), ex(t))<0 при x£l>t.	(80)
Выберем теперь некоторый способ варьирования управ¬
ления v(t) (см. стр. 98—99). Соответствующая варьирован¬
ная траектория (с прежним начальным условием, см. (59))
имеет вид:
y*(t) = y(t) + e6y(t) + o(s), 0< i < 71;	(81)
при этОхМ вектор Дг/ = 6у (Т) определяется формулой (22)*
гл. 2, в которой следует положить т = Т, 6t = 0 и от-
бросить координату х° (ибо рассматривается фазовое про¬
странство X, а не Ат). Пусть теперь е1, е2,.. . , sif. .. —
произвольная сходящаяся к нулю последовательность
положительных чисел. Траекторию (81), соответствующую
значению s = eit обозначим через у* (t), а соответствующее
управление — через v\ (t). Время преследования, соответ¬
ствующее управлению v*(t)y мы обозначим через tt:
h =
Таким образом,
jTi(*i)e2v г = 1,2,...	(82)
Из оптимальности пары управлений гг (г), v (t) вытекает,
что
tt<T9 г=1,2, ...	(83)
Далее, легко видеть, что
lim ti = Т.	(84)
оо
В самом деле, допустим, что соотношение (84) не вы¬
полнено. Переходя, если нужно, к подпоследовательно¬
сти, мы можем считать, что lim£. существует и <7\
i-^oo
17*

260
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
Положим limt{ = t. Так как Нте{ = 0, то из (81) следует,
i-*oo	i-voo
ЧТО
lim yt (ti) = y{t) .
оо
Далее, из (82), переходя к пределу, получаем
limyt (h) €	.
г~>оо
Таким образом, ?/(£)£ 2т, где £<Т, но это противоре¬
чит определению числа Т. Следовательно, соотношение (84)
выполнено.
Из (83) и (84) следует, что при достаточно большом
i определены числа т(^); мы будем считать (отбрасывая,
если нужно, несколько первых членов последовательности),
что числа т(tj) определены для всех i = 1, 2, . . . Далее,
из (78) и (84) следует, в силу непрерывности функции т(£),
что
Птт(£-) = Т.	(85)
i~> оо
Рассмотрим теперь векторы
ет(г), i = 1, 2, ... .	(86)
В силу компактности единичной сферы 72-мерного прост¬
ранства X, мы можем считать (перейдя, если нужно к
подпоследовательности), что векторы (86) сходятся при
i —> оо к некоторому единичному вектору е пространства X.
Пусть теперь х — произвольная внутренняя точка те¬
ла 2т- Тогда при достаточно большом i будет выполнено
включение х£ 2*. и потому
{x-y(ti), eT(ii))<0
(см. (80)). Переходя в этом соотношении к пределу при
7—> оо, мы получим (учитывая соотношение у(Т) = х(Т)
и соотношение (85)):
(ж-х(Г), е) < 0.	(87)
Соотношение (87) справедливо для всех внутренних точек х
тела 2т, а значит и для всех вообще точек х этого тела.

§28]	ОДНА ЗАДАЧА ПРЕСЛЕДОВАНИИ	261
Далее, из (82) следует, в силу (80), что
(У*(Ч)-У(Ь)’ ет(1{))<0,	1 = 1,2,...
или, согласно (81),
(е;бг/(^) + о(е)|Е=£., et{<{))<0, i=l, 2, ...
Разделив это соотношение на е. и переходя к пределу
при г—> оо, получим (в силу соотношения Пт —= 0)
е->0 е
(6у(П е)<0,
или, иначе,
(Ду, е)<0.	(88)
Наконец, рассмотрим функцию
фi(t) = (x(t)-y(t), et«.)).
Так как #(г)£2, при любом t, то из (80) следует, что
9i(^)<0. Далее, ф|(71) = 0, ибо х(Т) = у (Т). Кроме того,
функция ф|(£) имеет при достаточно большом i непрерыв¬
ную производную на отрезке ti < t < Т (ибо управления
u(t) и v(t) кусочно-непрерывны и имеет место соотноше¬
ние (84)). Поэтому существует такое число £., £.<£.<7\
что ф-(^)>0, т. е.
u(li))-g(y(l i), o(gt), li). ex(t.))> 0.
Переходя в этом соотношении к пределу при i—>оо, по¬
лучим
(w,	е)<0,	(89)
где
w = g(y(T),	v(T),	T)-f(z(T), и (Г)).	(90)
Обозначим теперь через Д гиперплоскость пространст¬
ва X, проходящую через точку х(Т) п ортогональную
вектору е. Кроме.того, будем считать векторы Ау и w
исходящими из точки	х(Т).	Тогда соотношения	(87), (88)
и (89)	показывают, что все	тело 2т и векторы Ду	и w
расположены по одну сторону гиперплоскости Д. Иначе
говоря, если мы обозначим через 2* выпуклую оболочку

262
РАЗНЫЕ ЗАДАЧИ
[ГЛ. 4
тела 2т и вектора до, то мы найдем, что тело S* и вектор
Ду лежат по одну сторону гиперплоскости Д. Поэтому
тело S* и вектор — Ду расположены в двух разных
замкнутых полупространствах, определяемых гиперпло¬
скостью Д. Отсюда мы, наконец, заключаем, что вектор
— Д2/, исходящий из точки х(Т), не проходит через вну¬
тренние точки тела S*.
Будем теперь рассматривать всевозможные способы
варьирования управления v(t), откладывая получающиеся
векторы Ау = 6у(Т) (см. (81)) из точки х (Т). Концы этих
векторов заполнят некоторое множество К в пространстве
X, являющееся, как легко видеть (ср. стр. 106 — 107) выпук¬
лым конусом с вершиной в точке х(Т). Концы векторов
— Ду заполняют выпуклый конус, симметричный конусу К
относительно точки х(Т). Этот конус мы обозначим через
— К. Из сказанного выше вытекает, что конус —К
не пересекается с внутренностью выпуклого тела S*.
Так как при этом тело S* содержит внутренние точки
(ибо тело St содержит внутренние точки), то тела S* и
— К являются разделяемыми. Иначе говоря, существует
в X такая гиперплоскость Д*, что тело S* содержится
в одном замкнутом полупространстве, определяемом гипер¬
плоскостью Д*, а конус — К в другом. Следовательно,
выпуклые множества S* и К расположены в одном замк¬
нутом полупространстве, определяемом гиперплоскостью
Д*. Обозначим через е* единичный вектор, исходящий из
точки х(Т), ортогональный гиперплоскости Д* и направ¬
ленный в полупространство, не содержащее тел S* и К.
Таким образом, вектор е* удовлетворяет соотношениям
Обозначим через ф(£) решение системы (63) с началь¬
ным условием \|э(Г) = е*, а через %(t) — решение системы
(64) с начальным условием % (Т) = е*. Мы покажем сей¬
час, что функции ф(£) и %(£) —искомые (т. е. они удо¬
(ср. (87), (88), (89)):
(х — х(Т), е*)<0 при z£St,
(Ду, е*)<0	при	Ау£К,
(до, е*)<0.
(91)
(92)
(93)

§ 28]
ОДНА ЗАДАЧА ПРЕСЛЕДОВАНИЯ
263
влетворяют условиям, указанным в теореме 21). Прежде
всего отметим, что в силу выбора начальных условий для
функций ф(/) и % (t) соотношение (68) выполнено. Далее, из
(90) и (93) непосредственно следует соотношение (67). На¬
конец, соотношения (65) и (66) доказываются, исходя из
неравенств (9:1) и (92), совершенно так же, как в главе 2
из неравенства (34) было доказано соотношение (11) (в до¬
казательстве должны быть сделаны очевидные изменения;
связанные с тем, что рассматривается пространство X,
а не X).
Итак, теорема 21 полностью доказана.

ГЛАВА 5
ПРИНЦИП МАКСИМУМА И ВАРИАЦИОННОЕ
ИСЧИСЛЕНИЕ
В этой главе мы рассмотрим связь, существующую
между теорией оптимальных процессов и классическим
вариационным исчислением. Будет показано, что оптималь¬
ная задача, изученная в главах 1 — 2, является обобще¬
нием задачи Лагранжа в вариационном исчислении и
эквивалентна ей в случае, когда область управления U
является открытым множеством г-мерного векторного про¬
странства Ег.
Далее, мы покажем, что в случае открытого мно¬
жества U из принципа максимума следуют все основные
необходимые условия, известные в вариационном исчис¬
лении (в частности, критерий Вейерштрасса). Однако в
случае, когда U — замкнутое множество пространства
Ет (не совпадающее со всем Ег), условие Вейерштрасса
перестает действовать, т. е. теорема о том, что для дости¬
жения минимума функционала необходимо выполнение
условия Вейерштрасса, становится неверной. Таким
образом, существенное преимущество принципа максимума
по сравнению с классическими теоремами вариационного
исчисления состоит в том, что он применим для любого
(в частности, замкнутого) множества U СИ Ег. Расшире¬
ние класса возможных областей управления U по
сравнению с классическим случаем открытых множеств
весьма существенно для технических приложений теории.
Именно случай замкнутого множества V CZ Ег наиболее
интересен в задачах оптимального управления и, в част¬
ности, в прикладных вопросах. Например, даже простейшие
задачи, приведенные в § 5, не могли бы быть рассмот-

§ 20]
ОСНОВНАЯ ЗАДАЧА
265
рены методами классического вариационного исчисления,
так как область управления U являлась замкнутым мно¬
жеством и значения оптимальных управлений во всех
примерах лежали на границе U. Если в любом из
этих примеров мы ограничимся рассмотрением открытого
множества, отбросив граничные точки области управления С/,
то классические теоремы дадут такой ответ: оптималь¬
ных управлений не существует. Это, конечно, может
служить указанием на то, что управляющий параметр дол¬
жен принимать значения на границе множества U, но
такого соображения отнюдь не достаточно для решения
задачи, ибо нужно знать, каким образом должен
изменяться управляющий параметр на границе области U.
Например, в случае линейных задач нужно знать, каково
может быть число переключений, из каких вершин много¬
гранника U в какие происходят переключения и т. п. На
эти вопросы классическая теория на может дать никакого
ответа; в то же время, как мы видели на примерах, прин¬
цип максимума содержит информацию, достаточную для
решения указанных вопросов.
В § 29 мы выведем из принципа максимума необхо¬
димые условия для основной задачи вариационного исчис¬
ления. В § 30 мы докажем эквивалентность задачи Ла¬
гранжа и оптимальной задачи гл. 2, а также выведем из
принципа максимума критерий Вейерштрасса в случае,
когда область управления U представляет собой откры¬
тое множество г-мерного векторного пространства Ег. Для
простоты изложения мы ограничимся рассмотрением силь¬
ных экстремумов вариационных задач.
§ 29. Основная задача вариационного исчисления
Хотя основная задача вариационного исчисления и
является частным случаем задачи Лагранжа, рассматри¬
ваемой в следующем параграфе, тем не менее мы посвя¬
щаем основной задаче отдельный параграф, так как связь
между принципом максимума и необходимыми условиями
вариационного исчисления особенно отчетливо выступает
в этом простейшем случае.

266	ВАРИАЦИОННОЕ	ИСЧИСЛЕНИЕ	[ГЛ.	5
Определения
Пусть в {п-\- 1)-мерном пространстве /?п+1 действитель¬
ных переменных (t, х1, ... , хп) = (t, х) задана кривая
x(t) уравнениями
xl = xl(t),	72,	£0<£<£r	(1)
Если функции яг(г), i=l, ... , п абсолютно непрерывны
и имеют ограниченные производные, т. е. во всякой точке
существования производной выполнено соотношение
dx1(t)
dt
< М = const, i = 1, ... , n,
то мы будем говорить, что кривая (1) абсолютно непре¬
рывна. Далее, обозначим точки x(t0) и x(tx) соответствен¬
но через х0 и хг; мы будем говорить, что кривая (1) соеди¬
няет точки (£0, х0) и (tv хг) или же что она удовлетворяет
краевым условиям
x(t0) = xо, x(t1) = x1.	(2)
Назовем б-окрестностью абсолютно непрерывной кривой
(1) множество всех абсолютно непрерывных кривых
х (t) = (х1 (/), . .. , хп (t)),
удовлетворяющих условию
| хх (I) — хъ (I) |<6 при t0<^t^tv i=l,2, . . . у п.
Пусть теперь G — некоторое открытое множество прост¬
ранства Z?n+* и пусть действительная функция
/ (t, х1, ... у х11у и1, ..., и11) = / (t, х, и)
определена для любой точки (t, x)£G и любых действи¬
тельных значений и1, ..., и11. Будем предполагать, кроме
того, что функция / непрерывна и непрерывно дифферен¬
цируема по всем аргументам.
Предположим, что кривая (1) целиком лежит в облас¬
ти G. Тогда определен интеграл
*i
/ = /(*)= $/(Ч x(t), ^Jdt,	(3)
*9

§ 29]
ОСНОВНАЯ ЗАДАЧА
267
который мы будем рассматривать как функционал от
вектор-функции x{t)y tQ^t^tv Очевидно, что для
любой кривой х (if),	<*!,	принадлежащей 6-окрест¬
ности кривой (1), функционал J (х) также определен, если
6>0 достаточно мало.
Абсолютно непрерывную кривую (1) назовем (сильной)
экстремалью для функционала (3), если существует такое
6>0, что на множестве всех кривых х (£), t0<t^tv
расположенных в 6-окрестности кривой (1) и удовле¬
творяющих тем же краевым условиям (2), функционал (3)
принимает свое наименьшее (или наибольшее) значение при
х = х. В дальнейшем мы будем рассматривать только
случай минимума. Таким образом, кривая (1) будет на¬
зываться экстремалью функционала (3), если существует
такое 6>0, что для любой абсолютно непрерывной кривой
x(t), t0<t<tv принадлежащей 6-окрестности кривой (1)
и удовлетворяющей краевым условиям х (t0) = xQf х (/2) = xv
выполнено неравенство J (х) > J (х).
Основная задача вариационного исчисления состоит в
нахождении всех экстремалей данного функционала (3)
при заданных (закрепленных) краевых условиях (2).
Уравнения Эйлера и условие Лежандра
Мы покажем сейчас, что всякая экстремаль является
оптимальной траекторией для некоторой оптимальной за¬
дачи. Рассмотрим следующую систему 72-го порядка:
(4)
и интегральный функционал
h
J = J(x, и) = ^ / (t, х1, . . . , хп, и1, . .. , Un) dt =
= ^ / (ty х, и) dt.	(5)
*0
Здесь гг = (гг1, ... , ггп) — управляющий параметр, который

2(38
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. В
выбирается в классе всех ограниченных измеримых век¬
тор-функций. Таким образом, область управления U сов¬
падает в данном случае со всем n-мерным пространством
Еп переменных гг1, , ггп.
Имея в виду применения к вариационному исчисле¬
нию, мы определим здесь оптимальные траектории задачи
(4), (5) несколько иначе, чем это было сделано в главах
1, 2. Именно, пусть пределы интегрирования в (5) фик¬
сированы. Измеримое ограниченное управление u(t)}
t0 < t < tv и соответствующую абсолютно непрерывную тра¬
екторию х (t) системы (4) с краевыми условиями (2) мы
будем называть оптимальными, если существует такое
6>0, что, каково бы ни было управление и (t), для кото¬
рого соответствующая траектория х (t) системы (4) удов¬
летворяет краевым условиям (2) и находится в б-окрест¬
ности кривой x(t), выполняется неравенство/^', гг) > / (ху гг).
Иначе говоря, здесь при определении оптимальных управ¬
лений и траекторий мы будем сравнивать траекторию х (t)
не со всеми другими траекториями х (£), а только с
траекториями, расположенными в 6-окрестности кривой
x(t). Всякая траектория, оптимальная в смысле гл. 1, 2,
является оптимальной и в смысле принятого здесь опре¬
деления, но, вообще говоря, не наоборот. Таким образом,
оптимальных управлений и траекторий в принятом здесь
смысле больше, чем оптимальных управлений и траек¬
торий в смысле глав 1, 2.
Нетрудно понять, однако, что принцип максимума, как
необходимое условие оптимальности, для оптималь¬
ных управлений и траекторий в принятом здесь смысле
сохраняется в той же самой формулировке. В самом деле,
при доказательстве принципа максимума в главе 2 мы
сравнивали траекторию х (t) только с траекториями вида
х* (*) = х (t) + гдх (t) + о (е),
где е—бесконечно малая величина. При достаточно малом
е траектория х* (t) лежит в 6-окрестности кривой х (t) (ка¬
ково бы ни было заданное число 6), и поэтому все рас¬
суждения главы 2 проходят без изменений для управ¬
лений и траекторий, оптимальных в рассматриваемом здесь
смысле.

§ 29]
ОСНОВНАЯ ЗАДАЧА
269
Сформулированная оптимальная задача (4), (5) являет¬
ся задачей с закрепленными концами и закрепленным
временем (см. § 8). Очевидно, что всякая оптимальная тра¬
ектория задачи (4), (5) является экстремалью интеграла
(3) и наоборот (достаточно, в силу (4), заменить в иитег-
dx i (t')
рале (5) величины и1 (t) производными —dt~)' Поэтому
принцип максимума, представляющий собой необходимое
условие оптимальности; является в то же время и необхо¬
димым условием для того, чтобы кривая x(t) была экстре¬
малью интеграла (3). Это простое соображение и позволяет
применять принцип максимума при решении вариацион¬
ной задачи (3).
В силу теоремы 6 для решения поставленной оптималь¬
ной задачи мы должны составить уравнения для вспомо¬
гательных неизвестных ф0> фх, . .. , и функцию
которые, в силу (4), принимают здесь вид
<з№ = Фо/ » х'> и) Ф^1 + Фг^2 + . . . + Фпмп, (6)
**о_п	1
dt	1
>	(7)
rfth	df(t,	X,	и)	J	,
dt	™	dxi	’	1	1	>•	•	•	’	п-	J
Условие максимума, указанное в теореме 6, дает
*(0> »(*)) =
п
= max(i>0/(t, x(t), «)+ 2 %(t)ua)	(8)
и£Еп	а=1
(почти всюду на отрезке	ср.	теорему	8).	Так
как область управления U совпадает со всем простран¬
ством Еп (для справедливости последующих рассужде¬
ний достаточно было бы потребовать, чтобы она была
открытым множеством в Еп), то точка максимума
и = и (t) функции	(ф (t),x (t)yt,u), рассматриваемой
как функция переменного гг £ ?7, является ее стацио¬
нарной точкой. Следовательно, из (8) вытекает, что

210
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. 5
(почти для всех t,	выполнены соотношения:
jzSfekb (t),x (t),t,u (0) =	(0	= о,
1=1, 2, .. ., п.
Из этих равенств следует, что ф0 =£ 0, так как в против¬
ном случае мы имели бы г|э. (t) = 0, i = О, 1, п. Сле¬
довательно, мы можем считать, что ф0 = —1, так как
ф0 = const < 0 (см. теорему 6), а величины яр0, ф15 ...
.. ., фп определены лишь с точностью до общего положи¬
тельного множителя пропорциональности. Полагая в пре¬
дыдущих равенствах ф0=—1, мы получаем (почти
всюду на отрезке
*«(*)= dfit’ Xa^U{t)) > f=l,	(9)
С другой стороны, подставляя в уравнения (7) ф0 = — 1
и интегрируя, мы находим
ч». w=■».(«.) + i int’ *£!• “(т)) dx,
to
г=1, ..., /г,	(10)
Из (9) и (10) мы получаехМ уравнения Эйлера в интег-
dx^ {£\
ралъной форме (подставив вместо и1 (t) производные ■ ^
(см. (4)):
v w у(=>) v дт +»(g.
to
i = 1, .. ., n,
где символ ( = ) означает, как и в главе 2, что равен¬
ства выполняются почти для всех £, £0<£<£г Диффе¬
ренцирование по t (при условии, что функция / и экстре¬
маль x(t) дважды непрерывно дифференцируемы) дает

§ 29]
ОСНОВНАЯ ЗАДАЧА
271
уравнения Эйлера в обычном виде
дх'1	dt	\	диi
i= 1, ..п.
( = ) о,
(10)
Предположим теперь, что функция f(t,x,u) имеет
вторые непрерывные частные производные по перемен¬
ным и1,	и11.	Тогда,	если	функция
как функция переменного и, достигает в точке и = и0
максимума, то квадратичная форма
неположительна (при любых ..., £п). Следовательно,
из условия максимума (8) вытекает, что почти для всех t,
*o<*<tv выполняется неравенство
Это условие, необходимое для того, чтобы кривая x(t)
была экстремалью интеграла (3), называется условием
Л ежанд ра.
Пусть, как и выше, гг (^), x(t), £0< tv — оптималь¬
ное управление и оптимальная траектория задачи (4), (5),
a яр(г) = (-1, яр, (<), ярп(г)) = (-1, яр (t)) - соответ-
ствующее им ненулевое абсолютно непрерывное решение
системы (7).
x(t), t, в) =
П
= f(t, x(t), и)+ 2 tya(t)ua,
а диадив 3е № W*•ио)	=
Канонические переменные

2?2	ЁАРЙАЦЙОННОЕ	ИСЧИСЛЕНИЕ	[ГЛ.	5
Обозначим через м (ф, ху t) точную верхнюю грань
значений функции gfe (ф, х, t, и) при фиксированных
ф = ( — 1, ф), х, t:
а£(\р, Ху 0 = SUpJ£?(\|), X, t, и) =
u£Eri
n
= sup( — f (t, X, M)+ 2 'I’ctM<1)-
u£K^i	d=	1
Предположим, что уравнение
ёв (ф, х, t, и) = м (ф, х, t)	(И)
имеет единственное решение
и = и(ф, rr, t),	(12)
определенное, непрерывное и непрерывно дифференцируе¬
мое по своим аргументам при
t0<t<tv \хг - хг (t) | < б, | ф. - ф{ (t) | < б,
i=l, .. ., /г,	(13)
где б — достаточно малое положительное число. При этих
условиях переменные (ж1,	хп)	= х, (ф1? фп) = ф
назовем каноническими переменными рассматриваемой
оптимальной задачи, а функцию
п
II (ф, Ху t)= — f(t, Ху и{ф, Ху t))-\- 2 фаИа(ф, Ху t)
а=1
— функцией Гамильтона.
Так как оптимальное управление u(t) почти всюду
на отрезке	удовлетворяет	условию максимума
(8) (напомним, что ф0 = — 1) и так как и(ф, х, t) —
единственное решение уравнения (И) (при усло¬
виях (13)), то (почти всюду на отрезке ^0<^<^)
и(0 = к(1>(0. Х(1), 0 = ^-	(14)
Можно даже утверждать, что равенство (14) выполняется
всюду на отрезке /0<£<£г В самом деле, так как

§ 29]
ОСНОВНАЯ ЗАДАЧА
273
равенство (14) выполняется почти всюду, то
t
x(t) = x{tQ) + ^ и(^(т), х(х), x)dx.
to
Но подынтегральная функция непрерывна пот (ибо
решение (12) непрерывно по совокупности своих аргумен¬
тов), и потому в каждой точке отрезка	про¬
изводная интеграла равна подынтегральной функции.
Из равенства (11) следует, что частные производные
функции е%?(ф,.х, t, и) по и1, £ = 1, ..., п, обращаются
в нуль при u = u(ty, х, t) (если выполнены условия (13)):
- 9f{t' X'l?’ *’ t)] +^i = 0, i = 1. .... п. (15)
Следовательно,
дН (г|5, х, г) _	”	df	диа	(-ф,	х,	t)	.	л	/	-	f)	.
Л диа (ф, х, t)
' 2j 'Фо	о!ф;
a=i	Yl
= мг(-ф, ж,
(9Я(ф, х, t) _ __ 9j_ _ yi д£ _ дца(т|), д, г)
а=1
=	У	Ль	_iTt	—	=	_^/(С	х,	м(ф,	»,Г))
^ 'ч £„<»/ 9x1	дх*
Полученные соотношения, в силу (14), (7), приводят нас
^8 л. С. Понтрягиц

274
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. 5
к каноническим уравнениям Эйлера — Гамильтона:
dx1	ОН	,
—j— =	,	I	=	1,	.	.	. , п,
dt dtyi
d^i	дН	.	.
-Г-L —	/	—	/2
df	ds*	'	’	‘	•	*’ ’
которым удовлетворяют в каждой точке отрезка
координаты вектор-функций х (t) = (.х1 (£), . . ., хп (t)) и
Ч>(0 = ('МО. • • •. 'Фп(О)-
Предположим, наконец, функцию / (t,x,u) дважды
непрерывно дифференцируемой по переменным и1, . . ., wn
и пусть определитель
д2
ди1 dui
f(t, x(t), и (г|) (I), x(t), t))
(16)
отличен от нуля при t0 < t < tv В этом случае система
уравнений
I	(t,	X,	и)	/-ч	.	j	/ л п\
—- = 0, 1 = 1	п,	17)
ди1
однозначно разрешима относительно и1, . . ., ип, если хх
и мало отличаются от xl (t) и (г), и, в силу (15),
решение этой системы совпадает с функцией (12). Таким
образом, данное нами выше определение канонических
координат согласуется с обычным определением этих
координат с помощью системы (17) при условии, что
определитель (16) не обращается в нуль.
Замечание. Если предполояшть, что функция
/(/, ху и) определена не для всех вещественных значений
переменных и1, . . ., unt а только при и£ U С1ЕПу где U —
некоторое открытое множество в ЕП) то (после очевидных
изменений в определении экстремалей для интеграла (3)),
все изложенное остается в силе. Надо только в соответ¬
ствующей оптимальной задаче (4), (5) в качестве области
управления взять не все пространство Еп, а его откры¬
тое подмножество U. Это замечание относится и к сле¬
дующему параграфу.

§ 30]
ЗАДАЧА ЛАГРАНЖА
275
§ 30* Задача Лагранжа
Формулировка задачи
Пусть заданы к функций
/*(*, х\	хп, и1, vn~k) =
= /l(£, X, v), i= 1, . .	/ь,
непрерывных и непрерывно дифференцируемых по всем
аргументам при (t, х) £ G и при любых значениях век¬
тора v = (v1,	vr), где г = п — к. Рассмотрим следую¬
щую систему из к дифференциальных уравнений с п
неизвестными функциями хг(1)у . .., xn(t):
Абсолютно непрерывную кривую x(t),
целиком лежащую в области G, будем называть допу¬
стимой, если она удовлетворяет краевым условиям (2),
а ее координаты — системе (18). Далее, абсолютно непре¬
рывную кривую x(t)y f0 <*<*!, мы будем называть
экстремалью для функционала (3) при заданных краевых
условиях (2) и заданной системе (18), если я (^ — допу¬
стимая кривая и существует такое 8 > 0, что J (х) <
< J (х) для любой допустимой кривой х (t), t0<t<tly
лежащей в 8-окрестности кривой х (t).
Задача Лагранжа (с закрепленными концами) при
заданных краевых условиях (2) и заданной системе (18)
заключается в нахождении всех экстремалей для функ¬
ционала вида (3).
Покажем, что эта задача сводится к некоторой опти¬
мальной задаче. Для симметрии введем обозначение
1=1, . .., к < п.
(18)
/° (t, х, v) =
— f(t, х, j1 (t, х, v), . ..fl(t, x, v), v1,	vr),	(19)
где функция f(t, x, и1, . . ., un) определена в предыдущем
параграфе.
18*

276
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. 5
Рассмотрим систему n-го порядка
в которой через v = (v1,	vr)	обозначен управляющий
вектор. Допустимыми будем считать любые измеримые
ограниченные управления, т. е. областью управления слу¬
жит все / -мерное пространство Ег переменных v1, vr.
Требуется найти допустимое управление v(t), кото¬
рому соответствует траектория х (£) системы (20), удов¬
летворяющая краевым условиям (2) и минимизирующая
интеграл
Очевидно, что всякое решение этой оптимальной задачи
(с закрепленным временем) является экстремалью для рас¬
смотренной задачи Лагранжа и, наоборот, произвольная
экстремаль х (t) = (xl (£), . .., х11 (/)), t0 < t < tv задачи
Лагранжа является оптимальной траекторией, соответст¬
вующей оптимальному управлению
Легко видеть, что и, обратно, всякая оптимальная
задача с закрепленным временем является задачей Лаг¬
ранжа (с закрепленными концами), если класс допусти¬
мых управлений состоит из произвольных ограниченных
измеримых управлений, а область управления совпадает
со всем пространством Ег.
Правило множителей Лагранжа
Пусть v(t), t0<Ct^tv— оптимальное управление,
а; (£) —соответствующая ему оптимальная траектория сис¬
темы (20), удовлетворяющая краевым условиям (2).
Пусть, далее, (t) = (i|)0 (t), . . ., \|)n (£)) — соответствую-
clxk+1 (t)
dt
• • »

§ 30]
ЗАДАЧА ЛАГРАНЖА
277
щая функциям x(t), v{t) ненулевая абсолютно непрерыв¬
ная вектор-функция. Функция т (-ф, х, t, v) имеет вид
(г|?, X, t, v) =
k	n—k
= г|)0f(t, x, v)+ 2 W°+ 2 ^k+avu.
a=l
a=l
Далее, мы имеем, в силу (19),
- =	+	У	г	=	1	п
1 дх1	диадх'’	’	'	'	'	’
а/» _ а/
дх{
(22)
<23>
д/о
dvi duk~^i ^ a^l dvi
Следовательно, система уравнений для вспомогательных
неизвестных ф^ имеет вид (см. теорему 6)
^Фо п
dt ’
1
dt
V dxi + диа dxi ) Фо ^ dxi фа» j
(24)
Из условия максимума (теорема 6) получаем почти
всюду на отрезке	(см.	(23))
lb se Ж<).* т.НО) (- > (та + 2 =; £ Н +
а=1
df
+ У! Г~7 фа + ф!i+j — 0»	/	—	1	>	•	•	•	>	п	—	к.	(25)
а=1 °v
Введем обозначения
dxi
dt
df
= хг, i — 1, .. ., п, (т. е.
dx
dt
= X
df
df
df
du'-	gxi ’	duh+> gxh*j ’
df'1 __ df
dvi	Qxk*j

278
В А РИ Л Ц И О Ы НО Е И С Ч И С Л Е Н И Е
[ГЛ. 5
Кроме того, имеем (см. (18)) при г = 1,	к
-^5-= 6),	1</	С/с,
дх>
дер1
9f
~—— ,	1	<	/	<	п	—	к.
(27)
дх
Перепишем теперь соотношения (24) в виде
у
а=1 -аха
г = 1, . . ., п.	(28)
Равенства (25) дают (см. (26))
w*)( = W-^o+ S	+
дхк+з а=1 dxh+J \ дх	J	J
j = 1, . . ., п — к.
Сравнивая полученные равенства с последними п — к
равенствами (28), получим
df
df r df
dxk+i
Г*+J,-£r( £♦.+*)<->
(29)
Наконец, введем /с измеримых и ограниченных на отрез¬
ке £0<£<£j функций kt(t), i= 1, ..., /с, равенствами
\(t) = df{t' x(t)’ ж(°Чо + ^(0. i=l, .... к, (30)
dxj

§ 30]
ЗАДАЧА ЛАГРАНЖА
279
и перепишем соотношения (28), (29) в виде
i = 1, . . п,
(31)
-Цк+}(*о)>	/'=	1.	П-к. (32)
Сформулируем и докажем теперь правило множите¬
лей Лагранжа.
Пусть абсолютно непрерывная кривая (1) является
экстремалью для интеграла (3) при заданных краевых
условиях (2) и заданной системе (18). Тогда найдутся
к таких измеримых и ограниченных функций 'ki{t), £0<
< I < tv называемых множителями Лагранжа, и такая
постоянная ф0 < 0, что функция
почти всюду на отрезке tQ^t^t1 удовлетворяет равен¬
ствам:
где С| — постоянные.
Доказательство. Определим множители (^),
=1,	равенствами (30), а за постоянную при¬
мем координату с нулевым индексом вектор-функции (I).
F (t, х (*), x(t)) =
k
■ф0/(г, x(t), x(t)) + 2 K(t)q>a(t, x(t), x(t))
a=l
dF (t, x (t), x (t))
dxl
i = 1, . . . , n,

280	ВАРИАЦИОННОЕ	ИСЧИСЛЕНИЕ	[ГЛ.	5
Тогда при l<i<A; равенства (27), (30), (31) дают
k
dF	.	df	I	v	i	дУа	,	df	,	*
77 'Фо “77 + ha —77 — — 'Фо Г- + i ~
дяг	а==1	&rl	дх1
k
= %(*) =	^0+	2	Ьа|£)*	+	'М*о)	=
/о	0=1
<о	а=1
= (<о)-
<о
Далее, из соотношений (32) получаем при / = 1, . . ., п — к
k
dF __	df	v	«9/а
-fe+. = )
dxk+J	dxk+1	a=1	dxh+J
<=> ■ к sfc +•■+ 2 *■»	+*•*><y=
<o	a=l
#0	a	=	l
t
= 5-7fcQ?T + tl+i(<o)-
h
Таким образом, правило множителей Лагранжа доказано.
Неравенство Вейерштрасса
Обозначим через I некоторый (к-\- 1)-мерный вектор
/==(/0, /1? ..., /Д pi определим функцию Вейерштрасса
jg(t, ж, xt £, /), зависящую от аргументов t, х = (ж1, ..., £п)>
г = (ж\ ,,,,хп), | = (|г	I")	И	/	=	(/0,	/j	у,

§ 30]
ЗАДАЧА ЛАГРАНЖА
281
формулой
<$(t, X, X, /) =
п
= F(t, X, I, l)-F(t, X, X, I)- У a°-xa)dF(t’ *' -’Л
«=;
где
k
F (t, x, x, Z) = — Z0/ (£, x, x) + ^ Za9a (t, x, x),
a=l
а функции /(£, x, x), фг = хг —/l(£, x, xft+1:,	x*1),
i = 1, . . ., /с, — те же, что и выше.
Для удобства обозначений последние га — /с координат
вектора £ будем обозначать через У1, . . ., yn~ft. первые
же к координат будем обозначать по-прежнему через
ъ\.... гк-
I = {i\	vn'h),	v = (v\ vn-k).
Вычислим теперь функцию Вейерштрасса в случае,
когда х = х (t) — экстремаль задачи Лагранжа при задан¬
ных уравнениях (18), х =	,	Z= А, (£) = (ф0,	(t),	...
..., hk(t)) (см. (30)), и первые к координат вектора
£ = (£\ ..., £/г, У1, ..., Уп_к) удовлетворяют уравнениям
Г-/{(г, х(0, V1, ..., У'1-*) =
= Г-/*(*. *(0. ^) = 0, г= 1, ..., fc. (33)
Из сделанных допущений следует, что (тг — А)-мер-
ная вектор-функция
v(t) = (v4t), .... vn-h(t)) = (ih*1(t),	xn(t))
является оптимальным управлением, соответствующим

282	ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ	[ГЛ. 5
траектории x(t) системы (20). Мы имеем (см. (18), (19), (33)):
F(t, x(t), x{t), l(t))=	x(l), x{t)) =
=	^(0- yW)-
F(t, x(t), I, X(t)) =
h
=	*(o.	i)+	2мо(г-/а(*,	*(о.ю)=
a=l
= - %f (t> x (t), l) = - %f° (t, X (1), V).
Далее, если i= 1, ..., &, то (см. 30))
-^r-F(t, x (t), x (t), a, (t)) = - ij)0 + a,j = \fi (0;
dz1	da;1
если же { = /c-)-/, /=Д ...,n — k, то (см. (19), (23), (25))
-4-F (t, x(t), x(t), %{t)) =
dx1
--*Jr-2<*w+-£iO	-
aTi	dxa	dxh*’
h
= ~^°£~	^*(o. «.u(0)+
a=l
тЬ *Ф.4+J (0-
Следовательно,
%{t, x{t), x(t), £, h{t)) =
=	x(t),	V)	+	^of°{t,	x(t),	v(t))-
k
- 2(/a(*. X(t), V) —/“ (i, X(i), t»(0))t|»a-
a=l
n—k
_ 2 (F“ - 0“ (0) (**+«(*) --^&eЖ*), *(0, <. 0(<)))=
a=l
= J2?(tJЭ (i), *(0- t> v(t)) —S&iW), x(t), t, V) +
n—k
+ 2 (Va —#*(*))-^rSViW), x(t), t, v(t)).	(34)
a=l

ЗАДАЧА ЛАГРАНЖА
283
Так как х (t) — экстремаль, то почти всюду на отрезке
выполняются равенства (25) и, следовательно,
из условия максимума почти для всех t следует нера¬
венство
%{t, x(t), x(t), g, %(t))>0,	(35)
которое и выражает необходимое условие Вейер-
ш т р а с с а: если х (t) — экстремаль рассмотренной нами
задачи Лагранжа, то найдутся такие ограниченные
и измеримые функции (t),' i= 1, . . ., /с, и4 такая непо¬
ложительная постоянная ф0, что почти для всех t вы¬
полняется неравенство (35) при любом выборе вектора
удовлетворяющего условиям (33).
Итак, в случае, когда область U изменения перемен¬
ных v1, . . ., vr совпадает со всем пространством Ег (или
является его открытым подмножеством), правило множи¬
телей Лагранжа и критерий Вейерштрасса вытекают из
принципа максимума.
Мы здесь подробно рассмотрели случай вариационной
задачи с закрепленными концами. Известные в вариа¬
ционном исчислении результаты для задач с п о д в и ж-
ными концами легко выводятся с помотцыо условий
трансверсальности (см. § 6).
Обсудим теперь вопрос о взаимоотношении принципа
максимума и критерия Вейерштрасса в случае, когда
множество U не является открытым. Полагая
V = v (t) + Да
и считая Av бесконечно малой, мы можем на основании
формулы Тейлора записать соотношение (34) (с точностью
до бесконечно малых более высокого порядка) в виде
g= 1 V Р&е (Ч> (0,f 09: b? W Диа At#. (36)
Z	Qvv>
а, 3=1
Это делает совершенно естественным условие Вейерштрасса
% > 0 во внутренних точках области возможных значе¬
ний U (ибо функция е%?, в силу теоремы 8, должна дости¬
гать при v = v(t) максимума, и, следовательно, v(t)
является стационарной точкой функции $в). Однако
в граничных точках, где, вообще говоря, перестают

284	ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ	[ГЛ.	5
обращаться в нуль производные —г (т. е. в разложении
dvl
функции фв (ty{t)>x {t),t,v{t)-\-kv) вблизи этих точек име¬
ются члены первого порядка малости относительно Ди),
неотрицательность функции % (имеющей второй порядок
малости) перестает быть необходимым условием максималь¬
ности функции фб. Иными словами, условие Вейерштрасса
% > О, вообще говоря, перестает быть справедливым в гра¬
ничных точках множества U.
Простой пример подтверждает сказанное. Рассмот¬
рим движение точки по закону
■§ = »2 (М<1),
где х и V — скалярные переменные. Очевидно, что движе¬
ние по закону v=l, х (t) = х0 +1 является оптимальным
по быстродействию (между любыми двумя точками), так
как скорость движения точки х, равная и2, не может
превосходить единицы. Здесь
/о = 1, /! = ^;
так как /° и /1 не зависят от х, то уравнения для ф0,
принимают вид
Ф0 = 0> ^1 = °’
т. е. ф0 = const, ty1 = const. Функция ф-в принимает вид
Вдоль рассматриваемой траектории v = 1, т. е. S& =
= ф0 + ф1? и потому (см. формулу (17) гл. 1) ф0 <0, грх > 0.
Выражение (36) для функции Вейерштрасса дает нам
теперь
Так как коэффициент — яр1 отрицателен, то условие Вейер¬
штрасса |>0 не выполняется.

ГЛАВА 6
ОПТИМАЛЬНЫЕ ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ
ФАЗОВЫХ КООРДИНАТАХ
В оптимальной задаче, изученной в главах 1 — 3,
ограничивалась лишь область U возможных значений
управляющего параметра и, в то время как на возмож¬
ные значения фазовой точки х не накладывалось никаких
ограничений и, следовательно, область возможных значе¬
ний фазовой точки совпадала со всем фазовым простран¬
ством X.
Поэтому не исключен случай, когда при оптималь¬
ном (в смысле гл. 1) переходе фазовой точки из началь¬
ного положения х0 в близкое к нему конечное положе¬
ние хг траектория х (t) сначала сильно отклонится от
точек х0, xv а уже потом попадет в положение хг
Однако часто в инженерной практике такое поведение
системы является не только нежелательным, но и недо¬
пустимым.
Дело в том, что в ряде случаев мощность допусти¬
мых сигналов управления вполне достаточна для пере¬
вода системы в состояние, недопустимое с точки зрения
безопасности или надежности работы (например, перегрев
в моторе, перегрузки и т. д.).
В этих случаях приходится ограничивать не только
область U возможных значений управляющего параметра,
но и область возможных значений фазовой точки. Другими
словами, разрешается выбирать только такие допустимые
управления, для которых соответствующие фазовые траек¬
тории лежат в заданной фиксированной области В,
выделенной наперед в н-мерном фазовом пространстве X.

286	ПРОЦЕССЫ	ПРИ	ОГРАНИЧЕННЫХ	КООРДИНАТАХ	[ГЛ.	6
В этом случае оптимальная задача состоит в выборе
такого допустимого управления, для которого соответ¬
ствующая траектория целиком лежит в области В
и удовлетворяет заданным краевым условиям, причем
минимизируется заданный функционал.
Полная система необходимых условий, которым удов¬
летворяют оптимальные управления и соответствующие
им оптимальные траектории этой обобщенной оптималь¬
ной задачи, дается теоремой 25 (см. стр. 341), которая
и является основным результатом настоящей главы.
Если область В — открытое множество фазового
пространства X, то сформулированная здесь оптималь¬
ная задача эквивалентна оптимальной задаче гл. 1, 2,
и ответ дается принципом максимума (так как при
доказательстве принципа максимума мы пользовались
лишь сколь угодно малой окрестностью оптимальной
траектории).
Новые трудности возникают в интересном для при¬
ложений случае, когда рассматривается замкнутая
область В (т. е. замыкание открытого в X множества)
и исследуемая оптимальная траектория частично или
целиком лежит на границе области В.
В дальнейшем мы будем предполагать, что В — замк¬
нутая область пространства X, а ее граница — гладкая
или кусочно-гладкая гиперповерхность пространства X.
Мы будем рассматривать только такие оптимальные
траектории, которые можно разбить на конечное число
участков, каждый из которых либо целиком лежит на
гладком куске границы области S, либо принадлежит
(за исключением, быть может, своих концов) открытому
ядру области В.
Участки оптимальной траектории, целиком лежащие
на гладком куске границы области В, удовлетворяют
необходимым условиям, указанным в теореме 22, анало¬
гичной принципу максимума. Формулировке и доказатель¬
ству этой теоремы, а также некоторым ее обобщениям
посвящены §§ 32 — 35 настоящей главы.
Участки оптимальной траектории, принадлежащие,
(за исключением, быть может, своих концов) открытому
ядру области В, удовлетворяют обычному принципу мак¬
симума (гл. 1 — 2).

§ 31]
ПОСТАНОВКА ЗАДАЧИ
287
Наконец, всякая пара примыкающих друг к другу
участков оптимальной траектории, один из которых
лежит в открытом ядре области В, а другой —на ее
границе, или лежащих на двух разных гладких кусках
границы области В, удовлетворяет некоторому условию
сопряжения, которое мы называем условием скачка
(теорема 24). Доказательству этого условия и некоторым
его приложениям посвящен § 36.
§ 31. Постановка задачи
Основные определения
В качестве допустимых управлений и теперь было бы
естественнее всего рассматривать кусочно-непрерывные
вектор-функции u(t), определенные на некотором отрезке
времени t0 < t < tv Однако имеющиеся доказательства
сформулированных в этой главе теорем проходят при
дополнительном предположении о кусочной гладко¬
сти управлений u(t).
Кроме того, областью U возможных значений допу¬
стимого управления будет теперь служить не произволь¬
ное подмножество 7-мерного пространства Ег, а множе¬
ство, которое в окрестности каждой своей граничной
точки имеет «регулярное» строение, точно определенное
ниже.
Поэтому в настоящей главе мы примем следующее
определение класса допустимых управлений (вполне
достаточное для всех технических приложений получен¬
ных результатов).
В качестве области управления U мы выберем про¬
извольное множество пространства Ег переменной и =
= (гг1, ...,ггг), устроенное в окрестности всякой своей
граничной точки «регулярным» в следующем смысле
образом.
Если их — произвольная граничная точка множества С/,
принадлежащая этому множеству, то найдутся такие
непрерывно дифференцируемые скалярные функции
q^u), г= 1, s, (s> 1),	(1)

288 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
что множество U в окрестности точки и1 задается сис¬
темой неравенств
9i(m)<0, .... qs(u)<0,
а в самой точке их выполнены равенства
?i(«i)= • • • = 9vK) = o>
и векторы
dq^l] = grad q, (и,)	 —= grad qs (щ)	(2)
линейно независимы.
Таким образом, (г — 1)-мерные грани области £/, примы¬
кающие к точке и15 определяются уравнениями
?1(в) = 0,	д,(в) = 0	(3)
и являются гладкими гиперповерхностями пространства ЕГУ
находящимися, в силу независимости векторов (2), в общем
положении в точке иг Сама точка их лежит на (r — s)~
мерном гладком «ребре» границы, определяемом как мно¬
жество решений системы (3), лежащих вблизи точки их.
Хотя функции (1) перечисленными условиями не опре¬
деляются однозначно, однако, как легко видеть, грани
всех размерностей множества U вблизи точки иг (в част¬
ности, (г— 5)-мерное «ребро» (3), и, следовательно,
число s) однозначно определены.
Формулировки основных теорем этой главы, есте¬
ственно, инвариантны относительно выбора функций (1)
для данной граничной точки uv Однако на некоторые
конструкции при доказательстве теорем этот выбор суще¬
ственно влияет, что значительно усложняет изложение.
Поэтому, во избежание такого произвола, мы для каждой
граничной точки ux^U зафиксируем одну из возможных
систем функций (1) и будем во всем дальнейшем изло¬
жении, говоря о функциях (1) для точки uv подразу¬
мевать именно эту систему.
Классом допустимых управлений мы назовем множе¬
ство всех кусочно-непрерывных, кусочно-гладких вектор-
функций и (t) = (и1 (t), ..., ur (t)) (с разрывами первого
рода), определенных на произвольном отрезке t0 < t < tx
(своем для каждой функции) и в каждый момент вре¬

§ 3 1]
ПОСТАНОВКА ЗАДАЧИ
281)
мени принимающих значения из области управления СЛ
Если в момент t' управление терпит разрыв, то мно¬
жеству U должны принадлежать обе точки u(t' — 0)
и и (£' + 0).
Допустимому управлению u(t), а также его производ¬
ной мы будем, как и в гл. 1, в момент разрыва припи¬
сывать значение, равное пределу слева.
Пусть в и-мерном фазовом пространстве X переменной
х = (я1, . . ., хп) дана замкнутая область В с гладкой
границей, определяемая вблизи границы неравенством
g(x) = g(x1, ..	я")<0,
где скалярная функция g (х) определена и имеет непре¬
рывные частные производные второго порядка вблизи
границы
g {х) = 0,
и вектор
^ = gradg(x) = (-!-,	JL')
нигде на границе в нуль не обращается.
Таким образом, граница области В — гладкая гипер¬
поверхность пространства X с непрерывно меняющейся
кривизной. Важный для приложений случай, когда
область В имеет кусочно-гладкую границу, обсуждается
ниже (см. стр. 341).
Формулировка задачи
Пусть заданы действительные скалярные функции
/°(ж, и), f (х, и),	/г,	непрерывные и непрерывно
дифференцируемые по всем координатам векторов х, и
на прямом произведении В* X U* ZD В X U, где В*, U* — от¬
крытые множества пространств X, Ет, содержащие соот¬
ветственно В, U.
Уравнение движения фазовой точки имеет, как и в гла¬
ве 1, вид
^ = /(*.«).	(4)
где
f(x, и) = (/! (X, и), fn (.Г, и)).
19 л. С. Понтряпш

290
ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. G
Поставим следующую задачу. В пространстве X заданы
две точки х0, xv принадлежащие замкнутой области В.
Среди всех допустимых управлений, переводящих фазовую
точку из положения х0 в положение xv причем так, что
соответствующая фазовая траектория х (t) целиком лежит
в замкнутой области В, требуется выбрать управление
u(t),	обращающее	в	минимум	интеграл
h
^ /° (х (t), и (t)) dt.
h
Чтобы дать вторую (эквивалентную) формулировку
нашей оптимальной задачи (ср. стр. 20), вводом (/?.-}1)-
мерное пространство X переменной
х = (х°, X1, . . ., хп) — (х°, х)у
где
X = (х\ . . ., хп) б X.
Всякую векторную или скалярную функцию F {х)у
зависящую от аргумента х£Х, можно, очевидно, считать
функцией от аргумента х = (х°, х) б X, полагая
F(x) = F(x°, x) = F(x)\
этим фактом мы будем в дальнейшем постоянно пользо¬
ваться.
Как и в главе 1, введем вектор
/(х, и) =/(х, и) = (f°(x, и), /1 (х, и), . .	/"	(х,	и)) —
= (/°(х, и), f(x, и)).
Обратим внимание на то обстоятельство, что функция
f(x, и) не зависит от координаты х°.
Через G обозначим прямое произведение замкнутой
области В на ось х°. Область G, так же как и В, заедается
в окрестности своей границы неравенством
g(x) = g(x°, x) = g(x)K 0.
Она имеет гладкую 72-мерную границу
g и=о

§ 31]
j юс т л н о в к л з лдлчи
с непрерывно меняющейся кривизной, и вектор
^5(ж)_=	,	Z	X	_dg_	dg
дх Ь % \	>	\	дх° ’ дх1 ’ ' ’ ’ ’ дхп J
= (ч°*	-&J = (°> §radS(-х))
нигде на границе области в нуль не обращается.
Рассмотрим в пространстве X уравнение
dX	гг /	ч
U),
объединяющее уравнение (4) и соотношение
dx°
dt
= г (ж> “)•
После введения этих обозначений можно дать сле¬
дующую эквивалентную формулировку нашей оптималь¬
ной задачи. Требуется выбрать допустимое управление
a(t), t0^Ct^.tv таким образом, чтобы конец х (^) соответ¬
ствующей траектории х (t) уравнения (5) с начальным
значением
эс(г0) = (0, х0)
лежал на прямой П CZ X, проходящей через точку (0, хг)
и параллельной оси х°, и чтобы при этом вся траектория
x(t), tn	целиком лежала в замкнутой области G,
а координата х° (^) принимала наименьшее возможное
значение.
В дальнейшем мы будем пользоваться преимущественно
второй формулировкой задачи.
Управления и траектории, удовлетворяющие этим усло¬
виям, будем называть оптимальными.
Некоторые дополните л ьные за мс ч а и и я
Кусочно-непрерывные управления мы назвали в гл. 1
«безынерционными управлениями», так как в случае надоб¬
ности такое управление может мгновенно перескакивать
с одного значения на другое. Однако в ряде случаев
«рули» обладают определенной инерцией, и, следовательно,
некоторые из функций и1^), ..., ur (£) (или даже все)

292	ПРОЦЕССЫ	ПРИ	ОГРАНИЧЕННЫХ	КООРДИНАТАХ	[ГЛ.	G
не только сами непрерывны, но и’обладают непрерывными
производными вплоть до некоторого порядка.
Оптимальные j задачи с инерционными управлениями
легко сводятся к сформулированной выше оптимальной
задаче. Пусть, например, допустимые управления — не¬
прерывные кусочно-гладкие функции, производные кото¬
рых ограничены по модулю одной и той же констан¬
той, например единицей, и пусть область управления
U — замкнутая область с кусочно-гладкой границей.
Для простоты допустим, что область возможных зна¬
чений фазовой точки х совпадает со всем простран¬
ством X.
Примем параметр и за фазовую переменную, а за
управляющий параметр примем производную от и. Тогда
вместо уравнения движения (4) в н-мерном фазовом про¬
странстве X мы получим систему
4г = /(*> “)■
du
в (п + 7')-мерном фазовом пространстве X х Ег, где
v = (и1, . . ., vr) — кусочно-непрерывное (безынерционное)
управление, областью возможных значений которого
является единичный г-мерный куб
|i/|< 1, i= 1, . . ., г,
а областью возможных значений фазовой точки (х, и)
является прямое произведение X X U.
Отметим еще, что принцип максимума справедлив для
оптимальных траекторий, которые лежат внутри от¬
крытого ядра G, за исключением концов, лежа¬
щих на границе этой области.
Пусть концы х (t0), х (£j) оптимальной траектории
х (£), t0 < t < tv лежат на границе g (х) = 0. Тогда участок
траектории при tQ + т< £< t1 — т, т > 0, целиком лежит
в открытом ядре области G, и потому существует функ¬
ция	т < t < t± — т, удовлетворяющая требова¬
ниям принципа максимума (теорема 1) применительно

§ 32]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ НА ГРАНИЦЕ
293
к участку x(t),	+	— т. Можно считать, что
длина вектора 'ф-г^ + т)	равна единице.
В силу компактности единичной сферы конечномерного
векторного пространства можно выбрать такую последова¬
тельность положительных чисел xv т2, . .., tt, . .., сходя¬
щуюся к нулю, что	последовательность векторов
Фт. (Л + Тг)’	2,	. . ., имеет предел Очевидно, что
функция я|) (£), £0 < £ <	соответствующая траекторий
x(t) и удовлетворяющая начальному условию 'ф(^0) = ,Фо’
внутри отрезка t0 < t < tx служит пределом функций
tf)T. (t), i= 1, 2, . . ., и потому является искомой.
§ 32. Оптимальные траектории, лежащие
на границе области
В этом параграфе сформулирована теорема 22, дающая
полную систему необходимых условий, которым удовле¬
творяет всякая регулярная оптимальная траектория, цели¬
ком лежащая на гладкой границе g (х) = 0 области G.
Необходимость ограничиться регулярными траекто¬
риями, определение которых приведено ниже, вызвана
не недостатком метода доказательства теоремы 22, а су¬
ществом вопроса. Дело в том, что при выводе любых
необходимых условий, которым удовлетворяет заданная
оптимальная траектория, ее нужно сравнить с другими
оптимальными траекториями, удовлетворяющими тем же
краевым условиям, т. е. включить (путем соответствую¬
щим образом выбранного метода вариаций) оптимальную
траекторию в некоторое «достаточно богатое» семейство
близких траекторий, лежащих в G. Однако нетрудно
привести пример оптимальной траектории, лежащей
на границе области G, любая вариация которой
выходит за пределы области G и для которой теорема
22 неверна.
Это исключительное явление не имеет места, если
рассматриваемая траектория регулярна. Именно, здесь
будет доказано, что соответствующими вариациями управ¬
ления всякую регулярную траекторию можно включить
в достаточно богатое семейство траекторий, лежащих
в замкнутой области G.

294	ПРОЦЕССЫ	ПРИ	ОГРАНИЧЕННЫХ	КООРДИНАТАХ	[ГЛ.	6
Основные определения
Введем обозначения:
*(*.“>=£^№“>=2 анх)
а=0
а=1
дха
/а (ж, и) =
(а?, м) _ { др др
дх
= ( О,
др
др ч\
’ ’ дя™ ) '
У ’
др (х, и)
да
др
да1
др
диг
(6)
Для того чтобы траектория x(t), £n<£<^, уравне¬
ния (5), соответствующая управлению u(t), целиком
лежала на границе g (х) = 0, очевидно, необходимо и до¬
статочно, чтобы выполнялись равенства
g(x(t0)) = 0,	p(w(t),	u(t))~	0,
первое из которых утверждает, что начальная точка
траектории лежит на границе области G, а второе—что
фазовая скорость движущейся вдоль траектории точки
в каждый момент времени касательна к границе.
Точку х £ X назовем регулярной относительно точки
их^и, если выполняются следующие условия:
1) р(х, Uj) = 0;
оч др(х, и{) л.
Z) Ш ф и’
3) если щ — граничная точка	множества	U	и q{ (и)>
i = 1, . . ., 5 — функции	(1) для	точки	uv то	векторы
др (х, щ)	ддг (ux)	dqs {и^}
да
ди
да
(7)
линеино независимы.
Остановимся на геометрическом смысле условия 3).
Прежде всего ясно, что условие 2) можно считать
частным случаем условия 3), если в последнем условии

§ 32]
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ 1IA ГРАНИЦЕ
295
полагать 5 = 0, когда ы1 — внутренняя точка множества U.
В дальнейшем мы так и будем поступать.
Из независимости векторов (7) следует, что гладкое
(/■ — 5)-мерное «ребро» (3) границы области U находится
в точке и] в общем положении с (/-—^-мерной гиперпо¬
верхностью, заданной в окрестности точки и1 уравне¬
нием р(х,и) = 0. Следовательно, 5<г — 1; другими сло¬
вами, иг не может быть вершиной границы множест¬
ва U, в которой сходятся г различных (г — 1)-мерных
граней.
Отметим еще тот очевидный факт, что понятие регу¬
лярности точки х относительно их не зависит от сделан¬
ного нами выбора функций (1) для точки иг
Обозначим через со (х) множество всех точек u£U,
относительно которых регулярна точка х. Множество
со (x)dU может, конечно, оказаться и пустым.
Траекторию х (t), t0 < t < tv уравнения (5), соответ¬
ствующую управлению и (t) и целиком лежащую на гра¬
нице области G, назовем регулярной, если и (t) £ со (х (t))
в каждой точке непрерывности t управления и (t) и если
и (t — 0) G со (х (t)),	u(t-\-	0)	£	со	(х	(t)),
когда t — точка разрыва управления u(t).
Для точек х, лежащих на границе области G, для
которых множество со (х) непусто, определим величину
/// (ф, х) равенством
171 (ф, Х) = Slip ёрр (ф, X, О) у
г<Е СО(се)
где, как и раньше,
п
Ж (ф, Ху и) = фа/а {х, и) = (ф, f(x, и)).
а=0
Если х — регулярная точка границы g (х) = 0 относи¬
тельно точки u£U и для некоторого вектора ф выпол¬
няется равенство
•Ж (ф, и) = т (ф, х),
то, по правилу множителей Лагранжа, существуют такие

296	ПРОЦЕССЫ	ПРИ	ОГРАНИЧЕННЫХ	КООРДИНАТАХ	[ГЛ.	6
действительные числа	К,	vv . . .,	vs, что
д&е (ф, х,	и) _	^ др (х, и)	,	у	v	дЧа (и)
ди	ди	'	а	ди у	'	•'
а=1
где д. (и), i = 1, . . ., 5, — функции (1) для точки w, а вектор
V
определяется форхмулои
дЖ = С дЖ	дЖ	\
ди ~~~ \ч ди1 ’ * * ‘ ’ дит J *
Кроме того, введем обозначения:
дЖ (ф, х, и) __ /	<9с^	дЖ	\	__	/'0
дх	v дх° ’ дх1 ’ * * ’ ’	#	/ у ’ дх1 ’ * * ' ’ д;гп ’
дЖ(^,х,и) / дЖ дЖ	дЖ\	ч
 Щ = (ж’ ж ц)-
^	дЖ	(ф,	х,	и)	дд (х, и)
Отметим, что векторы 			 , —^—- не зависят
от выбора функций qt (гг), г=1, .. ., 5. Далее, вектор
^	»	др (х, гг)
2j va —^— является параллельной направлению - ^—-
а=1
дЖ	.	ч
проекцией вектора — - на касательную плоскость (г —$)-
мерного «ребра» (3), также инвариантному относительно
выбора функций qi(u). Следовательно, множитель К в фор¬
муле (8) не зависит от выбора функций qt (и).
Если и — внутренняя точка множества £/, т. с. 5 = 0,
/оч	дЖ др (х, и)
то из (8) следует, что векторы	коллинеариы.
Теорема 22. Пусть x(t)y £0<£ <	— регулярная
оптимальная траектория уравнения (5), соответству¬
ющая оптимальному управлению u(t) и целиком лежащая
на границе области G. Тогда найдется такая непрерыв¬
ная вектор-функция ф (£) = (ф0 (t), . . ., фп (£)), t0^.t<Ctv
и такая кусочно-непрерывная, кусочно-гладкая скалярная
функция А,(£),	что	на отрезке t0 < t< t1 бу¬
дут выполняться нижеследующие равенства (9) —(11) и

§ 32]	ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ НА ГРАНИЦЕ	297
условия а) —в):
te =«й^)=/(1 и>1	(9)
= _»(»«■ “1 + >.(0 »?(». “> ,	(10)
ж(*)> М(0) = ™Ж0> x(t)) = 0,	(11)
г<9е	X	(£)	определяется из условия максимума	(11)	яа/г
множитель Лагранжа при векторе др ^ в формуле (8);
а) координата ф0 (t) = const < 0;
б) вектор ty(t0) отличен от нуля и касается гра¬
ницы g{x) = 0 в точке x(t0)\
в)	во	всех точках дифференцируемости функции 'k(t)
вектор
grad g (ж (<))
направлен внутрь области G или обращается в нуль
/'	dX (t) n\
(т• е- ~1Г<0)-
Сделаем несколько замечаний принципиального харак¬
тера, разъясняющих смысл условий а)— в).
Замечание 1. Равенство ф0 (t) = const следует из
независимости правой части уравнения (10) от коорди¬
наты х°.
Уравнения (9) —(11) и условие а) аналогичны прин¬
ципу максимума. Условия б) и в) специфичны для рас¬
сматриваемого случая и обсуждаются в замечаниях 4, 5.
Замечай и е 2. Из условия максимума непосред¬
ственно следует возможность подразделения отрезка
на частичные отрезки точками деления
*о = то < Ti < • • • < хи < *:t+1 = h
таким образом, что на отрезке T-<£<ti+1, i = 0, 1, . . к,
выпол яется равенство
д&6 (г|? (t)} х (t), и (0) _
да
. (л др (ж (0, u(t)) . 4)	(“(*))
=	 +	2j	v«	w—ш—•
а=1

298	ПРОЦЕССЫ	ПРИ	ОГРАНИЧЕННЫХ	КООРДИНАТАХ	[ГЛ.	6
где +Д, . .., +Д, s> 0 —функции (1) для точки и (tl + 0),
a х(Д(£), . ..,	(t)	- некоторые функции.
Это равенство эквивалентно на рассматриваемом от¬
резке системе г линейных уравнений относительно s + 1 < г
неизвестных X, х(Д, . . ., v(si} с кусочно-непрерывными,
кусочно-гладкими коэффициентами и свободными членами,
матрица которой имеет ранг 5+1. Следовательно, функ¬
цию X(t) можно представить на всем отрезке £0<£<£j
в виде
40= 2 'Ы0«а(*) = (Ч>(*)> «(*)),	(12)
а=0
где a (t) = (a0 (t), . . ., ап (£)) — кусочно-непрерывная, кусоч¬
но-гладкая вектор-функция.
Замечание 3. Уравнения (9) —(И) обращаются
в тождество, если ф (t) = 0, X ~ 0, £0	< +
Покажем, что если ф (t0) + 0, то ф (t) Ф 0 для любого t,
и наоборот, из ф(^0) = 0 следует ф (t) = 0, t0<CtKtv
В самом деле, подставив выражение (12) для % (t)
в уравнение (10), получим однородное линейное диф¬
ференциальное уравнение относительно ф (£), для которого
справедлива теорема единственности, откуда и следует
наше утверждение.
Замечай и е 4. Для выяснения смысла условия б)
заметим, что система (9) —(11) всегда имеет, кроме реше¬
ния u(t), x(t), ф (t) = 0, Л, (^) = С), еще следующее три¬
виальное решение:
u(t), x(t), ф(*) = vgradg(ac(0), X(t)~vt
где v — произвольное число. В этом легко убедиться
непосредственной подстановкой.
Легко проверить также, что если
u(i), x(t), ф(£), X(t)	(13)
— некоторое решение системы (9) —(И), то решением
является и
u(t), x(t), ф(0 + v grad g(x(t)), X (t) + v,
где v — произвольное число.

> 33]
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22
299
Следовательно, прибавлением к функциям гр(£), МО»
входящим в решение (13), членов вида v grad g (х (t)), v
мы всегда можем добиться того, чтобы начальное значе¬
ние (^0) + vgradg,(flc(^0)) лежало в касательной плоско¬
сти границы g(oc) = 0 в точке х (t0).
Если это начальное значение — нулевое, то исходное
решение было тривиальным, так как, учитывая замеча¬
ние 3, можно утверждать, что ф (0 = — v grad g (х (£)),
X(t) == -v.
Таким образом, из условия б) следует нстривиаль-
ность решения системы (9) —(11).
Из сказанного следует, что условие б) эквивалентно тре¬
бованию неколлинеарности векторов ф (£0) и grad g (х {tQ)).
Замечание 5. Условие в) возникает вследствие
того, что при варьировании траектория х (t) сравнивается
не только с соседними траекториями, так же как и x(t)
лежащими на границе g(x) = 0, но и со всеми близкими
траекториями, принадлежащими замкнутой области G.
Доказательству теоремы 22 посвящены следующие два
параграфа.
§ 33. Доказательство теоремы 22
(основные построения)
Некоторые обозначения
.Введем обозначение
ЛОЛ i = o 1 п / = 1
ди ч ди) J '	’	’	1	’
и будем рассматривать эту матрицу как оператор из
пространства Ет векторов и = (и1, . . ., ит) в пространство X
векторов х=(х°, х..., хп) и одновременно как опера¬
тор из пространства векторов ф = (ф0, ..., фп) в про¬
странство Ег:
bf_u_ у lLua	= fy	д^иа	у	дГ	а)
ди 2i диа	1 2j	диа U '	■■■’	2J	диа	J >
а=Л	а=1	а=1
д&6 (ф, х, и)
ди
и=0	а=0
Д (*■ц) яЬ _ (у dfa гЬ y dfa * ‘ -'
ди	dui	г^а’ •••’ 2j~wrva;~'

300
ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. G
Пусть А = (АД . . ., Хп) — вектор пространства X.
Матрицы
др (
дх	ч/v дх! j '
/=о,1	«
др
(Ж, К) f ^ i др (ж, и)~\	; п 4	„	„•	4
—“I*—Ты— 1>	I-U.1, .... п, 7 — 1,
также будем рассматривать как операторы, действующие
на векторы г|5, ас, и по формулам:
а=0
п
а-£ж=л01г’ аг)=Л2^жа-
а=0
Ли =	м')	=	ЛУ	—1ГМ“-
ди	\ди	J	Д
а=1
(14)
В этом параграфе ас (£),	£0 < t < £1} - произвольная
регулярная траектория уравнения (5), соответствующая
управлению и (t) и лежащая на границе g (ас) = 0 обла¬
сти G. В § 34 мы будем дополнительно предполагать, что
u(t)t x(t) оптимальны.
Построение функции i? (ас, и, ц)
Приступаем теперь к построению скалярной функции
R (ас, и, ц), играющей основную роль при доказатель¬
стве теоремы 22.
Зафиксируем s точек i= 1, ..., 5 (s>0), на
траектории ас (£), ни одна из которых не совпадает с кон¬
цом траектории ас(^); равенства g.=ac(£0) и ^ = при
i ф j возможны.
Через JSTi обозначим вектор, не касающийся грани¬
цы g (ас) = 0 в точке £. и направленный во вне области G;
в остальном вектор Xt произволен. Так как область G
в окрестности границы задается неравенством g (ас) < 0, то
(gradg(g.), JYJ > 0.

§ 33]
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22
301
Пусть — достаточно малая окрестность точки ^
в X, замыкание которой не содержит точки х (£х); един¬
ственное дополнительное требование, накладываемое на
заключается в том, что при ^ Ф х (t0) замыкание
окрестности 0^ не содержит также точки x(tQ). «Доста¬
точная малость» окресгаости характеризуется тем, что
скалярное произведение
(“' »,)>с>0	(15)
при ас£ 0^ г=1, .. ., s.
Через at (х) обозначим непрерывно дифференцируемую
скалярную функцию, удовлетворяющую условиям (х) = 1
в некоторой окрестности точки содержащейся в О£.,
аг (х) > 0 при х £	,	а{	(х)	=	0	вне	О^	.
Введем скалярную функцию
h (х, д) =g[x + \i 2 aa{x)Na^j ,	(16)
где д — скалярный параметр. Функция h(x, д) зависит,
очевидно, от выбора элементов at(x) и JVt, участвующих
в ее построении.
Если д > 0 достаточно мало и точка х, лежащая
вблизи границы области G, удовлетворяет уравнению
h (х, д) = О,
то x£G; если, кроме того, х не принадлежит объедине¬
нию окрестностей 0%. или если д = 0, то х лежит на
границе g (х) = 0. Если х не принадлежит объединению
окрестностей i = 1, .. ., s, или если д = 0, то h (х, д) =
= g (х) = 0, и утверждение справедливо. Пусть х £ 0£..
Тогда
h (ж, ц) = g ( ж -|- ц, 2 аа (ж) Жа
\	а=1
= g (ж) -1- ц	,	Д	а<х	И	лга)	+	о	(ц)	=	0.

ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. G
Но при достаточно малом ц в силу неравенств (15)
имеем:
S
^ аа(х)Жаj + o(n) >0,
а=1
следовательно, g (ас) < 0.
В дальнейшем параметр \х будет принимать близкие
к нулю значения вида ебц, где е имеет тот же смысл,
что и в главе 2, а бц —неотрицательное число. В опреде¬
ление функции /г(ас, ебц) входят точки ..., gs, функ¬
ции а1(х), ..., а3(х), векторы Nlt ..., JSrs и число бц.
Совокупность всех этих величин обозначим теперь через 6:
6 = {St. «»(*). бц}.	(17)
Чтобы подчеркнуть зависимость функции /г (ас, ебц) от
этих величин, мы будем теперь обозначать ее через
/го (ас, еб[х). Пусть Ъ± и Ь2 —два символа вида (17); запи¬
шем их в виде
6i = {£i> ai(x)> ^i>	* = 1> •••> sv
b2 = {Ei, ai(x), бц}, i = Sl+l, ...,sl + s2.
Символ b = {g^, at (ac), JSTit 6[x}, i = 1, . . ., s1 + s29 мы
будем называть суммой символов Ь2 и Ь2 и писать
Ь = Ьх + Ь2.
Произведение символа Ь = (£L, аь (ас), jVt, бц} на про¬
извольное неотрицательное число X определил!
формулой
Xb=[gL, at(x), JVi9 ^бц},
т. е. точки функции а{ (ас) и векторы остаются
прежними, а число бц умножается на X.
Таким образом, если Ь' и Ь" — два символа вида (17),
а X' и А/'— произвольные неотрицательные числа, то
определен символ Х'Ъ' + Х"Ь".

§ 33]
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22
303
Функцию R{x, и, ебц), зависящую от выбора символа
(17), определим равенством
It (Я, U, eSfl) 2 "" :'’,xa'J|" /“(*,") =
= (**<£^Й, /(*,«); (18)
(т. е. Я (ас, м, вбц) есть производная	в	силу’
уравнения (5)). Из (16) следует, что при 6ц = О
R (х, и, 0) =	, f(x, u) j = р[(х, и).	(19)
Чтобы подчеркнуть зависимость функции R (ас, гг, ебц)
от выбора символа (17), мы будем обозначать ее также
через /?о:
, д\ (х, ебц)	\
Rb (ас, гг, ебц) = (	—	, f{x, и)) .	(20)
Пусть функции v{t), y(t), г0<г<^, где v(t) — допу-
стимое управление, у (t) — непрерывная функция (не
обязательно принадлежащая области G), удовлетворяют
при некоторых в и 6ц системе
— = f(V v) I
dt	(21)
R(y,v,e6ц) = 0. J
В дальнейшем, говоря о решении v(t), y(t) этой си¬
стемы, мы всегда будем предполагать, что v (t) — допу¬
стимое управлегше, у (t) — непрерывная функция.
Если у (t) лежит достаточно близко от x(t) и
h(y(tо), ебц1) = 0, то y(t)£G при любом t, так как
d-t-/г (1/ (£), ебц ) = R(y(t),v(t), ебц) = О
и, следовательно,
h(y(t), ебц) == h(y(t0), ебц) = 0.
Управление u(t) и траектория x(t) удовлетворяют
системе (21) при 6ц = 0.

304
ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
Ниже мы опишем способ, позволяющий по заданной
начальной точке вида
«/(0) = as(0) + e6ase + o(e),	(22)
стандартным образом строить решение v (t), у (£), 0 < t < tly
системы (21), имеющее вид
v(t) = u (t)	+ ебu(t) -f- о (е),	(23)
y(t) = x {t)	+ гдх (t) -f о (е),	(24)
где бгг (t) — кусочно-непрерывная, кусочно-гладкая функ¬
ция, дх (t) — непрерывная функция.
Как уже отмечалось выше, если начальное значение (22)
удовлетворяет уравнению h(y(б), ебц) = 0, то вся тра¬
ектория у (t), 0 < t < tv принадлежит замкнутой области G.
Те участки траектории, которые не принадлежат объ¬
единению окрестностей	входящих	в	определение
функции h(y, ебц), лежат на границе g (х) — 0; если же
у (t) £ то у (t) принадлежит открытому ядру области G.
Следует в	заключение	отметить, что	формулой	(21)
определяется не одна система, а целое множество систем,
зависящих от выбора символа b (см. (17)).
Построение решения системы (21)
по начальному значению вида (22)
Отрезок t0<^t^tx подразделим точками
^0 = ^0 ^ ^1 ^	^	^/i	^	^к+1	==	G’
на частичные отрезки ti<^cti+1, i = 0,	1,	..., kf
достаточно малой длины. Точки xt выберем так, чтобы
среди них содержались все точки разрыва управления
и его производной. «Достаточная малость» длин частичных
отрезков характеризуется требованием выполнимости всех
описанных ниже построений. Будет непосредственно видно,
что, в силу регулярности траектории x(t), такой выбор
точек деления (естественно, неоднозначный) возможен.
Допустим, что решение v(t), у (t) системы (21), пред¬
ставимое в виде (23), (24) и удовлетворяющее началь¬
ному условию (22), уже построено на отрезке 0<£<тг
Продолжим это решение, сохранив непрерывность тра¬

§33]
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22
305
ектории у (I) и выраженные в равенствах (23), (24)
свойства, до точки Ti+1 включительно.
Пусть дь(и), i = 1,	s	(s > 0), — функции (1) для
точки и(ti-f-0). В силу (19) и регулярности траектории
х (t) [векторы
djR(cc(Tj), u(t;-|-0), £б}х)	^i(w(t7-	+ 0))	dqs	(и (т7 + 0)).
ди	’	ди	’	' * * ’	ди
линейно независимы. Так как длина отрезка т4<£<т1+1
мала, то линейно независимы и векторы
дЯ (х (t), и (t)f ебр) dq1(u(t))	dqs	(и	(t))
ди	’ ди	ди
на полуинтервале т- <	Пусть,	например,
Ф 0.	(25)
дЯ
dq 1
dqs
ди1
diO- • '
дЯ
3<71
dqs
ди* + 1
3ks+1 '
dus + 1
Следовательно, вблизи системы значений и(Т| + 0),
x(xi), еб|х = 0 система уравнений
R (у, v, ебц) = aj (v, t) = ... = as (v, t) = 0,	(26)
где ai(v, t) = qi(v) — qi(u(t)), i=l s, однозначно
разрешима относительно 5+1 переменных v1, ..., Vs*1:
vl = г\г(у, v$*2, .. vr, ебц, t), г = 1, ...,5+1, (27)
где г)1, t = 1, ..., 5 + 1, — непрерывно дифференцируемые
функции своих аргументов.
Подставив в (27) вместо Vs*2, . . ., zf соответственно
us*2 (t), ..., иг (I), получим 5+1 функций $г (у, ебц, t),
i= 1, ..., 5 + 1. Определим теперь вектор-функцию
v(y, ебц, t) равенством
v(y, ебр, t) =
= (&(У. ебц, г), ..., +,+1 (у, ебр, t), u^-(t) ur (t)).
(28)
Подставим, наконец, в уравнение
°)
вместо v функцию (28). Взяв решение полученного
таким образом дифференциального уравнения на
20 л. С. Понтрягип

>,00 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. Г>
отрезке ti < t < xi+1 с уже имеющимся начальным значением
//(т.), мы получим желаемое продолжение решения y(t).
Продолжением управления v(t) на полуинтервал
И < t < ti+1 служит функция
v(t) = v(y(t), ебц., *),	т4<*<т1+1,	(29)
которая получается подстановкой в (28) вместо 1/ про-
должения y(t), TL<^<Ti+1.
Свойства, выраженные в равенствах (23), (24), прове¬
ряются для полученных нами продолжений непосред¬
ственно. Допустимость управления (29) следует из ра¬
венств (26). В самом деле, для любого i= 1, ..., s
<Ji (» (t), t) = q. (v (t)) - qt (в (t)) = 0,
т. e.
?i (V (0) = ?i (M (*)) <0, ^ < f < ti+1.
Замечание. Описанная здесь конструкция определяет
решение системы (21) по заданному начальному значению
(22)	не однозначно, так как выбор точек деления т{,
i= 1, . . ., /с, а также выбор 5+1 переменных г+ относи¬
тельно которых разрешается система (26), не однозначен.
Легко, однако, видеть, что эту неоднозначность можно
устранить, зафиксировав для заданного управления и (t)
и регулярной траектории x(t), £0<£< + как точки
деления т., так и те 5+1 переменных (для каждого
отрезка tL<^<ri+1), относительно которых разрешается
система (26). После этого решение v (t), у (t) системы (21)
можно уже строить стандартным образом по начальному
значению (22). Во всех дальнейших построениях этого
параграфа, в которых применяется описанная здесь кон¬
струкция, упомянутая стандартизация будет предпола¬
гаться выполненной.
Уравнение в вариациях для системы (21)
Пусть v(t), y(t), 0<	—	решение системы (21),
построенное при помощи указанной выше конструкции
и удовлетворяющее начальному значению (22). Мы докажем
сейчас, что главная часть приращения y(t) — x(t) или,

§ 33]
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22
307
что то же самое, вектор-функция бx(t), 0<£< + одно¬
значно определяется главной частью начального смеще¬
ния (т. е. вектором 6xq) и удовлетворяет некоторому
линейному дифференциальному уравнению (см. уравне¬
ние (35)) с начальным значением 6xQ.
Для этого докажем прежде всего существование такой
кусочно-непрерывной, кусочно-гладкой вектор-функции
определенной на всем отрезке t0 < t < t± и зависящей
только от u(t), x(t) (и, следовательно, не зависящей
от вида функции i?), что главная (по е) часть бu(t)
разности v(t) — u(t) удовлетворяет на отрезке 0<^<^
уравнению
Тот факт, что Л (£), £0<£< + не зависит не только от
v(t)f но и от /?, играет в дальнейшем важную роль.
Для доказательства существования такой функции
предположим, что она уже построена на отрезке £0<£<т-,
г>0, и определим ее на полуинтервале ti<^<ti+1.
Точки т+ i=l, ..., /с, выбраны, как и выше.
Пусть на полуинтервале ti<£<Ti+1 система (26)
разрешалась, например, относительно первых 5+1 пере¬
менных v1, ..., vs+1. Тогда для каждого / = 0,1, . .., п
на этом полуинтервале определим 5+1 непрерывных
и гладких функций V (£),	(3	=	1,	...,	s, как реше¬
ние линейной неоднородной системы
где q1(u)J . .., qs (и) — функции (1) для точки ^(+ + 0).
(Индекс а в уравнениях (31) пробегает 5+1 значений,
соответствующих номерам переменных va, относительно
Л(<) = (^('>	>•"	<>)>■
[
df (ag (0, и (t))	д др (х (t),	и (t))
ди	“Г	\	/	qu
]вв(0 = 0. (30)
20’

308 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
которых разрешается система (26) на полуинтервале
х-ь < £<ti+1; в рассматриваемом случае а= 1, . .., s,+ 1.)
Система (31) разрешима, так как ее определитель
совпадает с определителем (25) при ебц = 0.
Вектор-функция (A. . ., Кп (*)), т{<^<т{+1> и яв¬
ляется желаемым продолжением.
Независимость функции Л (t) от функции R следует
из независимости матрицы коэффициентов и свободных
членов систем (31), / = 0, 1, ..., п, от R.
Докажем теперь формулу (30)’ для полуинтервала
т4<«<т4+1, е<т4.
Функция (23) имеет на полуинтервале t.<2<Ti+i
вид
v (t) = и (t) + еби (t) + о (е),
где
б и (t) = (б и1 (t), ..., бгг8+1 (0, 0, ..., 0),	(32)
так как
Vs+2 (t) = us+2 (£), . . ., vr (t) = ur (t).
Следовательно, умножая равенства (31) на биа и сум¬
мируя получающиеся соотношения по а = 1, 2, . .	5+1,
получим:
Определив вектор-функции L$(t) равенствами
!*(*) = $(*)> ••■.$(*)). P = l. •••>*>
перепишем равенства (33) в виде
(ш-+■Л<0 %■+ 2	(') 5)«“(') -1о-	<34>
Р=1
В силу (26) функция	v(t) = u (t) + ебгг (t) + о (е) удовле¬
творяет равенствам	(а =	1, ..	s):
ffa (и (0» 0 = Оа (И (0	+ ебгг (*) + о (е), £) =
дсг_, (к (г), t)	\
= Oa(u(t),t) + e( ^	,	6и(г))	+	о(е)	=	0.

§ 33]	ДОКАЗАТЕЛЬСТВО	ТЕОРЕМЫ 22	309
Но мы имеем:
Ста (и (*), t) = <7а (и [t)) — qa (и (t)) = 0,
dgg (» (t), Q _ дда (it (0)
0У	дм.	’
следовательно,
fdqa(u(t))	л
[-ЧГс ’ в»(0^1 = 0, 0=1, ..
ы соотношение (34) сводится к равенству
f—'+A (f) 6в (f) = О, Tt<«<ti+1,
\du r v> du
которое и является доказываемым равенством (30).
Подставив выражения (23), (24) в систему (21) и при¬
равняв члены при е, получим:
d {Ьх) = df(x(t),u(t)) Ьх + а/(х(0,«(0) бМ)
CLZ	ОЭО	OU
др (а? (0, и (t)) ^ dpjxjt), ujt))
дос	ди
дБ. jxjt), u(t), 0)	q
‘	<9(X
Умножив, далее, второе уравнение на A(t) и сложив его
с первым, получим, если учесть равенство (30), следую¬
щее соотношение:
=	“w> +АМ	|,)г)&*+
+ А (г) dR {Х {t)'d“{t)' 0) 6|Х.	(35)
Полученное линейное неоднородное уравнение относи¬
тельно бx(t) мы назовем уравнением в вариациях для
системы (21). Оно зависит только от самой системы (21),
и, следовательно, главная часть приращения бx(t) тра¬
ектории у (t) однозначно определяется начальным значе¬
нием 8xq и значением параметра бр.
По аналогии со сказанным в гл. 2 (стр. 95) мы бу¬
дем говорить, что векторы бx(t) получаются переносом
вектора бас(0) = басе, заданного в точке ас (6), вдоль

310 ПРОЦЕССЫ ПРИ ОГГАПИЧЕППЫХ КООРДИНАТАХ [ГЛ. 6
траектории х (t), и введем для операции переноса, завися¬
щей от параметра б(ы, обозначение
bx(t) = Pt^(b[i) Ьхв.
Следующие формулы очевидны:
Ptf 0 (6ц)	Ьх = А, т	(6ц) Рх,	8 (6ц) Ьх,	t > х > 0,
pt, 9 (убц)	ybx = уЛ, 0 (6ц)	Ьх,
>	(36)
Л, 0 (вцх + 6ц2) (6о+ + Ьх2) = Л, 0 (6ц2) 6»! +
+ А, 0 (бц2) Ьх2.
Обозначим через rP(x(t)) касательную плоскость
границы g(x) = 0 в точке *x(t). Если x(t) не принад¬
лежит объединению окрестностей 0^., участвующих в
определении символа (17), то, как уже отмечалось,
g (х (t) + sbx (t) + о (е)) = О
и, следовательно,
>6ж(о) = о,	(37)
т. е. bx(t)£T (x(t)). В частности, всегда
Ьх (tx) £ 1 (х (П))*
При 6ц = 0 уравнение (35) превращается в однород¬
ное уравнение
* (Ьх) = (дГ (ж и(г)) + Л (t) д-р {х +ц (+. Ьх. (38)
Наряду с этим уравнением рассмотрим сопряженное с ним
уравнение
«за;

§ 3 3]	ДОКАЗАТЕЛЬСТВО	ТЕОРЕМЫ	22	3]	]
Во избежание недоразумений запишем уравнения
(38), (39) покоординатно в виде двух систем (n-f-l)-ro
порядка:
а=0
Если 6x(t),	г|э(£),	—произвольные непре¬
рывные решения уравнений (38), (39) соответственно, то
(г|)(0, бас (0) = const.	(40)
(ср. стр. 97).
Фундаментальную систему решений уравнения (38)
обозначим через
Фо(0. • • •> ФтгС).
а сопряженную с ней систему решений уравнения (39) —
через
ф°(£), . . ., фп(£)>
Имеем:
(?«> й(0) = в‘-
Решение бx(t), Ql<Ct<b2> Ч <	<	^2 < неоднородного
уравнения (35), удовлетворяющее начальному условию
п
бас (0,) = У1 фа(01)бжа(0]),
а=0
запишется в виде
баг (t) = pi} в1 (6|Л) баг (0j) =
71	t
= 2 С) (бж“ (0i) + \ (■$“ (т). л со Щ ¥)dx) • (41)
а=0	0г

312 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
0	„	dR (х (0, и (Л, 0)
Вычисление производной —-—■■/>...■v —
Нам понадобится явный вид этой производной, по¬
этому займемся здесь ее вычислением.
Имеем:
S
h(x, |л) = g (х + ц 2 aa(x)Na) =
а=1
= g (z° + |I 2 Яа(ас) TVa, • • • , ж” + [А 2 аа (<*) Nl),
а=1
а=1
где Ni = (Nii . .., Ni). Введем обозначения:
Г]г = Xх + \1 2 аа (х) A a, i = 0, . .., и, к] = (т)°, . .., rf).
а=1
Тогда
R (х, и, |х) = 2
а, (3=0
dg(H) дг\а
Зг|а дх$
/Р (х, и) =
а=0
г=1
Следовательно,
dp
+ 2
a, (3=0
Л dg (ж)
V. <5 sc
i= 1
s n
г=1
(a?)
dx
ju=0
, f(x,u)) =
i=l a,(3=0

§ 33]
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22
313
s
i= 1
s
Итак,
dR (х (t), и
dp
s
Из определения сложения символов (17) непосредственно
следует:
В гл. 2 был определен сначала класс варьированных
управлений—вариаций исходного управления u(t), а затем
по заданному управлению, начальному отклонению и дей¬
ствительному числу бt строилась варьированная траек¬
тория (см. § 13).
Теперь мы уже не сможем независимо от варьирован¬
ных траекторий определить класс варьированных управ¬
лений и потом при помощи этих последних строить
варьированные траектории, так как они, вообще говоря,
будут вылезать из замкнутой области G (поскольку
траектория x(t) лежит на границе области). Здесь при¬
ходится варьированные управления и соответствующие
варьированные траектории строить одновременно, шаг за
шагом, чтобы иметь возможность в каждый момент вре¬
мени предотвратить упомянутую опасность и не выпу¬
скать варьированную траекторию за пределы области G.
Это оказывается возможным благодаря регулярности
траекторирг.
В соответствии со сказанным мы будем nppi строгих
формулировках говорить теперь не о вариациях управле-
нртя или вариациях траектории в отдельности, а о вариа¬
циях решения u(t), x(t), £0</<£j, системы (21)
м- °))
дВ^ (ж, гг, 0)	dR^	(х, и, 0)
Вариации решения u(t), x(t)

314 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
Таким образом, мы построим класс Ф варьированных
решений u*(t), ас* (t) системы (21) — вариаций решения
u(t)y х (t)y t0 <£<^, системы (21) при бц = 0. Строго
говоря, каждый элемент (и* (t), х* (t)) множества Ф будет
являться не одним решением системы (21), а целым
семейством решений, зависящих от положительного беско¬
нечно малого параметра е. Тем не менее мы для удоб¬
ства часто будем говорить о варьированном решении
(u*(t), x*(t))£ Ф, а также о вариации гг*(£) управления
u(t) или вариации х* (t) траектории x(t)y составляющих
данное решение u*(t)y х* (t) системы (21).
Отметим здесь же, что множество Ф будет состоять
из варьированных решений не одной какой-нибудь кон¬
кретной системы (21), а из варьированных решений
всех систем вида (21), зависящих от выбора функции R
(т. е. символа (17)). Однако каждый данный элемент
(w*(£), х*(£))£Ф будет являться семейством решений
одной и той же системы вида (21).
Варьированное управление строилось в гл. 2 зада¬
нием его параметров (см. определение символа а на
стр. 105). Точно так же и теперь каждое варьированное
решение н*(^), х* (t) системы (21) (точнее, семейство
варьированных решений) будет строиться при помощи
задания параметров этого решения. Поэтому мы определим
сначала параметры варьированного решения, а затем
опишем способ построения самого решения по заданным
параметрам.
Эти параметры естественно разбить на две группы:
параметры строящегося управления и* (t) и параметры
строящейся траектории x*(t).
Обозначения х1У . . ., т-,;	б£1? . . ., б/3, . . ., 1к\
viy	т,	Ы будут иметь здесь тот же смысл, что
и в § 13. Так как управление и (t) кусочно-непрерывно,
то х1У ..., т;. — точки непрерывности управления u(t).
Точку т мы всюду в дальнейшем будем считать совпа¬
дающей с концевой точкой tx отрезка £0<7<£1 (это воз¬
можно, так как управленле u(t) непрерывно в точке tj.
Далее, в качестве vv ...yvL мы разрешим брать только
такие точки области управления U, что для любого
i— 1, . . ., к точка х{х{) траектории x(t) регулярна отно¬
сительно точки vv Совокупность параметров т;, бt{y viy бty

§ 3d]
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22
315
входящих в определение варьированного управления и* (t)y
мы будем, как и в гл. 2, обозначать символом а. Однако
варьированное управление гг*(£), соответствующее сим¬
волу а, мы определим не так, как в гл. 2 (см. стр. 99),
а несколько иначе, проводя его построение одновременно
с построением соответствующей варьированной траектории
x*(t). Это объясняется тем, что при определении варьи¬
рованного управления по способу, принятому в гл. 2,
соответствующая варьированная траектория может на
отрезках 1Ь выйти за пределы области G.
В качестве параметров строящейся варьированной
траектории х* (t) мы примем величины, входящие в сим¬
вол Ъ (см. (17)).
Переходим к построению решения и* (t), х* (t) системы
(21), определяемого символами а, Ь. Это решение будет
определено на отрезке t0	+ Чтобы подчеркнуть
зависимость решения и* (t), х* (t) от выбора символов а,
6, мы будем обозначать функции п*, ас*, когда по¬
требуется, соответственно через
Начальное значение ас*(£0) траектории ас*(£) определим
формулой
Из (46) следует, что при достаточно малом е имеют
место соотношения
(44)
(45)
х* (t0) = х (t0) -f ебас0,
(46)
где
6ж0= -8ц 2 aa(x(t0))Na.
(47)
ai М) — (ЯС* (*„)), t Ь • • • > s> 0^)
причем (при достаточно малом е)
ai(x*(t0)) = ai(x(t0)) = 0 при &=£*(*„),
ai(x*(t0))=ai(x(t0))=l при ^ = x(t0).

316 ПРОЦЕССЫ IIPII ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
Из (47) и (48) мы получаем:
!г (ж* (t0), ебц.) = g (ж (t0) + е6ж0 + еб|л 2 «а («* (<<,)) -^а) =
= g(*(t0) = 0.	(49)
Из способа построения траектории (45) будет непосредст¬
венно следовать, что при е—>0 траектория ас* (t) равно¬
мерно по t стремится к x(t) на отрезке £0 <£<£]_. По¬
этому из (49) следует, что х* (t) целиком лежит в замк¬
нутой области G (см. стр. 303).
Как и в гл. 2 (ср. стр. 99), мы записываем полуин¬
тервал /. неравенствами
Ti + Eh < t < Ti + e (h + ^i)*
По заданному начальному значению (46) построим теперь
на отрезке £0< £< т^-f-(т. е. от начальной точки t0 до
левого конца полуинтервала /-,) при помощи конструкции,
описанной на стр. 304—306, решение системы (21) вида
(23), (24) и положим функции (44), (45) равными этому
решению на отрезке £0<£<т1 + е/1. Таким образом,
u* (t) — и (t) -f- гба (t) + о (е),
х* (t) = x(t)-\- ебх (t) + о (е), t0 < t < хг + dv
Следовательно, при t0 < t <	+ г1г функция бх (t)
является решением уравнения в вариациях (35):
бx(t) = PiiiQ(6\i) бx(t0).
Мы продолжим теперь решение и* (t), x*(t) с сохра¬
нением непрерывности функции х* (t) на полуинтервал 1г
(предполагая, что он не является пустым, т. е. б^ Ф 0)
при помощи следующей конструкции.
Точка х (rj по условию регулярна относительно vv
Обозначим через ^(и), ..., qs(v), s>0, функции (1) для
точки vv Тогда мы имеем (обозначая через R функцию
11^, где Ь — символ, входящий в определение строящегося
варьированного решения):
R (ж (г,), vv 0) = q1 (и,) = ... = cja (d,) = 0,

ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22
317
и система
R (у, v, ебц) =	(v) = ... = qs (v) = 0	(50)
разрешима относительно некоторых 5+1 координат век¬
тора v вблизи значений х (tj, vv ебц = 0, например,
относительно первых 5 + 1 координат:
vl = Ф1	(у,	+2, . . ., vr, ебц),
7 = 1,	. . . ,	5 + 1, 1 < 5 + 1 < 7%
где функции -д1, i= 1,	5+1, непрерывно дифферен¬
цируемы по всем аргументам. Очевидно, аргумент у
в функциях- '0,г может принимать значение х*(х1), так
как	при	е—>0 полуинтервал 1г стягивается	к	точке	хг и
X*	(Tj_ + е/-|)	= яс (т*]	+	~\~ ебзс (И. + e/j) + о (е)	—> х	(х^).
Подставив функции $+ 7 = 1, ...,5+1, в первое из
уравнений системы (21), получим:
=f(y, V1 {у, Vя*2, Vr, ебц,), .. ., yr) =
= /, (у, Vs*2, vr, ебц).	(51)
Подставим теперь в правую часть вместо параметров
us+2, . . ., vr соответствующие координаты v\+2, ..., v\
точки и j и возьмем решение полученного дифференци¬
ального уравнения с начальным значением х* (i:1 + &11)
на полуинтервале 1Г Это решение х* (t) и будет слу¬
жить на полуинтервале 1г продолжением решения х* (t),
t0<t +!	+ в/j.
Продолжение управления и* (t), t0 < t < х± + е/1? на
полуинтервал 1г зададим формулой
п* (t) = (й1 (ас* (t), v[+2, ...,t7[, ебц), ...
..., ■б'5'"1 (ас* (t), у®+2, • • •, v\, ебц), yf2, ..., v[), 1£ /г
Допустимость управления гг*(£), t £ 1г и равенство
Л (ас* (£), гг* (Z), ебц) = 0, t £ /2,
очевидны. Из построения, кроме того, следует, что
гг* (t) — непрерывная на полуинтервале 1Х функция, равно¬
мерно стремящаяся на этом полуинтервале к значению

3j8	ПРОЦЕССЫ IIPM ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. С
при в —> 0. Если = т2 = . . . = Xj < xj+1, то мы проде¬
лаем аналогичное построение на полуинтервалах /2, . . ., / •
(взяв вместо vx соответственно точки v2, .. ., +•) и опре¬
делим таким образом решение гг*(£), х* (I) на отрезке
Затем функции u*(t),x*(t) вновь продолжаются
на отрезок т/ < t < xj+1 + е/у+1	(т. е. вплоть до левого
конца полуинтервала Ij+1) при помощи конструкции,
изложенной на стр. 304—306 (с уже имеющимся началь¬
ным значением ж* (+•)) и т. д. вплоть до точки tv
Таким образом, если б£<0, то семейство варьиро¬
ванных решений u*(t), ас* (t), f0< t< t1 -f еб/, системы (21)
определено.
Пусть dt > 0. Решение и* (0, ос* (t) уже построено
на отрезке	Легко видеть, что точка ас* (£х)
регулярна относительно точки гг* (^) = гг* (t2 — 0). В самом
деле, первое условие регулярности следует из того, что
для значений t, близких к tv имеем:
R (ас* (t), гг* (£), ебц) = (ас* (£), гг* (£)) = 0,
ибо при этих значениях t точка ас*(£) лежит на границе
области G:
g (аз* (<)) = 0.
Второе и третье условия регулярности следуют из регу¬
лярности точки ас (£j) относительно и (^) = гг (£2 — 0)
и из соотношений ас* (^) —> ас (^), гг* (£2) —> гг (£2) прие—>0.
Следовательно, конструкция, при помощи которой мы
определили решение гг* (£), ас* (t) на полуинтервалах /{,
позволяет нам непрерывно продолжить функции гг* (t),
ас* (£) за вплоть до точки ^+еб^.
Таким образом, по заданным параметрам а, Ь мы
построили семейство варьированных решений системы (21).
Равенство (51), очевидно, выполняется и при £< t^edt.
Отметим, что траектория (45) не определяется пара¬
метрами а, Ъ однозначно. В самом деле, она зависит
от выбора переменных Vх, относительно которых разре¬
шается система уравнений (50) во время построения
варьированного решения на полуинтервалах IАнало¬
гичный произвол имеется при продолжении решения
на отрезок £<	+ еб£ в случае dt > 0. Этот произ¬

§ 33]
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22
319
вол легко устранить, зафиксировав для каждой точки u{t)
те переменные Vх, относительно которых резрешается
система (50) вблизи системы значений х(£), u(t), ебц = 0,
где Qi, . . ., gs, s > 0, — функции (1) для точки u(t).
(В случае, если t — точка разрыва управления u(t), то пе¬
ременные Vх, относительно которых разрешается система
(50), могут быть различными для точек и (t — 0) и и (t + 0).)
После принятых соглашений заданием символов а, Ь се-
мейство траекторий (48) однозначно определяется, так как
траектории этого семейства строятся на отрезках между
полуинтервалами 11 однозначно (см. замечание на стр. 306).
Построение конусов if*, /с*
Нас будет теперь, как и в гл. 2, интересовать откло¬
нение конца варьированной траектории (45) от точки х(^).
Совершенно так же, как это сделано в гл. 2 (стр. 100—
104), доказывается формула
х* (^гЬ ебг) = х (tj) + еДх* + о (е),	(52)
где вектор Дх* не зависит от е и определяется формулой
Дас* = Ptu ,0 (6ц) 6ас0 +/(х (<г), и (г3)) 6f +
k
+ У ЕыгДбМ-) [/(ас (ta), Va)—f(x(%a), u(ta))]6ta. (53)
a=l
Чтобы подчеркнуть зависимость вектора Дх* от выбора
символов а, Ьу мы будем (если нужно) обозначать этот
вектор символом Дх*
Из равенства (37), справедливого для близких к t±
значений t, следует, что
Дх*£Г(х(Ч)).	(54)
Пусть теперь а', Ъ' и а", Ь" — две пары символов,
определяющих варьирование управлений и траекторий,
а К' и %" — неотрицательные числа. Положим
а = %'а' + Я"а", b = A/b' + W.
Из свойств переноса (см. формулы (36)) и из того факта,
что в формулу (47) величина бц входит линейно,

320
процессы при ограниченных координатах
[ГЛ. 6
а в формулу (53) величины bx0, bt, 6ta входят линейно,
непосредственно вытекает, что
Д^а,Ь =	+ VAx£»t	(55)
Полученная формула показывает, что всевозможные
векторы вида Аха отложенные в пространстве X
от точки зс(^), образуют выпуклый конус с вер¬
шиной в точке ас(^), который мы будем обозначать
через Я*. Из (54) следует, кроме того, что конус Я*
лежит в касательной плоскости Т (х (^)) границы
g(x) = 0, проведенной в точке x(tx).
Конус Я* мы используем при доказательстве усло¬
вий скачка (§ 36). Для доказательства же теоремы 22
нам потребуется другой выпуклый конус /?*, содержа¬
щийся в Я*. Именно, будем рассматривать только такие
символы Ь, для которых ни одна из точек £• не совпа¬
дает с начальной точкой x(t0) траектории x(t). В этом
случае из формулы (47) следует, что 6х0 = 0, т. е. что
варьированная траектория х* (t) начинается в точке x(t0).
Если Ъ' и 6" — символы указанного вида (т. е. не содер¬
жащие точки x(t0) среди точек gj, а X', А," — неотрица¬
тельные числа, то А/Б' -f- А/'Б" — также символ того же
вида. Поэтому, откладывая от точки х (£х) всевозможные
векторы вида Дх* где Б —символы, не содержащие
точки x(t0) среди точек мы получаем выпуклый
конус с вершиной в точке x{t^), который будем обозна¬
чать через к*.
Так как A?* CZ Я* CZ Т (х (^)), то конусы к*, Я*
не более чем п-мерны. Поэтому внутренностью этих
конусов мы будем называть множество их внутренних
точек по отношению к плоскости Т (х (^)), а внутрен¬
ними лучами —лучи с вершиной в ас(^), принадлежащие
этим конусам и содержащие их внутренние точки.
§ 34. Доказательство теоремы 22 (окончание)
Для выполнимости всех построений предыдущего
параграфа достаточно потребовать, чтобы траектория
x(t), t0 <£<£15 лежащая на границе области G, была
регулярной.

§ 34] ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22 (ОКОНЧАНИЕ) 321
Предположим теперь дополнительно, что u(t) и х (t)
6п тим а льны.
Обозначим через L луч, выходящий из точки х (^)
и направленный вдоль отрицательной полуоси х°. Очевидно,
что LczT (xitj)).
Лемма I. Луч L не является внутренним лучом
конуса к*.
Доказательство. Обозначим через я проекцию
(например, ортогональную) пространства X на плоскость
(ас (^i)). Пусть ас* (£) —варьированная траектория, соот¬
ветствующая символам а, Ь, где Б — символ, не содер¬
жащий точки x(t0) среди точек £. (так что траектория
ас* (£) начинается в точке ас(£0)). Так как
ас* (гг + ебt) = ас (£х) + еДас* + о (е),
причем х (Ч) 6 Т (ас (£2)), Дас* £ Г (ас (^)), то
я (ас* (^ + еб£)) = ас (^) + еДас* + о (е).
Следовательно, главные (линейные по е) части векторов
я (ас* (£х+ ебt)) — ас (£х) и ас* (tx -(- еб£) — ас (£х)
совпадают и потому заполняют в Т (ас (£х)) один и тот же
конус /£*.
Допустим теперь, что луч L является внутренним
лучом конуса /£*. Тогда, в силу леммы 3 гл. 2, суще¬
ствуют такое е > 0 (которое можно предполагать как
угодно малым) и такие символы о, Ь, что им соответ¬
ствует варьированная траектория ас* (t), начинающаяся
в точке x(tQ) и кончающаяся в такой точке ас* (Ч + еб£),
что я (ас* (tx + гЫ)) — отличная от ас(^) точка луча L.
Отображение я, рассматриваемое на границе g (ас) = О,
является, вблизи точки ас (^), взаимно однозначным. Сле¬
довательно, если 1/— достаточно близкая к ас(^) точка
границы g (ас) = 0, то из я (у) £ L вытекает, что я (у) = у.
Так как при достаточно малом е точка ас* (^х + еб^)
(принадлежащая границе g (ас) = 0) как угодно близка
к точке ас(£х), то из соотношения я (ас* (t± + еб£)) £ L
вытекает, что ас* (£х +еб£) = я (ас* (£х + еб£)), и потому
ас* (£i -j- гЫ) есть отличная от ас (^) точка луча L. Однако
21 Л. С. Понтрягин

322 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. б
это противоречит предположению об оптимальности реше¬
ния u(t), x(t).
Таким образом, лемма I доказана.
Лемма II. Существует такое непрерывное решение
'Ф(0 = ('М<). 'МО. • • •> 'Фп(О).	/0<г<гл,	(56)
уравнения
__  С df (х (t), и (t)) . д/ ^ \ др (х (t), и (t)) \	(37)
dt	V дх	дх	'	'
-что <? каждой точке непрерывности оптимального управ¬
ления и (t) выполняется условие максимума
Ж (ф (*)» х (*)> w (0) = т (Ф (*)> я (0)»	(58)
гс ричем
т(^(^), ® (*,)) = О,	(59)
ц выполнены следующие условия:
а) Фо (0 ~ const < 0;
б) вектор ф(£0) коллинеарен вектору
grad g (ас (*0));
в) кусочно-гладкая скалярная функция X(t) =
= — (ф (£), Л (£)) такова, что о точках ее дифференци¬
руемости вектор
grad g (35(0)
направлен внутрь области G или обрагцается в нуль.
Доказательство. На основании леммы I через вер¬
шину х (^) конуса fe* С2Т (х (^)) можно провести (72 — 1)-
мерную плоскость Г, лежащую в 71 (ас (У) и отделяющую
конус fe* от луча L. Обозначим через % = (%0, Хп • • •> Хп)
лежащий в плоскости Т (х (^)) вектор, ортогональный
к плоскости Г и направленный таким образом, что луч L
лежит в том замкнутом полупространстве, определяемом
плоскостью Г, в которое направлен вектор %, а конус
fe* — в другом замкнутом полупространстве. Тогда %0<0
и для любого вектора Дас* £ fe* выполнено соотношение
(X, Дас*) < 0.
(60)

§ 34]	ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22	(ОКОНЧАНИЕ)	323
Далее, так	как	вектор % лежит в плоскости	T(x(t1)),
то векторы
X и gradg(*(^))	(61)
линейно независимы.
Определим искомую функцию ф(£) как решение урав¬
нения (57) с конечным значением
't(ii) = X-	(62)
Легко видеть, что равенство (58) выполняется. В самом
деле, пусть в некоторой точке непрерывности т2 упра¬
вления u(t) выполнено неравенство
'&€ (ф (Ы, Ж (tj), и (т,)) < т (ф (т,), х (Tj)),
т. е. существует такая точка х)г £ U, относительно кото¬
рой точка х(х^) регулярна, что
Ж (“Ф (Tj), X (Tj), t»x) > т (ф (т,), X (Tj), и (т,)).	(63)
Построим решение н* (£), х* (I), £0< £< tv системы (21),
взяв в качестве символа а символ {х1У vv dt1 = l, 8t = 0}
и в качестве Ъ символ, в котором s = 0 (т. е. £i,ai(ac),
отсутствуют) и 6р = 0. Из (53) следует, что в этом случае
Ax* = PhiXl(0)(f{x(x1), о1)-/(ав(т,), в(т,))).
Поэтому формулы (40), (63) дают
{%, Ах*) = (ф (*,), Р, ь (0) (,fix (т,), о,) -f(x (х,), и (т,))) =
= (Ф (И). /О* (п)> vi) - f(x (И). 11 Oi))) > 0.
что противоречит неравенству (60).
Доказательство равенства (59) и условия а) совпа¬
дает с доказательством соответствующих формул (12) гл. 2.
Условие б) следует из независимости векторов (61)
и равенства (62) (см. замечание 4 к теореме 22).
Докажем, наконец, условие в).
Пусть u*(t), x*(t), t0 t <; tly — решение системы (21),
соответствующее пустому символу а (т. е. символу, для
которого к = 0 и 8t = 0) и некоторому символу Ь, не со¬
держащему точки x(tQ) в качестве одной из точек £•.
21 *

324	ЕССЫ	ПРИ	ОГРАНИЧЕННЫХ КООРДИНАТАХ	[1'Л. 6
Из формул (53), (41) следует, что в этом случае
п	ti
Ах* = Ph, ,0 (бр) 0 = бр 2 фа (О 5 (Фа (0. л (*)) -S-dt-
а=0	/0
Формулы (62), (60) дают
п	1г
(х, Аж*) = бр 2 (ф (*i). Фа (tx) [ (фа (*). А (t))	A j =
а=0 4	t0
h	ti
= ¥ ^ (Ф(*)> А(*))-§^-Л = -бр J Х(/)-^Л<0,
*0	to
так как K(t)= — (ф(£), A(f)) и, в силу двойственности
систем функций (ф1; ..., ф„), (ф1, ..., ф"), имеем
П
2 (Ф(^)> Фа(^))Ф“(0=Ф(0-
а=0
Подставив в последнее неравенство выражение для -Щ-
из (42) и учитывая, что 6ц >0, получим:
N«)]dt>0.
t0	а=1
Интегрируя по частям и принимая во внимание равен¬
ства ai(x(t0)) = ai(x(t1)) = 0, i=l, .. ., s, получим:
\ чг 2 а“ (х W) > N-)dt < °-	(64)
to	а=1
Так как точки £. можно выбирать на траектории х (t)
произвольно (лишь бы они не совпадали с ее концами)
и так как, далее, окрестности 0^ сколь угодно малы,
функции а{{х(1)) неотрицательны и Ni — внешние век¬
торы (по отношению к области G), то из неравенства (64)
следует неравенство

§ 34] ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22 (ОКОНЧАНИЕ) 325
Это неравенство и выражает условие в), так как область G
задается вблизи границы неравенством g (х) < 0 и, сле¬
довательно, grad g (х (t)) — внешняя нормаль к границе
g (ас) = 0.
Для завершения доказательства теоремы 22
надо, во-первых, доказать, что скалярная функция
X(t)= — (ф(£), Л(£)) удовлетворяет соотношению
d&2(q>(t),x(t),u(t)) WA 0р(а>(*),и(О) , V v /-v^a(M(0)
a=l
и, во-вторых, доказать равенство
&е (ф (О» х (0> u(t — 0)) = m (ф (*), X (t))
в точках разрыва управления и (t) и постоянство функ¬
ции (t) = <Ж (ф {t)> % (t), и (t)) на отрезке ^0<£< +
В точках разрыва управления, согласно принятому усло¬
вию, полагаем
30 (t) = 3& (Ф (*).- * (0> м (t - 0)).
Для доказательства равенства (65) заметим, что коор¬
динаты вектора А (t) = (А,0 (£), . . ., %п (t)) удовлетворяют
уравнениям
dp	u{t))	.	у /А dP(x(t),u(t)) v	7У m
 ^+ ^ (0	^— + 2j	и>
/ = 0, 1, . . ., п, а = 1, . . ., 5 + 1.
Умножая это уравнение на ф;(£) и складывая по¬
лученные соотношения при всех / = 0, 1, . . ., п, получим
5 + 1 равенств (а=1, ...,5+1)
)(t), x(t), u(t))	«	dp {.г (I), и (t)) v	+
 ш =	—	+	2jvp
0=1
из которых функция X(t) однозначно определяется.
С другой стороны,
Зв (ф (t), х (t), и (t)) = яг (ф (0, х (0)

32G ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. G
и, по правилу множителей Лагранжа,
д&е{?\?(р, x(t) u(t)) _
ди
-1* (<) '"■ <*<;>' “(,)) + 2 Vt (0	;
а=1
следовательно, 'k(t) = rk* (t).
Докажем теперь равенство
(■ф (t), х (t), и (t)) = т (ф (0. X (t))	(66)
в точках разрыва управления u(t).
Пусть в точке разрыва т управления и (t) выполнено
соотношение
^(т) = Р%;(яр(т), ж(т), и(т —0)) ф т(яр(т), х(х)).
Тогда найдется такая точка £ со (зс (т)), что
<ёв (яр (т), X (т), и (т — 0)) < ёв (яр (т), X (т), и±).	(67)
Из условия м2£ со (х (т)) непосредственно следует
(см. стр. 294) существование такой непрерывной функции
u*(t), определенной для значений t, близких к т, что
и* (t) £ со (х (t)), и* (г) = uv Учитывая, что функция (ёв (яр (t),
x(t),u*(t)) непрерывна по t, а управление u{t) непре¬
рывно в точке т слева, мы для любой достаточно близ¬
кой к х точки t < х из неравенства (67) получим нера¬
венство
ёв (яр (*), х(t), и(*)) < ёв (яр(0> я00»	(0)-
Следовательно, для рассматриваемых t получаем
неравенство
ёв (яр (0, Ж (0, и (*)) < ёв (яр (*)» ж (0»	(0)	<	т	(яр (0* ж (0)>
противоречащее равенству (58). Равенство (66) доказано.
Аналогично доказывается и равенство
ёв (яр (t), х (t), u(t + 0)) = m (яр (t), х (t)).	(68)
Из равенств (66), (68) следует непрерывность функ¬
ции ёв (t) = т (яр (t), х (t)). Следовательно,, для доказа¬

§ 34]	ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 22 (ОКОНЧАНИЕ) 327
тельства постоянства функции <§$ (t) на отрезке
остается доказать, что она постоянна на каждом интер¬
вале одновременной дифференцируемости функций ф (t),
X (t), и (t).
Имеем (см. формулы (9), (10)):
d ы/л GdФ дЖ\ , fdffl dx\ . ГдШ du\
= ((	+ к m) ’ f)+(й"^’ f) +
a=l
-^g./)+r^.-§)+(s
a=l
s
= K (*) £ P (* (0. M (0) + 2 V“ (f) Й (0) =
a=l
s
= 2 va(0^?a («(«))•
a=l
Докажем, что в рассматриваемых точках t выполнены
dq (и (t))
соотношения —^	= 0, a = 1, .. ., s, и, следовательно,
dmt) _ VI /Л (“ (9) _ п
~ЧГ~ 2л М9 д -и-
а=1
Допустим противное; пусть, например, в точке т
fl?gl_(u_(T)) ^ a	(69)
Мы имеем:
?1(«(t))= ... =?|(ц(т)) = 0,
где дДи). ..., qs (и) — функции (1) для точки гг(т). Сле-
довательно, функция q± (и (t)) меняет знак в точке т, что,
однако, противоречит предположению о допустимости

328 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
управления гг (г), так как вблизи точки гг(т) множество U
задается неравенствами
^(гг)<0,	?8(в)<0,
и потому из допустимости управления u(t) следует, что
для любых достаточно близких к т значений t
Итак, теорема 22 полностью доказана.
§ 35. Некоторые обобщения
В этом параграфе мы приведем несколько очевидных
обобщений теоремы 22. Мы ограничимся формулировкой
результатов, так как их доказательства лишь незначи¬
тельно отличаются от доказательства теоремы 22.
При доказательстве теоремы 22 решающую роль играла
зависимость между векторами х, гг, заданная уравнением
р (х, гг) = 0.
Вид функции
р(ж, =	f(x, it)J
был использован лишь при доказательстве условий б) — в)
теоремы 22. Беглый анализ доказательства убеждает
нас в справедливости нижеследующей теоремы 23.
Пусть заданы т непрерывно дифференцируемых функ¬
ций Pi(x, гг), г = 1, . . ., ту не зависящих от координаты х°.
Регулярная относительно точки u0£U точка х, удовле¬
творяющая системе
Pi (*. ио) = • • • = Рш (х> ио) = °>
определяется так же, как и прежде, только в данном
случае вместо независимости векторов (7) надо потребо¬
вать независимость векторов
др1(х, и0)	дрт(х, ц0) ддх (и0)	dqs	(и0)
ди ’ * * ' ’ ди ’	ди	’ * * * ’ ди
Теорема 23. Пусть u(t), t0*Ct<^tv —оптимальное
управление a, x(t) — соответствующая регулярная

§3 5]	НЕКОТОРЫЕ ОБОБЩЕНИЯ	329
оптимальная траектория уравнения (5), удовлетворяющая
на отрезке	системе	уравнений:
р1 {ос (<), и (<)) = . . . = рт {х (г), и («)) = 0.	(70)
Тогда существует такая ненулевая непрерывная вектор-,
функция ф(£) = (ф0(г)> ••мФп(О)» t0<Ct<Ctv что на отрезке
t0<t^tx функции u(t), x(t), ф(0 удовлетворяют системе
уравнений
dx _	__	(ф,	X, и)
dt -]	U)-
dф _	^(ф,	X,	и)	Yv	дра(х*
dt ~~	дх	а	дх
а=1
и выполняется условие максимума
x{t), и(0)= m(q(t), x(t)),
причем
«(0) =
кусочно-гладкие функции Xt (t), 2 = 1, . .., m, t0^t<Ctv
определяются из условия максимума как множители
Лагранжа в формуле
т _	.	s	.	.	.
д&в (ф,	ху и) ^ л	Ра (х>	и) |	^	dqa (и)
ш =2j ^	ой	г	2j	Va_^r“;
а=1	а=1
кроме того,
ф0 = const <0.
К сформулированной теореме легко сводится решение
оптимальной задачи, в которой вместо равенств (70)
фигурируют неравенства
Р]_(х, 22) < 0, ..., рш(х, 22) <0.	(71)
В самом деле, введя m дополнительных скалярных
управляющих параметров щ, 2=1, ..., m, удовлетворяю¬
щих неравенствам щ > 0, и рассматривая вместо нера¬
венств (71) равенства
рх{х, и) + »!=... = ?т(ас, и) + уТ11 = О,
мы придем к условиям теоремы 23,

330 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
Наконец, отметим, что теорема 22 непосредственно
обобщается на тот случай, когда область G задана вблизи
границы несколькими, например двумя, неравенствами
gi(*)<0, g2(ac)<0,
а регулярная оптимальная траектория лежит на (п — 2)-
мерном «ребре», заданном уравнениями
g± (х) = g 2 (&)= 0;
при этом, естественно, предполагается, что гиперповерх¬
ности
gi (*) = 0. g2 И = 0
находятся в общем положении вдоль траектории, т. е. что
(х) dg2 (х)
векторы ^	,	ду линеино независимы.
§ 36. Условие скачка
Оптимальная траектория, лежащая в замкнутой обла¬
сти G, частично может лежать в открытом ядре области G,
частично — на границе области. Для того чтобы одно¬
значно проследить такую траекторию, недостаточно прин¬
ципа максимума и теоремы 22. В самом деле, принцип
максимума дает полную систему необходимых условий,
которым удовлетворяет всякий участок оптимальной
траектории, целиком лежащий в открытом ядре области G,
а теорема 22 дает необходимые условия, которым удовле¬
творяют участки, целиком лежащие на границе области G.
Недостает еще условия сопряжения, которому
удовлетворяет всякая пара примыкающих друг к другу
участков оптимальной траектории, один из которых лежит
в открытом ядре области G, а другой —на ее границе.
Это условие мы называем условием скачка для
вектор-функции ф(/), которая в момент перехода от одного
участка к другому может терпеть разрыв (см. формулировку
теоремы 24).
Докажем прежде всего одну простую лемму, которая
нам понадобится ниже.
Лемма. Пусть x(t),	—траектория	урав¬
нения (5), лежащая в замкнутой области G и со ответ-

§ 36]
УСЛОВИЕ СКАЧКА
331
ствующая некоторому допустимому управлению, и пусть
х (t0) — единственная точка траектории, лежащая на гра¬
нице g (х) = 0 области G. Если вектор дх (t0) не касается
границы g (х) = 0 в точке x{tQ) и направлен внутрь обла¬
сти Gy то варьированная траектория x*(t)y £0<£<G>
с начальным значением х* (t0) = х (tQ) -j- гЬх (t0) целиком
лежит в открытом ядре области G.
Доказательство. Мы имеем:
х* (t) = x(t) + едх (t) + о (е), (dg	,	Ьх	(t0)j = а < 0.
Следовательно, при достаточно малых 8 > 0 величина
g(x*(t)) = g(x(t)) + B(^M, 6x(t)j+o(e), t0<t<tr,
отрицательна. В самом деле, для значений t > t0, близких
к tQy это следует из неравенств
g{x{t)) < 0, а < 0.
Для значений t, удаленных от tQy величина \g(x(t))\
больше величины
*(4fx(t)) > бх(0) + о(е)
и, кроме того, g(x(t))<0.
Пусть и (t)y t0 < t < tv — допустимое управление,
a x(t) — соответствующая траектория (не обязательно опти¬
мальная) уравнения (5), целиком лежащая в замкнутой
области G. Некоторые участки траектории могут лежать
на границе области G, некоторые — внутри области, т. е.
в открытом ядре области G.
Точку х (т) траектории, лежащую на границе области
G, назовем точкой стыка у если t0 < т < t1 и существует
такое о > 0, что хотя бы один из участков траектории
х (t) при х — а < t < х или при х < t < х + а лежит
в открытом ядре области G. В дальнейшем для определен¬
ности будем всегда считать, что внутри области G лежит
участок траектории при т — а < t < т. Время х назовем
моментом стыка.
Мы будем рассматривать траектории с конечным
числом точех£ стыка, не оговаривая этого особо.

332 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
Траекторию х (t), £0< t < tv целиком лежащую в замк¬
нутой области G, назовем регулярной, если регулярен
всякий ее участок, лежащий на границе g(x) = 0 обла¬
сти G.
Предположим, что и (t),	t0 < t < £3, — оптималь¬
ное управление, a x{t)y £0 < t < ^ — соответствующая
оптимальная регулярная траектория уравнения (5), лежа¬
щая целиком в области G. Пусть х (т) — точка стыка
траектории х (t), t0 < t < £г Обозначим через < Z < т2
максимальный интервал отрезка £0<£<G.> содержащий
единственный момент стыка т. Таким образом, участок
траектории х (t) при тх < t < т лежит в открытом ядре
области G; что же касается участка этой траектории при
т < t < т2, то он либо целиком лежит на границе g (х) = О,
либо также принадлежит открытому ядру области G, и
тогда х (т) — единственная точка участка х (t),	< t < т2,
лежащая на границе области G.
Следовательно, участок x(t),	удовлетворяет
принципу максимума (ср. стр. 292). Соответствующая
этому участку ненулевая функция
Ф’(0 = (Фо (*)> Ф1(*)> •••> Фй(*))> *!<<<*,	(72)
непрерывна и удовлетворяет системе уравнений (15) гл. 1.
Участок x(t), т<£<т2, удовлетворяет либо требованиям
теоремы 22 (если он лежит на границе g(x) = 0), либо
принципу максимума (если он лежит внутри области G).
Соответствующая непрерывная ненулевая функция
Ф+(0 = (Фо(0, ФИО. ...,^(0), *<£<т2,	(73)
удовлетворяет либо системе (10), (И) и условиям а) — в)
теоремы 22, либо системе (15) гл. 1.
Мы будем говорить, что в точке стыка х (т) оптималь¬
ной регулярной траектории х (t), t0 < t < tly целиком лежа¬
щей в замкнутой области G, выполняется условие скачка,
если существует такой участок x(t), т1<^<т2, траекто¬
рии, что хг < t < т2 является максимальным интер¬
валом отрезка t0 < t < содержащим единственный
момент стыка т, и если для участков ас (t), хЛ < t < т,
ас(£), т<£<т2, определенные выше функции (72), (73)
можно подобрать таким образом, чтобы выполнялось одно

§ 36]	УСЛОВИЕ СКАЛКА	ЗАЗ
из следующих двух (как легко видеть, не совместных
между собой) условий:
Ф+ (т) — 'Ф (т) + Iх grad g (х (т)),	(74)
,t'(T) + M'gra(ig-(»:(T)) = 0, |л=£0,	(75)
где р,—действительное число. Если участок x(t), т< £<т2,
лежит на границе g(x) = 0, то условие (74) эквивалентно
условию
(т)=оо>
так как начальное значение i|)+ (т) функции ф+(0»
т<£<т2, можно изменять на произвольный вектор вида
ц grad g (х (т)) (см. замечание 4 к теореме 22).
Теорема 24 (условие скачка). Пусть регулярная
оптимальная траектория уравнения (5), лежащая в зам¬
кнутой области G, содержит конечное число точек стыка.
Тогда в каждой точке стыка выполняется условие скачка.
Доказательство. Пусть u(t), 70< t < tv — опти¬
мальное управление, х (t) — соответствующая оптималь¬
ная траектория, х (т) — точка стыка, x1<t<x2 — макси¬
мальный интервал, содержащий единственный момент
стыка т. Для определенности считаем, что участок x(t),
x1<t<x, принадлежит открытому ядру области G, а уча¬
сток х (£), т<£<т2, лежит на границе g (х) = 0.
Точка х(хг) может лежать как внутри области G, так
и на ее границе. Мы предположим сначала, что х{хЛ)
лежит внутри G; в этом случае, очевидно, xx = t0.
Введем уравнение
§=-/(&, О	(76)
и будем рассматривать его решения на отрезке 0<£<
< х — тх + еб0, где 60 — любое действительное число.
Очевидно, решением уравнения (76) являются функции
v (t) = и (т — t), \(t) = x(x—t), 0< t < х — хг-\- е60.	(77)
Обозначим через Ах-Хио оператор переноса вдоль траек¬
тории (77) уравнения (76) (см. стр. 95). Далее, пусть Д§
означает вектор смещения (ср. формулу (22) гл. 2) при про¬
извольном варьировании траектории (77) уравнения (76).
Наконец, пусть 6§0 — произвольный вектор, исходящий из

334 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. G
точки х (т) и либо направленный внутрь области G
(не касательный к границе области G), либо равный нулю.
Тогда определен вектор
й = Л-тьо(б|0) + А1.	(78)
который мы будем считать исходящим из точки х(х1).
Множество всех векторов (78) образует выпуклый конус Ж
с вершиной в точке х (тД = |(т — хг) (ср. стр. 106).
Через Ж* обозначим конус, определенный в § 33, рас¬
сматривая его для траектории х (Z), т<*< т2. Точка х (т2)
является вершиной конуса Ж*. Конус Ж* лежит в каса¬
тельной плоскости Т (х (т2)) границы g (х) = 0, про¬
веденной в точке х(т2), и образован всевозможными
векторами вида
6* = РХ2, т (бц) (Ьх (т)) + Ах*ajb	(79)
(см. формулу (53)), исходящими из точки х(т2).
Важно заметить, что варьированная траектория |*(£)
при достаточно малом е лежит вся в замкнутой области G.
В самом деле, если б|0 == 0, то начальный кусок траекто¬
рии S* (£) совпадает с траекторией £(£)> и потому точки
траектории !*(£) при £>0 являются внутренними точ¬
ками области G. Если же б|0 Ф 0, то, в силу выбора
вектора б|0, наше утверждение следует из леммы (стр. 330).
Траектория х* (I) также лежит в замкнутой области G
(см. § 33).
Рассмотрим теперь прямое произведение
Ж X Ж* cz X X Т (х (х2))	(80)
конусов Ж и Ж*. Это прямое произведение Ж X ЖГ* также
является выпуклым конусом.
Через (йГ обозначим содержащийся в Ж X Ж* выпук¬
лый конус, образованный всевозможными парами векто¬
ров (78), (79), для которых
б|о = бас(т).	(81)
Далее, обозначим через к выпуклый конус, опреде¬
ленный в § 14 и рассматриваемый для траектории £(£),
0<£<т — xv а через А)* —конус, определенный в § 33
и рассматриваемый для траектории x(t), т<Х<т2.

§ 36]	УСЛОВИЕ	СКАЧКА	ЗЗГ)
Очевидно, что к (ЦК,	и	потому
Ж Ц) к х х(т2), Ж ZD ас (г2) X к*.	(82)
Обозначим через L луч, выходящий из х(х2) и на¬
правленный вдоль отрицательной полуоси х°. Покажем, что
луч х (т3) X L, лежащий в прямом произведении /Г х
хТ(х(т2)), не является внутренним лучом конуса с/£\
Допустим обратное. Тогда совершенно так же, как
в § 34, для любого достаточно малого е > 0 . можно
доказать существование таких варьированных траекторий
| (t), 0<£<т —т^ + ебб, х* (£), т< г<т2 + еб£, (83)
начальные смещения которых удовлетворяют условию (81),
что точка
l*(t — т^ + ебб), ас*(т2 + еб<)	(84)
лежит на луче х (тх) X L и не совпадает с его началом
х (т3) х х (т2). Иначе говоря,
I* (т~Ti + ебе) = яс(т1),
х* (т2 + ебt) = х (т2) + К (— 1, 0, . .., 0),	(85)
где К > 0.
Определим допустимое управление u(t), хг — еб0<£<
< т2 + ебt, и соответствующую траекторию х (t), т3 — еб0 <
<£<т2 + еб£, уравнения (5) формулами:
и (t) = v* (т — t), х (t) = I* (т — t) при хг — ебб < t < т,
u(t) = u*(t), x(t) — x*(t) при т< т2еб£,
где (£), х* (t) — варьированные траектории (83), v* (t),
и* (t) — соответствующие им управления. Очевидно, функ¬
ции и (£), х (£), хг — ебб < t < т2 + ебt, удовлетворяют урав¬
нению (5), и, в силу условия (81), траектория x{t),
т3 — еб0 < t < т2 + еб£, непрерывна в точке х и, следователь¬
но, на всем отрезке т3 — еб0 < t < т2 + еб£. Кроме того,
согласно (85) имеем:
х (т1 — еб0) = х (т3),
х (т2 -f еб£) = (х° (т2) — Я, я1 (т2), . . ., £п (т2)), А* > 0.

336
ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ
[ГЛ. о
Но эти неравенства противоречат тому факту, что учас¬
ток x(t),	т1<^<т2,	оптимальной	траектории	x(t),
t0<Ct^tv также оптимален.
Итак, луч х(х1)хЬ не является внутренним лучом
для конуса о/С. Из включения (80) следует, что размер¬
ность dim о/С конуса о/С удовлетворяет неравенству
dim о/С < 2п + 1.
Следовательно, существует опорная 2гс-мерная плос¬
кость к конусу о/С в его вершине х (т2) X х (т2), лежа¬
щая в X X Т (х (т2)) и отделяющая конус о/С от луча
х (тА) X L. Обозначим через (/, %*) исходящий из точки
х (т2) х х (т2) вектор, ортогональный к этой плоскости,
лежащий в X X Т (х (т2)) и направленный таким образом,
что луч х (тх) X L лежит в том же замкнутом полупро¬
странстве, что и вектор (%, %*), а конус о/С — в другом.
Мы имеем:
Х* = (Хо*, хГ. ...,х:)£Т(х(т2)),	(86)
((X, X*)'	(*.	»*)) = (X. *) + (Х*>	<>*) < 0,	хо* < 0,	(87)
где векторы	6,	6* определяются	формулами	(78),	(79)
(при условии (81)). Далее,
(Х> X*) Ф 0	(88)
и потому векторы %, •%* одновременно в нуль не обра¬
щаются.
Обозначим через
£(*), 0<£<т —тх,	(89)
решение уравнения
= df(l(t),v(t)y
dt	д%
удовлетворяющее краевому условию
£(t-t1) = x.
где функция |(£) определена формулой (83), a v(t) —
соответствующее управление. Через
(t), т<£<т2,
(90)

§ 36]	УСЛОВИЕ	СКАЧКА	337
обозначим решение уравнения
d\|э _	и (t))
ИГ	to ^
с краевым условием
Ф(*2) = Х*-
Используя включения (82), так же как в гл. 2 и в § 34,
получаем:
(-&(*),	«(*)))	= je? (-2(0, Ш. о(0)=-	)
= ®®( —5(0. i(*)) = 0, 0<г<т —т1(
<$?(Ф+С);	“	С)) = w (Ф+ (*)> ж(0) = °>
ТГ<£<Т2.
Кроме второго равенства (91), функция я|)+(£)> т<г<т2,
удовлетворяет всем условиям теоремы 22, за исключе¬
нием, быть может, условия б), так как равенство = 0
и, следовательно, равенство ч>* (0 = 0 не исключены.
Пусть
ф~(0 = — SO — *)>	и<^<т.	(92)
Очевидно,
у. ф-(т.)--х, т,«<т.
©Ж'ОФ'Ч*)» ж(*)> и(^)) = <3^('ф“(^), a; (t)) = 0.
Из неравенства (88) следует, что хотя бы одна из
функций \JT (£), г|)+ (£) отлична от нуля. Ниже доказы¬
вается, что всегда я|Г(£)=£0 и, следовательно, функция
t|T (t) удовлетворяет всем условиям принципа максимума.
Докажем теперь, что либо
1|)+ (т) = 1|г (т) + (X grad g (ж (т)), i|f (t) Ф 0,
либо
Ф" (-Г) + ц gradg- (аг (т)) = 0, рфО.
Тем самым условия скачка будут доказаны, так как
функцию г|Г (£), тх< t <т, можно принять за функцию (72),
а функцию г]i+(t), т<г<т2 —за функцию (73), если
Ч>+(0=£0.
22 л. С. Понтрягин

338 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
Выберем варьированные траектории |* (£), х* (t) сле¬
дующим образом.
Положим
60 = 6< = 0,	v*(t) = v(t),	6|0=—^г,
где N — произвольный вектор, не касательный к границе
g (х) = 0 в точке х (т) и направленный во вые области
G. Эти данные однозначно определяют варьированную
траекторию |*(0- Для определения варьированной
траектории х* (t) мы будем считать символ а пустым,
а символ Ь — содержащим единственную точку = х (хг):
Ь = {Е1 = яс(т1), а, (ас), Ж, б[х= 1}.
Следовательно, в силу (47)
6ас(т) = -Ж= 610,
т. е. условие (81) выполняется.
Для векторов, определенных формулами (78), (79),
получим выражения (см. (53) и формулу (22) гл. 2):
п
6= -Л_т oW= - 2 фа(т-т,)ЛГа,	(93)
а=0
n	Т2
6* = 2 Фа (Т2) (	(Г	(0.	Л	(0)	-g-	Л, (94)
а=0	т
где
2 <Pa(0)7V“= 2 $а(т)ЛС = Ж
а=0	а=0
Здесь через <р0(£)> • ••, Фп(*)>	xv	обозначена
фундаментальная система решений уравнения в вариа¬
циях для уравнения (76).
Через я|э°(£), ..., фп(0 обозначим систему функций,
сопряженную с Ф0(£)> Ф,г(0- Мы имеем:
— (%> *)= 2 (Х> Фв(т-т2) 7Va) =
a=0
= 2 (ХрфР^-А). Фа(т-т1)Л^)= 2xa^Va = (S(0). .V),
а, 0=0	1	а=0

§ 36]	УСЛОВИЕ СКАЧКА	339
п
где £ (0) = J, XavF (0) — начальное значение функции (89).
а=1
Из равенства (92) следует:
(Х> S) = (^'C0, лт).	(95)
Аналогично равенство (94) дает:
*2
(Х*> 6*)= — (Ч>+(*). -ZV)+^ Сф+(0. A(t))^dt =
X
Т2
= -(i|>+ (т). JY)-^X(i)^dt,
X
где А,(£)= — (ф+(г)> Л(£)). Используя выражение (42) для
dR
и интегрируя по частям, получим:
(**.**)= -(**(*).•#)- [*■(<)«!(*(»)) х
х	^	|. + ^ Й в1 (в (<))	^	Л	_
т
--(ГМ. Д') + >-М(-%(ахТ>>'' It)+
+	Jv)*.
Складывая это равенство с (95) и учитывая неравен¬
ство (87), находим:
(X. ft) + (х*> 6*) = (V (т) - Ч>+ (*) + 00 dg(xjr))-, jv)+
+ ? чг	(х W) (;^г1' я) dt < °-	(96)
X
Величина
х
22*

340 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. б
может быть сделана сколь угодно малой при заданном N
за счет выбора малой окрестности 0^, входящей в опре¬
деление функции а1(х), в то время как первое слага¬
емое равенства (96) от этой окрестности не зависит.
Следовательно, для произвольного вектора Ж, не ка¬
сательного к границе g (х) = 0 в точке х (т) и направ¬
ленного наружу относительно области G, справедливо
неравенство
(Ф (х) ~ Ф+ (т) + ^ (т) grad g (х (т)), Лг)<0,	(97)
которое, в силу произвольности вектора Ж, эквивалентно
равенству
фЛ(т) = ф-(т) + ^гаа£ (х(х)).	(98)
Вектор г|Г (т) Ф 0, так как из равенства г|Г (т) = О
и неравенства (88) следует неравенство \р+ (т) Ф 0; с дру¬
гой стороны, из (98) получаем соотношение
Ф+ (т) = М- grad g (х (т)) ф 0.
которое в силу соотношения ф (т2) = %* противоречит
включению (86).
При г1)+(т) = 0 получаем:
Ф~ СО +Р grad g (х (т)) = °> РФ о.
Таким образом, теорема 24 доказана в том случае,
когда х (tj) — внутренняя точка области G.
Пусть теперь х (т2) лежит на границе g (х) = 0.
Этот случай легЕ^о сводится к рассмотренному:	до¬
статочно определить функцию фе (0 на отрезке
0<£<т, где хг < 0, и затем устремить точку 0 к Tjj
мы получим семейство функций фд (t), 6<£<т, для
которых существует искомая предельная функция
Ф"(0> т2<^<т.
Замечание 1. Если участок х (t), х < t < т2, также
принадлежит открытому ядру области G, то неравен¬
ство (97) заменится неравенством
(ф-(т)-ф+(т), Ж)< 0,

§ 37]
ФОРМУЛИРОВКА РЕЗУЛЬТАТА. ПРИМЕРЫ
341
из которого следует равенство
Ф+ СО = Ф" СО + и- grad 8 (х (т))> v > °*
Замечание 2. Если участок ас(0> т<£<т2, лежит
на границе g(x) = 0, то вектор grad g (х (т)) и вектор
/(х(х), и(т-}-0)) ортогональны и условие скачка дает:
(ф“(т), /(я(т), и{х 0))) =
= (i|)"(T) + |igradg(af(t)), (/(»(т), в(т + 0))) =
= ('ф'(т), /(ж(т), м(т+0))) = ^('ф" (т), :с(т)) = 0.
Отсюда вытекает, что если система уравнений относи¬
тельно и
СФ~С0> /(^(т)> и)) = сМ = 0
имеет единственное решение
и (т — 0) = и (т + 0),
то вектор
f(x(т), и(т — 0)) = f(x(x), 1г(т + 0))
касается границы g (х) = 0 в точке х (т); другими словами,
оптимальная траектория в точке стыка х (т) остается
гладкой.
Замечание 3. Если оптимальная траектория лежит
на кусочно-гладкой границе области G (до сих
пор мы рассматривали область G с гладкой границей),
то уравнения всякого участка траектории, целиком
лежащего на гладком куске границы, уже найдены в § 32.
При переходе траектории с одного гладкого куска гра¬
ницы на другой выполняются условия скачка, вполне
аналогичные условиям (74), (75).
§ 37. Формулировка основного результата. Примеры
Объединяя теоремы 22, 24 и принцип максимума, мы
приходим к следующей теореме, дающей полную систему
необходимых условий, которым удовлетворяет всякая
регулярная оптимальная траектория, являющаяся реше¬
нием оптимальной задачи § 31,

342 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. 6
Теорема 25. Пусть оптимальная траектория урав¬
нения (5) целиком лежит в замкнутой области G, содер¬
жит конечное число точек стыка, и пусть всякий ее
участок, лежащий на границе области G, регулярен.
Тогда всякий участок траектории, лежащий в откры¬
том ядре области G (за исключением, быть может, кон¬
цов траектории), удовлетворяет принципу максимума;
всякий ее участок, лежащий на границе области G, удо¬
влетворяет теореме 22; в каждой точке стыка выпол¬
няется условие скачка (теорема 24).
Пример 1
Условия скачка справедливы и для следующей опти¬
мальной задачи.
Пусть фазовое	пространство	X	разбито	на	две	части
Xv	Х2 гиперповерхностью g (х) =	0.	Пусть	в	части	Хг
уравнение движения фазовой точки имеет вид
dx jy ,	v
-5T=/i(*. и),
а в части Х2 вид]
doc /» /	\
ЧГ = Г,(х, и).
Требуется выбрать такое допустимое управление, чтобы
фазовая точка из начального положения х1£Х1 попала
на прямую П С Х2, параллельную оси х°, и координата х°
конца траектории обратилась в минимум.
Траектория движения в каждой из частей Xv Х2
будет удовлетворять принципу максимума, а в момент
перехода через границу раздела g (х) = 0 будет выпол¬
няться условие скачка.
При выводе условия скачка в рассматриваемом слу¬
чае начальное смещение варьированной траектории должно
лежать строго на границе раздела g(x) = 0. Поэтому
лемму, приведенную на стр. 330, невозможно использо¬
вать и доказательство § 36 проходит лишь если ни один
из векторов fx(x( т), и (г— 0)), f2(x(x)t и(т-{-0)) в точ¬
ке стыка х (т) не касается гиперповерхности g (х) = 0.

§ 37]	ФОРМУЛИРОВКА	РЕЗУЛЬТАТА.	ПРИМЕРЫ	343
Пример 2
Если изучается обычная вариационная задача, то из
условия скачка непосредственно следуют известные усло¬
вия преломления экстремалей. В качестве примера мы
выведем здесь эти условия для простейшей вариационной
задачи.
Пусть плоскость переменных ху у делится линией
S У)= О на Д1зе части Xv Х2 и пусть заданы две
точки (xv Уг)£Х1У (х2у у2)£Х2. Требуется соединить эти
точки непрерывной кусочно-гладкой линией у = у(х)
таким образом, чтобы обращался в минимум интеграл
Область управления U — открытое множество числовой
прямой. Принцип максимума записывается следующим
образом (легко доказать, что ф0 Ф 0 и, следовательно,
можно положить ф0 = —1):
'2
X.
где
1Лху У> у') при (х> у)€х1>
fAx> У у у') при (ХУ У)€х 2
и /1? /2 —гладкие функции своих аргументов.
Введем обозначения:
X
LlUs	п	/	/	\
~аг =	(х’	У’ у
^0 	 А
dt
dx1
dt
rftp! _ dF
dt	dx	’
d^2	dF
dt	dy	’
&€= —F{x, y, ?/') + гр! + -фа?/' = max = 0.

344 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ [ГЛ. О
Условия ё%? = тах и = 0 соответственно дают:
Из условия скачка = г|5 -f \i grad g (x,y) следует:
где (TV1, N2) — вектор нормали к линии g (х, у) = 0 в точке
перелома траектории. Обозначим через У тангенс угла
наклона касательной к кривой g = 0 в точке перелома.
Имеем:
откуда получаем известную формулу (см. Гюнтер Н. М.,
«Курс вариационного исчисления», М. —JI., 1941)
В качестве иллюстрации рассмотрим следующую гео¬
метрическую задачу. В п-мерном эвклидовом пространстве
X переменной х = (хг, ..., хп) задана замкнутая область
В неравенством g(:r)<0, причем граница
области В является гладкой регулярной поверхностью
с непрерывно меняющейся кривизной, т. е. функ¬
ция g (х) дважды непрерывно дифференцируема и вектор
grad g (я) нигде на поверхности (99) в нуль не обра¬
щается. В области В заданы две точки х0, хг Найти
в области В кривую С наименьшей длины, соединяющую
точки х0 и хг
ду’ ду'
1
У' ’
fi+w (у' - <у~у>=/*+■w(У'"{у+п
При м ер 3
g(x) = О
(99)

§ 37]
ФОРМУЛИРОВКА РЕЗУЛЬТАТА. ПРИМЕРЫ
3 45
Мы покажем, что из теоремы 25 вытекает следующий
геометрически очевидный результат. Пусть кривая С
наименьшей длины состоит из нескольких участков,
попеременно расположенных в открытом ядре области В
(кроме, быть может, кондов участка) и на границе (99).
Тогда участки, лежащие в открытом ядре области В,
являются отрезками прямых; участки, лежащие на гра¬
нице (99), являются геодезическими на поверхности (99)',
причем вектор главной нормали кривой С на этих
участках направлен во вые области В; наконец, в точках
стыка двух соседних участков прямолинейный участок,
проходящий в открытом ядре области В, касается поверх¬
ности (99). Таким образом, линия С не имеет угловых
точек.
Для доказательства рассмотрим следующую оптималь¬
ную задачу. Задана система уравнений
где управляющий вектор и = (и1, . . ., ип) подчинен
условию
т. е. областью управления U является единичный шар.
Требуется найти лежащую в В оптимальную по быстро¬
действию траекторию, соединяющую точки х0 и xv
Пусть х (*), t0 < £ < tv — оптимальная траектория,
являющаяся решением этой задачи и имеющая конечное
число участков, попеременно расположенных в открытом
ядре области В и на ее границе. Через u(t) обозначим
соответствующее оптимальное управление. Из условия
максимума (теоремы 2 и 22) непосредственно вытекает,
что |и(г)| = 1, и потому параметр t является длиной
дуги на линии x(t). Из этого следует, что линия х (t)
является решением поставленной геометрической задачи.
Докажем теперь сформулированные выше свойства кри¬
вой С. Тот факт, что расположенные в открытом ядре
участки кривой x(t) являются прямолинейными отрезками,
непосредственно вытекает из теоремы 2.
71

346 ПРОЦЕССЫ ПРИ ОГРАНИЧЕННЫХ КООРДИНАТАХ	[ГЛ.	6
Рассмотрим теперь участок, целиком расположенный
на границе области В. Область управления U опреде¬
ляется одним соотношением
q(u) = (a, и) — 1<0.	(100)
Далее, функция р(х, и) (см. (6)) имеет вид
р(х, и) = (gradg (х), и).	(101)
На рассматриваемом участке линии x(t) выполняется
соотношение
р(х, и) = (grad g {х), и) — 0.	(102)
Система уравнений для переменных ф| (см. (10)) имеет вид
= l Jp_ = X у d2g (х ^ иа = Х—	dg (х ^
dt	Qxi	J Qxi QyP*	dt	Qxi
a=l
1 = 1, . . ., ny
или иначе
4f = ^'i'Sradg(x(0).	(103)
Мы имеем:
^? = 'Фо + ('ф, и).	(104)
и потому ф0 Ф 0 (в противном случае было бы ф Ф 0
и тогда максимальное значение величины (ф, и) было бы
отличным от нуля, что противоречит соотношению (И)).
Следовательно, мы можем положить ф0 = — 1 и условие
максимума (И) принимает вид
(ф, и) = шах = 1.	(105)
Далее, в силу (100),
grad q (и) = 2м,	(106)
и потому (см. (104), (8), (101), (106))
^ = y = X^ + v-^ = Xg™d8(x) + 2vu- <107)
Умножая полученное соотношение ф = X grad g (х) + 2vu

§ 37]
ФОРМУЛИРОВКА РЕЗУЛЬТАТА. ПРИМЕРЫ
347
скалярно на iz, получаем, в силу (105), (102),
1 = (яр, ц) = % (^, grad g (я)) + 2v = 2v.
Таким образом, формула (107) принимает вид
ф = ^ grad g (х) + к,
и потому (см. (103))
коллинеарен нормали к поверхности (99), и потому
линия x(t) на рассматриваемом участке является геоде-
d2x(t)
зическои, причем вектор ее главной нормали
направлен во вне области В (см. условие в) в теореме 22).
Наконец, из условий скачка нетрудно вывести, что
кривая x(t) не имеет угловых точек.
-gLgradg(*(f))+-^ = 0.
Это означает, что

ГЛАВА 7
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ
Предыдущие главы были посвящены решению задачи
об оптимальном переводе управляемого объекта из одного
заданного положения в другое заданное положение (или
на заданное многообразие). Эту задачу можно трактовать
также как задачу об оптимальном достижении управляе¬
мым объектом другого, неподвижного объекта.
Однако в технике в ряде случаев возникает другая
задача — задача преследования управляемым объектом
другого, движущегося объекта. При этом о характере
движения второго объекта можно делать самые различные
предположения. Можно, например, считать, что второй
объект также является управляемым (ср. § 28). Пусть
при этом фазовое движение первого объекта х описы¬
вается системой обыкновенных дифференциальных урав¬
нений
х1 = f (х1, х2, . . ., хп, и1, и2, . . ., ur), i = 1, . . ., п,
а движение второго объекта у — системой уравнений
у1 = £ (г/1- У1 гЛ V1’ V2’ • • • - yS)> г’ = !> •••.«.
где иг — управляющие параметры первого объекта, со¬
управляющие параметры второго объекта, а х и у —
векторы одного и того же фазового пространства X.
Тогда можно ставить следующую задачу. Зная тех¬
нические возможности объекта у (т. е. соответствующую
систему дифференциальных уравнений) и положение

§ 38]
ПОНЯТИЕ О МАРКОВСКОМ ПРОЦЕССЕ
349
объекта у в каждый момент времени t, научиться выби¬
рать управления и объектом х в каждый момент времени t
таким образом, чтобы объект х достиг объекта у в крат¬
чайшее время (или оптимально в каком-либо другом
смысле); при этом — что очень существенно — не должно
предполагаться известным управление объектом у
в моменты времени, следующие за t.
В такой постановке задача преследования пока не
решена.
В настоящей главе мы решаем несколько иную
задачу преследования. Именно, мы считаем, что известен
лишь вероятностный закон поведения «убегающего»
объекта у, причем этот закон предполагается м а р к о в-
с к и м и описывается уравнением типа Фокера — Планка —
Колмогорова.
При решении этой задачи будут использованы неко¬
торые понятия и факты теории вероятностей. В §§ 38 и 40
мы сообщаем эти факты, не всегда приводя, однако, пол¬
ные доказательства, а ограничиваясь в основном неболь¬
шими пояснениями. У читателя, таким образом, не пред¬
полагается специальных знаний по теории вероятностей.
§ 38. Понятие о марковском процессе.
Дифференциальное уравнение Колмогорова
Пусть в тг-мерном фазовом пространстве R случайно
движется некоторая точка, причем если известно ее
положение х в момент а, то однозначно определена
вероятность Р (а, х, т, Е) ее нахождения в любом
измеримом подмножестве Е пространства R в про¬
извольный момент х > а. В таком случае процесс
движения случайной точки называют процессом без
последействия или процессом марковского типа. Полную
характеристику движения случайной точки дает функция
равная плотности вероятности Р(в,х,х,Е)
в точке у. Функция р (а, х, т, у) удовлетворяет, очевидно,
следующему соотношению:
р(о, х, т, у)
(1)
^ р(а, х, т, y)dy — \
(2)

350	ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА	[ГЛ. 7
(здесь, как и всюду в дальнейшем, интегрирование про¬
изводится по всему пространству R), если область инте¬
грирования специально не указана). Другое соотношение,
смысл которого также ясен, носит название тождества
Маркова
р (а, х, х, у) = ^ р (а, х, s, z) р (s, z, х, у) dz. (3)
Случайный процесс называется непрерывным, если
за малые промежутки времени лишь с малой вероятностью
координаты случайной точки могут получить заметные
по величине приращения. Мы потребуем от марковского
процесса несколько более сильной непрерывности,
а именно: каково бы ни было положительное число б,
имеет место соотношение
lim "hr *\ p(o-Aa,x,o,y)dy = 0.	(4)
До-*0 да , J .
| у—х I > 6
Мы сейчас выведем дифференциальное уравнение,
которому (при выполнении некоторых дополнительных
условий) удовлетворяет функция р(о, х,%, у). Это урав¬
нение впервые было получено А. Н. Колмогоровым
и носит название уравнения Колмогорова.
Предположим, что:
а) частные производные
др (а, х, т, у)	д2р (а, х, т, у)
дх1	9	dxldxi
существуют и непрерывны для любых а, ж, т > а, у\
б) каково бы ни было б > 0, существуют пределы
lim Д-	\	(у1 — х1)р(в—Аа,х, o,y)dy=bl	(о,х), (5)
Аа-*0 Д0 ,	J	.
I у — х I < 6
1 = 1» 2, ..., п,
lim Д- ^	(у1 - х5 (у1 - х}) р (о Аа, х, а,	у) dy =
Да-»0 Да . J. . .
| у-Х I < 6
= 2аг1(а,х), i, /= 1, 2, .. ., п, (6)

§ 38J	ПОНЯТИЕ	О	МАРКОВСКОМ	ПРОЦЕССЕ	351
причем сходимость в соотношениях (5) и (6) равно¬
мерна относительно х.
Покажем, что в этих предположениях функция
р(аух, т, у) как функция первой пары аргументов удов¬
летворяет дифференциальному уравнению втораго порядка
параболического типа {уравнению Колмогорова)
г, ;=1	i—1
Доказательство. В силу тождества Маркова (3)
мы имеем
р (а — Дет, х, т, у) = ^ р (а — Да, х, а, z) р (а, z, т, у) dz. (8)
Используя соотношение (8) и тождество
^ р (а — Да, х, а, z) dz = 1,	(9)
получаем:
р (а - Да, х, тУу)-р (а, х, т, у) =
= ^ р (а — Да, х, а, z) р (а, z, т, у) dz —
— р(а, х, т, г/)^ р(а — Да, х, а, z) dz =
= \[р (а, z, т, у) — р (а, х, т, ?/)] р (а - Да, х, а, z) dz.
Разбирая интеграл по пространству /? на два интеграла
соответственно по областям | z — х [ < 6 и	| z — х|	>б и	раз¬
лагая разность р(а, z, т, у) — р(о, х, т,	у)	по	степеням
zl — х1, находим
р (а —Да, ж, т, у) — р (о, х, т, у)
Ла
S [P(v>z,x,y)-p{G,x,T:,y)\p{e-ka,x,o,z)dz+
\Z -х|>6
+ S ^ (gg5 Т’У)	5	(zi	—	—Аа, x,a,z)dz +
i=l	|	z—эс |< б

352
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
1 д2р (а, х, т, у) 1
2	<9^	qxj	Дет
г, ;= 1	I	г—х|<
^	(^-ж^-ж^Х
2	(9х^ дх)
г, ;=1
X ^ о [| z — х |2] р (ег — Дет, ж, 0, z) dz. (10)
| Z-X |< 6
Перейдем теперь в соотношении (10) к пределу при
Да—>0. Первое слагаемое правой части, в силу (4), имеет
предел, равный нулю; предел второго слагаемого равен
(см. (5))
2	Ь*(о,	х)
Эр (а, X, г, у) .
дхг
г=1
третье слагаемое, ввиду (6), в пределе оказывается
равным
2 aij (о, х)
д2р (а, х, т, у)
дх1 dxi
iy 7=1
Наконец, последнее слагаемое стремится к нулю при
б—>0. Так как, однако, левая часть равенства (10) от б
не зависит, то предел правой части равен
г, ;=1	г=	1
Отсюда мы заключаем о существовании у левой части
равенства (10) предела, равного
др(а, х, т, у)
да
Итак, функция р(а, ж, т, у) является решением урав¬
нения (7).
Оказывается, что р (а, х, т, у) является фундамен¬
тальным решением уравнения (7). Это значит, что

§ 3bj	ПОНЯТИЕ О МАРКОВСКОМ ПРОЦЕССЕ	^
решение и, —и (о, х) уравнения (7), удовлетворяющее
наперед заданному начальному условию
и (at x)—-+F(x)>	(11)
где F (х) — заданная функция п переменных х19 х2, . . ., хп\
выражается по формуле
и{о,х)=^ р(о, х,х, y)F(y)dy.	(12).
Действительно, дифференцируя интеграл в правой части
соотношения (12) по параметрам о и х и используя урав¬
нение (7), мы получаем соотношение
2 ««(о,*) i^+	*>^	=	0.
i,j= 1	i=l
которое показывает, что функция и (сг, х) является реше¬
нием уравнения (7).
Формула (И) доказывается следующим образом.
Разобьем интеграл по пространству R, стоящий в правой
части равенства (12), на два интеграла соответственно по
областям \ у — х\ < б и \ у — х\> 6. Так как при (у — х | > б
ввиду непрерывности процесса, очевидно, справедливо
соотношение
Р (<*. х> у) °>
то
lim \ р (а, х, х, у) F (у) dy = lim \ р(а, х,х, y)F (у) dy.
ст~>т J	ст->т	,	_
I X-у |<б
Принимая во внимание соотношение (2) и учитывая, что
предел слева не зависит от б, заключаем, что
lim \ р (а, х, х, у) F {у) dy = F (ж),
(7->Т J
что и требовалось доказать.
Отметим еще одно важное свойство функции р (а, х, т, у),
нужное нам в дальнейшем. Пусть требуется решить
неоднородное параболическое уравнение
U+ 2	2	»>■	<13>
i, j= 1	i==l
23 л. С. Поптрягии

354
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
при нулевом начальном значении искомой функции.
Оказывается, что если р (о, х, т, у) — фундаментальное
решение соответствующего однородного уравнения, то
искомое решение дается формулой
х
и (а, X, т) = — ^	(а,	х,	s,	у)	Р (s, у) dy. (14)
G
Доказательство получается непосредственным дифферен¬
цированием.
§ 39. Точная постановка статистической задачи
В этой главе фазовые координаты управляемой точки
мы будем обозначать через z1, z2, . .., zn. Таким образом,
движение точки z в пространстве R описывается системой
обыкновенных дифференциальных уравнений
z1 = /1 (z1, z2, .. ., zn, и1, . . ., иг), г = 1,2, . . ., /г,	(15)
где и1, гг2, . . ., иг — управляющие параметры. Как и раньше,
функции f (z, гг) мы будем считать непрерывно зависящими
от всех переменных и непрерывно дифференцируемыми
ПО Z1, Z2, .. ., zn.
Предположим, что в пространстве R случайно движется
фазовая точка Q, причем так, что процесс ее движения
в пространстве R есть марковский процесс, удовлетворяю¬
щий условиям усиленной непрерывности. Как мы видели
в предыдущем параграфе, вероятностную характеристику
этого процесса дает функция р(а1х,х,у), которую мы
будем называть плотностью перехода случайной точки Q.
Плотность перехода является фундаментальным решением
уравнения (7). В дальнейшем мы будем считать, что про¬
цесс движения случайной точки задан функцией р (ст, ж, т, у).
Относительно коэффициентов уравнения (7) мы здесь
сделаем некоторые предположения. Именно, мы будем
считать, что:
1) коэффициенты aij (а, х), Ъг (а, х), г, / = 1, 2, . .., гг,
определены и непрерывны при а > 0 и при любом x^R\
2) все собственные значения матрицы |[ aij (о, х) || при
этих значениях аргументов ограничены сверху и снизу
положительными константами;

§ 39] ТОЧНАЯ ПОСТАНОВКА СТАТИСТИЧЕСКОЙ ЗАДАЧИ 355
3)	коэффициенты Ьг (а, х) при возрастании | х | возрас¬
тают ие быстрее чем e\xi
Пусть вместе с управляемой точкой z в пространстве R
движется некоторая ее окрестность 2Z, например шар
или вообще область, ограниченная произвольной кусочно¬
гладкой поверхностью, кусочно-гладко меняющейся
вместе с z. Тогда, если задан закон управления точкой
т. е. параметр и задан как кусочно-непрерывная функция
u = u(t) времени t, то система дифференциальных урав¬
нений (15) однозначно определяет непрерывное движение
точки z в пространстве R. Следовательно, если заданы
начальные положения управляемой точки z и случайной
точки Q, то однозначно определяется вероятность встречи
точки Q с окрестностью 2Z на конечном отрезке времени
о < t < х или на бесконечном отрезке времени а < t < оо
и т. п. Эта вероятность является, таким образом,
функционалом над управлением и (£). Естественно возникает
задача о таком выборе управления и (t) точкой z, при
котором этот функционал достигает максимального
значения.
Чтобы точно сформулировать задачу, введем в рас¬
смотрение неотрицательную и не превосходящую единицы
функцию h(t), определенную при 0<£<оо. Обозначим,
далее, через фи (а, х, т) вероятность того, что случайная
точка Q, находящаяся в момент времени о в положении х,
на отрезке времени а< t < т встретится с окрестностью 22
управляемой точки z (предполагается, конечно, что
начальное положение точки z, равное z(a), дано). Ста¬
вится следующая задача: выбрать управление и (t) точкой z
таким образом, чтобы функционал
достигал максимального значения. Функция h(t) опреде¬
ляет здесь, таким образом, постановку оптимальной
задачи; если, например,
оо
(16)
о
23*

356
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
ТО
/ =	(а,	х, т),
т. е. функционал (16) есть просто вероятность встречи
окрестности 2Z с точкой Q на отрезке времени сг<г<т.
Управление и (t) и соответствующую ему траекто¬
рию z(t) системы (15), обеспечивающие экстремум функ¬
ционалу (16), будем называть оптимальными. Решение
задачи, следовательно, сводится к вычислению функцио¬
нала (16) и последующему применению принципа макси¬
мума.
Конечно, функционал (16) зависит от размеров и формы
окрестности 2Z управляемой точки z. Как мы увидим
в следующем параграфе, для его вычисления надо решать
краевую задачу для параболического уравнения в част¬
ных производных (7). При этом нас будет интересовать
не факт существования решения, а эффективная (хотя бы
приближенная) формула для решения. Оказывается, что
такую формулу можно получить, если окрестность
считать малой. Но задача «накрыть» малой управляе¬
мой окрестностью случайную точку Q как раз является
естественной.
Таким образом, в последующем, начиная с § 41
настоящей главы, окрестность 2Z мы будем считать малой.
Для простоты мы будем считать, что 2Z есть /2-мерный
шар радиуса е с центром в точке z. Однако вниматель¬
ный читатель увидит, что наши рассуждения и сам
результат почти не изменятся, если под 2Z понимать
произвольную область малого «радиуса», ограниченную
кусочно-гладкой поверхностью, кусочно-гладко меняю¬
щейся вместе с z.
§ 40. Сведение вычисления функционала J к решению
краевой задачи для уравнения Колмогорова
Перед тем как указать подход к вычислению функ¬
ционала (16), сделаем одно общее замечание, относящееся
к произвольному марковскому процессу. Выделим в про¬
странстве R фиксированную область Г, ограниченную
(п — 1)-мерной кусочно-гладкой поверхностью S. Обозначим

§ 40]
ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J
357
теперь через q (а, х, т, у) плотность вероятности того, что
случайная точка, находящаяся в момент а в положении х,
окажется в момент т в положении у, не заходя при этом
на протяжении всего отрезка времени а< t < т в область Г.
Оказывается, что всюду вне области Г функция
q (а, х, т, у) удовлетворяет тому же уравнению (7), что
и функция р (o', х, т, у), и следующим начальному и гра¬
ничному условиям:
/•»
q(o, х, т, у) dy = lim \ р(о, х, x,y)dy=l, (17)
<^тя-г
^ д(а, х, т, y)dy—> 0 при я—(18)
я-г
Строгое доказательство этого факта можно найти
в специальной литературе по теории вероятностей. Мы
приведем здесь лишь наводящие соображения, вполне,
однако, достаточные для того, чтобы читатель уяснил
себе справедливость сформулированного предложения.
Соотношение (17) довольно очевидно.
Справедливость соотношения (18) будет достаточно
ясной, если процесс движения случайной точки Q пред¬
ставлять себе как броуновское движение частицы
(такая модель заключает в себе основные черты всякого
марковского процесса). Если частица Q находится
на границе мысленно выделенной в сосуде облас¬
ти Г, то вероятность ее захода в область Г за вре¬
мя 0<£<т равна единице. Этот факт и выражает соотно¬
шение (18).
Остается убедиться в том, что функция q(ay ху т, у)
всюду вне области Г удовлетворяет уравнению (7). Для
этого достаточно вновь внимательно просмотреть вывод
уравнения (7), данный в § 38. Весь этот вывод базиро¬
вался на тождестве Маркова (3), которое, очевидно,
справедливо и для функции q (а, ху т, у). Кроме тожде¬
ства Маркова, было также использовано соотношение (9).
В нашем случае
lim 'К
rr_vT J
^ q{o — Ao, X, a, y)dy Ф 1.
R—Г
(19)

358
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
Одиако из условия усиленной непрерывности (4) нетруд¬
но вывести соотношение
^ q	{о — Да, х, о, у) dy = 1 + о (Да),	(20)
я-г
которое и дает требуемый результат.
До сих пор область Г мы считали фиксированной.
Пусть	теперь	область Г не фиксирована, а движется
с течением времени, т. е. имеется однопараметрическое
семейство областей Г*. Обозначим через q (о, х, х, у)
плотность вероятности случайной точки Qy находящейся в
момент а в положении х, быть в момент х в положе¬
нии уу не встречаясь на протяжении времени а<£<т
с	движущейся	областью Г*. Тогда, очевидно, функция
^ q{a, х, х, y)dy	(21)
является решением уравнения (7) и удовлетворяет сле¬
дующему граничному условию:
^ д(сг, х, т, y)dy—>0 при х—>x0£So-	(22)
Теперь мы можем указать подход к вычислению
функционала (16). Пусть движущаяся область Г* представ¬
ляет собой окрестность управляемой точки z(t). В соот¬
ветствии со сказанным в § 39 мы будем обозначать ее
через	Положим
ф (сг, х, т) = 1 — ^ q (сг, х, х, у) dy.	(23)
Так как уравнение (7) линейно, то функция ф(сх, х, т)
по переменным о шх удовлетворяет уравнению (7). Далее,
из (17) и (22) следует, что начальное значение функции
ф(а, х, т) (при а = т) равно нулю, а краевое значение
на границе окрестности 2Z(a) равно единице:
ф(т, X, т) = 0, 1
*)|s0= !• J	^
Непосредственно из определения следует, что функ¬
ция ф(сг, х, т) представляет собой вероятность того, что

§ 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 359
случайная точка Q, находящаяся в момент времени а
в положении х, на отрезке времени а<£<т будет «на¬
крыта» окрестностью S2(o управляемой точки z. Таким
образом, функция ф(сг, х, т), определенная формулой (24),
совпадает с функцией фи, которая фигурирует в функцио¬
нале (16). Следовательно, для вычисления функционала
(16) мы должны решить уравнение
3+2 *и<*<*>
г, /= 1	г=1
со следующими начальным и граничным условиями:
ф (а, х, т) 0,	(26)
СГ^Т
ф(сг, х, т) —> 1 при х—>x0£So-	(27)
Как мы уже говорили раньше, мы будем решать эту
задачу для случая, когда окрестность управляемой
точки z представляет собой шар радиуса в. Мы увидим,
что в этом случае решение задачи (25),	(26), (27)
представляется в виде
ф(сг, х, т) = еп"'2Т’ (а, х, х) + о(еп“2),	(28)
и вычислим функционал	(а, х, т), представляющий
собой главную часть вероятности ф (а, ж, т). Отметим сразу,
что формула (28) справедлива лишь при п > 2. До конца
настоящей главы мы предполагаем, что размерность
фазового пространства R больше двух: п > 2.
§ 41. Вычисление функционала *7 в случае, когда
уравнение Колмогорова имеет постоянные коэффициенты
В этом параграфе вероятность ф(сг, х, т) и, следова¬
тельно, функционал (16) будут приближенно вычислены
для одного важного частного случая, а именно для слу¬
чая, когда уравнение (25) имеет постоянные коэффициен¬
ты. В процессе вычисления будут использованы неко¬
торые факты из теории интегральных уравнений, а также
понятие потенциала двойного слоя. Все это читатель
может найти в учебниках по теории дифференциальных
уравнений с частными производными, например в книге:

360	ОДНА	СТАТИСТИЧЕСКАЯ ЗАДАЧА	[ГЛ.	7
С. JL Соболев, «Уравнения математической физики»,
Гостехиздат, М., 1954. В соответствующих местах мы при¬
водим нужные определения и формулировки используе¬
мых теорем. Итак, мы будем решать уравнение
Z+ У й—+	= 0	(29)
дх1дх!	дх1
г, j— 1	г=1
(где а1* у Ь1 — постоянные коэффициенты) при начальных
и граничных условиях (26), (27), которые в дальнейшем
мы будем записывать в виде
ф(т, Ху т) = 0,	(30)
"Ф (<т> х> х) |sCT= 1;	(31)
через	St мы	обозначаем сферу	радиуса	е	с	центром
в точке z(t).
Прежде всего перейдем от этой задачи к задаче
с граничным	условием на сфере	радиуса	е	с	центром
в начале координат. Для этой цели в пространстве (z, t)
введем новые координаты по формулам
z = !i + z(£),	cr<£<s,	(32)
так что
''“5+z(0)' )	(331
у = 4+ .(>).	)	^ >
При таком преобразовании координат сфера S0 перейдет
в сферу SBt определяемую уравнением
(61)2 + (62)а+... + (Г)2 = е*.	(34)
Положим
ф(а, I, Т) = г1з(ст, £ + z(a),	т).	(35)
Для функции ф (сг, т) сразу же	получаем дифферен¬
циальное уравнение
Sr+	У. aiy-^T+y [Ъ- г*'(а)]-^	=	0	(36)
да	д£1д&	^	1	v /J дР1
I, y=i	b	i=l	ь
и условия
ф(т, |, т) = 0,	(37)
Ф («7. £. чг) lse = 1 •	(38)

§ 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ Ш
Для того чтобы решить уравнение (36) при условиях
(37), (38), нужны некоторые вспомогательные построения.
Нашим первым шагом будет построение некоторого
специального решения уравнения
W+ 2 “"Пт"0	<39>
i, ;=1 ь
с начальным условием
ф0 (т, I, т) = 0.	(40)
От	координат	£г,	. . ., перейдем	линейным	преоб¬
разованием к координатам . . ., |п
Г^!1,	(41)
в которых уравнение (39) имеет вид
^+Лф„ = 0,	(42)
где А	— оператор	Лапласа. При таком	преобразовании
координат сфера Se перейдет, очевидно, в эллипсоид Se
с уравнением
^(I1)2-!-... +Ьп(Г)2 = е2,	(43)
где
А,1, Г	(44)
— собственные значения матрицы (а13).
Докажем сначала следующее предложение.
Лемма	1. Исчезающее в бесконечности решение
внешней задачи Дирихле для уравнения
K~_d2v .	d2v А	/7гч
^ я?? + • • • + 7-2 — 0	(45)
дЦ	д1п
с граничным	условием
° (I) ье =1	(46)
на эллипсоиде (43) имеет вид
^~|) = 8п"2^-- + «(1. 8).	(47)

362
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
где а— положительная константа, однозначно опреде¬
ляемая размералш эллипсоида (43); г (|) — расстояние от
точки | до начала координат; функция я (|, е) при
|||<1 удовлетворяет следующим неравенствам:
Г" & 6) I < М	-	||г « (!. е) | < М	,	(48)
i = 1, ..., п	(И = const).
При доказательстве этой леммы нам понадобится по¬
нятие потенциала двойного слоя. Напомним читателю
определение этого потенциала, а также некоторые его
свойства.
Пусть S — гладкая замкнутая поверхность, располо¬
женная в и-мерном пространстве и х = (хг, . .., х11) —
точка вне поверхности S. Координаты точек, лежащих
на поверхности S, мы всегда будем обозначать через
у1 f . . ., у1. Положим
е (*. y) = v (х1 - У1)2 + ...+(хп- Уп)г. (49)
Функция
1 '\
Я (*) = 5 —ftp-(У) ds,	(50)
S
где ^ обозначает производную по внешней нормали к по¬
верхности S, называется потенциалом двойного слоя,
создаваемым поверхностью S в точке х, а функция
ц (у) — его плотностью. Легко доказываются следу¬
ющие свойства потенциала двойного слоя:
1. Всюду вне поверхности S функция п(х) является
гармонической:
Дя(ж) = 0.	(51)
2. Потенциал двойного слоя имеет смысл, если вместо
х подставить любую точку у поверхности S. Величину
функции п(х) на поверхности S будем обозначать
через п0(у).
3. Функция п(х) имеет предел при стремлении точки
х к любой точке поверхности S извне. Если этот предел

§ 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 363
обозначать через яе(у), то имеет место формула
пе(у)= -2яр(у) + я0(у).	(52)
4.	Обозначим через ф (п, q) угол, составленный на¬
правлением нормали в произвольной точке у поверхности
S с радиусом-вектором q, проведенным из этой точки у
в точку х. Тогда потенциал двойного слоя может быть
представлен в виде
я(*)= ^ \1(у) dS•
Все эти свойства непосредственно выводятся из опре¬
деления потенциала двойного	слоя.	Доказательства
читатель может провести сам или прочесть их в каком-
либо учебнике по теории уравнений с частными произ¬
водными, например в цитированной книге С. JI. Собо¬
лева.
Доказательство леммы 1. Будем искать ре¬
шение уравнения (45) с граничным условием (46) в сле¬
дующем виде:
=	+	(М)
где а —пока неопределенная константа, а я (^—потен¬
циал двойного слоя, создаваемый эллипсоидом (43)
в точке | с неизвестной пока плотностью ц (ц) (через г]
мы обозначаем координаты точек, лежащих на эллипсои¬
де Sе). Так как я (|) в силу свойства 1	является реше-
нием уравнения (45), а функция	■ - _2 ^	также удовлет¬
воряет уравнению (45) (что легко проверить простым
диффенцированием), то функция v (|), определяемая фор¬
мулой (53), удовлетворяет уравнению (45).
Граничное условие (43) дает нам
я,(л) = 1-а-^-	(54)
Гп 2(л)
для любого г] g Se. Но, в силу свойства (3), по формуле

ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
(52) имеем:
-2пц(т|) + я0 (л) = 1-а--е"*
Г (г|)
(55)
Вводя обозначения:
(56)
получаем неоднородное интегральное уравнение для не¬
известной плотности ц(ц):
Уравнение (57) является интегральным уравнением Фред-
гольма второго рода. Для таких уравнений имеет место
Теорема Фредгольма. Для	раз решимости
уравнения (57) необходимо и достаточно, чтобы его сво¬
бодный член был ортогонален ко всем собственным функ¬
циям сопряженного однородного интегрального уравнения
Доказательство этой теоремы читатель может найти
в уже цитированной книге. Там же доказано, что
если ядро К (г), rij) определяется формулой (56), то урав¬
нение (58) имеет только одну собственную функцию.
Обозначим эту функцию через v0 (г]) и будем считать ее
известной.
Условие ортогональности, о котором идет речь в фор¬
мулировке теоремы Фредгольма, дает возможность опре¬
делить значение константы а, при котором уравнение (57)
разрешимо относительно |х(ц). В самом деле, запишем это
условие ортогональности:
иОп)=Д К (ri, rij^TijGWe + OOn).	(57)
(58)

§ 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 365
Отсюда
^ V0 (Г))
dS 8
а =
е»-Л v.W dS
J Гп 2
(Л) ^8
В этой формуле величина а, казалось бы, зависит от
е. Зависимость эта, однако, лишь кажущаяся. В самом
деле, обозначим через S эллипсоид
X1 (р1)2 + X2 (р2)2 + • • • + Xй (pn)2 = 1,	(59)
получающийся из эллипсоида Se увеличением всех осей
1
в — раз. Мы без труда обнаружим, что
^ vo (л)
dS
а = ^—=■—• (60)
МЛ) ,т.
\ —
J Гп"2
"2 (р)
S
clS
Таким образом, число а не зависит от е и полностью
определяется собственными значениями матрицы
В формуле (60) под v0 (р) мы понимаем собственную
функцию интегрального уравнения (58), записанного для
поверхности S.
Итак, функция у(|), заданная формулой (53), при
значении а, определяемом из (60), является решением
задачи (45) —(46). Остается лишь проверить неравен¬
ства (48). Но они непосредственно вытекают из опреде¬
ления функции зх(|). В самом деле,
Я(£)=Др(Т1)	-Ф-	dSe.	61
j PV ^en-i(£| л)
S.

366
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
Следовательно,
е”'1 (£■ пер) <
< Мгп 1——— ,	М, /V — постоянные.
г"'1 (6)
Доказанная лемма будет использована позже. Сейчас
же мы воспользуемся лишь константой а, определенной
в ходе доказательства леммы. Константу а мы назовем
размером эллипсоида (59); размер эллипсоида, таким
образом, гладко зависит от собственных значений
матрицы (аг;).
Переходим к построению специального решения урав¬
нения (39), удовлетворяющего начальному условию (40).
Обозначим через g (a, g, т, rj) фундаментальное реше¬
ние тг-мерного уравнения теплопроводности
Известно, что это фундаментальное решение имеет сле¬
дующее явное выражение:
g(a, I, х, т]) =	*	_ехр|-1^-М}	.	(63)
[2 л (0 — т)] 2
Положим теперь
-Д £(<*. Ь t, ц) [е"'2 ^?^=. + п(ц, в)] rft|, (64)
или иначе
Фо(ст> I- тг) = Фо((Т. £. т) + бфДа, I, т),	(65)
где

§ 41]
ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 367
Очевидно, что функция ф* (а, т) является решением
уравнения (62) и удовлетворяет начальному условию
Перейдем теперь от координат	£п	к	коорди¬
натам	£п. Пусть при этом функции ф* (а,	т),
ф0(а, 1, т), 6ф0*(ст, 1, т), g\a, т, ц) перейдут соответ¬
ственно в функции ф*(а, £, т), ф0 (сг, т), 6ф* (сг, £, т),
g (а, £, ц, т). Нам впоследствии понадобится явное выра¬
жение для функции ф0 (сг, т). Чтобы выписать его,
надо знать, как запишутся в координатах £1, .. ., £п
функции г(£) и g(a, £, т, ц). Но это легко выяснить.
В самом деле, обозначим через atJ- элементы матрицы,
обратной матрице (alJ), так что
ФоК 'х) = ° ПРИ а = т*
(67)
п
2	=	К-
3— 1
(68)
Тогда без труда можно убедиться, что
(69)
П
л -11 = [ 2	(л1	-	П	(V	-	I1)]2 •
г, 1=1
Учтем еще, что
*Xndi\.
(70)
Таким образом, функция ф0 (а, т) имеет следующее
явное выражение:

ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
где
g (су, 6, t, Т]) =
г, ;=1
[2я (т — а)]
Л еХ^ I	4	(т	—	а)
2
. (72)
Итак, доказана следующая
Лемма 2. Функция ф* = ср0 (а, £, т) + 6ф*, опреде¬
ленная формулами (65), (71), (72), является решением
уравнения
дф* . I. V аИ ^2(Ро — Q	(73\
и удовлетворяет нулевому начальному условию
ФоС*. Ь т) — 0-	(74)
Следует отметить, что функция ф* (ст, т) не равна
единице на сфере SE. Однако, как будет выяснено впо¬
следствии, ее граничное значение в некотором смысле
лишь несущественно отличается от единицы.
Теперь уже все подготовлено для решения уравне¬
ния (36). Сначала мы найдем некоторое специальное
решение уравнения (36), удовлетворяющее нулевому
начальному условию. Оценив затем граничное значение
этого специального решения, мы увидим, что оно лишь
несущественно отличается от единицы. Отсюда мы выве¬
дем, что и само это специальное решение лишь несуще¬
ственно, с точностью до величин более высокого порядка
малости, чем е, отличается от точного решения задачи (36),
(37), (38). После этого полученное специальное решение
будет упрощено путем отбрасывания некоторых членов и,
таким образом, мы получим приближенное решение
задачи (36), (37), (38).
Приступим к осуществлению этой программы.
Будем искать специальное решение уравнения (36),
удовлетворяющее нулевому начальному условию, в виде
Ф*(а, I, т) = ф*(<т, I, т) + ф*(сг, I, т),	(75)

% 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 369
где ф* —только что построенное решение уравнения (73),
удовлетворяющее условию (74), а ф* — пока неизвестная
функция. Непосредственно проверяется, что функция ф*
должна удовлетворять следующему неоднородному пара¬
болическому уравнению:
Решить задачу (76), (77) во всем пространстве R
с помощью формулы, аналогичной формуле (14) § 38,
оказывается невозможным, так как правая часть урав¬
нения (76) при £ = 0 имеет полюс порядка п, получаю¬
щийся при дифференцировании функции я (£, е). Однако
эту трудность можно обойти, так как мы желаем знать
решение ф* (сг, т) лишь вне шара, ограниченного сфе¬
рой Se. Для этого привлечем к рассмотрению функцию
д(ст, х, s, 2/), введенную в § 40 и равную плотности
вероятности того, что случайная точка Q, находящаяся
в момент времени а в положении х, будет в момент s
находиться в положении у, не встречаясь при этом на
протяжении времени a</<s с шаром 2Z(n радиуса е
с центром в управляемой точке z(l). Очевидно, функция
(см. формулы (32), (33)) является вне сферы Se фунда¬
ментальным решением уравнения (36) и удовлетворяет
граничному условию
п
i=l
frpn	(76)
и нулевому начальному условию:
фЩ> I, Т) = 0.
(77)
q*{o, I, s, i\) = q(o, |+z(ct), s, T]+z(s)) =
= q{a, x, s, у)
(78)
(79)
l/2 24 Л. С. Понтрягин

370
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
а решением задачи (76), (77) вне сферы Se будет функция
= j [ q* (a, I, s, г]) ^ (bl - zV(s)) *** (8’ T) ] di\, (80)
rr R_	I
где Re обозначает дополнение в R к шару, ограничен¬
ному сферой Se. Очевидно, что
где ф* (o', £, т) определена формулой (65), а ф* (су, т)
формулой (80), является решением уравнения (36), удов¬
летворяет нулевому начальному условию Ф (т, т) = 0
и имеет те от граничные значения на сфере Se, что
и функция ф* (сг, £, т).
Теперь мы докажем, что функция Ф* (а, £, т) вне
сферы радиуса rQ (г0 —любое конечное, не зависящее от
в число) аппроксимирует решение задачи (36), (37), (38).
Доказательство этого факта базируется на одной
важной лемме об оценке решений параболического урав¬
нения. Сформулируем эту лемму.
Лемма 4 (об оценке решений параболического урав¬
нения), Пусть и (о, т) — решение параболического урав¬
нения
фГ(сг, I, т) =
т
71
a Re
71	П
удовлетворяющее условиям
и(х, I, т) = 0,
И (O', I, Т) kess = w (О, т),
(83)
где
ад (а, т)<
const при х — о< е,
б (е)	при т — а > е
(84)

§ 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 371
(6(e)—>0 при е—>0). Тогда для решения и {а, £, т) спра¬
ведлива оценка
I и {о, I, т) I < А (|, е) + 6 (е) % (о, £, т),	(85)
где Д (£, г) — положительная функция, имеющая при всех
|£| > г0 порядок о(еп"2), а %(а, ч) — решение уравне¬
ния (82), имеющее при а — т нулевые начальные значения
и на сфере Se принимающее значение единица.
Доказательство леммы 4 не просто и требует значи¬
тельных вычислений. В них существенно используются
различные оценки для решений уравнения теплопровод¬
ности
da L	dln2 J
Мы начнем с вывода этих оценок.
Фундаментальное решение уравнения (86) обозначим
здесь через g (а, £, т, г]):
! _
g{a, I, х, г]) =	^т-а).	(87)
[2л (т — Ст)р
Положим, как и раньше, г (£) = "Щ1'2-)- ... + и введем
следующие обозначения:
С*7- Ь х) = Д (ст’ 5. "П. х) йт1>	(88)
Т
Q, (а, I, х) = ДД g (а, £, тр т) - J- dx\.	(89)
а
Чтобы интегралы, стоящие в правых частях формул (88)
и	(89),	имели	смысл, мы	должны,	конечно, считать,
что к < п.
Нам	нужны	будут следующие	три неравенства, оце¬
нивающие функции со Да, £,	т) и	£2.	(а, т) при усло¬
вии, что точка £ принадлежит сфере ДД
<0,tК I»	х)	<4? при т-а>е>	(9°)
Щ {<*> I.	х)	<4 при т-<х<8,	(91)
5 t Se 8
Qt(o. I.	О	<4^-	(92)
V	;	€ Se	е'1"2
24*

372
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
Здесь С константа, не зависящая от е, a 6(e)—>0 при
е->0.
Вывод неравенств (90), (91). Легко видеть, что
со/4(а,	1п,	т) = со. (a, г(£), 0, ..., 0, т) =
,	r	(Tll-r(|))2+(T]2)2+>,,+(T1n)2
=	—	\	е	4	-— ch\.	(93)
} J	г (л)
[2л (т —а)]2
Положим
г]г = v (Е,) х1 у х — o=-r2(Qt.	(94)
Тогда из (93) мы получим:
<оА(а, I, г) = -Д—V(f),	(95)
где
,	-	(х1-1)2+(х2)2+ ... +(ХП)2
vw = —nV	4' тпах- (96)
- J	rk (x)
(2л t)2
Очевидно, что
V(/)—>1 при t—>0.	(97)
Для дальнейшего еще отметим, что при больших значе¬
ниях t функция V (t) имеет следующую асимптотику:
vw = 0/4-V	(98)
Действительно, если в (96) сделать замену
2 1/Ту1 = х\
то получим:
К Г ~\[yl—^'|2+(у2)2+ ... +(г/™)21	!
v(o-4)‘ 11 ,ul hbid!/’ (99)
t2
где К— константа, откуда следует соотношение (98).
Итак, мы имеем:
«т. s. т) <	v (.f^r; •	(*оо)

§ 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 373
Но легко видеть, что имеют место оценки
)<6(е) при Т-(Т>8> )
Х-аЧ	>	601)
V (	)	<	const	при	Т	—	CJ	<	8,	J
откуда и вытекают неравенства (90) и (91). Одновре¬
менно мы видели, что всегда
<в,(а,	т)<-^	.	(102)
г" (£)
Вывод неравенства (92). Легко видеть, что
Я(ст, I1,	lh, T) = Qlt(o, r(Q, 0,	0,	т)	=
Г г	1	(Г|1-Г(6))3+(Ч2)2+	+(ЛП)2	,
= \ ds \	  е	4 (s-c>	——	dr\.
I *	5	r	(И)
[2л (s — 0)]
Полагая r\’ — г (%)х’, s — o — r2(Qt, мы получим отсюда
т—о
i*7&)
Q,(a, I, х) = ^— \ V(t)dt,	(103)
rk2(t) <]
где V —функция, определенная формулой (96). В част¬
ности,
т—a
iYWdL	(104)
Учитывая	теперь асимптотику	функции V (t)	при	боль¬
ших значениях I (см. формулу	(98)), мы сразу	получаем
неравенства
т—a
82
(v(/)d/<Clne	при А; = 2,	(105)
0
т—о
е2
^V(t)dt<C	при к >2,	(106)

374	ОДНА	СТАТИСТИЧЕСКАЯ ЗАДАЧА	[ГЛ. 7
из которых и следует неравенство (92). Одновременно
мы видели, что
(107)
гк(1)
Замечание к неравенствам (90), (91), (92).
Пусть р* (а, £, г], ^ — фундаментальное решение уравне¬
ния (82). Исходя из этого фундаментального решения,
определим функции соДо, £, т) и £2Дсг, ^ соответст¬
венно по формулам (88), (89) (поставив в них вместо
g(a, g, т, г]) функцию р* (о, ц, 5)). Оказывается, что
для определенных таким образом функций о)/Ч (о, t) и
Qt(o, т) справедливы те же неравенства (90), (91),
(92). Действительно, в теории параболических уравне¬
ний доказывается, что при ограничениях на коэффициен¬
ты уравнения (82), которые мы предположили выполнен¬
ными в § 39, фундаментальное решение уравнения (82)
мажорируется фундаментальным решением некоторого
уравнения теплопроводности, т. е. для него имеет место
неравенство
Р*(о, 5, л) <  пе х~° >
(Т-0)2
где у — константа. Эта оценка обеспечивает возможность
буквального повторения вычислений, проведенных при
выводе неравенств (90), (91), (92).
После этих предварительных оценок мы можем осу¬
ществить
Доказательство леммы 4. Положим
w(a,	х) = w1(a, т)	+ о;2(а,	т),	(108)
где функции wx (о, т) и со2 (сг, т) определены следующим
образом:
_	f	С	при т — а < е,
w1(o,	т) =	|	л	(109)
1V	'	(	0	при т—о > е;	v '
_	(	0	при т — о < в,
W2,	Т) =	* / ч	^	(НО)
(	6(e)	при	т —	о > е.	v
Решения уравнения (82), имеющие нулевые начальные

§ 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 375
значения и краевые значения w (а, т), w1{a, т), w2(a, т),
обозначим соответственно через и (a, g, т), иДо, g, т),
*). Очевидно, что
к (а, g, т^к^а, g, т) + н2(о, g, т). (Ill)
Далее, на основании теоремы о максимальном значении
решений параболических уравнений решение и (a, g, т)
задачи (82), (83) оценивается следующим образом:
и (a, g, т) < и {a, g, т).	(112)
Оценим отдельно функции ггДсг, g, т) и и2 (a, g, т).
Для и2 (a, g, т) оценка сразу получается из той же
теоремы о максимальном значении решения параболиче¬
ского уравнения:
и2(ог, g, т)<6 (е)х(Щ g, т).	(ИЗ)
Для получения оценки функции иг (a, g, т) требуют¬
ся более тонкие рассуждения. Прежде всего оценим
(сг, g, т) при т — a <s. Положим
=	(114)
где К = const > С. Будем теперь искать решение урав¬
нения (82) с начальными значениями, равными у (g), и
с граничным	значением на сфере Se,	равным	К,	в	виде
v{a, I,	т) = у С) + о0 (а,	I, т).	(115)
Тогда	для	функции	v0 (сг, g, т) сразу же получаем не¬
однородное уравнение
W+ S	»-$—Ыт<*я.
i,j= 1	&	S	i= 1
(116)
которое мы должны решить при нулевых начальных и
при нулевых граничных условиях. Такое решение, как

376	ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА	[ГЛ.	7
мы знаем, вне сферы Se дается формулой
т
v0(a> £• т) = — ^ ds ^ q('a’ ^ Ч) Ыу (л)] *1- (117)
G Re
Итак,
т
o0(o, I. *) = Y (Е)-Д 9 (о, I. s, ri)L[Y(r))]dri.
о Re
(118)
Очевидно, что
£» т)<1/(а, £, т).	(119)
Нам остается,	таким	образом, оценить лишь функцию
v(a> т) ПРИ 1£| > го* Сначала заметим, что
I L	[Y («11<е^[ 75^ + ^]	’	(120>
где Av А2— достаточно большие константы. Далее, будем
иметь в виду следующее неравенство:
9(°. I.	т, т|)<^(о, I, т, rj).	(121)
Тогда из формулы (118) получаем:
т
0(0, i, t)<y(£)+^*$ р(сг, £, 5, Tl) s’"1 ^l(Tj}- dx\ +
a Re
X
+ \ds p(a, I, s,	йц.
a Re
(122)
Интегралы, стоящие в правой части неравенства (122),
обозначим соответственно через Iv /2. Оценим отдельно
величины 1г и /2. Мы имеем:
т
/, <	\	ds	[	р(а,	I,	s, п) —zv ( )dr\ =
a r£	r	™
T
= ^e„-2-v ^ ds.un-v(<J, I, s) + o(en~2).	(123)

§ 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 377
Принимая во внимание неравенство (102), отсюда сразу
же получаем:
т
h < АС 7^7	[ds	+ o (en-2),	(124)
где 0< v < 1. Следовательно, при т —ст<е имеет место
оценка
n-1-v
I, < М- ,	(125)
1 r~-v (Б) ’	1	'
т. е.
/1 = 0(еп-2)	(126)
при |£|>г0. Аналогично получим:
/2 = о (еп~2)	(127)
при 1> г0. Таким образом, функция v(a, £, т), мажо¬
рирующая на границе сферы Se решение щ (о, т) при
|^| >г0 и при т — о<е, имеет порядок о(еп_2). Отсюда
следует, что и само решение иг(ау т) при т — о<е и
при 1£| > г0 имеет порядок o(sn_2). Несколько изменяя
предыдущее построение, можно легко убедиться в том,
что такая же оценка для иг (о, £, т) имеет место и при
т — а > е. Лемма доказана.
Теперь мы можем доказать, что функция Ф* (а,	т),
фигурирующая в формулировке леммы 3, вне сферы лю¬
бого конечного радиуса с точностью до величин порядка
о(еп"2) аппроксимирует решение задачи (36), (37), (38).
Иными словами, справедлива следующая
Лемма 5. Пусть ф(а, т) — решение уравнения (36),
удовлетворяюгцее начальным и граничным условиям (37),
(38), а Ф*(а, т) — решение уравнения (36), определен¬
ное в лемме 3. Тогда для любого г0, не зависящего от е,
при |£| >г0 решение Ф*(сг, т) с точностью до величин
порядка о(еп~2) аппроксимирует решение ф(а, £, т):
ф(<*> Ъ> т)-Ф* (а, I, т) = о(еп'2).	(128)
Доказательство. Обозначим через и (о, т)
разность функций <р и Ф*:
и (а, т) = ср(о, т)-Ф*(<т, I, х).	(129)
25 л. С. Понтрягин

378
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
Функция и(o', g, т) является решением уравнения (36)
и удовлетворяет нулевым начальным условиям. Далее,
из формулы (80) видно, что граничные значения функ¬
ции и (а, g,- т) на сфере Se совпадают с граничными значе¬
ниями функции ф (а, т) — фо (а, g, т). Оценим эти послед¬
ние. Для этого запишем разность ф —фо в следующем
виде:
Ф(а, g, т) —ф5(а, g, т) =
= {ф(«, Е, T)-[e”--^ + S(I, е)]| —
~ ^8 (<*• I» т> Л) [ 8”'2 г11 ° (-} я (Л. е) ]	(13°)
(см. формулу (64)). Граничные значения слагаемого,
заключенного в фигурные скобки в правой части форму¬
лы (130), равны нулю. Остается, таким образом, оценить
лишь граничные значения второго слагаемого на сфере
Se (в координатах g1, .. ., gn —на эллипсоиде Se). Так как
для потенциала двойного слоя я (|, е) имеет место оценка
(48), то, очевидно, мы получим:
\g(a>Z> т> Л) [е”"2-^у +Я(Л.8)] dn
<
<^вп-Чи2(<У, Е. т) +Оп-Ло, g, т),	(131)
где Аг и А2 — постоянные, a con_2 и con_j — функции, опре¬
деленные формулой (88) соответственно при к = п — 2,
к = п—1. Используя теперь неравенства (90) и (91),
сразу же получаем, что граничные значения второго
слагаемого в формуле (130), а следовательно, и гранич¬
ные значения со (а, т) функции и (а, g, т) удовлетворяют
условиям леммы 4. Следовательно, на основании леммы 4
об оценке решений параболического уравнения мы можем
заключить, что соотношение (128) справедливо. Лемма 5,
таким образом, доказана.
Теперь нам остается лишь упростить полученное
приближенное решение Ф* (a, g, т), отбросив в нем вели¬
чины, имеющие при | g | > >‘0 порядок о (еп_2). Чтобы
сделать это, выпишем решение Ф* (a, g, т) в явном виде.
Вспоминая формулы (63), (64), (65), (75), (80), мы можем

§ 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 37у
написать:
ф* (<У, £, т) = ф0 (а,	т) + 6ф5 (а, I,	т) +
X	П
+ $ds \q* (0’ ^^ 2 tfel _ z%' j~i.x
cr	Re	i=l	^
X[%(s,r\,T) + 6<p t]dr]. (132)
Прежде всего ясно, что при 111 > г0
вфо(а,£, т) = о(8п"2).	(133)
Несколько сложнее упрощается интеграл, стоящий
в правой части формулы (132). Во-первых, можно отбро¬
сить член
L	IV
/l= \ ds 5 q*^°' ^ 2 \.bi-z%’ (s)]
a RP
i= 1
дбф* (я, Л. т)
В самом деле,
1Л1<
<
Р* (а, 6, s, ii)2 I 1,1 ~ z%' (s)
С fio
Так как, далее,
2=1
дбф*
дк\
дбф? (s, 11, Т)
дт[1
<8"-^ (Л)
(134)
<*1.(135)
(136)
(см. (65), (66)), где i?(rj) в нуле имеет полюс порядка
не более чем п, то
X	П
Hi I < en_1_v ^ ds ^ р*(а, I, s, л) 2 [| ^—гг' (s) |
a	Re	i= 1
где	(rj)	имеет	теперь в нуле полюс	порядка не более
чем	п — v	(0 < v	< 1). Таким образом,
/1==о(еп-2).	(137)
25*

380
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 1
Нам остается теперь лишь упростить член
х
п
X
71
h = \ ds J р* (a, I, s, т))2 [V - z*' (s)] ф0 (s, ц, т) *]+
о	i=	1	^
-f о (еп~2).	(139)
I2=\ds\ р*(°> s> Tl) S	^-ФоО.	11.0^+
o	i=	1
т	n
+	q*^	^	t6*	_	z‘'	0)]	f-	Фо	(*>	л.	О	+
a	Re	i=1
x	n
+ J* \ P* (O, 6, s, л) 2 ^	^	(01	Фо	0>	л-	T)	*]•
rr	T> Г?	J — 1	*
Последнее слагаемое в формуле (140) имеет, очевидно,
порядок о(еп"2). Обозначим второе слагаемое через
и (а, £, т). Функция гг (о, g, т) при а = т имеет нулевые
начальные значения и является в области Re решением
уравнения (36). Так как
Мы имеем:
X
71
о R—Re
(140)
<в*-1Д(т|),
дч\J
(141)

$ 41] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ЧАСТНОМ СЛУЧАЕ 381
где R(r\) имеет полюс порядка не более чем п — 1, то
граничные значения функции и(сг,	т) оцениваются сле¬
дующим образом:
I и (a, I, X) I < Мгп-^ (a, g, т) .	(142)
Stoe	Stog
Из неравенств	(152), (92) мы заключаем, что
I в (о, I, х) | ^ < б (в),
где 6(e)—> О при е—>0. Следовательно, всюду в обла¬
сти Re
I и (о, g, т) | < 6 (е) ф (о, е, т).	(143)
Лемма 5	и	полученные неравенства (133), (137), (143)
доказывают следующую лемму.
Лемма 6. Функция
Ф (с, t т) = ф0 (а, |, т) +
Т	П
+ \ ds § р*(а’ ^ s’ ^ 2	(у)]	афо(^’.11’ х) dr\, (144)
i=l
где ф0 (сг, т) определена формулой (71), при 1£1 > г0
(где г0 — произвольное положительное не зависящее от е
число) с точностью до величин порядка малости о (еп_2)
аппроксимирует, решение ф(а, |,т) уравнения (36), удов¬
летворяющее начальному и граничному условиям (37), (38).
Чтобы подвести итог всем рассмотрениям настоящего
параграфа, нам остается вновь возвратиться к старым
координатам х и у согласно формулам (32), (33). Проведя
соответствующие замены, мы можем на основании леммы 6
формулировать теперь следующее предложение.
Теорема 26. Пусть движение управляемой точки z,
имеющей в начальный момент времени а положение z(o),
описывается системой дифференциальных уравнений (15).
Пусть, далее, в пространстве R движется также слу¬
чайная точка Q, плотность вероятности перехода которой
/?(о, х, s, у) удовлетворяет параболическому дифференци¬
альному уравнению (29) с постоянными коэффициентами.
Обозначим через 2Z шар радиуса е с центром в точке z,
движущийся вместе с ъ. Обозначим, далее, через ф(сг, xt т)

382	ОДНА	СТАТИСТИЧЕСКАЯ ЗАДАЧА	[ГЛ.	7
вероятность того, что случайная точка Q, находящаяся
в момент сг в положении х> на отрезке времени	т
будет «накрыта» шаром 2 . Тогда вероятность oj^ (су, я, т),
являющаяся функционалом над управлением u(t), представ¬
ляется при | # — z (а) | > г0, где /■ 0 — произвольное положи¬
тельное число, в следующем виде:
ф (сг, ж, г) = еп“2 [ф0 (сг, ж, т) + фх (а, ж, т)] + о (еп_2). (145)
Чтобы выписать явные выражения для функций ф0 (а, ж, т)
гг фх (аг, х, т), введем следующие обозначения:
а) А,1, А2, . . ., Ап — собственные значения матрицы (аг;);
б) (abj) — матрица, обратная матрице (а1})\
в) G (а, х, т, г|) == g (а, ж — z (а), т, ц) =
гг
2 «г HV — * 4 + (°)) (V — 3:4 + (®))
1	\	г=1	1	.
= з ехр|	4(^=5)	;	’
[2я (т— ст)]2
г) а—константа, не зависящая от системы уравне¬
ний (15) и определенная формулой (60).
Тогда
Фо (^’	=			^32 —
П
]>] агУ (я* —** (а)) (ад —^ (а))
_д,У=1	J
f S “uWl
o,;= 1 J
т	n
% (а, ж, t) = ( rfs С p (a,"x, s, y) 2 [V-z1' (s)] (ДУ’T) dy.
a	i=l	27
Таким образом, теорема 26 дает явное выражение для
главного члена вероятности ф(а, ж, т) и, следовательно,
для главного члена функционала (16).

§ 42] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ОБЩЕМ СЛУЧАЕ 383
§ 42. Вычисление функционала J в общем случае
В настоящем параграфе вероятность (ст, х, т), а сле¬
довательно, и функционал (16) будут вычислены для
случая, когда коэффициенты уравнения Колмогорова
зависят от а их. Мы предполагаем, что эти коэффициенты
удовлетворяют условиям 1) —3), сформулированным в§ 39.
Схема вычисления в значительной степени воспроизводит
схему, которой мы следовали в предыдущем параграфе.
Поэтому мы часто будем отсылать читателя к предыду¬
щему параграфу, проводя подробно лишь существенно
новые построения.
Итак, нам нужно решить уравнение
Как и в § 41, с помощью замен (32), (33), (35) приведем
эту задачу к задаче решения уравнения
п
п
при условиях
^ (<у, х, т)
-ф (тг, х, т) = О,
x£Sa
= 1.
(147)
(148)
П
П
+ 2 [Ь1 (1 + z (а), а) - %' (а)] -	=	0	(149)
i= 1
при условиях
<р (т, I, т) = О,
(150)

384	ОДНА	СТАТИСТИЧЕСКАЯ ЗАДАЧА	[ГЛ.	7
Перепишем уравнение (149) в несколько иной форме:
*Р + у a1 l(a,z(a))-?X:+
до '	^	v v п дЪУ dV
i, /= 1
+ 2 [ail((y^ + z(o))-ail(a>z(c))}-£^-+
i, i= 1
+ 2	S + z^-z1''(a)] -5_ = °-	(152)
1=1
Нашим первым шагом будет конструкция некоторого
специального решения (сг, £, т) уравнения
2 «и(0.Мб))—=°	(153)
да	i	д%1 д1>
с начальным условием
Ф§(т. т) = 0.	(154)
Для того чтобы получить это специальное решение,
как и в § 41, перейдем с помощью линейного преобразо¬
вания от координат g1, £2, |п к координатам f1,12, .
в которых уравнение (153) запишется следующим образом:
-^ + Дф0 = 0.	(155)
Такое преобразование координат теперь уже зависит от
параметра 0. Тогда сфера S8 перейдет в эллипсоид
К1 (0) (I1)2 + ... + Xя (0) (Г)2 = 8^,	(156)
причем А,1(0), ..., ^п(0) — собственные значения матрицы
(а13 (0, z(0))). Почти буквальным повторением рассуждений
предыдущего параграфа доказывается следующее пред¬
ложение.
Лемма 1'. Исчезающее в бесконечности решение
внешней задачи Дирихле для уравнения
d2v	d2v

§ 42] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ОБЩЕМ^ СЛУЧАЕ 385
с граничным условием
7(1)1й5,-1.	(«8)
где £8 — эллипсоид (84), имеет вид
=	+	(«9)
Здесь а (б)— положительная константа, гладко завися¬
щая от параметра 0, и однозначно определяемая разме¬
рами эллипсоида Se, г (£) = V(I1)21!-* • -+(£п)2> а функция
я(£, е) и ее производные оцениваются неравенствами (48).
Доказательство этой леммы не нуждается в поясне¬
ниях.
Константа а(0) вычисляется по формуле (60), если
под S понимать эллипсоид
(Q) (Ч1)2 + # _ + г (0) (rf)2 = 1.	(160)
Введем функцию g0 (сг, £, т, ц) по формуле (63) и положим
Ф„*8 (сг, I, т) = 8»"	+	я	(1,	8)	-
г" 2(Е)
- J g* (и, т, ц) [ е”"2 -JgL-+nb{, е)] ch\,
(161)
или иначе
Фо*в = Ф§ + йф?,	(162)
где
Ф«(<т, I т) = 8"-*-^-^ - $ g (сг, I, т, л)
(163)
Очевидно, что^ функция ф*0 (а, т) является решением
уравнения (153) и удовлетворяет нулевому начальному
условию:
Ф*0(т, |, т) = 0.	(164)

386
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
Перейдем теперь от координат g1, £2, .. ., £п к коорди¬
натам £2, . . ., £п. Пусть при этом функции ф*8 (a, §, т),
Ф9, 6ф*°, g9.перейдут соответственно в функции ф*9 (а,	т),
Ф§> бфо0. £0- ^ьт можем выписать функцию ф*9 (сг, £, т)
в явном виде. Для этого, как и раньше, обозначим через
аи(0, z(0)) элементы матрицы, обратной матрице (alj (0, z(0))),
так что
У а1'(6, 2(0))а,,,(0, z(0)) = б1
;=1
Тогда
ф?(сг, S, г) = 8
п-2 _
а (8)
[ У аи (0, a (0)) Щ
i,j= 1
п—2
“2“
а(0) V" Я,1 (9) ... Хп (0)
[ У аИ (0> 2 (0)) 'П1’!
i, ;=1
п-2 ’
П 2
(165)
(166)
У <Ч;(0, 2(0)) W-Г) W-^')
i, У=1
4 (т — а)
(167)
где
=	"	пехР]
[2я (т — с)]2
Рассмотрим теперь функцию ФоСГ(ог> t), т. е. построен¬
ную функцию при значении параметра 0, равном а. Функ¬
ция Фоа(с», £, т) уже не удовлетворяет уравнению (153),
в коэффициентах которого вместо 0 подставлено а. Однако,
очевидно, справедлива следующая
Лемма 2'. Функция ф*а (сг, |, т) = ф£(ст, т) + йф*а,
где фо определена формулами (176), (177), (166), (167),
является решением дифференциального уравнения
°Фо
да
У aiy(<7, z(<r))
d2cpjc
г, 7=1
<90
Ке] „=а = 0 (168)

§ 42] ВЫЧИСЛЕНИЕ ФУНКЦИОНАЛА J В ОБЩЕМ СЛУЧАЕ 38'
и имеет нулевые начальные значения:
Теперь, как и в предыдущем параграфе, мы можем
искать специальное решение уравнения (149), имеющее
нулевые начальные значения, в следующем виде:
где ф*ог(сг, т) —только что построенное нами решение
уравнения (167), а ф* —пока неизвестная функция. Под¬
ставляя Ф* (сг, £, т) в уравнение (149) и учитывая лемму 2',
получим для ф* (а, т) следующее неоднородное пара¬
болическое уравнение:
Так как правая часть уравнения (171) имеет при £ = 0
полюс порядка лишь п (а не тг + 1), то мы можем
почти буквально повторить все рассуждения предыду¬
щего параграфа и доказать леммы, аналогичные леммам 3,
5, 6. Лемма, соответствующая лемме 6, формулируется
теперь следующим образом:
Ф? (сг, I, т) = 0 при а = т.
(169)
Ф*(ст, т) = ф*а(сх, I, т) + ф*(а, £, т),	(170)
п
5ср*
да
П
П
d<?*a(a,t х)
ag* d\i
г, j=i
n
g<Po*q (g, I. t)
dV
и начальное условие
<рГ (t, I, т) = 0.
(172)

38 Ь
ОДНА СТАТИСТИЧЕСКАЯ ЗАДАЧА
[ГЛ. 7
Лемма 6'. Функция
Ф (а, т) = ф® (а, I, т) +
X
п
+ ^ ds р (cr, I + Z (а), 5, Т] + Z (s)) | 2 [aii (*> Л + 2 (6‘)) -
где ф£ (сг, £, т) определена формулой (166)при 1£1 > г0 (г0 —
произвольное положительное число, we зависящее от е)
с точностью до величин порядка малости о (еп~2) аппро¬
ксимирует решение ф (а, £, т) уравнения (149), удовлетво¬
ряющее начальным и граничным условиям (150), (151).
Чтобы формулировать теперь окончательный резуль¬
тат, мы вновь должны перейти к координатам х и у по
формулам (31), (32). Тогда из леммы 6' следует теорема,
аналогичная теореме 26 предыдущего параграфа. Мы не
будем здесь выписывать окончательные формулы, так
как при желании читатель легко может сделать это сам.
а
п
дфо (s, Г], Т)
дцJ
(173)

ЛИТЕРАТУРА
К главе 1
1. Бсллман Р., Динамическое программирование, ИЛ, Москва,
1960.
2. Bellman R. Е., Glicksberg I., Gross О. A., Some
aspects of the mathematical theory of control processes, The
RAND corporation, Santa Monica, California, 1958.
3. Болтянский В. Г., Г а м к p e л и д з e Р. В., П о н т р я-
г и н Л. С., К теории оптимальных процессов, Доклады
Ак. наук СССР, 110, № 1 (1956), стр. 7 — 10.
4. Б о л т я и с к и й В. Г., Принцип максимума в теории опти¬
мальных процессов, Доклады Ак. наук СССР, 119, № 6 (1958),
стр. 1070 — 1073.
5. Болтянский В. Г., Гамкрелидзе Р. В., Понтря-
гин Л. С., Теория оптимальных процессов. I. Принцип
максимума, Изв. Ак. наук СССР, серия матем., 24, № 1
(1960), стр. 3 — 42.
6. Болтянский В. Г., Гамкрелидзе Р. В., Мищен¬
ко Е. Ф., Понтрягин Л. С., Принцип максимума в тео¬
рии оптимальных процессов, Первый конгресс ИФАК, Москва,
1960.
7. Гамкрелидзе Р. В., К общей теории оптимальных
процессов, Доклады Ак. наук СССР, 123, № 2 (1958), стр 223 —
226.
8. К р а с о в с к и й II. II., К теории оптимального регулирования,
Автоматика и телемеханика, 18, № И (1957), стр. 960 —970.
9. П о II т р я г и и Л. С., Оптимальные процессы регулирования,
Успехи матем. наук, 14, вып. 1 (1959), стр. 3 — 20.
10.	Розоноэр Л. И., Принцип максимума Л. С. Понтрягина
в теории оптимальных систем. I, II, III, Автоматика и теле¬
механика, 20, №№ 10 —12 (1959), стр. 1320—1334, 1441—1458,
1561-1578.
К главе 2
См. [4], [5], [7], [9].

390
ЛИТЕРАТУРА
К главе 3
См. [2], [6], [9].
11. Болтянский В. Г., Моделирование линейных оптималь¬
ных быстродействий при помощи релейных схем, Доклады
Ак. наук СССР, 139, № 2 (1961), стр. 19—22.
12. Bus haw D. W., Ph. D. Thesis, Department of Math. Prin¬
ceton Univ., 1952.
13. Гамкрелидзе P. В., К теории оптимальных процессов
в линейных системах, Доклады Ак. наук СССР, 116, № 1 (1957),
стр. 9 — И.
14. Гамкрелидзе Р. В., Теория оптимальных по быстродей¬
ствию процессов в линейных системах, Т1зв. Ак. наук СССР,
серия матем., 22, № 4 (1958), стр. 449 — 474.
15. La Salle J. P., The Time Optimal Control Problem, Contri¬
butions to the Theory of Nonlinear Oscillations, V, Princeton,
1959.
16. Фельдбаум А. А., О синтезе оптимальных систем с по¬
мощью фазового пространства, Автоматика и телемеханика,
16, № 2 (1955), стр. 129 — 149.
К главе 4
См. [5]
17. Б о л т я и с к и й В. Г., Оптимальные процессы с параметрами,
Доклады Ак. наук Узб. ССР, № 10 (1959), стр. 9 —13.
18. Б о л т я н с к и й В. Г., Применение теории оптимальных про¬
цессов к задачам приближения функций, Труды Матем. ин-та
им. В. А. Стеклова, 60, стр. 82—95.
19. X а р а т и ш в и л и Г. Л., Принцип максимума в теории
оптимальных процессов с запаздыванием, Доклады Ак. наук
СССР, 136, № 1 (1961), стр. 39-42.
К главе 5
20. Блисс Г. А., Лекции по вариационному исчислению, ИЛ,
Москва, 1950.
21. Me Shane, On Multipliers for Lagrange Problem, Amer.
Journ. Math., 61 (1939), стр. 809 — 819.
К главе 6
22. Гамкрелидзе Р. В., Оптимальные по быстродействию
процессы при ограниченных фазовых координатах, Доклады
Ак. наук СССР, 125, № 3 (1959), стр. 475 — 478.
23. Гамкрелидзе Р. В., Оптимальные процессы управления
при ограниченных фазовых координатах, Изв. Ак. наук СССР,
серия матем., 24, № 3 (1960), стр. 315 — 356.
24. Л е р и е р А. Я., О предельном быстродействии систем авто¬
матического управления, Автоматика и телемеханика, 15,
№ 6 (1954), стр. 461 — 477.

ЛИТЕРАТУРА
391
25. Розенман Е. А., О предельном быстродействии следящих
систем с ограниченным по мощности, моменту и скорости
исполнительным элементом, Автоматика и телемеханика, 19,
№ 7 (1958), стр. 633 — 653.
К главе 7
26. Kolmogoroff A. N., Ober die analytischen Met] oden
in der Wahrscheinlichheitsrechnung, Math. Ann., 104
(1931).
27. Мищенко E. Ф., Понтрягин JT. С., Одна статистиче¬
ская задача оптимального управления, Доклады Ак. наук СССР,
128, № 5 (1959), стр. 890-892.
28. Мищенко Е. Ф., П о н т р я г и н JT. С., Об одной стати¬
стической . задаче оптимального управления, Изв. Ак. наук
СССР, серия матем., 25 (1961).

Понтрягин Лев Семенович,
Болтянский Владимир Григорьевич,
Гамкрелидзе Реваз Валерианович,
Мищенко Евгений Фролович.
Математическая теория
оптимальных процессов.
Редактор Н. X. Розов.
Техн. редактор К. Ф. Брудно.
Корректор Л. О. Сечейко.
Сдано в набор 12/Y 1961 г. Подписано к печати
23/VIII 1961 г. Бумага 84 x108/32. Физ.
печ. л. 12,25. Условн. печ л. 20,09. Уч.-изд.
л. 18.66.Тираж 10000 экз. Т-08737.
Цена книги I р. 13 к. Заказ 1036.
Государственное издательство
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Московская типография № 5 Мосгорсовнархоза.
Москва, Трехпрудный пер., д. 9.