Author: Хатчер А.
Tags: алгебра геометрия топология высшая математика
ISBN: 978-5-94057-748-5
Year: 2011
Text
b^A.WiH ИЗ IMS,
АЛГЕБРАИЧЕСКАЯ
ТОПОЛОГИЯ
А. Хатчер
АЛГЕБРАИЧЕСКАЯ ТОПОЛОГИЯ
Перевод с английского В. В. Прасолова
Под редакцией Т. Е. Панова
Москва
Издательство МЦНМО
2011
УДК 512.515.14
ББК 22.152
Х25
Хатчер А.
Х25 Алгебраическая топология / Пер. с англ. В. В. Прасолова
под ред. Т. Е. Панова. — М.: МЦНМО, 2011. — 688 с: ил.
ISBN 978-5-94057-748-5
Книга представляет собой введение в алгебраическую топологию (до
спектральных последовательностей), включающее в себя как
гомотопическую топологию, так и теорию гомологии и когомологий (в том числе
двойственность Пуанкаре). Ориентированное на геометрические
аспекты предмета изложение является тем не менее строгим и подробным.
В книге имеется большое количество примеров и упражнений; в
дополнениях, занимающих почти половину книги, затрагиваются различные
более продвинутые сюжеты (когомологий с локальными коэффициентами,
теорема Брауна о представимости, когомологические операции, спектры
и пр.).
Для студентов Старших курсов, аспирантов и научных работников.
ББК 22.152
Algebraic Topology
ALLEN HATCHER
(Cambridge
UN1VIMITY ГАЕМ
Translation from the English language edition:
Algebraic topology by Allen Hatcher.
Cambridge University Press, 2002.
Аллен Хатчер
Алгебраическая топология
Подписано к печати 07.02.2011 г. Формат 70 х 100/16. Печать офсетная.
Объем 43 печ. л. Тираж 1000 экз. Заказ № 3655
Издательство Московского центра непрерывного математического образования.
119002, Москва, Бол. Власьевский пер., 11. Тел.: (499) 241-74-83.
Отпечатано с готовых диапозитивов в ГУЛ «Типография „Наука"».
199034, Санкт-Петербург, В. О., 9 линия, 12.
Книги издательства МЦНМО можно приобрести в магазине «Математическая книга»
Большой Власьевский пер., д. 11. Тел. (499) 241-72-85. E-mail: biblio«mccme .ru
ISBN 0-521-79160-Х
ISBN 978-5-94057-748-5
© Cambridge University Press, 2002.
© МЦНМО, 2011.
Оглавление
Предисловие 6
Глава О
Основные геометрические понятия 9
Гомотопии и гомотопический тип 9
Клеточные комплексы 13
Операции над пространствами 17
Два признака гомотопической эквивалентности 21
Свойство продолжения гомотопии 25
Глава 1
фундаментальная группа и накрытия 34
§ 1.1. Основные конструкции 38
Пути и гомотопии 39
Фундаментальная группа окружности 43
Индуцированные гомоморфизмы 50
§ 1.2. Теорема ван Кампена 57
Свободные произведения групп 58
Теорема ван Кампена 61
Приложения к клеточным комплексам 70
§1.3. Накрытия 77
Определения и примеры 77
Свойства поднятия 82
Классификация накрытий 85
Преобразования накрытий и действия групп 95
Дополнение ПО
§ 1.А. Графы и свободные группы НО
§1.В. Пространства K(G, 1) и графы групп 115
Глава 2
Гомологии 128
§ 2.1. Симплициальные и сингулярные гомологии . 133
А-комплексы 134
Симплициальные гомологии 137
Сингулярные гомологии 141
Гомотопическая инвариантность 145
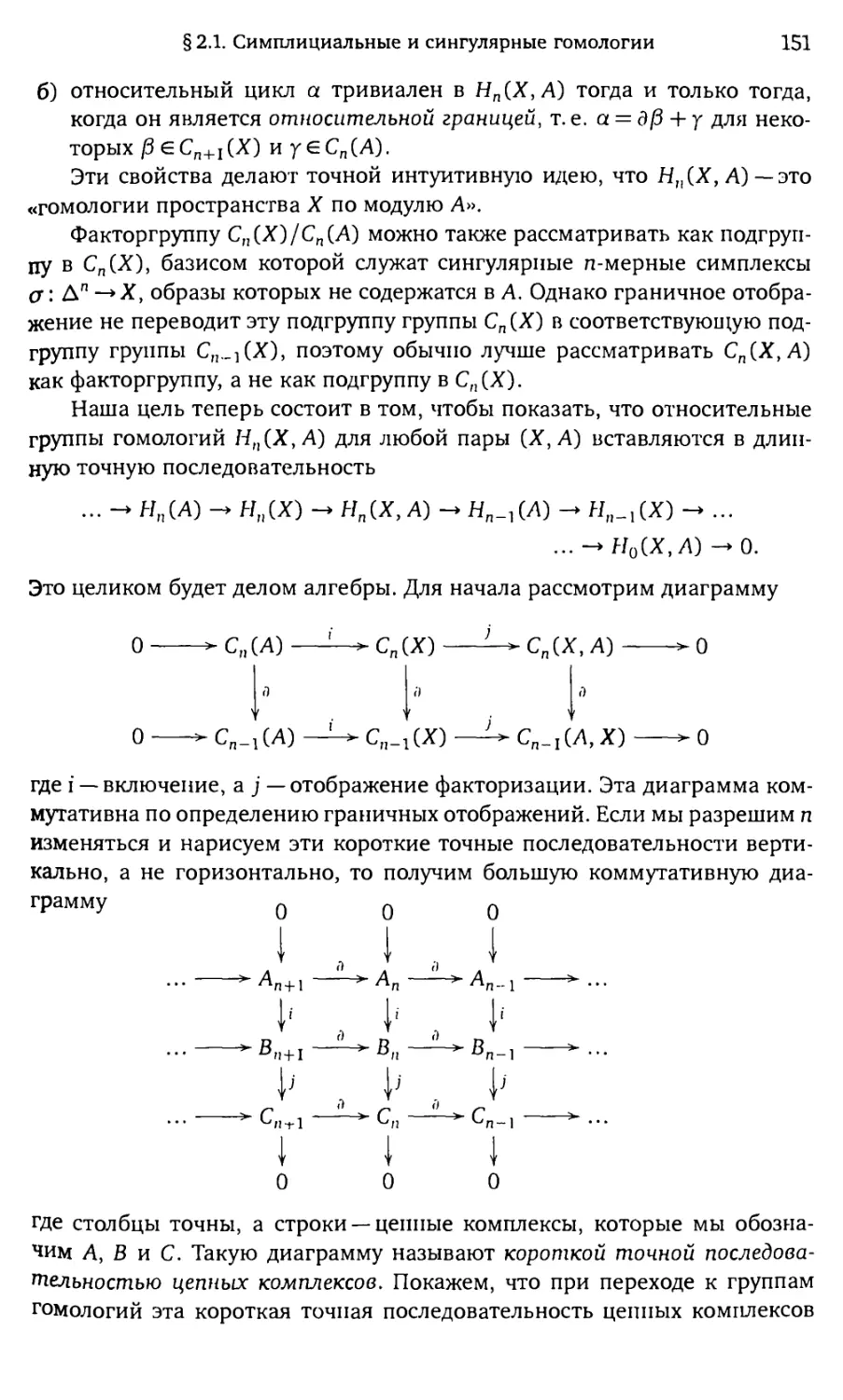
Точные последовательности и вырезание 148
Эквивалентность симплициальных и сингулярных гомологии 167
§ 2.2. Вычисления и приложения 174
Степень 174
Клеточные гомологии 178
Последовательности Майера—Вьеториса 193
Гомологии с коэффициентами 197
§ 2.3. Формальная точка зрения 206
Оглавление
Аксиомы гомологии 207
Категории и функторы ...... 209
Дополнение 214
§ 2.А. Гомологии и фундаментальная группа 214
§ 2.В. Классические приложения 217
§ 2.С. Симплициальная аппроксимация 227
Глава 3
Когомологий 238
§р.1. Группы когомологий 244
Теорема об универсальных коэффициентах 244
Когомологий пространств 253
§ 3.2. Умножение в когомологиях 264
Кольцо когомологий 271
Формула Кюннета 278
Пространства с полиномиальными когомологиями 285
8*3.3. Двойственность Пуанкаре 294
Ориентация и гомологии 297
Теорема двойственности 305
Связь с ^-произведением 317
Другие виды двойственности 322
Дополнение 332
§ З.А. Универсальные коэффициенты для гомологии 332
§ З.В. Общая формула Кюннета 340
§ З.С. Я-пространства и алгебры Хопфа 358
§3.D. Когомологий SO(n) 372
§З.Е. Гомоморфизмы Бокштейна 385
§3.F. Пределы и Ext 394
§ 3.G. Трансфер 407
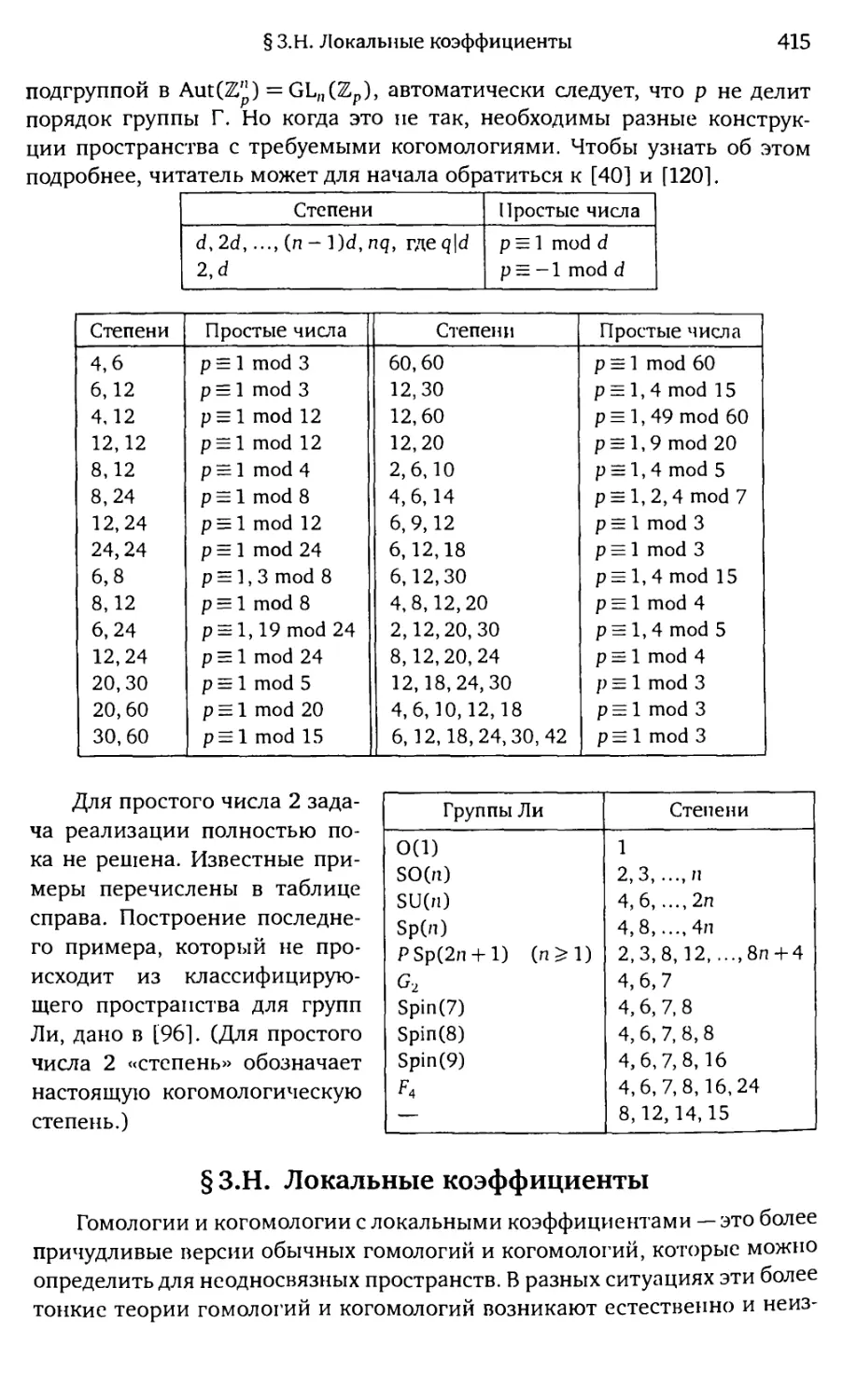
§ З.Н. Локальные коэффициенты 415
Глава 4
Теория гомотопий 428
§4.1. Гомотопические группы 430
Определения и основные конструкции 431
Теорема Уайтхеда 439
Клеточная аппроксимация 441
CW-аппроксимация 445
$ty.2t Элементарные методы вычислений 456
Вырезание для гомотопических групп 456
Теорема Гуревича 464
Локально тривиальные расслоения 474
Стабильные гомотопические группы 486
§ 4.3. Связь с когомологиями 497
Гомотопическое построение когомологий 498
Расслоения в смысле Гуревича 512
Башни Постникова 518
Теория препятствий 525
Дополнение 533
§4.А. Отмеченные точки и гомотопии 533
§ 4.В. Инвариант Хопфа 540
§4.С. Минимальные клеточные структуры 542
§4.D. Когомологии локально тривиальных расслоений 546
§4.Е. Теорема Брауна о представимости 567
§4.F. Спектры и теории гомологии 573
§4.G. Конструкции склейки 577
§4.Н. Двойственность Экмана—Хилтона 583
§4.1. Стабильные расщепления пространств 591
§ 4. J. Пространство петель для надстройки 595
§4.К. Теорема Дольда—Тома 601
§4.L. Квадраты и степени Стинрода 616
Приложение 658
Топология клеточных комплексов 658
Произведения CW-комплексов 664
Евклидовы окрестностные ретракты 666
Пространства, доминируемые CW-комплексами 669
Литература 676
Предметный указатель 682
Предисловие
Эта книга написана как доступное введение в алгебраическую
топологию с достаточно широким охватом этого предмета. Наш поход вполне
классический по духу и полностью остаётся в рамках чистой
алгебраической топологии. В некотором смысле, такая книга могла бы быть написана
30 или 40 лет назад, поскольку практически весь материал в ней по
крайней мере такой давности. Однако прошедшие годы помогли прояснить,
какие именно результаты и какая техника наиболее важны. Например,
CW-комплексы выдержали проверку временем как наиболее
естественный класс пространств для нужд алгебраической топологии, поэтому им
здесь уделяется гораздо больше внимания, чем в книгах прежнего
поколения. Это внимание показывает также направленность книги скорее на
геометрическую, чем на алгебраическую сторону предмета. Геометрия
алгебраической топологии столь красива, что было бы жаль пренебречь ей
и пропустить все те интуитивные представления, которые она предлагает.
На элементарном уровне алгебраическая топология естественно
разделяется на два широких русла — гомотопии и гомологии. В нашей
книге материал разделён на четыре главы, приблизительно по возрастанию
сложности, причём гомотопии распределены по главам 1 и 4, а
гомологии и их зеркальная версия, когомологии, — по главам 2 и 3. Однако эти
четыре главы не обязательно читать подряд. Можно начать с гомологии
и даже продолжить когомологиями, прежде чем обратиться к гомотопиям.
И наоборот, можно отложить гомологии и когомологии вплоть до
последних частей главы 4, причём если такую стратегию довести до её
естественного предела, то гомологии и когомологии можно ввести просто как
разделы теории гомотопии. Такой подход, хотя он и привлекателен с чисто
логической точки зрения, предъявляет больше требований к читателю,
а поскольку доступность является одним из главных приоритетов этой
книги, гомотопическая интерпретация гомологии и когомологии описана
уже после того, как эти теории были разработаны независимо от теории
гомотопии.
Перед этими четырьмя основными главами идёт предварительная
глава 0, в которой вводятся основные геометрические понятия и
конструкции, играющие главную роль как в гомотопических, так и в
гомологических сторонах предмета. Её можно либо прочитать до остальных глав,
либо пропустить и возвращаться к ней за справками по поводу именно
тех тем, в которых возникает потребность в последующих главах.
Каждая из четырёх основных глав завершается набором
дополнительных тем, которые читатель может выбирать по своему усмотрению,
независимо от основного ядра этой книги, содержащегося в предшествующих
Предисловие
7
частях глав. Многие из этих дополнительных тем в действительности
весьма важны в общей структуре алгебраической топологии, хотя они могут
и не втиснуться в сжатые по времени рамки вводного курса. В целом эти
дополнительные темы составляют почти половину книги, и они включены
сюда как для того, чтобы сделать книгу более исчерпывающей, так и для
того, чтобы предоставить читателю, который найдёт время в них
углубиться, более содержательные образцы истинного богатства и красоты
этого предмета.
Не включена в эту книгу важная, но несколько более изощрённая
тема — спектральные последовательности. Было очень соблазнительно
включить сюда что-нибудь об этом изумительном инструменте, но
спектральные последовательности —это столь обширная тема, что
представляется более предпочтительным начать ими заниматься в новом томе.
Он условно назван «Спектральные последовательности в алгебраической
топологии» (Spectral Sequences in Algebraic Topology) и в дальнейшем мы
ссылаемся на него как на [SSAT]. Готовится также третья книга, о
векторных расслоениях, характеристических классах и JC-теории, которая
будет в основном независима от [SSAT] и от большей части этой книги.
На неё мы ссылаемся как на [VBKT], а её предварительное название —
«Векторные расслоения и К-теория» (Vector Bundles and К-Theory).
Что касается предварительных сведений, в этой книге
предполагается, что читатель знаком с содержанием стандартных университетских
курсов по алгебре и теоретико-множественной топологии. В частности,
читатель должен иметь представление о факторпространствах, которые
весьма важны для алгебраической топологии. Это понятие хорошо
изложено1 в учебниках [7] и [39], указанных в списке литературы.
В книгах такого рода, как эта, целью которых является изложение
классического материала с весьма классической точки зрения, не место
для необузданных увлечений новшествами. Тем не менее, здесь есть
одна новая особенность изложения, которая заслуживает упоминания, хотя
в книге в целом она играет сравнительно небольшую роль. Это
—небольшое расширение классического понятия симплициального комплекса,
которое появляется в этой книге под названием Д-комплекс. Идея состоит
в том, чтобы отождествлять различные грани симплекса, так что
только внутренности симплексов вложены, и симплексы больше не
определяются единственным образом своими вершинами. (С технической
точки зрения упорядочение вершин каждого симплекса тоже является
частью структуры Д-комплекса.) Например, если взять стандартную
картинку тора как квадрата с отождествлёнными противоположными
сторонами и разделить его диагональю на два треугольника, то в результате
1 См. также О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов «Элементарная
топология» (М.: МЦНМО, 2010).— Прим. ред.
8
Предисловие
мы получим структуру Д-комплекса на торе, имеющую 2 треугольника,
3 ребра и 1 вершину. В противоположность этому, известно, что структура
симплициального комплекса на торе должна иметь по крайней мере 14
треугольников, 21 ребро и 7 вершин. Поэтому Д-комплексы
существенно повышают эффективность, что очень приятно с педагогической точки
зрения, поскольку это сокращает скучные вычисления в примерах.
Более основательная причина для рассмотрения Д-комплексов заключается
в том, что они представляются более естественными объектами с точки
зрения алгебраической топологии. Они являются естественной областью
определения для симплициальных гомологии, и многие стандартные
конструкции дают скорее Д-комплексы, нежели симплициальные
комплексы; например, сингулярный комплекс пространства или
классифицирующее пространство дискретной группы или категории. Несмотря на эту
естественность, Д-комплексы явно появлялись в литературе лишь изредка
и для них нет ещё стандартного названия.
Эта книга останется доступной в электронном виде и после того, как
будет издана традиционным образом. Адрес в Интернет такой: http://
www.math.cornell.edu/~hatcher Здесь также можно найти те части двух
других книг из этой серии, которые уже готовы. Хотя эта книга и
прошла через бесчисленные проверки, включая исправление многих мелких
ошибок, как типографских, так и математических, обнаруженных
внимательными читателями предыдущих версий, некоторые ошибки неизбежно
останутся, поэтому страница в Интернет будет содержать список опечаток
в изданной версии. Имея электронную версию, можно не только
исправить опечатки, но и сделать более существенные исправления и
дополнения. Просьба к читателям присылать замечания и предложения, а также
исправления по адресу электронной почты, указанному на моей странице
в Интернет.
Глава О
Основные геометрические понятия
Цель этой короткой вводной главы — ввести некоторые наиболее
общие геометрические понятия и конструкции в алгебраической топологии.
Изложение до некоторой степени неформальное, без теорем и
доказательств вплоть до нескольких последних страниц, и его следует читать
в таком же неформальном стиле, пропуская отдельные куски то здесь, то
там. На самом деле всю эту главу можно сейчас пропустить и обращаться
к ней позже по поводу основных определений.
Чтобы не злоупотреблять словом «непрерывный», мы принимаем
соглашение, что отображения между пространствами всегда
предполагаются непрерывными, если не оговорено противное.
Гомотопии и гомотопический тип
Одна из основных идей алгебраической топологии состоит в том,
чтобы рассматривать два пространства как эквивалентные, если они имеют
«одинаковую форму» в некотором смысле, более широком, чем
гомеоморфизм. Привести пример из обыденной жизни: буквы латинского алфавита
можно написать либо как объединения конечного числа прямолинейных
и криволинейных отрезков, либо в утолщённом виде как компактные
подмножества плоскости, ограниченные замкнутыми несамопересекающи-
мися кривыми. В каждом случае тонкая буква является подпространством
толстой буквы, и мы можем непрерывно сжать толстую букву в тонкую.
Хороший способ сделать это — представить толстую букву (назовём её X)
в виде объединения отрезков, соединяющих внешнюю границу буквы X
с единственной точкой внутренней тонкой буквы X, как показано на
рисунке. Затем мы можем сжать X на X, сдвигая каждую точку пространства
X — X до X вдоль отрезка, который её содержит. Точки, которые уже лежат
в X, не двигаются.
10 Глава 0. Основные геометрические понятия
Мы можем считать, что этот процесс продолжается во временном
интервале 0 ^ t ^ 1, и тогда он определяет семейство отображений ft: X —> X,
зависящих от параметра t е/ = [0,1], где ft(x) — это точка, в которую
данная точка х £ X передвигается за время t. Конечно, мы бы хотели, чтобы
точка ft(x) непрерывно зависела как от t, так и от х, и это будет
достигнуто, если мы будем двигать каждую точку xgX-X вдоль соответствующего
отрезка с постоянной скоростью так, чтобы она попала в свой образ в X
в момент t = 1, а все точки х е X будут неподвижны, как уже упоминалось.
Примеры такого рода приводят к следующему общему определению.
Деформационная ретракция пространства X на подпространство Л — это
семейство отображений /t: X —> X, t е /, для которого /0 = 1
(тождественное отображение), /i(X) = А и ft\A = 1 для всех t. Семейство /t должно
быть непрерывно в том смысле, что отображение Хх/^Х, заданное
формулой (х, 0 —►/гОО, непрерывно.
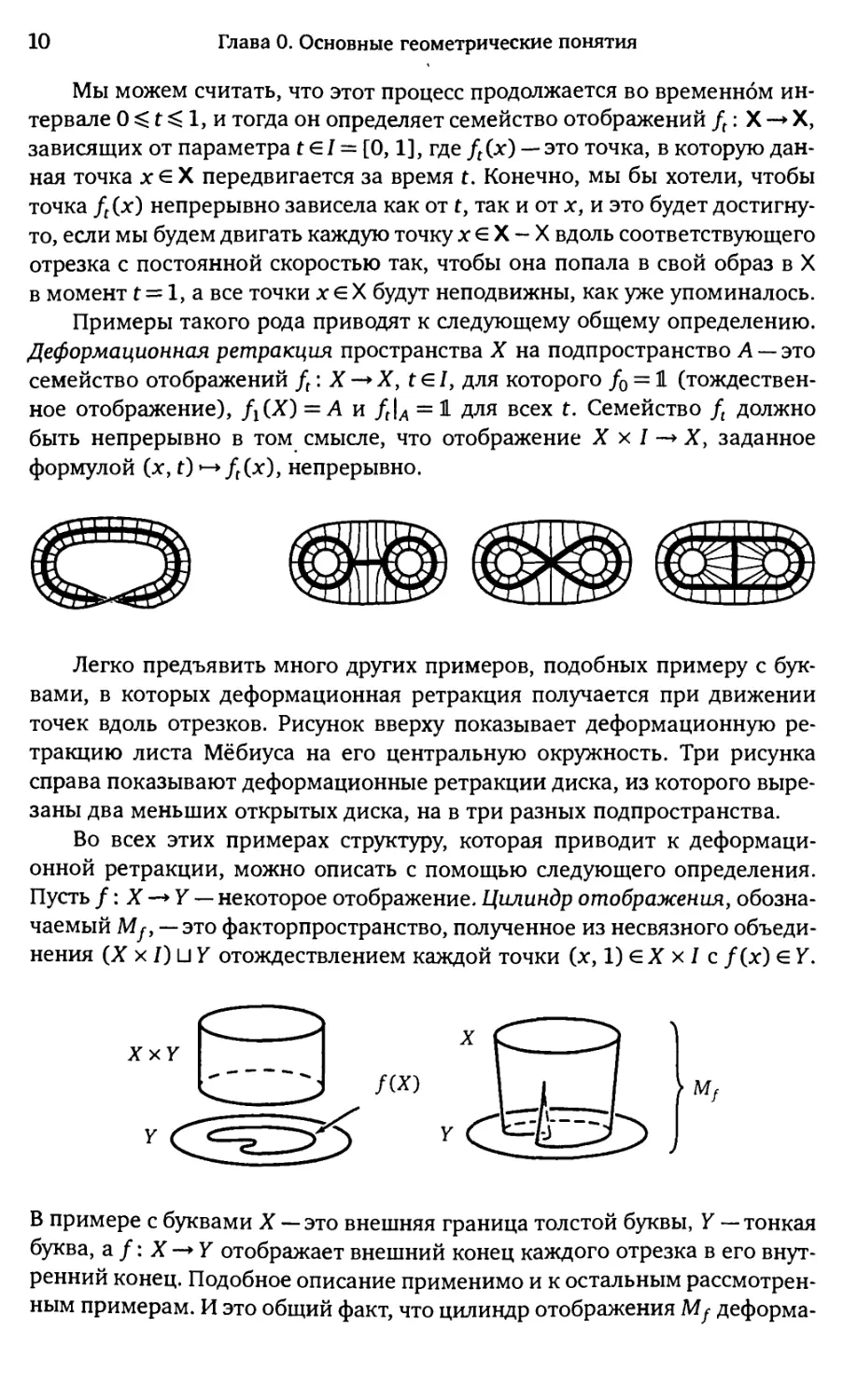
Легко предъявить много других примеров, подобных примеру с
буквами, в которых деформационная ретракция получается при движении
точек вдоль отрезков. Рисунок вверху показывает деформационную
ретракцию листа Мёбиуса на его центральную окружность. Три рисунка
справа показывают деформационные ретракции диска, из которого
вырезаны два меньших открытых диска, на в три разных подпространства.
Во всех этих примерах структуру, которая приводит к
деформационной ретракции, можно описать с помощью следующего определения.
Пусть /: X —► Y — некоторое отображение. Цилиндр отображения,
обозначаемый My, — это факторпространство, полученное из несвязного
объединения (X х /) u Y отождествлением каждой точки (х, 1) е X х / с /(*) е Y.
В примере с буквами X — это внешняя граница толстой буквы, Y —тонкая
буква, а /: X —> Y отображает внешний конец каждого отрезка в его
внутренний конец. Подобное описание применимо и к остальным
рассмотренным примерам. И это общий факт, что цилиндр отображения Mf деформа-
Глава 0. Основные геометрические понятия
11
ционно ретрагируется на подпространство У при движении каждой точки
(х, 0 вдоль отрезка {х} xI<zMf в его конец f(x)eY.
Однако не все деформационные ретракции возникают таким
способом из цилиндров отображений. Например, толстая буква X
деформационно ретрагируется в тонкую букву X, которая, в свою очередь,
деформационно ретрагируется в точку пересечения её перекладин. В результате
мы получаем деформационную ретракцию X в точку, в процессе которой
определённые пары точек движутся по путям, сливающимся до того, как
они достигают пункта назначения. Позже в этой главе мы опишем
существенно более сложный пример, так называемый «дом с двумя
комнатами», где деформационную ретракцию можно построить абстрактно, но
увидеть её невооружённым глазом поистине нелегко.
Деформационная ретракция /г: X —> X — это частный случай более
общего понятия гомотопии, являющейся просто семейством отображений
ft: X —> У, t е J, для которого отображение F: X х I —> У, заданное
формулой F(x, t) = ft О), непрерывно. Говорят, что два отображения /0, /i: X —> У
гомотопны, если существует связывающая их гомотопия /t; в таком
случае мы пишем fo—fi-
В таких терминах деформационная ретракция пространства X на
подпространство Л —это гомотопия тождественного отображения
пространства X в ретракцию X на А, т.е. в отображение г: X —>Ху для которого
г(Х) = Л и г|Л = 11. Можно также рассматривать ретракцию как
отображение X —> Л, ограничение которого на подпространство АсХ
тождественно. С более формальной точки зрения ретракция — это отображение
г: X —> X, для которого г2 = г, поскольку это соотношение в точности
означает, что г тождественно на своём образе. Ретракции — это
топологические аналоги проекторов, встречающихся в других областях математики.
Не все ретракции происходят из деформационных ретракций.
Например, любое пространство X всегда ретрагируется на произвольную
точку х0 е X посредством постоянного отображения, при котором всё
пространство X отображается в х0, но пространство, которое деформационно
ретрагируется на точку, должно быть линейно связным, поскольку
деформационная ретракция пространства X в точку х0 даёт путь, соединяющий
произвольную точку х £ X с х0. Не так тривиально показать, что
существуют линейно связные пространства, которые не ретрагируются
деформационно на точку. Можно ожидать, что такими будут «буквы с дырками»:
А, В, D, О, Р, Q, R. В главе 1 мы разовьём технику для доказательства этого
факта.
Гомотопия /г: X —> X, которая даёт деформационную ретракцию
пространства X на подпространство А, обладает тем свойством, что /Г|А = 1
для всех t. Вообще, гомотопию /г: X —> У, ограничение которой на
подпространство АсХ не зависит от t, называют гомотопией
относительно А или, короче, гомотопией относительно А. Таким образом, деформа-
12
Глава 0. Основные геометрические понятия
ционная ретракция пространства X на А — это гомотопия относительно А
тождественного отображения пространства X в ретракцию X на А.
Если пространство X деформационно ретрагируется на
подпространство А посредством отображения ft: X —> X, причём г: X —> А
обозначает результирующую ретракцию, a i: А —> X — включение, то мы имеем
ri = l и ir^l; последняя гомотопия задаётся посредством /г. Обобщая
эту ситуацию, отображение /: X—>Y называют гомотопической
эквивалентностью, если существует отображение g:Y —> X, для которого fg^t
и gf ^ 1. Пространства X и У называют тогда гомотопически
эквивалентными или имеющими один и тот же гомотопический тип. Обозначение:
X ^ У. Простое упражнение: показать, что это отношение
эквивалентности, в отличие от несимметричного понятия деформационной
ретракции. Например, три графа о—о, оо, аз гомотопически эквивалентны,
поскольку они являются деформационными ретрактами одного и того же
пространства, как мы видели раньше; но ни один из них не является
деформационным ретрактом никакого другого.
Верен общий факт, что два пространства X и У гомотопически
эквивалентны тогда и только тогда, когда существует третье пространство Z,
содержащее как X, так и У в качестве деформационных ретрактов. Менее
тривиален тот факт, что в качестве Z можно в действительности взять
цилиндр отображения Mf для произвольной гомотопической
эквивалентности /: X —> У. Мы уже отмечали, что Mf деформационно ретрагируется
на У, поэтому нужно только доказать, что Mf деформационно
ретрагируется также и на другое своё основание X, если / — гомотопическая
эквивалентность. Это показано в следствии 0.21.
Пространство, имеющее гомотопический тип точки, называют
стягиваемым. Это равносильно тому, что тождественное отображение
пространства должно быть гомотопно нулю, т.е. гомотопно постоянному
отображению. Вообще говоря, это несколько более слабое требование,
чем сказать, что пространство деформационно ретрагируется в точку;
см. упражнения в конце главы, в которых приводится пример, когда эти
понятия различны.
^
И
7\
т
^Ш1
\ WAX ъхШШьх^З
Опишем теперь пример двумерной поверхности в М3, известной под
названием дом с двумя комнатами, которая стягиваема, но не очевидным
образом. Чтобы построить это пространство, начнём с коробки,
разделённой на две комнаты горизонтальным прямоугольником, где под «пря-
Глава 0. Основные геометрические понятия
13
моугольником» мы понимаем не только четыре стороны
прямоугольника, но и его внутренность. Попасть в эти две комнаты снаружи можно
по двум вертикальным тоннелям. Верхний тоннель получен посредством
вырезания квадрата из верхней крышки коробки и ещё одного квадрата,
расположенного прямо под ним на среднем горизонтальном
прямоугольнике, а затем вставления четырёх вертикальных прямоугольников — стен
тоннеля. Этот тоннель позволяет попасть снаружи в нижнюю комнату.
Нижний тоннель устроен аналогичным образом; он позволяет попасть
в верхнюю комнату. Наконец, вставлены ещё два вертикальных
прямоугольника, образующих «опорные стены» двух тоннелей. Таким образом,
полученное в итоге пространство X состоит из трёх горизонтальных
частей, гомеоморфных кольцам, и всех вертикальных прямоугольников,
образующих стены двух комнат.
Чтобы убедиться, что X стягиваемо, рассмотрим замкнутую е-окрест-
ность N(X) множества X. Она, очевидно, деформационно ретрагируется
на X, если е достаточно мало. Действительно, N(X) представляет собой
цилиндр отображения для отображения граничной поверхности N(X) в X.
Менее очевиден тот факт, что пространство N(X) гомеоморфно D3,
единичному шару в R3. Чтобы убедиться в этом, представим, что мы
изготавливаем N(X) из глиняного шара, надавив на него пальцем, чтобы
получить верхний тоннель, а затем постепенно выдавив нижнюю
комнату, и аналогично, надавив пальцем, чтобы получить нижний тоннель,
и выдавив верхнюю комнату. Математически этот процесс даёт семейство
вложений ht: D3 —► R3, начинающееся с обычного вложения D3 <—> R3 и
заканчивающееся гомеоморфизмом на N(X).
Таким образом, X ~ N(X) = D3 ~ точка, поэтому X стягиваемо,
поскольку гомотопическая эквивалентность — отношение эквивалентности.
В действительности X деформационно ретрагируется в точку, поскольку
если /, —деформационная ретракция шара N(X) в точку х0 е X и если
г: N(X) —► X — ретракция (например, конечный результат
деформационной ретракции пространства N(X) на X), то ограничение композиции r/t
на X является деформационной ретракцией пространства X в х0. Однако
совсем непросто увидеть явно, как выглядит эта деформационная
ретракция.
Клеточные комплексы
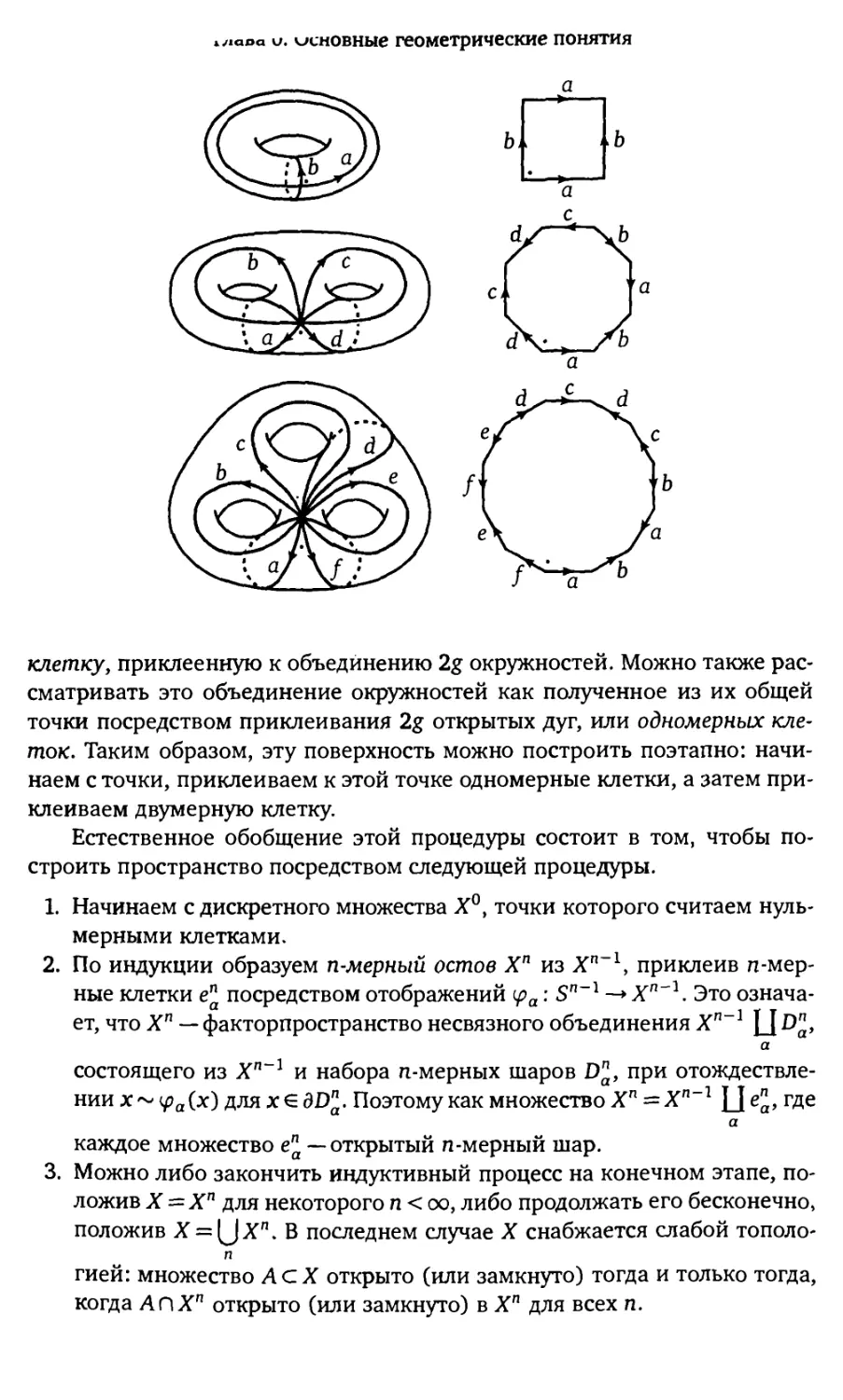
Обычный способ изготовления тора Sl *Sl —отождествление
противоположных сторон квадрата. Вообще, ориентируемую поверхность Mg
рода g можно получить из 4£-угольника, отождествляя пары его сторон,
как показано на рисунке для первых трёх случаев g= 1, 2, 3. При этом 4g
сторон многоугольника превращаются в 2g окружностей на полученной
поверхности, которые пересекаются ровно в одной точке. Внутренность
многоугольника можно представлять как открытый диск, или двумерную
wiaoa \j. основные геометрические понятия
клетку, приклеенную к объединению 2g окружностей. Можно также
рассматривать это объединение окружностей как полученное из их общей
точки посредством приклеивания 2g открытых дуг, или одномерных
клеток. Таким образом, эту поверхность можно построить поэтапно:
начинаем с точки, приклеиваем к этой точке одномерные клетки, а затем
приклеиваем двумерную клетку.
Естественное обобщение этой процедуры состоит в том, чтобы
построить пространство посредством следующей процедуры.
1. Начинаем с дискретного множества Х°, точки которого считаем
нульмерными клетками.
2. По индукции образуем n-мерный остов Хп из X""1, приклеив п-мер-
ные клетки епа посредством отображений ipa: Sn~l —> Хп~Л. Это
означает, что Хп — факторпространство несвязного объединения X"-1 Ц &а>
а
состоящего из Хп~1 и набора n-мерных шаров Dna, при
отождествлении х^уа О) для х € dDna. Поэтому как множество Хп =Xn~l \J ena, где
а
каждое множество епа —открытый n-мерный шар.
3. Можно либо закончить индуктивный процесс на конечном этапе,
положив Х = Хп для некоторого п < оо, либо продолжать его бесконечно»
положив X = (jxn. В последнем случае X снабжается слабой тополо-
п
гией: множество АсХ открыто (или замкнуто) тогда и только тогда,
когда АС\Хп открыто (или замкнуто) в Хп для всех п.
Глава 0. Основные геометрические понятия
15
Пространство X, построенное таким способом, называют клеточным
комплексом или CW-комплексом. Объяснение сокращения CW приведено
в приложении, где также доказаны многие основные свойства клеточных
комплексов. Читатель, которого интересуют различные
теоретико-множественные вопросы, скрытые за следующим далее обсуждением, должен
обратиться за подробностями к приложению.
Если X = Хп для некоторого п, то говорят, что комплекс X
конечномерен, а наименьшее такое п (наибольшую размерность клеток X) называют
размерностью комплекса X.
Пример 0.1. Одномерный клеточный комплекс Х = Х1—это то, что
в алгебраической топологии называют графом. Он состоит из вершин
(нульмерных клеток), к которым приклеены рёбра (одномерные клетки).
Оба конца ребра могут быть приклеены к одной и той же вершине.
Пример 0.2. Дом с двумя комнатами, нарисованный выше, имеет
наглядно очевидную структуру двумерного клеточного комплекса.
Нульмерные клетки — это вершины, в которых сходятся по крайней мере три из
нарисованных рёбер, а одномерные клетки —это внутренности рёбер,
соединяющих эти вершины. Это даёт одномерный остов X1, а двумерные
клетки —это компоненты связности оставшегося пространства Х-Х1.
Если сосчитать, то можно получить, что здесь 29 нульмерных клеток, 51
одномерная клетка и 23 двумерных клетки, причём альтернированная
сумма 29 — 51 + 23 равна 1. Это эйлерова характеристика, которая для
комплекса с конечным числом клеток определяется как число чётномер-
ных клеток минус число нечётномерных клеток. Как мы покажем в
теореме 2.44, эйлерова характеристика клеточного комплекса зависит только
от его гомотопического типа, поэтому тот факт, что дом с двумя
комнатами имеет гомотопический тип точки, влечёт то, что его эйлерова
характеристика должна быть равна 1, независимо от того, как именно он
представлен в виде клеточного комплекса.
Пример 0.3. Сфера Sn имеет структуру клеточного комплекса ровно
с двумя клетками, е° и е", причём n-мерная клетка приклеивается по
постоянному отображению S""1 -+е°. Это эквивалентно представлению
сферы Sn в виде факторпространства Dn/dDn.
Пример 0.4. Вещественное проективное пространство размерности п,
обозначаемое RPn, определяется как пространство всех прямых в Rn+1,
проходящих через начало координат. Каждая такая прямая задаётся
ненулевым вектором в Rn+1, который определён с точностью до умножения на
число, и топология на ЖРп задаётся как топология факторпространства
Rn+1 - {0} по отношению эквивалентности v ~ Av для всех чисел Я Ф 0.
Мы можем ограничиться векторами длины 1, поэтому RPn — это также
факторпространство Sn/(v ~ -v), т. е. сфера с отождествлёнными
диаметрально противоположными точками. Эквивалентно можно сказать, что
ЕРП —факторпространство полусферы Dn с отождествлёнными диамет-
16
Глава 0. Основные геометрические понятия
рально противоположными точками сферы 6D". Так как гШ" с
отождествлёнными диаметрально противоположными точками — это RP""1, мы
видим, что ЕР" получается из ЕР"-1 приклеиванием n-мерной клетки,
причём отображение приклеивания —это факторпроекция S""1 -*МР"~1.
Индукцией по п получаем, что MP" имеет структуру клеточного комплекса
е°Ue1 U... Uе" с одной клеткой е1 в каждой размерности £ ^ п.
Пример 0.5. Так как MP" получается из MP'1"1 приклеиванием п-мер-
ной клетки, бесконечное объединение RP°° = |J]RPn приобретает струк-
" " TV/T
туру клеточного комплекса с одной клеткой в каждой размерности. Мы
можем рассматривать RP00 как пространство всех прямых в M°° = lJlR",
проходящих через начало координат. п
Пример 0.6. Комплексное проективное пространство размерности п,
обозначаемое СРП, —это пространство всех комплексных прямых в С"+1,
проходящих через начало координат (т. е. одномерных подпространств в
С"4*1). Как и в случае ЕР", каждая прямая задаётся ненулевым вектором
в С"4"1, который определён однозначно с точностью до умножения на
число, и топология на СРП задаётся как топология факторпространства
С"+1 - {0} по отношению эквивалентности v ~ Av для Я Ф 0.
Эквивалентным образом, это факторпространство единичной сферы s2n+l с С"4*1 no
отношению эквивалентности v ~ Av при |А| = 1. Можно также получить
СР" как факторпространство шара D2" при отождествлении v ~ Av для
v е dD2n следующим образом. Векторы S2n+l с Сп+1, у которых
последняя координата вещественна и неотрицательна, — это в точности векторы
вида
(iv, y/l-\w\2) е С" х С, где М ^ 1.
Такие векторы образуют график отображения w —> у 1 — |iv|2. Это будет
диск D2", ограниченный сферой S2""1 с S2n+1, состоящей из векторов
(iv, 0) е С" х С, \w\ = 1. Каждый вектор из s2n+1 при отождествлении
v ~ Av эквивалентен вектору из D2", который единствен, если его
последняя координата ненулевая. Если же последняя координата нулевая, то мы
имеем как раз отождествление v ~ Av для v e S2" ~].
Из такого описания СРП как факторпространства D2" по
отождествлению v ~ Av для v GS2n_1 следует, что СР" получается из СР""1
приклеиванием клетки е2п посредством отображения факторизации S2""1 —*
-♦СР"-1. Поэтому индукцией по п мы получаем клеточную структуру
СР" = е° U е2 и ... и е2" с клетками только в чётных размерностях.
Аналогично СР00 имеет клеточную структуру с одной клеткой в каждой чётной
размерности.
После всех этих примеров вернёмся к общей теории. У каждой
клетки епа в клеточном комплексе X есть характеристическое отображение
*а '• £*а ~~* ^> которое продолжает отображение приклеивания ц>а и
является гомеоморфизмом внутренности D£ на е". А именно, в качестве Фа
Глава 0. Основные геометрические понятия
17
можно взять композицию D£ <-► Хп 2 [JD£ —> Хп <-► X, где среднее отоб-
а
ражение —это отображение факторизации, задающей Хп. Например, для
канонической клеточной структуры на Sn, описанной в примере 0.3,
характеристическое отображение для n-мерной клетки —это отображение
факторизации Dn —>Sn, стягивающее dDn в точку. Для ЕР"
характеристическое отображение для клетки е1 — это отображение факторизации
D1 —> ЕР' с ЕРП, отождествляющее диаметрально противоположные точки
3D1, и аналогично для СР".
Подкомплекс клеточного комплекса X — это замкнутое
подпространство Л с X, которое является объединением клеток из X. Поскольку А
замкнуто, образ характеристического отображения каждой клетки из А
содержится в Л; в частности, образ отображения приклеивания для
каждой клетки из А содержится в Л, а потому само А является клеточным
комплексом. Пару (Х,А), состоящую из клеточного комплекса X и его
подкомплекса А, будем называть CW-парой.
Например, каждый остов Xм клеточного комплекса X является
подкомплексом. Частные случаи этого — подкомплексы RPfc с ЕР" и СРк с СРП
при к ^ п. Они в действительности являются единственными
подкомплексами в RP" ивСРп.
Имеют место естественные включения S0 с S1 с ... с S", но эти под-
сферы не являются подкомплексами сферы Sn с её обычной клеточной
структурой ровно с двумя клетками. Однако мы можем снабдить Sn другой
клеточной структурой, относительно которой каждая подсфера Sk
является подкомплексом, считая, что каждая сфера Sk получена из её экватора
S^"1 приклеиванием двух /с-мерных клеток — компонент Sk — Sk~~l.
Бесконечномерная сфера S°° = IJ S" тогда тоже становится клеточным комплек-
/2
сом. Заметим, что отображение факторизации S°° —►ЕР00,
отождествляющее диаметрально противоположные точки в S00, переводит две п-мерные
клетки из S°° в одну n-мерную клетку из ЕР°°.
Во всех приведённых выше примерах клеточных комплексов
замыкание каждой клетки является подкомплексом и, более того, замыкание
любого набора клеток является подкомплексом. Большинство клеточных
структур, возникающих естественным образом, обладает этим свойством,
но в общем случае оно не обязано выполняться. Например, если мы
возьмём S1 с минимальной клеточной структурой и приклеим двумерную
клетку по отображению S1 —>S\ образ которого —нетривиальная дуга
окружности S1, тогда замыкание двумерной клетки — не подкомплекс,
потому что он содержит только часть одномерной клетки.
Операции над пространствами
У клеточных комплексов удачно сочетаются жёсткость и гибкость:
у них достаточно жёсткости, чтобы позволить проводить многие рассуж-
18 Глава 0. Основные геометрические понятия
дения комбинаторно, клетка за клеткой, и достаточно гибкости, чтобы
позволить совершать над ними многие естественные операции. Здесь
приведены примеры некоторых таких операций.
Произведения. Если X и У — клеточные комплексы, то X х У имеет
структуру клеточного комплекса, клетки которого — произведения e^xel
где е™ пробегает все клетки из X, a ej пробегает все клетки из У.
Например, клеточная структура на торе S1 х S1, описанная в начале этой
главы, получена таким способом из стандартной клеточной структуры на S1.
В случае совсем произвольных комплексов X и У есть, однако, небольшое
затруднение. Топология X х У как клеточного комплекса иногда слегка
мельче, чем топология произведения; в ней больше открытых множеств,
чем в топологии произведения. Но эти две топологии совпадают, если
либо в одном из комплексов X и У конечное число клеток, либо у каждого
из них не более чем счётное множество клеток. Это объясняется в
приложении. На практике эта тонкость теоретико-множественной топологии
редко вызывает проблемы.
Факторпространства. Если (X, А) — CW-napa, состоящая из
клеточного комплекса X и его подкомплекса А, то факторпространство Х/А
наследует от X структуру клеточного комплекса. Клетки Х/А — это клетки
из X — А плюс ещё одна новая 0-клетка, образ подкомплекса А в Х/А, Для
клетки епа из X — А, приклеенной посредством отображения уа: S""1 —>
—> Хп~1, отображение приклеивания для соответствующей клетки в Х/А —
это композиция S""1 —X"-1—Х""1/^-1.
Например, если мы снабдим Sn_1 произвольной клеточной
структурой и построим Dn из Sn~\ приклеив п-мерную клетку, то
факторпространство Dn/Sn~1 —это Sn с обычной клеточной структурой. Другой
пример такой: в качестве X возьмём замкнутую ориентируемую поверхность
с клеточной структурой, описанной выше,— с одной двумерной клеткой,
и пусть А —дополнение к этой двумерной клетке, т. е. одномерный остов
комплекса X. Тогда Х/А имеет клеточную структуру, состоящую из
нульмерной клетки и приклеенной к ней двумерной клетки, а есть только один
способ приклеить клетку к нульмерной клетке — по постоянному
отображению, поэтому Х/А — это S2.
Надстройка. Для пространства X надстройка SX — это фактор
комплекса X х J, полученный стягиванием X х {0} в одну точку и X х {1}
в другую точку. Мотивирующий пример —это пространство X = Sn, для
которого SX = Sn+1 с двумя «точками надстройки» в северном и
южном полюсе сферы Sn+1 — точками (0,..., 0, ±1). Можно рассматривать
SX как двойной конус над Ху объединение двух экземпляров конуса
СХ = (X х I)/{X х {0}). Если X-CW-комплекс, то SX и СХ тоже
будут CW-комплексами, как факторпространства комплекса X х I с
клеточной структурой произведения, где отрезок J снабжён стандартной
Глава 0. Основные геометрические понятия
19
клеточной структурой: две нульмерные клетки соединены
одномерной клеткой.
Значение надстройки возрастает по мере углубления
в алгебраическую топологию, хотя сразу не видно, почему
так должно быть. Одно из наиболее полезных свойств
надстройки заключается в том, что надстраивать можно не
только пространства, но и отображения. А именно, отображение f;X—>Y
надстраивается до отображения Sf: SX —> SY — факторотображения для
/х1:Хх/->Ух/.
Джойн. Конус СХ —это объединение всех отрезков, соединяющих
точки из X с некоторой внешней вершиной, и аналогично надстройка
SX — это объединение всех отрезков, соединяющих точки из X с двумя
внешними вершинами. Более общим образом, если дано пространство X
и другое пространство У, то можно рассмотреть пространство всех
отрезков, соединяющих точки из X с точками из Y. Это будет джойн1 X * У,
факторпространство X xY х I при отождествлениях (х, уь 0) ~ (х, у2, 0)
и (*!, у, 1) ~ (х2, у,1). Таким образом, мы сжимаем подпространство
X х У х {0} в X, а X х У х {1} — в У. Например, если оба пространства
X и У — замкнутые отрезки, то мы сжимаем две противоположные грани
куба в отрезки так, что куб превращается в тетраэдр. В общем случае
X * У содержит экземпляры X и У на своих «концах», а любая другая
точка (х, у, 0 из X * У принадлежит ровно одному отрезку, соединяющему
точку х е X с X * У с точкой y^Y с X * У; этот отрезок получается, когда
мы фиксируем л: и у и меняем координату t в (х, у, t).
гг~к
xN—^
J
Удобный способ представления точек из X * У — формальные
линейные комбинации txx + t2y, где 0^tz-^ 1 и ^ +12 = 1, подчиняющиеся
правилам Ox -fly = у и lx + Оу = л\ которые в точности соответствуют
отождествлениям, определяющим X * У. Аналогично можно построить
итерированный джойн XY * ... *ХП как пространство формальных линейных
комбинаций taха +... + tnxn, где 0 ^ t,- ^ 1 и ^ +... +1„ = 1, с соглашением,
что член Ох, можно опустить. В алгебраической топологии центральную
роль играет очень частный случай, когда каждое пространство Х{ — это
просто точка. Например, джойн двух точек —это отрезок, джойн трёх
точек—треугольник, а джойн четырёх точек —тетраэдр. Джойн п точек —
это выпуклый многогранник размерности п - 1, называемый симплексом.
Иногда употребляется термин соединение. —Прим. перев.
20
Глава 0. Основные геометрические понятия
В конкретном случае, когда выбранные п точек — это п стандартных
базисных векторов в Еп, их джойн —это пространство
Д""1 = {(tb ..., tn) e R" | t! + ... + tn = 1 и t,Z 0}.
Другой интересный пример получается, когда каждое пространство
X,—это S0, т.е. пара точек. Если в качестве этих двух точек из X, мы
возьмём два единичных вектора, направленных по z-й оси координат в Rn,
то джойн Xj * ... * Хп — это объединение 2П копий1 замкнутого симплекса
Д""1, и центральная проекция из начала координат даёт гомеоморфизм
между Хг*...*Хп и S'1"1.
Если X и Y — CW-комплексы, то на X * У есть естественная структура
CW-комплекса, для которой X и У — подкомплексы, а остальными
клетками служат произведения клеток пространства X х У х (0,1). Как и обычно
для произведений, CW-топология на X * У может быть слабее, чем фактор
топологии произведения на X х У х /.
Букет. Это довольно простая, но тем не менее весьма полезная
операция. Если даны пространства X и У с выделенными точками х0€Х
и у0 е У, то букет X V У — это фактор несвязного объединения X Ц У,
полученный отождествлением х0 и у0 в одну точку. Например, пространство
SlVSl гомеоморфно фигуре «8»—две окружности касаются в точке.
Вообще можно образовать букет V Ха произвольного набора пространств Ха,
а
взяв несвязное объединение Ц Ха и отождествив точки ха Е Ха в одну точ-
а
ку. В случае, когда Ха — клеточные комплексы, а точки ха — нульмерные
клетки, пространство \/Ха является клеточным комплексом, поскольку
а т т
оно получено из клеточного комплекса J_JXa стягиванием некоторого
подкомплекса в точку. а
Для любого клеточного комплекса X фактор Хп/Хп~1 является
букетом n-мерных сфер VSa> по одной сфере для каждой n-мерной клетки X.
a
Приведённое произведение. Как и для надстройки, важность этой
конструкции станет понятной только позже. Внутри произведения X х У
есть экземпляры пространств X и У, а именно X х {у0} и {х0} х У для
точек х0 G X и у0 е У. Эти два экземпляра X и У пересекаются в X х У только
в точке (х0, у0), поэтому их объединение можно отождествить с букетом
X V У. Тогда приведённое произведение X Л У определяется как факторпро-
странство X х Y/XVY. Можно представлять себе приведённое
произведение X Л У как версию произведения X х У, полученную стягиванием
тех частей, которые не являются подлинным произведением, — отдельных
множителей X и У.
При л = 3 получаем границу правильного октаэдра. — Прим. ред.
Глава 0. Основные геометрические понятия
21
Приведённое произведение X Л У клеточных комплексов X и У с
нульмерными клетками х0 и у0 является клеточным комплексом, если мы
снабжаем X х У топологией клеточного комплекса, а не топологией
произведения (в тех случаях, когда эти две топологии разные). Например,
Sm Л S" имеет клеточную структуру ровно с двумя клетками —
размерности Оиш + п, поэтому Sm ASn = Sm+n. В частности, когда т — п = 1, мы
видим, что стягивание меридиана и параллели тора в точку даёт двумерную
сферу.
Два признака гомотопической эквивалентности
Ранее в этой главе нашим основным инструментом для построения
гомотопических эквивалентностей служил тот факт, что цилиндр
отображения деформационно ретрагируется на основание, соответствующее
образу отображения. Применяя этот факт несколько раз, зачастую можно
построить гомотопические эквивалентности между пространствами,
выглядящими весьма по-разному. Однако на практике этот процесс может
оказаться громоздким, поэтому полезно иметь в распоряжении и другую
технику. Мы опишем здесь два широко распространённых метода. Первый
включает стягивание в точку некоторых подпространств, а второй
включает изменение того, как стыкуются друг с другом части пространства.
Стягивание подпространств
Операция стягивания подпространства в точку обычно коренным
образом изменяет гомотопический тип, но можно надеяться, что если
подпространство, намеченное для стягивания, уже имеет гомотопический
тип точки, то стягивание его в точку не изменит гомотопический тип
всего пространства. Вот положительный результат в этом направлении.
I Утверждение. Если (X, A) — CW-napa, состоящая из С1/^-комплек-
са X и стягиваемого подкомплекса Л, то отображение факторизации
Х-+Х/А является гомотопической эквивалентностью.
Доказательство будет дано позже, в предложении 0.17, а сейчас
давайте посмотрим на некоторые примеры, показывающие, как можно
применять этот результат.
Пример 0.7 (графы). Три графа о—о, оо, схэ гомотопически
эквивалентны, поскольку каждый из них является деформационным ретрактом
диска с двумя дырками, но это можно вывести также из
сформулированного выше признака со стягиваемым подпространством, поскольку
стягивание среднего ребра в первом и в третьем графе даёт второй граф.
Вообще пусть X — произвольный граф с конечным числом вершин
и рёбер. Если два конца некоторого ребра в X различны, то мы можем
стянуть это ребро в точку, получив при этом гомотопически
эквивалентный граф, у которого число рёбер на 1 меньше. Такое упрощение можно
повторять до тех пор, пока все рёбра графа X не станут петлями, а тогда
22 Глава 0. Основные геометрические понятия
каждая компонента графа X является либо изолированной вершиной,
либо букетом окружностей.
Из этого возникает вопрос, могут ли два таких графа, имеющих
только одну вершину в каждой компоненте, быть гомотопически
эквивалентными, если они не являются в действительности просто изоморфными
графами. Упражнение 12 в конце главы сводит этот вопрос к случаю
связных графов. А тогда задача состоит в том, чтобы доказать, что букет \/ S1,
т
состоящий из т окружностей, не гомотопически эквивалентен \/ S1 при
п
тфп. Утверждения такого рода трудно доказывать непосредственно.
Желателен некий алгебраический объект, который сопоставляется
пространствам, зависит только от их гомотопического типа и принимает разные
значения для \JS^ и для \JS1 при тфп.Ъ действительности этим усло-
т - п
виям удовлетворяет эйлерова характеристика, потому что для \/ S1 она
т
равна 1 — т. Но теорема о том, что эйлерова характеристика
пространства зависит только от его гомотопического типа, весьма нетривиальна.
Другой алгебраический инвариант, который для графов работает столь же
хорошо и строгое обоснование которого требует существенно меньших
усилий, чем для эйлеровой характеристики, — это фундаментальная
группа пространства, тема главы 1.
Пример 0.8. Рассмотрим пространство X, полученное из S2
приклеиванием двух концов дуги А к двум разным точкам этой сферы, скажем,
к северному и южному полюсу. Пусть
В—дуга на сфере S2, соединяющая две
точки, к которым приклеена дуга А.
Тогда X можно снабдить структурой
CW-комплекса с концами дуг Л и В в
качестве нульмерных клеток,
внутренними частями дуг Л и В в качестве
одномерных клеток и оставшейся частью
сферы S2 в качестве двумерной клетки.
Так как Л и В стягиваемы,
пространства Х/А и Х/В гомотопически эквивалентны X. Пространство Х/А — это
факторпространство S2/S°, сфера с двумя отождествлёнными точками,
а Х/В —это Sl VS2. Следовательно, S2/S° и S1 V S2 гомотопически
эквивалентны, что на первый взгляд не очевидно.
Пример 0.9. Пусть X — объединение тора и п меридиональных
дисков. Чтобы задать CW-структуру на X, выберем на торе параллель,
пересекающую каждый меридиональный диск в одной точке. Тогда эти точки
пересечения—нульмерные клетки, оставшиеся части параллели и
граничных окружностей меридиональных дисков — одномерные клетки, а
оставшиеся области на торе и внутренности меридиональных дисков — двумер-
Глава 0. Основные геометрические понятия
23
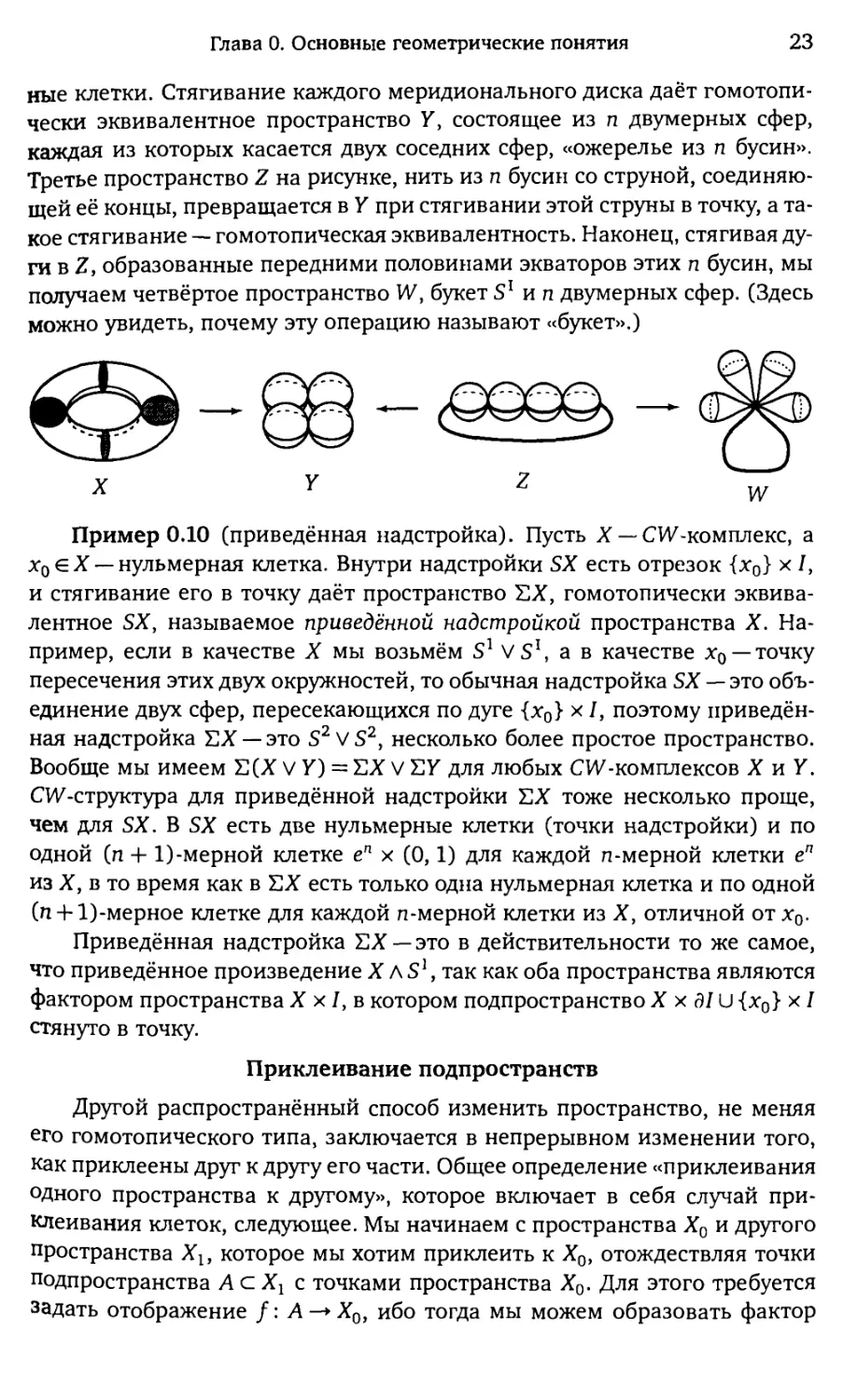
ные клетки. Стягивание каждого меридионального диска даёт гомотопи-
чески эквивалентное пространство У, состоящее из п двумерных сфер,
каждая из которых касается двух соседних сфер, «ожерелье из п бусин».
Третье пространство Z на рисунке, нить из п бусин со струной,
соединяющей её концы, превращается в У при стягивании этой струны в точку, а
такое стягивание — гомотопическая эквивалентность. Наконец, стягивая
дуги в Z, образованные передними половинами экваторов этих п бусин, мы
получаем четвёртое пространство W, букет S1 и п двумерных сфер. (Здесь
можно увидеть, почему эту операцию называют «букет».)
Пример 0.10 (приведённая надстройка). Пусть X —-СИ^-комплекс, а
х0 G X — нульмерная клетка. Внутри надстройки SX есть отрезок {х0} х J,
и стягивание его в точку даёт пространство ЕХ, гомотопически
эквивалентное SXy называемое приведённой надстройкой пространства X.
Например, если в качестве X мы возьмём S1 VS1, а в качестве х0 — точку
пересечения этих двух окружностей, то обычная надстройка SX — это
объединение двух сфер, пересекающихся по дуге {х0} х I, поэтому
приведённая надстройка ЕХ —это S2V S2y несколько более простое пространство.
Вообще мы имеем Е(Х V У) = ЕХ V ЕУ для любых CW-комплексов Х и У.
CW-структура для приведённой надстройки ЕХ тоже несколько проще,
чем для SX. В SX есть две нульмерные клетки (точки надстройки) и по
одной (п + 1)-мерной клетке еп х (0,1) для каждой n-мерной клетки еп
из X, в то время как в ЕХ есть только одна нульмерная клетка и по одной
(п-Ы)-мерное клетке для каждой n-мерной клетки из X, отличной от х0.
Приведённая надстройка ЕХ —это в действительности то же самое,
что приведённое произведение X Л S1, так как оба пространства являются
фактором пространства X х J, в котором подпространство X х dl U {х0} х I
стянуто в точку.
Приклеивание подпространств
Другой распространённый способ изменить пространство, не меняя
его гомотопического типа, заключается в непрерывном изменении того,
как приклеены друг к другу его части. Общее определение «приклеивания
одного пространства к другому», которое включает в себя случай
приклеивания клеток, следующее. Мы начинаем с пространства Х0 и другого
пространства Хь которое мы хотим приклеить к Х0, отождествляя точки
подпространства А с XY с точками пространства Х0. Для этого требуется
задать отображение /: А —► Х0, ибо тогда мы можем образовать фактор
24
Глава 0. Основные геометрические понятия
пространства Х0иХъ отождествляя каждую точку а е А с её образом
/(а)еХ0. Обозначим это факторпространство через XqU^-X! и назовём
его пространством Х0 с приклеенным к нему вдоль подмножества А по
отображению / пространством Хг. Если (Хь Л) = (Dn, S'l_1), то мы имеем
случай приклеивания n-мерной клетки к Х0 по отображению /: Sn~l —> Х0.
Цилиндры отображений тоже являются примерами этой
конструкции, поскольку цилиндр отображения Mf для отображения /: X —> 7
является пространством, которое получается из 7 приклеиванием
пространства X х / вдоль X х {1} посредством /. Тесно связан с
цилиндром отображения Mf конус отображения Cf — YUf СХ, где СХ —конус
(X х I)/{X х {0}), и мы приклеиваем его к Y вдоль X х {1} посредством
отождествления (х, 1) ~/(х). Например, когда X
—сфера S"-1, конус отображения С^ — это пространство,
полученное из У приклеиванием n-мерной клетки
посредством отображения /: S'1"1 —> У. Конус отображения
Cf можно также рассматривать как фактор Mf/X
цилиндра отображения Mf, в котором подпространство
X = X х {0} стянуто в точку.
Если заменить отображение приклеивания / на гомотопию /t, то
получим семейство пространств, форма которых непрерывно изменяется,
и можно ожидать, что все эти пространства имеют один и тот же
гомотопический тип. Так действительно часто бывает.
Утверждение. Если (Xj, Л) — CW-napa, а отображения приклеивания
/, g: А —> Х0 гомотопны, то X \Jf X} ^ X0 U^ X}.
Мы снова пока отложим доказательство и рассмотрим некоторые
примеры.
Пример 0.11. Давайте выведем снова результат примера 0.8 о том, что
сфера с двумя отождествлёнными точками гомотопически эквивалентна
S1^ S2. Сферу с двумя отождествлёнными точками 2 ^^—
можно получить, приклеив S2 к S1 по отображе- /—--/..
нию, которое наматывает на S1 замкнутую дугу А Г^_ /А
в S2, как показано на рисунке. Так как дуга А стя- г—-~Л"
гиваема, это отображение приклеивания гомотоп- \11Ш\-
но постоянному отображению, а приклеивание S2 ^^\
к S1 Посредством постоянного отображения дуги
А даёт S1 VS2. Из этого следует требуемый результат, поскольку (S2,A)
является CW-парой: сфера S2 получена из А приклеиванием двумерной
клетки.
Пример 0.12. Аналогично можно увидеть, что ожерелье из
примера 0.9 гомотопически эквивалентно букету окружности и п двумерных
сфер. Ожерелье можно получить из окружности, приклеив п двумерных
сфер вдоль дуг, поэтому ожерелье гомотопически эквивалентно простран-
о-:
Глава 0. Основные геометрические понятия
25
ству, полученному приклеиванием п двумерных сфер к окружности в
разных точках. Затем мы можем сдвинуть эти точки приклеивания по
окружности до тех пор, пока они не совпадут, что даёт букет.
Пример 0.13. Здесь мы применим упомянутый выше факт, что
сжатие в точку стягиваемого подкомплекса является гомотопической
эквивалентностью. Если (X, А) — CW-napa, состоящая из клеточного
комплекса X и его подкомплекса А, то Х/А ^ X и СА —конус отображения для
включения А<-*Х. Действительно, мы имеем X/A = (XUCA)/CA^XUCA,
поскольку СА — стягиваемый подкомплекс в X и СА.
Пример 0.14. Если (X, А) — CW-napa и подкомплекс А стягиваем в X
(т.е. включение А<^Х гомотопно постоянному отображению), то Х/А~
~ X V SA. А именно, согласно предыдущему примеру Х/А ~ X U СА, а так
как подкомплекс А стягиваем в X, конус отображения X U С А для
включения А <-* X гомотопически эквивалентен конусу отображения для
постоянного отображения, которым является X V SA. Например, Sn/Sl ^ Sn V Sl+1
при i < п, поскольку сфера S1 стягиваема в Sn при i < п. В частности, это
даёт S2/S° ca S2 V S1, а это снова результат примера 0.8.
Свойство продолжения гомотопии
В этом небольшом пункте мы докажем некоторые утверждения. В
частности, мы докажем два признака гомотопической эквивалентности,
сформулированные выше, а также тот факт, что любые два гомотопически
эквивалентных пространства можно вложить в качестве деформационных
ретрактов в одно и то же пространство.
Эти доказательства используют некое техническое свойство, которое
встречается и во многих других ситуациях. Рассмотрим следующую
задачу. Пусть задано отображение /0: X —> У, а на подпространстве АсХ
задана ещё и гомотопия ft: A^Y отображения fQ\Ay которую нужно
продолжить до гомотопии /t: X —► У данного отображения /0. Если пара (X, А)
такова, что эта задача продолжения всегда может быть решена, то говорят,
что пара (X, А) обладает свойством продолжения гомотопии. Таким
образом, (X, А) обладает свойством продолжения гомотопии, если любое
отображение Xx{0}UAxJ->y можно продолжить до отображения X х I -> У.
Утверждение. Пара (X, А) обладает свойством продолжения
гомотопии тогда и только тогда, когда X х {0} U А х / — ретракт пространства
Хх/.
Свойство продолжения гомотопии для пары (X, А) влечёт, что
тождественное отображение Xx{0}UAxJ->Xx{0}UAxJ продолжается до
отображения X х J — X х {0} U A x J, а потому X х {0} и А х / является
ретрактом пространства Хх/.
Доказать обратное столь же просто, если замкнуто А в X. В этом
случае любые два отображения Хх{0}->У иАх/->У, согласующиеся
26
Глава 0. Основные геометрические понятия
на Л х {0}, склеиваются в отображение X х {0} и Л х / —► У, непрерывное
постольку, поскольку непрерывны его ограничения на замкнутые
подмножества X х {0} и А х I. Взяв композицию отображения X х {0} и Д х / —► У
с ретракцией X х / —> X х {0} и Д х /, получаем продолжение X х I —► Y, так
что пара (X, А) обладает свойством продолжения гомотопии. Без условная
замкнутости А это утверждение так же верно, но доказательство при этом
более сложно.
Если X х {0} U Ах I — ретракт пространства X х / и X хаусдорфово,
то из этого на самом деле вытекает, что А замкнуто в X. В самом деле,
если г: X х / —► X х / — ретракция на X х {0} и А х /, то образ
отражения г состоит из точек % еХ х /, для которых r(z) = z, и это подмножество
вХ х / замкнуто, если Ххаусдорфово; стало быть, X х {0} и Л х / замкнуто
в X х /, откуда А замкнуто в X.
Простой пример пары (Х,Д) с замкнутым Д, для которой не
выполняется свойство продолжения гомотопии, даёт пара (/,Д), где Д =
= (0,1,1/2,1/3,1/4,.,.). Несложно показать, что не существует
непрерывной ретракции
/х/ -+/х{0}иДх/.
Нарушение свойства продолжения гомотопии здесь связано с плохой
структурой пары (Х,Д) вблизи точки 0. Если локально пара устроена
лучше, то, как показывает следующий пример, свойство продолжения
гомотопии выполняется.
Пример 0.15. Пара (X, А) обладает свойством продолжения
гомотопии, если у А есть окрестность в X, являющаяся цилиндром отображения;
под этим мы подразумеваем замкнутую окрестность Л/, содержащую такое
подпространство В (которое мы представляем себе как границу АО, что
N — В —открытая окрестность множества Д,
причём существуют отображение /: В —> А и
гомеоморфизм h: Mf —* N, для которого h\AvB = 1. Такого рода
окрестности, являющиеся цилиндрами отображений,
встречаются довольно часто. Например, толстые
буквы, которые обсуждались в начале этой главы,
являются такими окрестностями для тонких букв,
рассматриваемых как множества на плоскости. Чтобы
проверить свойство продолжения гомотопии, прежде всего заметим, что
/ х / ретрагируется на / х {0} и dl x J, а значит, В xl xl ретрагируется на
В х I х {0} и В х dl х /, и эта ретракция индуцирует ретракцию My x / на
Mf х {0} U (Л и В) х /. Таким образом, пара Ш/, А и В) обладает свойством
продолжения гомотопии. Поэтому им обладает и гомеоморфная ей пара
(N, А и В). Теперь если заданы отображение X —> Y и гомотопия его
ограничения на Л, то мы можем взять постоянную гомотопию на Х- (N-B),
а затем продолжить её на N, применив свойство продолжения гомотопии
для пары (N, А и В) к данной гомотопии на Л и постоянной гомотопии на В.
Глава 0. Основные геометрические понятия
27
I Предложение 0.16. Если (X, А) — CW-napa, то X х {0} U А х
/—деформационный ретракт пространства X х J, а потому (X, А) обладает
свойством продолжения гомотопии.
Доказательство. Существует ретракция г: Dn xI-^Dn x {0} U dDn x J
например, центральная проекция из точки (0, 2) е Dn x R. Затем,
полагая rt = tr + (1 - t)l, получаем деформационную ретракцию Dn x J на
Dn х {0} U <3Dn х /. Эта деформационная ретракция даёт деформационную
ретракцию X" х I на Хп х {0} U (Х""1 U Ап) х /, так как
Хп х / получается из Хп х {0} U (Xn_1 U Ап) х /
приклеиванием экземпляров Dn х I вдоль Dn х {0} U 3Dn х I.
Теперь будем совершать деформационную ретракцию Хп х J
на Хп х {0} U (Хп-1 и Ап) х I за время t из интервала
[1/2п+1,1/2п]. Тогда, взяв бесконечную композицию по
всем п, получим деформационную ретракцию X х / на
Хп х {0} U Л х I. Проблем с непрерывностью этой
деформационной ретракции при t = 0 нет, поскольку она непрерывна на Хп х /,
будучи там постоянной в течение времени t из интервала [0,1/2п+1],
а CW-комплексы снабжены слабой топологией относительно их остовов,
поэтому отображение непрерывно тогда и только тогда, когда непрерывно
его ограничение на все остовы. □
Докажем теперь сформулированное ранее утверждение, что
сжатие в точку стягиваемого подкомплекса — гомотопическая
эквивалентность.
I Предложение 0.17. Если пара (X, А) обладает свойством
продолжения гомотопии, причём А стягиваемо, то отображение факторизации
q: X—>Х/А является гомотопической эквивалентностью.
Доказательство. Пусть ft: X —> X — гомотопия, продолжающая
стягивание подпространства А, причём /0 = 1. Так как fc(A) с А для всех t,
композиция qfc: X —>Х/А переводит А в точку, а значит, представляется
в виде_композиции X —> Х/А —> Х/Л. Обозначив последнее отображение
через ft: Х/А —> Х/Л, мы имеем qfL = /tq в первой из двух диаграмм. Когда
* = 1, fi(A) есть точка —та самая точка, в которую стягивается А,
поэтому /l индуцирует отображение g: Х/А —> X, причём qg = /ь как во вто-
1>ой диаграмме. Следовательно, qg = fi, так как qgCx) = qgqO) = q/iU) =
^/iQOO = /i(x). Отображения g и q являются взаимно обратными
гомотопическими эквивалентностями, так как gq — /i ~ /0 = 1 посредством /t
и <Z£=Л ^ /о = 1 посредством /t.
X ^-^Х X ^—*Х
\я
Х/А —^ *М Х/А —5— Х/А
п
28
Глава 0. Основные геометрические понятия
Ещё одно приложение свойства продолжения гомотопии, дающее
несколько более тонкую версию одного из ранее сформулированных
признаков гомотопической эквивалентности, состоит в следующем.
(Предложение 0.18. Если (X!, А) — CW-napa, а отображения
приклеивания /, g: А —> Х0 гомотопны, то Х0 \jf Х} ~ Х0 Ug Хг относительно Х0.
Здесь определение гомотопической эквивалентности W ~ Z
относительно У для пар (W, У) и (Z, У) состоит в том, что существуют
отображения ip: W^>Zuip:Z^>W, ограничения которых на У тождественны,
и, кроме того, xpip c^t и ipxp c^t посредством гомотопии, ограничения
которых на Y тождественны в любой момент времени.
Доказательство. Если F: А х I —► Х0 — гомотопия отображения /
в отображение g, то рассмотрим пространство Х0 UF (X} х /). Оно
содержит оба пространства Х0 Uy X! и Х0 Ц X! в качестве подпространств.
Деформационная ретракция XY х I на X] х {0} иЛ х /, описанная в
предложении 0.16, индуцирует деформационную ретракцию Х0 UF (X} x /) на
Х0 Uf Хг. Аналогично Х0 UF (X! х /) деформационно ретрагируется на
Х0 \Jg X-i. Ограничения обеих деформационных ретракций на Х0
тождественны, поэтому вместе они дают гомотопическую эквивалентность
Х0 Lly XY с* Х0 L\g Xx относительно Х0. □
Мы завершим эту главу техническим результатом, доказательство
которого использует разные приложения свойства продолжения гомотопии.
Предложение 0.19. Предположим, что (X, А) и (У, Л)
удовлетворяют свойству продолжения гомотопии, а /: X —> Y — гомотопическая
эквивалентность, причём /|Л = 1. Тогда / — гомотопическая
эквивалентность относительно А.
I Следствие 0.20. Если (X, А) удовлетворяет свойству продолжения
гомотопии, а включение А <-* X является гомотопической
эквивалентностью, то Л —деформационный ретракт пространства X.
Доказательство. Достаточно применить предложение 0.19 к
включению А <-*Х. □
Следствие 0.21. Отображение /: X —> Y является гомотопической
эквивалентностью тогда и только тогда, когда X является
деформационным ретрактом цилиндра отображения My. Значит, два пространства
X и У гомотопически эквивалентны тогда и только тогда, когда
существует третье пространство, которое содержит как X, так и У в качестве
деформационных ретрактов.
Доказательство. На диаграмме отображения i и j —
включения, а г — каноническая ретракция, поэтому / — ri
и i^jf. Так как j и г — гомотопические эквивалентности,
получаем, что / является гомотопической
эквивалентностью тогда и только тогда, когда i — гомотопическая эк-
Глава 0. Основные геометрические понятия
29
вивалентность, поскольку композиция двух гомотопических эквивалент-
ностей — гомотопическая эквивалентность, а отображение, гомотопное
гомотопической эквивалентности, — гомотопическая эквивалентность.
Теперь применим предыдущее следствие к паре (М^,Х), которая
удовлетворяет свойству продолжения гомотопии согласно примеру 0.15 (нужно
воспользоваться окрестностью X х [0,1/2] подпространства X в Mf). □
Доказательство предложения 0.19. Пусть g: Y —> X — гомотопиче-
ски обратное отображение для /. Доказательство будет состоять из трёх
шагов:
1) построим гомотопию отображения g в отображение glt для которого
2) покажем, что gxf ~ 1 относительно А;
3) покажем, что /g: ~ 1 относительно А.
1. Пусть ht: X —* X — гомотопия, связывающая отображения gf = h0
и 1 = Ьг. Так как f\A = 1, мы можем рассматривать ht\A как гомотопию,
связывающую g\A и 1. Затем, так как по предположению (У, А) обладает
свойством продолжения гомотопии, мы можем продолжить эту
гомотопию до гомотопии g{: У —> X, связывающей отображение g = g0 с
отображением gl9 для которого giU = 1.
2. Гомотопия, связывающая отображения gxf и 1, задаётся формулами
1 \h2t,l9 1/2 ^ t ^ 1.
Заметим, что эти два определения согласованы для t = 1/2. Так как f\A = 1
и gt = ht на А, гомотопия /cJA начинается и заканчивается
тождественным отображением, а её вторая половина заключается просто в том, что
первая половина проходится в обратном направлении,
т.е. kt =fcw на А. Определим «гомотопию гомотопии»
ktu: А —> X с помощью рисунка, на котором изображена
область параметров / х / для пар (t, u) с горизонтальной
осью t и вертикальной осью и. На нижней стороне
квадрата мы полагаем kt0 = kt\A. Ниже «V» мы определяем ktu g^ gf t
так, что она не зависит от и, а выше «V» определяем ktu
так, что она не зависит от t. Эти условия не противоречат друг другу,
потому что kt = kx_t на А. Так как к0 = 1 на А, мы получаем кш = 1 для всех
(t, u), принадлежащих левой, правой и верхней сторонам квадрата. Затем
мы продолжаем ktu на всё X следующим образом. Так как (X, А)
обладает свойством продолжения гомотопии, (X х /, А х /) тоже обладает
свойством продолжения гомотопии согласно замечанию после определения
свойства продолжения гомотопии. Поэтому, рассматривая ktu как
гомотопию отображения kt\A, мы можем продолжить кш: А —* X до кш: X —> X, где
kt0 = kr Если мы ограничим это кш на левую, правую и верхнюю стороны
30
Глава 0. Основные геометрические понятия
квадрата в координатной плоскости (t, u), мы получим гомотопию glfc^t
относительно А.
3. Так как g1 s*g, мы имеем /gi —/g^l, а потому /gi^l и шаги1и2
можно повторить, заменив пару /, g на пару g:, /. В результате получим
отображение /г: X —> У, для которого /г|А = 1 и /1g1 ^ 1 относительно Л.
Следовательно, /г c*fl(glf) = (/1g1)/^/rel Л. Из этого мы заключаем, что
/gi-/igi^lrelA. п
Задачи
1. Постройте явно деформационную ретракцию тора с одной
выколотой точкой на граф, состоящий из двух окружностей, пересекающихся
в одной точке, а именно из параллели и меридиана тора.
2. Постройте явно деформационную ретракцию Rn - {0} на S""1.
3. а) Покажите, что композиция гомотопических эквивалентностей
X —► Y и Y —> Z является гомотопической эквивалентностью X —* Z.
Выведите из этого, что гомотопическая эквивалентность — отношение
эквивалентности.
б) Покажите, что отношение гомотопности между отображениями
X —► У — отношение эквивалентности.
в) Покажите, что отображение, гомотопное гомотопической
эквивалентности, является гомотопической эквивалентностью.
4. Деформационная ретракция в слабом смысле пространства X на
подпространство А — это гомотопия /£: X —> X, для которой /0 = 1, fx (X) =
= А и /Г(А) = А для всех t. Покажите, что если X деформационно ре-
трагируется на А в таком слабом смысле, то включение A<-* X является
гомотопической эквивалентностью.
5. Покажите, что если пространство X деформационно ретрагируется
в точку х € X, то для любой окрестности U точки х в X существует
окрестность V с U точки х, для которой включение У*-+и гомотопно нулю.
6. а) Пусть X — подпространство в R2, состоящее из
горизонтального отрезка [0,1] х {0} и вертикальных отрезков
{г} х [0,1 - г] для всех рациональных г из отрезка [0,1].
Покажите, что X деформационно ретрагируется в любую точку
отрезка [0,1] х {0}, но не ретрагируется деформационно ни
в какую другую точку. (Ср. с предыдущей задачей.)
б) Пусть Y — подпространство в R2, состоящее из бесконечного
числа экземпляров описанного выше пространства X, которые расположены
так, как показано на рисунке ниже. Покажите, что Y стягиваемо, но не
является деформационным ретрактом никакой точки.
Глава 0. Основные геометрические понятия
31
в) Пусть Z — идущее зигзагом подпространство в У, гомеоморфное Ж,
которое выделено на рисунке жирной линией. Покажите, что
существует деформационная ретракция в слабом смысле (см. задачу 4)
пространства У на Z, но не существует настоящей деформационной ретракции.
7. Восполните детали в следующей конструкции (из [99])
компактного подпространства Ус13 с теми же свойствами, что и у пространства
У из задачи 6, т. е. У стягиваемо, но не ретрагируется деформационно
ни в какую точку. Для начала рассмотрим пространство X — объединение
бесконечной последовательности конусов над канторовым множеством,
концы которых соединены так, как показано на рисунке. Затем
рассмотрим одноточечную компактификацию
пространства X х R. Она вкладывается в R3 как
замкнутый диск с искривлёнными «плавниками»,
приклеенными вдоль дуг окружностей, и с
одноточечной компактификацией пространства X в
качестве поперечного среза. Теперь требуемое
пространство У получается из этого
подпространства в R3 наматыванием ещё одного конуса над
канторовым множеством вдоль границы диска.
8. Для л > 2 постройте п-комнатный аналог дома с двумя комнатами.
9. Покажите, что ретракт стягиваемого пространства стягиваем.
10. Покажите, что пространство X стягиваемо тогда и только тогда,
когда любое отображение /: X —> У для произвольного пространства У
гомотопно постоянному. Аналогично покажите, что X стягиваемо тогда
и только тогда, когда любое отображение /: У —> X гомотопно
постоянному.
11. Покажите, что /: X —> У — гомотопическая эквивалентность, если
существуют отображения g, h: У —► X, для которых fg са 1и/|/^1. Вообще
покажите, что / — гомотопическая эквивалентность, если fguhf —
гомотопические эквивалентности.
12. Покажите, что гомотопическая эквивалентность /: X —> У
индуцирует взаимно однозначное соответствие между множеством компонент
линейной связности пространства X и множеством компонент линейной
связности пространства У и что ограничение / на компоненту линейной
связности пространства X — гомотопическая эквивалентность с
соответствующей компонентой линейной связности пространства У. Докажите
также соответствующее утверждение для компонент связности вместо
компонент линейной связности. Выведите, что если компоненты связности
пространства X совпадают с компонентами линейной связности, то это
верно и для любого пространства У, гомотопически эквивалентного X,
13. Покажите, что любые две деформационные ретракции г(° и г,1
пространства X на подпространство А можно соединить непрерывным
семейством деформационных ретракций rfs, 0 ^ 5 ^ 1, пространства X на А,
32
Глава 0. Основные геометрические понятия
где под непрерывностью подразумевается, что отображение X х / х / —> X,
переводящее 0,5, t) в г*(х), непрерывно.
14. Для заданных натуральных чисел v, e и /, удовлетворяющих
соотношению v — е + f = 2, постройте клеточную структуру на S2, имеющую v
нульмерных клеток, е одномерных и / двумерных.
15. Перечислите все подкомплексы в S00 для той клеточной структуры
на S°°, для которой S" является n-мерным остовом.
16. Покажите, что пространство S00 стягиваемо.
17. а) Покажите, что цилиндр отображения для любого отображения
/: S1 —► S1 является CW-комплексом.
б) Постройте двумерный CW-комплекс, который содержит как кольцо
S1 х /, так и лист Мёбиуса в качестве деформационных ретрактов.
18. Покажите, что Sl *SJ =S3 и вообще Sm *S" = Sm+n+1.
19. Покажите-, что пространство, полученное из S2 приклеиванием п
двумерных клеток вдоль любого набора из п окружностей на S2,
гомотопически эквивалентно букету п +1 двумерных сфер.
20. Покажите, что подпространство X с R3,
образованное бутылкой Клейна, пересекающей себя по
окружности, как показано на рисунке, гомотопически
эквивалентно S1 VS1 VS2.
21. Покажите, что если X — связное хаусдорфово пространство,
представляющее собой объединение конечного числа двумерных сфер, любые
две из которых имеют не более одной общей точки, то X гомотопически
эквивалентно букету нескольких S1 и нескольких S2.
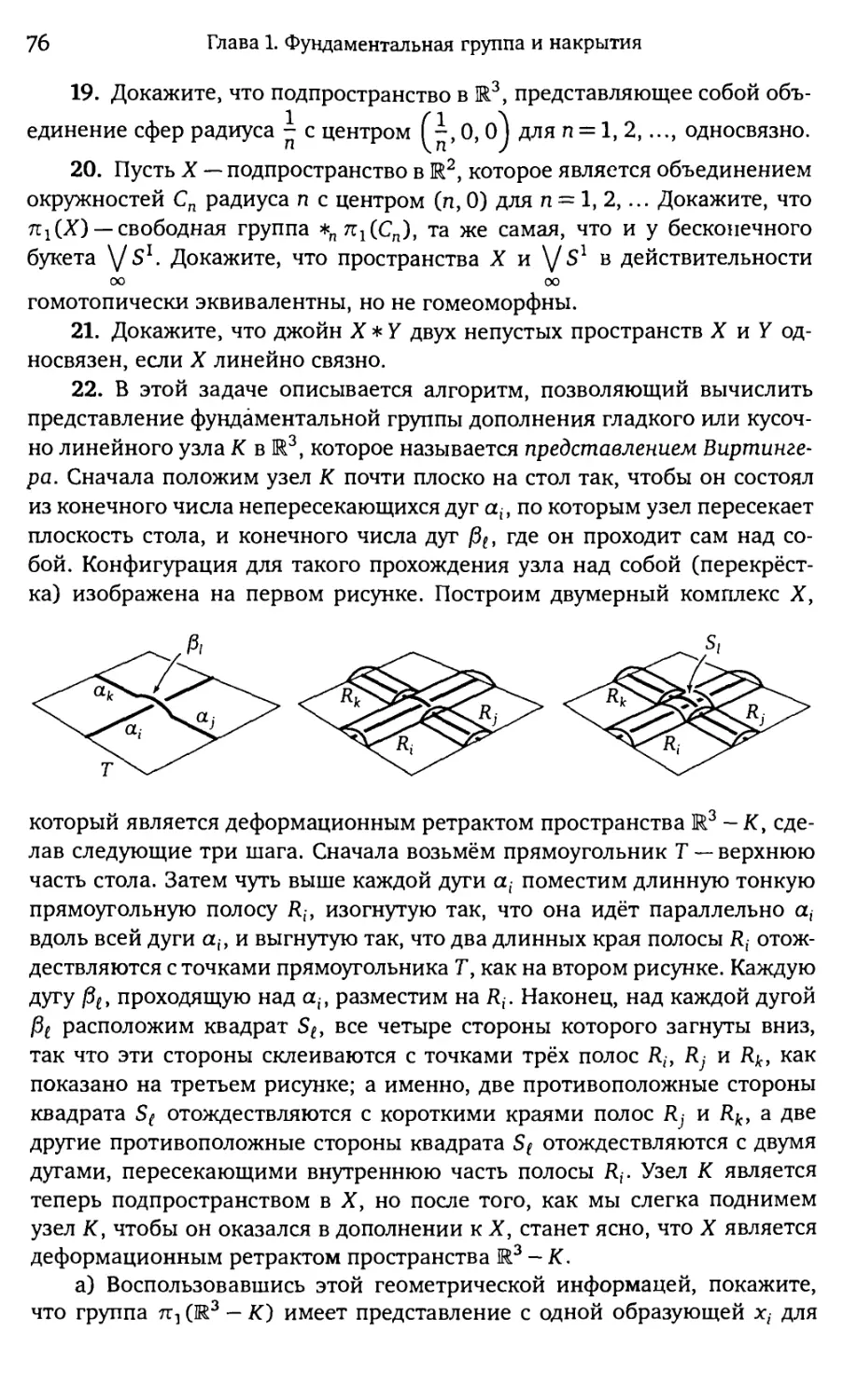
22. Пусть X — конечный граф, лежащий в полуплоскости Р с R3 и
пересекающий край полуплоскости Р по некоторому подмножеству своих
вершин. Опишите гомотопический тип «поверхности вращения»,
полученной при вращении X вокруг прямой —края полуплоскости Р.
23. Покажите, что С1У-комплекс стягиваем, если он является
объединением двух стягиваемых подкомплексов, пересечение которых тоже
стягиваемо.
24. Пусть X и У — CW-комплексы с нульмерными клетками х0 и у0.
Покажите, что факторпространства
Х*У/(Х*{у0}и{х0}*У) и S{XAY)/S{{x0}A{y0})
гомеоморфны, и выведите из этого, что X*Yc*S{X Л У).
25. Покажите, что если X — CW-комплекс с компонентами Ха, то
надстройка SX гомотопически эквивалентна У \/ SXa для некоторого графа У.
а
В случае, когда X — конечный граф, покажите, что надстройка SX
гомотопически эквивалентна букету окружностей и двумерных сфер.
26. Примените следствие 0.20, чтобы показать, что если (X, Л)
обладает свойством продолжения гомотопии, то X х / деформационно ре-
трагируется на X х {0}U A x /. Выведите из этого, что предложение 0.18
Глава 0. Основные геометрические понятия
33
выполняется в более общей ситуации — когда (Х^ А) обладает свойством
продолжения гомотопии.
27. Даны пара (X, А) и гомотопическая эквивалентность /: А—>В.
Покажите, что естественное отображение X —> В Uf X является
гомотопической эквивалентностью, если пара (X, А) обладает свойством
продолжения гомотопии. [Указание. Рассмотрите X U Mf и примените предыдущую
задачу.] Интересный случай возникает, когда / — отображение
факторизации, а значит, отображение X —> В Uf X — отображение факторизации,
которое переводит каждое множество /_1(Ь) в точку. Когда В состоит из
одной точки, это даёт другое доказательство предложения 0.17.
28. Покажите, что если (Хь А) обладает свойством продолжения
гомотопии, то им обладает и любая пара (Х0 Uf Хъ Х0), полученная
приклеиванием Х2 к пространству Х0 посредством отображения /: А—>Х0.
29. В случае, когда CW-комплекс Х получен из подкомплекса А
приклеиванием единственной клетки еп, опишите, как в точности выглядит
продолжение гомотопии ft: А —* У на пространство X, указанное в
доказательстве предложения 0.16. То есть для точки л:Ее" опишите путь ft[x)
для продолженного отображения ft.
30. Дано отображение /: X—> У. Докажите, что отображение g: У—>Х,
для которого gf ~ 1, существует тогда и только тогда, когда X является
ретрактом пространства Mf.
31. а) Предположим, что CW-комплекс Х является объединением
конечного числа подкомплексов X,, а подкомплекс Л с X является
объединением подкомплексов Д с X,-. Покажите, что если каждый комплекс Х{
деформационно ретрагируется на Ah а пересечение любого набора
комплексов X, деформационно ретрагируется на пересечение
соответствующего набора комплексов Ah то X деформационно ретрагируется на А. [По
индукции задача сводится к случаю, когда есть только два пространства
Х[ и два пространства А{. В этом частном случае покажите, что включения
А*-+Аи (Х2 ПХ2) «-♦X являются гомотопическими эквивалентностями.]
б) Используя цилиндры отображений, выведите более общий
результат, что отображение CW-комплексов /: X —> У является гомотопической
эквивалентностью, если являются гомотопическими эквивалентностями
его ограничения
x^n...nx^-^п...п^
для некоторых представлений комплексов X и У в виде конечных
объединений подкомплексов X,- с X и YJ с У, для которых /(X,-) с У|-.
Предположим, что / — клеточное отображение, переводящее n-мерный остов
в n-мерный остов для всех п. Это гарантирует, что цилиндр отображения
Mf является CW-комплексом. [Техника, описанная в §4.1, позволяет
показать, что предположение о клеточности можно опустить.]
32. Покажите, что n-мерный остов симплекса Ак имеет
гомотопический тип букета С?+1 сфер размерности п.
2 Зак. 3655
Глава 1
Алгебраическую топологию можно в первом приближении
определить как исследование методов создания алгебраических образов
топологических пространств. Чаще всего эти алгебраические образы — группы,
но встречаются и более сложные структуры, типа колец, модулей и алгебр.
Механизмы, которые создают эти образы (можно было бы сказать —
«фонари» алгебраической топологии), известны под названием функторов',
они отличаются тем, что они создают образы не только пространств, но
и отображений. Таким образом, непрерывные отображения между
пространствами превращаются в гомоморфизмы между их алгебраическими
образами, поэтому топологически связанные пространства имеют
алгебраически связанные образы.
С удобно сконструированными фонарями можно надеяться создать
достаточно детальные образы, по которым точно восстанавливаются
формы всех пространств, или по крайней мере обширных и важных классов
пространств. В этом одна из главных целей алгебраической топологии,
и она до удивительной степени хорошо достигнута. Конечно, фонари,
необходимые для этого, — весьма сложные механизмы. Но эти механизмы
тоже имеют свойственную им красоту.
В этой главе вводится один из самых простых и самых важных
функторов алгебраической топологии — фундаментальная группа, которая
создаёт алгебраический образ пространства при помощи петель в этом
пространстве, т.е. путей в пространстве, которые начинаются и
заканчиваются в одной и той же точке.
Идея фундаментальной группы
Чтобы получить представление, что же такое фундаментальная
группа, рассмотрим несколько предварительных примеров, прежде чем давать
формальные определения.
Рассмотрим две сцепленные окружности А и В в Ж\ как показано на
рисунке. Наш опыт с реальными зацеплениями и цепями подсказывает,
что, поскольку эти две окружности зацеплены, невозможно отделить В от
Глава 1. Фундаментальная группа и накрытия
35
.00.
А никаким непрерывным движением В типа
проталкивания, вытягивания или поворачивания. Мы
могли бы даже считать, что окружность В сделана
из резиновой или растягивающейся струны, и
разрешить любые её непрерывные деформации,
всегда оставаясь в дополнении к Л, и тогда всё ещё
будет невозможно оттащить В прочь от А. По крайней мере, именно это
подсказывает интуиция, и фундаментальная группа даёт способ сделать
эти интуитивные идеи математически строгими.
Вместо того чтобы зацепить окружность В с А только один раз, мы
могли бы зацепить её с А два или более раз, как на рисунках справа.
Кроме того, задав ориентацию на В, мы можем говорить об окружности В,
зацепленной с А положительное или
отрицательное число раз; скажем, положительное, когда В
проходит вперёд сквозь А, и отрицательное для
противоположного направления. Таким образом,
для каждого целого числа п, отличного от пуля,
мы имеем ориентированную окружность В„,
охватывающую п раз окружность А, где иод
«окружностью» мы подразумеваем кривую, гомеоморф-
ную окружности. Для удобства будем считать, что
окружность В0 вообще не зацеплена с А.
Вспомним теперь, что целые числа не только измеряют величины, но
и образуют группу относительно сложения. Можно ли интерпретировать
эту групповую операцию геометрически — как своего рода операцию
сложения на ориентируемых окружностях В, зацепленных с А?
Ориентируемую окружность В можно представлять себе как траекторию движения
точки, начинающуюся и заканчивающуюся в одной и той же точке х0,
в качестве которой мы можем выбрать любую точку на окружности. Такой
путь, начинающийся и заканчивающийся в одной и той же точке,
называют петлёй. Две различные петли В и В', которые начинаются и
заканчиваются в одной и той же точке х0> можно «сложить» и образовать новую
петлю В 4- В, которая проходит сначала вдоль В, затем вдоль В'. Например,
Ш
36
Глава 1. Фундаментальная группа и накрытия
если Bj и Bj —петли, каждая из которых зацеплена с А один раз в
положительном направлении, то их сумма В^+В'^ деформируется в петлю В2,
зацепленную с А дважды. Точно так же Вх +В_Х можно деформировать
в петлю В0, не зацепленную с Л. И вообще мы видим, что петлю Вт +ВП
можно деформировать в петлю Вт+п для любых целых чисел тип.
Заметьте, что при образовании сумм петель у нас возникают петли,
которые проходят через отмеченную точку не один раз. В этом одна из
причин, почему петли определены просто как непрерывные пути,
которые могут проходить через одну и ту же точку несколько раз. Поэтому
если представлять себе петлю как нечто изготовленное из растяжимой
струны, то эта струна должна обладать волшебным свойством проходить
через себя невредимой. Однако мы должны быть уверены, что наши петли
никогда не пересекают неподвижную окружность А, потому что иначе мы
всегда могли бы отцепить их от Л.
Рассмотрим теперь несколько более сложный вид зацепления,
включающий три окружности, которые образуют конфигурацию, известную
под названием кольца Борромео, изображённую на рисунке. Интересное
свойство этой конфигурации заключается в том, что если убрать любую
из этих трёх окружностей, то две оставшиеся будут не зацеплены.
Аналогично предыдущему будем рассматривать одну из окружностей,
скажем С, как петлю в дополнении к двум другим окружностям Л и В. Нас
интересует, можно ли непрерывно деформировать окружность С, чтобы
полностью отцепить её от Л и от В, всегда оставаясь в дополнении к Л и В
в процессе деформации. Мы можем сделать новый рисунок, потащив
отдельно Л и В в разные стороны; окружность С при этом тоже будет как-то
деформироваться. В результате С обмотается вперёд и назад между Л и В,
как показано на правом рисунке верху. При таком новом расположении,
если мы выходим из точки окружности С, выделенной на рисунке, и
совершаем обход в направлении, заданном стрелкой, то тогда мы проходим
последовательно: 1) вперёд сквозь А, 2) вперёд сквозь В, 3) назад сквозь А,
4) назад сквозь В. Если мы измеряем зацепленность С с Л и В парой целых
чисел, то «вперёд» и «назад» взаимно уничтожаются, поэтому оба целых
числа — нули. Это отражает тот факт, что С не зацеплено ни с Л, ни с В по
отдельности.
Глава 1. Фундаментальная группа и накрытия
37
Чтобы получить более точную меру того, как окружность С зацеплена
с Л и В в совокупности, мы рассмотрим четыре составные части 1)—4)
окружности С как упорядоченную последовательность. Учитывая
направления, в которых эти дуги кривой С проходят сквозь А и В, мы можем
деформировать С в сумму а + Ъ -а — Ъ четырёх петель, как показано на
рисунке. Мы записываем третью и четвёртую петли как первые две с
противоположным знаком, поскольку их можно продеформировать в две первые,
^о с противоположными ориентациями, а как мы видели в предыдущем
примере, сумма двух противоположно ориентированных петель
деформируется в тривиальную петлю, не зацепленную ни с чем. Мы хотели бы
рассмотреть выражение a+b—a — b как лежащее в неабелевой группе, чтобы
оно не получилось автоматически нулевым. Переходя к более привычным
^мультипликативным обозначениям для неабелевых групп, это выражение
можно записать как аЪа~1Ъ~1, т.е. как коммутатор петель а и Ь.
Чтобы лучше понять этот пример, изменим немного эту
конфигурацию, так чтобы окружности А и В были теперь зацеплены, как показано на
рисунке. Окружность С в таком случае можно продеформировать в
положение, изображённое справа, и тогда она снова представляет композицию
петель аЪсГ1Ъ~1у где а и Ъ — петли, охватывающие А и В. Но на левой
части рисунка показано, что в действительности С можно полностью
отцепить от А и В. Таким образом, в этом случае произведение аЬа~1Ь~х
должно быть тривиальным.
Фундаментальная группа пространства X будет определена так, что её
элементы — это петли в X, которые начинаются и заканчиваются в
фиксированной отмеченной точке х0 £ X, но две такие петли считаются
задающими один и тот же элемент фундаментальной группы, если одна
оетля может быть непрерывно продеформирована в другую в пределах
пространства X. (Все петли, которые встречаются в процессе деформации,
38
Глава 1. Фундаментальная группа и накрытия
должны тоже начинаться и заканчиваться в х0.) В первом из описанных
выше примеров пространство X — это дополнение к окружности Л, а в
других двух примерах X — это дополнение к двум окружностям Л и В. Во
втором параграфе этой главы мы покажем следующее.
• Фундаментальная группа дополнения окружности А в первом
примере является бесконечной циклической с петлёй В в качестве
образующей. Это означает, что каждую петлю в дополнении А можно
продеформировать в одну из петель В,р причём Вп нельзя продефор-
мировать в Вт, если пфт.
• Фундаментальная группа дополнения двух незацепленных
окружностей Л и В во втором примере является неабелевой свободной
группой с двумя образующими, представленными петлями а и Ь,
охватывающими окружности Л и В. В частности, коммутатор aba~lb~l
является нетривиальным элементом этой группы.
• Фундаментальная группа дополнения двух зацепленных окружностей
Л и В в третьем примере является свободной абелевой группой с
двумя образующими, представленными петлями а и Ь, охватывающими
окружности Л и В.
Как результат этих вычислений, мы получаем два способа выяснить,
когда пара окружностей Л и В зацеплена. Прямой подход даёт первый
пример, где одна окружность рассматривается как элемент
фундаментальной группы дополнения другой окружности. Альтернативный и несколько
более тонкий метод дают второй и третий примеры, где пара зацепленных
окружностей отличается от пары незацепленных окружностей
фундаментальной группой их дополнения, которая является абелевой в одном
случае и неабелевой в другом. Этот метод является намного более общим:
часто можно убедиться, что два пространства не гомеоморфны, показав,
что их фундаментальные группы не изоморфны, так как из определения
фундаментальной группы легко следует, что фундаментальные группы го-
меоморфных пространств изоморфны.
§ 1.1. Основные конструкции
Этот параграф начинается с основных определений и конструкций,
и затем мы быстро переходим к важному вычислению фундаментальной
группы окружности, опираясь на понятия, которые более подробно
обсуждаются в §1.3. Более систематические методы вычислений
приведены в § 1.2. Их достаточно, например, чтобы показать, что каждая группа
может быть представлена как фундаментальная группа некоторого
пространства. Эта идея используется в дополнении в конце главы, в котором
приведены некоторые примеры того, как алгебраические факты о группах
можно получить топологически. Там, в частности, доказан тот факт, что
каждая подгруппа свободной группы является свободной.
§1.1. Основные конструкции
39
Пути и гомотопии
Фундаментальная группа определяется в терминах петель и
деформаций петель. Иногда бывает полезно рассмотреть более общие понятия
путей и их деформаций, поэтому мы начнём с них.
Путём в пространстве X называют непрерывное отображение /: / —>Х,
где / — единичный отрезок [0,1]. Идея непрерывной деформации пути,
оставляющей неподвижными его концы, становится точной благодаря
следующему определению. Гомотопия путей в X — это семейство
отображений ft: / —> X, 0 ^ t ^ 1, обладающих следующими свойствами:
1) концы ft (0) = xQ и /Д1) = х} не зависят от t;
2) отображение F: / х / -»Х, заданное формулой F(s,0 = /,(s),
непрерывно.
Если два пути /0 и / связаны такой гомотопией /г, то говорят, что они
являются гомотопными. Гомотопность путей обозначается так: /0^/i-
Пример 1.1 (линейные гомотопии). Любые два пути /0 и /х в Еп
с общими концами х0 и хг гомотопны посредством гомотопии ft(s) =
= (1 — 0/0(5) +1/](5). При этой гомотопии каждая точка /0(s) движется
к точке / (s) по прямой с постоянной скоростью. Дело в том, что прямая,
проходящая через точки /0(s) и f (s), линейно параметризуется так:
/0(*) + t[/i(s)-/(,(*)] = (1-0/о(5)+ ГЛ(5),
причём отрезок, заключённый между точками /0(s) /i(s), соответствует
значениям t в интервале от 0 до 1, Если / (s) оказывается равным /0(s), то
этот отрезок вырождается в точку и / (s) =/0(5) для всех t. Это происходит,
в частности, для 5 = 0 и 5 = 1, таким образом, / для всех t является путём от
х0 до хг. Непрерывность гомотопии / как отображения / х / —► R" следует
из непрерывности /0 и /ь так как алгебраические операции сложения
векторов и умножения на скаляр в формуле для / непрерывны.
Эта конструкция показывает также, что для выпуклого подмножества
X с К" все пути в X с данными концами х0 и х} гомотопны, так как если
Л и Л лежат в X, то гомотопия / тоже лежит в X.
Прежде чем двигаться дальше, мы должны проверить следующее
техническое свойство.
Предложение 1.2. Отношение гомотопности для путей с
неподвижными концами в любом топологическом пространстве является
отношением эквивалентности.
Класс путей, гомотопных пути /, мы будем обозначать [/] и называть
Юмотопическим классом пути /.
40
Глава 1. Фундаментальная группа и накрытия
Доказательство. Рефлексивность очевидна, поскольку fc*f
посредством постоянной гомотопии /f =/. Симметричность тоже легко
доказывается, поскольку если /0 ^ /г посредством /t, то /i си /0 посредством
обратной гомотопии /i__t. Транзитивность доказывается следующим образом.
Если /о с* fi посредством ft и /г = g0, причём g0 ^ g! ^
посредством gt, то /о —gi посредством гомотопии /it,
которая равна f2t для 0 ^ t ^ ^ и #2t-i Д-71* 2 ^ r ^ 1#
1
Эти два определения согласованы при t = г, так как
по предположению /i = g0. Непрерывность
отображения Н(5, 0 = hf (5) следует из элементарного факта, который часто будет
использоваться без явного упоминания, а именно: функция, определённая
на объединении двух замкнутых множеств, непрерывна, если непрерывно
её ограничение на каждое из этих множеств. В рассматриваемом случае
Н(5, 0 =F(5, 20 приО^Г^! и
Я(5,0 = G(s,2t-l) при | ^ t ^ 1,
где F и G — отображения I x I -* X, относящиеся к гомотопиям ft и gf.
Так как отображение Я непрерывно на J х 0, « ина/х - 1 , оно
непрерывно на J x J. □
Если даны два пути /, g: I -* Ху для которых /(1) =g(0), то можно
определить композицию или произведение путей / • g как путь, который
проходит сначала вдоль /, а затем вдоль g, и задан формулой
7(25), 0^5^1/2;
g(2s-l), 1/2^5^1.
Таким образом, / и g проходятся с удвоенной скоростью, чтобы путь
/ • g оказался пройденным за единицу времени. Операция произведения
уважает гомотопические классы, поскольку если
/о — /i и £о — £1 посредством гомотопии /г и gf
и при этом /0(1) =go(0), чтобы путь /0 -g0 был
определён, то тогда путь ft • gt определён, и
семейство таких путей задаёт гомотопию /0 • g0 си
Ограничимся теперь путями /: J -»Х, у которых совпадают начало
и конец: /(0) =/(1) = х0еХ. Такие пути называют петлями, а их общее
начало и конец х0 называют отмеченной точкой. Множество всех
классов гомотопии [/] петель f: I -* X в отмеченной точке х0 обозначают
(Предложение 1.3. Множество пг(ХуХ0) является группой
относительно произведения [/] [g] = [/ • g].
Эту группу называют фундаментальной группой пространства X с
отмеченной точкой х0. Мы увидим в главе 4, что группа п1 (X, х0) является
/■g(5) =
§ 1.1. Основные конструкции
41
первой в последовательности групп тгп(Х, х0)у называемых
гомотопическими группами; они определяются совершенно аналогично, только
вместо отрезка / берётся п-мерный куб /п.
Доказательство. Ограничившись рассмотрением петель с
фиксированной отмеченной точкой х0 е X, мы получаем, что произведение / • g
любых двух таких петель определено. Мы уже отметили, что
гомотопический класс пути / • g зависит только от гомотопических классов путей /
и g; таким образом, произведение [/] [g] = [/ • g] корректно определено.
Остаётся проверить три аксиомы группы.
В качестве предварительного шага определим перепараметризацию
пути / как композицию ftp, где у: /—>/ —любое непрерывное
отображение, для которого (^(0) = 0 и ц>{\) = 1. Перепараметризация пути
сохраняет его гомотопический класс, так как fip^f посредством гомотопии /y?t,
где y?t(s) = (1 — Oy>(s) + te, так что щ — ¥> и ¥>i (5) =5- Заметим, что точка
(1 — t)ip(s) + ts расположена между (^(s) и s, а значит, принадлежит /;
поэтому композиция fy>t определена.
Если даны пути /, g, h, у которых /(1) = g(0) и g(l) = Л(0), то оба
произведения (/ • g) • h и / • (g • h) определены, причём / • (g • h), —
перепараметризация пути (f -g)-h кусочно линейной функцией
у>, график которой изображён на рисунке справа.
Следовательно, (/ • g) • h с* / ■ (g • h). Ограничивая рассмотрение
петлями в отмеченной точке х0у мы получаем, что произведение
в пг(Х, х0), ассоциативно.
Для данного пути /: / —> X пусть с —постоянный путь в точке /(1),
определённый так: c(s) = /(1) для всехsе/. Тогда f -с —
перепараметризация пути / посредством функции у>, график которой изображён на первом
рисунке справа; таким образом, f-ccaf. Аналогично с •/=*/, где теперь
с —постоянный путь в точке /(0) (теперь мы
применяем функцию перепараметризации на втором
рисунке). Если в качестве / взять петлю, то мы
получим, что класс гомотопии постоянного пути
в х0 — двусторонняя единица в т^ (X,х0).
Для пути /, идущего из х0 в хг, обратный путь /, идущий из хг назад
в х0, задан формулой /(s) = /(1 — s). Чтобы убедиться, что путь /•/
гомотопен постоянному пути, мы строим гомотопию hf — ft • gt, где /f — путь,
который равен / на отрезке [0,1 -1] и является постоянным
отображением в точку /(1 - О на отрезке [1 -1,1], a gt — обратный к /, путь. Можно
также описать ht с помощью соответствующего отображения Н: / х / —► X,
используя разбиение квадрата / х /, изображённое на рисунке.
На нижней стороне квадрата Я задаётся как / • /; ниже «V»
мы считаем H(s, О независимым от t, в то время как выше «V»
мы считаем H(s, t) независимым от s. Возвращаясь к первому
описанию гомотопии hf, мы видим, что, так как /0 = / и /т —
42
Глава 1. Фундаментальная группа и накрытия
постоянный путь с в точке х0, ft, — гомотопия, связывающая / • / и с • с = с.
Заменяя / на /, получаем, что / • / с* с, где с — постоянный путь в точке ^.
Взяв в качестве / петлю в отмеченной точке х0, получаем, что [/]
—двусторонний обратный элемент для [/] в Я] (X, х0). □
Пример 1.4. Для выпуклого множества ХвМ"с отмеченной точкой
х0 е X группа п} (X, х0) = 0 тривиальна, так как любые две петли /0 и fl9
которые начинаются и заканчиваются в х0, гомотопны посредством
линейной гомотопии
/,(s) = (l-0/o(s) + t/iW,
как описано в примере 1.1.
Не столь легко показать, что пространство имеет нетривиальную
фундаментальную группу, так как для этого нужно каким-то образом
проверить, что не существует гомотопии между некоторыми петлями.
Вскоре мы займёмся самым простым примером, вычислив фундаментальную
группу окружности.
Естественно поинтересоваться зависимостью группы я^Х, х0) от
выбора отмеченной точки х0. Поскольку пг (X, х0) вовлекает только
компоненту линейной связности пространства X, содержащую точку х0, мы
можем надеяться найти связь между пх (X, х0) и пг (X, xY) для двух
отмеченных точек х0 и хь только если х0 и хх лежат в одной и той же компоненте
линейной связности пространства X. Поэтому пусть ft: / —► X — путь из х0
в хъ a ft(s) = ft(l — s) — обратный путь из хг назад в х0. Тогда мы можем
сопоставить каждой петле / в точке Xj петлю
ft • / • ft в точке х0. Строго говоря, мы должны
выбрать порядок построения произведения ft -/-ft, х^ х\ ^ У
т. е. взять либо путь (ft • /) • ft, либо нугь ft • (/ * ft),
но эти два пути гомотопны, а нас здесь интересуют только
гомотопические классы. По-другому, чтобы избежать двусмысленности, мы могли бы
вообще определить n-кратное произведение /i -...■/„, в котором путь f(
Г/-1 П
проходится за время из отрезка , - .
(Предложение 1.5. Отображение /3h: яг(Х, х}) —> п} (X, х0), заданное
формулой /3}1 [/] = [ft •/ • ft], является изоморфизмом.
Доказательство. Если ft — гомотопия петель с началом и концом
в точке хъ то ft -ft • ft— гомотопия петель с началом и концом в точке х0,
поэтому отображение /3h определено корректно. Далее, /3/, —
гомоморфизм, поскольку
PhU-g] = [h'f-g-h] = [h.f-h-h-g-h]=ph[f]ph[g].
Наконец, ph — изоморфизм, а ^ — обратное отображение, так как
РнРкШ = PhVi'f'h] = [h-h-f-h-h] = [/]
и аналогично pfph [/] = [/]. □
§ 1.1. Основные конструкции 43
Таким образом, если X линейно связно, то группа тг^Х, х0) с
точностью до изоморфизма не зависит от выбора отмеченной точки х0. В этом
случае обозначение пг(Хух0) часто сокращают до тгДХ), а можно даже
пойти дальше и написать просто п^Х.
Вообще пространство называют односвязным, если оно линейно
связно и имеет тривиальную фундаментальную группу. Следующий результат
объясняет такое название.
Предложение 1.6. Пространство X односвязно тогда и только, когда
есть ровно один гомотопический класс путей, соединяющих любые две
точки в X.
Доказательство. Линейная связность означает, что существует путь,
соединяющий любую данную пару точек. Таким образом, нас интересует
только единственность соединяющих путей. Предположим, что пг(Х) =0.
Если / и g — два пути из х0 в хг, то / а* / ■ g • g с* g, поскольку каждая из
петель g -g и / -g гомотопна постоянной петле; в последнем случае
используется предположение пх(Х, х0) = 0. Наоборот, если есть только один
гомотопический класс путей, соединяющих отмеченную точку х0 с самой
собой, то все петли в х0 гомотопны постоянной петле и пл {X, х0) = 0. □
Фундаментальная группа окружности
Нашей первой настоящей теоремой будет вычисление группы n^S1) ^
^ Z. Помимо его самостоятельного интереса у этого важного результата
есть несколько существенных непосредственных применений, и он будет
исходной точкой для многих других вычислений в следующем
параграфе. Поэтому не должно вызывать удивления, что для его доказательства
требуется некоторая работа. Чтобы максимизировать отдачу этой работы,
доказательство написано так, чтоб его главные шаги были применимы
в более общей ситуации накрывающих пространств, которые являются
главной темой в § 1.3.
I Теорема 1.7. Отображение Ф: Z —> я} (S1), переводящее целое число п
I в гомотопический класс петли
I con(s) = (cos2rcns, sin2nns)
I с началом и концом в точке (1, 0), является изоморфизмом.
Доказательство. Основная идея заключается в том,
чтобы сравнить пути в S1 с путями в US при помощи
отображения р: Е —> S1, заданного формулой p(s) = (cos2rcs, sin2ns).
Это отображение можно представить геометрически, вложив
RbR3 как спираль, параметризованную как
s —► (cos2rcs, sin2rcs,s),
и тогда р — ограничение на спираль проекции пространства
К3 на М2, заданной формулой (х, у, z) —► (х,у), как показа-
44
Глава 1. Фундаментальная группа и накрытия
но на рисунке. Заметьте, что петля соп является композицией раЗ„, где
соп: 7 —> R — путь с5п (s) = ns, начинающийся в точке 0 и заканчивающийся
в точке п, который наматывается на спираль \п\ раз вверх, если п > О,
и вниз, если п < 0. Соотношение соп =ро>„ выражают словами, говоря, что
путь соп является поднятием пути соп.
Определение отображения Ф можно переформулировать, положив
Ф(п) равным гомотопическому классу петли р/, где / — любой путь в R
из точки 0 в точку п. Такой путь / гомотопен пути <5п_посредством
линейной гомотопии (1 — t)f + tconi следовательно, путь р/ гомотопен пути
рсоп = соп, и новое определение Ф(п) согласуется со старым.
Чтобы проверить, что Ф является гомоморфизмом, рассмотрим
перенос тш: R —> Е, заданный формулой т,п(х) = х + т. Тогда сот • (тта>п) —
путь в!из точки 0 в точку т + п, поэтому Ф(т + п) — гомотопический
класс петли в S1, который является образом этого пути при
отображении р. Этот образ равен просто сот • соп, следовательно, Ф(т + п) =
= Ф(т) -Ф(п).
При доказательстве того, что Ф является изоморфизмом, мы
применим два следующих факта.
а) Для каждого пути /: /—►S1 с началом в точке xQsSlji для каждой
точки х0ер~1(х0) существует единственное поднятие /: 7—>Е,
начинающееся в точке Зс0.
б) Для каждой гомотопии /t: 7 —> S1 путей, начинающихся в точке х0,
и для каждой точки 3?0 е р""1(х,0) существует единственное поднятие
гомотопии /t: / —> R путей, начинающихся в точке х0.
Прежде чем доказывать эти факты, покажем, как из них
выводится теорема. Чтобы проверить, что отображение Ф сюръективно, возьмём
петлю /: 7—>Sl в отмеченной точке (1,0), представляющую данный
элемент группы тг1(51). Согласно а) существует поднятие /, начинающееся
в точке 0. Этот путь / заканчивается в некотором целом числе п, так
как р/(1) = /(1) = (1, 0) и р-1 (1,0) = Z с R. По переформулированному
определению отображения Ф мы тогда получаем Ф(п) = [р/] = [/].
Следовательно, отображение Ф сюръективно.
Чтобы доказать, что отображение Ф инъективно, предположим, что
Ф(т) = Ф(п); это означает, что сот ^ соп. Пусть ft — гомотопия,
связывающая ojjvl= /0 и соп =/1в Согласно б) эта гомотопия поднимается до
гомотопии /t путей, начинающихся в точке 0. Единственность в утверждении
а) влечёт, что /0 = сот и fx — соп. Так как /t —гомотопия путей, конечная
точка /t(l) не зависит от t. При t = 0 эта конечная точка равна т, а для
t — 1 она равна п, таким образом, т = п.
Остаётся доказать факты а) и б). Оба эти утверждения могут быть
выведены из следующего более общего утверждения. _
в) Если даны отображение F: Y х 7 —> S1 и отображение F: У х {0} —> R,
которое является поднятием отображения F\Y x {0}, то существует
§ 1.1. Основные конструкции
45
единственное отображение F: У х / —► R, которое является поднятием
отображения F и имеет заданное ограничение F на У х {0}.
Утверждение а) — это частный случай, когда У является точкой, а
утверждение б) получается, если применить утверждение в) с У = /
следующим образом. Гомотопия ft в б) даёт отображение F: / х / —► S1, если
положить, как обычно, F(s, t) = /t(s). Единственное поднятие F: I х {0} —> R
получается с помощью утверждения а). Тогда утверждение в) даёт
единственное поднятие F: / х / —► R. Ограничения F|{0} x / и F|{1} x / — это
пути, которые являются поднятиями постоянных путей, следовательно,
они тоже должны быть постоянными путями согласно единственности
в утверждении а). Поэтому ft (s) = F(s, t) — гомотопия путей, и /t —
поднятие гомотопии /t, так как pF = F.
Мы докажем утверждение в), используя только одно специальное
свойство проекции р: R —* S1, а именно следующее.
(*) Существует такое открытое покрытие {Ua} окружности S1, что для
каждого а множество p~l (Ua) можно представить в виде объединения
непересекающихся открытых множеств, каждое из которых р
отображает гомеоморфно на Ua.
Например, можем взять покрытие {Ua}y состоящее из любых двух
открытых дуг в S1, объединение которых равно S1.
Чтобы доказать утверждение в), мы сначала построим поднятие
F: Nx —>1R, где N —некоторая окрестность в У данной точки y0€Y. Так
как отображение F непрерывно, для каждый точки (у0, t) € У х / можно
выбрать произведение окрестностей Nt x (a,, bt) так, что F(Nt x (at, bt)) cUa
для некоторого а. Ввиду компактности отрезка {у0} х / конечное число
таких произведений Nt x (at, bt) покрывает {у0} х /. Из этого следует, что
мы можем выбрать одну окрестность N точки у0 и выбрать разбиение
0 = t0 < tx < ... < tm = 1 отрезка / так, чтобы для каждого i множество
^(ЛГ х [th tl+1]) содержалось в некотором множестве Ua>^оторое мы
обозначаем [/,-. Предположим по индукции, что поднятие F уже построено
на N х [0, tj. По условию F(N x [th t,-+1]) с [/,, поэтому согласно
свойству (*) существует открытое множество U{ с R, которое проецируется
гомеоморфно на U{ отображением р и содержит точку F(y0, t(). Заменив
AT на меньшую^окрестность точки у0, мы можем считать, что F(N x {t{})
содержится в Uiy а именно, нужно заменить N х {t,} на его пересечение
с №\Nxitty)~l(Ui). Теперь мы можем определить F на N х [t,-,tl+1] как
композицию F с гомеоморфизмом р""1: [/, -> L/,. Повторив конечное число
раз шаг индукции, мы получим поднятие F: N х / —► R для некоторой
окрестности N точки у0.
Теперь мы докажем единственность в утверждении в) для
частного случая, когда У является точкой. В этом случае мы можем опустить
^ в наших обозначениях. Предположим, что F и F'— два поднятия пу-
46
Глава 1. Фундаментальная группа и накрытия
ти F: /—>S\ для которых F(0) =F/(0). Как и раньше, выберем
разбиение 0 = t0 < tx < ... < tm = 1 отрезка / так, чтобы для каждого i
множество F([t,,t{+1]) содержалось в некотором множестве £/,. Предположим
по индукции, что F = F' на [0,t,]. Так как отрезок [t,, tf+1] связен,
множество F([tp t,-+1]) тоже связно, поэтому оно должно лежать в одном из
непересекающихся открытых множеств Uit проецирующихся гомеоморф-
но на U( согласно свойству (*). По той же причине F'([th ti+l]) лежит
в одном множестве Ur Это множество совпадает с тем, которое содержит
F([tj, £,-+1]), так как F\t{) = F(tf). Поскольку отображение р инъективно на
и( и pF^pF', получаем, что F = F' на [th t,-+1], и шаг индукции доказан.
Последний шаг в доказательстве утверждения в) состоит в том, чтобы
заметить, что, так как отображения F, построенные выше на множествах
вида N х /, являются единственными при ограничениях на каждый
отрезок {у} х /, они должны быть согласованными всегда, когда два таких
множества N х / перекрываются. Таким образом, мы получаем корректно
определённое поднятие F на всём множестве Ух/. Это отображение F
непрерывно, так как оно непрерывно на каждом множестве N х /, и оно
единственно, так как является единственным на каждом отрезке {у} х I, □
Теперь мы обратимся к некоторым применениям этой теоремы. Хотя
обычно алгебраическая топология — это «алгебра, обслуживающая
топологию», их роли полностью меняются в следующем доказательстве
основной теоремы алгебры.
Теорема 1.8. У каждого непостоянного многочлена с
коэффициентами в С есть корень в С.
Доказательство. Можно считать, что многочлен имеет вид p(z) =
= zn + a1z;?_1 + ... +an. Если p(z) не имеет корней в С, то для каждого
вещественного числа г ^ 0 формула
, Р(ге2™)/р(г)
1Л5) |р(ге2^)/р(г)|
задаёт петлю на единичной окружности S1 с С с началом и концом в
точке 1. При изменении г получаем семейство отображений /г —гомотопию
петель с началом и концом в точке 1. Петля /0 тривиальна, поэтому класс
[/r] е я1(51) нулевой для всех г. Теперь выберем достаточно большое
значение числа г, а именно, больше чем |aa| -h... -h |an| и больше чем 1. Тогда
при \z\ = r получаем
|««| = rn = r.rn-1>(|a1| + ... + K|)|zn"1|^|a1^-1 + ... + an|.
Из неравенства |z"|> \а^п~1 + ...+an| следует, что многочлен pt(z) = zn +
+ t(aiZn~l + ...+a„) не имеет корней на окружности |z| = r, если O^t^l.
Заменив р на pt в формуле для /г, указанной выше, и разрешив t
изменяться от 1 до 0, мы получим гомотопию петли /г в петлю соп (s) = e2mns.
Согласно теореме 1.7 петля а>п представляет n-ю степень образующей
бесконечной циклической группы я1(51). Так как мы показали, что [соп] = [fr] =0,
§ 1.1. Основные конструкции
47
мы получаем, что п = 0. Таким образом, единственные многочлены без
корней в С — это константы. □
Наше следующее приложение —теорема Брауэра о неподвижной
точке в размерности 2.
Теорема 1.9. Любое непрерывное отображение h: D2 —> D2 имеет
неподвижную точку, т. е. точку х, для которой h(x) =x.
Здесь мы используем стандартное обозначение Dn для замкнутого
единичного шара (диска) в Rn, состоящего из векторов х длины \х\ ^ 1.
Таким образом, граница шара Dn —единичная сфера Sn~\
Доказательство. Предположим, что Ъ.(х)фх для всех x^D2. Тогда
можно определить отображение г: D2^>Sly взяв в качестве г{х) точку
окружности S1, в которой луч в R2, идущий из точки
h(x) в точку х, выходит за пределы D2.
Непрерывность отображения г очевидна, так как небольшое
изменение точки х приводит к небольшому
изменению точки h(x), а значит, и к небольшому изменению
луча, проходящего через эти две точки. Решающее
свойство отображения г, помимо непрерывности,
заключается в том, что г(х) = х для xeS1. Таким образом, г —ретракция
диска D2 на S1. Покажем, что никакой такой ретракции не может быть.
Пусть /0 — произвольная петля в S1. В D2 есть гомотопия петли /0
в постоянную петлю, например линейная гомотопия
/t(s) = (l-r)/o(s) + tx0,
где х0 — начало и конец петли /0. Так как ретракция г тождественна на S1,
композиция rft является гомотопией в S1 петли rf0 = f0 в постоянную
петлю в точке х0. Но это противоречит тому, что группа n}(Sl) отлична от
нуля. □
Эта теорема была доказана Брауэром около 1910 г., что явилось одним
из первых триумфов алгебраической топологии. Брауэр фактически
доказал соответствующий результат для шара D", и мы получим это обобщение
в следствии 2.15, используя группы гомологии вместо группы пл. Можно
было бы также применить высшую гомотопическую группу пп. Исходное
доказательство Брауэра не использовало ни группы гомологии, ни
гомотопические группы, которые в то время ещё не были изобретены. Вместо
этого оно использовало понятие степени отображения Sn —> Sn, которое
мы определим в § 2.2 с помощью гомологии, а сам Брауэр определял
непосредственно в более геометрических терминах.
Все эти доказательства используют рассуждение от противного, а
потому они показывают только существование неподвижных точек, не давая
никакого способа найти их для заданного явно отображения. Наше
доказательство основной теоремы алгебры похоже на них в этом отношении.
Известны другие доказательства теоремы Брауэра о неподвижной точке,
48
Глава 1. Фундаментальная группа и накрытия
которые несколько более конструктивны, например изящное и весьма
элементарное доказательство Шпернера (1928), которое очень хорошо
объяснено в [5].
Метод, использованный для вычисления группы n1{Sl)t можно
применить для доказательства теоремы Борсука—Улама в размерности 2.
I Теорема 1.10. Для любого непрерывного отображения /: S2 —>R2
существует пара диаметрально противоположных точек хи-х сферы S2,
для которых /(*) =/(-*).
Может оказаться, что есть только одна такая пара диаметрально
противоположных точек х и —х, например, если / — ортогональная проекция
стандартной сферы S2 CIR3 на плоскость.
Теорема Борсука—Улама выполняется также для отображений S" —> R",
как мы показываем в следствии 2.В.7. Доказательство для л = 1 получается
легко, так как разность /(*) - /(-*) изменяет знак, когда х проходит
половину пути вокруг окружности, а значит, эта разница должна быть
нулём для некоторого х. Для п ^ 2 теорема, конечно, уже менее очевидна.
Столь ли очевидно, например, что в любой момент времени должна
найтись пара диаметрально противоположных точек на поверхности земли,
в которых одинаковы температуры и одинаковы атмосферные давления?
Теорема говорит, в частности, что не существует взаимно
однозначного непрерывного отображения S2 в Ш2 и, таким образом, сфера S2 не
гомеоморфна подпространству в R2. Это интуитивно очевидный факт,
который нелегко доказать непосредственно.
Доказательство. Если утверждение теоремы ложно для отображения
/: S2 —> R2, то мы можем задать отображение g: S2^>Sl формулой
gW = (/W-/(-x))/|/U)-/(-x)|.
Определим петлю rj, обходящую вокруг экватора сферы S2 с Е3,
формулой г\(s) = (cos2tts, sin27rs, 0), и пусть h: I —> S1 —составная петля grj.
Так как g(-x) = -g(x), мы получаем соотношение h(s 4 1/2) = -h(s)
для всех s из отрезка [0,1/2]. Как мы показали при вычислении
группы KitS1), петлю h можно поднять и получить путь h: I —>R. Из
соотношения h(s 41/2) = -h(s) следует, что h(s 41/2) = h(s) 4 г Аля некоторого
нечётного целого числа q, которое могло бы зависеть от sG [0,1/2].
Но в действительности q не зависит от s, так как, решая уравнение
h(s 41/2) = h(s) +q/2 относительно qy мы видим, что q непрерывно
зависит от s € [0,1/2], а потому величина q должна быть постоянной, так как
значения этой величины ограничиваются целыми числами. В частности,
мы имеем
ft(l) = £(£)+§ = МО)+q.
Это означает, что петля h представляет q-ю степень образующей
группы ttjCS1). Так как число q нечётно, мы получаем, что петля h не го-
§ 1.1. Основные конструкции
49
мотопна нулю. Но ft-— это композиция gt)\ I —>S2 —>S\ причём петля rj,
очевидно, гомотопна нулю в S2, таким образом, петля gr] гомотопна нулю
в S1 (поскольку мы можем рассмотреть композицию стягивания петли г)
и отображения g). Получено противоречие. □
I Следствие 1.11. Если сфера S2 представлена как Объединение трёх
I замкнутых множеств Аъ А2 и А3, то по крайней мере одно из этих мно-
I жеств должно содержать пару диаметрально противоположных точек
Доказательство. Пусть dt: S2 —> Ж измеряет расстояние до А,-, т. е.
di(x) = infy6A.|x-y|.
Эта функция непрерывна, значит, мы можем применить теорему Борсу-
ка—Улама к отображению S2 —>R2, заданному формулой х—► (dj (х), d2M),
и получить пару диаметрально противоположных точек х и —х, для
которых dx(x) = dl(-x) и d2(x) = d2(-x). Если хотя бы одно из этих двух
расстояний равно нулю, то обе точки х и —х лежат в множестве Аг или
в множестве А2у так как эти множества замкнутые. С другой стороны, если
оба расстояния от х и —х до Ах и А2 строго положительны, то х и —х не
лежат ни в Аг, ни в А2, а потому они должны лежать в А3. П
Чтобы убедиться, что число «три» в этом результате нельзя увеличить,
рассмотрим сферу, вписанную в тетраэдр. Проецируя четыре грани
тетраэдра на сферу по радиусам, мы получаем покрытие сферы S2 четырьмя
замкнутыми множествами, ни одно из которых не содержит пару
диаметрально противоположных точек.
Если предполагать известной многомерную версию теоремы Борсу-
ка—Улама, то те же самые рассуждения показывают, что сферу Sn нельзя
покрыть п + 1 замкнутыми множествами без диаметрально
противоположных пар точек, хотя её можно покрыть гг + 2 такими множествами,
как это показывает многомерный аналог тетраэдра. Даже случай гг = 1
имеет некоторый интерес: если окружность покрыта двумя замкнутыми
множествами, то одно из них должно содержать пару диаметрально
противоположных точек. Это, конечно, неверно для незамкнутых множеств,
так как окружность можно представить в виде объединения двух
непересекающихся полуоткрытых полуокружностей.
Соотношение между фундаментальной группой произведения
пространств и фундаментальных групп множителей столь просто, сколь
можно было бы пожелать.
(Предложение 1.12. Фундаментальная группа nl(X x У) изоморфна
ях(Х) х Я!(У), если пространства X и У линейно связны.
Доказательство. Основное свойство топологии произведения
заключается в том, что отображение f:Z-+XxY непрерывно тогда и только
тогда, когда оба отображения g:Z—>X uh: Z—>У, определённые формулой
50
Глава 1. Фундаментальная группа и накрытия
/(z) = (g(z), h(z)), непрерывны. Следовательно, петля / в X х У с началом
и концом в точке (х0, у0) эквивалентна паре петель ghX иквУ с началом
и концом в точках х0 и у0 соответственно. Точно так же гомотопия ft петли
в X х У эквивалентна паре гомотопии gt и hf соответствующих петель в X
и У. Таким образом, мы получаем взаимно однозначное соответствие
тг^Х х У, (х0,Уо)) * *i(X,*o) х я,(У,у0). [/] ^ (И. №])■
Очевидно, что это гомоморфизм групп, а значит, изоморфизм. □
Пример 1.13 (тор). Согласно предыдущему предложению мы имеем
изоморфизм nA(Sl х S1) &Z x Z. При этом изоморфизме пара (р, q) eZ x Z
соответствует петле, которая наматывается р раз вокруг одного
множителя S1 тора и-q раз вокруг другого множителя S1,
например петле copq(s) = (cop(s), coq(s)). Интересно, что эту
петлю можно завязать узлом, как показано на рисунке для
случая р = 3, q = 2. Узлы, которые получаются таким
способом, так называемые торические узлы, изучаются в
примере 1.24.
Вообще n-мерный тор, который является произведением п
окружностей, имеет фундаментальную группу, изоморфную произведению п
экземпляров группы Z. Это доказывается индукцией по п.
Индуцированные гомоморфизмы
Пусть у: X —> Y — отображение, переводящее отмеченную точку х0£Х
в отмеченную точку у0 е У. Для краткости в такой ситуации мы будем
писать у: (X, х0) —>(У, у0). Тогда if индуцирует гомоморфизм <^#: пг (X, х0)—>
—►тгДУ,у0), который определяется как композиция петли /: J—>Х с
началом и концом в точке х0 и отображения <^, т.е., (£*[/] = [<£/]. Это
индуцированное отображение ^+ определено корректно, так как гомотопия
ft петель с началом и концом в точке х0 приводит к составной гомотопии
y>ft петель с началом и концом в точке у0, поэтому <£„ [/0] = [^/0] = [^/i ] =
= ^*[/i]» Кроме того, отображение <^ — гомоморфизм, так как v?(/-g) =
= (¥>/) • (<££)*> здесь оба отображения принимают значение (/?/(2s) при
0^s^l/2 и значение y?g(2s- 1) при 1/2^5^1.
Два основных свойства индуцированных гомоморфизмов таковы:
• (¥>i/0* = ¥>*i/>* Для композиции (X, х0) —►(У, у0) —►(Z, z0);
• 1+ = 1, что является кратким выражением того, что
тождественное отображение 1: X —> X индуцирует тождественное отображение
1: п^Х,х0)->л1(Х,х0).
Первое из них следует из того факта, что композиция отображений
ассоциативна, поэтому (iprp)f = 4>frpf), а второе очевидно. Эти два
свойства индуцированных гомоморфизмов делают фундаментальную группу
функтором. Формальное определение функтора требует, однако, введения
§ 1.1. Основные конструкции
51
некоторых других предварительных понятий, поэтому мы откладываем
его, пока оно не понадобится в § 2.3.
Если (£ —гомеоморфизм с обратным отображением xj>, то </>*,—
изоморфизм с обратным отображением *ф+, так как ¥>*г/>* = (<^)* = 1* = 1
и аналогично i/^* = 1. Мы применим этот факт при вычислении
фундаментальных групп многомерных сфер.
| Предложение 1.14. Если п ^ 2, то n^S71) = 0.
Доказательство. Пусть / — петля в Sn с началом и концом в
отмеченной точке х0. Если образ отображения / не содержит некоторую другую
точку xgS", to отображение / гомотопно нулю, так как пространство
Sn — {х} гомеоморфно пространству Rn, которое является односвязным.
Поэтому достаточно прогомотопировать отображение / так, чтобы оно
стало не сюръективным. Чтобы сделать это, рассмотрим малый открытый
шар В в Sn с центром в произвольной точке х Ф х0 и
убедимся, что / входит в В, проходит через точку х и выходит
из В конечное число раз, причём каждую из этих частей,
петли / можно сдвинуть с х, не изменяя остальных частей /.
На первый взгляд это может показаться трудновыполнимой
задачей, так как части петли / в В могут быть устроены
геометрически весьма сложно, например, они могут быть кривыми,
заполняющими пространство. Но в действительности это оказывается довольно
лёгким делом.
Множество /-1(В) открыто в (0,1), а потому является объединением
(возможно, бесконечного) набора непересекающихся открытых
интервалов (а,-, Ь(). Компактное множество f~l(x) содержится в объединении этих
интервалов, таким образом, оно должно содержаться в их конечном
объединении. Рассмотрим один из интервалов {ahbi)y содержащих /~Ч*).
Путь fh полученный при ограничении / на замкнутый отрезок [a,, b,L
лежит в замыкании шара В, а его концы /(а,-) и /(Ь,) лежат на границе
шара В. Если п ^ 2, то мы можем выбрать путь g,- из /(а,) в /(£>,-), который
лежит в замыкании шара В, но не проходит через х. Например, можно
выбрать g,- так, чтобы он лежал границе шара В, которая является сферой
размерности п — 1, а значит, линейно связна при п ^ 2. Так как замыкание
шара В гомеоморфно выпуклому подмножеству в ЯГ и, следовательно,
односвязно, путь f гомотопен пути gt согласно предложению 1.6. Таким
образом, мы можем прогомотопировать /, деформируя f в g,. Повторив
эту конструкцию для каждого из интервалов (а,, Ь,-), которые пересекают
/"" 00, мы получаем петлю g, которая гомотопна исходной петле / и при
этом g(J) не проходит через точку х. П
Пример 1.15. Для точки х в Еп дополнение Шп - {х} гомеоморфно
S""1 х К, таким образом, согласно предложению 1.12 группа я^К" - {х})
изоморфна ttjCS"-1) х пх(Ю. Следовательно, группа я^Е" - {х}) равна Z
при п = 2и тривиальна при п > 2.
52
Глава 1. Фундаментальная группа и накрытия
Вот приложение этого вычисления.
| Следствие 1.16. Пространство Ш2 не гомеоморфно R" при п Ф 2.
Доказательство. Предположим, что /: R2 —► R" — гомеоморфизм.
Случай п = 1 легко разбирается, так как пространство R2 — {0} линейно
связно, а гомеоморфное ему пространство R" — {/(0)} не линейно связно при
п = 1. Если п > 2, то мы не можем отличить R2 - {0} от R" - {/(0)} с
помощью числа компонент линейной связности, но предыдущее вычисление
группы Tii ДО" ~ {*}) позволяет различить их с помощью их
фундаментальных групп. □
Более общее утверждение о том, что пространство Rni не
гомеоморфно R" при тфп, можно доказать таким же способом, применяя высшие
гомотопические группы или группы гомологии. В действительности
непустые открытые множества в Rm и Rn могут быть гомеоморфными только
при т = п, как мы покажем в теореме 2.26 с помощью гомологии.
Индуцированные гомоморфизмы позволяют преобразовать
отношения между пространствами в отношения между их фундаментальными
группами. Вот иллюстрация этого принципа.
I Предложение 1.17. Если пространство X ретрагируется на подпро-
I странство А, то гомоморфизм
I t,: яг(Аух0) -► Я!(Х,х0),
К индуцированный включением t: ЛС-^Х, инъективен. Если А — дефор-
I мационный ретракт пространства X, то t* — изоморфизм.
Доказательство. Если г: X —► А — ретракция, то п = 1,
следовательно, r+t* = 1, а это влечёт, что гомоморфизм i* инъективен. Если rt: X —* X —
деформационная ретракция пространства X на Л, то r0 = I, rt\A = l и
гг (X) С А, поэтому для любой петли /: J —> X с началом и концом в точке
х0еА композиция rtf даёт гомотопию петли / в петлю в пространстве А,
таким образом, гомоморфизм t* является также и сюръективным. □
Это даёт другой способ убедиться, что окружность S1 не является
ретрактом диска D2 (этот факт мы проверили ранее при доказательстве
теоремы Брауэра о неподвижной точке). Действительно,
индуцированное включением отображение rc^S1)—►я^О2) является гомоморфизмом
Z —* 0, который не может быть инъективным.
Точный теоретико-групповой аналог ретракции — такой гомоморфизм
р группы G на подгруппу Н, что ограничение р на Н тождественно. В
приведённых выше обозначениях, если мы отождествим группу ях(Л) с её
образом при отображении £,, то получим, что г+ — именно такой
гомоморфизм группы ях(Х) на подгруппу пг(А). Существование гомоморфизма
ретракции р: G^>H является весьма сильным условием на Н. Если Н —
нормальная подгруппа, то из этого условия следует, что G — прямое
произведение группы И и ядра гомоморфизма р. Если подгруппа Н не нор-
§ 1.1. Основные конструкции
53
мальная, то группа G — это то, что в теории групп называют полупрямым
произведением группы Н и ядра гомоморфизма р.
Напомним, что в главе 0 было дано общее определение гомотопии
как семейства отображений ipt: X—>У, tel, для которого отображение
Ф: X х J —> У, заданное формулой Ф(х, t) = ipt(x), является непрерывным.
Если 4>t переводит подпространство Л с X в подпространство В с У для
всех t, то мы говорим о гомотопии отображений пар у>(: (X, А) —> (У, В).
В частности, гомотопна, сохраняющая отмеченную точку, </>t: (X, х0) —>
—> (У, у0), определяется условием ч>с(х0) = у0 Для всех г- Ещё °Дно важное
свойство индуцированных гомоморфизмов — их инвариантность
относительно таких гомотопии.
• Если ipt: (X, х0) —> (У, у0) — гомотопия, сохраняющая отмеченную
точку, то у?о* = 4>и-
Это выполняется, так как
¥>о*[/] = [^о/] = fVi/] = ¥>1*[Я;
здесь среднее равенство следует из гомотопии </>t/.
Для пространств с отмеченными точками имеется понятие
гомотопической эквивалентности. Говорят, что (Х,х0) ^ (У, у0), если существуют
отображения у>: (X, х0) —► (У, у0)и^: (У, у0) —> (X, х0) и существуют
гомотопии yip с*1 и трус*! в классе отображений, сохраняющих
отмеченные точки. В таком случае индуцированные отображения групп тсг
удовлетворяют условию ip*rp* — (уф)* = 1* = 1 и аналогично гр*ц>+= 1» таким
образом, у?+ и гр+ — взаимно обратные изоморфизмы 7ГХ (X, х0) ** 7Г2 (У, у0).
Это несколько формальное рассуждение даёт другое доказательство
того, что деформационная ретракция индуцирует изоморфизм
фундаментальных групп, так как если X деформационно ретрагируется на А, то
(X, х0) ~ (А, х0) для любой отмеченной точки х0 е Д.
Необходимость уделять так много внимания отмеченным точкам,
когда имеешь дело с фундаментальной группой, — нечто вроде досадной
помехи. Для гомотопических эквивалентностей не нужно быть столь же
осторожным, поскольку условия на отмеченные точки в действительности
можно убрать.
I Предложение 1.18. Если у>: X —> У — гомотопическая эквивалент-
I ность, то индуцированный гомоморфизм
I if,: пг{Х9х0) — Я1 (У,¥>(*(>))
I является изоморфизмом для всех х0 е X.
Доказательство использует простой факт о гомотопиях, которые не
сохраняют отмеченную точку.
I Лемма 1.19. Если tpt: X —> У — гомотопия, ah — путь крх О0), по
которому движется образ отмеченной точки х0 е X, то три отображения на
54
Глава 1. Фундаментальная группа и накрытия
диаграмме
nx[Y, </?0Uo))
удовлетворяют соотношению 4>o* = fih4>\*-
Доказательство. Пусть /^ — ограничение отображения ft на отрезок
[О, t], которое перепараметризовано так, чтобы область определения ftf
снова была отрезком [0,1]. Например, можно
положить ft, (s) —h(ts). Тогда если / — петля в X
с началом и концом в отмеченной точке х0, то
произведение ftt • {yj) • ftt даёт гомотопию
петель с началом и концом в точке у?0(*о)- Ес~ . ^
ли мы возьмем в этой гомотопии отображения,
соответствующие t = О и t = 1, то увидим, что
Vo*([/]) = i8fc(Vi.([/])). °
Доказательство предложения 1.18. Пусть отображение i/>: Y —> X
гомотопически обратно отображению </?, т.е. у? я/; с^1 и г/д/? ~1.
Рассмотрим отображения
яДХ,^) -^ Я! (Г, </>(*о)) -^ я^о/^Оо)) ^ я^У^^^^о))-
Композиция первых двух отображений является изоморфизмом, так как
из условия ipy ~1, согласно лемме следует, что ip*^* = /3Л для
некоторого ft. В частности, так как я/> *</?*-— изоморфизм, гомоморфизм (/>+
инъективен. То же самое рассуждение для второго и третьего отображений
показывает, что гомоморфизм гр+ инъективен. Таким образом, первые
два из трёх отображений инъективные, а их композиция— изоморфизм,
поэтому первое отображение </?* должно быть как сюръективным, так
и инъективным. □
Задачи
1. Докажите, что композиция путей обладает следующим свойством
сокращения: если f0'go-f\'Si и g0-gu T0 /о-Л-
2. Докажите, что гомоморфизм замены отмеченной точки (3h зависит
только от гомотопического класса пути ft.
3. Докажите, что для линейно связного пространства X группа п1 {X)
абелева тогда и только тогда, все гомоморфизмы замены отмеченной
точки (3h зависят только от концов пути ft.
4. Подмножество X с R" называют звёздным, если существует такая
точка х0еХ, что для всех хеХ отрезок с концами х0 и х целиком лежит
§ 1.1. Основные конструкции
55
в X. Докажите, что если подмножество ХсЕ" локально звёздное в том
смысле, что у каждой точки множества X есть звёздная окрестность в X,
то любой путь в X гомотопен в X кусочно линейному пути, т. е. пути,
состоящему из конечного числа отрезков, движение по которым происходит
с постоянной скоростью. Докажите, что это, в частности, имеет место,
когда X открыто или когда X является объединением конечного числа
замкнутых выпуклых множеств.
5. Докажите, что для пространства X следующие три условия
эквивалентны:
а) любое отображение S1 —> X гомотопно постоянному отображению,
образом которого является точка;
б) любое отображение S1 —»X продолжается до отображения D2 —> Х\
в) ях(Х, х0) = 0 для любой точки х0еХ.
Выведите из этого, что пространство X односвязно тогда и только
тогда, когда все отображения S1 —>Х гомотопны. [В этой задаче
«гомотопность» означает «гомотопность без каких-либо ограничений на
отмеченные точки».]
6. Мы можем рассматривать n1(Xtx0) как множество
гомотопических классов отображений (Sl,s0) —> (X, х0), сохраняющих отмеченную
точку. Пусть [S1, X] —множество гомотопических классов отображений
S1 —> X без каких-либо условий на отмеченные точки. Тогда есть
естественное отображение Ф: яг (X, х0) —> [S1, X], полученное забыванием
отмеченной точки. Докажите, что Ф сюрьективно, если X линейно связно,
и что Ф([/]) = Ф([^]) тогда и только тогда, когда [/] и [g] сопряжены
в ях(Х, х0). Следовательно, Ф индуцирует взаимно однозначное
соответствие между [S1, X] и множеством классов сопряжённости в ях(Х), если
X линейно связно.
7. Зададим отображение /: S1 х / —► S1 х / формулой
/(e,s) = (0 + 27rs,s),
так что ограничения / на две граничные окружности произведения S1 х /
тождественны. Докажите, что / гомотопно тождественному отображению
посредством гомотопии ft, которая постоянна на одной из граничных
окружностей, но не существует такой гомотопии /г, которая была бы
постоянной на обеих граничных окружностях. [Рассмотрите, что / делает
с путём s —> (0О, s) для фиксированной точки в0 е S1.]
8. Верна ли теорема Борсука—Улама для тора? Другими словами, для
любого ли отображения /: S1 x S1 —> R2 найдётся точка (x,y)eS] x S1, для
которой /(*, у) = /С-х, -у)?
9. Пусть Аъ А2у А3 — компактные множества в R3. С помощью
теоремы Борсука—Улама покажите, что существует плоскость Р сЕ3, которая
одновременно делит каждое множество А, на две части одинаковой меры.
56
Глава 1. Фундаментальная группа и накрытия
10. Из изоморфизма 7га (X х У, (х0, у0)) ** пг (X, х0) х кг (У, у0)
следует, что петли в X х {у0} и {х0} х У представляют коммутирующие
элементы группы кг (X х У, (х0, у0)). Постройте явно гомотопию,
показывающую это.
11. Докажите, что если Х0 — компонента линейной связности
пространства X, содержащая отмеченную точку х0, то включение Х0 <—* X
индуцирует изоморфизм п1 (Х0, х0) —> п} (X, х0).
12. Докажите, что любой гомоморфизм tt^S1) —* nl{Sl) можно
представить как индуцированный гомоморфизм у* для некоторого
отображения ч>\ Sl^>Sl.
13. Дано пространство X и линейно связное подпространство А,
содержащее отмеченную точку х0. Докажите, что отображение пг (А, х0) —>
—►тг1(Х,х0), индуцированное включением А <—* X, сюръективно тогда
и только тогда, когда каждый путь в X с концами в А гомотопен пути в А.
14. Докажите, что изоморфизм пх{Х хУ)% тг^Х) х тг^У) из
предложения L12 задаётся формулой [/] -> (pb([/]),p2*([/])), где рх и р2 —
проекции произведения X х У на оба множителя.
15. Даны отображение /: X —> У и путь /i: / —> X из х0 в хг. Покажите
что f+ph = pfhf* на диаграмме
ft,
пг (X, хг) >- тех (X, х0)
'4 , !'•
16. Докажите, что не существует ретракции г: X —> Л в следующих
случаях:
а) X = R3, а Л — любое подпространство, гомеоморфное S1;
б) X = Sl xD2, а Л —его граничный тор S1 xS1;
в) X = S1 х D2, а Л — окружность, изображённая на рисунке:
г) X = D2 V D2, а Л — его граница SlVSl;
д) X —диск с двумя отождествлёнными точками на его границе, а А —
его граница SlVSl;
е) X — лист Мёбиуса, а А — его граничная окружность.
17. Постройте бесконечно много негомотопных ретракций Sl V S1 —>
-s1.
18. Используя ту же технику, что и в доказательстве предложения 1.14,
покажите, что если пространство X получено из линейно связного
подпространства А приклеиванием клетки е", где п ^ 2, то включение А^Х
§ 1.2. Теорема ван Кампена
57
■индуцирует сюръекцию групп пг. Воспользуйтесь этим, чтобы показать
следующее:
а) букет S1 VS2 имеет фундаментальную группу Ъ\
б) для линейно связного CW-комплекса X отображение включения X1 *—>
<-+Х его одномерного остова индуцирует сюръекцию тг^Х1) —> ях(Х).
[По поводу случая, когда X имеет бесконечно много клеток, см.
предложение 1.А.1 в дополнении.]
19. Измените доказательство предложения 1.14 так, чтобы показать
что если X—линейно связный одномерный CW-комплекс с отмеченной
точкой х0, которая является нульмерной клеткой, то каждая петля в X
гомотопна петле, состоящей из конечной последовательности рёбер,
движение по которым монотонно. [Это даёт элементарное доказательство того,
что группа n^S1) является циклической группой, порождённой
стандартной петлёй, которая обходит один раз вокруг окружности. Поэтому более
трудная часть вычисления группы n^S1) заключается в доказательстве
того, что никакое кратное этой петли не гомотопно нулю.]
20. Пусть /f: X —* X — гомотопия, причём отображения /0 и /i
тождественные. С помощью леммы 1.19 покажите, что для любой точки х0 е X
петля /f(x0) представляет элемент центра группы nl(<Xix0). [По-другому
можно сказать, что петля представляет элемент центра группы тг^Х),
если она продолжается до петли в пространстве отображений X —> X.]
§ 1.2. Теорема ван Кампена
Теорема ван Кампена даёт метод вычисления фундаментальной
группы пространств, являющихся объединением более простых пространств,
фундаментальные группы которых уже известны. Систематически
применяя эту теорему, можно вычислить фундаментальные группы очень
многих пространств. Мы увидим, например, что для любой группы G
существует пространство Хс, фундаментальная группа которого изоморфна G.
Чтобы пояснить идею того, как можно было бы надеяться вычислить
фундаментальную группу, разбивая пространство на более простые части,
рассмотрим следующий пример. Пусть пространство X образовано двумя
окружностями Л и В, пересекающимися в единственной точке, которую
мы считаем отмеченной точкой х0. Согласно нашим
предыдущим вычислениям группа 7Га (А) бесконечная ^
Циклическая, порождённая петлёй а, которая обходит
один раз вокруг А. Аналогично группа п1(В) — ещё
одна группа Z, порождённая петлёй Ь, которая обходит один раз вокруг В.
Каждое произведение степеней элементов а и Ь даёт тогда элемент
группы ях(Х). Например, произведение a5b2a~3ba2 — это петля, которая
обходит пять раз вокруг А, затем два раза вокруг В, затем три раза вокруг А
в противоположном направлении, затем один раз вокруг В, затем два раза
ОО»
58
Глава 1. Фундаментальная группа и накрытия
вокруг А. Множество всех таких слов, состоящих из степеней элемента а,
чередующихся со степенями элемента Ь, образует группу, которую обычно
обозначают Z*Z. Умножение в этой группе определено так, как и
следовало бы ожидать, например, (Ъ*аъЪ2а~2){а%~1аЪ2) = Ъ*аъЪ2аЪ~1аЪ2.
Единичный элемент —пустое слово, а обратные элементы устроены так, как
и должны, например, {аЬ2а~3Ь~л)~г =b4a3b~2a~l. Было бы очень приятно,
если бы такие слова в алфавите, состоящем из букв а и Ь, в точности
соответствовали элементам группы п1{Х) и группа пл (X) была бы изоморфна
группе Z * Z. Из теоремы ван Кампена следует, что это действительно так.
Аналогично если X — объединение трёх окружностей, имеющих
единственную общую точку, из теоремы ван Кампена следует, что группа
тс1(Х) — это группа Z*Z*Z, состоящая из слов, образованных степенями
трёх букв а>Ь,с. Обобщение для объединения любого числа окружностей,
имеющих одну общую точку, тоже следует из теоремы ван Кампена.
Группа Ъ * Ъ является примером общей конструкции, которую
называют свободным произведением групп. Теорема ван Кампена будет
сформулирована в терминах свободных произведений, поэтому, прежде чем
формулировать эту теорему, мы сделаем алгебраическое отступление и
подробно опишем построение свободных произведений.
Свободные произведения групп
Предположим, что дан набор групп Ga и требуется построить одну
группу, содержащую все эти группы в качестве подгрупп. Один способ
сделать это состоит в том, чтобы взять прямое произведение П^а> эле~
а
менты которого можно рассматривать как отображения a>-*gaeiGa.
Можно также ограничиться отображениями, которые принимают значения,
отличные от единичного, лишь конечное число раз; тогда мы получим
прямую сумму 0Ga. Обе эти конструкции дают группы, содержащие все
a
группы Ga в качестве подгрупп, но при этом выполняется следующее
свойство: элементы различных подгрупп Ga коммутируют друг с другом. Для
неабелевых групп эта коммутативность неестественна, поэтому хотелось
бы иметь «неабелеву» версию групп П Ga уши 0 Ga. Так как прямая сумма
a a
ф Ga меньше и в некоторых отношениях проще, чем прямое
Произведшее
ние П^а> следует ожидать, что легче строить неабелеву версию прямой
a
суммы 0 Gai и именно эту версию даёт свободное произведение *a Ga.
а
Приведём теперь точное определение. Как множество, свободное
произведение *rt Ga состоит из всех слов g\g2---gm любой конечной длины
m ^ 0, где каждая буква g{ принадлежит группе Ga. и не равна
единичному элементу группы Ga., причём соседние буквы g, и gl41 лежат в раз-
§ 1.2. Теорема ван Кампена
59
ных группах Ga, т.е. a^a,^. Слова, удовлетворяющие этим условиям,
называют приведёнными; дело в том, что неприведённое слово всегда
можно преобразовать в приведённое, записав соседние буквы, которые
лежат в одной и той же группе Ga., как одну букву (которая является
их произведением в группе Ga) и удалив тривиальные буквы. Слову
разрешается быть пустым; пустое слово будет единичным элементом
в *a Ga. Групповая операция в *a Ga — это запись одного слова за другим:
(gi-.-Sm)№i---frn) = Si—SmV"V Это произведение может, однако,
оказаться неприведённым. Если g,n и hY лежат в одной и той же группе Ga,
то их нужно объединить в одну букву (gnth}) согласно умножению в Ga,
а если эта новая буква gmhY окажется единичным элементом группы Ga,
то её нужно убрать из произведения. После этого, возможно, придётся
объединить gm_j и h2 и, может быть, снова убрать единичный элемент.
Повторяя такие операции, в конце концов получим приведённое слово.
Например, в произведении (gi...gm)(g,7,1.--g1"1) всё сокращается, и мы
получаем единичный элемент группы *a Ga, т. е. пустое слово.
Непосредственная проверка того, что это умножение ассоциативно,
была бы довольно утомительной, но есть косвенный подход, который
дозволяет избежать большой работы. Пусть W — множество
приведённых слов gi...gm, которое включает и пустое слово. Каждому элементу
£G Ga сопоставим отображение Lg: W —> W, которое задаётся умножением
слева: L^^.gJ = ggl...gm, где мы объединяем g с ga, если gl e Ga,
♦гобы получилось приведённое слово ggi...gm. Ключевое свойство
сопоставления g »-» Lg — это формула Lgg. = LgLg> для элементов g, g' G Ga, т. е.
ffO^Cgi-.-gm)) = (£g')(gi...gm)- Этот частный случай ассоциативности
легка следует из ассоциативности произведения в Ga. Из формулы Lgg>=LgLg>
ргедует, что отображение Lg обратимо, причём обратное отображение —
iro Lg-i. Поэтому сопоставление g—*^ определяет гомоморфизм группы
Ga в группу P(W) всех перестановок элементов множества W. Вообще мы
Можем задать отображение L: W->P(W) формулой L(gl...gm) = Lg]...Lg
Для каждого приведённого слова gi...gm. Отображение L инъективно, так
как перестановка L(g1...gm) отображает пустое слово в gi-..gm. Операция
Произведения в W при отображении L переходит в композицию в P(W),
поскольку имеет место соотношение L^* = LgLg>. Так как композиция
в Р{у/) ассоциативна, мы получаем, что произведение в W ассоциативно.
В частности, мы получаем свободное произведение Z * Z, которое
было описано выше. Это пример свободной группы, т. е. свободного
произведения любого числа экземпляров группы Z, конечного или бесконечного.
Элементы свободной группы единственным образом представляются как
Приведённые слова от степеней образующих разных экземпляров
группы Z, по одной образующей для каждого экземпляра Z, как и в случае
группы Z * Z. Эти образующие называют базисом свободной группы, а
число элементов базиса называют рангом свободной группы. Абелианизация
60
Глава 1. Фундаментальная группа и накрытия
свободной группы — это свободная абелева группа, базисом которой
служит то же самое множество образующих, поэтому, так как ранг свободной
абелевой группы определён корректно и не зависит от выбора базиса, это
верно и для ранга свободной группы.
Интересным примером свободного произведения, которое не
является свободной группой, служит группа Z2*Z2. Она похожа на Z*Z, но
устроена более просто, поскольку а2 — е — Ъ2у а потому степени
элементов а и Ъ не нужны, и группа Z2 * Z2 состоит просто из слов с
чередующимися буквами а и b: a, b, аЪу Ъау аЪау ЬаЪу аЪаЪ, ЪаЪа, аЪаЪа, ... вместе
с пустым словом. Структуру группы Z2 *Z2 можно прояснить,
рассматривая гомоморфизм {р: Z2*Z2—>Z2, который сопоставляет каждому слову
его длину по модулю 2. Очевидно, что отображение (р сюръективно, а его
ядро состоит из слов чётной длины. Они образуют бесконечную
циклическую подгруппу, порождённую элементом аЬу так как Ъа = {ab)~] в группе
Z2*Z2. В действительности группа Z2*Z2 —это полупрямое
произведение подгрупп Z и Z2, порождённых элементами аЪ и а, с отношением
спряжения а(аЪ)а~1 = (ab)~}. Эту группу иногда называют бесконечной
диэдральной группой.
Для свободного произведения *aGa общего вида каждая группа Ga
естественно отождествляется с подгруппой группы *a Ga, которая состоит
из пустого слова и неединичных однобуквенных слов g e Ga. С такой
точки зрения пустое слово —общий единичный элемент всех подгрупп
Ga, которые во всём остальном не пересекаются. Из ассоциативности
следует, что любое произведение g}...gm элементов g, в группах Ga
имеет единственную приведённую форму —элемент группы *aGa, который
получается при выполнении умножений в любом порядке. Любую
последовательность операций приведения для неприведенного
произведения gi...gm (соединение соседних букв gf и gI+], которые лежат в одной
и той же группе Ga, или удаление элемента giy который является
единичным) можно рассматривать как способ расставить скобки в gi...gn,
и затем выполнить соответствующую последовательность умножений.
Таким образом, из ассоциативности следует, что любые две
последовательности операций приведения, применённые к одному и тому же
неприведенному слову, всегда приводят к одному и тому же приведённому
слову.
Основное свойство свободного произведения *a Ga заключается в том,
что любой набор гомоморфизмов (ра: Ga-+H единственным образом
продолжается до гомоморфизма у: *a Ga —> Н. А именно, значение
отображения (р на слове gi...gn, где gi^Ga.y должно быть равно 4>ai(gi)...4>an(gn)-
Эту формулу можно использовать для определения гомоморфизма </?; при
этом мы получаем корректно определённый гомоморфизм, так как
процесс сокращения неприведенного произведения в *a Ga, не изменяет его
образ при отображении у>. Например, для свободного произведения G*H
§ 1.2. Теорема ван Кампена
61
включения Gc-^GxHnH<-^GxH индуцируют сюръективный
гомоморфизм G*H—GxH.
Теорема ван Кампена
Предположим, что пространство X представлено в виде объединения
набора линейно связных открытых подмножеств Аа, каждое из которых
содержит отмеченную точку х0еХ. Согласно замечаниям в предыдущем
Параграфе гомоморфизмы ja: ni(Aa)—>я1(Х), индуцированные
включениями Аа t-> X, продолжаются до гомоморфизма Ф: *а тг^Ад) —> ях(Х).
Теорема ван Кампена покажет нам, что отображение Ф очень часто сюръ-
ективно, но у него может быть нетривиальное ядро, ибо если
lap' Пг(АаПАр) ->Я!(Аа)
— гомоморфизм, индуцированный включением Аа Г\Ар с—>Ла, то jaiap =
**jpipa и обе эти композиции индуцированы включением Аа ПАр С-^Х;
хаким образом, ядро гомоморфизма Ф содержит все элементы вида
ia/*(AOl0a(k>)~\ где со G пх(Аа П Ар). Теорема ван Кампена утверждает,
что при весьма общих предположениях это даёт полное описание
гомоморфизма Ф.
I Теорема 1.20. Если X — объединение линейно связных открытых мно-
I жеств Аа, каждое из которых содержит отмеченную точку х0 Е X, и
I если каждое пересечение Аа ПАр линейно связно, то гомоморфизм Ф:
I *a7u1(Aa) —* я^СХ) сюръективен. Кроме того, если каждое пересечение
I АаГ\АрГ\Ау линейно связно, то ядро гомоморфизма Ф — это нормаль-
I пая подгруппа N, порождённая всеми элементами вида iap(co)ipa{co)~l,
I а потому Ф индуцирует изоморфизм
Пример 1.21 (букет). В главе 0 мы определили букет \J Xa набора
a
Пространств Ха с отмеченными точками ха е Ха как факторпространство
Несвязного объединения [Ja Xa, в котором все отмеченные точки ха
отождествляются в одну точку. Если каждая точка ха— деформационный ре-
Тракт открытой окрестности Ua в Ха, то Ха—деформационный ретракт
своей открытой окрестности Аа =Ха \J Up. Пересечение двух или более
рфа
различных множеств Аа —это пространство \J Ua, которое деформацион-
a
■К> ретрагируется в точку. Из теоремы ван Кампена в таком случае следует,
***> *: *а пг (Ха) -> пх (V Ха) - изоморфизм.
а
Таким образом, для букета окружностей \JS\ группа ^\С\/Sla) сво-
,ж^Шая, а именно, является свободным произведением нескольких
экземпляров группы Z, по одному для каждой окружности S*. В частности,
62
Глава 1. Фундаментальная группа и накрытия
nl(SlvS1) — свободная группа Ъ*Z, как указано в примере в начале этого
параграфа.
Как мы покажем в §1.А, справедливо и более общее утверждение,
что фундаментальная группа любого связного графа является свободной.
Сейчас мы приведём пример, иллюстрирующий этот общий метод.
Пример 1.22. Пусть X — граф из двенадцати рёбер куба,
изображённый на рисунке. Семь выделенных рёбер образуют максимальное дерево
Т С X — стягиваемый подграф, содержащий все вершины
графа X. Мы утверждаем, что Я](Х) —свободное
произведение пяти экземпляров группы Z, по одному для каждого
ребра, не лежащего в Т. Чтобы вывести это из теоремы ван
Кампена, выберем для каждого ребра еа графа X - Т
открытую окрестность Аа множества Т и еа в X, которая
деформационно ретрагируется на TUea. Пересечение двух или более множеств
Аа деформационно ретрагируется на Г, а потому стягиваемо. Множества
Аа образуют покрытие графа X, удовлетворяющее условию теоремы ван
Кампена, а так как пересечение любых двух из них односвязно, мы
получаем изоморфизм ях(Х) ъ *a яДЛд). Каждое множество Аа
деформационно ретрагируется на окружность, поэтому я^Х) — свободная группа
с пятью образующими, что и требовалось. В качестве явных образующих
мы можем выбрать для каждого ребра еа графа X — Т петлю /а, которая
начинается в отмеченной точке графа Г, проходит в Г до одного конца
ребра еа, затем идёт вдоль ребра еа, а потом возвращается назад в
отмеченную точку по некоторому пути в Т.
Теорема ван Кампена часто применяется, когда покрытие
пространства X состоит только их двух множеств Аа и Ар. Тогда условие на тройные
пересечения АаПАрП Ау становится излишним и мы получаем
изоморфизм яДХ)^ (я1(Ла)*я1(Л/3))/Д^ при условии, что пространство Аа П Ар
линейно связно. Однако доказательство в этом частном случае
фактически совпадает с доказательством в общем случае.
Можно убедиться, что пересечения Аа П Ар должны быть линейно
связными, рассмотрев представление окружности S1 в виде объединения
двух открытых дуг. В этом случае гомоморфизм Ф не сюръективен. Чтобы
построить пример, показывающий, что тройные пересечения Аа ПАрПАг
должны быть линейно связными, возьмём в качестве X надстройку над
тремя точками а, Ь, с, и пусть Аа, Ар и Ау будут дополнениями этих трёх
точек. Теорему можно применить к покрытию {Аа,Ар}
и получить изоморфизмы ях(Х) ъп}(Аа) *я,(Л^) ^Z*Z,
так как пространство Аа П Ар стягиваемо. Если же мы
попытаемся использовать покрытие {Ла, Ар, Ау}, для
которого линейно связно любое двукратное (но не тройное) пересечение, то
получим, что Я] (X) «а z * Ъ * Z, но эта группа не изоморфна Ъ * Z, так как
у них разные абелианизации.
§ 1.2. Теорема ван Кампена
63
Доказательство теоремы ван Кампена. Сначала обсудим сюръек-
хивность отображения Ф. Мы утверждаем, что если дана петля f:I—*X
.с началом и концом в отмеченной точке х0, то существует такое разбиение
0 = 50 < Sj < ... < sm = 1 отрезка /, что образ каждого отрезка [s,_i, sf] при
отображении / целиком лежит в одном из множеств Аа. А именно, так как
/ непрерывно, каждая точка s е / имеет открытую окрестность Vs в /, образ
которой при отображении / лежит в одном из множеств Аа. В
действительности в качестве Vs мы можем взять открытый интервал, замыкание
которого отображается в одно из множеств Аа.
Из компактности отрезка / следует, что
конечное число таких интервалов покрывает /.
Тогда концы этих интервалов задают требуемое
разбиение отрезка /.
Обозначим множество Аа, содержащее
/([5,-1,5-]), через А,-, и пусть /j—путь,
полученный при ограничении / на [s^^s,-]. Тогда
/ — композиция Л •...•/„!, причём путь fa целиком лежит в А,-. Так как
мы предполагаем, что пространство A{CiAi+l линейно связно, мы можем
выбрать путь g( в А,- П А1+1, идущий из точки х0 в точку /(s,0 e А{ П А1+1.
Рассмотрим петлю
Cfrfi) * (Si 'Л *fo)' (fo'/з в1з)' -" (ftii-i */m)>
гомотопную /. Эта петля представляет собой композицию петель, каждая
из которых расположена в одном множестве А,-; такие петли заключены
в круглые скобки. Следовательно, [/] лежит в образе отображения Ф, а
потому Ф сюръективно.
Более трудная часть доказательства состоит в том, чтобы показать,
что ядро гомоморфизма Ф совпадает с N. Чтобы разъяснить суть дела,
введём несколько терминов. Под факторизацией элемента [/] е п1 (X) мы
будем подразумевать формальное произведение [/J.-.t/fc], где:
• каждый множитель f{ — это петля в некотором множестве Аа с
началом и концом в отмеченной точке х0, а [/•] е яi(Aa), —
гомотопический класс петли /•;
• петля / гомотопна f}- ...-fk в X.
Таким образом, факторизация гомотопического класса [/] — это
слово в ^anl(Aa)i возможно, неприведённое, которое переходит в [/] при
отображении Ф. Доказательство сюръективности гомоморфизма Ф
показывает, что у каждого элемента [/] еп^Х) есть факторизация.
Теперь нас будет интересовать единственность факторизации. Назовём
Две факторизации класса [/] эквивалентными, если они связаны
последовательностью преобразований следующих двух видов или обратных к ним:
• соседние члены [/•] [/j+i] объединяются в один член [f{ • fi+l], если [/■]
и [/-+1] лежат в одной и той же группе tt^Aq);
64
Глава 1. Фундаментальная группа и накрытия
• член [/j] e пг (Ла) рассматривается как лежащий в группе п^ 04^), а не
в группе яДЛа), если f{ — петля в АаГ\Ар.
Первое преобразование не изменяет элемент группы *а я^Ла),
определяемый факторизацией. Второе преобразование не изменяет образ
этого элемента в факторгруппе Q = *a n^A^/N согласно определению
группы N. Таким образом, эквивалентные факторизации дают один и тот же
элемент группы Q.
Если нам удастся показать, что любые две факторизации класса [/]
эквивалентны, то из этого будет следовать, что отображение Q —► яь (X),
индуцированное отображением Ф, инъективно, а потому ядро
гомоморфизма Ф совпадает с N, и доказательство будет завершено.
Пусть [/i]...[/J и [/^...[//l—две факторизации класса [/]. Тогда
составные пути Л *... • Л и /^ •... • /^ гомотопны, поэтому можно рассмотреть
гомотопию F: J x J —► X, связывающую /i •... • fk и f[ •... •//. Существуют
такие разбиения 0 = s0 <sx < ... <sm = 1 и 0 = t0 < tx < ... < tn = 1, что
образ каждого прямоугольника R{j = [5,_ь s{] x [t;_T, t;] при отображении F
лежит в одном множестве Aai которое мы обозначим A(j. Эти
разбиения можно получить, покрыв 1x1 конечным числом прямоугольников
[а,Ь] х [c,d], каждый из которых отображается в одно множество Ла,
используя рассуждения с компактностью, а затем разделив 1x1 всеми
горизонтальными и вертикальными прямыми, содержащими стороны этих
прямоугольников. Можно считать, что s-разбиение является
подразбиением тех разбиений, которые дают произведения /г •... • fk и // •... •//. Так
как F отображает окрестность прямоугольника R^
в А,-,, мы можем пошевелить вертикальные стороны
прямоугольников Rjj так, чтобы каждая точка
квадрата 1x1 принадлежала не более чем трём
прямоугольникам Rjj. Можно считать, что есть по крайней
мере три ряда прямоугольников, поэтому мы можем
сделать это шевеление только для прямоугольников
в промежуточных рядах, оставляя верхний и нижний ряд без изменений.
Занумеруем теперь новые прямоугольники Rb R2, ..., Rmn в таком
порядке, как показано на рисунке.
Если у —путь в J x J, идущий из точки левой стороны в точку
правой стороны, то ограничение F\y является петлёй с началом и концом
в отмеченной точке х0, так как F отображает левую и правую стороны
квадрата I x I в точку х0. Пусть уг —путь, отделяющий первые г
прямоугольников Rb ..., Rr от остальных прямоугольников. Тогда у0 —нижняя
сторона квадрата J x J, а утп — его верхняя сторона. Будем переходить от
пути уг к уг+1, протаскивая этот путь по прямоугольнику Rr+1.
Будем называть вершины прямоугольников Rr вершинами. Для
каждой вершины v, для которой F(v) ^х0, рассмотрим путь gv из х0 в F(v).
Мы можем выбрать путь gv так, чтобы он принадлежал пересечению двух
9
5
1
10 11 1
6
2
7
3
12
8
4
§ 1.2. Теорема ван Кампена
65
или трёх множеств A(j в соответствии с тем, сколько прямоугольников Rr
содержат вершину v, так как мы предполагаем, что пересечение любых
двух или трёх множеств A(j линейно связно. Если мы вставим в F\ yr
подходящие пути gvgv в последовательных вершинах, как при доказательстве
сюръективности отображения Ф, то мы получим факторизацию класса
[F\ yr], рассматривая петлю, соответствующую горизонтальному или
вертикальному отрезку между соседними вершинами, как лежащую в А-{] для
любого из прямоугольников Я5, содержащих этот отрезок. Если мы
выберем другой из этих прямоугольников Rs, то факторизация класса [F\ yr]
заменится на эквивалентную факторизацию. Более того, факторизации,
соответствующие последовательным путям уг и уг+1, эквивалентны, так
как протаскивание пути уг по прямоугольнику Яг+1, при котором
получается путь уг+1, заменяет F| yr Ha F\ yr+i посредством гомотопии в пределах
множества А,-,, соответствующего Яг+1, и мы можем выбрать такое
множество Ау для всех отрезков путей уг и уг+1, лежащих в Яг+1.
Мы можем добиться, чтобы факторизация, соответствующая у0, была
эквивалентна факторизации [/^...[Д], выбирая путь gv для каждой
вершины v вдоль нижней стороны квадрата / х / так, чтобы он принадлежал
не только двум множествам А,-,, соответствующим прямоугольнику Rsy
содержащему v, но также принадлежал и множеству Аа, соответствующему
пути f(, в области определения которого лежит точка v. В случае, когда v —
общий конец областей определения двух последовательных путей fh
выполняется равенство F(v) =x0, а тогда нет никакой надобности выбирать
путь gv. Аналогично мы можем считать, что факторизация,
соответствующая последнему пути утп, эквивалентна [f[]... [//]. Так как факторизации,
соответствующие всем путям уг, эквивалентны, мы получаем, что
факторизации [/х]...[/*] и [//]...[//] эквивалентны. □
Пример 1.23 (зацепленные окружности). Мы можем применить
теорему ван Кампена, чтобы вычислить фундаментальные группы трёх
пространств, которые обсуждались в вводной части этой главы, а именно
дополнений в Ш3 одной окружности, двух незацепленных окружностей
и двух зацепленных окружностей.
Дополнение Е3 — А одной окружности А деформационно ретрагиру-
ется на букет S1 V S2, вложенный в Е3 - А, как показано на первом из
двух рисунков ниже. Возможно, проще увидеть, что М3 - А
деформационно ретрагируется на объединение сферы S2 и её диаметра, как показано
DO
Глава 1. Фундаментальная группа и накрытия
на втором рисунке, где точки снаружи S2 деформационно ретрагируются
на S2, а точки, которые лежат внутри сферы S2, но не на окружности А,
можно отодвинуть от А по направлению к S2 или к диаметру» Помня эту
деформационную ретракцию, можно понять, как нужно её изменить, если
два конца диаметра постепенно сближаются друг с другом по экватору,
пока они не совпадут, образуя при этом окружность S1 в букете SlV S2.
Другой способ увидеть деформационную ретракцию пространства Ш3 - А на
S1 V S2 состоит в том, чтобы заметить сначала, что открытая е-окрестность
букета Sl VS2, очевидно, деформационно ретрагируется на SlvS2, если е
достаточно мало. Затем заметим, что эта окрестность гомеоморфна R3 - А
посредством гомеоморфизма, который тождествен на S1 V S2.
Действительно, окрестность можно постепенно увеличивать посредством
гомеоморфизма, пока она не совпадёт с R3 - А.
В любом случае, как только мы
убедились, что R3 - А деформационно
ретрагируется на Sl V S2, мы сразу получаем
изоморфизмы nl (R3 - А) « пг (S1 V S2) ъ Z, так как
nl(S2)=0.
Аналогично дополнение Е3 - (А и В) двух незацепленных
окружностей АиВ деформационно ретрагируется на Sx\/SlV S2 V S2, как на
рисунке справа. Из этого мы получаем пг (К3 - (АиВ)) ^Z*Z.
С другой стороны, если АиВ зацеплены, то R3 - (А и В)
деформационно ретрагируется на букет сферы S2 и тора
S1 х S1, разделяющего Л и В, как показано на рисунке
слева, следовательно, тг^К3 - (АиВ)) ъ tt1(S1 х S1) *
^ZxZ.
Пример 1.24 (торические узлы). Для взаимно простых
положительных целых чисел тип торический узел К = Ктп С1R3 определяется как
образ вложения /: S1 —> S1 х S1 с IR3, заданного формулой /(z) = (z'n, zn);
здесь тор S1 х Sl вложен в Ш3 стандартным способом. В целом узел К
обматывается вокруг тора т раз в направлении параллели и п раз в
направлении меридиана, как показано на рисунке для
случаев (т, п) = (2, 3) и (3,4). Нужно
предполагать, что числа тип взаимно простые,
чтобы отображение / было инъективным.
Без этого предположения отображение /
переводило бы d точек в одну, где d —
наибольший общий делитель чисел т и п, а образ отображения / был бы тогда
узлом Km/dM/d. Можно было бы позволить числам тип принимать
отрицательные значения, но от этого узел К мог бы измениться только на свой
зеркальный образ.
Давайте вычислим я1(К3~К). Вычисления будут немного проще,
если заменить пространство К3 на его одноточечную компактификацию S3.
§ 1.2. Теорема ван Кампена
67
Хворема ван Кампена показывает, что щ при этом не изменяется. А
именно, представим S3 — К в виде объединения Е3-Ки открытого шара В,
образованного точкой компактификации вместе с дополнением большого
замкнутого шара в R3, содержащего К. Оба пространства В и В П (R3 - К)
сдносвязны (последнее пространство гомеоморфно S2 х R). Поэтому из
теоремы ван Кампена следует, что включение R3 - К «-* S3 - К индуцирует
изоморфизм групп тс1.
Мы вычислим n^S3 -К"), показав, что это пространство
деформационно ретрагируется на двумерный комплекс X = Хшп, гомеоморфный фак-
торпространству цилиндра Sl xl при отождествлениях (z, 0) ~ (е2ш/тг, 0)
и (z, 1) ~ (e27n/nz, 1). Если Хт и Х;1 — части комплекса X, полученные
факторизацией подпространств S1 х 0, х и S1 х - 1 , то Хт и Ха —
цилиндры отображений z —* zm и z —* zn. Пересечение Хт П Х„ является
окружностью ^Х х { о j ~тем основанием каждого цилиндра отображения,
которое соответствует области определения.
Чтобы получить вложение пространства X в S3 — К в качестве
деформационного ретракта, мы воспользуемся стандартным представлением
сферы S3 в виде объединения двух полноторий Sl x D2 и D2 x S1, которое
получается, если рассматривать S3 как
d£>4 = a(D2xD2) = aD2xD2UD2xdD2.
Геометрически первое полноторие Sl x D2 можно отождествить с ком-
йактным множеством в 1R3, ограниченным стандартным тором S1 x S1,
Содержащим К, а второе полноторие D2 x S1 тогда будет замыканием
Дополнения первого полнотория вместе с бесконечно удалённой точкой
Компактификации. Обратите внимание, что меридианы в S1 x S1
ограничивают диски в первом полноторий, а параллели ограничивают диски во
втором полноторий.
В первом полноторий узел К пересекает каждый меридиан {х} х 3D2
3 m точках на равных расстояниях, как показано на рисунке, где
изображён меридиональный диск {х} х D2. Эти т точек
можно отделить друг от друга объединением т радиусов.
Когда х изменяется, эти радиусы заметают ^„ —
цилиндр отображения в первом полноторий.
Аналогично во втором полноторий содержится другой цилиндр
отображения Хп. Дополнение узла К в первом
полноторий деформационно ретрагируется на Хт, смещаясь на
каждом меридиональном диске по траекториям потока, изображённого
на рисунке. Точно так же дополнение узла К во втором полноторий
деформационно ретрагируется на Хп. Эти две деформационные ретракции
Не согласованы на их общей области определения S1 x S] - Ку но это легко
Исправить, изменив потоки в двух полноториях так, чтобы в S1 x S1 - К
68
Глава 1. Фундаментальная группа и накрытия
оба потока стали ортогональными к К, После этого изменения мы
получим корректно определённую деформационную ретракцию
пространства S3 — К на X. Описать эту ситуацию по-другому можно было бы,
сказав, что для открытой ^-окрестности N узла К, ограниченной тором Г,
дополнение S3 -N является цилиндром отображения Т—>Х.
Чтобы вычислить пА (X), мы применим теорему ван Кампена к
представлению пространства X в виде объединения множеств Хт и Хп, точнее
говоря, открытых окрестностей этих двух множеств, которые
деформационно ретрагируются на них. Пространства Хт и Хп являются
цилиндрами отображений, деформационно ретрагирующимися на окружности,
а Хт П Хп — окружность; таким образом, все три пространства имеют
фундаментальную группу Z. Петля в Хт ПХП, представляющая образующую
группы П\(Хт ПХП), гомотопна в Хт петле, представляющей гп-кратную
образующую, а в Хп — петле, представляющей п-кратную образующую.
Теорема ван Кампена говорит тогда, что п1 (X) — факторгруппа свободной
группы с образующими а и Ъ по нормальной подгруппе, порождённой
элементом атЬ~п.
Обозначим через Gmn группу я1(Хт>п), заданную двумя образующими
а и Ъ и одним соотношением ат = Ьп. Если т или п равно 1, то Gmn —
бесконечная циклическая группа, так как в этом случае соотношение просто
выражает одну образующую как степень другой. Чтобы описать строение
группы G,nn, когда т, п > 1, вычислим сначала центр группы Gmn, т.е.
подгруппу, состоящую из тех элементов, которые коммутируют со всеми
элементами группы Gmn. Элемент ат = ЬП коммутирует с а и Ь, поэтому
циклическая подгруппа С, порождённая этим элементом, лежит в центре.
В частности, подгруппа С нормальная, поэтому мы можем перейти к
факторгруппе Gmn/C, которая является свободным произведением Zni*Z„.
Согласно задаче 1 в конце этого параграфа свободное произведение
нетривиальных групп имеет тривиальный центр. Из этого следует, что С —это
в точности центр группы Gmjr Как мы увидим в примере 1.44, элементы
а и Ъ имеют бесконечный порядок в Gmn, поэтому группа С бесконечная
циклическая, но нам здесь этот факт не нужен.
Покажем теперь, что целые числа т и п (а значит, и группа Gmn)
однозначно определяются группой Ът * Zn. Абелианизация группы Ът * Ъп
есть группа Ът х Ъп\ она имеет порядок тп, поэтому произведение тп
однозначно определено группой Zm *Zn. Чтобы найти т и п по
отдельности, мы воспользуемся ещё одним утверждением из задачи 1 в конце
параграфа, а именно, что все элементы кручения в группе Ът * Zn
сопряжены элементам подгрупп Zm и Z„, а потому имеют порядок,
делящий т или п. Таким образом, максимальный порядок элементов кручения
в группе Zm *Zn равен наибольшему из чисел тип. Поэтому наибольшее
из этих двух чисел однозначно определяется группой Ът *Zn, а значит,
наименьшее тоже, так как их произведение определено однозначно.
§ 1.2. Теорема ван Кампена
69
Предыдущий анализ группы п1 (Хтп) не требовал предположения, что
числа тип взаимно простые; это условие нужно только для того,
чтобы соотнести Xmill с торическими узлами. Интересен тот факт, что Хтп
можно вложить в Е3 только в том случае, когда тип взаимно простые.
Это доказывается в замечаниях после следствия 3.45. Например, Хгг —
бутылка Клейна, так как это пространство представляет собой два
листа Мёбиуса Х2 с отождествлёнными граничными окружностями. Таким
образом, утверждение о невложимости обобщает тот факт, что бутылку
Клейна нельзя вложить в R3.
Алгоритм вычисления образующих и соотношений, задающих группу
ях(К3 — Ю для произвольного гладкого или кусочно линейного узла К,
описан в задаче 22 в конце этого параграфа, но вопрос о том, когда две из
этих фундаментальных групп изоморфны, в общем случае намного более
трудный, чем в частном случае торических узлов.
Пример 1.25 (букет стягивающихся окружностей). Рассмотрим
подпространство X с R2, которое является объединением окружностей Сп
радиуса - с центром (_,о) для п = 1,2,... На первый
взгляд X можно спутать с букетом бесконечного набора
окружностей, но мы сейчас покажем, что фундаментальная
группа у пространства X намного больше, чем у такого
букета. Рассмотрим ретракцию гп: X —► Сп, сжимающую все
окружности С,-, кроме С„, в одну точку — начало координат.
Каждая ретракция гп индуцирует сюръекцию р„: пг{X) —> пг{Сп) ъ%у где
в качестве отмеченной точки выбрано начало координат. Произведение
отображений рп — гомоморфизм
оо
в прямое произведение (не прямую сумму) бесконечного набора групп Z,
причём гомоморфизм р сюръективен, так как для каждой
последовательности целых чисел кп можно построить петлю /: J —> X, которая обходит
кп раз вокруг Сп за время из интервала [1 - 1/л, 1 - 1/л +1]. Эта
бесконечная композиция петель, очевидно, непрерывна в любой момент времени
меньше 1, и она непрерывна в момент 1, так как любая окрестность
отмеченной точки в X содержит все окружности Сп, кроме конечного числа.
Поскольку группа п1{Х) отображается на всю несчётную группу \\Ъ, она
оо
является несчётной. С другой стороны, фундаментальная группа букета
счётного набора окружностей счётно порождена, а значит, счётна.
Группа я1 (X) в действительности намного сложнее группы \\Ъ. На-
оо
пример, она неабелева, так как ретракция X —* Q и... и Сп, которая
стягивает все окружности внутри С„ в отмеченную точку, индуцирует сюръек-
70
Глава 1. Фундаментальная группа и накрытия
цию группы Tij {X) на свободную группу с п образующими. Полное
описание группы пг(Х) можно найти в [90].
В [128] доказана теорема, что для линейно связного локально линейно
связного компактного метрического пространства X группа пг(Х) либо
конечно порождённая, либо несчётная.
Приложения к клеточным комплексам
До конца этого параграфа мы будем рассматривать двумерные
клеточные комплексы, выясняя, как изменяется фундаментальная группа при
приклеивании двумерной клетки. Согласно примеру в конце этого
параграфа приклеивание клеток более высокой размерности не изменяет пх,
поэтому нас интересует лишь то, как приклеены двумерные клетки.
Предположим,, что пространство У получается приклеиванием набора
двумерных клеток е2а к линейно связному пространству X посредством
отображений tpa: S1 —>Х. Если s0 — отмеченная точка окружности S1, то
4>а определяет петлю с началом и концом в точке уа (s0). Мы будем
обозначать эту петлю ч>а, хотя мы определяли петли как отображения / —> X, а не
S1 —>Х. Для разных индексов а отмеченные точки ^a(s0) этих петель у>а,
возможно, не все совпадают. Чтобы это исправить, выберем отмеченную
точку х0еХ и путь уа в X из точки х0 в точку <£a(s0) для каждого
индекса а. Тогда yay>afa — петля в точке х0. Эта петля может быть не
гомотопной нулю в Ху но она обязательно будет гомотопной нулю после
приклеивания клетки е2а. Таким образом, нормальная подгруппа N с п1{Хух0))
порождённая всеми петлями Тач>ауа для разных а, лежит в ядре
отображения пг(Х,х0) —>7il(Y)x0), индуцированного включением Х<—>Y.
I Предложение 1.26. Включение X <-> У индуцирует сюръекцию
п1(Хух0) —> 7ti(Y,x0), ядро которой равно N. Таким образом, ти^У) «
Из этого, в частности, следует, что подгруппа N не зависит от
выбора путей уау но это можно доказать и непосредственно. Если мы
заменим уа другим путём г)а с теми же концами, то уац>ауа заменится на
VaVaVa = ^аГ^Та^аТа^Га^^у ПОЭТОМу ГаЧ>а?а И VaVaVa ОПредеЛЯЮТ СО-
пряжённые элементы группы п1 (X, х0).
Доказательство. Расширим У до несколько большего пространства Z,
которое деформационно ретрагируется на У и более удобно для приме-
§ 1.2. Теорема ван Кампена
71
нения теоремы ван Кампена. Пространство Z получается из Y
приклеиванием прямоугольных полос Sa = / х /, у каждой из которых нижний
Край / х {0} приклеивается вдоль уа, правый край {1} х / приклеивается
ВО дуге в е2а, а все левые края {0} х / разных полос склеиваются вместе.
Верхние края полос ни к чему не приклеиваются, и это позволяет нам
деформационно ретрагировать Z на Y.
В каждой клетке е2а выберем точку уа, не лежащую на дуге, по которой
приклеена полоса Sa. Пусть A = Z - |J {уа} и В = Z - X. Тогда А деформа-
а
ционно ретрагируется на X, а В стягиваемо. Так как пг (В) = 0, теорема ван
Кампена, применённая к покрытию {А, В}, утверждает, что группа nl(Z)
изоморфна факторгруппе группы ях(Л) по нормальной подгруппе,
порождённой образом отображения п1(<АПВ) —> п^А). Таким образом, остаётся
холько проверить, что группа пг(АГ\В) порождена петлями YaVaYa илиу
скорее, петлями в А П В, гомотопными этим петлям. Это можно показать,
ддё раз применив теорему ван Кампена, на этот раз к покрытию
пространства А ПВ открытыми множествами Аа — А ПВ — [J el. Так как Аа
Деформационно ретрагируется на окружность ве^- {уа}У мы получаем,
что группа п1(Аа) ъЪ порождена петлёй, гомотопной ya</?afa, что и
требовалось. □
В качестве первого приложения вычислим фундаментальную группу
ориентируемой поверхности Mg рода g. Она имеет клеточную структуру
С одной нульмерной клеткой, 2g одномерными клетками и одной
двумерной клеткой, как мы видели в главе 0. Одномерный остов —это букет 2g
окружностей; его фундаментальная группа — свободная группа с 2g
образующими. Двумерная клетка приклеена по петле, заданной
произведением коммутаторов этих образующих, скажем, [ab b}] •... • [ag, bg]. Поэтому
ях(Мр * (alybly...,ag,bg \ [al9bl]-...-[ag9bg])9
гДе (sa I rp) обозначает группу с образующими ga и соотношениями г$,
Другими словами, свободную группу с образующими ga по модулю
нормальной подгруппы, порождённой словами /^ из этих образующих1.
(Следствие 1.27. Поверхность Mg не гомеоморфна и даже не гомото-
пически эквивалентна поверхности МЛ, если g^h.
Доказательство. Абелианизация группы пг (Mg) — это прямая сумма
2g экземпляров группы Z. Поэтому если Mg^Mhy то ях(М^) ъ nx{Mh),
а значит, абелианизации этих групп изоморфны, что влечёт равенство
S = ft. □
Подобное задание группы образующими и соотношениями далее в этой главе будет
называться представлением (англ. presentation) группы. Его не нужно путать с представлением
Фундаментальной группы в линейном пространстве (англ. representation).— Прим. ред.
72
Глава 1. Фундаментальная группа и накрытия
Неориентируемые поверхности можно рассмотреть аналогично. Если
мы приклеиваем двумерную клетку к букету g окружностей по слову
a2v..a2 то получаем неориентируемую поверхность Ng. Например, N1 —
проективная плоскость RP2, которую можно представить как круг D2
с отождествлёнными диаметрально противоположными точками его
границы 3D2. Далее, N2 — бутылка Клейна, хотя более обычное её представ-
АГ, : ^^ N:
2-
ление — квадрат, у которого противоположные стороны отождествлены
посредством слова aba~lb. Если разрезать этот квадрат по диагонали,
а затем склеить два полученных треугольника, как показано на
рисунке, можно получить первое представление бутылки Клейна как
квадрата, стороны которого отождествлены посредством слова а2с2. Согласно
предложению n^Ng) ъ (аь ...,ag |а2...а2). Абелианизация этой группы
является прямой суммой группы Z2 и g — 1 экземпляров группы Z, так как
в этой абелианизации мы можем выбрать в качестве новых образующих
элементы аъ ..., ag_x и аг + ... + ag, для которых 2(ах + ... + ag) = 0.
Следовательно, поверхность Ng не гомотопически эквивалентна Nh, если
g^h, и не гомотопически эквивалентна никакой ориентируемой
поверхности М/,.
А вот ещё одно применение предыдущего предложения.
I Следствие 1.28. Для любой группы G существует двумерный
клеточный комплекс XG, для которого п^Х^ъС
Доказательство. Выберем представление G = (ga | Гд). Оно
существует, так как каждая группа является факторгруппой свободной группы,
поэтому в качестве ga можно взять образующие этой свободной группы, а в
качестве г^ —образующие ядра отображения этой свободной группы в G.
Теперь построим Хс из \/ Sla, приклеивая двумерные клетки el к петлям,
a
заданным словами г@. D
Пример 1.29. Если G — (а \ ап) = Zn, то Хс — это окружность S1 с
клеткой е2, приклеенной по отображению z*-*zn, если представлять себе S1
как единичную окружность в С. При п = 2 мы получаем Хс = З&Р2, но
при п > 2 пространство XG не является поверхностью, так как к каждой
точке окружности S1 с Хс приклеивается п «листов» клетки е2.
Например, при п = 3 можно построить окрестность N окружности S1 в Хс, взяв
произведение графа Y на отрезок /, а затем отождествив оба конца
этого произведения, повернув его на одну треть, как показано на рисунке.
§ 1.2. Теорема ван Кампена
73
Граница окрестности N состоит из одной
окружности, образованной тремя концами
каждого из поперечных сечений
множества N. Чтобы завершить построение
комплекса XG с помощью N, нужно приклеить
диск по граничной окружности
окрестности N. Этого нельзя сделать в R3, но можно сделать в Е4. Для п = 4 нужно
взять граф X вместо графа Y и поворот на одну четверть вместо поворота
на одну треть. Для большего п нужно взять n-конечную звезду и поворот
на 1/п.
Задачи
1. Докажите, что центр свободного произведения G*H
нетривиальных групп G и Н тривиален и что единственными элементами конечного
порядка в группе G*H являются элементы, сопряжённые элементам
конечного порядка в группах G и Н.
2. Пусть X с W" — объединение выпуклых открытых множеств Х]у...
...,ХП, причём Х{ DXjnXk^0 для всех *,;, к. Докажите, что
пространство X односвязно.
3. Докажите, что дополнение к конечному множеству точек в JR"
односвязно при ОЗ.
4. Пусть X с М? — объединение п прямых, проходящих через начало
координат. Вычислите л} (R3 - X).
5. Пусть X с R2 — связный граф, который является объединением
конечного числа отрезков. Докажите, что группа щ {X) свободная с
базисом, состоящим из петель, образованных границами ограниченных
областей дополнения к X, соединённых с отмеченной точкой путями в X.
[Предполагается известной теорема Жордана для полигональной
замкнутой несамопересекающейся кривой (такая кривая соответствует случаю,
когда граф X гомеоморфен S1).]
6. Предположим, что пространство Y получено из линейно связного
подпространства X приклеиванием n-мерных клеток, где п ^ 3
фиксировано. Докажите, что включение X <^-> Y индуцирует изоморфизм групп пх.
[См. доказательство предложения 1.26.] Выведите из этого, что
дополнение дискретного подпространства в Rn односвязно, если п ^ 3.
7. Пусть X — факторпространство сферы S2, полученное при
склеивании северного и южного полюсов в одну точку. Введите на X структуру
клеточного комплекса и примените её, чтобы вычислить группу пх{Х).
8. Вычислите фундаментальную группу пространства, полученного
из двух торов S1 х S1 отождествлением окружности S1 х {л:0} в одном торе
с соответствующей окружностью S1 х {л:0} в другом торе.
9. Пусть С — окружность на поверхности Mg рода g, разбивающая Mg
на две компактные подповерхности М\ и М£, которые получаются из за-
74
Глава 1. Фундаментальная группа и накрытия
мкнутых поверхностей Mh и Мк при вырезании из каждой из них
открытого диска. Докажите, что M'h не ретрагируется на свою граничную
окружность С, а значит, Mg не ретрагируется на С. [Указание: абелианизируйте
группу к1.] Докажите, что Mg ретрагируется, однако, на неразделяющую
окружность С', изображённую на рисунке.
10. Рассмотрим две дуги а и /3, вложенные
в D2 х /, как показано на рисунке. Петля у,
очевидно, гомотопна нулю в D2 х /. Докажите, однако, что
она не гомотопна нулю в дополнении к a U /3.
11. Тор отображения 7} для отображения /: X —► X — это факторпро-
странство пространства Хх/, полученное при отождествлении каждой
точки (х, 0) с (/00,1). В случае, когда X = Sl V S1, а отображение /
сохраняет отмеченную точку, вычислите представление группы пх {Tj) в
терминах индуцированного отображения /+: п^Х) —> я^Х). Сделайте то же
самое для X = Sl xSl. [Один из способов сделать это состоит в том, чтобы
рассмотреть пространство Tj как полученное из X V S1 приклеиванием
клеток.]
12. Бутылку Клейна обычно рисуют как подпространство в М3,
например, как подпространство X с №3, изображённое на первом рисунке справа.
Если нужна модель, которая
действительно могла бы служить бутылкой, то
можно удалить открытый диск, ограниченный
окружностью самопересечения
поверхности X, и получить подпространство У с X.
Докажите, что тг1(Х) ъ Ъ * Ъ и что группа
^!(У) имеет представление (a, b, c\aba~lb~lcbec~l), где е = ±1.
(Изменение знака для г даёт изоморфную группу, как это иногда бывает.)
Покажите также, что группа nl{Y) изоморфна tt1(R3 — Z) для графа Z,
изображённого на рисунке. Группы я^Х) и я^У) не изоморфны, но доказать
это нелегко; см. обсуждение в примере 1.В.13.
13. Пространство У из предыдущей задачи можно получить из
диска с двумя дырками, отождествляя три его граничные окружности. Есть
только два существенно различных способа отождествить эти три
граничные окружности. Докажите, что другой способ приводит к пространству Z
с группой ^(Z), не изоморфной nl{Y). [Абелианизируйте
фундаментальные группы, чтобы показать, что они не изоморфны.]
Ы
§ 1.2. Теорема ван Кампена 75
14. Рассмотрим факторпространство куба /3, полученное при
отождествлении каждой квадратной грани с противоположной квадратной
гранью посредством правостороннего винтового движения —
композиции переноса на одну единицу в направлении, перпендикулярном грани,
й одной четверти полного поворота грани вокруг её центра. Покажите,
что это факторпространство X является клеточным комплексом с
двумя нульмерными клетками, четырьмя одномерными, тремя двумерными
й одной трёхмерной. Используя эту структуру, покажите, что п1(Х) —
кватернионная группа {±1, ±i, ±j, ±k} порядка восемь.
15. Если дано пространство X с отмеченной точкой х0еХ, то можно
построить CW-KOMruieKc L(X), имеющий единственную нульмерную
клетку, одномерную клетку е1 для каждой петли у в X с началом и концом
в точке х0 и двумерную клетку е2 для каждого отображения т
стандартного треугольника PQR в пространство X, переводящего вершины Р, Q
И К в точку х0. Двумерная клетка е2 приклеивается к трём одномерным
клеткам, которые являются петлями, полученными при ограничении т
на три ориентированных ребра PQy PR и QR. Докажите, что естественное
отображение L(X) —► X индуцирует изоморфизм пг (L(X)) ^ пг (X, х0).
16. Докажите, что фундаментальная группа поверхности
бесконечного рода, изображённой ниже, является свободной группой с бесконечным
числом образующих.
Я) ■••
17. Докажите, что группа n^R2 -Q2) несчётна.
18. В этой задаче мы используем понятия надстройки,
приведённой надстройки, конуса и конуса отображения, введённые в главе 0.
Пусть X — подпространство в R, состоящее из последовательности точек
1,1/2,1/3,1/4,... вместе с её предельной точкой 0.
а) Для надстройки SX покажите что тс }(SX) — свободная группа со
Счётным множеством образующих, и выведите из этого, что группа 7ii(SX)
СЧётна. В противоположность этому приведённая надстройка ЕХ,
полученная из SX стягиванием отрезка {0} х [ в точку, является букетом
стягивающихся окружностей из примера 1.25, фундаментальная группа
которого несчётна.
б) Пусть С — конус факторотображения SX—>ЕХ. Докажите, что группа
Щ(.С) несчётна, построив гомоморфизм из пг (С) на всю группу П Z/ ® Z.
оо оо
Заметим, что С — приведённая надстройка над конусом СХ. Таким
образом, приведённая надстройка над стягиваемым пространством может
быть нестягиваемой, в отличие от неприведённой надстройки.
76
Глава 1. Фундаментальная группа и накрытия
19. Докажите, что подпространство в 1R3, представляющее собой
объединение сфер радиуса - с центром ( -, 0, 0) для п = 1, 2,..., односвязно.
20. Пусть X — подпространство в М2, которое является объединением
окружностей Сп радиуса п с центром (п, 0) для п = 1, 2,... Докажите, что
яi(X) — свободная группа *п тгДСД та же самая, что и у бесконечного
букета \J S1. Докажите, что пространства X и \/ S1 в действительности
00 00
гомотопически эквивалентны, но не гомеоморфны.
21. Докажите, что джойн X * Y двух непустых пространств X и Y од-
носвязен, если X линейно связно.
22. В этой задаче описывается алгоритм, позволяющий вычислить
представление фундаментальной группы дополнения гладкого или
кусочно линейного узла К в IR3, которое называется представлением Виртинге-
ра. Сначала положим узел К почти плоско на стол так, чтобы он состоял
из конечного числа непересекающихся дуг ait по которым узел пересекает
плоскость стола, и конечного числа дуг /3^, где он проходит сам над
собой. Конфигурация для такого прохождения узла над собой
(перекрёстка) изображена на первом рисунке. Построим двумерный комплекс X,
который является деформационным ретрактом пространства R3 — К,
сделав следующие три шага. Сначала возьмём прямоугольник Т — верхнюю
часть стола. Затем чуть выше каждой дуги а, поместим длинную тонкую
прямоугольную полосу Rh изогнутую так, что она идёт параллельно а,
вдоль всей дуги а,, и выгнутую так, что два длинных края полосы Я,
отождествляются с точками прямоугольника Г, как на втором рисунке. Каждую
дугу /3£, проходящую над а,, разместим на Я,. Наконец, над каждой дугой
/3£ расположим квадрат S^ все четыре стороны которого загнуты вниз,
так что эти стороны склеиваются с точками трёх полос Rh Rj и R^, как
показано на третьем рисунке; а именно, две противоположные стороны
квадрата S? отождествляются с короткими краями полос R; иКьа две
другие противоположные стороны квадрата S? отождествляются с двумя
дугами, пересекающими внутреннюю часть полосы R,. Узел К является
теперь подпространством в X, но после того, как мы слегка поднимем
узел К, чтобы он оказался в дополнении к X, станет ясно, что X является
деформационным ретрактом пространства Е3 — К.
а) Воспользовавшись этой геометрической информацей, покажите,
что группа 7г3 (R3 — К) имеет представление с одной образующей х, для
§ 1.3. Накрытия
77
каждой полосы R, и одним соотношением вида x(XjX~ =xk для каждого
квадрата Sh где индексы такие же, как на рисунках выше. [Чтобы
получить правильные знаки, следует использовать ориентацию узла К.]
б) Примените это представление, чтобы показать, что абелианизация
группы Я] (R3 - К) равна Z.
§1.3. Накрытия
Перейдём теперь ко второй основной теме этой главы, накрытиям,
фактически мы уже встретились с одним примером накрытия при
вычислении группы n{(Sl). Это было отображение Е—>S\ которое мы
представляли как проекцию спирали на окружность, причём спираль была
расположена выше окружности, «накрывая» её. Многое из того, что мы
доказали для этого накрытия, выполняется для всех накрытий, и поэтому
накрытия служат полезным общим методом вычисления фундаментальных
групп. Но связь между фундаментальной группой и накрытиями заходит
намного глубже этого, и во многом их можно рассматривать просто как
две точки зрения на одно и то же. Это означает, что алгебраические
свойства фундаментальной группы часто можно перевести на геометрический
язык накрытий. Это иллюстрируется одним из главных результатов этого
параграфа, дающим точное соответствие между различными связными
накрывающими пространствами данного пространства X и подгруппами
группы 7г1(Х). Это удивительно напоминает теорию Галуа, описывающую
соответствие между расширениями полей и подгруппами группы Галуа.
Определения и примеры
Начнём с определения. Накрывающее пространство данного
пространства X —-это пространство X и отображение р: X —>X, для которых
выполняется следующее условие: существует такое открытое покрытие
{Ua} пространства X, что для каждого а прообраз р~1(иа) является
объединением непересекающихся открытых множеств в X, каждое из
которых р гомеоморфно отображает на Ua. При этом допускается пустое
объединение, так что р не обязано быть сюръективным. Отображение р
Называют накрытием.
В примере со спиралью у нас есть отображение р: R —>Sl, заданное
формулой p(t) = (cos2nt, sin2rct), а требуемое покрытие {Ua} может
состоять из любых двух открытых дуг, объединение которых совпадает с S1.
Похожий пример — поверхность геликоида S СR3, состоящая из точек
вида (scos2nt,ssm2nt, t), где (s, t) e (0, оо) х R. Эта поверхность
проектируется на Ш2 - {0} посредством отображения (х, у, z) -* (х, у), и эта
проекция задаёт накрытие р: S -> IR2 - {0}, так как для каждого открытого
Диска U в R2 — {0} его прообраз p~l(U) состоит из счётного набора
непересекающихся открытых дисков в S, каждый из которых р отображает
Гомеоморфно на U. Ещё один пример — отображение р: S1 —*S\ заданное
78
Глава 1. Фундаментальная группа и накрытия
формулой p(z) = zn, где мы рассматриваем z как
комплексное число, у которого |z| = 1, а п —любое натуральное число.
Лучше всего представлять это накрытие как линейную
проекцию в трёхмерном пространстве, аналогичную проекции
спирали, нарисовав окружность, обматывающуюся вокруг
цилиндра п раз и пересекающую себя в п — 1 точках, которые
нужно считать не настоящими точками пересечения. Чтобы
нарисовать эту картинку по-другому, теперь уже без этого
дефекта, вложите S1 в граничный тор полнотория S1 x D2 так, чтобы она
монотонно наматывалась п раз вокруг множителя S1 без
самопересечений, а затем ограничьте проекцию Sl х D2 —>S] x {0} на эту вложенную
окружность.
Как покажет нам общая теория, эти примеры для п ^ 1 вместе с
примером спирали исчерпывают все связные накрывающие пространства
окружности S1. Есть много других несвязных накрывающих пространств
окружности S\ например п непересекающихся окружностей, каждая из
которых отображается гомеоморфно на S1, но эти несвязные
накрывающие пространства — просто несвязные объединения связных
накрывающих пространств. Обычно мы будем рассматривать связные
накрывающие пространства, поскольку они отражают большинство интересных
свойств накрывающих пространств.
Для накрытия р: X—>Х мощность множества р-1 (х)— локально
постоянная функция на X, поэтому если X связно, то мощность множества
р_1(х) не зависит от точки х; её называют числом листов накрытия.
Таким образом, накрытие S1 —>Sl, z^>z, является п-листным, а накрытие
R-^Sl является бесконечнолистным. Такая терминология возникает,
если рассматривать непересекающиеся множества p~l(Ua)> гомеоморфно
отображающиеся на Ua, из определения накрытия как отдельные «листы»
накрывающего пространства. Если пространство X несвязно, то число
листов может быть разным для разных компонент пространства X, и даже
может быть нулём над некоторыми компонентами, так как не требуется,
чтобы множество p~l(Ua) было непустым.
Накрывающие пространства букета S1 VS1 образуют чрезвычайно
богатое семейство, которое очень конкретно иллюстрирует основную часть
общей теории, поэтому давайте рассмотрим несколько из этих
накрывающих пространств, чтобы получить представление о том, что
происходит. Чтобы упростить обозначения, положим X = Sl V S1. Мы
рассматриваем это пространство как граф с одной верши- *—^ ^—-^
ной и двумя рёбрами. Обозначим эти рёбра а и Ь Ъ ( */\. )а
и выберем на них ориентации. Теперь пусть X — л ю- —
бой другой граф, у которого в каждой вершине
сходятся четыре ребра, причём мы будем предполагать, что рёбра графа X
помечены буквами а и Ъ и на них заданы ориентации так, что локаль-
§1.3. Накрытия
79
ная структура в окрестности каждой вершины такая же, как в графе X,
а именно, есть ребро а, направленное в вершину, ребро а, направленное
из вершины, ребро Ь, направленное в вершину, и ребро Ь, направленное
из вершины. Чтобы дать какое-то название этой структуре, будем
говорить, что X является 2-ориентированным графом.
Таблица на с. 80 показывает только некоторые из бесконечного
множества всех возможных примеров.
Для данного 2-ориентированного графа X можно построить
отображение р: X —»X, отобразив все вершины графа X в вершину графа X,
а каждое ребро графа X — в ребро графа X с той же самой пометкой
посредством отображения, которое является гомеоморфизмом на
внутренней части ребра и сохраняет ориентацию. Ясно, что для р
выполняются свойства накрытия. Обратное утверждение тоже верно. Любое
накрывающее пространство графа X является графом, который снабжён
2-ориентацией, индуцированной с графа X.
Как читатель обнаружит экспериментально, каждый граф, у которого
любой вершине инцидентны четыре ребра, можно 2-ориентировать. Для
конечных графов это можно доказать следующим образом. Есть вполне
классический и легко доказываемый факт, что любой конечный связный
граф с чётным числом рёбер, инцидентных каждой вершине, имеет
эйлеров обход — петлю, которая проходит по каждому ребру ровно один раз.
Если каждой вершине инцидентны ровно четыре ребра, то, помечая рёбра
эйлерова обхода поочерёдно буквами а и Ь, получаем в каждой вершине
два ребра а и два ребра Ъ. Тогда объединение рёбер а представляет собой
набор непересекающихся окружностей, как и объединение рёбер Ъ.
Выбирая ориентации для всех этих окружностей, получаем 2-ориентацию.
В теории графов есть теорема, что бесконечные графы, у которых
каждой вершине инцидентны четыре ребра, тоже можно 2-ориентировать;
доказательство имеется в главе 13 книги [44]. Известно также обобщение
для n-ориентированных графов, которые являются накрывающими
пространствами букета п окружностей.
Односвязное накрывающее пространство 4-f-f
Для X можно построить следующим образом.
Начнём с открытых интервалов (-1,1) на ко- 4.
ординатных осях в R2. Затем для фиксиро- * '* *' "*~
ванного числа Я, где 0 < Я < 1/2, например *+£ 1 И*
^ = 1/3, добавим четыре открытых отрезка 4-j-f ] -*f
Длины 2Л, расположенных на расстоянии Я от
концов предыдущих отрезков
перпендикулярно к ним так, что новые более короткие
отрезки делятся пополам прежними. На третьем
Щаге добавим перпендикулярные открытые отрезки длины 2Я2, располо
Женных на расстоянии Я2 от концов всех предыдущих отрезков и делящие
4-
4
4
+
*
80
Глава 1. Фундаментальная группа и накрытия
Накрывающие пространства S1 VS1
(1)
{a,b\bab~
(3)
а
Ъ ^а
(4)
а
Ъ ^а
1Гг <г
(а\Ь2уЬаЬ~])
{a,b\ba2b-\baba-]b-1)
(5) а
(6) а
(сЛЬ3,^-1,^)
(а3,Ь\аЬ,Ьа)
(а4,Ь4,аЬ,Ьа,а2Ь2)
(а2,Ь2,(аЬ)2, (Ъа)2,аЪ2а)
(а2,Ъ\аЬуЪа2Ь~\ЬаЪ-2)
(10) а а а
■ 0*0-0
а а а
(b2nab-2n-\b2n+xab-2"\neZ)
(П)
(b",ab-"|n€Z)
(12)
(а)
03)
<аЬ>
(И)
4
ьрьрь
(а.ЬаЬ"1)
§1.3. Накрытия
81
ся ими пополам. Затем этот процесс неограниченно повторяется, и на п-м
шаге добавляются открытые отрезки длины 2ЯП_1 на расстоянии А/1"1 от
всех концов полученных ранее отрезков. Объединение всех этих
открытых отрезков — граф, вершинами которого являются точки пересечения
горизонтальных и вертикальных отрезков, а рёбрами являются отрезки
между соседними вершинами. Мы помечаем все горизонтальные рёбра
буквой а и ориентируем направо, а все вертикальные рёбра помечаем
буквой Ъ и ориентируем вверх.
Это накрывающее пространство называют универсальный
накрытием пространства X, потому что, как покажет нам общая теория, оно
является накрывающим пространством любого другого связного
накрывающего пространства для X.
Все накрывающие пространства (1)—(14) в таблице неодносвязные.
Их фундаментальные группы свободные с базисами, представленными
петлями, которые задаются указанными словами из букв а и Ь; эти
петли начинаются и заканчиваются в отмеченной точке х0, выделенной на
рисунках. Это можно доказать в каждом случае, применяя теорему ван
Кампена. Можно также интерпретировать список слов как образующие
подгруппы рДят(Х, х0)) в группе 7гт(Х, х0) = (а, Ь). Общий факт, который
мы докажем о накрывающих пространствах, состоит в том, что
индуцированный гомоморфизм
р„: яДХДо) -* яДХ^о)
всегда инъективен. Таким образом, мы получаем парадоксальный, на
первый взгляд, факт, что свободная группа с двумя образующими содержит
в качестве подгруппы свободную группу с любым конечном числом
образующих и даже со счётным множеством образующих, как в примерах
(10) и (11). Другой общий факт, который мы тоже докажем, заключается
в том, что индекс подгруппы рЛп\ iX> *о)) в Я] (X, х0) равен числу листов
накрытия.
При замене отмеченной точки х0 на другую точку из р~1{х0)
подгруппа рДтг^Х, х0)) заменяется на сопряжённую подгруппу в п}(Х,х0).
При этом сопрягающий элемент группы тг^Х,.^) представляется любой
петлёй, которая является проекцией пути в X, соединяющего одну
отмеченную точку с другой. Например, накрывающие пространства (3) и (4)
различаются только выбором отмеченных точек, а соответствующие
подгруппы в 7гт(Х, х0) отличаются сопряжением посредством элемента Ь.
Основная классификационная теорема для накрывающих
пространств ^ггверждает, что если сопоставить накрытию р: X—>Х подгруппу
Р*Гтг1(Х, х0)), то мы получим взаимно однозначное соответствие
между всеми различными связными накрывающими пространствами для X
и классами сопряжённости подгрупп в п{(Х,х0). Если проследить за
отмеченной точкой х0еХ, то это будет взаимно однозначное соответствие
82
Глава 1. Фундаментальная группа и накрытия
между накрывающими пространствами р: (X, Зс0) —» (X, х0) и настоящими
подгруппами в тг^Х,^), а не классами сопряжённости. Конечно, чтобы
придать смысл этим утверждениям, нужно иметь точное определение
того, когда два накрывающих пространства одинаковы или «изоморфны».
В данном случае изоморфизм между накрывающими пространствами
для X — это просто изоморфизм графов, сохраняющий пометки и
ориентации рёбер. Таким образом, накрывающие пространства (3) и (4)
изоморфны, но не посредством изоморфизма, сохраняющего отмеченные точки,
поэтому две подгруппы в тг^Х, х0), соответствующие этим накрывающим
пространствам, разные, но сопряжённые. С другой стороны,
накрывающие пространства (5) и (6) не изоморфны, хотя эти графы гомеоморфны,
таким образом, соответствующие подгруппы в тг1(Х,х0) изоморфны, но
не сопряжены.
Некоторые из накрывающих пространств (1)—(14) более
симметричны, чем другие. Под «симметрией» здесь мы подразумеваем автоморфизм
графа, сохраняющий пометки и ориентации рёбер. Самые
симметричные накрывающие пространства —те, для которых найдётся симметрия,
переводящая любую вершину в любую другую. Примеры (1), (2), (5)—
(8) и (11) обладают этим свойством. Мы увидим, что накрывающее
пространство для X имеет максимальную симметрию в точности тогда, когда
соответствующая подгруппа в тг1(Х, х0) нормальная, и в этом случае
симметрии образуют группу, изоморфную факторгруппе группы пх (X, х0) по
этой нормальной подгруппе. Так как любая группа, порождённая двумя
элементами, является факторгруппой группы Z*Z, из этого следует, что
любая группа с двумя образующими является группой симметрии
некоторого накрывающего пространства для X.
Свойства поднятия
Накрытия определены в весьма геометрических терминах, как
отображения р: X —> X, которые являются локальными гомеоморфизмами
в довольно сильном смысле. Но с точки зрения алгебраической топологии
основное свойство накрытий —это их поведение по отношению к
поднятию отображений. Напомним терминологию из доказательства
теоремы 1.7: поднятие отображения /: У —»Х — это отображение /: У —*Х,
для которого р/ = /. Мы опишем три свойства поднятия для накрытий
и приведём некоторые их применения.
Прежде всего мы имеем свойство поднятия гомотопии или теорему
0 накрывающей гомотопии, как её иногда называют.
1 Предложение 1.30._Если даны накрытие р: X—>Х, гомотопия /,: У —►
I -* X и отображение £0: У —> X, поднимающее /0, то существует един-
I ственная гомотопия ft: У —>Х отображения /0, которая поднимает ft.
§ 1.3. Накрытия
83
Доказательство. Для накрытия р: R—>S это свойство в) из
доказательства теоремы 1.7, а приведённое там доказательство можно
применить к любому накрытию. □
Если в качестве Y взять точку, то получим свойство поднятия пути
для накрытия р: X —> X, которое говорит, что для любого пути /: / —> X
и любого поднятия х0 исходной точки /(0) — х0 существует единственный
путь /: J —»Х, поднимающий /, который начинается в х0. В частности,
из единственности поднятия следует, что любое поднятие постоянного
пути постоянно, но это проще выводится из того факта, что р~1(х0) имеет
дискретную топологию по определению накрытия.
Если в качестве Y взять /, то мы увидим, что любая гомотопия /г пути
/0 в X поднимается до гомотопии ft любого поднятия /0 пути /0. Поднятая
гомотопия /г является гомотопией путей, сохраняющей концы, так как
при изменении t каждый конец пути ft заметает путь, поднимающий
постоянный путь, а потому он должен быть постоянным.
Вот простое приложение.
I Предложение 1.31. Отображение
I р*: п1(Хух0) — TTjCX,^),
I индуцированное накрытием р: (X, х0) —> (X, х0), инъективно. Подгруп-
I па р*(тг1(Х, х0)) в 7Г] (X, х0) состоит из гомотопических классов петель
I в X с началом и концом в точке х0, поднятия которых в X с началом в х0
I являются петлями.
Доказательство. Любой элемент ядра отображения рж
представляется петлёй /0: / —> X, для которой есть гомотопия /г: / —> X петли /0 = р/0
в тривиальную петлю /г. Согласно замечаниям перед этим предложением
существует поднятие гомотопии петель ft, которая начинается петлёй /0
и заканчивается постоянной петлёй. Следовательно, [/0] =0 в тгДХ,х0)у
и гомоморфизм р+ инъективен.
Докажем теперь второе утверждения предложения. Петли с началом
и концом в х0, поднимающиеся до петель с началом и концом в Зс0,
очевидно, представляют элементы образа отображения р+: я^Х, х0) —> яДХ, х0).
Наоборот, петля, представляющая элемент образа отображения р+,
гомотопна петле, у которой есть такое поднятие, поэтому согласно свойству
поднятия гомотопии и у неё самой должно быть такое поднятие. П
I Предложение 1.32. Число листов накрытия р: (X, х0) —> (Х,х0), где
I пространства X и X является линейно связными, равно индексу под-
I группы р+ (щ(Х,х0)) в щ(Х,х0).
Доказательство. Для петли g в X с началом и концом в точке х0 пусть
£—- её поднятие в X, начинающееся в точке Зс0. Произведение h • g, где
[h] SH = р+(тг1(Х, Зс0)) имеет поднятие h-g, заканчивающееся в той же
самой точке, что и g, так как h — петля. Поэтому мы можем определить
84
Глава 1. Фундаментальная группа и накрытия
отображение Ф из смежных классов H[g] в р_1(*о)> переводящее H[g]
в g(l). Линейная связность пространства X влечёт, что Ф сюръективно,
так как точку х0 можно соединить с любой точкой в р-1 (х0) путём g,
проектирующимся в петлю g с началом и концом в х0. Чтобы убедиться, что
Ф инъективно, заметим, что из равенства ФСН^]) = Ф(И^2]) следует,
что g} • g2 поднимается до петли вХс началом и концом в Зс0, поэтому
[йП&Г1 еН, а значит, H[gl]=H[g2]. D
Важно также знать, как обстоит дело с существованием и
единственностью поднятий произвольных отображений, а не только гомотопий. Что
касается существования, ответ даёт следующий критерий поднятия.
I Предложение 1.33. Пусть дано накрывающее пространство р:
I (X, х0) —> (X, х0). и отображение /: (У, у0) —> (Х,л:0), причём нро-
I странство У линейно связно и локально линейно связно. Поднятие
I /: (У, у0) —> (X, х0) отображения / существует тогда и только тогда, ко-
I гдаД7г^У,у0))ср*(тсДХ,х0)).
Говоря, что какое-то пространство обладает определённым свойством
локально (например, является локально линейно связным), мы
подразумеваем, что любая его точка имеет сколь угодно малые открытые
окрестности, обладающие этим свойством. Таким образом, пространство У
локально линейно связно, если для любой точки у е У и любой окрестности
U точки у найдётся открытая окрестность V с U точки у, которая
является линейно связной. Некоторые авторы ослабляют требование
линейной связности V до условия, что любые две точки в V можно соединить
путём в U. Это более общее определение тоже годится для наших целей,
нужно лишь немного изменить доказательства, но для простоты мы будем
использовать более ограничительное определение.
Доказательство. Утверждение «только тогда» очевидно, так как /* —
= р*/*. Докажем обратное утверждение. Пусть у е У, и пусть у — путь в Y
из у0 в у. Путь fy в X, начинающийся в х0, имеет единственное поднятие
fy, начинающееся в Зс0. Положим /(у) = /у(1). Чтобы показать, что это
определение корректно, т. е^е зависит от выбора у, возьмём другой путь
/ из у0 в у. Тогда (/уО • (/у) —петля h0 с началом и концом в х0, для
которой [h0] е/+(я1(У, у0)) ср+(тг1(Х, Зс0)). Это означает, что существует
§1.3. Накрытия
85
гомотопия ht петли h0 в петлю hb которая поднимается до петли h^ в X
с началом и концом в х0. Применив свойство накрывающей гомотопии
к ht, получим поднятие hr Так как hT — петля с началом и концом в х0, h0 —
такая же петля. Согласно единственности поднятия пути первая половина
петли h0 —это путь fy'y а вторая половина — это путь /у, который
проходится в обратном направлении; точка /у(1) =/х/(1) У этих путей общая.
Это показывает, что отображение^/ определено корректно.
Докажем, что отображение / непрерывно. Пусть U с X — открытая
окрестность точки /(у), у которой есть такое поднятие (/сХ, содержащее
/(у)> что p. U -*U является гомеоморфизмом. Выберем линейно связную
открытую окрестность V точки у, для которой /(V) с U. В качестве путей
из Уо в разные точки у' е V можно взять фиксированный путь у из у0 в у,
который продолжается разными путями г\ в V из у в точки у'. Тогда пути
(/у)' С/1?) в X имеют поднятия (/у) • (/т)), где /т) = р"1/7/ и Р~!: ^ ~* ^ ~
отображение, обратное к р: U-+U. Таким образом, /(V) с U и/|V = p_1/,
поэтому отображение / непрерывно в точке у. □
Пример, показывающий необходимость предположения о локальной
линейной связности пространства Y, описан в задаче 7 в конце этого
параграфа.
Мы имеем также свойство единственности поднятия.
I Предложение 1.34. Пусть даны накрытие р: X —* X и отображение
I /: Y —> X вместе с двумя поднятиями fx, /2: Y —> X, которые согласованы
I в одной точке пространства Y. Тогда если Y связно, то эти два поднятия
| должны быть согласованы на всём пространстве Y.
Доказательство. Пусть точка у€У и U — такая открытая
окрестность точки /(у) в X, что р_1(^) является объединением
непересекающихся открытых множеств Ua, каждое из которых проекция р отображает
гомеоморфно на U. Пусть ил и L/2—те из множеств Ua, которые
содержат Д00 и /г(у) соответственно. В силу непрерывности отображений
Л i? /2 существует окрестность /V точки у, которую /j отображает в иг,
а /г отображает в U2z Если Л 00 ^ЛОО» то U\ Ф 02, а значит, ил и Ё2
Не Пересекаются, и /j ^ /2 во всей окрестности N. С другой стороны,
если /j(y) =/2(у)э то L?! = L?2, поэтому Л =Л на N, так как р/г = р/2
и отображение р^инъективно на Ul = L/2. Таким образом, множество
точек, в которых /i и /2 согласованы, является одновременно открытым
и замкнутым в 7. П
Классификация накрытий
Рассмотрим теперь задачу классификации всех различных
накрывающих пространств для фиксированного пространства X. Так как вся эта
глава —о путях, не стоит удивляться, что мы ограничимся рассмотрением
86
Глава 1. Фундаментальная группа и накрытия
пространств X, которые являются по крайней мере локально линейно
связными. Тогда компоненты линейной связности пространства X
совпадают с компонентами связности, и при классификации накрытий
пространства X мы ничего не потеряем, предположив, что X связно или,
что эквивалентно, линейно связно. Локальная линейная связность
наследуется накрывающими пространствами, поэтому они тоже связны тогда
и только тогда, когда они линейно связны. Основой классификации
будет соответствие Галуа между связными накрывающими пространствами
для X и подгруппами в 7Г](Х). После описания этого подхода мы опишем
ещё и другой метод классификации, который включает также несвязные
накрывающие пространства.
Соответствие Галуа происходит из отображения, которое
сопоставляет каждому накрытию р: (Х,3с0) ~* (^> *о) подгруппу рДтг^Х, 3?0))
в тг^Х,^)- Сначала мы выясним, сюръективно ли это отображение,
т.е. нас интересует, любая ли подгруппа в тс^Х,^) реализуется как
р+(я] (X, х0)) для некоторого накрытия р: (X, х0) —> (X, х0). В частности,
можно спросить, реализуется ли тривиальная подгруппа. Так как
гомоморфизм р+ всегда инъективен, это сводится к вопросу о том, есть ли у X
односвязное накрывающее пространство. Ответ на этот вопрос потребует
некоторой работы.
Необходимое условие для того, чтобы у пространства X было
односвязное накрывающее пространство, заключается в следующем: у любой
точки х е X есть такая окрестность I/, что индуцированное включением
отображение пг(и, х) —► я^Х, х) тривиально. Если такое свойство
выполняется, то говорят, что X полулокально односвязно. Чтобы понять, зачем
нужно это условие, предположим, что р: X —> X — накрытие с односвяз-
ным пространством X. У любой точки х е X есть окрестность [У, у которой
есть поднятие [У с X, проектирующееся гомеоморфно на U
отображением р. Любая петля в U поднимается до петли в [У, а поднятая петля
стягиваема в X, так как я1 (X) =0. Поэтому, взяв композицию этого стягивания
и отображения р, получаем, что исходная петля в U стягиваема в X.
Локально односвязное пространство, конечно, является полулокально
односвязным. Например, CW-комплексы обладают намного более
сильным свойством: они локально стягиваемы, как мы покажем в
приложении. Примером пространства, которое не полулокально односвязно,
служит букет стягивающихся окружностей, т. е. подпространство X с К2,
состоящее из окружностей радиуса 1/п с центром в точке (1/п,0) для
п = 1, 2,..., описанное в примере 125. С другой стороны, конус СХ =
= (X х 1)/{X х {0}) полулокально односвязен, так как он является
стягиваемым, но это пространство нелокально односвязно.
Теперь мы покажем, как построить односвязное накрывающее
пространство для X, если X линейно связно, локально линейно связно и
полулокально односвязно. Чтобы мотивировать это построение, предположим,
§ 1.3. Накрытия
87
*rro p: (X, *о) —> (X, х0) — односвязное накрывающее пространство. Тогда
согласно предложению 1.6 любую точку х е X можно соединить с
точкой х0 единственным с точностью до гомотопии путём, поэтому можно
рассматривать точки пространства X как гомотопические классы путей,
выходящих из точки Зс0. Преимущество такой точки зрения состоит в том,
что согласно свойству поднятия гомотопии гомотопические классы путей
в X, выходящих из точки Зс0, — это то же самое, что и гомотопические
классы путей в X, выходящих из точки х0. А это даёт способ описать X
в терминах пространства X.
Таким образом, если дано линейно связное, локально линейно
связное и полулокально односвязное пространство X с отмеченной точкой
Х0€Х, то мы приходим к следующему определению:
X = {[у] I У — путь в X, выходящий из точки х0 },
где, как обычно, [у] обозначает гомотопический класс пути у
относительно гомотопии, которые оставляют концы у(0) и у(1) неподвижными.
Тогда отображение р : X —> X, переводящее [у] в у(1), определено корректно.
Так как пространство X линейно связно, конец у(1) может быть любой
точкой в X, поэтому отображение р сюръективно.
Прежде чем определить топологию на X, сделаем несколько
предварительных замечаний. Пусть 9/ — множество всех таких линейно связных
открытых множеств U СХ, что отображение ti^L/) —> п1(Х) тривиально.
Отметим, что если отображение n^{U)—> яДХ) тривиально для какого-
то выбора отмеченной точки в L/, то оно тривиально для любого выбора
отмеченной точки, так как U линейно связно. Линейно связное
открытое подмножество VC[/G^ тоже содержится в °11', так как композиция
nx(V) —> n1(U) —> 7ii(X) тоже будет тривиальной. Из этого следует, что
fy — базис топологии на X, если X локально линейно связно и
полулокально односвязно
Если даны множество U е У/ и путь у в X из точки х0 в некоторую
точку в U, то положим
и[у] = {[у -г]] | Tj — путь в L/, для которого rjCO) = у(1) }.
Как указывают обозначения, U^ зависит только от гомотопического
класса [у]. Заметим, что отображение р: U^ —► U сюръективно, так как U
линейно связно, и инъективно, так как все пути tj, соединяющие у{\)
с фиксированной точкой х eU, гомотопны в X, поскольку отображение
%([/) —► я^Х) тривиально. Имеется также следующее свойство:
(*) и[у] = и[у>]у если [/] е и[у]\ действительно, если у' — у • rj, то
элементы множества U{r>] имеют вид [у • г\ • /i] и потому лежат в L/lrJ, в то
время как элементы множества UlY] имеют вид [у ■ ц] = [у ■ г\ • г\ • д] =
= [у/ * ^7 * М-] и потому лежат в U[Y^.
0 Глава 1. Фундаментальная группа и накрытия
оо
Этим можно воспользоваться, чтобы показать, что множества Uly]
образуют базис топологии на X. Действительно, если даны два таких
множества U[r]i У[у1] и элемент [у"] е Цу] П V[r^, то U[r] = U[r"j и VIy/, = V[y»j
согласно свойству (*). Поэтому если множество We^ содержится в U П V
и содержит r"G), то W[n С [/[П п У[уП и [/1 е W{y»v
Взаимно однозначное отображение р: t/[rl -> t/ является
гомеоморфизмом, так как оно даёт взаимно однозначное соответствие между
подмножествами V[r>] С U[y] и множествами VeW, содержащимися в U.
А именно, в одну сторону мы имеем р(У[г>\) = V, а в другую сторону
мы имеем р~1(У) П t/[rJ = V[f] для любого [у'] е U{r] с концом в V, так
как V[r/j с С/1г'] = С/[Г] и Vfr/] отображается на всё множество V взаимно
однозначным отображением р.
Из предыдущего- абзаца следует, что отображение р: X —> X
непрерывно. Мы также получаем, что это отображение — накрытие, так как для
фиксированного \]^°U множества Цу] для разных [у] задают разбиение
p~l(U) на непересекающиеся множества, потому что если [у"] £ЦГ] П[7[У>|,
то C/frj = l/[r»] = Цг^ согласно свойству (*).
Остаётся только показать, что пространство X односвязно. Для
данной точки [у] еХ пусть yt — путь в X, который совпадает с у на [0, г]
и остаётся в одной и той же точке y(t) на [г, 1]. Тогда отображение
t *"* [yf] представляет собой путь в X, поднимающий у, который
начинается в [х0] — гомотопическом классе постоянного пути в точке х0 — и
заканчивается в [у]. Так как [у] —произвольная точка в X, это показывает, что
пространство X линейно связно. Чтобы проверить, что К\(ХУ [х0]) = 0,
достаточно показать, что образ этой группы при гомоморфизме р*
тривиален, так как р+ инъективен. Элементы в образе гомоморфизма р+
представлены нетлями у с началом и концом в х0, которые поднимаются
до петель в X с началом и концом в точке [лг0]. Мы уже отметили, что
путь t —> [yf] является поднятием пути у, начинающимся в точке [>0], и то,
что этот поднятый путь является петлёй, означает, что [у}] = [х0]. Так как
Yi = у, это показывает, что [у] = [х0], а потому петля у стягиваема и образ
гомоморфизма р+ тривиален.
Это завершает построение односвязного накрывающего пространства
X — X.
В конкретных случаях обычно строят одиосвязное накрывающее
пространство более прямыми методами. Например, предположим, что X —
объединение подпространств Л и В, для которых односвязные
накрывающие пространства Л-»АиВ->В уже известны. Тогда можно попытаться
построить односвязное накрывающее пространство X —> X из нескольких
экземпляров пространств А и В. Например, пусть X = Sl V S1, а в качестве
А и В мы берём эти две окружности; тогда каждое из пространств А и В
равно R, и мы можем построить односвязное накрывающее пространство
X, описанное ранее в этом параграфе, склеивая вместе бесконечно много
§1.3. Накрытия
89
экземпляров пространств Л и В, которые соответствуют горизонтальным
и вертикальным прямым в X. А вот ещё одна иллюстрация этого метода.
Пример 1.35. Для целых чисел т, п ^ 2 пусть Хшп — факторпростран-
ство цилиндра Slxl при отождествлениях (z, 0)~ (е27г,/шг, 0) и (z, 1) ~
~ (e27r,/nz, 1). Пусть А с X и В с X получаются при факторизации
подпространств S1 х [0, 1/2] и S1 х [1/2, 1]; таким образом, Л и В —цилиндры
отображения для отображений z —* zm и z -> zn, причём Л П В = S1. Самый
простой случай т = п = 2; тогда Л и В —листы Мёбиуса, а Х22 — бутылка
Клейна. Мы уже встречались с комплексами Хтп при анализе дополнений
торических узлов в примере 1.24.
Рисунок из примера 1.29 в конце предыдущего параграфа
показывает, как выглядит А в типичном случае т = 3. У нас
тг^А) «a Z, а универсальное накрытие А гомеоморфно
произведению Ст х R, где Ст — граф, который является конусом над т
точками, как показано на рисунке справа. Ситуация для В
похожа, и пространство В гомеоморфно Сп х К. Теперь попытаемся
построить универсальное накрытие Хт п из экземпляров
пространств А и В. Начнём с одного экземпляра пространства А.
Его граница, т. е. внешние края его плавников, состоит из т
экземпляров пространства -R. Вдоль каждой из этих т. граничных прямых
мы приклеиваем экземпляр пространства В. У каждого из этих
экземпляров пространства В одна из границ приклеена к исходному экземпляру
пространства А, а остальные п — 1 граничных прямых свободны, и мы
приклеиваем новый экземпляр пространства А к каждой из этих свободных
граничных прямых. Таким образом, теперь у нас получилось т{п — 1) -Ь 1
экземпляров пространства А. Каждый из вновь приклеенных экземпляров
пространства А имеет т - 1 свободных граничных прямых, и к каждой из
этих прямых мы приклеиваем новый экземпляр пространства В. Дальше
это процесс повторяется до бесконечности очевидным способом. Пусть
Хт>п —полученное в результате пространство.
Структуры произведения А = Ст х 1R и В =
== Сп х IR дают для Хш>п структуру
произведения Ттп х ~R, где Ттм — бесконечный граф,
построенный по индуктивной схеме, точно такой
Же, как схема построения пространства ХШ1„.
Таким образом, Ттп —объединение
последовательности конечных подграфов, каждый из которых
получен из предыдущего приклеиванием новых
экземпляров пространства Ст или Сп. Каждый из
э1"Их конечных подграфов деформационно ретрагируется на предыдущий.
Бесконечная цепь этих деформационных ретракций, где /с-й граф
деформационно ретрагируется на предыдущий в течение времени из интерва-
ла [1/2 ,1/2/с~1], даёт деформационную ретракцию пространства Ттп на
90
Глава 1. Фундаментальная группа и накрытия
[гч
11
М-
Гп
1 '
к
к
к
1 \
к
\j
\Г
1
N
Й
г ]|
о
й
г 1
исходное пространство Сш. Так как Сш стягиваемо, это означает, что Ттп
стягиваемо, а значит, стягиваемо и пространство Хш>„, которое является
произведением Ттп х 3L В частности, пространство Хш„ односвязно.
Отображение, которое проектирует каждый
экземпляр пространства Л в Хтп на Л, а каждый
экземпляр пространства В на В, является накрытием.
Чтобы определить это отображение строго, выберем
точку х0 е S1; тогда образ отрезка {х0} х I в ХШ|П
пересекает Л по отрезку, прообраз которого в Л состоит из
бесконечного числа отрезков, встречавшихся на
предыдущем рисунке как горизонтальные отрезки,
расположенные по спирали вокруг центральной вертикальной
оси. Картина в В аналогична, и, когда мы склеиваем все экземпляры
пространства Л и В, чтобы построить Хт п, мы делаем это так, чтобы эти
горизонтальные отрезки всегда выстраивались точно в линию. Это даёт
разбиение пространства Хтп на бесконечно много прямоугольников, каждый
из которых получен из прямоугольника в Л и прямоугольника в В.
Накрывающая проекция Хшп -»Хш;1 — это отображение факторизации, которое
отождествляет все эти прямоугольники.
Вернёмся теперь к общей теории. Предположений, нужных для
построения односвязного накрывающего пространства для X, в
действительности достаточно для построения накрывающих пространств,
реализующих любую подгруппу в п1(Х).
Предложение 1.36. Предположим, что пространство X линейно
связно, локально линейно связно и полулокально односвязно. Тогда для
любой подгруппы НСпг (X, х0) существует такое накрытие р : Хн -»X, что
р+(я1(Хн, Зс0)) =Н при подходящем выборе отмеченной точки х0еХн.
Доказательство. Для точек [у] и [у'] в односвязном накрывающем
пространстве X, построенном выше, будем считать, что [у] ~ [у']
означает, что у(1) = у'(1) и [уу']еН. Легко видеть, что это отношение
эквивалентности, так как Я —подгруппа. Л именно, оно рефлексивно, так как Н
содержит единичный элемент; симметрично, так как Н замкнута
относительно обращения; транзитивно, так как Н замкнута относительно
умножения. Пусть Хи —факторпространство пространства X, полученное при
отождествлении [у] с [у'], если [у] ~ [у']. Заметим, что если у(1) = у'(1)у
то [у] ~ [у'] тогда и только тогда, когда [yrj] ~ [y'rj]. Это означает, что если
какие-нибудь две точки в базисных окрестностях U{y] и и^
отождествляются в Х/ь то тогда эти окрестности отождествляются целиком.
Следовательно, естественная проекция Хи —>Х, индуцированная отображением
[у] —> 7(1), является накрытием.
Если мы выберем в качестве отмеченной точки Зс0 е Хи класс
эквивалентности постоянного пути с в точке x0i то образ гомоморфизма
§ 1.3. Накрытия
91
рф: TtiCX//, xQ) —> пх(Х, Xq) в точности равен Н. Причина этого в том, что
для петли у в X с началом и концом в х0 её поднятие в точке X,
начинающееся в [с], заканчивается в [у], поэтому образ этого поднятого пути
в Хи будет петлёй тогда и только тогда, когда [у] ~ [с], а это эквивалентно
тому, что [у] е Я. П
Позаботившись о существовании накрытий пространства X,
соответствующих всем подгруппам в я^Х), обратимся теперь к вопросу
единственности. Точнее говоря, нас интересует единственность с
точностью до изоморфизма, где изоморфизм между накрытиями рх: X! —> X
ир2:Х2-> X —это такой гомеоморфизм /: Хх —> Х2, что р} = p2f. Это
условие означает, что / сохраняет структуру накрывающего
пространства, переводя pj"1 W в р^Ч*) для всеххеХ. Тогда обратное отображение
f"1 тоже изоморфизм, и композиция двух изоморфизмов — изоморфизм,
поэтому мы получаем отношение эквивалентности.
I Предложение 1.37. Если пространство X линейно связно и локаль-
I но линейно связно, то два линейно связных накрывающих простран-
I ства р}: Хх —> X и р2: Х2 —> X изоморфны посредством изоморфизма
I /: Хх —> Х2, переводящего отмеченную точку хг е р^"1 (jc0) в отмеченную
I точку х2 £ р"100), тогда и только тогда, когда
I Р\*(щ(ХиХг)) = р2*(я1(Х2,х2)).
Доказательство. Если существует изоморфизм
то из соотношений pj = р2/ и Рг — Pi/ 1 следует, что
Р^О^Х,,^)) = р2Лл1(Х2,Х2)).
Наоборот, предположим, что
рь(7Г1(Х1,Х1)) = Р2Дл1(Х2,Х2)).
В соответствии с критерием поднятия мы можем поднять рх до
отображения Pi • (Х\>х{)^+ (Х2, *г)> Для которого p2Pi = P\. Аналогично получаем
Р2: №2**2) —> (Хь ?!), где PiP2 = P2- Тогда согласно единственности
поднятия PiP2 = 1 и р2Р! = 1, так как эти композиции поднятий сохраняют
отмеченные точки. Таким образом, р, и р2 — обратные изоморфизмы. □
Мы доказали первую половину следующей теоремы классификации.
I Теорема 1.38. Пусть пространство X линейно связно, локально ли-
I нейно связно и полулокально односвязно. Тогда существует взаимно
I однозначное соответствие между множеством сохраняющих отмечен-
I ную точку классов изоморфных линейно связных накрывающих про-
I странств р: (X, х0) —> (Х,х0) и множеством подгрупп в тг^Х, Xq)*> это
I соответствие получается при сопоставлении подгруппы рДя^Х, х0))
92
Глава 1. Фундаментальная группа и накрытия
I накрывающему пространству (X, 3?0). Если отмеченные точки не учи-
I тываются, то такое сопоставление даёт взаимно однозначное соответ-
I ствие между классами изоморфных линейно связных накрывающих
I пространств р:Х->Хи классами сопряжённости подгрупп в пг (X, х0).
Доказательство. Остаётся доказать только последнее утверждение.
Покажем, что для накрытия р: (X, х0) —> (X, х0) изменение отмеченной
точки х0 в пределах р-1Оо) соответствует в точности замене подгруппы
р„ [пл (X, х0)) на некоторую сопряжённую ей подгруппу в п1 (X, х0). Пусть
хх —другая отмеченная точка в р-1 (х0) и у — путь из точки х0 в точку х^.
Тогда у проектируется в петлю у в X, представляющую некоторый элемент
ge TCjCX, х0). Положим Н,- = р*(я1(Х, jf,-)) для i = 0,1. Имеет место
включение g~[HQg с Нл, так как если / — петля с началом и концом в точке х{)у
то у/у — петля с началом и концом в точке хг. Аналогично gH^g~l CH().
Сопрягая последнее соотношение посредством элемента g"1, получаем
Нл Cg~[H0g, а потому g~lH0g = H]. Таким образом, изменение
отмеченной точки х0 на 5?! приводит к замене подгруппы Н0 на сопряжённую ей
подгруппу Нл =g~lHQg.
Наоборот, чтобы заменить подгруппу Н0 на сопряжённую ей
подгруппу Нг =g~lH0g, выберем петлю у, представляющую элемент g, поднимем
её до пути у, начинающегося в х0, и положим хг = у(1). Предыдущие
рассуждения тогда показывают, что имеет место требуемое соотношение
H,=g-lHog. a
Из критерия поднятия следует, что односвязное накрывающее
пространство линейно связного, локально линейно связного пространства X
является накрывающим пространством любого другого линейно связного
накрывающего пространства для X. Поэтому односвязное накрывающее
пространство для X называют универсальным накрытием. Оно
единственно с точностью до изоморфизма.
Вообще, можно ввести частичный порядок на всех линейно связных
накрывающих пространствах для X, согласно тому, накрывает ли одно
из них другое. Он соответствует частичному порядку, заданному
включением соответствующих подгрупп в тгДХ) или же классов сопряжённости
подгрупп, если отмеченные точки не учитываются.
Представление накрытий перестановками
Теперь мы хотим описать другой способ классификации различных
накрывающих пространств связного, локально линейно связного и
полулокально односвязного пространства X, не ограничиваясь только
связными накрывающими пространствами. Чтобы представить его идею,
рассмотрим трилистные накрывающие пространства окружности S1. Таких
пространств три: Хь Х2 и Х3> причём индекс указывает число компонент.
Для каждого из этих накрытий р: X, —►S1 три различных поднятия петли
§ 1.3. Накрытия
93
в S1, порождающей группу nl{S\x0)) определяют
перестановку множества р~1(х0), переводящую начальную точку
поднятия в конечную точку поднятия. Для Хх это будет циклическая
перестановка, для Х2 — транспозиция двух точек, сохраняющая
третью точку, а для Х3—тождественная перестановка. Эти
перестановки, очевидно, определяют накрывающие пространства
единственным образом с точностью до изоморфизма. То же
самое верно для п-листных накрытий окружности S1 для
произвольного п, даже для бесконечного п.
Накрывающие пространства букета SlVSl можно
закодировать с помощью той же самой идеи. Обращаясь вновь к
большой таблице примеров в начале этого параграфа, в случае накрывающего
пространства (1) мы видим, что петля а поднимается до тождественной
перестановки двух вершин, а петля Ъ поднимается до перестановки,
которая переставляет эти две вершины. В случае (2) обе петли а и Ъ
поднимаются до транспозиций двух вершин. В случаях (3) и (4) петли а и Ъ
поднимаются до транспозиций различных пар из трёх вершин, в то время
как в (5) и (6) они поднимаются до циклических перестановок всех
вершин. В (11) вершины можно занумеровать целыми числами Z так, что а
поднимается до тождественной перестановки, а Ъ поднимается до сдвига
п»-*п-Ы. Действительно, из этих примеров видно, что накрывающее
пространство букета Sl VS1 —это не что иное, как эффективное графическое
представление пары перестановок данного множества.
Идею поднимать петли до перестановок можно обобщить на
произвольные накрывающие пространства. Для накрытия р : X —>Х путь у в X
имеет единственное поднятие у, начинающееся в данной точке
множества р_1(у(0)), поэтому мы получаем корректно определённое
отображение hy\ p-1(y(0)) —>р-1(у(1)), переводя начальную точку f(0) каждого
поднятия у в его конечную точку 7(1). Очевидно, что Ly является
взаимно однозначным соответствием, так как отображение Ly ему обратно.
Для композиции путей уг\ мы имеем Ly7} = Lr?Lr, а не LrL7?, так как
композиция путей записывается слева направо, в то время как композиция
отображений записывается справа налево. Чтобы исправить это, изменим
определение, заменив отображение Ly обратным к нему. Таким образом,
новое Ly — это взаимно однозначное отображение р_1(уО)) —>р~1(7(0)),
и теперь Lyl] = LrL7?. Так как Ly зависит только от гомотопического
класса петли у, это означает, что если мы ограничимся петлями с началом
и концом в отмеченной точке х0 G X, то сопоставление у —»Ly даёт
гомоморфизм из п^ХуХц) в группу перестановок множества р"1{х0). Его
называют действием группы тс1(Х, х0) на слое р~](х0).
Посмотрим теперь, как можно восстановить накрывающее
пространство р: X —> X по соответствующему ему действию группы 7г,(Х,л:0) на
слое F — р_1(л:0), предполагая, что пространство X линейно связно, ло-
94
Глава 1. Фундаментальная группа и накрытия
кально линейно связно и полулокально односвязно, а потому у него есть
универсальное накрытие Х0 —>Х. В качестве точек пространства Х0
можно взять гомотопические классы путей в X, начинающихся в точке х0,
как в общей конструкции универсального накрытия. Рассмотрим
отображение h: Х0 х F—>Х, которое переводит пару ([у],х0) в f(l), где у —
поднятие пути у в X, начинающееся в точке xQ. Тогда h непрерывно, а в
действительности является локальным гомеоморфизмом, так как
окрестность точки ([у], Зс0) в Х0 х F состоит из пар ([yrj], 3t0), где rj —путь в
соответствующей окрестности точки у(1). Очевидно, что h сюръективно, так
как X линейно связно. Если бы отображение h было и инъективным, то
оно было гомеоморфизмом, что маловероятно, так как X, возможно, не
гомеоморфно Х0 х F. Несмотря на то что отображение h не инъективно,
оно будет индуцировать гомеоморфизм некоторого факторпространства
пространства Х0 х F на X. Чтобы понять, что это за
факторпространство, предположим, что h([y],x0) =
= h([y'],x'0). Тогда у и / — пути из точки х0 в одну
и ту же конечную точку, и из рисунка мы видим, что
JCQ = Lr/y(jf0). Если Я —петля у'у, то это означает, что
h([y]1x0) = h([Xy]iLx(x0)). Наоборот, для любой
петли Я мы получаем h([y]9x0) = /i([Ay], La(jc0)). Таким
образом, ft индуцирует корректно определённое
отображение в X из факторпространства пространства Х0 х F, полученного
при отождествлении ([у],х0) с ([Яу], LA(3c0)) для всех [Я] елДХ, х0).
Обозначим это факторпространство через Хр, где р—гомоморфизм группы
тг^Х, х0) в группу перестановок слоя F, заданный рассматриваемым
действием.
Заметим, что определение пространства Хр имеет смысл всегда, когда
задано действие р группы пх{Х,х0) на множестве F. Имеется
естественная проекция Хр —>Х, переводящая ([у], х0) в у(1), и она является
накрытием, так как если U С X — открытое множество, над которым
универсальное накрытие Х0 является произведением U х ttjCX, x0), to
отождествления, задающие Хр, просто сжимают U х пх (X, х0) х F в [/ х F.
Вернёмся к исходному накрытию X —>Х с соответствующим
действием р. Для него отображение Хр —>Х, индуцированное отображением ft,
взаимно однозначно, а поэтому является гомеоморфизмом, так как
отображение h было локальным гомеоморфизмом. Л так как этот
гомеоморфизм Хр —>Х переводит каждый слой накрытия Хр в соответствующий
слой накрытия X, он является изоморфизмом накрытий.
Если два накрытия р}: Хх —► X и р2: Х2 —> X изоморфны, можно
поинтересоваться, как связаны соответствующие действия группы п1 (X, х0)
на слоях Fj и F2 над точкой х0. Ограничение изоморфизма h: X] —> Х2
даёт взаимно однозначное отображение F} —> F2, причём очевидно, что
Lr(h(3c0)) = h(Lr(jf0)). Используя менее громоздкое обозначение ух0 для
§ 1.3. Накрытия
95
L (*о)> это соотношение можно более кратко записать как уН(х0) = Иух0).
Взаимно однозначное отображение FY —> F2 с таким свойством
естественно назвать изоморфизмом множеств с действием группы п] (X, х0). Таким
образом, изоморфные накрытия имеют изоморфные действия на слоях.
Обратное утверждение тоже верно и легко доказывается. Нужно только
заметить, что для изоморфных действий pY и р2 изоморфизм h: Fl^>F2
индуцирует отображение Xpi —>Хр2, a h~l индуцирует аналогичное
отображение в противоположном направлении, причём композиции этих двух
отображений в любом порядке —тождественные отображения.
Это показывает, что /7-листные накрытия пространства X
классифицируются классами эквивалентности гомоморфизмов 7r](X,x0) —> Е„,
где Еп — группа перестановок п символов, а отношение эквивалентности
отождествляет гомоморфизм р с каждым из сопряжённых с ним
гомоморфизмов h~lph для всех элементов hzY,n. Исследование гомоморфизмов
данной группы в группу Ип — классическая тема в теории групп, и мы
видим, что у этого алгебраического вопроса есть хорошая геометрическая
интерпретация.
Преобразования накрытий и действия групп
Для накрытия р: X —>Х изоморфизмы X—>Х называют
преобразованиями накрытия или преобразованиями скольжения. Они образуют
группу G(X) относительно композиций. Например, для накрытия р: 1R—> S\
проекции вертикальной спирали на окружность, преобразования
накрытия—это вертикальные переносы, отображающие спираль на себя; в этом
случае G(X) ъ%. Для п-листного накрытия S1 —>Sl, заданного
формулой z*-*zn, преобразования накрытия — вращения окружности S1 на углы,
кратные 2л:/п, поэтому G(X) — Ъп.
Согласно свойству единственности поднятия преобразование
накрытия полностью определяется тем, куда оно переводит одну точку, если
предположить, что пространство X линейно связно. В частности, только
тождественное преобразование накрытия может оставлять неподвижной
Хотя бы одну точку пространства X.
Накрытие р: X —> X называют нормальным., если для любой точки
х 6 X и любой пары поднятий х, х' точки х найдётся преобразование
Накрытия, переводящее х в х'. Например, накрытие $ —>Sl и п-листное
накрытие S1 —> S1 нормальны. Говоря неформально, нормальное
накрытие—это наиболее симметричное накрытие. Это можно усмотреть для
накрывающих пространств букета S1 V S\ изображённых в таблице в
начале этого параграфа, где нормальные накрывающие пространства —это
СП, (2), (5)—(8) и (11). Заметим, что в случае (7) группа преобразований
накрытия равна Z4, в то время как в случае (8) она равна Z2 х Ъг.
Часто нормальные накрытия называют регулярными накрытиями.
Термин «нормальное» мотивируется следующим результатом.
96
Глава 1. Фундаментальная группа и накрытия
I Предложение 1.39. Пусть р: (X,Зс0) —► (X, х0) —линейно связное на-
I крывающее пространство линейно связного, локально линейно связно-
I го пространства Хи Н —подгруппа р+(7Г! (X, -5с0)) стт^Х, х0). Тогда:
I а) это накрытие нормально тогда и только тогда, когда Н — нормаль-
I ная подгруппа в п] (X, х0);
I б) группа G(X) изоморфна факторгруппе N (Н)/Н, где N(H) — порма-
I лизатор подгруппы Н в тгДХ, х0).
I В частности, группа G(X) изоморфна п^Х, х0)/Н, если X —нормаль-
I ное накрытие. Следовательно, для универсального накрытия X —> X мы
I имеем GtJOfc^CX).
Доказательство. Мы видели ранее в доказательстве теоремы
классификации, что замена отмеченной точки x0Gp"l(x0) на хх ^р~1(х0) в
точности соответствует сопряжению подгруппы Н элементом [у] е пх(Ху х0),
где у поднимается до пути у из Зс0 в xv. Поэтому элемент [у] принадлежит
нормализатору N(H) тогда и только тогда, когда
р^тггСХДо)) = р,(тг1(Х,х1)),
а в соответствии с критерием поднятия это эквивалентно существованию
преобразования накрытия, переводящего х0 в х}. Следовательно,
накрытие нормально тогда и только тогда, когда N(H) = тг^Х,х0)у т.е. тогда
и только тогда, когда Н —нормальная подгруппа в тт, (X, х0).
Рассмотрим отображение ц>: N(H) —> G(X), которое переводит \у]
в преобразование накрытия т, отображающее точку х0 в точку х^, в ука*
занных выше обозначениях. Тогда у — гомоморфизм, поскольку если у' —
другая петля, соответствующая преобразованию накрытия т',
переводящему Зс0 в x'v то у • у' поднимается до у - (T(f')) — пути из х0 в т(*р =
= тт'(х0)] таким образом, тт' — преобразование накрытия,
соответствующее [у] [у7]. Согласно предыдущему абзацу гомоморфизм у сюрьекти^еи.
Его ядро состоит из классов [у], поднимающихся до петель в X. Такие
классы как раз и есть элементы группы рДя, (X, Зс0)) =-Н. П
Группа преобразований накрытия —это частный случай общего
понятия «группы, действующей на пространстве». Если даны группа G и
пространство У, то действие группы G на пространстве У—это
гомоморфизм р группы G в группу Нотео(У) всех гомеоморфизмов пространства
У в себя. Таким образом, каждому элементу g 6 G соответствует
гомеоморфизм р (g) :Y^>Y, который для простоты обозначений мы записываем
просто как g: Y ^>Y. Требование, что р — гомоморфизм, приводит к
условию, 4TOg1(g2(y))^(g1g2)(y) для всех gbg2GG иуеУ. Если р инъекти-
вен, то он отождествляет G с подгруппой в Нотео(У), и на практике мы не
много потеряем, предположив, что р — включение G1 <—> Нотео(У), так как
подгруппа p{G) сНотео(У) содержит всю топологическую информацию
об этом действии группы.
§ 1.3. Накрытия
97
Нас будут интересовать действия, удовлетворяющие следующему
условию:
(*) у любой точки у G У есть такая окрестность U, что все образы g(U) для
разных g e G не пересекаются; другими словами, если g^ (£/)ng2(LO/0,
TOg!=g2-
Действие группы преобразований накрытия G(X) на X удовлетворяет
условию (*). Чтобы убедиться в этом, предположим, что U с X
проектируется гомеоморфно на U С X. Если gi(U) П g2W) Ф 0 для некоторых
gi> Si е G(X), то gi (Зст) = g2(x2) Для некоторых хъ х2 G [/. Так как точки 3?!
и х2 должны лежать в одном и том же множестве р~1 (х), которое
пересекает t/ только в одной точке, мы получаем х\ = 3?2. Тогда g1"1g2 оставляет
эту точку неподвижной, поэтому g^]g2 = l и g] = g2.
Отметим, что в условии (*) достаточно считать gj единичным
элементом группы, так как условие g} (Ю ng2(L0 Ф0 эквивалентно условию
t/ng^1g2(t/) 7^0- Таким образом, мы имеем эквивалентное условие, что
UngW) ф0 только в том случае, когда g -— единичный элемент группы.
Если дано действие группы G на пространстве У, то можно
образовать пространство У/G-—факторпространство пространства У, в
котором каждая точка у отождествлена со всеми её образами g(y), когда
g пробегает по G. Точки пространства Y/G, таким образом,— это
орбиты Gy = ig(y) | g e G } в У, a Y/G называют пространством орбит
действия. Например, для нормального накрытия X —>Х пространство орбит
X/G{X)-это просто*.
I Предложение 1.40. Если действие группы G на пространстве Y удо-
I влетворяет условию (*), то
I а) отображение факторизации р: Y—>Y/G, заданное формулой р(у) =
I =Gy, является нормальным накрытием;
I б) G будет группой преобразований накрытия Y —► Y/G, если про-
I странство Y линейно связно;
I в) группа G изоморфна tTj (Y/G)/p* (tTj (У)), если пространство У ли-
I нейно связно и локально линейно связно.
Доказательство. Если дано такое открытое множество U с У, как
в условии (*), то отображение факторизации р просто отождествляет все
непересекающиеся гомеоморфные множества ig(U) | g e G} в одно
открытое множество p{V) в Y/G. По определению фактортопологии на Y/G
При ограничении р на g(U) получается гомеоморфизм g(U) на p(U) для
всех geG, таким образом, мы получаем накрытие. Каждый элемент
группы G действует как преобразование накрытия, причём накрывающее
пространство нормальное, так как g2g}1 переводит g^W в g2(L0. Эта группа
преобразований накрытия содержит G в качестве подгруппы, причём она
равна этой подгруппе, если У линейно связно. Действительно, если / —
• 4 3;)к. м>55
98
Глава 1. Фундаментальная группа и накрытия
некоторое преобразование накрытия, то для произвольной точки у е У
обе точки у и /(у) принадлежат одной орбите и существует элемент g e G,
для которого g(y)=/(y). Следовательно, / = g, так как преобразования
накрытия линейно связного накрывающего пространства единственным
образом задаются тем, куда они переводят одну точку. Последнее
утверждение предложения непосредственно следует из утверждения б)
предложения 1.39. П
Имея в виду предыдущее предложение, будем называть действие,
удовлетворяющее условию (*), действием накрытия. Это не стандартная
терминология, но общепринятого названия для действий, удовлетворяющих
условию (*), нет. Иногда их называют «вполне разрывными» действиями,
но часто этот довольно непривлекательный термин означает нечто более
слабое: у любой точки xgX есть такая окрестность L/, что множество
Ur\g(U) непусто лишь для конечного числа элементов geG. Многие
группы симметрии обладают таким свойством вполне разрывности, но при
этом не удовлетворяют условию (*), например группа симметрии
обычного замощения плоскости R2 правильными шестиугольниками. Причина,
по которой действие этой группы на R2 не может удовлетворять условию
(*), заключается в наличии неподвижных точек, т.е. точек у, для
которых есть такой нетривиальный элемент g ^G, что g{y) = у. Например,
вершины шестиугольников сохраняются при поворотах на 120° вокруг
них, а середины сторон сохраняются при поворотах на 180°. Действие
без неподвижных точек называют свободным действием. Таким образом,
для свободного действия группы G на У только единичный элемент
группы G оставляет неподвижной некоторую точку пространства У. Это
эквивалентно требованию, что все образы g(y) каждой точки у е У различны;
другими словами, gliy)—g2{y) только в том случае, когда g, =g2, так как
равенство gi(y)=g2(y) эквивалентно равенству g^g2(y) = У- Хотя
условие (*) влечёт свободность, обратное не всегда верно. Примером служит
действие группы Z на S1, при котором образующая группы Z действует
как поворот на угол а, являющийся иррациональным кратным числа 2тг.
В этом случае каждая орбита Ъу плотна в S1, поэтому условие (*) не может
выполняться, так как из него следует, что орбиты являются дискретными
подпространствами. Одна из задач в конце этого параграфа состоит в том,
чтобы показать, что для действий на хаусдорфовых пространствах из
свободное™ и вполне разрывности следует условие (*). Заметим, что вполне
разрывность автоматически выполняется для действия конечной группой.
Пример 1.41. Пусть У — замкнугая ориентируемая поверхность рода
11 (сфера с одиннадцатью ручками), изображённая на рисунке. Она
обладает пятикратной осевой симметреи, порождённой поворотом на угол
2я/5. Таким образом, мы имеем циклическую группу Z5, действующую
на Уу причём условие (*), очевидно, выполняется. Факторпространство
Y/Zs — это поверхность рода 3, которую можно получить из одной из пяти
§ 1.3. Накрытия
99
цодповерхностей в Y, отсекаемых окружностями
q ..., С5, склеив две граничные окружности С,
и С+1 так> чт°бы получилась окружность С, как
показано на рисунке. Таким образом, мы
имеем накрытие Мп-^> М3, где через Mg
обозначена замкнутая ориентируемая поверхность рода
g, В частности, мы видим, что яа(М3)
содержит «бблыиую» группу П}(Ми) в качестве
нормальной подгруппы индекса 5, причём
факторгруппа равна Ъъ. Этот пример допускает
очевидное обобщение: можно заменить два отверстия
в каждой «ручке» поверхности Мп на т
отверстий, а пятикратную симметрию на п-кратную
симметрию. Это даст накрытие М„ш+1 -*Мш+1.
В одной из задач в § 2.2 нужно показать с помощью эйлеровой
характеристики, что если существует накрытие Mg —* Mh, то g = ran +1 и h = т + 1
для некоторых тип.
Из последнего утверждения предыдущего предложения мы видим,
В частности, что для действия накрытия группы G на односвязном
локально линейно связном пространстве Y фундаментальная группа
пространства орбит Y/G изоморфна G. При этом изоморфизме элемент g^G
соответствует петле в Y/G, которая является проекцией пути в Y из выбранной
отмеченной точки у0 в g(y0). Любые два таких пути гомотопны, так как
Y односвязно, поэтому мы получаем корректно определённый элемент
Группы nl(Y/G)y соответствующий g.
Метод вычисления фундаментальной группы посредством действия
Группы на односвязном пространстве, по сути дела, такой же, каким мы
вычисляли группу TijCS1) в §1.1 посредством накрытия R—>Sl, которое
происходит из действия группы Ъ на R переносами. Это действительно
•есьма полезный общий метод вычисления фундаментальных групп.
Приведём некоторые примеры, иллюстрирующие эту идею.
Пример 1.42. Рассмотрим сетку в R2, образованную
горизонтальными и вертикальными прямыми, проходящими через точки из Z2. Украсим
эту решётку стрелками одним из двух способов, показанных на
рисунке; различие между этими двумя
случаями состоит в том, что во второмслучае
Горизонтальные стрелки на соседних
прямых противоположно направлены.
Группа G, состоящая из всех симметрии первой
Украшенной решётки, изоморфна группе
& * Z, так как она состоит из всех
переносов О, у) -» О + гп, у + п) для m, n e Z. Для второй решётки группа
симметрии G содержит подгруппу переносов вида О, у) —> О 4- т, у + 2п)
1 ► I ► I I ► I ► |
AAA AAA
I ► 1 ► I Ml*!
AAA AAA
1 ► I ► 1 1 ► 1 ► 1
100
Глава 1. Фундаментальная группа и накрытия
для т,п€:Ъ, но помимо них есть скользящие симметрии, каждая из
которых является композицией вертикального переноса на нечётное
расстояние и симметрии относительно вертикальной прямой решётки или
вертикальной прямой, равноудалённой от двух соседних прямых
решётки. Для обеих украшенных сеток существуют элементы группы G,
переводящие любой квадрат в любой другой, но только единичный элемент
группы G переводит квадрат в себя. Минимальное расстояние, на которое
любая точка перемещается нетривиальным элементом группы G, равно 1,
и из этого легко следует условие накрытия (*). Пространство орбит iR2/G
является факторпространством квадрата решётки, у которого
противоположные стороны отождествлены согласно стрелкам. Таким образом, мы
видим, что фундаментальные группы тора и бутылки Клейна являются
группами симметрии G в этих двух случаях. Во втором случае подгруппа
в G, образованная переносами, имеет индекс два, причём пространство
орбит для этой подгруппы — тор, двулистно накрывающий бутылку Клейна.
Пример 1.43 (пространство RPn). Антиподальное отображение
сферы Sn, заданное формулой л*—> —х, порождает действие группы Z2 на S'1
с пространством орбит RP", определённым в примере 0.4, —
вещественным проективным n-пространством. Действие здесь является действием
накрытия, так как каждое открытое полушарие в Sn не пересекается с его
образом. Как мы видели в предложении 1.14, сфера S" односвязна при
п ^ 2, поэтому из накрытия Sn —»RP" мы получаем, что тиДМР") ^Z2 для
п ^ 2. Образующая группы пг (МРП) — любая петля, являющаяся проекцией
пути в Sn, соединяющего две диаметрально противоположные точки.
Можно увидеть явно, что такая петля у имеет порядок два в группе щ (RP'1) при
п^2. Действительно, композиция y*Y поднимается до петли в S",
которую можно прогомотопировать в тривиальную петлю, так как nl(Sn) = 0,
поэтому проекция этой гомотопии в RP" даёт стягивание петли у - у.
Можно задать вопрос, есть ли другие конечные группы, которые
свободно действуют на S", определяя тем самым накрытие Sn —> Sn/G. Мы
покажем в предложении 2.29, что Z2 — единственная возможная группа
для чётного п, но для нечётного п вопрос намного более сложен. Легко
построить свободное действие любой циклической группы Ът на S2k~] —
действие, порождаемое вращением v —> e27n/n,v единичной сферы S2k"1
в С^ = R2fc. Это действие свободное, так как из уравнения v = e27r,£/mv, где
0 < I < т, следует, что v = 0, но 0 не является точкой сферы S2*"1.
Пространство орбит S2k'l/Zm —одно из семейства пространств, называемых
линзовыми пространствами, которые определяются в примере 2.43.
Есть также нециклические конечные группы, свободно действующие
на Sn поворотами для нечётного п > 1. Эти действия явно
классифицированы в книге [74]. В простейшем случае п — 3 примеры можно
построить следующим образом. Рассмотрим R4 как алгебру кватернионов 1HL
Умножение кватернионов обладает тем свойством, что \ab\ = |а||Ь|, где
§ 1.3. Накрытия
101
\а\ обозначает обычную евклидову длину вектора а е К4. Таким образом,
если а и Ъ — единичные векторы, то аЪ тоже единичный вектор, поэтому
умножение кватернионов задаёт отображение S3 x S3 —> S3. В
действительности оно превращает S3 в группу, хотя сейчас нам нужна только
ассоциативность, так как она влечёт, что любая подгруппа G в S3 действует
на S3 левым умножением: g(x) =gx. Это действие свободное, так как из
уравнения х = gx в алгебре с делением И следует, что g = 1 или х = 0. В
качестве конкретного примера группы G можно взять хорошо известную
кватернионную группу Q8 — {±1, ±i, ±;, ±k} из теории групп. Вообще для
любого натурального числа т путь Q4m — подгруппа в S3, порождённая
двумя кватернионами а = е"'/'ш и Ь=;. Таким образом, а имеет порядок
2m, a b имеет порядок 4. Из легко проверяемых соотношений ат = Ъ2 = — 1
и ЬаЬ-1 =а-1 следует, что подгруппа Z2mt порождённая элементом а,
нормальна и имеет индекс 2 в Q4;n. Следовательно, Q4,M — группа порядка 4т,
называемая обобщённой кватернионной группой. Другое
распространённое название этой группы — бинарная диэдральная группа D*;n, так как её
фактор по подгруппе {±1} является обычной диэдральной группой D2ni
порядка 2т.
Помимо групп Q4n, = £>4ni есТЬ только ТРИ другие нециклические
конечные подгруппы в S3: бинарные тетраэдральные, октаэдральные
и икосаэдральные группы Т2*4, 0*8 и /*20, порядки которых обозначены
индексами. Они проектируются (два элемента переходят в один) на
группы поворотных симметрии правильного тетраэдра, октаэдра (или куба)
и икосаэдра (или додекаэдра). В действительности нетрудно убедиться,
что гомоморфизм S3 —> SO(3), отображающий и е S3 с 1И в изометрию
v-*u~lvu пространства М3, которое рассматривается как пространства
чисто мнимых кватернионов v = а\ 4- bj 4- с/с, сюръективен и имеет ядро
{±1}. При этом группы D*m, T2*4, 048, /*20 —прообразы в S3 групп
поворотных симметрии правильного многоугольника или многогранника в R3.
Есть два условия, которым должна удовлетворять конечная группа G,
Действующая свободно на S":
а) любая абелева подгруппа в G является циклической; это эквивалентно
тому, что G не содержит никакой подгруппы Zp x 7L где р — простое
число;
б) группа G содержит не более одного элемента порядка 2.
Доказательство утверждения а) намечено в одной из задач в §4.2.
По поводу доказательства утверждения б) рекомендуется прочитать
статью [113]. Группы, удовлетворяющие условию а), полностью
классифицированы; подробности см. в [14], раздел VI.9. Примером группы,
удовлетворяющей условию а), но не условию б), служит диэдральная группа D2m для
нечётного т> 1.
Известно также намного более трудное обратное утверждение:
конечная группа, удовлетворяющая условиям а) и б), действует свободно
102
Глава 1. Фундаментальная группа и накрытия
на Sn для некоторого п. По поводу этого утверждения см. [108] и [92].
Известна также почти полная информация о том, какие числа гг возможны
для данной группы.
Пример 1.44. В примере 1.35 мы построили стягиваемый
двумерный комплекс Хтп = Ттп х К как универсальное накрытие конечного
двумерного комплекса Хтп> представляющего собой объединение двух
цилиндров отображений для отображений Sl —>S\ заданных формулами
z>-*zm и z>-*zn. Группа преобразований этого накрытия
—фундаментальная группа nl (Xnl п). По теореме ван Кампена, применённой к разбиению
пространства Xm n на два цилиндра отображения, получаем
представление (a,b|amb~n) для группы G^^tt^X,,^,,). Интересно внимательнее
посмотреть на действие группы Gm n на Хтп. Мы описали такое разбиение
пространства Хтп на прямоугольники, что Хтп — факторпространство
одного прямоугольника. Эти прямоугольники в действительности задают
клеточную структуру на Хт>п, поднимающую клеточную структуру на Хщп
с двумя вершинами, тремя рёбрами и одной двумерной клеткой. Группа
Gmn, таким образом, содержится в группе симметрии этой клеточной
структуры на Хт>п. Если мы ориентируем все три ребра комплекса Хт<п
и поднимем эти ориентации на рёбра комплекса ХпиП9 то Gtnn —группа
всех симметрии комплекса Хш/1, сохраняющих ориентации рёбер.
Например, элемент а действует как «винтовое движение» вдоль оси, которая
является вертикальной прямой {va} х М, где va —вершина комплекса 7'ш п,
а действие b аналогично для вершины vb.
Так как действие группы Gmn на Хтп сохраняет клеточную
структуру, оно также сохраняет структуру произведения Ттп х К. Это
означает, что существуют такие действия группы G,„ „ на Tmn и на Ж, что
действие на произведении Хтп = Тт>п х Ж является диагональным действием
g(*>.y) = (#(*)> g(y)) Для g^Gmn. Если мы изготовим прямоугольники
единичной высоты по координате Ж, то элемент ат = Ъп действует на R как
единичный перенос, в то время как а действует как перенос на 1/т, а Ь —
как перенос на 1/п. Действия элементов а и b на R переносами порождают
группу переносов прямой Ж, которая является бесконечной циклической,
порождаемый переносом на величину, обратную к наименьшему общему
кратному чисел тип.
Действие группы Gm>п на 7'шп имеет ядро, состоящее из степеней
элемента ат = ЬП. Эта бесконечная циклическая подгруппа в точности
совпадает с центром группы GHlf„, как мы видели в примере 1.24. Можно
рассмотреть индуцированное действие факторгруппы Ът *Z„ на 7'шл, но
это действие не свободное, так как элементы а и b и все элементы, с ними
сопряжённые, оставляют неподвижными вершины комплекса Ттп. С
другой стороны, если мы ограничим действие группы G„M, на 7ШП на ядро К
отображения Gm„ —>Z, заданного действием группы Gm<n на множителе :Я
в Хтп, то мы действительно получим свободное действие группы К на 7'„, ,г
§ 1.3. Накрытия
103
Так как это действие переводит вершины в вершины, а рёбра в рёбра, оно
будет действием накрытия. Таким образом, К — свободная группа, а
именно, фундаментальная группа графа Ттп/К. В одной из задач в конце этого
параграфа нужно определить Ттп/К явно и вычислить число образующих
группы К.
Комплексы Кэли
Накрытия можно использовать для изложения классического
метода геометрического описания групп при помощи графов. Напомним,
что в следствии 1.28 мы сопоставили каждому представлению группы
G= {ga I rj5) двумерный клеточный комплекс XG с яДХ^) % G, взяв букет
окружностей, по одной для каждой образующей ga, а затем приклеив
двумерную клетку для каждого соотношения fy. Мы можем построить
такой клеточный комплекс XG с действием накрытия группы G, что
XG/G = XG, следующим образом. Пусть вершинами комплекса XG будут
сами элементы группы G. Затем каждую вершину geG соединим ребром
с вершиной gga для всех выбранных образующих ga. Полученный при
этом граф называют графом Кэли группы G относительно образующих
ga. Этот граф связен, так как каждый элемент группы G является
произведением образующих ga, поэтому существует путь в графе,
соединяющий каждую вершину с вершиной, соответствующей единичному
элементу е. Каждое соотношение Гр задаёт петлю в графе, начинающуюся
в любой вершине g, и мы приклеиваем двумерную клетку по каждой
такой петле. Полученный в результате клеточный комплекс XG называют
комплексом Кэли группы G. Группа G действует на XG умножением
слева. Таким образом, элемент g е G переводит вершину g'eG в вершину
gg\ а ребро, соединяющее g; с g'ga, переводит в ребро, соединяющее
&g' c gg'ga- Действие продолжается на двумерные клетки очевидным
образом. Ясно, что это действие накрытия, а пространство орбит
—просто;^.
В действительности XG — универсальное накрытие пространства ХСп
так как оно односвязно. Это можно установить, рассматривая
гомоморфизм (/?: ят(Хс) —>G, определённый в доказательстве предложения 1.39.
Если еа — ребро в XG, соответствующее образующей ga группы G, то из
определения гомоморфизма у видно, что </>([ea]) =ga, таким образом (/? —
изоморфизм. В частности, ядро гомоморфизма </>, т.е. группа рДтгДХс)),
Нулевое; следовательно, группа пх (XG) тоже нулевая, так как гомоморфизм
Р* инъективен.
Давайте рассмотрим некоторые примеры комплексов Кэли.
Пример 1.45. В случае, когда G —свободная группа с двумя
образующими а и Ь, комплекс XG — это букет S1 V S\ а XG — граф Кэли груп-
Пы Z*Z, изображённый на рисунке. Действие элемента а на этом графе —
сДВиг вправо вдоль центральной горизонтальной оси, а элемент b действу-
104
Глава 1. Фундаментальная группа и накрытия
ет как сдвиг вверх вдоль центральной вертикальной оси. Композиция ab
этих двух сдвигов переводит вершину е в вершину ab. Аналогично
действие любого элемента w e Z * Z переводит вершину е в вершину w.
Пример 1.46. Для группы G = Z x Z с представлением (х, у \ хух~1у~^)
комплекс XG — это тор S1 x S1, а комплекс XG — плоскость R2, причём
вершины—узлы целочисленной решётки Z2 CIR2, а рёбра — горизонтальные
и вертикальные отрезки между этими точками решётки. Группа G
действует переносами О, у) •-+ (х + гп,у + п).
Пример 1.47. Для группы G = Z2 = (х \ х2 ) комплекс XG — плоскость
RP2, a XG = S2. Вообще для группы Zn = (х | хп ) комплекс XG> — это
окружность S1, к которой приклеен диск по отображению z —> zn, a XG состоит
из п дисков Db ..., DM, у которых отождествлены граничные окружности.
Образующая группы Zn действует на это объединение дисков, переводя
диск Df- в Df41 посредством поворота на угол 2тг/п; нижний индекс i
берётся по модулю п. Общая граничная окружность этих дисков
поворачивается на угол 2тг/п.
Пример 1.48. Если G = Z2 * Z2 = (а, Ь | а2, Ь2 ), то граф Кэли —
объединение бесконечной последовательности окружностей, каждая из которых
касается двух соседних с ней окружностей.
Комплекс XG получается из этого графа, если каждую окружность мы
рассмотрим как экватор двумерной сферы, получив при этом
бесконечную последовательность касающихся сфер. Элементы нормальной
подгруппы Z с Z2 * Z2 индекса два, порождённой элементом ab, действуют
на XG как переносы на чётное число, а любой из остальных элементов
группы Z2 * Z2 действует как антиподальное отображение одной из сфер
и переворачивает цепь сфер как единое целое вокруг этой сферы.
Пространство орбит XG — это IRP2 VIRP2.
§ 1.3. Накрытия
105
Нетрудно построить обобщение этого примера для группы Zm * Zn
с представлением (а, Ъ \ ат, Ъп) так, чтобы комплекс XG состоял из
бесконечного объединения экземпляров комплексов Кэли для Zm и Zn,
построенных в примере 1.47, которые расположены по образцу дерева. Случай
группы Z2 * Z3 изображён ниже.
Задачи
1- Для накрытия р: X —> X и подпространства А с. X положим А =
а=р"1(А). Докажите, что ограничение р: А—>А является накрытием.
2. Докажите, что если р1: Х1 —> Хт и р2: Х2 —> Х2 — накрытия, то их
произведение рх х р2: Хт х Х2 —>Х} х Х2 тоже является накрытием.
3. Пусть р: X—>Х— такое накрытие, что множество р~1(х) конечно
и непусто для всех хеХ, Докажите, что X —компактное хаусдорфово
пространство тогда и только тогда, когда X —компактное хаусдорфово
Пространство.
4. Постройте односвязное накрывающее пространство пространства
^CR3, которое является объединением сферы и диаметра. Сделайте то
Же самое, когда X — объединение сферы и окружности, пересекающей её
* Двух точках.
5. Пусть X — подпространство в R2, состоящее из четырёх сторон
Квадрата [0,1] х [0,1] и отрезков вертикальных прямых х = 1/2, 1/3,1/4,
•••> лежащих внутри этого квадрата. Докажите, что для любого накры-
***я X —> X существует окрестность левого края пространства X, которая
106
Глава 1. Фундаментальная группа и накрытия
поднимается гомеоморфно в X. Выведите из этого, что у X нет никакого
односвязного накрывающего пространства.
6. Пусть X — стягивающийся букет окружностей из примера 1.25,
и пусть X —его накрывающее пространство, изображённое на рисунке
внизу.
а^ь
Постройте такое двулистное накрывающее пространство У —>Х, что
композиция У —> X —> X этих двух накрытий не является накрытием. Заметьте,
однако, что композиция двух накрытий всегда обладает свойством
единственности поднятия пути.
7. Пусть У — квазиокружлостъ, изображённая на рисунке, т.е.
замкнутое подпространство в R2, состоящее из части графика функции
у = sin(l/x), отрезка [—1,1] на оси у и дуги,
соединяющей эти две части.
Стягивание в точку отрезка в Y на оси у, даёт фактор-
отображение /: У—►S1. Докажите, что / не поднимается
в накрытие К —> S1, несмотря на то что п}(У) — 0.
Таким образом, локальная линейная связность
пространства У — необходимое предположение в критерии поднятия.
8* Пусть X и У — односвязные накрывающие пространства линейно
связных, локально линейно связных пространств X и У. Докажите, что
если X ^ У, то X а У. [Здесь может оказаться полезной задача 11 из
главы 0.]
9. Докажите, что если линейно связное, локально линейно связное
пространство X имеет конечную фундаментальную группу пх{Х), то
любое отображение X —> S1 гомотопно нулю. [Воспользуйтесь накрытием
10. Найдите все связные двулистные и трёхлистные накрытия
букета S1 V S1 с точностью до изоморфизма накрытий без отмеченных точек.
11. Постройте конечные графы Хг иХ2, которые имеют общее ко-
нечное-листное накрывающее пространство Хг =Х2, но при этом не
существует пространства, которое накрывается каждым из пространств Хх
иХ2.
12. Пусть а и Ъ — образующие группы nl{Sl VS1), соответствующие
двум слагаемым S1. Нарисуйте накрывающее пространство букета S1 VS1,
соответствующее нормальной подгруппе, порождённой элементами а2, Ъ2
и {аЪ)л, и докажите, что это накрывающее пространство действительнс
то, которое нужно.
13. Найдите накрывающее пространство букета S1 V S\
соответствующее подгруппе в n^S1 VS1), порождённой кубами всех элементов. Этс
накрывающее пространство 27-листное, и его можно нарисовать на торе
§ 1.3. Накрытия
107
так, чтобы дополнительными областями были девять треугольников с
пометками ааа на сторонах, девять треугольников с пометками ЪЪЪ на
сторонах и девять шестиугольников с пометками аЪаЪаЪ на сторонах. [Для
аналогичной задачи с шестой степенью вместо кубов накрывающее
пространство имеет 228325 листов! А для fc-й степени, где к достаточно велико,
накрывающее пространство имеет бесконечно много листов. Лежащий
В основе этого вопрос из теории групп заключается в том, конечна ли
факторгруппа группы Z * Z по к-ы степеням всех элементов, и известен
под названием проблемы Бернсаида. Можно также задать такой вопрос
для свободной группы с п образующими.]
14. Найдите все связные накрывающие пространства для IRP2 V ЕР2.
15. Пусть р: X —> X — односвязное накрывающее пространство для X.
Пусть, далее, Л с X —линейно связное, локально линейно связное
подпространство, а А с X — компонента линейной связности пространства р~1 (А).
Докажите, что р: Л —> А — накрытие, соответствующее ядру отображения
*i(A)->*,(*).
16. Даны такие отображения X—>Y —>Z, что и отображение У—»Z,
И композиция X —> Z являются накрытиями. Докажите, что отображение
X-+Y является накрытием, если Z локально линейно связно. Докажите,
что это накрытие нормально, если X —» Z — нормальное накрытие.
17. Даны группа G и её нормальная подгруппа N. Докажите, что
существует нормальное накрывающее пространство X—>Х, для которого
ftjUO^G, 7ii(X)&N и группа G(X) преобразований накрытия изоморфна
G/N.
18. Пусть пространство X линейно связно, локально линейно связно
И полулокально односвязно. Тогда линейно связное накрывающее
пространство X —> X называется абелевым, если оно нормально и имеет абе-
леву группу преобразований накрытия. Докажите, что у X есть абелево
накрывающее пространство, которое является накрывающим
пространством любого другого абелева накрывающего пространства для X, причём
такое «универсальное» абелево накрывающее пространство единственно
С точностью до изоморфизма. Опишите это накрывающее пространство
явно для X = SlvSl и для X = SlvSlVSl.
19. С помощью предыдущей задачи докажите, что у замкнутой
ориентируемой поверхности М& рода g есть связное нормальное накрывающее
пространство с группой преобразований накрытия, изоморфной Ъп
(произведение п экземпляров группы Z), тогда и только тогда, когда п ^ 2g.
Для п = 3 и^З опишите такое накрывающее пространство явно как
Подпространство вЕ3с переносами в качестве преобразований
накрытия. Докажите, что такое накрывающее пространство в Ж3 существует
Тогда и только тогда, когда существует такое вложение поверхности Mg
в трёхмерный тор Т3 = S1 x S1 x S1, что индуцированное отображение
*i(Afg) —►7г1(7'3) сюръективно.
108
Глава 1. Фундаментальная группа и накрытия
20. Постройте накрытия бутылки Клейна бутылкой Клейна и тором,
не являющиеся нормальными.
21. Пусть X — пространство, полученное из тора S1 x S1
приклеиванием листа Мёбиуса посредством гомеоморфизма граничной окружности
листа Мёбиуса на окружность S1 х {л:0} в торе. Вычислите тгДХ),
опишите универсальное накрытие для X и опишите действие группы тг^Х)
на универсальном накрытии. Сделайте то же самое для пространства У,
полученного приклеиванием листа Мёбиуса к !^Р2 посредством
гомеоморфизма его граничной окружности на окружность в RP2, образованную
одномерным остовом обычной CW-структуры на RP2.
22. Даны действия накрытий для группы Gl на Хт и группы G2 на
Х2. Докажите, что действие группы GT x G2 на Х^ х Х2, заданное
формулой (gi,g2)(*i,*2) — (gi(^i)Jg2(x2))> является действием накрытия и что
(Хл х X2)/{GX x G2) гомеоморфно Xx/Gl x X2/G2.
23. Докажите, что если группа G действует свободно и вполне
разрывно на хаусдорфовом пространстве X, то это действие —действие
накрытия. (Здесь «вполне разрывно» означает, что у любой точки х е X
есть такая окрестность U, что множество { g e G | L/ П g(U) Ф 0} конечно.)
В частности, свободное действие конечной группы на хаусдорфовом
пространстве—действие накрытия.
24. Если дано действие накрытия группы G на линейно связном,
локально линейно связном пространстве X, то каждая подгруппа И с G
определяет композицию накрытий X —> Х/И —> X/G. Докажите, что
а) любое линейно связное накрывающее пространство между X и X/G
изоморфно Х/Н для некоторой подгруппы Н с G;
б) два таких накрывающих пространства Х/Н1 и Х/Н2 для X/G
изоморфны тогда и только тогда, когда И1и Н2 — сопряжённые подгруппы в G;
в) накрывающее пространство Х/Н —> X/G нормально тогда и только
тогда, когда Н — нормальная подгруппа в G, и в таком случае группа
преобразований этого накрытия изоморфна G/H.
25. Пусть кр\ R2—>]R2— линейное преобразование у>О,у) = (2л:,у/2).
Оно порождает действие группы Z на X = IR2 — {0}. Докажите, что это
действие является действием накрытия, и вычислите тгг (X/Z). Докажите, что
пространство орбит X/Z нехаусдорфово, и опишите его как объединение
четырёх подпространств, гомеоморфных пространству S1 x R, которые
происходят из компонент дополнения к оси х и оси у.
26. Для накрытия р : X —> X, где X связно, локально линейно связно
и полулокально односвязно, докажите, что
а) компоненты связности пространства X находятся во взаимно
однозначном соответствии с орбитами действия группы я^Х, л:0) на слое
p-1u0);
б) при соответствии Галуа между связными накрытиями пространства X
и подгруппами в n^{Xyx0) подгруппа, соответствующая компонен-
§ 1.3. Накрытия
109
те связности пространства X, содержащей данное поднятие х0
точки х0, — это стабилизатор точки Зс0, т. е. подгруппа, состоящая из
элементов, действие которых на слое оставляет точку х0 неподвижной.
27. Для универсального накрытия р: X —> X можно рассмотреть два
действия группы п1{Ху х0) на слое р~1(х0), а именно действие, заданное
поднятием петли с началом и концом в х0, и действие, заданное
ограничением на слой преобразований накрытия. Совпадают ли эти два действия
в случае, когда X = S1 V S1 или X = S1 x S1? Будут ли согласованы эти
действия, если группа тг, (X, х0) абелева?
28. Обобщите доказательство теоремы 1.7 и покажите, что для
действия накрытия для группы G на односвязном пространстве У группа
Hi(Y/G) изоморфна G. [Если У локально линейно связно, то это частный
случай утверждения б) из предложения 1.40.]
29. Пусть пространство У линейно связно, локально линейно связно
и односвязно. Пусть, далее, Gl и G2 — подгруппы в Нотео(У),
определяющие действия накрытия на У. Докажите, что пространства орбит Y/G^
и Y/G2 гомеоморфны тогда и только тогда, когда G: и G2 — сопряжённые
подгруппы в Нотео(У).
30. Нарисуйте граф Кэли группы Z * Ъ2 = (а, Ъ \ Ъ2 ).
31. Докажите, что нормальные накрывающие пространства
букета S1 VS1 — это в точности графы, которые являются графами Кэли групп
с двумя образующими. Вообще нормальные накрывающие пространства
букета п окружностей — это графы Кэли групп с п образующими.
32. Рассмотрим накрытия р: X —>Х, где X и X — связные СИ^-комп-
лексы, причём клетки комплекса X проектируются гомеоморфно на
клетки комплекса X. Тогда ограничение накрытия р на одномерный остов даёт
накрытие X1 —>Х1 над одномерным остовом комплекса X. Докажите, что
а) два таких накрытия XY —> X и Х2 —* X изоморфны тогда и только тогда,
когда их ограничения X* —>Х1 и Х\ —>Х1 изоморфны;
б) накрытие X —> X нормальное тогда и только тогда, когда накрытие
X1—>Х1 нормальное;
в) группы преобразований накрытий X —>Х и X1 —>Х1 изоморфны,
причём изоморфизм индуцируется отображением ограничения.
33. В примере 1.44 пусть d — наибольший общий делитель чисел т
и п, и пусть т' = m/d и n' = n/d. Докажите, что граф Ттп/К состоит из т!
вершин с пометками а, п' вершин с пометками Ъ и d рёбер, соединяющих
каждую вершину а с каждой вершиной Ъ. Выведите из этого, что
подгруппа К" с Gmn свободная с dm'n' — m' — n' + l образующими.
loffiiieffii
§ LA. Графы и свободные группы
Так как любую группу можно представить как фундаментальную
группу некоторого пространства, это открывает путь для применения
топологии в изучении алгебраических свойств групп. Этот и следующий
параграфы дают некоторые иллюстрации этого принципа, при этом используя
в основном теорию накрытий.
Напомним, что дополнение, которое завершают эту главу, не следует
считать неотъемлемой частью основного ядра книги. Читатели, которые
хотят перейти к новым темам, могуг пропустить его и идти вперёд.
По определению граф — это одномерный CW-комплекс, другими
словами, пространство X, которое получается из дискретного множества Х°
приклеиванием набора еа одномерных клеток. Таким образом, X
получается из несвязного объединения Х° и замкнутых отрезков 1а при
отождествлении двух концов каждого отрезка /а с точками множества Х°.
Точки множества Х° —это вершины, а одномерные клетки —это рёбра
графа X. Заметим, что при таком определении ребро не включает свои
концы, а потому ребро — открытое подмножество в X. Два конца ребра могут
быть одной и той же вершиной, поэтому замыкание еа ребра еа гомео-
морфно либо отрезку /, либо окружности S].
Так как пространство X снабжено фактортоиологией из несвязного
объединения Х°Ца/а, подмножество в X открыто (или замкнуто) тогда
и только тогда, когда оно пересекает замыкание ёа каждого ребра еа по
открытому (или замкнутому) в ёа множеству. Говорят, что X снабжено
слабой топологией относительно подпространств ёа. В этой топологии
последовательность точек, лежащих внутри различных рёбер, образует
замкнутое подмножество, а потому никогда не сходится. Это верно, в
частности, если все рёбра, содержащие эту последовательность, имеют общую
вершину, а последовательные точки выбираются так, чтобы они
располагались всё ближе и ближе к вершине. Таким образом, если есть вершина,
которая является концом бесконечного набора рёбер, то слабая топология
не может быть метрической топологией. В одной из задач в конце этого
параграфа нужно доказать обратное утверждение, что слабая топология
§ 1.А. Графы и свободные группы
111
является метрической топологией, если каждая вершина является концом
лишь конечного числа рёбер.
База топологии пространства Х состоит из открытых интервалов на
рёбрах вместе с линейно связными окрестностями вершин. Окрестность
последнего вида для вершины v представляет собой объединение
связных открытых окрестностей Ua точки v вёа для всех ёа, содержащих v.
В частности, мы видим, что пространство X локально линейно связно.
Следовательно, граф связен тогда и только тогда, когда он линейно связен.
Если у графа X есть только конечное число вершин и рёбер, то
X компактен, будучи непрерывным образом компактного пространства
Х°1_1а/а. Обратное утверждение тоже верно, и вообще компактное
подмножество С графа X может пересекать только конечное число вершин
и рёбер X. Чтобы убедиться в этом, рассмотрим подпространство D с С,
которое состоит из вершин в С, к которым добавлено по одной точке на
каждом ребре, пересекающем С. Тогда D — замкнутое подмножество X,
так как оно пересекает каждое множество ёа по замкнутому множеству.
По той же самой причине замкнуто любое подмножество множества D,
поэтому топология подпространства D дискретна. Но множество D
компактно, поскольку оно является замкнутым подмножеством
компактного пространства С, поэтому множество D должно быть конечным. По
определению множества D это означает, что С может пересекать только
конечное число вершин и рёбер.
Подграф графа X — это подпространство Y с X, которое является
объединением вершин и рёбер графа X, причём если е(1 с Y, то ёа с Y.
Последнее условие означает лишь то, что Y — замкнутое подпространство в X.
Дерево —это стягиваемый граф. Поддеревом в графе X мы подразумеваем
подграф, который является деревом. Дерево в X называют максимальным,
если оно содержит все вершины графа X. Как мы увидим ниже, это
эквивалентно более очевидному определению значению максимальности.
I Предложение 1.А.1. Любой связный граф содержит максимальное
дерево, и, более того, любое дерево в графе содержится в максимальном
дереве.
Доказательство. Пусть X — связный граф. Мы опишем конструкцию,
которая позволяет вложить произвольный подграф Х0 с X так, чтобы он
был деформационным ретрактом подграфа У с X, который содержит все
вершины графа X. Если выбирать в качестве Х0 произвольное поддерево
в X, например единственную вершину, то это докажет требуемое
утверждение.
В качестве предварительного шага мы построим последовательность
подграфов Х0 с Х1 с Х2 с ..., где Х,+1 получается из X, добавлением
замыканий ёп всех рёбер еа с X — X,, имеющих по крайней мере один
конец в Х(. Объединение (Jxr- открыто в X, так как окрестность точки в X,
112
Глава 1. Фундаментальная группа и накрытия
содержится в Х,+1. Более того, множество (Jx,- замкнуто, так как оно
i
представляет собой объединение замкнутых рёбер, а X снабжено слабой
топологией. Поэтому X = [Jxh так как граф X связен.
i
Теперь, чтобы построить Y, мы для начала положим Y0 = X0. Тогда по
индукции, предполагая, что граф YJ с X, уже построен так, что он содержит
все вершины графа X,-, рассмотрим граф Yi+l, который получается из Yh
если для каждой вершины графа Х,-+1 — X,- добавить одно ребро,
соединяющее её с Yh и положим V = IJVJ. Очевидно, что YJ+1 деформационно ре-
трагируется на Yh и мы можем получить деформационную ретракцию
графа Y на Y0 = X0, деформационно ретрагируя Yj-+1 на Y{ в течение времени
из промежутка [l/2'+l, 1/2']. Таким образом, точка xsYi+l — YJ остаётся
неподвижной до этого промежутка, во время которого она перемещается
в YJ-, а после этого продолжает перемещаться, пока не достигнет Y0.
Полученная в результате гомотопия ht: Y —> Y непрерывна, так как она
непрерывна на замыкании каждого ребра, a Y имеет слабую топологию. П
Если даны максимальное дерево 'Г с X и отмеченная вершина х0 е Г,
то каждое ребро еа графа X - Т определяет петлю fa в X, которая идёт
сначала из х0 в один из концов ребра еа по пути в Т, затем вдоль еа, а потом
назад в х0 по пути в Т. Строго говоря, мы должны сначала ориентировать
ребро еа, чтобы задать направление, в котором нужно его пройти.
Заметим, что гомотопический класс петли fa не зависит от выбора путей в Т,
так как Т односвязно.
I Предложение LA.2. Для связного графа X с максимальным
деревом Т группа TijCX) свободная и имеет базис из классов [/а],
соответствующих рёбрам еа графа X - Т.
В частности, из этого следует, что максимальное дерево максимально
в том смысле, что оно не содержится ни в каком большем дереве, так как
добавление любого ребра к максимальному дереву даёт граф с
нетривиальной фундаментальной группой. Другое следствие состоит в том, что
граф является деревом тогда и только тогда, когда он односвязен.
Доказательство. Отображение факторизации X —>Х/Т является
гомотопической эквивалентностью согласно предложению 0.17. Факторпро-
странство Х/Т является графом с единственной вершиной, а потому оно
является букетом окружностей, фундаментальная группа которого, как
было показано в примере 1.21, свободная, причём её базисом служат
петли, заданные рёбрами графа Х/Т, которые являются образами петель /„
вХ. D
Вот очень полезный факт о графах.
I Лемма 1.А.З. Любое накрывающее пространство графа тоже
является графом, вершины и рёбра которого — поднятия вершин и рёбер
исходного графа.
§ 1.А. Графы и свободные группы
113
Доказательство, Пусть р: X —> X — накрытие. В качестве вершин
Графа X мы берём дискретное множество Х° = р~1(Х°). Представив X
как факторпространство объединения X°UctIa, как в определении графа,
и применив свойство поднятия пути к получающимся в результате
отображениям 1а —> X, мы получим единственное поднятие /а —> X, проходящее
через каждую точку в р-10) Для х Е еа. Эти поднятия рёбер задают
структуру графа на X. Получающаяся при этом топология на X — та же
самая, что и исходная топология, так как обе топологии имеют одни и
те же базисные открытые множества, поскольку накрывающая проекция
Х-~>Х является локальным гомеоморфизмом. П
Теперь мы можем применить то, что доказали о графах и их
фундаментальных группах, для доказательства важного факта из теории групп.
| Теорема 1.А.4. Любая подгруппа свободной группы свободна.
Доказательство. Пусть дана свободная группа F. Выберем граф X,
для которого Ui(X)?vF, например букет окружностей, соответствующих
базису группы F. Для каждой подгруппы G в F согласно предложению 1.36
существует накрытие р: X —> X, для которого р+(п1 (X)) = G;
следовательно, п1(Х)ъС так как рА инъективно согласно предложению 1.31. Так
как согласно предыдущей лемме Х — граф, группа G % тг^Х) свободная
согласно предложению 1.А.2. □
Строение деревьев можно лучше понять, внимательно посмотрев на
конструкцию в доказательстве предложения 1.А.1. Если X —дерево, a v0 —
любая его вершина, то построение максимального дерева У с X,
начинающееся с Уо = {v()}, приводит к возрастающей последовательности
поддеревьев Уп с X, объединение которых —всё дерево X, так как у дерева
есть только одно максимальное поддерево, а именно
оно само. Можно представлять себе вершины графа
Уп — Yn_i расположенными на «высоте» п, причём рёбра
графа Уп — Yn_} соединяют эти вершины с вершинами,
расположенными на высоте п — 1. Таким образом, мы
получаем «функцию высоты» h: X —> R, которая
сопоставляет каждой вершине её высоту и монотонна на
рёбрах.
Для каждой вершины v этого дерева X есть ровно одно ребро,
ведущее из v вниз, поэтому если пойти по этим ведущим вниз рёбрам, то мы
получим путь из v в отмеченную вершину v0. Это один из примеров
рёберного пути, являющегося композицией конечного числа путей, каждый
из которых состоит из одного ребра, движение по которому монотонно.
Для любого рёберного пути из v в v0, кроме идущего вниз рёберного
пути, функция высоты не монотонна и, следовательно, имеет локальные
максимумы, которые встречаются тогда, когда рёберный путь идёт
назад, вновь возвращаясь на некоторое ребро, по которому он только что
прошёл. Таким образом, в дереве есть единственный не возвращающийся
114
Глава 1. Фундаментальная группа и накрытия
назад рёберный путь между любыми двумя точками. Все вершины и рёбра
вдоль этого рёберного пути различны.
Дерево не может содержать подграф, гомеоморфный окружности, так
как две вершины в таком подграфе можно было бы соединить более чем
одним невозвращающимся рёберным путём. Наоборот, если связный граф
X не содержит ни одного подграфа, гомеоморфного окружности, то он
должен быть деревом. Действительно, если Т — максимальное дерево в X,
которое не совпадает с X, то объединение некоторого ребра графа X -'/'
с невозвращающимся рёберным путём в Т, соединяющим концы этого
ребра, является подграфом в X, гомеоморфным окружности. Поэтому
если нет подграфов в X, гомеоморфных окружности, то мы получаем, что
Х = Г —дерево.
Для любого связного графа X и пары вершин v0 и Vj в нём существует
единственный невозвращающийся рёберный путь в каждом
гомотопическом классе путей из v0bv]. Это можно проверить, поднявшись в
универсальное накрытие X, которое является деревом, так как оно односвязио.
Если выбрать поднятие v0 вершины v0, то гомотопический класс путей из
v0 в V! поднимается до гомотопического класса путей, начинающихся в v0
и заканчивающихся в одном и том же поднятии v} вершины v^ Тогда
единственный невозвращающийся рёберный путь в X из v0 в V] проектируется
в требуемый невозвращающийся рёберный путь в X.
Задачи
1. Пусть X — граф, у которого каждая вершина является концом лишь
конечного числа рёбер. Докажите, что слабая топология на X является
метрической топологией.
2. Докажите, что связный граф ретрагируется на любой свой связный
подграф.
3. Для конечного графа X определим эйлерову характеристику #(Х)
как число вершин минус число рёбер. Докажите, что # (X) = 1, если X —
дерево, и что ранг (число элементов базиса) группы пг (X) равен 1 — % (X),
если граф X связен.
4. Докажите, что если X —конечный граф, а У — его подграф,
гомеоморфный S1 и содержащий отмеченную точку х0, то у группы 7Г](Х,л:0)
есть базис, в котором один из элементов представлен петлёй У.
5. Постройте связный граф X и отображения /, g: X —> X так, что
/g = l, но / и g не индуцируют автоморфизмы группы Я]. [Обратите
внимание, что из равенства /*g* = 1 следует, что гомоморфизм /+ сюръ-
ективен, a g+ инъективен.]
6. Пусть F — свободная группа с двумя образующими, a F' — её
коммутант. Найдите множество свободных образующих для F', рассматривая
накрывающее пространство графа S] VS1, соответствующее подгруппе F'.
§1.В. Пространства K(G, 1) и графы групп
115
7. Пусть F — конечно порождённая свободная группа, а N — её
нетривиальная нормальная подгруппа бесконечного индекса. Докажите,
используя накрытия, что группа N не является конечно порождённой.
8. Докажите, что конечно порождённая группа имеет лишь конечное
число подгрупп данного конечного индекса. [Сначала рассмотрите случай
свободных групп, используя накрывающие пространства графов. Общий
случай тогда следует из того, что любая группа — факторгруппа свободной
группы.]
9. Используя накрытия, докажите, что подгруппа И индекса п в
группе G имеет не более п сопряжённых подгрупп gHg~l в G. Воспользуйтесь
этим, чтобы показать, что существует такая нормальная подгруппа К С G
конечного индекса, что КсН. [Чтобы доказать последнее утверждение,
рассмотрите пересечение всех сопряжённых подгрупп gHg "1. Это
максимальная нормальная подгруппа в G, содержащаяся в Я.]
10. Пусть X— букет п окружностей с естественной структурой
графа. Пусть, далее, X —► X — накрывающее пространство с заданным
конечным связным подграфом У С X. Докажите, что существует конечный граф
Z Э У, который имеет те же самые вершины, что и У, и при этом проекцию
Y—>Х можно продолжить до накрытия Z-+X.
11. Примените две предыдущие задачи, чтобы показать, что если F —
конечно порождённая свободная группа и хе F — элемент, отличный от
единичного, то существует нормальная подгруппа Н с F конечного
индекса, для которой хфН. Следовательно, х имеет нетривиальный образ
в некоторой конечной факторгруппе группы F. В таком случае говорят,
что группа F остаточно конечная1,
12. Пусть F — конечно порождённая свободная группа, Н с F —
конечно порождённая подгруппа и xeF -Н. Докажите, что существует такая
подгруппа К конечного индекса в F, что КэН их£К. [Примените задачу
ю.]
13. Пусть х —нетривиальный элемент конечно порождённой
свободной группы F. Докажите, что существует подгруппа конечного индекса
Н с F, в которой х является одним из элементов базиса. [Здесь могут
оказаться полезными задачи 4 и 10.]
14. Докажите, что существование максимального дерева
эквивалентно аксиоме выбора.
§1.В. Пространства K(G, 1) и графы групп
В этом параграфе мы вводим класс пространств, гомотопический тип
Которых зависит только от фундаментальной группы. Эти пространства
часто возникают в топологии, особенно в её взаимодействии с теорией
групп.
По-англ. residually finite. — Прим. ред.
116
Глава 1. Фундаментальная группа и накрытия
Линейно связное пространство, фундаментальная группа которого
изоморфна данной группе G и которое имеет стягиваемое универсальное
накрывающее пространство, называют пространством типа K(G, 1) или
просто пространством K(Gy 1). Число 1 здесь относится к пх.
Пространства более общего вида K(G,ri) изучены в §4.2. Все такие пространства
называют пространствами Эйленберга—Маклейна, хотя в случае п = 1 их
изучал Гуревич, до того как Эйленберг и Маклейн рассмотрели общий
случай. Вот некоторые примеры.
Пример 1.В.1. Окружность S1 является пространством K"(Z, 1).
Вообще связный граф — пространство K(G, 1), где G —свободная группа, так
как согласно результатам § 1.А его универсальное накрытие — дерево, а
потому оно стягиваемо.
Пример 1.В.2. Замкнутые поверхности с бесконечной группой тгь
другими словами, все замкнутые поверхности, кроме S2 и КР2, являются
пространствами K(G, 1). Это будет доказано в примере 1.В.14 ниже. Это
следует также из теоремы в теории поверхностей, утверждающей, что
единственные односвязные поверхности без края —это S2 и 1R2, а потому
универсальное накрытие замкнутой поверхности с бесконечной
фундаментальной группой должно совпадать с R2, так как оно некомпактно.
Незамкнутые поверхности деформационно ретрагируются на графы,
поэтому такие поверхности — пространства K(G, 1) со свободной группой G.
Пример 1.В.З. Бесконечномерное проективное пространство RP00 —
пространство K(Z2,1), так как его универсальное накрытие —
бесконечномерная сфера S00, которая стягиваема. Чтобы доказать последний факт,
построим гомотопию тождественного отображения сферы S°° в
постоянное отображение в два шага следующим образом. Сначала рассмотрим
отображение ft: Ж°° —>R°°, заданное формулой
ft(x1,x29...) = 0—t)(xl,x2y...) + t(0,xl,x2,...).
Оно переводит ненулевые векторы в ненулевые для всех t е [0, 1], поэтому
ft/\ft\ даёт гомотопию тождественного отображения сферы S°° в
отображение Ох, х2, ...)—► (О, *!, х2у ...). Далее, гомотопия этого отображения
в постоянное отображение задаётся семейством отображений1 gt/\gt\t где
gt(xl,x2,...) = (l-t)(0,xl,x2y...) + t(l,090,...).
Пример 1.В.4. Обобщая предыдущий пример, можно построить
К(Ът, 1) как бесконечномерное линзовое пространство S°°/Zm, где группа
Ът действует на сфере S00, которую мы рассматриваем как единичную
сферу в С°°, умножением координат на корни т-й степени из единицы;
образующая этого действия —отображение (г^, z2,...) —► e2rr'/n,(z1, z2, ..•)•
Легко проверить, что это действие накрытия.
1 Для того чтобы значение gt{x]yx2,...) принадлежало единичной сфере S°°, лучше
определить gt(x]t х2у ...) = V 1 -г2(0, *!, х2, ...) + гП,0, 0, ...).— Прим. ред.
§1.В. Пространства K(G, 1) и графы групп
117
Пример 1.В.5. Произведение K(G, 1) х К{НУ 1) является
пространством K(G х Н, 1), так как его универсальное накрытие —произведение
универсальных накрытий пространств K(G, 1) и К(Н, 1). Поэтому, взяв
произведения окружностей и бесконечномерных линзовых пространств,
мы получим пространство K{G, 1) для любой конечно порождённой абе-
левой группы G. Например, n-мерный тор Г", т. е. произведение п
окружностей, является пространством K{Zn, 1).
Пример 1.В.6. Для замкнутого непустого связного подпространства
К в S3, его дополнение 53 — К является пространством K{G, 1). Это
теорема из теории трёхмерных многообразий, но в частном случае, когда К —
торический узел, этот результат следует из нашего исследования
дополнений торических узлов в примерах 1.24 и 1.35. А именно, мы показали, что
если К — торический узел /СШ|П, то существует деформационная
ретракция пространства S3 - К на некий двумерный комплекс Хти,
универсальное накрытие которого стягиваемо. Тогда свойство поднятия гомотопии
влечёт, что универсальное накрытие пространства S3 — К гомотопически
эквивалентно универсальному накрытию комплекса Х„, п, а потому тоже
стягиваемо.
Пример 1.В.7. Несложно построить пространство K{G, 1) для
произвольной группы G, используя понятие А-комплекса, введённое в §2.1.
Пусть EG — Д-комплекс, n-мерные симплексы которого — упорядоченные
наборы [g0, ..., gn] из п + 1 элементов группы G. Такой n-мерный симплекс
прилегает к (п — 1)-мерным симплексам [g0, ...,g,-, ...,gn] очевидным
образом, точно так же, как стандартный симплекс прилегает к своим
граням. (Обозначение g, означает, что соответствующая вершина удалена.)
Комплекс EG можно стянуть посредством гомотопии hr, которая сдвигает
каждую точку х 6 [g0, ...,gn] по отрезку в симплексе [е, g0, ...,£„],
соединяющему точку х и вершину [е], где е —единичный элемент группы G. Эта
гомотопия является корректно определённой в EG, так как если мы
рассмотрим её ограничение на грань [g0, ..., gh ..., gM], то получим линейную
Деформацию к точке [е] в грани [е,g0, ...,g,-, ...,g„]. Заметим, что h(
переносит [е] вдоль петли [е, е], поэтому hr в действительности не является
деформационной ретракцией пространства EG на [е].
Группа G действует на EG левым умножением, при этом элементg^G
линейно отображает симплекс [g0, ..., gn] на симплекс [gg0, ..., gg„].
Только тождественный элемент е переводит любой симплекс в себя, поэтому
согласно одной из задач в конце этого параграфа действие группы G на
EG— действие накрытия. Следовательно, факторотображение EG^EG/G
является универсальным накрытием пространства орбит BG = EG/G, а
потому BG — пространство K{G, 1).
Так как G действует на EG, свободно переставляя симплексы,
пространство BG наследует из EG структуру Д-комплекса. Действие группы G
на EG отождествляет все вершины комплекса EG, поэтому у BG есть толь-
118
Глава 1. Фундаментальная группа и накрытия
ко одна вершина. Чтобы явно описать структуру Л-комплекса на BG,
заметим сначала, что каждый п-мерный симплекс в EG можно единственным
образом записать в виде
Образ этого симплекса в BG можно однозначно обозначить символом
[gilg2l---lgj- В эт°й системе обозначений с «перегородками» элементы g,-
и их упорядоченные произведения можно использовать для того, чтобы
помечать рёбра, рассматривая пометку ребра как отношение двух
пометок вершин — концов ребра, как показано на рисунке. При такой системе
обозначений граница симплекса [gi|...|gn] комплекса BG состоит из
симплексов [g2|...|gn], [gi|...|gn-i] И [gI|...|gl-g|-+1|...|g,J ДЛЯ1 = 1,...,П-1.
go£i£2
g0g\g2g3
g2 g\g2g3
gogi
goglg-2
I gl
go g, gogi
Эта конструкция K(G, 1) даёт довольно большое пространство, так
как BG всегда бесконечномерно, а если группа G бесконечна, то BG
имеет бесконечное число клеток в каждой положительной
размерности. Например, ВЪ намного больше окружности S1, самого удобного
пространства K(Z,1). С другой стороны, комплекс BG обладает тем
достоинством, что он функториален: гомоморфизм /: G -* И индуцирует
отображение Bf: BG-+BH, переводящее симплекс [gi|...|gj в симплекс
[/(gi)!---l/(gn)]- ДРУгая конструкция пространства K(G, 1) приведена в
§4.2. Она начинается с произвольного двумерного комплекса с
фундаментальной группой G, например комплекса XGi соответствующего
представлению группы G. Затем приклеивают клетки размерности 3 и выше так,
чтобы универсальное накрытие стало стягиваемым, но при этом группа
пг не изменилась. В общем случае трудно как-нибудь проконтролировать
число многомерных клеток, необходимых для этой конструкции, поэтому
она тоже может быть весьма неэффективной. В действительности найти
удобное пространство K(G, 1) для данной группы G часто бывает трудной
задачей.
Интересен и почти парадоксален тот факт, что если группа G
содержит хотя бы один элемент конечного порядка, то любой CW-комплекс
типа K(G, 1) должен быть бесконечномерным. Это доказано в
предложении 2.45. В частности, бесконечномерное линзовое пространство из
§1.В. Пространства K(G, 1) и графы групп
119
примера 1.В.4, которое является пространством K(Zm, 1), нельзя заменить
никаким конечномерным комплексом.
Несмотря на большой произвол в построении пространств К (G, 1), они
обладают очень важным свойством единственности с точностью до гомото-
пии, которое во многом обусловливает интерес к пространствам K(G, 1).
I Теорема 1.В.8. Гомотопический тип О/У-комплекса типа K(G, 1)
однозначно определяется группой G.
Единственность гомотопического типа пространства X(G, 1),
соответствующего данной группе G, означает, что алгебраические инварианты
пространств, которые зависят только от гомотопического типа, например
группы гомологии и когомологий, превращаются в инварианты групп.
Это оказалось весьма плодотворной идеей и было подробно изучено как
с алгебраической, так и с топологической точки зрения. В обсуждении
после предложения 2.45 приведено несколько соответствующих ссылок.
Предыдущая теорема легко выводится из следующего предложения.
I Предложение 1.В.9. Пусть X — связный CW-комплекс, и пусть У —
I пространство X(G, 1). Тогда любой гомоморфизм п} (X, х0) —> п} (У, у0)
I индуцирован отображением (Х,х0) —> (У,у0), которое единственно с
| точностью до гомотопии, сохраняющей точку х0.
Чтобы вывести теорему из этого предложения, возьмём в качестве X
и Y CW-комплексы K(G, 1) с изоморфными фундаментальными группами.
Предложение даёт отображения /: (X, х0) ->(У, у0) и g: (У, у0) ->(X, х0)9
индуцирующие взаимно обратные изоморфизмы ят(Х, х0) ъ ттДУ, у0).
Тогда отображения / g и gf индуцируют тождественные отображения групп
пъ а потому гомотопны тождественным отображениям.
Доказательство предложения 1.В.9. Рассмотрим сначала случай,
Когда у X есть только одна нульмерная клетка, а именно отмеченная
точка х0. Если дан гомоморфизм (/?: nl(Xix0) —> я^У,^), то мы начнём
построение отображения /: (X, х0) —> (У, у0), для которого /* = </>, положив
/О^сО — Уо- Замыканием любой клетки е\ комплекса X является
окружность, задающая элемент [е^] е тгДХ, х0), и мы определяем / на
замыкании клетки е1а как отображение, представляющее элемент ^([е^]). Если
i- X1 с-*Х обозначает включение, то i/>i* = /*, так как группа я^Х1,^)
Порождается элементами [е^].
тгДХ1,^) МУ.Уо)
7Ti(X,x0)
Чтобы продолжить / на клетку ei с отображением приклеивания
*Фр\ S1 —>Х], нам нужно лишь, чтобы композиция /г/'/з была гомотопна
Нулю. Если выбрать отмеченную точку 50 е S1 и путь в X1 из я/'/з(5о)
в х0, то \j)p определяет элемент [1/J/3] е я^Х1, х()), и гомотопность нулю
120
Глава 1. Фундаментальная группа и накрытия
отображения fipp эквивалентна тому, что /ДЬ/^]) равно нулю в п1 (У, у0).
Мы имеем кИ'Фр]) = 0, так как клетка el обеспечивает гомотопию в нуль
отображения^ в X. Следовательно,/+([,0/?]) = ^i+(['0^]) = O, а потому/
можно продолжить на el.
Продолжение / индуктивно на клетки е" где п > 2, возможно, так
как для отображений приклеивания ipy: Sn~l —>Xn_1 композиции f\pY:
Sn~l —> У гомотопны нулю. Дело в том, что fipy поднимается в
универсальное накрытие комплекса У при п > 2, а это накрытие стягиваемо но
предположению, поэтому поднятие отображения fxpy гомотопно нулю,
а значит, и само отображение f\py тоже.
Обратимся теперь к утверждению о единственности. Если два
отображения /0, /j: (X, х0) —> (У, у0) индуцируют один и тот же гомоморфизм
групп яь то мы сразу видим, что их ограничения на X1 гомотопны,
причём гомотопия сохраняет х0. Чтобы продолжить полученное
отображение X1 х / и X х д1 —> У на остальные клетки еп х (0,1) комплекса X х /,
мы можем поступить точно так же, как в предыдущем абзаце, поскольку
эти клетки имеют размерность п -Ь 1 > 2. Так мы получаем гомотопию
ft: (Х,х0) —> (У,у0)> что и завершает доказательство в случае, когда у X
есть только одна нульмерная клетка.
Случай, когда у X больше одной нульмерной клетки, можно
разобрать, слегка уточнив предыдущие рассуждения. Выберем максимальное
дерево ТсХ. Чтобы построить отображение /, реализующее данный
гомоморфизм if у сначала положим /(Т) = у0. Тогда каждое ребро е1а в X - Т
задаёт элемент [е^] е 7rI(X,x0), и мы определим / на замыкании
клетки е^ как отображение, представляющее элемент </>(|V]). Продолжение
отображения / на многомерные клетки тогда происходит так же, как
и раньше. В построении гомотопии fti соединяющей два данных
отображения /0 и /,, для которых /о, = fi*, тоже есть дополнительный шаг.
Пусть ht: X1 —>X1 —гомотопия, которая начинается с й0 = 1, причём её
ограничение является деформационной ретракцией дерева Т на х0.
(Легко продолжить такую деформационную ретракцию до гомотопии,
определённой на всём пространстве X1.) Мы можем построить гомотопию
отображения f0\X] в /jlX1, сначала продеформировав f0\Xl и fx\Xl так,
чтобы дерево Т отображалось в у0, взяв для этого композицию с htt а затем
применив предыдущие рассуждения, чтобы получить гомотопию между
модифицированными отображениями f0\Xl и fx\Xl. Построив гомотопию
/0|Х! ^fi\Xl, мы продолжаем её на весь комплекс X таким же способом,
как и раньше. О
Первая часть предыдущего доказательства проходит также для
двумерных комплексов XG, соответствующих представлениям групп. Таким
образом, любой гомоморфизм G —> Н реализуется как индуцированный
гомоморфизм для некоторого отображения Хс —> Хн. Однако для таких
§1.В. Пространства K(G, 1) и графы групп
121
отображений нет никакого утверждения единственности, и легко может
случиться, что разные представления группы G дают гомотопически не
эквивалентные комплексы XG.
Графы групп
В качестве иллюстрации того, как пространства K(G, 1) могут
оказаться полезными в теории групп, мы опишем процедуру соединения
вместе набора пространств K(G, 1) в пространство AT(G, 1) для большей
группы G. С точки зрения теории групп это даёт способ собрать меньшие
группы вместе и образовать из них большую группу, который обобщает
понятие свободных произведений.
Пусть Г —граф, который связен и ориентирован, т.е. его рёбра
рассматриваются как стрелки: у каждого ребра есть направление.
Предположим, что в каждой вершине v графа Г мы помещаем группу Gv,
а на каждом ребре е графа Г мы помещаем гомоморфизм ус из группы
3 начале ребра в группу в конце ребра. Назовём эти данные графом
групп. Теперь построим пространство ВГ, поместив пространство BGV
из примера 1.В.7 в каждой вершине v графа Г, а затем приставим
цилиндр отображения Ву>е к каждому ребру е графа Г, отождествив два
конца цилиндра отображения с двумя пространствами BGV на концах
ребра е. Полученное пространство ВГ тогда будет CW-комнлексом, так
как отображения Вуе переводят все п-мерные клетки гомеоморфно на
л-мерные клетки. В действительности клеточную структуру на ВГ можно
канонически подразделить так, что получится структура Д-комплекса;
для этого нужно применить призменную конструкцию из доказательства
теоремы 2.10, но нам сейчас это не нужно.
Вообще вместо BGV можно взять любой CW-комплекс /C(GV, 1) в
вершине v, а затем к рёбрам приставить цилиндры отображений,
реализующих гомоморфизмы [ре. Мы оставляем читателю проверку того, что
-Полученное в результате пространство КГ гомотопически эквивалентно
Пространству ВГУ построенному выше.
Пример 1.В.10. Предположим, что граф Г состоит из одной централь-
Ной вершины и нескольких рёбер, выходящих из неё, а группа Gv в этой
•Центральной вершине тривиальна, а потому и все рёберные
гомоморфизмы тоже. Тогда теорема ван Кампена показывает, что nl (КТ) — свободное
произведение групп, стоящих во всех внешних вершинах.
Имея в виду этот пример, назовём группу пх{КТ) для общего графа
^упп Г граф-произведением групп Gv, стоящих в вершинах,
относительно рёберных гомоморфизмов ipe. В литературе для я^КТ) обычно
используется довольно неуклюжее название «фундаментальная группа
графа групп».
Основной результат, который мы докажем о графах групп, состоит
в бедующем.
122
Глава 1. Фундаментальная группа и накрытия
I Теорема 1.В.11. Если все рёберные гомоморфизмы кре инъективны,
то КГ — пространство K{G, 1) и включения K(GVi 1) <->КГ индуцируют
инъективные отображения групп тг^
Прежде чем приступить к доказательству, давайте рассмотрим
некоторые интересные частные случаи.
Пример 1.В.12 (свободные произведения с амальгамацией).
Предположим, что граф групп имеет вид Л <— С-+Ву причём оба отображения —
мономорфизмы. Можно рассматривать эти данные как указание
вложений группы С в группы Л и В в качестве подгруппы. Применяя теорему
вен Кампена к представлению пространства КГ в виде объединения двух
цилиндров отображений, мы видим, что п1(КГ) — факторгруппа
группы Л* В, полученная при отождествлении подгруппы С с Л с подгруппой
С с В. Обычно эту группу обозначают Л *с В и называют свободным
произведением групп Л и В, амальгамированных но подгруппе С. По
теореме 1.В.11 группа А*СВ содержит обе группы Л и В в качестве подгрупп.
Например, свободное произведение с амальгамацией Z *z Z можно
реализовать цилиндрами отображений Sl <— S1 —♦S1, которые являются
m-листным и n-листным накрытиями соответственно. Мы изучили этот
случай в примерах 1.24 и 1.35, где было показано, что комплекс /СГ —
деформационный ретракт дополнения торического узла в S3, если тип
взаимно просты. Один из основных результатов в теории трёхмерных
многообразий заключается в том, что дополнение каждого гладкого узла в S3
можно построить, если повторить конструкцию графа групп с инъектив-
ными рёберными гомоморфизмами, начиная её со свободных групп.
Поэтому из теоремы 1.В.11 следует, что дополнение любого узла
—пространство K(G, 1). В действительности их универсальные накрытия всегда R3.
Пример 1.В.13 (HNN-расширения). Рассмотрим граф групп С =^ Л ,
где оба отображения ц> и я/) — мономорфизмы. Это похоже на
предыдущий случай А<г- с -^>В, но теперь две группы Л и В соединились в одну
группу. Группа п1(КГ)1 которая в предыдущем случае обозначалась А*СВ,
теперь обозначается Л*с. Чтобы понять, как выглядит эта группа,
давайте рассмотрим пространство КГ как полученное из К(Л, 1)
приклеиванием цилиндра К (С, 1) х / вдоль обоих концов К (С, 1) х а/ посредством
отображений, реализующих мономорфизмы у и гр. Используя комплекс
К (С, 1) с единственной нульмерной клеткой, мы видим, что КГ можно
получить из К (Л, 1) VS1, приклеивая клетки размерности два и выше,
поэтому пг(КГ) — факторгруппы группы Л*^, причём нетрудно понять,
что соотношения, задающие эту факторгруппу, имеют вид r^(c)r_1 =\j)(c),
где г —образующая множителя Z, ас пробегает всю группу С или набор
образующих группы С. Проверке этого посвящена одна из задач в конце
параграфа.
§1.В. Пространства K(G, 1) и графы групп
123
Весьма специальный случай, когда ц> = гр = 1, даёт Л*д = Л х Z, так
как в этом случае мы можем взять КГ = К(А, 1) х S1. Вообще, если </? = И,
а ^ — произвольный автоморфизм группы Л, то мы реализуем любое
полупрямое произведение групп А и Z как А*Л. Например, бутылка Клейна
получается таким способом, если у? реализовано тождественным
отображением окружности S1, a i/j реализовано симметрией. В тех случаях,
когда (/? = 1, мы можем реализовать ту же самую группу ttj (/СГ), используя
немного более простой граф групп с одной вершиной, помеченной А,
и одним ребром, помеченным ip.
А вот ещё один частный случай. Возьмём тор, вырежем малый
открытый диск, а затем отождествим полученную при этом граничную
окружность с параллелью тора. Это даёт пространство X, которое оказывается
гомеоморфным подпространству в стандартной картинке бутылки
Клейна в R3; см. задачу 12 в §1.2. Фундаментальная группа Я](Х) имеет вид
(Z*Z) *z Z с определяющим соотношением tb±lt~l —aba~xb~l, где а —
меридиональная петля, а Ъ — продольная петля (параллель) на торе. Знак
показателя степени в члене b±l несуществен, так как оба способа
приклеивания граничной окружности к параллели дают гомеоморфные
пространства. При абелианизации из группы п1 (X) = (a, b, 11 tbt"laba~lb~l)
получается группа Z x Z, но доказательство того, что группа п] (X) не
изоморфна Z*Z, требует некоторой работы. Есть сюръекция nl(X) —>Z*Z,
которая получается, если положить Ь = 1. Она имеет нетривиальное ядро,
так как элемент b нетривиален в ят(Х) согласно предыдущей теореме.
Если бы группа 7ГТ(Х) была изоморфна Z*Z, то мы получили бы сюръек-
тивный гомоморфизм Z * Z —> Z * Z, который не является изоморфизмом.
Однако в теории групп есть теорема, что свободная группа F является
хопфовой — любой сюръективный гомоморфизм F —>F должен быть инъ-
ективным. Следовательно, группа пл(Х) не свободна
Пример 1.В.14 (замкнутые поверхности). Замкнутую ориентируемую
поверхность М рода два или больше можно разрезать по окружности па
две компактные поверхности М2 и М2 так, что замкнутые поверхности,
полученные из М2 и М2, заклеиванием их граничной окружности диском,
имеют род меньше, чем М. Каждая из поверхностей М} и М2 — цилиндр
отображения из S1 в конечный граф. А именно, рассмотрим
поверхность М, как полученную из замкнутой поверхности вырезанием
открытого диска из внутренности двумерной клетки в стандартной CW-структуре,
описанной в главе 0, так, что М, становится цилиндром отображения
приклеивания двумерной клетки. Это отображение приклеивания не
гомотопно нулю, поэтому оно индуцирует инъективное отображение групп
Я], поскольку свободные группы не имеют кручения. Так мы реализовали
исходную поверхность М как пространство КГ, где Г —граф групп вида
Р\ <—Z—>F2 со свободными группами F} и F2 и двумя инъективными
отображениями. Теорема LB.11 тогда говорит, что М — пространство K(Gy 1).
124
Глава 1. Фундаментальная группа и накрытия
Такие же рассуждения годятся для замкнутых неориентируемых
поверхностей, кроме RP2. Например, бутылка Клейна получается из двух
листов Мёбиуса отождествлением их граничных окружностей, а лист
Мёбиуса — цилиндр отображения для двулистного накрытия S1 —> S1.
Доказательство теоремы 1.В.11. Мы будем строить накрывающее
пространство К-+КГ, склеивая экземпляры универсальных
накрывающих пространств для различных цилиндров отображений, из которых
состоит КТ, таким способом, что К окажется стягиваемым. Тогда К будет
универсальным накрытием над AT, которое поэтому должно быть
пространством К (G, 1).
Сначала сделаем предварительное наблюдение. Если дано
универсальное накрывающее пространство р: X —>Х и такое связное, локально
линейно связное подпространство Л С X, что включение А <—* X
индуцирует инъективное отображение групп тс], то каждая компонента Л
пространства р-1 (Л) —универсальное накрытие над Л. Чтобы убедиться в этом,
заметим, что р: Л —► Л — накрытие, а потому композиция инъективных
отображений пл (А) —► п^А) —► л} (X) пропускается через пх (X) — 0,
следовательно тгДАЭ^О. Например, если X — тор S1 x S1, а А —окружность
S1 х {х0}, то р~1(А) состоит из бесконечного набора параллельных
прямых в М2, каждая из которых —универсальное накрытие над А.
Для отображения /: А—►£ между связными CW-комплексами пусть
р: Mf —>М^ — универсальное накрытие цилиндра отображения Mf. Тогда
пространство Mf само является цилиндром отображения
f'.p-'W^p-'W,
так как отрезки в структуре цилиндра отображения на Mf поднимаются до
отрезков в My, определяющих структуру цилиндра отображения. Так как
Mj — цилиндр отображения, он деформационно ретрагируется на р 1(В),
поэтому пространство р~\В) тоже односвязно, а значит, являются
универсальным накрытием над В. Если / индуцирует инъективное
отображение групп 7ГЬ то можно применить рассуждение из предыдущего
абзаца, поэтому компоненты пространства р~] (А) —универсальные накрытия
над А. Если мы дополнительно предположим, что А и В — пространства
K(Gy 1), то Mf и компоненты пространства р~л(А) стягиваемы, и мы
можем утверждать, что Mf деформационно ретрагируется на каждую
компоненту А пространства р~1(А). Действительно, включение A^-+Mf
является гомотопической эквивалентностью, так как оба пространства
стягиваемы. Тогда следствие 0.20 влечёт, что Mf деформационно ретрагируется
на А, так как пара (М^, А) обладает свойством продолжении гомотопии,
как показано в примере 0.15.
Теперь мы можем описать построение накрывающего пространства
К для КГ. Оно представляет собой объединение возрастающей последо-
§ 1.В. Пространства K(G, 1) и графы групп
125
вательности пространств Кх сК2 с ... На первом шаге пусть
^—универсальное накрытие одного из цилиндров отображения My, из которых
состоит КГ. Согласно предыдущим замечаниям оно содержит
различные непересекающиеся экземпляры универсальных накрытий двух^про-
странств K(GV, 1) на основаниях цилиндра Mf. Затем мы строим К2 из
Кг приклеивая к каждому из этих универсальных накрытий
пространства K(GVi 1) экземпляр универсального накрытия каждого из
цилиндров отображения Mg, из которых состоит КТ, пересекающего My в его
основании. Теперь повторим процесс, чтобы построить К3, приклеивая
универсальные накрытия цилиндров отображения во всех универсальных
накрытиях пространств K(GV, 1), построенных на предыдущем шаге.
Точно так же мы строим Кп+1 по Кп для всех п, а затем полагаем K = {jKu.
п
Заметим, что пространство Кп+1 деформационно ретрагируется на Кп,
так как оно получается приклеиванием к Кп кусков, деформационно ре-
трагирующихся на подпространства, вдоль которых они приклеены,
согласно предыдущим замечаниям. Из этого следует, что пространство К
стягиваемо, так как мы можем деформационно ретрагировать /Сп+1 на Кп
в течение времени из интервала [1/2пИ, 1/2"], а затем стянуть
пространство К1 в точку в течение времени из интервала [1/2,1].
Естественная проекция К—*КГ, очевидно, является накрытием, что
и завершает доказательство того, что КГ является пространством K{G, 1).
Оставшееся утверждение, что каждое включение K(GV, 1) с-> КГ
индуцирует инъективное отображение групп пъ легко выводится из
предыдущих построений. Действительно, предположим, что петля у: S] —> K(GVi l)
гомотопна нулю в КГ. Согласно критерию поднятия для накрывающих
пространств существует поднятие у: S1 —> К. Его образ содержится в одном
ТО экземпляров универсального накрытия над K(GV, 1), поэтому петля у
гомотопна нулю в этом универсальном накрытии, а значит, петля у
гомотопна нулю в K(GV, 1). □
Разные цилиндры отображений, которые составляют универсальное
накрытие над КТ, упорядочены по образцу дерева. Это дерево (назовём
его ТГ) имеет по одной вершине для каждого экземпляра
универсального накрытия пространства K{GVi 1) в К, причём две вершины соединены
Ребром, если два универсальных накрытия над K(GV, 1), соответствующие
этим вершинам, соединены отрезком, поднимающим отрезок в структуре
Цилиндра отображения для одного из цилиндров отображения, из которых
состоит КГ. Индуктивное построение пространства К отражено в
индуктивном построении пространства ТГ как объединения возрастающей
последовательности поддеревьев Тт с Т2 с ... Пространству Кх соответствует
Поддерево Тх сТГ, состоящее из центральной вершины с набором рёбер,
^Ходящих из неё — «звёздочка», у которой может быть бесконечно много
Ребер. Когда мы увеличиваем Кх до К2, 7\ соответственно увеличивается
126
Глава 1. Фундаментальная группа и накрытия
до дерева Т2 посредством приклеивания такого вида звёздочек в каждой
внешней вершине графа Ть и каждое последующее увеличение устроено
таким же образом. Действие группы тг1(К'Г) на К преобразованиями
накрытия индуцирует действие на дереве ТГ, при котором переставляются
его вершины и рёбра, причём пространство орбит дерева ТГ при этом
действии —это просто исходный граф Г. Действие на ТГ, вообще говоря,
не будет свободным действием, так как элементы подгруппы Gv с пх(КГ)
оставляют неподвижной вершину графа 7Т, соответствующую одному из
универсальных накрытий над K(GV, 1).
В действительности есть точное соответствие между графами групп
и группами, действующими на деревья. Эта довольно красивая теория
описана в [124]. С точки зрения групп, действующих на деревьях, обычно
используется более ограничительное определение графа групп, чем то,
которое использовали мы. А именно, рассматриваются только
ориентируемые графы, которые получаются из неориентируемого графа
подразделением каждого ребра посредством добавления вершины в середине
ребра, а затем два полученных при этом ребра ориентируются наружу,
в направлении от новой вершины.
Задачи
1. Предположим, что группа G действует симплициально на Д-ком-
плексе X, где «симплициально» означает, что каждый элемент группы G
отображает каждый симплекс комплекса X на другой симплекс линейным
гомеоморфизмом. Докажите, что если это действие свободно, то оно
является действием накрытия.
2. Пусть X — связный CW-комплекс, а группа G такова, что любой
гомоморфизм nl(X) -* G тривиален. Докажите, что любое отображение
X-*K(G, 1) гомотопно нулю.
3. Докажите, что любое граф-произведение тривиальных групп
свободно.
4. Применяя теорему ваи Кампена, вычислите Л*с как факторгруппу
группы А*Z, как предлагается в тексте.
5. Рассмотрим граф групп Г с одной вершиной, помеченной Z, и
одним ребром, помеченным отображением Z -* Z, которое является
умножением на 2, реализованным двулистным накрытием 51 -*Sl.
Докажите, что группа 7г1(КТ) имеет представление (a,b\bab~xa~2), и
опишите явно универсальное накрытие над КГ как произведение 7' х Ж, где
Т —дерево. [Группа тг^/СГ) является первой в семействе групп,
называемых группами Баумслага—-Солитера, которые имеют представления вида
(a,b\bamb~]a~n). Они являются HNN-расширениями группы Z*7.|
6. Докажите, что для графа групп, у которого все рёберные
гомоморфизмы — инъективные отображения Z-» Z, можно выбрать КГ так, чтобы
§1.В. Пространства K(G, 1) и графы групп
127
его универсальное накрытие было произведением Т х R, где Т — дерево.
Разберите подробно случай, когда граф групп — бесконечная
последовательность Z —>Ъ —>Z —>Z —>..., где отображение Z—»Z — умножение на п.
Докажите, что в этом случае группа л1(КГ) изоморфна Q. Как нужно
изменить этот пример, чтобы получить группу п^КГ), изоморфную
подгруппе в Q, состоящую из рациональных чисел со всевозможными
знаменателями вида 2к?
7. Докажите, что любое граф-произведение групп можно реализовать
графом, вершины которого разбиты на два подмножества так, что каждое
ориентированное ребро направлено из вершины в первом подмножестве
к вершине во втором подмножестве.
8. Докажите, что конечное граф-произведение конечно
порождённых групп конечно порождено, и аналогично для конечно представимых
групп.
9. Докажите, что конечное граф-произведение конечных групп (если
все рёберные гомоморфизмы инъективны) имеет свободную подгруппу
конечного индекса, построив конечнолистное накрытие пространства КГ
из универсальных накрытий цилиндров отображения, из которых
состоит КГ. [Обратное утверждение тоже верно для конечно порождённых
групп; см. [124].]
Глава 2
Гомологии
Фундаментальная группа яг(Х) наиболее полезна для изучения
пространств малой размерности, как можно ожидать из её определения,
которое использует только отображения пространств малой размерности в X
(а именно, петли / —> X и гомотопии петель, т. е. отображения / х / —> X).
Определение в терминах объектов, которые имеют размерность не
выше двух, проявляется, например, в том, что если X — CW-комплекс, то
группа пх{Х) зависит только от двумерного остова комплекса X.
Ввиду маломерной природы фундаментальной группы не следует ожидать,
что она будет очень точным инструментом для работы с многомерными
пространствами. В частности, она не может различить сферы Sn, n ^ 2.
Это ограничение малыми размерностями можно устранить,
рассматривая естественные многомерные аналоги группы я ,(Х) —гомотопические
группы 7г„ (X), которые определяются в терминах отображений п-мерного
куба /" в X и гомотопии Г х / —> X таких отображений. Неудивительно,
что если X — CW-комплекс, то яп(Х) зависит только от (п + 1)-мерного
остова комплекса X. И, как следовало ожидать, гомотопические группы
действительно различают сферы всех размерностей, так как группа tt,-(S")
равна 0 для i < п и Z для f = п.
Однако многомерные гомотопические группы имеют серьёзный
недостаток: их чрезвычайно трудно вычислять в общем случае. Даже для
такого простого пространства, как сферы, вычисление групп п((БП) для i>n
оказывается очень тяжёлой задачей. К счастью, есть более вычислимая
альтернатива гомотопическим группам: группы гомологии НП(Х). Как
и группа яп(Х), группа гомологии ЯП(Х) для CW-комплекса Х зависит
только от его (п + 1)-мерного остова. Для сфер группы гомологии //,-(5")
изоморфны гомотопическим группам rc,(Sn) при 1 ^i^n, но группы
гомологии имеют то преимущество, что H,-(S/l) = 0 при i > п.
К сожалению, вычислимость групп гомологии не достаётся бесплатно.
Определение групп гомологии гораздо менее прозрачно, чем определение
гомотопических групп, и, как только нужно выйти за пределы
определения, сразу требуется большое количество технических средств, с
которыми нужно освоиться перед любыми реальными вычислениями и приложе-
Глава 2. Гомологии
129
ниями. В нашем изложении мы подходим к определению группы Нп(Х)
в два предварительных этапа: сначала нестрого приводится несколько
мотивирующих примеров, а затем строится ограниченная модель теории
гомологии, называемая симплициальными гомологиями. И лишь после
этого мы погружаемся в общую теорию, известную под названием
сингулярных гомологии. После того как определение сингулярных гомологии
будет усвоено, начинается настоящая работа по выяснению их основных
свойств. Это занимает около 20 страниц, и в это время ещё не будет
понятно, почему эта тема заслуживает таких усилий. В этом заключается
основная часть первого параграфа главы, в котором помимо этого есть
только небольшие отступления, связанные с приложениями к двум
классическим теоремам Брауэра: теореме о неподвижной точке и теореме об
«инвариантности размерности».
Во втором параграфе главы будет уже больше приложений, в том
числе гомологическое определение эйлеровой характеристики и понятие
степени для отображений Sn —>S", введённое Брауэром. Однако в основном
этот параграф направлен на разработку методов эффективного
вычисления групп гомологии. Наиболее эффективный метод известен под
названием клеточных гомологии. Сила его, вероятно, в том, что он является
«гомологией, возведённой в квадрат» — гомологии определяются в
терминах гомологии. Другой весьма полезный инструмент
—последовательности Майера—Вьеториса, аналог для гомологии теоремы ван Кампена для
фундаментальной группы.
Интересная особенность гомологии, которая начинает выявляться
после того, как с ними поработаешь некоторое время, состоит в том, что
чаще всего используются именно основные свойства гомологии, а не само
их определение. Это позволяет предположить, что к гомологиям возможен
аксиоматический подход. Это действительно так, и в третьем параграфе
этой главы мы перечисляем аксиомы, которые полностью характеризуют
группы гомологии для CW-комплексов. Можно принять такую точку
зрения, что эти весьма алгебраические аксиомы представляют собой всё то,
что действительно важно знать о группах гомологии, а геометрия,
участвующая в определении гомологии, вторична — она нужна только для того,
чтобы показать, что аксиоматическая теория не пустая. В какой степени
каждый принимает эту точку зрения — вопрос вкуса, и наше изложение,
при котором аксиомы откладываются до тех пор, пока теория не будет
хорошо усвоена, — это лишь один из нескольких возможных подходов.
Глава завершается тремя необязательными параграфами дополнения.
Первый из них, довольно короткий, устанавливает связь между Н^Х)
и я1№, а в двух других содержатся избранные классические приложения
гомологии. Они включают п-мерную версию теоремы Жордана о кривой
и теорему об «инвариантности области» (обе они доказаны Брауэром),
а также теорему Лефшеца о неподвижной точке.
Зак 3655
130
Глава 2. Гомологии
Идея гомологии
Трудность с высшими гомотопическими группами пп заключается
в том, что их нельзя непосредственно вычислять по клеточной структуре
как группу п1. Например, у двумерной сферы нет никаких клеток в
размерностях выше 2, но её n-мерная гомотопическая группа nn(S2) отлична
от нуля для бесконечно многих значений п. Группы гомологии, в отличие
от этого, весьма непосредственно связаны с клеточной структурой, и в
действительности их можно рассматривать просто как алгебраизацию
геометрии первого уровня в клеточной структуре: как клетки
размерности п приклеиваются к клеткам размерности п — 1.
Давайте посмотрим на некоторые примеры, чтобы понять, в чём здесь
идея. Рассмотрим граф Хъ изображённый на рисунке, состоящий из двух
вершин, соединённых четырьмя рёбрами. При изу- у
чении фундаментальной группы графа Х} мы
рассматриваем петли, образованные
последовательностями рёбер, которые начинаются и
заканчиваются в фиксированной отмеченной точке. Например,
если отмечена точка х, петля ab~l проходит
вперёд по ребру а, а затем назад по Ь, что обозначено
показателем степени — 1. Примером более сложной
петли служит ac~lbd~lca~l. Характерной особенностью фундаментальной
группы является то, что она, вообще говоря, неабелева, что и обогащает,
и усложняет теорию. Предположим, что мы упрощаем ситуацию, переходя
к абелианизации. Тогда, например, две петли аЪ~] и b~la нужно считать
равными, если мы заставляем а коммутировать с Ь"1. Эти две петли ab~]
и b~la в действительности являются одной и той же окружностью, но на
ней по-разному выбрана точка, в которой начинается и заканчивается
петля: х для ab~l и у для Ь-1 а. То же самое происходит для всех петель.
Выбор другой отмеченной точки для петли просто переставляет её буквы
циклически, поэтому побочным продуктом абелианизации является то,
что мы больше не должны прикреплять все петли к фиксированной
отмеченной точке. Так петли становятся циклами, на которых отмеченная
точка не выбирается.
Произведя абелианизацию, давайте перейдём к аддитивной системе
обозначений, так чтобы циклы стали линейными комбинациями рёбер
с целочисленными коэффициентами, например, а — Ъ + c — d. Будем
называть эти линейные комбинации цеттми рёбер. Некоторые цепи
можно разложить в циклы несколькими различными способами, например
(а - с) + (Ь - d) = (а - d) -f (b — с), и если мы принимаем алгебраическую
точку зрения, то мы не хотим различать эти разные разложения.
Поэтому мы расширим значение термина «цикл», чтобы он просто означал
любую линейную комбинацию рёбер, для которой существует по край-
Глава 2. Гомологии
131
ggH мере одно разложение в циклы в предыдущем более геометрическом
сцысле.
Каково условие на цепь, чтобы она была циклом в этом более
алгебраическом смысле? Геометрический цикл, который мы представляем себе
vjtK траекторию движения, характеризуется тем свойством, что он входит
В каждую вершину столько же раз, сколько выходит из этой вершины. Для
произвольной цепи ка + 1Ъ + тс + nd полное число раз, когда эта цепь
входит в у, равно к +1 + т + п, так как каждое из рёбер а, Ь, с и d входит
ъу один раз. Аналогично каждое из этих четырёх рёбер выходит из х один
ваз, поэтому полное число раз, когда цепь ка + 1Ъ + тс + nd входит в х,
равно -k — i-m — n. Поэтому условие, что цепь ка Л-lb Л-тс Л- nd является
циклом, состоит просто в том, что /с + £ + т + п = 0.
Опишем этот результат так, чтобы его можно было обобщить на все
графы. Для этого рассмотрим свободную абелеву группу Сь базисом ко-
здрой служат рёбра а, Ь, с, d, и свободную абелеву группу С0, базисом ко-
фрой служат вершины х, у. Элементы группы Cj —это цепи из рёбер, т. е.
Одномерные цени, а элементы группы С0-—линейные комбинации вер-
щдан, т.е. нульмерные цепи. Определим гомоморфизм д: CY —>С0, отобра-
ЯИВ каждый элемент базиса а, Ь, с, d в у - х, вершина в конце ребра минус
Вершина в начале. Таким образом, мы имеем
d{ka + tb + mc + nd) = (/с +1 + т + п)у- (Лс + £ + т + п)дг,
В циклы — это в точности ядро гомоморфизма д. Простые вычисления
показывают, что a -b, b - с и с- d образуют базис этого ядра. Поэтому
Наждый цикл в графе Хх единственным образом представляется в виде ли-
Щейной комбинации этих трёх наиболее очевидных циклов. Посредством
язгих трёх основных циклов мы выражаем геометрическую информацию,
Шо у графа Хг есть три видимых «дырки» — пустых пространства между
|етырьмя рёбрами.
Давайте теперь увеличим предыдущий граф Xlt
Приклеив двумерную клетку Л по циклу а - Ъ и
получив при этом двумерный клеточный комплекс Х2.
Если мы считаем, что двумерная клетка Л
ориентирована по часовой стрелке, то мы можем
рассматривать её границу как цикл а — Ъ. Этот цикл теперь
Яомотопически тривиален, так как мы можем стя-
Иутъ его в точку, скользя по Л. Другими словами, он больше не охватывает
ЯЫрку в х2. Это наводит на мысль профакторизовать группу циклов из
предыдущего примера по подгруппе, порождённой циклом а - Ъ. В этой
факторгруппе циклы а — с\\Ъ — с, например, эквивалентны, что согласу-
**Ся с тем фактом, что они гомотопны в Х2.
С алгебраической точки зрения мы можем теперь определить два
"Моморфизма С2 -*Ci^* C0, где С2 — бесконечная циклическая группа,
132
Глава 2. Гомологии
порождённая клеткой А, а д2(А) = а — Ъ. Отображение дх —граничный
гомоморфизм в предыдущем примере. Факторгруппа, которая нас
интересует, — это Кег д1/ Im д2, т. е. одномерные циклы по модулю тех, которые
являются границами, т. е. по модулю кратных элемента а — Ъ. Эта
факторгруппа—группа гомологии Н1(Х2). Предыдущий пример тоже
вписывается в эту схему, если взять группу С2 нулевой, так как в Х7 нет никаких
двумерных клеток; поэтому в этом случае Н}(Х}) = Kerdj/Im*^ = Kerdb
что, как мы видели, является свободной абелевой группой с тремя
образующими. В новом примере группа Н^Х-^ свободная абелева с двумя
образующими Ь — сис — d; это выражает геометрический факт, что, заклеив
одну «дырку» двумерной клеткой А, мы уменьшили число дырок в нашем
пространстве с трёх до двух.
Предположим, что мы увеличиваем Х2 до пространства Х3,
приклеивая вторую двумерную клетку В по тому же самому циклу а — Ъ.
Это даёт двумерную группу цепей С2, состоящую из линейных
комбинаций клеток Л и В, а граничный гомоморфизм д2: С2—>СХ отображает
как А, так и В в а - Ъ. Группа гомологии Н1(Х3) =
= КегЭ1/1гп(92 та же самая, что и у Х2, но теперь д2
имеет нетривиальное ядро — бесконечную
циклическую группу, порождённую элементом А — В. Мы
рассматриваем А — В как двумерный цикл,
порождающий группу гомологии Н2(Х3) =Kerd2 ^ Z.
Топологически цикл А — В является сферой,
образованной клетками Л и В вместе с их общей граничной
окружностью. Этот сферический цикл обнаруживает присутствие «дырки»
в Х3 — недостающей внутренней части сферы. Однако, так как эта дырка
охватывается сферой, а не окружностью, она другого рода, нежели дырки,
обнаруживаемые группой Н{(Х3) *vZ x Z, т.е. обнаруживаемые циклами
Ъ-с и c — d.
Сделаем ещё один шаг и построим по Х3 комплекс Х4, приклеив
трёхмерную клетку С по двумерной сфере, образованной клетками Л и В. Это
даёт группу цепей С3, порождённую этой трёхмерной клеткой С, и мы
определим граничный гомоморфизм д3: С3 —► С2, отобразив С в А — В,
так как цикл А — В следует рассматривать как границу клетки С
аналогично тому, что одномерный цикл а - Ь —это граница клетки А.
Теперь у нас есть последовательность из трёх граничных гомоморфизмов
'^3 ^2 f^J
С3 —* С2 —* С?! —* С0, и факторгруппа Я2(Х4) = Kerd2/Imd3 становится
тривиальной. Кроме того, Н3(Х4) = Кегд3 = 0. Группа Н} (Х4) та же самая, что
и Н1(Х3)У а именно Z x Z, таким образом, это единственная
нетривиальная группа гомологии комплекса Х4.
Ясна общая схема этих примеров. Для клеточного комплекса X для
каждого п рассматривается группа цепей СП(Х) — свободная абелева
группа, базисом которой служат n-мерные клетки комплекса Х\ имеются так-
§ 2.1. Симплициальные и сингулярные гомологии
133
же граничные гомоморфизмы дп: С„(Х) —> С^.ДХ), с помощью которых
определяются группы гомологии Hn(X) = Kerd„/Imd,I+1. Основная
трудность состоит в том, как определить дп в общем случае. Для п — 1 это
легко: граница ориентируемого ребра —это вершина в его конце минус
вершина в его начале. Следующий случай п = 2 тоже несложен, по
крайней мере для клеток, приклеенных по циклам, которые являются просто
петлями из рёбер, ибо тогда граница клетки — как раз этот цикл из рёбер
с соответствующими знаками, учитывающими ориентацию. Но для п > 2
ситуация становится более сложной. Даже если ограничиться
клеточными комплексами, образованными полиэдральными клетками с хорошими
отображениями приклеивания, нужно ещё разобраться с ориентацией.
Наилучшее решение этой задачи даёт, видимо, применение
косвенного подхода. Произвольные многогранники всегда можно подразделить
на специальные многогранники, называемые симплексами (треугольник
и тетраэдр — двумерный и трёхмерный симплексы). Поэтому,
ограничиваясь симплексами, мы не потеряем в общности, хотя поначалу будет
некоторая потеря в эффективности. Для симплексов не возникает трудности
при определении граничных отображений или при работе с ориентацией.
Таким образом, мы получаем теорию гомологии, называемую симпли-
циальными гомологиями, для клеточных комплексов, состоящих из
симплексов. Однако это весьма ограниченный класс пространств, да и сама
теория обладает определённой жёсткостью, которая делает её неудобной
для работы.
Способ обойти эти препятствия состоит в том, чтобы оставить в
стороне геометрию пространств, разбитых на симплексы, и рассмотреть
вместо этого нечто на первый взгляд представляющееся гораздо более
сложным, а именно набор всех непрерывных отображений симплексов в
данное пространство X. Эти отображения порождают чрезвычайно большие
группы цепей СП(Х), но факторгруппы НП(Х) = Кегд„/1тдп.и,
называемые сингулярными группами гомологии, как оказывается, намного
меньше, по крайней мере для достаточно хороших пространств X. В частности,
для пространств такого рода, как в четырёх рассмотренных выше
примерах, сингулярные группы гомологии совпадают с группами гомологии,
которые мы вычисляли по клеточным цепям. И как мы позже увидим в этой
главе, сингулярные гомологии позволяют определить эти замечательные
группы клеточных гомологии для всех клеточных комплексов и, в
частности, решить задачу определения граничного отображения для клеточных
Цепей.
§ 2.1. Симплициальные и сингулярные гомологии
Самую важную теорию гомологии в алгебраической топологии
называют сингулярными гомологиями; мы будем заниматься почти только
ими. Так как технический аппарат сингулярных гомологии довольно ело-
134
Глава 2. Гомологии
жен, мы сначала представим более примитивную их версию, называемую
симплициальными гомологиями, чтобы показать, как часть технического
аппарата работает в этой более простой ситуации, прежде чем приступить
к общей теории.
Естественная область определения для симплициальных гомологии —
класс пространств, которые мы называем Д-комплексами; они являются
небольшим обобщением более классического понятия симплициального
комплекса. Современное определение сингулярных гомологии было
впервые дано Эйленбергом [98], а Д-комплексы были введены вскоре после
этого в [22], где их называли полусимплициальными комплексами. В
течение нескольких лет так называли то, что сами Эйленберг и Зильбер
называли полными полусимплициальными комплексами, и потом было ещё
одно изменение в терминологии, так как последние объекты стали
называть симплициальными множествами. Теоретически это позволяет
использовать термин «полусимплициальный комплекс» в его
первоначальном значении, но во избежание возможной путаницы лучше ввести новое
название, а название «Д-комплекс» имеет, по крайней мере, достоинство
краткости.
Д-комплексы
Тор, проективную плоскость и бутылку Клейна можно получить из
квадрата, отождествляя противоположные стороны способом,
показанным стрелками на следующих рисунках:
Г:
V
а <
Ь
и /
Ус
/ L
w
а'
Ь
U /
Ус
/ L
К:
Разрезание квадрата по диагонали даёт два треугольника, поэтому
каждую из этих поверхностей можно также построить из двух
треугольников, отождествляя пары их рёбер.
Таким же способом многоугольник с любым числом сторон можно
разрезать по диагоналям на треугольники, поэтому в действительности
все замкнутые поверхности можно построить из
треугольников, отождествляя их стороны. Поэтому у нас
есть единый стандартный блок —треугольник, из
которого можно построить все поверхности.
Используя только треугольники, мы можем также построить
большой класс двумерных пространств, которые не
являются поверхностями в строгом смысле, позволив
отождествлять одновременно более двух сторон.
§ 2.1. Симплициальные и сингулярные гомологии 135
v0 v0 vT v3
Идея Д-комплекса состоит в том, чтобы обобщить такие
конструкции для любых размерностей. Для треугольника п-мерный аналог —это
n-мерный симплекс. Он представляет собой наименьшее выпуклое
множество в евклидовом пространстве Жт, содержащее п + 1 точек v0,..., vn,
которые не лежат в гиперплоскости размерности меньше п, где под
гиперплоскостью мы подразумеваем множество решений системы линейных
уравнений. Эквивалентное условие состоит в том, что векторы разностей
Vi — v0, ..., vn - v0 линейно независимы. Точки v, —это вершины симплекса,
а сам симплекс обозначают [v0,..., vn]. Например, есть
стандартный n-мерный симплекс
Дп = { (t0, ..., tj G RM+1 \Yti = 1 и t,Z 0 для всех i},
i
вершины которого — единичные векторы, направленные
по координатным осям.
Для целей гомологии будет важно следить за порядком вершин
симплекса, поэтому «n-мерный симплекс» будет в действительности означать
«n-мерный симплекс с указанным порядком его вершин». Побочным
продуктом указания порядка вершин симплекса [v0, ...,vn] является то, что
оно определяет ориентации рёбер [v,, v;] согласно возрастанию индексов,
как показано на двух предыдущих рисунках. Задание порядка вершин
также определяет канонический линейный гомеоморфизм стандартного
n-мерного симплекса Дп на любой другой n-мерный симплекс [v0,..., vn],
сохраняющий порядок вершин, а именно
(t0,...,tj^^tfvr,
i
Коэффициенты t,- — барицентрические координаты точки J] t,-v, в
симплексе [v0, ...,vn].
Если мы удалим одну из п -I-1 вершин n-мерного симплекса [v0, ..., v„],
то оставшиеся п вершин порождают (п - 1)-мерный симплекс,
называемый гранью симплекса [v0,..., vn]. Мы принимаем следующее соглашение.
Вершины грани или любого подсимплекса, порождённого некоторым
подмножеством вершин, всегда будут упорядочиваться согласно их
порядку в большем симплексе.
§>■■
136
Глава 2. Гомологии
Объединение всех граней симплекса Дп — это граница симплекса Дп,
обозначаемая дДп. Открытый симплексАп —это Ап — дДп, т.е.
внутренность симплекса Д" \
Структура А-комплекса на пространстве X — это такой набор
отображений аа: Дл —> X, где л зависит от индекса а, что выполняются
следующие условия.
1. Ограничение аа |Д" инъективно, причём каждая точка
пространства X содержится в образе ровно одного такого ограничения аа \Ап.
2. Каждое ограничение отображения аа на грань симплекса Дп—это
одно из отображений а^: Д""1 -*Х. Здесь мы отождествляем грань
симплекса Дп с Д""1 посредством канонического линейного
гомеоморфизма между ними, который сохраняет порядок вершин.
3. Множество Аа X открыто тогда и только тогда, когда множество
сг"1 (Л) открыто в Дп для всех аа.
Помимо прочего последнее условие исключает тривиальную
возможность считать все точки пространства X отдельными вершинами.
Рассмотренные ранее разбиения тора, проективной плоскости и бутылки
Клейна на два треугольника, три ребра и одну или две вершины задают
структуры Д-комплекса в общей сложности с шестью отображениями
аа для тора и для бутылки Клейна и семью для проективной плоскости.
Ориентации рёбер на рисунках совместимы с единственным порядком
вершин каждого симплекса, и эти порядки определяют отображения аа.
Из условия 3 следует, что X можно построить как факторпростран-
ство набора непересекающихся симплексов Д£, по одному для каждого
отображения аа: Дп —► X. Это факторпространство получается при
отождествлении каждой грани симплекса Апа с симплексом ДГ1,
соответствующим ограничению ар отображения аа на рассматриваемую грань, как
в условии 2. Можно представлять себе построение факторпространства по
индукции, начиная с дискретного множества вершин, к которым потом
приклеиваются рёбра, чтобы получился граф, затем к графу
приклеиваются двумерные грани и т.д. С этой точки зрения мы видим, что данные,
определяющие Д-комплекс, можно описать чисто комбинаторно как
наборы п-мерных симплексов Д£ для каждого п вместе с отображениями,
сопоставляющими каждой грани каждого п-мерного симплекса Апа
некоторый (п - 1)-мерный симплекс До"*1.
Вообще Д-комплекс можно построить по набору непересекающихся
симплексов, отождествляя различные подсимплексы, порождённые
подмножествами вершин, причём отождествления осуществляются с
помощью канонических линейных гомеоморфизмов, которые сохраняют
порядок вершин. Рассмотренные ранее структуры Д-комплексов на торе,
1 При этом для п = 0 принимается соглашение, что внутренность О-симнлекса (точки)
совпадает с ним самим. —Прим. ред.
§ 2.1. Симплициальные и сингулярные гомологии
137
проективной плоскости и бутылке Клейна можно получить таким
способом, отождествляя пары рёбер двух двумерных симплексов. Если
начать с одного двумерного симплекса и отождествить все три ребра в
одно ребро, сохраняя ориентации, заданные порядком вершин, то это даст
Д-комплекс, известный под названием «шутовской колпак». В отличие от
этого, если три грани двумерного
симплекса отождествлены с сохранением
циклической ориентации этих трёх рёбер,
как на первом рисунке, то не даст
структуры Д-комплекса, хотя если этот
двумерный симплекс разбит на три меньших двумерных симплекса вокруг
центральной вершины, то тогда действительно получается структура
Д-комплекса на факторпространстве.
Представляя себе Д-комплекс X как факторнространство набора
непересекающихся симплексов, нетрудно увидеть, что пространство X
должно быть хаусдорфовым. Из условия 3 тогда следует, что каждое
ограничение сга|Д" является гомеоморфизмом на свой образ, который является
поэтому открытым симплексом в X. Предложение П.2 из приложения влечёт,
что эти открытые симплексы сга(дп) — клетки епа структуры CW-комплекса
на X с характеристическими отображениями аа. Нам этот факт сейчас,
однако, не нужен.
Симплициальные гомологии
Теперь наша цель состоит в том, чтобы определить группы симпли-
циальных гомологии Д-комплекса X. Пусть ДП(Х) —свободная абелева
группа, базисом которой служат открытые п-мерные симплексы епа
комплекса X. Элементы группы ДЛ(Х), называемые n-мерными цепями, могут
быть записаны в виде конечных формальных сумм 2паеа с коэффици-
а
ентами па eZ. Эквивалентным образом мы могли написать ^пааа, где
а
сга: д" —*Х — характеристическое отображение клетки е£, образ
которого—замыкание клетки е£, как описано выше. Такую сумму ^пааа можно
а
представлять себе как конечный набор, или «цепь», п-мерных симплексов
в X с целочисленными коэффициентами па.
Как можно увидеть на следующем рисунке, граница п-мерного
симплекса [v0,..., vn] состоит из различных (п — 1)-мерных симплексов [v0, ...
-..,v-,..., vn], где символ ~ над v,- указывает, что эта вершина удалена из
последовательности v0,..., v„. В терминах цепей тогда возникает желание
сказать, что граница симплекса [v0,..., v,J — это (п - 1)-мерная цепь,
образованная суммой граней [v0,..., vj,..., v„]. Оказывается, однако, что лучше
вставить определённые знаки и вместо этого считать границей симплекса
Kb ••., vn] цепь J](—l)'[v0,..., v-, ..., vn]. Подходя к этому эвристически, мы
АА
138 Глава 2. Гомологии
расставляем знаки с учётом ориентации, чтобы все грани симплекса были
ориентированы согласованно, как показано на следующем рисунке.
V(J Z » tVl 3[v0jv1] = [v1]-[v0]i
d[v0, vlf v2] = [vj, v2] - [v0, v2] + [v0, v, ],
v2 d[v0, v,, v2, v3] = [vj, v2, v3] - [v0, v2, v3] +
+ [v()3v1)v3]-[v0,v1)v2].
В последнем случае две грани на заднем плане тоже ориентированы
против часовой стрелки, если смотреть на них снаружи трёхмерного
симплекса.
Используя эти геометрические соображения, определим для
произвольного Л-комплекса X граничный гомоморфизм дп: Ап{Х) —> Ап_1(Х))
задав его значения на элементах базиса:
d„(ae) = 2(-l)l'aa|[v0,...,^...,vn].
Заметим, что правая часть этого равенства действительно лежит в A„_2 (X),
так как каждое ограничение аа\ [v0,..., vh ..., vn] является
характеристическим отображением (п — 1)-мерного симплекса комплекса X.
Лемма 2.1. Композиция ДП(Х) —* ДП-1(Х) —» ДЛ_2(Х) — нулевое
отображение.
Доказательство. Имеет место равенство
drt(^) = 2(-l)l"a|[v0>...,^...>vn]>
i
а потому
d„-A(a) = 2(-1)Ч-1Уа| [v0>.... v,.,...,% ..., vj +
+ S(-1),(-1)J"lal [v0' — ^ — 9i> •- v»]'
Последние две суммы взаимно сокращаются, так как после
перестановки i и j во второй сумме она становится первой суммой со знаком
минус. С
§ 2.1. Симплициальные и сингулярные гомологии
139
Теперь мы находимся в следующей алгебраической ситуации: имеется
последовательность гомоморфизмов абелевых групп
... —> Сл+1 > Сп —> Сп_! —> ... —> Cj —> С0 —> О,
причём дпдл+1 = 0 для всех п. Такую последовательность называют цепным
комплексом. Обратите внимание, что мы дополнили последовательность
нулём справа и отображением д0 = 0. Из равенства дпдп+г =0 следует, что
Imdn+1 с Кег д„, где Im и Кег обозначают образ и ядро. Поэтому мы можем
определить n-ю группу гомологии цепного комплекса как факторгруппу
Hn = Kerdn/Imdn4.1. Элементы ядра Кетдп называют циклами, а элементы
образа Imdn+1 —границами. Элементы группы Нп —смежные классы
группы Imdn+1, называемые классами гомологии. Два цикла, представляющие
один и тот же класс гомологии, называют гомологичными. Это означает,
что их разница является границей.
Возвращаясь к случаю Сп = ДП(Х), группу гомологии Kerdn/Imd,I+1
мы будем обозначать H,f (X) и называть n-й группой симплициалъных
гомологии комплекса X.
Пример 2.2. Пусть X = S1 с одной вершиной v и одним ребром е. Тогда
обе группы AqCS1) и AjCS1) равны Z, а граничное отображение д{ нулевое,
так как де = v — v. Группы An(Sl) равны 0 при п ^ 2, так как е
никаких симплексов в этих размерностях нет. Следовательно,
л . [Ъ при п = 0,1;
{ 0 при п Z 2. v
Это иллюстрирует тот общий факт, что если все граничные отображения
В цепном комплексе нулевые, то группы гомологии комплекса изоморфны
самим группам цепей.
Пример 2.3. Пусть Х = Т — тор с изображённой ранее структурой
Д-комплекса с одной вершиной, тремя рёбрами а, Ъ и с и двумя
двумерными симплексами U и L. Как и в предыдущем примере, д{ = 0, поэтому
Н£(Т) ^ Z. Так как d2U = а + Ъ — с = d2L, а {а, Ь, а + Ъ - с} — базис для
Ai(T), получаем, что HjA(T)^Z$Z с базисными классами гомологии
[а] и [Ь]. Так как никаких трёхмерных симплексов нет, группа Н£(Т)
равна группе Кегд2, которая является бесконечной циклической группой,
порождённой цепью U - L, так как d{pU + qL) = (р -f q){a + b — с) = 0
только при p = -q. Таким образом,
(Z0Z прип = 1;
Z при п = 0, 2;
0 при п ^ 3.
Пример 2.4. Пусть X = IRP2 — проективная плоскость, как она
изображалась ранее, с двумя вершинами v и w, тремя рёбрами а, Ъ и с и двумя
хлава z. гомологии
двумерными симплексами U и L. Тогда Imd] порождается цепью w — v,
поэтому Н^(Х) «*Z, причём в качестве образующей можно взять любую
вершину. Так как д21/ = -а + b -f с и d2L = а — b -f с, мы видим, что
гомоморфизм д2 инъективен, поэтому Я^(Х) = 0. Далее, Kerd^ %Z®Zc базисом
а - Ъ и с, a Imd2 является подгруппой индекса два в группе Кегдь так как
мы можем выбрать сиа-Ь+св качестве базиса для Кегд1} а а-Ъ + с
и 2с = (а - Ъ + с) + (-а + b + с) в качестве базиса для Im d2. Таким образом,
Пример 2.5. Мы можем получить структуру Д-комплекса на Sn, взяв
два экземпляра симплекса Л'1 и отождествив их границы посредством
тождественного отображения. Если пометить эти два п-мерных
симплекса буквами U и L, то очевидно, что группа Кегд„ является бесконечной
циклической, порождаемой цепью U — L. Поэтому tf,f (Sn) ^Z для такой
структуры Л-комплекса на S". Вычисление других групп гомологии будет
более трудным. .
Без больших затруднений можно разобрать много аналогичных
примеров; в частности, можно рассмотреть другие замкнутые ориентируемые
и неориентируемые поверхности. Однако вычисления имеют тенденцию
быстро усложняться, особенно для многомерных комплексов.
Напрашиваются некоторые очевидные общие вопросы. Зависят ли
группы tfff (X) от выбора структуры Л-комплекса на X? Другими словами,
если два Л-комплекса гомеоморфны, то будут ли их группы гомологии
изоморфны? Более общий вопрос: будут ли изоморфны группы
гомологии, если пространства лишь гомотопически эквивалентны? Чтобы
ответить на эти вопросы и разработать общую теорию, лучше выйти за рамки
довольно жёстких симплициальыых конструкций и ввести сингулярные
группы гомологии. У них есть дополнительное преимущество в том, что
они определены для всех пространств, а не только для Д-комплексов.
В конце этого параграфа, после того как будет разработана некоторая
теория, мы покажем, что для Д-комплексов симплициальные и сингулярные
группы гомологии совпадают.
Традиционно симплициальные гомологии определяют для симпли-
циалъиых комплексов, являющихся Д-комплексами, симплексы которых
единственным образом задаются их вершинами. По-другому можно
сказать, что любой п-мерный симплекс имеет п +1 разных вершин и нет
другого n-мерного симплекса с тем же самым множеством вершин. Таким
образом, симплициальный комплекс можно описать комбинаторно как
множество Х0 вершин вместе с множествами Х„ — и-мерными симплексами,
которые являются (п +1)-элементными подмножествами в Х0.
Единственное требование состоит в том, что каждое (/с + 1)-элементное
подмножество вершин п-мерного симплекса в Хп является к -мерным симплексом
в Хк. По этим комбинаторным данным можно построить Д-комплекс X,
как только мы выберем частичный порядок вершин Х0, ограничение ко-
§ 2.1. Симплициальные и сингулярные гомологии
141
торого на вершины любого симплекса в Хп является линейным порядком.
Например, мы могли бы выбрать просто линейный порядок на всех
вершинах. Для больших множеств вершин это могло бы потребовать
привлечения аксиомы выбора.
Одна из задач в конце этого параграфа состоит в том, чтобы
показать, что каждый Д-комплекс можно подразделить так, что он станет сим-
плициальным комплексом. В частности, любой Д-комплекс гомеоморфен
симплициальному комплексу.
По сравнению с симплициальными комплексами Д-комплексы имеют
то преимущество, что вычисления с ними проще, поскольку требуется
меньше симплексов. Например, чтобы ввести структуру симплициального
комплекса на торе, нужно по крайней мере 14 треугольников, 21 ребро
и 7 вершин, а для IRP2 нужно по крайней мере 10 треугольников, 15 рёбер
И 6 вершин. Это существенно замедлило бы вычисления!
Сингулярные гомологии
Сингулярный n-мерный симплекс в пространстве X — это по
определению, просто отображение а: Дп —>Х. Слово «сингулярный»
используется здесь, чтобы показать, что отображение а не должно быть
вложением, но может иметь «особенности», где его образ вовсе не похож на
симплекс. Единственное, что требуется от а, —это непрерывность. Пусть
Сп(Х) — свободная абелева группа, базисом которой служит множество
сингулярных гг-мерных симплексов в X. Элементы группы СП(Х),
называемые n-мерными цепями (точнее, сингулярными п-мерными цепями),
являются конечными формальными суммами £] п(аь где n, e Z и сг{: Д" —> X.
i
Граничное отображение дп: СЛ(Х) —>СЛ_1(Х) задаётся той же самой
формулой, что и раньше:
I
В этой формуле неявно используется каноническое отождествление [v0,...
...,^-,..., vn] с Д""1, сохраняющее порядок вершин, так что а\ [v0,..., vj,...
.,., vn] рассматривается как отображение Дп-1 —>ХУ т.е. как сингулярный
(и — 1)-мерный симплекс.
Обычно мы записываем граничное отображение дп из СЛ(Х) в С,,.^)
просто как д, когда это не приводит к недоразумениям. Доказательство
леммы 2.1 применимо и к сингулярным симплексам; оно показывает, что
dndn+1 = 0, или, короче, д2 = 0. Поэтому мы можем определить группу
сингулярных гомологии Нп (X) = Кег дп/ Im д„+1.
Из определения очевидно, что гомеоморфные пространства имеют
Изоморфные группы сингулярных гомологии Нп, в отличие от ситуации
Для Н*. С другой стороны, так как группы СЛ(Х) столь велики, что
число сингулярных гг-мерных симплексов в X обычно несчётно, непонятно,
142
Глава 2. Гомологии
почему для А-комплекса X с конечным числом симплексов группа Нп (X)
должна быть конечно порождённой для всех п и должна быть нулевой,
если п больше размерности комплекса X; эти два свойства тривиальны
дляЯ*(Х).
Хотя сингулярные гомологии выглядят намного более общими, чем
симплициальные гомологии, в действительности их можно
рассматривать как частный случай симплициальных гомологии посредством
следующей конструкции. Для произвольного пространства X определим
сингулярный комплекс S(X) как А-комплекс, имеющий по одному п-мерному
симплексу А" для каждого сингулярного п-мерного симплекса а: А" —> X,
причём Д£ приклеивается очевидным способом к (п — 1)-мерным
симплексам комплекса S(X), которые являются ограничениями
отображения а на разные (п — 1)-мерные симплексы в <ЗА". Из определений ясно,
что группа Н* (S(X)) совпадает с Нп (X) для всех п, и в этом смысле группа
сингулярных гомологии Нп (X) является частным случаем группы
симплициальных гомологии. Можно рассматривать S(X) как модель
А-комплекса для X, хотя это, как правило, чрезвычайно большой объект по
сравнению с X.
Циклы в сингулярных гомологиях определяются алгебраически, но
им можно дать несколько более геометрическую интерпретацию в
терминах отображений из конечных А-комплексов. Чтобы увидеть это, прежде
всего заметим, что сингулярную п-мерную цепь Е, всегда можно записать
в виде Yi ei(Jb гДе £i =±1, если допустить повторение сингулярных п-мер-
ных симплексов а(. Если дана такая п-мерная цепь С = 5]^'(71» то> К0ГДа
мы вычисляем <3£ как сумму сингулярных (п — 1)-мерных симплексов со
знаками ±1, может произойти сокращение пары, состоящей из двух
одинаковых сингулярных (п — 1)-мерных симплексов с противоположными
знаками. Выбирая максимальный набор таких сокращающихся пар,
построим п-мерный А-комплекс К% из несвязного объединения п-мерных
симплексов А", по одному для каждого <тг, отождествляя пары (п — 1)-мерных
граней, соответствующие выбранным сокращающимся парам. Тогда
отображения а, индуцируют отображение К^ —>Х. Если £ — цикл, то любой
(п - 1)-мерный симплекс комплекса К^ происходит из сокращающейся
пары, а потому является гранью ровно двух п-мерных симплексов комплекса
К^. Таким образом, К^ — пространство, локально гомеоморфное R" всюду,
за исключением подкомплекса размерности не больше п - 2. Все п-мер-
ные симплексы комплекса К^ можно согласовано ориентировать,
учитывая знаки перед ah поэтому К^ в действительности является
ориентируемым многообразием вне его особых точек. Более внимательное изучение
показывает, что К^ является многообразием и около внутренних точек
(п — 2)-мерных симплексов, и, таким образом, особые точки комплекса К?
в действительности имеют размерность не больше п — 3. Однако вполне
§ 2.1. Симплициальные и сингулярные гомологии
143
может случиться, что около внутренних точек (п — 3)-мерных симплексов
Кг уже не будет многообразием.
В частности, элементы группы НХ(Х) представляются наборами
ориентированных нетель в X, а элементы группы Н2(Х) представляются
отображениями замкнутых ориентированных поверхностей в X.
Потрудившись ещё немного, можно показать, что ориентированный одномерный
цикл Ц ^а ""* * является нулём в Нх (X) тогда и только тогда, когда он
а
продолжается до отображения ориентированной поверхности в X;
аналогичное утверждение есть и для двумерных циклов. В начале развития
теории гомологии верили, по крайней мере надеялись, что эта тесная
связь с многообразиями продолжается на все высшие размерности, но
оказалось, что это не так. Есть своего рода теория гомологии, построенная
из многообразий, которую называют бордизмами, но она гораздо более
сложная, чем теория гомологии, которую мы изучаем здесь.
После этих предварительных замечаний давайте посмотрим, что
можно доказать о сингулярных гомологиях.
I Предложение 2.6. Разбиению пространства X на компоненты ли-
I нейной связности Ха соответствует изоморфизм группы НП(Х) на пря-
I мую сумму фН„(Ха).
I а
Доказательство. Так как образ сингулярного симплекса всегда
линейно связен, группа СП(Х) расщепляется как прямая сумма своих
подгрупп Сп(Ха). Граничные отображения дп сохраняют это разложение
в прямую сумму, переводя Сп(Ха) в Cn_j(Xa), поэтому Кегд,, и Imdn+1
аналогично расщепляются как прямые суммы. Следовательно, группы
гомологии также расщепляются: Нп(X) ъ 0Нп(Ха). □
а
I Предложение 2.7. Если пространство X непусто и линейно связ-
I но, то Я0(Х) ^ Z. Следовательно, для любого пространства X группа
I Н0(Х) —прямая сумма групп Z, по одной для каждой компоненты ли-
I нейной связности пространства X.
Доказательство. По определениюH0(X)=C0(X)/Imдг, так как д0=0.
Определим гомоморфизм е: С0(Х) —> Z, положив e(2nf<7i) =Snr Он>
очевидно, сюръективен, если пространство X непусто. Утверждение
состоит в том, что Kere = ImdIf если пространство X линейно связно, а
значит, е индуцирует изоморфизм H0(X)&Z.
Чтобы доказать это утверждение, заметим сначала, что Imdj cKere,
так как для сингулярного одномерного симплекса о\ Д1 —► X мы
имеем ед^а) = е(сг| [vj - a\ [v0]) = 1-1 = 0. Для доказательства обратного
включения Kerf clmdj предположим, что е(£]п,-сг,-) = 0> т-е. £]пг- = 0.
Отображения а, — сингулярные нульмерные симплексы, которые
являются просто точками в X. Выберем путь т,-: I —>Х из отмеченной точки х0
144
Глава 2. Гомологии
в сг,-О0), и пусть а0 — сингулярный нульмерный симплекс с образом х0.
Мы можем рассматривать т, как сингулярный одномерный симплекс, т. е.
отображение т,-: [v0, vj —>Х, а тогда мы имеем дт,- = а,- — а0.
Следовательно,
i i i i
так как ^п, =0. Таким образом, ^п^сг, —граница, а это показывает, что
Кег е с Im д х. D
| Предложение 2.8. Если X — точка, то Нп (X)=0 при п > 0 и Я() (X) «* Z.
Доказательство. В этом случае есть единственный сингулярный
n-мерный симплекс ап для каждого п, а Э(сгп) = 5](-1),ап_1 — сумма п-hi
членов, которая равна 0 для нечётного п и а,,.! для чётного п, п ^ 0. Таким
образом, мы получаем цепной комплекс
в котором граничные отображения поочерёдно являются изоморфизмами и
тривиальными отображениями, за исключением последней группы Z.
Группы гомологии этого комплекса тривиальны за исключением Н0ъг£. □
Часто гораздо более удобной оказывается слегка изменённая версия
гомологии, для которой точка имеет тривиальные группы гомологии во
всех размерностях, включая нуль. Для этого определяются приведённые
группы гомологии Н„(Х) как группы гомологии увеличенного цепного
комплекса или цепного комплекса с аугментацией
... -> С2(Х) % С, (X) ^ С0(Х) Д Z - 0,
где e(Yjniai) =2П1> как в доказательстве предложения 2.7; это отобра-
жение называют аугментацией1. Здесь мы должны потребовать, чтобы
пространство X было непустым, чтобы избежать появления
нетривиальной группы гомологии в размерности —1. Так как edi = 0, отображение
е обращается в нуль на Im^! и, следовательно, индуцирует отображение
Н0(Х) —> Z с ядром Н0(Х)} поэтому Я0(Х) ъ Н0(Х) Ф Ъ. Очевидно, что
Нп(Х)ъНп(Х) прип>0.
Формально можно думать о дополнительной группе Z в
увеличенном цепном комплексе как порождённой единственным отображением
[0] —> X, где [0] — пустой симплекс, без вершин. Тогда отображение
аугментации е— это обычное граничное отображение, так как d[v0] =
= [vo] = [0].
Читатели, которые знают о фундаментальной группе тгДХ), могут,
опережая события, заглянуть в § 2.А, где показано, что группа //] (X) явля-
1 От английского augmentation. — Прим. перев.
§ 2.1. Симплициальные и сингулярные гомологии
145
ется абелианизацией группы Я] (X), если пространство X линейно связно.
Этот результат, однако, не понадобится в других местах этой главы.
Гомотопическая инвариантность
Первый существенный результат, который мы докажем о сингулярных
гомологиях, состоит в том, что гомотопически эквивалентные
пространства имеют изоморфные группы гомологии. Мы сделаем это, показав, что
отображение /: X —> Y индуцирует гомоморфизм /*: НЛ(Х) —* НП(У) для
всех п и что /+ является изоморфизмом, если / — гомотопическая
эквивалентность.
Для отображения /: X —* Y индуцированный гомоморфизм /fi: Сп (X) —*
—>Cn(Y) определяется как композиция каждого сингулярного п-мерного
симплекса а: Ап —* X с отображением /, которая даёт сингулярный п-мер-
ный симплекс /д(сг) = fa: Дп —* Y, с последующим продолжением по
линейности посредством формулы
i i i
Отображения /3: Cn (X) —> Cn(Y) удовлетворяют соотношению f:d = d/ц, так
как
/sa(a) = /.(S(-iya|tv0>.
= £(-1)'/ct|[v0,
Таким образом, мы имеем диаграмму
vi.-.vn]) =
.,v[-, ...,vn] = d/j,(a).
Jn+1
W-
■c„(X)—^c^w
-c„+100
-c„-i(n
в которой в каждом квадрате композиция f^d равна композиции д/д.
Диаграмму отображений, которая обладает тем свойством, что любые две
композиции отображений, исходящие из одной и той же точки диаграммы
и заканчивающиеся в некоторой другой точке, равны, называют
коммутативной диаграммой. В данном случае коммутативность диаграммы
эквивалентна соотношению коммутативности f$d — df:i но коммутативные
диаграммы могут содержать коммутативные треугольники,
пятиугольники и т.д., а не только коммутативные квадраты.
Тот факт, что отображения ff СП(Х) —>СП(У) удовлетворяют
соотношению f:d = d/-, выражают также, говоря, что отображения /й определяют
цепное отображение сингулярного цепного комплекса X в сингулярный
цепной комплекс Y. Соотношение /ид = д/ц влечёт, что /: переводит циклы
146
Глава 2. Гомологии
в циклы, так как из равенства да = О следует, что д(/-а) =/,(да) = 0. Кроме
того, /й переводит границы в границы, так как f^(dl3) = d(<f:l3).
Следовательно, /: индуцирует гомоморфизм /+: Нп(Х) —>Hn(Y). Алгебраическое
утверждение, которое мы только что доказали, состоит в следующем.
(Предложение 2.9. Цепное отображение цепных комплексов
индуцирует гомоморфизмы групп гомологии этих двух комплексов.
Вот два основных свойства индуцированных гомоморфизмов,
которые важны, несмотря на их тривиальность:
S I
1) (/&)* = /*g* Для композиции отображений X —* У —> Z (это следует из
a g f
ассоциативности композиций Лп —> X —> У —»Z);
2) 1* = 1, где 1 обозначает тождественное отображение пространства
или группы.
Менее тривиально следующее утверждение.
I Теорема 2.10. Если два отображения /, g: X —> У гомотопны, то они
индуцируют один и тот же гомоморфизм /* = g*: Ни (X) —> Яп(У).
Если учесть формальные свойства (/g)+ = /*g* и!, = 1, то немедленно
получаем следующей результат.
I Следствие 2.11. Отображения /*: Нп(Х) —> Ни(У), индуцированные
гомотопической эквивалентностью /: X—* У, являются
изоморфизмами для всех п.
Например, если пространство X стягиваемо, то Нп{Х) =0 для всех п.
Доказательство теоремы 2.10. Существенной составляющей
доказательства является построение разбиения цилиндра А" х J на (п 4-
^-мерные симплексы. На рисунке изображены случаи п = 1, 2. В Д" х J пусть
Дп х {0} = [v0, ...,vn] и Д" х {1} = [w0,..., wM], где v,- и w( имеют один
и тот же образ при проекции Д" х / —► Дп.
Симплекс [v0,..., Vj, wl4!,..., wn] размерности n — это
график линейной функции у?,: Дп —> J,
заданной в барицентрических координатах формулой
4>i(t0, ..., tn) =tI+i 4-... 4-tn, так как вершины
симплекса [v0,..., Vj, w/+1,..., w„] лежат на графике
функции </>, и этот симплекс проектируется гомео-
морфно на Дп при проекции Дп х / —► Д". График
функции </>,- расположен ниже графика функции
</>,■-!, так как </?,- ^ </>,•_ i, и область между этими
двумя графиками —симплекс [v0,..., v,-,w,-,..., wn].
Это действительно (п 4-1)-мерный симплекс, так
как w, не лежит на графике функции у?,- и,
следовательно, не принадлежит n-мерному
симплексу [v0,..., v(, wi+1,..., wn]. Из последовательности
неравенств 0 = ipn ^ у> j ^ ... ^ у?0 ^ ^-1 = 1 мы
§ 2.1. Симплициальные и сингулярные гомологии
147
получаем, что Дп х / — объединение (п + 1)-мерных симплексов [v0, ...
..., vf, wh ..., wn], каждый из которых пересекает следующий за ним по
грани— n-мерному симплексу.
Если дана гомотопия F: X х / —> У отображения / в отображение g, то
можно определить призменные операторы Р: СП(Х) —> Сп+1(У), положив
Р(<7) = J](-DrFo (а х 1)| [v0, ..., v;, wh ..., wn]
i
для а: Д" —►X, где F о (а х 1) — композиция Дпх/—>Х xl —► У. Мы
покажем, что призменные операторы удовлетворяют соотношению
ap = gE-/s-Pd.
С точки зрения геометрии левая часть этого уравнения представляет
границу призмы, а три члена в правой части представляют верхнее
основание Д" х {!}, нижнее основание Дп х {0} и боковую поверхность с)Дп х /
призмы. Чтобы доказать это соотношение, приведём вычисление:
дР(а) = ]Г(-Щ-1);> о (а х 1)| [v0,..., vj9..., v,-, iv,-,..., wn] +
+ ]Г(-1)Ч-1У+1Ро (а x 1}l [v°' — v" w<' •'" ™i> -' w"]-
Члены с i = j в этих двух суммах взаимно сокращаются, за исключением
члена
Fo(axl)|[v0,w0, ...,wn],
который равен goor = g:(or), и члена — Fо (а х 1)| [v0, ..., v„, fi>„], который
равен —/оа = —/с(а). Члены с i ^J —-это в точности -Рд(сг), так как
Рд(а) = ^(-1)Ч-1);>о (а х 1)| [v0,..., v,-, iv,-,..., wj9 .... wn] +
«<i
+ X|(-l)r'"1(-lVFo (a x 1)| Lv0, ..., vj9..., vf, wi9..., wn].
«>;
Теперь мы можем завершить доказательство теоремы. Если а е Сп (X) —
цикл, то мы получаем g-(a) -/,(a) =dP(a)+Pd(a) =ЭР(а),так как да = 0.
Таким образом, g- (a) - /:(a) — граница, а потому gc (a) и /, (а) определяют
один и тот же класс гомологии, а это означает, что g* совпадает с /+ на
классе гомологии цикла а. □
Соотношения дР + Pd = gj, - /, выражают, говоря, что Р — цепная
гомотопия между цепными отображениями /с и gn. Мы только что доказали
следующее утверждение.
148
Глава 2. Гомологии
I Предложение 2.12. Цепно гомотопные цепные отображения
индуцируют один и тот же гомоморфизм гомологии.
Есть также индуцированные гомоморфизмы /+: Нп {X) —► Нп (Y) для
приведённых групп гомологии, так как /;;£ = £/:. Свойства
индуцированных гомоморфизмов, доказанные выше, выполняются и для приведённых
гомологии; доказываются они точно так же.
Точные последовательности и вырезание
Было бы хорошо, если бы всегда имелись простые соотношения между
группами гомологии пространства X, подпространства А и факторпро-
странства Х/А. Действительно, тогда можно было бы надеяться найти
группы гомологии пространств типа CW-комплексов, индуктивно
получаемых из подпространств, сложность которых последовательно
возрастает. По-видимому, наиболее простые соотношения получились бы, если
бы группа НЛ(Х) содержала Нп(А) в качестве подгруппы, а факторгруппа
Нп(Х)/Нп{А) была бы изоморфна Нп(Х/А). Хотя это действительно так
в некоторых случаях, но если бы это выполнялось всегда, то теория
гомологии полностью выродилась бы, поскольку любое пространство X
можно вложить в качестве подпространства в пространство с тривиальными
группами гомологии, а именно в конус СХ = {X х I)/(X х {0}), который
является стягиваемым.
Оказывается, эту чересчур простую модель не нужно менять слишком
сильно, чтобы получить соотношение, которое справедливо в весьма
общей ситуации. Новое свойство реального соотношения состоит в том, что
оно вовлекает группы НП(Х), Нп(А) и Нп{Х/А) для всех значений п
одновременно. На практике это не столь плохо, как могло бы показаться;
кроме того, это имеет приятный побочный эффект, иногда позволяя
вычислять группы гомологии высокой размерности в терминах групп меньшей
размерности, которые могут быть уже известны, например, по индукции.
Чтобы сформулировать искомое соотношение, нам понадобится
алгебраическое определение, которое играет ключевую роль в
алгебраической топологии. Последовательность гомоморфизмов
a/!+l aH
_» А > А —U А —>
называют точной, если Кегал =1тал+1 для всех п. Включения 1та„+1 с
с Кегап эквивалентны тому, что апап+1 = 0, поэтому такая
последовательность—цепной комплекс, а противоположные включения Keran clman+1
выражают тот факт, что группы гомологии этого цепного комплекса
тривиальны.
Многие основные алгебраические понятия можно выразить в
терминах точных последовательностей, например:
§ 2.1. Симплициальные и сингулярные гомологии
149
1) последовательность 0 —> А —► В точна тогда и только тогда, когда
Кега = 0, т.е. гомоморфизм а инъективен;
2) последовательность Л —► В —> О точна тогда и только тогда, когда
Ima = B, т.е. гомоморфизм а сюръективен;
3) согласно п. 1 и 2 последовательность 0 —> А —> В —> О точна тогда и
только тогда, когда а — изоморфизм;
a P
4) последовательность О—► А —► В —> С —► О точна тогда и только тогда,
когда гомоморфизм а инъективен, гомоморфизм /3 сюръективен
и Ker/3 = Ima, поэтому /3 индуцирует изоморфизм C^B/Ima; это
можно записать как СъВ/А, если мы представляем себе а как
включение группы Л в группу В в качестве подгруппы.
Точную последовательность0—► А —>В —>С —► О, рассмотренную в
примере 4, называют короткой точной последовательностью.
Точные последовательности дают правильный инструмент, чтобы
связать группы гомологии пространства, подпространства и
соответствующего факторпространства.
I Теорема 2.13. Если X — некоторое пространство, а А —его непустое
I замкнутое подпространство, которое является деформационным ре-
I трактом некоторой своей окрестности в X, то существует точная после-
I довательность
I ... - НП(А) ^ НЛ(Х) ^ Нп{Х/Х) Л Нп_,{А) ^ Яп_!(X) - ...
I ...-Н0(Х/А)-0,
I где i — включение А с-* X, а j — отображение факторизации X —> Х/А.
Отображение <1 будет построено по ходу доказательства. Идея его
построения состоит в том, что элемент хеНп(Х/А) можно представить
такой цепью а в X, что да — цикл в А, класс гомологии которого и есть
дхеНп_,№-
Пару пространств (Х,А), удовлетворяющую условию теоремы,
будем называть хорошей парой. Например, если X — CW-комплекс, а А —
его непустой подкомплекс, то (X, А)— хорошая пара согласно
предложению П.5 из приложения.
I Следствие 2.14. Hn(Sn) ъЪ и H((Sn) = 0 при \фп.
Доказательство. Для п > 0 положим (X, А) = (Dn, Sn_1); тогда Х/А =
= Sn. Члены H,(Dn) в длинной точной последовательности для этой пары
являются нулями, так как шар D" стягиваем. Тогда из точности
последовательности следует, что отображения Н((Бп) -^Hf_1(S"~1)— изоморфизмы
При i > 0 и Я0(5") = 0. Требуемое утверждение теперь получается
индукцией по п, начиная со случая S0, для которого оно выполняется согласно
предложениям 2.6 и 2.8. □
150
Глава 2. Гомологии
Как приложение этого вычисления мы получаем следующую
классическую теорему Брауэра, двумерный случай которой был доказан в § 1.1.
Следствие 2.15. Сфера dDn не является ретрактом шара Dn.
Следовательно, каждое отображение /: Dn —>Dn имеет неподвижную точку.
Доказательство. Если г: Dn —> tiDn — ретракция, то п = 1 для
отображения включения i: 3Dn —>Dn. Композиция
Hn-d<lDn) ^ H.-iCD") -^ Hn_1{dDn)
тогда является тождественным отображением на Hn_}(dDn) &Z. Но оба
отображения iM и г* нулевые, так как //„^(D") = 0, и мы получаем
противоречие. Утверждение о неподвижных точках доказывается так же, как
и в теореме 1.9. □
Вывод точной последовательности групп гомологии для хорошей
пары (X, А) будет весьма длинным. Фактически мы получим более общую
точную последовательность, которая имеет место для любых пар (X, Л),
но в ней группы гомологии факторпространства Х/А заменяются на
относительные группы гомологии, обозначаемые НП(Х, А). Эти группы
оказываются весьма полезными также и для многих других целей.
Относительные группы гомологии
Иногда случается, что если забыть про некоторые данные или
структуры, то получается более простая и более гибкая теория, которая, как это
ни парадоксально, может дать результаты, не сразу получающиеся в
исходной ситуации. Хорошо известный пример — арифметика по модулю п, где
игнорируются кратные числа п. Относительные гомологии —другой
пример. В этом случае игнорируются все сингулярные цепи, образы которых
лежат в данном подпространстве.
Относительные группы гомологии определяются следующим
образом. Если даны пространство X и подпространство Л с X, то пусть
СЛ(Х, А) —факторгруппа С„(Х)/СЛ04). Таким образом, цепи в А
тривиальны в СЛ(Х,Л). Так как граничное отображение д: СЛ(Х) —> Cn_j(X)
переводит СП(Л) в СП_](Л), оно индуцирует граничное факторотображе-
ние д: СЛ(Х, А) —> С^СХ, А). Меняя п, мы получаем последовательность
граничных отображений
... ^ Сп{Х9А) -^ Сп_^Х9А) ^ ...
Соотношение д2 = 0 выполняется для этого граничного отображения, так
как оно выполнялось до перехода к факторгруппам. Поэтому мы
получаем цепной комплекс, и группы гомологии Kerd/Imd этого цепного
комплекса—по определению относительные группы гомологии ЯП(Х, А). Из
определения относительного граничного отображения мы видим, что
а) элементы из Н„(Х,Л) представлены относительными циклами, т.е.
такими n-мерными цепями аеСп(Х), что даеС^^);
§ 2.1. Симплициальные и сингулярные гомологии
151
б) относительный цикл а тривиален в Нп{Х,А) тогда и только тогда,
когда он является относительной границей, т. е. а = др + у для
некоторых р еСл+1(Х) и уеСп(А)-
Эти свойства делают точной интуитивную идею, что Ни(Х, А)— это
«гомологии пространства X по модулю А».
Факторгруппу Сп(Х)/Сп(А) можно также рассматривать как
подгруппу в СП(Х), базисом которой служат сингулярные п-мерные симплексы
а: Ап —*Х, образы которых не содержатся в А, Однако граничное
отображение не переводит эту подгруппу группы СП(Х) в соответствующую
подгруппу группы С^СХ), поэтому обычно лучше рассматривать Сп(Х,А)
как факторгруппу, а не как подгруппу в СП(Х).
Наша цель теперь состоит в том, чтобы показать, что относительные
группы гомологии Н„(Х, А) для любой пары (X, А) вставляются в
длинную точную последовательность
... -* ниш -> ни(х) -* нп(х, А) -* нп_,ш -> нп-1(х) -* ...
...-*Н0(Х,А)->0.
Это целиком будет делом алгебры. Для начала рассмотрим диаграмму
О >- СпШ —^ СЛ(Х) '-+ СЛ(Х, А) ^ О
л л л
т т т
О >- С^гСА) —U- СП_Т(Х) —^ С^СА, X) ^ О
где i —включение, a j —отображение факторизации. Эта диаграмма
коммутативна по определению граничных отображений. Если мы разрешим п
изменяться и нарисуем эти короткие точные последовательности
вертикально, а не горизонтально, то получим большую коммутативную
диаграмму
О
О
О
1 . )
лп + 1
+ Ап
+ А
п--1
I' . 1'
[1
вп
\> . \>
-*с,
11+1
■*с„
о
о
->п-1
■*сп_,
I
о
где столбцы точны, а строки — ценные комплексы, которые мы
обозначим А, В и С. Такую диаграмму называют короткой точной
последовательностью цепных комплексов. Покажем, что при переходе к группам
гомологии эта короткая точная последовательность цепных комплексов
152
Глава 2. Гомологии
растягивается в длинную точную последовательность групп гомологии
групп
... - НпШ ^ Нп(В) ± Нп{С) Л Нп^{А) - Нп_х(В) - ...,
где Я„(А) обозначает группу гомологии Kerd/Imd в члене Ап в цепном
комплексе Л, а Н„(£0 и НЛ(С) определяются аналогично.
Коммутативность квадратов в короткой точной последовательности
цепных комплексов означает, что i и ; —цепные отображения.
Поэтому они индуцируют отображения i* и j+ для гомологии. Чтобы
определить граничное отображение д: Нп(С) —>Нп_х(А)у допустим, что сеСп —
цикл. Так как j — отображение на, с = ДЬ) для некоторого элемента ЬеВп.
Элемент db е Вп_х лежит в Ker j, так как j(db) = dj(b) = дс = 0. Поэтому
db = i(a) для некоторого оеЛ,^, так как Ker; =Imi. Заметим, что da = 0,
так как i(da) = di(a) = ddb = 0 и гомоморфизм i инъективен. Определим
d: Н„ (С) —> Н;?_] (Л); отобразив класс гомологии цикла с в класс гомологии
цикла а, т. е. положив d[с] = [а]. Это отображение определено корректно,
поскольку имеют место следующие утверждения:
а
Т т
<!'
сп
а) элемент а однозначно определяется элементом db, так как
гомоморфизм i инъективен;
б) если бы мы выбрали Ь' вместо Ь, то получили бы ДЬ') = ДЬ), поэтому
Ь'— b лежит в Ker; = Imi. Таким образом, Ь' — b = i(a0 для
некоторого а', поэтому Ь' = Ъ + i(<*')• Замена b на b -f i(aO приводит к
тому, что а заменяется на гомологичный ему элемент a -f da', так как
i(a + da7) = i(a) + i(daO = db + di(aO = d(b + i(aO);
в) другой элемент, выбранный вместо с в пределах его класса гомологии,
должен иметь вид с + дс'. Так как с'= ДЬ') для некоторого Ь', мы
тогда получаем с + дс' = с + dj(b') = с + j(db') = j (b 4- dbO, поэтому Ь
заменяется на b -f db', a db при этом не изменяется, поэтому а тоже не
изменяется.
Отображение д: Нп (С) —>Hn_j(Л) — гомоморфизм, так как если dic^ —
= [aj и d[c2] = [a2] посредством элементов Ъх и Ь2, как и выше, то
ДЬ! +Ь2) = ЯЬХ) -f ДЬ2) = с} + с2
и
i(ai+a2) = i'(ai) + i(a2) = dbi+db2 = д{Ьх+Ъ2),
таким образом, dCtcJ + [с2]) = [aj -f [a2].
§ 2.1. Симплициальные и сингулярные гомологии
153
I Теорема 2.16. Последовательность групп гомологии
... - НП(А) -^ НП(В) ± ЯП(С) Л НпМ(А) -^ Н^СВ) - ...
| точная.
Доказательство. Нужно проверить шесть утверждений.
1. Imi* с Кег;*. Это очевидно, так как из равенства ji — О следует, что
;'Л = 0.
2. Im;* с Кег д. Мы получаем д;* = О, так как в этом случае дЪ — О по
определению отображения д.
3. ImdcKeri*. Здесь i+d = 0, так как i+д переводит [с] в [db] = 0.
4. Kerj* clmi^. Класс гомологии в Кег;'* представляется циклом ЬеВп,
для которого ;(Ь) —граница, поэтому j(b) = dc для некоторого с' е
еСп+1. Так как гомоморфизм ; сюръективен, с' = j(b') для некоторого
Ь' е Вп+1. Мы получаем ; (Ь - (ЭЬО = ; (Ь) - ; (db') = ; (b) - dj (b') = 0, так
как d;(b') = дс' = ;(Ь). Поэтому Ь — (ЭЬ7 = i(a) для некоторого aeAn.
Этот элемент а — цикл, так как i(da) = di(a) = d(b- db') = db = 0, а
гомоморфизм i инъективен. Следовательно, i*[a] = [b - db'] = [Ь], а это
показывает, что образ отображения £* содержит всю группу Кег;*.
5. Kerdclm;+. В обозначениях, использованных при определении
отображения д, если с представляет класс гомологии в Кег д, то а = да' для
некоторого а' е А„. Элемент Ъ - i(a') — цикл, так как
д(Ъ - i(a')) = (9b - di'Ca') = db - i(da') = db - f(a) = 0.
Далее,
;(b~i(a/)) = ;(b)-;i(a,) = j(b) = c,
поэтому ;* переводит элемент [b — i(a0] в [с].
6. Кеп+ с Imd. Если дан такой цикл а е Ап_ь что i(a) = (9b для
некоторого b€Bni то ;(Ь) является циклом, так как d;(b) = ;(db) = ;i(a) = 0
и (9 переводит [;(Ь)] в [а]. □
Эта теорема одна из начальных в гомологической алгебре. Метод её
Доказательства иногда называют диаграммным поиском.
Если вернуться к топологии, то предыдущая алгебраическая теорема
приводит к длинной точной последовательности групп гомологии:
- -* ЯП(Л) -^ НП(Х) ± ЯП(Х, Л) Л НП_}(А) -^ ЯП_}(Х) - ...
...-Н0(Х,А)^0.
Граничное отображение (9: НП(Х, А) —►#„_} (А) имеет очень простое
°писание. Если класс [а]еЯ(1(Х,А) представлен относительным
циклом а, то д[а]— класс цикла (9а в ЯП_1(А). Это видно непосредственно
из алгебраического определения граничного гомоморфизма в длинной
154
Глава 2. Гомологии
точной последовательности групп гомологии, соответствующей короткой
точной последовательности цепных комплексов.
Эта длинная точная последовательность даёт аккуратную
формулировку идеи, что группы Нп{Х,А) измеряют различие между группами
НП(Х) и ЯП(Л). В частности, из точности следует, что если Нп(Х, А) = 0
для всех п, то включение А <—>Х индуцирует изоморфизмы Ни(А) ъНп(Х)
для всех л согласно замечанию 3 после определения точности. Обратное
утверждение тоже верно согласно одной из задач в конце этого параграфа.
Имеется совершенно аналогичная длинная точная
последовательность групп приведённых гомологии для пары (X, Л), где Аф®. Она
возникает при применении предыдущей алгебраической техники к короткой
точной последовательности цепных комплексов, образованной
короткими точными последовательностями 0 —* Сп(А) —* СП(Х) —* СП(Х, А) —► 0
в неотрицательных размерностях и дополненной короткой точной после-
довательностью 0—*Z—>Z—>0—*0 в размерности — 1. В частности, это
означает, что группа Нп(X, А) та же самая, что и Нп(Х, Л), для всех п, если
Л^0.
Пример 2.17. В длинной точной последовательности групп
приведённых гомологии для пары (Dn, dDn) отображения Hz(Dn, dDn) -Uh^jCS""1)
являются изоморфизмами для всех i > 0, так как остальные члены H,(Dn)
нулевые для всех i. Так, мы можем вычислить
( Z при i = п;
у 0 в остальных случаях.
Пример 2.18. Применяя длинную точную последовательность групп
приведённых гомологии к паре (X, х0), где х0^Ху получаем изоморфизмы
Нп(X, х0) «й Ип(X) для всех п, так как Нп (*0) = 0 для всех л.
Для относительных гомологии имеются и индуцированные
гомоморфизмы, точно так же, как и в не относительном или «абсолютном» случае.
Отображение /: X—► У, для которого /(Л) с В, или, короче, отображение
пар/: (X, Л) -»(У, В), индуцирует гомоморфизмы /и: СП(Х, Л)—>СП(У,В),
так как цепное отображение /2: СП(Х) -♦СпСУ) переводит Сп{А) в СП(В),
поэтому мы получаем корректно определённое отображение факторгрупп
ff СП(Х, Л) -» СП(У, В). Соотношение /сд = д/п выполняется для
относительных цепей, так как оно выполняется для абсолютных цепей. Тогда
согласно предложению 2.9 мы получаем индуцированные гомоморфизмы
Ъ:НП{ХУА)-*НП(У,В).
I Предложение 2.19. Если два отображения /, g: (X, Л) -»(У, В)
гомотопны в классе отображения пар (X, Л) —► (У, В), то /* =g+: НП(Х, Л) —►
->НП(У,В).
Доказательство. Призменный оператор Р из доказательства
теоремы 2.10 переводит Сп{А) в Сп+1 (В), поэтому он индуцирует относительный
§ 2.1. Симплициальные и сингулярные гомологии
155
призменный оператор Р: СП(Х, Л) —»СП+1(У, В). Так как мы просто
переходим к факторгруппам, формула дР + Рд = g: - /fi, остаётся справедливой.
Поэтому отображения /, и gB на относительных группах цепей являются
цепно гомотопными, а значит, они индуцируют один и тот же
гомоморфизм относительных групп гомологии. □
Несложным обобщением длинной точной последовательности пары
(X, Л) является длинная точная последовательность тройки (ХУАУВ)У где
ВСЛСХ:
... -> НП(Л, В) - ЯП(Х, В) -> Н„(Х, Л) - Я,., (Л, В) - ...
Это длинная точная последовательность групп гомологии, связанная с
короткой точной последовательностью цепных комплексов, образованных
короткими точными последовательностями
О -> Сп{А, В) - СП(Х, В) -> С„(Х, Л) -> 0.
Например, если в качестве В взять точку, то длинная точная
последовательность тройки {Х,А,В) превращается в длинную точную
последовательность приведённых гомологии для пары (X, Л).
Вырезание
Важное свойство относительных групп гомологии даёт следующая
теорема вырезания, которая описывает, когда относительные группы
Нп{Х,А) не изменяются при удалении, или вырезании, подмножества
ZcA.
I Теорема 2.20. Пусть даны такие подпространства Z с Л с X, что за-
I мыкание пространства Z содержится во внутренности пространства Л.
I Тогда включение (X — Z,A — Z) ^-> (X, Л) индуцирует изоморфизмы
I Нп{Х - Z,A — Z) —* НП(Х, Л) для всех п. Эквивалентная формулиров-
I ка такова: для подпространств Л,ВсХ, внутренности которых по-
I крывают X, включение (В, Л П В) ^-> (X, Л) индуцирует изоморфизмы
I НП(В,ЛПВ)-*НП(Х,Л) для всех п.
Соответствие между этими двумя версиями
формулировки получается, если положить B = X — ZwZ =
= X — В.Тогда ЛПВ = Л — Z,aусловиеclZсintЛ
эквивалентно тому, что X = int Л U int В, так как X - int В =
= clZ.
Доказательство теоремы вырезания довольно длинное и техническое.
Оно использует конструкцию, известную под названием
«барицентрическое подразделение», которая позволяет вычислять группы гомологии,
используя лишь малые сингулярные симплексы. В метрическом
пространстве «малость» можно определить в терминах диаметров, но для общих
пространств она будет определена в терминах покрытий.
Для пространства X пусть <?/ = {Uj} — набор подпространств в X,
внутренности которых образуют открытое покрытие пространства X, и пусть
156
Глава 2. Гомологии
С*'(X) —подгруппа в С„(Х), состоящая из таких цепей Xln/°"i> что °б-
i
раз каждого отображения а, содержится в некотором множестве из
покрытия °1/. Граничное отображение д: СП(Х) —>Сп_г{Х) переводит С^(Х)
в C^ijCX), поэтому группы СП^(Х) образуют цепной комплекс. Обозначим
группы гомологии этого цепного комплекса через Н^(Х).
I Предложение 2.21. Включение t: С'* (X) ^-> Сп (X) является цепной
I гомотопической эквивалентностью, т.е. существует такое цепное отоб-
I ражение р: СП(Х) —> С*'(Х), что Lp и рб цепно гомотопны тожде-
I ственным отображениям. Следовательно, t индуцирует изоморфизмы
I Н*(X) ъ Яп (X) для всех п.
Доказательство. Процесс барицентрического подразделения будет
выполнен в четыре этапа начиная с самого геометрического и постепенно
будет становиться всё более и более алгебраическим.
1. Барицентрическое подразделение симплексов. Точки симплекса
[v0,..., vn]—это линейные комбинации ХЛу/> гДе 2fi = 1 и t,- ^ 0 для
всех i. Барицентрf или «центр тяжести», симплекса [v0,..., vfl] —это точка
b — ^tiVj, у которой все барицентрические координаты tt равны, а имен-
но t, = l/(n 4- 1) для всех f. Барицентрическое подразделение
симплекса [v0,..., vfl] —это разбиение симплекса [v0,..., vn] на п-мерные
симплексы [Ь, u>0, ...,wn_1], где, по индукции, [и>0,..., wn_{[ —это (п-1)-мерный
симплекс барицентрического подразделения грани [v0,..., vj,..., vn].
Индукция начинается со случая п = О, когда барицентрическое
подразделение для точки [v0] определяется просто как сама точка [v0].
Следующие два случая п = 1, 2 и часть случая п = 3 изображены на рисунке.
Из индуктивного определения следует, что вершины симплексов в
барицентрическом подразделении симплекса [v0,..., vn]—это в точности
барицентры всех fc-мерных граней [v,o,..., v,- ] симплекса [v0, ...,vn] для
О ^ к ^ п. При к = О это даёт исходные вершины vt, так как барицентр
нульмерного симплекса —это он сам. Барицентр симплекса [v,o,...,vfJ
имеет барицентрические координаты t£ = l/(fc + l) при / = i0j ...,^ и t,- = 0
в остальных случаях.
§2.1. Симплициальные и сингулярные гомологии
157
Симплексы размерности п барицентрического подразделения
симплекса Дп вместе со всеми их гранями действительно образуют структуру
д-комплекса на Дп, и даже структуру симплициального комплекса, хотя
уго и не требуется нам для дальнейших рассуждений.
Факт, который нам нужен, состоит в том, что диаметр каждого
симплекса барицентрического подразделения симплекса [v0,..., vn] не
превосходит диаметра симплекса [v0,..., v„], умноженного на п/(п + 1). Здесь
по определению диаметр симплекса — это наибольшее расстояние между
любыми двумя из его точек, и мы используем метрику из объемлющего
евклидова пространства Жп\ содержащего [v0,..., vn]. Диаметр симплекса
равен наибольшему расстоянию между любыми из его вершин, потому
что расстояние между точками v и 5]t,v- симплекса [v0,..., v„]
удовлетворяет неравенству '
I I I I
Чтобы получить оценку n/(n-f 1) для отношения диаметров, мы должны
проверить, что расстояние между любыми двумя вершинами Wj и wk
симплекса [w0,..., wn] барицентрического подразделения симплекса [v0,..., vn]
на превосходит диаметра симплекса [v0,..., v„], умноженного на п/(п +1).
Если ни точка w;, ни точка wk не являются барицентром Ъ симплекса
[v0,..., v„], то эти две точки лежат в некоторой грани симплекса [v0,..., vn],
и мы получаем требуемое индукцией по п. Поэтому мы можем
предположить, что, скажем, точка Wj совпадает с барицентром Ь, и тогда согласно
доказанному ранее неравенству мы можем взять в качестве wk вершину
Vj. Пусть Ь| —барицентр симплекса [v0,..., v),..., v„]; все его
барицентрические координаты равны 1/п, за исключением t, =0. Тогда мы получаем
Ь= ~rTvi H—ХТ^г Сумма этих двух коэффи- ^^.
циентов равна 1, поэтому точка Ъ лежит на от- ^^^L^-^^^1
резке [Vj, Ь,-], соединяющем v, и Ъь причём рас- v, -^~~~ " \
стояние от Ъ до v, равно длине отрезка [v,-, Ь,-],
умноженной на п/{п +1). Следовательно, расстояние от Ъ до v,
ограничено диаметром симплекса [v0,..., vn], умноженным на п/(п + 1).
Значение множителя п/(п +1) в том, что, повторяя барицентрическое
подразделение, мы можем получить симплексы сколь угодно малого
диаметра, так как (п/(п 4- 1))г стремится к 0, когда г стремится к
бесконечности. Существенно, что оценка п/(п + 1) не зависит от формы симплекса,
так как повторение барицентрического подразделения даёт симплексы
Многих разных форм.
2. Барицентрическое подразделение линейных: цепей. Основная часть
доказательства состоит в построении оператора подразделения S: С„(Х)—*
—>СП(Х) и проверке того, что он цепно гомотопен тождественному отоб-
158
Глава 2. Гомологии
ражению. Сначала мы будем строить S и цепную гомотопию в частном
линейном случае.
Для выпуклого множества У в евклидовом пространстве линейные
отображения Л" —* У порождают подгруппу LCn(Y) в СП(У), состоящую
из линейных цепей. Граничное отображение д: Cn(Y) —> Сп_г(У)
переводит LCn(Y) в LCn_!(y), поэтому линейные цепи образуют подкомплекс
в сингулярном цепном комплексе Y. Мы можем однозначно обозначить
линейное отображение Я: Л'1 -»У через [wQ,..., и/„], где w,—образ f-й
вершины симплекса Д'1 при отображении Я. Чтобы не делать исключения
для нульмерных симплексов, удобно увеличить комплекс LC{Y), положив
LC^{Y) =Z (группа, порождённая пустым симплексом [0]) и d[w0] = [01
для всех нульмерных симплексов [w0].
Для каждой точки ЬеУ рассмотрим гомоморфизм b: £СП(У) -*
-»LCn+1(y), заданный на элементах базиса формулой b([w0y..., wn]) =
= [b, w0,..., wn]. Геометрически гомоморфизм Ь можно представить как
конический оператор, переводящий линейную цепь в конус, основание
которого —эта линейная цепь, а вершина —точка Ъ. Применяя обычную
формулу для д, мы получаем соотношение
db([w0,..., wn]) = [w0,..., wn]-b(d[w09..., u/J).
По линейности из этого следует, что дЪ{а) — а — Ъ{да) для всех aeLCn(Y).
Это выражает алгебраически геометрический факт, что граница конуса
состоит из его основания и конуса над границей его основания.
Соотношение дЪ{а) — а — Ь(да) можно переписать в виде db + bd = l, поэтому
Ъ — цепная гомотопия между тождественным отображением и нулевым
отображением на аугментированном цепном комплексе LC{Y).
Теперь мы определим гомоморфизм подразделения S: LCn(Y)—*LCn(Y)
индукцией по п. Пусть Я: Дп —> У — образующая группы LCn(Y), а ЬА —
образ барицентра симплекса Дл при отображении Я. Тогда индуктивная
формула для S имеет вид S(A) = bx{Sdh), где b?: LCn_x(Y) —*LC„(y) —
конический оператор, определённый в предыдущем абзаце. Индукция
начинается с S([0]) = [0], поэтому S — тождественное отображение на
LC_l{Y). Оно также тождественно на 7,С0(У), так как при п = 0 формула
для S превращается в
S([w0]) = w0(Sd[w0]) = wo(S([0])) = wo([0]) = [w0].
Если Я — вложение, образом которого является настоящий п-мерный
симплекс [w0)..., wn], то S(A) — сумма п-мерных симплексов
барицентрического подразделения симплекса [w0,..., wn] с некоторыми знаками,
которые можно вычислить явно. Это видно из сравнения индуктивного
определения гомоморфизма S с индуктивным определением
барицентрического подразделения симплекса.
Давайте проверим, что отображения S удовлетворяют соотношению
dS = Sd, а потому задают цепное отображение цепного комплекса LC{Y)
§ 2.1. Симплициальные и сингулярные гомологии
159
в себя. Так как S = 1 на LC0(Y) и на LC_^ (У), мы, конечно, получаем дБ = S3
на LC0(Y). Требуемое утверждение для п > О доказывает следующее
вычисление, в котором мы опускаем некоторые круглые скобки, чтобы не
загромождать формулы:
dSX = d(bx(SdX)) =
= SdX - bx{dSdX) = (так как дЬх + Ъхд = 1)
= SdX — bx(SddX) = (согласно индукции по п)
= SdA (так как дд = 0).
Теперь мы построим цепную гомотопию 7': LCn{Y) -*1С„+1(У) между
S и тождественным отображением, включающуюся в диаграмму
+ LC2(Y)
LC,(Y)
0
LC2(Y)
LC^Y)
LC0{Y)
LC.^Y)
LC^(Y) ^0
Мы определяем Т на LCn{Y) по индукции, полагая Т = 0 при п = -1
и ГЯ = ЬЯ(Я — ТдА) при п ^ 0. Геометрической мотивацией этой формулы
служит индуктивное определение подразделения призмы Д" х /,
полученное в результате соединения всех симплексов в Ап х {0} U ЭДП х /
с барицентром симплекса Дп х {1}, как показано на рисунке в случае
п = 2. Фактически Т вычисляет образ этого подразделения при проекции
Дпх/->ДП.
Формула цепной гомотопии дТ + Тд = 1 - S тривиальна на ЬС_}^),
где Т = 0и5 = И.На LCn{Y), где п^О, эта формула проверяется
вычислением:
ЭТА = Э(ЬА(А-7ЭА)) =
= А-7ЭА-ЬА(Э(А-7ЭА)) =
= А - ТдХ - bA(SdA + ТддЛ.) =
= X-TdX-SX
(так как дЪх = 1- Ъхд)
(индукцией по п)
(так как дд = 0 и SX = bA(SflA)).
Теперь мы завершили индуктивные рассуждения и можем отказаться
°т группы LC^l(Y)} которая была нужна только для удобства.
Соотношение dT + Td = t-S будет выполняться и без LC. г (Y), так как отображение
Г было нулевым на LC_}(Y).
160
Глава 2. Гомологии
3. Барицентрическое подразделение произвольных цепей. Определим
отображение S: СП(Х) -» СП(Х), полагая Scr = cr^SA" для сингулярного
п-мерного симплекса а: Ап —* X. Так как SAn — сумма п-мерных
симплексов барицентрического подразделения симплекса Дп с некоторыми
знаками, Scr — сумма с соответствующими знаками ограничений а на
п-мерные симплексы барицентрического подразделения симплекса Д".
Оператор S — цепное отображение, так как
dSa = da^SA" = a«dSAn = a:SdAn =
= CT|.S(5]("-1)'A") = (гДе Д" —это i-я грань симплекса Дп)
i
= Ц(-1)^|5Д? = 2(-l)'S(a| Др = S(2(-1)''<t| Д;.') = S(d<7).
i i i
Аналогично.мы определяем Т: СП(Х)-»СП+1(Х) формулой To^cr-jrA",
и это даёт цепную гомотопию между S и тождественным отображением,
так как формула дТ + Тд = 1 - S проверяется вычислением:
дТа = да:ТАп = а^дТА" = а^Ап - SAn - ТдА") =
= <j-S<j- а^ТдА" =<j-S<j- Т(дсг),
где последнее равенство доказывается точно так же, как в предыдущем
выделенном вычислении, с заменой S на Т.
4. Итерированное барицентрическое подразделение. Цепная гомото-
пия между II и итерацией Sm задаётся оператором Dm = J] TS1, так как
dDm + Dmd= £] (дТ81 + Т&д) = £] (дТ31 + Тд81) =
= J] (3T + 73)S'= J] (1-S)S'= J] (S'-S,+1)=l-Sra.
0^i<m 0$i<m 0^i<m
Для каждого сингулярного п-мерного симплекса а: Дп -»X можно
выбрать m так, что Sm(cO лежит в С*;/(Х), так как диаметры
симплексов в Sm(An) будут меньше числа Лебега покрытия симплекса А"
открытыми множествами a~](intUj), если m достаточно велико. (Напомним,
что число Лебега открытого покрытия компактного метрического
пространства — это такое число е > 0, что любое множество, диаметр
которого меньше е, лежит в некотором множестве покрытия; такое число
существует согласно элементарным рассуждениям с компактностью.) Нельзя
ожидать, что одно и то же число m годится для всех а, поэтому определим
гл(сг) как наименьшее т, для которого Sma принадлежит С'^(Х).
Предположим, что мы определяем D: СП(Х) -» СП+1(Х) формулой
Da =Dm(a)a. Чтобы понять, является ли D цепной гомотопией,
преобразуем уравнение цепной гомотопии
dDmiCT)a + Dmia)da = a-Smi(7)a
§ 2.1. Симплициальные и сингулярные гомологии
161
в уравнение с левой частью dDa + Dda, перенеся второй член из левой
части в другую часть уравнения и прибавив Dda к обеим частям:
dDa + Dd(j = (J- [SmMa + Dm{(j)(da)-D{da)].
Если мы определим р(сг) как выражение в скобках в последнем
уравнении, то это уравнение примет вид
dDa + Dda = а-р{а). (*)
Мы утверждаем, что р(сг) € С^(Х). Это очевидно для члена S"'(or)cr. Для
остальной части Dm(cr)(da) -D(dcr) заметим сначала, что если а-}
обозначает ограничение отображения а на ;-ю грань симплекса Ап, то т(сг;) ^
^т(сг), поэтому каждый член TSl{<jj) в D(dcr) будет членом в D,;i((j)(dcr).
Таким образом, Dmi(J)(da) -D (дет) —сумма членов TSl(<Jj), где z ^т(сг;),
и эти члены лежат в С'*'(Х), так как Т переводит С^СХ) в С'*'(Х).
Поэтому мы можем рассматривать уравнение (*) как определение
отображения р : Сп{Х) -» С^(Х). Эти отображения р для всевозможных п
образуют цепное отображение, так как из (*) следует, что др(сг) = да -
-dDd(a) = р(да). Уравнение (*) говорит, что dD + Dd = l — tp для
включения i: C^(X)^->Cn(X). Кроме того, pt = l, так как D тождественно
равно нулю на С^(Х), поскольку гл(сг) =0, если а принадлежит С^{Х), а
потому Da определяется как сумма по пустому множеству. Таким образом,
мы показали, что отображение р цепно гомотопически обратно к i. □
Доказательство теоремы вырезания. Мы будем доказывать
вторую версию, в которой участвует разложение X = AU В. Для покрытия
^/ = {А,В} мы будем обозначать группы С^(Х) через СП(Л-ЬВ), что
указывает на то, что они состоят из сумм цепей в Л и цепей в В. В
конце предыдущего доказательства мы получили формулы 3D + Dd — 1 - tp
и pi = t. Все отображения, встречающиеся в этих формулах, переводят
цепи в Л в цепи в А, поэтому они выдерживают факторизацию по цепям
в А. Полученные факторотображения автоматически удовлетворяют тем
же самым двум формулам, поэтому включение
Сп{А + В)/Сп№ -> СП(Х)/СП(Л)
индуцирует изоморфизм гомологии. Отображение
Сп{В)/Сп{АПВ) - СП(Л + В)/СП(Л),
индуцированное включением, очевидно, является изоморфизмом, так как
обе факторгруппы свободные и их ёбазисом служат сингулярные п-мер-
ные симплексы в В, не лежащие в А. Следовательно, мы получаем
требуемый изоморфизм Нп(В,АПВ)ъНп(Х, Л), индуцированный
включением. □
Всё, что остаётся для доказательства теоремы 2.13, — это заменить
относительные группы гомологии абсолютными группами гомологии. Это
Позволяет сделать следующий результат.
(>3ак. М)55
162
Глава 2. Гомологии
I Предложение 2.22. Для хороших пар (X, А) факторотображение
I q: (X, Л) -»{XIАу А/А) индуцирует изоморфизмы
I q*:Hn{X,A)->Hn{X/A,A/A)*Hn{X/A) для всех п.
Доказательство. Пусть V — окрестность А в X, деформационно ре-
трагирующаяся на А. Мы имеем коммутативную диаграмму
Нп (X, А) > Нп (X, V) * Нп (X - А, V - А)
U. <?. <?.
Нп {XIА, А/А) ► Яп (Х/Л, V/Л) -< Нп {X/А - A/A, V/A - А/А)
Горизонтальное отображение вверху слева — изоморфизм, так как в
длинной точной последовательности тройки (X, V, Л) группы H„(V, Л)
нулевые для всех л, потому что деформационная ретракция V на Л даёт
гомотопическую эквивалентность пар (V, Л) ^ (Л, Л), а НП(Л, Л) =0.
Деформационная ретракция V на Л индуцирует деформационную
ретракцию V/Л на А/А, поэтому то же самое рассуждение показывает, что
горизонтальное отображение внизу слева тоже изоморфизм. Другие два
горизонтальных отображения — изоморфизмы по теореме вырезания. Правое
вертикальное отображение q+ —изоморфизм, так как ограничение q на
дополнение множества Л — гомеоморфизм. Из коммутативности
диаграммы следует, что левое отображение q¥ — изоморфизм. □
Это предложение показывает, что относительные гомологии можно
представить как приведённые абсолютные гомологии в случае хороших
пар (X, Л). В действительности есть способ сделать это
и для произвольных пар. Рассмотрим пространство X U
иСЛ, где СА — конус (Л х/)/(Л х {0}), основание Л х {1}
которого мы отождествляем с Л с X. Используя терми- X
нологию, введённую в главе 0, X U СА можно также
описать как конус отображения включения Л С->Х. Утверждение состоит
в том, что группа ЯП(Х, Л) изоморфна Hn{X\JCA) для всех л посредством
последовательности изоморфизмов
Яп(ХиСЛ) ъ Hn{XUCA,CA) ъ Hn{XUCA- {р}, СА-{р})ъНп{Х,А),
где р € СА — вершина конуса. Первый изоморфизм происходит из
точной последовательности пары, если воспользоваться тем фактом, что
пространство СА стягиваемо. Второй изоморфизм — изоморфизм вырезания,
а третий изоморфизм происходит из деформационной ретракции
пространства СА — {р} на Л.
Вот применение предложения 2.22.
§ 2.1. Симплициальные и сингулярные гомологии
163
Пример 2.23. Давайте найдём явные циклы, представляющие
образующие бесконечных циклических групп Hn(D'\dDn) и Hn(Sn). Заменив
ф", SDn) на эквивалентную пару (Дп, дДп), мы покажем индукцией по п,
что тождественное отображение in: Д" —* Д", рассматриваемое как
сингулярный n-мерный симплекс, является циклом, порождающим группу
Яп(Дп,дДп)- Ясно, что это цикл, так как мы рассматриваем
относительные гомологии. При п = 0 он, конечно, представляет образующую.
Чтобы доказать шаг индукции, рассмотрим Л с Д" —объединение всех
(п — 1)-мерных граней симплекса Дп, кроме одной. Мы утверждаем, что
имеют место изоморфизмы
ни(&\дА") -н^сад'и) -^нп_1(дп-\здп-1).
Первый изоморфизм —граничное отображение в длинной точной
последовательности тройки (Дп, ЭД", Л), в которой третьи члены Н((Ап, Л)
нулевые, так как Дп деформационно ретрагируется на Л, а потому (Дп, Л) с*
с* (Л, Л). Второй изоморфизм следует из предыдущего предложения, так
как мы имеем дело с хорошими парами, а включение Д"-1 <-> ЭДП в
качестве грани, не содержащейся в Л, индуцирует гомеоморфизм факторпро-
странств Дп-1/дД"-1 ъдАп/А. Шаг индукции этим доказывается, так как
первый изоморфизм переводит цикл in в цикл din, который равен ±in_i_
вСп_х{дАп,А).
Чтобы найти цикл, порождающий группу Hn(Sn), давайте рассмотрим
S" как два n-мерных симплекса Д" и Д!], границы которых отождествлены
очевидным способом, с сохранением порядка вершин. Разность Д" - Д£,
рассматриваемая как сингулярная n-мерная цепь, тогда является циклом.
Мы утверждаем, что этот цикл представляет образующую группы Hn(Sn),
если предположить, что п > О, так что последняя группа бесконечная
циклическая. Чтобы убедиться в этом, рассмотрим изоморфизмы
Hn(stl) - Hn{s\ д!р - нп(А"]уэд;),
где первый изоморфизм происходит из длинной точной
последовательности пары (Sn,A%)> a второй изоморфизм проверяется переходом к фак-
Торпространствам, как и раньше. При этих изоморфизмах цикл Д" - Д1[
в первой группе соответствует циклу Д" в третьей группе, который
представляет образующую этой группы, как мы уже видели. Поэтому Д" - Д£
Представляет образующую группы Hn(Sn).
Из предложения 2.22 следует, что свойство вырезания выполняется
также для подкомплексов CW-комплексов.
I Следствие 2.24. Если GW-комплекс Х является объединением
подкомплексов Л и В, то включение (В, АПВ)<-> (X, А) индуцирует
изоморфизмы Нп(В,АПВ) -> Пп(Х, А) для всех п.
164
Глава 2. Гомологии
Доказательство. Так как CW-пары хорошие, предложение 2.22
позволяет нам перейти к факторпространствам В/(АГ\Е) и Х/А, которые го-
меоморфны, если предположить, что у нас не тривиальный случай, когда1
ДПВ = 0. □
А вот ещё одно применение предложения 2.22.
I Следствие 2.25. Для букета V Ха включения ia : Ха ^-> \J Ха индуци-
I а а
I руют изоморфизмы
I ©1'«.:®ВД«)-нп(\/*«>
I а а а
I при условии, что в букете отождествляются такие отмеченные точки
I ха € Ха, что пары (Ха, ха) являются хорошими.
Доказательство. Так как приведённые гомологии — это то же самое,
что гомологии относительно отмеченной точки, это следует из
предложения, если положить
(Х,Д)=(Ц*а,Ц{*а}). D
а а
Теперь применим разработанную нами технику, чтобы получить
классический результат Брауэра, который примерно с 1910 г. известен под на-
званием «инвариантность размерности». Он утверждает, в частности, что
пространство Шт не гомеоморфно R", если тфп.
Теорема 2.26. Если непустые открытые множества U с IRm и VcLf
гомеоморфны, тот = п.
Доказательство. Для х € U мы имеем
Hk(U, U - {*}) ъ Hfc(Rm, Rm - {*})
согласно вырезанию. Из длинной точной последовательности для пары
(Rm, Шт ~ {х}) мы получаем
Hk(Rm, Шт - {х}) « Нк_г (Rm - {*}).
Так как Шт - {х} деформационно ретрагируется на сферу S'"""1, мы
заключаем, что Hk(U\U - {л:}) —это Z для к = т и 0 в остальных случаях.
Согласно тем же самым рассуждениям Нк(У, V — {у}) — это Z для к = п
и 0 в остальных случаях. Так как гомеоморфизм h: U -* V индуцирует
изоморфизмы Hk(U, U - {х}) -*Нк(У, V - {h(x)}) для всех /с, у нас должно
бытьт = п. □
Обобщая идею этого доказательства, определим локальные группы
гомологии пространства X в точке XGX как группы Нп(Х,Х - {х}). Для
1 В этом тривиальном случае эти факторпространства также гомеоморфны, так как
каждое из них представляет собой несвязное объединение пространства В и точки. —Прим. ред.
§ 2.1. Симплициальные и сингулярные гомологии
165
любой открытой окрестности U точки х вырезание даёт изоморфизмы
Нп{Х,Х-{х})ъНп{и,и-{х}),
следовательно, эти группы зависят только от локальной топологии
пространства X вблизи точки х. Гомеоморфизм f:X-*Y должен
индуцировать изоморфизмы НП(Х, X - {х}) ^ Hn{Y, Y - {/(х)}) для всех х и п.
Таким образом, эти локальные группы гомологии можно применить,
чтобы выяснить, когда пространства не являются локально гомеоморфными
в некоторых точках, как в предыдущем доказательстве. В задачах даны
некоторые дополнительные примеры этого применения.
Естественность
Точные последовательности, которые мы построили, имеют
дополнительное свойство, которое позже будет важным в ключевых моментах
многих рассуждений, хотя на первый взгляд оно может показаться просто
бесполезной технической деталью, не представляющей интереса. Мы
обсудим это свойство сразу, чтобы в дальнейшем не прерывать рассуждения
для его проверки, но читатель может пока отложить внимательное чтение
этого обсуждения.
Это свойство называют естественностью. Например, если мы
говорим, что длинная точная последовательность пары является
естественной, то это означает, что для отображения /: (X, А) -* (У, В) диаграмма
Ни(Л)
НП{Х) -^ НП(Х, А) —^ Нп-гШ
и
л
/.
... - НП{В) —+ НП(У) -^- НП(У, В) —l-^ H^iB) - ...
коммутативна. Коммутативность квадратов, в которые входят i* и ;„,
следует из очевидной коммутативности соответствующих квадратов групп
Цепей, где вместо Нп стоит Сп. Для оставшегося квадрата, когда мы
определяли индуцированные гомоморфизмы, мы видели, что f$d = df~ на
Уровне цепей. Тогда для класса [а] еНп{Х, А), представленного
относительным циклом а, мы получаем
/Ма] = Д[йа] - [/„За] - Ща] = Э[/„а] - ЭД[а].
Мы могли бы также сослаться на общий алгебраический факт, что
Длинная точная последовательность групп гомологии, связанная с
короткой точной последовательностью цепных комплексов, является
естественной: для коммутативной диаграммы коротких точных последовательно-
166
Глава 2. Гомологии
стеи цепных комплексов
+ А'
п + 1
А'
Y
А'
Лп-1
-^д
■п + 1
+ в'
V
+ Ап
-> А
П + 1
в' -
11-1
■* B-+i
lJ"
■*в„
^в
Г~р С"+1
I''
п-1
У.
V
) у "-1
■*с,
п+1
о
■*сП
■+С,
\
о
п-1
I
о
о
индуцированная диаграмма
н„Ш-
р.
Нп(С)
-**„_! (А)
«*
НП(В;) -^ Нп(С0 -^ Нп_, (АО
... ^Нп(А0-
коммутативна. Коммутативность первых двух квадратов очевидна, так
как из равенства fii = i'a следует, что /3*i* = i^a*, а из yj = j'ft следует
Y*J* = J'*P*- Что же касается третьего квадрата, то напомним, что
отображение д: ff„(C) -*Hn_](A) определялось как д[с] = [а], где с = ;(Ь)
и i(a) = db. Тогда d[y(c)] = [a(a)], так как y{c) = yj(b)=j'(f5{b)) и i'(a(a)) =
= /?i(a) = /3d(b) = d/?(b). Следовательно, ду#[с] = a*[a] = а+д[с]. Из этого
алгебраического факта также следует также естественность длинной
точной последовательности тройки и длинной точной последовательности
приведённых гомологии пары.
Наконец, имеет место естественность длинной точной
последовательности в теореме 2.13, т. е. коммутативна следующая диаграмма:
... ^ НП(А) -^ НП(Х) -^ Нп{Х/А) —U- Нп.г{А) ^ ...
т
Н„(В)
-^- Яп (7) -^* Нп (Y/B) —^ Яп_, (В)
§ 2.1. Симплициальные и сингулярные гомологии
167
где через i и q обозначены включение и отображение факторизации,
а отображение /: Х/Л —> Y/В индуцировано отображением /. Первые два
квадрата коммутативны, так как fi = if и fq = qf'. Третий квадрат можно
расширить до
Нп(Х/А) -£-*- Нп(Х/А, А/А) *Л- Н„(Х, А)
Нп (У /В) —^ Нп {Y IB, В/В) <Л- Нп (У, В)
Н„_,(А)
+ Нп^(У,В)
Мы доказали коммутативность первого и третьего квадратов, а второй
квадрат коммутативен, так как fq—qf.
Эквивалентность симплициальных и сингулярных гомологии
Мы можем применить полученные ранее результаты, чтобы показать,
что группы симплициальных и сингулярных гомологии Д-комплекса
всегда изоморфны. Для доказательства удобно рассматривать также и
относительный случай, поэтому пусть X — Д-комплекс, а А с X — его
подкомплекс. Таким образом, Л —это Д-комплекс, образованный
объединением некоторых симплексов комплекса X. Относительные группы Н* (X, А)
можно определить таким же способом, как и для сингулярных гомологии,
посредством относительных цепей Ап(Х,А) = Ап(Х)/Ап(А). Это
приводит к длинной точной последовательности групп симплициальных
гомологии для пары (X, А) с помощью тех же самыми алгебраических
рассуждений, что и для сингулярных гомологии. Имеет место канонический
гомоморфизм Н*(X, А) —>Нп{Х, Л), индуцированный цепным
отображением ДП(Х, А) —> С„(Х, Л), переводящим каждый п-мерный симплекс
комплекса X в его характеристическое отображение о: Д" —>Х. Не
исключена возможность Л = 0, когда относительные группы сводятся к
абсолютным группам.
I Теорема 2.27. Гомоморфизмы Н^(Х, Л) —> НП(Х, Л) — изоморфизмы
для всех п и всех пар Д-комплексов (X, Л).
Доказательство. Сначала мы разберём случай, когда комплекс X
конечномерен, а подкомплекс Л пуст. Если Хк — это fc-мерный остов
комплекса X, состоящий из всех симплексов размерности к или меньше, то
Мы имеем коммутативную диаграмму точных последовательностей
ЯГ1(Х,Л)—^ЙП_!(Л)
Нп{Х/А)-^Нп{Х/А,А/А) -4г
/.
/.
/.
Hn{Y/B) -^ Hn(Y/B, В/В) ^— НИ(У, В)
Л
H„-!(B)
Сначала покажем, что первое и четвёртое вертикальные отображения —
Изоморфизмы для всех п. Группа симплициальных цепей Ап(Хк, Xfc_1) ну-
168
Глава 2. Гомологии
левая при п Ф к и свободная абелева, базисом которой служат /с-мерные
симплексы комплекса X, при п = к. Следовательно, Н^{Хк,Хк~1) имеет
точно такое же описание. Соответствующие группы сингулярных
гомологии Нп(Хк, Хк~г) можно вычислить, рассматривая отображение
Ф: Ц(Д*,ЭД*)-(Х*,Х'С-1),
а
образованное характеристическими отображениями Д* -* X для всех
/с-мерных симплексов комплекса X. Так как Ф индуцирует гомеоморфизм
факторпространств
Цька/Цдька»хк/хк-\
а а
оно индуцирует изоморфизмы для всех групп сингулярных гомологии.
Таким образом, Нп (Хку Хк~1) — нуль при п Ф ку в то время как при п = к эта
группа свободная абелева с базисом, представленным относительными
циклами, заданными характеристическими отображениями всех
/с-мерных симплексов комплекса X, вследствие того факта, что Нк{Ак, дАк)
порождается тождественным отображением 5к —> 5к, как мы показали в
примере 2.23. Поэтому отображение Я* (Х^Х*-1) -*Нк(Хку Хк~1) —
изоморфизм.
Применяя индукцию по /с, мы можем предположить, что второе и
пятое вертикальные отображения в предыдущей диаграмме тоже
изоморфизмы. Тогда следующая часто используемая важная алгебраическая
лемма влечёт, что среднее вертикальное отображение —изоморфизм. Это
завершает доказательство в случае, когда комплекс X конечномерен и
Л = 0.
I 5-лемма. Если в коммутативной диаграмме абелевых групп
I A —U-B—]-^C—k-+D—^E
■ Т Y т т »
I Л' -^ В' -L» С -^ D' -^ Е'
I обе строки точны и а, /3, 5, е — изоморфизмы, то у тоже изоморфизм.
Доказательство. Достаточно доказать следующее:
а) гомоморфизм у сюръективен, если /3 и 5 сюръективны, а е инъективен;
б) гомоморфизм у инъективен, если /3 и 5 инъективны, а а сюръективен.
Доказательство этих двух утверждений — прямой диаграммный
поиск. В действительности рассуждение проводится единственно
возможным путём, и было бы хорошим упражнением для читателя закрыть
сейчас книгу и воспроизвести доказательство, не заглядывая в неё.
Чтобы доказать а), начнём с элемента с' € С'. Тогда /с7(с7) = 5{d) для
некоторого d € D, так как гомоморфизм 5 сюръективен. Так как
гомоморфизм е инъективен и el(d)=l'5(d)=tk'(c')=0t мы получаем, что
§ 2.1. Симплициальные и сингулярные гомологии
169
1(d) = 0, значит, d = fc(c) для некоторого с^С согласно точности
верхней строки. Разность с' — у (с) переходит в 0 при отображении fc', так как
Jt'(c') - fcV(c) = к'(с') - 5к(с) = к'(с') - 5(d) = 0. Поэтому с' - у (с) = j'(b')
для некоторого Ъ' е В' согласно точности. Так как /3 сюръективен, b/ = /3(b)
для некоторого Ь е В, и тогда г(с + j(b)) = г(с) + ГДЬ) = У 00 + У^(Ь) =
= у00 +j'(b') = с', а это показывает, что гомоморфизм у сюръективен.
Чтобы доказать б), предположим, что у (с) = 0. Так как 5 инъективен,
равенство 5к(с) = JcY00 =0 влечёт, что fc(c) = 0, поэтому с = ;(Ь) для
некоторого b GВ. Для элемента /3(b) имеют место равенства j'/3(b) = yj(b) =
= у(с) = 0, поэтому /3(b) = i'(a') для некоторого о! е А'. Так как а
сюръективен, а' — а(а) для некоторого а е А. Так как /3 инъективен, равенство
/3(i(a)-b) = /3i(a)-/3(b) = i'a(a)-/3(b) = i'(a') ~/3(b) = 0
влечёт, что i(a)-b = 0. Таким образом, b = i(a), поэтому c=;(b)=./i(a) = 0,
так как ;i = 0. Это показывает, что ядро гомоморфизма у тривиально. □
Возвращаясь к доказательству теоремы, мы теперь рассмотрим
случай, когда комплекс X бесконечномерный. Мы воспользуемся следующим
фактом: компактное множество в X может пересекать только конечное
число открытых симплексов в X, т. е. симплексов, у которых удалены все
собственные грани. Это общий факт о CW-комплексах, доказанный в
приложении, но вот его прямое доказательство для Д-комплексов. Если бы
компактное множество С пересекало бесконечно много открытых
симплексов, то оно содержало бы бесконечную последовательность точек xh
любые две из которых лежали бы в разных открытых симплексах. Тогда
множества Ul=Х — |J{x;} (которые являются открытыми, так как их про-
образы при характеристических отображениях всех симплексов,
очевидно, открыты) образуют открытое покрытие множества С, у которого нет
конечного подпокрытия.
Этим можно воспользоваться, чтобы доказать, что отображение
Н^(Х)-*Нп(Х) сюръективно. Представим данный элемент группы Ип(Х)
сингулярным л-мерным циклом z. Он представляет собой линейную
комбинацию конечного числа сингулярных симплексов с компактными
образами, пересекающими лишь конечное число открытых симплексов в X,
а потому содержится в Хк для некоторого к. Мы показали, что
отображение Н*(Хк) —> Нп(Хк) — изоморфизм; в частности, оно сюръективно.
Таким образом, z гомологичен в Хк (а значит, и в X) симплициальному
циклу. Это доказывает сюръективность. Инъективность доказывается
аналогично. Если симплициальный гг-мерный цикл z является границей
сингулярной цепи в X, то эта цепь имеет компактный образ, а потому должна
лежать в некотором остове Хк. Таким образом, цикл z представляет элемент
ядра отображения Н*(Хк)->Нп(Хк). Но мы знаем, что это отображение
инъективно, поэтому z — симплициальная граница в Хк, а потому и в X.
170
Глава 2. Гомологии
Остаётся разобрать случай, когда X произвольно и Л -ф 0, но он
следует из абсолютного случая, если применить 5-лемму к каноническому
отображению из длинной точной последовательности групп симплици-
альных гомологии для пары (X, А) в соответствующую длинную точную
последовательность групп сингулярных гомологии. G
Из этой теоремы можно вывести, что группа НМ(Х) конечно
порождённая, если X — Д-комплекс с конечным числом п-мерных симплексов.
Действительно, в этом случае группа симплициальных цепей ДП(Х)
конечно порождённая, следовательно, её подгруппа циклов тоже, а потому
и факторгруппа Н*{Х) также конечно порождённая. Если мы запишем
Нп(Х) в виде прямой суммы циклических групп, то число слагаемых вида
Z известно под названием n-го числа Бетти пространства X, а целые
числа, указывающие порядки конечных циклических слагаемых, называют
коэффициентами кручения.
Интересно, что гомологии первоначально представляли себе не как
последовательность групп, а как числа Бетти и коэффициенты кручения.
Можно ведь вычислить числа Бетти и коэффициенты кручения по симпли-
циальным граничным отображениям, не упоминая группы гомологии.
Такая вычислительная точка зрения, что гомологии являются числами, а не
группами, преобладала со времени, когда Пуанкаре впервые начал
серьёзную работу с гомологиями приблизительно в 1900 г., и вплоть до 1920-х
годов, когда в обиход вошла более абстрактная групповая точка зрения. В
течение этого периода под «гомологиями» подразумевались прежде всего
«симплициальные гомологии», и прошло ещё 20 лет до того, как переход
к сингулярным гомологиям был завершён. Окончательное определение
сингулярных гомологии появляется только в 1944 г. в статье Эйленберга,
использовавшего вклад многих других математиков, особенно Александе-
ра и Лефшеца. В течение нескольких следующих лет была сформирована
оставшая часть структурной теории гомологии, изложенная нами. Первое
полное изложение появилось в классической книге [21].
Задачи
1. Каким известным пространством является Д-комплекс,
полученный из двумерного симплекса [v0,v1,v2] при отождествлении граней
[v0, vj и [у1э v2] с сохранением порядка вершин?
2. Докажите, что Д-комплекс, полученный из Д3 при отождествлении
рёбер [v0, vx] ~ [vb v3] и [v0, v2] ^ [v2, v31, деформационно ретрагируется на
бутылку Клейна. Укажите другие пары отождествляемых рёбер, которые
дают Д-комплексы, деформационно ретрагирующиеся на тор, двумерную
сферу и MP2.
3. Постройте структуру Д-комплекса на RPn путём факторизации
структуры Д-комплекса на Sn, имеющей в качестве вершин два вектора
единичной длины на каждой координатной оси в Rn+1.
§ 2.1. Симплициальные и сингулярные гомологии
171
4. Вычислите группы симплициальных гомологии треугольного
парашюта, полученного из Д2 отождествлением трёх его вершин в одну точку.
5. Вычислите группы симплициальных гомологии бутылки Клейна,
используя структуру Д-комплекса, описанную в начале этого параграфа.
6. Вычислите группы симплициальных гомологии Д-комплекса,
полученного из п-f 1 двумерных симплексов Д2,..., Д2 отождествлением
всех трёх рёбер симплекса Д2 в одно ребро, а при i > 0 отождествлением
рёбер [vqjVJ и [v1}v2] симплекса Д2 в одно ребро и его ребра [v0,v2]
с ребром [v0, vj симплекса Д?_г
7. Найдите способ отождествления пар граней симплекса Д3,
дающий структуру Д-комплекса на S3 с единственным трёхмерным
симплексом, и вычислите группы симплициальных гомологии этого Д-комплекса.
8. Построим трёхмерный Д-комплекс X из п тетраэдров Т], ..., Тп в два
шага следующим образом. Сначала расположим тетраэдры циклически,
как показано на рисунке, чтобы каждый тетраэдр 7) имел общую
вертикальную грань с двумя своими соседями ^_х и 7}+1,
где индексы берутся по модулю п. Затем
отождествим нижнюю грань тетраэдра 7) с верхней
гранью тетраэдра 7)+1 для каждого i. Покажите, что
группы симплициальных гомологии комплекса X
в размерностях 0, 1, 2, 3 равны Z, Z„, О, Z соответственно. [Пространство
X — это один из примеров линзового пространства; общий случай описан
в примере 2.43.]
9. Вычислите группы гомологии Д-комплекса X, полученного из Дп
отождествлением всех граней одной и той же размерности. Таким
образом, у X есть ровно один fc-мерный симплекс для каждого к ^ п.
10. а) Докажите, что факторпространство конечного набора
непересекающихся двумерных симплексов, полученное при отождествлении пар
рёбер, всегда является поверхностью, локально гомеоморфной R2.
б) Докажите, что рёбра всегда можно ориентировать так, чтобы
задать структуру Д-комплекса на поверхности, полученной при такой
факторизации. [Это труднее.]
11. Покажите, что если А — ретракт пространства X, то отображение
НП(Д)—>НП(Х), индуцированное включением АсХ, инъективно.
12. Покажите, что цепная гомотопия цепных отображений —
отношение эквивалентности.
13. Проверьте, что из условия / си g следует равенство /# = g+ для
индуцированных гомоморфизмов приведённых групп гомологии.
14. Выясните, существует ли короткая точная последовательность
0 —> Z4 —> Z8 Ф Z2 —* Z4 —> 0. Вообще, выясните, какие абелевы группы А
включаются в короткую точную последовательность 0—>Zp„, —> Л —>Z;,» —*0,
где р — простое число. Что можно сказать в случае коротких точных
последовательностей 0->Z->A->Zn->0?
172
Глава 2. Гомологии
15. Для точной последовательности A—+B—*C—+D—*E покажите,
что С = О тогда и только тогда, когда отображение А —> В сюръективно
и отображение D —> Е инъективно. Значит, для пары пространств (X, А)
включение А<-»X индуцирует изоморфизмы всех групп гомологии тогда
и только тогда, когда НП(Х, Л) =0 для всех п.
16. а) Докажите, что Н0(Х, Л) = 0 тогда и только тогда, когда Л
пересекает каждую компоненту линейной связности пространства X.
б) Докажите, что Н1(Х,А) = 0 тогда и только тогда, когда
гомоморфизм Нг{А) —>Нг(Х) сюръективен и каждая компонента линейной
связности пространства X содержит не более одной компоненты линейной
связности пространства Л.
17. а) Вычислите группы гомологии Нп{Х,А), когда X—это S2 или
S1 х S1, а Л —- конечный набор точек в X.
б) Вычислите группы Нп(Х,А) и Нп(Х,В)
для замкнутой ориентируемой поверхности X
рода два с окружностями Л и В, указанными на
рисунке. [Что такое пространства Х/А и Х/В?]
18. Покажите, что для подпространства Q С R относительная группа
гомологии HY(R, Q) свободная абелева, и найдите базис.
19. Вычислите группы гомологии подпространства в / х /, состоящего
из четырёх граничных рёбер и всех внутренних точек, первая координата
которых рациональна.
20. Покажите, что НП(Х) &Hn+l(SX) для всех п, где SX — надстройка
над X. Вообще, представляя SX как объединение двух конусов СХ с
отождествлёнными основаниями, вычислите приведённые группы гомологии
объединения п конусов СХ с отождествлёнными основаниями.
21. Сделайте предыдущую задачу более конкретной, построив явные
цепные отображения s: Cn{X) —>Cn+1(SX)y индуцирующие изоморфизмы
Hn(X)->Hn+1(SX).
22. Докажите индукцией по размерности следующие факты о го-
мологиях конечномерного CW-комплекса Х, используя наблюдение, что
Хп/Хп_1 является букетом п-мерных сфер.
а) Если X имеет размерность п, то Н,(Х) = 0 при i > п и группа Н,?(Х)
свободна.
б) Если нет клеток размерностей п — 1 и п +1, то группа НП(Х) является
свободной, причём её базис находится во взаимно однозначном
соответствии с п-мерными клетками.
в) Если у X есть к клеток размерности п, то группа Нп{Х) порождается
не более чем к элементами.
23. Покажите, что второе барицентрическое подразделение Д-ком-
плекса является симплициальным комплексом. А именно, покажите, что
первое барицентрическое подразделение даёт Д-комплекс, обладающий
тем свойством, что у каждого его симплекса все вершины различны, а за-
§ 2.1. Симплициальные и сингулярные гомологии
173
тем покажите, что для Д-комплекса с таким свойством барицентрическое
подразделение даёт симплициальный комплекс.
24. Покажите, что каждый л-мерный симплекс в барицентрическом
подразделении симплекса Дп задаётся л неравенствами t^^t^^.-.^t,- в
барицентрических координатах, где (*0,..., *п) — перестановка чисел (0,..., л).
25. Найдите явную, неиндуктивную формулу для оператора
барицентрического подразделения S: СП(Х)-*СП(Х).
26. Покажите, что группа Нг(Х,Л) не изоморфна Н-1(Х/А)> если
Х = [О,1] и А — последовательность 1,1/2,1/3,... вместе с её пределом 0.
[См. пример 1.25.]
27. Пусть /: (X, А) -* (У, В) ~ отображение, для которого как само
отображение /: X —* Yy так и его ограничение /: А —> В являются
гомотопическими эквивалентностями.
а) Докажите, что /*: НП(Х, Л)~>ЯЛ(7, В) — изоморфизм для всех п.
б) Для включения /: (Dn, S""1) <-> (D", Dn - {0}) покажите, что / не
является гомотопической эквивалентностью пар, т.е. не существует
такого отображения g: (Dn, Dn - {0}) —> (Dn, S""1), что /g и gf гомотопны
тождественным отображениям в классе отображений пар. [Заметьте, что
гомотопическая эквивалентность пар (X, А) ~► (У, В) является также
гомотопической эквивалентностью для пар, полученных при замене А и В
их замыканиями.]
28. Пусть X — конус над одномерным остовом симплекса Д3, т. е.
объединение всех отрезков, соединяющих точки шести рёбер симплекса Д3 с
его барицентром. Вычислите локальные группы гомологии Нп (X, X - {х})
для всех хеХ. Определим ЭХ как подпространство таких точек х, что
Нп(Ху X — {х}) = 0 для всех л; вычислите локальные группы гомологии
Нп(дХ, дХ — {х}). Применяя эти вычисления, выясните, какие
подмножества А с X обладают тем свойством, что /(Л) с А для всех
гомеоморфизмов/: Х-*Х.
29. Покажите, что группы гомологии для пространств S1 x S1 и S1 V
V Sl v S2 изоморфны во всех размерностях, а для их универсальных
накрывающих пространств — нет.
30. В каждой из следующих коммутативных диаграмм
предполагается, что все отображения, кроме одного, —изоморфизмы. Докажите, что
остающееся отображение тоже должно быть изоморфизмом.
А ^В А ^В А ^В
I I \
т т I
С С ^D С ^D
31. В обозначениях 5-леммы приведите пример, когда отображения а,
/3, 5 и е нулевые, а отображение у отлично от нуля. Это можно сделать
с короткими точными последовательностями, в которых все группы
равны или Z, или 0.
\/
174
Глава 2. Гомологии
§ 2.2. Вычисления и приложения
Теперь, когда основные свойства гомологии установлены, мы
получим большую свободу действий. Наша первая тема, в которой
используется вычисление группы Hn(Sn), — брауэровское понятие степени для
отображений Sn —>Sn. Исторически введение этого понятия Брауэром в 1910—
1912 гг. предшествовало строгому описанию гомологии. Таким образом,
его определение было совсем другим; оно использовало метод симпли-
циальной аппроксимации, который мы разъясняем в §2.С. Более
позднее определение в терминах гомологии, конечно, более изящно, хотя при
этом, возможно, происходит некоторая потеря геометрической интуиции.
Духу определения Брауэра больше соответствует третий подход,
использующий дифференциальную топологию, весьма прозрачно изложенный
в [54].
Степень
Для отображения /: S" —> S", где п > 0, индуцированное
отображение /*: Hn(Sn) —>Hn(Stl) —гомоморфизм бесконечной циклической
группы в себя, а потому он должен иметь вид /*(а) = da для некоторого целого
числа d, зависящего только от /. Это число называют степенью
отображения / и обозначают deg/. Вот некоторые основные свойства степени.
а) degl = l, так как 1* = 1.
б) deg/ = 0, если отображение / не сюръективно. Действительно, если
мы выберем точку х0 €S" — /(S"), то / можно представить в виде
композиции Sn —> Sn -{xQ}<-^Sny aHn(S" -{x0}) = 0, так как пространство
Sn — {х0} стягиваемо. Следовательно, /* = 0.
в) Если / ^g, то deg/ = degg, так как /* = g*. Обратное утверждение,
что /^g, если deg/ = degg,— это фундаментальная теорема Хопфа
примерно 1925 г., которую мы доказываем в следствии 4.25.
г) deg/g = deg/degg, так как (/g)*=/*g*. Как следствие получаем, что
deg/ = dbl, если / гомотопическая эквивалентность, так как из
условия / g ы 1 следует, что deg / deg g = deg 1 = 1.
д) Если / — симметрия сферы S", которая оставляет неподвижными
точки под сферы Sn~l и переставляет две дополнительные полусферы, то
deg/ = — 1. Действительно, мы можем снабдить Sn структурой Д-ком-
плекса с этими двумя полусферами в качестве двух её п-мерных
симплексов Д^ и Д!}. Тогда п-мерная цепь Д" - Д^ представляет
образующую группы Hn(Sn), как мы видели в примере 2.23. Поэтому
симметрия, переставляющая Д" и Д£, переводит эту образующую в её саму
с противоположным знаком.
е) Антиподальное отображение -1: S" —> S", заданное формулой дг —»—дг,
имеет степень (-1)п4"\ так как оно является композицией п + 1
симметрии, каждая из которых меняет знак одной координаты в Rn+1.
§ 2.2. Вычисления и приложения
175
ж) Если отображение /: S" —* Sn не имеет неподвижных точек, то deg/ =
= (—l)n+1. Действительно, если /00 фх, то отрезок с концами /00
и —х, заданный формулой t —> (1 — 0/00 - t;t для 0 $ t $ 1, не
проходит через начало координат. Следовательно, если / не имеет
неподвижных точек, то формула
/ U) = [(1 - О/0О - tjc]/|(l - t)/Q0 - tx\
определяет гомотопию отображения / в антиподалыюе отображение.
Заметьте, что антиподальное отображение не имеет неподвижных
точек, поэтому тот факт, что отображения без неподвижных точек
гомотопны антиподальному отображению, — это своего рода обратное
утверждение.
Вот интересное применение степени отображения.
Теорема 2.28. На сфере Sn есть непрерывное поле касательных
векторов, отличных от нуля, тогда и только тогда, когда п нечётно.
Доказательство. Предположим, что # —> vOO — касательное
векторное поле на Sn, сопоставляющее вектору xGSn касательный вектор vOO
к сфере Sn в точке х. Если рассматривать vOO как вектор в начале
координат, а не в х, то касание означает просто, что векторы х иу(х)
ортогональны в Еп+1. Если vOO 7^0 для всех х, то мы можем нормализовать
векторное поле так, что |v0OI = 1 для всех х, заменив vOO на v(jc)/|v(jc)|. Тогда
векторы (cos0*+ (sin 0v 00 лежат на единичной окружности в
плоскости, порождённой х и vOO- Меняя t от 0 до тг, мы получаем гомотопию
/00 = (cos0* + (sinOvOO тождественного отображения сферы Sn в
антиподальное отображение -1. Из этого следует, что deg(-l) = degl, а
потому (—1)п+1 = 1 и число п должно быть нечётным.
Наоборот, если число п нечётно, скажем п = 2fc - 1, мы можем
положить v(*l5 x2f..., х2к_ъ х2к) = (-х2, *i, ..., -x2kf х2к_г). Тогда вектор v(x)
ортогонален х, поэтому v — касательное векторное поле на S", и |v(jc)| = 1
для всех х GS". D
По поводу гораздо более трудной задачи нахождения максимального
числа касательных векторных полей на сфере S", линейно независимых
в каждой точке, см. [VBKT] или [36].
Другим интересным применением степени, дающим частичный ответ
на вопрос, поставленный в примере 1.43, является следующий результат.
I Предложение 2.29. Группа Z2 является единственной
нетривиальной группой, которая может действовать свободно на S", если число п
четно.
Напомним, что действие группы G на пространстве X — это
гомоморфизмом группы G в группу Нотео(Х) гомеоморфизмов X —*Х, и действие
свободно, если гомеоморфизм, соответствующий каждому нетривиальному
элементу группы G, не имеет неподвижных точек. В случае сферы Sn
антиподальное отображение х-+—х порождает свободное действие группы Z2.
176
Глава 2. Гомологии
Доказательство. Так как степень гомеоморфизма должна быть равна
±1, действие группы G на Sn определяет функцию степени d: G -+ {±1}.
Это гомоморфизм, так как deg/g = deg/ degg. Если действие свободно, то
d переводит каждый нетривиальный элемент группы G в (—1)"+1 согласно
свойству ж), упомянутому выше. Таким образом, когда п четно,
гомоморфизм d имеет тривиальное ядро, а потому G с Z2. G
Теперь мы опишем метод вычисления степени, который можно
применить к большинству отображений, возникающих на практике.
Предположим, что отображение /: Sn -+ S", где п > 0, обладает тем свойством,
что для некоторой точки у €Sn прообраз /_1 (у) состоит только из
конечного числа точек, скажем, хъ ..., хт. Пусть С/ь ..., lfm — непересекающиеся
окрестности этих точек, которые отображение / переводит в окрестность
V точки у. Тогда /(17,- -х,-) с V-у для всех i, и мы получаем
коммутативную диаграмму
Hn Щ-, U( - jc.O — Нп (V, К - у)
H„(Sn, Sn-x{) ■«-£- Hn(S", S" -/"'Су)) ^— "n(S", S" -y)
Hn(Sn) £ Hn(Srt)
где все отображения очевидны, в частности, к, и р, индуцированы
включениями. Два изоморфизма в верхней половине диаграммы получаются из
свойства вырезания, а два нижних изоморфизма получаются из точных
последовательностей пар. Посредством этих четырёх изоморфизмов две
верхние группы в диаграмме можно отождествить с Hn(Sn) &Z, причём
тогда верхний гомоморфизм /+ становится умножением на целое число,
которое называют локальной степенью отображения / в точке х{ и
обозначают deg/jx,.
Например, если / — гомеоморфизм, то точка у может быть любой,
и есть только одна соответствующая ей точка xit таким образом, все
отображения в диаграмме —изоморфизмы, и deg/| x,-= deg/= ±1.
Вообще, если / отображает каждую окрестность U( гомеоморфно на V, то
deg/|x,- = ±l для всех i. Такая ситуация весьма часто встречается в
приложениях, и обычно не составляет труда правильно определить знаки.
Вот формула, которая сводит вычисление степени к вычислению
локальных степеней.
I Предложение 2.30. Справедливо равенство deg / = £ deg /1 х(.
Доказательство. Согласно свойству вырезания центральный член
Hn(Sn,Sn — /_1(у)) в предыдущей диаграмме—прямая сумма групп
Н„Щ-, Ц-— х() &Z, причём к{ — отображение включения для i-го слага-
§ 2.2. Вычисления и приложения
177
емого, причём к,-— отображение включения для £-го слагаемого, а р, —
проекция на i-e слагаемое. Отождествляя внешние группы в диаграмме
с Z, как и ранее, из коммутативности нижнего треугольника мы получаем,
что р,-Д1) = 1, а потому ;(1) = (1,..., l) = ^fcr(l). Коммутативность верх-
него квадрата означает, что средний гомоморфизм /+ отображает fc,-(l)
в deg/|xf, а потому ^к((1)= j{l) отображается в £deg/|xr. Коммута-
i i
тивность нижнего квадрата тогда даёт требуемую формулу
deg/ = 2deS/l*.- П
Пример 2,31. Мы можем применить этот результат, чтобы построить
отображение Sn —> Sn любой заданной степени для каждого л ^ 1. Пусть
q: Sn —> VSn — отображение факторизации, полученное при стягивании
к
в точку дополнения к к непересекающимся открытым дискам В, в Sn, и
пусть р: \/ Sn-*Sn отождествляет все слагаемые с одной сферой. Рассмот-
к
рим композицию / = pq. Для почти всех точек у € S" прообраз /_1(у)
состоит из одной точки х( в каждом диске В,. Локальная степень
отображения / в точке х( равна ±1, так как / — гомеоморфизм вблизи х(. Взяв при
необходимости перед отображением р симметрию слагаемого из \J Sn, мы
к
можем добиться, чтобы каждая локальная степень была равна -1-1 или — 1,
как мы пожелаем. Так мы можем получить отображение Sn-*Sn
степени ±к.
Пример 2.32. В случае окружности S1 отображение /(z) = zk, где мы
рассматриваем S1 как единичную окружность в С, имеет степень к. Это
очевидно в случае к = 0, так как тогда отображение / постоянно. Случай
к < 0 сводится к случаю к> 0, если рассмотреть композицию данного
отображения с отображением z—*z_1, которое является симметрией и имеет
степень — 1. Чтобы вычислить степень при к > 0, заметим сначала, что
для любой точки у € S1 прообраз /_1(у) состоит из к точек х1у ...,х/с,
в окрестности каждой из которых / является локальным
гомеоморфизмом, растягивающим дугу окружности с коэффициентом к. Это локальное
растяжение можно устранить деформацией отображения / вблизи точки
xh которая не изменяет локальную степень, поэтому локальная степень
в точке х( та же самая, что и у поворота окружности S1. Поворот является
гомеоморфизмом, поэтому его локальная степень в любой точке равна
его глобальной степени, которая равна +1, так как поворот гомотопен
тождественному отображению. Следовательно, deg/|x, = 1 и deg/ = k.
Другой способ получить отображение Sn —> Sn степени к состоит в том,
Чтобы взять многократную надстройку отображения z —* zk из
примера 2.32. Как показывает следующий результат, надстройка сохраняет
степень.
178
Глава 2. Гомологии
Предложение 2.33. Имеет место равенство degS/= deg/, где Sf:
Sn+l -»Sn+1 — надстройка отображения f:Sn-*Sn.
Доказательство. Пусть CSn обозначает конус (Sn x /)/(Sn x 1) с
основанием S" = Sn х 0 с CSn\ таким образом, CSn/Sn — надстройка над S".
Отображение / индуцирует отображение С/: {CSn, Sn) -* (CSn, Sn) с фак-
торотображением Sf. Естественность граничных отображений в длинной
точной последовательности пары (CSn,Sn) тогда даёт коммутативность
следующей диаграммы:
Hn+1(Sn+1)^Hn(S»)
H„+1(S',+1)^Hn(Sn)
Следовательно, если /* — умножение на d, то S/* тоже. □
Заметим, что для /: Sn -* Sn надстройка Sf отображает только
одну точку в каждый из двух «полюсов» сферы Sn+1. Из этого следует, что
локальная степень отображения Sf в каждом полюсе должна равняться
глобальной степени отображения Sf. Поэтому локальная степень
отображения Sn —* Sn может быть любым целым числом, если п ^ 2, точно так же,
как сама степень может быть любым целым числом при п ^ 1.
Клеточные гомологии
Клеточные гомологии — очень эффективный инструмент для
вычисления групп гомологии CW-комплексов, основанный на вычислении
степени. Прежде чем давать определения клеточных гомологии, мы докажем
несколько вспомогательных фактов.
I Лемма 2.34. Если X — CW-комплекс, то
I а) группа Нк(Хп,Хп~1) нулевая при кфптл свободная абелева при
I /с = п, причём её базис находится во взаимно однозначном соот-
I ветствии с п -мерными клетками комплекса X;
I б) Нк{Хп) =0 при к> п; в частности, если комплекс X конечномерен,
I то Нк{Х) =0 при fc >dimX;
I в) включение i: Хп ^-> X индуцирует изоморфизм i*: Нк{Хп) -»Нк(Х)
| при к<п.
Доказательство. Утверждение а) немедленно следует из замечания,
что пара (Хп, Хп_1) является хорошей, а Хп/Хп~} —букет п-мерных сфер,
по одной для каждой п-мерной клетки комплекса X. Здесь мы используем
предложение 2.22 и следствие 2.25.
Чтобы доказать утверждение б), рассмотрим длинную точную
последовательность пары (Хп, Хп_1), которая содержит участок
Нм{Хп, X""1) -> Нк{Хп~') -> Нк(Хп) -> Нк(Хп, Хп~}).
Если к не равно п или п - 1, то обе внешние группы нулевые
согласно утверждению а), поэтому мы получаем изоморфизмы Нк(Хп~~}) ъ
§ 2.2. Вычисления и приложения
179
ъ Нк(Хп) при к Ф п, п - 1. Таким образом, если к>п) то мы имеем
Hfc(Xn)^^(^'^1)^^(^n"2)^--^^W°) = 0J что и доказывает
утверждение б). Далее, если к < п, то Hfc(Xn) **Hfc(Xn+1) « ... *Н*(ХИ+'П) для всех
m ^ 0, что и доказывает утверждение в), если комплекс X конечномерен.
Доказательство утверждения в) для бесконечномерного комплекса X
требует дополнительных усилий, и его можно получить двумя разными
способами. Более прямой подход состоит в том, чтобы спуститься на
уровень цепей и воспользоваться тем фактом, что сингулярная цепь в X
имеет компактный образ, а потому пересекает только конечное число клеток
комплекса X согласно предложению П.1 из приложения. Таким образом,
каждая цепь лежит в конечном остове Хт. Поэтому /с-мерный цикл в X
является циклом в некотором X"1, а тогда согласно конечномерному
случаю утверждения в) этот цикл гомологичен циклу в X" при п > к, а значит,
гомоморфизм I*: Нк(Хп) —> Ик(Х) сюръективен. Аналогично для инъек-
тивности: если к-мерный цикл в X" ограничивает цепь в X, то эта цепь
лежит в некотором остове Хгп, где т ^ п, а потому согласно
конечномерному случаю этот цикл ограничивает цепь в X" при п > к.
Другой подход более общий. Согласно длинной точной
последовательности пары (X, Хп) достаточно показать, что Hfc(X, Хп) = 0 при к $ п. Так
как Нк{Х, X") ъ Нк{Х/Хп), это сводит нашу задачу к доказательству
следующего утверждения:
(*) Нк(Х) = 0 при к ^ п, если п-мерный остов комплекса X является
точкой.
Когда комплекс X конечномерен, утверждение О) непосредственно
следует из конечномерного случая утверждения в), который мы уже
доказали. Поэтому достаточно свести бесконечномерный случай к
конечномерному. Это сведение будет получено посредством растяжения X до
комплекса, который является по крайней мере локально конечномерным,
с помощью частного случая «телескопа отображения» —конструкции,
описанной в более общем виде в §3.F.
Рассмотрим X х [0, оо) с клеточной структурой произведения, где
мы снабжаем [0, оо) клеточной структурой с целочисленными точками
в качестве нульмерных клеток. Пусть T~[JXl х [i, оо) —подкомплекс
в X х [0, оо). На рисунке схематично изображён
комплекс Т с лучом [0, оо) в горизонтальном —\ \ \ -f-
направлении и подкомплексами X1 х [ij ■+- 1]
в виде прямоугольников, размер которых
увеличивается с ростом [, так как X' с Х'+1. Прямую с пометкой R можно пока
проигнорировать. Мы утверждаем, что Тс^Х, а потому Нк(Х) ъНк(Т) для
всех к. Так как X— деформационный ретракт пространства X х [0, оо),
достаточно показать, что X х [0, оо) тоже деформационно ретрагирует-
ся на Т. Пусть У; = Г и (X х [i,oo)). Тогда У{ деформационно ретраги-
180
Глава 2. Гомологии
руется на Yj-+1, так как X х [i,i + 1] деформационно ретрагируется на
Xх х [i, i + 1] UX х {i + 1} согласно предложению 0.16. Если мы выполняем
деформационную ретракцию пространства Y{ на Yi+l в течение времени
t из интервала [1 — 1/2', 1 - 1/2,+1], то это даёт деформационную
ретракцию ft пространства X х [0, оо) на Т, причём точки в X1 х [0, оо) остаются
неподвижными при отображении /t, если t ^ 1 - 1/2'"1'1. Непрерывность
следует из того факта, что CW-комплексы снабжены слабой топологией
относительно их остовов, а потому отображение непрерывно, если его
ограничение на каждый остов непрерывно.
Вспомним, что Х° является точкой. Пусть R с Т— луч Х° х [0, оо),
и пусть Z с Т — объединение этого луча со всеми подкомплексами X1 х {i}.
Тогда пространство Z/R гомеоморфно \J Х\ букету конечномерных ком-
i
плексов с п-мерными остовами, состоящими из одной точки, а потому из
конечномерного случая утверждения (*) вместе со следствием 2.25,
описывающим гомологии букета, следует, что Hk(Z/R) = 0 при к $ п. Поэтому
то же самое верно для Z согласно длинной точной последовательности
пары (Z, Я), так как пространство R стягиваемо. Точно так же T/Z — букет
конечномерных комплексов с (п-f 1)-мерными остовами, состоящими из
одной точки, поскольку если мы сначала стягиваем каждый подкомплекс
Xх х {{} комплекса Т в точку, то мы получаем бесконечную
последовательность надстроек SX', «насаженных» на луч Я, и если мы затем стягиваем R
в точку, то мы получаем \/ЕХ', где ЕХ'—приведённая надстройка над
i
X1, полученная из SX1 стягиванием отрезка Х° х [i, i+ 1] в точку.
Поэтому (п + 1)-мерный остов комплекса ЕХ' состоит из одной точки. Таким
образом, Нк(Т/Z) =0 при к $ п + 1, а тогда из длинной точной
последовательности пары (Т, Z) следует, что Нк(Т) = 0 при к $ п, и утверждение (*)
доказано. D
Пусть X—CW-комплекс. Используя лемму 2.34, вставим участки
длинных точных последовательностей для пар (ХП+1,ХП), (ХП,ХП_1) и
(ХП_1,ХП-2) в диаграмму
^0
0^ Hn{X»+i) ъ Н„{Х)
ХП,ХП"
- -> НП+1(ХП+1,ХП) ^+ Ни{Хп, Хп~1) ^ Нп_, (Хп-\ Xм"2)
0^
где гомоморфизмы dn+1 и dn определяются как композиции jndn+\ и jn-\dn,
и являются просто относительными версиями абсолютных граничных
§ 2.2. Вычисления и приложения
181
отображений дп+1 и Эп. Композиция dndn+1 включает два
последовательных отображения из одной и той же точной последовательности,
следовательно, она нулевая. Таким образом, горизонтальная строка в этой
диаграмме—цепной комплекс, называемый клеточным цепным комплексом
для X. Группа НП(Х",Х"-1) свободная абелева, а её базис находится во
взаимнооднозначном соответствии с п-мерными клетками комплекса X.
Потому элементы из Л„(ХП, Хп_1) можно представлять как линейные
комбинации п-мерных клеток комплекса X. Группы гомологии клеточного
цепного комплекса называют группами клеточных гомологии
комплекса X. Мы будем временно обозначать их Н™{Х).
I Теорема 2.35. Имеет место изоморфизм Н™(Х) ъНп(Х).
Доказательство. Из записанной выше диаграммы видно, что группу
Нп(Х) можно отождествить с Нп(Х")/1тдп+1. Так как гомоморфизм jn
инъективен, он отображает Imd,1+I изоморфно на Im(jndri+1) == Imdn+1,
а ЯП(ХП) изоморфно на Im;'n = Kerdn. Так как гомоморфизм ju^
инъективен, Kerd„ = Kerdn. Таким образом, ;„ индуцирует изоморфизм
факторгруппы Нп(Хп)/1тдп+1 на Kerdn/Imdn+1. D
Вот несколько непосредственных приложений.
1. Если X — CW-комплекс без п-мерных клеток, то Нп(Х) = 0.
2. Вообще, если X — CW-комплекс с к клетками размерности п, то
группа Нп(Х) порождена не более чем к элементами. Действительно, так
как Нп{ХпуХп~1) — свободная абелева группа с к образующими,
подгруппа Kerd„ тоже должна порождаться не более чем к элементами,
а потому и факторгруппа Kerdn/Imd„+] тоже.
3. Если X — CW-комплекс, у которого нет пар клеток в соседних
размерностях, то НП(Х) —свободная абелева группа, базис которой
находится во взаимно однозначном соответствии с п-мерными клетками
комплекса X. Это так, потому что клеточные граничные отображения dn
в этом случае автоматически являются нулевыми.
Последнее наблюдение применимо, например, к пространству СР",
которое имеет CW-структуру с одной клеткой каждой чётной размерности
2к ^ 2п, как мы видели в примере 0.6. Таким образом,
f Z для[ = 0,2,4, ...,2п,
Н:(СРП) « <
^ 0 иначе.
Другой простой пример —гомологии произведения S" x S'\ где п > 1, если
воспользоваться клеточной структурой произведения, состоящей из нуль-
Мерной клетки, двух п-мерных клеток и 2п-мерной клетки.
Можно доказать утверждения 1—3 для конечномерных CW-комплек-
сов индукцией по размерности, не используя клеточных гомологии,
опираясь лишь на основные результаты предыдущего параграфа. Однако под-
182
Глава 2. Гомологии
ход с точки зрения клеточных гомологии делает утверждения 1—3
особенно прозрачными.
Теперь мы опишем, как можно вычислить клеточное граничное
отображение dn. При п = 1 это легко, так как граничное отображение
d^CX1,*0)-^*0)
— это то же самое, что и симплициальное граничное отображение Д1 (X) —►
—* Д0(Х). В случае, когда комплекс X связен и имеет только одну
нульмерную клетку, отображение dx должно быть нулевым, поскольку иначе
группа Н0(Х) не была бы равна Z. При п > 1 мы покажем, что dn можно
вычислить в терминах степеней следующим образом.
Формула для клеточного оператора границы. Имеет место
равенство dn(e^) = 2]с*а/зея~1> где dap — степень отображения S^~l -* Xn~l -*
/з •
—*S"~\ которое является композицией отображения приклеивания для
клетки епа и отображения факторизации, стягивающего Хп~1 - е"-1
в точку.
Здесь мы отождествляем клетки епа и е^"1 с образующими
соответствующих слагаемых клеточных групп цепей. Сумма в этой формуле содержит
лишь конечное число членов, так как образ отображения приклеивания
для клетки епа компактен, а потому этот образ пересекает лишь конечное
число клеток еГ1.
Чтобы получить формулу для клеточного оператора границы,
рассмотрим коммутативную диаграмму
Hn{Dna9dDna)-
+ НпЛдОпа)-
±ар>
-Hn-iCST1)
♦«.
4/1.
Нп(Х\ X'-1) =—*■ Н^СХ""1)
<*,.
Нп_1(Х"-\Х"-2) —^Н,,,,^"-1/*
-^н„_,(х"-7х"-2)
м-1/ум-2 уп-2 I уп-2
IX"-*)
где
Фа — характеристическое отображение клетки епа, а ца — её
отображение приклеивания;
q: Xм"1 -*Хп~1/Хп~2 — отображение факторизации;
qp\ Xn~l/Xn~2 -* S'jf1 стягивает дополнение клетки еп„~1 в точку,
получающаяся при факторизации сфера отождествляется с S""1 =
= D«~1/clD2"1 посредством характеристического отображения Ф^;
Аар : dD^-*Sn~l — это композиция qpqy>a, другими словами, за
отображением приклеивания клетки епа следует факторотображение X""1 -»
Ър , стягивающее в точку дополнение к е^
§ 2.2. Вычисления и приложения
183
Отображение Фа* переводит образующую [D£] eHn{Dr^, dDJJ) в
образующую слагаемого Z группы НП(ХП, Xм"1), соответствующего клетке епа.
Если обозначить эту образующую е£, то из коммутативности левой
половины диаграммы даёт dn(e£) = ;n_-,(/?a¥a[DJJ]. В терминах базиса для
Я _i(Xn~\ X'1"2), соответствующего клеткам е"-1, отображение q^+ — это
проекция группы Hn_i(X""V^n"2) на её слагаемое Z, соответствующее
клетке е"-1. Коммутативность диаграммы приводит к формуле для dn,
приведённой выше.
Пример 2.36. Пусть М^ —замкнутая ориентируемая поверхность
рода g с обычной CW-структурой, состоящей из одной нульмерной клетки,
2g клеток размерности 1 и одной двумерной клетки, приклеенной по
произведению коммутаторов [с^, bj]...[ag,bg]. Соответствующий клеточный
цепной комплекс имеет вид 0 —> Z —> Zzg —> Z —> 0. Как было замечено
выше, отображение dT должно быть нулевым, так как есть только одна
нульмерная клетка. Кроме того, отображение d2 нулевое, потому что
каждое ребро а,- и Ь, появляется в произведении [а1} bl]...[agi bg] вместе с его
обратным, а значит, отображения Аар гомотопны постоянным
отображениям. Так как оба отображения dY или d2 нулевые, группы гомологии
комплекса Mg такие же, как клеточные группы цепей, а именно, они равны Z
В размерностях 0 и 2 и равны Z2g в размерности 1.
Пример 2.37. Замкнутая неориентируемая поверхность N^ рода g
Имеет клеточную структуру с одной нульмерной клеткой, g клетками раз-
Мерности 1 и одной двумерной клеткой, приклеенной по слову а^а^-*^'
Снова dT =0, а d2: Z—>ZS задаётся уравнением d2(l) = (2, ..., 2), так как
каждое ребро а, появляется в слове приклеивания двумерной клетки
с полной степенью 2, а это означает, что каждое отображение Aa^
гомотопно отображению z —» z2 степени 2. Так как d2(l) = (2,..., 2),
отображение d2 инъективно, а потому H2{Ng) = 0. Если мы изменим базис
группы Zg, заменив последний стандартный базисный элемент (0, ..., 0, 1)
На (1,..., 1), то мы увидим, что H^(Ng)^Zg~l 0Z2.
Эти два примера иллюстрируют общий факт, что ориентируемость
замкнутого связного многообразия М размерности п обнаруживает группа
НпШ), которая равна Z, если М ориентируемо, и равна 0 в противном
случае. Это доказано в теореме 3.26.
Пример 2.38 (ацикличное пространство). Пусть пространство X
получено из S1 VS1 приклеиванием двух двумерных клеток но словам а5Ь~3
иЬ3(аЬ)"2. Тогда отображение d2: Z2—>Z2 задаётся матрицей
В которой столбцы получаются при абелианизации слов а5Ь~3 и ЬЛ(аЬУ'2
8 5а - ЗЬ и -2а -f b в аддитивных обозначениях. Определитель этой
матрицы равен -1, поэтому d2 — изоморфизм и Н,(Х) = 0 для всех i. Такое
Пространство X называют ацикличным.
5 -2
-3 1
184
Глава 2. Гомологии
Мы можем убедиться, что это ацикличное пространство не стягиваемо,
рассмотрев лг(Х), которая имеет представление (а, Ъ | а5Ь~3, Ъ'л{аЪ)~2 ).
Имеется нетривиальный гомоморфизм из этой группы в группу G
поворотных симметрии правильного додекаэдра, переводящий элемент а в
поворот ра на угол 2тг/5 относительно оси, проходящей через центр
пятиугольной грани, а элемент Ъ — в поворот рь на угол 2тг/3 относительно
оси, проходящей через вершину этой грани. Композиция рарь —это
поворот на угол п относительно оси, проходящей через середину ребра,
содержащего эту вершину. Таким образом, соотношения а5 = Ь3 = (аЬ)2,
определяющие группу тг^Х), превращаются в соотношения р*=р^ = (раРь)2 = 1
в группе G, а это означает, что существует корректно определённый
гомоморфизм р: п1{Х) —> G, переводящий а в pQ и 5 в рь. Легко видеть, что
группа G порождается элементами ра и р5, поэтому гомоморфизм р сюръ-
ективен. Потрудившись, можно вычислить, что ядро гомоморфизма р —
это подгруппа Z2, порождённая элементом а5 = Ь3 = (аЬ)2, и эта
подгруппа Z2 в действительности является центром группы п^{Х). В частности,
порядок группы ях(Х) равен 120, так как порядок группы G равен 60.
После этих двумерных примеров перейдём к размерности 3, где у нас
появляется дополнительная задача вычисления клеточного граничного
отображения d3.
cs
к
а
а
■'»-■
71
7
СА
W
\
0 1
а
а '
1 s ' *
7\
т
Ь
7
Пример 2.39. Трёхмерный тор Г3 = Sl x S1 x S1 можно полнить из
куба, отождествляя каждую пару противоположных квадратных граней
так, как показано на первом из двух рисунков. На втором рисунке
изображён немного другой способ отождествления противоположных граней,
когда передняя и задняя грани отождествляются посредством поворота
куба вокруг горизонтальной оси, идущей слева направо. Пространство,
полученное при таком отождествлении, — это произведение К х S1
бутылки Клейна и окружности. Для обоих пространств Т3 и К х S1 мы имеем
СУУ-структуру с одной трёхмерной клеткой, тремя двумерными клетками,
тремя одномерными клетками и одной нульмерной клеткой. Клеточные
цепные комплексы, таким образом, имеют вид
о - z - z3 ^ z3 Л ъ -> о.
В случае трёхмерного тора Г3 клеточное граничное отображение d2
нулевое согласно тем же самым вычислениям, что и для двумерного тора.
Мы угверждаем, что отображение d3 тоже пулевое. Другими словами, три
§ 2.2. Вычисления и приложения
185
отображения Аар: S2 —► S2, соответствующие трём двумерным клеткам,
имеют степень нуль. Каждое Аа^ гомеоморфно отображает внутренности
двух противоположных граней куба на дополнение точки в S2 и
отображает остальные четыре грани в эту точку. Вычисляя локальные
степени в центрах двух противоположных граней, мы видим, что локальная
степень равна -1-1 в одном из них и -1 в другом, так как ограничения
отображения Аар на эти две грани отличаются на симметрию границы
куба относительно плоскости, равноудалённой от них, а симметрия имеет
степень — 1. Так как все клеточные граничные отображения нулевые, мы
получаем, что группа Н,(Г3) равна Z при i = О, 3, равна Z3 при i = 1, 2
и равна 0 при \ > 3.
В случае К х S1, когда мы вычисляем локальные степени для передней
и задней граней, мы получаем, что степени имеют теперь одинаковые,
а не противоположные знаки, так как ограничения отображения Аар на
эти две грани отличаются не на симметрию, а на поворот границы куба.
Локальные степени для всех других граней те же самые, что и раньше.
Обозначая буквами Л, В и С двумерные клетки, заданные гранями,
ортогональными рёбрам а, Ъ и с соответственно, мы получаем формулы для
граничного отображения: d3e3 = 2С, d2A = 2b, d2B = 0 и d2C — 0. Из них
следует, что Н3(К х S1) = 0, И2{К х S1) = Z0 Z2 и Нг (К х S1) = Z 0Z 0 Z2.
Аналогично можно было бы разобрать ещё много примеров такого
рода —факторпространства куба или другого многогранника с гранями,
отождествлёнными каким-то образом. Но давайте вместо этого
обратимся к некоторым многомерным примерам.
Пример 2.40 (пространства Мура). Для данной абелевой группы G и
целого числа п ^ 1 мы будем строить такой CW-комплекс X, что Нп{Х) w G
и Н{(Х) =0 при [фп. Такое пространство называют пространством Мура
и обычно обозначают M{G, п), чтобы указать зависимость от G и п.
Вероятно, в определение пространства Мура лучше включить условие, что
пространство M(G, п) односвязно, если п > 1. Пространства, которые мы
построим, будут обладать этим свойством.
В простом частном случае, когда G = Zni, мы можем взять в качестве
X сферу Sn, к которой приклеена клетка en+1 по отображению S" —► Sn
степени т. Вообще любую конечно порождённую группу G можно
реализовать, взяв букеты пространств такого типа для конечных циклических
слагаемых группы G и сфер S" для бесконечных циклических слагаемых
группы G.
В общем случае пусть F —♦ G — гомоморфизм свободной абелевой
группы F на G, переводящий базис группы F в некоторое множество
образующих группы G. Ядро К этого гомоморфизма —подгруппа свободной
абелевой группы, а потому она сама свободная абелева. Выберем базис
{ха} для F и базис {yft} для К и запишем у^ =Yi^i3axa- Пусть Хп =
V а7
186
Глава 2. Гомологии
а потому Hn{Xn)^F согласно следствию 2.25. Мы будем строить ХпоХ",
приклеивая клетки е^"1"1 посредством таких отображений fp : Sn —*Хп, что
композиция отображения fp с проекцией на слагаемое S£ имеет степень
dpa. Тогда клеточное граничное отображение d,I+1 будет включением
К<—»F, а потому X будет иметь требуемые группы гомологии.
Построение отображения fp обобщает построение отображения Sn —>
—*Sn данной степени из примера 2.31. А именно, мы можем считать, что fp
отображает дополнение к J] \dpa\ непересекающимся шарам в Sn в нуль-
а
мерную клетку комплекса Xй и отображает \dpa\ шаров на слагаемое S"
посредством отображений степени -1-1, если dpa > 0, и степени -1, если
dpa<0.
Пример 2.41. Взяв букет пространств Мура, построенных в
предыдущем примере, и изменяя п, мы получим связный CW-комплекс с
произвольной заданной последовательностью групп гомологии размерностей
1,2,3,...
Пример 2.42. Вещественное проективное пространство ЖРп. Как мы
видели в примере 0.4, пространство lRPn имеет CW-структуру с одной
клеткой ек в каждой размерности к $ п, причём отображение
приклеивания для клетки efc—это двулистное накрытие \р: Sk~l —*H£Pfc~1. Чтобы
вычислить граничное отображение dk, вычислим степень композиции
где q — отображение факторизации. При ограничении на каждую
компоненту связности пространства Sk~] — Sk~2 отображение qy> является
гомеоморфизмом, и эти два гомеоморфизма получаются друг из друга
посредством композиции с предшествующим им антиподальным
отображением сферы Sfc_1, которое имеет степень (—1)к. Следовательно, degq^ =
= degl + deg(-l) = 14- (-1)\ а потому dk является либо нулём, либо
умножением на 2, в соответствии с тем, нечётно или четно число к. Таким
образом, клеточный цепной комплекс для RP" имеет вид
2 0 2 0 2 0
0->Z-->Z—>...—>Z—>Z—>Z—>Z->0, если п четно;
0 2 2 0 2 0
0-*Z—>Z—>... —>Z—>Z—>Z—>Z-*0, если п нечётно.
Из этого следует, что
при к = 0 и при нечётном к — п;
Нк{ЖУх) = { Z2 при нечётном к, где 0 < к < п;
в остальных случаях.
Пример 2.43 (линзовые пространства). Этот пример несколько более
сложен. Для данного целого число т > 1 и целых чисел ilt..., tn, взаимно
простых с т, определим линзовое пространство L = L„,(£1, ..., £п) как про-
§ 2.2. Вычисления и приложения
187
странство орбит S2""1 /Хт единичной сферы S2""1 с Сп по действию
группы Zm, порождённому поворотом рО]} ..., zn) = (e27r!*,/nlz1,..., e2,T^"//",zn),
при котором ;-й множитель С в Сп поворачивается на угол 2nCj/m. В
частности, если т = 2, а р -- антиподальное отображение, то L гг^Р2""1. В
общем случае проекция S2n_1 -> L — накрытие, так как действие группы Z„,
на S2nM свободно. Действительно, только единичный элемент оставляет
неподвижными все точки сферы S2n"\ так как любая точка сферы S2""1
имеет некоторую координату я;-, отличную от нуля, а тогда из
предположения, что 1} взаимно просто с ш, следует, что e2rn/cVmz;- ф %} при 0 < fc < гл.
Построим CW-структуру на! с одной клеткой ек для всех fc ^ 2п — 1
и покажем, что при этом получается клеточный цепной комплекс
г» ° ™ '» ™ 0 0 „, ш „ 0 „
О -» Z -> Z -> Z -» ... -» Z -» Z -» Z -> О,
в котором граничные отображения поочерёдно равны 0 и умножению
на гл. Следовательно,
Z при*с = 0,2п-1;
tfk(An^i> •••»^п)) = { zm ПРИ нечётном fc, где 0 < fc < 2п-1;
О в остальных случаях.
Чтобы получить CW-структуру, сначала рассмотрим подразделение
единичной окружности С в п-м множителе С пространства Сп, взяв в
качестве вершин точки е2т^т е С для j = 1,..., гл. Соединяя j-ю вершину
окружности С с единичной сферой S2n~3 с С""1 дугами больших
окружностей в S2n~\ получим (2п - 2)-мерный шар В2п~2, ограниченный сферой
S2""3. А именно, В2""2 состоит из точек cos в(О, ..., О, e2™i/m) + sin0(zlf...
..., 2n_1} 0), где 0^ в ^ я/2. Аналогично, соединив точки ;-го ребра
окружности С с S2n~3, получим шар В2""1, ограниченный шарами В2п~2 и В2""2,
где индексы берутся по модулю т. Поворот р переводит S2n~3 в себя и
поворачивает С на угол 2п£п/т, следовательно, р переставляет шары В2п~2
и шары В2""1. Подходящая степень р, а именно рг, где г£„ = 1 mod m,
переводит каждый шар В2п"2 и В2п~] в следующий за ним. Так как элемент
рг имеет порядок ш, он тоже является образующей группы поворотов Zm,
а значит, мы можем получить L как факторпространство одного из шаров
В2""1, отождествляя две его грани В2"™2 и B2"j2 посредством
отображения рг.
В частности, когда п = 2, В2""1 — это трёхмерный шар, имеющий
форму линзы. Тогда I получается из этого шара отождествлением двух его
граней, имеющих форму искривлённых кругов, посредством отображения рг.
Это отображение можно описать как композицию симметрии
относительно плоскости, содержащей ободок линзы, которая переводит одну грань
линзы в другую, и последующего поворота этой грани на угол 2nt/m, где
188
Глава 2. Гомологии
t=r£}. На рисунке изображён случай (т, £) = (7, 2), причём две
выделенные точки — это типичная пара отождествляемых точек верхней и нижней
граней линзы. Так как линзовое пространство L задаётся углом поворота
2тг£/т, его удобно обозначить 1цт. Ясно, что
существенны лишь значения £ по модулю т.
Классическая теорема Рейдемейстера,
доказанная в 1930-е годы, гласит, что 1цт гомеоморф-
но Li'/m' тогда и только тогда, когда т' = т
и I1 = ±l±} mod т. Например, при т = 7 есть
только два разных линзовых пространства Llp
и /,2/у Утверждение «тогда» в этой теореме
простое: зеркальная симметрия линзы показывает, что ^/ш^£_£/,„, а меняя
местами оба множителя С в С2, получаем 1цт ^Lf-ym. Что же касается
обратного утверждения, то из гомеоморфизма L^/,,, ^Lr/f„'> очевидно,
следует равенство т = т\ так как 7i}(L^m)^Znr Доказательство оставшейся
части теоремы требует значительно больше труда и использует либо
специальную трёхмерную технику, либо более алгебраические методы,
которые можно обобщить для получения классификации многомерных
линзовых пространств. Последний подход изложен в книге [16].
Возвращаясь к построению CW-структуры на Lnl(£j, ..., £п), заметим,
что (2п - 3)-мерное линзовое пространство 1т(1\, >.., £„-i) содержится
в Lm(£b ..., £„) как факторпространство сферы S2n~3, причём Lni{i},..., £,,)
получается из этого подпространства приклеиванием двух клеток
размерностей 2п — 2 и 2п - 1, которые получаются из внутренности шара В2""1
и двух его отождествляемых граней В2п~2 и В2""2. По индукции это даёт
CW-структуру на Lm(tl9..., £м) с одной клеткой ек в каждой размерности
Граничные отображения в соответствующем клеточном цепном
комплексе вычисляются следующим образом. Первое из них, d2n-\, является
нулевым, так как отождествление двух граней шара В2п_1 происходит
посредством симметрии (имеющей степень —1) шара В2п_1, оставляющей
неподвижной сферу S2"-3, и последующего поворота (имеющего степень
+ 1), поэтому d2n-i(e2ri~l) =e2n~2 -е2п-2 = 0. Следующее граничное
отображение d2n-2 переводит е2п~2 в те2п"3, так как отображение
приклеивания для е2"-2 —это отображение факторизации S2n~3 -^Ln](il} ...,£„._!),
а шары В?""3 в S2""3, которые проектируются на е2п_3, переставляются
циклически поворотом р, имеющим степень -1-1. По индукции
последующие граничные отображения dk поочерёдно являются нулевыми и
умножениями на т.
Представляют интерес также и бесконечномерные линзовые
пространства Lm(£1,£2, ...) = S°°/Zm, которые определяются таким же
образом, как и в конечномерном случае, начиная с последовательности
§ 2.2. Вычисления и приложения
189
целых чисел £i,£2, •••> взаимно простых cm, Пространство Lm(£b£2, •••) —
объединение возрастающей последовательности конечномерных
линзовых пространств Lm(li,..., £„) для п = 1, 2,..., каждое из которых
—подкомплекс последующего в клеточной структуре, которую мы только что
построили. Поэтому Lm(£b £2, •••) тоже CW-комплекс. Его клеточный
цепной комплекс состоит из группы Z в каждой размерности с граничными
отображениями, поочерёдно равными 0 и т, поэтому его приведённые
группы гомологии состоят из группы Zm в каждой нечётной размерности.
В терминологии § 1.В бесконечномерное линзовое пространство
LmU\>^2y -О является пространством Эйленберга—Маклейна К(2Ш, 1),
поскольку его универсальное накрытие S00, как было там показано,
стягиваемо. Согласно теореме 1.В.8 гомотопический тип пространства Lm(£a, £2> •••)
зависит только от т и не зависит от чисел £,-. Это неверно в
конечномерном случае: два линзовых пространства Lni(£b ...,£„) и Lm(t'ly • ••>£'„)
имеют один и тот же гомотопический тип тогда и только тогда, когда
ll...£n = ±kutl...l'n mod m для некоторого целого числа к. Доказательство
этого намечено в задаче 2 из §З.Е и задаче 29 из §4.2. Например,
трёхмерные линзовые пространства L1/5 и L2/5 не являются гомотопически
эквивалентными, хотя они имеют одну и ту же фундаментальную группу
и одинаковые группы гомологии. С другой стороны, линзовые
пространства L1/7 и L2/7 гомотопически эквивалентны, но не гомеоморфны.
Эйлерова характеристика
Для конечного CW-комплекса Х эйлерова характеристика #(Х)
определяется как альтернированная сумма £(-1)псп, где с„ — число п-мерных
клеток комплекса X, что обобщает знакомую нам формулу
вершины —рёбра Л-грани
для двумерных комплексов. Следующий результат показывает, что число
#(Х) можно определить в терминах гомологии, а потому оно зависит
только от гомотопического типа комплекса X. В частности, /(X) не
зависит от выбора CW-структуры на X.
I Теорема 2.44. Справедливо равенство %(Х) = S(-l)n rankHn(X).
n
Здесь ранг конечно порождённой абелевой группы —число
слагаемых Z в представлении группы в виде прямой суммы циклических
Групп. Нам будет нужен следующий факт, доказательство которого мы
оставляем в качестве упражнения. Если Q-+A-+B-+C-* 0 —короткая
точная последовательность конечно порождённых абелевых групп, то
rank В = rank А + rank С.
Доказательство теоремы 2.44 чисто алгебраическое. Рассмотрим
Цепной комплекс
О -* Ск —► Ск_г ~> ... -* Cj —► С0 -* О
190
Глава 2. Гомологии
конечно порождённых абелевых групп; Zn =Kerdn — циклы, Вп = Imdn+1 —
границы, Нп =Zn/Bn — гомологии. У нас есть короткие точные
последовательности 0 -* Zn -* Сп -> Ви_} -* 0 и 0-» Вп -* Zn -* Нп -* 0; следовательно,
rankC,, = rankZ„-f rankB„_I}
rankZ71 — rank Bn-f rankHn.
Подставим теперь второе уравнение в первое, умножим полученное
уравнение на (—1)" и просуммируем по л. В результате получим
J](-l)nrankC„ = ][](-1)пгапк//п.
Применив это утверждение к Сп = Нп{Х'\ Хп~]), получим доказательство
теоремы. О.
Например, поверхности Mg и Ng имеют эйлеровы характеристики
#(Mg) = 2 - 2g и /(Ng) = 2- g. Таким образом, все ориентируемые
поверхности Mg различаются их эйлеровыми характеристиками, и то же
верно для неориентируемых поверхностей Ng. Имеются лишь
соотношения xiMg) =*(N2g).
Расщепимые точные последовательности
Предположим, что задана ретракция г: X —* Л, так что п" = 1, где
i: А —* X — включение. Тогда индуцированное отображение 1*ж: Нп(А) —*
—> Нп(Х) инъективно, так как r+i* = l. Из этого следует, что граничные
отображения в длинной точной последовательности для пары (X, А)
нулевые, а потому длинная точная последовательность разбивается в короткие
точные последовательности
0 -> Нп (Л) ^ Нп (X) ^ Н„ (X, Л) -> 0.
Как видно из следующего элементарного алгебраического утверждения,
соотношение rj* = 1в действительности даёт больше информации.
Лемма о расщеплении. Для короткой точной последовательности
0—* А —> В —> С —* 0 абелевых групп следующие утверждения
эквивалентны:
а) существует гомоморфизм р: В-*А, для которого pi = 1: Л-»Л;
б) существует гомоморфизм 5: С-*В, для которого js = l: C—*C\
в) существует изоморфизм В ад Л Ф С, задающий коммутативную
диаграмму
В
-^0
ЛФС
где нижние отображения очевидны, а именно, а —»(а, 0) и (а, с) —> с.
§ 2.2. Вычисления и приложения
191
Если эти условия выполняются, то точную последовательность
называют расщепимой. Заметьте, что условие в) симметрично: нет никакой
существенной разницы между группами А и С.
Набросок доказательства. Для доказательства импликации а) => в)
нужно проверить, что отображение В —* А $ С, заданное формулой Ъ —►
»-* (р(Ь), j(b)), является изоморфизмом с требуемыми свойствами. Для
доказательства импликации б) => в) нужно взять вместо этого
отображение АФС-»В, (а,с)—►i(a)+5(c). Обратные импликации в)=>а) и в) =>б)
довольно очевидны. Если нужно доказать б) => а) непосредственно, то
можно положить p(b) = i_1(b-5J(b)). Дальнейшие подробности
оставляются читателю. □
За исключением импликаций б) => а) и б) => в) это доказательство
годится и для неабелевых групп. В неабелевом случае условие б) явно
слабее, чем а) и в), и короткие точные последовательности,
удовлетворяющие условию б), определяют В лишь как полупрямое произведение
групп А и С. Трудность состоит в том, что 5(C) может не быть нормальной
подгруппой в В. В неабелевом случае «расщенимость» означает
выполнение условия б).
Как в абелевой, так и в неабелевой ситуации, если группа С свободна,
то любая точная последовательность
0-* A -Ub ^С-*0
расщепляется, так как можно определить гомоморфизм 5: С—>В, выбрав
базис {са} для группы С и взяв в качестве s(ca) произвольный элемент
Ьа€В, для которого j(ba) = ca. Обратное утверждение тоже верно:
если любая короткая точная последовательность, заканчивающаяся
группой С, расщепляется, то группа С свободна. Действительно, для любой
группы С есть короткая точная последовательность 0—* А —* В —* С —»0 со
свободной группой В: выберем образующие для группы С, и пусть базис
группы В находится во взаимно однозначном соответствии с этими
образующими; затем пусть гомоморфизм В-*С переводит каждый элемент
базиса в соответствующую образующую. Тогда если последовательность
О—* А —* В —* С—* О расщепляется, то группа С изоморфна подгруппе
свободной группы, а потому сама является свободной.
Из леммы о расщеплении и предыдущих замечаний мы получаем, что
ретракция г: Х-*А даёт расщепление
НП(Х)*НП(А)ФН„(Х,А).
Этим можно воспользоваться, чтобы показать, что такой ретракции не
существует в некоторых случаях, например в ситуации теоремы Брауэра
о неподвижной точке, где ретракция D" —*S"-1 привела бы к
невозможному расщеплению H^iD") ^Hn_^Sn~l) eH^CD", S""1). Чтобы получить
Немного более тонкий пример, рассмотрим цилиндр отображения Mf для
192
Глава 2. Гомологии
отображения f:Sn-+Sn степени т, где т > 1. Если бы пространство Mr
ретрагировалось на сферу Sn с Mf, соответствующую области значений /,
мы получили бы расщепление короткой точной последовательности
О ^ Hn(Sn) ^ Hn(Mf) >• Hn{Mfy Sn) - О
О ^ Z - >■ Z >- Zm ^ О
Но эта последовательность не расщепляется, так как группа Z не
изоморфна Z ф Zm, если m > 1, поэтому такой ретракция не может быть.
В простейшем случае отображения Sl ^>S* степени 2, заданного формулой
z —> z2, это означает, что лист Мёбиуса не ретрагируется на его граничную
окружность.
Гомологии групп
В § 1.В для каждой группы G мы построили CW-комплекс K(G, 1), для
которого универсальное накрытие стягиваемо, и показали, что
гомотопический тип такого пространства K(G, 1) единственным образом
определяется группой G. Поэтому группы гомологии Нп(К{С, 1)) зависят только
от G, и их обычно обозначают просто Hn(G). Вычисления для линзовых
пространств в примере 2.43 показывают, что Hn(Zn,) —это Zm для
нечётного п и 0 для чётного п > 0. Так как окружность S1 —это пространство
X(Z, 1), а тор — это пространство К[Ъ х Z, 1), мы знаем также и гомологии
этих двух групп. Вообще гомологии конечно порождённых абелевых групп
можно вычислить на основе этих примеров, используя формулу Кюннета
из § З.В и тот факт, что произведение X(G, 1) х К{НУ 1) является
пространством типа K{G х Н, 1).
Вот применение вычисления группы Hn(Zni).
I Предложение 2.45. Если конечномерный CW-комплекс Х является
пространством X(G, 1), то группа G^tt^X) должна быть свободной от
кручения.
Это можно применить к довольно многим многообразиям, например
к замкнутым поверхностям, кроме S2 и Ш>2, а также ко многим
трёхмерным многообразиям, в частности к дополнениям узлов в S3.
Доказательство. Если бы группа G имела кручение, то у неё была бы
конечная циклическая подгруппа Ът для некоторого т > 1, а
накрывающим пространством для X, соответствующим этой подгруппе в G = тг1 (X),
было бы пространство K(Zm, 1). Так как X — конечномерный
CW-комплекс, таким же должно быть и его накрывающее пространство K(Zm, 1),
а потому гомологии пространства X(Zni, 1) будут отличны от нуля только
для конечного числа размерностей. Но это противоречит тому факту, что
группы Hfl(Z,„) отличны от нуля для бесконечно многих значений п. □
§ 2.2. Вычисления и приложения
193
Гомологии групп отражают богатство теории групп и были изучены
весьма тщательно. Хорошим начальным курсом для тех, кто хочет более
подробно познакомиться с ними, является учебник [14]. Более
продвинутые книги [4] и [10] рассматривают эту тему в основном с топологической
точки зрения.
Последовательности Майера—Вьеториса
Наряду с длинной точной последовательностью групп гомологии для
пары (X, А) имеется другая длинная точная последовательность,
известная под названием последовательность Майера—Вьеториса, столь же
мощная, но иногда более удобная для применения. Для пары таких
подпространств Л, В с X, что X является объединением внутренностей Л и В,
эта точная последовательность имеет вид
... -> нп(лпв) Д нпшеяп(в) Л нп(Х) Л нп_г(Апв) ->...
... -W/0(X)->0.
Помимо её полезности для вычислений, последовательность
Майера—Вьеториса часто применяется в рассуждениях по индукции, когда известно,
что некое утверждение верно для А, В и АПВ согласно индукции, а затем
с помощью этой точной последовательности доказывается, что оно верно
для ДиВ.
Последовательность Майера—Вьеториса легко получить, применяя
технику из § 2.1. Пусть См (Л + В) — подгруппа в С„ (X), состоящая из цепей,
которые являются суммами цепей в Л и цепей в В. Обычный граничный
гомоморфизм (1: С„(Х) -* Сп^(Х) переводит Си(А + В) в Сп_г(А + В),
поэтому группы Сп (Л -I- В) образуют цепной комплекс. Согласно
предложению 2.21 включения Сп(А + В) С-*С„(Х) индуцируют изоморфизмы групп
гомологии. Последовательность Майера—Вьеториса — это длинная точная
последовательность групп гомологии, связанная с короткой точной
последовательностью цепных комплексов, образованных короткими точными
последовательностями
0 -> СП(ДПВ) ^ Сп{А)®Сп{В) ^ Сп{А + В) -> 0,
где (/?(*) = (*, ~х) и гр(х, у) = х + у. Точность этой короткой точной
последовательности можно проверить следующим образом. Прежде всего
Кег {р == 0, так как цепь в А П В, которая является нулевой как цепь в А (или
в В), должна быть нулевой цепью. Далее, Imc/? cKeri/;, так как я/;У> =0.
Кроме того, Кегя/> с Im у>, так как для пары Qt, у) е СП(Л) Ф Сп{В) условие
х + у = 0 влечёт, что х — -у, поэтому х — цепь и в Л, и в В, т. е. х е С„ (Л П В)
и (*> у) = (*, -*) £ Imy?. Наконец, точность в члене СМ(Л + В)
непосредственно следует из определения групп Сп(А + В).
7 3ак ЛЛ55
194
Глава 2. Гомологии
Граничное отображение д: Нп(Х) -♦Н^СЛ ПВ) легко описать явно.
Пусть класс а€Н„(Х) представлен циклом z. С помощью
барицентрического подразделения или каким-нибудь другим методом мы можем
выбрать цикл z так, чтобы он был суммой х + у цепей в Л и В соответственно.
При этом х и у не обязательно являются циклами по отдельности, но
дх = -ду, так как а(х + у) = 0. Тогда элемент даеНп_1(ЛПВ) представлен
циклом дх = —ду, как видно из определения граничного отображения
в длинной точной последовательности групп гомологии, связанных с
короткой точной последовательностью цепных комплексов.
Имеется также формально такая же последовательность Майера—Вье-
ториса для приведённых групп гомологии, которая получается при
увеличении предыдущей короткой точной последовательности цепных
комплексов очевидным способом:
О ^ С0(Л ПВ) —£->- С0(А)®С0(В) —^ С0(А + В) ^ О
Т . т г/? *
о ^z ^zez ■ ^z ^о
Последовательности Майера—Вьеториса можно рассматривать как
аналоги теоремы ван Кампена, так как если пространство АПВ линейно
связно, то члены Нг приведённой последовательности Майера—Вьеториса
дают изоморфизм
Н^Х) * (Н1(Л)0Н1(В))/1тФ.
Это в точности абелианизованное утверждение теоремы ван Кампена,
a Нг — это абелианизация группы п1 для линейно связных пространств,
как показано в § 2.А.
Имеются также последовательности Майера—Вьеториса для таких
разложений X = A U В, что Л и В являются деформационными ретрактами
окрестностей U и V, причём U П V деформационно ретрагируется на
АПВ. При таких предположениях из 5-леммы следует, что отображения
Сп(А + В) -* Cn(U + V) индуцируют изоморфизмы гомологии, а потому то
же верно и для отображений Сп(А + В) -* СП(Х). Лишь это требуется для
построения последовательности Майера—Вьеториса. Например, если X —
CW-комплекс, а Л и В — его подкомплексы, то мы можем выбрать в
качестве U и V окрестности вида Ne(A) и АГДВ), построенные в приложении,
которые обладают тем свойством, что Ne (Л) П N£ (В) = Ne (Л П В).
Пример 2.46. Возьмём X = Sn, и пусть Л и В — северная и южная
полусферы, причём AC\B = Sn~K Тогда в приведённой последовательности
Майера—Вьеториса члены Н{(А) (ВН[(В) нулевые, поэтому мы получаем
изоморфизмы H,(S'1) ъ Hi_l(Sn~l). Это даёт другой способ вычисления
групп гомологии сферы S" по индукции.
§ 2.2. Вычисления и приложения
195
Пример 2.47. Мы можем представить бутылку Клейна К в виде
объединения двух листов Мёбиуса Л и В, склеенных по гомеоморфизму их
граничных окружностей. Тогда А, В и АГ)В гомотопически эквивалентны
окружностям, поэтому интересная часть приведённой
последовательности Майера—Вьеториса для разложения К = А и В — это участок
О -* Н2(К) -> Н,(АПВ) -^ Н,(А) ФН^В) -> ЯДЮ -> 0.
Отображение Ф: Z -* Z 0 Z задаётся формулой 1 —► (2, -2), так как
граничная окружность листа Мёбиуса дважды наматывается на центральную
окружность. Так как гомоморфизм Ф инъективен, мы получаем Н2(К) = 0.
Кроме того, H1(JO^Z0Z2, так как мы можем выбрать (1,0) и (1,-1)
в качестве базиса группы Z 0 Z. Все группы гомологии пространства К
более высоких размерностей нулевые согласно предыдущему участку
последовательности Майера—Вьеториса.
Пример 2.48. Опишем теперь точную последовательность, которая
похожа на последовательность Майера—Вьеториса и в некоторых случаях
обобщает её. Если заданы два отображения /, g: X-+Y, то мы можем
рассмотреть факторпространство Z несвязного объединения пространств
X х / и У посредством отождествления (х, 0) ~/(х) и (х, 1) ~g(x); таким
образом, один конец X х / приклеивается к У посредством /, а другой
конец — посредством g. Например, если оба отображения / и g — это
тождественное отображение X -*Х, то тогда Z = X x S1. Если только одно из
отображений / и g, например /, является тождественным, то
пространство Z гомеоморфно так называемому тору отображения g, т. е. фактор-
пространству цилиндра X xl при отождествлениях (х,0)~ (g(x), 1).
Примером служит бутылка Клейна; для неё g — симметрия Sl -*Sl.
Нужная нам точная последовательность имеет вид
... - яп(х) ^> нпт ±> нпц) - нп_г(х) ^ нп_гт -..., w
где i — очевидное включение Y<-^Z. Чтобы получить эту точную
последовательность, рассмотрим отображение q: (X х /, X х 31) -* (Z, У), которое
является ограничением на X х / отображения факторизации X х /иУ-*Z.
Отображение q индуцирует отображение длинных точных
последовательностей:
... -^ Нп+1(Х х1,Ххд1)-^ Нп(Х х 31) -^ Нп(Х х I) -Л- ...
... - Нп+1(7, У) ^— HU(Y) -^-^ Hn{Z) -^ ...
В верхней строке средний член —прямая сумма двух экземпляров
группы Ни(Х), и отображение i* сюръективно, так как X х I
деформационно ретрагируется на X х {0} и на X х {1}. Сюръективность
отображений i+ в верхней строке влечёт, что следующие за ними отображения
196
Глава 2. Гомологии
нулевые, откуда, в свою очередь, следует, что отображения д инъективны.
Таким образом, отображение д в верхней строке даёт изоморфизм группы
Ип+1(Х х /, X х д/) на ядро гомоморфизма £*, которое состоит из пар
(ау~а), где а€Нп(Х). Это ядро —экземпляр группы НП(Х), и среднее
вертикальное отображение q* переводит {а,-а) в /Да) -g+(a).
Отображение q+ слева является изоморфизмом, так как мы имеем дело с
хорошими парами и отображение q индуцирует гомеоморфизм фактор-
пространств (X х I)/{X х д/) —* Z/Y. Следовательно, если мы заменим
группу Hn+1(Z, У) в нижней точной последовательности на изоморфную
ей группу НП(Х) ^Кеп*, то мы получим желаемую длинную точную
последовательность.
В случае тора отображения для симметрии g: S1 —*S], когда Z —
бутылка Клейна, интересна следующая часть точной
последовательности (*):
О -*- H2(Z) -*■ H^S1) ^ H^S1) -— H^Z) -— HofS1) ^ HqCS1)
Z —>Ъ Z —^Z
Таким образом, H2(Z) = 0, и мы имеем короткую точную
последовательность 0 -* Z2 -* H: (Z) -»Z -»0. Она расщепима, так как группа Z свободна;
поэтому Hl (Z) яй Z2 Ф Z. Другие примеры приведены в задачах.
Если У — несвязное объединение пространств ^ и У2, причём /: Х->У:
и g: X —* У2, то Z состоит из цилиндров отображений для этих двух
отображений, у которых отождествлены концы, соответствующие области
определений. Предположим, например, что мы представили CW-комплекс
в виде объединения двух подкомплексов Л и В, а в качестве fug взяли
включения Л П В <—► Л и Л П В <—► В. Тогда двойной цилиндр
отображения Z гомотопически эквивалентен A U В, так как мы можем
рассмотреть Z как пространство (А П В) х /, к концам которого приклеены А
и Bt a затем сдвинуть приклеивание А вниз к концу В и получить A U В
с приклеенным по одному из концов пространством (АПВ) х /. Согласно
предложению 0.18 эта операция сдвига сохраняет гомотопический тип,
поэтому мы получаем гомотопическую эквивалентность Z ~ A U В. Точная
последовательность (*) в этом случае совпадает с последовательностью
Майера—Вьеториса.
Иногда бывает полезна относительная последовательность Майера—
Вьеториса. Если дана такая пара пространств (X, У) = (Л U В, С U D), где
С с Л и D с В, что X является объединением внутренностей множеств А
и В, а У является объединением внутренностей множеств С и D, то имеет
место относительная последовательность Майера—Вьеториса
...->Ни(ЛПВ,СпО) -^НМ(Л,С)ФН„(В^) ^НП(Х,У) Л...
§ 2.2. Вычисления и приложения
197
Чтобы получить её, рассмотрим коммутативную диаграмму
0 0 0
i 1,1
0 ^С„(СП0) —^С„(С)ФС„(0) ^—+C„(C + D) ^0
О ^СП(АПВ) ^—^СП(А)ФСП(В) ^—^СП(Л + В) ^0
Т Т I, Y
0-^Cn(AnB,CriD)-!^Cn(A,C)©Cn(B>D)-i-Cn(A+B,C + D)-^0
Y Y I
0 0 0
где СП(А -I- В, С -I- D) —факторгруппа подгруппы СП(Л -I- В) с С„(Х) по её
подгруппе Cn{C + D) ССП(У). Таким образом, все три столбца диаграммы
точные. Мы уже знаем, что первые две строки точные, и мы утверждаем,
что третья строка (с отображениями кр игр, индуцированными
отображениями с/? и гр во второй строке) тоже точная. Так как во второй строке
xj)ip = 0, это равенство выполняется и в третьей строке, поэтому третья
строка, во всяком случае, является цепным комплексом. Если
рассматривать эти три строки как цепные комплексы, то тогда диаграмма
представляет собой короткую точную последовательность цепных комплексов.
В соответствующей ей длинной точной последовательности групп
гомологии два из каждых трёх членов нулевые, так как первые две строки
диаграммы точные. Следовательно, остальные группы гомологии тоже
нулевые, а потому третья строка тоже точная.
Третий столбец отображается на 0 —> С„(У) —> С„(Х) —> СП(Х, У) —> 0,
что индуцирует отображения групп гомологии, которые являются
изоморфизмами для членов X и У, как мы видели выше. Поэтому
согласно 5-лемме отображения Сп{А + В, С -I- D) —> Cn(X, Y) тоже индуцируют
изоморфизмы групп гомологии. Тогда относительная последовательность
Майера—Вьеториса — это длинная точная последовательность групп
гомологии, соответствующая короткой точной последовательности цепных
Комплексов, заданной третьей строкой диаграммы.
Гомологии с коэффициентами
Есть простое обобщение теории гомологии, рассматриваемой нами
До сих пор, которое ведёт себя во многом похоже, но иногда предоставляет
Технические преимущества. Обобщение состоит в использовании цепей
вида Хп1сг1' гДе crt — сингулярный п-симплекс в X, как и раньше, но те-
Перь коэффициенты п,- берутся в фиксированной абелевой группе G, а не
в Z. Такие п-мерные цепи образуют абелеву группу С„(Х; G), и у неё то-
198
Глава 2. Гомологии
же есть относительная версия СП(Х, Л; G) = СП(Х; G)/Cn(A; G). Прежнюю
формулу для граничного отображения д можно использовать и для
произвольной группы G, а именно, д(£п1ад = I](-~l);ni0"r| tvo> •••» V/,..., vn].
Вычисление снова показывает, что д2 = 0, поэтому группы Cn(X;G) и
Cn(X, A; G) образуют цепные комплексы. Получающиеся при этом группы
гомологии Hn(X\G) и Hn(X, A; G) называют группами гомологии с кгоэф-
фициентами в G. Приведённые группы НП(Х; G) определяются с помощью
аугментированного цепного комплекса ...—>С0(Х; G) —► G —>0, где
отображение е снова определяется как суммирование коэффициентов.
Случай G = Ъ2 особенно простой, так как нужно считать суммы
сингулярных симплексов с коэффициентами 0 или 1, поэтому, отбрасывая
члены с коэффициентом 0, можно представлять себе цепи просто как
конечные «объединения» сингулярных симплексов. Формулы для границы
также упрощаются, так как больше не нужно заботиться о знаках. Так
как знаки являются алгебраическим выражением для ориентации, можно
игнорировать также и ориентации. Это означает, что гомологии с
коэффициентами в Z2 обычно наиболее естественный инструмент в неориен-
тируемом случае.
Вся теория, которую мы разработали в §2.1 для группы
коэффициентов Z, непосредственно переносится на общие группы коэффициентов G
без изменения в доказательствах. Это относится и к последовательности
Майера—Вьеториса. Различия между Hn(X; G) и НП(Х) появляются только
тогда, когда начинаются вычисления. Если X — это точка, то метод,
использованный нами для вычисления НП(Х), показывает, что группа Hn(X\G)
равна G при п = 0 и равна 0 при п > 0. Из этого следует, так же как и для
G = Z, что группа Ип (Sfc; G) равна G при п = к и равна 0 в остальных случаях.
Клеточные гомологии тоже обобщаются на гомологии с
коэффициентами: группа клеточных цепей Нп(Хп,Хп~1) заменяется на группу
ЯП(ХП, Xn~l\ G), которая является прямой суммой групп G, по одной
для каждой n-мерной клетки. Доказательство того, что группы
клеточных гомологии Н™(Х) совпадают с группами сингулярных гомологии
НП(Х), переносится на общий случай непосредственно и даёт
изоморфизм Н™(Х; G)wHn(X; G). Клеточные граничные отображения задаются
той же самой формулой, что и для группы коэффициентов Z, а именно,
dn(Snaea) = S^n^e^1. Прежнее доказательство применимо, но для
того, чтобы знать, что коэффициенты dnp будут те же самые, что и раньше,
необходим следующий результат.
Лемма 2.49. Если отображение /: Sk —>Sk имеет степень т, то
гомоморфизм /*: Hk(Sk; G)-*Hk(Sk; G) представляет собой умножение на т.
Доказательство. Прежде всего заметим, что гомоморфизм уэ: GX-*G2
индуцирует отображения <р„: Сп(Х, A; GO -* СП(Х,Л; G2), коммутирую-
§ 2.2. Вычисления и приложения
199
щие с граничными отображениями, поэтому возникают индуцированные
гомоморфизмы </v ЯП(Х, A; Ga) -* Н„(Х, Л; G2). Они обладают
различными свойствами естественности. Например, они дают коммутативную
диаграмму, отображающую длинную точную последовательность
гомологии для пары (X, А) с коэффициентами в Gj в соответствующую
последовательность с коэффициентами в G2. Кроме того, отображения (/?*
коммутируют с гомоморфизмами /*, индуцированными отображениями
/:(Х,Л)->(У,В).
Пусть теперь отображение /: Sk-+Sk имеет степень т, и пусть ц>: Z—*G
переводит 1 в данный элемент g^G. Тогда мы получаем коммутативную
диаграмму
Z w Hfc(Sfc; Z) —£-*- fy (Sfc; Z) ** Z
G ъ Hfc(S*; G) -^ /^(S*; G) * G
в которой коммутативность двух внешних квадратов следует из
индуктивного вычисления этих групп гомологии, сводящегося к случаю fc = 0, когда
коммутативность очевидна.
Так как диаграмма коммутативная, из предположения о том, что
верхнее отображение переводит 1 в т, следует, что нижнее отображение
переводит g в mg. □
Пример 2.50. Поучительно посмотреть, что происходит с гомология-
ми пространства RPrt, когда в качестве группы коэффициентов G выбрана
аддитивная группа поля F. Тогда клеточный цепной комплекс имеет вид
0 2 0 2 0
... -^F->F-*F->F->F->0.
Следовательно, если характеристика поля F равна 2, например, если
F = Z2, то Hfc(RPn;F)**F для 0^/с^п; это более единообразный ответ,
чем для группы коэффициентов Z. С другой стороны, если характеристика
2
поля F отлична от 2, то тогда граничные отображения F —*F —
изоморфизмы, а потому группа Hk(RPn; F) равна F при fc = 0 и при нечётном fc = п,
а во всех остальных случаях она нулевая.
В §З.А мы увидим, что имеется общая алгебраическая формула,
выражающая гомологии с произвольными коэффициентами в терминах
гомологии с коэффициентами в Z. Некоторые её простые частные случаи,
которые во многом дают представление об общем результате, приведены
в качестве задач.
Несмотря на то что гомологии с коэффициентами в Z полностью
определяют гомологии с коэффициентами в других группах, есть много
ситуаций, когда гомологии с удачно выбранной группой коэффициентов дают
больше информации, чем гомологии с коэффициентами в Z. Хорошим
200
Глава 2. Гомологии
примером этого является доказательство теоремы Борсука—Улама в §2.В,
использующее коэффициенты в Z2.
В качестве другой иллюстрации мы сейчас приведём пример
отображения /: X —* У, которое обладает тем свойством, что индуцированные
отображения /* тривиальны для гомологии с коэффициентами в Z, но не
для гомологии с коэффициентами в Zm для подходящим образом
выбранного т. Таким образом, гомологии с коэффициентами в Ът показывают,
что отображение / не гомотопно постоянному, причём мы не смогли бы
этого узнать, используя только группу коэффициентов Z.
Пример 2.51. Пусть X — пространство Мура M(Z„,, л), полученное из
Sn приклеиванием клетки еп+1 по отображению степени т. Отображение
факторизации /: X—*X/Sn—Sn+l индуцирует тривиальные
гомоморфизмы приведённых гомологии с коэффициентами в Z, так как отличные от
нуля приведённые группы гомологии пространств X и Sn+1 встречаются
в разных размерностях. Но для коэффициентов в Zn, ситуация другая,
как видно из длинной точной последовательность пары (X, Sn), которая
содержит участок
0 = Hn+1(Sn; ZJ -> Hn+1(X; Zm) ±* Hn+1(X/Sn; Z,M).
Точность показывает, что гомоморфизм /* инъективен, а потому
отличен от нуля, так как группа ЯП+1(Х; Zm) равна Zni, поскольку клеточное
граничное отображение Hn+l(Xn+l, Xn\ Zm) -*НП(ХП, X""1; Zm) имеет вид
Zm —Zm.
Задачи
1. Докажите теорему Брауэра о неподвижной точке для отображений
/: Dn -*Dn, применив теорию степени к отображению Sn -»Sn, которое
переводит и северную, и южную полусферы сферы S'1 в южную полусферу
посредством /. [Таким было исходное доказательство Брауэра.]
2. Дано отображение /: S2n —*S2n. Докажите, что существует точка
х € S2n, для которой либо /О) =х, либо /О) = —х. Выведите из этого, что
любое отображение RP2n —* RP2n имеет неподвижную точку. Постройте
отображение RP2""1 -♦RP2"""1 без неподвижных точек с помощью
линейного преобразования R2n —*R2n, у которого нет собственных векторов.
3. Пусть f:Sn-*Sn — отображение степени нуль. Докажите, что
существуют точки *, у еSn, для которых /00 =х и /(у) = —у. Воспользуйтесь
этим, чтобы доказать, что если F —такое непрерывное векторное поле,
определённое на единичном шаре Dn в Rn, что F(x) Ф 0 для всех х, то
существует точка края 3D'1, в которой вектор F направлен по радиусу
наружу, и другая точка края dDny в которой вектор F направлен по радиусу
внутрь.
4. Постройте сюръективное отображение S" —* S" нулевой степени
для каждого л ^ 1.
§ 2.2. Вычисления и приложения
201
5. Докажите, что любые две симметрии сферы Sn относительно
разных п-мерных гиперплоскостей гомотопны, причём гомотопны в классе
симметрии. [Здесь может оказаться полезной формула из линейной
алгебры для симметрии в терминах скалярного произведения.]
6. Докажите, что любое отображение Sn —> Sn гомотопно
отображению, которое имеет неподвижную точку, если п > 0.
7. Для обратимого линейного отображения /: Rn —> lRn докажите, что
индуцированное отображение групп Hn(Rn,3T - {0}) я* W^CR" - {0})ъ
ыЪ — это 1 или —1 в соответствии с тем, положителен или
отрицателен определитель отображения /. [С помощью метода Гаусса покажите,
что матрицу отображения / можно соединить путём, состоящим из
обратимых матриц, с диагональной матрицей с элементами ±1 на
диагонали.]
8. Многочлен /(z) с комплексными коэффициентами,
рассматриваемый как отображение С —> С, всегда можно продолжить до непрерывного
отображения одноточечной компактификации /: S2-*S2. Докажите, что
степень отображения / равна степени / как многочлена. Докажите также,
что локальная степень отображения / в корне многочлена / равна
кратности этого корня.
9. Вычислите группы гомологии следующих двумерных комплексов.
а) Факторпространство сферы S2, полученное при отождествлении
северного и южного полюса в одну точку.
б) Пространство S1 x (SlVSl).
в) Пространство, полученное из D2 при вырезании внутренностей двух
непересекающихся дисков, расположенных внутри D2, и
последующего отождествления всех трёх полученных граничных окружностей
в одну посредством гомеоморфизмов, сохраняющих ориентации по
часовой стрелке этих окружностей.
г) Факторпространство тора S1 x S1, полученное при отождествлении
точек окружности S1 х {х0}, которые отличаются поворотом на 2тг/т,
и отождествлении точек окружности {xQ} x S1, которые отличаются
поворотом на 2п/п.
10. Пусть X — факторпространство сферы S2 при отождествлениях
х ~ — х для точек ху лежащих на экваторе S1. Вычислите группы гомологии
Hf(X). Сделайте то же самое для сферы S3 с отождествлёнными
диаметрально противоположными точками экватора S2 с S3.
11. В одной из задач в §1.2 описан трёхмерный CW-комплекс,
полученный из куба /3 при отождествлении противоположных граней
посредством поворота на четверть оборота. Вычислите группы гомологии этого
комплекса.
12. Докажите, что отображение факторизации S1 x S1 ->S2,
стягивающее в точку подпространство Sl V S1, не гомотопно нулю, показав, что
оно индуцирует изоморфизм групп Н2. С другой стороны, докажите с по-
202
Глава 2. Гомологии
мощью накрывающих пространств, что любое отображение S2-+Sl x S1
гомотопно нулю.
13. Пусть X—- двумерный комплекс, полученный из окружности S1
с обычной клеточной структурой приклеиванием двух двумерных клеток
по отображениям степеней 2 и 3 соответственно.
а) Вычислите группы гомологии всех подкомплексов Л с X и
соответствующих факторкомплексов Х/А.
б) Докажите, что X ~ S2 и что единственный подкомплекс Л с X, для
которого отображение факторизации X —* Х/А является
гомотопической эквивалентностью,— это тривиальный подкомплекс, т.е.
нульмерная клетка.
14. Отображение /: Sn -»Sn, для которого /О) = /(-*) для всех х,
называют чётным отображением. Докажите, что чётное отображение
Sn —* Sn должно иметь чётную степень и что степень должна быть в
действительности нулём, когда п четно. Когда п нечётно, докажите, что
существуют чётные отображения любой данной чётной степени. [Указания.
Если отображение / четно, то его можно представить в виде композиции
Sn —* RPn —* S". Используя вычисление группы Hn(RPrt) в тексте книги,
докажите, что индуцированное отображение Hn(Sn) —>H„(RPn) переводит
образующую в удвоенную образующую, когда п нечётно. Может оказаться
полезным показать, что отображение факторизации МРП —* МР"/КРП-1
индуцирует изоморфизм групп Ни, когда п нечётно.]
15. Докажите, что если Х-—CW-комплекс, то группа Н„(ХМ)
свободная, отождествив её с ядром клеточного граничного отображения
яп(хп,х"-1)-яп_1(хм-1,х"-2).
16. Пусть симплекс А" = [v0,..., vM] снабжён естественной структурой
А-комплекса с k-мерными симплексами [v, , ..., V; ] для f0 < ... < ifc.
Вычислите ранги симплициальных (или клеточных) групп цепей А,(А") и
подгрупп циклов и границ. [Указание: треугольник Паскаля.] Воспользуйтесь
этим, чтобы показать, что для k-мерного остова комплекса Ап группа
гомологии Н{ ((А77)*) равна 0 при f < к и является свободной группой ранга
С*+1при1 = 1к.
17. Докажите, что изоморфизм между клеточными и сингулярными
гомологиями естествен в следующем смысле. Отображение /: X—>У,
которое является клеточным, т.е. обладает тем свойством, что /(Хп) с Yn
для всех п, индуцирует цепное отображение /+ между клеточными
цепными комплексами для X и У, и отображение /*: Н™(Х) -*H%w(Y)t
индуцированное этим цепным отображением, соответствует отображению
/#: Нп (X) -> Нп (У) при изоморфизме Н™ ъ Нп.
18. Для CW-пары (Х, Л) покажите, что существует относительный
клеточный цепной комплекс, образованный группами H,(X',X'_1 U Л'),
группы гомологии которого изоморфны НП(Х, Л).
§ 2.2. Вычисления и приложения
203
19. Вычислите Н((ШРп/ЖРт) при m < n с помощью клеточных
гомологии, используя стандартную CW-структуру на RP" с IRPm в качестве т-мер-
ного остова.
20. Для конечных CW-комплексов X и У докажите, что #(Х х У) =
21. Докажите, что если конечный CW-комплекс X является
объединением подкомплексов А и В, то х СЮ = X W) + X (Я) — X (^ п Я)•
22. Докажите, что если X —конечный CW-комплекс, а р: Х-*Х —
п-листное накрытие, то # (X) = п# (X).
23. Докажите, что если замкнутая ориентируемая поверхность Mg
рода g является накрывающим пространством для Mh, то g = п(ft - 1) +1, где
п — число листов накрытия. [Наоборот, если g = n(h — 1) + 1, то
существует п-листное накрытие Mg-*Mh, как мы видели в примере 1.41.]
24. Предположим, что мы строим S2 из конечного набора
многоугольников, отождествляя пары их сторон. Докажите, что в полученной при
этом СW-структуре на S2 одномерный остов не может быть ни одним
из двух нарисованных справа графов с пятью
и шестью вершинами. [Это один из шагов в
доказательстве того, что ни один из этих графов
не вкладывается в R2.]
25. Докажите, что для каждого n € Z есть единственная функция ip,
которая сопоставляет каждому конечному CW-комплексу целое число,
обладающее следующими свойствами: а) у>(Х) — ч>(У), если X и У го-
меоморфны; б) ip(X) = i/?(A) + ip(X/A)> если А — подкомплекс в X; в)
ip(S°) = n. Для такой функции ip докажите, что (/?(Х) = i/?(7), еслиХ^У.
26. Для пары (X, Л) пусть X и СА— это пространство X, к которому
приклеен конус над Д.
а) Докажите, что X является ретрактом пространства X и СА тогда
и только тогда, когда А стягиваемо в X, т. е. существует гомотопия
/,: А -* X, где /0 — включение А <-► X, а /: — постоянное отображение.
б) Докажите, что если А стягиваемо в X, то
Н„(ХМ)^Нп(Х)еЙп_1(А)>
воспользовавшись тем фактом, что (ХиСА)/Х является надстройкой
SA над А.
27. Короткие точные последовательности
0 -> С„(А) -> СП(Х) -> С„(Х, А) - 0
всегда расщепляются, но почему это не всегда приводит к расщеплениям
НП(Х)*НП(А)ФНП(Х,А)?
28. а) Используя последовательность Майера—Вьеториса, вычислите
группы гомологии пространства, полученного из тора S1 x S1
приклеиванием листа Мёбиуса посредством гомеоморфизма граничной окружности
листа Мёбиуса на окружность S1 х {х0} в торе.
#
204
Глава 2. Гомологии
б) Сделайте то же самое для пространства, полученного
приклеиванием листа Мёбиуса к Ж?2 посредством гомеоморфизма его граничной
окружности на стандартное подпространство IRP1 CRP2.
29. Поверхность Mg рода g, вложенная в R3 стандартным способом,
ограничивает компактное множество R. Два экземпляра R, склеенные по
тождественному отображению их граничных поверхностей Mg>
образуют замкнутое трёхмерное многообразие X. Вычислите группы гомологии
многообразия X с помощью последовательности Майера—Вьеториса для
этого разбиения X на два экземпляра R. Вычислите также относительные
группы Hi(R,Mg).
30. Пусть Ту —тор отображения для отображения /: X —> X. В
примере 2.48 мы построили длинную точную последовательность
... - НП(Х) ±±+ НП(Х) -> Нп(7>) - НП_,(Х) - ...
Воспользуйтесь ей, чтобы вычислить гомологии тора отображения для
следующих отображений.
а) Симметрия S2—>S2.
б) Отображение S2 —> S2 степени 2.
в) Отображение S] x Sl ^>Sl x S1, которое тождественно на одном
множителе и является симметрией па другом.
г) Отображение Sl xSl ^>S^ xS^, которое является симметрией на
каждом множителе.
д) Отображение S1 xSl^>Sl x S1, которое переставляет множители, а
затем отражает симметрично один из множителей.
31. Используя последовательность Майера—Вьеториса, докажите, что
если отмеченные точки в X и У, которые отождествляются в X V У,
являются деформационными ретрактами окрестностей L/ с X и V с У, то
имеют место изоморфизмы ЙП(Х \/У)^Нм(Х)ФНп(У).
32. Для SX (надстройки над X) докажите с помощью
последовательности Майера—Вьеториса, что имеют место изоморфизмы Hn{SX)&
^Hn_](X) для всех п.
33. Предположим, что пространство X — объединение таких
открытых множеств Aj, ..., Ап, что каждое пересечение А, П ... ПА,- либо пусто,
либо имеет тривиальные приведённые группы гомологии. Докажите, что
Н,(Х) = 0 при i ^ п - 1, и приведите пример, показывающий, что это
неравенство нельзя улучшить ни для какого п.
34. Выведите длинную точную последовательность пары (X, А) из
последовательности Майера—Вьеториса, применённой к X U СА, где СА —
конус над А. [Для сведения к случаю CW-nap (X, А) можно использовать
сингулярные комплексы S(X) и S{A).]
35. Используя последовательность Майера—Вьеториса, покажите, что
неориентируемую замкнутую поверхность, и вообще конечный симпли-
циальный комплекс X, для которого группа Нл (X) имеет кручение, нельзя
§ 2.2. Вычисления и приложения
205
вложить как подпространство в R3 таким образом, чтобы у него была
окрестность, гомеоморфная цилиндру отображения для некоторого
отображения из замкнутой ориентируемой поверхности в X. [Предположение
об окрестностях в действительности не нужно, если доказывать это
утверждение с помощью двойственности Александера из §3.3.]
36. Докажите что Н,(Х х Sn) ** Н((Х) ф Н,_П(Х) для всех i и п, где по
определению И{ = 0 при z < 0. А именно, докажите, что
Н{(Х х Sn) w Н{(Х) ®Н{{Х х Sn, X х {х0})
Н,(Х х Sn, X х {х0}) ъ Н^СХ х Sn~\ X х {jf0}).
[Относительная последовательность Майера—Вьеториса приводит к
простому доказательству последнего изоморфизма.]
37. Дайте элементарный вывод последовательности
Майера—Вьеториса для симплициальных гомологии Д-комплекса X, представленного
в виде объединения подкомплексов Л и В.
38. Докажите, что коммутативная диаграмма
-л+1
£n+i
\
в„
сп
в
Al-1
Dn
л-1
*Vi
с двумя точными последовательностями, нижней и верхней, приводит
к точной последовательности ... —*Еп+1 —*ВП —*Cn $Dn —*Е„ -»ВП_! —*...,
где отображения получены из отображений в диаграмме очевидным
образом, за исключением того, что отображение Вп-+Сп $Dn имеет минус по
одной из координат.
39. Воспользуйтесь предыдущей задачей, чтобы получить
относительную последовательность Майера—Вьеториса для CW-пары (Х, У) =
= (AUB, CUD), гдеЛ = ВилиС = 0.
40. Выведите непосредственно из длинной точной
последовательности групп гомологии, связанной с короткой точной последовательностью
Цепных комплексов 0 -» С,(Х) —> С,(Х) -»Q(X; Zn) -» 0, что имеют место
короткие точные последовательности
0 -> Н[{Х)1пН[{Х) -> Ht(X; Zn) -> (n-кручение Н^СХ)) -* 0,
где гькручение группы G —это ядро отображения G —> G, заданного
формулой g —* ng. Воспользуйтесь этим, чтобы показать, что H,(X;Zp) = 0
Для всех i и всех простых р тогда и только тогда, когда Я,(X) —линейное
пространство над Q для всех i.
206
Глава 2. Гомологии
41. Пусть X — конечный CW-комплекс, а F — поле. Докажите, что
эйлерову характеристику # (X) можно также вычислить по формуле
;№ = 2(-1)ndimH"(X;F)>
п
как альтернированную сумму размерностей линейных пространств
Hn(X\F).
42. Пусть X — конечный связный граф, у которого нет вершин,
являющихся концом ровно одного ребра. Предположим, что Нх(Х)Ъ)—~
свободная абелева группа ранга п > 1, а потому группа автоморфизмов
группы Hj(X;Z) — это GLn(Z), группа обратимых матриц размера пхп
с целочисленными элементами, для которых обратная матрица тоже
целочисленная. Докажите, что если G — конечная группа гомеоморфизмов
графа X, то гомоморфизм G—>GL„(Z), сопоставляющий гомеоморфизму
g: X—>Х индуцированный гомоморфизм g*: Hj(X; Z) —► HjfX; Z), инъек-
тивен. Докажите, что это утверждение остаётся верным, если заменить
группу коэффициентов Z на Z,n, где m > 2. Что будет плохо при т = 2?
43. а) Докажите, что цепной комплекс свободных абелевых групп
Сп можно представить в виде прямой суммы подкомплексов 0 —> Ln+1 —>
—> JCn —> 0, в каждом из которых не более двух членов, отличных от нуля.
[Докажите, что короткая точная последовательность 0 —> Кегд —> Сп —>
—> Im 6 —* 0 расщепима, и положите Кп = Кег д.]
б) В случае, когда группы Сп конечно порождённые, докажите, что
возможно дальнейшее разложение на слагаемые 0—>Z—>0 иО—>Z—>Z—>0.
[Приведите матрицу граничного отображения LM+I -*1Са к ступенчатому
виду элементарными преобразованиями строк и столбцов.]
в) Докажите, что если X — CW-комплекс с конечным числом клеток
в каждой размерности, то Н„(Х; G) — прямая сумма следующих групп:
• одного экземпляра группы G для каждого слагаемого Z в группе
НП(Х);
• одного экземпляра группы G/mG для каждого слагаемого Ът в группе
Н„(Х);
• одного экземпляра ядра отображения G ^>G для каждого слагаемого
Ът в группе Нп_х(Х).
§ 2.3. Формальная точка зрения
Иногда бывает полезно отстраниться от многочисленных
подробностей и выяснить общую структуру. В этом весьма коротком параграфе мы
сначала опишем общую структуру гомологии посредством аксиом, а затем
рассмотрим некоторые общие формальные свойства, которыми обладают
многие из наших конструкций, используя язык категорий и функторов,
ставший обычным во многих областях современной математики.
§ 2.3. Формальная точка зрения
207
Аксиомы гомологии
Для простоты давайте ограничимся CW-комплексами и будем
рассматривать только приведённые гомологии, чтобы не пришлось
упоминать про относительные гомологии. (Приведённая) теория гомологии
сопоставляет каждому непустому CW-комплексу X последовательность абе-
левых групп hn(X), а каждому отображению /: X -* Y одного CW-kom-
плекса в другой — последовательность гомоморфизмов /*: hn(X) -*hn(Y)
так, что (/g)* = /*g* и 1* = 1, и при этом должны выполняться следующие
три аксиомы.
LEcли/^g:X-,У,тoЛ=g+:hn(X)-*hп(У)^
2. Существуют граничные гомоморфизмы д: hn(X/A) -*hn_1(A),
которые определены для каждой CW-пары (Х, Л), причём они включаются
в точную последовательность
... - ЙП(А) - ft„(X) -hn(X/A)^hn4(A) - ...,
где i —включение, a q — отображение факторизации. Кроме того,
граничные отображения естественны в следующем смысле: для отображения
/: (X, Л) -* (У, В), индуцирующего факторотображение /: Х/А -* У/В,
имеют место коммутативные диаграммы
hn(X/A)^^hn^(A)
J/. J/-
йду/вз-^/^св)
3. Для букета X = \J Xa с включениями ia: Xa <-» X прямая сумма отоб-
a
ражений ©ia+: фйп(Ха) -*hn(X) является изоморфизмом для всех п.
а а
Индексы п могут принимать отрицательные значения. Обычные
сингулярные гомологии нулевые в отрицательных размерностях по
определению, но существуют интересные теории гомологии с нетривиальными
группами в отрицательных размерностях.
Третья аксиома может показаться менее важной, чем первые две.
В действительности для конечных букетов её можно вывести из первых
Двух аксиом, но, вообще говоря, это неверно для бесконечных букетов, как
показывает одна из приводимых ниже задач.
Можно сформулировать аксиомы и для неприведённых теорий
гомологии, и это не намного сложнее. Предположим, что определены
относительные группы /i„(X, Л), частным случаем которых являются
абсолютные группы, если положить /in(X) = ftn(X, 0). Аксиома 1 заменяется на её
очевидную относительную версию, а аксиома 2 разбивается на две части,
в первой из них предполагается существование длинной точной
последовательности для этих относительных групп с естественными граничными
отображениями, а во второй утверждается некоторая версия вырезания,
208
Глава 2. Гомологии
например, hn(X, А) ъ1гп(Х/А,А/А) в случае CW-nap. В аксиоме 3 букет
заменяется на несвязное объединение.
Эти аксиомы для неприведённых гомологии, по сути, те же самые,
что и первоначально предложенные в оказавшей большое влияние
книге [21], за исключением того, что там не было аксиомы 3, так как речь
там шла в основном о конечных комплексах, и была другая аксиома, в
которой утверждалось, что группы hn (точка) нулевые при п ф0у как для
сингулярных гомологии. Это аксиому называли «аксиомой размерности»,
по-видимому, из-за того, что она утверждает, что точка имеет
нетривиальные гомологии только в нулевой размерности. Её можно
рассматривать как аксиому нормализации, так как можно тривиальным образом
определить теорию гомологии, для которой она не выполняется, положив
hn(X, А) = Hn+/c(X, А) для фиксированного целого числа fc, отличного от
нуля. В то время не было известно никаких интересных теорий гомологии,
для которых аксиома размерности не выполнялась. Однако вскоре
топологи начали изучать теорию гомологии, называемую бордизмами, которая
обладает тем свойством, что группы бордизмов точки отличны от нуля
в бесконечно многих размерностях. Аксиома 3 впервые появилась, по-
видимому, в статье [116].
Приведённые и неприведённые теории гомологии, по сути дела,
эквивалентны. Из неприведённой теории h можно получить
приведённую теорию h, положив группу hn(X) равной ядру канонического
отображения hn(X) —>пп(точка). В обратном направлении можно положить
h„(X) = hn(X.f), где Х+ —несвязное объединение пространства X и
точки. Мы оставляем в качестве задачи доказательство того, что эти два
преобразования между приведёнными и неприведёнными гомологиями
обратны друг другу. Точно так же, как и для обычных гомологии, получаем,
что hn(X)^hn(X)©hn(x0) ДЛЯ любой точки х0еХ, так как длинная
точная последовательность пары (X, х0) расщепляется посредством ретракции
пространства X на х{). Отметим, что hn(x0) = 0 ддя всех п, как показывает
длинная точная последовательность приведённых групп гомологии пары
(*о »*<>)•
Группы hn(x0) **hn(S°) называют коэффициентами теорий гомологии
h и h по аналогии со случаем сингулярных гомологии с коэффициентми.
Любую последовательность абелевых групп G, легко можно реализовать
как группы коэффициентов теории гомологии, положив
/111(х,л) = 0ни(х)Д;С1).
Вообще говоря, теория гомологии не определяется однозначно
своими группами коэффициентов, но для сингулярных гомологии это
верно. Если h — теория гомологии, определённая для CW-nap, для
которой группы коэффициентов hu(x0) нулевые при л ф 0, то тогда для всех
§ 2.3. Формальная точка зрения
209
CW-nap (X, Л) и всех п существуют естественные изоморфизмы hn(Xf А) ъ
^НГ1(Х, Л; G), где G = h0(x0). Это доказано в теореме 4.59.
Мы видели, что последовательность Майера—Вьеториса может быть
весьма полезной для сингулярных гомологии, и в действительности
каждая теория гомологии имеет последовательности Майера—Вьеториса, но
крайней мере для CW-комплексов. Их можно получить непосредственно
из аксиом следующим образом. Для CW-комплекса X = A U В с
подкомплексами АиВ включение (В, Л ПВ) <—> (X, Л) индуцирует коммутативную
диаграмму точных последовательностей
... -*- fcM+1(B, Л ПВ) -*• К(ЛПВ) — h„(B) — hn(B, АПВ) -*- ...
Ь lib
... ^ h„+iW, Л) ^ ЬП(Л) ^ h„(X) ^ ftn(X, А) ^ ...
Вертикальные отображения между относительными группами являются
изоморфизмами, так как В/(ЛПВ) = Х/Л. Но имеет место чисто
алгебраический факт (доказательству которого посвящена задача 38 в
конце предыдущего параграфа), что диаграмма такого вида, в которой
каждое третье вертикальное отображение является изоморфизмом, приводит
к длинной точной последовательности, включающей оставшиеся
неизоморфные члены. В нашем случае она принимает вид последовательности
Майера—Вьеториса
... -* йп(апв) - hnwehn{B) ^ hn{x) Л К_,(Апв) - ...
Категории и функторы
Сингулярные гомологии можно формально рассматривать как
последовательность «функций» Нп, сопоставляющих каждому пространству X
абелеву группу Нп (X), а каждому отображению /: X -* Y — гомоморфизм
Нп(/) =/*: Нп(Х) -*НМ(У), и аналогично для относительных групп
гомологии. Такого рода ситуации возникают весьма часто, и не только в
алгебраической топологии. Поэтому полезно ввести для этого некую общую
терминологию. Грубо говоря, «функции», подобные Нп, называют
функторами, и области определения и области значений этих функторов
называют категориями. Таким образом, для Ип категория области
определения состоит из топологических пространств и непрерывных отображений
(в относительном случае — из пар пространств и непрерывных
отображений пар), а категория области значений состоит из абелевых групп и
гомоморфизмов. Важно, что нас интересуют не только объекты категории,
например пространства или группы, но также и отображения, или мор-
физмы, между этими объектами.
Теперь приведём точные определения. Категория с€ состоит из трёх
вещей:
210
Глава 2. Гомологии
1) набора ОЬС#) объектов;
2) множества Мог(Х, У) морфизмов для каждой пары X, У € ОЬ(^),
включая выделенный «тождественный» морфизм 1 = 1Х € Мог(Х, X)
для каждого X;
3) отображения композиции морфизмов о; Мог(Х, У) х Mor(y,Z) —>
-+Mor(X,Z) для каждой тройки X, Y,Z € Ob(^), обладающего
следующими свойствами: /ol = /, 1о/ = /и (/og)o/i = /o (go/i).
Имеется много очевидных примеров категорий.
• Категория топологических пространств с непрерывными
отображениями в качестве морфизмов. Мы могли бы также ограничиться
специальными классами пространств, например CW-комплексами, оставляя
непрерывные отображения в качестве морфизмов. Мы могли бы также
ограничить набор морфизмов, например, гомеоморфизмами.
• Категория групп с гомоморфизмами в качестве морфизмов или
подкатегория абелевых групп, снова с гомоморфизмами в качестве
морфизмов. Обобщением этого является категория модулей над фиксированным
кольцом с гомоморфизмами модулей в качестве морфизмов.
• Категория множеств с произвольными отображениями в качестве
морфизмов. Также морфизмами можно считать только инъективные,
сюръективные или взаимно однозначные отображения.
Есть также много категорий, в которых морфизмы —это не просто
отображения. Вот несколько таких примеров.
• Любую группу G можно рассматривать как категорию с
единственным объектом и с G в качестве морфизмов этого объекта. При этом
условие 3 выражает две из трёх аксиом для группы. Если мы требуем
выполнения только этих двух аксиом, т. е. ассоциативности и существования
левого и правого единичного элемента, то мы получаем «группу без обратных
элементов», обычно называемую моноидом, так как это то же самое, что
и категория с одним объектом.
• Частично упорядоченное множество (X, ^) можно рассматривать
как категорию, объекты которой — элементы множества X, причём
существует единственный морфизм из * в у, если х $ у. Отношение х ^х даёт
морфизм 1, а транзитивность даёт композицию
MorOt, у) х Mor(y, z) —> Mor(x, z).
Условие, что х $ у и у ^х влекут х = у, означает, что существует не более
одного морфизма между любыми двумя объектами.
• Имеется «гомотопическая категория», объекты которой —
топологические пространства, а морфизмы — гомотопические классы
отображений, а не настоящие отображения. Здесь используется тот факт, что
композиция корректно определена на гомотопических классах: /0go — /i£i>
если/о^Л Hgo^gi.
• Цепные комплексы являются объектами категории, морфизмы
которой — цепные отображения. У этой категории имеются разные интерес-
§ 2.3. Формальная точка зрения
211
ные подкатегории, возникающие при наложении ограничений на
объекты. Например, мы можем рассматривать цепные комплексы, группы
которых нулевые в отрицательной размерности или нулевые вне конечного
диапазона. Также мы могли бы ограничиться точными
последовательностями или короткими точными последовательностями. В каждом случае
в качестве морфизмов мы берём цепные отображения, которые
являются коммутативными диаграммами. Можно пойти дальше, рассмотрев
категорию, объекты которой — короткие точные последовательности
цепных комплексов, а морфизмы — коммутативные диаграммы отображений
между такими короткими точными последовательностями.
Функтор F из категории ^ в категорию 2? сопоставляет каждому
объекту X в св объект F(X) в Ф, а каждому морфизму / € Мог(Х, У) в св —
такой морфизм F(/) € Mor(F(X),F(Vr)) в @, что F(l) = 1 и F(/ о g) =
= F(/) oF(g). в случае функтора сингулярных гомологии Н„ последние
два условия —это знакомые нам свойства 1, = 1и (/g)* = /*g*
индуцированных отображений. Точнее говоря, мы определили ковариантный
функтор. Контравариантный функтор отличается от него тем, что
морфизму / €Mor(X, Y) он сопоставляет морфизм «в обратном направлении»
F(/)€Mor(F(7),F(X)), причём F(l) = l и F(/ og) = F(g) oF(/).
Классический пример— функтор двойственного векторного пространства,
который сопоставляет векторному пространству V над фиксированным полем
скаляров К двойственное векторное пространство F(V) = V*, состоящее
из линейных отображений V —* К, а каждому линейному отображению
/: V—* W— двойственное отображение
F(/) = /*: W*->V\
идущее в обратном направлении. В следующей главе мы будем изучать кон-
травариантную версию гомологии, которую называют когомологиями.
Многие из конструкций, изученных нами в этой главе, являются
функторами.
• Функтор сингулярного цепного комплекса сопоставляет
пространству X цепной комплекс сингулярных цепей в X, а отображению /: X —* Y —
индуцированное цепное отображение. Это функтор из категории
пространств и непрерывных отображений в категорию цепных комплексов
и цепных отображений.
• Алгебраический функтор гомологии сопоставляет цепному
комплексу последовательность его групп гомологии, а цепному
отображению—индуцированные гомоморфизмы гомологии. Это функтор из
категории цепных комплексов и цепных отображений в категорию, объекты
которой — последовательности абелевых групп, а морфизмы —
последовательности гомоморфизмов.
• Композиция двух предыдущих функторов —это функтор,
сопоставляющий пространству группы его сингулярных гомологии.
212
Глава 2. Гомологии
• Первый из приведённых выше примеров, функтор сингулярного
цепного комплекса, можно, в свою очередь, рассмотреть как композицию
двух функторов. Первый из этих функторов сопоставляет пространству X
его сингулярный комплекс S(X) (некоторый А-комплекс), а второй
функтор сопоставляет А-комплексу его симплициальный цепной комплекс. Так
эти два функтора действуют на объектах, а их действие на морфизмах
можно описать следующим образом. Отображение пространств f:X—*Y
индуцирует отображение /*: S(X)-*S(Y) посредством композиции
сингулярных симплексов Ап —* X с /. Отображение /+— это отображение
А-комплексов, переводящее выделенные характеристические
отображения в А-комплексе, который является областью определения, в
выделенные характеристические отображения в А-комплексе, который
является областью значений. Назовём такие отображения ^-отображениями
и будем считать их морфизмами в категории А-комплексов. Заметим,
что А-отображение индуцирует цепное отображение симплициальных
цепных комплексов, которое переводит базисные элементы в базисные
элементы; таким образом, мы получаем функтор симплициального
цепного комплекса, переводящий категорию А-комплексов и А-отображений
в категорию цепных комплексов и цепных отображений.
• Имеется функтор, сопоставляющий паре пространств (X, А)
соответствующую ей длинную точную последовательность групп гомологии.
Морфизмы в категории, которая является областью определения, —это
отображения пар, а морфизмы в категории, которая является областью
значений, —это отображения между точными последовательностями,
задающие коммутативные диаграммы. Этот функтор — композиция двух
функторов, первый из которых сопоставляет паре (X, А) короткую точную
последовательность цепных комплексов, а второй сопоставляет такой
короткой точной последовательности соответствующую ей длинную
точную последовательность групп гомологии. Морфизмы в промежуточной
категории —очевидные коммутативные диаграммы.
Нам встречались также операции ещё одного вида: преобразование
одного функтора в другой. Вот примеры таких операций.
• Граничные гомоморфизмы Нп(Х, А)-*Нп_1 (Л) в теории сингулярных
гомологии, а в действительности —в любой теории гомологии.
• Гомоморфизмы замены коэффициентов НП(Х; Gj)—>Hn(X; G2),
индуцированные гомоморфизмом Gj —*G2, как в доказательстве леммы 2.49.
Вообще, если даны два функтора F,G: *& —* ^, то F(f)
естественное преобразование Т из F в G сопоставляет F(X) >- F (Y)
каждому объекту X € ^ морфизм Тх: F(X) -* G(X)
так, что для любого морфизма /: X —* Y в категории
с€ квадрат на рисунке коммутативен. Случай, когда
F и G контравариантны, а не ковариантны,
аналогичен.
§ 2.3. Формальная точка зрения
213
Мы описали переход от топологии к абстрактному миру категорий
и функторов, но имеется также следующая замечательная конструкция,
действующая в противоположном направлении.
• Каждой категории ^ можно сопоставить Л-комплекс Вс€',
называемый классифицирующим пространством категории с€, п-мерные
симплексы которого — последовательности Х0 —» Х1 —»...—» Хп морфизмов
в категории Ч?. Грани этого симплекса получаются при удалении Х{ и (при
i^O, п) замене двух соседних морфизмов на их композицию. Таким
образом, при п = 2 три грани симплекса Х0 -* Хг —> Х2 — это Х0 -* Х^, Хг —> Х2
и морфизм Х0 —> Х2, который является композицией. В случае, когда в с€
есть только один объект, а морфизмы категории с€ образуют группу G,
классифицирующее пространство Вс€ — это то же самое, что Д-комплекс
BG, построенный в примере 1.В.7, т.е. K(G, 1). Однако в общем случае
пространство В^€ не обязано быть пространством K{G, 1). Например, если
мы начнём с Д-комплекса X и рассмотрим множество его симплексов как
частично упорядоченное множество ^(Х) относительно включения
граней, то тогда В^(Х) —это барицентрическое подразделение комплекса X.
• Функтор F: ^ -* ^ индуцирует отображение Вс€ —> ВО). Оно
является Д-отображением, которое переводит п-мерный симплекс Х0 —* Х} —*...
,..-*Хп в п-мерный симплекс F(XQ)-*F(Xl)-*...-*F(Xu).
• Естественное преобразование из функтора F в функтор G
индуцирует гомотопию между индуцированными отображениями
классифицирующих пространств. Мы оставляем читателю описать эту гомотопию явно,
используя подразделение комплекса Дп х I на (п -I-1)-мерные симплексы,
описанное ранее в этой главе.
Задачи
1. Пусть Г„(Х,А) обозначает подгруппу кручения в H„(X,A;Z).
Докажите, что функторы (X, А) -* 7'„(Х, А) с очевидными
индуцированными гомоморфизмами Тп(Х, А) —* Tn(Y, В) и граничными отображениями
ТП(Х, А) -»Тп_т (А) не определяют теорию гомологии. Докажите то же
самое для функтора «по модулю кручения» МТп(X, А) = Н„(X, A; Z)/Tn (X, A).
2. Определите кандидата на роль приведенной теории гомологии на
CW-комилексах, положив/1п(Х)=ПЙ,(Х)/фН,(Х).Таким образом, груп-
па hn(X) не зависит от п и равна нулю, если комплекс X конечномерен, но
она отлична от нуля, например, для X = \J S1. Докажите, что выполняются
все аксиомы теории гомологии, за исключением аксиомы букета.
3. Докажите, что если h — приведённая теория гомологии, то для
всех п hn (точка) =0. Выведите из этого, что для всех п имеют место
изоморфизмы надстройки hn(X) ъйп+](БХ).
4. Докажите, что аксиома букета для теории гомологии следует из
Других аксиом в случае конечных букетов.
§Щопошещё
§ 2.А. Гомологии и фундаментальная группа
Имеется тесная взаимосвязь между Н^ (X) и п1(Х), основанная на том
факте, что отображение /: / —* X можно рассматривать либо как путь,
либо как сингулярный одномерный симплекс. Если / — петля, для которой
/(0) = /(1), то этот сингулярный одномерный симплекс является циклом,
таккакд/ = /(1)-/(0).
Теорема 2.А.1. Рассматривая петли как сингулярные одномерные
циклы, мы получаем гомоморфизм h: iii(X,x0) —* Hj(X). Если
пространство X линейно связно, то гоморфизм h сюръективен, а его ядро —
это коммутант группы пх{Х). Таким образом, h индуцирует
изоморфизм абелианизации группы ^(Х) на Я^Х).
Доказательство. Напомним обозначение / ы g для отношения
гомотопности путей / и g в классе путей с фиксированными концами. Для
цепей / и g запись f^g будет означать, что цепь / гомологична g, т.е.
/-g —граница некоторой двумерной цепи. Перечислим некоторые
факты об этом отношении.
1. Если / — постоянный путь, то /~0. А именно, / — цикл, так как
он является петлёй, а так как Ну (точка) = 0, петля / тогда должна быть
границей. Явным образом / можно представить как границу постоянного
сингулярного двумерного симплекса а, имеющего тот же самый образ,
что и /, так как
dC7 = O-|[vljV2J-C7|[v0>V2]+O-|[v0,V1] = /-/ + / = /.
2. Если / с* g, то / ~ g. Чтобы доказать это,
рассмотрим гомотопию F: I x I -> X отображения /
в отображение g. Она приводит к паре сингулярных
двумерных симплексов о-] и сг2 в X, если разбить
квадрат / х / на два треугольника [v0, vb v3] и fv0, v2, v3],
как показано на рисунке. При вычислении d(o"i — о*2)
два ограничения отображения F на диагональ
квадрата взаимно уничтожаются, и остаётся / - g вместе с двумя постоянными
сингулярными одномерными симплексами, соответствующими левой и
§ 2.A. Гомологии и фундаментальная группа
215
правой сторонам квадрата. По свойству 1 они являются v2
границами, поэтому / — g тоже является границей.
3. /■£ ~ / + g, где /-g обозначает произведение
путей / и g. Действительно, если сг: Д2-*Х —
композиция ортогональной проекции симплекса Л2 =
= tvo> vi> v2l на ребро [v0, v2] и следующего за ней отоб- v° f м
ражения /-g: [v0, v2]_-> X, то да = g - f-g + /.
4. / ~ — /, где / — обратный путь для пути /. Это следует из трёх
предыдущих замечаний, которые доказывают, что / + /~/"/~0.
Применив утверждения 2 и 3 к петлям, получим, что у нас имеется
корректно определённый гомоморфизм ft: 7i^(X,x0)—>H^(X), отображающий
гомотопический класс петли / в класс гомологии одномерного цикла /.
Покажем, что гомоморфизм ft сюръективен, когда пространство X
линейно связно. Пусть ^]Hj-cr, —одномерный цикл, представляющий данный
i
элемент группы НХ(Х). Изменив индексы у сг,-, мы можем считать, что
каждое число п, равно ±1. Согласно свойству 4 в действительности мы
можем считать, что каждое число п, равно +1, поэтому наш одномерный
цикл имеет вид ^сг,-. Если какой-то из путей а, — не петля, то из условия
i'
d(S °"i) = 0 следует, что должен быть другой путь ор для которого опреде-
i
лено произведение путей сг--сг;-. Согласно утверждению 3 мы можем тогда
объединить члены сг, и о ^ в один член сг,"сг;. Повторяя эту операцию,
мы приходим к случаю, когда каждый путь сг, является петлёй. Так как
пространство X линейно связно, мы можем взять путь у, из точки х0
в отмеченную точку петли сг,. Из свойств 3 и 4 следует, что у^оуу, ~ сг,,
поэтому мы можем считать, что все пути сг, —петли с началом и концом
в точке х0. Тогда мы можем объединить все пути сг, в один путь сг согласно
свойству 3. Это означает, что данный элемент группы НДХ) содержится
в образе гомоморфизма ft.
Коммутант группы п^(Х) содержится в ядре гомоморфизма ft,
поскольку группа Н] (X) абелева. Чтобы получить обратное включение,
покажем, что каждый класс [/], содержащийся в ядре гомоморфизма ft,
тривиален в абелианизации n}(X)ab группы яДХ).
Если элемент [/] е п{(Х) лежит в ядре гомоморфизма ft, то /, как
одномерный цикл, является границей двумерной цепи ^п^сг,. Мы снова
I*
можем предположить, что каждое число п, равно ±1. Как и в
обсуждении перед предложением 2.6, мы можем сопоставить
Цепи $]п,сг,- двумерный Д-комплекс К, взяв двумер-
ный симплекс Д2 для каждого симплекса сг,- и
отождествив некоторые пары граней этих двумерных
симплексов. А именно, если мы применим обычную фор-
Глава 2. Гомологии
мулу для границы и напишем да, = тю - тп -I- т,-2 для сингулярных
одномерных симплексов т,-,, то тогда из формулы
/ = з(2>.-<г.-) = Z^ao-i = £(-i)4-t,7
i i ij
следует, что мы можем сгруппировать все т1;-, кроме одного, в пары так,
что коэффициенты (-1);п, в каждой паре —это -1-1 и -1. Оставшийся
сингулярный симплекс Хц равен /. Затем мы отождествляем рёбра
симплексов Д?, соответствующие объединённым в пары симплексам т,-,, сохраняя
ориентации этих рёбер, так, чтобы получился Д-комплекс К.
Отображения а{ согласованы, поэтому из них можно составить
отображение а: К—>Х. Можно следующим образом продеформировать
отображение а, не изменяя его на ребре, соответствующем циклу /, так, чтобы
каждая вершина отображалась в отмеченную точку х0. Пути из образов
этих вершин в точку х0 определяют нужную нам гомотопию на
объединении нульмерного остова комплекса К с ребром, соответствующим
циклу /, а затем мы можем воспользоваться свойством продолжения гомото-
пии из предложения 0.16 и продолжить эту гомотопию на весь комплекс К.
Это продолжение несложно было бы построить и непосредственно.
Ограничивая новое отображение а на симплексы Д?, мы получаем новую цепь
^г^сг,, граница которой равна /, причём все т,;- — петли с началом и кон-
{
цом в точке х0.
Используя аддитивную систему обозначений в абелевой группе Я] (Х)аЬ,
мы имеем формулу [/] = ][](—1Уп,-[т^-], поскольку пары iV} сокращают-
ся. Мы можем записать сумму ^](—l)Jn, [т1;] как ^^[дсг,], где [да,] =
= [т,о] ~ tT<i] + [Ti2]« Так как °"i Дают стягивание составной петли т,0 -
- Гц + т,-2, мы получаем, что [/]=0 в п^Х)^. О
Окончание этого доказательства станет понятнее, если более
внимательно посмотреть на геометрию. Комплекс К" —это фактически
компактная поверхность с краем, состоящим из одной окружности,
образованной ребром, соответствующим циклу /. Это связано с тем, что при
любом отождествлении пар рёбер конечного набо- с
ра непересекающихся двумерных симплексов
получается компактная поверхность с краем. Мы
оставляем читателю в качестве задачи проверку того, что
из алгебраической формулы / = d(2ni°"i)> где п,-=
t
= ±1, следует, что К является ориентируемой
поверхностью. Согласно основной теореме о строении
компактной ориентируемой поверхности компонента комплекса Ку
содержащая граничную окружность, —это стандартная замкнутая ориентируемая
поверхность некоторого рода g, из которой вырезан открытый диск. Если
§ 2.B. Классические приложения
217
снабдить эту поверхность клеточной структурой, изображённой на
рисунке, то станет ясно, что / гомотопно произведению g коммутаторов
в группе п^{Х).
Отображение h: пл(Х,х0) -*НХ(Х) можно также задать формулой
Л ([/])= /Л°0> гДе /: S1 ~*^ представляет данный элемент группы пг (X, х0),
/# — индуцированное отображение групп Яъ а а — образующая группы
HI(5I)^Z, представленная стандартным отображением a: I-*S], a{s) =
— е2гш. Это следует из того, что оба элемента [/] <Е п, (X, х0) и /+ (а) <Е Я] (X)
представлены петлёй fa: /—*Х. Из этого определения следует, что /?([/]) =
= ft([g])> если / и g — гомотопные отображения S1 —* X, так как /* = g*
согласно теореме 2.10.
Пример 2.А.2. Для замкнутой ориентируемой поверхности М рода g
абелианизация группы Я](М) изоморфна Z2g — произведению 2g
экземпляров группы Z, а базис группы Я] (М) состоит из одномерных циклов,
представленных одномерными клетками в М со стандартной CW-структу-
рой. Можно также представить базис петлями а, и Д, изображёнными на
рисунке, так как эти петли гомотопны петлям, представленными
одномерен а2 а3 ал
ными клетками, как можно увидеть на изображении г. _.„
клеточной структуры в главе 0. С другой стороны /^-«sTTx^S^v
петли Yi гомологически тривиальны, так как часть Щъ }Д\ /1)
поверхности М, расположенная по одну сторону от ^&te^o**Nte<^/
Yi, является компактной поверхностью, ограниченной ^^м-—L """""^
петлёй, а значит, как мы недавно видели, петля у,- гомотопна петле,
которая является произведением коммутаторов. Петля а'{ представляет тот же
самый класс гомологии, что и а,, так как область, заключённая между у,
и a, U а', задаёт гомотопию между у,- и произведением двух петель, одна из
которых гомотопна а,, а другая — обратной к а\, поэтому а, - а\ ~у,- ~0,
а значит, а^а^.
§ 2.В. Классические приложения
В этом параграфе мы применим теорию гомологии, чтобы доказать
несколько интересных теорем из топологии и алгебры. Из формулировок
этих теорем совершенно не ясно, что в доказательствах может быть
применена алгебраическая топология.
218
Глава 2. Гомологии
Для начала вычислим гомологии дополнений к сферам и дискам,
вложенным в сферу. Напомним, что вложение —это отображение, которое
является гомеоморфизмом на свой образ.
I Предложение 2.В.1. 1. Для вложения h: Dk —> S" имеет место равен-
I ство Н,(Sn - h(Dk)) = О для всех i.
I 2. Для вложения h: Sk -> S", где к < п, группа H,(Sn - h(Sk)) равна Z
I при i = n - /с - 1 и равна 0 в остальных случаях.
В качестве частного случая утверждения 2 мы получаем теорему Жор-
дана о кривой: подпространство в S2, гомеоморфное S1, разбивает S2 на
два связных подпространства, или, что эквивалентно, два линейно
связных подпространства, так как открытые подмножества в Sn локально
линейно связны. Здесь можно также взять R2 вместо S2, так как
выкалывание точки из открытого множества в S2 не влияет на его связность.
Вообще из п. 2 следует, что подпространство в Sn, гомеоморфное Sn-1,
разбивает сферу на две связные компоненты, причём эти компоненты
имеют такие же группы гомологии, как и точка. До некоторой
степени удивительно, что существуют вложения, для которых дополнительные
компоненты не односвязны, поскольку они односвязны для стандартного
вложения. Примером служит рогатая сфера Александера в S3, которую мы
подробно опишем после доказательства предложения. Все эти сложности,
связанные с вложениями Sn_I в Sn, полностью локальны по своей
природе, так как известно, что любое локально хорошее вложение S"-1 в Sn
эквивалентно стандартному вложению Sn~l с S" в том смысле, что
существует гомеоморфизм сферы S", переводящий данную вложенную сферу
£п-1 в стандартную сферу Sn_1. В частности, обе дополнительные области
гомеоморфны открытым шарам. Точную формулировку и доказательство
можно найти в [89]. Для п = 2 есть классическая теорема Шёнфлиса, что
все вложения Sl ^->S2 эквивалентны.
В противоположность этому, когда мы переходим к вложениям Sn~2
в Sn, даже локально хорошие вложения не обязаны быть эквивалентны
стандартному. Этим занимается теория узлов, включая классический
случай заузленных вложений S1 в S3 или в Ж3. Согласно предложению 2.В.1
для вложений S""2 в S" дополнение всегда имеет те же самые
гомологии, что и S1, но фундаментальные группы могут быть совсем разными.
Несмотря на то, что гомологии дополнения узла не обнаруживают зауз-
ленность, теорию гомологии всё же можно применять для различения
узлов, рассматривая гомологии накрывающих пространств их дополнений.
Доказательство. Докажем утверждение 1 индукцией по /с. Если /с=0, то
S" -h(D°) гомеоморфно R"; этот случай тривиален. Для доказательства
шага индукции удобно заменить диск Dk (на котором определено отображение
h)HaKy6/;c.nycrbA=Sn-h(/fc-,x[0, l/2]),MnycrbB=Sn-ha/c-1x[l/2, 1]).
Таким образом, AnB = Su -h(Ik), и AUB = Sn -h(Ik~l x {1/2}). По ин-
§ 2.B. Классические приложения
219
дукции ЯДА U В) = 0 для всех i, поэтому последовательность Майера—
Вьеториса даёт изоморфизмы Ф: /?,(S" -h{Ik)) —>НДА) еНу(В) для всех i.
С точностью до знака обе компоненты отображения Ф индуцированы
включениями Sn - h(Ik) ^ А и Sn - h{Ik) <^-> В, поэтому если существует
i-мерный цикл а в Sn —hUk), который не является границей в Sn — h0k),
то тогда а не будет границей и по крайней мере в одном из пространств
А и В. (При i = 0 слово «цикл» здесь нужно понимать в смысле аугмента-
рованных цепных комплексов, так как мы имеем дело с приведёнными
гомологиями.) Повторяя эту процедуру, мы получим последовательность
вложенных замкнутых интервалов Jx э J2 Э ... по последней координате
куба Ikt стягивающуюся к некоторой точке ре/, причём а— не граница
bS"- h(Ik~] x Jm) Для любого m. С другой стороны, согласно индукции
по к мы знаем, что а —граница цепи /3 в Su -h(Ik~l x {р}). Эта цепь /3 —
конечная линейная комбинация сингулярных симплексов с компактными
образами в Sn -hVk~l х {p}). Объединение этих образов покрыто
последовательностью вложенных открытых множеств S" — h(/fc_1 x Jrn), поэтому
из компактности следует, что /3 должна быть в действительности цепью
в Sn — h{Ik~} x Im) для некоторого m. Это противоречие показывает, что
цикл а должен быть границей в S" -h(Ik), что завершает шаг индукции.
Утверждение 2 тоже доказывается индукцией по /с, начиная с
тривиального случая к = 0, когда пространство Sn - h{S°) гомеоморфно
Sn~] x R. Для доказательства шага индукции представим Sk в виде
объединения полусфер D^ и D*, пересекающихся по Sfc_1. Тогда
последовательность Майера—Вьеториса для пространств A = Sn —h(D+) и В = S" — h(D^),
имеющих тривиальные приведённые гомологии согласно утверждению 1,
даёт изоморфизмы
H,(Sn-fc(Dfc)) «U+^-ftCS*-1)). П
Если мы применим последнюю часть этого доказательства к
вложению h: Sn —>S", то последовательность Майера—Вьеториса закончится
членами H0(A)®H0(B)->£0(Sn -ftCS"-1)) ->0. Обе группы Й0(А) и Н0(В)
нулевые, поэтому из точности следовало бы, что H0(S" — h(S'1-1)) = 0,
а это противоречит тому факту, что S" - MS"-1) имеет две
компоненты линейной связности. Единственный выход из этой ситуации состоит
в том, что отображение h должно быть сюръективным, чтобы множество
An В было пустым, а тогда в конце последовательности
Майера—Вьеториса вместо члена 0 стоит группа Н_} (0), которая равна Z, а не 0.
Это, в частности, показывает, что Sn нельзя вложить в Мм, так как
это привело бы к несюръективному вложению в Sn. Следовательно, не
существует вложения Шт ^Жп при т>п, так как иначе его можно было
бы ограничить до вложения сферы S" cR"1 в R". И вообще, не существует
непрерывного инъективного отображения Жт —> R" при m > п, так как оно
тоже дало бы вложение S" ^-> 3£п.
220
Глава 2. Гомологии
Пример 2.В.2. Рогатая сфера Александера — это такое
подпространство ScR3, гомеоморфное S2, что неограниченная компонента
пространства R3 — S неодносвязна, в отличие от стандартного вложения S2 с R3.
Мы будем строить S, задавая последовательность компактных
подпространств Х0 D X1 D ... в R3, пересечение которых гомеоморфно шару, и
тогда S будет граничной сферой этого шара.
Начнём с Х0 — полнотория S1 x D2, полученного из шара В0
приклеиванием ручки / х D2 по д! х D2. На рисунке эта ручка изображена как
объединение двух «рогов», приклеенных к
шару, вместе с более короткой ручкой,
нарисованной пунктирными линиями. Чтобы
получить пространство Хх с Х0, мы удаляем
часть короткой ручки так, что остаётся
пара зацепленных ручек, приклеенных к
шару Bj — объединению шара В0 с этими двумя
рогами. Чтобы получить Х2, повторяем
процесс: представим каждую из ручек,
полученных на втором шаге, как пару рогов и
короткую ручку, а затем удалим часть короткой
ручки. Точно так же Хп индуктивно
строится по Хп_!. Таким образом, Хп — шар Вп с 2"
приклеенными ручками, а Вп получается из
Яп_] приклеиванием 2П ручек. Существуют
гомеоморфизмы hn: BM_1-*Bn, которые тождественны вне малых
окрестностей множеств Вп — Вп-1. Когда п стремится к бесконечности,
композиция hn...hl сходится к отображению /: B0-*R3, которое является
непрерывным, так как сходимость равномерная. Множество точек в В0, где / не
равно hn...h! для большого п, — это канторово множество, образ которого
при отображении / — пересечение всех ручек. Нетрудно убедиться, что /
взаимно однозначно. Из компактности следует, что / — гомеоморфизм на
свой образ. Этот образ— шар BcR3, граничная сфера которого /(дВ0) —
это рогатая сфера Александера S.
Вычислим теперь tt^R3 -В). Заметим, что В—это пересечение
множеств Хи, поэтому R3 - В — это объединение дополнений У„ к множествам
Хп, которые образуют возрастающую последовательность У0 с ^i с ••• По-
кажем, что группы тт^У,,) тоже образуют возрастающую
последовательность постепенно увеличивающихся групп, объединение которых равно
TTjCR3 —В). Сначала у нас есть пх(У())^1,у так как Х0 — полноторие,
стандартно вложенное в R3. Чтобы вычислить tcj (Vi), рассмотрим У0
—замыканием множества У0 в У^ Тогда У() - У0 —открытое круглое кольцо А,
а группа Я)(У0) тоже равна Z. Мы получаем Ух из У0, приклеивая
пространство Z = Ух — У0 по А. Группа кх(Z) —это свободная группа F2 с
двумя образующими aj и а2, представленными петлями, зацепленными за
№)
§ 2.В. Классические приложения
221
две ручки, так как пространство Z — А гомеоморфно открытому шару, из
которого вырезаны две прямые трубки. Петля а, порождающая группу
Я] (А), представляет коммутатор [а1? а2]; в этом можно убедиться,
заметив, что замыкание множества Z получается из Z присоединением двух
непересекающихся поверхностей, каждая из которых гомеоморфна тору
с вырезанным открытым диском; граница этого диска гомотопна петле а,
а также гомотопна коммутатору двух окружностей в торе — меридиана
и параллели, которые соответствуют петлям ах и а2. Теперь из теоремы
ван Кампена теперь следует, что включение Y0 <—► Y1 индуцирует инъекцию
группы tz^Yq) в 7Г] (Vj) как бесконечной циклической подгруппы,
порождённой элементом [а:, а2].
Аналогично можно рассматривать Уп+1 как пространство, полученное
из Yn приклеиванием 2П экземпляров пространства Z. Предположим по
индукции, что 7ii(Yn) — свободная группа F2» с образующими,
представленными петлями, надетыми на 2п наименьших ручек пространства Хп.
Тогда каждый экземпляр пространства Z, приклеенный к У„, изменяет
группу тг^У,,), превращая одну из образующих в коммутатор двух
новых образующих. Заметим, что приклеивание экземпляра пространства
Z индуцирует инъективное отображение групп тгь так как
индуцированный гомоморфизм — свободное произведение инъективного отображения
пг (Л) —* пi (Z) и тождественного отображения на дополнительном
свободном множителе. Таким образом, отображение я1(Уп) —► 7Z\(Yn+0 —
инъекция F2„ —*F2,n. Группа TTjCR3 — В) изоморфна объединению этой
возрастающей последовательности групп в силу компактности: образ каждой
петли в R3 - В компактен, а потому она должна лежать в некотором Yn\
для гомотопий петель рассуждения аналогичны.
В частности, мы видим, почему абелианизация группы tt^IR3 -В)
тривиальна: потому что каждая из её образующих в точности равна
коммутатору двух других образующих. Такое индуктивное построение, в
котором каждая образующая свободной группы превращаются в коммутатор
двух новых образующих, по-видимому, является самым простым способом
построить нетривиальную группу с тривиальной абелианизацией, и
достойно изумления, что для этой конструкции есть столь приятная
геометрическая интерпретация. С наивной точки зрения может показаться
немного странным, что в высшей степени несвободную группу можно
построить как объединение возрастающей последовательности свободных
групп, но это может легко случиться и для абелевых групп, поскольку,
например, Q — объединение возрастающей последовательности
бесконечных циклических подгрупп.
Следующая теорема гласит, что для подпространства в Rn свойство
быть открытым — топологический инвариант. Этот результат известен под
классическим названием «инвариантность области»; слово «область» —
это устаревшее название открытого множества в Жп.
222
Глава 2. Гомологии
I Теорема 2.В.З. Если I/— открытое множество в Rn, то для любого
вложения ft: U -* Rn образ h(L7) должен быть открытым множеством
вГ.
Доказательство. Если представить S" как одноточечную компакти-
фикацию пространства Кп, то эквивалентное утверждение заключается
в том, что h{U) открыто в S", и именно это мы докажем. Каждая
точка х € U является центром шара D" с U, Достаточно будет доказать, что
множество h(Dn - 0D") открыто в S". Согласно предложению 2.В.1
пространство Sn — h(dDn) имеет две компоненты линейной связности. Эти
компоненты линейной связности — h(Du - 0Dn) и S" - h(D"), так как эти
два подпространства не пересекаются, причём первое из них линейно
связно, поскольку оно гомеоморфно Dn - dDn, а второе линейно связно
согласно предложению. Так как множество S" - h{dDn) открыто в S", его
компоненты линейной связности — это то же самое, что и его
компоненты связности. Компоненты связности пространства с конечным числом
компонент связности открыты, поэтому множество h(Dn — dDn) открыто
в Sn -h(dDn), а значит, и в Sn, □
А вот применение этого результата, которое использует понятие п
-мерного многообразия, т. е. хаусдорфова пространства, локально гомеоморф-
ного пространству R".
I Следствие 2.В.4. Если М —компактное п-мерное многообразие, а
N — связное п-мерное многообразие, то вложение ft: M —> N должно
быть сюръективным, а потому—гомеоморфизмом.
Доказательство. Множество h(M) замкнуто в N, так как оно
компактно, а N хаусдорфово. Поскольку N связно, достаточно показать, что
h{M) также открыто в N, а это непосредственно следует из теоремы. □
Инвариантность области и п-мерное обобщение теоремы Жордана
о кривой были впервые доказаны Брауэром около 1910 г. на очень ранней
стадии развития алгебраической топологии.
Алгебры с делением
Здесь мы приведём алгебраическое приложение теории гомологии,
принадлежащее X. Хоифу.
I Теорема 2.В.5. R и С —это единственные конечномерные алгебры
с делением над R, которые коммутативны и обладают единичным
элементом.
По определению структура алгебры на R" — просто билинейное
отображение умножения R" x R" -» R", (а, Ъ) —> аЪ. Таким образом,
произведение обладает свойствами левой и правой дистрибутивности, т.е.
a(b -f с) = ab + ас и (а + Ъ)с = ас + Ьс, и ассоциативности относительно
скаляров, т.е. а{аЪ) = {aa)b = a(ab) для a€R. Коммутативность, настоящая
ассоциативность и существование единичного элемента не предполагают-
§ 2.В. Классические приложения
223
ся. Алгебра является алгеброй с делением, если уравнения ах = Ь ил*а = Ь
всегда разрешимы при а Ф 0. Другими словами, линейные
преобразования х —► ах и х —► ха являются сюръективными при а Ф О. Они являются
линейными отображениями Rn —►!&", таким образом, сюръективность
эквивалентна тривиальности ядра, что, в свою очередь, означает отсутствие
делителей нуля.
Четыре классических примера —это R, С, алгебра кватернионов И,
и алгебра октав О. Фробениус доказал в 1877 г., что R, С, и Н —это
единственные конечномерные ассоциативные алгебры с делением над R с
единичным элементом. Для произведения, которое удовлетворяет равенству
|ab| = |а||Ь|, как в классических примерах, Гурвиц показал в 1898 г., что
размерность алгебры должна быть равна 1, 2, 4 или 8, а другие потом
показали, что такие алгебры с единичным элементом— только
классические. Полное обсуждение этих результатов, включая некоторые примеры,
показывающие необходимость предположения о существовании
единичного элемента, можно найти в [20]. Как и следует ожидать,
доказательства этих результатов алгебраические, но если отбросить условие, что
|ab| = |a||b|, то, по-видимому, необходимы более топологические
доказательства. Мы покажем в теореме 3.20, что конечномерная алгебра с
делением над Е должна иметь размерность, равную степени числа 2. Тот
факт, что размерность не может быть больше 8, — это известная теорема;
см. [85] и [106]. Дополнительные комментарии на эту тему приводятся
в§4.В.
Доказательство. Предположим сначала, что Rn обладает структурой
коммутативной алгебры с делением. Зададим отображение /: S"""1 —> Sn_1
формулой /far) = jc2/|jc2(. Оно определено корректно, так как в
алгебре с делением из того, что х Ф 0, следует, что х2 Ф 0. Отображение /
непрерывно, так как отображение умножения iRn x Rn —> Rn является
билинейным, а потому и непрерывным. Так как /(—х) = f(x) для всех х,
отображение / индуцирует факторотображение /: 2Р"-1 —>Sn~l.
Следующее рассуждение показывает, что отображение / инъективно. Равенство
/М=/(у) влечёт, что*2 = а2у2, где а = (|лг2|/|у2|)1/'2 >0. Таким образом,
мы получаем х2 - а2у2 = 0, что можно разложить как (х + ау) (х — ау) = 0,
используя коммутативность и тот факт, что а — действительное число. Так
как никаких делителей нуля нет, мы получаем, что х = ±ау. Так как х
и у— единичные векторы, а а действительное число, это приводит к
равенству х = ±у, поэтому * и у задают одну и ту же точку в RP"""1, а это
означает, что отображение / инъективно.
Так как / —инъективное отображение компактных хаусдорфовых
пространств, оно должно быть гомеоморфизмом на свой образ. Согласно
следствию 2.В.4 отображение / в действительности должно быть сюръ-
ективным, если мы рассматриваем не тривиальный случай п = 1. Таким
образом, мы получаем гомеоморфизм W?n"x wS"-1. Из этого следует, что
224
Глава 2. Гомологии
п = 2, так как если п > 2, то пространства МРП_1 и Sn~l имеют разные
группы гомологии (или разные фундаментальные группы).
Остаётся показать, что двумерная коммутативная алгебра А с
делением с единицей изоморфна С. Это элементарная алгебра. Пусть элемент
j^A не является вещественным кратным единичного элемента 1еА.
Запишем j2 = a + bj для ауЪеИ. Тогда (j -b/2)2 = a + b2/4, поэтому, выбрав
j по-другому, мы можем считать, что j2 = а Е К. Пусть а ^ 0, например,
а = с2, тогда из равенства j2 = с2 следует, что (j + c)(j - с) = 0, а потому
j = ±с, но это противоречит выбору элемента j. Следовательно, j2 = —с2, и,
умножив j на вещественное число, мы можем считать, что j2 = — 1. Таким
образом, алгебра А изоморфна С. □
Если забыть про последний абзац, то это доказательство
показывает, что конечномерная коммутативная алгебра с делением, но не
обязательно с единичным элементом, должна иметь размерность не более 2.
Это весьма странно, но существуют двумерные коммутативные алгебры
с делением без единичных элементов, например алгебра С с изменённым
умножением z • w = zwy где черта обозначает комплексное сопряжение.
Теорема Борсука—Улама
В теореме 1.10 мы доказали двумерный случай теоремы
Борсука—Улама, а теперь приведём доказательство для всех размерностей, используя
следующую теорему Борсука.
Предложение 2.В.6. Нечётное отображение /: S" —> S", для которого
/(-*) = -/О) для всех х, должно иметь нечётную степень.
Аналогичное утверждение, что чётные отображения имеют чётную
степень, доказывается проще; оно было сформулировано в качестве
задачи 14 в §2.2.
Доказательство покажет нам, что иногда использование гомологии
с группой коэффициентов, отличной от Z, может давать существенное
преимущество. Главной составной частью доказательства будет точная
последовательность, связанная с двулистным накрытием р: X —» X,
имеющая вид
... -> НП(Х; Z2) ^ Н„(Х; Z2) - НП(Х; Z2) -> Нп_, (X; Z2) -> ...
Это длинная точная последовательность групп гомологии, связанных с
короткой точной последовательностью цепных комплексов, состоящих из
коротких точных последовательностей групп цепей
0 -> С„(Х; Z2) -^ СП(Х; Z2) ^ СП(Х; Z2) - 0.
Отображение р. сюръективно, так как сингулярные симплексы а: Д" —> X
всегда можно поднять в X, поскольку симплекс Д" односвязен. Каждый
сингулярный симплекс а имеет в действительности ровно два поднятия
§ 2.В. Классические приложения
225
аг и С72. Поскольку мы используем коэффициенты Z2, ядро отображения
Рц порождается суммами а1 + ст2. Поэтому если мы рассмотрим
гомоморфизм т, который переводит каждый сингулярный симплекс а: Ам —* X
в сумму двух его поднятий в А", то образ гомоморфизма т —это ядро
гомоморфизма рч. Очевидно, что гомоморфизм т инъективен, поэтому
мы получаем указанную короткую точную последовательность. Так как
тир- коммутируют с граничными отображениями, мы получаем
короткую точную последовательность цепных комплексов, которая приводит
к длинной точной последовательности групп гомологии.
Отображение т* — это частный случай более общего гомоморфизма,
который называют трансфером; мы рассмотрим его в §3.G. Поэтому мы
будем называть длинную точную последовательность, включающую
отображения т+, последовательностью трансфера. Эту последовательность
можно также рассматривать как частный случай последовательностей Ги-
зина, обсуждаемых в §4.D. Имеется также обобщение последовательности
трансфера на гомологии с другими коэффициентами, но , как мы покажем
в §З.Н, оно использует гомологии более сложного вида, называемые гомо-
логиями с локальными коэффициентами.
Доказательство предложения 2.В.6. Доказательство будет
использовать последовательность трансфера для накрытия р: S" —* RP". Она
имеет следующий вид, где для упрощения обозначений мы сокращаем RP" до
Рп и не указываем явно группу коэффициентов Ъг\
о— нп{Рп) -^ Hn(sn) Х- "„a"1) s- h„-i(p") — о — ...
... -*■ О -*- Н{Рп) -f Н{ .j(P") — 0 — ...
... _^ 0 — Н{(Р») -^ Н0(РП) -+ H0{S") -^ Н0(Рп) — 0.
Начальный член 0 —это группа Hu+l{Pn'y Z2), которая обращается в нуль,
так как Р" является п-мерным CW-комплексом. Другие члены, которые
являются нулями, — это группы Н((Бп), где 0 < i < п. Мы предполагаем, что
п > 1, предоставляя читателю сделать необходимые небольшие изменения
для случая п = 1. Клеточные гомологии показывают, что все ненулевые
члены равны Ъг. С другой стороны, эту точную последовательность можно
было бы применить для вычисления групп гомологии H,-(RP"; Z2), если бы
мы их не знали. Так как все ненулевые группы в этой последовательности
равны Z2, точность вынуждает все отображения быть изоморфизмами
или нулевыми, как это указано.
Нечётное отображение /: Sn—* Sn индуцирует факторотображение
/: RP" -*;RPM. Эти два отображения индуцируют отображение
последовательности трансфера в себя, и нам нужно проверить, что квадраты
в полученной диаграмме коммутативные. Это будет вытекать из есте-
8 За к .V»*5
226
Глава 2. Гомологии
ственности длинной точной последовательности гомологии, связанной
с короткой точной последовательностью цепных комплексов, как только
мы проверим коммутативность диаграммы
О —^ С((Рп) -^ Q(Sn) А Q(Pn) —*. О
1* т i«, I*
о —^ с{(Рп) -^ c{(sn) -^ q(pn) —*- о
Здесь правый квадрат коммутативен, так как pf = fp. Левый квадрат
коммутативен, поскольку для сингулярного i-мерного симплекса а: А1 —*Р"
с поднятиями ах и а2 двумя поднятиями для fa являются fax и fa2, так
как / переводит диаметрально противоположные точки в диаметрально
противоположные точки.
Теперь утверждение о том, что все отображения /+ и /* в
коммутативной диаграмме последовательностей трансфера —изоморфизмы,
получается индукцией по размерности с использованием очевидного факта,
что если три отображения в коммутативном квадрате — изоморфизмы,
то и четвёртое тоже. Индукция начинается с тривиального факта, что /*
и /* — изоморфизмы в размерности нуль.
В частности, мы получаем, что отображение /*: Hn(Sn; Z2) —>Hn(Sn; Z2)
является изоморфизмом. Согласно лемме 2.49 это отображение —
умножение на степень отображения / по модулю 2, поэтому степень
отображения / должна быть нечётной. □
Из этого факта, что нечётные отображения имеют нечётную степень,
легко получить следующую теорему Борсука—Улама.
Следствие 2.В.7. Для любого отображения g: Sn -*Шп существует
точка xeS", для которой g(x)=g(-x).
Доказательство. Положим /О) = g(x) - g(—jc); тогда отображение
/ нечётно. Мы должны доказать, что /О) = 0 для некоторого х. Если
это не так, то мы можем заменить /О) на /00/1/001 и получить
новое отображение /: Sn —*S"~\ которое всё ещё является нечётным. Тогда
ограничение этого отображения / на экватор Sn~l имеет нечётную
степень согласно предложению. Но это ограничение гомотопно постоянному
отображению; гомотопия строится посредством ограничения / на одну из
полусфер с границей S"-1. □
Задачи
1. Вычислите H((Sn — X), где X — подпространство в Sn, гомеоморф-
ное SkVSe или SkUSe.
2. Докажите, что Hi(Sn -X)^Hn_i_l(<X)t если X гомеоморфно
конечному связному графу. [Сначала разберите случай, когда граф —дерево.]
§ 2.C. Симплициальная аппроксимация
227
3. Пусть (D, S) с (D'^S"-"1) —пара подпространств, гомеоморфных
(Dfc, Sk~l), причём D П Sn~l = S. Докажите, что включение Sn~l - S с—>
<-+ Dn - D индуцирует изоморфизм гомологии. [Вклейте два экземпляра
пары (Dn, D) по обеим компонентам границы в (S'1"1 x J, S х /), получив
fc-мерную сферу в Sn. Затем рассмотрите последовательность Майера—
Вьеториса для дополнения этой fc-мерной сферы.]
4. В единичной сфере Sp+q~l CR^ пусть Sp'1 и S^"1—подсферы,
состоящие из точек, у которых соответственно q последних и р первых
координат равны нулю.
а) Докажите, что Sp+q~l —Sp~l деформационно ретрагируется на Sq~l
и в действительности гомеоморфно Sq~l x Rp.
б) Докажите, что Sp~l и Sq~~} не могут быть границами никакой пары
непересекающихся вложенных дисков Dp и Dq в Dp+(]. [Здесь может
оказаться полезной предыдущая задача.]
5. Пусть S — fc-мерная сфера, вложенная в S", для которой существует
диск D" С S", пересекающий S по диску Dk cDnt определяемому
первыми к координатами диска Dn. Пусть Dn~k с Dn —диск, определяемый
последними п — к координатами, с граничной сферой Sn~k~l. Докажите, что
включение sn~k~} c—>Sn —S индуцирует изоморфизм групп гомологии.
6. Измените построение рогатой сферы Александера,
чтобы получить вложение S2 с—> R3, для которого ни одна /TWy^?^
из компонент пространства IR3 — S2 не односвязна. I \ ^\М /
7. Выясните, что происходит, когда число ручек в
основном стандартном блоке для рогатой сферы
Александера удваивается, как на рисунке справа.
8. Докажите, что R2n+1 не является алгеброй с делени- \-^""""^"^ /
ем над R при п > О, посмотрев, как изменился бы опреде- ^' "^
литель линейного отображения х-*ах, заданного умножением в алгебре
с делением, когда а обходит путь в R2n+l - {0}, соединяющий две
диаметрально противоположные точки.
9. Запишите последовательность трансфера явно в случае
тривиального накрытия X -* X, где X =Х х S0.
10. Применяя последовательность трансфера для накрытия S°° —>
— RP00, вычислите НП(»Р°°; Z2).
11. Применяя последовательность трансфера для накрытия X х S°° —>
-> X х RP00, получите изоморфизмы ЯП(Х х RP00; Z2) ^ ©Н,(Х; Z2) для
всех п.
§ 2.С. Симплициальная аппроксимация
Многие пространства, представляющие интерес для алгебраической
топологии, можно снабдить структурой симплициального комплекса, и в
начале истории этого предмета такая структура использовалась как один
из основных технических инструментов. Позднее CW-комплексы в основ-
228
Глава 2. Гомологии
ном заменили симплициальные комплексы в этой роли, но есть всё же
некоторые ситуации, когда дополнительная структура симплициального
комплекса может оказаться весьма полезной. Это будет хорошо видно
в доказательстве классической теоремы Лефшеца о неподвижной точке
в этом параграфе.
Одно из хороших свойств симплициальных комплексов состоит в том,
что любые непрерывные отображения между ними всегда можно про-
деформировать в отображения, которые линейны на симплексах
некоторого подразделения комплекса — области определения. В этом
заключается идея «симплициальной аппроксимации», разработанной Брауэром
и Александером к 1920 г. Соответствующее определение выглядит так.
Пусть К и L — симплициальные комплексы, тогда отображение /: К —* L
является симплициалъным, если оно переводит каждый симплекс
комплекса К в симплекс комплекса L посредством линейного отображения,
переводящего вершины в вершины. В барицентрических координатах
линейное отображение симплекса [v0,..., vj имеетвид £t,-v,-—>£t,-/(v,-). Так
i i
как линейное отображение симплекса в симплекс однозначно задаётся
своими значениями на вершинах, это означает, что симплициальное
отображение однозначно задаётся своими значениями па вершинах. Легко
видеть, что отображение вершин комплекса К в вершины комплекса L
продолжается до симплициального отображения тогда и только тогда,
когда оно переводит вершины любого симплекса комплекса К в вершины
некоторого симплекса комплекса L.
Вот наиболее стандартная формулировка теоремы о симплициальной
аппроксимации.
I Теорема 2.С.1. Если К" —конечный симплициальный комплекс, a L —
I произвольный симплициальный комплекс, то любое отображение /:
I /С —> L гомотопно отображению, которое симплициально относитель-
I но несколько раз повторённого барицентрического подразделения ком-
I плекса К.
Чтобы убедиться, что переход к подразделению комплекса К
бывает необходим, рассмотрите случай отображений Sn —>Sn. Для
фиксированных симплициальных структур на области определения и на области
значений имеется лишь конечное число симплициальных отображений,
так как отобразить вершины на вершины можно лишь конечным числом
способов. Следовательно, симплициальными отображениями
относительно фиксированных симплициальных структур реализуется лишь конечное
число значений степени отображения. Это остаётся верным, даже если
разрешить менять симплициальную структуру на сфере — области
значений, так как если у области значений больше вершин, чем у области
определения, то отображение не может быть сюръективным, а потому должно
иметь степень нуль.
§ 2.С. Симплициальная аппроксимация
229
Прежде чем доказывать теорему о симплициальной аппроксимации,
нам нужно ввести некоторые термины и доказать лемму. Звезда St о-
симплекса а в симилициальном комплексе X определяется как подкомплекс,
состоящий из всех симплексов комплекса X, которые содержат ст. Тесно
связана с этим понятием открытая звезда stcr, которая является
объединением внутренностей всех симплексов, содержащих ст, где внутренность
симплекса т по определению равна т-дт. Таким образом, st а —
открытое множество в X, замыкание которого совпадает с St о-.
I Лемма 2.С.2. Для набора вершин v1}...,vM симплициального ком-
I плекса X пересечение stvl П ... ristv,, пусто, если только vb ..., vn не яв-
I ляются вершинами некоторого симплекса о- в X, а в этом случае
I stv1 n...nstv„ = st о-.
Доказательство. Пересечение stvl П ... Пstvfl состоит из
внутренностей всех тех симплексов т, наборы вершин которых содержат {v1} ..., vr?}.
Если множество stvT П ... nstv„ непусто, то такой симплекс т
существует и содержит симплекс а = [у1}...,ум] с X. Симплексы т, содержащие
{vls ..., v,,}, —это в точности те симплексы, которые содержат ст, поэтому
StVi n...nstVM=St<7. D
Доказательство теоремы 2.С.1. Выберем метрику на К,
ограничение на которой на каждый симплекс в К является стандартной
евклидовой метрикой. Например, К можно считать подкомплексом
симплекса 5N, вершины которого —это все вершины комплекса К] тогда
мы можем взять ограничение стандартной метрики на 5N и получить
требуемую метрику на К. Пусть е — число Лебега для открытого
покрытия {/_1(stw) | iv-вершина в L] комплекса К. Повторяя несколько раз
барицентрическое подразделения комплекса К, мы можем добиться того,
чтобы диаметр каждого симплекса стал меньше е/2. Замкнутая звезда
каждой вершины v комплекса К имеет тогда диаметр меньше е,
следовательно, отображение / переводит эту замкнутую звезду в открытую звезду
некоторой вершины g(v) комплекса L. Таким образом, полученное в
результате отображение g: К0 —> L0 удовлетворяет условию /(Stv) с stg(v)
для всех вершин v комплекса К.
Чтобы проверить, что g продолжается до симплициального
отображения g: К —> L, рассмотрим задачу продолжения g на симплекс [vj,..., vn]
комплекса К. Внутренняя точка х этого симплекса лежит в stv, для всех i,
поэтому f(x) лежит в stg(v,) для всех i, так как /(stvf) cstg(v,) по
определению g(v,). Таким образом, stg(v1)n...fistg(vn)^0, поэтому [gOi),...
•••>gO'n)] является симплексом в L согласно лемме, и мы можем
продолжить g на [v,, ..., vn ] по линейности. Обе точки /00 и gOO лежат в одном
симплексе комплекса /,,так как gOO лежит в [gOJ,..., g(vM)J, а/00 лежит
в звезде этого симплекса. Поэтому линейный путь (1 - 0/00 + tgM>
О ^ t ^ 1, в симплексе, содержащем /00 и gOO, определяет гомото-
230
Глава 2. Гомологии
пию отображения / в отображение g. Чтобы проверить непрерывность
этой гомотопии, достаточно ограничиться симплексом [vlf...,vn], где
непрерывность очевидна, так как f(x) изменяется непрерывно в звезде
симплекса [g(yx), ...,g(vn)], a g(x) изменяется непрерывно в симплексе
[gCva.^gCvj]. а
Заметим, что если / изначально переводит некоторые вершины
комплекса К в вершины комплекса L, то мы можем выбрать отображение g
так, чтобы оно было равно / на этих вершинах, а тогда гомотопия
отображения / в отображение g будет постоянной на этих вершинах. Это бывает
удобно, когда требуются отображения и гомотопии, оставляющие
неподвижными отмеченные точки.
Из этого доказательства видно также, что симплициальную
аппроксимацию g можно выбрать не только гомотопной отображению /, но и сколь
угодно близкой к /, если мы разрешим подразделять не только К, но и L.
Теорема Лефшеца о неподвижной точке
Это классическое приложение гомологии является значительным
обобщением теоремы Брауэра о неподвижной точке. Оно также связано с
формулой для эйлеровой характеристики.
Для гомоморфизма у: Ъп -*Zn с матрицей [а^] след trc/?
определяется как £ап~сумма диагональных элементов матрицы [а,-,-]. Так как
i
tr([afj-][by]) = tr([by][a/;]), подобные матрицы имеют одинаковые следы,
а из этого следует, что tr</? не зависит от выбора базиса в Zn. Для
гомоморфизма у: А -* А конечно порождённой абелевой группы А мы
можем тогда определить try? как след индуцированного гомоморфизма
<J5: А/кручение -* Л/кручение.
Ддя отображения /: X -* X конечного CW-комплекса Х или вообще
любого пространства, группы гомологии которого конечно порождены
и обращаются в нуль в достаточно больших размерностях, число
Лефшеца т(/) определяется как £(-1)п tr(/*: НП(Х) -*НП(Х)). В частности, ес-
п
ли /—тождественное или гомотопное тождественному отображение, то
т(/) — это эйлерова характеристика #(Х), так как след единичной
матрицы размера пхп равен п.
Вот теорема Лефшеца о неподвижной точке.
I Теорема 2.С.З. Если X — конечный симплициальный комплекс или
хотя бы ретракт конечного симплициального комплекса, а /: Х-»Х —
отображение, для которого т(/) Ф0, то / имеет неподвижную точку.
Как показано в теореме П.7 в приложении, каждое компактное
локально стягиваемое пространство, которое вкладывается в Еп для
некоторого п, является ретрактом конечного симплициального комплекса. Сюда
входят, например, компактные многообразия и конечные CW-комплексы.
Предположение о компактности существенно, так как для параллельного
§ 2.C. Симплициальная аппроксимация
231
переноса в К имеет место равенство т = 1, но у переноса нет
неподвижных точек. В качестве примера, показывающего, что локальные свойства
тоже существенны, рассмотрим X —компактное
подпространство в R2, состоящее из двух концентрических
окружностей вместе с экземпляром пространства R
между ними, концы которого приближаются по
спирали к этим двум окружностям, оборачиваясь вокруг них
бесконечно много раз, и пусть /: X —> X —
гомеоморфизм, не имеющий неподвижных точек, сдвигающий
пространство R по себе и вращающий окружности. Так как отображение /
гомотопно тождественному, мы получаем т(/) = #(Х), что равно 1, так
как три компоненты линейной связности пространства X — это две
окружности и прямая.
Если группы гомологии пространства X такие же, как у точки, по
крайней мере по модулю кручения, то тогда теорема 2.С.З
утверждает, что любое отображение X —>X имеет неподвижную точку. Это
выполняется, например, для ШРп, если п четно. Случай проективных
пространств интересен из-за из связи с линейной алгеброй. Обратимое
линейное преобразование /: Rn —>R" переводит прямые, проходящие
через 0, в прямые, проходящие через 0, а потому оно индуцирует
отображение /: RPn_1 —>RPn-1. Неподвижные точки отображения / эквивалентны
собственным векторам отображения /. Характеристический многочлен
отображения / имеет нечётную степень, если п нечётно, следовательно,
он имеет действительный корень; таким образом, в этом случае
существует собственный вектор. Это согласуется со сделанным выше замечанием,
что любое отображение RP2k —> RP2k имеет неподвижную точку. С другой
стороны, поворот пространства R2fc, заданный формулой
f(Xi, ...,Х2к) = \х2» ~~х\>х<\> ~х3> •••>х2к> ~X2k-0>
не имеет собственных векторов, и его проективизация /: КР2^1 —> KP2fc_1
не имеет неподвижных точек.
Аналогично в комплексном случае обратимое линейное
преобразование /: Сп —> С" индуцирует отображение /: СРП~! —>СРП_1, которое всегда
имеет неподвижную точку, так как характеристический многочлен всегда
имеет комплексный корень. Однако, как и в вещественном случае,
существует отображение СР2/с~] —>CP2fc_1 без неподвижных точек. А именно,
рассмотрим отображение /: С2* —>С2к, заданное формулой
/(Z,, ...,22fc) = (22, -ZbZ4, -Z3, —>Z2k,-Z2k-0-
Это отображение лишь «сопряжённо-линейно» над С, но и этого
достаточно для того, чтобы / индуцировало корректно определённое
отображение / на СР2*"1, и легко проверить, что / не имеет неподвижных точек.
Аналогия между вещественным и комплексным случаями сохраняется и в
232
Глава 2. Гомологии
том факте, что любое отображение СР2/с —>СР имеет неподвижную
точку. Однако вывод этого утверждения из теоремы Лефшеца о неподвижной
точке требует дополнительной структуры по сравнению с гомологиями.
Мы оставим его в качестве задачи к §3.2, решение которой использует
произведение в когомологиях.
Можно пойти дальше и рассмотреть кватернионный случай. Антипо-
дальное отображение сферы S4 = HP] не имеет неподвижных точек, но
любое отображение HP" —»HP" при п > 1 имеет неподвижную точку. Это
показано в примере 4.L.4 с использованием гораздо более сложной
техники.
Доказательство теоремы 2.С.З. Общий случай легко сводится к
случаю конечных симплициальиых комплексов. Действительно,
предположим, что г: К —>X — ретракция конечного симплициалыюго комплекса К
на X. Тогда для.отображения /: X —> X композиция /г: К —> X с К имеет
в точности те же неподвижные точки, что и /. Так как г*: Нп (К) —> Нп (X) —
проекция на прямое слагаемое, мы, очевидно, имеем tr(/*rj = tr/L, а
потому T(/*rJ = т(/+).
Пусть X — конечный симплициальный комплекс. Предположим, что
отображение /: X—*Х не имеет неподвижных точек. Мы утверждаем,
что существуют подразделение L комплекса X, дальнейшее подразделение
К комплекса L, а также такое симплициальное отображение g: К —> L,
гомотопное отображению /, что g(a) Пег = 0 для любого симплекса а
комплекса К. Чтобы доказать это, сначала выберем метрику d на X, как
в доказательстве теоремы о симплициальной аппроксимации. Так как /
не имеет неподвижных точек, d(x,/(x)) >0 для всех хеХ, поэтому из
компактности пространства X следует, что существует такое е: > 0, что
d(x,/00) > t: для всех х. Выберем подразделение L комплекса X так,
чтобы диаметры звёзд всех симплексов были меньше е/2. Согласно
теореме о симплициальной аппроксимации существует подразделение К
комплекса L и симплициальное отображение g: K—*L, гомотопное
отображению /. По построению g обладает тем свойством, что для любого
симплекса сг комплекса К множество /(сг) содержится в звезде симплекса
g(cr). Тогда g(cr) Па = 0 для любого симплекса сг комплекса К, так как для
любой выбранной точки хеа мы получаем d(x,/00) >е, в то время как
g(cr) лежит на расстоянии не более в/2 от /00, а сг лежит на расстоянии
не более е/2 от ху что следует из того факта, что а содержится в симплексе
комплекса L, а комплекс К является а подразделением комплекса L.
Числа Лефшеца т(/) и z(g) равны, так как / и g гомотопны. Так как
отображение g симплициальное, оно переводит /i-мерный остов К11
комплекса К в п-мерный остов L" комплекса L для всех п. Так как К является
подразделением комплекса L, остов L" содержится в Кп\ следовательно,
g(Kn) <z К" для всех п. Таким образом, g индуцирует цепное отображение
клеточного цепного комплекса {Нп(К'\ Кп~])} в себя. Этим можно вое-
§2.С. Симплициальная аппроксимация
233
пользоваться, чтобы вычислить r(g) по формуле
т(£)= J](-irtr(g,:HM(r,K'l-1)->Hn(Kn,KM-1)).
п
Это аналог теоремы 2.44 для следа вместо ранга, и доказывается он точно
тем же способом, с помощью элементарного алгебраического факта, что
след является аддитивной функцией для эндоморфизмов коротких точных
последовательностей. А именно, если дана коммутативная диаграмма
сточными строками, то tr/3 = traH-try. Этот алгебраический факт можно
доказать, сведя его к простому случаю, когда группы А, В и С свободные,
сначала отфакторизовав кручение в В, а потому и кручение в А, а затем
уничтожив всё остающееся кручение в С с помощью замены А на большую
подгруппу А' с В, для которой А имеет конечный индекс в А\ Подробности
этого рассуждения остаются читателю.
Наконец, заметим, что g*: Нп(Кп, К'3"1) -*Hu(Kn, Ku~l) имеет след О,
так как у матрицы для g* на диагонали стоят нули, потому что g (cj) П а = 0
для любого п-мерного симплекса ст. Поэтому т(/) = r(g)=0. □
Пример 2.С.4. Проверим эту теорему на примере. Пусть X —
замкнутая ориентируемая поверхность рода 3, как показано на рисунке внизу,
а отображение /: X —>X — поворот на 180° вокруг вертикальной оси,
проходящей через центральное отверстие поверхности X. Так как / не имеет
неподвижных точек, должно выполняться равенство т(/) = 0.
Индуцированное отображение /#: Н0(Х) —*Н0(Х) тождественное, как и для любого
линейно связного пространства, поэтому оно даёт вклад 1 вт(/).В
примере 2.А.2 мы видели, что шесть петель а, и Д являются представителями
базиса группы Н1(Х). Отображение /# переставляет классы гомологии
нетель а1 и а3, и аналогично для петель ft и ft, в то время как петля ft
переводится в себя, а петля а2 переводится в а2> которая гомологична а2,
как мы видели в примере 2.А.2. Таким образом, /+: Нл (X) —»//] (X) вносит
вклад -2 в т(/). Остаётся проверить, что отображение/,,: Н2(Х) -* Н2(Х)
234
Глава 2. Гомологии
тождественное, что мы делаем с помощью коммутативной диаграммы
Н2(Х) - -Н2(Х)
I- , I-
Н2(Х, X - {*}) -^ Н2(Х, X - {у})
где х — точка поверхности X в центральном торе, а у = /(>). Мы
можем убедиться, что вертикальное отображение слева — изоморфизм,
рассматривая длинную точную последовательность тройки (X, X - {*}, X1),
где X1 —одномерный остов поверхности X с её обычной CW-структурой,
а точка х выбрана в X - X1; тогда X - {х} деформационно ретрагиру-
ется на X1 и Нп(Х — {х},Х1) = 0 для всех л. Те же самые рассуждения
показывают, что вертикальное отображение справа —изоморфизм. Есть
и аналогичная коммутативная диаграмма, в которой / заменено на
гомеоморфизм g, гомотопный тождественному и равный / в окрестности
точки х, причём g тождественно вне диска в X, содержащего хиу. Так как
отображение g гомотопно тождественному, оно индуцирует
тождественное отображение вдоль верхней строки диаграммы, а так как
отображение g равно / вблизи х, оно индуцирует то же самое отображение, что и /
в нижней строке диаграммы, согласно вырезанию. Из этого следует, что
отображение /+ в верхней строке тождественное.
Этот пример обобщается на поверхности любого нечётного рода
добавлением симметричных пар торов слева и права. Примеры для
поверхностей чётного рода описаны в одной из задач.
Теория неподвижных точек —это хорошо разработанная область
алгебраической топологии, но мы касаемся её в этой книге лишь изредка.
Хорошим введением в эту теорию является книга [15].
Симплициальные аппроксимации CW-комплексов
Теорема о симплициальной аппроксимации позволяет заменить
произвольные непрерывные отображения гомотопными им симплициальны-
ми отображениями во многих случаях, и можно задаться аналогичным
вопросом для пространств: какие пространства гомотопически
эквивалентны симплициальным комплексам? Мы покажем, что это верно для
наиболее общего класса пространств в алгебраической топологии — для
CW-комплексов. В приложении этот вопрос обсуждается и для некоторых
других классов пространств.
I Теорема 2.С.5. Любой CW-комплекс Х гомотопически эквивалентен
I симплициальному комплексу, который можно выбрать той же самой
I размерности, что и X, конечным, если X конечный, и счётным, если X
I счётный.
Мы будем строить симплициальный комплекс Y ^ X по индукции
как возрастающее объединение подкомплексов Yfl, гомотопически экви-
§ 2.C. Симплициальная аппроксимация
235
валентных остовам Хп. Чтобы сделать шаг индукции, предположим, что
мы уже построили Уп ^Хп, и пусть еп_и — это (п + 1)-мерная клетка
комплекса X, приклеенная по отображению у?: Sn —>ХП. Отображение Sn —► Уп,
соответствующее отображению у при гомотопической эквивалентности
Yn ^Хп, гомотопно симплициальному отображению /: Sn —>Yn по теореме
о симплициальной аппроксимации, и нетрудно убедиться, что
пространства Хп U^ en+1 и YJ, Uy еп_и гомотопически эквивалентны (индексы
обозначают приклеивание еп+1 посредством ip и / соответственно); см.
предложение 0.18. Мы можем рассматривать Уп и^еп+1 как конус отображения
Cf, полученный из цилиндра отображения для / стягиванием в точку
основания, соответствующего области определения. Если бы мы знали, что
конус отображения для симплициального отображения является симпли-
циальным комплексом, то тогда, делая то же самое построение для всех
(п + 1)-мерных клеток комплекса X, мы завершили бы шаг индукции.
К сожалению (и это несколько удивительно), конусы отображения и
цилиндры отображения — весьма неудобные объекты в симплициальной
категории. Чтобы избежать этих неудобств, мы будем вместо этого строить
симплициальные аналоги конусов и цилиндров отображений, которые
обладают всеми важными свойствами настоящих конусов и цилиндров
отображений.
Давайте сначала построим симплициальный аналог цилиндра
отображения. Для симплициального отображения f:K—*L это будет
симплициальный комплекс М(/), содержащий как L, так и барицентрическое
подразделение К' комплекса К, в качестве подкомплексов, причём
существует деформационная ретракция rt комплекса М(/) на L, для которой
ri|^/ = /« На рисунке изображён случай, когда / является
симплициальной сюръекцией А2 —> Д1. Построение идёт по одному симплексу
комплекса К за шаг, индукцией по размерности. Начинаем мы с обычного
цилиндра для отображения f: К0 -+L, который можно взять в качестве
М(/|К"°). Предположим по индукции, что мы уже построили M(f\Kn~l).
Пусть а — n-мерный симплекс комплекса К, и пусть т = /(ст) — симплекс
комплекса L размерности п или меньше.
Согласно предположению индукции мы уже
построили М(/: да —> т) с требуемыми
свойствами. Выберем в качестве М(/: а —> т) конус над
М(/: да —> т), как показано на рисунке.
Пространство М(/: да —» т) стягиваемо, так как
по индукции оно деформационно ретрагирует-
ся на пространство т, которое является стягиваемым. Конус М(/: а —»т),
очевидно, стягиваем, поэтому включение пространства М(/: да —» т)
в М(/: а —>т) является гомотопической эквивалентностью. Из этого
вытекает, что М(/: а —> т) деформационно ретрагируется на М(/: да —> т)
согласно следствию 0.20, а можно доказать это и непосредственно, ис-
236
Глава 2. Гомологии
пользуя тот факт, что пространство М(/: да —> т) стягиваемо. Приклеивая
М(/:ст->т) к M(f\K'1'1) по отображению М(/: Ост -> т) CM(/(/С""1)
для всех п-мерпых симплексов ст комплекса К, мы получаем M(f\Kn)
вместе с деформационной ретракцией на M{f\Ku~x). Взяв объединение
по всем п, получим M(f) вместе с деформационной ретракцией г, на L,
которая представляет собой соединение бесконечного числа
предыдущих деформационных ретракций, когда деформационная ретракция
пространства М(/|К") на M(/|JC"~l) выполняется за время t из интервала
[1/2"+1,1/2"]. Отображениег}\К необязательно равно/, но оно
гомотопно отображению / посредством линейной гомотопии f/+ (1 — Qru
которая определена, так как г, (а) с/(а) для всех симплексов ст комплекса /С.
Применяя свойство продолжения гомотопии к гомотопии отображения г},
которая равна t/ + (1 — t)^ па tf и тождественному отображению на L, мы
можем исправить нашу деформационную ретракцию пространства М(/)
на L так, чтобы её ограничение на К в момент времени 1 было равно /.
С помощью симплициального аналога М(/) цилиндра
отображения мы строим симплициальный «конус отображения» С(/), приклеивая
обычный конус над К' к подкомплексу К' сМ(/).
Доказательство теоремы 2.С.5. Для каждого п мы построим GW-kom-
плекс Z7J, содержащий Xй в качестве деформационного ретракта, а также
содержащий в качестве деформационного ретракта подкомплекс У„,
который является симплициальным комплексом. Начинаем с у0 = /0 = Х°.
Предположим по индукции, что мы уже построили У„ и Z„. Пусть клетки
е£+1 комплекса X приклеиваются по отображениям <p(l: S" —> X'J. Согласно
теореме о симплициальной аппроксимации существует гомотопия
отображения </?и в симплициальное отображение /а : S" —»У„. CW-комплекс
Wn=Zn{JM{fa)
а
содержит симплициальный подкомплекс Sna, гомеоморфпый S", на одном
из концов цилиндра отображения М(/а)э причём гомеоморфизм S"^S"a
гомотопен в Wn отображению /ttl а потому и отображению ^,. Пусть Z„.rl
получается из Z„ приклеиванием пространств Df"+1 x / посредством этих
гомотопии между отображениями </?„ и включениями S£ с—► W;r Таким
образом, Z,Hl содержит X"+l па одном конце, а па другом конце у нас
есть симплициальный комплекс Уп+1 = y„lJC(/a), где С(/(Х) получается
а
из М(/(Х) приклеиванием конуса над подкомплексом SJJ. 'Гак как D'""1 х /
деформационно ретрагируется на 3Du+l x / UD"+1 x {1}, мы видим, что
Znfl деформационно ретрагируется на пространство Z„ иУ„+ь которое,
в свою очередь, деформационно ретрагируется на У„ U У„+1 = У/Н j по
индукции. Аналогично Zn+1 деформационно ретрагируется па пространство
X'I+1 UW„, которое деформационно ретрагируется на Х"и UZ„, а потому
ипаХ"+1иХ"=Х"м по индукции.
§ 2.C. Симплициальная аппроксимация
237
Пусть Y = {jYn и z = {JZn- Деформационные ретракции Zn на Хп да-
п п
ют деформационные ретракции Xl)Zn на X, а соединение бесконечного
числа последних деформационных ретракций даёт деформационную
ретракцию Z па X. Точно так же Z деформационно ретрагируется на У. □
Задачи
1. Каково минимальное число рёбер в структурах симплициальных
комплексов К и L на S1, для которых существует симплициальное
отображение К —»L степени п?
2. Применяя теорему Лефшеца о неподвижной точке, докажите, что
отображение S" —> S" имеет неподвижную точку, если его степень не равна
степени антиподального отображения х—» — х.
3. Проверьте, что формула
задаёт отображение /: С2к —► C2fc, индуцирующее факторотображение
(£p2fc-i _^^p2fc-i ge3 неподвижных точек.
4. Пусть X — конечный симплициальный комплекс, а /: X —> X —
симплициальный гомеоморфизм. Докажите, что число Лефшеца т(/)
равно эйлеровой характеристике множества неподвижных точек
отображения /. В частности, т(/) — это число неподвижных точек, если
неподвижные точки изолированные. [Указание. Рассмотрите барицентрическое
подразделение комплекса X, чтобы неподвижные точки образовывали
подкомплекс]
5. Пусть М —замкнутая ориентируемая поверхность, вложенная в !R3
так, что симметрия относительно плоскости Р задаёт гомеоморфизм
г: М-^М, оставляющий неподвижным МПР —набор окружностей.
Можно ли прогомотопировать г в отображение без неподвижных точек?
6. Получите аналог примера 2.С.4 для чётного рода, заменив
центральный тор сферой и считая, что / — гомеоморфизм, ограничение
которого на эту сферу является антиподальным отображением.
7. Проверьте, что теорема Лефшеца о неподвижной точке
выполняется также и тогда, когда т(/) определяется с помощью гомологии с
коэффициентами в ноле F.
8. Пусть пространство X гомотопически эквивалентно конечному
симплициальному комплексу, а пространство Y гомотопически
эквивалентно конечному или счётному бесконечному симплициальному
комплексу. Применив теорему о симплициальной аппроксимации, докажите,
что множество гомотопических классов отображений X —> У не более чем
счётно.
9. Докажите, что имеется лишь счётное множество гомотопических
типов конечных CW-комплексов.
Глава 3
Когомологий
Когомологий — это алгебраический вариант гомологии, который
получается в результате простой дуализации определения. Неудивительно,
что группы когомологий Н1(Х) удовлетворяют аксиомам, очень похожим
на аксиомы для гомологии, за исключением того, что индуцированные
гомоморфизмы идут в противоположном направлении из-за дуализации.
Таким образом, основное различие между гомологиями и когомологиями
состоит в том, что группы когомологий являются контравариаитными
функторами, в то время как группы гомологии ковариантны. В терминах
внутренних свойств, однако, нет большой разницы между группами гомологии
и группами когомологий. Группы гомологии пространства полностью
определяют его группы когомологий, и обратное утверждение тоже верно, по
крайней мере в случае, когда группы гомологии конечно порождённые.
Что немного удивительно, так это то, что контравариантность
приводит к дополнительной структуре в когомологиях. Это прежде всего
проявляется в естественном произведении, называемом ^-произведением,
которое превращает группы когомологий пространства в кольцо. Эта
дополнительная структура чрезвычайно полезна, и основная часть этой главы
посвящена изучению этих произведений, которые являются гораздо более
чувствительными, чем просто аддитивная структура когомологий.
Как контравариантность приводит к произведению в когомологиях,
которого нет в гомологиях? В действительности в гомологиях есть
естественное произведение, но оно имеет вид несколько другого
отображения НДХ) х Hj(Y) —>HI+j(X x Y)y называемого внешним гомологическим
произведением. Если и X и У — CW-комплексы, то внешнее произведение
в гомологиях индуцировано отображением клеточных цепей,
переводящим пару (е1, ej), состоящую из клетки комплекса X и клетки комплекса У,
в произведение клеток е1 х е; в X х Y. Подробности этой конструкции
описаны в § З.В. Положив X = У, мы получаем так первую половину
гипотетического произведения
H,(X) х Hj(X) -> Hi+j{X x X) -> Я/+;(Х).
Трудность заключается в определении второго отображения. Естественно
было бы, чтобы оно было индуцированно отображением X х X —> X. Отоб-
Глава 3. Когомологии
239
ражение умножения в топологической группе и вообще в Н-пространстве
является таким отображением, и, как мы покажем в § З.С , получающееся
в результате произведение Понтрягина может быть весьма полезным для
изучения этих пространств. Но для произвольного пространства X
единственные естественные отображения X х X —> X — проекции на один из
множителей, а так как эти проекции стягивают другой множитель в точку,
получающееся при этом произведение в гомологиях весьма тривиально.
С когомологиями, однако, дело обстоит лучше. Снова имеется
внешнее произведение Н'(Х) х HJ(7) —>HI+J(X x У), которое строится почти
так же, как для гомологии, поэтому снова можно положить X = Y и
получить первую половину произведения
Н'(Х) х H'(JO -> Hi+j(X х X) -> Hi+j(X).
Но теперь по контравариантности второе отображение должно быть
индуцировано отображением X —> X х X, и есть очевидный кандидат для
такого отображения —диагональное отображение А(х) = (х, х). Это, как
оказывается, блестяще срабатывает и даёт произведение в когомологиях,
которое очень хорошо себя ведёт, — w-произведение.
Другая дополнительная структура в когомологиях, существование
которой обусловлено контравариантностью, задаётся когомологическими
операциями. Они превращают группы когомологии пространства в
модуль над неким весьма сложным кольцом. Когомологические операции
лежат несколько глубже, чем структура w-произведения, поэтому мы
отложим их изучение до § 4.L.
Поначалу может показаться, что дополнительная прослойка алгебры
в когомологиях, которая появляется из-за дуализации, участвующей в их
определении, удаляет их от топологии, но есть много топологических
ситуаций, где когомологии возникают весьма естественно. Одна из них —
двойственность Пуанкаре, которой посвящен третий параграф этой
главы. Другая — теория препятствий, которая обсуждается в §4.3.
Характеристические классы в теории векторных расслоений (см. [55] или [VBKT])
предоставляют ещё один пример.
С точки зрения теории гомотопий когомологии являются до
некоторой степени более важными, чем гомологии. Как мы увидим в §4.3,
когомологии можно описать в терминах гомотопических классов
отображений. Это описание похоже на определение гомотопических групп, и в
определённом смысле двойственно ему. Имеется аналог и для гомологии,
описанный в §4.F, но соответствующая конструкция более сложная.
Идея когомологии
Давайте рассмотрим несколько примеров в малых размерностях,
чтобы понять, как можно естественно прийти к рассмотрению групп кого-
240
Глава 3. Когомологии
мологий, и посмотрим, какие свойства пространства они могли бы
измерять. Ради простоты мы рассматриваем симплициальные когомологии
Д-комплексов, а не сингулярные когомологии более общих пространств.
Рассмотрим сначала простейший случай, когда X является
одномерным Д-комплексом, другими словами, ориентируемым графом. Для
фиксированной абелевой группы G множество всех функций на вершинах
графа X со значениями в G тоже образует абелеву группу, которую мы
обозначим Д°(Х; G). Аналогично множество всех функций,
сопоставляющих элемент группы G каждому ребру графа Ху образует абелеву группу
Д1 (X; G). Пас будет интересовать гомоморфизм 5: Д°(Х; G) —> Д1 (X; G),
переводящий с/?е Д°(Х; G) в функцию 5yG Д!(Х; G), значение которой на
ориентированном ребре [v0,v,] равно разности c/pfv,) — i/?(v0). Например,
X мог бы быть графом, образованным лыжнями на горе, с вершинами
в точках пересечения лыжней. Функция с/? могла бы тогда сопоставлять
каждой точке пересечения её высоту над уровнем моря; в таком случае
5 с/? измеряет изменение высоты по лыжне от одной точки пересечения до
следующей. Или граф X мог бы изображать простую электрическую цепь
с функцией с/?, измеряющей напряжения в точках соединения (вершинах);
в таком случае 5 с/? измеряет изменения напряжения вдоль компонент
цепи, задаваемых рёбрами.
Если рассмотреть отображение 5: А°(Х] G) —> А} (Х\ G) как цепной
комплекс с нулями до и после этих двух членов, то группы гомологии
такого цепного комплекса — это по определению группы симплициальных
когомологии графах, а именно Н°(Х; G) = Кег5 с Д°(Х; G) \\Hl(X\G) =
= Д!(Х; G)/Im5. Для простоты мы используем здесь те же обозначения,
которые затем будут использоваться в этой главе для сингулярных
когомологии, предвосхищая теорему о том, что, как мы покажем в §3.1, эти
две теории совпадают для Д-комплексов.
Группу Н°(Х; G) легко описать явно. Функция с/? е Д°(Х; G) обладает
свойством 5(/? = 0 тогда и только тогда, когда с/? принимает одно и то
же значение в обоих концах каждого ребра графа X. Это эквивалентно
тому, что с/? постоянна на каждой компоненте связности графа X. Таким
образом, H°(X;G)—это группа всех функций на множестве компонент
графа X со значениями в G. Она представляет собой прямое произведение
групп G, но одной для каждой компоненты графа X.
Группа когомологии Н](Х; G) = Д](Х; G)/Im5 тривиальна тогда и
только тогда, когда уравнение 5 с/? = xj) имеет решение с/? е Д°(Х; G) для
любого гр е А](Х\ G). Решить это уравнение означает выяснить,
определяет ли задание изменения у вдоль каждого ребра графа X настоящую
функцию [р е Д°(Х; G). Это очень похоже на задачу из анализа о
нахождении функции, имеющей заданную производную; оператор разности 5
здесь играет роль дифференцирования. Как и в анализе, если решение
уравнения 5ip=ip существует, то оно будет единственным с точностью до
Глава 3. Когомологии
241
прибавления элемента ядра оператора 5, т. е. функции, которая постоянна
на каждой компоненте графа X.
Уравнение 5ц> = хр всегда разрешимо, если X —дерево, поскольку если
мы выберем произвольно значение функции у в отмеченной точке v0, то
затем изменение ip вдоль каждого ребра графа X единственным образом
определяет значение функции у в любой другой вершине v индукцией
по длине единственного пути в дереве из v0 в v. Если X —не дерево, то
мы сначала выберем максимальное дерево в каждой компоненте графа X.
Тогда, так как каждая вершина лежит в одном из этих максимальных
деревьев, значения функции гр на рёбрах максимальных деревьев определяют
<р на каждой компоненте графа X единственным образом с точностью до
константы. Но для того, чтобы уравнение <5^>=i/J выполнялось, значение
функции -ф на каждом ребре, не лежащем ни в одном из максимальных
деревьев, должно равняться разности уже полученных значений
функции {р в концах этого ребра. Это условие не обязано выполняться, так как
%j) может иметь произвольные значения на этих рёбрах. Таким образом,
мы видим, что группа когомологии Hl(X; G) — это прямое произведение
групп G, по одной для каждого ребра графа X, не принадлежащего ни
одному из выбранных максимальных деревьев. Это можно сравнить с
группой гомологии Н\(Х; G), которая состоит из прямой суммы групп G, по
одной для каждого ребра графа X, не лежащего ни в одном из
максимальных деревьев. Заметьте, что связь между Я1 (X; G) и Н, (X; G) такая же, как
и связь между Н°(Х; G) и Н0(Х; G), поскольку группа Н°(Х; G) является
прямым произведением групп G, а группа Н0(Х; G) —прямой суммой, по
одному экземпляру для каждой компоненты графа X в обоих случаях.
Теперь давайте увеличим размерность, взяв в качестве X двумерный
Д-комплекс. Определим, как и раньше, Д°(Х; G) и Д' (X; G) как функции
на вершинах и рёбрах комплекса X со значениями в абелевой группе G,
и определим Д2(Х;С) как функции на двумерных симплексах
комплекса X со значениями в G. Гомоморфизм 5: Д1 (X; G) —> Д2(Х; G)
определяется формулой
бч/'(1>0, ^ , V2]) = ^([V0l V, ]) +l/'([V1, V2D - l/'ClVo, V2^>
как сумма со знаками значений функции ч/1 на трёх рёбрах,
принадлежащих границе симплекса [v0,vbv2], точно так же, как значение 5^([v0, v,])
для^е Д°(Х; G) было суммой со знаками значений функции ip на границе
симплекса [v0,v,]. Эти два гомоморфизма Д°(Х; G)-*Al(X\ 0-»Д2(Х; G)
образуют цепной комплекс, так как для ip € Д°(Х; G) мы получаем
Добавим к этому цепному комплексу нули с обоих концов. Полученные
при этом группы гомологии по определению и есть группы когомологии
Hl'(X;G).
242
Глава 3. Когомологии
На формулу для отображения 5: ДЧХ; G) —»Д2(Х; G) можно
посмотреть с нескольких разных точек зрения. По-видимому, самая простая из
них связана с замечанием, что 5\р = 0 тогда и только тогда, когда яр
удовлетворяет свойству аддитивности
lMI>0> Ы) = V>(l>o, vlD + V>(l>b V2]),
где мы представляем ребро [v0, v2] как сумму рёбер [v0, vj и [vx, v2].
Таким образом, 5т/> измеряет отклонение функции яр от того, чтобы быть
аддитивной.
С другой точки зрения 5^ можно рассмотреть как препятствие для
нахождения функции \р е Д°(Х; G) с яр = 5(/>, поскольку если яр = 5ц>,
то тогда 5т/; = 0, так как 55(/> = 0, как мы проверили выше. Мы можем
представлять себе функцию 5яр как локальное препятствие к построению
решения уравнения яр = 5 у, так как она зависит только от значений
функции яр в пределах отдельного двумерного симплекса комплекса X. Если
это локальное препятствие обращается в нуль, то яр определяет элемент
группы Hl(X;G), который является нулём тогда и только тогда, когда
уравнение яр = 5^ имеет настоящее решение. Таким образом, этот класс
в Hl(X\G) является глобальным препятствием для построения решения
уравнения яр = 5ip. Эта ситуация похожа на задачу в анализе о
выяснении того, является ли данное векторное поле векторным полем градиента
некоторой функции. Локальное препятствие здесь — обращение в нуль
ротора векторного поля, а глобальное препятствие —обращение в нуль всех
интегралов по замкнутым контурам в области определения векторного
поля.
Условие 5\р = 0 имеет более геометрическую интерпретацию, когда
X — поверхность, а группа G — это Ъ или Z2. Рассмотрим сначала более
простой случай G = Z2. Условие 5 яр = 0
означает, что количество раз, когда \р
принимает значение 1 на рёбрах каждого
двумерного симплекса, четно, т.е. равно 0
или 2. Это означает, что мы можем
сопоставить функции \р такой набор С^,
непересекающихся кривых в X,
пересекающих одномерный остов трансверсально,
что число пересечений С^, с каждым
ребром равно значению функции яр на этом ребре. Если яр = 5 у для
некоторой функции \р, то кривые из набора С^ делят X на две области Х0 и Xlf
где индекс указывает значение функции ip на всех вершинах в данной
области.
Когда G = Z, мы можем уточнить эту конструкцию, строя С^ из
нескольких дуг в каждом двумерном симплексе, причём на каждой дуге
задана трансверсальная ориентация, которая согласована или не согла-
Глава 3. Когомологии
243
v2 v2
сована с ориентацией каждого ребра в соответствии со знаком значения
функции гр на этом ребре, как на рисунке вверху. Получающийся при этом
набор С^ непересекающихся кривых в X можно представлять как нечто
вроде линий уровня для функции у с 5(/> =я/>, если такая функция
существует. Значение у? изменяется на 1 при каждом пересечении кривой из
набора Сф. Например, если X — это диск, то мы покажем, что Я1 (X; Z) = 0;
таким образом, равенство 5гр = 0 влечёт, что ip = 5(/? для
некоторого (р, поэтому любая трансверсальная система кривых С^ образует линии
уровня некой функции ц>. С другой стороны, если X — кольцо, то это не
всегда верно, как показывает пример, изображённый 1
на рисунке справа, где уравнение ip = 5ц>, очевидно,
не имеет решения, несмотря на то что 5гр = 0.
Отождествляя внутреннюю и внешнюю граничные
окружности этого кольца, мы получаем аналогичный
пример на торе. Даже для G = Z2 уравнение гр = 5(/? не
имеет решений, так как кривая С^, не разбивает X на
две области Х0 и Х:.
Ключ к связи между группами когомологии и группами гомологии
Даёт наблюдение, что функция на множестве i-мерных симплексов
комплекса X со значениями в G — это то же самое, что гомоморфизм группы
симплициальных цепей А,(Х) в G. Дело в том, что Д;(Х) — свободная
абелева группа, базисом которой служат z-мерные симплексы
комплекса X, а гомоморфизм свободной абелевой группы однозначно задаётся
значениями на элементах базиса, причём эти значения могут быть
произвольными. Таким образом, мы получаем отождествление группы Al(X\ G)
с группой Hom(A,(X), G) гомоморфизмов А,(Х) —> G, которую называют
двойственной группой для А,(Х). Есть также простое соотношение
двойственности между гомоморфизмом 5: Д' (X; G) -»5,+1 (X; G) и граничным
244
Глава 3. Когомологии
гомоморфизмом д: Д,+1 (X) —> Д,(Х). Общая формула для 5 имеет вид
5(/?([v0,..., vf+1 ]) = ^(-D;V([v0, ..., vj9..., v/+1]),
а последняя сумма —это просто (/?(r)[v0,..., v,-+,]). Таким образом, имеет
место соотношение 5(/? = </>Э. Другими словами, 5 переводит каждый го-
д у
моморфизм ^еНот(Д,(Х), G) в композицию Д/+1(Х) —> Д,(Х) —*G, а это
на языке линейной алгебры означает, что 5 —двойственное к д
отображение.
Таким образом, возникает алгебраическая задача— выяснить
соотношения между группами гомологии цепного комплекса и группами
гомологии двойственного комплекса, полученного при применении функтора
C—»Hom(C, G). Такова первая тема этой главы.
§ 3.1. Группы когомологии
Группы гомологии Нп(Х) получаются как результат процесса,
состоящего из двух шагов. Сначала строится цепной комплекс ... —> Сп —►
—*С„_] —>... сингулярных, симплициальных или клеточных цепей, а
затем берутся группы гомологии этого цепного комплекса Кетд/ Im<9. Чтобы
получить группы когомологии H"(X;G), мы вставляем промежуточный
шаг, заменяя группы цепей С„ двойственными группами Hom(C„, G),
а граничные отображения с)—двойственными к ним отображениями <5,
прежде чем строить группы когомологии Ker5/Im<5. План этого
параграфа такой. Сначала мы разберёмся в алгебре этого процесса дуализации
и покажем, что группы когомологии полностью алгебраически
определяются группами гомологии, хотя и довольно тонким способом. После этого
отклонения в алгебру мы определим группы когомологии пространств
и покажем, что они удовлетворяют основным свойствам, очень похожим
на свойства гомологии. Польза от всей этой формальной работы
постепенно станет понятной в последующих параграфах.
Теорема об универсальных коэффициентах
Начнём с простого примера. Рассмотрим цепной комплекс
О —^ Z -^ Z -^ Z -^ Z —*■ О
II II II II
Оз ^2 Cj С0
где Z—>Z — отображение х—>2х. Если мы дуализируем его, взяв Hom(-, G)
с G = Z, to мы получим коцепной комплекс
о ^— z ^- z -Д- z ^- z ^— о
II II II II
г* с* с* г*
^з ^2 W о
§ 3.1. Группы когомологий
245
В исходном цепном комплексе группы гомологии равны Ъ в
размерностях 0 и 3 и Z2 в размерности 1. Группы гомологии двойственного ко-
цепного комплекса, которые называют группами когомологий, чтобы
подчеркнуть двойственность, снова равны Ъ в размерностях 0 и 3, но группа
Z2 одномерных гомологии исходного комплекса переместилась в другую
размерность и стала группой Z2 двумерных когомологий.
Можно рассмотреть вообще любой цепной комплекс конечно
порождённых свободных абелевых групп. Такой цепной комплекс всегда
раскладывается в прямую сумму элементарных комплексов вида 0 —> Ъ —* О
и О—*7А—>Z —>0 согласно задаче 43 в §2.2. Применяя Hom(-, Z) к этой
прямой сумме элементарных комплексов, мы получаем прямую сумму
соответствующих двойственных комплексов 0 <— Z <— 0 и 0 <— Z <— Z <— 0.
Таким образом, группы когомологий —то же самое, что и группы
гомологии, за исключением того, что кручение смещается на одну размерность.
Мы увидим позже в этом параграфе, что такое же соотношение между
гомологиями и когомологиями всегда выполняется, если группы
гомологии конечно порождённые, даже когда группы цепей не являются конечно
порождёнными. В этом примере также легко понять, что происходит при
замене Hom(-, Z) на Нот(-, G), так как двойственные элементарные ко-
цепные комплексы тогда имели бы вид 0 <— G <— 0 и 0 <— G <— G <— 0.
Рассмотрим теперь произвольный цепной комплекс С свободных
абелевых групп
Чтобы дуализовать этот комплекс, заменим каждую группу цепей Сп
на двойственную к ней группу коцепей С* = IIom(C„, G), т.е. на
группу гомоморфизмов С„ —> G, и заменим каждое граничное отображение
д: Сп~^Сп_1 на двойственное ему кограничное отображение 5 = д*: С*_}—*
—* С*. Причина, по которой 5 идёт в противоположном направлении
по сравнению с г), увеличивая, а не уменьшая размерность, чисто
формальная. Для гомоморфизма а: Л—>В двойственный гомоморфизм а*:
Hom(B,G) -»Нот(Л, G) определяется как а*(с/?) = ^а> поэтому а*
переводит B^G в композицию А —> В ^ G. Двойственные гомоморфизмы,
очевидно, удовлетворяют соотношениям (а/3)* = /Га*, V = 1 и 0* = 0.
В частности, так как дд — 0, из этого следует, что 55 = 0, и группу
когомологий Н"(С) G) можно определить как «группу гомологии» Ker5/Im5
в члене С* в коцепном комплексе
< ^* J_ ^ J_ ^* <
п\-\ п /i-l
Наша цель состоит в том, чтобы показать, что группы
когомологий Нп(С\ G) полностью определяются группой G и группами гомологии
Нп(С) = Кегд/ \тд. Первой догадкой могло бы быть предположение, что
группа Нп{С\ G) изоморфна Hom(H„(C), G), но это чересчур оптимистич-
246
Глава 3. Когомологии
но, как показывает рассмотренный выше пример, где группа Я2 была
нулевой, в то время как группа Я2 была отлична от нуля. Тем не менее,
имеется естественное отображение h: Я" (С; G) —>Нот(Яп(С), G), которое
определяется следующим образом. Обозначим циклы и границы через
Zn = KerdcCn иВп = 1тдсСп. Класс в Нп(С; G) представлен
гомоморфизмом (/>: Cn^>G, для которого 5(/> = 0, т. е. ipd = 0, или, другими словами,
^р обращается в нуль на Вп. Ограничение c/?0 = (/>|Zn тогда индуцирует
гомоморфизм факторизации (р0: Zn/Bu —>G, который является элементом
группы Hom(Hn(C), G). Если (р лежит в Im5, скажем, (р = 5гр = грд, то
</> обращается в нуль на Zn, поэтому с/?0 = 0, а значит, ^0 = 0. Таким
образом, получаем корректно определённое отображение факторизации
h: Hn(C; G) —> Нот(Яп(С), G), переводящее класс когомологии
гомоморфизма у в ф0. Очевидно, что h —гомоморфизм.
Легко видеть, что h сюръективен. Короткая точная
последовательность
0->Zn->Cn^Bn_1-0
расщепляется, поскольку группа Вп_г свободна как подгруппа свободной
абелевой группы Сп^, Таким образом, имеется гомоморфизм проекции
р: Сп —>Zn, ограничение которого на Zn тождественно. Композиция с р
даёт способ продолжить гомоморфизмы с/?0: Zn —» G до гомоморфизмов
с/? = с/?0р: Сп —> G. В частности, это позволяет продолжить гомоморфизмы
Zn—*G, которые обращаются в нуль на Вп, до гомоморфизмов Cn—>G,
которые тоже обращаются в нуль на Вп; другими словами, это позволяет
продолжить гомоморфизмы Нп(С) —»G до элементов группы Кег5. Таким
образом, мы получаем гомоморфизм Нот(Яп(С), G) —>Кег5. Взяв
композицию с отображением факторизации Ker5 —*Hn(C; G), получаем
гомоморфизм из Нот(Яп(С), G) в Яп (С; G). Если мы применим после этого
отображение h, то получим тождественное отображение на Нот(Яп(С), G), так
как эффект от композиции с h состоит в том, что просто уничтожается
эффект от продолжения гомоморфизмов посредством р. Это показывает,
что гомоморфизм h сюръективен. В действительности это показывает, что
мы имеем расщепимую короткую точную последовательность
0 -> Kerft -> Нп(С; G) -^ Нот(Яп(С), G) -> 0.
Остаётся изучить Kerh. Для этого мы рассмотрим не только цепной
комплекс С, но и его подкомплексы, состоящие из циклов и границ. Таким
образом, мы имеем коммутативную диаграмму коротких точных
последовательностей
о —- zn+, —- cn+1 -JL- вп о
|о L |о О)
0 -Zn "- Сп —5__ в ^о
§ 3.1. Группы когомологий
247
где вертикальные граничные отображения групп Zn+1 и Вп являются
ограничениями граничного отображения в комплексе С, а потому они
нулевые. Дуализация диаграммы (1) даёт коммутативную диаграмму
о-—*„%.,-—с*п+1* в*п
о-—к*—с,:-—ви-—о
(2)
Строки здесь точны, поскольку, как мы уже отмечали, строки в
диаграмме (1) расщепимы, а двойственная к расщепимой короткая точная
последовательность — расщепимая короткая точная последовательность
вследствие естественного изоморфизма
Нот(Л0В, G) ъ Hom(A, G) 0Нот(В, G).
Мы можем рассмотреть диаграмму (2) аналогично (1), как часть
короткой точной последовательности цепных комплексов. Так как когранич-
ные отображения в комплексах Z* и В* нулевые, соответствующая
длинная точная последовательность групп гомологии имеет вид
-*-К*-К - H»{C;G)*-B*n_x*-rn_x - ... (3)
«Граничные отображения» Z* —>В* в этой длинной точной
последовательности в действительности просто двойственные отображения i* для
включений in: Bn—*Zn. Для доказательства этого достаточно вспомнить, как
эти граничные отображения определяются: в диаграмме (2) нужно взять
элемент группы Z*, перенести его назад в С*, применить 5, получив
элемент группы С*+1, а затем перенести его назад в В*. На первом из этих
шагов гомоморфизм с/?0: Zn —> G продолжается до (/?: Сп —> G, на втором
шаге берётся композиция (/? с д, а на третьем шаге мы забываем про
композицию и берём ограничение с/? на Вп. Окончательный результат —
просто ограничение ц>0 с Zn на В„.
Длинную точную последовательность всегда можно разбить на
короткие точные последовательности, и применение этой операции к
последовательности (3) приводит к коротким точным последовательностям
О — КегГ — Нп(С; G) «- Cokeri*.1 — 0. (4)
Группу Keri* можно естественно отождествить с Hom(Hn(C), G), так как
элементы группы Keri* — это гомоморфизмы Zn —»G, которые обращаются
в нуль на подгруппе Вп, а такие гомоморфизмы — это то же самое, что
И гомоморфизмы Zn/Bn —* G. При таком отождествлении группы Keri*
с Hom(Hn(C), G) отображение Нп(С; G) ->Keri* в последовательности (4)
превращается в рассмотренное ранее отображение h. Таким образом, мы
можем переписать (4) как расщепимую короткую точную
последовательность
0 -> Cokeri* -» НП(С; G) -^ Hom(Hn(C), G) -> 0. (5)
хлсша j. когомологии
Наша цель теперь состоит в том, чтобы показать, что наиболее
таинственный член Coker/*_j зависит только от НП_Г(С) и G, причём
естественным, функториальным образом. Сначала давайте заметим, что член
Сокеп'*_1 был бы нулём, если бы всегда было верно, что двойственная
к короткой точной последовательности тоже точная, так как
последовательность, двойственная к короткой точной последовательности
О - В„_, ^ Z„_, - Hn_,(С) - 0, (6)
имеет вид
O^B*n_1^Z'a_l+-Hn_l(C)*+-0 (7)
и если бы она была точной в члене В*_р то гомоморфизм (*г_г был бы
сюръективным, а потому член Cokerf*^ был бы нулём. Это рассуждение
можно применить, если группа Нп^{С) окажется свободной, так как
последовательность (6) в этом случае расщепима, а это влечёт, что (7)
тоже расщепимая точная последовательность. Следовательно, в этом случае
отображение h в последовательности (5) —изоморфизм. Однако в общем
случае легко найти короткие точные последовательности, двойственные
к которым не точны. Например, если мы дуализуем последовательность
О—»Z <— Ъ—*Ъп—» О, применив Hom(-, Z), то получим
последовательность 0 <— Z <— Z <— 0 <— 0, которая не может быть точной в левом члене Z,
ровно в том месте, которое нас интересует в связи с Cokeri*_r
Можно упомянуть вскользь, что нарушение точности в левом конце
короткой точной последовательности после дуализации —это в
действительности единственное нарушение точности ввиду следующего факта.
Упражение. Если последовательность А —> В —> С —> 0 точная, то дуа-
лизация посредством применения Hom(-, G) приводит к точной
последовательности Л* <— В* <— С* <— 0.
Однако в дальнейшем этот факт нам не будет нужен.
Точная последовательность (6) обладает специальным свойством, что
обе группы Вп_! и Zn_i свободные, поэтому её можно рассматривать как
свободную резольвенту группы Нп,г(С), где свободная резольвента абеле-
вой группы Я — это точная последовательность
в которой каждая группа Fn свободная. Если мы дуализуем эту свободную
резольвенту, применив Hom(-,G), то мы можем потерять точность, но
по крайней мере мы получим цепной комплекс (возможно, следует
говорить «коцепной комплекс», но алгебраически нет никакой разницы). Этот
двойственный комплекс имеет вид
§3.1. Группы когомологий
249
Давайте временно использовать обозначение Hn(F; G) для группы
гомологии Ker/n*+I/Im/n* этого двойственного комплекса. Заметим, что
группа Сокеп*_г, которая нас интересует, является группой Hl(F; G), где F —
свободная резольвента в последовательности (6). Поэтому утверждение 2
следующей леммы показывает, что Cokeri*_1 зависит только от Hn_Y(C)
и G.
I Лемма 3.1. 1. Пусть даны свободные резольвенты F и F' абелевых
I групп И и Н'. Тогда любой гомоморфизм а: Н —>Н* можно продолжить
I до цепного отображения из F в Ff\
I ... >■ F2 ^i7! >- F0 ^Н ^0
I «2 «I «0 Q
I У г/ V ,■/ У Г Т
I ... >■ F2 >- F2 5- t0 >■ Я - 0
I Более того, любые два таких цепных отображения, продолжающие го-
I моморфизм а, цепно гомотопны.
I 2. Для любых двух свободных резольвент F и F' группы Н существуют
I канонические изоморфизмы Hn(F; G) %Hn(F/; G) для всех п.
Доказательство. Гомоморфизмы а, мы построим по индукции. Так
как группы F, свободны, достаточно определить каждый гомоморфизм а,
на базисе группы F,-. Чтобы определить а0, заметим, что из сюръектив-
ности гомоморфизма /0' следует, что для любого базисного элемента х
группы F0 существует элемент x'gFq, для которого /q(*') = а/о 00,
поэтому можно положить а000 = *'. Мы хотим определить а] таким же
образом, отображая базисный элемент xeFY в элемент х' eFj, для которого
//С*') = a0/i00. Такой *' существует, если а0/2(х) лежит в Im/,' = Кег/0',
а это действительно так, потому что /^ao/i = а/0/г = 0. Такая же процедура
определяет все последующие гомоморфизмы а,.
Если у нас есть другое цепное отображение, продолжающее
гомоморфизм а, заданное отображениями а[: F, —* Ff, то разности Д = а, - а|
задают цепное отображение, продолжающее нулевое отображение fi: И —> Я'.
Достаточно построить отображения A,-: Fi—*F'i+l, определяющие цепную
гомотопию отображения Д в 0, т.е. удовлетворяющие соотношениям
А' = f!+\K: + Л-i-ifi- Отображения А,- строятся по индукции посредством
процедуры, очень похожей на построение отображений а,. При i =0 мы
выбираем отображение А_1: Н —>F('} нулевым, а тогда требуемое
соотношение принимает вид До —//^о- Этого можно добиться, считая, что А0
переводит базисный элемент* в элементx'gF[, для которого f[{xf) = /3000-
Такой элемент х' существует, так как Im/j' = Ker/J и /0'j8000 = Pf0M = 0.
Для доказательства шага индукции нам нужно определить отображение
А,-, переводящее базисный элемент xeF, в элемент x'eF^j, для которого
■/f+iOO = Д0О - А^/ОО- Это можно сделать, если Д00 - А^/ОО ле-
250
Глава 3. Когомологии
жит в Im^/+1 =Ker/j/, а это будет так, если f!(f5{ - ^-ifi) =0. Применяя
соотношение f!f5{ = Д-i/ и соотношение Д_х = yj-/AI-_1 -f Я/_2/_1, которое
выполняется по предположению индукции, получаем
/;/(/3i-ai-_1/;) = /;'/3i-a--i/- =
= &-ifi-flh-ifi = (Pi-i-f^i-Ofi = *i-2fi-Ji = о,
что и требовалось. Это завершает доказательство утверждения 1.
При дуализации отображений ап, построенных в утверждении 1,
получаются отображения a*: F'* —>F*, образующие цепное отображение
междудвойственными комплексами F'* и F*. Поэтому мы получаем
индуцированные гомоморфизмы когомологии a*: H"(F'\ G) —>Hn(F\ G). Они не
зависят от выбора отображений ап, так как любые другие выбранные а'п
цепно гомотопны, скажем, посредством цепной гомотопии Ям, а тогда
а* и а'* цепно гомотопны посредством двойственных отображений Я*,
так как двойственное к а,- - а- = ^+1Я, + Я,_т/| соотношение имеет вид
а*-< = А*/7+1+^А*_г
Индуцированные гомоморфизмы a*: Hn(Ff\ G) —*Hn(F; G)
удовлетворяют соотношению (/За)* = а*/3* для композиции Н -+Hf -+ Я" (где
задана также свободная резольвента F" для Я"), так как в качестве
продолжения отображения /За можно выбрать композиции /Зма„, где а„ —
продолжение а и /3„ — продолжение отображения /3. В частности, если мы
в качестве а возьмём изоморфизм, а в качестве /3 обратный ему
изоморфизм, причём F" = F, то тогда а*/3* = (/За)* = 1; последнее равенство
получается из очевидного продолжения отображения 1: Н —> Я
тождественным отображением группы F. Те же самые рассуждения показывают, что
/3*а* = 1, поэтому а* — изоморфизм. Наконец, если мы выберем
гомоморфизм а ещё более специальным образом, чтобы он был тождественным,
но с двумя разными свободными резольвентами F и F', то мы получим
канонический изоморфизм 1*: Hn(F';G)->Hn(F;G). □
У любой абелевой группы Я есть свободная резольвента вида 0—*F1—*
—> F0 —» Я —> 0 с F,: = 0 при i > 1, которая строится следующим
образом. Выберем набор образующих для Я, и пусть F0 —свободная абелева
группа, базис которой находится во взаимно однозначном соответствии
с этими образующими. Тогда мы получаем сюръективный гомоморфизм
/0: F0 —>Я, который переводит элементы базиса в выбранные
образующие. Ядро гомоморфизма /0 свободно как подгруппа свободной абелевой
группы, поэтому мы можем взять в качестве FT это ядро, а в качестве
/х: Fx —> F0 взять включение, и тогда мы можем взять F,- = 0 при i > 1.
Для этой свободной резольвенты мы, очевидно, имеем Hn(F; G) =0 при
п > 1, поэтому это должно быть верным и для всех свободных резольвент.
Таким образом, единственная интересная группа Hn(F;G)— это группа
Hl(F\ G). Как мы видели, эта группа зависит только от Н и G, и обычно
§ 3.1. Группы когомологий
251
её обозначают Ext(H, G). Такое обозначение связано с тем фактом, что
Ext(H, G) можно интерпретировать как множество классов
эквивалентности расширений1 группы G посредством группы Я, т. е. коротких точных
последовательностей О—> G —> J —> Н —> О с естественным определением
изоморфизма между такими точными последовательностями. Это
объясняется в книгах по гомологической алгебре, например [14], [34], или [46].
Однако эта интерпретация группы Ext(H, G) редко бывает нужна в
алгебраической топологии.
Суммируя изложенное выше, получаем следующий алгебраический
результат.
I Теорема 3.2. Если группы гомологии цепного комплекса С, состоя-
I щего из свободных абелевых групп, равны Нп(С), то группы когомоло-
I гий HU(C; G) коцепного комплекса Hom(Cn, G) определяются расщепи-
I мыми точными последовательностями
I 0->Ext(Hn_!(C),G) ->Hn(C\G) -^Hom(Hn(C),G) -> 0.
Это утверждение известно под названием теорема об универсальных
коэффициентах для когомологий, потому что оно формально похоже на
теорему об универсальных коэффициентах для гомологии из § З.А,
которая выражает гомологии с произвольными коэффициентами в терминах
гомологии с коэффициентами в Z.
Вычислить Ext(H, G) для конечно порождённой группы Н несложно,
используя следующие три свойства:
• Ext(H0H', G)^Ext(H,G)eExt(H',G);
• Ext(H, G) =0, если группа Н свободная;
• Ext(Zn, G)^G/nG.
Первое из них можно получить, используя прямую сумму свободных
резольвент для Н и Hf как свободную резольвенту для Н $ Н'. Если группа
Н свободная, то свободная резольвента 0 —» Н —>Н —> 0 доказывает
второе свойство, а третье получается при дуализации свободной резольвенты
0—> Z <— Z —> Zn —► 0, дающей точную последовательность
0 •<— Ext(Zn, G) ^— Hom(Z, G) ^- Hom(Z, G) ^— Hom(Zn, G) ^— 0
G/nG * G ^ " G
В частности, из этих трёх свойств следует, что группа Ext(H, Z) изоморфна
подгруппе кручения в Н, если Н конечно порождённая. Так как группа
Hom(H, Z) изоморфна свободной части группы Н, если Н конечно
порождённая, мы получаем следующее утверждение.
По-английски extension, откуда и происходит обозначение. — Прим. перев.
252
Глава 3. Когомологии
I Следствие 3.3, Если группы гомологии Нп и Нп^} цепного комплек-
I са С, состоящего из свободных абелевых групп, конечно порождён-
I ные с подгруппами кручения Тп с Нп и 7м_1сНп_1> то //"(C;Z)^
| *(Hn/Tn)(BTn_v
Во многих ситуациях бывает полезно знать, что короткие точные
последовательности в теореме об универсальных коэффициентах
естественны в том смысле, что цепное отображение а между ценными комплексами
С и С', состоящими из свободных абелевых групп, индуцирует
коммутативную диаграмму
О -^ ExtCH^CC), G) —>• НП(С, G)'—*- HomC/Z^CC), G) —* О
|(а.Г fa' t(rt.)'
О -^ ExtCW^CC), G) — /-/"(С, G)''— Hom(//n_I(G/), G) — О
Это станет очевидно, если вспомнить конструкцию; очевидным
образом получается отображение между короткими точными
последовательностями (4), содержащими Keri* и Сокеп*м, отождествление Кеп* =
= Hom(H„(C), G), разумеется, естественно, а доказательство леммы 3.1
показывает, что Ext(H, G) естественно зависит от И.
Однако расщепление в теореме об универсальных коэффициентах не
естественное, так как оно зависит от выбора проекций р: Сп -»Zn. В
одной из задач в конце этого параграфа приведён топологический пример,
показывающий, что это расщепление действительно не может быть
естественным.
Свойство естественности вместе с 5-леммой доказывает следующее.
I Следствие 3.4. Если цепное отображение между цепными комплек-
I сами свободных абелевых групп индуцирует изоморфизм групп гомоло-
I гий, то оно индуцирует изоморфизм групп когомологии с коэффициен-
I тами в любой группе G.
Можно попытаться обобщить алгебраический механизм теоремы об
универсальных коэффициентах, заменив абелевы группы модулями над
фиксированным кольцом R, а Нот на Нотя — гомоморфизмы R-модулей.
Ключевой факт об абелевых группах, который был нам нужен, состоял
в том, что подгруппы свободных абелевых групп являются свободными.
Подмодули свободного Я-модуля свободны, если R — область главных
идеалов. Таким образом, в этом случае обобщение получается
автоматическим. Имеют место естественные расщепимые короткие точные
последовательности
О - ExtR(Hn.-i(C), G) -> //"(С; G) -^ HomKy/M(C), G) - О,
где С — цепной комплекс свободных R-модулей, в котором граничные
отображения являются гомоморфизмами R-модулей, а группа
коэффициентов G тоже является R-модулем. Если R —это, например, поле, то
§ 3.1. Группы когомологий
253
Я-модули всегда свободны, а потому член ExtR всегда нулевой, так как
можно выбрать свободные резольвенты вида 0—* F0 —> Н —* 0.
Интересно отметить, что доказательство леммы 3.1 о единственности
свободных резольвент годится для модулей над произвольным кольцом Я.
Кроме того, у любого Я-модуля Н есть свободная резольвента, которую
можно построить следующим образом. Выберем набор образующих для И
как Я-модуля, и пусть F0 — свободный Я-модуль, базис которого находится
во взаимно однозначном соответствии с этими образующими. Таким
образом, у нас есть сюръективный гомоморфизм /0: F0-+H, переводящий
элементы базиса в выбранные образующие. Теперь повторим этот процесс
с Кег/0 вместо Н и построим гомоморфизм /г: F^ —* F0, переводящий базис
свободного Я-модуля F1 в образующие модуля Кег/0. По индукции с
помощью той же самой процедуры построим гомоморфизм /„: Fn —> F„_i, образ
которого равен Кег/П_т.
Согласно лемме 3.1 группы Hn(F; G) зависят только от Н и G; от
свободной резольвенты группы F они не зависят. Обычно группу Hn(F\G)
обозначают Ext" (H, G). Для достаточно сложных колец Я группы Ext" (H, G)
могут быть отличными от нуля при п > 1. В некоторых более сложных
разделах алгебраической топологии эти группы Ext" играют существенную
роль.
Теперь сделаем последнее замечание по поводу определения
группы Ext^(H, G). Согласно упражнению на с. 248 точность
последовательности F} —* F0 —* Н —* 0 влечёт точность последовательности F* «— F^ «—
«— Я* «— 0. Это означает, что группа ^(F^G), как она определена
выше, нулевая. Чтобы группа Ext" (H, G) не оказывалась автоматически ну-
левой, лучше определить Hn(F\ G) как п-ю группу гомологии комплекса
...«— Fj"«— Fq «— 0 с пропущенным членом Н\ Это можно рассматривать
как определение групп Hn(F;G) так, чтобы они были неприведёнными
группами когомологий. Для такого слегка изменённого определения мы
получаем Ext(^(H, G) =H°(F; G) -H* =HomR(H, G) согласно точности
последовательности F* «— Fq «— Н* «— 0. Настоящая причина, по которой
неприведённые группы Ext лучше, чем приведённые группы, связана, по-
видимому, с некоторыми точными последовательностями, включающими
Ext и Нот, построенными в §3.F, которые бы не работали при замене
членов Нот нулями.
Когомологий пространств
Вернёмся теперь к топологии. Пусть даны пространство X и абелева
группа G. Определим группу Cn(X]G) сингулярных n-мерных коцепей с
коэффициентами в G как двойственную группу Hom(CM(X), G) для
сингулярной группы цепей СМ(Х). Таким образом, п-мерная коцепь у> еС"(Х; G)
сопоставляет каждому сингулярному п-мерному симплексу ст: А" —* X
254
Глава 3. Когомологии
значение ц>(сг) eG. Так как сингулярные n-мерные симплексы образуют
базис группы СП(Х), эти значения можно выбирать произвольно, поэтому
n-мерные коцепи в точности эквивалентны функциям на сингулярных
n-мерных симплексах со значениями в G.
Отображение кограницы 5: СП(Х; G) —> СП+1(Х; G) является
двойственным отображением Э*, поэтому для коцепи (/? е СП(Х; G) её когра-
л ^
ница 5(/? —это композиция СМ+1(Х) —> СП(Х) —» G. Это означает, что для
сингулярного (п + 1)-мерного симплекса а: Д"+1 —> X мы имеем
5(/>(ст) = 5](-D WI К, ...Д, ..., vn+1]).
Мы автоматически получаем, что 52 = 0, так как отображение 52
двойственно отображению д2 = 0. Поэтому можно определить группу
когомологии Нп(Х; G) с коэффициентами в G как факторгруппу Ker5/ Im5 в члене
СП(Х; G) коцепного комплекса
... «- СП+1(Х; G) ^ С"(Х; G) £ С"-1(Х; G) *- ... «- С°(Х; G) — 0.
Элементы группы Кег<5 —это коциклы, а элементы группы Im 5 —
кограницы. Коцепь (/? является коциклом, когда 5ф = ц>д = 0, другими словами,
когда if обращается в нуль на границах.
Так как группы цепей Сп(Х) свободны, алгебраическая теорема об
универсальных коэффициентах принимает топологический облик
расщепляющихся коротких точных последовательностей
0 — ExtCH^CJO, G) — НП(Х; G) — Hom(Hn(X), G) — 0.
которые описывают, как группы когомологии с произвольными
коэффициентами определяются чисто алгебраически группами гомологии с
коэффициентами в Z. Например, если группы гомологии пространства X
конечно порождённые, то следствие 3.3 показывает, как вычислить группы
когомологии НП(Х; Z) по группам гомологии.
При п = 0 члена Ext нет, и теорема об универсальных
коэффициентах сводится к изоморфизму Н°(Х; G) ^Hom(H0(X), G). Его можно
доказать и непосредственно из определений. Так как сингулярные нульмерные
симплексы — это просто точки пространства X, коцепь в C°(X;G) —это
произвольная функция </>: X —> G, не обязательно непрерывная. Она
является коциклом, если для любого сингулярного одномерного симплекса
о"- [v0, vj —>Х мы имеем 5</>(сг) = ф(дсг) = ^(crO^)) - ^(o"(vo)) =0- Это
эквивалентно тому, что (/? постоянна на компонентах линейной связности
пространства X. Таким образом, Н°(Х; G) — это все функции на
множестве компонент линейной связности пространства X со значениями в G.
Это в точности то же самое, что и Hom(H0(X), G).
Аналогично в случае группы Hl(X;G) теорема об универсальных
коэффициентах даёт изоморфизм Hl(X;G) ** Нот(Н,(Х), G), так как
§ 3.1. Группы когомологий
255
Ext(H0(X), G) =0, поскольку группа Н0(Х) свободна. Если пространство X
линейно связно, то группа Нг (X) — это абелианизация группы кг (X), и мы
можем отождествить Нот(Нг(Х),0 с НотСя^Х), G), так как группа G
абелева.
Теорема об универсальных коэффициентах имеет более простой вид,
когда мы берём коэффициенты в поле F и для гомологии, и для
когомологий. В §2.2 мы определили группы гомологии Hn(X;F) как
группы гомологии цепного комплекса, состоящего из свободных F-модулей
Cn(X;F), где базисом Cn(X;F) служат сингулярные n-мерные симплексы
в X. Двойственный комплекс HomF(Gn(X; F),F), состоящий из
гомоморфизмов F-модулей,— это то же самое, что и Hom(Cn(X),F), так как и то
и другое можно отождествить с функциями на множестве сингулярных
n-мерных симплексов со значениями в F. Следовательно, группы
гомологии двойственного комплекса HomF(Cn(X; F), F) — это группы
когомологий ЯП(Х; F). В обобщении теоремы об универсальных коэффициентах
на случай модулей над областью главных идеалов члены ExtF обращаются
в нуль, так как F — поле, поэтому мы получаем изоморфизмы
Hn(X;F)*HomF(H„(X;F),F).
Таким образом, когомологий с коэффициентами в поле в точности
двойственны гомологиям. Заметим, что, когда F = Zp или Q, для любых
F-модулей G и И мы имеем HomF(H, G) = Hom(H, G) —группа гомоморфизмов.
В оставшейся части этого параграфа мы вспомним основные свойства
сингулярных гомологии и проверим, что они без особого труда
переносятся на когомологий.
Приведённые группы. Приведённые группы когомологий НП(Х; G)
можно определить, дуализовав аугментированный цепной комплекс
...->G0(X)-^Z->0,
а затем взяв Ker/Im. Как и для гомологии, это даёт НП(Х; G) =НП(Х; G)
при п > 0, и теорема об универсальных коэффициентах отождествляет
Н°(Х; G) с Hom(H0(X), G). Мы можем описать разницу между Й°(Х; G)
и H°(X\G) более явно, используя интерпретацию группы H°(X',G) как
функции X —> G, которые постоянны на компонентах линейной
связности. Вспомните, что отображение аугментации е: G0(X) —>Z переводит
каждый сингулярный нульмерный симплекс а в 1, поэтому
двойственное отображение е* переводит гомоморфизм кр\ Ъ—* G в композицию
G0(X) ^ Ъ —+ G, которая является функцией а —► с/?(1). Это постоянная
функция X —> G, а так как с/?(1) может быть любым элементом группы G,
образ отображения е* состоит в точности из постоянных функций. Таким
образом, Н°(Х; G) —это все функции X —► G, которые постоянны на
компонентах линейной связности, по модулю функций, которые постоянны
на всём пространстве X.
256
Глава 3. Когомологии
Относительные группы и длинная точная последовательность
пары. Чтобы определить относительные группы Нп(Х, A\G) для пары
(X, Л), мы сначала дуализуем короткую точную последовательность
О - Сп(А) -U С„(Х) ^ С„(Х, А) - О,
применив Hom(-, G) и получив
О «- С"(Л; G) «^ СП(Х; G) «^ C"U, A; G) «- 0, (8)
где по определению С"(Х, Л; G) = Нот(С„(Х, Л), G). Эта
последовательность точна согласно следующим непосредственным рассуждениям.
Отображение Г ограничивает коцепь на X до коцепи на Л. Поэтому для
функции, сопоставляющей сингулярному n-мерному симплексу в X элемент
группы G, образ этой функции при отображении i* получается
посредством ограничения области определения функции до сингулярных п-мер-
ных симплексов в Л. Каждую функцию, переводящую сингулярные п-мер-
ные симплексы в Л в элементы группы G, можно продолжить так, чтобы
она была определена на всех сингулярных п-мерных симплексах в X,
например, сопоставив значение 0 всем сингулярным N-мерным симплексам,
не лежащим в Л, поэтому гомоморфизм i* сюръективен. Ядро
гомоморфизма Г состоит из коцепей, принимающих значение 0 на сингулярных
n-мерных симплексах в Л. Такие коцепи —это то же самое, что и
гомоморфизмы С„(Х, Л) = Сп(Х)/Сп(А) —> G, поэтому ядро гомоморфизма Г — это
как раз Сп{Х,А\ G) = Нот(С„(Х, Л), G), что и даёт требуемую точность.
Заметим, что мы можем рассматривать Cn{XyA\G) как функции,
сопоставляющие сингулярному n-мерному симплексу в X элемент группы G,
которые обращаются в нуль на симплексах в Л, так как базис группы
С„(Х), состоящий из сингулярных n-мерных симплексов в X, представляет
собой объединение двух непересекающихся множеств: симплексов с
образом, содержащимся в А, и симплексов с образом, не содержащимся в Л.
Относительные отображения кограницы 5: С/1 (X, Л; G)—>Сп+] (X, Л; G)
получаются как ограничения абсолютных отображений 5; так мы
получаем определение групп относительных когомологии Н"(Х, Л; G). Тот факт,
что группа относительных коцепей является подгруппой абсолютных
коцепей, а именно коцепей, обращающихся в нуль на цепях в Л, означает,
что относительные когомологии концептуально устроены немного более
просто, чем относительные гомологии.
Отображения Г и j* коммутируют с 5, так как i и j коммутируют с Я,
поэтому короткая точная последовательность (8) групп коцепей является
частью короткой точной последовательности коцепных комплексов,
дающей соответствующую длинную точную последовательность групп
когомологии
... -> tf"(X,/\;G) ^//"(X;G) ^>Hn(A\G) Л tf"H(X, Л; С) - ...
§ 3.1. Группы когомологии
257
Аналогично можно получить длинную точную последовательность
приведённых групп когомологии для пары (X, А) с непустым А, где НМ(Х, А\ G) =
= Н"(Х, A; G) для всех п, как и для гомологии. Если в качестве А взять
точку х0, то эта точная последовательность даёт отождествление группы
HnU;G)cH"U,x0;G).
Имеется и более общая длинная точная последовательность для
тройки (X, А, В), которая получается из коротких точных последовательностей
О *- СЧА, В; G) £- СпW, В; G) J- Cn(X, A; G) «- 0.
Длинную точную последовательность приведённых когомологии можно
рассматривать как частный случай, когда В —точка.
Как и следовало ожидать, имеется соотношение двойственности
между связывающими гомоморфизмами
5:H"(A;G)->H'l+1U,A;G) и д: Н11+1(Х, А) -> Н„(А).
Оно имеет вид коммутативной диаграммы
Нп04; G) ^ НпИ(Х Л; G)
/i к
Hom(H„(A), G) -£► Hom(ffn+I(X, A), G)
Чтобы проверить коммутативность, вспомним, как эти два связывающих
гомоморфизма определялись посредством диаграмм
СП+1(Х; G) — С"+ЧХ, A; G) СП+1(Х; G) — СП+,(Х, Л; G)
^-"""y _ -- ^~ y
С»(A; G) ^- СЧХ] G) СМ(Л; G) ^— Cn(X; G)
Связывающие гомоморфизмы представлены пунктирными стрелками,
которые корректно определены только тогда, когда группы цепей и
коцепей заменяются на группы гомологии и когомологии. Чтобы показать,
что h5 — d*h, начнём с элемента аеН!1(А\ G), представленного коциклом
(f€Cn(A\ G). Чтобы вычислить 5(a), мы сначала продолжим кр до коцепи
Ф £СП(Х; G), скажем, считая, что новая коцепь принимает значение 0 на
сингулярных симплексах, не лежащих в А. Затем мы возьмём
композицию (р с д\ СП+1(Х) —> Сп(Х) и получим коцепь (рд е С,1+1(Х; G), которая
в действительности лежит в СП+1(Х, А\ G), так как исходная коцепь с/?
была коциклом в А. Эта коцепь (/>деСп+1(Х, A; G) представляет класс 5(a)
в Hn^(X,A\G). Теперь мы применяем отображение h, которое просто
ограничивает область определения отображения (рд до относительных
циклов в СМ+1(Х, А), т.е. до (и + 1)-мерных цепей в X, границы которых
лежат в А. Для таких цепей мы получаем Ipd = c/?d, так как продолжение </>
до (р несущественно. В результате получаем, что класс h5(a) представлен
'Пик. V>55
258
Глава 3. Когомологии
элементом с/?Э. Сравним его с d*h(a). Применение h к (/? ограничивает
его область определения до циклов в Л. А тогда применение отображения
Э* соответствует композиции с отображением, которое переводит
относительный (п 4- 1)-мерный цикл в X в его границу в А. Таким образом, класс
d*h(a) представлен тем же самым элементом ц>д, которым был
представлен класс h<5(a), а потому квадрат коммутативен.
Индуцированные гомоморфизмы. Двойственными к цепным
отображениям /:: Cn(X) -* Cn(Y), индуцированным отображением /: X -> У,
являются коцепные отображения р\ Cn{Y\G) —> C\X\G). При дуали-
зации соотношения /цд = д/ц получается соотношение 5/* = /"5,
поэтому /tt индуцирует гомоморфизмы /*: Hn(Y;G) —>Hn(X;G). В
относительном случае те же самые рассуждения показывают, что отображение
/: (X, Л) —(У, В) индуцирует гомоморфизмы/*: ЯП(У, В; G)->Hn(X, А\ G),
а в действительности / индуцирует отображение между короткими
точными последовательностями коцепных комплексов, а значит,
отображение между длинными точными последовательностями групп
когомологии, с коммутативными квадратами. Из свойств (/g)0 — g*P и Iй = 1
следует, что (/g)*=g*/* и 1* = 1, поэтому Х-*НП (X; G) и (X, Л) — Нп(X, Л; G) -
контравариантные функторы; «контра» указывает, что индуцированные
отображения идут в обратном направлении.
Алгебраическая теорема об универсальных коэффициентах
применима также и к относительным когомологиям, так как относительные
группы цепей СП(Х,Д) являются свободными, и имеет место утверждение
о естественности: отображение /: (Х,Д) -* (У, В) индуцирует
коммутативную диаграмму
О -*- Ext(Hn_3(X, A), G) -* Нп№, Л; G) -i Hom(H„(X, Л), G) -^ О
(/.Г
Г
(ЛГ
О -** ExtfH^^y, В), G) -*- Н"^, В; G) Л- Нот(Н„(У, В), G) -Ь- О
Это следует из естественности алгебраических последовательностей
универсальных коэффициентов, так как вертикальные отображения
индуцированы цепными отображениями /д: С,,(Х,Д) -* С„(У,В). Когда
подпространства Л и В пустые, мы получаем абсолютные версии этих
утверждений.
Гомотопическая инвариантность. Утверждение состоит в том, что
если fc*g: (X, Д) — (У, В), то /*=g*: Hn(Y, В) -> Н"(Х, А). Это
доказывается непосредственной дуализацией доказательства для гомологии. Из
доказательства теоремы 2.10 мы имеем цепную гомотопию Р,
удовлетворяющую соотношению g$ - /- = ЭР + Рд. При дуализации этого
соотношения получаем gfl - /: = Р*5 + 5Р*, таким образом, Р* — цепная гомотопии
§ 3.1. Группы когомологий
259
между отображениями /B,gB: Cn(Y\ G)-+Cn(X; G). Её можно также
ограничить до цепной гомотопии между /- и g* на относительных коцепях,
т. е. коцепях, обращающихся в нуль на сингулярных симплексах в
подпространствах В и А. Так как /с и g> цепно гомотопны, они индуцируют один
и тот же гомоморфизм /* = g* когомологий.
Вырезание. Для когомологий это утверждение состоит в том, что для
таких подпространств Z с А с X, что замыкание пространства Z
содержится во внутренности пространства А, включение i: (X - Z, Л - Z) с-> (X, Л)
индуцирует изоморфизмы**: Н"(Х, A; G) —>Hn(X~Z, A-Z; G) для всех п.
Это следует из соответствующего результата для гомологии в силу
естественности теоремы об универсальных коэффициентах и 5-леммы. По-
другому, если не хочется обращаться к теореме об универсальных
коэффициентах, доказательство свойства вырезания для гомологии легко дуа-
лизуется на когомологий следующим образом. В доказательстве для
гомологии рассматривались такие цепные отображения t: Cn(A-f В) —* СП(Х)
и р: СП(Х) -+Сп(А + В), что pi = 1 и t~ip=dD + Dd для цепной
гомотопии D. Дуализуя, т.е. применяя Hom(-, G), мы получаем отображения
р* и t* между С'104 + В; G) и Cn(X; G), и они индуцируют изоморфизмы
когомологий, так как t*p* = 1 и 1 - pV =D*5 + 5D*. Согласно 5-лемме
отображения СП(Х,Д; G) —► СП(А + В, Л; G) тоже индуцируют
изоморфизмы когомологий. Имеется очевидное отождествление Сп(А + В, А\ G)
с СП(В,Д П В; G), поэтому мы получаем изоморфизмы Hn(X,A\G)) ъ
ъНп(В,АПВ; G), индуцированные включением (В, АПВ) '-►(Х, А).
Аксиомы для когомологий. Они в точности двойственны аксиомам
для гомологии. Если мы снова ограничимся CW-комплексами, то
(приведённая) теория когомологий — это последовательность контравариант-
ных функторов hn из С1У-комплексов в абелевы группы вместе с
естественными гомоморфизмами кограницы 5: hn(A) —► hn+1(X/A) для CW-nap
(X, А), которая удовлетворяет следующим аксиомам.
1. Если fc*g:X^Y,to f* = g*:hn(Y)-*hn(X).
2. Для каждой CW-пары (Х, А) имеет место длинная точная
последовательность
... -^ hu(X/A) ^ hn(X) -^ hn№ -^ hM+1(X/A) ^ ...,
где i — включение, a q — отображение факторизации.
3. Для букета X = VaXa с включениями ia: Xa c-> X произведение
отображений П1*: hn(X)-+Y\hn(Xa) — изоморфизм для всех п.
a a
Мы уже видели, что первая аксиома выполняется для сингулярных
когомологий. Вторая аксиома следует из вырезания точно так же, как и для
гомологии, посредством изоморфизмов Н"(Х/А; G) ъ НП(Х, A; G).
Заметим, что в третьей аксиоме участвует прямое произведение, а не прямая
260
Глава 3. Когомологии
сумма, которая встречается в гомологической версии. Так получается из-
за естественного изоморфизма Нот(фАа, G) ^ J~[Hom(Aa> G), из которо-
а а
го следует, что коцепной комплекс несвязного объединения Ц Ха являет-
а
ся прямым произведением коцепных комплексов отдельных пространств
Ха, и это разложение в прямое произведение переходит на группы
когомологии. То же самое рассуждение применимо и в относительном случае,
поэтому мы получаем изоморфизмы Нп(ЦХа, JJЛа; G)^f]tf'(Xa, Aa\ G).
а а а
Третья аксиома получается, если в качестве пространств Аа взять
отмеченные точки ха и перейти к факторпространству Ц Ха/ Ц ха = VaXa.
a a
Соотношение между приведённой и неприведённой теориями
когомологии такое же, как и для гомологии, как это описано в § 2.3.
Симплициальные когомологии. Если X — Д-комплекс и АсХ-
его подкомплекс, то группы симплициальных цепей Д„(Х, А) дуализуют-
ся в группы симплициальных коцепей ДП(Х, A; G) — Нот(Дп(Х, A), G),
и получающиеся при этом группы когомологии — это по определению
группы симплициальных когомологии H^(X,A;G). Так как включения
ДП(Х, А) с СП(Х, А) индуцируют изоморфизмы H,f (X, А)ъНп(Х, А),
следствие 3.4 влечёт, что двойственные отображения СП(Х, A; G)-^>An(X,A\ G)
тоже индуцируют изоморфизмы НП(Х, A; G) ъН^(Х, А\ G).
Клеточные когомологии. Для С1У-комплекса X они определяются
посредством комплекса клеточных коцепей, образованного
горизонтальной последовательностью в следующей диаграмме, где подразумеваются
коэффициенты в данной группе G, а клеточные отображения кограницы
dn —это композиции 5njny что делает треугольники коммутативными.
Заметим, что dndn_j =0, так как ;„§„_! =0.
0
н"-'(Xя"1, хп~2) d"] > нчхп, хл-]) -i. я"+1 (х"+\ хм)
tf"(Xn)
H"(X)^HM(X"+l)
§3.1. Группы когомологий
261
I Теорема 3.5. Имеет место изоморфизм НП(Х; G) ъ Kerd^/Imd,,..!.
I Кроме того, комплекс клеточных коцепей {НМ(ХП, X"-1; G), d„} изомор-
I фен комплексу, двойственному комплексу клеточных цепей, полученно-
I му применением Hom(-, G).
Доказательство. Из теоремы об универсальных коэффициентах
следует, что Нк(Хп, Xм"1; G) = 0 для кфп. Тогда длинная точная
последовательность пары (Хп, X'1"1) даёт изоморфизмы Нк(Хп\ G) ^нЧх"-1; G) для
fc ф п, п - 1. Следовательно, индукцией по п мы получаем, что Hfc (Хп; G) = О
при к> п. Таким образом, диагональные последовательности в
предыдущей диаграмме точны. Теорема об универсальных коэффициентах
даёт также равенство Нк(Х, Xn+1; G) = 0 при к $ п + 1, таким образом,
ЯП(Х; G)^H"(Xn+1; G). Тогда наша диаграмма приводит к изоморфизмам
Н'ЧХ; G) « H"(*"+1; G) « Ker5„ w KerdJImS^i w Kerdjlmd,,^.
Для доказательства второго утверждения теоремы рассмотрим диаграмму
Нк(Хк9 Хк~{; G) >- Hfc(Xfc; G) —*- Hk+1tffc+1, Xfc; G)
I" Ih . 1"
Hom(Hk(Xk, Xk~l), G) -*- Hom(H^(Xfc), G) -^ Hom(Hfc+1(X*+\ Xfc), G)
Клеточное отображение кограницы — композиция двух верхних
отображений, и мы хотим проверить, что это то же самое, что и композиция
двух нижних отображений. Первое и третье вертикальные отображения —
изоморфизмы согласно теореме об универсальных коэффициентах,
поэтому достаточно доказать, что диаграмма коммутативная. Первый
квадрат коммутативен согласно естественности отображения h, а
коммутативность второго квадрата была доказана при обсуждении длинной точной
последовательности групп когомологий пары (X, Л). □
Последовательности Майера—Вьеториса. В абсолютном случае они
принимают вид
... -> НЧХ; G) -^ Нп(А; G) ФН"(В; G) -^ Нп(АпВ; G) -> НП+1(Х; G) — ...,
где X — объединение внутренностей множеств А и В. Это длинная точная
последовательность, соответствующая короткой точной
последовательности коцепных комплексов
0^CnG4 + B,G) icnO4;G)0Cn(B;G) ^Cn(AnB;G) -> 0.
Здесь группа Сп(А + В; G) двойственна подгруппе С„(А + В) с С„(Х),
состоящей из сумм сингулярных n-мерных симплексов, лежащих в А или
в В. Включение С„(А + В) с С„(Х) является цепной гомотопической
эквивалентностью согласно предложению 2.21, поэтому двойственное ему
отображение ограничения Cn(X]G) -» С"(А + B;G) тоже цепная гомото-
262
Глава 3. Когомологии
пическая эквивалентность, следовательно, она индуцирует изоморфизм
когомологии, как было показано при обсуждении вырезания несколько
страниц назад. Отображение ip согласует оба ограничения на Л и на В,
а <р вычисляет разность ограничений на А П В, поэтому очевидно, что ц> —
эпиморфизм, причём его ядро равно образу отображения ip.
Имеется и относительная последовательность Майера—Вьеториса
... ->Hn(X,y;G) ->Hn(A,C;G)®Hn(B,D;G)->Hn(AnB,CnD;G) -> ...
для пары (X, У) = (Л U В, С U D), где С С Л и D С В таковы, что X является
объединением внутренностей множеств Л и В, в то время как У —
объединение внутренностей множеств С и D. Чтобы получить её, рассмотрим
сначала отображение коротких точных последовательностей коцепных
комплексов
О > СП(Х, У; G) ^ СП(Х; G) ^ Cn(Y; G) —^ О
Т У Т
О -> CnC4 + B, C + D; G) -> СПС4 + В; G) -*- С'ЧС + D; G) -> О
Здесь СП(Л + В, С + D; G) определяется как ядро отображения
ограничения Сп(Л + В; G) -* Сп (С + D; G), поэтому вторая последовательность
точная. Вертикальные отображения — это отображения ограничения. Второе
и третье из них индуцируют изоморфизмы когомологии, как мы уже
видели, поэтому согласно 5-лемме первое вертикальное отображение
тоже индуцирует изоморфизм когомологии. Относительная
последовательность Майера—Вьеториса — это длинная точная последовательность,
соответствующая короткой точной последовательности коцепных комплексов
0->Cn04 + B,C + D;G) Л Cn(A,C;G)®Cn(ByD;G) ^
^>Cn(APiB,CnD]G) — 0.
Эта последовательность точная, так как она двойственна короткой точной
последовательности
0 — СП(ДПВ,СГШ) — CnG4,C)eCn(B,D) ->Cn(A + B,C + D) — 0,
построенной в §2.2, которая расщепима, так как Сп(А-\-В,С + D) —
свободная группа, базисом которой служат сингулярные n-мерные
симплексы в А или в В, которые не лежат в С или в D.
Задачи
1. Докажите, что Ext(H, G) — контравариантный по Н функтор для
фиксированной группы G и ковариантный по G функтор для
фиксированной группы Н.
2. Докажите, что отображения G —> G и Н —> Н, умножающие каждый
элемент на целое число п, индуцируют умножение на п в Ext(H, G).
§ 3.1. Группы когомологий
263
3. Рассматривая Z2 как модуль над кольцом Z4, постройте
резольвенту группы Z2 свободными модулями над Z4 и воспользуйтесь этим, чтобы
показать, что группа Ext^ (Z2, Z2) отлична от нуля для всех п.
4. Что происходит, когда группы гомологии h„(X;G) определяются
как группы гомологии цепного комплекса
... -> Hom(G, Cn(JO) — Hom(G, С^СХ)) ->...?
Более конкретно, что такое группы h„(X; G) для G = Z, Zm и Q?
5. Рассматривая коцепи (/? еСг(Х; G) как функции на множестве
путей в X со значениями в G, покажите, что если (р — коцикл, то
а) ip(feg) = 4>(f) + 4>(gy,
б) (/> принимает значение 0 на постоянных путях;
в) </>(/) = ч>№>если/-г;
г) с/? является кограницей тогда и только тогда, когда </?(/) зависит
только от концов пути / для всех /.
[В частности п. а) и в) дают отображение Н1 (X; G) —»НотСтг^Х), G),
которое согласно теореме об универсальных коэффициентах является
изоморфизмом, если пространство X линейно связно.]
6. а) Исходя непосредственно из определений вычислите группы сим-
плициальных когомологий пространства S1 x S1 с коэффициентами в Z
и в Z2, используя структуру Д-комплекса, приведённую в § 2.1.
б) Сделайте то же самое для RP2 и для бутылки Клейна.
7. Докажите, что функторы hn(X) = Hom(Hn(X), Z) не определяют
теорию когомологий на категории СН^-комплексов.
8. Многие из основных гомологических рассуждений по-прежнему
работают для когомологий, несмотря на то что отображения идут в
противоположном направлении. Проверьте это в следующих случаях.
а) Вычислите Н'(5П; G) индукцией по п двумя способами: применяя
длинную точную последовательность пары и применяя
последовательность Майера—Вьеториса.
б) Докажите, что если Л— замкнутое подмножество в X, которое
является деформационным ретрактом некоторой окрестности, то
отображение факторизации X —> Х/А индуцирует изоморфизмы ЯП(Х,Л; G) ъ
^H"(X/A;G) для всех п.
в) Докажите, что если А — ретракт пространства X, то Hn(X;G) ъ
^Hn(A;G)0Hn(X,A;G).
9. Докажите, что если отображение f:Sn—*Sn имеет степень dt то
/*: Нп (Sn; G) -> Нп (Sn; G) — умножение на d.
10. Для линзового пространства Lm(ilt ...,£„), определённого в
примере 2.43, вычислите группы когомологий, используя клеточный коцеп-
ной комплекс и выбирая коэффициенты в Z, Q, Zm и Zp для простого р.
Проверьте, что эти ответы согласуются с теми, которые даёт теорема об
универсальных коэффициентах.
264
Глава 3. Когомологии
11. Пусть X — пространство Мура M(Zm, п), полученное из Sn
приклеиванием клетки en+1 по отображению степени т.
а) Докажите, что отображение факторизации X—>X/Sn = Sn+1
индуцирует тривиальное отображение на Я,(—; Z) для всех z, но не на
Н"+1(—; Z). Выведите из этого, что расщепление в теореме об
универсальных коэффициентах для когомологии не может быть естественным.
б) Докажите, что включение S" <—>Х индуцирует тривиальное
отображение на //'(—; Z) для всех z, но не на Нп(—; Z).
12. Докажите, что нЧх, X";G)=0, если X — CW-комплекс и /с $ п,
применив когомологическую версию второго доказательства
соответствующего утверждения для гомологии в лемме 2.34.
13. Пусть (X, Y) обозначает множество классов отображений X—>Y,
сохраняющих отмеченную точку, гомотопных в классе отображений,
сохраняющих отмеченную точку. Используя предложение 1.В.9, покажите,
что если X —связный CW-комплекс, a G—абелева группа, то
отображение <X,K(G, 1)> —* Н](Х; G), переводящее отображение /: X —* K(G, 1)
в индуцированный гомоморфизм /„: ЯДХ) -> H}(K(G, 1)) « G,
является взаимно однозначным отображением, где мы отождествляем Н1 (X; G)
с HomCHj (X), G) посредством теоремы об универсальных коэффициентах.
§ 3.2. Умножение в когомологиях
Во введении к этой главе мы дали набросок определения ^-произве-
дения в терминах другого произведения, называемого внешним
произведением. Однако определение внешнего произведения с самого начала
требует некоторой работы, поэтому мы будем действовать в обратном
порядке: сначала дадим элементарное определение ^-произведения
явной формулой с симплексами, а потом определим внешнее произведение
в терминах ^-произведения. Другой подход к определению ^-произведе-
ния через внешнее произведение объясняется в конце § З.В.
Чтобы определить ^-произведение, мы рассмотрим когомологии с
коэффициентами в кольце R; наиболее распространённые случаи — кольца
Z, Zn и Q. Для коцепей у? е Ск(Х; R) и гр е Сс (X; R) ^-произведение у^гре
€Ck+i(X; R)—это коцепь, значение которой на сингулярном симплексе
а: д^+* _» х задаётся формулой
(Y?wi//)(ct) = 4>(<r\[v0, ...,vk])*l)((T\[vk, ...,vk+f]),
где выражение в правой части —произведение в R. Чтобы убедиться, что
это ^-произведение коцепей индуцирует ^-произведение классов
когомологии, нам нужна формула, связывающая его с отображением кограницы.
Лемма 3.6. Для у eCk(X;R) и -ф eCc(X;R) выполняется равенство
5(<р wi/0 = 5с/? w^-f (—l)kc/? ^5-ф.
§ 3.2. Умножение в когомологиях
265
Доказательство. Для а: Ак+(+1 —>Х мы имеем
к+1
{5ч>^ф)(сг) = J](-1)V(ct| [v0, ...,% ..., vfc+1])^(or| [vfc+1, ..., vfc+,+1]),
1=0
(-l)k(^5t/0(cr)= J] (-l)V(cT|[v0,...,v,])i/;((7|[vb...,^,...,v^+1]).
Когда мы сложим эти два выражения, последний член первой суммы
взаимно уничтожится с первым членом второй суммы, а остающиеся
члены—это в точности 5(с/? w0)(a) = (с/? ^я/0(дсг), так как
k+i+\
дСГ= J] (-1)'C7|[V0, ...,v;-,...,Vfc+( + I]. □
1=0
Из формулы 5((/?и^) = 5(/> w0 ± «^ w 5i/j видно, что w-произведе-
ние двух коциклов снова является коциклом. Кроме того, ^-произведение
коцикла и кограницы (в любом порядке) является кограницей, так как
{р w 5ip = ±5((/> w я/j), если 5(/> = 0, и 5(/> wi/j = 5((/> w t/0, если 5i/j = 0. Из
этого следует, что определено индуцированное ^-произведение
Hk(X;R) xHe(X]R) <^-Hk+i(X;R).
Оно ассоциативно и дистрибутивно, так как на уровне коцепей w-npo-
изведение, очевидно, обладает этими свойствами. Если в кольце R есть
единичный элемент, то есть и единичный элемент для w-произведения —
класс 1еН°(Х; Я), заданный нульмерным коциклом, принимающим
значение 1 на любом сингулярном нульмерном симплексе.
Произведение для симплициальных когомологий можно задать той же
самой формулой, что и для сингулярных когомологий, поэтому
канонический изоморфизм между симплициальными и сингулярными когомология-
ми сохраняет произведения. Теперь приведём три примера
непосредственных вычислений w-произведений для симплициальных когомологий.
Пример 3.7. Пусть М — замкнутая ори- а2
ентируемая поверхность рода g ^ 1 со
структурой А-комплекса, изображённой на
рисунке для случая g — 2. Представляющее интерес
^-произведение — это отображение Н1Ш) х
хН1(М)—>Н2(М)- Для коэффициентов Z ба- 2
зис группы НХ(М) образован рёбрами а, и Ь,-,
как было показано в примере 2.36, когда мы
вычислили гомологии поверхности М,
используя клеточные гомологии. Мы получаем
HY(M) ъНот(Н^Ш), Ю с помощью клеточных когомологий или с
помощью теоремы об универсальных коэффициентах. Базис Н{(М) определяет
266
Глава 3. Когомологий
двойственный базис Нот (Я] (М), Z) так, что двойственный к а, класс ко-
гомологий а, принимает значение 1 на а, и 0 на других элементах базиса,
и аналогично мы имеем классы когомологий Д, двойственные к Ь,.
Чтобы представить а, симплициальным коциклом ц>{, мы должны
задать значения ip{ на рёбрах, выходящих из центральной вершины, так, что
5^ = 0. Это «условие коцикличности», которое обсуждалось во введении
в эту главу, где мы видели, что оно имеет геометрическую интерпретацию
в терминах кривых, трансверсальных рёбрам в М. Помня об этой
интерпретации, рассмотрим дугу, помеченную а{ на рисунке, которая
представляет петлю в М, пересекающую а, в единственной точке и не
пересекающую все остальные базисные элементы а; и Ь;. Мы определим коцикл
<£,• так, чтобы он принимал значение 1 на рёбрах, пересекающих дугу ah
и значение 0 на всех остальных рёбрах. Таким образом, </?,- вычисляет
число пересечений каждого ребра с дугой а,. Аналогично мы получаем
коцикл iph вычисляющий число пересечений с дугой Д, и %р{ представляет
класс когомологий Д, двойственный к Ь,.
Теперь мы можем вычислить w-произведения, используя
определение. Помня, что упорядочение вершин каждого двумерного симплекса
согласованно с указанными ориентациями его рёбер, мы видим, например,
что коцикл {рх \j гр} принимает значение 0 на всех двумерных симплексах,
кроме симплекса с внешним ребром bl в нижней правой части рисунка,
на котором он принимает значение 1. Таким образом, 4>\^>ipi принимает
значение 1 на двумерной цепи с, образованной суммой всех двумерных
симплексов со знаками, указанными в центре рисунка. Несложное
вычисление показывает, что дс = 0. Так как никаких трёхмерных симплексов
нет, коцикл с — не граница, поэтому он представляет отличный от нуля
элемент группы Н2(М). Из того факта, что (ipl wi/^XO является
образующей группы Z, следует как то, что с представляет образующую группы
Н2Ш) **Z, так и то, что с/?т wi/^ представляет двойственную
образующую у группы Н2(М) ** Нот(Я2(М), Z) ^ Z. Таким образом, а1 w Д = у.
Аналогичные вычисления показывают, что
(*i^Pj = \Q • / .[ = -(А^аД а{^а} = 0, ft^^ = 0.
Эти соотношения полностью определяют w-произведение Н1{М)*НХ(М)'^
-+Н2(М), так как w-произведение дистрибутивно. Заметим, что в этом
примере w-произведение не коммутативно, так как a, w Д = — (Д w а,).
Мы покажем в теореме 3.14, что это самое худшее, что может случиться:
w-произведение коммутативно с точностью до знака, зависящего только
от размерностей; здесь мы предполагаем, что кольцо коэффициентов само
коммутативно.
Из этого примера видно, что ненулевые w-произведения различных
классов а, или Д встречаются в точности тогда, когда соответствующие
§ 3.2. Умножение в когомологиях
267
петли а, или /3,- пересекаются. Это также верно для w-произведений а, или
j3j- с самими собой, если мы разрешаем брать два экземпляра
соответствующей петли и деформировать одну из них так, чтобы она не пересекала
другую.
Пример 3.8. Замкнутую неориентируемую поверхность N рода g
можно рассмотреть аналогичным образом, если мы используем
коэффициенты Z2. Если мы выберем структуру Д-комплекса, изображённую
на рисунке, то рёбра а,- задают базис группы
Hi(N;Z2)f а двойственные базисные
элементы a,-eH1(N;Z2) можно представить
коциклами, которые вычисляют количество
пересечений с дугами, помеченными а, на рисунке.
Тогда можно вычислить, что а{ w a, — отлич- a4
ный от нуля элемент группы H2(N;Z2) &Z2
и а{ \j dj = 0 при 1ф). В частности, при g = 1
мы получаем N = RP2, и произведение
образующей группы НЧ^Р2; Z2) с собой —это об- " аг
разующая группы Н2(ЕР2; Z2).
Замечания в абзаце, предшествующем этому примеру, здесь тоже
применимы, но со следующим отличием: если попытаться продеформировать
второй экземпляр петли а, в нашем примере, чтобы она не пересекалась
с исходным экземпляром, то лучшее, чего можно добиться, — это
заставить её пересекать исходную петлю в одной точке. Это отражает тот факт,
что a, w af теперь отлично от нуля.
Пример 3.9. Пусть X—двумерный CW-комплекс, полученный
приклеиванием двумерной клетки к S1 по отображению S1 —> S1, z*-+zmt
степени т. Применяя клеточные когомологии или клеточные
гомологии и теорему об универсальных коэффициентах, мы видим, что группа
НП(Х; Z) есть Z при п = Ои Z„, при п = 2, поэтому структура w-произве-
дения с коэффициентами Z неинтересна. Однако с коэффициентами Zm
мы получаем Hl(X\ Zm) ^ Ът при i = 0,1, 2, поэтому произведение двух
одномерных классов может оказаться нетривиальным.
Чтобы построить структуру Д-комплекса на X, w e w
возьмём правильный m-угольник, разбитый на т
треугольников Th окружающих центральную
вершину v, как показано на рисунке для случая т = 4;
затем отождествим все внешние рёбра поворота- е
ми m-угольника. Это задаёт на X структуру
Д-комплекса с двумя вершинами, т + 1 рёбрами и т
двумерными симплексами. Образующая а
группы H}(X;Zm) представлена коциклом (/?,
принимающим значение 1 на ребре е, которое порождает группу И{(Х).
Условие, что (/? является коциклом, означает, что </?(е,-) + с/?(е) = с/?(е1+1) для
268
Глава 3. Когомологий
всех i, где индексы берутся по модулю т. Поэтому мы можем считать,
что (/?(е,) = i EZm. Следовательно, (^ w </?)(7}) = с/?(е,)с/?(е) = i.
Отображение h: Н2(Х; Zm) •-> Hom(H2(X; Z,M), Z;„) является изоморфизмом, так как
YtЪ■— образующая группы 772(Х; Ът) и существуют двумерные коциклы,
принимающие значения 1 на J]7], например коцикл, принимающий зна-
чение 1 на одном 7} и 0 на всех остальных. Коцикл с/? w у принимает
значение 0+ 1 + ... + (т — 1) па J]7}, поэтому он представляет умножен-
i
ную на 0+ 1 + ... + (т - 1) образующую ft группы Н2(Х; Ът). В Ът сумма
0+ 1 + ... + (т — 1) равна 0, если т нечётно, и равна /с, если т — 2к, так
как члены 1 и m — 1 сокращаются, 2 и m - 2 сокращаются, и т.д. Таким
образом, обозначив а^а через а2, мы получаем а2 = 0, если т нечётно,
и а2 = /с/3, если т = 2к.
В частности, если m = 2, то X —это RP2, и а2 = /3 в H2CRP2; Z2), как
мы уже показали в примере 3.8.
Формула для ^-произведения
(у? ^я/0(сг) = ¥>(сг| [v0,..., vfc])T/i(cr| [vfc>..., vfc+f])
даёт также относительные w-произведения
Ик{Х\ Я) х 7/'(Х, Л; Я) -^ Hfc+'(X, Л; Я),
НЧХ, Л; Я) х НЧХ; Я) ^ Н*+Чх, Л; Я),
//ЧХ, А; Я) х НЧХ, Л; Я) ^ Hfc+'(X, Л; Я),
так как если у или я/; обращаются в нуль на цепях в Л, то это верно и для
(/? ui/i, Имеется и более общее относительное ^-произведение
7/Чх, Л; Я) х НЧХ, Б; Я) ^ Н*+Чх, AUB; Я),
где Л и В —открытые подмножества в X или подкомплексы
CW-комплекса X. Оно получается следующим образом. Абсолютное
^-произведение ограничивается до ^-произведения Ск(Х, Л; Я) х С^(Х, В; Я) —>
->Ск+/(Х, А + В; Я), где С"(Х, А + В; Я) -подгруппа в СП(Х; Я), состоящая
из коцепей, обращающихся в нуль на суммах цепей в А и цепей в В. Если
А и В открыты в X, то включения CU(X, A U В; Я) «-> СП(Х, Л + В; Я)
индуцируют изоморфизмы когомологий посредством 5-леммы и того факта,
что отображения ограничения
Cn(AUB\R)->Cl(A + B\R)
индуцируют изоморфизмы когомологий, как мы видели при обсуждении
вырезания в предыдущем параграфе. Поэтому ^-произведение
СЧХ, А; Я) х СЧХ, В; Я) -* Cfc+'(X, А + В; Я)
§ 3.2. Умножение в когомологиях
269
индуцирует требуемое относительное ^-произведение
Нк{Х9 A; Я) х Н*(Х, В; Я) -> Нк+с(Х, A UB; Я).
Это верно также в случае, когда X — СН^-комплекс с подкомплексами А
И В, так как тогда отображения Cn(AUB; Я) —>Cn(A + B\ R) снова
индуцируют изоморфизмы когомологии, как мы видели для гомологии в § 2.2.
Предложение 3.10. Для отображения /: X —> Y индуцированные
отображения /*: Hn(Y\R) —> НП(Х;Я) удовлетворяют соотношению
/*(aw/3)=/*(a) ^/*(j3), и аналогично в относительном случае.
Доказательство. Это следует из формулы /Ч</0 ^/:СФ) = /s(¥> ^i/>)
для коцепей:
(/V w/^)((7) = /^01 [V0, ..., Vfc])/ty(cr| [Vfcl ..., Vfc+,]) =
= v(/^|[vo.-.vfc])^(/or|[vit>...>vfc+f]) =
= (^^)(/(7)=/:(^^)((7). П
Определим теперь внешнее произведение. В абсолютном и в общем
относительном случае это отображения
н*(Х; Я) х н*(У; я) ^ н*+'(х x У;Я),
НЧХ, A; R) х Н'(У, В; Я) Д Н* И(Х х У, А х У UX х В; Я),
заданные формулой a x b = pj(a) ^pJCW, где рг и р2 — проекции X х 7 на
Хи на 7.
Пример 3.11 (n-мерный тор). Покажем, что для n-мерного тора Гп,
т.е. для произведения п окружностей, все классы когомологии являются
Произведениями одномерных классов. Точнее говоря, мы покажем, что
Нк(Тп\ Я) — свободный Я-модуль, базисом которого служат произведения
Щг^...^а(к для ia < ...<ik, причём а{еН}(Тп\К) —это р*(а), где а
—образующая группы Нl (S1; Я) и р, — проекция тора Гп на его i-й множитель.
В качестве предварительного шага докажем, что для образующей а
Группы ^U.dl-.R) отображение
Нп (У; Я) -> Н"+1 (/ х У, а/ х Y; Я), /3 — a x /3,
является изоморфизмом для любого пространства У. Это доказательство
Использует коммутативность следующего квадрата:
Нк{А\ Я) х H\Y\ Я) -^ Н*+1(Х, Л; Я) х Н'(У\ Я)
Hfc+4A х Г; Я) 5—^ Нк+ш(Х X У, Л х Г; Я)
Чтобы проверить её, начнём с элемента верхнего левого произведения,
Представленного коциклами ф eCfc(A; Я) и ч/;еС'(У; Я). Продолжим ф до
270
Глава 3. Когомологии
коцепи (р е Ск(Х; Я). Тогда пара (с/?, гр) отображается направо в (5(р, ^),
а затем вниз в p\(5ip) ^pl(xjj). При обходе квадрата в другом направлении
(ifyijj) отображается вниз в pJ(</0 ^pjjO/O, а затем направо в <5(pJ(iJ?)w
^piW)> таккакр;((£)^р£(^) продолжает рJ (^^р^ВД на X х У.
Наконец, 5(pj((^) ^р^О/О) =р\(5{р)^>р1(гр), так как 5^ = 0.
Вернёмся к произведению / х У. Длинная точная последовательность
пары (/ xY,dI х У) разбивается на расщепимые короткие точные
последовательности
0 -> Нп(/ х У; Я) — НП(Э/ хУ;Я)Л Нп+1 (/ х У, Э/ х У; Я) — 0.
Отображение 5 является изоморфизмом при ограничении на
экземпляр группы Hn(Y; Я), соответствующий {0} х У. Этот экземпляр группы
Hn(Y; R) состоит из элементов вида 10 х /3, где элемент 10 €Н°(д/; R)
представлен коциклом, который равен 1 на Оед/ и 0 на 1 еэ/. Из
коммутативности рассмотренного выше квадрата следует, что 5(10 х /3) = 5(10) х /3.
Элемент 5(10) —образующая группы нЧЛЭ/;^) согласно случаю, когда
У — точка. Любая другая образующая а равна элементу 5(10),
умноженному на единицу кольца Я, таким образом, это показывает, что отображение
j3^axj3- изоморфизм.
Эквивалентное утверждение заключается в том, что отображение
Нп(У; R) -> H^CS1 х У, {s0} х У; Я), заданное формулой р -> a x 0,
является изоморфизмом; теперь а —образующая группы H1(S1,50;R). Из
длинной точной последовательности пары (S1 х У, {s0} x У) следует, что
отображение
Hn+\Y; R) х Hn(Y; Я) — Hn+1(S] x У; Я), (ft, j82) -> 1 x ft + a x /32,
является изоморфизмом; здесь a —образующая группы Н1^1; Я). В
частности, а случае п-мерного тора мы получаем индукцией по п, что Нк(Т"; Я)
имеет структуру, описанную в начале примера.
Мы можем применить это вычисление, чтобы доказать факт,
который скоро нам понадобится для вычисления произведений в проективных
пространствах. Записав n = i + ;, можно представить куб /" в виде
произведения V х V. Утверждение состоит в том, что внешнее произведение
образующих групп Hl{I\ Э/'; Я) и W(V > Э/;; Я) является образующей
группы Нп(Г, дГ; Я), где мы используем первое из следующих трёх внешних
произведений:
Н'(7\дГ;Я) х W{J*,dV\R) -^HnUn,dIn;R),
Н1{Т\ Г; Я) х Hj(V, Г; Я) Д Нп(Тпу tn; Я),
Н((Г\К) х Hj(Tj;R) Д Hn(Tn;R).
§ 3.2. Умножение в когомологиях
271
Во втором внешнем произведении точки обозначают удаление клетки
наибольшей размерности. Все эти три внешних произведения
эквивалентны. Это очевидно для первого и второго, если представлять себе тор
как факторпространство куба. Для второго и третьего заметим, что все
клеточные граничные отображения для Тп с коэффициентами Ъ должны
быть тривиальными, поскольку иначе группы когомологий были бы
меньше, чем вычисленные выше. Следовательно, все клеточные кограничные
отображения с произвольными коэффициентами нулевые, и отображение
Нп(Тпу t"; R) —>Нп(Тп; К) является изоморфизмом. Соответствующие
результаты для V иГ, конечно, тоже верны.
Так как внешнее произведение ассоциативно, предыдущее
вычисление показывает, что для последнего из этих трёх внешних произведений
внешнее произведение образующих является образующей, следовательно,
это верно и для первого внешнего произведения.
Кольцо когомологий
Так как w-произведение ассоциативно и дистрибутивно,
естественно попытаться использовать его для введения кольцевой структуры на
группах когомологий пространства X. Это легко сделать, если мы просто
определим Н*(Х; R) как прямую сумму групп Hn(X; R). Элементы группы
Н*(Х;Я) — это конечные суммы £а,-, где а,еН'(^;Д)> и произведение
i
двух таких сумм определяется как (£] a,-) (£] 0/) = X а,-j8j. Несложная про-
i ) ч
верка показывает, что это превращает Н*(Х; R) в кольцо, причём с
единицей, если Я — кольцо с единицей. Аналогично Н*(Х,А;Я) превращается
в кольцо посредством относительного w-произведения. Учитывая
скалярное умножение на элементы из Я, эти кольца можно также рассматривать
как алгебры над R.
Например, вычисления в примере 3.8 или в примере 3.9 показывают,
что H*(IRP2; Z2) состоит из многочленов а0 + а1а + а2а2 с
коэффициентами az-€Z2, таким образом, H*Q&P2; Z2) — факторкольцо Z2[a]/(a3) кольца
многочленов Z2[a] по идеалу, порождённому классом а3.
Этот пример показывает, что H*(X;R) часто имеет более
компактное описание, чем последовательность отдельных групп ЯП(Х; R),
поэтому есть определённая экономия при изменении точки зрения, когда мы
начинаем рассматривать все группы Я"(Х; R) как часть единого объекта
Н*(Х;Я).
Сложение классов когомологий разных размерностей,
использованное при определении кольца Н*(Х; Я), —это удобный формальный
аппарат, но он не имеет почти никакого топологического смысла. Кольцо
когомологий всегда рассматривают как градуированное кольцо, т.е. кольцо А
с таким разложением в сумму © Ак аддитивных подгрупп Ак> что уМНОЖе-
272
Глава 3. Когомологии
ние переводит Ак х А^ в Ак+(. Указывая, что элемент а еД лежит в Ак) мы
пишем \а\ = к. Это применимо, в частности, к элементам группы Hk(X;R).
Некоторые авторы называют \а\ «степенью» элемента а, но мы будем
использовать термин «размерность», который более геометричен и его
нельзя спутать со степенью многочлена.
Одни из наиболее простых градуированных колец —кольца
многочленов R[a] и их срезанные версии Я[а]/(а'?), состоящие из
многочленов степени меньше п. Пример, который мы уже встретили,— кольцо
Н*(ШР2; Z2) ъ Z2[a]/(a3). Обобщая его, мы имеем следующее
утверждение.
I Теорема 3.12. H*(5№n; Z2) *<Z2[a]/(a',+1) и /-/*(ВР°°; Х2) *Z2[a], где
|а| = 1. В комплексном случае Н*(СРМ; Z) ^Z[a]/(an+1) и Н'ССР00; Z) *
wZ[a], где |а| = 2.
Этот результат оказывается весьма важным, и его можно доказать
многими разными способами. Доказательство, которое мы приведём
здесь, заключается в прямом сведении к вычислению относительного
произведения в примере 3.11. Другое доказательство, использующее
двойственность Пуанкаре, будет приведено в примере 3.40. Третье
доказательство содержится в §4.D как одно из приложений последовательности
Гизина.
Доказательство. Сначала разберём случай RP". Чтобы упростить
обозначения, мы сократим IRPn до Р" и не будем упоминать явно группу
коэффициентов Z2. Так как включение Рп~] <-* Рп индуцирует изоморфизм
групп Н' при i $ п - 1, для доказательства индукцией по п достаточно
показать, что w-произведение образующей группы ЯП-1(РП) и образующей
группы Н1(Р11) — это образующая группы Нп(Рп). Не потребует большего
труда доказательство более общего утверждения, что ^-произведение
образующей группы Н1(Рп) и образующей группы Нп~1(Рп) — это
образующая группы Нп(Рп). Чтобы ещё упростить обозначения, положим j = n~ f;
таким образом, i4-; = п.
Доказательство использует до некоторой степени геометрическую
структуру пространства Рп. Напомним, что Рп состоит из ненулевых
векторов (%...,xn)eR"+1 по модулю умножения на ненулевые скаляры.
Внутри Рп есть экземпляр пространства Р', представленный векторами,
у которых последние j координат х/+1,...,хп нулевые. Там есть также
экземпляр пространства PJ, представленный точками, у которых первые f
координат х0,..., х,_! нулевые. Пересечение Р? С\Р} состоит из
единственной точки р, представленной векторами, у которых только координата
х{ отлична от нуля. Пусть [/ — подпространство в Р", представленное
векторами с отличной от нуля координатой х{. Каждую точку из U можно
представить единственным вектором, у которого *,■ = 1, а остальные п
координат произвольные, поэтому пространство U гомеоморфно К'\ причём
§3.2. Умножение в когомологиях
273
при этом гомеоморфизме точка р соответствует
точке 0. Мы можем записать это пространство
Шп как R1 х R;, где R1 соответствует
координатам х0, ...,*,■_!, a RJ — координатам xi+u ...,х,г
На рисунке пространство Р" представлено в
виде диска с отождествлёнными диаметрально
противоположными точками его граничной сферы, из которой получается
Р"-1сРп, причём U = Pn -Рп~т —внутренность диска.
Рассмотрим диаграмму
Н((Рп)хН^(Рп) ^Нп(Р")
А А
Н[{Р\Рп - Pj) х W{P\ Pn-P() ^ Нп(Р\ Ри - {р})
\ \
H'(R", К" - R0 х Н1(Ж"ЛП -Ю *- H"(R", R" - {0})
которая коммутативна в силу естественности w-цроизведепия. Самое
нижнее отображение ^-произведения переводит образующую,
умноженную на образующую, в образующую, как было показано в примере 3.11
в эквивалентной ситуации произведения кубов. То же самое будет верно
для самой верхней строки, если четыре вертикальных отображения
являются изоморфизмами, таким образом, именно это остаётся доказать.
Нижнее отображение в правом столбце является изоморфизмом
согласно вырезанию. Для верхнего отображения в этом столбце тот факт,
что Рп — {р} деформационно ретрагируется на Рп~х, даёт изоморфизм
Нп(Рп, Рп - {р})ъНп(Рп, Р""1), который получается применением 5-лем-
мы, к длинным точным последовательностям этих пар. Используя
клеточные когомологии, получаем изоморфизм Нп(Р'\ Р'1~1)^Нп(Рп).
Чтобы убедиться, что вертикальные отображения в левом столбце
являются изоморфизмами, мы воспользуемся следующей коммутативной
диаграммой:
Н{(Рп) *— Н{(Р'\ Р1'-1) *— Н((Рп, Pn-Pj) *- НЧЖ", Им - №')
Y т т т
Н'(РП) -<— И1(Р\ Р1'1) *— Н{(Р\ Р1 - {р}) —>• №№'", R''- {0})
Если мы сможем показать, что все эти отображения — изоморфизмы, то
тогда то же самое рассуждение можно применить, поменяв местами i и j,
и доказательство для iRPM будет завершено.
Левый квадрат состоит из изоморфизмов согласно клеточным когомо-
логиям. Правое вертикальное отображение, очевидно, изоморфизм. Ниж-
274
Глава 3. Когомологии
нее правое горизонтальное отображение —изоморфизм согласно
вырезанию, а отображение слева от него —изоморфизм, так как Р1 — {р}
деформационно ретрагируется на Р'-1. Оставшиеся отображения будут
изоморфизмами, если среднее отображение в верхней строке —изоморфизм.
А это отображение действительно изоморфизм, потому что Рп — Р-*
деформационно ретрагируется на Р1-1 посредством следующего
рассуждения. Подпространство Рп - PJ с Рп состоит из точек, представленных
векторами v = (х0, ...,хп), у которых по крайней мере одна из координат
х0, ...,х,_1 отлична от нуля. Формула /f(v) = (x0, ...,х,_ь txh ..., txu) для t,
убывающего от 1 до 0, даёт корректно определённую деформационную
ретракцию пространства Рп -Р} на Р'"1, так как /f(Av) = A/f(v) для
скаляров AeR.
Случай пространства R?°° следует из конечномерного случая, так как
включение М>п «-> MP00 индуцирует изоморфизмы групп H\-\Z2) при
i ^ п согласно клеточным когомологиям.
Для комплексных проективных пространств доказательство то же
самое, нужно только использовать коэффициенты Z и заменить каждую
группу Нк на Н2к и R на С. □
Имеются также кватернионные проективные пространства HP'7 и
HP00, которые определяются точно так же, как и в комплексном
случае, с CW-структурами вида е° U e4 U es U ... Ассоциативность умножения
кватернионов необходима для того, чтобы отождествление v ~ Av было
отношением эквивалентности, поэтому такое определение не
позволяет построить октавные проективные пространства, хотя есть октавная
проективная плоскость ОР2, которая будет определена в §4.3. Структура
^-произведения в кватернионных проективных пространствах точно
такая же, как в комплексных проективных пространствах, за исключением
того, что образующая четырёхмерная:
H*(MP°°;Z) *Z[a] и Я*(МРП; Z) ъ Z[a]/(an+1), где |a| = 4.
То же самое доказательство, что и в действительном и в комплексном
случаях, применимо также и в этом случае.
Структуру ^-произведения для RP°° с коэффициентами в Z можно
легко вывести из структуры ^-произведения с коэффициентами в Z2
следующим образом. Гомоморфизм колец R —> S всегда индуцирует гомоморфизм
колец Н*(Х, Л; R) -> Н*(Х, Л; S). В случае проекции Z —> Z2 мы получаем
для RP00 индуцированное цепное отображение клеточных коцепных
комплексов с коэффициентами в Z и в Z2:
... ^—z Д—z Д^—z Д—z Д^—z^—о
у у { Y у
... ^— z2 -Д- z2 «Д- z2 Д- z2 Д- z2 -<— о
§ 3.2. Умножение в когомологиях
275
Из этого мы видим, что гомоморфизм колец Н*(МР°°; Z) —> H*(RP°°; Z2)
инъективен в положительных размерностях, причём его образ —чёт-
номерная часть H*GRP°°; Z2). По-другому это можно вывести из
теоремы об универсальных коэффициентах. Следовательно, мы получаем
Н*»Р°°;^)^^[а]/(2а),где|а| = 2.
Структуру ^-произведения в H*(RPn; Z) можно вычислить
аналогичным способом, но описание получается несколько громоздким:
H*(RP2k; Z) ъ Z[a]/(2a, ak+l), \a\ = 2;
H*(RP2M; Z) ъ Z[a, /3]/(2a, ak+\ ft2, a/3), \a\ = 2, |jS| = 2fc + 1.
Здесь /3 — образующая группы H2/c+1(RP2/c+1; Z) ^Z. Из этого вычисления
мы видим, что кольца H*(R?2k+l;Z) и Н*(Ш>2к V S2fc+1; Z) изоморфны,
хотя для коэффициентов в Z2 это неверно, так как для образующей а е
gH1(KP2/c+1; Z2) имеем а2к~*~1 ^0, в то время как a2k+l = 0 для образующей
aGH]№P2/cVS2;c+1;Z2).
Индуцированные гомоморфизмы являются гомоморфизмами колец
согласно предложению ЗЛО. Вот пример, иллюстрирующий этот факт.
Пример 3.13. Изоморфизм Н*ГЦХа;я) ^>Y\H*(Xa'>Ry)> покоорди-
натно индуцированный включениями ia: Ха<-+\\Ха, является
изоморфизмом колец относительно обычного покоординатного умножения в
произведении колец, потому что каждая координатная функция i* является
гомоморфизмом колец. Аналогично для букета изоморфизм H*(VaXa; R)%
^f~[H*(Xa;R) является изоморфизмом колец. Здесь мы рассматриваем
a
приведённые когомологии как когомологии относительно отмеченной
точки и применяем относительные w-произведения. Мы должны сделать
предположение, что отмеченные точки ха е Ха являются
деформационными ретрактами окрестностей, чтобы быть уверенными, что требуемый
изоморфизм действительно имеет место.
Эту структуру произведения колец для букетов можно иногда
использовать, чтобы доказать невозможность представления пространства
в виде букета с точностью до гомотопической эквивалентности.
Например, рассмотрим пространство СР2, которое представляет собой сферу
S2 с клеткой е4, приклеенной по отображению /: S3 —> S2. Используя
гомологии или только аддитивную структуру когомологии, нельзя сделать
вывод, что СР2 не гомотопически эквивалентно S2 V S4 и, следовательно,
что отображение / не гомотопно постоянному. Однако с помощью
^-произведения мы можем различить эти два пространства, так как квадрат
любого элемента из H2(S2 V S4; Z) равен нулю ввиду изоморфизма
колец H*(S2 V S4; Z) ъ H*(S2; Z) 0 H*(S*; Z), а квадрат образующей группы
Н2(СР2; Z) отличен от нуля по теореме 3.12.
276
Глава 3. Когомологии
Вообще w-произведения позволяют различить бесконечно много
разных гомотопических классов отображений sAn~l—*S2n для всех п^1. Это
систематизируется в понятии инварианта Хопфа, который изучается в §4.В.
Ответ на естественный вопрос, является ли кольцо когомологии
коммутативным, даёт следующее утверждение.
Теорема 3.14. Равенство a w (5 = (—l)w/3 w а выполняется для всех
а^Нк{Ху Л; R) и /ЗеН{{ХуА; Я), если кольцо R коммутативно.
Положив а = /3, получим, в частности, что если а —элемент группы
Нк(Х, A; R), где к нечётно, то 2а2 = 0 в Н2к(Ху A; R). Следовательно, если
H2k(XyA\R) не имеет элементов порядка 2, то а2 =0. Например, если
X — двумерный комплекс, полученный при приклеивании диска к S1 по
отображению степени т, как в примере 3.9, то мы можем сделать вывод,
что квадрат образующей группы Н1^; Ът) равен нулю, если т нечётно,
и равен либо нулю, либо единственному элементу порядка два в группе
И2{Х)Ът) ъЖщ, если т четно. Как было показано ранее, этот квадрат
в действительности отличен от нуля, когда т четно.
Градуированное кольцо, удовлетворяющее свойству
коммутативности из теоремы 3.14, в алгебраической топологии обычно называют
просто коммутативным у несмотря на возможные недоразумения. В старых
книгах и статьях можно найти термины, дающие меньше поводов для
путаницы, например градуированно коммутативное, антикоммутативное
или косокоммутативное кольцо.
Доказательство. Рассмотрим сначала случай А — 0. Для коцепей
ц> eCk(X;R) и я/j е СЧХ; Я) из определения видно, что ^-произведения
с/? kj гр и \j) w у различаются только перестановкой вершин симплекса
Ак+С. Идея доказательства состоит в том, чтобы изучить самую хорошую
перестановку вершин, а именно ту, которая полностью обращает их
порядок, заменяя [v0, ..., vn] на [vn,..., v0]. Она обладает удобным свойством
обращения порядка вершин любой грани.
Для сингулярного n-мерного симплекса a: [v0, ...,v„] —» X пусть а
будет сингулярным n-мерным симплексом, полученным при
композиции а с предшествующим ему линейным гомеоморфизмом симплекса
[v0,..., vj, обращающим порядок вершин. Таким образом, cj(v,) =a(v;j_,).
Эта перестановка вершин в обратном порядке представляет собой
произведение п + (п - 1) + ... + 1 = п(п + 1)/2 транспозиций соседних вершин,
каждая из которых обращает ориентацию n-мерного симплекса, так как
она является симметрией относительно (и — 1)-мерной гиперплоскости.
Поэтому, учитывая ориентацию, следует ожидать, что должен быть
вставлен знак еп = (-i)n(n+^/2. Таким образом, мы определим гомоморфизм
р: С„(Х)->СП(Х) формулой р(а) = епа.
Покажем, что р — цепное отображение, ценно гомотопное
тождественному, а потому оно индуцирует тождественное отображение кого-
§3.2. Умножение в когомологиях
277
мологий. Из этого немедленно следует теорема. Л именно, формулы
(p>wp*^)(a) = ^(efca|[vjt,...,Vo])V4e£or|Ivfc+f.---»vjtl)>
p44^w)((7) = ek^(a\[vk.H,...yvk])y(cr\[vk,...,v0])
показывают, что еке^(р*^ w р*я/0 = ek+(p*(xl) w ^)> так как МЫ
предполагаем, что кольцо R коммутативное. Простое вычисление даёт ek+i =
= (-l.)fcfefc£f, следовательно, р*у> ^p*ip = (-1)нрж0/'^у0- Так как р цеп-
но гомотопно тождественному отображению, при переходе к классам ко-
гомологии р* можно опустить, поэтому мы получаем требуемую формулу
Свойство др = рд цепного отображения можно проверить
вычислением. Для сингулярного п-мерного симплекса сг имеем
др(сг) = fc'„^](-l)lC7|[v„,...,vn4, ...,v0],
i
pfl(or) = p(5](-l)4[vo.-.V(>...,vn]) =
= en_,J](-l)n-ICT|[vn>...>vn..,-, ...,v0],
J
что приводит нас к легко проверяемому тождеству еп = (—l)nf„-i-
Образцом для определения цепной гомотопии между р и
тождественным отображением служит построение призменного оператора Р в
доказательстве того, что гомотопные отображения индуцируют один и тот
же гомоморфизм гомологии в теореме 2.10. Главной частью конструкции
оператора Р было подразделение комплекса Д" х / на (п + 1)-мерные
симплексы с вершинами v, в Д" х {0} и w( в Дм х {1}, причём вершина w{
лежит непосредственно над v,-. Используя то же самое подразделение и
задавая л: Ап х I ^> Ап как проекцию, мы теперь определяем отображение
Р:Сп(Х)^Сп+1(Х) формулой
Р(сг) = ^(-l)4-i(<™)| [v0,..., v,-, w„,..., и/,-],
i
Таким образом, вершины w написаны в обратном порядке, и введён
компенсирующий знак £„_,. Можно рассматривать эту формулу как
происходящую из структуры Д-комплекса на Д" х /, в которой вершины
расположены в порядке v0,..., v„, w„,..., vv0, а не в более естественном порядке
vo>-..,vri,u/0, ...,w„.
Чтобы показать, что дР + Рд = р — 1, мы сначала вычислим дР, опустив
Для краткости сг и an:
dP = 2(-iy(-1Venw[vo,...,v;.,...,vI->Wri,...lwI.] +
278
Глава 3. Когомологии
Члены с j = i в этих двух суммах дают
fn[wn,...,w0]+^]fn_I[v0, ..^V^W,,, ..^И^Ч-
+ J](-l)n+l+1fM_I[v0, ...tvifwn,...,wi+l]-[v0, ...,v„].
В этом выражении две суммы взаимно уничтожаются, так как замена z
на i - 1 во второй сумме приводит к новому знаку (—1)п+,£п_,-+1 = -£n-i-
Оставшиеся два члена £n[wni..., w0] и — [v0, ..., vn] представляют р(а) -а.
Поэтому, чтобы показать, что дР + Рд = р - 1, остаётся проверить, что
в приведённой выше формуле для дР члены с ; Ф i дают -Рд. Вычисляя
Рд непосредственно по определению, получаем
Рд = ^](-l)4-l)JCn-i-i 1>о> •-•> vp wn> •••> %> ..., w(] +
+ ^(-l)'~4-l);en-^vo>->Vy, ...,v,-,wn, ...,wf].
«>j
Так как е„_,- = (—1)п~,еп_,-^1, это завершает проверку того, что дР -\-Рд —
= р — 1, и тем самым теорема доказана в случае А = 0. То же самое
доказательство применимо и в случае Л Ф 0, так как отображения р и Р
переводят цепи в Л в цепи в Л, поэтому двойственные гомоморфизмы р*
и Р* действуют на относительных коцепях. □
Пример 3.15 (внешние алгебры). В общем случае внешняя алгебра
±R[ab а2, ...] над коммутативным кольцом R с единицей —это
свободный R-модуль, базисом которого служат конечные произведения а, ...а,- ,
i1<...<ifc, с ассоциативным и дистрибутивным умножением, которое
определяется правилами a,a; = —a;-a,- при z ^ ; и a^ = 0. Пустое
произведение элементов а{ тоже допускается, и оно равно единичному элементу
1 в dbR[aba2, ...]. Вычисление ^-произведений для n-мерных торов Ти
в примере 3.11 показывает, что И*(Тп; R) — внешняя алгебра ±R [аг,..., ап].
Это верно и вообще для любого произведения нечётномерных сфер
согласно доказанной ниже теореме 3.16 (это можно также вывести,
непосредственно обобщив рассуждения для тора Тп).
Формула Кюннета
Можно догадаться, что должна быть какая-то связь между w-произ-
ведением и произведениями пространств. Это действительно так, что мы
и покажем в этом пункте.
Для начала определим внешнее произведение, или, как его иногда
называют, внешнее ^-произведение. Это отображение
Н*{Х\ R) х H*(Y\ R) -^ Н*{Х х У\ Д),
§3.2. Умножение в когомологиях
279
заданное формулой а х Ь = р{(а) ^ р*2{Ъ), где р} и р2 — проекции
произведения X х Y на X и Y. Так как w-произведение дистрибутивно,
внешнее произведение билинейно, т.е. линейно по каждой переменной по
отдельности. Мы могли бы надеяться, что отображение внешнего
произведения во многих случаях будет изоморфизмом, давая тем самым
хорошее описание колец когомологий произведений пространств. Однако
билинейные отображения редко бывают гомоморфизмами, а потому они
едва ли могут быть изоморфизмами. К счастью, есть хорошее
алгебраическое решение этой проблемы: нужно заменить прямое произведение
H*(X\R)xH*(Y;R) тензорным произведением H*(X;R)®RH*(У;R).
Напомним определение и основные свойства тензорного
произведения. Для абелевых групп Л и В тензорное произведение А ® В
определяется как абелева группа с образующими а ® Ъ для а е А, Ъ е В и
соотношениями (а -Ь а') (8> Ь = а ® Ь -Ь а' ® Ь и а <8> (Ь + Ь') = а <8> Ь 4- а <8> Ь'.
Таким образом, нулевой элемент группы А<8>В — это 0®0 = 0®Ь = а®0,
и - (а (8> Ь) = — а <8> Ь = а (8) (—Ь). Вот некоторые легко проверяемые
элементарные свойства:
1) А®ВъВ®А\
2) (фД-)®В*©(А®В);
3) (Л®В)®С^Л®(В®С);
4) Z®A*M;
5) £п®Д^А/пЛ;
6) пара гомоморфизмов /: Л—»Л' и g:B-► В' индуцирует
гомоморфизм / ® g: А ® В -» Л' ® В' посредством формулы (/ ® g)(a ® Ь) =
= /(a)®g№);
7) билинейное отображение с/?: Л х В -* С индуцирует гомоморфизм
А&В-+С, переводящий a®b в с/?(а, Ь).
В п. 1—5 изоморфизмы очевидные, например, а <&Ъ ^>Ъ ® а в п.1
и n ® a »-> na в 4. Свойства 1, 2, 4 и 5 позволяют вычислить тензорные
произведения конечно порождённых абелевых групп.
Легко строится обобщение тензорного произведения для модулей над
коммутативным кольцом R. Определим А ®н В для R-модулей Л и В как
модуль, получаемый факторизацией модуля А ® В по дополнительным
соотношениям га ® Ъ = а ® rb для г е R, а е Д и b е В. Эти соотношения
гарантируют, что Д®д В снова будет R-модулем. В случае, когда кольцо R
не коммутативное, нужно предполагать, что Л —правый R-модуль, а В —
левый R-модуль, а соотношение нужно записать в виде аг ® Ъ = а ® rb
(в этом случае Л ®R В — это лишь абелева группа, но не всегда R-модуль).
Проверка того, что AxRB = A®B, если R равно Zm или Q, — лёгкое
упражнение по алгебре. Но в общем случае A<8>RB — это не то же самое, что
Л® В. Например, если R = Q(>/2) —двумерное линейное пространство над
Q, то R ®R R = R, но R ® R ~ четырёхмерное линейное пространство над Q.
280
Глава 3. Когомологии
Утверждения 1—3, 6 и 7 остаются верными для тензорных
произведений Я-модулей. Обобщение утверждения 4 —канонический изоморфизм
R<8RA&A, г<8>а—>га.
Свойство 7 тензорных произведений гарантирует, что внешнее
произведение, как оно определено выше, приводит к гомоморфизму
Н*(Х; Я) ®л Н*(У\ Я) ^ Н\Х х У; Я), a <8>Ь -> а х Ь,
который мы также назовём внешним произведением. Это отображение
становится гомоморфизмом колец, если мы определим умножение в
тензорном произведении градуированных колец формулой (а <8> Ъ)(с ® d) =
= (-l)'b"c'ac<8>bd, где \х\ обозначает размерность элемента х. А именно,
отображение внешнего произведения переводит элемент (a <8>b)(c<8>d) =
= (-l)|b!iC'ac<8>bd в элемент
(-l)|b||c|acxbd = (-l)|b||c|p;(awc)wp24bwd) =
- (-l)|b!|c|p^(a)wp;(c)wp^b)wp*(d) -
= p;(a)wp;(b)wp;(c)wp*(d) = (axb)(cxd),
который является произведением образов элементов а <8>Ь и c<8>d.
I Теорема 3.16. Внешнее произведение
I H*(X\R)®RH*(Y;R) ->Н*(ХхУ;Я)
I является изоморфизмом колец, если X и У — CW-комплексы, а Hfc (У; Я) —
I конечно порождённый свободный Я-модуль для всех к.
Результаты такого типа, дающие вычисления гомологии или
когомологии произведения пространств, известны как формулы Кюннета.
Предположение о том, что X и У — CW-комплексы, не является необходимым;
это будет показано в §4.1, когда мы рассмотрим CW-аппроксимации
произвольных пространств. С другой стороны, без предположения о
свободное™ не всегда можно обойтись, как мы увидим в § З.В, когда получим
совсем общую формулу Кюннета для гомологии произведения пространств.
Из теоремы 3.16 следует, что кольцевая структура в Н*(Х х У; Я)
определяется кольцевыми структурами в Н*(Х\ Я) и в Н*(У; Я). Однако,
пример З.Е.6 показывает, что некоторые предположения необходимы для
того, чтобы это было верно.
Прежде чем доказывать теорему, рассмотрим некоторые примеры.
Пример 3.17. Теорема 3.16 утверждает, что Н*(^Р°° х 1P°°;Z2) из°"
морфно Н*№Р°°; Z2) ОНЧ^Р00; Z2) как кольцо. Согласно теореме 3.12 оно
равно Z2[a] <8>Z2[/3], что является просто кольцом многочленов Z2[a, [3].
Вообще мы видим по индукции, что для произведения п экземпляров
пространства ]£Р°° когомологии с коэффициентами в Z2—это кольцо
многочленов от п переменных. Аналогичные замечания относятся также к ко-
гомологиям пространств СР°° и ЕР°° с коэффициентами в произвольном
коммутативном кольце.
§ 3.2. Умножение в когомологиях
281
Пример 3.18. Внешняя алгебра Л/?[а], а2,...] — это градуированное
тензорное произведение над R внешних алгебр от одной переменной
AR[a(], где все а, имеют нечётную размерность. Формула Кюннета
даёт тогда изоморфизм H*(Sk* х ... х Sk"; Z) % Лй[аь ..., ап], если все
размерности к( нечётны. Если некоторые fc, четны, то полнится тензорное
произведение внешней алгебры для нечётномерных сфер и срезанных
колец многочленов Z[a]/(a2) для чётномерных сфер. Конечно, Az[a]
и Z[a]/(a2) изоморфны как кольца, но, когда берутся тензорные
произведения в градуируемом смысле, важно различать их как градуированные
кольца, поскольку элемент а нечётномерный в Az[a] и чётномерный
в Z[a]/(a2). Эти замечания применимы вообще для любого кольца
коэффициентов R вместо Z, но при R = Z2 нет никакой надобности различить
нечётномерный случай и чётномерный, так как знаки тогда становятся
несущественными.
Идея доказательства теоремы состоит в том, чтобы рассмотреть для
фиксированного СН^-комплекса У функторы
ЪЧх,л) = ф(нчхИ;Ю®кНп-ЧУ;Ю);
кп(Х,А) = Нм(ХхУ,ДхУ;Я).
Внешнее произведение, или его относительная версия, определяют
отображение /i: /?П(Х, А) —> fcM(X, А), про которое мы хотим доказать, что оно
является изоморфизмом, когда X— CW-комплекс и А = 0. Мы покажем
следующее:
1) h* и к* — теории когомологий на категории CW-nap;
2) (л является естественным преобразованием: оно коммутирует с
индуцированными гомоморфизмами и с гомоморфизмами кограницы
в длинных точных последовательностях пар.
Очевидно, что отображение /i: hn(X) —>Jc"(X) является изоморфизмом,
когда X—точка, так как в этом случае мы получаем отображение
умножения на скаляр Я ®л Hn(Y\R) —>НП(У; R). Тогда теорема вытекает из
следующего общего факта.
I Предложение 3.19. Если естественное преобразование между непри-
I ведёнными теориями когомологий на категории CW-nap является изо-
I морфизмом для CW-пары вида (точка, 0), то оно является изоморфиз-
I мом для всех CW-iiap.
Доказательство. Пусть ju: ft*(X, A) —> к*(X, А) —естественные
преобразования. Согласно 5-лемме достаточно показать, что (л —
изоморфизм, когда Д = 0.
Сначала мы разберём случай конечномерного X индукцией но
размерности. Индукция начинается со случая, когда X нульмерно и
требуемое утверждение выполняется согласно предположению и аксиоме для
282
Глава 3. Когомологии
несвязных объединений. Чтобы доказать шаг индукции, заметим, что //
задаёт отображение между двумя длинными точными
последовательностями пары (Хп, Х"^1) с коммутативными квадратами, так как \х является
естественным преобразованием. 5-лемма сводит шаг индукции к
доказательству того, что \х является изоморфизмом для (X, Л) = (Х^Х""1).
Пусть Ф: Ц(#а, dD1^) —> (ХП,ХП~[)— набор характеристических отобра-
жений для всех n-мерных клеток комплекса X. Согласно вырезанию Ф* —
изоморфизм для h* и /с*; поэтому в силу естественности достаточно
показать, что \х является изоморфизмом для (X, А) = JJ(D£, д^)- Аксиома
а
для несвязных объединений даёт дальнейшую редукцию к случаю пары
(Dn, <9Dn), а этот случай сразу получается, если применить 5-лемму к
длинным точным последовательностям этой пары, так как диск D" стягиваем,
а потому уже покрыт нульмерным случаем, а комплекс <9D" имеет
размерность (п-1).
Случай, когда комплекс X бесконечномерный, сводится к
конечномерному случаю телескопическим рассуждением, как при доказательстве
леммы 2.34. Мы оставляем это читателю, так как конечномерный случай
вполне достаточен для тех специальных теорий h* и к*у которые мы
рассматриваем, поскольку h'(X,Xn) и к'(Х,Х") равны нулю при n ^i (это
видно, например, из клеточных когомологии). □
Доказательство теоремы 3.16. Остаётся проверить, что h* и к* —
теории когомологии и что \х является естественным преобразованием.
Так как мы имеем дело с неприведёнными теориями когомологии, нужно
проверить четыре аксиомы.
1. Гомотопическая инвариантность: из f^g следует, что /*=g*. Это
очевидно как для 7Г, так и для /с*.
2. Вырезание: h*(X, Л) ^ h*(B,A ПВ) для любых подкомплексов А и В
в CW-комплексе Х = АиВ. Это очевидно, а потому верно и
соответствующее утверждение для к*, так как (А х У) и (В х У) = (А и В) х У
и (AxY)n(BxY) = (AnB)xY.
3. Длинная точная последовательность пары. Это тривиально для /с*,
но нужно сказать несколько пояснительных слов для /i*, где
требуемая точная последовательность строится в два шага. На первом
шаге нужно тензорно умножить длинную точную последовательность
обычных групп когомологии для пары (X, А) на свободный Я-модуль
Hn(Y;R) для фиксированного п. Это снова приводит к точной
последовательности, поскольку Нп (У; R) — прямая сумма нескольких
экземпляров Я, а потому в результате тензорного умножения точной
последовательности на эту прямую сумму просто получается прямая
сумма нескольких экземпляров точной последовательности, что снова
является точной последовательностью. На втором шаге нужно
разрешить п изменяться, взяв прямую сумму построенных ранее точных
§ 3.2. Умножение в когомологиях
283
последовательностей для всех п и при этом сдвинув n-ю точную
последовательностью вверх на п размерностей.
4. Несвязные объединения. Эта аксиома снова очевидным образом
выполняется для /с*, но для h* требуются некоторые рассуждения. Нам
нужен следующий алгебраический факт: имеет место канонический
изоморфизм (П^О ®я N ъ П [Ма ®к N) для К-модулей Ма и ко-
а а
нечно порождённого свободного R-модуля N. Так как /V —прямое
произведение конечного числа экземпляров Rp кольца К, Ма ®я А/ —
прямое произведение соответствующих экземпляров Ма^ = Ма ®д К^
модуля Ма, и требуемое соотношение превращается в соотношение
ПП^а^ПП^а^ которое, очевидно, верно.
Р а ар
Остаётся проверить естественность преобразования ju.
Естественность относительно отображений пространств непосредственно следует
из естественности w-произведений. Естественность относительно
отображений кограницы в длинных точных последовательностях — это
коммутативность квадрата из примера 3.11. □
Следующая теорема Хопфа — хорошее алгебраическое приложение
структуры произведения в H*(RP" x Ш>п\Х2), описываемой формулой
Кюннета.
Теорема 3.20. Если R" имеет структуру алгебры с делением над
полем R, то число п должно быть степенью двойки.
Доказательство. Если задана структура алгебры с делением на RJ\ то
можно рассмотреть отображение g: S""1 x Sn~l -*S"~\ заданное
формулой g(x,y) =xy/\xy\. Это определение корректно, так как нет делителей
нуля, и непрерывно вследствие билинейности умножения. Из
соотношений (-х)у = ~(ху) = х(-у) следует, что g(-x, у) = -g(x, у) = g(x, -у).
Поэтому g индуцирует факторотображение h: RPn-1 x RP17""1 -* MP'1-1.
Мы утверждаем, что h*: НЧЖР""1; Z2) — НЧ^Р"'1 х ЯР""1; Z2) -это
отображение h*(j) = a + /3, где у порождает группу Hl(jRPn'l]Z2)) а
элементы а и 15 индуцируются элементом у при проекциях КР""1 х RP""1
на оба множителя. Это можно доказать следующим образом. Можно
считать, что п > 2, поэтому тг1(КРп"1) ъ Z2. Пусть Я: / -* S^1 —путь,
соединяющий точку л: с диаметрально противоположной ей точкой —лг.
Тогда для фиксированной точки у путь 5 -»g(A(5),y) соединяет gO, у)
с g(-x, у) = — gO, у). Следовательно, при отождествлении диаметрально
противоположных точек отображение h переводит нетривиальную петлю
в первом множителе IRP""1 произведения ЖРп'^ х RP^1 в нетривиальную
петлю в RP""1. Те же самые рассуждения годятся и для второго
множителя, поэтому ограничение отображения h на одномерный остов S1 V S1
гомотопно отображению, которое включает каждое слагаемое S1 букета
S^ v S1 в iRP^1 в качестве одномерного остова. Так как ограничение
284
Глава 3. Когомологии
на одномерный остов является изоморфизмом групп H1(~~]7j2) как для
RPn~\ так и для UPn~l xRPn_1, из этого следует, что h*(y) = a + /3.
Так как у11 = О, мы получаем
О = /Г(Г») = (а + Р)п = ^С*акр
п-к
Это соотношение имеет место в кольце
НЧйР""1 х RP""1; Z2) « Z2[a> j8]/(a", j8"),
поэтому коэффициент С* должен быть нулём в Z2 для всех к в
диапазоне 0 < к < п. В теории чисел известен весьма простой факт, что такое
бывает только тогда, когда п — степень двойки. А именно, очевидным
образом эквивалентное утверждение заключается в том, что в кольце
многочленов Z2[x] равенство (1 + х)п = 1+х" выполняется только тогда,
когда п — степень двойки. Чтобы доказать последнее утверждение,
запишем п как сумму степеней двойки: п = п{ + ... + пк> где пг < ... < пк.
Тогда (1 +х)п = (1 + jf)"1 ...(1 + *)"* = (1 +х",)...(1 +*"*), так как возведение
в квадрат —аддитивный гомоморфизм в случае коэффициентов Z2. При
вычислении произведения (1 +дг",)...(1 +х"к) никакие члены не
объединяются и не уничтожаются, так как n, ^ 2ni..l для всех i, а потому
полученный в результате многочлен имеет 2к членов. Таким образом, если
этот многочлен равен l+x", то обязательно к = 1, а это означает, что п —
степень двойки. □
Иногда бывает важно иметь относительную версию формулы Кюнне-
та в теореме 3.16. Относительное внешнее произведение
/Г(Х, Л; Я) <8>я H*(Y, В; Я) Д Н*(Х х У, Л х У и X х В; Я)
для CW-пар (Х, Л) и (У, В) определяется так же, как и в абсолютном
случае, формулой а х Ь = р^а) ^р^Ь), где р|(а)бН*(Х х У, А х У; Я)
ир*(Ь)(=Н*(ХхУ,ХхВ;Я).
Теорема 3.21. Для CW-nap (X, Л) и (У, В) гомоморфизм внешнего
произведения Н*(Х, Л; Я) ®к Н*(У, В; Я) -> Н*(Х х У, Л х У и X х В; Я)
является изоморфизмом колец, если Н^(У, В; Я)— конечно
порождённый свободный Я-модуль для всех к.
Доказательство. Случай В = 0 был разобран по ходу доказательства
абсолютного случая, поэтому достаточно вывести случай В^0 из случая
В = 0.
Следующая коммутативная диаграмма показывает, что стягивание В
в точку сводит доказательство к случаю, когда В — точка:
Н*(Х, Л) <8>я H4Y, В) ^ Н*(Х, Л) <8>я HM(Y/B9 В/В)
X X
т т
Н*(Х х У, Л х У и X х В) ^— Н*(X х (У/В), Л х (Y/В) U X х (В/В))
§ 3.2. Умножение в когомологиях
285
Нижнее отображение является изоморфизмом, так как факторпростран-
ства (X х У)/(7\ хУиХхВ)и(Хх (У/В))/(Д х (У/В)UX х (В/В))
совпадают.
В случае, когда В —это точка y0^Y', рассмотрим коммутативную
диаграмму
H*{X,A)®RH-(Y,yQ) *H*(X,A)®RW(Y) >H'tX,A)®RH4{yn)
т
Н*(Хху0,Аху0)
т т ,-~-"~— I
Н*(Х х У, X х у0и А х У) ->. Н*(Х х У, X, Л х У) ->• Н*(Х х у() и А х У, Л х У)
Так как у()—ретракт пространства У, верхняя строка этой
диаграммы — расщепимая короткая точная последовательность. Нижняя строка —
длинная точная последовательность тройки, и она также является рас-
щепимой короткой точной последовательностью, так как (X х у0, А х у0)
является ретрактом пары (X х У, Л х У). Среднее и правое отображения
внешнего произведения — изоморфизмы согласно случаю, когда В = 0,
так как Нк (У; Я) — конечно порождённый свободный Я-модуль, если
таковым является Hk{Yy y0; Я). Тогда из 5-леммы следует, что левое
отображение внешнего произведения тоже изоморфизм. □
Относительное внешнее произведение для пар (Х,х0) и (Y,y0) даёт
приведённое внешнее произведение
Н*(Х; R) <8>кН*(У; Я) Д Н*(ХЛ У; Я),
где X Л У — приведённое произведение X х У/(Х х {у()} и {х0} х У). Из
предыдущей теоремы следует, что это приведённое внешнее
произведение—изоморфизм, если хотя бы один из модулей Н*(Х; Я) и H*(Y;R)
является свободным и конечно порождённым в каждой размерности.
Например, мы имеем изоморфизмы Н"(Х; R) ъНп+к(Х ASk; R) посредством
внешнего произведения на образующую модуля Hk(Sk] R) ^Я.
Пространство X Л Sk — приведённая /с-кратная надстройка Т.кХ над X, поэтому мы
видим, что изоморфизмы надстройки Нп(Х\ Я) ъНп+к(Т,кХ; Я), которые
получаются элементарными рассуждениями с точными
последовательностями, можно также получить посредством внешнего произведения на
образующую модуля H*(Sk\ Я).
Пространства с полиномиальными когомологиями
Мы видели в теореме 3.12, что кольца когомологий пространств 1RP00,
СР°° и HP00 являются алгебрами многочленов. Теперь мы опишем
конструкцию, позволяющую расширить S2n до пространства J(S2n), кольцо
когомологий которого H*(J(S2n); Z) —это почти кольцо многочленов Ъ\х\
286
Глава 3. Когомологии
от образующей х размерности 2п. И если мы заменим коэффициенты Z на
Q, то тогда H*(J(S2n)\ Q) — это в точности кольцо многочленов Q[x]. Эта
конструкция, известная под названием приведённого произведения
Джеймса, интересна ещё и из-за её связи с пространствами петель, описанной
b§4.J.
Для пространства X рассмотрим Хк — произведение к экземпляров
пространства X. По несвязному объединению Ц Хк построим фактор-
пространство J(X), отождествив (хъ ...,xh ...,хк) с (xlt ..., xh ...,*fc), если
х, = е — выбранная отмеченная точка пространства X. Таким образом,
точки пространства J(X) можно представлять себе как наборы из к
точек Qq, ...,хк), к ^ 0, причём все х, отличны от е. В J(X) есть
подпространство J,„(X), состоящее из точек (хь ...,хк), к^т. Его можно
рассматривать как факторпространство пространства Хт при
отождествлениях (хъ ...,хье, ...,хт) *~ (хъ ...,е,хь ...,хт). Например, 3Л(Х) = X и
J2(X) = Х х X/U, е) ^ (е,х). Если X — CVV-комплекс, причём отмеченная
точка е является его нульмерной клеткой, то отображение
факторизации Хт —> Jm(X) склеивает т подкомплексов комплекса-произведения
Хт, заданных тем, что одна координата равна е. Эти склеивания
осуществляются гомеоморфизмами, переводящими клетки в клетки, поэтому
Jm(X) наследует CW-структуру из Хт. Имеются естественные включения
Jm(X) с Jm+1(X) в качестве подкомплексов, причём J(X) — объединение
этих подкомплексов, а потому тоже CW-комплекс.
I Предложение 3.22. Пусть п > 0. Тогда W{J(SU)\Z) состоит из Z
I в каждой размерности, кратной п. Если п четно, то i-я степень образую-
I щей группы Hn[j(Sn); Z) равна умноженной на i! образующей группы
I Hin(j(Sn);Z) для любого i^l.
Таким образом, для чётного п H*(J(Sn)\Z) можно отождествить
с подкольцом кольца многочленов Q[x], аддитивно порождённого
мономами xl/i\. Это подкольцо называют алгеброй разделённых степеней и
обозначают Tz[x]. Одна из задач в конце этого параграфа заключается в том,
чтобы показать, что, когда п нечётно, H*(J(Sn);Z) как градуированное
кольцо изоморфно H*(Sn] Z) <8>H*(J(S2"); Z) —тензорному произведению
внешней алгебры и алгебры разделённых степеней.
Доказательство. Если снабдить Sn обычной CW-структурой, то
полученная в результате CW-структура на J(Sn) состоит ровно из одной
клетки в каждой размерности, кратной п. Таким образом, если п > 1, то мы
немедленно выводим из клеточных когомологии, что H*(j(Sn)\ Z)
состоит в точности из групп Z в размерностях, кратных п. Альтернативное
рассуждение, которое работает также в случае, когда п = 1, заключается в
следующем. Рассмотрим отображение факторизации q: (S")'" —> Jm(Sn). Оно
гомеоморфно отображает каждую клетку из (S"),M на клетку из Jm(S")-
В частности, q —клеточное отображение, переводящее fc-мерный остов
§ 3.2. Умножение в когомологиях
287
в fc-мерный остов для каждого /с, поэтому q индуцирует цепное
отображение клеточных цепных комплексов. Это цепное отображение сюръек-
тивно, так как каждая клетка из Jm(Sn) является гомеоморфным образом
клетки из (Sn)m. Следовательно, все клеточные граничные отображения
для Jm (Sn) будут тривиальными, если они тривиальны для (Sn)'n, а это
действительно должно быть верно, чтобы кольцо H*((Sn)m; Z) имело
структуру, указанную в теореме 3.16.
Так как q отображает каждую из т клеток размерности п в (Sn)m
гомеоморфно на п-мерную клетку в J^S"), мы видим из клеточных когомо-
логий, что образующая a eH"(Jm(Sn); Z) переводится отображением q*
в сумму aY 4-... 4- ат образующих группы Нп ((Sn)fn; Z), соответствующих
n-мерным клеткам в (Sn)'". Если п четно, то структура ^-произведения
в H*(J(Sn)\ Z) строго коммутативна и
H*((Sn)m; Z) « Z[ab ..., am]/(a2v ..., a*).
Степень ат тогда отображается в
(а^+... + ат)т = т!^...^,,
где произведение а1.,.ат порождает группу Hmn((Sn)m; Z) ^Z.
Отображение q гомеоморфно отображает mn-мерную клетку в (Sn)m на шп-мерную
клетку в Jm(Sn), поэтому q* — изоморфизм на Нтп. Из этого следует, что
ат — это умноженная на т\ образующая группы H'"n(Jm(Sn); Z). Так как
клетки комплекса J(Sn) - Jm(Sn) имеют размерность по крайней мере
(т4- 1)п, включение Jm(Sn) С J(Sn) индуцирует изоморфизмы на Н1 при
i $ тп. Таким образом, если мы обозначим через х{ образующую группы
Hln[j(Sn); Z), то получим х™ =±m!xm для всех т. Выбирая при
необходимости хт по-другому, можно добиться, чтобы получился знак плюс. □
В Tz[jc] С Q[jc], если мы положим хг ~х1/И> мультипликативная
структура задаётся формулой x^Xj = Cli+.xj+j. Вообще для любого
коммутативного кольца R мы можем определить Гя[х] как свободный R-модуль с
базисом #0 = 1, х1у х2у ... и умножением, заданным формулой XjXj = C]i+.xi+j. Из
предложения 3.22 следует, что H*(J(S2n)\R) ъ rR[x]. Когда R = Q), ясно,
что rQ[jc] — это просто Q[jc]. Однако для R = Zp, где р —простое число,
происходит нечто совсем другое: имеет место изоморфизм
rzJx]*Zp[xbxp,xp2,..J/0t^
как мы покажем в §З.С, где мы увидим также, что алгебры разделённых
степеней в определённом смысле двойственны алгебрам многочленов.
Примеры проективных пространств естественно приводят к
следующему вопросу. Пусть даны кольцо коэффициентов R и целое число
d >0. Существует ли пространство X, для которого Н*(Х; R) ^ R[a],
причём |a| = d? Исторически потребовалось существенное развитие теории,
288
Глава 3. Когомологии
чтобы ответить на этот выглядящий
простым вопрос. Вот таблица,
дающая все возможные значения d для
некоторых из самых очевидных и
важных колец R, а именно Z, Q, Z2 и Zp,
где р — нечётное простое число. Как
мы видели, проективные
пространства дают примеры для Z и Z2. Примеры для Q —это пространства J{Sd)t
а примеры для Zp построены в §3.G. Доказательство того, что никакие
другие значения d не могут встретиться, требует гораздо больше
труда. Тот факт, что число d должно быть чётным, когда R Ф Z2, следует
из свойства коммутативности ^-произведения. В теореме 4.L.9 и в
следствии 4.L.10 мы разберём случай R = Z и покажем, что число d должно
быть степенью двойки для R = Z2 и степенью числа р, умноженной на
чётный делитель числа 2(р - 1), для R = Zp, где р нечётно. Исключить
оставшиеся случаи лучше всего с помощью К -теории, как в [VBKT] или
в классической работе [78]. Однако есть один несколько аномальный
случай, R = Z2, d = 8, который требует специальных рассуждений; см. [131].
Интересно, что для любого чётного d существует СW-комплекс Xih
который является одновременно примером для всех допустимых
коэффициентов R в таблице. Более того, Xd можно выбрать так, чтобы у немо
была самая простая CW-структура, которая совместима с его когомоло-
гиями, а именно, в каждой размерности, кратной d, была
единственная клетка. Р1апример, мы можем взять Х2=СРСС и Х4 = НР°°.
Следующее пространство Х6 должно иметь когомологии /Г(Х6; 7/Jp) ^Zp[a] для
р = 7,13, 19, 31, ..., т.е. для простых чисел вида 35 + 1, поскольку условие
6|2(р — 1) эквивалентно тому, что р — 3.s 4-1. (Согласно известной теореме
Дирихле в любой такой арифметической прогрессии содержится
бесконечно много простых чисел.) Заметим, что в терминах коэффициентов Ъ
пространство Xd должно обладать тем свойством, что для образующей а
группы Hd{Xd\ Z) каждая степень а1 равна образующей группы Hdl(Xd\ Z),
умноженной на целое число ah причём а, ^ 0, если H*(Xd; Q) ^ Q[a],
и а,- взаимно просто с р, если H*(Xd; Zp)^Zp\d\. Конструкция
пространства Xd приведена в [SSAT] и в исходной работе [102].
Можно также поинтересоваться реализацией срезанного кольца
многочленов Я[а]/(ап^), имея в виду примеры, которые дают MP", CP"
и НРП, оставляя в стороне тривиальный случай п = 1, где примеры дают
сферы. Результаты для колец многочленов позволяют также выяснить,
какие срезанные кольца многочленов реализуются; помимо полных колеи
многочленов есть очень мало таких примеров.
Имеется также вопрос о реализации колец многочленов R[au ..., a;I]
с образующими а, заданных размерностей d,. Так как R[ab ..., ат] ®н
®RR\f}u...9f}n] равно R\au ...,aMI,^1, ..., Д,1, произведение двух про-
R
Z
Q
\%2
к,
d 1
2,4 1
любое чётное число
1,2,4
любой чётный делитель числа
2(р-1)
§ 3.2. Умножение в когомологиях
289
странств с полиномиальными когомологиями снова является
пространством с полиномиальными когомологиями, если предположить, что число
полиномиальных образующих конечно в каждой размерности.
Например, п-кратное произведение (СР°°)П имеет когомологии H*((€P°°)n; Z) **
fc*Z[ai,..., a„], где каждая образующая а, двумерна. Аналогично
произведения пространств J(Sd0 реализуют все наборы чётных d{ для
коэффициентов Q.
Однако для коэффициентов Z и Zp произведения примеров с одной
переменной не исчерпывают все возможности. Как мы покажем в §4.D,
имеются ещё следующие три основных примера с коэффициентами Z.
1. Обобщая пространство СР00 комплексных прямых, проходящих через
начало координат в С00, можно определить многообразие Грассмана
Gn(C°°), состоящее из n-мерных векторных подпространств в С00,
и оно имеет когомологии H*(Gn(C°°); Z) *sZ[alt..., a„], где \at\ = 2i.
Это пространство известно также как BU(n), «классифицирующее
пространство» унитарной группы U(n). Оно играет важнейшую роль
в исследовании векторных расслоений и в Х-теории.
2. Заменяя С на Н, можно определить кватернионное многообразие
Грассмана Gn(H°°), известное также как BSp(n), классифицирующее
пространство для симплектической группы Sp(n). Для него //*(Gn(!Hl0C); Z)&
wZCaj,..., an], где |a,| = 4i.
3. Имеются классифицирующие пространства BSU(n) для специальной
унитарной группы SU(n), когомологии которых получаются из
когомологии пространств BU(n) отбрасыванием первой образующей а};
таким образом, H*(BSU(n); Z)*Z[a2, ...,aj> где \a(\ = 2i.
Эти примеры и их произведения составляют все реализуемые
полиномиальные кольца ^-произведения с коэффициентами в Z согласно
теореме, доказанной в [80]. Ситуация для коэффициентов Zp более сложная; её
мы обсудим в § 3.G.
В связи с этим возникает следующий очевидный общий вопрос.
Проблема реализации. Какие градуированно коммутативные
алгебры над R являются алгебрами ^-произведения Н*(Х; R) некоторого
пространства XI
Это трудная проблема, степень трудности которой сильно зависит от
кольца коэффициентов R. Наиболее доступен случай R = Q, где по сути
Дела любая градуированно коммутативная алгебра над Q реализуема, как
показано в [121]. Следующий по трудности случай K = Zp, где р простое.
Этот случай намного сложнее, чем случай кольца Q, и известны лишь
частичные результаты, достигнутые тяжёлым трудом, в основном о
реализации колец многочленов. Наконец, есть случай R = Z, о котором известно
очень мало помимо того, что следует из случая Zp.
Юзак 3655
290
Глава 3. Когомологии
Алгебры многочленов дают примеры свободных градуированно
коммутативных алгебр, где «свободность» означает, грубо говоря, отсутствие
необязательных соотношений. Вообще, свободная градуированно
коммутативная алгебра —это тензорное произведение свободных
градуированно коммутативных алгебр с одной образующей. Последние алгебры —это
либо алгебры многочленов R[a] от образующих а чётной размерности,
либо факторалгебры R[a]/(2a2), где образующая а нечётномерная.
Заметим, что если R —поле, то R[a]/(2a2) является либо внешней алгеброй
AR[a], если характеристика поля R отлична от 2, либо алгеброй
многочленов R[a] в противном случае. Ясно, что любая градуированно
коммутативная алгебра является факторалгеброй свободной алгебры.
Пример 3.23 (подкомплексы n-мерного тора). Чтобы показать лишь
малую часть бесконечного разнообразия несвободных алгебр
^-произведения, которые могут быть реализованы, рассмотрим подкомплексы
n-мерного тора Г" —произведения п экземпляров окружности S1. Здесь
мы снабжаем S1 стандартной минимальной клеточной структурой и
снабжаем Т" получающейся при этом клеточной структурой произведения.
Мы знаем, что Н*(Тп; Z) —внешняя алгебра Лг[аг,..., а„], причём
моном air..aik соответствует посредством клеточных когомологии /с-мер-
ной клетке е? х ... х ej. Поэтому если мы перейдём к подкомплексу
ХсГ, выбросив некоторые клетки, то Н*(Х;%,) — это факторкольцо
кольца Л%[а19..., a,J, которое получается, если считать мономы,
соответствующие выброшенным клеткам, равными нулю. Так как мы имеем
дело с кольцами, мы производим факторизацию по некоторому идеалу
в A^Jctj,..., an], а именно по идеалу, порождённому мономами,
соответствующими «минимальным» выброшенным клеткам, т.е. тем, граница
которых целиком содержится в X. Например, если мы берём в качестве
X подкомплекс в Т3, полученный при выбрасывании клеток е\ х е\ х е^
ие\х е\, то Н*(Х; Z)f*Az[al9a2, a3]/(a2a3).
Сколько имеется разных подкомплексов в Г"? Каждому
подкомплексу X с Тп можно сопоставить конечный симплициальный комплекс Сх
посредством следующей процедуры. Рассмотрим Тп как факторпростран-
ство n-мерного куба /п = [0,1]п с К", полученное при отождествлении
противоположных граней. Если мы пересечём куб Г гиперплоскостью
Xj + ... + хп = е для малого е > 0, то получим симплекс Дп-1. Тогда для
отображения факторизации q: /" —► Тп в качестве Сх мы берём Д"~ П
nq-1(X). Это подкомплекс в Д,,_1, у которого /с-мерные симплексы
соответствуют в точности (/c-f 1)-мерным клеткам комплекса X. Ясно, что
пространство X однозначно определяется симплициальным комплексом
Сх, и легко видеть, что любой подкомплекс в Д'2-1 получается как Сх
для некоторого подкомплекса X в Vх. Так как любой симплициальный
комплекс с п вершинами является подкомплексом в Дп~ г, мы видим, что
Тп имеет весьма много различных подкомплексов при больших п. Кольца
§ 3.2. Умножение в когомологиях
291
когомологий H*(X\Z) принадлежат к типу колец, который был
полностью классифицирован в [100а, теорема 3.1], и из этой классификации
вытекает, что кольцо Н*(Х; Z) (и даже Н*(Х\ Z2)) однозначно определяет
комплекс X, с точностью до перестановки п окружностей в Т\
Несколько более сложные примеры можно получить, рассмотрев
подкомплексы в произведении п экземпляров СР°°. В этом случае кольца
когомологий изоморфны кольцам многочленов по модулю идеалов,
порождённых мономами. Можно было бы также взять подкомплексы в
произведении нескольких S1 и нескольких СР00. Но и это всё ещё намного проще
общего случая, когда берутся свободные алгебры по модулю идеалов,
порождённых произвольными многочленами, все мономы которых имеют
одинаковую размерность.
Завершим этот параграф примером кольца когомологий, которое не
слишком сильно отличается от кольца многочленов.
Пример 3.24 (кольца Коэна—Маколея). Пусть X — факторпростран-
ство СР^/СР"^1. Отображение факторизации СР00 -»X индуцирует инъ-
ективное отображение Н*(Х; Z) -* Н*(СР°°; Z), вкладывающее Н*{Х\Ъ)
в Z[a] в качестве подкольца, порождённого 1, a",a"+1,... Если мы
рассмотрим это подкольцо как модуль над Z[an], то он свободный с
базисом {1, an+1, ап+2,..., а2""1}. Таким образом, Я*(X; Z) — пример
кольца Коэна—Маколея, т. е. кольца, содержащего полиномиальное подкольцо,
над которым оно является конечно порождённым свободным модулем.
В то время как полиномиальные кольца w-произведения весьма редки,
кольца Коэна—Маколея w-произведения встречаются гораздо более часто.
Задачи
1. Предполагая известной структуру w-произведения на торе S1 х S1,
вычислите структуру w-произведения в H*(Mg), где Mg — замкнутая
ориентируемая поверхность рода g, используя отображение факторизации из
Mg в букет g торов, изображённое ниже.
2. Используя w-произведенис
Нк(Х, А\ К) х НЧХ, В; К) — Hk+t(X, AUВ; Я),
«окажите, что если X — объединение стягиваемых открытых
подмножеств А и В, то все w-произведения классов положительной размерности
292
Глава 3. Когомологии
в H*(X;R) нулевые. Это применимо, в частности, когда X — надстройка.
Обобщите это утверждение на случай, когда X — объединение п
стягиваемых открытых подмножеств, показав, что все п-кратные произведения
классов положительной размерности нулевые.
3. а) Используя структуру ^-произведения, докажите, что не
существует отображения Ж?" —>RPm, индуцирующего нетривиальное
отображение Hl(RPm\ Z2) -^H](RPn; Z2), если п>т. Как выглядит
соответствующий результат для отображений СР" —> СРт?
б) Докажите теорему Борсука—Улама следующим образом.
Предположим от противного, что отображение /: S" —>ЕП обладает тем свойством,
что fW^f(-x) для всех х. Тогда зададим отображение g: S" —>Sn-1
формулой
gW = {fix) - f{-x))/\f(x) -/(-дг)|.
Таким образом, g{-x) = -gO), ng индуцирует отображение !RP" —»RP""1.
Покажите, что утверждение а) можно применить к этому отображению.
4. Применяя теорему Лефшеца о неподвижной точке, покажите, что
любое отображение /: СР" —>СР" имеет неподвижную точку, если п
четно, воспользовавшись тем, что /*: H*(CP";Z) —> H¥(CP"; Z)—
гомоморфизм колец. Для нечётного п покажите, что неподвижная точка
существует, если только не выполняется равенство /*(а) = -а, где а — образующая
группы Н2(СР"; Z). [См. задачу 3 в §2.С по поводу примера отображения
без неподвижных точек в этом исключительном случае.]
5. Докажите, что кольцо H*(IRP°°; Z2k) изоморфно кольцу
Z2Ja,/3]/(2a,2/3,a2-fc/3),
где \а\ = 1 и |/3| = 2. [Примените отображение коэффициентов Ъ2к ~* ^2
и доказательство теоремы 3.12.]
6. Применяя ^-произведение, вычислите отображение Н*(СРП; Z) ~*
—>Н*(СР"; Z), индуцированное отображением СР"—>СРП, которое
является факторотображепием для отображения C"+1 —>C"+1, возводящего
каждую координату в степень d, т.е. (z0,..., zn) —> (zjj, ...,z^) для
фиксированного целого числа d > 0. [Сначала разберите случай п = 1.]
7. Применяя ^-произведение, докажите, что пространства !RP и
MP2 V S3 гомотопически не эквивалентны.
8. Пусть X — это СР2 с клеткой е3, приклеенной по отображению S —*
-»СР1 С СР2 степени р, и пусть У = М(Ъру 2) V S4. Таким образом, X и Y
имеют один и тот же трёхмерный остов, но различаются тем, как
приклеены их четырёхмерные клетки. Докажите, что X и У имеют изоморфные
кольца когомологии с коэффициентами в Z, но не с коэффициентами в Ъг
9. Докажите, что если группа Hn(X;Z) свободная для всех п, то
Н*(Х; Zp) и И*(Х; Z) <8>Zp изоморфны как кольца, поэтому, в частности,
кольцевая структура с коэффициентами в Z полностью определяет
кольцевую структуру с коэффициентами в Zp.
§ 3.2. Умножение в когомологиях
293
10. Докажите, что отображение внешнего произведения H*(X;Z)<8>
®H*(Y;Z) -» Н*{Х х У\Ъ) — не изоморфизм, если X и У—бесконечные
дискретные множества. [Это показывает необходимость предположения
о конечной порождённости в теореме 3.16.]
11. С помощью w-произведения докажите, что любое отображение
Sk+i —>Sk x Sc индуцирует тривиальный гомоморфизм
HM(SkH) — Hk+l(Sk xs'), если к > 0 и I > 0.
12. Докажите, что пространства (S1 х CP°°)/(S1 х {х0}) и S3 х СР°°
имеют изоморфные кольца когомологий с коэффициентами в Z и с
любыми другими коэффициентами. [В одной из задач в §4.L требуется
доказать, что эти два пространства гомотопически не эквивалентны.]
13. Опишите Н^ССР^/СР1; Z) как кольцо с конечным набором
мультипликативных образующих. Как это кольцо соотносится с H*(S6 x ЫР°°; Z)?
14. Пусть q: 1RP°° —> СР°° — естественное факторотображение,
полученное при рассмотрении обоих пространств как факторпростраиств
сферы S°° по модулю умножения на действительные скаляры в одном случае
и на комплексные скаляры в другом. Докажите, что индуцированное
отображение q*: H*(CP°°; Z) ->H*(RP°°; Z) сюръективно в чётных
размерностях, показав сначала геометрическим рассуждением, что ограничение
q: MP2—>CPT индуцирует сюръекцию на Н2, а затем воспользовавшись
структурами w-произведения. Далее, рассмотрим факторпространство X
пространства КР°°1_1СРП, полученное при отождествлении каждой
точки хеКР2п с qQc)eCP". Докажите, что существуют изоморфизмы колец
H*(X;Z)^Z[a]/(2an+1) и Н*(Х; Z2) « Z2[a, /3]/(/32 - a2"+1), где |a| = 2
и |/3| = 2n+ 1. Проанализируйте аналогичные конструкции для фактор-
отображения q : СР°° -» НР°°.
15. Для фиксированного поля коэффициентов F определим ряд
Пуанкаре пространства X как формальный степенной ряд p(t) = ^а^1, где а, —
i
размерность Hl (X; F) как линейного пространства над F, предполагая, что
эта размерность конечна для всех i. Докажите, что р{Х х У) ~ р{Х)р{У).
Вычислите ряд Пуанкаре для S", RP", i£P°°, CP", СР°° и пространств
из предыдущих трёх задач.
16. Докажите, что если X и У — конечные CW-комплексы, для
которых группы Н*(Х\ Z) и Я*(Y; Z) не содержат элементов, порядка равному
степени данного простого числа р, то тогда то же самое верно и для X х Y.
[Примените теорему 3.16 с коэффициентами в разных полях.]
17. Докажите, что H*(J(Sn); Z) для нечётного п изоморфно
H4Sn;Z)®H*(J(S2n);Z)
Как градуированное кольцо. [Рассмотрите естественное факторотображе-
-Ние sn х S" х J2fc_i(Sn) -*J2fc+i(s") и примените индукцию по к.)
294
Глава 3. Когомологии
18. Для замкнутой ориентируемой поверхности М рода g ^ 1
покажите, что для любого элемента a^Hl(M\ Z), отличного от нуля, существует
элемент fi ^Hl{M\ Z), для которого а/3 фО. Выведите из этого, что
пространство М гомотопически не эквивалентно букету Xv Y CW-комплек-
сов с нетривиальными приведёнными гомологиями. Сделайте то же самое
для замкнутых неориентируемых поверхностей, используя когомологии
с коэффициентами в Z2.
§ 3.3. Двойственность Пуанкаре
Алгебраическая топология чаще всего занимается теми свойствами
пространств, которые зависят только от гомотопического типа, поэтому
локальные топологические свойства не играют важной роли.
Несколько отступая от такой точки зрения, мы изучаем в этом параграфе класс
пространств, самое важное свойство которых —их локальная топология,
а именно многообразия, т. е. пространства, которые локально гомеоморф-
ны пространству Rn. До некоторой степени удивительно, что одного лишь
этого локального свойства однородности вместе с глобальной
компактностью достаточно, чтобы наложить сильное условие симметрии на
группы гомологии и когомологии этих пространств, а также сильное условие
нетривиальности ^-произведений. Эти условия даёт теорема
двойственности Пуанкаре, одна из самых ранних теорем в этой области. В
действительности исходная работа Пуанкаре о свойстве двойственности
появилась ещё до того, как гомологии и когомологии были должным образом
определены, и потребовалось много лет, чтобы понятия гомологии и
когомологии были достаточно усовершенствованы для того, чтобы поставить
двойственность Пуанкаре на прочную основу
Начнём с некоторых определений. Многообразие размерности п, или
n-мерное многообразие, — это хаусдорфово пространство, в котором
каждая точка имеет открытую окрестность, гомеоморфную R". Размерность
многообразия М внутренним образом характеризуется тем фактом, что
для хеМ локальная группа гомологии Н((М, М - {х}; Z) отлична от нуля
только для i = n:
2Н,.(М, М - {*}; Z) % H,-(R", R" - {0}; Z), по вырезанию,
% //,-_! (Rn - {0}; Z), так как Rn стягиваемо,
* Hf-iCS""1; Z), так как R" - {0} - Sn'\
Компактные многообразия часто называют замкнутыми, чтобы отличить
их от более общих компактных многообразий с краем, которые
рассматриваются далее в этом параграфе. Например, S" — замкнутое
многообразие, как и RPn и линзовые пространства, поскольку S" их накрывает.
Ещё одно замкнутое многообразие — СР". Оно компактно, так как
является факторпространством сферы S2""1"1, а свойство многообразия выпол-
§ 3.3. Двойственность Пуанкаре
295
няется, так как есть открытое покрытие подмножествами, гомеоморф-
ными IR2n, а именно множествами U{ = { [z0,..., zn] е СРП | zt = 1}. То же
самое рассуждение можно применить и для кватернионных проективных
пространств. Другие примеры замкнутых многообразий можно получить,
используя тот очевидный факт, что произведение замкнутых
многообразий размерностей тип является замкнутым многообразием размерности
т + п.
Двойственность Пуанкаре в её самом простом виде утверждает, что
для замкнутого ориентируемого многообразия М размерности п имеют
место изоморфизмы Нк{М\Ъ) fc*H"~*(M;Z) Для всех к. Здесь неявно
используется соглашение, что группы гомологии и когомологий
отрицательной размерности нулевые, таким образом, теорема двойственности
включает тот факт, что все нетривиальные гомологии и когомологий
многообразия М лежат в размерностях от 0 до п. Определение
«ориентируемости» будет приведено ниже. Без предположения об ориентируемости
имеет место более слабое утверждение, что Нк{М\ Z2) ъ*Нп~к(М\ Z2) для
всех к. Как мы покажем в следствиях П.8 и П.9 в приложении, все группы
гомологии замкнутого многообразия конечно порождённые. Поэтому
посредством теоремы об универсальных коэффициентах двойственность
Пуанкаре для замкнутого ориентируемого п-мерного многообразия М
можно сформулировать в терминах одних гомологии: по модулю подгрупп
кручения группы Нк(М\ Т) и Нп_к(М; Z) изоморфны, кроме того,
подгруппы кручения Нк[М\ Z) и Hn_fc_j(M; Z) изоморфны. Однако формулировка
в терминах когомологий более естественна.
Таким образом, двойственность Пуанкаре выражает некоторую
симметрию в гомологиях замкнутых ориентируемых многообразий.
Рассмотрим, например, п-мерный тор Тп —произведение п окружностей.
Индукцией по п из формулы Кюннета (или из её простого частного случая
Ht(X х S1; Z) &Н{(Х; Х)®Н(_г(Х; Z), который был одной из задач в §2.2)
получаем, что группа Нк(Тп\ Z) изоморфна прямой сумме Ск экземпляров
группы Z. Таким образом, двойственность Пуанкаре отражена в
соотношении Ск — С"~к. Читатель может также проверить, что двойственность
Пуанкаре совместима с нашими вычислениями гомологии проективных
пространств и линзовых пространств, все из которых ориентируемы, за
исключением Ж?п с чётным п.
Для многих многообразий есть хорошее геометрическое
доказательство двойственности Пуанкаре, использующее понятие двойственных
клеточных структур. Истоки этой идеи восходят к пяти правильным плато-
новым телам: тетраэдру, кубу, октаэдру, додекаэдру и икосаэдру. У
каждого из этих многогранников есть двойственный многогранник, вершины
которого —центры граней данного многогранника. Таким образом, кубу
двойствен октаэдр, и наоборот. Аналогично додекаэдр и икосаэдр двои-
ственны друг другу, а тетраэдр двойствен самому себе. Можно считать,
296
Глава 3. Когомологии
что каждый из этих многогранников задаёт клеточную структуру С на S2
с двойственной клеточной структурой С*, заданной двойственным
многогранником. Каждая вершина структуры С лежит в двойственной
двумерной клетке структуры С*, каждое ребро в С пересекает двойственное
ребро в С*, а каждая двумерная клетка в С содержит двойственную
вершину в С*. На первом рисунке справа изображён случай куба и октаэдра.
Здесь нет необходимости
ограничиваться правильными
многогранниками, и можно даже рассмотреть
более общую ситуацию, заменив S2
на любую поверхность. Участок
более или менее произвольной пары
двойственных клеточных структур
изображён на втором рисунке. Для
тора, если мы поднимем
двойственную пару клеточных структур в его
универсальное накрытие К2, то
получим двойственную пару
периодических замощений плоскости, как
на следующих трёх рисунках.
Последние два рисунка показывают, что стандартная CW-структура на
поверхности рода g, полученная из 4#-угольника при отождествлении его
сторон посредством произведения коммутаторов [аъ b^]...[agi bg]y гомео-
морфна своей двойственной структуре.
Если задана пара двойственных клеточных структур С и С* на
замкнутой поверхности М, то спаривание клеток с двойственными клетками
даёт отождествление групп клеточных цепей С* = С2, С* = Сх и С* = С0.
Когда мы используем коэффициенты Z, эти отождествления не вполне
канонические, так как имеется неоднозначность в выборе знака для
каждой клетки, соответствующая выбору образующей для
соответствующего слагаемого Z клеточного цепного комплекса. Этой неоднозначности
можно избежать, рассматривая более простой случай коэффициентов Z2,
где отождествления Q^C*^ полностью канонические. Основное
наблюдение теперь состоит в том, что при этих отождествлениях клеточное
граничное отображение д: Ci->Ci_l превращается в клеточное когранич-
ное отображение 5: C*_f—► С*_/+1, так как д сопоставляет клетке
сумму клеток, которые являются её гранями, в то время как 5
сопоставляет клетке сумму клеток, гранью которых она является. Таким
образом, Н((С; Z2) ъН2~((С*; Z2), а потому Н{{№\ Z2) ^H2-l*(M; Z2), так как С
и С* —клеточные структуры на одной и той же поверхности М.
Чтобы перенести это рассуждение на коэффициенты Z, нужно
обратиться к проблеме знаков. Изучив ситуацию более тщательно,
можно убедиться, что если М ориентируемо, то можно последовательно вы-
§ 3.3. Двойственность Пуанкаре
297
брать ориентации всех клеток в С и С* так, чтобы граничные
отображения в С были согласованы с кограничными отображениями в Сж;
поэтому мы получаем изоморфизмы Н((С; Z) ъН2~1(С*; Z), следовательно,
Hf(M;Z)*H2-4M;Z).
Для многообразий более высокой размерности ситуация
совершенно аналогична. Нужно рассмотреть двойственные клеточные структуры
С и С* на замкнутом n-мерном многообразии М, для которых каждая
i-мерная клетка в С двойственна ровно одной (п - f)-мерной клетке
в С*, которая пересекает её в одной точке «трансверсально». Например,
на трёхмерном торе Sl x Sl x S1 можно взять стандартную клеточную
структуру, которая поднимается до разбиения универсального накрытия
Е3 на кубы с вершинами в узлах целочисленной решётки Z3, и тогда
двойственная клеточная структура получается из неё сдвигом на вектор
(1/2,1/2, 1/2). У каждого ребра в любой из этих клеточных структур тогда
есть двойственная двумерная клетка, которую оно пересекает
ортогонально, и каждая вершина лежит в двойственной трёхмерной клетке.
Все многообразия, которые обычно встречаются, например все
дифференцируемые многообразия, имеют двойственные клеточные
структуры, обладающие теми свойствами, которые должны выполняться, чтобы
можно было провести доказательство двойственности Пуанкаре,
набросок которого мы только что сделали. Однако для построения этих
клеточных структур нужно довольно сильно углубиться в теорию многообразий.
Чтобы избежать этого, а заодно и получить теорему, которая относится ко
всем многообразиям, мы применим совсем другой подход, использующий
алгебраическую топологию вместо геометрии двойственных клеточных
структур.
Ориентация и гомологии
Рассмотрим вопрос о том, как можно было бы определить
ориентируемость для многообразий. Прежде всего возникает локальный вопрос:
что такое ориентация пространства R"? Чем бы эта ориентация ни была,
она должна обладать такими свойствами: она сохраняется при поворотах
и обращается при отражениях. Например, в !R2 понятия «по часовой
стрелке» и «против часовой стрелки», конечно, обладают этими свойствами,
так же как и «правая система координат» и «левая система координат»
в R3. Мы примем точку зрения, что эти свойства характеризуют
ориентацию, т.е. всё, что обладает этими свойствами, можно рассматривать как
ориентацию.
Помня об этом, мы предлагаем следующее определение в
алгебраической топологии: ориентация пространства R" в точке х — это выбор
образующей бесконечной циклической группы H„(!Rn,IR" - {*}), где
отсутствие в обозначениях группы коэффициентов означает, что мы берём
коэффициенты в Z. Чтобы проверить, что характеризующие свойства ориен-
298
Глава 3. Когомологии
тации выполняются, мы воспользуемся изоморфизмами Hn(Rn, Rn-{x})^
ъНп_г(Еп -{х}) ъНп_г (S""1), где Sn~l — сфера с центром в точке х. Так как
эти изоморфизмы естественные, а повороты сферы S"~l имеют степень 1,
поскольку они гомотопны тождественному отображению, в то время как
отражения имеют степень — 1, мы видим, что поворот р пространства
Rn, оставляющий неподвижной точку х, переводит образующую а группы
HnCRn, Rn - {х}) в себя, т. е. рЛа) = а, в то время как отражение
переводит а в —а.
Заметим, что при таком определении ориентация Еп в точке х задаёт
ориентацию в любой другой точке у посредством канонических
изоморфизмов
НП(ЗГ, Еп - {х}) w Hn(iRn, R" -В) * НП(ЕП, Rn - {у}),
где Б —любой шар, содержащий обе точки х и у.
Преимущество такого определения локальной ориентации состоит
в том, что его можно применить к любому п-мерному многообразию М:
локальная ориентация многообразия М в точке х — это выбор
образующей цх бесконечной циклической группы Нп(М9 М — {х}).
Соглашение об обозначениях. В дальнейшем нам придётся очень
часто рассматривать группы гомологии вида Нп(Х, Х- А). Чтобы
упростить обозначения, мы будем записывать группуНп(Х, X — А) как Нп(Х\ А)
или Нп(Х\А\ G), если нужно указать группу коэффициентов G. Согласно
вырезанию группа Ни(Х\А) зависит только от окрестности замыкания
множества А в X, поэтому имеет смысл рассматривать Нп(Х\А) как
локальные гомологии X в А.
Установив, что такое локальные ориентации в точках многообразия,
глобальную ориентацию следует определить как «согласованный выбор
локальных ориентации во всех точках». Мы придадим этому точный
смысл следующим определением. Ориентация п-мерного многообразия
М —это функция х—►jtijr, сопоставляющая каждой точке хеМ локальную
ориентацию {лх € Нп(М|х), которая удовлетворяет условию «локальной
согласованности», что у каждой точки хеМ есть окрестность Rn сМ,
содержащая такой открытый шар В конечного радиуса с центром х, что все
локальные ориентации \iy в точках у е В являются образами одной
образующей juB группы Нп(М\В)ъНп(Шп\В) при естественных отображениях
Нп(М\В) —>Н„(М|у). Если для многообразия М существует ориентация,
то М называют ориентируемым.
У каждого многообразия М есть ориентируемое двулистное
накрывающее пространство М. Например, ЕР2 накрывается сферой S2, а для
бутылки Клейна двулистным накрывающим пространством является тор.
Общая конструкция устроена следующим образом. Определим множество
М = {tix | х е М, a jUjj. — это локальная ориентация для М в точке х }.
§ 3.3. Двойственность Пуанкаре
299
Отображение цх —> х определяет сюръекцию М —>М, переводящую две
точки в одну, и мы хотим ввести топологию на М так, чтобы это
отображение было проекцией накрывающего пространства. Пусть дан
открытый шар BcRn CM конечного радиуса и дана образующая дйе НП(М| В).
Определим U((jlb) как множество всех таких ц,х е М, что х е В и /^ является
образом цв при естественном отображении НП(М|В) —>Нп(М|х). Легко
проверить, что эти множества U(jjlb) образуют базу топологии на М и что
проекция М—*М является накрытием. Многообразие М ориентируемо,
так как каждая точка ^gM имеет каноническую локальную ориентацию,
заданную элементом ц>х е НГ1(М| /1Х), соответствующим ц,х при
изоморфизмах НпШ\Ц>х)ъHU(U(fJiH)\ fj,x)ъНп(В\х), а по построению эти локальные
ориентации удовлетворяют условию локальной согласованности, которое
необходимо для того, чтобы определить глобальную ориентацию.
I Предложение 3.25. Если М связно, то М ориентируемо тогда и толь-
I ко тогда, когда М имеет две компоненты. В частности, М ориентируемо,
I если оно односвязно или, вообще, если в группе пл(М) нет подгрупп
I индекса два.
Первое утверждение — это формулировка интуитивного понятия
неориентируемости как возможности обойти вдоль некоторого замкнутого
контура и вернуться назад с противоположной ориентацией, так как в
терминах накрывающего пространства М —*М этот обход соответствует
петле в М, которая поднимается до пути в М, соединяющего две разные точки
с одним и тем же образом в М. Существование таких путей эквивалентно
связности пространства М.
Доказательство. Если М связно, то М имеет либо одну, либо две
компоненты связности, так как оно является двулистным накрывающим
пространством над М. Если оно имеет две компоненты, то каждая из
них отображается гомеоморфно на М при накрывающей проекции, таким
образом, М ориентируемо, поскольку оно гомеоморфно компоненте
связности ориентируемого многообразия М. Наоборот, если М ориентируемо,
то оно имеет ровно две ориентации, так как оно связно, и каждая из
этих ориентации определяет одну компоненту многообразия М.
Последнее утверждение предложения следует из того, что двулистные накрытия
пространства М соответствуют подгруппам индекса два в пл (М) согласно
классификации накрытий. □
Накрывающее пространство М —> М можно вложить в большее
накрывающее пространство Mz —* М, где Mz состоит из всех элементов
ах еНп(М|х), где точка х пробегает М. Как и раньше, мы вводим
топологию на Mz посредством базы из множеств U(aB), состоящих из
элементов аХУ где х еВ и ах — образ элемента авеН„(М|В) при отображении
Нп(М|В)->Нп(М|х). Накрытие МЪ->М бесконечнолистное, так как для
фиксированного х е М элемент ах пробегает бесконечную циклическую
300
Глава 3. Когомологии
группу Нп(М\х). Накладывая условие, что ах равно нулю, мы
получаем экземпляр М0 многообразия М в Мъ. Оставшаяся часть Mz состоит
из бесконечной последовательности экземпляров Мк многообразия М,
к = 1, 2, ..., где Мк состоит из тех элементов ах, которые равны любой из
образующих группы Н„(М|х), умноженной на к.
Непрерывное отображение М —► Мх вида х —> ах е Нп (М| х) называют
сечением накрытия. Ориентация многообразия М —это то же самое, что
такое сечение х—► (лх, что цх является образующей группы Нп(М\х) для
всех х.
Можно обобщить определение ориентации, заменив группу
коэффициентов Z на любое коммутативное кольцо Я с единицей. Тогда Я-
ориентация многообразия М сопоставляет каждой точке х е М
образующую группы Нп(М|х;Я)«Я, удовлетворяющую соответствующему
условию локальной согласованности, где «образующая» кольца Я —это
такой элемент и, что Ru = R. Так как мы предполагаем, что в R есть
единичный элемент, это эквивалентно тому, что и является единицей, т. е.
обратимым элементом кольца R. Определение накрывающего
пространства Mz немедленно обобщается до накрытия MR —>М, и Я-ориентация—
это сечение этого накрытия, значение которого в каждой точке х е М —
образующая группы Нп(М|х; Я).
Легко описать строение пространства MR. Ввиду канонического
изоморфизма
Нп(М|х;Я) *НП(М|*)®Я
каждый элемент reR определяет накрывающее подпространство МгвМк,
состоящее из точек ±цх ® г е Нп(М|х; Я), где цх — образующая группы
Нп(М\х). Если г имеет порядок 2 в Я, то г = -г, поэтому Мг — это просто
копия многообразия М, а в противном случае Мг изоморфно
двулистному накрытию М. Накрывающее пространство MR —объединение этих
пространств Мг, причём они не пересекаются, если не считать равенства
В частности, мы видим, что ориентируемое многообразие Я-ориенти-
руемо для всех Я, в то время как неориентируемое многообразие Я-ори-
ентируемо тогда и только тогда, когда Я содержит единицу порядка 2, что
эквивалентно равенству 2 = 0 в кольце Я. Таким образом, любое
многообразие Z2-opHeHTHpyeMo. На практике это означает, что два наиболее
важных случая — это Я = йиЯ = й2.В дальнейшем читателю следует помнить
прежде всего об этих двух случаях, но мы обычно будем формулировать
результаты для произвольного Я.
Ориентируемость замкнутого многообразия отражается в строении
его гомологии согласно следующему результату.
Теорема 3.26. Пусть М — замкнутое связное многообразие
размерности п. Тогда
§ 3.3. Двойственность Пуанкаре
301
I а) если М является R-ориентируемым, то отображение Нп(М',Ю—>
I —> Нп (М | х; R) ъ R — изоморфизм для всех х € М;
I б) если М не является R-ориентируемым, то отображение Нп (М; R) —>
I —>Hn(M|x; R)&R инъективно, причём его образ равен {r€R|2r =
I = 0} для всех х€М;
I в) Н{(М\ Ю = 0 при i> п.
В частности, группа Нп(М\ Z) равна Z или 0 в зависимости от того,
является М ориентируемым или нет, и в любом случае Нп{М\ Z2) = Z2.
Элемент группы Нп (M',R), образ которого в Нп (М| х; R) — образующая
для всехх, называют фундаментальным классом для М с коэффициентами
в R. Согласно теореме 3.26 фундаментальный класс существует, если М
замкнуто и R-ориентируемо. Покажем, что обратное утверждение тоже
верно. Пусть ju€Hn(M; R) — фундаментальный класс. Обозначим через \хх
его образ в Нп (М | х; R). Тогда функция х —► /^ является R-ориентацией, так
как отображение Нп{М\ R) —>Hn(M|x; R) пропускается сквозь НМ(М| В; R),
где В — произвольный открытый шар в М, содержащий х. Кроме того,
М должно быть компактным, так как \хх может быть отличным от нуля
только для точек х, лежащих в образе цикла, представляющего класс ju,
а этот образ компактен. Эти замечания показывают, что
фундаментальный класс можно было бы также назвать классом ориентации для
многообразия М.
Теорема легко вытекает из следующего более технического
утверждения.
I Лемма 3.27. Пусть М — многообразие размерности п, и пусть ЛсМ-
I компактное подмножество. Тогда
I а) если х »-» ах — сечение накрытия MR-^>M, то существует един-
I ственный класс аА€Нп(М| Л; R), образ которого в Hn(M|x; R) ра-
I вен ах для всех х€ А\
I б) Hi(M\A\R) = 0npni>n.
Чтобы вывести теорему из этой леммы, положим А = М, что
является компактным множеством по предположению. Утверждение в)
теоремы непосредственно следует из утверждения б) леммы. Чтобы
получить утверждения а) и б) теоремы, рассмотрим ГК(М) —множество
сечений накрытия MR —> М. Сумма двух сечений является сечением,
и скалярное кратное сечения тоже является сечением, поэтому ГК(М) —
это R-модуль. Существует гомоморфизм Нп(М\ Ю —> ГК(М), переводящий
класс а в сечение х »-» ах, где ax —образ класса а при отображении
Hn(M; R) —>Hn(M|x; R). Согласно утверждению а) леммы этот
гомоморфизм—изоморфизм. Если М связно, то любое сечение единственным
образом определяется его значением в одной точке, поэтому утверждения
а) и б) теоремы очевидно следуют из строения пространства MR, которое
мы обсудили ранее.
302
Глава 3. Когомологии
Доказательство леммы 3.27. Кольцо коэффициентов R не будет
играть никакой особой роли в рассуждениях, поэтому мы опустим его в
обозначениях. Доказательство разбивается на четыре шага.
1. Прежде всего заметим, что если лемма верна для компактных
множеств А, В и А П В, то она верна для AU В. Чтобы увидеть это, рассмотрим
последовательность Майера—Вьеториса
о-+нпш\лив) 1+нпш\А)®н„ш\в) ^>нп(м\Апв).
Здесь нуль слева возникает из предположения, что Нп+г (М| А п В) = 0.
Отображение Ф задаётся формулой Ф(а) = (а, -а), а Ф — формулой Ф(а, (3) =
= а + /3, где мы опускаем обозначения для отображений гомологии,
индуцированных включением. Члены Н,(М| AUB) ещё дальше слева в этой
последовательности зажаты между группами, которые являются
нулевыми по предположению, таким образом, Н,(М| A U В) = 0 при i > п. Это
доказывает утверждение б). Докажем существование в утверждении а).
Если х —» ах — сечение, то по предположению мы имеем единственные
классы
аА€Н,?(М|А), ав€Нп(М\В) и аАпВ € НП(М| An В),
имеющие образ а^ для всех х в А, В или А П В соответственно. Образы
элементов аА и ав в НП(М|АПВ) удовлетворяют свойству,
определяющему элемент алпНу следовательно они должны быть равны аАпв. Тогда
точность последовательности влечёт, что (аА, —аи) = Ф(аАив) для
некоторого аАиВ €Н„(М| A UВ). Это означает, что аАиВ отображается в аА и в а/3,
поэтому образ элемента аАиВ равен ах для всех jc€AUB, так как аА и ав
обладают этим свойством. Чтобы проверить, что элемент аАиВ единствен,
заметим, что если класс a€Hn(M|AUB) имеет нулевой образ в Нп(М\х)
для всех x€AUB, то его образы в НП(М|А) и Нп(М|В) тоже обладают
этим свойством, а потому равны нулю по предположению, поэтому и сам
элемент а должен быть нулевым, так как Ф ииъективно. Единственность
элемента аАив получается, если применить это наблюдение к разности
двух элементов, выбранных в качестве аАин.
2. Сведём всё к случаю М = Rn. Компактное множество А С М можно
представить в виде объединения конечного числа компактных множеств
А!,..., Аш, каждое из которых содержится в открытом множестве R"cM.
Мы применяем результат пЛк множествам А{ U ... U Ат_х и Ат.
Пересечение этих двух множеств —это (Аг П Аш) U ...U (Аш_! П Аш), объединение
т — 1 компактных множеств, каждое из которых содержится в открытом
множестве М"СМ. Индукция по т позволяет свести ситуацию к случаю
т = 1. При т = 1 вырезание позволяет заменить М на окрестность Жп СМ.
3. Если M = Rn и А — объединение выпуклых компактных множеств
Аъ ..., А,п, то такое же рассуждение по индукции, как и в п. 2 позволяет
свести всё к случаю, когда само множество А выпуклое. Если множество
§ 3.3. Двойственность Пуанкаре
303
А выпуклое, то требуемое утверждение очевидно, так как отображение
H,(IRn|i4) ~>H,(RM|x) является изоморфизмом для любой точки хеА,
поскольку оба множества Ж1 —А и R11 - {х} деформационно ретрагируются
на сферу с центром в точке х.
4. Для произвольного компактного множества А с IR" пусть класс
aGHf(lR"|i4) представлен относительным циклом z, и пусть С с Rn —A —
объединение образов сингулярных симплексов из dz. Так как множество
С компактное, оно находится на положительном расстоянии 5 от А. Мы
можем покрыть А конечным числом замкнутых шаров радиуса
меньше 5 с центрами в точках множества А. Пусть К — объединение этих
шаров; тогда К не пересекается с С. Относительный цикл z определяет
элемент ак е/7,-(!&")/(), отображающийся в данный элемент aeH,(Rn| А).
Если i > п, то согласно п.З мы получаем H,-(R"|/C) =0, поэтому ак = 0,
а из этого следует, что а = 0 и, таким образом, /7,(1£П|Д) = 0. Если i = n
и ах = 0 в H„(!R"|x) для всех х е А, то в действительности это
выполняется для всех х е /С, где под ах в этом случае подразумевается образ
элемента ак. Дело в том, что К — объединение шаров В, пересекающих А,
и Нп(Жп\В) —>Нп(Ж'1\х) — изоморфизм для всех xGB. Так как ах = 0 для
всех х е К, шаг 3 тогда даёт, что элемент ак равен нулю, а потому
элемент а тоже равен нулю. Это завершает доказательство единственности
в утверждении а). Существование доказывается легко, так как мы можем
считать, что аА — образ элемента ав, соответствующего произвольному
шару В э Л. □
Для замкнутого п-мерного многообразия, обладающего структурой
А-комплекса, есть более явная конструкция фундаментального класса.
Рассмотрим случай коэффициентов Z. В симплициальных гомологиях
фундаментальный класс должен быть представлен некоторой линейной
комбинацией ^fc^cr,- симплексов сг,- размерности п комплекса М. Усло-
вие, что фундаментальный класс отображается на образующую группы
Яп (М| х; Z) для точек х внутри симплексов сг,-, означает, что каждый
коэффициент /с, должен быть равен ±1. Кроме того, коэффициенты /с, должны
быть такими, что 5]к,-сг,- является циклом. Из этого следует, что если ст,
i
и <jj имеют общую (п - 1)-мерную грань, то /с, определяет /с; и наоборот.
Изучив это более внимательно, можно показать, что выбор знаков для /с,,
при котором XI k,°",- становится циклом, возможен тогда и только тогда,
когда многообразие М ориентируемо, и если такой выбор возможен, то
цикл Y^kiCTj задаёт фундаментальный класс. Для коэффициентов Ъг нет
проблемы знаков и £] 0\ всегда определяет фундаментальный класс.
Из предыдущей теоремы также можно получить некоторую
информацию о Нп._!(М).
304
Глава 3. Когомологии
I Следствие 3.28. Пусть М —связное замкнутое n-мерное
многообразие. Тогда подгруппа кручения в Hn^i(M\ Z) тривиальна, если М
ориентируемо, и равна Z2, если М неориентируемо.
Доказательство. Это утверждение получается применением
теоремы об универсальных коэффициентах для гомологии с использованием
того факта, что группы гомологии многообразия М конечно порождённые
согласно следствиям П.8 и П.9 в приложении. В ориентируемом случае,
если бы группа Hj^y^M; Z) содержала элементы кручения, то для некоторого
простого р группа Нп(М\ Zp) была бы больше группы Zp, получающейся
из H„(M;Z). В неориентируемом случае группа Hn(M;Z,„) равна Z2 или
0 в зависимости от того, четно m или нечётно. Это заставляет подгруппу
кручения в Hn_l{M] Z) быть равной Z2. D
Читатель, знакомый с гомоморфизмом Бокштейна, который
обсуждается в §З.Е, поймёт, что подгруппа Z2 в H„_!(M;Z) в неориентируемом
случае — это образ гомоморфизма Бокштейна
Нп{М'/£2)-^Нп_у{М'Ъ)у
возникающего из короткой точной последовательности групп
коэффициентов 0-> Z-> Z-> Z2-»0.
Структуру групп Hn[M\G) и Hn_i(M',G) для замкнутого п-мерного
многообразия М легко объяснить в терминах клеточных гомологии в
случае, когда М обладает структурой CW-комплекса с единственной п-мер-
ной клеткой, что имеет место для очень многих многообразий. Заметим,
что не может быть клеток более высокой размерности, так как клетка
максимальной размерности даёт нетривиальные локальные гомологии
в соответствующей размерности. Рассмотрим клеточное граничное
отображение d: Сп(М) —» Сп_х(М) с коэффициентами в Z. Так как у М есть
только одна п-мерная клетка, мы получаем C„(M) = Z. Если М
ориентируемо, отображение d должен быть нулевым, так как Нп{М\ Z) =Z. Тогда,
так как отображение d нулевое, группа Hn-i(M;Z) должна быть
свободной. С другой стороны, если М неориентируемо, то d должно
переводить образующую группы Сп(М) в удвоенную образующую а слагаемого Z
в Сп__] (М), чтобы группа Ип{М\ Zp) была нулевой для нечётных простых р
и была равна Z2 для р = 2. Клеточная цепь а должна быть циклом, так как
2а —граница, а потому —цикл. Из этого следует, что подгруппа кручения
в Нп_{(М; Z) должна быть группой Z2, порождённой элементом а.
Имеется следующее общее утверждение о гомологиях некомпактных
многообразий.
Предложение 3.29. Если М —связное некомпактное п-мерное
многообразие, то Н, (М; R) = 0 при i ^ п.
Доказательство. Представим элемент группы Н{(М\ R) циклом z. Его
образ в М компактен, поэтому существует открытое множество U с М,
§ 3.3. Двойственность Пуанкаре 305
содержащее образ цикла z и имеющее компактное замыкание 0 с М.
Положим V — М — П. Часть длинной точной последовательности тройки
(М, U U V, V) можно вставить в коммугативную диаграмму
Н^СМ, UU V; R) -*- HfCUU V, V; R) ^ 7/,(М, V; R)
Если i > п, то две группы по обе стороны от H,(L7 U V, V; Я) нулевые
согласно лемме 3.27, так как U и V и V—дополнения компактных
множеств в М. Следовательно, H,-(lf; R) — 0, таким образом, z — граница в U,
а поэтому и в М, и мы получаем, что И{{М\ Я) = 0.
Если i = п, то класс [z] sHn(M\R) задаёт сечение х —► [г]д.
накрытия MR. Так как М связно, это сечение полностью определяется значением
в одной точке, поэтому класс [z]x будет нулевым для всех х, если он будет
нулевым для некоторого х, а это должно быть так, поскольку z имеет
компактный образ, а М некомпактно. Согласно лемме 3.27 цикл z тогда
представляет нуль в Нп(М, V; R), а потому и в HM(lf; R), поскольку первый
член в верхней строке указанной выше диаграммы нулевой при i = п,
снова согласно лемме 3.27. Поэтому \z] = 0 в группе Нп(М\ К), а значит,
Нп{М\ R) = 0, так как [z] был произвольным элементом этой группы. D
Теорема двойственности
Версия двойственности Пуанкаре, которую мы докажем, угверждает,
что для R-ориентируемого замкнутого n-мерного многообразия
некоторое естественным образом определённое отображение
Hk(M]R)^H,^k(M\R)
является изоморфизмом. Определение этого отображения будет дано
в терминах более общей конструкции, называемой ^-произведением,
которая тесно связана с ^-произведением.
Для произвольного пространства X и кольца коэффициентов R
определим R-билинейное /^-произведение
rs: Q(X; R) x С((Х; R) — Cfc_f (X; R)
при k^t, положив
а^у = Y?H[v0, ...,v^)ct|[v£,...,vJ
для <т: Ак —>Х и (реСс(Х) R). Чтобы доказать, что оно индуцирует
^-произведение в гомологиях и когомологиях, мы воспользуемся формулой
д(сг r\{p) = (—lYidcrr^ip —су г^8 с/?),
306
Глава 3. Когомологии
которая проверяется вычислением:
е
дсг^ч> = ]T(--1)V(>| [v0, ...,vh ..., v/+1])a| [vM,..., vk] +
к
сгг,5ч> = ]T(-1)VM [v0, ..., v;-, ..., vm])cr| [v,+1, ..., vj;
/ = o
к
d(ar^y) = ^(-iy~lv(a\[v0, ...,v(])a\[vt, ...9vh ...,vk].
i=(
Из соотношения д(а r\ с/?) = ±(Эсг o,^ — <j^5(/?) следует, что
^-произведение цикла а и коцикла кр является циклом. Далее, если да = О, то
Э(сггм/?) = ±(сго>5у0, таким образом, ^-произведение цикла и
кограницы является границей. А если 5с/? = 0, то д(а ^ </?) = ±(Эа о» </?), таким
образом, ^-произведение границы и коцикла является границей. Из этих
фактов следует, что определено индуцированное ^-произведение
Нк(Х; Я) х НС(Х; Я) ^ Н^(Х; Я),
которое Я-линейно по каждой переменной.
Используя те же самые формулы, можно проверить, что у
^-произведения есть относительные версии
Нк(Х, A; Я) х Нс(X; Я) -^ Я^_ДХ, А\ Я);
Н*(Х, Л; Я) х Н£(Х, Л; Я) -^ Hfc_£(X; Я).
Например, во втором случае ограничение ^-произведения Ck(X;R) x
х С£(Х; Я) -> Q_£(X; Я) на подмодуль Q(A; Я) х С^Х, Л; Я) нулевое,
таким образом определено индуцированное ^-произведение Q(X, Л; Я) х
х сЧх, Л; Я) —* С^_ДХ; Я). Формула для д(сг г\ (/?) по-прежнему
выполняется, поэтому можно перейти к группам гомологии и когомологии. Есть
также более общее относительное ^-произведение
Нк(Х, ЛUВ; Я) х ЯЧХ, Л; Я) -^ Н*_ДХ, В; Я),
которое определяется, когда А и В — открытые множества в X, с помощью
того факта, что Hk(X,A\JB;R) можно вычислить, используя группы
цепей С„(Х,Л + В; Я) =СП(Х;Я)/СП(Л + В;Я), как в выводе относительной
последовательности Майера—Вьеториса в § 2.2.
Отметим, что ^-произведение обладает свойством естественности,
которое формулируется немного сложнее, чем соответствующий
результат для ^-произведения, потому что в нём участвуют как ковариантный,
так и контравариантный функтор. Для данного отображения /: X —» Y со-
§ 3.3. Двойственность Пуанкаре
307
ответствующие индуцированные отображения гомологии и когомологий
включаются в диаграмму
Xk(X)xHc(X)^^Hk_t(X)
!'• V !'•
Xk(Y)xHl(Y)-^Hk_((Y)
Не вполне уместно говорить, что эта диаграмма коммутативная, но
подобие коммутативности содержится в формуле
которая получается при подстановке fa вместо а в определение
^-произведения: fa^ip = [p[f<j\ [v0,..., V{]) fa\ [vh ..., vk]. Имеются также
очевидные относительные версии свойства естественности.
Теперь мы можем сформулировать двойственность Пуанкаре для
замкнутых многообразий.
Теорема 3.30 (двойственность Пуанкаре). Если М — замкнутое R-ори-
ентируемое n-мерное многообразие с фундаментальным классом [М] е
еНиШ',Ю, то отображение D: Нк(М',Ю ->Нп_к(М)Ю, заданное
формулой D(a) = [М] г\а, является изоморфизмом для всех к.
Напомним, что фундаментальный класс для М — это элемент
группы Нп(М; R), образ которого в Нп(М|х; R) является образующей для всех
хеМ. Существование такого класса доказано в теореме 3.26.
Пример 3.31 (поверхности). Пусть М — замкнутая ориентируемая
поверхность рода g, полученная, как обычно, из 4£-угольника
отождествлением пар сторон в соответствии со словом a 1b1a^1b~1...agbga"1b~1.
Структура Л-комплекса на М получается, если взять конусы над сторонами
4g-yranbHHKa с вершиной в его центре, как
показано на рисунке в случае g = 2. Можно
вычислить ^-произведения, используя сим-
плициальные гомологии и когомологий, так
как ^-произведения определены для симпли-
циальных гомологии и когомологий той же о.
самой формулой, что и для сингулярных
гомологии и когомологий, поэтому
изоморфизм между симплициальной и сингулярной
теориями уважает гл-произведения.
Фундаментальный класс [М], порождающий
группу Н2Ш)> представлен двумерным циклом, образованным суммой всех
4g двумерных симплексов с указанными знаками. Рёбра а, и Ь,
образуют базис группы Н](М). При изоморфизме Н[(М) ^Hom(Hx(M), Ъ) класс
когомологий а,, соответствующий ребру а,, принимает значение 1 на а,
и 0 на остальных элементах базиса. Этот класс а, представлен коцик-
308
Глава 3. Когомологии
лом (j)h принимающим значение 1 на одномерных симплексах,
пересекающих дугу, помеченную а, на рисунке, и 0 на остальных одномерных
симплексах. Аналогично мы получаем класс Д, соответствующий ребру bh
представленный коциклом xph принимающим значение 1 на одномерных
симплексах, пересекающих дугу Д, и 0 на остальных одномерных
симплексах. Применяя определение ^-произведения, получаем [М] rs^z-= fc>(.
и [М] r\ i/;,- = ~ah так как в обоих случаях есть ровно один двумерный
симплекс [v0, v}, v2], для которого </>,- или ipi отличны от нуля на ребре [v0, vj.
Таким образом, класс Ъ{ двойствен по Пуанкаре к а,-, а -а, двойствен по
Пуанкаре к Д. Если мы интерпретируем двойственность Пуанкаре
полностью в терминах гомологии, отождествляя класс а, с его двойственным
относительно Нот классом а,, а Д — с Ь,, то классы а, и Ь, двойственны по
Пуанкаре друг другу, по крайней мере с точностью до знака.
Геометрически двойственность Пуанкаре отражается в том факте, что петли а, и Ь,
гомотопны, так же как и петли Д и az.
Замкнутую неориентируемую поверхность N рода g можно разобрать
таким же способом, если мы используем коэффициенты Z2. Будем считать,
что поверхность N получена из 2g-yronbHHKa отождествлением
последовательных пар сторон в соответствии со
словом а?...а^. У нас есть классы с^-еЯ1^;^?)» ^ Д к
представленные коциклами </>,, принимающи- / \' «з / tv 2
ми значение 1 на рёбрах, пересекающих ду- / \ / ' \
гу а,. Тогда [N] ^ </>,- = а,, таким образом, а,
двойствен по Пуанкаре классу а,. В терминах а4
гомологии класс а^ двойствен относительно
Нот классу ah таким образом, он двойствен
по Пуанкаре сам себе. Геометрически петля a^\j ' \/ 1
а, на поверхности N гомотопна двойственной а,
по Пуанкаре петле а,.
Наше доказательство двойственности Пуанкаре, как и построение
фундаментального класса, будет проведено по индукции, с помощью
последовательности Майера—Вьеториса. Для шага индукции понадобится
версия двойственности Пуанкаре для открытых подмножеств в М,
которые являются некомпактными и могут удовлетворять двойственности
Пуанкаре лишь в том случае, когда используется другой вид когомологии,
которые называют когомологиями с компактными носителями.
Когомологии с компактными носителями
Прежде чем давать общее определение, рассмотрим концептуально
более простое понятие симплициальных когомологии с компактными
носителями. Они определяются для Д-комплекса X, который является
локально компактным. Это эквивалентно тому, что у каждой его точки есть
окрестность, которая пересекает лишь конечное число симплексов. Рас-
§ 3.3. Двойственность Пуанкаре
309
смотрим подгруппу Alc(X; G) в группе симплициальных коцепей А' (X; G),
состоящую из коцепей, которые имеют компактный носитель в том
смысле, что они принимают отличные от нуля значения лишь на конечном
числе симплексов. Кограница такой коцепи у может принимать отличное
от нуля значение только на (i + 1)-мерных симплексах, имеющих грань,
на которой {р принимает отличное от нуля значение. Так как согласно
предположению о локальной компактности имеется лишь конечное число
таких симплексов, 5<р лежит в A[.+1(X;G). Таким образом, мы получаем
подкомплекс симплициального коцепного комплекса. Группы когомоло-
гий этого подкомплекса будем временно обозначать Н[(Х\ G).
Пример 3.32. Вычислим эти группы когомологий, когда X = Ж со
структурой А-комплекса с вершинами в целых точках. Чтобы симпли-
циальная нульмерная коцепь была коциклом, она должно принимать
одно и то же значение на всех вершинах, но тогда, если эта коцепь
лежит в 5°(Х), она должна быть тождественно нулевой. Таким
образом, Hc°(iR;G) = 0. Однако группа H^(R]G) отлична от нуля. Л именно,
рассмотрим отображение И: Aj(M; G) —► G, переводящее каждую коцепь
в сумму её значений на всех одномерных симплексах. Отметим, что И не
определено на всей группе А!(Х), а определено только на А^(Х).
Отображение И обращается в нуль на кограницах, поэтому оно индуцирует
отображение Ht] (!R; G) —> G. Это отображение сюръективно, так как любой
элемент группы А^(Х)— коцикл. Проверка того, что это отображение
инъективно, —лёгкое упражнение, поэтому Н1 (!R; G) % G.
Клеточные когомологий с компактными носителями для локально
компактного GW-комплекса можно было бы определить аналогично,
используя клеточные коцепи, которые отличны от пуля лишь на конечном
числе клеток. Однако на самом деле нам нужны сингулярные когомологий
с компактными носителями для пространства без симплициальнои или
клеточной структуры. Самое простое их определение следующее. Пусть
Clc(X; G) — подгруппа в Gr(X; G), состоящая из коцепей кр : Q(X) —>G, для
каждой из которых существует такое компактное множество К ~К'..с X,
что <р обращается в нуль на всех цепях в X — К. Заметим, что тогда 5ip
тоже обращается в нуль на цепях в X -К, поэтому 5у> лежит в С1сАЛ(Х; G)
и группы С'(Х; G) с меняющимся индексом i образуют подкомплекс
комплекса сингулярных коцепей в X. Группы когомологий №(Х; G) этого
подкомплекса—группы когомологий с компактными носителями.
Коцепи в С'.(Х; G) имеют компактные носители лишь в весьма слабом
смысле. Более сильное и, возможно, более естественное условие
заключается в том, что коцепи должны быть отличны от пуля лишь па
сингулярных симплексах, содержащихся в некотором компактном множестве,
зависящем от коцепи. Однако коцепи, удовлетворяющие этому условию,
вообще говоря, не образуют подкомплекса в комплексе сингулярных
коцепей. Например, если X = R, а \р — нульмерная коцепь, которая принимает
310
Глава 3. Когомологии
отличное от нуля значение в одной точке пространства R и нулевое
значение во всех других точках, то 5ц> принимает отличное от нуля значение
на сколь угодно большом одномерном симплексе.
Полезно иметь другое определение группы Н[(Х\ G). Группа коцепей
С[(Х\ G) является объединением своих подгрупп С(Х, X - К; G), где К
пробегает все компактные подмножества в X. Любое включение К" <-» L
индуцирует включения С (X, X - К; G) <-> С1 (X, X - L; G) для всех i, поэтому
имеются индуцированные отображения Н1(Х, X - К; G) -* Н'(Х, X - L; G).
Они не обязаны быть инъективными, но можно всё же надеяться, что
Hlc(X\ G) так или иначе поддаётся описанию в терминах семейства групп
Н1 (X, X — К; G) с переменным множеством К. Это действительно так, и
такое описание обеспечивают алгебраические пределы.
Предположим, что даны абелевы группы Ga, занумерованные
некоторым частично упорядоченным множеством индексов /, которое
обладает тем свойством, что для любой пары индексов а, /3 € / существует
индекс у €/, для которого а ^ у и Р ^ Y- Такое множество / называют
направленным множеством. Предположим также, что для любой пары
а ^ /3 задан такой гомоморфизм fap : Ga —► Gp, что faa = И для всех а,
а если a ^ /3 ^ у, то /ar — композиция гомоморфизмов /а/3 и fpr. Если есть
такие данные, которые называют направленной системой групп, то
можно двумя эквивалентными способами определить прямой предел групп
limGa. Более короткое определение такое: HmGa является факторгруппой
прямой суммы ф Ga по подгруппе, порождённой всеми элементами вида
a
a - /a^(a) для a € Ga, где мы рассматриваем каждую группу Ga как
подгруппу в Ф Ga. Другое определение, которое часто бывает более удобным
a
для работы таково. Определим отношение эквивалентности на множестве
[jGa следующим образом: а^Ъ, если /ar(a) = fpr(b) для некоторого у,
a
где aeGa и beGjg. Это отношение, очевидно, рефлексивно и
симметрично, а транзитивность следует из свойства направленного множества. Его
можно также описать как отношение эквивалентности, порождаемое эк-
вивалентностями а~/а^(а). Любые два класса эквивалентности [а] и [Ь]
имеют представителей а/ и Ь', лежащих в одной и той же группе Gr,
поэтому положим [а] + [Ь] = [а' + Ь']. Можно проверить, что это
определение корректно и задаёт структуру абелевой группы на множестве классов
эквивалентности. Далее, легко проверить, что отображение, переводящее
класс эквивалентности [а] в класс смежности элемента а в HmGa>
—гомоморфизм, причём обратное отображение индуцировано отображением
2ai,~>2[ai]i гДе а;€(^а,- Таким образом, мы можем отождествить HmGa
с группой классов эквивалентности [а].
Полезное следствие этого результата такое: если у нас есть
подмножество J с/, обладающее тем свойством, что для любого а€/ существует
§ 3.3. Двойственность Пуанкаре
311
j8 e J, для которого а ^ /3, то тогда limG„ не зависит от того, вычисляем ли
мы его для а, меняющихся по / или только по J. В частности, если в I есть
максимальный элемент у, мы можем взять J = {у}, и тогда limGa = Gv.
Предположим теперь, что пространство X представлено в виде
объединения набора подпространств Ха, образующих направленное
множество относительно отношения включения. Тогда группы H,-(Xa;G) для
фиксированных i и G образуют направленную систему, если использовать
гомоморфизмы, индуцированные включениями. Естественные
отображения H,(Xa; G) —> Н,(Х; G) индуцируют гомоморфизм limH,(Xa; G) —>
-H,(X;G). ~~*
I Предложение 3.33, Если пространство X — объединение направлен-
I ного множества подпространств Ха, обладающих тем свойством, что лю-
I бое компактное множество в X содержится в некотором Ха, то естествен-
I ное отображение limH;(Xa; G) —> Н,(Х; G) — изоморфизм для всех i и G.
Доказательство. Для доказательства сюръективности представим
цикл в X в виде конечной суммы сингулярных симплексов. Объединение
образов этих сингулярных симплексов компактно в X, поэтому оно лежит
в некотором множестве Ха, следовательно, отображение limH,(Xa; G) —>
-+Н,(Х; G) сюръективно. Инъективность доказывается аналогично. Если
цикл в некотором Ха является границей в X, то из компактности следует,
что он является границей в некотором Х^ эХа, поэтому он представляет
нуль в lim Я, (Xa; G). D
Теперь мы можем дать другое определение когомологий с
компактными носителями в терминах прямых пределов. Для пространства X
компактные подмножества К с X образуют направленное множество
относительно включения, так как объединение двух компактных множеств
компактно. Каждому компакту К с X мы сопоставим группу Н1(Х, X - К\ G),
где i и группа коэффициентов G фиксированы, а каждому включению
К с L компактных множеств мы сопоставим естественный гомоморфизм
Н'(Х, X - К; G) -» Н'(Х, X - L; G). Получающаяся предельная группа
HmH'(X, X-K; G) тогда равна Н[{Х\ G), так как каждый элемент этой
предельной группы представлен коциклом в СГ(Х, X - К\ G) для некоторого
компакта К, причём такой коцикл равен нулю в limH' (X, X — К; G) тогда
и только тогда, когда он является кограницей коцепи в С'-1(Х, X — L\G)
для некоторого компакта Lz>K.
Заметим, что если X компактно, то Hlc(X; G) = Hl(X] G), так как
имеется единственное максимальное компактное множество К С X, а именно
само X. Это непосредственно видно и из первоначального определения,
так как С^(Х; G) = С(X; G), если X компактно.
Пример 3.34 (Н*(1Г; G)). Чтобы вычислить limН'"(IX", lRn - К; G),
достаточно рассмотреть случай, когда в качестве множеств К берутся шары
Вк целочисленного радиуса к с центром в начале координат, так как лю-
312
Глава 3. Когомологии
бое компактное множество содержится в таком шаре. Поскольку группа
Н' (Rn, 1R" —Bk;G) отлична от нуля лишь при i = n (в этом случае она равна
G), а отображения
нпдеп, кп -вк; G) — яп(»я, кп -Bjt+i; G)
являются изоморфизмами, мы получаем, что tf!(:Rn;G) = 0 при i ^ г?
HHcn(K";G)^G.
Этот пример показывает, что когомологии с компактными
носителями—не инвариант гомотопического типа. Это может приводить к
сложностям с индуцированными отображениями. Например, постоянное
отображение Жп в точку не индуцирует отображения когомологии с
компактными носителями. Отображения, которые действительно
индуцируют отображения групп Я*, —это собственные отображения, т.е. те, для
которых прообраз любого компактного множества компактен. Однако
для доказательства двойственности Пуанкаре нам будут нужны
индуцированные отображения другого вида, которые идут в направлении,
противоположном обычному для когомологии, а именно отображения
Hlc{U;G) —► Hlc{V;G), связанные с включениями U <—> V открытых
множеств в фиксированном многообразии М.
Согласно вырезанию группа Hl(X, X — K;G) для компактного К
зависит только от окрестности К в Ху если предположить, что X хаусдорфово
и замкнуто. Эту группу удобно для краткости обозначить Hl{X\K\ G) по
аналогии с обозначениями, использованными ранее для локальных
гомологии. Можно представлять себе когомологии с компактными носителями
как предел этих «локальных групп когомологии в компактных
подмножествах».
Двойственность для некомпактных многообразий
Для R-ориентируемого n-мерного многообразия М, возможно
некомпактного, можно определить отображение двойственности DM : Hk (М; R) —*
—»H/z_fc(M;R) предельным процессом следующим образом. Для
компактных множеств К с L с М мы имеем диаграмму
HnW\L;R)xHkW\L;R)^~
Hn_k{M;R)
Ип{М\К\ К) х Нк(М\ К\ R) ^
где НП(М| Л; R) = НпШ, М - A; R) и Нк{М\ А\ R) = НкШ, М-А; К).
Согласно лемме 3.27 существуют единственные элементы /!к € Нп(М| К; R) и fiL €
€Hn(M|L;R), при ограничении которых получается данная ориентация
многообразия М в каждой точке множеств К и L соответственно. Из
единственности мы получаем i*(jLiL) =Дк. Естественность ^-произведения
влечёт, что i*(ju;) ^ х = jul ^ i*(jc) для всех х € H*(M|JC; R), а значит,
§ 3.3. Двойственность Пуанкаре
313
lxKr^x — yLLrs i*0). Поэтому, когда К пробегает компактные подмножества
в М, гомоморфизмы Нк(М\К] R) —* Hn_k(M\ R), лг—♦ fiK r^x, индуцируют
в пределе гомоморфизм двойственности DM : Нк{М; R) —* Нп_к(М\ К).
Так как Н*(М\ Ю =Н*Ш'> Ю, если М компактно, следующая теорема
обобщает двойственность Пуанкаре для замкнутых многообразий.
Теорема 3.35. Отображение двойственности
DM:Hk{M;R)^Hn_k{M;R)
— изоморфизм для всех /с, если М является R-ориентируемым п-мерным
многообразием.
Доказательство будет несложным, как только мы установим
технический результат, сформулированный в следующей лемме, по поводу
коммутативности некоторой диаграммы. Такого рода утверждения о
коммутативности обычно доказываются рутинно, но это, по-видимому, является
исключением. Читатель, который обратится к другим книгами за
альтернативным подходом, найдёт неожиданно непростые изложения этого
технического результата, и доказательство, которое мы приводим, тоже не
так просто, как хотелось бы.
Кольцо коэффициентов R будет одним и тем же во всём
доказательстве, и для краткости мы опустим его в обозначениях для гомологии и ко-
гомологий.
Лемма 3.36. Если М — объединение двух открытых множеств U и V,
то существует диаграмма последовательностей Майера—Вьеториса,
коммутативная с точностью до знака:
^Hk+\unv) —^...
■H*(unv)
Vvnv
H*(W*Hkc(V)
DyQ-Dv
нкс(М)
Hn_k(UnV) — Hn_k(U) x Hn_k{V) — Htl..k(M)
fyjrV
T
■//„_*_,«/rw)
Доказательство. Компактные множества К с U и L с V приводят
к последовательности Майера—Вьеториса в верхней строке следующей
диаграммы, нижняя строка которой тоже последовательность Майера—
Вьеториса:
... —^НкШ\КПЬ) *HkW\K)®HkW\L)-+HkW\KUL)-+ ...
Hk(UCiV\KnL)
■н
Hk(U\K)®Hk(V\L)
+ Hn-k(U)xHn-k{V)-
ИК-.Л'
^Нп'К(М) >■ ...
Два отображения, помеченные как изоморфизмы, получаются из
вырезания. Предположив, что эта диаграмма коммутативная, рассмотрим пере-
314
Глава 3. Когомологии
ход к пределу по компактным множествам К с U и L с V. Так как
каждое компактное множество в UnV содержится в пересечении Kf)L
компактных множеств К <ZU и L с V и аналогично для V и V, эта диаграмма
индуцирует предельную диаграмму, которая имеет такой вид, как
утверждается в лемме. Первая строка этой предельной диаграммы точная, так
как прямой предел точных последовательностей точен. Это одна из задач
в конце этого параграфа; она легко следует из определения прямых
пределов.
Остаётся установить коммутативность предыдущей диаграммы,
вовлекающей К и L. В двух изображённых квадратах, не включающих
отображений границы или кограницы, коммутативность легко проверяется на
уровне циклов и коциклов. Менее тривиален третий квадрат, который мы
перепишем следующим образом:
Hk(M\K\JL)-^Hk+l(M\KnL)^Hk+lWc\V\KCM)
(*)
Нп.к(М)
Если положить А = М—К и В = М ~ L, то отображение 5 — это
отображение кограницы в последовательности Майера—Вьеториса, полученной
из короткой точной последовательности коцепных комплексов
О -» С*{М,А + В) -» С*(М, А)0 С*Щ, В) -» С*(М,АПВ) -» О,
где С*{М, А 4-В) состоит из коцепей на М, обращающихся в нуль на цепях
в А и цепях в В. Вычислим кограничное отображение
Майера—Вьеториса 5 на классе когомологии, представленном коциклом у^С*(М,АС\В).
Первый шаг состоит в том, чтобы написать у = уА — ц>в для <рА е С*(М, А)
и ipe е С*(М,В). Тогда класс 5[</?] представлен коциклом 5ц>А = 5ipB e
€С*(М> АН-В), где равенство, 5ц>А—5{рв следует из того, что у является
коциклом, а потому 5<р = 5</?А - 5^в = 0. Аналогично граничное
отображение д в гомологической последовательности Майера—Вьеториса
получается, если представить элемент группы Н,(М) циклом z, который
является суммой цепей z^C,-(10 и z^eQfV), и тогда d[z] = [dza].
С помощью барицентрического подразделения класс iiKuL можно
представить цепью а, которая является суммой av_L + aunv 4- av._K цепей
§ 3.3. Двойственность Пуанкаре
315
в U — L, U(IV иУ — К соответственно, так как эти три открытых
множества покрывают М. Цепь aunv представляет класс fJLKnL, так как другие
две цепи av_L и av_K лежат в дополнении множества К П L, а потому
обращаются в нуль в
НП(М| К П L) ** Нп (и П V| /С П lV
Аналогично цепь а^-/, + aanv/ представляет класс /iK.
В квадрате (*) пусть </? — коцикл, представляющий элемент группы
h4m|/CUL). При отображении 5 он переходит в класс когомологий
коцикла 5(/?л. Перемещаясь в Hn_k_l(UDV), мы получаем коцикл aunv ^~-
^ 5ц>А, который лежит в том же самом классе гомологии, что и daunv -—
^Ч>А, так как
d(<*unv ~ Ч>а) = (-Dk(daunv — ipA-aUnv — 5ipA)9
a aunv ^ </?А является цепью в U П V.
Если обходить квадрат (*) по другому пути, то у отображается
сначала в агмр. Чтобы применить к нему граничное отображение Майера—
Вьеториса Э, сначала запишем а^<р в виде суммы цепи в U и цепи в V:
Затем мы берём границу первой из этих двух цепей, получая при этом
класс гомологии [d{av_L ^ у)] е Hn_k_](U n V). Чтобы сравнить его с
[daunv г\ ц>А], запишем
д(аи_1/^{р) = (—1)кдаи_1г^ф) так как ду = О,
= (—1) dau_Lr^y)Al так как dau_l/sipB = 0, потому что у?д
обращается в нуль на цепях в В = М -I,
где последнее равенство следует из того факта, что d{au^L + aVnv)^{pA = 01
так как d(av_L + aanv/) является цепью bU -К (согласно сделанному
ранее наблюдению, что av_l +avrw представляет класс [1К), а у>А обращает-
ся в нуль на цепях в Л = М - К.
Таким образом, квадрат (*) коммутативен с точностью до знака,
зависящего только от к. □
Доказательство двойственности Пуанкаре, Начнём с двух шагов
индукции, конечного и бесконечного.
А. Если М — объединение открытых множеств U и V, причём D(;, Dv
и Dunv — изоморфизмы, то DM тоже изоморфизм. Это непосредственно
следует из предыдущей леммы и 5-леммы.
Б. Если М — объединение последовательности открытых множеств
иг с U2 с ..., причём каждое отображение двойственности Da : Н*Щ-) —*
-»Hn_k([/,-) — изоморфизм, то DM тоже изоморфизм. Чтобы доказать это,
ivui иМОЛОГИИ
мы сначала заметим, что согласно вырезанию Н*Ш,-) можно
рассматривать как предел групп Нк(М\К), когда К пробегает компактные
подмножества в и{. Тогда имеются естественные отображения Н^ОД) ~*
—*H*(L/,-+1), так как вторые из этих групп —пределы по большему набору
множеств К. Таким образом, мы можем образовать предел НтН^Щ),
который, очевидно, изоморфен Н*(М), так как компактные множества
в М — это просто компактные множества во всех множествах [/,-. Согласно
предложению 3.33 имеем Hn__k(M) ъ \\mHn_k{Uj). Поэтому отображение
DM является пределом изоморфизмов Ои, следовательно, оно является
изоморфизмом.
После этих предварительных замечаний мы можем доказать теорему
за три несложных шага.
1. Случай М = :&" можно доказать, рассматривая К" как внутренность
симплекса Л". Тогда отображение DM можно отождествить с
отображением Нк(Ап, дА11) ~* Н„_.^(А"), заданным как ^-произведение на
образующую \Ап'\ еНп(Ап, дА'1), определённую тождественным
отображением симплекса Л", которое является относительным циклом.
Единственное нетривиальное значение /с — это к = п, когда отображение
^-произведения является изоморфизмом. Действительно, образующая группы
Н"(А}\ дАп) ъ Нот (Я„(ДП, dAu),R) представлена коциклом </?,
принимающим значение 1 на Д". Поэтому по определению ^-произведения
Дп^(/?~это последняя вершина симплекса Д", представляющая
образующую группы Н0(Ап).
2. Докажите теперь, что DM — изоморфизм в более общем случае
произвольного открытого множества М п У, Сначала представим М как
счётное объединение непустых ограниченных выпуклых открытых
множеств Uh например открытых шаров, и положим V{ = [J Uj. Оба множе-
}<i
ства Vj и Ui П Vj — объединения i —1 ограниченных выпуклых открытых
множеств, поэтому, используя индукцию по числу таких множеств в
покрытии, мы можем предположить, что Dv и Рцпу—изоморфизмы.
Согласно случаю 1 отображение 0и —изоморфизм, так как множество У,-
гомеоморфно 1R". Следовательно, DU[jV —изоморфизм согласно п.А. Так
как М — возрастающее объединение множеств Vif причём каждое
отображение Dv — изоморфизм, отображение DM тоже является изоморфизмом
согласно п. Б.
3. Если М — конечное или счётное бесконечное объединение
открытых множеств I/,-, гомеоморфных R", то теорема теперь доказывается
такими же рассуждениями, как и в п. 2 нужно только каждый раз заменять
слова «ограниченное выпуклое открытое множество» на «открытое
множество в -R"». Таким образом, доказательство завершено для замкнутых
многообразий, так же как и для всех некомпактных многообразий,
которые реально встречаются на практике.
§ 3.3. Двойственность Пуанкаре
317
Чтобы разобраться с наиболее общим некомпактным
многообразием М, мы применим рассуждение с леммой Цорна. Рассмотрим набор всех
открытых множеств 1/сМ, для которого отображения двойственности Du
являются изоморфизмами. Этот набор частично упорядочен
относительно включения, и объединение любого вполне упорядоченного гюднабора
снова принадлежит этому набору согласно рассуждению из п. Б, в
котором в действительности не использовало предположение, что набор {(/,}
занумерован натуральными числами. Тогда из лемма Цорна следует, что
существует максимальное открытое множество U, для которого теорема
верна. Если [/ ^ М, то выберем точку х € М — U и открытую окрестность V
точки х, гомеоморфную Ж". Теорема верна для V и Un V согласно п. 1 и 2,
а для U она верна по предположению, поэтому согласно п. А она верна для
U U V, что противоречит максимальности множества U. П
Следствие 3.37. Эйлерова характеристика замкнутого многообразия
нечётной размерности равна нулю.
Доказательство. Пусть М — замкнутое п-мерное многообразие. Если
М ориентируемо, то мы получаем rank H,(M; Z) = rankHn~l(M\ Z);
последний ранг равен rankHn_,(M; Z) согласно теореме об универсальных
коэффициентах. Таким образом, если п нечётно, то все слагаемые в сумме
]Г(-1)' rankHt(M; Z) попарно сокращаются,
i
Если М не ориентируемо, то мы применяем те же самые рассуждения,
используя коэффициенты Z2 и заменяя rankH{(M;Z) на dimH;(M;Z2) —
размерность линейного пространства над Z2, чтобы получить, что
2](-l)zdimHI(M;Z2) = 0.
Остаётся проверить, что эта альтернированная сумма равна эйлеровой
характеристике ^(—l)'rankH,(M; Z). Это можно сделать, воспользовав-
шись изоморфизмами Н{{М\ Z2) ъН\М\ Z2) и применив теорему об
универсальных коэффициентах для когомологий. Каждое слагаемое Z группы
Н{{М\ Z) даёт слагаемое Z2 группы Hl(M\ Z2). Каждое слагаемое Ът
группы H,(M;Z) с чётным m даёт слагаемые Z2 в Н{(М\Ъ2) и Н'+1(М,2£2),
вклады которых в £](-l)'dimH,(M; Z2) взаимно уничтожаются. А сла-
гаемые Ът группы H,(M;Z) с нечётным т. не дают никакого вклада
bH*(M;Z2). □
Связь с ^-произведением
^- и ^-произведение связаны формулой
(*)
■ф(а^у) = (</>wa/>)(a),
«^xo
Глава 3. Когомологии
где а е Ck+t{X\ R), ц> е Ск(Х; R) и -ф е С*(Х; R). Она верна, так как для
сингулярного (fc + О-мерного симплекса a: Ak+t —>Х мы имеем
•ф{агмр) = ^0(сг| [v0,..., vk])a\ [vb ..., v^]) =
= Ч>(°\ [vo>.... vj)^(cr| [vb .... vM]) = (</> kj VO(cr).
Формула (*) означает, что отображение y?w: Се(Х; Я) -»Скч"'(Х; R)
совпадает с отображением HomK(Q(X; R),R) —> HomR(Q+f(X; Ю,Ю,
двойственным к ^(^. Переходя к гомологиям и когомологиям, получаем
коммутативную диаграмму
НС(Х; R) —^ НотдСЯДХ; R), R)
)^ [(^'
Н*+ЧХ; R) -^ Hom^OW*; R), R)
Если отображения h являются изоморфизмами, например, когда R —
поле или когда R = Z, а группы гомологии пространства X свободные,
то отображение ц> ^ двойственно к г\(р. Таким образом в этих случаях
\j- и /^-произведения определяют друг друга (по крайней мере, если
сделать предположение о конечной порождённое™, чтобы когомологии
определяли гомологии и обратно). Однако имеются примеры, в которых
\j- и ^-произведения не эквивалентны, когда R = Z и в гомологиях есть
кручение.
Посредством формулы (*) двойственность Пуанкаре накладывает
нетривиальные ограничения на структуру ^-произведения для
многообразий. Для замкнутого R-ориентируемого n-мерного многообразия М
рассмотрим спаривание, определённое ^-произведением:
Hk(M\R) х H"-k(M;R) —>R, (¥>,ч/0 — (¥?^г/0[М].
Такое билинейное спаривание Ах B-^R называют невырожденным, если
оба отображения A-»Hom(£,R) и Я—>Hom(A, R), полученные при
рассмотрении спаривания как функции от каждой переменной по
отдельности, являются изоморфизмами.
I Предложение 3.38. Спаривание посредством ^-произведения для
замкнутого R-ориентируемого многообразия невырожденно, если R — поле
или если R = Z и произведена факторизация по кручению в Н*(М; Z).
Доказательство. Рассмотрим композицию
Нп~к{М\ R) -^ HomR(Hn_fc(M; R), R) -^ Нотл(Н*(М; R), R),
где h — отображение (появляющееся в теореме об универсальных
коэффициентах), индуцированное вычислением значений коцепей на
цепях, a D* —отображение, Horn-двойственное двойственности Пуанкаре
D: Hk -*Un_k. Композиция D*h переводит \j>eHn' k(M;R) в гомоморфизм
<р -* г/>([М] ^ (/?) = ((/? ч^ xj))[M]. Для коэффициентов в поле или для целых
§ 3.3. Двойственность Пуанкаре
319
коэффициентов с отфакторизованным кручением h — изоморфизм.
Невырожденность спаривания по одной из переменных тогда эквивалентна
тому, что D —изоморфизм. Невырожденность по другой переменной
следует из коммутативности ^-произведения. □
I Следствие 3.39. Если М —замкнутое связное ориентируемое л-мер-
I ное многообразие, то для любого элемента aeHk(M',Z) бесконечного
I порядка, который не является нетривиальным кратным другого элемен-
I та, существует такой элемент (5 е Ип~к{М\ Z), что a w /3 является обра-
I зующей группы Нп(М\ Z) ъ Z. Для коэффициентов в поле то же самое
I верно для любого а фО.
Доказательство. Условия на элемент а означают, что он порождает
слагаемое Z в Нк{М\Ъ). Тогда имеется гомоморфизм у: Hk(M\Z) —► Z,
для которого <р(а) = 1. Согласно невырожденности спаривания, заданного
^-произведением, </? реализуется взятием ^-произведения с элементом
/ЗеНп~~к{М', Z) и вычислением значения полученного класса когомологий
на [М]. Таким образом, элемент а w/З порождает группу Н"(М; Z). Случай
коэффициентов в поле аналогичен. □
Пример 3.40 (проективные пространства). Структуру
^-произведения в H*(CP";Z), задаваемую отождествлением со срезанным кольцом
многочленов Z[a]/(an+1), где \а\ =2, можно легко вывести следующим
образом. Включение СР"~] <—>СР" индуцирует изоморфизм групп Н1 при
i ^ 2л — 2, поэтому индукция по л показывает, что группа H2'(CP";Z)
порождена элементом а1 при i < л. Согласно следствию 3.39
существует такое целое число т, что произведение а^тап~^ =тап порождает
группу H2n(CPn;Z). Это может случиться, только если m = ±1, а
потому H*(CPn;Z) ^Z[a]/(an+1). To же самое рассуждение показывает, что
H*(HPn;Z)^Z[a]/(an+1), где |а| = 4. Для КРП можно применить те же
самые рассуждения с коэффициентами в Z2 и получить, что Н*(^РП; Z2) ^
^Z2[a]/(an+1), где |а| = 1. Структура ^-произведения в
бесконечномерных проективных пространствах следует из конечномерного случая, как
мы видели в доказательстве теоремы 3.12.
Существует ли замкнутое многообразие, когомологий которого
аддитивно изоморфны когомологиям СРП, но с другой структурой w-произве-
дения? При л = 2 ответ отрицательный, так как из двойственности
следует, что квадрат образующей группы И2 должен быть образующей
группы Н4. При л = 3 двойственность говорит, что произведение образующих
групп Н2 и Я4 должно быть образующей группы Н6, но ничего не
говорится о квадрате образующей группы Ы2. Действительно, для пространства
S2 х S4, когомологий которого имеют ту же самую аддитивную структуру,
Что и для СР3, квадрат образующей группы H2(S2 x S4; Z) равен нулю,
Так как эта образующая получается из образующей группы H2(S2', Z) при
отображении, индуцированном проекцией S2 x S4 —> S2, а в i/*(S2; Z)
квадрат образующей группы И2 равен нулю. В одной из задач в § 4.D описан бо-
320
Глава 3. Когомологии
лее общий пример замкнутого 6-мерного многообразия с теми же самыми
группами когомологии, что и у СР3, но для которого квадрат образующей
группы II2 — произвольное кратное образующей группы И4.
Пример 3.41 (линзовые пространства). В линзовых пространствах
^-произведения можно вычислить таким же образом, как в
проективных пространствах. Для линзового пространства /,2""н размерности 2п + 1
с фундаментальной группой Z,„ мы вычислили в примере 2.43, что группа
Н,(/,2"м; Z) равна Z для i = 0 и 2п + 1, равна Ът для нечётного i < In + 1
и равна 0 в остальных случаях. В частности, из этого следует, что
многообразие L2n+] ориентируемо; это можно также вывести из того факта,
что L2n+i — пространство орбит действия группы Ът на S2,lM
сохраняющими ориентацию гомеоморфизмами, используя одну из задач в
конце этого параграфа. Согласно теореме об универсальных коэффициентах
группа H'"a2n+1; Zm) равна Z„, для всех i $2п + 1. Пусть aeHl(L2n+]] Zm)
и (5 €H2(L2n+1; Z,„) — образующие. Мы хотим доказать следующее
утверждение:
• (Р1 при;=21,
группа W (L и; Zm) порождена классом <
(а/31 при j =2f + l.
Индукция по п позволяет предположить, что это верно для j $ 2п - 1, так
как у нас есть линзовое пространство 12п~] с L2""1 л, причём это вю1ючение
индуцирует изоморфизм групп Н; при ; ^ 2п — 1, в чём можно убедиться,
сравнив клеточные цепные комплексы для L2n~x и L2"""1. Следствие 3.39
нельзя применить непосредственно для коэффициентов Z,„ с
произвольным т, но его доказательство позволяет это сделать, так как отображения
h: H'"a2n+1; z,„) - Hom(//za2',fl; z,M), z,„)
являются изоморфизмами. Мы делаем вывод, что класс /3 w/ca/З"-1
порождает группу H2',+ ,(L2ntl; Zm) для некоторого целого числа к.
Число /с должно быть взаимно простым с т, поскольку иначе произведение
(3 w kafin~l = ка(Зп имело бы порядок меньше т и не могло бы порождать
группу H2""M(£2"+1; Zm). Тогда, так как к взаимно просто с гл, класс а/Зм
тоже образующая группы H2n+l(L2n+l'> Z,„). Из этого следует, что элемент
/3м должен порождать группу H2n(L2n+l\ Z,„), поскольку иначе он имел бы
порядок меньше т, а тогда элемент а/3" тоже имел бы порядок меньше т.
Оставшуюся часть структуры w-произведения на H*(L2u~[; Zm) можно
определить, выразив элемент а2 как кратное элемента /3. Когда ш нечётно,
из формулы коммутативности для w-произведения следует, что а2 = 0.
Когда ш четно, коммутативность влечёт лишь то, что элемент а2 является
либо нулём, либо единственным элементом группы f/2(L2/U1; Zm) ^ Z„}
порядка два. В действительности имеет место последний вариант, так как
двумерный остов L2 —это окружность L1 с двумерной клеткой,
приклеенной по отображению степени ш, а мы вычислили структуру w-произве-
дения в этом двумерном комплексе в примере 3.9. По-видимому, нельзя
§3.3. Двойственность Пуанкаре
321
вывести нетривиальность класса а2 из одной лить двойственности
Пуанкаре, помимо случая, когда т = 2.
Структура w-произведения для бесконечномерного линзового
пространства L°° следует из конечномерного случая, так как отображение
ограничения Hj(L°°\ Z,„) -* H;"(L2n+1; Z;M) — изоморфизм при j $ 2л + 1.
Как и для IRP'1, кольцевая структура в Н* (L2n+ ]; Z) определяется кольцевой
структурой в H*(L2n+1; Zm), и аналогично для L00, где структура немного
более простая: /-/"(L00; Z) %Z[a]/(ma), причём |a| = 2. Случай L2n+I
получается из этого, если положить а"41 = 0 и присоединить дополнительно
Z»H2,l+1a2n+1;Z).
Другой вывод структуры w-произведения в линзовых пространствах
приведён в примере З.Е.2.
Временно будем использовать обозначение м£ее(М) для группы Нк(М)
по модулю её подгруппы кручения. Из предыдущего предложения
следует, что для замкнутого ориентируемого многообразия М размерности 2п
спаривание /"/"ree(M) x Нг^с(М) -* Z, заданное ^-произведением в
средней размерности, является неособой билинейной формой на Н" (М). Эта
форма симметрическая или кососимметрическая в соответствии с тем,
четно или нечётно л. Алгебра в кососимметрическом случае довольно
простая. При подходящем выборе базиса матрицу кососимметрической
неособой билинейной формы над Z можно привести к стандартному виду,
состоящему из блоков ( на диагонали и нулей на остальных
местах, согласно алгебраической задаче в конце этого параграфа. В
частности, ранг группы /7"(М2") должен быть чётным, когда л нечётно. Мы уже
знакомы с этими фактами в случае л = 1 на основании явных вычислений
w-произведений для поверхностей в §3.2.
Симметрический случай намного более интересен с точки зрения
алгебры. Имеется лишь конечное число классов изоморфных
симметрических невырожденных билинейных форм над Z фиксированного ранга, но
это «конечное число» растёт очень быстро, например, оно больше 80
миллионов для ранга 32; изложение этого красивого раздела теории чисел
дано в [63]. Известно, что для любого чётного л ^ 2 каждая
симметрическая невырожденная форма реализуется как спаривание посредством
w-произведения на некотором замкнутом многообразии М2п. Можно даже
выбрать М2п односвязным и имеющим самые минимальные гомологии:
Z в размерностях 0 и 2 л и Zk в размерности л. Для л = 2 есть не более двух
не гомеоморфных односвязиых замкнутых четырёхмерных многообразий
с одной и той же билинейной формой. А именно, имеются два
многообразия с одной и той же формой, если квадрат а^а некоторого элемента
a e Н2(М4)— нечётное кратное образующей группы НЛ(МЛ) (например,
это верно для СР2), а иначе М4 единственно (например, это верно для S
или S1 х S2); см. [26]. В §4.С мы делаем первый шаг в этом направлении,
322
Глава 3. Когомологии
доказывая классический результат Уайтхеда о том, что гомотопический
тип односвязного замкнутого четырёхмерного многообразия однозначно
определяется его структурой w-произведения.
Другие виды двойственности
Обобщая понятие многообразия, определим n-мерное многообразие
с краем М как хаусдорфово пространство, в котором любая точка имеет
открытую окрестность, гомеоморфную либо Rn, либо полупространству
Ж" = {(л^, ..., л:м) еR" |л:п ^ 0}. Если точка хеМ соответствует при таком
гомеоморфизме точке (л*!,..., хи) € R'j, xn = 0, то согласно вырезанию мы
имеем
Нп (М, М - {х}; Z) » Нп {Ж% RI - {0}; Z) = 0,
а если х соответствует точке (л*ь ..., хп) € R" , хм > 0, или точке
пространства R", то НпШ, М - {л:}; Z) «Hn(Kn, R'1 - {0}; Z) «Z. Поэтому точки х,
для которых Нп(М,М — {x};Z) = 0, образуют корректно определённое
подпространство, которое называют краем многообразия М и
обозначают дМ. Например, ЭК" =R"_1 и dDn=Sn_1. Очевидно, что ЭМ является
(п - 1)-мерным многообразием с пустым краем.
Если М — многообразие с краем, то воротник края дМ в М — это
открытая окрестность, гомеоморфная дМ х [0,1) при гомеоморфизме,
переводящем дМ в дМ х {0}.
Предложение 3.42. Если М — компактное многообразие с краем, то
дМ имеет воротник.
Доказательство. Пусть М' — это М с приклеенным внешним
воротником, т. е. факторпространство несвязного объединения М и дМ х [0,1], в
котором точка хедМ отождествляется с (х, 0)едМ х [0,1]. Достаточно
построить гомеоморфизм h: М—>М', так как дМ\ очевидно, имеет воротник.
Так как М компактно, его замкнутое подпространство дМ тоже
компактно. Из этого следует, что можно выбрать конечное число
непрерывных функций (/?,-: дМ —> [0,1] так, что множества V{ = с/?"1 (0,1] образуют
открытое покрытие края дМ и замыкание каждого множества V(
содержится в открытом множестве U{ с М, гомеоморфном полупространству
R". После деления каждой функции <£,• на ]>]</>, мы можем считать, что
i
Пусть т/^ = у>3 +... 4- у>ь и пусть Мк с М' —объединение М с
точками (л*, 0 € ЭМ х [0,1], для которых t $ ij'kW- По определению t/>0 = О
и М0 = М. Построим гомеоморфизм /ifc: Mk_] —»Mfc следующим образом.
Гомеоморфизм l/fc ^R'J. даёт воротник d£/fc x [-1, 0] множества dUk в Uk,
причём точка л*е dUk соответствует точке (х, 0) е dl/fc x [—1, о]. При
помощи внешнего воротника дМ х [0,1] мы можем построить вложение dllk *
х [-1,1] аМ'. Определим hk как тождественное отображение вне этого
множества dUk х [—1,1], а для хе dUk мы будем считать, что hk линей-
§ 3.3. Двойственность Пуанкаре
323
но растягивает отрезок {х} х [-1, грк_1{х)] на отрезок {х} х [-1, грк(х)].
Композиция всех гомеоморфизмов hk даёт тогда гомеоморфизм М ъ М'',
что и завершает доказательство. □
Вообще воротник можно построить для края паракомпактного
многообразия таким же способом.
Компактное многообразие М с краем называют Я-ориентируемым,
если М — дМ является Я-ориентируемым как многообразие без края.
Если дМ х [0,1) —воротник края дМ в М, то группа Н{(М, дМ; Я)
естественно изоморфна Н((М - дМ, дМ х (0, е); Я), поэтому, когда М
является Я-ориентируемым, лемма 3.27 даёт относительный фундаментальный
класс [М] в Нп(М,дМ\К), ограничение которого даёт данную
ориентацию в каждой точке многообразия М - дМ.
Не составит труда вывести следующее обобщение двойственности
Пуанкаре на многообразия с краем из той версии, которую мы уже доказали
для некомпактных многообразий.
Теорема 3.43. Предположим, что М — компактное Я-ориентируемое
п-мерное многообразие, край которого дМ представлен в виде
объединения двух компактных (п - 1)-мерных многообразий Л и В с
общим краем дА = дВ = АГ) В. Тогда ^-произведение с
фундаментальным классом [М] е Нп(М, дМ\ Я) даёт изоморфизм DM : Hk{M, А\ Я) —>
—>Нп_к(М, В; Я) для всех fc.
Не исключается возможность, что А, В или АПВ являются пустыми.
Случаи А = 0 и В = 0 иногда называют двойственностью Лефшеца.
Доказательство. Отображение ^-произведения DM : Hk{M,A\R) —>
->Hn_fc(M, В; Я) определено, поскольку из существования воротников для
АПВвДивВи для дМ в М следует, что А и В —деформационные ретрак-
ты таких открытых окрестностей U и V в М, что U U V деформационно
ретрагируется на АиВ = дМ, a t/nl/ деформационно ретрагируется на
АПВ.
Случай В = 0 доказывается применением теоремы 3.35 к М - дМ.
Рассматривая воротник края <Ш, мы видим, что
НкШ, дМ; Я) ъ Нк(М - дМ; Я),
и имеются очевидные изоморфизмы Ип_к[М\ Я) ъ Нп_к(М - <Ш; Я).
Общий случай сводится к случаю В = 0 применением 5-леммы к
следующей диаграмме, где коэффициенты в Я явно не указываются:
Нк(М,дМ)
\му
Нп_к{М)
■НкШ,А)-*-
\
Нп-к(
[МЬ
'
М,В)->
Нк(дМ,М)
1-
Нк(В,дВ)
>
" Нп-к
-i(B)
Нк+1(М,дМ)
ту
Н„
-ЛМ)
324
Глава 3. Когомологии
Для доказательства коммутативности среднего квадрата нужно проверить,
что граничное отображение W„(M, <Ш)—>H„_T(dM) переводит
фундаментальный класс многообразия М в фундаментальный класс многообразия
дМ. Мы оставляем это в качестве задачи в конце этого параграфа. □
Теперь мы обратимся к двойственности Александера.
Теорема 3.44. Если К — компактное локально стягиваемое непустое
собственное подпространство в Sn, то H,(S" - К; Z) ъ Нп~1~1(К\ Ж) для
всех z".
Частный случай, когда К — сфера или диск, был разобран более
элементарными средствами в предложении 2.В.1. Как там отмечено,
интересно, что гомологии пространства Sn - К не зависят от того, как
именно К вложено в S". Возможны локальные патологии, как в случае
рогатой сферы Александера, или глобальные сложности, как для заузленных
окружностей в S3, но они никак не влияют на гомологии дополнения.
Единственное требование состоит в том, чтобы само пространство К не
было слишком плохим. Пример, когда теорема оказывается неверной без
предположения о локальной стягиваемости, —«квазиокружность»,
определённая в одной из задач в § 1.3. Это компактное подпространство К с R2
можно рассматривать как подпространство в S2, если добавить
бесконечно удалённую точку. Тогда мы имеем H0(S2 - К; Z) ъ Z, так как S2 - К
имеет две компоненты линейной связности, но НХ(К\ Z) = 0, так как
пространство К односвязное.
Доказательство. Мы получим требуемый изоморфизм при i Ф 0 как
композицию из пяти изоморфизмов:
ъ limH;,-'(Sn-iC, U-К) « ljmHn"'(Sn, U) «
wlimH""1'1^, велико,
где всюду в доказательстве будут неявно использоваться
коэффициенты Z, а прямые пределы берутся относительно открытых окрестностей U
множества К. Первый изоморфизм—двойственность Пуанкаре. Второй —
определение когомологии с компактными носителями. Третий
—вырезание. Четвёртый получается из длинных точных последовательностей пар
(S'\ U). Что касается последнего изоморфизма, имеется простой частный
случай, когда у К есть окрестность, которая является цилиндром
отображения для некоторого отображения X —> К, как в «примерах с буквами»
в начале главы 0. В этом случае мы можем вычислить прямой предел,
используя окрестности U, которые являются частями цилиндра
отображения, деформационно ретрагирующегося на К.
Чтобы получить последний изоморфизм в общем случае, нужно
применить теорему П.7 из приложения, в которой утверждается, что К — Ре~
§ 3.3. Двойственность Пуанкаре
325
тракт некоторой окрестности U0 в S", так как К локально стягиваемо. При
вычислении прямых пределов мы можем тогда ограничиться открытыми
множествами L/cl/0, каждое из которых ретрагируется на К посредством
ограничения ретракции из U0. Из этого следует, что естественное
отображение ограничения limH*(L0 —► Н*(К) сюръективно, так как мы можем
перенести назад в прямой предел любой элемент группы Н*(К)
посредством ретракции U —>К".
Чтобы проверить инъективность отображения limH*(L0 —> 77* (Ю>
мы сначала покажем, что любая окрестность U с U0 множества К
содержит такую окрестность V, что включение V <—» U гомотопно
ретракции V —>К с U. А именно, если рассматривать U как подпространство
в IRn с S", то линейная гомотопия U х I —► У тождественного отображения
в ретракцию U —> К переводит К х I в /С, а потому переводит V х I в U для
некоторой окрестности V множества К согласно компактности отрезка /.
Так как включение V <-> U гомотопно ретракции V —>К с (У, ограничение
H*(U) —>H*(V) пропускается сквозь 77х (К), и поэтому если элемент
группы 77* (^0 при отображении ограничения в Н*(К) переходит в нуль, то
он переходит в нуль и при отображении ограничения в 77* (V). Из этого
следует, что отображение lim 77* (10 —>77*(/0 инъективно.
Единственная трудность в случае i = 0 заключается в том, что
четвёртого из указанных выше пяти изоморфизмов нет и вместо пего у нас есть
только короткая точная последовательность
О — Й'^ОО ->Hn(Sn,U) ->H"(S") ->0.
Чтобы обойти эту небольшую проблему, заметим, что все группы,
участвующие в первых трёх из этих пяти изоморфизмов отображаются
естественно на соответствующие группы с пустыми множествами К и U. То-
£да если мы возьмём ядра этих отображений, то получим изоморфизм
Ro(Sn —К) %Нт/-/"_1([/), а мы уже видели, что последняя группа
изоморфна Я""1 {К). П
(Следствие 3.45. Если пространство X с Жп компактно и локально
стягиваемо, то группа 77,(X; '£) равна 0 при 1>пи свободна от кручения
при i = n — 1 и п -2.
Например, замкнутое неориентируемое п-мерное многообразие М
нельзя вложить в качестве подпространства в !Rn_M, так как группа Нп,л{М\ 7S)
Содержит подгруппу Z2 согласно следствию 3.28. Таким образом,
бутылку Клейна нельзя вложить в R3. И вообще, двумерный комплекс Хти,
изученный в примере 1.24, т.е. факторпространство цилиндра S1 х I при
Отождествлениях (z, 0) ~ (e2~'/mz, 0) и (z, 1) ~ (e2",7"z, 1), нельзя вложить
ЫК3, если числа m и п не взаимно просты, так как группа Н^ {Хти7/,) равна
Z х Zdi где d — наибольший общий делитель чисел т и п. Бутылка Клейна
'Получается в случае m = и = 2.
326
Глава 3. Когомологии
Доказательство. Рассмотрим X как подпространство в
одноточечной компактификации, т.е. в S". Двойственность Александера даёт
изоморфизм Hl(X; Z)^//n_,_1(S"-X; Z). Последняя группа нулевая при i^n
и свободна от кручения при i = п — 1, поэтому требуемое утверждение
следует из теоремы об универсальных коэффициентах, так как группы
гомологии пространства X конечно порождённые. D
А вот другой вид двойственности, которая обобщает вычисление
групп локальных гомологии Я, (!Rn, К" - {х}; Z).
I Предложение 3.46. Если К — компактное локально стягиваемое
подпространство ориентируемого п-мерного многообразия М, то имеют
место изоморфизмы Н,(М,М-К; Ц)ъНп~1(К\ Z) для всех i.
Доказательство. Пусть [7 —открытая окрестность множества К в М,
и пусть V — дополнение некоторого компактного множества в М. Мы
будем предполагать, что 1/П\/ = 0. Тогда ^-произведение с
фундаментальными классами даёт коммутативную диаграмму с точными строками
... —*н(ш-ю ^и{ш)—*н{ш,м-к) « н,о/,и-ю-^...
\ \ \
... -+Hn4(M,UUV) -+Hn4{M,V)-**Hn-iWuV,V) » Нп~1Ш) ^.--
Если перейти к прямому пределу по убывающим U э К и V, то первые две
вертикальные стрелки станут изоморфизмами двойственности Пуанкаре
Н,-(М -К) *НСП~'(М -К) и Н^М)*^'^!^)* Тогда 5-лемма даёт
изоморфизм Н{{М,М - К) ъ limH"~"4L0. Последняя группа изоморфна Нп~1(К)
согласно рассуждениям из доказательства теоремы 3.44 при условии, что
К — ретракт некоторой окрестности в М. Чтобы получить такую
ретракцию, можно сначала построить для некоторого большого к отображение
М «-* Ек, которое является вложением вблизи компактного множества К
методом, применённым для доказательства следствия П.9 в приложении.
Тогда окрестность множества К в Rk ретрагируется на К согласно
теореме П.7 из приложения, таким образом, ограничение этой ретракции на
окрестность К в М завершает доказательство. D
Есть способ распространить двойственность Александера и
двойственность из предыдущего предложения на компактные множества К,
которые не являются локально стягиваемыми, заменив сингулярные
когомологии К на когомологии другого вида, называемые когомологиями
Чеха. Они определяются следующим образом. Каждому открытому
покрытию °l/ — {Ua} данного пространства X можно сопоставить симпли-
циальный комплекс N(4/), называемый нервом покрытия 9/. У него есть
вершина va для каждого Ua, причём на множество из к + 1 вершин натянут
к -мерный симплекс в том случае, когда пересечение соответствующих
к -f 1 множеств Ua непусто. Если другое покрытие У = {Vp} является
§ 3.3. Двойственность Пуанкаре
327
измельчением покрытия °Ы, т. е. каждое множество Vjg содержится в
некотором Ua, то эти включения индуцируют симплициальное отображение
N(V)-+N(W), которое корректно определено с точностью до гомотопии.
Тогда можно образовать прямой предел \\mH{{N(<9/)\ G) относительно
всё более и более мелких открытых покрытий °11. Эта предельная группа
и есть по определению группа когомологий Чеха НХ{Х\ G). Полное
изложение этой теории когомологий можно найти в книге [21]. Оказывается,
если аналогично определить относительные группы, то когомологий Чеха
удовлетворяют тем же самым аксиомам, что и сингулярные когомологий,
и в действительности имеет место более сильная аксиома вырезания:
отображение (X, Л) —> (F, В), для которого ограничение X - А —> Y - В
является гомеоморфизмом, индуцирует изоморфизмы групп когомологий
Чеха. Для пространств, гомотопически эквивалентных CW-комплексам,
когомологий Чеха совпадают с сингулярными когомологиями, но для
пространств, локально устроенных сложно, они часто ведут себя более
разумно. Например, если X — подпространство в R3, состоящее из сфер
радиуса 1/л с центрами (1/л, 0, 0) для л = 1, 2,..., то, вопреки
ожидаемому, группа Я3(Х; Z) отлична от нуля, как показано в [81]. Но Н3(Х; Z) =0,
а Н2(Х\ Z) = Z°° — это прямая сумма счётного набора групп Z.
Достаточно странно, что соответствующие группы гомологии Чеха,
определяемые с помощью обратных пределов, не столь хороши. Это
связано с тем, что аксиома точности нарушается из-за того
алгебраического факта, что обратный предел точных последовательностей не обязан
быть точным, в отличие от прямого предела; см. § 3.F. Однако есть способ
обойти эту проблему, используя более тонкое определение. Это теория
гомологии Стинрода, о которой читатель может узнать из [118].
Задачи
1. Покажите, что существуют неориентируемые одномерные
многообразия, если из определения многообразия убрать условие хаусдорфовости.
2. Покажите, что выкалывание точки из многообразия размерности
более 1 не влияет на ориентируемость многообразия.
3. Покажите, что любое накрывающее пространство ориентируемого
многообразия является ориентируемым многообразием.
4. Пусть для группы G задано действие накрытия на ориентируемом
многообразии М сохраняющими ориентацию гомеоморфизмами.
Докажите, что M/G тоже ориентируемо.
5. Докажите, что М х N ориентируемо тогда и только тогда, когда оба
многообразия М и N ориентируемы.
6. Пусть даны два непересекающихся связных л-мерных
многообразия Мг и М2. Связное п-мерное многообразие М<[$М2, называемое их
связной суммой, можно построить, вырезав внутренности замкнутых л-мер-
328
Глава 3. Когомологии
ных шаров В1 с Мг и В2 с М2 и отождествив полученные при этом гра.
ничные сферы дВг и дВ2 посредством некоторого гомеоморфизма между
ними. (Предполагается, что каждый шар В, хорошо вкладывается в
некоторый больший шар в М,.)
а) Докажите, что если многообразия Мг и М2 замкнутые, то имеют
место изоморфизмы Hi(Ml$M2] Z) % Н{Ши Z) 0 Н((М2; Z) при 0 < i < п
с единственным исключением: если М, и М2 неориентируемы, то группа
H^CMJM^Z) получается из Hn_](M];Z)eHn_1(M2>Z) заменой одного
из двух слагаемых Z2 слагаемым Z. [Чтобы разобраться в исключительном
случае, можно применить эйлерову характеристику.]
б) Докажите, что
ДГ(М1ЛМ2) = ^(М1) + ^(М2)-г(5я),
если многообразия Мг и М2 замкнутые.
7. Для отображения /: М —> N связных замкнутых ориентируемых
n-мерных многообразий с фундаментальными классами [М] и [N]
степень f определяется как целое число d, для которого /*([М]) = d[N]; таким
образом, знак степени зависит от выбора фундаментальных классов.
Докажите, что для любого связного замкнутого ориентируемого п-мерного
многообразия М существует отображение М -*Sn степени 1.
8. Дано отображение f:M-*N связных замкнутых ориентируемых
п-мерных многообразий. Предположим, что существует такой шар BCN,
что /-1(B) является объединением непересекающихся шаров В,, каждый
из которых / отображает гомеоморфно на В. Докажите, что степень
отображения / равна Y*ei> гДе ei Равно +1 или -1 в соответствии с тем,
сохраняет или изменяет отображение f \ В{-*В локальные ориентации,
индуцированные изданных фундаментальных классов [М] и [N].
9. Докажите, что р-листное накрытие М -+N имеет степень ±р, если
М и N — связные замкнутые ориентируемые многообразия.
10. Докажите, что для отображения f:M-*N степени 1 связных
замкнутых ориентируемых многообразий индуцированное отображение
/*: пхМ —> nxN сюръективно; следовательно, отображение /+: Н\{М)~^
-*H\{N) тоже сюръективно. [Поднимите / в накрывающее пространство
N -+N, соответствующее подгруппе Im/* с n^N, а затем рассмотрите два
случая, когда это накрытие конечнолистное и когда оно бесконечнолист-
ное.]
11. Пусть Mg обозначает замкнутую ориентируемую поверхность
рода g. Докажите что отображение Mg —> Mh степени 1 существует тогда
и только тогда, когда g^h.
12. В качестве алгебраического приложения предыдущей задачи
докажите, что в свободной группе F с базисом jq, ...,x2k произведение
коммутаторов [xi,x2]...[x2k_ux2k] не равно произведению менее чем к
коммутаторов [v,, vvr] элементов vhw(eF. [Напомним, что двумерная клетка
§ 3.3. Двойственность Пуанкаре
329
комплекса Мк приклеена по произведению [xi,x2]---[*2fc-b*2fc]- По
соотношению [x<[9x2\...[x2k-i,X2k] = [vl,wl]...[Vj,Wj] в группе F постройте
отображение М; —>Мк степени 1.]
13. Пусть Mfh<zMg — компактная подповерхность рода h с одной
граничной окружностью, т.е. M'h гомеоморфна Mh с вырезанным открытым
диском. Докажите, что не существует ретракции Mg —> M'h, если h > g/2.
[Примените предыдущую задачу, используя тот факт, что поверхность
Mg - M'h имеет род g-h.]
14. Пусть X —- букет стягивающихся окружностей из примера 1.25, т. е.
подпространство в :R2, состоящее из окружностей радиуса 1/пс центрами
(1/п,0)дляп = 1,2,...
а) Пусть /„:/—> X — петля с началом и концом в начале координат,
один раз обходящая окружность с номером п. Покажите, что бесконечное
произведение коммутаторов [/ь /2][/3, /4]... определяет петлю в X,
которая нетривиальна в Hj(X). [Воспользуйтесь задачей 12.]
б) Рассмотрим X как букет подпространств Л и В, состоящих из
окружностей с чётными номерами и с нечётными номерами соответственно.
Воспользуйтесь той же самой петлёй, чтобы показать, что отображение
Hi(X) —►Н^Л) 0Hi(B), индуцированное ретракциями пространства X на
А и на В, — не изоморфизм.
15. Для n-мерного многообразия М и компактного подпространства
АсМ докажите, что группа Нп(М,М — А\К) изоморфна группе VR(A)
сечений накрытия MR —► М над Л, т. е. отображений Л —► MR, композиция
которых сМй->М-тождественное отображение.
16. Докажите, что
для всех аеQ(X; R), 4>eCJ(X;R) и яреСт(Х\ R). Выведите из этого, что
^-произведение превращает НДХ; R) в правый Я*(Х; К)-модуль.
17. Докажите, что прямой предел точных последовательностей точен.
И вообще, докажите, что гомологии коммутируют с прямыми
пределами: если {Са, /ад} — направленная система цепных комплексов, в которой
отображения fap: Са —► Сд цепные, то H„(limC„) = Нт Н„(Са).
18. Докажите, что прямой предел HmGa абелевых групп без кручения
Ga не имеет кручения. И вообще, докажите, что любая конечно
порождённая подгруппа в limGa реализуется как подгруппа в некоторой группе Ga.
19. Докажите, что прямой предел счётных абелевых групп по
счётному множеству индексов счётен. Примените это, чтобы доказать, что если
•X" —открытое множество в Еп, то группа Н;(Х; Z) счётна для всех i\
20. Докажите, что Нс°(Х; G) = 0, если пространство X линейно связно
И некомпактно.
21. Для пространства X обозначим через Х+ его одноточечную ком-
Пактификацию. Пусть у добавленной точки, обозначенной оо, есть окрест-
330
Глава 3. Когомологии
ность в Х+, которая является конусом с вершиной оо. Докажите, что
очевидное отображение Н"(Х; G) —>НП(Х+, оо; G) — изоморфизм для всех п.
[Вопрос: верно ли это, когда X = Z x Ш]
22. Докажите, что Нсп(Х х Е; G)*H?-l(X; G) для всех п.
23. Докажите, что для локально компактного Д-комплекса X группы
симплициальных и сингулярных когомологии Hlc(X;G) изоморфны. Это
можно сделать, показав, что Д[.(Х; G) является объединением своих
подгрупп Д'(Х, A; G), когда А пробегает подкомплексы в X, которые содержат
все симплексы, кроме конечного числа, и аналогично Clc(X\ G)
—объединение своих подгрупп С'(Х, А\ G) для того же самого семейства
подкомплексов А.
24. Пусть М — связное замкнутое трёхмерное многообразие.
Запишем Н{ (М; Z) в виде И Ф F, т. е. в виде прямой суммы свободной абелевой
группы ранга г и конечной группы F. Докажите, что группа H2(M;Z)
равна Zr, если М ориентируемо, и равна Zr~] 9Z2, если М неориенти-
руемо. В частности, г ^ 1, когда М неориентируемо. Используя задачу б,
постройте примеры, показывающие, что нет никаких других ограничений
на группы гомологии замкнутого трёхмерного многообразия. [В неориен-
тируемом случае рассмотрите многообразие N, полученное из S2 х / при
отождествлении S2 х {0} с S2 х {1} посредством зеркальной симметрии
сферы S2,]
25. Докажите, что если у замкнутого ориентируемого
многообразия М размерности 2fc группа Hk_{W, Z) свободна от кручения, то группа
Ик{М\ Z) тоже свободна от кручения.
26. Вычислите структуру ^-произведения в H*(S2 x S8|JS4 x S6; Z) и,
в частности, покажите, что единственные нетривиальные произведения —
это те, которые предписаны двойственностью Пуанкаре. [См. задачу б.
Этот результат имеет очевидное обобщение для связных сумм
многообразий S1 х Sn~l с фиксированным п и переменным £.]
27. Докажите, что после подходящей замены базиса кососимметричс-
скую невырожденную билинейную форму над Z можно представить мат-
- * (° -А
рицеи, состоящей из блоков I на диагонали и нулей в остальных
местах. [Для матрицы билинейной формы следующую операцию можно
реализовать заменой базиса. Прибавим целое кратное z'-й строки к j-й
строке и прибавим то же самое целое кратное i-ro столбца к j-му столбцу.
Используйте эту операцию, чтобы привести к требуемому виду каждый
столбец по очереди. Заметим, что у кососимметрической матрицы на
диагонали должны стоять нули.]
28. Докажите, что невырожденное симметрическое или кососиммет-
рическое билинейное спаривание над полем F, имеющее вид F" x F" —► F,
не может быть тождественно нулевым при ограничении на все пары
векторов v, w в Je-мерном подпространстве V с F", если к > п/2.
§ 3.3. Двойственность Пуанкаре
331
29. Используя предыдущую задачу, покажите, что если замкнутая
ориентируемая поверхность Mg рода g ретрагируется на граф X с Mgi то
Нг(Х) имеет ранг не более g. Получите из этого другое решение задачи 13
и постройте ретракцию Mg на букет к окружностей для каждого k^g.
30. Докажите, что край R-ориентируемого многообразия тоже К-ори-
ентируем.
31. Докажите, что если М —компактное R-ориентируемое гс-мерное
многообразие, то граничное отображение Ип{М, dM; R) —> Нп_х{дМ\ К)
переводит фундаментальный класс для (М, дМ) в фундаментальный класс
для дМ.
32. Докажите, что компактное многообразие не ретрагируется на
свой край.
33. Докажите, что если М — компактное стягиваемое n-мерное
многообразие, то дМ — гомологическая (/7 - 1)-мерная сфера, т. е. Н({дМ] Z) ъ
^Ht(Sn~l;Z) для всех/.
34. Для компактного многообразия М проверьте, что следующая
диаграмма, связывающая двойственность Пуанкаре для М и дМ,
коммутативна, по крайней мере с точностью до знака:
HK~l(dM;R)
нп_к№\Ю
НкЩ,дМ;Ю
+ Hk(M;R)
ип.к{М\ Ю -*• нп_кщ, дМ] ю
■нкШ\Ю
[ДМ И
■нп_к_х№\Ю
35. Пусть М —некомпактное К-ориентируемое n-мерное
многообразие с краем дМ, имеющим воротник в М. Докажите, что для всех к имеют
место изоморфизмы двойственности Пуанкаре Нк(М\ Я)ъНп_к(М, dM; R).
Используйте 5-лемму и следующую диаграмму:
Hk~\dM;R)
Hn.k{dM;R)
Hk{M,dM;R)
\DM
Hk(M',R)
Hn„kW\ Ю — Hn_k(Mt Ж\ R)+H
Hk(dM;R)
П_Ы(ЙМ;Ю
§ З.А. Универсальные коэффициенты для гомологии
Главная цель этого параграфа —алгебраическая формула для
вычисления гомологии с произвольными коэффициентами в терминах
гомологии с коэффициентами в Z. Эта теория очень похожа на теорему об
универсальных коэффициентах для когомологий из §3.1.
Первый шаг состоит в том, чтобы сформулировать определение
гомологии с коэффициентами в терминах тензорных произведений. Группа
цепей С„(Х; G), как она определялась в §2.2, состоит из конечных
формальных сумм ][]£,сГр gjGG и оу. Д" —>Х. Это означает, что С„(Х; G) — прямая
£
сумма экземпляров группы G, по одному экземпляру для каждого
сингулярного п-мерпого симплекса в X. Более общая относительная группа
цепей С„(Х, Л; G) = Cn(X\ G)/Cn(A\ G) —этотоже прямая сумма
экземпляров группы G, по одному экземпляру для каждого сингулярного /2-мерного
симплекса в Ху не содержащегося в А. Из основных свойств тензорных
произведений, перечисленных при обсуждении формулы Кюниета в §3.2,
следует, что группа G„(X,A;G) естественно изоморфна C„(X,A)®G
посредством соответствия $]&<7|• —► ^сг,;<8>gr При этом изоморфизме гра-
ничиое отображение С„(Х, A; G) —► СП_,(Х, A; G) превращается в отобра-
жение д® 1: С„(Х, A) ®G — Сп_, (X, A) ®G, где д: СМ(Х, А) — Сп_, (X, А) -
обычное граничное отображение для коэффициентов в Z. Таким образом,
мы получаем следующую алгебраическую задачу.
Дан цепной комплекс ... —> Сп -^ Сп_{ —» ... свободных абелевых
групп С„. Можно ли вычислить группы гомологии Н„(С; G) соот-
ветствующего цепного комплекса ... —»С„ ® G ► GM_] ® G —>...
в терминах только группы G и групп гомологии Нп(С) исходного
комплекса?
Идея подхода к этой задаче состоит в том, чтобы сравнить цепной
комплекс С с двумя более простыми подкомплексами —подкомплексами,
состоящими из циклов и границ вС,-и посмотреть, что происходит при
тензорном умножении всех трёх комплексов на G.
§ З.Л. Универсальные коэффициенты для гомологии 333
Пусть Zn = Kerdn с Сп и Вп = Imdn+1 с Сп. Ограничения отображения
дп на эти две подгруппы нулевые, следовательно, эти подгруппы можно
рассматривать как подкомплексы Z и В в С с тривиальными граничными
отображениями. Таким образом, мы получаем короткую точную
последовательность цепных комплексов, состоящую из коммутативных диаграмм
О
+ Zn
+ Q
О
-zn_
п-1
-с
л
"и
«V
]
в
и-1
в„
-^0
(1)
■о
Строки этой диаграммы расщепимы, так как каждая группа Вп свободна
как подгруппа свободной группы Сп. Поэтому Сп &Zn ФВ„_Ь но цепной
комплекс С не является прямой суммой цепных комплексов Z и В
тривиальны, так как хотя граничные отображения в Z и В тривиальны, но
граничные отображения в С могут быть нетривиальными. Теперь умножим
тензорно на G, получив коммутативную диаграмму
0 ^ Zn 0 G
+ Cn®G ^ Bn_Y(S>G ^ 0
й„®1
0
,®1
,®i
(2)
->- ^п-i ®G ^ Cn_j OG —^ Bn_2®G
0
Строки здесь точные, так как строки в диаграмме (1) расщепимы, а
тензорные произведения удовлетворяют соотношению
(A®B)®G*A®G®B®G,
таким образом, строки в диаграмме (2) тоже расщепимые точные
последовательности. Поэтому мы получаем короткую точную
последовательность цепных комплексов 0—*Z®G —>C®G—>B®G—► 0. Так как
граничные отображения тривиальны bZ®GhB®G, соответствующая длинная
точная последовательность групп гомологии имеет вид
Bn®G ->Zn®G-> Нп(С; G) — Вп_г ОG -* Zn_^G
(3)
«Граничные» отображения Bn®G^>Zn®G в этой последовательности —
это просто отображения in ® 1, где in: Вп —> Zn — включение. Это очевидно
из определения граничного отображения в длинной точной
последовательности групп гомологии: в диаграмме (2) нужно взять элемент группы
B„-i ® G, перенести его посредством (дп ОН)"1 в Сп ® G, затем применить
дп® 1, чтобы попасть в Сп_х ®G, а затем вернуться назад в Zn_j ®G.
Длинную точную последовательность (3) можно разбить на короткие
точные последовательности
0->Coker(i„®l) -+Hn(C;G) — Ker(i„_i ®l) — 0, (4)
334
Глава 3. Когомологии
где Coker(in ® 1) = (Z„ ® G)/ Im(i„ ® 1). Следующая лемма показывает, что
это коядро — это просто Нп (С) ® G.
I Лемма З.А.1. Если последовательность абелевых групп А —► В —► С —>
I —► О точная, то последовательность А ® G —> В ® G —> С ® G —> 0 тоже
I точная.
Доказательство. Ясно, что композиция двух соседних отображений
во второй последовательности равна нулю. Кроме того, отображение
j ® 1, очевидно, сюръективно, так как j сюръективно. Чтобы
проверить точность в члене В ® G, достаточно показать, что отображение
В ® G/Im(i ® 1) —> С ® G, индуцированное отображением j ® 1, является
изоморфизмом, что мы сделаем, построив обратное отображение.
Зададим отображение у>: С х G —> B®G/ Im(i ® U) формулой ^(с, g) = Ъ ® g,
где ;(Ь) = с. Это отображение (/? определено корректно, так как если
j(b) = ){У) = с, то Ъ -Ъ' — \{а) для некоторого а е Л в силу точности,
поэтому Ъ ® g - b' ® g = (b - У) ® g = Ца) ® g е Im(i ® 1). Так как
отображение ц> — гомоморфизм по каждой переменной по отдельности, оно
индуцирует гомоморфизм C®G^>B®G/Im(i® 1). Он, очевидно, обратен
отображению В ® G/ Im(i ® 1) —> С® G. D
Остаётся разобраться с ядром Kerfi,,.^ ® 1), или, что эквивалентно,
с Ker(in ® 1). Ситуация здесь такая, что тензорное умножение короткой
точной последовательности
О — Вп ±> Zn —> Нп(С) — 0 (5)
на G даёт последовательность, которая становится точной только после
добавления дополнительного члена Ker(in ® 1):
О — Ker(in ® 1) —>Bn®G -^> Zn®G —> Hn(C)®G-> 0. (6)
Мы покажем, что Ker(i„ ® 1) действительно зависит не от групп Вп и /„,
а только от факторгруппы Нп(С) и, конечно, от G.
Последовательность (5) — свободная резольвента группы Нп(С), где,
как и в § 3.1, свободная резольвента абелевой группы Н — это точная
последовательность
...—» fAfAfo^h-^ о,
в которой все группы Fn свободные. Тензорное умножение свободной
резольвенты такого вида на фиксированную группу G даёт цепной комплекс
... —>Fj®G^—>F0®G::i—>H®G —>0.
Согласно предыдущей лемме он точен в членах F0 ® G и Н ® G, но слева
от этих двух членов он, возможно, не точен. Временно обозначим через
Hn(F ® G) группу гомологии Кег(/П ® 1)/ Im(/n+1 ® 1).
§ З.А. Универсальные коэффициенты для гомологии 335
I Лемма З.А.2. Для любых двух свободных резольвент F и F' группы Н
существуют канонические изоморфизмы Hn(F ® G) ъ Hn(F' ® G) для
всех п.
Доказательство. Воспользуемся леммой 3.1 п.1. В ситуации,
описанной там, у нас есть две свободные резольвенты F и F' вместе с цепным
отображением между ними. Если мы тензорно умножим эти две
свободные резольвенты на G, то получим цепные комплексы F ® G и F' ® G
с отображениями afl ® 1, образующими цепное отображение между ними.
При переходе к гомологиям это цепное отображение индуцирует
гомоморфизмы а*: Hn(F®G)-+ Hn(F'®G)t которые не зависят от выбора
отображений ап, так как если ап и а!п цепно гомотопны посредством цепной
гомотопии Ап, то ап ® 11 и а'п ® 1 цепно гомотопны посредством гомото-
пии Ап®1.
Для композиции Н —* Н' —* Н", когда заданы также свободные
резольвенты F, F' и F" этих трёх групп, индуцированные гомоморфизмы
удовлетворяют соотношению {(За), = /3+а*, так как в качестве цепного
отображения F —» F" можно вывести композицию цепных отображений
F ^>F' -*F". В частности, если мы выберем в качестве а изоморфизм,
а /3—обратный изоморфизм и F" = F, то /3*аж = (/За) + = 1^ = 1, и
аналогично для (3 и а, переставленных местами. Таким образом, а+ —
изоморфизм, если а— изоморфизм. Рассмотрим ещё более частный случай,
выбрав в качестве а тождественное отображение, но с двумя разными
свободными резольвентами F и F'. В результате получим канонический
изоморфизм !„: Hn(F<8> G) -+ Hn(F'®G). □
Группу Hn(F ® G), которая зависит только от Н и G, обозначают
Тогл(Н, G). Так как всегда существует свободная резольвента вида О—>FX —►
—>F0—>H—>0, как отмечено в §3.1, из этого следует, что Torn(H, G)=0 при
п> 1. Обычно группу Тог}(H,G) обозначают просто Tor(H, G). Как мы
позже увидим, Tor(H, G) оценивает меру общего кручения групп Н и G,
отсюда и происходит название «Тог»1.
Определена ли группа Tor0(H,G)? При определении, данном выше,
она была бы нулевой, так как из леммы З.А.1 следует, что
последовательность Fj®G—>F0®G—>H®G—>0 точная. Возможно, лучше изменить
определение групп Нп (F&G), чтобы они были группами гомологии
последовательности ... —> Fj ® G —> F0 ® G —► 0, пропуская член Н ® G, который
можно рассматривать как своего рода аугментацию. При таком
исправленном определении лемма З.А.1 даёт изоморфизм Tor0(H, G)?vH<8G.
Следует отметить, что Tor(H, G) —функтор и от G, и от Н:
гомоморфизмы а: Н-*Н' и (3: G-+G' индуцируют гомоморфизмы а*: Tor(H, G) —>
-*Tor(H', G) и j3,: Tor(H, G) —>Tor(H, G'), удовлетворяющие
соотношениям (аа')* = а*а*, (РР')* = Р*Р'* и 1, = 1. Индуцированное отображение а*
1 От torsion — «кручение». — Прим. перев.
336
Глава 3. Когомологии
было построено в доказательстве леммы З.А.2, а для /3 построение
гомоморфизма р+ очевидно.
Прежде чем перейти к вычислениям групп Tor(H, G), давайте
завершим анализ полученной ранее точной последовательности (4). Вспомним,
что у нас есть цепной комплекс С свободных абелевых групп, группы
гомологии которого обозначены ЯП(С), и тензорное умножение С на G даёт
другой комплекс C&G, группы гомологии которого обозначены Нп{С\ G).
Следующий результат известен под названием теорема об универсальных
коэффициентах для гомологии, так как он описывает гомологии с
произвольными коэффициентами в терминах гомологии с «универсальной»
группой коэффициентов Z.
I Теорема З.А.З. Если С — цепной комплекс свободных абелевых групп,
I то имеют место естественные короткие точные последовательности
I 0 - /-/„(С)®G - ЯП(С; G) - TorCH^CC), G) - О
I для всех п и всех G, причём эти последовательности расщепляются, хотя
I и не естественно.
Естественность означает, что цепное отображение С —* С индуцирует
отображение между соответствующими короткими точными
последовательностями с коммутативными квадратами.
Доказательство. Рассматриваемая точная последовательность —это
последовательность (4), так как мы показали, что можно отождествить
Coker(/„ ®1) с Нп(С) ® G, a Kcrzn_1 с Tor(H„_! (G), G). Доказательство
естественности этой последовательности —устное упражнение па проверку
определения, которое мы оставляем читателю.
Расщепление получается следующим образом. Мы уже заметили
ранее, что короткая точная последовательность 0 —> Zn —> Сп —* Вп...} —* О
расщепима, поэтому есть проекция р: Сп —» Zn, ограничение которой
на Z„ тождественно. Отображение р даёт продолжение фактороотобра-
жения Zn —»Н„(С) до гомоморфизма Сп -*Нп(С). Разрешив п меняться,
мы получаем цепное отображение С-*Н(С), где группы Нп(С)
рассматриваются как цепной комплекс с тривиальными граничными
отображениями, поэтому условие, что отображение цепное, выполняется
автоматически. Теперь, умножив тензорно на G, получим цепное
отображение С ® G —» Н(С) <8> G. Взяв группы гомологии, мы получаем
индуцированные гомоморфизмы /7n(C;G) -» //„(С) ® G, так как граничные
отображения в ценном комплексе J7(C)®G тривиальны. Гомоморфизмы
Нп(С; G)->Hn(G) ® G дают требуемое расщепление, так как на уровне
цепей они тождественны на циклах в G по определению отображения р. J
I Следствие З.А.4. Для каждой пары пространств (X, А) имеют место
I расщепимые точные последовательности
| 0 -> Н„(Х, A)®G-> Н„(Х, A; G) -» Тог(/■/„_., (X, A), G) -> О
§З.А. Универсальные коэффициенты для гомологии 337
для всех л, причём эти последовательности естественны относительно
отображений (X, А) —> {У, В).
Расщепление не является естественным, поскольку если бы это было
так, то отображение X —> У, индуцирующее тривиальные отображения
НП(Х) —>Hn(Y) и Нп_1(Х) —►НП_1(У), должно было бы индуцировать
тривиальные отображения //„(X; G) —> Н„(У; G) для всех G, но в примере 2.51
мы встретились с ситуацией, когда это не так, а именно, для отображения
факторизации M(Zm, л) —►S'1"'"1 в случае группы G = Znr
Основные инструменты для вычисления Тог приводятся в следующем
предложении.
I Предложение З.А.5. Справедливо следующие утверждения:
I 1. Тог(А,В)*Тог(В,А);
I 2. ТогСфА^В^фТогСА-.В);
I
I 3. Тог(Л, В) = 0, если группа А или В свободна, или хотя бы свободна
I от кручения;
I 4. Тог (Л, В) % Тог (74 Л), В), где Г (Л) — подгруппа кручения в Л;
I 5. Tor(Zn>A)wKer(A^A);
I 6. каждой короткой точной последовательности 0—► В —> С —> D —> 0
I естественно сопоставляется точная последовательность
I 0 — Тог(А,В) — Tor(A,C) — Tor(A,D) — ЛОВ — А®С-> Ag>D — 0.
Доказательство. Утверждение 2 доказывается легко, так как в
качестве свободной резольвенты для ©А, можно взять прямую сумму сво-
i
бодных резольвент для Л,. Столь же легко доказывается угверждение 5,
которое получается при тензорном умножении свободной резольвенты
0->Z^Z — ZM — 0 на Л.
Что касается доказательства свойства 3, то у свободной группы А есть
свободная резольвента с Fn = 0 при л ^ 1, поэтому Тог(А, В) = 0 для всех В.
С другой стороны, если группа В свободная, то тензорное умножение
свободной резольвенты для А на В сохраняет точность, так как
тензорное умножение последовательности на прямую сумму групп Z даёт
просто прямую сумму нескольких копий этой последовательности. Поэтому
Тог(Л, В) = 0 и в этом случае тоже. Обобщение на случай группы А или В
без кручения будет приведено ниже.
Для доказательства утверждения 6 выберем свободную резольвенту
0 -* Fj —> F0 —> А —> 0 и, тензорно умножив её на данную короткую точную
Последовательность, получим коммутативную диаграмму
0—*b\®B—^F{®C—^F^D—^0
I ' I
Y Y T
0 —*- F0®B —* F0®C —* F0®D —>- 0
338
Глава 3. Когомологии
Её строки точные, так как тензорное умножение на свободную группу
сохраняет точность. Продолжая три полученных столбца нулями сверху
и снизу, мы получаем короткую точную последовательность цепных
комплексов, для которой соответствующая ей длинная точная
последовательность групп гомологии —требуемая шестичленная точная
последовательность.
Чтобы доказать утверждение п.1, применим утверждение п. 6 к
свободной резольвенте 0 -» Fx -» F0 -» В -» 0. Так как Тог(Л, F}) и Тог(Л, F0)
обращаются в нуль согласно той части утверждения 3, которую мы
доказали, шестичленная последовательность в п. 6 сводится к первой строке
следующей диаграммы:
0 —>- Тог(Л, В) —^ Л ® Fj —* Л ® F0 —*- ЛОВ —>■ 0
Л (g> Fj —^ Л ® F0 —*- ЛОВ —>■
Fj®A—^0®Л—^В®Л—^
0 —^ Тог(В, Л) -
Вторая строка получается из определения группы Тог (В, Л). Вертикальные
изоморфизмы возникают из естественной коммутативности тензорного
произведения. Так как квадраты коммутативны, существует
индуцированное отображение Тог(Л, В) —>Тог(В, Л), которое является изоморфизмом
согласно 5-лемме.
Теперь мы можем доказать утверждение 3 в случае групп без круче-
ний. Для свободной резольвенты 0 —> F} —>F0 —> Л —> 0 мы хотим показать,
что гомоморфизм </? ® 1: F^B-^FoiS^B инъективен, если группа В без
кручения. Предположим, что элемент £]*i ® b,- лежит в ядре отображения
<£ ® 1. Это означает, что ]>] <р0О ® Ь,- можно превратить в 0, конечное чис-
ло раз применяя определяющие соотношения для тензорного
произведений. Лишь конечное число элементов группы В участвует в этом процессе.
Они лежат в конечно порождённой подгруппе В0 с В, поэтому элемент
£лг, ® Ь,- лежит в ядре отображения </? ® 1: Fx ® В0 —> F0 ® В0. Это ядро
1
нулевое, так как Тог(Л, В0) = 0, поскольку группа В0 конечно порождённая
и без кручения, а потому свободная.
Наконец, мы можем получить утверждение 4, применив утверждение
6 к короткой точной последовательности 0 —> Г (Л) —> Л —> Л/7 (Л) —> 0, так
как группа А/Т {А) без кручения. О
В частности, утверждение 5 даёт изоморфизм Tor(Zm,Zn) ^Zq, где
q—-наибольший общий делитель чисел тип. Таким образом, группа
Tor(Zm, Z„) изоморфна Zm ® Z„, хотя это до некоторой степени случайное
совпадение. Комбинируя этот изоморфизм со свойствами 2 и 3, мы видим,
что для конечно порождённых групп Л и В группа Тог(Л, В) изоморфна
тензорному произведению подгрупп кручения в Л и в В, или, грубо говоря,
§ З.А. Универсальные коэффициенты для гомологии 339
общему кручению групп Л и В. В этом одна из причин введения
обозначения Тог; оправдывают это обозначение также свойства 3 и 4.
Гомологические вычисления часто упрощаются, если взять
коэффициенты в поле, обычно в Q или Zp для простого р. В общем случае это
даёт меньше информации, чем для коэффициентов в Z, но некоторые из
существенных свойств всё же сохраняются, как показывает следующий
результат.
I Следствие З.А.6. 1. Hn(X; Q) ** Hn(X; Z) ® Q, поэтому, когда группа
I Hn(X;Z) конечно порождённая, размерность H„(X;(Q)) как линейного
I пространства над Q равна рангу группы НП(Х; Z).
I 2. Если группы Н„(Х; Z) и Н^ДХ; Z) конечно порождённые, то для
I простого р группа Н„(Х; Zp) состоит из:
I а) слагаемого Zp для каждого слагаемого Z в группе НП(Х; Z);
I б) слагаемого Zp для каждого слагаемого Zp* в группе Н„(Х; Z), где
I к>\\
I в) слагаемого Zp для каждого слагаемого Zp* в группе Н„_Т(Х; Z), где
Даже в случае не конечно порождённых групп гомологии,
коэффициенты в поле всё ещё дают хорошую качественную информацию.
I Следствие З.А.7. 1. ЯП(Х; Z) = 0 верно для всех п тогда и только то-
I гда, когда Нп (X; Q) = 0 и Ни(X; Zp) = 0 для всех п и всех простых р.
I 2. Отображение /: X —> У индуцирует изоморфизмы групп гомоло-
I гий с коэффициентами в Z тогда и только тогда, когда оно индуцирует
I изоморфизмы групп гомологии с коэффициентами в Q и в Zp для всех
I простых р.
Доказательство. Утверждение 2 следует из п. 1 при переходе к конусу
отображения /. Теорема об универсальных коэффициентах даёт
утверждение «только тогда» в п. 1. Для угверждения «тогда» достаточно
показать, что если абелева группа А такова, что А ® Q = 0 и Tor(A, Zp) = О
для всех простых р, то А = 0. Для коротких точных последовательностей
О—»Z-^Z—»Zp—>0и0—»Z—»Q—► Q/Z —> 0 шестичленные точные
последовательности в утверждении 6 из предложения З.А.5 принимают вид
О -» Tor(A, Zp) — А — рА — А ® Zp — О,
О — Tor(A, Q/Z) — A — А ® Q — A® Q/Z — 0.
Если Tor(A, Zp) = 0 для всех р, то из точности первой последовательности
р
следует, что гомоморфизм А^>А инъективен для всех р, поэтому группа
А без кручения. Тогда Tor(A, Q/Z) = 0 согласно утверждению 3 или 4
предложения З.А.5. Таким образом, из второй последовательности следует, что
гомоморфизм A^>A®<Q инъективен, поэтому А = 0, если А ® Q = 0. □
Алгебраическая конструкция, посредством которой функтор Тог
получается из тензорных произведений, имеет очень естественное обобще-
34U
Глава 3. Когомологии
ние, в котором абелевы группы заменяются модулями над
фиксированным кольцом R с единицей, если воспользоваться определением
тензорного произведения R-модулей, данным в §3.2. Свободные резольвенты
R-модулей определяются так же, как и для абелевых групп, с помощью
свободных R-модулей, которые являются прямыми суммами нескольких
экземпляров кольца R. Леммы ЗЛЛ и З.А.2 переносятся в этот контекст без
изменений, а потому определены функторы Тог^(А, Б). Однако не всегда
имеет место равенство Тог^(Д, В) = 0 при п > 1. Причина, по которой это
было верно для R = Z, состоит в том, что подгруппы свободных групп
являются свободными, но подмодули свободных R-модулей, вообще
говоря, не обязаны быть свободными. Если R —область главных идеалов,
то подмодули свободного R-модуля свободны, таким образом, в этом
случае оставшаяся часть алгебраической конструкции, в частности
применение теоремы об универсальных коэффициентах, проходит без изменений.
Когда Я —это поле F, любой модуль свободен и Torfj (Л, В) =0 для л > 0
ввиду наличия свободной резольвенты 0 —► А —► А —> 0. Таким образом,
Нп(С <8>F G) % Нп (С) <g>F G, если F - поле.
Задачи
1. Используя теорему об универсальных коэффициентах, докажите,
что если группа НДХ; Z) конечно порождённая, а значит, определена
эйлерова характеристика #(Х) = £(~l)nrankH;l(X; Z), то для любого поля
п
коэффициентов F выполняется равенство # (X) = ^(—1УгdimHn(X\ F).
п
2. Докажите, что группа Tor(A, Q/Z) изоморфна подгруппе кручения
в А. Выведите из этого, что группа А свободна от кручения тогда и только
тогда, когда Тог(Л, В) =0 для всех В.
3. Докажите, что если группы Hn(X;Q>) и Нп{Х\Ър) нулевые для
всех л и всех простых р, то НП(Х; Z) = 0 для всех л, а потому НП(Х; G)~0
для всех G и п.
4. Докажите, что функторы ® и Тог коммутируют с прямыми
пределами: (lim Ад) ® В = Ит(Аа 0В) и Torflim Аа,В) = ИтТог(Аа, В).
5. Из того факта, что Тог (А, В) =0, если группа А свободная,
выведите, что Тог(А, В) = 0, если группа А без кручения, применив предыдущую
задачу к направленной системе конечно порождённых подгрупп Аа в А.
6. Покажите, что группа Тог(А, В) всегда состоит из элементов
конечного порядка и что Тог(А, В) содержит элемент порядка л тогда и только
тогда, когда обе группы А и В содержат элементы порядка л.
§ З.В. Общая формула Кюннета
Формулы Кюннета описывают гомологии или когомологии
произведения пространств в терминах гомологии или когомологии множи-
§ З.В. Общая формула Кюннета
341
«гелей. В хороших случаях эти формулы принимают вид f/ДХ х Y\ R) ^
»Н*(Х;Д)<8>НДУ;К) или Н*(* х У; R) **H*(X; R) <g>H*(V; Я) для кольца
коэффициентов К. В случае когомологии такая формула приводилась
9 теореме 3.16 при предположении о конечной порождённое™ и
свободное™ когомологии одного множителя. Если нужно получить общую
формулу без этих предположений, то оказывается, что гомологии более
естественны, чем когомологии, и основная цель этого параграфа состоит
В том, чтобы получить общую формулу Кюннета для гомологии. Новое
свойство общего случая —это то, что необходим дополнительный член
Тог, чтобы полностью описать гомологии произведения.
Внешнее произведение в гомологиях
Основная составляющая формулы Кюннета — внешнее произведение,
т. е. отображение
Н£Х\ Ю х Н;(У; К) Д Н,Ч;(Х х У; R).
Его можно определить двумя способами. Один из них —прямое
определение для сингулярных гомологии, включающее явные симплициальные
формулы. Более поучительным, однако, является определение в
терминах клеточных гомологии. Для него необходимо считать X и Y CW-kom-
плексами, но это предположение можно потом убрать методом CW-an-
йроксимации из §4.1. Поэтому мы сосредоточимся на клеточном
определении и приведём симплициальное определение позже в этом параграфе
для тех, кому интересно знать, как оно выглядит.
Ключевой составляющей в определении клеточного внешнего
произведения является тот факт, что клеточное граничное отображение
удовлетворяет соотношению d(el x e;) = del x e; -f (-l)'e' x deK В правой
части этой формулы неявно использовано соглашение рассматривать
символ х как билинейную операцию на клеточных цепях. При таком
соглашении мы можем сказать, что вообще d{a x b) = da x Ъ + (-l)'a x db,
когда а —клеточная /-мерная цепь, а Ъ — клеточная j-мерная цепь. Из
Этой формулы видно, что внешнее произведение двух циклов является
Циклом. Кроме того, произведение границы и цикла — граница, так как
da х b = d(a x b), если db = 0, и аналогично a x db= (-l)'d(a x b), если
da = 0. Следовательно, возникает индуцированное билинейное
отображение Н,(Х; R) х Hj(Y\ R) —> H(+j(X x У\ Ю, которое по определению
является внешним произведением в клеточных гомологиях. Так как это
отображение билинейно, его можно также рассматривать как гомоморфизм
**iCX; Ю ®RHj(Y; R) ->Hi+j(X х У; Я). В любой из этих форм внешнее
произведение оказывается независимым от клеточных структур на X и на Y.
Наша задача теперь состоит в том, чтобы выразить граничные
отображения в клеточном ценном комплексе СДХ х Y) для X х Y в терминах
граничных отображений в клеточных цепных комплексах СЖ{Х) и С\(У). Для
342
Глава 3. Когомологии
простоты мы здесь рассмотрим гомологии с коэффициентами в Z, но та же
самая формула для произвольных коэффициентов немедленно следует из
этого частного случая. Для коэффициентов в Z группа клеточных цепей
С,(Х) свободная с базисом, состоящим из i-мерных клеток в X, но при
этом имеется неоднозначность с выбором знака для элемента базиса,
соответствующего клетке е\ а именно с выбором образующей для слагаемого
Z группы Н^Х1, Х1~}), соответствующего клетке е'. Лишь при i = 0 этот
выбор является каноническим. Мы будем называть такой выбор «выбором
ориентации клеток». Выбор этих ориентации позволяет однозначно
представить клеточную i-мерную цепь в виде линейной комбинации i-мерных
клеток.
Формула d(e' x ej) = del х eJ -Ь (-l)'e' x de; не вполне каноническая,
так как она содержит знак (—1)', но не (-1)J. Очевидно, между двумя
множителями е{ х ej делается некоторое различие. Поскольку знаки
возникают как результат ориентации, нужно описать явно, как ориентации
клеток е1 и е; определяет ориентацию клетки е1 х е;. При помощи
характеристических отображений ориентации можно получить из ориентации
шаров, на которых заданы характеристические отображения. Удобно
рассматривать эти шары как кубы, поскольку произведение двух кубов —это
снова куб. Таким образом, для клетки е1а мы берём характеристическое
отображение Фа: /' —►Х, где /' — произведение i отрезков [0, 1].
Ориентация куба /' —это образующая группы H,-(J', dV), а образ этой образующей
при отображении Фа* даёт ориентацию клетки е1а. Для любой точки х
внутри /' можно отождествить Н{(Г, 3I1) с Н,(Г, V - {*}), а тогда
ориентация определена линейным вложением А1 —> V с точкой х, выбранной
внутри образа этого вложения. Это вложение задаётся его
последовательностью вершин v0,..., v,. Векторы vl - v0,..., v{ - v0 линейно независимы
в кубе /', который мы рассматриваем как единичный куб в R1. Таким
образом, ориентация в нашем смысле эквивалентна ориентации в
смысле линейной алгебры, т. е. классу эквивалентности упорядоченных
базисов, где два упорядоченных базиса считаются эквивалентными, если они
получаются друг из друга линейным преобразованием с положительным
определителем. (Упорядоченный базис можно непрерывно продеформи-
ровать в ортонормированный базис с помощью процесса Грама—Шмидта,
и два ортонормированных базиса связаны либо поворотом, либо
поворотом с последующей зеркальной симметрией, в соответствии со знаком
определителя преобразования, переводящего один базис в другой.)
Помня об этом, мы принимаем соглашение, что ориентация
произведения V х /; =V+J получается при выборе упорядоченного базиса,
состоящего из упорядоченного базиса для 1\ после которого идёт
упорядоченный базис для V. Отметим, что тогда изменение ориентации для /' или для
V изменяет ориентацию для /'+;, поэтому реально имеет значение только
порядок двух множителей в /' х /;.
§ З.В. Общая формула Кюннета
343
I Предложение З.ВЛ. Граничное отображение в клеточном цепном
I комплексе СДХ х У) определяется граничными отображениями в кле-
I точных цепных комплексах СДХ) и С*(У) посредством формулы
] d(e{ х ej) = de[ x ej + (-l)'V x deK
Доказательство. Сначала рассмотрим частный случай куба /п.
Зададим на I структуру CW-комплекса с двумя вершинами и одним ребром.
Тогда i-й экземпляр отрезка / имеет одномерную клетку е, и нульмерные
клетки 0, и 1,, причём de{ = 1, - 0,. Клеткой размерности п в
произведении 7П является ех х ... х еп, и мы утверждаем, что граница этой клетки
задаётся формулой
(*) d(ex х ... х еп) = ^(-1)'"+1е, x ... х de{ x ... х еп.
Эта формула верна по модулю знаков отдельных членов ех х ... х 0,- х ...
... х еп и ех х ... х 1, х ... х еп, так как они представляют собой в точности
(п - 1)-мерные клетки в граничной сфере д1п куба 1п. Чтобы получить
знаки в формуле (*), заметим, что перестановка двух концов множителя
I в 1п даёт зеркальную симметрию сферы 0J", точно так же, как и
перестановка двух соседних множителей /. Поскольку зеркальные симметрии
имеют степень —1, из этого следует, что формула (*) верна с точностью до
полного знака. Этот окончательный знак можно определить, посмотрев
на любой член, например, на член 0l x e2 x ... х еПУ который в формуле
(*) имеет знак минус. Чтобы проверить, что этот знак правильный,
рассмотрим n-мерный симплекс [v0,..., vn] с вершиной v0 в начале координат
и вершиной vk — концом единичного вектора, направленного по к-й
координатной оси при к> 0. Этот симплекс определяет «положительную»
ориентацию куба /п, как описано ранее, и в обычной формуле для границы
грань [v0, v2,..., vn], которая определяет положительную ориентацию для
грани 0: х е2 х ... х еп куба Г\ имеет знак минус.
Если мы запишем J" =/' х /•>, где i + j = п, и положим е' =ех х ... х е,-
и eJ =е,+1 х ... х еп, то формула (*) превращается в формулу d(el x eJ) =
^del x ej 4- (-l)V x de}. Мы воспользуемся естественностью, чтобы
свести общий случай формулы границы к этому частному случаю. Если иметь
Дело с клеточными гомологиями, то отображения /: X —► У, которые
индуцируют цепные отображения /+: С„(Х) —> С*(У) клеточных цепных
комплексов,—это клеточные отображения, переводящие Хп в У" для всех п,
а значит, переводящие (Х",ХП-1) в (УП,УП_1). Тогда необходимое нам
Утверждение о естественности заключается в следующем.
I Лемма З.В.2. Для клеточных отображений f: X —> Z и g: У —> W
I клеточные цепные отображения /,: СДХ) -> СЛ%), g*> С (У) -* СЛЮ
I и (/ х g)*: СДХ х Y) -> CSZ х W) связаны соотношением (/ х g)+ =
■ =/*xg*.
344
Глава 3. Когомологии
Доказательство. Соотношение (/ х g), = /„ х g„ означает, что если
/*(<)=1>*гег и8*(е4)=1]п/95е^то
г б
(/ х £)*(< х е£) = Yjm*YnP5K х Ф«
Коэффициент тау — это степень композиции
где первое и третье отображения индуцированы характеристическими
отображениями1 для клеток е'а и el a среднее отображение
индуцировано клеточным отображением /. При естественном выборе отмеченных
точек в этих факторпространствах отображение far сохраняет
отмеченные точки. Коэффициенты пр5 получаются аналогично из отображений
gp5: Sj -^Sj. Для f x g отображение (/ x g)apfY5: Sl+j -> Sl+;", степень
которого—коэффициент при el x eJ5 в (/ хg)*(ela хер, получается из
произведения отображений
/ауХ£(35'.&Х& ^S(XSJ
при стягивании в точку (i 4- j — 1)-мерного остова комшшкса Sl x SK
Другими словами, (/ хg)apy5 — приведённое произведение отображений
fay А £{35- Нам нужно доказать формулу deg(/ Л g) = deg(/)deg(g) для
сохраняющих отмеченную точку отображений /: S1 —> S1 и g: SJ' —► S'.
Так как / Л g — это композиция отображений / Л1 и 1Лg, достаточно
доказать, что deg(/ Л 1) = deg(/) и deg(l Л g) = deg(g). Мы сделаем это,
связав приведённые произведения с надстройкой. Приведённое
произведение X A S] можно рассматривать как X х lj{X x dl U {х0} х 7), таким
образом, это приведённая надстройка 2Х, т. е. факторпространство
обычной надстройки SX, полученное при стягивании отрезка {х0} х I в точку.
Если X — CW-комплекс с нульмерной клеткой х0, то отображение
факторизации SX —>Х AS1 индуцирует изоморфизм гомологии, так как оно
переводит в точку стягиваемый подкомплекс. Взяв X = Sl, мы получим
коммутативную диаграмму
S{S() -^ S(S()
\ ,t i
i /At -,
SlAS] ^S'AS1
и из индуцированной коммутативной диаграммы групп гомологии //,-~i
мы выводим, что отображения Sf и / Л1 имеют одну и ту же степень. Так
как надстройка сохраняет степень согласно предложению 2.33, мы
получаем, что deg(/ Л1) = deg(/). В этой формуле 1 — тождественное отображе-
1 Третье отображение —это ретракция букета сфер Z'/Z'~] на сферу, соответствуют/10
клетке е1 .—Прим. ред.
§ З.В. Общая формула Кюннета
345
ние окружности S , и итеративно мы получаем тот же самый результат для
тождественного отображения сферы S;, так как SJ является приведённым
произведением j экземпляров окружности S1. Из этого также следует, что
deg(l Л#) = deg(g), так как перестановка координат в S'+; не влияет на
степень отображения S'+J —► Sl+jf. П
Теперь, чтобы закончить доказательство предложения, рассмотрим
ф: J' —► X' и Ф: V —> УJ — характеристические отображения клеток e[z с X
и ei с У. Ограничение отображения Ф на dV —это отображение
приклеивания для е1а. Можно предварительно сделать гомотопию этого
отображения приклеивания dV -*X'_1 так, чтобы оно стало клеточным. Для этого
нет никакой надобности обращаться к теореме о клеточной
аппроксимации, так как это легко доказать непосредственно. Сначала продефор-
мируем отображение приклеивания так, чтобы оно переводило в точку
все грани куба /', кроме одной, что можно сделать, так как
объединение этих граней стягиваемо, затем сделаем дальнейшую деформацию так,
чтобы точка, которая является образом этого объединения граней, стала
нульмерной клеткой, Гомотопия отображения приклеивания dV —► Х'"1 не
затрагивает клеточную границу dela, так как dela определяется индуциро-
ранным отображением H^idV)^>Н^^Х1'1)^>Н(_}(Х1~\ Х1~2). Поэтому
можно считать, что отображение Ф клеточное, и аналогично для Ф,
следовательно, отображение Ф х Ф тоже клеточное. Отображение клеточных
цепных комплексов, индуцированное клеточным отображением CW-kom-
плексов, — цепное отображение, коммутирующее с клеточными
граничными отображениями.
Если е'— i-мерная клетка куба /', а е} — j-мерная клетка куба Jj, то
Ф*(е')=ед, ФДе;) = во и (Ф х Ф)*(е' xe^)=ela xel, следовательно,
d(e^ х eJ) =а((Фх Ф)¥(е£ х ej)) =
= (Ф х ФЗ^Се1 х е;), так как (Ф хФ),- цепное отображение,
= (Ф х Ф)+Уе' х е; + (-l)'e' x de;), согласно частному случаю,
= Ф+(de') х ФДеО-Ь(-1УФ*(е') хФ+Ие;), согласно лемме,
= dФж(e,) х ФДеО -Ь (-1)'Ф*(е') х dФ+(ej), так как Ф.иФ,-
цепные отображения,
= de'ax^ + (-l)'e'exde^
Что и завершает доказательство предложения. П
Пример З.В.З. Рассмотрим X х Sk, где мы снабжаем Sk обычной
CW-структурой с двумя клетками. Формула границы в СЖ(Х х Sk)
принимает вид d(a xb)=daxb1 так как d = 0 в C*(Sk). Поэтому цепной комплекс
С*(Х х Sk) — это просто прямая сумма двух экземпляров цепного комплек-
Са С*(Х), причём в одном из экземпляров размерность сдвинута вверх
На fc. Следовательно, Я,?(Х х Sk\ Ж) ъ Н„(Х; Z) 9 Нп_к(Х\ Z) для всех п.
346
Глава 3. Когомологии
В частности, мы видим, что все классы гомологии в X х Sk являются
внешними произведениями классов гомологии в X и Sk.
Пример З.В.4. Более тонкие свойства проявляются, когда оба
пространства X и Y имеют кручение в гомологиях. Рассмотрим самый
простой случай, когда X — это S1 с клеткой е2, приклеенной по отображению
Sl ~^>Sl степени т. Таким образом, Н\{Х\Ъ)ъЪт и Н{(Х\ Z) = 0 при {>1,
Точно так же, пусть Y получено из S1 приклеиванием двумерной клетки
по отображению степени п. Таким образом, каждое из пространств X
и Y имеет CW-структуру с тремя клетками, поэтому X х Y имеет девять
клеток. Они обозначены точками на диаграмме
-<-
—л
-«г-
т
т
е° е1 е2
где пространство X расположено в горизонтальном направлении, a Y —
в вертикальном направлении. Стрелками обозначены клеточные
граничные отображения, отличные от нуля. Например, две стрелки, выходящие
из точки в верхнем правом углу, указывают, что д{е2 х е2) = m(e1 x е2) +
+ п(е2 хе1). Очевидно, что группа Нх {X х У; Z) равна Zm®Zn. В
размерности 2 группа Kerr) порождена элементом е1 хе1, а образ граничного
отображения в размерности 3 состоит из элементов (1т — кп)(ех х е1). Они
образуют циклическую группу, порождённую элементом q{el x e1), vj\eq —
наибольший общий делитель чисел тип; таким образом, Н2(Х х Y; Z)&Zq.
В размерности 3 циклы — кратные элемента (m/q)(el xe2) + (n/q)(e2xe1),
и наименьшее такое кратное, которое является границей, — это
q[(m/q)(el х е2) + (n/q)(e2 х е1)] = т{е1 х е2) + п(е2 х е1);
таким образом, Н3(Х х Y; Z) &Zq. Так как у X и Y нет гомологии в
размерности выше 1, эти трёхмерные гомологии пространства X х Y не
могут быть реализованы внешними произведениями. Как покажет
общая теория, H2(Xx7;Z)-3T0 H^X; Z) <g> H^Y; Z), а Я3(Х х Y\Z)-oro
Tox(H^(X\Z)>Hl(Y\Z)).
Этот пример легко обобщается на более высокие размерности, если
положить X = Sl Uez+1 и У = S; Ue;+1, где отображения приклеивания
имеют степени тип соответственно. По существу то же самое вычисление
показывает, что у X х Y обе группы Н;Ч;- и Н,+;+1 изоморфны Zq.
Следует сказать несколько слов о том, почему внешнее произведение
не зависит от CW-структуры. Для этого нам понадобится утверждение о
§ З.В. Общая формула Кюннета
347
том, что любое отображение С\У-комплексов гомотопно клеточному
отображению, доказанное в следующей главе в теореме 4.8. Как мы уже
упоминали ранее, клеточное отображение индуцирует цепное отображение
клеточных цепных комплексов. Из эквивалентности клеточных и
сингулярных гомологии легко видеть, что отображение клеточных гомологии,
индуцированное клеточным отображением, —- это то же самое, что и
индуцированное отображение сингулярных гомологии. Теперь предположим,
что у нас есть клеточные отображения /:X->Z Hg: y->W. Тогда
лемма З.В.2 влечёт, что диаграмма
Ht(X; Z) х Н;(У; Z) -^ Ht+f(X х У; Z)
Hr(Z; Z) x H}[W\ Z) -^ Ht+f{Z x W; Z)
коммутативна. Теперь возьмём в качестве Z и W те же самые
пространства, что и X и У, но с другими CW-структурами, и пусть / и g
—клеточные отображения, гомотопные тождественному. Тогда вертикальные
отображения в диаграмме тождественные, а коммутативность диаграммы
означает, что внешние произведения, определённые при помощи разных
CW-структур, совпадают.
Внешнее произведение, очевидно, является билинейным, или,
другими словами, дистрибутивным. Нетрудно проверить, что оно также
ассоциативно. Как обстоят дела с коммутативностью? Если Т: X xY —>Y х X —
перестановка множителей, то можно спросить, равны ли ТДа х Ь) и b x а.
Единственный эффект, который производит перестановка множителей на
определение внешнего произведения, связан с соглашением о том, что
ориентация произведения /' х /; задаётся упорядоченным базисом в
первом множителе, после которого идёт упорядоченный базис во втором мно-
'Жителе. Перестановку этих двух множителей можно получить,
переставляя каждую из i координат в Г с каждой из координат в /;. Всего для
этого требуется ij перестановок соседних координат, каждая из которых
реализуется зеркальной симметрией, поэтому возникает знак (—1)^.
Таким образом, правильная формула имеет вид T*{a x b) = (—l)';'b x а, где
аеН^ЮиЬеНДУ).
Алгебраическая формула Кюннета
Соединяя вместе всевозможные внешние произведения, мы получаем
отображение
(^{Н^Х- Z) ® НП_,(У; Z)) — Нп{Х х У; Z),
и естественно задаться вопросом, будет ли оно изоморфизмом.
Приведённый выше пример З.В.4 показывает, что так бывает не всегда, хотя
это и верно в примере З.В.З. Наша главная цель сейчас состоит в том,
348
Глава 3. Когомологии
чтобы показать, что это отображение всегда инъективно и что его
коядром является группа ф Тог (Я,-(X; Z), H„_,-_2 (У; Z)). Мы рассмотрим также
i
и другие коэффициенты, отличные от Z, и покажем, в частности, что j\nn
коэффициентов в поле это отображение —изоморфизм.
Для С W-комплексов X и У связь между клеточными цепными
комплексами СДХ), СДУ), и СДХ х У) хорошо выражается в терминах
тензорных произведений. Так как п-мерные клетки в X х У—это
произведения /-мерных клеток в X на (п-0-мерные клетки в У, мы получаем
СП(Х х У) ^0(С,(Х) 0С„_,(Г)), причём е1' х е'} соответствует е' ®ej. При
таком отождествлении формула для границы из предложения З.ВЛ
принимает вид d(e' ® е;) = def ® eJ -f (~l)lel ®dej. Наша задача теперь
становится чисто алгебраической: вычислить гомологии цепного комплекса
СДХ х У) по гомологиям цепных комплексов СДХ) и СДУ).
Предположим, что заданы цепные комплексы С и С/ абелевых групп С„
и Сп или вообще Я-модули над коммутативным кольцом R. Тогда
тензорное произведение цепных комплексов C®R С определяется как (С®д С'),, =
= ф(С; ®я С'^.) с отображениями границы, заданными формулой д(с®с') =
i
= дс®с/ + (~1)|'с®г)с/длясеС,- ис'еС^.. Знак (-1)' гарантирует, чтод2 = 0
в С ®д С', так как
д2(с®с) = d(dc®c'+(-l)'c®dc/) =
= d2c®c4(-l)'~Idc®dc4(-l)'dc®dc4c®dV = a
Из формулы для границы г)(с ® с') = (9с ® с + (-l)'c ® дс' следует, что
тензорное произведение циклов —цикл, а тензорное произведение цикла
и границы (в любом порядке) является границей, так же, как и для
внешнего произведения, определённого ранее. Таким образом, существует
естественное индуцированное отображение групп гомологии /7, (С) ®r
®я НпЧ(С') -* НП(С ®R СО- Суммирование по г тогда даёт отображение
® (НДС) ®R Н^ДС')) — НП(С ®R С'). Оно участвует в следующей алгеб-
i
раической версии формулы Кюннета.
I Теорема З.В-5. Пусть R —область главных идеалов, а R-модули С,-
I свободные. Тогда для любого п существует естественная короткая точ-
I пая последовательность
I о - ф(я,(С) «„^,..,(0) - н„(с®„ с') -
I - ф(Тогк(Н,(С), «„..-^(С')) ^ °'
I
I причём эта последовательность расщепима.
§ З.В. Общая формула Кюннета
349
Это обобщение теоремы об универсальных коэффициентах для
гомологии, которая получается, когда С' состоит только из группы
коэффициентов G в нулевой размерности. Доказательство тоже будет естественным
обобщением доказательства теоремы об универсальных коэффициентах.
Доказательство. Прежде всего разберём частный случай, когда все
отображения границы в С нулевые, таким образом, Н{{С) = С,. В этом
случае d(c®c') = (-l)lc®dc' и цепной комплекс C®RC — это просто прямая
сумма комплексов С, ®R С', каждый из которых —прямая сумма
нескольких экземпляров модуля С', так как модуль С, свободный. Следовательно,
Hn(Q®RC') « QQkH^C') = H{-(C)®RHn_,(C').
Суммирование по i даёт изоморфизм Нп(С®R С') ^ ф(Н,(С) ®R Hn .((С)),
/*
который и является утверждением теоремы, так как никаких членов Тог
нет, поскольку модуль H^O^Ci свободный.
В общем случае пусть Z, С С, и В,- С Q обозначают ядро и образ
граничных гомоморфизмов в С. Они задают цепные подкомплексы Z и В в С
С тривиальными граничными отображениями. Мы имеем короткую
точную последовательность цепных комплексов О—>Z —>С —> В —> О,
составленную из коротких точных последовательностей 0 —> Z,- —► Q -^ B,_! —> О,
каждая из которых расщепима, так как модуль В,_! свободен,
поскольку он является подмодулем в модуле Q_l5 который свободен по
предположению. Ввиду расщепимости, умножив тензорно последовательность
О—►Z—►С—►В—►ОнаС', мы получим другую короткую точную
последовательность цепных комплексов, а потому длинную точную
последовательность гомологии
...-h^z^^cO-h^c^^cO-h^^b^cO-h^^z^c')-...,
где мы встречаем Ип^^(В ®R С') вместо ожидаемого Нп(В ®R С'), так как
Ь\С-+В уменьшает размерность на единицу. Проверка определения
показывает, что «граничное» отображение Нп_}(В ®R С') —> Hn_x{Z ®R С')
* предыдущей длинной точной последовательности — это просто
отображение, индуцированное естественным отображением В ®R С —> Z ®R С,
возникающим из включения BcZ.
Так как Z и В — цепные комплексы с тривиальными граничными
отображениями, частный случай, разобранный в начале доказательства,
позволяет преобразовать предыдущую точную последовательность в
последовательность
i I
H0(z,.®RHn_1-.1(C))-...
350 Глава 3. Когомологии
Таким образом, мы получаем короткие точные последовательности
0 -> Сокепп -> Hn(C®RC') — Кеп,,^ -> 0,
где
Cokerin = (B(zi®RHn-i(C'))/Imint
i
что равняется ф(Н,-(С) ®ЯЯГ,_,(С')) согласно лемме З.А.1. Остаётся отож-
i
дествить Keri„_, с 0Тогя(Н,(С), Нп_,(С')).
I
Согласно определению Тог тензорное умножение свободной
резольвенты 0 —> В,г —> Z, —> Я, (С) —> 0 на Яп_, (СО приводит к точной
последовательности
о - тог* (якс),я,,-_,.(с')) -в,:®янп._({С) ^г{®кнп_{(С) -
-я,(С)®яЯп_,(с')~-а
Следовательно, суммируя по i, получаем
Кеп„ = фТогя(Н,-(С),Нп-,(С')).
I
Естественность достаточно очевидна, и мы предлагаем читателю
восполнить детали.
Покажем, что короткая точная последовательность в утверждении
теоремы расщепима, если предположить, что обе группы С и С'
свободные. Этого достаточно для наших потребностей. Дополнительные
рассуждения, необходимые для доказательства расщепимости в случае, когда
группа С' не свободная, можно найти в [34].
Расщепление осуществляется гомоморфизмом
Hn(C®RC) -» 0(Н,(С)®дНп_,-(С')),
I
который строится следующим образом. Как уже было отмечено,
последовательность 0 —> Z, —> С, —> Bj_! —> 0 расщепляется, поэтому отображения
факторизации Z, —> Н((С) продолжаются до гомоморфизмов С{—*Н{(С).
Аналогично мы получаем С'.^>Н}(С), если группа С' свободная.
Рассматривая последовательности групп гомологии Н({С) и Я;(С0 как цепные
комплексы Н(С) и Я(С0 с тривиальными граничными отображениями,
мы получаем цепные отображения С —>Я(С) и С' —> Я (СО, тензорное
произведение которых — цепное отображение С ®RC -> Я (С) ®я Я(С').
Индуцированное отображение гомологии для последнего цепного
отображения—требуемое расщепляющее отображение, так как цепной комплекс
H(C)®RH(C') равен своим собственным гомологиям, поскольку
граничные отображения тривиальные. ^
§ З.В. Общая формула Кюннета
351
Топологическая формула Кюннета
Теперь мы можем применить предыдущие алгебраические
конструкции, чтобы получить искомое топологическое утверждение.
I Теорема З.В.6. Если X и У — CW-комплексы, a R — область главных
I идеалов, то существуют естественные короткие точные последователь-
I ности
I 0 - 0(Н,№ Ю ®R НП_;(У; R)) - НП(Х х У; R) -+
I
I - 0TorR(H,(X; R),Hn_,^Y; R)) - 0,
I
I причём эти последовательности расщепимы.
Естественность означает, что отображения X —> X' и У —> У'
индуцируют отображение из короткой точной последовательности для X х У в
соответствующую короткую точную последовательность для X' х У' с
коммутативными квадратами. Расщепление, однако, не является естественным,
как показывает одна из задач в конце этого параграфа.
Доказательство. При работе с произведениями CW-комплексов
всегда приходится сталкиваться с тем неприятным фактом, что компактно
порождённая CW-топология может оказаться отличной от топологии
произведения. Однако в нашем контексте это не вызывает серьёзных
проблем. Так как у этих двух топологий одни и те же компактные множества,
у них одни и те же сингулярные симплексы и, следовательно, одни и те же
группы сингулярных гомологии.
Пусть C = C+(X;R) и С' = С+ (У; R) — клеточные цепные комплексы
с коэффициентами в R. Тогда
C®RC' = СДХхУ;Я)
согласно предложению З.В.1, поэтому алгебраическая формула Кюннета
даёт требуемые короткие точные последовательности. Их естественность
следует из естественности в алгебраической формуле Кюннета, так как мы
можем прогомотопировать произвольные отображения X —> X1 и Y ^>Yf
так, чтобы они стали клеточными, согласно теореме 4.8, а это
гарантирует, что они индуцируют цепные отображения клеточных цепных
комплексов. □
Для коэффициентов в поле формула Кюннета упрощается, потому что
члены Тог над полем всегда нулевые.
I Следствие З.В.7. Если F — поле, а X и У — CW-комплексы, то отобра-
I жение внешнего умножения
I h: ®{Hi{X-F)®FHn_l(Y;F))^Hn(XxY;F)
I
I — изоморфизм для всех п.
352
Глава 3. Когомологии
Имеется также относительная версия формулы Кюннета для CW-nap
(X, Л) и (У, В). Это расщепимая короткая точная последовательность
О - 0(/7, (X, Л; R) ®„ 11„_{(У, В; Ю) - Н„ (X х У, Л х У и X х В; R) ->
- 0Toir('W A; Я), Н„..,_1(У, В; R)) - О,
где R—-область главных идеалов. Это также следует из алгебраической
формулы Кюннета, так как изоморфизм клеточных цепных комплексов
С,(Х х У) ъСЛХ)®Сщ(У) опускается до факторизоморфизма
СДХ х У)/СДА х У UX х Б) % СЛЮ/СЛА)®СЛУ)/СЛВ),
поскольку базисы этих трёх относительных клеточных цепных
комплексов находятся во-взаимно однозначном соответствии с клетками в (X — А) х
х (У —Б), X -Л и У -В соответственно.
Рассмотрим частный случай, когда Л и В —отмеченные точки х{)еХ
и у0еУ. Тогда подкомплекс Л х У иX х В можно отождествить с букетом
X V У и факторпространство X х У/Х V У — это приведённое
произведение X Л У. Так мы получаем приведённую формулу Кюннета
° -> 0(Д-(Х; Л) ®Лям-,-(У; Ю) - н„(х л У; к) -
- 0TorR(H,-(X; Я), Н„_,-_,(У; Я)) - 0.
I
Если мы возьмём, например, Y = Skt то XASfc —это /с-кратная
приведённая надстройка над X и мы получаем изоморфизмы
Hn{X\R)*Hn+k{XASk]R).
Совместно применив формулу Кюннета и теорему об универсальных
коэффициентах, можно получить более короткую формулу Н„(Х х У; R) %
« 0Н,-(Х;//п_,-(У; Д)). Естественность этого изоморфизма, однако, пе-
сколько проблематична, так как он использует расщепимость в
формуле Кюннета и в теореме об универсальных коэффициентах. Используя
некоторые дополнительные алгебраические соображения, можно
показать, что эта формула верна вообще для любой группы коэффициентов G
вместо Я; см. [33].
Имеется аналогичная формула 11„(Х Л У; Я) «* ®Н,(Х; Н„.((У; R))-
i
В частном случае, когда У— пространство Мура M(G,/с), мы получаем
изоморфизмы Н„(Х; G)fc*HM+/f(XAM(G, fc);Z). Естественность снова
проблематична, но в этом случае имеется естественный изоморфизм,
который получается, если применить теорему 4.59 из §4.3 и проверить,
§З.В. Общая формула Кюннета
353
что функторы hn(X) = Нп+к(Х Л M(G,/c);Z) определяют приведённую
теорию гомологии, а это нетрудно. Наличие изоморфизма H„(X;G)^
«Hn+k(X AM(G, к); Z) говорит о том, что гомологии с произвольными
коэффициентами можно получить из гомологии с коэффициентами в Z,
применив топологическую конструкцию вместо алгебраической конструкции
тензорных произведений. Для общих теорий гомологии эту формулу
можно использовать в качестве определения гомологии с коэффициентами.
Можно задать вопрос о когомологической версии формулы Кюннета.
Если взять коэффициенты в поле F и воспользоваться естественным
изоморфизмом Нот(Л ® В, С) % Нот(Д, Нот(В, С)), то формула Кюннета для
гомологии и теорема об универсальных коэффициентах дают изоморфизмы
НП(Х х У; F) % Homf.(H„(X x У; F), F) *
w 0HomF(Hr-(X; Р)®Нп_{(У; F), F) *
i
« 0HomF(H,(X; в, Нотн{НпЧ(У; F), F)) %
* 0HomF(H,(X; F), //"-'(Г; F)) * фн'(Х; Я"-''(У; F)).
I I
Имеют место и более общие изоморфизмы
Н"(Х х У; G) « 0НЧХ; НП"ЧУ; С))
для любой группы коэффициентов G; см. [33]. Однако на практике обычно
бывает достаточно применить формулу Кюннета для гомологии и теорему
об универсальных коэффициентов для когомологий по отдельности.
Кроме того, теорема 3.16 показывает, что при более сильных предположениях
можно получить более сильные выводы, используя ^-произведения.
Симплициальное внешнее произведение
Объясним схематично, как можно определить внешнее произведение
Hm(X; R) (8>НП(У; R) —>Нт+п(Х х У; R) непосредственно в терминах
сингулярных гомологии. В действительности необходимо внешнее
произведение на уровне сингулярных цепей, С,„(Х; R) ® Cn(Y\ R) —> Cm+„(X x У; R).
Если заданы сингулярные симплексы /: Дш —> X и g: Д" —> У, то возникает
Произведение отображений / х g: Дш х Д" —► X х У, и идея состоит в том,
чтобы разбить Дш х Д" на симплексы размерности т + п, а затем взять
сумму ограничений отображения / х g на эти симплексы с
соответствующими знаками.
В частных случаях, когда т или п равно 1, мы уже видели, как разбить
дш х дм на СИМШ1ексы, ПрИ построении призменных операторов в §2.1.
Обобщение па Дш х Д", однако, не вполне очевидно. Пометим вершины
12 Ък. ЗГ.>5
354
Глава 3. Когомологии
симплекса Ат символами v0,vb...,vm, а вершины симплекса Ап —
символами vv0, W],..., wn. Будем представлять себе пары (f,j), для которых
О $ i $ m и 0^;$п, как узлы прямоугольной целочисленной решётки
размером тхпв 1R2. Пусть а — путь, образованный последовательностью
изт + п горизонтальных и вертикальных рёбер этой решётки,
начинающийся в точке (0,0) и заканчивающийся в точке [уплп), всегда идущий
либо направо, либо вверх. Такому пути а мы сопоставляем линейное
отображение tG: Ат+п -► А'п х Д", переводящее вершину к симплекса Ат+и
в О^, Wjk), где (i\,;^) —fc-я вершина ломаного пути а. Тогда мы
определяем симплициальное внешнее произведение
Cm(X; R)® С„(У; R) Д С„|+П(Х х У; R)
формулой
а
где |сг| —число квадратов решётки, лежащих ниже пути а. Обратите
внимание, что символ «х» имеет разный смысл в разных частях
уравнения. При таком определении доказательство того, что d(/ x g) = д/ х g -f
-f (—l)m/ x dg, — это несложное вычисление. Из этого следует, что
внешнее произведение двух циклов —цикл, а внешнее произведение цикла
и границы —граница, поэтому в сингулярных гомологиях возникает
индуцированное внешнее произведение.
Можно проверить, что образы отображений 1а задают симплициаль-
ную структуру на Дш х Дп, следующим образом. Можно рассмотреть Ат
как подпространство в Rm, заданное неравенствами 0 ^ х{ $ ... ^ хт ^ 1,
причём вершина v,—это точка, у которой m - i координат —нули, а
после них идут i единиц. Аналогично мы имеем Л"с1" с координатами
0 $ ух $ ... $ уп $ 1. Тогда произведение Аш х А" состоит из наборов
т + п чисел (хь ..., хт,уъ ...,у„), удовлетворяющих обеим системам
неравенств. Объединение неравенств 0 $ хг $ ... $ хт $ ух $ ... ^ уп ^ 1 задаёт
симплекс дш+п в Аш х Дп, и любая другая точка в Дш х А" удовлетворяет
аналогичной системе неравенств, полученных из неравенств 0 ^ х{ ^ ...
••• ^ хт ^ Ух ^ ••• ^ Уп ^ 1 перестановкой переменных,
«перетасовывающей» переменные у; и переменные1 х(. Каждой такой перетасовке
соответствует путь сг, состоящий из идущей вправо стороны для каждого *,
и идущей вверх стороны для каждого у- в перетасованной
последовательности. Так мы получаем представление А"' х Дп в виде объединения
симплексов А™+п, занумерованных путями о. Можно проверить, что эти
симплексы хорошо стыкуются вместе и образуют структуру А-комплекса на
1 Имеется в виду перестановка, сохраняющая порядок переменных х, и порядок
переменных у, (по-английски такая перестановка называется «shuffle» по аналогии с «перетасовкой»
колоды карт). — Прим. ред.
§ З.В. Общая формула Кюннета
355
Дш х Ап, которая является также структурой симплициального
комплекса, см. [21]. В действительности этой конструкции достаточно, чтобы
естественным образом превратить произведение любых двух А-комплексов
в Д-комплекс.
Когомологическое внешнее произведение
В § 3.2 мы определили внешнее произведение
Нк(Х; Я) х И1 (У; Я) Д Hk+i(X х Y; Я)
в терминах w-произведения. Теперь мы опишем другой подход, при
котором внешнее произведение определяется непосредственно через
клеточные когомологии, а затем ^-произведение определяется в терминах этого
внешнего произведения.
Клеточное определение когомологического внешнего произведения
очень похоже на определение для гомологии. Если даны С1У-комплексы X
и Y, то определим внешнее произведение клеточных коцепей </? е Ск(Х; Я)
и я/> е Cl(Y\ Я), положив
мы предполагаем, что </? х гр принимает значение 0 на (к + £)-мерных
клетках в X х У, которые не являются произведением /с-мерной клетки в X
на £-мерную клетку в Y. По-другому это можно сказать, используя
соглашение, что клеточная коцепь в Ск{Х\ Я) принимает значение 0 на клетках
размерности, отличной от к\ тогда можно положить (</? х гр)(е™ х е'1) =
= Y?(ea )^(ej) для всех тип.
Клеточная формула кограницы б(</? хгр) = 5ц> х г/> -Ь (-l)fcy? x 5i/j для
клеточных коцепей </? еCfc(X; Я) H^GCf(y; Я) легко следует из
соответствующей формулы для границы из предложения З.В.1, а именно,
5(v> х г/0 (е™ х е£) = (</> х t/О (Э(е™ х ер) =
= (V х я/0(с< хе; + (-1)ше™ x dejp =
= 6V(eJ)^(^) + (-l)nV(ea)5^(^) =
= (5^x1/i + (-l)Vx5^)(eJxeJ),
где коэффициент (—I)"1 в предпоследней строке можно заменить на
(—l)fc, так как (/?(е™) = 0, кроме случая, когда к = т. Из формулы б(</? х я/>) —
= 5у? х я^-Ь (-l)fcy? х 5i/> также, как для гомологии и для w-произведения,
следует, что возникает индуцированное внешнее произведение в
клеточных когомологиях.
Чтобы проверить, что новое определение согласовано с
предыдущим определением, мы можем сначала свести ситуацию к случаю, когда
X имеет тривиальный (к - 1)-мерный остов, а Y имеет тривиальный
356
Глава 3. Когомологии
{(. — 1)-мерный остов, с помощью коммутативной диаграммы
Нк{Х/Хк~х; R) х Нс(Y/Y(-x; R) -А- Нш(Х/Хк~х х Y/Y(~x; R)
I J
Нк(Х; R) х Н1 (У; R) ^ Нк+с(Х х У; R)
Левое вертикальное отображение сюръективно, поэтому из
коммутативности следует, что если два определения внешнего произведения
согласованы для верхней строки, то они согласованы и для нижней строки. Затем,
предполагая, что Хк~1 и У*""1 тривиальны, рассмотрим коммутативную
диаграмму
Н*(Х; Ю х H*(Y; R) —^ НШ(Х х У; R)
- j i
Н*(Х*; R) х НЧ^; R) -^ Н*+'(Х* x У<; R)
Вертикальные отображения здесь инъективны, поскольку Хк х Y(
является (/с -f О-мерным остовом X х У, поэтому достаточно проверить, что
два определения согласованы в нижней строке. Мы имеем Хк = VaS^
и У£ = VjgSi, поэтому при ограничении на эти слагаемые букета вопрос
сводится, наконец, к случаю произведения Ska x Si. В этом случае для
R = Z мы показали в теореме 3.16, используя исходное определение
внешнего произведения, что рассматриваемое внешнее произведение —это
отображение Z x Z->Z, переводящее (1,1) в ±1. То же самое, очевидно,
верно, если использовать клеточное внешнее произведение. Итак, для
R = Z оба внешних произведения согласованы с точностью до знака, а из
этого следует, что это верно и для произвольного R. Мы предоставляем
читателю самостоятельно разобраться со знаками.
Чтобы связать внешнее произведение с ^-произведением, мы
воспользуемся диагональным отображением А: X ->Х х X, дг —> (х,х). Если
у нас определено внешнее произведение, то мы можем определить w-npo-
изведение как композицию
Нк(Х; R) х НС(Х; R) Д НМ(Х xX;R)^> НШ(Х; R).
Это согласуется с исходным определением ^-произведения, так как мы
имеем 5*(а х b) = 8*(p*(d) w р*2(Ь)) = 5*(р\Ца)) ^ 5*(р*2(Ъ)) = а w Ь,
поскольку обе композиции рх5 и р25 являются тождественным
отображением пространства X.
К сожалению, определение клеточного внешнего произведения
нельзя объединить с А, чтобы получить определение w-произведения на
уровне клеточных коцепей. Это связано с тем, что А —не клеточное
отображение, а потому оно не индуцирует отображения клеточных
коцепей. Можно прогомотопировать А в клеточное отображение согласно
§ З.В. Общая формула Кюннета
357
теореме 4.8, но при этом возникает произвол в выборе клеточного
отображения. Например, диагональ квадрата можно протащить по любому из
соседних с ней треугольников. В частных случаях можно надеяться понять
геометрию достаточно хорошо, чтобы явно вычислить клеточную
аппроксимацию диагонального отображения, но обычно более предпочтительны
другие методы вычисления w-произведений.
Когомологическое внешнее произведение удовлетворяет тому же
самому соотношению коммутативности, что и для гомологии, а именно,
Т*(а xb) = (-1)*'Ь х а, где Г: X х Y —>Y х X — отображение
транспозиции, a eHfc(Y; R) и Ь еН((Х; R). Доказательство такое же, как и для
гомологии. Положив X = Y и заметив, что ТЛ = А, мы получаем новое
доказательство свойства коммутативности ^-произведения.
Задачи
1. Вычислите группы H,(RPm x RPn; G) и H'ORP"1 x RP"; G) для G = Z
и Z2 с помощью клеточных цепных и коцепных комплексов. [См.
пример З.В.4.]
2. Пусть С и С' — цепные комплексы, а / — цепной комплекс, состоя-
щий из Z в размерности 1 и Z х Z в размерности 0, с граничным
отображением, переводящим образующую е в размерности 1 в разность vT - v0
образующих v, двух групп Z в размерности 0. Докажите, что цепное
отображение /: / <8> С —> С — это то же самое, что цепная гомотопия между
двумя цепными отображениями /J: С ^>С\ с —> /О,- ® с), i = 0,1. [Цепная
гомотопия здесь задаётся формулой ft (с) =/(е® с).]
3. Докажите, что расщепление в топологической формуле Кюннета не
может быть естественным, рассмотрев отображение
/ х 1: M(Z,„, n) х M(Z,„, n) — Sn+1 x M(Zm, n),
где / стягивает n-мерный остов комплекса M(Z,n, n) =S" Uen+1 в точку.
4. Докажите, что внешнее произведение фундаментальных классов
замкнутых R-ориентируемых многообразий М и N равно
фундаментальному классу для MxJV.
5. Докажите, что косые произведения
Нп{Х х У; R) х Н'(У; R) - НП_,-(Х; К), (е' х е\ ц>) ~ </>(е'У,
НП(Х х У; R) х НДУ; R) — НП^(Х; R), (<?, е') ~ (е' -> </>(е'" х еО),
можно определить посредством указанных клеточных формул. [Эти
«произведения» в некотором отношении больше похожи на деление, чем на
умножение, и это отражено в общепринятой системе обозначений для
них: а/Ъ или а\Ь, когда множители переставлены. Первое из этих двух
косых произведений связано с ^-произведением так же, как внешнее
произведение когомологий связано с w-произведением.]
358
Глава 3. Когомологии
§З.С. Н-пространства и алгебры Хопфа
Из трёх аксиом группы, казалось бы, наименее тонкая —
существование единичного элемента. Однако мы увидим в этом параграфе, что,
когда добавляется топология, аксиома о единичном элементе становится
намного более мощной. Чтобы дать имя объектам, которые мы будем
рассматривать, назовём пространство X Н-пространством, где «Я» пишется
в честь Хопфа (Hopf), если существуют непрерывное отображение
умножения ц,: X х X —»X и «единичный» элемент е €Х, для которых оба
отображения X —> X, заданные формулами х —► /iO, е) и х —» /i(e, x)>
гомотопны тождественному отображению в классе отображений (X, е) —> (X, е).
В частности, это влечёт, что /i(e, e) = е.
Это определение находится где-то посередине: можно ослабить
определение, отбросив.условие, что гомотопии сохраняют отмеченную
точку е, а можно усилить его, потребовав, чтобы элемент е был настоящим
единичным элементом, без каких-либо гомотопии. В одной из задач в
конце этого параграфа требуется доказать, что все три эти определения
эквивалентны, если X —CW-комплекс. Преимущество использования
гомотопии в определении состоит в том, что пространство, гомотопически
эквивалентное (с сохранением отмеченных точек) Я-пространству,
снова является Я-пространством. Наложение условий на отмеченные точки
довольно стандартно в теории гомотопии, и обычно оно не приводит к
существенным ограничениям.
Самый классический пример Н-пространства —топологическая
группа, т.е. пространство X с такой структурой группы, что отображение
умножения X хХ->Х и отображение обращения X—>Х, х>->х~1,
непрерывны. Например, группа GLn(M) обратимых матриц размера пхпс
вещественными элементами —топологическая группа, если топология на ней
задана как топология подпространства в п2-мерном линейном
пространстве Mn(R) всех матриц размера пхп над R. Это открытое
подпространство, так как обратимые матрицы —это матрицы с определителем,
отличным от нуля, а определитель Мп (Ж) —> R является непрерывной функцией.
Матричное умножение, конечно, непрерывно, так как оно определяется
простыми алгебраическими формулами, и нетрудно видеть, что
обращение матриц тоже непрерывно, если вспомнить, например, классическое
выражение обратной матрицы через алгебраические дополнения.
Аналогично GLn(C) —топологическая группа, так же как и её кватер-
нионный аналог GL„(H), хотя в последнем случае нужны несколько
другие обоснования, так как определители кватернионных матриц не
обладают необходимыми хорошими свойствами. Так как группы GLn над R,
С и Н —открытые подмножества евклидова пространства, они
являются примерами групп Ли, которые можно определить как топологические
группы, являющиеся одновременно многообразиями. Группы GLn неком-
§З.С. Н-пространства и алгебры Хопфа
359
пактны, поскольку они являются открытыми подмножествами евклидова
пространства, но они имеют гомотопический тип компактных групп Ли
О(п), U(n) и Sp(n). Это объясняется в §3.D для GLn(R), а два других случая
аналогичны.
Среди самых простых с топологической точки зрения Я-пространств
выделим единичные сферы S1 в С, S3 в пространстве кватернионов Н, и S7
в пространстве октав О. Они являются Я-пространствами, так как
умножение в этих алгебрах с делением непрерывно, поскольку оно определено
полиномиальными формулами, и сохраняет норму, \ab\ = |а||Ь|, поэтому
умножение можно ограничить на сферу, причём в каждом случае
единичный элемент алгебры с делением принадлежит единичной сфере. Оба
пространства S1 и S3 — группы Ли, так как умножение вСивМ ассоциативно,
а обратный элемент существует, поскольку аа = \а\2 = 1, если \а\ = 1.
Однако S7 — не группа, так как умножение октав не ассоциативно. Конечно,
S° = {±1} тоже топологическая группа, что очевидно. Известная теорема
Адамса утверждает, что S°, S1, S3 и S7 — единственные сферы, которые
являются Я-пространствами; более подробное обсуждение см. в §4.В.
Опишем теперь некоторые ассоциативные Я-пространства, в
которых обратные элементы отсутствуют. Умножение многочленов задаёт
структуру Я-пространства на СР00 следующим образом. Ненулевой
многочлен а0 Н- ах% Н-... Н- anzn с коэффициентами а,- еС соответствует точке
(а0, ...,ап,0, ...) е С00 - {0}. Умножение двух таких многочленов
определяет умножение С00 - {0} х С00 - {0} —> С00 - {0}, которое является
ассоциативным, коммутативным и имеет единичный элемент (1,0,...).
Так как умножение в С коммутативно, мы можем вынести за скобки
ненулевой общий множитель и получить индуцированное произведение
СР00 х СР00 —►СР00 с теми же самыми свойствами. Таким образом, СР00 —
ассоциативное коммутативное Я-пространство с настоящим единичным
элементом. Вместо того чтобы выносить за скобки произвольный
ненулевой общий множитель, мы могли выносить за скобки только скаляры вида
pe2mk/q^ где р _ произвольное положительное число, к — произвольное
Целое число, a q — фиксированное натуральное число. Факторпростран-
ство С00 — {0} при таком отождествлении — бесконечномерное линзовое
пространство L00 с n^L00) ^ Zq, которое поэтому также является
ассоциативным коммутативным Я-пространством. Этот пример включает,
в частности, КР00.
Пространства J(X), определённые в §3.2, также являются
Я-пространствами с умножением, заданным формулой
(*i,...,*m)(yi,...,y„) = Ui, ...,*т,У1,...,У„),
Которое является ассоциативным и имеет единичный элемент (е), где
е — отмеченная точка в X. Можно было бы описать J(X) как свободное
ассоциативное Я-пространство, порождённое точками пространства X.
360
Глава 3. Когомологии
Имеется также коммутативный аналог пространства J(X), называемый
бесконечным симметричным произведением SP(X), которое
определяется следующим образом. Пусть SPn (X) — факторпространство п-кратного
произведения Хп, полученное при отождествлении всех наборов п
точек (*!,..., х„), которые отличаются только перестановкой их координат.
Включение Xм <—> Xn+l, (x1? ...,хп)-> (хь ...,хп,е), индуцирует включение
SP„(X)*—>SP„+1(X), и SP(X) определяется как объединение этой
возрастающей последовательности пространств SP„(X) со слабой топологией.
По-другому SP(X) можно определить как факторпространство
пространства J(X), полученное при отождествлении точек, которые отличаются
только перестановкой координат. Структура Н-пространства на J(X)
индуцирует структуру Н-пространства на SP(X), которая дополнительно
обладает свойством коммутативности, а не только ассоциативности, и
имеет настоящий единичный элемент. Пространства SP(X) изучаются более
подробно в §4.К.
Цель этого параграфа состоит в том, чтобы описать дополнительную
структуру, которую умножение в Н-пространстве привносит в его
гомологии и когомологии. Эта структура представляет большой интерес, так
как многие из наиболее важных пространств в алгебраической топологии
оказываются Я-пространствами.
Алгебры Хопфа
Обсудим сначала когомологии. Выбирая коммутативное кольцо R
в качестве кольца коэффициентов, мы можем рассматривать кольцо
когомологии Н*(Х; R) пространства X как алгебру над R. Предположим, что
X — это Я-пространство, удовлетворяющее следующим двум условиям:
1) пространство X линейно связно, а потому Я°(Х; R) ъ R;
2) модуль ЯП(Х; R) — конечно порождённый свободный R-модуль для
всех п, таким образом, внешнее произведение Я*(Х; R) ®R Я*(Х; R) —>
—>Н*(Х хХ;К)—изоморфизм.
Умножение /i: X х X —> X индуцирует отображение /!*: Н*(Х; R) —>
—>Я*(Х х X; R), Взяв его композицию с изоморфизмом внешнего
произведения из п. 2, получим отображение
Я*(Х; R) — Я*(Х; R) ®RЯ*№; R),
которое является гомоморфизмом алгебр, так как и отображение (л\
и изоморфизм внешнего произведения — гомоморфизмы алгебр.
Оказывается, ключевое свойство отображения А состоит в том, что для любого
элемента а^Ип{Х\ К), п>0, мы имеем
А(а) =а®1 + 1®а + ^Га|®а", где \а\\ > Ои \а"\ > 0.
§ З.С. Н-пространства и алгебры Хопфа
361
Чтобы проверить это, возьмём i:X->Xx X —включение х —* О, е), где
е — единичный элемент в X, и рассмотрим коммутативную диаграмму
H*U; R) * И\Х х X; R) *- Я*(Х; R)
Н*(Х; R)®RH*(X; R) — H*(X; R) ®RH*(e; R)
Отображение Р определено как композиция, и, рассматривая нижний
правый треугольник, мы видим, что Р(а ® 1) = а и Р(а ® /3) = 0, если
|]3| > 0. Свойство Н-пространства влечёт, что pti ^ 1, поэтому РЛ = 1. Из
этого следует, что Л (а) имеет компоненту в Н"(Х; R) ®R Н°(Х; R), равную
а® 1. Аналогичное рассуждение показывает, что Л(а) имеет компоненту
bH°(X;R)®rH"U;R), равную 1®а.
Все вместе эти свойства выражают тот факт, что H*{X\R) является
алгеброй Хопфа, т. е. градуированной алгеброй Д=0Л" над
коммутативно
ным кольцом R, удовлетворяющей следующим двум условиям.
1. Существует единичный элемент 1еА°, для которого отображение
R^>A°, г—>г-1, является изоморфизмом. В таком случае говорят, что
алгебра А связная.
2. Существует диагональ, или копроизведение, — гомоморфизм
градуированных алгебр Л: А^>А®А, удовлетворяющий условию Д(а)=а®1-Ь
+ 1®а + ]>]а;®а" при |а||>0и \а"\ >0, для всех а, |а|>0.
Здесь и далее ® означает ®R. Умножение в А ® А задаётся стандартной
формулой (а® /3)(у ® 5) = (-1)^1,г1(ау ® ^5). Для общей алгебры Хопфа
умножение не предполагается ассоциативным или коммутативным (в
градуированном смысле), хотя в случае H*(X]R), где X —Н-пространство,
алгебра является, конечно, ассоциативной и коммутативной.
Пример З.С.1. Одна из самых простых алгебр Хопфа — кольцо
многочленов R[a]. Копроизведение Л(а) должно быть равно а ® 1 + 1 ® а, так
как единственные элементы в R[a] более низкой размерности, чем а,—
это элементы кольца R в нулевой размерности, поэтому члены а[ и а"
Ь формуле копроизведения Л (а) = а ® 1 + 1 ® а + XI а\ ® аГ Должны быть
i
нулевыми. Требование, чтобы отображение Л было гомоморфизмом
алгебры, тогда полностью определяет копроизведение Л. Чтобы описать Л
явно, мы разберём два случая. Если размерность элемента а четна или
*сли 2 = 0 в кольце R, то умножение в R[a] ®R[a] строго коммутативно
И Л(ап) = (а ® 1 4-1 ® а)п = ^Спа! ® ап~'. А в случае, когда элемент а
i
Имеет нечётную размерность, Л (а2) = (а ® 1 + 1 ® а)2 = а2®1 + 1®а ,
Так как (а ® 1) (1 ® а) = а ® а и (1 ® а) (а ® 1) = -а ® а. Поэтому если мы
362
Глава 3. Когомологии
положим /3 = а2, то элемент /3 имеет чётную размерность, и мы получаем
Д(а2п) = Д(/?п) = (/?®1 + 1®/?)п= ^С1пР1®рпЧ
i
и
А(а2п+1) = А(а/Зп) = А(а)А(/?п) = ^Спа^' ®^П"'+2]Сп^' ® а^М"'-
Пример З.С.2. Внешняя алгебра Ля[а] с образующей а нечётной
размерности — алгебра Хопфа с копроизведением А(а) = а®1 + 1®а.
Чтобы убедиться, что А является гомоморфизмом алгебры, нужно
проверить, что А(а2) = А(а)2; другими словами, так как а2 = 0, нужно
доказать, что А (а)2 = 0. Как и в предыдущем примере, мы получаем
А(а)2 = (а ® 1 + 1 ® а)2 = а2 ® 1 + 1 ® а2, поэтому А(а)2 действительно
равно 0. Заметим, что если бы образующая а имела чётную размерность,
мы вместо этого получили бы А(а)2 = а2 ® 1 + 2а ® а + 1 ® а2, а это
выражение равно 0 в AR[a] ®Лд[а] только в том случае, когда 2 = 0
в кольце R.
Элемент а алгебры Хопфа называют примитивным, если А (а) =
= а®1 + 1®а. Из предыдущих примеров видно, что если алгебра Хопфа
порождается как алгебра примитивными элементами, то копроизведе-
ние А единственным образом определяется произведением. Это
случается во многих интересных частных случаях, но, конечно, не всегда, как
мы увидим позже.
Существование копроизведения в алгебре Хопфа, как оказывается,
сильно ограничивает мультипликативную структуру. Вот важный пример,
иллюстрирующий это явление.
Пример З.С.З. Предположим, что срезанная алгебра многочленов
F[a]/(an) над полем F —алгебра Хопфа. Тогда элемент а примитивен,
поскольку он лежит в F[a]. Если мы предположим что либо а имеет
чётную размерность, либо F имеет характеристику 2, то соотношение
ап = 0 приводит к уравнению
0 = Д(ап) = ап®1 + 1®ап+ ]>] Спа*®апЧ= ^ С\ха}®ап-\
0<i<n 0<i<n
из которого следует, что Сп = 0 в поле F для всех f, удовлетворяющих
неравенствам 0 < i < п. Этого не может быть, если F имеет характеристику 0,
а если характеристика поля F равна р > 0, то это бывает только тогда,
когда п — степень числа р. Для р = 2 это было показано в доказательстве
теоремы 3.20, и рассуждение, приведённое там, работает точно так же для
нечётных простых чисел. Наоборот, легко проверить, что если F имеет
характеристику р, то F[a]/(ap') — алгебра Хопфа (мы по-прежнему
предполагаем, что элемент а имеет чётную размерность, если р нечётно).
В случае характеристики 0 из этого результата следует, что СРП —это
не Н-пространство для конечного п, в отличие от пространства СР00,
которое является Я-пространством, как мы видели ранее. Точно так же, взяв
§ З.С. Н-пространства и алгебры Хопфа
363
F = Z2, мы получаем, что МРП может быть Н-пространством только в том
случае, когда n-f 1— степень 2. Действительно, RP1 = S] /±1, EP3 = S3/±1
и ЕР7 = S7/±l имеют факторструктуры Н-пространств, полученных из
S1, S3 и S7, так как -1 коммутирует со всеми элементами в S1, S3 и S7.
Однако это единственные случаи, когда RPn является Я-пространством.
Это следует из задачи в конце этого параграфа о том, что универсальное
накрытие Н-пространства является Н-пространством, и упомянутой
ранее теоремы Адамса, согласно которой S1, S3 и S7 — единственные сферы,
которые являются Н-пространствами.
Несложно проверить, что тензорное произведение алгебр Хопфа —
снова алгебра Хопфа, с копроизведением Л(а <8> /3) = Л(а) <8> Д(/3).
Таким образом, предыдущие примеры приводят ко многим другим алгебрам
Хопфа— тензорным произведениям полиномиальных, срезанных
полиномиальных и внешних алгебр от любого числа образующих. Следующая
теорема Хопфа представляет собой частичное обращение этого утверждения.
I Теорема З.С.4. Пусть А — коммутативная ассоциативная алгебра Хоп-
I фа над полем F характеристики 0, причём пространство А'1 конечномер-
I но над F для всех п. Тогда А изоморфна как алгебра тензорному про-
I изведению внешней алгебры от нечётномерных образующих и алгебры
I многочленов от чётномерных образующих.
Имеется аналогичная теорема Бореля в случае конечного поля F
характеристики р. В этом случае алгебра А снова изоморфна тензорному
произведению алгебр Хопфа с одной образующей, которые имеют один
из следующих видов:
• F[a]y где элемент а чётномерный, если рф2\
• AF[a], где элемент а нечётномерный;
• F[a]/(ap)y где элемент а чётномерный, если рф2.
Доказательство можно найти в [83] или Г40].
Доказательство теоремы З.С.4. Так как подпространство Ап
конечно порождённое над F для всех п, мы можем выбрать образующие
*1,х2> ••• алгебры А так, что \х(\ $ |*,+il для всех i. Пусть Ап—
подалгебра, порождённая элементами хи ..., хп. Она является подалгеброй
Хопфа в Л, т.е. А(Л„) СЛ„ ® А„, поскольку в А(х,) встречаются только
Х( и члены меньшей размерности. Можно считать, что хп не лежит в Ап _л.
Так как алгебра А ассоциативна и коммутативна, имеется естественная
сюръекция Лп_] ®F[xM] ->А„, если \хп\ четно, или Ап_х ® Лр[хп] —> Ап,
если \хп\ нечётно. Для применения индукции по п достаточно
доказать, что эти сюръекции инъективны. Таким образом, в двух
рассматриваемых случаях мы должны исключить нетривиальные соотношения
XiaiXln = 0 и a0-ha^xn = 0 соответственно с коэффициентами a,eAM_i.
1 Пусть / — идеал в АПУ порождённый элементом х?} и элементами из
\-i положительной размерности; таким образом, / состоит из многочле-
364
Глава 3. Когомологии
нов X!ai*/i с коэффициентами а,- € Ап-1, причём первые два коэффициент
i
та а0 и а{ имеют тривиальные компоненты в А0. Заметим, что хп&1у так
как элементы идеала /, имеющие размерность \хп\, должны лежать в А„_,.
Рассмотрим композицию
Д q
Ап -+ Ап®Ап -+АпЪ{Ап/1\
где q — естественное отображение факторизации. По определению
идеала / эта композиция qA переводит а€An_^ в а® 1, а х„ — в лгп ®1 +1 ®х„,
где хп —образ элемента хп в Ап/7. В случае, когда \хп\ четно, применяя дД
к нетривиальному соотношению ^щх1п = 0, получаем
О = £](<*, ®1)(хп® 1 + 1®*,,)' = (£]«,•<) ®1 + 2'а'"хя"' ®*"-
I I I
Так как Xlai*n ~ ^> из этого следует, что элемент ^ia,*)"1 ® *„ равен
?' i
нулю в тензорном произведении Ап ® (Ап/1), поэтому ^ia,-*,',""1 =0, так
i
как, если хп &I, то j?„ ^0. Соотношение ^Ш{ХХ~Х = 0 имеет более низкую
i
степень, чем исходное соотношение, и оно не тривиальное, так как F
имеет характеристику 0, а потому если at ф 0, то i a,- 5^ 0 при i > 0. Так как
мы могли предположить, что исходное соотношение имеет минимальную
степень, мы приходим к противоречию.
Случай нечётного |х„| аналогичен. Применение дД к соотношению
а0 + агхп = 0 даёт
0 = а0®1 + (а1®1)(хи®1 + 1®хп) = (ao + a^J^l + a!®^,.
Так как a0 + a,xn =0, мы получаем а1 ® хп = 0, а это влечёт, что сц = 0 и,
значит, а0 = 0. □
Структура алгебр Хопфа над Z намного более сложна, чем над полем.
Вот пример, который является всё ещё довольно простым.
Пример З.С.5 (алгебры разделённых степеней). В предложении 3.22
было показано, что если л четно, то для Н-пространства J(SM) алгебра
H*(J(Sn); Z) —это алгебра разделённых степеней, т. е. алгебра I\[a] с
аддитивными образующими а, в размерности ni и умножением, заданным
формулой а\ = к\ак) из которой следует, что a,a; =Cj+jaI+j. Копроизведе-
ние в Гг[а] однозначно определяется мультипликативной структурой, так
как
Д(a^) = (a1®l^-l®a1)': = 2C^ai(8>al"',
I
а из этого следует, что A(a\/k\)=^l(a\/i\)^{a\~l/{k — i)\)y т.е. А(ак)-
i
= 2ai ® aJt-r Таким образом, в этом случае копроизведение имеет более
простое описание, чем произведение.
§ З.С. Н-пространства и алгебры Хопфа
365
Интересно посмотреть, что происходит с алгеброй разделённых
степеней Г7Да], когда мы переходим к коэффициентам в поле. Ясно, что
Га [а] —это то же самое, что и Q[a]. В отличие от этого, алгебра Гй [а]
с умножением, заданным формулой а{а} = С!+.а,-+;-, оказывается, как мы
сейчас покажем, изоморфна бесконечному тензорному произведению
(g)Zp[ap.]/(ap,). Однако как алгебры Хопфа эти два объекта разные, так
f*o р
как элемент ар, примитивен в ®Zp[ap.]/(ap,), но не в Гъ [а], если f> О,
поскольку копроизведение в Тъ [а] задаётся формулой A(afc)=^]a,®afc_t-.
Теперь давайте покажем, что существует изоморфизм алгебр
rZp[a]«®Zp[ap,-]/(aJ,.).
Так как Tz [a] = Tz[a] ® Zp, это эквивалентно следующему:
(*) элемент а\°апК,,ап\ в Тг[а\ делится на р тогда и только тогда, когда
л,- ^ р для некоторого i.
Произведение а[°ап\..аПкк равно тап для п = п0 + пгр + ... + пкрк
и некоторого целого числа т. Вопрос состоит в том, делится ли р на т.
Мы покажем следующее:
(**) апарк делится на р тогда и только тогда, когда пк — р — 1, если
предположить, что л,- < р для всех i.
Это позволяет доказать утверждение (*) рассуждением по индукции,
в котором мы строим произведение, повторяя умножение справа на
члены api.
Чтобы доказать утверждение (**), вспомним, что апарк =Сп косп+рк.
Значение по модулю р этого биномиального коэффициента можно
вычислить с помощью леммы З.С.6, приведённой ниже. Предположим, что л,- < р
для всех i и что л^ + 1 < р. Тогда р-адические представления для л -Ь рк
и л отличаются только коэффициентом при рк, поэтому по модулю р мы
получаем Сп к = С"1к+1 = пк +1. Это равенство остаётся верным и в случае
пк + 1 = р, когда р-адические представления для п + рк и п отличаются
также и коэффициентом при pk+l. Из этого следует утверждение (**).
I Лемма З.С.6. Если число р простое, то С^ = П^п' moc* Р> где л = ^л,р'
I '
I нк=^к(р1, 0^л,<р иО$*с,<р, — р-адические представления для л и к.
I
Здесь используется соглашение, что Ск = О, если л < fc, и С^ = 1 для всех
Доказательство. В Zp[x] имеет место тождество (1 + х)р = 1 + *р,
так как р, очевидно, делит Ск = р\/к\(р - к)\ при 0 < к < р. По индукции
из этого следует, что (1 + х)р' = 1 + хр'. Следовательно, если л = X! niP' ~~
366
Глава 3. Когомологии
р-адическое представление для п, то
= [1 + с! x+cix2+... + cp-lxp-1]x
х [1 + С,; *р + С,2*2р + ... + СГ1*(р~1)р1 х
х [i+c,;*p2+cn2*2p2+...+cnp-1*(p~1)',2i х...
Производя умножения, мы видим, что никакие члены не объединяются,
а коэффициент при хк — это просто П^п» где ^ = £ ^Р* ~~Р -адическое
i i
представление для к. О
Произведение Понтрягина
Ещё одно специфическое свойство Н-пространств заключается в том,
что на их группах гомологии определена операция произведения,
называемая произведением Понтрягина. Для Н-пространства X с умножением
jjl: X х X —>Х это произведение определяется как композиция
НДХ;Д)<8>НДХ;Д) ^НДХхХ;Д) ^Я+(Х;Д),
где первое отображение — внешнее произведение, определённое в §З.В.
Таким образом, произведение Понтрягина состоит из билинейных
отображений Я,(Х; К) х Hj(X; R) —>HI+;(X; R). В отличие от ^-произведения,
произведение Понтрягина, вообще говоря, не ассоциативно. Оно будет
таковым, если (л ассоциативно с точностью до гомотопии, в том смысле, что
отображения X х X х X —>X, заданные формулами О, у, z) —»//(х, //(у, z))
и 0,у, z) •->//(//О, y),z), гомотопны. К счастью, большинство Н-прост-
ранств, встречающихся на практике, обладают этим свойством
ассоциативности. Но при этом произведение Понтрягина, вообще говоря, не
является коммутативным, даже в градуированном смысле, если умножение /х
не является коммутативным или коммутативным с точностью до
гомотопии, что бывает довольно редко для Н-пространств. Мы вкратце приведём
примеры, когда произведение Понтрягина не является коммутативным.
В случае, когда X — СW-комплекс, а \х ■— клеточное отображение,
произведение Понтрягина можно вычислить, используя клеточные
гомологии, с помощью клеточного цепного отображения
С,(Х; Я) х Cj{X; Ю ^ Q+;(X xX;R)^> Q+j(X; Я),
где отображение внешнего произведения переводит образующие,
соответствующие клеткам е1 и е;, в образующую, соответствующую
произведению клеток е1 х е;, а затем //* применяется к этому произведению клеток.
Пример З.С.7. Вычислим произведение Понтрягина для J(SM). Здесь
есть одна клетка е,п для каждого i ^ О, и (л отображает произведение
клеток eln xejn гомеоморфно на клетку e(l+J)n. Это означает, что НДДЯ"); Z) —
§ З.С. Н-пространства и алгебры Хопфа
367
просто кольцо многочленов Z[x] от л-мерной образующей х. Это верно
как для нечётных л, так и для чётных л, поэтому произведение Понт-
рягина не должно удовлетворять тому же самому общему соотношению
коммутативности, что и для ^-произведения. В этом примере структура
произведения Понтрягина проще, чем структура ^-произведения, хотя
для некоторых Н-пространств бывает и наоборот. В приложениях часто
бывает удобно иметь возможность выбирать, какую именно структуру
произведения использовать.
Это вычисление немедленно обобщается на J(X), где X — любой
связный CW-комплекс, все клеточные граничные отображения
которого тривиальны. Тогда клеточные граничные отображения в
произведении Хш, содержащем т множителей X, тривиальны, как показывает
индукция по т, использующая предложение З.В.1. Потому все
клеточные граничные отображения в J(X) тривиальны, так как отображение
факторизации Хш —> Jm(X) является клеточным, и каждая клетка в Jm(X)
является гомеоморфным образом клетки в Хт. Таким образом, модуль
НДДХ); Z) свободный, причём его аддитивным базисом служат
произведения е"1 х ... х еПк клеток положительной размерности в X, а
мультипликативная структура — это структура многочленов от некоммутирующих
переменных, соответствующих клеткам положительной размерности в X.
По-другому кольцо H*{J(X)\ Z) можно описать как тензорную алгебру
TH*(X;Z). Для градуированного R-модуля М, который тривиален в
нулевой размерности (как приведённые гомологии линейно связного
пространства), тензорная алгебра ТМ — это прямая сумма л-кратных
тензорных произведений модуля М на себя для всех л ^ 1 вместе с экземпляром R
в нулевой размерности, с очевидным умножением, которое получается из
тензорного произведения и скалярного умножения.
Обобщая предыдущий пример, мы получаем следующее.
I Предложение З.С.8. Пусть X —связный CW-комнлекс, для которого
H*(X;R) —свободный R-модуль. Тогда модуль H*(J(X)',R) изоморфен
тензорной алгебре ТН*(Х\ R).
Это можно перефразировать, сказав, что гомологии свободного
Н-пространства, порождённого пространством со свободными гомологиями, —
свободная алгебра, порождённая гомологиями пространства.
Доказательство. Будем рассматривать гомологии с
коэффициентами в R. Пусть у>: ТН*(Х) —>H*(J(X)) —гомоморфизм, ограничение
которого на л-кратное тензорное произведение Н+(Х)®П является композицией
НДХГ* - Н+(Х)®П Д НЛХп) - H*(JM(X)) - H*(J(X)),
где предпоследнее отображение индуцировано отображением
факторизации Хп —> Jn(X). Ясно, что у является гомоморфизмом колец, так как
произведение в J(X) индуцировано естественным отображением Хгм х X —>
-+ХШ+П. Чтобы показать, что ^— изоморфизм, рассмотрим следующую
368
Глава 3. Когомологии
коммутативную диаграмму коротких точных последовательностей:
О Тп_гН.{Х) ТпНЛХ) >- НЛХ)*п О
Y т '
о —- HAJn-i(X)) —^ ад,(Х)) —- н,(хл") —^ о
В^ верхней строке ТШЯ,(Х) обозначает прямую сумму произведений
Н*(Х)®к для к $ т, таким образом, эта строка точная. Вторая строка —
гомологическая точная последовательность пары (Jn(X),Jtl_.}(X)) с фак-
торпространством Jn(X)/Jn_l(X), являющимся n-кратпым приведённым
произведением ХА'\ Эта длинная точная последовательность разбивается
на короткие точные последовательности, как указано, согласно
коммутативности правого квадрата и тому факту, что вертикальное
отображение справа является изоморфизмом по формуле Кюннета (здесь мы
пользуемся нашим предположением, что модуль НДХ) свободен над
данным кольцом коэффициентов). Используя индукцию по п и 5-лемму,
мы получаем из этой диаграммы, что с/?: ТпН¥(Х) —>H+(J„(X))
—изоморфизм для всех п. Переходя к пределу п к оо, мы получаем из этого, что
у?: ТИ+(Х) —> Н+(J(X)) —изоморфизм, так как в любой фиксированной
размерности ТПН*(Х) не зависит от п, когда п достаточно велико, и то же
самое верно для H*(jn(X)) согласно второй строке диаграммы. □
Двойственные алгебры Хопфа
Имеется тесная связь между произведением Понтрягина в гомологиях
и структурой алгебры Хопфа в когомологиях. Предположим, что X — такое
Н-пространство, что для коэффициентов в поле R линейные пространства
Нп (X; R) конечномерны для всех п. По-другому можно было бы взять R = Ъ
и предположить, что группы //„(X; Z) конечно порождённые и свободные
для всех п. В обоих случаях мы имеем НП(Х;Д) = HomR(H„(X; R), R).
Отсюда вытекает, что произведение Понтрягина ДДХ; R) ® Н*(Х; R) —►
— НДХ;Я) и копроизведение Л: Н*(Х; Я) — Н*(Х; К) <8> Н*{Х\ К)
двойственны друг другу, поскольку оба они индуцированы произведением
ji\ X х X —>X в Н-пространстве. Поэтому копроизведение в когомологиях
определяет произведение Понтрягина в гомологиях, и наоборот. В
частности, компонента А,-,-: Н'+;(Х; R) —>Н[{Х\ R) ®Н;(Х; R) копроизведения
А двойственна произведению Н,(Х; R) ®Н;(Х; R)—>Н,-+;-(Х;Я).
Пример З.С.9. Рассмотрим пространство J(Sn) с чётным п. Тогда
H*(J(Sn); Z)— алгебра разделённых степеней Гй[а]. В примере З.С.5 мы
получили формулу A(afc) = 2ai ® afc-i Для копроизведения. Таким об-
разом, Ау переводит aI+; в a^aj, поэтому если ^—образующая
группы Hin(J(Sn); Z), двойственная к а,-, то jr,-*, = *,-+;-. Это означает, что
Н+ (J(Sn); Z) — кольцо многочленов Z[jr]. Мы уже показали это в приме-
§ З.С. Н-пространства и алгебры Хопфа
369
ре З.С.7, используя клеточную структуру комплекса J(Sn), но приведённое
здесь доказательство использует исключительно алгебраическую
структуру ^-произведения.
Теперь мы хотим показать, что соотношение между НЖ(Х; R) и Н+(Х; R)
совершенно симметричное: они являются двойственными алгебрами
Хопфа. Это чисто алгебраический факт.
I Предложение 3.СЮ. Пусть Л —алгебра Хопфа над Я, которая яв-
I ляется конечно порождённым свободным Я-модулем в каждой раз-
I мерности. Тогда для произведения я: Л ® Л —► А и копроизведения
I Л: А —► А ® А имеются двойственные отображения я*: Аж —► А* ® Аж
I и Л*: А* ® А* —> А*, которые задают на А* структуру алгебры Хопфа.
Доказательство. Это станет очевидным, если мы интерпретируем
структуру алгебры Хопфа на А формально как пару гомоморфизмов
градуированных Я-модулей я: Л®Л—>А и А: А—>А®А вместе с элементом
1е А0, обладающих следующими свойствами.
1. Обе композиции А-^А®А —> А и Д-^А^дАл, где i((a) = а ® 1
и 1г(а) = 1 ® а, являются тождественными отображениями. Это означает,
что 1 —двусторонняя единица для умножения в А.
A Pi A P,
2. Обе композиции А—>А®А—>АиА—>А®А—>А, где рДа ® 1) = а =
= рг(1®а)э pf (а ®Ь) =0, если |Ь| >0, и рг(а®Ь) =0, если |а| >0 является
тождественными преобразованиями. Это просто формула Д(а) = а ® 1 -Ь
+1 ® а Н- XIа • ® а" Для копроизведения.
3. Диаграмма
А® А ^—^ А
А® А® А® А -
коммутативна; здесь T(a®b®c®d) = (-l)lbl|C|a ®c®b®d. Это —условие,
что Д является гомоморфизмом алгебр, так как если мы применим к
элементу а®Ъ стрелки из верхней части диаграммы, то получим Д(аЬ),
в то время как нижний маршрут даёт сначала Д (а) ® Д (Ь) = (]>] а'{ ® а") ®
® (2^' ®Ь"), а после применения т и я® я получаем
что равно Д(а)Д(Ь).
Условие 1 для А двойственно к условию 2 для А*, и аналогично
условие 2 для А двойственно к условию 1 для А\ Условие 3 для А двойственно
к условию 3 для А\ D
^ А® А
■*■ А® А® А®А
370
Глава 3. Когомологии
Пример З.С.11. Вычислим двойственную алгебру для алгебры
многочленов R[x]. Предположим сначала, что х имеет чётную размерность»
Тогда А(хп) = {х ® 1 -Ь 1 ® х)п = ^С^х1 ® x""z» П0ЭТ0МУ если элемент а,-
i
двойствен х1, то член С^х' ® хп~1 в Д(хп) даёт соотношение для
произведения а{ап_{ = С„ап- Это совпадает с правилом умножения в алгебре
разделённых степеней, таким образом, двойственная к R[x] алгебра Хопфа —
это Гн [а], если размерность элемента х четна. Это верно также, если 2 = 0
в R, так как чётномерность элемента х использовалась только для того,
чтобы доказать, что алгебра R[x] ® R[x] строго коммутативна.
В случае, когда х имеет нечётную размерность, мы видели в
примере З.С.1, что если мы положим у = х2, то получим
А(уп) = (у® 1 + 1®у)п = ]Г СУ®УП~[
и
Д(^п) = ДМД(уп) = ^С^'®У""'+ 2С^'0 ^"",'
i i
Эти формулы для А означают, что двойственная к R[x] алгебра Хопфа —
это AR[a] ® Гн[/?], где элемент а двойствен к х, а /? двойствен к у.
Эти алгебраические рассмотрения позволяют вывести структуру
^-произведения на H*(J(Sn); Я) из геометрического вычисления H*(J(Sn); R) ъ
&R[x] в примере З.С.7. Чтобы получить ещё одно приложение, напомним,
что ранее в этом параграфе говорилось, что MP00 и СР00 являются Я-про-
странствами, поэтому из их структур w-произведения мы можем сделать
вывод, что кольца Понтрягина ДД2&Р00; Z2) и Н*(СР°°; Z) являются
алгебрами разделённых степеней.
В этих примерах алгебра Хопфа порождается как алгебра
примитивными элементами, таким образом, произведение определяет копроизве-
дение и, следовательно, двойственную алгебру. Это, однако, не всегда
верно. Например, мы видели, что алгебра Хопфа Тъ [а] изоморфна как
алгебра (8>^р[ар;]/(ар,), но если мы рассмотрим последнее тензорное
произведение как тензорное произведение алгебр Хопфа Zp [ар.-]/(ар,), то
элементы ар, примитивные, хотя они и не примитивные в Тг [а] при i > 0.
В действительности алгебра Хопфа ® Zp[api]/(ap,) двойственна сама се-
бе согласно одной из приведённых ниже задач, но двойственная к Тг [а]
алгебра Хопфа — это Zp [a].
Задачи
1. Предположим, что X — CW-комплекс с отмеченной точкой ееХ,
являющейся нульмерной клеткой. Докажите, что X — Н-пространство,
если существует такое отображение /i: X х X —*Х, что отображения Х-*Х,
§З.С. Н-пространства и алгебры Хопфа
371
х*-+1л(х, е) и х —>/i(e, х), гомотопны тождественному отображению.
[Иногда именно это берётся в качестве определения Н-пространства, а не
более ограничительное условие из определения, данного нам ранее.] При
тех же самых предположениях покажите также, что /! можно прогомото-
пировать так, чтобы элемент е стал строгим двусторонним единичным
элементом.
2. Докажите, что ретракт Н-пространства является Н-пространством,
если он содержит единичный элемент.
3. Докажите, что в гомотопически ассоциативном Н-пространстве,
множество компонент линейной связности которого — группа
относительно умножения, индуцированного структурой Н-пространства, все
компоненты линейной связности гомотопически эквивалентны.
[Гомотопическая ассоциативность означает ассоциативность с точностью до
гомотопии.]
4. Докажите, что структуру Н-пространства или топологической
группы на линейно связном локально линейно связном пространстве можно
поднять до такой же структуры на его универсальном накрытии. [Для
группы SO(n), рассматриваемой в следующем параграфе,
универсальное накрытие при п > 2 —двулистное накрытие группой, называемой
Spin(n).]
5. Докажите, что если (X, е) является Н-пространством, то группа
я^Х, е) абелева. [Ср. обычную композицию feg петель с произведением
/i(/(t),g(0), получающимся из умножения /! в Н-пространстве.]
6. Докажите, что Sn является Н-пространством тогда и только тогда,
когда отображение приклеивания 2п-мерной клетки для J2(Sn)
гомотопически тривиально,
7. Каковы примитивные элементы алгебры Хопфа Zp [x] для
простого р?
8. Докажите, что тензорное произведение двух алгебр Хопфа —
алгебра Хопфа.
9. С помощью теорем Хопфа и Бореля докажите, что для
Н-пространства X, которое является связным конечным СУУ-комплексом с НДХ; Z) ф
фОу эйлерова характеристика #(Х) равна 0.
10. Пусть X —линейно связное Н-пространство, для которого модуль
Н*(Х; Ю свободный и конечно порождённый в каждой размерности. Для
отображений /, g: X —> X определим произведение fg: X —> X формулой
(f g)(x) = f(x)g(x), используя произведение в Н-пространстве.
а) Докажите, что (/g)*(a) = /*(а) +g*(a) для примитивных элементов
аеН*(Х;Я).
б) Выведите из этого, что отображение возведения в /с-ю степень, х —> хк,
индуцирует отображение а*-> к а на примитивных элементах а. В
частности, отображение возведения кватернионов в fc-ю степень, S3 —>S3,
имеет степень к.
372
Глава 3. Когомологии
в) Докажите, что любой многочлен апхпЬп +... + a1xbl + а0 ненулевой
степени с коэффициентами в Ш имеет корень в Н. [См. теорему 1.8.]
И. Для n-мерного тора Т" (произведения п окружностей)
докажите, что кольцо Понтрягина Н¥(Тп; Z) — внешняя алгебра А7\хъ ..., хп]
12. Вычислите структуру произведения Понтрягина в H*(L;Zp), где
L — бесконечномерное линзовое пространство S°°/Zp, для нечётного
простого р, используя копроизведение в H*(L; Zp).
13. Проверьте, что алгебры Хопфа AR[a] и Zp[a]/(ap) двойственны
сами себе.
14. Докажите, что копроизведение в алгебре Хопфа Н*(Х;Я),
двойственной к H*(X;R), индуцировано диагональным отображением X -*
-♦X х X, х—» U,x).
15. Пусть X—такое линейно связное Я-пространство, что модуль
H*(X;Z) свободный и конечно порождённый в каждой размерности,
а Н*(Х; Q) — кольцо многочленов Q[a]. Докажите, что кольцо Понтрягина
Н*(Х; Z) коммутативно и ассоциативно, причём его структура однозначно
определяется кольцом Н*{Х\ Z).
16. Классифицируйте алгебраически такие алгебры Хопфа А над Z,
что модуль Л" является свободным для каждого п и j4®<Q>^Q>[a]. В
частности, выясните, какие алгебры Хопфа Д® Zp получаются из таких Л.
§3.D. Когомологии SO(п)
После общего обсуждения гомологических и когомологических свойств
Н-пространств в предыдущем параграфе мы обратимся теперь к
семейству очень интересных и тонких примеров, к ортогональным группам
О(п). Мы вычислим их гомологии и когомологии, построив хорошие
CW-структуры на них. Эти вычисления хорошо иллюстрируют общие
структурные теоремы из последнего параграфа. Разобравшись с
ортогональными группами, мы затем опишем прямое обобщение этих
результатов для многообразий Штифеля, которые тоже являются весьма важными
объектами в алгебраической и геометрической топологии.
Ортогональную группу О(п) можно определить как группу изометрий
пространства Мп, сохраняющих начало координат. Эквивалентное
определение: это — группа таких матриц А размера пхпс коэффициентами в 1R,
что АА{ =/, где А{ —транспонированная матрица. С этой точки зрения
2
О(п) топологизируется как подпространство в пространстве Rn ,
координатами которого служат п2 элементов матрицы п х п. Так как столбцы
матрицы из О(п) — единичные векторы, О(п) можно также рассматривать
как подпространство в произведении п сфер Sn_1. Это подпространство
замкнутое, так как условие, что столбцы ортогональны, задаётся
полиномиальными уравнениями. Следовательно, пространство О(п) компакт-
§3.D. Когомологии SO(n)
373
ное. Отображение О(п) х O(n) —> О(п), заданное матричным умножением,
непрерывно, так как оно задаётся многочленами. Отображение
обращения А*->А~1 = А*, очевидно, непрерывно. Таким образом, О(п)—
топологическая группа и, в частности, Н-пространство.
Отображение О(п) —> {±1}, сопоставляющее матрице её
определитель, — сюръективный гомоморфизм, таким образом, его ядро SO(n),
«специальная ортогональная группа», является подгруппой индекса два.
Два смежных класса SO(n) и O(n) — SO(n) гомеоморфны друг другу, так
как для фиксированной матрицы ВеО(п) с определителем —1
отображения А —► АВ и А —> АВ~1 —взаимно обратные гомеоморфизмы между
этими двумя смежными классами. Подгруппа SO(/z) является
объединением компонент связности пространства О(п), так как образ отображения
О(п) —> {±1} дискретен. В действительности пространство SO(/z) линейно
связно, так как в линейной алгебре доказывается, что любое
преобразование Д е SO(n) — это поворот, т. е. композиция поворотов в наборе
ортогональных двумерных подпространств в R" и тождественного
отображения на подпространстве, ортогональном ко всем этим плоскостям. Такой
поворот можно, очевидно, соединить с тождественным преобразованием
путём, состоящим из поворотов в тех же самых плоскостях, уменьшая
углы поворота. Другая причина, по которой пространство SO(n) связно,
заключается в том, что оно имеет CW-структуру с единственной нульмерной
клеткой, как мы покажем в предложении 3.D.I. В одной из задач в конце
этого параграфа нужно доказать, что топологическая группа с
конечномерной CW-структуро й — ориентируемое многообразие, таким образом,
SO(п) — замкнутое ориентируемое многообразие. Из CW-структуры этого
многообразия следует, что его размерность равна п(п - 1)/2. Эти факты
можно также доказать, используя локально тривиальные расслоения.
Группа О(п) является подгруппой в GL„(R) —«полной линейной
группе» всех обратимых матриц размера пхпе элементами из !R, которая
обсуждалась в начале §З.С. Процесс ортогонализации Грама—Шмидта,
применённый к столбцам матриц из GLn(R), даёт ретракцию г: GLn(R)—>0(п);
непрерывность отображения г очевидна из явных формул для процесса
Грама—Шмидта. Вставляя подходящие скалярные множители в эти
формулы, легко убедиться, что в действительности О(п) —деформационный
ретракт пространства GLn(IR). Используя полярное разложение из
алгебры, можно показать, что пространство GLn(M) в действительности гомео-
морфно О(п) xRky где к = п(п +1)/2.
Топологическое строение группы SO(n) для небольших п можно
описать в терминах более знакомых пространств.
• Пространство SO(l) является точкой.
• Пространство SO(2), повороты плоскости R2, гомеоморфпо (и
изоморфно как группа) окружности S\ которую нужно представлять себе как
множество комплексных чисел, по модулю равных 1.
374
Глава 3. Когомологии
• Пространство SO(3) гомеоморфно IRP3. Чтобы убедиться в этом,
рассмотрим отображение у>: D3 —>SO(3), переводящее ненулевой вектор х
в поворот на угол \х\п относительно оси, образованной прямой,
проходящей через начало координат в направлении вектора х. Чтобы сделать это
определение однозначным, необходимо соглашение об ориентации, типа
«правила правой руки». Тогда по непрерывности отображение с/?
переводит 0 в тождественное отображение. Обе диаметрально противоположные
точки сферы S2 = dD3 отображаются в один и тот поворот на угол я,
таким образом, {р индуцирует отображение (р: RP3 —> SO(3), если
рассматривать Ш>3 как шар D3 с отождествлёнными диаметрально
противоположными граничными точками. Отображение ф, очевидно, инъективно, так
как ось нетривиального поворота единственным образом определяется
как множество его неподвижных точек. Кроме того, (р сюръективно, так
как несложная линейная алгебра показывает, что любой элемент группы
SO(3), отличный от единичного, является поворотом вокруг некоторой
оси. Из этого следует, что <р — гомеоморфизм RP3 ъ SO(3).
• Пространство SO (4) гомеоморфно S3 x SO(3). Если отождествить
R4 с кватернионами И, a S3 —с группой единичных кватернионов, то
умножение кватернионов v —► vw для фиксированного w е S3
определяет изометрию pw € 0(4), так как |vw| = |v||w| = |v|, если |w| = 1. Точки
пространства 0(4)—это четвёрки (ул,..., v4) ортонормированных
векторов v,€H = E4, и мы рассматриваем 0(3) как подпространство, для
которого Vj = 1. Определим гомеоморфизм S3 х 0(3) —* 0(4), переводящий
(v, (l,v2,v3,v4)) в
(v, v2v, v3v, v4v) = pv(1, v2, v3, v4);
обратное отображение имеет вид
(v,v2,v3,v4) -> iy9(l9v2v"l9v3v~\vAv'1)) = (v,pv-i(v,v2,v3,v4)).
Взяв ограничение на компоненты связности единичного элемента, мы
получаем гомеоморфизм S3 x S0(3) ^ SO(4). Он, однако, не является
изоморфизмом групп. Можно показать (хотя мы и не будем здесь
этого делать), что гомоморфизм я/>: S3 x S3 —> SO(4), переводящий пару
единичных кватернионов (u, v) в изометрию w *-» uwv~l пространства
Н, сюръективен и имеет ядро Z2 = {±(1,1)} и что отображение -ф
является накрытием, представляя S3 x S3 как двулистное накрытие над
SO (4), причём это накрытие универсальное. Ограничение гр на диагональ
S3 = {(u,u)}cS3 xS3 даёт универсальное накрытие S3—*S0(3), таким
образом, группа S0(3) изоморфна факторгруппе группы S3 по нормальной
подгруппе {±1}.
Используя октавы, можно таким же способом построить
гомеоморфизм S0(8) ъБ7 х S0(7). Но во всех других случаях SO(n) — лишь
«скрученное произведение» пространств SO(n - 1) и Sn_1; см. пример 4.55 и
обсуждение после следствия 4.D.3.
§ 3.D. Когомологии SO(n)
375
Клеточная структура
Наша первая задача состоит в том, чтобы построить CW-структуру на
SO(n). Она будет получена вместе с очень хорошим клеточным
отображением р: RPn_1 xRPn~2 x ,,. xRP1 —► SO(n). Чтобы упростить обозначения,
мы будем писать Р1 вместо Ж?1.
Каждому ненулевому вектору v e Rn можно сопоставить симметрию
г (у) е О(п) относительно гиперплоскости, состоящей из всех векторов,
ортогональных к v. Так как г(v) —зеркальная симметрия, она имеет
определитель — 1, поэтому, чтобы получить элемент из SO(n), мы
рассмотрим композицию p(v) = r(v)r(e1), где ег —первый стандартный базисный
вектор (1, 0,..., 0). Так как p(v) зависит только от прямой, порождённой
вектором v, мы имеем отображение р : Pn_1 —► SO(n). Это отображение
инъективно, так как оно является композицией отображения v —► r(v),
которое, очевидно, является инъективным отображением пространства
Рп~1 в О(п) - SO(n), и гомеоморфизма О(п) - SO(n) —> SO(n), заданного
умножением справа на г(ег). Так как отображение р инъективно, а Рп_1 —
компактное хаусдорфово пространство, мы можем представлять себе р
как вложение Р""1 в качестве подпространства в SO(n).
Вообще для последовательности / = (ilt..,, im), где все i; меньше п,
мы определим отображение р: Р1 = Ph х ... х Р1>» —► SO(n), взяв в
качестве p{ylt.,., vm) композицию p(yi)^.p(ym). Если </?': Dz —>Р'
—стандартное характеристическое отображение для i-мерной клетки в Р',
ограничением которого является двулистное накрытие 3D1 —► Р'~1, то
произведение у1: D7 —>Р7 соответствующих отображений </Л —характеристическое
отображение для клетки максимальной размерности в Р7. Больше всего
нас будут интересовать последовательности / = С^,..., im),
удовлетворяющие неравенствам п > i} > ... > im > 0, Такие последовательности будем
называть допустимыми, как и последовательность, состоящую из одного 0.
I Предложение 3.D.I. Отображения ру1: D1 —> SO(n) для /, пробегаю-
I щих по всем допустимым последовательностям, являются характери-
I стическими отображениями CW-структуры на SO(n), для которой отоб-
| ражение р: Р""1 х Р"~2 х ... х Р1 —► SO(n) является клеточным.
В частности, есть только одна нульмерная клетка е° = {!}, поэтому
пространство SO(n) линейно связно. Другие клетки е1 = е'1...е'"' —
произведения клеток е' с Рп_1 с SO(n), полученные посредством групповой
операции в SO(n).
Доказательство. Согласно предложению П.2 из приложения, чтобы
показать, что мы действительно получаем CW-структуру, нужно
проверить следующие три утверждения.
1. Для каждой убывающей последовательности / отображение ру>' —
гомеоморфизм внутренности шара D1 на его образ.
376
Глава 3. Когомологии
2. Все получающиеся при этом клетки-образы е не пересекаются и
покрывают SO(n).
3. Для каждой клетки е1 множество pip^dD1) содержится в объединении
клеток меньшей размерности, чем е'.
Чтобы начать проверку этих свойств, определим р: SO(n) -*Sn_1 как
применение изометрии к вектору еп = (0,..., 0,1), т.е. р(а) = а(еп). Изо-
метрии из Рп~2 С Рп~1 С SO(n) оставляют вектор еп неподвижным,
поэтому р(Р"~2) = {еп}. Мы утверждаем, что р — гомеоморфизм из Рп-1 -Рп~2
на Sn~l — {еп}. В этом можно убедиться следующим образом. Если
представлять себе точку в Р""1 как вектор v, то отображение р переводит её
в p(v)(en) = r(v)r(e])(en), что равно r(v)(en), так как
еп лежит в гиперплоскости, ортогональной
вектору в]. Из рисунка справа тогда ясно, что р
просто растягивает нижнюю половину каждой
меридиональной окружности в S""1 на всю меридиональную
окружность, удваивая угол, отсчитываемый от
южного полюса. Таким образом, пространство Р""1 — Рп~2,
представленное векторами, у которых последняя ко- ~~еп
ордината отрицательна, отображается гомеоморфно
HaS,,-1-{en}.
Следующее утверждение заключается в том, что отображение
h: (Pn~1xSO(n-l),Pn~2xSO(n'l)) -> (SO(n), SO(n- 1)),
h(y,a) = p(y)a,
является гомеоморфизмом пространства (Р""1 - pn~2) x SO(n — 1) на
SO(n) - SO(n - 1). Здесь мы рассматриваем SO(n - 1) как подгруппу
в SO(n), оставляющую неподвижным вектор еп. Чтобы построить
гомеоморфизм, обратный к этому гомеоморфизму, предположим, что задан
элемент ft е SO(n) - SO(n - 1). Тогда /3(еп) ^ е„, поэтому согласно
предыдущему абзацу есть единственная точка v^ e P""1 — Р"~2, для которой
p(v^)(en) = /3(еп), причём v^ непрерывно зависит от /3, так как /?(е„)
непрерывно зависит от р. Композиция а^ = p(v/3)~1/3 тогда оставляет
вектор еп неподвижным, следовательно, а^ лежит в SO(n - 1). Так как
p(v^)a/3 = ^, отображение Р*-*{уру а^) обратно к h на SO(n)-SO(n- 1).
Утверждения 1 и 2 можно теперь доказать индукцией по п.
Отображение р переводит Рп~2 в SO(n - 1), поэтому можно предположить по
индукции, что отображения ру' для /, пробегающих все допустимые
последовательности с первым членом i-[<n- 1, — характеристические
отображения для CW-структуры на SO(n — 1) с клетками, соответствующими
произведениям е1. Тогда допустимые последовательности J с i] = п — 1
дают непересекающиеся клетки е7, покрывающие SO(n) - SO (n - 1),
согласно тому, что было показано в предыдущем абзаце. Поэтому свойства 1
И 2 выполняются для SO(n).
§ 3.D. Когомологии SO(n)
377
Чтобы доказать свойство 3, достаточно показать, что имеется
включение1 в SO(n) PlPl сР'Р'"1. Действительно, для допустимой
последовательности J отображение р: Р1 —>SO(n) переводит границу клетки
наибольшей размерности в Р1 в образ произведений PJ с
последовательностями J у полученными из J уменьшением одного члена ij на 1. Любая
такая последовательность является допустимой, за исключением,
возможно, того, что у неё есть два последовательных равных члена. Предваряя
доказательство того, что Р[Р1 с PlPl~l, заметим, что для а G О(п) мы
имеем r(a{v)) — ar{y)a~l. Следовательно, p(v)p(w) = r{v)r(e1)r(w)r(e]) =
= r(v)r(w'), где и/ = r(ex)w. Таким образом, чтобы показать, что Р1Р] с
С PlPl~l, достаточно найти для каждой пары v, w G R'+1 пару х G R'+1,
yGR1, для которой r(v)r(w) = r(x)r(y).
Пусть Vcll+1 — двумерное подпространство, содержащее v и w. Так
как VniR' имеет размерность не менее 1, мы можем выбрать единичный
вектор у G V П R'. Пусть а G 0(i -f 1) переводит V в R2, а у — в ех. Тогда
сопряжённое отображение аг(у)г(и/)а-1 =r(a(v))r(a(w)) лежит в SO(2),
а потому имеет вид р(z) — r(z)r(e{) для некоторого zel2 согласно
утверждению 2 для п = 2. Поэтому
r(v)r(iv) = оГ^Ме^а - r(a-1{z))r(a~] (e{)) = rU)r(y)
длях = а_1(2)еМ'41 иуеМ'.
Остаётся показать, что отображение р : Рп_1 х Рм~2 х ... х Р1 —► SO(n)
клеточное. Это следует из включений Р[Р1 СР'Р1"1, полученных выше,
вместе с другим семейством включений Р^Р} с Р}Р1 для i < ;'. Чтобы
доказать последние включения, запишем формулы
p(v)p{w) = г*0)г(и/), где и/ = r(ex)w, как и раньше
— r(v)r(w')r(v)r(v) =
= r(r(v)w')r(v), поскольку r(a(v)) = ar(v)a~\
= KrOMeJwMv) = r(pO)w)rO) =
— p(p(v)w)p(v'), где v' = г(ех)у, поэтому v = rfe^v'.
В частности, взяв v G Rt+1 и w G R;41 с i < ;, получаем p(v)w G R;_rl,
и произведение p(v)p(w) G P'P; равно произведению p(p{v)w)p(v') €
ePjP\ □
Гомологии и когомологии по модулю 2
Каждая клетка в SO(n) —образ клетки в Рп_1 х Рп"2 х ... х Р1 при
некотором гомеоморфизме. Таким образом, клеточное цепное
отображение, индуцированное отображением р: Рп_1 х Рп"2 х ... х Р1 —> SO(n),
1 Здесь обозначения Р1Р1 используют для изометрий из SO(n), получаемых как
композиции двух изометрий из Р1 с SO(п). —Прим. ред.
о/о
Глава 3. Когомологии
сюръективно. Из этого следует, что для коэффициентов в Z2 все
клеточные граничные отображения для SO(n) тривиальны, так как это верно
в Р1 и, следовательно, в Р""1 х Рп~2 х ... х Р1 согласно предложению 3.B.L
Таким образом, tf#(SO(n); Z2) имеет слагаемое Z2 для каждой клетки
в SO(n). Можно перефразировать это, сказав, что имеют место
изоморфизмы H,(SO(n);Z2) ^Hi(Sn~l x Sn~2 x ... х SJ;Z2) для всех iy так как
у этого произведения сфер клетки также находятся во взаимно
однозначном соответствии с допустимыми последовательностями. Полностью
структуру колец гомологии и когомологии с коэффициентами в Ъг
описывает следующее утверждение.
I Теорема 3.D.2. 1. Имеет место изоморфизм
I H*(SO(n);Z2)* (g) Z^AIA/?/''),
I i нечётное
I где |/3J = i, a pt — наименьшая степень 2, для которой \р?'* | ^ п.
I 2. Кольцо Понтрягина H*(SO(n); Z2) — внешняя алгебра Л^Де1,...
I ....е"-1].
Здесь е' обозначает класс клеточных гомологии клетки е1 сР""1 с
cSO(n), а /3,— двойственный к е' класс, представленный клеточной
коцепью, принимающей значение 1 на клетке е' и 0 на всех других i-мерных
клетках.
Доказательство. Как мы отметили выше, р индуцирует сюръек-
цию на клеточных цепях. Поскольку клеточные граничные
отображения с коэффициентами в Z2 тривиальны как для Р""1 х ... х Р1, так
и для SO(n), из этого следует, что р* сюръективен на H*(~;Z2), а р¥
инъективен на Н*(-;^2). Мы знаем, что H*(Pn~l x ... х Рк, Z2)~кольцо
многочленов Z2[ab .♦., ап_}]7 срезанное соотношениями aj+1 = 0. Для
класса /3, е H2(SO(n); Z2), двойственного классу е', мы получаем, что
Р*(/3,) = 2а' —это класс, сопоставляющий 1 каждой i-мерной клетке
;'
в множителе Р} в Р'1""1 х ... х Р1 и 0 всем другим i-мерным клеткам,
которые являются произведениями клеток меньшей размерности и,
следовательно, отображаются на клетки в SO(n), не пересекающиеся с е'.
Сначала мы покажем, что мономы /3/ = /3^ ...)3,-(11, соответствующие
допустимым последовательностям /, линейно независимы в H*(SO(n); Z2),
а потому являются базисом линейного пространства. Так как р*
инъективен, мы можем отождествить каждый элемент /3, с его образом Х!а;
в срезанном кольце многочленов Z2[a1,,.., Vil/^, ♦♦♦, <*n_i)-
Предположим, что имеет место линейное соотношение 5]Ь7Д = 0, где b, eZ2 и /
пробегает по всем допустимым последовательностям. Так как каждый
элемент /37 — произведение разных /3,, мы можем записать это соотношение
в форме хр} + у = 0, где ни в х, ни в у не входит множитель рг. Так как
§3.D. Когомологии SO(n)
379
множитель ах встречается только в члене /3: двучлена xpY -f у, где он
имеет показатель 1, мы получаем х{5х -f у = хах + z, где ни в ху ни в z
не встречается аг. Из соотношения xa1-fz = 0 в Z2[ab ..., o^.J/fa2, ...
...,an_i) тогда следует, что х = 0. Таким образом, мы можем
предположить, что в исходном соотношении не встречается /3^ Теперь мы
повторим это рассуждение для /32. Запишем соотношение в виде xfi2 -f у = 0, где
ни в х, ни в у не входит /32 или /Зг. Переменная а2 тогда встречается только
в члене /32 двучлена xfi2 + у, где он имеет показатель 2. Таким образом, мы
получаем х/32 + у = ха2 + z, где ни в х, ни в z не входят аг или а2. Тогда
ха^ + z = 0 влечёт, что х = 0, и мы получаем соотношение, в котором не
встречаются ни /Зь ни /32. Продолжая рассуждения по индукции, мы в
конце концов получаем, что все коэффициенты Ъ{ в исходном соотношении
2 Ь//3/ — 0 должны быть нулевыми.
7 Заметим теперь, что /З2 = fl2h если 2i < п, и /З2 = 0, если 2£ ^ п, так
как (2а') —Serf- Факторалгебра Q алгебры Z2[/3b/32, ...] по соотно-
шениям /З2 = {52i и /3; = 0 для j ^ n тогда отображается на всю алгебру
H*(SO(n); Z2). Это отображение Q—>H*(SO(n); Z2) является также инъек-
тивным, так как соотношения, задающие Q, позволяют представить
каждый элемент в Q в виде линейной комбинации допустимых мономов j3h
а допустимые мономы линейно независимы в H*(SO(n); Z2). Алгебру Q
можно также описать как тензорное произведение в утверждении 1
теоремы, так как соотношения /З2 = /32, позволяют записать допустимые
мономы единственным образом как мономы от степеней Д с нечётными i,
а соотношение /3; = 0 для j ^ п принимает вид в /3,р = /3tp' = 0, где j = iph
причём i нечётно, а р, — степень 2. Для данного i это соотношение
выполняется тогда и только тогда, когда ipi ^ п, или, другими словами, тогда
и только тогда, когда |/3fp'| ^ п. Это завершает доказательство
утверждения 1.
Что же касается утверждения 2, заметим сначала, что групповое
умножение SO(n) x SO(n) —> SO(n) является клеточным отображением
ввиду включений Р'Р' с Р'Р'-1 и Р1Р} с Р;Р' для i < ;. Таким образом,
мы можем вычислить произведения Понтрягина на клеточном уровне.
Мы знаем, что имеет место по крайней мере аддитивный изоморфизм
H*(SO(n);Z2) ^A^fe1,..., en_1], так как произведения е1 =е1{ ...е1>" с
допустимыми / образуют базис для H„(SO(n); Z2). Тогда из включения Р1Р1 с
с Р'Р1-1 следует, что произведение Понтрягина (е1)2 равно 0. Остаётся
только проверить соотношение коммутативности е'е;'= е;'е\ Включение
Plpj сР;Р' для/<; было получено из формулы p(v)p(w) — p(p(v)w)p(v')
для v e R'+1, w G Ei+I и v' = rfe^v. Отображение f:P(x Pj — P; x P',
/(v, vv) = (p(v)w, v'), является гомеоморфизмом, так как это композиция
гомеоморфизмов (v, w) -* (v,p(v)w) -> (V, p(v)vv) -^ (p(v)vv, v'). Первое
из этих отображений отображает е' х е; гомеоморфно на себя, так как
JOU
Глава 3. Когомологии
p(v)(e-/) = е;, если i < j. Очевидно, второе отображение тоже
отображает е' х е; гомеоморфно на себя, в то время как третье отображение
просто переставляет эти два множителя. Таким образом, ограничение
/ на е' х е) является гомеоморфизмом на е; х е\ а потому е'е; = e;V
BH,(SO(n);Z2). D
Структуры w-ироизведения и произведения Понтрягина в этой
теореме могут показаться, на первый взгляд, не связанными друг с другом, но
в действительности связь между ними довольно прямая. Как мы видели
в предыдущем параграфе, двойственная алгебра для алгебры
многочленов Z2[x] —это алгебра разделённых степеней Г2 [а], а для
коэффициентов bZ2 последняя алгебра является внешней алгеброй ЛйДа0, аь ..,], где
|а,-| = 2'|х|. Если мы срежем алгебру многочленов соотношением хт =0,то
это лишь исключает образующие а, для \ ^ п. Ввиду этого если бы
образующие Д для алгебры H*(SO(n); Z2) оказались примитивными, то тогда
H*(SO(n); Z2) как алгебра Хопфа была бы изоморфна тензорному
произведению алгебр Хопфа с одной образующей Z2[j3,-]/(j3f?'), i = l, 3, ... В этом
случае, двойственная алгебра H+(SO(n); Z2) была бы тензорным
произведением соответствующих алгебр разделённых степеней, другими
словами, внешней алгеброй, как только что было объяснено. Это в
действительности структура H+(SO(n); Z2), поэтому, так как произведение Понтрягина
в H¥(SO(n); Z2) определяет копроизведепие в H*(SO(n); Z2) единственным
образом, все Д действительно должны быть примитивными.
Нетрудно дать прямое доказательство того, что каждый элемент Д
примитивный. Копроизведепие
Л: H*(SO(n); z2) -> //*(SO(n); Z2) <8>H+(SO(n); Z2)
индуцировано умножением в группе fi: SO(n) x SO(n) -* SO(n). Мы
должны показать, что значение Д(Д) на е1 ®eJ, которое мы обозначим
(Д(Д), е{ ® eJ), совпадает со значением (Д <8> 1 + 1 <8> Д, el ® eJ) для всех
клеток е' и eJ, размерности которых в сумме дают i. Так как Л = /^*, мы
имеем (Л(Д), е/ (2)^) — (Д, /i^(V ®eJ)). Поскольку/i — отображение
умножения, дСе' х eJ) содержится в Р1Р'1. Если мы воспользуемся
соотношениями pip} с pjpi~l и Р^ с РкР> для ; < к, чтобы переставить множители Р]
в Р1Р3 так, чтобы их размерности были расположены в порядке убывания,
то получить в конце концов член Р' можно лишь тогда, когда мы начинаем
с PlPJ, равного Р'Р° или Р°Р1. Таким образом, (Д, /i*(e' ® eJ)) = О, за
исключением тех случаев, когда е1 <8> eJ равно е1 ® е° или е° <8> е1.
Следовательно, А(Д) не содержит никаких других членов, кроме Д <8> 1 +1 ® Д,
и элемент Д примитивный.
Целочисленные гомологии и когомологии
Для коэффициентов в Z гомологии и когомологии пространства SO(n)
оказываются намного более сложными, чем для коэффициентов в Ъ2-
§ 3.D. Когомологии SO(n)
381
Часть этой сложности можно увидеть уже для небольших значений п,
когда гомеоморфизмы SO(3) ^RP3 и SO(4) ъБ3 х 1RP3 позволяют вычислить
аддитивную структуру как прямую сумму некоторого числа групп Z и Z2.
Для всех значений п аддитивная структура качественно та же самая.
■ Предложение 3.D.3. Группа H+(SO(n);Z) является прямой суммой
групп Z и Z2.
Доказательство. Вычислим клеточный цепной комплекс для SO(n)
и покажем, что его можно представить в виде тензорного произведения
более простых комплексов. Для клетки е1 с Рп_1 с SO(n) клеточная
граница de' равна 2е'-1 для чётного i > 0 и 0 для нечётного i. Чтобы
вычислить клеточную границу клетки eh...elniy мы можем перенести её
назад в клетку е'1 х ... х е1,и в Р"-1 х ... х Р1, клеточная граница которой
согласно предложению З.В.1 равна ^(-l^e'1 x ... х de'> x ... х е'»«, где
j
о,-= ii-f ...+ i;-_i. Следовательно, d(eh...e'"») = S(-l)C7je'1...de''...e'"', где
;'
подразумевается, что eh...del>...elm равно нулю, если z- = i-+1 -f 1, так как
pij-ip'j-i содержится в Р'^Р';-2, т.е. в остове меньшей размерности.
Чтобы представить клеточный цепной комплекс C¥(SO(n)) в виде
тензорного произведения меньших цепных комплексов, рассмотрим С2' —
подкомплекс в C+(SO(n)), базисом которого служат клетки е°, е2', е21"1
и е2'е2'-1. Это действительно подкомплекс, так как de2'-1 = 0, de2' =2e2'-1,
а в Р2' х Р2'"1 имеем
d(e2' х е2'"1) = de2' х е2'"1 + е2'' х de2'"1 = 2е2'~] х е2'"1,
следовательно, dCe^e2'"1) =0, таккакР2'_1Р2'-1 с Р2'"^2'"2. Утверждение
состоит в том, что имеют место изоморфизмы цепных комплексов
C+(SO(2fc + l)) ^C2®C4g>...g>C2fc,
C+(SO(2fc + 2)) ^C^C^.^C2^^1,
где C2/f+1 имеет базис е° и e2fc+1. Конечно, эти изоморфизмы имеют место
для самих групп цепей, поэтому нужно только проверить, что граничные
отображения согласованы. В случае комплекса C+(SO(2fc-f 1)) это можно
доказать индукцией по fc, в чём читатель может легко убедиться. Затем
случай комплекса C+(SO(2fc + 2)) сводится к первому случаю
аналогичным рассуждением.
Так как И^{СЪ) состоит из групп Z в размерностях 0 и А\ — 1 и
группы Z2 в размерности 2f - 1, а Я+(С2/с+1) состоит из групп Z в
размерностях 0 и 2к + 1, мы получаем из алгебраической формулы Кюннета, что
H+(SO(n); Z) — это прямая сумма групп Z и Z2. О
Заметим, что это вычисление показывает, что SO(2fc) и SO(2fc - 1) х
х S2k~] имеют изоморфные группы гомологии во всех размерностях.
382
Глава 3. Когомологии
Предложение 3.D.3 позволяет получить довольно полную информацию
0 H*(SO(n); Z), рассматривая естественные отображения в H*(SO(n); Z2)
и в факторгруппу по подгруппе кручения. Обозначим эту факторгруппу
Hfec(SO(n); Z). Та же самая стратегия столь же хорошо применима и к
когомологиям, а теорема об универсальных коэффициентах даёт
изоморфизм Hf*ree(SO(n); Z)*H*ee(SO(n); Z).
Доказательство предложения 3.D.3 показывает, что аддитивная
структура в H^rce(SO(n); Z) довольно проста:
H^ree(SO(2/c +1); Z) % H,(S3 х S7 x ... х S4*-1),
tt[rce(SO(2/c + 2); Z) * H+(S3 х S7 х ... х S4*"1 x S2k+l).
Мультипликативная структура также настолько проста, насколько
возможно.
1 Предложение 3.D.4. Кольцо Понтрягина Hfrce(SO(n); Z) — это внеш-
I няя алгебра
I Hfee(SO(2k + l);Z) « Az[a3,a7, ....a^-iL где |a,| = i,
I Hfrec(SO(2fc + 2);Z)«Az[a3>a7,...>a4Jt_lla2Jt+1].
I Образующие a, примитивные, поэтому двойственная алгебра Хопфа
I ^free^O(n)' ^ ~~ это внешняя алгебра от двойственных образующих а,.
Доказательство. Как и в случае коэффициентов в Z2, мы можем
работать на уровне клеточных цепей, так как умножение в SO(n) кле-
точно. Рассмотрим сначала случай n = 2fc + l. Пусть Я1—цикл е2'е2'"\
порождающий слагаемое Z группы H„(SO(n); Z). Согласно доказанному
выше произведения Eh...Eln,t ix> ...> imJ образуют аддитивный базис для
H[rce(SO(n);Z), поэтому мы должны только проверить, что умножение
устроено так, как во внешней алгебре от классов £'. Отображение / в
доказательстве теоремы 3.D.2 даёт гомеоморфизм е1 х е; ъ е; х е', если i < j,
причём этот гомеоморфизм имеет локальную степень (-1)/;+1, так как
он является композицией (v, w) —► (v, p(v)w) —► (V, p(v)w) —► (p(v)w, v')
гомеоморфизмов с локальными степенями +1,-1 и (—1)^'. Применим
это четыре раза, чтобы преобразовать Е1Е> = е2'е2'"1е2;е2;-1 в Е*Е1 =
= e2^e2;_1e2ze2'Jl. Три из этих четырёх перестановок дают знаки — 1, а
четвёртая даёт знак+1, поэтому мы получаем, что£'Е; = — Е}Е\ если* <;\
Когда i = j, мы получаем (Е')2 = 0, так как e2le2l_1e2,e2'"1 = e2re2/e2'"1e21"1, что
лежит в остове меньшей размерности из-за соотношения ръръ с ръръ~ .
Таким образом, мы показали, 4ToH*(SO(2/c-f 1); Z) содержит AZ[E\ •••
..., Ек] в качестве подалгебры. Те же самые рассуждения показывают, что
H+(SO(2/c + 2); Z) содержит подалгебру AZ[E\ ..., Ек, e2fc+1]. Эти внешние
подалгебры отвечают за всё, кроме кручения, в H¥(SO(n);Z), поэтому
структура произведения в H^rcc(SO(n); Z) именно такая, как угверждается
в формулировке.
§3.D. Когомологии SO(n)
383
Теперь мы покажем, что образующие Е1 и e2k+l примитивные в
Hhee(.SO(n); Z). Глядя на формулу для граничного отображения в
клеточном цепном комплексе для SO(n), мы видим, что этот цепной комплекс —
прямая сумма подкомплексов С(гп) с базисом из гп-кратных произведений
eI'1...elm, где il > ...>im>0. Здесь может быть гп = 0, и С(0) имеет базис,
состоящий из нульмерной клетки в SO(n). Прямая сумма С(0)ф...ФС(гп) —
клеточный цепной комплекс подкомплекса в SO(n) состоящего из клеток,
которые являются произведениями не более т клеток е'. В частности,
взяв т = 2, мы получаем подкомплекс X с SO(n), гомологии которого,
по модулю кручения, состоят из Z в нулевой размерности и групп Z,
порождаемых клетками Е', причём вместе с клеткой е2к+х при n = 2fc-H2.
Включение X«—> SO(n) индуцирует коммутативную диаграмму
Hfree(x. z) А ^ Hfree(X; Z) 0Н<тее(Х; z)
т т
H+free(SO(n); Z) —^ H+frce(SO(n); Z) ® H*ee(SO(n); Z)
где нижнее отображение Л — копроизведение в H[ree(SO(n); Z), а
верхнее отображение Д — его аналог для X, получающийся из диагонального
отображения X —► X х X и формулы Кюннета. Классы Е1 в нижней левой
группе поднимаются до элементов в верхней левой группе, которые мы
обозначаем Е1. Так как они имеют нечётную размерность, a H[Tee(X;Z)
обращается в нуль в чётных положительных размерностях, образы А(Е')
не могут иметь компонент вида а®Ъ, где оба элемента а и Ъ имеют
положительную размерность. Поэтому то же самое верно и для Л(Е1) в силу
коммутативности диаграммы, таким образом, классы Е1 примитивные.
Это рассуждение работает также для e2k+l, когда п = 2к -Ь 2.
Так как образующие внешней алгебры для H^ree(SO(n); Z)
примитивные, эта алгебра раскладывается как алгебра Хопфа в тензорное
произведение внешних алгебр Л^[а,] с одной образующей. Поэтому двойственная
алгебра Хопфа Hf*ee(SO(n); Z) раскладывается в тензорное произведение
Двойственных внешних алгебр Лй[а,-], следовательно, Hf*ee(SO(n); Z) тоже
внешняя алгебра. D
Точную кольцевую структуру H*(SO(n);Z) можно вывести из этих
результатов посредством гомоморфизмов Бокштейна, как мы покажем
в примере З.Е.7, хотя этот процесс несколько трудоёмкий, а ответ не очень
приятный.
Многообразия Штифеля
Рассмотрим многообразие Штифеля Vnk, точки которого — ортонор-
Мированные fc-реперы в Мп, т.е. наборы из к ортонормированных
векторов. Таким образом, Vnk — подмножество в произведении к экземпляров
384
Глава 3. Когомологии
сферы S""1, и оно снабжается топологией подпространства. В частных
случаях мы имеем Vnn =0(n) и Vnл =Sn~\ Кроме того, Vn2 можно
отождествить с пространством единичных касательных векторов к S""1, так
как вектор v в точке xeS"'1 касается S"-1 тогда и только тогда, когда
он ортогонален х. Можно также отождествить Vnu_x с SO(n), так как есть
только один способ дополнить ортонормированный (п - 1)-репер до
положительно ориентированного ортонормированного п-репера.
Имеется естественная проекция р: О(п) —» Vlhk, переводящая аеО(п)
в /е-репер, состоящий из последних к столбцов матрицы а, которые
являются образами при отображении а последних к векторов стандартного
базиса в 1R". Эта проекция — отображение на, а прообразы точек —это
в точности смежные классы аО(п - к), где мы вкладываем 0(п - к) в О(п)
как ортогональные преобразования первых п — к координат в Rn. Таким
образом, Vtltk можно рассматривать как пространство 0(гс)/0(п - к) таких
смежных классов с фактортопологией из О(п). Это то же самое, что и
определённая ранее топология на V,hk, так как проекция О(п) —> Vn^ является
сюръективным отображением компактных хаусдорфовых пространств.
При к < п проекция р: SO(n) —» Vnk сюръективна, и Vnk можно
также рассматривать как факторпространство SO(n)/SO(n — к). Мы
можем воспользоваться этим, чтобы индуцировать CW-структуру на V„tk из
CW-структуры на SO(n). Клетками являются множества смежных классов
вида el SO(n - к) = el]...elnt SO(n - /с), где п > 1г > ... > im ^ и - к, вместе
с самим смежным классом SO(n —к) в качестве нульмерной клетки в Vllk.
Эти множества смежных классов —объединения клеток в SO(n), так как
SO(n - к) состоит из клеток eJ = e;i.. .eJ', где п — к> jx> ...> jc. Из этого
следует, что Vnk — объединение этих непересекающихся клеток, и граница
каждой клетки содержится в клетках меньшей размерности, таким
образом, мы действительно получаем CW-структуру.
Так как проекция SO(n) —> Vnk является клеточным отображением,
структуру клеточного цепного комплекса для Vnki можно легко вывести
из такой же структуры для SO(n). Например, клеточный ценной комплекс
для V2k+],2 —это комплекс С2/с, определённый ранее, в то время как для
V2k2 все клеточные граничные отображения тривиальны. Следовательно,
ненулевые группы гомологии Vn2 такие:
[Ъ при1 =0, 4/с-1;
у L2 при i = 2/с — 1;
Ili(V2k2) Z) = Z при i =0, 2/с - 2, 2/с - 1, 4/е - 3.
Таким образом, SO(n), имеет те же самые группы гомологии и
когомологии, что и произведение пространств V22 x V52 х ... х 1^+1,2 ПРИ л = 2/с +
или V32 х V52 x ... х V2k+l2 x S2k^ при п =2к + 2. Однако наши
вычисления показывают, что SO(n) отличается от этих произведений структур»11
§ З.Е. Гомоморфизмы Бокштейна
385
^-произведения с коэффициентами в Z2, по крайней мере при п ^ 5, так
как элемент (3* отличен от нуля в H4(SO(n); Z2), если п ^ 5, в то время как
для произведений пространств нетривиальный элемент группы Нг(—; Z2)
должен лежать в множителе V32, а Н4(1/32; Z2) =0. При п = 4 пространство
SO(4) гомеоморфно SO(3) x S3 = V3>2 x S3, как мы уже отметили в начале
этого параграфа. Кроме того, SO(3) = V3,2 и SO(2) =SJ.
Задачи
1. Докажите, что топологическая группа, которая имеет
конечномерную СW-структуру, является ориентируемым многообразием.
[Рассмотрите гомеоморфизмы л:—>xg для фиксированного элемента группы g.]
2. Используя CW-структуру на SO(n), докажите, что пх SO(n) % Z2 для
П^З. Укажите петлю, представляющую образующую, и опишите, как эта
удвоенная петля стягивается в точку.
3. Вычислите структуру кольца Понтрягина в H+(SO(5); Z).
§ З.Е. Гомоморфизмы Бокштейна
Гомологии и когомологии с коэффициентами в поле, особенно в поле
Zp с простым р, часто имеют дополнительные структуры, и их легче
вычислять, чем для коэффициентов в Z. Конечно, переход от коэффициентов
В Z к коэффициентам в Zp может привести к определённой потере
информации, размывая более тонкие различия. Например, Zp„ в целочисленных
гомологиях превращается в пару групп Zp в гомологиях или когомологиях
с коэффициентами в Ъ таким образом, показатель степени п теряется
для коэффициентов в Zp. В этом параграфе мы введём гомоморфизмы
бокштейна, которые во многих интересных случаях позволяют
восстановить информацию для коэффициентов в Z по информации для коэффи-
диентов в Zp. Гомоморфизмы Бокштейна также обеспечивают некоторую
дополнительную внутреннюю структуру на самих гомологиях и когомоло-
Айях с коэффициентами в Zp, которая может оказаться весьма полезной.
Мы сконцентрируемся на когомологиях, чтобы иметь в своём
распоряжении w-произведения, но основные конструкции столь же хорошо
работают и для гомологии. Если мы возьмём короткую точную
последовательность 0—> G —»// —»К —»0 абелевых групп и применим ковариантный
функтор Нот(См(Х), -), то получим последовательность
0 -> СМ(Х; G) -+ С"(Х; И) -> СМ(Х; К) -+ 0,
которая является точной, так как группа С„(Х) свободная. Разрешив п
изменяться, мы получим короткую точную последовательность цепных
комплексов, поэтому имеется соответствующая ей длинная точная
последовательность
... -+ Нп(X; G) — //"(X; Н) -> Н"(Х; К) -> Н'н '(X; G) -> ...,
Нак. м>\<
386
Глава 3. Когомологии
«граничное» отображение в которой Нп(Х; K)—>Hn+l(X; G) называют го-
моморфизмом Бокштейна.
Нас прежде всего будет интересовать гомоморфизм Бокштейна /3:
Нп(Х; Zm) —>Hn+l(X; Z,„), связанный с последовательностью
коэффициентов т
О -> Zni -> ZWI2 -* Zm - О,
особенно для простого т, но пока нам не нужно это предположение.
Тесно связан с /3 гомоморфизм Бокштейна /3: Нп{Х\ Zm) ->Hn+l(X; Z),
соответствующий последовательности 0 —* Z —> Z —* Ът —* 0. Из естественного
отображения последней короткой точной последовательности на
предыдущую мы получаем соотношение /3 =р/3, где р: Н*(Х; Z) -* Н*(Х; 2Ж) —
гомоморфизм, индуцированный отображением Z —*Zm, приводящим
коэффициенты по модулю т. Таким образом, мы получаем коммутативный
треугольник в следующей диаграмме:
H"(X;Z) P > Hn(X;ZJ
верхняя строка которой — точная последовательность, содержащая (3.
Пример З.Е.1. Пусть X — это пространство K(Zmi 1), например RP00
для m = 2 или бесконечномерное линзовое пространство с
фундаментальной группой Zm для произвольного т. Из гомологических вычислений
в примерах 2.42 и 2.43, воспользовавшись теоремой об универсальных
коэффициентах или клеточными когомологиями, мы получаем Нп{Х\ Z,M)«
^ Zm для всех п. Давайте покажем, что отображение /3: Hn(X;Zm) -*
—► Нп+}(Х] Zm) — изоморфизм для нечётных п и нулевое для чётных п.
Если п нечётно, то вертикальное отображение р в приведённой выше
диаграмме сюръективно для X = K(Zmi 1), как и отображение /3,
поскольку отображение m тривиально. Поэтому отображение /3 сюръективно,
а значит, оно является изоморфизмом. С другой стороны, когда п четно,
первое отображение р в этой диаграмме сюръективно, таким образом,
/3 =0 согласно точности, следовательно, /3 = 0.
Полезный факт о гомоморфизме /3 состоит в том, что он
удовлетворяет свойству дифференцирования
(*) /3(а^Ь) =/3(a) ^Ъ+(-1)^а^/3(b),
которое получается из соответствующей формулы для обычной
кограницы. А именно, пусть у> и я/' — коциклы с коэффициентами в Zm,
представляющие классы а и Ь, и пусть (^и^-их поднятия до коцепей с
коэффициентами в Zm2. Конкретно можно рассмотреть у игр как функции на
сингулярных симплексах со значениями в {0, 1, ..., т - 1}, а затем в каче-
*Hn+1(X;Z)
^Hn+l(X]Z)
H"+1(X;Zm)
§ З.Е. Гомоморфизмы Бокштейна
387
стве (р и ip можно взять те же самые функции, но теперь {0,1, ..., т — 1}
рассматривается как подмножество в Zmi. Тогда 5(p = mri и 5гр = m[i для
коциклов т)и/2С коэффициентами в Zp, представляющих /3(a) и [3(b).
Если рассмотреть ^-произведения, то (р^гр —коцепь с коэффициентами
в Zm2, которая является поднятием коцикла \р wi/> с коэффициентами
в^т,и
5{(р^гр) = 5(р^гр±(рку5'ф = шт} wi/;±<£wrn/i = m (17 wi/j ± (/? w /i),
где знак ± равен (—1)'°'. Следовательно, tj wi/> -f (-1)'а|(/> v^/i представляет
класс |S(awb), что и даёт формулу (*).
Пример З.Е.2 (w-произведения в линзовых пространствах).
Структура w-произведения для линзовых пространств была вычислена в
примере 3.41 с помощью двойственности Пуанкаре, но, применяя
гомоморфизмы Бокштейна, мы можем вывести её из структуры ^-произведе-
ния в СР°°, которая была вычислена в теореме 3.12 без использования
двойственности Пуанкаре. Рассмотрим сначала бесконечномерное
линзовое пространство L = S°°/Z,„, где Zm действует на единичной сфере S°°
в С°° умножением на скаляры, таким образом, это действие
порождается поворотом v —* e2nilmv. Факторотображение S°° —> СР00 пропускается
сквозь L, таким образом, мы получаем проекцию L —> СР°°. Глядя на
клеточную структуру на L, описанную в примере 2.43, мы видим, что
каждая клетка в L чётной размерности проектируется гомеоморфно на
соответствующую клетку в СР°°. А именно, 2п-мерная клетка в L — это
гомеоморфный образ 2п-мерной клетки в S2n_Hl с Сп+1, образованной
точками cos0(zb ...,zn,O) + sin0(O, ...,0,1), для которых $]z? = l и О<0^тг;
то же самое верно для 2п-мерных клеток в СР°°. Если рассмотреть
клеточные когомологии, то из этого следует, что отображение L—►СР00
индуцирует изоморфизмы когомологии чётной размерности с коэффициентами
в Zm. Так как Н*(СР°°; Zm) — кольцо многочленов, мы получаем, что
если у е H2(L; Zm) — образующая, то ук порождает группу H2k(L\Zm) для
.Всех к.
Согласно примеру З.Е.1 существует образующая хбН1^;^), для
которой /ЗО) = У- Из формулы для произведения (*) получаем f3(xyk) =
= Р(х)ук - х/3(ук) = yk+l. Таким образом, /3 переводит хук в
образующую, следовательно, элемент хук должен быть образующей группы
H2/c+1(L; Z,„). Это полностью определяет структуру w-произведения в
Н*Щ Zm), если т нечётно, так как из свойства коммутативности w-npo-
изведения следует, что в этом случае х2 = 0. Результат состоит в том, что
H*(L; Zm) а» \z [x] ®Z,n[y] для нечётного т. Когда т четно, это
утверждение нужно немного изменить, добавив уловие, что л:2 — единственный
элемент порядка 2 в H2(L; Z,„) «» Z,„, как мы показали в примере 3.9 явным
вычислением в двумерном остове комплекса L.
388
Глава 3. Когомологии
Структура ^-произведения в конечномерных линзовых
пространствах следует из этого, поскольку конечномерное линзовое пространство
вкладывается в бесконечномерное линзовое пространство как остов, а
гомотопический тип бесконечномерного линзового пространства
определяется его фундаментальной группой, так как оно является пространством
типа К (я, 1). Из этого следует, что структура ^-произведения на линзовом
пространстве S2',+1/Z„, с коэффициентами в Zm получается из
предыдущего вычисления срезанием посредством соотношения^""1"1 =0.
Из соотношения /3 = р /3 следует, что /З2 = pfip /3 = 0, так как /Зр = о
в длинной точной последовательности, содержащей /3. Поскольку /З2 = 0,
группы Hn(X;Zm) образуют цепной комплекс с гомоморфизмами Бокш-
тейна /3 в качестве «граничных» отображений. Мы можем тогда построить
соответствующие группы когомологии Бокштейна Кег/3/ Im/З, которые мы
обозначаем ВНп(Х; Zm) в размерности п. Наиболее интересный случай —
когда т равно простому числу р, поэтому в дальнейшем мы будем это
предполагать.
I Предложение З.Е.З. Если группы Hn(X;Z) конечно порождённые
I для всех л, то группы когомологии Бокштейна ВНп(Х; Zp) находятся по
I следующим правилам:
I а) каждое слагаемое Z группы Нп(Х; Z) даёт слагаемое Zp в группе
I BH'l{X;Zp);
I б) каждое слагаемое Zpk группы Нп(Х; Z) с /с > 1 даёт слагаемые Ър
I как в ВНп-\Х\ Zp), так и в ВНп(Х', Zp);
I в) слагаемое Zp группы Нп(Х; Z) даёт слагаемые Zp вНп~1(Х; Zp) ив
I Я" (X; Zp), причём /3 — изоморфизм между этими двумя слагаемы-
I ми, поэтому оно не даёт никакого вклада в ВН*(Х; Zp).
Доказательство. Мы будем использовать алгебраическое понятие
минимального цепного комплекса. Предположим, что С —цепной
комплекс свободных абелевых групп, для которых группы гомологии Нп{С)
конечно порождённые для всех п. Выберем разложение каждой группы
Нп(С) в виде прямой суммы циклических групп. Этих циклических групп
счётное множество, поэтому мы можем перечислить их как G{, G2,... Для
каждой группы G, выберем образующую g,- и определим соответствующий
цепной комплекс M(g() по следующему правилу. Если g,- имеет
бесконечный порядок в G, с Нп (С), то M(g,) состоит только из Z в размерности л,-
с образующей z,. С другой стороны, если g{ имеет конечный порядок к
в Нп.(С), то M(g;) состоит из групп Z в размерностях п, и 72, +1,
порождаемых элементами х,- и у,- соответственно, причём ду{ = /сх,. Пусть М —
прямая сумма цепных комплексов M(g(). Определим цепное отображение
а: М —> С так, что оно переводит z{ и х, в циклы £,- и £,-,
представляющие соответствующие классы гомологии для g,, а у, —в цепь г/,, для
которой drj, = /с£,. Цепное отображение а индуцирует изоморфизм го-
§ З.Е. Гомоморфизмы Вокштейна
389
мологий, а значит, и когомологий с любыми коэффициентами согласно
следствию 3.4. Двойственный коцепной комплекс М*, полученный в
результате применения Hom(—, Z), раскладывается в прямую сумму
двойственных комплексов M*(gi)- Поэтому в когомологиях с коэффициентами
в Ъ элемент двойственного базиса z* порождает слагаемое Ъ в
размерности nh в то время как у* порождает слагаемое Тк в размерности п, + 1,
так как Ьх[ — ку%{. Для коэффициентов в Z/;, где число р простое, z* даёт
слагаемое Zp в группе Нп,(М\ Zp), в то время как х* и у* дают слагаемые
Ър в ЯП/(М; Ър) и в Нп, + 1(М\ %р), если р делит /с, а иначе они ничего не
дают.
Отображение а индуцирует изоморфизм между соответствующими
длинными точными последовательностями групп когомологий Бокштей-
на, причём с коммутативными квадратами. Таким образом, мы^можем
использовать комплекс М* для вычисления гомоморфизмов /? и /3, и мы
можем провести это вычисление отдельно на каждом слагаемом M*(g,).
Очевидно, что (5 и (5 обращаются в нуль на у* и на z*. Когда р
делит /с, мы получаем класс х* GH"'(M; Zp), а по определению
гомоморфизмов Бокштейна из этого следует, что /3U*) = (к/р)у* е H"i+1(M; z)
и /3(х*) = (/с/р)у-* е Нп,+г(М; Ър). Последний элемент отличен от нуля
тогда и только тогда, когда к не делится на р2. □
I Следствие З.Е.4. В ситуации, описанной в предыдущем предложе-
I нии, группа 1Г(Х\ Z) не содержит элементов порядка р2 тогда и только
I тогда, когда размерность BH1l{X\ Zp) как линейного пространства над
I Zp равна рангу группы Нп(Х\ Z) для всех п. В этом случае отображение
I р: Н*(Х; Z) —>Н*(Х; Zp) инъективно на р-кручении, причём образ это-
I го р-кручения при отображении р равен Im/3.
Доказательство. Первое утверждение очевидно следует из
предложения. Инъективность отображения р на р-кручении в действительности
эквивалентна отсутствию элементов порядка р2. Равенство Imp = Im/3
следует из того факта, что в коммутативной диаграмме в начале этого
параграфа Im/3=p(Im/3)=p (Ker m), и того, что для m = p ядро отображения
т—-это в точности р-кручение, если нет элементов порядка р2. □
Пример З.Е.5.Применим гомоморфизмы Бокштейна, чтобы
вычислить группы Н*(-КР°° х RP00; Z). По-другому это можно было бы сделать,
сначала вычислив гомологии посредством общей формулы Кюннета, а
затем применив теорему об универсальных коэффициентах, но с
гомоморфизмами Бокштейна нам будет нужна только более простая формула
Кюннета из теоремы 3.16 для коэффициентов в поле. Структуру w-произве-
дения в H*(RP°° х RP00; Z) тоже будет легко определить с помощью
гомоморфизмов Бокштейна.
Для нечётного простого числа р мы имеем /7*(RP°°; Zp) = 0,
следовательно, H*(RP°° х RP00; Zp) = 0 согласно теореме 3.16. По теореме об
390
Глава 3. Когомологии
универсальных коэффициентах тогда получаем, что H*(RP°° xRP°°;Z)
целиком состоит из элементов, порядки которых — степени числа 2. Из
примера З.Е.1 мы знаем, что гомоморфизмы Бокштейна в H*(RP°°; Z2) ъ
ъ%2[х] задаются формулой /3(х2к~1) = х2к и /3(х2к) = О, В H'CRP00 x
х RP00; Z2) ^Z2[jc,y] мы можем тогда вычислить /3 по формуле
произведения Р(хтуп) = (I3xm)ytl + xm(l3yn). Ответ представлен графически на
рисунке. Здесь точка, ромб или окруж- 6
ность в точке с координатами (т, п) пред- Т Т Т Т Т I Y
ставляют моном хтуп, а отрезки указы- У' • *—* *—^ А—6
вают нетривиальные гомоморфизмы Бок- у* « о—о о о о—о
штейна. Например, нижний левый квад- ч I I I I I I I
рат представляет собой запись формул ^
/3(ху) = х2у + ху2у/3(х2у) = х2у2 = 13(ху2) у2 о о—о с—о *—о
и /3(х2у2) = 0. Таким образом, для этого I 1 1 I I II
квадрата мы видим, что Ker/3 = Im/3,
причём образующими являются «диагональ- 1 ° •—о •—о •—о
нал» сумма х2у + ху2 и х2у2. То же самое 1 х х2 х3 хА х5 хь
происходит во всех других квадратах,
поэтому очевидно, что Кег /3 = Im /3, за исключением нульмерного класса «1».
Согласно предыдущему следствию это означает, что все нетривиальные
элементы группы H*(RP°° x IRP°°; Z) имеют порядок 2. Кроме того, Im/3
состоит из подкольца Z2[x2,y2], обозначенного на рисунке
окружностями, вместе с элементами, которые получаются из х2у + ху2 при
умножении на элементы кольца Z2j>2, у2]. Из этого следует, что имеет место
изоморфизм колец
H*(RP°° х RP00; Z) w Z[A, /i, v]/(2A, 2ju, 2v, v2 +A2ju +Aju2),
где p(A) = л:2, р(м) = у2, p(v) = x2y + ху2, а соотношение v2 + A2/i +
+ А/х2 = 0 выполняется, так как (х2у + ху2)2 = xAу2 + x2y4.
Это вычисление иллюстрирует общий принцип, что структуры w-npo-
изведения с коэффициентами в Z склонны оказываться гораздо более
сложными, чем с коэффициентами в поле. Можно получить ещё более
поразительное свидетельство этого, вычислив H*(RP°° x RP00 x RP°°;Z)
тем же самым методом.
Пример З.Е.6. Построим конечные CW-комплексы Xl9 Х2 и У, для
которых кольца H*(^;Z) и H*(X2;Z) изоморфны, но Н*(Хг х Y;Z) и
Н*(Х2 х У; Z) изоморфны только как группы, но не как кольца. Согласно
теореме 3.16 это может случиться, только если у всех трёх пространств
X-i, Х2 и У есть кручение в когомологиях с коэффициентами в Z.
Пространство Хх получается из S2 x S2 приклеиванием трёхмерной клетки
е3 ко второму множителю S2 по отображению степени 2. Таким
образом, Х} имеет CW-структуру с клетками е°, е2, е2, е3 и е4, причём клетка
е3 приклеена к двумерной сфере е0 и е2< Пространство Х2 получено из
§ З.Е. Гомоморфизмы Бокштейна
391
S2 V S2 V S4 приклеиванием трёхмерной клетки ко второму слагаемому S2
по отображению степени 2, таким образом, оно имеет CW-структуру с тем
же самым набором из пяти клеток; единственное различие заключается
в том, что в Х2 четырёхмерная клетка приклеена тривиально. В качестве
пространства У мы выберем пространство Мура M(Z2, 2) с клетками,
помеченными /°, /2, /3; здесь трёхмерная клетка приклеена по
отображению степени 2.
Из клеточных когомологий можно видеть, что как H*{XY\Z)y так и
Н*{Х2\ Z) состоят из Z в размерностях 0, 2 и 4 и из Z2 в размерности 3.
В обоих случаях все произведения классов положительной размерности
нулевые, так как по причинам размерности единственное возможное
нетривиальное произведение является квадратом двумерного класса, но
оно равно нулю, в чём легко убедиться, ограничившись подкомплексом
S2 х S2 или S2 V S2 V S4. Для пространства У мы получаем, что Н*(У; Z)
состоит из Z в размерности 0 и из Z2 в размерности 3, таким образом,
структура ^-произведения здесь тоже тривиальна.
С коэффициентами в Z2 все клеточные коцепные комплексы для Xh
Y и Xt, х У тривиальны, поэтому мы можем отождествить их клетки с
базисом для когомологий с коэффициентами в Z2. В X, и в У единственные
нетривиальные гомоморфизмы Бокштейна с коэффициентами bZ2- это
)8(е2) = е3 и /3(/2) =/3. Гомоморфизмы Бокштейна в X, х У можно тогда
вычислить, используя формулу произведения для /3, которая применима
к внешнему произведению, как и к ^-произведению, поскольку внешнее
произведение определено в терминах ^-произведения. Полученные
результаты изображены в виде следующей таблицы, где стрелка обозначает
нетривиальный гомоморфизм Бокштейна.
е°х/° е2х/° е3х/° е4х/° е2х/3 е4х/2-^е4х/3
е2х/° е°х/3 е2х/2 е3х/2-^е3х/3
е°х/2 е2х/2-^е2х/3
Две стрелки, выходящие из е2 х /2, означают, что /3(е2 х /2) = е3 х /2 +
+ е2 х /3. Очевидно, что ВН*(Х{ х У\ Z2) состоит из групп Z2 в
размерностях 0, 2 и 4, поэтому из предложения 3.F.3 следует, что свободная
часть группы Н*(Х, х У; Z) состоит из групп Z в этих размерностях.
Кроме того, согласно следствию З.Е.4 2-кручение в /7*(Х, х У\ Z)
соответствует образу отображения /3 и состоит из групп Z2 x Z2 в
размерностях 3 и 5 вместе с группами Z2 в размерностях 6 и 7. В частности,
есть слагаемое Z2, соответствующее классу е3 х /2 + е2 х /3 в
размерности 5. Никакого р-кручения для нечётных простых р нет, так как кольцо
Н*(Х( х У; Zp) ^H*(X,-; Zp) <8>H*(Y; Zp) отлично от нуля только в чётных
размерностях.
392
DiaDa 3. Когомологии
Теперь мы можем убедиться, что для коэффициентов в Z w-произве-
дение Н2 х Н5 -+Н7 нетривиально для Х{ х У, но тривиально для Х2 х Y.
Действительно, в Н*(Х, х Y;Z2) мы ползаем, используя соотношение
(а х b) w (с х d) = (а^ с) х (b w d) (которое следует непосредственно из
определения внешнего произведения), что
1) е\х f° ^е2 х р = (е2^е2) х (f° ^ f3) = 0, так как е2^е2 = 0,
2) e5x/^(e3x/2 + e22x/3) = (e^e3)x(/^/2) + (e^e22)x(/(>w^) =
= (e2we2) х/3, так как e2we3 = 0,
а в Н7(Х{ х У; Z2) ^ H7(Xi x Y; Z) мы получаем (е2 w е2) х /3 = е4 х /V О
для i = 1, но (е2 w е2) х /3 = 0 х /3 = 0 для i = 2.
Таким образом, кольцо когомологии произведения пространств не
всегда определяется кольцами когомологии множителей.
Пример З.Е.7.. Можно применить гомоморфизмы Вокштейна, чтобы
получить более полное представление о структуре кольца H*(SO(n); ЭД.
Будем использовать ту же систему обозначений, что и в предыдущем
параграфе. Мы знаем из вычислений для ^RP°° в примере З.Е.1, что/3(^]а?'"*1) =
j
= Y*af и ^(Saf) -°> следовательно, Р(Ръ-\) = Ри и j8(j82,-) = 0. Напри-
j )
мер, в случае п = 5 мы получаем tf*(SO(5); 12)ъг£2[(Зъ j83]/(j8f, Д2).
Верхняя часть приведённой ниже таблицы показывает нетривиальные
гомоморфизмы Вокштейна. Снова две стрелки, выходящие из одного элемента,
означают «сумму», например /3(Д /33) = Рф\)/33 + Р\Р(/?з) = РгРз + Р\Ра =
= Р2Рз + /?f- Эти данные о гомоморфизмах Вокштейна позволяют
вычислить H'(SO(5); Z) по модулю нечётного кручения, если воспользоваться
также результатами из остальной части таблицы, где вертикальные
стрелки обозначают отображение р. Как было показано в предложении 3.1).3,
никакого нечётного кручения нет, таким образом, это фактически даёт
полное вычисление групп H'(SO(5); Z).
1 Pi - j8f
$
&
foh + Pfc
if*
X
3?&
Ж
tffti
0?ft - tfft tf &
0 '£-> Ъ
x'] — y2 x2y, z
Pt
P'f fii+Рз Pi /»?+/»? A.
tf
tf+tfft,
A.,y = r,
Д»ГЛ*
уг
P?ft
Важно, что для образующей у 6 H3(SO(5); Z) a» Z квадрат у2
нетривиален, так как это влечёт, что кольцевые структуры для H*(SO(5);Z)
§ З.Е. Гомоморфизмы Бокштейна
393
и H*(RP7 х S3; Z) не изоморфны, несмотря на то что группы когомологий
и кольца когомологий с коэффициентами в Ъг у этих двух пространств
одни и те же. В одной из задач в конце этого параграфа нужно доказать, что
в действительности пространство SO(5) не гомотопически эквивалентно
произведению никаких двух CW-комплексов с нетривиальными когомо-
логиями.
Естественно описывать H*(SO(5);Z) как факторалгебру свободной
градуированпо коммутативной ассоциативной алгебры F[x, у, zj над Z
с |х| = 2, \у\ = 3, и |z| = 7. Элементы алгебры F[x,y,z] представляются
в виде многочленов р(лг, у, z), подчинённых только соотношениям, накла-
дываемым коммутативностью. В частности, так как у и z имеют нечётную
размерность, мы получаем, что yz — —zy, а у2 и z2 — ненулевые элементы
порядка 2 в F[x, y,z]. Любой моном, содержащий множитель у2 или z2,
тоже имеет порядок 2. В этих терминах вычисление кольца Я* (SO(5); Z)
можно записать так:
H4SO{5y,Z)**F[x,y,z]/{2x,x\y\z2,xz,x*-y2).
На следующем рисунке указаны нетривиальные гомоморфизмы
Бокштейна для H"(SO(7); Z2). Здесь числа вверху указывают размерность;
последнее число 21 —это размерность многообразия SO(7). Пометки на
точках относятся к базисным произведениям разных Д. Например, точка,
помеченная 135, —это fiJ33f35.
О 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
_ 2356 12356 13456 123456
0 I 2 Г7*4 УГ\15ц~Т24 l54~234 1?345*6 1^6~236 3^^5б/ч ^"Й45б"~23456 *
12 13 23 24 34 *\~А. / / 1256 135614562456 3456
"" " Н5\ 123И2ЛЙГ 13452345
>4в XX \ \l2345f2346
136 24?
Т26у/\Ч//\ 345~~34б 13462346
»246
Лево-правая симметрия рисунка изображает графически
двойственность Пуанкаре. Обратите внимание, что соответствующая диаграмма для
SO(5), представленная слегка иначе, чем предыдущий рисунок,
встречается в левом верхнем углу как поддиаграмма с пометками от 1 до 4. Эта
поддиаграмма тоже обладает симметрией двойственности Пуанкаре.
Из этой диаграммы после некоторых усилий можно получить
структуру ^-произведения в f/*(SO(7); Z), но ответ довольно сложен, как и сама
диаграмма:
F[x, у, z, v, wl/(2x, 2v, х4, у4, z2, v2, w2, xz, vz, vw, y2w, x3y2v,
y2z-x2v,xw -y2v -x*v),
394
Глава 3. Когомологии
где х, у, z, v и w имеют размерности 2, 3, 7, 7 и 11 соответственно.
Интересно, что соотношение х3 = у2 в H*(SO(5);Z) уже не выполняется
bH*(SO(7);Z).
Задачи
1. Докажите, что если к делит ш, то кольцо H*(K(Zm, I); //^)
изоморфно кольцу /r(K(Z,„, 1); Z,„) ® ZA.. В частности, если /и//с четно, то это
кольцо изоморфно кольцу AZk [х] ® Zk[y].
2. В этой задаче мы получим половину классификации линзовых
пространств с точностью до гомотопической эквивалентности, показав, что
если/,гтД^,...^^-/1т(Г1,...,^,),то£1...£п-±Г1...£;?/с'1тос1т для
некоторого целого числа к. Обратное утверждение —задача 29 из §4.2.
1. Пусть L = Lm(tly...,(„), и пусть Ъ\п —мультипликативная группа
обратимых элементов в Z,„. Определим элемент t e Z;4n уравнением
ху""1 = tz, где х — образующая группы Hl(L\Zm)y у = fi(x), азе
е H2n~\L; Z,„) — образ образующей группы H2n_1U;Z). Докажите,
что образ t(L) элемента t в факторгруппе Z*}/±(Z*f)" зависит только
от гомотопического типа пространства /,.
2. Пусть даны ненулевые целые числа к]9...,кп. Определим
отображение /: S2n_1 —>S2n\ которое переводит единичный вектор (rxcl0\...
..., г^е'0") из Сп в (^е'4'1^1,..., гпе'ч'"а"). Докажите, что
а) / имеет степень кj...fc,f;
б) / индуцирует факторотображение f:L->L' для // = Lm(^'p ...,/'//,)
при условии, что /с;^; =£^. mod m для всех ;;
в) / индуцирует изоморфизм групп пх> а значит, и групп f/Ч—; Zm);
г) /имеет степень/с ^../С;,, т.е./+ —умножение на к]...кп вН2„...|(-; Z).
3. Используя отображение / из п. б), докажите, что T(L) = fc1...fcMT(L/).
4. Выведите из этого, что если L,„(£,, ...,£„) ^ 1*п№\> •■•> О» то f ,...£„ =
= ±f/1...^zfc" по модулю m для некоторого целого числа /с.
3. Пусть X — приведённое произведение к экземпляров пространства
Мура M(Z;,,n), где р — простое число. Вычислите гомоморфизмы Бокш-
тейна в H*(X\Zp) и примените это вычисление, чтобы описать кольцо
H*(X;Z).
4. Используя структуру ^-произведения в H*(SO(5);Z), докажите,
что пространство SO(5) не может быть гомотопически эквивалентно
произведению двух CW-комплексов с нетривиальными когомологиями.
§ 3.F. Пределы и Ext
Часто случается, что задан CW-комилекс Х, представленный в виде
объединения возрастающей последовательности подкомплексов Х() с X, с
С Х2 С ... Например, X,- может быть i-мерным остовом комплекса X, или
пространства X, могут быть конечными комплексами, объединение
которых равно X. В ситуациях такого рода предложение 3.33 утверждает,
§3.F. Пределы и Ext
395
что Hn(X; G) — прямой предел limHM(X,; G). Наша цель в этом параграфе
состоит в том, чтобы показать, что это верно и в более общем случае для
любой гомологической теории, и получить соответствующую формулу для
теорий когомологий, которая немного более сложна даже для обычных ко-
гомологий с коэффициентами в Z. Для обычных гомологии и когомологий
эти результаты применимы в несколько более общей ситуации, чем
только к CVY-комплексам. Если пространство X — объединение возрастающей
последовательности подпространств Xh для которых каждое компактное
множество в X содержится в некотором X,, то сингулярный комплекс
пространства X — объединение сингулярных комплексов пространств Х{.
Таким образом, это позволяет свести ситуацию к случаю CW-комплексов.
Переход к пределам часто может приводить к не конечно
порождённым группам гомологии и когомологий. В конце этого параграфа мы
частично опишем довольно тонкое поведение функтора Ext для не конечно
порождённых групп.
Прямые и обратные пределы
Как частный случай общего определения из § 3.3, прямой предел lim G,
последовательности гомоморфизмов абелевых групп Gx —> G2 -^ G:i —>...
определяется как факторгруппа прямой суммы 0G, по подгруппе, состо-
ящей из элементов вида (gb g2 — «ifei),g3 ~~ а2(&г)> •••)• Из этого
определения легко видеть, что любой элемент из lim G, представлен элементом
gi e G, для некоторого i, причём два таких представителя g,- e G, и gj e Gj
определяют один и тот же элемент в limG, тогда и только тогда, когда
совпадают их образы в некоторой группе Gk при соответствующей
композиции гомоморфизмов а(. Если все гомоморфизмы а, инъективны и
рассматриваются как включения подгрупп, то limG, —это просто IJG,.
i'
Пример 3.F.I. Для простого р рассмотрим последовательность Z —>
р р
—► Z —► Z —>..., где все отображения — умножения на р. Тогда lim Gj можно
отождествить с подгруппой Z[l/p] в Q, состоящей из рациональных
чисел, знаменатели которых — степени р. Вообще можно реализовать любую
подгруппу в Q как прямой предел последовательности Z —> Z —> Z —> ...,
соответствующим образом выбрав отображения. Например, если
отображение с номером п — это умножение на п, то прямой предел —это сама
группа Q.
Пример 3.F.2. Прямым пределом последовательности инъективных
р р
отображений Ър —> Zp* —> Zps —»..., где число р простое, является группа,
которую мы обозначим Ър™. Она изоморфна Z[l/p]/Z — подгруппе bQ/Z,
представленной дробями, знаменатели которых —степени р. В
действительности группаQ/Z изоморфна прямой сумме подгрупп Z[l/p]/Z^Zp™
для всех простых р. Нетрудно найти все подгруппы в Q/Z и убедиться,
396
Глава 3. Когомологии
что каждую из них можно реализовать как прямой предел конечных
циклических групп с ипъективными отображениями между ними. Наоборот,
любой такой прямой предел изоморфен некоторой подгруппе в Q/Z.
Мы можем реализовать эти алгебраические примеры топологически
следующей конструкцией. Определим телескоп отображений для
последовательности отображений Х0 -^> X] -^ Х2 —> ... как объединение
цилиндров отображения Mfj, причём копии пространства X, в Mj и в М.
отождествляются для всех i. Таким
образом, телескоп отображений —это
факторпространство несвязного
объединения в котором
каждая точка (xh i + 1) е X,- х fi, i + 1 ]
отождествлена с (/,Qr,), i + 1) е Х,-+1 х -
х [f +1, i + 2], В телескопе отображений 7' пусть 7} обозначает
объединение первых i цилиндров отображений. Это пространство деформационно
ретрагируется на X, при поочерёдной деформационной ретракции
каждого цилиндра отображения на его правый конец. Если все отображения f{
клеточные, то каждый цилиндр отображения является CW-комплексом,
и телескоп Т —это объединение возрастающей последовательности
подкомплексов 7J ^ X,-. Тогда из предложения 3.33 (или приводимой ниже
теоремы 3.F.8) следует, что Н„(7'; G)^lim//„(X,; G).
Пример 3.F.3. Предположим, что каждое f( — это отображение S" —► S"
степени р для фиксированного простого числа р. Тогда //„(Т)
—прямой предел последовательности Ъ—>Z —>Z —>..., рассмотренной в
примере 3.F.1 выше, причём Нк(Т) = 0 при кфп, таким образом, 7'
—пространство Мура M(Z[l/p], n).
Пример 3.F.4. В предыдущем примере, если мы приклеим клетку
е'1_м к первой сфере Sn в Т посредством тождественного отображения
сферы S", то получим пространство X, которое является пространством Мура
MCZpoo, п), так как X — объединение своих подпространств X,- = 7} Ue'Ml,
которые являются пространствами Мура M(Zp., п), а включение X, с Х,-.м
индуцирует включение Zp, cZp,.i для групп Н„.
Обобщая эти два примера, можно получить пространства Мура М(С7, /О
для произвольных подгрупп G в Q или в Q/Z, выбирая отображения
/i: S" -*S" подходящих степеней.
Поведение групп когомологии более сложно. Если X— объединение
возрастающей последовательности подкомплексов X,, то группы
когомологии H,2(X,;G) для фиксированных пиС образуют последовательность
гомоморфизмов
... —* Go ~^ G ] —► Go
Если дана такая последовательность гомоморфизмов групп, то
обратный предел limG, определяется как подгруппа в [~[Gh состоящая из по-
§3.F. Пределы и Ext
397
следователыюстей (g,), a^gi) = g,-^ для всех i. Имеется естественное
отображение Я: Н"(Х; G) —> limH"(X,; G), переводящее элемент группы
Нп(Х\ О) в последовательность его образов в Нп(Х{\ G) при
отображениях ЯП(Х; G) —> Н"(Х,; G), индуцированных включением. Можно было бы
надеяться, что Я —изоморфизм, но это, как мы вскоре увидим, не всегда
верно. Однако для некоторых групп G это верно.
Предложение 3.F.5. Если CW-комплекс Х является объединением
возрастающей последовательности подкомплексов X, и если G — это
одно из полей Q или Zp, то Я: Н"(Х; G)—>НтНм(Х,-; G) — изоморфизм для
всех п.
Доказательство. Сначала отметим простой алгебраический факт:
если дана последовательность гомоморфизмов абелевых групп G} —>
-^>G2-^G3—>..., то Нот (limG,-, G) = limHom(G,, G) для любой группы G.
А именно, из определения Нт G, следует, что гомоморфизм у?: lim G^G —
это то же самое, что последовательность гомоморфизмов (/?,: G, —* G,
<ft = <£,■+ia» Для всех !- Такая последовательность (с/?,)—это в точности
элемент группы HmHom(G,, G).
Теперь если G — поле Q или Zp, то мы получаем
ЯП(Х; G) = Hom(H„(X; G), G) = HomQim//„(*,•; G), G) =
= ИтНот(Нп(Х,; G), G) = ИтНп(Х,; G). П
Давайте проанализируем, что происходит для когомологий с
произвольной группой коэффициентов и вообще для любой теории
когомологий. Если дана последовательность гомоморфизмов абелевых групп
... —> G2 -^ G^ —►, G0
то зададим отображение 5 : О ^/ ~> П G\ формулой
<5(...,g,-,...) = (...,g/-a,+i(g,M),^0;
тогда limG, —это ядро отображения А. Обозначая коядро отображения 5
через lirr^G,, мы получаем точную последовательность
О -> limG,- -> J~[Gf -^ J^G,- ->Hrr/G,
0.
i
Это можно сравнить с соответствующей ситуацией для прямого предела
последовательности G1 —*G2—*G3 —>... В этом случае получается
короткая точная последовательность
0-©С,--^фс(-1ипС1--0,
I I
где 5(...,£,-, ...) = (...,g,- - al-..I(gl-_1),...), поэтому отображение б инъек-
тивно и нет никакого члена lim1 G,, аналогичного lirr^G,.
398
Глава 3. Когомологии
Вот несколько простых замечаний о lim и lim .
1. Если все отображения а,—изоморфизмы, то limG/^G() и Iim'G/^O.
В действительности lim1 G, = 0, если все отображения а, сюръективны,
ибо для того, чтобы реализовать данный элемент (ft,-) e J~[ G, как fi(g(),
мы можем положить g() = 0, а затем решить уравнения tf^gO = -/10>
a2(S2)=Si-fti. •••
2. Если все отображения а,- нулевые, то limG,■ = lim1Gi= 0.
3. Удаление конечного числа членов последовательности ... —>G, —> G()
не влияет ни на limG,-, ни на limJG,-. Вообще limG, и lin^G,- не
изменяются, если мы заменим последовательность ... —>GX —» G() на
подпоследовательность, в которой отображениями являются композиции
некоторых а;.
Пример 3.F.6. Рассмотрим последовательность естественных сюръ-
екций ... -»Zp:» —»Zp2 —»Zp, где р — простое число. Обратный предел этой
последовательности —известный объект в теории чисел, называемый р-
адическими целыми числами. Мы будем обозначать их Zp. В
действительности это коммутативное кольцо, а не просто группа, так как проекции
ZpMi -+Zpi являются кольцевыми гомоморфизмами, но нас будет
интересовать только аддитивная структура группы. Элементы из Ър — такие
бесконечные последовательности (...,a2,<3i), ахег£рЧ что а, получается
из aI+I приведением по модулю р'. Для каждого выбранного числа а,
есть ровно р возможностей выбрать aJ+1, таким образом, множество %р
несчётное. Имеется естественное включение Z с Zp как постоянных
последовательностей a,=neZ. Легко убедиться, что группа Ър не имеет
кручения, проверив, что она не имеет элементов простого порядка.
Есть другой способ посмотреть на Zp. Элемент группы Zp имеет
единственное представление в виде последовательности („.уа2у<1\) целых
чисел а,-, где 0 $ а, < р' для всех i. Каждое число а, можно единственны!^
образом записать в виде b^rf1'1 + ... +bxp + b0t где O^b,- <p. Тот факт,
что при приведении ai+l по модулю р' получается а,, означает, что числа
bj зависят только от элемента (...,а2, аг) GZ/r Поэтому мы можем
рассматривать элементы группы Ър как бесконечные в р-ичной системе
счисления числа ...Ь^о, О^Ь, <р для всех i, с обычным правилом сложения
в р-ичной системе счисления. Конечные выражения Ьп...Ь{Ь0
соответствуют неотрицательным целым числам, но разложения отрицательных целых
чисел бесконечные. Например, для —1 получаем Ьх—р — Л для всех i, в чём
легко убедиться, прибавив к этому числу 1.
Так как отображения Zp.-i —► Zp, сюръективны, lim'Zy =0.
Следующий пример показывает, как р-адические целые числа могут также
приводить к ненулевому члену lim1.
§3.F. Пределы и Ext
399
Пример 3.F.7. Рассмотрим последовательность ... —> Z —> Z —> Z для
простого р. В этом случае обратный предел равен нулю, так как целое
число, отличное от нуля, можно разделить на р только конечное число раз.
Член lim1 —это коядро отображения 5: ]~{Z—>]~{Z, заданного формулой
* эо ос-
6(Уг,У2> •••) — (У1 ~~ РУъУг ~ РУз> •••). Мы утверждаем, что отображение
£ /Z—>Coker<5, переводящее р-адическое число ...b^b0i как и в
предыдущем примере, в (Ь01Ь}, ...), является изоморфизмом. Чтобы убедиться
в этом, заметим, что образ элемента 5 состоит из сумм yj (1, 0, ...) +
+ У2(~Р> 1>0' •••) + Уз(0> "Р, li 0, ...) + ... Члены после у,(1, 0,...) дают
в точности соотношения, которые выполняются для р-адических чисел
...Ь^о и, в частности, позволяют приводить произвольную
последовательность (b0, bj,...) к единственной последовательности, для которой
0^bt <p для всех I. Член yjQ, 0, ...) соответствует подгруппе ZcZp.
Перейдём теперь к главному результату этого параграфа.
I Теорема 3.F.8. Для CW-комплекса X, который является объединена
I ем возрастающей последовательности подкомплексов Х0 с Хт с ..., име-
I ет место точная последовательность
I 0 -> limV^CX,) -> Vх(X) -^ lim h" ОД -> О,
I где ft* — любая приведённая или неприведённая теория когомологий.
I Для любой теории гомологии ft+, приведённой или неприведёпной,
I естественные отображения limft,,(X,) —>ftM(X) — изоморфизмы.
Доказательство. Пусть Т — телескоп отображений для
последовательности включений Х0 <-* X] *-> ... Он является подкомплексом в X х
х [0, оо), где пространство [0, со) снабжено CW-структурой с
целочисленными точками в качестве нульмерных клеток. Мы получаем Т ~ X,
поскольку Т—деформационный ретракт пространства X х [0, со), как
мы показали в доказательстве леммы 2.34 в частном случае, когда X,
является i-мерным остовом комплекса X, но эти рассуждения точно так
же работают для произвольных подкомплексов X,.
Пусть ?! с Т — объединение произведений X, х [i,i + 1] для
нечётных i, а Т2 — соответствующее объединение для чётных i. Таким образом,
7\ п Т2 = Ц X,- и 7'j U Т2 = Т. Для неприведённой теории когомологий ft* мы
имеем тогда последовательность Майера—Вьеториса
h*1'1^) ©ftn" \Т2) ■>• кп-х{Тг ПТ2) - hn{T) + h"^) ehn(T2) ■>• h'1^ ПТ2)
й й й Я й
nr/i"-4x,) —^-- пг/1,1_1од -*• Ь'ЧХ) —^ nf/in(x,) —^ nfhn(x,)
Отображения с/?, делающие диаграмму коммутативной, задаются
формулой </>(..., g,-, ...) = (..., (-l),'"l(gI--p(gl-+i)),.. О, где отображения р-это
4VV
Глава 3. Когомологии
соответствующие отображения ограничения. Это отличается от 5 только
знаком в чётных координатах, поэтому если мы изменим изоморфизм
hk(T} ПТ2) ^П^(Х,), вставив знак минус в чётные координаты, то мы мо-
жем заменить во второй строке диаграммы (р на 5. Эта строка тогда
приводит к короткой точной последовательности 0 —» Coker<5 —> hn{X; G) —>
—» Ker<5 —> 0, что и завершает доказательство для неприведённых
когомологии.
То же самое рассуждение годится и для приведённых когомологии,
если мы будем использовать приведённый телескоп, полученный из 7'
стягиванием подпространства {х0} х [0, оо) в точку; здесь х() —
отмеченная точка, которая является нульмерной клеткой комплекса Х0. Тогда
Г, ПГ2 = V,-X(-, а не Цх,, и остальные рассуждения проходят без изме-
нений. Это доказательство применимо также к теориям гомологии, если
во второй строке диаграммы заменить прямые произведения на прямые
суммы. Как мы уже отметили ранее, в случае прямого предела Кег5 = 0,
aCoker5 = lim. G
Пример 3.F.9. Как и в примере 3.F.3, рассмотрим телескоп
отображений Т для последовательности отображений S" —> Sn —» ... степени р.
Пусть 7^—объединение первых i цилиндров отображений в телескопе.
Тогда включения 7^ <—*Т2<—* ... индуцируют на Нп(—\Ъ) последователь-
р
ность ...—>Z—>Z из примера 3.F.7. Из теоремы 3.F.8 мы выводим, что
Нп+\Т; Z)**Zp/Z и Нк(Т;'£) = 0 для fc^n + l. Таким образом, мы имеем
довольно странную ситуацию, когда CW-комплекс Т является
объединением подкомплексов 7), у каждого из которых когомологии состоят
только из Z в размерности п, а сам комплекс Т имеет нулевые когомологии
в размерности п, по вместо этого имеет огромную несчётную группу
когомологии Zp/Z в размерности n-f 1. Это резко отличается от того, что
происходит для гомологии, где группы Н„(7)) ^Z хорошо стыкуются
вместе и дают Hn(T)^Z[l/p].
Пример 3.F.10. Более разумное поведение проявляется, если мы
рассматриваем пространство X = M(Zp^,n) из примера 3.F.4
представленным в виде объединения его подпространств X,. Согласно теореме об
универсальных коэффициентах приведённые когомологии пространства
X, с коэффициентами в Ъ состоят из Z/;, = Ext(Z;)., Z) в размерности п + 1.
Включение X,- <—* Xf>1 индуцирует включение Zp; <-* Z/;.n па Нп, а
соответствующее отображение на группах Ext —сюръекция Z/;.n —»2у, в чём
можно убедиться, посмотрев на диаграмму (слева) свободных резольвент:
О -*- Z Х- Z -+ Zp, —* 0 0 •<— Kxt(7v, Z) ■<— Hom(Z, Z)
Y p»-i Y У i I
0 -^Z-^Z^-Z ,♦. -^0 0*- Ext(Z ,-,,Z) ^-Hom(Z, Z) -«- ...
§3.F. Пределы и Ext
401
Применяя Hom(-, Z) к этой диаграмме, мы получаем диаграмму (справа),
строки которой точные, а вертикальное отображение слева —сюръекция,
так как вертикальное отображение справа от него сюръективно. Таким
образом, последовательность ...—>Н'НЛ(Х2\ Z) —>Hn+}(Xl\ Z) является
последовательностью из примера 3.F.6, и мы получаем, что Нп~*~1(Х; Z) %Zp,
р-адические целые числа —и Нк(Х\ Z) — 0 при кфп + 1.
Этот пример можно связать с предыдущим. Если мы рассматриваем X
как конус отображения для включения 5" <—* Т одного конца телескопа, то
длинные точные последовательности групп гомологии и когомологии для
пары (Г, Sn) приводят к коротким точным последовательностям:
0 —> Hn(S") - //„(Г) Нп(Х) — 0
Z Z[l/p] Zp^
0 —^ Hn{Sn) —^ Hnf ] (X) —> Нп+](Т) —^ 0
Z % Ър/Ъ
Из этих примеров и из теоремы об универсальных коэффициентах
мы получаем изоморфизмы Ext(Zpx;, Z) ^Zp и Ext(Z[l/p], Z) ^Zp/Z. Их
можно также получить непосредственно из определения группы Ext. В
качестве свободной резольвенты для Zp^ можно взять
о -> z°° Д z°° — zp. -> о,
где Z00 — прямая сумма бесконечного числа групп Z; она состоит из
последовательностей Оь х2, ...) целых чисел, все из которых, кроме конечного
числа, равны нулю, и у переводит Оь х2,...) в (рх1 - х2, рх2 - лг3> ••■)•
Можно рассматривать ^ как линейное отображение, соответствующее
бесконечной матрице с элементами р на диагонали, -1 непосредственно
выше диагонали и 0 во всех остальных местах. Ясно, что Ксг кр — 0, так как
целые числа нельзя делить па р бесконечное число раз. Образ
отображения кр порождается векторами (р, 0,...), (-1,р, 0, ...), (0, —1, р, 0, ...),...,
поэтому Coker</? *fc Zpoo. Дуализуя посредством применения Hom(-,Z),
мы получаем Нот(Z00, Z)— бесконечное прямое произведение групп Z,
и у?*(УъУ2, •••) = (РУъ РУг "УьРУз ~Уг> •••), что соответствует
транспонированной матрице отображения у. По определению Ext(Zp-v, Z)=Cokerv?".
Образ отображения </?* состоит из бесконечных сумм У](р, — 1, 0...) +
+ У2&> Р> ~~1> 0> •••) + •••> таким образом, Cokery?* можно отождествить
с Zp, переписав последовательность (zl5z2,...) как р-адическое число
...z2z^. ^
Вычисление Ext(Z[l/p], Z) ^Zp/Z совершенно аналогично.
Свободную резольвенту для Z[l/pJ можно получить из свободной резольвенты
402
Глава 3. Когомологии
для Zpco, удалив первый столбец матрицы отображения кр и для удобства
изменив знак. Это даёт формулу
ip(xux2f...) = (xl,x2-pxux3-px2,...),
причём образ отображения </> порождается элементами (1, -р, 0,...),
(0,1, -р, 0,...), ••• Двойственное отображение </?* задаётся формулой
^*(УьУ2» ■■■) = (У\ "* РУ2>У2 ~ РУз>---) и его образ состоит из сумм
Ух(1, 0...) + У2(~~Р> 1» °> •••) + УзСО, -р, 1, 0, ...) + ..., таким образом, мы
получаем Ext(Z[l/p], Z) = Cokerc/?* a»Zp/Z. Отметим, что с/?* —это в
точности отображение б из примера 3.F.7.
Интересно также отметить, что отображение <f: Z°° —> Z00 в обоих
случаях, для Z v и для Z[l/p], является в точности клеточным
граничным отображением Нп+1 (Х'и'\ Хп) —>НП(Х", X"-1) для пространства Мура
M(Zpoo, п) или M(Z[l/p], п), построенного как телескоп отображений для
последовательности отображений S" —>SM —>... степени р, с клеткой е"41,
приклеенной к первой сфере S" в случае Zp*:,
Ещё об Ext
Функторы Нот и Ext ведут себя достаточно просто для конечно
порождённых групп, когда когомологии и гомологии —это, по существу,
одно и то же, за исключением сдвига размерности для кручения. Но дело
обстоит более сложно в не конечно порождённом случае. Полезный
инструмент для того, чтобы научиться преодолевать эти трудности, заключается
в следующем.
I Предложение 3.F.1L Для данной абелевой группы G и короткой точ-
I ной последовательности абелевых групп 0—>А —>В—>С —> 0 имеют ме-
I сто точные последовательности
I 0 — Hom(G, Л) — Hom(G, В) — Hom(G, С) —
I — Ext(G, А) — Ext(G, В) — Ext(G, С) — 0,
I 0 — Hom(C, G) — Нот(В, G) — Нот(/\, G) —
I — Ext(C, G) — Ext(B, G) — Ext(A, G) — 0.
Доказательство. Свободная резольвента 0—>FX—> F0 —>G—>0
приводит к коммугативной диаграмме
0 -*• Hom(F0, Л) -*• Hom(F0, В) -+ Hom(F0, С)-** 0
\ \ I
О -*• Y\om[h\yA) -*- Hom(Fb В) -*■ Hom(F,, С) -*- 0
Так как группы F0 и Fi свободные, обе строки точные, поскольку они —
просто прямые произведения нескольких копий точной последовательно-
§3.F. Пределы и Ext
403
0
1
-Fl
I
■+-FQ-
1
-*~A-
1
0
0
1
-Fl
1
-K
\
—^B-
1
0
0
1
-Fl"
1
-K
\
—*c-
\
0
-*0
^0
-*0
сти 0—>A—>B—»С —> 0; это следует из общего факта, что
Нот(фс,,н) =[~[Hom(G„H).
Дополнив диаграмму нулями сверху и снизу, получаем короткую точную
последовательность цепных комплексов, и соответствующая ей длинная
точная последовательность групп гомологии является первой из двух
требуемых точных шестичленных последовательностей.
Чтобы получить другую точную последовательность, построим
коммутативную диаграмму на рисунке, где столбцы — свободные
резольвенты, а строки точные. Начнём с того, что в
качестве F0 —> А и F(" —> С возьмём сюръекции
свободных абелевых групп на Л и С. Затем
положим Fq — F0B Fq с очевидными отображе- 0
ниями во второй строке, включением и
проекцией. Отображение Fq^>B определяется на о
слагаемом F0 так, чтобы сделать нижний
левый квадрат коммугативным, а на слагаемом q .
F{{ оно определяется тем, что переводит
элементы базиса группы Fq в элементы группы В,
отображающиеся на образы этих элементов
базиса в С, поэтому нижний правый квадрат тоже коммутативный.
Теперь у нас есть две нижние строки диаграммы, и мы можем
рассмотреть эти две строки как короткую точную последовательность двучленных
цепных комплексов. Соответствующая ей длинная точная
последовательность групп гомологии имеет шесть членов: первые три —это ядра трёх
вертикальных отображений в Л, В и С, а последние три —коядра этих
отображений. Так как вертикальные отображения в Л и С сюръективны,
Четвёртая и шестая из шести групп гомологии обращаются в нуль,
следовательно, пятая тоже, а это означает, что вертикальное отображение в В
сюръективно. Первые три из исходных шести групп гомологии образуют
короткую точную последовательность, и мы берём её в качестве верхней
строки диаграммы; она образована ядрами вертикальных отображений
в Л, В и С. Эти ядра —подгруппы свободных абелевых групп, поэтому они
тоже свободные. Таким образом, рассматриваемые три столбца
—свободные резольвенты. Верхние два квадрата автоматически коммутативны,
поэтому построение диаграммы завершено.
Первые две строки диаграммы расщепимы вследствие свободности,
поэтому применение Hom(—, G) приводит к диаграмме
0 -*- Hom(F(", G) -*- Hom(F^, G) -*• Hom(F0, G) -** 0
у y i
0 -*■ HomCF,", G) -*■ Hom(Fj, G) -*• Нот(^, G) -*• 0
404
Глава 3. Когомологии
с точными строками. Снова рассмотрим её как короткую точную
последовательность цепных комплексов. Соответствующая ей длинная точная
последовательность групп гомологии —это вторая требуемая шестачлен-
ная точная последовательность. □
Вторая последовательность из предложения 3.F.11 означает, в
частности, что инъективное отображение А —> В индуцирует сюръекцию
Ext(£, С) —> Ext (Л, С) для любой группы С. Например, если Л имеет
кручение, то это означает, что группа Ext(/1, Z) отлична от нуля, так как она
отображается на Ext(Z„, Z) %Z„ для некоторого п > 1. Вычисление группы
Kxt(Zr*, Z) ^ Z;), проведённое ранее в этом параграфе, показывает, что
кручение в А не обязательно приводит к кручению в Ext(A, Z).
Полезны также формулы
Ехг(0Л1,й)^[^Ехс(Л1,В), Ext(A,0Bi) ^©ExtW,^),
доказательсгво которых мы оставляем в качестве задач. Например, так как
Q/Z = ®Z/}v, из вычисления Ext(Zp^, Z)^Zp, мы получаем Ext(Q/Z,Z)^
л
% J~]Zp. Тогда из точной последовательности 0 —► Z —► Q —> Q/Z —► 0, ис-
л
пользуя вторую точную последовательность из предложения З.Е.П,
получаем Ext(Q, Z) ъ (ПZp)/Z.
л
В этих примерах группы Ext(A, Z) являются довольно большими,
и следующий результат показывает, что это часть более общей ситуации.
| Предложение 3.F.12. Если группа А не конечно порождённая, то ли-
I бо группа Нот(Л, Z), либо группа Ext(y4, Z) несчётна. Следовательно,
I если группа Нп(Х; Z) не конечно порождённая, то либо группа НП(Х; Z),
I либо группа Нп^х{Х\ Z) несчётна.
Обе возможности могут встретиться, как мы видим из примеров
Hom«BZ, Z) %flz и Ext(Zpnc, Z) *Zp.
ОС 00
Это предложение имеет некоторые интересные топологические
следствия. Прежде всего, оно влечёт, что если для пространства X имеет
место равенство H*(X;Z) =0, то H*(X;Z) = 0, так как случай конечно
порождённых групп гомологии следует из наших более ранних
результатов. А во-вторых, оно означает, что не всегда можно построить
пространство X с предписанными группами когомологии Ип{Х\ Z), как это
можно сделать для гомологии. Например, не существует пространства,
у которого единственная ненулевая группа Hn(X;Z) —счётная не
конечно порождённая группа, как Q или Q/Z. Даже в конечно порождённом
случае размерность п = 1 до некоторой степени особая, так как группа
Hl(X; Z^HomCf/^X), Z) всегда не имеет кручения.
§3.F. Пределы и Ext
405
Доказательство. Рассмотрим отображение А —► А, а —> ра, —
умножение на натуральное число р. Обозначим ядро, образ и коядро этого
отображения рА, рА и Ар соответственно. Короткие точные
последовательности 0—►рД—>Д—>рА—>0 и 0—>рД—>Д—►Др—>0 дают две шестичленные
точные последовательности, включающие Hom(-, Z) и Ext(-, Z). Нам
понадобятся следующие фрагменты этих точных последовательностей:
0 — Нот(рД, Z) -^ Нот(А, Z) — Нот(рД, Z) = 0,
Нот(рА, Z) — Ext(Ap, Z) — Ext(A, Z),
причём член Нот(рА, Z) в первой последовательности нулевой, так как
рА — это группа кручения.
Пусть теперь р —простое число, таким образом, Ар —линейное
пространство над Zp. Если это линейное пространство бесконечномерное, то
оно является бесконечной прямой суммой группl Zp, а группа Ext(Ap, Z) —
прямое произведение бесконечного числа групп Zp, а потому она
несчётна. Тогда точность второй из приведённых выше последовательностей
влечёт, что один из двух соседних членов, Ext(A, Z) или Hom(pA,Z)^
«Hom(A, Z), должен быть несчётным, и таким образом, мы разобрали
случай, когда группа Ар бесконечная.
Противоположная крайность —случай, когда Ар — 0. Это означает, что
А = рА, таким образом, каждый элемент группы А делится на р.
Следовательно, если группа А нетривиальна, то она содержит подгруппу,
изоморфную либо Z[l/pl, либо Zp*.. Мы уже видели, что Ext(Z[l/p], Z)%Zp/Z
и Ext(Zpoc, Z) ^Zp, и обе эти группы несчётные. Как было замечено ранее,
включение В <—> А индуцирует сюръекцию Ext (A, Z) —> Ext(E, Z), поэтому
из этого следует, что группа Ext(A, Z) несчётна, когда Ар = 0 и А Ф 0.
Оставшийся случай, когда Ар —конечная прямая сумма групп Zp,
можно свести к случаю Ар — 0. Выберем для этого конечное число
элементов группы А, образы которых в Ар—набор образующих, и пусть
В с А — подгруппа, порождённая этими элементами. Таким образом,
отображение Вр —► Др, индуцированное включением В <—► А, сюръективно.
Функтор А —> Ар — это то же самое, что А *-» А <8> Zp, поэтому точность
последовательности В —> А —> А/В —► 0 влечёт точность последовательности
Др —► Ар —► (А/В)р —> 0, а потому (А/В)р — 0. Если группа А не конечно
порождённая, то группа А/В отлична от нуля, поэтому из предыдущего
случая следует, что группа Ext (А/В, Z) несчётная. Из этого следует, что
На самом деле группа Ар может быть намного больше, чем бесконечная прямая
сумма. Она может быть несчётной. Например, если А —это бесконечное прямое произведение
Групп Zp, то А = Ар — несчётная группа. Однако если группа Ар бесконечна, то она содержит
бесконечную прямую сумму групп 7,р. Отсюда вытекает, что имеется сюръективный
гомоморфизм из \Lx\{Ap,Z) в бесконечное прямое произведение групп Т.р. А значит, Ext(Ap,Z)
также несчётная группа, и дальше рассуждение проходит как указано. — Прим. ред.
406
Глапа 3. Когомологии
группа Ext(A, Z) тоже несчётная, как показывает точная
последовательность Hom(B, Z) —► Ext(A/B, Z) —► Ext(A, Z), поскольку группа Нот(В, Ъ)
конечно порождённая, а потому счётная. □
На основании этого предложения можно подумать, что группы
когомологии с коэффициентами в Ъ либо конечно порождённые, либо несчётные.
Как было объяснено в §3.1, функтор Ext можно обобщить до
последовательности функторов Ext" для модулей над кольцом R. При таком
обобщении шестичленные последовательности из предложения 3.F.11
превращаются в длинные точные последовательности групп Ext" соответ-
А
ствующие коротким точным последовательностям R-модулей. Они
получаются аналогичным способом посредством построения коротких точных
последовательностей свободных резольвент. Имеются также аналогичные
длинные точные последовательности для функторов Тог*, которые
становятся шестичленными последовательностями при R = Z. Однако эти
шестичленные последовательности, по-видимому, менее полезны, чем их
аналоги для Ext, так как функтор Тог менее загадочен для не конечно
порождённых групп, чем функтор Ext, поскольку он коммутирует с прямыми
пределами согласно одной из задач в § З.А.
Задачи
1. Даны отображения ff: Х{ —► JO+i для целых чисел i < 0. Докажите,
что «обратный телескоп отображений», полученный склеиванием вместе
цилиндров отображений fh очевидным способом деформационно ретра-
гируется на Х0. Аналогично, если отображения f{: Х{ —> Xi+l заданы для
всех i GZ, докажите, что получающийся «двойной телескоп отображений»
деформационно ретрагируется на любой из обычных телескопов
отображения, содержащихся в нём, т. е. на объединение цилиндров отображений
ft для I, превосходящих данное число и.
1 а2
2. Докажите, что IinrG,- = 0, если последовательность ... —> G2 —*
—>G! —>G0 удовлетворяет условию Миттаг-Леффлера, которое
заключается в том, что для любого i образы отображений С,-.,.п —> G,- не зависят от п
для достаточно большого п.
3. Докажите что Ext(A,Q) = 0 для всех А. [Рассмотрите гомологии
пространства Мура М(АУ п) с коэффициентами в Q.]
4. Говорят, что абелева группа G делима, если отображение G —> G,
g>-*ng, сюръективно для всех п > 1. Докажите, что группа является
делимой тогда и только тогда, когда она является факторгруппой прямой
суммы групп Q. Выведите из предыдущей задачи, что если группа G делима,
то Ext(A, G) = 0 для всех А.
5. Докажите, что группа Ext(A, Z) изоморфна коядру отображения
Hom(A, Q) —► Нот(А, Q/Z), индуцированного отображением факториза-
§3.G. Трансфер
407
ции Q —> Q/Z. Воспользуйтесь этим, чтобы получить другое
доказательство того, что Ext(Zp~, Z) ^Zp для простого р.
6. Докажите, что Ext(Zp«x,, Ър)ъЪр.
7. Докажите, что для короткой точной последовательности абелевых
груии 0—> А —> В —>С —► 0 пространство Мура М(С, п) можно реализовать
как факторпространство М(В, п)/М(А, п). Применяя длинную точную
последовательность когомологий для пары (М(В, п),М(А, п)) с
произвольной группой коэффициентов G, получите точную последовательность
0 -» HomCC, G) -* Нот(В, G) -* Нот(А, G) -* Ext(C, G) -*
— Ext(B, G) -* Ext(A, G) -* 0.
8. Докажите, что для пространства Мура M(G> n) длинная точная
последовательность Вокштейна для когомологий, соответствующая
короткой точной последовательности групп коэффициентов 0—> А —>В —>С—>0,
приводит к точной последовательности
0 — Hom(G, А) — Hom(G, В) -* Hom(G, С) -* Ext(G, A) -*
-> Ext(G, В) -* Ext(G, С) -* 0.
9. Для абелевой группы А пусть р: А—>А — умножение на р, и пусть
рА = Кегр, рА = Imp и Ар = Cokerp, как в доказательстве
предложения 3.F.12. Докажите, что шестичленные точные последовательности,
включающие Hom(-,Z) и Ext(-,Z), связанные с короткими точными
последовательностями 0—> рА —> А—> рА —> 0 и 0 —> рА —> А —> Ар —> 0,
можно соединить вместе и получить верхнюю точную последовательность
в следующей диаграмме:
Hom(pA, Z) -*- Ext(Ap, Z) -^ Ext (A, Z) ^-*- Ext(pA, Z) -*> Ext(pA, Z) -^ 0
X /-
Ext(pA, Z)
0-*Нот(рА, Z) ^>Hom(A, Z) ->0 0
где отображение, обозначенное «р», — это умножение на р.
Воспользуйтесь этим, чтобы показать следующее:
а) группа Ext(A, Z) делима тогда и только тогда, когда группа А не имеет
кручения;
б) группа Ext(A, Z) не имеет кручения, если группа А делима; обратное
утверждение верно, если Hom(A, Z) = 0.
§3.G. Трансфер
Имеется простая конструкция, называемая «трансфер» или
«гомоморфизм переноса», которая предоставляет очень полезную
информацию о гомологиях и когомологиях конечнолистных накрывающих про-
4U8
Глава 3. Когомологии
странств. Сначала мы дадим определение трансфера и докажем несколько
его элементарных свойств, а затем применим трансфер для построения
многочисленных пространств, когомологии которых с коэффициентами
bZp- кольца многочленов.
Пусть я: X —» X — /2-листное накрытие для некоторого конечного п.
Помимо индуцированного отображения сингулярных цепей я:: Ск(Х)~~*
—> Ск(Х) имеется также гомоморфизм в противоположном
направлении т: Ск(Х) —> Q(X), который сопоставляет сингулярному
симплексу сг: бк —» X сумму п различных поднятий а: 6"^ —> X. Это,
очевидно, цепное отображение, коммутирующее с граничными
гомоморфизмами, поэтому оно индуцирует гомоморфизмы т+: Нк(Х\ G) —> Ик{Х\ G)
и т*: Ик{Х\ G) -+Нк(Х\ G) для любой группы коэффициентов G. Каждый
из этих гомоморфизмов называют трансфером. В дальнейшем мы
сосредоточимся на когомологиях, но аналогичные утверждения верны также
и для гомологии.
Ясно, что композиция я-т — это умножение на п, значит, т*я*=п.
Из этого следует, что ядро отображения я*: Hk(X\G) —> IIk(X;G)
состоит из элементов кручения, порядок которых делит и, так как равенство
п*(а) =0 влечет равенство т*я*(а) = па = 0. Таким образом,
когомологии пространства X должны быть «больше», чем когомологии
пространства X, за исключением, возможно, элементов кручения, порядок которых
делит ?7. Это исключение действительно может встретиться, как видно из
примера сферы Sm, накрывающей ЖРт и линзовые пространства.
Вообще, если Sm —► X — какое-нибудь гс-листное накрытие, то из соотношения
т*я* — п следует, что Н*(Х; Z) целиком состоит из элементов кручения,
порядок которых делит /2, кроме, возможно, Z в размерности т. (Так как
X — замкнутое многообразие, его группы гомологии конечно
порождённые согласно следствиям П.8 и П.9 из приложения.)
Изучая другую композицию я*т*, мы докажем следующее
утверждение.
I Предложение 3.G.I. Пусть я: X —> X — /z-листное накрытие, задап-
I ное действием группы Г на X. Тогда для коэффициентов в поле F, харак-
I теристика которого —это 0 или простое число, не делящее /7, отображс-
I ние я*: Ик{Х\ F) -^Нк(Х; F) ипъективно, причём его образ —подгруппа
I Н*(Х; F)1 , состоящая из таких классов а, что у* (а) = а для всех ye.Y.
Доказательство. Мы уже убедились, что элементы ядра
отображения я* имеют конечный порядок, делящий /2, поэтому гомоморфизм я
инъективен для тех нолей коэффициентов, которые мы рассматриваем
здесь. Остаётся описать образ отображения я*. Заметим сначала, что тя:
переводит сингулярный симплекс Д^Хв сумму всех его образов при
действии Г. Следовательно, я*т¥(а)= ^ У^а^ Для «еН^(Х; F). Ксли эле-
уеГ
§ 3.G. Трансфер
409
мент а неподвижен относительно действия группы Г' на Нк(Х\ F), то
сумма ^]у*(а) равна па, поэтому если характеристика поля коэффициен-
тов F — это 0 или простое число, не делящее п, то мы можем написать
а = тг*т*(а/л), а значит, а лежит в образе отображения п\ Наоборот,
так как пу = я для всех у е Г, мы получаем у* я* (а) = я" (а) для всех а,
а потому образ отображения я* содержится в 1Г(Х\ F)T. 3
Пример 3.G.2. Пусть X = Sl V S*, где /с> 1, а X — это п-листное
накрывающее пространство, соответствующее подгруппе индекса пн л} (X).
Таким образом, X — это окружность, к которой приклеены п сфер Sk в
точках, делящих окружность на равные части. Группа преобразований
накрытия Ъп действует, вращая окружность и циклически переставляя сферы Sk.
Следовательно, для любой группы коэффициентов G инвариантные кого-
мологии Н*{Х\ G)/j" —это все группы Н° и Н1 целиком плюс ещё группа G
в размерности /с, состоящая из клеточных классов когомологий, которые
сопоставляют один и тот же элемент группы G каждой сфере Sk. Таким
образом, Я'(Х; G)L,> —это в точности образ отображения я* при / = 0 и /с,
в то время как образ отображения я* в размерности 1—это подгруппа
nHl{X\G). Равна она Hx{X\G)*'n или нет, зависит от группы G. Мы
получаем равенство для G = Q или Zp, где р не делит п но не для G — Z
или Zp, где р делит п. В последнем случае отображение п< не инъективно
на Я1.
Пространства с полиномиальными когомологиями
по модулю р
Интересный частный случай общей задачи реализации градуирован-
но коммутативных колец как колец ^-произведения пространств —это
случай колец многочленов Zp[xx,..., л:,,] над полем коэффициентов Z/M где
р простое. Основной вопрос здесь такой: какие наборы чисел <Jb ...,dtl
реализуются как размерности |х,-| образующих л:,? Из §3.2 у нас есть
примеры произведений пространств СР00 и НР°°, для которых числа d, равны
2 или 4, для произвольного р, а когда р = 2, мы можем также взять Е^Р°°,
для которого числа d, равны 1.
В качестве применения трансфера мы построим некоторые примеры,
Для которых числа d{ больше. В случае многочленов одной переменной
оказывается, что эти примеры реализуют всё, что только можно
реализовать. Но для двух или более переменных необходимы более сложные
методы, чтобы реализовать все реализуемые случаи; дальнейшие замечания
По этому поводу см. в конце этого параграфа.
Конструкцию можно вкратце описать следующим образом. Начнем
с пространства У, про которое уже известно, что оно имеет
полиномиальные когомологий H*(Y\Zp)=Zp[yb ...,У„], и предположим, что па У
задано действие конечной группы Г. Простой трюк, называемый конструк-
410
Глава 3. Когомологии
цией Бореля, показывает, что без потери общности мы можем
предположить, что действие свободно, а потому оно определяет накрытие У —> У/Г.
Тогда согласно предложению 3.G.1, если р не делит порядок группы Г, то
кольцо Н*(У/Г; Zp) изоморфно иодкольцу в Z.p[yl, ..., у„], состоящему из
многочленов, инвариантных при индуцированном действии группы Г на
Я*(У; Zp). И в некоторых случаях это подкол ьцо само является кольцом
многочленов.
Например, если У — произведение п экземпляров пространства СРХ,
то симметричная группа Еп действует на У, переставляя множители, а
индуцированное действие на H*(Y; Zp) tvZp[y{, ..., уп] переставляет
переменные у,. Стандартная теорема из алгебры утверждает, что
инвариантные многочлены образуют кольцо многочленов Zp [а,,..., ап ], где а, — это
1-й элементарный симметричный многочлен, т.е. сумма всевозможных
мономов степени f без кратных степеней. Таким образом,
сг,—однородный многочлен степени i. Порядок группы Е„ равен л!, поэтому условие,
что р не делит порядок группы Г, сводится к тому, что р > л. Таким
образом, мы реализовали кольцо многочленов Zp[xXi ...,х„], |x,-| = 2i, при
условии, что р>п.
Этот пример не оптимальный, так как имеется другое пространство —
многообразие Грассмана n-мерных линейных подпространств в С00,
когомологии которого с коэффициентами в любом кольце R равны R[xlt..., лг„],
\Xi\ = 2f, как мы покажем в §4.D. Поэтому ограничение р > п в
действительности не является необходимым.
Чтобы получить другие примеры, мы заменим СР°° пространством
с теми же самыми когомологиями с коэффициентами в Zpi но с «большей
симметрией», которое допускает действия больших групп Г.
Конструкция будет использовать пространства /С(тг, 1), которые были определены
в §1.В. Для группы л мы построили там Д-комплекс Вп со стягиваемым
универсальным накрытием Еп. Построение функториально:
гомоморфизм {р: л—► п1 индуцирует отображение Ву\ Втс—►Втг', B(^([g1|...|gr,]) =
= [{P(g\)\---\iP(gn)]> удовлетворяющее свойствам функтора: В{^р^) = В^>Вф
и Ы = 1. В частности, если Г —группа автоморфизмов группы тг, то Г
действует на Б тт.
Другая составляющая, которая нам понадобится, — конструкция
Бореля, преобразующая действие группы Г на пространстве У в свободное
действие группы Г на гомотопически эквивалентном пространстве У •
А именно, возьмём У' = У х ЕТ с диагональным действием группы I,
Y(y,z) = (ТУ> Yz^> гДе Г действует на ЕГ как преобразование накрытия.
Это диагональное действие свободно: на самом деле оно является
действием накрытия, так как это верно для действия по второй координате.
Пространство орбит диагонального действия обозначают У хгЕГ.
Пример 3.G.3. Пусть n = Zp, и пусть Г —полная группа
автоморфизмов Aut(Zp). Автоморфизмы группы Zp имеют вид х —>тх, где (/», р) ~ *■>
§3.G. Трансфер
411
таким образом, Г — мультипликативная группа обратимых элементов
поля Ър. Согласно элементарной теории полей эта группа циклическая,
порядка р - 1. Предыдущие конструкции тогда дают накрытие K(Zp, 1) —>
-*K(Zp, 1)/Г, причём H*(K(ZP, l)/r;Zp)«H*(K(Zp, l); Zp)r. Можно
считать, что мы рассматриваем нетривиальный случай р > 2. На основании
вычисления структуры ^-произведения для линзовых пространств в
примере 3.41 или примере З.Е.2 мы получаем H~(K(l.pi l);Zp)**Az [a]®Zp[/31,
\а\ = 1 и |/31 = 2, и мы должны выяснить, как группа Г действует на этом
кольце когомологий.
Пусть у^Г— образующая, например, у(х)=тх. Индуцированное
действие элемента у на n^KiZp, 1) тоже умножение на т, так как мы взяли
JC(Zp, l) = BZp х ЯГ, а у переводит петлю-ребро [g] на BZp, в [yr(g)] = [mgl.
Следовательно, у действует на Hi{K{Zp, 1);Z) как умножение на гл. Из
этого следует, что у(а) = та и f(/3) = m/3, так как HJ(K(Zp, 1); Zp) %
^Hom(H1(K(Zp,l)),Zp), /J2(K(Zp, l);Zp)^Ext(H1(K(Zp,l)),Zp) и
имеет место общий факт, легко следующий из определений, что
умножение на целое число т в абелевой группе Н индуцирует умножение на т
вНот(Я, G) HBExt(H,G).
Таким образом, уфк) = тк13к и у(аРк) = тк*1а13к. Так как число т
выбрано так, что оно является образующей мультипликативной группы
обратимых элементов в Zp, из этого следует, что единственные
элементы в H*(K(Zp, 1); Zp), неподвижные относительно у (а значит, и
относительно Г),— это скалярные кратные /З'(р"п и а/3|(р~|)_1- Таким образом,
H*(X(Zp, l);Zp)r = A^[a/3p_2](g>Zp[^p"1]. Тем самым мы построили
пространство, у которого кольцо когомологий с коэффициентами в Zp равно
^z [*2р-з] ® ^р[У2р-2]> гДе индексы указывают размерность.
Пример 3.G.4. Как простое обобщение предыдущего примера,
можно заменить группу Г на подгруппу в Aut(Zp) порядка d, где
d—любой делитель числа р — 1. Новая группа Г порождается автоморфизмом
x»->m(p~I)/dx, и тот же самый анализ показывает, что мы получаем
пространство с Zp-когомологиями Az>[x2d-.i] ® Zp[y2d]> гДе индексы снова
обозначают размерность. Для данного выбора числа d условие, что d
делит р — 1, означает, что р = 1 mod d, а это соотношение выполняется
Для бесконечно многих р согласно классической теореме Дирихле.
Пример 3.G.5. Два предыдущих примера можно изменить так, чтобы
убрать множители, являющиеся внешними алгебрами, заменив Zp па
2роо — объединение возрастающей последовательности Zp с Zp2 с Zp3 с ...
Первый шаг-показать, что H*(K(Zpx>, 1); Zp)wZp[j3], где |j3| = 2. Мы
знаем, что H+(K(Zp., 1); Z) состоит из групп Zp. в нечётных размерностях.
Включение Zp. *-> Zp.-*i индуцирует отображение K(Zp., 1) -> K(Zp.+i, l),
Которое единственно с точностью до гомотопии. В качестве этого
отображения можно взять р-листное накрытие, так как накрывающее
пространство для K(Zp.h, 1), соответствующее единственной подгруппе ин-
412
Глава 3. Когомологии
декса р в ^/((Zp.,), 1), —это К(г£р>, 1). Формула для гомологического
трансфера 7г+т* = р показывает, что образ индуцированного отображения
H„(K(Zpi, 1); Z)->Hn(K(Zp.ri, 1); Z) для нечётного п содержит кратные р,
следовательно, это отображение— включение Zp, <-+ Zp,n. Мы можем
использовать теорему об универсальных коэффициентах, чтобы
вычислить индуцированное отображение H*(K(Zp.+i, 1); Zp)-+Hx(K(Zp.-, 1); Zp).
А именно, включение Zp, <—> Zp.+i индуцирует тривиальное отображение
Hom(Zp,M, Zp) —>Hom(Zp., Zp), поэтому на нечётномерных когомологиях
индуцированное отображение тривиально. С другой стороны,
индуцированное отображение на чётномерных когомологиях —изоморфизм, так
как отображение свободных резольвент
О >Z
т
о—*ъ
дуализуется в отображение
О -< Ext(Zp,, Z;,) ■< Hom(Z, Zp)
t i-
0 -<— Ext(Zp.+i, Zp) •<— Hom(Z, Zp)
Так как Zp* —объединение возрастающей последовательности
подгрупп Zpi, пространство BZp*> —объединение возрастающей
последовательности подкомплексов £ZpI. Поэтому можно применить
предложение 3.F.5 и сделать вывод, что группы H*(/((Zp.*, 1); Zp) нулевые в
нечётных размерностях, в то время как в чётных размерностях
отображение H*(K(Zp*, 1); Яр) -> H*(K(Zp9 1); Zp), индуцированное включением
Zp^Zp-*, — изоморфизм. Таким образом, H*(K(Zp*., 1); Zp)**Zp[/3], что
и требовалось.
Теперь мы покажем, что отображение Aut(Zp*0 —>Aut(Zp),
полученное ограничением на подгруппу Zp с Zp^, — расщепляющаяся сюръекция.
Автоморфизмы группы Zpf —это отображения х—>тх, где (т, р) = 1,
поэтому отображение ограничения Aut(Zp,n) —>Aut(Zp;) сюръективно. Так
как Aut(Zp-v) = lim Aut(Zp(), отображение ограничения Aut(ZpxO —> Aut(Zp)
тоже сюръективно. Порядок мультипликативной группы Aut(Zp.)
обратимых элементов в Zp., равен р' -р'"1 =р1'1(р — 1), а число р — 1 взаимно
просто с р'~\ таким образом, абелева группа Aut(Zp.) содержит
подгруппу порядка р — 1. Эта подгруппа отображается на циклическую группу
Aut(Zp) того же самого порядка, поэтому Aut(Zp0 —> Aut(Zp) —
расщепляющаяся сюръекция, следовательно, таким же является и отображение
AutCZ,^)—Aut(Zp).
-^ z ^ zpl ^ о
Г I''
р.*. + +
^ Z ^ Z,,,. ^ О
^-Hom(Z,Zp)
1
^-Hom(Z,Zp)
§3.G. Трансфер
413
Таким образом, мы получаем действие группы Г = Aut(Zp) на BZLx,
продолжающее её естественное действие на £Zp. Конструкция Норе-
ля тогда даёт включение ВЪр хг ЕГ <-* BZpx. хгЕГ, индуцирующее
изоморфизм алгебры HY(BZ;^ xrEr;Zp) на чётномерную часть алгебры
H*(BZp хгЕГ;2/;), которая является алгеброй многочленов Ър\у2р-г\-
Аналогично если d — любой делитель числа р — 1, то, взяв в качестве Г
подгруппу в Aut(Zp) порядка d, получим пространство, у которого кого-
мологии с коэффициентами в Zp — кольцо многочленов Zp[y2dJ.
Пример 3.G.6. Теперь мы расширим предыдущий пример, взяв
произведения и рассмотрев действие группы подстановок. В результате
получим пространство, у которого когомологии с коэффициентами в Ър —это
кольцо многочленов Zp[y2d,y4d, ...,y2,jdL гДе d —произвольный делитель
числа р — 1 и р > п. Пусть X — произведение п экземпляров пространства
BZp^, и пусть Г1 —группа гомеоморфизмов пространства X, порождённая
перестановками множителей вместе с действием Zd на каждом
множителе, построенном в предыдущем примере. Мы можем рассмотреть Г как
группу матриц размера п х п с элементами в Ър\ эти матрицы получаются
при замене некоторых элементов 1 в матрице перестановок на
элементы из Zp, мультипликативный порядок которых —делитель числа d.
Таким образом, имеется расщепимая короткая точная последовательность
О—> (Zd)" —> Г—> Ц, —> 0, и порядок группы Г' равен dnn\. Пространство-
произведение X имеет когомологии Н*(Х\ Zp)**Z [(3lf..., Д], где |Д| = 2,
поэтому
H\X*vET\Zp)**Zp[fa,...,pnf
при условии, что р не делит порядок группы Г, а это означает, что р>п.
Чтобы многочлен был инвариантным при действии Zd на каждом
множителе, он должен быть многочленом от степеней Д^, а чтобы быть
инвариантным при перестановках переменных, он должен быть
симметричным многочленом от этих степеней. Так как симметричные многочлены —
это в точности многочлены от элементарных симметрических функций,
многочлены от переменных Д, инвариантные относительно действия Г,
образуют кольцо многочленов Zp[y2d,y4(i, ••^УгнсЛ» гДе У2/с — сумма всех
произведений к разных степеней (if.
Пример 3.G.7. Чтобы получить другой вариант предыдущего
примера, выберем делитель q числа d и заменим группу Г на её подгруппу,
состоящую из матриц, для которых произведение q-x степеней отличных
от нуля элементов равно 1. В результате этого кольцо инвариантных
многочленов увеличивается. Можно показать, что инвариантные многочлены
образуют кольцо многочленов Zp[y2(i,y4(i, ••-.Угсп-ПсьУгш/]» гДе последняя
образующая y2tld заменяется на уЪщ — П Р?- Например, если л = 2 и q = 1,
i
томы получаем Zr[y4, у2(/], гдеу4 = ^/32 и у2({ = (3d{ + /3^. гРУппа г в этом
случае оказывается изоморфной группе диэдра порядка 2d.
414
Глава 3. Когомологии
Общие замечания
Задача реализации градуированного кольца многочленов Ъ [у] от
одной переменной как кольца ^-произведения пространства обсуждалась
в §3.2, а пример 3.G.5 предоставляет остающиеся примеры, показывая,
что \у\ может быть любым чётным делителем числа 2(р - 1). В случае
многих переменных задача реализации кольца Zp[yu ...,у„] с данными
размерностями |у| более трудная, но она была решена для нечётных
простых р. Приведём краткий ответ.
Мы предполагаем, что число р нечётно, а размерности |у| четны.
Назовём число d,- = |у|/2 степенью переменной у,-. В приведённых выше
примерах это действительно была степень у, как многочлена от
двумерных классов /3j, инвариантных относительно действия группы Г.
В работе [95] было доказано, что любая реализуемая алгебра
многочленов %р[у\, ..., уп) — кольцо инвариантных многочленов %р [/Зи ..., Д,)[ для
действия некоторой конечной группы Г на ^р[/?ь ..., /3„], где |Д| — 2.
Основные примеры, произведения которых дают вес реализуемые алгебры
многочленов, можно разделить на две категории. Прежде всего имеются
классифицирующие пространства групп Ли, каждое из которых реализует
некоторую алгебру многочленов для всех простых р, кроме конечного
числа. Они перечислены в следующей таблице.
Группа Ли
"£■
SU(n)
Sp(n)
SO(2fc)
G2
1 F«
£'o
1 E?
[£«
Степени
1
2,3,...,л
2, 4,...,2л
2, 4,..M2fc-2.it
2,6
2,6,8,12
2,5,6,8,9,12
2,6,8,10,12,14
2,8,12,14,18,20,24,30
Простые числа
все
все
все
р>2
р>2
р>3
р>3
р>3
р>5
Остальные примеры приходится строить вручную. Они образуют
два бесконечных семейства и ещё 30 спорадических исключений,
приведённых в двух таблицах на следующей странице. Первая строка —
примеры, которые мы построили, хотя наше построение нуждалось
в дополнительном условии, что числа р не делят порядок группы Г.
Для всех элементов в обеих таблицах порядок группы Г, для которой
%р[Уи ••^yJ ~^p[P\,..., Д,]г, оказывается равным произведению
степеней. Когда р не делит этот порядок, метод, который мы использовали
для первой строки, можно также применить для того, чтобы построить
примеры для всех остальных строк. В некоторых случаях из соотношений
сравнения для р, которые необходимы для того, чтобы группа Г была
§ З.Н. Локальные коэффициенты
415
подгруппой в Aut(Z") = GL„(Zp), автоматически следует, что р не делит
порядок группы Г. Но когда это не так, необходимы разные
конструкции пространства с требуемыми когомологиями. Чтобы узнать об этом
подробнее, читатель может для начала обратиться к [40] и [1201.
Степени
d,2d,..., (n-l)d, nq, meq|d
2,d
Простые числа |
p = 1 mod d
p = -l mod d
Степени
4,6
6,12
4,12
12,12
i 8,12
8,24
I 12,24
24,24
6,8
8,12
6,24
12,24
20,30
20,60
30,60
Простые числа |
p = 1 mod 3
p = 1 mod 3
p = l mod 12
p = l mod 12
p = 1 mod 4
p = 1 mod 8
p = l mod 12
p = 1 mod 24
p = 1, 3 mod 8
p = 1 mod 8
p = 1,19 mod 24
p = 1 mod 24
p = 1 mod 5
p = 1 mod 20
p = l mod 15
Степени
60,60
1 12,30
12,60
12,20
2,6,10
4,6,14
6,9,12
6,12,18
6,12,30
4,8,12,20
2,12,20,30
8,12,20,24
12,18,24,30
4,6,10,12,18
6,12,18,24,30,42
Простые числа |
p = 1 mod 60
p = l,4 mod 15
p = 1,49 mod 60
p = l,9mod20
p = l,4mod5
p = l,2,4 mod 7
p = 1 mod 3
p = 1 mod 3
p = l,4 mod 15
p = l mod 4
p = 1, 4 mod 5
p = 1 mod 4
p = 1 mod 3
p = l mod 3
p= 1 mod 3
Для простого числа 2
задача реализации полностью
пока не решена. Известные
примеры перечислены в таблице
справа. Построение
последнего примера, который не
происходит из
классифицирующего пространства для групп
Ли, дано в [96]. (Для простого
числа 2 «степень» обозначает
настоящую когомологическую
степень.)
Группы Ли
I 0(1)
SO(/i)
SU(n)
Sp(n)
PSp(2n + l) (Ol)
G2
Spin(7)
Spin(8)
Spin(9)
F*
—
Степени
1
2,3,...,n
4,6, ...,2n
4,8,...,4n
2,3,8,12, ...,8n+4
4,6,7
4,6, 7, 8
4, 6, 7, 8, 8
4,6,7,8,16
4,6,7,8,16,24
8,12,14,15
§ З.Н. Локальные коэффициенты
Гомологии и когомологий с локальными коэффициентами — это более
причудливые версии обычных гомологии и когомологий, которые можно
определить для неодносвязных пространств. В разных ситуациях эти более
тонкие теории гомологии и когомологий возникают естественно и неиз-
416
Глава 3. Когомологии
бежно. Например, единственный способ распространить двойственность
Пуанкаре с коэффициентами в Ъ на неориентируемые многообразия
состоит в том, чтобы использовать локальные коэффициенты. Однако
в алгебраической топологии в целом роль локальных коэффициентов
довольно скромная. Локальные коэффициенты приводят к дополнительным
сложностям, которых хочется избежать, когда это возможно. Имея это
в виду, мы не приводим полное их описание, а только сделаем набросок
основных идей, предоставляя заинтересованному читателю восполнить
технические детали.
План этого параграфа такой: сначала мы дадим беглое
алгебраическое определение гомологии и когомологии с локальными
коэффициентами, а затем переформулируем это определение более геометрическим
способом, который больше похож на обычные гомологии и когомологии. Эта
переформулировка позволяет также перенести знакомые нам свойства
гомологии и когомологии на случай локальных коэффициентов с малыми
усилиями.
Локальные коэффициенты как модули
Пусть X—линейно связное пространство с универсальным
накрытием X и фундаментальной группой я, так что X —факторпрострап-
ство пространства X относительно действия группы я
преобразованиями накрытия х^+уех для у е я и 3?еХ. Действие группы я па X
индуцирует действие группы я на группе СП(Х) сингулярных п-мерных
цепей в X, переводящее сингулярный n-мерный симплекс <т: Д" —> X
в композицию Д" —> X —* X. Действие группы я на С„(Х) превращает
С„(Х) в модуль над групповым кольцом Z[tt], которое состоит из
конечных формальных сумм £]m,-y,-, m, e Z и у{ е я, с естественным сложе-
i
нием SmiTi+Sn.Ti = SCm» + rli)ri и умножением (£miTi) (Т*п]У]) =
i i i i" j
= ^гп,п;у,уу. Отображения границы <1: СП(Х) —> С„_|(Х) являются гомо-
'.)
морфизмами 2^[я]-модулей, так как действие группы я на этих группах
получается из действия на X.
Если М — произвольный модуль над Z[rc"|, то мы хотели бы определить
Сп(Х\М) как Сп(Х)®2Мтг] М, но для тензорных произведений над
некоммутативным кольцом нужно соблюдать некоторую осторожность с левой
и правой структурами модуля. В общем случае, если R — кольцо, возможно
некоммутативное, тензорное произведение А ®к В правого R-модуля А
и левого R-модуля В определяется как абелева группа с образующими
а ® Ъ для а е А и be В, связанными соотношениями дистрибутивности
и ассоциативности:
1) (ат+ а2)®Ь = а] <8>Ь + а2®Ь и а®^ +b2) = a®b] +a®b2\
2) ar(S)b = a<S)rb.
§З.Н. Локальные коэффициенты
417
В случае, когда R = Z[rc], левый ZOl-модуль А можно рассматривать как
правый Z[7r]-модуль, положивау = у~1 а для уея. Таким образом,
определено тензорное произведение двух левых Z[я]-модулей А и Я, причём
соотношение ay®b = a®yb принимает вид у~']а®Ь = а<8>уЬ, или, что
эквивалентно, a!<8>b = ya'®yb, где а/ = у"1а. Таким образом, тензорное
умножение над Z[tz] производит эффект факторизации по действию группы
я. Чтобы упростить систему обозначений, запишем А<8>7\г] Б как Л®г В,
подчёркивая тот факт, что существенной частью структуры Z|rc] -модуля
является действие группы тт.
В частности, группа Сп(Х) ®ГМ определена, если М—левый
Z[^-модуль. Группы цепей С„(Х; М) = Сп{Х) ®r M образуют цепной комплекс
с граничными отображениями д <8> 1. Группы гомологии Нп{Х\М) этого
цепного комплекса суть по определению группы гомологии с локальными
коэффициентами.
Для когомологии можно в качестве Си{Х\ М) взять Hom?j-j(C„(X), M),
т.е. группу гомоморфизмов Z[n] -модулей Си(Х)—>М. Эти группы Сп{Х; М)
образуют коцепной комплекс, группы когомологии которого Нп{Х\ М) —
это группы когомологии с локальными коэффициентами.
Пример З.Н.1. Проверим, что если М—тривиальный Z[ я]-модуль,
для которого ут = т для всех у е я и т е М, то Пи(Х\ М) — это просто
обычные гомологии с коэффициентами в абелевой группе М. Для
сингулярного п-мерного симплекса а: А'1 —> X разные поднятия а: Д" —> X
образуют орбиту действия группы я на С„(Х). В С„(Х) &_ М все эти
поднятия отождествлены посредством соотношения а®т = усг <8>ут = уст ®т.
Таким образом, мы можем отождествить (^(Х) &_ М с СП(Х) <8> М, т.е.
с группой цепей, обозначаемой С„(Х;М) в обычной теории гомологии,
поэтому Ни{Х\М) сводится к обычным гомологиям с коэффициентами
в М. Аналогичное утверждение для когомологии тоже верно, так как
элементы группы Ыот::[7Г|(Сп(Х), М) — это функции на множестве
сингулярных п-мерных симплексов а: Л"->ХкМ, принимающие одно и то же
значение на всех элементах орбиты действия группы я, так как действие
я на М тривиально. Поэтому Нот:1\гЛ{Сп{Х),М) можно отождествить
с Нот(С„(Х), М) — обычными коцепями с коэффициентами в М.
Пример З.Н.2. Предположим, что мы берём модуль M=Z[rc],
рассматриваемый как модуль над самим собой посредством его кольцевой
структуры. Для кольца R с единицей группа А ®л R естественно изоморфна
группе А посредством соответствия а®г*->аг. Таким образом, мы
получаем естественное отождествление СП(Х) ®я^[я] с С„(Х) и,
следовательно, изоморфизм //„(X; Z[tt]) «Н„(Х). Чтобы обобщить это, рассмотрим
накрытие X' —> X, соответствующее подгруппе я' с я. Тогда свободная
абелева группа Z[rc/rc'l, базисом которой служат смежные классы уп\
является Z| я 1-модулем и С„(Х) ®^l7r] 7,[п/к\ ъС„(Х'), таким образом,
Hn(X\rLln I п' \) ъ Hn{Xf). Вообще, если Л —абелева группа, то АО/я'] —
418
Глава 3. Когомологий
это £[7г]-модуль и НМ(Х; А[п/п']) ъ Нп(Х'\А). Поэтому гомологии
накрывающего пространства —частный случай гомологии с локальными
коэффициентами. Однако для когомологий соответствующие утверждения
неверны, как мы увидим позже в этом параграфе.
Для Ъ\п\-модуля М обозначим через тгх ядро гомоморфизма р: я-*
—►Aut(M), определяющего структуру модуля, т.е. заданного формулой
р(у)(т) = угп; здесь Aut(M) —группа автоморфизмов абелевой группы М.
Если X' —> X — накрытие, соответствующее нормальной подгруппе п'
группы тг, то Сп(Х)®пМъСп(Х')®кМъСп(Х')®и„/г<]М. Это даёт более
эффективное описание группы ЯП(Х; М).
Пример З.Н.З. Рассмотрим частный случай, когда М = Z; таким
образом, Aut(Z)^Z2 = {±l}. Для нетривиальной структуры Х[7г]-модуля на М
подгруппа п' имеет индекс 2, а отображение X' —>Х является двулистным
накрытием. Если т— нетривиальное преобразование накрытия X', то
положим С+(Х') = {аеСп(Х')\т:(а) = а} и С^(Х') = {аеСп(Х')\т:(а) = -а}.
Легко проверить, что С* (Xх) имеет базис из цепей а ± та для а: Л" —> X',
и мы ползшем короткие точные последовательности
о - с-(Xх) - сп(х') - сп+(х') - о,
О - С+СХ') — СП(Х') - С,; (Xх) - О,
где Е(а) = а + т.Са) и Л(а) = а - т:(а). Гомоморфизм СП(Х) —► С(^(Х'),
переводящий сингулярный симплекс в X в сумму двух его поднятий
в X7, — изоморфизм. Факторотображение Сп (X') —> С„ (Xх) &>„. Z имеет ядро
С* (Xх), поэтому вторая короткая точная последовательность даёт
изоморфизм С~(Х0 ^ Сп(Х') ®к Z. Эти изоморфизмы —изоморфизмы цепных
комплексов, а короткие точные последовательности —короткие точные
последовательности цепных комплексов. Поэтому из первой короткой
точной последовательности мы получаем длинную точную
последовательность групп гомологии
... - НМ(Х; Z) - НМ(ХХ) - НМ(Х) - Н^СХ; Z) - ...,
где символ Z указывает на локальные коэффициенты в модуле Z, а
отображение р* индуцировано отображением накрытия р: Xх —>Х.
Применим эту точную последовательность в случае, когда X —неори-
ентируемое п-мерное многообразие М, которое замкнуто и связно. Мы
будем использовать терминологию и обозначения из §3.3. Можно
рассмотреть Z как Z[ftiM]-модуль, считая, что петля у в М действует на Ъ
как умножение на +1 или на —1 в соответствии с тем, сохраняет или
изменяет у локальные ориентации многообразия М. Тогда двулистное
накрытие Xх —>Х— это двулистное накрытие М —> М, где М
ориентируемо. Неориентируемость многообразия М влечёт, что Нп(М) = 0. Так
как Нп+1(М) = 0, приведённая выше точная последовательность даёт
§ З.Н. Локальные коэффициенты
419
НП(М; Z) ^ ЯМ(М) ^ Z. Это можно интерпретировать как наличие
фундаментального класса в гомологиях с локальными коэффициентами для
неориентируемого многообразия.
Локальные коэффициенты как ансамбли групп
Теперь мы хотим интерпретировать гомологии и когомологии с
локальными коэффициентами в более геометрических терминах, сделав их
более похожими на обычные гомологии и когомологии.
Сначала мы определим накрытия специального вида с
дополнительной алгебраической структурой. Ансамбль групп — это такое отображение
р: Е-^Х вместе со структурой группы на каждом подмножестве р~1(х),
что все группы р_10) изоморфны фиксированной группе G следующим
специальным способом: каждая точка в X имеет окрестность L/, для
которой существует гомеоморфизм hu : p~l(U) —>UxG, переводящий
каждую группу р_10) в {х} х G посредством некоторого изоморфизма групп.
Так как пространство G снабжено дискретной топологией, проекция р
является накрытием. Заимствуя терминологию из теории локально
тривиальных расслоений, подмножества р_10) называют слоями
отображения р: Е —► X и говорят о Е как об ансамбле групп со слоем G. Следует
отметить, что если мы изменим это определение, заменив всюду слово
«группа» на «линейное пространство», то мы получим намного более
распространённое понятие векторного расслоения; см. [VBKT].
Тривиальный пример предоставляет произведение Е = Х х G.
Нетривиальные примеры, которые мы уже рассмотрели, —накрытия M7j-+M
неориентируемых многообразий М, определённые в §3.3. Здесь группа
G — это группа коэффициентов Z для гомологии, но аналогично можно
было бы определить ансамбль групп Ма —> М для любой абелевой группы
коэффициентов G.
Группы гомологии пространства X с коэффициентами в ансамбле Е
абелевых групп можно определить следующим образом. Рассмотрим
конечные суммы ^]п,-с7,-, где каждый символ сг,: Д" —>Х обозначает сингу-
i
лярный n-мерный симплекс в X, а п,: Д" —►£ — поднятие симплекса сг,-.
Сумма двух поднятий /i, и ш, одного и того же симплекса сг,
определяется формулой (н,- + w,)(s) = ri;(s) + /и,(5); она тоже является поднятием
симплекса а,. Таким образом, конечные суммы ][]п,-сг,- образуют абеле-
ву группу С„(Х;Е), если мы разрешим удалять члены п,сг,, где
п,—поднятие, всюду принимающее нулевое значение. Граничный гомоморфизм
д: С„(Х; E)-+Cn_i(X; Е) определяется формулой
(1(^ni^i) =^(-l)4-a,-|[v0,...,v,, ...,v„l,
i i.i
420
Глава 3. Когомологии
где «п,» в правой части уравнения означает ограничение поднятия, т.е.
n-t\ [v0, ...,v;, ..., v,J. Доказательство того, что обычный граничный
гомоморфизм д удовлетворяет соотношению д2 = 0, работает и в нашей
ситуации, поэтому группы Сп(Х\ Е) образуют цепной комплекс. Мы обозначим
группы гомологии этого цепного комплекса через Н„(Х; Е).
В случае, когда ансамбль групп £ является произведением ХхС,
поднятия п, —это просто элементы группы G, таким образом, Нп(Х\ Е) =
= Нп(Х\ G) —обычные гомологии. В общем случае поднятие п,: Д" -* Е
единственным образом определяется своим значением в одной точке
5£ Д", и это значение может быть произвольным, так как пространство
Д'г односвязно, таким образом, п, можно представлять себе как элементы
группы р"1 (о*,-($)), изоморфной G. Однако если Е — не произведение, то
нет канонического изоморфизма между разными слоями р _10), поэтому
Нп(Х\ Е) нельзя отождествить с обычными гомологиями.
Альтернативный подход мог бы состоять в том, чтобы взять в качестве
коэффициентов п,- элементы группы слоя над выбранной точкой в <уХ&п),
скажем, cr,-(v0). Однако при таком определении формула для граничного
оператора д становится более сложной, так как в симплексе Д" нет точки,
которая принадлежит всем его граням сразу.
Наша задача теперь состоит в том, чтобы соотнести группы гомологии
Нп(Х\ Е) с группами гомологии с коэффициентами в модуле,
определёнными ранее. В §1.3 мы описали, как можно классифицировать
накрывающие пространства над X с данным слоем F в терминах действия
группы Л! (X) на F, если предположить, что пространство X линейно связно
и имеет локальные свойства, гарантирующие существование
универсального накрытия. Легко проверить, что накрывающие пространства,
являющиеся ансамблями групп со слоем G, эквивалентны действиям
группы п1(Х) на G автоморфизмами группы G, т.е гомоморфизмам из тгДХ)
BAut(G).
Например, для ансамбля Мг-*М действие петли у на слое Ъ — это
умножение на ±1 в соответствии с тем, сохраняет или изменяет у
ориентацию многообразия М, т.е. поднимается у до замкнутой петли в
ориентируемом двулистном накрытии М —> М или нет. Другой пример, действие
группы пх(Х) на себе внутренними автоморфизмами, соответствует
ансамблю групп р: Е—»Х со слоями р~~1(х) ~пх{Х, х). Этот пример
довольно похож но духу на примеры Мт —> М. В обоих случаях имеется функтор,
сопоставляющий группу каждой точке пространства, причём все группы
в разных точках изоморфны, но не канонически. Различные выборы
изоморфизмов получаются при выборе разных путей между двумя точками,
и петли приводят к действию группы пх на слоях.
В случае ансамбля групп р: Е—>Х, слой G которого абелев, действие
группы пх(Х) на G автоморфизмами—это то же самое, что структура
ZtTrjXJ-модуля на G.
§ З.Н. Локальные коэффициенты
421
I Предложение З.Н.4. Если X — линейно связное пространство, у ко-
I торого есть универсальное накрывающее пространство, то группы
I Нп(Х; Е) естественно изоморфны группам гомологии Ип(Х; G) с локаль-
I ными коэффициентами в ^[тг]-модуле G, соответствующем ансамблю Е,
I где тг = п^Х).
Доказательство. Как было отмечено ранее, задание ансамбля групп
Е-+Х со слоем G эквивалентно заданию действия группы п па G. В более
явном виде это означает, что если X— универсальное накрытие над X,
то Е отождествляется с факторпространством X х G по диагональному
действию группы к, у(х, g) — (уху yg), где действие по первой
координате—преобразования накрытия X. Для цепи ^П/Ст, е CM(X; E) коэффици-
i
ент г\[ даёт поднятие симплекса сг,- в Е, a nh в свою очередь, имеет
разные поднятия в X х G. Таким образом, мы получаем естественные сюръ-
екции Сп(Х х G) —> С„(Е) —> С„(Х; Е), представляющие каждую из этих
групп как факторгруппу предыдущей. Точнее говоря, если отождествить
Сп(Х х G) с СМ(Х) <8>Z[G] очевидным образом, то С„(£) — факторгруппа
СП(Х) ® Z1[G] при отождествлениях а ® g ~ утст ® ycg. Эта
факторгруппа—тензорное произведение С„(Х) <£>-/Z[G]. Чтобы перейти к
факторгруппе СП(Х;Е) группы С„(Е) = С„(Х)®7Г ZLG], мы должны учесть
операцию суммы в С„(Х; Е), сложение поднятий п,: Лм —>Е. Это означает, что
в сумме а <8> gl + a <8> g2 = a <g> (g! + g2) luien gj + g2 нужно
интерпретировать не в ^[G], а в естественной факторгруппе G группы Z[G].
Следовательно, СП(Х; Е) отождествляется с факторгруппой С„(Х) &_ G группы
СП(Х) <8>к Z[G]. Это естественное отождествление коммутирует с
граничными гомоморфизмами, поэтому группы гомологии также
отождествляются. □
В общем случае, если X содержит несколько компонент линейной
связности Ха с универсальными накрытиями Ха, то
C,IU;£) = 0(Cn(XQ)OJ.,[,!WJ|G)>
(X
поэтому Ни(Х;Е) раскладывается соответствующим образом в прямую
сумму групп гомологии с локальными коэффициентами для компонент
линейной связности Ха.
Обратимся теперь к вопросу о том, удовлетворяют ли гомологии с
локальными коэффициентами аксиомам, подобным аксиомам для обычных
гомологии. Основное отличие связано с поведением индуцированных
гомоморфизмов. Чтобы отображение /: X —> X' индуцировало
отображение гомологии с локальными коэффициентами, у пас должны быть
ансамбли групп Е —> X и Е' -* X', связанные некоторым образом.
Естественно пред положить, что имеет место^ коммутативная диаграмма на
Рис., причём ограничение отображения / на любой слой является гомо-
422
Глава 3. Когомологии
морфизмом. При таком предположении существует цеп- ?
ной гомоморфизм /-: СП(Х; Я) —> СП(Х'; Я'), полненный Е ^ Е/
при композиции сингулярных симплексов с /, а их под- \р \р
нятий —с /; следовательно, определён индуцированный 1 / *
гомоморфизм /+: Нп(Х; Я) —>НП(Х'; Я'). Слои ансамблей Е
и Я' не обязаны быть изоморфными группами, поэтому гомоморфизмы
замены коэффициентов Нп(Х; GT) —>Н„(Х; G2) для обычных гомологии —
частный случай такого гомоморфизма. Чтобы избежать этих
дополнительных осложнений, мы рассмотрим только случай, когда ограничение
отображения / на каждый слой — изоморфизм. При таком условии
изображённую коммутативную диаграмму называют отображением ансамблей.
Опишем метод построения отображений ансамблей. Начнём с
отображения /: X—>Х' и ансамбля групп р'': Я'—>Х'. Положим
E = {(x,e/)eXxE'\f(x) = p'(e/)}.
Это множество можно вставить в приведённую выше коммутативную
диаграмму, если положить р(х, е')=хи /О, е/) = е/. В частности, слой р~[(х)
состоит из таких пар О, е'), что р'(е') = /00; таким образом, / —
взаимно однозначное отображение этого слоя па слой ансамбля Я' —> X' над
точкой /О)- Воспользуемся этим взаимно однозначным отображением,
чтобы снабдить р~Л(х) структурой группы. Проверим, что р: Я —»X
является ансамблем групп. Пусть ti\ (рО'Ч^') —* I/' x G —изоморфизм из
ансамбля групп. Зададим h: p~l(U) —► [/ х G над I/ = /~1([//) формулой
h(x, е') = (х,/^(е')), где h^ —вторая координата для h'. Обратное
отображение для h —это О, g)e(x, (ftO_I(/M,g)), и ясно, что h —изоморфизм
на каждом слое. Таким образом, р: Е —► X — ансамбль групп, который
называется ансамблем, индуцированным из отображения Е/ —► X'
посредством отображения /. Для индуцированного ансамбля часто используется
обозначение /*(£')•
Если дано любое отображение ансамблей Я—>Я', как на приведённой
выше диаграмме, то стандартная проверка показывает, что отображение
Я —► /*(£'), е —► (р(е),/(е)), является изоморфизмом ансамблей групп
над X, поэтому конструкция индуцированного ансамбля групп даёт все
отображения ансамблей. Здесь мы видим одну из причин, по которой
гомологии с локальными коэффициентами несколько более сложные:
НП(Х; Е) в действительности является функтором по двум переменным,
ковариантным по X и контравариантным по Я.
Можно рассматривать ансамбли групп над X как Z^X]-модули.
Тогда построение индуцированного ансамбля соответствует превращению
1\П\Х'}-модуля в 2[я,Х]-модуль при помощи формулы Y8~ f*WS Д-Ля
/*: щ{Х) —► тг,{X'). Это легко получить из определений. В частности, из
этого следует, что гомотопные отображения /0, /,: X —> X' индуцируют
изоморфные индуцированные ансамбли /0¥(Я'),//(Я')- Следовательно,
§ З.Н. Локальные коэффициенты
423
отображение f¥\ НМ(Х; Е) —> Нп(Х'; £'), индуцированное отображением
ансамблей, зависит только от гомотопического класса отображения /.
Обобщение определения Нп(Х;Е) для пар (Х,А) получается
непосредственно. Начнём с определения Нп(Х, А\ Е) как n-й группы гомологии
цепного комплекса факторгрупп С„(Х; Е)/Сп(Л\ Е), где р : Е —>Х
становится ансамблем групп над А при ограничении на р~у(А). Тогда паре (X, А)
соответствует длинная точная последовательность групп гомологии с
локальными коэффициентами в ансамбле Е. Свойство вырезания можно
доказать, как и для обычных гомологии, повторяя несколько раз
барицентрическое подразделение. Последуя аксиома для гомологии, в которую входят
несвязные объединения, тривиально переносится на гомологии с
локальными коэффициентами. Симплициальные и клеточные гомологии тоже без
труда переносятся на случай локальных коэффициентов, как и
доказательство того, что эти разновидности гомологии согласуются с
сингулярными гомологиями для Д-комплексов и CW-комнлексов соответственно. Мы
оставляем проверку всех этих угверждений усердному читателю.
Теперь обратимся к когомологиям. Можно было бы попытаться
определить Н"(Х; Е) непосредственной дуализацией, взяв Hom(C„(X), E), но
это не имеет смысла, так как Е не группа. Вместо этого группа
коцепей Сп(Х\Е) определяется как множество всех отображений (/?,
сопоставляющих каждому сингулярному симплексу а: Л" —* X поднятие
4>(а): Д" —► Е. В случае, когда Е — произведение X х G, это приводит
к сопоставлению элемента группы G каждому симплексу а, таким
образом, это определение обобщает обычные когомологии. Кограничные
отображения 5: С"(Х; Е)—>С"+1(Х; Е) определяются точно так же, как для
обычных когомологии; они удовлетворяют соотношению 52 = 0, поэтому
мы получаем группы когомологии Ип{Х\Е), а в относительном случае
группа НП(Х, А; Е) определяется с помощью относительных коцепей
Сп(Х,А\Е) = Ker(Gn(X;E) -* Сп(А;Е)).
Для линейно связного пространства X с универсальным накрытием
X и фундаментальной группой я мы можем отождествить Нп(Х\Е) с
НП(Х; G), когомологиями с локальными коэффициентами в £[я]-модуле G,
соответствующем ансамблю Е, отождествив С"(Х; Е) с Нот7Лг] (СП(Х), G)
следующим образом. Элемент i^eC"(X;£) сопоставляет каждому
симплексу а: Д" —► X поднятие в Е. Если рассматривать Е как факторпро-
странство X х G по диагональному действию группы я, то поднятие
симплекса а в Е — это то же самое, что орбита поднятия в X х G. Такая
орбита — это отображение /, сопоставляющее каждому поднятию а: Д" —► X
такой элемент /(от) € G, что f(ya) = у/(or) для всех у е G, т. е. элемент
группы Hom?[rT,(Gn(X), G).
Основные свойства обычных когомологии из §3.1 переносятся без
большого труда на группы когомологии с локальными коэффициентами.
424
Глава 3. Когомологий
Чтобы определить отображение
индуцированное, как и раньше, отображением ансамблей, достаточно
заметить, что сингулярный симплекс а: Д" —> X и поднятие а': Д" —> Е'
симплекса fa определяют поднятие а — (сг, а'): Лп —>/*(Ю симплекса а.
Чтобы показать, что /^g влечёт fx —g\ нужна некоторая модификация
доказательства соответствующего результата для обычных когомологий
из § 3.1, которая получается дуализацией доказательства для гомологии.
В случае локальных коэффициентов можно построить цепную гомотопию
Р*у удовлетворяющую соотношению g: — р = Рж5 + 5Р+,
непосредственно по подразделению комплекса Дп х /, использованному в
доказательстве соответствующего результата для гомологии. Аналогичные
замечания относятся к доказательствам свойства вырезания и
последовательности Майера—Вьеториса для когомологий с локальными коэффициентами.
Чтобы доказать, что симплициальные и клеточные когомологий
эквивалентны сингулярным когомологиям в случае локальных коэффициентов,
нужно применить рассуждения с телескопом из доказательства леммы
2.34 и показать, что Нп(Хк\Е)ы Нп(Х;Е) при к > п. Подробности снова
оставляются читателю.
Различие между гомологиями с локальными коэффициентами и ко-
гомологиями с локальными коэффициентами проясняется при сравнении
следующего предложения с полученным ранее отождествлением группы
НДХ; 2[тг1Х]) с обычными гомологиями универсального накрытия
пространства X.
I Предложение З.Н.5. Если X — конечный CW-комнлекс с упивереаль-
I ным накрытием X и фундаментальной группой я, то для всех п группа
I Н"(Х\ Z[tt]) изоморфна Н'^Х', Z), когомологиям пространства X с ком-
I пактными носителями и обычными целочисленными коэффициентами.
Например, рассмотрим n-мерный тор Т\ произведение п
окружностей, с фундаментальной группой п — Ъи и универсальным накрытием .'&".
Мы получаем Н,(Т"; Ъ[п\) %H,(Rn), что равно нулю, за исключением Ъ
в размерности 0, но Hx{Jn\ Z\n]) ъН1с(Мп) обращается в нуль, за
исключением Z в размерности п, как мы видели в примере 3.34.
Чтобы доказать это предложение, мы воспользуемся некоторыми
общими фактами о когомологиях с компактными носителями. Одно из
существенных различий между обычными когомологиями и когомологмими
с компактными носителями связано с индуцированными отображениями.
Отображение f: X -+Y индуцирует отображения р: C"(Y; G) —> C'cl(X\ G)
и, следовательно, /*: H"{Y\ G) —>Н"(Х] G) при условии, что
отображение / собственное, т. е. прообраз /~](Ю каждого компактного множества
К в Y компактен в X. Таким образом, если Lp e Gn(Y;G) обращается
в нуль на цепях в Y - /С, то /-(</?) е Сп(Х\ G) обращается в нуль па цепях
§ З.Н. Локальные коэффициенты
425
в X - f"l(K). Далее, чтобы гарантировать, что f ^ g влечёт /+ — g*, мы
должны ограничиться гомотопиями, которые являются собственными как
отображения Хх/->У. Относительные группы Н"(Х, Л\ G) определены,
когда Л —замкнутое подмножество в X, поскольку это гарантирует, что
включение A t-> X — собственное отображение. При таких ограничениях
основная теория из § 3.1 без труда переносится на когомологии с
компактными носителями.
В частности, для локально компактного CW-комплекса Х можно
вычислить H*(X;G), используя конечные клеточные коцепи, т.е.
клеточные коцепи, обращающиеся в нуль па всех клетках, кроме конечного
числа. Л именно, чтобы вычислить Н"(Х", X"'1; G), используя
вырезание, сначала нужно отождествить эту группу с H'?(XM, N(X',_1); G), где
N(Xn~l) —замкнутая окрестность Х"~] в Xй, полученная при вырезании
открытого п-мерпого шара из внутренности каждой л-мерной клетки.
Если комплекс X локально компактен, то очевидная деформационная
ретракция пространства N(Xn~l) на X""'1 —собственная гомотопическая
эквивалентность. Следовательно, с помощью длинных точных
последовательностей и 5-леммы, мы получаем изоморфизмы Н"(Х", Х"~]; G) %
^Н"(ХП, N(X"_1); G), a no свойству вырезания последнюю группу можно
отождествить с конечными коцепями.
Доказательство предложения З.Н.5. Как отмечено выше, мы
можем вычислить /7*(Х; Z), используя группы С"(Х; Z) конечных клеточных
коцепей </?: С„—>Z, где С„ = НДХП, X""1). Снабдим X СW-структурой,
подняв CW-структуру комплекса X. Тогда, так как пространство X компактно,
конечные клеточные коцепи —это такие гомоморфизмы <р: Сп —> Z, что
для каждой клетки еп в X значение ^р(уеп) отлично от нуля только для
конечного числа преобразований накрытия уея. Такой гомоморфизм </?
определяет отображение (р: С„—»Z[7r], если положить (£(еп)=2 (/7(Т~1еП)У-
г
Отображение (/? является ZfTrJ-гомоморфизмом, так как если мы заменим
индекс суммирования у в правой части равенства <p(r]en) = 4£iip(y~xr]e'1)y
г
на г)у, то получим ^у(у~1еп)г1у. Отображение у >-+(р определяет
гомоморфизм г
С}{Х\Ъ) - Homz(7rJ(CM,Z[rc]),
который инъективен, так как кр восстанавливается по (р как
коэффициент при у— 1. Кроме того, этот гомоморфизм сюръективен, так как
21[я]-гомоморфизм я/л М —> Z[n] имеет вид \j>(x) — ^1рг(х)у, где я/'г G
г
£Hom>:(M, Z) удовлетворяет условию я/;у (л-) = я/^ (у !*), поэтому я/'i
определяет я/'. Изоморфизмы С"(Х; Z) ^Homy.f7:](Crp Z[7i]) являются
изоморфизмами коцепных комплексов, поэтому соответствующие группы
когомологии /-/"(X; Z) и //"(X; Z[rr]) изоморфны. И
426
Глава 3. Когомологий
Отметим, что ^- и ^-произведения легко вводятся для коэффициентов
в ансамбле колец; последнее понятие определяется очевидным образом,
^-произведением можно воспользоваться, чтобы получить версию
двойственности Пуанкаре для замкнутого п-мерного многообразия М,
используя коэффициенты в ансамбле колец Е. При этом необходимо делать то же
предположение, что и для обычных коэффициентов, а именно, что
существует фундаментальный класс [М] еНп(М; Е), при ограничении которого
получается образующая группы Ни(М, М - {х}\ Е) для всех хе М. Согласно
вырезанию последняя группа изоморфна кольцу Я —слою ансамбля Е. То
же самое доказательство, что и для обычных коэффициентов, тогда
показывает, что [М]гл: Нк(М] Е) ^>Нп_к(М;Е) — изоморфизм для всех к.
Если взять в качестве R одно из стандартных колец Ъ, Q или Ъ то мы
не получим ничего нового, так как единственным кольцевым
автоморфизмом для этих колец является тождественный, а значит, ансамбль колец Е
должен быть произведением М х R. Чтобы получить что-то более
интересное, предположим, что в качестве R мы берём кольцо Ъ\\\ комплексных
целых чисел, т.е. комплексных чисел a -f bi, a,b€Z. В этом кольце
определено комплексное сопряжение а + Ы*->а — Ы, которое является
изоморфизмом колец. Если М неориентируемо и связно, то мы можем
воспользоваться гомоморфизмом со: я,(М)—>{=Ы}, который определяет ансамбль
групп Mz, чтобы построить ансамбль колец Е, соответствующий действию
группы пхШ) на Z[i]t заданному формулой у(а + Ы) = a-f со(у)Ы. Группы
гомологии и когомологий многообразия М с коэффициентами в Е зависят
только от аддитивной структуры кольца Z[i], поэтому они
раскладываются в прямую сумму действительных и мнимых частей, которые являются
просто группами гомологии и когомологий с обычными коэффициентами
в Z и скрученными коэффициентами в Ъ соответственно.
Фундаментальный класс в Нп(М\7л)> построенный в примере З.Н.З, можно
рассматривать как чисто мнимый фундаментальный класс [М] ^Нп(М\ Е). Так как
^-умножение на [М] переставляет действительную и мнимую части, мы
получаем следующую теорему.
I Теорема З.Н.6. Если М — замкнутое неориентируемое связное /ьмер-
I ное многообразие, то ^-умножение на чисто мнимый фундамепталь-
I ный класс [М] даёт изоморфизмы Нк(М\ Z)^Hn_/c(M; Z) и H*(M;Z)«
I **Нп_кШ\%).
Это верно и в более общем случае, когда Z заменяется на другие
кольца, вроде Q или Zp. Имеется также версия для некомпактных
многообразий, использующая когомологий с компактными носителями.
Задачи
1. Вычислите H+(5K,E) и H*(Sl',E) для нетривиального ансамбля
Е—>Sl со слоем Ъ.
§ З.Н. Локальные коэффициенты
427
2. Вычислите группы гомологии с группой локальных
коэффициентов Нп(М\ М7) для замкнутой неориентируемой поверхности М.
3. Пусть <#(Х; G) —множество классов изоморфных ансамблей групп
Е —► X со слоем G, и пусть £0 —> ВAut(G) —ансамбль, соответствующий
«тождественному» действию р: Aut(G) —► Aut(G). Докажите, что
отображение [X, BAut(G)] -* Я(Х, G), [/] -*/*(Яо), является взаимно
однозначным, если X — GW-KOMiuieKc. Здесь [X, У1 обозначает множество
гомотопических классов отображений X —* Y.
4. Докажите, что если конечные связные GW-комплексы Х и Y гомо-
топически эквивалентны, то их универсальные накрытия X и У
собственно гомотопически эквивалентны.
5. Пусть X—конечный неодносвязный граф. Докажите, что группа
Hn(X; Z[7rjX]) нулевая, за исключением случая п = 1, когда она
является прямой суммой счётного множества групп Ъ. [Воспользуйтесь
предложением З.Н.5 и вычислите Н"(Х) как 1\тНп(Х, X - 7)) для подходящей
последовательности конечных поддеревьев 7^ С Т2 с ... в X, для которой
i
6. Докажите, что группы гомологии HlJ(X; G) можно определить,
используя локально конечные цепи, которые являются такими формальными
суммами ]£g(Jcr сингулярных симплексов а: Д" —>Х с коэффициентами
ga € G, что у каждой точки х е X есть окрестность, содержащая образы
лишь конечного числа симплексов сг, g^ Ф 0. Разработайте эту теорию
гомологии в достаточной степени, чтобы можно было доказать, что для
локально компактного GW-комплекса Х группу Н^(Х; G) можно
вычислить, используя бесконечные клеточные цепи ^£аеа-
и
Глава 4
Теория гомотопий начинается с гомотопических групп тг„(Х),
которые являются естественными многомерными аналогами
фундаментальной группы. У этих высших гомотопических групп есть некоторое
формальное сходство с группами гомологии. Например, группа пп(Х) всегда
оказывается абелевой при п ^ 2, и есть относительные гомотопические
группы, которые включаются в точно такую же длинную точную
последовательность, как длинная точная последовательность групп гомологии.
Однако высшие гомотопические группы гораздо труднее вычислять, чем
группы гомологии или фундаментальную группу, потому что пи свойство
вырезания для гомологии, ни теорема вап Кампена для nY не
выполняются для высших гомотопических групп.
Несмотря на эти вычислительные трудности, гомотопические группы
имеют большое теоретическое значение. Одна из причин этого
—теорема Уайтхеда о том, что отображение СW-комплексов, индуцирующее
изоморфизм всех гомотопических групп, является гомотопической
эквивалентностью. Однако более сильное утверждение, что два CW-комплекса
с изоморфными гомотопическими группами гомотопически
эквивалентны, обычно бывает неверно. Один из редких случаев, когда
гомотопический тип CW-комплекса действительно единственным образом
определяется его гомотопическими группами, —это когда комплекс имеет только
одну нетривиальную гомотопическую группу. Оказывается, такие
пространства, известные под названием пространств Эйленберга—Маклей-
на, играют фундаментальную роль в алгебраической топологии по
многим причинам. Возможно, самая важная из них —их тесная связь с ко-
гомологиями: классы когомологий для CW-комплекса находятся во
взаимно однозначном соответствии с гомотопическими классами
отображений из этого комплекса в пространство Эйленберга—Маклейпа. Таким
образом, когомологий имеют чисто теоретико-гомотопическую
интерпретацию, и есть аналогичная, но более тонкая теоретико-гомотопическая
интерпретация гомологии, которая объясняется в §4.F.
Более элементарную и прямую связь между гомотопиями и гомологи-
ями устанавливает теорема Гуревича, утверждающая, что первая
ненулевая гомотопическая группа лп(Х) односвязиого пространства X изоморф-
Глава 4. Теория гомотетий
429
на первой ненулевой группе гомологии Нп(Х). Этот результат, вместе с его
относительной версией, является одним из краеугольных камней
алгебраической топологии.
Хотя свойство вырезания не всегда выполняется для гомотопических
групп, в некоторых важных частных случаях есть диапазон размерностей,
в которых оно выполняется. Это приводит к идее стабильных
гомотопических групп, основе стабильной теории гомотопий. Возможно, главная
нерешённая задача в алгебраической топологии —вычисление
стабильных гомотопических групп сфер. Ближе к концу §4.2 мы приводим
некоторые таблицы известных вычислений, которые весьма ясно показывают
сложность этой задачи.
В §4.2 включено краткое введение в теорию локально тривиальных
расслоений, которые обобщают накрытия и играют похожую роль для
высших гомотопических групп. Локально тривиальным расслоениям, и
даже частному случаю векторных расслоений, легко можно было бы
посвятить целую книгу, но здесь мы используем локально тривиальные
расслоения лишь для того, чтобы получить несколько основных примеров
и мотивировать изучение их более гибкого теоретико-гомотопического
обобщения, расслоения в смысле Гуревича, которые играют большую
роль в §4.3. Помимо всего прочего расслоения в смысле Гуревича
позволяют описать, по крайней мере теоретически, как гомотопический тин
произвольного CW-комплекса восстанавливается по его гомотопическим
группам при помощи индуктивной процедуры построения «скрученных
произведений» пространств Эйленберга—Маклейна. Это понятие башни
Постникова. В благоприятных случаях, включающих все односвязные
CW-комплексы, также можно описать дополнительные данные,
необходимые наряду с гомотопическими группами для определения
гомотопического типа. Это последовательность классов когомологий, называемых
/с-инвариантами пространства. Если все они нулевые, то пространство
гомотопически эквивалентно произведению пространств Эйленберга—
Маклейна, а в противном случае —нет. К сожалению, ^-инварианты —
классы когомологий, вообще говоря, весьма сложных пространств. Таким
образом, это не приводит к практическому способу классификации
гомотопических типов, но бывает полезно для разных более теоретических
целей.
Эта глава устроена так, что она начинается с чисто
теоретико-гомотопических понятий, в основном независимых от теории гомологии и
когомологий, роль которой постепенно возрастает в последующих параграфах
этой главы. Поэтому можно прочитать значительную часть этой главы
сразу после главы 1, лишь с редкими обращениями к главе 2 по поводу
алгебраических определений, в частности понятия точной
последовательности, которая столь же важна в теории гомотопий, как и в теории
когомологий и гомологии.
430
Глава 4. Теория гомотопий
§ 4.1. Гомотопические группы
По-видимому, самые простые нестягиваемые пространства —сферы,
поэтому, чтобы получить хотя бы небольшое представление о сложности,
свойственной гомотопическим группам, давайте посмотрим на
некоторые результаты вычислений групп 7i,(S"). Небольшой список,
приведённый ниже в таблице, взят из книги 170].
r4(Sa)
п 1
1 2
1 3
4
5
| 6
7
8
i
1
Z
0
0
0
0
0
0
0
2
0
ъ
0
0
0
0
0
0
3
0
ъ
ъ
0
0
0
0
0
4
0
z2
ъ2
z
0
0
0
0
5
0
г2
ъ2
.z2
Z
0
0
0
6
0
z12
ZI2
z2
z2
z
0
0
7
0
7L2
7L2
Z x Zu
z2
z2
z
0
8
0
z2
z2
Z2 x Z2
z24
*'2
z2
z
9
0
z,
z.
Z2 x Z2
Z2
z24
z2
z2
10
0
Zis
^,5
-^24 X Лсд
z2
0
Z24
z2
11
0
z.
z2
Zis
z2
z
0
z24
12
0
Z2 x Z2
Z2 x 7L2
Z2
Z:«)
Z-,
0
0
Здесь странная смесь порядка и хаоса. Самая очевидная
закономерность—большая область нулей ниже диагонали, и действительно,
тг,-(5п) =0 для всех / < п, как мы покажем в следствии 4.9. Есть также
последовательность нулей в первом ряду, позволяющая предположить,
что 7Г,-(Sl) =0 для всех i > 1. Это тоже довольно элементарный факт,
частный случай предложения 4.1, легко следующий из теории накрывающих
пространств.
Трудно не заметить совпадений во второй и третьей строке. Они
относятся к случаю п = 1 изоморфизмов тгД£2") ъп{._х{$2п~х} х 7i,(S4"" !),
которые имеют место для п = 1, 2, 4 и всех i. Следующий случай п = 2 говорит,
что каждый элемент четвёртой строки — произведение элемента,
расположенного от него по диагонали выше и слева, и элемента на три строки
ниже его. В действительности изоморфизмы тг,-(52") ^л,-.^^2"-1) х тг(-(£4"'" ])
имеют место для всех п, если профакторизовать по 2-кручению, т.е. по
элементам, порядок которых —степень числа 2. Это теорема Джеймса,
которая будет доказана в [SSAT].
Следующая закономерность в таблице —последовательность групп Z
на диагонали. Это иллюстрирует теорему Гуревича, которая угверждает,
что для односвязного пространства X первая ненулевая гомотопическая
группа я„(Х) изоморфна первой ненулевой группе гомологии Н„(Х).
Можно также увидеть, что все группы выше диагонали конечны, за
исключением групп tt3(S2), tt7(S4) и яп(56). В §4.С мы применим ^-про-
изведение в когомологиях, чтобы показать, что группа nAk_}(S2k)
содержит прямое слагаемое Ъ для всех к ^ 1. Имеется теорема Серра,
доказательство которой можно найти в [SSAT], угверждающая, что группа тг, (S")
§4.1. Гомотопические группы
431
конечна при i > n, за исключением групп nAk_^(S2k), которые являются
прямой суммой группы Z и конечной группы. Итак, вся сложность
гомотопических групп сфер обитает в конечных абелевых группах. Задача,
таким образом, сводится к вычислению р-кручения в 7r,-(S") для каждого
простого числа р.
Наиболее интересное свойство таблицы заключается в том, что на
каждой диагонали группы nn+k(Sn) с фиксированным к и переменным п
в конце концов становятся независимыми от п для достаточно большого п.
Это свойство стабильности — теорема Фрейденталя о надстройке,
доказанная в §4.2, где мы приводим более обширные таблицы этих
стабильных гомотопических групп сфер.
Определения и основные конструкции
Пусть Г —единичный п-мерный куб, произведение п экземпляров
отрезка [0,1]. Граница дГ1 куба /" — подпространство, состоящее из точек,
у которых по крайней мере одна координата равна 0 или 1. Для
пространства X с отмеченной точкой х0£Х определим я„(Х,л:0) как множество
гомотопических классов отображений /: (Г\дГ) —* (Х,х0), где гомото-
пии ft должны обладать свойством ft(dln) =xQ для всех t. Это определение
можно распространить и на случай п = 0, считая, что /° — точка, а гЭ/° —
пустое множество; таким образом, я0(Х, х0) —это просто множество
компонент линейной связности пространства X.
При п ^2 операция суммы в тг„(Х, *0), обобщающая операцию
композиции в 7г1? определяется так:
C/ + g)Cs1,S2> ...,5„) =
/(2sbs2,...,s„),
s} e [0,1/2];
l,s2,...,s„), «м е [1/2,1].
Очевидно, что эта сумма корректно определена для гомотопических
классов. Так как в операции суммы участвует только первая координата,
те же самые рассуждения, что и для Tij, показывают, что пп(Х,х{)) —
группа, причём единичный элемент —постоянное отображение,
переводящее 1п в лг0> а обратный элемент задаётся формулой -/(s,,s2, ...,s„) =
Аддитивная система обозначений для операции группы здесь
используется потому, что группы пп (X, Хц) абелевы при п ^ 2. А именно, / + g ^ g + /
посредством гомотопии, изображённой на следующих рисунках.
/
8
8
f
Сначала гомотопия сжимает области определения отображений / и g
в меньшие кубы в /п, а область вне этих кубов отображается в отмеченную
432
Глава 4. Теория гомотопий
точку. Когда это будет сделано, появится свободное пространство, в
котором можно сдвигать эти два куба куда угодно в /", пока они остаются
непересекающимися, поэтому если п ^ 2, то их можно сдвинуть мимо друг
друга, переставив их. Затем, чтобы завершить построение гомотопий,
области определения отображений / и g можно снова увеличить до их
исходного размера. Если угодно, то всё это можно сделать, используя только
координаты S] и s2, оставляя все другие координаты без изменений.
Отображения (/", 01п) —> (Х,х()) — это то же самое, что
отображения факторпространства 1п/д1п = 5" в X, переводящие отмеченную
точку 50 = dln/dln в х0. Это означает, что мы можем рассмотреть группы
я„(Х, х0) и как гомотопические классы отображений (Sri, s0) —> (X, х0), где
берутся гомотопий в классе отображений того же самого вида (S",s0) —>
—►(Х,х0). При такой интерпретации групп пп(Х,х0) сумма /H-g
—композиция S" —> S" V Sn —^ X, где отображение с стягивает экватор S"~ l
в сфере 5" в точку, и мы выбираем отмеченную точку s0 так, чтобы она
принадлежала этому экватору 5""1.
Теперь мы покажем, что если X— линейно связное пространство, то
разные способы выбора отмеченной точки х0 всегда производят к
изоморфным группам тг„(Х, х0), как и для т^, поэтому в этом случае
оправдана запись тсп(Х) для 7гп(Х,х0). Если задан путь у: I —» л-0
—> X изх0 = у(0) в другую отмеченную точку х} = у(1), [\\\\1 ////i
то мы можем сопоставить каждому отображению /:
U'\(lln) -> (Х,х}) новое отображение yf: (/", Л/")->
—► (X, х()), сжав область определения отображения /
в меньший концентрический куб в /", а затем вставив
путь у на каждом радиальном отрезке в промежутке
между этим меньшим кубом и <11п. При п = 1 отображение yf —
композиция трёх путей: у, / и обратного к у, поэтому обозначение yf не
согласуется с обозначением для композиции путей. Так как здесь нас в основном
интересует случай п > 1, мы оставляем читателю сделать необходимые
изменения обозначений для п = 1.
Гомотопия у или / в классе отображений, сохраняющих 01 или 01п
соответственно, приводит к гомотопий yf в классе отображений (/", <)1п) —>
—► (X, х"0). Вот ещё три важных свойства:
2) (rW^rO?/);
3) 1/~/, где 1 обозначает постоянный путь.
Г/777ТГ^
§4.1. Гомотопические группы
433
Гомотопии отображений в свойствах 2 и 3 очевидны. Для
доказательства свойства 1 мы сначала деформируем / и g так, чтобы они были
постоянны на правой и левой половинах куба /" соответственно, получив
при этом отображения, которые можно назвать / + 0 и 0 + g, а затем
вырезаем постепенно всё более широкий симметричный пласт в середине
y(/ + 0) + y(0 + g), пока не получится y(/ + g):
wm-шша isssmz
ks
а/
ш
Х\
W^t/777
ES3
/
4±
У7Ш
■Ml////]
w
7ТШЯ
а/
ш
ШЛ
g Щ
Явная формула для этой гомотопии такова:
■r(/ + 0)((2-0s1,52l...tsn)>
hf(s1,s2, ...,s„) =
5, efO, 1/2];
r(0 + g)((2-t)5,+t-l,52,...,5„), 5l G [1/2,1].
Таким образом, мы получаем y(/ + g)^y(/ + 0) + y(Q + g) ~yf + yg-
Если определить преобразование изменения отмеченной точки /Зг:
тгп(Х, jfi) —> тг„(Х, х0) формулой /Зг([/]) = Г у/1, то свойство 1 показывает,
что Рг — гомоморфизм, в то время как из свойств 2 и 3 следует, что /Зг —
изоморфизм с обратным отображением (3^ где у— обратный путь для
пути у, т.е. y(s) — у(1 — s). Таким образом, если пространство X линейно
связно, то разные способы выбора отмеченной точки х0 приводят к
изоморфным группам тг„(Х, лг0), которые можно поэтому обозначить просто
Ограничимся теперь петлями у в отмеченной точке х0. Так как fiyr) =
= flrl3v, сопоставление [у] —* /Зу определяет гомоморфизм из тг^Х,^)
в Aut(^M(X, х0)), группу автоморфизмов группы яп(Х,х0). Эту
операцию называют действием группы яг на яп; каждый элемент группы ят
действует как автоморфизм [/] —> [у/] группы пп. При п = 1 это
действие группы 7Г] на себе внутренними автоморфизмами. Когда п > 1,
это действие превращает абелеву группу ям(Х, х0) в модуль над
групповым кольцом Ъ\пх{Х, х0)]. Элементы из 7А[п\] —конечные суммы ]>]",•)',■,
i
где п,-е Z и у,-€я,, причём умножение определяется
дистрибутивностью и умножением в я3. Структура модуля на лп задаётся формулой
(SniT»)a — 2пД/|а) Для я £ ?V Для краткости иногда говорят, что тг„
i
является 7ггмодулем, а не Z[яjl-модулем.
В литературе пространство с тривиальным действием пх па пп
называют «п-простым», а «простое» означает «^-простое для всех /7». Было бы
хорошо использовать термины, лучше описывающие эти свойства. В этой
книге мы будем называть пространство абелевым, если для него действие
гРуппы тгj на всех гомотопических группах пп тривиальное, так как при
434
Глава 4. Теория гомотопий
п = 1 это условие означает, что группа я3 абелева. Эта терминология
согласуется с традиционным использованием термина «нильпотентное»,
относящегося к пространствам с нильпотентной группой кх и нильпо-
тентным действием тгт на всех высших гомотопических группах; см. [35].
Заметим теперь, что пп — функтор. А именно, отображение у : (X, х())—>
-^(У,Уо) индуцирует отображение (/?,: тгГ1(Х,х0) — 7гп(У,у0),
определённое формулой ¥?*([/]) = [у?/]. Непосредственно из определений следует,
что отображение ^>„ определено корректно и является гомоморфизмом
при п ^ 1. Свойства функториалыюсти {yip)* — У+'Ф* и 14 = 1 тоже
очевидны, как и тот факт, что если у?,: (Х,х0) —> (У, у0) — гомотопия, то </?0, = '^1ж.
В частности, гомотопическая эквивалентность (X, х0) ^ (У,у())
пространств с отмеченными точками индуцирует изоморфизм всех
гомотопических групп пп. Это верно даже тогда, когда отмеченные точки не
обязаны быть постоянными в процессе гомотопий. Мы показали это для п^
в предложении 1.18, а обобщение для остальных и — одна из задач в конце
этого параграфа.
Гомотопические группы ведут себя очень хорошо относительно
накрывающих пространств.
Предложение 4.1. Отображение накрытия р: (Х,3с0)—> (Х,х0)
индуцирует изоморфизмы р*: тг„(Х, х0) —> тг„(Х, х0) для всех п ^ 2.
Доказательство. Для доказательства сюръективности отображения
р, мы применим критерий поднятия из предложения 1.33, из которого
следует, что любое отображение (S",s0)—> (Х,л:0) поднимается в (Х,х0),
поскольку при п ^ 2 сфера Sn односвязна. Инъективность отображения
р+ непосредственно следует из свойства накрывающей гомотопий, так же
как и в предложении 1.31, где рассматривался случай п = 1. !И
В частности, лп(Х,л:0) = 0 при п ^ 2, если универсальное накрытие
пространства X стягиваемо. Это можно применить, например, к S\
поэтому мы получаем первую строку таблицы гомотопических групп сфер,
приведённой ранее. Верно и более общее утверждение: n-мерный тор Г",
произведение п окружностей, имеет универсальное накрытие Ж'\ поэтому
7Ti(TM) = 0 при i > 1. Это разительно отличается от групп гомологии Я, (Г"),
которые отличными от нуля /\ля всех / ^ п. Пространства, у которых я„ = О
для всех п ^ 2, иногда называют асферичными.
Поведение гомотопических групп относительно произведений очень
простое.
I Предложение 4.2. Для произведения ПаХа произвольного набора
линейно связных пространств Ха имеют место изоморфизмы пп(ПаХа) ^
«а Паям(Х„) для всех п.
Доказательство. Отображение /: У —► ПаХа — это то же самое, что
набор отображений fa: У —> Ха. Взяв в качестве У пространства S" и S" х /,
получаем требуемое LJ
§4.1. Гомотопические группы
435
Очень полезное обобщение гомотопических групп пп(Х,х0)
—относительные гомотопические группы пп(Х,А,х0) для пары (Х,А) с
отмеченной точкой х0еА. Чтобы определить их, рассмотрим 7м'"1 как грань
куба 7" с последней координатной sn = 0 и обозначим через J'1"1
замыкание дополнения д1п — 7"'"1, т.е. объединение остальных граней куба Г.
Тогда яп(Х, А, х0) для п ^ 1 определяется как множество гомотопических
классов отображений (7м, 0Г\ J"""1) —> (X, А, х0) с гомотопиями в классе
отображений того же самого вида. По-видимому, нет вполне
удовлетворительного способа определить п0(Х,А,х0), поэтому мы оставим этот
объект без определения (одно из возможных определений дано в задачах
в конце этого параграфа). Заметим, что яп(Х, х0, х0) = я„(Х, х0), поэтому
абсолютные гомотопические группы —частный случай относительных
гомотопических групп.
Операция суммы определяется в яп(Х, А, х0) теми же самыми
формулами, что и для 7гп(Х, х0), за исключением того, что координата sn теперь
играет особую роль, и её больше нельзя использовать для операции
суммы. Таким образом, ям(Х, А, х0) — группа при п ^ 2, и эта группа абелева
при п ^3. При п = 1 мы получаем 71 = [0, 1], 7° = {0} и J° = {1}, таким
образом, пг (X, А, х0) — это множество гомотопических классов путей в X из
переменной точки в Л в фиксированную отмеченную точку х0 € А. Вообще
говоря, это множество нельзя превратить в группу никаким естественным
способом.
Точно так же, как элементы группы ям(Х, х0) можно рассматривать
как гомотопические классы отображений (S",s0) —> (X, х0), имеется
альтернативное определение 7гп(Х,А,х0) как множества гомотопических
классов отображений (D", S"-I,.s0) —► (Х,А,х0), так как стягивание
подпространства J11"1 в точку преобразует (/", дГ\ J""1) в (Dn, S"-1,.s0). Сэтой
точки зрения сложение задаётся посредством отображения с: Dn-+DnVDnt
стягивающего D/,_I CD" в точку.
Полезная и более понятная переформулировка того, что означает
тривиальность элемента группы лп(Х, А,х0), даётся следующим критерием
сжатия.
Отображение /: (D/?, Sn~\sQ) —> (X, А, х0) представляет нуль в группе
7гп(Х, Л, х0) тогда и только тогда, когда оно гомотопно относительно
S""1 отображению с образом, содержащимся в А.
Действительно, если существует такая гомотопия в отображение g, то
Ш = Lgl в 7гп(Х, А, х0) и [g] =0 посредством гомотопии, полученной в
результате композиции g с деформационной ретракцией диска D" на sC).
Наоборот, если [/] =0 посредством гомотопии F: D" х 7 —>Х, то,
ограничивая F на семейство п-мерных дисков в Dn х 7, начинающееся с D" х {0},
заканчивающееся диском D" x {1}USM_1 x 7 и такая, что все диски в этом
семействе имеют одну и ту же границу, мы получаем гомотопию
отображения / в некоторое отображение в А, постоянное на S""1.
436
Глава 4. Теория гомотопий
Отображение кр: (X, Д, х0) —> (Y, В, у0) индуцирует отображения
if,: тгм (X, Д, х0) -> 7Г„ (Г, В, у0),
которые являются гомоморфизмами при 02и обладают свойствами,
аналогичными свойствам в абсолютном случае: (i/?V;L = ^*i/'-» ^* — 2.
и ^, = i/>*, если i/?^^ в классе отображений (X, Л, х0)—► (7, B,y0).
Самое полезное свойство относительных групп тг,ДХ, Д,х0),
возможно, состоит в том, что они включаются в длинную точную
последовательность
... — тг„(Л, х0) -^ я,ДХ, х0) -^ я„(Х, Л, х0) -U яп_! (Д, х0) —... — я0(Х, ха).
Здесь i и j — включения (Д, х0) <-* (X, х0) и (X, х0, х0) <-* (X, Д, х0).
Отображение Л получается при ограничении отображения (Г1, г)/", J"-1) —►
—►(Х,Д,х0) на 7"-1 или при ограничении отображения (DM, S"-1, s0) —►
—>(Х,Д, х0) на Sn~]. Отображение д, называемое граничным
отображением, является гомоморфизмом при п > 1.
| Теорема 4.3. Эта последовательность точна.
В самом конце последовательности, где структуры группы не
определены, точность всё ещё имеет смысл: образ одного отображения —это
ядро следующего, т. е. множество элементов, отображающихся в
гомотопический класс постоянного отображения.
Доказательство. С чуть большими усилиями мы можем получить
длинную точную последовательность тройки (X, Д, В, х0), где х0 е В с А с
СХ:
... -> я,ДД, В,х0) ^ я,ДХ,В,х0) ±+ тг„(Х, A,xQ) -^ пп_х{А9 В,х0) — ...
... — тгДХ.Д,^))
Когда В = х0, это сводится к точной последовательности для пары (X, А, х0),
однако последняя последовательность продолжается ещё на два шага до
я0(Х,х0), Проверка точности для этих двух последних шагов остаётся
в качестве простого упражнения.
Точность в члене я,ДХ, В, х0). Сначала заметим, что композиция
jj* равна нулю, так как любое отображение (/", дГ\ J""1) —► (Д, В, *())
представляет нуль в я,ДХ,Д,х0) в соответствии с критерием сжатия.
Чтобы убедиться, что Kerj* с Imi*, предположим, что отображение /:
(/", Э/", J""1) — (X, В,х0) представляет нуль в я,ДХ,Д,х0). Тогда снова
в соответствии с критерием сжатия / гомотопно относительно д!п
отображению, образ которого содержится в Д. Следовательно, класс [/) <=
е яп(Х, В, х0) лежит в образе отображения i+.
Точность в члене я,ДХ,Д,х0). Композиция г);+ равна нулю, так как
ограничение отображения {Г\ дГ\ J"~]) —> (X, В, х0) на /м_1 имеет образ,
лежащий в В, а потому представляет нуль в пп_х{Ау В, х0). Наоборот, пред
§4.1. Гомотопические группы
437
/
-А-
F
положим, что ограничение отображения
f:On,dI",Jn-l)^{X,A,x0)
на J"~l представляет нуль в я„_т(Л, В, х0). Тогда
отображение /|/м_1 гомотопно отображению с образом,
лежащим в В, посредством гомотопии F: Г1~] х / —► Л Л
относительно г)/"-1. Мы можем приставить F к/,
получив новое отображение (Г\ дГ\ J""1) —> (X, В, х0), ко- в
торое, как отображение (/", dl'\ J""1) —> (X, Л, х0), гомотопно
отображению / посредством гомотопии, приставляющей постепенно, всё более
и более длинные начальные участки отображения F. Поэтому [/] elmj*.
Точность в члене тгп(Л,В, х0). Композиция i*d равна нулю, так как
ограничение отображения /: (/"+1, d/'7+1, J") —> (X, Л, х0) на /" гомотопно
относительно д1п постоянному отображению посредством самого
отображения /. Включение Ker j+ с \тд, очевидно, имеет место, если В — точка, так
как гомотопия ft: (/", дГ1) —► (X, х0) отображения /0: (/", дГ) —► (Л, х0) в
постоянное отображение даёт отображение F: (/"+1, rJ/"+1, J")—>(Х, Л, х0),
для которого r)([F]) = [/0]. Таким образом, в этом случае
доказательство завершено. Для произвольного В пусть F — гомотопия отображения
/: (/", дГ\ J""1) —> (Л, В, х0) в постоянное отображение в классе
отображений (/", д/п, J"-1) —> (Х,В, х0), и пусть g — это ограничение отображения F
на /п~г х /, как на первом из двух приведённых ниже рисунков.
/
/
Перепараметризуя п-ю и (п + 1)-ю координаты так, как показано на
втором рисунке, мы видим, что отображение / с приставленным к нему
отображением g лежит в образе отображения д. Но, как мы отметили в
предыдущем абзаце, приставление g к/ даёт тот же самый элемент группы
яп(Л,В,х0). □
Пример 4.4. Пусть СХ — конус над линейно связным
пространством X, т.е. факторпространство цилиндра X х /, полученное при
стягивании основания X х {0} в точку. Мы можем рассматривать X как под-
Пространство X х {1} с СХ. Так как пространство СХ стягиваемо, длинная
точная последовательность гомотопических групп для пары (СХ, X) даёт
Изоморфизмы пп(СХ,Х,х0)^ки_](Х,х0) для всех п ^ 1. Положив п = 2,
Мы можем реализовать любую группу G, абелеву или нет, как
относительную группу 7г2, выбрав пространство X так, что я-^Х) ^G.
Длинная точная последовательность гомотопических групп, очевидно,
естественна: отображение троек с отмеченными точками (Х,Л,В,х0)—>
438
Глава 4. Теория гомотетий
—> (У, С, D,y0) индуцирует отображение соответствующих длинных
точных последовательностей с коммутативными квадратами.
Для относительных гомотопических групп имеются
изоморфизмы изменения отмеченной точки /Зу, аналогичные
изоморфизмам в абсолютном случае. Начнём с пути у
в А с X из лг0 в хг. Он индуцирует отображение (Зу:
ям(Х, А, х^ — я„(Х, А,х0), если положить /Зг([/]) = [у/], г л 7~
где отображение у/ определено так, как на рисунке справа.
Область определения отображения / размещена в меньшем кубе
с гранью /""\ расположенной в центре соответствующей грани большего
куба. Эта конструкция обладает теми же самыми основными свойствами,
что и в абсолютном случае; доказательства вполне аналогичны, и мы
оставляем их в качестве задач. Доказательства для абсолютных и
относительных групп требуется провести отдельно, так как определение
yf в абсолютном случае не является частным случаем определения yf
в относительном случае.
Изоморфизмы /Зу показывают, что я„(Х, А, х0) не зависит от х0, если
пространство А линейно связно. В этом случае я„(Х, А, х0) часто
обозначают просто как я„(Х, А).
Если ограничиться петлями с началом и концом в отмеченной
точке, то сопоставление у *-> /3V определяет действие группы п1{А,х0) на
я„(Х, А, лг0), аналогичное действию группы я^Х, л:0) на я„(Х, х0) в
абсолютном случае. На самом деле, как видно из определений, группа
Я! (А, х0) действует на всю длинную точную последовательность
гомотопических групп для (X, А, х0), причём это действие коммутирует с
разными отображениями в последовательности.
Пространство X с отмеченной точкой л:0 называют тквязным, если
я,(Х, л:0) —0 при i $ п. Таким образом, 0-связность означает линейную
связность, а односвязность означает односвязность. Так как п-связность
влечёт 0-связность, выбор отмеченной точки л:0 несуществен. Условие,
что пространство п-связно, можно выразить без упоминания об
отмеченной точке, так как легко проверить, что следующие три условия
эквивалентны:
1) любое отображение 51 —► X гомотопно постоянному отображению;
2) любое отображение S1 —>Х продолжается до отображения D1+) —>Х\
3) я,(Х,л:0) =0 для всех х0еХ.
Таким образом, пространство X является п-связным, если любое из
этих трёх условий выполняется для всех i $ п. Аналогично в
относительном случае легко убедиться, что следующие четыре условия эквивалентны
при i >0:
1) любое отображение (D\ dDl) —> (X, А) гомотопно относительно д&
отображению D1 —► А;
р
i:
щ
/
уО\
§4.1. Гомотопические группы
439
2) любое отображение (D', dDl) —> (X, Л) гомотопно в классе таких
отображений отображению D' —> Л;
3) любое отображение (D1, dD') —> (X, А) гомотопно в классе таких
отображений постоянному отображению D' —> А;
4) 7Г((Х, Л,х0)=0для всехх0еЛ.
Для i = 0 мы не определяли относительное множество тг0, а каждое из
свойств 1—3 эквивалентно высказыванию, что любая компонента
линейной связности пространства X содержит точки из Д, так как D0 — это
точка, а множество dD° пустое. Пару (X, А) называют п-связной, если
свойства 1—4 выполняются для всех i $ л, i > 0, а свойства 1—3 выполняются
И при i = 0.
Заметим, что пространство X является л-связным тогда и только
тогда, когда пара (Х,х0) является л-связной для некоторой точки х0, а
значит, и для всех х0.
Теорема Уайтхеда
Так как CW-комплексы строятся с помощью отображений
приклеивания, области определения которых —сферы, не должно быть слишком
удивительно, что гомотопические группы CW-комплексов несут много
информации. Теорема Уайтхеда выражает это в явном виде.
I Теорема 4.5. Если отображение /: X—>Y связных CW-комплексов
I индуцирует изоморфизмы /*: пп(Х) —> пп{У) для всех п, то / —гомото-
I пическая эквивалентность. В случае, когда / — включение подкомплек-
1 са Xе-* Y, справедливо более сильное утверждение: X —деформацион-
I ный ретракт пространства Y.
Доказательство легко следует из более технического результата,
который оказывается очень полезным во многих рассуждениях. Для удобства
ссылок мы назовём его леммой о сжатии.
I Лемма 4.6. Пусть (X, А) — CW-napa, а (У, В)—любая пара сВ^0.
I Предположим, что 7Г„(У, В, у0) = 0 для всех л, для которых X — А име-
I ет клетки размерности л, и всех у0 е В. Тогда любое отображение
I /: (X, А) —> (У, В) гомотопно относительно А отображению X —> В.
При л = 0 условие, что 7Г„(У, В,у0) =0для всех у0е В, следует
рассматривать как утверждение, что пара (У, В) является 0-связной.
Доказательство. Предположим по индукции, что отображение / уже
Прогомотопировано так, что оно переводит остов Хк~] в В. Если Ф —
Характеристическое отображение клетки ек из X - Д то композицию
/Ф: (Dfc, dDk) —* (У, В) можно прогомотопировать в В относительно dDk
^гласно предположению о том, что як(У,В, у0) =0, если /с > 0, или что
йаРа (У, В) является 0-связной, если /с = 0. Эта гомотопия отображения
/Ф индуцирует на факторпространстве Х^1 Ue^ пространства Х^"1 UD
К>Мотопию отображения / относительно Хк~\ Сделав это для всех /с-мер-
440
Глава 4. Теория гомотопии
ных клеток в X - А одновременно и взяв постоянную гомотопию на А, мы
получаем гомотопию отображения /| Хк и А в отображение в В. Согласно
свойству продолжения гомотопии из предложения 0.16 эту гомотопию
можно продолжить до гомотопии, определённой на всём пространстве X,
и тем самым доказательство шага индукции завершено.
Применив конечное число шагов индукции, получим доказательство
в случае, когда клетки комплекса X - А имеют ограниченную
размерность. В общем случае мы выполняем гомотопию на к-м шаге индукции
в течение времени г из интервала [1 - 1/2*, 1 - l/2fc+1]. Любой конечный
остов Хк в конце концов станет стационарным при этих гомотопиях,
поэтому мы получаем корректно определённую гомотопию/,, te [0, 1],
причём /j(X) С В. □
Доказательство теоремы Уайтхеда. В частном случае, когда / —
включение подкомплекса, рассмотрим длинную точную
последовательность гомотопических групп для пары (У, X). Так как / индуцирует
изоморфизмы всех гомотопических групп, все относительные группы пп{У, X)
нулевые. Применение леммы к тождественному отображению (Y, X) —► (У, X)
тогда даёт деформационную ретракцию пространства Y на X.
Общий случай можно доказать, используя цилиндры отображений.
Напомним, что цилиндр отображения Mj для отображения /: X —> Y —
это факторпространство несвязного объединения пространств X х I и У
при отождествлениях (х, 1) ~ /00- Таким образом, Mj содержит как
Х = Х х {0}, так и Y в качестве подпространств, и My деформационно
ретрагируется на У. Отображение / представляется в виде композиции
включения X <—> My и ретракции My —> У. Так как эта ретракция —
гомотопическая эквивалентность, достаточно доказать, что М,- деформационно
ретрагируется на X, если / индуцирует изоморфизмы гомотопических
групп, или, что эквивалентно, если все относительные группы 7in(Mf, X)
нулевые.
Если отображение / оказалось клеточным, т. е. оно переводит
/2-мерный остов комплекса X в п-мерный остов комплекса Y для всех п, то
[Mf, X) — CW-napa, поэтому в соответствии с первым абзацем
доказательства мы получаем требуемое. Если отображение / не клеточное, то мы
можем обратиться к теореме 4.8, которая утверждает, что отображение j
гомотопно клеточному отображению, или же мы можем использовать
следующее рассуждение. Сначала применим предыдущую лемму, чтобы
получить гомотопию относительно X включения {X U Y, X) <-^> (My, X) в
отображение в X. Так как пара (М(ДиУ), очевидно, обладает свойством
продолжения гомотопии, эта гомотопия продолжается до гомотопии
тождественного отображения пространства My в отображение g: Mf —>M^
переводящего X и У в X. Затем, применив ещё раз лемму к композиции
{X х / Ц У, X х dl U Y) -> (М/-, X и Y) -^ (Mf, X), завершим построение
деформационной ретракции пространства Mj ни X. D
§4.1. Гомотопические группы
441
Теорема Уайтхеда не утверждает, что два CW-комплекса X и У с
изоморфными гомотопическими группами будут гомотопически
эквивалентны, так как есть большая разница между утверждением, что X и У
имеют изоморфные гомотопические группы, и утверждением, что существует
отображение X—>У, индуцирующее изоморфизм гомотопических групп.
Например, рассмотрим пространства X = IRP2 и У = S2 x IRP30. У них обоих
фундаментальная группа равна Z2, и согласно предложению 4.1 их высшие
гомотопические группы изоморфны, так как их универсальные накрытия
S2 и S2 х S°° гомотопически эквивалентны, поскольку пространство S°°
стягиваемо. Но 1RP2 и S2 x 1RP00 не гомотопически эквивалентны, так как
их группы гомологии совсем разные: у пространства S2 x IRP00 имеются
ненулевые гомологии в бесконечно многих размерностях, так как оно
ретрагируется на RP°°. Другая пара CW-комплексов, которые не являются
гомотопически эквивалентными, но имеют изоморфные гомотопические
группы, —это S2 и S3 х СР°°, как мы увидим в примере 4.51.
Очень частный случай, когда гомотопический тип CW-комплекса
определяется его гомотопическими группами, —это когда все его
гомотопические группы тривиальны, поскольку тогда отображение вложения
нульмерной клетки в комплекс индуцирует изоморфизм гомотопических
групп, а потому комплекс деформационно ретрагируется на нульмерную
клетку.
Следующая достаточно важная лемма о продолжении до некоторой
степени похожа на лемму о сжатии.
I Лемма 4.7. Пусть даны CW-napa (X, А) и отображение /: А —>У, при-
I чём У линейно связно. Тогда отображение / можно продолжить до отоб-
I ражения X —> У, если пп_х(У) = 0 для всех таких п, что X - А имеет
I клетки размерности п.
Доказательство. Предположим по индукции, что / продолжено на
(п - 1)-мерный остов. Продолжение на n-мерные клетки существует
тогда и только тогда, когда композиция отображения приклеивания клетки
Sn~]—►Х'1"1 и отображения /: Х"~] —>У гомотопна нулю. П
Клеточная аппроксимация
Когда мы доказывали в предложении 1.14, что nx{Sk) = 0 при /с> 1, мы
сначала показали, что любую петлю в Sk можно продеформировать так,
чтобы она не проходила по крайней мере через одну точку, если к > 1,
а затем использовали тот факт, что дополнение точки в Sk стягиваемо,
чтобы закончить доказательство. Ту же самую стратегию можно было бы
применить, чтобы доказать, что nt](Sk) —0 при п < /с, если бы мы смогли
сделать первый шаг, т.е. деформировать отображение S" —>Sk так, чтобы
оно стало не сюръективным. На первый взгляд может показаться, что
этот шаг не нужен, потому что никакое непрерывное отображение Sn —> S
442
Глава 4. Теория гомотопий
не может быть сюръективным при п < /с, но нетрудно использовать
заполняющие пространство кривые из общей топологии, чтобы построить
такие отображения. Поэтому нужно проделать некоторую работу, чтобы
построить гомотопий, устраняющие это довольно неприятное поведение
отображений.
Оказывается, в случае отображений CW-комплексов для этого, как
и для многих других целей в теории гомотопий, достаточно только по«
требовать, чтобы клетки отобрались на клетки той же самой или
меньшей размерности. Отображение /: X —» Y, удовлетворяющее условию
f{Xn) с Yn для всех л, называют клеточным отображением. Имеет место
фундаментальный факт, что любое отображение можно продеформиро-
вать так, чтобы оно стало клеточным. В этом и состоит теорема о
клеточной аппроксимации.
I Теорема 4.8.- Любое отображение /: X —* Y CW-комплексов гомотоп-
I но клеточному отображению. Если / уже является клеточным на под-
I комплексе А С X, то гомотопию можно выбрать так, чтобы она была
I постоянной на А.
I Следствие 4.9. nu{Sk) = 0 при п <к.
Доказательство. Если S" и Sk снабжены их обычными CW-струк-
турами с нульмерными клетками в качестве отмеченных точек, то любое
отображение Sn -^Sk, сохраняющее отмеченную точку, можно прогомото-
пировать с сохранением отмеченной точки так, чтобы оно стало
клеточным, а потому постоянным, если п < к. □
Линейные отображения не могут увеличить размерность, поэтому
можно попытаться доказать, что любое отображение можно прогомотопи-
ровать в отображение, обладающее своего рода свойствами линейности.
Один из самых старых таких результатов —теорема о симплициальной
аппроксимации из §2.С. Клеточную аппроксимацию можно
рассматривать как аналог для CW-комплексов симплициальной аппроксимации
для симплициальных комплексов, так как симплициальные отображения
являются клеточными. Однако симплициальные отображения намного
более жёсткие, чем клеточные отображения, что, возможно, объясняет,
почему подразделение области определения необходимо для
симплициальной аппроксимации, но не для клеточной аппроксимации. Основой
доказательства клеточной аппроксимации будет слабая форма
симплициальной аппроксимации, которую можно доказать довольно элементарным
прямым рассуждением.
Доказательство теоремы 4.8. Предположим по индукции, что
отображение/: X—>Y уже клеточное на остове X""1, и пусть е" —это п-мерная
клетка в X. Замыкание клетки е" в X компактно, поскольку оно
является образом характеристического отображения для е". Таким образом.
/ переводит замыкание клетки е" в компактное множество в Y. Так как
§4.1. Гомотопические группы
443
компактное множество в CW-комплексе может пересекать только
конечное число клеток согласно предложению 4.АЛ из приложения, из этого
следует, что f{en) пересекает только конечное число клеток в Y. Пусть
ек (ZY — клетка самой высокой размерности, с которой пересекается /(еп).
Мы можем считать, что к >п, поскольку иначе отображение / уже
клеточное на еп. Ниже мы покажем, что можно деформировать отображение
/|Xn_1 U е" так, чтобы оно оставалось неподвижным на Хп~] и чтобы
множество /(еп) не содержало некоторую точку р еек. Тогда можно
деформировать f\Xn~l Uen относительно Xn_1 так, чтобы множество /(еп)
не содержало всю клетку ек, взяв композицию с деформационной
ретракцией пространства Yk - {р} на Yk -ek. Повторяя этот процесс конечное
число раз, мы в конце концов добьёмся того, чтобы множество /(еп) не
пересекалось со всеми клетками размерности больше п. Делая это для всех
n-мерных клеток и оставляя при этом неподвижным на п-мерных клетках
в А, где оно уже клеточное, мы получим гомотопию /|Х"ге1 X""1 U А"
в клеточное отображение. Шаг индукции тогда можно завершить,
обратившись к свойству продолжения гомотопии из предложения 0.16, чтобы
продолжить эту гомотопию, вместе с постоянной гомотопией на А, до
гомотопии, определённой на всём пространстве X. Переходя к пределу
по п —> оо, получаем, возможно, бесконечную последовательность
гомотопии, которую можно реализовать как одну гомотопию, выполняя
гомотопию с номером п в течение времени t из интервала [1 - 1/2", 1 - 1/2"+1].
Это имеет смысл, так как каждая точка комплекса X лежит в некотором
остове X", который в конце концов становится стационарным в
бесконечной цепи гомотопии.
Чтобы заполнить недостающий шаг в этом рассуждении, нам
понадобится следующее техническое утверждение.
I Лемма 4.10. Пусть /: /" —> Z — отображение, где Z получено из своего
I подпространства W, приклеиванием клетки ек. Тогда / гомотопно отно-
I сительно /_1(W) отображению fl} для которого существует такой сим-
I плекс Ак с ек, что f~l{&k) — объединение (возможно, пустое) конечно-
I го числа выпуклых многогранников, на каждом из которых fx является
I ограничением линейной сюръекции Еп —> Rk.
Здесь выпуклый многогранник в Г с ■&" — любое подпространство,
которое можно получить как пересечение конечного числа
полупространств, заданных линейными неравенствами вида ^]а,-х,- ^ Ь.
Прежде чем доказывать эту лемму, покажем, как она позволяет
завершить доказательство теоремы о клеточной аппроксимации. Взяв
композицию данного отображения /: Xм"1 ие" —> Yk с характеристическим
отображением Iй —> X для е", мы получим такое отображение /, как в лемме,
с Z = Yk и W = Yk' — ек. Гомотопия, которую даёт лемма, неподвижна на
д/п, поэтому она индуцирует гомотопию ft отображения /|Х"-1 Ue", непо-
444 I лани 4. Теории гомотопиЛ
движную на Л"' "\ Нсли к > п, го не существует сюръективных линейных
отображений У:"' —► .'.Чк\ таким образом, множество /,'ЧД*) должно быть
пустым, и мы можем выбрать в качестве р любую точку симплекса Л:'. ;;j
Доказательство леммы 4.10. Отождествим е* с У/. Пусть В:, /i^Cc* -
замкнутые шары радиусов 1 и 2 с центром в начале координат.
Множество f~\B:,) замкнуто, а потому компактно в /'. Из этого следует, что
отображение / |)авномерно непрерывно па / ](В-,). Полому существует
такое f > 0. что неравенство х - у < f влечет |/(.v) f(yV < 1/2 ^г/л
всех x.ycf (В}). Разобьём отрезок / так, чтобы для индуцированного
разбиения куба I'' на кубы каждый куб лежал и шаре диаметра меньше *:,
Пусть К- —объединение всех замкнутых кубов, пересекающих множество
/""(/*;). и пусть К2—объединение всех замкнутых кубов, пересекающих
множество X,. Тогда мы получаем включения / 1(В) с К* с. К:. с/ ill);
последнее включение имеет место потому, что точки из/(А',) удалены па
расстояние меньше 1/2 от/(К]}, а точки из f(K^) удалены на расстояние
меньше 1/2 от В:.
Мы можем рассматривать К2 какСМ'-комплекс, i-мерные клетки
которого— i-мерные открытые кубы, внутренности /-мерных граней /с-мернмх
кубов из К2 для /$ к. барицентрическое подразделение этой кубический
клеточной структуры является структурой симплициального комплекса
на А':», вершины которой -центры клеток. Можно построить эту симали-
циальпую структуру индукцией по остовам кубической клеточной
структуры; шаг индукции состоит в том, чтобы взять конус над симплициадь-
ной структурой на границе каждой кубической клетки с вершиной в
центре этой клетки.
Пусть g\ К1—> с" = У." - отображение, которое совпадает с / на всех
вершинах симплексов подразделения и линейно на каждом симплексе.
Зададим iомотопню /,: К2- »е* формулой (1 -tj)f -4 (t^)g> где j: К"*
—> |0, 1 ] — отображение, для которого ^(/WJ " 0 и ^(К) = 1. Таким
образом, /{: = / и /|1Х, • £JA',. 'Так как /, -постоянная гомотопна на 'Я-
мы можем продолжить её так, чтобы она было постоянной гомого;аиИ
отображения / на остальной части куба /".
Мы утверждаем, чю существует окрестное:т> N точки 0 в />,, дли )<°'
юрой / '(\:) с К,. Это эквивалентно утверждению, что / переводиi i()'
$4.1. Гомотопические группы
445
долненпе к К] и дополнение к /V, Сточками дополнения к К:! все ясно, гак
как назтих точках /: -/ и / переводит дополнение к К? в дополнение к В{,
для точек и:* К2 ■ К-. рассмотрим симплекс с/ из подразделения комплек
са К2- Отображение / переводит каждую его точку в точку :пара Я,,
радиуса 1/2. Гак как шар В0 выпуклый, £ тоже отображает сх в В.т, а потому
я /j тоже. Пели а не содержится в K]t то Нх! пересекает внешность шара
Ву и, следовательно, не пересекает некоторую окрестность точки U в В-.
Так как число симплексов ст конечно, существуем окрестность -V точки О
вВр не пересекающая образы /:(а) всех симплексов сг, не содержащихся
р Kj. Для :л'ОЙ окрестности .V мы получаем f"l{N) С К-.
Дли симплекса Ак с /V прообраз / ' (А') с К- является объединением
его пересечений с симплексами а в А'-, и каждое такое пересечение —
выпуклый многогранник, так как он является пересечением (т с
выпуклым многогранником 1.~',] (А14), где /..,: "*.'' —» .г.' — линейное отображение.
ограничение которого на сг совпадает eg. (Напомним, что / % на К,.)
Чтобы завершить доказательство, достаточно выбрать симплекс Д* так,
чтобы 01! не пересекался с образами всех несюръектпвпых отображении
l(J> что, очевидно, возможно, так как эти образы состоят из конечного
числа подпространств размерности меньше к.
Пример 4Л1 (клеточная аппроксимация для пар). Любое
отображение /: (А', Л) --► (У\ В) CVV-nap можно продеформировать в классе
отображений (X. А) * (У, В) в клеточное отображение. Это следует из нашей
теоремы, если сначала продеформировать ограничение /: А—>В так, чтобы
оно стало клеточным, затем продолжить эту гомотошпо до гомотопии /
на всём пространстве X, а затем продеформировать полученное
отображение так, чтобы получилось клеточное отображение, причём гомотопия
была неподвижна на А. Как дальнейшее уточнение, гомотошпо
отображения/ можно выбрать постоянной на любом подкомплексе в X, на котором
/уже клеточное.
Вот простое следствие :зтого результата.
I Следствие 4.12. CVV-napa (Л\ А) является п-связной, если все клетки
I В Х- А имеют размерность больше п. В частности, пара (X, X') явля-
I ется нсвязной, поэтому включение Х-"«—*А' индуцирует изоморфизмы
I групп г, для i <п и сюръекцию групп г.,.
Доказательство. Применяя клеточную аппроксимацию к
отображениям {!)'. д!У) -> (X, А) для i ^ и. получаем первое утверждение.
Последнее утверждение след\*ет из длинной точной последовательности пары
(*>ХП).
CW-аппроксимация
Отображение / : X * Y называют слабой голюпюпическои эккиаапсигп-
Ностью, если оно индуцирует изоморфизмы ,тДХ. .v:J ■» г. (V. M-v,)) лля
446
Глава 4. Теория гомотопий
всех п ^ 0 и всех способов выбора отмеченной точки х0. Теорему Уайт-
хеда можно переформулировать, сказав, что слабая гомотопическая
эквивалентность между CW-комплексами является гомотопической
эквивалентностью. Легко убедиться, что это верно и для пространств, гомото-
пически эквивалентных CW-комплексам. В общем случае, однако, слабая
гомотопическая эквивалентность строго слабее, чем гомотопическая
эквивалентность. Например, существуют нестягиваемые пространства, все
гомотопические группы которых тривиальны, например
«квазиокружности», как показывает одна из задач в конце этого параграфа. Для таких
пространств отображение в точку —слабая гомотопическая
эквивалентность, которая не является гомотопической эквивалентностью.
Один из наиболее важных результатов этого пункта состоит в том,
что для любого пространства X существуют CW-комплекс Z и слабая
гомотопическая эквивалентность /: Z —> X. Такое отображение f:Z—*X
называют CW-аппроксимацией пространства X. Мы покажем, что слабая
гомотопическая эквивалентность индуцирует изоморфизмы всех групп
гомологии и когомологий, поэтому CW-апироксимации позволяют свести
многие общие утверждения алгебраической топологии к случаю CW-ком-
плексов, где часто можно применять рассуждения поклеточно.
Метод построения CW-аппроксимаций можно также использовать
и для других целей. Начнём с того, что можно попытаться найти
относительную версию, в которой предполагается, что X содержит
подпространство А, которое уже является CW-комплексом, и построено такое
пространство Z, что оно содержит А в качестве подкомплекса, причём
ограничение отображения /: Z—>Х на Л —тождественное отображение.
Далее, если пара (X, А) является п-связной, то можно попытаться сделать
пару (Z, А) п-связной в том сильном геометрическом смысле, чтобы все
клетки комплекса Z — А имели размерность больше п. В действительности
оказывается, что можно сделать построение, удовлетворяющее
последнему условию, даже если пара (X, А) не п-связна, но в этом случае группа
тг,-(Z) при i < n будет изоморфна 71,04), а не я,(Х).
Приведём определение, которое является достаточно общим, чтобы
покрыть все эти случаи. Пусть дана пара (Х,Л), где подпространство
А с X — непустой CW-комплекс. Тогда п-связиая CW-модель для (X, А) —
это такая п-связная CW-пара (Z, А) и такое отображение /: Z —> X, для
которого ограничение /| А тождественно, что отображение /*: 7r,(Z)—►тгДХ)
является изоморфизмом при i > п и инъекцией при i = п для всех
способов выбора отмеченной точки. Так как пара (Z,A) является п-связной,
отображение тг,(Д) —> tt,(Z) является изоморфизмом при i <п и сюрьек-
цией при i = п. В критической размерности п отображения Л1—*/—*Х
индуцируют композицию тг„(А) —> rr„(Z) —► 7Г„(Х), которая даёт
представление отображения гг„(Л) -* тгп(Х) в виде композиции сюръекции с
последующей инъекцией, точно так же, как любой гомоморфизм (/?: G —* Н
§4.1. Гомотопические группы
447
можно представить (единственным образом) как композицию сюръекции
у\ G—>Im(f с последующей инъекцией 1глу>(—>Н. Можно представлять
себе Z как своего рода теоретико-гомотопический гибрид пространств А
и X. При возрастании п этот гибрид всё больше похож на Л и всё меньше
похож на X.
Частным случаем этого определения является введённое ранее
понятие CW-аппроксимации; нужно взять п = Ои считать, что А состоит из
одной точки в каждой компоненте линейной связности пространства X. Это
вынуждает отображение /+: n0(Z) —> тг0(Х) быть сюръективным, а также
инъективным.
I Предложение 4.13. Для любой пары (X, А), где А — непустой CW-kom-
I плекс, существует п-связная CW-модель /: (Z, А) —> (X, А) для всех п ^ О,
I и эти модели можно выбрать так, чтобы они обладали дополнительным
I свойством, что Z получается из А приклеиванием клеток размерности
I больше п.
Заметим, что из условия, что Z — А состоит из клеток размерности
больше п, автоматически следует, что пара (Z, А) является п-связиой; это
доказывается с помощью клеточной аппроксимации.
Доказательство. Будем строить Z как объединение подкомплексов
A = Zn с Z„+1 с ..., где Zk получается из Zk_x приклеиванием /с-мерных
клеток. Предположим по индукции, что мы уже построили Zk и
отображение /: Zk —>Х, ограничение которого на А тождественно, причём
индуцированное отображение групп тг, инъективно при п $ f <к и сюръек-
тивно при п < i $ к по отношению к выбору в качестве отмеченной точки
нульмерной клетки ху в каждой компоненте связности Ау пространства А.
Индукция начинается с к = п и Zn = Л, когда эти условия пустые.
Для доказательства шага индукции выберем клеточные
отображения у>а: Sk —> Zki представляющие образующие ядра отображения /+:
nk(Zki xY) —> пк(Х, ху) для всех у. Приклеим клетки ека+] к Zk посредством
этих отображений </?а и обозначим полученный комплекс Y^i- Так как
композиции /</?а гомотопны нулю, мы можем продолжить / на Yk+{,
Отображение /,: nk(Yk+lixy) —* iTk(X, xy) тогда инъективно, так как
каждый элемент ядра, представлен клеточным отображением, образ которого
лежит в Zk, а такие отображения гомотопны нулю в Vj.Ml по построению.
Продолженное отображение / всё ещё индуцирует сюръекцию групп пк,
так как композиция nk{Zk) —> nk(Yk+l) —> пк(Х) сюръективна.
Гомотопические группы п{ для 1 < к не изменяются при приклеивании клеток
еа+1. При /с = 0 это построение нужно сделать по-другому, так как на я0
Нет структуры группы. Вместо всего этого мы строим YXy приклеивая
одномерные клетки, соединяющие все отмеченные точки (нульмерные
клетки Ху), лежащие в одной и той же компоненте линейной связности
пространства X.
448
Глава 4. Теория гомотопий
Теперь выберем отображения я/^: S —> X, порождающие группы
пк.п(Х,хг) для всех ^- Пусть ZfcH — букет пространства У^+1 и сфер s}^"1
в соответствующих отмеченных точках ху. Продолжим / на Zk+l, считая его
равным ipp на Si+i. Это гарантирует, что индуцированное отображение
Л: ^/с-Ы C^/c-f-i, ^г) — ЯМ,(Х, Ху)
сюръективно. Включение V^+1 *—* 7.клЛ индуцирует изоморфизм групп
п{ для f ^/с: сюръективность получается из клеточной аппроксимации,
а инъективность — из ретракции Zk+{ на Yk+l. Это завершает
доказательство шага индукции.
Так как отображения /ж: 7r,(Z, лу) —> я,(Х, лу) зависят только от (i + 13-
мерного остова комплекса Z, они являются изоморфизмами для всех i > /7
и инъективны при i = п. В действительности это верно для всех
отмеченных точек в Z, а не только для лу, так как любую точку в Z можно
соединить путём с некоторой точкой ху. П
Пример 4.14. Когда пространство X линейно связно, а Л —точка,
построение 0-связной CVV-модели для (X, А) даёт CW-аппроксимацию
пространства X с единственной нульмерной клеткой, причём все клетки
более высокой размерности приклеиваются по отображениям,
сохраняющим отмеченную точку. В частности, любой связный CW-комплекс гомо-
топически эквивалентен CW-комплексу с этими свойствами.
Пример 4.15. Можно применить предложение 4.13, чтобы получить
CW-аппроксимацию произвольной пары (X, Х0). Сначала построим CW-an-
проксимацию /0: Z0 —* Х0, затем построим 0-связную CW-модель (Z, Z0) -»
—> (М,г0), где М — цилиндр отображения для композиции отображения
/0 и включения Х0<—*Х. Взяв композицию отображения Z—*М и
ретракции пространства М на X, мы получим продолжение отображения /0
до CW-апироксимации /: Z—>Х. Из 5-леммы следует, что отображение
(Z, Z0) —* (X, Х0) индуцирует изоморфизмы относительных
гомотопических групп, так же как и абсолютных.
А вот совсем другое применение предложения 4.13, дающее более
геометрическую интерпретацию /7-связности.
I Следствие 4.16. Если (X, А) — /7-связная CW-napa, то существует
такая CW-пара (Z, А) с± (X, A) rel А, что все клетки комплекса Z - А имеют
размерность больше п.
Доказательство. Задаваемая предложением 4.13 n-связная
СW-аппроксимация /: (Z, А) —> (X, А) будет обладать требуемыми свойствами.
Сначала мы проверим, что / индуцирует изоморфизмы 7r,(Z) ъ 7Г,(Х) для
всех I. Это верно для i > п по определению, а для i < п это верно, так
как оба включения A<—*Z и А<—*Х индуцируют изоморфизмы на этих
гомотопических группах более низкой размерности. При f = n
отображение / индуцирует инъективное отображение групп пп по определению.
Так как включение А <-* X индуцирует сюръекцию групп тгм, отображе-
§4.1. Гомотопические группы
449
ние / также индуцирует сюръекцию ввиду разложения в композицию
лп(Л)-я„(г)->7гп(Х).
Так как отображение / индуцирует изоморфизм всех гомотопических
групп, оно является гомотопической эквивалентностью. Чтобы убедиться,
что оно также является гомотопической эквивалентностью относительно
Д, рассмотрим факторпространство W цилиндра отображения Mfj
полученное при стягивании каждого отрезка {а} х / в точку для всех а£ А.
Если предположить, что отображение / было сделано клеточным, то W —
CW-комплекс, содержащий X и '/. в качестве подкомплексов, причём W,
как и Mf, деформационно ретрагируется на X. Кроме того, 7U,(W,Z) = 0
для всех I, так как / индуцирует изоморфизм всех гомотопических групп,
поэтому W деформационно ретрагируется па Z. Эти две деформационные
ретракции пространства W на X и на Z постоянны на Д, следовательно,
они дают гомотопическую эквивалентность X~Zrel Л. □
Пример 4.17 (башни Постникова). Для CW-комплекса X, который
можно считать связным, мы построим последовательность пространств
Хп) для которых 7Г,-(Х„) ^ тг,(Х) при i $ л и я,-(Х„) — 0 при i > л.
Выберем клеточные отображения ip(2: S"1"1 —> X, порождающие группу 7г„.ц,
и воспользуемся ими, чтобы приклеить клетки е"*2 к X, получив при этом
CW-комнлекс У. Согласно клеточной аппроксимации включение Х^->У
индуцирует изоморфизмы групп я, при i ^ л, а тс„+1(У) = 0, так как
любой элемент группы я„+1(У) представляется отображением в X согласно
клеточной аппроксимации, а такие отображения гомотопны нулю в У
по построению. Теперь можно повторить этот процесс для У вместо X
и заменив пнап + 1, чтобы получить пространство с нулевыми группами
яп+2 и Япи» приклеивая (л 4-3)-мерные клетки. Повторяя это бесконечно
много раз, мы расширим X до такого CW-комплекса Х„, что включение
X <—► Хп индуцирует изоморфизм групп тг,- при i $ л и я,(Хп) = 0 при
i > л. Эта конструкция в действительности — частный случай конструкции
CW-моделей; здесь (ХП,Х)—это (л 4- 1)-связная CW-модель для (СХ, X),
где СХ — конус над X.
Включение Х<—>ХП продолжается до отображения Х„+1 —>Х„, так как
Хп+1 получено из X приклеиванием клеток размерности л 4- 3 и выше,
а я,(Хп) = 0 при / > л, поэтому можно применить лемму 4.7 (лемму о
продолжении). Таким образом, мы получаем так называемую
башню Постникова для пространства X (см. рис.). Можно рас- :
сматривать пространства Хп как срезы пространства X, кото- |
рые последовательно всё лучше и лучше приближают X при ^
возрастании л. Башни Постникова оказываются весьма мощ- , , *
ными инструментами для доказательства общих теорем, и мы / *
изучим их далее в § 4.3. / 2
После этого примера можно поинтересоваться, всегда ли // т
п-связные CW-модели (Z„,A) для произвольной пары (Х,Д) х *" лэ
15'Зак Vos
450
Глава 4. Теория гомотетий
вписываются в башню. Следующее предложение позволит нам построить
такие башни, и не только их.
Предложение 4.18. Предположим, что нам даны: z ^ X
1) л-связная CW-модель /: (Z, А) —* (Я\ А), }\ \
2) л'-связная CW-модель /': (Z', А') -> (Х\ А'), \ /' ^
3) отображение g: (X, А) — (*', А')■ Z ** Х'
Тогда если л ^ л', то существует такое отображение h : Z —» Z', что
h|A = g и gfmf'hrcl А; таким образом, диаграмма является
коммутативной с точностью до гомотопии относительно А. Кроме того, такое
отображение h единственно с точностью до гомотопии относительно А.
Доказательство. Согласно следствию 4.16 мы можем предположить,
что все клетки комплекса Z — А имеют размерность больше л. Пусть W —
это факторпространство цилиндра отображения для отображения /',
полученное при стягивании каждого отрезка {ri} х / в точку для всех а1 е А'.
Мы можем представлять себе W как относительный цилиндр
отображения; как и обычный цилиндр отображения, W содержит экземпляры
пространств Z' и Х\ причём последнее пространство —как деформационный
ретракт. Из предположения, что (Z', А') является л'-связной CW-моделью
для (X'.A'), следует, что относительные группы n^W^Z') нулевые при
i>ri.
Посредством включения X' с—> W мы можем рассматривать gf как
отображение Z -+W'. Как отображение пар (Z, А) —> (W, Z7), отображение
gf гомотопно относительно А отображению h с образом в Z' согласно
лемме о сжатии и предположению, что л ^ ri. Это доказывает первое
утверждение. Для доказательства второго предположим, что h{) и hl —
два отображения Z —* Z', композиции которых с /' гомотопны
отображению gf относительно А. Таким образом, если мы рассмотрим /i0 и h{
как отображения в W, то они гомотопны относительно А. Такая гомото-
пия даёт отображение (Z х /, Z x 31 U А х /) —> (W, Z'), и снова согласно
лемме о сжатии это отображение можно продеформировать относительно
Z х 31U А х / ь отображение с образом в Z', что и даёт требуемую гомото-
нию h0^.hl rel A. О
Следствие 4.19. л-связная CW-модель для пары №,А)
единственна с точностью до гомотопической эквивалентности относителыю А.
В частности, CW-аппроксимации пространств единственны с
точностью до гомотопической эквивалентности.
Доказательство. Если даны две л-связные CW-модели (Z, А) и (/', M
для {X, А), то, применяя предложение 4.18 дважды, взяв в качестве g
тождественное отображение, мы получим отображения h: Z —»Z' и h': Z' -*%•
Утверждение о единственности даёт гомотопии hh' ~1и h'h ^ H rel A. ^
Взяв п = ri в предложении 4.18, мы получаем свойство функториаль-
ности для п-связных CW-моделей. Например, отображение X —> X ин-
§4.1. Гомотопические группы
451
дуцирует отображение CW-аппроксимаций Z-+Z', которое единственно
с точностью до гомотопии. .
Предложение 4.18 позволяет связать п-связные
СУИ-модели (ZM,A) для (X, Л) при разных п
посредством отображений Zn—>Zn_-,, образующих башню,
показанную на диаграмме в которой треугольники
коммутативны, а треугольники справа коммутативны
с точностью до гомотопии. Можно сделать
треугольники справа строго коммутативными, заменив
отображения Zn —> X композициями сквозь Z0.
Пример 4.20 (башни Уайтхеда). Пели мы возьмём
в качестве X произвольный CW-комплекс с подпространством Л — точкой,
то получающаяся башня п-связных CW-моделей представляет собой
последовательность отображений
... -^> Z2 -+ Zi —> Z0 —> X,
Где пространство Z„ является n-связным, а отображение Zn —> X
индуцирует изоморфизм всех гомотопических групп п{ для f > п. Пространство
Z0 линейно связно и гомотопически эквивалентно компоненте
пространства X, содержащей подпространство А, поэтому можно также
предположить, что Z0 равно этой компоненте. Следующее пространство Z{ одно-
связно, а отображение Zl -^ X имеет гомотопические свойства
универсального накрытия компоненты Z0 пространства X. Для больших
значений /1 можно но аналогии рассматривать отображение Z„ —> X как
«п-связное накрытие» пространства X. Для п > 1 они, по-видимому, не
встречаются в жизни так же часто, как в случае п = 1. Одно из редких
Исключений — отображение Хопфа S3 -^>S2, определённое в примере 4.45,
Которое является двусвязным накрытием.
Теперь давайте покажем, что CW-аппроксимации хорошо себя ведут
по отношению к гомологиям и когомологиям.
Предложение 4.21. Слабая гомотопическая эквивалентность /: X —>
—> У индуцирует изоморфизмы
/,://MU;G)-H„(y;G) и /+: Нп{У\ G) - Н"(Х; G)
для всех п и всех групп коэффициентов G.
Доказательство. Заменив У на цилиндр отображения My и
рассмотрев длинные точные последовательности гомотопических групп, групп
гомологии и когомологий для (My, X), мы увидим, что достаточно доказать
следующее:
если (Z, X) есть n-связная пара линейно связных пространств, то
1^ (Z, X; G) = 0 и Н'(Z, X; G) = 0 для всех !$пи всех G.
Пусть а = XInj°"jf—относительный цикл, представляющий элемент
j
группы Hk(Z,X; G); здесь а}-,: Ак ->Z — сингулярные /с-мерные симплек-
452
Глава 4. Теория гомотопий
сы. Построим конечный Л-комплекс К, взяв несвязное объединение к
-мерных симплексов, по одному для каждого (7;, и отождествив все (к —
13-мерные грани этих /с-мерных симплексов, для которых соответствующие
ограничения отображений о} равны. Таким образом, сингулярные симплексы
aj индуцируют отображение a: K-^Z. Так как а — относительный цикл,
да — цепь в X. Пусть L с К — подкомплекс, состоящий из {к- 1)-мерных
симплексов, соответствующих сингулярным {к— 1)-мерным симплексам
в да] таким образом, a(L) с X. Цепь а является образом при цепном
отображении ас некоторой цепи а в К, причём да — цепь в L. В
относительных гомологиях мы тогда получаем сгж[5] = fa]. Если мы
предположим, что tt,-(Z, X) = 0 для i $ /с, то отображение а: {К, L) -* (Z, X)
гомотопно относительно L отображению, образ которого лежит в X,
согласно лемме о сжатии. Следовательно, сгж(5] лежит в образе отображения
Hk(Xt X] G) — Hk(Z, X; G), а так как Н*(Х,Х; G) = 0, мы получаем, что
[а] = сг+[2] =0. Это доказывает требуемое утверждение для гомологии,
а утверждение для когомологий следует из теоремы об универсальных
коэффициентах. О
CW-аппроксимациями можно воспользоваться для того, чтобы
свести многие утверждения об общих пространствах к частному случаю
CW-комплексов. Например, версию формулы Кюннета из теоремы 3.16,
в которой утверждается, что при определённых условиях Я+(Х х У; R) ^
ъ Н¥(Х; R) 0 H*(Y] R), можно теперь распространить и на пространства,
не являющиеся CW-комплексами, так как если X и У — CW-аппроксима-
ции пространств Z и W соответственно, то X х У — CW-аппроксимация
пространства Z xW. Здесь мы снабжаем X х У топологией CVV, а не
топологией произведения, но это никак не влияет на гомотопические группы,
так как у этих двух топологий одни и те же компактные множества, как
объяснено в приложении. Точно так же общая формула Кюннета для
гомологии из §З.В верна для произвольных произведений X х У.
Условие, что отображение Y -+Z является слабой гомотопической
эквивалентностью, использует только отображения сфер в Y и в Z, по в
действительности слабые гомотопические эквивалентности Y —* Z хорошо
себя ведут относительно отображений произвольных СИЛкомплексои в Y
и в Z, а не только сфер. Б следующем предложении приведена точная
формулировка этого утверждения, использующая обозначение [X, У] Для
множества гомотопических классов отображений X —> Y и (X, У) для
множества гомотопических классов отображений X —* У, сохраняющих
отмеченную точку. (Обозначение (X, У) нестандартное; оно предназначено
для указания на «пунктированные гомотопические классы».)
I Предложение 4.22. Слабая гомотопическая эквивалентность /: '
—> Z индуцирует взаимно однозначные отображения [Х,У] -* 1^'
и (X, У) —>(X, Z) для всех CW-комплексов Х.
§4.1. Гомотопические группы
453
Доказательство. Рассмотрим сначала отображение [X, Y] —> [X,Z].
Можно предположить, что / — включение, заменив Z на цилиндр
отображения Mf9 как обычно. Тогда группы nn(Z,Y,y0) нулевые для всех
л и всех отмеченных точек у0 € Y, таким образом, из леммы о сжатии
следует, что любое отображение X —> Z можно прогомотопировать так,
чтобы его образ лежал в Y. Это доказывает сюръективность
отображения [X, Y] —► [X,Z]. Относительная версия этого рассуждения
доказывает инъективность, поскольку мы можем деформировать гомотопию
(X х /, X х д!) —► (Z, Y) так, чтобы её образ лежал в Y.
В случае (X, Y) —> (X,Z) то же самое рассуждение можно применить,
заменив Mj на приведённый цилиндр отображения, т.е. на факторпро-
странство цилиндра My, полученное при стягивании отрезка {у()} х /
в точку, где у0 — отмеченная точка в Y. Этот стянутый отрезок тогда
служит общей отмеченной точкой пространств У, Z и приведённого
цилиндра отображения. Приведённый цилиндр отображения
деформационно ретрагируется на Z точно так же, как и неприведённый, но тем
с преимуществом, что отмеченная точка не двигается. П
Задачи
1. Предположим, что сумма fYg отображений/^: (Г\ <11п) —►(Х,х0)
Определена с помощью координаты в Г, отличной от первой координаты.
Проверьте формулу (/ 4- g) +' (h + к) = (/ +' h) + (g +' к) и выведите из
неё, что / +' к ~/ 4- к, так что эти две суммы согласованы на 7г„(Х,х0).
Проверьте также, что g +' h ^ h + g, так что сложение является
коммутативным.
2. Докажите, что если </?: X —> Y — гомотопическая эквивалентность,
То индуцированные гомоморфизмы '>/>*• л„(Х,х0) ~^ тсп(У, ^(хо))
являются изоморфизмами для всех /7. [Случай п = 1 —это предложение 1.18.]
3. Для Я-пространства (X, х0) с умножением (л: X х X —> X докажите,
Что групповую операцию в 7Г„(Х, х0) можно также определить по правилу
(/ + g)(x)=/i(/(x),g(x)).
4. Пусть р: X—>Х — универсальное накрытие линейно се*язного
пространства X. Докажите, что при изоморфизме яп(Х) ^ я„(Х), который
имеет место при п ^ 2, действие группы тт^Х) на тт„(Х) соответствует
действию группы 7г,(Х) на тг„(Х), индуцированному действием группы тгДХ)
На X посредством преобразований накрытия. Точнее, докажите формулу
Vp*(a) = p+(/Jr.(7,(a))), где уетг^Х,^), a e тгп(Х, х()), а у, обозначает
^Моморфизм, индуцироЕ^анный действием элемента у на X.
5. Для пары (X, А) линейно связных пространств докажите, что
множество Я!(Х,>\,х0) можно естественным образом отождествить с
множеством смежных классов ail подгруппы 11 с tt^XjXq), представленной
петлями в Л с началом и концом в точке х0.
I Лава 4. Теория гомотопий
6. Докажите, что если р: (X, AJcq) —> (X, А, х0) — накрытие, причём
Л = р~1(А), то отображение р+: я„(Х, А, 3?0) —»я„(Х, Л, х0) — изоморфизм
для всех п > 1.
7. Перенесите доказанные в начале этого параграфа результаты об
отображениях изменения отмеченной точки /Зу на случай относительных
гомотопических групп.
8. Докажите, что последовательность
пх(Х,Хо) — кх(Х9А9х0) -^ 7Г0(Л,х0) -* я0(Х, х0) точная.
9. Предположим, что мы определяем я0(Х, Л, х0) как
фактормножество тг0(Х,х0)/л:0(Л,х0), так что длинная точная последовательность
гомотопических групп для пары (X, Л) продолжается до последовательности
... — тг0(Х, х0) — тг0(Х, Ау х0) — 0.
а) Докажите, что тогда 5-лемма верна для отображения длинных точных
последовательностей, индуцированного отображением (Х,А, х0)-*
—> (У, В, у0), в следующем виде: одно из отображений этих двух
последовательностей будет взаимно однозначным, если четыре соседних
с ним отображения взаимно однозначные для всех способов выбора
точки л:0.
б) Докажите, что длинную точную последовательность тройки (X, А, В, х0)
можно продолжить, вообще говоря, только до члена я0(Л, В, л:0) и что
5-лемма верна для этого продолжения.
10. Докажите, что «квазиокружность», описанная в примере 7 в § 1.3,
имеет тривиальные гомотопические группы, но не стягиваема, а потому
она не может иметь гомотопический тип CW-комплекса.
11. Докажите, что CW-комплекс стягиваем, если он является
объединением возрастающей последовательности подкомплексов Xj с Х2 с ...,
для которой каждое включение X, с-> Xi+l гомотопно нулю; это условие
иногда выражают, говоря, что пространство X, стягиваемо в Xi+1.
Примером служит S00, и вообще бесконечная надстройка S°°X любого
CW-комплекса X — объединение итерированных надстроек SUX.
12. Докажите, что n-связный п-мерный CW-комплекс стягиваем.
13. С помощью леммы о продолжении докажите, что CW-комплекс
ретрагируется па любой свой стягиваемый подкомплекс.
14. С помощью клеточной аппроксимации покажите, что п-мерные
остовы гомотопически эквивалентных CW-комплексов без клеток
размерности п 4-1 тоже гомотопически эквивалентны.
15. Докажите, что любое отображение /: S" —> Sn гомотопно кратному
тождественного отображения, сделав следующие таги.
а) С помощью леммы 4.10 (или симплициальной аппроксимации,
теорема 2.С.1) сведите задачу к случаю, когда существует точка q €S'1, для
которой f~l(q) = {Pii ••♦, Pk} и / — обратимое линейное отображение
вблизи каждой точки рг
§4.1. Гомотопические группы
455
б) Для такого отображения /, как в п. а), рассмотрите композицию gf,
где g: Sn —»S" стягивает дополнение малого шара с центром q в
отмеченную точку. Воспользуйтесь этим, чтобы свести п. а) далее к случаю
fc=l.
в) Завершите рассуждение, показав, что обратимую матрицу размера
пхп можно соединить путём, состоящим из обратимых матриц,
либо с единичной матрицей, либо с матрицей зеркальной симметрии.
(Воспользуйтесь, например, методом Гаусса.)
16. Докажите, что отображение /: X —* Y связных CW-комплексов
представляется в виде композиции X —*Zn —> Y, где первое отображение
индуцирует изоморфизмы групп я,- при i $ л, а второе отображение
индуцирует изоморфизмы групп л:{ при i ^ л +1.
17. Докажите, что если X и Y — CW-комплексы, причём X является
m-связным, a Y — п-связным, то пара (ХхК,Х\/У)-(ш-|-п + 1)-связнал,
как и приведённое произведение X AY.
18. Приведите пример слабой гомотопической эквивалентности X —>
—»У', для которой не существует слабой гомотопической эквивалентности
Y-+X.
19. Рассмотрим отношение эквивалентности ^w, порождённое
слабой гомотопической эквивалентностью: X ^w Y, если существуют
пространства Х=ХЪ Х2, ..., Xn = Y со слабыми гомотопическими эквивалентнос-
тями X, —> Хт или X,-«— Х,+1 для всех i. Докажите, что X^WY тогда и
только тогда, когда пространства X и У имеют общую CW-аппроксимацию.
20. Докажите, что множество [X, Y] конечно, если X — конечный
связный CW-комплекс и множество я,-(У) конечно при i'^dimX.
21. В этой задаче удобно использовать обозначение Хп для n-го этажа
башни Постникова для X и обозначение Хт для (т — 1)-связного
накрывающего пространства над X, где X — связный
CW-комплекс. Докажите, что (Хп)т ^ (Хт)п, а потому обозначе- Хт —^ Х^
ние Хг'^ не приводит к недоразумениям. Таким образом, I I
яДХ;'^) % я,(Х) при m ^ i ^ л, а все остальные гомотопиче- * „
ские группы пространства Х;" нулевые.
22. Докажите, что линейно связное пространство X слабо гомотопи-
чески эквивалентно CW-комплексу со счётным множеством клеток тогда
и только тогда, когда множество яп(Х) счётно для всех л.
[Воспользуйтесь результатами о симплициалыюй аппроксимации отображений и
пространств из §2.С]
23. Пусть /: X —» Y — отображение пространств X и У, гомотопически
эквивалентных CW-комплексам. Докажите, что пара (Му, X)
гомотопически эквивалентна CW-nape, где Му — цилиндр отображения. Выведите
из этого, что конус отображения Cf имеет гомотопический тип СИ/~ком-
плекса.
456
Глава 4. Теория гомотопий
§ 4.2. Элементарные методы вычислений
Мы до сих пор не вычислили никаких ненулевых гомотопических
групп 7i„(X) при п ^ 2. В главе 1 двумя основными инструментами,
которые мы использовали для вычисления фундаментальных групп, были
теорема ван Кампена и накрывающие пространства. В этом параграфе
мы изучим многомерные их аналоги: теорему о вырезании для
гомотопических групп и локально тривиальные расслоения. Оба эти метода
гораздо слабее, чем их аналоги для фундаментальной группы; это связано
с тем, что они не вычисляют непосредственно гомотопические группы,
а только дают соотношения между гомотопическими группами разных
пространств. Возможности их применения, таким образом, более
ограничены, но достаточны для многих интересных вычислений, например для
вычисления я„(5п) и для доказательства более общей теоремы Гуревича,
связывающей первую ненулевую гомотопическую группу и первую
ненулевую группу гомологии пространства. Ещё одно важное приложение —
теорема Фрейденталя о надстройке, которая приводит к стабильным
гомотопическим группам и в действительности ко всей стабильной теории
гомотопий.
Вырезание для гомотопических групп
Что делает гомотопические группы гораздо более трудными для
вычислений, чем группы гомологии, —это отсутствие свойства вырезания.
Однако есть определённый диапазон размерности, зависящий от степени
связности пространств, в котором вырезание в действительности имеет
место и для гомотопических групп.
I Теорема 4.23. Пусть X — CW-комплекс, представленный в виде объ-
I единения подкомплексов Л и В с непустым связным пересечением
I С = АП В. Если пара (Л, С) является m-связной, а пара (В, С) является
I п-связной, где т,п^0, то отображение я,(Л, С) —> тг,(Х, В), индуци-
I рованное включением,— изоморфизм при i<m + n и сюръекция при
I I = 771 + П .
Это приводит к теореме Фрейденталя о надстройке.
I Следствие 4.24. Отображение надстройки тс, (SM) —> я,чj(S"+1) — изо-
I морфизм при i < 2п — 1 и сюръекция при i = 2п — 1. Это верно и вооб-
I ще для любой надстройки тг((Х) —> 7i(+1(SX), если X — (п - 1)-связный
I CW-комплекс.
Доказательство. Представим надстройку SX в виде объединения
двух конусов СЛ.Х и С. X, пересекающихся по экземпляру пространства X.
Отображение надстройки —то же самое, что и отображение
Щ{Х) ъ 7r,,tl(CfX,X) - тгт(SX,C_X) * 7i,H0SX),
§4.2. Элементарные методы вычислений
457
где оба изоморфизма получаются из длинных точных
последовательностей пар, а среднее отображение индуцировано включением. Из
длинной точной последовательности нары (С±Х,Х) мы видим, что эта пара
n-связна, если пространство X является (п — 1)-связным. Предыдущая
теорема тогда говорит, что среднее отображение — изоморфизм при i 4-1 < 2п
и сюръекция при i 4-1 = 2п. □
I Следствие 4.25. Группа 7r„(S") изоморфна Z и порождается тожде-
I ственным отображением для всех п ^ 1. В частности, отображение
I пп (S11) —> Z, сопоставляющее каждому отображению его степень, — изо-
I морфизм.
Доказательство. Из предыдущего следствия мы знаем, что в
последовательности надстройки
первое отображение сюръективно, а все последующие отображения —
изоморфизмы. Так как группа n^S1) изоморфна Ъ и порождается
тождественным отображением, из этого следует, что nn(Sn) при п ^2 —это
конечная или бесконечная циклическая группа, не зависящая от п,
порождаемая тождественным отображением. Гот факт, что эта
циклическая группа бесконечная, можно вывести из теории гомологии, так как
существуют сохраняющие отмеченные точки отображения S" —> Sn
произвольной степени, а степень —гомотопический инвариант. По-другому,
чтобы избежать обращения к теории гомологии, можно воспользоваться
расслоением Хопфа S1 —> S* —> S2, описанным в примере 4.45, длинная
точная последовательность гомотопических групп которого даёт изоморфизм
^(S'^MS2).
Отображение nn(Sn) —>Ъ, сопоставляющее каждому отображению его
степень, является изоморфизмом, так как согласно предложению 2.33
отображение z —+ zk окружности Sx имеет степень /с, так же, как и его
Итерированные надстройки. □
Доказательство теоремы 4.23. Мы будем постепенно разбирать всё
более и более общие случаи. Первый случай содержит главное
рассуждение; его достаточно, чтобы вычислить n,7(S").
Случай 1: пространство А получено из С приклеиванием клеток
е£+1, а В получено из С приклеиванием клетки е'м1. Чтобы доказать
сюръективность отображения я, (Л, С) —> я,(Х, В), начнём с отображения
/: (I\dI\J1' х) —> (Х,В,х0). Образ отображения / компактен, а потому
он пересекает лишь конечное число этих клеток е|"м и е"+1.
Применяя несколько раз лемму 4.10, мы можем прогомотопировать / в классе
отображений (/', i)l\ J'"1) -> (Х,В,х0) так, чтобы прообразы / Ч^Г1)
И/~1(Д""Ь1) симплексов в е^11 и в еп+1 были конечными объединениями
Выпуклых многогранников, на каждом из которых / является
ограничением линейной сюръекции из Ж1 на IR"'"^1 или на 1R"+1.
458
Глапа 4. Теория гомотетий
I Утверждение. Если i ^ m + п, то существу-
I ют точки ра G А™~и и q G Дп_м и отображение
I </?: J'"1 —> [0,1), для которых: /
I а) /~] (q) лежит ниже графика отображения
I у? в/1""1 х/ = /';
I б) /_1(ра) лежит выше графика отображе-
I ния {р для всех а;
I в) у>=0на а/'"1.
Предположим, что это утверждение верно. Пусть /г — гомотопия
отображения /, вырезающая область под графиком отображения у
посредством ограничения / на область выше графика отображения ty для
О $ t $ 1. Согласно п. б) множество /Д/'"1) не пересекается с Р = \J{pa}
а
для всех Г, а согласно п. а) множество fx (/') не пересекается с Q = {q}. Это
означает, что в коммутативной диаграмме
тг,(АС) -тг,-(Х,В)
I У
7r,(X-Q,X-Q-P) 7T,U,X-P)
данный элемент [/] в верхней справа группе, рассматриваемый как
элемент нижней справа группы, равен элементу [/J, лежащему в образе
нижнего горизонтального отображения. Так как вертикальные
отображения—изоморфизмы, это доказывает сюръективность.
Теперь мы докажем утверждение. Для любой точки q e An+l
множество f~l(q) представляет собой конечное объединение выпуклых
многогранников размерности не выше f - п — 1, так как /_1(A"+I) — конечное
объединение выпуклых многогранников, на каждом из которых /
является ограничением линейной сюръекции Ш1 —>Rn+l. Мы хотим выбрать
точки ра е Д™+1 так, чтобы не только множество /~Чч") не пересекалось
с /"*1 (ра) для каждого а, но и чтобы образы /"] (q) и /~1 (ра) при проекции
я: V —>Il~l не пересекались. Это эквивалентно тому, что f~l(pa) He пеРе"
секается с множеством Т = тс~х (тгС/""1^))) —объединением всех отрезков
{х} х /, пересекающих /^Чч")- Множество Т является конечным
объединением выпуклых многогранников размерности не выше f - п, так как
/_1(ч") —конечное объединение выпуклых многогранников размерности
не выше i — п — 1. Так как линейное отображение не может увеличить
размерность, /(]')ПДдИ тоже конечное объединение выпуклых
многогранников размерности не выше f — п. Таким образом, если m + l>i — ny то
существует точка раеА™+], не принадлежащая /(Г). Тогда /_1(Рп) П7' = 0«
если i ^тп + п. Следовательно, мы можем выбрать окрестность U
множества 7i(f~l(q)) в J'-1, не пересекающую множества 7i(/_1 (ра)) для всех
а. Тогда существует такое отображение у: J'-1 —> [0, 1) с носителем в V,
§4.2. Элементарные методы вычислений
459
что f~l(q) лежит под графиком отображения (/?. Это как раз такое
отображение, какое требовалось, поэтому доказательство сюръективности в
случае 1 завершено.
Для доказательства инъективности в случае 1 рассуждение очень
похожее. Предположим, что даны два отображения /0, /,: (/', дГ, Jl~l) -+
—► (А, С, лг0), представляющие элементы группы тг,-(А, С, х0), образы
которых в я,(Х,В,л:0) совпадают. Таким образом, есть гомотопия,
соединяющая /о с /ъ которая представляет собой отображение F: (/', <9Г, J'"1) x
X [0,1] —* (X, В, х0). После предварительной деформации отображения F
на основе леммы 4.10 мы построим функцию </?: 7'""1 х / —* [0, 1),
отделяющую F~l(q) от множеств F-1^), как и раньше. Это позволяет нам
вырезать F~l(q) из области определения отображения F, а из этого
следует, что /0 и /т представляют один и тот же элемент группы тг,(А, С, л:0).
Так как /' х / теперь играет роль /', размерность f заменяется на i + 1,
и ограничение на размерность i ^ m + л превращается в f + 1 ^ т + л, т. е.
1<т + л.
Случай 2: пространство Л получено из С приклеиванием (гл + 1)-мер-
ных клеток, как и в случае 1, а В получено из С приклеиванием клеток
размерности не меньше л + 1. Чтобы доказать сюръективпость отображения
я,-(А, С)—>тг,(Х, В), рассмотрим отображение /: (/', dl\ J'"1)-» (Х,В,х0),
представляющее некоторый элемент группы я,(Х, В). Образ отображения
/ компактен, поэтому он пересекает лишь конечное число клеток;
применив несколько раз случай 1, мы можем сдвинуть / с клеток
комплекса В — С, по одной на каждом шаге, в порядке уменьшения
размерности. Инъективность доказывается аналогично: мы начинаем с гомотопии
F: (J1, dVfJl~]) х [0, 1] -* (X, В, х0) и сдвигаем её с клеток комплекса В - С.
Случай 3: пространство А получено из С приклеиванием клеток
размерности не меньше гл +1, а В такое же, как в случае 2. Можно считать,
что все клетки комплекса А — С имеют размерность не выше т + л + 1,
так как клетки более высокой размерности не влияют на тс, при i ^ гл + л
согласно теореме о клеточной аппроксимации. Пусть Ak<z А~
объединение комплекса С и клеток комплекса А размерности не выше к, и пусть
Хк = Ак и В. Мы докажем требуемое для отображений п{(Ак, С) -* п{(Хк, В)
индукцией по к. Индукция начинается с к = т + 1, что соответствует
случаю 2. Для доказательства шага индукции рассмотрим следующую
коммутативную диаграмму, образованную точными последовательностями тро-
ек(АьАи,С)и(^Дл.„В):
Я1+1(АЬ Д^) -» я,-(А*_1, С) -*- 7Г,-(АЪ С) -» тг;(Ль Ак_,) -*- tt.-^OV,, С)
X Т V Т У
«i+iWkJfc-i) — t,W*-i> Д) — *,■(**, в) — я,.(хь хк_,) — тг,ч(хы, в)
При i < гл + л первое и четвёртое вертикальные отображения
являются изоморфизмами согласно случаю 2, а но предположению индукции
460
Плана 4. Теория гомотопий
второе и пятое отображения тоже изоморфизмы, таким образом,
среднее отображение —изоморфизм согласно 5-лемме. Точно так же, когда
i = m -f n, второе и четвёртое отображения сюръективны, а пятое
отображение инъективно; этого достаточно для сюръективиости среднего
отображения согласно 5-лемме. При i = 2 диаграмма может содержать
неабелевы группы и два члена справа могут не быть группами, по 5-лемма
для такого обобщения остаётся справедливой, с тривиальными
модификациями доказательства из §2.1. При i = 1 утверждение об
отображении я, (Л, С) —> пх (X, В) доказывается прямым рассуждением: если т ^ 1,
то оба члена тривиальны, а если /п = 0, то п ^ 1 и требуемое утверждение
следует из клеточной аппроксимации.
После этих частных случаев мы можем теперь легко разобрать общий
случай. Из предположений о связности для пар (Л, С) и (В, С) получаем,
согласно следствию 4.16, что эти пары гомотопически эквивалентны
таким парам (А', С) и (В', С), как в случае 3, посредством гомотопических
эквивалентпостей, неподвижных на С. Таким образом, эти
гомотопические эквивалентности можно состыковать и получить гомотопическую
эквивалентность AUB^ A1U В''. Поэтому общий случай сводится к
случаю 3. D
Пример 4.26. Вычисление группы nn(Sn) можно обобщить и
показать, что rc„(VrtS£) при п ^ 2 —свободная абелева группа, базисом которой
служат гомотопические классы включений 5^°-* Vrt5(". Предположим
сначала, что есть лишь конечное число слагаемых Su. Мы можем
рассматривать yaSna как л-мерный остов произведения Пп5^ где сферы S'la снабжены
обычной CW-структурой, а пространство П„5^ снабжено CW-структурой
произведения. Так как X\aS"(i имеет клетки только размерностей,
кратных п, пара (n„S£, VrxS£) является (2п - 1)-связпой. Поэтому из длинной
точной последовательности гомотопических групп для этой пары мы
видим, что включение V(2S^c->nttS" индуцирует изоморфизм групп яП1 если
п ^ 2. Согласно предложению 4.2 мы получаем, что яп (II„S[p ы 0 пп (S[[) —
а
свободная абелева группа, базисом которой служат включения S'([<—> П„5^,
поэтому то же самое верно и для VaS^. Это даёт доказательство в случае
конечного числа сфер 5"х.
Чтобы свести случай бесконечного букета сфер S'(\ к конечному
случаю, рассмотрим гомоморфизм
*: ®«H(s;;)-n„(ves;;),
а
индуцированный включениями S,([{—^\/CJSt(lr Гомоморфизм Ф сюръективен,
так как любое отображение /: S" —> VttS'fJ имеет компактный образ,
содержащийся в букете конечного числа сфер S". Поэтому согласно уже
доказанному конечному случаю [/] лежит в образе Ф. Аналогично гомотопий,
соединяющая / с постоянным отображением, имеет компактный образ,
§4.2. Элементарные методы вычислений
461
содержащийся в конечном букете сфер S„, поэтому из конечного случая
следует, что гомоморфизм Ф инъективен.
Пример 4.27. Покажем, что группа nn{Sl V Sn) при п ^2
—свободная абелева со счётным множеством образующих. Согласно предложению
4.1 мы можем вычислить ti^S1 VS") при i^ 2, переходя к
универсальному накрытию. Оно состоит из прямой R, в каждой целочисленной точке
k € R которой приклеена сфера SJJ; таким образом, оно гомотопически
эквивалентно V^SJJ. Предыдущий пример 4.26 показывает, что 7r„(VfcSJJ) —
свободная абелева группа с базисом, представленным включениями сфер
в этот букет. Поэтому базис группы тг„ универсального накрытия S1 VS"
представлен отображениями, которые являются поднятиями
отображений, полученных из включения Sn c-* Sl V S" действием разных
элементов группы Ti! (S1 V S") яз z. Это означает, что nu(Sl V S") —свободный
Z[tii(S1 У5п)]-модуль с единственным базисным элементом —
гомотопическим классом включения S" <-* S1 VS". Если обозначить образующую
группы 7Г] (S1 VS") через t, то групповое кольцо Ъ[п^ (S1 VS")J
превращается в Z[t, t_I] — кольцо многочленов Лорана от t и t_1 с коэффициентами
bZ, и мы получаем ^„(S1 VS") ^Z[t, Г!].
Этот пример показывает, что в отличие от групп гомологии
гомотопические группы конечного CW-комплекса не обязаны быть конечно
порождёнными. Однако если мы ограничимся пространствами с
тривиальным действием группы пг на всех группах 7гп, то теорема Серра,
доказательство которой можно найти в [SSAT], утверждает, что гомотопические
группы такого пространства конечно порождённые тогда и только тогда,
когда группы гомологии конечно порождённые.
В этом примере группа тс,, (S1 VS") конечно порождается как
^[тг^-модуль, но существует конечные CW-комплексы, для которых даже это
неверно. Такой пример даёт также группа t^CS1 VS2) согласно задаче 38
в конце этого параграфа. В §4.А мы построим более сложные примеры
для каждой группы тг„, где п > 1, в частности для тг2.
Полезный инструмент для более сложных вычислений даёт
следующий общий результат.
I Предложение 4.28. Если CW-napa (X, А) является г-связной, а иро-
I странство А — s-связным, где г, s ^ 0, то отображение
I щ{Х,А)-*7Т{{Х/А),
I индуцированное отображением факторизации X —> Х/А} — изоморфизм
I при i $r + s и сюръекция при i = г4-s4-1 -
Доказательство. Рассмотрим XI) СА — комплекс, полученный из X
приклеиванием конуса СА по подпространству А сХ. Так как СЛ
—стягиваемый подкомплекс вХи СА, отображение факторизации X и СА —*
-+ {X и СА)/СА = Х/А является гомотопической эквивалентностью
согласно предложению 0.17. Таким образом, мы получаем коммутативную диа-
Глава 4. Теория гомотопий
грамму
щ(Х,А) >• щ(ХиСА9СА) —*- яДХиСЛ/СД) = п^Х/А)
тг,(ХиСЛ)
где вертикальный изоморфизм получается из длинной точной
последовательности. Теперь применим теорему о вырезании к первому
отображению в этой диаграмме, используя тот факт, что пара (СЛ, А) является
(5 +1)-связной, если пространство А является s-связным, который
получается из точной последовательности для пары (СЛ, А). п
Пример 4.29. Предположим, что пространство X получено из букета
сфер VaS^ приклеиванием клеток eV'1 но отображениям у>р\ S" -» VaS'^,
сохраняющим отмеченные точки, причём п > 2. Клеточная
аппроксимация показывает, что я,(Х) = 0 при i < п, и мы покажем, что яп(Х) —
факторгруппа свободной абелевой группы nn(w(IS'(1i) ^©Z по подгруп-
пе, порождённой классами [^]. Любую подгруппу можно реализовать
таким образом, выбирая отображения у>£ так, чтобы они представляли
набор образующих для подгруппы, поэтому из этого следует, что
любую абелеву группу можно реализовать как пп(Х) для такого
пространства Х= (vaS£) (Je'rM. Это многомерный аналог конструкции из след-
ствия 1.28 двумерного CW-комплекса с предписанной фундаментальной
группой.
Чтобы проверить, что группа пп(Х) именно такая, как сказано,
рассмотрим следующий участок длинной точной последовательности пары
%i№ vasna) -U nn&asna) —> тгп(х) — о.
Факторпространство X/vaS^ является букетом сфер S«+\ поэтому из
предыдущего предложения и примера 4.26 следует, что группа л„+1(Х, VaS"z)
свободная, причём её базисом служат характеристические отображения
клеток ej4"1. Граничное отображение д переводит их в классы [ipp], что
и доказывает требуемое.
Пространства Эйленберга—Маклейна
Пространство X, имеющее только одну нетривиальную
гомотопическую группу rcri(X)^G, называют пространством Эйленберга—Маклейна
K(G,n). Случай п = 1 рассмотрен в §1.В, где условие, что л,(Х) = 0 для
i > 1, было заменено условием, что X имеет стягиваемое универсальное
накрытие; эти условия эквивалентны для пространств, у которых существует
универсальное накрытие, имеющее гомотопический тип CW-комплекса.
Можно следующим образом построить СW-комплекс /£(£, л) для
произвольных Сип, если предполагать, что группа G абелева при п > 1. Пусть
X —такой (п - 1)-связный CW-комплекс размерности п + 1, что пп(Х) ъС\
§4.2. Элементарные методы вычислений
463
такой комплекс был построен в примере 4.29 при п > 1 и в следствии 1.28
при п = 1. Далее, мы показали в примере 4.17, как нужно приклеить
многомерные клетки к X, чтобы сделать группу щ тривиально при i > п, не
меняя пп и гомотопические группы более низкой размерности.
Если брать произведения пространств K(G, и) для разных п, можно
реализовать любую последовательность групп Gn (абелевых при п > 1) как
гомотопические группы яп некоторого пространства.
Многочисленные пространства K(G, 1) естественно возникают во
многих контекстах, и некоторые из них упомянуты в §1.В. В отличие
от этого естественное появление пространств K(G,n) при п ^ 2
встречается редко. По-видимому, единственный настоящий такой пример —
пространство СР00, которое является пространством K(Z, 2), как мы
увидим в примере 4.50. Можно, конечно, тривиально обобщить этот пример,
взяв произведение пространств СР00, чтобы получить K(G, 2), где G —
произведение групп Z.
В действительности есть довольно естественная конструкция
пространства К{Ъ,п) для любого п — бесконечная симметрическая степень
SP(S"), которая определялась в §З.С. В §4.К мы докажем, что функтор SP
обладает удивительным свойством преобразовывать группы гомологии
в гомотопические группы, а именно, rc,(SP(X)) %f/,(X; Z) для всех i > 0
и всех связных CW-комплексов X. Взяв в качестве X сферу, мы
получим, что SP(S") —пространство K(Z, п). Верно и более общее
утверждение: SP (M(G, п)) —пространство K(G, п) для любого пространства Мура
M(G, л).
Доказав существование пространств K(G, гг), мы теперь рассмотрим
вопрос о единственности, ответ на который оказывается наилучшим.
Предложение 4.30. Гомотопический тип CW-комплекса К(G, п)
единственным образом определяется группой G и числом п.
Доказательство будет основано на следующем более техническом
утверждении.
I Лемма 4.31. Пусть X — С^-комплекс вида (v„S^) UeS+1 для некот°-
I Р
I рого п ^ 1. Тогда для любого гомоморфизма i/j: тг„(Х) —► nu(Y), где про-
I странство У линейно связно, существует отображение /: X—► У, для
I которого /+ = V'-
Доказательство. Начнём с отображения /, которое переводит
естественную отмеченную точку пространства V„S'^ в выбранную
отмеченную точку у0 е У. Продолжим / на каждую сферу S£ посредством
отображения, представляющего класс i/j([ia])> ГДС ia —включение S^<—^X. Таким
образом, для отображения /: X" -* У, построенного на этом этапе, мы
получаем /„([.i„D = V'(f^l) Для всех я> следовательно, /*(Г^1) = iMtV-D
для всех отображений ц>\ S" —>ХМ, сохраняющих отмеченные точки, так
464
Глаиа 4. Теория гомотопий
как классы отображений ia порождают группу пп(Хп). Чтобы можно было
продолжить / на клетку е1^ \ нам нужно только убедиться, что
композиция отображения приклеивания с/?^: S"—> Xй для этой клетки с
отображением / гомотопна нулю в У. Но эта композиция /<^ представляет элемент
Д([^|з]) = ^([¥>р])» а ^([^/з!) = 0> потому что [<^] — нулевой элемент
группы тг„(Х), так как ц>р можно прогомотопировать в нуль в X
посредством характеристического отображения клетки е»41. Таким образом, мы
получаем продолжение /: X —► У. Для него /+ = г/>, так как элементы [ifi]
порождают группу тгп(Хп), а значит, и группу тгг,(Х) но теореме о
клеточной аппроксимации. U2
Доказательство предположения 4.30. Предположим, что К и К' —
CW-комнлексы типа K(G, п). Так как гомотопическая эквивалентность —
отношение эквивалентности, не будет потери общности, если мы
предположим, что К — специальное пространство /C(G, п), а именно то, которое
построено по такому пространству X, как в лемме, приклеиванием
клеток размерности п + 2и выше. Согласно лемме существует отображение
/: X—>К\ индуцирующее изоморфизм групп п,г Чтобы продолжить это
отображение / на К, мы будем действовать по индукции. Для каждой
клетки е"+2 композиция её отображения приклеивания с отображением /
гомотопна нулю в К', так как 7гп.н (К') = 0, таким образом, / продолжается
на эту клетку. То же самое рассуждение можно поочерёдно применить для
всех клеток большей размерности. Полученное в результате отображение
f:K-^K/ является гомотопической эквивалентностью, так как оно
индуцирует изоморфизмы всех гомотопических групп. П
Теорема Гуревича
Используя приведённое выше вычисление гомотопических групп, мы
можем легко доказать самые простые и чаще всего используемые случаи
теоремы Гуревича.
I Теорема 4.32. Если пространство X является (п - 1)-связным, где
I п^2, то Н,(Х) = 0 при i <п и 7Гп(Х)^//„(Х). Если пара (X, Л) является
I (п - 1)-связной, где л ^ 2, а пространство Л одпосвязио и непусто, то
I Hf(X, А) = 0 при i<n и 7ГП(Х,Д)^/-/„(Х,А).
Таким образом, первая ненулевая гомотопическая группа и первая
ненулевая группа гомологии одпосвязного пространства встречаются в
одной и той же размерности, и эти группы изоморфны. Не следует
ожидать никаких хороших соотношений между тг,(Х) и Н((Х) помимо этого.
Например, сфера S" имеет тривиальные группы гомологии выше
размерности п, но у неё есть много нетривиальных гомотопических групп в этом
диапазоне при л ^ 2. Наоборот, пространства Эйленберга—Маклейна,
например СР^, имеют тривиальные высшие гомотопические группы, но
у них есть много нетривиальных групп гомологии.
§4.2. Элементарные методы вычислений
465
Теоремой 4.32 можно иногда воспользоваться, чтобы вычислить
группу л2(Х), если Х~линейно связное пространство, достаточно хорошее
для того, чтобы у него было универсальное накрытие. В самом деле, если
X — универсальное накрытие, то 7i2(X) % тг2(Х), а последняя группа
изоморфна Н2(Х) по теореме Гуревича. Поэтому если можно описать X
достаточно хорошо, чтобы вычислить Н2(Х), то можно вычислить и п2(Х).
По поводу той части теоремы, в которой идёт речь об относительных
группах, заметим, что пространство X должно быть односвязным, так же,
как и А, поскольку пара (X, А) является односвязной по предположению.
Имеет место более общая версия относительной теоремы Гуревича,
которая позже будет приведена в теореме 4.37; в ней допускаются неодио-
связные пространства А и X, но для этого нужно заменить я„(Х, А) на
некоторую факторгруппу.
Доказательство. Мы можем предположить, что X — CW-komiuickc,
а (X, А) — CW-napa, взяв CW-аппроксимации к X и к (X, А). Для CW-nap
относительный случай тогда сводится к абсолютному случаю, так как
7i,(X, А) ъ я,(Х/А) при i ^ п согласно предложению 4.28, в то время как
Н2(Х, А) ^Я,(Х/А) для всех i согласно предложению 2.22.
В абсолютном случае мы можем применить следствие 4.16, чтобы
заменить комплекс X гомотопически эквивалентным ему CW-комплексом,
у которого (п — 1)-мерный остов состоит из одной точки,
следовательно, Н,(Х) =0 при i < п. Чтобы доказать, что тгм(Х) ^ Н,?(Х), мы можем
сделать дальнейшее упрощение, выбросив клетки размерности больше
п + 1, так как они не влияют на пп и на Нп. Таким образом, X имеет
вид (vaS^) lJeeJ ]- Мы можем считать, что отображения у>р приклеивания
ft
клеток e"+L сохраняют отмеченные точки, как описано в доказательстве
следствия 4.16. Тогда пример 4.29 показывает, что я„(Х) есть коядро
граничного отображения яп И(Х, Xм) —> тсп(Xм) — отображения ®Z—»®Z.
ft «
Это отображение — то же самое, что клеточное граничное отображение
d: Hn+1(Xn+1, Xм) ->Hn(X\XM_I), так как для клетки е£+1 коэффициенты
в de"+1 —степени композиций qaipp, где qa стягивает все n-мерные
клетки, кроме е", в точку, а изоморфизм rzu(Sn) %Z в следствии 4.25
задаётся степенью. Так как нет никаких (п — 1)-мерных клеток, мы получаем
H„(X)%Cokerd. П
Так как группы гомологии обычно легче вычислять, чем
гомотопические группы, часто бывает легче применять следующую версию теоремы
Уайтхеда.
I Следствие 4.33. Отображение f:X-*Y односвязных CW-комилек-
сов является гомотопической эквивалентностью, если /*: Я„(Х) —*
—*//„(У) — изоморфизм для всех п.
466
Глава 4. Теория гомотопий
Доказательство. Заменив У на цилиндр отображения My, мы можем
считать, что / — включение Xе-» У. Так как X иУ односвязны, мы
получаем Tti(Y, X) = 0. Относительная теорема Гуревича тогда показывает, что
первая ненулевая группа л,, (У, X) изоморфна первой ненулевой группе
НП(У, X). Длинная точная последовательность гомологии показывает, что
все группы Нп(У, X) нулевые, поэтому все группы яп(У, X) тоже нулевые.
Это означает, что включение X с-> У индуцирует изоморфизм всех
гомотопических групп, а потому это включение —гомотопическая
эквивалентность. □
Пример 4.34 (единственность пространств Мура), /(окажем, что
гомотопический тип CW-комплекса, являющегося пространством Мура
M(G, л), единственным образом задаётся группой G и числом л при
условии л > 1, обеспечивающем односвязность пространства M(G, л).
Пусть пространство X —это пространство Мура M(G, л), которое было
построено в примере 2.40 приклеиванием (л + 1)-мерных клеток к букету
п-мерных сфер, и пусть У —любой другой CW-комплекс типа M(G,n).
Согласно лемме 4.31 существует отображение /: X —> У, индуцирующее
изоморфизм групп тг„. Если мы сможем показать, что / индуцирует также
изоморфизм групп Н„, то из предыдущего следствия мы получим
требуемое утверждение.
Один из способов доказать, что / индуцирует изоморфизм групп Нп)
мог бы состоять в том, чтобы воспользоваться более тонкой версией
теоремы Гуревича, дающей изоморфизм между пп и Нп, являющийся
естественным относительно отображений пространств, как в теореме 4.37,
сформулированной ниже. Однако мы приведём здесь прямое
рассуждение, которое позволяет избежать вопроса о естественности. Для цилиндра
отображения Mj мы знаем, что я,(Му,Х) =0 при i ^ п. Если это верно
и для i = л -f 1, то из относительной теоремы Гуревича получаем, что
Н,(Муг, X) = 0 при i ^ л + 1 и, следовательно, что fM будет изоморфизмом
групп f/„. Чтобы это рассуждение сработало, давайте временно увеличим
пространство У, приклеив к нему (л 4-2)-мерные клетки, чтобы сделать
группу ;гпЧ.! нулевой. Тогда для нового цилиндра отображения Му-мы
получим ям+1(Му, X) = 0 из длинной точной последовательности пары.
Поэтому для увеличенного пространства У отображение / индуцирует
изоморфизм групп IIп. Но приклеивание (л-Ь2)-мерных клеток никак не влияет
на НПУ поэтому исходное отображение /: X —► У должно быть
изоморфизмом групп Н,г
Конечно, отображение неодносвязных пространств может индуцирО"
вать изоморфизмы всех групп гомологии, но не гомотопических групп-
Неодносвязные ациклические пространства, для которых отображение
включения точки индуцирует изоморфизм гомологии, реализуют это
явление в его самой чистой форме. По-видимому, самое простое
нетривиальное ациклическое пространство —двумерный комплекс, построен-
§4.2. Элементарные методы вычислений
467
ный в примере 2.38, с фундаментальной группой (а,Ь \ а5 = Ь3 = (ab)2}
порядка 120.
Может также случиться, что отображение пространств с абслевыми
фундаментальными группами индуцирует изоморфизмы групп гомологии,
но не высших гомотопических групп, как показывает следующий пример.
Пример 4.35. Построим такое пространство X = (S1 V Sn) U еп+] для
произвольного п > 1, что включение S1 <-> X индуцирует изоморфизм всех
групп гомологии и групп я,- при i < п, но не групп яп. Из примера 4.27
мы получаем nn(Sl VS") я» Z[t, г-1]. Пусть пространство X получено из
S1 vSn приклеиванием клетки еп+1 по отображению S" —*S1 VS",
соответствующему элементу 2t - 1 eZ[t, t"1]. Рассматривая универсальное
накрытие, мы видим, что rc„(X)^Z[t, f~l]/(2t- 1), где (2t - 1) обозначает
идеал в Z[t, Г""1], порождённый элементом 2t — 1. Заметим, что, положив
t = 1/2, мы получим включение кольца Z[t, t_1]/(2t - 1) в Q в качестве
подкольца Z[l/2], состоящего из дробей, знаменатели которых — степени
числа 2. Из длинной точной последовательности гомотопических групп
для (п — 1)-связной пары (X, S1) мы видим, что включение кольца S1<—> X
индуцирует изоморфизм групп я, при i < п. Тот факт, что это
включение индуцирует также изоморфизм всех групп гомологии, можно
получить из клеточных гомологии. Ключевой момент состоит в том, что
клеточное граничное отображение Н„+1(Х'Н \ X") —► Я„(Х", Xм-1) является
изоморфизмом, так как степень композиции отображения приклеивания
Sn-+SlV S" клетки en+1 и стягивания S1 V S" — Sn равна 2-1 = 1.
Этот пример во многом основан на нетривиальности действия группы
тг^Х) на я„(Х), поэтому можно поинтересоваться, нельзя ли ослабить
предположение об односвязности в следствии 4.33 до тривиальности
действия группы Я] на всех группах я„. Это действительно так, и мы это
докажем в предложении 4.74.
В приведённой выше версии теоремы Гуревича утверждается лишь
существование изоморфизма между гомотопическими группами и
группами гомологии, но может понадобиться более точное утверждение,
которое говорит, что некоторое специальное отображение —изоморфизм.
В действительности всегда существуют естественные отображения из
гомотопических групп в группы гомологии, которые определяются
следующим образом. Будем представлять себе группу пп(Х,А,х{)) при п > 0
Как множество гомотопических классов отображений /: (D", dDn,s0) —>
-* (X, А, х0). Тогда отображение Гуревича h: я„(Х, А, х0) —» НП(Х, А)
определяется как h([/]) =/*(«), где а —фиксированная образующая группы
Hn(Dn, сШ") ^ Z, а отображение /+: tfn(DM, <ШП) — Н„(Х, Л)
индуцировано отображением /. Если задана гомотопия / ~ g в классе
отображений (D", сШм, 5()) -» (X, Л, х0), или даже в классе отображений (D", AD") -»
""* (X, Л), не сохраняющих отмеченную точку, то /+ =g+, поэтому
отображение h определено корректно.
468
Плана 4. Теория гомотопий
Предложение 4.36, Пусть п > 1, тогда отображение Гуревича h:
ггп(Х, Л, х0) —>Нп(Х, А) является гомоморфизмом.
Доказательство. Достаточно доказать, что для отображений /, g;
(Dn, <lDn) —> (X, А) индуцированные отображения гомологии
удовлетворяют соотношению (/4 g)¥=/y4- g,, поскольку если это так, то ft([/ + g]) =
= (/ + g)*(«) = /«(a)4-g„(a) = h(I./]) 4- h([g]). Наше доказательство того,
что (/ + g)+ = /+ + g*, в действительности будет годиться для любой теории
гомологии.
Пусть с: D" —> D" V Dn—отображение, стягивающее экватор Оп"]
в точку, и пусть qi,q2: ^" v ^" —^"—отображения факторизации, т.е.
отображения на одно из этих двух слагаемых, при которых другое
слагаемое стягивается в точку. Тогда мы получаем диаграмму
Hn{D\i)Dn) • '' > Hn(DnVDn,dDnV<lDn) ——+Нп(Х,Л)
Hn{Dn,dDn)®Hn{D\<Wn)
Отображение qu $ q2v — изоморфизм, причём обратным к нему
является отображение ib -f i2*, где ^ и i2 —включения этих двух слагаемых
D" <-»/}" VD". Так как отображения дтс и q2c гомотопны тождественному
в классе отображений (Dn,dDn)-* (Dn,dDn), композиция (ql5K Ф q2Jt\ —
диагональное отображение х—»(х,х). Из равенств (/Vg)/^/ и (f\Zg)i2 =
= g мы получаем, что (/ V g)Mu + *2*) переводит 0,0) в /+U) и (0, х)
в g*0), а потому оно переводит О, х) в /+0) 4- g+(x). Таким образом,
композиция отображений в верхней части диаграммы —это отображение
jc-»/+0) -fg*0). С другой стороны, /4g=(/Vg)c, таким образом, эта
композиция равна также (/ + g)„. U
Существует также абсолютное отображение Гуревича h: nn(X,x{)) —>
—>Нп(Х), которое определяется аналогично: мы полагаем ft([/]) =/Да)
для отображения /: (Sn,s0) —> (X, jc0) и выбранной образующей а группы
Hn(Sn). Например, если X=S", то /Да) равно (deg/)a по определению
степени, таким образом, в этом случае мы можем рассматривать h как
отображение степени nn(Sn)—>Z, которое, как мы знаем, является
изоморфизмом согласно следствию 4.25. Доказательство предыдущего
предложения легко изменить, чтобы показать, что абсолютное отображение
h — гомоморфизм при п ^ 1.
Абсолютные и относительные отображения Гуревича можно
объединить в диаграмме длинных точных последовательностей
... -+пп(Л,х0) —*• 7Zn(X,xQ)—>nn(X,Atx0) —^я„_,(А,х0) ~^ •••
\h lh \h i"
... —^нпш >iinW -//„(x, д) *нп_М) —- ...
§4.2. Элементарные методы вычислений
469
Простая проверка определений, которую мы оставляем читателю,
показывает, что эта диаграмма коммутативна, по крайней мере с точностью
до знака. Позаботившись о выборе образующих а, эту диаграмму можно
сделать действительно коммутативной.
Другое элементарное свойство отображений Гуревича состоит в том,
что они естественны: отображение /: (X, х{)) —> (У, у0) индуцирует
коммутативную диаграмму
кп(Х9х0) —>■ nn(Y, у0)
I r \
нпю—^пп(У)
и аналогично в относительном случае.
Легко построить нетривиальные элементы ядра гомоморфизма
Гуревича h: я„(Х, х0) —> //П(Х), если я^Х, х()) нетривиально действует на
яп(Х,х0): это элементы вида [y][f] - [/]. Дело в том, что yf и /,
рассматриваемые как отображения S" —> X, гомотопны, если мы не требуем,
чтобы отмеченная точка оставалась неподвижной в процессе гомотопии.
Поэтому (yf)Да) = /Да) для образующей а группы Hn(Sn).
В относительном случае ядро отображения h : я„(Х, Д, х0) —>Н„(Х, А)
содержит элементы вида [у] [/] - [/ ] для [у] е п} (А, х0). Например,
отображение Гуревича nn(S] V SU,S]) —> Hn(S] \/S'l,S1)— это гомоморфизм
ЩЛ, Г1] —>Z, переводящий все степени t в 1. Так как пара (S1 VS^S1)
является (п - 1)-связной, этот пример показывает, что условие п1 (Л, х0) = О
в доказанной ранее относительной версии теоремы Гуревича опустить
нельзя.
Если мы определим тг^(Х, А, х0) как факторгруппу группы яп(Х, А, х0)
по подгруппе, порождённой всеми элементами вида [у][/] - [/I, или по
нормальной подгруппе, порождённой такими элементами в случае п = 2,
когда группа я2(Х, Л, х()), возможно, неабелева, то h индуцирует
гомоморфизм ti': n'n{X, Л, jc0) —>ПП(Х, А). Теорема Гуревича общего вида
описывает свойства этого гомоморфизма.
I Теорема 4.37. Если (Х,Л) —(л - 1)-связная пара линейно связных
пространств, причём п ^ 2 и А Ф 0, то Ы: я'} (X, Л, х0) —> Нп(X, Л) —
изоморфизм и //,(Х, Л) = 0 при i <п.
Отметим, что это утверждение включает абсолютную версию
теоремы Гуревича, если взять в качестве А отмеченную точку.
Перед началом доказательства этой общей теоремы Гуревича мы
сделаем предварительный шаг.
I Лемма 4.38. Если X—связный CW-комплекс, к которому ириклеи-
I ваются клетки е" фиксированной размерности n ^ 2, образуя CW-kom-
I плекс W = X(Je^, то ^„(W, X)—свободный я2(Х)-модуль, базисом ко-
I а
I торого служат гомотопические классы характеристических отображе-
470
Глапа 4. Теория гомотопий
I ний Фа клеток е£, при условии, что отображение пх(Х) —> nx(W)y инду-
I цированное включением, — изоморфизм. В частности, это всегда имеет
I место при п ^ 3. В общем случае при п = 2 группа я2(Ж X) порожда-
I ется классами характеристических отображений клеток е2 вместе с их
I образами под действием группы яДХ).
Если характеристические отображения Фа : (D'?, dD") —> (W, X) не
переводят отмеченную точку s0 в дОп в отмеченную точку х0 в X, то они
определяют элементы группы rrM(VU,X,x0) только после выбора пути из
точки Ф„(50) в точку х0, задающего изменение отмеченной точки. Разные
способы выбора таких путей приводят к элементам группы ttm(VU, X, х()),
связанным действием группы я^Х, х0); таким образом, базис модуля
rrM(VU, X, х()) определён корректно с точностью до умножения на
обратимые элементы кольца Z[tIj (X)].
Ситуация, когда л = 2 и отображение пх(Х) —> Я] (VU) не является
изоморфизмом, более сложная, потому что относительная группа я2
в этом случае может быть неабелевой. Уайтхед проанализировал эту
ситуацию и показал, что я2(И/, X) имеет структуру «свободного скрещенного
я^Х)-модуля». См. [135] или [127].
Доказательство, Так как W/X = VaS^, для односвязного комплекса X
мы получаем ttm(VU, X) % 7rft(VaS^) согласно предложению 4.28.
Утверждение леммы в этом случае следует непосредственно из примера 4.26.
Если комплекс X не односвязен, но включение X с-> W индуцирует
изоморфизм групп яь то универсальное накрытие комплекса W
получается из универсального накрытия комплекса X приклеиванием п-мерных
клеток, которые являются поднятиями клеток епа. Если мы выбираем одно
такое поднятие е^ клетки е", то все остальные её поднятия — образы уё^
клетки е^ при преобразованиях накрытия, соответствующих элементам
yGn1(X). Частный случай, доказанный в предыдущем абзаце,
показывает, что относительная группа я„ для универсального накрытия
—свободная абелева группа с базисом, соответствующим клеткам уе7^. Согласно
относительной версии предложения 4.1 проекция универсального накрытия
для W на комплекс W индуцирует изоморфизм относительных групп я„.
Поэтому я„(И/, X)— свободная абелева группа, базисом которой служат
классы [уе^], где у пробегает я^Х), или, другими словами, свободный
Я! (X)-модуль, базисом которого служат клетки e'j.
Остаётся рассмотреть случай и = 2в общем виде. Так как обе пары
(W, X) и (X1 [Jea> *2) являются односвязными, из гомотопической теоре-
а
мы о вырезании следует, что отображение
а
сюръективно. Это позволяет свести всё у случаю, когда комплекс X
одномерен. Мы можем также предположить, что двумерные клетки cf приклее*
§4.2. Элементарные методы вычислений
471
ны по петлям, проходящим через отмеченную точку — нульмерную клетку
Х0, так как этого можно добиться гомотопией отображений
приклеивания, которая не влияет на гомотопический тип пары (W, X).
В замыкании каждой двумерной клетки е2а выберем вложенный диск
р2, который содержит точку х0, но во всём остальном лежит целиком во
внутренности клетки е2п. Пусть У = X[jD2 — букет комплекса X и дис-
а
ков D2, и пусть Z = W - IJint(D^), таким образом, Y и Z—двумерные
а
CW-комплексы с общим одномерным остовом У1 — '/} — Y C\Z = X V(I <1D2.
Включение (W, X)«—»(W, Z) является гомотопической эквивалентностью
пар. Гомотопическое вырезание даёт сюръекцию я2(У, У1) —► n2(W, Z).
Универсальное накрытие Y комплекса Y получается из универсального
накрытия X комплекса X взятием букета с поднятиями D2„ дисков D2.
Следовательно, мы имеем изоморфизмы
тг2(У, У1) ъ n2(Y, У1), где У1 —одномерный остов накрытия У,
** 7r2(va/3^/3, Va^aD^), так как X стягиваемо,
^ п\ (УардВ2а„) так как Va/3I)L стягиваемо.
Последняя группа свободная, причём её базисом служат петли dD2*,
поэтому включения D^ ^ V^D^ образуют базис для rr2(Va/3D^, V^dD^).
Из этого следует, что n2(Y, У1) порождается включениями D2 <—> У и их
образами под действием петель в X. То же самое верно для 7i2(W, Z),
как показывает сюръекция я2(У, У1) —» 7r2(W, Z). Используя изоморфизм
7r2(W, Z) ^ 7i2(W, X), мы получаем, что tt2(W, X) порождается
характеристическими отображениями клеток е2а и их образами под действием
ГРУППЫ Я !(Х). □
Доказательство общей теоремы Гуревича. Как и для предыдущей
версии этой теоремы, мы можем считать, что (X, А) —такая CW-пара, что
клетки комплекса X — А имеют размерность не меньше п.
Сначала докажем теорему, предполагая, что л:, (А) —* пх (X) —
изоморфизм. Это всегда имеет место, если л ^ 3, таким образом, это даст нам
Доказательство теоремы, кроме случая л = 2. Мы можем также
предполагать, что Х = ХМ_Ь1, так как клетки большей размерности не влияют на пп
И на Н„. Рассмотрим коммутативную диаграмму
яп+1(Х, X" U А) -^ я71(Х"иЛ, А) -^ тг71(Х, Л) —>• О
Y , Y (-/ t
<1+1 (х, х" и Л) ^ п'п (xfI и л, Л) — < (х, л) -— о
У ., Y ,•' I
Hn , 1 (X, Xм U Л) -^ Н„ (Xм U Л, Л) —^ Нп (X, Л) --* О
472
Глава 4. Теория гомотопий
Первая и третья строки — точные последовательности для тройки (X, Xй и
ил, Л). Отображение h' слева —изоморфизм. Действительно, по
предыдущей лемме тгг1+1(Х, X" и Л) — свободный я!-модуль, базисом которого
служат характеристические отображения (п 4- 1)-мерных клеток
комплекса X - Л. Поэтому я'п+1(Х, X" U Л) —свободная абелева группа с тем же
самым базисом. Группа Нл+1(Х,ХпиЛ) тоже свободная с базисом из
(п4- 1)-мерных клеток комплекса X - Л. Аналогично из предыдущей
леммы следует, что среднее отображение Ы — изоморфизм, так как из
предположения, что Я] (Л) —> пх (X) — изоморфизм, следует, что отображение
пх{А)^> Я] (Xм U Л) инъективно, а потому является изоморфизмом при
Тогда 5-лемма влечёт, что изображение h' справа —изоморфизм.
Остаётся доказать теорему в случае, когда п = 2 и отображение
к1 (Л) —> Я] (X) — не изоморфизм. Приведённое выше доказательство
можно будет применить, если мы покажем, что среднее отображение /i'
в диаграмме —изоморфизм. Из предыдущей леммы следует, что группа
я^(Х2и Л, Л) порождается характеристическими отображениями
двумерных клеток комплекса X -Л. Образы этих образующих при отображении
h' являются базисом для Н2(Х2 и Л, Л). Поэтому ti~ гомоморфизм из
группы, которая согласно доказываемой ниже лемме является абелевой,
в свободную абелеву группу, переводящий набор образующих в базис,
следовательно, h' — изоморфизм. С
Лемма 4.39. Для любой тройки (X, Л, х0) формула а 4- b - а = {<)а)Ь
выполняется для всех а, Ьея2(Х, A,jc0), гдед: я2(Х, Л,х0) —> я^Л, х0) —
обычное граничное отображение, а (да)Ь обозначает действие элемента
да на Ь. Следовательно, группа я2(Х, Л, х0) абелева.
Здесь 4- и - в выражении а + Ь — а относятся к групповой операции
в неабелевой группе я2(Х, Л, х0).
Доказательство. Требуемая формула получается посредством
гомотопий отображения а + Ь — а в отображение (да)Ь, которая устроена так,
как показано на приведённом ниже рисунке. П
а
Ь
—а
а
*о
Ъ
—а
=щ
да
да
Плюс-конструкция
В алгебраической топологии возникает много ситуаций, когда
наличие нетривиальной фундаментальной группы сильно затрудняет работу.
Мы сейчас опишем конструкцию, которая при определённых условиях
§4.2. Элементарные методы вычислений
473
позволяет изменить пространство так, чтобы устранить его
фундаментальную группу или по крайней мере упростить её, не меняя гомологии
и когомологий. Вот самый простой случай этой конструкции.
I Предложение 4.40. Пусть X является связным CW-комплексом,
причём НХ(Х) = 0. Тогда существуют односвязный CW-комплекс Х~ и
отображение X —> Х+, индуцирующее изоморфизмы всех групп гомологии.
Доказательство. Выберем петли уи: S1 -+ Х\ порождающие группу
rii(X). Приклеив по ним клетки е2а к X, получим односвязный
CW-комплекс X'. Гомологическая точная последовательность
0 — Н2(Х) -> Н2(Х') — Н2(Х', X) — 0 = ПХ{Х)
расщепляется, так как группа Н2(Х', X) свободная; её базисом служат
клетки е^. Таким образом, мы получаем изоморфизм /72(Х') ^ /72(Х) ф
фН2(Х', X). Так как пространство X' односвязно, теорема Гуревича даёт
изоморфизм Н2(Х') ^ 7т2(Х'), а потому мы можем представить базис
свободного слагаемого Н2(Х', X) отображениями гра: S2 -+ X'. Можно
считать, что все они — клеточные отображения. Воспользуемся ими, чтобы
приклеить клетки е3а к X'. В результате получим односвязный
CW-комплекс Х+, причём включение X <-+ Х^ индуцирует изоморфизм всех групп
гомологии. D
В предыдущем предложении условие НДХ) =0 означает, что группа
пх(Х) совпадает со своим коммутантом, т.е. яДХ) — совершенная
группа. Рассмотрим более общую ситуацию, когда X — связный CW-комплекс,
аНс тг^Х)—совершенная подгруппа. Пусть р: X -* X накрытие,
соответствующее подгруппе Н; таким образом, группа тг^Х) ы Н
совершенная, и Н\(Х) = 0. Из предыдущего предложения мы получаем включение
ХС-^Х+. Пусть пространство Х+ получено из несвязного объединения Х+
и цилиндра отображения Мр отождествлением экзем- ^ ~+
пляров пространства X в этих двух пространствах. То- I i
гда мы получаем коммутативную диаграмму вложений j |
(см. рис.). По теореме ван Кампена индуцированное х^М >■ Х+
отображение п1(Х) —► тгДХ4) сюръективно, причём р
его ядром является нормальная подгруппа, порождённая подгруппой //.
Далее, так как пространство X*/Мр гомеоморфно Х^/Х, мы получаем
Н*(Х+, Мр) = НЖ(Х", X) = 0, поэтому отображение X -* Х+ индуцирует
изоморфизм гомологии.
Эта конструкция X —> X"1, убивающая совершенную подгруппу в тг1 (X),
сохраняя при этом гомологии, известна под названием шиос-конструкции
Квиллена. В ряде важных приложений X — пространство типа K(G, 1), где
Коммутант группы G — совершенная группа. Таким образом, отображение
-Х"-*Х+ абелианизирует группу пи сохраняя гомологии. Пространство Х~
йе обязано иметь тип К(я, 1), и в действительности его гомотопические
гРуппы могут быть весьма интересными. Самый поразительный пример —
474
Глава 4. Теория гомотопий
G = EOOJ бесконечная симметрическая группа, состоящая из перестановок
символов 1,2,..., оставляющая неподвижными все из них, кроме
конечного числа; коммутант этой группы —бесконечная знакопеременная
группа Л^, которая является совершенной. В этом случае известная теорема
Баррата—Кана—Придди и Квиллена говорит, что гомотопические группы
я^С/ССЕ^, 1)f) —стабильные гомотопические группы сфер!
Однако убивать подгруппы в я^Х), не меняя гомологии
пространства X, можно лишь до некоторого предела. Например, для X ~ Sl V S1
нельзя убить коммутант группы я^Х), сохраняя гомологии. Дело в том,
что согласно задаче 23 в конце этого параграфа любое пространство с
фундаментальной группой Z х Ъ должно иметь нетривиальную группу Н2.
Локально тривиальные расслоения
«Короткая точная последовательность» пространств A *—> X —* Х/А
приводит к длинной точной последовательности групп гомологии, но не
к длинной точной последовательности гомотопических групп из-за
нарушения свойства вырезания. Однако есть другая «короткая точная
последовательность» пространств, которая действительно даёт длинную точную
последовательность гомотопических групп. Такая короткая точная после-
р
довательность F —> Е —* В, называемая локально тривиальным,
расслоением, отличается от последовательности A *—> X —» Х/А большей
однородностью: все подпространства р'^(Ь) с £, которые называют слоями t го-
меоморфны. Например, Е может быть произведением FxB,ap:E-*B-
проекцией. Общие локально тривиальные расслоения можно
представлять себе как скрученные произведения. Знакомые нам примеры—лист
Мёбиуса, который является скрученным круговым кольцом с отрезками
в качестве слоев, и бутылка Клейна, которая является скрученным тором
с окружностями в качестве слоев.
Топологическая однородность всех слоев локально тривиального
расслоения весьма похожа на алгебраическую однородность в короткой
точной последовательности групп 0—> К —> G —»Н —> О, где «слои» р~] (Ю —
это смежные классы К в G. В некоторых локально тривиальных
расслоениях F —> Е —> В пространство Е действительно бывает группой, /' — её
подгруппой (хотя и очень редко нормальной подгруппой), а В —
пространством левых или правых смежных классов. Один из самых приятных таких
примеров — расслоение Хопфа S1 —»S3 —> S2, где S3 — группа кватернионов
единичной длины, a S1 —подгруппа комплексных чисел, модуль которых
равен 1. Для этого расслоения длинная точная последовательность
гомотопических групп принимает вид
... - я.-CS1) - я^3) - я,(52) - Щ_х&1) - tt^CS3) - ...
В частности, эта точная последовательность даёт изоморфизм п-?{$ '
ъ я1(51), так как два соседних члена n2(S3) и Я](£3) нулевые по тео-
§4.2. Элементарные методы вычислений
475
реме о клеточной аппроксимации. Таким образом, мы получаем прямое
теоретико-гомотопическое доказательство того, что n2(S2) ъЪ. Кроме
того, так как rc,(S]) =0 при i > 1 согласно предложению 4.1, из этой
точной последовательности следует, что имеют место изоморфизмы rc,(S3) ъ
fc*7T,-(S2) для всех / ^ 3. Поэтому, в частности, rc3(S2) ъ ^3(S3), а согласно
следствию 4.25 последняя группа равна Z.
После этих предварительных замечаний начнём с того, что
определим свойство, которое приводит к длинной точной последовательности
гомотопических групп. Говорят, что отображение р: Е-+В обладает
свойством поднятия гомотопии относительно пространства X, если для
данной гомотопии gt: X -+ В и данного отображения g0: X -* Я,
поднимающего g0 (т. е. pg0 =go)> существует гомотопия gt: X —»£, поднимающая gt.
С формальной точки зрения это можно рассматривать как частный случай
свойства поднятия продолжения для пары (2,Л), которое означает, что
для любого отображения Z —> В существует поднятие Z —> Е,
продолжающее данное поднятие, заданное на подпространстве AdZ. Случай, когда
(Z, А) = (X х /, X х {0}), —это свойство поднятия гомотопии.
Расслоение в смысле Гуревича] — это отображение р\Е—*В,
обладающее свойством поднятия гомотопии относительно всех пространств X.
Например, проекция, В х F —> В является расслоением в смысле Гуреви-
ча, так как мы можем выбрать поднятия вида gfO) = (grM>hto), где
$>(*) = (&)(*)> Л(*))•
I Теорема 4.41. Предположим, что отображение р: Е —> В обладает
I свойством поднятия гомотопии относительно дисков Dk для всех к ^ 0.
I Выберем отмеченные точки Ь{)еВ и x0eF = p~](bQ). Тогда отображе-
I ние р+: я„(£, F, х0) —> яп(В, Ь0) является изоморфизмом для всех п ^ 1.
I Следовательно, если пространство Б линейно связно, то имеет место
I длинная точная последовательность
I ... -* яп(Т,х0) -* яп(Е,х0) -* я„(В,Ь0) -* я,,..,^, *0) -* ■■•
I ... -> я0(Е,х0) — 0.
Доказательство будет использовать относительную версию свойства
поднятия гомотопии. Говорят, что отображение р: Е—* В обладает
свойством поднятия гомотопии для пары (Х,Л), если любую гомотопию
ft'. X -* В можно поднять до гомотопии gt: X -* Е, начинающейся с
данного поднятия g0 и продолжающей данное поднятие g,: Л —* Е. Другими
словами, свойство поднятия гомотопии для (X, А)— это свойство
поднятия продолжения для (X х /, X х {0}иД х /).
Так как пары (Dk х /, Dk x {0}) и (D* х /, 1)к х {0} U гШ* х /) гомео-
Морфиы, свойство поднятия гомотопии для Dk эквивалентно свойству
1 По-английски ото называется одним словом fibration, но в русском языке нет разных
Терминов для расслоений с разными свойствами. — Прим. перса.
476
Глава 4. Теория гомотолий
поднятия гомотопии для (Dk,dDk). Из этого следует, что свойство
поднятия гомотопии для дисков эквивалентно свойству поднятия гомотопии
для всех CW-пар (Х,Л). Действительно, индукция по остовам комплекса
X показывает, что достаточно строить поднятие gt для одной клетки
комплекса X - А на каждом шаге. Композиция с характеристическим
отображением клетки Ф: Dk —* X тогда позволяет свести ситуацию к случаю
(X, А) = (Dk, dDk). Отображение р: Е-*В, обладающее свойством
поднятия гомотопии для дисков, иногда называют расслоением в смысле Серра.
Доказательство. Сначала мы покажем, что р+ —отображение на.
Представим элемент группы я„(#, Ь0) отображением /: (7м, 31й) —* (В, Ь0).
Постоянное отображение в точку х{) задаёт поднятие отображения /
в Е над подпространством J'1"1 с /", поэтому свойство поднятия
относительной гомотопии для (i'1"1, d/"~l) позволяет продолжить его до
поднятия /: 1п —> Е, а это поднятие обладает свойством /(д/") с F, так как
/(дГ) = Ь0. Тогда / представляет элемент группы я„(£, F, х0), для
которого р«([/]) = L/J, так как р/ = /.
Инъективность отображения рж доказывается аналогично. Пусть
даны такие отображения /0>/i: (/", г>/", J""'1) —> (Я, F, jc0), что р*([/0]) =
=j)*([/i]), и пусть G: (/п х /, о/" х /) —» (В, Ь0) — гомотопия отображения
р/0 в отображение р/а. У нас есть частичное поднятие G, заданное
отображением /0 на /" х {0}, отображением f} на J" x {]} и постоянным
отображением в х0 на J""1 х /. После перестановки последних двух координат
в /" х I свойство поднятия относительной гомотопии даёт продолжение
этого частичного поднятия до полного поднятия G: /" х / —» И. Оно
представляет собой ^омотопию ft: (/", d/", J""1) —* (F,F,x0) отображения /()
в отображение fx. Таким образом, гомоморфизм р+ инъективен.
Для доказательства последнего утверждения теоремы мы подставим
пп(В, Ь0) вместо я„(Я, F, х0) в длинной точной последовательности пары
(F, F). Отображение я„(£, х0) —> я„(Я, F, х0) в точной последовательности
р.
тогда становится композицией я„(Е, х0) —* я„(£, F, х0) —> я„(#, Ь0),
которая является просто отображением рж: я„(Е, х0) —> я„(В, Ь0). Нуль в
конце последовательности, т.е. сюръективность отображения я0(Е,л:0) —*
—>я0(Е,х0), возникает из условия, что пространство В линейно связно,
так как путь в Е из произвольной точки хе Е к F можно получить,
поднимая путь в В из точки р(х) в точку Ь0. D
Структура локально тривиального расслоения на пространстве Е со
слоем F состоит из такого отображения проекции р : F —»В, что у любой
точки пространства Я есть окрестность 1У, для которой существует
гомеоморфизм h : р""1 ((У) —* U х F делающий диаграмму
р-,О0 "!—*UxF
§ 4.2. Элементарные методы вычислений
477
коммутативной; здесь непомеченное отображение —проекция на первый
множитель. Коммутативность диаграммы означает, что ft отображает
каждый слой Fb = p~](b) гомеоморфно на копию {b} х F пространства /«'.
Таким образом, слои Еь локально устроены так, как в произведении В х Fy
хотя глобально это не обязательно так. Такое отображение ft, как указано
выше, называют локальной тривиализацией расслоения. Так как первая
координата отображения ft — это просто р, отображение ft определяется
второй координатой, т. е. отображением p~l(U) —■> F, которое является
гомеоморфизмом на каждом слое Fb.
Структура локально тривиального расслоения полностью
определяется отображением проекции р: Е—>£, но, чтобы указать, какой у нас слой,
мы иногда записываем локально тривиальное расслоение как «короткую
точную последовательность пространств» F —>Е—*В. Пространство В
называют базой расслоения, а Е — пространством расслоения.
Пример 4.42. Локально тривиальное расслоение, слоем которого
является дискретное пространство,— это накрытие. Наоборот, накрытие,
все слои которого имеют одно и то же количество элементов, например
накрытие над связной базой, является локально тривиальным
расслоением с дискретным слоем.
Пример 4.43. Одно из простейших нетривиальных локально
тривиальных расслоений —лист Мёбиуса, являющегося расслоением над S1,
слоем которого служит отрезок. А именно, возьмём в качестве Е фак-
ториространство произведения / х [-1, 1] при отождествлениях (0, v) ~
~ (1, -v), и пусть отображение р: Е —> S1 индуцировано проекцией / х
х [-1, 1] —>/, таким образом, слой —это [-1, 1]. Склеив два экземпляра Е
по тождественному отображению их граничных окружностей, мы
получим бутылку Клейна, расслоение над S1 со слоем S1.
Пример 4.44. Проективные пространства приводят к интересным
локально тривиальным расслоениям. В действительном случае мы
получаем уже знакомые нам накрытия S" —*1RP" со слоем S0. Над
комплексными числами аналог этого —локально тривиальное расслоение
si _>s2,l+1 ->СРМ.
Здесь s2"'H —единичная сфера в С'н \ а СРП рассматривается как фактор-
пространство сферы s2""rl при отношении эквивалентности
(z0, ...,z„) ~ A(z0, ...,z„)
для AeS1 — единичной окружности в С. Проекция р: S2/I+1-^CPM
переводит (z0, ..., z„) в его класс эквивалентности [z0,..., z„], поэтому слои —
окружности S1. Убедимся, что условие локальной тривиальности
расслоения выполняется. Пусть U{ сСРп —открытое множество классов
эквивалентности [z0, ...,zj с 2| фО. Зададим отображение ft,-: p~x{U{) —* U( x S]
формулой ft,(z0, ...,z„) = ([z0, ..., zM], z,/|z,|). Оно переводит слои в слои
478
Глава 4. Теория гомотопий
и является гомеоморфизмом, поскольку, как легко можно проверить
вычислением, ему обратно отображение ([z0, ...,zn], X)^X\zi\zTl{z<d, ...,z„).
Конструкция расслоения S1 —► S2""1"1 —>CP" годится и для и = оо,
поэтому есть локально тривиальное расслоение S1 —> S°° —> СР°°.
Пример 4.45. Случай л = 1 особенно интересен, так как СР1 = S2
и расслоение принимает вид S1 —► S3 —> S2, где слой, пространство
расслоения и база —сферы. Это расслоение известно под названием
расслоение Хопфа; оно имеет достаточно малую размерность, что
позволяет описать его явно. Можно считать, что проекция S3 —> S2 имеет вид
(z0, 2]) —» z0/z] G С U {оо} = S2. В полярных координатах мы получаем
р(г0е'°°, ^е'01) = (r0/rL)e'(0°~0,), где г2 + г2 = 1. Для фиксированного
отношения р —г^/г-^ G (0, оо) углы 00 и 0j независимо пробегают окружность
S1, поэтому точки (/oe'^rje'^1) образуют тор Тр CS3. При изменении р
эти непересекающиеся торы Тр заполняют S3, если мы включаем
предельные случаи 7'0 и 7^, когда радиусы г0 и ^ обращаются в нуль, а торы
Т0 и 7^ вырождаются в окружности. Эти две окружности —единичные
окружности в двух множителях С пространства С2, поэтому при
стереографической проекции сферы S3 из точки (0, 1) на :R3 они переходят в
единичную окружность в плоскости ху и ось z. Концентрические торы Тр
тогда устроены так, как показано на следующем рисунке.
Каждый тор Тр является объединением слоев-окружностей —пар {90, щ)
с постоянной разностью 0О — 0{. Эти слои-окружности имеют наклон 1 на
торе, обматываясь один раз по широте и один раз по меридиану. По
отношению к объемлющему пространству, возможно, точнее было бы сказать,
что они имеют наклон р. Когда р меняется от 0 до оо, слои-окружност
приближаются к окружностям Г() и 7'^, которые тоже являются слоями- ^
рисунке изображены четыре из этих торов, разбитых на слои.
§4.2. Элементарные методы вычислений
479
Пример 4.46. Если заменить поле С на поле кватернионов Н, то та
же самая конструкция приводит к локально тривиальным расслоениям
g3 __> £4п+3 _> IHIP" над кватернионным проективным пространством И-Р".
Здесь слой S3 является множеством единичных кватернионов, a S4,H'3 —
единичная сфера в Н"+1. Положив п = 1, мы получим второе расслоение
Хопфа S3^S7^S4 = MP1.
Пример 4.47. Ещё одно расслоение Хопфа S7 —» 515 —»S8 можно
определить, используя алгебру октав О. Элементы алгебры О —пары
кватернионов (аь а2) с умножением, заданным формулой
(аиа2){Ъ],Ь2) = (атЬ, -b2a2, ^bj -fb^).
Если рассматривать S15 как единичную сферу в 16-мерном линейном
пространстве Q2, то отображение проекции р: S15 —* S8 = О U {оо} задаётся
как (z0, ^i) —>z0zj"1, точно так же, как и для других расслоений Хопфа. Но
поскольку алгебра О не ассоциативна, тот факт, что это локально
тривиальное расслоение со слоем S7 — единичные октавы, нуждается в
дополнительных пояснениях. Пусть U{) и L/T —дополнения к оо и 0 в базе Ои {оо}.
Зададим отображения /i,: p~1(Ui)—*Ui x S7 и g-: L/, x S7->p_1(^,) так:
ho(zo>zi) = (znz\\z\l\z\\)> go(z,w) = (zw, w)/|(zw,w)|,
Mzo>zi) = (vr^o/lzol), gi(z,w) = (и/^-^З/Ки/^"^)!.
Если принять на веру известный факт, что любая подалгебра в О,
порождённая двумя элементами, ассоциативна, то легко проверить, что g{ и h{ —
обратные гомеоморфизмы, поэтому мы получаем локально тривиальное
расслоение S7 —* S15 —*58. В действительности для вычисления, которое
показывает, что g,- и h, — обратные отображения, нужны только
следующие более элементарные факты об октавах z, w, где сопряжённый
элемент z для z = (аиа2) определяется, как и следовало ожидать, формулой
2=(аь-а2):
1) rz = zr для всех г € IR и z € О, где R с О как пары (г, 0);
2) |z|2 = zz = zz, следовательно, z"1 = z/|z|2;
3) |zw| = |z||w|;
4) zw = wzy следовательно, (zvv)-1 ^w"1^"1;
5) z(zw) = (zz)w и (zw)w = z(ww), значит, z(z~xw) — w и (zm/)w"! =z.
Эти факты можно проверить несколько утомительным прямым
вычислением. Более изящный их вывод можно найти в главе 8 книги [20].
Существует октавная проективная плоскость ОР2, которая получается
Приклеиванием клетки е16 к S8 по отображению Хопфа S15 —»S8, точно
Так же, как CP2 и 1H1P2 получаются из других отображений Хопфа.
Однако нет никакого октавного аналога для !RP", CP" и MP" при п > 2, так
как ассоциативность умножения необходима для того, чтобы отношение
'*о> -..,z„) ~A(z0, ...,z„) было отношением эквивалентности.
480
Глава 4. Теория гомотопий
Нет никаких локально тривиальных расслоений, для которых слой,
пространство расслоения и база являются сферами размерностей,
отличных от тех, которые встречаются в этих примерах расслоений Хопфа. Это
обсуждается в одной из задач в §4.D, которая сводит этот вопрос к
известной проблеме об инварианте Хонфа, равном 1.
I Предложение 4.48. Локально тривиальное расслоение р: Е-+В
обладает свойством поднятия гомотопий относительно всех CW-nap {X, Л).
Теорема Хюбша и Гуревича, доказываемая в главе 2.7 книги [64],
утверждает, что локально тривиальные расслоения над иаракомиактной
базой —расслоения в смысле Гуревича, обладающие свойством поднятия
гомотопий относительно всех пространств. Однако этот более сильный
результат редко бывает необходимым в алгебраической топологии.
Доказательство. Как было отмечено ранее, свойство поднятия
гомотопий для CW-nap эквивалентно свойству поднятия гомотопий для
дисков, или, что равносильно, кубов. Пусть G: /" х/ —>В, G(x, t) = grO) — ro-
мотопия, которую мы ходим поднять, начиная с заданного поднятия g0
отображения g0. Выберем открытое покрытие {U(l} пространства В
вместе с локальными тривиализациями ha: p~l (Ua) —* U(t х F. Используя
компактность пространства /" х /, мы можем разбить /" на меньшие кубы
С, а / — на отрезки /,- = [f;,t;+J так, чтобы каждое произведение С х /;
отображалось посредством G в одно множество Ua. Применяя индукцию
по п, мы можем предположить, что гомотопия gt уже построена на ОС
для каждого из меньших кубов С. Чтобы продолжить эту гомотопию gt на
куб С, мы можем действовать постепенно, строя g, для г в каждом
интервале /;- последовательно. Это в действительности приводит нас к случаю,
когда никакое подразделение куба /" х / не нужно; поэтому мы считаем,
что G отображает весь куб /" х / на одно множество Ua, Тогда мы получаем
G(/n х {0} U дГ1 х/)срч (Ua), и композиция поднятия G с локальной три-
виализацией ha приводит пас к случаю расслоения-произведения Ua x F.
В этом случае первая координата поднятия gt является просто данным
отображением gt, поэтому нужно построить только вторую координату. Не'
можно получить как композицию/" х/-»/" x{0}\JdIn xj—*F, где первое
отображение—ретракция, а второе отображение —то, которое нам дано. ^
Пример 4.49. Если применить эту теорему к накрытию р: Е-* В
с линейно связными пространствами Е и В и дискретным слоем /'', т0
получающаяся при этом длинная точная последовательность
гомотопических групп приводит нас к предложению 4.1, утверждающему, чт0
р*: тгп(£) —* пп(В) — изоморфизм при п ^ 2. Мы также получаем короткую
точную последовательность 0—* п}{Е) —* п^В) -* п{)(Е) -* 0, которая
согласуется с фактами из теории накрытий, что гомоморфизм р.: К\(Ю~*
—* 7Г,(Б) инъективен и что слой F можно отождествить посредством под-
нятия путей с множеством смежных классов подгруппы р.^п^Е) н ^\\PJ-
§4.2. Элементарные методы вычислений
481
Пример 4.50. Из расслоения S1 —>S°°—► СР00 мы получаем тгДСР00) %
«7Г/_1 (51) для всех I, так как пространство S°° стягиваемо. Таким образом,
СР00 — пространство типа К (Z, 2). Аналогично расслоение S3 —* S°° —> НР^
даёт 7Г,(НР°°) ^ 7Tr_-, (S3) для всех i, но эти гомотопические группы
намного сложнее, чем для СР°° и S1. В частности, ЕР00 — не пространство типа
K(Z,4).
Пример 4.51. Длинная точная последовательность для расслоения
Хопфа S1->S3 — S2 даёт изоморфизмы я2(52) ^ я, (S1) и tt„(S3) ^ tim(S2)
для всех п ^ 3. Положив п = 3, мы видим, что я3 (S2) — бесконечная
циклическая группа, порождённая отображением Хонфа S3—>S2.
Из этого и предыдущего примеров мы видим, что S2 и S3 х СР00 —
односвязные CW-комплексы с изоморфными гомотопическими группами,
хотя они и не гомотонически эквивалентны, так как у них весьма разные
группы гомологии.
Пример 4.52 (произведения Уайтхеда). Вычислим группу ^(N^S2),
показав, что она является свободной абелевои с базисом, состоящим из
отображений Хопфа S3 —> S2 с VaS2 вместе с отображениями
приклеивания S3 -* S2 V Si с VaS2 клеток е2 х е2 в произведениях S2 x S2 для всех
неупорядоченных пар аф р.
Предположим сначала, что число слагаемых S2 конечно. Для
конечного произведения ПпХп линейно связных пространств отображение
пп{\/аХа) —> 7ГМ(П„Х„), индуцированное включением, сюръективно, так
как группа пп (П(Да) % 0 пп (Ха) порождается подгруппами пп (Ха). Таким
а
образом, длинная точная последовательность гомотопических групп /для
пары (ПпХа, VaX(X) разбивается на короткие точные последовательности
О - тгн.н(Пд*„, VaXa) - пп{УаХа) - пп(ПаХа) - 0.
Эти короткие точные последовательности расщенимы, так как
включения Ха <-> УаХа индуцируют отображения пп(Ха) —* 7in(V(tXa), а потому
и расщепляющий гомоморфизм 0 пп(Ха) -* яп(\/иХа). Положив Ха =S2t
а
Им = 3, мы получаем изоморфизм
а
Множитель 0 7r3(S^) является свободной группой с базисом из отображе-
**ий Хопфа S3 —>S2 согласно предыдущему примеру. Для другого
множителя мы получаем ;r4(nfiS2, V„S2) ^ 7r4(naS2/ Va S2) согласно
предложению 4.28. Для факторпространства Yl(XS2 / V(XS2 пятимерный остов —тго
бУКет сфер S^ для а ф [3, поэтому группа тг4(П^2/ v„ S2) % тг4(У^.^)
свободная, и её базисом служат включения S*t„ <—» va/^/r Следовательно,
группа 7i4(na,S2, VUS2) свободная и её базисом служат
характеристические отображения четырёхмерных клеток с2 х е*. Если учесть иньеш
хлава 4. Теория гомотопий
ность отображения д: TC4(naS^, v„S^) —► ^3(vaS^), то это означает, что
отображения приклеивания клеток е£ х е\ образуют базис для слагаемого
\тд группы n3(\taS2a). Это завершает доказательство в случае конечного
числа слагаемых S2a. Случай бесконечного числа сфер Sz сразу из него
следует, так как любое отображение S3 —> vaS'£ имеет компактный образ,
лежащий в конечном объединении слагаемых, и то же самое верно для
любой гомотопий между такими отображениями.
Отображения S3 -*S^ V Si в этом примере можно выразить в
терминах произведения в гомотопических группах, которое называется
произведением Уайтхеда и определяется следующим образом. Пусть даны
отображения /: Sk —> X и g: S* -* X, сохраняющие отмеченные точки. Зададим
отображение [/, g]: S^"1 —>Х как композицию Sk+i~{ -+SkVS{ —^Х, где
первое отображение — отображение приклеивания (к + О-мерной клетки
комплекса Sk x S( с его обычной СW-структурой. Так как гомотопий
отображений / или g дают нам гомотопию отображения ("/,#], мы получаем
корректно определённое произведение як(Х) х яДХ) —> я^.^_](Х).
Обозначение [/, g] используется потому, что для /с = € = 1 это отображение
является просто коммутатором в ях(Х). Несложно проверить, что, когда
к = 1 и I > 1, [/, g] — это разность между g и его образом при я {-действии
элементом /.
В этих терминах отображение 53 -*S^ V Si в предыдущем примере —
произведение Уайтхеда [frt, i^] двух включений пространства S2 в S^ VS£.
Другой пример произведения Уайтхеда, с которым мы уже встречались,—
отображение [1,1]: S2'1"1 -* S", являющегося отображением
приклеивания 2п-мерной клетки пространства J(SM), рассмотренного в §3.2.
Вычисление группы я3(\/а52) —первый нетривиальный случай более
общей теоремы Хилтона, позволяющей вычислить все гомотопические
группы любого букета сфер в терминах гомотопических групп сфер,
используя произведения Уайтхеда. Дальнейшее обобщение этой теоремы
Милнором распространяет её на букеты надстроек над произвольными
связными СУУ-комплексами. Сведения о произведениях Уайтхеда можно
найти в книге [73].
Пример 4.53 (многообразия Штифеля и Грассмана). Локально
тривиальные расслоения с пространством расслоения —сферой, а базой —
проективным пространством, которое были рассмотрены выше, — это
случаи п = 1 следующих семейств локально тривиальных расслоений в
вещественном, комплексном и кватернионном случае:
0(п) - Ц,№*) - Gn('Rk) O(n) - ^(S00)
1Д/0 - Vn(Ck) - Gn(Ck) U(n) - Vn{C*)
Spin) - V„(H*) - G„(K*) Sp(n) - Vn(E*)
-G^R00),
->Gn(C°°),
-GM(H°°).
§4.2. Элементарные методы вычислений
483
Рассмотрим сначала вещественный случай. Многообразие Штифеля
у(Е.к) — это пространство n-реперов в Rk, т.е. наборов из п ортонор-
щированных векторов в Rk. Топология на нём задаётся как топология
подпространства в произведении п единичных сфер в Rk.
Многообразие Грассмана Gn(Rk)-- это пространство n-мерных векторных
подпространств в Rk. Существует естественная сюръекция р: V„CRfc) -> Gn(lRfc),
переводящая и-репер в подпространство, которое на него натянуто, и на
G (Мк) задаётся топология факторпространства относительно этой
проекции. Слои отображения р являются пространствами n-реперов в
фиксированном n-мерном подпространстве в Rk, а потому они гомеоморф-
ны УП(1КП). Ясно, что n-репер в R" — это то же самое, что ортогональная
матрица размера пх п, столбцы которой мы рассматриваем как векторы
n-репера, поэтому слой можно также описать как ортогональную группу
О(м). В этих определениях без труда можно положить к = оо, и в
действительности
V;i(R00) = (Jvn(K*) и Gn(R°°) = (jG„(Kfc).
к к
Комплексные и кватернионные многообразия Штифеля и
многообразия Грассмана определяются таким же способом с помощью обычных
эрмитовых скалярных произведений в С1' и в Ик. Унитарная группа U(n)
состоит из матриц размера пхп, столбцы которых образуют ортонорми-
рованные базисы в С", а симплектическая группа Sp(n) —её кватернион-
ный аналог.
Необходимо объяснить, почему все эти разные проекции Vn —> Gn —
локально тривиальные расслоения. Рассмотрим для определённости
вещественный случай, хотя рассуждение будет одинаковым во всех
случаях. Если мы фиксируем n-мерное подпространство PsGu(Rk) и выберем
В Р ортонормированный базис, то мы получим непрерывно
изменяющиеся ортонормированные базисы во всех n-мерных подпространствах Р'
В окрестности U точки Р, проектируя базис в подпространстве Р
ортогонально на Р' и применяя ортогонализацию Грама—Шмидта к этому
базису, чтобы сделать его ортонормированным. Формулы для ортогона-
лизации Грама—Шмидта показывают, что полученные базисы меняются
Непрерывно. Получив ортонормированные базисы для всех n-мерных под-
Пространств из L7, мы можем воспользоваться ими, чтобы отождествить
эти n-мерные подпространства с R'\ а значит, n-реперы в этих п-мерных
Пространствах отождествляются с п-реперами в R", и, таким образом,
P~T(U) отождествляется с U х У„(КП). Это рассуждение проходит для к = оо
точно так же, как и для конечного к.
В случае п = 1 пространства расслоения Ул являются сферами, которые
Имеют высокую связность, и то же самое верно в общем случае:
• VJ,(lRfc) является {к - п - 1)-связным;
• Vn(.Ck) является (2/с -2п)-связным;
484
Глава 4. Теория гомотетий
• Vn(Кк) является (4/с - 4п + 2)-связным;
• l/„№°°), Vn(C°°) и Vn(K°°) стягиваемы.
Первые три утверждения будут доказаны в следующем примере. Для
последнего утверждения рассуждения аналогичны, поэтому рассмотрим
только вещественный случай. Зададим гомотопию ht: R°° —> R00 формулой
ht(x{ix2, ...) = (l-t)(xbx2, ...) + t(0,xbx2>...).
Она является линейным отображением для каждого t, причём ядро этого
линейного отображения, как легко проверить, тривиально. Поэтому если
мы применим ht к п-реперу, то получим п линейно независимых векторов,
которые можно сделать ортонормированными с помощью формул Гра-
ма—Шмидта. Таким образом, мы получаем деформационную ретракцию
(в слабом смысле) пространства Vf7(R°°) па подпространство л-реперов,
для которых первая координата нулевая. Повторяя это л раз, мы ироде-
формируем наше пространство в подпространство п-реперов, для которых
первые л координат пулевые. Для такого n-репера (vb ..., v„) определим
гомотопию (1 - t)(V!,..., v„) -f t(e1?..., еп), где е, — стандартный базисный
1-й вектор в R00. Эта гомотопия сохраняет линейную независимость,
поэтому после применения ортогонализации Грама—Шмидта мы снова
получаем деформацию в классе п-реперов, что и завершает построение
стягивания пространства VJ^R00).
Так как Vn(R°°) стягиваемо, мы получаем изоморфизмы тг,-0(п) ъ
^rc^G^CR00) для всех f и п, и аналогично в комплексном и кватерни-
онном случаях.
Пример 4.54. При т < л ^ к существуют локально тривиальные
расслоения
Vn.m№k-m)^Vn{Rk)^Vm{Rk),
где проекция р переводит п-репер в ш-репер, образованный его
первыми т векторами; таким образом, слой состоит из (п — ш)-реперов
в (к — ш)-мерном пространстве, ортогональном данному m-реперу.
Локальные тривиализации можно построить следующим образом. Для ш-ре-
пера F выберем ортонормированный базис в (/с - т)-мерном
подпространстве, ортогональном к F. Это определяет ортонормированные
базисы в (/с - ш)-мерных подпространствах, ортогональных всем близким
m-реперам, посредством ортогональной проекции и ортогонализации
Грама—Шмидта, как в предыдущем примере. Тем самым эти (к — ш)-меР~
ные подпространства отождествляются с 'Rk~m, и, в частности, слои
вблизи p~l(F) отождествляются с V„_m(Rk~m), что и даёт локальную тривилли-
зацию.
Имеются также аналогичные расслоения в комплексном и кватернион-
ном случаях, причём локальная тривиальность доказывается точно так #е-
Если т = ], получаются расслоения У„._] ('Rk ]) -> У„(."К*) -> Sk~[. P<'lC"
сматривая соответствующую им длинную точную последовательность то-
§4.2. Элементарные методы вычислений
485
мотопических групп и используя индукцию по п, получаем, что
пространство У„0^) является (/с - п - 1)-связным. В комплексном и кватернион-
ном случаях то же самое рассуждение приводит к другим утверждениям
о связности, сформулированным в предыдущем примере.
При к = пу получаем локально тривиальные расслоения 0(/с - /п) —■>
—* O(Jc) —* V„,C&k). Их слои в действительности просто смежные классы
аО(к - т) для а е 0(/с), где 0(/с - ш) рассматривается как подгруппа
в О(/0, сохраняющая первые т стандартных базисных векторов. Таким
образом, мы видим, что Ц7?(^') отождествляется с факторпространством
0(/с)/0(/с - ш), или, другими словами, с пространством орбит свободного
действия группы 0(/с — т) на 0(/с) умножением справа. Аналогично
можно показать, что Gm(Rk) — факторпространство 0(/с)/(0(/п) x 0(/c -m)),
где подгруппа О(гп) х 0(/с-ш) сО(/с) состоит из ортогональных
преобразований, переводящих т-мерное подпространство, натянутое на первые
т стандартных базисных векторов, в себя. Соответствующие рассуждения
применимы также в комплексном и кватернионном случаях для
унитарных и симилектических групп.
Пример 4.55 (периодичность Ботта). Взяв частный случай
предыдущего примера, когда ш = 1 и к — п, мы получаем расслоения
0(п-1) —О(п) -^Sn"\
U(n-l) —UCrO-^S2"-1,
Sp(n-l) —Sp(n) As4'1"1.
Отображение р можно описать как вычисление значения
ортогонального, унитарного или симплектического преобразования на фиксированном
единичном векторе. Эти расслоения показывают, что вычисление
гомотопических групп пространств О(п), U(n) и Sp(n) должно быть по
крайней мере столь же трудным, как вычисление гомотопических групп сфер.
Например, если бы мы знали гомотопические группы пространств О(п)
И 0(п - 1), то из длинной точной последовательности гомотопических
Групп для первого расслоения можно было бы кое-что сказать о
гомотопических группах сферы S"-1.
Из приведённых выше расслоений следует очень интересное
свойство стабильности. В вещественном случае включение 0(п - 1) <-*0(п)
Индуцирует изоморфизм групп я, при i < п - 2 согласно длинной точной
Последовательности первого расслоения. Следовательно, группы тг(0(п)
Не зависят от п, если п достаточно велико, и то же самое верно для групп
^,U(n) и тг, SpOO, как показывают два других расслоения. Один из
наиболее удивительных результатов во всей алгебраической топологии —
теорема периодичности Нотта, которая утверждает, что эти стабильные группы
Повторяются периодически, с периодом 8 для О и Sp и с периодом 2 для U.
486 Глава 4. Теория гомотопий
Их значения приведены в следующей таблице:
i mod 8
я, О (л)
7T(U(/0
rc,-Sp(n)
0
г2
0
0
1
z2
г
0
2
0
0
0
3
ъ
Z
z
4
0
0
z2
5
0
Z
z2
6
0
0
0
7
Z
Z
Z
Стабильные гомотопические группы
В следствии 4.24 мы показали, что для п-связного CW-комплекса Х
отображение надстройки п((Х)-* 7tf+1(SX) является изоморфизмом при
i < 2п Н- 1. В частности, это верно для i^i п, поэтому пространство SX
является (п 4- 1)-связным. Из этого следует, что в последовательности
итерированных надстроек
Щ(Х) - 7rr-+I(SX) - ni+2(S2X) - ...
все отображения в конце концов становятся изоморфизмами, даже без
какого-либо предположения о степени связности самого X. Получающаяся
в результате стабильная гомотопическая группа обозначается 7Г^(Х).
Особенно интересен случай группы тг*(5°), которая равна тг,-н,(5п)
для п > i H-1. Обозначение этой стабильной гомотопической группы часто
сокращается до п*. Имеет место теорема Серра, которую мы доказываем
в [SSAT], о том, что группа я? всегда конечна при i > 0.
Стабильные гомотопические группы сфер —одни из самых
фундаментальных объектов в топологии, и было приложено немало усилий для
их вычисления. В настоящее время полные вычисления известны только
приблизительно i = 60. Ниже приведена таблица для z $ 19, взятая из кни-
i
Ks
i
1
Z
2
Ъ2
3
z24
4
0
5
0
6
Z2
7
^240
8
1,2 x Z2
9
Z2 x Z2 x Z2
10
7*
11
^504
12
0
13 14 15 16 17 18 19
Z3 Z2 x Z2 ZA80 xZ2 Z2x Z2 Z2xZ2x7l2x Z2 ZH x Z2 Z2bA x ^2
Закономерности в этом видимом хаосе начинают появляться, только если
рассмотреть проекции группы п* на её р-компоненты, т. е. факторгруппы
по всем элементам, порядок которых взаимно прост с простым числом р-
Для i>0 р-компонента ря*, конечно, изоморфна подгруппе в тг\
состоящей из элементов, порядки которых —степени числа р, но точка зрени
факторизации в некоторых отношениях более предпочтительна. 5
На рисунке изображена принципиальная схема 2-компопепт групп ,•
для i $ 60. Вертикальная цепочка из п точек в z-м столбце иредставля
§ 4.2. Элементарные методы вычислений
487
слагаемое Ъ2* группы я*. Нижняя точка такой цепи обозначает
образующую этого слагаемого, а вертикальные отрезки обозначают умножение
на 2, таким образом, вторая точка —удвоенная образующая, следующая
точка —учетверённая образующая, и т.д. Три образующие 7), v и <т в
размерностях 1, 3 и 7 представлены отображениями Хопфа S3 —>S2, S7—>S4
и S15 -*S8, определёнными в примерах 4.45, 4.46 и 4.47.
Д>/| [//! k/! м k/i k^ k/i
13 7 11 15 19 23 27 31 35 39 43 47 51 55 59
Горизонтальные и диагональные отрезки на рисунке
предоставляют некоторую информацию о композициях отображений сфер. А
именно, определены произведения я* x п5. —* я? ., заданные композициями
Si+J+b-+sj+k-+Sk.
Предложение 4.56. Композиционные произведения л* х ns. —► nsi+j
индуцируют структуру градуированного кольца на я* = 0я*,
удовлетворяющую соотношению коммутативности а/3 = (-1),;/За для а е я*
H/3€7TJ.
Это мы докажем в конце этого пункта. Из предложения 4.56 следует,
что прямая сумма ря* р-компонент ря* тоже является градуированным
Кольцом, удовлетворяющим тому же самому свойству коммутативности.
В 2я* многие из композиций с надстройками отображений Хопфа г\ и v
Нетривиальны, и эти нетривиальные композиции обозначены на
диаграмме идзоцими вправо отрезками длины 1 или 3 единицы, по диагонали
*ля т\ и горизонтально для v. Таким образом, например, мы видим
соотношение т)3 — 4v в 2^3. Запомним, что 2ks3 ъ Z8 — факторгруппы группы
^з^^24> гДе в действительности имеет место соотношение т)3 = 12v, так
Как 2т) = 0 влечёт, что 2т)3 — 0, таким образом, т)3 — единственный элемент
Порядка два в этой группе Z24.
Вдоль основания диаграммы встречаются повторяющиеся пары
«зубцов». Такие пары продолжаются до бесконечности, хотя их пики в
размерностях 8к - 1 не все будут одной высоты, а именно, пик в размерности
488
Diana 4. Теория гомотетий
2т(2п +1) - 1 имеет высоту m + 1. В верхней части диаграммы, однако,
заметно меньше регулярности, и эта сложность, по-видимому,
сохраняется также и в более высоких размерностях.
На следующей диаграмме изображены 3-компонеиты групп тг? для
/' ^ 100, и увеличение регулярности весьма заметно. Здесь вертикальные
отрезки обозначают умножение на 3, а другие сплошные отрезки
обозначают композицию с элементами ах €зяз и fi{ e3n\0. Значение
пунктирных линий будет объяснено ниже. Самая регулярная часть диаграммы —
«триадическая линейка» вдоль основания. Она продолжается по тому же
самому образцу всюду дальше, с пиками высоты ш + 1 в размерности
4/с - 1, где Зш — наибольшая степень числа 3, делящая 4/с. Посмотрев
снова на диаграмму для р = 2, можно увидеть, что вертикальные отрезки
«зубцов» образуют «диадическую линейку».
Р'.мгш-' Рь/:*- ^*£ ^»
«>. . : . . i . . { . . : . . i . . 1 . . : . . i . .
3 7 1115 19 23 27 31 35 39 43 47 51 55 59 63 67 71 75 79 83 87 91 95 99 103
Рлцё больше закономерностей появляется для больших простых чисел,
начиная со случая р = 5, изображённого на следующей диаграмме. Снова
имеется бесконечная линейка, на этот раз «пентадическая» линейка, но
много закономерностей присутствует также и в остальной части
диаграммы. Четыре точки вблизи правого края диаграммы, помеченные
вопросительными знаками под ними, гипотетические: вычисления б [57] не
позволяют сказать, существуют ли на самом деле эти возможные элементы
групп 5п* для i =932, 933, 970 и 971.
Эти три диаграммы извлечены из таблиц, опубликованных в [42)
и [107] для р = 2 и в [57] для р = 3, 5.
Для каждого р существуют подобные «р-адические линейки»,
соответствующие циклическим подгруппам порядка pm+1 в рп*{1)_ 1 для всех j,
где рш — наибольшая степень числа р, делящая j. Эти подгруппы являются
р-компонентами некоторой циклической подгруппы в пАк_ p известной
как ImJ — образ гомоморфизма J: п4к_}(0)-^п*Ак_г Имеются также
подгруппы Ъ2 в п* для i = 8/с, 8/с + 1, образующие для ImJ в этих размерностях.
20/4/.
2°/По4 21*
20/2* 2-19*
18
17/""»"
/^7*
„*ч
15/4 Д , - - ,
15/з{| ™*^~±f~^
15<* > ,.*—V* ?♦ ?•
15/2*2-14 * «г" V" V- V '
1/f ^—?*. *•<:—7^—Г*
14 * >* «г * v
^г^
10/4/
12 4——-♦ ** *■ —*г
,0* ^^^Z^Sv' / /^7'-/'-/--7/^7
ю/3^4 1
20/5 /''/
/ ./'
/ . „' /-,
10/2* 2-9 *-
9 *■
П *TZ *Х *~Z 5»
5/4/.
/^.
в/^7'-«^г
/■>■." ^*»,Л^
<*~z—*^—*т—=*
/ /- Л^ ЛЕ7
^—=*Т—*Т—з*~;—з*х
15/5
/
>-—;».» /
* ♦* 4
-«> , V
/
TBte
V—^-"* «# * ■"•
5/2* 2-4/^/^/^7^^1
4/ / / / ^
3 />7%~7%~У^7 Ю/5 ,
2Л^У^7^7 /./^^^Т^^^^^^^^^Ч^^^
г v ># * •*> %• * *> w w-T—V-^—V-^-—-W
.2—I—2—2.
J....:....!....:....:....!....!....:....:....:....!.
.!....!....!....!.
Л....!....!....!.
39 79 119 159 199 239 279 319 359 399 439 479 519 559 599 639 679 719 759 799 839 879 919 959 999
000
4*
CD
I
2
x
s
s
I
s
Sc
-^
490
Глава 4. Теория гомотопий
В диаграмме для 2п1 они являются частями зубцов, связанных с пиком
в размерности 8/с - 1. Гомоморфизм J будет подробно изучен в [VBKT].
Известно ещё несколько других бесконечных семейств в я*; наиболее
примечательно семействы элементов /3„ ерп2( 2_Пп_2) Для р ^ 5 и
семейство ynepns2{ 3_I)n_2p2_2 +i для Р ^ ?• Элемент Д, появляется в диаграмме
для р = 5 как элемент в верхней части диаграммы, помеченный числом п.
Эти элементы /3„ порождают полосы на идущей вверх диагонали, кроме
тех случаев, когда п кратно 5, и тогда полоса порождается элементом
PiPn-iy a не Рп- Существуют также элементы Д, для некоторых дробных
значений п. Элемент у2 порождает длинную полосу, начинающуюся в
размерности 437, но у3 = 0. Элемент у4 в размерности 933 — это один из
элементов, отмеченных вопросительным знаком. Теория, лежащая в основе
этих семейств /3„ и уп и их возможных обобщений (см. [57], [58]), является
одной из самых таинственных ветвей алгебраической топологии.
В я* есть много композиций, равных нулю. Можно получить
некоторое представление об этом из приведённых выше диаграмм, где все
последовательности отрезков вскоре прерываются. Как частный случай
обращения в нуль произведений, формула коммутативности из
предложения 4.56 гарантирует, что квадрат нечётномерного элемента нечётного
порядка равен нулю. И вообще, теорема Нисиды утверждает, что любой
элемент а е я* положительной размерности нильпотентен, т. е. а" = 0 для
некоторого п. Например, для элемента /3j е5Яз8 наименьшее такое п
равно 18.
Частое обращение в нуль произведений в я* можно расценить как
их малую полезность для описания структуры я*. Но этим можно также
воспользоваться для построения новых элементов в я*. Предположим, что
I Ч h
заданы такие отображения W —> X -^ Y —>Z, что обе композиции gf и hg
гомотопны постоянным отображениям. Гомотопия отображения gf в
постоянное отображение даёт продолжение отображения gf до отображения
F: CW —> У, а стягивание отображения hg даёт продолжение отображения
hg до отображения G: CX—*Z. Рассматривая надстройку SW как
объединение двух конусов CW, определим скобку 'Годы (/, g, h): SW —»Z как
композицию G(Cf) на одном конусе и hF на другом.
Отображение (/, g, h) определяется отображениями fygwh
неоднозначно, так как оно зависит от выбора стягиваний отображений. В случае
§4.2. Элементарные методы вычислений
491
л1 разные скобки (/,g, h) пробегают смежный класс некоторой
подгруппы, описанной в одной из задач в конце этого параграфа.
Имеются также скобки Тоды высшего порядка (/ь ...,/„),
определяемые похожим способом. Пунктирные линии на диаграммах для Зя*
и 5^* соединяют элемент х со скобкой (ах,..., а]ух). Большинство
непомеченных элементов выше линеек во всех трёх диаграммах
получается из маркированных элементов композициями и скобками. Например,
8-мерный элемент в 2^ —это (v,rj,v)» а 14-мерные элементы —это сг2
и (v,(v,rj,v>,2,rj>.
Доказательство предложения 4.56. Нужно проверить только
дистрибутивность и коммутативность. Один из законов дистрибутивности
доказывается легко: если даны/, g: s'+;'+*-*S;'+* и h: Sj+k-+Sk, то h(f + g) =
= hf -f hg, так как оба выражения равны hf и hg на двух полусферах
в Sl+j*k. Другой закон дистрибутивности следует из этого закона
дистрибутивности и соотношения коммутативности.
Чтобы доказать соотношение коммутативности, будет удобно
выразить надстройку в терминах приведённого произведения. Приведённое
произведение Sn A S1 можно рассматривать как факторпространство
цилиндра S" х /, полученное в результате стягивания S" х 31 и {х0} х / в
точку. Это то же самое, что факторпространство надстройки Sn+I над
сферой S", полученное при стягивании в точку надстройки над х0.
Стягивание этой дуги в Sn+I в точку снова приводит к Sn+1, поэтому мы
получаем таким образом гомеоморфизм, отождествляющий Sn AS1 с Sn+I. При
этом отождествлении надстройка Sf над сохраняющим отмеченную
точку отображением /: S" —>S" превращается в приведённое произведение
/ Л1: S" Л S1 —► S" Л S1. Повторяя это, получаем, что fc-кратная надстройка
Skf соответствует отображению / Л1: S" Л Sk —>Sn A Sk.
Теперь проверим соотношение коммутативности. Пусть даны
отображения /: Si+k -*Skng:Sj+k^Sk. Можно считать, что fc четно. Рассмотрим
коммутативную диаграмму
S'-+* Л &+к -^ sk л у+к -^ sk л sk
SJ+kASk^SkASk
где ант переставляют соответствующие пары множителей. Если
представлять себе S;4fc и Sfc как приведённые произведения окружностей,
то а— это композиция fc(j + fc) транспозиций соседних множителей —
окружностей. Такая транспозиция имеет степень — 1, так как её можно
реализовать как симметрию сферы S2 = Sl AS1, входящей как
множитель в соответствующее пространство. Следовательно, сг имеет степень
(-l)fc(;'+fc), что равно +1, так как fc четно. Таким образом, отображение
сг гомотопно тождественному. Точно так же отображение т гомотопно
ч-y^J
Глава 4. Теория гомотолий
тождественному. Следовательно, / Ag = (1 Ag)(f A S) гомотопно
композиции (g л 1)(/ л И), которая стабильно эквивалентна композиции £/\
По симметрии /g стабильно гомотопно отображению g A f. Поэтому
достаточно доказать, что / Ag ~ (-l)'-'g л/. Мы сделаем это с помощью
коммутативной диаграммы
S*kAS^k^Sk/\Sk
где а и т —снова транспозиции двух множителей. Как и раньше,
отображение т гомотопно тождественному, но теперь а имеет степень
(-l)(MfcKj4fc), что равно (-1)';, так как fc четно. Композиция (g A f)cj
гомотопна отображению (—l)';(g л/), так как аддитивные обратные в
гомотопических труппах получаются при взятии композиции с симметрией
(выполняемой в первую очередь), которая имеет степень —1. Таким
образом, из коммутативности этой диаграммы мы получаем соотношение
/Ag-(-l)*gA/. П
Задачи
1. Используя гомотопические группы, докажите, что не существует
ретракции IRP" -* Г&Р*, если п > к > 0.
2. Докажите, что действие группы тг^Р") на я„С&Р") *.7L
тривиально для нечётного п и нетривиально для чётного п.
3. Пусть X получено из линзового пространства размерности 2п + 1
выкалыванием точки. Вычислите я2„(Х) как модуль над й[я,(Х)].
4. Пусть X с I*;"'4 —объединение бесконечной последовательности
сфер££ с радиусами 1/fc и центрами (l/fc,0,..., 0). Докажите, что я,-(Х)=0
при i <п, и постройте гомоморфизм группы я„(Х) на nfc7r„(SJJ).
5. Пусть /: S^ V So —* 5^ V Sj!j—отображение, которое
тождественно на слагаемом S2a, а на слагаемом So является суммой
тождественного отображения и гомеоморфизма S\—*S*V Пусть X— тор
отображения /, т.е. факториространство цилиндра (S^V Si) x / при
отождествлениях (х,0) ~ (/(*), j)- 'lop отображения для ограничения / па Sjt
образует подпространство Л = S1 x S^ С X. Докажите, что отображения
я2(Д) —* я2(Х) —* я2(Х, Л) образуют короткую точную
последовательность 0 —* Z —* Z Ф Z —* Z —* 0, и вычислите действие группы я ДА) на
этих трёх группах. В частности, докажите, что действие группы я, (Л)
тривиально на я2(Л) и па я2(Х, Л), но не тривиально па я2(Х).
6. Докажите, что из относительной версии теоремы Гуревича в
размерности п следует абсолютная версия в размерности п - 1. Для этого
рассмотрите пару (СХ, X), где СХ — конус над X.
§4.2. Элементарные методы вычислений
493
7. Постройте CW-комплекс X с предписанными гомотопическими
группами я,(Х) и предписанными действиями группы пх{Х) на группах
8. Докажите, что надстройка над ацикличным CW-комплексом
стягиваема.
9. Докажите, что отображение односвязных CW-komidickcob является
гомотопической эквивалентностью, если его конус отображения
стягиваем. Используя предыдущую задачу, приведите пример, когда это неверно
в неодпосвязном случае.
10. Пусть CW-комплекс X получен из Sl V S", где п ^ 2,
приклеиванием клетки en+l по отображению, представляющему многочлен p(t) €
eZ[t,rl]^nn{Sl VS"); таким образом,
rrM(X)^Z[t,r1]/(p(t)).
Покажите, что группа п'п{Х) циклическая и выразите её порядок в
терминах р(г). Приведите примеры, показывающие, что группа, тг„(Х) может
быть или не быть конечно порождённой, независимо от того, конечна или
бесконечна группа тг'ДХ).
11. Пусть X — связный CW-комплекс с одномерным остовом X1.
Докажите, что
п2(Х,Х1) ъл2(Х)хК,
где К — ядро отображения тг^Х1) —> тгДХ); К — свободная группа.
Докажите также, что
n^(X,X])*n^X)xK',
где К' — факторгруппа группы К по действию группы tcjCX1)
спряжениями. Отметим, что группа К' абелева.
12. Докажите, что отображение /: X —> Y связных CW-комплексов
является гомотопической эквивалентностью, если оно индуцирует
изоморфизм групп п1 и если поднятие /: X—>Y в универсальные накрытия
индуцирует изоморфизм гомологии. [Последнее условие можно
переформулировать в терминах гомологии с локальными коэффициентами, сказав,
что /+: НДХ; Ъ[плХ]) -> ЯДУ; Z[nxY\) - изоморфизм; см. § З.Н.]
13. Докажите, что отображение связных п-мерных CW-комплексов
является гомотопической эквивалентностью, если оно индуцирует
изоморфизм групп пi при i ^ п. [Перейдите к универсальным накрытиям и
воспользуйтесь гомологиями.]
14. Пусть п-мерный CW-комплекс Х содержит подкомплекс У, гомо-
топически эквивалентный S". Докажите, что отображение пп{У) —> тг„(Х),
индуцированное включением, инъективно. [Воспользуйтесь
гомоморфизмом Гуревича.]
15. Докажите, что замкнугое односвязное трёхмерное многообразие
гомотопически эквивалентно S3. [Воспользуйтесь двойственностью
Пуанкаре, а также тем фактом, что замкнутые многообразия гомотопически
494
Глава 4. Теория гомотопий
эквивалентны СУУ-комплексам согласно следствию П.12 из приложения.
Более сильное утверждение, что замкнутое односвязное трёхмерное
многообразие гомеоморфно S3, — это гипотеза Пуанкаре, в итоге доказанная
Перельманом. Её многомерный аналог, что замкнутое n-мерное
многообразие, гомотопически эквивалентное S", гомеоморфно S", был доказан
ранее для всех п ^ 4.]
16. Докажите, что замкнутые поверхности с бесконечной
фундаментальной группой являются пространствами типа К(я, 1), показав, что их
универсальные накрытия стягиваемы используйте теорему Гуревича и
результаты § 3.3.
17. Докажите, что отображение (X, У) —>Нот(я„(Х), тгп(У)), [/] -*/м
взаимно однозначно, если X — (п - 1 )-связный CW-комплекс, а У —
линейно связное пространство с я,-(У) =0 при i > гг. Выведите из этого, что
ОУ-комплекс типа K(G, n) определён однозначно с точностью до
гомотопического типа группой G и числом п.
18. Пусть X и У—такие односвязные СУУ-комплексы, что группы
Я((Х) и Hj(Y) конечны и имеют взаимно простые порядки для всех пар
(f,;'). Докажите, что включение X V У <—> X х У является гомотопической
эквивалентностью, а пространство X Л У стягиваемо. [Воспользуйтесь
формулой Кюннета.]
19. Докажите, что если X — CW-комплекс типа K(G, 1), то группа
яп (Хп) свободная абелева при п ^ 2.
20. Пусть G — группа, а X — односвязное пространство. Докажите, что
для произведения K(G, 1) х X действие группы пх на пп тривиально для
всех п> 1.
21. Дана последовательность CW-комплексов типа K(G,V n), п = 1, 2,...
Пусть Хп — СУУ-комплекс, представляющий собой произведение первых
гг их этих комплексов JC(Gfpn). Посредством включений X„._j С Х,р
которые возникают, если рассматривать Х„_2 как подкомплекс в Хп с п-й
координатой, равной отмеченной точке —нульмерной клетке комплекса
K(Gn,n), мы можем сформировать объединение всех комплексов Х„ —
CW-комплекс X. Докажите, что яп(Х) ^ G„ для всех п.
22. Докажите, что Hn+1(iC(G, п); Z) =0, если гг > 1. [Постройте K(G, n)
из пространства Мура MiG.n), приклеивая клетки размерности больше
гг + 1.]
23. Уточните теорему Гуревича, показав, что если X —(п -
^-связный CW-комплекс, то гомоморфизм Гуревича h: я,,^ (X) —► HtH {(X) сюръ-
ективен при п > 1, а при гг = 1 покажите, что существует изоморфизм
Я2(Х)//г(я2(Х))^Я2(К(я1(Х),1)). [Постройте К(яп(Х),п) из X,
приклеивая клетки размерности гг + 2 и выше, а затем рассмотрите
гомологическую последовательность пары (У, X), где У —это X с приклеенными
(гг + 2)-мерными клетками комплекса К(я„(Х), гг). Заметим, что образ
граничного отображения ЯП+2(У, X) —> Н„ М(Х) совпадает с образом отоб-
§4.2. Элементарные методы вычислений
495
ражения h и Нп+1 (У) ^Нп.м (К(7Г„(Х), л)). Предыдущая задача
необходима для случая п > 1.]
24. Докажите, что пространство Мура M(G, 1) с я} (M(G, 1)) % G
существует тогда и только тогда, когда H2{K(G, 1); Z) = 0. [Воспользуйтесь
предыдущей задачей. Постройте такое пространство M(G, 1) из
двумерного остова К2 пространства K(G, 1), приклеивая трёхмерные клетки
согласно базису свободной группы H2(X2;Z).] В частности, не существует
пространства M(Z", 1) с фундаментальной группой Z" —свободной абеле-
вой группой ранга л, если п ^ 2.
25. Пусть X — CW-комплекс, и пусть тг, (X) = 0 при 1 < i < л для
некоторого п £2. Докажите, что Hn(X)/h(nn(X)) ^Нп(К(п}(Х), 1)), где h-
гомоморфизм Гуревича.
26. Обобщая пример RP2 и S2 х 3£Р°°, докажите, что если X — связный
конечномерный CW-комплекс с универсальным накрытием X, то X и Хх
xKin^ (X), 1) имеют изоморфные гомотопические группы, но не гомотопи-
чески эквивалентны, если тгДХ) содержит элементы конечного порядка.
27. Выведите из леммы 4.39, что образ отображения тг2(Х, х()) -»
—»тг2(Х, Л, х0) лежит в центре группы тг2(Х, А, х{)).
28. Докажите, что группа Zp x Zp, где р —простое число, не может
действовать свободно ни на какой сфере S", восполнив детали следующего
рассуждения. Такое действие определило бы накрывающее пространство
Sn—*M, где М —замкнутое многообразие. При п > 1 постройте
пространство К(Ър х Zp, 1) из М, приклеив единственную (п 4-1)-мерную клетку,
а затем клетки более высокой размерности. Выведите из этого, что группа
Hn+l(K(Zp х Zp, l);Zp) равна Zp или 0, что приводит к противоречию.
(Случай п = 1 более элементарен.)
29. Завершите гомотопическую классификацию линзовых
пространств, начатую в задаче 2 из §З.Е, показав, что два линзовых
пространства Lm((,}, ..., Сп) и Lm(t\, ..., ^) гомотопически эквивалентны, если
1\...1п = ±k'4'r..Cn mod m для некоторого целого числа /с, посредством
следующих шагов.
а) Сведите ситуацию к случаю к = 1, показав, что Lm(l'v ..., £'п) =
= L„}(fc£j, ..., fc^), если /с взаимно просто с гл. [Выберите по-другому
образующую действия Ът на S2"^1.]
б) Пусть /: L —> V — отображение, построенное так, как в части б)
задачи из §З.Е. Постройте отображение g: I -»I/ как композицию L-*
—» L V S2n_I —► L V S2n_1 —► I/, где первое отображение стягивает границу
Малого шара в точку, второе отображение — букет тождественного
отображения на L и отображения некоторой степени d на S2"-1, а третье
отображение—это / на L и проекция S2n_1 —> I/ на S2n_1. Докажите, что g
имеет степень kj.../с,, + dm, т.е. g индуцирует умножение на к}...кп + dm
в группе H2„_.i(-;Z). [Докажите сначала, что поднятие отображения g
в универсальное накрытие S2n_1 имеет именно такую степень.]
^УО
Глава 4. Теория гомотопий
в) Если £{...£„ ~±£\..Л\ mod ш, то выберите с/ так, что к]...кп -f <7ш =
= ±1, и покажите, что из этого следует, что g индуцирует изоморфизм всех
гомотопических групп, а значит, является гомотопической
эквивалентностью. [Для П/, где ! > 1, рассмотрите поднятие отображения g в
универсальное накрытие.]
30. Пусть Е — подпространство в R2, полученное удалением
некоторого подпространства в {0} х :&. Для каких из этих подпространств Е
проекция Е —> R, О, у) -+ ху является локально тривиальным расслоением?
31. Пусть для локально тривиального расслоения F —> /Г —> В
включение F <~> Е гомотопно постоянному отображению. Докажите, что
длинная точная последовательность гомотопических групп разбивается на рас-
щенимые короткие точные последовательности, дающие изоморфизмы
пп(В) & тг„(Е) $ яп_.!(Р). В частности, для расслоений Хопфа S3 —>S7 -->S4
и S7 —>S15 -*SS это приводит к изоморфизмам
nn(S*)*nn{S7)®nn^(S*)9
nn(Ss)*nu{S]5)enn_x{S7).
Таким образом, группы 7i7(S4) и rcl5(S8) содержат слагаемое Z.
32. Докажите, что если Sk —>Sm —>Sn —локально тривиальное
расслоение, то к — п - 3 и m = 2и — 1. [Рассмотрите длинную точную
последовательность гомотопических групп.]
33. Докажите, что если бы существовали локально тривиальные
расслоения Sn"1 —>S2'?~~I ~>S" для всех п, то группы 7tt-(S") были бы конечно
порождёнными свободными абелевыми группами, вычислимыми по
индукции и отличными от нуля при i ^ п ^ 2.
34. Пусть р: S3 —* S2 — расслоение Хоифа, и пусть q: Т3 —► S3 —
отображение факторизации, стягивающее дополнение шара в трёхмерном торе
73 = S1 xS] xS1 в точку. Докажите, что отображение pq: Тл —>S2
индуцирует тривиальное отображение на тг* и на Н*, но не гомотопно
постоянному отображению.
35. Докажите, что локально тривиальное расслоение S3 —> S4"+-* —> lii'P"
приводит к локально тривиальному факторрасслоению S2 —> СР2пИ —> !п!Р"
посредством факторизации по действию S1 на S4"к3 умножением на
комплексные скаляры.
36. Для сохраняющих отмеченную точку отображений /: S1 —> X
и g: S" —>Х, где п > 1, докажите, что произведение Уайтхеда [f,g] равно
±(g - /g), где fg обозначает действие / па g.
37. Докажите, что все произведения Уайтхеда в линейно связном /7-
пространстве тривиальны.
38. Докажите, что тг3(51 VS2) не конечно порождён как модуль над
Z[nx(S] V52)], рассмотрев произведения Уайтхеда в универсальном
накрытии и воспользовавшись результатами из примера 4.52. Обобщите
этот резутьтат на ni+j__l(S'i vS' VS') для it j> 3.
§4.3. Связь с когомологиями
497
39. Докажите, что неопределённость скобки Тоды (/, g, h), где /е n*t
gen) и йетф —это подгруппа fe п)Ак^л+кек]+}лх группы ^.w>jt+1.
§ 4.3. Связь с когомологиями
Теорема Гуревича показывает, что гомотопические группы тесно
связаны с гомологиями, а потому косвенным образом и с когомологиями. Но
есть и более прямая связь с когомологиями совсем другого рода. Мы
покажем, что для любого CW-комплекса Х имеет место естественное
взаимно однозначное отображение между Нп(Х; G) и множеством (X, K(G, л))
гомотопических классов сохраняющих отмеченную точку отображений
из X в K(G, л). Мы также определим естественную структуру группы на
{X,K(G,n)), которая превращает это взаимно однозначное отображение
в изоморфизм групп. Первое, что здесь удивляет, — это сам факт, что
существует вообще какая-то связь между когомологиями и гомотопическими
классами отображений, а второе —то, что здесь участвуют пространства
Эйленберга—Маклейпа, так как их определение даётся полностью в
терминах гомотопических групп и, на первый взгляд, не имеет никакого
отношения к когомологиям.
После доказательства основного изоморфизма IIn(X; G) ъ (X, K(G, л))
и разбора нескольких его непосредственных применений последующие
части этого параграфа нацелены на дальнейшее исследование башен
Постникова, которые были вкратце описаны в §4.1. Они предоставляют
общий теоретический метод для того, чтобы реализовать
произвольный CVU-комплекс как своего рода скрученное произведение пространств
Эйленберга—Маклейпа с точностью до гомотопической
эквивалентности. Наиболее геометрическая интерпретация фразы «скрученное
произведение»—это понятие локально тривиального расслоения, введённое
в предыдущем параграфе. Однако здесь понадобится более теоретико-
гомотопическое понятия расслоения в смысле Гуревича, поэтому, прежде
чем начать обсуждение башен Постникова, мы сначала уделим несколько
страниц изложению основных конструкций и результатов об этих
расслоениях.
Как мы увидим, башни Постникова можно представить как
последовательности расслоений в смысле Гуревича, слои которых —пространства
Эйленберга—Маклейпа, поэтому мы снова можем ожидать тесных связей
с когомологиями. Одна из таких связей предоставляется к-иивариаитами,
которые описывают, по крайней мере в принципе, как башни Постникова
для весьма широкого класса пространств задаются последовательностью
классов когомологий. Другое применение этих идей, описанное в конце
этого параграфа, — техника разложения основных задач в теории гомото-
пий, задач продолжения и поднятия отображений, в последовательность
более простых задач, решения которых эквивалентны обращению в нуль
498
Глава 4. Теория гомотопий
определённых классов когомологий. Эта техника известна под несколько
претенциозным названием теории препятствий, хотя в действительности
она имеет весьма простое выражение в терминах башен Постникова.
Гомотопическое построение когомологий
Основной результат этого пункта — следующие фундаментальные
соотношения между сингулярными когомологиями и пространствами Эй-
ленберга—Маклейна.
I Теорема 4.57. Имеют место естественные взаимно однозначные
I отображения Г: (X, K(G, n)> —> Нп(Х; G) для всех CW-комплексов Х
I и всех п > О, где G — любая абелева группа. Такое отображение Т
I имеет вид Т([/]) = /*(«) для некоторого фиксированного класса ае
I eH'l(K(G,n);G).
По ходу доказательства мы определим естественную структуру группы
на (X, K{G, n)), для которой преобразование Т является изоморфизмом.
Класс аеЯп(К(С,п);С), который обладает свойством, указанным
в теореме, называют фундаментальным классом. Доказательство теоремы
приведёт нас к явному выражению для фундаментального класса. А
именно, он является элементом группы H"(K(G, n); G) % Нот(Нп(К; Z), G),
заданным как обратное отображение для изоморфизма Гуревича G =
= 7i,1(K'(G, п)) —►НГ|(ЛГ; Z). Говоря более конкретно, если мы выберем в
качестве K(G, п) CW-комплекс, (п - 1)-мерный остов которого состоит из
одной точки, то фундаментальный класс представлен клеточной коцепью,
сопоставляющей каждой п-мерной клетке комплекса K(G,n) элемент
группы nn(K(G, п)), представленный характеристическим отображением
для этой п-мерной клетки.
Теорема также остаётся верной при замене (X, /C(G, n)) на [X,#(G, н)1,
т.е. на гомотопические классы, не сохраняющие отмеченную точку. Это
легко видеть для п > 1, так как любое отображение X —> K(G, n) можно
прогомотопировать так, чтобы оно переводило отмеченную точку в
отмеченную точку, и любую гомотопию между сохраняющими
отмеченную точку отображениями можно прогомотопировать так, чтобы гомо-
топия сохраняла отмеченную точку, если пространство K(G,n) (область
значений) односвязно. Для п = 1 равенство [X, K(G> n)] = (X, K{G, n)) —
одна из задач в §4.А, использующая предположение, что группа G
абелева. Для п = 0 элементарно проверяется, что /Y°(X; G) = [X,K(G,0)1 и
H°(X;G) = (X,K(G,0)).
Можно дать прямое доказательство этой теоремы «голыми руками»,
строя отображения и гомотопий для клетки за клеткой. Это даёт
хорошее геометрическое понимание того, почему результат верен, но, к
сожалению, технические детали этого доказательства довольно утомительны.
Поэтому мы применим другой подход, преимущество которого в том, что
§4.3. Связь с когомологиями
499
он помещает этот результат в его естественный контекст посредством
общей техники, которая оказывается весьма полезной и в других ситуациях.
Двумя главными шагами будут следующие утверждения.
1) Функторы hn(X) = (X, K(G, п)> определяют приведённую теорию ко-
гомологий на категории CW-комплексов с отмеченной точкой.
2) Если приведённая теория когомологий /Г, определённая на GW-kom-
плексах, имеет группы коэффициентов hu(S°), равные нулю при п ^0,
то существуют естественные изоморфизмы h"(X)^H"(X; h{)(S°)) для
всех CW-комплексов Х и всех п.
Для доказательства 1 мы изучим более общий вопрос: когда
последовательность пространств Кп определяет теорию когомологий, если
положить ftn(X) = (X, Ки)? Заметим, что это будет приведённая теория
когомологий, так как (X, Кп) тривиально, когда X —точка.
Первый вопрос, к которому надо обратиться, —это введение
структуры группы на множестве (X, К). Для этого требуется, чтобы либо X, либо
К имели какую-то специальную структуру. Когда X = S", мы получаем
(Sn, К) = 7Г„(Ю, что имеет структуру группы при п > 0. Определение этой
структуры группы работает и в более общем случае, когда S" заменяется
на надстройку SX, причём сумма отображений /, g: SX -^K определяется
как композиция SX —» SX V SX —> К, где первое отображение стягивает
«экватор» X CSX в точку, а второе отображение состоит из / и g на двух
полученных слагаемых букета. Однако для того, чтобы это имело смысл,
мы должны говорить о сохраняющих отмеченную точку отображениях,
и есть проблема с тем, где выбрать отмеченную точку в SX. Если х0 —
отмеченная точка в X, то отмеченная точка в SX должна быть где-то
на отрезке {х{)} х I cSX, наиболее вероятно —в его конце или середине,
но никакой единственный выбор такой отмеченной точки не даёт
корректно определённую сумму. Сумма была бы корректно определённой,
если бы мы ограничились отображениями, переводящими весь отрезок
{jc0} х / в отмеченную точку. Это эквивалентно рассмотрению
отображений ЕХ —> К, сохраняющих отмеченную точку, где EX = SX/({x0} x /)
и образ подпространства {х0} х / в ЕХ выбран в качестве отмеченной
точки. Если X — CW-комплекс, в котором отмеченная точка х0 — нульмерная
клетка, то отображение факторизации SX —> ЕХ является гомотопической
эквивалентностью, так как оно стягивает стягиваемый в SX подкомплекс
в точку, поэтому мы можем отождествить (SX, К) с (ЕХ, К). Пространство
ЕХ называют приведённой надстройкой над X, когда мы хотим отличить
её от обычной надстройки SX.
Легко проверить, что (ЕХ, К) —группа относительно суммы,
определённой выше; обратный элемент получается отражением координаты /
в надстройке. Однако на самом деле мы хотели бы получить структуру
группы на (Х,/С), получающуюся из специальной структуры на Кл а не
500
Глава 4. Теория гомотопий
на X. Её можно получить, используя следующее основное соотношение
сопряжённости.
Справедливо равенство (ЕХ, К) = (X, С1К), где Q.K — пространство
петель в пространстве К с началом и концом в его отмеченной точке,
а постоянная петля взята в качестве отмеченной точки в £Ж.
На пространстве Г2К, называемом пространством петель в К,
топология задаётся как топология подпространства в пространстве К1 всех
отображений I -*К, где К1 снабжено компактно-открытой топологией; см.
приложение по поводу определения и основных свойств этой топологии.
Соотношение сопряжённости (ЕХ, К) = (X, Q.K) выполняется потому, что
сохраняющие отмеченную точку отображения ЕХ —* К — это в точности то
же самое, что и сохраняющие отмеченную точку отображения X —>£Ж;
соответствие задаётся так: отображению /: ЕХ—►/( сопоставляется
семейство петель, полученных при ограничении / на образы отрезков {*} х /
в EX.
Полагая в соотношении сопряжённости X=S'\ мы видим, что тгп.и (/() =
= 7ГП(£Ж) для всех п ^ 0. Поэтому переход от пространства к его
пространству петель приводит к сдвигу гомотопических групп на размерность 1
вниз. В частности, мы видим, что <ЛК(0,п)— это K(Gyn - 1). Этот факт
окажется важным в дальнейшем.
Заметим, что сопоставление X—>Г1Х является функтором:
сохраняющее отмеченную точку отображение /: X —* У индуцирует отображение
£lf: D.X —► Г2У посредством композиции с /. Гомотопия f^g
индуцирует гомотонию rtfartg, таким образом, из этого формально следует, что
Хс*У влечёт ПХ^£7У.
Имеет место теорема (см. [115]), что пространство петель CW-kom-
плекса имеет гомотопический тип CW-комплекса. Это может
показаться немного странным, так как пространства петель обычно весьма
большие, хотя, конечно, CW-комплексы тоже могуг быть весьма большими,
если иметь в виду число клеток. На практике часто случается, что если
CW-комплекс Х имеет только конечное число клеток в каждой
размерности, то пространство ПХ гомотопически эквивалентно CW-комплексу
с тем же самым свойством. Мы увидим явно, как это происходит для
X = S",b§4.J.
Композиция петель определяет отображение D.K х D.K-+D.K, и оно
задаёт операцию суммы в (X, £Ж)> если считать, что (/' + g)(x) = f {x)eg(x) —
композиция петель f(x) и gO). При соотношении сопряжённости эта
операция переходит в сумму в (ЕХ, К), определённую ранее. Если мы
берём композицию петель в качестве операции суммы, то тогда, возможно,
несколько легче увидеть, что (X, £Ж) — группа, так как можно применить
то же самое рассуждение, что и для доказательства того, что тс^К) —
группа.
§4.3. Снязь с когомологиями
501
Поскольку группы когомологий абелевы, мы бы хотели, чтобы
группа (X, ПК) была абелевой. Этого можно добиться, повторяя операцию
образования пространств петель. Есть двукратное пространство петель
<Л2К = Г1(£1К), и но индукции можно определить п-кратное пространство
петель ПпК — £1(Г1п~1К). Очевидное взаимно однозначное отображение
KYxZ ъ (KY)Z является гомеоморфизмом для локально компактных хау-
сдорфовых пространств У и Z, как показано в предложении 11.16 в
приложении. Из этого следует но индукции, что ПпК можно рассматривать
как пространство отображений Iй—>КУ переводящих dln в отмеченную
точку. Положив п = 2, мы видим, что рассуждение, которое показывает,
что группа 7i2{K) абелева, доказывает и более общее утверждение, что
(X, П2К) — абелева группа. Итерация соотношения сопряжённости даёт
(ЕПХ, К) = (X, ПпК), таким образом, эта группа абелева для всех п ^ 2.
Таким образом, чтобы последовательность пространств Кп
определяла теорию когомологий h"(X) = (X, Кп), можно потребовать, чтобы
каждое Кп было пространством петель, и даже двукратным пространством
петель. В действительности нам не нужно, чтобы Кп было настоящим
пространством петель, так как достаточно, чтобы оно было гомотоиически
эквивалентно пространству петель, поскольку (Х,Кп) зависит только от
гомотопического типа пространства Кп. Па самом деле достаточно иметь
только слабую гомотопическая эквивалентность Кп —> FLLn для некоторого
пространства L,p так как она индуцирует взаимно однозначное
отображение (Х,Кп) = (Х,Ш,„) согласно предложению 4.22. В частном случае,
когда Кп =K(G, п) для всех н, мы можем положить Ln = К"„П =K(G, п + 1)
в соответствии со сделанным ранее наблюдением, что £IK(G, n + 1)
является пространством типа К (С, п). Таким образом, если мы выбираем
пространства K(G, n) так, чтобы они были CW-комплексами, то отображение
/Сп—»ftK„.;.j —это просто CW-аппроксимация K(G, п)-+Г1К(С,п + 1).
Есть и другой повод искать слабые гомотопические эквивалентности
Кп —►£lKn+i. Для приведённой теории когомологий hu(X) имеют место
естественные изоморфизмы hn(X) ъН'п [0£Х), возникающие из длинной
точной последовательности пары (СХ, X), где СХ —конус над X, поэтому
если hn(X) = (Х,Кп) для всех п, то изоморфизм h"(X) ъИп*1СЕХ)
превращается во взаимно однозначное отображение (Х,Кп) ъ (>~1Х, Кп.,,) =
= (X, £Ж„+1), и наиболее естественным было бы, чтобы оно получалось из
слабой эквивалентности Кп —> Г2КМ г х. Слабые эквивалентности такого
вида дали бы также слабые эквивалентности Кп —»ftK„+1 —>П2К",М 2, и, таким
образом, мы автоматически получили бы структуру абелевой группы па
(Х,Кп)ъ(Х,П2К,и.2).
Эти наблюдения приводят к следующему определению. Г1-спектр —
это последовательность CW-комилексов К{УК2, ... вместе со слабыми
гомотопическими эквивалептпостями Кп -*SlKn+l для всех п. Если
воспользоваться упомянутой выше теоремой Милнора, то можно заменить в этом
502
Глава 4. Теория гомотопий
определении «слабую гомотопическую эквивалентность» на
«гомотопическую эквивалентность». Это не приводит к существенному упрощению,
разве что психологически так легче.
Отметим, что если у нас отсутствует конечное число пространств Кп
в начале ft-спектра Кь К2, ..., то эти пропущенные члены можно
восстановить по остальным пространствам К1п так как каждое пространство Кп
определяет Кп^ как CW-аппроксимацию к £Ж„. Поэтому неважно, что
последовательность начинается с Кх. Кроме того, это позволяет нам
продолжить последовательность Кп на все отрицательные значения п. Это
существенно, потому что общая теория когомологий hn(X) не должна
обращаться в нуль для отрицательных п.
I Теорема 4.58. Если {Кп} — ft-спектр, то функторы
I X^>hn(X) = (X, Kn)t neZ,
I определяют приведённую теорию когомологий на категории CW-kom-
I плексов с отмеченными точками и сохраняющих отмеченную точку
I отображений.
Весьма удивительно, что обратное утверждение тоже верно: любая
приведённая теория когомологий на CW-комплексах возникает таким
образом из Г2-спектра. В этом состоит теорема Брауна о представимости,
которая будет доказана в §4.Е.
Пространство Кп в £7-спектре иногда называют бесконечнократным
пространством петель, так как имеют место слабые гомотопические
эквивалентности +k для всех к. Многие важные
пространства в алгебраической топологии оказываются бесконечнократными
пространствами петель. Помимо пространств Эйлеиберга—Маклейн два
других примера —бесконечномерные ортогональные и унитарные группы О
и U, для которых существуют слабые гомотопические эквивалентности
О —> П80 и U —> ft2U согласно сильной форме теоремы периодичности
Ботта, которую мы доказываем в [VBKT]. Таким образом, О и U дают
периодические ft-спектры, а значит, периодические теории когомологий,
известные как вещественная и комплексная К -теория. Как более
подробное введение в теорию бесконечнократных пространств петель можно
рекомендовать книгу [3].
Доказательство. Две из трёх аксиом теории когомологий, аксиому
гомотопий и аксиому букета, проверить очень легко. Что касается
аксиомы гомотопий, сохраняющее отмеченную точку отображение /: X —*У
индуцирует отображение /*: (У, Кп) —» (Х,Кп) посредством композиции,
переводя отображение У —> Кп в X —> Y —> Кп. Ясно, что /* зависит
только от гомотопического класса отображения / в классе отображений,
сохраняющих отмеченную точку, и очевидно, что /* является
гомоморфизмом, если мы заменим Кп на Г1Кп^ и воспользуемся композицией петель,
§4.3. Связь с когомологиями
503
чтобы определить структуру группы. Аксиома букета выполняется, так
как в классе отображений, сохраняющих отмеченную точку, отображение
УаХа -* Кп — это то же самое, что набор отображений Ха -+ Кп,
Существенная часть доказательства основана на сопоставлении
каждой CW-nape (X, А) некоторой длинной точной последовательности. В
качестве первого шага построим следующую диаграмму:
ас—^хс—^хисдс—^ (хисл)исхс—> «хисл)исх)ис(хисд)
II 1 - -lf
II И Y ||
Ас >■ X -»■ XIА ^ SA ^ SX
Первая строка получается из включения A *—> X повторением
конструкции «приклеим конус над предыдущим подпространством», как показано
на рисунке ниже. Три идущие вниз стрелки на диаграмме (1) — отобра-
~т^ -^ ет^
жения факторизации, стягивающие в точку конус, приклеенный на
последнем таге. Так как конусы стягиваемы, эти идущие вниз
отображения — гомотопические эквивалентности. Второе и третье из них имеют го-
мотопически обратные отображения — очевидные включения,
обозначенные идущими вверх стрелками. В нижней строке диаграммы
отображения очевидные, за исключением отображения X/A-+SA, которое
является композицией гомотопически обратного к отображению факторизации
X U СА -> X)А и отображений X U СА -> (X U CA) U СХ -* SA. Таким
образом, квадрат, содержащий это отображение, коммутативен с точностью до
гомотопии. Легко проверить, что то же самое верно также и для правого
квадрата.
Всю конструкцию можно теперь повторить для SA^SX вместо Л'-»X,
затем для двукратных надстроек и т.д. Получающуюся при этом
бесконечную последовательность можно записать в любом из следующих двух
видов:
Д->Х -*X\JCA-*SA-+SX — S(XUCA) — S2A — S2X — ...,
A->X -> X)A — SA ->SX — SX/SA — S2A — S2X -> ...
В первой версии мы используем очевидное равенство SXUCSA — S(XUCA).
Первая версия имеет то преимущество, что отображение ХиСА—>SA
легко описываемое и каноническое, тогда как во второй версии
соответствующее отображение Х/А —> SA определено только с точностью до
гомотопии, так как оно зависит от выбора гомотопически обратного к
отображению факторизации ХиСЛ—>Х/Д. Вторая версия имеет, однако,
преимущество краткости.
А
i п)
504
Глава 4. Теория гомотопий
Когда важны отмеченные точки, удобнее использовать приведённые
конусы и приведённые надстройки, которые получаются из обычных
конусов и надстроек стягиванием отрезка {х0} х 7, где х0 — отмеченная
точка. Точка —образ этого отрезка —в приведённом конусе или в
приведённой надстройке тогда служит естественной отмеченной точкой в фак-
торпрострапстве. Если предположить, что х0 —нульмерная клетка, то эти
стягивания отрезка {х0} х /— гомотопические эквивалентности.
Использование приведённых конусов и надстроек в предыдущей конструкции
приводит к последовательности
А ^ X -+ X/А -* ЕЛ ^ ЕХ -+ Е(Х/Л) -+ Е2Л *-* Е2Х -> ..., (2)
где мы отождествляем EX/ЕЛ с Е(Х/Л), и все последующие
отображения в этой последовательности —надстройки первых трёх отображений.
Эту последовательность или её пеприведённую версию называют
последовательностью корасслоения или последовательностью Пуппе для пары
(Х,Л). Она обладает очевидным свойством естественности, а именно,
отображение (X, А) —> (У, В) индуцирует отображение между
последовательностями корассллоений этих двух пар с гомотоиически
коммутативными квадратами:
А ■->- X —^ XIА —^ ЕЛ —*- ЕХ —>- Е(Х/Л) —*- Е2Л —>- ...
| | I | I I |
В —*• Г -^ У/13 —^ ЕВ — >- ЕУ —^ Е(У/В) —>- Е2В —*- ...
Если взять гомотопические классы отображений, сохраняющих
отмеченную точку, из пространств в последовательности (2) в фиксированное
пространство К, то мы получим последовательность
(Л, К) «- (X, К) «- (Х/Д, К) — (ЕЛ, К} «- (ЕХ, К) — ..., (3)
в которой отображения определяются как композиции с отображениями
из последовательности (2). Например, отображение (X, К) —> (Л, К)
переводит отображение Х—>К в Л —>X —>К. Множества в последовательности
(3) являются группами начиная с (ЕЛ, К) и абелевыми группами начиная
с (Е2Л, К) и далее. Легко видеть, что отображения между этими
группами — гомоморфизмы, так как отображения в (2) — надстройки с ЕЛ —»ЕХ
и далее. Вообще говоря, первые три члена в (3) —только множества с
выделенными «нулевыми» элементами —постоянными отображениями.
Ключевое наблюдение состоит в том, что последовательность (3)
точна. Чтобы убедиться в этом, заметим сначала, что диаграмма (1)
показывает, что с точностью до гомотопической эквивалентности каждый член
последовательности (2) получен из двух предыдущих членов одной и той
же процедурой образования конуса отображения, поэтому достаточно
доказать, что последовательность (Л, К) <— (X, К)<— (ХиСЛ, К) точная. Это
§4.3. Связь с когомологиями
505
просто: отображение f:X-*K переходит в нуль в (Л, К) тогда и только
тогда, когда его ограничение на А гомотопно нулю с сохранением
отмеченной точки, а это эквивалентно тому, что / продолжается до отображения
XUCA-+K.
Если мы имеем слабую гомотопическую эквивалентность К —> £Ж' для
некоторого пространства К', то последовательность (3) можно
продолжить на три шага влево посредством коммутативной диаграммы
(Л, К)) — (X, К) — (Х/Л, К) — ...
Y Y Y
(ОА, К') ■<- (ПХ, 1С') ^ (ПХ/Л, /С') ^ ...
II I
(Л, 1С') ^ (X, К') ■<- (Х/Л, Г) ^ (ЕЛ, /С') ^ (ЕХ, К') + (ЕХ/Л, /С') ^ ...
Таким образом, если у нас есть последовательность пространств Ки
вместе со слабыми гомотопическими эквивалентностями Кп —»£ЖМ.Н, то мы
можем бесконечно продолжать последовательность (3) влево, получая при
этом длинную точную последовательность
... - (Л,Кп) - (Х,Кп) - (Х/Л,Кп) - (*,*„_!> - (Х,*,,.,) - ... (4)
Все члены здесь — абелевы группы и гомоморфизмы отображений. Эта
длинная точная последовательность естественна относительно
отображений (X, Л) —» (У, В), так как последовательности корасслоений
естественны. П
Нет никакой существенной разницы между теориями когомологий
на CVU-комплексах с отмеченными точками и теориями когомологий на
CW-комплексах без отмеченных точек. Если дана приведённая теория
когомологий /Г с отмеченными точками, то мы получаем неприведённую
теорию, полагая fr"(X, A) = hn{X/A), где Х/0 = Х, —объединение
пространства X и не принадлежащей ему отмеченной точки. Это теория без
отмеченных точек, так как любое отображение X —> У индуцирует
отображение Х+ —> Kf, сохраняющее отмеченную точку. Кроме того, неприведён-
ная теория h* без отмеченных точек даёт приведённую теорию, если
положить hn(X) = Coker(h"(точка)—> h"(X)), где отображение индуцировано
постоянным отображением X—>точка. Можно также привести
рассуждение, использующее надстройку, которая всегда является изоморфизмом
для приведённых теорий и которая осуществляет переход из категории
без отмеченных точек в категорию с отмеченными точками.
I Теорема 4.59. Если /Г — неприведённая теория когомологий на кате-
I гории CW-пар и hn (точка) =0 при и т^О, то имеют место естественные
I изоморфизмы /i"(X, Л) ** Н"(Х, А\ Л°(точка)) для всех CW-nap (X, Л)
I и всех п. Соответствующее утверждение для теорий гомологии тоже
I верно.
506
Глава 4. Теория гомотопий
Доказательство. Случай гомологии немного проще, поэтому
рассмотрим сначала его. Для CW-комилексов относительные группы
гомологии сводятся к абсолютным группам, поэтому достаточно разобраться
с последними. Для CW-комплекса X длинные точные последовательности
групп гомологии /iT для пар (Х",Х"~]) приводят к клеточному цепному
комплексу
... — hllTl (X"+I, X") ^ hn{Xn, X"-1) i /iM-1 (X»-1, X"-2) —+ ...
точно так же, как и для обычных гомологии. Из предположения, что
/i,, (точка) = 0 при /7^0, следует, что этот ценной комплекс имеет
группы гомологии hn(X); при этом используются те же рассуждения, что
и для обычных гомологии. Главное, что теперь нужно проверить, —это
то, что полученный клеточный цепной комплекс изоморфен клеточному
цепному комплексу для обычных гомологии с коэффициентами в группе
G = /г0(точка). Ясно, что клеточные группы цепей в обоих случаях
изоморфны, поскольку они являются прямыми суммами групп G, по одной
для каждой клетки, таким образом, мы должны только проверить, что
клеточные граничные отображения те же самые.
В действительности нет необходимости рассматривать клеточное
граничное отображение d, из одномерных цепей в нульмерные, так как
всегда можно перейти от X к ИХ, поскольку изоморфизм надстройки
—естественный изоморфизм в любой теории гомологии, а в двукратной
надстройке Е2Х нет никаких одномерных клеток.
Вычисление клеточных граничных отображений dn при п > 1 в
терминах степеней некоторых отображений сфер работает столь же хорошо для
теории гомологии /7*, где «степень» теперь означает степень относительно
теории h„. Поэтому нам нужен тот факт, что отображение S" —»S"
степени т в обычном смысле индуцирует умножение на т в ft„(S") ъС. Это,
очевидно, верно для степеней 0 и 1, представленных постоянным
отображением и тождественным отображением. Так как rr„(SM) ъХ, любое
отображение Sn —> S" гомотопно некоторому кратному тождественного
отображения, таким образом, общий случай будет доказан, если мы
удостоверимся, что степень в теории h+ аддитивна относительно операции суммы
в 7rn(S"). Это частный случай следующего более общего утверждения.
I Лемма 4.60. Если функтор h из CW-комплексов с отмеченными точ-
I ками в абелевы группы удовлетворяет аксиомам гомотопий и буке-
I та, то для любых двух сохраняющих отмеченные точки отображений
I /, g: EX —> К выполняются равенства (/ + g)+ =/* +&*, если h ковари-
I антен, и (/ + §)*=/* -f g*, если h контравариантен.
Доказательство. Отображение f + g —это композиция ИХ —> ЕХ V
VEX—>К, где с —отображение факторизации, стягивающее
экваториальную копию пространства X. В ковариантном случае рассмотрим диа-
§4.3. Связь с когомологиями
507
грамму
h(EX) -^ ИТ.Х V ЕХ) ^^ h(K)
h(SX)©h(SX)
где i] и i2 — включения ЕХ <-* ИХ V EX. Пусть qb q2: EX V EX -» EX —
отображения факторизации, которые тождественны на слагаемом,
соответствующем индексу, а другое слагаемое переводят в точку. Тогда
отображение qu ® 4*2* обратно отображению iu 012ж, так как q^ik
—тождественное отображение для j = к и постоянное отображение для )фк.
Элемент х группы h(EX) слева на диаграмме переводится
композицией (q1+ 0 ч*2*)с* в элемент О, х) нижней группы ft(EX) 0 fr(EX),
так как qxc и q2c гомотопны тождественному отображению.
Композиция (/Vg)*(iu 0i2J переводит (х, 0) в /„(*), а (0, у) в g„(y), так как
(/V£)i'i=/h (/Vg)i2 = g. Следовательно, (х,у) переходит в /Дх) +#Ду).
Объединяя эти факты, мы видим, что композиция вдоль верхней
части диаграммы —это х —> /LU) + g+(x). Но эта композиция равна также
(/ + g)*, так как / + g = (/ V g)c. Это завершает доказательство в ковари-
антном случае.
Контравариантный случай аналогичен. Нужно воспользоваться такой
же диаграммой со стрелками, направленными в противоположную
сторону. Обратное к i* 0i* отображение —это снова q* 0q*, согласно тому же
самому рассуждению. Элемент и в группе h(K) справа отображается в
элемент (/*("), g*(u)) в нижней группе ft(EX) 0fr(EX), так как (/Vg)^ = /
и (/ vg)l2 — &• Элемент (х, 0) в нижней группе в диаграмме отображается
в элемент х в группе слева, так как отображение q^c гомотопно
тождественному, и аналогично (0, у) отображается в у. Следовательно, {х, у)
отображается в х + у в группе слева. Мы получаем, что элемент u eh (К)
отображается композицией вдоль верхней части диаграммы в элемент
/*(и) +£¥(и) группы ft(EX). Но эта композиция по определению и есть
(/ + *)'• □
Возвращаясь к доказательству теоремы 4.59, мы видим, что
клеточные цепные комплексы для h*(X) и НДХ; G) изоморфны, поэтому мы
получаем изоморфизмы hn(X) ъ //„(X; G) для всех п. Чтобы проверить,
что эти изоморфизмы естественны относительно отображений /: X—* К,
мы можем сначала продеформировать такое отображение / так, чтобы
оно стало клеточным. Тогда / переводит любую пару (Х",ХМ !) в пару
(Yn, Y'1'1), следовательно, / индуцирует цепное отображение клеточных
цепных комплексов в теории h*, так же как и для НД-; С). Чтобы
вычислить это цепное отображение, мы можем перейти к факторотображе-
ниям Хи/Хп~l ->Yn/Y"- ]. Они имеют вид VaS£ —v^, поэтому индуци-
508
Глава 4. Теория гомотопий
рованные отображения /. на hn определяются своими компонентами —
отображениями fM\ S^-^S'L. Это в точности та же самая ситуация, что
и раньше для клеточных граничных отображений, где мы видели, что
степень отображения S" —> S" определяет индуцированное отображение
на /i„. Мы делаем вывод, что клеточное цепное отображение,
индуцированное отображением / в теории Лк, в точности согласуется с клеточным
цепным отображением для /-/*(—;G). Из этого следует, что изоморфизм
между этими двумя теориями естествен.
Ситуация для когомологий весьма похожая, но есть одно место в
рассуждениях, где нужно сказать ещё несколько слов. Для теорий
когомологий клеточные группы коцепей —прямые произведения, а не прямые
суммы, групп коэффициентов С = и°(точка), по одной для каждой клетки.
Это означает, что в случае бесконечного числа клеток данной
размерности не получается автоматически, что клеточные кограпичпые
отображения единственным образом определяются тем, как они отображают
множители одного прямого произведения на множители другого
прямого произведения. Л именно, рассмотрим клеточное кограиичное
отображение d„: h"(X", X""1)—>hn+[(Xn: \ X"). Представляя последнюю группу
как произведение групп G, по одной для каждой (п + 1)-мерной клетки,
мы видим, что dn определяется отображениями hu(Xn/X"~]) —>hn(S"t)t
соответствующими отображениям приклеивания фа клеток е"г1''\ Надо
обратить внимание на то, что образ отображения </?а компактен, поэтому
он пересекает конечное число п-мерных клеток, а значит, отображение
h"(Xn/Xn~l) —>h"(S"x) имеет конечный носитель в том смысле, что
существует такое разложение области определения в произведение конечного
числа множителей и произведение оставшегося, возможно, бесконечного
числа множителей, что отображение пулевое на последнем
произведении. Отображения с конечным носителем обладают тем хорошим
свойством, что они определяются своими ограничениями на множители G
в h"(Xn/Xn" ]). Из этого мы получаем, используя лемму, что клеточные
пограничные отображения в теории h* согласуются с такими
отображениями для обычных когомологий с коэффициентами в G. Это дополнительное
рассуждение необходимо также для того, чтобы доказать естественность
изоморфизмов 1\"(Х)ъНп(Х\ С).
Это завершает доказательство теоремы 4.59. —
Доказательство теоремы 4.57. Функторы h"(X) = (X, K{G, n))
определяют приведённую теорию когомологий, а группы коэффициентов
h"(S') = 7i,(X(G, /7)) совпадают с Hu(Sl\ G); таким образом, теорема 4.59,
переведённая на язык приведённых когомологий, даёт естественные
изоморфизмы Т: (X, K(G, /1)) —>//"(*; G) для всех GW-комплексов Х.
Остаётся убедиться в том, что Г([/]) =/*(а) для некоторого а £
GH"(i((G, /1); G), не зависящего от/. Это делается чисто формально:
возьмём а = Т(2)у где И —тождественное отображение пространства K(GjO-
§4.3. Связь с когомологиями
509
Тогда естественность даёт Т([/]) = Г(/*(1)) = /*Г(1) =/*(a), где первое
отображение /т— индуцированный гомоморфизм для функтора ft", что
означает композицию с /. □
Фундаментальный класс а = ГЦ) можно представить более явно, если
мы выберем в качестве X(G, п) CW-комплекс /С, у которого (п - 1)-мерный
остов состоит из одной точки. Обозначив (X,X(G, л)) через ft"(X), мы
тогда получаем
ft"(X) * ft"(Kn+1) % Kerd: ft"(X") — ft"+1(K"+1, X").
Отображение d является клеточной кограницей в когомологиях ft*, так
как мы имеем ft"(X") = ft"(X", X""1), потому что X""1 —точка, a ft"1
—приведённая теория. Изоморфизм группы ft"(X) на группу Kerd задаётся
ограничением отображений X —> К на X", поэтому элемент Heft"(X),
определяющий фундаментальный класс Т(1), при изоморфизме ft"(X)^Kerd
соответствует включению X" ^->Х, рассматриваемому как элемент
группы ft"(X"). Как клеточный коцикл, этот элемент сопоставляет каждой
п-мерной клетке в X элемент группы коэффициентов G = я„(Х), заданный
включением замыкания этой клетки в X. Это означает, что
фундаментальный класс aeHu(K\G) представлен клеточным коциклом,
сопоставляющим каждой п-мерной клетке элемент группы тг„(Х), заданный
характеристическим отображением для этой клетки.
Из естественности зоморфизма Т следует, что для клеточного
отображения /: X -* X соответствующий элемент группы //"(X; G)
представлен клеточным коциклом, переводящим каждую n-мерную клетку в X
в элемент группы G = 7in(X), представленный композицией отображения
/ с характеристическим отображением для этой клетки.
Естественный изоморфизм Н"(Х; G) ъ (X, X(G, п)) приводит к
основному принципу, который появляется во многих местах в
алгебраической топологии: возможность или невозможность определённого
явления управляется тем, что происходит в единственном частном случае,
универсальном примере. Чтобы проиллюстрировать это, давайте докажем
следующий специальный факт.
Отображение Н](Х; Z) —>Н2(Х; Z), а-* а2, тождественно нулевое для
всех пространств X.
Взяв CW-аппроксимацию пространства X, мы сводим ситуацию к
случаю, когда X —CW-комплекс. В этом случае любой элемент группы
Я!(Х; Z) имеет вид /*(а) для некоторого /: X —>X(Z, 1), где а
—фундаментальный класс в H!(X(Z, 1); Z). Это дальнейшее упрощение приводит
нас к проверке требуемого угверждения для этого единственного а,
«универсального примера». А для этого универсального а очевидно, что а = 0,
так как S] является пространством типа X(Z, 1) и H2(Sl\ Z) = 0.
Обобщается ли этот факт? Он, безусловно, перестаёт быть верным,
если мы заменим кольцо коэффициентов Z на Z2, так как H'CRP**"* <*У =
510
Глава 4. Теория гомотопий
= Z2M. Действительно, пример пространства 'КР°° показывает более
общее свойство, что фундаментальный класс а е Пи(К(7.2, п); Z2)
порождает подалгебру многочленов Z2[a] с //*(K(Z2, n); Z2) для любого
п ^ 1, так как существует отображение /: ^Р°° —> K(Z2,n), для
которого /*(a) = jf", а все степени монома хп отличны от нуля, а потому
и все степени класса а тоже. Применяя те же самые рассуждения, мы
видим, что пример пространства С?10 показывает, что
фундаментальный класс а е f/2"(X(Z, 2л); Z) порождает подалгебру многочленов Z[a]
в H"(K(Z,2h);Z). Как мы увидим в [SSAT], H*(K(Z, 2п); Z)/кручение-
в точности эта алгебра многочленов Z[a].
Более тонкий вопрос —нахождение подалгебры в НЖ(К(Ж, n); Z),
порождённой фундаментальным юшссом а, для нечётного л ^ 3. По свойству
коммутативности w-произведения мы знаем, что а2 — это либо нуль, либо
элемент порядка два. Чтобы убедиться, что элемент а2 отличен от нуля,
достаточно найти одно пространство X с таким элементом у eH"(X;Z),
что у2 ф0. Первым кандидатом могло бы быть пространство RP°°, но его
когомологии с коэффициентами в Z сконцентрированы в чётных
размерностях. Вместо этого рассмотрим пространство X = Rl:pu x RP00. Его
когомологии с коэффициентами в Z2 равны Z2[x,y], и пример З.Е.5
показывает, что его когомологии с коэффициентами в Z —это Z2[x2,
у2[-подмодуль, порождённый элементами 1 и х2у + гу2, конечно, кроме нулевой
размерности, где 1 порождает Z, а не Z2. В частности, мы можем взять
z — x2k(x2y -\-ху2) для любого к ^ 0, и тогда все степени zm отличны от
нуля, так как мы находимся в кольце многочленов Z2[x,y]. Из этого
следует, что подалгебра в H*(K(Z, n); Z), порождённая классом а, равна
Z[a]/(2a2) для нечётного л $?3.
Эти примеры побуждают задаться вопросом, насколько сложны
когомологии пространств K(G, л). Общая конструкция K(G,n) не очень
полезна для ответа на этот вопрос. Рассмотрим, например, случай G = Z.
Здесь можно было бы начать с S" и приклеить (п 4- 2)-мерные клетки,
чтобы убить 7T„H(SM). Так как группа nn+l(S") оказывается циклической,
необходима только одна (л + 2)-мерпая клетка. Чтобы продолжать, нам
придётся вычислить образующие группы тг„+2 полученного пространства
S"Ue"'f2 и, воспользовавшись ими, приклеить (л ■+- 3)-мерные клетки,
затем вычислить полученную группу 7т,1+3 и т.д. Для каждой последующей
размерности. Для п = 2 эта процедура, как оказывается, работает очень
чётко и даёт в качестве K(Z, 2) комплекс CP°° с его обычной
CW-структурой, с одной клеткой в каждой чётной размерности, согласно одной из
задач в конце этого параграфа. Однако для больших л использовать эту
процедуру затруднительно, так как гомотопические группы весьма трудно
вычислять. Можно получить некоторое представление о сложности
следующего случая л =3, рассматривал группы гомологии пространства K(Z, 3).
Используя методы из [SSAT], можно вычислить группы H((K(Z, 3); Z) Д71Я
§4.3. Связь с когомологиями
511
0^1^12:
Z, 0, 0, Z, О, Z2> О, Z3, Z2l Z2> Z3, Z10, Z2.
Чтобы получить эту последовательность групп гомологии, потребовалось
бы довольно много клеток, и ситуация только ухудшается в более высоких
размерностях, где группы гомологии не всегда циклические.
Можно было бы предположить, что вычисление групп гомологии
пространств K(Z, л) столь же сложно, как вычисление гомотопических
групп сфер, но некоторым чудесным образом дело обстоит не так.
Вычисления действительно сложные, но они были полностью проделаны
Серром и Картаном в 1950-е годы, и не только для пространств K(Z,n),
но и для всех K(G, n), где G — конечно порождённая абелева группа.
Например, Н*(К(Z, 3); Z2) — алгебра многочленов Z2[jc3, jcs, jc9, *1?>*зз> •••]
с образующими размерностей 2' +1, обозначенных нижними индексами.
И вообще, для конечно порождённой абелевой группы G когомологии
H*(K(G, n);Zp) —алгебра многочленов от образующих указанных явно
размерностей, если р равно 2, в то время как для нечётного простого
числа р получаем тензорное произведение кольца многочленов от
образующих чётных размерностей и внешней алгебры от образующих нечётных
размерностей, причём размерности образующих можно указать явно. Для
группы коэффициентов Ъ структура когомологии, однако, далеко не столь
регулярна. Мы изучим эти вопросы подробнее в [SSAT].
Существенный интерес к когомологиям пространств K(G,n) вызван
наличием эквивалентностей НП(Х; G) % (X, K(G, л)). Если взять для
простоты группу коэффициентов Z, то элемент группы H'"(K(Z, n); Z)
соответствует отображению в : K(Z, n) -*K(Z, m). Мы можем взять
композицию отображения 0 с любым отображением /: X -*K(Z, п) и получить
отображение 0/: X -*K(Z, m). Разрешив / изменяться и фиксировав 0,
мы получим отображение НМ(Х; Z) -*Н"'(Х; Z), которое зависит только
от в. В этом состоит идея когомологических операций, которые мы изучим
более подробно в §4.L.
Эквивалентность Я" (X; G) % (X,K(G, n)) приводит также к новой
точке зрения на w-произведения. Возьмём в качестве G кольцо R и положим
Кп = K(R, л). Тогда если заданы отображения /: X —* Кт и g: У —> К„, то
мы можем определить внешнее произведение соответствующих классов
когомологии посредством композиции
X х У > К,„ х Ки —* Кт Л К„ —* Кт+п,
где среднее отображение — отображение факторизации, а д можно
определить следующим образом. Пространство Кт Л Ки является (т + л — 3 )-связ-
Ным, поэтому согласно теореме Гуревича и формуле Кюинета для
приведённых гомологии мы получаем изоморфизмы
1„н,(К,„ЛК„) « Нт+п{КтЛК„) « H„,(Km)®H„(K„) « «®R-
512
Глапа 4. Теория гомотопий
Тогда согласно леммам 4.7 и 4.31 существует отображение д: Кт л Кп —»
—>/(,„+„, индуцирующее отображение умножения Я®К—>Я на 7гП1+;1. При
другом подходе мы могли воспользоваться изоморфизмом
Н,п+ЧКт Л К„; Я) * Hom(//M1+„(KMI л/С„), Я)
и взять в качестве и отображение, соответствующее классу когомологий,
заданному гомоморфизмом умножения R<8>R—>R.
Случай R — Ъ особенно прост. Возьмём S'" в качестве (ш 4-1)-мерпо-
го остова комплекса Кт, и аналогично для Кп, поэтому Кт /\Кп содержит
Sm AS" в качестве (т + п 4- 1)-мериого остова, и мы можем получить д,
продолжая включение Sm Л Sn = Srn'f" с-> Кщ+п.
Используя это определение, нетрудно доказать основные свойства
w-произведепия; в частности, свойство коммутативности с этой
точки зрения становится несколько более прозрачным. Например, когда
R = '£, коммутативность сводится просто к тому факту, что отображение
Sm Л S" —> Sn Л S'", переставляющее множители, имеет степень (-1)'"",
когда его рассматривают как отображение сферы S'M~".
Расслоения в смысле Гуревича
Напомним, что в §4.2 расслоение в смысле Гуревича определялось
как отображение р: Е—>Я, обладающее свойством поднятия гомотопий
относительно всех пространств. В локально тривиальном расслоении все
слои гомеоморфпы по определению, но это не всегда верно для
расслоений в смысле Гуревича. Примером служит линейная проекция
двумерного симплекса на одну из его граней, которая является расслоением
в смысле Гуревича согласно одной из задач в конце этого параграфа.
Следующий результат до некоторой степени свидетельствует о том, что
расслоения в смысле Гуревича нужно представлять себе как теоретико-
гомотопический аналог локально тривиальных расслоений.
I Предложение 4.61. Для расслоения в смысле Гуревича р: Е —* В все
слои Еь — р~]{Ъ) над каждой компонентой линейной связности
пространства В гомотопически эквивалентны.
Доказательство. Путь у: I —> В приводит к гомотопий gt: Еу(0) ~~* ^
с &(^у(о)) = У(0- Включение Fr(0)^>£ обеспечивает поднятие g(), поэтому
по свойству поднятия гомотопий мы получаем гомотопию g,: /\.(0) ■"* £
с gt(Fv(0)) с Fr(() для всех Г. В частности, gY даёт отображение Ly: /\(o) "*
—*Еу{{). Сопоставление у—► /,у обладает следующими основными
свойствами:
а) если y~/rel 1)1, то Lr^LY-\ В частности, гомотопический класс
отображения L не зависит от выбора поднятия g{ гомотопий &,;
б) для композиции путей уу' отображение /,,у гомотопно композиции
l.fLY.
§4.3. Связь с когомологиями
513
Из этих утверждений следует, что Ly — гомотопическая
эквивалентность с гомотопически обратным отображением 1^, где у — обратный путь
для пути у.
Прежде чем доказывать утверждение а), заметим, что расслоение
в смысле Гуревича обладает свойством поднятия гомотопии для пар
(X х /, X х Л/), так как пары (/ х /, / х {0} и dl х /) и (7 х /, / х {0}) гомео-
морфны, а значит, то же самое верно и после взятия произведений с X.
Докажем свойство а). Пусть y(s, r) — гомотопия отображения y(t)
в отображение y'(t), (s, г)е/ х /. Она определяет семейство gst: Fr(0) —►В,
где gst(Fr(0)) ==У(5. О- Пусть g0f и glr — поднятия, задающие отображения
1Г и 1у, и пусть g50 — включение FyC0) «->Е для всех s. Используя свойство
поднятия гомотопии для пары (FrC0) x /, Fy(0) x 31), мы можем продолжить
эти поднятия до поднятий gst для (5, 0 е / х /. Тогда при t = 1 мы получаем
гомотопию Ly ^ /,г/.
Свойство б) выполняется, так как для поднятий gt и g', задающих
отображения Ly и /у, мы получаем поднятия, задающие отображения Lyr>,
взяв£2г при0^г^1/2и^_^г при 1/2^t^l. П
Можно поинтересоваться, обладают ли расслоения в смысле
Гуревича гомотопическим аналогом свойства локальной тривиальности.
Заметим сначала, что для расслоения в смысле Гуревича р: Е -* В
ограничение р: р~х(А) -+ А — расслоение в смысле Гуревича для любого
подпространства Ас В. Таким образом, мы можем спросить, у любой ли точки
пространства В есть окрестность L/, для которой расслоение p~x(U)~» U
эквивалентно в некотором теоретико-гомотопическом смысле проекции
U х F —+U. Естественное понятие эквивалентности для расслоений в
смысле Гуревича определяется следующим образом. Пусть даны расслоения
в смысле Гуревича рл: Е} -*В и р2: Е2—>В. Отображение /: Е} -+Е2
называют послойным., если р} = p2f, или, другими словами, f(p^x(b)) Ср~1(Ъ)
для всех Ъ^В. Послойное отображение f \ ЕЛ-* Е2 является послойной
гомотопической эквивалентностью, если существует послойное
отображение g: E2-*E]t для которого обе композиции fg и gf гомотопны
тождественному отображению в классе послойных отображений. Послойную
гомотопическую эквивалентность можно представлять себе как
семейство гомотопических эквивалентностей между соответствующими
слоями расслоений Ех и Е2. Интересен тот факт, что послойное отображение,
которое является гомотопической эквивалентностью, является послойной
гомотопической эквивалентностью; это одна из задач в §4.11.
Покажем, что расслоение в смысле Гуревича р: Е -* В является
локально послойно гомотопически тривиальным в смысле, описанном
выше, если пространство В локально стягиваемо. Но перед этим мы сначала
сделаем отступление, чтобы ввести другое фундаментальное понятие.
Если дано расслоение в смысле Гуревича р: Е—> В и отображение
/• А —> В, то можно определить индуцированное расслоение /ЧЮ ~* ^>
17 Зак. V)S<
^i*t
Глава 4. Теория гомотопий
положив /*(Е) = {(а, в) е А х Е|/(а) = р(е)}; проекции f*(£) ^ £
/*(Е) на А и на Е задают коммутативную диаграмму i i
(см. рис.). Свойство поднятия гомотопий выполняется \ f \р
для отображения /* (Е) —* Л, так как гомотопия gt: X —> А А >- В
задаёт первую координату поднятия g(: X —►/*(#)> а вторая координата —
поднятие в Е гомотопий, которая является композицией f gr
I Предложение 4,62. Пусть даны расслоение в смысле Гуревича р;
Е —► В и гомотопия /j: А —► В. Тогда индуцированные расслоения /0*(Е) —>
—►Ли /^(Е) —*Л послойно гомотопически эквивалентны.
Доказательство. Пусть F: А х / —►В — это гомотопия /,. Расслоение
F*(E) -»Д х / содержит /0*(Е) и /*(Е) над Л х {0} и над Л х {1}. Таким
образом, достаточно доказать следующее: для расслоения р: Е -+ В х I
все расслоения Es = p~l[B x {s}) -+ В, являющиеся его ограничениями,
послойно гомотопически эквивалентны для s€ ГО, 1].
Идея доказательства этого утверждения состоит в имитации
построения гомотопических зквивалентностей Ly из доказательства
предложения 4.61. Путь у: [0,1] -*/ даёт послойное отображение Ly: Er(0) -*Еу(1)
посредством поднятия гомотопий
&: Ey(0) ->BxI, gtM = (рО), у (О),
начинающегося с включения Еу(0) ^-> Е. Как и раньше, можно доказать два
основных свойства а) и б), заметив, что в п. а) гомотопия Ly^h ,
послойная, так как она получена поднятием гомотопий h{: Еу(0) х [0,1] -*В х /
вида ht О, и) = (р(х), -). Из п. а) и б) следует, что /,у — послойная
гомотопическая эквивалентность с обратным отображением Ly. □
I Следствие 4.63. Расслоение в смысле Гуревича Е —* В над
стягиваемой базой В послойно гомотопически эквивалентно расслоению-
произведению В xF-+B.
Доказательство. Расслоение, индуцированное из Е тождественным
отображением В —>В, — это само Е, в то время как расслоение,
индуцированное постоянным отображением В—*В, — произведение В xF. □
Таким образом, мы видим, что если пространство В локально
стягиваемо, то любое расслоение над В локально послойно гомотопически
эквивалентно расслоению-произведению.
Конструкции с пространством путей
Существует просгой, но чрезвычайно полезный способ превратить
произвольное отображение в расслоение. Если дано отображение /: Д-*В, то
пусть Ej — пространство пар (а, у), где аеДи/:/—>В — путь в В, для
которого у(0) =/(а). Мы тогюлогизируем Ef как подпространство вЛхВ', где
В1 —пространство отображений / —>В с компактно-открытой топологией.
Определение и основные свойства этой топологии можно найти в
приложении, см. также предложение П.14, которым мы вскоре воспользуемся.
§4.3. Связь с когомологиями
515
Предложение 4.64. Отображение р: Ef-^B, p(a, у) = у(1), является
расслоением в смысле Гуревича.
Доказательство. Непрерывность отображения р следует из
утверждения а) предложения П.14 в приложении, согласно которому
отображение В7 х/-*В, (r,s)->y(s), непрерывно.
Чтобы проверить свойство расслоения, предположим, что даны
гомотопия gt: X -+В и поднятие g0: X-*Ef отображения g0. Запишем g0(x) =
= (ftО), Yx) Для h: X -* А и ух: I —> В. Определим поднятие gt: X —► Ef
формулой
где вторая координата — это путь уХУ после которого проходится путь,
заметаемый точкой gs(x) за время 0 ^ s ^ t. Эта композиция путей
определена, так как g0(x) = pg0M — T.vO)- Чтобы проверить, что гомотопия
gt непрерывна, мы рассмотрим её как отображение X х I -+ Ef (Z А х В1,
а затем применим утверждение б) из предложения П.14, которое в
данном контексте означает, что непрерывность отображения X х I —> А х В1
эквивалентна непрерывности соответствующего отображения X xl xl —►
->ДхВ. D
Мы можем рассматривать А как подпространство в Ej, состоящее
из пар (а, у), где у — постоянный путь в точке /(а), и Ej
деформационно ретрагируется на это подпространство, если ограничивать все
пути у всё более и более короткими начальными отрезками. Отображение
р: Ef—*B ограничивается до / на подпространстве А, поэтому мы
получаем представление произвольного отображения /: А-*В в виде
композиции А <^-> Ej -+ В гомотопической эквивалентности и расслоения в
смысле Гуревича. Мы можем также представлять себе эту конструкцию как
продолжение отображения / на расслоение Ef -* В, увеличивая его
область определения до гомотопически эквивалентного пространства. Слой
Ff расслоения Ej-*B называют гомотопическим слоем отображения /. Он
состоит из всех пар (а, у), где аеЛиу- путь в В из точки /(а) в
отмеченную точку Ь0^В.
Если /: А -* В — включение подпространства, то Ef — пространство
путей в В, начинающихся в точках подпространства А. В этом случае
отображение (/, + 1, d/'+I, J1) —> (В, Л, х0) —то же самое, что и отображение
(/', dV) -* (fy, y0)i гДе То ~~ постоянный путь в точке jc0, a Ff —слой
расслоения Ef над х0. Это означает, что 7Г/+1(В, Л, х0) можно отождествить
с 7T,-(Fy, y0), следовательно, длинные точные последовательности
гомотопических групп пары (В, А) и расслоения Ef-*B можно отождествить.
Важный частный случай получается, когда / — включение
отмеченной точки Ь0 в В. Тогда Ef — пространство РВ путей в В, начинающихся
в Ь0, и р: РВ —* В отображает каждый путь в его конец. Слой р~ (Ь0) —
Пространство петель ПВ, состоящее из всех петель в В с началом и кон-
516
Глава 4. Теория гомотопий
цом в Ь0. Так как пространство РВ можно стянуть, постепенно
укорачивая пути, длинная точная последовательность гомотопических групп для
расслоения путей РВ —»В приводит к другому доказательству того, что
лп(Х, х0) ъ пп^(ПХ9 х0) для всех а.
Как мы уже упоминали при обсуждении пространств петель ранее
в этом параграфе, имеет место теорема (см. [115]) о том, что
пространство петель CW-комплекса гомотопически эквивалентно CW-комплексу.
Теорема Милпора в действительности немного более общая, и из неё
следует, в частности, что гомотопический слой произвольного отображения
CW-комплексов имеет гомотопический тип CW-комплекса. Обычно
можно избежать ссылки на эти результаты, воспользовавшись СУУ-аппрокси-
мациями, но будет спокойней, если знать, что эту теорему можно
применить при необходимости или если не хочется иметь дело с CW-аппрокси-
мациями.
Если конструкцию расслоения / —» Ej применить к отображению
р: Е—*В, которое уже является расслоением, то можно ожидать, что
полученное расслоение Ер—*В будет тесно связано с исходным расслоением
Е —* Б. Это действительно так.
I Предложение 4.65. Если р: Е —> Б — расслоение в смысле Гуревича,
I то включение Е с-> Ер —послойная гомотопическая эквивалентность.
I В частности, гомотопические слои отображения р гомотопически экви-
I валентны настоящим слоям.
Доказательство. Применим свойство поднятия гомотопий к
гомотопий gt: Efi —> Б, gt(e,f) = y(i), с начальным поднятием g0: Ер —* Е,
£о(е>У) = е- Тогда поднятие g,: Ер—>Е — первая координата гомотопий
ht: Ер —> Ер, вторая координата которой — ограничение путей у на отрезок
[f,l]. Так как концы путей у не изменяются, гомотония ht послойная.
Мы получаем h0 = 1, h{(Ep) с Я и h((£) <zE для всех t. Если обозначить
через i включение Е<—^Ер9 то ih{ ~1 посредством гомотопий ht и h}i^l
посредством гомотопий ht\E, таким образом, i —послойная
гомотопическая эквивалентность. □
Мы видели, что пространства петель встречаются в качестве слоев
расслоений РВ —> В со стягиваемым пространством расслоения РВ. Вот
нечто вроде обратного утверждения.
I Предложение 4.66. Если F —>£ —>Б — расслоение в смысле Гуревича
или локально тривиальное расслоение, для которого Е стягиваемо, то
существует слабая гомотопическая эквивалентность F —>£1В.
Доказательство. Если мы рассмотрим композицию стягивания
пространства Е и проекции р: Е —> Б, то получим для каждой точки х € Е путь
ух в В из точки рО) в отмеченную точку Ь0 = р(х()), где х0 — точка, в
которую стягивается Е. Это даёт отображение Е—*РВ, jc-*f_v, композиция
которого с расслоением РВ—>В равна р. При ограничении оно даёт отоб-
§4.3. Связь с когомологиями
517
ражение F —► ПВ, где F = р-1 (Ь0), и длинная точ- „ ^ тг
нал последовательность гомотопических групп для i i ^ ,,
F —> Я —> В отображается на длинную точную после- | j ||
довательность для QB -^> РВ-+ В. Так как простран- &>В ^ РВ >- в
ства Е и РВ стягиваемы, из 5-леммы следует, что
отображение F —> QB — слабая гомотопическая эквивалентность. □
Примеры, возникающие из локально тривиальных расслоений,
построенных ранее в этой главе, —это 0(п) ^ ftG^R00), U(n) ~ ^GM(C^)
HSpCn^ftG^E00). В частности, взяв в последних двух примерах п — 1, мы
получаем S1 ~^СР°° и Я^ГШР00. Отметим, что во всех этих примерах
пространству петель гомотопически эквивалентна топологическая
группа. В [112] показано, что для любой топологической группы G
существует локально тривиальное расслоение G—► EG -^ BG со стягиваемым
пространством EG; следовательно, согласно предложению 4.66 существует
слабая гомотопическая эквивалентность G^QBG. Верно также обратное
утверждение: пространство петель любого CVU-комплекса гомотопически
эквивалентно топологической группе.
Связь между X и QX была подробно изучена, особенно случай, когда
£1Х имеет гомотопический тип конечного CW-комплекса, который
представляет большой интерес из-за примеров классических групп Ли, таких
какО(п), U(n) и Sp(n). Введение в эту тематику можно найти в книге [40J.
Интересно посмотреть, что происходит, когда процесс образования
гомотопических слоев повторяется. Если дано расслоение р: Е —> В со
слоем F = p~l(b0), то мы знаем, что включение пространства F в
гомотопический слой Fp — гомотопическая эквивалентность. Напомним, что F
состоит из пар (е, у), где ее£ и у — путь в В из р(е) в Ь0. Включение Fc—>F
продолжается до отображения [\ Fp-+Ey i(e, у) = е, и это отображение,
очевидно, является расслоением в смысле Гуревича. В действительности
оно индуцировано посредством проекции р из расслоения путей РВ—* В.
Это позволяет нам повторить конструкцию, взяв гомотопический слой F,-
вместе с его отображением в Fp и т.д., как в первой строке следующей
диаграммы:
... ^ Fj ^ F,- —U- Fp —U- F —^ Б
**| *!! -| II II
!y п р К I II II
... ^ ft£ —U- ЛВ > F ^ F —-^ Б
Настоящий слой отображения i над точкой е0ер" Т(Ь0) состоит из пар
(е0, у), где у — петля в Б с началом и концом в отмеченной точке Ь0, таким
образом, этот слой —просто QB, а включение QB*-* F, — гомотопическая
эквивалентность. Во второй строке диаграммы отображение QB —>F —
композиция VLB ^-> F, —> Fp —> F, где последнее отображение —
гомотопические обратное к включению F c-^ F поэтому квадрат в диаграмме, со-
518
Глава 4. Теория гомотопий
держащей эти отображения, коммутативен с точностью до гомотопий.
Гомотопический слой F, состоит из пар (у, rj), где г\ — путь в Е,
заканчивающийся в е0, а у —путь в В из р(г)(0)) в Ь0. Отображение, гомотопически
обратное к включению VLB<—* F,-, — ретракция F, -* ftB, переводящая (у, г\)
в петлю, полученную при композиции обратного пути для рг\ с у. Эти
конструкции можно теперь повторять неограниченно.
Так мы получаем последовательность
... — П2В — VLF — ftE — ПВ — F — Е — В,
где любые два последовательных отображения образуют расслоение в
смысле Гуревича с точностью до гомотопической эквивалентности и все
отображения слева от VLB получены применением функтора VL к
последующим отображениям. Мы оставляем читателю проверить, что длинная
точная последовательность гомотопических групп для любого расслоения
из этой последовательности совпадает с длинной точной
последовательностью для F -+Е-+В.
Башни Постникова
Башня Постникова для линейно связного пространства :
X — это коммутативная диаграмма справа, в которой:
1) отображение X—> Хп индуцирует изоморфизм групп я,-
при i^n;
2) я,-(Х„) = 0 при |>п.
Как мы видели в примере 4.17, любой связный CW-kom-
плекс X имеет башню Постникова, причём она
единственна с точностью до гомотопической эквивалентности согласно
следствию 4.19.
Если мы превратим отображение Хп-+Хп_х в расслоение, то его слой
Fn является пространством типа К(япХ,п), что сразу видно из длинной
точной последовательности гомотопических групп для расслоения:
*i+iW -* Я|+](*„-1) -* Щ&п) — я,(Хп) -* щ{Хп-0.
Мы можем заменить каждое отображение Хп —> Хп_^ на расслоение
Х'п -* Х'п_г последовательно, начиная с Х2-+Х{ и идя вверх. Для
доказательства шага индукции мы преобразуем композицию с „,
Хп-*Хп_г t-^X/n_ml в расслоение X'n-*X' v которое
вписывается в коммутативную диаграмму справа. Так мы
получим башню Постникова, удовлетворяющую дополни- %' с ^ х'
тельному условию
3) отображение Хп —>X„_i —расслоение в смысле Гуревича со слоем
К(япХ,п).
В той же степени, в какой расслоения в смысле Гуревича можно
рассматривать как скрученные произведения с точностью до
гомотопической эквивалентности, пространства Хп в башне Постникова для X можно
§ 4.3. Связь с когомологиями
519
представлять себе как скрученные произведения пространств Эйленбер-
га—Маклейна К(тгм(Х),п).
Для многих целей CW-комллекс X можно заменить на один из
этажей Хп башни Постникова для X, например, если нас интересуют
гомотопические группы или группы гомологии лишь в конечном диапазоне
размерностей. Однако, чтобы определить полный гомотопический тип
пространства X по его башне Постникова, необходим своего рода
предельный процесс. Давайте исследуем этот вопрос в несколько большей
общности.
Пусть дана последовательность отображений ... —>Х2 -»Х1.
Определим её обратный предел lim Xn как подпространство в произведении П„ХП,
состоящее из таких последовательностей точек хп е Хп, что хп
переходит в хп_! при отображении Х„-*ХП_1. Соответствующее
алгебраическое понятие —обратный предел ПтХ„ последовательности
гомоморфизмов групп ... —» G2 —>G^, который является подгруппой в n„G„, состоящей
из таких последовательностей элементов gM е G„, что gn переходит в gn_j
при гомоморфизме Gn —>Gf,_1.
I Предложение 4.67. Для любой последовательности расслоений ... —»
I -*Х2-*Х1 естественное отображение А: 7r,(limXn) -*Птя,-(Х„) сюръек-
I тивно, и А инъективно, если отображения тг/+1(Хп) —> тг[+1(Хп„1) сюръ-
I ективны для достаточно больших п.
Доказательство. Представим элемент группы Нттг,-(ХП)
отображениями /„: (Sl,sQ) —> (Хм,хп). Так как проекция рп: Хп —> Хп_: переводит
[/п] в [/„_!], применяя свойство поднятия гомотопии для пары (Sl,s0),
мы можем прогомотопировать/м, оставляя точку s0 неподвижной, так, что
Рп/п =/n-i' Делая это по индукции для п = 2, 3,..., мы получаем р„/п = /„_i
для всех п одновременно, что и даёт сюръективность отображения А.
Для доказательства инъективности сначала заметим, что обратные
пределы не замечают отбрасывания конечного числа членов в конце
последовательности пространств или групп, поэтому мы можем считать,
что отображения тг,-+1(Хп) —» тг,Ч1(Хп_1) сюръективны для всех п. Пусть
дано отображение /: S' -*ИтХп. Предположим, что имеются гомотопии
Fn: DI+1 -*Х„, связывающие с постоянным отображением координатные
функции /п: S1 —>ХП отображения /. Мы получаем pnFn — Fn_^ на S',
поэтому pnFn и Fn_! можно рассматривать как ограничения на две
полусферы в S'+1 некоторого отображения gn_i: S'+1 -♦Хп_1. Если отображение
я|-+1(Хп) —> 7г,-+1(Хп_г) сюръективно, мы можем по-другому выбрать Fn так,
чтобы новое отображение gfl_^ было гомотопно постоянному, т. е. так, что
pnFn ~Fn_1rel S'. Применяя свойство поднятия гомотопии для (Dl+1,Sl),
мы можем добиться того, что pnFn =F„_1. Делая это по индукции для
п = 2, 3,..., мы видим, что отображение /: S' -*ИтХп гомотопно
постоянному и А инъективно. О
520
Глапа 4. Теория гомотопий
Может понадобиться описание ядра отображения А в случае
произвольной последовательности расслоений ...--> Х2-* Xlf хотя к нашим
непосредственным целям этот вопрос не имеет отношения. В
действительности КегА естественно изоморфно группе lim17r/H_1(Xn)> где lim1 —
функтор, определённый в § 3.F. А именно, если отображение /: S'-*
—> lim Xn определяет элемент из Кег А, то последовательность отображений
gn: S,+1 —>ХП, построенных выше, даёт элемент из Ппяг>1(Хп), который
корректно определён с точностью до выбора гомотопий Fu. Любой
другой выбор Fn получается прибавлением отображения Gn: S,+1 —»Х„ к Fn.
Эффект от этого состоит в замене gn на gn +Gn и gn_, на gn_} - pnG„. Так
как lim1я|Ч {(Х„) — факторгруппа произведения П„ я,+1 (Х„) в точности для
таких отождествлений, мы получаем КегА^ lim1 я^СХ,,). Таким образом,
для каждого i > 0 имеет место естественная точная последовательность
0 -> \ип]пИ](Хп) -> я,(НтХп) -> Нтя,(Х„) -> 0.
Предложение 4.67 говорит нам, что член lim1 обращается в нуль, если
отображения я|Ч1(Х„) —► я^СХ,,^) сюръективны для достаточно
больших п.
Следствие 4.68. Для башни Постникова связного CW-комплекса Х
естественное отображение X—> lim X,2 — слабая гомотопическая
эквивалентность, таким образом, X является CW-аппроксимацией к limXM.
Доказательство. Композиция я, (X)—> я, (lim XJ—> lim я, (Х„)—
изоморфизм, так как я,(Х) —» я,(Х,2) — изоморфизм для достаточно
большого п. П
Посмотрев, как раскладывается пространство X в члены в его башне
Постникова, мы рассмотрим теперь обратный процесс построения башни
Постникова, начиная сХ3 как К(п, 1) и индуктивно строя Хм поХп_}. Было
бы очень хорошо, если бы расслоение К(п,п) —>ХП —►Хм_1 можно было
продолжить ещё одним членом справа, образуя при этом
последовательность расслоения
поскольку это означало бы, что Хп —гомотопический слой
отображения Хп_х -*К(тг,п -Ь 1), а гомотопические классы таких отображений
находятся во взаимно однозначном соответствии с элементами
группы Нп+1(Хп .у', я) согласно теореме 4.57. Так как гомотопический слой
отображения Хп_{ —► К (я, п + 1) —то же самое, что расслоение,
индуцированное из расслоения путей РК(п,п ■+■ 1) —> К(пуп + 1), его
гомотопический тип зависит только от гомотопического класса отображения
Xn._i —> К(я, п 4-1) согласно предложению 4.62. Заметим, что последний
член /С(я, п + 1) в приведённой выше последовательности расслоения не
§4.3. Связь с когомологиями
521
может быть ничем, кроме К (л, л 4-1), так как его пространство петель
должно быть гомотопически эквивалентно первому члену в
последовательности, т. е. К(п, л).
В общем случае расслоение F—>Е —>В называют главным, если
существует коммутативная диаграмма
F ^Е ^В
Y Y Y
ПВ' >- F* >- А" >- В'
вторая строка которой —последовательность расслоения, а вертикальные
отображения — слабые гомотопические эквивалентности. Таким образом,
если все расслоения в башне Постникова для X окажутся главными, то мы
имеем диаграмму
К(я3Х, 3) >» Х3 —^-*- К(я4Х, 5)
К(я2Х, 2) >- Х3 —^ К(я3Х, 4)
J.
К^Х, 1) = Х1 —U- К(я2Х, 3)
где каждое пространство Х,2+1 с точностью до слабой гомотопической
эквивалентности является гомотопическим слоем отображения fc„: Хп —>
—>/C(7r„_i_1, п И-2). Отображение fc„ эквивалентно классу вЯ""|_2(Х„; я„+1Х),
называемому п-м k-инвариантом пространства X. Эти классы
определяют, как строить X по индукции из пространств Эйленберга—Маклей-
на. Например, если все кп равны нулю, то X — просто произведение
пространств К(ппХ, л), а в общем случае X —своего рода скрученное
произведение пространств К(ппХ, л).
Реальное построение пространства по его /с-инвариантам — обычно
слишком громоздкая процедура, чтобы выполнять её практически, но как
теоретический инструмент эта процедура может быть весьма полезной.
Следующий результат говорит нам, когда этим инструментом можно
воспользоваться.
I Теорема 4.69. Связный CW-комплекс Х имеет башню Постникова из
главных расслоений тогда и только тогда, когда действие группы я] (X)
на яп(Х) тривиально для всех л > 1.
Заметим, что в определении главного расслоения отображение F —*
—>QB' автоматически существует и является слабой гомотопической
эквивалентностью, как только есть правый квадрат в коммутативной
диаграмме с вертикальными отображениями —слабыми гомотопическими
522
Глава 4. Теория гомотопий
эквивалентностями. Таким образом, вопрос о том, является ли
расслоение главным, можно переформулировать следующим образом. Пусть дано
отображение А —>X (которое, если угодно, всегда можно заменять
эквивалентным расслоением); существуют ли расслоение F -* Е -* В и такой
коммутативный квадрат на рисунке, в котором вертикальные
отображения — слабые гомотопические эквивалентности? Ее- , ^ .
ли заменить Л и X их CW-аппроксимациями и преобразовать | |
получающееся при этом отображение А -* X во включение но- F —*■ К
средством цилиндра отображения, то вопрос становится
таким: эквивалентна ли CW-napa (X, А) паре расслоения (F,F), т.е.
существуют ли расслоение F -+Е-+В и отображение (X, А) -* (F, F), для
которых оба отображения X —► Е и А —► F являются слабыми гомотопическими
эквивалентностями. В общем случае ответ редко бывает утвердительным,
так как гомотопический слой отображения А с—► X должен тогда иметь
слабый гомотопический тип пространства петель, что является довольно
серьёзным ограничением. Однако в случае башен Постникова
гомотопический слой — пространство типа К(7г, п) с абелевой группой я при п ^2,
таким образом, это пространство петель. Но есть ещё одно требование:
действие группы кх(А) на ям(Х, А) должно быть тривиальным для всех
п ^ 1. Это эквивалентно тому, что действие группы tc^F) на ям(£, F)
тривиально, а это всегда имеет место для расслоения, так как при
изоморфизме р*: 7T„(E,F) —>nn(B,xQ) элементуа-а, гдеу€ TCj(F) и a€rcM(F,F),
переходит в элемент рж()0р*(а) - рг(а), который равен нулю, поскольку
рДу) лежит в тривиальной группе tz^Xq).
Относительная группа ям(Х, А) всегда изоморфна группе тгм_1
гомотопического слоя включения А <—* X, поэтому в нашем случае, когда
гомотопический слой— пространство К(пу п), единственная нетривиальная
относительная гомотопическая группа — это 7гп+ х (X, А) ъ п. В этом случае
необходимое условие тривиальности действия оказывается также и
достаточным.
I Лемма 4.70. Пусть (X, Л)—такая CW-napa со связными простран-
I ствами X и Л, что гомотопический слой включения А с—► X является
I пространством типа К(п, п), п^ 1. Расслоение F-+E-+ В и отображение
I (Х,Л) —► (Е, F), индуцирующее слабые гомотопические эквивалентно-
I сти X —* Е и Л -* F, существует тогда и только тогда, когда действие
| группы яг(А) на л„+1(Х, А) тривиально.
Доказательство. Остаётся доказать только утверждение «тогда». Как
мы отметили как раз перед формулировкой этой леммы, группы 7Г,(Х, Л)
нулевые, за исключением 7гп;1(Х, Л) ъ л. Если действие группы пх(А)
на тгп+1(Х, А) тривиально, то относительная теорема Гуревича даёт
изоморфизм ям+1(Х, А) ^НМ+1(Х, А). Так как пара (X, А) является п-связной,
мы можем предположить, что А содержит п-мерный остов комплекса X.
§4.3. Связь с когомологиями
523
поэтому пространство Х/А является п-связным, и абсолютная теорема
Гуревича даёт изоморфизм пп+}(Х/А) ъНп+](Х/А). Следовательно,
отображение факторизации X —> Х/А индуцирует изоморфизм тгм+1(Х,Л)^
«яп+1 (Х/А), так как аналогичное утверждение для гомологии, очевидно,
верно.
Так как тгп+1 (Х/А) as я, мы можем построить К (я, п 4-1) из Х/А,
приклеивая клетки размерности n + Зи выше. Это приводит к коммутативной
диаграмме
А ^Х + Х/А
К(я,п + 1)
где вертикальные отображения —включения, а нижняя строка получена
при преобразовании отображения к в расслоение. Отображение A-+Fk
является слабой гомотопической эквивалентностью согласно 5-лемме,
применённой к отображению между длинными точными
последовательностями гомотопических групп для пар (X, А) и {Ек, Fk)y так как
единственные нетривиальные относительные группы —это группа я,|+1, обе из
которых отображаются изоморфно на яп+1(/С(тг, п + 1)). □
Доказательство теоремы 4.69. Лемма 4.70 показывает, что нужно
только отождествить действие группы ят(Х) на яп(Х) с действием
группы Ях(Хп) на nn+i(Xn^lt Хп) при п ^ 2, представляя себе отображение
Хп—>Х„_! как включение. Из точной последовательности
0 = пп^(Хп^) - яп+1(Хп_ьХп) Л Яп(х„) - *„(*„_,) = 0
мы получаем изоморфизм я^^Х,,.!, Х„) ^ я„(Хп), уважающий действие
группы я^Х,,). А отображение X—>Х„ индуцирует изоморфизмы для п}
и ял, и, таким образом, доказательство завершено. □
Рассмотрим теперь естественное обобщение
башен Постникова, в котором мы начинаем с
отображения /: X—► У линейно связных пространств, а не
просто с одного пространства X. Башня
Мура—Постникова для отображения / — коммутативная
диаграмма справа в которой каждая композиция X —► Zn —> У
гомотопна отображению / и при этом выполняются
следующие условия.
1. Отображение X—>Zn индуцирует изоморфизм групп
я, при i <п и сюръекцию при i = n.
2. Отображение Zn —► У индуцирует изоморфизм групп я, при i > п
и инъекцию при i = n.
3. Отображение Zn+1 —> Zn — расслоение в смысле Гуревича со слоем
K(nuFy n), где F — гомотопический слой отображения /.
524
Глава 4. Теория гомотопии
Из башни Мура—Постникова получается, в частности, башня
Постникова, если мы возьмём в качестве Y точку, а затем положим Xn=Zn+b
отбросив пространство Z]y гомотопические группы которого тривиальны.
I Теорема 4.71. Любое отображение /: X —► У связных CW-комилексов
I имеет башню Мура—Постникова, причём единственную с точностью
I до гомотопической эквивалентности. Башня Мура—Постникова, состо-
I ящая из главных расслоений, существует тогда и только тогда, когда
I действие группы яДХ) на яп(Мг,Х) тривиально для всех п > 1, где
J My — цилиндр отображения /.
Доказательство. Существование и единственность диаграммы,
удовлетворяющей условиям 1 и 2 и при этом коммутативной, по крайней
мере с точностью до гомотопии, следуют из предложений 4.13 и 4.18,
применённых к паре (My, X), где My— цилиндр отображения /. Имея такую
диаграмму, мы действуем так же, как в рассмотренном ранее случае
башен Постникова, заменяя каждое отображение Zn —>Zn...} гомотопически
эквивалентным ему расслоением, начиная с Z2 —*Z\ и двигаясь вверх. Мы
можем затем применить свойство поднятия гомотопии, чтобы сделать все
треугольники в левой половине башни строго коммутативными. После
того как это сделано, треугольники в правой половине диаграммы
коммутативны с точностью до гомотопии, и чтобы сделать их строго
коммутативными, мы можем просто заменить каждое отображение в У на
композицию, проходящую через Zx.
Чтобы убедиться, что слои отображений Zn+] —*Zn
являются пространствами Эйленберга—Маклейна, как
в условии 3, рассмотрим два последовательных этажа
башни на рисунке. Мы можем добиться, чтобы
отображения X —> Z„+1 —> Zn —> У были включениями, взяв
цилиндры отображений сначала для X—>Zn+ly затем для нового
отображения Z„ + 1 —>ZU, а затем для нового отображения Zn —► Y. Из
треугольника слева мы видим, что отображение Zn+] —*Zn индуцирует изоморфизм
групп я,- при i <п и сюръекцию при i = n, следовательно, яД^,, Z,,^])-О
при i < п + 1. Аналогично другой треугольник даёт яД£„, ZM+1) =0 при
i > л + 1. Чтобы доказать, что я„+1 (Z,„ Zu^) ъ яп+1 (У, X), мы
воспользуемся следующей диаграммой:
Y Y Y Y т
яп+1(/„+1) —*■ ям.м(У) —*• я„ч(У,£м+1) --*■ nn{Zn+{) —>- я,ДУ)
! t- t f- !"
n„+](X) > n„+l(Y) п„и(У, X) n„(X) —+n„(Y)
Верхнее справа вертикальное отображение инъективно, а нижнее ел
ва вертикальное отображение сюръективно, поэтому из 5-лсммы следу
Z„,
У
s
§4.3. Связь с когомологиями
525
ет, что два средних вертикальных отображения —изоморфизмы. Так как
у гомотопического слоя включения А<-^В группа я,- равна я,Ч1(В, А), мы
видим, что условие 3 выполняется.
Утверждение о башне, состоящей из главных расслоений, можно
получить, применив лемму 4.70. Как мы видели в предыдущем абзаце, имеют
место изоморфизмы
причём они уважают действие группы Я](Х) ъ rci(Zn+1), поэтому лемма
4.70 даёт требуемое утверждение. □
Помимо случая, когда У —точка, который приводит к башням
Постникова, другой интересный частный случай башен Мура—Постникова
получается, когда X—точка. В этом случае
пространство Zn — это n-связное накрытие
пространства У, как в примере 4.20. Можно также получить
n-связное накрытие пространства Y как гомотопи- Л ^ к(п Y 41
ческий слой п-го этажа Y —> Yn башни Постникова .
для Y. Башню n-связных накрытий пространства Y \
можно реализовать главными расслоениями, взяв Zx ^K(n2Y,2)
в качестве Zn гомотопический слой отображения I
Zn-i~+K(nnY, п), т.е. первого нетривиального эта- т
жав башне Постникова для Zn_1. ^ "*" К(ям > *■)
Обобщение предыдущей теории, допускающее нетривиальные
действия группы Я], можно найти в [123].
Теория препятствий
Очень часто в алгебраической топологии встречаются ситуации,
когда нужно продолжить или поднять данное отображение. Очевидные
примеры—продолжение гомотопии и свойство поднятия гомотопии. В
простейшем виде задачи продолжения и поднятия обычно можно
сформулировать одним из следующих двух способов.
Задача продолжения. Даны CVU-пара (W,A) и отобра- л ^х
Жение А —> X; можно ли продолжить его до отображения i у*
Задача поднятия. Даны расслоение X—>Y и отображе-
Ние W —> Y; существует ли поднятие W —► X? *
Чтобы задача поднятия включала также, например, и /' |
свойство поднятия гомотопии, её нужно обобщить до отно- VV >■ Y
Отельной версии.
Относительная задача поднятия. Даны CVU-пара (W,A), A ^ X
Расслоение в смысле Гуревича X —> Y и отображение W —> Y; | у' I
ЕУЩествует ли поднятие W —► X, продолжающее заданное на у, '_ ^ у
А Поднятие?
526
Глава 4. Теория гомотопий
Помимо того что относительная задача сводится к абсолютной задаче
о поднятии, когда Л = 0, она включает и задачу о продолжении, если в
качестве Y взять точку. Конечно, можно было бы расширить эти задачи,
отбросив требования, что (W, А) должно быть CW-парой и что отображение
X -* У должно быть расслоением. Однако эти условия часто выполняются
в интересных случаях, и они намного облегчают поиск решений.
Термин «теория препятствий» относится к процедуре определения
последовательности классов когомологии, которые являются
препятствиями для нахождения решения задачи продолжения, поднятия или
относительного поднятия. В наиболее благоприятных случаях эти препятствия
лежат в группах когомологии, которые все равны нулю, поэтому задача
имеет решение. Но даже когда препятствия отличны от нуля, может
оказаться очень полезным переформулировать задачу в когомологических
терминах.
Есть два способа развивать теорию препятствий, которые в конце
приводят, по сути, к одному и тому же результату. При более
элементарном подходе мы пытаемся строить продолжение или поднятие для
одной клетки комплекса W на каждом шаге, применяя индукцию по
остовам комплекса. Этот подход привлекателен прямотой, но технические
детали работы на уровне коцепей, возможно, несколько утомительны.
Вместо того чтобы следовать этой прямой дорогой, мы применим второй
подход, который немного более сложен, но имеет то преимущество, что
теория оказывается почти тривиальным применением башен
Постникова для задачи о продолжении или башен Мура—Постникова для задачи
о поднятии. Клеточный подход объясняется в [VBKT], где он появляется
в исследовании характеристических классов векторных расслоений.
Рассмотрим сначала задачу о продолжении, когда мы хотим
продолжить отображение А -* X на больший комплекс W. Предположим, что у X
есть башня Постникова из главных расслоений. Тогда у нас есть
коммутативная диаграмма
1
Х3 *К(п4Х,5)
/ Х2 + К(п3Х,4)
А ^ X *- X, >■' К(я2Х, 3)
W *- Х0 »? К(я,Х, 2)
где мы увеличили башню, добавив в основании пространство Х0,
являющееся просто точкой. Отображение X, —>Х0 тогда является расслоением
§4.3. Связь с когомологиями
527
в смысле Гуревича, и то, что оно главное, означает, что пространство Хь
которое в любом случае является пространством типа К(пАХ, 1), в нашем
случае является пространством петель в К(пгХу 2), следовательно, группа
7г1(Х) должна быть абелевой. Наоборот, если группа п^(Х) является абе-
левой и действует тривиально на всех высших гомотопических группах
пространства X, то, как указано, существует увеличенная башня
Постникова главных расслоений.
Наша стратегия будет состоять в том, чтобы попытаться поднять
постоянное отображение W -* Х0 до отображений W -* Хп для п = 1, 2, ...
последовательно, продолжая при этом данные отображения А —>Хп. Если
мы сможем найти все эти поднятия W —> Хп, то не составит никакого труда
построить требуемое продолжение W —>Х.
Для доказательства шага индукции рассмотрим коммутативную
диаграмму
А *Хп >РК
ТУТ
W * Хп_} >- К = К(япХ, п + 1)
Так как Хп — индуцированное расслоение, его точки —пары, состоящие
из точки в Хп..] и пути из её образа в К в отмеченную точку. Поэтому
поднятие W —► Хп эквивалентно гомотопии композиции W —► Хп_1 —► К
в постоянное отображение. У нас уже есть такое поднятие, определённое
на А, т. е. гомотопия отображения А —► К в постоянное отображение, и мы
хотим построить гомотопию отображения W —► К в постоянное
отображения, продолжающую эту гомотопию на пространстве А.
Отображение W —► К вместе с заданной гомотопией на А даёт
отображение W U СА -* К", где СЛ — конус над Л. Так как К — пространство типа
*С(тгпХ, п + 1), отображение W и СЛ —► /С определяет препятствие — класс
con€Hn+1(WuCA;^X)%Hn+1(VU,A;7rMX).
Предложение 4.72. Поднятие W —> Хп, продолжающее данное
отображение А -+ Хп, существует тогда и только тогда, когда соп = 0.
Доказательство. Мы должны показать, что отображение W U СА -+
—► К продолжается до отображения CW -* К тогда и только тогда, когда
wn = 0, или, другими словами, тогда и только тогда, когда отображение
W и СА —► /С гомотопно постоянному отображению.
Предположим, что gr: WUCA—>K — такая гомотопия. Тогда постоянное
отображение g^ продолжается до постоянного отображения g]: CW —> К,
поэтому по свойству продолжения гомотопии для пары (CW, VUUCA),
применённому к обращенной гомотопии g^_t, мы получаем гомотопию
£t: CW —► /С, продолжающую предыдущую гомотопию gt: W U СА -+ К.
Отображение g0: CW —► К тогда продолжает данное отображение W и
UCA-+K.
bZU
Глава 4. Теория гомотопий
Наоборот, если у нас есть продолжение CW —> К, то оно гомотопно
нулю, так как конус CW стягиваем, и мы можем ограничить на W U СЛ
эту гомотопию, связывающую данное отображение с постоянным. П
Если мы сможем построить продолжение поднятия А —> Хп до
поднятия W —* Хп для всех п, то мы получим отображение W —►limX,,,
продолжающее данное отображение Л —► X —*limXn. Пусть М —цилиндр
отображения X —> ПтХп. Так как ограничение отображения W —► \\тХп с М
на А пропускается сквозь X, это даёт гомотопию, связывающую это
ограничение с отображением Л —> X с М. Продолжив её до гомотопий
отображения W —>М, получим отображение (W,A)—-> (M,X). Так как
отображение X —>\\тХп является слабой гомотопической эквивалентностью,
тг,(М,Х) —0 для всех z, поэтому согласно лемме 4.6 (лемма о сжатии)
отображение (W, А) —> (М,Х) можно прогомотопировать в отображение
W —> X, продолжающее данное отображение А —> X, и мы решили задачу
продолжения.
Таким образом, если случилось так, что на каждом этапе индуктивного
процесса построения поднятий W—> Хп препятствие соп еЯгН [{W, Л; nnX)
обращается в нуль, то задача продолжения имеет решение. В частности,
это даёт следующее утверждение.
I Следствие 4.73. Если X — связный абелев CW-комплекс, a (W, А) —
такая CW-napa, что #П+1(1У, Д; ппХ) = 0 для всех п, то любое
отображение А —> X можно продолжить до отображения W —> X.
Это существенно уточняет более элементарный результат, что
продолжения существуют, если пп (X) = 0 для всех тех п, для которых W - А имеет
клетки размерности п -Ы (см. лемму 4.7).
Мы можем применить теорему Гуревича и теорию препятствий,
чтобы распространить гомологическую версию теоремы Уайтхеда на CW-kom-
плексы с тривиальным действием группы тг, на всех гомотопических
группах.
I Предложение 4.74. Если X и Y — связные абелевы CW-комнлексы, то
отображение f:X-+Y, индуцирующее изоморфизмы всех групп
гомологии, является гомотопической эквивалентностью.
Доказательство. Взятие цилиндра отображения / приводит нас к
случаю включения X <-> Y подкомплекса. Если мы сможем показать, что
группа тг^Х) действует тривиально на nn(Y, X) для всех п, то из
относительной теоремы Гуревича будет следовать, что 7ГП(У, X) = 0 для всех п, таким
образом, X —> Y будет слабой гомотопической эквивалентностью. Наши
предположения гарантируют, что я^Х) —► п1 (У) — изоморфизм, поэтому
мы знаем, по крайней мере, что 7ij(Y, Х) = 0.
Мы можем воспользоваться теорией препятствий, чтобы продолжить
тождественное отображение X —> X до ретракции Y —>Х. Чтобы
применить эту теорию, нам нужно, чтобы группа 7rt(X) действовала тривиально
§4.3. Связь с когомологиями
529
на яп(Х), а это выполняется по предположению. Так как включение X с—> У
индуцирует изоморфизмы гомологии, мы получаем //ДУ, X) = О,
следовательно, Hn'l(Y, X; я„(Х)) = 0 для всех п по теореме об универсальных
коэффициентах. Поэтому нет никаких препятствий, и ретракция У —> X
существует. Из этого следует, что отображения тг„(У) -* тгм(У, X) являются
отображениями на, поэтому из тривиальности действия группы яДХ) на
яп(У) следует тривиальность действия на я,,(У, X) согласно
естественности действия. П
Обобщение предыдущего анализа задачи продолжения на случай
относительной задачи поднятия получается непосредственно.
Предположим, что у расслоения р: X -+Y из формулировки задачи поднятия
существует башня Мура—Постникова, состоящая из главных расслоений.
Тогда мы получаем такую диаграмму:
А -X ^
у /} \^ у
W ^У
Первый шаг состоит в том, чтобы поднять отображение W —>Y в Z,,
продолжив заданное на Л поднятие. В качестве 7,х можно взять накрывающее
пространство над У, соответствующее подгруппе рДяДХ)) в я^У).
Теория накрытий говорит нам, что в таком случае мы можем поднять
отображение W —>Y в Z]. Мы можем воспользоваться свойством
единственности поднятия для накрытий, чтобы выяснить, можно ли это поднятие
выбрать так, чтобы оно было согласованно с поднятием на А; проблемы
могут возникнуть только тогда, когда А имеет больше одной компоненты
связности.
Если поднятие в Zx уже построено, то анализ проходит точно так же,
как и раньше. У нас получается последовательность препятствий а>п е
SHn+[(W,A\ япР), если предположить, что группа n^F абелева в случае
п = 1. Поднятие в X, продолжающее заданное на А поднятие, существует,
если каждый последовательный класс соп нулевой.
Можно задать обратный вопрос: если поднятие существует, то должны
ли все препятствия а>п быть нулевыми? Так как предложение 4.72 является
утверждением «тогда и только тогда», можно было бы ожидать, что ответ
утвердительный, но при более внимательном рассмотрении дело
становится менее ясным. Трудность состоит в том, что даже если на некотором
^К(я2Р,3)
-К(я^,2)
530
Глава 4. Теория гомотопий
этапе препятствие соп равно нулю, а потому поднятие в Z,l+1 существует,
может быть много разных способов выбрать такое поднятие, а разные
способы выбора могут привести к разным классам соп+]у одни из которых
равны нулю, а другие отличны от нуля. Примеры таких
неопределённостей легко построить, как для задачи поднятия, так и для задачи
продолжения, причём неопределённости становятся только хуже с каждым
последующим выбором поднятия. Поэтому лишь при довольно специальных
обстоятельствах можно утверждать, что существуют корректно
определённые препятствия. Одним из простых случаев— когда я,(Р) =0при i<n
и, таким образом, факторизация Мура—Постникова начинается с Zn, как
на диаграмме
Zn+2 -К(я,н_2Р,п + 3)
/\
А X —— Z,1+, K(7rn+1F, n + 2)
W >■ Y = Zn -> K(nnF, n +1)
В этом случае композиция вдоль основания диаграммы даёт корректно
определённое примарное препятствие соп€Яп+1(Мг, A\ nnF).
Задачи
1. Докажите, что существует отображение R?°° -> СР°° = K(Z, 2),
которое индуцирует тривиальное отображение на ЯД-; Z), но нетривиальное
отображение на Н*(—; Z). Как это согласуется с теоремой об
универсальных коэффициентах?
2. Докажите, что структура группы на S1, возникающая из умножения
в С, индуцирует такую структуру группы на {X, S1), что взаимно
однозначное отображение (X, S1) -*Hl(X\ Z) из теоремы 4.57 является
изоморфизмом.
3. Предположим, что CW-комплекс Х содержит такой подкомплекс S1,
что включение S1 <—► X индуцирует инъективное отображение /^ (S1; Z) -*
—>Н}(Х;Г£), образ которого — прямое слагаемое группы ttjCXjZ).
Докажите, что S1 — ретракт пространства X.
4. Даны абелевы группы G и Я и CW-комплексы типа K(G,n) и
/С(Я,п). Докажите, что отображение (K(G, n)tK(Hy п)) —»Hom(G, Я),
переводящее гомотопический класс [/] в индуцированный гомоморфизм
/*: ntl(K(G, п)) —♦ тгп(К(Я, п)), является взаимно однозначным
отображением.
§ 4.3. Связь с когомологиями
531
5. Докажите, что [X, Sn] ъ НП(Х; Z), если X —n-мерный CW-kom-
плекс. [Постройте K(Z, п) из Sn, приклеивая клетки размерности не
меньше п + 2.]
6. Используя задачу 4, постройте мультипликативное изображение
pt: K(G, п) х K(G, n) -+K(G, n) для любой абелевой группы G. Тем самым
CW-комплекс превращается в Ы-пространство с коммутативным и
ассоциативным с точностью до гомотопии умножением и гомотопическим
обратным. Покажите также, что такое умножение /i единственно с
точностью до гомотопии.
7. Используя Н-пространственное умножение \х на /C(G, п),
определите сложение в (X, K(G, n)) по формуле [/] + [g] = [/i(/, g)] и докажите,
что при взаимно однозначном отображении Нп(Х\ G) % (X, K(G,n)) это
сложение соответствует обычному сложению в когомологиях.
8. Докажите, что отображение р: Е-+В является расслоением в
смысле Гуревича тогда и только тогда, когда отображение п: Е1 -* Ер, тс (у) =
= (у(0),ру), имеет сечение, т.е. такое отображение s: Fp—>£', что ns — t.
9. Докажите, что линейная проекция двумерного симплекса на одну
из его граней — расслоение в смысле Гуревича, но не локально
тривиальное расслоение. [Воспользуйтесь предыдущей задачей.]
10. Дано расслоение в смысле Гуревича F —»Е —»В. Используя
свойство поднятия гомотопии, определите действие группы пл(Е) на тг„(Р) —
такой гомоморфизм пл{Е) -*Aut(rcn(F)), что композиция
7i1(F)-,^1(E)-Aut(^n(F))
является обычным действием группы nx{F) на 7i„(F). Выведите из этого,
что если тт1 (F) = 0, то действие группы тсх(Р) на тсп (F) тривиально.
11. Для данного пространства В обозначим через &{В) множество
классов послойной гомотопической эквивалентности расслоений в
смысле Гуревича Е -+ В. Докажите, что отображение /: Вх -* В2 индуцирует
отображение /*: &{В2) -*«^'(В1), зависящее только от гомотопического
класса отображения /, причём отображение /* взаимно однозначное,
если / — гомотопическая эквивалентность.
12. Докажите, что для гомотопных отображений /, g: А-^В
расслоения Ef —* В и Eg -* В послойно гомотопически эквивалентны.
13. Даны отображение /:Д-+Ви гомотопическая эквивалентность
g: С —► А. Докажите, что расслоения Ej-+B и Efg-+B послойно
гомотопически эквивалентны. [Один из подходов состоит в том, чтобы
воспользоваться следствием 0.21 и свести ситуацию к случаю деформационных
ретракций.]
14. Для данного пространства В пусть Ж {В) обозначает множество
классов эквивалентности отображений /: А —* В, где fx: Ах —» В
эквивалентно /2: А2 —* В, если существует такая гомотопическая
эквивалентность g: Ах -* А2> что /i — hS- Докажите, что естественное отображение
532
Глава 4. Теория гомотопий
&{В) -*Ж{В) является взаимно однозначным отображением. [См. задачи
11 и 13.]
15. Докажите, что если расслоение в смысле Гуревича р: Е-+ В
является гомотопической эквивалентностью, то р — послойная
гомотопическая эквивалентность расслоения Е с тривиальным расслоением 1: В —* В.
16. Докажите, что отображение /: X —> У связных CW-комнлексов
является гомотопической эквивалентностью, если оно индуцирует
изоморфизм групп я1? а для его гомотопического слоя Fy верно, чтоЯЛ^у; Z)=0.
17. Докажите, что ПХ является /^-пространством с умножением —
композицией петель.
18. Докажите, что последовательность расслоений ... —> ПВ —> F->
-+Е-+В индуцирует длинную точную последовательность ...—> (X, QB) —►
—► (X, F) —► (X, Я) -* (X, В) групп и гомоморфизмов группы, за
исключением последних трёх членов, и абелевых групп, за исключением последних
шести членов.
р
19. Дано расслоение F —► Е —» В. Определите естественное действие
Н-пространства ПВ на гомотопическом слое Ff) и воспользуйтесь им,
чтобы показать, что точность в члене (X, F) в длинной точной
последовательности в предыдущей задаче можно уточнить так: образы двух элементе»
из (X,F) в (Х,Е) совпадают тогда и только тогда, когда они
принадлежат одной и той же орбите индуцированного действия группы (X, ПВ) на
(X, F).
20. Докажите, что, применяя функтор пространства петель к башне
Постникова для X, мы получим башню Постникова из главных
расслоений для ПХ.
21. Докажите, что в башне Постникова для tf-пространства все
пространства являются Я-пространствами, а отображения являются
Н-отображениями, коммутирующими с умножением с точностью до
гомотопий.
Р о
22. Докажите, что главное расслоение ПС-*Е—*В послойно гомото-
пически эквивалентно произведению ПС х В тогда и только тогда, когда
у него есть сечение, т. е. отображение 5: В —► Е, для которого ps = l.
23. Докажите следующий результат единственности для
плюс-конструкции Квиллена. Пусть дан связный CW-комплекс Х. Тогда если
существуют абелев CW-комплекс Y и отображение X —>У, индуцирующее
изоморфизм H*(X;Z) ^H*(Y\Z), то такой комплекс Y единствен с
точностью до гомотопической эквивалентности. [Воспользуйтесь следствием
4.73, взяв в качестве W цилиндр отображения X -* У.]
24. В ситуации относительной задачи поднятия предположим, что
есть два разных поднятия W—>Х, которые согласованы на
подпространстве А с W. Докажите, что препятствия к построению гомотопий
относительно Л между этими двумя поднятиями лежат в группах H"(W, A; л„П-
ДсшсШн^нйе
§ 4.А. Отмеченные точки и гомотопии
В первой части этого параграфа мы применим действие группы пх
на я,,, чтобы описать разницу между тг„(Х,х0) и множеством
гомотопических классов отображений S'1 —> X без условий на отмеченные точки.
Более общим образом, мы сравним множество (Z, X) сохраняющих
отмеченную точку гомотопических классов отображений {Z,z0) —> (Х,х0)
с множеством [Z,X] гомотопических классов отображений Z —> X без
ограничений, где Z —произвольный CW-комплекс с отмеченной точкой
z0, являющейся нульмерной клеткой. Параграф завершается обобщённым
примером, демонстрирующим некоторые довольно тонкие явления не
конечной порождённое™ в гомотопических группах и группах гомологии.
Мы начнём с построения действия группы 7Г](Х,х0) на (Z,X), когда
Z —CW-комплекс с отмеченной точкой z0, являющейся нульмерной
клеткой. Если даны петля у в X с началом и концом в точке х{) и
отображение /0: (Z, z0) —► (X, х0), то согласно свойству продолжения гомотопии
существует такая гомотопия fs: Z —► X отображения /0, что /s(z0) является
петлёй у. Можно попробовать определить действие группы 71{{Х,х()) на
(Z, X) формулой [у] [/0] = [/]], но это определение приводит к небольшой
проблеме, когда мы составляем петли вместе. Действительно, если г\ —
другая петля в точке х0, то, применяя свойство продолжения гомотопии
ещё раз, мы получаем гомотопию отображения /l5 ограничением которой
на х0 служит петля rj, и эти две гомотопии вместе дают соотношение
([y][^J)l/o] = f^/]([yJ[/о!) ввиду нашего соглашения, что произведение
уг\ означает, что сначала проходится у, а затем г/. Это не совсем то
соотношение, которое нам нужно, но его легко исправить, считая, что группа
действует справа, а не слева. Таким образом, мы полагаем [/0][у] = [/J,
итогда[/0](М[т»]) = ([/(,][г.1)[ч].
Проверим, что это правое действие определено корректно. Пусть мы
начинаем с отображений /0>£о: (Z,z0)-^ (Х,х0)> представляющих один
и тот же класс в (Z, X), вместе с такими гомотопиями /s и g, отображений
/о и go, что /Дг0) и gs(z0) являются гомотопными петлями. Эти разные
534
Глава 4. Теория гомотопий
гомотопии определяют отображение
Н: Z х / х dl U Z х {0} х / и {z0} х / х / -> X,
которое совпадает с f на Z х / х {0}, с gs на Z х / х {1}, является
сохраняющей отмеченную точку гомотопией отображения /0 в
отображение g0 на Z х {0} х / и гомотопией отображения /s(z0) в отображение
g5(z0) на {z0} х / х /. Мы хотим продолжить отображение Н на Z х / х /.
Пара (/ х /, / х dl U {0} х /) гомеоморфна паре (/ х /, / х {0}), и
посредством этого гомеоморфизма мы можем рассматривать Я как отображение
Z х / х {0} U {z0} х / х / —> X, т. е. отображение Z х / —> X вместе с
гомотопией на подкомплексе {z0} x /. Это означает, что можно применить
свойство продолжения гомотопии, получив продолжение исходного
отображения И на Z х / х /. Ограничивая это продолжение отображения И на
Z х {1} х /, получаем сохраняющую отмеченную точку гомотопию fx ^g,,
которая показывает, что действие [/0] [у] определено корректно.
Отметим, что в этом рассуждении мы не пользовались тем, что
гомотопии /s и gs были построены с помощью свойства продолжения
гомотопии. Таким образом, мы доказали следующее утверждение.
Предложение 4.А.1. Формула [/0] [у] = [/,] определяет правое
действие группы пл (X, х0) на (Z, X), если существует такая гомотопия f: Z —>X
отображения /0 в отображение /ъ что f(zQ) является петлёй у или любой
петлёй, гомотопной у.
Легко преобразовать это правое действие в левое действие, положив
[у][/о] = f/olM"1- При этом просто выбирается гомотопия /, так, чтобы
/s(z0) был обратным путём для у.
Когда Z = Sn, это действие сводится к обычному действию группы
пх (X, х0) на тгп (X, х{)), так как в исходном определении действия yf в
терминах отображений (/", д/") —> (Х,х0) гомотопия отображения yf в
отображение / получается при ограничении yf на всё меньшие и меньшие
концентрические кубы, а на «отмеченной точке» <3/п эти гомотопии
высекают петлю у.
I Предложение 4.А.2. Если (Z, z0) — CW-пара, а X—линейно связное
I пространство, то естественное отображение (Z, X) —> [Z, X] индуцирует
I взаимно однозначное отображение множества орбит (Z, Х)/Я](Х, л*0)
[ на [Z.X].
Из этого, в частности, следует, что [Z, X] = (Z, X), если пространство
X односвязно.
Доказательство. Так как X линейно связно, любое отображение
/: Z —>X можно прогомотопировать так, чтобы оно переводило z0 в
отмеченную точку х0, посредством продолжения гомотопии. Поэтому
отображение (Z, X) —► [Z, X] является отображением на. Если /0 и /,
—сохраняющие отмеченную точку отображения, которые гомотопны посредством
гомотопии/,: Z —> X, то по определению f/J = [/0][у] для петли y(s) = /<(z0).
§4.А. Отмеченные точки и гомотопии
535
Поэтому [/о] и [/J лежат в одной и той же орбите относительно действия
группы ttj (X, х0). Наоборот, два сохраняющих отмеченную точку
отображения, лежащие в одной и той же орбите, очевидно, гомотопны. □
Пример 4.А.З. Если X — /-/-пространство с единичным элементом х0,
то действие группы тг, (X, х0) на (Z, X) тривиально, так как для
отображения /: (Z, z0) —> (X, х0) и петли у в X с началом и концом в точке х0
умножение в X определяет гомотопию /s(z) = /(z)y(s). Она начинается и
заканчивается отображением, гомотопным /, а петля /Дя0) гомотопна у,
причём обе эти гомотопии сохраняют отмеченную точку по определению
Н-пространства.
Множество орбит действия группы П\ на тг„, вообще говоря, не
наследует структуру группы из я„. Например, при п = 1 орбиты —это просто
классы сопряжённости в тгь а они образуют группу, только если группа
Tij абелева. Таким образом, отмеченные точки— необходимое
техническое приспособление для задания структуры группы в гомотопических
группах, хотя, как мы показали, их можно игнорировать в односвязных
пространствах.
Условие, что набор отображений S" —>Х порождает тгм(Х) как модуль
над Z[rr„(X)], означает, что все элементы группы пп(Х) можно
представить в виде сумм этих отображений вдоль произвольных путей в X,
причём разрешается изменять ориентации, чтобы получить отрицательные
коэффициенты, и разрешается повторно брать отображение, чтобы
получить произвольные целые кратные. Примеры конечных CW-комилек-
сов X, для которых тг„(Х) как модуль над Z[rrn(X)] не является конечно
порождённым, приведены в задаче 38 в §4.2 для n ^ 3. Построение такого
примера для п = 2 представляется более трудным. Оставшаяся часть этого
параграфа будет посвящена довольно сложной конструкции, которая даёт
такой пример, а также интересна и по другим причинам.
Пример не конечной порождённости
Мы построим конечный CW-комплекс, у которого тг„ как
Ъ[п{\-модуль для данного целого числа n ^ 2 не конечно порождён. Этот комплекс
будет подкомплексом в К(я,1), обладающим интересными
гомологическими свойствами: это (п + 1)-мерный CW-комплекс, у которого группа
Нп+1 не конечно порождена, но его n-мерный остов конечен, поэтому
группа Н, конечно порождена при i: ^ п и группа п конечно представи-
ма при п > 1. Первый такой пример был найден в [129] для п = 2. Наша
конструкция будет, по существу, n-мерным обобщением этого примера,
но представленным более геометрическим способом (см. [82]), который
даёт общий метод построения многочисленных примеров такого вида.
Начнём с пространства X —произведения п копий букета S] V S]. Так
KaKS1 VS1 —одномерный остов тора T2 = Sl x S1 с его обычной CW-струк-
турой, X можно рассматривать как подкомплекс 2п-мерного тора Т2п, про-
536
Глава 4. Теория гомотопий
изведения 2г? окружностей. Зададим отображение /: Т2п —> Sx формулой
/(#i,..-, в2п) = Oi + ... + 02„, гДе координаты 0{ eS] рассматриваются как
углы в радианах. Пространство Z = Xn/_1(0) даёт пример, который нам
нужен. Как мы увидим, Z — конечный CW-комплекс размерности п - 1?
причём nn__x(Z) как модуль над TijCZ) не конечно порождён, если п ^ 3.
Мы также увидим, что 7t,(Z) =0 при I < i < п - 1.
Индуцированный гомоморфизм /„: тгДТ2'1) -* я1(51) — Ъ переводит
каждую образующую, возникающую из множителя S\ в 1. Пусть Г2" -*
—>Т2п — это накрытие, соответствующее ядру гомоморфизма /+. Это
накрытие регулярное, так как оно соответствует нормальной подгруппе,
и группа преобразований накрытия равна Z. Подкомплекс в 7'2п,
проектирующийся на X, —нормальное накрывающее пространство X —> X с той
же самой группой преобразований накрытия. Так как я^Х) —
произведение п свободных групп с двумя образующими, X —накрывающее
пространство над X, соответствующее ядру гомоморфизма я,(Х) —>Z,
переводящего каждую из двух образующих каждого свободного множителя
в 1. Так как X — пространство типа К(я, 1), X тоже пространство такого
типа. Например, когда п=1, X—объединение двух винтовых линий па
бесконечном цилиндре Т2:
О X X X ;< X X ~Х1
Отображение / поднимается до отображения /: Т2п -*J£, и Z
поднимается гомеоморфпо до подпространства ZcX, а именно /_1(0)ПХ. Мы
покажем следующее:
(*) пространство X гомотопически эквивалентно пространству У,
полученному из Z приклеиванием бесконечной последовательности
n-мерных клеток.
Если это верно, то группа Н„(У) не конечно порождена, так как в
точной последовательности
Hn(Z) - Hn(Y) - H„(y,Z) - H„_,(Z)
первый член нулевой, а последний ^шеи конечно порождён (поскольку
Z является конечным CW-комплексом размерности п — 1), в то время
как третий член — бесконечная сумма групп Z, по одной для каждой
п-мерной клетки комплекса У. Если бы nn.\{Z) был конечно порождён
как кi(Z)-модуль, то, приклеив к пространству Z конечное число п-мер-
ных клеток, мы смогли бы сделать его (п — 1)-связным, так как оно уже
(п - 2)-связно как (п - 1)-остов комплекса У, имеющего тип К(п, 1)-
Тогда, приклеивая клетки размерности больше л, мы смогли бы построить
пространство типа К (я, 1) с конечным n-остовом. Но это противоречит
тому факту, что группа Н„(У) не конечно порождена.
§4.Л. Отмеченные точки и гомотопии
537
Проверку утверждения (*) мы начнём с того, что рассмотрим тор Т".
Стандартная клеточная структура на V" поднимается до кубической
клеточной структуры на универсальном накрытии Rm с вершинами в
целочисленной решётке Z"'. Функция / поднимается до линейной проекции
I: Шт —> R, Ц*1, ...,^ш) =х} + ... + хт. Плоскости из L~l[7J) разрезают
кубы в Rm на выпуклые многогранники, которые мы назовём плитами.
В каждом т-мерном кубе есть т плит. Граница плиты
в l'llU * + 1] состоит из боковых граней, которые
являются плитами для кубов меньшей размерности, вместе
с нижней гранью в плоскости /,_1(0 и верхней гранью
в IT1 (i Ч-1). В каждом кубе есть две исключительные
плиты, у которых нижняя или верхняя грань вырождается
в точку. Это плиты, содержащие вершины куба, в которых
L достигает своего максимального или минимального значения. Плита
деформационно ретрагируется на объединение её нижней и боковых
граней, при условии, что у плиты есть верхняя грань, которая отлична от
точки. В противном случае плита — m-мерный симплекс, и мы в
дальнейшем будем называть такие плиты конусами. Они являются плитами,
содержащими вершину куба, в которой L принимает максимальное значение.
Боковые грани конуса —тоже конусы, меньшей размерности.
Плиты, вместе со всеми их гранями меньшей размерности, задают
CW-структуру на Rm с плоскостями из L~l(Z) в качестве подкомплексов.
Эта структура сохраняется при преобразованиях накрытия Жт —> Т",
поэтому на факторпространстве Т" имеется индуцированная CW-структура
с/-1(0) в качестве подкомплекса.
Если X — произвольный подкомплекс в Тт с его исходной
кубической клеточной структурой, то CW-структура плит на Тт ограничивается
до С W-структуры на X. В частности, мы получаем CW-структуру на / =
= ХП/_1(0). Аналогично мы получаем поднятую CW-структуру на
накрытии Xcf". Пусть X[i,j] =Xn/_1[i,j]. Деформационные ретракции
неконических плит на их боковые и нижние грани приводят к
деформационной ретракции пространства X[i, i +1] на X[i] UC,, где С, состоит из
всех конусов в X[i9 i + 1]. Эти конусы приклеены по их нижним граням,
и все они имеют одну и ту же вершину в X[i +1], поэтому само
пространство С, —конус в обычном смысле, приклеенный к X[i] по его основанию.
Для того конкретного комплекса X, который нас интересует, мы
утверждаем, что каждое пространство С,—n-мерный диск, приклеенный
по своей граничной сфере. Для п — 1 это очевидно из приведённого ранее
описания комплекса X как объединения двух винтовых линий на
цилиндре. Для больших п мы рассуждаем по индукции. Переход от п к п + 1
заменяет X двумя копиями пространства X х S1, пересекающимися по X,
по одной копии для каждого из дополнительных множителей S] в 7'""
Замена X на X х S1 превращает С, в его джойн с точкой в основании
538
Глава 4. Теория гомотопий
нового С/. Повторение этой операции дважды даёт надстройку над Q,
приклеенную по надстройке над основанием.
То же самое рассуждение показывает, что X[-i - 1, —i]
деформационно ретрагируется на Х[—f] с приклеенной /i-мерной клеткой. Мы строим
пространство У и гомотопическую эквивалентность g: У —> X по
индукции, начиная с Y0 = Z. Предполагая, что пространство У{ и
гомотопическая эквивалентность g{\ Vj—>X[-i,i] уже построены, мы образуем У|Чь
приклеивая две n-мерные клетки по отображениям, полученным из
отображений приклеивания двух /i-мерных клеток в X[—i - 1, i +1] —X[-i, i]
композицией с отображением, гомотопически обратным к g,. Это
позволяет продолжить g, до гомотопической эквивалентности g^i-' ^m-i ~~*
—> X[-i - 1, i + 1]. Взяв объединение по f, получаем g: У —> X. Можно
проверить, что это отображение —гомотопическая эквивалентность,
убедившись, что оно. индуцирует изоморфизмы всех гомотопических групп;
для этого используется стандартное рассуждение с компактностью. Это
завершает проверку свойства (*).
Интересно посмотреть, как выглядит комплекс Z в случае л = 3,
когда он двумерен и его группа тг2 не конечно порождённая над 7j[n{(Z)].
В этом случае X — произведение трёх пространств Sl V S1, таким образом,
X —объединение восьми трёхмерных торов, полученных при выборе
одного из двух слагаемых S1 в каждом множителе Sl VS1. Мы обозначим эти
трёхмерные торы Sl± х S]± х Sl±. Рассматривая каждый из этих трёхмерных
торов как куб на предыдущем рисунке с отождествлёнными
противоположными гранями, мы видим, что Z —объединение восьми двумерных
торов, образованных двумя наклонными треугольниками в каждом кубе.
Два из этих двумерных торов пересекаются по окружности, когда
соответствующие трёхмерные торы пространства X пересекаются по двумерному
тору. Это происходит, когда тройки знаков ± для этих двух трёхмерных
торов отличаются ровно одним элементом. Поэтому схему пересечения
этих восьми двумерных торов пространства Z можно описать
комбинаторно посредством одномерного остова куба с вершинами (±1, ±1, ±1).
Каждой вершине куба соответствует тор пространства Z, причём два тора
пересекаются по окружности, если соответствующие вершины куба
соединены ребром. Все восемь торов содержат единственную нульмерную
клетку комплекса Z.
Чтобы получить модель самого комплекса Z,
рассмотрим правильный октаэдр, вписанный в куб с
вершинами (±1, ±1, ±1). Если мы отождествим каждую
пару противоположных граней октаэдра, то каждая
пара противоположных треугольных граней
превратится в тор. Однако есть лишь четыре пары
противоположных граней, поэтому мы получаем таким
способом лишь четыре тора, а не восемь. Чтобы исправить это, рассмот-
§ 4.A. Отмеченные точки и гомотопии
539
рим каждую треугольную грань октаэдра как две копии одного и того
же треугольника, которые отличаются друг от друга выбором
нормального направления —стрелки, приложенной к треугольнику и
направленной внутрь октаэдра или наружу, т.е. либо к самой близкой вершине
объемлющего куба, либо к противоположной его вершине. Тогда каждая
пара противоположных треугольников октаэдра, имеющих нормальные
векторы, направленные к одной и той же вершине куба, задаёт тор, когда
противоположные грани отождествляются так же, как и раньше. Каждое
ребро исходного октаэдра тоже заменено двумя рёбрами. Вершины
октаэдра можно не удваивать, так как они в любом случае будут все
отождествлены в одну точку. Для этой схемы два тора, соответствующие вершинам
в концах ребра куба, пересекаются по окружности, как и должны, а другие
пары торов пересекаются только в нульмерной клетке комплекса Z.
Эта модель комплекса Z имеет то преимущество, что на ней видна
группа симметрии куба —группа порядка 48, как группа симметрии
комплекса Z, соответствующая симметриям пространства X,
переставляющим три множителя S^ У S} и два слагаемых S1 в каждом букете S} У S}.
Несомненно, на Z было бы очень приятно посмотреть, если бы мы
жили в пространстве достаточно высокой размерности, чтобы можно было
охватить это всё одним взглядом.
Интересно было бы явно описать множество отображений S2—^Z,
порождающих 7i2(Z) как 2[я1]-модуль. Можно также спросить, существуют
ли более простые примеры этих явлений не конечной порождённое™.
Задачи
1. Докажите непосредственно, что если X — топологическая
группа с единичным элементом xQj то любые два гомотопных отображения
/, g: (Z, zQ) —► (X, х0) гомотопны также в классе отображений,
сохраняющих отмеченную точку.
2. Докажите, что при отображении (X, У) —»Нот(яп(Х, *0), лп(У, у{))),
[/]—*/*, действие группы л}(У,у0) на (X, У) соответствует композиции
с действием на я„(У, у0), т.е. (у/)* = j3y/*. Получите взаимно однозначное
отображение из [X, К(7Г, 1)] на множество орбит в НотСяДХ), п) при
композициях с внутренними автоморфизмами группы п. В частности,
если группа п абелева, то
[X, К(тг, 1)] = (X, К(тг, 1)) = НотСтг, (X), к).
3. Для пространства X обозначим через Aut(X) группу
гомотопических классов гомотопических эквивалентностей X —► X. Докажите, что
для CW-комплекса типа К(я, 1) группа Аш(К(я, 1)) изоморфна группе
внешних автоморфизмов группы я, т. е. группе автоморфизмов по модулю
внутренних автоморфизмов.
эч-и
Глава 4. Теория гомотопий
4. В обозначениях предыдущей задачи докажите, что Aut(V„S ) ^
^GLn(Z) при к> 1, где v„S* обозначает букет п копий сферы Sky a GL„(Z) —
группа матриц размера пхпс элементами из Z, имеющих обратную
матрицу того же самого вида. [GL„(Z)—это группа автоморфизмов группы
%n**izk(vnSk)**Hk(vnSk).]
5. В этой задаче участвуют пространства, построенные в последней
части этого параграфа.
а) Вычислите группы гомологии комплекса он в случае п = 3, когда Z
двумерен.
б) Пусть Хп обозначает n-мерпый комплекс X. Докажите, что Х„
можно получить по индукции из Хп_х как объединение двух экземпляров тора
отображения для образующей Хи_л -*Х„_1 группы преобразования
накрытия, где оба экземпляра Хп_х в этих двух торах отображения
отождествлены. Таким образом, существует локально тривиальное расслоение
Xn-+Sx\/Sx со слоем X,,..!.
в) Используя п. б), найдите представление группы я, (Хп) и покажите,
что это представление приводит к конечному представлению, если п >2,
и к представлению с конечным числом образующих, если п = 2. В
последнем случае докажите, что у группы П\(Х2) нет никакого конечного
представления, используя тот факт, что группа Н2(Х2) не конечно
порождённая.
§4.В. Инвариант Хопфа
В §2.2 мы применили гомологии, чтобы отличить разные
гомотопические классы отображений S" —> S" посредством понятия степени.
Здесь мы покажем, что нечто подобное можно сделать и для
отображений S2n~l -*S'\ применив когомологическое умножение. Первоначально
это сделал Хопф, используя более геометрические конструкции, ещё до
изобретения когомологий и ^-произведений.
Для любого отображения /: Sm —> S1", т^ п, мы можем построить
CW-комплекс Су, приклеив клетку еш+х к Sn по отображению /.
Гомотопический тип комплекса Cf зависит только от гомотопического класса
отображения / согласно предложению 0.18. Поэтому для отображений
/, g: Sm —>Sn любой инвариант гомотопического типа, который
отличает Cf от Cg, покажет, что / не гомотопно g. Например, если т~п и /
имеет степень d, то из клеточного цепного комплекса для Cf мы видим,
что Hn(CyO^Z|€j|, поэтому гомологии комплекса Cf распознают степень
отображения / с точностью до знака. При т > п, однако, гомологии
комплекса Cf состоят из групп Z в размерностях 0, п и т+1, независимо
от /. То же самое верно для групп когомологий, но для v^-произведений
есть шанс, что они могут быть нетривиальными в H*(Cj) при т = 2п - 1.
В этом случае, если мы выберем образующие ае/-/"(Су) и /3 e/J2"(Cy), то
мультипликативная структура кольца H*(Cf) определяется соотношением
§4.В. Инвариант Хопфа
541
а2 = Н(/)/3 для некоторого целого числа Н(/), называемого
инвариантом Хопфа отображения /. Знак числа Н(/) зависит от выбора
образующей /3, но его можно определить, потребовав, чтобы (3
соответствовала фиксированной образующей группы H2"(D2'\ dD2n) при отображении
H2n(Cf)KH2n(Cf, Sn)->H2n(D2n, dD2n)y индуцированном
характеристическим отображением клетки е2п, которое задаётся отображением /. Мы
можем тогда изменить знак числа Н(/), взяв композицию / с зеркальной
симметрией сферы S2""1, имеющей степень — 1. Если /^g, то при
гомотопической эквивалентности Cf^Cg выбранные образующие /3 для H2"(Q)
и H2n(CR) соответствуют друг другу, поэтому число Н(/) зависит только
от гомотопического класса отображения /.
Если / — постоянное отображение, то Cf = S" V S2n и И (/) = 0, так как
С с ретрагируется на S". Кроме того, число Н(/) всегда равно нулю для
нечётного п, так как в этом случае а2— —а2 по свойству коммутативности
^-произведения, а значит, а2 = 0.
Три основных примера отображений с инвариантом Хопфа, отличным
от нуля, —это отображения, задающие три расслоения Хопфа в примерах
4.45, 4.46 и 4.47. Первое из этих отображений Хопфа —отображение
приклеивания /: S3 —»S2 для четырёхмерной клетки в СР2. Для него Н(/) = 1,
так как ЬГ(СР2; Z) ъг£[а]/(а3) по теореме 3.12. Аналогично HP2 приводит
к отображению S7 —*S4 с инвариантом Хопфа 1. В случае октавной
проективной плоскости (ОР2, которая строится по отображению S]* —*SS,
определённому в примере 4.47, можно показать, что H*(QP2] Z) ^Z[a]/(a3),
воспользовавшись либо двойственностью Пуанкаре, как в примере 3.40,
либо задачей 4.D.5 в конце §4.D.
Имеет место фундаментальная теорема (см. [75]), утверждающая, что
отображение /: s2n"1 —*Sn с инвариантом Хопфа 1 существует только для
л = 2, 4, 8. Она имеет много очень интересных следствий, например:
а) R" является алгеброй с делением только при п = 1, 2, 4, 8;
б) S" является //-пространством только при п = 0, 1, 3, 7;
в) на S" есть п линейно независимых касательных векторных полей
только при п = 0, 1, 3, 7;
г) локально тривиальные расслоения Sp —> Sq —* Sr существуют только
для (р, с?, г) =(0,1, 1), (1, 3, 2), (3, 7, 4) и (7,15, 8).
Первое и третье утверждения были фактически доказаны в ГЮ6]
и [114] незадолго до появления теоремы Адамса как приложения теоремы
Ботта о том, что 7r2„U(n) я* Zn!. Подробное обсуждение этих вопросов
и доказательство теоремы Адамса содержатся в [VBKT].
Хотя отображения с инвариантом Хопфа 1 встречаются редко,
отображения S2""1 —*S" с инвариантом Хопфа 2 существуют для всех чётных п.
А именно, рассмотрим пространство J2(Sn), построенное в § 3.2. Оно
имеет CW-структуру с тремя клетками размерностей 0, п и 2п, поэтому J-ziS )
имеет вид Сг для некоторого отображения/: S2""1 —>Sn. Мы показали, что
мг
Глава 4. Теория гомотопий
если п четно, то квадрат образующей группы Hn(J2(Sn); Z) —это удвоен-
нал образующая группы H2n(J2(Sn)> ^)> таким образом, H{f) = ±2.
Из этого примера мы можем получить отображение с любым чётным
инвариантом Хопфа, когда п четно, воспользовавшись следующим
фактом.
(Предложение 4.В.1. Инвариант Хопфа И: п2п.л (Sn) —► Z является
гомоморфизмом.
Доказательство. Для ftg: S2n_l —> Sn давайте сравним Cf+д с
пространством CfVgy полученным из 5" приклеиванием двух 2гьмерных
клеток посредством отображений / и g. Имеется естественное
отображение факторизации q: Cy+g —> C/V£> стягивающее экваториальный диск
2гьмерной клетки комплекса Cj+g в точку. Индуцированное клеточное
цепное отображение q¥ переводит e2fn в e?'4ef. В когомологиях из
этого следует, что q*(j8y) =q*(j8p = j8y+s, где /3fy fiH и j3/+g — классы ко-
гомологий, двойственные 2п-мерным клеткам. Пусть o.f+% и «/v^ ~
классы когомологий, соответствующие п-мерным клеткам. Тогда мы
получаем q*(ay-v#) = а/+#> так как Я —гомеоморфизм на n-мерных клетках.
Взяв ограничение на подпространства Cj и С^ в Cyvg, мы видим, что
a2fvg = H(f)Pf + H(g)Pg. Таким образом,
af+* =4+(a/vP = H(/)q*(/8/) + H(g)q*(/3g) = (H(/)+H(g))jB/4r □
I Следствие 4.В.2. Группа rc2n-i(S") содержит прямое слагаемое Z,
если п четно.
Доказательство. Либо Я, либо Н/2 —сюръективиый гомоморфизм
n2n_x(Sn)->'L. D
Задачи
1. Докажите, что инвариант Хопфа композиции S2'1-1 —> S2n"1 ~-> S"
задаётся формулой H(gf) = (deg/)H(g), а для композиции S2""'1 —»S" —>S"
инвариант Хопфа удовлетворяет соотношению H(gf) = (degg)2H(/).
2. Докажите, что если Sk -^Sm —> pSn —локально тривиальное
расслоение, то m = 2n - 1 и /с = п - 1, а когда п > 1, Н(р) = ±1. [Докажите, что
Ср —многообразие, и примените двойственность Пуанкаре.]
§4.С. Минимальные клеточные структуры
Мы можем применить гомологическую версию теоремы Уайтхеда
(следствие 4.33), чтобы показать, что любой односвязный CW-комплекс
с конечно порождёнными группами гомологии гомотопически
эквивалентен CW-комплексу, имеющему минимальное число клеток, совместимое
с его гомологиями, а именно, но одной n-мерной клетке для каждого
§4.С. Минимальные клеточные структуры
543
слагаемого Z в Нп и по паре клеток размерностей пип + 1 для каждого
слагаемого Zk в Нп.
| Предложение 4.С.1. Пусть дан односвязный CW-комплекс Х и дано
I представление каждой из его групп гомологии НП(Х) в виде прямой
I суммы циклических групп с указанными образующими. Тогда существу-
I ют CW-комплекс Z и такая клеточная гомотопическая эквивалентность
I гомотопии /: Z —> X, что каждая клетка в Z является либо:
I а) п-мерной клеткой-образующей е£, которая является циклом в кле-
I точных гомологиях, переходящим при отображении / в клеточный
I цикл, представляющий указанную образующую а одного из цик-
I лических слагаемых группы НП(Х), либо
I б) (п 4-1)-мерной клеткой-соотношением е'^+1, клеточная граница ко-
I торой равна кратному образующей п-мерной клетки е£, в случае,
I когда элемент а имеет конечный порядок.
В неодносвязном случае этот результат может легко может оказаться
неверным; контрпримеры даются ациклическими пространствами и
пространством X = (S1 V Sn) U еп+1, построенным в примере 4.35, которое
имеет те же самые гомологии, что и S1, но у которого должны быть клетки
размерности больше 1, чтобы группа пп была нетривиальной.
Доказательство. Мы строим Z индукцией по остовам, начиная с
комплекса Z1, состоящего из одной точки, так как пространство X одно-
связно. Чтобы сделать шаг индукции, предположим, что мы построили
отображение /: Zn —> X, индуцирующее изоморфизм групп Н, при i < п
и сюръекцию групп Нп. Для цилиндра отображения Mf мы тогда
получаем Н(Ш/> Zn) = 0 при i^n и Нп+1Ш/, Z") % пп+\Ш/, Z") по теореме
Гуревича. Чтобы построить Zn+1, воспользуемся следующей диаграммой:
Нп+,№) nn+](Mf,Zn) НП(Х)
й й й
Я„+1 (м/) * «п+1 (М/, Zn) — Hn(Z») — НП(М/) — О
т т || t
Hn+1(Z"+1) — Hn+1(Zn+1,Zn) ^Hn{Zn) — Hn(Z"+1) — 0
По индукции мы полностью знаем отображение Hn(Z")—»Н„(М^)^НП(Х),
а именно, Z" имеет п-мерные клетки-образующие, которые являются
клеточными циклами, отображающимися в данные образующие группы
НП(Х), а также п-мерные клетки-соотношения, которые не дают
вклада в Hn{Zn). Таким образом, Hn{Zn)— свободная абелева группа,
базисом которой служат п-мерные клетки-образующие, а ядро отображения
Hn(Zn) —»НП(Х) — свободная абелева группа с базисом, заданным
определёнными кратными некоторых из образующих п-мерных клеток. Выберем
элементы-соотношения р, в Нп+} (My, Z"), отображающиеся на этот базис
544
Глава 4. Теория гомотопий
в ядре, и пусть элементы-образующие у,-е H„+1(My,Z") будут образами
выбранных образующих группы Hn+l(Mf) ^ЯМ+1(Х).
Посредством изоморфизма Гуревича Нп+1Ш/, %п)ъпп±] Ш/, Z")
классы гомологии р, и Yi представляются отображениями
r,ia.:(D"-r,lS")-(M/,Zn).
Мы строим Z""rl из Z", приклеивая (/т-Ь 1)-мерные клетки посредством
ограничений отображений г, и g, на S". Сами отображения г{ и g,-
тогда дают продолжение включения Z"<—* My до отображения Zn+1 —>Mj,
композиция которого с ретракцией Mj —* X — продолженное отображение
/: Z"+1 —* X. Это даёт нам нижнюю строку предыдущей диаграммы,
причём квадраты коммутативны. По построению подгруппа в HM^1(Z""rI,Z"),
порождённая (/i + 1)-мерпыми клетками-соотношениями, отображается
инъективно в Hn(Zn), причём образ этого отображения —ядро
отображения Hn(Zu) ->7/M(X), поэтому /„: tf„(Z'Hl) -* НмРО— изоморфизм.
Элементы группы Н;Н.] (Zn+1, Z"), представленные образующими (п +
^-мерными клетками, отображаются в элементы yh следовательно, они
отображаются в нуль в H„(Z"), так как ввиду точности второй строки эти
(и + 1)-мерные образующие-клетки являются клеточными циклами,
представляющими элементы группы //„+1(ZM+I), которые при отображении
/„ переходят в данные образующие группы Н,?.Н(Х). В частности,
гомоморфизм /ж: HMH(Z'HI) —> НМ+1(Х) сюръективен, и доказательство шага
индукции завершено.
Сделав это для всех п, мы построим CW-комнлекс Z и отображение
/: Z—>Х, обладающие требуемыми свойствами. □
Пример 4.С.2. Предположим, что X—такой односвязный CW-kom-
плекс, что для некоторого п ^ 2 единственными приведёнными группами
гомологии пространства Ху отличными от нуля, являются группа НДХ),
которая конечно порождена, и группа //„ r x (X), которая конечно
порождена и свободна. Тогда предложение 4.С.1 говорит, что комплекс X гомото-
иически эквивалентен CW-комнлексу Z, полученному из букета п-мерных
сфер приклеиванием (п + 1)-мерных клеток. Отображения приклеивания
этих клеток определены с точностью до гомотопий клеточным
граничным отображением НмН (Z" и, Z") -> W„(Z"), так как tt„(Zm) ^ /7M(Z").
Поэтому отображения приклеивания либо тривиальны (в случае
образующих (и 4- 1)-мерных югеток), либо представляют некоторое кратное
включения одного из слагаемых букета (в случае (п + 1)-мерной клетки-
соотношения). Следовательно, Z — букет сфер S" и S""'"1 вместе с
пространствами Мура M(Z„,,n) вида 5"ие"'м. В частности, гомотопический тип
пространства X однозначно определяется его группами гомологии.
I Предложение 4.С.3. Пусть X— такое односвязное пространство, го-
мотопически эквивалентное CW-комнлексу, что единственными
нетривиальными приведёнными группами гомологии X являются Н2(Х) ыЪт
§4.С. Минимальные клеточные структуры
545
I и Я4(Х) ъ Ъ. Тогда гомотопический тип пространства X однозначно
I определён кольцом Н*(Х; Z) с ^-произведением. В частности, это мож-
I но применить к любому односвязному замкнутому четырёхмерному
I многообразию.
Доказательство. Согласно предыдущему предложению мы можем
считать, что X — комплекс X,, полученный из букета V;S2, состоящего
из т двумерных сфер S?, приклеиванием клетки е4 по отображению
с/?: S3-* VjS?. Как показано в примере 4.52, группа n3(\/jS'j) свободная,
причём её базисом служат отображения Хопфа т};-: S3 —♦ S2 и произведения
Уайтхеда [ij,ifcL j <ку где z'j — включение S2<—> V,S2. Так как гомотопия
отображения у> не изменяет гомотопический тин пространства Х^, мы
можем считать, что у —линейная комбинация Xl0;7); + S ад[*л U- Мы
j )<k
должны понять, как коэффициенты а} и а-)к определяют w-произведение
Н2(Х; Z) х Н2(Х; Z) -> Н4(Х; Z).
Это w-произведение можно представить симметрической матрицей
(bjk) размера т х гп, где произведение классов когомологий,
двойственных j-й и /с-й двумерным клеткам,— это умноженный на bjk класс,
двойственный четырёхмерной клетке. Мы утверждаем, что Ь;/с = а^к для j < к
и bjj^dy Если кр — одна из образующих rj,- или [i,,^], то это очевидно,
так как если у = У)р то Х^ —букет пространства СР2 и m — 1 двумерных
сфер, в то время как если у? = [ij, zfc], то Х^ — букет пространства S? x S2
и m — 2 двумерных сфер. Утверждение также верно, когда </? = —г}; или
~[ij, ifc], так как изменение знака для кр достигается композицией кр с
зеркальной симметрией сферы S3, которая действует на образующую
группу Н4(Х^; Z) обращением знака. Общий случай теперь доказывается по
индукции с помощью утверждения, что матрица (bj7c) для Х^+Яу, является
суммой соответствующих матриц для Х^ и Х^,. Это утверждение можно
доказать следующим образом. Приклеивая две четырёхмерные клетки
к VjS2 по отображениям с/? и я/;, мы получаем комплекс Х.^,, который
можно рассматривать как X^UXV,. Имеется отображение факторизации
Ч: ^hv ~~*^гм/"> котоРое является гомеоморфизмом на двумерном
остове и стягивает в точку замыкание экваториального трёхмерного диска
в четырёхмерной клетке комплекса Х^,. Индуцированное отображение
q*: Н4(Х^ ^) -* Н4(Х^+^,) переводит каждую из двух образующих,
соответствующих четырёхмерным клеткам комплекса Х^,, в образующую, что
и доказывает требуемое утверждение.
Теперь предположим, что кольца когомологий пространств Х^ и Х^,
изоморфны. Это означает, что базисы в Н*{Ху, Z) и Н*{Х^\ Z) можно
выбрать так, чтобы матрицы, определяющие w-произведение Н2 х Н2 -*НА
относительно этих базисов, были одинаковыми. Предыдущее
предложение говорит, что любой выбор базиса можно реализовать как двойствен-
18 3ак. «о>
546
Глава 4. Теория гомотопий
ный базис для клеточной структуры на CW-комплексе, гомотопически
эквивалентном данному комплексу. Поэтому мы можем считать, что
матрицы (Ь;/с) для Ху и Х^ одинаковые. Согласно тому, что мы показали
в предыдущем абзаце, это означает, что отображения ip и я/' гомотопны,
следовательно, Х^ и Х^ гомотопически эквивалентны.
Что касается утверждения об односвязных замкнутых
четырёхмерных многообразиях, то согласно следствиям П.8 и П.9 и предложению
П.11 из приложения такое многообразие М имеет гомотопический тип
CW-комплекса с конечно порождёнными группами гомологии. Тогда из
двойственности Пуанкаре и теоремы об универсальных коэффициентах
следует, что единственные нетривиальные группы гомологии //,(М) — это
Z при i = 0, 4 и Zm при i = 2 для некоторого т ^ 0. D
Этот результат и пример перед ним — частные случаи гомотопической
классификации Уайтхеда односвязных CW-комплексов с клетками
положительной размерности в трёх соседних размерностях п, п -4-1 и п. + 2; см.
полное изложение в [9J.
§ 4.D. Когомологии локально тривиальных
расслоений
В то время как гомотопические группы трёх пространств в
локально тривиальном расслоении вписываются в длинную точную
последовательность, соотношение между их группами гомологии или когомологии
гораздо сложнее. Формула Кюннета показывает, что некоторая тонкость
имеется даже для расслоения-произведения, а для общих расслоений
требуется уже механизм спектральных последовательностей, описанный в
[SSAT]. В этом параграфе мы описываем несколько специальных типов
локально тривиальных расслоений, где достаточно более элементарных
методов. В качестве приложения мы вычисляем кольца когомологии
некоторых важных пространств, тесно связанных с группами Ли. В частности,
мы находим много пространств, кольца когомологии которых —внешние
и полиномиальные.
Теорема Лере—Хирша
Эта теорема будет основой для всех остальных результатов в этом
параграфе. Она описывает условия, достаточные, чтобы гарантировать,
что локально тривиальное расслоение имеет когомологии, очень похожие
на когомологии расслоения-произведения.
I Теорема 4.D.I. Пусть F -> Е —► Б — такое локально тривиальное рас-
I слоение, что для некоторого коммутативного кольца коэффициентов Я
I выполнены следующие условия:
I a) Hn(F\ R) — конечно порождённый свободный R-модуль для всех и;
§4.D. Когомологии локально тривиальных расслоений 547
I б) существуют классы Cj еН^(£; R), для которых ограничения f*(cj)
I образуют базис в H*(F\ R) для каждого слоя F, где i: F —> £ — вклю-
I чение.
I Тогда отображение
I Ф:НЧВ;Ю®яН*(^;Я)->Н¥(£;Я), J]bf ®i*(Cj) - £У(Ь'° -с;,
I у О'
I является изоморфизмом.
Другими словами, Н*(Е; R) —свободный Н*(В; R)-модуль с базисом
{Cj}y где мы рассматриваем H¥(£;R) как модуль над кольцом H*(B;R),
определяя умножение на скаляр формулой be = p*(b) wc, bG H*(B\ R)
ис€Н*(Н;Я).
В случае произведения £ = В х Fc модулем Н*(£; Ю, свободным над R,
мы можем индуцировать базис в H*(F;R) посредством проекции £ —> F
и получить классы с,-. Таким образом, теорема Л ере—Хирша обобщает
версию формулы Кюннета, в которой участвуют ^-произведения (теорему
3.16), по крайней мере в том, что касается аддитивной структуры и
структуры модуля над ir(B;R). Однако теорема Лере—Хирша не утверждает,
что изоморфизм FT(£; Ю ^ Н*(В; Ю ®к H*(F\ R) является кольцевым
изоморфизмом, и в действительности это не всегда верно, как мы увидим
позже на конкретном примере.
Примером расслоения, для которого не существует классов с-р служит
расслоение Хопфа S1 ->S3 ->S2, так как H4S3) j*H*{S2) ®H\Sl).
Доказательство. Мы сначала докажем требуемое утверждение для
конечномерных CW-комплексов В индукцией по размерности комплекса.
Случай, когда комплекс В нульмерен, тривиален. Для доказательства шага
индукции предположим, что В имеет размерность п, и пусть В' С В
—подпространство, полученное удалением точки ха из внутренности каждой
n-мерной клетки е^ комплекса В. Положим Е' = р~1{В'). Тогда мы
получаем следующую коммутативную диаграмму, где подразумеваются
коэффициенты в R:
... - Н*(В, ВО ®я Н*(£) -*■ Н*(В) ®R H*(F) - Н*(В') ®R H*(F) - ...
|ф 1ф |ф
... ^ НЧ£, £0 *■ Н*№') *■ Н*{Е') ^ ...
Отображение Ф слева определяется точно так же, как в абсолютном
случае, с помощью относительного ^-произведения
H*(E,E')QRH*(E) -+ Н*(Е,Е').
Первая строка диаграммы точна, так как тензорное умножение на
свободный модуль сохраняет точность. Вторая строка, конечно, тоже
точна. Коммутативность диаграммы следует из очевидной естественности
отображения Ф в случае двух изображённых квадратов. Для оставшего-
548
Глава 4. Теория гомотопий
ся квадрата, в который входят отображения кограницы, если мы
начнём с элемента b<8>i*(cj) eH*(B0 <8RH*(F) и отобразим его
горизонтально, то получим элемент 5b<8>i*(Cj), который отображается вертикально
в р*(5Ь) ^с;, тогда как если мы сначала отобразим исходный элемент
вертикально, то получим элемент р*(Ь)^С/, который отображается
горизонтально в 5(p*(b)^Cj) = 5p*(b)^Cj = p*(5b)^Cj, так как 5с;=0.
Пространство В' деформационно ретрагируется на остов Вп~\ и ш
следующей леммы вытекает, что включение р"^{Вп~1) <^->Е' является
слабой гомотопической эквивалентностью, а потому индуцирует
изоморфизм всех групп когомологий.
I Лемма 4.D.2. Пусть даны локально тривиальное расслоение р: Е-+В
и такое подпространство Л с В, что пара (В, А) является к -связной.
Тогда пара (£, р~1(А)) тоже является к -связной.
Доказательство.' По предположению для отображения
g:(D\3D')- (E,p-]G4)), ; О,
существует гомотопия ft: (D', 3D1) —»(В, А) отображения f0~pg в
отображение /j с образом в А. Свойство поднятия гомотопий тогда даёт гомото-
пию gt: (D', 3D1) —> (Е, р_1(А)) отображения g в отображение с образом
вр~\А). D
Теорема для конечномерного В доказывается теперь индукцией но п
с помощью 5-леммы, как только мы покажем, что отображение Ф в левой
части диаграммы — изоморфизм.
По свойству локально тривиального расслоения существуют такие
открытые шаровые окрестности Ua с епа точек ха, что расслоение
является произведением над каждым множеством Ua. Пусть U = {JUa и пусть
а
U' = U ПВ\ Согласно свойству вырезания мы получаем Я*(В> В')ъН*{и, U')
и Н*(Е,Е') ъ Н* (p~l (U), p~l (U')). Это сводит нашу задачу к
доказательству того, что отображение
Ф: H\Uy U')®RH*(F) -> H\U xF,U'x F)
является изоморфизмом. Для этого мы можем либо обратиться к
относительной формуле Кюннета из теоремы 3.21, либо снова рассуждать по
индукции, применяя 5-лемму к той же самой диаграмме, в которой (В, В )
заменяется на ([/,[/'). Тогда по индукции получаем, что теорема верна
для U и U', так как они деформационно ретрагируются на комплексы
размерностей Оип-1 соответственно, а согласно лемме мы можем
ограничиться расслоениями над этими комплексами.
Теперь рассмотрим случай, когда В —бесконечномерный CW-kom-
плекс. Так как пара (В, Вп) является n-связной, из леммы следует, что
то же самое верно для (£, р_1(В")). Следовательно, в коммутативной
§4.D. Когомологии локально тривиальных расслоений 549
диаграмме
/Г(Ю ^Н*(р'1(Вп))
горизонтальные отображения — изоморфизмы в размерностях ниже п.
Тогда из этого факта следует, что отображение Ф справа является, как мы
уже показали, изоморфизмом, следует, что отображение Ф слева
—изоморфизм в размерностях ниже п. Так как число п любое, это доказывает
теорему для всех CW-комплексов В.
Чтобы распространить доказательство на случай произвольной
базы В, нам нужно понятие индуцированного расслоения, которое весьма
часто используется в теории расслоений. Пусть даны локально тривиальное
расслоение р:К->Ви отображение /: А—* В, Положим /*(£) — {(а,е) е
еА х £ /(а) = р(е)}. Тогда имеет место коммутативная диаграмма
Г(Е) -£
т т
А ^В
где два отображения из /*(£) задаются формулами (а, е) —>а и (а, е) —>е.
Простая проверка показывает, что проекция /*(£) —> А является локально
тривиальным расслоением с тем же самым слоем, что и £ —* В, так как
локальная тривиализация расслоения £ —> В над СУ с В приводит к локальной
тривиализации расслоения /*(£) —* А над f~l(U).
Если /: А —> В — CW-аппроксимация произвольного базового
пространства В, то отображение /*(£)—>£ индуцирует изоморфизм
гомотопических групп согласно 5-лемме, применённой к длинным точным
последовательностям гомотопических групп для двух расслоений £ —> В
и /*(£)—>А со слоем F. Следовательно, отображение /*(£)—>£
индуцирует также изоморфизм когомологии. Классы с; индуцируют классы
в Н*(/*(£); R), ограничения которых всё ещё являются базисом в каждом
слое, а потому естественность отображения Ф сводит теорему для £ —* В
к случаю /*(£)-* А. □
I Следствие 4.D.3. Имеют место следующие изоморфизмы:
I a) H*(U(n); Z) ъ Az[xlyx3, ...,x2n-"J —внешняя алгебра от образую-
I щих х, нечётной размерности i;
I б) H4SU(n);Z)^[x3>*5>...,*2M-i];
| в) H*(Sp(rO;Z)^Ax[x3,*7>--.,*4n-i].
Эта довольно простая структура сильно контрастирует с когомологи-
ями О(п) и SO(n), которые значительно сложнее, как показано в §3.D.
Доказательство. Для доказательства утверждения а) предположим по
индукции, что оно верно для U(n - 1). Рассматривая расслоение U(n- 1)—>
550 Глава 4. Теория гомотопий
—>U(n)—>S2"-1, мы видим, что пара (U(n), U(n — 1)) является (2п-2)-связ-
ной, поэтому
//'(U(n); Z) -> Н'ОДп - 1); Z)
— отображение на при i ^ 2п — 3, и классы
существующие по индукции, являются ограничениями классов с ь..., с2;?_3б
eH*(U(n); Z). Произведения разных х, образуют базис в H*(U(n - 1); Z) ^
^ Л7Д-^1, •••, *2п-з1> и эти произведения —ограничения соответствующих
произведений элементов с,. Поэтому можно применить теорему Лере—
Хирша, и она даёт изоморфизм
/ГОДп); Z) ъ Н*ЦДп - 1); Z) ®/r(S2'1-1; Z).
Согласно свойству коммутативности ^-произведения это тензорное
произведение—внешняя алгебра от образующих xlt...,*2h-i нечётной
размерности.
То же самое доказательство годится для Sp(n), если воспользоваться
расслоением Sp(n - 1) —>Sp(n) —>S4"-1. В случае SU(n) нужно
воспользоваться расслоением SU(n - 1) ^SU(n) —►S2""1. Так как SU(1)
—тривиальная группа, расслоение SU(1) —> SU(2) —> S3 показывает, что SU(2)=53,
поэтому первая образующая — это х3. □
Поучительно посмотреть более внимательно на то, как гомологии
и когомологии О(п), U(n) и Sp(n) связаны со структурами расслоений на
них. Для U(n) есть последовательность расслоений
S1 = U(l)c >- U(2)c ^ U(3)c >• ...с *- U(n - 1)с ^ U(n)
Y Y Y Y
s3 ss s2"-3 s2""1
Если бы все они были расслоениями-произведениями, то пространство
U(n) было бы гомеоморфно произведению S1 х S3 х ... х S2u~l. В
действительности расслоения нетривиальны, но гомологии и когомологии для
U(n) те же самые, что и у этого произведения сфер, включая структуру
w-произведения. Для Sp(n) ситуация весьма похожая, причём
соответствующее произведение сфер имеет вид S3 х S7 х ... х 54"-1. Для О(п)
соответствующая последовательность расслоений такова:
S° = 0(1)с *- 0(2)с > 0(3)с ^ ...с *- 0(п - 1)с >- О(п)
Y Y Y Y
Sl S2 S"-'2 S""1
Вычисления в §3.D показывают, что
H+(0(n);Z2) *HAS°xSl x...x5n_1;Z2),
§ 4.D. Когомологии локально тривиальных расслоений 551
но для коэффициентов в Z это уже не верно. Вместо этого рассмотрим
более грубую последовательность расслоений
5° = 0(1)с *■ 0(3)с ^ 0(5)С ^ ...с—s- 0(2fc - 1)с—^ 0(2fc)
Y Y т I
У2(Ж3) V2CR5) V2(R2fc_1) S2*"1
где последнее расслоение 0(2fc) —> S2k~l опускается, если п = 2fc - 1. Как
мы заметили в конце §3.D для случая SO(n), группа О(п) имеет те же
самые целочисленные гомологии и когомологии, как если бы эти
расслоения были произведениями, но структура w-произведения для О(п)
с коэффициентами в Z не такая, как в этом произведении.
Когомологии грассманианов
Вот важное приложение теоремы Лере—Хирша, обобщающее
вычисление колец когомологии проективных пространств.
I Теорема 4.D.4. Если Gn(С00)— многообразие Грассмана п-мерных
I векторных подпространств в С°°, то H*(Gn(C°°); Z) — кольцо много-
I членов Z[c!,...,cn] от образующих с, размерности 2t. Аналогично
I H*(Gn(jR°°); Z2) —кольцо многочленов Z2[wly..., vvn] от образующих vvf
I размерности i, a H*(Gn(EI00);Z) ъ Z[qx, ...,qn], где q,- имеет размер-
I ность 4i.
План доказательства состоит в том, чтобы применить теорему Лере—
р
Хирша к локально тривиальному расслоению F -* £ —* Gn(C°°), где £
имеет то же самое кольцо когомологии, что и произведение п экземпляров
пространства СР°°, т.е. кольцо многочленов Ъ\хъ ..., хп], где все Xi
имеют размерность 2. Индуцированное отображение р*: H*(Gn(C°°); Z) —>
-*H*(£;Z) будет инъективным, и мы покажем, что его образ состоит из
симметрических многочленов в Ъ\х1у..., хп], т.е. многочленов,
инвариантных относительно перестановок переменных х(. Классическая теорема
из алгебры утверждает, что сами симметрические многочлены образуют
кольцо многочленов Z[cr,,..., сгп], где сг, — некоторый симметрический
многочлен степени i, а именно сумма всех произведений i разных Xj. Это
Доказывает требуемое утверждение для Gn(C°°), и то же самое
рассуждение можно применить в вещественном и в кватернионном случаях.
Доказательство. Определим п-флаг в Ск как упорядоченный набор п
ортогональных одномерных векторных подпространств в Ск.
Эквивалентным образом п-флаг можно определить как последовательность
векторных подпространств V} с ... с Vn в Ск, где V( имеет размерность i. Почему
эти объекты нужно называть «флагами», не совсем понятно, но это
традиционное название. Множество всех п-флагов в Ск образует
подпространство Fn(Ck) в произведении п экземпляров СР*"1. Существует естествен-
552
Глава 4. Теория гомотетий
ное локально тривиальное расслоение
где р отображает набор п ортогональных прямых в п-мерное
подпространство, которое на них натянуто. Свойство локальной тривиальности можно
проверить так же, как мы это делали для аналогичного расслоения Шти-
феля Vn (С") -> Vn (Ск) -> Gn(Ck) в примере 4.53. Случай к = оо можно
разобрать тем же самым рассуждением, и в этом случае получается расслоение
F—► £ —> G„(C°°), которое упоминалось в абзаце перед доказательством.
Первый шаг доказательства —проверка того, что
H'tfnQC00);® **Z[xl9 ...,хп],
где элемент х{ индуцирован из образующей группы Н2(СР°°; Z) при
отображении Fn(C°°) —►СР00, проектирующем п-флаг на его прямую с
номером i. В этом можно убедиться, рассматривая локально тривиальное
расслоение
Сроо _^ рп(с°°) Д F^CC00),
где р проектирует п-флаг на (п - 1)-флаг, полученный при отбрасывании
его последней прямой. Свойство локальной тривиальности можно
проверить рассуждением из примера 4.54. Теорема Лере—Хирша применима,
так как степени элемента хп образуют базис в Я*(СР°°; Z) при
ограничении на слои СР00, где каждый слой является пространством прямых в
векторном подпространстве С°° стандартного пространства С00. Элементы х{
при i < п индуцированы посредством р из элементов в H*(Fn_1(C00); Z),
определённых таким же образом. По индукции H*(Fn^I(C0C); Z) —кольцо
многочленов от этих элементов. По теореме Лере—Хирша мы получаем,
что произведения степеней элемента х( для 1 ^ i $ п образуют аддитивный
базис в H*(Fn(C°°);Z), следовательно, это кольцо — кольцо многочленов
от переменных х{.
Имеется соответствующий результат для F„(Cfc), согласно
которому группа H*(F,?(Cfc);Z) свободна, причём её базисом служат мономы
х^.^х^1, ij ^ к - j для каждого j. Это доказывается точно тем же способом,
если мы применим индукцию по п и воспользуемся локально
тривиальным расслоением CPk"n —>Fn(Cfc) -+Fn_i(Ck). Таким образом, группы
когомологий пространства Fn (Ck) изоморфны группам когомологий
пространства CPfc~! х ... х СР*""".
После этих предварительных замечаний можно начать основное
рассуждение, применяя локально тривиальное расслоение
Предыдущие вычисления показывают, что теорема Лере—Хирша
применима, поэтому H*(F„(C°°); Z) — свободный модуль над /Г(СП(С°°); Z),
базисом из мономов х|\..х£' cij^n- j для каждого j. В частности, так как
§4.D. Когомологии локально тривиальных расслоений 553
1 содержится среди элементов базиса, гомоморфизм р* инъективен, а его
образ —прямое слагаемое в H*(Fn(C°°); Z). Остаётся показать, что образ
гомоморфизма р* —это в точности симметрические многочлены.
Чтобы показать, что образ гомоморфизма р* содержится в
симметрических многочлен, рассмотрим отображение п: F„(C°°) —> F^CC00),
переставляющее прямые в каждом n-флаге в соответствии с данной
перестановкой чисел 1, ..., п. Индуцированное отображение п* на H*(Fn(C0C); Z) ъ
ъ Z[xl5 ...Ухп] — это соответствующая перестановка переменных х(. Так
как перестановка прямых в n-флаге не влияет на n-мерное
подпространство, которое на них натянуто, мы получаем ртт = р, а потому тг*р* = р\
а это означает, что многочлены в образе гомоморфизма р* инвариантны
относительно перестановок переменных.
Как отмечалось ранее, симметрические многочлены в Z[xlt ..., хп]
образуют кольцо многочленов Z[crb ..., сг„], где ст, имеет степень i. Мы
показали, что образ гомоморфизма р* — прямое слагаемое, поэтому, чтобы
проверить, что р* —отображение на все симметрические многочлены,
достаточно показать, что градуированные кольца H*(GM(C°°); Z) и "£[аъ ...
..., <7П] имеют одинаковый ранг в каждой размерности, где ранг конечно
порождённой свободной абелевой группы —это количество слагаемых Ъ.
Для градуированного свободного Z-модуля А = @А{ определим его
ряд Пуанкаре как формальный степенной ряд рА(0 =^а^1, где а{ — ранг
i
группы А,, который мы предполагаем конечным для всех i. Нам
понадобится формула Ра<8)в(0 = P/\(Opzj(t), которая непосредственно следует из
определения градуированного тензорного произведения.
В нашем случае все когомологии, отличные от нуля, сосредоточены
в чётных размерностях, поэтому давайте упростим обозначения, считая,
что А,—это 21-мерные когомологии рассматриваемого пространства.
Так как ряд Пуанкаре для Z[x] равен ^]t' = (1 - t)"1, ряд Пуанкаре для
H*(Fn(C°°); Z) равен (1 - t)_n. Для H*(Fn(Cn); %) ряд Пуанкаре равен
л п
Cl4-t)(14-t4-t2)...Cl-bt4-...4-tr'-1) = Пт^Т = Cl-t)-"P](l-t?).
Из аддитивного изоморфизма
H*(Fn(C0O);Z)^H*(Gn(C0O);Z)(8)H4Fn(Cn);Z)
мы видим, что ряд Пуанкаре p(t) для H*(GM(C°°); Z) удовлетворяет
соотношению
P(t)(l-tr"P](i-t'') = (l-trn, а потому РСО = ПО -г'")-1.
554
Глава 4. Теория гомотопий
Это в точности ряд Пуанкаре для Z[ab ..., cj,J, так как а{ имеет степень i.
Как уже было отмечено, из этого следует, что образ гомоморфизма р* —
все симметрические многочлены.
Это завершает доказательство для Gn(C™). Те же самые рассуждения
применимы в других двух случаях, если использовать коэффициенты Z2
всюду в вещественном случае и заменить «ранг» на «размерность» для
линейных пространств над Z2. G
Эти вычисления показывают, что изоморфизм
Я*(Я; Я) * Я*(В; Я) ®ЛЯ*(Р; Я)
из теоремы Лере—Хирша не всегда является изоморфизмом колец,
поскольку если бы это было так, то кольцо многочленов Н* (**',, (С00); Z)
содержало бы H*(F„(€");Z) в качестве подкольца, но в последнем кольце
некоторая степень каждого элемента положительной размерности равна
нулю, так как Hk(Fn(Cn); Z) = 0 для достаточно большого к.
Последовательность Гизина
Помимо теоремы Лере—Хирша, которая имеет дело с локально
тривиальными расслоениями, когомологически похожими на произведения,
существует другой специальный класс локально тривиальных расслоений,
для которых элементарный анализ их структуры когомологий оказьша-
ется возможным. Это локально тривиальные расслоения S" —* Е —► В,
удовлетворяющие условию ориентируемости, которое всегда
выполняется, если В односвязно или если мы берём когомологий с коэффициентами
в Z2. Для таких расслоений мы покажем, что имеет место точная
последовательность, называемая последовательностью Гизина:
... -> Н'"П(В; К) ^ #'(£; К) -^ Н((Е\ Я) -> Н('п+1(В; Я) -> ...,
где е — так называемый «эйлеров класс» в Hn(B;R). Так как bV(B\ R)=Q
при i < 0, начальный участок последовательности Гизина даёт
изоморфизм р*: Hl(B\ R) -^ Н'(Е; Я) при i < n - 1, а более интересная часть
последовательности начинается с
0 -> Нп~\В; Я) ^ Нп'1{Е; Я) -> Н°(В; Я) -^ Н"(В; К) ^ Н"№; Я) ^ ...
В случае расслоения-произведения £ = S"~1 x В существует сечение, т.е.
отображение 5: В —► £, для которого ps = 1, таким образом,
последовательность Гизина разбивается на расщенимые короткие точные
последовательности
о -> н\в\ я) ^ f/'cs""1 хв-,ю^ н'"-',+,(В; Ю ->о,
что согласуется с формулой Кюннета
H*(Sn'1 *В;Юъ H*(Sn~l\ R) ®//*(В; Ю-
§4.D. Когомологии локально тривиальных расслоений 555
Расщепление имеет место всегда, когда расслоение имеет сечение, даже
если это расслоение —не произведение.
Например, рассмотрим расслоение Sn_I —> У2(!^п+1) —>Sn. Точки
пространства V2№n+I) — пары (v1,v2) ортогональных единичных векторов
в Rn+\ и p(vb v2) = Vj. Если мы представляем себе v} как точку сферы Sn,
a v2 — как единичный касательный вектор к S" в точке vb то V^C^"4"1) —
это в точности расслоение касательных единичных векторов к S".
Сечение этого расслоения —поле единичных касательных векторов к SM, а по
теореме 2.28 такое векторное поле существует тогда и только тогда, когда
п нечётно. Из того факта, что последовательность Гизина расщепляется,
когда существует сечение, следует, что V2(Rn+1) имеет те же самые
когомологии, что и произведение Sn~l x S", если п нечётно, по крайней мере
для п > 1, когда базовое пространство S" односвязно и предположение
об ориентируемости выполняется. Когда п четно, вычисления в конце
§3.D показывают, что H*(V2(M"+1); Z) состоит из групп Ъ в размерностях
О и 2п - 1 и группы Ъ2 в размерности п. Последняя группа появляется
в последовательности Гизина как
H°{Sn) ^Hn(Sn) —^Нп0дан■*)) _* Hj(S")
II II II II
ъ ъ ъ2 о
следовательно, эйлеров класс е должен быть удвоенной образующей
группы Hn(Sn) в случае, когда п четно. Когда п нечётно, он должен быть
нулевым, чтобы последовательность Гизина была расщепимой.
Этот пример иллюстрирует теорему из дифференциальной
топологии, которая объясняет, почему эйлеров класс так называется: эйлеров
класс расслоения единичных касательных векторов для замкнутого
ориентируемого гладкого п-мерного многообразия М равен эйлеровой
характеристике #(М), умноженной на образующую группы Нп(М\ %)•
— 1 р
Всегда, когда расслоение S" —>Е-^>В имеет сечение, эйлеров класс е
должна быть нулевым в силу точности последовательности Я0(В) -^-»
we p'
—*Нп(В) —> Н"(Е), так как гомоморфизм р* инъективен, если существует
сечение. Таким образом, эйлеров класс можно рассматривать как
препятствие к существованию сечения: если эйлеров класс отличен от нуля, то
не может существовать никакого сечения. Это качественное утверждение
можно сделать более точным с помощью техники теории препятствий,
как объяснено в [55] или в [VBKT].
Перед выводом последовательности Гизина давайте рассмотрим
некоторые примеры того, как её можно использовать для вычисления ^-про-
изведений.
Пример 4.D.5. Рассмотрим расслоение S"-1 —>£—>Я, где Е
стягиваемо, например расслоение S1 -*S0C-*CP°° или его вещественный или ква-
556
Глава 4. Теория гомотопий
тернионныи аналог. Длинная точная последовательность гомотопических
групп расслоения показывает, что пространство В является (п —
^-связным. Таким образом, если п > 1, то В односвязно, и мы получаем
последовательность Гизина для когомологий с коэффициентами в Z. Для
п = 1 мы берём коэффициенты Z2. Если п > 1, то, так как £
стягиваемо, из последовательности Гизина следует, что Hl(B; Z) = 0 при 0 < i < п
и что we: Н'(В; Z)—* Н1+П(В; Z)— изоморфизм при i ^ 0. Из этого
следует, что IV (В\ Z) — кольцо многочленов Z[e]. При п = 1 отображение
р*: Hn~l{B\ Z2) —* Нп_1(£; Z2) в последовательности Гизина сюръектив-
но, поэтому мы видим, что ^е: H'(B;Z2) —»НИ""(В; Z2) —снова
изоморфизм для всех i ^ 0, а значит, H*(B;Z2) ^Z2[e]. Таким образом,
последовательность Гизина даёт новый вывод структуры ^-произведения для
проективных пространств. Кроме того, так как кольца многочленов ZTe]
реализуются как Н*(Х; Z), только если е имеет размерность 2 или 4, как
мы покажем в следствии 4.L.10, мы можем сделать вывод, что расслоения
Sn_1 —>£—>В со стягиваемым пространством £ существуют, только если п
равно 1, 2 или 4.
Пример 4.D.6. Для многообразия Грассмана Gn = G,,^00) мы
имеем ^](Gn) ^ тг0О(п) ^Z2, поэтому универсальное накрытие над G„ даёт
расслоение 5° —> Gn —* G„. Можно рассматривать Gn как пространство
ориентированных п-мерных подпространств в К00, которое является,
очевидно, двулистным накрывающим пространством над Gn, а потому
универсальным накрытием, так как оно линейно связно, будучи фактор-
пространством VJjCR^/SOCn) стягиваемого пространства V^CIR00). Один
из участков последовательности Гизина для расслоения S0 —* Gu —> G„
имеет вид H°(Gn;Z2) ^ Hl{Gn\Z2)-^ Hl{Gn\Z2). Последняя группа
пулевая, так как пространство Gn односвязно, и H^[Gn\Z2) ** Z2, так как
H*(Gn;Z2) ^Z2[vt/j, ...,и/п], как мы уже показали в этом параграфе.
Поэтому е = wY и отображение we: H*(G„; Z2) —> H*(G„\ Z2) инъективно.
Последовательность Гизина тогда разбивается на короткие точные
последовательности
0 - Я''(СП; Z2) ^ Н'"+1(СП; Z2) - H'41(G„; Z2) - 0,
из которых следует, что #*(G„; Z2) —это факторкольцо
Z2[w,,..., и/J/OVi) я» Z2[vi/2,..., и/J.
Пример 4.D,7. Комплексный аналог расслоения из предыдущего
примера—расслоение Sl -»Gn(C°°) -^„(С00), где пространство ^„(С00)
является двусвяз ным. Его можно построить следующим образом.
Имеется детермииантный гомоморфизм U(n)—>Sl с ядром
SU(n)—унитарными матрицами с определителем 1, поэтому S1 —это факторпространство
U(n)/SU(n), и, ограничивая на SU(n) действие группы U(n) на простран-
§ 4.D. Когомологии локально тривиальных расслоений 557
стве УЯ(С°°), мы получаем вторую строку коммутативной диаграммы
Un > Vn(C°°) G^C00)
1 1 II
S1— Vn(C°°)/SU(n)-*- Gn(C™)
Эта вторая строка— локально тривиальное расслоение согласно
обычному рассуждению с выбором непрерывно меняющегося ортонормирован-
ного базиса в п -мерных подпространствах вблизи данного п -мерного
подпространства. Легко проверить, что пространство Gn (С00) = Vn (С00)/ SU(n)
является двусвязным, посмотрев на соответствующий участок диаграммы
гомотопических групп, связанных с этими двумя расслоениями:
О 7r2(G„) -V тчОЯл)) - О
II ; ь
О — rc2(Gn) — 7r2(Gn) -^ ^(S1) tt^G,) —^ О
Второе вертикальное отображение— изоморфизм, так как S1
вкладывается в U(n) как подгруппа U(l). Так как граничное отображение в верхней
строке — изоморфизм, граничное отображение в нижней строке тоже
будет изоморфизмом, а тогда точность влечёт, что пространство Gn является
двусвязным.
Последовательность Гизина для S1 —> G„(C°°) —> Gn(C°°) можно
проанализировать точно так же, как в предыдущем примере. Один из
участков последовательности имеет вид
H°(Gn] Z) ^ H\Gn; Z) - H\Gn; Z),
и последняя группа нулевая, так как пространство Gn является
двусвязным, поэтому элемент е должен быть образующей группы H2(Gn\ Z) ъЪ.
Так как H*(Gn; Z)—алгебра многочленов Z[cb ..., с„], мы должны
получить е = ±сь поэтому отображение ^е: H*(Gn; Z) —> H*(Gn; Z) инъектив-
но, последовательность Гизина, разбивается на короткие точные
последовательности и H*(Gn; Z) —это факторкольцо
Z[c1,...,cn]/(c])^Z[c2, ...,cj.
Пространства G„ из последних двух примеров часто обозначают
BSO(n) и BSU(n), выражая тот факт, что они связаны с группами SO(n)
и SU(n) посредством расслоений SO(n) -> Vn(R°°) -> BSO(n) и SU(n) ->
-** ^П(С°°) —> BSU(n) со стягиваемым тотальным пространством Vn.
Никакого кватернионного аналога для BSO(n) и BSU(n) нет, так как при
л = 2 он давал бы пространство с кольцом когомологии Ъ\х\ от 8-мерной
образующей, а это невозможно согласно следствию 4.L.10.
Теперь мы обратимся к выводу последовательности Гизина, который
идёт весьма окольным путём:
558
Глава 4. Теория гомотопий
1) выводим относительную версию теоремы Лере—Хирша из
абсолютного случая;
2) применяем её в частном случае расслоений с шаровым слоем, что
приводит к основному результату, называемому изоморфизмом Тома;
3) показываем, что это рассуждения применимо ко всем ориентируемым
расслоениям с шаровым слоем;
4) выводим последовательность Гизина, вставляя изоморфизм Тома в
длинную точную последовательность групп когомологий для пары,
состоящей из шарового расслоения и его граничного сферического
расслоения.
1. Пара локально тривиальных расслоений состоит из локально
тривиального расслоения р: Е —> В со слоем F вместе с таким подпространством
Е1 С £, что р: Е' —> В —расслоение со слоем F' С F, причём локальные
тривиализации для Е' получаются как ограничения локальных тривиали-
заций для Е. Например, если £ —> В — расслоение со слоем D", а Е' СЕ —
объединение граничных сферических слоев, то (£, £') — пара локально
тривиальных расслоений, так как локальные тривиализации расслоения F
при ограничении дают локальные тривиализации расслоения £' ввиду
того факта, что гомеоморфизмы п-мерного шара на п-мерный шар при
ограничении дают гомеоморфизмы их граничных сфер, поскольку
граница и внутренность шара Dn различаются локальными группами гомологии
Hn(D",Dn-{x};Z).
I Теорема 4.D.8. Предположим, что (F, F') —» (Е, £') —> В — такая па-
I ра локально тривиальных расслоений, что //*(£, F'; Я) —свободный
I R-модуль, конечно порождённый в каждой размерности. Если суще-
I ствуют классы с, €Н*(Е, £'; Я), ограничения которых образуют базис
I для H*(FyF';R) в каждом слое (£,£'), то Н*(£, E';R) как модуль над
| Н*(В; R) является свободным модулем с базисом {с;}.
Структура модуля определяется точно так же, как в абсолютном
случае, формулой Ьс = р*(Ь)^с, но теперь мы используем относительное
произведение Н*(£; Я) х Н*(£, Е'\ R) ->Н*(Е, Е'\ Я).
Доказательство. Построим расслоение £ —> В из £, приклеив
цилиндр отображения М для отображения р: Е' —► В к £ и отождествив
тем самым подпространства Е' С Е и Е'сМ. Таким образом, слои F
расслоения £ получаются из слоев F приклеиванием конусов CF' над
подпространствами F' с F. Рассматривая В как подпространство в Я в
одном из оснований цилиндра отображения М, мы получаем //*(£, /Vf; Я) ~
« Н*(£ - В, М - В; Я) « Н*(£, £'; Я) посредством вырезания и очевидной
деформационной ретракции пространства £ — В на £. Длинная точная
последовательность тройки даёт изоморфизм Н*(£, М\ Я) ^ f/+(E, В; Я), так
как М деформационно ретрагируется на В. Все эти изоморфизмы являют^
ся изоморфизмами Н*(В; Я)-модулей. Так как В —ретракт пространства Е
§4.D. Когомологии локально тривиальных расслоений 559
при проекции Ё-*В, мы получаем расщепление Н*(£; R) % Н*(£, В; R) ф
ф Н*(В; R) как Н*(В; К)-модулей. Пусть класс с) е H*(£; R) соответствует
классу
с; eH*(£,£';R) *sH*(E,B;R)
в этом расщеплении. Классы с-} вместе с 1 при ограничении дают базис для
Я*(£; R) в каждом слое F = FuC/;/, поэтому из абсолютной версии
теоремы Лере—Хирша следует, что Н*(£; Ю —свободный Н*(В; К)-модуль с
базисом {1, <Г;}. Из этого следует, что {с;} —базис свободного Н*(В\
R)-модуля «*№,£'; Ю. □
2. Теперь мы применим это к частному случаю пары локально
тривиальных расслоений (D", S""*1) — (£, £') -^В. Элемент се//"(£, £'; R),
ограничение которого на каждый слой (D", S"""1) является образующей группы
Hn(Dn,Su~l;R)& R, называют классом Тома для расслоения. Нас больше
всего интересуют случаи R = Z и Z2> но R может быть любым
коммутативным кольцом с единицей, и тогда «образующая» — это элемент, для
которого существует мультипликативный обратный, таким образом, все
элементы кольца R кратны образующей. Класс Тома для коэффициентов Ъ
приводит к классу Тома для любого другого кольца коэффициентов R при
гомоморфизме Нп(£, £'; Z) -*Н"(£, £'; Ю, индуцированном
гомоморфизмом Z—*R, переводящим 1 в единичный элемент кольца R.
I Следствие 4.D.9. Если шаровое расслоение (D", S"-1) -* (£, £') —> В
I имеет класс Тома с€Нп(Е, £'; R), то отображение
I Ф: H\B;R) -> Hi+n(E,E']R)y Ф(Ь) = р¥(Ь) ис,
I является изоморфизмом для всех 1^0иН'(Е, £'; R) = 0 при i <п.
Изоморфизм Ф называют изоморфизмом Тома. Следствие 4.D.9
можно превратить в утверждение об абсолютных когомологиях, определив
пространство Тома Т(Е) как факторпространство £/£'. Каждый шаровой
слой D" расслоения £ превращается в сферу Sn в Т(£), и все эти сферы,
получающиеся из разных слоев, не пересекаются, за исключением общей
отмеченной точки х0 = £'/£'. Класс Тома можно рассматривать как элемент
группы Hn(T(E)txQ\ R) ^ H"(T(£); R), ограничение которого на каждый
«слой» S" в Т(£) является образующей группы H"(Sn;R), и изоморфизм
Тома превращается в Н((В; R) %НП+'(Т(£); Я).
3. Главный остающийся шаг в выводе последовательности Гизина
должен связать существование класса Тома для шарового расслоения
Dn -^ Е —* В с понятием ориентируемости расслоения. Сначала мы
определим ориентируемость для сферического расслоения Sn~] -*£'—> В. В
доказательстве предложения 4.61 мы описали процедуру поднятия пути у
в В до гомотопической эквивалентности Ly между слоями над концами
пути у. Мы сделали это для расслоений в смысле Гуревича, а не для
560
Глава 4. Теория гомотопий
локально тривиальных расслоений, но этот метод применим и к локально
тривиальным расслоениям, слой которых — CW-комплекс, так как
свойство поднятия гомотопий использовалось только для слоя и для
произведения слоя па /. В случае сферического расслоения S""1 —>Е/ —>В, если у~~
петля в В, то Ly — гомотопическая эквивалентность слоя S'J_1 над
отмеченной точкой петли у в себя, и мы говорим, что сферическое расслоение
ориентируемо, если Ly индуцирует тождественное отображение группы
Hn~l(Sn~]; Z) для каждой петли у в В.
Например, бутылка Клейна, рассматриваемая как расслоение над S1
со слоем S1, неориентируема, так как при обходе пути, наматывающегося
один раз на окружность — базу расслоения, соответствующие окружности-
слои заметают всю бутылку Клейна, заканчиваясь там, где они
начинались, но с изменённой ориентацией. Те же самые рассуждения
показывают, что тор, рассматриваемый как расслоение окружностей над S1,
является ориентируемым. И вообще, любое сферическое расслоение, которое
является произведением, ориентируемо, так как отображения Ly можно
взять тождественными для всех петель у. Кроме того, сферическое
расслоение над односвязной базой ориентируемо, так как у ^ г/ влечёт Ly ^ Lip
а потому все отображения 1у гомотопны тождественному, так как все
петли у гомотопны нулю.
Можно было бы определить ориентируемость для шарового
расслоения Dn —>Е—>В, взяв относительную версию предыдущего определения
и строя поднятия Ly, которые являются гомотопическими эквивалентио-
стями пар (Dn, Sn~l) в слое. Однако, так как группа Hn(Dn, Sn"]\ Z)
канонически изоморфна Hn~l(Sn~l]Z) посредством отображения кограницы
в длинной точной последовательности пары, проще получить то же самое,
сказав, что расслоение Е ориентируемо, если его граничное сферическое
подрасслоение Е' ориентируемо.
I Теорема 4.D.10. Любое шаровое расслоение имеет класс Тома с
коэффициентами в Z2 и любое ориентируемое шаровое расслоение имеют
класс Тома с коэффициентами в Z.
В одной из задач в конце этого параграфа нужно показать, что обратное
утверждение для последнего утверждения тоже верно: шаровое расслоение
ориентируемо, если оно имеет класс Тома с коэффициентами в Ъ,
Доказательство. Случай, когда база В не является CW-комнлексом,
сводится к CW-случаю переходом к расслоению, индуцированному
посредством СУУ-аипроксимации к В. Это делается как в доказательстве
теоремы Лере—Хирша, с применением 5-леммы, чтобы показать, что
индуцированное расслоение имеет изоморфные гомотопические группы, а
значит, изоморфные абсолютные и относительные группы когомологий. Из
определения индуцированного расслоения непосредственно следует, что
расслоение, индуцированное ориентируемым сферическим расслоением,
§4.D. Когомологии локально тривиальных расслоений 561
ориентируемо. Без вреда можно считать базу, CW-комплекс В, связным.
Мы докажем следующее:
(*) если шаровое расслоение Dn —> £ —> В ориентируемо, а В является
связным CW-комплексом, то отображение ограничения //'(£> Е'\ Z) —>
—> Н'(^, S""1; Z) — изоморфизм для всех слоев D", xGB, и для всех
Для коэффициентов Z2 мы увидим, что утверждения (*) выполняется
и без предположения об ориентируемости. Следовательно, для
коэффициентов Z или Z2 образующая группы Нп(£, £') ^/in(D",S^-1) — класс Тома.
Если шаровое расслоение Dn -+ Е -+В ориентируемо, то, выбрав
изоморфизм Hn(D", S""1; Z) ^Z для одного слоя D", мы получим такие
изоморфизмы для всех слоев посредством композиции с изоморфизмами
L* которые зависят только от концов пути у. Сделаем такой выбор;
тогда если утверждение (*) верно, то получаем выделенный изоморфизм
Нп(£, E';Z) ^ Z, при ограничении которого па каждый слой получается
выбранный изоморфизм Hn(D", S"_1; Z) **Z. Так происходит потому, что
для пути 7 из х в у включение (D", S"-1) <-» (£, £') гомотопно композиции
отображения Ly и включения (D" Sn~]) <-> (£, £')• Мы воспользуемся этим
выделенным изоморфизмом Нп(£, E';Z)^Z в индуктивном
доказательстве утверждения (*), приведённом ниже. В случае коэффициентов Z2
может быть только один изоморфизм группы с группой Z2, поэтому никакого
выбора делать не нужно и ориентируемость несущественна. Мы докажем
утверждение (*) в случае коэффициентов Z, предоставляя читателю всюду
в доказательстве заменить все Z на Ъъ чтобы получить доказательство
в случае Z2.
Предположим сначала, что CW-комплекс В имеет конечную
размерность к. Пусть U с В —подпространство, полученное выкалыванием
одной точки из внутренности каждой /с-клетки комплекса В, и пусть V С В —
объединение открытых fc-мерных клеток. Таким образом, В = U U V. Для
подпространства Л С В пусть £А —> А и Ед —> А — шаровое и сферическое
расслоения, которые получаются, если взять подпространства в £ и в £',
проектирующиеся на А. Рассмотрим следующий участок
последовательности Майера—Вьеториса с коэффициентами в Z, которые мы отныне не
указываем:
Нп (£, £') - Нп (£„, £[,) Ф Н" (£„ £(,) - Я" (Е^пу, E'UnV).
Первое отображение инъективно, так как предыдущий член в
последовательности нулевой согласно индукции по /с, поскольку U DV
деформационно ретрагируется на несвязное объединение (к - 1)-мерных
сфер, и мы можем применить лемму 4.D.2, чтобы заменить EunV на
часть расслоения £ над этим объединением (к- 1)-мерных сфер. Тогда
из точности мы получаем изоморфизм //П(Е, Е') ъ КегФ. Аналогично,
562
Глава 4. Теория гомотопий
воспользовавшись леммой 4.D.2 и индукцией, получаем, что каждый из
членов Нп(Еи,Е'и)у Hn(Ev,E'v) и Hn(EunVi E'unv) — произведение групп Z,
по одному множителю Z для каждой компоненты присутствующих здесь
пространств, причём проекция на множитель Z задаётся ограничением
на любой слой в этой компоненте. Элементы группы КегФ —это пары
(а, /3) еНп[Еи, Е'и) ФН"(£\/' E'v), которые имеют одно и то же ограничение
на Hn(EUnv,E'unv). Так как В связно, это означает, что все Z-координаты
элементов аи/JB предыдущем разложении в прямое произведение
должны быть равны, так как любые две компоненты пространств U или V
можно соединить конечной последовательностью компонент пространств
U и V поочерёдно так, каждая компонента в этой последовательности
пересекалась со своими соседями. Таким образом, КегФ —это группа Z,
причём ограничение на слой является изоморфизмом Нп(Е, Е')ъЪ.
Чтобы завершить доказательство утверждения (*) для
конечномерного В, остаётся проверить, что Hl{Ey E') = 0 при i < п, но это немедленно
следует из рассмотрения предыдущего участка последовательности Май-
ера—Вьеториса, где два члена, соседние с Н'(Е, £')> обращаются в нуль по
индукции.
Доказательство утверждения (*) для бесконечномерного CW-kom-
плекса В сводится к конечномерному случаю, как в теореме Лере—Хир-
ша, так как нас интересуют когомологии только в конечном диапазоне
размерностей. П
4. Теперь мы можем получить последовательность Гизина для сфе-
рического расслоения Sn —> Е —> В. Рассмотрим цилиндр отображения
р
Мр} который является шаровым расслоением Dn -^>Мр-+В, причём £ —
его граничное сферическое расслоение. Предположим, что класс Тома
с е НпШр,Е;Ю существует (а это верно для ориентируемого £ и для
R = Z2). Длинная точная последовательность групп когомологии для пары
Шр, Е) даёт первую строку следующей коммутативной диаграммы, где
подразумеваются коэффициенты в R:
— Н{ШР, Е) -U- W(MP) —* Н'(£) -— Н'+1(Мр, Е) —*■
*|ф <4р-
^ //''""(В) -^U- И'{В) -£*■ Н1
яз|ф
СЕ) •>Н1'-"+1(В) •-
Отображения Ф —изоморфизмы Тома, а вертикальное отображение р+ —
изоморфизм, так как Мр деформационно ретрагируется на В. Эйлеров
класс е е Hn(B;R) определяется как класс (р*)_1;*(с), где с —класс
Тома. Квадрат, содержащий отображение ие, коммутативен, так как для
beHl~n(B; R) мы получаем
§4.D. Когомологии локально тривиальных расслоений 563
что равно р*(Ъ^е)=р*{Ъ)^р¥(е), так как р*(е) =;*(с). По-другому можно
определить е как класс, соответствующий классу c\jc при изоморфизме
Тома, так как Ф(е) = р*(е) wc = j*(c) ^sc = c wc.
Наконец, нижняя строка диаграммы —это по определению и есть
последовательность Гизина. □
В завершении этого параграфа мы воспользуемся следующим весьма
частным применением последовательности Гизина, чтобы получить ещё
несколько примеров пространств с полиномиальными когомологиями.
I Предложение 4.D.11. Пусть S2/f_1 —► Е —> В — такое ориентируемое
I сферическое расслоение, что Я*(Е;К) является кольцом многочленов
I R[xlt ...,Х(] от чётномерных образующих *,. Тогда ЬГ(В\Н) =K[yll ...
I •••> Ус eL 1'Де е —эйлеров класс расслоения и р*(у,0 =*,• для всех /.
Доказательство. Рассмотрим три члена
НЧ/3; R) ^ Hi+2k(B\ R) -* И1:г2к{Е] R)
последовательности Гизина. Если / нечётно, то третий член нулевой, так
как у Е нет нечётномерных когомологии. Следовательно, отображение ^е
сюръективно, и индукцией по размерности из этого получаем, что группы
Н*(В; Ю нулевые в нечётных размерностях. Это означает, что
последовательность Гизина сводится к коротким точным последовательностям
О -> Н2'(В; R) ^ H2r42fc(B; R) ^ H2'+2fc (E; Ю -> 0.
Так как гомоморфизм р* сюръективен, мы можем выбрать элементы
y;-eH*(B;R) так, что p*tyj) = Xj. Остаётся проверить, что H*(B\R) =
= R[yi, ...,yf,e], а эта проверка сводится к элементарной алгебре.
Действительно, если дан элемент beH*(B;R), то элемент р*(Ь) должен быть
многочленом /Оь ..., хс), поэтому b — f(yu ...ууц) лежит в ядре
гомоморфизма р*, и точность даёт уравнение Ъ - f{y\, •••, У() = Ь' ^ е для
некоторого fe'eH^BiR)- Так как Ь' имеет более низкую размерность, чем Ь,
мы можем предположить по индукции, что Ь' — многочлен от ух, ..., у(, е.
Следовательно, Ъ = /(yl5..., ус) + b' w e тоже многочлен от Уь ...,Ус е.
Поэтому естественное отображение R[yb ...,Уо е] —>Н*(В; R)
сюръективно. Чтобы проверить, что оно инъективно, предположим, что имеется
полиномиальное соотношение f(yx, ...,У{, е) = 0 в Н*(В\ R). Применяя р\
получаем /Оь ...,;*>, 0) =0, так как р*(у,) =х, и р*0) =0 согласно
короткой точной последовательности. Соотношение /Ol5 ...,.ху,0) = 0
выполняется в кольце многочленов R[xb ...,л>], поэтому /(уь ,.., У(, 0) = 0
в R[yi, ...,У(,е\, а значит, /(уь ...,#, е) делится на е, скажем, / = ge для
некоторого многочлена g. Соотношение/(yls ...,yf, e) =0 в Н + (В; R) тогда
имеет вид g(yb ...,^,с)^е = 0. Так как гомоморфизм ^е инъективен, это
даёт полиномиальное соотношение g(y(,..., yh e) = 0, где g имеет степень
564
Глава 4. Теория гомотопий
ниже, чем /. По индукции мы получаем, что g должен быть нулевым
многочленом, следовательно, / тоже. П
Пример 4.D.12. Применим этот результат, чтобы получить другое
доказательство того, что fr(G„(C°°); Z) является кольцом многочленов
Z[cb ..., с„], где |с/| =2/. Мы воспользуемся двумя локально тривиальными
расслоениями:
S2"-1 _* Е _* сп(С°°), S°° ^ Е — G^CC00).
Тотальное пространство Е в обоих случаях —это пространство пар (Р, v),
где Р —n-мерное подпространство в С00, a v — единичный вектор в Р.
В первом расслоении отображение £^Gn(C°°) задаётся формулой (Р, v) »-*
-*Р; слой этого расслоения —сфера S2""1. Для второго расслоения
отображение Е—►Gj^fC00) переводит (Р,v) в (п — 1)-мерное
подпространство в Р, ортогональное вектору v; слой этого расслоения —сфера S00,
состоящая из всех единичных векторов в С00, ортогональных данному
(п - 1)-мерному подпространству. Локальная тривиальность для этих двух
расслоений проверяется обычным способом. Так как пространство S00
стягиваемо, отображение Е —► G^^C00) индуцирует изоморфизмы всех
гомотопических групп, а значит, и всех групп когомологий. Тогда
индукцией по п мы получаем Н*(£;Z)^Z[съ ...9сп^]. Первое расслоение
ориентируемо, так как пространство GniC™) односвязно, поэтому
предложение 4.D.11 даёт изоморфизм H*(Gn(C°°); Z)^Z[c1? ...,сп], где с„ = е.
То же самое рассуждение годится и в кватернионном случае. По
поводу версии этого рассуждения в вещественном случае см. §3.3 книги
[VBKT].
Прежде чем обратиться к следующему примеру, заметим, что
последовательность Гизина с фиксированным кольцом коэффициентов R
имеет место для любого ориентируемого локально тривиального рас-
р
слоения F —> Е —► В, слой которого — CW-комплекс F с когомологиями
H*(F\ R)fvH*(Sn~l; Я). Ориентируемость определяется так же, как и
раньше, в терминах индуцированных отображений V : Яп_1 (F; R)-+Hn"] (F; Ю-
Чтобы получить этот более общий случай, никаких изменений в выводе
последовательности Гизина не нужно, если в качестве соответствующего
«шарового» расслоения снова берётся цилиндр отображения CF -+Мр-+ В.
Пример 4.D.13. Мы вычислили когомологий Gn(E°°) с
коэффициентами в Z2 и получили, что это кольцо многочленов от образующих
размерностей от 2 до п. Теперь мы вычислим когомологий с коэффициентами
в Zp, где р —нечётное простое число. Ответом снова будет алгебра
многочленов, но на этот раз от чётномерных образующих, причём вид ответа
зависит от чётности п. Рассмотрим сначала случай, когда п нечётно,
скажем, п = 2к -4-1. Имеем два локально тривиальных расслоения
V2(R2*+1) -> Е - G2M(R°°)y V2(JR°°) ^E^ G2*-i(R°°);
§4.D. Когомологий локально тривиальных расслоений 565
здесь Е — пространство троек (P,vl5v2), где Р — ориентируемое (2/сН-
^-мерное подпространство в iR00, a v, и v2 — два ортогональных единичных
вектора в Р. Отображение проекции в первом расслоении — это (Р, Vj, v2) »-* Р,
а во втором расслоении проекция переводит (Р, V], v2) в ориентированное
(2/с - 1)-мерное подпространство в Р, ортогональное к vx и v2, с
ориентацией, заданной, например, тем, что пара vb v2, после которой идёт
положительно ориентируемый базис для ортогонального (2fc — 1)-мерпого
подпространства, является положительно ориентированным базисом для
р. Оба расслоения ориентируемы, так как их базы GM (R™) односвязны, что
видно из расслоения SO(n) -> Vn(К00) -* Gn(Ж00).
Слой V^CIR00) второго расслоения стягиваем, поэтому когомологий у Е
те же самые, что и у G^jCR00). Слой первого расслоения имеет те же
самые когомологий с коэффициентами в Zp, что и сфера S4k"\ если р
нечётно, согласно вычислениям в конце §3.D. Поэтому если мы
предположим по индукции, что H4G2*-i№°°); Zp) ъZp[pb ..., pfc«i], где |р,| =4/, то
из предложения 4.D.11 следует, что H*(G2fc+i№°°); ^P) ^^PtPi> ■••» Р^1> гДе
р^ = е имеет размерность 4/с. Индукцию можно начинать с пространства
GxCIR00), которое является просто сферой S00, так как ориентированная
прямая в IR00 содержит единственный единичный вектор положительного
направления.
Чтобы разобраться со случаем С„№°°), где число п — 2/с четно, мы
поступим так же, как в примере 4.D.12, рассматривая расслоения
S2k"1 -> Е -> G2k(R°°), S°° -*E-* G^OO.
Согласно случаю, когда п нечётно, мы получаем H*(G2fc._1(l00); Zp) ^
«* Zptp], ..., p^_i], где |p-| = 4i, таким образом, из предложения 4.D.11
следует, что fTCG^CIR00); Zp) —кольцо многочленов от этих образующих
и от образующей размерности 2fc.
Итак, для нечётного простого числа р мы показали следующее:
H¥(G2Jt+ICR°°); Zp) * Zp[Pl, .... pk], |p,-| - 4i,
/Г (G2Jt(R°°); Zp) * Zp[Pl)..., p^l5 e], |p,| - 4i, |e| - 2k.
To же самое верно и для коэффициентов Q. В действительности наше
доказательство годится для любого кольца коэффициентов, в котором
элемент 2 имеет мультипликативный обратный, так как единственное, что
нам нужно,— это изоморфизм Н*(У2(Ж2*+1); R) ^H*(S4k~ *; R). По поводу
вычислений когомологий G,,©00) с коэффициентами в Z см. [VBKT].
Оказывается, все элементы кручения имеют порядок 2, а по модулю этого
кручения целочисленные когомологий снова являются кольцом
многочленов от образующих р, и е. Аналогичные результаты верны также для
когомологий неориентированного многообразия Грассмана GM(1R°°), но
образующая е заменяется на рк, когда п = 2к.
566
Глава 4. Теория гомотопий
Задачи
1. Согласно задаче 35 из §4.2 существует расслоение S2 —>СР3 —>S4.
Пусть расслоение S2 —>Ek—>S4 индуцировано из этого расслоения
посредством отображения SA —> S4 степени к, где к > 1. Применяя теорему Ле-
ре—Хирша, чтобы доказать, что кольцо Н*(Ек\Ъ) аддитивно изоморфно
Н*(СР3; Z), но имеет другую структуру ^-произведения, в которой
квадрат образующей группы Н2(Ек\ Z) является к -кратной образующей группы
H4(£bZ).
2. Применяя теорему Лере—Хирша к расслоению S1 —>S°°/Zp —>СР°°,
вычислите 1Г(К(1р, 1); Zp) no H*(CP°°; Zp).
3. Используя теорему Лере—Хирша, как в следствии 4.D.3, чтобы
вычислить H*(Vn(Cfc);Z) ^Az[jf2jt-2n+i,^2*-2n+3>---.^2fe-]] и аналогично
в кватернионном случае. .
4. Для пространства флагов Fn(C") покажите, что W(Fn{Cn)\ Z) %
**Z[*i, ...^„l/Ccr,, ...,сг„), где crf — i-й элементарный симметричный
многочлен.
5. Используя последовательность Гизина, покажите, покажите, что
для локально тривиального расслоения Sk —> S'n —► Sn должны выполняться
равенства к — п — 1 и m = 2п — 1. Затем с помощью изоморфизма Тома
покажите, что инвариант Хопфа отображения р должен быть равен ±1.
[Следовательно, п = 1, 2, 4, 8 согласно теореме Адамса.]
6. Докажите, что если М — многообразие размерности 2/7, для
которого существует локально тривиальное расслоение S] —>S2n+1 —>М, то М
односвязно и Н*(М; Ъ) %Н*(СР"; Z) как кольца. Наоборот, докажите, что
если М односвязно и Н*(М; Z) ^ Я*(СРМ; Z) как кольца, то существует
расслоение S1 —> Е -+ М, где Е ^ S2n+1. [Для п > 1 существуют примеры,
в которых М не гомеоморфно СР'\]
7. Докажите, что если шаровое расслоение Dn —> Е —> В имеет класс
Тома с коэффициентами в Z, то оно ориентируемо.
8. Пусть Е — расслоение-произведение В х D", причём В — CW-kom-
плекс. Докажите, что пространство Тома Т(Е) гомотопически
эквивалентно n-кратной приведённой надстройке £"В, причём изоморфизм Тома
превращается в изоморфизм надстройки Н1(В\ К) ы Hn+l(T,nB] R),
заданный приведённым внешним произведением из §3.2.
9. Докажите, что включение подгруппы диагональных матриц Тп с-^
c->U(n)гомотопно отображению Ти —> U(l) «-►LKn), переводящему набор
из п комплексных чисел единичной длины (zb ...,z,?) в (1 х 1)-матрицу
(zl4..zn). Сделайте то же самое для диагональной подгруппы в Sp(n).
[Указание: диагональные матрицы в U(n) соответствуют композициям
умножений на скаляр в п различных прямых в С", а пространство СРП-1 связно.]
10. Восполнив детали следующего рассуждения, докажите, что любая
(п х п)-матрица Л с элементами из К имеет собственное значение в Н.
§4.Е. Теорема Брауна о представимости
567
(Обычное рассуждение над С, использующее корни
характеристического многочлена, здесь не работает, потому что нет хорошего кватерни-
онного определителя.) Для t е [0,1] и Я <Е S3 с R рассмотрим матрицу
tA/ + (1 ~~ 0Л- Если у /\ нет собственных значений, то эта матрица
обратима для всех t. Поэтому отображение S3 —> GL„(iH[), Я—> А/, гомотопно нулю.
Но согласно предыдущей задаче и задаче 10 6) из §З.С это отображение
представляет п-кратную образующую группы 7i3GL„(IHi).
§4.Е. Теорема Брауна о представимости
В теореме 4.58 в §4.3 мы показали, что ^-спектры задают теории
когомологии, а теперь мы докажем обратное утверждение, что все теории
когомологии на CW-категории возникают таким образом из ^-спектров.
I Теорема 4.ЕЛ. Любая приведённая теория когомологии на катего-
I рии CW-комплексов с отмеченной точкой и сохраняющих отмеченную
I точку отображений имеет вид h"(X) = (X, Кп) для некоторого ^-спектра
I «пЬ
Мы также увидим, что пространства Кп единственны с точностью до
гомотопической эквивалентности.
Эта теорема даёт другое доказательство того, что обычные
когомологии представимы как отображения в пространства Эйлепберга—Маклей-
на, так как для пространств Кп в ft-спектре, представляющем теорию
Н*(~; G), мы получаем 7i/(/Cn) = (S,,/Cn)=H"(S'; R), поэтому Кп— это
пространство типа K(G, n).
Прежде чем перейти к доказательству теоремы, заметим, что
последовательности корасслоения, построенные в §4.3, позволяют нам
сформулировать определение приведённой теории когомологии немного короче
следующим образом. Приведённая теория когомологии на категории с^,
объекты которой —CW-комплексы с выбранной в качестве отмеченной
точки нульмерной клеткой, а морфизмы — сохраняющие отмеченную
точку отображения, является последовательностью функторов hn, nGZ, из
категории с€ в категорию абелевых групп вместе с естественными
изоморфизмами hn(X) ^/iM+1(EJO для всех X в %', причём для каждого hn
выполняются следующие аксиомы.
1. Если/^g: X —* Y с сохранением отмеченной точки, то/* = g*: hu[Y)-+
-+h"{X).
2. Для любого включения А <-* X в %' последовательность 1\и(Х/А) —>
->hn(X)-*h"{A) точна.
3. Для букета Х = УаХа с включениями ia: Xac-*X отображение
произведения П„/*: hn{X) —* Uahn(Xa) — изоморфизм.
Чтобы убедиться, что этих аксиом достаточно, чтобы определить теорию
когомологии, прежде всего заметим, что последовательность корасслое-
568
Глава 4. Теория гомотопий
ния А —> X —> Х/Л —> ЕЛ —>... позволяет нам построить длинную точную
последовательность пары точно так же как мы делали в случае функторов
hn{X) = (X, Кп). Наоборот, если у нас есть естественные длинные точные
последовательности пар, то, применяя их к парам вида (СХ, X), мы
получаем естественные изоморфизмы hn(X) яз hn^l(T,X). Заметим, что эти
естественные изоморфизмы, возникающие из отображений кограницы
для пар (СХ, X), единственным образом определяют отображения
кограницы для всех пар (X, А) посредством диаграммы
hnW ^ hn+1(X/A)
hn+l(CA/A) —^— hn+l(CX/A)
где отображения из hn(A)— это отображения кограницы для пар и
диаграмма коммутативна в силу естественности этих отображений
кограницы. Изоморфизм возникает из деформационной ретракции пространства
СХ на СА. Легко проверить, что эти процедуры преобразования одного
определения теории когомологий в другое обратны друг другу.
Основная работа по представлению теорий когомологий Г2~спектрами
будет состоять в реализации одного функтора hn теории когомологий как
{—, Кп) для некоторого пространства Кп. Поэтому давайте посмотрим,
какими свойствами обладает функтор h(X) = (X, К), где К —фиксированное
пространство с отмеченной точкой. Прежде всего, это контравариантный
функтор из категории CW-комплексов с отмеченной точкой в категорию
пунктированных множеств, т. е. множеств с выделенным элементом, в
нашем случае гомотопическим классом постоянного отображения. Морфиз-
мы в категории пунктированных множеств— это отображения,
сохраняющие выделенный элемент. Мы уже видели в §4.3, что h(X) удовлетворяет
трём аксиомам 1—3. Ещё одно свойство —это следующая аксиома Майе-
ра—Вьеториса.
Пусть CW-комплекс Х является объединением подкомплексов А и В,
содержащих отмеченную точку. Тогда если a eh(A) и Ъ eh(B) при
ограничении дают один и тот же элемент группы ft(AnB), то
существует элемент x€h(X), ограничения которого на Л и на В—данные
элементы а и Ь.
Здесь и далее термин «ограничение» означает отображение,
индуцированное включением. В случае, когда h(X) = (Х,К), эта аксиома-
непосредственное следствие свойства продолжения гомотопий.
Функторы ft" в любой теории когомологий тоже удовлетворяют этой аксиоме,
поскольку в любой теории когомологий есть точные последовательности
Майера—Вьеториса, как мы видели в § 2.3 в аналогичной ситуации теории
гомологии.
§4.Е. Теорема Брауна о представимости
569
I Теорема 4.Е.2. Если ft — контравариантный функтор из категории
I связных CW-комплексов с отмеченной точкой в категорию пунк-
I тированных множеств, удовлетворяющий аксиоме гомотопии 1, ак-
I сиоме Майера—Вьеториса и аксиоме букета 3, то существуют связ-
I ный CW-комплекс К и такой элемент uGh(K), что преобразование
I Ти: {ХУК) —>ft(X), Tu(/) = /*(u), является взаимно однозначным отоб-
I ражением для всех X.
Такую пару (К, и) называют универсальной для функтора ft.
Непосредственно из определения следует, что пространство К в универсальной
паре (К", и) единственно с точностью до гомотопической эквивалентности.
Действительно, пусть пара (К\ и') тоже универсальна для ft. Будем
использовать обозначение /: (/С, и) —> {К\ и') для такого отображения /: К—* К',
что /*(V) = и. Из универсальности следует, что существуют
отображения /: (Ж, и) —► (К"', и') и g: {К\ и') —> {К, и), причём они единственны
с точностью до гомотопии. Аналогично композиции gf: (К", и) —> (К, и)
и fg: (К\ и') —> (К', и') единственны с точностью до гомотопии, поэтому
они гомотопны тождественным отображениям.
Перед началом доказательства этой теоремы сделаем два
предварительных комментария по поводу аксиом.
1. Из аксиомы букета следует, что множество ft (точка) тривиально.
Чтобы убедиться в этом, нужно просто воспользоваться тем фактом, что
для любого X мы получаем X N/точка = Х, поэтому отображение ft(X) x
х ft(точка) —>ft(X), индуцированное включением первого слагаемого,
взаимно однозначное, но это отображение — проекция (а,Ь)—>а,
следовательно, множество ft (точка) должно состоять только из одного элемента.
2. Из аксиомы 1, 3 и аксиома Майера—Вьеториса следует аксиому
2. А именно, утверждение 2 эквивалентно точности последовательности
h(A)«— ft(X) <— ft(XUG4), где СА — приведённый конус, так как мы
работаем в пунктированной категории. Включение Im С Кег имеет место, так
как композиция А —> X U СА гомотопна постоянному отображению,
поэтому индуцированное отображение пропускается сквозь ft (точка) =0.
Чтобы получить противоположное включение Кег dm, разложим XUCA на
два подпространства У и Z, сделав разрез по экземпляру пространства А
на полпути от вершины конуса СА до его основания; таким образом, Y —
уменьшенная копия конуса СА, a Z — приведённый цилиндр отображения
Для включения А <—> X. Если дан элемент х е ft(X), то его можно
продолжить до элемента zeft(Z), так как Z деформационно ретрагируется на X.
Если х при ограничении даёт тривиальный элемент в ft (Л), то z при
ограничении даёт тривиальный элемент в ft (У HZ). Последний элемент можно
Продолжить до тривиального элемента в ft (У), поэтому из аксиомы
Майера—Вьеториса следует, что в ft(XUCA) существует элемент, который при
ограничении даёт элемент z в ft(Z) и, таким образом, элемент х в ft(X).
570
Глава 4. Теория гомотопий
Основная часть доказательства теоремы содержится в двух
приведённых ниже леммах. Чтобы сформулировать первую из них, рассмотрим
пару (К, и), где К — связный CW-комплекс с отмеченной точкой и и £/7(К),
где h удовлетворяет предположениям теоремы. Назовём такую пару (X, и)
п-униоерсалъной, если отображение Ти : я,(К) —>/i(S'), Ta(f) =/*(")> сюръ-
ективно при i ^ /I и имеет тривиальное ядро при i < п. Обратите внимание,
что тривиальность ядра, возможно, не то же самое, что ипъективиость,
поскольку здесь мы имеем дело не с гомоморфизмами групп. Назовём
пару (Ж, и) г:^-универсальнойу если она н-универсальна для всех п.
I Лемма 4.Е.З. Для любой данной пары (Z, я), где Z — связный CW-kom-
плекс и zeh(Z), существует тг^-универсальная пара (К, и), для которой
Z — подкомплекс в К и u|Z = 2.
Доказательство. Мы построим К из Z по индукции, приклеивая
клетки. Начнём с Kh=Z Va S^, где а пробегает по всем элементам
множества h(Sl). По аксиоме букета существует элемент u1 €h(K]), для которого
ux\Z = z и Uj|S^ = a, поэтому пара (/Сь Uj) является 1-универсалыюй.
Для доказательства шага индукции предположим, что мы уже
построили п-универсальную пару (Кп, и„), причём ZcKu и i/„|Z = z. Представим
каждый элемент а из ядра отображения Тм : пп(Кп) —»h(S") некоторым
отображением /a: S" —»Кп. Пусть / = Va/a: Va S£ —* Kn. Приведённый
цилиндр отображения My деформационно ретрагируется на Кп, поэтому мы
можем рассмотреть ип как элемент множества ft (My), причём этот
элемент при ограничении даёт тривиальный элемент множества ft(VaS") по
определению отображения /. Из свойства точности для h тогда следует,
что для приведённого конуса отображения Cf = Mf/ va S|* существует
элемент vveft(Cy), дающий элемент ип при ограничении на Кп. Заметим,
что Cf получается из Кп приклеиванием клеток е£+1 по отображениям fir
Чтобы завершить построение комплекса Kn+l9 положим Kn+l —CjVpSy ,
где /5 пробегает по h(Sn4_1). Снова по аксиоме букета существует элемент
ип+г €МКп_ц), ПРИ ограничении которого получаются элемент w на Cf
и элемент ^ па S'I+1.
Чтобы проверить, что пара (Kn+1,u„+]) является (п-Ы)-универсаль-
ной, рассмотрим коммутативную диаграмму
тгда »мкп+д
ft(S')
Так как Кпл1 получается из Кп приклеиванием (п + 1)-мерных клеток,
верхнее отображение — изоморфизм при i<n и сюръекция при i = n. По
индукции отображение 7'„ имеет тривиальное ядро при i < п и сюръектив-
но при I $ п, поэтому то же самое верно для Ти f . Ядро отображения TUn+}
§ 4.E. Теорема Брауна о представимости
571
тривиально при i =п, так как элемент этого ядра при индуцировании
попадает в Ker Tu С яп(/Сп) согласно сюръективности верхнего отображения
при i = n, а мы приклеивали клетки к Кп по отображениям,
представляющим все элементы из KerTU/. Наконец, отображение TU| ( сюръективпо
при i = п +1 по построению.
Теперь пусть К =(J/CM. Применим рассуждение с телескопом отоб-
п
ражений, как в доказательствах леммы 2.34 и теоремы 3.F.8, чтобы
показать, что существует элемент ueh(K), при ограничении которого на
Кп получается элемент ип для всех п. Телескоп отображений для
включений К{ <-> К2*-+ ...—это подкомплекс Т = {JK( x [iyi + 1] в К х [1, оо).
i
Здесь «х» означает приведённое произведение, в котором произведение
отмеченной точки на отрезке стягивается в точку. Естественная проекция
Т-+К является гомотопической эквивалентностью, поскольку К х [1, оо)
деформационно ретрагируется на Г, как мы показали в доказательстве
леммы 2.34. Пусть А С Г—это объединение подкомплексов К, х [i, i + 1]
для нечётных /, а В — соответствующее объединение для чётных i. Таким
образом, AUB — Ty АПВ = \/(КЬ Ac*V,-JC2i-i и B^v,/C2l. По аксиоме букета
существуют элементы ash(A) и beh(B), при ограничении которых
получается Ui на каждом К,. Тогда, воспользовавшись тем, что и,ч.1|К,- = и,-, по
аксиоме Майера—Вьеториса получаем, что а и Ъ — ограничения
некоторого элемента tG h(T). При изоморфизме h(T)&h(K) этот элемент t
соответствует элементу и Gh(K), при ограничении которого получаем элемент и„
на Кп для всех п.
Чтобы проверить, что пара (iC,ii) является я+-универсальной,
воспользуемся коммутативной диаграммой
щ{Кп) ^тгДО
has1)
При n>i-hl верхнее отображение— изоморфизм, а отображение TU| сюръ-
ективно и имеет тривиальное ядро, поэтому то же самое верно для Ти. П
I Лемма 4.Е.4. Пусть (/С, и) является тг+-универсальной парой, и пусть
I (X, А) — CW-napa с отмеченной точкой. Тогда для любого х ^h(X) и лю-
I бого отображения /: А-+К со свойством /* {и) = х\ А существует отоб-
I ражение g: X —> К, продолжающее /, для которого g* {и) — х.
Схематично можно выразить так: диагональная стрелка в диаграмме
(Х,х)
где отображение i —включение, всегда существует.
572
Глава 4. Теория гомотопий
Доказательство. Замена К на приведённый цилиндр отображения /
приводит нас к случаю, когда / — включение подкомплекса. Пусть Z—-
объединение пространств X и К с отождествлёнными двумя
экземплярами пространства Л. По аксиоме Майера—Вьеториса существует элемент
z€ft(Z), для которого z\X~x и z\K = и. Согласно предыдущей лемме
мы можем вложить (Z, z) в яж-универсальную пару (Xх, и'). Включение
(X, и) <-> (Xх, и') индуцирует изоморфизм гомотопических групп, так как
оба элемента и и и' являются т^-универсальными, поэтому К1
деформационно ретрагируется на К. Эта деформационная ретракция индуцирует
гомотопию относительно Л включения X с-> К' в отображение g: X —> К.
Соотношение g¥(u) =х выполняется, так как и/|К = и и u'|X = x. G
Доказательство теоремы 4.Е.2. Достаточно доказать, что тг*-уни-
версальная пара (X, и) является универсальной. Применив предыдущую
лемму в случае, когда Л —точка, получаем, что отображение Ти: (X, К) —►
—>ft(X) сюръективно. Чтобы доказать инъективность, предположим, что
7L(/о) = <ru(/i)» T-e- /о С") =/Г("). Мы применим предыдущую лемму для
(X х /, X х 61) в роли (X, Л), используя отображения /0 и /i на X х Э/ и взяв
в качестве х элемент p*/0*(u) = p*/I*(u), где р —проекция X х /—>Х. Здесь
X х / должно быть приведённым произведением, в котором
подпространство отмеченная точка х / стянуто в точку. Тогда лемма даёт гомотопию
отображения /0 в отображение /^ D
Доказательство теоремы 4.Е.1. Так как надстройка является
изоморфизмом в любой приведённой теории когомологий, а надстройка над
любым CW-комплексом связна, можно ограничиться связными CW-kom-
плексами. Как мы отметили ранее, каждый функтор hn удовлетворяет
аксиомам гомотопий, букета и Майера—Вьеториса, поэтому предыдущая
теорема даёт CW-комнлексы Хп, для которых h"(X) = (Х,Кп). Остаётся
показать, что естественные изоморфизмы ft"(X) ъЬ1Н !(£Х)
соответствуют слабым гомотопическим эквивалентностям Кп —>QXn+1. Естественный
изоморфизм ft" СЮ &hu+l(yiX) соответствует естественному взаимно
однозначному отображению (Х,Кп) ъ (ЕХ, Кп+1) = (X, QXrHl), которое мы
обозначим Ф. Естественность этого взаимно однозначного отображения
даёт для любого отображения /: X —► Хп коммутативную диаграмму
(Кп,Кп) — (Х,КМ)
ф I ф
Положим е„ = Ф(1): Хм —>ПКп+1. Тогда, воспользовавшись
коммутативностью, получаем Ф(/) =Ф/*(1) =/*Ф(1) = /*(£,,) = £„/» а это означает, что
отображение Ф: (X, Хм) -»(X, ПК,,.,.,) является композицией с etr
Отображение Ф взаимно однозначное, поэтому если в качестве X мы возьмём
5', то увидим, что отображение еп индуцирует изоморфизм групп я, для
§4.F. Спектры и теории гомологии
573
всех I, а значит, еп —слабая гомотопическая эквивалентность, и мы
получаем Г2-спектр.
Последнее, что осталось проверить,—это то, что взаимно
однозначное соответствие ftn(X) = (X, Кп) является изоморфизмом групп, где
множество (Х,Кп) снабжено структурой группы, возникающей из
отождествления этого множества с (X, Ш(п+1) = (SX, /Сп+1). Применив естественный
изоморфизм ftn(X) ^hn+1(SX), мы видим, что это эквивалентно
утверждению, что взаимно однозначное соответствие ftM+1(£X) = (¥,X,Kn+])
сохраняет структуру группы. Для отображений /, g: ИХ —> К соотношение
Tu(f + g) = Tu(J) + Tu(g) означает, что (/ + g)*{u) =/*(")+ g¥00, а это
верно, так как (/4-g)*=/*+g*: ft (Ю ->ft(EX) по лемме 4.60. П
§ 4.F. Спектры и теории гомологии
Мы видели в §4.3 и в предыдущем параграфе, что теории кого-
мологий имеют теоретико-гомотопическую интерпретацию в терминах
Г2-спектров, и естественно попытаться найти соответствующее описание
теорий гомологии. В этом случае у нас уже нет
теоретико-гомотопического описания обычных гомологии, которое послужило бы отправным
пунктом. Но есть другая теория гомологии, уже знакомая нам, которая
действительно имеет вполне теоретико-гомотопический вид.
I Предложение 4.F.I. Стабильные гомотопические группы я*п(Х)
определяют приведённую теорию гомологии на категории CW-комплексов
с отмеченной точкой и отображений, сохраняющих отмеченную точку.
Доказательство. В предыдущем параграфе мы переформулировали
аксиомы для теории когомологий так, что в аксиоме точности
требуется только точность последовательности ftn(X/A) —> ftn(X) —► ftn(A) для
CW-пар (X, А). Чтобы можно было получать длинные точные
последовательности, переформулированные аксиомы требуют также, чтобы
естественные изоморфизмы надстройки ftn(X) & ftn+l(EX) были определены
как часть теории когомологий. Аналогичная переформулировка аксиом
для теории гомологии тоже справедлива, как показывают те же самые
рассуждения, и мы будем пользоваться этим в дальнейшем.
Для стабильных гомотопических групп изоморфизмы надстройки
я*(Х) ъ 7r*41(£X) имеют место автоматически, поэтому остаётся
проверить три аксиомы. Аксиома гомотопии очевидна. Точность
последовательности я* (А) —> я* (X) —> тг*п(Х/А) следует из точности
последовательности пп(А) —► я„(Х) —► я,?(Х, А) и из изоморфизма яп(Х, А) ^ тг,?(Х/А),
имеющего место при предположениях о связности, которые достигаются
после достаточного количества надстроек. Аксиома букета rc*(V„Xtt) ^
^фя^(Хд) сводится к случаю конечного числа слагаемых обычными
а
Рассуждениями с компактностью, а случай конечного числа слагаемых
574
Глава 4. Теория гомотопий
сводится к случаю двух слагаемых по индукции. Затем мы получаем
изоморфизмы
тг^СЕ'Х V ЕТ) * ПП^{Т!Х х Е'У) * nn+i№X) © тги4,-(Г'П,
первый из которых имеет место, когда п + i < 2i — 1, т. е. i > п -f 1, так
как Е'Х V Е'У—это (2z - 1)-мерный остов комплекса Е'Х х Е'У.
Переходя к пределу по возрастающим i, мы ползаем требуемый изоморфизм
nsn(XvY)*n>n{X)®7TJn(Y). С
Небольшое обобщение этой теории гомологии можно получить,
положив fr;j(X) — п*п(Х ЛК) для фиксированного комплекса К. Проверка
аксиом гомологии сводится непосредственно к случаю стабильных
гомотопических групп согласно основным свойством приведённого произведения:
а) ЛП(Х) ъ Л„+1(ЕХ), так как Е(Х Л К) = (ЕХ) Л К, поскольку оба
пространства совпадают с S1 Л X Л К;
б) аксиома точности' выполняется, так как (X Л К)/(А Л К) = (Х/Л) Л К,
поскольку оба пространства получаются из X х К при стягивании иод-
пространства Л х К и X х {fc0} в точку;
в) аксиома букета следует из дистрибутивности: (VaXa) Л К = Va(Xa Л К).
Коэффициентами этой теории гомологии являются hn(S{)) = я* (S° Л К) =
= я* (/С). Предположим, например, что К — пространство Эйленберга—
Маклейна K(G, n). Поскольку пространство K(G, п) является (п - 1)-связ-
ным, его стабильные гомотопические группы —это то же самое, что его
нестабильные гомотопические группы в размерностях ниже 2и. Таким
образом, если мы сдвинем размерности, положив /?,(Х) = п*+п (X Л K(G, /О),
то получим теорию гомологии, группы коэффициентов которой в
размерностях ниже п —это обычные гомологии с коэффициентами в G. Из
этого следует, как и в теореме 4.59, что эта теория гомологии согласована
с обычной теорией гомологии для CW-комплексов размерности меньше
п-1.
Это ограничение на размерности можно было бы устранить, если
бы существовало «стабильное пространство Эйленберга—Маклейна»,
стабильные гомотопические группы которого нулевые, кроме одной
размерности. Однако это требование слишком сильное, и вместо этого
попробуем образовать предел групп я|+г?(ХЛК(С, //)), устремив п к
бесконечности. Пространства К(6, и) для разных п связаны слабыми
гомотопическими эквивалентностями K(Gy n)—>r2K(G, n-f 1). Так как надстройка играет
очень большую роль в наших рассуждениях, мы можем преобразовать
последнее отображение в EK(G, n) ~> K{G, n + 1), или, в более краткой
записи, Е/С,? —>К;н1. Оно индуцирует отображение
nU„(XAK„) = я;Н1+1(хле/с„) - 7г;+п+1(хл*„+1).
Тогда при посредстве этих отображений имеет смысл рассмотреть
прямой предел, устремив п к бесконечности, и получить группу
= Ит7г?+п(Х ЛК,,). Это даёт теорию гомологии, так как прямые преДелЬ
§ 4.F. Спектры и теории гомологии
575
сохраняют точность последовательностей и тем самым аксиома точности
выполняется. Прямые пределы сохраняют изоморфизмы, поэтому
изоморфизм надстройки и аксиома букета тоже верны. Группы коэффициентов
этой теории гомологии те же самые, что и для обычных гомологии с
коэффициентами в G, так как группа hy(S°) = Птя"+;](/Сп) нулевая, кроме
случая i = 0, когда она равна G. Следовательно, эта теория гомологии
совпадает с обычными гомологиями согласно теореме 4.59.
Чтобы привести этот результат в его естественной общности,
определим спектр как последовательность CW-комплексов Ки вместе с
сохраняющими отмеченную точку отображениями Т,Ки —> Кп+1. Это обобщает
понятие fi-спектра, где отображения Т,Кп —> Кп^ возникают из слабых
гомотопических эквивалентностей Кп —♦£Жп+1. Другое очевидное
семейство примеров — спектры надстройки, когда мы начинаем с
произвольного CW-комплекса X и полагаем Кп = Т,'1Х, а Т,Кп —>Кп+1 —тождественное
отображение.
Гомотопические группы спектра К определяются как
я,(Ю = l\mni+n(Kn),
где прямой предел вычисляется с помощью композиций
последнее отображение индуцировано данным отображением Т,Кп —>
-+Кп+Х. Таким образом, в случае спектра надстройки для пространства
X гомотопические группы спектра —это то же самое, что стабильные
гомотопические группы пространства X. Для общего спектра К тоже можно
описать п{(К) как lim тг? (К„), так как композиция ni+n(Kn)^>ni+n+j(Kn+j)
пропускается сквозь 7ii+n+J{T,jKn). Поэтому гомотопические группы
спектра—это «стабильные гомотопические группы», по сути, по определению.
Вернёмся теперь к контексту теорий гомологии. Если даны спектр К
и CW-комплекс X, то мы получаем спектр X Л К с (X Л К)п = X Л Кп,
используя очевидные отображения Е(Х Л Кп) = X Л ЛКп —> X Л К,?+1. Группы
7tf(X Л К) —это группы Итп*+п(Кп), рассмотренные ранее в случае
спектра Эйленберга—Маклейна, и рассуждения, приведённые там,
показывают следующее.
I Предложение 4.F.2. Для спектра К группы ft,-(X) = я,(Х Л К) обра-
I зуют приведённую теорию гомологии. Когда К — спектр Эйленберга—
I Маклейна с Кп — K(G, n), эта теория гомологии —обычные гомологии,
I поэтому я,-(X Л Ю^Д-(Х;0.
Если бы мы хотели сопоставить теорию когомологий
произвольному спектру /С, то первым побуждением было бы в качестве hl(X) взять
um(E"X, Kn+i)f прямой предел относительно композиций
(Е'X,/С,н,) —> (Е X,HKn+i) —» (Е' Х,К„.ь,-+1).
576
Глава 4. Теория гомотопий
Например, в случае спектра сфер S = {S"} это определение приводит
к стабильным когомотопическим группам я^(Х) = lim(EnX, S',+'). К
сожалению, для определения ft'СЮ = lim(EnX, Kn+i) возникают трудности
с аксиомой букета, так как прямой предел произведения не обязан быть
равен произведению прямых пределов. Для конечных букетов никаких
трудностей нет, поэтому мы действительно получаем теорию когомологий
для конечных CW-комплексов. Но для общих CW-комплексов необходимо
другое определение. Проще всего было бы сопоставить каждому спектру
К некоторый ^-спектр К' и положить hn{X) = {Х,К'п). Можно получить
К' из К, если в качестве К'п взять limfi'KM.H— телескоп отображений для
последовательности Кп —> ПКм+1 —> £12Кп+2 —>... Структура ^-спектра
задаётся эквивалентностями
К'п = \\тП%,н * ИтП/+,/Сп41-+1 - ПНтП%,+,Ч1 = ^Cr
Первая гомотопическая эквивалентность возникает посредством
удаления первого члена последовательности Ки —>ШСмИ —►Г22К„.|_2—► ••••> что не
влияет на телескоп отображений. Следующее отображение к* —частный
случай естественной слабой эквивалентности limfiZ,, —>filimZ„, которая
имеет место для любой последовательности Zj —>Z2—>... Строго говоря,
мы должны взять в качестве К'п CW-аппроксимацию к телескопу
отображений Шп£У/Сп+|-, чтобы получить спектр, состоящий из CW-комплексов,
в соответствии с нашим определением спектра.
В случае, когда мы начинаем со спектра надстройки Кп = Е"К, нет
необходимости брать телескопы отображения, так как в качестве К'п
можно взять просто (Jn'E'+nK=lJfi'E'Kn —объединение относительно есте-
ственных включений П'Е'КП с П'+1Е'+1К„. Объединение IJft'E'X обыч-
но сокращённо обозначают ft^E^X, По-другому это объединение часто
обозначают QX. Таким образом, n^QX) = я*(Х), поэтому Q —функтор,
преобразующий стабильные гомотопические группы в обычные
гомотопические группы.
Непосредственно из определений следует, что теория гомологии,
заданная спектром —это то же самое, что теория гомологии, заданная
соответствующим ^-спектром. Можно поинтересоваться, любая ли
теория гомологии задаётся спектром, как мы показали для когомологий.
Ответ утвердительный, если заменить аксиому букета более сильной
аксиомой прямого предела: ft,(X) = limft,-(Xtt), где прямой предел берётся но
конечным подкомплексам Ха комплекса X. Теория гомологии, заданная
спектром, удовлетворяет этой аксиоме, а обратное утверждение доказано
в [79].
Спектры стали наиболее распространённым языком для описания
многих стабильных явлений в алгебраической топологии. Увеличение
§4.G. Конструкции склейки
577
гибкости спектров, однако, не проходит даром, так как многие понятия,
элементарные для пространств, становятся намного более сложными для
спектров, например правильное определение отображения спектров или
приведённого произведения двух спектров. Для читателя, который хочет
больше узнать об этом языке, хорошим вводным курсом послужит [2].
Задачи
1. Предполагая, что верны первые две аксиомы для теории гомологии
на CW-категории, покажите, что из аксиомы прямого предела следует
аксиома букета. Докажите, что обратное утверждение тоже верно для
счётных CW-комплексов.
2. Для CW-комплексов Х и У рассмотрим последовательность
надстройки
(X, У) ^ (ZX, ЪУ) ^ (Е2Х, Е2У) -» ...
Докажите, что если X — конечный комплекс, то эти отображения в конце
концов становятся изоморфизмами. [Примените индукцию по числу
клеток комплекса X и 5-лемму.]
3. Докажите, что для любой последовательности Zx —>Z2 —>...
естественное отображение limftZ,, —> filimZ,, является слабой гомотопической
эквивалентностью; здесь прямые пределы означают телескопы
отображений.
§4.G. Конструкции склейки
В алгебраической топологии часто приходится склеивать
пространства, чтобы получить более сложные пространства. В этом параграфе мы
описываем две общие процедуры таких конструкций. Первая довольно
прямолинейная, но и весьма жёсткая; ей недостаёт свойства
гомотопической инвариантности. Второй тип конструкций склейки избегает этого
недостатка, систематически используя цилиндры отображений. Мы уже
встречали много частных случаев обеих конструкций, и наличие общей
структуры, охватывающей все эти частные случаи, должно внести
некоторую концептуальную ясность.
Диаграмма пространств состоит из ориентированного графа Г,
каждой вершине v которого сопоставлено пространство Xv, а каждому
ребру е, идущему из вершины v в вершину w, сопоставлено отображение
fe: Xv —>Xw'y слова «из вершину» и «в вершину» относятся к заданной
ориентации ребра е. Коммутативность диаграммы не предполагается.
Обозначив такую диаграмму пространств просто через X, мы определим
пространство UX как факторпространство несвязного объединения всех
пространств XVi сопоставленных вершинам графа Г, при отождествлениях
х~/еО) для всех отображений /с, сопоставленных рёбрам графа Г. Будем
Называть UX амальгамацией диаграммы X. Вот некоторые примеры.
19 За к Уо5*
578
Глава 4. Теория гомотопий
1. Если диаграмма пространств имеет простой вид Х0 *— Ас-* Хх, то UX —-
пространство X0Uj- Хх, полученное из Х0 приклеиванием Х} вдоль Л
по отображению /.
2. Последовательность включений X, С->Х1 с-*... определяет диаграмму
пространств X, для которой UX — это пространство [Jxi со слабой
топологией. Это верно и в более общем случае, когда пространства
X,- занумерованы любым направленным множеством.
3. По покрытию °2/ = {X,} пространства X подпространствами X, мы
можем построить диаграмму пространств Х,у/, вершины которой —
непустые конечные пересечения Х?) П...ПХ, с разными индексами i• ,
а рёбра —всевозможные включения, полненные исключением
некоторых из подпространств в таком пересечении, например включения
X, П Xj с-> X,. Тогда UX,^ равно X как множество, хотя, возможно,
имеет другую топологию. Если данное покрытие открытое или если X —
CW-комплекс, а все X,—-подкомплексы, то эта топология совпадает
с исходной топологией на X.
4. Действие группы G на пространстве X определяет диаграмму
пространств Хг;, где единственным пространством является само X,
а отображения —гомеоморфизмы g: X—> X, g£G, заданные
действием. В этом случае \JXG — пространство орбит X/G.
5. Можно рассматривать Д-комнлекс X как диаграмму пространств Хд,
где каждый симплекс X даёт вершинное пространство XVJ которое
является симплексом той же самой размерности, а рёберные
отображения—включения граней в симплексы, которые их содержат. Тогда
ихд = х.
Легко может случиться, что для диаграммы пространств X
рассматривать амальгамацию UX совершенно бесполезно, потому что
происходит так много отождествлений, что от исходной диаграммы почти
ничего не остаётся. Например, рассмотрим диаграмму X вида Х() <— Х0 х
х X! -+X-L, отображения в которой —проекции на оба множителя. В этом
случае UX —просто точка. Чтобы справиться с такими проблемами и
получить понятие с более хорошими теоретико-гомотопическими
свойствами, мы введём гомотопическую версию пространства UX, которую мы
обозначим ДХ и назовём реализацией диагаммы X. Здесь мы снова
начинаем с несвязного объединения всех вершинных пространств Хг, но
вместо перехода к факторпространству этого несвязного объединения
мы увеличиваем его, вставляя цилиндр отображения Mf для каждого
отображения / из диаграммы, отождествляя оба основания этого
цилиндра с соответствующими пространствами Xv. В случае диаграммы-
проекции Х0 <— Х() х X, —> X! объединение двух цилиндров
отображения—это то же самое, что факторпространство цилиндра Х0 х Xj x /,
в котором Х0 х Хх х {0} стягивается в Х0, а Х0 х Xj x {1} стягивает-
§4.G. Конструкции склейки
579
ся в XY. Таким образом, 5Х— это джойн Х0*ХЬ определённый в
главе 0.
Мы уже встречались со многими другими частными случаями
конструкции АХ. Для диаграммы, состоящей только из одного отображения
/: Х0-^Х1) мы получаем, конечно, просто цилиндр отображения My. Для
/ н
диаграммы Х0 ±—Х^—*Х2 реализация АХ —это двойной цилиндр
отображения. В случае, когда Х2 — точка, это будет конус отображения /. Когда
в диаграмме есть только одно пространство и одно отображение из этого
пространства в себя, АХ—тор отображения. Для диаграммы, состоящей
из двух отображений /, g: X0—>ХЬ пространство АХ изучалось в примере
2.48. Телескопы отображений относятся к последовательности
отображений Х0~>Х] —>... В §1.В мы рассматривали общие диаграммы, в которых
пространствами являются пространства типа K(G, 1).
Существует естественное обобщение конструкции АХ, в котором мы
начинаем с А-комплекса Г и диаграммы пространств, связанных с
одномерным остовом комплекса Г так, что отображения, соответствующие
граням каждого n-мерного симплекса в Г, где п > 1, образуют
коммутативную диаграмму. Назовём эти данные комплексом пространств. Если
X — комплекс пространств, то для каждого /i-мерного симплекса в Г мы
получаем последовательность отображений
Х—1*. V lib ^" V
0 * л1 * •■■ лм>
и мы определим итерированный цилиндр отображения M(flf ...,/„) как
обычный цилиндр отображения при п = 1, а при п> \ по индукции, как
цилиндр отображения композиции М(/ь ...,/r,-i) """* Хп_х -^Хм, где
первое отображение — каноническая проекция цилиндра отображения на его
основание, соответствующее образу отображения. Имеется естественная
проекция М(/ь ..., /п) —> Ап, и над каждой гранью комплекса Ам имеется
итерированный цилиндр отображения для отображений, связанных с
рёбрами этой грани. Например, при п = 2 мы получаем три цилиндра
отображений МС/т), М(/2) и M(f2f\) над тремя рёбрами симплекса А2. Все эти
итерированные цилиндры отображений над разными симплексами
комплекса Г, таким образом, стыкуются вместе и образуют пространство АХ
с канонической проекцией АХ —> Г. Мы снова назовём АХ реализацией
комплекса пространств X и назовём Г базой для X или АХ.
Некоторые из наших предыдущих примеров диаграмм пространств
можно естественным образом рассматривать как комплексы пространств.
1. Для покрытия °U = {X,} пространства X диаграмма пространств
Key, вершины которой — конечные пересечения пространств Х?, а рёбра —
включения, является комплексом пространств с n-мерными симплексами,
соответствующими n-кратным включениям. База Г для этого комплекса
Пространств —барицентрическое подразделение нерва покрытия. Напом-
ssu
Глава 4. Теория гомотопий
ним, что в конце § 3.3 нерв покрытия определялся как симплициальный
комплекс, n-мерные симплексы которого — непустые (п + 1)-кратные
пересечения множеств из покрытия.
2. Диаграмма пространств Хс, соответствующая действию группы G
на пространстве X, является комплексом пространств, n-мерные
симплексы которого соответствуют n-кратным композициям
Базисный А-комплекс Г —это пространство типа K(G, 1), которое мы
в §1.В назвали BG. Там оно было пространством орбит свободного
действия группы G на стягиваемом А-комплексе EG. Проверяя определения,
можно убедиться, что пространство ДХ^ в этом случае можно
рассматривать как факторпространство произведения X х EG при диагональном
действии группы G, g(x,y) = (gOO,g(y))« Это именно то пространство,
которое в §3.G мы назвали конструкцией Бореля и обозначили X xcEG.
Под отображением /: X —* У комплексов пространств над одной и той
же базой Г мы подразумеваем набор отображений /v: Xv —> Yv для всех
вершин комплекса Г с коммутативными квадратами над всеми рёбрами
комплекса Г. Тогда определено индуцированное отображение А/: АХ—> АУ.
I Предложение 4.G.I. Если все отображения /v, составляющие отобра-
I жение комплексов пространств /: X—>У, являются гомотопическими
I эквивалентностями, то и отображение А/: АХ—> АУ является гомото-
I пической эквивалентностью.
Доказательство. Цилиндры отображений M(/v) образуют комплекс
пространств М(/) над той же самой базой Г, причём пространство АМ(/)
является цилиндром отображения М(А/). Оно деформационно
ретрагируется на АУ, поэтому достаточно показать, что оно также
деформационно ретрагируется на АХ.
Пусть М'ЧА/)—часть пространства М(А/), лежащая над п-мерным
остовом комплекса Г. Мы утверждаем, что пространство МП(А/) и АХ
деформационно ретрагируется на Mn~l(Af)u AX. Достаточно доказать это
для Г = Д ". В этом случае / — отображение из Х0 —>...—> Хп в У0 —>... —* У„.
Согласно следствию 0.20 достаточно доказать, что включение Mn~l (A/) U
U АХ *—^М(А/) является гомотопической эквивалентностью и что пара
(М(А/), M"~Z(A/) U АХ) обладает свойством продолжения гомотопий.
Последнее утверждение вытекает из примера 0.15, так как для этой пары
легко строится окрестность, являющаяся цилиндром отображения. Для
доказательства второго условия заметим, что, применяя индукцию по
размерности комплекса Г, мы можем предположить, что Mn~l(Af)
деформационно ретрагируется на часть пространства АХ, лежащую над дДм.
Кроме того, включение АХС~^М(А/) является гомотопической
эквивалентностью, так как оно эквивалентно отображению Хп —> Yn, которое
является гомотопической эквивалентностью по условию. Поэтому можно
§4.G. Конструкции склейки
581
применить следствие 0.20, и утверждение о том, что Mn(Af) и АХ
деформационно ретрагируется на М"-1 (А/) и АХ, доказано.
Меняя л, получаем бесконечный набор этих деформационных
ретракций за время t из интервала Г1/2"4"1,1/2п], который даёт
деформационную ретракцию пространства М(А/) на АХ. □
Существует каноническое отображение АХ —* UX, индуцированное
ретракцией каждого цилиндра отображения на его основание,
соответствующее области значений. В некоторых случаях оно является
гомотопической эквивалентностью, например, для диаграммы Х0 <— А с-> X!, где
пара (Х^Л) обладает свойством продолжения гомотопии. Другой
пример—последовательность включений Х0С->Х1 с->..., где пары (Х^Х,,^)
обладают свойством продолжения гомотопии; это проверяется
рассуждениями с телескопом отображения из доказательства леммы 2.34. Однако
без каких-либо условий на отображения не всегда верно, что АХ —* UX
является гомотопической эквивалентностью, как показывает приведённый
ранее пример проекций Х0 <— Х0 х X! —►Хр Даже для отображений
вложения мы не всегда получаем АХ ~ UX, если база Г не стягиваема.
Тривиальный пример —диаграмма, состоящая из двух пространств 5° и А1 и двух
отображений /0, fY: А0 —> А1, которые имеют один и тот же образ.
Таким образом, можно ожидать, что отображение АХ —* UX
является гомотопической эквивалентностью только при специальных условиях.
Вот одна из таких ситуаций.
I Предложение 4.G.2. Если Х0// — комплекс пространств, связанных с
I открытым покрытием °1/ — {Х{) паракомпактного пространства X, то
I отображение р: АХ,# —»UX7/ = X является гомотопической эквивалент-
I ностью.
Доказательство. Реализацию АХ„и можно также описать как фак-
торпростраиство несвязного объединения всех произведений
Х,йП...П^хДп,
где наборы индексов пробегают по множествам из п +1 разных индексов
иОО, при отождествлениях над гранями симплекса Ап посредством
включений
X: П...ПХ; <— X; П...ПХ; П...ПХ; .
С этой точки зрения точки пространства АХ.9/ в данном «слое» р~1(х)
можно записать в виде конечных линейных комбинаций J] t,or,, где J] t,■ = 1
/ i
и х,- — это точка х, рассматриваемая как точка пространства X,, для тех X,,
которые содержат х.
Так как пространство X паракомпактно, существует разбиение
единицы, подчинённое покрытию °U. Оно является семейством
отображений </>а: Х—> [0, 1], удовлетворяющих трём условиям: носитель каждого
отображения уа содержится в некотором множестве Х,(а); лишь конечное
582
Глава 4. Теория гомотопий
число значений ц>а отличны от нуля вблизи каждой точки пространства X;
2^я = 1. Определим сечение s: X —> AX,f/ для отображения р, положив
а
s(x) =5]^аМх,-(а). На рисунке изображён случай X = S]
а
с покрытием двумя дугами; выделенная линия
обозначает образ отображения s. В общем случае сечение s
вкладывает X в качестве ретракта пространства ЛХ7/, причём
это деформационный ретракт, так как точки в каждом
слое р~1(х) можно линейно сдвигать по отрезкам к точке s(x). □
I Следствие 4.G.3. Если °U — такое открытое покрытие паракомпакт-
I ного пространства X, что каждое непустое пересечение конечного
I числа множеств из °U стягиваемо, то X гомотопически эквивалентно
I нерву №?/.
Доказательство. Предложение 4.G.2 даёт гомотопическую
эквивалентность X ~ ДХ#. Так как непустые конечные пересечения множеств из
41 стягиваемы, из предложения 4.G.1 следует, что отображение ДХУ/ —> Г,
индуцированное тем, что каждое пересечение отображается в точку,
является гомотопической эквивалентностью. Так как Г —барицентрическое
подразделение комплекса №2/, получаем требуемое утверждение. G
Завершим этот параграф некоторыми комментариями по поводу
терминологии. Для некоторых диаграмм пространств, например для
последовательностей X! -+Х2—>..., амальгамацию UX можно рассматривать как
прямой предел вершинных пространств в Xv относительно рёберных
отображений /е. В соответствии с этим замечанием пространство UX обычно
называют прямым пределом для произвольных диаграмм, даже конечных.
Если рассматривать UX как прямой предел, то ЛХ превращается в своего
рода гомотопический прямой предел. По причинам, которые объясняются
в следующем параграфе, прямые пределы часто называют «копределами».
Это привело к весьма неудачному термину «hocolim» для ЛХ
—сокращению для «homotopy colimit». Мы предпочли ему термин «реализация», как
из-за его существенных достоинств, так и потому, что пространство ЛХ
тесно связано с тем, что называют геометрической реализацией симпли-
циального пространства.
Задачи
1. Докажите, что для последовательности отображений Х()—->Х} -^ •••
бесконечный итерированный цилиндр отображений M(fltf2t ...), который
является объединением конечных итерированных цилиндров отображении
M(/i, ..., /„), деформационно ретрагируется на телескоп отображений.
2. Докажите, что если X — комплекс пространств, в котором все
отображения являются гомеоморфизмами, то проекция ДХ —> Г является
локально тривиальным расслоением.
§4.И. Двойственность Экмана—Хилтона
583
3. Как устроен нерв покрытия симплициального комплекса
открытыми звёздами его вершин? [См. лемму 2.С.2.]
4. Докажите, что предложение 4.G.2 и его следствие верны также для
CW-комплексов и покрытий семействами подкомплексов. [CW-комплек-
сы паракомпактны; см. [VBKT].]
§4,Н. Двойственность Экмана—Хилтона
В теории гомотопий имеет место очень хороший принцип
двойственности. В более систематическом виде этот принцип известен под
названием двойственности Экмана—Хилтона, но лежащая в его основе идея очень
проста и заключается в том, чтобы обратить направление всех стрелок
в некоторой данной конструкции. Например, если в
определении расслоения как отображения, обладающего свой- А —L-^ X
ством поднятия гомотопий, мы обратим направление всех , yf
стрелок, то получим двойственное понятие корасслоения. в ' Sn
Это отображение i: A —> В, обладающее следующим
свойством. Если заданы отображение g0:B->X и гомотопия gt: A —>Х, для
которых g0i = g0, то существует гомотопия gt: В —> X, для которой gfi = gt.
В частном случае, когда i — включение подпространства, это свойство
продолжения гомотопий, и следующее предложение утверждает, что это
в действительности общий случай. Таким образом, корасслоение —это то
же самое, что включение, обладающее свойством продолжения
гомотопий.
Предложение 4.Н.1. Если i: A-+B — корасслоение, то отображение i
инъективио и является гомеоморфизмом на свой образ.
Доказательство. Рассмотрим цилиндр отображения М,, т. е. фактор-
пространство пространства А х / Ц В, в котором точка (а, 1)
отождествляется с г (а). Пусть gf: А —> М, — гомотопия, отображающая абД в образ
точки (а, 1 - О е А х / в М,-, и пусть g0 —включение В ^-> М,. Свойство
корасслоения даёт гомотопию gt: В^>М[у для которой gfi=gr. Фиксируя
t > 0, из этого получаем, что отображение i инъективно, так как gt
инъективио. Кроме того, так как gt —гомеоморфизм на свой образ А х {1 - t},
из соотношения gti — gt следует, что отображение g~lgt: i(A) —> А является
непрерывным обратным к г. А —> i(A). D
Многие конструкции для расслоений имеют аналоги для
корасслоений, и наоборот. Например, для произвольного отображения /: А^>В
включение A<-^>Mf, очевидно, является корасслоением, поэтому аналог
разложения А °-> Ef —> В отображения / в композицию гомотопической
эквивалентности и последующего расслоения — это разложение A<-^>Mj^>B
в композицию корасслоения с последующей гомотопической
эквивалентности. Даже определение пространства My в некотором роде двойственно
определению пространства Ef, так как Ef можно определить как перетас-
584
Глава 4. Теория гомотопий
кивание1 назад (индуцирование), a Mj можно определить как
двойственное выдавливание.
Ef >• В1 А ^ В
т Y т У
А >- В Axl ^ Mf
В общем случае выдавливание отображений f\Z^>Xug:Z-*Y
определяется как фактор пространства XUY при отождествлениях /(z)^g(z).
Таким образом, выдавливание — факторпространство для X Ц Y, в то
время как перетаскивание назад отображений X —> Z и Y —> Z является под-
объектом в X х У. Мы видим здесь два проявления двойственности:
двойственность между несвязным объединением и произведением и
двойственность между подобъектами и факторобъектами. Первая из них легко
объясняется, так как набор отображений Ха —> X эквивалентен
отображению ЦХа—>Х, в то время как набор отображений X —> Ха эквива-
а
лентен отображению X—>ПаХа. Обозначение JJ для «копроизведения»
было выбрано, чтобы указать на то, что оно двойственно к f]. Если бы
мы имели дело с пространствами с отмеченной точкой и отображениями,
сохраняющими отмеченные точки, то копроизведение было бы букетом.
В категории абелевых групп копроизведение — прямая сумма.
Двойственность между подобъектами и факторобъектами ясна для
абелевых групп, где подобъекты — ядра, а факторобъекты — коядра.
Точный топологический аналог ядра —слой расслоения. Двойственным
образом, топологический аналог коядра — косяой В/А корасслоения А^В.
Если мы превратим произвольное отображение /: А —> В в корасслоение
A^Mf, то кослой —конус отображения Cj — Mf/{A x {0}).
На диаграмме, изображающей Ej и My как перетаскивание назад
и выдавливание, видно нечто вроде двойственности между членами А х /
и В1. Это приводит к вопросу о том, двойственны ли X х J и X1 каким-
то образом. Действительно, если игнорировать топологию и мыслить
теоретико-множественно, то это частный случай знакомой нам
двойственности произведение-копроизведение, так как произведение
экземпляров X с индексами / — это множество X1 всех функций / —> X, в то
время как копроизведение экземпляров X с индексами / — это множество
X х /, т.е. несвязное объединение множеств X х {t} для t€/.
Возвращаясь назад из категории множеств в топологическую категорию, мы
можем рассматривать X1 как «непрерывное произведение» экземпляров
пространства X, а X х / — как «непрерывное копроизведение».
На менее абстрактном уровне тот факт, что отображение А х / —> В —
это то же самое, что отображение Л—>ВУ, указывает на какую-то двой-
1 В русской математической терминологии до сих пор нет адекватного аналога очень
распространённого английского термина pullback. — Пром. перев.
§4.Н. Двойственность Экмана—Хилтона
585
ственность между Л х / и В1. Она приводит к двойственности между
надстройкой и пространством петель, так как ЕЛ — факторпространство
пространства Л х /, a Q.B — подпространство в В1. Эта двойственность
выражена в соотношении сопряжённости (EX, Y) = (X, QY) из §4.3. Сочетая эту
двойственность между Е и £1 с двойственностью между слоями и косло-
ями, мы получаем соотношение двойственности между
последовательностями расслоения и корасслоения из §4.3:
... -* CIF -* ПЕ -* ПВ -* F -* Е -* В,
Л — X — Х/Л — ЕЛ — ЕХ -» Е(Х/Л) — ...
Конструкции выдавливания и перетаскивания назад можно обобщить
на произвольные диаграммы. В случае выдавливания это было сделано
в §4.G, где мы сопоставили пространство UX диаграмме пространств X.
Оно было факторпространством копроизведения \JXV, где v пробегает
v
по всем вершинам диаграммы, при отождествлениях х~/еО) для всех
отображений /с, соответствующих рёбрам е диаграммы. Двойственная
конструкция ПХ должна быть подпространством в произведении UvXVi
состоящим из таких наборов OJ, что /eOv) =xxv для всех отображений
fe: Xv —> Xw в этой диаграмме. Возможно, в алгебраической топологии
более полезен гомотопический вариант этого понятия, полученный дуа-
лизацией определения пространства ДХ из предыдущего параграфа. Это
будет пространство VX, состоящее из всех возможных точек xv в каждом
пространстве Xv и пути ус в пространстве — области значений каждого
рёберного отображения fe: Xv —►Х^, для которого уе(0) =/Ov) и уе(1) =xw.
Подпространство, в котором все пути постоянные, — это ПХ. В случае
диаграммы ... —► Х2 -»Xj (например, башни Постникова) эта конструкция
даёт нечто немного отличающееся от просто превращения каждого
последовательного отображения в расслоение посредством обычной конструкции
пространства путей, начиная с Х2 -* Хг и идя вверх по башне, как мы это
делали в §4.3. Последняя конструкция скорее является двойственной
итерированному цилиндру отображения: в ней используются пространства
отображений Л" -* Xv вместо просто пространств путей. Можно
использовать такие пространства отображений, чтобы обобщить определение
пространства VX с диаграмм пространств на комплексы пространств.
Как частные случаи конструкций UX и ПХ мы получаем прямые
пределы и обратные пределы для диаграмм Х0 -* Хт -*... и ... —> XY -* Х0
соответственно. Так как обратный предел связан с произведением, а прямой
предел — с копроизведением, в некоторых кругах обычно используют
обратную логику и называют обратный предел просто «пределом», а прямой
предел — «копределом». Гомотопические версии тогда называют «holim»
Для VX и «hocolim» для ЛХ. Эта терминология часто используется также
для более общих диаграмм.
586
Глава 4. Теория гомотопий
Гомотопические группы с коэффициентами
Существует более глубокая двойственность между
гомотопическими группами и когомологиями, которая проявляется в том факте, что
группы когомологий —гомотопические классы отображений в
пространство с единственной ненулевой гомотопической группой, в то время
как гомотопические группы —гомотопические классы отображений из
пространства с единственной ненулевой группой когомологий. Эта
двойственность, однако, в одном неполна, а именно, утверждение о когомо-
логиях имеет место для произвольной группы коэффициентов, но мы
пока не определяли гомотопические группы с коэффициентами. Помня
об этой двойственности, можно было бы попытаться определить яи(Х\ G)
как множество сохраняющих отмеченную точку гомотопических классов
отображений из когомологического аналога пространства Мура М(6\ п)
в X. Когомологическим аналогом пространства M(G,n) должно быть
пространство Y, у которого единственная группа когомологий //'(Y;Z),
отличная от нуля, равна G для i = n. К сожалению, такое пространство
существует не для любой группы G, например, его не существует для
G = Q, так как мы показали в предложении 3.F.12, что если все группы
когомологий пространства счётны, то все они конечно порождены.
В качестве первого приближения к nn(X;G) давайте рассмотрим
(M(G,n), X) — множество сохраняющих отмеченную точку
гомотопических классов отображений M(G,n)^>X. Чтобы в названии этого
множества было указание на его смысл, обозначим его /i„(X;G). Мы должны
предположить, что п > 1, чтобы гарантировать, что гомотопический тип
пространства M(G, п) корректно определён, как показано в примере 4.34.
Если п > 1, то цп(Х; G) —группа, так как мы можем выбрать в качестве
M(G,n) надстройку над M(G,n - 1). А если п > 2, то группа [лп(Х;С)
абелева, так как мы можем выбрать в качестве M(G,n) двукратную
надстройку.
Для групп /in(X; G) имеет место утверждение, похожее на теорему об
универсальных коэффициентах.
I Предложение 4.Н.2. Для п > 1 имеются естественные короткие точ-
I ные последовательности
I 0-> Ext(G, nn+x(X)) -> jLt„(X;G) -» Hom(G, тг„(Х)) — 0.
Сходство с теоремой об универсальных коэффициентах для
когомологий очевидно, но с перестановкой переменных в членах Ext и Нот. Это
отражает тот факт, что 1ЛП(Х; G) является ковариантным функтором по X
и контравариантным функтором no G, точно так же, как Ext и Нот.
Доказательство. Пусть 0—>Я—►F—>G—►() — свободная резольвента
для G. Отображение / включения реализуется отображением M(R,n)~+
—>М(Р, п), где M(Ryn) и M(Fy /i) — букеты сфер S'\ соответствующих ба-
§4.Н. Двойственность Экмана—Хилтона
587
зисам для F и R. Превратим это отображение в корасслоение посредством
цилиндра отображения. Его кослоем является пространство M(G, п), как
видно из длинной точной последовательности групп гомологии. Как и в
§4.3, последовательность корасслоения
М(Д, п) -> M(F, п) -> M(G, п) -> M(R, п + 1) -> M(F, п +1)
приводит к точной последовательности в верхней части следующей
диаграммы:
/iII+1 (X; F) >■ ^ 1 (X; R) —>/ifl(X; G)—> /i„(X; F) ^ /i„(X; R)
i .. i » . i
Hom(F, nn^ (X)) 4- Hom(R, n„n (X)) Hom(F, тт„(Х)) -*- Hom(R, 7t„(X))
Четыре внешних члена этой точной последовательности можно
отождествить с указанными гомоморфизмами, так как отображение букета
сфер S" в X сводится к выбору элемента группы яДХ) для каждого
слагаемого букета. Ядро и коядро гомоморфизма Г—это по определению
Hom(G, —) и Ext(G, —), а потому мы получаем искомую короткую точную
последовательность. Проверка естественности оставляется читателю. □
В отличие от того, что происходит в теоремах об универсальных
коэффициентах для гомологии и когомологий, короткая точная
последовательность из предложения 4.Н.2, вообще говоря, не расщепляется. В
качестве соответствующего примера можно взять G = Z2 и X = M(Z2, п) для
п ^ 2, где тождественное отображение пространства M(Z2, п) определяет
элемент группы /i^M(Z2, n); Z2) = (M(Z2, n), M(Z2, п)), имеющий
порядок 4, как мы покажем в примере 4.L.7, в то время как два внешних члена
в короткой точной последовательности могут содержать только элементы
порядка 2, так как G = Z2. Этот пример показывает также, что группа
/i,j(X; Zm) не обязана быть модулем над Zm, в отличие от групп гомологии
и когомологий с коэффициентами в Ът.
Из предложения 4.Н.2 следует, что первая ненулевая группа /х, (Sn; ZM))—
это группа /iM_i(Sn; Zm) = Z,„, происходящая из члена Ext. Этот результат
выглядел бы более понятным, если бы мы изменили обозначения, заменив
нижний индекс п — 1 на п. Поэтому введём определение
ям(Х; ZJ = (M(Z,„, п - 1), X) = /i^CX; Z,n).
Имеется два основания считать это определение правильным. Первое
формальное: пространство M(Z„,,n — 1)—это «когомологическое
пространство M(Zm,n)», так как его единственная нетривиальная группа
когомологий Hl(M(Zm> п - 1); Z) равна Zm в размерности п. Вторая
причина более геометрическая: элементы группы nn{X\Zm) должны быть
гомотопическими классами— «теоретико-гомотопическими циклами по
модулю т», что означает отображения D" —> X, граница которых не
обязательно постоянное отображение, как для 7i„(X), а является умноженным
588
Глава 4. Теория гомотопий
на т циклом Sn~l -* X. Это в точности отображения M(Z,n, п — 1) -* X,
если мы выберем в качестве M(Zm, п - 1) сферу S'1"1 с клеткой е",
приклеенной по отображению степени т.
Помимо вычисления nn(Sn; Zm) ъ Zm предложение 4.Н.2 приводит
также к изоморфизму 7rn(M(Z,„, n); Zm) ъ Ext(Z,„, Zm) = Zm. В
действительности оба этих результата — частные случаи теоремы, похожей на
теорему Гуревича, связывающей группы ям(Х; Z,„) и Н„(Х; Z,„); эта теорема
доказана в [119].
Наряду с Z и Ът ещё одна чрезвычайно полезная группа
коэффициентов для гомологии и когомологий — группа Q. Мы отметили выше
трудность, состоящую в том, что нет когомологического аналога пространства
M(Q, п). С группами /i„(X; Q) тоже есть сложности. Например,
предложение 4,Н.2 показывает, что iin_x{Sn\ Q) ъ Ext((Q), Z), а это сложная
несчётная группа, как мы показали в § 3.F. Однако существует альтернативный
подход, который, как оказывается, работает очень хорошо. Определим
рациональные гомотопические группы просто как rcM(X)®(Q>,
аналогично изоморфизму Н„(Х; Q) ъ Hn(X; Z) (g) Q из теоремы об универсальных
коэффициентах для гомологии. Подробнее об этом см. в [SSAT].
Гомологические разложения
Двойственность Экмана—Хилтона может оказаться чрезвычайно
полезной как организационный принцип, значительно сокращая то, что
нужно запомнить, и давая ценные подсказки, как действовать в разных
ситуациях. Чтобы проиллюстрировать это, давайте посмотрим, что
произойдёт, если мы дуализируем понятие башни Постникова из главных
расслоений, где пространство представлено как обратный предел
последовательности слоев отображений в пространства Эйленберга—Маклей-
на. В двойственном представлении пространство должно быть
представлено как прямой предел последовательности кослоёв отображений из
пространств Мура.
Опишем это подробнее. Предположим, что задана
последовательность абелевых групп Gn, п ^ 1, и мы строим CW-комплекс Х, для которого
Hn{X)^Gn для всех п, конструируя по индукции возрастающую
последовательность подкомплексов Хх с Х2 с ..., для которых Н{ (Х„) ъ G, при i ^ п
и Н,(Хп) = 0 при f >п, где:
1) Xj—пространство Мура M(Gb 1);
2) Х„+1 —конус отображения для такого клеточного отображения
ft„:M(G„+1>n)-Xn,
что индуцированное отображение hn*: Hn(M(Gn+l> п)) —>Н„(Х„)
тривиально;
3) X = {JXn.
п
§4.Н. Двойственность Экмана—Хилтона
589
По индукции можно доказать, что Хп+1 имеет требуемые группы
гомологии, сравнив длинные точные последовательности пар (ХП+1,ХП)
и (СМ, М), где M = M(Gn+l, п), а СМ -конус М х I/M х {0}:
Hn+1(CM,M)Hr"«tt«*Gn+1
Предположение, что отображение ftn* тривиально, означает, что
граничное отображение в верхней строке нулевое, следовательно, Нп+1(Хм+1) ъ
wGn+1. Остальные группы гомологии у Хп+1 те же самые, что и у Хп, так
какН,-(Хп+1, ХП)^Н,(СМ, М) для всех i согласно вырезанию, а Н{(СМ, М)^
«H/.jCM), так как пространство GM стягиваемое.
В случае, когда все отображения ftn тривиальные, X —это букет
пространств Мура M(Gn, n), так как в этом случае конструкция конуса
отображения в п. 2 даёт букет с надстройкой над M(Gn+1, n), т.е. с пространством
MypaM(Gn+1,n + l).
Для пространства У гомотопическая эквивалентность /: X -+Y, где
пространство X построено так, как в п. 1—3, называют гомологическим
разложением пространства У.
Теорема 4.Н.З. У любого односвязного CW-комплекса существует
гомологическое разложение.
Доказательство. Для данного односвязного GW-комплекса Y
положим Gn = НП(У). Предположим по индукции, что мы уже построили
Хп посредством отображений ft,, как в п. 2, и построили отображение
/: Хп —> У, индуцирующее изоморфизм групп Н, при i ^ п. Индукцию
можно начать, взяв в качестве Хх точку, так как Y односвязно.
Чтобы построить Xn+i, мы сначала заменим Y на цилиндр отображения
/: Хп —> У, превратив / во включение. Воспользовавшись теоремой Гу-
ревича и гомологической точной последовательностью пары (У,ХП),
получаем 7гп+1 (У, Хп) ъ Нп+1 (У, Хп) ъ Нп+1 (У) = Gn+1. Этот изоморфизм нам
понадобится для построения отображения ftn: M(Gn+l, n) -+ Хп и
продолжения/: Хп+1-*У.
Стандартная конструкция пространства M(Gn+l,n) представляет
собой букет сфер Sna, соответствующих образующим ga группы Gn+1, с
клетками е'1+\ приклеенными в соответствии с определёнными линейными
комбинациями r^ =Sna/5^a> которые равны нулю в Gn+1. При изоморфиз-
а
Me Gn+1 ъ яп+1 (У, Хп) каждая образующая ga соответствует сохраняющему
отмеченную точку отображению fa: (CSn,Sn) -* (У,ХП), где CSn — конус
над Sn. Ограничения этих отображений fa на Sn определяют отображение
hn- Va Sna -> Хп, а сами отображения /a: CSn -> У задают продолжения
отображения /: Хп -* У на конус отображения для ft,?: va Sna -+ Хп. Каж-
590
Глава 4. Теория гомотетий
дое соотношение Гр даёт гомотопию Fp: {CSn, Sn) х / —► (У, Хп)
отображения ^пар/а в постоянное отображение. Мы воспользуемся отображением
а
Fp\ Sn x {0}, чтобы приклеить клетку c*+I; тогда Fp\ Sn x / задаёт
отображение hn на eV'\ a F^ даёт продолжение отображения / на конус над е«+1.
Эта конструкция гарантирует, что отображение /+: Я„+1(Хп+1, Хм) —>
—>Н,,+1(У, Х„) является изоморфизмом, поэтому из 5-леммы,
применённой к длинным точным последовательностям этих пар, мы получаем, что
/*: Я,-(Х„+1) —> Я/(У) —изоморфизм при t ^ n + 1. Это завершает
доказательство шага индукции. Мы можем считать, что отображения fa и Fp
клеточные, поэтому X = (JX„ —-С1У-комплекс с подкомплексами Хп. Так как
отображение /: X—>У односвязных CW-комплексов индуцирует
изоморфизм всех групп гомологии, оно является гомотопической
эквивалентностью. П
В качестве примера предположим, что У — односвязный
CW-комплекс, у которого все группы гомологии свободные. Тогда в качестве
пространств Мура, используемых при построении пространства X,
можно взять букеты сфер, а потому Х„ получается из Хм_ L приклеиванием
гс-мериой клетки для каждого слагаемого Z а группе ЯМ(У).
Отображения приклеивания можно выбрать клеточными, что превращает X
в CW-комплекс, клеточный цепной комплекс которого имеет
тривиальные граничные отображения. Аналогично конечные циклические
слагаемые группы Я„(У) можно реализовать букетом пространств вида S""1 ие"
в М(ЯП(У), п - 1), дающих в X следующий вклад: одну п-мерпую клетку
и одну (п 4-1)-мерную. Это в точности предложение 4.С.1, но в более
сильной форме, потому что теперь конечное циклическое слагаемое группы
Нп можно реализовать за один шаг, приклеив конус над пространством
Мура M(Zk, n — 1), а не за два шага, приклеив п-мерную клетку а затем
(п + 1)-мерную.
Задачи
1. Докажите, что если А <-* X — корасслоение компактных хаусдорфо-
вых пространств, то для любого пространства У отображение Vх —> Ул,
полученное в результате ограничения отображений, является расслоением
в смысле Гуревича. [Если А <—* X — корасслоение, то АхУ^ХхУ тоже
корасслоение для любого пространства У.]
2. Рассмотрим диаграмму выдавливания (см. рис.), a j > j$
где BUf X —это В, к которому приклеено X по подпро- Г
странству А посредством отображения /. Докажите, что |
если А с-> X — корасслоение, то В <-> В Uy X тоже корас- J, ^ В U - X
слоение. -'
3. Для расслоений в смысле Гуревича Е{ —>В и Е2 —* В докажите, что
сохраняющее слои отображение Е} —> Е2> которое является гомотопиче-
§4.1. Стабильные расщеплния пространств
591
ской эквивалентностью, в действительнее™ является послойной
гомотопической эквивалентностью. [Это утверждение двойственно
предложению 0.19.]
4. Определите точно двойственный объект для итерированного
цилиндра отображения в терминах отображений из Д" и воспользуйтесь им,
чтобы дать определение VX— двойстве шого объекта для ДХ, где X —
комплекс пространств.
§4.1. Стабильные расщегления пространств
Иногда случается, что надстраивание пространства приводит к
упрощению его гомотопического типа, поскаьку надстройка оказывается го-
мотопически эквивалентной букету меньших пространств. Основной
интерес к таким стабильным расщепленшм связан с тем фактом, что они
предоставляют геометрическое объяснение алгебраических расщеплений
групп гомологии и когомологий, а так<е других алгебраических
инвариантов пространств, которые не изменится при надстройке, например
когомологических операций, изученныхв §4.L.
Самый простой пример стабильной расщепления даёт тор S1 x S1.
Для него приведённая надстройка ECS1 < S1) гомотопически
эквивалентна S2 V S2 V S3, так как T,(S] x S1) — эт> S2 V S2 с трёхмерной клеткой,
приклеенной по надстройке над отображением приклеивания двумерной
клетки тора, но последнее отображение приклеивания —это коммутатор
двух включений S1 e-^Sl VS1, и надстройка над этим коммутатором
тривиальна, так как она лежит в абелевой руппе n2{S2 VS2).
Несложным геометрическим рассуждением мы докажем более общее
утверждение.
Предложение 4.1.1. Если X и У — С V-комплексы, тоЕ(ХхУ)^ ЕХ V
VEyvE(XA7).
Например, £(S'" x S") ^S",+I VS"4"1 'Sm+n'\ Структура w-произведе-
ния на H*(S1U х S") показывает, что такого расщепления Sm x S" не может
быть до надстройки.
Доказательство. Рассмотрим джойн X * У, определённый в главе 0,
состоящий из всех отрезков, соединяюдих точки из X с точками из Y.
Для наших непосредственных целей у/:обпо использовать приведённую
версию джойна, которая получается при стягивании в точку отрезка, со-
592
Глава 4. Теория гомотопий
единяющего отмеченные точки х0еХ и у0 е Y. Мы будем по-прежнему
обозначать этот приведённый джойн X*Y. Рассмотрим пространство,
полученное из X * Y приклеиванием приведённых конусов СХ и CY к
экземплярам пространств X и Y на обоих концах X*Y. Если мы сожмём
каждый из этих конусов в точку, то получим приведённую надстройку
Т,(Х х Y). Так как каждый конус стягиваем, сжимание конусов даёт
гомотопическую эквивалентность X * Y U СХ U CY ^ E(X x Y). Джойн X * Y
также содержит конусы х0*У иХ*у0, пересекающиеся по одной точке.
Стягивание этих конусов превращает X*Y в £(Х А У), a X*Y UCXUCY
BT,(XAY)VT,XVTtY. □
Этот результат можно применять индуктивно, чтобы получать
расщепления для надстроек произведений более чем двух пространств,
используя тот факт, что приведённая надстройка —это приведённое
произведение с S1, а приведённое произведение ассоциативно и коммутативно.
Например,
E(XxyxZ) ~
- EXVEyvEZVEUAy)VE(XAZ)VE(yAZ)vE(XAyAZ).
В нашем следующем примере участвует приведённое произведение
Джеймса J(X), определённое в §3.2. Интересным случаем является
пространство J(Sn), которое имеет CW-структуру вида Sn Ue2" Ue3M U ... Все
клетки ет для1>1 приклеены нетривиально, так как H*(J(S"); Q) — кольцо
многочленов <Q[x] для чётного п и тензорное произведение Q[x] ® А.г>[у]
для нечётного п. Однако после перехода к надстройке I^JiS") все
отображения приклеивания удивительным образом становятся тривиальными.
I Предложение 4.1.2. T.J(Sn)c*Sn+l vS2n+I vS3n+I V ... И вообще, если
X —связный CW-комплекс, то T,J(X) ~ Vn£XAn, где ХАп обозначает
приведённое произведение п экземпляров пространства X.
Доказательство. Пространство J(X) является объединением
возрастающей последовательности подкомплексов Jk{X), где Jk{X) — фак-
торпространство /с-кратного произведения Ххк. Факторпрострапство
Jk{X)/Jk_l{X) —это ХАк. Таким образом, мы получаем отображения
Ххк -> Jk(X) - ХАк = Jk{X)/Jk_^X).
Повторное применение предыдущего предложения показывает, что Т,ХАк —
слагаемое букета для ЛХхк с точностью до гомотопической
эквивалентности. Из доказательства также видно, что существует такое отображение
Т,ХАк — Т,Ххк, что композиция Т,ХАк — ?,Х*к -> ЕХЛ* гомотопна
тождественному отображению. Эта композиция раскладывается так:
ШАк -> ЕХХ/С -> ВДХ) -> SXA/c,
поэтому мы получаем такое отображение sk: Т,ХАк —> DJ^(X), что
отображение EXAfc -^ EJ^(X) —> Т,ХАк гомотопно тождественному.
§4.1. Стабильные расщепления пространств
593
Отображение sk индуцирует расщепление длинной точной
последовательности групп гомологии для пары (EJ^CX), EJ^-iCX)). Следовательно,
отображение i V sk: EJ^CX) V EXAfc —► T,Jk(X) индуцирует изоморфизм
гомологии, где i обозначает отображение вложения. По индукции полу-
п п
чаем, что отображение \J sk: \J ЕХА/с -» EJ„(X) индуцирует изоморфизм
к=\ fc=i
гомологии для всех конечных п. Из этого следует соответствующее
утверждение для п = оо, так как пространство ХА" является (п — 1)-связным,
если X связно. Поэтому мы получаем отображение VfcEXAfc —»EJ(X),
индуцирующее изоморфизм гомологии. По теореме Уайтхеда это
отображение—гомотопическая эквивалентность, так как данные пространства —
односвязные CW-комплексы. П
В нашем заключительном примере стабильное расщепление будет
построено с помощью структуры группы на (ЕХ, У) —множестве
сохраняющих отмеченную точку гомотопических классов отображений ЕХ —+ Y.
I Предложение 4.1.3. Для любой степени простого числа рп надстрой-
I ка EK(Zp-., 1) гомотопически эквивалентна букету Хг V ... vXp._l5 где
I X, — CW-комплекс, у которого группы НДХ,; Z) отличны от нуля только
I в размерностях, сравнимых с 2f mod 2p - 2.
Этот результат является наилучшим в следующем смысле: сколько
бы раз ни надстраивать любое из пространств X,, оно никогда не станет
гомотопически эквивалентным нетривиальному букету. Это будет
доказано в примере 4.L.3 посредством изучения когомологических операций
в H*{K{Zp»t l);Zp). Существует также несколько более простое
объяснение этого факта с помощью К-теории; см. [VBKT].
Доказательство. Пусть К = /C(Zp»., 1). Мультипликативная группа
ненулевых элементов поля Zp циклическая, поэтому пусть целое число г
представляют образующую. Согласно предложению 1.В.9 существует
отображение /: К —> К, индуцирующее умножение на г в группе я2 (/С). А нам
нужно, чтобы / индуцировало умножение на г1 в группе Н2|-] (X; Z) ^Zp„,
и в этом можно убедиться следующим образом. Из естественного
изоморфизма п^ {К) рп Н^/С; Z) вытекает, что / индуцирует умножение на г
в группе f/] (X; Z). Из теоремы об универсальных коэффициентах следует,
что / индуцирует также умножение на г в группах Н! (К; Zp„) и Н2 (К; Zp,).
Структура ^-произведения в H*(X;Zp-.), вычисленная в примерах 3.41
и З.Е.2, тогда показывает, что / индуцирует умножение на г' в группе
H2,_1(X;ZpO, поэтому то же самое верно для группы H2i-\(K\Z)t как
вытекает опять же из теоремы об универсальных коэффициентах.
Для каждого целого числа ; ^ 0 пусть ft;: Е/С —> ЕК — это разность
Е/ - rjl; таким образом, h} индуцирует умножение на г1 - г; в группе
H2,(E/C;Z) ^Zp». В силу выбора числа г мы знаем, что р делит г' - rj
тогда и только тогда, когда f = j mod p — 1. Это означает, что отображе-
594
Плана 4. Теория гомотопий
ние, индуцированное отображением ft,- на Н2/(Е£; Z), имеет
нетривиальное ядро тогда и только тогда, когда i = j mod p — 1. Поэтому
композиция mi = h-[ о ... oft-_j oft|.+1...ftp_I индуцирует изоморфизм на НДЕ/С; Z)
в размерностях, сравнимых с 2i mod 2p - 2, и имеет нетривиальное
ядро в остальных размерностях, для которых группа гомологии отлична от
нуля. Когда есть нетривиальное ядро, некоторая степень числа т{
индуцирует нулевое отображение, так как мы имеем дело с гомоморфизмами
Zpn —► Zp».
Пусть X, — телескоп отображений для последовательности ЕК —>
—> ЕК -*..., где каждое отображение —это т{. Так как гомологии
коммутируют с прямыми пределами, включение первого множителя ЕК <—> X,
индуцирует изоморфизм на Н+ в размерностях, сравнимых с 2i mod 2p -2,
и НДХ,; Z) = 0 во всех остальных размерностях. Сумма этих включений —
отображение ЕК —* X] V ... vXp_b индуцирующее изоморфизм всех групп
гомологии. Так как эти комплексы односвязны, требуемое утверждение
следует из теоремы Уайтхеда. D
Построение пространств X, как телескопов отображений приводит
к довольно большим пространствам, с бесконечным числом клеток в
каждой размерности. Однако согласно предложению 4.С.1 каждое
пространство Х| гомотопически эквивалентно CW-комплексу с минимальной
конфигурацией клеток, совместимой с его гомологиями, а именно, с одной
нульмерной клеткой и одной /с-мерной клеткой для каждого fc,
сравнимого с 2i или 2i 4-1 mod 2p — 2.
Стабильные расщепления пространств /C(G, 1) для конечных групп G
хорошо изучены; это вопрос сложный и тонкий. Если взять самый простой
нециклический пример, то из предложения 4.1.1 следует, что EK(Z2xZ2, 1)
расщепляется как букет двух экземпляров E/C(Z2,1) и Е(/С(Й2,1)Л/С(Й2,1)),
но последнее слагаемое можно расщепить далее согласно результату из
[101], который утверждает, что если G —прямая сумма к групп Zp.., то
EK(G,1) расщепляется канонически как букет пространств, имеющих
ровно рк - 1 разных гомотопических типов. Некоторые из этих слагаемых
встречаются не один раз, как мы видим на примере группы Z2 x Z2.
Задачи
1. Докажите, что если связный CW-комплекс Х ретрагируется на
подкомплекс Л, то ЕХ~ЕА VE(X/A). [Один из возможных подходов такой:
докажите, что отображение Er + Eq: EX -* ЕЛ V Е(Х/Д) индуцирует
изоморфизм гомологии, где г: X -+ А — ретракция, a q : X -* Х/А —
отображение факторизации.]
2. Используя формулу Кюннета, докажите, что
EK(Zm xZ„, 1) с* EK(Z,M, 1) VEK(Z,?, 1),
§4 J. Пространство петель для надстройки
595
если т и п — взаимно простые числа. Таким образом, чтобы найти
стабильные расщепления для K(Zn, 1), достаточно разобрать случай, когда
п — степень простого числа, как в предложении 4.1.3.
3. Обобщая предложение 4.1.3, докажите, что (2/с + 1)-мерный остов
надстройки над линзовым пространством с фундаментальной группой
порядка рп гомотопически эквивалентен букету (2/с + 1)-мерных остовов
пространств Xh если эти Х{ выбраны так, что у них минимальное число
клеток в каждой размерности, как описано в замечании после
доказательства этого предложения.
§ 4.J. Пространство петель для надстройки
Пространства петель кажутся на первый взгляд безнадёжно
сложными объектами, но если нас интересует только гомотопический тип, то
во многих случаях возможны существенные упрощения. Один из самых
хороших таких случаев — пространство петель для сферы. Мы покажем
в этом параграфе, что £lSn+l имеет слабый гомотопический тип
приведённого произведения Джеймса 7(5"), введённого в §3.2. Мы докажем
и более общее утверждение, что Q.HX имеет слабый гомотопический тип
пространства J(X) для любого связного CW-комплекса Х. При желании
можно усилить «слабый гомотопический тип» до «гомотопического типа»,
сославшись на теорему Милнора, упомянутую в §4.3, которая
утверждает, что пространство петель CW-комплекса имеет гомотопический тип
CW-комплекса.
Интерес к пространству Q.Y.X частично вызван его тесной связью с
гомоморфизмом надстройки я, (X) —> я,+1 (ЕХ). Мы применим слабую
гомотопическую эквивалентность пространства Q.HX с J(X), чтобы получить
другое доказательство того, что гомоморфизм надстройки является
изоморфизмом в размерностях до приблизительно удвоенной связности
пространства X. Кроме того, мы получим точную последовательность,
которая измеряет отклонение отображения надстройки от изоморфизма в
размерностях между удвоенной и утроенной связностью пространства X. Это
вместе с результатами, доказанными в других местах в этой книге,
позволяет легко вычислить я,н1(5п) и яп+2(5") для всех п.
В качестве грубого первого приближения к Г25п+1
можно взять естественное включение 5м в Г25'?+1,
которое получается, если мы рассматриваем 5П+1 как
приведённую надстройку L'S", т.е. факторпростран-
ство (5" х /)/(5" х г?/ и {е} х /), где е — отмеченная
точка сферы 5'\ а затем сопоставляем каждой
точке хе5" петлю А(х) в £5", заданную формулой £-»(*, О- Рисунок
показывает, как выглядят несколько таких петель. Однако мы не можем
ожидать, что включение S" <-> £lSn+l будет гомотопической эквивалент-
596
Глава 4. Теория гомотопий
ностью, так как f2Sn+I всегда является Н-пространством, а сфера S"
является Н-пространством только при п = 1, 3, 7 по теореме Адамса,
обсуждавшейся в §4.В. Самый простой способ исправить этот недостаток
сферы Sn мог бы состоять в том, чтобы заменить её на свободное Н-
пространство, которое она порождает, т, е. на приведённое произведение
Джеймса J(Sn). Напомним из §3.2, что точка пространства J(SI])— это
формальное произведение х1...хк точек Jt, e Sn с отмеченной точкой е,
действующей как единичный элемент для умножения, полученного при
конкатенации этих формальных произведений. Мы хотели бы определить
отображение A: J(Sn) —>fiSn+1, положив AC*!...**) = А(дг1)...А(дг*)
произведение петель АО,). Единственная трудность заключается в
параметризации этого произведения, которую нужно выбрать так, чтобы
отображение А было непрерывно. Проблема в том, что, когда некоторая точка х{
стремится к отмеченной точке eeSn, нужно, чтобы петля АО,) постепенно
исчезала из произведения А01)...АОД не нарушая параметризацию, как
случилось бы при простом удалении А(е). Этого можно добиться, сначала
сделав время, которое требуется для прохождения каждой петли АО<),
равным расстоянию от лг, до отмеченной точки сферы Sn, а затем
нормализовав полученное произведение петель так, чтобы оно занимало единицу
времени, давая отображение J —► ES".
Более общим образом, та же самая процедура определяет
отображение А: J{X) —> Г2ЕХ для любого связного CW-комплекса Х, если заменить
«расстояние до отмеченной точки» любым отображением d: X—» [0, 1*1,
где d~l (0) = е — отмеченная точка пространства X.
Теорема 4.J.I. Отображение А: J(X) —»Г2ЕХ является слабой
гомотопической эквивалентностью для любого связного CW-комплекса Х.
Доказательство. Основной шаг —вычисление гомологии
пространства Г2ЕХ. После того как это сделано, легко проверить, что отображение
А индуцирует изоморфизм гомологии, воспользовавшись вычислением
гомологии пространства J(X) в предложении З.С.8, а из этого делается
вывод, что А — слабая гомотопическая эквивалентность. Как выяснится,
достаточно рассмотреть гомологии с коэффициентами в поле F. Мы
знаем, что Н*(7(Х); F) —тензорная алгебра ТН*(Х; F) согласно предложению
З.С.8, поэтому нужно показать, что НДГ2ЕХ; F) имеет ту же самую
структуру; впервые это было доказано в [84].
Представим приведённую надстройку У = ЕХ в виде объединения
двух приведённых конусов У+ = С+Х и У_ = С_Х, пересекающихся по
экваториальному пространству X с EX. Рассмотрим расслоение путей
р: PY -► У со слоем ПУ. Пусть Р+У = р-1(У+) и Р_У = р~!(Х); таким
образом, Р+У состоит из путей в У, начинающихся в отмеченной точке
и заканчивающихся в У+, и аналогично для Р_У. Тогда Р+УпР_У —это
Р~1{Х) — пути из отмеченной точки в точку в X. Так как У+ и У. являются
§4.J. Пространство петель для надстройки
597
деформационными ретрактами таких открытых окрестностей U+ и Ц_ в У,
что 1/+ П 1/_ деформационно ретрагируется на Y+r\Y_= X, из свойства
поднятия гомотопии следует, что P+Y, Р_У и р^У П Р_У являются
деформационными ретрактами в слабом смысле открытых окрестностей p~!(Lf+),
р_1(Ю и р-1(У+) П p~4LL) соответственно. Поэтому имеется
гомологическая последовательность Майера—Вьеториса для представления
пространства PY в виде Р+У иР_У. Взяв приведённые гомологии и используя
тот факт, что пространство PY стягиваемо, получаем изоморфизм
Ф:НДР+УпР_У;Р) -^ H^P+Y',F)®HAP-Y\F). (1)
Две координаты отображения Ф индуцированы включениями, со знаком
минус в одном из случаев, но Ф останется изоморфизмом, если убрать этот
знак минус, поэтому мы можем считать, что его убрали.
Мы утверждаем, что изоморфизм Ф можно переписать как
изоморфизм
в: НДПУ xX;F)^ Й*(ПУ; F)®H^Y\ F). (2)
Чтобы убедиться в этом, заметим, что расслоение P+Y —* У+
послойно гомотопно тривиальному. Это верно, потому что конус У+
стягиваем, но нам будет нужна явная послойная гомотопическая
эквивалентность P+Y n£lY х У+| и её легко построить следующим образом.
Зададим отображение Д: P+Y —♦ £IY х У+ формулой Д(у) = (у£Уу»у)> гДе
у = у(1), a Y~t — очевидный путь в У+ из у = О, t) в отмеченную точку
вдоль отрезка {х} х J. Отображение в противоположном направлении
g+: £IY хУ+-> P+Y зададим формулой g+(y, у) = yef *, где черта
обозначает обратный путь. Тогда f+g+ и g+f+ послойно гомотопны
соответствующим тождественным отображениям, так как fteTt и Y~te7t гомотопны
постоянным путям.
Аналогично расслоение P_Y —*У_ послойно гомотопически
тривиально посредством отображений /_ и g_. Ограничивая послойную
гомотопическую тривиализацию для P+Y или P_Y на P+Y DP_Y, мы видим, что
расслоение P+Y ПР_У послойно гомотопически эквивалентно произведению
£IY х X. Давайте сделаем это, использую послойную гомотопическую
тривиализацию для Р_У. Группы из (1) можно теперь заменить группами из
(2). Координаты отображения Ф индуцированы включениями, и из этого
следует, что координаты соответствующего отображения 8 из (2)
индуцированы двумя отображениями £IY х X-* Г2У, (у, х) —»уеЛ(х) и (у, х) —> у.
А именно, первая координата отображения О индуцирована
отображением f+g_\QY х X, после которого берётся проекция на Г2У, а вторая
координата такая же, но вместо f+g_ берётся /_g_.
Если записать две координаты отображения О как 8т и 02, то тот
факт, что 8 — изоморфизм, означает, что ограничение отображения 0: на
ядро отображения 82 — изоморфизм. С помощью формулы Кюннета мы
598
Глапа 4. Теория гомотопий
можем записать НЖ(Г2У xX;F) как
(НДПУ; F) ® Я,(Х; F)) ФНД^Г; F),
где проекция на последнее слагаемое— это Э2. Следовательно, G} даёт
изоморфизм первого слагаемого H*(f2K; F) ® НДХ; F) на НДГ2У; F). Так
как 0] (у, х) = (уеАО)), это означает, что композиция отображений
НЛПУ; F) <g>H+(X; F) -^> Н,(ПУ; F) ® НДПУ; F) —> НДПУ; F),
где второе отображение —произведение Понтрягина, является
изоморфизмом. Теперь, чтобы завершить вычисление //ДГ2У; F) как тензорной
алгебры ТН+(Х; F), мы применим следующую алгебраическую лемму для
A = H„№Y\F)yV = H,(X\F) И1=АФ.
I Лемма 4.J.2. Пусть Л— градуированная алгебра над полем F, при-
I чём А0 = F, и пусть V — градуированное линейное пространство над F,
I причём V0 = 0. Предположим, что задано такое линейное отображе-
I ние /: V —>А, сохраняющее градуировку, что отображение умножения
I ju: A®V —> A, /Да ® v) =af(v), является изоморфизмом. Тогда канони-
I ческий гомоморфизм алгебр i: TV -+А, продолжающий отображение i,
I является изоморфизмом.
Например, если V —одномерное линейное пространство над F, как
для случая X = S", то это означает, что если отображение Д —> А, заданное
умножением справа на элемент a = i(v), — изоморфизм, то А — алгебра
многочленов F[a]. Общий случай можно рассматривать как естественное
обобщение этого утверждения на многочлены от любого числа некомму-
тирующих переменных.
Доказательство. Так как // — изоморфизм, каждый элемент a€.A]V
п > 0, можно единственным образом записать в виде
; i
где VjGl/ и а} € Ап{)), причём n(j) < п, так как V0 — 0. Индукцией по п
получаем, что aj —i{aj) для единственного а} € {TV)n{}). Таким образом,
a = i (2aj ® vj)' поэтому гомоморфизм i сюръективен. Так как эти пред-
j
ставления единственны, гомоморфизм i также инъективен. Индукция
начинается с предположения, что A0 = F —скаляры в TV. ^
Снова возвращаясь к доказательству теоремы, заметим, что Я —это
Н-отображение: два отображения ДХ) х J(X) —> QY.X, (х,у) —> ?Л*У^
и О, у) —► Х(х)Х(у), гомотопны, так как петли \{ху) и ЯО)Я(у)
отличаются только их параметризациями. Так как Я —это Н-отображение,
§4.J. Пространство петель для надстройки
599
отображения Xе-* J{X) —+QT.X индуцируют коммутативную диаграмму
ТЙЛХ\Р)
H,U(X)',F) >■ /UftEX; F)
Мы показали, что правое диагональное отображение —изоморфизм, и то
нее самое верно для левого согласно вычислениям H+(J(X); F) в
предложении З.С.8. Следовательно, А* — изоморфизм. Согласно следствию З.А.7
это верно также и для коэффициентов Z. Если пространство X односвяз-
но, то J(X) и Г2ЕХ тоже, поэтому после перехода к CW-аппроксимации
пространства £1Т,Х теорема Уайтхеда показывает, что Я —слабая
гомотопическая эквивалентность. В общем случае, когда пространство X лишь
связно, мы приходим к тому же самому выводу, применяя обобщение
теоремы Уайтхеда на абелевы пространства (предложение 4.74), так как
J(X) и QT.X являются Н-пространствами, а значит, для них п{ действует
на всех гомотопических группах тривиально. □
Если воспользоваться естественным отождествлением я,(Г2Х!Х) =
= TTf+j (EX), то включение X с-> Г2ЕХ индуцирует отображение надстройки
TZiiX) —► я|+1(Х]Х). Так как это включение пропускается сквозь J(X), мы
можем отождествить относительные группы я,(Г2£Х,Х) с я,С/(Х),Х).
Если пространство X является п-связным, то пара (J(X),X) является
(2п + 1)-связной, так как мы можем заменить X комплексом, у которого
n-мерный остов состоит из одной точки, а тогда (2и + 1)-мерный остов
комплекса J(X) содержится в X. Таким образом, мы получаем следующее
утверждение.
I Следствие 4.J.3. Отображение надстройки я,(Х) —> я,-г1(ЕХ) для
п-связного CW-комплекса Х — изоморфизм при i ^ 2п и сюръекция при
i = 2n + l.
В случае сферы мы можем описать, что происходит в первой
размерности, когда надстройка не является изоморфизмом, а именно, для
отображения надстройки rc2n_,(SM) —► n2n(Sn^1), когда следствие гарантирует
только то, что отображение сюръективно. CW-структура на J(Sn) состоит
из единственной клетки в каждой размерности, кратной п; поэтому из
точности последовательности
7i2„(J(S"),S") Д 7r2n_,(Sn) - 7r2ll(S"+1)
Мы видим, что ядро отображения надстройки 7t2n..\{.Su) —> K2n{Su~[)
порождено отображением приклеивания 2и-мерной клетки в J(SU). Это
отображение приклеивания —произведение Уайтхеда [Д, 3.], как мы
отменили в § 4.2, когда определяли произведения Уайтхеда после примера 4.52.
Когда п четно, гомоморфизм инварианта Хопфа я2м_1(Ь1") -+7Л принимает
600
Глава 4. Теория гомотопий
значения ±2 на [1,1], как мы видели в §4.В. Если не существует
отображения с инвариантом Хопфа ±1, то из этого следует, что [1,1] порождает
слагаемое Z в n2n-i(Sn)y и, таким образом, надстроечный гомоморфизм
просто убирает это слагаемое из тг2п_1 CS'1)- По теореме Адамса это имеет
место для всех чётных п, кроме 2, 4 и 8.
Для п — 2 мы получаем группу rr3(S2) »Z, порождённую
отображением Хопфа г\ с инвариантом Хопфа 1, поэтому 2г\ = ±[1,1] порождает ядро
гомоморфизма надстройки. Из этого получаем такое следствие.
I Следствие 4.J.4. Группа 7in+l(Sn) равна Z2 при п ^ 3; она
порождается надстройкой или итерированной надстройкой над отображением
Хопфа.
Ситуация для п = 4и8 более тонкая. Здесь нам недоступна
техника, позволяющая произвести соответствующее вычисление, но если мы
обратимся к таблице в начале §4.1, то увидим, что надстройка tt7(S4) ->
—► тг8(S5) — это отображение Z $ ZI2 —* Z24- Из наших предыдущих
замечаний мы знаем, что это отображение сюръективно с ядром, порождённым
единственным элементом [1,1]. С алгебраической точки зрения должно
произойти следующее: координата элемента [1,1] в слагаемом Z является
удвоенной образующей, в то время как координата в слагаемом Z12 —это
образующая. Поэтому образующая слагаемого Z, в качестве которой
можно взять отображение Хопфа S7 —►S4, при надстройке переходит в
образующую группы Z24. Для п = 8 ситуация совершенно аналогичная; в этом
случае надстройка rr15(S8) —>rr16(S9) — это гомоморфизм Z0Z12o—>^24о-
Можно также получить некоторую информацию о надстройке за
пределами стабильного диапазона размерностей. Так как сфера S" является
(п - 1)-связной, а пара (J(Sn), Sn) — (2n - 1)-связной, мы получаем
изоморфизмы 7T,(J(Sn),Sn) Kii{{J{Sn)lSn) при i^3n-2 согласно
предложению 4.28. Группа 7T,-C/(S")/Sn) изоморфна n{{S2n) в том же самом
диапазоне i $ Зп - 2, так как для комплекса J(Sn)/Sn сфера S2n является его
(Зп — 1)-мерным остовом. Поэтому заключительную часть длинной
точной последовательности пары (J(Sn), Sn), начиная с члена n3n_2(Sn),
можно записать в виде
*3„-2(Sn) - n3n_I(S"+I) - 7T3n_2(S2") - rc3n_3(S") - K3n_2(Sn+1) - ...
Она известна под названием последовательность ЕНР, так как три
входящих в неё отображения первоначально обозначали Е, Н и Р. (По-немецки
слово «надстройка» начинается с буквы Е, Н относится к обобщению
инварианта Хопфа, а Р обозначает связь с произведениями Уайтхеда;
подробности см. в [73].) Отметим, что члены 7r,(S2n) в последовательности ЕНР
стабильные гомотопические группы, так как i ^ Зп — 2. Таким образом,
мы получаем любопытную ситуацию, когда стабильные гомотопические
группы измеряют отклонение от стабильности групп 7r,(Sn) в диапазоне
2п — 1 ^ i; $: Зп — 2, так называемом метастабильном диапазоне.
§ 4.K. Теорема Дольда—Тома
601
В первом интересном случае п = 2 эта последовательность принимает
ЭВД
n4(S2) _iL^ Я5(53) ^ ti4(S4) ^ rr3(S2) _^_ rr4(S3) ^ 0
й Я Я Я
z2 z z z2
Из расслоения Хопфа S1 —► S3 -* S2 мы получаем rr4(S2) % rr4(S3) « Z2,
причём группа rr4(S2) порождается композицией rjCErj), где 17 — отображение
Хопфа S3 -* S2. Из точности последней части рассматриваемой
последовательности мы делаем вывод, что отображение tt4(S4) -* rr3(S2) инъектив-
но, а значит, надстройка rr4(S2) -* rr5(S3) сюръективна, поэтому группа
тг5(£3) равна Z2 или 0. По общей теореме о надстройке гомоморфизм
надстройки 7i5(S3) -* rr6(S4) тоже сюръективен, а последняя группа находится
в стабильном диапазоне. Мы покажем в предложении 4.L.11, что
стабильная группа тг2 отлична от нуля, и /таким образом, мы заключаем, что
7in+2(S") % Z2 для всех п ^ 2, причём эта группа порождается композицией
Мы увидим в [SSAT], что последовательность ЕНР продолжается
влево, образуя бесконечную точную последовательность, когда п нечётно,
а когда п четно, справедливо более слабое утверждение:
последовательность продолжается после факторизации по всему нечётному кручению.
Если заменить S" любым (п - 1)-связным CW-комплексом X, наш
вывод конечной последовательности ЕНР немедленно обобщается и даёт
точную последовательность
Язп-гУО ^ я3п-1(ЕХ) -* ^зп-2№АХ) - я3п.3») ^ я3„_2(ЕХ) "* —
если воспользоваться тем фактом, что J2(X)/X = XAX.
Обобщение результатов этого параграфа на ПП£ПХ, как оказывается,
имеет некоторое значение в теории гомотопии. Если мы не дойдём до
этой темы в [SSAT], то читатель может начать знакомство с ней по [91].
Задача
1. Докажите, что QEX для несвязного CW-комплекса X сводится
к связному случаю, показав, что каждая компонента линейной
связности пространства QEX гомотопически эквивалентна ft£(vaXa), где
пространства Ха —это компоненты пространства X.
§ 4.К. Теорема Дольда—Тома
В предыдущем параграфе мы изучили свободный моноид ДХ),
порождённый пространством X, а в этом займёмся его коммутативным
аналогом — свободным абелевым моноидом, порождённым пространством X.
602
Глава 4. Теория гомотопий
Это пространство —бесконечное симметрическое произведение
(симметрическая степень) SP(X), кратко описанное в §З.С. Главным нашим
результатом будет теорема (см. [93]), утверждающая, что rz^ SP(X)«-H,(X; Z)
для всех связных CW-комплексов Х. В частности, мы получаем
удивительный факт, что SP(S") является пространством типа К(Ъ, п) и что, вообще,
функтор SP переводит пространство Мура M(G,/i) в пространство Эй-
ленберга—Маклейна K(Gy n). Это приводит к общему результату, что для
любого связного CW-комплекса Х пространство SP(X) имеет
гомотопический тип произведения пространств Эйленберга—Маклейна. Другими
словами, все k-инварианты пространства SP(X) тривиальны.
Основной шаг в доказательстве теоремы Дольда—Тома состоит в том,
чтобы показать, что гомотопические группы тг¥ SP(X) определяют теорию
гомологии. Простое вычисление групп коэффициентов 7i+ SP(S") тогда
покажет, что они должны.давать обычную теорию гомологии с
коэффициентами в Ъ. Новая идея, необходимая для доказательства основного
тага,—понятие квазирасслоения, обобщающее расслоения в смысле Гуреви-
ча и локально тривиальные расслоения. Чтобы доказать несколько
основных фактов о квазирасслоениях, мы сначала сделаем небольшое
отступление для доказательства довольно элементарного факта об относительных
гомотопических группах.
Свойство Майера—Вьеториса для гомотопических групп
В этом пункте пас будут в основном интересовать относительные
гомотопические группы, и нельзя будет избежать того неудобного факта,
что нет никакого хорошего способа определить относительное множество
тг0. Пойдя на компромисс, мы определим я0(Х, А, х0) как фактормножество
7С0(Х, х0)/я0(Д, х0). Это, по крайней мере, позволяет закончить длинную
точную последовательность гомотопических групп для (X, А) членами
тг0(Л,х0) -* я0(Х,х0) -» я0(Х, А,х0) -» 0.
Одна из задач в §4.1 показывает, что 5-лемму можно применить к
отображению длинных точных последовательностей, индуцированных
отображением (X, А) —> (К, В), если отмеченной точке разрешено изменяться.
Однако длинную точную последовательность тройки нельзя продолжить
членами 7г0 с таким определением, поэтому нужно действовать осторожно.
В теореме вырезания для гомологии участвует пространство X с
такими подпространствами Л и В, что X является объединением
внутренностей подпространства Л и В. В такой ситуации мы называем (X; Л, Я)
вырезаемой триадой. Под отображением /: (X; Л, В) —» (У; С, D) мы
подразумеваем отображение /: X —* У, для которого /(Л) с С и /(В) с D.
I Предложение 4.К.1. Пусть/: (X; А, В) —> (У; С, D) —отображение вы-
I резаемых триад. Если индуцированные отображения
I тг,(А,АПВ) -» я,(С, CDD) и гч(В,АПВ) -» 7r,(D,CnD)
§4.К. Теорема Дольда—Тома
603
являются биекциями при f <п и сюръекциями при i =п для всех
способов выбора отмеченных точек, то то же самое верно для
индуцированных отображений я,(Х, А) —> тг,(У, С). По симметрии это верно также
и для отображений я,(Х, В) —* я,(У, D).
Соответствующее утверждение для гомологии —тривиальное
следствие вырезания, которое говорит, что
Н,-(Х,А) ^Н,(В,АПВ) и Н,(Т,С) */-/,-(/), СПD),
поэтому нет необходимости что-либо предполагать об отображении
Н,(А,АПВ) — H.-CCCnD).
Ввиду отсутствия свойства вырезания для гомотопических групп
неудивительно, что условие на отображение я, (А, А П В) —* 71,(0, С П D)
нельзя отбросить. Соответствующий пример даёт отображение факторизации
/: D2 —*S2, стягивающее 3D2 в северный полюс сферы S2; в качестве С и D
можно взять северное и южное полушария сферы S2, а в качестве А и В —
их прообразы при отображении /.
Доказательство. Сначала мы установим общий факт об
относительных гомотопических группах. Рассмотрим включение (X, А) <-> (У, С). Мы
покажем, что следующие три условия эквивалентны для любого п ^ 1.
1. Для всех способов выбора отмеченных точек отображение я,(X, А) —>
—► 7Г((У, С), индуцированное включением, сюръективно при i = n
и имеет тривиальное ядро при i = п — 1.
2. Пусть пространство dDM представлено в виде
объединения полусфер 5^D" и 5_D", пересекающихся *-
по S" 2. Тогда любое отображение
(D" х {0} U 5.rDn х J, 5_D" x {0} US""2 x /)
(У, С),
переводящее (5 rDn х {1}, Sn"2 x {1}) в (Х,А),
продолжается до отображения (D" х J, 5_D" x J) —>
-> (У, С), переводящего (D" x {1},5_D'? x {1}) в
(Х,А).
3. Условие 2 с дополнительным предположением, что ограничение
данного отображения на 5+Dn x J не зависит от координаты J.
Очевидно, что условия 2 и 3 эквивалентны, так как выполнения более
сильного предположения в условии 3 всегда можно добиться, взяв
композицию с гомотопией пространства DM x J, которая сжимает 5<D" x J
b5+D"x{1}.
Убедимся, что из 3 следует 1. Пусть
/:(5,.D'?x{l},S''-2x{l})->(X,A)
представляет элемент из яп_1(Х, А). Если он лежит в ядре отображения
в TZj^W, С), то мы получаем продолжение отображения / па D" х {0} U
604
Глава 4. Теория гомотопий
U<5+Dn х /, причём гомотопия на 5+D" х / постоянная и (Dn x {0}, 5_Dn x
х {0}) отображается в (У, С). Условие 3 тогда даёт продолжение на Dn x /
ограничение которого на Dn х {1} показывает, что / представляет нулъ
в яп^(Х, А), поэтому ядро отображения я^СХ, Л) —► nn_x(Y3 С)
тривиально. Чтобы проверить сюръективностьотображения 7Г„(Х, А)—►тгДУ, С),
представим элемент из тгп(У, С) отображением /: Dn x {0} —> У,
переводящим 5_D'1 х {0} в С, a 5+Dn x {0} —в выбранную отмеченную точку.
Продолжим / на 5+Dn x / посредством постоянной гомотопий, а затем
продолжим на D" х /, применяя условие 3. В результате получим гомо-
топию данного отображения / в отображение, представляющее элемент
образа отображения я„(Х,А)—► nn(Y, С).
Теперь мы покажем, что из 1 следует 2. Пусть
дано такое отображение /, как в условии 2. Тогда часть
условия 1, относящаяся к инъективности, даёт
продолжение отображения / на D" х {1}. Выберем
небольшой диск Еп с 5_D" х /, заштрихованный на рисунке,
пересекающий 5_Dn x {1} по полусфере 5+Еп его
границы. Можно считать, что продолженное
отображение / принимает постоянное значение х0еА на 5+Еп.
Если рассматривать продолженное отображение / как представитель
элемента из яп(У, С, лс0), то часть условия 1, относящаяся к сюръективно-
сти, даёт продолжение отображения / на D" х /, переводящее (Еп, 5„Еп)
в (X, А), а остальную часть подпространства 5_Dn x / — в С. Чтобы
завершить рассуждение, нужно взять композицию этого продолженного
отображения / с деформацией пространства D" х /, сжимающей Еп в Dn x {1}.
Показав эквивалентность условий 1—3, давайте докажем само
предложение. Мы можем свести ситуацию к случаю, когда данное
отображение /: (X; А, В) —> (У; С, D) — включение, воспользовавшись цилиндрами
отображения. Первое, что приходит в голову, — заменить (Y\C,D)
триадой цилиндров отображений (Му-; М^, Му(в), где мы рассматриваем /| А
как отображение А—>С, а /|В —как отображение B^>D. Однако триада
Ш/\ М/1л, М/|й) не обязана быть вырезаемой, например, если X состоит
из двух точек А и В, а У — это одна точка. Чтобы справиться с этой
проблемой, заменим пространство Mf\A на его объединение с /_1(С) х (1/2,1)
в My и аналогично увеличим Му|В.
Теперь мы докажем предложение для включения (X; А, В) *-* (У; С, #)•
Случай п = 0 тривиально получается из определений, поэтому будем
считать, что п > 1. Ввиду эквивалентности условия 1 с условиями 2 и 3,
достаточно доказать, что из условия 2 для включений (A, AnB)c->(CyCOD)
и (ВуАГ\В)<-> (D, CHD) следует условие 3 для включения (X, А) <-+ (У, О-
Пусть дано такое отображение /: D" х {0} U 5+Dn х / —> У, как в условии 3.
Рассуждения будут использовать разбиение диска Dn на меньшие диски,
а для этого удобнее вместо диска D" использовать куб /". Так что даиаи-
§4.К. Теорема Дольда—Тома
605
хе отождествим /п с D" таким способом, что 5_Dn соответствует грани
[п~1 х {1}, которую мы обозначим 5_/п, a 5+Dn соответствует остальным
граням куба /п, которые мы обозначим 5+/п. Таким образом, задано
отображение / на J" х {0}, переводящее 5+1п х {0} в X, а 5_/п х {0} — в С, и на
5+/п х J У нас есть постоянная гомотопия.
Так как (У; С,D)—вырезаемая триада, мы можем разбить каждый
множитель / в J" х {0} на меньшие отрезки так, чтобы / переводило
каждый из полученных при этом п-мерных подкубов в Г х {0} либо в С, либо
в D. Продолжение отображения /, которое мы построим, будет обладать
следующим ключевым свойством:
(*) если К"— один из подкубов в /п х {0} или грань меньшей размерности
такого куба, то продолжение отображения / переводит (Кх/Д х {1})
в (С, А) или в (D, В), когда / переводит К" в С или в D соответственно.
Первоначально у нас есть отображение /, определённое на 5+In x /,
с образом в X, не зависящее от координаты /, и мы можем
предположить, что условие (*) выполняется, так как мы можем предположить, что
А = ХПС и В — XnD; эти условия выполняются для конструкции с
цилиндром отображения, описанной выше.
Рассмотрим задачу продолжения отображения / на К х /, когда К —
один из подкубов. Можно предположить, что / уже было продолжено
на 5+К х / так, что выполняется условие (*), применив индукцию по п
и по последовательности отрезков разбиения для последней координаты
в 1п х {0}. Чтобы продолжить / на К х /, давайте сначала разберёмся
со случаями, когда данное отображение / переводит
(К, 5_К) в (C,Cr\D) или в (D,Cr\D). Тогда по
условию 2 для включения (А, А П В) с-> (С, С П D) или
(В, АП В) с-> (D, С П D) мы можем продолжить / на К х /
так, чтобы условие (*) всё ещё выполнялось. Если же
ни один из этих двух случаев не имеет места, то данное
отображение / переводит (К,5_К) просто в (С, С) или в (D,D), и мы
Можем тривиально применить условие 2, чтобы построить требуемое
продолжение / на К х /. □
I Следствие 4.К.2. Пусть даны отображение /:Х->7и открытые по-
I крытия {I/,-} пространства X и Щ} пространства У, причём /((У,-) с VJ
I для всех I. Тогда если любое ограничение /: £/,■—> Vj и вообще любое
I ограничение /: и(]Г\... П Uin —> V^ П ... П VJ является слабой гомотони-
I ческой эквивалентностью, то и само отображение /: X —> У тоже.
Доказательство. Сначала разберём случай покрытий двумя
множествами. Согласно 5-лемме из этих предположений следует, что
отображение лп ([/,•, иг П U2) -> 7in(V;, V\ П V2) биективно для i = 1, 2, п > 0, и для всех
способы выбора отмеченных точек. Предыдущее предложение тогда
показывает, что отображения яп(Х, £Л)->тгп(У, V^) — изоморфизмы. Из этого,
^s
606
Глава 4. Теория гомотопии
снова применяя 5-лемму, получаем, что отображения яп(Х) —> nn(Y) тоже
изоморфизмы.
По индукции случай конечных покрытий к > 2 множествами
сводится к случаю покрытий двумя множествами, если в качестве одного из
двух множеств взять объединение первых к - 1 данных множеств, а дру.
гого — к-е множество. Случай бесконечных покрытий сводится к
конечному случаю, так как для доказательства сюръективности отображения
7ГП(Х) —>7t„(V) можно воспользоваться тем, что отображение S" —>У
имеет компактный образ, покрытый конечным числом множеств Vh и
аналогично для доказательства инъективности. □
Квазирасслоения
Отображение р: Е —> В, где пространство В линейно связно, называют
квазирасслоением, если индуцированное отображение
р,: щ(Е,р^(Ъ),х0) -> ЩЦ*,Ъ)
— изоморфизм для всех beB, xQe р"1 (Ь) и i ^ 0. Мы показали в теореме
4.41, что локально тривиальные расслоения и расслоения в смысле Гуре-
вича обладают этим свойством для i > 0, как следствие свойства поднятия
гомотопии, и то же самое рассуждение можно применить при i = 0, так
как мы предполагаем, что В линейно связно.
Например, рассмотрим естественную проекцию My —> 1 цилиндра
отображения для отображения /: X —► У, Эта проекция будет
квазирасслоением тогда и только тогда, когда / — слабая гомотопическая
эквивалентность, так как последнее условие эквивалентно тому, что
я,-(My, р-1(Ь)) =0 = 7г,-(/,Ь) для всех i и всех bel.
Заметим, что если / не сюръективно, то существуют пути в /,
которые не поднимаются до путей в My с предписанной
начальной точкой, поэтому р в таких случаях не будет
расслоением в смысле Гуревича.
Альтернативное условие, чтобы отображение р: Е—*В было
квазирасслоением, состоит в том, что включение каждого слоя p~l(b) в
гомотопический слой Fb отображения р над Ъ является слабой гомотопической
эквивалентностью. Напомним, что Fb — пространство всех пар О, у), где
х € Е, а у — путь в В из точки рО) в точку Ь. Настоящий слой р 1{Ь)
включается в Fb как пары, для которых xep~l(b), а у — постоянный путь
в точке х. Чтобы убедиться в эквивалентности этих двух определений,
рассмотрим коммутативный треугольник
я.-СЕ.р-1 («)—*■ rti(Ep9Fh)
\ /
§4.К. Теорема Дольда—Тома
607
где Fb —* Ер —* В — обычная конструкция расслоения путей, применённая
к р. Правое отображение в диаграмме — изоморфизм для всех i ^ 0, а
верхнее отображение будет изоморфизмом для всех i ^ 0 тогда и только тогда,
когда включение р_1(Ь) <-*Еь является слабой эквивалентностью, так как
£ ~Ер. Следовательно, эти два определения эквивалентны.
Напомним из предложения 4.61, что все слои расслоения в смысле
Гуревича над линейно связной базой гомотопически эквивалентны. Так
как мы рассматриваем квазирасслоения только над линейно связными
базами, из этого следует, что все слои квазирасслоения имеют один и тот
же слабый гомотопический тип. Квазирасслоения над базой, которая не
линейно связна, рассматриваются в задачах, но нам эта общность в
дальнейшем не потребуется.
Следующая техническая лемма даёт различные условия,
позволяющие выяснить, что данное отображение является квазирасслоепием; они
нам понадобятся для доказательства теоремы Дольда—Тома.
I Лемма 4.К.З. Отображение р: Е—>В является квазирасслоением, ес-
I ли выполнено одно из следующих условий:
I 1. В можно представить в виде объединения открытых множеств V}
I и V2 так, что каждое из ограничений p~l(Vx) —>VXi р~х(У2) —* V2
I и р"1 (V} П V2) —* Vl П V2 является квазирасслоением;
I 2. В является объединением такой возрастающей последовательно-
I сти подпространств В1 сВ2 с ... (со слабой топологией или топо-
I логией прямого предела), что каждое ограничение р~1(Вп) —*Вп
I является квазирасслоением;
I 3. существует такая деформация F, пространства Е в подпростран-
I ство Е\ накрывающая деформацию F£ пространства В в подпро-
I странство В', что ограничение Е' —* В' является квазирасслоением,
I a Fj: р~х{Ъ) —> p_1(FT(b)) —слабая гомотопическая эквивалент-
I ность для всех ЬеВ.
Под «деформацией» в п. в) мы подразумеваем деформационную
ретракцию в слабом смысле, как она определена в задачах к главе 0, где
гомотопия не обязана быть тождественной на подпространстве.
Доказательство. 1. Чтобы избежать утомительных подробностей, мы
рассмотрим только случай, когда слои отображения р линейно связны,
который достаточен для наших нынешних целей, оставив общий случай
в качестве задачи для читателя. Это предположение о слоях
гарантирует, что все множества тг0, возникающие в доказательстве, тривиальны.
В частности, согласно одной из задач из §4.1 это позволяет закончить
длинные точные последовательности гомотопических групп троек нулями
на месте я().
Пусть и}=р~'[(Ух) и и2=р~^{У2). Применяя 5-лемму к длинным точным
последовательностям гомотопических групп троек (Uk, Ux nU2, P~l(b)) и
608
Глава 4. Теория гомотопий
(Уь V\ П У2> Ь), получаем, что отображения я,(1^, l^Dl^)—>я,(\4, Цп1/2) —
изоморфизмы для к = 1,2 и всех /. Тогда из предложения 4.К.1 следует,
что отображения тгДЕ, l/j)—> я((В, Ц) —изоморфизмы. Поэтому из
предположения, что отображения n^U^, p~l(b)) —> я,-^, b) являются
изоморфизмами, с учётом 5-леммы следует, что отображения п{{Е, p~l(b)) -*
—» я,(В, Ь) — изоморфизмы.
2. Доказательство— стандартное рассуждение с компактностью для
прямых пределов. Каждое компактное подпространство в £ лежит в одном
из подпространств Еп = р'1^^, поэтому я, (Е, p~4b))—прямой предел
lim я, (Е,р р_1(Ь)), следовательно, отображение п{(Е, р~}(Ь)) —> п{(В,Ъ)
является изоморфизмом, если все отображения п{[ЕПУ р_1(Ь)) —> я^СВ, Ъ) —
изоморфизмы.
3. Рассмотрим коммутативную диаграмму
(Е)Р-](Ъ)) -^+ (Е^р-^Р^Ъ))) —^ (Е.р-Ч^СЬ)))
I f i
где верхнее отображение справа —включение. Композиция вдоль
верхней части диаграммы индуцирует изоморфизм относительных
гомотопических групп посредством 5-леммы и предположения, что F}: р'ЧЬ)—►
—>р-1 (F\{b)) является слабой гомотопической эквивалентностью. Так как
включение Е' <-► Е является гомотопической эквивалентностью, верхнее
правое отображение тоже индуцирует изоморфизмы относительных
гомотопических групп. Следовательно, верхнее левое отображение Fx
индуцирует изоморфизмы относительных гомотопических групп. Нижнее
отображение Fl является гомотопической эквивалентностью, поэтому из
коммутативности диаграммы мы получаем, что левое вертикальное
отображение индуцирует изоморфизмы гомотопических групп, так как это
верно для правого вертикального отображения по предположению. С
Симметрические произведения
Напомним определение из §З.С. Для пространства X его п-кратиос
симметрическое произведение SPfI(X)— это факторпространство
произведения п экземпляров пространства X по действию симметрической
группы, переставляющему множители. Выбор отмеченной точки е е X
даёт включения SP,7(X) <-* SP^CX), индуцированные отображениями
(х1? ...,*„) -* (xlt ...,хп,е), и SP(X) определяется как объединение этой
возрастающей последовательности пространств с топологией прямого*
предела. Заметим, что SP,? — гомотопический функтор: отображение /'•
X —> Y индуцирует отображение /4: SP„ (X) —> SP„ (У), причём fug влечёт
/+~g+. Следовательно, Х^У влечёт SP„(X) ^ SPn(Y). Аналогично SP —
гомотопический функтор на категории пространств с отмеченной точкой
§4.К. Теорема Дольда—Тома
609
и сохраняющих отмеченную точку гомотопических классов отображений.
Из этого следует, что X ^ У влечёт SP(X) ^ SP(Y) для связных CW-kom-
плексов X и У, так как в этом случае требование, чтобы отображения
и гомотопии сохраняли отмеченные точки, не влияет на отношение
гомотопической эквивалентности.
Пример 4.К.4. Интересен частный случай, когда X = S2, потому что
в этом случае SP(S2) можно отождествить с СРЖ следующим образом.
Сначала мы отождествим СР" с ненулевыми многочленами степени
степени не выше п и с коэффициентами в С по модулю умножения на
скаляр, считая, что а0 + ... + anzn соответствует прямой, содержащей
точку (а0,..., ап). Рассмотрим сферу S2 как С U {оо} и определим
отображение /: (S2)" —> СР", положив /(а^ ..., а„) = (z + aA)...{z + а„) и опуская
при этом множители z-foo. Поэтому, в частности, /(оо,..., оо) = 1. Чтобы
проверить, что отображение / непрерывно, предположим, что некоторая
точка ah например ам, стремится к оо, а все остальные точки а} конечны.
Тогда если мы запишем
= z" + (a1 + ... + a;i)z'I", + ...+ ]>] alV..ar-,z"-fc + ...H-a1...af!,
i)<...<ik
то, поделив на aM и устремив a„ к оо, мы увидим, что этот многочлен
стремится к
z"-, + (a, + ...+all_!)z',-2 + ... + a]...an_1 = О + aJ...U + a,,..,).
То же самое рассуждение можно применить, когда несколько точек а,
стремятся к оо одновременно.
Значение /(аь ...,а„) не изменяется при перестановке точек ah
поэтому определено индуцированное отображение SP„(S2) —>СР", которое
является непрерывной биекцией, а потому гомеоморфизмом, так как оба
пространства компактны и хаусдорфовы. Перейдя к пределу по п, мы
ползаем гомеоморфизм SP(S2) ^СР°°.
Теми же самыми рассуждениями можно воспользоваться, чтобы
показать, что SP^CS1) ^S1 для всех п, включая п =оо. А именно, предыдущее
рассуждение показывает, что SP„(C- {0}) можно отождествить с
многочленами zn -f Qu-\Zn l -f ... + a0, а()7^0, или, другими словами, с наборами
п чисел (а0,..., а„_,) gC\ где а0^0, а это подпространство в С"
деформационно ретрагируется на окружность.
Симметрические произведения сфер высшей размерности устроены
более сложно, хотя дела обстоят не так уж плохо для двукратного
симметрического произведения.
Пример 4.К.5. Покажем, что пространство SP2(S") гомеоморфно
конусу отображения £"RP"_1 —>S". Тогда
//A(SP2(Sn)) ъ H^Sn)©/7.(E"","1XP"~1)
610
Глава 4. Теория гомотоиий
из длинной точной последовательности групп гомологии для пары
(SP2(S"), S"), так как SP2(S")/S" — это пространство E^RP""1, у
которого отсутствуют приведённые гомологии размерности ниже п + 2.
Если мы рассмотрим S" как Dn/dDn3 то SP2(S") становится
определённым факторпространством для D" x D". Рассматривая D" x D" как
конус над его границей Dn x r)D" U r)D" x D", мы видим, что
отождествления, которые дают SP2(S"), уважают разные концентрические копии
этой границы, которые заполняют внутренность произведения D" x D".
Поэтому достаточно проанализировать отождествления во всех этих
копиях границы. Отождествления на самой границе произведения D'; x D"
дают S". Дело в том, что отождествление (х, у)~(у,х) преобразует
Dn х dDn UdDn x D" в Dn x dDn и все точки пространства <Юп
отождествляются в пространстве S".
Остаётся убедиться, что отождествления (х, у) ~ (у, х) на каждой
концентрической копии границы во внутренности произведения D" x D"
дают E"RPn_I. Обозначим через Z факторпространство произведения
Dn х r)D" U r)D" x Dn при этих отождествлениях. Это то же самое, что
факторпространство для D" x dD" при отождествлениях (х, у) ~ (у, х) для
(x,y)edDnxdD".
Зададим отображение /: D" х КР"""1 -»Z формулой f(x,L) = (vv,s),
где и/ и z определяются так, как на рисунке, т.е. точка х
равноудалена от точек z e dDn и w € Dn на прямой, прове- ^^_^^
денной через х параллельно L. Заметим, что если f S^\^-'£
точка х окажется серединой отрезка zz\ то iv = z' [J^^^^^X
и нет никакого способа различить w и z, но, так как z \\^^0 J
f принимает значения в факторпространстве Z, ^\. J
с этим нет проблем. Если хедП'\ то w = z = x иеза- ^ S
bhchmootL.EoihxgD" - dDn, tow^z, и наоборот,
если дана пара (w, z) eDn x dD"3 и/^z, то существует единственная пара
(х, L), для которой /(х, L) = (iv,z), а именно, х —середина отрезка u>s,
a L —прямая, параллельная этому отрезку. Из этих замечаний мы видим,
что Z —факторпространство произведения D" х КР""1 при
отождествлениях (x,L) ~ (х, Z/), если x€dD". Это факторпространство —в точности
ЕПКРП_1.
Этот пример показывает, что переход от CW-структуры на X к
CW-структуре на SPn(X) или на SP(X) совсем не прямой. Но если X —
симнлициальный комплекс, то существует естественный способ ввести
структуры Д-комплексов на SP„(X) и на SP(X) следующим образом.
Структура симплициалыюго комплекса на X задаёт CW-структуру на
произведении п экземпляров пространства X, клетки которой —п-кратпые
произведения симплексов. Такое произведение имеет каноническое
барицентрическое подразделение — симнлициальный комплекс; его
вершинами являются точки, координаты которых — барицентры симплексов
§ 4.K. Теорема Дольда—Тома
611
в X. Индукцией по остовам мы просто берём конусы симплициальной
структуры на границе каждой клетки произведения. Эта симплициальная
структура на произведении п экземпляров пространства X в
действительности является структурой А-комплекса, так как вершины каждого из
её симплексов имеют естественный порядок, заданный размерностями
клеток, барицентрами которых они являются. Действие симметрической
группы, переставляющей координаты, уважает эту структуру Д-комплек-
са, отображая симплексы гомеоморфно на симплексы, сохраняя порядок
вершин, поэтому на факторпространстве SPn(X) имеется индуцированная
структура А-комплекса. Если в качестве отмеченной точки в X
выбрана вершина, то SPn(X)— подкомплекс в SPn+1(X), поэтому естественная
структура А-комнлекса имеется также и на бесконечном симметрическом
произведении SP(X).
Как обычно бывает для произведений, CW-топология на SP,?(X) и
SP(X), вообще говоря, отличается от топологии, возникающей из
исходного определения в терминах топологии произведения, но можно
проверить, что эти две топологии имеют одни и те же компактные множества,
поэтому их различие не имеет значения для наших нынешних целей. Для
определённости в дальнейшем мы будем использовать CW-топологию.
Это означает, что мы ограничиваемся пространствами X, которые
являются симшшциальными комплексами. Так как каждый CW-комплекс
гомотопически эквивалентен симплициальному комплексу по теореме
2.С.5, a SPn и SP — гомотопические функторы, не будет никакой
существенной потери общности, если вместо CW-комплексов мы ограничимся
симплициальиыми комплексами.
Вот основной результат этого параграфа.
I Теорема 4.К.6 (Дольда—Тома). Функтор X —>ti,SP(X) при i^l
совпадает с функтором X —> Н,(Х; Z) на категории связных CW-комплексов
с отмеченной точкой.
В частности, это означает, что SP(Sn) — это пространство типа KCZ, п)
и что, вообще, для пространства Мура М(G, п) пространство SP(M(G, п)) —
это K(G, п).
Тот факт, что SP(X) является коммутативным ассоциативным
Н-пространством со строгим единичным элементом, накладывает
существенные ограничения на его слабый гомотопический тип.
I Следствие 4.К.7. Линейно связное коммутативное ассоциативное
Н-пространство со строгим единичным элементом имеет слабый
гомотопический тип произведения пространств Эйленберга—Маклейна.
В частности, если Х~ связный CW-комплекс, то пространство SP(X)
линейно связно и имеет слабый гомотопический тип ПП/С(//П(Х), п).
Таким образом, функтор SP приводит, по сути, к пространствам
Эйленберга—Маклейна.
612
Глава 4. Теория гомотопий
Доказательство. Пусть X— линейно связное коммутативное
ассоциативное /-/-пространство со строгим единичным элементом, и пусть
Gn = пп(Х). По лемме 4.31 существует отображение M(Gnt п) —* X,
индуцирующее изоморфизм групп 7гп, когда п > 1, или изоморфизм групп Нь
когда п = 1. Мы можем выбрать эти отображения так, чтобы они
сохраняли отмеченные точки, а тогда их можно объединить и получить
отображение vnM(Gn, п) —>Х. Очень специальная структура Н-прострапства на X
позволяет нам продолжить его до гомоморфизма /: SP(V„M(G,P п)) —>Х.
В общем случае SP(VaXa) можно отождествить с пространством П„ SP(Xa),
где подразумевается «слабое» бесконечное произведение, т. е.
объединение конечных произведений. Как мы увидим в конце доказательства
теоремы Дольда—Тома, из этого утверждения и из того общего факта,
что отображение я,(Х) —> пх;SP(X) = H{(X\ Z), индуцированное
включением X = SP,(X) «—> SP(X), является гомоморфизмом Гуревича,
следует, что отображение / индуцирует изоморфизм всех гомотопических
групп. Поэтому мы получаем слабую гомотопическую эквивалентность
n„SP(M(G„, /i)) —>Х, а выше мы отметили, что SP(M(G,P п)) —это
пространство типа K(Gn, п). Наконец, так как каждый множитель SP(M(G„, п))
имеет только одну нетривиальную гомотопическую группу, слабое
бесконечное произведение имеет тот же самый слабый гомотопический тип,
что и обычное бесконечное произведение. Г.1
Основной шаг в доказательстве теоремы будет состоять в
доказательстве того, что для симплициальной пары (Х,Л), где оба пространства X
и А связные, существует длинная точная последовательность
... -> щ SP(A) -> 7i, SP(X) -> тг, SP(X/A) -> я,_ { SP(A) -> ...
Это сразу получилось бы, если бы отображения SP(A) —* SP(X) —* SP(X/A)
образовывали локально тривиальное расслоение или расслоение в смысле
Гуревича. Есть причина полагать, что это может быть верным, потому что
все слои проекции SP(X) —* SP(X/A) гомеоморфиы SP(A). Действительно,
в терминах структуры Я-пространства на SP(X) как свободного абелева
моноида, порождённого пространством X, слои —это в точности
смежные классы подмоноида SP(A). Однако для проекции SP(X) —> SP(X/A)
не выполняется свойство поднятия гомотопий, и даже его частный
случай—поднятие путей. В самом деле, пусть хп t е [0, 1), —путь в X — А,
приближающийся к точке х7 = a е А, отличной от отмеченной точки. Тогда
если рассматривать xt как путь в SP(X/A), то любое его поднятие в SP(X)
имело бы вид xtan at eSP(A), заканчиваясь в точке х^а{ ~аа] —точке
пространства SP(A), которая является кратным точки а. Поэтому, в
частности, не может существовать поднятия, заканчивающегося в отмеченной
точке пространства SP(X).
Мы покажем, что проекция SP(X) —>SP(X/A) имеет вместо этого
более слабую структуру квазирасслоепия, которая всё же достаточно хоро-
§4.К. Теорема Дольда—Тома
613
ina, чтобы получить длинную точную последовательность гомотопических
групп.
Доказательство теоремы 4.К.6. Как мы уже сказали, основной шаг
будет состоять в том, чтобы сопоставить длинную точную
последовательность гомотопических групп каждой симплициальной паре (X, А) со
связными X и Л. Это будет длинная точная последовательность
гомотопических групп, возникающая из квазирасслоения S?(A) —> SP(X) —> SP(X/A),
поэтому основная работа будет заключаться в проверке свойства
квазирасслоения. Так как SP —гомотопический функтор, мы можем заменить
(X, А) на гомотоиически эквивалентную пару, поэтому давайте заменим
(Х,Л) на (М,А)У где М — цилиндр отображения для включения Л <-> X.
Как мы увидим позже в процессе доказательства, эта новая пара, которую
мы по-прежнему обозначаем (X, Л), обладает некоторыми техническими
преимуществами.
Чтобы начать доказательство того, что проекция р: SP(X) —> SPCX/Л)
является квазирасслоением, положим Bn = SPn(X/A) и Еп = р~1(Вп). Таким
образом, Еп состоит из точек в SP(X), имеющих не более п координат из
X — Л. Согласно лемме 4.К.З (2) достаточно доказать, что р: Еп —> Вп —
квазирасслоение. Доказательство этого проведём индукцией по п, начиная
с тривиального случая п = 0, когда й0— точка. Шаг индукции
заключается в следующем: мы доказываем, что р является квазирасслоепием над
окрестностью множества Вм_1 и над Вп - /Зм_т, а затем применяем лемму
4.К.З(1). Сначала мы займёмся доказательством свойства
квазирасслоения над окрестностью множества В,,-].
Пусть ft: X —> X — гомотопия тождественного отображения,
деформационно ретрагирующая окрестность N множества Л на Л. Так как
мы заменили исходное пространство X на цилиндр отображения для
включения ЛС->Х, мы можем выбрать гомотопию /,, чтобы она просто
сдвигала точки по отрезкам {а} х / в цилиндре отображения, и взять
N = Л х [0, 1/2). Пусть множество U с Еп состоит из точек, у которых
есть по крайней мере одна координата из А/, или, другими словами, из
произведений по крайней мере с одним множителем из N. Таким образом,
U — окрестность множества Еп..1 в Еп, a p{U) — окрестность множества
В„-, вВп.
Гомотопия /, индуцирует гомотопию F{: £„—>£„, ограничение
которой на U —деформация U в £„_], где под «деформацией» мы
подразумеваем деформационную ретракцию в слабом смысле. Так как отображение
ft тождественно на Л, гомотопия Ff — поднятие гомотопии Ft: Вп —> Я,р
ограничение которой даёт деформацию V~p{U) в Вп.{. Мы докажем, что
проекция U —> U — квазирасслоение, воспользовавшись леммой 4.К.З (3).
Чтобы применить её в рассматриваемом случае, мы должны проверить,
что Fj: р"1(Ь)—>p_1(Fi(b)) —слабая эквивалентность для всех Ь. Каждая
точка w G р_1(Ь) — коммутативное произведение точек из X. Пусть w —
614
Глава 4. Теория гомотопий
часть этого произведения, множители которого —точки из X - А, таким
образом, мы имеем w = vvv, где v—произведение точек из А. Так как
отображение /, тождественно на A, a F} —гомоморфизм, мы получаем
Fy(w) = F1(iv)v, что можно записать как F^T^v'v, где v' тоже
произведение точек из Л. Если мы фиксируем iv и разрешим v пробегать SP(A),
то мы получаем все точки из р~}(Ь) ровно по одному разу, или, другими
словами, мы получаем выражение р~}(Ь) как смежного класса vvSP(A).
Отображение F]t wv—» F^l^v'v, переводит этот смежный класс в
смежный класс Fj С~и) SP(A) посредством отображения, которое было бы
гомеоморфизмом, если бы отсутствовал множитель v'. Так как пространство А
связное, существует путь vf' из v' в отмеченную точку, а потому, заменяя
v' на v't в произведении F,C~$v'v, мы получаем гомотопию отображения
F\: Р"1 СЬ) —> р~] (F^b)) "в гомеоморфизм, следовательно, это
отображение—гомотопическая эквивалентность, что и требовалось.
Остаётся проверить, что р — квазирасслоение над Вп — В„_1 и над
пересечением этого множества с 0. Рассуждение будет одним и тем же в
обоих случаях.
Если отождествить Вп -Вп_х с SPn(X -А), то проекция р: £,, —£„ _г—►
—>ВП—Вп_! —это то же самое, что оператор w—>w. Включение SP„(X—A)c->
<->£„ — £„_! даёт сечение для р: Еп - Еи_} —> Вм - В„_ь поэтому
отображение р+: тг,-(£„ - £„_ь p~L(b)) —> тг,-(Вп -Вп_ьЬ) сюръективно. Чтобы
проверить, что оно также и инъективно, представим элемент его ядра
отображением g: (D', dD1) —> (£„ -£„-i, p-I(b)). Гомотопия отображения
pg в постоянное отображение даёт гомотопию отображения g,
меняющую только его координаты в X - А. Это гомотопия в классе
отображений (D',dD')—► (£п - £n-i,p-I(b)), а заканчивается она отображением
в p~l(b), поэтому ядро отображения р* тривиально. Таким образом,
проекция Еп — £„_1 —> В„ -£„_!—квазирасслоение, по крайней мере, если
пространство Вп — Вп_х линейно связно. Но, заменив исходное
пространство X на цилиндр отображения для включения А<—>Х, мы
гарантируем, что пространство X — А линейно связно, так как оно деформационно
ретрагируется на X. Следовательно, пространство Вп -BM_i — SPn(X -А)
тоже линейно связно.
Это рассуждение столь же хорошо работает над любым открытым
подмножеством в Ви — Вп_и которое является линейно связным, в частности
над U П (В„ — Вп_1), поэтому с учётом леммы 4.К.З (1) это завершает
доказательство того, что SP(A)—>SP(X)—>SP(X/A) является квазирасслоеиием.
Так как аксиома гомотопий очевидна, это даёт нам первые две из трёх
аксиом, которые нужны для того, чтобы группы /?,(Х) = я, SP(X)
определяли приведённую теорию гомологии. Остаётся только аксиома букета
а
§4.К. Теорема Дольда—Тома
615
но она непосредственно следует из того очевидного факта, что SP(vaXa) =
= Па SP(Xa), где имеется в виду «слабое» произведение, т. е. объединение
произведений конечного числа множителей.
Теория гомологии /тДХ) определена на категории связных симпли-
циальных комплексов с отмеченной точкой и с сохраняющими
отмеченную точку отображениями. Коэффициенты этой теории гомологии,
группы h,-(S"), те же самые, что и для обычных гомологии с
коэффициентами в Z, так как мы знаем, что это верно для п — 2 согласно
гомеоморфизму SP(S2) ^CP00, и в любой приведённой теории гомологии
имеют место изоморфизмы h,(X) %h/+1(EX). Если бы теория гомологии
h+(X) была определена на категории всех симплициальиых комплексов
без отмеченных точек, то теорема 4.59 дала бы естественные
изоморфизмы h,(X) ы Н,(Х; 7i) для всех X и доказательство было бы
завершено. Однако этого легко добиться, определив новую теорию гомологии
h|(X) — h/+](EX), так как надстройка над произвольным комплексом
связна, а надстройка над произвольным отображением сохраняет
отмеченную точку, если выбрать в качестве отмеченной точки одну из вершин
надстройки. Так как группа h'(X) естественно изоморфна h;(X), если X
связно, доказательство завершено. D
Следует заметить, что отображение я,(Х) —* 7r,SP(X) = Н,-(Х; Z),
индуцированное включением X = SP,(X) <-* SP(X), — это гомоморфизм Гу-
ревича. Действительно, согласно определению гомоморфизма Гуревича
и естественности ситуация сводится к случаю X = S', где отображение,
SP^S') c-> SP(S') индуцирует на группах п{ гомоморфизм Z —> Z, для
которого нужно только проверить, что он — изоморфизм, поскольку
гомоморфизм Гуревича определяется только до с точностью знака.
Изоморфизм надстройки даёт дальнейшее сведение к случаю i = 1, где включение
SP^S1) c-> SPGS1) является гомотопической эквивалентностью, а значит,
индуцирует изоморфизм групп тг^
Задачи
1. Докажите, что следствие 4.К.2 остаётся справедливым, когда X
и У — CW-комплексы, а подпространства Ui и ^—подкомплексы, а не
открытые множества.
2. Докажите, что симплициальное отображение f:K—*L является
гомотопической эквивалентностью, если пространство /-100 стягиваемо
для всех xgL. [Рассмотрите покрытие комплекса L открытыми звёздами
симплексов и покрытие комплекса К прообразами этих открытых звёзд.]
3. Докажите, что SP„(/) = Д".
4. Докажите, что SP2CS1) —лист Мёбиуса, и что это согласуется с
описанием пространства SP2(S") как конуса отображения, приведённым
в примере 4.К.5.
616
Глава 4. Теория гомотопий
5. Отображение р: Е —* В, где В не обязательно линейно связно, но
определению называют квазирасслоением, если выполнены следующие
эквивалентные условия:
1) для всех ЬеБ^оер^ЧЬ) отображение pY: п((Еу р_1(Ь),д:())—>7Г,(73; Ь) —
изоморфизм для f>0, последовательность я0(р_1(Ь), х0)—>тг0(£, jc0)—>
—>я0(В, Ь) точная;
2) включение слоя p~l(b) в гомотопический слой Fb отображения р над
Ь —слабая гомотопическая эквивалентность для всех be В;
3) ограничение отображения р на каждую компоненту линейной
связности пространства В — квазирасслоение, как оно определялось в этом
параграфе.
Докажите, что эти три условия эквивалентны, и докажите лемму 4.К.З для
квазирасслоений над не линейно связными базовыми пространствами.
6. Пусть X — комплекс пространств над Л-комплексом Г, как он
определён в §4.G. Докажите, что естественная проекция ДХ —> Г является
квазирасслоением, если все отображения в X, связанные с гранями
комплекса Г,— слабые гомотопические эквивалентности.
§ 4.L. Квадраты и степени Стинрода
Основной объект исследования в этом параграфе —некоторые
гомоморфизмы, называемые квадратами Стинрода и степенями Стинрода:
Sq/':///?(X;Z2) — Hn+i(X; Z2),
Р': НП(Х; Ър) — //',+2'"С/'~1)(Х; Zp) для нечётных простых р.
Названия «квадраты» и «степени» связаны с тем фактом, что Sql и Р'
связаны с отображениями а —* а2 и а —> ар> переводящими класс когомологий а
в двукратное или р-кратное произведение с самим собой. В отличие от
произведений, однако, операции Sq* и Р' стабильны, т.е. инвариантны
относительно надстройки.
Операции Sql порождают такую алгебру .с/2> называемую алгеброй
Стинрода, что 1Г(Х; Z2) является модулем над Л2 Для любого
пространства X, причём отображения пространств индуцируют гомоморфизмы
^2_м°дулей. Аналогично для нечётных простых чисел р, /7*(Х;й/)) —
модуль над соответствующей алгеброй Стинрода ..<#р, порождённой
гомоморфизмами Бокштейна и операциями Р'. Как и кольцевая структура,
заданная ^-произведением, эти структуры модуля налагают сильные
ограничения на пространства и отображения. Например, мы воспользуемся
ими, чтобы показать, что не существует пространства X, для которого
Н*(X; Z) — кольцо многочленов Z[a], если размерность а не равна 2
или 4, когда есть уже знакомые нам примеры пространств СР°° и IHiP* .
Этот довольно длинный параграф разделён на две части. В первой
части описаны основные свойства квадратов и степеней Стинрода и при-
§4.L. Квадраты и степени Стинрода
617
ведено много примеров и приложений. Вторая часть посвящена
построению квадратов и степеней и доказательству того, что они обладают
основными свойствами, перечисленными в первой части. Более обширные
приложения будут даны в [SSATJ, после того как будут введены
спектральные последовательности. Большинство приложений квадратов и степеней
Стинрода зависит не от того, как эти операции в действительности
построены, а только от их основных свойств. Это похоже на ситуацию для
обычных гомологии и когомологий, где аксиом обычно достаточно для
большинства приложений. Построение квадратов и степеней Стинрода
и проверка их основных свойств, или аксиом, довольно интересны сами
по себе, но требуют большой работы, особенно для степеней Стинрода,
и именно но этой причине мы откладываем эту работу до второй части
этого параграфа.
Начнём с нескольких общих определений. Когомологическая
операция—это преобразование 9 = 9Х : H,U(X\ G) —► Нп{Х\ //), определённое
для всех пространств X для фиксированных ш, п, G и И и
удовлетворяющее условию естественности, т.е. обладающее тем свойством, что для
всех отображений f: X ~>Y существует коммутативная диаграмма
Hm(Y\G) 9> > /Г(У;Н)
Т Y
Hm(X\G) —"-^НЦХ'Л)
Например, для коэффициентов в кольце R преобразование /7m(X;R) —>
-^Н"Ф(Х; R), а —» ар, является когомологической операцией, так как
/*(ар) = (/*(а))р. Если взять R — Ъ, то этот пример показывает, что
когомологические операции не обязаны быть гомоморфизмами. С
другой стороны, когда R — Zpy где р — простое число, операция а —> ар —
гомоморфизм. Другие примеры когомологических операций, с которыми
мы уже встречались, —гомоморфизмы Бокштейпа, определённые в §З.Н.
Приведём более простой пример: гомоморфизм G —> И индуцирует
гомоморфизмы замены коэффициентов Hm(X; G)~>Hm(X\ H), которые можно
рассматривать как когомологические операции.
Несмотря на их довольно общее определение, когомологические
операции можно описать в несколько более конкретных терминах.
I Предложение 4.L.I. Для фиксированных ш, п, G и /7 имеется вза-
I имно однозначное соответствие между множеством всех когомологиче-
I ских операций 9: 1Гп(Х; G) — Нп{Х\ Н) и группой //n(K(G, ш); //), за-
I данное формулой 9—>9(0, где ieH"l(K(G,m); G) —фундаментальный
I класс.
Доказательство. CW-аппроксимации пространств позволяют
ограничиться CW-комплексами,, поэтому мы можем отождествить Нт(Х\ G) с
618
Глава 4. Теория гомотопий
(X, K(G, m)) при т > 0, как в теореме 4.57, и с [X, K(G, 0)] при т = 0.
Пусть элемент а е Ит (X; G) соответствует отображению ip : X -» /C(G, m),
т.е. y?*(i) = a. Тогда G(a) = G(c£*(0) = 9*(G(0) и G однозначно
определяется элементом G(t)« Поэтому отображение G—►G(i) инъективно. Для
доказательства сюръективности возьмём элемент a£:Hn(K(Gym)', H),
соответствующий отображению 0: K(G,m) -* К(Н,п), тогда композиция с 0
определяет преобразование (X, K(Gy m))-*(X, К(ИУ п)>, т. е. в: Hm(X; G)->
-*/-/"(X; Н), где G(t) = а. Свойство естественности для G эквивалентно
ассоциативности композиций
X -4 У Д K(G, ш) Л /С(Я, п),
поэтому G — когомологическая операция. D
Одно из следствий предложения 4.L.1 заключается в том, что
нетривиальные когомологические операции не могут уменьшать размерность, так
как пространство K(G, т) является (т — 1)-связным. Кроме того, так как
Hm(K(G, m)\ H) %Hom(G, /-/), мы получаем, что единственные
когомологические операции, которые сохраняют размерность, задаются
гомоморфизмами коэффициентов.
Квадраты Стинрода Sql: Н" (X; Ъ2) -* Н" И(Х\ Z2), / ^ 0, будут обладать
свойствами из следующего списка, начинающегося с естественности:
1) 5дЧГ(а))=Г(5д'(а))для/:Х-У;
2) Sq4a + j8)=Sq4a)+Sq4j8);
3) Sq,'(av-/j8)=J]SqJ'(a)^Sql'"J"(^) (формула Картана);
4) Sq'(o"(a)) = cr(Sq'(a)), где a: H"(X;Z2) -* Н"М(^Х; Z2)
-изоморфизм надстройки, заданный приведённым внешним произведением
с образующей группы H](S]; Z2);
5) Sq'CoO^a2, если i = |a|, и Sq'(a)=0, если i> |a|;
6) Sq° = t — тождественное отображение;
7) Sq1 является гомоморфизмом Бокштейна /3, соответствующим
последовательности коэффициентов 0 -* г£2 —* ЪА —* Ъ2 —* 0.
Первая часть свойства 5 означает, что квадраты Стинрода являются
обобщением операции возведения в квадрат а —► а2, которая обладает тем
хорошим свойством, что она является гомоморфизмом для
коэффициентов в Z2. Свойство 4 означает, что Sql —стабильные операции, т.е. они
инвариантны относительно надстройки. Настоящая операция возведения
в квадрат а^а1 не обладает этим свойством, так как для надстройки Т>Х
все ^-произведения классов положительной размерности нулевые
согласно одной из задач в § 3.2.
Тот факт, что квадраты Стинрода являются стабильными операциями,
обобщающими операцию возведения в квадрат для ^-произведения,
приводит к следующей теореме, из которой следует, что стабильные
гомотопические группы сфер я]', 7Гз и тг* нетривиальны.
§4.L. Квадраты и степени Стинрода
619
Теорема 4.L.2. Если отображение f: S2n l -* S" имеет инвариант
Хопфа 1, то элемент [/] е п*}_1 отличен от нуля, поэтому все
итерированные надстройки T,kf: 52n+/c-1 -*Sn+k гомотопически нетривиальны.
Доказательство. Отображению f:S(—* Sm соответствует конус
отображения Cf = Sm Uf ef+I с клеткой е(+\ приклеенной посредством
отображения /. Предположив, что / сохраняет отмеченные точки, мы получаем
соотношение (7^ = 1! Су, где Е обозначает приведённую надстройку.
Если отображение /: s2""1 —*Sn имеет инвариант Хопфа 1, то
согласно свойству 5 отображение Sqn: Hn{Cj\ Z2) -* НЪ\С;\ Z2) нетривиально.
Согласно свойству 4 то же самое верно для отображения
Sq": Hn+k(£kCf\ Z2) -> H2n+k(£kCf\ Z2) для всех it.
Если бы отображения T,kf были гомотопически тривиальны, то мы
получили бы ретракцию г: EfcCy -*S" t'/c. Диаграмма
Hn+*(Sn+*; Z2) —^— Hn+k&kCf; Z2)
Sq"
.Sq"
H2n+fc(sn+*. Za) __!_^ н^+Ч^Су; Z2)
тогда была бы коммутативной в силу естественности операций Sq", а так
как группа в нижнем левом углу диаграммы нулевая, это приводит к
противоречию. П
Операции степеней Стинрода Р': Н"(Х\ Zp) -> Hn+2l4p~1)(*; Zp) для
нечётных простых чисел р будут обладать аналогичными свойствами:
1) РЧГ(а))=/*(РЧа)) для/:Х->У;
2) P4a + j8) = P4a) + Pf"(j8);
3) P4a^j3)=£pJ(a)^P''-J"(j3) (формула Картана);
)
4) Р'(сг(а)) = сг(Р'(а)), гдесг: И"{Х\ Zp) -> tf"+1(EX; Zp) -изоморфизм
надстройки, заданный приведённым внешним произведением на
образующую группы Н1($1\Ър)\
5) Р'"(а) = ар, если21 = |а|, и Р'"(а)=0, если 2i>|a|;
6) P° = t— тождественное отображение.
Выполнения порождающего свойства Р'(а) =арпп. 5 можно ожидать
только для классов а чётной размерности, так как для нечетномерного
а из свойства коммутативности ^-произведения следует, что а2 = О для
коэффициентов в Zp, если р нечётно, а тогда ар =0, так как а2 = 0.
Отметим, что из формулы Р'(а) = ар для \а\ = 2i следует, что Р' увеличивает
размерность на 2i(p — 1), что объясняет появление этого числа.
Гомоморфизм Бокштейна ft: H"(X; Zp)-* НП+1(Х; Zp) не
встречается как одно из Р\ но это в основном вопрос удобства обозначений. Как
620 Глапа 4. Теория гомотопий
мы увидим позже, когда будем обсуждать соотношения Адсма, операция
Sq2l+l —это то же самое, что композиция Sq}Sq21 = (3Sq2t, поэтому
операции Sq21 можно рассматривать как Р1 для р = 2.
Можно поинтересоваться, существуют ли в я* элементы,
обнаруживаемые степенями Стинрода таким же образом, как отображения Хопфп
обнаруживаются квадратами Стинрода. Как мы покажем в примере 4.L.6,
ответ положительный для операции Р1. Возможно, неутешителен факт,
что никакие другие квадраты или степени помимо Sq1, Sq2, Sq4, Sqb и Р1
не обнаруживают элементов гомотопических групп сфер {Sq1
обнаруживает отображение Sn—> Sn степени 2). Мы докажем это для некоторых
операций Sq1 и Р1 позже в этом параграфе. Общий случай для р = 2 — это
теорема Адамса об инварианте Хопфа, обсуждавшаяся в §4.В, а случай
нечётного р доказан в [78]; см. также [VBKT].
Формулы Картана можно выразить в более краткой форме,
определив полные операции квадрата и степеней Стинрода, положив Sq = Sq° +
+ Sql + ... и Р = Р° + Р1 + ... Они действуют на H*(X;Zp), так как по
свойству 5 только конечное число операций Sq1 или Р1 может быть
отлично от нуля на данном классе когомологий. Тогда по формулам Картана
Sq(aw/3) = Sq(a)^Sq(/?) и Р(а^ /3) = P(a)^ P(/3), и таким образом, Sq
и Р —кольцевые гомоморфизмы.
Мы можем применить Sq и Р, чтобы вычислить операции Sq1 и Р' для
проективных пространств и линзовых пространств посредством
следующих общих формул:
Sq^a") = C\an+i для а е Н[{Х; Z2),
с*}
Р*{а") = c,naa+ilp-" для a € Н2(Х; Zp).
Чтобы получить первую формулу, применим свойства 5 и 6; из них
следует, что Sq(a) = а + а2 — а(1 + а), таким образом,
Sq(an) = Sq(a)n = a"(l + a)" = ^Cnan+i,
i
а потому Sq1(an) = Clnatl+l. Вторая формула получается аналогично: Р(а) =
= а + ар = а(1 -hap_1), поэтому
i
В лемме З.С.6 мы описали, как можно вычислять биномиальные
коэффициенты по модулю простого числа р:
C,n = n,C,modp,
где т = ^] rriip1 и п = J] п,р' — р-ичные разложения чисел т и п. Например,
для р = 2 крайние случаи двоичных разложений, состоящие только из
§4.L. Квадраты и степени Стинрода
621
одной цифры 1 или всех цифр 1, дают
Sq{a2 ) = a2 +a2 ,
Sqia2"'1) = a2""4a24a24l+... + a2UI"2
для а<^Нх(Х\ Z2). Более общим образом, коэффициенты для Sq{an)
можно прочитать в (п + 1)-й строке треугольника Паскаля по модулю 2, часть
которого изображена на рисунке, где точки обозначают нули.
1 1
1 • 1
1111
1 • • • 1
1 1 • • 1 1
1 • 1 ■ 1 • 1
11111111
1 1
11- -11
1 ■ 1 • -1-1
1111 -1111
1 ... 1 ■ 1 • • ■ ]
1 1 • • 1 1 • • 1 1 • • 1 1
1 • 1 ■ 1 • 1 . 1 • 1 ■ 1 ■ 1
1111111111111111
Пример 4.L.3 (стабильные расщепления). Формула (*) говорит нам,
как вычислить квадраты Стинрода для 1RP00, а значит, и для любой
надстройки над RP°°. Приведённые выше явные формулы для Sq(aT) и
Sq(a2 ~l) показывают, что все степени образующей aetf^RP00; Z2)
связаны вместе квадратами Стинрода, так как первая формула связывает а
индуктивно со всеми степенями вида а2 , а вторая формула связывает эти
степени со всеми остальными степенями. Это показывает, что никакая
надстройка E^IRP00 не может иметь гомотопический тип букета X V Y,
где оба пространства X и У имеют нетривиальные когомологии. В случае
самого пространства 1RP00 мы могли бы вывести это из структуры кольца
Н*(!RP°°; Z2) ^Z2[aJ, но ^-произведения становятся тривиальными в
надстройке.
Те же самые рассуждения показывают, что у СР°° и у ЕР00 нет никаких
нетривиальных стабильных расщеплений. Когомологии с
коэффициентами в Z2 в этих случаях снова имеют вид Z2[a], хотя а более не является
одномерным классом. Однако мы снова получаем Sq(a) = a + a2, так как
у этих пространств нет никаких нетривиальных когомологии в
размерностях между а и а2, поэтому Sq2i{an)=Cnan+l для СР~ и Sq4l(an) = cy}+i
для ЕР00. Тогда рассуждения из вещественного случая полностью
переносятся на эти случаи, если воспользоваться операциями Sq21 и Sq '
вместо Sq'.
622
Глава 4. Теория гомотопий
Предположим теперь, что мы рассматриваем тот же самый вопрос для
iC(Z3,1) вместо Ш)0°. Если взять когомологии с коэффициентами в Z3, то
гомоморфизм Бокштейна /3 отличен от нуля на иечётномерных классах
в H*(K"(Z3,1); Z3), связывая их таким образом с чётномерными классами,
поэтому мы должны только понять, какие чётномерные классы связаны
операциями Р1. Чётномерная часть кольца H*(X(Z3, 1); Z3) — это алгебра
многочленов Z3[a], где |а| = 2, таким образом, мы имеем
Pi(an)=Cinan+i{p' -1) = Спап+2(
согласно полученной ранее формуле. Так как Р1 увеличивает размерность
на 4z, когда р = 3, нет никаких шансов, что все чётномерные
когомологии будут связаны операциями Р'. В действительности мы показали
в предложении 4.1.3, что EK"(Z3> 1) ^Х1 V Х2> где Х{ имеет когомологии
пространства 5JK(Z3,1) в размерностях, сравнимых с 2 и 3 mod 4, в то
время как Х2 имеет'все остальные когомологии. Поэтому лучшее, на что
можно надеяться, —это на то, что все нечётные степени элемента а
связаны операциями Р' и аналогично связаны все чётные степени, так как
из этого следовало бы, что ни Xlf ни Х2 не расщепляется нетривиально.
Это действительно так, что показывает анализ коэффициентов в формуле
Р'(а") = С1паи+2'. В треугольнике Паскаля по
модулю 3, изображённом на рисунке, P(atl) j l
определяется (n -f 1)-й строкой. Например, 1 2 1
шестая строка говорит, что 1 о о 1
Р(а5) = a5 + 2a7 + a9 + a1I+2aI3 + a15. 12 112 1
Недолгие размышления показывают, что в ] п°? ? о i * i
строках, которые вычисляют Р(ап) для л = 121212121
= Зкт - 1, все элементы отличны от нуля i 000000001
и этих строк вместе со строками сразу после
них достаточно, чтобы связать степени элемента а требуемым способом.
Поэтому у Х1 и Х2 нет никаких стабильных расщеплений. Можно также
проверить, что пространства Т,2Х} и Х2 не гомотопически эквивалентны,
даже стабильно, так как операции Р' по-разному действуют в этих двух
пространствах. Например, операция Р2 тривиальна на надстройках
элемента а, но не на надстройках элемента а2.
Ситуация для iC(Zp, 1) для других простых чисел р совершенно
аналогична; при этом EiC(Zp, 1) расщепляется как букет р - 1 пространств. Те
же самые рассуждения годятся и для iC(Zp», 1), хотя при i > 1 обычный
гомоморфизм Бокштейна (3 является тождественно нулевым, поэтому
нужно воспользоваться вместо этого гомоморфизмом Бокштейна, связанным
с коэффициентами "£р,. Мы оставляем подробности этих рассуждений в
качестве задач.
Пример 4.L.4 (отображения пространства HP00). Мы можем
применить операции Р' и некоторые результаты из теории чисел, чтобы про-
§4.L. Квадраты и степени Стинрода
623
демонстрировать интересное различие между КР00 и СР°°. А именно, мы
покажем, что, если для отображения /: HP00 —> E^IP00 выполняется
равенство /*(у) = dy, где у — образующая группы H4(2iP(X;Z), то целое
число d, которое мы называем степенью отображения /, должно быть полным
квадратом. В отличие от этого, так как для СР00 есть K(Z, 2), существуют
отображения СР^-^СР™, переводящие образующую aGH2(CP0C; Z) в
любое её кратное. Такие отображения можно описать явно, а именно,
отображение z—>zr/, zeC, индуцирует отображение / пространства СР00, для
которого /* (а) = da. Для этой конструкции требуется коммутативность С,
поэтому она не переносится на кватернионный случай.
Мы выведем действие степеней Стинрода на H"0HLP°°; Zp) из их
действия на Н*(СР°°; Zp), описанного ранее формулой (*), которая говорит,
что P'(an) = c;|an+'(P"1J, где а —образующая группы Н2(СР°°; Z;)).
Имеется естественное факторотображение СР°° —>HP°°, возникающее из
определения обоих пространств как факторпространств сферы S°°. Оно
отображает четырёхмерную клетку в СР°° гомеоморфно на четырёхмерную
клетку в НР°°, поэтому индуцированное отображение когомологий
переводит образующую у €Н4ЩР°°; Zp) в а2, а значит, уп —в а2п. Поэтому из
формулы Р((а2п) = С2па2п+Кр~1) следует, что Р\уп) = Цпгп+'(р"1)/2.
Например, Р1 (Г) = 2г(р+1)/2.
Теперь пусть /: НР°° —»НР°° —произвольное отображение. Применяя
формулу Рг(у) = 2у(р_|"1)/2 двумя способами, получаем
р7ж(Г) -ГрЧг) = Г(2Г(я+1)/2) = 2d('+1)/y',41)/2
и Plf*{y)=Pl{dy) = 2dy{pJfl)/2.
Следовательно, степень d удовлетворяет сравнению d(/,+1)/2 =d mod р для
всех нечётных простых чисел р. Таким образом, либо d = 0 mod p, либо
^(р-1)/2 = 2 mocj р в обоих случаях d — квадрат по модулю р, так как
сравнение d(p~1)/2 = 1 mod p эквивалентно тому, что d является ненулевым
квадратом по модулю р, поскольку мультипликативная группа ненулевых
элементов поля Zp —это циклическая группа порядка р - 1.
Доказательство завершается применением результата из теории
чисел, гласящего, что целое число, которое является квадратом по модулю р
для всех достаточно больших простых чисел р, само должно быть
квадратом. Это можно вывести из квадратичного закона взаимности и
теоремы Дирихле о простых числах в арифметических прогрессиях
следующим образом. Предположим от противного, что утверждение неверно для
некоторого целого числа d. Рассмотрим простые числа р, не делящие d.
Так как произведение двух квадратов в Zp снова является квадратом, мы
можем считать, что d — произведение различных простых чисел q1} .••>Яп>
где одному из этих простых чисел разрешается быть равным -1, если d
отрицательно. В терминах символа Лежапдра ( - ), который но определе-
624
Глава 4. Теория гомотопий
нию равен +1, если d —квадрат по модулю р, и -1 в противном случае,
мы получаем
00=0047}
Выражение в левой части равно -hi для всех достаточно больших р по
предположению, поэтому достаточно убедиться, что р можно выбрать так,
чтобы каждый член в правой части принимал произвольное заданное
значение. Значения символов Лежандра ( — ) и 1 — 1 зависят только от р
mod 8, и четыре комбинации их значений реализуются четырьмя
остатками 1, 3, 5, 7 mod 8. Если фиксировать значение р mod 8, то квадратичный
закон взаимности говорит, что для нечётных простых чисел q задание
значения ( - ] эквивалентно заданию значения ( ~~ )• Таким образом, мы
должны просто выбрать р в соответствующих классах вычетов по
модулю 8 и по модулю q{ для каждого нечётного q{. По китайской теореме об
остатках это означает задать р по модулю умноженного на 8 некоторого
произведения нечётных простых чисел. Теорема Дирихле гарантирует, что
в действительности существует бесконечно много простых чисел р,
удовлетворяющих этому сравнению.
Известно, что целые числа, реализуемые как степени отображений
HP00 —♦ КР00, — это в точности нечётные квадраты и нуль. Конструкция
отображений, степени которых —нечётные квадраты, будет приведена
в [SSAT] с помощью техники локализации, следуя [130]. Исключить
чётные квадраты, отличные от нуля, можно с помощью ^-теории; см. [100],
где рассматриваются также отображения КР" —* КР".
Предыдущие вычисления можно также применить для того,
чтобы показать, что любое отображение ЕР'1 —* Б-Р" должно иметь
неподвижную точку, если п > 1. Действительно, если положить р = 3, то
элемент Р](у) лежит в группе /78(КР"; Z3), которая отлична от нуля при
п > 1, поэтому, когда в предыдущих рассуждениях мы возьмём
частный случай р = 3, сравнение d(/H IJ/2 = d mod p превращается в
уравнение d2 = d в Z3, которому в Z3 удовлетворяют только элементы О
и 1. В частности, d не равно — 1. Отсюда вытекает, что число Лефшеца
А(/) = 1 +d + ... + d" = (d'Ifl - l)/(d - 1) не равно пулю, так как
единственными целыми корнями из единицы являются ±1. Поэтому теорема
Лефшеца о неподвижной точке даёт требуемое.
Пример 4.L.5 (векторные поля на сферах). Применим теперь
квадраты Стинрода, чтобы определить максимальное число ортопормированных
касательных векторных полей на сфере в тех случаях, когда размерность
сферы не сравнима с -1 mod 16. Первый шаг состоит в
переформулировке этого вопроса в терминах многообразий Штифеля. Напомним из
конца §3.0 и примера 4.53, что Vnk — это пространство ортопормированных
/с-реперов в ?Л Проекция /с-репера па его первый вектор даёт отобра-
§4.L. Квадраты и степени Стинрода
625
жение р: Vnk -»Sn_1, и сечения для этой проекции, т.е. такие
отображения /: S"-1 -* Vnk, что р/ = 1, — это в точности множество наборов к - 1
ортонормированных касательных векторных полей vb ..., v^, на сфере
Sn-\ так как / сопоставляет каждой точке xeS""1 ортонормированный
/с-репер (х,у^х),...,ук^(х)).
Мы описали клеточную структуру на Vnk в конце § 3.D, и утверждаем,
что (п - 1)-мерный остов этой клеточной структуры — это RPn~ VlKPn~fc~\
если 2к - 1 $ п. Клетками в Vnk были произведения е'1 х ... х е'"', где
п > ц > ... > im ^ п — к, поэтому произведения с единственным
множителем отвечают за весь (2п — 2/0-мерный1 остов, следовательно, они
отвечают за весь (п - 1)-мерный остов, если п - 1 ^ 2п — 2к, т.е. если
2к — 1 ^ п. Клетки, которые являются произведениями с единственным
множителем, —это гомеоморфные образы клеток в IRP""1 при
отображении RPn_I -* SO(n) -* SO(n)/SO(n - fc) = Ц1Л. Это отображение
стягивает RPn~fc_1 в точку, поэтому мы получаем требуемый вывод, что
Ш)П~1/Ш)П"~'С~1 является (п - 1)-мерным остовом комплекса Vnk, если
2/с-1^п.
Теперь предположим, что задано отображение /: Sn~l —* Vnk, для
которого р/ = 1. В частности, /* сюръективно на Н"_1(-; Z2). Если мы про-
деформируем / в клеточное отображение с образом в (п - 1)-мерном
остове, то в соответствии с предыдущим абзацем это даст отображение
g: S""1 -* RPn_1/KP"'"lc~"1, если 2к - 1 ^ п, и это отображение всё ещё
будет индуцировать сюръекцию на Нп_1 (-; Z2), а потому изоморфизм. Если
число к окажется таким, что С*~* = 1 mod 2, то по предыдущей формуле
(*) операция
sqfc-^H'I-fc(RPn-VRPn"fc~1;z2)^Hn"1№Pn"1/KPn"fc"1;z2)
будет отлична от нуля, что противоречит существованию отображения g,
так как очевидно, что операция
Sqfc-1:Hn-k(Sn-1;Z2)-Hn-1(Sn"1;Z2)
является нулевой.
Чтобы гарантировать, что С*"^ = 1 mod 2, запишем п = 2r(2s + 1) и
выберем к = 21 -f1. Временно предположим, что s ^ 1. Тогда С*^ = С*'.,.. r
и согласно правилу для вычислительных биномиальных коэффициентов
в Z2 это число отлично от нуля, так как двоичное разложение для 2'+1s - 1
заканчивается последовательностью из цифр 1, включая 1 в том
единственном месте, где разложение для 2Г отлично от нуля. Отметим, что
сформулированное раннее условие 2к — 1 ^ п выполняется, так как оно
превращается в неравенство 2Г+1 +1 ^ 2r+1s + 2Г, а мы предположили, что
1 Потому что произведения с двумя множителями имеют размерность но меньше 2и -
— 2/с 4-1. — Прим. перев.
?1 1л k 3(>V
626
Глава 4. Теория гомотопий
Итак, мы показали, что для n = 2r(2s+ 1) на сфере Sn-1 не может
быть 2Г ортонормированных касательных векторных полей, если s ^ 1.
Это также по очевидным причинам верно для s = 0, так как на сфере S"-1
не может быть п ортонормированных касательных векторных полей.
Легко убедиться, что этот результат наилучший возможный при г $ 3,
явно построив 2Г - 1 ортонормированных касательных векторных полей
на Sn_1 для п~2гт. При г = 1 представим Sr,_1 как единичную сферу в С",
и тогда x*-*ix определяет касательное векторное поле, так как
комплексные числа единичной длины 1 и i ортогональны, а умножение на
комплексное число единичной длины — изометрия на С, поэтому х и ijc
ортогональны в каждой координате пространства Сш, а потому ортогональны.
При г = 2 годится та же самая конструкция с Н вместо С, использующая
отображения x—*ixt x^jx и х>-*кху чтобы задать три
ортонормированных касательных векторных поля на единичной сфере в Нш. При г^Змы
можем воспользоваться той же самой процедурой с октавами, строя семь
ортонормированных касательных векторных полей к единичной сфере
в От посредством ортонормированиого базиса 1, i, ;, /с,... в О.
Верхняя оценка 2Г — 1 для числа ортонормированных векторных
полей на сфере Sn'-1 не является наилучшей возможной в оставшемся
случае п = 0 mod 16. Оптимальная верхняя граница получается, если вместо
квадратов Стинрода применить К -теорию; см. [VBKT] или [36].
Построение требуемого числа векторных полей снова является алгебраическим,
на этот раз с помощью алгебр Клиффорда.
Пример 4.L.6 (отображение с инвариантом Хопфа mod р, равным 1).
Здесь мы опишем построение такого отображения /: S2p -* S3, что в
конусе отображения Су = S3Ufe2p+l первая степень Стинрода Р1: H3(Cy;Zp)-*
-»H2p+1 (Cf; Zp) отлична от нуля, а значит, / отлично от нуля в п&2 3.
Построение начинается с того факта, что образующая группы H2(K(Zp, 1); Zp)
имеет нетривиальную р-ю степень, поэтому операция
Р1: H2(K(Zp, 1); Zp) - H2p(K(Zpy 1); Zp)
нетривиальна по свойству 5. Это остаётся верным и после того, как
мы перейдём к надстройке EK(Zp, 1), а мы показали в предложении
4.1.3, что EK(Zp, 1) имеет гомотопический тип букета CW-комплексов
Xh 1 ^ i ^ р - 1, для которых ЯДХ,-; Z) состоит только из Zp в каждой
размерности, сравнимой с 2\ mod 2p - 2. Сейчас нас интересует
пространство Х~ХЛ, которое имеет нетривиальные когомологии с
коэффициентами в Zp в размерностях 2, 3, 2р, 2р + 1, ... Так как X, с
точностью до гомотопий, является слагаемым букета для EK(Zp, 1), операция
Р1: Я3(Х; Zp) -* Н1рлЛ{Х\ Zp) нетривиальна. Так как пространство X од-
носвязно, конструкция из §4.С показывает, что мы можем выбрать
комплекс X так, чтобы его (2р + 1)-мерный остов имел вид S2 U е3 и е2р и е2р •
В действительности, используя понятие гомологического разложения из
§4.L. Квадраты и степени Стинрода
627
§4.Н, мы можем выбрать этот остов так, чтобы он был приведённым
конусом отображения Cg для отображения g: M(Zp, 2p - 1) —» M(Zp, 2)
пространств Мура. Следовательно, факторпространство Cg/S2 — это
приведённый конус отображения для композиции
h: M(Zp, 2p - 1) Л M(Zp, 2) - M(Zp, 2)/S2 = S3.
Ограничение h| S2/)_1 представляет элемент группы 7r2p_j(S3), который
либо тривиален, либо имеет порядок р, так как это ограничение
продолжается на 2р-мерную клетку комплекса M(Zp, 2p-l), которая приклеена по
отображению S2p~] —>S2p~] степени р. В действительности отображение
h|S2p_1 гомотопно нулю, поскольку, как мы увидим в [SSAT] с помощью
спектральной последовательности Серра, группа rc,(S3) не содержит
элементов порядка р, если i: ^ 2р — 1. Из этого следует, что пространство
Ch—CgIS2 гомотопически эквивалентно CW-комплексу Y, полученному
из S3 VS2p приклеиванием клетки е2р+]. Факторпространство Y/S2p тогда
имеет вид S3 U е2р41, поэтому оно является конусом отображения для
отображения /: S2p —♦ S3. По построению существует отображение Cg —> Су,
индуцирующее изоморфизм когомологий с коэффициентами в Zp в
размерностях 3 и 2р +1, поэтому операция Р1 нетривиальна в H*(Cf) Zp), так
как это было верно для Cg — (2р Н- 1)-мерного остова комплекса X.
Пример 4.L.7 (пространства Мура). Применим операцию Sq2,
чтобы показать, что при п ^ 2 тождественное отображение пространства
M(Z2, n) имеет порядок 4 в группе гомотопических классов сохраняющих
отмеченную точку отображений M(Z2, n) —♦ M(Z2, n) со сложением,
определённым посредством структуры надстройки на M(Z2, n) = EM(Z2, n-1).
Согласно предложению 4.Н.2 эта группа —средний член в короткой
точной последовательности, остальные члены которой содержат только
элементы порядка 2. Следовательно, если тождественное отображение
пространства M(Z2, n) имеет порядок 4, то эта короткая точная
последовательность не может быть расщепимой.
Ввиду наличия упомянутой короткой точной последовательности
достаточно показать, что удвоенное тождественное отображение
пространства M(Z2,n) не гомотопно нулю. Если бы удвоенное тождественное
отображение было гомотопно нулю, то конус отображения С для этого
отображения имел бы гомотопический тип букета M(Z2, n) V EM(Z2, n).
Это вынудило бы операцию Sq2: Н"(С; Z2) —»Н""|"2(С; Z2) быть
тривиальной, так как две группы, область определения и область значений,
возникают из разных слагаемых букета. Однако мы сейчас покажем, что эта
операция Sq2 нетривиальна. Удвоенное тождественное отображение
пространства M(Z2, n) можно рассматривать как приведённое произведение
отображения S1 —>S\ z —> z2, степени 2 на тождественное отображение
пространства M(Z2, п - 1). Если мы возьмём приведённое произведение
последовательности корасслоения S1 —> Sl —>RP2 для этого отображения
628
Глава 4. Теория гомотопий
степени 2 на M(Z2, п — 1), то получим последовательность корасслоения
M(Z2, п) -> M(Z2, п) -»С ввиду тождества (Х/А) Л У = (X Л У)/(Л Л У). Это
означает, что мы можем рассматривать С как IRP2 AM(Z2, п — 1). Формула
Картана, переведённая на язык внешних произведений, принимает вид
Sq2{a х /3) = Sq°a х Sq2/3+Sqia x Sq}/3+Sq2a x Sq°/3.
Это равенство выполняется для приведённых произведений, как и для
обычных произведений, согласно естественности. Выбрав в качестве а
образующую группы H4RP2;Z2), а в качестве /3 — образующую группы
Hn~r(M(Z2, n-l);Z2), мы получаем Sq2a = 0 = Sq2/3, но Sqla и Sq{/3
отличны от нуля, так как Sql — гомоморфизм Бокштейна. По формуле Кюн-
нета Sqla х Sq}/3 тогда порождает группу Hn+2(RP2 Л M(Z2, п - 1); Z2),
и доказательство завершено.
Соотношения Адема и алгебра Стинрода
Композиции квадратов или степеней Стинрода удовлетворяют
определённым соотношениям, к сожалению, довольно сложным, которые
известны под названием соотношений Адема:
SqaSqb = 2Cb-/-iS9fl+b";'s9;. если а < 2Ь>
)
р"рь = 2(-1)в+УсоГ-'?)»-л-1р0+ь";р;- если a < pb>
р"^6=Е(-1)а+;с(7Л)(ь-л^ра+ь";р) -
)
- £(-ОвЧ"-щн)-1 Ра+ЬЧРР], если а ^ рЬ.
Здесь мы используем соглашение, что биномиальный коэффициент CJJ,
считается равным нулю, если m или п отрицательно или если т<п. Кроме
того, С° = 1 для т ^ 0.
Например, взяв a = 1 в соотношении Адема для квадратов Стинрода,
мы получаем Sq}Sqb = (b~l)Sqb+lt поэтому Sq]Sq2i=Sq2i+} и Sq*Sq2i+l=0.
Соотношения SqlSq21 =Sq2,+} и Sql = /3 объясняют сделанный ранее
комментарий, что Sq21 является аналогом операции Р' для р = 2.
Алгебра Стинрода j#2 определяется как алгебра над Z2, которая
является факторалгеброй алгебры многочленов от некоммутирующих
переменных Sq1, Sq2,... по двустороннему идеалу, порождённому
соотношениями Адема, т.е. многочленами, заданными как разности между левыми
и правыми частями соотношений Адема, Аналогично jtf для
нечётного р определяется как алгебра над Zp, образованная многочленами от
некоммутирующих переменных /3, Pl, P2, ... по модулю соотношений
Адема и соотношения /З2 = 0. Таким образом, для каждого пространства X
§ 4.L. Квадраты и степени Стинрода
629
на H*(X;Zp) есть структура модуля над jtfp для всех простых чисел р.
Алгебра Стинрода — градуированная алгебра; элементы степени /с —это
те, которые отображают Нп{Х\ Zp) в Нп+к(Х; Zp) для всех п.
Из следующего предложения следует, что .stf2 порождена как алгебра
элементами Sq2 , в то время как jtfp для нечётного р порождена /3 и
элементами Рр .
1 Предложение 4.L.8. Имеет место соотношение
I Sq1 = Yj ajSqi4Sqi
I 0<j<i
I с коэффициентами a; eZ2, если i не является степенью числа 2. Ана-
I логично если i не является степенью р, то имеет место соотношение
I Р'"= Е ajPi^P^aj^Zp.
I 0<j<[
Доказательство. Рассуждение одно и то же для р = 2 и и для
нечётного р, поэтому мы обсудим только последний случай. Идея состоит в том,
чтобы записать i в виде такой суммы а + Ъ целых чисел a > 0 и Ъ > О,
где a < pb, что коэффициент члена j = 0 в соотношении Адема для РаРь
отличен от нуля. Тогда можно решить это соотношение для ра+ь = р1.
Пусть р-ичная запись числа f имеет вид i — f0 -f- i}p + ... + ikPk, где
ik ф 0. Положим b = pk и a = i - pk, таким образом, b > 0 и a > 0, если
i не является степенью числа р. Утверждение состоит в том, что
число С(а 1)Ь_г представляет ненулевой элемент в Zp. Число (р — 1)Ь — 1 =
— (pfc+1 - 1) _ рк в р-ичной системе счисления запишется как
(р-1)-Ир-1)р + ...4-(р-2)р\
а число а —как i0 + i\P + ••• + (i* - l)pfc. Следовательно, C(ap__1)b_1 =Ср°_г..
...C'kJ2 , причём в каждом множителе последнего произведения числитель
представляет ненулевой элемент в Zpi поэтому произведение
представляет ненулевой элемент в Ър. Когда р = 2, последний множитель
пропускается, и произведение всё ещё отлично от нуля в Z2. □
Это предложение говорит, что большинство операций Sq1 и Р1
разложимо (элемент а градуированной алгебры, например, .*/р, называют раз-
ложшиьш, если его можно представить в виде J]a,b,, где каждый элемент
а{ и Ъ{ имеет степень ниже, чем а). Операция Sq2 неразложима, так как
для образующей а группы H^IRP00; Z2) мы видели, что Sq2 (a2 ) = а2 ,
но Sql(a2 ) = 0 для 0 < i < 2к. Аналогично операция Рр неразложима, так
как если аеН2(CP°°;Zp)-образующая, то Рр\арк) = арк"\ но P''(a',l)=0
для 0 < i < pfc и, кроме того, /?(аг ) = 0.
Вот применение предыдущего предложения.
630
Глава 4. Теория гомотопий
I Теорема 4.L.9. Предположим, что Н*(Х; Zp) — алгебра многочленов
I Zp[a] от образующей а размерности пу возможно, срезанная соотно-
I шением ат = 0 для т > р. Тогда если р = 2У то число п должно быть
I степенью 2, а если р — нечётное простое число, то п должно иметь вид
I рк1, где I —чётный делитель числа 2(р - 1).
Как мы упоминали в §3.2, имеет место более сильная теорема, что
п должно быть равно 1, 2, 4 или 8, когда р = 2, и п должно быть
чётным делителем числа 2(р - 1), когда р — нечётное простое число. Мы
также приводили примеры, показывающие необходимость предположения
т>р в случае срезанной алгебры многочленов.
Доказательство. В случае р = 2 получаем Sqn(a) = а2 Ф 0. Если п не
является степенью числа 2, то Sqn разлагается в композиции Sqn~^Sq\
0 < j < п. Такие композиции должны быть нулевыми, так как они
пропускаются сквозь группу Hn+j(X; Z2), которая является нулевой при 0< j <n.
Для нечётного р из того факта, что элемент а2 ненулевой, следует,
что п четно, скажем, п = 2/с. Тогда Рк(а) = ар ф 0. Так как Рк можно
выразить в терминах операций Рр\ некоторая операция Рр' должна быть
ненулевой в Н*(Х; Zp). Из этого следует, что величина 2р'(р - 1), на
которую Рр' увеличивает размерность, должна быть кратна п, так как группы
Н*(Х; Zp) сосредоточены в размерностях, кратных п. Так как число п
делит 2р' (р - 1), оно должно быть степенью р, умноженной на делитель
числа 2 (р — 1), причём этот делитель должен быть чётным, так как п четно,
а р нечётно. D
Следствие 4.L.10. Если Н*(Х; Z)— алгебра многочленов Z[a],
возможно, срезанная соотношением ат = 0, где т > 3, то \а\ = 2 или 4.
Доказательство. Если перейти от коэффициентов Z к
коэффициентам Z2, то из теоремы следует, что \а\ — степень числа 2, а взяв
коэффициенты Z3, мы видим, что \а\ —степень числа 3, умноженная на делитель
числа 2(3-1) =4. □
В частности, октавная проективная плоскость ОР2, построенная в
примере 4.47 приклеиванием 16-мерной клетки к S8 посредством
отображения Хопфа S15 —>S8, не обобщается до октавного проективного п-мерного
пространства <ОРп при п ^ 3.
Аналогично из разложимости следует, что если элемент группы п\
обнаруживается операцией Sql или Р1, то i должно быть степенью 2 для
Sql и степенью р для Р1. Действительно, если операция Sql разложимая, то
отображение Sql: Hn(Cf: Z2) -> Hn+i(Cf; Z2) должно быть тривиальным,
так как оно является суммой композиций, которые пропускаются сквозь
тривиальные группы когомологий, и аналогично для Р'.
Интересно, что соотношения Адема можно также применить
положительным способом для обнаружения элементов группы я*, как покажет
доказательство следующего результата.
§4.L. Квадраты и степени Стинрода 631
I Предложение 4.L.11. Если элемент r\ е п\ представлен отображени-
I ем Хопфа S3 —> S2, то элемент г)2 отличен от нуля в тс*. Аналогично
I другие два отображения Хопфа представляют элементы v Е я* и а € я*7,
I квадраты которых нетривиальны в я£ и в п\л.
Доказательство. Пусть r\\ Sn+1 —> S" — надстройка над
отображением Хопфа; конус отображения С^ получается из S" приклеиванием клетки
е"+2 по отображению т). Если мы предположим, что композиция (£77)77
гомотопна постоянному отображению, то мы можем определить
отображение /: Sn+3 —> С^ следующим образом. Представим Sn+3 в виде
объединения двух конусов CSn+2. Пусть на одном из этих конусов отображение /
будет гомотопией отображения (£77)77 в постоянное отображение. На
другом конусе зададим / как композицию CSn+2 —> CSn+l —> Сг/, где первое
отображение получено как конус над Иг), а второе отображение —
характеристическое отображение для клетки еп+2.
Воспользуемся отображением /, чтобы приклеить клетку еп+4 к С^,
образовав при этом пространство X. Его (п 4- 2)-мерным остовом
является С поэтому Sq2: Н"(Я; Z2) -*Hn+2(X; Z2) — изоморфизм.
Отображение Sq2: НП+2(Х; Z2) —>НП+4(Х; Z2) тоже является изоморфизмом, так как
отображение факторизации X-+X/Sn индуцирует изоморфизм групп ко-
гомологий размерности выше п, а пространство X/Sn гомотопически
эквивалентно конусу отображения для отображения £2г). Таким образом,
композиция Sq2Sq2: Нп (X; Z2) —► НП+4(Х; Z2) — изоморфизм. Но этого не
может быть ввиду соотношения Адема Sq2Sq2 = Sq3Sql, так как операция
Sq1 тривиальна на НП(Х; Z2).
То же самое рассуждение показывает, что v2 и а2 нетривиальны, если
воспользоваться соотношениями
Sq4SqA = Sq7Sql+Sq6Sq2 и SqsSqs = Sql5Sql +SqlASq2 + Sq]2SqA. □
Эта схема рассуждений не работает для нечётных простых чисел и
элемента а€ тг2 з» обнаруживаемого операцией Р1, так как соотношением
Адема для Р1?1 является Р1?1 = 2Р2, которое бесполезно. И в
действительности а2 = 0 по свойству коммутативности произведения в группе я*.
Когда мы имеем дело с л/2, часто бывает удобно сократить систему
обозначений, записав моном Sq^Sq'2... как Sq7, где / — конечная после-
632
Глава 4. Теория гомотопий
довательность неотрицательных целых чисел ilt i2, ••• Назовём моном Sq
допустимым, если к нему нельзя применить никакое соотношение Адема,
т. е. если i • 5 2ij+1 для всех j. Из соотношений Адема следует, что каждый
моном Sq моном записать в виде суммы допустимых мономов.
Действительно, если моном Sq1 не допустимый, то он содержит пару Sq(lSqb, к
которой можно применить соотношение Адема, что даёт сумму членов SqJ,
для которых J > I относительно лексикографического порядка на
конечных последовательностях целых чисел. Эти члены SqJ имеют ту же самую
степень iY + ... 4- ik, что и Sq1, а так как число мономов Sq1
фиксированной степени конечно, последовательные применения соотношений Адема
в конце концов приводят любой моном Sq1 к сумме допустимых мономов.
Для нечётного р элементы алгебры ,srfp —это линейные комбинации
мономов /З^Р'1/?^?'2..., где каждое £j равно 0 или 1. Такой моном
допустим, если ij ^ Ej+i +pij+] для всех j, и это снова означает, что к такому
моному нельзя применить никакое соотношение Адема. Как и для j^2,
соотношений Адема достаточно, чтобы привести каждый моном к линейной
комбинации допустимых мономов; это показывают те же самые
рассуждения, что и раньше, но на этот раз с использованием лексикографического
порядка на наборах (£j -fpi'i, £2 + Ph> ••-)•
Определим избыточность допустимого монома Sq1 как сумму
j
— эта его численная мера допустимости. Для нечётного р можно было
бы ожидать, что избыточность допустимого монома 13Ь]Р1]/3Е2Р12... будет
определена как сумма ^](^ — pij+i — £;-ц), но вместо этого она определя-
)
ется как сумма ][](2i;- - 2piJ+1 ~ £,+]) по причинам, которые станут понят-
)
ны позже.
Как мы объяснили в начале этого параграфа, когомологические
операции соответствуют элементам в когомологиях пространств Эйленбер-
га—Маклейна. Вот довольно важная теорема, которая будет доказана
в [SSAT], так как доказательство существенно использует спектральные
последовательности.
I Теорема. Для любого простого р алгебра Я* {К (Zp, n); Z,,) —свободная
I коммутативная алгебра от образующих 9(tn), где tnGHn{K{Zpi n); Zp) —
I образующая, a G пробегает по всем допустимым мономам с избыточно-
I стью меньше п.
Здесь «свободная коммутативная алгебра» означает «алгебру
многочленов», когда р = 2, и «алгебру многочленов от образующих чётной
размерности, тензорно умноженную на внешнюю алгебру от образующих
нечётной размерности», когда р нечётно. Мы вскоре сделаем некоторые
пояснения по поводу условия «с избыточностью меньше п».
§4.L. Квадраты и степени Стинрода
633
Применяя теорему к первым двум случаям п = 1, 2, мы получаем
следующие алгебры когомологий:
JC(Z2,1) : Z2[i],
K(Zp,l): AZji[i]®Zp[j8i],
K(Z2, 2) : Z2[t, Sq4, Sq2Sq4, Sq^Sq'i, ...],
K(Zp, 2) : Zp[i, PP1Pi, I3PpP}I3l, /3PpVp]j8i, ...] ®
® AZ|i[j8i, P1^, pPp^t, Pp2ppPlf5i, ...].
Из этой теоремы следует, что допустимые мономы в j^p линейно
независимы, а потому образуют базис для jrfp как линейного пространства над
Zp. Действительно, если бы некоторая линейная комбинация допустимых
мономов была равна нулю, то она давала бы нуль при применении к
классу in, но если мы выберем п больше, чем избыточность каждого монома
в этой линейной комбинации, то это будет противоречить противоречило
бы тому, что алгебра H*(K(Zp, n); Zp) свободна. Несмотря на то что
мультипликативная структура алгебры Стинрода весьма сложна, соотношения
Адема предоставляют способ выполнять вычисления алгоритмически,
систематически приводя все произведения к суммам допустимых мономов.
Доказательство линейной независимости допустимых мономов,
использующее более элементарную технику, можно найти в [66].
Ещё одно следствие теоремы состоит в том, что все когомологические
операции с коэффициентами в Zp являются многочленами от операций
Sql при р = 2 и многочленами от Р' и /3 при нечётном р, как видно
из предложения 4.L.I. Мы можем также сделать вывод, что j4v состоит
в точности из всех когомологических операций с коэффициентами в Zp:
которые стабильны, т. е. коммутируют с надстройкой. Действительно,
рассмотрим отображение E/C(Zp, п) —► K(Zp, п + 1), для которого
индуцированное отображение когомологий переводит tn+1 в надстройку над t„. Этс
отображение индуцирует изоморфизм в гомотопических группах я, пр^
i ^ 2п и сюръекцию при i = 2п + 1 согласно следствию 4.24, поэтому тс
же самое верно для гомологии и когомологий. Тогда, если устремить г
к бесконечности, предел limH*(X(Zp> n); Zp) существует в строгом смыс
ле. С одной стороны, этот предел —в точности множество стабильны)
операций согласно предложению 4.L.1 и определению стабильной опера
ции. С другой стороны, из предыдущей теоремы следует, что этот преде;
равен .^р, так как эта теорема утверждает, что все элементы алгебрь
H*(K(Zp, n); Zp) размерности ниже 2п единственным образом представ
ляются в виде сумм допустимых мономов, применённых к t„.
Давайте теперь объясним, почему условие «с избыточностью мень
ше п» в этой теореме естественно. Для монома Sq1 =SqhSqh.-- определ
ние избыточности е{1) можно переписать как уравнение i} =e(/) +12
634
Глава 4. Теория гомотопий
4- i3 4-... Таким образом, если е(7) >п, то мы получаем ^ > |Sq'2Sq,3...(i,j)|,
следовательно, Sq'O,,) = 0. А если е(/) = п, то Sq'OJ = CSq'2Sql3...(iM))2
и либо операция Sql'2Sqh... имеет избыточность меньше п, либо она
имеет избыточность, равную п, и мы можем повторить процесс, написав
Sq,2Sq,3...(i„) = (Sq,J...(in))2, и т. д. В итоге получим уравнение Sq\tn) =
= (SqJ(in)) , где e(J) < n, так что Sq'(tn) уже принадлежит алгебре,
порождённой элементами SqJ(i„), для которых e(J) < п. Ситуация для
нечётного р аналогична. Для допустимого монома Р1 = (3E]Pl][3F2Pl2...
определение избыточности даёт 2\г = е(7) 4- е2 4- 2(р - l)i2 4-... Поэтому
если e(J) > п, то мы должны получить Р^Ьц) = 0, а если e(J) = п, то либо
Р'Он) — степень (PJ(in))p , e(J) < п, либо если Р7 начинается с /3, то
p'(iri) =/3((PJ(t,l))p") =0 согласно формуле |3(х"1) = rnx'^'^x), которая
имеет место, когда |х| четно, и мы можем считать, что это так, поскольку
иначе (PJ(in))p =0 согласно коммутативности ^-произведения.
Имеется другой набор соотношений между квадратами Стинрода,
эквивалентных соотношениям Адема и несколько более лёгкий для
запоминания:
Y,CJkSq2n~k-j-lSqn+j = 0.
j
При к = 0 это будет просто соотношение Sq2n~lSqn = 0, а случаи при fc > 0
получаются из него посредством треугольника Паскаля. Например, из
Sq7Sq4~0 мы получаем следующую таблицу соотношений:
Sq7Sq4 = 0,
SqeSq* 4- Sq^q3 = 0,
Sq5Sq4 4- Sq7Sq2 = 0,
Sq4Sq4 + SqsSq:* 4- SqbSq2 + Sq7Sq] = 0,
Sq:,Sq4 + Sq7Sq°= 0,
Sq2Sq4 4- Sq:,Sq3 4- Sq6Sq° = 0,
Sq*Sq4 4- Sq3Sq2 + Sq5Sq° = 0,
Sq°Sq4 + SqlSq* 4- SqzSq2 4- Sq*Sql 4- 5q45q° = 0.
Эти соотношения записаны не в самой простой форме. Например,
SqsSq3 = 0 в четвёртой строке и Sq3Sq2 = 0 в седьмой строке — частные
случаи соотношения Sq2n~[Sqn = 0. Для степеней Стинрода имеют место
аналогичные соотношения ]Г]С^Ррп~*";'"1РгН";'= 0, которые получаются из
;'
основного соотношения рРп~1р" — 0. Мы оставляем заинтересованному
читателю доказательство того, что эти соотношения следуют из
соотношений Адема.
Построение квадратов и степеней
Теперь мы обратимся к построению квадратов и степеней Стинрода
и доказательству их основных свойств, включая соотношения Адема. Как
§4.L. Квадраты и степени Стинрода
635
мы увидим, это построение тесно связано с тем фактом, что когомологии
являются отображениями в пространства Эйленберга—Маклейна. Случай
р = 2 несколько проще, чем случай нечётного р, поэтому в первой части
изложения мы считаем, что р равно 2, всякий раз, когда есть
существенное различие между этими двумя случаями.
Прежде чем изложить подробную конструкцию, опишем идею в
самом простом случае р = 2. Квадрат (относительно w-произведения) а2
элемента a€Hn(X;Z2) можно рассматривать как композицию X —* X х
х X-+K(Z2,2n), где первое отображение— диагональное отображение,
а второе отображение представляет внешнее произведение ах а. Так как
мы рассматриваем коэффициенты Z2, w-произведение и внешнее
произведение являются строго коммутативными, поэтому если Т: X х X —>
-* X х X — отображение, переставляющее два множителя, Т(хих2) =
= Qc2, хх), тоГ(аха) = ах а. Если представлять себе ах а как
отображение X х X —> iC(Z2, 2п), то это означает, что существует гомотопия ft
отображения ахав отображение (a x а)Т. Если мы после гомотопии ft
сделаем ещё гомотопию ftT, то получим гомотопию отображения ахав
отображение (а х а)Т, а затем —в отображение (a x а)Т2 — ах а, т.е. петлю,
состоящую из отображений X х Х-*К(7А2, 2п). Мы можем рассматривать
эту петлю как отображение S1 х X х X -* K{Z2i 2п). Если гомотопия /г
выбрана подходящим образом, то петля отображений будет гомотопна
нулю, т. е. её можно продолжить до отображения D2 х X х X -*К(7А2, 2п).
Если рассматривать D2 как верхнюю половину сферы S2, то это даёт
половину отображения S2 х X х X —* K(Z2, 2n), и мы снова получаем
другую половину посредством композиции с Т. Действуя аккуратно, этот
процесс можно повторить бесконечно много раз и получить отображение
S°° х X х X—>K(Z2) 2п), которое каждую пару точек (5, хь х2) и (-5, jc2, jcj)
переводит в одну и ту же точку в K(Z2, 2п). Это означает, что когда мы
берём композицию с очевидным отображением 5°° х X -» 5°° х X х X,
существует индуцированное факторотображение кР°° х X -* iC(Z2, 2п).
Это отображение представляет класс в Я2'1 (RP00 х X\Z2).
Воспользовавшись формулой Кюннета и тем фактом, что НХ(ЖР°°; Z2) является кольцом
многочленов Z2[co], этот класс когомологии в Н2п(Ш>°° х X\Z2) можно
записать в виде J] w"~' x ah где а{ €Я"+|(Х;Щ. Тогда мы полагаем по
i
определению Sql (a) = a,.
Отображение
S°°xXxX-»IC(Z2>2h)
будет строиться поклеточно, поэтому удобно убрать все ненужные клетки.
Это делается заменой X х X на приведённое произведение X Л X и
факторизацией по поперечному срезу S°° в S°° x ХлХ. Дальнейшее
упрощение будет использовать естественность, чтобы свести ситуацию к случаю
X = K(Z2,n).
636
Глава 4. Теория гомотопий
Перейдём к самой конструкции. Для пространства X с отмеченной
точкой х0 пусть ХАр обозначает X Л ... Л X — приведённое произведение
р экземпляров пространства X. Рассмотрим отображение Т: ХАр -*ХАр,
заданное формулой Т(хг, ...,хр) = (х2,..., хр, jfi), которое циклически
переставляет множители. Заметим, что при р = 2 это отображение
—просто транспозиция Оъ х2) *-> (х2) х}). Отображение Т порождает действие
группы Zp на ХАр. Есть также стандартное действие группы Zp на сфере
S°°, рассматриваемой как объединение единичных сфер S2n~l в Сп:
образующая группы Zp поворачивает каждый множитель С на угол 2п/р; фак-
торпространство для этого действия —бесконечномерное линзовое
пространство L00 либо RP°° при р = 2. Тогда на произведении S°° x ХАр есть
диагональное действие gCs,*)1^ (g(s),gOO) для#ейр. Пусть ГХ
обозначает пространство орбит (S00 х ХАр)/7,р этого диагонального действия. Это
пространство — то же самое, что конструкция Бореля S°° x7 ХДр,
описанная в §3.G. Проекция S°° x ХАр -*S°° индуцирует проекцию п: ГХ ->/,°°,
причём n~l(z) = ХАр для всех zeL00, так как действие группы Zp на 5°°
свободное. В действительности эта проекция ГХ —* L°°— локально
тривиальное расслоение, хотя нам этот факт не будет нужен, а потому мы
оставляем его доказательство в качестве задачи. Действие группы Zp на
ХАр оставляет неподвижной отмеченную точку х0 еХЛр, поэтому
включение S°° х {х{)} <—> S°° х ХАр индуцирует включение L°° <—> ГХ. Композиция
L°° <—»ГХ -* L°° — тождественное отображение, поэтому на языке локально
тривиальных расслоений это подпространство L°° с ГХ является сечением
расслоения. Пусть АХ обозначает факторпространство ГХ/L00,
полученное при стягивании сечения L°° в точку. Заметим, что слои ХАр в ГХ всё
ещё остаются вложенными в факторпространство ЛХ, так как каждый
слой пересекает сечение L°° в единственной точке.
Если мы заменим в этом определении S°° на S1, то получим
подпространства ГгХ С ГХ и Л!Хс АХ. Все эти пространства имеют
естественные CW-структуры, если X — CW-комплекс, у которого х0 — нульмерная
клетка. А именно, L°° снабжается стандартной CW-структурой с одной
клеткой в каждой размерности. Она поднимается до CW-структуры на
S°° с р клетками в каждой размерности, и тогда Т свободно переставляет
клетки произведения S°° x ХЛр, поэтому на ГХ имеется индуцированная
факторструктура CW-комплекса. Сечение L°° с ГХ — подкомплекс,
поэтому факторпространство АХ наследует CW-структуру из ГХ. Например,
если п-мерный остов комплекса X —это сфера S" с её обычной CW-струк-
турой, то рп-мерный остов комплекса АХ — это сфера Spn с её обычной
CW-структурой.
Заметим также, что Г, Г1, Л и Л1 —функторы: отображение
f:(X,x0)->(Y,y0)
индуцирует отображения Г/: ГХ-*ГУ и т.д. очевидным образом.
§ 4.L. Квадраты и степени Стинрода
637
Для краткости будем записывать H*(-;Zp) просто как #*(—). Для
п > О пусть Кп обозначает CW-комплекс K(Zpt п) с (п - 1)-мерным
остовом из одной точки и n-мерным остовом Sn. Пусть t e Нп(Кп) —
канонический фундаментальный класс, описанный в обсуждении после теоремы
4.57. С точки зрения обозначений будет удобно рассматривать элемент
а<ЕНп(Х) ещё и как отображение а: X—>КЛ, для которого a*(t) = a. Здесь
мы предполагаем, что X — CW-комплекс.
Из §3.2 нам знакомо приведённое р-кратное внешнее
произведение H*U)®P -^H*(XAp), где Н*(Х)0р обозначает р-кратное тензорное
произведение Н*(Х) на себя. Это отображение внешнего произведения
Н*(Х)®Р —► Н*(ХАр) является изоморфизмом, так как мы используем
коэффициенты в Zp. Помня об этом изоморфизме, мы будем использовать для
р-кратных внешних произведений в Н*(ХАр) обозначение al ® ...®ар>
а не aj x ... х ар. В частности, для каждого элемента аеНл(Х), п>0, мы
получаем его р-кратное внешнее произведение а®р еН*(ХАр). Нашей
первой задачей будет построение элемента А(а) е Нрп(ЛХ), ограничением
которого на каждый слой ХАр С ЛХ является а®р. В силу естественности
достаточно построить A(i) ЕНрп(ЛКп).
Ключевой момент в построении элемента A(i) —тот факт, что T*(i®p) =
= t®p. В терминах отображений КАр —>Крп это означает, что композиция
i0p Г гомотопна t®p с сохранением отмеченных точек. Такую гомотопию
можно построить следующим образом. Остов размерности рп для КАр —
это (Sn)Ap = Spn, причём Т переставляет множители циклически. Если
представлять себе Sn как (Sl)An, то перестановка Т является
произведением (р — 1)п транспозиций соседних множителей, поэтому Т имеет
степень (—1)(Р~1)л на Spn. Если р нечётно, то эта степень равна 4-1,
поэтому ограничение отображения Т на этот остов гомотопно
тождественному отображению, следовательно, отображение t®p T гомотопно t0p на
этом остове. Это рассуждение проходит также для р = 2, поскольку знаки
в этом случае несущественны, так как мы имеем дело с отображениями
S2"—>К2п, а7Г2/7(/С2Л)=22. Если задана гомотопия 1®р Г^ч®р нарп-мерном
остове, то нет никаких препятствий для продолжения этой гомотопии на
все многомерные клетки е1 х (0,1), так как 71((Крп) =0 при 1>рп.
Гомотопия i®p Т^а®р: КАр^>Крп определяет отображение Г1^ —>Крп,
так как ГТХ — факторпространство произведения / х ХЛр при
отождествлениях (0, х) ~ (1, ГО)). Эта гомотопия сохраняет отмеченные точки,
поэтому отображение Г1^ —>Крп опускается до факторотображепия
Aj: Л Кп —> Крп.
Так как Кп получается из Sn приклеиванием клеток размерности больше п,
пространство АКи получается из А1Кп приклеиванием клеток
размерности больше рп 4-1. Тогда нет никаких препятствий к продолжению
отображения Аг до отображения А: АКп^>Крп, так как тг,-(КрП)=0 при i>pn.
638
Глава 4. Теория гомотопий
Отображение Я даёт требуемый элемент A(i) € Hpn (ЛК„), так как
ограничение отображения Я на каждый слой К*р гомотопно i®p. Отметим, что
это свойство определяет Я однозначно с точностью до гомотопий, так как
отображение ограничения Нрп(АКп) —>Нрп(К*р) инъективно, поскольку
pn-мерный остов комплекса АКп содержится в К*р. Нам придётся
воспользоваться этим рассуждением в доказательстве ещё раз, поэтому будем
ссылаться на него как на «рассуждение о единственности».
Для любого а€Ип(Х) пусть Х(а) обозначает композицию
АХ^АКп^Крп.
Её ограничением на каждый слой ХАр является а®р, так как при
ограничении Ла на каждый слой получается а®р.
Теперь мы готовы определить некоторые когомологические
операции. Определим включение /,°° х X <—> ГХ как факторотображение
диагонального вложения S00 х X <—> S°° x ХЛр, заданного формулой (s,x) —*
—► (s, х,..., х). Взяв композицию с факторотображением ГХ —»ЛХ, мы
получим отображение V: L00 х X —►ЛХ, индуцирующее отображение
V*: Я*(ЛХ) - H\L°° х X) w H*(L°°)®H*(X).
Для любого а€Н"(Х) элемент V*U(a)) e Hpn(L°° x X) можно записать
в виде
V*(A(a))=J]w(p.I)n.I-®0|.(a)>
i
где соj — образующая группы Hj(L°°), а 0|(а)еЯп"4"Ч^г). Таким образом, б,-
увеличивает размерность на i. При р = 2 в выборе образующей coj нет
неопределённости. Для нечётного р в качестве а>} мы выбираем класс,
двойственный одномерной клетке комплекса L°° со стандартной
клеточной структурой, затем мы берём в качестве со2 элемент /За>ь где /3 —
гомоморфизм Бокштейна, и далее полагаем со2} =со}2и co2}^\~^>\<^2^
Ясно, что 0t-— когомологическая операция, так как 0,-(a) = a*(0,-(O).
Для р = 2 мы полагаем Sql{a) = 0,(a). Для нечётного р мы покажем, что
0,- = 0, кроме случаев, когда f = 2/с(р - 1) или 2к(р - 1) + 1. Операция
Рк будет определена как некоторая константа, умноженная на 02к(р-п>
а #2к(р-1)+1 будет константой, умноженной на /ЗРк, где /3 — гомоморфизм
Бокштейна по модулю р.
| Теорема 4.L.12. Операции Sql удовлетворяют свойствами 1—7.
Доказательство. Мы уже отметили, что 0, — когомологические
операции, поэтому свойство 1 выполняется. Поскольку когомологические
операции не могут уменьшать размерность, мы получаем 0, =0 для i <0.
Кроме того, 0, = 0 при i > (р - 1)п, так как множитель со(р_1)п_{ в этом
случае обращается в нуль. Из основного свойства, что Л.(а) при ограничении
§4.L. Квадраты и степени Стинрода
639
на каждый слой даёт а®р, следует, что 0Ср_1)м(а) = ар, так как со0 = 1. Это
доказывает свойство 5.
Чтобы доказать свойство аддитивности 2, мы покажем, что A (a -f fi) =
= А(а) 4- А(/3), используя следующую диаграмму:
ЛХ > Л(Х х X) *• Л(К„ х Кп) *- АКи
Y ЛахЛ/3 ,^4.,ч>-
ЛХ х ЛХ -^ ЛКМ х Л/С„ — ^- Л/С
Р"
Здесь Д — общее обозначение для диагональных отображений х—> (х, х).
Они связывают внешнее произведение с ^-произведением посредством
формулы A*((£ ® г/0 = ¥> ^^- Два вертикальных отображения без пометок
индуцированы отображением
(s,*i,yi,...,*p,yp) -> (5,х1,...,Хр,5,у1,...,Ур).
Очевидно, что коммутативен центральный квадрат в диаграмме, а также
левый и верхний справа треугольники. Чтобы доказать, что оставшийся
треугольник коммутативен, достаточно показать это в случае, когда мы
рассматриваем ограничение на слой (Кп х Кп)Лр, согласно рассуждению
о единственности, использованному ранее, так как (Кп х Ки)Ар содержит
рп-мерный остов комплекса А(Кп х Кп). На слое два пути в Крп задаются
отображениями i®p ® 1 4-1 ® t®p и (t ® 1 4-1 ® t)®p. Они равны, так как
возведение в степень р — аддитивный гомоморфизм поля Zp.
Композиция ЛХ—►ЛК,,-—это Л(а4-/5), поэтому композиция ЛХ—^/Срп
вдоль верхней части диаграммы равна А(а4-/3). Идя из ЛХ в Крп вдоль
нижней части диаграммы, получаем А(а) 4-А(/3), так как второй и третий
шаги этой композиции дают А (а) ® 1 4- 1 ® А(/3) и Д*(</> ® я/») = кр w г/;.
Таким образом, А(а + /3) = А(а) 4- А(/3), а из этого следует, что каждое
отображение 0,-— аддитивный гомоморфизм.
Теперь мы обратимся к формуле Картана. Для любого простого р мы
покажем, что А(а w (3) = (-1)р(р"1)т'?/2А(сОА(/3), где т = |а| и л = |]3|. В
случае р = 2 из этого следует свойство 3, так как если мы положим со = сои
а значит, coj = аУ, то
^Sq4a^^)®co"+m-' = V*(A(aw^)) = V*(A(a) wA(j8)) =
= V*(A(a))wV*(A(^))=J]sqJ'(a)®con-Jw^Sq4^)®w'"""'C =
= 2(1] V(a)^Sq4j8))®ft>n+m"f.
640
Глава 4. Теория гомотопий
Чтобы получить формулу А(а ^ /3) = ±А(а)
граммой, очень похожей на предыдущую:
МЛ) 4 ,„ . ,„ Л(аЛ0)
'А(/3), мы воспользуемся диа-
АХ
А(ХлХ)
АХ А АХ
ЛалЛ/?
А(КтЛКп)
АКт Л ЛК„
Л(|,„®1„)
- ЛК„
рт+рп
Композиция АХ —> Крт+рп, идущая вдоль верхней части диаграммы, равна
А(а ^ /3), так как отображение АХ —> ЛКт+п — это А(а ^ /3). Композиция
АХ Л АХ —► Крт+рп — это Я(а) 0 А(/3), поэтому композиция АХ -* Крт+рп
вдоль нижней части диаграммы — это Я(а)^Яф). Коммутативность
квадрата и двух верхних треугольников очевидна из определений. Остаётся
убедиться, что нижний треугольник коммутативен с точностью до
знака (-i)P0>-i)»"i/2# так как (Кт лКп)Др включает (рш + рп)-мерный остов
комплекса А(КШ /\Кп), ограничение на этот слой инъективно на Нрш+рп.
На этом слое два пути по треугольнику дают (i,M ® in)®p и t®p 0 i®p. Они
отличаются перестановкой, которая является произведением (р — 1) +
+ (р - 2) + ... + 1 = р(р - 1)/2 транспозиций соседних множителей. Так
как ьт и i„ имеют размерности тип, эта перестановка приводит к знаку
(__1)/>(р-1)»1л/2 по СВОИСТВу коммутативности ^-произведения. Это
завершает проверку формулы Картана для р = 2.
Прежде чем двигаться дальше, мы должны провести явное
вычисление, чтобы показать, что операция Sq° тождественна на H](Sl). Если
рассматривать S1 как одноточечную компактификацию пространства К
с бесконечно удалённой точкой в качестве отмеченной точки, то
двумерная сфера S1 AS1 становится одноточечной компактификацией
пространства К2. Отображение Т: Sl AS1 —>S] AS1 тогда соответствует отражению
^R2 относительно прямой r = y, поэтому после поворота осей координат
оно превращается в симметрию сферы S2 относительно экватора.
Следовательно, Г1^1 получается из скорлупы I x S2 отождествлением её
внутренней и внешней граничных сфер посредством симметрии относительно
экватора. Диагональ RP1 х S1 с Г1^1 —это тор, полученный из
экваториального кольца J х S1 С J х S2 отождествлением двух его концов
посредством тождественного отображения, так как экватор неподвижен при
рассматриваемой симметрии. Это пространство IRP1 xS1 представляет тот же
§ 4.L. Квадраты и степени Стинрода
641
самый элемент группы H2(TlSl; Z2), что и сферический слой S1 AS1, так
как верхняя половина скорлупы — трёхмерная клетка, граница которой по
модулю 2bF1S1- объединение этих двух поверхностей.
Для образующей aeHl(Sl) рассмотрим элемент V*(A(a)) в
H2(RP°° х S1) % Нот(Н2(КР°° х S1; Z2), Z2).
Базис для H2(M?°° x S1; Z2) представлен подпространствами IRP2 х {х0} и
MP1 х S1. Коцикл, представляющий элемент V*(A(a)), принимает
значение 0 на RP2 х {х0>, так как КР00 х {х0> стягивается в точку в AS1 и А(а)
лежит в H2(ASl). На MP1 x S1 коцикл V*(A(a)) принимает значение 1, так
как, когда А(а) переносится назад в VS1 индуцированным отображением,
он принимает одно и то же значение на гомологичных циклах RPl x S1
и S1 AS1, а именно, 1 согласно определяющему свойству для А(а), так
как a®a£H2(Sl AS1) —образующая. Таким образом, V*(A(a)) = (^1 ®a,
а потому Sq°(a) — а по определению операции Sq°.
Мы воспользуемся этим вычислением, чтобы доказать, что Sq1
коммутирует с надстройкой а, которая определяется формулой сг(а) — е ® а €
€H*(S1 АХ), где е — образующая группы Н1^1), а а€Н*(^0- Мы только
что убедились, что Sq°(е) = е. По свойству 5 Sql (е) = е2 = 0 и Sql (е) — 0 при
i > 1. Тогда формула Картана показывает, что
Sq'"(cr(a)) = Sqf(e®a) = ^Sqj(e)®Sq'"~j(a) = e®Sq'"(a) = cr(Sq'(a)).
Из этого следует, что операция Sq° тождественна на Hn(Sn) для всех
п > 0. Так как Sn —это п-мерный остов комплекса Кп, из этого следует, что
операция Sq° тождественна на фундаментальном классе tn, а потому она
тождественна на всех классах положительной размерности.
Свойство 7 доказывается аналогично: Sq1 совпадает с
гомоморфизмом Бокштейна /3 на образующей coeHl(JRP2), так как обе эти операции
дают со2. Следовательно, Sq1 = /3 на итерированных надстройках над со,
а п-кратная надстройка над RP2 — это (п + 2)-мерный остов комплекса
Теорема 4.L.13. Для квадратов Стинрода выполняются соотношения
Адема.
Доказательство. Идея состоит в том, чтобы имитировать
конструкцию пространства АХ, воспользовавшись группой Ър х Ър вместо Zp.
Соотношения Адема тогда появятся из симметрии группы ZpxZp,
переставляющей два её множителя.
Действие группы Ър х Ър на S00 x S00 задаётся формулой (g, h)(s, О =
= (g(s),h(0), причём факторпространством является L°° x L°°. Имеется
также действие группы Zp x Zp на ХЛр , которое получается, если записать
точки пространства ХЛр как наборы р2 точек О,-,) с индексами i и ;,
меняющимися от 1 до р, а затем разрешить первой группе Ър действовать
642
Глава 4. Теория гомотопий
на первом индексе, а второй группе Zp — на втором. Факторизация по
диагональному действию группы Zp х Zp на S°° x S°° x ХАр даёт факторпро-
странство Г2Х. Оно проектируется на L00 x L°° с сечением, и стягивание
этого сечения даёт А2Х. Слои проекции A2X~+L°° х L°° —этоХДр\ так как
действие группы Zp x Zp на S00 x S°° свободное. Мы можем также
получить А2Х из произведения S00 x S°° x Хр , сначала стянув подпространство
точек, имеющих по крайней мере одну координату по X, равную
отмеченной точке х0, а затем профакторизовав по действию группы Zp x Zp.
Полезно сравнить А2Х с Л(ЛХ). Последнее пространство —фактор-
пространство произведения S°° x (S00 х Хр)р, в котором сначала
отождествлены все точки, имеющие по крайней мере одну координату по X,
равную xQi а затем произведена факторизация по действию веночного
произведения1 Zp \Ър. Это группа порядка pp+l, которая определяется
посредством расщепимой точной последовательности
o-z|;-zp;zp-zp-o,
где сопряжение элементами факторгруппы Zp задаётся циклическими
перестановками р множителей Zp в Zp В координатах
(5, tb хи>..., xlpi..., tp, хрЪ ..., хрр)
множитель Zp с номером i в Ър действует на блоке (t,, xn, ..., xip), и
факторгруппа Zp действует циклическими перестановками индекса i и
вращением по координате s. Существует естественное отображение А2Х —>
-*Л(ЛХ), индуцированное отображением
(S, t, Jfj], ..., Xip, ..., Xpi, ..., Xpp) ►—> (S, t, Хц, ..., Л"1р, ..., t, Jfpi, ..., Xpp).
В Л2Х происходит факторизация по действию группы Zp x Zp. Она
является подгруппой в Zp I Zp, полученной при ограничении действия
факторгруппы Zp на группе Zp на диагональную подгруппу Zp cZjJ, где это
действие становится тривиальным, поэтому мы получаем прямое
произведение Zp х Zp.
Так как достаточно доказать, что соотношения Лдема
выполняются для класса i е Нп(Кп), мы возьмём X = Кп. Имеется отображение
Я2: А2Кп -* Кр2п, ограничение которого на каждый слой —это t®p . Оно
строится тем же самым методом, которым мы воспользовались для
построения Я. Начинаем с отображения, представляющего t®p в некотором
слое, затем продолжаем его на ту часть А2Кп, которая проектируется
в одномерный остов комплекса L00 x L°°, и, наконец, продолжаем его по
индукции на клетки комплекса А2Ки более высокой размерности,
используя тот факт, что Кр2п является пространством Эйленберга—Маклейна.
По англ. wreath product. — Прим. ред.
§4.L. Квадраты и степени Стинрода 643
Отображение А2 можно включить в диаграмму
L^xL^x Кп —U- Л2К„ — ^ Кр2п
L°°xAK„—^Л(ЛК„)
где отображение V2 индуцировано отображением (s, г, х) -^ (s, f, х, ..., х)
и отображение без пометки —это отображение, определённое выше.
Ясно, что квадрат коммутативен. Коммутативность с точностью до гомото-
пии треугольника следует из того факта, что отображение Я2 определено
однозначно, с точностью до гомотопии, его ограничениями на слои.
Элемент V*А*(0 можно записать в виде ^ cor <8> <os ® iprs> и мы утвер-
ждаем, что элементы yrs удовлетворяют соотношению симметрии iprs =
= (-l)rs4 p(p_1)'l/2^sr. Чтобы проверить это, мы воспользуемся
коммутативной диаграммой
L^xL^x Кп —^ A2K„
I00 х L°° х К„ —i- A2i<:n
где отображение т слева меняет местами два множителя L00, а
отображение т справа индуцировано перестановкой двух множителей S00
в S00 х S°° х К*р и перестановкой множителей приведённого
произведения К„, меняющей местами оба индекса в наборе р2 точек (x(J). Эта
перестановка является произведением р(р - 1)/2 транспозиций, по одной
для каждой пары (t,j), где 1 ^ i<j ^p, поэтому в слое класс <,®р переходит
в (—i)P(p-i)n/2t®p по свойству единственности для Я2 это означает, что
т*А*(0 = (-1)р(р_1)п/2А*(0. Из коммутативности квадрата тогда получаем
(-l)P<p-"n/2v*A*(t) = у*т*А*2(0 = t*V*A;(i) = 5](-l)rV,® cor® V„,
где последнее равенство следует из свойства коммутативности внешних
произведений. Соотношение симметрии iprs = (-1)''5+р(р~1)м/2(,9лТ
доказывается перестановкой индексов г и s в последней сумме.
Если мы вычислим V*A*(t), используя нижний путь в приведённой
ранее диаграмме, содержащей отображение А2, то получим
«J
644 Глава 4. Теория гомотопий
Теперь мы рассмотрим случай р = 2, таким образом, 0,= Sql для всех i.
Формула Картана преобразует последнюю из написанных выше сумм в
сумму вида
]Гсо2""' ® Sqk{ojn~j) ® Sq(-kSq*(i).
ij,k
Подставляя значения для Sqk{con~J), вычисленные в обсуждении,
предшествующем примеру 4.L.3, получаем
X! Сп-;^2П~' ® w"~j+* ® Sqf-kSq^(О-
Чтобы записать эту сумму более симметрично по отношению к двум
членам со, положим п — j + k = 2n — t. Тогда мы получаем
Ввиду свойства симметрии для iprs, которое принимает вид tprs = ц$г для
р = 2, перемена местами i и I в этой формуле не меняет её. Следовательно,
мы получаем соотношение
Оно выполняется для всех n, i и £, и идея состоит в том, чтобы выбрать
эти числа так, чтобы в левой части этого равенства был только один
ненулевой член. Для данных целых чисел г и s положим п = 2Г - 1 + s
и £ = n + s; тогда С"*;~ = С^ГД,: ,.}. Если г достаточно велико, то этот
биномиальный коэффициент равен 0 по модулю 2, кроме случая, когда
j =s. Дело в том, что двоичная запись числа 2Г - 1 целиком состоит из
цифр 1, поэтому в двоичной записи числа 2Г - 1 - (j - 5) будет стоять 0 на
тех местах, где в записи числа j — s стоят 1, следовательно, мы получаем
соответствующий множитель С^ = 0 в C^i-c -s)* Таким образом, для пи(,
выбранных, как показано выше, соотношение (*) принимает вид
Sq'Sq40 ^cZzlZt'-'Sq'+'-JSqtb) ^C^^Sq^SqHO,
j )
где последнее равенство возникает из общего соотношения С^ = Схх'у.
Последний шаг —доказательство того, что Cl^Js_j_l = C^.i7, если
i < 2s. Оба эти биномиальных коэффициента равны нулю, если i < 2j. Если
i ^ 2j, то мы получаем 2) ^ i < 25, поэтому j < 5, а значит, 5 — j — 1 ^ 0.
Тогда член 2Г не влияет на Cl~^}s_.v если г достаточно велико, так как этот
член 21 даёт только одну цифру 1 в двоичной записи числа 2Г +s — j - 1,
стоящую далеко слева от всех ненулевых цифр в двоичной записи чисел
s — j — 1 и i — 2j.
§4.L. Квадраты и степени Стинрода
645
Это даёт соотношения Адема для классов i размерности п = 2Г - 1-f s,
где г велико. Следовательно, эти соотношения выполняются для всех
классов такой размерности в силу естественности. Так как мы можем
несколько раз сделать надстройку, чтобы любой класс приобрёл размерность
такого вида, соотношения Адема должны выполняться для всех классов ко-
гомологий. D
Степени Стинрода
Нам остаётся проверить аксиомы и соотношения Адема для степеней
Стинрода для нечётного простого р. К сожалению, это гораздо сложнее,
чем в случае р = 2, в основном потому, что нужно быть очень
осторожными при вычислении многочисленных коэффициентов в Zpi которые здесь
возникают. Даже для невинно выглядящей аксиомы Р° = 1 потребуются
три страницы вычислений нормализационных констант, чтобы
убедиться, что эта аксиома выполняется. Желательно найти менее запутанное
доказательство.
I Лемма 4.L.14. в{ = 0, за исключением случаев, когда i = 2/с(р — 1) или
2fc(p-l) + l.
Доказательство. Так как р простое, группа автоморфизмов поля Ър
есть группа Z* его ненулевых элементов, причём эта группа
циклическая порядка р — 1; пусть г — её образующая. Определим отображение
Ч>: S00 х ХАр —>S°° х ХЛр, переставляющее сомножители Х; в ХЛр по
правилу i/?(s, Xj — (sr, Xrj), где нижние индексы рассматриваются как вычеты
по модулю р, а отображение sr возводит в степень г каждую координату
вектора 5, рассматриваемого как единичный вектор в С°° (с последующей
нормировкой до вектора единичной длины). Если теперь у — образующая
действия Zp на S00 х ХЛр, то имеем
¥>(r(s,X,-)) = 4>b2nUps.Xhl) = (e2rm7V,Xrj_r) = rXs,X,)).
Значит, ip переводит орбиты в орбиты и тем самым индуцирует
отображения (р: ГХ —» ГХ и у: АХ -* ЛХ. Ограничивая на первую координату,
получаем также индуцированное отображение у: L°° —>L°°. Если положить
X = Кп, то эти отображения включаются в следующую диаграмму:
I00 х Кп -2-* ЛК„ -±- Kpn
т
L°° х Кп -^ \Кп
В этой диаграмме квадрат, очевидно, коммутативен, а треугольник
коммутативен с точностью до гомотопии и знака (-1)п. В самом деле,
последнее достаточно проверить на pn-остове пространства (S")Ap, a на
нём отображение у является нечётной перестановкой множителей S":
646
Глава 4. Теория гомотопий
это циклическая перестановка чётного порядка р — 1, а перестановка двух
множителей S" имеет знак 1, если п четно, и — 1, если п нечётно.
Предположим сначала, что п четно. Тогда коммутативность
диаграммы означает, что сумма S/^Cp-i)»-» ® ^'М инвариантна относительно
отображения ^*®1, откуда Ч>* (со{р_1)п_{) = со{р_1)п_1, если #,(0^0.
Отображение у> индуцирует на л{ (L00) (а тем самым и на H^L00) и Н1 (X00, Zp))
умножение на г: со - 1 —► га>{. Поскольку по построению а>2 было
результатом применения гомоморфизма Бокштейна к а>1} оно также умножается
на г. Выберем г таким образом, чтобы оно имело порядок р — 1 вР;
тогда у>*(а>£) = со( в том и только том случае, когда общее количество
сомножителей сох и со2 в со^ кратно р — 1. Если со( = со*, это означает, что
I = (р - 1)п — z = 2/с(р - 1), а если а>( = со - lco^'1, то это означает, что
£ = 2/с (р — 1) — 1 — на единицу меньше. Решая эти уравнения
относительно z, получаем, что i — ^n -2/с)(р- 1) или z = (n -2/с)(р — 1)4-1. Поскольку
п четно, это означает, что i сравнимо с 0 или 1 по модулю 2(р — 1), что и
требовалось.
Если п нечётно, то условие ^*(со^) = cot превращается в (/?*(^) = -а>(.
В циклической группе 7/ элемент —1 — единственный элемент порядка 2,
и он равен (р — 1)/2-й степени образующей, так что общее количество
сомножителей сох и со2 в со( должно быть равно (2/с +1)(р — 1)/2 для
некоторого целого к. Отсюда следует, что£ равно (р — l)n —z = 2(2fc + l)(p- l)/2
или (p-l)n-z = 2(2fc + l)(p-l)/2-l, откуда! равно (n-2fc-1)(р-1)
или (п — 2fc — 1)(р - 1) + 1. Так как п нечётно, отсюда опять следует, что i
сравнимо с 0 или 1 по модулю 2(р - 1). D
Так как 0О: Нп{Х) -*Нп(Х) — когомологическая операция,
сохраняющая размерность, она должна быть некоторым гомоморфизмом
коэффициентов Zp —► Zp, т.е. умножением на некоторый элемент ап € Zp. Мы
утверждаем, что эти элементы ап удовлетворяют соотношениям
а«+п = (-l)p(p-1)nm/2aman и ап = (-lyXp-'Mn-i)/^
Чтобы убедиться в этом, вспомним формулу
A(aw0) = (-l)^-1)m,,/2A(a)A(j8)
для \а\=т и |/3| =п. Из определения операций 0,- тогда следует, что
d0(a\j /3) = (-l)p(p"~I)n,n/20o(a)0o(/3)> и это даёт первую часть
утверждения. Вторая часть следует из неё индукцией по п.
Лемма 4.L.15. Для т = (р — 1)/2, т. е. р = 2т 4-1, выполняется
равенство а{ =±т\.
Доказательство. Достаточно вычислить 0о(а), где а—любой
ненулевой одномерный класс, поэтому проще всего выбрать класс а так, чтобы
он был образующей группы Hl(Sl), скажем, образующей, возникающей
из образующей группы Hl{Sl\ Z). Это определяет а с точностью до знака.
Так как Hl(Sl) = 0 при i > 1, мы получаем 0,(а) = 0 при z > 0, поэтому
§4.L. Квадраты и степени Стинрода
647
определяющая формула для в0(а) имеет вид V*(A(a)) = сор^1 0 #0(а) =
= aicop-i ® а в НР(ЬЖ х 51). Чтобы вычислить аь можно без вреда
заменить L°° на конечномерное линзовое пространство, скажем, на Lp,
р-мерный остов комплекса L°°. Таким образом, мы можем ограничить
расслоение AS1 —* L°° до расслоения APSX —*LP с теми же самыми слоями
(S!)Ap = Sp. Мы рассматриваем S1 как одноточечную компактификацию
пространства Ж с отмеченной точкой—добавленной бесконечно
удалённой точкой, и тогда (S1)Ap превращается в одноточечную
компактификацию пространства Rp, на которой Zp действует циклическими
перестановками координат в Rp, сохраняя начало координат и бесконечно
удалённую точку. Это действие определяет расслоение rpSl —* Lp со слоями
Sp, содержащими нулевое сечение и сечение на бесконечности, и APS]
получается в результате стягивания сечения на бесконечности. Мы можем
также описать ApSl как одноточечную компактификацию дополнения
к сечению на бесконечности в rpS!, так как базовое пространство Lp
компактно. Дополнение к сечению на бесконечности — это расслоение
Е —* Lp со слоями Жр. В общем случае одноточечную компактификацию
локально тривиального расслоения Е над компактной базой со слоями
Rn называют пространством Тома Т(Е) расслоения, а класс в //П(Т(£)),
ограничение которого на одноточечную компактификацию каждого слоя
Rn является образующей группы Нп, называют классом Тома. В нашей
ситуации А (а) —такой класс Тома.
Наша первая задача — построить подрасслоения E0tElt ...,EJU в Е,
где Е0 имеет слой R, а остальные Ej имеют слой R2, таким образом,
р = 2га + 1. Расслоение Е происходит из линейного преобразования Т:
Шр —*ЖР, переставляющего координаты циклически. Мы угверждаем, что
существует такое разложение
^р = ур0ФУ,Ф...еурш,
где пространство V0 одномерно, а остальные пространства Vj
двумерные, что T(Vj) =Vj для всех ;, причём отображение Т\ V0 тождественное,
а T\Vj; —поворот на угол 2nj/p для j > 0. Таким образом, Т определяет
действие группы Zp на V,, и мы можем определить Ej точно так же, как
было определено Е, т. е. как факторпространство (Sp x Vj)/Zp
относительно диагонального действия.
Простой способ получить разложение IRP = V0 ф V, ф ... Ф Vm состоит
в том, чтобы рассмотреть Rp как модуль над областью главных
идеалов R[t], положив tv = T(v) для v e Rp. Тогда Жр как модуль
изоморфен модулю R[f]/(tp — 1), так как Т переставляет координаты
циклически; это приводит к отождествлению стандартных базисных
векторов vu...tvp в Rp с 1, г,..., tp~]. Многочлен tp - 1 разлагается над С
на линейные множители t - е27Г,;/р для j = 0, ..., р - 1. Если объединить
комплексные сопряжённые множители, то это даёт разложение над В:
648
Глава 4. Теория гомотопий
tp - 1 = (t - l)n1^;^m(t2 - 2(cos(fj)t + 1), где ifj = 2nj/p. Эти
множители—неприводимые многочлены со старшим коэффициентом 1, поэтому
модуль R[t]/(tp — 1) разлагается в прямую сумму
R[r]/(r-l) 0 K[t]/(t2-2(cos^)t+l)
согласно теореме о структуре модулей над областью главных идеалов.
Этому разложению соответствует разложение
Шр = VoGVi©...©^,
где T(Vj-) с V;. Здесь VQ соответствует модулю R[t]/(t - 1) «1R с
тождественным действием t, а V, при ; > 0 соответствует модулю
R[t]/(t2-2(cos^;)t+l).
Последний модуль изоморфен плоскости R2, на которой t действует как
поворот на угол (/?;, поскольку характеристический многочлен этого
поворота, как показывают простые вычисления, равен t2 - 2(cos(/?;)t + 1,
следовательно, этот поворот удовлетворяет соотношению t2 - 2(cos y>j)t + 1 =
= 0, таким образом, существует гомоморфизм модулей
IR[t]/(t2 - 2(costpfit + 1) -* R2,
который, очевидно, является изоморфизмом.
Из разложения Rp = VQ 0 VY 0 ... 0 V,„ и действия Г на каждом
множителе легко видеть, что все векторы, которые Т оставляет
неподвижными, лежат на прямой V0. Векторы (х, ...,х) остаются неподвижными
при действии Г, поэтому пространство VQ должно быть этой диагональной
прямой.
Теперь мы вычислим классы Тома для расслоений Е;-. Это легко
сделать для расслоения Е0> которое является произведением Lp х R, поэтому
проекцию Е0 -* R одноточечная компактификация преобразует в
отображение Г(£0) —►S1, и мы можем при помощи индуцированного
отображения перенести назад выбранную образующую aeHl(Sl) в класс Тома
для Е0. Остальные расслоения Е} имеют двумерные слои, которые мы
теперь рассматриваем как С, а не как R2. По аналогии с представлением
Ej в виде факторпространства произведения Sp х С при
отождествлениях 0,z) ~ (e2nilpv,e2ni*lpz) мы можем определить расслоение Ё; -* СР'"
со слоем С посредством отождествлений О, z) ~ (Av, A;z) для А е S] с С.
Тогда мы получаем левую половину коммутативной диаграммы
ч - 7
Ej * Ej >- Ех
I \ f \
lp JL*. ср'» -U. СРШ
§ 4.L. Квадраты и степени Стинрода
649
где ограничение факторотображения q на каждый слой является
гомеоморфизмом. Отображения / и / индуцированы отображением SpxC->
—> Sp x С, переводящим (v,z) в (V, z), где vJ означает возведение
каждой координаты v в степень j, а затем пе£енормировку, чтобы
получить вектор единичной длины. Отображение / определено корректно, так
как эквивалентные пары 0,2;) ~ (Av, AJz) в Ё} переходят в пары (v;, z)
и (AJV, Ajz), которые эквивалентны в Ё1.
Так как ограничения обоих отображений q и / на каждый слой
являются гомеоморфизмами, они продолжаются до отображений пространств
Тома, и индуцированные ими отображения переносят класс Тома для Ё^
назад в классы Тома для Ё} и для Еу Чтобы построить класс Тома для Ё},
заметим, что пространство Тома Т(Ёг) гомеоморфно СРШ+1. Именно,
рассмотрим сферу Sp =S2m+l как единичную сферу в Сш+1, и тогда включение
SpxC^Cm+1 х С = Сш+2 индуцирует отображение g: Ёг -»СР"Н\ так как
отношение эквивалентности, определяющее Ёь — это (v, z) ~ (Av, Az) для
AeS1. Очевидно, что g — гомеоморфизм на дополнение к точке [0, ...,0, 1]
в CPm+1, поэтому, отображая бесконечно удалённую точку в Т{Ё{) в точ-
ку [0, ..., О, 1], получаем продолжение отображения g до гомеоморфизма
Т(Ёг) «a CPm+1. При этом гомеоморфизме одноточечные компактифика-
ции слоев расслоения Ёх соответствуют двумерным сферам S2, состоящим
из точки [0,..., 0,1] и точек [v, z] eCPm+I с фиксированной точкой veSp
и меняющимся числом zeC. Каждая сфера S2 — это подпространство СР1
в CPm+1, эквивалентное стандартному подпространству СР1 при
гомеоморфизме пространства СРП1+1, возникающем из линейного
изоморфизма пространства Ст+2, поэтому образующая у группы H2(CPm+1) — это
класс Тома, ограничение которого является образующей группы H2(S2)
для всех v. Мы выберем образующую у так, чтобы она получалась
приведением к коэффициентам в Ър образующей группы H2(CP"1+l;Z); таким
образом, у определена с точностью до знака.
Нам будет полезен немного другой взгляд на классы Тома. Для E—*LP,
например, мы получаем изоморфизмы
Н*(Т(Е)) ъ Н*(Т(Е), оо), где оо —точка компактификации,
ъ Н*(ПЮ, Т(Е) - Lp), где Lp вложено в Г(£) как нулевое
сечение, поэтому Т(Е) - Lp деформационно ретрагируется на оо,
ъ Н*(Е, E — Lp)y согласно вырезанию.
Таким образом, мы можем считать, что класс Тома лежит в Н*(Е, Е — Lp),
и аналогично для расслоений Е}.
Мы получаем проекции п),: Е—►£; посредством проекций V0®V\ ©...
... 0 Vm -> Vj в слоях. Если т; е H*(Ejt Е; - Lp) обозначает класс Тома,
построенный выше, то мы получаем индуцированный класс я*(т;) е
eH*(E,E-7i71(Lp)), и ^-произведение П;7г*(т;) bH*(E,E-Lp) является
650
Глава 4. Теория гомотопий
классом Тома для Е, в чём легко убедиться, применив вычисление в конце
примера 3.11 к каждому слою. При изоморфизме /Г(Е, E — Lp) ъН*{Т(Е))
класс TljitUzj) соответствует ±А(а), так как оба класса при ограничении
на каждый слой Sp с 7(E) дают ±а®р, а класс Я (а) однозначно
определяется его ограничениями на слои.
Теперь мы можем завершить доказательство леммы. Класс V*(A(a))
получается при ограничении класса А(а) еЯ;)(Т(Е)) на диагональ Г(Е0)
и последующем переносе на Lp х S1 посредством отображения,
индуцированного отображением факторизации Lp х S1 —* Т(Е0)У которая
стягивает в точку сечение на бесконечности. Ограничение П;я*(т^) на
HP(E0,E0-Lp)^Hp(T(E0)) даётт0^е1^...^еш, где е; €Я2(Е0)-образ
класса т; при отображении
HhE^.Ej -Lp) -> H2(Ej) w Я2(//) * Я2(Е0);
здесь последние два изоморфизма возникают из включений Lp в Е; и в
Е0 как нулевых сечений, к которым они деформационно ретрагируются.
Чтобы вычислить ej, мы воспользуемся диаграммой
Я2(Е;-, E}-Lp) ^— H2[Ej, Ej-CP"1) ^— Н2(ЁЪ Ел - СР'")
H2(Ej) - - Я2^) * - Я2^)
н2ар) -*— я2(ср'м) ■<— я2(срш)
Класс Тома для Ej лежит в верхней справа группе. Если этот класс
отобразить сначала вдоль верхней части диаграммы, а затем вниз, в нижний
левый угол, то получим элемент ef. Чтобы вычислить е;, мы выберем другой
маршрут через нижний правый угол диаграммы. Образ класса Тома для Ег
в нижней справа группе Я2(СРШ) —образующая уу так как T{El)=£PmrX-
Отображение /* является умножением на j, так как / имеет степень j на
СР1 с СР'". A q*(y) = ±oj2, так как ограничение q на двумерные клетки
комплекса Lp с СW-структурой, определённой в примере 2.43, является
гомеоморфизмом. Таким образом, е; =±jcd2, а потому
Класс т0 был индуцирован из а посредством проекции Т(Е0) -*Sl,
поэтому, когда мы переносим т0 назад в Lp x S1 посредством V, мы получаем
1<8>а, а значит, Tq^^ ^... ^em переносится индуцированным
отображением в ±т\сор_] ® а. Следовательно, аг =±т\. D
Из этой леммы следует, в частности, что аи — ненулевой элемент в Zp,
поэтому у ап есть мультипликативный обратный элемент а"1 в Ър. Тогда
§ 4.L. Квадраты и степени Стинрода
651
мы определим
Р((а) = (-lya-^p-i)^) Для а G H"M •
Множитель а"1 гарантирует, что Р° — тождественное отображение. Как
мы сейчас покажем, коэффициент (-1)' вставлен для того, чтобы
выполнялось равенство P'(a) = ap, если |a|=2i. Мы знаем, что #2f(p-i)(°0 — aP>
поэтому нужно показать, что (—l)'^,1 = 1, или, что эквивалентно, а2, =
= (-!)''.
Для этого нам нужен следующий факт из теории чисел:
((р - 1)/2)!2 = С—1)Ср+1)/2 mod p.
Чтобы доказать его, сначала заметим, что произведение всех элементов
±1, ±2, ..., ±(р - 1)/2 группы Z* равно ((р - 1)/2) !2(-1)(р'1)/2. С другой
стороны, эта группа является циклической группой чётного порядка,
поэтому произведение всех её элементов — единственный элемент
порядка 2, т.е. — 1, так как все другие нетривиальные элементы в этом
произведении взаимно сокращаются со своими обратными. Таким образом,
((р - 1)/2)!2(-1)(р-!>/2 = -1, а значит, ((р - 1)/2) !2 = (-1)^+1)/2 mod p.
Тогда используя формулы an = (-l)p(p-1)n(n~1)/4aj и а1=±((р-1)/2)!,
мы получаем
a2i = (-iyip-im2i-l)'\tp-l)/2)l2i =
_ (_1)pt(p-l)/2].(2.-l)^_1y(p + l)/2 _
= (^i)'(p-i)/2(_1y(P+D/2j так как р и 2i - 1 нечётны ,
= (—1)ф = (-1)', так как р нечётно.
Теорема 4.L.16. Операции Р1 удовлетворяют свойствам 1—6 и
соотношениям Адема.
Доказательство. Первые два свойства, естественность и
аддитивность, наряду с тем фактом, что Р1(а) =0 при 2i > |a|, наследуются из
свойств операций в{. Свойство 6 и другая половина свойства 5 только что
были доказаны выше. Докажем формулу Картана. Для а<ЕНт и^еНп мы
получаем A(a^j8) = (-1)р(р~1)тп/2Я(а)Я(^), а потому
2w(P-i)(m+n)-i®^(aw/5) -
= (-1)р(р-1)п'п/2 g] "(р_1)ш_; ® 0, (a)) (£ со(р_.1)п_, в 0fc(0)) •
Напомним, что а>2г = сог2 и w2r-ri — ^1^2» ПРИЧ^М °>\ = °- Поэтому члены
с чётными i в левой части этого равенства могут возникнуть только из
членов с чётными ; и к в правой части. Это даёт второе равенство в еле-
652 Глава 4. Теория гомотопий
дующей последовательности:
Р''(а^/3) = (-l)4~,l,Acp-i)(a^) =
= (-1),^1,1(-1)р(р-1,","/2Е^о-лсР-1)С«)02Лр-1)Ф) =
= £c-i)'-4;4.w>cpM>cax-i)44cp-i>03) =
i
Свойство 4, инвариантность операций Р1 относительно надстройки,
следует из формулы Картана точно так же, как в случае р = 2, с помощью того
факта, что Р° является единственной из операций Р\ которая может быть
ненулевой на одномерных классах согласно свойству 5.
Остаётся доказать соотношения Адема для степеней Стинрода. Нам
понадобится вычисление гомоморфизма Бокштейна.
| Лемма 4.L.17. рв2к = -в2к+1.
Доказательство. Прежде всего сведём задачу к доказательству того,
что/ЗУ*(А(0) = 0. Если мы вычисляем /3V*(A(0)> используя формулу
произведения для /3, то получаем
0(2"(р-1)п^®0КО)=2^
1 I
Так как t3co2j__l = co2j и /3a>2j=0, члены с i = 2k и i — 2fc + 1 дают
к
и
^(p-l)n-2*-l ® 002fc+l(O
соответственно. Таким образом, коэффициент при ^^„^„„г/с в /3V*(A(0)
равен /}02fc(O + 02fc+iM> поэтому если мы предположим, что /3V*(A(0) =0,
то этот коэффициент должен обратиться в нуль, так как мы
находимся в тензорном произведении H*(L°°) ® Н*(Кп). Поэтому мы получаем
I362k(t) = -02k+iM> а значит, 13в2к{а) = -02fc+i(a) Для всех а- Отметим,
что 13в2к+1 = 0, как видно из коэффициента при C0(p_1)n_2k-i' Это также
следует из формулы /302* = ~#2к+ь так как /З2 = 0.
Чтобы показать, что /3V*(A(t)) = 0, мы сначала вычислим /?А(0-
Можно считать, что Кп имеет единственную n-мерную клетку и единственную
(п + 1)-клетку, приклеенную по отображению степени р. Пусть у и ip —
клеточные коцепи, принимающие значение 1 на n-мерной и (п +
^-мерной клетках соответственно, таким образом, 5ц> = р*ф. В К*р мы тогда
§ 4.L. Квадраты и степени Стинрода
653
получаем
5(^®P) = 5](-l),'Ve,'®5v®^®Cp",""1) =
где знак ® означает клеточное внешнее произведение, так что, например,
(/?®р — это клеточная коцепь, двойственная к пр-мерной клетке е" х ... х еп
комплекса К*р. Формула (*) выполняется также и в ЛКП, так как
последнее пространство имеет лишь одну (пр + 1)-мерную клетку, не лежащую
в К*р, с клеточной границей, равной нулю. А именно, эта клетка
—произведение одномерной клетки в L°° и пр-мерной клетки в К*р, причём один
конец этого произведения приклеен к пр-мерной клетке по
тождественному отображению, а другой конец —по циклической перестановке Г,
которая имеет степень +1, так как р нечётно. Таким образом, эти два члена
в границе этой клетки взаимно сокращаются, а никаких других членов
нет, так как остальные приклеивания для этой клетки производятся к
отмеченной точке.
Гомоморфизмы Бокштейна можно вычислять, используя клеточные
коцепные комплексы, поэтому формула (*) говорит, что коцепь
представляет класс /3A(i). Индуцированное отображение для фактор-
отображения ГКп —* АКп переносит класс А(0 в класс y(t). При этом
класс /3у(0 также представлен коцепью $](—1)"V®' ®i/> ® </>®(р~1_1). Что-
i
бы понять, что происходит, когда мы переносим назад класс /3/(0 в
/3V*(A(0) посредством индуцированного отображения для включения
L°° х Кп <—> ГКП, рассмотрим коммутативную диаграмму
Н*(ГКп) —£->. H\S°° х КпДр) —U* Н*(ГКп)
tit
H*tt°° х Кп) -^ H*(S°° х Кп) —^ Н*а°° х Кп)
В левом квадрате отображения я* индуцированы проекциями накрытий
я: S00 х КДр -* ГКП и тг: S00 х Кп -* L00 х Кп, возникающих из свободных
действий группы Zp. Вертикальные отображения индуцированы
диагональным включением S°° х К <—> S°° x КДр. Отображения т
—гомоморфизмы переноса, определённые в § 3.G. Напомним их определение. Рхли
я: X -* X — р-листное накрытие, то цепное отображение СДХ) -* СДХ)
опредено тем, что оно переводит сингулярный симплекс а: 5к -+ X в
сумму его р поднятий в X, а т — индуцированное отображение когомоло-
гий. Ключевое свойство гомоморфизма т состоит в том, что
отображение тя*: Н*(Х) —>Н*(Х) является умножением на р для любого выбора
654
Глава 4. Теория гомотопий
группы коэффициентов, так как, когда мы проектируем р поднятий
симплекса а: Ак —* X назад в X, мы получаем per. Если X — CW-комплекс,
а пространство X снабжено поднятой СW-структурой, то т можно также
определить в клеточных когомологиях той же самой процедурой.
Вычислим значение верхнего гомоморфизма т в диаграмме на коцепи
1®i/j® с/?®(р_1), где «1» — клеточный коцикл, принимающий значение 1 на
каждой нульмерной клетке комплекса S00. По определению
гомоморфизма т мы получаем
т(1 ® я/' ® у®[р~})) = 2 Г {яр ® ^®(р_1)),
i
где Г: К*р -> К^р переставляет множители циклически. Не имеет
значения, сдвигает Т координаты на одну позицию влево или вправо, так как
мы суммируем по всем степеням Г, поэтому будем считать, что Т сдвигает
координаты вправо. Тогда r(i/j® ^®(р_1)) = ^®i/j ® t/?®(p_2), где последняя
коцепь tp переставлена на первую позицию. Такого перемещения можно
добиться, переставляя эту коцепь у с каждой из р — 2 стоящих перед
ней коцепей ip и с ip. Перестановка двух коцепей у вносит знак (—1)'г,
а перестановка (/? с гр вносит знак (—1)п(п+1) =+1 по свойству
коммутативности внешнего произведения. Таким образом, полный знак, который
вносит Г, равен (—1)" (р_2), что равно (-1)п, так как р нечётно. Каждая
последовательная итерация Т тоже вносит знак (-1)", поэтому V вносит
знак (-1)'" для 0^1 ^р — 1. Таким образом,
т(1 ®яр ® ^®(р"1}) = ^]г'СФ ® ^®(р"1}) - ^C-iV'V®1' ®'Ф ® ^®^р-'-1).
Как отмечено ранее, последний коцикл представляет класс /3/(0-
Так как /3^(0 лежит в образе верхнего гомоморфизма т в диаграмме,
образ класса /3^(0 в Н*(Х°° х ^п)» который равен V*(0A(O), лежит в
образе нижнего гомоморфизма т, так как правый квадрат коммутативен.
Отображение я* в нижней строке, очевидно, является отображением на,
так как пространство S°° стягиваемо; таким образом, V*(/?A(0) лежит
в образе композиции ттг* вдоль нижней части диаграммы. Но эта
композиция—умножение на р, а это отображение нулевое для коэффициентов
Zpi поэтому /3V4A(0) = V*Q3A(0) = 0. П
Вывод соотношений Адема теперь следует своему образцу для случая
р = 2. Мы получили формулу
Так как мы полагаем р = 2гп + 1, её можно переписать в виде
§4.L. Квадраты и степени Стинрода 655
Единственные ненулевые операции 0, — это 02i(p-i) — (_1)'ап^' и
02«чР~1)+1 = ~рвъ{Р-\)> поэтому мы получаем
Ч
-2(-l)'+ja2mna^^^
i>j
Так как т. и п в нашем обсуждении будут фиксированными, мы
можем вынести за скобки постоянный ненулевой множитель а2тпап- Тогда,
применяя формулу Картана, чтобы выразить члены Р', и используя также
формулы Рк(со2г) = Скгсо2г+2к{р_1) и ^(co2r+1) = Cffcco2r+2fc(p_1H1, доказан-
ные ранее в этом параграфе, мы получаем
2(-1)|>;"с*(п_2^
-2(-1),+JC*'Cn-2j)W2m(pn-2,>l®W2m(n-2j+2fc)®
"2](-1)'+^(п-2ЛМ^^
Если положить £ = mn 4- j - к, так что п - 2j + 2/c = рп — 2£, то первая из
этих пяти сумм превращается в
и аналогично для четырёх остальных сумм.
Теперь мы воспользуемся свойством симметрии ч>Г5 = (-1У*+тпрф$г>
где, как и раньше, V^A^CO = j£ a>r ® a>s ® yrs. Из наших пяти сумм только
в первой есть слагаемые, у которых оба члена со имеют чётные индексы,
а именно, г = 2т(рп - 20 и s = 2m(рп - 20- Поэтому коэффициент при
656
Глава 4. Теория гомотопий
сог <8> со$ в этой сумме должен быть симметричен относительно
перестановки i и (. с точностью до знака, который будет положительным, если мы
выберем число п так, чтобы оно было чётным, и так мы и сделаем. Это
даёт соотношение
Yi^iy+icz%pi+e~"m4piM=Xti~1)t+ic""n-2i\pi+t~mn~ipi^- (1)
i )
Аналогично во вторую, третью и четвёртую сумму входят со с индексами
противоположной чётности, что приводит к соотношению
^(-iy+icX-2jUpi+l~mn~iPpi^=:
j
= %{-1У+*с™+%РрМ~шЧр)Ы ~
j
-%{-1)<+*с™£ир'+1~тпЧРр]'М- (2)
j
Соотношения (1) и (2) приведут нас к двум соотношениям Адема, поэтому
нет необходимости рассматривать соотношение, происходящее из пятой
суммы.
Чтобы получить первое соотношение Адема из соотношения (1), мы
выберем пиЕ так, чтобы в левой части (1) был только один член, а именно,
мы положим л = 2(1 + р + ... + рг~]) + 2s и E = mn + s для данных целых
чисел г и s. Тогда
ЧиСп-2;) ~- V-I-CP-DO'-O'
и если г достаточно велико, то этот биномиальный коэффициент равен 1
для j = s и 0 в остальных случаях, так как если самая правая ненулевая
цифра в р-ичной записи «знаменателя» j — s равна х, то соответствующая
цифра «числителя» (р - 1)[(1 + р + ... +pr_l) — (j — s)] получается
приведением (р — 1)(1 — л1) mod р, что даёт х — 1, а Схх_л = 0. Тогда соотношение
(1) принимает вид
или Р'РЧО = ^(-1)'+;С^ так как Е = s mod 2,
= X;(-l)'+yCi2;)P,+s-J>a), так как Cjf = С?"'.
j
Zj{ j S'+cp-dcs-»-^ r ^-
j
Если г велико и i <psy то член рг в биномиальном коэффициенте
можно опустить, так как можно считать, что i ^ р/, а значит, j < s, поэтому
§4.L. Квадраты и степени Стинрода
657
— 1 + (р - l)Cs — j) ^ 0 и рг никак не влияет на биномиальный
коэффициент. Это показывает, что первое соотношение Адема выполняется для
класса с, а общий случай следует из этого, как и в случае р = 2.
Чтобы получить второе соотношение Адема, мы выберем л = 2рг + 2s
и £ = тп +s. Если рассуждать так же, как и раньше, то левая часть (2)
равна (-1)'"КчР'^Р'ч(0 и (2) принимает вид
;"
-S(-l)'+;c!p-Si.+s-;1-.P'+'"^P^0.
;
На этот раз член рг можно опустить, если г велико и f ^ ps. П
Задачи
1. Найдите все когомологические операции Hl(X\Z)-* Hn(X\Z),
/72(Х; Z) -*H"(X\ Z) и //ЧХ; Zp) ->H"(*I Zp) для простого числа р.
2. Используя когомологические операции, покажите, что
пространства (S1 х СР00)/^1 х {х0}) и S3 х СР00 гомотопически неэквивалентны.
3. Так как согласно примеру 35 из §4.2 существует локально
тривиальное расслоение S2-*CP5-*HP2, можно поинтересоваться, существует
ли аналогичное расслоение S4-*HP5 —>OP2. Используя степени Стинрода
для простого числа 3, покажите, что такое расслоение не может
существовать. [Можно воспользоваться последовательностью Гизина, чтобы
определить отображение когомологий, индуцированное проекцией
расслоения MP5->QP2.]
4. Докажите, что не существует локально тривиального расслоения
S7 -*S23 —>OP2. [Вычислите кольцо когомологий конуса отображения для
проекции S23 —»ОР2 при помощи двойственности Пуанкаре или
изоморфизма Тома.J
5. Докажите, что подалгебра в .я/2, порождённая операциями Sq1 для
i ^ 2, имеет размерность 8 как линейное пространство над Z2, причём её
мультипликативная структура отражена в следующей диаграмме:
Sq1 Sq2Sql
/ \
] Sq2 Sq2Sq2 Sq2Sq2Sq2
Sq2Sq1 Sq2SqlSq2
где диагональные линии обозначают умножение слева на Sq1, а
горизонтальные линии обозначают умножение слева на Sq2.
Приложение
Топология клеточных комплексов
Здесь для удобства ссылок собраны основные топологические факты
о CW-комплексах. Доказано также несколько связанных с CW-комнлек-
сами фактов о многообразиях.
Напомним сначала из главы 0, что CW-комплекс — это
пространство X, построенное следующим образом.
1. Начинаем с дискретного множества Х° нульмерных клеток
комплекса X.
2. По индукции строим /7-мерный остов Xй по X""1, приклеивая п-мер-
ные клетки спа посредством отображений <ра: Sn"1 —* X"-1. Это
означает, что Xй — факторпрострапство несвязного объединения Xu~l \JO^
а
при отождествлениях х^уи(х) для xe5D"r Клетка епа — гомеоморф-
ный образ пространства D"2 - 5Dua при отображении факторизации.
3. Зададим на X = (JX" слабую топологию: множество АсХ открыто
л
(или замкнуто) тогда и только тогда, когда множество АПХ'1 открыто
(или замкнуто) в Хп для всех п.
Отметим, что условие 3 излишне, когда комплекс X конечномерен,
т.е. X — Хп для некоторого п. Действительно, если множество А открыто
в Х = Х", то из определения фактортопологии на Хп следует, что
множество АГ\Хп~] открыто в Хп~\ а тогда согласно тому же самому
рассуждению множество АПХп~2 открыто в Xм"2, и аналогично для всех остовов
Х""'.
У каждой клетки еп есть своё характеристическое отображение Фа,
которое по определению является композицией
D£<-> X"'1 Ц^-* Xй <-> X.
а
Оно непрерывно, так как является композицией непрерывных
отображений; включение Xй с-> X непрерывно но свойству 3. Ограничение
отображения Фи на внутренность шара Dua — гомеоморфизм на клетку е"х.
Другой способ описания топологии на X состоит в том, чтобы сказать,
что множество АсХ открыто (или замкнуто) тогда и только тогда, когда
Ф~Ч^) открыто (или замкнуто) в D"a для любого характеристического
отображения Фа. В одну сторону это следует из непрерывности
отображений Ф„, а чтобы получить доказательство в другую сторону,
предположим, что множество Ф"1^) открыто в £)'* для всех Фа, и предположим,
применяя индукцию по /?, что множество АГ\Х"~ 1 открыто в X""1. Тогда,
Топология клеточных комплексов
659
так как множество Ф~ЧА) открыто в D'(\ для всех а, множество А П Хп
открыто в X" по определению фактортопологии на Xй. Следовательно, по
свойству 3 множество А открыто в X.
Из этого описания топологии на X следует, что X является факторпро-
странством пространства LI^".
Подкомплекс CW-комплекса Х— это такое подпространство А с X,
являющееся объединением клеток комплекса X, что замыкание каждой
клетки в А содержится в А. Таким образом, для каждой клетки в А образ
её отображения приклеивания содержится в Л, поэтому пространство Л
само является СW-комплексом. Топология CW-комплекса на нём —то же
самое, что топология, индуцированная из X, поскольку легко проверить
по индукции, что эти две топологии согласованы на Ап ~АпХп. Легко
доказать индукцией по остовам, что подкомплекс —это замкнутое
подпространство. Наоборот, подкомплекс можно определить как замкнутое
подпространство, которое является объединением клеток.
Конечный CW-комплекс, т.е. комплекс с конечным числом клеток,
компактен, так как приклеивание одной клетки сохраняет компактность.
Вот утверждение, своего рода обратное к этому.
Предложение П.1. Компактное подпространство CW-комплекса
содержится в конечном подкомплексе.
Доказательство. Сначала мы покажем, что компактное множество С
в CW-комплексе Х может пересекать только конечное число клеток
комплекса X. Предположим от противного, что есть такая бесконечная
последовательность точек х( е С, что все они расположены в разных клетках.
Тогда множество S = {хх, х2,...} замкнуто в X. А именно, применяя
индукцию по п, предположим, что множество SHX""1 замкнуто в Xм"1; тогда
для каждой клетки епа комплекса X множество ip~l{S) замкнуто в 5D"it
а Фц!(5) состоит из не более чем одной точки множества D^, поэтому
множество Ф~:(5) замкнуто в DJJ. Следовательно, множество S П X"
замкнуто в Xм для всех п, а потому S замкнуто в X. То же самое рассуждение
показывает, что любое подмножество множества S замкнуто, таким
образом, топология множества S дискретная. Но это множество компактно,
поскольку оно является замкнутым подмножеством компактного
множества С. Поэтому множество S должно быть конечным, что противоречит
нашему предположению.
Так как С содержится в конечном объединении клеток, достаточно
доказать, что конечное объединение клеток содержится в конечном
подкомплексе комплекса X. Конечное объединение конечных подкомплексов —
это снова конечный подкомплекс, поэтому всё сводится к доказательству
того, что одна клетка епа содержится в конечном подкомплексе. Образ
отображения приклеивания ц>п для еп компактен, поэтому индукция по
размерности показывает, что этот образ содержится в конечном подком-
660
Приложение
плексе ЛсХп_1. Таким образом, епа содержится в конечном
подкомплексе Ли епа. П
Теперь мы можем объяснить таинственные буквы CW, относящиеся
к следующим двум свойствам, которыми обладают СУУ-комплексы.
1. Closure-finiteness (конечные замыкания): замыкание любой клетки
пересекает только конечное число других клеток. Это следует из
предыдущего предложения, так как замыкание клетки компактно,
поскольку оно является образом характеристического отображения.
2. Weak topology (слабая топология): множество замкнуто тогда и только
тогда, когда оно пересекает замыкание каждой клетки по
замкнутому множеству. Действительно, если множество пересекает замыкание
каждой клетки по замкнутому множеству, то его прообраз при любом
характеристическом отображении замкнут, а потому само множество
замкнуто согласно сделанному ранее замечанию.
В первоначальном определении CW-комплексов, которое предложил
Дж. Г. К. Уайтхед, эти два свойства играли центральную роль. Следующее
предложение содержит, по сути, это определение.
I Предложение П.2. Пусть даны хаусдорфово пространство X и семей-
I ство отображений Фи: D'^ —>Х. Эти отображения являются характери-
I стическими отображениями для некоторой структуры CW-комплекса
I на X тогда и только тогда, когда:
I 1) каждое отображение Фа инъективно на intD^, а потому ограниче-
I ние Фа на intD^ — гомеоморфизм на клетку епа с X; все эти клетки
I не пересекаются, причём их объединение равно Х\
I 2) для каждой клетки е" множество Фа(гШ^) содержится в объедине-
I нии конечного числа клеток размерности меньше п;
I 3) подмножество в X замкнуто тогда и только тогда, когда оно пе-
I ресекает замыкание каждой клетки комплекса X по замкнутому
I множеству.
Часть «а потому» вп.1 следует из того факта, что Фа отображает
компактное множество Dna на хаусдорфово пространство, поэтому, так как Фа
переводит компактные множества в компактные множества, оно
переводит замкнутые множества в замкнутые множества, а это означает, что
отображение Ф~ ]: е11а —> intD^ непрерывно. Согласно тем же самым
рассуждениям с компактностью свойства 3 можно переформулировать, сказав,
что множество С с X замкнуто тогда и только тогда, когда множество
Ф~](С) замкнуто в D" для всех а. В частности, свойство 3 выполняется
автоматически, если число клеток конечно, так как проекция LJDJJ —*Х
а
является отображением компактного пространства на хаусдорфово
пространство, а потому —отображением факторизации.
Топология клеточных комплексов
661
Чтобы получить пример, когда выполняются все условия, кроме
предположения о конечности в 2, возьмём такой комплекс X: диск D2 с его
внутренностью в качестве двумерной клетки и каждой точкой
границы 3D2 в качестве нульмерной клетки. Тождественное отображение диска
D2 служит характеристическим отображением Фа для двумерной клетки.
Свойство 3 выполняется, так как оно нетривиально только для двумерной
клетки.
Доказательство. Мы уже доказали утверждение «только тогда». Для
доказательства обратного утверждения предположим по индукции, что
объединение Хп~1 всех клеток размерности меньше п является CW-kom-
плексом с соответствующими Фа в качестве характеристических
отображений. Индукцию можно начать с X~l ~<Z). Пусть отображение
f-.xn~] J_Jd;;->x"
а
задано включением на X"""1 и отображениями Фа для всех п-мерных
клеток комплекса X. Это отображение— непрерывная сюръекция, и если мы
сможем показать, что она является отображением факторизации, то X"
будет получаться из Хп~] приклеиванием и-мерной клетки епа. Таким
образом, если подмножество С С Xй таково, что множество /'"1 (С) замкнут,
то нам нужно показать, что множество Спё"* замкнуто для всех клеток е',"
комплекса X; здесь черта обозначает замыкание.
Здесь возможны три случая. Если т < п, то замкнутость f~] (С) влечёт
замкнутость прообраза СПХП_1, следовательно, СПёУ замкнуто, так как
в'!} с Xм"1. Если т = а, то е"1 —одна из клеток е£, поэтому замкнутость
прообраза f"l(C) влечёт, что /_1(C)nD£ замкнуто, а значит, компактно;
следовательно, его образ СПёпа при отображении / является компактным,
а потому замкнутым. Осталось разобрать случай т > п. В этом случае
условие С с Хп влечёт Спё'р с Ф^(SO?). Последнее пространство содержится
в конечном объединении множеств ё* с i < т. Индукция по т показывает,
что все множества С П ё( замкнуты. Следовательно, пересечение
множества С с объединением конечного числа множеств ё(у замкнуто.
Рассматривая пересечение этого замкнутого множества с e"J9 мы получаем, что
множество СПё"1 замкнуто.
Остаётся только проверить, что X имеет слабую топологию
относительно остовов Xм, т.е. множество в X замкнуто тогда и только тогда,
когда оно пересекает каждое множество Хп по замкнутому множеству.
Предыдущее рассуждение для С = Хп показывает, что множество Xй
замкнуто, поэтому замкнутое множество пересекает каждый остов X" по
замкнутому множеству. Наоборот, если множество С пересекает X" по
замкнутому множеству, то С пересекает каждое множество ё" по замкну-
662
Приложение
тому множеству, следовательно, множество С замкнуто в X согласно
свойству 3. □
Теперь мы опишем удобный способ строить открытые окрестности
Л/ДА) подмножеств А в CW-комплексе Х, где в — функция,
сопоставляющая число еа > 0 каждой клетке еиа комплекса X. Построение
проведём индукцией по остовам X", поэтому предположим, что мы уже
построили окрестность N"(A) множества А П Хп в X", начиная процесс
с N®(A) —АГ\Х°. Тогда мы определим множество N't!+l(А), указав его
прообраз при характеристическом отображении Фа: D"4'1 —*Х каждой
клетки e^+I, а именно, Ф"1 (N"+1 (Л)) —объединение двух частей: открытой
еа-окрестности множества Ф"1 (А) - 51)п м в D'H l - 5Durl и произведения
(1 - еа, 1] х Ф~!(ЛГ"(А)) относительно «сферических» координат (г, 0)
в D'H1, где re [0, 1]— радиальная координата, а 9 лежит в 5D""1 =Sn.
Тогда мы полагаем Nf.(A) = (J/V"(A). Это множество открыто в X, так как
п
его прообраз при каждом характеристическом отображении открыт.
Предложение П.З. CW-комплексы являются нормальными
пространствами, в частности, они хаусдорфовы.
Доказательство. Точки замкнуты в CW-комплексе Х, так как их
пробразы при всех характеристических отображениях Фа замкнуты. Для
непересекающихся замкнутых множеств А и Б в X мы покажем, что МДА)
и Л/Д/3) не пересекаются для достаточно малых ен. Будем строить эти
открытые множества но индукции. Предположим, что N"(A) и Л/"(В)
были выбраны так, что они не пересекаются. Для характеристического
отображения Фп: D"+I —*Х заметим, что множества Ф"1 (ЛГ"(А)) и Ф~ЧВ)
расположены на положительном расстоянии друг от друга, так как
иначе в силу компактности мы получили бы последовательность в Ф~1(В),
сходящуюся к точке множества Ф~а1(В) в 5Dn^1 на пулевом расстоянии от
Ф~!(М"(А)), но это невозможно, так как Ф~!(М"(В)) —окрестность
множества Ф~ДЯ) П <5D"+1 в б/У'"1"1, не пересекающаяся с Ф"1 (ЛГ'(А)).
Аналогично множества Ф'^Л^ЧЯ)) и Фг/ДА) находятся на положительном
расстоянии друг от друга. Кроме того, Ф~ЧА) и Ф~ЧВ) находятся на
положительном расстоянии друг от друга. Поэтому для достаточно малых еа
множества Ф"1 (n;.'+1(A)) и Ф"1 (ЛГ,_и(В)) не пересекаются bD"h. □
I Предложение П.4. У любой точки CW-комплекса существуют сколь
угодно малые стягиваемые открытые окрестности; таким образом,
CW-комплексы локально стягиваемы.
Доказательство. Пусть даны точка х CW-комплекса Х и
окрестность U точки х в X. Тогда мы можем выбрать еа столь малыми, что
А/Дх)с[/, потребовав, чтобы замыкание множества N"(x) содержалось
в V для всех п. Остаётся убедиться, что пространство Л/Дх) стягиваемо.
Если х G Хт — Х"1-1 и п > т, то мы можем построить деформационную
ретракцию пространства /V"(>) на N"~l(x), двигая точки в направлении
Топология клеточных комплексов
663
наружу по радиальным отрезкам в клетках е£ (радиальные отрезки в
клетках определяются как образы радиусов в D" при
характеристических отображениях). Деформационная ретракция пространства NF(x) на
N"'00 тогда получается, если мы выполняем деформационную
ретракцию пространства N"(x) на N"-100 в течение времени Г из
интервала [1/2п, 1/2""1], причём точки множества N"(x) - N""l{x) остаются
неподвижными вне этого интервала времени г. Остаётся заметить, что
N"'00 — открытый шар, содержащий точку х, поэтому оп деформационно
ретрагируется на х. П
В частности, CW-комилексы локально линейно связны. Таким
образом, CW-комплекс линейно связен тогда и только тогда, когда он связен.
Предложение П.5. Для подкомплекса Л в CW-комплексе Х открытая
окрестность NF(A) деформационно ретрагируется на Л, если £а < 1 для
всех а.
Доказательство. В каждой клетке из X - Л множество А/ДА) имеет
структуру произведения подмножества границы этой клетки на
полуоткрытый интервал, поэтому деформационную ретракцию множества А/ДА)
на А можно построить так же, как в предыдущем доказательстве. □
Отметим, что для подкомплексов Л и В комплекса X мы получаем
А/ДА) П А/ДВ) = А/ДА ПВ), Из этого следует, например, что теорема ван
Кампена и последовательность Майера—Вьеториса справедливы для
представлений Х = ЛиВ в виде объединения подкомплексов Л и В, как и для
представлений в виде объединения открытых множеств Л и В.
Отображение /: X —» У, где X — CW-комплекс, непрерывно тогда
и только тогда, когда его ограничения на замыкания ёпа всех клеток е"х
непрерывны, и было бы полезно знать, что то же свойство верно для
гомотопий ft: X —>Y. Помня об этом свойстве, давайте введём некоторую
терминологию. Топологическое пространство X называют порождённым
набором подпространств Ха, если X~\JXa и множество АаХ замкнуто
а
тогда и только тогда, когда множества АГ)Ха замкнуты в Ха для всех а.
Эквивалентным образом мы могли здесь сказать «открыто» вместо
«замкнуто», но замкнутые множества более удобны для наших нынешних
целей. Как было отмечено ранее, хотя в других терминах, CW-комплекс Х
порождается замыканиями ёпа его клеток епа. Так как любой конечный
подкомплекс в X является конечным объединением замыканий ё£, комплекс
X порождается также своими конечными подкомплексами. Из этого
следует, что X порождается также своими компактными подпространствами,
или, короче, пространство X компактно порождено.
Предложение П.15, которое будет доказано позже в этом приложении,
утверждает, что если X — компактно порождённое хаусдорфово
пространство, a Z —локально компактное пространство, то пространство X х Z
с топологией произведения компактно порождено. В частности, простран-
664
Приложение
ство X х / компактно порождено, если X — CW-комплекс. Так как любое
компактное подмножество в X х / содержится в произведении
компактного подпространства в X на /, а потому в произведении конечного
подкомплекса в X на /, такие произведения тоже порождают пространство X х L
Так как такое произведение является конечным объединением
произведений ё"х х /, верно также, что X х I порождается своими
подпространствами ёпа х I. Из этого следует, что гомотопия F: X х I —► У непрерывна
тогда и только тогда, когда её ограничения на подпространства ёпа х I
непрерывны, что мы и хотели доказать.
Произведения CW-комплексов
При работе с произведениями CW-комилексов возникает
неожиданная тонкость из общей топологии. Как мы покажем, произведение двух
CW-комплексов имеет естественную ClV-структуру, но её топология,
вообще говоря, более тонкая, т. е. имеет больше открытых множеств, чем
топология произведения. Однако различие между этими двумя топологиями
довольно небольшое и в действительности несущественно в большинстве
интересных случаев. Таким образом, в этом нет никакой настоящей
проблемы для алгебраической топологии.
Пусть даны пространство X и набор подпространств Ха, объединение
которых равно X. Эти подпространства порождают, возможно, более
тонкую топологию на X, если мы будем считать множество ДсХ открытым
тогда и только тогда, когда множество АГ\Ха открыто в Ха для всех а.
Аксиомы топологии для этого определения легко проверяются. В случае,
когда {Ха}— набор компактных подмножеств в X, мы будем обозначать
эту новую компактно порождённую топологию через Хг. Легко видеть, что
у X и Хс одни и те же компактные подмножества, причём обе
индуцированные топологии на этих компактных подмножествах совпадают. Если
пространство X компактно или хотя бы локально компактно, то Х^Х^,
т.е. X компактно порождено.
I Теорема П.6. Для CW-комплексов Х и Y с характеристическими
I отображениями Фа и Ф^ произведения отображений Фа х Ф^ являются
I характеристическими отображениями для структуры CW-комплекса па
I (X х У)с. Если одно из пространств X или У компактно или хотя бы
I локально компактно, то (X х У)С = Х x Y. Кроме того, (X х У)С = Х х Yy
I если у обоих комплексов X и У множество клеток не более чем счётно.
Доказательство. Для доказательства первого утверждения
достаточно проверить, что выполнены три условия из предложения П.2, когда
мы берём в качестве пространства X из этого предложения пространство
(X х У)с.. Первые два условия очевидны. Для доказательства третьего,
которое утверждает, что пространство (X х Y)c порождается
произведениями ё'(" х e'L заметим, что каждое компактное множество в X х Y содер-
Произведения CW-комплексоп
665
жится в произведении его проекций на X и па Y, причём эти проекции
компактны и, следовательно, содержатся в конечных подкомплексах
комплексов X и Y. Поэтому исходное компактное множество содержится в
конечном объединении произведений ё™ х ё" Следовательно, произведения
ё^1 х ё'р порождают пространство (X х У)с.
Второе утверждение теоремы — это частный случай предложения П.15,
не имеющего никакого отношения к CW-комплексам, которое гласит, что
произведение X х Y компактно порождено, если X компактно порождено
и хаусдорфово, a Y локально компактно.
Чтобы доказать последнее утверждение теоремы, предположим, что
каждый из комплексов X и Y имеет не более чем счётное множество
клеток. Для открытого множества W с (X х У)с и точки (a, b) <EW мы
должны найти произведение U х V с W, где U — открытая окрестность
точки а в X, а V — открытая окрестность точки Ъ в У. Выберем
конечные подкомплексы Хх с Х2 с ... в X, для которых X =[jxh и аналогично
для У. Можно считать, что аеХ, и be У,. Так как обе рассматриваемые
топологии согласованы на Хх х Уь существует компактная окрестность-
произведение Кх х L3 с W точки (а,Ь) в X, х УР Предполагая по
индукции, что произведение К, х L,- с W уже построено в X, х У,, мы хотим
построить K,V1 х L,-+1 с W как компактную окрестность множества К, х L,
в Х,Ч1 х Yi+l. Чтобы сделать это, мы сначала выберем для каждой
точки jeK,- компактные окрестности Кх точки х в X,V1 и Lx множества L,
в Yi+l так, что Кх х Lx с W, пользуясь компактностью множества L,. В силу
компактности множества К, конечное число множеств Кх покрывает К{.
Пусть К141 —объединение этих множеств Кх, и пусть JJ|41 —пересечение
соответствующих множеств Lx. Это определяет требуемое произведение
/С,-+1 х LIfl. Пусть С/, — внутренность множества К, в X,, таким образом,
U{ с С/,+1 для всех /. Объединение U = |J С/,- тогда открыто в X, так как оно
i
пересекает каждое множество X, по объединению открытых множеств,
а множества X, порождают X. Аналогично множества L, определяют
открытое множество V в У. Таким образом, мы получаем произведение
открытых множеств U х V с W, содержащее точку (а, Ь). П
Мы опишем теперь пример из [94], где топология произведения па
X х У отличается от CW-топологии. Оба комплекса X и У будут графами,
состоящими из бесконечного числа рёбер, выходящих из одной вершины,
причём множество рёбер X несчётно, а множество рёбер У счётно.
Пусть X — У ls, где /^—экземпляр отрезка [0,1J, а индекс s
пробегает по всем бесконечным последовательностям s = (sus2,...) натуральных
чисел. Букет образуется в конце 0 отрезка /s. Аналогично пусть У = V^»
но здесь j пробегает только множество натуральных чисел. Пусть pSj —
точка (l/s;-, l/Sj) e /s. х /; с X х У, и пусть множество Р состоит из всех
666
Приложение
этих точек pSj. Таким образом, Р содержит единственную точку в
каждой двумерной клетке комплекса X х Y, поэтому множество Р замкнуто
в CW-топологии на X х Y. Мы докажем, что это множество не замкнуто
в топологии произведения, показав, что точка (х0, у0) лежит в его
замыкании, где х() —общий конец отрезков Js, а у0 — общий конец отрезков /;.
Базисное открытое множество, содержащее О0,у0)> в топологии
произведения имеет вид V х V, где U = Vs[0, as) и V — Vj[0, b}). Достаточно
доказать, что Р имеет непустое пересечение с U х V. Выберем
последовательность t= (t^ £2, •••), где г- >; и tj > l/bj для всех ;, и выберем целое
число к> l/af. Тогда tk>k> l/ar, a значит, l/tfc <ar Кроме того, l/tfc <Ь^.
Поэтому (l/tfc, l/tk) —точка множества Р, которая лежит в [0, а,) х [0, Ък)
и, значит, в U х I/.
Евклидовы окрестностные ретракты
В некоторых местах в этой книге желательно знать, что данное
компактное пространство является ретрактом конечного симплициалыюго
комплекса или, что эквивалентно (как мы увидим), окрестностным
ретрактом в некотором евклидовом пространстве. Например, это условие
встречается в теореме Лефшеца о неподвижной точке, и оно
использовалось в доказательстве двойственности Александера. Поэтому давайте
изучим эту ситуацию более подробно.
I Теорема П.7. Компактное подпространство К в Rn является ретрак-
I том некоторой своей окрестности тогда и только тогда, когда К локаль-
I но стягиваемо в слабом смысле, т. е. для любой точки х е К и любой
I окрестности U точки х в К существует такая окрестность V с U точки х,
| что включение V (—> U гомотопно нулю.
Заметим, что если пространство К — ретракт некоторой своей
окрестности, то оно является ретрактом любой меньшей окрестности просто при
ограничении ретракции. Поэтому можно потребовать, чтобы окрестности
были открытыми. Аналогично можно потребовать, чтобы окрестности U
и V в утверждении теоремы были открытыми.
Доказательство. Разберём сначала более трудную часть, построив
ретракцию окрестности множества К на К в предположении локальной
стягиваемости. Первый шаг состоит в том, чтобы ввести СW-структуру на
открытом множестве X = Ж'1 - К, размер клеток которой стремится к нулю
вблизи К. Рассмотрим разбиение пространства R" на единичные кубы
размерности п с вершинами в точках с целочисленными координатами.
Обозначим этот набор кубов С0. Для любого целого числа к> 0 мы можем
подразделить кубы из С0, взяв п-мерные кубы с ребром 1/2*, вершины
которых имеют координаты вида i/2k для / е Ъ. Обозначим этот набор
кубов Ск. Пусть Л0 с С() — множество кубов, не пересекающихся с К, и по
индукции пусть Ак с Ск — множество кубов, не пересекающихся с К и не
Евклидовы окрестностные ретракты
667
содержащихся в кубах из А} для j < к. Тогда открытое множество X —это
объединение всех кубов в объединённом наборе
A = {jAk.
к
Заметим, что набор А локально конечен: у любой точки множества X
есть окрестность, пересекающая только конечное число кубов в Л, так как
эта точка находится на положительном расстоянии от замкнутого
множества К.
Если два куба из Л пересекаются, то их пересечение —это [-мерная
грань одного из них для некоторого i < п. Аналогично, когда две грани
кубов из А пересекаются, их пересечение — грань одного из них. Из этого
следует, что открытые грани кубов из А, которые являются
минимальными относительно включения среди граней такого вида, образуют клетки
CW-структуры на X, так как граница такой грани — объединение граней
такого вида. Вершины этой CW-структуры, таким образом, —это
вершины всех кубов из Л, а n-мерные клетки —внутренности кубов из Л.
Теперь мы определим по индукции подкомплекс Z этой
CW-структуры на X и отображение г: Z —> К. Нульмерные клетки комплекса Z —
это в точности нульмерные клетки комплекса Ху и мы полагаем, что г
переводит каждую нульмерную клетку в самую близкую к ней точку
множества К, а если такая точка не единственна, то в любую из самых близких
точек К. Предположим по индукции, что Zk и г: Zk —> К уже определены.
Для клетки еклл комплекса X с границей в Zk, если ограничение
отображения г на эту границу продолжается на ek+l, то мы включаем ек+х в Zk^x,
и полагаем, что отображение г на ек+] —это такое продолжение, которое
при этом не слишком велико, скажем, продолжение, для которого
диаметр его образа r(efc+1) меньше, чем удвоенная нижняя грань диаметров
всех возможных продолжений. Это даёт определение подкомплекса Zk^]
и отображения г: Zk+X —>K. Завершив индукцию, мы полагаем Z = Zn.
Остаётся проверить, что, положив г равным тождественному
отображению на К, мы получим непрерывную ретракцию ZUК —»К и что Zl)K
содержит окрестность множества К. Для данной точки х е К пусть U —
шар в метрическом пространстве К с центром в точке х. Так как
пространство К локально стягиваемо, мы можем выбрать конечную
последовательность шаров в К с центрами в точке х вида
[i = [i,1DVI1D[i/HDV1,,D...Dli0Dl/0)
где каждый шар имеет радиус, равный некоторой небольшой части
радиуса предыдущего шара, причём Ц стягиваемо в [/,-. Пусть В с Rn —шар
с центром в точке ху радиус которого меньше половины радиуса шара V0,
и пусть У — подкомплекс в X, образованный клетками, замыкания
которых содержатся в В. Таким образом, У U К содержит окрестность точки х
в Rn. Согласно выбору В и определению отображения г на нульмерных
668
Приложение
клетках мы получаем r(Y°) с V{). Так как пространство V0 стягиваемо в U0y
отображение г определено на одномерных клетках комплекса Y. Кроме
того, r(Yl) с V} согласно определению отображения г на одномерных
клетках и тому факту, что U0 намного меньше, чем V,. Аналогично по
индукции мы получаем отображение г, определённое на Y\ причём r(Yl) с Vl
для всех /. В частности, г отображает Y в U. Так как шар U может быть
произвольно малым, это показывает, что продолжение г на К
тождественным отображением даёт непрерывное отображение г: Z U К —> К. А так как
Y CZ, мы видим, что ZUK содержит окрестность множества К согласно
сделанному ранее замечанию, что Y U К содержит окрестность точки х.
Таким образом, отображение г: ZUK—*K ретрагирует окрестность
множества К на К.
Теперь докажем обратное утверждение. Так как открытые множества
в 'Rn локально стягиваемы, достаточно показать, что ретракт
локально стягиваемого пространства является локально стягиваемым. Пусть
г: X —» А — ретракция, и пусть U с А — окрестность данной точки хеЛ.
Если X является локально стягиваемым, то внутри открытого множества
r~x(U) существует окрестность V точки х, стягиваемая в г l(U)f скажем,
гомотопией/,: V—>r~](U). Тогда множество V ПА стягиваемо в U
посредством ограничения композиции rfr П
Пространство X называют евклидовым окрестностным ретрактом
или ENR (от английского Euclidean neighborhood retract), если для
некоторого п существует такое вложение i: X <—>Rn, что i(X) является ретрактом
некоторой окрестности в R". Из предыдущей теоремы следует, что
существование ретракции не зависит от выбора вложения, по крайней мере,
когда X компактно.
1 Следствие П.8. Компактное пространство является ENR тогда и толь-
I ко тогда, когда его можно вложить как ретракт в некоторый конечный
1 симплициальный комплекс. Следовательно, группы гомологии и фунда-
I ментальная группа компактного ENR конечно порождены.
Доказательство. Конечный симплициальный комплекс К с п
вершинами—подкомплекс симплекса Л"-1, следовательно, он вкладывается
в R". Тогда из предыдущей теоремы следует, что К — ретракт некоторой
окрестности в R", поэтому любой ретракт комплекса К является также
ретрактом такой окрестности посредством композиции этих двух
ретракций. Наоборот, пусть К — компактное пространство, которое является
ретрактом некоторой открытой окрестности [/ в 1". Так как множество К
компактно, оно ограничено, т.е. лежит в некотором достаточно большом
симплексе Лп с R". Подразделим Д", скажем, повторяя несколько раз
барицентрическое подразделение, чтобы все симплексы подразделения
имели диаметр меньше, чем расстояние от К до дополнения к U. Тогда
объединение всех симплексов в этом подразделении, которые пересекают К,—
Пространства, доминируемые CW-комилексами 669
конечный симплициальный комплекс, который ретрагируется на К
посредством ограничения ретракции U —> К. □
I Следствие П.9. Каждое компактное многообразие, с краем или без,
является ENR.
Доказательство. Многообразия локально стягиваемы, поэтому
достаточно показать, что компактное многообразие М можно вложить в R*"
для некоторого к. Если М не замкнуто, то оно вкладывается в замкнутое
многообразие, полученное из двух экземпляров многообразия М
отождествлением их краёв. Поэтому достаточно рассмотреть случай, когда М
замкнуто. В силу компактности существует конечное число замкнутых
шаров В" сМ, внутренности которых покрывают М; здесь п — размерность
многообразия М. Пусть f(: М —> S" — отображение факторизации,
стягивающее дополнение к внутренности шара В" в точку. Эти отображения ft —
компоненты отображения /: М—»(S")m, которое является инъективпым,
так как если х и у — разные точки многообразия М, причём точка х лежит
внутри, скажем, шара В", то /j(.v) Ф /1-(у). Взяв композицию
отображения / с каким-нибудь вложением (S")''1 с-^^/с, например с произведением
стандартных вложений Sn с—> RtH ], мы получим непрерывное ииъективпое
отображение М <—» Жк, и оно является гомеоморфизмом па свой образ, так
как М компактно. П
| Следствие ПЛО. Любой конечный CVV-комплекс является ENR.
Доказательство. Так как CW-комнлексы локально стягиваемы,
достаточно показать, что конечный СЧУ-комплекс можно вложить в
некоторое пространство Жп. Это доказывается индукцией по числу клеток.
Предположим, что CW-комплекс Х получен из подкомплекса А приклеиванием
клетки ек по отображению /: Sk'~l —* А, и предположим, что у нас есть
вложение А<-* R"'. Тогда мы можем вложить X и :Ак х R"! x IR как
объединение множеств Dk х {0} х {0}, {0} х А х {1} и всех отрезков, соединяющих
точки (х,0,0) и (0,/(х),1) дляхе^'"1. □
Пространства, доминируемые CW-комплексами
Мы рассмотрели пространства, которые являются ретрактами
конечных симплициальных комплексов, а теперь мы покажем, что такие
пространства имеют гомотопический тип CtV-комплексов. В
действительности мы можем столь же легко доказать немного более общее утверждение.
Пространство У называют доминируемым пространством X, если
существуют отображения У —* X -^ У, для которых ri ~ 1. Это превращает
понятие ретракта в нечто зависящее только от гомотопических типов
участвующих пространств.
Предложение П.11. Пространство, доминируемое CtV-комплексом,
гомотопически эквивалентно СИ/-комллексу.
670
Приложение
Доказательство. Как известно из §3.F, что телескоп отображений
Т(/ь/2, ...) Лля последовательности отображений Хх -U Х2 ^ Х3 ^—
это факторпространство объединения Ц(Х, х [/, i + 1.1), полученное при
i
отождествлении О, / + 1) е Х> х [i,i + 1] с (f(x),i + l)eXi+] x \i + l9 i+2J.
Нам будут нужны следующие элементарные факты:
1) T(f\>h> —)-T(g\,g2> ••■), если ft^g{ для всех г,
2) nfx,f2,...)*nf2,&,...)-,
Второй факт очевиден. Чтобы доказать остальные два, мы
воспользуемся предложением 0.18, доказательство которого применимо не только
к CW-парам, но и к любой паре (Х1уА), для которой существует
деформационная ретракция пространства Хх х I на Х{ х {0} U Д х /.
Чтобы доказать 1, рассмотрим пространство T(fltf2, ...) как полученное из
JJ(Xj х {i}) приклеиванием пространства Ц(^, x [i,i'-f Г]). Тогда мы
i i
можем получить T(gl,g2,...), меняя отображение приклеивания на
гомотопное. Чтобы доказать 3, мы рассмотрим пространство Т(/ь/2, ...) как
полученное из несвязного объединения цилиндров отображений М(/2,-)
приклеиванием пространства I_J(^2f-i x [2i — l,2i]). Сдвигая прикле-
ивание пространства X2i_} x [2i — l,2i] к X2i cM(/2l) вниз по
последнему цилиндру отображения к X2i+ly мы преобразуем М(/2,_,) и М(/2,)
в M(/2,/2i-i) uM(/2l). Последнее пространство деформационно ретраги-
руется на M(/2,-/2,-_i). Сделав это для всех i, получаем гомотопическую
эквивалентность в утверждении 3.
Теперь докажем само предложение. Пусть пространство Y доминиру-
ется CW-комплексом X посредством отображений Y —> X —> Y у для
которых п' ~ 1. Согласно фактам 2 и 3 мы получаем
T(ir, iry...) ~ 7'(У, I, г, I,...) ^ T(i, г, I, г,...) ^ Т(п', п', ...).
Так как ri ~ 1, пространство Т(п', п',...) гомотопически эквивалентно
телескопу тождественных отображений У —*Y —*Y —*..., который совпадает
с Y х [0, оо) ^ У. С другой стороны, отображение ir гомотопно
клеточному отображению /: X —*Х, поэтому T(ir, iry...) ~ Т(/, /, ...), а последнее
пространство является СУУ-комплексом. □
Можно поинтересоваться, будет ли пространство, доминируемое
конечным CW-комплексом, гомотопически эквивалентно конечному CW-kom-
плексу. В односвязном случае это следует из предложения 4.С.1, так как
такое пространство имеет конечно порождённые группы гомологии. Но
в общем случае есть контрпримеры; см. [133].
Если воспользоваться следствием П.10, то из предыдущего
предложения вытекает следующее.
Пространства, доминируемые CW-комплекса ми
671
Следствие П.12. Компактное многообразие гомотопически
эквивалентно CW-комплексу.
Можно задать и более тонкие вопросы. Например, любое ли
компактное многообразие имеет структуру CW-комплекса или даже структуру
симплициального комплекса? Ответы на эти вопросы получить гораздо
труднее. Если ограничиться для простоты замкнутыми многообразиями,
то нынешний статус этих вопросов таков. На многообразии
размерности меньше 4 всегда существует структура симплициального
комплекса. В размерности 4 существуют замкнутые многообразия, па которых
нельзя ввести структуру симплициального комплексна, в то время как
существование СИ/-структур — открытый вопрос. В размерностях выше 4
CW-структуры всегда существуют, по всегда ли существуют симилициаль-
ные структуры, неизвестно. При этом известно, что существуют п-мер-
ные многообразия, не имеющие симплициальных структур, локально
изоморфных какому-либо линейному симплициалыюму подразделению R'1,
для всех л > 4. Подробнее об этих вопросах см. [43] и L26].
Задачи
1. Докажите, что накрывающее пространство CW-комплекса тоже
является CW-комплексом, клетки которого проектируются гомеоморфно на
клетки исходного комплекса.
2. Пусть X — CW-комплекс, а х{) — произвольная точка комплекса X.
Постройте на X новую структуру CW-комплекса, для которой х{) является
нульмерной клеткой и при этом каждая из исходных клеток является
объединением новых клеток. Последнее условие выражают, говоря, что новая
CW-структура — подразделение старой.
3. Докажите, что CW-комплекс линейно связен тогда и только тогда,
когда его одномерный остов линейно связен.
4. Докажите, что CW-комплекс локально компактен тогда и только
тогда, когда у любой его точки существует окрестность, которая
пересекает только конечное число клеток.
5. Докажите, что для любого пространства X тождественное
отображение Хс —> X индуцирует изоморфизм групп тгь где Хс обозначает X
с компактно порождённой топологией.
Компактно-открытая топология
По определению компактно-открытая топология па пространстве Ху
отображений /: Y —* X имеет предбазу1, состоящую из множеств М(К, 10
1 Напомним, что предбазой топологии на множестве X называется такой набор открытых
множеств, что их всевозможные конечные пересечения образуют базу топологии, т. е. любое
открытое множество в X представляется в виде объединения некоторого набора конечных
пересечении множеств из предбазы.— Прим. ред.
672
Приложение
отображений, переводящих компактное множество К с У в открытое
множество U с X. Таким образом, база топологии для XY состоит из множеств
отображений, переводящих конечное число компактных множеств К,- с У
в открытые множества И{ сХ. Если пространство У компактно, а только
этот случай мы рассматриваем в этой книге, то сходимость k/gXv
означает, грубо говоря, что всё более и более мелкие компактные покрытия
{К{} пространства У отображаются во всё меньшие и меньшие открытые
покрытия {£/,} пространства /(7). Один из наиболее интересных
случаев в теории гомотопий —когда У = /, таким образом, X1 — пространство
путей в X. В этом случае можно проверить, что система базисных
окрестностей пути /: / —»X состоит из открытых множеств f)M(Kh £/,), где К{ —
разбиения отрезка / на неперекрывающиеся замкнутые отрезки, a U{ —
открытая окрестность множества /(£<■).
Компактно-открытая топология —это во многих случаях то же самое,
что топология равномерной сходимости.
I Предложение П.13. Если X — метрическое пространство, а простран-
I ство У компактно, то компактно-открытая топология на XY —это то же
I самое, что топология, заданная метрикой
I d(/,g)=supd(/(y),g(y)).
I y<=Y
Доказательство. Сначала покажем, что любой открытый s-шар BF (/)
с центром /еХк содержит окрестность точки / в компактно-открытой
топологии. Так как пространство /(У) компактно, его можно покрыть
конечным числом шаров В,./з(/(.У«))- Пусть К{ с У —замыкание
множества /^(Яр/зС/СУ,-))), таким образом, К{ компактно, У =(Jtf,- и /(К,-) с
i
с Bf/2(/(/i)) = Uh следовательно, / е f]M{Kh L/,). Чтобы показать, что
i
f)M(Kh и() СЙД/), предположим, что gef)M(Kh I/,). Для любого у еУ,
скажем, для у е Kit мы получаем d(g(y), /(у,-)) < е/2, так как g(K() с U(.
Аналогично получаем d(/(y),/(y,-)) <tf/2, поэтому
d(/(y),g(y))^d(/(y),/(y,))+d(g(y),/(y))<f.
Так как точка у была произвольная, это показывает, что ge/ЗД/).
Наоборот, покажем, что для любого открытого множества M{KyU)
и любой точки f e M(K,U) существует шар ВД/) с М(Ж, U). Так как
множество f(K) компактно, оно удалено на расстояние е > 0 от
дополнения к U. Тогда из неравенства d(/,g) < е/2 следует, что g{K) с [/,
так как g(K) содержится в £/2-окрестности множества /(К). Поэтому
Bf/2(/)cM(K,l/). □
Следующее предложение содержит важные свойства
компактно-открытой топологии с точки зрения алгебраической топологии.
Пространства, доминируемые CW-комплексами 673
I Предложение П.14. Если пространство У локально компактно, то
I а) отображение вычисления е: XY x У —> X, задаваемое формулой
I е(/,у)=/(у), непрерывно;
I б) отображение /: У х Z —> X непрерывно тогда и только тогда, ко-
I гда отображение /: Z -* Ху, заданное формулой f(z)(y) = /(y,z),
I непрерывно.
В частности, утверждение б) предоставляет обще-топологическое
оправдание соотношения сопряжённости (ЕХ, У) = (X, ПУ) в § 4.3, так как из
него следует, что отображение ЕХ —> У непрерывно тогда и только тогда,
когда соответствующее ему отображение X —> ПУ непрерывно, и
аналогично для гомотопий таких отображений. А именно, будем представлять
себе сохраняющее отмеченные точки отображение ЕХ -* У как
отображение /: / х X -* У, переводящее 5/хХи {л:0} х / в отмеченную точку
пространства У\ тогда образ соответствующего ему отображения /: X —> У1
лежит в подпространстве ПУ с У1. Гомотопия ft: ЕХ —> У даёт
отображение F: I х X х I -*У, переводящее 5/хХх/и/х {л:0} х / в отмеченную
точку, и при этом отображение F: X х / —> ПУ с У1 определяет гомотопию
ft в классе отображений, сохраняющих отмеченную точку.
Доказательство, а) Для точки (/, у)еХухУ пусть U сX — открытая
окрестность точки /(у). Так как пространство У локально компактно, из
непрерывности отображения / следует, что существует такая компактная
окрестность К с У точки у, что f(K) с U. Тогда М{КУ U) х К — окрестность
точки (/,у) в XY х У, которую отображение е переводит в U, поэтому е
непрерывно в точке (/, у).
б) Предположим, что отображение /: У х Z —> X непрерывно. Чтобы
доказать непрерывность отображения /, достаточно показать, что для
множества M(K,U)cXY из пред базы множество
Г1 (М(К, U)) = { z Е Z | /(К, z) с L7}
открыто в Z. Пусть ze/"1 (М(К, [/)). Так как /_1(£Л — открытая
окрестность компактного множества К х {z}, существуют открытые
множества V с У и W a Z, произведение которых V х W обладает тем
свойством, что К х {z} с V х W <zf~l(U). Поэтому W — окрестность точки z
в f~x (M(X, (У)). (Предположение, что пространство У локально
компактно, здесь не нужно.)
Для доказательства обратного утверждения в п. б), заметим, что / —
композиция У х2^>У хХу -*Х отображения lx/и отображения
вычисления, поэтому требуемый результат следует из и. а). □
I Предложение П.15. Если X —компактно порождённое хаусдорфово
пространство, а У — локально компактное пространство, то топология
произведения на X х У компактно порождена.
Доказательство. Сначала сделаем предварительное наблюдение:
функция /: X х У —>Z непрерывна тогда и только тогда, когда её ограниче-
674
Приложение
ния /: С х У —* Z непрерывны для всех компактных подмножеств С с X.
Действительно, если воспользоваться утверждением б) из предыдущего
предложения, то первое утверждение эквивалентно тому, что
отображение /: X —*ZY непрерывно, а второе утверждение эквивалентно тому, что
отображение /: С —> ZY непрерывно для всех компактных подмножеств
С с X. Так как пространство X компактно порождённое, последние два
утверждения эквивалентны.
Чтобы доказать предложение, мы должны только показать, что
тождественное отображение X х У —* (X х У)с непрерывно. В соответствии
с предыдущим абзацем это эквивалентно непрерывности отображений
включения С х Y —* (X х Y)c для всех компактных подмножеств С с X. Так
как пространство У локально компактно, оно компактно порождённое;
пространство С компактное хаусдорфово, следовательно, локально
компактное. Поэтому те же самые рассуждения показывают, что
непрерывность отображения С х Y —»(X х Y)c эквивалентна непрерывности
отображения С х С' —»(X х Y)c для всех компактных подмножеств С;сК. Но на
компактном множестве С х С' обе рассматриваемые топологии на X х Y
согласованы, что и завершает доказательство. (Это доказательство взято
из [19].) П
I Предложение П.16. Отображение XYx/ —»[XYY\ f^f, является
гомеоморфизмом, если пространство Y локально компактное
хаусдорфово, а пространство Z хаусдорфово.
Доказательство. Сначала мы покажем, что иредбаза топологии для
XYxZ образована множествами М(А х В, С/), где Л и В пробегают
компактные множества в У и Z соответственно, a U пробегает открытые
множества в X. Для данного компактного множества К с Y x Z и точки
f eM{K,U) пусть KY и JCZ—проекции пространства К на Y и Z. Тогда
пространство Ку х К? компактно и хаусдорфово, а значит, нормальное,
поэтому для каждой точки k е К существуют такие компактные
множества Ак с Y и Вк с Z, что Ак х Вк является компактной окрестностью
точки к в f~l(U) П (iCy х iCz). В силу компактности пространства К конечное
число произведений Ак х Вк покрывает его. Отбросив остальные, мы
получаем / е f)M(Ak х Bki U) с М{К, (У), а это показывает, что множества
к
М{Ах В, С/) образуют предбазу.
При биекции XYxZ —»(Х^)2 эти множества М(Л х В, С/) соответствуют
множествам М(В, М(Л, 10), поэтому достаточно показать, что последние
множества образуют предбазу для (Xv)z. Мы докажем более общее
утверждение, что в качестве предбазы для XY можно взять множества М{К, V),
где V пробегает по предбазе для X, а К пробегает по компактным
множествам в У, если предположить, что пространство Y хаусдорфово.
Пусть дана точка f eM(Ky U). Представим U в виде объединения
множеств Ua из базы, где каждое множество Ua является пересечением ко-
Пространства, доминируемые CW-комплексами
675
немного числа множеств Vaj из данной предбазы. Из покрытия
пространства К открытыми множествами f~l(Ua) можно выбрать конечное
подпокрытие, скажем, открытыми множествами /_1(^,)- Так как
пространство К компактное хаусдорфово, а потому нормальное, мы можем
представить К в виде объединения компактных подмножеств Kh для которых
К{с/^Щ). Тогда точка / лежит в M^KhUi) = M^KhP\Vij) = ^[M^KhVi})
/ )
для всех i\ Следовательно, / лежит в f]M(Kh V{j) = P|M(K,-, [/,) <ZM{K,U).
Так как f)M(Kh Ц;)— конечное пересечение, это показывает, что множе-
ства М{К, V) образуют предбазу для (Xv)z. G
I Предложение П.17. Если /: X —>У — отображение факторизации, то
и/х1:Хх2-»Ухг тоже отображение факторизации при условии,
что пространство Z локально компактно.
Это предложение можно применить в случае, когда Z = l, чтобы
показать, что гомотопия, определённая на факторпространстве, непрерывна.
Доказательство. Рассмотрим диаграмму
где W — это У х Z с фактортопологией из пространства X х Z, g
—отображение факторизации, а отображение h тождественное. Каждое открытое
множество в У х Z открыто в W, так как отображение /xl непрерывно,
поэтому достаточно показать, что отображение h непрерывно.
Так как отображение g непрерывно, соответствующее ему
отображение g: X —> Wz тоже непрерывно согласно предложению П.14. Из этого
следует, что отображение h: Y —>WZ непрерывно, так как / —
отображение факторизации. Применяя ещё раз предложение П.14, мы получаем,
что отображение h непрерывно. □
Литература
1. Adams J.F. Algebraic Topology: a Student's Guide. Cambridge Univ. Press, 1972.
2. Adams J. F. Stable Homotopy and Generalised Homology. Univ. of Chicago Press,
1974.
3. Adams J.F. Infinite Loop Spaces //Ann. of Math. Studies. 1978. V. 90. (Имеется
русский перевод: Адаме Дж. Бесконечнократные пространства петель. М:
Мир, 1982.)
4. Adem A., Milgram R.J. Cohomology of Finite Groups. Springer-Verlag, 1994.
5. Aigner M., Ziegler G. Proofs from THE BOOK. Springer-Verlag, 1999. (Имеется
русский перевод: Айгнер М., Циглер Г. Доказательства из Книги. Лучшие
доказательства со времён Евклида до наших дней. М.: Мир, 2006.)
6. AlexandroffR, HopfH. Topologie. Chelsea, 1972 (reprint of original 1935 edition).
7. Armstrong M. A. Basic Topology. Springer-Verlag, 1983.
8. Atiyah M. F. ^-Theory. W. A. Benjamin, 1967. (Имеется русский перевод: Атъя М.
Лекции по К -теории. М.: Мир, 1967.)
9. Baues H.J. Homotopy Type and Homology. Oxford Univ. Press, 1996.
10. Benson D.J. Representations and Cohomology. V. II: Cohomology of Groups and
Modules. Cambridge Univ. Press, 1992.
11. Benson D.J. Polynomial Invariants of Finite Groups. Cambridge Univ. Press, 1993.
12. Bott K.t Tu L. Differential Forms in Algebraic Topology. Springer-Verlag, 1982.
(Graduate texts in mathematics; V82). (Имеется русский перевод: Ботт Р.,
Ту Л. В. Дифференциальные формы в алгебраической топологии. М.: Наука,
1989.)
13. Bredon G. Topology and Geometry. Springer-Verlag, 1993. (Graduate texts in
mathematics; V.139).
14. Brown K. Cohomology of Groups. Springer-Verlag. 1982. (Graduate texts in
mathematics; V. 87). (Имеется русский перевод: Браун К. С. Когомологии
групп. М.: Наука, 1987. 383 с.)
15. Brown R. The Lefschetz Fixed Point Theorem. Scott Foresman, 1971. (Имеется
русский перевод: Браун К. С. Когомологии групп. М.: Наука, 1987.)
16. Cohen М. A Course in Simple-Homotopy Theory. Springer-Verlag, 1973. (Graduate
texts in mathematics; V. 10).
17. Dieudonne J. A History of Algebraic and Differential Topology 1900—1960. Birk-
hauser, 1989.
18. Dold A. Lectures on Algebraic Topology. Springer-Verlag, 1980. (Имеется русский
перевод: Дольд А. Лекции по алгебраической топологии. М.: Мир, 1976.)
19. Dugundji J. Topology. Allyn & Bacon, 1966.
20. Ebbinghaus H.-D. et al. Numbers. Springer-Verlag, 1991. (Graduate texts in
mathematics; V. 123).
21. Eilenberg 5., Steenrod N. Foundations of Algebraic Topology. Princeton Univ. Press,
1952. (Имеется русский перевод: Стинрод Н., Эйяенберг С. Основания
алгебраической топологии. М.: Физматгиз, 1958.)
22. Eilenberg S., ZilberJ.A. Semi-simplicial complexes and singular homology // Ann.
of Math. 1950. V. 51. P. 499-513.
Литература
677
23. Felix Y., Halperin S., Thomas J.-C. Rational Homotopy Theory. Springer-Verlag,
2001. (Graduate texts in mathematics; V. 205).
24. Fenn R. Techniques of Geometric Topology. Cambridge Univ. Press, 1983.
25. Фоменко А. Т., Фукс Д. Б. Курс гомотопической топологии. М.: Наука, 1989.
26. Freedman М., Quinn F. Topology of 4-Manifolds. Princeton Univ. Press, 1990.
27. Fulton W. Algebraic Topology: A First Course. Springer-Verlag, 1995. (Graduate
texts in mathematics; V. 153).
28. Gray B. Homotopy Theory. Academic Press, 1975.
29. Greenberg M., Harper J. Algebraic Topology: A First Course. Addison-Wesley, 1981.
30. Griffiths P., Morgan J. Rational Homotopy Theory and Differential Forms. Birk-
hauser, 1981. (Имеется русский перевод: Гриффите Ф.А., Морган Д. В.
Рациональная теория гомотопия и дифференциальные формы. М.: Наука, 1990.)
31. Hilton P.J. An Introduction to Homotopy Theory. Cambridge University Press,
1953.
32. Hilton P. J. Homotopy Theory and Duality. Gordon and Breach, 1966.
33. Hilton P. J., Wylie S. Homology Theory. Cambridge Univ. Press, 1967. (Имеется
русский перевод: Хилтон П.Дж., Уайли С. Теория гомологии. Введение в
алгебраическую топологию. М.: Мир, 1966.)
34. Hilton P. J.yStammbach U. A Course in Homological Algebra. Springer-Verlag, 1970.
(Graduate texts in mathematics; V.4).
35. Hilton P. J., Mislin G., Roitberg J. Localization of Nilpotent Groups and Spaces.
North-Holland, 1975.
36. Husemoller D. Fibre Bundles. McGraw-Hill, 1966 (later editions by Springer-
Verlag). (Имеется русский перевод: Хьюзмоллер Д. Расслоенные пространтва.
М.: Мир, 1970.)
37. James /. M. (ed.) Handbook of Algebraic Topology. North-Holland, 1995.
38. James I. M. (ed.) History of Topology. North-Holland, 1999.
39. Janich K. Topology. Springer-Verlag, 1984.
40. Kane R. M. The Homology of I lopf Spaces. North-I lolland, 1988.
41. Kirby R.t Siebenmann L Foundational F.ssays on Topological Manifolds, Smooth-
ings, and Triangulations // Ann. of Math. Studies. 1977. V. 88.
42. Kochman S. Stable Homotopy Groups of Spheres // Springer Lecture Notes. 1990.
V 1423.
43. Kochman S. Bordism, Stable Homotopy and Adams Spectral Sequences // Fields
Institute Monographs. AMS, 1996. V.7.
44. Konig D. Theory of Finite and Infinite Graphs. Birkhauser, 1990.
45. Lundell Д., Weingram S. The Topology of CW Complexes. Van Nostrand Reinhold,
1969.
46. MacLane S. Homology. Springer-Verlag, 1963. (Имеется русский перевод: Ma-
клейн С. Гомология. М.: Мир, 1966.)
47. MacLane S. Categories for the Working Mathematician. Springer-Verlag, 1971.
(Graduate texts in mathematics; V. 5). (Имеется русский перевод: Маклейн С.
Категории для работающего математика. М.: Физматлит, 2004.)
48. Madsen /., Milgram R. The Classifying Spaces for Surgery and Cobordism of
Manifolds // Ann. of Math. Studies. 1979. V. 92.
678
Литература
49. Massey W. Algebraic Topology: An Introduction. Harcourt: Brace & World, 1967
(reprinted by Springer-Verlag). (Имеется русский перевод в книге: Массы У,
Столпите Дж. Алгебраическая топология. Введение. М.: Мир, 1977. 344 с.)
50. Massey W. A Basic Course in Algebraic Topology. Springer-Verlag, 1993. (Graduate
texts in mathematics; V. 127).
51. Maunder C.R.F. Algebraic Topology. Cambridge Univ. Press, 1980 (reprinted by
Dover Publications).
52. May J. P. Simplicial Objects in Algebraic Topology. Van Nostrand, 1967 (reprinted
by Univ. Chicago Press).
53. May J. P. A Concise Course in Algebraic Topology. Univ. Chicago Press, 1999.
54. Milnor ./. Topology from the Differentiable Viewpoint. Univ. Press of Virginia,
1965. (Имеется русский перевод: Милнор Дж. Топология с
дифференциальной точки зрения // Милнор Дж., Уоллес А. Дифференциальная топология:
Начальный курс. М.: Мир, 1972.)
55. Milnor ./., StasheffJ. Characteristic Classes // Ann. of Math. Studies. 1974. V.76.
(Имеется русский перевод: Милнор Дж., Сташеф Дж. Характеристические
классы. М.: Мир, 1979.)
56. Mosher R., Tangora M. Cohomology Operations and Applications in Homotopy
Theory. Harper and Row, 1968. (Имеется русский перевод: Мошер Р., Тангора М.
Когомологические операции и их приложения в теории гомотопий. М.: Мир,
1970.)
57. Ravenel D. Complex Cobordism and Stable Homotopy Groups of Spheres.
Academic Press, 1986.
58. Ravenel D. Nilpotence and Periodicity in Stable Homotopy Theory // Ann. of Math.
Studies. 1992. V. 128.
59. Rees £., Jones J.D.S. (eds.) Homotopy Theory: Proceeding of the Durham
Symposium 1985. Cambridge Univ. Press, 1987.
60. Rolfsen D. Knots and Links. Publish or Perish, 1976.
61. Seifert //., Threlfall W. Lehrbuch der Topologie. Teubner, 1934. (Имеется русский
перевод: Зейферт Г., Трелъфалль В. Топология. М.; Л.: ОНТИ, 1938.)
62. Selick P. Introduction to Homotopy Theory // Fields Institute Monographs 9. AMS,
1997.
63. Serre J.-P. A Course in Arithmetic. Springer-Verlag, 1973. (Graduate texts in
mathematics; V. 7). (Имеется русский перевод: Серр Ж.-П. Курс арифметики.
М.: Мир, 1972.)
64. Spanier E. Algebraic Topology. McGraw-Hill, 1966 (reprinted by Springer-Verlag).
(Имеется русский перевод: Спеньер Э. Алгебраическая топология. М.: Мир,
1971.)
65. Steenrod N. The Topology of Fibre Bundles. Princeton Univ. Press, 1951. (Имеется
русский перевод: Cmunpod H. Тология косых произведений. М.: ИЛ, 1953.)
66. Steenrod A/., Epstein D. Cohomology Operations // Ann. of Math. Studies. 1962.
V. 50. (Имеется русский перевод: Cmunpod H., Эпстейн Д. Когомологические
операции. М.: Наука, 1983.)
67. Stong R. Notes on Cobordism Theory. Princeton Univ. Press, 1968. (Имеется
русский перевод: Стонг Р. Заметки по теории кобордизмоп. М.: Мир, 1973.)
Литература
679
68. Sullivan D. Geometric Topology. Xeroxed notes from MIT, 1970. (Имеется русский
перевод: Суляиван Д. Геометрическая топология. М.: Мир, 1975.)
69. Switzer R. Algebraic Topology. Springer-Verlag, 1975. (Имеется русский перевод:
Свипщер P.M. Алгебраическая топология —гомотопии и гомологии. М.:
Наука, 1985.)
70. Toda И. Composition Methods in Homotopy Groups of Spheres // Ann. of Math.
Studies. 1962. V.49. (Имеется русский перевод: Тода X. Композиционные мет-
доы в теории гомотопических групп сфер. М.: Наука, 1982.)
71. Varadarajan К. The Finiteness Obstruction of С. Т. С. Wall. Wiley, 1989.
72. Weibel C. An Introduction to Homological Algebra. Cambridge Univ. Press, 1994.
73. Whitehead G. Elements of Homotopy Theory. Springer-Verlag 1978. (Graduate texts
in mathematics; V. 62).
74. Wolf J. Spaces of Constant Curvature. Publish or Perish, 1984.
Papers
75. Adams J.F. On the non-existence of elements of Hopf invariant one // Ann. of
Math. 1960. V. 72. P. 20-104.
76. Adams J. F. Vector fields on spheres // Ann. of Math. 1962. V. 75. P. 603-632.
77. Adams J. R On the groups J(X). IV // Topology. 1966. V. 5. P. 21-71.
78. Adams J. F, Atiyah M. F. К-theory and the Hopf invariant // Quart. J. Math. 1966.
V. 17. P. 31-38.
79. Adams J. F. A variant of E. H. Brown's representability theorem // Topology. 1971.
V. 10. P. 185-198.
80. Adams J. F, Wilkerson С Finite H-spaces and algebras over the Steenrod algebra //
Ann. of Math. 1980. V. 111. P. 95-143.
81. Barratt M., Milnor J. An example of anomalous singular homology // Proc. AMS.
1962. V. 13. P. 293-297.
82. Bestvina M., Brady N. Morse theory and finiteness properties of groups // Invent.
Math. 1997. V. 129. P. 445-470.
83. Borel A. Sur la cohomologie des espaces fibres principaux // Ann. of Math. 1953.
V. 57. P. 115-207.
84. Bott R., Samelson H. On the Pontryagin product in spaces of paths // Comment.
Math. Helv. 1953. V. 27. P. 320-337.
85. Bott Я., Milnor J. On the parallelizability of spheres // Bull. AMS. 1958. V.64.
P. 87-89.
86. Boff R. The stable homotopy of the classical groups // Ann. of Math. 1959. V.70.
P. 313-337.
87. Brown £., Copeland A. An homology analog of Postnikov systems // Michigan
Math. J. 1959. V. 6. P. 313-330.
88. Brown E. Cohomology theories // Ann. of Math. 1962. V.75. P. 467—484.
89. Brown M. A proof of the generalized Schoenflies theorem / Bull. AMS. 1960. V. 66.
P. 74-76.
90. Cannon J., Conner G. The combinatorial structure of the Hawaiian earring group /
Top. and its Appl. 2000. V. 106. P. 225-271.
91. Carlsson G., Milgram R.J. Stable homotopy and iterated loopspaces / Handbook
of Algebraic Topology / Ed. I. M. James. Elsevier, 1995. P. 505—583
680
Литература
92. Davis J., Milgram R.J. A survey of the spherical space form problem // Math.
Reports. Harwood Acad. Pub., 1985. V.2. P. 223—283.
93. Dold A, Thom R. Quasifaserungen und unendliche symmetrischen Produkte //
Ann. of Math. 1958. V. 67. P. 239-281.
94. Dowker С Topology of metric complexes // Am. J. Math. 1952. V. 74. P. 555—577.
95. Dwyer W.y Miller H., Wilkerson С Homotopical uniqueness of classifying spaces //
Topology. 1992. V. 31. P. 29-45.
96. Dwyer W., Wilkerson С A new finite loop space at the prime two // Journal AMS.
1993. V. 6. P. 37-63.
97. Dyer £., Vasquez A. Some small aspherical spaces // J. Austral. Math. Soc. 1973.
V.16. P. 332-352.
98. Eilenberg S. Singular homology theory // Ann. of Math. 1944. V. 45. P. 407—447.
99. Edwards R. A contractible, nowhere locally connected compactum // Abstracts
AMS. 1999. V. 20. P. 494.
100. Feder S., Gitler S. Mappings of quaternionic projective spaces // Bol. Soc. Mat.
Mexicana. 1978. V. 18. P. 33-37.
100a. Gubeladze J. The isomorphism problem for commutative monoid rings // J. Pure
Appl. Alg. 1998. V. 129. P. 35-65.
101. Harris J., Kuhn N. Stable decompositions of classifying spaces of finite abelian
p-groups // Math. Proc. Camb. Phil. Soc. 1988. V.103. P. 427-449.
102. Hoffman P., Porter G. Cohomology realizations of Q[x], Ox // Q. 1973. V. 24.
P. 251-255.
103. Holzsager R. Stable splitting of K{G, 1) // Proc. AMS. 1972. V. 31. P. 305-306.
104. /-/op/ H. Uber die Abbildungen der dreidimensionalen Sphare auf die Kugel-
flache // Math. Ann. 1931. V. 104. P. 637-665.
105. James I. M. Reduced product spaces // Ann. of Math. 1955. V. 62. P. 170-197.
106. Kervaire M. Non-parallelizability of the п-sphere for n > 7 // Proc. N.A.S. 1958.
V. 44. P. 280-283.
107. Kochman S.yMahowald M. On the computation of stable stems // Contemp. Math.
1995. V. 181. P. 299-316.
108. Madsen /., Thomas С. R, Wall C.T.C. The topological spherical space form
problem. II: Existence of free actions // Topology. 1976. V. 15. P. 375—382.
109. May J. P. A general approach to Steenrod operations // Springer Lecture Notes.
1970. V. 168. P. 153-231.
110. May J. P. Weak equivalences and quasifibrations // Springer Lecture Notes. 1990.
V. 1425. P. 91-101.
111. Miller С The topology of rotation groups // Ann. of Math. 1953. V. 57. P. 95—110.
112. Milnor J. Construction of universal bundles. 1, II // Ann. of Math. 1956. V. 63.
P. 272-284, 430-436.
113. Milnor J. Groups which act on Sn without fixed points // Am. J. Math. 1957. V. 79.
P. 623-630.
114. Milnor J. Some consequences of a theorem of Bott // Ann. of Math. 1958. V. 68.
P. 444-449.
115. Milnor J. On spaces having the homotopy type of a CW complex // Trans. AMS.
1959. V. 90. P. 272-280.
116. Milnor J. On axiomatic homology theory // Рас. J. Math. 1962. V. 12. P. 337-341.
Литература
681
117. Milnor J., Moore J. On the structure of Hopf algebras // Ann. of Math. 1965. V. 81.
P. 211-264.
118. Milnor J. On the Steenrod homology theory // Novikov Conjectures, Index
Theorems, and Rigidity / Ed. S. Ferry, A. Ranicki, J. Rosenberg. Cambridge Univ.
Press, 1995. P. 79—96.
119. Neisendorfer J. Primary homotopy theory // Mem. AMS. 1980. V. 232.
120. Notbohm D. Spaces with polynomial mod-p cohomology // Math. Proc. Camb. Phil.
Soc. 1999. P. 277-292.
121. Quillen D. Rational homotopy theory // Ann. of Math. 1969. V. 90. P. 205-295.
122. Rector D. Loop structures on the homotopy type of S:i // Springer Lecture Notes.
1971. V. 249. P. 99-105.
123. Robinson C. Moore-Postnikov systems for non-simple fibrations // 111. J. Math.
1972. V. 16. P. 234-242.
124. Scott P., Wall T. Topological methods in group theory // London Math. Soc. Lecture
Notes. 1979. V. 36. P. 137-203.
125. Serre J.-P. Homologie singuliere des espaces fibres // Ann. of Math. 1951. V. 54.
P. 425-505.
126. Serre J.-P. Groupes d'homotopie et classes de groupes abeliens // Ann. of Math.
1953. V. 58. P. 258-294.
127. Sieradski A. Algebraic topology for two dimensional complexes // Two-Dimensional
Homotopy and Combinatorial Group Theory / Ed. С Hog-Angeloni, W. Metzler,
A. Sieradski. Cambridge Univ. Press, 1993. P. 51—96.
128. Shelah S. Can the fundamental group of a space be the rationals? // Proc. AMS.
1988. V. 103. P. 627-632.
129. Stallings J. A finitely presented group whose 3-dimensional integral homology is
not finitely generated // Am. J. Math. 1963. V. 85. P. 541—543.
130. Sullivan D. Genetics of homotopy theory and the Adams conjecture // Ann. of
Math. 1974. V. 100. P. 1-79.
131. Toda И. Note on the cohomology ring of certain spaces // Proc. AMS. 1963. V. 14.
P. 89-95.
132. van Kampen E. On the connection between the fundamental groups of some
related spaces // Am. J. Math. 1933. V.55. P. 261-267.
133. Wall С. Г. С. Finiteness conditions for CW complexes // Ann. of Math. 1965. V.81.
P. 56-69.
134. Whitehead G. Generalized homology theories // Trans. AMS. 1962. V.102.
P. 227—283.
135. Whitehead J. И. С Combinatorial homotopy. II // Bull. AMS. 1949. V.55.
P. 453-496.
Предметный указатель
BSO(n) 557
BSU(n) 557
г\ произведение 305
Д-комплекс 136
Ext 251, 401, 402
lim-один 397
lim1 520
П-спектр 501
Sp(n) 289
Spin(ri) 371
ENR 668
hocolim 585
holim 585
Tor 335, 340
U(n) 289
CW-аппроксимация 446
CW-комплекс 15, 658
CW-napa 17
//-пространство 532
/-/-пространство 358, 541
HNN-расширение 122
J-гомоморфизм 488
ЛХ) 286
fc-инвариант 521
/с-инварианты 602
р-адические целые числа 398
5-лемма 168
абелево пространство 433, 528
Адаме 541
аксиома Майера—Вьеториса 568
алгебра разделённых степеней 286,
364, 370
— с делением 223, 283, 541
— свободная 290
— Стинрода 628
— Хопфа 361
Алексаидер 228
Александера 170
— рогатая сфера 218, 220
амальгамация 577
ансамбль групп 419
асферичное пространство 434
аугментация 144
ацикличное пространство 183
база 477
базис 59
барицентр 156
барицентрические координаты 135
барицентрическое подразделение 156
башня Мура—Постникова 523
— Постникова 449, 518
— Уайтхеда 451
Бернсайда проблема 107
бесконечное симметричное
произведение 360
бесконечнократное пространство
петель 502
Бетти число 170
биномиальный коэффициент 365, 620
Бореля конструкция 580
— теорема 363
Борсука—Улама теорема 48, 55
Брауэр 47,164, 174, 222, 228
Брауэря теорема 150
букет 20, 61, 164, 207, 259, 481, 591
— стягивающихся окружностей 69, 75,
86,106, 329
бутылка Клейна 72,100,123, 134
ван Кампена теорема 61
векторное поле 175, 624
вершина ПО, 135
вещественное проективное
пространство 15, 100
Виртингера представление 76
внешнее ^-произведение 278
— произведение 269, 278, 285, 341, 353,
355
внешняя алгебра 278, 362
воротник 322
Предметный указатель
683
вполне разрывное действие 98
выдавливание 584, 590
вырезаемая триада 602
вырезание 155, 259, 456
Галуа соответствие 86
гипотеза Пуанкаре 494
гомологии групп 192
— клеточные 181
— локально конечные 427
— локальные 164
— приведённые 144
— с локальными коэффициентами 417
— симнлициальные 139,167
— сингулярные 141
— Стинрода 327
— Чеха 327
гомологии группа 139
— класс 139
— теория 207
гомологическое разложение 589
гомологичные циклы 139
гомоморфизм Бокштейна 386, 617
— Гуревича 467, 615
— индуцированный 50,145, 146,154
гомотопическая группа 431
с коэффициентами 586
— эквивалентность 12,53, 439
послойная 513
гомотопически эквивалентные
пространства 12
гомотопический класс 39
— тип 12
гомотопия 11, 39
— накрывающая 82
— относительно подпространства 11
— сохраняющая отмеченную точку 53,
452, 533
— цепная 147
гомотопное нулю отображение 12
гомотопные отображения 11
— пути 39
градуированная алгебра связная 361
граница 139
— относительная 151
— симплекса 136
граничный гомоморфизм 138,141,152
грань 135
грассманиан 564
граф 15, ПО
— групп 121
— Кэли 103
граф-произведение групп 121
группа гомологии 139
относительная 150
— действующая на сфере 100,175
— диэдральная 101
— когомологий 245, 254
— Ли 358
— ортогональная О(п) 550
— свободная 103,113
— симплектическая Sp(n) 549
— унитарная U(n) 549
— фундаментальная 40
группы действие 96
— действующие свободно на сферах
495
— когомотопические 576
двойственная алгебра Хопфа 369
двойственность Александера 324
— Лефшеца 323
— Пуанкаре 307, 313, 323, 426
— Экмана—Хилтона 583
двумерная клетка 14
действие я 1 на тг„ 433, 438, 533
— л, на слое 93
— вполне разрывное 98
— группы 96, 578
— накрытия 98
— свободное 98
действий изоморфизм 95
дерево 111
— максимальное 111
деформационная ретракция 10, 663
в слабом смысле 30
деформационный ретракт 52, 439
Джеймса приведённое произведение
286, 359, 366, 368, 592, 595
джойн 19, 579, 591
диагональ 361
диаграмма коммутативная 145
684
Предметный указатель
— пространств 577, 585
диэдральная группа 101
длинная точная последовательность
гомологии 149,153
когомологий 256
— точная последовательность
гомологии 151
гомология 152
гомотопическая 436
додекаэдральная группа 184
дом с двумя комнатами 12
допустимый моном 632
евклидов окрестностныи ретракт 668
единственность поднятия 85
естественное преобразование 212
естественность 165
задача поднятия 525
— продолжения 525
замкнутое многообразие 294
зацепление 65
звезда 229
звёздное множество 54
избыточность 632
изменение отмеченной точки 42, 433
изоморфизм действий 95
— накрытий 91
— Тома 559
инвариант Хопфа 541, 566, 619, 620
инвариантность области 221
— размерности 164
индуцирование 584
индуцированное расслоение 549
индуцированный гомоморфизм 50,
145, 146, 154, 258, 275
категория 209
квазиокружность 106
квазирасслоение 606
кватернион 100
кватернионы 223, 359, 374, 566
Квиллен 473
класс гомологии 139
— гомотопический 39
— ориентации 301
— Тома 559, 647
классифицирующее пространство 213
Клейна бутылка 72,100, 123,134
клетка двумерная 14
— одномерная 14
клеточное отображение 202, 343, 442
клеточные гомологии 181,198
— когомологий 260
клеточный комплекс 15
— цепной комплекс 181
ковариантный функтор 211
когомологий с компактными
носителями 308, 309
— с локальными коэффициентами 417,
423
— Чеха 327
когомологическая операция 617
кограница 254
кограницы отображение 254
кограничное отображение 245
кольцо когомологий 271
— Коэна—Маколея 291
коммутативная диаграмма 145
коммутативное градуированное
кольцо 276
коммутативность w-произведения 276
компактные носители 308, 424
комплекс клеточный 15
— Кэли 103
— пространств 579, 585, 591
— симплициальный 140
— сингулярный 142
— цепной 139
комплексное проективное
пространство 16
конечная порождённость для
гомотопий 461
конечно порождённая гомология 496,
535, 668
конструкция Вореля 410
контравариантный 258
— функтор 211
конус 18
— отображения 24, 235
координаты барицентрические 135
Предметный указатель
685
копредел 585
копроизведение 361, 584
корасслоение 583
короткая точная последовательность
149,151
кослой 584
коцепь 245, 253
коцикл 254
коэффициент кручения 170
коэффициенты 198, 208, 254, 586
край 322
кручения коэффициент 170
Кэли граф 103
— комплекс 103
лемма о продолжении 441
— о сжатии 439
Лефшец 170, 230
Лефшеца теорема 292
— число 230
линзовое пространство 100,116,186,
320, 359, 387, 394, 495
лист 78
локальная ориентация 298
— стягиваемость 662
— тривиализация 477
локально линейно связное
пространство 84
— тривиальное расслоение 476, 546
локальные гомологии 164, 326
Майера—Вьеториса
последовательность 193
максимальное дерево 111
Милнор 516, 517
минимальный цепной комплекс 388
многообразие 294, 669, 671
— Грассмана 289, 483, 551, 556
— односвязное четырёхмерное 545
— с краем 322
— Штифеля 383, 483, 552, 566, 624
многочлены симметрические 551
моноид 210
морфизм 210
Мура пространство 185
надстройка 18, 177, 285, 591, 599
— приведённая 23
накрывающая гомотопия 82
накрывающее пространство 77, 408,
434
накрытие 77, 477
— п-связное 525
— нормальное 95
— универсальное 81, 92
накрытий изоморфизм 91
накрытия действие 98
— преобразование 95
направленное множество 310
невырожденное спаривание 318
неподвижная точка 47, 98,150, 230, 624
нерв 326, 579
нормальное накрытие 95
обратный предел 396, 519, 585
— путь 41
объект 210
одномерная клетка 14
односвязное пространство 43
окружность 43
октавы 223, 359, 374, 479, 630
оператор призменный 147
орбит пространство 97
орбита 97
ориентация 138, 298, 300
ориентируемое многообразие 298
— сферическое расслоение 560
ортогонализация Грама—Шмидта 373,
483, 484
ортогональная группа 372, 392
основная теорема алгебры 46
остов 14, 658
отмеченная точка 40, 42
относительная гомотопическая группа
435
— граница 151
— группа гомологии 150
относительные когомологии 256
относительный цикл 150
отображение гомотопное нулю 12
— послойное 513
— характеристическое 16
— Хопфа 479, 481, 487, 541, 545, 631
686
Предметный указатель
— цепное 145
отображения гомотопные 11
пара п-связная 439
— хорошая 149
перепараметризация 41
перестановка 92
перетасовка 354
периодичность Ботта 485, 502
петля 35, 40
плоскость проективная 72, 134,139
плюс-конструкция 473, 532
поверхность 71, 116, 123, 134, 183, 265,
307, 494
подграф 111
подкомплекс 17, 659
поднятие 44
— гомотопии 82
— отображения 82
— пути 83
поднятия единственность 85
— критерий 84
подразделение 671
— барицентрическое 156
покрытие открытое 581
полная линейная группа GLri 373
полулокально односвязное
пространство 86
последовательность ЕНР 600
— Гизина 554, 562
— корасслоения 504, 585
— Майера-Вьеториса 205, 209, 261
— Пуппе 504
— расслоения 518, 585
— точная 148
предел 585
представление Виртингера 76
препятствие 527
— примарное 530
приведённая надстройка 23, 499
приведённое произведение 20
приведённые гомологии 144
— когомологии 255
призменный оператор 147
приклеивание 24
— пространства 578
примитивный элемент 362, 380
проблема Бернсайда 107
проективная плоскость 72, 134, 139,
271, 479
проективное пространство
вещественное 15, 100,116,186,199,
231, 272, 409, 555, 621
действительное 293, 319
кватернионное 274, 288, 293, 319,
409, 479, 481, 556, 621, 622
комплексное 16,181, 272, 288,
293, 319, 359, 409, 481, 555, 621
произведение 317
— Д-комплексов 355
— СW-комплексов 664
— косое 357
— Понтрягина 366, 380
— приведённое 20, 285, 344
— пространств 49, 340, 434, 673
— путей 40
— свободное 58
— симплексов 354
— Уайтхеда 482, 545
пространства гомотопически
эквивалентные 12
— Эйленберга—- Маклсйна 498
пространство п-связное 438
— доминируемое 669
— классифицирующее 213
— линзовое 116, 186
— локально стягиваемое 666
— Мура 185, 352, 396, 407, 495, 586, 588,
602
— накрывающее 77
— односвязное 43
— орбит 97, 578
— петель 500, 515, 595
— полулокально односвязное 86
— путей 514
— расслоения 477
— стягиваемое 12
— типаК(6\1) 116
— Тома 559, 647
— функциональное 671
— Эйленберга—Маклсйна 116, 462, 518,
574, 602
Предметный указатель
ЬЬ/
прямой предел 310, 395, 576, 582, 585
Пуанкаре 170
путей произведение 40
пути гомотопные 39
путь 39
— обратный 41
— рёберный 113
разложимая операция 629
размерность 15
ранг 59, 189
расслоение в смысле Гуревича 475
Серра 476
— главное 521, 532
— индуцированное 513
— Хопфа 457, 474, 478, 479, 496
расщеиимая точная
последовательность 191
реализация 578
ребро 110
резольвента свободная 248
ретракт 52, 150, 666
— деформационный 52
ретракция 11,191
— деформационная 10
в слабом смысле 30
рёберный путь 113
ряд Пуанкаре 293, 553
свободная группа 59,103, 113
— резольвента 334
свободное действие 98
— произведение 58
с амальгамацией 122
свойство поднятия гомотопии 475, 480
— продолжения гомотопии 25
связная сумма 327
симметрическая степень 463
симметрическое произведение 608
симплекс 19, 135
— сингулярный 141
симплектическая группа 289, 483
симплициальное отображение 228
симплициальные гомологии 139,167
— когомологии 260
симплициальный комплекс 140
сингулярные гомологии 141
сингулярный комплекс 142
— симплекс 141
скобка Тоды 490
скольжение 95
слабая гомотопическая
эквивалентность 445
— топология ПО
слой 474
— гомотопический 515, 583, 606
соответствие Галуа 86
соотношение сопряжённости 500
соотношения Адема 628, 634
сопряжённость 585
спектр 575
— надстройки 575
срезанная алгебра многочленов 362
стабильная гомотопическая группа
486, 573
стабильные расщепления 621
степень 174, 328
— локальная 176
Стинрода квадраты 616
— степени 616
стягиваемое пространство 12
стягиваемость 203
сферическое расслоение 559, 563
телескоп отображений 179, 396, 579,
670
тензорная алгебра 367, 596
тензорное произведение 279, 416
цепных комплексов 348
теорема алгебры основная 46
— Баррата—Кана—Придди 474
— Борсука—Улама 48, 55, 226
— Брауна о представимости 567
— Брауэра150
— ван Кампена 61
— вырезания 155
— Гуревича 469, 471, 494
— Дольда—Тома 611
— Жордана 218
— Лере—Хирша 546
— о клеточной аппроксимации 442
— о накрывающей гомотопии 82
688
Предметный указатель
— о симплициальной аппроксимации
228
— об универсальных коэффициентах
336
— об универсальных коэффициентах
251, 586
— Уайтхеда 439, 465, 528
— Фрейденталя о надстройке 456
— Шёнфлиса 218
теория гомологии 399, 575
— когомологий 259, 399, 567, 575
— препятствий 526
топологическая группа 358
топология компактно порождённая
663, 673
— компактно-открытая 671
— слабая ПО
тор 50,100,134, 139, 290
— отображения 74,195, 579
торический узел 50, 66
точка неподвижная 47, 98, 150
— отмеченная 40
точная последовательность 148
гомологии 149,151-153
короткая 151
расслоения 475
тройки 155
трансфер 225, 408
тройка 436
тройки точная последовательность 155
узел торический 50, 66
универсальное накрытие 81, 92
унитарная группа 289, 483
условие Миттаг-Леффлера406
флаг 551, 566
формула Картаиа 618, 619
— Кюннета 280, 340, 348, 351, 452, 547
фундаментальная группа 40
фундаментальный класс 301, 498
функтор 211
характеристика эйлерова 15, 114
характеристическое отображение 16,
658
Хопф 174, 222, 283, 358, 363
Хопфа отображение 600, 601
хорошая пара 149
цепная гомотопия 147
цепное отображение 145
цепной комплекс 139
клеточный 181
цепь 137, 141
цикл 139
— относительный 150
циклы гомологичные 139
цилиндр отображения 10, 235, 440, 578,
583
итерированный 579, 591
число Нетти 170
— Лефшеца 230
— листов 78
Эйленберг170
Эиленберга—Маклеина пространство
116
эйлеров класс 554, 562
эйлерова характеристика 15,114,189
эквивалентность гомотопическая 53
Книга представляет собой введение в алгебраическую
топологию (до спектральных последовательностей),
включающее в себя как гомотопическую топологию,
так и теорию гомологии и когомологий (в том числе
двойственность Пуанкаре). Ориентированное на
геометрические аспекты предмета изложение является
тем не менее строгим и подробным.
В книге имеется большое количество примеров
и упражнений; в дополнениях, занимающих почти
половину книги, затрагиваются различные более
продвинутые сюжеты (когомологий с локальными
коэффициентами, теорема Брауна о представимости,
когомологические операции, спектры и пр.).
Для студентов старших курсов, аспирантов
и научных работников.